"
+ ]
+ },
+ "execution_count": 2,
+ "metadata": {},
+ "output_type": "execute_result"
+ }
+ ],
+ "source": [
+ "import importlib\n",
+ "\n",
+ "importlib.reload(peft)"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "id": "da74b569",
+ "metadata": {
+ "id": "8d0850ac"
+ },
+ "outputs": [],
+ "source": [
+ "# creating model\n",
+ "peft_config = IA3Config(task_type=TaskType.SEQ_2_SEQ_LM, inference_mode=False, feedforward_modules=[])\n",
+ "\n",
+ "model = AutoModelForSeq2SeqLM.from_pretrained(model_name_or_path)"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 4,
+ "id": "df33fce2",
+ "metadata": {
+ "colab": {
+ "base_uri": "https://localhost:8080/"
+ },
+ "id": "e10c3831",
+ "outputId": "e69c5e07-ae58-446c-8301-e99ac6b85d62"
+ },
+ "outputs": [
+ {
+ "data": {
+ "text/plain": [
+ "MT5ForConditionalGeneration(\n",
+ " (shared): Embedding(250112, 1024)\n",
+ " (encoder): MT5Stack(\n",
+ " (embed_tokens): Embedding(250112, 1024)\n",
+ " (block): ModuleList(\n",
+ " (0): MT5Block(\n",
+ " (layer): ModuleList(\n",
+ " (0): MT5LayerSelfAttention(\n",
+ " (SelfAttention): MT5Attention(\n",
+ " (q): Linear(in_features=1024, out_features=1024, bias=False)\n",
+ " (k): Linear(in_features=1024, out_features=1024, bias=False)\n",
+ " (v): Linear(in_features=1024, out_features=1024, bias=False)\n",
+ " (o): Linear(in_features=1024, out_features=1024, bias=False)\n",
+ " (relative_attention_bias): Embedding(32, 16)\n",
+ " )\n",
+ " (layer_norm): MT5LayerNorm()\n",
+ " (dropout): Dropout(p=0.1, inplace=False)\n",
+ " )\n",
+ " (1): MT5LayerFF(\n",
+ " (DenseReluDense): MT5DenseGatedActDense(\n",
+ " (wi_0): Linear(in_features=1024, out_features=2816, bias=False)\n",
+ " (wi_1): Linear(in_features=1024, out_features=2816, bias=False)\n",
+ " (wo): Linear(in_features=2816, out_features=1024, bias=False)\n",
+ " (dropout): Dropout(p=0.1, inplace=False)\n",
+ " (act): NewGELUActivation()\n",
+ " )\n",
+ " (layer_norm): MT5LayerNorm()\n",
+ " (dropout): Dropout(p=0.1, inplace=False)\n",
+ " )\n",
+ " )\n",
+ " )\n",
+ " (1-23): 23 x MT5Block(\n",
+ " (layer): ModuleList(\n",
+ " (0): MT5LayerSelfAttention(\n",
+ " (SelfAttention): MT5Attention(\n",
+ " (q): Linear(in_features=1024, out_features=1024, bias=False)\n",
+ " (k): Linear(in_features=1024, out_features=1024, bias=False)\n",
+ " (v): Linear(in_features=1024, out_features=1024, bias=False)\n",
+ " (o): Linear(in_features=1024, out_features=1024, bias=False)\n",
+ " )\n",
+ " (layer_norm): MT5LayerNorm()\n",
+ " (dropout): Dropout(p=0.1, inplace=False)\n",
+ " )\n",
+ " (1): MT5LayerFF(\n",
+ " (DenseReluDense): MT5DenseGatedActDense(\n",
+ " (wi_0): Linear(in_features=1024, out_features=2816, bias=False)\n",
+ " (wi_1): Linear(in_features=1024, out_features=2816, bias=False)\n",
+ " (wo): Linear(in_features=2816, out_features=1024, bias=False)\n",
+ " (dropout): Dropout(p=0.1, inplace=False)\n",
+ " (act): NewGELUActivation()\n",
+ " )\n",
+ " (layer_norm): MT5LayerNorm()\n",
+ " (dropout): Dropout(p=0.1, inplace=False)\n",
+ " )\n",
+ " )\n",
+ " )\n",
+ " )\n",
+ " (final_layer_norm): MT5LayerNorm()\n",
+ " (dropout): Dropout(p=0.1, inplace=False)\n",
+ " )\n",
+ " (decoder): MT5Stack(\n",
+ " (embed_tokens): Embedding(250112, 1024)\n",
+ " (block): ModuleList(\n",
+ " (0): MT5Block(\n",
+ " (layer): ModuleList(\n",
+ " (0): MT5LayerSelfAttention(\n",
+ " (SelfAttention): MT5Attention(\n",
+ " (q): Linear(in_features=1024, out_features=1024, bias=False)\n",
+ " (k): Linear(in_features=1024, out_features=1024, bias=False)\n",
+ " (v): Linear(in_features=1024, out_features=1024, bias=False)\n",
+ " (o): Linear(in_features=1024, out_features=1024, bias=False)\n",
+ " (relative_attention_bias): Embedding(32, 16)\n",
+ " )\n",
+ " (layer_norm): MT5LayerNorm()\n",
+ " (dropout): Dropout(p=0.1, inplace=False)\n",
+ " )\n",
+ " (1): MT5LayerCrossAttention(\n",
+ " (EncDecAttention): MT5Attention(\n",
+ " (q): Linear(in_features=1024, out_features=1024, bias=False)\n",
+ " (k): Linear(in_features=1024, out_features=1024, bias=False)\n",
+ " (v): Linear(in_features=1024, out_features=1024, bias=False)\n",
+ " (o): Linear(in_features=1024, out_features=1024, bias=False)\n",
+ " )\n",
+ " (layer_norm): MT5LayerNorm()\n",
+ " (dropout): Dropout(p=0.1, inplace=False)\n",
+ " )\n",
+ " (2): MT5LayerFF(\n",
+ " (DenseReluDense): MT5DenseGatedActDense(\n",
+ " (wi_0): Linear(in_features=1024, out_features=2816, bias=False)\n",
+ " (wi_1): Linear(in_features=1024, out_features=2816, bias=False)\n",
+ " (wo): Linear(in_features=2816, out_features=1024, bias=False)\n",
+ " (dropout): Dropout(p=0.1, inplace=False)\n",
+ " (act): NewGELUActivation()\n",
+ " )\n",
+ " (layer_norm): MT5LayerNorm()\n",
+ " (dropout): Dropout(p=0.1, inplace=False)\n",
+ " )\n",
+ " )\n",
+ " )\n",
+ " (1-23): 23 x MT5Block(\n",
+ " (layer): ModuleList(\n",
+ " (0): MT5LayerSelfAttention(\n",
+ " (SelfAttention): MT5Attention(\n",
+ " (q): Linear(in_features=1024, out_features=1024, bias=False)\n",
+ " (k): Linear(in_features=1024, out_features=1024, bias=False)\n",
+ " (v): Linear(in_features=1024, out_features=1024, bias=False)\n",
+ " (o): Linear(in_features=1024, out_features=1024, bias=False)\n",
+ " )\n",
+ " (layer_norm): MT5LayerNorm()\n",
+ " (dropout): Dropout(p=0.1, inplace=False)\n",
+ " )\n",
+ " (1): MT5LayerCrossAttention(\n",
+ " (EncDecAttention): MT5Attention(\n",
+ " (q): Linear(in_features=1024, out_features=1024, bias=False)\n",
+ " (k): Linear(in_features=1024, out_features=1024, bias=False)\n",
+ " (v): Linear(in_features=1024, out_features=1024, bias=False)\n",
+ " (o): Linear(in_features=1024, out_features=1024, bias=False)\n",
+ " )\n",
+ " (layer_norm): MT5LayerNorm()\n",
+ " (dropout): Dropout(p=0.1, inplace=False)\n",
+ " )\n",
+ " (2): MT5LayerFF(\n",
+ " (DenseReluDense): MT5DenseGatedActDense(\n",
+ " (wi_0): Linear(in_features=1024, out_features=2816, bias=False)\n",
+ " (wi_1): Linear(in_features=1024, out_features=2816, bias=False)\n",
+ " (wo): Linear(in_features=2816, out_features=1024, bias=False)\n",
+ " (dropout): Dropout(p=0.1, inplace=False)\n",
+ " (act): NewGELUActivation()\n",
+ " )\n",
+ " (layer_norm): MT5LayerNorm()\n",
+ " (dropout): Dropout(p=0.1, inplace=False)\n",
+ " )\n",
+ " )\n",
+ " )\n",
+ " )\n",
+ " (final_layer_norm): MT5LayerNorm()\n",
+ " (dropout): Dropout(p=0.1, inplace=False)\n",
+ " )\n",
+ " (lm_head): Linear(in_features=1024, out_features=250112, bias=False)\n",
+ ")"
+ ]
+ },
+ "execution_count": 4,
+ "metadata": {},
+ "output_type": "execute_result"
+ }
+ ],
+ "source": [
+ "model"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 5,
+ "id": "63d7bc2d",
+ "metadata": {
+ "colab": {
+ "base_uri": "https://localhost:8080/"
+ },
+ "id": "05978e96",
+ "outputId": "ea9b7d40-010f-4df0-ec64-a7146a5f8b08"
+ },
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "trainable params: 282,624 || all params: 1,229,863,936 || trainable%: 0.0230\n"
+ ]
+ },
+ {
+ "data": {
+ "text/plain": [
+ "PeftModelForSeq2SeqLM(\n",
+ " (base_model): IA3Model(\n",
+ " (model): MT5ForConditionalGeneration(\n",
+ " (shared): Embedding(250112, 1024)\n",
+ " (encoder): MT5Stack(\n",
+ " (embed_tokens): Embedding(250112, 1024)\n",
+ " (block): ModuleList(\n",
+ " (0): MT5Block(\n",
+ " (layer): ModuleList(\n",
+ " (0): MT5LayerSelfAttention(\n",
+ " (SelfAttention): MT5Attention(\n",
+ " (q): Linear(in_features=1024, out_features=1024, bias=False)\n",
+ " (k): Linear(\n",
+ " (base_layer): Linear(in_features=1024, out_features=1024, bias=False)\n",
+ " (ia3_l): ParameterDict( (default): Parameter containing: [torch.FloatTensor of size 1024x1])\n",
+ " )\n",
+ " (v): Linear(\n",
+ " (base_layer): Linear(in_features=1024, out_features=1024, bias=False)\n",
+ " (ia3_l): ParameterDict( (default): Parameter containing: [torch.FloatTensor of size 1024x1])\n",
+ " )\n",
+ " (o): Linear(in_features=1024, out_features=1024, bias=False)\n",
+ " (relative_attention_bias): Embedding(32, 16)\n",
+ " )\n",
+ " (layer_norm): MT5LayerNorm()\n",
+ " (dropout): Dropout(p=0.1, inplace=False)\n",
+ " )\n",
+ " (1): MT5LayerFF(\n",
+ " (DenseReluDense): MT5DenseGatedActDense(\n",
+ " (wi_0): Linear(in_features=1024, out_features=2816, bias=False)\n",
+ " (wi_1): Linear(\n",
+ " (base_layer): Linear(in_features=1024, out_features=2816, bias=False)\n",
+ " (ia3_l): ParameterDict( (default): Parameter containing: [torch.FloatTensor of size 2816x1])\n",
+ " )\n",
+ " (wo): Linear(in_features=2816, out_features=1024, bias=False)\n",
+ " (dropout): Dropout(p=0.1, inplace=False)\n",
+ " (act): NewGELUActivation()\n",
+ " )\n",
+ " (layer_norm): MT5LayerNorm()\n",
+ " (dropout): Dropout(p=0.1, inplace=False)\n",
+ " )\n",
+ " )\n",
+ " )\n",
+ " (1-23): 23 x MT5Block(\n",
+ " (layer): ModuleList(\n",
+ " (0): MT5LayerSelfAttention(\n",
+ " (SelfAttention): MT5Attention(\n",
+ " (q): Linear(in_features=1024, out_features=1024, bias=False)\n",
+ " (k): Linear(\n",
+ " (base_layer): Linear(in_features=1024, out_features=1024, bias=False)\n",
+ " (ia3_l): ParameterDict( (default): Parameter containing: [torch.FloatTensor of size 1024x1])\n",
+ " )\n",
+ " (v): Linear(\n",
+ " (base_layer): Linear(in_features=1024, out_features=1024, bias=False)\n",
+ " (ia3_l): ParameterDict( (default): Parameter containing: [torch.FloatTensor of size 1024x1])\n",
+ " )\n",
+ " (o): Linear(in_features=1024, out_features=1024, bias=False)\n",
+ " )\n",
+ " (layer_norm): MT5LayerNorm()\n",
+ " (dropout): Dropout(p=0.1, inplace=False)\n",
+ " )\n",
+ " (1): MT5LayerFF(\n",
+ " (DenseReluDense): MT5DenseGatedActDense(\n",
+ " (wi_0): Linear(in_features=1024, out_features=2816, bias=False)\n",
+ " (wi_1): Linear(\n",
+ " (base_layer): Linear(in_features=1024, out_features=2816, bias=False)\n",
+ " (ia3_l): ParameterDict( (default): Parameter containing: [torch.FloatTensor of size 2816x1])\n",
+ " )\n",
+ " (wo): Linear(in_features=2816, out_features=1024, bias=False)\n",
+ " (dropout): Dropout(p=0.1, inplace=False)\n",
+ " (act): NewGELUActivation()\n",
+ " )\n",
+ " (layer_norm): MT5LayerNorm()\n",
+ " (dropout): Dropout(p=0.1, inplace=False)\n",
+ " )\n",
+ " )\n",
+ " )\n",
+ " )\n",
+ " (final_layer_norm): MT5LayerNorm()\n",
+ " (dropout): Dropout(p=0.1, inplace=False)\n",
+ " )\n",
+ " (decoder): MT5Stack(\n",
+ " (embed_tokens): Embedding(250112, 1024)\n",
+ " (block): ModuleList(\n",
+ " (0): MT5Block(\n",
+ " (layer): ModuleList(\n",
+ " (0): MT5LayerSelfAttention(\n",
+ " (SelfAttention): MT5Attention(\n",
+ " (q): Linear(in_features=1024, out_features=1024, bias=False)\n",
+ " (k): Linear(\n",
+ " (base_layer): Linear(in_features=1024, out_features=1024, bias=False)\n",
+ " (ia3_l): ParameterDict( (default): Parameter containing: [torch.FloatTensor of size 1024x1])\n",
+ " )\n",
+ " (v): Linear(\n",
+ " (base_layer): Linear(in_features=1024, out_features=1024, bias=False)\n",
+ " (ia3_l): ParameterDict( (default): Parameter containing: [torch.FloatTensor of size 1024x1])\n",
+ " )\n",
+ " (o): Linear(in_features=1024, out_features=1024, bias=False)\n",
+ " (relative_attention_bias): Embedding(32, 16)\n",
+ " )\n",
+ " (layer_norm): MT5LayerNorm()\n",
+ " (dropout): Dropout(p=0.1, inplace=False)\n",
+ " )\n",
+ " (1): MT5LayerCrossAttention(\n",
+ " (EncDecAttention): MT5Attention(\n",
+ " (q): Linear(in_features=1024, out_features=1024, bias=False)\n",
+ " (k): Linear(\n",
+ " (base_layer): Linear(in_features=1024, out_features=1024, bias=False)\n",
+ " (ia3_l): ParameterDict( (default): Parameter containing: [torch.FloatTensor of size 1024x1])\n",
+ " )\n",
+ " (v): Linear(\n",
+ " (base_layer): Linear(in_features=1024, out_features=1024, bias=False)\n",
+ " (ia3_l): ParameterDict( (default): Parameter containing: [torch.FloatTensor of size 1024x1])\n",
+ " )\n",
+ " (o): Linear(in_features=1024, out_features=1024, bias=False)\n",
+ " )\n",
+ " (layer_norm): MT5LayerNorm()\n",
+ " (dropout): Dropout(p=0.1, inplace=False)\n",
+ " )\n",
+ " (2): MT5LayerFF(\n",
+ " (DenseReluDense): MT5DenseGatedActDense(\n",
+ " (wi_0): Linear(in_features=1024, out_features=2816, bias=False)\n",
+ " (wi_1): Linear(\n",
+ " (base_layer): Linear(in_features=1024, out_features=2816, bias=False)\n",
+ " (ia3_l): ParameterDict( (default): Parameter containing: [torch.FloatTensor of size 2816x1])\n",
+ " )\n",
+ " (wo): Linear(in_features=2816, out_features=1024, bias=False)\n",
+ " (dropout): Dropout(p=0.1, inplace=False)\n",
+ " (act): NewGELUActivation()\n",
+ " )\n",
+ " (layer_norm): MT5LayerNorm()\n",
+ " (dropout): Dropout(p=0.1, inplace=False)\n",
+ " )\n",
+ " )\n",
+ " )\n",
+ " (1-23): 23 x MT5Block(\n",
+ " (layer): ModuleList(\n",
+ " (0): MT5LayerSelfAttention(\n",
+ " (SelfAttention): MT5Attention(\n",
+ " (q): Linear(in_features=1024, out_features=1024, bias=False)\n",
+ " (k): Linear(\n",
+ " (base_layer): Linear(in_features=1024, out_features=1024, bias=False)\n",
+ " (ia3_l): ParameterDict( (default): Parameter containing: [torch.FloatTensor of size 1024x1])\n",
+ " )\n",
+ " (v): Linear(\n",
+ " (base_layer): Linear(in_features=1024, out_features=1024, bias=False)\n",
+ " (ia3_l): ParameterDict( (default): Parameter containing: [torch.FloatTensor of size 1024x1])\n",
+ " )\n",
+ " (o): Linear(in_features=1024, out_features=1024, bias=False)\n",
+ " )\n",
+ " (layer_norm): MT5LayerNorm()\n",
+ " (dropout): Dropout(p=0.1, inplace=False)\n",
+ " )\n",
+ " (1): MT5LayerCrossAttention(\n",
+ " (EncDecAttention): MT5Attention(\n",
+ " (q): Linear(in_features=1024, out_features=1024, bias=False)\n",
+ " (k): Linear(\n",
+ " (base_layer): Linear(in_features=1024, out_features=1024, bias=False)\n",
+ " (ia3_l): ParameterDict( (default): Parameter containing: [torch.FloatTensor of size 1024x1])\n",
+ " )\n",
+ " (v): Linear(\n",
+ " (base_layer): Linear(in_features=1024, out_features=1024, bias=False)\n",
+ " (ia3_l): ParameterDict( (default): Parameter containing: [torch.FloatTensor of size 1024x1])\n",
+ " )\n",
+ " (o): Linear(in_features=1024, out_features=1024, bias=False)\n",
+ " )\n",
+ " (layer_norm): MT5LayerNorm()\n",
+ " (dropout): Dropout(p=0.1, inplace=False)\n",
+ " )\n",
+ " (2): MT5LayerFF(\n",
+ " (DenseReluDense): MT5DenseGatedActDense(\n",
+ " (wi_0): Linear(in_features=1024, out_features=2816, bias=False)\n",
+ " (wi_1): Linear(\n",
+ " (base_layer): Linear(in_features=1024, out_features=2816, bias=False)\n",
+ " (ia3_l): ParameterDict( (default): Parameter containing: [torch.FloatTensor of size 2816x1])\n",
+ " )\n",
+ " (wo): Linear(in_features=2816, out_features=1024, bias=False)\n",
+ " (dropout): Dropout(p=0.1, inplace=False)\n",
+ " (act): NewGELUActivation()\n",
+ " )\n",
+ " (layer_norm): MT5LayerNorm()\n",
+ " (dropout): Dropout(p=0.1, inplace=False)\n",
+ " )\n",
+ " )\n",
+ " )\n",
+ " )\n",
+ " (final_layer_norm): MT5LayerNorm()\n",
+ " (dropout): Dropout(p=0.1, inplace=False)\n",
+ " )\n",
+ " (lm_head): Linear(in_features=1024, out_features=250112, bias=False)\n",
+ " )\n",
+ " )\n",
+ ")"
+ ]
+ },
+ "execution_count": 5,
+ "metadata": {},
+ "output_type": "execute_result"
+ }
+ ],
+ "source": [
+ "model = get_peft_model(model, peft_config)\n",
+ "model.print_trainable_parameters()\n",
+ "model"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 6,
+ "id": "155b8728",
+ "metadata": {
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 140,
+ "referenced_widgets": [
+ "bbfb7533b5ca459194e171df56b79566",
+ "c894e8237aa34c56bb250acab1466005",
+ "a5a126b229064812bf3dcb228118be50",
+ "661e1b29c59a4295b594edfa4f50ff87",
+ "1bcba805972b484d8b6aa6542c81841c",
+ "e71f5c7f1d5d4f83b58c68d2fa310d9c",
+ "6a567e0a1a5447519c5df10e777520cf",
+ "7aeca19b84904906a04c12659f84ff9e",
+ "dd4b895874ce46ceb1ad0d9bc973f98f",
+ "b138f91be7f94008806eaf0a6988bc3f",
+ "da14180f51ab44b48470cb9ea74d3864",
+ "9e12d97af6124a5a8c6627708b300c1e",
+ "faa18df899c14e9cac6721253e6c9128",
+ "79d0ede7a5b24756aa6d34fda8c29159",
+ "3b175b452f4347558aa3c4501cc90030",
+ "fc4637a1b37e4e90874c71aa4271ac74",
+ "1b8aada826a0451bb60c418b19178c8c",
+ "a91916e02e9c424e881e45b3aa978574",
+ "ca509bd409624c998e555c9a779b8aae",
+ "9c890fc422954347b86d3bde7a421caf",
+ "6f9453484ea94587a64d70f1b3a1f6e4",
+ "48770ef159f44c01be2a75c75aecd80f",
+ "0c561dab67914ea9b6e1aab803600551",
+ "1e021a1954b44d69a90101a96c360661",
+ "013e3343285f437a893bdd673fb90e22",
+ "28802da68fb04d70b1c6bc511a04676f",
+ "94174da0d6554be087d4527bea5b511a",
+ "dc8ab16a1e6c4e6893c95ccd16568f9a",
+ "72383136663448d89cf3b82b87cbb392",
+ "5b1bdaf16cbc473081e4237f839167b9",
+ "51f8fb45485540bb985b606d43ae04ea",
+ "f760cd4758334ca9a43fd15612fd808b",
+ "f60e9915d2a74ca7bc010d7684f5acf6"
+ ]
+ },
+ "id": "4ee2babf",
+ "outputId": "3c413083-247d-47da-f25c-032764be0beb"
+ },
+ "outputs": [
+ {
+ "name": "stderr",
+ "output_type": "stream",
+ "text": [
+ "Using the latest cached version of the dataset since financial_phrasebank couldn't be found on the Hugging Face Hub\n",
+ "Found the latest cached dataset configuration 'sentences_allagree' at /root/.cache/huggingface/datasets/financial_phrasebank/sentences_allagree/1.0.0/550bde12e6c30e2674da973a55f57edde5181d53f5a5a34c1531c53f93b7e141 (last modified on Thu Jul 31 03:15:41 2025).\n"
+ ]
+ },
+ {
+ "data": {
+ "application/vnd.jupyter.widget-view+json": {
+ "model_id": "43b03e9b6de94bf0921228482d7be1e5",
+ "version_major": 2,
+ "version_minor": 0
+ },
+ "text/plain": [
+ "Map: 0%| | 0/2037 [00:00 Tensor(a!)\n",
+ " registered at /pytorch/build/aten/src/ATen/RegisterSchema.cpp:6\n",
+ " dispatch key: XPU\n",
+ " previous kernel: registered at /pytorch/aten/src/ATen/VmapModeRegistrations.cpp:37\n",
+ " new kernel: registered at /build/intel-pytorch-extension/build/Release/csrc/gpu/csrc/gpu/xpu/ATen/RegisterXPU_0.cpp:172 (function operator())\n"
+ ]
+ },
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "[2025-07-31 07:06:51,984] [INFO] [real_accelerator.py:254:get_accelerator] Setting ds_accelerator to xpu (auto detect)\n"
+ ]
+ },
+ {
+ "name": "stderr",
+ "output_type": "stream",
+ "text": [
+ "/usr/bin/ld: cannot find -laio: No such file or directory\n",
+ "collect2: error: ld returned 1 exit status\n"
+ ]
+ },
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "[2025-07-31 07:06:52,955] [INFO] [logging.py:107:log_dist] [Rank -1] [TorchCheckpointEngine] Initialized with serialization = False\n"
+ ]
+ },
+ {
+ "name": "stderr",
+ "output_type": "stream",
+ "text": [
+ "No label_names provided for model class `PeftModelForSeq2SeqLM`. Since `PeftModel` hides base models input arguments, if label_names is not given, label_names can't be set automatically within `Trainer`. Note that empty label_names list will be used instead.\n"
+ ]
+ },
+ {
+ "data": {
+ "text/html": [
+ "\n",
+ " \n",
+ " \n",
+ "
\n",
+ " [1275/1275 03:31, Epoch 5/5]\n",
+ "
\n",
+ " \n",
+ " \n",
+ " | Epoch | \n",
+ " Training Loss | \n",
+ " Validation Loss | \n",
+ " Accuracy | \n",
+ "
\n",
+ " \n",
+ " \n",
+ " \n",
+ " | 1 | \n",
+ " 2.169900 | \n",
+ " 0.507156 | \n",
+ " 0.621145 | \n",
+ "
\n",
+ " \n",
+ " | 2 | \n",
+ " 0.537700 | \n",
+ " 0.430996 | \n",
+ " 0.651982 | \n",
+ "
\n",
+ " \n",
+ " | 3 | \n",
+ " 0.482200 | \n",
+ " 0.426718 | \n",
+ " 0.696035 | \n",
+ "
\n",
+ " \n",
+ " | 4 | \n",
+ " 0.459700 | \n",
+ " 0.470894 | \n",
+ " 0.682819 | \n",
+ "
\n",
+ " \n",
+ " | 5 | \n",
+ " 0.436000 | \n",
+ " 0.409604 | \n",
+ " 0.718062 | \n",
+ "
\n",
+ " \n",
+ "
"
+ ],
+ "text/plain": [
+ ""
+ ]
+ },
+ "metadata": {},
+ "output_type": "display_data"
+ },
+ {
+ "data": {
+ "text/plain": [
+ "TrainOutput(global_step=1275, training_loss=0.8170911183076747, metrics={'train_runtime': 213.5513, 'train_samples_per_second': 47.693, 'train_steps_per_second': 5.97, 'total_flos': 344546979840000.0, 'train_loss': 0.8170911183076747, 'epoch': 5.0})"
+ ]
+ },
+ "execution_count": 5,
+ "metadata": {},
+ "output_type": "execute_result"
+ }
+ ],
+ "source": [
+ "# training and evaluation\n",
+ "\n",
+ "\n",
+ "def compute_metrics(eval_preds):\n",
+ " preds, labels = eval_preds\n",
+ " preds = tokenizer.batch_decode(preds, skip_special_tokens=True)\n",
+ " labels = tokenizer.batch_decode(labels, skip_special_tokens=True)\n",
+ "\n",
+ " correct = 0\n",
+ " total = 0\n",
+ " for pred, true in zip(preds, labels):\n",
+ " if pred.strip() == true.strip():\n",
+ " correct += 1\n",
+ " total += 1\n",
+ " accuracy = correct / total\n",
+ " return {\"accuracy\": accuracy}\n",
+ "\n",
+ "\n",
+ "training_args = Seq2SeqTrainingArguments(\n",
+ " \"out\",\n",
+ " per_device_train_batch_size=batch_size,\n",
+ " learning_rate=lr,\n",
+ " num_train_epochs=num_epochs,\n",
+ " eval_strategy=\"epoch\",\n",
+ " logging_strategy=\"epoch\",\n",
+ " save_strategy=\"no\",\n",
+ " report_to=[],\n",
+ " predict_with_generate=True,\n",
+ " generation_config=GenerationConfig(max_length=max_length),\n",
+ ")\n",
+ "trainer = Seq2SeqTrainer(\n",
+ " model=model,\n",
+ " processing_class=tokenizer,\n",
+ " args=training_args,\n",
+ " train_dataset=train_dataset,\n",
+ " eval_dataset=eval_dataset,\n",
+ " data_collator=default_data_collator,\n",
+ " compute_metrics=compute_metrics,\n",
+ ")\n",
+ "trainer.train()"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 6,
+ "id": "a8de6005",
+ "metadata": {
+ "ExecuteTime": {
+ "end_time": "2023-05-30T09:53:13.045146Z",
+ "start_time": "2023-05-30T09:53:13.035612Z"
+ }
+ },
+ "outputs": [],
+ "source": [
+ "# saving model\n",
+ "peft_model_id = f\"{model_name_or_path}_{peft_config.peft_type}_{peft_config.task_type}\"\n",
+ "model.save_pretrained(peft_model_id)"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "id": "bd20cd4c",
+ "metadata": {
+ "ExecuteTime": {
+ "end_time": "2023-05-30T09:53:15.240763Z",
+ "start_time": "2023-05-30T09:53:15.059304Z"
+ }
+ },
+ "outputs": [],
+ "source": [
+ "ckpt = f\"{peft_model_id}/adapter_model.safetensors\"\n",
+ "!du -h $ckpt"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 8,
+ "id": "76c2fc29",
+ "metadata": {
+ "ExecuteTime": {
+ "end_time": "2023-05-30T09:53:25.055105Z",
+ "start_time": "2023-05-30T09:53:17.797989Z"
+ }
+ },
+ "outputs": [],
+ "source": [
+ "from peft import PeftModel, PeftConfig\n",
+ "\n",
+ "peft_model_id = f\"{model_name_or_path}_{peft_config.peft_type}_{peft_config.task_type}\"\n",
+ "\n",
+ "config = PeftConfig.from_pretrained(peft_model_id)\n",
+ "model = AutoModelForSeq2SeqLM.from_pretrained(config.base_model_name_or_path)\n",
+ "model = PeftModel.from_pretrained(model, peft_model_id)"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 9,
+ "id": "d997f1cc",
+ "metadata": {
+ "ExecuteTime": {
+ "end_time": "2023-05-30T09:53:26.777030Z",
+ "start_time": "2023-05-30T09:53:26.013697Z"
+ }
+ },
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "EPS grew to 0.04 eur from 0.02 eur .\n",
+ "{'input_ids': tensor([[ 3, 24935, 3, 4774, 12, 4097, 6348, 3, 1238, 45,\n",
+ " 4097, 4305, 3, 1238, 3, 5, 1]]), 'attention_mask': tensor([[1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1]])}\n",
+ "tensor([[ 0, 1465, 1]])\n",
+ "['positive']\n"
+ ]
+ }
+ ],
+ "source": [
+ "model.eval()\n",
+ "i = 107\n",
+ "inputs = tokenizer(dataset[\"validation\"][text_column][i], return_tensors=\"pt\")\n",
+ "print(dataset[\"validation\"][text_column][i])\n",
+ "print(inputs)\n",
+ "\n",
+ "with torch.no_grad():\n",
+ " outputs = model.generate(input_ids=inputs[\"input_ids\"], max_new_tokens=10)\n",
+ " print(outputs)\n",
+ " print(tokenizer.batch_decode(outputs.detach().cpu().numpy(), skip_special_tokens=True))"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "id": "fb746c1e",
+ "metadata": {},
+ "outputs": [],
+ "source": []
+ }
+ ],
+ "metadata": {
+ "kernelspec": {
+ "display_name": "Python 3 (ipykernel)",
+ "language": "python",
+ "name": "python3"
+ },
+ "language_info": {
+ "codemirror_mode": {
+ "name": "ipython",
+ "version": 3
+ },
+ "file_extension": ".py",
+ "mimetype": "text/x-python",
+ "name": "python",
+ "nbconvert_exporter": "python",
+ "pygments_lexer": "ipython3",
+ "version": "3.11.13"
+ },
+ "toc": {
+ "base_numbering": 1,
+ "nav_menu": {},
+ "number_sections": true,
+ "sideBar": true,
+ "skip_h1_title": false,
+ "title_cell": "Table of Contents",
+ "title_sidebar": "Contents",
+ "toc_cell": false,
+ "toc_position": {},
+ "toc_section_display": true,
+ "toc_window_display": false
+ },
+ "varInspector": {
+ "cols": {
+ "lenName": 16,
+ "lenType": 16,
+ "lenVar": 40
+ },
+ "kernels_config": {
+ "python": {
+ "delete_cmd_postfix": "",
+ "delete_cmd_prefix": "del ",
+ "library": "var_list.py",
+ "varRefreshCmd": "print(var_dic_list())"
+ },
+ "r": {
+ "delete_cmd_postfix": ") ",
+ "delete_cmd_prefix": "rm(",
+ "library": "var_list.r",
+ "varRefreshCmd": "cat(var_dic_list()) "
+ }
+ },
+ "types_to_exclude": [
+ "module",
+ "function",
+ "builtin_function_or_method",
+ "instance",
+ "_Feature"
+ ],
+ "window_display": false
+ },
+ "vscode": {
+ "interpreter": {
+ "hash": "aee8b7b246df8f9039afb4144a1f6fd8d2ca17a180786b69acc140d282b71a49"
+ }
+ }
+ },
+ "nbformat": 4,
+ "nbformat_minor": 5
+}
diff --git a/peft/examples/conditional_generation/requirements.txt b/peft/examples/conditional_generation/requirements.txt
new file mode 100644
index 0000000000000000000000000000000000000000..9571ec3501248ebd05f2442a9a6d7ba6555f22bf
--- /dev/null
+++ b/peft/examples/conditional_generation/requirements.txt
@@ -0,0 +1,8 @@
+transformers
+accelerate
+evaluate
+deepspeed
+tqdm
+datasets
+safetensors
+scikit-learn
\ No newline at end of file
diff --git a/peft/examples/corda_finetuning/README.md b/peft/examples/corda_finetuning/README.md
new file mode 100644
index 0000000000000000000000000000000000000000..d39d2cc09e13a1b7988fbbb8ae905ab598f60da6
--- /dev/null
+++ b/peft/examples/corda_finetuning/README.md
@@ -0,0 +1,257 @@
+# CorDA: Context-Oriented Decomposition Adaptation of Large Language Models for Task-Aware Parameter-Efficient Fine-tuning
+
+## Introduction
+
+
+Existing PEFT methods are mostly agnostic of the context of a task of concern, e.g., a downstream task to learn or some pre-trained world knowledge to maintain.
+[CorDA](https://openreview.net/pdf?id=Gi00NVru6n) builds task-aware LoRA adapters from weight decomposition oriented by the context of the task concerned.
+
+Concretely, CorDA randomly collects a few (by default 256 in our `preprocess.py`) data samples from a target task, e.g. questions from a QA dataset or instructions to write a code or solve a math problem, and feeds these samples into a pre-trained LLM. We can obtain the covariance matrix of the input activation of each linear layer, i.e., $C=XX^T\in\mathcal{R}^{d_{in}\times d_{in}}$.
+We then perform singular value decomposition (SVD) for the weight $W\in \mathcal{R}^{d_{out}\times d_{in}}$ multiplied by the covariance matrix, i.e., $\verb|SVD|(WC) = U\Sigma V^T$. In this way, the context expressed by these representative covariance matrices is able to orientate the decomposition, such that the principal components (the singular vectors with the largest singular values) are most associated with the task of concern (please refer to Fig.2 of our paper for the advantage of our decomposition over the plain SVD). To ensure the same inference result with the pre-trained model at the start of adaptation, we multiply the inverse of these covariance matrices with the decomposed components, i.e., $\hat{W}=U\Sigma V^T C^{-1}$.
+
+Thanks to the task-awareness, you can choose how to utilize the task-specific principal components. For examples, if you want to adapt a model to a new task without losing the knowledge of a question-answering dataset, e.g., TriviaQA and NQopen, you can sample questions from this dataset to collect covariance matrices, and keep the principal components frozen because they compact the ability of this dataset, while using the lowest components with the smallest $r$ singular values to initialize the learnable LoRA adapters. This is achieved by the **knowledge-preserved mode (KPM)** of CorDA, which learns new tasks effectively while keeping the world knowledge you are concerned about as sound as possible. Alternatively, when your primary objective is to maximize performance on the finetuning task, disregarding the preservation of world knowledge, the **instruction-previewed mode (IPM**) will be favored. In this mode, CorDA uses the instruction and response from the fine-tuning task (e.g., Math or Code) to produce the covariance matrices. The principal components with the largest $r$ singular values, capturing the characteristics of the finetuning task in advance, can better adapt to the new ability, so they are used to initialize the LoRA adapters, with the remaining components frozen. IPM can further accelerate convergence to enhance the fine-tuning performance on downstream tasks.
+
+
+The implementations of KPM and IPM are compared as follows:
+
+| Mode | Collect covariance from | LoRA $A$ | LoRA $B$ |
+|---|---|---|---
+|KPM | questions from the knowledge benchmark to maintain | $A=\sqrt{\Sigma}\_{[-r:]}(V^T C^{-1})\_{[-r:,:]}$ | $B=U_{[:,-r:]}\sqrt{\Sigma}_{[-r:]}$ |
+IPM | instructions and responses from the downstream task to learn | $A= \sqrt{\Sigma}\_{[:r]} (V^T C^{-1})\_{[:r,:]}$ | $B =U_{[:,:r]} \sqrt{\Sigma}_{[:r]}$ |
+
+### Comparison with alternative methods
+
+The distinction between CorDA with other similar LoRA initialization methods is summarized as follows:
+
+| Method | Initialization for | SVD on | Data-driven | Supports knowledge maintenance |
+| - | - | - | - | - |
+| PiSSA | $A$ and $B$ | weights | no | no |
+| EVA | $A$ | activations | yes | no |
+|CorDA | $A$ and $B$ | weights (oriented by covariance) | yes | yes |
+
+"Supports knowledge maintenance" denotes the ability of explicitly associating a knowledge benchmark with some components of the pre-trained weights after decomposition, and keeping these components frozen during fine-tuning.
+
+### Some Results
+
+- Performance with knowledge-preserved mode (sample from NQopen, fine-tune on Math)
+
+| Method | Model | NQ open | GSM8k | Math | Avg. |
+|---|---|---|---|---|---|
+|Pre-trained|Llama-2-7b| 14.99 | -| - | - |
+|LoRA|Llama-2-7b|1.27| 42.68 | 5.88 | 16.61 |
+|**CorDA (KPM)** |Llama-2-7b| **8.20** | **46.32** | **7.00** | **20.51** |
+|Pre-trained|Llama-2-13b|23.63|-|-|-|
+|LoRA|Llama-2-13b| 16.26 | 57.24 | 8.92 | 27.47 |
+|**CorDA (KPM)** |Llama-2-13b| **19.86** | **59.29** | **9.62** | **29.59** |
+|Pre-trained|Llama-3-8b|13.41|-|-|-|
+|LoRA|Llama-3-8b| 8.75 | 72.33 | 24.04| 35.04 |
+|**CorDA (KPM)** |Llama-3-8b| **9.61** | **74.68** | **25.34** | **36.54** |
+|Pre-trained|Gemma-2-9b|12.85|-|-|-|
+|LoRA|Gemma-2-9b| 9.28 | 83.47 | 42.30| 45.02 |
+|**CorDA (KPM)** |Gemma-2-9b|**10.17** | **84.08** | **42.64** | **45.63** |
+
+- Performance with instruction-previewed mode (sample from Math, fine-tune on Math)
+
+| Method | Model | GSM8k | Math |
+| --- | --- | --- | ---|
+|LoRA| Llama-2-7b | 42.68 | 5.88 |
+|PiSSA | Llama-2-7b | 51.63 | 7.32 |
+| **CorDA (IPM)** | Llama-2-7b | **53.45** | **8.64** |
+|LoRA| Llama-2-13b | 57.24 | 8.92 |
+|PiSSA | Llama-2-13b |60.88 | 11.08|
+| **CorDA (IPM)** | Llama-2-13b | **62.47** |**11.54** |
+|LoRA| Gemma-2-9b | 83.47 | 42.30 |
+|PiSSA | Gemma-2-9b | 84.23 | 43.52|
+| **CorDA (IPM)** | Gemma-2-9b | **84.45** | **43.88** |
+
+
+## Quick Start
+
+### Knowledge-preserved adaptation mode
+
+```py
+import torch
+from peft import LoraConfig, get_peft_model
+from transformers import AutoTokenizer, AutoModelForCausalLM
+from peft.tuners.lora.config import CordaConfig
+from peft.tuners.lora.corda import preprocess_corda
+from trl import SFTConfig, SFTTrainer
+from datasets import load_dataset
+
+model = AutoModelForCausalLM.from_pretrained("meta-llama/Llama-2-7b-hf", torch_dtype=torch.bfloat16, device_map="auto")
+tokenizer = AutoTokenizer.from_pretrained("meta-llama/Llama-2-7b-hf")
+tokenizer.pad_token_id = tokenizer.eos_token_id
+sampled_dataset = load_dataset("wikitext", "wikitext-2-raw-v1", split="train[:256]")
+dataset = load_dataset("imdb", split="train[:256]")
+
+
+def run_model():
+ for batch in sampled_dataset:
+ input_ids = batch["text"]
+ input_ids = input_ids.to(model.device)
+ with torch.no_grad():
+ model(input_ids)
+
+
+corda_config = CordaConfig(
+ corda_method="kpm",
+)
+lora_config = LoraConfig(
+ init_lora_weights="corda",
+ corda_config=corda_config,
+)
+
+# Call `preprocess_corda` first to collect covariance matrix and build SVD result for model
+# For more details, please refer to documentation of `preprocess_corda`
+preprocess_corda(model, lora_config, run_model=run_model)
+
+# Call `get_peft_model` after preprocessing, or else you'll encounter error
+peft_model = get_peft_model(model, lora_config)
+peft_model.print_trainable_parameters()
+
+training_args = SFTConfig(dataset_text_field="text", max_seq_length=128)
+trainer = SFTTrainer(
+ model=peft_model,
+ args=training_args,
+ train_dataset=dataset,
+ processing_class=tokenizer,
+)
+trainer.train()
+peft_model.save_pretrained("corda-llama-2-7b")
+```
+
+### Instruction-previewed adaptation mode
+
+```py
+# Get model and dataset identically as KPM...
+
+# Different from KPM, we run the model on dataset of the downstream task to collect covariance matrices
+def run_model():
+ for batch in dataset:
+ input_ids = batch["text"]
+ input_ids = input_ids.to(model.device)
+ with torch.no_grad():
+ model(input_ids)
+
+# Different from KPM, we set `corda_method` to `"ipm"`
+corda_config = CordaConfig(
+ corda_method="ipm",
+)
+
+# The rest of training process is identical to KPM...
+```
+
+## Advanced Usage
+
+### Preprocessing
+
+`preprocess.py`: This script builds CorDA adapters for a model, and saves the adapters initial weights and residual model weights to a specified directory. Example usage:
+
+#### Knowledge-preserved adaptation mode
+
+```bash
+export CUDA_VISIBLE_DEVICES=0 # force to use device 0 of CUDA GPU
+export ZE_AFFINITY_MASK=0 # force to use device 0 of Intel XPU
+
+python -u preprocess.py --model_id="meta-llama/Llama-2-7b-hf" \
+ --r 128 --seed 233 \
+ --save_model --save_path {path_to_residual_model} \
+ --calib_dataset "nqopen"
+```
+Arguments:
+
+- `--model_id` is the pre-trained model for decomposition.
+- `--r` is the low rank of LoRA, e.g. 128.
+- `--calib_dataset` specifies the dataset to sample data to obtain covariance matrices. KPA mode uses QA datasets such as `"nqopen"`, `"traivia_qa"`, or other choices.
+- `--save_model` saves the initialized model in `--save_path`.
+
+#### Instruction-previewed adaptation mode
+
+```bash
+export CUDA_VISIBLE_DEVICES=0 # force to use device 0 of CUDA GPU
+export ZE_AFFINITY_MASK=0 # force to use device 0 of Intel XPU
+
+python -u preprocess.py --model_id="meta-llama/Llama-2-7b-hf" \
+ --r 128 --seed 233 \
+ --save_model --save_path {path_to_residual_model} \
+ --first_eigen --calib_dataset "MetaMATH"
+```
+
+Arguments:
+
+- `--first_eigen` uses the largest $r$ singular values and vectors to initialize the learnable adapter for the instruction-previewed adaptation mode.
+- `--calib_dataset` specifies the dataset to sample data to obtain covariance matrices. Instruction-previewed mode uses the downstream task dataset you are learning, such as `"MetaMATH"`, `"codefeedback"`, `"WizLMinstruct"`, `"alpaca"`, or other choices.
+
+#### Note about memory consumption
+
+The process of collecting covariance matrices is performed in `torch.float32` by default. If you would like to reduce the memory consumption of preprocessing, you can specify `use_float16_for_covariance=True` in `CordaConfig` to collect covariance matrices in `torch.float16`. But this may cause numerical instability only in a few cases, such that the initialized model does not ensure the exact same inference result as the original model. So it is suggested to check, e.g., comparing the inference result of Wiki/PTB perplexity before and after preprocessing, if you choose to perform in `torch.float16`.
+
+### Fine-tuning
+
+`corda_finetuning.py`: This script fine-tunes the preprocessed model built above on a downstream task.
+
+Example usage:
+
+```bash
+python corda_finetuning.py \
+ --model_name_or_path {path_to_residual_model} \
+ --output_dir {path_to_output_model} \
+ --corda_mode True \
+ --data_path meta-math/MetaMathQA \
+ --dataset_split "train[:100000]" \
+ --dataset_field query response \
+ --num_train_epochs 1 \
+ --per_device_train_batch_size 1 \
+ --gradient_accumulation_steps 32 \
+ --save_strategy "steps" \
+ --save_steps 100 \
+ --save_total_limit 1 \
+ --learning_rate 2e-5 \
+ --weight_decay 0. \
+ --warmup_ratio 0.03 \
+ --lr_scheduler_type "cosine" \
+ --logging_steps 1 \
+ --bf16 True \
+ --tf32 True \
+ --report_to none
+```
+
+### Convert CorDA to LoRA
+
+The main advantage of CorDA is concentrated during the training phase. For a trained CorDA adapter, we recommend converting it equivalently to the LoRA adapter for using and sharing.
+
+```python
+# The fine-tuned matrices $A$ and $B$ in CorDA adapter is saved and should be combined with the residual model.
+peft_model.save_pretrained(output_dir)
+# Given the matrices $A_0$ and $B_0$, initialized by CorDA and untrained, and the trained matrices $A$ and $B$,
+# we can convert these to LoRA by setting $\Delta W = A \times B - A_0 \times B_0 = [A \mid A_0] \times [B \mid -B_0]^T = A'B'$.
+peft_model.save_pretrained(output_dir, path_initial_model_for_weight_conversion="corda_init")
+```
+
+This conversion enables the loading of LoRA on top of a standard base model:
+
+```python
+import torch
+from peft import PeftModel
+from transformers import AutoModelForCausalLM
+
+model = AutoModelForCausalLM.from_pretrained(
+ "meta-llama/Llama-2-7b-hf", torch_dtype=torch.bfloat16, device_map="auto"
+)
+# No SVD is performed during this step, and the base model remains unaltered.
+peft_model = PeftModel.from_pretrained(model, "corda-llama-2-7b-lora")
+```
+
+Utilizing the converted LoRA does not require modifying the parameters of the base model. When multiple converted LoRAs are needed simultaneously, each adapter operates independently without interference, allowing for the adapters to be freely deleted or added.
+
+Note that this conversion is not supported if `rslora` is used in combination with `rank_pattern` or `alpha_pattern`.
+
+## Citation
+```
+@inproceedings{yangcorda,
+ title={CorDA: Context-Oriented Decomposition Adaptation of Large Language Models for Task-Aware Parameter-Efficient Fine-tuning},
+ author={Yang, Yibo and Li, Xiaojie and Zhou, Zhongzhu and Song, Shuaiwen Leon and Wu, Jianlong and Nie, Liqiang and Ghanem, Bernard},
+ booktitle={The Thirty-eighth Annual Conference on Neural Information Processing Systems},
+ year={2024},
+}
+```
diff --git a/peft/examples/corda_finetuning/corda_finetuning.py b/peft/examples/corda_finetuning/corda_finetuning.py
new file mode 100644
index 0000000000000000000000000000000000000000..42b80ee48e723aafa722126fdbd2e5dcfa0fd08f
--- /dev/null
+++ b/peft/examples/corda_finetuning/corda_finetuning.py
@@ -0,0 +1,276 @@
+# Copyright 2024-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+import copy
+import os
+from collections.abc import Sequence
+from dataclasses import dataclass, field
+from typing import Optional
+
+import torch
+import transformers
+from datasets import load_dataset
+from transformers import Trainer
+
+from peft import LoraConfig, PeftModel, get_peft_model
+
+
+IGNORE_INDEX = -100
+
+PROMPT = (
+ "Below is an instruction that describes a task. "
+ "Write a response that appropriately completes the request.\n\n"
+ "### Instruction:\n{instruction}\n\n### Response:"
+)
+
+
+def get_nb_trainable_parameters(model) -> tuple[int, int]:
+ r"""
+ Returns the number of trainable parameters and the number of all parameters in the model.
+ """
+ trainable_params = 0
+ all_param = 0
+ for _, param in model.named_parameters():
+ num_params = param.numel()
+ # if using DS Zero 3 and the weights are initialized empty
+ if num_params == 0 and hasattr(param, "ds_numel"):
+ num_params = param.ds_numel
+
+ # Due to the design of 4bit linear layers from bitsandbytes
+ # one needs to multiply the number of parameters by 2 to get
+ # the correct number of parameters
+ if param.__class__.__name__ == "Params4bit":
+ num_bytes = param.quant_storage.itemsize if hasattr(param, "quant_storage") else 1
+ num_params = num_params * 2 * num_bytes
+
+ all_param += num_params
+ if param.requires_grad:
+ trainable_params += num_params
+
+ return trainable_params, all_param
+
+
+@dataclass
+class TrainingArguments(transformers.TrainingArguments):
+ model_name_or_path: Optional[str] = field(default="facebook/opt-125m")
+ data_path: str = field(default=None, metadata={"help": "Path to the training data."})
+ dataset_split: str = field(default="train[:100000]", metadata={"help": "(`['train', 'test', 'eval']`):"})
+ dataset_field: list[str] = field(default=None, metadata={"help": "Fields of dataset input and output."})
+ dataloader_num_proc: int = field(default=16, metadata={"help": "Number of processes to load dataset"})
+ dataloader_batch_size: int = field(
+ default=3000,
+ metadata={
+ "help": "batch size to load dataset. To set the batch size for training, you should pass --batch_size argument instead."
+ },
+ )
+ optim: str = field(default="adamw_torch")
+ model_max_length: int = field(
+ default=512,
+ metadata={"help": "Maximum sequence length. Sequences will be right padded (and possibly truncated)."},
+ )
+ lora_r: int = field(
+ default=None,
+ metadata={"help": "The rank of LoRA adapter. When passing `None`, CorDA or full fine-tuning is used."},
+ )
+ corda_mode: bool = field(default=True, metadata={"help": "True for CorDA mode"})
+
+
+def safe_save_model_for_hf_trainer(trainer: transformers.Trainer, output_dir: str):
+ """Collects the state dict and dump to disk."""
+ state_dict = trainer.model.state_dict()
+ if trainer.args.should_save:
+ cpu_state_dict = {key: value.cpu() for key, value in state_dict.items()}
+ del state_dict
+ trainer._save(output_dir, state_dict=cpu_state_dict) # noqa
+
+
+def smart_tokenizer_and_embedding_resize(
+ special_tokens_dict: dict,
+ tokenizer: transformers.PreTrainedTokenizer,
+ model: transformers.PreTrainedModel,
+):
+ """Resize tokenizer and embedding.
+
+ Note: This is the unoptimized version that may make your embedding size not be divisible by 64.
+ """
+ num_new_tokens = tokenizer.add_special_tokens(special_tokens_dict)
+ model.resize_token_embeddings(len(tokenizer))
+
+ if num_new_tokens > 0:
+ input_embeddings = model.get_input_embeddings().weight.data
+ output_embeddings = model.get_output_embeddings().weight.data
+
+ input_embeddings_avg = input_embeddings[:-num_new_tokens].mean(dim=0, keepdim=True)
+ output_embeddings_avg = output_embeddings[:-num_new_tokens].mean(dim=0, keepdim=True)
+
+ input_embeddings[-num_new_tokens:] = input_embeddings_avg
+ output_embeddings[-num_new_tokens:] = output_embeddings_avg
+
+
+def _tokenize_fn(strings: Sequence[str], tokenizer: transformers.PreTrainedTokenizer) -> dict:
+ """Tokenize a list of strings."""
+ tokenized_list = [
+ tokenizer(
+ text,
+ return_tensors="pt",
+ padding="longest",
+ max_length=tokenizer.model_max_length,
+ truncation=True,
+ )
+ for text in strings
+ ]
+ input_ids = labels = [tokenized.input_ids[0] for tokenized in tokenized_list]
+ input_ids_lens = labels_lens = [
+ tokenized.input_ids.ne(tokenizer.pad_token_id).sum().item() for tokenized in tokenized_list
+ ]
+ return {
+ "input_ids": input_ids,
+ "labels": labels,
+ "input_ids_lens": input_ids_lens,
+ "labels_lens": labels_lens,
+ }
+
+
+def preprocess(
+ sources: Sequence[str],
+ targets: Sequence[str],
+ tokenizer: transformers.PreTrainedTokenizer,
+) -> dict:
+ """Preprocess the data by tokenizing."""
+ examples = [s + t for s, t in zip(sources, targets)]
+ examples_tokenized, sources_tokenized = (_tokenize_fn(strings, tokenizer) for strings in (examples, sources))
+ input_ids = examples_tokenized["input_ids"]
+ labels = copy.deepcopy(input_ids)
+ for label, source_len in zip(labels, sources_tokenized["input_ids_lens"]):
+ label[:source_len] = IGNORE_INDEX
+ return {
+ "input_ids": input_ids,
+ "labels": labels,
+ }
+
+
+@dataclass
+class DataCollatorForSupervisedDataset:
+ """Collate examples for supervised fine-tuning."""
+
+ tokenizer: transformers.PreTrainedTokenizer
+
+ def __call__(self, instances: Sequence[dict]) -> dict[str, torch.Tensor]:
+ input_ids, labels = tuple([instance[key] for instance in instances] for key in ("input_ids", "labels"))
+ input_ids = [torch.tensor(x) for x in input_ids]
+ input_ids = torch.nn.utils.rnn.pad_sequence(
+ input_ids, batch_first=True, padding_value=self.tokenizer.pad_token_id
+ )
+ labels = [torch.tensor(x) for x in labels]
+ labels = torch.nn.utils.rnn.pad_sequence(labels, batch_first=True, padding_value=IGNORE_INDEX)
+ return {
+ "input_ids": input_ids,
+ "labels": labels,
+ "attention_mask": input_ids.ne(self.tokenizer.pad_token_id),
+ }
+
+
+def train_tokenize_function(examples, tokenizer, query, response):
+ sources = [
+ PROMPT.format_map(
+ {
+ "instruction": instruction,
+ }
+ )
+ for instruction in examples[query]
+ ]
+ targets = [f"{output}{tokenizer.eos_token}" for output in examples[response]]
+ data_dict = preprocess(sources, targets, tokenizer)
+ return data_dict
+
+
+def train():
+ parser = transformers.HfArgumentParser(TrainingArguments)
+ script_args = parser.parse_args_into_dataclasses()[0]
+ print(script_args)
+
+ if script_args.corda_mode:
+ print("Train in CorDA mode")
+ res_model = transformers.AutoModelForCausalLM.from_pretrained(
+ script_args.model_name_or_path,
+ device_map="auto",
+ )
+ model = PeftModel.from_pretrained(
+ res_model, script_args.model_name_or_path, subfolder="corda_init", is_trainable=True
+ )
+ elif script_args.lora_r is not None:
+ print("Train in LoRA mode")
+ model = transformers.AutoModelForCausalLM.from_pretrained(
+ script_args.model_name_or_path,
+ device_map="auto",
+ )
+ lora_config = LoraConfig(
+ r=script_args.lora_r,
+ lora_alpha=script_args.lora_r,
+ init_lora_weights=True, # script_args.init_lora_weights,
+ target_modules=["q_proj", "o_proj", "k_proj", "v_proj", "gate_proj", "up_proj", "down_proj"],
+ lora_dropout=0,
+ bias="none",
+ task_type="CAUSAL_LM",
+ )
+ model = get_peft_model(model, lora_config)
+ else:
+ print("Train in Full Finetuning mode")
+ model = transformers.AutoModelForCausalLM.from_pretrained(
+ script_args.model_name_or_path,
+ torch_dtype=torch.bfloat16,
+ device_map="auto",
+ )
+ trainable_params, all_param = get_nb_trainable_parameters(model)
+ print(
+ f"trainable params: {trainable_params:,d} || all params: {all_param:,d} || trainable%: {100 * trainable_params / all_param}"
+ )
+ tokenizer = transformers.AutoTokenizer.from_pretrained(
+ script_args.model_name_or_path,
+ model_max_length=script_args.model_max_length,
+ padding_side="right",
+ use_fast=True,
+ trust_remote_code=True,
+ )
+ tokenizer.pad_token_id = tokenizer.eos_token_id
+
+ raw_train_datasets = load_dataset(script_args.data_path, split=script_args.dataset_split)
+ train_dataset = raw_train_datasets.map(
+ train_tokenize_function,
+ batched=True,
+ batch_size=script_args.dataloader_batch_size,
+ num_proc=script_args.dataloader_num_proc,
+ remove_columns=raw_train_datasets.column_names,
+ load_from_cache_file=True,
+ desc="Running tokenizer on train dataset",
+ fn_kwargs={
+ "tokenizer": tokenizer,
+ "query": script_args.dataset_field[0],
+ "response": script_args.dataset_field[1],
+ },
+ )
+
+ data_collator = DataCollatorForSupervisedDataset(tokenizer=tokenizer)
+ data_module = {
+ "train_dataset": train_dataset,
+ "data_collator": data_collator,
+ }
+ trainer = Trainer(model=model, processing_class=tokenizer, args=script_args, **data_module)
+ trainer.train()
+ trainer.save_state()
+ model.save_pretrained(os.path.join(script_args.output_dir, "ft"))
+
+
+if __name__ == "__main__":
+ train()
diff --git a/peft/examples/corda_finetuning/datautils.py b/peft/examples/corda_finetuning/datautils.py
new file mode 100644
index 0000000000000000000000000000000000000000..3e612b07af57f57023e8b1a319f38047e2e7c54d
--- /dev/null
+++ b/peft/examples/corda_finetuning/datautils.py
@@ -0,0 +1,235 @@
+# Copyright 2024-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+import os
+import random
+
+import numpy as np
+import torch
+from datasets import load_dataset
+
+
+"""
+doc https://huggingface.co/docs/datasets/loading
+doc https://huggingface.co/docs/datasets/process
+doc https://huggingface.co/blog/llama2#how-to-prompt-llama-2
+"""
+
+
+def set_seed(seed):
+ np.random.seed(seed)
+ torch.random.manual_seed(seed)
+
+
+def sample_train_loaders(name, tokenizer, nsamples=128, seed=0, seqlen=2048):
+ set_seed(seed)
+ if "wikitext2" in name:
+ traindata = load_dataset(
+ "wikitext",
+ "wikitext-2-raw-v1",
+ split="train",
+ )
+ traindata = "\n\n".join(traindata["text"])
+ elif "c4" in name:
+ traindata = load_dataset(
+ "allenai/c4",
+ "allenai--c4",
+ data_files={"train": "en/c4-train.00000-of-01024.json.gz"},
+ split="train",
+ )
+ traindata = "\n\n".join(traindata["text"])
+ else:
+ raise NotImplementedError
+
+ trainloader = []
+ for _ in range(nsamples):
+ i = random.randint(0, len(traindata) - seqlen * 2 - 1)
+ j = i + seqlen * 2
+ # breakpoint()
+ trainenc = tokenizer(traindata[i:j], return_tensors="pt")
+ inp = trainenc.input_ids[:, :seqlen]
+ trainloader.append(inp)
+ return trainloader
+
+
+def get_redpajama_train(tokenizer, percent=10, seed=3, batch_size=128, max_length=2048):
+ def tokenization(example):
+ return tokenizer(example["text"], truncation=True, max_length=max_length)
+
+ if percent != 100:
+ split = f"train[:{int(850000 * percent / 100)}]"
+ else:
+ split = "train"
+ dataset = load_dataset("togethercomputer/RedPajama-Data-1T-Sample", split=split)
+
+ processed_dataset = dataset.map(tokenization, batched=True, batch_size=batch_size, num_proc=os.cpu_count())
+ return processed_dataset
+
+
+def get_english_quote(dataset_name, tokenizer):
+ data = load_dataset(dataset_name)
+ data = data.map(lambda samples: tokenizer(samples["quote"]), batched=True)
+ return data["train"]
+
+
+def get_qat_dataset(name, tokenizer, data_percent):
+ if name == "red_pajama":
+ data = get_redpajama_train(tokenizer, data_percent)
+
+ elif name == "Abirate/english_quotes":
+ data = get_english_quote(name, tokenizer)
+ else:
+ raise NotImplementedError
+ data = data.shuffle()
+ return data
+
+
+llama_chat_format = """[INST] <>
+"Below is an instruction that describes a task. Write a response that appropriately completes the request."
+<>
+
+{instruction} [/INST] {response}
+"""
+
+
+def get_calib_data(name, tokenizer, model_id, nsamples, seqlen=2048, seed=3):
+ print(f" get_data_from: {name}, nsamples={nsamples}, seqlen={seqlen}, {seed}")
+ cache_file = f"cache/{name}_{model_id.replace('/', '_')}_{nsamples}_{seqlen}_{seed}.pt"
+ traindataset = []
+ if not os.path.exists("cache"):
+ os.makedirs("cache")
+ if os.path.exists(cache_file):
+ print(f"found data file: {cache_file}")
+ traindataset = torch.load(cache_file)
+ print("loaded ...")
+ return traindataset
+ if name == "c4":
+ traindata = load_dataset(
+ "allenai/c4",
+ "allenai--c4",
+ data_files={"train": "en/c4-train.00000-of-01024.json.gz"},
+ split="train",
+ )
+ tot_text = "\n\n".join(traindata["text"])
+ elif name == "wikitext2":
+ traindata = load_dataset("wikitext", "wikitext-2-raw-v1", split="train")
+ tot_text = "\n\n".join(traindata["text"])
+ elif name == "ptb":
+ traindata = load_dataset(
+ "ptb_text_only",
+ "penn_treebank",
+ split="train",
+ )
+ tot_text = "\n\n".join(traindata["sentence"])
+ elif name == "traivia_qa":
+ traindata = load_dataset("trivia_qa", "rc", split="train")
+ tot_text = "\n\n".join(traindata["question"])
+ elif name == "nqopen":
+ traindata = load_dataset("nq_open", split="train")
+ tot_text = "\n\n".join(traindata["question"])
+ elif name == "alpaca":
+ selected_data_dict = load_dataset("iboing/alpaca_data", split="train").shuffle(seed=seed).take(nsamples)
+ for example in selected_data_dict:
+ if example.get("input", "") == "":
+ s = llama_chat_format.format(instruction=example["instruction"], response=example["output"])
+ trainenc = tokenizer(s, return_tensors="pt")
+ inp = trainenc.input_ids[:, :seqlen]
+ attention_mask = torch.ones_like(inp)
+ traindataset.append({"input_ids": inp, "attention_mask": attention_mask})
+ print("example instruction:", s)
+ torch.save(traindataset, cache_file)
+ return traindataset
+ elif name == "MetaMATH":
+ selected_data_dict = load_dataset("iboing/MetaMathQA-395K", split="train").shuffle(seed=seed).take(nsamples)
+ for example in selected_data_dict:
+ if example.get("input", "") == "":
+ s = llama_chat_format.format(instruction=example["query"], response=example["response"])
+ trainenc = tokenizer(s, return_tensors="pt")
+ inp = trainenc.input_ids[:, :seqlen]
+ attention_mask = torch.ones_like(inp)
+ traindataset.append({"input_ids": inp, "attention_mask": attention_mask})
+ print("example instruction:", s)
+ torch.save(traindataset, cache_file)
+ return traindataset
+ elif name == "codefeedback":
+ selected_data_dict = (
+ load_dataset("iboing/CodeFeedback-Filtered-Instruction", split="train").shuffle(seed=seed).take(nsamples)
+ )
+ for example in selected_data_dict:
+ if example.get("input", "") == "":
+ s = llama_chat_format.format(instruction=example["query"], response=example["answer"])
+ trainenc = tokenizer(s, return_tensors="pt")
+ inp = trainenc.input_ids[:, :seqlen]
+ attention_mask = torch.ones_like(inp)
+ traindataset.append({"input_ids": inp, "attention_mask": attention_mask})
+ print("example instruction:", s)
+ torch.save(traindataset, cache_file)
+ return traindataset
+ elif name == "WizLMinstruct":
+ selected_data_dict = (
+ load_dataset("iboing/WizardLM_evol_instruct_V2_143k", split="train").shuffle(seed=seed).take(nsamples)
+ )
+ for example in selected_data_dict:
+ if example.get("input", "") == "":
+ s = llama_chat_format.format(
+ instruction=example["conversation"][0]["human"], response=example["conversation"][0]["assistant"]
+ )
+ trainenc = tokenizer(s, return_tensors="pt")
+ inp = trainenc.input_ids[:, :seqlen]
+ attention_mask = torch.ones_like(inp)
+ traindataset.append({"input_ids": inp, "attention_mask": attention_mask})
+ print("example instruction:", s)
+ torch.save(traindataset, cache_file)
+ return traindataset
+ else:
+ raise NotImplementedError
+ print(f"tot_text={len(tot_text)}")
+ for _ in range(nsamples):
+ i = random.randint(0, len(tot_text) - seqlen - 1)
+ j = i + seqlen * 10
+ trainenc = tokenizer(tot_text[i:j], return_tensors="pt")
+ inp = trainenc.input_ids[:, :seqlen]
+ attention_mask = torch.ones_like(inp)
+ traindataset.append({"input_ids": inp, "attention_mask": attention_mask})
+ torch.save(traindataset, cache_file)
+ return traindataset
+
+
+def get_eval_loaders(name, tokenizer):
+ if "wikitext2" in name:
+ testdata = load_dataset(
+ "wikitext",
+ "wikitext-2-raw-v1",
+ split="test",
+ )
+ testenc = tokenizer("\n\n".join(testdata["text"]), return_tensors="pt")
+ return testenc
+ if "ptb" in name:
+ valdata = load_dataset(
+ "ptb_text_only",
+ "penn_treebank",
+ split="validation",
+ )
+ testenc = tokenizer("\n\n".join(valdata["sentence"]), return_tensors="pt")
+ return testenc
+ if "c4" in name:
+ testdata = load_dataset(
+ "allenai/c4",
+ "allenai--c4",
+ data_files={"validation": "en/c4-validation.00000-of-00008.json.gz"},
+ split="validation",
+ )
+ testenc = tokenizer("\n\n".join(testdata["text"]), return_tensors="pt")
+ return testenc
+ raise NotImplementedError
diff --git a/peft/examples/corda_finetuning/preprocess.py b/peft/examples/corda_finetuning/preprocess.py
new file mode 100644
index 0000000000000000000000000000000000000000..765242f15e46ff08939702dea4f3b0e73ba93a2c
--- /dev/null
+++ b/peft/examples/corda_finetuning/preprocess.py
@@ -0,0 +1,165 @@
+# Copyright 2024-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+import argparse
+import os
+
+import numpy as np
+import torch
+from datautils import get_calib_data
+from tqdm import tqdm
+from transformers import AutoModelForCausalLM, AutoTokenizer
+
+from peft import get_peft_model
+from peft.tuners.lora.config import CordaConfig, LoraConfig
+from peft.tuners.lora.corda import preprocess_corda
+
+
+@torch.no_grad()
+def run_model(model, calib_loader):
+ model.eval()
+ for batch in tqdm(calib_loader):
+ batch = {k: v.to(model.device) for k, v in batch.items()}
+ model(**batch)
+
+
+def main(args):
+ # Setting random seed of numpy and torch
+ np.random.seed(args.seed)
+ torch.manual_seed(args.seed)
+ if torch.cuda.is_available():
+ torch.cuda.manual_seed_all(args.seed)
+ elif torch.xpu.is_available():
+ torch.xpu.manual_seed_all(args.seed)
+ torch.use_deterministic_algorithms(True)
+
+ # Load model
+ model_id = args.model_id
+ tokenizer = AutoTokenizer.from_pretrained(model_id, trust_remote_code=True)
+
+ model = AutoModelForCausalLM.from_pretrained(
+ model_id, device_map="auto", torch_dtype=torch.float16, trust_remote_code=True
+ )
+
+ # Collect data
+ calib_loader = get_calib_data(args.calib_dataset, tokenizer, model_id, args.calib_loader_size, seed=args.seed)
+
+ # Evaluate the original model
+ print("\n---- model before svd ---\n")
+ print(model)
+
+ # Perform decomposition
+ corda_config = CordaConfig(
+ corda_method="ipm" if args.first_eigen else "kpm",
+ )
+ lora_config = LoraConfig(
+ init_lora_weights="corda",
+ target_modules=["q_proj", "o_proj", "k_proj", "v_proj", "gate_proj", "up_proj", "down_proj"],
+ r=args.r,
+ lora_alpha=args.r,
+ corda_config=corda_config,
+ )
+ preprocess_corda(
+ model,
+ lora_config,
+ run_model=lambda: run_model(model, calib_loader),
+ )
+ model = get_peft_model(model, lora_config)
+
+ # Evaluate again to check if the model is consistent
+ # Using `model.model` here because `get_peft_model` wraps a layer to the model
+ print("\n---- model after svd ---\n")
+ print(model)
+
+ # Save as hugging face model
+ if args.save_model:
+ assert args.save_path is not None
+ save_path = args.save_path
+
+ # Save CorDA modules
+ model.peft_config["default"].init_lora_weights = True
+ model.save_pretrained(os.path.join(save_path, "corda_init"))
+
+ # Save residual model
+ model = model.unload()
+ model.save_pretrained(save_path)
+
+ # Save tokenizer
+ tokenizer.save_pretrained(save_path)
+ print(f"Done building CorDA huggingface model in {save_path}")
+
+
+if __name__ == "__main__":
+ parser = argparse.ArgumentParser()
+ parser.add_argument(
+ "--model_id",
+ type=str,
+ default="meta-llama/Llama-2-7b-hf",
+ help="Pretrained model ID",
+ )
+ parser.add_argument(
+ "--calib_loader_size",
+ type=int,
+ default=256,
+ help="number of samples used for covariance matrices",
+ )
+ parser.add_argument(
+ "--calib_dataset",
+ type=str,
+ default="wikitext2",
+ choices=[
+ "wikitext2",
+ "c4",
+ "ptb",
+ "traivia_qa",
+ "nqopen",
+ "MetaMATH",
+ "codefeedback",
+ "WizLMinstruct",
+ "alpaca",
+ ],
+ help="calibration dataset",
+ )
+ parser.add_argument(
+ "--eval_mmlu",
+ action="store_true",
+ help="evaluate mmlu",
+ )
+ parser.add_argument(
+ "--seed",
+ type=int,
+ default=233,
+ help="random seed",
+ )
+ parser.add_argument(
+ "--r",
+ type=int,
+ default=None,
+ )
+ parser.add_argument(
+ "--first_eigen",
+ action="store_true",
+ )
+ parser.add_argument(
+ "--save_model",
+ action="store_true",
+ )
+ parser.add_argument(
+ "--save_path",
+ type=str,
+ default=None,
+ )
+ args = parser.parse_args()
+
+ main(args)
diff --git a/peft/examples/cpt_finetuning/README.md b/peft/examples/cpt_finetuning/README.md
new file mode 100644
index 0000000000000000000000000000000000000000..2c84ce91c95e4480168fca7971d3cae188348fea
--- /dev/null
+++ b/peft/examples/cpt_finetuning/README.md
@@ -0,0 +1,64 @@
+
+# Context-aware Prompt Tuning: Advancing In-Context Learning with Adversarial Methods
+## Introduction ([Paper](https://huggingface.co/papers/2410.17222), [Code](https://github.com/tsachiblau/Context-aware-Prompt-Tuning-Advancing-In-Context-Learning-with-Adversarial-Methods), [Notebook](cpt_train_and_inference.ipynb), [Colab](https://colab.research.google.com/drive/1UhQDVhZ9bDlSk1551SuJV8tIUmlIayta?usp=sharing))
+
+> Large Language Models (LLMs) can perform few-shot learning using either optimization-based approaches or In-Context Learning (ICL). Optimization-based methods often suffer from overfitting, as they require updating a large number of parameters with limited data. In contrast, ICL avoids overfitting but typically underperforms compared to optimization-based methods and is highly sensitive to the selection, order, and format of demonstration examples. To overcome these challenges, we introduce Context-aware Prompt Tuning (CPT), a method inspired by ICL, Prompt Tuning (PT), and adversarial attacks. CPT builds on the ICL strategy of concatenating examples before the input, extending it by incorporating PT-like learning to refine the context embedding through iterative optimization, extracting deeper insights from the training examples. Our approach carefully modifies specific context tokens, considering the unique structure of the examples within the context. In addition to updating the context with PT-like optimization, CPT draws inspiration from adversarial attacks, adjusting the input based on the labels present in the context while preserving the inherent value of the user-provided data. To ensure robustness and stability during optimization, we employ a projected gradient descent algorithm, constraining token embeddings to remain close to their original values and safeguarding the quality of the context. Our method has demonstrated superior accuracy across multiple classification tasks using various LLM models, outperforming existing baselines and effectively addressing the overfitting challenge in few-shot learning.
+
+
+
+
+

+
\n",
+ " \n",
+ "
\n",
+ " [500/500 01:28, Epoch 5/5]\n",
+ "
\n",
+ " \n",
+ " \n",
+ " | Step | \n",
+ " Training Loss | \n",
+ "
\n",
+ " \n",
+ " \n",
+ " \n",
+ " | 100 | \n",
+ " 0.400800 | \n",
+ "
\n",
+ " \n",
+ " | 200 | \n",
+ " 0.036000 | \n",
+ "
\n",
+ " \n",
+ " | 300 | \n",
+ " 0.026300 | \n",
+ "
\n",
+ " \n",
+ " | 400 | \n",
+ " 0.016100 | \n",
+ "
\n",
+ " \n",
+ " | 500 | \n",
+ " 0.011600 | \n",
+ "
\n",
+ " \n",
+ "
"
+ ]
+ },
+ "metadata": {}
+ },
+ {
+ "output_type": "execute_result",
+ "data": {
+ "text/plain": [
+ "TrainOutput(global_step=500, training_loss=0.09815525007247924, metrics={'train_runtime': 90.6767, 'train_samples_per_second': 5.514, 'train_steps_per_second': 5.514, 'total_flos': 79477977907200.0, 'train_loss': 0.09815525007247924, 'epoch': 5.0})"
+ ]
+ },
+ "metadata": {},
+ "execution_count": 10
+ }
+ ],
+ "source": [
+ "training_args = TrainingArguments(\n",
+ " output_dir='../.',\n",
+ " use_cpu=False,\n",
+ " auto_find_batch_size=False,\n",
+ " learning_rate=1e-4,\n",
+ " logging_steps=100,\n",
+ " per_device_train_batch_size=1,\n",
+ " save_total_limit=1,\n",
+ " remove_unused_columns=False,\n",
+ " num_train_epochs=5,\n",
+ " fp16=True,\n",
+ " save_strategy='no',\n",
+ " logging_dir=\"logs\",\n",
+ " report_to=\"none\"\n",
+ ")\n",
+ "\n",
+ "trainer = Trainer(\n",
+ " model=model,\n",
+ " args=training_args,\n",
+ " train_dataset=cpt_train_dataset, # Custom CPT training dataset.\n",
+ " data_collator=CPTDataCollatorForLanguageModeling(tokenizer, training=True, mlm=False)\n",
+ ")\n",
+ "\n",
+ "trainer.train()"
+ ],
+ "metadata": {
+ "ExecuteTime": {
+ "end_time": "2024-10-22T09:25:27.599132Z",
+ "start_time": "2024-10-22T09:25:13.906685Z"
+ },
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 268
+ },
+ "id": "1a865c2ad2dc7218",
+ "outputId": "c4bfd785-e354-4ee6-a87e-63c17bfd2605"
+ },
+ "id": "1a865c2ad2dc7218",
+ "execution_count": 10
+ },
+ {
+ "cell_type": "markdown",
+ "source": [
+ "# Model Evaluation\n",
+ "\n",
+ "---"
+ ],
+ "metadata": {
+ "collapsed": false,
+ "id": "b799ea89a567590f"
+ },
+ "id": "b799ea89a567590f"
+ },
+ {
+ "cell_type": "code",
+ "outputs": [
+ {
+ "output_type": "stream",
+ "name": "stderr",
+ "text": [
+ "100%|██████████| 100/100 [00:00<00:00, 1972.82it/s]\n"
+ ]
+ },
+ {
+ "output_type": "stream",
+ "name": "stdout",
+ "text": [
+ "Sentence: input: it 's a charming and often affecting journey . output: positive \n",
+ " \t The prediction is: positive\n",
+ " \t The GT is positive\n",
+ "Sentence: input: unflinchingly bleak and desperate output: negative \n",
+ " \t The prediction is: negative\n",
+ " \t The GT is negative\n",
+ "Sentence: input: allows us to hope that nolan is poised to embark a major career as a commercial yet inventive filmmaker . output: positive \n",
+ " \t The prediction is: positive\n",
+ " \t The GT is positive\n",
+ "Sentence: input: the acting , costumes , music , cinematography and sound are all astounding given the production 's austere locales . output: positive \n",
+ " \t The prediction is: positive\n",
+ " \t The GT is positive\n",
+ "Sentence: input: it 's slow -- very , very slow . output: negative \n",
+ " \t The prediction is: negative\n",
+ " \t The GT is negative\n",
+ "Sentence: input: although laced with humor and a few fanciful touches , the film is a refreshingly serious look at young women . output: positive \n",
+ " \t The prediction is: positive\n",
+ " \t The GT is positive\n",
+ "Sentence: input: a sometimes tedious film . output: negative \n",
+ " \t The prediction is: negative\n",
+ " \t The GT is negative\n",
+ "Sentence: input: or doing last year 's taxes with your ex-wife . output: negative \n",
+ " \t The prediction is: negative\n",
+ " \t The GT is negative\n",
+ "Sentence: input: you do n't have to know about music to appreciate the film 's easygoing blend of comedy and romance . output: positive \n",
+ " \t The prediction is: positive\n",
+ " \t The GT is positive\n",
+ "Sentence: input: in exactly 89 minutes , most of which passed as slowly as if i 'd been sitting naked on an igloo , formula 51 sank from quirky to jerky to utter turkey . output: negative \n",
+ " \t The prediction is: negative\n",
+ " \t The GT is negative\n",
+ "Sentence: input: the mesmerizing performances of the leads keep the film grounded and keep the audience riveted . output: positive \n",
+ " \t The prediction is: positive\n",
+ " \t The GT is positive\n",
+ "Sentence: input: it takes a strange kind of laziness to waste the talents of robert forster , anne meara , eugene levy , and reginald veljohnson all in the same movie . output: negative \n",
+ " \t The prediction is: negative\n",
+ " \t The GT is negative\n",
+ "Sentence: input: ... the film suffers from a lack of humor ( something needed to balance out the violence ) ... output: negative \n",
+ " \t The prediction is: negative\n",
+ " \t The GT is negative\n",
+ "Sentence: input: we root for ( clara and paul ) , even like them , though perhaps it 's an emotion closer to pity . output: positive \n",
+ " \t The prediction is: positive\n",
+ " \t The GT is positive\n",
+ "Sentence: input: even horror fans will most likely not find what they 're seeking with trouble every day ; the movie lacks both thrills and humor . output: negative \n",
+ " \t The prediction is: negative\n",
+ " \t The GT is negative\n",
+ "Sentence: input: a gorgeous , high-spirited musical from india that exquisitely blends music , dance , song , and high drama . output: positive \n",
+ " \t The prediction is: positive\n",
+ " \t The GT is positive\n",
+ "Sentence: input: the emotions are raw and will strike a nerve with anyone who 's ever had family trauma . output: positive \n",
+ " \t The prediction is: positive\n",
+ " \t The GT is positive\n",
+ "Sentence: input: audrey tatou has a knack for picking roles that magnify her outrageous charm , and in this literate french comedy , she 's as morning-glory exuberant as she was in amélie . output: positive \n",
+ " \t The prediction is: positive\n",
+ " \t The GT is positive\n",
+ "Sentence: input: ... the movie is just a plain old monster . output: negative \n",
+ " \t The prediction is: negative\n",
+ " \t The GT is negative\n",
+ "Sentence: input: in its best moments , resembles a bad high school production of grease , without benefit of song . output: negative \n",
+ " \t The prediction is: negative\n",
+ " \t The GT is negative\n",
+ "Sentence: input: pumpkin takes an admirable look at the hypocrisy of political correctness , but it does so with such an uneven tone that you never know when humor ends and tragedy begins . output: negative \n",
+ " \t The prediction is: negative\n",
+ " \t The GT is negative\n",
+ "Sentence: input: the iditarod lasts for days - this just felt like it did . output: negative \n",
+ " \t The prediction is: negative\n",
+ " \t The GT is negative\n",
+ "Sentence: input: holden caulfield did it better . output: negative \n",
+ " \t The prediction is: positive\n",
+ " \t The GT is negative\n",
+ "Sentence: input: a delectable and intriguing thriller filled with surprises , read my lips is an original . output: positive \n",
+ " \t The prediction is: positive\n",
+ " \t The GT is positive\n",
+ "Sentence: input: seldom has a movie so closely matched the spirit of a man and his work . output: positive \n",
+ " \t The prediction is: positive\n",
+ " \t The GT is positive\n",
+ "Sentence: input: nicks , seemingly uncertain what 's going to make people laugh , runs the gamut from stale parody to raunchy sex gags to formula romantic comedy . output: negative \n",
+ " \t The prediction is: negative\n",
+ " \t The GT is negative\n",
+ "Sentence: input: the action switches between past and present , but the material link is too tenuous to anchor the emotional connections that purport to span a 125-year divide . output: negative \n",
+ " \t The prediction is: negative\n",
+ " \t The GT is negative\n",
+ "Sentence: input: it 's an offbeat treat that pokes fun at the democratic exercise while also examining its significance for those who take part . output: positive \n",
+ " \t The prediction is: positive\n",
+ " \t The GT is positive\n",
+ "Sentence: input: it 's a cookie-cutter movie , a cut-and-paste job . output: negative \n",
+ " \t The prediction is: negative\n",
+ " \t The GT is negative\n",
+ "Sentence: input: i had to look away - this was god awful . output: negative \n",
+ " \t The prediction is: negative\n",
+ " \t The GT is negative\n",
+ "Sentence: input: thanks to scott 's charismatic roger and eisenberg 's sweet nephew , roger dodger is one of the most compelling variations on in the company of men . output: positive \n",
+ " \t The prediction is: positive\n",
+ " \t The GT is positive\n",
+ "Sentence: input: ... designed to provide a mix of smiles and tears , `` crossroads '' instead provokes a handful of unintentional howlers and numerous yawns . output: negative \n",
+ " \t The prediction is: negative\n",
+ " \t The GT is negative\n",
+ "Sentence: input: a gorgeous , witty , seductive movie . output: positive \n",
+ " \t The prediction is: positive\n",
+ " \t The GT is positive\n",
+ "Sentence: input: if the movie succeeds in instilling a wary sense of ` there but for the grace of god , ' it is far too self-conscious to draw you deeply into its world . output: negative \n",
+ " \t The prediction is: negative\n",
+ " \t The GT is negative\n",
+ "Sentence: input: it does n't believe in itself , it has no sense of humor ... it 's just plain bored . output: negative \n",
+ " \t The prediction is: negative\n",
+ " \t The GT is negative\n",
+ "Sentence: input: a sequence of ridiculous shoot - 'em - up scenes . output: negative \n",
+ " \t The prediction is: negative\n",
+ " \t The GT is negative\n",
+ "Sentence: input: the weight of the piece , the unerring professionalism of the chilly production , and the fascination embedded in the lurid topic prove recommendation enough . output: positive \n",
+ " \t The prediction is: positive\n",
+ " \t The GT is positive\n",
+ "Sentence: input: ( w ) hile long on amiable monkeys and worthy environmentalism , jane goodall 's wild chimpanzees is short on the thrills the oversize medium demands . output: negative \n",
+ " \t The prediction is: negative\n",
+ " \t The GT is negative\n",
+ "Sentence: input: as surreal as a dream and as detailed as a photograph , as visually dexterous as it is at times imaginatively overwhelming . output: positive \n",
+ " \t The prediction is: positive\n",
+ " \t The GT is positive\n",
+ "Sentence: input: escaping the studio , piccoli is warmly affecting and so is this adroitly minimalist movie . output: positive \n",
+ " \t The prediction is: positive\n",
+ " \t The GT is positive\n",
+ "Sentence: input: there 's ... tremendous energy from the cast , a sense of playfulness and excitement that seems appropriate . output: positive \n",
+ " \t The prediction is: positive\n",
+ " \t The GT is positive\n",
+ "Sentence: input: this illuminating documentary transcends our preconceived vision of the holy land and its inhabitants , revealing the human complexities beneath . output: positive \n",
+ " \t The prediction is: positive\n",
+ " \t The GT is positive\n",
+ "Sentence: input: the subtle strength of `` elling '' is that it never loses touch with the reality of the grim situation . output: positive \n",
+ " \t The prediction is: positive\n",
+ " \t The GT is positive\n",
+ "Sentence: input: holm ... embodies the character with an effortlessly regal charisma . output: positive \n",
+ " \t The prediction is: positive\n",
+ " \t The GT is positive\n",
+ "Sentence: input: the title not only describes its main characters , but the lazy people behind the camera as well . output: negative \n",
+ " \t The prediction is: positive\n",
+ " \t The GT is negative\n",
+ "Sentence: input: it offers little beyond the momentary joys of pretty and weightless intellectual entertainment . output: negative \n",
+ " \t The prediction is: positive\n",
+ " \t The GT is negative\n",
+ "Sentence: input: a synthesis of cliches and absurdities that seems positively decadent in its cinematic flash and emptiness . output: negative \n",
+ " \t The prediction is: negative\n",
+ " \t The GT is negative\n",
+ "Sentence: input: a subtle and well-crafted ( for the most part ) chiller . output: positive \n",
+ " \t The prediction is: positive\n",
+ " \t The GT is positive\n",
+ "Sentence: input: has a lot of the virtues of eastwood at his best . output: positive \n",
+ " \t The prediction is: positive\n",
+ " \t The GT is positive\n",
+ "Sentence: input: it 's hampered by a lifetime-channel kind of plot and a lead actress who is out of her depth . output: negative \n",
+ " \t The prediction is: negative\n",
+ " \t The GT is negative\n",
+ "Sentence: input: it feels like an after-school special gussied up with some fancy special effects , and watching its rote plot points connect is about as exciting as gazing at an egg timer for 93 minutes . output: negative \n",
+ " \t The prediction is: positive\n",
+ " \t The GT is negative\n",
+ "Sentence: input: for the most part , director anne-sophie birot 's first feature is a sensitive , extraordinarily well-acted drama . output: positive \n",
+ " \t The prediction is: positive\n",
+ " \t The GT is positive\n",
+ "Sentence: input: mr. tsai is a very original artist in his medium , and what time is it there ? output: positive \n",
+ " \t The prediction is: positive\n",
+ " \t The GT is positive\n",
+ "Sentence: input: sade is an engaging look at the controversial eponymous and fiercely atheistic hero . output: positive \n",
+ " \t The prediction is: positive\n",
+ " \t The GT is positive\n",
+ "Sentence: input: so devoid of any kind of intelligible story that it makes films like xxx and collateral damage seem like thoughtful treatises output: negative \n",
+ " \t The prediction is: negative\n",
+ " \t The GT is negative\n",
+ "Sentence: input: a tender , heartfelt family drama . output: positive \n",
+ " \t The prediction is: positive\n",
+ " \t The GT is positive\n",
+ "Sentence: input: ... a hollow joke told by a cinematic gymnast having too much fun embellishing the misanthropic tale to actually engage it . output: negative \n",
+ " \t The prediction is: negative\n",
+ " \t The GT is negative\n",
+ "Sentence: input: the cold turkey would 've been a far better title . output: negative \n",
+ " \t The prediction is: negative\n",
+ " \t The GT is negative\n",
+ "Sentence: input: manages to be both repulsively sadistic and mundane . output: negative \n",
+ " \t The prediction is: negative\n",
+ " \t The GT is negative\n",
+ "Sentence: input: it 's just disappointingly superficial -- a movie that has all the elements necessary to be a fascinating , involving character study , but never does more than scratch the surface . output: negative \n",
+ " \t The prediction is: negative\n",
+ " \t The GT is negative\n",
+ "Sentence: input: this is a story of two misfits who do n't stand a chance alone , but together they are magnificent . output: positive \n",
+ " \t The prediction is: positive\n",
+ " \t The GT is positive\n",
+ "Sentence: input: schaeffer has to find some hook on which to hang his persistently useless movies , and it might as well be the resuscitation of the middle-aged character . output: negative \n",
+ " \t The prediction is: negative\n",
+ " \t The GT is negative\n",
+ "Sentence: input: the primitive force of this film seems to bubble up from the vast collective memory of the combatants . output: positive \n",
+ " \t The prediction is: positive\n",
+ " \t The GT is positive\n",
+ "Sentence: input: on this tricky topic , tadpole is very much a step in the right direction , with its blend of frankness , civility and compassion . output: positive \n",
+ " \t The prediction is: positive\n",
+ " \t The GT is positive\n",
+ "Sentence: input: the script kicks in , and mr. hartley 's distended pace and foot-dragging rhythms follow . output: negative \n",
+ " \t The prediction is: positive\n",
+ " \t The GT is negative\n",
+ "Sentence: input: you wonder why enough was n't just a music video rather than a full-length movie . output: negative \n",
+ " \t The prediction is: negative\n",
+ " \t The GT is negative\n",
+ "Sentence: input: if you 're hard up for raunchy college humor , this is your ticket right here . output: positive \n",
+ " \t The prediction is: positive\n",
+ " \t The GT is positive\n",
+ "Sentence: input: a fast , funny , highly enjoyable movie . output: positive \n",
+ " \t The prediction is: positive\n",
+ " \t The GT is positive\n",
+ "Sentence: input: good old-fashioned slash-and-hack is back ! output: positive \n",
+ " \t The prediction is: positive\n",
+ " \t The GT is positive\n",
+ "Sentence: input: this one is definitely one to skip , even for horror movie fanatics . output: negative \n",
+ " \t The prediction is: negative\n",
+ " \t The GT is negative\n",
+ "Sentence: input: for all its impressive craftsmanship , and despite an overbearing series of third-act crescendos , lily chou-chou never really builds up a head of emotional steam . output: negative \n",
+ " \t The prediction is: negative\n",
+ " \t The GT is negative\n",
+ "Sentence: input: exquisitely nuanced in mood tics and dialogue , this chamber drama is superbly acted by the deeply appealing veteran bouquet and the chilling but quite human berling . output: positive \n",
+ " \t The prediction is: positive\n",
+ " \t The GT is positive\n",
+ "Sentence: input: uses high comedy to evoke surprising poignance . output: positive \n",
+ " \t The prediction is: positive\n",
+ " \t The GT is positive\n",
+ "Sentence: input: one of creepiest , scariest movies to come along in a long , long time , easily rivaling blair witch or the others . output: positive \n",
+ " \t The prediction is: positive\n",
+ " \t The GT is positive\n",
+ "Sentence: input: a string of rehashed sight gags based in insipid vulgarity . output: negative \n",
+ " \t The prediction is: negative\n",
+ " \t The GT is negative\n",
+ "Sentence: input: among the year 's most intriguing explorations of alientation . output: positive \n",
+ " \t The prediction is: positive\n",
+ " \t The GT is positive\n",
+ "Sentence: input: the movie fails to live up to the sum of its parts . output: negative \n",
+ " \t The prediction is: negative\n",
+ " \t The GT is negative\n",
+ "Sentence: input: the son 's room is a triumph of gentility that earns its moments of pathos . output: positive \n",
+ " \t The prediction is: positive\n",
+ " \t The GT is positive\n",
+ "Sentence: input: there is nothing outstanding about this film , but it is good enough and will likely be appreciated most by sailors and folks who know their way around a submarine . output: positive \n",
+ " \t The prediction is: positive\n",
+ " \t The GT is positive\n",
+ "Sentence: input: this is a train wreck of an action film -- a stupefying attempt by the filmmakers to force-feed james bond into the mindless xxx mold and throw 40 years of cinematic history down the toilet in favor of bright flashes and loud bangs . output: negative \n",
+ " \t The prediction is: negative\n",
+ " \t The GT is negative\n",
+ "Sentence: input: the draw ( for `` big bad love '' ) is a solid performance by arliss howard . output: positive \n",
+ " \t The prediction is: positive\n",
+ " \t The GT is positive\n",
+ "Sentence: input: green might want to hang onto that ski mask , as robbery may be the only way to pay for his next project . output: negative \n",
+ " \t The prediction is: positive\n",
+ " \t The GT is negative\n",
+ "Sentence: input: it 's one pussy-ass world when even killer-thrillers revolve around group therapy sessions . output: negative \n",
+ " \t The prediction is: negative\n",
+ " \t The GT is negative\n",
+ "Sentence: input: though it 's become almost redundant to say so , major kudos go to leigh for actually casting people who look working-class . output: positive \n",
+ " \t The prediction is: positive\n",
+ " \t The GT is positive\n",
+ "Sentence: input: the band 's courage in the face of official repression is inspiring , especially for aging hippies ( this one included ) . output: positive \n",
+ " \t The prediction is: positive\n",
+ " \t The GT is positive\n",
+ "Sentence: input: the movie achieves as great an impact by keeping these thoughts hidden as ... ( quills ) did by showing them . output: positive \n",
+ " \t The prediction is: positive\n",
+ " \t The GT is positive\n",
+ "Sentence: input: the film flat lines when it should peak and is more missed opportunity and trifle than dark , decadent truffle . output: negative \n",
+ " \t The prediction is: negative\n",
+ " \t The GT is negative\n",
+ "Sentence: input: jaglom ... put ( s ) the audience in the privileged position of eavesdropping on his characters output: positive \n",
+ " \t The prediction is: positive\n",
+ " \t The GT is positive\n",
+ "Sentence: input: fresnadillo 's dark and jolting images have a way of plying into your subconscious like the nightmare you had a week ago that wo n't go away . output: positive \n",
+ " \t The prediction is: positive\n",
+ " \t The GT is positive\n",
+ "Sentence: input: we know the plot 's a little crazy , but it held my interest from start to finish . output: positive \n",
+ " \t The prediction is: positive\n",
+ " \t The GT is positive\n",
+ "Sentence: input: it 's a scattershot affair , but when it hits its mark it 's brilliant . output: positive \n",
+ " \t The prediction is: positive\n",
+ " \t The GT is positive\n",
+ "Sentence: input: hardly a masterpiece , but it introduces viewers to a good charitable enterprise and some interesting real people . output: positive \n",
+ " \t The prediction is: positive\n",
+ " \t The GT is positive\n",
+ "Sentence: input: you wo n't like roger , but you will quickly recognize him . output: negative \n",
+ " \t The prediction is: positive\n",
+ " \t The GT is negative\n",
+ "Sentence: input: if steven soderbergh 's ` solaris ' is a failure it is a glorious failure . output: positive \n",
+ " \t The prediction is: negative\n",
+ " \t The GT is positive\n",
+ "Sentence: input: byler reveals his characters in a way that intrigues and even fascinates us , and he never reduces the situation to simple melodrama . output: positive \n",
+ " \t The prediction is: positive\n",
+ " \t The GT is positive\n",
+ "Sentence: input: this riveting world war ii moral suspense story deals with the shadow side of american culture : racial prejudice in its ugly and diverse forms . output: negative \n",
+ " \t The prediction is: positive\n",
+ " \t The GT is negative\n",
+ "Sentence: input: it 's difficult to imagine the process that produced such a script , but here 's guessing that spray cheese and underarm noises played a crucial role . output: negative \n",
+ " \t The prediction is: positive\n",
+ " \t The GT is negative\n",
+ "Sentence: input: no sophomore slump for director sam mendes , who segues from oscar winner to oscar-winning potential with a smooth sleight of hand . output: positive \n",
+ " \t The prediction is: positive\n",
+ " \t The GT is positive\n",
+ "Sentence: input: on the whole , the movie lacks wit , feeling and believability to compensate for its incessant coarseness and banality . output: negative \n",
+ " \t The prediction is: negative\n",
+ " \t The GT is negative\n",
+ "Sentence: input: why make a documentary about these marginal historical figures ? output: negative \n",
+ " \t The prediction is: negative\n",
+ " \t The GT is negative\n",
+ "The model Acc is 90.0%\n"
+ ]
+ }
+ ],
+ "source": [
+ "model.eval()\n",
+ "\n",
+ "# Select relevant columns from the test dataset\n",
+ "test_dataset = test_dataset.select_columns(['sentence', 'label_text'])\n",
+ "\n",
+ "# Convert the test dataset to a CPT-compatible format\n",
+ "cpt_test_dataset = CPTDataset(test_dataset, tokenizer, templates)\n",
+ "\n",
+ "# Get the device where the model is loaded (CPU, GPU or XPU)\n",
+ "device = model.device\n",
+ "list_bool_predictions = []\n",
+ "\n",
+ "for i in range(len(test_dataset)):\n",
+ " input_ids, input_type_mask = cpt_test_dataset[i]['input_ids'], cpt_test_dataset[i]['input_type_mask']\n",
+ "\n",
+ " # Pass the inputs through the model\n",
+ " outputs = model(\n",
+ " input_ids=torch.Tensor(input_ids).long().to(device=device).view(1, -1),\n",
+ " labels=torch.Tensor(input_ids).long().to(device=device).view(1, -1),\n",
+ " input_type_mask=torch.Tensor(input_type_mask).long().to(device=device).view(1, -1)\n",
+ " )\n",
+ "\n",
+ " # Shift logits to exclude the last token and match the labels\n",
+ " shifted_logits = outputs.logits[..., :-1, :].contiguous().to(model.dtype)[0, -len(input_ids) + 1:]\n",
+ " shift_labels = torch.Tensor(input_ids).long().to(device=device).view(1, -1)[0, 1:].contiguous().to(device)\n",
+ " shifted_input_type_mask = torch.Tensor(input_type_mask).long().to(device=device).view(1, -1)[..., 1:].contiguous().to(device)\n",
+ "\n",
+ " # Create a mask for the type `4` tokens (label tokens)\n",
+ " mask = torch.Tensor(shifted_input_type_mask).long().to(device=device).view(-1,) == 4\n",
+ "\n",
+ " # Extract logits and labels corresponding to the mask\n",
+ " logit = shifted_logits[mask]\n",
+ " label = shift_labels[mask]\n",
+ "\n",
+ " # All possible label tokens for `negative` and `positive`\n",
+ " all_labels = torch.Tensor([tokenizer(i, add_special_tokens=False)[\"input_ids\"] for i in ['negative', 'positive']]).long().to(device).view(-1,)\n",
+ "\n",
+ " # Compare logits with label tokens and infer prediction\n",
+ " prediction = logit[0, torch.Tensor([tokenizer(i, add_special_tokens=False)[\"input_ids\"] for i in ['negative', 'positive']]).long().to(device).view(-1,)].argmax()\n",
+ " prediction_text = 'negative' if prediction == 0 else 'positive'\n",
+ " print(f\"Sentence: {tokenizer.decode(input_ids)} \\n \\t The prediction is: {prediction_text}\\n \\t The GT is {tokenizer.decode(label)}\")\n",
+ " list_bool_predictions.append(prediction_text == tokenizer.decode(label))\n",
+ "\n",
+ "print(f'The model Acc is {100 * np.mean(list_bool_predictions)}%')"
+ ],
+ "metadata": {
+ "ExecuteTime": {
+ "end_time": "2024-10-22T09:25:28.252009Z",
+ "start_time": "2024-10-22T09:25:27.598326Z"
+ },
+ "id": "48e7d976e6e01212",
+ "colab": {
+ "base_uri": "https://localhost:8080/"
+ },
+ "outputId": "40dd1226-fa31-4e77-dc7e-e06a3600304e"
+ },
+ "id": "48e7d976e6e01212",
+ "execution_count": 11
+ }
+ ],
+ "metadata": {
+ "kernelspec": {
+ "display_name": "Python 3",
+ "name": "python3"
+ },
+ "language_info": {
+ "codemirror_mode": {
+ "name": "ipython",
+ "version": 2
+ },
+ "file_extension": ".py",
+ "mimetype": "text/x-python",
+ "name": "python",
+ "nbconvert_exporter": "python",
+ "pygments_lexer": "ipython2",
+ "version": "2.7.6"
+ },
+ "colab": {
+ "provenance": [],
+ "gpuType": "T4"
+ },
+ "accelerator": "GPU",
+ "widgets": {
+ "application/vnd.jupyter.widget-state+json": {
+ "72a5be4b77ec4d5994bcace9d462da84": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_name": "HBoxModel",
+ "model_module_version": "1.5.0",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_bed78529ff2c4d08befca97c50cb5efc",
+ "IPY_MODEL_cf7077acfce04aff8af0a2483dbf094c",
+ "IPY_MODEL_910462d70d944d00ba54958d77bee755"
+ ],
+ "layout": "IPY_MODEL_a899818bdad0415b860eaac4afe31f30"
+ }
+ },
+ "bed78529ff2c4d08befca97c50cb5efc": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_name": "HTMLModel",
+ "model_module_version": "1.5.0",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_3d78a6c8923547cf8c75bc8c10125eda",
+ "placeholder": "",
+ "style": "IPY_MODEL_8083f95a673a423286ade63051de757d",
+ "value": "Map: 100%"
+ }
+ },
+ "cf7077acfce04aff8af0a2483dbf094c": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_name": "FloatProgressModel",
+ "model_module_version": "1.5.0",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "FloatProgressModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "ProgressView",
+ "bar_style": "success",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_13fc203ab1b44c83b6cfcc1e171d26ad",
+ "max": 100,
+ "min": 0,
+ "orientation": "horizontal",
+ "style": "IPY_MODEL_663a0196d2b547fd8a6890b8a86080c2",
+ "value": 100
+ }
+ },
+ "910462d70d944d00ba54958d77bee755": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_name": "HTMLModel",
+ "model_module_version": "1.5.0",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_72be01164e974d59b05bee716e9bc978",
+ "placeholder": "",
+ "style": "IPY_MODEL_4cedaf37e79e4ff1a10ffb96ec543e81",
+ "value": " 100/100 [00:00<00:00, 1327.06 examples/s]"
+ }
+ },
+ "a899818bdad0415b860eaac4afe31f30": {
+ "model_module": "@jupyter-widgets/base",
+ "model_name": "LayoutModel",
+ "model_module_version": "1.2.0",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "3d78a6c8923547cf8c75bc8c10125eda": {
+ "model_module": "@jupyter-widgets/base",
+ "model_name": "LayoutModel",
+ "model_module_version": "1.2.0",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "8083f95a673a423286ade63051de757d": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_name": "DescriptionStyleModel",
+ "model_module_version": "1.5.0",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "13fc203ab1b44c83b6cfcc1e171d26ad": {
+ "model_module": "@jupyter-widgets/base",
+ "model_name": "LayoutModel",
+ "model_module_version": "1.2.0",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "663a0196d2b547fd8a6890b8a86080c2": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_name": "ProgressStyleModel",
+ "model_module_version": "1.5.0",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "72be01164e974d59b05bee716e9bc978": {
+ "model_module": "@jupyter-widgets/base",
+ "model_name": "LayoutModel",
+ "model_module_version": "1.2.0",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "4cedaf37e79e4ff1a10ffb96ec543e81": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_name": "DescriptionStyleModel",
+ "model_module_version": "1.5.0",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ }
+ }
+ }
+ },
+ "nbformat": 4,
+ "nbformat_minor": 5
+}
diff --git a/peft/examples/dna_language_models/dna_lm.ipynb b/peft/examples/dna_language_models/dna_lm.ipynb
new file mode 100644
index 0000000000000000000000000000000000000000..70360879dec511676290762c6e8bd67a9c6221de
--- /dev/null
+++ b/peft/examples/dna_language_models/dna_lm.ipynb
@@ -0,0 +1,2860 @@
+{
+ "cells": [
+ {
+ "cell_type": "markdown",
+ "id": "db4dc272-88fe-47ad-98fd-b94d4f840dca",
+ "metadata": {
+ "id": "db4dc272-88fe-47ad-98fd-b94d4f840dca"
+ },
+ "source": [
+ "# PEFT with DNA Language Models"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "d381f473-0d37-4b5b-ae9e-d2b32bab7c04",
+ "metadata": {
+ "id": "d381f473-0d37-4b5b-ae9e-d2b32bab7c04"
+ },
+ "source": [
+ "This notebook demonstrates how to utilize parameter-efficient fine-tuning techniques (PEFT) from the PEFT library to fine-tune a DNA Language Model (DNA-LM). The fine-tuned DNA-LM will be applied to solve a task from the nucleotide benchmark dataset. Parameter-efficient fine-tuning (PEFT) techniques are crucial for adapting large pre-trained models to specific tasks with limited computational resources."
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "23f460c3-d7e5-437f-a5e9-d029cd225bf8",
+ "metadata": {
+ "id": "23f460c3-d7e5-437f-a5e9-d029cd225bf8"
+ },
+ "source": [
+ "### 1. Import relevant libraries"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "29a35f95-738a-4f5e-88ce-dc5f8f9be5dc",
+ "metadata": {
+ "id": "29a35f95-738a-4f5e-88ce-dc5f8f9be5dc"
+ },
+ "source": [
+ "We'll start by importing the required libraries, including the PEFT library and other dependencies."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 1,
+ "id": "0a40abdf-ca1c-436f-a2af-603cd67a45a4",
+ "metadata": {
+ "id": "0a40abdf-ca1c-436f-a2af-603cd67a45a4"
+ },
+ "outputs": [
+ {
+ "name": "stderr",
+ "output_type": "stream",
+ "text": [
+ "/opt/homebrew/anaconda3/envs/peft/lib/python3.12/site-packages/tqdm/auto.py:21: TqdmWarning: IProgress not found. Please update jupyter and ipywidgets. See https://ipywidgets.readthedocs.io/en/stable/user_install.html\n",
+ " from .autonotebook import tqdm as notebook_tqdm\n"
+ ]
+ }
+ ],
+ "source": [
+ "import torch\n",
+ "import transformers\n",
+ "import peft\n",
+ "import tqdm\n",
+ "import numpy as np"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "a445f8be-545d-4085-a5f9-c64983655224",
+ "metadata": {
+ "id": "a445f8be-545d-4085-a5f9-c64983655224"
+ },
+ "source": [
+ "### 2. Load models\n"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "63782b55-1c38-4e44-b003-e57daa813bed",
+ "metadata": {
+ "id": "63782b55-1c38-4e44-b003-e57daa813bed"
+ },
+ "source": [
+ "We'll load a pre-trained DNA Language Model, \"SpeciesLM\", that serves as the base for fine-tuning. This is done using the transformers library from HuggingFace.\n",
+ "\n",
+ "The tokenizer and the model comes from the paper, \"Species-aware DNA language models capture regulatory elements and their evolution\". [Paper Link](https://www.biorxiv.org/content/10.1101/2023.01.26.525670v2), [Code Link](https://github.com/gagneurlab/SpeciesLM). They introduce a species-aware DNA language model, which is trained on more than 800 species spanning over 500 million years of evolution."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 2,
+ "id": "dac961f4-c450-4124-923e-f4ba9bbd5e07",
+ "metadata": {
+ "id": "dac961f4-c450-4124-923e-f4ba9bbd5e07"
+ },
+ "outputs": [],
+ "source": [
+ "from transformers import AutoTokenizer, AutoModelForMaskedLM"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 3,
+ "id": "e73fae58-03e9-4acc-b0fc-9bc810c7d366",
+ "metadata": {
+ "id": "e73fae58-03e9-4acc-b0fc-9bc810c7d366"
+ },
+ "outputs": [],
+ "source": [
+ "tokenizer = AutoTokenizer.from_pretrained(\"gagneurlab/SpeciesLM\", revision = \"downstream_species_lm\")\n",
+ "lm = AutoModelForMaskedLM.from_pretrained(\"gagneurlab/SpeciesLM\", revision = \"downstream_species_lm\")"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "id": "ca43b893-2d66-4e93-a08f-b17a92040709",
+ "metadata": {
+ "colab": {
+ "base_uri": "https://localhost:8080/"
+ },
+ "id": "ca43b893-2d66-4e93-a08f-b17a92040709",
+ "outputId": "ccbac964-a329-414d-f537-3cae7da66cf2"
+ },
+ "outputs": [
+ {
+ "data": {
+ "text/plain": [
+ "BertForMaskedLM(\n",
+ " (bert): BertModel(\n",
+ " (embeddings): BertEmbeddings(\n",
+ " (word_embeddings): Embedding(5504, 768, padding_idx=0)\n",
+ " (position_embeddings): Embedding(512, 768)\n",
+ " (token_type_embeddings): Embedding(2, 768)\n",
+ " (LayerNorm): LayerNorm((768,), eps=1e-12, elementwise_affine=True)\n",
+ " (dropout): Dropout(p=0.1, inplace=False)\n",
+ " )\n",
+ " (encoder): BertEncoder(\n",
+ " (layer): ModuleList(\n",
+ " (0-11): 12 x BertLayer(\n",
+ " (attention): BertAttention(\n",
+ " (self): BertSdpaSelfAttention(\n",
+ " (query): Linear(in_features=768, out_features=768, bias=True)\n",
+ " (key): Linear(in_features=768, out_features=768, bias=True)\n",
+ " (value): Linear(in_features=768, out_features=768, bias=True)\n",
+ " (dropout): Dropout(p=0.1, inplace=False)\n",
+ " )\n",
+ " (output): BertSelfOutput(\n",
+ " (dense): Linear(in_features=768, out_features=768, bias=True)\n",
+ " (LayerNorm): LayerNorm((768,), eps=1e-12, elementwise_affine=True)\n",
+ " (dropout): Dropout(p=0.1, inplace=False)\n",
+ " )\n",
+ " )\n",
+ " (intermediate): BertIntermediate(\n",
+ " (dense): Linear(in_features=768, out_features=3072, bias=True)\n",
+ " (intermediate_act_fn): GELUActivation()\n",
+ " )\n",
+ " (output): BertOutput(\n",
+ " (dense): Linear(in_features=3072, out_features=768, bias=True)\n",
+ " (LayerNorm): LayerNorm((768,), eps=1e-12, elementwise_affine=True)\n",
+ " (dropout): Dropout(p=0.1, inplace=False)\n",
+ " )\n",
+ " )\n",
+ " )\n",
+ " )\n",
+ " )\n",
+ " (cls): BertOnlyMLMHead(\n",
+ " (predictions): BertLMPredictionHead(\n",
+ " (transform): BertPredictionHeadTransform(\n",
+ " (dense): Linear(in_features=768, out_features=768, bias=True)\n",
+ " (transform_act_fn): GELUActivation()\n",
+ " (LayerNorm): LayerNorm((768,), eps=1e-12, elementwise_affine=True)\n",
+ " )\n",
+ " (decoder): Linear(in_features=768, out_features=5504, bias=True)\n",
+ " )\n",
+ " )\n",
+ ")"
+ ]
+ },
+ "execution_count": 12,
+ "metadata": {},
+ "output_type": "execute_result"
+ }
+ ],
+ "source": [
+ "lm.eval()\n",
+ "device = torch.accelerator.current_accelerator().type if hasattr(torch, \"accelerator\") else \"cuda\"\n",
+ "lm.to(device);"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "c1bda6f2-34bb-4ce2-aa3f-3013548b0a28",
+ "metadata": {
+ "id": "c1bda6f2-34bb-4ce2-aa3f-3013548b0a28"
+ },
+ "source": [
+ "### 2. Prepare datasets"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "f4c61e59-457c-47d9-8929-5e8cd32d3125",
+ "metadata": {
+ "id": "f4c61e59-457c-47d9-8929-5e8cd32d3125"
+ },
+ "source": [
+ "We'll load the `nucleotide_transformer_downstream_tasks` dataset, which contains 18 downstream tasks from the Nucleotide Transformer paper. This dataset provides a consistent genomics benchmark with binary classification tasks."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "id": "f5c0b3df-911a-4645-9140-99ee489515e8",
+ "metadata": {
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 145,
+ "referenced_widgets": [
+ "03bba232d3974119acf8031bc086a072",
+ "9107f7bfc8d3483390f802b0458e9380",
+ "f5c80fa70ead4c86aa3b2a046061b901",
+ "57966a469ca1458daab74e81672ae855",
+ "1464502dc3dd46308be8b4fcc9d5ddb9",
+ "92f64c7e088342b9b3c070ba7a295ed0",
+ "ab0aa8af3816422e9d97934f12af842c",
+ "ff89a891bd9c42a8be164587a94ccac1",
+ "e113a50f8ed2410ca12ce7cb38a1681d",
+ "1afa6e9b69c74136863b7747e62a0608",
+ "0838d19b226d486285a26ce0b04d7e15",
+ "7bdab33f4b244fc89408b91755bf17c5",
+ "4d4ce0d35c124690b3427e84a9a128b1",
+ "33be6b0ca8fd44188f834a48a9574a72",
+ "74e9bc1ead434ae78077df6b85f1df58",
+ "e1acc6e70b9246a5b063b3e262f01c81",
+ "078c6877377a491d97d6fadd27064a76",
+ "d46ee1c39bac44c2b541a88c883de1cb",
+ "12f1de7122a7471e90f01d9e7be81178",
+ "dad286d42a514c9ca6bb01bfe9e9c4be",
+ "c028ed977b5e479fbd93b8add588a6dc",
+ "6d80dec073e449efba272fa9f3527922",
+ "c311b777514f41ef986756a386c0bb34",
+ "e2e4bf053ce442f6aee6ffab5f76525f",
+ "c88cf701e20b4354a63ac7d8645d1df9",
+ "f71c252ada474be882b0335ed9a0a1c3",
+ "e059c665229e46ea905dcbd6fc179c88",
+ "bd5273325a4b453e8053d98a09fe9493",
+ "8f20ed2b74d84e80a8d403793354adea",
+ "57c9af47364d48ffbb4ffbdd2c951ede",
+ "fa9d75fcb1d5400c8ca1d1d13d28d0c7",
+ "682644a713b145f0b2dcff99790c6d4d",
+ "9b9b9d573d44464f9a6f5030a40245fe",
+ "ec165fdbe87a4b00a6c288ef1e85c0a9",
+ "17859b793a304e389d1ea0b9ccc3646f",
+ "34921fd116cc42b7b530174d9f61e71e",
+ "2d5466a5e98849c5a09f16faa98f91da",
+ "952397f9c91c480184fa57e175ab1b4c",
+ "86bcccb842244f4f9add58f62facaace",
+ "78b5bbf4c8ac4fe5961776fded4d5798",
+ "c80062a855cb41a28ac625ab03635da2",
+ "aecd740c17c84d45b0615d4fc4196035",
+ "39640709e7174f84a50da05764abbf99",
+ "7114a029e75c4ed5b966eddd3a3c919d"
+ ]
+ },
+ "id": "f5c0b3df-911a-4645-9140-99ee489515e8",
+ "outputId": "15315be1-9d07-4c46-acda-c65cb5a05250"
+ },
+ "outputs": [
+ {
+ "data": {
+ "application/vnd.jupyter.widget-view+json": {
+ "model_id": "03bba232d3974119acf8031bc086a072",
+ "version_major": 2,
+ "version_minor": 0
+ },
+ "text/plain": [
+ "Downloading data: 0%| | 0.00/3.50M [00:00\n",
+ " \n",
+ " \n",
+ " [65/65 01:43, Epoch 5/5]\n",
+ " \n",
+ "
\n",
+ " \n",
+ " \n",
+ " | Epoch | \n",
+ " Training Loss | \n",
+ " Validation Loss | \n",
+ "
\n",
+ " \n",
+ " \n",
+ " \n",
+ " | 1 | \n",
+ " 0.887400 | \n",
+ " 0.685295 | \n",
+ "
\n",
+ " \n",
+ " | 2 | \n",
+ " 0.644700 | \n",
+ " 0.682495 | \n",
+ "
\n",
+ " \n",
+ " | 3 | \n",
+ " 0.599600 | \n",
+ " 0.680431 | \n",
+ "
\n",
+ " \n",
+ " | 4 | \n",
+ " 0.892800 | \n",
+ " 0.679170 | \n",
+ "
\n",
+ " \n",
+ " | 5 | \n",
+ " 0.663800 | \n",
+ " 0.678761 | \n",
+ "
\n",
+ " \n",
+ "
"
+ ],
+ "text/plain": [
+ ""
+ ]
+ },
+ "metadata": {},
+ "output_type": "display_data"
+ },
+ {
+ "data": {
+ "text/plain": [
+ "TrainOutput(global_step=65, training_loss=0.7263066686116733, metrics={'train_runtime': 104.8696, 'train_samples_per_second': 9.536, 'train_steps_per_second': 0.62, 'total_flos': 0.0, 'train_loss': 0.7263066686116733, 'epoch': 5.0})"
+ ]
+ },
+ "execution_count": 36,
+ "metadata": {},
+ "output_type": "execute_result"
+ }
+ ],
+ "source": [
+ "from transformers import Trainer, TrainingArguments\n",
+ "\n",
+ "\n",
+ "# Define training arguments\n",
+ "training_args = TrainingArguments(\n",
+ " output_dir='./results',\n",
+ " eval_strategy=\"epoch\",\n",
+ " learning_rate=2e-5,\n",
+ " per_device_train_batch_size=16,\n",
+ " per_device_eval_batch_size=16,\n",
+ " num_train_epochs=5,\n",
+ " weight_decay=0.01,\n",
+ " eval_steps=1,\n",
+ " logging_steps=1,\n",
+ ")\n",
+ "\n",
+ "# Initialize Trainer\n",
+ "trainer = Trainer(\n",
+ " model=classification_model,\n",
+ " args=training_args,\n",
+ " train_dataset=train_dataset,\n",
+ " eval_dataset=val_dataset,\n",
+ " tokenizer=tokenizer,\n",
+ " data_collator=data_collator,\n",
+ ")\n",
+ "\n",
+ "# Train the model\n",
+ "trainer.train()"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "ebc7e33a-caad-4412-84e3-3e1ce7d02ccd",
+ "metadata": {
+ "id": "ebc7e33a-caad-4412-84e3-3e1ce7d02ccd"
+ },
+ "source": [
+ "### 5. Evaluation"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 37,
+ "id": "38eb0273-ce7e-4770-8457-2f9609f6843b",
+ "metadata": {
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 124
+ },
+ "id": "38eb0273-ce7e-4770-8457-2f9609f6843b",
+ "outputId": "2b0b93c9-0199-4e71-9825-9f6a2bd199d0"
+ },
+ "outputs": [
+ {
+ "data": {
+ "text/html": [],
+ "text/plain": [
+ ""
+ ]
+ },
+ "metadata": {},
+ "output_type": "display_data"
+ },
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "[0 1 1 1 1 1 1 1 1 0 1 0 1 1 1 1 0 1 1 0 1 1 0 1 1 1 1 0 1 0 0 0 1 1 0 1 1\n",
+ " 1 1 1 0 1 1 1 0 1 1 0 1 1 1 1 1 1 1 1 0 1 0 0 1 1 1 1 1 0 0 0 1 0 1 1 0 1\n",
+ " 0 1 1 0 1 1 1 0 0 1 0 1 0 1 0 1 1 1 0 1 1 1 1 0 1 0 0 0 0 1 0 1 0 0 1 1 1\n",
+ " 1 0 1 1 0 0 1 1 1 0 1 1 1 1 0 0 1 1 1 1 0 0 1 1 1 0 0 1 1 0 1 1 0 1 1 0 1\n",
+ " 1 1 1 1 1 1 0 0 1 1 1 1 1 1 1 1 0 0 1 0 1 1 1 1 1 1 1 0 1 1 1 0 0 1 1 1 1\n",
+ " 0 1 1 1 1 0 1 1 0 0 1 0 1 1 0]\n"
+ ]
+ }
+ ],
+ "source": [
+ "# Generate predictions\n",
+ "\n",
+ "predictions = trainer.predict(test_dataset)\n",
+ "logits = predictions.predictions\n",
+ "predicted_labels = logits.argmax(axis=-1)\n",
+ "print(predicted_labels)"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "ae4c7bca",
+ "metadata": {
+ "id": "ae4c7bca"
+ },
+ "source": [
+ "Then, we create a function to calculate the accuracy from the test and predicted labels."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 38,
+ "id": "327a1c3b-88d6-4430-8978-73a7cbdbb697",
+ "metadata": {
+ "colab": {
+ "base_uri": "https://localhost:8080/"
+ },
+ "id": "327a1c3b-88d6-4430-8978-73a7cbdbb697",
+ "outputId": "f03ad54d-d35f-4fcc-e709-c24d14906e25"
+ },
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "Accuracy: 0.53\n"
+ ]
+ }
+ ],
+ "source": [
+ "def calculate_accuracy(true_labels, predicted_labels):\n",
+ "\n",
+ " assert len(true_labels) == len(predicted_labels), \"Arrays must have the same length\"\n",
+ " correct_predictions = np.sum(true_labels == predicted_labels)\n",
+ " accuracy = correct_predictions / len(true_labels)\n",
+ "\n",
+ " return accuracy\n",
+ "\n",
+ "accuracy = calculate_accuracy(test_labels, predicted_labels)\n",
+ "print(f\"Accuracy: {accuracy:.2f}\")"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "9p0fFXKTZz9Q",
+ "metadata": {
+ "id": "9p0fFXKTZz9Q"
+ },
+ "source": [
+ "The results aren't that good, which we can attribute to the small dataset size."
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "e681864c-f15a-40a6-ac34-0e631d68d5c8",
+ "metadata": {
+ "id": "e681864c-f15a-40a6-ac34-0e631d68d5c8"
+ },
+ "source": [
+ "### 7. Parameter Efficient Fine-Tuning Techniques"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "9141fabe-417b-4fbb-bd3e-244ad84e3010",
+ "metadata": {
+ "id": "9141fabe-417b-4fbb-bd3e-244ad84e3010"
+ },
+ "source": [
+ "In this section, we demonstrate how to employ parameter-efficient fine-tuning (PEFT) techniques to adapt a pre-trained model for specific genomics tasks using the PEFT library."
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "71b8a749-461e-4533-b1d0-cebc924d3dc0",
+ "metadata": {
+ "id": "71b8a749-461e-4533-b1d0-cebc924d3dc0"
+ },
+ "source": [
+ "The LoraConfig object is instantiated to configure the PEFT parameters:\n",
+ "\n",
+ "- task_type: Specifies the type of task, in this case, sequence classification (SEQ_CLS).\n",
+ "- r: The rank of the LoRA matrices.\n",
+ "- lora_alpha: Scaling factor for adaptive re-parameterization.\n",
+ "- target_modules: Modules within the model to apply PEFT re-parameterization (query, key, value in this example).\n",
+ "- lora_dropout: Dropout rate used during PEFT fine-tuning."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "id": "021641ae-f604-4d69-8724-743b7d7c613c",
+ "metadata": {
+ "colab": {
+ "base_uri": "https://localhost:8080/"
+ },
+ "id": "021641ae-f604-4d69-8724-743b7d7c613c",
+ "outputId": "d7c41fca-1c6b-46fd-9116-01f42d1d6ddf"
+ },
+ "outputs": [
+ {
+ "data": {
+ "text/plain": [
+ "DNA_LM(\n",
+ " (model): BertModel(\n",
+ " (embeddings): BertEmbeddings(\n",
+ " (word_embeddings): Embedding(5504, 768, padding_idx=0)\n",
+ " (position_embeddings): Embedding(512, 768)\n",
+ " (token_type_embeddings): Embedding(2, 768)\n",
+ " (LayerNorm): LayerNorm((768,), eps=1e-12, elementwise_affine=True)\n",
+ " (dropout): Dropout(p=0.1, inplace=False)\n",
+ " )\n",
+ " (encoder): BertEncoder(\n",
+ " (layer): ModuleList(\n",
+ " (0-11): 12 x BertLayer(\n",
+ " (attention): BertAttention(\n",
+ " (self): BertSdpaSelfAttention(\n",
+ " (query): lora.Linear(\n",
+ " (base_layer): Linear(in_features=768, out_features=768, bias=True)\n",
+ " (lora_dropout): ModuleDict(\n",
+ " (default): Dropout(p=0.01, inplace=False)\n",
+ " )\n",
+ " (lora_A): ModuleDict(\n",
+ " (default): Linear(in_features=768, out_features=8, bias=False)\n",
+ " )\n",
+ " (lora_B): ModuleDict(\n",
+ " (default): Linear(in_features=8, out_features=768, bias=False)\n",
+ " )\n",
+ " (lora_embedding_A): ParameterDict()\n",
+ " (lora_embedding_B): ParameterDict()\n",
+ " )\n",
+ " (key): lora.Linear(\n",
+ " (base_layer): Linear(in_features=768, out_features=768, bias=True)\n",
+ " (lora_dropout): ModuleDict(\n",
+ " (default): Dropout(p=0.01, inplace=False)\n",
+ " )\n",
+ " (lora_A): ModuleDict(\n",
+ " (default): Linear(in_features=768, out_features=8, bias=False)\n",
+ " )\n",
+ " (lora_B): ModuleDict(\n",
+ " (default): Linear(in_features=8, out_features=768, bias=False)\n",
+ " )\n",
+ " (lora_embedding_A): ParameterDict()\n",
+ " (lora_embedding_B): ParameterDict()\n",
+ " )\n",
+ " (value): lora.Linear(\n",
+ " (base_layer): Linear(in_features=768, out_features=768, bias=True)\n",
+ " (lora_dropout): ModuleDict(\n",
+ " (default): Dropout(p=0.01, inplace=False)\n",
+ " )\n",
+ " (lora_A): ModuleDict(\n",
+ " (default): Linear(in_features=768, out_features=8, bias=False)\n",
+ " )\n",
+ " (lora_B): ModuleDict(\n",
+ " (default): Linear(in_features=8, out_features=768, bias=False)\n",
+ " )\n",
+ " (lora_embedding_A): ParameterDict()\n",
+ " (lora_embedding_B): ParameterDict()\n",
+ " )\n",
+ " (dropout): Dropout(p=0.1, inplace=False)\n",
+ " )\n",
+ " (output): BertSelfOutput(\n",
+ " (dense): Linear(in_features=768, out_features=768, bias=True)\n",
+ " (LayerNorm): LayerNorm((768,), eps=1e-12, elementwise_affine=True)\n",
+ " (dropout): Dropout(p=0.1, inplace=False)\n",
+ " )\n",
+ " )\n",
+ " (intermediate): BertIntermediate(\n",
+ " (dense): Linear(in_features=768, out_features=3072, bias=True)\n",
+ " (intermediate_act_fn): GELUActivation()\n",
+ " )\n",
+ " (output): BertOutput(\n",
+ " (dense): Linear(in_features=3072, out_features=768, bias=True)\n",
+ " (LayerNorm): LayerNorm((768,), eps=1e-12, elementwise_affine=True)\n",
+ " (dropout): Dropout(p=0.1, inplace=False)\n",
+ " )\n",
+ " )\n",
+ " )\n",
+ " )\n",
+ " )\n",
+ " (classifier): Linear(in_features=768, out_features=2, bias=True)\n",
+ ")"
+ ]
+ },
+ "execution_count": 40,
+ "metadata": {},
+ "output_type": "execute_result"
+ }
+ ],
+ "source": [
+ "# Number of classes for your classification task\n",
+ "num_labels = 2\n",
+ "classification_model = DNA_LM(lm, num_labels)\n",
+ "classification_model.to(device);"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 41,
+ "id": "6c223937-86ea-42ef-991a-050f23b21ef9",
+ "metadata": {
+ "id": "6c223937-86ea-42ef-991a-050f23b21ef9"
+ },
+ "outputs": [],
+ "source": [
+ "from peft import LoraConfig, TaskType\n",
+ "\n",
+ "peft_config = LoraConfig(\n",
+ " r=8,\n",
+ " lora_alpha=32,\n",
+ " target_modules=[\"query\", \"key\", \"value\"],\n",
+ " lora_dropout=0.01,\n",
+ ")"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 42,
+ "id": "e7a9fe7d-e3ac-4ffa-9a9b-2067fb09b885",
+ "metadata": {
+ "colab": {
+ "base_uri": "https://localhost:8080/"
+ },
+ "id": "e7a9fe7d-e3ac-4ffa-9a9b-2067fb09b885",
+ "outputId": "02a6c65f-7474-4bc1-bfab-c05532e350a5"
+ },
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "trainable params: 442,368 || all params: 90,121,730 || trainable%: 0.4909\n"
+ ]
+ }
+ ],
+ "source": [
+ "from peft import get_peft_model\n",
+ "\n",
+ "peft_model = get_peft_model(classification_model, peft_config)\n",
+ "peft_model.print_trainable_parameters()"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 43,
+ "id": "22064519-eaab-4142-8618-d1210d05c6bd",
+ "metadata": {
+ "colab": {
+ "base_uri": "https://localhost:8080/"
+ },
+ "id": "22064519-eaab-4142-8618-d1210d05c6bd",
+ "outputId": "ca3f764d-cdb4-4525-c541-8eabfb4cde57"
+ },
+ "outputs": [
+ {
+ "data": {
+ "text/plain": [
+ "PeftModel(\n",
+ " (base_model): LoraModel(\n",
+ " (model): DNA_LM(\n",
+ " (model): BertModel(\n",
+ " (embeddings): BertEmbeddings(\n",
+ " (word_embeddings): Embedding(5504, 768, padding_idx=0)\n",
+ " (position_embeddings): Embedding(512, 768)\n",
+ " (token_type_embeddings): Embedding(2, 768)\n",
+ " (LayerNorm): LayerNorm((768,), eps=1e-12, elementwise_affine=True)\n",
+ " (dropout): Dropout(p=0.1, inplace=False)\n",
+ " )\n",
+ " (encoder): BertEncoder(\n",
+ " (layer): ModuleList(\n",
+ " (0-11): 12 x BertLayer(\n",
+ " (attention): BertAttention(\n",
+ " (self): BertSdpaSelfAttention(\n",
+ " (query): lora.Linear(\n",
+ " (base_layer): Linear(in_features=768, out_features=768, bias=True)\n",
+ " (lora_dropout): ModuleDict(\n",
+ " (default): Dropout(p=0.01, inplace=False)\n",
+ " )\n",
+ " (lora_A): ModuleDict(\n",
+ " (default): Linear(in_features=768, out_features=8, bias=False)\n",
+ " )\n",
+ " (lora_B): ModuleDict(\n",
+ " (default): Linear(in_features=8, out_features=768, bias=False)\n",
+ " )\n",
+ " (lora_embedding_A): ParameterDict()\n",
+ " (lora_embedding_B): ParameterDict()\n",
+ " )\n",
+ " (key): lora.Linear(\n",
+ " (base_layer): Linear(in_features=768, out_features=768, bias=True)\n",
+ " (lora_dropout): ModuleDict(\n",
+ " (default): Dropout(p=0.01, inplace=False)\n",
+ " )\n",
+ " (lora_A): ModuleDict(\n",
+ " (default): Linear(in_features=768, out_features=8, bias=False)\n",
+ " )\n",
+ " (lora_B): ModuleDict(\n",
+ " (default): Linear(in_features=8, out_features=768, bias=False)\n",
+ " )\n",
+ " (lora_embedding_A): ParameterDict()\n",
+ " (lora_embedding_B): ParameterDict()\n",
+ " )\n",
+ " (value): lora.Linear(\n",
+ " (base_layer): Linear(in_features=768, out_features=768, bias=True)\n",
+ " (lora_dropout): ModuleDict(\n",
+ " (default): Dropout(p=0.01, inplace=False)\n",
+ " )\n",
+ " (lora_A): ModuleDict(\n",
+ " (default): Linear(in_features=768, out_features=8, bias=False)\n",
+ " )\n",
+ " (lora_B): ModuleDict(\n",
+ " (default): Linear(in_features=8, out_features=768, bias=False)\n",
+ " )\n",
+ " (lora_embedding_A): ParameterDict()\n",
+ " (lora_embedding_B): ParameterDict()\n",
+ " )\n",
+ " (dropout): Dropout(p=0.1, inplace=False)\n",
+ " )\n",
+ " (output): BertSelfOutput(\n",
+ " (dense): Linear(in_features=768, out_features=768, bias=True)\n",
+ " (LayerNorm): LayerNorm((768,), eps=1e-12, elementwise_affine=True)\n",
+ " (dropout): Dropout(p=0.1, inplace=False)\n",
+ " )\n",
+ " )\n",
+ " (intermediate): BertIntermediate(\n",
+ " (dense): Linear(in_features=768, out_features=3072, bias=True)\n",
+ " (intermediate_act_fn): GELUActivation()\n",
+ " )\n",
+ " (output): BertOutput(\n",
+ " (dense): Linear(in_features=3072, out_features=768, bias=True)\n",
+ " (LayerNorm): LayerNorm((768,), eps=1e-12, elementwise_affine=True)\n",
+ " (dropout): Dropout(p=0.1, inplace=False)\n",
+ " )\n",
+ " )\n",
+ " )\n",
+ " )\n",
+ " )\n",
+ " (classifier): Linear(in_features=768, out_features=2, bias=True)\n",
+ " )\n",
+ " )\n",
+ ")"
+ ]
+ },
+ "execution_count": 43,
+ "metadata": {},
+ "output_type": "execute_result"
+ }
+ ],
+ "source": [
+ "peft_model"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 45,
+ "id": "d3812e96-6b49-4911-8b21-d8871b7c06a5",
+ "metadata": {
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 268
+ },
+ "id": "d3812e96-6b49-4911-8b21-d8871b7c06a5",
+ "outputId": "8d497e30-1d3f-457a-f62a-244731698cb2"
+ },
+ "outputs": [
+ {
+ "data": {
+ "text/html": [
+ "\n",
+ " \n",
+ " \n",
+ "
\n",
+ " [65/65 01:39, Epoch 5/5]\n",
+ "
\n",
+ " \n",
+ " \n",
+ " | Epoch | \n",
+ " Training Loss | \n",
+ " Validation Loss | \n",
+ "
\n",
+ " \n",
+ " \n",
+ " \n",
+ " | 1 | \n",
+ " 0.625700 | \n",
+ " 0.777132 | \n",
+ "
\n",
+ " \n",
+ " | 2 | \n",
+ " 0.717200 | \n",
+ " 0.773871 | \n",
+ "
\n",
+ " \n",
+ " | 3 | \n",
+ " 0.768200 | \n",
+ " 0.771541 | \n",
+ "
\n",
+ " \n",
+ " | 4 | \n",
+ " 0.687400 | \n",
+ " 0.769679 | \n",
+ "
\n",
+ " \n",
+ " | 5 | \n",
+ " 0.552000 | \n",
+ " 0.768947 | \n",
+ "
\n",
+ " \n",
+ "
"
+ ],
+ "text/plain": [
+ ""
+ ]
+ },
+ "metadata": {},
+ "output_type": "display_data"
+ },
+ {
+ "data": {
+ "text/plain": [
+ "TrainOutput(global_step=65, training_loss=0.74742647592838, metrics={'train_runtime': 100.8429, 'train_samples_per_second': 9.916, 'train_steps_per_second': 0.645, 'total_flos': 0.0, 'train_loss': 0.74742647592838, 'epoch': 5.0})"
+ ]
+ },
+ "execution_count": 45,
+ "metadata": {},
+ "output_type": "execute_result"
+ }
+ ],
+ "source": [
+ "# Define training arguments\n",
+ "training_args = TrainingArguments(\n",
+ " output_dir='./results',\n",
+ " eval_strategy=\"epoch\",\n",
+ " learning_rate=2e-5,\n",
+ " per_device_train_batch_size=16,\n",
+ " per_device_eval_batch_size=16,\n",
+ " num_train_epochs=5,\n",
+ " weight_decay=0.01,\n",
+ " eval_steps=1,\n",
+ " logging_steps=1,\n",
+ ")\n",
+ "\n",
+ "# Initialize Trainer\n",
+ "trainer = Trainer(\n",
+ " model=peft_model.model,\n",
+ " args=training_args,\n",
+ " train_dataset=train_dataset,\n",
+ " eval_dataset=val_dataset,\n",
+ " tokenizer=tokenizer,\n",
+ " data_collator=data_collator,\n",
+ ")\n",
+ "\n",
+ "# Train the model\n",
+ "trainer.train()"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "76dbd948-d919-4ade-a405-cec297979577",
+ "metadata": {
+ "id": "76dbd948-d919-4ade-a405-cec297979577"
+ },
+ "source": [
+ "### 8. Evaluate PEFT Model"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 46,
+ "id": "58cf70ba-47d5-4111-bb12-830ae04c6285",
+ "metadata": {
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 124
+ },
+ "id": "58cf70ba-47d5-4111-bb12-830ae04c6285",
+ "outputId": "0abc56a9-bd68-4e4e-9f13-756e8c9ffa3e"
+ },
+ "outputs": [
+ {
+ "data": {
+ "text/html": [],
+ "text/plain": [
+ ""
+ ]
+ },
+ "metadata": {},
+ "output_type": "display_data"
+ },
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "[1 0 1 0 0 1 1 0 1 1 1 1 0 1 1 1 0 1 0 0 1 0 0 0 0 1 0 0 0 0 0 1 1 0 0 1 1\n",
+ " 1 1 1 0 1 1 0 1 0 0 1 0 0 1 1 0 1 1 0 0 1 1 0 0 1 1 0 0 0 0 0 0 0 1 1 0 1\n",
+ " 1 0 1 0 0 1 1 0 1 0 1 0 1 0 0 1 1 0 0 0 1 1 1 0 1 1 0 1 0 0 1 1 0 1 1 1 0\n",
+ " 1 1 0 0 1 0 1 1 1 0 1 1 0 1 1 0 0 0 0 1 1 0 1 1 1 1 1 0 1 0 1 0 1 1 0 1 1\n",
+ " 0 1 1 1 1 1 1 1 0 1 1 0 1 0 0 0 0 0 0 1 1 0 0 0 1 1 1 1 1 0 0 1 0 1 0 1 0\n",
+ " 0 1 1 0 0 0 1 0 1 1 1 0 1 1 0]\n"
+ ]
+ }
+ ],
+ "source": [
+ "# Generate predictions\n",
+ "\n",
+ "predictions = trainer.predict(test_dataset)\n",
+ "logits = predictions.predictions\n",
+ "predicted_labels = logits.argmax(axis=-1)\n",
+ "print(predicted_labels)"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 47,
+ "id": "4bd38fe5-6513-4c88-afee-0cc4e1781fdd",
+ "metadata": {
+ "colab": {
+ "base_uri": "https://localhost:8080/"
+ },
+ "id": "4bd38fe5-6513-4c88-afee-0cc4e1781fdd",
+ "outputId": "a50a91d0-d04d-4620-9006-868716bb992d"
+ },
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "Accuracy: 0.52\n"
+ ]
+ }
+ ],
+ "source": [
+ "def calculate_accuracy(true_labels, predicted_labels):\n",
+ "\n",
+ " assert len(true_labels) == len(predicted_labels), \"Arrays must have the same length\"\n",
+ " correct_predictions = np.sum(true_labels == predicted_labels)\n",
+ " accuracy = correct_predictions / len(true_labels)\n",
+ "\n",
+ " return accuracy\n",
+ "\n",
+ "accuracy = calculate_accuracy(test_labels, predicted_labels)\n",
+ "print(f\"Accuracy: {accuracy:.2f}\")"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "4ba5af69",
+ "metadata": {},
+ "source": [
+ "As we can see, the PEFT model achieves similar performance to the baseline model, demonstrating the effectiveness of PEFT in adapting pre-trained models to specific tasks with limited computational resources.\n",
+ "\n",
+ "With PEFT, we only train 442,368 parameters, which is 0.49% of the total parameters in the model. This is a significant reduction in computational resources compared to training the entire model from scratch.\n",
+ "\n",
+ "We can improve the results by using a larger dataset, fine-tuning the model for more epochs or changing the hyperparameters (rank, learning rate, etc.).\n"
+ ]
+ }
+ ],
+ "metadata": {
+ "accelerator": "GPU",
+ "colab": {
+ "gpuType": "T4",
+ "provenance": []
+ },
+ "kernelspec": {
+ "display_name": "Python 3",
+ "name": "python3"
+ },
+ "language_info": {
+ "codemirror_mode": {
+ "name": "ipython",
+ "version": 3
+ },
+ "file_extension": ".py",
+ "mimetype": "text/x-python",
+ "name": "python",
+ "nbconvert_exporter": "python",
+ "pygments_lexer": "ipython3",
+ "version": "3.12.3"
+ },
+ "widgets": {
+ "application/vnd.jupyter.widget-state+json": {
+ "03bba232d3974119acf8031bc086a072": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_9107f7bfc8d3483390f802b0458e9380",
+ "IPY_MODEL_f5c80fa70ead4c86aa3b2a046061b901",
+ "IPY_MODEL_57966a469ca1458daab74e81672ae855"
+ ],
+ "layout": "IPY_MODEL_1464502dc3dd46308be8b4fcc9d5ddb9"
+ }
+ },
+ "078c6877377a491d97d6fadd27064a76": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "0838d19b226d486285a26ce0b04d7e15": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "12f1de7122a7471e90f01d9e7be81178": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "1464502dc3dd46308be8b4fcc9d5ddb9": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "17859b793a304e389d1ea0b9ccc3646f": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_86bcccb842244f4f9add58f62facaace",
+ "placeholder": "",
+ "style": "IPY_MODEL_78b5bbf4c8ac4fe5961776fded4d5798",
+ "value": "Generating test split: 100%"
+ }
+ },
+ "1afa6e9b69c74136863b7747e62a0608": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "2d5466a5e98849c5a09f16faa98f91da": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_39640709e7174f84a50da05764abbf99",
+ "placeholder": "",
+ "style": "IPY_MODEL_7114a029e75c4ed5b966eddd3a3c919d",
+ "value": " 1497/1497 [00:00<00:00, 41394.98 examples/s]"
+ }
+ },
+ "33be6b0ca8fd44188f834a48a9574a72": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "FloatProgressModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "FloatProgressModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "ProgressView",
+ "bar_style": "success",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_12f1de7122a7471e90f01d9e7be81178",
+ "max": 390606,
+ "min": 0,
+ "orientation": "horizontal",
+ "style": "IPY_MODEL_dad286d42a514c9ca6bb01bfe9e9c4be",
+ "value": 390606
+ }
+ },
+ "34921fd116cc42b7b530174d9f61e71e": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "FloatProgressModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "FloatProgressModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "ProgressView",
+ "bar_style": "success",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_c80062a855cb41a28ac625ab03635da2",
+ "max": 1497,
+ "min": 0,
+ "orientation": "horizontal",
+ "style": "IPY_MODEL_aecd740c17c84d45b0615d4fc4196035",
+ "value": 1497
+ }
+ },
+ "39640709e7174f84a50da05764abbf99": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "4d4ce0d35c124690b3427e84a9a128b1": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_078c6877377a491d97d6fadd27064a76",
+ "placeholder": "",
+ "style": "IPY_MODEL_d46ee1c39bac44c2b541a88c883de1cb",
+ "value": "Downloading data: 100%"
+ }
+ },
+ "57966a469ca1458daab74e81672ae855": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_1afa6e9b69c74136863b7747e62a0608",
+ "placeholder": "",
+ "style": "IPY_MODEL_0838d19b226d486285a26ce0b04d7e15",
+ "value": " 3.50M/3.50M [00:00<00:00, 26.3MB/s]"
+ }
+ },
+ "57c9af47364d48ffbb4ffbdd2c951ede": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "682644a713b145f0b2dcff99790c6d4d": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "6d80dec073e449efba272fa9f3527922": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "7114a029e75c4ed5b966eddd3a3c919d": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "74e9bc1ead434ae78077df6b85f1df58": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_c028ed977b5e479fbd93b8add588a6dc",
+ "placeholder": "",
+ "style": "IPY_MODEL_6d80dec073e449efba272fa9f3527922",
+ "value": " 391k/391k [00:00<00:00, 3.34MB/s]"
+ }
+ },
+ "78b5bbf4c8ac4fe5961776fded4d5798": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "7bdab33f4b244fc89408b91755bf17c5": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_4d4ce0d35c124690b3427e84a9a128b1",
+ "IPY_MODEL_33be6b0ca8fd44188f834a48a9574a72",
+ "IPY_MODEL_74e9bc1ead434ae78077df6b85f1df58"
+ ],
+ "layout": "IPY_MODEL_e1acc6e70b9246a5b063b3e262f01c81"
+ }
+ },
+ "86bcccb842244f4f9add58f62facaace": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "8f20ed2b74d84e80a8d403793354adea": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "9107f7bfc8d3483390f802b0458e9380": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_92f64c7e088342b9b3c070ba7a295ed0",
+ "placeholder": "",
+ "style": "IPY_MODEL_ab0aa8af3816422e9d97934f12af842c",
+ "value": "Downloading data: 100%"
+ }
+ },
+ "92f64c7e088342b9b3c070ba7a295ed0": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "952397f9c91c480184fa57e175ab1b4c": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "9b9b9d573d44464f9a6f5030a40245fe": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "ab0aa8af3816422e9d97934f12af842c": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "aecd740c17c84d45b0615d4fc4196035": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "bd5273325a4b453e8053d98a09fe9493": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "c028ed977b5e479fbd93b8add588a6dc": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "c311b777514f41ef986756a386c0bb34": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_e2e4bf053ce442f6aee6ffab5f76525f",
+ "IPY_MODEL_c88cf701e20b4354a63ac7d8645d1df9",
+ "IPY_MODEL_f71c252ada474be882b0335ed9a0a1c3"
+ ],
+ "layout": "IPY_MODEL_e059c665229e46ea905dcbd6fc179c88"
+ }
+ },
+ "c80062a855cb41a28ac625ab03635da2": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "c88cf701e20b4354a63ac7d8645d1df9": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "FloatProgressModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "FloatProgressModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "ProgressView",
+ "bar_style": "success",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_57c9af47364d48ffbb4ffbdd2c951ede",
+ "max": 13468,
+ "min": 0,
+ "orientation": "horizontal",
+ "style": "IPY_MODEL_fa9d75fcb1d5400c8ca1d1d13d28d0c7",
+ "value": 13468
+ }
+ },
+ "d46ee1c39bac44c2b541a88c883de1cb": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "dad286d42a514c9ca6bb01bfe9e9c4be": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "e059c665229e46ea905dcbd6fc179c88": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "e113a50f8ed2410ca12ce7cb38a1681d": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "e1acc6e70b9246a5b063b3e262f01c81": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "e2e4bf053ce442f6aee6ffab5f76525f": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_bd5273325a4b453e8053d98a09fe9493",
+ "placeholder": "",
+ "style": "IPY_MODEL_8f20ed2b74d84e80a8d403793354adea",
+ "value": "Generating train split: 100%"
+ }
+ },
+ "ec165fdbe87a4b00a6c288ef1e85c0a9": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_17859b793a304e389d1ea0b9ccc3646f",
+ "IPY_MODEL_34921fd116cc42b7b530174d9f61e71e",
+ "IPY_MODEL_2d5466a5e98849c5a09f16faa98f91da"
+ ],
+ "layout": "IPY_MODEL_952397f9c91c480184fa57e175ab1b4c"
+ }
+ },
+ "f5c80fa70ead4c86aa3b2a046061b901": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "FloatProgressModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "FloatProgressModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "ProgressView",
+ "bar_style": "success",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_ff89a891bd9c42a8be164587a94ccac1",
+ "max": 3495021,
+ "min": 0,
+ "orientation": "horizontal",
+ "style": "IPY_MODEL_e113a50f8ed2410ca12ce7cb38a1681d",
+ "value": 3495021
+ }
+ },
+ "f71c252ada474be882b0335ed9a0a1c3": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_682644a713b145f0b2dcff99790c6d4d",
+ "placeholder": "",
+ "style": "IPY_MODEL_9b9b9d573d44464f9a6f5030a40245fe",
+ "value": " 13468/13468 [00:00<00:00, 193879.37 examples/s]"
+ }
+ },
+ "fa9d75fcb1d5400c8ca1d1d13d28d0c7": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "ff89a891bd9c42a8be164587a94ccac1": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ }
+ }
+ }
+ },
+ "nbformat": 4,
+ "nbformat_minor": 5
+}
diff --git a/peft/examples/dora_finetuning/QDoRA_finetuning.ipynb b/peft/examples/dora_finetuning/QDoRA_finetuning.ipynb
new file mode 100644
index 0000000000000000000000000000000000000000..e0582a9eff8437a27c38bde39a675f9b787efb70
--- /dev/null
+++ b/peft/examples/dora_finetuning/QDoRA_finetuning.ipynb
@@ -0,0 +1,8545 @@
+{
+ "cells": [
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "CV_gQs58bsvM"
+ },
+ "source": [
+ "# Fine-tuning [Llama-3-8B](https://huggingface.co/meta-llama/Meta-Llama-3-8B) on [timdettmers/openassistant-guanaco](https://huggingface.co/datasets/timdettmers/openassistant-guanaco) Dataset using QDora (quantized Lora w/ use_dora=True)."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 2,
+ "metadata": {
+ "colab": {
+ "base_uri": "https://localhost:8080/"
+ },
+ "id": "FuXIFTFapAMI",
+ "outputId": "b95d8260-65bd-405f-f1e2-8d353aa46814"
+ },
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "\u001b[2K \u001b[90m━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━\u001b[0m \u001b[32m119.8/119.8 MB\u001b[0m \u001b[31m7.2 MB/s\u001b[0m eta \u001b[36m0:00:00\u001b[0m\n",
+ "\u001b[2K \u001b[90m━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━\u001b[0m \u001b[32m21.3/21.3 MB\u001b[0m \u001b[31m37.3 MB/s\u001b[0m eta \u001b[36m0:00:00\u001b[0m\n",
+ "\u001b[?25h Installing build dependencies ... \u001b[?25l\u001b[?25hdone\n",
+ " Getting requirements to build wheel ... \u001b[?25l\u001b[?25hdone\n",
+ " Preparing metadata (pyproject.toml) ... \u001b[?25l\u001b[?25hdone\n",
+ " Building wheel for transformers (pyproject.toml) ... \u001b[?25l\u001b[?25hdone\n",
+ " Installing build dependencies ... \u001b[?25l\u001b[?25hdone\n",
+ " Getting requirements to build wheel ... \u001b[?25l\u001b[?25hdone\n",
+ " Preparing metadata (pyproject.toml) ... \u001b[?25l\u001b[?25hdone\n",
+ "\u001b[2K \u001b[90m━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━\u001b[0m \u001b[32m309.4/309.4 kB\u001b[0m \u001b[31m6.0 MB/s\u001b[0m eta \u001b[36m0:00:00\u001b[0m\n",
+ "\u001b[?25h Building wheel for peft (pyproject.toml) ... \u001b[?25l\u001b[?25hdone\n",
+ " Installing build dependencies ... \u001b[?25l\u001b[?25hdone\n",
+ " Getting requirements to build wheel ... \u001b[?25l\u001b[?25hdone\n",
+ " Preparing metadata (pyproject.toml) ... \u001b[?25l\u001b[?25hdone\n",
+ " Building wheel for accelerate (pyproject.toml) ... \u001b[?25l\u001b[?25hdone\n",
+ "\u001b[2K \u001b[90m━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━\u001b[0m \u001b[32m547.8/547.8 kB\u001b[0m \u001b[31m7.4 MB/s\u001b[0m eta \u001b[36m0:00:00\u001b[0m\n",
+ "\u001b[2K \u001b[90m━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━\u001b[0m \u001b[32m40.8/40.8 MB\u001b[0m \u001b[31m28.4 MB/s\u001b[0m eta \u001b[36m0:00:00\u001b[0m\n",
+ "\u001b[2K \u001b[90m━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━\u001b[0m \u001b[32m116.3/116.3 kB\u001b[0m \u001b[31m16.3 MB/s\u001b[0m eta \u001b[36m0:00:00\u001b[0m\n",
+ "\u001b[2K \u001b[90m━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━\u001b[0m \u001b[32m64.9/64.9 kB\u001b[0m \u001b[31m10.5 MB/s\u001b[0m eta \u001b[36m0:00:00\u001b[0m\n",
+ "\u001b[2K \u001b[90m━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━\u001b[0m \u001b[32m194.1/194.1 kB\u001b[0m \u001b[31m27.5 MB/s\u001b[0m eta \u001b[36m0:00:00\u001b[0m\n",
+ "\u001b[2K \u001b[90m━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━\u001b[0m \u001b[32m134.8/134.8 kB\u001b[0m \u001b[31m20.1 MB/s\u001b[0m eta \u001b[36m0:00:00\u001b[0m\n",
+ "\u001b[?25h\u001b[31mERROR: pip's dependency resolver does not currently take into account all the packages that are installed. This behaviour is the source of the following dependency conflicts.\n",
+ "cudf-cu12 24.4.1 requires pyarrow<15.0.0a0,>=14.0.1, but you have pyarrow 16.1.0 which is incompatible.\n",
+ "google-colab 1.0.0 requires requests==2.31.0, but you have requests 2.32.3 which is incompatible.\n",
+ "ibis-framework 8.0.0 requires pyarrow<16,>=2, but you have pyarrow 16.1.0 which is incompatible.\u001b[0m\u001b[31m\n",
+ "\u001b[0m"
+ ]
+ }
+ ],
+ "source": [
+ "# Install the libraries\n",
+ "!pip install -q -U bitsandbytes\n",
+ "!pip install -q -U git+https://github.com/huggingface/transformers.git\n",
+ "!pip install -q -U git+https://github.com/huggingface/peft.git\n",
+ "!pip install -q -U git+https://github.com/huggingface/accelerate.git\n",
+ "!pip install -q datasets"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 3,
+ "metadata": {
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 145,
+ "referenced_widgets": [
+ "8cc86330c2af436c9af314e8c04c8c2b",
+ "e25f9ca445b14e3f8397779df071dfb4",
+ "8365680c634a44aa880317e36fa5e46e",
+ "0c4ac7c3db0b431397cc812f7c9e785c",
+ "c84f542c863043dea8a3675fa153e78d",
+ "b3b3f4ddd4ed4d938c923887939a0440",
+ "35186465f87341f683affb9399661540",
+ "791df472db174df69b8c9f0e200af254",
+ "6bb9c7182d2a464ea21809e59043562a",
+ "31c574113731403b88edc5bb0798bc6d",
+ "3b8bc5b9392e45758813a1db9db824a9",
+ "90661b333d6f496ca606b3046622660e",
+ "5f551f9b217e44cf8b5433f314b3844b",
+ "d2d81cc8296c4b10bf80b86c0a3302d3",
+ "7e3a386e672f4748882211227b7721a9",
+ "57f251691b4c453896b2508c431dfc2f",
+ "4bdb196cd1494f809829651ec5b6cbf8",
+ "7cd50bcc8fcc4b83abcda6d3604bd4cc",
+ "7a00aa4a97a34da39cc052c6926dbe13",
+ "14c73d88df9e46e3bbb6690fdb48ad07",
+ "0e2beab611114239b6ee48a3cbb09c49",
+ "006b78b5191b4fb888d98bdf6c20ec1e",
+ "5f6ffa1d929443a5bd9c7c550f0690f0",
+ "668a7f88506148a9ba2b48920afc028f",
+ "57b0096985ab44aea342e52795c4f999",
+ "a4c404e420cc4ce781ce569f9ab3f987",
+ "ee4e4af964ec4dd597cb04a90f0697f9",
+ "974e3687f18a4e1a975969b880d086aa",
+ "93a50117ece543d4857ba02505dc4514",
+ "71a3a56edbdb45669d382fef4b097e1b",
+ "53f287d4927541d08e2ae7d4d0b3c396",
+ "afa442ab223b46cb82569438c0047823"
+ ]
+ },
+ "id": "wAAPv5CRmg7e",
+ "outputId": "687f979a-04c1-4160-d71c-4de8ecdb07d9"
+ },
+ "outputs": [
+ {
+ "data": {
+ "application/vnd.jupyter.widget-view+json": {
+ "model_id": "8cc86330c2af436c9af314e8c04c8c2b",
+ "version_major": 2,
+ "version_minor": 0
+ },
+ "text/plain": [
+ "VBox(children=(HTML(value=' \n",
+ " \n",
+ " \n",
+ " [10/10 03:56, Epoch 0/1]\n",
+ " \n",
+ " \n",
+ " \n",
+ " \n",
+ " | Step | \n",
+ " Training Loss | \n",
+ "
\n",
+ " \n",
+ " \n",
+ " \n",
+ " | 1 | \n",
+ " 1.276300 | \n",
+ "
\n",
+ " \n",
+ " | 2 | \n",
+ " 1.877700 | \n",
+ "
\n",
+ " \n",
+ " | 3 | \n",
+ " 1.983800 | \n",
+ "
\n",
+ " \n",
+ " | 4 | \n",
+ " 2.011400 | \n",
+ "
\n",
+ " \n",
+ " | 5 | \n",
+ " 1.997800 | \n",
+ "
\n",
+ " \n",
+ " | 6 | \n",
+ " 1.648100 | \n",
+ "
\n",
+ " \n",
+ " | 7 | \n",
+ " 1.576000 | \n",
+ "
\n",
+ " \n",
+ " | 8 | \n",
+ " 0.916400 | \n",
+ "
\n",
+ " \n",
+ " | 9 | \n",
+ " 1.523100 | \n",
+ "
\n",
+ " \n",
+ " | 10 | \n",
+ " 1.814500 | \n",
+ "
\n",
+ " \n",
+ "
"
+ ],
+ "text/plain": [
+ ""
+ ]
+ },
+ "metadata": {},
+ "output_type": "display_data"
+ },
+ {
+ "data": {
+ "text/plain": [
+ "TrainOutput(global_step=10, training_loss=1.662518608570099, metrics={'train_runtime': 269.3407, 'train_samples_per_second': 0.149, 'train_steps_per_second': 0.037, 'total_flos': 530537216679936.0, 'train_loss': 1.662518608570099, 'epoch': 0.004062563477554337})"
+ ]
+ },
+ "execution_count": 10,
+ "metadata": {},
+ "output_type": "execute_result"
+ }
+ ],
+ "source": [
+ "import transformers\n",
+ "\n",
+ "tokenizer.pad_token = tokenizer.eos_token\n",
+ "\n",
+ "trainer = transformers.Trainer(\n",
+ " model=model,\n",
+ " train_dataset=data[\"train\"],\n",
+ " args=transformers.TrainingArguments(\n",
+ " per_device_train_batch_size=1,\n",
+ " gradient_accumulation_steps=4,\n",
+ " warmup_steps=2,\n",
+ " max_steps=10,\n",
+ " learning_rate=2e-4,\n",
+ " fp16=True,\n",
+ " logging_steps=1,\n",
+ " output_dir=\"path/to/your/HF/repo\", # change it to your desired repo!\n",
+ " optim=\"paged_adamw_8bit\",\n",
+ " ),\n",
+ " data_collator=transformers.DataCollatorForLanguageModeling(tokenizer, mlm=False),\n",
+ ")\n",
+ "model.config.use_cache = False # silence the warnings. Please re-enable for inference!\n",
+ "trainer.train()"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "Mr3rLrHwqhf6"
+ },
+ "source": [
+ "## Usage Example"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 11,
+ "metadata": {
+ "collapsed": true,
+ "id": "9mrOJ9l8SMHv"
+ },
+ "outputs": [],
+ "source": [
+ "model.config.use_cache = True\n",
+ "model.eval();"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 122
+ },
+ "id": "AM6FNOFzqKfI",
+ "outputId": "fdbe28b1-e440-45d3-bd6d-c15e744ad23d"
+ },
+ "outputs": [
+ {
+ "name": "stderr",
+ "output_type": "stream",
+ "text": [
+ "Setting `pad_token_id` to `eos_token_id`:128001 for open-end generation.\n"
+ ]
+ },
+ {
+ "data": {
+ "application/vnd.google.colaboratory.intrinsic+json": {
+ "type": "string"
+ },
+ "text/plain": [
+ "\"A chat between a curious human and an artificial intelligence assistant. The assistant gives helpful, detailed, and polite answers to the user's questions. ### Human: What is the purpose of quantization in LLMs?### Assistant: Quantization is a technique used to reduce the size of a model without significantly impacting its performance. In the context of language models, quantization is the process of converting floating-point numbers (which are used to represent the weights and activations of a model) to smaller, fixed-point numbers. This can be done by grouping the weights into small chunks and assigning each chunk a single, fixed-point number. Quantization can significantly reduce the size of a model, making it more efficient to train and deploy. In addition, quantization can improve the performance of a model on low-power devices, such as mobile phones\""
+ ]
+ },
+ "execution_count": 11,
+ "metadata": {},
+ "output_type": "execute_result"
+ }
+ ],
+ "source": [
+ "from transformers import GenerationConfig\n",
+ "\n",
+ "max_new_tokens = 120\n",
+ "top_p = 0.9\n",
+ "temperature = 0.7\n",
+ "user_question = \"What is the purpose of quantization in LLMs?\"\n",
+ "device = torch.accelerator.current_accelerator().type if hasattr(torch, \"accelerator\") else \"cuda\"\n",
+ "\n",
+ "\n",
+ "prompt = (\n",
+ " \"A chat between a curious human and an artificial intelligence assistant. \"\n",
+ " \"The assistant gives helpful, detailed, and polite answers to the user's questions. \"\n",
+ " \"### Human: {user_question}\"\n",
+ " \"### Assistant: \"\n",
+ ")\n",
+ "\n",
+ "\n",
+ "def generate(model, user_question, max_new_tokens=max_new_tokens, top_p=top_p, temperature=temperature):\n",
+ " inputs = tokenizer(prompt.format(user_question=user_question), return_tensors=\"pt\").to(device)\n",
+ "\n",
+ " outputs = model.generate(\n",
+ " **inputs,\n",
+ " generation_config=GenerationConfig(\n",
+ " do_sample=True,\n",
+ " max_new_tokens=max_new_tokens,\n",
+ " top_p=top_p,\n",
+ " temperature=temperature,\n",
+ " ),\n",
+ " )\n",
+ "\n",
+ " text = tokenizer.decode(outputs[0], skip_special_tokens=True)\n",
+ " # print(text)\n",
+ " return text\n",
+ "\n",
+ "\n",
+ "generate(model, user_question)"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "id": "T5t_gl2_f5OO"
+ },
+ "outputs": [],
+ "source": [
+ "# trainer.push_to_hub()"
+ ]
+ }
+ ],
+ "metadata": {
+ "accelerator": "GPU",
+ "colab": {
+ "gpuType": "T4",
+ "provenance": []
+ },
+ "gpuClass": "standard",
+ "kernelspec": {
+ "display_name": "Python 3",
+ "name": "python3"
+ },
+ "language_info": {
+ "codemirror_mode": {
+ "name": "ipython",
+ "version": 3
+ },
+ "file_extension": ".py",
+ "mimetype": "text/x-python",
+ "name": "python",
+ "nbconvert_exporter": "python",
+ "pygments_lexer": "ipython3",
+ "version": "3.1.-1"
+ },
+ "widgets": {
+ "application/vnd.jupyter.widget-state+json": {
+ "00371a48e64c45cd97020a78b710e64c": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_3f9fa554747743f8a86b40a4f7530617",
+ "placeholder": "",
+ "style": "IPY_MODEL_ffe561df8772443ebf40a3b8b656079f",
+ "value": " 50.6k/50.6k [00:00<00:00, 3.65MB/s]"
+ }
+ },
+ "006b78b5191b4fb888d98bdf6c20ec1e": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "LabelModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "LabelModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "LabelView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_ee4e4af964ec4dd597cb04a90f0697f9",
+ "placeholder": "",
+ "style": "IPY_MODEL_974e3687f18a4e1a975969b880d086aa",
+ "value": "Your token has been saved in your configured git credential helpers (store)."
+ }
+ },
+ "026072374b7d47c194707a50f5c99099": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "02d6cc4c2717434c895798601bda7c86": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "03dd6c24f6d94fe7ab85b79d6f6cbeaf": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_cc5ce633746949ed98418cae9f68afe3",
+ "placeholder": "",
+ "style": "IPY_MODEL_4b1f795c4c004cacbf3660d935e52995",
+ "value": "Downloading data: 100%"
+ }
+ },
+ "04188e0cec0542818894ebc6a534fb51": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "061c45266c484ff6807dcaf4722fd73b": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "068eb104d5d346b1897f8cbe9860d267": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "0711e28e06a440c2a241acbc1f90d1e8": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_f4ca7b63d7d749ff83a848e250f03ec1",
+ "placeholder": "",
+ "style": "IPY_MODEL_8c149bc655a34fe5b91853c66db458a9",
+ "value": "model.safetensors.index.json: 100%"
+ }
+ },
+ "076357d4bb9943bdaa1d6846897786af": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "07e0aed682fd4cc88fa75c0592dc04a7": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_47944ad8cadf4a57b170193c46d4389c",
+ "placeholder": "",
+ "style": "IPY_MODEL_db05b25cb38140bdb21e6f3b7fde7e66",
+ "value": "model-00001-of-00004.safetensors: 100%"
+ }
+ },
+ "082b6990ce5e4812adc0ad6a7b376dac": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "0aad2d9d1cba40cbb64308ede3242ed7": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_0711e28e06a440c2a241acbc1f90d1e8",
+ "IPY_MODEL_77704d2e27e94cd3a0c5f6b5ceeffd1c",
+ "IPY_MODEL_3b82b8d41b134bec9bd77ed8d4f00eb4"
+ ],
+ "layout": "IPY_MODEL_25fef90e209f4b14a73f3e39d226d913"
+ }
+ },
+ "0b145e421f4840f2872c29256b49f168": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "0c4ac7c3db0b431397cc812f7c9e785c": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "CheckboxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "CheckboxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "CheckboxView",
+ "description": "Add token as git credential?",
+ "description_tooltip": null,
+ "disabled": false,
+ "indent": true,
+ "layout": "IPY_MODEL_90661b333d6f496ca606b3046622660e",
+ "style": "IPY_MODEL_5f551f9b217e44cf8b5433f314b3844b",
+ "value": true
+ }
+ },
+ "0d2ae3466a3447c58e23ccd2b3733deb": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_921a1a037f7b47f8b57d1da8192a437a",
+ "placeholder": "",
+ "style": "IPY_MODEL_892ff4e2f0e44c23bc5c2be7547cf0bd",
+ "value": "generation_config.json: 100%"
+ }
+ },
+ "0e2beab611114239b6ee48a3cbb09c49": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "LabelModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "LabelModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "LabelView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_57b0096985ab44aea342e52795c4f999",
+ "placeholder": "",
+ "style": "IPY_MODEL_a4c404e420cc4ce781ce569f9ab3f987",
+ "value": "Token is valid (permission: write)."
+ }
+ },
+ "0ec2643d9fd44785addb37d9ecd23989": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "0f4c664612364dc89acf78eb1c740980": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "0f54e8fda93144f6a95493e6ec535e9d": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "0f60f9aa76b941809e013ffcae83604a": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "124a70bfad434c5c946f611c04a91c8f": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "14bf612f6ad7416c8ddd6085c72eee0e": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "14c73d88df9e46e3bbb6690fdb48ad07": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "1561cd47c42e46368677d34e7b7084cd": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_04188e0cec0542818894ebc6a534fb51",
+ "placeholder": "",
+ "style": "IPY_MODEL_4a13203d132b45beadf140c02dc8a566",
+ "value": " 518/518 [00:00<00:00, 976.36 examples/s]"
+ }
+ },
+ "156f95b0012449e8a0c604e6e03bf35f": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "17c797e08bd2493fa685918129415309": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "191caf3a38eb4191a35f623ce25238f9": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "1ae1d2702da5483a85504f59939ffa39": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "FloatProgressModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "FloatProgressModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "ProgressView",
+ "bar_style": "success",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_8cd63d3908e4411c9fcb42bc32c8dd16",
+ "max": 73,
+ "min": 0,
+ "orientation": "horizontal",
+ "style": "IPY_MODEL_64624b26145b42db82f7afc36c32e117",
+ "value": 73
+ }
+ },
+ "1b2abf90003e4165a3293acd6a5ea9ff": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_cffdf12fbe97462ab74e88ccca943aeb",
+ "placeholder": "",
+ "style": "IPY_MODEL_bcaf4c81ba9d437bb6223dbb22d011ed",
+ "value": " 73.0/73.0 [00:00<00:00, 4.75kB/s]"
+ }
+ },
+ "1bd0a270c7ee409c970763398e54fc36": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_076357d4bb9943bdaa1d6846897786af",
+ "placeholder": "",
+ "style": "IPY_MODEL_7b3e136fc9e74a699497a947006f4f1d",
+ "value": " 1.11M/1.11M [00:00<00:00, 8.23MB/s]"
+ }
+ },
+ "1d27ab2bc6ae463a806292b68b7891f8": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "1f0efc167b3744b38ff832b71d529318": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_64911f0e52e74067a1a986c5edfc7f59",
+ "placeholder": "",
+ "style": "IPY_MODEL_b4a274fc9e324b80bf559c4dbd05e319",
+ "value": "Downloading readme: 100%"
+ }
+ },
+ "1f59dd66813f419999336e59a3efc56a": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "1f75d85e6c7e4eb6a91b03f0c8adb644": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "1f82a5685eef4b47a2dbf7618362907c": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "21bf14b771c14d2dab9e98a326302e14": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "23012118a7314a3f838870a2aee9ec90": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_e297072ab5d64815b90bc89d22503378",
+ "placeholder": "",
+ "style": "IPY_MODEL_67fbabb9082c4241b8f937b24e0cdd03",
+ "value": " 395/395 [00:00<00:00, 16.6kB/s]"
+ }
+ },
+ "2540d57e3bf545e3812da1ee72b85fc8": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "2558c2dd7d394ecf9fc67a69ce8fc97a": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "25fc6aaf37fc49fa822df29236bf2f90": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "25fef90e209f4b14a73f3e39d226d913": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "27a587021d854b79a279a510a55f9d73": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_d4092198673141d3b4a824d629d73f64",
+ "placeholder": "",
+ "style": "IPY_MODEL_d3cbfd564fe8485ba7afdb1cc54abed3",
+ "value": "Map: 100%"
+ }
+ },
+ "2a57bb48e1c6475abba242994a79d44a": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "2ab86b3fbd49488bb02f8205a572e752": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "30b74bd2db8d40d08408013cebcd7661": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "317cda72329c4043ab0b224b46b259d3": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "31c10fa464e24f97b379675a204a09b5": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "FloatProgressModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "FloatProgressModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "ProgressView",
+ "bar_style": "success",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_1d27ab2bc6ae463a806292b68b7891f8",
+ "max": 654,
+ "min": 0,
+ "orientation": "horizontal",
+ "style": "IPY_MODEL_2a57bb48e1c6475abba242994a79d44a",
+ "value": 654
+ }
+ },
+ "31c574113731403b88edc5bb0798bc6d": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "347540dc03d34e65b7ffbb0f5fc569aa": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "34e381adbd9242759b57f2a305c5d2e3": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "35186465f87341f683affb9399661540": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": "center",
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": "flex",
+ "flex": null,
+ "flex_flow": "column",
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": "50%"
+ }
+ },
+ "353bf45a4bbc46d6a798175f152399cb": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_740604526cc44cd58b811827d4787d96",
+ "placeholder": "",
+ "style": "IPY_MODEL_2558c2dd7d394ecf9fc67a69ce8fc97a",
+ "value": "Generating test split: 100%"
+ }
+ },
+ "35c2c635c2024bcda3265bf95d330f63": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "37523a6cac1047e9a261698212d47737": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "FloatProgressModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "FloatProgressModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "ProgressView",
+ "bar_style": "success",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_191caf3a38eb4191a35f623ce25238f9",
+ "max": 20877686,
+ "min": 0,
+ "orientation": "horizontal",
+ "style": "IPY_MODEL_30b74bd2db8d40d08408013cebcd7661",
+ "value": 20877686
+ }
+ },
+ "3b614b9712874fac990d2c557b0791a6": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "3b82b8d41b134bec9bd77ed8d4f00eb4": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_14bf612f6ad7416c8ddd6085c72eee0e",
+ "placeholder": "",
+ "style": "IPY_MODEL_f7e59b47f9b74523843f37268212d566",
+ "value": " 23.9k/23.9k [00:00<00:00, 1.51MB/s]"
+ }
+ },
+ "3b8bc5b9392e45758813a1db9db824a9": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "3d9d8278667d496aaea1eaaa4d24ae93": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "3e45aea9f7444a4db885c4cca4c9c4ff": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "3f9fa554747743f8a86b40a4f7530617": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "4227474e986546d1a7d31dce35a2410c": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "FloatProgressModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "FloatProgressModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "ProgressView",
+ "bar_style": "success",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_7e51e8e0612e46b1a3403d448b39aa50",
+ "max": 518,
+ "min": 0,
+ "orientation": "horizontal",
+ "style": "IPY_MODEL_061c45266c484ff6807dcaf4722fd73b",
+ "value": 518
+ }
+ },
+ "42eb041021214110a860924d28d73409": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_4c369386ba5f4862b11a50e50130663b",
+ "placeholder": "",
+ "style": "IPY_MODEL_bbdf3bb657e64fc2b0a90e78e8886480",
+ "value": " 5.00G/5.00G [00:24<00:00, 249MB/s]"
+ }
+ },
+ "434fe18d50a14920b30fd2d0650297ac": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_353bf45a4bbc46d6a798175f152399cb",
+ "IPY_MODEL_bfcbfe4184774fd3a8320f4f0e1baf54",
+ "IPY_MODEL_99c5c846cc5e43429905f071670b4310"
+ ],
+ "layout": "IPY_MODEL_8d988c86648244788f6dc5aa0fea38fd"
+ }
+ },
+ "43d12a98d90a4bf7a96c033172c646e2": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_c35b16156253402f90a432f3f07c2e0a",
+ "IPY_MODEL_1ae1d2702da5483a85504f59939ffa39",
+ "IPY_MODEL_1b2abf90003e4165a3293acd6a5ea9ff"
+ ],
+ "layout": "IPY_MODEL_3e45aea9f7444a4db885c4cca4c9c4ff"
+ }
+ },
+ "47944ad8cadf4a57b170193c46d4389c": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "4a13203d132b45beadf140c02dc8a566": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "4a7c8dfd88db4bc893da2bced0560d47": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_27a587021d854b79a279a510a55f9d73",
+ "IPY_MODEL_4227474e986546d1a7d31dce35a2410c",
+ "IPY_MODEL_1561cd47c42e46368677d34e7b7084cd"
+ ],
+ "layout": "IPY_MODEL_8b9e961c837a464fb7a8c44756dc41e7"
+ }
+ },
+ "4b1f795c4c004cacbf3660d935e52995": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "4bc1fd9d480a4799954c69031c071b30": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_068eb104d5d346b1897f8cbe9860d267",
+ "placeholder": "",
+ "style": "IPY_MODEL_b621c6a8c0e9440fa840d75a1b1b02fc",
+ "value": " 9846/9846 [00:00<00:00, 38881.08 examples/s]"
+ }
+ },
+ "4bdb196cd1494f809829651ec5b6cbf8": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "4c369386ba5f4862b11a50e50130663b": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "4c8e98294bd240a6869cb199caee66e1": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "4e1f5423311b4dc0930c21c9ad5a88f5": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "51180cce01564821a170d1d4b8a9a918": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_03dd6c24f6d94fe7ab85b79d6f6cbeaf",
+ "IPY_MODEL_f2ab2fa803e94328a237e84cd4ea0027",
+ "IPY_MODEL_1bd0a270c7ee409c970763398e54fc36"
+ ],
+ "layout": "IPY_MODEL_e92b30d0b4234af6b5a33bff989b1b45"
+ }
+ },
+ "51b3af446ace409dbcdf5de499552061": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "53f287d4927541d08e2ae7d4d0b3c396": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "546b76a22f1046cd856a8fa2f9ff2d9f": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "5690d92586494b9187147f32fa708405": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "57b0096985ab44aea342e52795c4f999": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "57f251691b4c453896b2508c431dfc2f": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "57f87d4780634d36ae8159d987c22993": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_58ea619f81bf42ddb8b166db3deb0e86",
+ "IPY_MODEL_8bb83ae3229e4f38b1733f92f536fad0",
+ "IPY_MODEL_5c0104210ee34ca8a072ee5121f424a1"
+ ],
+ "layout": "IPY_MODEL_34e381adbd9242759b57f2a305c5d2e3"
+ }
+ },
+ "58ea619f81bf42ddb8b166db3deb0e86": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_e4e1a4338c5e46b3ba5a3bb960da7107",
+ "placeholder": "",
+ "style": "IPY_MODEL_9a5072b8d16d4a1eb0652da61bda0ac8",
+ "value": "Loading checkpoint shards: 100%"
+ }
+ },
+ "5924b266e95a42039634a334ff561a82": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_eadeec171e7b4c0f9e26964f031cfb71",
+ "IPY_MODEL_feae525923d5407bb69a922954c474f7",
+ "IPY_MODEL_00371a48e64c45cd97020a78b710e64c"
+ ],
+ "layout": "IPY_MODEL_156f95b0012449e8a0c604e6e03bf35f"
+ }
+ },
+ "5962e77eea5a4d88ba6dbc5e9f51c709": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "5a8ac674153248999007a713299b2644": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "5b2a671976fa446db408d58a215b8249": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "FloatProgressModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "FloatProgressModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "ProgressView",
+ "bar_style": "success",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_63899ac621ff4e9cb8e215d5ab63bef8",
+ "max": 4,
+ "min": 0,
+ "orientation": "horizontal",
+ "style": "IPY_MODEL_6b2b59d2b62b4f7da8c60ff783138397",
+ "value": 4
+ }
+ },
+ "5b56ac3009714a5a84dd8749db4a7bce": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_51b3af446ace409dbcdf5de499552061",
+ "placeholder": "",
+ "style": "IPY_MODEL_9a12124915994b70a71ebd64b99e93e9",
+ "value": " 1.17G/1.17G [00:09<00:00, 45.8MB/s]"
+ }
+ },
+ "5c0104210ee34ca8a072ee5121f424a1": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_604582e8cbff4dc9876551a3307b5b77",
+ "placeholder": "",
+ "style": "IPY_MODEL_a98165ee656643ad85ac9ea1447cc775",
+ "value": " 4/4 [01:13<00:00, 15.74s/it]"
+ }
+ },
+ "5cf4a57d21a545029b6448258a5ebd84": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_0d2ae3466a3447c58e23ccd2b3733deb",
+ "IPY_MODEL_ba7f32c41f9247ec9d4c40e6396b55a9",
+ "IPY_MODEL_ea1bdb5f2da64332960bccd967a84b4a"
+ ],
+ "layout": "IPY_MODEL_b08631e4cffa445c912da0c8eac2ef23"
+ }
+ },
+ "5f551f9b217e44cf8b5433f314b3844b": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "5f60910d1e744432bdf87518f0f45874": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "5f6ffa1d929443a5bd9c7c550f0690f0": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "LabelModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "LabelModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "LabelView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_93a50117ece543d4857ba02505dc4514",
+ "placeholder": "",
+ "style": "IPY_MODEL_71a3a56edbdb45669d382fef4b097e1b",
+ "value": "Your token has been saved to /root/.cache/huggingface/token"
+ }
+ },
+ "5fb4a4ef8afe4ea4af6655faea17f354": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "604582e8cbff4dc9876551a3307b5b77": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "610e1ddfb7a44d51a54ebea6dad3a5f0": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "6149752353fe4f9cbb7b26bcc25199a9": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_6cb8065803724d80b82b06dc95ded91e",
+ "placeholder": "",
+ "style": "IPY_MODEL_8301c6302df54bbc9f15295f11cec208",
+ "value": " 654/654 [00:00<00:00, 46.9kB/s]"
+ }
+ },
+ "63899ac621ff4e9cb8e215d5ab63bef8": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "63ac7dafeb27446cb30aaddf4cd27c9f": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "64624b26145b42db82f7afc36c32e117": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "64911f0e52e74067a1a986c5edfc7f59": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "661f76474252493caae8f7d6aa8f99b7": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_83c355e1418140a5bbad11bf0646b332",
+ "placeholder": "",
+ "style": "IPY_MODEL_84d6d2a6afcd423f9b609cbb2d10f00e",
+ "value": " 20.9M/20.9M [00:00<00:00, 44.7MB/s]"
+ }
+ },
+ "668a7f88506148a9ba2b48920afc028f": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "LabelModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "LabelModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "LabelView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_53f287d4927541d08e2ae7d4d0b3c396",
+ "placeholder": "",
+ "style": "IPY_MODEL_afa442ab223b46cb82569438c0047823",
+ "value": "Login successful"
+ }
+ },
+ "67b4473eb8a44a96ba34983762ab38fa": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "FloatProgressModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "FloatProgressModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "ProgressView",
+ "bar_style": "success",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_6f474268da0f4337a2ccecc1ca2098a1",
+ "max": 4976698672,
+ "min": 0,
+ "orientation": "horizontal",
+ "style": "IPY_MODEL_c2ceccfdb59b4336a24003cd6bc2403d",
+ "value": 4976698672
+ }
+ },
+ "67fbabb9082c4241b8f937b24e0cdd03": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "6b0ec8d5f7294d44a5fa15d8ef12471e": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_8ea89e52123643268857285e0e1db1c0",
+ "placeholder": "",
+ "style": "IPY_MODEL_a8514e34378d47a28fbf0831a14ede8f",
+ "value": "tokenizer.json: 100%"
+ }
+ },
+ "6b2b59d2b62b4f7da8c60ff783138397": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "6b6ed29053ec4aaa8fc5526a35f17c2b": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "6bb9c7182d2a464ea21809e59043562a": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "6cb8065803724d80b82b06dc95ded91e": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "6f474268da0f4337a2ccecc1ca2098a1": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "7037c32dfce84e70ac86537dbbc6a495": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_0f4c664612364dc89acf78eb1c740980",
+ "placeholder": "",
+ "style": "IPY_MODEL_0f60f9aa76b941809e013ffcae83604a",
+ "value": "config.json: 100%"
+ }
+ },
+ "71a3a56edbdb45669d382fef4b097e1b": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "7243d8e2e1cc4043a2ee310eabd0ac09": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "740604526cc44cd58b811827d4787d96": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "7504986b8d8d4d0da58ad79e80a81948": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "7725e9d443e249ada02e5ac7056d00db": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "77704d2e27e94cd3a0c5f6b5ceeffd1c": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "FloatProgressModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "FloatProgressModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "ProgressView",
+ "bar_style": "success",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_0f54e8fda93144f6a95493e6ec535e9d",
+ "max": 23950,
+ "min": 0,
+ "orientation": "horizontal",
+ "style": "IPY_MODEL_880124db7dc04aaea09edd75e1ec7921",
+ "value": 23950
+ }
+ },
+ "791df472db174df69b8c9f0e200af254": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "7a00aa4a97a34da39cc052c6926dbe13": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "7ac8e88f29f04b859f592a003d39836b": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "7b3e136fc9e74a699497a947006f4f1d": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "7cd50bcc8fcc4b83abcda6d3604bd4cc": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "LabelModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "LabelModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "LabelView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_7a00aa4a97a34da39cc052c6926dbe13",
+ "placeholder": "",
+ "style": "IPY_MODEL_14c73d88df9e46e3bbb6690fdb48ad07",
+ "value": "Connecting..."
+ }
+ },
+ "7d3a7be9ed6f48988a2c4a1a4a2271cf": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "FloatProgressModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "FloatProgressModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "ProgressView",
+ "bar_style": "success",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_f86b969ef69b48119619e1a424b50460",
+ "max": 9085698,
+ "min": 0,
+ "orientation": "horizontal",
+ "style": "IPY_MODEL_7725e9d443e249ada02e5ac7056d00db",
+ "value": 9085698
+ }
+ },
+ "7e2e097c703a4a0d8556733a0739469c": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_e0fd6d00f0ba4e59bdaa5779556ec4ea",
+ "IPY_MODEL_cd318c6bfc8e421a9bfcdab16be5eaa7",
+ "IPY_MODEL_4bc1fd9d480a4799954c69031c071b30"
+ ],
+ "layout": "IPY_MODEL_25fc6aaf37fc49fa822df29236bf2f90"
+ }
+ },
+ "7e3a386e672f4748882211227b7721a9": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ButtonStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ButtonStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "button_color": null,
+ "font_weight": ""
+ }
+ },
+ "7e51e8e0612e46b1a3403d448b39aa50": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "800e9453214848b69bc4c6ca2d5e8f79": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_6b0ec8d5f7294d44a5fa15d8ef12471e",
+ "IPY_MODEL_7d3a7be9ed6f48988a2c4a1a4a2271cf",
+ "IPY_MODEL_c40f583823574e40b6b29d4914143c0e"
+ ],
+ "layout": "IPY_MODEL_a4368e6da8f046aaa32f3152b7d333d1"
+ }
+ },
+ "8301c6302df54bbc9f15295f11cec208": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "8365680c634a44aa880317e36fa5e46e": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "PasswordModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "PasswordModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "PasswordView",
+ "continuous_update": true,
+ "description": "Token:",
+ "description_tooltip": null,
+ "disabled": false,
+ "layout": "IPY_MODEL_31c574113731403b88edc5bb0798bc6d",
+ "placeholder": "",
+ "style": "IPY_MODEL_3b8bc5b9392e45758813a1db9db824a9",
+ "value": ""
+ }
+ },
+ "83c355e1418140a5bbad11bf0646b332": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "849cdc1912aa4df4b0c721a8c63ca0f9": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "84d6d2a6afcd423f9b609cbb2d10f00e": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "854e35df771f470b82a59f878a2a6a46": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "8800c351b6da450eace0c3890d36c8d7": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_7037c32dfce84e70ac86537dbbc6a495",
+ "IPY_MODEL_31c10fa464e24f97b379675a204a09b5",
+ "IPY_MODEL_6149752353fe4f9cbb7b26bcc25199a9"
+ ],
+ "layout": "IPY_MODEL_0b145e421f4840f2872c29256b49f168"
+ }
+ },
+ "880124db7dc04aaea09edd75e1ec7921": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "88024cd312ee42c2925ebfbe52077780": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "892ff4e2f0e44c23bc5c2be7547cf0bd": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "8a7c82dcbd414b24b67ccfbc562b2e38": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "8b9e961c837a464fb7a8c44756dc41e7": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "8bb83ae3229e4f38b1733f92f536fad0": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "FloatProgressModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "FloatProgressModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "ProgressView",
+ "bar_style": "success",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_1f75d85e6c7e4eb6a91b03f0c8adb644",
+ "max": 4,
+ "min": 0,
+ "orientation": "horizontal",
+ "style": "IPY_MODEL_9da33f07ea354b5798e85298e132b017",
+ "value": 4
+ }
+ },
+ "8c149bc655a34fe5b91853c66db458a9": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "8c4d6f4eea3742289a2604e66b0c6182": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "8cc86330c2af436c9af314e8c04c8c2b": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "VBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "VBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "VBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_0e2beab611114239b6ee48a3cbb09c49",
+ "IPY_MODEL_006b78b5191b4fb888d98bdf6c20ec1e",
+ "IPY_MODEL_5f6ffa1d929443a5bd9c7c550f0690f0",
+ "IPY_MODEL_668a7f88506148a9ba2b48920afc028f"
+ ],
+ "layout": "IPY_MODEL_35186465f87341f683affb9399661540"
+ }
+ },
+ "8cd63d3908e4411c9fcb42bc32c8dd16": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "8d0f1d547c384094b10aa00a3ede3c06": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_082b6990ce5e4812adc0ad6a7b376dac",
+ "placeholder": "",
+ "style": "IPY_MODEL_610e1ddfb7a44d51a54ebea6dad3a5f0",
+ "value": "model-00003-of-00004.safetensors: 100%"
+ }
+ },
+ "8d988c86648244788f6dc5aa0fea38fd": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "8ea89e52123643268857285e0e1db1c0": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "8f5b8c513b164dab9e0892422163c483": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_cd11fb7d54bb43ae821f2272d075a1b3",
+ "placeholder": "",
+ "style": "IPY_MODEL_fbc6a2834c5442fbb6667f1b3612bb5b",
+ "value": "Downloading shards: 100%"
+ }
+ },
+ "90661b333d6f496ca606b3046622660e": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "921a1a037f7b47f8b57d1da8192a437a": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "93a50117ece543d4857ba02505dc4514": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "974e3687f18a4e1a975969b880d086aa": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "99529129d7f0435da0fdcfc9803a2f11": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "FloatProgressModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "FloatProgressModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "ProgressView",
+ "bar_style": "success",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_5a8ac674153248999007a713299b2644",
+ "max": 1168138808,
+ "min": 0,
+ "orientation": "horizontal",
+ "style": "IPY_MODEL_1f82a5685eef4b47a2dbf7618362907c",
+ "value": 1168138808
+ }
+ },
+ "99c5c846cc5e43429905f071670b4310": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_a2c543008f444cf49972a4f35c32b8e3",
+ "placeholder": "",
+ "style": "IPY_MODEL_bb7b8a9e42f6478f851236685a1392d6",
+ "value": " 518/518 [00:00<00:00, 13408.85 examples/s]"
+ }
+ },
+ "9a0b012915c54abeb100f466fa99d303": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_fffbf696c07744fc8e3d81ab51dc9c90",
+ "placeholder": "",
+ "style": "IPY_MODEL_a153cc3ca0cc45c18a941bd57e363ec3",
+ "value": "model-00004-of-00004.safetensors: 100%"
+ }
+ },
+ "9a12124915994b70a71ebd64b99e93e9": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "9a5072b8d16d4a1eb0652da61bda0ac8": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "9bdebf06b6874bbb88404f4ad14e1dbc": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "FloatProgressModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "FloatProgressModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "ProgressView",
+ "bar_style": "success",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_5f60910d1e744432bdf87518f0f45874",
+ "max": 4915916176,
+ "min": 0,
+ "orientation": "horizontal",
+ "style": "IPY_MODEL_2ab86b3fbd49488bb02f8205a572e752",
+ "value": 4915916176
+ }
+ },
+ "9cfaf17064bc49a5aded0fc53dd7cd7f": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_ede66e196fa9482498f58dcdffd494a2",
+ "IPY_MODEL_a26cc7fea1a64d7bac1769d33cc74e28",
+ "IPY_MODEL_c2f24a8930be4b70b4bbbcf5d908b01d"
+ ],
+ "layout": "IPY_MODEL_1f59dd66813f419999336e59a3efc56a"
+ }
+ },
+ "9da33f07ea354b5798e85298e132b017": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "9f13437a44b8434b9cc3afab998e8d3c": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "a06b2bd0236249999adffa44e53cf80e": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "FloatProgressModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "FloatProgressModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "ProgressView",
+ "bar_style": "success",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_5fb4a4ef8afe4ea4af6655faea17f354",
+ "max": 395,
+ "min": 0,
+ "orientation": "horizontal",
+ "style": "IPY_MODEL_b1a03a5e9bae46129830daeeb23bf6ff",
+ "value": 395
+ }
+ },
+ "a153cc3ca0cc45c18a941bd57e363ec3": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "a2249f364b914662b54045a1f8d6dfd1": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_9f13437a44b8434b9cc3afab998e8d3c",
+ "placeholder": "",
+ "style": "IPY_MODEL_8a7c82dcbd414b24b67ccfbc562b2e38",
+ "value": " 4.92G/4.92G [00:32<00:00, 171MB/s]"
+ }
+ },
+ "a26cc7fea1a64d7bac1769d33cc74e28": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "FloatProgressModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "FloatProgressModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "ProgressView",
+ "bar_style": "success",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_854e35df771f470b82a59f878a2a6a46",
+ "max": 9846,
+ "min": 0,
+ "orientation": "horizontal",
+ "style": "IPY_MODEL_d1cbe0ab9379453588eb438d13fd272d",
+ "value": 9846
+ }
+ },
+ "a2a7b715b16a41a288209dee1de5d2d1": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "a2c543008f444cf49972a4f35c32b8e3": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "a34b3fd5859a441f89cbe7f6e6df9da9": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_8f5b8c513b164dab9e0892422163c483",
+ "IPY_MODEL_5b2a671976fa446db408d58a215b8249",
+ "IPY_MODEL_c934919f617447cfb9226929e7a68d79"
+ ],
+ "layout": "IPY_MODEL_124a70bfad434c5c946f611c04a91c8f"
+ }
+ },
+ "a4368e6da8f046aaa32f3152b7d333d1": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "a4c404e420cc4ce781ce569f9ab3f987": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "a53b4776f95f4dd38197193e6c5f649e": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_aea74071600f483b9e6de1a61743c03a",
+ "placeholder": "",
+ "style": "IPY_MODEL_21bf14b771c14d2dab9e98a326302e14",
+ "value": "model-00002-of-00004.safetensors: 100%"
+ }
+ },
+ "a8514e34378d47a28fbf0831a14ede8f": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "a8999d04e4114693bb6be358bdbe9b83": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "a98165ee656643ad85ac9ea1447cc775": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "aea74071600f483b9e6de1a61743c03a": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "afa442ab223b46cb82569438c0047823": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "b08631e4cffa445c912da0c8eac2ef23": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "b0b7457a8b47496483da1506fb2505b3": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "b1a03a5e9bae46129830daeeb23bf6ff": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "b1de7b283eeb41828e8093e60c83f2c4": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_bb640a5c858349d29c13ce5629e72f22",
+ "IPY_MODEL_37523a6cac1047e9a261698212d47737",
+ "IPY_MODEL_661f76474252493caae8f7d6aa8f99b7"
+ ],
+ "layout": "IPY_MODEL_849cdc1912aa4df4b0c721a8c63ca0f9"
+ }
+ },
+ "b2a19b6092c44b20886987b30f1bf48a": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_1f0efc167b3744b38ff832b71d529318",
+ "IPY_MODEL_a06b2bd0236249999adffa44e53cf80e",
+ "IPY_MODEL_23012118a7314a3f838870a2aee9ec90"
+ ],
+ "layout": "IPY_MODEL_dcff079d850c423a83eb70105b816ee4"
+ }
+ },
+ "b3b3f4ddd4ed4d938c923887939a0440": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_57f251691b4c453896b2508c431dfc2f",
+ "placeholder": "",
+ "style": "IPY_MODEL_4bdb196cd1494f809829651ec5b6cbf8",
+ "value": "\nPro Tip: If you don't already have one, you can create a dedicated\n'notebooks' token with 'write' access, that you can then easily reuse for all\nnotebooks.
"
+ }
+ },
+ "b4a274fc9e324b80bf559c4dbd05e319": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "b4ba435f6d1c448f99b533bc6df32e76": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "FloatProgressModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "FloatProgressModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "ProgressView",
+ "bar_style": "success",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_35c2c635c2024bcda3265bf95d330f63",
+ "max": 4999802720,
+ "min": 0,
+ "orientation": "horizontal",
+ "style": "IPY_MODEL_ec014d847e394a309b6a82c30a6fdfc5",
+ "value": 4999802720
+ }
+ },
+ "b621c6a8c0e9440fa840d75a1b1b02fc": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "ba7f32c41f9247ec9d4c40e6396b55a9": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "FloatProgressModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "FloatProgressModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "ProgressView",
+ "bar_style": "success",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_4c8e98294bd240a6869cb199caee66e1",
+ "max": 177,
+ "min": 0,
+ "orientation": "horizontal",
+ "style": "IPY_MODEL_4e1f5423311b4dc0930c21c9ad5a88f5",
+ "value": 177
+ }
+ },
+ "bac377ed96ae4e8db9b298bb623888ec": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "bb640a5c858349d29c13ce5629e72f22": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_5962e77eea5a4d88ba6dbc5e9f51c709",
+ "placeholder": "",
+ "style": "IPY_MODEL_f07c8a6ec12f46ea9e32a2208e70bccd",
+ "value": "Downloading data: 100%"
+ }
+ },
+ "bb7b8a9e42f6478f851236685a1392d6": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "bbdf3bb657e64fc2b0a90e78e8886480": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "bcaf4c81ba9d437bb6223dbb22d011ed": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "bf77e5aaab0547f7b2beb015687552ef": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "bfcbfe4184774fd3a8320f4f0e1baf54": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "FloatProgressModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "FloatProgressModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "ProgressView",
+ "bar_style": "success",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_a2a7b715b16a41a288209dee1de5d2d1",
+ "max": 518,
+ "min": 0,
+ "orientation": "horizontal",
+ "style": "IPY_MODEL_bf77e5aaab0547f7b2beb015687552ef",
+ "value": 518
+ }
+ },
+ "c27e8ce031884a90b41d8220b1870bc4": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "c2ceccfdb59b4336a24003cd6bc2403d": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "c2f24a8930be4b70b4bbbcf5d908b01d": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_b0b7457a8b47496483da1506fb2505b3",
+ "placeholder": "",
+ "style": "IPY_MODEL_c7dc386d978a44ff885763ecec94dc38",
+ "value": " 9846/9846 [00:09<00:00, 1066.17 examples/s]"
+ }
+ },
+ "c35b16156253402f90a432f3f07c2e0a": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_6b6ed29053ec4aaa8fc5526a35f17c2b",
+ "placeholder": "",
+ "style": "IPY_MODEL_e69cd88ccbae4bb7b238fa112a60f0f9",
+ "value": "special_tokens_map.json: 100%"
+ }
+ },
+ "c40f583823574e40b6b29d4914143c0e": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_f81756eb9e554899b0778311f2c407c4",
+ "placeholder": "",
+ "style": "IPY_MODEL_3b614b9712874fac990d2c557b0791a6",
+ "value": " 9.09M/9.09M [00:00<00:00, 19.3MB/s]"
+ }
+ },
+ "c56d8289513441688f9bc5f4b52d60a0": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_a53b4776f95f4dd38197193e6c5f649e",
+ "IPY_MODEL_b4ba435f6d1c448f99b533bc6df32e76",
+ "IPY_MODEL_42eb041021214110a860924d28d73409"
+ ],
+ "layout": "IPY_MODEL_17c797e08bd2493fa685918129415309"
+ }
+ },
+ "c7dc386d978a44ff885763ecec94dc38": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "c7e06fd82f7f4f9fb81c68e8758f2de1": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_a8999d04e4114693bb6be358bdbe9b83",
+ "placeholder": "",
+ "style": "IPY_MODEL_2540d57e3bf545e3812da1ee72b85fc8",
+ "value": " 4.98G/4.98G [00:34<00:00, 232MB/s]"
+ }
+ },
+ "c84f542c863043dea8a3675fa153e78d": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ButtonModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ButtonModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "ButtonView",
+ "button_style": "",
+ "description": "Login",
+ "disabled": false,
+ "icon": "",
+ "layout": "IPY_MODEL_d2d81cc8296c4b10bf80b86c0a3302d3",
+ "style": "IPY_MODEL_7e3a386e672f4748882211227b7721a9",
+ "tooltip": ""
+ }
+ },
+ "c934919f617447cfb9226929e7a68d79": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_c27e8ce031884a90b41d8220b1870bc4",
+ "placeholder": "",
+ "style": "IPY_MODEL_88024cd312ee42c2925ebfbe52077780",
+ "value": " 4/4 [01:41<00:00, 22.30s/it]"
+ }
+ },
+ "cc5ce633746949ed98418cae9f68afe3": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "cd11fb7d54bb43ae821f2272d075a1b3": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "cd318c6bfc8e421a9bfcdab16be5eaa7": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "FloatProgressModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "FloatProgressModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "ProgressView",
+ "bar_style": "success",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_d10ba011d05045b18bbfeb9660e4d9d3",
+ "max": 9846,
+ "min": 0,
+ "orientation": "horizontal",
+ "style": "IPY_MODEL_e56c22f77c884caaacfafd48dfa51a55",
+ "value": 9846
+ }
+ },
+ "cf6d1be81b6c4ffc81ce8fdabfc5ad28": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_07e0aed682fd4cc88fa75c0592dc04a7",
+ "IPY_MODEL_67b4473eb8a44a96ba34983762ab38fa",
+ "IPY_MODEL_c7e06fd82f7f4f9fb81c68e8758f2de1"
+ ],
+ "layout": "IPY_MODEL_3d9d8278667d496aaea1eaaa4d24ae93"
+ }
+ },
+ "cffdf12fbe97462ab74e88ccca943aeb": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "d10ba011d05045b18bbfeb9660e4d9d3": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "d1508f5cde9a43d8abc26dd2d0c34dbd": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_9a0b012915c54abeb100f466fa99d303",
+ "IPY_MODEL_99529129d7f0435da0fdcfc9803a2f11",
+ "IPY_MODEL_5b56ac3009714a5a84dd8749db4a7bce"
+ ],
+ "layout": "IPY_MODEL_546b76a22f1046cd856a8fa2f9ff2d9f"
+ }
+ },
+ "d1cbe0ab9379453588eb438d13fd272d": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "d2d81cc8296c4b10bf80b86c0a3302d3": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "d3cbfd564fe8485ba7afdb1cc54abed3": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "d4092198673141d3b4a824d629d73f64": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "d7ef74cf4a914ad38a69c84c34fff393": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_8d0f1d547c384094b10aa00a3ede3c06",
+ "IPY_MODEL_9bdebf06b6874bbb88404f4ad14e1dbc",
+ "IPY_MODEL_a2249f364b914662b54045a1f8d6dfd1"
+ ],
+ "layout": "IPY_MODEL_7504986b8d8d4d0da58ad79e80a81948"
+ }
+ },
+ "db05b25cb38140bdb21e6f3b7fde7e66": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "dcff079d850c423a83eb70105b816ee4": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "de3757d6125a4c07b502dd60816bafec": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "e0fd6d00f0ba4e59bdaa5779556ec4ea": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_7ac8e88f29f04b859f592a003d39836b",
+ "placeholder": "",
+ "style": "IPY_MODEL_0ec2643d9fd44785addb37d9ecd23989",
+ "value": "Generating train split: 100%"
+ }
+ },
+ "e25f9ca445b14e3f8397779df071dfb4": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_791df472db174df69b8c9f0e200af254",
+ "placeholder": "",
+ "style": "IPY_MODEL_6bb9c7182d2a464ea21809e59043562a",
+ "value": "
Copy a token from your Hugging Face\ntokens page and paste it below.
Immediately click login after copying\nyour token or it might be stored in plain text in this notebook file. "
+ }
+ },
+ "e297072ab5d64815b90bc89d22503378": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "e4e1a4338c5e46b3ba5a3bb960da7107": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "e56c22f77c884caaacfafd48dfa51a55": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "e69cd88ccbae4bb7b238fa112a60f0f9": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "e92b30d0b4234af6b5a33bff989b1b45": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "ea1bdb5f2da64332960bccd967a84b4a": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_347540dc03d34e65b7ffbb0f5fc569aa",
+ "placeholder": "",
+ "style": "IPY_MODEL_7243d8e2e1cc4043a2ee310eabd0ac09",
+ "value": " 177/177 [00:00<00:00, 11.4kB/s]"
+ }
+ },
+ "eadeec171e7b4c0f9e26964f031cfb71": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_de3757d6125a4c07b502dd60816bafec",
+ "placeholder": "",
+ "style": "IPY_MODEL_8c4d6f4eea3742289a2604e66b0c6182",
+ "value": "tokenizer_config.json: 100%"
+ }
+ },
+ "ec014d847e394a309b6a82c30a6fdfc5": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "ede66e196fa9482498f58dcdffd494a2": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_026072374b7d47c194707a50f5c99099",
+ "placeholder": "",
+ "style": "IPY_MODEL_63ac7dafeb27446cb30aaddf4cd27c9f",
+ "value": "Map: 100%"
+ }
+ },
+ "ee4e4af964ec4dd597cb04a90f0697f9": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "f07c8a6ec12f46ea9e32a2208e70bccd": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "f2ab2fa803e94328a237e84cd4ea0027": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "FloatProgressModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "FloatProgressModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "ProgressView",
+ "bar_style": "success",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_5690d92586494b9187147f32fa708405",
+ "max": 1105272,
+ "min": 0,
+ "orientation": "horizontal",
+ "style": "IPY_MODEL_317cda72329c4043ab0b224b46b259d3",
+ "value": 1105272
+ }
+ },
+ "f4ca7b63d7d749ff83a848e250f03ec1": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "f7e59b47f9b74523843f37268212d566": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "f81756eb9e554899b0778311f2c407c4": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "f86b969ef69b48119619e1a424b50460": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "fbc6a2834c5442fbb6667f1b3612bb5b": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "feae525923d5407bb69a922954c474f7": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "FloatProgressModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "FloatProgressModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "ProgressView",
+ "bar_style": "success",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_bac377ed96ae4e8db9b298bb623888ec",
+ "max": 50566,
+ "min": 0,
+ "orientation": "horizontal",
+ "style": "IPY_MODEL_02d6cc4c2717434c895798601bda7c86",
+ "value": 50566
+ }
+ },
+ "ffe561df8772443ebf40a3b8b656079f": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "fffbf696c07744fc8e3d81ab51dc9c90": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ }
+ }
+ }
+ },
+ "nbformat": 4,
+ "nbformat_minor": 0
+}
diff --git a/peft/examples/dora_finetuning/README.md b/peft/examples/dora_finetuning/README.md
new file mode 100644
index 0000000000000000000000000000000000000000..91ffb2a529f6fb88c03a1e7e7ae8de07b9304969
--- /dev/null
+++ b/peft/examples/dora_finetuning/README.md
@@ -0,0 +1,105 @@
+# DoRA: Weight-Decomposed Low-Rank Adaptation
+
+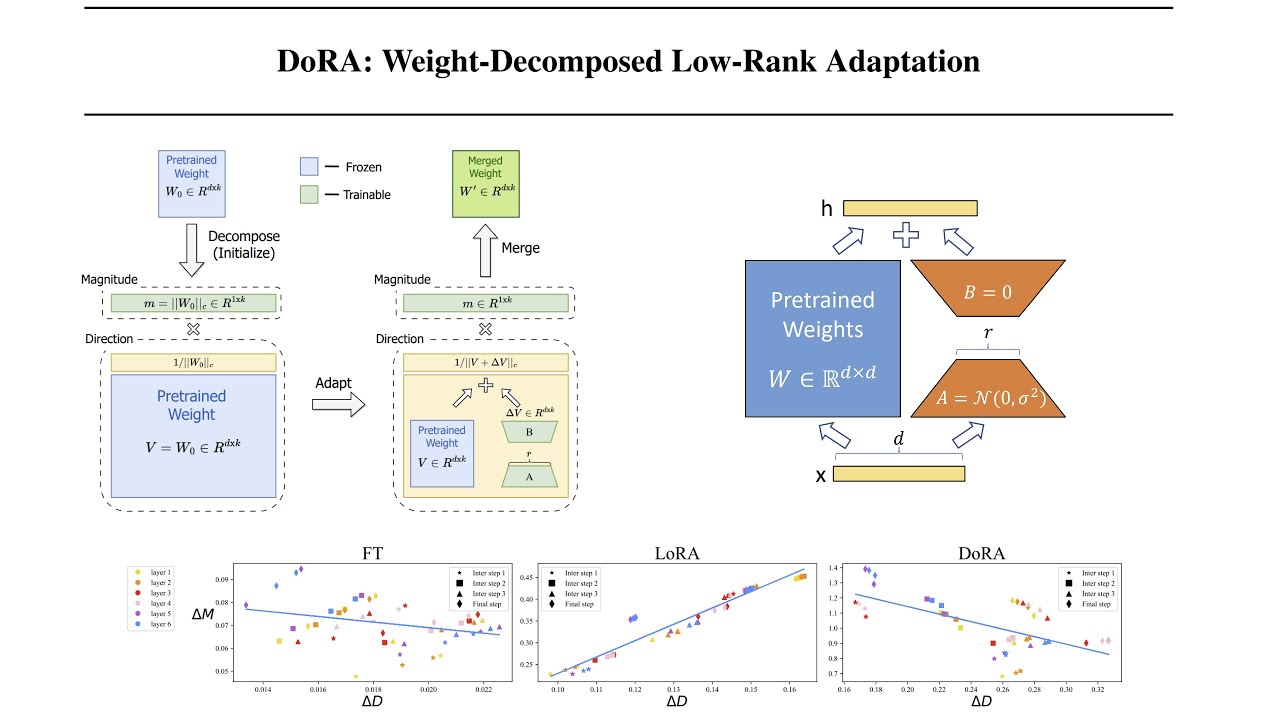
+
+
+## Introduction
+[DoRA](https://huggingface.co/papers/2402.09353) is a novel approach that leverages low rank adaptation through weight decomposition analysis to investigate the inherent differences between full fine-tuning and LoRA. DoRA initially decomposes the pretrained weight into its magnitude and directional components and finetunes both of them. Because the directional component is large in terms of parameter numbers, we further decompose it with LoRA for efficient finetuning. This results in enhancing both the learning capacity and training stability of LoRA while avoiding any additional inference overhead.
+
+## Quick start
+```python
+import torch
+from peft import LoraConfig, get_peft_model
+from transformers import AutoTokenizer, AutoModelForCausalLM, Trainer
+from datasets import load_dataset
+
+model = AutoModelForCausalLM.from_pretrained("huggyllama/llama-7b", device_map="auto")
+tokenizer = AutoTokenizer.from_pretrained("huggyllama/llama-7b")
+dataset = load_dataset("timdettmers/openassistant-guanaco", split="train")
+lora_config = LoraConfig(
+ use_dora=True
+)
+peft_model = get_peft_model(model, lora_config)
+trainer = transformers.Trainer(
+ model=peft_model,
+ train_dataset=dataset,
+ dataset_text_field="text",
+ max_seq_length=2048,
+ tokenizer=tokenizer,
+)
+trainer.train()
+peft_model.save_pretrained("dora-llama-3-8b")
+```
+
+There is no additional change needed to your standard LoRA procedure, except for specifying `use_dora = True` option in your lora configuration.
+
+
+Run the finetuning script simply by running:
+```bash
+python examples/dora_finetuning/dora_finetuning.py --base_model meta-llama/Meta-Llama-3-8B --data_path timdettmers/openassistant-guanaco
+```
+This 👆🏻 by default will load the model in peft set up with LoRA config. Now if you wanna quickly compare it with Dora, all you need to do is to input ` --use_dora` in the command line. So same above example would be 👇🏻;
+
+```bash
+python examples/dora_finetuning/dora_finetuning.py --base_model meta-llama/Meta-Llama-3-8B --data_path timdettmers/openassistant-guanaco --use_dora
+```
+
+DoRA also supports quantization. To use 4-bit quantization try:
+
+```bash
+python examples/dora_finetuning/dora_finetuning.py --base_model meta-llama/Meta-Llama-3-8B --quantize
+```
+
+Similarly, by default the LoRA layers are the attention and MLP layers of LLama model, if you get to choose a different set of layers for LoRA to be applied on, you can simply define it using:
+```bash
+python examples/dora_finetuning/dora_finetuning.py --lora_target_modules "q_proj,k_proj,v_proj,o_proj"
+```
+
+### Full example of the script
+```bash
+python dora_finetuning.py \
+ --base_model "PATH_TO_MODEL" \
+ --data_path "PATH_TO_DATASET" \
+ --output_dir "PATH_TO_OUTPUT_DIR" \
+ --batch_size 1 \
+ --num_epochs 3 \
+ --learning_rate 3e-4 \
+ --cutoff_len 512 \
+ --val_set_size 500 \
+ --use_dora \
+ --quantize \
+ --eval_step 10 \
+ --save_step 100 \
+ --lora_r 16 \
+ --lora_alpha 32 \
+ --lora_dropout 0.05 \
+ --lora_target_modules "q_proj,k_proj,v_proj,o_proj" \
+ --hub_model_id "YOUR_HF_REPO" \
+ --push_to_hub
+```
+## Use the model on 🤗
+You can load and use the model as any other 🤗 models.
+```python
+from transformers import AutoModel
+model = AutoModel.from_pretrained("ShirinYamani/huggyllama-llama-7b-finetuned")
+```
+
+## DoRA vs. LoRA
+In general, DoRA finetuning on diffusion models is still experimental and is likely to require different hyperparameter values to perform best compared to LoRA.
+
+Specifically, people have noticed 2 differences to take into account in your training:
+
+1. LoRA seem to converge faster than DoRA (so a set of parameters that may lead to overfitting when training a LoRA may be working well for a DoRA)
+
+2. DoRA quality superior to LoRA especially in lower ranks: The difference in quality of DoRA of rank 8 and LoRA of rank 8 appears to be more significant than when training ranks of 32 or 64 for example.
+
+
+## Citation
+```
+@article{liu2024dora,
+ title={DoRA: Weight-Decomposed Low-Rank Adaptation},
+ author={Liu, Shih-Yang and Wang, Chien-Yi and Yin, Hongxu and Molchanov, Pavlo and Wang, Yu-Chiang Frank and Cheng, Kwang-Ting and Chen, Min-Hung},
+ journal={arXiv preprint arXiv:2402.09353},
+ year={2024}
+}
+```
\ No newline at end of file
diff --git a/peft/examples/dora_finetuning/dora_finetuning.py b/peft/examples/dora_finetuning/dora_finetuning.py
new file mode 100644
index 0000000000000000000000000000000000000000..c8d281fc617a96958b96fbbb91fb2514a875a03e
--- /dev/null
+++ b/peft/examples/dora_finetuning/dora_finetuning.py
@@ -0,0 +1,208 @@
+import os
+
+import torch
+from datasets import load_dataset
+from transformers import (
+ AutoModelForCausalLM,
+ AutoTokenizer,
+ BitsAndBytesConfig,
+ DataCollatorForLanguageModeling,
+ Trainer,
+ TrainingArguments,
+)
+
+from peft import LoraConfig, get_peft_model, prepare_model_for_kbit_training
+
+
+def train_model(
+ base_model: str,
+ data_path: str,
+ output_dir: str,
+ batch_size: int,
+ num_epochs: int,
+ learning_rate: float,
+ cutoff_len: int,
+ val_set_size: int,
+ use_dora: bool,
+ quantize: bool,
+ eval_step: int,
+ save_step: int,
+ device: str,
+ lora_r: int,
+ lora_alpha: int,
+ lora_dropout: float,
+ lora_target_modules: str,
+ hub_model_id: str,
+ push_to_hub: bool,
+):
+ os.environ["TOKENIZERS_PARALLELISM"] = "false"
+ hf_token = os.getenv("HF_TOKEN")
+
+ # Setup device
+ if device == "auto":
+ device = torch.accelerator.current_accelerator().type if hasattr(torch, "accelerator") else "cuda"
+ else:
+ device = torch.device(device)
+ print(f"Using device: {device}")
+
+ # load tokenizer
+ tokenizer = AutoTokenizer.from_pretrained(base_model, token=hf_token)
+
+ # QDoRA (quantized dora): IF YOU WANNA QUANTIZE THE MODEL
+ if quantize:
+ if (torch.cuda.is_available() and torch.cuda.is_bf16_supported()) or torch.xpu.is_available():
+ bnb_4bit_compute_dtype = torch.bfloat16
+ else:
+ bnb_4bit_compute_dtype = torch.float16
+ model = AutoModelForCausalLM.from_pretrained(
+ base_model,
+ token=hf_token,
+ quantization_config=BitsAndBytesConfig(
+ load_in_4bit=True,
+ bnb_4bit_compute_dtype=bnb_4bit_compute_dtype,
+ bnb_4bit_use_double_quant=True,
+ bnb_4bit_quant_type="nf4",
+ ),
+ )
+ # setup for quantized training
+ model = prepare_model_for_kbit_training(model, use_gradient_checkpointing=True)
+ else:
+ model = AutoModelForCausalLM.from_pretrained(base_model, token=hf_token)
+ # LoRa config for the PEFT model
+ lora_config = LoraConfig(
+ use_dora=use_dora, # to use Dora OR compare to Lora just set the --use_dora
+ r=lora_r, # Rank of matrix
+ lora_alpha=lora_alpha,
+ target_modules=(
+ lora_target_modules.split(",")
+ if lora_target_modules
+ else ["q_proj", "k_proj", "v_proj", "o_proj", "gate_proj", "up_proj", "down_proj"]
+ ),
+ lora_dropout=lora_dropout,
+ bias="none",
+ )
+
+ # get the peft model with LoRa config
+ model = get_peft_model(model, lora_config)
+
+ model.to(device) # MODEL TO GPU/CUDA
+ tokenizer.pad_token = tokenizer.eos_token
+
+ # Load the dataset
+ dataset = load_dataset(data_path)
+
+ def tokenize_function(examples):
+ inputs = tokenizer(examples["text"], padding="max_length", truncation=True, max_length=cutoff_len)
+ inputs["labels"] = inputs["input_ids"].copy() # setting labels for a language modeling task
+ return inputs
+
+ # Tokenize the dataset and prepare for training
+ tokenized_datasets = dataset.map(tokenize_function, batched=True, remove_columns=dataset["train"].column_names)
+
+ # Data collator to dynamically pad the batched examples
+ data_collator = DataCollatorForLanguageModeling(tokenizer, mlm=False)
+
+ # Define training arguments
+ training_args = TrainingArguments(
+ output_dir=output_dir,
+ num_train_epochs=num_epochs,
+ per_device_train_batch_size=batch_size,
+ per_device_eval_batch_size=batch_size,
+ warmup_steps=100,
+ weight_decay=0.01,
+ logging_dir="./logs",
+ logging_steps=eval_step,
+ save_steps=save_step,
+ save_total_limit=2,
+ push_to_hub=push_to_hub,
+ hub_model_id=hub_model_id,
+ gradient_accumulation_steps=16,
+ fp16=True,
+ learning_rate=learning_rate,
+ hub_token=hf_token,
+ )
+
+ # Clear device cache to free memory
+ if torch.cuda.is_available():
+ torch.cuda.empty_cache()
+ elif torch.xpu.is_available():
+ torch.xpu.empty_cache()
+
+ # Initialize the Trainer
+ trainer = Trainer(
+ model=model,
+ args=training_args,
+ train_dataset=tokenized_datasets["train"],
+ eval_dataset=tokenized_datasets["test"],
+ data_collator=data_collator,
+ )
+
+ # Start model training
+ trainer.train()
+
+ # Save and push the trained model and tokenizer
+ if push_to_hub:
+ # Push the main model to the hub
+ trainer.push_to_hub(commit_message="Fine-tuned model")
+
+ # Save the model and tokenizer locally
+ model.save_pretrained(output_dir)
+ tokenizer.save_pretrained(output_dir)
+
+
+if __name__ == "__main__":
+ import argparse
+
+ parser = argparse.ArgumentParser(description="Fine-tune LLaMA with DoRA and PEFT")
+ parser.add_argument("--base_model", type=str, default="huggyllama/llama-7b", help="Base model path or name")
+ parser.add_argument(
+ "--data_path", type=str, default="timdettmers/openassistant-guanaco", help="Dataset path or name"
+ )
+ parser.add_argument(
+ "--output_dir", type=str, default="path/to/output", help="Output directory for the fine-tuned model"
+ )
+ parser.add_argument("--batch_size", type=int, default=1, help="Batch size")
+ parser.add_argument("--num_epochs", type=int, default=1, help="Number of training epochs")
+ parser.add_argument("--learning_rate", type=float, default=3e-4, help="Learning rate")
+ parser.add_argument("--cutoff_len", type=int, default=512, help="Cutoff length for tokenization")
+ parser.add_argument("--val_set_size", type=int, default=500, help="Validation set size")
+ parser.add_argument("--use_dora", action="store_true", help="Apply Dora")
+ parser.add_argument("--quantize", action="store_true", help="Use quantization")
+ parser.add_argument("--eval_step", type=int, default=10, help="Evaluation step interval")
+ parser.add_argument("--save_step", type=int, default=100, help="Save step interval")
+ parser.add_argument("--device", type=str, default="auto", help="Device to use for training")
+ parser.add_argument("--lora_r", type=int, default=8, help="LoRA rank")
+ parser.add_argument("--lora_alpha", type=int, default=16, help="LoRA alpha")
+ parser.add_argument("--lora_dropout", type=float, default=0.05, help="LoRA dropout rate")
+ parser.add_argument(
+ "--lora_target_modules", type=str, default=None, help="Comma-separated list of target modules for LoRA"
+ )
+ parser.add_argument(
+ "--hub_model_id",
+ type=str,
+ default="path/to/repo",
+ help="Repository name to push the model on the Hugging Face Hub",
+ )
+ parser.add_argument("--push_to_hub", action="store_true", help="Whether to push the model to Hugging Face Hub")
+ args = parser.parse_args()
+ train_model(
+ base_model=args.base_model,
+ data_path=args.data_path,
+ output_dir=args.output_dir,
+ batch_size=args.batch_size,
+ num_epochs=args.num_epochs,
+ learning_rate=args.learning_rate,
+ cutoff_len=args.cutoff_len,
+ val_set_size=args.val_set_size,
+ use_dora=args.use_dora,
+ quantize=args.quantize,
+ eval_step=args.eval_step,
+ save_step=args.save_step,
+ device=args.device,
+ lora_r=args.lora_r,
+ lora_alpha=args.lora_alpha,
+ lora_dropout=args.lora_dropout,
+ lora_target_modules=args.lora_target_modules,
+ hub_model_id=args.hub_model_id,
+ push_to_hub=args.push_to_hub,
+ )
diff --git a/peft/examples/ephemeral_gpu_offloading/load_with_dora.py b/peft/examples/ephemeral_gpu_offloading/load_with_dora.py
new file mode 100644
index 0000000000000000000000000000000000000000..cc61925f9008af2f526c145fca9689587d75cd65
--- /dev/null
+++ b/peft/examples/ephemeral_gpu_offloading/load_with_dora.py
@@ -0,0 +1,103 @@
+# Copyright 2024-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""
+Example script demonstrating the time difference loading a model with a DoRA using ephemeral GPU offloading vs doing it purely on the CPU.
+
+Example outputs:
+$ python load_with_dora.py
+--- Loading model ---
+Loading checkpoint shards: 100%|████████████████████████████████████████████████████████████████████████████████████████████████████| 4/4 [00:04<00:00, 1.03s/it]
+--- Loading PeftModel ---
+--- Done ---
+Model loading time: 4.83s
+PeftModel loading time: 28.14s
+Use ephemeral GPU offloading: False
+
+(Note: if this was the first time you ran the script, or if your cache was cleared, the times shown above are invalid, due to the time taken to download the model and DoRA files. Just re-run the script in this case.)
+
+$ python load_with_dora.py --ephemeral_gpu_offload
+--- Loading model ---
+Loading checkpoint shards: 100%|████████████████████████████████████████████████████████████████████████████████████████████████████| 4/4 [00:03<00:00, 1.11it/s]
+--- Loading PeftModel ---
+--- Done ---
+Model loading time: 4.28s
+PeftModel loading time: 16.59s
+Use ephemeral GPU offloading: True
+
+(Note: if this was the first time you ran the script, or if your cache was cleared, the times shown above are invalid, due to the time taken to download the model and DoRA files. Just re-run the script in this case.)
+"""
+
+import argparse
+import time
+
+from huggingface_hub import snapshot_download
+from transformers import AutoModelForCausalLM
+
+from peft import PeftModel
+
+
+def main():
+ parser = argparse.ArgumentParser(description="Load a model with DoRA using ephemeral GPU offloading")
+ parser.add_argument("--model", type=str, default="NousResearch/Hermes-2-Pro-Mistral-7B", help="Model to load")
+ parser.add_argument(
+ "--dora",
+ type=str,
+ default="peft-internal-testing/DoRA-Hermes-2-Pro-Mistral-7B",
+ help="DoRA to use",
+ )
+ parser.add_argument("--ephemeral_gpu_offload", action="store_true", help="Use ephemeral GPU offloading")
+ parser.add_argument(
+ "--merge_model_path", type=str, help="Merge the model with the DoRA model and save to the given path"
+ )
+ args = parser.parse_args()
+
+ peft_model_kwargs = {
+ "ephemeral_gpu_offload": args.ephemeral_gpu_offload,
+ "max_memory": {"cpu": "256GiB"},
+ "device_map": {"": "cpu"},
+ }
+
+ # Predownload
+ try:
+ snapshot_download(repo_id=args.model)
+ except Exception as e:
+ print(f"Failed to download model: {e}")
+ # We continue anyway as this might be e.g. a local directory or something
+ try:
+ snapshot_download(repo_id=args.dora)
+ except Exception as e:
+ print(f"Failed to download DoRA: {e}")
+ # We continue anyway as this might be e.g. a local directory or something
+
+ start = time.perf_counter()
+ print("--- Loading model ---")
+ model = AutoModelForCausalLM.from_pretrained(args.model)
+ model_time = time.perf_counter() - start
+ print("--- Loading PeftModel ---")
+ peft_model = PeftModel.from_pretrained(model, args.dora, **peft_model_kwargs)
+ print("--- Done ---")
+ peft_model_time = time.perf_counter() - start
+
+ print(f"Model loading time: {model_time:.2f}s")
+ print(f"PeftModel loading time: {peft_model_time:.2f}s")
+ print(f"Use ephemeral GPU offloading: {args.ephemeral_gpu_offload}")
+
+ if args.merge_model_path is not None:
+ merged_model = peft_model.merge_and_unload(progressbar=True)
+ merged_model.save_pretrained(args.merge_model_path)
+
+
+if __name__ == "__main__":
+ main()
diff --git a/peft/examples/eva_finetuning/README.md b/peft/examples/eva_finetuning/README.md
new file mode 100644
index 0000000000000000000000000000000000000000..0c710410059719eb7b50b043fa94437a45bfec28
--- /dev/null
+++ b/peft/examples/eva_finetuning/README.md
@@ -0,0 +1,159 @@
+# EVA: Explained Variance Adaptation
+## Introduction ([Paper](https://huggingface.co/papers/2410.07170), [code](https://github.com/ml-jku/EVA))
+Explained Variance Adaptation (EVA) is a novel initialization method for LoRA style adapters which initializes adapter weights in a data driven manner and adaptively allocates ranks according to the variance they explain. EVA improves average performance on a multitude of tasks across various domains, such as Language generation and understanding, Image classification, and Decision Making.
+
+The abstract from the paper is:
+
+*Foundation models (FMs) are pre-trained on large-scale datasets and then fine-tuned on a downstream task for a specific application. The most successful and most commonly used fine-tuning method is to update the pre-trained weights via a low-rank adaptation (LoRA). LoRA introduces new weight matrices that are usually initialized at random with a uniform rank distribution across model weights. Recent works focus on weight-driven initialization or learning of adaptive ranks during training. Both approaches have only been investigated in isolation, resulting in slow convergence or a uniform rank distribution, in turn leading to sub-optimal performance. We propose to enhance LoRA by initializing the new weights in a data-driven manner by computing singular value decomposition on minibatches of activation vectors. Then, we initialize the LoRA matrices with the obtained right-singular vectors and re-distribute ranks among all weight matrices to explain the maximal amount of variance and continue the standard LoRA fine-tuning procedure. This results in our new method **E**xplained **V**ariance **A**daptation (EVA). We apply EVA to a variety of fine-tuning tasks ranging from language generation and understanding to image classification and reinforcement learning. EVA exhibits faster convergence than competitors and attains the highest average score across a multitude of tasks per domain.*
+
+## Quick Start
+Below is an example of how to use EVA with a causal language model. For a more detailed example see [eva_finetuning.py](https://github.com/huggingface/peft/blob/main/examples/eva_finetuning/eva_finetuning.py).
+```python
+import torch
+from datasets import load_dataset
+from torch.utils.data import DataLoader
+from transformers import AutoModelForCausalLM, AutoTokenizer
+
+from peft import EvaConfig, LoraConfig, get_peft_model, initialize_lora_eva_weights
+
+
+# config
+model_name = "meta-llama/Llama-3.1-8B"
+max_seq_len = 512
+rank = 16
+alpha = 1
+rho = 2.0
+target_modules = ["q_proj", "k_proj", "v_proj", "o_proj"]
+svd_batch_size = 4 # can be different from the batch size used in finetuning
+
+# load model and tokenizer
+model = AutoModelForCausalLM.from_pretrained(model_name)
+tokenizer = AutoTokenizer.from_pretrained(model_name)
+tokenizer.pad_token = tokenizer.eos_token
+
+# load dataset
+dataset = load_dataset("Rowan/hellaswag")
+dataset = dataset.map(
+ lambda x: tokenizer(x["ctx"], padding="max_length", truncation=True, max_length=max_seq_len),
+ batched=True,
+ remove_columns=dataset["train"].column_names,
+)
+dataset.set_format(type="torch")
+
+# create dataloader for SVD
+# typically this is the same as the dataloader used for finetuning
+dataloader = DataLoader(
+ dataset["train"],
+ batch_size=svd_batch_size,
+ collate_fn=lambda examples: {k: torch.stack([v[k] for v in examples], dim=0) for k in examples[0].keys()},
+)
+
+# setup peft config
+eva_config = EvaConfig(
+ rho=rho
+)
+peft_config = LoraConfig(
+ r=rank,
+ lora_alpha=alpha,
+ target_modules=target_modules,
+ init_lora_weights="eva",
+ eva_config=eva_config
+)
+
+# move model to accelerator
+device = torch.accelerator.current_accelerator().type if hasattr(torch, "accelerator") else "cuda"
+model = model.to(device)
+
+# to optimize memory usage during EVA initialization, set low_cpu_mem_usage=True
+peft_model = get_peft_model(model, peft_config, low_cpu_mem_usage=True)
+
+initialize_lora_eva_weights(peft_model, dataloader)
+```
+`initialize_lora_eva_weights` will compute the SVD and load the components into the model. After this continue with standard LoRA finetuning.
+
+## Using EVA with Bitsandbytes
+EVA is fully compatible with bitsandbytes. Simply initialize the pretrained model with a BitsAndBytesConfig and then use the peft model with EVA.
+```python
+from transformers import BitsAndBytesConfig
+from peft import prepare_model_for_kbit_training
+
+model = AutoModelForCausalLM.from_pretrained(
+ "meta-llama/Llama-3.1-8B",
+ quantization_config=BitsAndBytesConfig(load_in_4bit=True)
+)
+model = prepare_model_for_kbit_training(model)
+peft_model = get_peft_model(model, peft_config)
+initialize_lora_eva_weights(peft_model, dataloader)
+```
+
+## Getting the EVA state_dict without loading the adapter weights
+In some cases you might just want to get the state_dict after EVA initialization without loading the adapter weights. This can be useful for example if:
+- you want to precompute and store the state_dict for different downstream tasks.
+- you need to quantize the model for finetuning but want to perform EVA initialization with model weights in full/half precision.
+- you do not intend to use a peft model for LoRA finetuning.
+- you would like to leverage multiple accelerators for EVA initialization. (At the moment this is not directly supported by `initialize_lora_eva_weights`)
+
+You can do this by calling `get_eva_state_dict` directly (you only need to pass `peft_config` if `model` is not a PeftModel):
+```python
+from peft import get_eva_state_dict
+
+eva_state_dict = get_eva_state_dict(model, dataloader, peft_config)
+```
+Later you can load the state_dict into a `PeftModel` by using the `eva_state_dict` argument in `initialize_lora_eva_weights`:
+```python
+initialize_lora_eva_weights(peft_model, eva_state_dict=eva_state_dict)
+```
+
+## Leveraging multiple accelerators
+
+EVA initialization can be parallelized across multiple accelerators. In this case inputs from multiple accelerators are gathered before computing the SVD for the batch. This requires that the model is wrapped in a `torch.nn.DataParallel` or `torch.nn.DistributedDataParallel` class. An example of how to use this can be found in [eva_finetuning_multi_accelerator.py](https://github.com/huggingface/peft/blob/main/examples/eva_finetuning/eva_finetuning_multi_accelerator.py).
+
+## Customizing EVA
+
+By default, EVA is designed to work with standard transformer language models. However we integrated three different parameters which can be used to customize EVA for other types of models.
+1. `forward_fn`: Defines how the forward pass during EVA initialization should be computed.
+2. `prepare_model_inputs_fn`: Can be used if it is necessary to use information contained in the original model_input to prepare the input for SVD in individual layers.
+3. `prepare_layer_inputs_fn`: Defines how layer inputs should be prepared for SVD.
+
+All three parameters can be passed to `initialize_lora_eva_weights` and `get_eva_state_dict`.
+
+### forward_fn
+
+`forward_fn` defines how the forward pass during EVA initialization should be computed. `forward_fn` receives two arguments: `model` and `inputs`. By default this is set to `forward_fn_dict` which simply returns `model(**inputs)`.
+
+### prepare_model_inputs_fn
+
+`prepare_model_inputs_fn` can be used if it is necessary to use information contained in the original model_input to prepare the input for SVD in individual layers. `prepare_model_inputs_fn` receives two arguments: `model_input` and `peft_config`. This component is separate from `prepare_layer_inputs_fn` as the output only needs to be computed once per batch. By default this parameter is set to `prepare_model_inputs_fn_language_modeling` which is used get a subset of indices based on attention and label mask to avoid including padding tokens in the SVD computation. If you would like to not use this component set `prepare_model_inputs_fn` to None. The default logic is:
+```python
+def prepare_model_inputs_fn_language_modeling(model_input, peft_config: LoraConfig):
+ mask = model_input.get("attention_mask", torch.ones_like(model_input["input_ids"])).bool()
+ if peft_config.eva_config.use_label_mask and hasattr(model_input, "labels"):
+ mask = torch.logical_and(mask, model_input["labels"] != peft_config.eva_config.label_mask_value)
+ return mask.nonzero()
+```
+
+### prepare_layer_inputs_fn
+
+`prepare_layer_inputs_fn` can be used to preprocess the layer inputs before passing them to the SVD algorithm. `prepare_layer_inputs_fn` receives three arguments: `layer_input`, `model_input` and `layer_name`. It can either be a callable or a dictionary where the keys are the layer names and the values are callables. If it is a dictionary, functions are assigned to adapter layers based on the layer names. By default a language modeling setting is assumed where model_inputs are the outputs of `prepare_model_inputs_fn_language_modeling` which is a mask of indices. If this parameter is set to None, only two modifications are made to the layer inputs
+- take the first element incase of a tuple or list.
+- if the input has more than 2 dimensions, we flatten all but the last dimension.
+
+Must always return a tensor. The default logic is:
+```python
+def prepare_layer_inputs_fn_default(layer_input, model_input, layer_name) -> torch.Tensor:
+ if isinstance(layer_input, (tuple, list)):
+ layer_input = layer_input[0]
+ return layer_input[model_input.T.unbind()]
+```
+
+## Citation
+In case you find our work useful, please consider citing it.
+
+```
+@article{paischer2024eva,
+ title={One Initialization to Rule them All: Fine-tuning via Explained Variance Adaptation},
+ author={Fabian Paischer, Lukas Hauzenberger, Thomas Schmied, Benedikt Alkin, Marc Peter Deisenroth, Sepp Hochreiter},
+ journal={arXiv preprint arXiv:2410.07170},
+ year={2024}
+}
+```
diff --git a/peft/examples/eva_finetuning/eva_finetuning.py b/peft/examples/eva_finetuning/eva_finetuning.py
new file mode 100644
index 0000000000000000000000000000000000000000..4901770f0b58170fea3e2ecb9bb5fb6746d2be9e
--- /dev/null
+++ b/peft/examples/eva_finetuning/eva_finetuning.py
@@ -0,0 +1,96 @@
+# Copyright 2024-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+import torch
+from datasets import load_dataset
+from torch.utils.data import DataLoader
+from transformers import AutoModelForCausalLM, AutoTokenizer, Trainer, TrainingArguments
+from utils import DataCollator, TokenizerMetaMath
+
+from peft import EvaConfig, LoraConfig, get_peft_model, initialize_lora_eva_weights
+
+
+DEVICE = torch.accelerator.current_accelerator().type if hasattr(torch, "accelerator") else "cuda"
+
+# config
+model_name = "meta-llama/Llama-3.1-8B"
+max_seq_len = 512
+rank = 16
+alpha = 1
+rho = 2.0
+target_modules = ["q_proj", "k_proj", "v_proj", "o_proj"]
+svd_batch_size = 4 # can be different from the batch size used in finetuning
+batch_size = 4
+learning_rate = 5e-4
+gradient_accumulation_steps = 8
+num_epochs = 1
+output_dir = "outputs"
+bf16 = True
+
+
+# load model and tokenizer
+model = AutoModelForCausalLM.from_pretrained(model_name)
+tokenizer = AutoTokenizer.from_pretrained(model_name)
+
+# load dataset
+dataset = load_dataset("meta-math/MetaMathQA")
+dataset = dataset.map(
+ TokenizerMetaMath(model_name),
+ batched=True,
+ remove_columns=dataset["train"].column_names,
+)
+dataset.set_format(type="torch")
+
+# data collator
+data_collator = DataCollator(tokenizer.eos_token_id, max_length=max_seq_len)
+
+# dataloader
+dataloader = DataLoader(
+ dataset["train"],
+ batch_size=svd_batch_size,
+ collate_fn=data_collator,
+)
+
+# setup peft config
+eva_config = EvaConfig(rho=rho)
+peft_config = LoraConfig(
+ r=rank, lora_alpha=alpha, target_modules=target_modules, init_lora_weights="eva", eva_config=eva_config
+)
+
+# move model to accelerator
+model = model.to(DEVICE)
+
+# to optimize memory usage during eva initialization, set low_cpu_mem_usage=True
+peft_model = get_peft_model(model, peft_config, low_cpu_mem_usage=True)
+initialize_lora_eva_weights(peft_model, dataloader)
+
+# setup training arguments
+training_args = TrainingArguments(
+ per_device_train_batch_size=batch_size,
+ learning_rate=learning_rate,
+ gradient_accumulation_steps=gradient_accumulation_steps,
+ num_train_epochs=num_epochs,
+ output_dir=output_dir,
+ remove_unused_columns=False,
+ bf16=bf16,
+)
+
+# continue with standard finetuning
+trainer = Trainer(
+ model=peft_model,
+ args=training_args,
+ train_dataset=dataset["train"],
+ data_collator=data_collator,
+)
+trainer.train()
diff --git a/peft/examples/eva_finetuning/eva_finetuning_multi_accelerator.py b/peft/examples/eva_finetuning/eva_finetuning_multi_accelerator.py
new file mode 100644
index 0000000000000000000000000000000000000000..447137e3b13e79adee85676493fc37d0da316a60
--- /dev/null
+++ b/peft/examples/eva_finetuning/eva_finetuning_multi_accelerator.py
@@ -0,0 +1,132 @@
+# Copyright 2024-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+import os
+
+import torch
+import torch.distributed as dist
+from datasets import load_dataset
+from torch.nn.parallel import DistributedDataParallel as DDP
+from torch.utils.data import DataLoader
+from torch.utils.data.distributed import DistributedSampler
+from transformers import AutoModelForCausalLM, AutoTokenizer, Trainer, TrainingArguments
+from utils import DataCollator, TokenizerMetaMath
+
+from peft import EvaConfig, LoraConfig, get_eva_state_dict, get_peft_model, initialize_lora_eva_weights
+
+
+# run this script e.g. with: torchrun --nproc_per_node=4 eva_finetuning_multi_gpu.py
+
+# config
+model_name = "meta-llama/Llama-2-7b-hf"
+max_seq_len = 512
+rank = 16
+alpha = 1
+rho = 2.0
+target_modules = ["q_proj", "k_proj", "v_proj", "o_proj"]
+svd_batch_size = 4 # can be different from the batch size used in finetuning
+batch_size = 4
+learning_rate = 5e-4
+gradient_accumulation_steps = 8
+num_epochs = 1
+output_dir = "outputs"
+bf16 = True
+
+
+# Initialize distributed environment
+if torch.cuda.is_available():
+ local_rank = int(os.environ.get("LOCAL_RANK", -1))
+ torch.cuda.set_device(local_rank)
+ dist.init_process_group("nccl")
+ world_size = dist.get_world_size()
+elif torch.xpu.is_available():
+ local_rank = int(os.environ.get("LOCAL_RANK", -1))
+ torch.xpu.set_device(local_rank)
+ dist.init_process_group("xccl")
+ world_size = dist.get_world_size()
+else:
+ local_rank = -1
+ world_size = 1
+
+
+# load model and tokenizer
+model = AutoModelForCausalLM.from_pretrained(model_name)
+tokenizer = AutoTokenizer.from_pretrained(model_name)
+
+# load dataset
+dataset = load_dataset("meta-math/MetaMathQA")
+dataset = dataset.map(
+ TokenizerMetaMath(model_name),
+ batched=True,
+ remove_columns=dataset["train"].column_names,
+)
+dataset.set_format(type="torch")
+
+# data collator
+data_collator = DataCollator(tokenizer.eos_token_id, max_length=max_seq_len)
+
+# Create sampler for distributed training
+sampler = DistributedSampler(dataset["train"], num_replicas=world_size, rank=local_rank)
+
+# dataloader
+dataloader = DataLoader(
+ dataset["train"],
+ batch_size=svd_batch_size,
+ collate_fn=data_collator,
+ sampler=sampler,
+ shuffle=False,
+)
+
+sampler.set_epoch(0)
+
+# Wrap model in DDP
+model = model.to(local_rank)
+model = DDP(model, device_ids=[local_rank], output_device=local_rank)
+
+# setup peft config
+eva_config = EvaConfig(rho=rho)
+peft_config = LoraConfig(
+ r=rank, lora_alpha=alpha, target_modules=target_modules, init_lora_weights="eva", eva_config=eva_config
+)
+
+# EVA initialization
+eva_state_dict = get_eva_state_dict(model, dataloader, peft_config)
+eva_state_dict = {".".join(["base_model.model"] + k.split(".")[1:]): v for k, v in eva_state_dict.items()}
+
+# cleanup ddp
+model = model.module
+
+# initialize peft model
+peft_model = get_peft_model(model, peft_config, low_cpu_mem_usage=True)
+initialize_lora_eva_weights(peft_model, eva_state_dict=eva_state_dict)
+
+# setup training arguments
+training_args = TrainingArguments(
+ per_device_train_batch_size=batch_size,
+ learning_rate=learning_rate,
+ gradient_accumulation_steps=gradient_accumulation_steps,
+ num_train_epochs=num_epochs,
+ output_dir=output_dir,
+ remove_unused_columns=False,
+ bf16=bf16,
+)
+
+# continue with standard finetuning
+trainer = Trainer(
+ model=peft_model,
+ args=training_args,
+ train_dataset=dataset["train"],
+ data_collator=data_collator,
+)
+trainer.train()
diff --git a/peft/examples/eva_finetuning/utils.py b/peft/examples/eva_finetuning/utils.py
new file mode 100644
index 0000000000000000000000000000000000000000..df7f069a07e461e7851e9515cf912497ff28c310
--- /dev/null
+++ b/peft/examples/eva_finetuning/utils.py
@@ -0,0 +1,76 @@
+# Copyright 2024-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+import torch
+from transformers import AutoTokenizer
+
+
+class TokenizerMetaMath:
+ PROMPT_NO_INPUT = (
+ "Below is an instruction that describes a task. Write a response that appropriately completes the request.\n\n"
+ "### Instruction:\n{query}\n\n### Response: "
+ )
+ PROMPT = (
+ "Below is an instruction that describes a task, paired with an input that provides further context. "
+ "Write a response that appropriately completes the request.\n\n"
+ "### Instruction:\n{query}\n\n### Input:\n{input}\n\n### Response: "
+ )
+
+ def format_prompt(self, query):
+ query = query.split("\n", 1)
+ if len(query) == 1 or query[1].strip("\n") == "":
+ return self.PROMPT_NO_INPUT.format(query=query[0])
+ else:
+ return self.PROMPT.format(query=query[0], input=query[1])
+
+ def __init__(self, tokenizer_path):
+ self.tokenizer = AutoTokenizer.from_pretrained(tokenizer_path)
+
+ def __call__(self, examples):
+ prompts = [self.format_prompt(text) for text in examples["query"]]
+ completions = examples["response"]
+ return self._tokenize_fn(prompts, completions)
+
+ def _tokenize_fn(self, prompts, completions):
+ prompt_tokens = self.tokenizer(prompts, add_special_tokens=False)["input_ids"]
+ input_tokens = self.tokenizer([x + y for x, y in zip(prompts, completions)], add_special_tokens=False)[
+ "input_ids"
+ ]
+ input_tokens = [[self.tokenizer.bos_token_id] + x + [self.tokenizer.eos_token_id] for x in input_tokens]
+ prompt_length = [len(x) + 1 for x in prompt_tokens] # +1 for the bos token
+ input_length = [len(x) for x in input_tokens]
+ return {"input_ids": input_tokens, "prompt_length": prompt_length, "input_length": input_length}
+
+
+class DataCollator:
+ def __init__(self, eos_token_id, max_length=None):
+ self.eos_token_id = eos_token_id
+ self.max_length = max_length
+
+ def __call__(self, batch):
+ batch = {k: [item[k] for item in batch] for k in batch[0]}
+ input_lengths = torch.stack(batch["input_length"])
+ prompt_lengths = torch.stack(batch["prompt_length"])
+ input_ids = torch.nn.utils.rnn.pad_sequence(
+ batch["input_ids"], batch_first=True, padding_value=self.eos_token_id
+ )
+ col_indices = torch.arange(input_ids.size(1)).unsqueeze(0)
+ attention_mask = col_indices < input_lengths.unsqueeze(1)
+ label_mask = torch.logical_or(col_indices < prompt_lengths.unsqueeze(1), ~attention_mask)
+ labels = input_ids.masked_fill(label_mask, -100)
+ if self.max_length is not None:
+ input_ids = input_ids[:, : self.max_length]
+ attention_mask = attention_mask[:, : self.max_length]
+ labels = labels[:, : self.max_length]
+ return {"input_ids": input_ids, "attention_mask": attention_mask, "labels": labels}
diff --git a/peft/examples/evaluation/lora-lm-eval.ipynb b/peft/examples/evaluation/lora-lm-eval.ipynb
new file mode 100644
index 0000000000000000000000000000000000000000..253c6da49b9a3346f3a8e27c6c83282f57efadb3
--- /dev/null
+++ b/peft/examples/evaluation/lora-lm-eval.ipynb
@@ -0,0 +1,4252 @@
+{
+ "cells": [
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "qAkXdLL2D25p"
+ },
+ "source": [
+ "## Peft model evaluation using [lm-eval-harness](https://github.com/EleutherAI/lm-evaluation-harness)\n",
+ "\n",
+ "In this notebook, we are going to learn how to evaluate the finetuned lora model on the hellaswag task using lm-eval-harness toolkit."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 1,
+ "metadata": {
+ "colab": {
+ "base_uri": "https://localhost:8080/"
+ },
+ "id": "o52TJHcYD25q",
+ "outputId": "c5482c79-ff56-4ffa-d20c-46c3d30d2cd5"
+ },
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "\u001b[33m DEPRECATION: Building 'rouge-score' using the legacy setup.py bdist_wheel mechanism, which will be removed in a future version. pip 25.3 will enforce this behaviour change. A possible replacement is to use the standardized build interface by setting the `--use-pep517` option, (possibly combined with `--no-build-isolation`), or adding a `pyproject.toml` file to the source tree of 'rouge-score'. Discussion can be found at https://github.com/pypa/pip/issues/6334\u001b[0m\u001b[33m\n",
+ "\u001b[0m\u001b[33m DEPRECATION: Building 'sqlitedict' using the legacy setup.py bdist_wheel mechanism, which will be removed in a future version. pip 25.3 will enforce this behaviour change. A possible replacement is to use the standardized build interface by setting the `--use-pep517` option, (possibly combined with `--no-build-isolation`), or adding a `pyproject.toml` file to the source tree of 'sqlitedict'. Discussion can be found at https://github.com/pypa/pip/issues/6334\u001b[0m\u001b[33m\n",
+ "\u001b[0m\u001b[33m DEPRECATION: Building 'word2number' using the legacy setup.py bdist_wheel mechanism, which will be removed in a future version. pip 25.3 will enforce this behaviour change. A possible replacement is to use the standardized build interface by setting the `--use-pep517` option, (possibly combined with `--no-build-isolation`), or adding a `pyproject.toml` file to the source tree of 'word2number'. Discussion can be found at https://github.com/pypa/pip/issues/6334\u001b[0m\u001b[33m\n",
+ "\u001b[0m\u001b[33mWARNING: Running pip as the 'root' user can result in broken permissions and conflicting behaviour with the system package manager, possibly rendering your system unusable. It is recommended to use a virtual environment instead: https://pip.pypa.io/warnings/venv. Use the --root-user-action option if you know what you are doing and want to suppress this warning.\u001b[0m\u001b[33m\n",
+ "\u001b[0m\n",
+ "\u001b[1m[\u001b[0m\u001b[34;49mnotice\u001b[0m\u001b[1;39;49m]\u001b[0m\u001b[39;49m A new release of pip is available: \u001b[0m\u001b[31;49m25.1.1\u001b[0m\u001b[39;49m -> \u001b[0m\u001b[32;49m25.2\u001b[0m\n",
+ "\u001b[1m[\u001b[0m\u001b[34;49mnotice\u001b[0m\u001b[1;39;49m]\u001b[0m\u001b[39;49m To update, run: \u001b[0m\u001b[32;49mpython3 -m pip install --upgrade pip\u001b[0m\n"
+ ]
+ }
+ ],
+ "source": [
+ "# Install LM-Eval\n",
+ "!pip install -q datasets evaluate lm_eval"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "uhUflrJXD25q"
+ },
+ "source": [
+ "### First we will check the accuracy score on the hellaswag task for the base bert without finetuning"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 3,
+ "metadata": {
+ "colab": {
+ "base_uri": "https://localhost:8080/"
+ },
+ "id": "hwJIYD5KD25q",
+ "outputId": "51e69f81-d048-46b2-9699-658d3ffc5f08"
+ },
+ "outputs": [
+ {
+ "name": "stderr",
+ "output_type": "stream",
+ "text": [
+ "If you want to use `BertLMHeadModel` as a standalone, add `is_decoder=True.`\n"
+ ]
+ },
+ {
+ "data": {
+ "application/vnd.jupyter.widget-view+json": {
+ "model_id": "7b1ea8948a0747bc98795d6459270044",
+ "version_major": 2,
+ "version_minor": 0
+ },
+ "text/plain": [
+ "README.md: 0.00B [00:00, ?B/s]"
+ ]
+ },
+ "metadata": {},
+ "output_type": "display_data"
+ },
+ {
+ "data": {
+ "application/vnd.jupyter.widget-view+json": {
+ "model_id": "4ec51e06812446899b66826c41697f8d",
+ "version_major": 2,
+ "version_minor": 0
+ },
+ "text/plain": [
+ "data/train-00000-of-00001.parquet: 0%| | 0.00/24.4M [00:00\n",
+ " \n",
+ " \n",
+ " [3910/3910 40:13, Epoch 5/5]\n",
+ " \n",
+ " \n",
+ " \n",
+ " \n",
+ " | Epoch | \n",
+ " Training Loss | \n",
+ " Validation Loss | \n",
+ " Accuracy | \n",
+ "
\n",
+ " \n",
+ " \n",
+ " \n",
+ " | 1 | \n",
+ " 0.353800 | \n",
+ " 0.261258 | \n",
+ " 0.901160 | \n",
+ "
\n",
+ " \n",
+ " | 2 | \n",
+ " 0.277400 | \n",
+ " 0.221651 | \n",
+ " 0.912480 | \n",
+ "
\n",
+ " \n",
+ " | 3 | \n",
+ " 0.244500 | \n",
+ " 0.216107 | \n",
+ " 0.918200 | \n",
+ "
\n",
+ " \n",
+ " | 4 | \n",
+ " 0.197000 | \n",
+ " 0.215257 | \n",
+ " 0.920040 | \n",
+ "
\n",
+ " \n",
+ " | 5 | \n",
+ " 0.157700 | \n",
+ " 0.215050 | \n",
+ " 0.923240 | \n",
+ "
\n",
+ " \n",
+ "
"
+ ],
+ "text/plain": [
+ ""
+ ]
+ },
+ "metadata": {},
+ "output_type": "display_data"
+ },
+ {
+ "data": {
+ "application/vnd.jupyter.widget-view+json": {
+ "model_id": "7298a140779d4fd88a65a191af265821",
+ "version_major": 2,
+ "version_minor": 0
+ },
+ "text/plain": [
+ "Downloading builder script: 0.00B [00:00, ?B/s]"
+ ]
+ },
+ "metadata": {},
+ "output_type": "display_data"
+ },
+ {
+ "data": {
+ "application/vnd.jupyter.widget-view+json": {
+ "model_id": "3c6b99b4b5854527a8b34b92a8d2986b",
+ "version_major": 2,
+ "version_minor": 0
+ },
+ "text/plain": [
+ "Downloading builder script: 0.00B [00:00, ?B/s]"
+ ]
+ },
+ "metadata": {},
+ "output_type": "display_data"
+ },
+ {
+ "data": {
+ "text/plain": [
+ "TrainOutput(global_step=3910, training_loss=0.24082870385835847, metrics={'train_runtime': 2416.0772, 'train_samples_per_second': 51.737, 'train_steps_per_second': 1.618, 'total_flos': 3.300271872e+16, 'train_loss': 0.24082870385835847, 'epoch': 5.0})"
+ ]
+ },
+ "execution_count": 8,
+ "metadata": {},
+ "output_type": "execute_result"
+ }
+ ],
+ "source": [
+ "# Configure training arguments\n",
+ "training_args = TrainingArguments(\"bert-lora-imdb\",\n",
+ " eval_strategy=\"epoch\",\n",
+ " per_device_train_batch_size=32, # decrease this for OOM error\n",
+ " per_device_eval_batch_size=64,\n",
+ " save_strategy=\"epoch\",\n",
+ " learning_rate=2e-3,\n",
+ " num_train_epochs=5,\n",
+ " weight_decay=0.01,\n",
+ " load_best_model_at_end=True,\n",
+ " do_eval=True,\n",
+ " do_predict=True,\n",
+ " metric_for_best_model=\"accuracy\",\n",
+ " report_to=\"none\")\n",
+ "\n",
+ "# Initialize the Trainer for the model training loop\n",
+ "trainer = Trainer(\n",
+ " model=model,\n",
+ " args=training_args,\n",
+ " train_dataset=train_dataset,\n",
+ " eval_dataset=eval_dataset,\n",
+ " compute_metrics=compute_metrics,\n",
+ ")\n",
+ "\n",
+ "#start training\n",
+ "trainer.train()"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "34h3g_eED25s"
+ },
+ "source": [
+ "### Now take the finetuned lora checkpoint and check the accuracy score on hellaswag task."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "id": "7tgAq7nLD25s"
+ },
+ "outputs": [],
+ "source": [
+ "# use the path of your checkpoint here\n",
+ "output = lm_eval.simple_evaluate(model = 'hf',\n",
+ " model_args = {\n",
+ " 'pretrained' : 'bert-base-cased',\n",
+ " 'peft' : './bert-lora-imdb/checkpoint-3910',\n",
+ " 'dtype' : 'bfloat16'},\n",
+ " tasks = 'hellaswag',\n",
+ " device = device,\n",
+ " batch_size = 128,\n",
+ " log_samples = False)\n",
+ "\n",
+ "output[\"results\"]"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {},
+ "outputs": [],
+ "source": []
+ }
+ ],
+ "metadata": {
+ "accelerator": "GPU",
+ "colab": {
+ "gpuType": "T4",
+ "provenance": []
+ },
+ "kaggle": {
+ "accelerator": "nvidiaTeslaT4",
+ "dataSources": [],
+ "dockerImageVersionId": 30787,
+ "isGpuEnabled": true,
+ "isInternetEnabled": true,
+ "language": "python",
+ "sourceType": "notebook"
+ },
+ "kernelspec": {
+ "display_name": "Python 3 (ipykernel)",
+ "language": "python",
+ "name": "python3"
+ },
+ "language_info": {
+ "codemirror_mode": {
+ "name": "ipython",
+ "version": 3
+ },
+ "file_extension": ".py",
+ "mimetype": "text/x-python",
+ "name": "python",
+ "nbconvert_exporter": "python",
+ "pygments_lexer": "ipython3",
+ "version": "3.11.13"
+ },
+ "widgets": {
+ "application/vnd.jupyter.widget-state+json": {
+ "00a9858d90d6430eaab54f9e013f077b": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "03f7cfca9e634cf69e3cc70f24832ba3": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_886443acd2f14cff93059c093f98cc1b",
+ "placeholder": "",
+ "style": "IPY_MODEL_24abe5089abc4ecfab75f7601bc98e68",
+ "value": " 25000/25000 [00:25<00:00, 1037.33 examples/s]"
+ }
+ },
+ "0649702ad9764ad8bf3dfbaa6739686e": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "0bee940b8667495f9e685f7ba6c3706f": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "0dc109378f1c43a7b18b1be03cce32ce": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_db789da312a24fc9944ecb8b617109e7",
+ "placeholder": "",
+ "style": "IPY_MODEL_0bee940b8667495f9e685f7ba6c3706f",
+ "value": " 7.81k/7.81k [00:00<00:00, 580kB/s]"
+ }
+ },
+ "10335d3ada7f428588c4faa3f57bbd51": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "122d7dd4d02d4df0b6573e100b5e46e3": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_db0b4bb4c7a642fb9e8d5c7738e90afc",
+ "IPY_MODEL_f8b71d5cb37549fba6559e2d83531319",
+ "IPY_MODEL_30d18e09421b42c985904750e68740d1"
+ ],
+ "layout": "IPY_MODEL_f67b5bbf7ccb475abe41e08316dc5b37"
+ }
+ },
+ "15dc2c4e42ab48c9ad09aafff29f9278": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_1fea1738e9fe48629b09e2ec9351fcd2",
+ "IPY_MODEL_2e2fc856557e40df8400e4b69f7143fc",
+ "IPY_MODEL_bce88474ca6745da99d79bc07216333c"
+ ],
+ "layout": "IPY_MODEL_99bab394a68140f79def33bc6f6499b2"
+ }
+ },
+ "16afa8cf9ca64a59afd7a4c4f293b479": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "17c7d8bb89184c26966a33dc27ef5517": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "1882e91f0b264cbeb90b99a69c7de7f5": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_8e862faf12804eaebfd7692db348842b",
+ "placeholder": "",
+ "style": "IPY_MODEL_7812641b79ae46d48bc88b4c773344c0",
+ "value": " 21.0M/21.0M [00:00<00:00, 189MB/s]"
+ }
+ },
+ "1c07d8f701604da0989d5f8d88d4bbcd": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_f8d90231390a4211b698e700a66fcb0f",
+ "placeholder": "",
+ "style": "IPY_MODEL_aa7697dbb00641f19491f13b1a643197",
+ "value": " 50000/50000 [00:00<00:00, 142668.00 examples/s]"
+ }
+ },
+ "1dfc470241c44ce1a0f9ae71fdfdbdf6": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_da7f0a799616427ba7e93b0080d26d37",
+ "placeholder": "",
+ "style": "IPY_MODEL_9931cc064e2c400e9830e448c8ef4655",
+ "value": " 20.5M/20.5M [00:00<00:00, 214MB/s]"
+ }
+ },
+ "1fea1738e9fe48629b09e2ec9351fcd2": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_60695bb251124317a897a6fc56b754ac",
+ "placeholder": "",
+ "style": "IPY_MODEL_d0582455fe3c449dbde19a47561770b4",
+ "value": "Generating train split: 100%"
+ }
+ },
+ "20cd23dc1cd840c89741957f3fcbfdb8": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "FloatProgressModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "FloatProgressModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "ProgressView",
+ "bar_style": "success",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_16afa8cf9ca64a59afd7a4c4f293b479",
+ "max": 50000,
+ "min": 0,
+ "orientation": "horizontal",
+ "style": "IPY_MODEL_4a025adc548b4fcb8c5637f8f6dabc81",
+ "value": 50000
+ }
+ },
+ "24abe5089abc4ecfab75f7601bc98e68": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "24cbed7481774ef793a8f204ba5b604b": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "2bbd92cebbf445d087bcadf82625c6d5": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "2be4c676b5834100b31d7f42ab8bab85": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "2cd718fb166641d59c8df64cbc637d9c": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "2d2adb2b7a3b41d28736a8b7aba258b1": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "2d46765961fe453597645a0b56a9cbc7": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "2d76c76bc4a6433b8fe2b28a1c887ada": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_31aa04d4f32a411293f2f729889984b8",
+ "IPY_MODEL_87de47c8821f423d9efc5c7e85297e32",
+ "IPY_MODEL_5f0dfd26cb484695b85d021a5d687503"
+ ],
+ "layout": "IPY_MODEL_d1414b66bc0f4a088c5e4551e8f4ee72"
+ }
+ },
+ "2e2fc856557e40df8400e4b69f7143fc": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "FloatProgressModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "FloatProgressModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "ProgressView",
+ "bar_style": "success",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_92b9e59f9038485e839598237ec3fd8c",
+ "max": 25000,
+ "min": 0,
+ "orientation": "horizontal",
+ "style": "IPY_MODEL_d69df0074246435f8481fd803863cdb1",
+ "value": 25000
+ }
+ },
+ "30d18e09421b42c985904750e68740d1": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_71a7cf52600f4288bd725b7bb93e7299",
+ "placeholder": "",
+ "style": "IPY_MODEL_e3082a5e8a4144f5982ad478d9a54a2c",
+ "value": " 50000/50000 [00:44<00:00, 1214.24 examples/s]"
+ }
+ },
+ "3142f29a154c4a33a161237d4c605c50": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_9b39cdb9f7a14ab4865f360f3c1537dc",
+ "IPY_MODEL_798c00bf640e483cbc4fea744b268461",
+ "IPY_MODEL_1882e91f0b264cbeb90b99a69c7de7f5"
+ ],
+ "layout": "IPY_MODEL_17c7d8bb89184c26966a33dc27ef5517"
+ }
+ },
+ "31664fd452bb43e3aefb87542c747b74": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "31aa04d4f32a411293f2f729889984b8": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_da58efd0f2b5442c8a284a948f2614f8",
+ "placeholder": "",
+ "style": "IPY_MODEL_2cd718fb166641d59c8df64cbc637d9c",
+ "value": "Map: 100%"
+ }
+ },
+ "31bad1f4c7c047a280d490b854a6e911": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "336ffca0a89e4255a62564ec2600318c": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "34f8bcc1d9954fb8ba8ecca7a6bd04cd": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "FloatProgressModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "FloatProgressModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "ProgressView",
+ "bar_style": "success",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_336ffca0a89e4255a62564ec2600318c",
+ "max": 25000,
+ "min": 0,
+ "orientation": "horizontal",
+ "style": "IPY_MODEL_2bbd92cebbf445d087bcadf82625c6d5",
+ "value": 25000
+ }
+ },
+ "38fd040b3a0d44d2adf13c2476f4505a": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_a9548c2f9fd54f73abc3e9c3c0bc9fda",
+ "placeholder": "",
+ "style": "IPY_MODEL_faa9b111dd9745a29bf7494b95619a1b",
+ "value": "test-00000-of-00001.parquet: 100%"
+ }
+ },
+ "3a99edeb7d5e43048fdce29b880c19a5": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "FloatProgressModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "FloatProgressModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "ProgressView",
+ "bar_style": "success",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_81eef7f1d0c7461cb443b996a5d5163f",
+ "max": 20470363,
+ "min": 0,
+ "orientation": "horizontal",
+ "style": "IPY_MODEL_b832fdc7655b4f88a15e19fc8381db47",
+ "value": 20470363
+ }
+ },
+ "3cc5521074d3411cbc24d0348d3fc314": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "3d6b95a9f8774341be1976f10fb74679": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "3ec913f1b93d4097ad9729156295f9e9": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "404088a4057546968f4e8cfc9e7461e1": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "47789088bcfa4c96a5fd898812c23d17": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_8ac5b5baeefb4078a74d8c8b2fed6d93",
+ "placeholder": "",
+ "style": "IPY_MODEL_4bbb4bf49e50489abc875881958c00aa",
+ "value": "Map: 100%"
+ }
+ },
+ "4a025adc548b4fcb8c5637f8f6dabc81": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "4bbb4bf49e50489abc875881958c00aa": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "4c55b2c1daa4497abf9c9f53e23f83b8": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "4f7b2a1359bf41cab2ed5663643509a6": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "4fe02a8771814e22b8d954cfdd8b9f86": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_d52e5c49b80348fbb55ab39ce0a13f7e",
+ "IPY_MODEL_51f4dabc59d04f0c89128d41d4c184a1",
+ "IPY_MODEL_803fcea81b7b47fb91fb108e2170fa75"
+ ],
+ "layout": "IPY_MODEL_ee5722120e1045e985e5e4ca29a2e192"
+ }
+ },
+ "51f4dabc59d04f0c89128d41d4c184a1": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "FloatProgressModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "FloatProgressModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "ProgressView",
+ "bar_style": "success",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_3d6b95a9f8774341be1976f10fb74679",
+ "max": 41996509,
+ "min": 0,
+ "orientation": "horizontal",
+ "style": "IPY_MODEL_3ec913f1b93d4097ad9729156295f9e9",
+ "value": 41996509
+ }
+ },
+ "55cab288802d49efb930c7641b036f44": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "568c0efe6ced432d81f45af4acaa921e": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "580a3b71b23f4a72be9e8633c04e9276": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "FloatProgressModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "FloatProgressModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "ProgressView",
+ "bar_style": "success",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_5b346ce1eaf649d195fa7dd6058dd196",
+ "max": 25000,
+ "min": 0,
+ "orientation": "horizontal",
+ "style": "IPY_MODEL_d7b4684e53d445e58de1fe155315e093",
+ "value": 25000
+ }
+ },
+ "5b346ce1eaf649d195fa7dd6058dd196": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "5ce04c799bb0430386e39af4734e80e6": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "5f0dfd26cb484695b85d021a5d687503": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_b1c37874948c459583a9f33dc77a6f55",
+ "placeholder": "",
+ "style": "IPY_MODEL_24cbed7481774ef793a8f204ba5b604b",
+ "value": " 25000/25000 [00:23<00:00, 1166.56 examples/s]"
+ }
+ },
+ "60695bb251124317a897a6fc56b754ac": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "6eea630bd65745739ff646fbb172f426": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "716d24b9c1b340a2bf9045b0bf4e7e34": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_47789088bcfa4c96a5fd898812c23d17",
+ "IPY_MODEL_580a3b71b23f4a72be9e8633c04e9276",
+ "IPY_MODEL_03f7cfca9e634cf69e3cc70f24832ba3"
+ ],
+ "layout": "IPY_MODEL_987a633e24594228b82e162397a63141"
+ }
+ },
+ "71a7cf52600f4288bd725b7bb93e7299": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "7812641b79ae46d48bc88b4c773344c0": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "7823f9d79e1d4350b385e6dfef84b021": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_c006e4b791204d10a9d8e7fbc4bceb81",
+ "placeholder": "",
+ "style": "IPY_MODEL_31664fd452bb43e3aefb87542c747b74",
+ "value": "Generating unsupervised split: 100%"
+ }
+ },
+ "798c00bf640e483cbc4fea744b268461": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "FloatProgressModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "FloatProgressModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "ProgressView",
+ "bar_style": "success",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_d406b18b855d488cac92b9b96073ba43",
+ "max": 20979968,
+ "min": 0,
+ "orientation": "horizontal",
+ "style": "IPY_MODEL_eee89779493748d38c01bb0a74b29e38",
+ "value": 20979968
+ }
+ },
+ "7f78e58f4e9c457a9c2d121759efdb09": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_f1574df0debf4e1b8617e24ffcc39e16",
+ "placeholder": "",
+ "style": "IPY_MODEL_a9cbf2bbb1f14894886617ce8e60de12",
+ "value": " 25000/25000 [00:00<00:00, 104177.91 examples/s]"
+ }
+ },
+ "803fcea81b7b47fb91fb108e2170fa75": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_b29cde97f90f4c489c5cdfd007c96d4f",
+ "placeholder": "",
+ "style": "IPY_MODEL_d8c8ee9f63b14182a9ded152435c510f",
+ "value": " 42.0M/42.0M [00:00<00:00, 163MB/s]"
+ }
+ },
+ "806a2b3f4c4c4ba59370a46c0f8faa85": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_38fd040b3a0d44d2adf13c2476f4505a",
+ "IPY_MODEL_3a99edeb7d5e43048fdce29b880c19a5",
+ "IPY_MODEL_1dfc470241c44ce1a0f9ae71fdfdbdf6"
+ ],
+ "layout": "IPY_MODEL_feb83525a43a4c2d818f3ef1ae69d581"
+ }
+ },
+ "81eef7f1d0c7461cb443b996a5d5163f": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "87de47c8821f423d9efc5c7e85297e32": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "FloatProgressModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "FloatProgressModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "ProgressView",
+ "bar_style": "success",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_2be4c676b5834100b31d7f42ab8bab85",
+ "max": 25000,
+ "min": 0,
+ "orientation": "horizontal",
+ "style": "IPY_MODEL_6eea630bd65745739ff646fbb172f426",
+ "value": 25000
+ }
+ },
+ "886443acd2f14cff93059c093f98cc1b": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "8ac5b5baeefb4078a74d8c8b2fed6d93": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "8e862faf12804eaebfd7692db348842b": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "8fcd7e9ed5f54287b5cda0ad52a277f4": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "92b9e59f9038485e839598237ec3fd8c": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "93dd1cc84f26479caaa1ded80bbea5ff": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "FloatProgressModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "FloatProgressModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "ProgressView",
+ "bar_style": "success",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_b3cde05a07b2437b935083d6aac25913",
+ "max": 7809,
+ "min": 0,
+ "orientation": "horizontal",
+ "style": "IPY_MODEL_31bad1f4c7c047a280d490b854a6e911",
+ "value": 7809
+ }
+ },
+ "987a633e24594228b82e162397a63141": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "9931cc064e2c400e9830e448c8ef4655": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "99bab394a68140f79def33bc6f6499b2": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "9b39cdb9f7a14ab4865f360f3c1537dc": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_55cab288802d49efb930c7641b036f44",
+ "placeholder": "",
+ "style": "IPY_MODEL_0649702ad9764ad8bf3dfbaa6739686e",
+ "value": "train-00000-of-00001.parquet: 100%"
+ }
+ },
+ "9b4b309603db4847a0d94da76db15116": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_568c0efe6ced432d81f45af4acaa921e",
+ "placeholder": "",
+ "style": "IPY_MODEL_f402e8e510d64d0ca4d4ae2c09a7ddfc",
+ "value": "README.md: 100%"
+ }
+ },
+ "a9548c2f9fd54f73abc3e9c3c0bc9fda": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "a9cbf2bbb1f14894886617ce8e60de12": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "aa7697dbb00641f19491f13b1a643197": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "b1c37874948c459583a9f33dc77a6f55": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "b29cde97f90f4c489c5cdfd007c96d4f": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "b3cde05a07b2437b935083d6aac25913": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "b832fdc7655b4f88a15e19fc8381db47": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "bce88474ca6745da99d79bc07216333c": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_3cc5521074d3411cbc24d0348d3fc314",
+ "placeholder": "",
+ "style": "IPY_MODEL_4c55b2c1daa4497abf9c9f53e23f83b8",
+ "value": " 25000/25000 [00:00<00:00, 113831.51 examples/s]"
+ }
+ },
+ "c006e4b791204d10a9d8e7fbc4bceb81": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "d0582455fe3c449dbde19a47561770b4": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "d1414b66bc0f4a088c5e4551e8f4ee72": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "d406b18b855d488cac92b9b96073ba43": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "d52e5c49b80348fbb55ab39ce0a13f7e": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_8fcd7e9ed5f54287b5cda0ad52a277f4",
+ "placeholder": "",
+ "style": "IPY_MODEL_10335d3ada7f428588c4faa3f57bbd51",
+ "value": "unsupervised-00000-of-00001.parquet: 100%"
+ }
+ },
+ "d69df0074246435f8481fd803863cdb1": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "d7b4684e53d445e58de1fe155315e093": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "d8c8ee9f63b14182a9ded152435c510f": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "da58efd0f2b5442c8a284a948f2614f8": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "da7f0a799616427ba7e93b0080d26d37": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "db0b4bb4c7a642fb9e8d5c7738e90afc": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_e0e6445a2a774ae89729b7e2fb4a14b3",
+ "placeholder": "",
+ "style": "IPY_MODEL_fdd99c599f9c4ac88c09939ec397ca46",
+ "value": "Map: 100%"
+ }
+ },
+ "db1b2639fc4944bcbbdfbdaf9150409f": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "db789da312a24fc9944ecb8b617109e7": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "e0e6445a2a774ae89729b7e2fb4a14b3": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "e3082a5e8a4144f5982ad478d9a54a2c": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "e85940da7bc24b8bb29ce609ba6e5613": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_4f7b2a1359bf41cab2ed5663643509a6",
+ "placeholder": "",
+ "style": "IPY_MODEL_db1b2639fc4944bcbbdfbdaf9150409f",
+ "value": "Generating test split: 100%"
+ }
+ },
+ "ebf724c3ad1443e98763dd279e6fc996": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_9b4b309603db4847a0d94da76db15116",
+ "IPY_MODEL_93dd1cc84f26479caaa1ded80bbea5ff",
+ "IPY_MODEL_0dc109378f1c43a7b18b1be03cce32ce"
+ ],
+ "layout": "IPY_MODEL_2d2adb2b7a3b41d28736a8b7aba258b1"
+ }
+ },
+ "ee5722120e1045e985e5e4ca29a2e192": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "eee89779493748d38c01bb0a74b29e38": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "f1574df0debf4e1b8617e24ffcc39e16": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "f402e8e510d64d0ca4d4ae2c09a7ddfc": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "f4d35fb98b0048ca8bdbe856d182d561": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_e85940da7bc24b8bb29ce609ba6e5613",
+ "IPY_MODEL_34f8bcc1d9954fb8ba8ecca7a6bd04cd",
+ "IPY_MODEL_7f78e58f4e9c457a9c2d121759efdb09"
+ ],
+ "layout": "IPY_MODEL_2d46765961fe453597645a0b56a9cbc7"
+ }
+ },
+ "f67b5bbf7ccb475abe41e08316dc5b37": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "f8b71d5cb37549fba6559e2d83531319": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "FloatProgressModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "FloatProgressModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "ProgressView",
+ "bar_style": "success",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_5ce04c799bb0430386e39af4734e80e6",
+ "max": 50000,
+ "min": 0,
+ "orientation": "horizontal",
+ "style": "IPY_MODEL_404088a4057546968f4e8cfc9e7461e1",
+ "value": 50000
+ }
+ },
+ "f8d90231390a4211b698e700a66fcb0f": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "faa9b111dd9745a29bf7494b95619a1b": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "fdd4b9937b7744d98ba1163efbe1310b": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_7823f9d79e1d4350b385e6dfef84b021",
+ "IPY_MODEL_20cd23dc1cd840c89741957f3fcbfdb8",
+ "IPY_MODEL_1c07d8f701604da0989d5f8d88d4bbcd"
+ ],
+ "layout": "IPY_MODEL_00a9858d90d6430eaab54f9e013f077b"
+ }
+ },
+ "fdd99c599f9c4ac88c09939ec397ca46": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "feb83525a43a4c2d818f3ef1ae69d581": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ }
+ }
+ }
+ },
+ "nbformat": 4,
+ "nbformat_minor": 4
+}
diff --git a/peft/examples/feature_extraction/peft_lora_embedding_semantic_search.py b/peft/examples/feature_extraction/peft_lora_embedding_semantic_search.py
new file mode 100644
index 0000000000000000000000000000000000000000..8ed8babb7ea00acf556d16e3abc60c85d650f3d9
--- /dev/null
+++ b/peft/examples/feature_extraction/peft_lora_embedding_semantic_search.py
@@ -0,0 +1,502 @@
+# Copyright 2023-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+import argparse
+import logging
+import math
+import os
+import random
+from pathlib import Path
+
+import datasets
+import evaluate
+import torch
+import transformers
+from accelerate import Accelerator
+from accelerate.logging import get_logger
+from accelerate.utils import set_seed
+from datasets import DatasetDict, load_dataset
+from huggingface_hub import HfApi
+from torch import nn
+from torch.utils.data import DataLoader
+from tqdm import tqdm
+from transformers import AutoModel, AutoTokenizer, SchedulerType, default_data_collator, get_scheduler
+
+from peft import LoraConfig, TaskType, get_peft_model
+
+
+logger = get_logger(__name__)
+
+
+def parse_args():
+ parser = argparse.ArgumentParser(description="Training a PEFT model for Semantic Search task")
+ parser.add_argument("--dataset_name", type=str, default=None, help="dataset name on HF hub")
+ parser.add_argument(
+ "--max_length",
+ type=int,
+ default=128,
+ help=(
+ "The maximum total input sequence length after tokenization. Sequences longer than this will be truncated,"
+ " sequences shorter will be padded if `--pad_to_max_length` is passed."
+ ),
+ )
+ parser.add_argument(
+ "--model_name_or_path",
+ type=str,
+ help="Path to pretrained model or model identifier from huggingface.co/models.",
+ required=True,
+ )
+ parser.add_argument(
+ "--per_device_train_batch_size",
+ type=int,
+ default=8,
+ help="Batch size (per device) for the training dataloader.",
+ )
+ parser.add_argument(
+ "--per_device_eval_batch_size",
+ type=int,
+ default=8,
+ help="Batch size (per device) for the evaluation dataloader.",
+ )
+ parser.add_argument(
+ "--learning_rate",
+ type=float,
+ default=5e-5,
+ help="Initial learning rate (after the potential warmup period) to use.",
+ )
+ parser.add_argument("--weight_decay", type=float, default=0.0, help="Weight decay to use.")
+ parser.add_argument("--num_train_epochs", type=int, default=3, help="Total number of training epochs to perform.")
+ parser.add_argument(
+ "--max_train_steps",
+ type=int,
+ default=None,
+ help="Total number of training steps to perform. If provided, overrides num_train_epochs.",
+ )
+ parser.add_argument(
+ "--gradient_accumulation_steps",
+ type=int,
+ default=1,
+ help="Number of updates steps to accumulate before performing a backward/update pass.",
+ )
+ parser.add_argument(
+ "--lr_scheduler_type",
+ type=SchedulerType,
+ default="linear",
+ help="The scheduler type to use.",
+ choices=["linear", "cosine", "cosine_with_restarts", "polynomial", "constant", "constant_with_warmup"],
+ )
+ parser.add_argument(
+ "--num_warmup_steps", type=int, default=0, help="Number of steps for the warmup in the lr scheduler."
+ )
+ parser.add_argument("--output_dir", type=str, default=None, help="Where to store the final model.")
+ parser.add_argument("--seed", type=int, default=None, help="A seed for reproducible training.")
+ parser.add_argument("--push_to_hub", action="store_true", help="Whether or not to push the model to the Hub.")
+ parser.add_argument(
+ "--hub_model_id", type=str, help="The name of the repository to keep in sync with the local `output_dir`."
+ )
+ parser.add_argument("--hub_token", type=str, help="The token to use to push to the Model Hub.")
+ parser.add_argument(
+ "--checkpointing_steps",
+ type=str,
+ default=None,
+ help="Whether the various states should be saved at the end of every n steps, or 'epoch' for each epoch.",
+ )
+ parser.add_argument(
+ "--resume_from_checkpoint",
+ type=str,
+ default=None,
+ help="If the training should continue from a checkpoint folder.",
+ )
+ parser.add_argument(
+ "--with_tracking",
+ action="store_true",
+ help="Whether to enable experiment trackers for logging.",
+ )
+ parser.add_argument(
+ "--report_to",
+ type=str,
+ default="all",
+ help=(
+ 'The integration to report the results and logs to. Supported platforms are `"tensorboard"`,'
+ ' `"wandb"`, `"comet_ml"` and `"clearml"`. Use `"all"` (default) to report to all integrations.'
+ "Only applicable when `--with_tracking` is passed."
+ ),
+ )
+ parser.add_argument(
+ "--sanity_test",
+ action="store_true",
+ help="Whether to enable sanity test.",
+ )
+ parser.add_argument(
+ "--use_peft",
+ action="store_true",
+ help="Whether to use PEFT.",
+ )
+ args = parser.parse_args()
+
+ if args.push_to_hub:
+ assert args.output_dir is not None, "Need an `output_dir` to create a repo when `--push_to_hub` is passed."
+
+ return args
+
+
+def save_model_hook(models, weights, output_dir):
+ for i, model in enumerate(models):
+ model.save_pretrained(output_dir, state_dict=weights[i])
+ # make sure to pop weight so that corresponding model is not saved again
+ weights.pop()
+
+
+def load_model_hook(models, input_dir):
+ while len(models) > 0:
+ model = models.pop()
+ # pop models so that they are not loaded again
+ if hasattr(model, "active_adapter") and hasattr(model, "load_adapter"):
+ model.load_adapter(input_dir, model.active_adapter, is_trainable=True)
+
+
+class AutoModelForSentenceEmbedding(nn.Module):
+ def __init__(self, model_name, tokenizer, normalize=True):
+ super().__init__()
+
+ self.model = AutoModel.from_pretrained(
+ model_name
+ ) # , quantizaton_config=BitsAndBytesConfig(load_in_8bit=True), device_map={"":0})
+ self.normalize = normalize
+ self.tokenizer = tokenizer
+
+ def forward(self, **kwargs):
+ model_output = self.model(**kwargs)
+ embeddings = self.mean_pooling(model_output, kwargs["attention_mask"])
+ if self.normalize:
+ embeddings = torch.nn.functional.normalize(embeddings, p=2, dim=1)
+
+ return embeddings
+
+ def mean_pooling(self, model_output, attention_mask):
+ token_embeddings = model_output[0] # First element of model_output contains all token embeddings
+ input_mask_expanded = attention_mask.unsqueeze(-1).expand(token_embeddings.size()).float()
+ return torch.sum(token_embeddings * input_mask_expanded, 1) / torch.clamp(input_mask_expanded.sum(1), min=1e-9)
+
+ def __getattr__(self, name: str):
+ """Forward missing attributes to the wrapped module."""
+ try:
+ return super().__getattr__(name) # defer to nn.Module's logic
+ except AttributeError:
+ if name == "model": # see #1892: prevent infinite recursion if class is not initialized
+ raise
+ return getattr(self.model, name)
+
+
+def get_cosing_embeddings(query_embs, product_embs):
+ return torch.sum(query_embs * product_embs, axis=1)
+
+
+def get_loss(cosine_score, labels):
+ return torch.mean(torch.square(labels * (1 - cosine_score) + torch.clamp((1 - labels) * cosine_score, min=0.0)))
+
+
+def main():
+ args = parse_args()
+
+ accelerator_kwargs = {"gradient_accumulation_steps": args.gradient_accumulation_steps}
+ if args.with_tracking:
+ accelerator_kwargs["log_with"] = args.report_to
+ accelerator_kwargs["project_dir"] = args.output_dir
+ accelerator = Accelerator(**accelerator_kwargs)
+
+ # Make one log on every process with the configuration for debugging.
+ logging.basicConfig(
+ format="%(asctime)s - %(levelname)s - %(name)s - %(message)s",
+ datefmt="%m/%d/%Y %H:%M:%S",
+ level=logging.INFO,
+ )
+ logger.info(accelerator.state, main_process_only=False)
+ if accelerator.is_local_main_process:
+ datasets.utils.logging.set_verbosity_warning()
+ transformers.utils.logging.set_verbosity_info()
+ else:
+ datasets.utils.logging.set_verbosity_error()
+ transformers.utils.logging.set_verbosity_error()
+
+ # If passed along, set the training seed now.
+ if args.seed is not None:
+ set_seed(args.seed)
+
+ # Handle the repository creation
+ if accelerator.is_main_process:
+ if args.push_to_hub:
+ api = HfApi(token=args.hub_token)
+
+ # Create repo (repo_name from args or inferred)
+ repo_name = args.hub_model_id
+ if repo_name is None:
+ repo_name = Path(args.output_dir).absolute().name
+ repo_id = api.create_repo(repo_name, exist_ok=True).repo_id
+
+ with open(os.path.join(args.output_dir, ".gitignore"), "w+") as gitignore:
+ if "step_*" not in gitignore:
+ gitignore.write("step_*\n")
+ if "epoch_*" not in gitignore:
+ gitignore.write("epoch_*\n")
+ elif args.output_dir is not None:
+ os.makedirs(args.output_dir, exist_ok=True)
+ accelerator.wait_for_everyone()
+
+ # get the tokenizer
+ tokenizer = AutoTokenizer.from_pretrained(args.model_name_or_path)
+
+ # dataset download and preprocessing
+ if args.sanity_test:
+ train_dataset = load_dataset("smangrul/amazon_esci", split="train[:1024]")
+ val_dataset = load_dataset("smangrul/amazon_esci", split="validation[:1024]")
+
+ dataset = DatasetDict({"train": train_dataset, "validation": val_dataset})
+ else:
+ dataset = load_dataset(args.dataset_name, revision="main")
+
+ def preprocess_function(examples):
+ queries = examples["query"]
+ result = tokenizer(queries, padding="max_length", max_length=70, truncation=True)
+ result = {f"query_{k}": v for k, v in result.items()}
+
+ products = examples["product_title"]
+ result_products = tokenizer(products, padding="max_length", max_length=70, truncation=True)
+ for k, v in result_products.items():
+ result[f"product_{k}"] = v
+
+ result["labels"] = examples["relevance_label"]
+ return result
+
+ processed_datasets = dataset.map(
+ preprocess_function,
+ batched=True,
+ remove_columns=dataset["train"].column_names,
+ desc="Running tokenizer on dataset",
+ )
+
+ # Log a few random samples from the training set:
+ for index in random.sample(range(len(processed_datasets["train"])), 3):
+ logger.info(f"Sample {index} of the training set: {processed_datasets['train'][index]}.")
+
+ # base model
+ model = AutoModelForSentenceEmbedding(args.model_name_or_path, tokenizer)
+
+ if args.use_peft:
+ # peft config and wrapping
+ peft_config = LoraConfig(
+ r=8,
+ lora_alpha=16,
+ bias="none",
+ task_type=TaskType.FEATURE_EXTRACTION,
+ target_modules=["key", "query", "value"],
+ )
+ model = get_peft_model(model, peft_config)
+ model.print_trainable_parameters()
+
+ accelerator.print(model)
+
+ # get dataloaders
+ train_dataloader = DataLoader(
+ processed_datasets["train"],
+ shuffle=True,
+ collate_fn=default_data_collator,
+ batch_size=args.per_device_train_batch_size,
+ pin_memory=True,
+ )
+
+ eval_dataloader = DataLoader(
+ processed_datasets["validation"],
+ shuffle=False,
+ collate_fn=default_data_collator,
+ batch_size=args.per_device_eval_batch_size,
+ pin_memory=True,
+ )
+
+ optimizer = torch.optim.Adam(model.parameters(), lr=args.learning_rate)
+
+ # Scheduler and math around the number of training steps.
+ overrode_max_train_steps = False
+ num_update_steps_per_epoch = math.ceil(len(train_dataloader) / args.gradient_accumulation_steps)
+ if args.max_train_steps is None:
+ args.max_train_steps = args.num_train_epochs * num_update_steps_per_epoch
+ overrode_max_train_steps = True
+
+ lr_scheduler = get_scheduler(
+ name=args.lr_scheduler_type,
+ optimizer=optimizer,
+ num_warmup_steps=args.num_warmup_steps,
+ num_training_steps=args.max_train_steps,
+ )
+
+ # Prepare everything with our `accelerator`.
+ model, optimizer, train_dataloader, eval_dataloader, lr_scheduler = accelerator.prepare(
+ model, optimizer, train_dataloader, eval_dataloader, lr_scheduler
+ )
+
+ # We need to recalculate our total training steps as the size of the training dataloader may have changed
+ num_update_steps_per_epoch = math.ceil(len(train_dataloader) / args.gradient_accumulation_steps)
+ if overrode_max_train_steps:
+ args.max_train_steps = args.num_train_epochs * num_update_steps_per_epoch
+ # Afterwards we recalculate our number of training epochs
+ args.num_train_epochs = math.ceil(args.max_train_steps / num_update_steps_per_epoch)
+
+ # Figure out how many steps we should save the Accelerator states
+ checkpointing_steps = args.checkpointing_steps
+ if checkpointing_steps is not None and checkpointing_steps.isdigit():
+ checkpointing_steps = int(checkpointing_steps)
+
+ # We need to initialize the trackers we use, and also store our configuration.
+ # The trackers initializes automatically on the main process.
+ if args.with_tracking:
+ experiment_config = vars(args)
+ # TensorBoard cannot log Enums, need the raw value
+ experiment_config["lr_scheduler_type"] = experiment_config["lr_scheduler_type"].value
+ accelerator.init_trackers("peft_semantic_search", experiment_config)
+
+ metric = evaluate.load("roc_auc")
+
+ total_batch_size = args.per_device_train_batch_size * accelerator.num_processes * args.gradient_accumulation_steps
+
+ if args.use_peft:
+ # saving and loading checkpoints for resuming training
+ accelerator.register_save_state_pre_hook(save_model_hook)
+ accelerator.register_load_state_pre_hook(load_model_hook)
+
+ logger.info("***** Running training *****")
+ logger.info(f" Num examples = {len(processed_datasets['train'])}")
+ logger.info(f" Num Epochs = {args.num_train_epochs}")
+ logger.info(f" Instantaneous batch size per device = {args.per_device_train_batch_size}")
+ logger.info(f" Total train batch size (w. parallel, distributed & accumulation) = {total_batch_size}")
+ logger.info(f" Gradient Accumulation steps = {args.gradient_accumulation_steps}")
+ logger.info(f" Total optimization steps = {args.max_train_steps}")
+
+ # Only show the progress bar once on each machine.
+ progress_bar = tqdm(range(args.max_train_steps), disable=not accelerator.is_local_main_process)
+ completed_steps = 0
+ starting_epoch = 0
+ # Potentially load in the weights and states from a previous save
+ if args.resume_from_checkpoint:
+ if args.resume_from_checkpoint is not None or args.resume_from_checkpoint != "":
+ accelerator.print(f"Resumed from checkpoint: {args.resume_from_checkpoint}")
+ accelerator.load_state(args.resume_from_checkpoint)
+ path = os.path.basename(args.resume_from_checkpoint)
+ else:
+ # Get the most recent checkpoint
+ dirs = [f.name for f in os.scandir(os.getcwd()) if f.is_dir()]
+ dirs.sort(key=os.path.getctime)
+ path = dirs[-1] # Sorts folders by date modified, most recent checkpoint is the last
+ # Extract `epoch_{i}` or `step_{i}`
+ training_difference = os.path.splitext(path)[0]
+
+ if "epoch" in training_difference:
+ starting_epoch = int(training_difference.replace("epoch_", "")) + 1
+ resume_step = None
+ completed_steps = starting_epoch * num_update_steps_per_epoch
+ else:
+ # need to multiply `gradient_accumulation_steps` to reflect real steps
+ resume_step = int(training_difference.replace("step_", "")) * args.gradient_accumulation_steps
+ starting_epoch = resume_step // len(train_dataloader)
+ resume_step -= starting_epoch * len(train_dataloader)
+ completed_steps = resume_step // args.gradient_accumulation_steps
+
+ # update the progress_bar if load from checkpoint
+ progress_bar.update(completed_steps)
+
+ for epoch in range(starting_epoch, args.num_train_epochs):
+ model.train()
+ total_loss = 0
+ if args.resume_from_checkpoint and epoch == starting_epoch and resume_step is not None:
+ # We skip the first `n` batches in the dataloader when resuming from a checkpoint
+ active_dataloader = accelerator.skip_first_batches(train_dataloader, resume_step)
+ else:
+ active_dataloader = train_dataloader
+ for step, batch in enumerate(active_dataloader):
+ with accelerator.accumulate(model):
+ query_embs = model(**{k.replace("query_", ""): v for k, v in batch.items() if "query" in k})
+ product_embs = model(**{k.replace("product_", ""): v for k, v in batch.items() if "product" in k})
+ loss = get_loss(get_cosing_embeddings(query_embs, product_embs), batch["labels"])
+ total_loss += accelerator.reduce(loss.detach().float(), reduction="sum")
+ accelerator.backward(loss)
+ optimizer.step()
+ lr_scheduler.step()
+ model.zero_grad()
+
+ # Checks if the accelerator has performed an optimization step behind the scenes
+ if accelerator.sync_gradients:
+ progress_bar.update(1)
+ completed_steps += 1
+
+ if (step + 1) % 100 == 0:
+ logger.info(f"Step: {step + 1}, Loss: {total_loss / (step + 1)}")
+ if args.with_tracking:
+ accelerator.log({"train/loss": total_loss / (step + 1)}, step=completed_steps)
+
+ if isinstance(checkpointing_steps, int):
+ if completed_steps % checkpointing_steps == 0:
+ output_dir = f"step_{completed_steps}"
+ if args.output_dir is not None:
+ output_dir = os.path.join(args.output_dir, output_dir)
+ accelerator.save_state(output_dir)
+
+ if completed_steps >= args.max_train_steps:
+ break
+
+ model.eval()
+ for step, batch in enumerate(eval_dataloader):
+ with torch.no_grad():
+ query_embs = model(**{k.replace("query_", ""): v for k, v in batch.items() if "query" in k})
+ product_embs = model(**{k.replace("product_", ""): v for k, v in batch.items() if "product" in k})
+ prediction_scores = get_cosing_embeddings(query_embs, product_embs)
+ prediction_scores, references = accelerator.gather_for_metrics((prediction_scores, batch["labels"]))
+ metric.add_batch(
+ prediction_scores=prediction_scores,
+ references=references,
+ )
+
+ result = metric.compute()
+ result = {f"eval/{k}": v for k, v in result.items()}
+ # Use accelerator.print to print only on the main process.
+ accelerator.print(f"epoch {epoch}:", result)
+ if args.with_tracking:
+ result["train/epoch_loss"] = total_loss.item() / len(train_dataloader)
+ accelerator.log(result, step=completed_steps)
+
+ if args.output_dir is not None:
+ accelerator.wait_for_everyone()
+ if accelerator.is_main_process:
+ if isinstance(checkpointing_steps, str):
+ accelerator.save_state(os.path.join(args.output_dir, f"epoch_{epoch}"))
+ accelerator.unwrap_model(model).save_pretrained(
+ args.output_dir, state_dict=accelerator.get_state_dict(accelerator.unwrap_model(model))
+ )
+ tokenizer.save_pretrained(args.output_dir)
+ if args.push_to_hub:
+ commit_message = (
+ f"Training in progress epoch {epoch}"
+ if epoch < args.num_train_epochs - 1
+ else "End of training"
+ )
+ api.upload_folder(
+ repo_id=repo_id,
+ folder_path=args.output_dir,
+ commit_message=commit_message,
+ run_as_future=True,
+ )
+ accelerator.wait_for_everyone()
+ accelerator.end_training()
+
+
+if __name__ == "__main__":
+ main()
diff --git a/peft/examples/feature_extraction/peft_lora_embedding_semantic_similarity_inference.ipynb b/peft/examples/feature_extraction/peft_lora_embedding_semantic_similarity_inference.ipynb
new file mode 100644
index 0000000000000000000000000000000000000000..ded221bbce4417334a5129e6e1deb1cd6859347f
--- /dev/null
+++ b/peft/examples/feature_extraction/peft_lora_embedding_semantic_similarity_inference.ipynb
@@ -0,0 +1,1808 @@
+{
+ "cells": [
+ {
+ "cell_type": "code",
+ "execution_count": 1,
+ "id": "3e7b6247",
+ "metadata": {},
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "[2023-06-29 09:08:24,868] [INFO] [real_accelerator.py:110:get_accelerator] Setting ds_accelerator to cuda (auto detect)\n",
+ "\n",
+ "===================================BUG REPORT===================================\n",
+ "Welcome to bitsandbytes. For bug reports, please run\n",
+ "\n",
+ "python -m bitsandbytes\n",
+ "\n",
+ " and submit this information together with your error trace to: https://github.com/TimDettmers/bitsandbytes/issues\n",
+ "================================================================================\n",
+ "bin /home/sourab/miniconda3/envs/ml/lib/python3.11/site-packages/bitsandbytes/libbitsandbytes_cuda118.so\n",
+ "CUDA SETUP: CUDA runtime path found: /home/sourab/miniconda3/envs/ml/lib/libcudart.so\n",
+ "CUDA SETUP: Highest compute capability among GPUs detected: 7.5\n",
+ "CUDA SETUP: Detected CUDA version 118\n",
+ "CUDA SETUP: Loading binary /home/sourab/miniconda3/envs/ml/lib/python3.11/site-packages/bitsandbytes/libbitsandbytes_cuda118.so...\n"
+ ]
+ },
+ {
+ "name": "stderr",
+ "output_type": "stream",
+ "text": [
+ "/home/sourab/miniconda3/envs/ml/lib/python3.11/site-packages/bitsandbytes/cuda_setup/main.py:149: UserWarning: Found duplicate ['libcudart.so', 'libcudart.so.11.0', 'libcudart.so.12.0'] files: {PosixPath('/home/sourab/miniconda3/envs/ml/lib/libcudart.so'), PosixPath('/home/sourab/miniconda3/envs/ml/lib/libcudart.so.11.0')}.. We'll flip a coin and try one of these, in order to fail forward.\n",
+ "Either way, this might cause trouble in the future:\n",
+ "If you get `CUDA error: invalid device function` errors, the above might be the cause and the solution is to make sure only one ['libcudart.so', 'libcudart.so.11.0', 'libcudart.so.12.0'] in the paths that we search based on your env.\n",
+ " warn(msg)\n"
+ ]
+ }
+ ],
+ "source": [
+ "import argparse\n",
+ "import json\n",
+ "import logging\n",
+ "import math\n",
+ "import os\n",
+ "import random\n",
+ "from pathlib import Path\n",
+ "from tqdm import tqdm\n",
+ "\n",
+ "import datasets\n",
+ "from datasets import load_dataset, DatasetDict\n",
+ "\n",
+ "import evaluate\n",
+ "import torch\n",
+ "from torch import nn\n",
+ "from torch.utils.data import DataLoader\n",
+ "\n",
+ "import transformers\n",
+ "from transformers import AutoTokenizer, AutoModel, default_data_collator, SchedulerType, get_scheduler\n",
+ "from transformers.utils import check_min_version, get_full_repo_name, send_example_telemetry\n",
+ "from transformers.utils.versions import require_version\n",
+ "\n",
+ "from huggingface_hub import Repository, create_repo\n",
+ "\n",
+ "from accelerate import Accelerator\n",
+ "from accelerate.logging import get_logger\n",
+ "from accelerate.utils import set_seed\n",
+ "\n",
+ "from peft import PeftModel\n",
+ "\n",
+ "import hnswlib"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 2,
+ "id": "c939b4fd",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "class AutoModelForSentenceEmbedding(nn.Module):\n",
+ " def __init__(self, model_name, tokenizer, normalize=True):\n",
+ " super(AutoModelForSentenceEmbedding, self).__init__()\n",
+ "\n",
+ " self.model = AutoModel.from_pretrained(model_name) # , quantizaton_config=BitsAndBytesConfig(load_in_8bit=True), device_map={\"\":0})\n",
+ " self.normalize = normalize\n",
+ " self.tokenizer = tokenizer\n",
+ "\n",
+ " def forward(self, **kwargs):\n",
+ " model_output = self.model(**kwargs)\n",
+ " embeddings = self.mean_pooling(model_output, kwargs[\"attention_mask\"])\n",
+ " if self.normalize:\n",
+ " embeddings = torch.nn.functional.normalize(embeddings, p=2, dim=1)\n",
+ "\n",
+ " return embeddings\n",
+ "\n",
+ " def mean_pooling(self, model_output, attention_mask):\n",
+ " token_embeddings = model_output[0] # First element of model_output contains all token embeddings\n",
+ " input_mask_expanded = attention_mask.unsqueeze(-1).expand(token_embeddings.size()).float()\n",
+ " return torch.sum(token_embeddings * input_mask_expanded, 1) / torch.clamp(input_mask_expanded.sum(1), min=1e-9)\n",
+ "\n",
+ " def __getattr__(self, name: str):\n",
+ " \"\"\"Forward missing attributes to the wrapped module.\"\"\"\n",
+ " try:\n",
+ " return super().__getattr__(name) # defer to nn.Module's logic\n",
+ " except AttributeError:\n",
+ " return getattr(self.model, name)\n",
+ "\n",
+ "\n",
+ "def get_cosing_embeddings(query_embs, product_embs):\n",
+ " return torch.sum(query_embs * product_embs, axis=1)"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 3,
+ "id": "8b5d9256",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "model_name_or_path = \"intfloat/e5-large-v2\"\n",
+ "peft_model_id = \"smangrul/peft_lora_e5_semantic_search\"\n",
+ "dataset_name = \"smangrul/amazon_esci\"\n",
+ "max_length = 70\n",
+ "batch_size = 256"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "id": "f190e1ee",
+ "metadata": {},
+ "outputs": [
+ {
+ "name": "stderr",
+ "output_type": "stream",
+ "text": [
+ "Found cached dataset parquet (/raid/sourab/.cache/huggingface/datasets/smangrul___parquet/smangrul--amazon_esci-321288cabf0cc045/0.0.0/14a00e99c0d15a23649d0db8944380ac81082d4b021f398733dd84f3a6c569a7)\n"
+ ]
+ },
+ {
+ "data": {
+ "application/vnd.jupyter.widget-view+json": {
+ "model_id": "43b84641575e4ce6899a3e6f61d7e126",
+ "version_major": 2,
+ "version_minor": 0
+ },
+ "text/plain": [
+ " 0%| | 0/2 [00:00\n",
+ "\n",
+ "\n",
+ " \n",
+ " \n",
+ " | \n",
+ " index | \n",
+ " product_title | \n",
+ "
\n",
+ " \n",
+ " \n",
+ " \n",
+ " | 0 | \n",
+ " 0 | \n",
+ " RamPro 10\" All Purpose Utility Air Tires/Wheel... | \n",
+ "
\n",
+ " \n",
+ " | 1 | \n",
+ " 1 | \n",
+ " MaxAuto 2-Pack 13x5.00-6 2PLY Turf Mower Tract... | \n",
+ "
\n",
+ " \n",
+ " | 2 | \n",
+ " 2 | \n",
+ " NEIKO 20601A 14.5 inch Steel Tire Spoon Lever ... | \n",
+ "
\n",
+ " \n",
+ " | 3 | \n",
+ " 3 | \n",
+ " 2PK 13x5.00-6 13x5.00x6 13x5x6 13x5-6 2PLY Tur... | \n",
+ "
\n",
+ " \n",
+ " | 4 | \n",
+ " 4 | \n",
+ " (Set of 2) 15x6.00-6 Husqvarna/Poulan Tire Whe... | \n",
+ "
\n",
+ " \n",
+ " | ... | \n",
+ " ... | \n",
+ " ... | \n",
+ "
\n",
+ " \n",
+ " | 476273 | \n",
+ " 476273 | \n",
+ " Chanel No.5 Eau Premiere Spray 50ml/1.7oz | \n",
+ "
\n",
+ " \n",
+ " | 476274 | \n",
+ " 476274 | \n",
+ " Steve Madden Designer 15 Inch Carry on Suitcas... | \n",
+ "
\n",
+ " \n",
+ " | 476275 | \n",
+ " 476275 | \n",
+ " CHANEL Le Lift Creme Yeux, Black, 0.5 Ounce | \n",
+ "
\n",
+ " \n",
+ " | 476276 | \n",
+ " 476276 | \n",
+ " Coco Mademoiselle by Chanel for Women - 3.4 oz... | \n",
+ "
\n",
+ " \n",
+ " | 476277 | \n",
+ " 476277 | \n",
+ " Chânél No. 5 by Chânél Eau De Parfum Premiere ... | \n",
+ "
\n",
+ " \n",
+ "
\n",
+ "476278 rows × 2 columns
\n",
+ ""
+ ],
+ "text/plain": [
+ " index product_title\n",
+ "0 0 RamPro 10\" All Purpose Utility Air Tires/Wheel...\n",
+ "1 1 MaxAuto 2-Pack 13x5.00-6 2PLY Turf Mower Tract...\n",
+ "2 2 NEIKO 20601A 14.5 inch Steel Tire Spoon Lever ...\n",
+ "3 3 2PK 13x5.00-6 13x5.00x6 13x5x6 13x5-6 2PLY Tur...\n",
+ "4 4 (Set of 2) 15x6.00-6 Husqvarna/Poulan Tire Whe...\n",
+ "... ... ...\n",
+ "476273 476273 Chanel No.5 Eau Premiere Spray 50ml/1.7oz\n",
+ "476274 476274 Steve Madden Designer 15 Inch Carry on Suitcas...\n",
+ "476275 476275 CHANEL Le Lift Creme Yeux, Black, 0.5 Ounce\n",
+ "476276 476276 Coco Mademoiselle by Chanel for Women - 3.4 oz...\n",
+ "476277 476277 Chânél No. 5 by Chânél Eau De Parfum Premiere ...\n",
+ "\n",
+ "[476278 rows x 2 columns]"
+ ]
+ },
+ "execution_count": 5,
+ "metadata": {},
+ "output_type": "execute_result"
+ }
+ ],
+ "source": [
+ "product_dataset_for_indexing"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 6,
+ "id": "85840ec6",
+ "metadata": {},
+ "outputs": [
+ {
+ "data": {
+ "text/html": [
+ "\n",
+ "\n",
+ "
\n",
+ " \n",
+ " \n",
+ " | \n",
+ " index | \n",
+ " product_title | \n",
+ "
\n",
+ " \n",
+ " \n",
+ " \n",
+ " | 34710 | \n",
+ " 34710 | \n",
+ " ROK 4-1/2 inch Diamond Saw Blade Set, Pack of 3 | \n",
+ "
\n",
+ " \n",
+ " | 277590 | \n",
+ " 277590 | \n",
+ " WSGG Medical Goggles, FDA registered, Safety Goggles, Fit Over Glasses, Anti-Fog, Anti-Splash (1 pack) | \n",
+ "
\n",
+ " \n",
+ " | 474000 | \n",
+ " 474000 | \n",
+ " iJDMTOY 15W CREE High Power LED Angel Eye Bulbs Compatible With BMW 5 6 7 Series X3 X5 (E39 E60 E63 E65 E53), 7000K Xenon White Headlight Ring Marker Lights | \n",
+ "
\n",
+ " \n",
+ " | 18997 | \n",
+ " 18997 | \n",
+ " USB Charger, Anker Elite Dual Port 24W Wall Charger, PowerPort 2 with PowerIQ and Foldable Plug, for iPhone 11/Xs/XS Max/XR/X/8/7/6/Plus, iPad Pro/Air 2/Mini 3/Mini 4, Samsung S4/S5, and More | \n",
+ "
\n",
+ " \n",
+ " | 208666 | \n",
+ " 208666 | \n",
+ " AOGGY Compatible with MacBook Air 13 inch Case A1466/A1369 (2010-2017 Release) Glitter Fluorescent Color Plastic Hard Case, with Older Version MacBook Air 13 inch Keyboard Cover - Gold | \n",
+ "
\n",
+ " \n",
+ " | 326614 | \n",
+ " 326614 | \n",
+ " CUTE STONE Little Kitchen Playset, Kitchen Toy Set with Realistic Sound &Light, Play Sink, Cooking Stove with Steam, Play Food and Kitchen Accessories, Great Kitchen Toys for Toddlers Kids | \n",
+ "
\n",
+ " \n",
+ " | 105637 | \n",
+ " 105637 | \n",
+ " Milwaukee Electric Tool 2470-21 M12 Cordless Shear Kit, 12 V, Li-Ion | \n",
+ "
\n",
+ " \n",
+ " | 342392 | \n",
+ " 342392 | \n",
+ " chouyatou Women's Short Sleeve/Strap Open Bust Bodysuit Shapewear Firm Control Body Shaper (X-Small, Nude Sleeve) | \n",
+ "
\n",
+ " \n",
+ " | 319970 | \n",
+ " 319970 | \n",
+ " AMT 256 Hz Medical-Grade Tuning Fork Instrument with Fixed Weights, Non-Magnetic Aluminum Alloy (C 256) | \n",
+ "
\n",
+ " \n",
+ " | 416956 | \n",
+ " 416956 | \n",
+ " Timberland HIKER-ROUND 54 BROWN | \n",
+ "
\n",
+ " \n",
+ "
\n",
+ "
\n",
+ " \n",
+ " \n",
+ " | Epoch | \n",
+ " Training Loss | \n",
+ " Validation Loss | \n",
+ " Accuracy | \n",
+ "
\n",
+ " \n",
+ " \n",
+ " \n",
+ " | 1 | \n",
+ " No log | \n",
+ " 0.506871 | \n",
+ " 0.896000 | \n",
+ "
\n",
+ " \n",
+ " | 2 | \n",
+ " 2.162700 | \n",
+ " 0.189141 | \n",
+ " 0.946000 | \n",
+ "
\n",
+ " \n",
+ " | 3 | \n",
+ " 0.345100 | \n",
+ " 0.144759 | \n",
+ " 0.960000 | \n",
+ "
\n",
+ " \n",
+ " | 4 | \n",
+ " 0.211600 | \n",
+ " 0.150886 | \n",
+ " 0.958000 | \n",
+ "
\n",
+ " \n",
+ " | 5 | \n",
+ " 0.171100 | \n",
+ " 0.149751 | \n",
+ " 0.958000 | \n",
+ "
\n",
+ " \n",
+ "
"
+ ],
+ "text/plain": [
+ ""
+ ]
+ },
+ "metadata": {},
+ "output_type": "display_data"
+ },
+ {
+ "name": "stderr",
+ "output_type": "stream",
+ "text": [
+ "***** Running Evaluation *****\n",
+ " Num examples = 500\n",
+ " Batch size = 128\n",
+ "Saving model checkpoint to vit-base-patch16-224-in21k-finetuned-lora-food101/checkpoint-9\n",
+ "Configuration saved in vit-base-patch16-224-in21k-finetuned-lora-food101/checkpoint-9/config.json\n",
+ "Model weights saved in vit-base-patch16-224-in21k-finetuned-lora-food101/checkpoint-9/pytorch_model.bin\n",
+ "Image processor saved in vit-base-patch16-224-in21k-finetuned-lora-food101/checkpoint-9/preprocessor_config.json\n",
+ "Image processor saved in vit-base-patch16-224-in21k-finetuned-lora-food101/preprocessor_config.json\n",
+ "***** Running Evaluation *****\n",
+ " Num examples = 500\n",
+ " Batch size = 128\n",
+ "Saving model checkpoint to vit-base-patch16-224-in21k-finetuned-lora-food101/checkpoint-18\n",
+ "Configuration saved in vit-base-patch16-224-in21k-finetuned-lora-food101/checkpoint-18/config.json\n",
+ "Model weights saved in vit-base-patch16-224-in21k-finetuned-lora-food101/checkpoint-18/pytorch_model.bin\n",
+ "Image processor saved in vit-base-patch16-224-in21k-finetuned-lora-food101/checkpoint-18/preprocessor_config.json\n",
+ "Image processor saved in vit-base-patch16-224-in21k-finetuned-lora-food101/preprocessor_config.json\n",
+ "***** Running Evaluation *****\n",
+ " Num examples = 500\n",
+ " Batch size = 128\n",
+ "Saving model checkpoint to vit-base-patch16-224-in21k-finetuned-lora-food101/checkpoint-27\n",
+ "Configuration saved in vit-base-patch16-224-in21k-finetuned-lora-food101/checkpoint-27/config.json\n",
+ "Model weights saved in vit-base-patch16-224-in21k-finetuned-lora-food101/checkpoint-27/pytorch_model.bin\n",
+ "Image processor saved in vit-base-patch16-224-in21k-finetuned-lora-food101/checkpoint-27/preprocessor_config.json\n",
+ "Image processor saved in vit-base-patch16-224-in21k-finetuned-lora-food101/preprocessor_config.json\n",
+ "***** Running Evaluation *****\n",
+ " Num examples = 500\n",
+ " Batch size = 128\n",
+ "Saving model checkpoint to vit-base-patch16-224-in21k-finetuned-lora-food101/checkpoint-36\n",
+ "Configuration saved in vit-base-patch16-224-in21k-finetuned-lora-food101/checkpoint-36/config.json\n",
+ "Model weights saved in vit-base-patch16-224-in21k-finetuned-lora-food101/checkpoint-36/pytorch_model.bin\n",
+ "Image processor saved in vit-base-patch16-224-in21k-finetuned-lora-food101/checkpoint-36/preprocessor_config.json\n",
+ "Image processor saved in vit-base-patch16-224-in21k-finetuned-lora-food101/preprocessor_config.json\n",
+ "***** Running Evaluation *****\n",
+ " Num examples = 500\n",
+ " Batch size = 128\n",
+ "Saving model checkpoint to vit-base-patch16-224-in21k-finetuned-lora-food101/checkpoint-45\n",
+ "Configuration saved in vit-base-patch16-224-in21k-finetuned-lora-food101/checkpoint-45/config.json\n",
+ "Model weights saved in vit-base-patch16-224-in21k-finetuned-lora-food101/checkpoint-45/pytorch_model.bin\n",
+ "Image processor saved in vit-base-patch16-224-in21k-finetuned-lora-food101/checkpoint-45/preprocessor_config.json\n",
+ "Image processor saved in vit-base-patch16-224-in21k-finetuned-lora-food101/preprocessor_config.json\n",
+ "\n",
+ "\n",
+ "Training completed. Do not forget to share your model on huggingface.co/models =)\n",
+ "\n",
+ "\n",
+ "Loading best model from vit-base-patch16-224-in21k-finetuned-lora-food101/checkpoint-27 (score: 0.96).\n"
+ ]
+ }
+ ],
+ "source": [
+ "trainer = Trainer(\n",
+ " lora_model,\n",
+ " args,\n",
+ " train_dataset=train_ds,\n",
+ " eval_dataset=val_ds,\n",
+ " processing_class=image_processor,\n",
+ " compute_metrics=compute_metrics,\n",
+ " data_collator=collate_fn,\n",
+ ")\n",
+ "train_results = trainer.train()"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "b2NENHxHCejv"
+ },
+ "source": [
+ "In just a few minutes, we have a fine-tuned model with 96% validation accuracy. Also, note that we used a very small subset of the training dataset which is definitely impacting the results. "
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 21,
+ "metadata": {
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 198
+ },
+ "id": "_MAd2906jQKG",
+ "outputId": "7b825531-4e8d-4666-d6fc-eaa1accf3bb6"
+ },
+ "outputs": [
+ {
+ "name": "stderr",
+ "output_type": "stream",
+ "text": [
+ "***** Running Evaluation *****\n",
+ " Num examples = 500\n",
+ " Batch size = 128\n"
+ ]
+ },
+ {
+ "data": {
+ "text/html": [
+ "\n",
+ " \n",
+ " \n",
+ "
\n",
+ " [4/4 01:48]\n",
+ "
Copy a token from your Hugging Face\ntokens page and paste it below.
Immediately click login after copying\nyour token or it might be stored in plain text in this notebook file. "
+ }
+ },
+ "dfe97442852c4338843c65333b25623d": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "dffe636233c84dcd9d75f34baf40fa1d": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "e0d98c36e5d242b2905adf8167ac348a": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_ddf88cbfaaef4a55babf480816db7d28",
+ "placeholder": "",
+ "style": "IPY_MODEL_38f30da546444f8199673003d0a92dda",
+ "value": " 5.64k/5.64k [01:17<?, ?B/s]"
+ }
+ },
+ "e0f2599ed04c424f896e503630034e84": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_7e243f4a30c645b080e688fb706b4548",
+ "placeholder": "",
+ "style": "IPY_MODEL_db6b68a237cf4e93ae6383448b773e47",
+ "value": " 1/1 [00:14<00:00, 14.25s/it]"
+ }
+ },
+ "e302923a9df24e5fa8fff79c203ead9f": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "e3047557ae7f40e2aecccf1afad36f3f": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "e33243b001274d02a25f5940ba41ecf6": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "FloatProgressModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "FloatProgressModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "ProgressView",
+ "bar_style": "success",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_40a5a50aeca24f0d8990da97971004d1",
+ "max": 2688263,
+ "min": 0,
+ "orientation": "horizontal",
+ "style": "IPY_MODEL_be71e6438e0e49759d2f72feec520cae",
+ "value": 2688263
+ }
+ },
+ "e4074e524a19455fab810ec454fe8bf1": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "e4694cffcb574863a255e9022c8ddf5d": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "e4a4122ff32a41a1917459709224fc6a": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_8ba66e043f8a4975bd77ecd343401260",
+ "IPY_MODEL_2e0bb2dcd85640d7b85d80469ea9f9f3",
+ "IPY_MODEL_1c208beced884b9291c5bcb7b4f71680"
+ ],
+ "layout": "IPY_MODEL_3f188d6d34774154afc297b13a3eb9e8"
+ }
+ },
+ "e54b7fc2f9b94118ab97f2736862f77d": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "e667b14a3c0e41c6a16c4be453f10378": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "e6ce3e626b1744c7ba3da26d1fde5fa5": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "e6e36d744e1244aeb7eb0c4ce392372d": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "e7144551e74b46529b00a61f580a183d": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "e8026bcb0e2c4b14bc6c84537c8c4ae9": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "e83fd078f467406da0baf26e18b39e89": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_9b4b67731a7a4bc59be132b53c24eae8",
+ "IPY_MODEL_e33243b001274d02a25f5940ba41ecf6",
+ "IPY_MODEL_06e4c619e366427a8ff4c358196ecd12"
+ ],
+ "layout": "IPY_MODEL_bacd429b42d843299cb75224db3afb1e"
+ }
+ },
+ "e88c3ad56ef24e4d8281898b08ff6f4b": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_1fdc59cbb8724c618ce6e586e2c9723f",
+ "placeholder": "",
+ "style": "IPY_MODEL_dbaa70ad4f1d4496a670601fe447116d",
+ "value": " 5.64k/5.64k [01:17<?, ?B/s]"
+ }
+ },
+ "e8c2cfdaf0eb413189d93924eae757c7": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "ea2217bba8574c7890a411f27da0c147": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_b1b6922df40c4af69b00b4e85db770c4",
+ "IPY_MODEL_2b8bc04ac3104592bf950e349c034c2d",
+ "IPY_MODEL_cf815c0979644cd6ad2c681fa96c0648"
+ ],
+ "layout": "IPY_MODEL_7541b2304cc5466cb2369c0025d2d243"
+ }
+ },
+ "eaf2c76a172d4da6846c6face18a3b58": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "eb864284052c46b28b93fc79bfed740f": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "eca3b1f4ad76430483a221470e592c13": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_e302923a9df24e5fa8fff79c203ead9f",
+ "placeholder": "",
+ "style": "IPY_MODEL_f7b9abca32ec42edad5ec6e52882f732",
+ "value": " 5.64k/5.64k [01:17<00:00, 61.4B/s]"
+ }
+ },
+ "ecf73dd75420460399bfd04d8cd81f90": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "edb0d1ba5e114af9b6705969f58ece7b": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "edc0742a08a445a594139200c7f03c60": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "ee103846621b4c0e8e1266599b99f6ee": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_e7144551e74b46529b00a61f580a183d",
+ "placeholder": "",
+ "style": "IPY_MODEL_9b1bfa11ee3746c38155c4505abfaa86",
+ "value": "Generating train split: 100%"
+ }
+ },
+ "eef81e9bea0c4f5d85e7efa8ebe0463a": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ButtonModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ButtonModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "ButtonView",
+ "button_style": "",
+ "description": "Login",
+ "disabled": false,
+ "icon": "",
+ "layout": "IPY_MODEL_c778798c234d45b5a4ae2f250e3706f9",
+ "style": "IPY_MODEL_d5c5396ea2f54ff0aeb9be58b59c253b",
+ "tooltip": ""
+ }
+ },
+ "ef7c7fe37c8d459da6d20f4ccbea3fb8": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_4ee1fde44dcf49eda97e1a05173e5bb1",
+ "placeholder": "",
+ "style": "IPY_MODEL_a0929e66406644dbb09bbdc9c58d488d",
+ "value": "Downloading (…)rocessor_config.json: 100%"
+ }
+ },
+ "f02443fbda394fefa162f4ff5b2d2ce7": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "f031aaf7fbc648a7b8a2e5faf37df14d": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "f0b0cad40fbd461ca7bdcdbb5f442f57": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_76cf84387a7c43608ad018188eef4114",
+ "IPY_MODEL_68ef0c8550ee4c00aa8b284d48572610",
+ "IPY_MODEL_58e7f5c36d8b4836a868ce89838f1896"
+ ],
+ "layout": "IPY_MODEL_9b216287b8694bcc9960a356adf15504"
+ }
+ },
+ "f22598cf4ade4427a1b437fd45aabcc4": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "f34be236ef9c42448ecf2957160990f7": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "f3991aaad13a4c50a7809483b7907b7b": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "FloatProgressModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "FloatProgressModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "ProgressView",
+ "bar_style": "success",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_4a118fa87e424664a2d2ed7c7f58f3fd",
+ "max": 5773,
+ "min": 0,
+ "orientation": "horizontal",
+ "style": "IPY_MODEL_852b01d8592b4d8aa2c4297d6cf75f78",
+ "value": 5773
+ }
+ },
+ "f5041033ddf94f459ed8d1747f6b2d6e": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "f544720498e44c49add78550b46edb3a": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "FloatProgressModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "FloatProgressModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "ProgressView",
+ "bar_style": "success",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_9281c5aec5b84411a05e4762125388d9",
+ "max": 5777,
+ "min": 0,
+ "orientation": "horizontal",
+ "style": "IPY_MODEL_f5b5d6ace35a4a82bfcf2549b93c8558",
+ "value": 5777
+ }
+ },
+ "f5b5d6ace35a4a82bfcf2549b93c8558": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "f6a9243d46cb4c0fbdf3f80f7074f6c5": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "f7b9abca32ec42edad5ec6e52882f732": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "f96302d0c2d849c5b5a0206b65e461ab": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "f981fb4aae504045aa10889dceeb6cac": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "fc612aaed5644b84959a1958b0240dda": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "fc9d0c314ca14826993fe1f24b070b5d": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "fcc7ad16a0b14d96acd9be9e03ac6af9": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "fcc8254622324f8ea965e12e4d4966cd": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "fd9df81594724b88b54b4e3e1b19370a": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_c8267c689fb14afc9a8eb3ecb6f4fd4c",
+ "IPY_MODEL_adb09cebab13484a8d75a338eaba7b0c",
+ "IPY_MODEL_d68194cf7d264df7820f27eb4d070de2"
+ ],
+ "layout": "IPY_MODEL_8bf8a843d65142bbad81de74aa8573f6"
+ }
+ },
+ "fdb3673fdbf24468a9965f13196b78ed": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_0b82dbc29d514f4e9e012fd755948e52",
+ "IPY_MODEL_af1a42626ba7452189fbb5987b159b9c",
+ "IPY_MODEL_93788683ef8e4c71bc1c0b3b9cc7219c"
+ ],
+ "layout": "IPY_MODEL_6e4983016e4f465b85ab7a472d0e986e"
+ }
+ },
+ "fdf282b234fe4a1a8ab452ac04511b7d": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_59792e1ee7074f998d5d4494c09061c6",
+ "IPY_MODEL_cd5b2433cc404ac7b1bb35c6a55f6874",
+ "IPY_MODEL_7c1b6f271fff4d60be39d291c73bfb75"
+ ],
+ "layout": "IPY_MODEL_074f38bd3a9d49719188e8860fb1b5d3"
+ }
+ },
+ "fe93399cc15f4f29b6a37f6a65cf8c9b": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "fea27a80cd2f4b4dba84ecdfefd2722c": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "fee3db0deefb410db4c572efd95575bf": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "fee4fba960ac41ed97984467da41f319": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_ee103846621b4c0e8e1266599b99f6ee",
+ "IPY_MODEL_dcd1c1f4fc014c4aa9ebdaf3c533a061",
+ "IPY_MODEL_a29d758fb7f147c7ad1108f140caf23a"
+ ],
+ "layout": "IPY_MODEL_cb52fa97c659430a8bd71dcd76245a7f"
+ }
+ },
+ "ff39519704b64e68b69ec06aea02791e": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "FloatProgressModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "FloatProgressModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "ProgressView",
+ "bar_style": "success",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_dcefc9ba538e4da2b75f9372a4c5b5bf",
+ "max": 1,
+ "min": 0,
+ "orientation": "horizontal",
+ "style": "IPY_MODEL_77df794cb4e4491e80ee20bbd2801a89",
+ "value": 1
+ }
+ },
+ "ffc13c11355b46bb9cafcb17f3e1535e": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ }
+ }
+ }
+ },
+ "nbformat": 4,
+ "nbformat_minor": 1
+}
diff --git a/peft/examples/image_classification/image_classification_timm_peft_lora.ipynb b/peft/examples/image_classification/image_classification_timm_peft_lora.ipynb
new file mode 100644
index 0000000000000000000000000000000000000000..1e2f2225055ef8d0542d66b77d089806ae9015cd
--- /dev/null
+++ b/peft/examples/image_classification/image_classification_timm_peft_lora.ipynb
@@ -0,0 +1,744 @@
+{
+ "cells": [
+ {
+ "cell_type": "markdown",
+ "id": "4ef57047",
+ "metadata": {},
+ "source": [
+ "# Using PEFT with timm"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "80561acc",
+ "metadata": {},
+ "source": [
+ "`peft` allows us to train any model with LoRA as long as the layer type is supported. Since `Conv2D` is one of the supported layer types, it makes sense to test it on image models.\n",
+ "\n",
+ "In this short notebook, we will demonstrate this with an image classification task using [`timm`](https://huggingface.co/docs/timm/index)."
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "aa26c285",
+ "metadata": {},
+ "source": [
+ "## Imports"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "552b9040",
+ "metadata": {},
+ "source": [
+ "Make sure that you have the latest version of `peft` installed. To ensure that, run this in your Python environment:\n",
+ " \n",
+ " python -m pip install --upgrade peft\n",
+ " \n",
+ "Also, ensure that `timm` is installed:\n",
+ "\n",
+ " python -m pip install --upgrade timm"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 1,
+ "id": "e600b7d5",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "import timm\n",
+ "import torch\n",
+ "from PIL import Image\n",
+ "from timm.data import resolve_data_config\n",
+ "from timm.data.transforms_factory import create_transform"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 2,
+ "id": "73a2ae54",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "import peft\n",
+ "from datasets import load_dataset"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 3,
+ "id": "82c628fd",
+ "metadata": {},
+ "outputs": [
+ {
+ "data": {
+ "text/plain": [
+ ""
+ ]
+ },
+ "execution_count": 3,
+ "metadata": {},
+ "output_type": "execute_result"
+ }
+ ],
+ "source": [
+ "torch.manual_seed(0)"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "701ab69c",
+ "metadata": {},
+ "source": [
+ "## Loading the pre-trained base model"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "20bff51a",
+ "metadata": {},
+ "source": [
+ "We use a small pretrained `timm` model, `PoolFormer`. Find more info on its [model card](https://huggingface.co/timm/poolformer_m36.sail_in1k)."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 4,
+ "id": "495cb3d6",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "model_id_timm = \"timm/poolformer_m36.sail_in1k\""
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "2dc06f9b",
+ "metadata": {},
+ "source": [
+ "We tell `timm` that we deal with 3 classes, to ensure that the classification layer has the correct size."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 5,
+ "id": "090564bc",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "model = timm.create_model(model_id_timm, pretrained=True, num_classes=3)"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "beca5794",
+ "metadata": {},
+ "source": [
+ "These are the transformations steps necessary to process the image."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 6,
+ "id": "9df2e113",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "transform = create_transform(**resolve_data_config(model.pretrained_cfg, model=model))"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "3f809dfa",
+ "metadata": {},
+ "source": [
+ "## Data"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "a398fe22",
+ "metadata": {},
+ "source": [
+ "For this exercise, we use the \"beans\" dataset. More details on the dataset can be found on [its datasets page](https://huggingface.co/datasets/beans). For our purposes, what's important is that we have image inputs and the target we're trying to predict is one of three classes for each image."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 7,
+ "id": "0fddc704",
+ "metadata": {
+ "scrolled": true
+ },
+ "outputs": [
+ {
+ "name": "stderr",
+ "output_type": "stream",
+ "text": [
+ "Found cached dataset beans (/home/vinh/.cache/huggingface/datasets/beans/default/0.0.0/90c755fb6db1c0ccdad02e897a37969dbf070bed3755d4391e269ff70642d791)\n"
+ ]
+ },
+ {
+ "data": {
+ "application/vnd.jupyter.widget-view+json": {
+ "model_id": "05592574da474b81ab736d6babb5e19d",
+ "version_major": 2,
+ "version_minor": 0
+ },
+ "text/plain": [
+ " 0%| | 0/3 [00:00"
+ ]
+ },
+ "execution_count": 9,
+ "metadata": {},
+ "output_type": "execute_result"
+ }
+ ],
+ "source": [
+ "ds_train[0][\"image\"]"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "880ea6c4",
+ "metadata": {},
+ "source": [
+ "We define a small processing function which is responsible for loading and transforming the images, as well as extracting the labels."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 10,
+ "id": "142df842",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "def process(batch):\n",
+ " x = torch.cat([transform(img).unsqueeze(0) for img in batch[\"image\"]])\n",
+ " y = torch.tensor(batch[\"labels\"])\n",
+ " return {\"x\": x, \"y\": y}"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 11,
+ "id": "9744257b",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "ds_train.set_transform(process)\n",
+ "ds_valid.set_transform(process)"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 12,
+ "id": "282374be",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "train_loader = torch.utils.data.DataLoader(ds_train, batch_size=32)\n",
+ "valid_loader = torch.utils.data.DataLoader(ds_valid, batch_size=32)"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "5dcd3329",
+ "metadata": {},
+ "source": [
+ "## Training"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "969bc374",
+ "metadata": {},
+ "source": [
+ "This is just a function that performs the train loop, nothing fancy happening."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 13,
+ "id": "b9fc9588",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "def train(model, optimizer, criterion, train_dataloader, valid_dataloader, epochs):\n",
+ " for epoch in range(epochs):\n",
+ " model.train()\n",
+ " train_loss = 0\n",
+ " for batch in train_dataloader:\n",
+ " xb, yb = batch[\"x\"], batch[\"y\"]\n",
+ " xb, yb = xb.to(device), yb.to(device)\n",
+ " outputs = model(xb)\n",
+ " lsm = torch.nn.functional.log_softmax(outputs, dim=-1)\n",
+ " loss = criterion(lsm, yb)\n",
+ " train_loss += loss.detach().float()\n",
+ " loss.backward()\n",
+ " optimizer.step()\n",
+ " optimizer.zero_grad()\n",
+ "\n",
+ " model.eval()\n",
+ " valid_loss = 0\n",
+ " correct = 0\n",
+ " n_total = 0\n",
+ " for batch in valid_dataloader:\n",
+ " xb, yb = batch[\"x\"], batch[\"y\"]\n",
+ " xb, yb = xb.to(device), yb.to(device)\n",
+ " with torch.no_grad():\n",
+ " outputs = model(xb)\n",
+ " lsm = torch.nn.functional.log_softmax(outputs, dim=-1)\n",
+ " loss = criterion(lsm, yb)\n",
+ " valid_loss += loss.detach().float()\n",
+ " correct += (outputs.argmax(-1) == yb).sum().item()\n",
+ " n_total += len(yb)\n",
+ "\n",
+ " train_loss_total = (train_loss / len(train_dataloader)).item()\n",
+ " valid_loss_total = (valid_loss / len(valid_dataloader)).item()\n",
+ " valid_acc_total = correct / n_total\n",
+ " print(f\"{epoch=:<2} {train_loss_total=:.4f} {valid_loss_total=:.4f} {valid_acc_total=:.4f}\")"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "3fd58357",
+ "metadata": {},
+ "source": [
+ "### Selecting which layers to fine-tune with LoRA"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "7987321c",
+ "metadata": {},
+ "source": [
+ "Let's take a look at the layers of our model. We only print the first 30, since there are quite a few:"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 14,
+ "id": "55a7be4d",
+ "metadata": {
+ "scrolled": true
+ },
+ "outputs": [
+ {
+ "data": {
+ "text/plain": [
+ "[('', timm.models.metaformer.MetaFormer),\n",
+ " ('stem', timm.models.metaformer.Stem),\n",
+ " ('stem.conv', torch.nn.modules.conv.Conv2d),\n",
+ " ('stem.norm', torch.nn.modules.linear.Identity),\n",
+ " ('stages', torch.nn.modules.container.Sequential),\n",
+ " ('stages.0', timm.models.metaformer.MetaFormerStage),\n",
+ " ('stages.0.downsample', torch.nn.modules.linear.Identity),\n",
+ " ('stages.0.blocks', torch.nn.modules.container.Sequential),\n",
+ " ('stages.0.blocks.0', timm.models.metaformer.MetaFormerBlock),\n",
+ " ('stages.0.blocks.0.norm1', timm.layers.norm.GroupNorm1),\n",
+ " ('stages.0.blocks.0.token_mixer', timm.models.metaformer.Pooling),\n",
+ " ('stages.0.blocks.0.token_mixer.pool', torch.nn.modules.pooling.AvgPool2d),\n",
+ " ('stages.0.blocks.0.drop_path1', torch.nn.modules.linear.Identity),\n",
+ " ('stages.0.blocks.0.layer_scale1', timm.models.metaformer.Scale),\n",
+ " ('stages.0.blocks.0.res_scale1', torch.nn.modules.linear.Identity),\n",
+ " ('stages.0.blocks.0.norm2', timm.layers.norm.GroupNorm1),\n",
+ " ('stages.0.blocks.0.mlp', timm.layers.mlp.Mlp),\n",
+ " ('stages.0.blocks.0.mlp.fc1', torch.nn.modules.conv.Conv2d),\n",
+ " ('stages.0.blocks.0.mlp.act', torch.nn.modules.activation.GELU),\n",
+ " ('stages.0.blocks.0.mlp.drop1', torch.nn.modules.dropout.Dropout),\n",
+ " ('stages.0.blocks.0.mlp.norm', torch.nn.modules.linear.Identity),\n",
+ " ('stages.0.blocks.0.mlp.fc2', torch.nn.modules.conv.Conv2d),\n",
+ " ('stages.0.blocks.0.mlp.drop2', torch.nn.modules.dropout.Dropout),\n",
+ " ('stages.0.blocks.0.drop_path2', torch.nn.modules.linear.Identity),\n",
+ " ('stages.0.blocks.0.layer_scale2', timm.models.metaformer.Scale),\n",
+ " ('stages.0.blocks.0.res_scale2', torch.nn.modules.linear.Identity),\n",
+ " ('stages.0.blocks.1', timm.models.metaformer.MetaFormerBlock),\n",
+ " ('stages.0.blocks.1.norm1', timm.layers.norm.GroupNorm1),\n",
+ " ('stages.0.blocks.1.token_mixer', timm.models.metaformer.Pooling),\n",
+ " ('stages.0.blocks.1.token_mixer.pool', torch.nn.modules.pooling.AvgPool2d)]"
+ ]
+ },
+ "execution_count": 14,
+ "metadata": {},
+ "output_type": "execute_result"
+ }
+ ],
+ "source": [
+ "[(n, type(m)) for n, m in model.named_modules()][:30]"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "09af9349",
+ "metadata": {},
+ "source": [
+ "Most of these layers are not good targets for LoRA, but we see a couple that should interest us. Their names are `'stages.0.blocks.0.mlp.fc1'`, etc. With a bit of regex, we can match them easily.\n",
+ "\n",
+ "Also, we should inspect the name of the classification layer, since we want to train that one too!"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 15,
+ "id": "8b98d9ef",
+ "metadata": {
+ "scrolled": true
+ },
+ "outputs": [
+ {
+ "data": {
+ "text/plain": [
+ "[('head.global_pool.flatten', torch.nn.modules.linear.Identity),\n",
+ " ('head.norm', timm.layers.norm.LayerNorm2d),\n",
+ " ('head.flatten', torch.nn.modules.flatten.Flatten),\n",
+ " ('head.drop', torch.nn.modules.linear.Identity),\n",
+ " ('head.fc', torch.nn.modules.linear.Linear)]"
+ ]
+ },
+ "execution_count": 15,
+ "metadata": {},
+ "output_type": "execute_result"
+ }
+ ],
+ "source": [
+ "[(n, type(m)) for n, m in model.named_modules()][-5:]"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "00e75b78",
+ "metadata": {},
+ "source": [
+ " config = peft.LoraConfig(\n",
+ " r=8,\n",
+ " target_modules=r\".*\\.mlp\\.fc\\d|head\\.fc\",\n",
+ " )"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "23814d70",
+ "metadata": {},
+ "source": [
+ "Okay, this gives us all the information we need to fine-tune this model. With a bit of regex, we match the convolutional layers that should be targeted for LoRA. We also want to train the classification layer `'head.fc'` (without LoRA), so we add it to the `modules_to_save`."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 16,
+ "id": "81029587",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "config = peft.LoraConfig(r=8, target_modules=r\".*\\.mlp\\.fc\\d\", modules_to_save=[\"head.fc\"])"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "e05876bc",
+ "metadata": {},
+ "source": [
+ "Finally, let's create the `peft` model, the optimizer and criterion, and we can get started. As shown below, less than 2% of the model's total parameters are updated thanks to `peft`."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "id": "8cc5c5db",
+ "metadata": {},
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "trainable params: 1,064,454 || all params: 56,467,974 || trainable%: 1.88505789139876\n"
+ ]
+ }
+ ],
+ "source": [
+ "device = torch.accelerator.current_accelerator().type if hasattr(torch, \"accelerator\") else \"cuda\"\n",
+ "peft_model = peft.get_peft_model(model, config).to(device)\n",
+ "optimizer = torch.optim.Adam(peft_model.parameters(), lr=2e-4)\n",
+ "criterion = torch.nn.CrossEntropyLoss()\n",
+ "peft_model.print_trainable_parameters()"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 18,
+ "id": "9e557e42",
+ "metadata": {},
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "epoch=0 train_loss_total=1.2999 valid_loss_total=1.0624 valid_acc_total=0.4436\n",
+ "epoch=1 train_loss_total=1.0200 valid_loss_total=0.8906 valid_acc_total=0.7594\n",
+ "epoch=2 train_loss_total=0.8874 valid_loss_total=0.6894 valid_acc_total=0.8045\n",
+ "epoch=3 train_loss_total=0.7440 valid_loss_total=0.4797 valid_acc_total=0.8045\n",
+ "epoch=4 train_loss_total=0.6025 valid_loss_total=0.3419 valid_acc_total=0.8120\n",
+ "epoch=5 train_loss_total=0.4820 valid_loss_total=0.2589 valid_acc_total=0.8421\n",
+ "epoch=6 train_loss_total=0.3567 valid_loss_total=0.2101 valid_acc_total=0.8722\n",
+ "epoch=7 train_loss_total=0.2835 valid_loss_total=0.1385 valid_acc_total=0.9098\n",
+ "epoch=8 train_loss_total=0.1815 valid_loss_total=0.1108 valid_acc_total=0.9474\n",
+ "epoch=9 train_loss_total=0.1341 valid_loss_total=0.0785 valid_acc_total=0.9699\n",
+ "CPU times: user 4min 3s, sys: 36.3 s, total: 4min 40s\n",
+ "Wall time: 3min 32s\n"
+ ]
+ }
+ ],
+ "source": [
+ "%time train(peft_model, optimizer, criterion, train_loader, valid_dataloader=valid_loader, epochs=10)"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "94162859",
+ "metadata": {},
+ "source": [
+ "We get an accuracy of ~0.97, despite only training a tiny amount of parameters. That's a really nice result."
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "9c16bad8",
+ "metadata": {},
+ "source": [
+ "## Sharing the model through Hugging Face Hub"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "2e1e16c7",
+ "metadata": {},
+ "source": [
+ "### Pushing the model to Hugging Face Hub"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "ec596b3b",
+ "metadata": {},
+ "source": [
+ "If we want to share the fine-tuned weights with the world, we can upload them to Hugging Face Hub like this:"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 19,
+ "id": "b583579d",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "user = \"BenjaminB\" # put your user name here\n",
+ "model_name = \"peft-lora-with-timm-model\"\n",
+ "model_id = f\"{user}/{model_name}\""
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 20,
+ "id": "f1db67e4",
+ "metadata": {},
+ "outputs": [
+ {
+ "data": {
+ "application/vnd.jupyter.widget-view+json": {
+ "model_id": "aed1f9c3fa334be1b5f208efe5ba27e6",
+ "version_major": 2,
+ "version_minor": 0
+ },
+ "text/plain": [
+ "Upload 1 LFS files: 0%| | 0/1 [00:00\n",
+ " \n",
+ " \n",
+ " [255/255 06:13, Epoch 1/1]\n",
+ " \n",
+ " \n",
+ " \n",
+ " \n",
+ " | Epoch | \n",
+ " Training Loss | \n",
+ " Validation Loss | \n",
+ "
\n",
+ " \n",
+ " \n",
+ " \n",
+ " | 1 | \n",
+ " No log | \n",
+ " 0.017228 | \n",
+ "
\n",
+ " \n",
+ "
"
+ ],
+ "text/plain": [
+ ""
+ ]
+ },
+ "metadata": {},
+ "output_type": "display_data"
+ },
+ {
+ "name": "stderr",
+ "output_type": "stream",
+ "text": [
+ "Saving model checkpoint to temp/checkpoint-100\n",
+ "Trainer.model is not a `PreTrainedModel`, only saving its state dict.\n",
+ "/usr/local/lib/python3.8/dist-packages/bitsandbytes/autograd/_functions.py:298: UserWarning: MatMul8bitLt: inputs will be cast from torch.float32 to float16 during quantization\n",
+ " warnings.warn(f\"MatMul8bitLt: inputs will be cast from {A.dtype} to float16 during quantization\")\n",
+ "Saving model checkpoint to temp/checkpoint-200\n",
+ "Trainer.model is not a `PreTrainedModel`, only saving its state dict.\n",
+ "/usr/local/lib/python3.8/dist-packages/bitsandbytes/autograd/_functions.py:298: UserWarning: MatMul8bitLt: inputs will be cast from torch.float32 to float16 during quantization\n",
+ " warnings.warn(f\"MatMul8bitLt: inputs will be cast from {A.dtype} to float16 during quantization\")\n",
+ "***** Running Evaluation *****\n",
+ " Num examples = 227\n",
+ " Batch size = 8\n",
+ "\n",
+ "\n",
+ "Training completed. Do not forget to share your model on huggingface.co/models =)\n",
+ "\n",
+ "\n"
+ ]
+ },
+ {
+ "data": {
+ "text/plain": [
+ "TrainOutput(global_step=255, training_loss=0.2569344015682445, metrics={'train_runtime': 377.3565, 'train_samples_per_second': 5.398, 'train_steps_per_second': 0.676, 'total_flos': 1181084919791616.0, 'train_loss': 0.2569344015682445, 'epoch': 1.0})"
+ ]
+ },
+ "execution_count": 8,
+ "metadata": {},
+ "output_type": "execute_result"
+ }
+ ],
+ "source": [
+ "trainer.train()"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "r98VtofiGXtO",
+ "metadata": {
+ "id": "r98VtofiGXtO"
+ },
+ "source": [
+ "## Qualitatively test our model"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "NIm7z3UNzGPP",
+ "metadata": {
+ "id": "NIm7z3UNzGPP"
+ },
+ "source": [
+ "Let's have a quick qualitative evaluation of the model, by taking a sample from the dataset that corresponds to a positive label. Run your generation similarly as you were running your model from `transformers`:"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "id": "c95d6173",
+ "metadata": {
+ "colab": {
+ "base_uri": "https://localhost:8080/"
+ },
+ "id": "c95d6173",
+ "outputId": "ed03a1dc-597a-4053-99d6-eca2cc6da253"
+ },
+ "outputs": [
+ {
+ "name": "stderr",
+ "output_type": "stream",
+ "text": [
+ "Generate config GenerationConfig {\n",
+ " \"_from_model_config\": true,\n",
+ " \"decoder_start_token_id\": 0,\n",
+ " \"eos_token_id\": 1,\n",
+ " \"pad_token_id\": 0,\n",
+ " \"transformers_version\": \"4.27.0.dev0\",\n",
+ " \"use_cache\": false\n",
+ "}\n",
+ "\n",
+ "/usr/local/lib/python3.8/dist-packages/bitsandbytes/autograd/_functions.py:298: UserWarning: MatMul8bitLt: inputs will be cast from torch.float32 to float16 during quantization\n",
+ " warnings.warn(f\"MatMul8bitLt: inputs will be cast from {A.dtype} to float16 during quantization\")\n",
+ "/usr/local/lib/python3.8/dist-packages/transformers/generation/utils.py:1374: UserWarning: You are calling .generate() with the `input_ids` being on a device type different than your model's device. `input_ids` is on cpu, whereas the model is on cuda. You may experience unexpected behaviors or slower generation. Please make sure that you have put `input_ids` to the correct device by calling for example input_ids = input_ids.to('cuda') before running `.generate()`.\n",
+ " warnings.warn(\n"
+ ]
+ },
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "input sentence: In January-September 2009 , the Group 's net interest income increased to EUR 112.4 mn from EUR 74.3 mn in January-September 2008 .\n",
+ " output prediction: ['positive']\n"
+ ]
+ }
+ ],
+ "source": [
+ "model.eval()\n",
+ "input_text = \"In January-September 2009 , the Group 's net interest income increased to EUR 112.4 mn from EUR 74.3 mn in January-September 2008 .\"\n",
+ "inputs = tokenizer(input_text, return_tensors=\"pt\").to(model.device)\n",
+ "\n",
+ "outputs = model.generate(input_ids=inputs[\"input_ids\"], max_new_tokens=10)\n",
+ "\n",
+ "print(\"input sentence: \", input_text)\n",
+ "print(\" output prediction: \", tokenizer.batch_decode(outputs.detach().cpu().numpy(), skip_special_tokens=True))"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "9QqBlwzoGZ3f",
+ "metadata": {
+ "id": "9QqBlwzoGZ3f"
+ },
+ "source": [
+ "## Share your adapters on 🤗 Hub"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "NT-C8SjcKqUx",
+ "metadata": {
+ "id": "NT-C8SjcKqUx"
+ },
+ "source": [
+ "Once you have trained your adapter, you can easily share it on the Hub using the method `push_to_hub` . Note that only the adapter weights and config will be pushed"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "id": "bcbfa1f9",
+ "metadata": {
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 359,
+ "referenced_widgets": [
+ "5bb29f3102954b06bec825f6b3a7aaa7",
+ "90516032070a40979181d1d27db10c4f",
+ "4b7dc0fb222b4e2a9bb2ef2501e9fd30",
+ "06069855ef82484f9985e4619095dbe8",
+ "1ece69c53e37413caad8db70d9160ad5",
+ "7ce90db727ea47cc9344176858a2225b",
+ "64f2b70b63cd4e7eb9e22ac2de5589c9",
+ "57dea1b3e04142bb91868a474774d86a",
+ "8ac43334e0ad4a78acda3b876fead058",
+ "04da98e400514cf2847d172916cd0081",
+ "4dbe49547fe94010ad5a30818cfc35bc",
+ "99091ca45c1b4809ba0a1b01af85f528",
+ "06ec124c3dac4fe6b152fb812d20d86d",
+ "7561c47a97444666816422a0418e1675",
+ "45ab5d7049e34dfd8a067643ae887a31",
+ "434e308cac5847f0bee431c7dbb4c04a",
+ "dd993a4a7cdf40448098544c95468a10"
+ ]
+ },
+ "id": "bcbfa1f9",
+ "outputId": "91ef770e-9fc4-4eb2-b02b-24e635101f97"
+ },
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "Token is valid.\n",
+ "Your token has been saved in your configured git credential helpers (store).\n",
+ "Your token has been saved to /root/.cache/huggingface/token\n",
+ "Login successful\n"
+ ]
+ }
+ ],
+ "source": [
+ "from huggingface_hub import notebook_login\n",
+ "\n",
+ "notebook_login()"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "id": "rFKJ4vHNGkJw",
+ "metadata": {
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 152,
+ "referenced_widgets": [
+ "00f7d043cb184d69b828c204dac2c0ab",
+ "1e409cd3d3a04b558d989d63f0b3b5f7",
+ "d48cbb38078b456fab1634bec5b0a1ba",
+ "9030744dbca9427ba8a036a76b5c8bf7",
+ "53dd4444c0e14e16a912532898b32d92",
+ "5287ac638c22412ab91c55f3316c9b63",
+ "a43ddb478f044f17adbcfae841ec2114",
+ "45141234ce584f208a9d301faadf75d2",
+ "f62ffbdc24734b999f36058d9edca81f",
+ "972ddebd536d4685bfc3c7c13e5bd8be",
+ "64156e2c54b44fb9aec661d9b57da962",
+ "050de732f51f4af8bb41ab3cad0090a4",
+ "7960ed3beb2a429ba2aca1c6ed032f64",
+ "726a2eedc7434210bc5aa4d0a772b313",
+ "07bf5d621cf944258aaf13954669df56",
+ "93a0896ca66b4111bc4cabe6e1278440",
+ "cfc78731f7d543ce8529cc254d92ddf5",
+ "eacf8e9ed6e847faae2b8ecab283ddc4",
+ "bef1971d92e6479696e3f9a27a757b8a",
+ "821f2f296acb40ae9bb40fc3faf4103d",
+ "11efd993475a4f2aabe7df605bab04dd",
+ "406e4d8561f64d2a94d93a606d02d7d3"
+ ]
+ },
+ "id": "rFKJ4vHNGkJw",
+ "outputId": "07425379-64ad-47e8-ba8f-8d9dc26252b6"
+ },
+ "outputs": [
+ {
+ "name": "stderr",
+ "output_type": "stream",
+ "text": [
+ "Uploading the following files to ybelkada/flan-t5-large-lora: adapter_model.bin,adapter_config.json\n"
+ ]
+ },
+ {
+ "data": {
+ "application/vnd.jupyter.widget-view+json": {
+ "model_id": "00f7d043cb184d69b828c204dac2c0ab",
+ "version_major": 2,
+ "version_minor": 0
+ },
+ "text/plain": [
+ "Upload 1 LFS files: 0%| | 0/1 [00:00Pro Tip: If you don't already have one, you can create a dedicated\n'notebooks' token with 'write' access, that you can then easily reuse for all\nnotebooks. "
+ }
+ },
+ "7cfda0921e5a4f378e90e057447f3b3d": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_10aa4e3aca57438ea7af97b60208ac81",
+ "placeholder": "",
+ "style": "IPY_MODEL_f14657da8e1e4298a96e3885eb4eee93",
+ "value": "Downloading builder script: 100%"
+ }
+ },
+ "7fb7e3e2c75d4d03a98e581d4ead0f00": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "FloatProgressModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "FloatProgressModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "ProgressView",
+ "bar_style": "success",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_43d7a9b421be430286b5eb8441d6d465",
+ "max": 2201,
+ "min": 0,
+ "orientation": "horizontal",
+ "style": "IPY_MODEL_ebc26228160046c48279d71770c928d8",
+ "value": 2201
+ }
+ },
+ "8035fd17e29a48d7b415c531607216a6": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "808a41f78a7c4ae0b6aafee59c6234ae": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "808cea6c94264f0c9990d6dbcf538419": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "81d2f0953e104fc1ad57295819b6b689": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_bcda86e43607436583f1fbfee08a9786",
+ "placeholder": "",
+ "style": "IPY_MODEL_55cf3bcee7c745948b39eea5f65fc62b",
+ "value": " 3.13G/3.13G [00:18<00:00, 182MB/s]"
+ }
+ },
+ "821f2f296acb40ae9bb40fc3faf4103d": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "8252a05cb70b46ec8b0480062ea1cb71": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_8669a890db6c456cbc3ada28976be30b",
+ "placeholder": "",
+ "style": "IPY_MODEL_9e5afa2048c74754816b34a34171fcb0",
+ "value": "Downloading (…)lve/main/config.json: 100%"
+ }
+ },
+ "82849bb4d5da452e87a18ca749ce5d7b": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_2b4d68606bdf4758b812f5a8057af595",
+ "placeholder": "",
+ "style": "IPY_MODEL_f9620e01cd6749f88b722a42ff68c502",
+ "value": "Downloading (…)"spiece.model";: 100%"
+ }
+ },
+ "83f196eb5d9549cda4d48008fa7b1386": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "85ae7ed1ec244a89aeb9f4552c2c9462": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "85e5c1a9b7ac4e6e884213a636d0aaa1": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "8669a890db6c456cbc3ada28976be30b": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "87ce7c58b18146f3ac73970d7f8079ac": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "8a2bd1b4d9ba47ef9e77048e3d2d1e83": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "8ac43334e0ad4a78acda3b876fead058": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "8b41d2e9f7424dc898446e7f428dc757": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "8d35a041dbfb4747aea427e76890551a": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_74efd6bfe71e4dc599a7fc76574ff154",
+ "IPY_MODEL_1ed1bfefa6534085869130ea533ff4b1",
+ "IPY_MODEL_fd08c4fbe5d84dd893d87a5e2f2d082d"
+ ],
+ "layout": "IPY_MODEL_87ce7c58b18146f3ac73970d7f8079ac"
+ }
+ },
+ "8d79b7d0c3cb4f8d99fb20941c35856f": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "8ef94158b0584f0eb55582bf8b6594c6": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "8f339c9070f046dab46ebc35c1cc2dba": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "FloatProgressModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "FloatProgressModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "ProgressView",
+ "bar_style": "success",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_d618ec6be7d14a239b3bc74172616bf2",
+ "max": 13677,
+ "min": 0,
+ "orientation": "horizontal",
+ "style": "IPY_MODEL_3c8349539946412a93a51d9087306ea4",
+ "value": 13677
+ }
+ },
+ "8fceec1018574003884e082b2a5c23bf": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "9030744dbca9427ba8a036a76b5c8bf7": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_972ddebd536d4685bfc3c7c13e5bd8be",
+ "placeholder": "",
+ "style": "IPY_MODEL_64156e2c54b44fb9aec661d9b57da962",
+ "value": " 1/1 [00:02<00:00, 2.11s/it]"
+ }
+ },
+ "90516032070a40979181d1d27db10c4f": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_57dea1b3e04142bb91868a474774d86a",
+ "placeholder": "",
+ "style": "IPY_MODEL_8ac43334e0ad4a78acda3b876fead058",
+ "value": "
Copy a token from your Hugging Face\ntokens page and paste it below.
Immediately click login after copying\nyour token or it might be stored in plain text in this notebook file. "
+ }
+ },
+ "924e6a8308fc47af929aca1987a12f09": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "93a0896ca66b4111bc4cabe6e1278440": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "93fe5a8fafbc44b496309d1a8da77ac5": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "94437f56e5a44fa3bb08c9d798b2eaeb": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_0f091d25adf34ade835b094eb5b952a3",
+ "IPY_MODEL_9d599c2a4d9f4f2db1e4b3183c18eb94",
+ "IPY_MODEL_aa91ad725da147bc8cab70f931d82672"
+ ],
+ "layout": "IPY_MODEL_fb6877c376e0430296b2746513f60931"
+ }
+ },
+ "945ac449c2e84fd6b5a7805b017343f2": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "96e2d208830f48cd821be7e59643c93e": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_2fe0a2fa22a0498da983ec38150216e6",
+ "placeholder": "",
+ "style": "IPY_MODEL_f3784e85cef34bdba64b611a1f5883e4",
+ "value": " 792k/792k [00:00<00:00, 7.01MB/s]"
+ }
+ },
+ "96e4e44a789a46ce8239b260bf6e3dc8": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "972ddebd536d4685bfc3c7c13e5bd8be": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "978bbbf33d304588af971d22bb2a3690": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "99091ca45c1b4809ba0a1b01af85f528": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "9d0500a0f5f74be39e5edfbbcd7a64fc": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "9d599c2a4d9f4f2db1e4b3183c18eb94": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "FloatProgressModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "FloatProgressModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "ProgressView",
+ "bar_style": "success",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_bf7a49e0e4a64df6b1b1c66e5e73c3a6",
+ "max": 8862,
+ "min": 0,
+ "orientation": "horizontal",
+ "style": "IPY_MODEL_d27ff6c2869242b98564b0e03d68b413",
+ "value": 8862
+ }
+ },
+ "9d68afcb8e26420cb91ea1eb872c80c4": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_a72073cfb8b4422a98ca581c4e5d18b8",
+ "placeholder": "",
+ "style": "IPY_MODEL_3a5712c976b04af0975804b34344dfcf",
+ "value": "100%"
+ }
+ },
+ "9e5afa2048c74754816b34a34171fcb0": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "a0186b2194df4a0a9cd1ac49054d68da": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "a10078c15aae4ec6a849f1b58c6b1cc2": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_223848818aff4af1ab5d5e14271408e3",
+ "placeholder": "",
+ "style": "IPY_MODEL_4b4b31109a9746e88ffa9b47bab00e53",
+ "value": " 1/1 [00:00<00:00, 12.10ba/s]"
+ }
+ },
+ "a38c0fedf90a4f3cbb4680b5f85bbf2f": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "a3bb3f44c1754082a4f5169431c5b760": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "a43ddb478f044f17adbcfae841ec2114": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "a4857f97132a41acbe4535b03cd8d94a": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "a4d6de73a37148bf9303a273d13cd091": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "a72073cfb8b4422a98ca581c4e5d18b8": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "a9effc13b52044a5bc0d6a2a1088396f": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "aa2c51ad05c14a02a13e5c047779fc05": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_2ce6779fa5904471945fa5738510af64",
+ "IPY_MODEL_bdff3b35dcdf49e5ba2c5c2498773cb7",
+ "IPY_MODEL_6994741f3113493b9d5bba278b8732f5"
+ ],
+ "layout": "IPY_MODEL_808a41f78a7c4ae0b6aafee59c6234ae"
+ }
+ },
+ "aa91ad725da147bc8cab70f931d82672": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_8a2bd1b4d9ba47ef9e77048e3d2d1e83",
+ "placeholder": "",
+ "style": "IPY_MODEL_dbd908538859410f9c20536fe5acb328",
+ "value": " 8.86k/8.86k [00:00<00:00, 381kB/s]"
+ }
+ },
+ "aaa1477cfabb4767b755e902d3b99e61": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "FloatProgressModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "FloatProgressModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "ProgressView",
+ "bar_style": "success",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_a38c0fedf90a4f3cbb4680b5f85bbf2f",
+ "max": 6036,
+ "min": 0,
+ "orientation": "horizontal",
+ "style": "IPY_MODEL_c6a28dcd88c1487ab17aef6946ada876",
+ "value": 6036
+ }
+ },
+ "b560fc36ee8f424f9590e04a042046fe": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_f2a36b126c1b41848e61b0c581ff8c4b",
+ "placeholder": "",
+ "style": "IPY_MODEL_6a40d6535f9e4b5b9c9283a1cd67687a",
+ "value": "Downloading (…)okenizer_config.json: 100%"
+ }
+ },
+ "b718fba0f1514025a0ca22e7f780a2fc": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_0271e1cc4e2d43c69d4959e46eddec9a",
+ "IPY_MODEL_601fb3752e134641b28da908d4e7b65a",
+ "IPY_MODEL_e002207d6982491cbef196f25fc891f8"
+ ],
+ "layout": "IPY_MODEL_a4857f97132a41acbe4535b03cd8d94a"
+ }
+ },
+ "b77afc7c1f184de0970feb2df8ac5285": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "FloatProgressModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "FloatProgressModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "ProgressView",
+ "bar_style": "success",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_5bfebc75ec424c6cb41b33d210d28d2b",
+ "max": 662,
+ "min": 0,
+ "orientation": "horizontal",
+ "style": "IPY_MODEL_ef2fa44d0105457c9aed3812633dd329",
+ "value": 662
+ }
+ },
+ "b8087054f46c44cab9bd62fa23fbf9de": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_5192bc282c4847cb9df8365fc22a6cc2",
+ "placeholder": "",
+ "style": "IPY_MODEL_608e9f7a14054573b9bd07f0f74b6345",
+ "value": " 2.20k/2.20k [00:00<00:00, 84.9kB/s]"
+ }
+ },
+ "b8944b7027d449b4a7fc752978f463b1": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_390b88f67b84451999b0845483905144",
+ "placeholder": "",
+ "style": "IPY_MODEL_be9c243b74d944eb82ca1fe4ada6721d",
+ "value": " 1303/2264 [00:00<00:00, 4889.47 examples/s]"
+ }
+ },
+ "b8bb0aed01d04e8dad560df1b051e1e4": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_93fe5a8fafbc44b496309d1a8da77ac5",
+ "placeholder": "",
+ "style": "IPY_MODEL_a9effc13b52044a5bc0d6a2a1088396f",
+ "value": " 3/3 [00:00<00:00, 17.02ba/s]"
+ }
+ },
+ "baf53867f52046c182a2b1755f02e136": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": "hidden",
+ "width": null
+ }
+ },
+ "bc24304c057d4b5898e832818de55caa": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "bca79be79b6d4a68b148255bba86ea96": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_74e88bd01bf14e0e9f772f993c92eb77",
+ "placeholder": "",
+ "style": "IPY_MODEL_401bd48c5b2d48eb86a1499912ee2b44",
+ "value": " 682k/682k [00:00<00:00, 6.99MB/s]"
+ }
+ },
+ "bcda86e43607436583f1fbfee08a9786": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "bdfb4a04e48246a4b0890f52d6dd424b": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "bdff3b35dcdf49e5ba2c5c2498773cb7": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "FloatProgressModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "FloatProgressModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "ProgressView",
+ "bar_style": "success",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_df8fbdbe9bc341e3a39a7bda99b70be2",
+ "max": 147,
+ "min": 0,
+ "orientation": "horizontal",
+ "style": "IPY_MODEL_179a912bbd1e454eba503782b675efa8",
+ "value": 147
+ }
+ },
+ "be11f6865f6c41b5a57b2b7f4a85e14c": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_85e5c1a9b7ac4e6e884213a636d0aaa1",
+ "placeholder": "",
+ "style": "IPY_MODEL_216e5237b31944cbab006d9761ade0a1",
+ "value": "Downloading data: 100%"
+ }
+ },
+ "be9c243b74d944eb82ca1fe4ada6721d": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "bef1971d92e6479696e3f9a27a757b8a": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "bf7a49e0e4a64df6b1b1c66e5e73c3a6": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "c0deb08457be4a3ebb3947e33f7ce1df": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_cba58e0b316b439ab035b917a40c630c",
+ "placeholder": "",
+ "style": "IPY_MODEL_de6718209a7a42b0809e97fcd97e09ed",
+ "value": "100%"
+ }
+ },
+ "c149c1c53e9d44008a86944ef8c261c5": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "c1757a5b684f4496a4b0e3db544bf44b": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "c31cffaa6934407399856235a2f3af54": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "FloatProgressModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "FloatProgressModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "ProgressView",
+ "bar_style": "success",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_a4d6de73a37148bf9303a273d13cd091",
+ "max": 681890,
+ "min": 0,
+ "orientation": "horizontal",
+ "style": "IPY_MODEL_f79eeece093f4b0e9de6dbc346a3fa19",
+ "value": 681890
+ }
+ },
+ "c6a28dcd88c1487ab17aef6946ada876": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "c708031a279e4e55ac7833e6697f93bd": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "c7771479ae4e4efab744fad6da586fd3": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "cba58e0b316b439ab035b917a40c630c": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "cce112d791dd4b748908756e785ab555": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_be11f6865f6c41b5a57b2b7f4a85e14c",
+ "IPY_MODEL_c31cffaa6934407399856235a2f3af54",
+ "IPY_MODEL_bca79be79b6d4a68b148255bba86ea96"
+ ],
+ "layout": "IPY_MODEL_5093700dd3a14cc1a283d18a4a0e17a7"
+ }
+ },
+ "ce0213e9d6aa45c5a9ac9954fbe15f62": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_7cfda0921e5a4f378e90e057447f3b3d",
+ "IPY_MODEL_aaa1477cfabb4767b755e902d3b99e61",
+ "IPY_MODEL_7b6bddd4ca51495dbc2fceba7c50706f"
+ ],
+ "layout": "IPY_MODEL_6317d49813234f5b9103b249cf648c2c"
+ }
+ },
+ "cfc78731f7d543ce8529cc254d92ddf5": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "cfc7aa04c11d408c9c12cdbd9cff4bb5": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "d27ff6c2869242b98564b0e03d68b413": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "d48cbb38078b456fab1634bec5b0a1ba": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "FloatProgressModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "FloatProgressModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "ProgressView",
+ "bar_style": "success",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_45141234ce584f208a9d301faadf75d2",
+ "max": 1,
+ "min": 0,
+ "orientation": "horizontal",
+ "style": "IPY_MODEL_f62ffbdc24734b999f36058d9edca81f",
+ "value": 1
+ }
+ },
+ "d5b57d3c74d14e5d80d1ef634c103a40": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "d618ec6be7d14a239b3bc74172616bf2": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "d72e8b3419f240f2bdce253cce9d24e3": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "d7d9e2e2090d4226ad89e5ba9cec33df": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_5cc620a232bf4d418c3fc882f4c1cd0c",
+ "IPY_MODEL_f742450a607c4ed0bff98ac9b7685d40",
+ "IPY_MODEL_e87b05e685b040f7a99450bfbab72433"
+ ],
+ "layout": "IPY_MODEL_e1c8e6f843604161bbb6cbd269488469"
+ }
+ },
+ "da99eed13d524b8fb95dbc563eb2d044": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "dbd908538859410f9c20536fe5acb328": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "dbdb787728184aa1a6906f96c5e6f929": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_e3be963920c84c7fbe7e0bc61b8e778d",
+ "IPY_MODEL_1275c5a5c88b435a897f88a19c54a0a5",
+ "IPY_MODEL_81d2f0953e104fc1ad57295819b6b689"
+ ],
+ "layout": "IPY_MODEL_61ab054f49884b1fadf529a39ccc37dc"
+ }
+ },
+ "dd53a486f7b5403a81e2be89cbbda719": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "dd993a4a7cdf40448098544c95468a10": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "de6718209a7a42b0809e97fcd97e09ed": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "df8fbdbe9bc341e3a39a7bda99b70be2": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "e002207d6982491cbef196f25fc891f8": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_1d11cb45c5cb472aa86722e4dbb8c085",
+ "placeholder": "",
+ "style": "IPY_MODEL_34142a8e97594931b316970911679e55",
+ "value": " 3/3 [00:00<00:00, 2.89ba/s]"
+ }
+ },
+ "e1769695dffd4ebeb79a63ff4812fa9e": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_f66e179caa8b4393bed19a0488821c47",
+ "placeholder": "",
+ "style": "IPY_MODEL_cfc7aa04c11d408c9c12cdbd9cff4bb5",
+ "value": " 2.54k/2.54k [00:00<00:00, 95.8kB/s]"
+ }
+ },
+ "e1c8e6f843604161bbb6cbd269488469": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "e24115bb662c428e89c2c4421915e632": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "e293930c8e2c4eadbda53005e21ec450": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "e3be963920c84c7fbe7e0bc61b8e778d": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_924e6a8308fc47af929aca1987a12f09",
+ "placeholder": "",
+ "style": "IPY_MODEL_c1757a5b684f4496a4b0e3db544bf44b",
+ "value": "Downloading (…)"pytorch_model.bin";: 100%"
+ }
+ },
+ "e87b05e685b040f7a99450bfbab72433": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_06cea508d7504b228f6cebc66742d200",
+ "placeholder": "",
+ "style": "IPY_MODEL_9d0500a0f5f74be39e5edfbbcd7a64fc",
+ "value": " 2.42M/2.42M [00:00<00:00, 4.03MB/s]"
+ }
+ },
+ "eacf8e9ed6e847faae2b8ecab283ddc4": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "ebc26228160046c48279d71770c928d8": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "ec73524ed7f14ea0b67f07d72eada173": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "ef2fa44d0105457c9aed3812633dd329": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "f00b73eb32374c33882c1bfc49822e44": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "f061a6deaa73484aa04f219bba6a4329": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "f14657da8e1e4298a96e3885eb4eee93": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "f2a36b126c1b41848e61b0c581ff8c4b": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "f2dc5e8a31c348358aca916274899e8b": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_2bfb7c240e154769a0d58a3ceaa20212",
+ "IPY_MODEL_8f339c9070f046dab46ebc35c1cc2dba",
+ "IPY_MODEL_34db70b6e6ec475699fd23a2d6c3a973"
+ ],
+ "layout": "IPY_MODEL_e24115bb662c428e89c2c4421915e632"
+ }
+ },
+ "f3784e85cef34bdba64b611a1f5883e4": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "f48454eadbfb4953b719bdf44555c90e": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_3c5affff513341b29e6a2c1c90bfe334",
+ "IPY_MODEL_0bbeca449a814d95bec438a9141b2b6b",
+ "IPY_MODEL_a10078c15aae4ec6a849f1b58c6b1cc2"
+ ],
+ "layout": "IPY_MODEL_06e8fd84d6224e5096088d66aad71961"
+ }
+ },
+ "f4ff06e2c48d4e58abe64cb7f41dd886": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_4f57cfa7cb3b4199babf82dc9d93b074",
+ "placeholder": "",
+ "style": "IPY_MODEL_053de11f995247f6b851909a6a8dfc16",
+ "value": "Downloading (…)cial_tokens_map.json: 100%"
+ }
+ },
+ "f62ffbdc24734b999f36058d9edca81f": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "f66e179caa8b4393bed19a0488821c47": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "f742450a607c4ed0bff98ac9b7685d40": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "FloatProgressModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "FloatProgressModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "ProgressView",
+ "bar_style": "success",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_e293930c8e2c4eadbda53005e21ec450",
+ "max": 2424064,
+ "min": 0,
+ "orientation": "horizontal",
+ "style": "IPY_MODEL_945ac449c2e84fd6b5a7805b017343f2",
+ "value": 2424064
+ }
+ },
+ "f79eeece093f4b0e9de6dbc346a3fa19": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "f9620e01cd6749f88b722a42ff68c502": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "fb6877c376e0430296b2746513f60931": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "fd08c4fbe5d84dd893d87a5e2f2d082d": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_6f30253108fb4dce9c3de029457ef6f1",
+ "placeholder": "",
+ "style": "IPY_MODEL_1fa2a7e3ff3c4c99ab95e96a28624846",
+ "value": " 1/1 [00:00<00:00, 22.88ba/s]"
+ }
+ }
+ }
+ }
+ },
+ "nbformat": 4,
+ "nbformat_minor": 5
+}
diff --git a/peft/examples/int8_training/Finetune_opt_bnb_peft.ipynb b/peft/examples/int8_training/Finetune_opt_bnb_peft.ipynb
new file mode 100644
index 0000000000000000000000000000000000000000..99ab2a30e763d8fe6dce3ce9637bb629a73f10b9
--- /dev/null
+++ b/peft/examples/int8_training/Finetune_opt_bnb_peft.ipynb
@@ -0,0 +1,9276 @@
+{
+ "cells": [
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "WE5GJ6s7y0Xo"
+ },
+ "source": [
+ "## Fine-tune large models using 🤗 `peft` adapters, `transformers` & `bitsandbytes`\n",
+ "\n",
+ "In this tutorial we will cover how we can fine-tune large language models using the very recent `peft` library and `bitsandbytes` for loading large models in 8-bit.\n",
+ "The fine-tuning method will rely on a recent method called \"Low Rank Adapters\" (LoRA), instead of fine-tuning the entire model you just have to fine-tune these adapters and load them properly inside the model. \n",
+ "After fine-tuning the model you can also share your adapters on the 🤗 Hub and load them very easily. Let's get started!"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "TfBzP8gWzkpv"
+ },
+ "source": [
+ "### Install requirements\n",
+ "\n",
+ "First, run the cells below to install the requirements:"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "colab": {
+ "base_uri": "https://localhost:8080/"
+ },
+ "id": "otj46qRbtpnd",
+ "outputId": "2aa109f6-3f4e-4887-a16e-336f51e7cc9a"
+ },
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "\u001b[2K \u001b[90m━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━\u001b[0m \u001b[32m76.3/76.3 MB\u001b[0m \u001b[31m10.3 MB/s\u001b[0m eta \u001b[36m0:00:00\u001b[0m\n",
+ "\u001b[2K \u001b[90m━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━\u001b[0m \u001b[32m462.8/462.8 KB\u001b[0m \u001b[31m25.4 MB/s\u001b[0m eta \u001b[36m0:00:00\u001b[0m\n",
+ "\u001b[2K \u001b[90m━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━\u001b[0m \u001b[32m199.7/199.7 KB\u001b[0m \u001b[31m25.5 MB/s\u001b[0m eta \u001b[36m0:00:00\u001b[0m\n",
+ "\u001b[2K \u001b[90m━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━\u001b[0m \u001b[32m190.3/190.3 KB\u001b[0m \u001b[31m23.1 MB/s\u001b[0m eta \u001b[36m0:00:00\u001b[0m\n",
+ "\u001b[2K \u001b[90m━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━\u001b[0m \u001b[32m213.0/213.0 KB\u001b[0m \u001b[31m26.4 MB/s\u001b[0m eta \u001b[36m0:00:00\u001b[0m\n",
+ "\u001b[2K \u001b[90m━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━\u001b[0m \u001b[32m132.0/132.0 KB\u001b[0m \u001b[31m18.5 MB/s\u001b[0m eta \u001b[36m0:00:00\u001b[0m\n",
+ "\u001b[2K \u001b[90m━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━\u001b[0m \u001b[32m140.6/140.6 KB\u001b[0m \u001b[31m20.2 MB/s\u001b[0m eta \u001b[36m0:00:00\u001b[0m\n",
+ "\u001b[?25h Installing build dependencies ... \u001b[?25l\u001b[?25hdone\n",
+ " Getting requirements to build wheel ... \u001b[?25l\u001b[?25hdone\n",
+ " Preparing metadata (pyproject.toml) ... \u001b[?25l\u001b[?25hdone\n",
+ " Installing build dependencies ... \u001b[?25l\u001b[?25hdone\n",
+ " Getting requirements to build wheel ... \u001b[?25l\u001b[?25hdone\n",
+ " Preparing metadata (pyproject.toml) ... \u001b[?25l\u001b[?25hdone\n",
+ "\u001b[2K \u001b[90m━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━━\u001b[0m \u001b[32m7.6/7.6 MB\u001b[0m \u001b[31m72.4 MB/s\u001b[0m eta \u001b[36m0:00:00\u001b[0m\n",
+ "\u001b[?25h Building wheel for transformers (pyproject.toml) ... \u001b[?25l\u001b[?25hdone\n",
+ " Building wheel for peft (pyproject.toml) ... \u001b[?25l\u001b[?25hdone\n"
+ ]
+ }
+ ],
+ "source": [
+ "!pip install -q datasets==3.6.0 accelerate\n",
+ "!pip install -q git+https://github.com/bitsandbytes-foundation/bitsandbytes.git\n",
+ "!pip install -q git+https://github.com/huggingface/transformers.git@main git+https://github.com/huggingface/peft.git"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "FOtwYRI3zzXI"
+ },
+ "source": [
+ "### Model loading\n",
+ "\n",
+ "Here let's load the `opt-6.7b` model, its weights in half-precision (float16) are about 13GB on the Hub! If we load them in 8-bit we would require around 7GB of memory instead."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 4,
+ "metadata": {
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 408,
+ "referenced_widgets": [
+ "d4de260ffd8a440eb87eb900fc1bb1d3",
+ "8602b545a9f8474dbb3cc178ac0b8e60",
+ "b46919912ee54f6f9f2ce9080be1c61a",
+ "50374e3ab81c4626a182e61fc03b94ce",
+ "2144bc2897dc40b29f060e30ace12275",
+ "949ca70002ca4472bbc21fea4d7ac745",
+ "49943c9dadca43a584b3f354ba45280c",
+ "6123e53fb26b41f0af9a3a3348ae1afd",
+ "285ef943d540400ab827c462945a259c",
+ "95727290446244ccb9626f4594949675",
+ "61b54aa6c9e94ee1bc45c15a9e3f7917",
+ "fc2d5ffe254d425b939252ec46ec27cc",
+ "f65af2e868244edeb0cc9402534874a8",
+ "e466054f08004bbcabb24e400cb3c7fc",
+ "6ea40800dfd849e3b106bae71fc53ae3",
+ "722a01f42b7d4c38836a4546ecb38108",
+ "1bd5179cdb474b65aa06eca3520ad37b",
+ "04d367124a3b419ab1fa1dfd4f9004c3",
+ "4ea667f48b9f4e1f9da7c5a0d3025b85",
+ "9b96c63630654773acd38b8b88371f28",
+ "cb69ae47666a4603a07a8778e2ae7d6e",
+ "8f5e9f2d11d54fd2a08dcbff9f6da05c",
+ "c6f712eadc4d49019b2bd355968cc155",
+ "5fd979c05fd34311af877ce1a988ead8",
+ "179165ff4c0e4586aaf3a40b8502f428",
+ "cad1d8326e474a4f9ee13db9005121dd",
+ "b049ac0b3d2e44ba9b1fc1cb2dd3de62",
+ "921c268ecd724b6a8869dae8f81d558a",
+ "4cf85a85c0764f15b5134c81b360e910",
+ "5936d9eb59e147eea6482006decfe0ee",
+ "fad61c68edc84c8197afeafded84280d",
+ "451309d8b3ca4cd9b6f538640477039e",
+ "c7621e14aa16421d9758321e433b92e4",
+ "5aa74b9b30614172b07f88873cf89471",
+ "cf39fb025e3d4635a5695135a56d9f64",
+ "deaf9732f33446a3be015d2ec16aba76",
+ "bdfd856dd8ee4ae09205ad9d1b9cc806",
+ "7a49f7a55b054b6d829f290a1a426a7a",
+ "5b695486a0ac442b8b6a8ef2ebf4e57a",
+ "03be7cb91cba4afab795aab7aa242ee1",
+ "8f7890f54d514f80b1eb17905cf0f964",
+ "ae660d51267544a89f0ad199cc12b6fa",
+ "d5bb8d7359274c8e9cc79df563175137",
+ "98d5a80ec50c46c18f9ee991e2982115",
+ "e73e5388182040a8937ccf1748171a87",
+ "f797f7b8b13f4b3cb871522d34498631",
+ "41f47c864e094cacb1c550d37ddfe80e",
+ "104d982b444947fe8e4fbb2c2f082616",
+ "2cf8581583c641fb95d1e16aff7d4cd1",
+ "11808e9097424dd0b22a5af6c77813f3",
+ "dc08d237860e4788a8ceeff4518c2612",
+ "7bbf2c40a4ae46fe9e5885db08975263",
+ "f00cbc4a89f5492787ec489da65ff70b",
+ "8a7cd2194113493a841b00d034b5f1ba",
+ "e9673363e85448d494ac9ac5d7ba0efb",
+ "a994beafbf3f4c20880a7bbe3898db36",
+ "7769c261781f4f5483c7e9d58c1a5573",
+ "4a713a8fe16f4e81aa841c69711fa136",
+ "08d036904ecf47ed88e129ba6e2b285c",
+ "9f1182fdddab43b59ee98bc701965a17",
+ "c2302f535b114ad780bfa440445c2e28",
+ "8fe032f285ba4858b8efd68119c217b0",
+ "4ca695fca3d140c6ab4e1e1d34df807b",
+ "b77ceaf55dc04810963cdd01126478f6",
+ "0ccdefcb25e14d229b2634ffae4a6d3d",
+ "11d6b952503c4824b36b66e228f87599",
+ "1e9391f6c89c4d08859ef3413edb19be",
+ "039bbda2402f469eb21ba7ec7ea589a6",
+ "5da6eef8fb0048219159f38a68727b64",
+ "c006e62ee6d04831b2b89273ef04a8ac",
+ "af0634c2539a43989902daef47776901",
+ "62fea00ef0364af287e6097b964d00c4",
+ "9e5ef73f8b244845a6b9002fa5c35d15",
+ "5cb09c84e1e144e0a92580fb5e1ce2fe",
+ "0f561c1660744251a8f710b69d434c87",
+ "9e5f870ef80242f5af09fad70f84ea62",
+ "6f173ca73dd545deb22b8cd0470d925f",
+ "4e6d5943bc374b388b93ed115e44b6a5",
+ "cbe2a6ea41834e95a27d6f02c3c0eeec",
+ "7beb5f4efefc4593abac253df74d1405",
+ "370cefbaeebf41f582b7507ad493055f",
+ "e3df9dda16e244aa9b61d54f9e21ef40",
+ "23d2ad64a17041b7a006dad1e041e0a1",
+ "c1fd6a1234274a44b838a09f3f5380c6",
+ "81bb51d088374394becd9a45ec3b17d4",
+ "9e762779e5434bb7afcc295b61c2f4e4",
+ "f539b7a4665449de9eac209a20629969",
+ "32d528db79ad4f6f836ab2e0df5ac426",
+ "1ca7684b79c5438fa06b047bd2b3283f",
+ "a07688185bff4c4b8cbed3af3b4cf802",
+ "0272f1d9f93f4dd788363a8409cdfd69",
+ "27b41d23d2c64127ba3ae8464958f855",
+ "2b54032c0d8e4a2897aed1ac1c79af14",
+ "ed8fa1048e814f2fa3666899fc42e55a",
+ "97daf559100c44ac983562fea93c5fac",
+ "72e511b775604d899ff5b3fa2ebe9fc4",
+ "da946f86590447d2ab98b9da468fa66b",
+ "54fe79d5c7254117a2209927a7248dd4",
+ "1d122e4eaad54e06961288484f31e18b",
+ "d46b5725c35142a89617e46c0e8d3679",
+ "c5493c23fd5542738ffd1ff5f09a6a67",
+ "a1a80d3460984c2496ada5a634875934",
+ "598c5584ffba4f26815c4e87bb1595c4",
+ "fe93f25323604447be0bb1d24a0c2c59",
+ "00c2e2d3ee8b45818ba84da12c6b11e2",
+ "6ccea64c2e614a9fbdcc2f716cecaea0",
+ "63fc9a9eebca4f2db2ed8a385fc5e204",
+ "9a4860dfeac944db85e6e532599bc1cb",
+ "3b946e1bbab24629b98307275fbe7cbb",
+ "d9d36f8ff5f747bf90fbc8a7d35a6664"
+ ]
+ },
+ "id": "cg3fiQOvmI3Q",
+ "outputId": "135a7675-6a4d-4786-b5dc-34cb867f40c7"
+ },
+ "outputs": [
+ {
+ "data": {
+ "application/vnd.jupyter.widget-view+json": {
+ "model_id": "bee2f575b3e64c30b2f3afa137802406",
+ "version_major": 2,
+ "version_minor": 0
+ },
+ "text/plain": [
+ "Loading checkpoint shards: 0%| | 0/2 [00:00\n",
+ " \n",
+ " \n",
+ " [153/200 26:04 < 08:06, 0.10 it/s, Epoch 0.97/2]\n",
+ " \n",
+ " \n",
+ " \n",
+ " \n",
+ " | Step | \n",
+ " Training Loss | \n",
+ "
\n",
+ " \n",
+ " \n",
+ " \n",
+ " | 1 | \n",
+ " 2.364400 | \n",
+ "
\n",
+ " \n",
+ " | 2 | \n",
+ " 2.200400 | \n",
+ "
\n",
+ " \n",
+ " | 3 | \n",
+ " 2.302300 | \n",
+ "
\n",
+ " \n",
+ " | 4 | \n",
+ " 2.184700 | \n",
+ "
\n",
+ " \n",
+ " | 5 | \n",
+ " 1.878700 | \n",
+ "
\n",
+ " \n",
+ " | 6 | \n",
+ " 2.307200 | \n",
+ "
\n",
+ " \n",
+ " | 7 | \n",
+ " 2.193800 | \n",
+ "
\n",
+ " \n",
+ " | 8 | \n",
+ " 2.446200 | \n",
+ "
\n",
+ " \n",
+ " | 9 | \n",
+ " 2.458900 | \n",
+ "
\n",
+ " \n",
+ " | 10 | \n",
+ " 2.020000 | \n",
+ "
\n",
+ " \n",
+ " | 11 | \n",
+ " 1.941200 | \n",
+ "
\n",
+ " \n",
+ " | 12 | \n",
+ " 1.931000 | \n",
+ "
\n",
+ " \n",
+ " | 13 | \n",
+ " 2.055900 | \n",
+ "
\n",
+ " \n",
+ " | 14 | \n",
+ " 1.975100 | \n",
+ "
\n",
+ " \n",
+ " | 15 | \n",
+ " 2.015100 | \n",
+ "
\n",
+ " \n",
+ " | 16 | \n",
+ " 2.095600 | \n",
+ "
\n",
+ " \n",
+ " | 17 | \n",
+ " 1.768300 | \n",
+ "
\n",
+ " \n",
+ " | 18 | \n",
+ " 2.155700 | \n",
+ "
\n",
+ " \n",
+ " | 19 | \n",
+ " 2.402300 | \n",
+ "
\n",
+ " \n",
+ " | 20 | \n",
+ " 2.124600 | \n",
+ "
\n",
+ " \n",
+ " | 21 | \n",
+ " 2.314900 | \n",
+ "
\n",
+ " \n",
+ " | 22 | \n",
+ " 1.908500 | \n",
+ "
\n",
+ " \n",
+ " | 23 | \n",
+ " 2.078800 | \n",
+ "
\n",
+ " \n",
+ " | 24 | \n",
+ " 1.941900 | \n",
+ "
\n",
+ " \n",
+ " | 25 | \n",
+ " 1.879800 | \n",
+ "
\n",
+ " \n",
+ " | 26 | \n",
+ " 1.927500 | \n",
+ "
\n",
+ " \n",
+ " | 27 | \n",
+ " 1.371400 | \n",
+ "
\n",
+ " \n",
+ " | 28 | \n",
+ " 1.977600 | \n",
+ "
\n",
+ " \n",
+ " | 29 | \n",
+ " 2.055000 | \n",
+ "
\n",
+ " \n",
+ " | 30 | \n",
+ " 1.915800 | \n",
+ "
\n",
+ " \n",
+ " | 31 | \n",
+ " 1.958100 | \n",
+ "
\n",
+ " \n",
+ " | 32 | \n",
+ " 2.195900 | \n",
+ "
\n",
+ " \n",
+ " | 33 | \n",
+ " 2.001000 | \n",
+ "
\n",
+ " \n",
+ " | 34 | \n",
+ " 2.025000 | \n",
+ "
\n",
+ " \n",
+ " | 35 | \n",
+ " 1.576900 | \n",
+ "
\n",
+ " \n",
+ " | 36 | \n",
+ " 1.879800 | \n",
+ "
\n",
+ " \n",
+ " | 37 | \n",
+ " 1.821600 | \n",
+ "
\n",
+ " \n",
+ " | 38 | \n",
+ " 1.727800 | \n",
+ "
\n",
+ " \n",
+ " | 39 | \n",
+ " 1.995700 | \n",
+ "
\n",
+ " \n",
+ " | 40 | \n",
+ " 1.698600 | \n",
+ "
\n",
+ " \n",
+ " | 41 | \n",
+ " 2.129300 | \n",
+ "
\n",
+ " \n",
+ " | 42 | \n",
+ " 2.025800 | \n",
+ "
\n",
+ " \n",
+ " | 43 | \n",
+ " 1.696500 | \n",
+ "
\n",
+ " \n",
+ " | 44 | \n",
+ " 1.984700 | \n",
+ "
\n",
+ " \n",
+ " | 45 | \n",
+ " 2.051100 | \n",
+ "
\n",
+ " \n",
+ " | 46 | \n",
+ " 2.054400 | \n",
+ "
\n",
+ " \n",
+ " | 47 | \n",
+ " 1.765600 | \n",
+ "
\n",
+ " \n",
+ " | 48 | \n",
+ " 2.063100 | \n",
+ "
\n",
+ " \n",
+ " | 49 | \n",
+ " 1.746900 | \n",
+ "
\n",
+ " \n",
+ " | 50 | \n",
+ " 1.873000 | \n",
+ "
\n",
+ " \n",
+ " | 51 | \n",
+ " 2.391300 | \n",
+ "
\n",
+ " \n",
+ " | 52 | \n",
+ " 2.494100 | \n",
+ "
\n",
+ " \n",
+ " | 53 | \n",
+ " 2.072300 | \n",
+ "
\n",
+ " \n",
+ " | 54 | \n",
+ " 1.808000 | \n",
+ "
\n",
+ " \n",
+ " | 55 | \n",
+ " 1.911900 | \n",
+ "
\n",
+ " \n",
+ " | 56 | \n",
+ " 2.168100 | \n",
+ "
\n",
+ " \n",
+ " | 57 | \n",
+ " 2.166100 | \n",
+ "
\n",
+ " \n",
+ " | 58 | \n",
+ " 1.921500 | \n",
+ "
\n",
+ " \n",
+ " | 59 | \n",
+ " 1.856000 | \n",
+ "
\n",
+ " \n",
+ " | 60 | \n",
+ " 1.652800 | \n",
+ "
\n",
+ " \n",
+ " | 61 | \n",
+ " 1.605000 | \n",
+ "
\n",
+ " \n",
+ " | 62 | \n",
+ " 2.032500 | \n",
+ "
\n",
+ " \n",
+ " | 63 | \n",
+ " 1.822100 | \n",
+ "
\n",
+ " \n",
+ " | 64 | \n",
+ " 1.623600 | \n",
+ "
\n",
+ " \n",
+ " | 65 | \n",
+ " 1.923200 | \n",
+ "
\n",
+ " \n",
+ " | 66 | \n",
+ " 2.053200 | \n",
+ "
\n",
+ " \n",
+ " | 67 | \n",
+ " 2.114300 | \n",
+ "
\n",
+ " \n",
+ " | 68 | \n",
+ " 1.807700 | \n",
+ "
\n",
+ " \n",
+ " | 69 | \n",
+ " 1.857800 | \n",
+ "
\n",
+ " \n",
+ " | 70 | \n",
+ " 1.854600 | \n",
+ "
\n",
+ " \n",
+ " | 71 | \n",
+ " 2.023000 | \n",
+ "
\n",
+ " \n",
+ " | 72 | \n",
+ " 1.864900 | \n",
+ "
\n",
+ " \n",
+ " | 73 | \n",
+ " 1.769300 | \n",
+ "
\n",
+ " \n",
+ " | 74 | \n",
+ " 1.837700 | \n",
+ "
\n",
+ " \n",
+ " | 75 | \n",
+ " 1.742200 | \n",
+ "
\n",
+ " \n",
+ " | 76 | \n",
+ " 1.895900 | \n",
+ "
\n",
+ " \n",
+ " | 77 | \n",
+ " 1.922800 | \n",
+ "
\n",
+ " \n",
+ " | 78 | \n",
+ " 2.325300 | \n",
+ "
\n",
+ " \n",
+ " | 79 | \n",
+ " 2.231200 | \n",
+ "
\n",
+ " \n",
+ " | 80 | \n",
+ " 2.309500 | \n",
+ "
\n",
+ " \n",
+ " | 81 | \n",
+ " 1.945700 | \n",
+ "
\n",
+ " \n",
+ " | 82 | \n",
+ " 2.072100 | \n",
+ "
\n",
+ " \n",
+ " | 83 | \n",
+ " 1.917400 | \n",
+ "
\n",
+ " \n",
+ " | 84 | \n",
+ " 2.004600 | \n",
+ "
\n",
+ " \n",
+ " | 85 | \n",
+ " 1.951700 | \n",
+ "
\n",
+ " \n",
+ " | 86 | \n",
+ " 1.450600 | \n",
+ "
\n",
+ " \n",
+ " | 87 | \n",
+ " 1.785600 | \n",
+ "
\n",
+ " \n",
+ " | 88 | \n",
+ " 1.668000 | \n",
+ "
\n",
+ " \n",
+ " | 89 | \n",
+ " 1.903100 | \n",
+ "
\n",
+ " \n",
+ " | 90 | \n",
+ " 1.709800 | \n",
+ "
\n",
+ " \n",
+ " | 91 | \n",
+ " 2.312900 | \n",
+ "
\n",
+ " \n",
+ " | 92 | \n",
+ " 2.092100 | \n",
+ "
\n",
+ " \n",
+ " | 93 | \n",
+ " 2.319600 | \n",
+ "
\n",
+ " \n",
+ " | 94 | \n",
+ " 1.603100 | \n",
+ "
\n",
+ " \n",
+ " | 95 | \n",
+ " 1.740000 | \n",
+ "
\n",
+ " \n",
+ " | 96 | \n",
+ " 1.670500 | \n",
+ "
\n",
+ " \n",
+ " | 97 | \n",
+ " 1.611600 | \n",
+ "
\n",
+ " \n",
+ " | 98 | \n",
+ " 1.728900 | \n",
+ "
\n",
+ " \n",
+ " | 99 | \n",
+ " 2.285200 | \n",
+ "
\n",
+ " \n",
+ " | 100 | \n",
+ " 1.957800 | \n",
+ "
\n",
+ " \n",
+ " | 101 | \n",
+ " 1.676700 | \n",
+ "
\n",
+ " \n",
+ " | 102 | \n",
+ " 1.656300 | \n",
+ "
\n",
+ " \n",
+ " | 103 | \n",
+ " 1.612400 | \n",
+ "
\n",
+ " \n",
+ " | 104 | \n",
+ " 1.848900 | \n",
+ "
\n",
+ " \n",
+ " | 105 | \n",
+ " 1.870000 | \n",
+ "
\n",
+ " \n",
+ " | 106 | \n",
+ " 1.954000 | \n",
+ "
\n",
+ " \n",
+ " | 107 | \n",
+ " 2.192200 | \n",
+ "
\n",
+ " \n",
+ " | 108 | \n",
+ " 1.637600 | \n",
+ "
\n",
+ " \n",
+ " | 109 | \n",
+ " 1.208700 | \n",
+ "
\n",
+ " \n",
+ " | 110 | \n",
+ " 2.254200 | \n",
+ "
\n",
+ " \n",
+ " | 111 | \n",
+ " 1.832100 | \n",
+ "
\n",
+ " \n",
+ " | 112 | \n",
+ " 2.119600 | \n",
+ "
\n",
+ " \n",
+ " | 113 | \n",
+ " 2.126400 | \n",
+ "
\n",
+ " \n",
+ " | 114 | \n",
+ " 1.915700 | \n",
+ "
\n",
+ " \n",
+ " | 115 | \n",
+ " 1.587500 | \n",
+ "
\n",
+ " \n",
+ " | 116 | \n",
+ " 1.564800 | \n",
+ "
\n",
+ " \n",
+ " | 117 | \n",
+ " 1.742700 | \n",
+ "
\n",
+ " \n",
+ " | 118 | \n",
+ " 1.712600 | \n",
+ "
\n",
+ " \n",
+ " | 119 | \n",
+ " 1.727900 | \n",
+ "
\n",
+ " \n",
+ " | 120 | \n",
+ " 2.361500 | \n",
+ "
\n",
+ " \n",
+ " | 121 | \n",
+ " 2.070300 | \n",
+ "
\n",
+ " \n",
+ " | 122 | \n",
+ " 1.878500 | \n",
+ "
\n",
+ " \n",
+ " | 123 | \n",
+ " 1.846600 | \n",
+ "
\n",
+ " \n",
+ " | 124 | \n",
+ " 2.061700 | \n",
+ "
\n",
+ " \n",
+ " | 125 | \n",
+ " 2.149700 | \n",
+ "
\n",
+ " \n",
+ " | 126 | \n",
+ " 1.940600 | \n",
+ "
\n",
+ " \n",
+ " | 127 | \n",
+ " 2.098300 | \n",
+ "
\n",
+ " \n",
+ " | 128 | \n",
+ " 1.734100 | \n",
+ "
\n",
+ " \n",
+ " | 129 | \n",
+ " 2.111700 | \n",
+ "
\n",
+ " \n",
+ " | 130 | \n",
+ " 1.887600 | \n",
+ "
\n",
+ " \n",
+ " | 131 | \n",
+ " 1.716300 | \n",
+ "
\n",
+ " \n",
+ " | 132 | \n",
+ " 2.070000 | \n",
+ "
\n",
+ " \n",
+ " | 133 | \n",
+ " 1.782200 | \n",
+ "
\n",
+ " \n",
+ " | 134 | \n",
+ " 1.955200 | \n",
+ "
\n",
+ " \n",
+ " | 135 | \n",
+ " 1.762900 | \n",
+ "
\n",
+ " \n",
+ " | 136 | \n",
+ " 1.954700 | \n",
+ "
\n",
+ " \n",
+ " | 137 | \n",
+ " 1.687100 | \n",
+ "
\n",
+ " \n",
+ " | 138 | \n",
+ " 1.979100 | \n",
+ "
\n",
+ " \n",
+ " | 139 | \n",
+ " 1.634600 | \n",
+ "
\n",
+ " \n",
+ " | 140 | \n",
+ " 1.801200 | \n",
+ "
\n",
+ " \n",
+ " | 141 | \n",
+ " 1.954100 | \n",
+ "
\n",
+ " \n",
+ " | 142 | \n",
+ " 1.833900 | \n",
+ "
\n",
+ " \n",
+ " | 143 | \n",
+ " 2.051400 | \n",
+ "
\n",
+ " \n",
+ " | 144 | \n",
+ " 1.921200 | \n",
+ "
\n",
+ " \n",
+ " | 145 | \n",
+ " 1.787500 | \n",
+ "
\n",
+ " \n",
+ " | 146 | \n",
+ " 1.825400 | \n",
+ "
\n",
+ " \n",
+ " | 147 | \n",
+ " 1.363400 | \n",
+ "
\n",
+ " \n",
+ " | 148 | \n",
+ " 1.977400 | \n",
+ "
\n",
+ " \n",
+ " | 149 | \n",
+ " 1.768300 | \n",
+ "
\n",
+ " \n",
+ " | 150 | \n",
+ " 2.226700 | \n",
+ "
\n",
+ " \n",
+ " | 151 | \n",
+ " 1.945500 | \n",
+ "
\n",
+ " \n",
+ "
"
+ ],
+ "text/plain": [
+ ""
+ ]
+ },
+ "metadata": {},
+ "output_type": "display_data"
+ }
+ ],
+ "source": [
+ "import transformers\n",
+ "from datasets import load_dataset\n",
+ "\n",
+ "data = load_dataset(\"Abirate/english_quotes\")\n",
+ "data = data.map(lambda samples: tokenizer(samples[\"quote\"]), batched=True)\n",
+ "\n",
+ "trainer = transformers.Trainer(\n",
+ " model=model,\n",
+ " train_dataset=data[\"train\"],\n",
+ " args=transformers.TrainingArguments(\n",
+ " per_device_train_batch_size=4,\n",
+ " gradient_accumulation_steps=4,\n",
+ " warmup_steps=100,\n",
+ " max_steps=200,\n",
+ " learning_rate=2e-4,\n",
+ " fp16=True,\n",
+ " logging_steps=1,\n",
+ " output_dir=\"outputs\",\n",
+ " ),\n",
+ " data_collator=transformers.DataCollatorForLanguageModeling(tokenizer, mlm=False),\n",
+ ")\n",
+ "model.config.use_cache = False # silence the warnings. Please re-enable for inference!\n",
+ "trainer.train()"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "Duak7T_B3VpJ"
+ },
+ "source": [
+ "## Share adapters on the 🤗 Hub"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 331,
+ "referenced_widgets": [
+ "262f01ffc5824b5faa8a61afac12ff67",
+ "c1af10b599da43a3a848f3ba816d7acc",
+ "be673691e713472980fa1132465714b4",
+ "01f8b90f0f184dfdb92c0c3bffb28b0f",
+ "9ad2bd0e92174d339a3a91a38253a180",
+ "bff17ef6aabd4aa681bfd5ad64b808d9",
+ "55633800b60a4336abea6a4adfcfdec1",
+ "73d5c6b4034d49b392b103d889bfb3b4",
+ "a55954b8d7bf4057b0d7aa6a1cb9e91a",
+ "4da42eb3846f423d88e2a6462a0cfce8",
+ "dab39ef354a84be3b37b6f151f9d9b9d",
+ "b88b03326f464c96a5656eef774e36d5",
+ "4eccb670e98043b3b2702821a3060ece",
+ "a333501a50df4b9fa9546d8d965e0dc3",
+ "1f173cb95c5c44f4b32f6cfe10ee3b03",
+ "52c8a7e673f24276a07042388a13b58f",
+ "a0f323ccfbc14fc4b7a5e7046b221ce3"
+ ]
+ },
+ "id": "DpYr24pR8T_0",
+ "outputId": "20186456-1bd4-4655-b2f2-8f24f9f37fcc"
+ },
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "Token is valid.\n",
+ "Your token has been saved to /root/.cache/huggingface/token\n",
+ "Login successful\n"
+ ]
+ }
+ ],
+ "source": [
+ "from huggingface_hub import notebook_login\n",
+ "\n",
+ "notebook_login()"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 133,
+ "referenced_widgets": [
+ "3dbe077ed0c34e4eb1628418138ccbc6",
+ "a579cb7804774ca3aa9efd800d1af57e",
+ "9f44e3175835470aba43e239661037b2",
+ "549bd12e3af64256a7534903688835a8",
+ "a18d9beb34b848ff8cc541d2cb290c4c",
+ "876cb42184f54b749c442163290c2c45",
+ "43b14e0e1263499dbd592b280cff21b0",
+ "7164feaf360d4300a5083f95064b144a",
+ "bd7547126a874a45b608afed7ab2958b",
+ "26e4b6b94e4540728c59df8e481ce43d",
+ "9d1b77500f1c45308d4791a9c443e307",
+ "b2693135b6954d35afb3120f3caf4000",
+ "aeca2429ee48450a814515cb06acbc3e",
+ "434c09950be04d728cd7ca8d6c134dc6",
+ "34f58c132d2e4249b1e62a0b57c85999",
+ "d148369be26a43949257790cb202728d",
+ "0ecf58c5cbcd40908595fccddff1c6d4",
+ "fc2314656a2745eb921f636cc3451381",
+ "7817f8669b7f449fadf02d7145fa89e2",
+ "06e012eea9714ed589344a362b7421bb",
+ "504e9e5ced0348cc87aafae0c1c372eb",
+ "5b538e8389fb4574a5dfdc554624e3c8"
+ ]
+ },
+ "id": "VxB6UV5XAvvP",
+ "outputId": "c3b0133b-f5b1-4283-8367-f06524bea46c"
+ },
+ "outputs": [
+ {
+ "name": "stderr",
+ "output_type": "stream",
+ "text": [
+ "Uploading the following files to ybelkada/opt-6.7b-lora: adapter_config.json,adapter_model.bin\n"
+ ]
+ },
+ {
+ "data": {
+ "application/vnd.jupyter.widget-view+json": {
+ "model_id": "3dbe077ed0c34e4eb1628418138ccbc6",
+ "version_major": 2,
+ "version_minor": 0
+ },
+ "text/plain": [
+ "Upload 1 LFS files: 0%| | 0/1 [00:00Pro Tip: If you don't already have one, you can create a dedicated\n'notebooks' token with 'write' access, that you can then easily reuse for all\nnotebooks. "
+ }
+ },
+ "c006e62ee6d04831b2b89273ef04a8ac": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_9e5f870ef80242f5af09fad70f84ea62",
+ "placeholder": "",
+ "style": "IPY_MODEL_6f173ca73dd545deb22b8cd0470d925f",
+ "value": " 685/685 [00:00<00:00, 34.4kB/s]"
+ }
+ },
+ "c1af10b599da43a3a848f3ba816d7acc": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_73d5c6b4034d49b392b103d889bfb3b4",
+ "placeholder": "",
+ "style": "IPY_MODEL_a55954b8d7bf4057b0d7aa6a1cb9e91a",
+ "value": "
Copy a token from your Hugging Face\ntokens page and paste it below.
Immediately click login after copying\nyour token or it might be stored in plain text in this notebook file. "
+ }
+ },
+ "c1fd6a1234274a44b838a09f3f5380c6": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "c2302f535b114ad780bfa440445c2e28": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "c2b42681b8bb47e3895d6105240c5812": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "c41a9d785e884ab0a58117d17ac7d228": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "c423a3cc0b504828b11077c77268ed92": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "c4ab408eb1344da0bb15a9a6760818e4": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "c5493c23fd5542738ffd1ff5f09a6a67": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_00c2e2d3ee8b45818ba84da12c6b11e2",
+ "placeholder": "",
+ "style": "IPY_MODEL_6ccea64c2e614a9fbdcc2f716cecaea0",
+ "value": "Downloading (…)cial_tokens_map.json: 100%"
+ }
+ },
+ "c57c7cf35bf04f3bb3b2b0d8ce7feb31": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "c6f712eadc4d49019b2bd355968cc155": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_5fd979c05fd34311af877ce1a988ead8",
+ "IPY_MODEL_179165ff4c0e4586aaf3a40b8502f428",
+ "IPY_MODEL_cad1d8326e474a4f9ee13db9005121dd"
+ ],
+ "layout": "IPY_MODEL_b049ac0b3d2e44ba9b1fc1cb2dd3de62"
+ }
+ },
+ "c7621e14aa16421d9758321e433b92e4": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "c81d20fe47ce4b7594427830d71504d7": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_a14542c8431c48b48a614cfd0d41f03c",
+ "IPY_MODEL_856f3dcf949741acb394f252186a1d7e",
+ "IPY_MODEL_865bae11c917492a9a1ef7286a493bd5"
+ ],
+ "layout": "IPY_MODEL_2561b7a7c1694f229d30d2b1eeb14b2f"
+ }
+ },
+ "c9b718882fec4254bce1f33fa9373921": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "FloatProgressModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "FloatProgressModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "ProgressView",
+ "bar_style": "success",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_4884bf82f5814e049c47cf6d496aab08",
+ "max": 1,
+ "min": 0,
+ "orientation": "horizontal",
+ "style": "IPY_MODEL_432fc8277ebc492f91d6b46ed073ccb4",
+ "value": 1
+ }
+ },
+ "cad1d8326e474a4f9ee13db9005121dd": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_451309d8b3ca4cd9b6f538640477039e",
+ "placeholder": "",
+ "style": "IPY_MODEL_c7621e14aa16421d9758321e433b92e4",
+ "value": " 9.96G/9.96G [03:05<00:00, 63.7MB/s]"
+ }
+ },
+ "cb69ae47666a4603a07a8778e2ae7d6e": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "cbe2a6ea41834e95a27d6f02c3c0eeec": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_23d2ad64a17041b7a006dad1e041e0a1",
+ "placeholder": "",
+ "style": "IPY_MODEL_c1fd6a1234274a44b838a09f3f5380c6",
+ "value": "Downloading (…)olve/main/vocab.json: 100%"
+ }
+ },
+ "ce6de6f9ddde4a6d8094a2b96eac3a4e": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "ce8d4bac782949579a2e52864455d9de": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "cf39fb025e3d4635a5695135a56d9f64": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_5b695486a0ac442b8b6a8ef2ebf4e57a",
+ "placeholder": "",
+ "style": "IPY_MODEL_03be7cb91cba4afab795aab7aa242ee1",
+ "value": "Downloading (…)00002-of-00002.bin";: 100%"
+ }
+ },
+ "d148369be26a43949257790cb202728d": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "d3511ce1754b41969e5c36a5b33ac466": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "d46b5725c35142a89617e46c0e8d3679": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_c5493c23fd5542738ffd1ff5f09a6a67",
+ "IPY_MODEL_a1a80d3460984c2496ada5a634875934",
+ "IPY_MODEL_598c5584ffba4f26815c4e87bb1595c4"
+ ],
+ "layout": "IPY_MODEL_fe93f25323604447be0bb1d24a0c2c59"
+ }
+ },
+ "d4de260ffd8a440eb87eb900fc1bb1d3": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_8602b545a9f8474dbb3cc178ac0b8e60",
+ "IPY_MODEL_b46919912ee54f6f9f2ce9080be1c61a",
+ "IPY_MODEL_50374e3ab81c4626a182e61fc03b94ce"
+ ],
+ "layout": "IPY_MODEL_2144bc2897dc40b29f060e30ace12275"
+ }
+ },
+ "d4f5b19f75e246df9c688f625792e8ba": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "FloatProgressModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "FloatProgressModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "ProgressView",
+ "bar_style": "success",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_a6ce291698ad460394433a49000c1d25",
+ "max": 646739,
+ "min": 0,
+ "orientation": "horizontal",
+ "style": "IPY_MODEL_aa54b2a9b43848b0902d135beffb806b",
+ "value": 646739
+ }
+ },
+ "d54e8d69575f49eb977da64abc5ceb0c": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "d5bb8d7359274c8e9cc79df563175137": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "d72bd17e161442b0979dceaaef66d82c": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "FloatProgressModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "FloatProgressModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "ProgressView",
+ "bar_style": "success",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_4f592d7632fd440aac0bf97ceed2de75",
+ "max": 33601485,
+ "min": 0,
+ "orientation": "horizontal",
+ "style": "IPY_MODEL_1b515483e5884479b2101127c16321d4",
+ "value": 33601485
+ }
+ },
+ "d7e33c29d410414eb452d121edd9920e": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "d9d36f8ff5f747bf90fbc8a7d35a6664": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "da946f86590447d2ab98b9da468fa66b": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "dab39ef354a84be3b37b6f151f9d9b9d": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "dc08d237860e4788a8ceeff4518c2612": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "ddc333530c13446a91cf332846bfa22f": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_d7e33c29d410414eb452d121edd9920e",
+ "placeholder": "",
+ "style": "IPY_MODEL_d3511ce1754b41969e5c36a5b33ac466",
+ "value": " 0/0 [00:00<?, ? examples/s]"
+ }
+ },
+ "ddc36fdbdd634dc489f658bead61e7ee": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "deaf9732f33446a3be015d2ec16aba76": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "FloatProgressModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "FloatProgressModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "ProgressView",
+ "bar_style": "success",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_8f7890f54d514f80b1eb17905cf0f964",
+ "max": 3356360185,
+ "min": 0,
+ "orientation": "horizontal",
+ "style": "IPY_MODEL_ae660d51267544a89f0ad199cc12b6fa",
+ "value": 3356360185
+ }
+ },
+ "e1f62cbd805d4b8aa9aba7e345c21c82": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "e3df9dda16e244aa9b61d54f9e21ef40": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "e466054f08004bbcabb24e400cb3c7fc": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "FloatProgressModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "FloatProgressModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "ProgressView",
+ "bar_style": "success",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_4ea667f48b9f4e1f9da7c5a0d3025b85",
+ "max": 41937,
+ "min": 0,
+ "orientation": "horizontal",
+ "style": "IPY_MODEL_9b96c63630654773acd38b8b88371f28",
+ "value": 41937
+ }
+ },
+ "e73e5388182040a8937ccf1748171a87": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_f797f7b8b13f4b3cb871522d34498631",
+ "IPY_MODEL_41f47c864e094cacb1c550d37ddfe80e",
+ "IPY_MODEL_104d982b444947fe8e4fbb2c2f082616"
+ ],
+ "layout": "IPY_MODEL_2cf8581583c641fb95d1e16aff7d4cd1"
+ }
+ },
+ "e9673363e85448d494ac9ac5d7ba0efb": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "ed2736d862a94d8f9db9ba6037016071": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "FloatProgressModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "FloatProgressModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "ProgressView",
+ "bar_style": "info",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_3185bd8ecbde4f26b8ed0f92cf79e14f",
+ "max": 1,
+ "min": 0,
+ "orientation": "horizontal",
+ "style": "IPY_MODEL_ddc36fdbdd634dc489f658bead61e7ee",
+ "value": 1
+ }
+ },
+ "ed8fa1048e814f2fa3666899fc42e55a": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "f00cbc4a89f5492787ec489da65ff70b": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "f27905d0073e493cb9dcd174c0f15e35": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_c423a3cc0b504828b11077c77268ed92",
+ "placeholder": "",
+ "style": "IPY_MODEL_668dd47eec9942bcad0af209772cf8e6",
+ "value": " 1/1 [00:00<00:00, 9.58it/s]"
+ }
+ },
+ "f357166c6e5f43f39d0a287ca6d6f60e": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_805a10c2fd794ff692e8ebeefd65f2eb",
+ "IPY_MODEL_3730f843399d4ba48e98383563283e94",
+ "IPY_MODEL_f855aced7ca2485ea720604359deaa18"
+ ],
+ "layout": "IPY_MODEL_6d728366de1a4bacb1ba1939c5e0146f"
+ }
+ },
+ "f51c7f18977447e2bca36e1da3e1be4f": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "f539b7a4665449de9eac209a20629969": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "f65af2e868244edeb0cc9402534874a8": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_1bd5179cdb474b65aa06eca3520ad37b",
+ "placeholder": "",
+ "style": "IPY_MODEL_04d367124a3b419ab1fa1dfd4f9004c3",
+ "value": "Downloading (…)model.bin.index.json: 100%"
+ }
+ },
+ "f797f7b8b13f4b3cb871522d34498631": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_11808e9097424dd0b22a5af6c77813f3",
+ "placeholder": "",
+ "style": "IPY_MODEL_dc08d237860e4788a8ceeff4518c2612",
+ "value": "Loading checkpoint shards: 100%"
+ }
+ },
+ "f855aced7ca2485ea720604359deaa18": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_49504531deaf4449938bea751d1ec4e7",
+ "placeholder": "",
+ "style": "IPY_MODEL_7dfe540a75864cf390b3bed20ab1dcd9",
+ "value": " 5.55k/5.55k [00:00<00:00, 156kB/s]"
+ }
+ },
+ "fad61c68edc84c8197afeafded84280d": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "faf24b3ed994422f8dd806ae0cc30531": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_86dff0987bf040da99c8f2846da26d86",
+ "placeholder": "",
+ "style": "IPY_MODEL_63f8ad255d2147128bdc26f47fdf2528",
+ "value": " 3/3 [00:02<00:00, 1.18ba/s]"
+ }
+ },
+ "fc15c6d6eb3049a3b8542b332dd8a3f2": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "fc2314656a2745eb921f636cc3451381": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "fc2d5ffe254d425b939252ec46ec27cc": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_f65af2e868244edeb0cc9402534874a8",
+ "IPY_MODEL_e466054f08004bbcabb24e400cb3c7fc",
+ "IPY_MODEL_6ea40800dfd849e3b106bae71fc53ae3"
+ ],
+ "layout": "IPY_MODEL_722a01f42b7d4c38836a4546ecb38108"
+ }
+ },
+ "fe93f25323604447be0bb1d24a0c2c59": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "ff2454cf69b346fea70070522cf93689": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_87b36eb4ad3b4047a32c7d67a5aabc5e",
+ "IPY_MODEL_8bf9fd4bd28e4bc1b5895bc9315e727e",
+ "IPY_MODEL_01845549768a4db580b5555809e83342"
+ ],
+ "layout": "IPY_MODEL_a490025901df478f93be1f19c1be4b09"
+ }
+ }
+ }
+ }
+ },
+ "nbformat": 4,
+ "nbformat_minor": 0
+}
diff --git a/peft/examples/int8_training/config.yaml b/peft/examples/int8_training/config.yaml
new file mode 100644
index 0000000000000000000000000000000000000000..c5d87a578372648e677ce66828e35aec5b49e9e5
--- /dev/null
+++ b/peft/examples/int8_training/config.yaml
@@ -0,0 +1,19 @@
+compute_environment: LOCAL_MACHINE
+debug: false
+distributed_type: MULTI_XPU
+downcast_bf16: 'no'
+enable_cpu_affinity: false
+gpu_ids: all
+ipex_config:
+ ipex: false
+machine_rank: 0
+main_training_function: main
+mixed_precision: 'no'
+num_machines: 1
+num_processes: 4
+rdzv_backend: static
+same_network: true
+tpu_env: []
+tpu_use_cluster: false
+tpu_use_sudo: false
+use_cpu: false
diff --git a/peft/examples/int8_training/fine_tune_blip2_int8.py b/peft/examples/int8_training/fine_tune_blip2_int8.py
new file mode 100644
index 0000000000000000000000000000000000000000..1b67013783a0721b2bac5d53d8ba22aec82043c4
--- /dev/null
+++ b/peft/examples/int8_training/fine_tune_blip2_int8.py
@@ -0,0 +1,104 @@
+# Copyright 2023-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+import torch
+from datasets import load_dataset
+from torch.utils.data import DataLoader, Dataset
+from transformers import AutoModelForVision2Seq, AutoProcessor, BitsAndBytesConfig
+
+from peft import LoraConfig, get_peft_model
+
+
+# Let's define the LoraConfig
+config = LoraConfig(
+ r=16,
+ lora_alpha=32,
+ lora_dropout=0.05,
+ bias="none",
+)
+
+# We load our model and processor using `transformers`
+model = AutoModelForVision2Seq.from_pretrained(
+ "Salesforce/blip2-opt-2.7b", quantization_config=BitsAndBytesConfig(load_in_8bit=True)
+)
+processor = AutoProcessor.from_pretrained("Salesforce/blip2-opt-2.7b")
+
+# Get our peft model and print the number of trainable parameters
+model = get_peft_model(model, config)
+model.print_trainable_parameters()
+
+# Let's load the dataset here!
+dataset = load_dataset("ybelkada/football-dataset", split="train")
+
+
+class ImageCaptioningDataset(Dataset):
+ def __init__(self, dataset, processor):
+ self.dataset = dataset
+ self.processor = processor
+
+ def __len__(self):
+ return len(self.dataset)
+
+ def __getitem__(self, idx):
+ item = self.dataset[idx]
+ encoding = self.processor(images=item["image"], padding="max_length", return_tensors="pt")
+ # remove batch dimension
+ encoding = {k: v.squeeze() for k, v in encoding.items()}
+ encoding["text"] = item["text"]
+ return encoding
+
+
+def collator(batch):
+ # pad the input_ids and attention_mask
+ processed_batch = {}
+ for key in batch[0].keys():
+ if key != "text":
+ processed_batch[key] = torch.stack([example[key] for example in batch])
+ else:
+ text_inputs = processor.tokenizer(
+ [example["text"] for example in batch], padding=True, return_tensors="pt"
+ )
+ processed_batch["input_ids"] = text_inputs["input_ids"]
+ processed_batch["attention_mask"] = text_inputs["attention_mask"]
+ return processed_batch
+
+
+train_dataset = ImageCaptioningDataset(dataset, processor)
+train_dataloader = DataLoader(train_dataset, shuffle=True, batch_size=2, collate_fn=collator)
+
+optimizer = torch.optim.AdamW(model.parameters(), lr=5e-5)
+
+device = torch.accelerator.current_accelerator().type if hasattr(torch, "accelerator") else "cuda"
+
+model.train()
+
+for epoch in range(50):
+ print("Epoch:", epoch)
+ for idx, batch in enumerate(train_dataloader):
+ input_ids = batch.pop("input_ids").to(device)
+ pixel_values = batch.pop("pixel_values").to(device, torch.float16)
+
+ outputs = model(input_ids=input_ids, pixel_values=pixel_values, labels=input_ids)
+
+ loss = outputs.loss
+
+ print("Loss:", loss.item())
+
+ loss.backward()
+
+ optimizer.step()
+ optimizer.zero_grad()
+
+ if idx % 10 == 0:
+ generated_output = model.generate(pixel_values=pixel_values)
+ print(processor.batch_decode(generated_output, skip_special_tokens=True))
diff --git a/peft/examples/int8_training/peft_adalora_whisper_large_training.py b/peft/examples/int8_training/peft_adalora_whisper_large_training.py
new file mode 100644
index 0000000000000000000000000000000000000000..3e2b07d7b5a03aef58ef2b2a37336ff54329f5b5
--- /dev/null
+++ b/peft/examples/int8_training/peft_adalora_whisper_large_training.py
@@ -0,0 +1,817 @@
+import argparse
+import gc
+import json
+import logging
+import math
+import os
+from dataclasses import dataclass
+from datetime import datetime
+from pathlib import Path
+from random import randint
+from typing import Any, Union
+
+# datasets imports
+import datasets
+
+# metric imports
+import evaluate
+import numpy as np
+import torch
+import transformers
+import wandb
+
+# accelerate imports
+from accelerate import Accelerator, dispatch_model
+from accelerate.logging import get_logger
+from datasets import Audio, DatasetDict, IterableDatasetDict, interleave_datasets, load_dataset
+
+# hf imports
+from huggingface_hub import HfApi
+from torch.utils.data import DataLoader
+from tqdm import tqdm
+from transformers import (
+ BitsAndBytesConfig,
+ SchedulerType,
+ WhisperForConditionalGeneration,
+ WhisperProcessor,
+ get_scheduler,
+ set_seed,
+)
+from transformers.models.whisper.english_normalizer import BasicTextNormalizer
+
+# peft imports
+from peft import AdaLoraConfig, LoraConfig, PeftModel, get_peft_model
+
+
+logger = get_logger(__name__, log_level="INFO")
+
+
+def parse_args():
+ parser = argparse.ArgumentParser(description="Whisper Fine-Tuning with AdaLora")
+ parser.add_argument(
+ "--model_name_or_path",
+ type=str,
+ help="Path to pretrained model or model identifier from huggingface.co/models.",
+ required=True,
+ )
+ parser.add_argument("--language", type=str, help="Language to use for training; e.g., 'Hindi' ", required=True)
+ parser.add_argument("--language_abbr", type=str, help="Language to use for training; e.g., 'hi' ", required=True)
+ parser.add_argument(
+ "--task", type=str, default="transcribe", help="Task to use for training; e.g., 'transcribe' ", required=False
+ )
+ parser.add_argument(
+ "--dataset_name",
+ type=str,
+ default="mozilla-foundation/common_voice_11_0",
+ help="Dataset to use for training; e.g., 'whisper' ",
+ required=False,
+ )
+ parser.add_argument(
+ "--dataset_in_streaming_mode",
+ action="store_true",
+ help="Whether to use streaming mode for the dataset.",
+ )
+ parser.add_argument(
+ "--do_lower_case", action="store_true", help="lowercase the transcribed text before tokenizing"
+ )
+ parser.add_argument(
+ "--do_remove_punctuation", action="store_true", help="remove punctuation from the transcribed text"
+ )
+ parser.add_argument("--push_to_hub", action="store_true", help="Whether or not to push the model to the Hub.")
+ parser.add_argument(
+ "--overwrite_cache", type=bool, default=False, help="Overwrite the cached training and evaluation sets"
+ )
+ parser.add_argument("--max_audio_input_length", type=float, default=30.0, help="Maximum audio length in seconds.")
+ parser.add_argument(
+ "--preprocessing_num_workers",
+ type=int,
+ default=None,
+ help="The number of processes to use for the preprocessing.",
+ )
+ parser.add_argument(
+ "--per_device_train_batch_size",
+ type=int,
+ default=8,
+ help="Batch size (per device) for the training dataloader.",
+ )
+ parser.add_argument(
+ "--per_device_eval_batch_size",
+ type=int,
+ default=8,
+ help="Batch size (per device) for the evaluation dataloader.",
+ )
+ parser.add_argument(
+ "--buffer_size",
+ type=int,
+ default=5000,
+ help="Number of samples to prefetch in the streaming mode.",
+ )
+ parser.add_argument(
+ "--dataloader_pin_memory",
+ action="store_true",
+ help="Whether or not to pin memory for the DataLoader.",
+ )
+ parser.add_argument(
+ "--dataloader_num_workers",
+ type=int,
+ default=0,
+ help="Number of subprocesses to use for data loading.",
+ )
+ parser.add_argument(
+ "--learning_rate",
+ type=float,
+ default=5e-5,
+ help="Initial learning rate (after the potential warmup period) to use.",
+ )
+ parser.add_argument("--weight_decay", type=float, default=0.0, help="Weight decay to use.")
+ parser.add_argument("--num_train_epochs", type=int, default=3, help="Total number of training epochs to perform.")
+ parser.add_argument(
+ "--max_train_steps",
+ type=int,
+ default=None,
+ help="Total number of training steps to perform. If provided, overrides num_train_epochs.",
+ )
+ parser.add_argument(
+ "--gradient_accumulation_steps",
+ type=int,
+ default=1,
+ help="Number of updates steps to accumulate before performing a backward/update pass.",
+ )
+ parser.add_argument(
+ "--lr_scheduler_type",
+ type=SchedulerType,
+ default="linear",
+ help="The scheduler type to use.",
+ choices=["linear", "cosine", "cosine_with_restarts", "polynomial", "constant", "constant_with_warmup"],
+ )
+ parser.add_argument(
+ "--num_warmup_steps", type=int, default=0, help="Number of steps for the warmup in the lr scheduler."
+ )
+ parser.add_argument("--output_dir", type=str, default=None, help="Where to store the final model.")
+ parser.add_argument("--seed", type=int, default=None, help="A seed for reproducible training.")
+ parser.add_argument(
+ "--load_best_model",
+ action="store_true",
+ help="Whether to load the best model at the end of training",
+ )
+ parser.add_argument(
+ "--with_tracking",
+ action="store_true",
+ help="Whether to enable experiment trackers for logging.",
+ )
+ parser.add_argument(
+ "--report_to",
+ type=str,
+ default="all",
+ help=(
+ 'The integration to report the results and logs to. Supported platforms are `"tensorboard"`,'
+ ' `"wandb"` and `"comet_ml"`. Use `"all"` (default) to report to all integrations.'
+ "Only applicable when `--with_tracking` is passed."
+ ),
+ )
+ parser.add_argument("--hub_token", type=str, help="The token to use to push to the Model Hub.")
+ parser.add_argument(
+ "--hub_model_id", type=str, help="The name of the repository to keep in sync with the local `output_dir`."
+ )
+ parser.add_argument(
+ "--checkpointing_steps",
+ type=int,
+ default=500,
+ help="Whether the various states should be saved at the end of every n steps, or 'epoch' for each epoch.",
+ )
+ parser.add_argument(
+ "--logging_steps",
+ type=int,
+ default=100,
+ help="Whether the various states should be saved at the end of every n steps, or 'epoch' for each epoch.",
+ )
+ parser.add_argument(
+ "--evaluation_steps",
+ type=int,
+ default=500,
+ help="Whether the various states should be saved at the end of every n steps, or 'epoch' for each epoch.",
+ )
+ parser.add_argument(
+ "--resume_from_checkpoint",
+ type=str,
+ default=None,
+ help="If the training should continue from a checkpoint folder.",
+ )
+
+ # lora/adalora specific args
+ parser.add_argument(
+ "--use_peft",
+ action="store_true",
+ help="Whether to use PEFT",
+ )
+ parser.add_argument(
+ "--use_adalora",
+ action="store_true",
+ help="Whether to use AdaLoRA or LoRA. If set, uses AdaLoRA instead of the default LoRA.",
+ )
+ parser.add_argument(
+ "--init_r",
+ type=int,
+ default=12,
+ help="Initial AdaLoRA rank",
+ )
+ parser.add_argument(
+ "--target_r",
+ type=int,
+ default=4,
+ help="Target AdaLoRA rank",
+ )
+ parser.add_argument(
+ "--tinit",
+ type=int,
+ default=200,
+ help="number of warmup steps for AdaLoRA wherein no pruning is performed",
+ )
+ parser.add_argument(
+ "--tfinal",
+ type=int,
+ default=1000,
+ help=" fix the resulting budget distribution and fine-tune the model for tfinal steps when using AdaLoRA ",
+ )
+ parser.add_argument(
+ "--delta_t",
+ type=int,
+ default=10,
+ help="interval of steps for AdaLoRA to update rank",
+ )
+ parser.add_argument(
+ "--lora_alpha",
+ type=int,
+ default=32,
+ help="LORA alpha",
+ )
+ parser.add_argument(
+ "--r",
+ type=int,
+ default=8,
+ help="LORA rank",
+ )
+ parser.add_argument(
+ "--lora_dropout",
+ type=float,
+ default=0.1,
+ help="LORA dropout",
+ )
+ parser.add_argument(
+ "--orth_reg_weight",
+ type=float,
+ default=0.5,
+ help="Orthogonal regularization weight",
+ )
+ parser.add_argument(
+ "--debug_mode",
+ action="store_true",
+ help="Whether to use debug mode",
+ )
+
+ args = parser.parse_args()
+
+ if args.push_to_hub:
+ assert args.output_dir is not None, "Need an `output_dir` to create a repo when `--push_to_hub` is passed."
+
+ return args
+
+
+def load_streaming_dataset(dataset_name, dataset_config_name, split, **kwargs):
+ if "+" in split:
+ # load multiple splits separated by the `+` symbol *with* streaming mode
+ dataset_splits = [
+ load_dataset(dataset_name, dataset_config_name, split=split_name, streaming=True, **kwargs)
+ for split_name in split.split("+")
+ ]
+ # interleave multiple splits to form one dataset
+ interleaved_dataset = interleave_datasets(dataset_splits)
+ return interleaved_dataset
+ else:
+ # load a single split *with* streaming mode
+ dataset = load_dataset(dataset_name, dataset_config_name, split=split, streaming=True, **kwargs)
+ return dataset
+
+
+def prepare_dataset_wrapper(do_lower_case, do_remove_punctuation, processor, normalizer):
+ def prepare_dataset(batch):
+ # load and (possibly) resample audio data to 16kHz
+ audio = batch["audio"]
+
+ # compute log-Mel input features from input audio array
+ batch["input_features"] = processor.feature_extractor(
+ audio["array"], sampling_rate=audio["sampling_rate"]
+ ).input_features[0]
+ # compute input length of audio sample in seconds
+ batch["input_length"] = len(audio["array"]) / audio["sampling_rate"]
+
+ # optional pre-processing steps
+ transcription = batch["sentence"]
+ if do_lower_case:
+ transcription = transcription.lower()
+ if do_remove_punctuation:
+ transcription = normalizer(transcription).strip()
+
+ # encode target text to label ids
+ batch["labels"] = processor.tokenizer(transcription).input_ids
+ return batch
+
+ return prepare_dataset
+
+
+def save_model_hook(models, weights, output_dir):
+ for model in models:
+ model.save_pretrained(output_dir)
+ # make sure to pop weight so that corresponding model is not saved again
+ weights.pop()
+
+
+def load_model_hook(models, input_dir):
+ while len(models) > 0:
+ model = models.pop()
+ # pop models so that they are not loaded again
+ PeftModel.from_pretrained(model.base_model.model, input_dir)
+
+
+@dataclass
+class DataCollatorSpeechSeq2SeqWithPadding:
+ processor: Any
+
+ def __call__(self, features: list[dict[str, Union[list[int], torch.Tensor]]]) -> dict[str, torch.Tensor]:
+ # split inputs and labels since they have to be of different lengths and need different padding methods
+ # first treat the audio inputs by simply returning torch tensors
+ input_features = [{"input_features": feature["input_features"]} for feature in features]
+ batch = self.processor.feature_extractor.pad(input_features, return_tensors="pt")
+
+ # get the tokenized label sequences
+ label_features = [{"input_ids": feature["labels"]} for feature in features]
+ # pad the labels to max length
+ labels_batch = self.processor.tokenizer.pad(label_features, return_tensors="pt")
+
+ # replace padding with -100 to ignore loss correctly
+ labels = labels_batch["input_ids"].masked_fill(labels_batch.attention_mask.ne(1), -100)
+
+ # if bos token is appended in previous tokenization step,
+ # cut bos token here as it's append later anyways
+ if (labels[:, 0] == self.processor.tokenizer.bos_token_id).all().cpu().item():
+ labels = labels[:, 1:]
+
+ batch["labels"] = labels
+
+ return batch
+
+
+def get_audio_length_processor(max_input_length):
+ def is_audio_in_length_range(length):
+ return length < max_input_length
+
+ return is_audio_in_length_range
+
+
+def evaluation_loop(model, eval_dataloader, processor, normalizer, metric, forced_decoder_ids, accelerator):
+ model.eval()
+ predictions = []
+ references = []
+ normalized_predictions = []
+ normalized_references = []
+ device_type = torch.accelerator.current_accelerator().type if hasattr(torch, "accelerator") else "cuda"
+ for _, batch in enumerate(tqdm(eval_dataloader)):
+ with torch.amp.autocast(device_type=device_type):
+ with torch.no_grad():
+ generated_tokens = (
+ model.generate(
+ input_features=batch["input_features"],
+ forced_decoder_ids=forced_decoder_ids,
+ max_new_tokens=255,
+ )
+ .cpu()
+ .numpy()
+ )
+ labels = batch["labels"].cpu().numpy()
+ labels = np.where(labels != -100, labels, processor.tokenizer.pad_token_id)
+ decoded_preds = processor.tokenizer.batch_decode(generated_tokens, skip_special_tokens=True)
+ decoded_labels = processor.tokenizer.batch_decode(labels, skip_special_tokens=True)
+ predictions.extend(decoded_preds)
+ references.extend(decoded_labels)
+ normalized_predictions.extend([normalizer(pred).strip() for pred in decoded_preds])
+ normalized_references.extend([normalizer(label).strip() for label in decoded_labels])
+ del generated_tokens, labels, batch
+ gc.collect()
+ wer = 100 * metric.compute(predictions=predictions, references=references)
+ normalized_wer = 100 * metric.compute(predictions=normalized_predictions, references=normalized_references)
+ eval_metrics = {"eval/wer": wer, "eval/normalized_wer": normalized_wer}
+ if accelerator.get_tracker("wandb"):
+ sample_size = min(len(predictions), 256)
+ ids = [randint(0, len(predictions) - 1) for p in range(0, sample_size)]
+ sample_predictions = [predictions[i] for i in ids]
+ sample_references = [references[i] for i in ids]
+ sample_normalized_predictions = [normalized_predictions[i] for i in ids]
+ sample_normalized_references = [normalized_references[i] for i in ids]
+ table_rows = [
+ list(r)
+ for r in zip(
+ sample_predictions, sample_references, sample_normalized_predictions, sample_normalized_references
+ )
+ ]
+ eval_metrics["eval_samples"] = wandb.Table(
+ columns=["predictions", "references", "normalized_predictions", "normalized_references"],
+ rows=table_rows,
+ )
+ return eval_metrics
+
+
+def main():
+ args = parse_args()
+
+ accelerator_kwargs = {"gradient_accumulation_steps": args.gradient_accumulation_steps}
+ if args.with_tracking:
+ accelerator_kwargs["log_with"] = args.report_to
+ accelerator_kwargs["project_dir"] = args.output_dir
+ accelerator = Accelerator(**accelerator_kwargs)
+
+ # Make one log on every process with the configuration for debugging.
+ logging.basicConfig(
+ format="%(asctime)s - %(levelname)s - %(name)s - %(message)s",
+ datefmt="%m/%d/%Y %H:%M:%S",
+ level=logging.INFO,
+ )
+ logger.info(accelerator.state, main_process_only=False)
+ if accelerator.is_local_main_process:
+ datasets.utils.logging.set_verbosity_warning()
+ transformers.utils.logging.set_verbosity_info()
+ else:
+ datasets.utils.logging.set_verbosity_error()
+ transformers.utils.logging.set_verbosity_error()
+
+ # If passed along, set the training seed now.
+ if args.seed is not None:
+ set_seed(args.seed)
+
+ # Handle the repository creation
+ if accelerator.is_main_process:
+ if args.push_to_hub:
+ api = HfApi(token=args.hub_token)
+
+ # Create repo (repo_name from args or inferred)
+ repo_name = args.hub_model_id
+ if repo_name is None:
+ repo_name = Path(args.output_dir).absolute().name
+ repo_id = api.create_repo(repo_name, exist_ok=True).repo_id
+
+ with open(os.path.join(args.output_dir, ".gitignore"), "w+") as gitignore:
+ if "step_*" not in gitignore:
+ gitignore.write("step_*\n")
+ if "epoch_*" not in gitignore:
+ gitignore.write("epoch_*\n")
+ elif args.output_dir is not None:
+ os.makedirs(args.output_dir, exist_ok=True)
+ accelerator.wait_for_everyone()
+
+ # load dataset either in streaming mode or not
+ processor = WhisperProcessor.from_pretrained(args.model_name_or_path, language=args.language, task=args.task)
+ normalizer = BasicTextNormalizer()
+ prepare_dataset = prepare_dataset_wrapper(args.do_lower_case, args.do_remove_punctuation, processor, normalizer)
+ is_audio_in_length_range = get_audio_length_processor(args.max_audio_input_length)
+ data_collator = DataCollatorSpeechSeq2SeqWithPadding(processor=processor)
+
+ if args.dataset_in_streaming_mode:
+ raw_datasets = IterableDatasetDict()
+ loading_method = load_streaming_dataset
+ else:
+ raw_datasets = DatasetDict()
+ loading_method = load_dataset
+
+ if args.debug_mode:
+ train_split = "train[:100]"
+ test_split = "test[:10]"
+ else:
+ train_split = "train+validation"
+ test_split = "test"
+
+ raw_datasets["train"] = loading_method(args.dataset_name, args.language_abbr, split=train_split)
+ raw_datasets["test"] = loading_method(args.dataset_name, args.language_abbr, split=test_split)
+ raw_datasets = raw_datasets.cast_column("audio", Audio(sampling_rate=16000))
+
+ logger.info("Dataset loaded: %s", raw_datasets)
+ logger.info(f"{raw_datasets['train'][0]}")
+
+ vectorized_datasets = raw_datasets.map(
+ prepare_dataset,
+ remove_columns=list(next(iter(raw_datasets.values())).features),
+ num_proc=args.preprocessing_num_workers,
+ ).with_format("torch")
+
+ if args.dataset_in_streaming_mode:
+ vectorized_datasets["train"] = vectorized_datasets["train"].shuffle(
+ buffer_size=args.buffer_size,
+ seed=args.seed,
+ )
+
+ # filter out audio files that are too long from the training set
+ is_audio_in_length_range = get_audio_length_processor(args.max_audio_input_length)
+ vectorized_datasets["train"] = vectorized_datasets["train"].filter(
+ is_audio_in_length_range, input_columns=["input_length"]
+ )
+
+ # get dataloaders
+ train_dataloader = DataLoader(
+ vectorized_datasets["train"],
+ batch_size=args.per_device_train_batch_size,
+ shuffle=True,
+ collate_fn=data_collator,
+ num_workers=args.dataloader_num_workers,
+ pin_memory=args.dataloader_pin_memory,
+ )
+ eval_dataloader = DataLoader(
+ vectorized_datasets["test"],
+ batch_size=args.per_device_eval_batch_size,
+ collate_fn=data_collator,
+ num_workers=args.dataloader_num_workers,
+ pin_memory=args.dataloader_pin_memory,
+ )
+
+ # metric
+ metric = evaluate.load("wer")
+
+ # model
+ model = WhisperForConditionalGeneration.from_pretrained(
+ args.model_name_or_path, quantization_config=BitsAndBytesConfig(load_in_8bit=True)
+ )
+ model.config.forced_decoder_ids = None
+ model.config.suppress_tokens = []
+ if hasattr(model, "hf_device_map") and len(set(model.hf_device_map.values()).intersection({"cpu", "disk"})) > 0:
+ raise ValueError("Training on CPU or disk is not supported.")
+ if hasattr(model, "hf_device_map") and len(set(model.hf_device_map.values())) > 1:
+ device_map = model.hf_device_map.copy()
+ # required because `labels` are on main execution device (0) while the output of `proj_out` is on other device.
+ # So, this leads to device mismatch error when calculation cross-entropy between logits and labels.
+ # Won't arise during inference as `labels` aren't supplied during that time
+ # instead of changing device of one of the tied modules, I have to do this for all tied modules
+ # else the execution device of remaining tied modules isn't changed
+ device_map["model.decoder.embed_tokens"] = model._hf_hook.execution_device
+ device_map["model.decoder.embed_positions"] = model._hf_hook.execution_device
+ device_map["proj_out"] = model._hf_hook.execution_device
+ dispatch_model(model, device_map=device_map)
+
+ # preparing peft model
+ if args.use_peft:
+ from peft import prepare_model_for_kbit_training
+
+ model = prepare_model_for_kbit_training(model)
+
+ # as Whisper model uses Conv layer in encoder, checkpointing disables grad computation
+ # to avoid this, make the inputs trainable
+ def make_inputs_require_grad(module, input, output):
+ output.requires_grad_(True)
+
+ model.model.encoder.conv1.register_forward_hook(make_inputs_require_grad)
+
+ # Calculate total steps first for AdaLoRA
+ if args.max_train_steps is None:
+ num_update_steps_per_epoch = math.ceil(len(train_dataloader) / args.gradient_accumulation_steps)
+ total_steps = args.num_train_epochs * num_update_steps_per_epoch
+ else:
+ total_steps = args.max_train_steps
+
+ # wrapping model with adalora tuner
+ if args.use_adalora:
+ config = AdaLoraConfig(
+ init_r=args.init_r,
+ target_r=args.target_r,
+ beta1=0.85,
+ beta2=0.85,
+ tinit=args.tinit,
+ tfinal=args.tfinal,
+ deltaT=args.delta_t,
+ lora_alpha=args.lora_alpha,
+ lora_dropout=args.lora_dropout,
+ target_modules=["k_proj", "q_proj", "v_proj", "out_proj", "fc1", "fc2"],
+ orth_reg_weight=args.orth_reg_weight,
+ total_step=total_steps,
+ )
+ else:
+ config = LoraConfig(
+ r=args.r,
+ lora_alpha=args.lora_alpha,
+ target_modules=["q_proj", "v_proj"],
+ lora_dropout=args.lora_dropout,
+ )
+
+ model = get_peft_model(model, config)
+ model.print_trainable_parameters()
+
+ # optimizer
+ optimizer = torch.optim.AdamW(model.parameters(), lr=args.learning_rate, weight_decay=args.weight_decay)
+
+ if args.max_train_steps is None:
+ num_update_steps_per_epoch = math.ceil(len(train_dataloader) / args.gradient_accumulation_steps)
+ args.max_train_steps = args.num_train_epochs * num_update_steps_per_epoch
+ else:
+ args.num_train_epochs = math.ceil(args.max_train_steps / num_update_steps_per_epoch)
+
+ # scheduler
+ lr_scheduler = get_scheduler(
+ name=args.lr_scheduler_type,
+ optimizer=optimizer,
+ num_warmup_steps=args.num_warmup_steps,
+ num_training_steps=args.max_train_steps,
+ )
+
+ # Prepare everything with our `accelerator`.
+ model, optimizer, train_dataloader, eval_dataloader, lr_scheduler = accelerator.prepare(
+ model, optimizer, train_dataloader, eval_dataloader, lr_scheduler
+ )
+
+ accelerator.print(model)
+
+ # Note here that the max steps is adjusted by the accelerator's num_processes
+ args.max_train_steps = math.ceil(args.max_train_steps / accelerator.num_processes)
+ if args.use_peft and args.use_adalora:
+ # Update the total_step in the config to reflect the adjusted max_train_steps
+ # Handle DDP case where model is wrapped
+ if hasattr(model, "module"):
+ # DDP case
+ model.module.base_model.peft_config["default"].total_step = args.max_train_steps
+ else:
+ # Non-DDP case
+ model.base_model.peft_config["default"].total_step = args.max_train_steps
+
+ # We need to initialize the trackers we use, and also store our configuration.
+ # The trackers initializes automatically on the main process.
+ if args.with_tracking:
+ run_name = f"run-{datetime.now().strftime('%Y-%m-%d_%H-%M-%S')}"
+ experiment_config = vars(args)
+ # TensorBoard cannot log Enums, need the raw value
+ experiment_config["lr_scheduler_type"] = experiment_config["lr_scheduler_type"].value
+ accelerator.init_trackers(
+ "Whisper PEFT Fine-Tuning", config=experiment_config, init_kwargs={"wandb": {"name": run_name}}
+ )
+
+ # saving and loading checkpoints for resuming training
+ accelerator.register_save_state_pre_hook(save_model_hook)
+ accelerator.register_load_state_pre_hook(load_model_hook)
+
+ total_batch_size = args.per_device_train_batch_size * accelerator.num_processes * args.gradient_accumulation_steps
+ logger.info("***** Running training *****")
+ logger.info(f" Num Epochs = {args.num_train_epochs}")
+ logger.info(f" Instantaneous batch size per device = {args.per_device_train_batch_size}")
+ logger.info(f" Total train batch size (w. parallel, distributed & accumulation) = {total_batch_size}")
+ logger.info(f" Gradient Accumulation steps = {args.gradient_accumulation_steps}")
+ logger.info(f" Total optimization steps = {args.max_train_steps}")
+ # Only show the progress bar once on each machine.
+ progress_bar = tqdm(range(args.max_train_steps), disable=not accelerator.is_local_main_process)
+ global_step = 0
+ starting_epoch = 0
+ best_metric = None
+ resume_step = 0
+ forced_decoder_ids = processor.get_decoder_prompt_ids(language=args.language, task=args.task)
+
+ # Potentially load in the weights and states from a previous save
+ if args.resume_from_checkpoint:
+ accelerator.load_state(args.resume_from_checkpoint)
+ path = os.path.basename(args.resume_from_checkpoint)
+ training_difference = os.path.splitext(path)[0]
+ global_step = resume_step = int(training_difference.replace("step_", ""))
+ starting_epoch = resume_step // len(train_dataloader)
+ resume_step -= starting_epoch * len(train_dataloader)
+
+ # We need to adjust the progress bar to the current step
+ progress_bar.update(resume_step)
+ for epoch in range(starting_epoch, args.num_train_epochs):
+ model.train()
+ if args.with_tracking:
+ total_loss = 0
+ running_loss = 0
+ for step, batch in enumerate(accelerator.skip_first_batches(train_dataloader, num_batches=resume_step)):
+ with accelerator.accumulate(model):
+ outputs = model(**batch)
+ loss = outputs.loss
+ accelerator.backward(loss)
+ optimizer.step()
+ lr_scheduler.step()
+
+ # Update the importance of low-rank matrices
+ # and allocate the budget accordingly.
+ # This is only needed for AdaLora.
+ # Note that this requires parameter gradients.
+ # Hence being called before optimizer.zero_grad().
+ if args.use_peft and args.use_adalora:
+ # Handle DDP case where model is wrapped
+ if hasattr(model, "module"):
+ # DDP case
+ peft_model = model.module
+ else:
+ # Non-DDP case
+ peft_model = model
+
+ # Check if rank_pattern exists before calling update_and_allocate
+ if (
+ hasattr(peft_model, "peft_config")
+ and peft_model.peft_config["default"].rank_pattern is not None
+ and global_step >= args.tinit # Only start updating after tinit steps
+ ):
+ peft_model.update_and_allocate(global_step)
+
+ optimizer.zero_grad()
+ global_step += 1
+ progress_bar.update(1)
+
+ if args.with_tracking:
+ step_loss = accelerator.reduce(loss.detach().clone()).item()
+ total_loss += step_loss
+ running_loss += step_loss
+
+ if global_step % args.checkpointing_steps == 0:
+ output_dir = os.path.join(args.output_dir, f"step_{global_step}")
+ accelerator.save_state(output_dir)
+
+ if global_step % args.logging_steps == 0:
+ if args.with_tracking:
+ accelerator.log({"train/running_loss": running_loss / args.logging_steps}, step=global_step)
+ running_loss = 0
+
+ if global_step % args.evaluation_steps == 0:
+ eval_metrics = evaluation_loop(
+ model, eval_dataloader, processor, normalizer, metric, forced_decoder_ids, accelerator
+ )
+ if args.with_tracking:
+ logger.info(f"Step {global_step} eval metrics: {eval_metrics}")
+ accelerator.log(eval_metrics, step=global_step)
+ if best_metric is None or eval_metrics["eval/wer"] < best_metric:
+ best_metric = eval_metrics["eval/wer"]
+ accelerator.save_state(os.path.join(args.output_dir, "best_checkpoint"))
+ model.train()
+
+ if global_step >= args.max_train_steps:
+ break
+
+ if args.with_tracking:
+ train_epoch_loss = total_loss / (step + 1)
+ logger.info(f"Epoch {epoch} train loss: {train_epoch_loss}")
+ accelerator.log({"epoch/train_loss": train_epoch_loss}, step=epoch)
+
+ if args.push_to_hub and epoch <= args.num_train_epochs - 1:
+ accelerator.wait_for_everyone()
+ unwrapped_model = accelerator.unwrap_model(model)
+ unwrapped_model.save_pretrained(args.output_dir, is_main_process=accelerator.is_main_process)
+ # evaluate the model at the end of training
+ eval_metrics = evaluation_loop(
+ model, eval_dataloader, processor, normalizer, metric, forced_decoder_ids, accelerator
+ )
+ if args.with_tracking:
+ logger.info(f"Step {global_step} eval metrics: {eval_metrics}")
+ accelerator.log(eval_metrics, step=global_step)
+ if best_metric is None or eval_metrics["eval/wer"] < best_metric:
+ best_metric = eval_metrics["eval/wer"]
+ accelerator.save_state(os.path.join(args.output_dir, "best_checkpoint"))
+
+ if accelerator.is_main_process:
+ processor.tokenizer.save_pretrained(args.output_dir)
+ api.upload_folder(
+ repo_id=repo_id,
+ folder_path=args.output_dir,
+ commit_message=f"Training in progress epoch {epoch}",
+ run_as_future=True,
+ )
+
+ if args.load_best_model:
+ # load the best model
+ accelerator.load_state(os.path.join(args.output_dir, "best_checkpoint"))
+ # Handle DDP case where model is wrapped
+ if hasattr(model, "module"):
+ # DDP case
+ peft_model = model.module
+ else:
+ # Non-DDP case
+ peft_model = model
+
+ # Only resize if rank_pattern exists
+ if hasattr(peft_model, "peft_config") and peft_model.peft_config["default"].rank_pattern is not None:
+ peft_model.resize_modules_by_rank_pattern(peft_model.peft_config["default"].rank_pattern, "default")
+
+ eval_metrics = evaluation_loop(
+ model, eval_dataloader, processor, normalizer, metric, forced_decoder_ids, accelerator
+ )
+ if args.with_tracking:
+ best_metrics = {"best_" + k: v for k, v in eval_metrics.items()}
+ accelerator.log(best_metrics, step=global_step)
+
+ accelerator.wait_for_everyone()
+ unwrapped_model = accelerator.unwrap_model(model)
+ unwrapped_model.save_pretrained(args.output_dir, is_main_process=accelerator.is_main_process)
+ if accelerator.is_main_process:
+ processor.tokenizer.save_pretrained(args.output_dir)
+ if args.push_to_hub:
+ api.upload_folder(
+ repo_id=repo_id,
+ folder_path=args.output_dir,
+ commit_message="End of training",
+ )
+
+ with open(os.path.join(args.output_dir, "all_results.json"), "w") as f:
+ eval_metrics.pop("eval_samples")
+ json.dump(eval_metrics, f)
+
+
+if __name__ == "__main__":
+ main()
diff --git a/peft/examples/int8_training/peft_bnb_whisper_large_v2_training.ipynb b/peft/examples/int8_training/peft_bnb_whisper_large_v2_training.ipynb
new file mode 100644
index 0000000000000000000000000000000000000000..41c92c6166f9214f687b9a0fe729e262a61f66ae
--- /dev/null
+++ b/peft/examples/int8_training/peft_bnb_whisper_large_v2_training.ipynb
@@ -0,0 +1,20610 @@
+{
+ "cells": [
+ {
+ "cell_type": "markdown",
+ "id": "5cefac89",
+ "metadata": {},
+ "source": [
+ "# Finetuning Whisper-large-V2 on Colab using PEFT-Lora + BNB INT8 training"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "090fa3ed",
+ "metadata": {},
+ "source": [
+ "In this Colab, we present a step-by-step guide on how to fine-tune Whisper for any multilingual ASR dataset using Hugging Face 🤗 Transformers and 🤗 PEFT. Using 🤗 PEFT and `bitsandbytes`, you can train the `whisper-large-v2` seamlessly on a colab with T4 GPU (16 GB VRAM). In this notebook, with most parts from [fine_tune_whisper.ipynb](https://colab.research.google.com/github/sanchit-gandhi/notebooks/blob/main/fine_tune_whisper.ipynb#scrollTo=BRdrdFIeU78w) is adapted to train using PEFT LoRA+BNB INT8.\n",
+ "\n",
+ "For more details on model, datasets and metrics, refer blog [Fine-Tune Whisper For Multilingual ASR with 🤗 Transformers](https://huggingface.co/blog/fine-tune-whisper)\n",
+ "\n"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "625e47a0",
+ "metadata": {},
+ "source": [
+ "## initial Setup"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "id": "eJrPyQM5Xhv5",
+ "metadata": {
+ "colab": {
+ "base_uri": "https://localhost:8080/"
+ },
+ "id": "eJrPyQM5Xhv5",
+ "outputId": "cfd6d8c9-964c-492b-b641-8e80e337f783"
+ },
+ "outputs": [],
+ "source": [
+ "!add-apt-repository -y ppa:jonathonf/ffmpeg-4\n",
+ "!apt update\n",
+ "!apt install -y ffmpeg"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "id": "r_Ivl7qlX0dz",
+ "metadata": {
+ "colab": {
+ "base_uri": "https://localhost:8080/"
+ },
+ "id": "r_Ivl7qlX0dz",
+ "outputId": "2caa9eed-f01a-4603-a527-fe3b0b58b6e2"
+ },
+ "outputs": [],
+ "source": [
+ "!pip install datasets==3.6.0\n",
+ "!pip install git+https://github.com/huggingface/transformers\n",
+ "!pip install librosa\n",
+ "!pip install evaluate>=0.30\n",
+ "!pip install jiwer\n",
+ "!pip install gradio\n",
+ "!pip install -q datasets accelerate\n",
+ "!pip install -q git+https://github.com/bitsandbytes-foundation/bitsandbytes.git\n",
+ "!pip install -q git+https://github.com/huggingface/transformers.git@main git+https://github.com/huggingface/peft.git@main"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "8a528c1a",
+ "metadata": {},
+ "source": [
+ "Linking the notebook to the Hub is straightforward - it simply requires entering your Hub authentication token when prompted. Find your Hub authentication token [here](https://huggingface.co/settings/tokens):"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "id": "ed0OpduhX2JF",
+ "metadata": {
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 303,
+ "referenced_widgets": [
+ "c60690c2aee74763bf23115553f4e640",
+ "7d3d6c198e794219ab5db59f0228c8ab",
+ "5d5ea0207c6148769ad9f15b7b3dd92d",
+ "642e28d258ca4c30a5df94c5cf7e0471",
+ "170ee581427d4f30925dc393d124c1be",
+ "d5d5aa24182a4e04b3fdae1ca7fad52a",
+ "6dba643113a547ac9b6e121d008791d6",
+ "cd9bda1053a14890ad9091c63c0a0acf",
+ "4522666ebbcf4647b06ce81a6316fbbb",
+ "989b3df296504f34a62d31ca0d6d88bb",
+ "e8a7a34c6fb146f0b38a40f389a617fa",
+ "960553d142c446cd8852523887a5cc04",
+ "441820fb176048109e0f8f7e9519d735",
+ "0bb38c654e18429a8396466ebab84504",
+ "1acfc4a2809e41dd995817c3526650dd",
+ "6d5801774beb4b529b227ef2f098614e",
+ "dfdf23cde48c421caebb573060641d6a"
+ ]
+ },
+ "id": "ed0OpduhX2JF",
+ "outputId": "ecc2048a-b46a-4b20-b94a-5912924feb3d"
+ },
+ "outputs": [],
+ "source": [
+ "from huggingface_hub import notebook_login\n",
+ "\n",
+ "notebook_login()"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "id": "e1da5fff",
+ "metadata": {
+ "id": "e1da5fff"
+ },
+ "outputs": [],
+ "source": [
+ "# Select CUDA device index\n",
+ "import os\n",
+ "\n",
+ "os.environ[\"CUDA_VISIBLE_DEVICES\"] = \"0\"\n",
+ "model_name_or_path = \"openai/whisper-large-v2\"\n",
+ "language = \"Marathi\"\n",
+ "language_abbr = \"mr\"\n",
+ "task = \"transcribe\"\n",
+ "dataset_name = \"mozilla-foundation/common_voice_11_0\""
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "805b1c56",
+ "metadata": {},
+ "source": [
+ "## Load Dataset"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "id": "a2787582-554f-44ce-9f38-4180a5ed6b44",
+ "metadata": {
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 1000,
+ "referenced_widgets": [
+ "020176f5aa0a4d489d022ef5e41ef3f6",
+ "cbbba08d9e634560a6c0429e32166fe5",
+ "6d9d1609edc8471dafe653e4da32eeeb",
+ "435b5708e6cf487ebb1799c7b64a8218",
+ "931b96b21b39482298f40449424fdd34",
+ "79da882ea494477a8c94fdac7acd644e",
+ "f14847261aa247fb9561373e0495f3e5",
+ "ce8f306e745d4b158c58058d471de037",
+ "0bd122731d674cdab803a9981eb28237",
+ "46211764bc6641b4b693c16c90747021",
+ "f1884e5a392941bfa8c484496d87084c",
+ "6b1cdae6f5e34d1d9a0b5e7adf5183db",
+ "4d29aa0885214a2aa79701cc226edaef",
+ "5411f018d4464e839f2fb21ad3f026aa",
+ "5fb8e97b25b44e0dae9715eeb97acc5d",
+ "783d4d18627646648f8c120b728babe1",
+ "1a721ed289684104b0fbdc8147c2311b",
+ "4880366554ad4f6687a25b5a17877dcf",
+ "283f5528547b457698ced126c25c2a44",
+ "7c90db94a11e4a5aa432e664b2af4e7e",
+ "7f6a466819bb45e880eb989f388a7523",
+ "d96245da43944c4b8235e0cd02c1aa4c",
+ "41187d9a120448fab6c8608f226971fa",
+ "1d4bd11921d145c7bfd1a8ce0700a666",
+ "2853a43036244f54b74db99311bc580d",
+ "d9a85d7c76b54199bbf7646448e3458c",
+ "b09d153958cf4a28baad268bbda78236",
+ "003227997471488dae9ae26dcbff89ea",
+ "deb18822d58b4b60bb75460f0a5fe921",
+ "e6cf97ef7bc541d0b9c6de206a3a45b0",
+ "a4b16b5279504dd694090798f5925d65",
+ "564cd321c06440e9856f10f5c40c20be",
+ "8a91574c4b6e4745b2b65885323b4d25",
+ "9202065d8e6f425d88e4514dde70992d",
+ "f7b4ec74e2ac45bbbf0265d0363f4d9f",
+ "3a083523ae604362901e4e31c39fe949",
+ "d1bc2ce48c3e481b9059e882b5102946",
+ "30c688df949042ce89337643f6178230",
+ "2bc85a5bde9a454990d3bb7de5e3c7c1",
+ "2ab45b22ce3f400a81cc451b9d7c9eb8",
+ "cdd08679c28642a184805912c07b324e",
+ "90744e5529c04f18b11e00326649abe5",
+ "11b9c50e720a466aa92c64b254d40778",
+ "8f856d6bde4041149324e1f53d19c1cb",
+ "49545bfc91c848b8a465e13d0b45fa34",
+ "45a85ceb24ea444ab18a6985884be966",
+ "ac9c1141ca7c453f84a8ab62b2de9158",
+ "bd4e3eb14252470d9c8ac60a32948a72",
+ "75dfc66dab48405b85073317c8dff155",
+ "b16e3a75acd0403f865849f1de6ca654",
+ "78fb0d05929849ad9aa7a7ded63c7b6b",
+ "3fd0fd7cbbef4785b360891c12017f48",
+ "a9c132959dae4303bcf6015106ce3453",
+ "2ef66808d51d440b9998064e212df420",
+ "45478f2ce991441c8ceaef9acf745084",
+ "c1f019686c564cca87c240a75ab71ad3",
+ "54589117bf244027ba024ea85bd1fd77",
+ "7b7986ad93f64956b8d198d2cb4acb60",
+ "dbc1a016a69b4ad7811d2701a9520a2f",
+ "72f8e7de2a5d4155a9e9146f12e14b19",
+ "46e44f07b96d4c32bbe75bb89159f093",
+ "90b53e96b3f04c2993969b17547ae0d5",
+ "8843f70cfa1f45299a588e96e9c1159a",
+ "8b2e2c650f4b4bee9e763b7c59525ec8",
+ "fb9f013a6188463fad6db70702576c37",
+ "93e2efbb5da747d4b94c916153ee9706",
+ "c44f472624d84e16a0f380580d36ca61",
+ "65188c1fdba2421ba85c2cc349709600",
+ "0683cbffd97a4b75bd5e00a05d541fef",
+ "4573606592ce4b2a914ed0a70b69f9af",
+ "efb85d003fb54f55aa4eadf2ab8b1684",
+ "a235cb3d4d424efeb30901f63fc1dbe5",
+ "2452ab9f6f974d1d831f7c81e884d00e",
+ "bd7da2671a22431889fbfa2ae1e0fe2c",
+ "47ee1eec97cf4af58ed4f50944386a7e",
+ "a05426c8e5f849b7a972dc0df3cd84ef",
+ "1e8cdf737c93431e841e129abb541e22",
+ "91fc5846a32f44d5bc5fa30fdcb3c638",
+ "daf4005d1d334608846d0fb2fe4f837a",
+ "ba48d89cab9346ed92dc338779f9f828",
+ "6b0e0694d895445c9bf7c955a116953f",
+ "ecb7ffba323743c68961e294e74b337b",
+ "460be80f176849e0b1241e3a4fc18b74",
+ "74e2bcef1ce94234bbf6ba0d6488279d",
+ "73bde731e20d48de8ce66b9d72fb95cb",
+ "9afdb23ba9ee47709f194e0e92de0edf",
+ "621f989f46f84d73b96a37c954e92b8d",
+ "89bb7bbcaa194a23bf3d908a4782ccb8",
+ "59e79d9132964429a2a2abbdf4bdbf32",
+ "2e5c1a371742446e8bc416d4735c9ce3",
+ "e57b15cc74e7474083e87722d6acde47",
+ "e899060f1edc43b980fe6f3bbe13c609",
+ "a6963ce72cb3425791804abf1718ba90",
+ "41a7cc33e0bc4bc5bc04dfc72bab7a81",
+ "28279812acfb4272a1c28ed70aa1362d",
+ "451d3851e29e4efabbc2c235dea718da",
+ "18dfdd09a3af49f5b17cda27872d0ba3",
+ "aaeec2b7986d493e8d238aa14f2e5937",
+ "0894264041854eea960707529f3fb8c7",
+ "3a4965f422f14e1ca2a63e1852235507",
+ "e590170f306347f3a82b76a25d37b652",
+ "384f4d9515d1431589a3cc934bcf5ea7",
+ "edc24ce2510f45f8adde0a187016259f",
+ "c2c2608dd091493795d975f1a3cc3762",
+ "1dedb58d31dd43db96ddd7315bb7e2ee",
+ "308e1ee4593b454a84681bda10921207",
+ "8f52bab9ebd049d6a57686d621f407ac",
+ "2958a33cff794de1aa8128327bf405f1",
+ "1b2780d8137042449bd6779c70bf43ca",
+ "ddc2a8e8ef4d429f95081c4c5baf1fb3",
+ "ce06b2a0de6c4fb8bae36bc4d7f63270",
+ "c4cca1778f314ce582bd09b9b2494f82",
+ "3bd70d937e924f61b943acb0aaf15619",
+ "c81c5d3a4dc5409e95a6410e67fa9857",
+ "dd02d1b31bfd4b19ad626d6691a9b293",
+ "b1d780c721b840d7a06661a7a5e63236",
+ "d19402df47464044b36fb5ee4a0c1c4d",
+ "b1221f4e0a57482682ea4bd6ae245da3",
+ "64533507b97148008548e55623b6c2a3",
+ "33888a5cafe6495782309dae44531dd3",
+ "7d5ff2f1b8794bad8286e90307bd6a61",
+ "7a2d45b371ba47a994e4372437f51cff",
+ "dec9f287435e4c6b9fb1d1ead2ded576",
+ "db5e1bf1871546408f233f0cbc37b136",
+ "af44aa66372a43beb9812ad9895d8d1f",
+ "9b427631384c47ab89ee1352c0236afd",
+ "00071f8cf276478fb2740684552f1275",
+ "64378b1064dc4036a9a4c8813013e210",
+ "ed7daa32c94648d5951876229f9835b3",
+ "eb883a37a9cf4945bd864decb4fc87ea",
+ "7b190bb2bd234b7997ca041baddd511f",
+ "7549fd0b38364d8580f8eb1549558a33",
+ "5cba5542df344d54bb80dcf7be56b2ae",
+ "8daed385e6564c7897fb6553669a9065",
+ "25fcd4b584a143058266f7f3a650d69a",
+ "58a15b8df2d54f89828bcd205d6bf298",
+ "8b51633b2fe5479db0fc73cd3f0ebaea",
+ "d2c1704e34c34d12b99c31d64fce88cc",
+ "6bdce3b33872457ea67a3a3191f438ca",
+ "c8ba787279ea43aa97b134c134d4f183",
+ "6efc3be410ef4710a59dea8dbdabcdf3",
+ "6f9d8dc63c494c76b36074af773330ce",
+ "64c0bac85ee446e284ed85ec0eb5ad44",
+ "5162987085ce45d88233f34ca3a41ce0",
+ "00819c11ea23467689e78a00d89d1b09",
+ "65dbf3c3a80b468aa8717e97c14db6a2",
+ "8cb910ad08024c818b99c2e30e30b039",
+ "0235efbdc6a74cce8050ab1116466427",
+ "ee1ae17fdf4143ae8125ce5e2a7e9066",
+ "481ebdff3ccc40fcb7a8d848b01ae8db",
+ "6117f9e9718c4f4388bd1feec34578b4",
+ "623d0c6427964291b5c74fb18bfb4ce4",
+ "14bca5cf764d4464a186961ccc6bdb3d",
+ "75c793c91b9e4aa994c2d34ebb16f7d4",
+ "3502b5f8aeab4bfd89c83b99ab308b9e",
+ "c43169085f2949f1b8259cd0b767d121",
+ "4903414a865c4813a9371e8b301f1af7",
+ "ec7e7e3811e34b4a8c8cc31cd021cf20",
+ "a22db8523d44457bb96448d08129988f",
+ "9980bca9b1334893bf6583c325122f50",
+ "931fc769fbeb42bf82df6ef5f914bf48",
+ "e944fa694d824042845364bdba72d642",
+ "3785471f614f47c78e3000a303b11ca6",
+ "dd634585d5e64c97881b132b1d59083e",
+ "785f3df156b946449c492f1296656a70",
+ "47a25de2e10d4b55a9e6827b85e49c3a",
+ "898c7b43a5e94601bc093e0cde28c2ec",
+ "a03430c0cdcb47bfbd2ffd754074d692",
+ "cda6af0ca01d4053bcebe06f3c41d887",
+ "abe561c67f1f42b29c33d4c296221b2f",
+ "21ca204b93994e8790c9eb7b0722761f",
+ "f628cb62f5fa446eb608467c1ecea526",
+ "e20264d19e804f9dba3e3867ef9b31bd",
+ "43141dcab2324fc6a12f9b8198e10154",
+ "f773a61b1dba4e3eb0df36162efe9abc",
+ "bfc9036c9c5f4be7ab191b92d92f1352",
+ "0f534e081ec64883a5f88d06f93aeb00",
+ "3a94afa1e03544f68df7752a4f503fbc",
+ "32ed17ecaf7548d5a80b27eb97cd78af",
+ "56817cd3b11e46f187dc13e71b7ec97d",
+ "3d30c20af23e495999646521d39e8e66",
+ "bafada4a1f29442296c47018dcaedb77",
+ "6cd3baac550741ba866ce2cd2dcaebdf",
+ "bc9c3ba4bc6d4623a764d92890536935",
+ "719f2b2ab9eb4e348ae902d063c27e2d",
+ "5e09bdca5081429ab82b488a3e016fbf",
+ "200bc7d8c2bc494399a4560dabd64293",
+ "91c3b5ddf5fb4c7aa835d992b4c7b4e7",
+ "52ff6528abdd4a9e9b85f4b355b2391d",
+ "6bb6737e22bd48d786b02051d077e8cc",
+ "e97a0201b81446b882ba802a5a3b00e8",
+ "c1a89a042b044278a8666da306e6a481",
+ "21ce216193f346c09a04a1d64bc0cd8a",
+ "23ee9c5c18c64305adc55ee218afd7a9",
+ "1f632bdc00e84422b64c0a4b8e238f34",
+ "8d50d82f9d94482c9883f99ea5c7d704",
+ "6a2dea21e7ce4eda8953995497308327",
+ "2f3d1d2f1c92402cadc4cfa1b0094238",
+ "844caba5ebdd48189517a10705543292",
+ "2d667cd4bc134a44958d17ef75d86321",
+ "acfb7b6734884939a753fc19047bb9bc",
+ "73cd51c6c43b40cab25d411e7c0f6ad1",
+ "19c7ea1e9364437a9c0bf6b4e645f854",
+ "8675aad817a44ab39b097ec864669833",
+ "5664e1233a904f4bb4af9c5322517fab",
+ "0ae5110b687440e89ebebfb847985aa1",
+ "85509b0aafec47e5ad540abc7ae4ab7d",
+ "d3d7c15d53c8498e823c84fe609321dd",
+ "80de3739b91a45478cb6a00dcaeae756",
+ "7c99e16722cf4fab866732557769b921",
+ "00834c084ddb4f46ac29f14575a2383d",
+ "4ce1e695a6ab4906ba0817005cf58d55",
+ "eb03476353ef4568b94a3071918e72f2",
+ "1b8307d133bf4280845f7d3a302b3a2b",
+ "daee15869a92459aabcd9128526183d5",
+ "5ddd9e1a1fab4531930acaf08cc45c73",
+ "4081e141986f4abba15477a12a752ca0",
+ "892e150a80464f8198024587a47186ba",
+ "9f9e15ff2e394ee7a7776e3e7f4b7d30",
+ "7e264d54d38e4d02acfd47e4e533b49d",
+ "746302ee5d21495db5d9a13789c5256c",
+ "47f7ff7b213e405a822ad6fe2e5de431",
+ "e4810a798c0f47b6b54f84ff4ffec608",
+ "8e480fe546f24afebb1ea723bff84456",
+ "0cf925f582374cd197164625f0ddf27d",
+ "aa7557fbffc54ed3a9c58c1531fd93f6",
+ "061c90e4148b43b8ba65848ca4c1ba46",
+ "f617d181ffdb4b1e8d81fbb393923a6e",
+ "a26ddb684a07496da4290e3f6031b685",
+ "f20fc82bcbf245619ad4dec04d0f999d",
+ "8016eabfc7aa48c2bc0bf3a13919a675",
+ "83cb83e404a24fba8cf43610cb1696fc",
+ "7b70db203ee644fe81006f5d48aa426d",
+ "efd9d5724dbd435991052b4445c6970f",
+ "41f65340441f419d91e1d3841921f48a",
+ "58aba8edefa44c60818891a2651137be",
+ "e5e8f119a91944f296ff821dd7ecfb1b",
+ "568a85caf800461b8571e3d206854e6b",
+ "e2a8a379bd0d4cbdb22fbc3bbb4fdc7a",
+ "2c7d952f958247b681301d1c6bff4fa7",
+ "27649a0d303643d8985caf506ef66fc3",
+ "1855ae0388074d08a4763b7ac76c6948",
+ "7e5252f608d6468f80deb468cb2556fd",
+ "bce6b62300d942a1ab89a6f0ceb16d30",
+ "0239f7263d1a4e8b9475ae48379c068d",
+ "5b527e45d6a946b28047115fa6b5aa3a",
+ "3c5eb07f0bff43948ff1f283c3c56b0f",
+ "3545fcc1e9d7453099c4931f658e0bc8",
+ "2f314258091a430095794c3fe0aea7e3",
+ "0ebfa123462342e99ad81b7e5ee00eac",
+ "8af6bd6e8cae4964a2e372be30220bd9",
+ "4184f160ab6d4f58bc921fb7ba89cf60",
+ "575c4d8d503244d8a9f2a5709021b5b2",
+ "ffce35af1ad84a2c838cca55a26dd3c4",
+ "d21cd4878c6e49d38dd3abb2e3b3f566",
+ "969e3cf7f3634c3f90b5fea38c5797ca",
+ "78501c2a5ac84f9ca0d20bbef340fc9f",
+ "5b4fbd1102a84670a1eed6f3d25c0bcd",
+ "621880c98245427881dd5b004b480c6a",
+ "65c2716dd7f14afa93d3bfaebe85c44f",
+ "2ff541d18f5844408690be00c7259d59",
+ "679fa9d2a703494dbb10fbfd19879f1a",
+ "6717b182e5674afb90006b50dea98cae",
+ "0887c7aabbbe4d4e8fdc64d2e2657cc7"
+ ]
+ },
+ "id": "a2787582-554f-44ce-9f38-4180a5ed6b44",
+ "outputId": "b1729004-591e-41c2-c206-9d0e572eb8e5"
+ },
+ "outputs": [],
+ "source": [
+ "from datasets import load_dataset, DatasetDict\n",
+ "\n",
+ "common_voice = DatasetDict()\n",
+ "\n",
+ "common_voice[\"train\"] = load_dataset(dataset_name, language_abbr, split=\"train+validation\")\n",
+ "common_voice[\"test\"] = load_dataset(dataset_name, language_abbr, split=\"test\")\n",
+ "\n",
+ "print(common_voice)"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "id": "20ba635d-518c-47ac-97ee-3cad25f1e0ce",
+ "metadata": {
+ "colab": {
+ "base_uri": "https://localhost:8080/"
+ },
+ "id": "20ba635d-518c-47ac-97ee-3cad25f1e0ce",
+ "outputId": "dd81bced-f544-4d55-9669-5babb901f842"
+ },
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "DatasetDict({\n",
+ " train: Dataset({\n",
+ " features: ['audio', 'sentence'],\n",
+ " num_rows: 3927\n",
+ " })\n",
+ " test: Dataset({\n",
+ " features: ['audio', 'sentence'],\n",
+ " num_rows: 1816\n",
+ " })\n",
+ "})\n"
+ ]
+ }
+ ],
+ "source": [
+ "common_voice = common_voice.remove_columns(\n",
+ " [\"accent\", \"age\", \"client_id\", \"down_votes\", \"gender\", \"locale\", \"path\", \"segment\", \"up_votes\"]\n",
+ ")\n",
+ "\n",
+ "print(common_voice)"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "2d63b2d2-f68a-4d74-b7f1-5127f6d16605",
+ "metadata": {
+ "id": "2d63b2d2-f68a-4d74-b7f1-5127f6d16605"
+ },
+ "source": [
+ "## Prepare Feature Extractor, Tokenizer and Data"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "id": "bc77d7bb-f9e2-47f5-b663-30f7a4321ce5",
+ "metadata": {
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 49,
+ "referenced_widgets": [
+ "4d25d9919acf44a19f1b6f8fd625f808",
+ "b041efb27b6149fcaf206590f1c1b961",
+ "4668602d021a400a8b0ec88599abc85c",
+ "92d9732acb964601b27695041f9fbb72",
+ "c3ea17f7dd94462986d30b751664d77b",
+ "1b1dc31d9a2b4357a71119300c6d899a",
+ "7a24ae9d13fb4e82b1993b05f8d71d11",
+ "e1141861d9f44d4c95313fd432795b70",
+ "6ef55b5db76d4c78854fa0c27165e480",
+ "91b103ac79e641b190416acdeb55902c",
+ "e9e10f1e53b74509bfc9c0bf11502c5e"
+ ]
+ },
+ "id": "bc77d7bb-f9e2-47f5-b663-30f7a4321ce5",
+ "outputId": "7abb2062-e755-4f1a-e88b-9b7bf2986dbf"
+ },
+ "outputs": [],
+ "source": [
+ "from transformers import WhisperFeatureExtractor\n",
+ "\n",
+ "feature_extractor = WhisperFeatureExtractor.from_pretrained(model_name_or_path)"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "id": "c7b07f9b-ae0e-4f89-98f0-0c50d432eab6",
+ "metadata": {
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 209,
+ "referenced_widgets": [
+ "f436e6a7d3014e2ca44c94455bfeace8",
+ "f9d6d41ffeba43cf94ec9d7a96af6617",
+ "bed65245e7234977874d35bf78694e35",
+ "c28c2fc81e0e467cbc0ded0205d1ee85",
+ "ea941a078b984f51b66b5f1e8f3d1d82",
+ "e3f1244dbe2c48bc8102f958c3df6467",
+ "786d3d34cfd24f81996797c55b10b443",
+ "3a4bb5b9cf864265af8f1a0b989dff2c",
+ "ac2e1977ddaf4b948c9cc24d84c08b83",
+ "dd339bf6baf6433e92665e30dc30b062",
+ "6a544d6dd5954beab32ce3089d8d2aac",
+ "f933fbdcc26d41b0bb294dabd0337834",
+ "950e74921e6042868ab6b7b9070d6f69",
+ "82dc91c5b065459d827863699a9710e1",
+ "5b7b6f08765c4c1989f945414f2c3cf4",
+ "735c3606df924b9297ddc05fae3e92d5",
+ "d5d632dd16f147e090c62aad38c45d3c",
+ "24191f38e3654b86a5da3576615e2229",
+ "4b1f4abe697948d5a1cca9b45b2a6f87",
+ "8527f474f1a549abafe9519e2b4bd338",
+ "1031dc4b5d2d45f3b14ab12dbd9bca56",
+ "ab40616ed9b74f438e74d403f848bed4",
+ "e6c2dc814c324a0c8cb744ca16707479",
+ "a615446a48624d0f9a009c1f6d8b1a54",
+ "383d6e891c5249b4b2fabb60d4900488",
+ "3c3214f235a54864848902f7e53662db",
+ "73f6e6860b64491284c9442f0deae8b6",
+ "6d9826a5adb847e8b4cc4486a31b52ce",
+ "e8b3093587e44164b0ac043414cea0fa",
+ "96266c5722f54eeeb682b2707b8025dd",
+ "f0be69583cd1410da6dbc18302d4439b",
+ "c24ddbaafa5f4a63b391d981a4f10354",
+ "629725dfcc684b1db1a57850c3bc7bc3",
+ "add0f175631742d49dd4695bc004e81a",
+ "5871a46d60f14da99e4bb8ee74405319",
+ "64b308019fff4095ab7f1812aab4676a",
+ "03f62b3f5aa64b6390b157cb3f9d2b9f",
+ "59657f26f4af490980b1d9bea1526e5e",
+ "1571fa5d8f494704949c5809f3409fa7",
+ "5ef218872f2646249888def0abed7149",
+ "03fcbc61c50c4ddc9c3684e4c085bffb",
+ "e4234c7c29744fc4be99b8b2ebedc9d1",
+ "70aa1fc14b09473e911dad3f9030b15b",
+ "008bead021ea416eb31dd9143d5ae5b9",
+ "ebd79e22ad4e4256a6d88883af2c1eef",
+ "c47ba0b11e074f708338863a35a78f7b",
+ "72b715be2c774235a21602b18d71e75a",
+ "ff9a0ed54bab49aca6f27bf1be66958e",
+ "15b5e415b62146ba96215458cf116431",
+ "8b0dd001d5b04647b1c480aab83d03a2",
+ "0af935ad4f694fb48094e6a119cbcf82",
+ "7cfbb542eba34459ba64b881c1040eee",
+ "fe48e65b2371445bbb01a8d3e9af1f67",
+ "b8d3539c8a454217a3b6ffab51259054",
+ "05e96819517e417aaf05f5f38c0c8b76",
+ "b600ead93bbf44a3a3fe229589c63a61",
+ "3d4c614fb775434fb0c5b02d46246ee0",
+ "344d1cc53e28411cae839a4ebba1bf58",
+ "a1578c0c777f4780a3fdd1635a0909d9",
+ "41faf55c8878475f8a986b02ad73e8ce",
+ "b5c8221a09df4dfdb74017d4af544b95",
+ "65e4b8dae1e4435cb7737a8d5dd13d91",
+ "6d932eadfd6a448a9a71d741bb64f428",
+ "dce0d285c7d947dfba9ee5bc1a6ebece",
+ "bde010029c374a0eb2bb942f380f0e8b",
+ "a91f37ce798d411ea2a33cfdb1f01251"
+ ]
+ },
+ "id": "c7b07f9b-ae0e-4f89-98f0-0c50d432eab6",
+ "outputId": "4c094075-3f95-42db-9f4b-4db0c2fbeb91"
+ },
+ "outputs": [],
+ "source": [
+ "from transformers import WhisperTokenizer\n",
+ "\n",
+ "tokenizer = WhisperTokenizer.from_pretrained(model_name_or_path, language=language, task=task)"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "id": "77d9f0c5-8607-4642-a8ac-c3ab2e223ea6",
+ "metadata": {
+ "id": "77d9f0c5-8607-4642-a8ac-c3ab2e223ea6"
+ },
+ "outputs": [],
+ "source": [
+ "from transformers import WhisperProcessor\n",
+ "\n",
+ "processor = WhisperProcessor.from_pretrained(model_name_or_path, language=language, task=task)"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "381acd09-0b0f-4d04-9eb3-f028ac0e5f2c",
+ "metadata": {
+ "id": "381acd09-0b0f-4d04-9eb3-f028ac0e5f2c"
+ },
+ "source": [
+ "### Prepare Data"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "id": "6e6b0ec5-0c94-4e2c-ae24-c791be1b2255",
+ "metadata": {
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 72
+ },
+ "id": "6e6b0ec5-0c94-4e2c-ae24-c791be1b2255",
+ "outputId": "1f1fe2d1-3ad2-42d4-e6f0-f0929785ae8e"
+ },
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "{'audio': {'path': '/root/.cache/huggingface/datasets/downloads/extracted/f7e1ef6a2d14f20194999aad5040c5d4bb3ead1377de3e1bbc6e9dba34d18a8a/common_voice_mr_30585613.mp3', 'array': array([-1.3727526e-15, -1.2400461e-13, -1.5159097e-13, ...,\n",
+ " 4.7928120e-06, 3.5631349e-06, 1.6352631e-06], dtype=float32), 'sampling_rate': 48000}, 'sentence': 'आईचे आजारपण वाढत चालले, तसतशी मथीही नीट खातपीतनाशी झाली.'}\n"
+ ]
+ }
+ ],
+ "source": [
+ "print(common_voice[\"train\"][0])"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "5a679f05-063d-41b3-9b58-4fc9c6ccf4fd",
+ "metadata": {
+ "id": "5a679f05-063d-41b3-9b58-4fc9c6ccf4fd"
+ },
+ "source": [
+ "Since \n",
+ "our input audio is sampled at 48kHz, we need to _downsample_ it to \n",
+ "16kHz prior to passing it to the Whisper feature extractor, 16kHz being the sampling rate expected by the Whisper model. \n",
+ "\n",
+ "We'll set the audio inputs to the correct sampling rate using dataset's \n",
+ "[`cast_column`](https://huggingface.co/docs/datasets/package_reference/main_classes.html?highlight=cast_column#datasets.DatasetDict.cast_column)\n",
+ "method. This operation does not change the audio in-place, \n",
+ "but rather signals to `datasets` to resample audio samples _on the fly_ the \n",
+ "first time that they are loaded:"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "id": "f12e2e57-156f-417b-8cfb-69221cc198e8",
+ "metadata": {
+ "id": "f12e2e57-156f-417b-8cfb-69221cc198e8"
+ },
+ "outputs": [],
+ "source": [
+ "from datasets import Audio\n",
+ "\n",
+ "common_voice = common_voice.cast_column(\"audio\", Audio(sampling_rate=16000))"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "00382a3e-abec-4cdd-a54c-d1aaa3ea4707",
+ "metadata": {
+ "id": "00382a3e-abec-4cdd-a54c-d1aaa3ea4707"
+ },
+ "source": [
+ "Re-loading the first audio sample in the Common Voice dataset will resample \n",
+ "it to the desired sampling rate:"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "id": "87122d71-289a-466a-afcf-fa354b18946b",
+ "metadata": {
+ "colab": {
+ "base_uri": "https://localhost:8080/"
+ },
+ "id": "87122d71-289a-466a-afcf-fa354b18946b",
+ "outputId": "727a709a-2b21-4c54-807f-efd40ea1719c"
+ },
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "{'audio': {'path': '/root/.cache/huggingface/datasets/downloads/extracted/f7e1ef6a2d14f20194999aad5040c5d4bb3ead1377de3e1bbc6e9dba34d18a8a/common_voice_mr_30585613.mp3', 'array': array([-4.4097186e-14, -9.4153831e-14, 3.4645775e-13, ...,\n",
+ " -7.6018655e-06, -1.8617659e-06, 4.4520480e-06], dtype=float32), 'sampling_rate': 16000}, 'sentence': 'आईचे आजारपण वाढत चालले, तसतशी मथीही नीट खातपीतनाशी झाली.'}\n"
+ ]
+ }
+ ],
+ "source": [
+ "print(common_voice[\"train\"][0])"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "91edc72d-08f8-4f01-899d-74e65ce441fc",
+ "metadata": {
+ "id": "91edc72d-08f8-4f01-899d-74e65ce441fc"
+ },
+ "source": [
+ "Now we can write a function to prepare our data ready for the model:\n",
+ "1. We load and resample the audio data by calling `batch[\"audio\"]`. As explained above, 🤗 Datasets performs any necessary resampling operations on the fly.\n",
+ "2. We use the feature extractor to compute the log-Mel spectrogram input features from our 1-dimensional audio array.\n",
+ "3. We encode the transcriptions to label ids through the use of the tokenizer."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "id": "6525c478-8962-4394-a1c4-103c54cce170",
+ "metadata": {
+ "id": "6525c478-8962-4394-a1c4-103c54cce170"
+ },
+ "outputs": [],
+ "source": [
+ "def prepare_dataset(batch):\n",
+ " # load and resample audio data from 48 to 16kHz\n",
+ " audio = batch[\"audio\"]\n",
+ "\n",
+ " # compute log-Mel input features from input audio array\n",
+ " batch[\"input_features\"] = feature_extractor(audio[\"array\"], sampling_rate=audio[\"sampling_rate\"]).input_features[0]\n",
+ "\n",
+ " # encode target text to label ids\n",
+ " batch[\"labels\"] = tokenizer(batch[\"sentence\"]).input_ids\n",
+ " return batch"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "70b319fb-2439-4ef6-a70d-a47bf41c4a13",
+ "metadata": {
+ "id": "70b319fb-2439-4ef6-a70d-a47bf41c4a13"
+ },
+ "source": [
+ "We can apply the data preparation function to all of our training examples using dataset's `.map` method. The argument `num_proc` specifies how many CPU cores to use. Setting `num_proc` > 1 will enable multiprocessing. If the `.map` method hangs with multiprocessing, set `num_proc=1` and process the dataset sequentially."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "id": "7b73ab39-ffaf-4b9e-86e5-782963c6134b",
+ "metadata": {
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 197,
+ "referenced_widgets": [
+ "466eeda389c442e487742faff05eeb81",
+ "664ff40a4e7346869652ba3be663acf2",
+ "3d8f10b5726b46de934dd0f7ed7244e4",
+ "b803893882ac4358a4676964dfb3fb31",
+ "4ff7e3d07f6a48f8935f0f42b86fc20c",
+ "3e5db1000a6c4871936614e712e769db",
+ "21dcf39a421847a78ea685eec0983fc6",
+ "c4119f7ec7464aab90f17d022e674999",
+ "965ac01b68064dc5a9fc3bb3f244c804",
+ "f5d7433d15de45e997d12568cac536fc",
+ "14e284f308844311a9ad40415091d93f",
+ "58c3766293e64116a131357f6cc66fe5",
+ "abc8f69eae7b46b1b430cf3b7a231b05",
+ "979edd227f0840a4be0233082e452b5a",
+ "12dedd9f089c42f3a8bba9adb01cf9d3",
+ "3042d874fcf544fabc4701938bca7cf3",
+ "baa8f739bb7e402bae7ee479e282e813",
+ "54509d703b7d4416bdee59157f918396",
+ "ec6017ce2fb3431ab823bde05f977a61",
+ "1a540a7cba794122abdb1900061479e2",
+ "d046a46c70ea46ffbb04a3c9f55637d5",
+ "99b628071c814d88a3cd5d72e4c95f01",
+ "e213d1c919314315ada180d49e27dfb6",
+ "0ea1f163e4174684bd6efc2e2433c1d3",
+ "09511a81a89d4754897a3507a84405be",
+ "8338339ab8a242c1a485bce8558f9c39",
+ "8e84abf61e3e45d58efc7ccd0bfe8d37",
+ "47a5e0cfb3564c16acaedb88613b9020",
+ "09e357a7187044b0bd2b841893a2601f",
+ "65e8c45d05be4d41b136439d9785a09c",
+ "1442a54fad7d44ddbafdacaf7f95279a",
+ "4bea6b0455ae4019b33d45491dbf4584",
+ "9c928a14371a4d9aa521953e287fff54",
+ "b8acdb71c3564972a6c8b27e964ec061",
+ "688f552e85714fe6a5d3eda82be0106a",
+ "a8aac44a077040bd9f4638c0c8f7a877",
+ "89f8ede64593475da4e056e9907f370f",
+ "851902cb2b0e494998684409d82dafd1",
+ "328f4d11886d48f49d4578e8e352097f",
+ "a25ef41450eb42ff9b8b618b40080ac0",
+ "04144ed3ff5f423f99179702cee5343f",
+ "8c41e1ee1a2c49b8b3d3d320fbf26262",
+ "4edf0948ed1346ceba1c0148e9c6fe1c",
+ "40f2b2ff75ca4562808fc2c7a870901e"
+ ]
+ },
+ "id": "7b73ab39-ffaf-4b9e-86e5-782963c6134b",
+ "outputId": "eecac4c8-c5f8-427b-a2ba-0d51fae825ac"
+ },
+ "outputs": [],
+ "source": [
+ "common_voice = common_voice.map(prepare_dataset, remove_columns=common_voice.column_names[\"train\"], num_proc=2)"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "id": "c4be572c",
+ "metadata": {
+ "colab": {
+ "base_uri": "https://localhost:8080/"
+ },
+ "id": "c4be572c",
+ "outputId": "0383124a-d4b1-4abe-a8a1-868ce6b3884e"
+ },
+ "outputs": [
+ {
+ "data": {
+ "text/plain": [
+ "Dataset({\n",
+ " features: ['input_features', 'labels'],\n",
+ " num_rows: 3927\n",
+ "})"
+ ]
+ },
+ "execution_count": 18,
+ "metadata": {},
+ "output_type": "execute_result"
+ }
+ ],
+ "source": [
+ "common_voice[\"train\"]"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "263a5a58-0239-4a25-b0df-c625fc9c5810",
+ "metadata": {
+ "id": "263a5a58-0239-4a25-b0df-c625fc9c5810"
+ },
+ "source": [
+ "## Training and Evaluation"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "8d230e6d-624c-400a-bbf5-fa660881df25",
+ "metadata": {
+ "id": "8d230e6d-624c-400a-bbf5-fa660881df25"
+ },
+ "source": [
+ "### Define a Data Collator"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "id": "8326221e-ec13-4731-bb4e-51e5fc1486c5",
+ "metadata": {
+ "id": "8326221e-ec13-4731-bb4e-51e5fc1486c5"
+ },
+ "outputs": [],
+ "source": [
+ "import torch\n",
+ "\n",
+ "from dataclasses import dataclass\n",
+ "from typing import Any, Dict, List, Union\n",
+ "\n",
+ "\n",
+ "@dataclass\n",
+ "class DataCollatorSpeechSeq2SeqWithPadding:\n",
+ " processor: Any\n",
+ "\n",
+ " def __call__(self, features: List[Dict[str, Union[List[int], torch.Tensor]]]) -> Dict[str, torch.Tensor]:\n",
+ " # split inputs and labels since they have to be of different lengths and need different padding methods\n",
+ " # first treat the audio inputs by simply returning torch tensors\n",
+ " input_features = [{\"input_features\": feature[\"input_features\"]} for feature in features]\n",
+ " batch = self.processor.feature_extractor.pad(input_features, return_tensors=\"pt\")\n",
+ "\n",
+ " # get the tokenized label sequences\n",
+ " label_features = [{\"input_ids\": feature[\"labels\"]} for feature in features]\n",
+ " # pad the labels to max length\n",
+ " labels_batch = self.processor.tokenizer.pad(label_features, return_tensors=\"pt\")\n",
+ "\n",
+ " # replace padding with -100 to ignore loss correctly\n",
+ " labels = labels_batch[\"input_ids\"].masked_fill(labels_batch.attention_mask.ne(1), -100)\n",
+ "\n",
+ " # if bos token is appended in previous tokenization step,\n",
+ " # cut bos token here as it's append later anyways\n",
+ " if (labels[:, 0] == self.processor.tokenizer.bos_token_id).all().cpu().item():\n",
+ " labels = labels[:, 1:]\n",
+ "\n",
+ " batch[\"labels\"] = labels\n",
+ "\n",
+ " return batch"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "3cae7dbf-8a50-456e-a3a8-7fd005390f86",
+ "metadata": {
+ "id": "3cae7dbf-8a50-456e-a3a8-7fd005390f86"
+ },
+ "source": [
+ "Let's initialise the data collator we've just defined:"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "id": "fc834702-c0d3-4a96-b101-7b87be32bf42",
+ "metadata": {
+ "id": "fc834702-c0d3-4a96-b101-7b87be32bf42"
+ },
+ "outputs": [],
+ "source": [
+ "data_collator = DataCollatorSpeechSeq2SeqWithPadding(processor=processor)"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "d62bb2ab-750a-45e7-82e9-61d6f4805698",
+ "metadata": {
+ "id": "d62bb2ab-750a-45e7-82e9-61d6f4805698"
+ },
+ "source": [
+ "### Evaluation Metrics"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "66fee1a7-a44c-461e-b047-c3917221572e",
+ "metadata": {
+ "id": "66fee1a7-a44c-461e-b047-c3917221572e"
+ },
+ "source": [
+ "We'll use the word error rate (WER) metric, the 'de-facto' metric for assessing \n",
+ "ASR systems. For more information, refer to the WER [docs](https://huggingface.co/metrics/wer). We'll load the WER metric from 🤗 Evaluate:"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "id": "b22b4011-f31f-4b57-b684-c52332f92890",
+ "metadata": {
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 49,
+ "referenced_widgets": [
+ "215c3486e13343e091a26d658e1030d2",
+ "999382fb9e764a98893bd5269261d70b",
+ "4e9729771294424f959bbfb6bf8b60f3",
+ "3d2249516ecd43a08b5fba53fddb32e8",
+ "681711ebd0c64a63bee6b5337ef401db",
+ "d37791ea2b6c4152991295ca0edb0fb7",
+ "730f4d93bbd94452a59de43bf3d0a266",
+ "048e5c87cea34014a8f8a4538f4126bd",
+ "fbd27061ff114846aedc99bc2d17f7a7",
+ "5a306409e9e045b2b936267c520f935c",
+ "9f0638198f544a3bbb31a3a78b7bd2c2"
+ ]
+ },
+ "id": "b22b4011-f31f-4b57-b684-c52332f92890",
+ "outputId": "b0a08086-69b9-4ab4-97ac-dbed295f2e15"
+ },
+ "outputs": [],
+ "source": [
+ "import evaluate\n",
+ "\n",
+ "metric = evaluate.load(\"wer\")"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "4f32cab6-31f0-4cb9-af4c-40ba0f5fc508",
+ "metadata": {
+ "id": "4f32cab6-31f0-4cb9-af4c-40ba0f5fc508"
+ },
+ "source": [
+ "We then simply have to define a function that takes our model \n",
+ "predictions and returns the WER metric. This function, called\n",
+ "`compute_metrics`, first replaces `-100` with the `pad_token_id`\n",
+ "in the `label_ids` (undoing the step we applied in the \n",
+ "data collator to ignore padded tokens correctly in the loss).\n",
+ "It then decodes the predicted and label ids to strings. Finally,\n",
+ "it computes the WER between the predictions and reference labels:"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "id": "23959a70-22d0-4ffe-9fa1-72b61e75bb52",
+ "metadata": {
+ "id": "23959a70-22d0-4ffe-9fa1-72b61e75bb52"
+ },
+ "outputs": [],
+ "source": [
+ "def compute_metrics(pred):\n",
+ " pred_ids = pred.predictions\n",
+ " label_ids = pred.label_ids\n",
+ "\n",
+ " # replace -100 with the pad_token_id\n",
+ " label_ids[label_ids == -100] = tokenizer.pad_token_id\n",
+ "\n",
+ " # we do not want to group tokens when computing the metrics\n",
+ " pred_str = tokenizer.batch_decode(pred_ids, skip_special_tokens=True)\n",
+ " label_str = tokenizer.batch_decode(label_ids, skip_special_tokens=True)\n",
+ "\n",
+ " wer = 100 * metric.compute(predictions=pred_str, references=label_str)\n",
+ "\n",
+ " return {\"wer\": wer}"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "daf2a825-6d9f-4a23-b145-c37c0039075b",
+ "metadata": {
+ "id": "daf2a825-6d9f-4a23-b145-c37c0039075b"
+ },
+ "source": [
+ "### Load a Pre-Trained Checkpoint"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "437a97fa-4864-476b-8abc-f28b8166cfa5",
+ "metadata": {
+ "id": "437a97fa-4864-476b-8abc-f28b8166cfa5"
+ },
+ "source": [
+ "Now let's load the pre-trained Whisper `small` checkpoint. Again, this \n",
+ "is trivial through use of 🤗 Transformers!"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "id": "5a10cc4b-07ec-4ebd-ac1d-7c601023594f",
+ "metadata": {
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 220,
+ "referenced_widgets": [
+ "d8c1a66480204f1095ff5f6a7dd2e477",
+ "9dc736113ef6477d91aaf71c9969ca74",
+ "79521628c64b4d6f9f22e73749298693",
+ "c7268972f75e4824893ebe7d893a18e1",
+ "a87598d464174703b5f5a5eca23543f3",
+ "e0529b81739144db8912c2d6789e729a",
+ "13d0a97497274652b081cbcefb3fd17d",
+ "08b26adf061b48f59078bf0c0b59e643",
+ "ef056ad59e314089a012acaa73a54e4f",
+ "7935e298049f4deeaeb278ba3de92291",
+ "3afca90970fc4925a05a9a1aa5c8d2f2",
+ "40aba44ef0a74c0d9a385c803c1365a6",
+ "ae54388d78dc4b7ebd1b21860421ffe4",
+ "bb4a47c63d254d4aa3220e85f86d37c4",
+ "cd585c98560b42c8b4a08df5b853b23c",
+ "a140cd385e5a4c0a88c5562370982d2e",
+ "fce64f5690024c698701330f0e5d039a",
+ "abd0e7c414974e51b280a29bf978f776",
+ "bf7961a79c2f403a89a4fb6d4b1a02e5",
+ "1d8636d1d1c3442fbbc2fc83cd03fa44",
+ "313090dc1f034ab19d5ffc573ea1aa5c",
+ "966c0400dafe4e3ea2c9baebc2e104fa",
+ "9087be5d992c4198b3ec2c61f4021164",
+ "6bc07db3471342a6bbc1b86ca734b3e6",
+ "4f167e9657274d56b8568d48262d1ee6",
+ "b7fbaa9d4bcd40b5bcf8d1475658c5b1",
+ "ba21f5ddf2434cc792b70a70c8c1079e",
+ "21bc84c704874455a57c47239984d28d",
+ "5b226e580df94448bed54b400c7a9a25",
+ "b0237154051343adaa076a9cc6dd711d",
+ "64756452791144859b9c803886c6dc77",
+ "f027b4358c2c41a8a93c617641135bcd",
+ "42cb6114956c4a86980c8dafd5a734ae"
+ ]
+ },
+ "id": "5a10cc4b-07ec-4ebd-ac1d-7c601023594f",
+ "outputId": "163d4b39-7e5d-4126-8d78-846c5d94dca6"
+ },
+ "outputs": [],
+ "source": [
+ "from transformers import WhisperForConditionalGeneration, BitsAndBytesConfig\n",
+ "\n",
+ "model = WhisperForConditionalGeneration.from_pretrained(model_name_or_path, quantization_config=BitsAndBytesConfig(load_in_8bit=True))\n",
+ "\n",
+ "# model.hf_device_map - this should be {\" \": 0}"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "a15ead5f-2277-4a39-937b-585c2497b2df",
+ "metadata": {
+ "id": "a15ead5f-2277-4a39-937b-585c2497b2df"
+ },
+ "source": [
+ "Override generation arguments - no tokens are forced as decoder outputs (see [`forced_decoder_ids`](https://huggingface.co/docs/transformers/main_classes/text_generation#transformers.generation_utils.GenerationMixin.generate.forced_decoder_ids)), no tokens are suppressed during generation (see [`suppress_tokens`](https://huggingface.co/docs/transformers/main_classes/text_generation#transformers.generation_utils.GenerationMixin.generate.suppress_tokens)):"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "id": "62038ba3-88ed-4fce-84db-338f50dcd04f",
+ "metadata": {
+ "id": "62038ba3-88ed-4fce-84db-338f50dcd04f"
+ },
+ "outputs": [],
+ "source": [
+ "model.config.forced_decoder_ids = None\n",
+ "model.config.suppress_tokens = []"
+ ]
+ },
+ {
+ "attachments": {},
+ "cell_type": "markdown",
+ "id": "bR-_yaEOPsfQ",
+ "metadata": {
+ "id": "bR-_yaEOPsfQ"
+ },
+ "source": [
+ "### Post-processing on the model\n",
+ "\n",
+ "Finally, we need to apply some post-processing on the 8-bit model to enable training, let's freeze all our layers, and cast all non `int8` layers in `float32` for stability."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "id": "Cl_ZQualPt9R",
+ "metadata": {
+ "id": "Cl_ZQualPt9R"
+ },
+ "outputs": [],
+ "source": [
+ "from peft import prepare_model_for_kbit_training\n",
+ "\n",
+ "model = prepare_model_for_kbit_training(model)"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "Vjl4j4RJPmPR",
+ "metadata": {
+ "id": "Vjl4j4RJPmPR"
+ },
+ "source": [
+ "### Apply LoRA\n",
+ "\n",
+ "Here comes the magic with `peft`! Let's load a `PeftModel` and specify that we are going to use low-rank adapters (LoRA) using `get_peft_model` utility function from `peft`."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "id": "DQtpDPRHPyOL",
+ "metadata": {
+ "colab": {
+ "base_uri": "https://localhost:8080/"
+ },
+ "id": "DQtpDPRHPyOL",
+ "outputId": "1effcbde-7acc-4f62-f24b-e6236a43f833"
+ },
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "trainable params: 15728640 || all params: 1559033600 || trainable%: 1.0088711365810203\n"
+ ]
+ }
+ ],
+ "source": [
+ "from peft import LoraConfig, PeftModel, LoraModel, LoraConfig, get_peft_model\n",
+ "\n",
+ "config = LoraConfig(r=32, lora_alpha=64, target_modules=[\"q_proj\", \"v_proj\"], lora_dropout=0.05, bias=\"none\")\n",
+ "\n",
+ "model = get_peft_model(model, config)\n",
+ "model.print_trainable_parameters()"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "3906d436",
+ "metadata": {},
+ "source": [
+ "We are ONLY using **1%** of the total trainable parameters, thereby performing **Parameter-Efficient Fine-Tuning**"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "2178dea4-80ca-47b6-b6ea-ba1915c90c06",
+ "metadata": {
+ "id": "2178dea4-80ca-47b6-b6ea-ba1915c90c06"
+ },
+ "source": [
+ "### Define the Training Configuration"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "c21af1e9-0188-4134-ac82-defc7bdcc436",
+ "metadata": {
+ "id": "c21af1e9-0188-4134-ac82-defc7bdcc436"
+ },
+ "source": [
+ "In the final step, we define all the parameters related to training. For more detail on the training arguments, refer to the Seq2SeqTrainingArguments [docs](https://huggingface.co/docs/transformers/main_classes/trainer#transformers.Seq2SeqTrainingArguments)."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "id": "0ae3e9af-97b7-4aa0-ae85-20b23b5bcb3a",
+ "metadata": {
+ "id": "0ae3e9af-97b7-4aa0-ae85-20b23b5bcb3a"
+ },
+ "outputs": [],
+ "source": [
+ "from transformers import Seq2SeqTrainingArguments\n",
+ "\n",
+ "training_args = Seq2SeqTrainingArguments(\n",
+ " output_dir=\"temp\", # change to a repo name of your choice\n",
+ " per_device_train_batch_size=8,\n",
+ " gradient_accumulation_steps=1, # increase by 2x for every 2x decrease in batch size\n",
+ " learning_rate=1e-3,\n",
+ " warmup_steps=50,\n",
+ " num_train_epochs=3,\n",
+ " eval_strategy=\"epoch\",\n",
+ " fp16=True,\n",
+ " per_device_eval_batch_size=8,\n",
+ " generation_max_length=128,\n",
+ " logging_steps=25,\n",
+ " remove_unused_columns=False, # required as the PeftModel forward doesn't have the signature of the wrapped model's forward\n",
+ " label_names=[\"labels\"], # same reason as above\n",
+ ")"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "b3a944d8-3112-4552-82a0-be25988b3857",
+ "metadata": {
+ "id": "b3a944d8-3112-4552-82a0-be25988b3857"
+ },
+ "source": [
+ "**Few Important Notes:**\n",
+ "1. `remove_unused_columns=False` and `label_names=[\"labels\"]` are required as the PeftModel's forward doesn't have the signature of the base model's forward.\n",
+ "\n",
+ "2. INT8 training required autocasting. `predict_with_generate` can't be passed to Trainer because it internally calls transformer's `generate` without autocasting leading to errors. \n",
+ "\n",
+ "3. Because of point 2, `compute_metrics` shouldn't be passed to `Seq2SeqTrainer` as seen below. (commented out)"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "id": "d546d7fe-0543-479a-b708-2ebabec19493",
+ "metadata": {
+ "colab": {
+ "base_uri": "https://localhost:8080/"
+ },
+ "id": "d546d7fe-0543-479a-b708-2ebabec19493",
+ "outputId": "e2fabe64-2c50-42ff-a7ca-7773813e9408"
+ },
+ "outputs": [
+ {
+ "name": "stderr",
+ "output_type": "stream",
+ "text": [
+ "The model is loaded in 8-bit precision. To train this model you need to add additional modules inside the model such as adapters using `peft` library and freeze the model weights. Please check the examples in https://github.com/huggingface/peft for more details.\n",
+ "Using cuda_amp half precision backend\n"
+ ]
+ }
+ ],
+ "source": [
+ "from transformers import Seq2SeqTrainer, TrainerCallback, TrainingArguments, TrainerState, TrainerControl\n",
+ "from transformers.trainer_utils import PREFIX_CHECKPOINT_DIR\n",
+ "\n",
+ "\n",
+ "class SavePeftModelCallback(TrainerCallback):\n",
+ " def on_save(\n",
+ " self,\n",
+ " args: TrainingArguments,\n",
+ " state: TrainerState,\n",
+ " control: TrainerControl,\n",
+ " **kwargs,\n",
+ " ):\n",
+ " checkpoint_folder = os.path.join(args.output_dir, f\"{PREFIX_CHECKPOINT_DIR}-{state.global_step}\")\n",
+ "\n",
+ " peft_model_path = os.path.join(checkpoint_folder, \"adapter_model\")\n",
+ " kwargs[\"model\"].save_pretrained(peft_model_path)\n",
+ "\n",
+ " pytorch_model_path = os.path.join(checkpoint_folder, \"pytorch_model.bin\")\n",
+ " if os.path.exists(pytorch_model_path):\n",
+ " os.remove(pytorch_model_path)\n",
+ " return control\n",
+ "\n",
+ "\n",
+ "trainer = Seq2SeqTrainer(\n",
+ " args=training_args,\n",
+ " model=model,\n",
+ " train_dataset=common_voice[\"train\"],\n",
+ " eval_dataset=common_voice[\"test\"],\n",
+ " data_collator=data_collator,\n",
+ " # compute_metrics=compute_metrics,\n",
+ " processing_class=processor.feature_extractor,\n",
+ " callbacks=[SavePeftModelCallback],\n",
+ ")\n",
+ "model.config.use_cache = False # silence the warnings. Please re-enable for inference!"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "id": "ee8b7b8e-1c9a-4d77-9137-1778a629e6de",
+ "metadata": {
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 1000
+ },
+ "id": "ee8b7b8e-1c9a-4d77-9137-1778a629e6de",
+ "outputId": "cdea5268-f33a-4d48-ea4a-a9c71576f81d"
+ },
+ "outputs": [
+ {
+ "name": "stderr",
+ "output_type": "stream",
+ "text": [
+ "/usr/local/lib/python3.8/dist-packages/transformers/optimization.py:346: FutureWarning: This implementation of AdamW is deprecated and will be removed in a future version. Use the PyTorch implementation torch.optim.AdamW instead, or set `no_deprecation_warning=True` to disable this warning\n",
+ " warnings.warn(\n",
+ "***** Running training *****\n",
+ " Num examples = 3927\n",
+ " Num Epochs = 3\n",
+ " Instantaneous batch size per device = 8\n",
+ " Total train batch size (w. parallel, distributed & accumulation) = 8\n",
+ " Gradient Accumulation steps = 1\n",
+ " Total optimization steps = 1473\n",
+ " Number of trainable parameters = 15728640\n",
+ "/usr/local/lib/python3.8/dist-packages/torch/utils/checkpoint.py:31: UserWarning: None of the inputs have requires_grad=True. Gradients will be None\n",
+ " warnings.warn(\"None of the inputs have requires_grad=True. Gradients will be None\")\n",
+ "/usr/local/lib/python3.8/dist-packages/bitsandbytes/autograd/_functions.py:298: UserWarning: MatMul8bitLt: inputs will be cast from torch.float32 to float16 during quantization\n",
+ " warnings.warn(f\"MatMul8bitLt: inputs will be cast from {A.dtype} to float16 during quantization\")\n"
+ ]
+ },
+ {
+ "data": {
+ "text/html": [
+ "\n",
+ " \n",
+ " \n",
+ "
\n",
+ " [1473/1473 3:20:30, Epoch 3/3]\n",
+ "
\n",
+ " \n",
+ " \n",
+ " | Epoch | \n",
+ " Training Loss | \n",
+ " Validation Loss | \n",
+ "
\n",
+ " \n",
+ " \n",
+ " \n",
+ " | 1 | \n",
+ " 0.255800 | \n",
+ " 0.262023 | \n",
+ "
\n",
+ " \n",
+ " | 2 | \n",
+ " 0.166500 | \n",
+ " 0.221193 | \n",
+ "
\n",
+ " \n",
+ "
\n",
+ "
\n",
+ " \n",
+ "
\n",
+ " [ 62/227 04:52 < 13:11, 0.21 it/s]\n",
+ "
\n",
+ " \n",
+ "
\n",
+ " [1473/1473 3:38:43, Epoch 3/3]\n",
+ "
\n",
+ " \n",
+ " \n",
+ " | Epoch | \n",
+ " Training Loss | \n",
+ " Validation Loss | \n",
+ "
\n",
+ " \n",
+ " \n",
+ " \n",
+ " | 1 | \n",
+ " 0.255800 | \n",
+ " 0.262023 | \n",
+ "
\n",
+ " \n",
+ " | 2 | \n",
+ " 0.166500 | \n",
+ " 0.221193 | \n",
+ "
\n",
+ " \n",
+ " | 3 | \n",
+ " 0.083900 | \n",
+ " 0.215908 | \n",
+ "
\n",
+ " \n",
+ "
"
+ ],
+ "text/plain": [
+ ""
+ ]
+ },
+ "metadata": {},
+ "output_type": "display_data"
+ },
+ {
+ "name": "stderr",
+ "output_type": "stream",
+ "text": [
+ "\n",
+ "\n",
+ "Training completed. Do not forget to share your model on huggingface.co/models =)\n",
+ "\n",
+ "\n"
+ ]
+ },
+ {
+ "data": {
+ "text/plain": [
+ "TrainOutput(global_step=1473, training_loss=0.20080567288382556, metrics={'train_runtime': 13136.6638, 'train_samples_per_second': 0.897, 'train_steps_per_second': 0.112, 'total_flos': 2.52799085113344e+19, 'train_loss': 0.20080567288382556, 'epoch': 3.0})"
+ ]
+ },
+ "execution_count": 36,
+ "metadata": {},
+ "output_type": "execute_result"
+ }
+ ],
+ "source": [
+ "trainer.train()"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "id": "0576aa2a",
+ "metadata": {
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 116,
+ "referenced_widgets": [
+ "f309d7a096df4f119e6e6871b56913f1",
+ "5f283548f34848af90affe55a169b5a9",
+ "51a4d85c08d745bda70ba0db731dca68",
+ "eb46a602b3ef484daddbcb847957c3e5",
+ "8e2e49c6046e4dc0a0a810b4e58f80cc",
+ "f3f191968f724e9bbb710b86d3657a66",
+ "d97f77f45e1e400494c2fbf2cd9d69a3",
+ "10e52425e59d4c2c8d2a1239b24e5a95",
+ "9ca0667998cb443d9df29fdd09cf90ff",
+ "f22aa0a93d8b44d0a4c412343ec1f48b",
+ "6e6a59f8e7454c2d886634eade47a21f",
+ "92ae14b97e814d51b016e2a14f227a15",
+ "fb8aca596a1c4ac4a7428248b6c6f8b1",
+ "31de6bfcde21400ab02af4fb31d409da",
+ "3c45a19fdf664b92a27be16abf537a03",
+ "9827e382bf3b49b092969d5656dcad7a",
+ "168e19229aa5404bb151e4547bb31283",
+ "d140f5373bf144d1ae5d282e1a65647e",
+ "fa137c931d2c4e579c27893ca8ee1848",
+ "93647f2d98a74109bfc5ca7a9cc23eed",
+ "a478b23c34654615aad4202b8c7089f6",
+ "4553ba4c0ed645dbb9ddfcc88975ab5f"
+ ]
+ },
+ "id": "0576aa2a",
+ "outputId": "6d3fe4aa-f42a-4428-e070-2272f3b87f5c"
+ },
+ "outputs": [
+ {
+ "name": "stderr",
+ "output_type": "stream",
+ "text": [
+ "Uploading the following files to smangrul/openai-whisper-large-v2-LORA-colab: adapter_model.bin,adapter_config.json\n"
+ ]
+ },
+ {
+ "data": {
+ "application/vnd.jupyter.widget-view+json": {
+ "model_id": "f309d7a096df4f119e6e6871b56913f1",
+ "version_major": 2,
+ "version_minor": 0
+ },
+ "text/plain": [
+ "Upload 1 LFS files: 0%| | 0/1 [00:00
Copy a token from your Hugging Face\ntokens page and paste it below.
Immediately click login after copying\nyour token or it might be stored in plain text in this notebook file. "
+ }
+ },
+ "7d5ff2f1b8794bad8286e90307bd6a61": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "7e2534cfd8564dbd9bddaa2217f2dda4": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "7e264d54d38e4d02acfd47e4e533b49d": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "7e5252f608d6468f80deb468cb2556fd": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_bce6b62300d942a1ab89a6f0ceb16d30",
+ "IPY_MODEL_0239f7263d1a4e8b9475ae48379c068d",
+ "IPY_MODEL_5b527e45d6a946b28047115fa6b5aa3a"
+ ],
+ "layout": "IPY_MODEL_3c5eb07f0bff43948ff1f283c3c56b0f"
+ }
+ },
+ "7f6a466819bb45e880eb989f388a7523": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "7fbb2599863f45f49ad4925d75ef5f77": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "8016eabfc7aa48c2bc0bf3a13919a675": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "80de3739b91a45478cb6a00dcaeae756": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "812f78ca88234efa9b2ccc001245290c": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "82dc91c5b065459d827863699a9710e1": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "FloatProgressModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "FloatProgressModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "ProgressView",
+ "bar_style": "success",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_4b1f4abe697948d5a1cca9b45b2a6f87",
+ "max": 1036558,
+ "min": 0,
+ "orientation": "horizontal",
+ "style": "IPY_MODEL_8527f474f1a549abafe9519e2b4bd338",
+ "value": 1036558
+ }
+ },
+ "830245f63f1947e18b29986d9a091c0a": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_b0efdb97594b4997a8cb148aa03f9a6b",
+ "placeholder": "",
+ "style": "IPY_MODEL_66bdd68e31204abc92fafc0e29860d1c",
+ "value": " 829/829 [00:00<00:00, 42.4kB/s]"
+ }
+ },
+ "8338339ab8a242c1a485bce8558f9c39": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_4bea6b0455ae4019b33d45491dbf4584",
+ "placeholder": "",
+ "style": "IPY_MODEL_9c928a14371a4d9aa521953e287fff54",
+ "value": " 908/908 [03:07<00:00, 3.87ex/s]"
+ }
+ },
+ "83a7cd2ce4074720acc6236aaf24014d": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "83cb83e404a24fba8cf43610cb1696fc": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_7b70db203ee644fe81006f5d48aa426d",
+ "IPY_MODEL_efd9d5724dbd435991052b4445c6970f",
+ "IPY_MODEL_41f65340441f419d91e1d3841921f48a"
+ ],
+ "layout": "IPY_MODEL_58aba8edefa44c60818891a2651137be"
+ }
+ },
+ "844caba5ebdd48189517a10705543292": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_2d667cd4bc134a44958d17ef75d86321",
+ "IPY_MODEL_acfb7b6734884939a753fc19047bb9bc",
+ "IPY_MODEL_73cd51c6c43b40cab25d411e7c0f6ad1"
+ ],
+ "layout": "IPY_MODEL_19c7ea1e9364437a9c0bf6b4e645f854"
+ }
+ },
+ "845211300fbd49f480d056bba9de83e1": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "851902cb2b0e494998684409d82dafd1": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "8527f474f1a549abafe9519e2b4bd338": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "85509b0aafec47e5ad540abc7ae4ab7d": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "85cdb3ecd88d426a8e517b3c8c8a8307": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "86692318e7584e62b4143c1b2eca5935": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "8675aad817a44ab39b097ec864669833": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "87d251db4a6e495cb1d59d276e823bf2": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "8843f70cfa1f45299a588e96e9c1159a": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "892e150a80464f8198024587a47186ba": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "898c7b43a5e94601bc093e0cde28c2ec": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_21ca204b93994e8790c9eb7b0722761f",
+ "placeholder": "",
+ "style": "IPY_MODEL_f628cb62f5fa446eb608467c1ecea526",
+ "value": "Downloading data: 100%"
+ }
+ },
+ "89bb7bbcaa194a23bf3d908a4782ccb8": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "89f8ede64593475da4e056e9907f370f": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_4edf0948ed1346ceba1c0148e9c6fe1c",
+ "placeholder": "",
+ "style": "IPY_MODEL_40f2b2ff75ca4562808fc2c7a870901e",
+ "value": " 908/908 [03:10<00:00, 4.49ex/s]"
+ }
+ },
+ "8a91574c4b6e4745b2b65885323b4d25": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "8af6bd6e8cae4964a2e372be30220bd9": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "8b0dd001d5b04647b1c480aab83d03a2": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "8b2e2c650f4b4bee9e763b7c59525ec8": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "8b51633b2fe5479db0fc73cd3f0ebaea": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "8b9324f5c0e24576a9733f30a8945edd": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "FloatProgressModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "FloatProgressModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "ProgressView",
+ "bar_style": "success",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_ad8b6c32caa4493ebadf7691ed1546d4",
+ "max": 2064,
+ "min": 0,
+ "orientation": "horizontal",
+ "style": "IPY_MODEL_85cdb3ecd88d426a8e517b3c8c8a8307",
+ "value": 2064
+ }
+ },
+ "8ba244a082284f6dbac1c8f689c527a8": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "8c010800d6d945fe965fd5b9c6ab2ec4": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "FloatProgressModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "FloatProgressModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "ProgressView",
+ "bar_style": "success",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_4568923487c44041ab985ee326842d15",
+ "max": 358,
+ "min": 0,
+ "orientation": "horizontal",
+ "style": "IPY_MODEL_352a2237356846af836779413e584fee",
+ "value": 358
+ }
+ },
+ "8c41e1ee1a2c49b8b3d3d320fbf26262": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "8cb910ad08024c818b99c2e30e30b039": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_14bca5cf764d4464a186961ccc6bdb3d",
+ "placeholder": "",
+ "style": "IPY_MODEL_75c793c91b9e4aa994c2d34ebb16f7d4",
+ "value": " 782k/782k [00:00<00:00, 972kB/s]"
+ }
+ },
+ "8d50d82f9d94482c9883f99ea5c7d704": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "8daed385e6564c7897fb6553669a9065": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_d2c1704e34c34d12b99c31d64fce88cc",
+ "placeholder": "",
+ "style": "IPY_MODEL_6bdce3b33872457ea67a3a3191f438ca",
+ "value": "Downloading data files: 100%"
+ }
+ },
+ "8e2e49c6046e4dc0a0a810b4e58f80cc": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "8e480fe546f24afebb1ea723bff84456": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_f20fc82bcbf245619ad4dec04d0f999d",
+ "placeholder": "",
+ "style": "IPY_MODEL_8016eabfc7aa48c2bc0bf3a13919a675",
+ "value": " 1682/0 [00:14<00:00, 2245.17 examples/s]"
+ }
+ },
+ "8e84abf61e3e45d58efc7ccd0bfe8d37": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "8f52bab9ebd049d6a57686d621f407ac": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "8f856d6bde4041149324e1f53d19c1cb": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "90744e5529c04f18b11e00326649abe5": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "9087be5d992c4198b3ec2c61f4021164": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_6bc07db3471342a6bbc1b86ca734b3e6",
+ "IPY_MODEL_4f167e9657274d56b8568d48262d1ee6",
+ "IPY_MODEL_b7fbaa9d4bcd40b5bcf8d1475658c5b1"
+ ],
+ "layout": "IPY_MODEL_ba21f5ddf2434cc792b70a70c8c1079e"
+ }
+ },
+ "90b53e96b3f04c2993969b17547ae0d5": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "91b103ac79e641b190416acdeb55902c": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "91c3b5ddf5fb4c7aa835d992b4c7b4e7": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_52ff6528abdd4a9e9b85f4b355b2391d",
+ "IPY_MODEL_6bb6737e22bd48d786b02051d077e8cc",
+ "IPY_MODEL_e97a0201b81446b882ba802a5a3b00e8"
+ ],
+ "layout": "IPY_MODEL_c1a89a042b044278a8666da306e6a481"
+ }
+ },
+ "91fc5846a32f44d5bc5fa30fdcb3c638": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_daf4005d1d334608846d0fb2fe4f837a",
+ "IPY_MODEL_ba48d89cab9346ed92dc338779f9f828",
+ "IPY_MODEL_6b0e0694d895445c9bf7c955a116953f"
+ ],
+ "layout": "IPY_MODEL_ecb7ffba323743c68961e294e74b337b"
+ }
+ },
+ "9202065d8e6f425d88e4514dde70992d": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_f7b4ec74e2ac45bbbf0265d0363f4d9f",
+ "IPY_MODEL_3a083523ae604362901e4e31c39fe949",
+ "IPY_MODEL_d1bc2ce48c3e481b9059e882b5102946"
+ ],
+ "layout": "IPY_MODEL_30c688df949042ce89337643f6178230"
+ }
+ },
+ "921fd273a7254447a93fb997773aedab": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "925f7aad24b547cc8071ee9bda713d7c": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_7e2534cfd8564dbd9bddaa2217f2dda4",
+ "placeholder": "",
+ "style": "IPY_MODEL_a5bd56eb69524729afdfdd14b55b6130",
+ "value": "Downloading (…)lve/main/config.json: 100%"
+ }
+ },
+ "92ae14b97e814d51b016e2a14f227a15": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_fb8aca596a1c4ac4a7428248b6c6f8b1",
+ "IPY_MODEL_31de6bfcde21400ab02af4fb31d409da",
+ "IPY_MODEL_3c45a19fdf664b92a27be16abf537a03"
+ ],
+ "layout": "IPY_MODEL_9827e382bf3b49b092969d5656dcad7a"
+ }
+ },
+ "92d9732acb964601b27695041f9fbb72": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_91b103ac79e641b190416acdeb55902c",
+ "placeholder": "",
+ "style": "IPY_MODEL_e9e10f1e53b74509bfc9c0bf11502c5e",
+ "value": " 185k/185k [00:00<00:00, 656kB/s]"
+ }
+ },
+ "92debeaea5cc4136bb37703947e825e0": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_7aca78c9768a48a7ab0a8220a3b364b9",
+ "placeholder": "",
+ "style": "IPY_MODEL_7213f79093f74df996f8dbe7fe816ea0",
+ "value": " 63.1M/63.1M [00:00<00:00, 108MB/s]"
+ }
+ },
+ "931b96b21b39482298f40449424fdd34": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "931fc769fbeb42bf82df6ef5f914bf48": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "93647f2d98a74109bfc5ca7a9cc23eed": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "93e2efbb5da747d4b94c916153ee9706": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "950e74921e6042868ab6b7b9070d6f69": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_d5d632dd16f147e090c62aad38c45d3c",
+ "placeholder": "",
+ "style": "IPY_MODEL_24191f38e3654b86a5da3576615e2229",
+ "value": "Downloading (…)olve/main/vocab.json: 100%"
+ }
+ },
+ "960553d142c446cd8852523887a5cc04": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "96266c5722f54eeeb682b2707b8025dd": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "965ac01b68064dc5a9fc3bb3f244c804": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "966c0400dafe4e3ea2c9baebc2e104fa": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "969e3cf7f3634c3f90b5fea38c5797ca": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "FloatProgressModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "FloatProgressModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "ProgressView",
+ "bar_style": "info",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_2ff541d18f5844408690be00c7259d59",
+ "max": 1,
+ "min": 0,
+ "orientation": "horizontal",
+ "style": "IPY_MODEL_679fa9d2a703494dbb10fbfd19879f1a",
+ "value": 1
+ }
+ },
+ "96c0b77f9a5e473b8b5dc92bde0f4a9c": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "979edd227f0840a4be0233082e452b5a": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "FloatProgressModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "FloatProgressModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "ProgressView",
+ "bar_style": "success",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_ec6017ce2fb3431ab823bde05f977a61",
+ "max": 1963,
+ "min": 0,
+ "orientation": "horizontal",
+ "style": "IPY_MODEL_1a540a7cba794122abdb1900061479e2",
+ "value": 1963
+ }
+ },
+ "980e87bb43d54306aba5019964857b89": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "9827e382bf3b49b092969d5656dcad7a": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "989b3df296504f34a62d31ca0d6d88bb": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "9980bca9b1334893bf6583c325122f50": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "999382fb9e764a98893bd5269261d70b": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_d37791ea2b6c4152991295ca0edb0fb7",
+ "placeholder": "",
+ "style": "IPY_MODEL_730f4d93bbd94452a59de43bf3d0a266",
+ "value": "Downloading builder script: 100%"
+ }
+ },
+ "99b628071c814d88a3cd5d72e4c95f01": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "9abe7ed3e3d347b6bad7d1252bde226f": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "9afdb23ba9ee47709f194e0e92de0edf": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "9b427631384c47ab89ee1352c0236afd": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "9c928a14371a4d9aa521953e287fff54": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "9ca0667998cb443d9df29fdd09cf90ff": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "9dc736113ef6477d91aaf71c9969ca74": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_e0529b81739144db8912c2d6789e729a",
+ "placeholder": "",
+ "style": "IPY_MODEL_13d0a97497274652b081cbcefb3fd17d",
+ "value": "Downloading (…)lve/main/config.json: 100%"
+ }
+ },
+ "9f0638198f544a3bbb31a3a78b7bd2c2": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "9f9e15ff2e394ee7a7776e3e7f4b7d30": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "a03430c0cdcb47bfbd2ffd754074d692": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "FloatProgressModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "FloatProgressModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "ProgressView",
+ "bar_style": "success",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_e20264d19e804f9dba3e3867ef9b31bd",
+ "max": 615674,
+ "min": 0,
+ "orientation": "horizontal",
+ "style": "IPY_MODEL_43141dcab2324fc6a12f9b8198e10154",
+ "value": 615674
+ }
+ },
+ "a05426c8e5f849b7a972dc0df3cd84ef": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "a140cd385e5a4c0a88c5562370982d2e": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "a1578c0c777f4780a3fdd1635a0909d9": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_bde010029c374a0eb2bb942f380f0e8b",
+ "placeholder": "",
+ "style": "IPY_MODEL_a91f37ce798d411ea2a33cfdb1f01251",
+ "value": " 2.06k/2.06k [00:00<00:00, 75.3kB/s]"
+ }
+ },
+ "a22db8523d44457bb96448d08129988f": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "a235cb3d4d424efeb30901f63fc1dbe5": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "a25ef41450eb42ff9b8b618b40080ac0": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "a26ddb684a07496da4290e3f6031b685": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "a478b23c34654615aad4202b8c7089f6": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "a4b16b5279504dd694090798f5925d65": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "a5bd56eb69524729afdfdd14b55b6130": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "a615446a48624d0f9a009c1f6d8b1a54": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_6d9826a5adb847e8b4cc4486a31b52ce",
+ "placeholder": "",
+ "style": "IPY_MODEL_e8b3093587e44164b0ac043414cea0fa",
+ "value": "Downloading (…)olve/main/merges.txt: 100%"
+ }
+ },
+ "a6963ce72cb3425791804abf1718ba90": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "a87598d464174703b5f5a5eca23543f3": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "a8aac44a077040bd9f4638c0c8f7a877": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "FloatProgressModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "FloatProgressModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "ProgressView",
+ "bar_style": "success",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_04144ed3ff5f423f99179702cee5343f",
+ "max": 908,
+ "min": 0,
+ "orientation": "horizontal",
+ "style": "IPY_MODEL_8c41e1ee1a2c49b8b3d3d320fbf26262",
+ "value": 908
+ }
+ },
+ "a91f37ce798d411ea2a33cfdb1f01251": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "a9c132959dae4303bcf6015106ce3453": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "aa7557fbffc54ed3a9c58c1531fd93f6": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "aaeec2b7986d493e8d238aa14f2e5937": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "ab40616ed9b74f438e74d403f848bed4": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "ab4ae16fa4f448838f677ea60523c905": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "abc8f69eae7b46b1b430cf3b7a231b05": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_baa8f739bb7e402bae7ee479e282e813",
+ "placeholder": "",
+ "style": "IPY_MODEL_54509d703b7d4416bdee59157f918396",
+ "value": "#1: 100%"
+ }
+ },
+ "abd0e7c414974e51b280a29bf978f776": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "abe561c67f1f42b29c33d4c296221b2f": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "ac2e1977ddaf4b948c9cc24d84c08b83": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "ac9c1141ca7c453f84a8ab62b2de9158": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "FloatProgressModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "FloatProgressModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "ProgressView",
+ "bar_style": "success",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_3fd0fd7cbbef4785b360891c12017f48",
+ "max": 12179,
+ "min": 0,
+ "orientation": "horizontal",
+ "style": "IPY_MODEL_a9c132959dae4303bcf6015106ce3453",
+ "value": 12179
+ }
+ },
+ "acfb7b6734884939a753fc19047bb9bc": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "FloatProgressModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "FloatProgressModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "ProgressView",
+ "bar_style": "success",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_0ae5110b687440e89ebebfb847985aa1",
+ "max": 5,
+ "min": 0,
+ "orientation": "horizontal",
+ "style": "IPY_MODEL_85509b0aafec47e5ad540abc7ae4ab7d",
+ "value": 5
+ }
+ },
+ "ad8b6c32caa4493ebadf7691ed1546d4": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "add0f175631742d49dd4695bc004e81a": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_5871a46d60f14da99e4bb8ee74405319",
+ "IPY_MODEL_64b308019fff4095ab7f1812aab4676a",
+ "IPY_MODEL_03f62b3f5aa64b6390b157cb3f9d2b9f"
+ ],
+ "layout": "IPY_MODEL_59657f26f4af490980b1d9bea1526e5e"
+ }
+ },
+ "ae54388d78dc4b7ebd1b21860421ffe4": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_fce64f5690024c698701330f0e5d039a",
+ "placeholder": "",
+ "style": "IPY_MODEL_abd0e7c414974e51b280a29bf978f776",
+ "value": "Downloading (…)"pytorch_model.bin";: 100%"
+ }
+ },
+ "af44aa66372a43beb9812ad9895d8d1f": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_7b190bb2bd234b7997ca041baddd511f",
+ "placeholder": "",
+ "style": "IPY_MODEL_7549fd0b38364d8580f8eb1549558a33",
+ "value": " 5/5 [00:03<00:00, 1.15it/s]"
+ }
+ },
+ "af56501692b84e718fe3e8b1e452b7c2": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "FloatProgressModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "FloatProgressModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "ProgressView",
+ "bar_style": "success",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_e53d35abac8241bcaf6d3b0f732d1bb9",
+ "max": 184990,
+ "min": 0,
+ "orientation": "horizontal",
+ "style": "IPY_MODEL_87d251db4a6e495cb1d59d276e823bf2",
+ "value": 184990
+ }
+ },
+ "b0237154051343adaa076a9cc6dd711d": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "b041efb27b6149fcaf206590f1c1b961": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_1b1dc31d9a2b4357a71119300c6d899a",
+ "placeholder": "",
+ "style": "IPY_MODEL_7a24ae9d13fb4e82b1993b05f8d71d11",
+ "value": "Downloading (…)rocessor_config.json: 100%"
+ }
+ },
+ "b09d153958cf4a28baad268bbda78236": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "b0e084a4c551427bb176061df894fdf6": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "b0efdb97594b4997a8cb148aa03f9a6b": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "b1183b9042744d3fa7437e2ec55b6cdd": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_c643b8650c31466a8614510928ab5d2e",
+ "placeholder": "",
+ "style": "IPY_MODEL_58e46e1d355244bcab90b32c163e2877",
+ "value": " 1.97k/1.97k [00:00<00:00, 31.4kB/s]"
+ }
+ },
+ "b1221f4e0a57482682ea4bd6ae245da3": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "b16e3a75acd0403f865849f1de6ca654": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "b19431ca425341568c2b3a8556431a8f": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_6072c153de2540bf9e1227db5057fffc",
+ "placeholder": "",
+ "style": "IPY_MODEL_b7d9e1bf1d2e48e59c4dca38a638d4b4",
+ "value": " 494k/494k [00:00<00:00, 3.65MB/s]"
+ }
+ },
+ "b1d780c721b840d7a06661a7a5e63236": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "b3a59b83acaa4864be23e10d90560139": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "FloatProgressModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "FloatProgressModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "ProgressView",
+ "bar_style": "success",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_7b8266519f0a41cd9a065b9e795d7e84",
+ "max": 2108,
+ "min": 0,
+ "orientation": "horizontal",
+ "style": "IPY_MODEL_658361b3d5054f44a5c21df747537bdd",
+ "value": 2108
+ }
+ },
+ "b5c8221a09df4dfdb74017d4af544b95": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "b600ead93bbf44a3a3fe229589c63a61": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_3d4c614fb775434fb0c5b02d46246ee0",
+ "IPY_MODEL_344d1cc53e28411cae839a4ebba1bf58",
+ "IPY_MODEL_a1578c0c777f4780a3fdd1635a0909d9"
+ ],
+ "layout": "IPY_MODEL_41faf55c8878475f8a986b02ad73e8ce"
+ }
+ },
+ "b7d9e1bf1d2e48e59c4dca38a638d4b4": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "b7fbaa9d4bcd40b5bcf8d1475658c5b1": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_f027b4358c2c41a8a93c617641135bcd",
+ "placeholder": "",
+ "style": "IPY_MODEL_42cb6114956c4a86980c8dafd5a734ae",
+ "value": " 3.49k/3.49k [00:00<00:00, 142kB/s]"
+ }
+ },
+ "b803893882ac4358a4676964dfb3fb31": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_f5d7433d15de45e997d12568cac536fc",
+ "placeholder": "",
+ "style": "IPY_MODEL_14e284f308844311a9ad40415091d93f",
+ "value": " 1964/1964 [06:56<00:00, 4.82ex/s]"
+ }
+ },
+ "b8acdb71c3564972a6c8b27e964ec061": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_688f552e85714fe6a5d3eda82be0106a",
+ "IPY_MODEL_a8aac44a077040bd9f4638c0c8f7a877",
+ "IPY_MODEL_89f8ede64593475da4e056e9907f370f"
+ ],
+ "layout": "IPY_MODEL_851902cb2b0e494998684409d82dafd1"
+ }
+ },
+ "b8d3539c8a454217a3b6ffab51259054": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "ba21f5ddf2434cc792b70a70c8c1079e": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "ba48d89cab9346ed92dc338779f9f828": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "FloatProgressModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "FloatProgressModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "ProgressView",
+ "bar_style": "success",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_73bde731e20d48de8ce66b9d72fb95cb",
+ "max": 65484800,
+ "min": 0,
+ "orientation": "horizontal",
+ "style": "IPY_MODEL_9afdb23ba9ee47709f194e0e92de0edf",
+ "value": 65484800
+ }
+ },
+ "baa8f739bb7e402bae7ee479e282e813": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "bafada4a1f29442296c47018dcaedb77": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "bb1bcdfd39bb430c8a453d7a4c3a5e3d": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "bb4a47c63d254d4aa3220e85f86d37c4": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "FloatProgressModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "FloatProgressModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "ProgressView",
+ "bar_style": "success",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_bf7961a79c2f403a89a4fb6d4b1a02e5",
+ "max": 6173629930,
+ "min": 0,
+ "orientation": "horizontal",
+ "style": "IPY_MODEL_1d8636d1d1c3442fbbc2fc83cd03fa44",
+ "value": 6173629930
+ }
+ },
+ "bbc5dbbb8b3548d485b878e194683cf2": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_c0432026ca204c4e89721fb22589c576",
+ "IPY_MODEL_c5672e82461148e29dc93af865e259ff",
+ "IPY_MODEL_f8053b94954d401a85ead90319aa4690"
+ ],
+ "layout": "IPY_MODEL_cfee6cbc1d15435bad0bc4a193542c10"
+ }
+ },
+ "bc2b317065ed4b658995663ff202108a": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "bc9c3ba4bc6d4623a764d92890536935": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "bce6b62300d942a1ab89a6f0ceb16d30": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_3545fcc1e9d7453099c4931f658e0bc8",
+ "placeholder": "",
+ "style": "IPY_MODEL_2f314258091a430095794c3fe0aea7e3",
+ "value": "Generating other split: "
+ }
+ },
+ "bd4e3eb14252470d9c8ac60a32948a72": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_2ef66808d51d440b9998064e212df420",
+ "placeholder": "",
+ "style": "IPY_MODEL_45478f2ce991441c8ceaef9acf745084",
+ "value": " 12.2k/12.2k [00:00<00:00, 142kB/s]"
+ }
+ },
+ "bd7da2671a22431889fbfa2ae1e0fe2c": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "bde010029c374a0eb2bb942f380f0e8b": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "be90fac89e5243fb82389ed06d094c10": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "FloatProgressModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "FloatProgressModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "ProgressView",
+ "bar_style": "success",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_845211300fbd49f480d056bba9de83e1",
+ "max": 63056269,
+ "min": 0,
+ "orientation": "horizontal",
+ "style": "IPY_MODEL_df4435b0da414c3880adf33a50c465e5",
+ "value": 63056269
+ }
+ },
+ "bed65245e7234977874d35bf78694e35": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "FloatProgressModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "FloatProgressModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "ProgressView",
+ "bar_style": "success",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_3a4bb5b9cf864265af8f1a0b989dff2c",
+ "max": 829,
+ "min": 0,
+ "orientation": "horizontal",
+ "style": "IPY_MODEL_ac2e1977ddaf4b948c9cc24d84c08b83",
+ "value": 829
+ }
+ },
+ "bf7961a79c2f403a89a4fb6d4b1a02e5": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "bfc9036c9c5f4be7ab191b92d92f1352": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "c0432026ca204c4e89721fb22589c576": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_35e6c9e3c5ea47a89cd0cbebfd197bde",
+ "placeholder": "",
+ "style": "IPY_MODEL_f81bffac74ff4b07a09760a00620610c",
+ "value": "Downloading (…)olve/main/vocab.json: 100%"
+ }
+ },
+ "c1a89a042b044278a8666da306e6a481": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "c1f019686c564cca87c240a75ab71ad3": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_54589117bf244027ba024ea85bd1fd77",
+ "IPY_MODEL_7b7986ad93f64956b8d198d2cb4acb60",
+ "IPY_MODEL_dbc1a016a69b4ad7811d2701a9520a2f"
+ ],
+ "layout": "IPY_MODEL_72f8e7de2a5d4155a9e9146f12e14b19"
+ }
+ },
+ "c24ddbaafa5f4a63b391d981a4f10354": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "c28c2fc81e0e467cbc0ded0205d1ee85": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_dd339bf6baf6433e92665e30dc30b062",
+ "placeholder": "",
+ "style": "IPY_MODEL_6a544d6dd5954beab32ce3089d8d2aac",
+ "value": " 829/829 [00:00<00:00, 34.3kB/s]"
+ }
+ },
+ "c2c2608dd091493795d975f1a3cc3762": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "c3ea17f7dd94462986d30b751664d77b": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "c4119f7ec7464aab90f17d022e674999": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "c43169085f2949f1b8259cd0b767d121": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_9980bca9b1334893bf6583c325122f50",
+ "placeholder": "",
+ "style": "IPY_MODEL_931fc769fbeb42bf82df6ef5f914bf48",
+ "value": "Downloading data: 100%"
+ }
+ },
+ "c44f472624d84e16a0f380580d36ca61": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_65188c1fdba2421ba85c2cc349709600",
+ "IPY_MODEL_0683cbffd97a4b75bd5e00a05d541fef",
+ "IPY_MODEL_4573606592ce4b2a914ed0a70b69f9af"
+ ],
+ "layout": "IPY_MODEL_efb85d003fb54f55aa4eadf2ab8b1684"
+ }
+ },
+ "c47ba0b11e074f708338863a35a78f7b": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_8b0dd001d5b04647b1c480aab83d03a2",
+ "placeholder": "",
+ "style": "IPY_MODEL_0af935ad4f694fb48094e6a119cbcf82",
+ "value": "Downloading (…)in/added_tokens.json: 100%"
+ }
+ },
+ "c4cca1778f314ce582bd09b9b2494f82": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_b1d780c721b840d7a06661a7a5e63236",
+ "placeholder": "",
+ "style": "IPY_MODEL_d19402df47464044b36fb5ee4a0c1c4d",
+ "value": "Downloading data: 100%"
+ }
+ },
+ "c4e7cf4e42554d61aa055da47ab0ee22": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "c5672e82461148e29dc93af865e259ff": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "FloatProgressModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "FloatProgressModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "ProgressView",
+ "bar_style": "success",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_cb55e8ca8bf4477bb323ae45a6c60500",
+ "max": 1036558,
+ "min": 0,
+ "orientation": "horizontal",
+ "style": "IPY_MODEL_3e154f89e56146438bc45030e5254d8d",
+ "value": 1036558
+ }
+ },
+ "c60690c2aee74763bf23115553f4e640": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "VBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "VBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "VBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_7d3d6c198e794219ab5db59f0228c8ab",
+ "IPY_MODEL_5d5ea0207c6148769ad9f15b7b3dd92d",
+ "IPY_MODEL_642e28d258ca4c30a5df94c5cf7e0471",
+ "IPY_MODEL_170ee581427d4f30925dc393d124c1be",
+ "IPY_MODEL_d5d5aa24182a4e04b3fdae1ca7fad52a"
+ ],
+ "layout": "IPY_MODEL_6dba643113a547ac9b6e121d008791d6"
+ }
+ },
+ "c643b8650c31466a8614510928ab5d2e": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "c6c9fa535ff4458ba966183e1489905b": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_56e8812fa66e40b0896a19dd3be7330c",
+ "placeholder": "",
+ "style": "IPY_MODEL_116c89bb3a2045f28123e4f36067a7e5",
+ "value": " 185k/185k [00:00<00:00, 2.18MB/s]"
+ }
+ },
+ "c7268972f75e4824893ebe7d893a18e1": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_7935e298049f4deeaeb278ba3de92291",
+ "placeholder": "",
+ "style": "IPY_MODEL_3afca90970fc4925a05a9a1aa5c8d2f2",
+ "value": " 1.97k/1.97k [00:00<00:00, 70.2kB/s]"
+ }
+ },
+ "c78544f32b564ba6832120b3167a2162": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "c80954848a4a499a87708548bed8e7cc": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "c81c5d3a4dc5409e95a6410e67fa9857": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_33888a5cafe6495782309dae44531dd3",
+ "placeholder": "",
+ "style": "IPY_MODEL_7d5ff2f1b8794bad8286e90307bd6a61",
+ "value": " 91.0M/91.0M [00:02<00:00, 43.0MB/s]"
+ }
+ },
+ "c89cb73d51dd457d8c17ff97e74b7ca1": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "c8ba787279ea43aa97b134c134d4f183": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "cb55e8ca8bf4477bb323ae45a6c60500": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "cbbba08d9e634560a6c0429e32166fe5": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_79da882ea494477a8c94fdac7acd644e",
+ "placeholder": "",
+ "style": "IPY_MODEL_f14847261aa247fb9561373e0495f3e5",
+ "value": "Downloading builder script: 100%"
+ }
+ },
+ "cd585c98560b42c8b4a08df5b853b23c": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_313090dc1f034ab19d5ffc573ea1aa5c",
+ "placeholder": "",
+ "style": "IPY_MODEL_966c0400dafe4e3ea2c9baebc2e104fa",
+ "value": " 6.17G/6.17G [00:31<00:00, 201MB/s]"
+ }
+ },
+ "cd9bda1053a14890ad9091c63c0a0acf": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "cda6af0ca01d4053bcebe06f3c41d887": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_f773a61b1dba4e3eb0df36162efe9abc",
+ "placeholder": "",
+ "style": "IPY_MODEL_bfc9036c9c5f4be7ab191b92d92f1352",
+ "value": " 616k/616k [00:00<00:00, 1.31MB/s]"
+ }
+ },
+ "cdd08679c28642a184805912c07b324e": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "ce06b2a0de6c4fb8bae36bc4d7f63270": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_c4cca1778f314ce582bd09b9b2494f82",
+ "IPY_MODEL_3bd70d937e924f61b943acb0aaf15619",
+ "IPY_MODEL_c81c5d3a4dc5409e95a6410e67fa9857"
+ ],
+ "layout": "IPY_MODEL_dd02d1b31bfd4b19ad626d6691a9b293"
+ }
+ },
+ "ce8f306e745d4b158c58058d471de037": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "cfee6cbc1d15435bad0bc4a193542c10": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "d046a46c70ea46ffbb04a3c9f55637d5": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "d140f5373bf144d1ae5d282e1a65647e": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "d19402df47464044b36fb5ee4a0c1c4d": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "d1bc2ce48c3e481b9059e882b5102946": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_11b9c50e720a466aa92c64b254d40778",
+ "placeholder": "",
+ "style": "IPY_MODEL_8f856d6bde4041149324e1f53d19c1cb",
+ "value": " 60.9k/60.9k [00:00<00:00, 169kB/s]"
+ }
+ },
+ "d21cd4878c6e49d38dd3abb2e3b3f566": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_621880c98245427881dd5b004b480c6a",
+ "placeholder": "",
+ "style": "IPY_MODEL_65c2716dd7f14afa93d3bfaebe85c44f",
+ "value": "Generating invalidated split: "
+ }
+ },
+ "d2c14b2486e24150a8242ca37f4200f4": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "d2c1704e34c34d12b99c31d64fce88cc": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "d37791ea2b6c4152991295ca0edb0fb7": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "d3d7c15d53c8498e823c84fe609321dd": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "d5d5aa24182a4e04b3fdae1ca7fad52a": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_6d5801774beb4b529b227ef2f098614e",
+ "placeholder": "",
+ "style": "IPY_MODEL_dfdf23cde48c421caebb573060641d6a",
+ "value": "\nPro Tip: If you don't already have one, you can create a dedicated\n'notebooks' token with 'write' access, that you can then easily reuse for all\nnotebooks. "
+ }
+ },
+ "d5d632dd16f147e090c62aad38c45d3c": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "d65e79ed6a9f4daea04e098959f12c80": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "FloatProgressModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "FloatProgressModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "ProgressView",
+ "bar_style": "success",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_c89cb73d51dd457d8c17ff97e74b7ca1",
+ "max": 3486,
+ "min": 0,
+ "orientation": "horizontal",
+ "style": "IPY_MODEL_921fd273a7254447a93fb997773aedab",
+ "value": 3486
+ }
+ },
+ "d8c1a66480204f1095ff5f6a7dd2e477": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_9dc736113ef6477d91aaf71c9969ca74",
+ "IPY_MODEL_79521628c64b4d6f9f22e73749298693",
+ "IPY_MODEL_c7268972f75e4824893ebe7d893a18e1"
+ ],
+ "layout": "IPY_MODEL_a87598d464174703b5f5a5eca23543f3"
+ }
+ },
+ "d92259acf9704ef9be6eced8a5f25dab": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "d96245da43944c4b8235e0cd02c1aa4c": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "d97f77f45e1e400494c2fbf2cd9d69a3": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "d9a85d7c76b54199bbf7646448e3458c": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_564cd321c06440e9856f10f5c40c20be",
+ "placeholder": "",
+ "style": "IPY_MODEL_8a91574c4b6e4745b2b65885323b4d25",
+ "value": " 3.44k/3.44k [00:00<00:00, 71.6kB/s]"
+ }
+ },
+ "daee15869a92459aabcd9128526183d5": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "daf4005d1d334608846d0fb2fe4f837a": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_460be80f176849e0b1241e3a4fc18b74",
+ "placeholder": "",
+ "style": "IPY_MODEL_74e2bcef1ce94234bbf6ba0d6488279d",
+ "value": "Downloading data: 100%"
+ }
+ },
+ "db5e1bf1871546408f233f0cbc37b136": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "FloatProgressModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "FloatProgressModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "ProgressView",
+ "bar_style": "success",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_ed7daa32c94648d5951876229f9835b3",
+ "max": 5,
+ "min": 0,
+ "orientation": "horizontal",
+ "style": "IPY_MODEL_eb883a37a9cf4945bd864decb4fc87ea",
+ "value": 5
+ }
+ },
+ "dbc1a016a69b4ad7811d2701a9520a2f": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_fb9f013a6188463fad6db70702576c37",
+ "placeholder": "",
+ "style": "IPY_MODEL_93e2efbb5da747d4b94c916153ee9706",
+ "value": " 5/5 [00:24<00:00, 5.01s/it]"
+ }
+ },
+ "dbe19b9505884a958e832c0362d547df": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_6a40bc08e55a4605b478edf01ff088df",
+ "placeholder": "",
+ "style": "IPY_MODEL_fbd304c2564e4acba84809377ba19e25",
+ "value": "Downloading (…)"pytorch_model.bin";: 100%"
+ }
+ },
+ "dce0d285c7d947dfba9ee5bc1a6ebece": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "dd02d1b31bfd4b19ad626d6691a9b293": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "dd339bf6baf6433e92665e30dc30b062": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "dd634585d5e64c97881b132b1d59083e": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "ddc2a8e8ef4d429f95081c4c5baf1fb3": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "deb18822d58b4b60bb75460f0a5fe921": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "dec9f287435e4c6b9fb1d1ead2ded576": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_00071f8cf276478fb2740684552f1275",
+ "placeholder": "",
+ "style": "IPY_MODEL_64378b1064dc4036a9a4c8813013e210",
+ "value": "Extracting data files: 100%"
+ }
+ },
+ "df4435b0da414c3880adf33a50c465e5": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "dfdf23cde48c421caebb573060641d6a": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "e0529b81739144db8912c2d6789e729a": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "e1141861d9f44d4c95313fd432795b70": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "e166fb45a33c495e9428bcdef8cd8813": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_098e92acdc444f64a031bd0daf070604",
+ "placeholder": "",
+ "style": "IPY_MODEL_6feb1c05469b4bc8ac9c98cdf29fdd57",
+ "value": " 2.06k/2.06k [00:00<00:00, 70.6kB/s]"
+ }
+ },
+ "e1fef249d35d482681cd39eefb7e0d7e": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "FloatProgressModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "FloatProgressModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "ProgressView",
+ "bar_style": "success",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_54af0365067b498d86d23c453c5e38f1",
+ "max": 52666,
+ "min": 0,
+ "orientation": "horizontal",
+ "style": "IPY_MODEL_ab4ae16fa4f448838f677ea60523c905",
+ "value": 52666
+ }
+ },
+ "e20264d19e804f9dba3e3867ef9b31bd": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "e213d1c919314315ada180d49e27dfb6": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_0ea1f163e4174684bd6efc2e2433c1d3",
+ "IPY_MODEL_09511a81a89d4754897a3507a84405be",
+ "IPY_MODEL_8338339ab8a242c1a485bce8558f9c39"
+ ],
+ "layout": "IPY_MODEL_8e84abf61e3e45d58efc7ccd0bfe8d37"
+ }
+ },
+ "e2a8a379bd0d4cbdb22fbc3bbb4fdc7a": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": "20px"
+ }
+ },
+ "e3f1244dbe2c48bc8102f958c3df6467": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "e4234c7c29744fc4be99b8b2ebedc9d1": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "e4810a798c0f47b6b54f84ff4ffec608": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "FloatProgressModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "FloatProgressModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "ProgressView",
+ "bar_style": "info",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_f617d181ffdb4b1e8d81fbb393923a6e",
+ "max": 1,
+ "min": 0,
+ "orientation": "horizontal",
+ "style": "IPY_MODEL_a26ddb684a07496da4290e3f6031b685",
+ "value": 1
+ }
+ },
+ "e53d35abac8241bcaf6d3b0f732d1bb9": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "e57b15cc74e7474083e87722d6acde47": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "FloatProgressModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "FloatProgressModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "ProgressView",
+ "bar_style": "success",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_451d3851e29e4efabbc2c235dea718da",
+ "max": 69713920,
+ "min": 0,
+ "orientation": "horizontal",
+ "style": "IPY_MODEL_18dfdd09a3af49f5b17cda27872d0ba3",
+ "value": 69713920
+ }
+ },
+ "e590170f306347f3a82b76a25d37b652": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_1dedb58d31dd43db96ddd7315bb7e2ee",
+ "placeholder": "",
+ "style": "IPY_MODEL_308e1ee4593b454a84681bda10921207",
+ "value": "Downloading data: 100%"
+ }
+ },
+ "e5e8f119a91944f296ff821dd7ecfb1b": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "e6c2dc814c324a0c8cb744ca16707479": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_a615446a48624d0f9a009c1f6d8b1a54",
+ "IPY_MODEL_383d6e891c5249b4b2fabb60d4900488",
+ "IPY_MODEL_3c3214f235a54864848902f7e53662db"
+ ],
+ "layout": "IPY_MODEL_73f6e6860b64491284c9442f0deae8b6"
+ }
+ },
+ "e6cf97ef7bc541d0b9c6de206a3a45b0": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "e6dcbcdf41c34e418be0b0b86e44d3f1": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "e7be6d842a0c4ba485dfa8e58338eed4": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "e899060f1edc43b980fe6f3bbe13c609": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_aaeec2b7986d493e8d238aa14f2e5937",
+ "placeholder": "",
+ "style": "IPY_MODEL_0894264041854eea960707529f3fb8c7",
+ "value": " 69.7M/69.7M [00:03<00:00, 22.6MB/s]"
+ }
+ },
+ "e8a7a34c6fb146f0b38a40f389a617fa": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "e8b3093587e44164b0ac043414cea0fa": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "e944fa694d824042845364bdba72d642": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "e97a0201b81446b882ba802a5a3b00e8": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_6a2dea21e7ce4eda8953995497308327",
+ "placeholder": "",
+ "style": "IPY_MODEL_2f3d1d2f1c92402cadc4cfa1b0094238",
+ "value": " 789k/789k [00:00<00:00, 1.10MB/s]"
+ }
+ },
+ "e9e10f1e53b74509bfc9c0bf11502c5e": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "ea941a078b984f51b66b5f1e8f3d1d82": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "eb03476353ef4568b94a3071918e72f2": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_9f9e15ff2e394ee7a7776e3e7f4b7d30",
+ "placeholder": "",
+ "style": "IPY_MODEL_7e264d54d38e4d02acfd47e4e533b49d",
+ "value": " 2245/0 [00:15<00:00, 2226.90 examples/s]"
+ }
+ },
+ "eb0d8c3f6de3468fb2b41ddf940de999": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_3547b43905c94f479248a29b60e5a1ce",
+ "placeholder": "",
+ "style": "IPY_MODEL_02ec476d0571401eb18332d2af3a13fd",
+ "value": "Downloading (…)/adapter_config.json: 100%"
+ }
+ },
+ "eb46a602b3ef484daddbcb847957c3e5": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_f22aa0a93d8b44d0a4c412343ec1f48b",
+ "placeholder": "",
+ "style": "IPY_MODEL_6e6a59f8e7454c2d886634eade47a21f",
+ "value": " 1/1 [00:03<00:00, 3.39s/it]"
+ }
+ },
+ "eb883a37a9cf4945bd864decb4fc87ea": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "ebd79e22ad4e4256a6d88883af2c1eef": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_c47ba0b11e074f708338863a35a78f7b",
+ "IPY_MODEL_72b715be2c774235a21602b18d71e75a",
+ "IPY_MODEL_ff9a0ed54bab49aca6f27bf1be66958e"
+ ],
+ "layout": "IPY_MODEL_15b5e415b62146ba96215458cf116431"
+ }
+ },
+ "ec6017ce2fb3431ab823bde05f977a61": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "ec7e7e3811e34b4a8c8cc31cd021cf20": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_dd634585d5e64c97881b132b1d59083e",
+ "placeholder": "",
+ "style": "IPY_MODEL_785f3df156b946449c492f1296656a70",
+ "value": " 581k/581k [00:00<00:00, 1.91MB/s]"
+ }
+ },
+ "ecb7ffba323743c68961e294e74b337b": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "ed7daa32c94648d5951876229f9835b3": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "ed80930617a64700a92b3bcff97c2885": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_0dc05bee870740ffa72af34ace8c05d9",
+ "placeholder": "",
+ "style": "IPY_MODEL_7a8b8f2a2160441dbdc54a62de83d297",
+ "value": "Downloading (…)"adapter_model.bin";: 100%"
+ }
+ },
+ "edc24ce2510f45f8adde0a187016259f": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_1b2780d8137042449bd6779c70bf43ca",
+ "placeholder": "",
+ "style": "IPY_MODEL_ddc2a8e8ef4d429f95081c4c5baf1fb3",
+ "value": " 110M/110M [00:04<00:00, 30.6MB/s]"
+ }
+ },
+ "ee1ae17fdf4143ae8125ce5e2a7e9066": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "ef01f9efbfb749a3999c5b89ba0ee370": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "ef056ad59e314089a012acaa73a54e4f": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "efb85d003fb54f55aa4eadf2ab8b1684": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "efd9d5724dbd435991052b4445c6970f": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "FloatProgressModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "FloatProgressModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "ProgressView",
+ "bar_style": "info",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_e2a8a379bd0d4cbdb22fbc3bbb4fdc7a",
+ "max": 1,
+ "min": 0,
+ "orientation": "horizontal",
+ "style": "IPY_MODEL_2c7d952f958247b681301d1c6bff4fa7",
+ "value": 1
+ }
+ },
+ "f027b4358c2c41a8a93c617641135bcd": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "f09d5d5e7faf48f5adbaa90cbcf55162": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_3ff0c6a4f4fc4b72a5163a7da50af4da",
+ "IPY_MODEL_e1fef249d35d482681cd39eefb7e0d7e",
+ "IPY_MODEL_0a8ca977f9db4d7794dcbcaca3c5cb96"
+ ],
+ "layout": "IPY_MODEL_e7be6d842a0c4ba485dfa8e58338eed4"
+ }
+ },
+ "f0be69583cd1410da6dbc18302d4439b": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "f14847261aa247fb9561373e0495f3e5": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "f1884e5a392941bfa8c484496d87084c": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "f20fc82bcbf245619ad4dec04d0f999d": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "f22aa0a93d8b44d0a4c412343ec1f48b": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "f309d7a096df4f119e6e6871b56913f1": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_5f283548f34848af90affe55a169b5a9",
+ "IPY_MODEL_51a4d85c08d745bda70ba0db731dca68",
+ "IPY_MODEL_eb46a602b3ef484daddbcb847957c3e5"
+ ],
+ "layout": "IPY_MODEL_8e2e49c6046e4dc0a0a810b4e58f80cc"
+ }
+ },
+ "f3f191968f724e9bbb710b86d3657a66": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "f436e6a7d3014e2ca44c94455bfeace8": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_f9d6d41ffeba43cf94ec9d7a96af6617",
+ "IPY_MODEL_bed65245e7234977874d35bf78694e35",
+ "IPY_MODEL_c28c2fc81e0e467cbc0ded0205d1ee85"
+ ],
+ "layout": "IPY_MODEL_ea941a078b984f51b66b5f1e8f3d1d82"
+ }
+ },
+ "f5d7433d15de45e997d12568cac536fc": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "f5ff1816a56243e4872ddfcd35331ad8": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "f617d181ffdb4b1e8d81fbb393923a6e": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": "20px"
+ }
+ },
+ "f628cb62f5fa446eb608467c1ecea526": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "f773a61b1dba4e3eb0df36162efe9abc": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "f7b4ec74e2ac45bbbf0265d0363f4d9f": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_2bc85a5bde9a454990d3bb7de5e3c7c1",
+ "placeholder": "",
+ "style": "IPY_MODEL_2ab45b22ce3f400a81cc451b9d7c9eb8",
+ "value": "Downloading extra modules: 100%"
+ }
+ },
+ "f8053b94954d401a85ead90319aa4690": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_9abe7ed3e3d347b6bad7d1252bde226f",
+ "placeholder": "",
+ "style": "IPY_MODEL_8ba244a082284f6dbac1c8f689c527a8",
+ "value": " 1.04M/1.04M [00:00<00:00, 5.93MB/s]"
+ }
+ },
+ "f81bffac74ff4b07a09760a00620610c": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "f933fbdcc26d41b0bb294dabd0337834": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_950e74921e6042868ab6b7b9070d6f69",
+ "IPY_MODEL_82dc91c5b065459d827863699a9710e1",
+ "IPY_MODEL_5b7b6f08765c4c1989f945414f2c3cf4"
+ ],
+ "layout": "IPY_MODEL_735c3606df924b9297ddc05fae3e92d5"
+ }
+ },
+ "f93f87ef211446379963df5bbb2e4ff0": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "f96c7014b47d4d048ff50d6f1f2da200": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_925f7aad24b547cc8071ee9bda713d7c",
+ "IPY_MODEL_4043e3ceb27c435d83913b3796bd9927",
+ "IPY_MODEL_b1183b9042744d3fa7437e2ec55b6cdd"
+ ],
+ "layout": "IPY_MODEL_20a0694ee1684ffc8289af9094e812e1"
+ }
+ },
+ "f9d6d41ffeba43cf94ec9d7a96af6617": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_e3f1244dbe2c48bc8102f958c3df6467",
+ "placeholder": "",
+ "style": "IPY_MODEL_786d3d34cfd24f81996797c55b10b443",
+ "value": "Downloading (…)okenizer_config.json: 100%"
+ }
+ },
+ "f9e5029c15054f5a9cbcda1ed5878995": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_4cc5b0a5c84e43f3bb185c63bc1f9a56",
+ "IPY_MODEL_af56501692b84e718fe3e8b1e452b7c2",
+ "IPY_MODEL_c6c9fa535ff4458ba966183e1489905b"
+ ],
+ "layout": "IPY_MODEL_b0e084a4c551427bb176061df894fdf6"
+ }
+ },
+ "fa137c931d2c4e579c27893ca8ee1848": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "fab643980982452988a02c14132c73ca": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_062727d821f248c9958ecc2d79237e5b",
+ "IPY_MODEL_2c264564d4c642ebb033703b1df02c69",
+ "IPY_MODEL_b19431ca425341568c2b3a8556431a8f"
+ ],
+ "layout": "IPY_MODEL_441e89acb62e47dab61b32b5a97110f3"
+ }
+ },
+ "fb8aca596a1c4ac4a7428248b6c6f8b1": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_168e19229aa5404bb151e4547bb31283",
+ "placeholder": "",
+ "style": "IPY_MODEL_d140f5373bf144d1ae5d282e1a65647e",
+ "value": "adapter_model.bin: 100%"
+ }
+ },
+ "fb9f013a6188463fad6db70702576c37": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "fbd27061ff114846aedc99bc2d17f7a7": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "fbd304c2564e4acba84809377ba19e25": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "fce64f5690024c698701330f0e5d039a": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "fe48e65b2371445bbb01a8d3e9af1f67": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "ff9a0ed54bab49aca6f27bf1be66958e": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_b8d3539c8a454217a3b6ffab51259054",
+ "placeholder": "",
+ "style": "IPY_MODEL_05e96819517e417aaf05f5f38c0c8b76",
+ "value": " 2.11k/2.11k [00:00<00:00, 124kB/s]"
+ }
+ },
+ "ffce35af1ad84a2c838cca55a26dd3c4": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_d21cd4878c6e49d38dd3abb2e3b3f566",
+ "IPY_MODEL_969e3cf7f3634c3f90b5fea38c5797ca",
+ "IPY_MODEL_78501c2a5ac84f9ca0d20bbef340fc9f"
+ ],
+ "layout": "IPY_MODEL_5b4fbd1102a84670a1eed6f3d25c0bcd"
+ }
+ }
+ }
+ }
+ },
+ "nbformat": 4,
+ "nbformat_minor": 5
+}
diff --git a/peft/examples/int8_training/requirements.txt b/peft/examples/int8_training/requirements.txt
new file mode 100644
index 0000000000000000000000000000000000000000..9a53bafca0e0ab1d4a7af59c921cd1ca5f5f69aa
--- /dev/null
+++ b/peft/examples/int8_training/requirements.txt
@@ -0,0 +1,9 @@
+accelerate
+git+https://github.com/bitsandbytes-foundation/bitsandbytes.git
+datasets==3.6.0
+evaluate
+jiwer
+librosa
+soundfile
+transformers==4.52.4
+wandb
diff --git a/peft/examples/int8_training/run_adalora_whisper_int8.sh b/peft/examples/int8_training/run_adalora_whisper_int8.sh
new file mode 100644
index 0000000000000000000000000000000000000000..39bd69d5f1287401b2bf54bd345b76c8f039d50b
--- /dev/null
+++ b/peft/examples/int8_training/run_adalora_whisper_int8.sh
@@ -0,0 +1,37 @@
+accelerate launch --config_file config.yaml peft_adalora_whisper_large_training.py \
+ --model_name_or_path "openai/whisper-large-v2" \
+ --language "Marathi" \
+ --language_abbr "mr" \
+ --task "transcribe" \
+ --dataset_name "mozilla-foundation/common_voice_11_0" \
+ --push_to_hub \
+ --preprocessing_num_workers 2 \
+ --per_device_train_batch_size 8 \
+ --per_device_eval_batch_size 8 \
+ --dataloader_pin_memory \
+ --dataloader_num_workers 2 \
+ --learning_rate 1e-3 \
+ --weight_decay 1e-4 \
+ --num_train_epochs 3 \
+ --gradient_accumulation_steps 1 \
+ --lr_scheduler_type "linear" \
+ --num_warmup_steps 50 \
+ --output_dir "adalora_whisper_large_marathi_multi_adapter" \
+ --seed 42 \
+ --load_best_model \
+ --with_tracking \
+ --report_to "wandb" \
+ --hub_token $HUB_TOKEN \
+ --checkpointing_steps 2000 \
+ --evaluation_steps 2000 \
+ --logging_steps 25 \
+ --use_peft \
+ --use_adalora \
+ --init_r 12 \
+ --target_r 8 \
+ --tinit 100 \
+ --tfinal 800 \
+ --delta_t 10 \
+ --lora_alpha 32 \
+ --lora_dropout 0.1 \
+ --orth_reg_weight 0.5
\ No newline at end of file
diff --git a/peft/examples/loftq_finetuning/LoftQ_weight_replacement.ipynb b/peft/examples/loftq_finetuning/LoftQ_weight_replacement.ipynb
new file mode 100644
index 0000000000000000000000000000000000000000..b03d8524cc73b04c4296f55fd2a26a5e14774323
--- /dev/null
+++ b/peft/examples/loftq_finetuning/LoftQ_weight_replacement.ipynb
@@ -0,0 +1,801 @@
+{
+ "cells": [
+ {
+ "cell_type": "markdown",
+ "id": "546b6c6d-f949-4387-9c41-6989223911f8",
+ "metadata": {},
+ "source": [
+ "# Initializing weights with LoftQ by replacing LoRA weights in-place"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "d041ecb4-6957-467e-8f3e-d4a12c674e9f",
+ "metadata": {},
+ "source": [
+ "This notebook shows how to apply [LoftQ](https://huggingface.co/papers/2310.08659) initialization on our QLoRA model.\n",
+ "\n",
+ "In short, the idea behind LoftQ is the following. When we use QLoRA, i.e. we quantize the base model with bitsandbytes to save memory, and then train LoRA weights on top of this base model, we expect a certain performance gap. This is partly due to the fact that quantization is onyl an approximation of the \"real\" weights and thus introduces a quantization error. By default, LoRA weights are initialized such that they are a no-op at the start of the training. However, we can instead initialize them so that they minimize the quantization error. This is the idea behind LoftQ.\n",
+ "\n",
+ "Note that this only influences the initialization of the model. Everything that follows stays the same as always."
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "90d5420f-de32-42fa-8792-247f60e3647d",
+ "metadata": {},
+ "source": [
+ "## Imports"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 1,
+ "id": "a2c69b7c-c922-405f-aae1-ccc4f6911155",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "import os\n",
+ "import torch"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 2,
+ "id": "22be0432-8798-44a2-9014-d929525e3059",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "from transformers import AutoModelForCausalLM, AutoTokenizer, BitsAndBytesConfig"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 3,
+ "id": "f087ce0f-71b4-45ec-b2f9-197677bbc1ee",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "from peft import get_peft_model, LoraConfig, replace_lora_weights_loftq"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "63fdf18e-4ac4-409e-8475-88147cf85067",
+ "metadata": {},
+ "source": [
+ "## Functions"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 4,
+ "id": "af14bd0a-597e-446c-800b-619fc0599ee0",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "def get_mae(x, y):\n",
+ " return (x - y).abs().mean()\n",
+ "\n",
+ "\n",
+ "def get_mse(x, y):\n",
+ " return torch.pow(x - y, 2).mean()\n",
+ "\n",
+ "\n",
+ "def error_report(x, y):\n",
+ " mae = get_mae(x, y)\n",
+ " mse = get_mse(x, y)\n",
+ " print(\n",
+ " f\"Mean absolute error: {mae:>8.5f}\\n\"\n",
+ " f\"Mean squared error: {mse:>8.5f}\"\n",
+ " )"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "1bc01a5f-7ee8-400f-8e80-3f2b7df29882",
+ "metadata": {},
+ "source": [
+ "## Base model"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "fdc447d9-2f4f-4d0f-afdb-1cf5c4237321",
+ "metadata": {},
+ "source": [
+ "First, let's load a base model and calculate some logits. These logits are the baseline, i.e. we try to match their values as best as possible. We only need these logits for demonstration purposes. In practice, it is not necessary to load the non-quantized weights to apply LoftQ initialization.\n",
+ "\n",
+ "**Note**: We have to choose a model with a `model.safetensors` file. As PyTorch checkpoints (pickle) cannot be loaded lazily, we have to use [safetensors](https://huggingface.co/docs/safetensors/index). If those don't exist for your model, save the pretrained model as a safetensors file using `safe_pretrained` and pass the model path to `replace_lora_weights_loftq`."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 5,
+ "id": "0cb29074-d180-4fdc-8a47-27d2b9857264",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "model_id = \"bigscience/bloomz-560m\""
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 6,
+ "id": "e7ddd6a2-04dd-42ec-9f48-100a3946ae04",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "tokenizer = AutoTokenizer.from_pretrained(model_id)"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 7,
+ "id": "1f5b27db-51cc-41da-a21d-049ff747a149",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "model = AutoModelForCausalLM.from_pretrained(model_id)"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 8,
+ "id": "51548b6a-945c-4797-b02a-0e3fc77d1242",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "s = \"\"\"Beautiful is better than ugly.\n",
+ "Explicit is better than implicit.\n",
+ "Simple is better than complex.\n",
+ "Complex is better than complicated.\n",
+ "Flat is better than nested.\n",
+ "Sparse is better than dense.\n",
+ "Readability counts.\n",
+ "Special cases aren't special enough to break the rules.\n",
+ "Although practicality beats purity.\n",
+ "Errors should never pass silently.\n",
+ "Unless explicitly silenced.\n",
+ "In the face of ambiguity, refuse the temptation to guess.\n",
+ "There should be one-- and preferably only one --obvious way to do it.\n",
+ "Although that way may not be obvious at first unless you're Dutch.\n",
+ "Now is better than never.\n",
+ "Although never is often better than *right* now.\n",
+ "If the implementation is hard to explain, it's a bad idea.\n",
+ "If the implementation is easy to explain, it may be a good idea.\n",
+ "Namespaces are one honking great idea -- let's do more of those!\"\"\""
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 9,
+ "id": "ce72d923-5283-48ba-96ef-7f859309ad84",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "inputs = tokenizer(s.splitlines(), return_tensors=\"pt\", padding=True)"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "3bfe54cb-76ef-4981-ba25-3e544d264c62",
+ "metadata": {},
+ "source": [
+ "Our baseline logits:"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 10,
+ "id": "04bebcaa-3a05-4621-9a03-e25de72fa27c",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "logits_base = model(**inputs).logits"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "fa9c9001-8ade-422d-92f8-bcafa50917c7",
+ "metadata": {},
+ "source": [
+ "## Normal LoRA model"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "8024390b-736a-4b21-848b-aa4f30951d51",
+ "metadata": {},
+ "source": [
+ "Now we load the model quantized with bitsandbytes. For now, only 4bit is supported."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 11,
+ "id": "01d1912a-646e-42d2-8292-6702b77d1948",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "bnb_config = BitsAndBytesConfig(\n",
+ " load_in_4bit=True,\n",
+ " bnb_4bit_use_double_quant=True,\n",
+ " bnb_4bit_compute_dtype=torch.float16,\n",
+ ")"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 12,
+ "id": "b1218717-4db4-48ce-978d-c05dc190fa91",
+ "metadata": {},
+ "outputs": [
+ {
+ "name": "stderr",
+ "output_type": "stream",
+ "text": [
+ "`low_cpu_mem_usage` was None, now set to True since model is quantized.\n"
+ ]
+ }
+ ],
+ "source": [
+ "model = AutoModelForCausalLM.from_pretrained(model_id, quantization_config=bnb_config)"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "a0b4e4c5-3932-4d9a-9457-41a05f24d556",
+ "metadata": {},
+ "source": [
+ "Next we create a LoRA model using PEFT and compute the logits of that model."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 13,
+ "id": "4741bce0-cd2b-4f05-a50c-4f9e56b43e72",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "lora_config = LoraConfig(task_type=\"CAUSAL_LM\", target_modules=\"all-linear\")"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 14,
+ "id": "cf55cc48-b55d-4806-b6ab-e9b8035ed526",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "peft_model = get_peft_model(model, lora_config)"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 15,
+ "id": "f2f11e25-4a1e-485b-be4c-65aec62ac207",
+ "metadata": {},
+ "outputs": [
+ {
+ "name": "stderr",
+ "output_type": "stream",
+ "text": [
+ ".../bitsandbytes/nn/modules.py:391: UserWarning: Input type into Linear4bit is torch.float16, but bnb_4bit_compute_dtype=torch.float32 (default). This will lead to slow inference or training speed.\n",
+ " warnings.warn('Input type into Linear4bit is torch.float16, but bnb_4bit_compute_dtype=torch.float32 (default). This will lead to slow inference or training speed.')\n"
+ ]
+ }
+ ],
+ "source": [
+ "logits_lora = peft_model(**inputs).logits"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "5bc0cde7-0b9f-4305-ac0e-e3a6d2cfa401",
+ "metadata": {},
+ "source": [
+ "Let's check the influence of the quantization error on our logits:"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 16,
+ "id": "6f404c0d-f428-4923-9122-7b830410f089",
+ "metadata": {},
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "Mean absolute error: 3.61113\n",
+ "Mean squared error: 36.53259\n"
+ ]
+ }
+ ],
+ "source": [
+ "error_report(logits_base, logits_lora)"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "58c437e1-4fae-4a2f-9c42-ada6bedb9a4d",
+ "metadata": {},
+ "source": [
+ "## LoftQ"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "1af05376-c8b0-48ec-8d80-7d7f4d32bbd7",
+ "metadata": {},
+ "source": [
+ "Next, let's use LoftQ initialization and see if it helps reduce the error."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 17,
+ "id": "890e6108-3f02-469c-9e7d-f2144448227c",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "replace_lora_weights_loftq(peft_model)"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 18,
+ "id": "b452db0e-a510-42d3-bef5-f567186e26c2",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "logits_loftq = peft_model(**inputs).logits"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 19,
+ "id": "456dc564-f268-4cf3-9d59-a6942d3733ad",
+ "metadata": {},
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "Mean absolute error: 3.24111\n",
+ "Mean squared error: 31.13725\n"
+ ]
+ }
+ ],
+ "source": [
+ "error_report(logits_base, logits_loftq)"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "1ddf9e0f-3f78-426c-be59-77c6481674ec",
+ "metadata": {},
+ "source": [
+ "We can see that LoftQ initialization helped a little bit, but the difference is not huge."
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "0dd344f2-249c-4fe9-8357-7fe3bcd1e82f",
+ "metadata": {},
+ "source": [
+ "## LoftQ with callback"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "e2fd7dd5-88b3-40b8-95c2-3f3895d8093d",
+ "metadata": {},
+ "source": [
+ "To help with this, let's write a small callback function and pass it to `replace_lora_weights_loftq`. What this function does is that each time one weight is being replaced with LoftQ-initialized weights, we perform a test if the quantization error is actually reduced. If it it is not, we roll back the replacement. This way, we keep only those replacements that improve the results."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 20,
+ "id": "1f882802-22b7-4969-919e-120b1f2893d2",
+ "metadata": {},
+ "outputs": [
+ {
+ "name": "stderr",
+ "output_type": "stream",
+ "text": [
+ "`low_cpu_mem_usage` was None, now set to True since model is quantized.\n"
+ ]
+ }
+ ],
+ "source": [
+ "# Since PEFT has modified the base model, we should reload it\n",
+ "model = AutoModelForCausalLM.from_pretrained(model_id, quantization_config=bnb_config)"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 21,
+ "id": "c6438363-b66e-4507-8667-5a6df379a03f",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "peft_model = get_peft_model(model, lora_config)"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 22,
+ "id": "7b93d082-0fcb-4b20-982e-c1aaf0c71d13",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "current_mse = float(\"inf\")"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 23,
+ "id": "e22eb18d-b06e-47fe-91ba-ff34cbf62f60",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "def my_callback(model, module_name):\n",
+ " \"\"\"Callable to replace weights with LoFTQ if the mse is lower than the current best one.\"\"\"\n",
+ " global current_mse\n",
+ "\n",
+ " logits = model(**inputs).logits\n",
+ " mse = get_mse(logits_base, logits)\n",
+ " if mse < current_mse:\n",
+ " current_mse = mse\n",
+ " print(f\"MSE improved for module {module_name}\")\n",
+ " return True\n",
+ " print(f\"MSE did not improve for module {module_name}\")\n",
+ " return False"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 24,
+ "id": "44ee90d1-e15a-4740-a39d-ebf9e7adb79c",
+ "metadata": {
+ "scrolled": true
+ },
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "MSE improved for module transformer.h.0.self_attention.query_key_value\n",
+ "MSE did not improve for module transformer.h.0.self_attention.dense\n",
+ "MSE improved for module transformer.h.0.mlp.dense_h_to_4h\n",
+ "MSE improved for module transformer.h.0.mlp.dense_4h_to_h\n",
+ "MSE did not improve for module transformer.h.1.self_attention.query_key_value\n",
+ "MSE did not improve for module transformer.h.1.self_attention.dense\n",
+ "MSE did not improve for module transformer.h.1.mlp.dense_h_to_4h\n",
+ "MSE improved for module transformer.h.1.mlp.dense_4h_to_h\n",
+ "MSE improved for module transformer.h.2.self_attention.query_key_value\n",
+ "MSE improved for module transformer.h.2.self_attention.dense\n",
+ "MSE improved for module transformer.h.2.mlp.dense_h_to_4h\n",
+ "MSE did not improve for module transformer.h.2.mlp.dense_4h_to_h\n",
+ "MSE improved for module transformer.h.3.self_attention.query_key_value\n",
+ "MSE did not improve for module transformer.h.3.self_attention.dense\n",
+ "MSE improved for module transformer.h.3.mlp.dense_h_to_4h\n",
+ "MSE improved for module transformer.h.3.mlp.dense_4h_to_h\n",
+ "MSE improved for module transformer.h.4.self_attention.query_key_value\n",
+ "MSE did not improve for module transformer.h.4.self_attention.dense\n",
+ "MSE improved for module transformer.h.4.mlp.dense_h_to_4h\n",
+ "MSE did not improve for module transformer.h.4.mlp.dense_4h_to_h\n",
+ "MSE did not improve for module transformer.h.5.self_attention.query_key_value\n",
+ "MSE improved for module transformer.h.5.self_attention.dense\n",
+ "MSE improved for module transformer.h.5.mlp.dense_h_to_4h\n",
+ "MSE did not improve for module transformer.h.5.mlp.dense_4h_to_h\n",
+ "MSE improved for module transformer.h.6.self_attention.query_key_value\n",
+ "MSE did not improve for module transformer.h.6.self_attention.dense\n",
+ "MSE improved for module transformer.h.6.mlp.dense_h_to_4h\n",
+ "MSE did not improve for module transformer.h.6.mlp.dense_4h_to_h\n",
+ "MSE improved for module transformer.h.7.self_attention.query_key_value\n",
+ "MSE improved for module transformer.h.7.self_attention.dense\n",
+ "MSE did not improve for module transformer.h.7.mlp.dense_h_to_4h\n",
+ "MSE did not improve for module transformer.h.7.mlp.dense_4h_to_h\n",
+ "MSE did not improve for module transformer.h.8.self_attention.query_key_value\n",
+ "MSE did not improve for module transformer.h.8.self_attention.dense\n",
+ "MSE improved for module transformer.h.8.mlp.dense_h_to_4h\n",
+ "MSE did not improve for module transformer.h.8.mlp.dense_4h_to_h\n",
+ "MSE improved for module transformer.h.9.self_attention.query_key_value\n",
+ "MSE did not improve for module transformer.h.9.self_attention.dense\n",
+ "MSE did not improve for module transformer.h.9.mlp.dense_h_to_4h\n",
+ "MSE did not improve for module transformer.h.9.mlp.dense_4h_to_h\n",
+ "MSE did not improve for module transformer.h.10.self_attention.query_key_value\n",
+ "MSE did not improve for module transformer.h.10.self_attention.dense\n",
+ "MSE did not improve for module transformer.h.10.mlp.dense_h_to_4h\n",
+ "MSE improved for module transformer.h.10.mlp.dense_4h_to_h\n",
+ "MSE did not improve for module transformer.h.11.self_attention.query_key_value\n",
+ "MSE did not improve for module transformer.h.11.self_attention.dense\n",
+ "MSE did not improve for module transformer.h.11.mlp.dense_h_to_4h\n",
+ "MSE improved for module transformer.h.11.mlp.dense_4h_to_h\n",
+ "MSE improved for module transformer.h.12.self_attention.query_key_value\n",
+ "MSE did not improve for module transformer.h.12.self_attention.dense\n",
+ "MSE improved for module transformer.h.12.mlp.dense_h_to_4h\n",
+ "MSE did not improve for module transformer.h.12.mlp.dense_4h_to_h\n",
+ "MSE improved for module transformer.h.13.self_attention.query_key_value\n",
+ "MSE improved for module transformer.h.13.self_attention.dense\n",
+ "MSE did not improve for module transformer.h.13.mlp.dense_h_to_4h\n",
+ "MSE improved for module transformer.h.13.mlp.dense_4h_to_h\n",
+ "MSE did not improve for module transformer.h.14.self_attention.query_key_value\n",
+ "MSE improved for module transformer.h.14.self_attention.dense\n",
+ "MSE did not improve for module transformer.h.14.mlp.dense_h_to_4h\n",
+ "MSE improved for module transformer.h.14.mlp.dense_4h_to_h\n",
+ "MSE did not improve for module transformer.h.15.self_attention.query_key_value\n",
+ "MSE did not improve for module transformer.h.15.self_attention.dense\n",
+ "MSE did not improve for module transformer.h.15.mlp.dense_h_to_4h\n",
+ "MSE improved for module transformer.h.15.mlp.dense_4h_to_h\n",
+ "MSE did not improve for module transformer.h.16.self_attention.query_key_value\n",
+ "MSE did not improve for module transformer.h.16.self_attention.dense\n",
+ "MSE improved for module transformer.h.16.mlp.dense_h_to_4h\n",
+ "MSE improved for module transformer.h.16.mlp.dense_4h_to_h\n",
+ "MSE did not improve for module transformer.h.17.self_attention.query_key_value\n",
+ "MSE did not improve for module transformer.h.17.self_attention.dense\n",
+ "MSE improved for module transformer.h.17.mlp.dense_h_to_4h\n",
+ "MSE did not improve for module transformer.h.17.mlp.dense_4h_to_h\n",
+ "MSE improved for module transformer.h.18.self_attention.query_key_value\n",
+ "MSE did not improve for module transformer.h.18.self_attention.dense\n",
+ "MSE did not improve for module transformer.h.18.mlp.dense_h_to_4h\n",
+ "MSE did not improve for module transformer.h.18.mlp.dense_4h_to_h\n",
+ "MSE did not improve for module transformer.h.19.self_attention.query_key_value\n",
+ "MSE improved for module transformer.h.19.self_attention.dense\n",
+ "MSE improved for module transformer.h.19.mlp.dense_h_to_4h\n",
+ "MSE improved for module transformer.h.19.mlp.dense_4h_to_h\n",
+ "MSE improved for module transformer.h.20.self_attention.query_key_value\n",
+ "MSE did not improve for module transformer.h.20.self_attention.dense\n",
+ "MSE did not improve for module transformer.h.20.mlp.dense_h_to_4h\n",
+ "MSE improved for module transformer.h.20.mlp.dense_4h_to_h\n",
+ "MSE did not improve for module transformer.h.21.self_attention.query_key_value\n",
+ "MSE improved for module transformer.h.21.self_attention.dense\n",
+ "MSE did not improve for module transformer.h.21.mlp.dense_h_to_4h\n",
+ "MSE did not improve for module transformer.h.21.mlp.dense_4h_to_h\n",
+ "MSE improved for module transformer.h.22.self_attention.query_key_value\n",
+ "MSE improved for module transformer.h.22.self_attention.dense\n",
+ "MSE improved for module transformer.h.22.mlp.dense_h_to_4h\n",
+ "MSE improved for module transformer.h.22.mlp.dense_4h_to_h\n",
+ "MSE improved for module transformer.h.23.self_attention.query_key_value\n",
+ "MSE did not improve for module transformer.h.23.self_attention.dense\n",
+ "MSE improved for module transformer.h.23.mlp.dense_h_to_4h\n",
+ "MSE did not improve for module transformer.h.23.mlp.dense_4h_to_h\n"
+ ]
+ }
+ ],
+ "source": [
+ "replace_lora_weights_loftq(peft_model, callback=my_callback)"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 25,
+ "id": "e31adc81-a090-49b2-90f6-9906743c76ae",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "logits_loftq_callback = peft_model(**inputs).logits"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 26,
+ "id": "7c640092-1f26-48be-bea4-487511205440",
+ "metadata": {},
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "Mean absolute error: 1.79576\n",
+ "Mean squared error: 8.47075\n"
+ ]
+ }
+ ],
+ "source": [
+ "error_report(logits_base, logits_loftq_callback)"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "1896857e-3d87-44a9-887f-90c765bc8d91",
+ "metadata": {},
+ "source": [
+ "We can see that applying LoftQ with the help of the callback reduced the error quite significantly."
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "8eaf86cf-4fb4-455d-ab07-892591564303",
+ "metadata": {},
+ "source": [
+ "## Applying LoftQ multiple times"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "70836a75-5c6d-4b7b-9175-f395aef8383b",
+ "metadata": {},
+ "source": [
+ "It is possible to run `replace_lora_weights_loftq` multiple times on the same model when using the callback."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 27,
+ "id": "8e5ee38c-007c-4c75-9248-005d94b19445",
+ "metadata": {
+ "scrolled": true
+ },
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "MSE did not improve for module transformer.h.0.self_attention.query_key_value\n",
+ "MSE did not improve for module transformer.h.0.self_attention.dense\n",
+ "MSE did not improve for module transformer.h.0.mlp.dense_h_to_4h\n",
+ "MSE did not improve for module transformer.h.0.mlp.dense_4h_to_h\n",
+ "MSE improved for module transformer.h.1.self_attention.query_key_value\n",
+ "MSE did not improve for module transformer.h.1.self_attention.dense\n",
+ "MSE did not improve for module transformer.h.1.mlp.dense_h_to_4h\n",
+ "MSE did not improve for module transformer.h.1.mlp.dense_4h_to_h\n",
+ "MSE did not improve for module transformer.h.2.self_attention.query_key_value\n",
+ "MSE did not improve for module transformer.h.2.self_attention.dense\n",
+ "MSE did not improve for module transformer.h.2.mlp.dense_h_to_4h\n",
+ "MSE did not improve for module transformer.h.2.mlp.dense_4h_to_h\n",
+ "MSE did not improve for module transformer.h.3.self_attention.query_key_value\n",
+ "MSE did not improve for module transformer.h.3.self_attention.dense\n",
+ "MSE did not improve for module transformer.h.3.mlp.dense_h_to_4h\n",
+ "MSE did not improve for module transformer.h.3.mlp.dense_4h_to_h\n",
+ "MSE did not improve for module transformer.h.4.self_attention.query_key_value\n",
+ "MSE did not improve for module transformer.h.4.self_attention.dense\n",
+ "MSE did not improve for module transformer.h.4.mlp.dense_h_to_4h\n",
+ "MSE did not improve for module transformer.h.4.mlp.dense_4h_to_h\n",
+ "MSE did not improve for module transformer.h.5.self_attention.query_key_value\n",
+ "MSE did not improve for module transformer.h.5.self_attention.dense\n",
+ "MSE did not improve for module transformer.h.5.mlp.dense_h_to_4h\n",
+ "MSE did not improve for module transformer.h.5.mlp.dense_4h_to_h\n",
+ "MSE did not improve for module transformer.h.6.self_attention.query_key_value\n",
+ "MSE improved for module transformer.h.6.self_attention.dense\n",
+ "MSE did not improve for module transformer.h.6.mlp.dense_h_to_4h\n",
+ "MSE did not improve for module transformer.h.6.mlp.dense_4h_to_h\n",
+ "MSE did not improve for module transformer.h.7.self_attention.query_key_value\n",
+ "MSE did not improve for module transformer.h.7.self_attention.dense\n",
+ "MSE did not improve for module transformer.h.7.mlp.dense_h_to_4h\n",
+ "MSE did not improve for module transformer.h.7.mlp.dense_4h_to_h\n",
+ "MSE did not improve for module transformer.h.8.self_attention.query_key_value\n",
+ "MSE did not improve for module transformer.h.8.self_attention.dense\n",
+ "MSE did not improve for module transformer.h.8.mlp.dense_h_to_4h\n",
+ "MSE did not improve for module transformer.h.8.mlp.dense_4h_to_h\n",
+ "MSE did not improve for module transformer.h.9.self_attention.query_key_value\n",
+ "MSE did not improve for module transformer.h.9.self_attention.dense\n",
+ "MSE did not improve for module transformer.h.9.mlp.dense_h_to_4h\n",
+ "MSE did not improve for module transformer.h.9.mlp.dense_4h_to_h\n",
+ "MSE did not improve for module transformer.h.10.self_attention.query_key_value\n",
+ "MSE did not improve for module transformer.h.10.self_attention.dense\n",
+ "MSE improved for module transformer.h.10.mlp.dense_h_to_4h\n",
+ "MSE did not improve for module transformer.h.10.mlp.dense_4h_to_h\n",
+ "MSE did not improve for module transformer.h.11.self_attention.query_key_value\n",
+ "MSE did not improve for module transformer.h.11.self_attention.dense\n",
+ "MSE did not improve for module transformer.h.11.mlp.dense_h_to_4h\n",
+ "MSE did not improve for module transformer.h.11.mlp.dense_4h_to_h\n",
+ "MSE did not improve for module transformer.h.12.self_attention.query_key_value\n",
+ "MSE improved for module transformer.h.12.self_attention.dense\n",
+ "MSE did not improve for module transformer.h.12.mlp.dense_h_to_4h\n",
+ "MSE did not improve for module transformer.h.12.mlp.dense_4h_to_h\n",
+ "MSE did not improve for module transformer.h.13.self_attention.query_key_value\n",
+ "MSE did not improve for module transformer.h.13.self_attention.dense\n",
+ "MSE did not improve for module transformer.h.13.mlp.dense_h_to_4h\n",
+ "MSE did not improve for module transformer.h.13.mlp.dense_4h_to_h\n",
+ "MSE did not improve for module transformer.h.14.self_attention.query_key_value\n",
+ "MSE did not improve for module transformer.h.14.self_attention.dense\n",
+ "MSE did not improve for module transformer.h.14.mlp.dense_h_to_4h\n",
+ "MSE did not improve for module transformer.h.14.mlp.dense_4h_to_h\n",
+ "MSE did not improve for module transformer.h.15.self_attention.query_key_value\n",
+ "MSE did not improve for module transformer.h.15.self_attention.dense\n",
+ "MSE did not improve for module transformer.h.15.mlp.dense_h_to_4h\n",
+ "MSE did not improve for module transformer.h.15.mlp.dense_4h_to_h\n",
+ "MSE improved for module transformer.h.16.self_attention.query_key_value\n",
+ "MSE did not improve for module transformer.h.16.self_attention.dense\n",
+ "MSE did not improve for module transformer.h.16.mlp.dense_h_to_4h\n",
+ "MSE did not improve for module transformer.h.16.mlp.dense_4h_to_h\n",
+ "MSE improved for module transformer.h.17.self_attention.query_key_value\n",
+ "MSE did not improve for module transformer.h.17.self_attention.dense\n",
+ "MSE did not improve for module transformer.h.17.mlp.dense_h_to_4h\n",
+ "MSE did not improve for module transformer.h.17.mlp.dense_4h_to_h\n",
+ "MSE did not improve for module transformer.h.18.self_attention.query_key_value\n",
+ "MSE did not improve for module transformer.h.18.self_attention.dense\n",
+ "MSE did not improve for module transformer.h.18.mlp.dense_h_to_4h\n",
+ "MSE did not improve for module transformer.h.18.mlp.dense_4h_to_h\n",
+ "MSE did not improve for module transformer.h.19.self_attention.query_key_value\n",
+ "MSE did not improve for module transformer.h.19.self_attention.dense\n",
+ "MSE did not improve for module transformer.h.19.mlp.dense_h_to_4h\n",
+ "MSE did not improve for module transformer.h.19.mlp.dense_4h_to_h\n",
+ "MSE did not improve for module transformer.h.20.self_attention.query_key_value\n",
+ "MSE did not improve for module transformer.h.20.self_attention.dense\n",
+ "MSE did not improve for module transformer.h.20.mlp.dense_h_to_4h\n",
+ "MSE did not improve for module transformer.h.20.mlp.dense_4h_to_h\n",
+ "MSE did not improve for module transformer.h.21.self_attention.query_key_value\n",
+ "MSE did not improve for module transformer.h.21.self_attention.dense\n",
+ "MSE did not improve for module transformer.h.21.mlp.dense_h_to_4h\n",
+ "MSE did not improve for module transformer.h.21.mlp.dense_4h_to_h\n",
+ "MSE did not improve for module transformer.h.22.self_attention.query_key_value\n",
+ "MSE did not improve for module transformer.h.22.self_attention.dense\n",
+ "MSE did not improve for module transformer.h.22.mlp.dense_h_to_4h\n",
+ "MSE did not improve for module transformer.h.22.mlp.dense_4h_to_h\n",
+ "MSE did not improve for module transformer.h.23.self_attention.query_key_value\n",
+ "MSE did not improve for module transformer.h.23.self_attention.dense\n",
+ "MSE did not improve for module transformer.h.23.mlp.dense_h_to_4h\n",
+ "MSE did not improve for module transformer.h.23.mlp.dense_4h_to_h\n"
+ ]
+ }
+ ],
+ "source": [
+ "replace_lora_weights_loftq(peft_model, callback=my_callback)"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 28,
+ "id": "2abe2702-9510-4814-b5f2-63140a102c17",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "logits_loftq_callback_twice = peft_model(**inputs).logits"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 29,
+ "id": "e908de14-01f9-4fdc-91b5-61118a3ce6cb",
+ "metadata": {},
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "Mean absolute error: 1.76357\n",
+ "Mean squared error: 8.33938\n"
+ ]
+ }
+ ],
+ "source": [
+ "error_report(logits_base, logits_loftq_callback_twice)"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "5b8b09fe-d369-4444-b6e2-cd514e775637",
+ "metadata": {},
+ "source": [
+ "There are further gains, but they are not very big."
+ ]
+ }
+ ],
+ "metadata": {
+ "kernelspec": {
+ "display_name": "Python 3 (ipykernel)",
+ "language": "python",
+ "name": "python3"
+ },
+ "language_info": {
+ "codemirror_mode": {
+ "name": "ipython",
+ "version": 3
+ },
+ "file_extension": ".py",
+ "mimetype": "text/x-python",
+ "name": "python",
+ "nbconvert_exporter": "python",
+ "pygments_lexer": "ipython3",
+ "version": "3.10.11"
+ }
+ },
+ "nbformat": 4,
+ "nbformat_minor": 5
+}
diff --git a/peft/examples/loftq_finetuning/README.md b/peft/examples/loftq_finetuning/README.md
new file mode 100644
index 0000000000000000000000000000000000000000..b8d204d3cea02c7a71ce61252d390c696c74d759
--- /dev/null
+++ b/peft/examples/loftq_finetuning/README.md
@@ -0,0 +1,144 @@
+# LoftQ: LoRA-fine-tuning-aware Quantization
+
+## Introduction
+
+LoftQ finds quantized LoRA initialization: quantized backbone Q and LoRA adapters A and B, given a pre-trained weight W.
+
+## Quick Start
+Steps:
+
+1. Apply LoftQ to a full-precision pre-trained weight and save.
+2. Load LoftQ initialization and train.
+
+For step 1, we have provided off-the-shelf LoftQ initializations (see [supported model list](#appendix-off-the-shelf-model-list))
+in [Huggingface Hub LoftQ](https://huggingface.co/LoftQ).
+If you want to do it yourself, jump to [LoftQ DIY](#loftq-diy).
+
+For step 2, below is an example of loading 4bit Mistral-7B with 64rank LoRA adapters from Huggingface Hub.
+```python
+import torch
+from transformers import AutoModelForCausalLM, BitsAndBytesConfig
+from peft import PeftModel
+
+MODEL_ID = "LoftQ/Mistral-7B-v0.1-4bit-64rank"
+
+base_model = AutoModelForCausalLM.from_pretrained(
+ MODEL_ID,
+ torch_dtype=torch.bfloat16, # you may change it with different models
+ quantization_config=BitsAndBytesConfig(
+ load_in_4bit=True,
+ bnb_4bit_compute_dtype=torch.bfloat16, # bfloat16 is recommended
+ bnb_4bit_use_double_quant=False,
+ bnb_4bit_quant_type='nf4',
+ ),
+)
+peft_model = PeftModel.from_pretrained(
+ base_model,
+ MODEL_ID,
+ subfolder="loftq_init",
+ is_trainable=True,
+)
+
+# Do training with peft_model ...
+```
+
+## LoftQ DIY
+
+### Apply LoftQ and save
+We provide [quantize_save_load.py](quantize_save_load.py) as an example to apply LoftQ with
+different bits(`--bits`), ranks(`--rank`), and alternating steps (`--iter`, a hyper-parameter in LoftQ, see Algorithm 1 in [LoftQ paper](https://huggingface.co/papers/2310.08659)). Currently, this example supports
+`llama-2`, `falcon`, `mistral`, `bart`, `t5`, `deberta`, `bert`, `roberta`.
+
+Below is an example of obtaining 4bit LLAMA-2-7b with 16-rank LoRA adapters by 5 alternating steps.
+```sh
+SAVE_DIR="model_zoo/loftq/"
+python quantize_save_load.py \
+ --model_name_or_path meta-llama/Llama-2-7b-hf \ # high-precision model id in HF
+ --token HF_TOKEN \ # your HF token if the model is private, e.g., llama-2
+ --bits 4 \
+ --iter 5 \
+ --rank 16 \
+ --save_dir $SAVE_DIR
+```
+
+The above commands end up with creating the model directory under `$SAVE_DIR`.
+Specifically, the model directory is named as
+
+`MODEL_DIR = SAVE_DIR + f"{args.model_name_or_path.split('/')[-1]}-{args.bits}bits-{args.rank}rank"`
+
+In this example, `MODEL_DIR="model_zoo/loftq/Llama-2-7b-hf-4bit-16rank"`, where the backbone is stored in `$MODEL_DIR`
+and the LoRA adapters are at the sub-folder `$MODEL_DIR/loftq_init`.
+
+### Load and train
+Similar to loading from Huggingface Hub, we only need to change the `MODEL_ID` to the `MODEL_DIR`.
+
+```python
+import torch
+from transformers import AutoModelForCausalLM, BitsAndBytesConfig
+from peft import PeftModel
+
+MODEL_DIR = "model_zoo/loftq/Llama-2-7b-hf-4bit-16rank"
+
+base_model = AutoModelForCausalLM.from_pretrained(
+ MODEL_DIR,
+ torch_dtype=torch.bfloat16,
+ quantization_config=BitsAndBytesConfig(
+ load_in_4bit=True,
+ bnb_4bit_compute_dtype=torch.bfloat16,
+ bnb_4bit_use_double_quant=False,
+ bnb_4bit_quant_type='nf4',
+ ),
+)
+peft_model = PeftModel.from_pretrained(
+ base_model,
+ MODEL_DIR,
+ subfolder="loftq_init",
+ is_trainable=True,
+)
+# Do training with peft_model ...
+```
+
+## LoftQ Fine-tuning
+
+We also provide an example to fine-tune LoftQ on GSM8K.
+We load the quantized backbone and LoRA adapters from the [LoftQ Huggingface hub](https://huggingface.co/LoftQ).
+
+```sh
+python train_gsm8k_llama.py \
+ --model_name_or_path LoftQ/Llama-2-13b-hf-4bit-64rank \
+ --output_dir exp_results/gsm8k/llama-2-13b/bit4-rank64/lr1e-4 \
+ --learning_rate 1e-4 \
+ --weight_decay 0.1 \
+ --lr_scheduler_type cosine \
+ --num_warmup_steps 100 \
+ --seed 202 \
+ --dataset_name gsm8k \
+ --dataset_config main \
+ --pad_to_max_length \
+ --max_source_length 128 \
+ --max_target_length 256 \
+ --num_train_epochs 5 \
+ --per_device_train_batch_size 4 \
+ --per_device_eval_batch_size 4 \
+ --gradient_accumulation_steps 4 \
+ --with_tracking \
+ --report_to tensorboard
+```
+
+
+## Appendix: Off-the-shelf Model List
+| Model Name | Bits | Ranks |
+| ----------- | ---- | ----- |
+| LLAMA-2-7b | 4 | 64 |
+| LLAMA-2-13b | 4 | 64 |
+| LLAMA-2-70b | 4 | 64 |
+| Mistral | 4 | 64 |
+| Mistral | 4 | 32 |
+| BART-large | 4 | 8 |
+| BART-large | 4 | 16 |
+| BART-large | 4 | 32 |
+| BART-large | 2 | 8 |
+
+## In-place application of LoftQ initialization
+
+PEFT provides a convenience function `replace_lora_weights_loftq` to apply LoftQ initialization in-place to the quantized model. Check out [this notebook](https://github.com/huggingface/peft/blob/main/examples/loftq_finetuning/LoftQ_weight_replacement.ipynb) for an example.
diff --git a/peft/examples/loftq_finetuning/quantize_save_load.py b/peft/examples/loftq_finetuning/quantize_save_load.py
new file mode 100644
index 0000000000000000000000000000000000000000..2110ed908684a658896bbfbe065130cfa35490a6
--- /dev/null
+++ b/peft/examples/loftq_finetuning/quantize_save_load.py
@@ -0,0 +1,193 @@
+# Copyright 2023-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+import argparse
+import os
+
+import torch
+import torch.nn as nn
+from transformers import (
+ AutoModelForCausalLM,
+ AutoModelForSeq2SeqLM,
+ AutoModelForSequenceClassification,
+ AutoTokenizer,
+)
+
+from peft import LoftQConfig, LoraConfig, TaskType, get_peft_model
+
+
+class Shell(nn.Module):
+ def __init__(self, weight, bias=None):
+ super().__init__()
+ self.weight = nn.Parameter(weight, requires_grad=False)
+ if bias is not None:
+ self.bias = nn.Parameter(bias, requires_grad=False)
+
+
+def unwrap_model(model, sub_module_name=".base_layer"):
+ sub_module_name_list = [k.split(sub_module_name)[0] for k in model.state_dict().keys() if sub_module_name in k]
+ sub_module_name_set = set(sub_module_name_list)
+ for name in sub_module_name_set:
+ # get the parent of the submodule
+ name_parent = ".".join(name.split(".")[:-1])
+ name_child = name.split(".")[-1]
+ sub_module = model.get_submodule(name_parent)
+ print(sub_module)
+
+ # replace with shell
+ child = getattr(sub_module, name_child)
+ weight = getattr(child.base_layer, "weight", None)
+ bias = getattr(child.base_layer, "bias", None)
+ shell = Shell(weight, bias)
+
+ setattr(sub_module, name_child, shell)
+
+ print("You have unwrapped the model. Use it on your own risk.")
+
+
+def print_model(model, name):
+ print("=" * 10 + name + "=" * 10)
+ print(model)
+ for name, param in model.named_parameters():
+ if torch.is_tensor(param):
+ if param.dtype in [torch.float32, torch.float16]:
+ print(
+ name,
+ param.shape,
+ param.device,
+ param.dtype,
+ param.requires_grad,
+ param.mean().item(),
+ param.max().item(),
+ )
+ else:
+ print(name, param.shape, param.device, param.dtype, param.requires_grad)
+
+
+def arg_parse():
+ parser = argparse.ArgumentParser(description="Quantize a model with LoftQ.")
+ parser.add_argument(
+ "--model_name_or_path",
+ type=str,
+ default=None,
+ required=True,
+ help="The name or path of the fp32/16 model.",
+ )
+ parser.add_argument(
+ "--token",
+ type=str,
+ default=None,
+ help="The access token to download model from HuggingFace Hub.",
+ )
+ parser.add_argument(
+ "--bits",
+ type=int,
+ default=4,
+ help="The quantized bits",
+ )
+ parser.add_argument(
+ "--iter",
+ type=int,
+ default=1,
+ help="The alternating steps in LoftQ",
+ )
+ parser.add_argument(
+ "--rank",
+ type=int,
+ default=16,
+ help="The rank of the LoRA adapter",
+ )
+ parser.add_argument(
+ "--save_dir",
+ type=str,
+ default="./model_zoo/loftq/",
+ help="The rank of the LoRA adapter",
+ )
+ args = parser.parse_args()
+ return args
+
+
+def quantize_and_save():
+ args = arg_parse()
+
+ # Download weights and configure LoRA
+ tokenizer = AutoTokenizer.from_pretrained(args.model_name_or_path, token=args.token, trust_remote_code=True)
+ if any(name in args.model_name_or_path.lower() for name in ["llama", "mistral", "falcon"]):
+ model = AutoModelForCausalLM.from_pretrained(args.model_name_or_path, token=args.token, trust_remote_code=True)
+ task_type = TaskType.CAUSAL_LM
+ target_modules = ["q_proj", "k_proj", "v_proj", "o_proj", "up_proj", "down_proj", "gate_proj"]
+
+ elif any(name in args.model_name_or_path.lower() for name in ["bart", "t5"]):
+ model = AutoModelForSeq2SeqLM.from_pretrained(args.model_name_or_path, token=args.token)
+ task_type = TaskType.SEQ_2_SEQ_LM
+ target_modules = ["q_proj", "k_proj", "v_proj", "fc1", "fc2", "out_proj"]
+
+ elif any(name in args.model_name_or_path.lower() for name in ["deberta", "roberta", "bert"]):
+ model = AutoModelForSequenceClassification.from_pretrained(args.model_name_or_path, token=args.token)
+ task_type = TaskType.SEQ_CLS
+ target_modules = ["query_proj", "key_proj", "value_proj", "dense"] # embeddings not supported by peft
+ else:
+ raise NotImplementedError("Other models not supported yet.")
+
+ # Config of LoftQ
+ loftq_config = LoftQConfig(loftq_bits=args.bits, loftq_iter=args.iter)
+
+ lora_config = LoraConfig(
+ task_type=task_type,
+ inference_mode=True,
+ r=args.rank,
+ lora_alpha=16 if task_type is TaskType.CAUSAL_LM else args.rank,
+ lora_dropout=0.1,
+ target_modules=target_modules,
+ init_lora_weights="loftq",
+ loftq_config=loftq_config,
+ )
+
+ # Obtain LoftQ model
+ lora_model = get_peft_model(model, lora_config)
+ base_model = lora_model.get_base_model()
+
+ # Save LoftQ model
+ model_name = args.model_name_or_path.split("/")[-1] + f"-{args.bits}bit" + f"-{args.rank}rank"
+ base_model_dir = os.path.join(args.save_dir, model_name)
+ lora_model_dir = os.path.join(args.save_dir, model_name, "loft_init")
+
+ # save lora adapters first
+ lora_model.base_model.peft_config[
+ "default"
+ ].base_model_name_or_path = base_model_dir # This can be a local path or Hub model id
+ lora_model.base_model.peft_config["default"].init_lora_weights = True # Don't apply LoftQ when loading again
+
+ lora_model.save_pretrained(lora_model_dir)
+ print_model(lora_model, "lora_model")
+
+ # remove lora adapters and save the backbone
+ unwrap_model(base_model)
+ base_model.save_pretrained(base_model_dir)
+ tokenizer.save_pretrained(base_model_dir)
+
+ print_model(base_model, "base_model")
+
+ return base_model_dir, lora_model_dir
+
+
+if __name__ == "__main__":
+ base_dir, lora_dir = quantize_and_save()
+
+# example command:
+# python quantize_save_load.py \
+# --model_name_or_path meta-llama/Llama-2-7b-hf \
+# --token XXX \
+# --bits 4 --iter 5 --rank 16 \
+# --save_dir ./model_zoo/loftq/
diff --git a/peft/examples/loftq_finetuning/train_gsm8k_llama.py b/peft/examples/loftq_finetuning/train_gsm8k_llama.py
new file mode 100644
index 0000000000000000000000000000000000000000..66b83d55e38d9c7c20231d08e371ed15aea23ca9
--- /dev/null
+++ b/peft/examples/loftq_finetuning/train_gsm8k_llama.py
@@ -0,0 +1,851 @@
+# Copyright 2023-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+import argparse
+import copy
+import logging
+import math
+import os
+import random
+import re
+from pathlib import Path
+
+import datasets
+import torch
+import transformers
+from accelerate import Accelerator, DistributedType
+from accelerate.logging import get_logger
+from accelerate.utils import set_seed
+from datasets import load_dataset
+from huggingface_hub import HfApi
+from torch.utils.data import DataLoader
+from tqdm.auto import tqdm
+from transformers import (
+ CONFIG_MAPPING,
+ MODEL_MAPPING,
+ AutoConfig,
+ AutoModelForCausalLM,
+ AutoTokenizer,
+ BitsAndBytesConfig,
+ SchedulerType,
+ default_data_collator,
+ get_scheduler,
+)
+from transformers.utils import send_example_telemetry
+from transformers.utils.versions import require_version
+
+from peft import PeftModel
+
+
+# Will error if the minimal version of Transformers is not installed. Remove at your own risks.
+# check_min_version("4.32.0.dev0")
+
+logger = get_logger(__name__)
+
+require_version("datasets>=1.8.0", "To fix: pip install -r examples/pytorch/language-modeling/requirements.txt")
+
+MODEL_CONFIG_CLASSES = list(MODEL_MAPPING.keys())
+MODEL_TYPES = tuple(conf.model_type for conf in MODEL_CONFIG_CLASSES)
+
+
+def parse_args():
+ parser = argparse.ArgumentParser(description="Finetune a transformers model on a causal language modeling task")
+ parser.add_argument(
+ "--dataset_name",
+ type=str,
+ default=None,
+ help="The name of the dataset to use (via the datasets library).",
+ )
+ parser.add_argument(
+ "--dataset_config_name",
+ type=str,
+ default=None,
+ help="The configuration name of the dataset to use (via the datasets library).",
+ )
+ parser.add_argument(
+ "--train_file", type=str, default=None, help="A csv, txt or a json file containing the training data."
+ )
+ parser.add_argument(
+ "--validation_file", type=str, default=None, help="A csv, txt or a json file containing the validation data."
+ )
+ parser.add_argument(
+ "--validation_split_percentage",
+ default=5,
+ help="The percentage of the train set used as validation set in case there's no validation split",
+ )
+ parser.add_argument(
+ "--model_name_or_path",
+ type=str,
+ help="Path to pretrained model or model identifier from huggingface.co/models.",
+ required=False,
+ )
+ parser.add_argument(
+ "--config_name",
+ type=str,
+ default=None,
+ help="Pretrained config name or path if not the same as model_name",
+ )
+ parser.add_argument(
+ "--tokenizer_name",
+ type=str,
+ default=None,
+ help="Pretrained tokenizer name or path if not the same as model_name",
+ )
+ parser.add_argument(
+ "--use_slow_tokenizer",
+ action="store_true",
+ help="If passed, will use a slow tokenizer (not backed by the 🤗 Tokenizers library).",
+ )
+ parser.add_argument(
+ "--per_device_train_batch_size",
+ type=int,
+ default=8,
+ help="Batch size (per device) for the training dataloader.",
+ )
+ parser.add_argument(
+ "--per_device_eval_batch_size",
+ type=int,
+ default=8,
+ help="Batch size (per device) for the evaluation dataloader.",
+ )
+ parser.add_argument(
+ "--learning_rate",
+ type=float,
+ default=5e-5,
+ help="Initial learning rate (after the potential warmup period) to use.",
+ )
+ parser.add_argument("--weight_decay", type=float, default=0.0, help="Weight decay to use.")
+ parser.add_argument("--num_train_epochs", type=int, default=3, help="Total number of training epochs to perform.")
+ parser.add_argument(
+ "--max_train_steps",
+ type=int,
+ default=None,
+ help="Total number of training steps to perform. If provided, overrides num_train_epochs.",
+ )
+ parser.add_argument(
+ "--gradient_accumulation_steps",
+ type=int,
+ default=1,
+ help="Number of updates steps to accumulate before performing a backward/update pass.",
+ )
+ parser.add_argument(
+ "--lr_scheduler_type",
+ type=SchedulerType,
+ default="linear",
+ help="The scheduler type to use.",
+ choices=["linear", "cosine", "cosine_with_restarts", "polynomial", "constant", "constant_with_warmup"],
+ )
+ parser.add_argument(
+ "--num_warmup_steps", type=int, default=0, help="Number of steps for the warmup in the lr scheduler."
+ )
+ parser.add_argument("--output_dir", type=str, default=None, help="Where to store the final model.")
+ parser.add_argument("--seed", type=int, default=None, help="A seed for reproducible training.")
+ parser.add_argument(
+ "--model_type",
+ type=str,
+ default=None,
+ help="Model type to use if training from scratch.",
+ choices=MODEL_TYPES,
+ )
+ parser.add_argument(
+ "--ignore_pad_token_for_loss",
+ type=bool,
+ default=True,
+ help="Whether to ignore the tokens corresponding to padded labels in the loss computation or not.",
+ )
+ parser.add_argument(
+ "--max_source_length",
+ type=int,
+ default=128,
+ help=(
+ "The maximum total input sequence length after "
+ "tokenization.Sequences longer than this will be truncated, sequences shorter will be padded."
+ ),
+ )
+ parser.add_argument(
+ "--max_target_length",
+ type=int,
+ default=128,
+ help=(
+ "The maximum total sequence length for target text after "
+ "tokenization. Sequences longer than this will be truncated, sequences shorter will be padded."
+ "during ``evaluate`` and ``predict``."
+ ),
+ )
+ parser.add_argument(
+ "--pad_to_max_length",
+ action="store_true",
+ help="If passed, pad all samples to `max_length`. Otherwise, dynamic padding is used.",
+ )
+ parser.add_argument(
+ "--preprocessing_num_workers",
+ type=int,
+ default=None,
+ help="The number of processes to use for the preprocessing.",
+ )
+ parser.add_argument(
+ "--overwrite_cache", action="store_true", help="Overwrite the cached training and evaluation sets"
+ )
+ parser.add_argument(
+ "--no_keep_linebreaks", action="store_true", help="Do not keep line breaks when using TXT files."
+ )
+ parser.add_argument("--push_to_hub", action="store_true", help="Whether or not to push the model to the Hub.")
+ parser.add_argument(
+ "--hub_model_id", type=str, help="The name of the repository to keep in sync with the local `output_dir`."
+ )
+ parser.add_argument("--hub_token", type=str, help="The token to use to push to the Model Hub.")
+ parser.add_argument(
+ "--trust_remote_code",
+ type=bool,
+ default=False,
+ help=(
+ "Whether or not to allow for custom models defined on the Hub in their own modeling files. This option"
+ "should only be set to `True` for repositories you trust and in which you have read the code, as it will"
+ "execute code present on the Hub on your local machine."
+ ),
+ )
+ parser.add_argument(
+ "--checkpointing_steps",
+ type=str,
+ default=None,
+ help="Whether the various states should be saved at the end of every n steps, or 'epoch' for each epoch.",
+ )
+ parser.add_argument(
+ "--resume_from_checkpoint",
+ type=str,
+ default=None,
+ help="If the training should continue from a checkpoint folder.",
+ )
+ parser.add_argument(
+ "--with_tracking",
+ action="store_true",
+ help="Whether to enable experiment trackers for logging.",
+ )
+ parser.add_argument(
+ "--report_to",
+ type=str,
+ default="tensorboard",
+ help=(
+ 'The integration to report the results and logs to. Supported platforms are `"tensorboard"`,'
+ ' `"wandb"`, `"comet_ml"` and `"clearml"`. Use `"all"` (default) to report to all integrations.'
+ "Only applicable when `--with_tracking` is passed."
+ ),
+ )
+ parser.add_argument(
+ "--low_cpu_mem_usage",
+ action="store_true",
+ help=(
+ "It is an option to create the model as an empty shell, then only materialize its parameters when the pretrained weights are loaded."
+ "If passed, LLM loading time and RAM consumption will be benefited."
+ ),
+ )
+ ##########################
+ # Generation Config #
+ ##########################
+ parser.add_argument(
+ "--temperature",
+ type=float,
+ default=0.8,
+ help="temperature of 1.0 has no effect, lower tend toward greedy sampling",
+ )
+ parser.add_argument("--k", type=int, default=40, help="Choose k candidate words")
+ parser.add_argument("--p", type=float, default=0.95, help="The sum of probability of candidate words is 0.9 ")
+
+ ##########################
+ # Exp Args #
+ ##########################
+ parser.add_argument(
+ "--adapter_name_or_path",
+ type=str,
+ default=None,
+ help=(
+ "The LoRA adapter checkpoint. Set None if you want to fine-tune from LoftQ."
+ "Specify a path if you want to evaluate."
+ ),
+ )
+
+ args = parser.parse_args()
+
+ # Sanity checks
+ if args.dataset_name is None and args.train_file is None and args.validation_file is None:
+ raise ValueError("Need either a dataset name or a training/validation file.")
+ else:
+ if args.train_file is not None:
+ extension = args.train_file.split(".")[-1]
+ assert extension in ["csv", "json", "txt"], "`train_file` should be a csv, json or txt file."
+ if args.validation_file is not None:
+ extension = args.validation_file.split(".")[-1]
+ assert extension in ["csv", "json", "txt"], "`validation_file` should be a csv, json or txt file."
+
+ if args.push_to_hub:
+ assert args.output_dir is not None, "Need an `output_dir` to create a repo when `--push_to_hub` is passed."
+
+ return args
+
+
+def main():
+ args = parse_args()
+
+ # Sending telemetry. Tracking the example usage helps us better allocate resources to maintain them. The
+ # information sent is the one passed as arguments along with your Python/PyTorch versions.
+ send_example_telemetry("run_clm_no_trainer", args)
+
+ # Initialize the accelerator. We will let the accelerator handle device placement for us in this example.
+ # If we're using tracking, we also need to initialize it here and it will by default pick up all supported trackers
+ # in the environment
+ accelerator_log_kwargs = {}
+
+ if args.with_tracking:
+ accelerator_log_kwargs["log_with"] = args.report_to
+ accelerator_log_kwargs["project_dir"] = args.output_dir
+
+ accelerator = Accelerator(gradient_accumulation_steps=args.gradient_accumulation_steps, **accelerator_log_kwargs)
+
+ # Make one log on every process with the configuration for debugging.
+ logging.basicConfig(
+ format="%(asctime)s - %(levelname)s - %(name)s - %(message)s",
+ datefmt="%m/%d/%Y %H:%M:%S",
+ level=logging.INFO,
+ )
+ logger.info(accelerator.state, main_process_only=False)
+ if accelerator.is_local_main_process:
+ datasets.utils.logging.set_verbosity_warning()
+ transformers.utils.logging.set_verbosity_info()
+ else:
+ datasets.utils.logging.set_verbosity_error()
+ transformers.utils.logging.set_verbosity_error()
+
+ # If passed along, set the training seed now.
+ if args.seed is not None:
+ set_seed(args.seed)
+
+ # Handle the repository creation
+ if accelerator.is_main_process:
+ if args.push_to_hub:
+ api = HfApi(token=args.hub_token)
+
+ # Create repo (repo_name from args or inferred)
+ repo_name = args.hub_model_id
+ if repo_name is None:
+ repo_name = Path(args.output_dir).absolute().name
+ repo_id = api.create_repo(repo_name, exist_ok=True).repo_id
+
+ with open(os.path.join(args.output_dir, ".gitignore"), "w+") as gitignore:
+ if "step_*" not in gitignore:
+ gitignore.write("step_*\n")
+ if "epoch_*" not in gitignore:
+ gitignore.write("epoch_*\n")
+ elif args.output_dir is not None:
+ os.makedirs(args.output_dir, exist_ok=True)
+ accelerator.wait_for_everyone()
+
+ # Get the datasets: you can either provide your own CSV/JSON/TXT training and evaluation files (see below)
+ # or just provide the name of one of the public datasets available on the hub at https://huggingface.co/datasets/
+ # (the dataset will be downloaded automatically from the datasets Hub).
+ #
+ # For CSV/JSON files, this script will use the column called 'text' or the first column if no column called
+ # 'text' is found. You can easily tweak this behavior (see below).
+ #
+ # In distributed training, the load_dataset function guarantee that only one local process can concurrently
+ # download the dataset.
+ if args.dataset_name is not None:
+ # Downloading and loading a dataset from the hub.
+ raw_datasets = load_dataset(args.dataset_name, args.dataset_config_name)
+ if "validation" not in raw_datasets.keys():
+ raw_datasets["validation"] = load_dataset(
+ args.dataset_name,
+ args.dataset_config_name,
+ split=f"train[:{args.validation_split_percentage}%]",
+ )
+ raw_datasets["train"] = load_dataset(
+ args.dataset_name,
+ args.dataset_config_name,
+ split=f"train[{args.validation_split_percentage}%:]",
+ )
+ else:
+ data_files = {}
+ dataset_args = {}
+ if args.train_file is not None:
+ data_files["train"] = args.train_file
+ if args.validation_file is not None:
+ data_files["validation"] = args.validation_file
+ extension = args.train_file.split(".")[-1]
+ if extension == "txt":
+ extension = "text"
+ dataset_args["keep_linebreaks"] = not args.no_keep_linebreaks
+ raw_datasets = load_dataset(extension, data_files=data_files, **dataset_args)
+ # If no validation data is there, validation_split_percentage will be used to divide the dataset.
+ if "validation" not in raw_datasets.keys():
+ raw_datasets["validation"] = load_dataset(
+ extension,
+ data_files=data_files,
+ split=f"train[:{args.validation_split_percentage}%]",
+ **dataset_args,
+ )
+ raw_datasets["train"] = load_dataset(
+ extension,
+ data_files=data_files,
+ split=f"train[{args.validation_split_percentage}%:]",
+ **dataset_args,
+ )
+
+ # See more about loading any type of standard or custom dataset (from files, python dict, pandas DataFrame, etc) at
+ # https://huggingface.co/docs/datasets/loading_datasets.html.
+
+ # Load pretrained model and tokenizer
+ #
+ # In distributed training, the .from_pretrained methods guarantee that only one local process can concurrently
+ # download model & vocab.
+ if args.config_name:
+ config = AutoConfig.from_pretrained(
+ args.config_name,
+ trust_remote_code=args.trust_remote_code,
+ )
+ elif args.model_name_or_path:
+ config = AutoConfig.from_pretrained(
+ args.model_name_or_path,
+ trust_remote_code=args.trust_remote_code,
+ )
+ else:
+ config = CONFIG_MAPPING[args.model_type]()
+ logger.warning("You are instantiating a new config instance from scratch.")
+
+ if args.tokenizer_name:
+ tokenizer = AutoTokenizer.from_pretrained(
+ args.tokenizer_name, use_fast=not args.use_slow_tokenizer, trust_remote_code=args.trust_remote_code
+ )
+ elif args.model_name_or_path:
+ tokenizer = AutoTokenizer.from_pretrained(
+ args.model_name_or_path,
+ use_fast=not args.use_slow_tokenizer,
+ trust_remote_code=args.trust_remote_code,
+ )
+ else:
+ raise ValueError(
+ "You are instantiating a new tokenizer from scratch. This is not supported by this script."
+ "You can do it from another script, save it, and load it from here, using --tokenizer_name."
+ )
+
+ ##########################
+ # Tokenizer #
+ ##########################
+ tokenizer.pad_token_id = 0 # unk. we want this to be different from the eos token
+ tokenizer.padding_side = "left" # Allow batched inference
+ tokenizer.truncation_side = "left"
+
+ if args.model_name_or_path:
+ model = AutoModelForCausalLM.from_pretrained(
+ args.model_name_or_path,
+ from_tf=bool(".ckpt" in args.model_name_or_path),
+ config=config,
+ low_cpu_mem_usage=True,
+ quantization_config=BitsAndBytesConfig(
+ load_in_4bit=True,
+ bnb_4bit_use_double_quant=False,
+ bnb_4bit_quant_type="nf4",
+ bnb_4bit_compute_dtype=config.torch_dtype,
+ ),
+ )
+ else:
+ logger.info("Training new model from scratch")
+ model = AutoModelForCausalLM.from_config(config, trust_remote_code=args.trust_remote_code)
+
+ ##########################
+ # Peft Model #
+ ##########################
+ if args.adapter_name_or_path is None:
+ model = PeftModel.from_pretrained(model, args.model_name_or_path, subfolder="loftq_init", is_trainable=True)
+ else:
+ model = PeftModel.from_pretrained(model, args.adapter_name_or_path, is_trainable=True)
+ model.print_trainable_parameters()
+
+ # We resize the embeddings only when necessary to avoid index errors. If you are creating a model from scratch
+ # on a small vocab and want a smaller embedding size, remove this test.
+ embedding_size = model.get_input_embeddings().weight.shape[0]
+ if len(tokenizer) > embedding_size:
+ model.resize_token_embeddings(len(tokenizer))
+
+ # Preprocessing the datasets.
+ # First we tokenize all the texts.
+ ##########################
+ # GSM8K dataset #
+ ##########################
+
+ # Preprocessing the datasets.
+ # First we tokenize all the texts.
+ column_names = raw_datasets["train"].column_names
+
+ # Get the column names for source/target.
+ source_column, target_column = "question", "answer"
+
+ # Temporarily set max_target_length for training.
+ padding = "max_length" if args.pad_to_max_length else False
+ task_prompt = "\nAnswer the above question. First think step by step and then answer the final number.\n"
+
+ def prompt_process(sent_1, sent_2, prompt_1="", prompt_2="", prompt_3=""):
+ sent_2 = sent_2.replace("####", "The final answer is")
+ return prompt_1 + sent_1 + prompt_2 + sent_2 + prompt_3
+
+ def preprocess_function_train(examples):
+ sources = examples[source_column]
+ targets = examples[target_column]
+
+ inputs = [prompt_process(source, target, prompt_2=task_prompt) for (source, target) in zip(sources, targets)]
+
+ model_inputs = tokenizer(
+ inputs,
+ max_length=args.max_source_length + args.max_target_length,
+ padding=padding,
+ truncation=True,
+ return_tensors="pt",
+ )
+
+ labels = copy.deepcopy(model_inputs)
+
+ # If we are padding here, replace all tokenizer.pad_token_id in the labels by -100 when we want to ignore
+ # padding in the loss.
+ if padding == "max_length" and args.ignore_pad_token_for_loss:
+ # get the length of the target tokens. -1 to kick out the token
+ target_tokens = tokenizer(targets, padding=False)
+ target_len = [len(label) - 1 for label in target_tokens["input_ids"]]
+
+ # don't calculate the loss from source and padding (left padding)
+ for i in range(len(labels["input_ids"])):
+ labels["input_ids"][i, : -target_len[i]] = -100
+
+ model_inputs["labels"] = labels["input_ids"]
+ return model_inputs
+
+ def preprocess_function_test(examples):
+ sources = examples[source_column]
+ labels = examples[target_column]
+
+ inputs = [source + task_prompt for source in sources]
+
+ model_inputs = tokenizer(inputs, max_length=args.max_source_length, padding=padding, truncation=True)
+ labels = tokenizer(labels, max_length=args.max_target_length, padding=padding, truncation=True)
+
+ model_inputs["labels"] = labels["input_ids"]
+
+ return model_inputs
+
+ with accelerator.main_process_first():
+ train_dataset = raw_datasets["train"].map(
+ preprocess_function_train,
+ batched=True,
+ num_proc=args.preprocessing_num_workers,
+ remove_columns=column_names,
+ load_from_cache_file=not args.overwrite_cache,
+ desc="Running tokenizer on training dataset",
+ )
+
+ eval_dataset = raw_datasets["test"].map(
+ preprocess_function_test,
+ batched=True,
+ num_proc=args.preprocessing_num_workers,
+ remove_columns=column_names,
+ load_from_cache_file=not args.overwrite_cache,
+ desc="Running tokenizer on test dataset",
+ )
+
+ # Log a few random samples from the set:
+ for index in random.sample(range(len(train_dataset)), 2):
+ logger.info(f"Sample {index} of the training set: {train_dataset[index]}.")
+ for index in random.sample(range(len(eval_dataset)), 2):
+ logger.info(f"Sample {index} of the validation set: {eval_dataset[index]}.")
+
+ # DataLoaders creation:
+ train_dataloader = DataLoader(
+ train_dataset, shuffle=True, collate_fn=default_data_collator, batch_size=args.per_device_train_batch_size
+ )
+ eval_dataloader = DataLoader(
+ eval_dataset, collate_fn=default_data_collator, batch_size=args.per_device_eval_batch_size
+ )
+
+ # Optimizer
+ # Split weights in two groups, one with weight decay and the other not.
+ no_decay = ["bias", "layer_norm.weight"]
+ optimizer_grouped_parameters = [
+ {
+ "params": [p for n, p in model.named_parameters() if not any(nd in n for nd in no_decay) and "lora" in n],
+ "weight_decay": args.weight_decay,
+ },
+ {
+ "params": [p for n, p in model.named_parameters() if any(nd in n for nd in no_decay)],
+ "weight_decay": 0.0,
+ },
+ ]
+ optimizer = torch.optim.AdamW(optimizer_grouped_parameters, lr=args.learning_rate)
+
+ # Scheduler and math around the number of training steps.
+ overrode_max_train_steps = False
+ num_update_steps_per_epoch = math.ceil(len(train_dataloader) / args.gradient_accumulation_steps)
+ if args.max_train_steps is None:
+ args.max_train_steps = args.num_train_epochs * num_update_steps_per_epoch
+ overrode_max_train_steps = True
+
+ lr_scheduler = get_scheduler(
+ name=args.lr_scheduler_type,
+ optimizer=optimizer,
+ num_warmup_steps=args.num_warmup_steps * args.gradient_accumulation_steps,
+ num_training_steps=args.max_train_steps * args.gradient_accumulation_steps,
+ )
+
+ # Prepare everything with our `accelerator`.
+ model, optimizer, train_dataloader, eval_dataloader, lr_scheduler = accelerator.prepare(
+ model, optimizer, train_dataloader, eval_dataloader, lr_scheduler
+ )
+
+ # On TPU, the tie weights in our model have been disconnected, so we need to restore the ties.
+ if accelerator.distributed_type == DistributedType.TPU:
+ model.tie_weights()
+
+ # We need to recalculate our total training steps as the size of the training dataloader may have changed.
+ num_update_steps_per_epoch = math.ceil(len(train_dataloader) / args.gradient_accumulation_steps)
+ if overrode_max_train_steps:
+ args.max_train_steps = args.num_train_epochs * num_update_steps_per_epoch
+ # Afterwards we recalculate our number of training epochs
+ args.num_train_epochs = math.ceil(args.max_train_steps / num_update_steps_per_epoch)
+
+ # Figure out how many steps we should save the Accelerator states
+ checkpointing_steps = args.checkpointing_steps
+ if checkpointing_steps is not None and checkpointing_steps.isdigit():
+ checkpointing_steps = int(checkpointing_steps)
+
+ # We need to initialize the trackers we use, and also store our configuration.
+ # The trackers initializes automatically on the main process.
+ if args.with_tracking:
+ experiment_config = vars(args)
+ # TensorBoard cannot log Enums, need the raw value
+ experiment_config["lr_scheduler_type"] = experiment_config["lr_scheduler_type"].value
+ accelerator.init_trackers("clm_no_trainer", experiment_config)
+
+ # Train!
+ total_batch_size = args.per_device_train_batch_size * accelerator.num_processes * args.gradient_accumulation_steps
+
+ logger.info("***** Running training *****")
+ logger.info(f" Num examples = {len(train_dataset)}")
+ logger.info(f" Num Epochs = {args.num_train_epochs}")
+ logger.info(f" Instantaneous batch size per device = {args.per_device_train_batch_size}")
+ logger.info(f" Total train batch size (w. parallel, distributed & accumulation) = {total_batch_size}")
+ logger.info(f" Gradient Accumulation steps = {args.gradient_accumulation_steps}")
+ logger.info(f" Total optimization steps = {args.max_train_steps}")
+ # Only show the progress bar once on each machine.
+ progress_bar = tqdm(range(args.max_train_steps), disable=not accelerator.is_local_main_process)
+ completed_steps = 0
+ starting_epoch = 0
+
+ # Potentially load in the weights and states from a previous save
+ if args.resume_from_checkpoint:
+ if args.resume_from_checkpoint is not None or args.resume_from_checkpoint != "":
+ checkpoint_path = args.resume_from_checkpoint
+ path = os.path.basename(args.resume_from_checkpoint)
+ else:
+ # Get the most recent checkpoint
+ dirs = [f.name for f in os.scandir(os.getcwd()) if f.is_dir()]
+ dirs.sort(key=os.path.getctime)
+ path = dirs[-1] # Sorts folders by date modified, most recent checkpoint is the last
+ checkpoint_path = path
+ path = os.path.basename(checkpoint_path)
+
+ accelerator.print(f"Resumed from checkpoint: {checkpoint_path}")
+ accelerator.load_state(path)
+ # Extract `epoch_{i}` or `step_{i}`
+ training_difference = os.path.splitext(path)[0]
+
+ if "epoch" in training_difference:
+ starting_epoch = int(training_difference.replace("epoch_", "")) + 1
+ resume_step = None
+ completed_steps = starting_epoch * num_update_steps_per_epoch
+ else:
+ # need to multiply `gradient_accumulation_steps` to reflect real steps
+ resume_step = int(training_difference.replace("step_", "")) * args.gradient_accumulation_steps
+ starting_epoch = resume_step // len(train_dataloader)
+ resume_step -= starting_epoch * len(train_dataloader)
+ completed_steps = resume_step // args.gradient_accumulation_steps
+
+ # update the progress_bar if load from checkpoint
+ progress_bar.update(completed_steps)
+
+ for epoch in range(starting_epoch, args.num_train_epochs):
+ model.train()
+ if args.with_tracking:
+ total_loss = 0
+ if args.resume_from_checkpoint and epoch == starting_epoch and resume_step is not None:
+ # We skip the first `n` batches in the dataloader when resuming from a checkpoint
+ active_dataloader = accelerator.skip_first_batches(train_dataloader, resume_step)
+ else:
+ active_dataloader = train_dataloader
+ for step, batch in enumerate(active_dataloader):
+ with accelerator.accumulate(model):
+ outputs = model(**batch)
+ loss = outputs.loss
+ # We keep track of the loss at each epoch
+ if args.with_tracking:
+ total_loss += loss.detach().float()
+ accelerator.backward(loss)
+ if completed_steps % 50:
+ accelerator.print(f"Epoch: {epoch} | Step: {completed_steps} | Loss: {loss}")
+ optimizer.step()
+ lr_scheduler.step()
+ optimizer.zero_grad()
+
+ # Checks if the accelerator has performed an optimization step behind the scenes
+ if accelerator.sync_gradients:
+ progress_bar.update(1)
+ completed_steps += 1
+
+ if isinstance(checkpointing_steps, int):
+ if completed_steps % checkpointing_steps == 0:
+ output_dir = f"step_{completed_steps}"
+ if args.output_dir is not None:
+ output_dir = os.path.join(args.output_dir, output_dir)
+ accelerator.save_state(output_dir)
+ if completed_steps >= args.max_train_steps:
+ break
+
+ model.eval()
+ gen_kwargs = {
+ "max_new_tokens": args.max_target_length,
+ "temperature": args.temperature,
+ "top_k": args.k,
+ "top_p": args.p,
+ "do_sample": True,
+ }
+ ans_pred_list = []
+ ans_gold_list = []
+ for step, batch in enumerate(eval_dataloader):
+ with torch.no_grad():
+ gen_kwargs["input_ids"] = batch["input_ids"]
+ gen_kwargs["attention_mask"] = batch["attention_mask"]
+ generated_tokens = accelerator.unwrap_model(model).generate(**gen_kwargs)
+
+ pred_tokens = generated_tokens[:, args.max_source_length :]
+ pred_tokens = accelerator.pad_across_processes(pred_tokens, dim=1, pad_index=tokenizer.pad_token_id)
+ gold_tokens = batch["labels"]
+
+ if not args.pad_to_max_length:
+ # If we did not pad to max length, we need to pad the labels too
+ gold_tokens = accelerator.pad_across_processes(
+ batch["labels"], dim=1, pad_index=tokenizer.pad_token_id
+ )
+
+ pred_tokens, gold_tokens = accelerator.gather_for_metrics((pred_tokens, gold_tokens))
+ pred_tokens, gold_tokens = pred_tokens.cpu().numpy(), gold_tokens.cpu().numpy()
+
+ if isinstance(pred_tokens, tuple):
+ pred_tokens = pred_tokens[0]
+ decoded_pred = tokenizer.batch_decode(pred_tokens, skip_special_tokens=True)
+ decoded_gold = tokenizer.batch_decode(gold_tokens, skip_special_tokens=True)
+
+ # Extract the numbers in sentences
+ accelerator.print(decoded_pred)
+ ans_pred_list += [extract_answer_number(sentence_pred) for sentence_pred in decoded_pred]
+ ans_gold_list += [extract_answer_number(sentence_gold) for sentence_gold in decoded_gold]
+
+ accelerator.print(ans_pred_list)
+ accelerator.print(ans_gold_list)
+ accuracy = compute_accuracy(ans_gold_list, ans_pred_list)
+
+ logger.info(f"epoch {epoch}: accuracy: {accuracy}")
+
+ if args.with_tracking:
+ accelerator.log(
+ {
+ "accuracy": accuracy,
+ "train_loss": total_loss.item() / len(train_dataloader),
+ "epoch": epoch,
+ "step": completed_steps,
+ },
+ step=completed_steps,
+ )
+
+ if args.push_to_hub and epoch < args.num_train_epochs - 1:
+ accelerator.wait_for_everyone()
+ unwrapped_model = accelerator.unwrap_model(model)
+ unwrapped_model.save_pretrained(
+ args.output_dir, is_main_process=accelerator.is_main_process, save_function=accelerator.save
+ )
+ if accelerator.is_main_process:
+ tokenizer.save_pretrained(args.output_dir)
+ api.upload_folder(
+ repo_id=repo_id,
+ folder_path=args.output_dir,
+ commit_message=f"Training in progress epoch {epoch}",
+ run_as_future=True,
+ )
+
+ if args.checkpointing_steps == "epoch":
+ output_dir = f"epoch_{epoch}"
+ if args.output_dir is not None:
+ output_dir = os.path.join(args.output_dir, output_dir)
+ accelerator.save_state(output_dir)
+
+ if args.with_tracking:
+ accelerator.end_training()
+
+ if args.output_dir is not None:
+ accelerator.wait_for_everyone()
+ unwrapped_model = accelerator.unwrap_model(model)
+ unwrapped_model.save_pretrained(
+ args.output_dir, is_main_process=accelerator.is_main_process, save_function=accelerator.save
+ )
+ if accelerator.is_main_process:
+ tokenizer.save_pretrained(args.output_dir)
+ if args.push_to_hub:
+ api.upload_folder(
+ repo_id=repo_id,
+ folder_path=args.output_dir,
+ commit_message="End of training",
+ )
+
+
+PATTERN_NUMBER = re.compile(r"-?\d+\.?\d*")
+
+
+def extract_answer_number(sentence: str) -> float:
+ sentence = sentence.replace(",", "")
+ pred = PATTERN_NUMBER.findall(sentence)
+ if not pred:
+ return float("inf")
+ segment = sentence.split("The final answer is ")
+ if len(segment) > 1:
+ pred_answer = segment[1]
+ pred_answer = PATTERN_NUMBER.findall(pred_answer)
+ if len(pred_answer) > 0:
+ pred_answer = pred_answer[0]
+ else:
+ pred_answer = float(pred[-1])
+ else:
+ pred_answer = float(pred[-1])
+
+ if isinstance(pred_answer, str):
+ try:
+ pred_answer = float(pred_answer)
+ except ValueError:
+ pred_answer = float("inf")
+ return pred_answer
+
+
+def compute_accuracy(pred: list, gold: list):
+ acc = 0.0
+ for p, g in zip(pred, gold):
+ if p == g:
+ acc += 1
+
+ return acc / len(pred)
+
+
+if __name__ == "__main__":
+ main()
diff --git a/peft/examples/lora_dreambooth/colab_notebook.ipynb b/peft/examples/lora_dreambooth/colab_notebook.ipynb
new file mode 100644
index 0000000000000000000000000000000000000000..91ac558aaf6728e2b9d0e501d99cbed0f053c3a5
--- /dev/null
+++ b/peft/examples/lora_dreambooth/colab_notebook.ipynb
@@ -0,0 +1,54 @@
+{
+ "cells": [
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "id": "kdOhtpergLCQ"
+ },
+ "outputs": [],
+ "source": [
+ "!git clone https://huggingface.co/spaces/smangrul/peft-lora-sd-dreambooth"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "id": "_LuGk9mihPx7"
+ },
+ "outputs": [],
+ "source": [
+ "%cd \"peft-lora-sd-dreambooth\"\n",
+ "!pip install -r requirements.txt"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "id": "BYKO8e5ElJOX"
+ },
+ "outputs": [],
+ "source": [
+ "!python colab.py"
+ ]
+ }
+ ],
+ "metadata": {
+ "accelerator": "GPU",
+ "colab": {
+ "provenance": []
+ },
+ "gpuClass": "premium",
+ "kernelspec": {
+ "display_name": "Python 3",
+ "name": "python3"
+ },
+ "language_info": {
+ "name": "python"
+ }
+ },
+ "nbformat": 4,
+ "nbformat_minor": 0
+}
diff --git a/peft/examples/lora_dreambooth/convert_kohya_ss_sd_lora_to_peft.py b/peft/examples/lora_dreambooth/convert_kohya_ss_sd_lora_to_peft.py
new file mode 100644
index 0000000000000000000000000000000000000000..a691ba7d053d83f64611db2763c5717d29abe7d3
--- /dev/null
+++ b/peft/examples/lora_dreambooth/convert_kohya_ss_sd_lora_to_peft.py
@@ -0,0 +1,175 @@
+import argparse
+import os
+from collections import Counter
+from dataclasses import dataclass
+from typing import Optional
+
+import safetensors
+import torch
+from diffusers import UNet2DConditionModel
+from transformers import CLIPTextModel
+
+from peft import LoraConfig, get_peft_model, get_peft_model_state_dict, set_peft_model_state_dict
+
+
+# Default kohya_ss LoRA replacement modules
+# https://github.com/kohya-ss/sd-scripts/blob/c924c47f374ac1b6e33e71f82948eb1853e2243f/networks/lora.py#L661
+UNET_TARGET_REPLACE_MODULE = ["Transformer2DModel", "Attention"]
+UNET_TARGET_REPLACE_MODULE_CONV2D_3X3 = ["ResnetBlock2D", "Downsample2D", "Upsample2D"]
+TEXT_ENCODER_TARGET_REPLACE_MODULE = ["CLIPAttention", "CLIPMLP"]
+LORA_PREFIX_UNET = "lora_unet"
+LORA_PREFIX_TEXT_ENCODER = "lora_te"
+
+
+@dataclass
+class LoRAInfo:
+ kohya_key: str
+ peft_key: str
+ alpha: Optional[float] = None
+ rank: Optional[int] = None
+ lora_A: Optional[torch.Tensor] = None
+ lora_B: Optional[torch.Tensor] = None
+
+ def peft_state_dict(self) -> dict[str, torch.Tensor]:
+ if self.lora_A is None or self.lora_B is None:
+ raise ValueError("At least one of lora_A or lora_B is None, they must both be provided")
+ return {f"{peft_key}.lora_A.weight": self.lora_A, f"{peft_key}.lora_B.weight": self.lora_A}
+
+
+def construct_peft_loraconfig(info: dict[str, LoRAInfo]) -> LoraConfig:
+ """Constructs LoraConfig from data extracted from kohya checkpoint
+
+ Args:
+ info (Dict[str, LoRAInfo]): Information extracted from kohya checkpoint
+
+ Returns:
+ LoraConfig: config for constructing LoRA
+ """
+
+ # Unpack all ranks and alphas
+ ranks = {x[0]: x[1].rank for x in info.items()}
+ alphas = {x[0]: x[1].alpha or x[1].rank for x in info.items()}
+
+ # Determine which modules needs to be transformed
+ target_modules = list(info.keys())
+
+ # Determine most common rank and alpha
+ r = Counter(ranks.values()).most_common(1)[0]
+ lora_alpha = Counter(alphas.values()).most_common(1)[0]
+
+ # Determine which modules have different rank and alpha
+ rank_pattern = dict(filter(lambda x: x[1] != r, ranks.items()))
+ alpha_pattern = dict(filter(lambda x: x[1] != lora_alpha, alphas.items()))
+
+ config = LoraConfig(
+ r=r,
+ lora_alpha=lora_alpha,
+ target_modules=target_modules,
+ lora_dropout=0.0,
+ bias="none",
+ init_lora_weights=False,
+ rank_pattern=rank_pattern,
+ alpha_pattern=alpha_pattern,
+ )
+
+ return config
+
+
+def combine_peft_state_dict(info: dict[str, LoRAInfo]) -> dict[str, torch.Tensor]:
+ result = {}
+ for key_name, key_info in info.items():
+ result[f"base_model.model.{key_name}.lora_A.weight"] = key_info.lora_A
+ result[f"base_model.model.{key_name}.lora_B.weight"] = key_info.lora_B
+ return result
+
+
+if __name__ == "__main__":
+ parser = argparse.ArgumentParser()
+
+ parser.add_argument("--sd_checkpoint", default=None, type=str, required=True, help="SD checkpoint to use")
+
+ parser.add_argument(
+ "--kohya_lora_path", default=None, type=str, required=True, help="Path to kohya_ss trained LoRA"
+ )
+
+ parser.add_argument("--dump_path", default=None, type=str, required=True, help="Path to the output model.")
+
+ parser.add_argument("--half", action="store_true", help="Save weights in half precision.")
+ args = parser.parse_args()
+
+ # Load all models that we need to add adapter to
+ text_encoder = CLIPTextModel.from_pretrained(args.sd_checkpoint, subfolder="text_encoder")
+ unet = UNet2DConditionModel.from_pretrained(args.sd_checkpoint, subfolder="unet")
+
+ # Construct possible mapping from kohya keys to peft keys
+ models_keys = {}
+ for model, model_key, model_name in [
+ (text_encoder, LORA_PREFIX_TEXT_ENCODER, "text_encoder"),
+ (unet, LORA_PREFIX_UNET, "unet"),
+ ]:
+ models_keys.update(
+ {
+ f"{model_key}.{peft_key}".replace(".", "_"): peft_key
+ for peft_key in (x[0] for x in model.named_modules())
+ }
+ )
+
+ # Store conversion info (model_type -> peft_key -> LoRAInfo)
+ lora_info: dict[str, dict[str, LoRAInfo]] = {
+ "text_encoder": {},
+ "unet": {},
+ }
+
+ # Open kohya_ss checkpoint
+ with safetensors.safe_open(args.kohya_lora_path, framework="pt", device="cpu") as f:
+ # Extract information about LoRA structure
+ metadata = f.metadata()
+
+ # Iterate through available info and unpack all the values
+ for key in f.keys():
+ kohya_key, kohya_type = key.split(".")[:2]
+
+ # Find which model this key belongs to
+ if kohya_key.startswith(LORA_PREFIX_TEXT_ENCODER):
+ model_type = "text_encoder"
+ elif kohya_key.startswith(LORA_PREFIX_UNET):
+ model_type = "unet"
+ else:
+ raise ValueError(f"Cannot determine model for key: {key}")
+
+ # Find corresponding peft key
+ if kohya_key not in models_keys:
+ raise ValueError(f"Cannot find corresponding key for diffusers/transformers model: {kohya_key}")
+ peft_key = models_keys[kohya_key]
+
+ if peft_key not in lora_info[model_type]:
+ lora_info[model_type][peft_key] = LoRAInfo(kohya_key=kohya_key, peft_key=peft_key)
+
+ if kohya_type == "alpha":
+ lora_info[model_type][peft_key].alpha = f.get_tensor(key).item()
+ elif kohya_type == "lora_down":
+ tensor = f.get_tensor(key)
+ lora_info[model_type][peft_key].lora_A = tensor
+ lora_info[model_type][peft_key].rank = tensor.shape[0]
+ elif kohya_type == "lora_up":
+ tensor = f.get_tensor(key)
+ lora_info[model_type][peft_key].lora_B = f.get_tensor(key)
+ lora_info[model_type][peft_key].rank = tensor.shape[1]
+ else:
+ raise ValueError(f"Unknown weight name in key: {key} - {kohya_type}")
+
+ # Process each model
+ for model, model_name in [(text_encoder, "text_encoder"), (unet, "unet")]:
+ config = construct_peft_loraconfig(lora_info[model_name])
+ model = get_peft_model(model, config)
+
+ keys_peft = list(get_peft_model_state_dict(model).keys())
+ keys_new = list(combine_peft_state_dict(lora_info[model_name]).keys())
+
+ set_peft_model_state_dict(model, combine_peft_state_dict(lora_info[model_name]))
+
+ if args.half:
+ model.to(torch.float16)
+
+ # Save model to disk
+ model.save_pretrained(os.path.join(args.dump_path, model_name))
diff --git a/peft/examples/lora_dreambooth/convert_peft_sd_lora_to_kohya_ss.py b/peft/examples/lora_dreambooth/convert_peft_sd_lora_to_kohya_ss.py
new file mode 100644
index 0000000000000000000000000000000000000000..97f964844ebb79546cbe5fa8dc5d15e48dd11a74
--- /dev/null
+++ b/peft/examples/lora_dreambooth/convert_peft_sd_lora_to_kohya_ss.py
@@ -0,0 +1,100 @@
+import argparse
+import os
+
+import torch
+from diffusers import UNet2DConditionModel
+from safetensors.torch import save_file
+from transformers import CLIPTextModel
+
+from peft import PeftModel, get_peft_model_state_dict
+
+
+# Default kohya_ss LoRA replacement modules
+# https://github.com/kohya-ss/sd-scripts/blob/c924c47f374ac1b6e33e71f82948eb1853e2243f/networks/lora.py#L664
+LORA_PREFIX_UNET = "lora_unet"
+LORA_PREFIX_TEXT_ENCODER = "lora_te"
+LORA_ADAPTER_NAME = "default"
+
+
+def get_module_kohya_state_dict(
+ module: PeftModel, prefix: str, dtype: torch.dtype, adapter_name: str = LORA_ADAPTER_NAME
+) -> dict[str, torch.Tensor]:
+ kohya_ss_state_dict = {}
+ for peft_key, weight in get_peft_model_state_dict(module, adapter_name=adapter_name).items():
+ kohya_key = peft_key.replace("base_model.model", prefix)
+ kohya_key = kohya_key.replace("lora_A", "lora_down")
+ kohya_key = kohya_key.replace("lora_B", "lora_up")
+ kohya_key = kohya_key.replace(".", "_", kohya_key.count(".") - 2)
+ kohya_ss_state_dict[kohya_key] = weight.to(dtype)
+
+ # Set alpha parameter
+ if "lora_down" in kohya_key:
+ alpha_key = f"{kohya_key.split('.')[0]}.alpha"
+ kohya_ss_state_dict[alpha_key] = torch.tensor(module.peft_config[adapter_name].lora_alpha).to(dtype)
+
+ return kohya_ss_state_dict
+
+
+if __name__ == "__main__":
+ parser = argparse.ArgumentParser()
+
+ parser.add_argument(
+ "--sd_checkpoint",
+ default=None,
+ type=str,
+ required=True,
+ help="Path to pretrained model or model identifier from huggingface.co/models.",
+ )
+
+ parser.add_argument(
+ "--sd_checkpoint_revision",
+ type=str,
+ default=None,
+ required=False,
+ help="Revision of pretrained model identifier from huggingface.co/models.",
+ )
+
+ parser.add_argument("--peft_lora_path", default=None, type=str, required=True, help="Path to peft trained LoRA")
+
+ parser.add_argument(
+ "--dump_path",
+ default=None,
+ type=str,
+ required=True,
+ help="Path to the output safetensors file for use with webui.",
+ )
+
+ parser.add_argument("--half", action="store_true", help="Save weights in half precision.")
+ args = parser.parse_args()
+
+ # Store kohya_ss state dict
+ kohya_ss_state_dict = {}
+ dtype = torch.float16 if args.half else torch.float32
+
+ # Load Text Encoder LoRA model
+ text_encoder_peft_lora_path = os.path.join(args.peft_lora_path, "text_encoder")
+ if os.path.exists(text_encoder_peft_lora_path):
+ text_encoder = CLIPTextModel.from_pretrained(
+ args.sd_checkpoint, subfolder="text_encoder", revision=args.sd_checkpoint_revision
+ )
+ text_encoder = PeftModel.from_pretrained(
+ text_encoder, text_encoder_peft_lora_path, adapter_name=LORA_ADAPTER_NAME
+ )
+ kohya_ss_state_dict.update(
+ get_module_kohya_state_dict(text_encoder, LORA_PREFIX_TEXT_ENCODER, dtype, LORA_ADAPTER_NAME)
+ )
+
+ # Load UNet LoRA model
+ unet_peft_lora_path = os.path.join(args.peft_lora_path, "unet")
+ if os.path.exists(unet_peft_lora_path):
+ unet = UNet2DConditionModel.from_pretrained(
+ args.sd_checkpoint, subfolder="unet", revision=args.sd_checkpoint_revision
+ )
+ unet = PeftModel.from_pretrained(unet, unet_peft_lora_path, adapter_name=LORA_ADAPTER_NAME)
+ kohya_ss_state_dict.update(get_module_kohya_state_dict(unet, LORA_PREFIX_UNET, dtype, LORA_ADAPTER_NAME))
+
+ # Save state dict
+ save_file(
+ kohya_ss_state_dict,
+ args.dump_path,
+ )
diff --git a/peft/examples/lora_dreambooth/lora_dreambooth_inference.ipynb b/peft/examples/lora_dreambooth/lora_dreambooth_inference.ipynb
new file mode 100644
index 0000000000000000000000000000000000000000..a94358c6f11927f8f3006e8e8f8cdd4a0791535d
--- /dev/null
+++ b/peft/examples/lora_dreambooth/lora_dreambooth_inference.ipynb
@@ -0,0 +1,497 @@
+{
+ "cells": [
+ {
+ "cell_type": "code",
+ "execution_count": 2,
+ "id": "acab479f",
+ "metadata": {},
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "\n",
+ "===================================BUG REPORT===================================\n",
+ "Welcome to bitsandbytes. For bug reports, please submit your error trace to: https://github.com/TimDettmers/bitsandbytes/issues\n",
+ "================================================================================\n"
+ ]
+ }
+ ],
+ "source": [
+ "import argparse\n",
+ "import gc\n",
+ "import hashlib\n",
+ "import itertools\n",
+ "import logging\n",
+ "import math\n",
+ "import os\n",
+ "import threading\n",
+ "import warnings\n",
+ "from pathlib import Path\n",
+ "from typing import Optional\n",
+ "import psutil\n",
+ "import json\n",
+ "\n",
+ "import torch\n",
+ "import torch.nn.functional as F\n",
+ "import torch.utils.checkpoint\n",
+ "from torch.utils.data import Dataset\n",
+ "\n",
+ "import datasets\n",
+ "import diffusers\n",
+ "import transformers\n",
+ "from accelerate import Accelerator\n",
+ "from accelerate.logging import get_logger\n",
+ "from accelerate.utils import set_seed\n",
+ "from diffusers import AutoencoderKL, DDPMScheduler, DiffusionPipeline, UNet2DConditionModel\n",
+ "from diffusers import DDPMScheduler, PNDMScheduler, StableDiffusionPipeline\n",
+ "from diffusers.pipelines.stable_diffusion import StableDiffusionSafetyChecker\n",
+ "from diffusers.optimization import get_scheduler\n",
+ "from diffusers.utils import check_min_version\n",
+ "from diffusers.utils.import_utils import is_xformers_available\n",
+ "from huggingface_hub import HfFolder, Repository, whoami\n",
+ "from PIL import Image\n",
+ "from torchvision import transforms\n",
+ "from tqdm.auto import tqdm\n",
+ "from transformers import AutoTokenizer, PretrainedConfig, CLIPFeatureExtractor\n",
+ "from peft import PeftModel, LoraConfig, get_peft_model_state_dict, set_peft_model_state_dict\n",
+ "\n",
+ "# Will error if the minimal version of diffusers is not installed. Remove at your own risks.\n",
+ "check_min_version(\"0.10.0.dev0\")\n",
+ "\n",
+ "logger = get_logger(__name__)\n",
+ "\n",
+ "\n",
+ "MODEL_NAME = \"CompVis/stable-diffusion-v1-4\" # \"stabilityai/stable-diffusion-2-1-base\"\n",
+ "INSTANCE_PROMPT = \"a photo of sks dog\"\n",
+ "base_path = \"/home/sourab/temp/\""
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "id": "06cfd506",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "def get_lora_sd_pipeline(\n",
+ " ckpt_dir, base_model_name_or_path=None, dtype=torch.float16, device=\"auto\", adapter_name=\"default\"\n",
+ "):\n",
+ " if device == \"auto\":\n",
+ " device = torch.accelerator.current_accelerator().type if hasattr(torch, \"accelerator\") else \"cuda\"\n",
+ "\n",
+ " unet_sub_dir = os.path.join(ckpt_dir, \"unet\")\n",
+ " text_encoder_sub_dir = os.path.join(ckpt_dir, \"text_encoder\")\n",
+ " if os.path.exists(text_encoder_sub_dir) and base_model_name_or_path is None:\n",
+ " config = LoraConfig.from_pretrained(text_encoder_sub_dir)\n",
+ " base_model_name_or_path = config.base_model_name_or_path\n",
+ "\n",
+ " if base_model_name_or_path is None:\n",
+ " raise ValueError(\"Please specify the base model name or path\")\n",
+ "\n",
+ " pipe = StableDiffusionPipeline.from_pretrained(\n",
+ " base_model_name_or_path, torch_dtype=dtype, requires_safety_checker=False\n",
+ " ).to(device)\n",
+ " pipe.unet = PeftModel.from_pretrained(pipe.unet, unet_sub_dir, adapter_name=adapter_name)\n",
+ "\n",
+ " if os.path.exists(text_encoder_sub_dir):\n",
+ " pipe.text_encoder = PeftModel.from_pretrained(\n",
+ " pipe.text_encoder, text_encoder_sub_dir, adapter_name=adapter_name\n",
+ " )\n",
+ "\n",
+ " if dtype in (torch.float16, torch.bfloat16):\n",
+ " pipe.unet.half()\n",
+ " pipe.text_encoder.half()\n",
+ "\n",
+ " pipe.to(device)\n",
+ " return pipe\n",
+ "\n",
+ "\n",
+ "def load_adapter(pipe, ckpt_dir, adapter_name):\n",
+ " unet_sub_dir = os.path.join(ckpt_dir, \"unet\")\n",
+ " text_encoder_sub_dir = os.path.join(ckpt_dir, \"text_encoder\")\n",
+ " pipe.unet.load_adapter(unet_sub_dir, adapter_name=adapter_name)\n",
+ " if os.path.exists(text_encoder_sub_dir):\n",
+ " pipe.text_encoder.load_adapter(text_encoder_sub_dir, adapter_name=adapter_name)\n",
+ "\n",
+ "\n",
+ "def set_adapter(pipe, adapter_name):\n",
+ " pipe.unet.set_adapter(adapter_name)\n",
+ " if isinstance(pipe.text_encoder, PeftModel):\n",
+ " pipe.text_encoder.set_adapter(adapter_name)\n",
+ "\n",
+ "\n",
+ "def merging_lora_with_base(pipe, ckpt_dir, adapter_name=\"default\"):\n",
+ " unet_sub_dir = os.path.join(ckpt_dir, \"unet\")\n",
+ " text_encoder_sub_dir = os.path.join(ckpt_dir, \"text_encoder\")\n",
+ " if isinstance(pipe.unet, PeftModel):\n",
+ " pipe.unet.set_adapter(adapter_name)\n",
+ " else:\n",
+ " pipe.unet = PeftModel.from_pretrained(pipe.unet, unet_sub_dir, adapter_name=adapter_name)\n",
+ " pipe.unet = pipe.unet.merge_and_unload()\n",
+ "\n",
+ " if os.path.exists(text_encoder_sub_dir):\n",
+ " if isinstance(pipe.text_encoder, PeftModel):\n",
+ " pipe.text_encoder.set_adapter(adapter_name)\n",
+ " else:\n",
+ " pipe.text_encoder = PeftModel.from_pretrained(\n",
+ " pipe.text_encoder, text_encoder_sub_dir, adapter_name=adapter_name\n",
+ " )\n",
+ " pipe.text_encoder = pipe.text_encoder.merge_and_unload()\n",
+ "\n",
+ " return pipe\n",
+ "\n",
+ "\n",
+ "def create_weighted_lora_adapter(pipe, adapters, weights, adapter_name=\"default\"):\n",
+ " pipe.unet.add_weighted_adapter(adapters, weights, adapter_name)\n",
+ " if isinstance(pipe.text_encoder, PeftModel):\n",
+ " pipe.text_encoder.add_weighted_adapter(adapters, weights, adapter_name)\n",
+ "\n",
+ " return pipe"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 4,
+ "id": "d4e888d2",
+ "metadata": {},
+ "outputs": [
+ {
+ "data": {
+ "application/vnd.jupyter.widget-view+json": {
+ "model_id": "9f12b2cca0784cba9dc14ec48de929d5",
+ "version_major": 2,
+ "version_minor": 0
+ },
+ "text/plain": [
+ "Fetching 19 files: 0%| | 0/19 [00:00"
+ ]
+ },
+ "execution_count": 8,
+ "metadata": {},
+ "output_type": "execute_result"
+ }
+ ],
+ "source": [
+ "prompt = \"sks dog playing fetch in the park\"\n",
+ "negative_prompt = \"low quality, blurry, unfinished\"\n",
+ "image = pipe(prompt, num_inference_steps=50, guidance_scale=7, negative_prompt=negative_prompt).images[0]\n",
+ "image"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 9,
+ "id": "1e1d1f30",
+ "metadata": {},
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "CPU times: user 7.74 ms, sys: 0 ns, total: 7.74 ms\n",
+ "Wall time: 7.31 ms\n"
+ ]
+ }
+ ],
+ "source": [
+ "%%time\n",
+ "set_adapter(pipe, adapter_name=\"toy\")"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 13,
+ "id": "0c50c03d",
+ "metadata": {},
+ "outputs": [
+ {
+ "data": {
+ "application/vnd.jupyter.widget-view+json": {
+ "model_id": "4f978437709b44b391744cf972415027",
+ "version_major": 2,
+ "version_minor": 0
+ },
+ "text/plain": [
+ " 0%| | 0/50 [00:00"
+ ]
+ },
+ "execution_count": 13,
+ "metadata": {},
+ "output_type": "execute_result"
+ }
+ ],
+ "source": [
+ "prompt = \"narendra modi rendered in the style of <1>\"\n",
+ "negative_prompt = \"low quality, blurry, unfinished\"\n",
+ "image = pipe(prompt, num_inference_steps=50, guidance_scale=7, negative_prompt=negative_prompt).images[0]\n",
+ "image"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 24,
+ "id": "e3b9a681",
+ "metadata": {},
+ "outputs": [
+ {
+ "data": {
+ "application/vnd.jupyter.widget-view+json": {
+ "model_id": "8871731127904802ba6123128ba22ecf",
+ "version_major": 2,
+ "version_minor": 0
+ },
+ "text/plain": [
+ " 0%| | 0/50 [00:00"
+ ]
+ },
+ "execution_count": 24,
+ "metadata": {},
+ "output_type": "execute_result"
+ }
+ ],
+ "source": [
+ "set_adapter(pipe, adapter_name=\"dog\")\n",
+ "prompt = \"sks dog in a big red bucket\"\n",
+ "negative_prompt = \"low quality, blurry, unfinished\"\n",
+ "image = pipe(prompt, num_inference_steps=50, guidance_scale=7, negative_prompt=negative_prompt).images[0]\n",
+ "image"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 15,
+ "id": "a659ca6e",
+ "metadata": {},
+ "outputs": [
+ {
+ "data": {
+ "application/vnd.jupyter.widget-view+json": {
+ "model_id": "b701336557e4417d8d39d500699c298b",
+ "version_major": 2,
+ "version_minor": 0
+ },
+ "text/plain": [
+ " 0%| | 0/50 [00:00"
+ ]
+ },
+ "execution_count": 15,
+ "metadata": {},
+ "output_type": "execute_result"
+ }
+ ],
+ "source": [
+ "set_adapter(pipe, adapter_name=\"toy\")\n",
+ "prompt = \"superman rendered in the style of <1>, close up potrait\"\n",
+ "negative_prompt = \"low quality, blurry, unfinished\"\n",
+ "image = pipe(prompt, num_inference_steps=50, guidance_scale=7, negative_prompt=negative_prompt).images[0]\n",
+ "image"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 34,
+ "id": "1f0ecb40",
+ "metadata": {},
+ "outputs": [
+ {
+ "data": {
+ "application/vnd.jupyter.widget-view+json": {
+ "model_id": "b47385e953b14c768d82bea776129904",
+ "version_major": 2,
+ "version_minor": 0
+ },
+ "text/plain": [
+ " 0%| | 0/50 [00:00"
+ ]
+ },
+ "execution_count": 34,
+ "metadata": {},
+ "output_type": "execute_result"
+ }
+ ],
+ "source": [
+ "set_adapter(pipe, adapter_name=\"toy_dog\")\n",
+ "prompt = \"sks dog rendered in the style of <1>, close up potrait, 4K HD\"\n",
+ "negative_prompt = \"low quality, blurry, unfinished\"\n",
+ "image = pipe(prompt, num_inference_steps=50, guidance_scale=7, negative_prompt=negative_prompt).images[0]\n",
+ "image"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "id": "29720cdb",
+ "metadata": {},
+ "outputs": [],
+ "source": []
+ }
+ ],
+ "metadata": {
+ "kernelspec": {
+ "display_name": "Python 3 (ipykernel)",
+ "language": "python",
+ "name": "python3"
+ },
+ "language_info": {
+ "codemirror_mode": {
+ "name": "ipython",
+ "version": 3
+ },
+ "file_extension": ".py",
+ "mimetype": "text/x-python",
+ "name": "python",
+ "nbconvert_exporter": "python",
+ "pygments_lexer": "ipython3",
+ "version": "3.10.4"
+ },
+ "vscode": {
+ "interpreter": {
+ "hash": "aee8b7b246df8f9039afb4144a1f6fd8d2ca17a180786b69acc140d282b71a49"
+ }
+ }
+ },
+ "nbformat": 4,
+ "nbformat_minor": 5
+}
diff --git a/peft/examples/lora_dreambooth/requirements.txt b/peft/examples/lora_dreambooth/requirements.txt
new file mode 100644
index 0000000000000000000000000000000000000000..ec1a3dcd9922d0a01cb636f5cd0c57f6aac5b3d3
--- /dev/null
+++ b/peft/examples/lora_dreambooth/requirements.txt
@@ -0,0 +1,11 @@
+transformers
+accelerate
+evaluate
+tqdm
+datasets
+diffusers
+Pillow
+torchvision
+huggingface_hub
+safetensors
+wandb
\ No newline at end of file
diff --git a/peft/examples/lora_dreambooth/train_dreambooth.py b/peft/examples/lora_dreambooth/train_dreambooth.py
new file mode 100644
index 0000000000000000000000000000000000000000..2bbc39cc758701e9eeac77061034e7e0417c915e
--- /dev/null
+++ b/peft/examples/lora_dreambooth/train_dreambooth.py
@@ -0,0 +1,1107 @@
+import argparse
+import gc
+import hashlib
+import itertools
+import logging
+import math
+import os
+import threading
+import warnings
+from contextlib import nullcontext
+from pathlib import Path
+
+import datasets
+import diffusers
+import numpy as np
+import psutil
+import torch
+import torch.nn.functional as F
+import torch.utils.checkpoint
+import transformers
+from accelerate import Accelerator
+from accelerate.logging import get_logger
+from accelerate.utils import set_seed
+from diffusers import (
+ AutoencoderKL,
+ DDPMScheduler,
+ DiffusionPipeline,
+ DPMSolverMultistepScheduler,
+ UNet2DConditionModel,
+)
+from diffusers.optimization import get_scheduler
+from diffusers.utils import check_min_version
+from diffusers.utils.import_utils import is_xformers_available
+from huggingface_hub import HfApi
+from PIL import Image
+from torch.utils.data import Dataset
+from torchvision import transforms
+from tqdm.auto import tqdm
+from transformers import AutoTokenizer, PretrainedConfig
+
+from peft import LoraConfig, get_peft_model
+
+
+# Will error if the minimal version of diffusers is not installed. Remove at your own risks.
+check_min_version("0.10.0.dev0")
+
+logger = get_logger(__name__)
+
+UNET_TARGET_MODULES = ["to_q", "to_v", "query", "value"] # , "ff.net.0.proj"]
+TEXT_ENCODER_TARGET_MODULES = ["q_proj", "v_proj"]
+
+
+def import_model_class_from_model_name_or_path(pretrained_model_name_or_path: str, revision: str):
+ text_encoder_config = PretrainedConfig.from_pretrained(
+ pretrained_model_name_or_path,
+ subfolder="text_encoder",
+ revision=revision,
+ )
+ model_class = text_encoder_config.architectures[0]
+
+ if model_class == "CLIPTextModel":
+ from transformers import CLIPTextModel
+
+ return CLIPTextModel
+ elif model_class == "RobertaSeriesModelWithTransformation":
+ from diffusers.pipelines.alt_diffusion.modeling_roberta_series import RobertaSeriesModelWithTransformation
+
+ return RobertaSeriesModelWithTransformation
+ else:
+ raise ValueError(f"{model_class} is not supported.")
+
+
+def parse_args(input_args=None):
+ parser = argparse.ArgumentParser(description="Simple example of a training script.")
+ parser.add_argument(
+ "--pretrained_model_name_or_path",
+ type=str,
+ default=None,
+ required=True,
+ help="Path to pretrained model or model identifier from huggingface.co/models.",
+ )
+ parser.add_argument(
+ "--revision",
+ type=str,
+ default=None,
+ required=False,
+ help="Revision of pretrained model identifier from huggingface.co/models.",
+ )
+ parser.add_argument(
+ "--tokenizer_name",
+ type=str,
+ default=None,
+ help="Pretrained tokenizer name or path if not the same as model_name",
+ )
+ parser.add_argument(
+ "--instance_data_dir",
+ type=str,
+ default=None,
+ required=True,
+ help="A folder containing the training data of instance images.",
+ )
+ parser.add_argument(
+ "--class_data_dir",
+ type=str,
+ default=None,
+ required=False,
+ help="A folder containing the training data of class images.",
+ )
+ parser.add_argument(
+ "--instance_prompt",
+ type=str,
+ default=None,
+ required=True,
+ help="The prompt with identifier specifying the instance",
+ )
+ parser.add_argument(
+ "--class_prompt",
+ type=str,
+ default=None,
+ help="The prompt to specify images in the same class as provided instance images.",
+ )
+ parser.add_argument(
+ "--with_prior_preservation",
+ default=False,
+ action="store_true",
+ help="Flag to add prior preservation loss.",
+ )
+ parser.add_argument("--prior_loss_weight", type=float, default=1.0, help="The weight of prior preservation loss.")
+ parser.add_argument(
+ "--num_class_images",
+ type=int,
+ default=100,
+ help=(
+ "Minimal class images for prior preservation loss. If there are not enough images already present in"
+ " class_data_dir, additional images will be sampled with class_prompt."
+ ),
+ )
+ parser.add_argument(
+ "--validation_prompt",
+ type=str,
+ default=None,
+ help="A prompt that is used during validation to verify that the model is learning.",
+ )
+ parser.add_argument(
+ "--num_validation_images",
+ type=int,
+ default=4,
+ help="Number of images that should be generated during validation with `validation_prompt`.",
+ )
+ parser.add_argument(
+ "--validation_steps",
+ type=int,
+ default=100,
+ help=(
+ "Run dreambooth validation every X steps. Dreambooth validation consists of running the prompt"
+ " `args.validation_prompt` multiple times: `args.num_validation_images`."
+ ),
+ )
+ parser.add_argument(
+ "--output_dir",
+ type=str,
+ default="text-inversion-model",
+ help="The output directory where the model predictions and checkpoints will be written.",
+ )
+ parser.add_argument("--seed", type=int, default=None, help="A seed for reproducible training.")
+ parser.add_argument(
+ "--resolution",
+ type=int,
+ default=512,
+ help=(
+ "The resolution for input images, all the images in the train/validation dataset will be resized to this"
+ " resolution"
+ ),
+ )
+ parser.add_argument(
+ "--center_crop", action="store_true", help="Whether to center crop images before resizing to resolution"
+ )
+ parser.add_argument("--train_text_encoder", action="store_true", help="Whether to train the text encoder")
+
+ # lora args
+ parser.add_argument("--use_lora", action="store_true", help="Whether to use Lora for parameter efficient tuning")
+ parser.add_argument("--lora_r", type=int, default=8, help="Lora rank, only used if use_lora is True")
+ parser.add_argument("--lora_alpha", type=int, default=32, help="Lora alpha, only used if use_lora is True")
+ parser.add_argument("--lora_dropout", type=float, default=0.0, help="Lora dropout, only used if use_lora is True")
+ parser.add_argument(
+ "--lora_bias",
+ type=str,
+ default="none",
+ help="Bias type for Lora. Can be 'none', 'all' or 'lora_only', only used if use_lora is True",
+ )
+ parser.add_argument(
+ "--lora_text_encoder_r",
+ type=int,
+ default=8,
+ help="Lora rank for text encoder, only used if `use_lora` and `train_text_encoder` are True",
+ )
+ parser.add_argument(
+ "--lora_text_encoder_alpha",
+ type=int,
+ default=32,
+ help="Lora alpha for text encoder, only used if `use_lora` and `train_text_encoder` are True",
+ )
+ parser.add_argument(
+ "--lora_text_encoder_dropout",
+ type=float,
+ default=0.0,
+ help="Lora dropout for text encoder, only used if `use_lora` and `train_text_encoder` are True",
+ )
+ parser.add_argument(
+ "--lora_text_encoder_bias",
+ type=str,
+ default="none",
+ help="Bias type for Lora. Can be 'none', 'all' or 'lora_only', only used if use_lora and `train_text_encoder` are True",
+ )
+
+ parser.add_argument(
+ "--num_dataloader_workers", type=int, default=1, help="Num of workers for the training dataloader."
+ )
+
+ parser.add_argument(
+ "--no_tracemalloc",
+ default=False,
+ action="store_true",
+ help="Flag to stop memory allocation tracing during training. This could speed up training on Windows.",
+ )
+
+ parser.add_argument(
+ "--train_batch_size", type=int, default=4, help="Batch size (per device) for the training dataloader."
+ )
+ parser.add_argument(
+ "--sample_batch_size", type=int, default=4, help="Batch size (per device) for sampling images."
+ )
+ parser.add_argument("--num_train_epochs", type=int, default=1)
+ parser.add_argument(
+ "--max_train_steps",
+ type=int,
+ default=None,
+ help="Total number of training steps to perform. If provided, overrides num_train_epochs.",
+ )
+ parser.add_argument(
+ "--checkpointing_steps",
+ type=int,
+ default=500,
+ help=(
+ "Save a checkpoint of the training state every X updates. These checkpoints can be used both as final"
+ " checkpoints in case they are better than the last checkpoint, and are also suitable for resuming"
+ " training using `--resume_from_checkpoint`."
+ ),
+ )
+ parser.add_argument(
+ "--resume_from_checkpoint",
+ type=str,
+ default=None,
+ help=(
+ "Whether training should be resumed from a previous checkpoint. Use a path saved by"
+ ' `--checkpointing_steps`, or `"latest"` to automatically select the last available checkpoint.'
+ ),
+ )
+ parser.add_argument(
+ "--gradient_accumulation_steps",
+ type=int,
+ default=1,
+ help="Number of updates steps to accumulate before performing a backward/update pass.",
+ )
+ parser.add_argument(
+ "--gradient_checkpointing",
+ action="store_true",
+ help="Whether or not to use gradient checkpointing to save memory at the expense of slower backward pass.",
+ )
+ parser.add_argument(
+ "--learning_rate",
+ type=float,
+ default=5e-6,
+ help="Initial learning rate (after the potential warmup period) to use.",
+ )
+ parser.add_argument(
+ "--scale_lr",
+ action="store_true",
+ default=False,
+ help="Scale the learning rate by the number of accelerators, gradient accumulation steps, and batch size.",
+ )
+ parser.add_argument(
+ "--lr_scheduler",
+ type=str,
+ default="constant",
+ help=(
+ 'The scheduler type to use. Choose between ["linear", "cosine", "cosine_with_restarts", "polynomial",'
+ ' "constant", "constant_with_warmup"]'
+ ),
+ )
+ parser.add_argument(
+ "--lr_warmup_steps", type=int, default=500, help="Number of steps for the warmup in the lr scheduler."
+ )
+ parser.add_argument(
+ "--lr_num_cycles",
+ type=int,
+ default=1,
+ help="Number of hard resets of the lr in cosine_with_restarts scheduler.",
+ )
+ parser.add_argument("--lr_power", type=float, default=1.0, help="Power factor of the polynomial scheduler.")
+ parser.add_argument(
+ "--use_8bit_adam", action="store_true", help="Whether or not to use 8-bit Adam from bitsandbytes."
+ )
+ parser.add_argument("--adam_beta1", type=float, default=0.9, help="The beta1 parameter for the Adam optimizer.")
+ parser.add_argument("--adam_beta2", type=float, default=0.999, help="The beta2 parameter for the Adam optimizer.")
+ parser.add_argument("--adam_weight_decay", type=float, default=1e-2, help="Weight decay to use.")
+ parser.add_argument("--adam_epsilon", type=float, default=1e-08, help="Epsilon value for the Adam optimizer")
+ parser.add_argument("--max_grad_norm", default=1.0, type=float, help="Max gradient norm.")
+ parser.add_argument("--push_to_hub", action="store_true", help="Whether or not to push the model to the Hub.")
+ parser.add_argument("--hub_token", type=str, default=None, help="The token to use to push to the Model Hub.")
+ parser.add_argument(
+ "--hub_model_id",
+ type=str,
+ default=None,
+ help="The name of the repository to keep in sync with the local `output_dir`.",
+ )
+ parser.add_argument(
+ "--logging_dir",
+ type=str,
+ default="logs",
+ help=(
+ "[TensorBoard](https://www.tensorflow.org/tensorboard) log directory. Will default to"
+ " *output_dir/runs/**CURRENT_DATETIME_HOSTNAME***."
+ ),
+ )
+ parser.add_argument(
+ "--allow_tf32",
+ action="store_true",
+ help=(
+ "Whether or not to allow TF32 on Ampere GPUs. Can be used to speed up training. For more information, see"
+ " https://pytorch.org/docs/stable/notes/cuda.html#tensorfloat-32-tf32-on-ampere-devices"
+ ),
+ )
+ parser.add_argument(
+ "--report_to",
+ type=str,
+ default="tensorboard",
+ help=(
+ 'The integration to report the results and logs to. Supported platforms are `"tensorboard"`'
+ ' (default), `"wandb"` and `"comet_ml"`. Use `"all"` to report to all integrations.'
+ ),
+ )
+ parser.add_argument(
+ "--wandb_key",
+ type=str,
+ default=None,
+ help=("If report to option is set to wandb, api-key for wandb used for login to wandb "),
+ )
+ parser.add_argument(
+ "--wandb_project_name",
+ type=str,
+ default=None,
+ help=("If report to option is set to wandb, project name in wandb for log tracking "),
+ )
+ parser.add_argument(
+ "--mixed_precision",
+ type=str,
+ default=None,
+ choices=["no", "fp16", "bf16"],
+ help=(
+ "Whether to use mixed precision. Choose between fp16 and bf16 (bfloat16). Bf16 requires PyTorch >="
+ " 1.10.and an Nvidia Ampere GPU or Intel XPU. Default to the value of accelerate config of the current system or the"
+ " flag passed with the `accelerate.launch` command. Use this argument to override the accelerate config."
+ ),
+ )
+ parser.add_argument(
+ "--prior_generation_precision",
+ type=str,
+ default=None,
+ choices=["no", "fp32", "fp16", "bf16"],
+ help=(
+ "Choose prior generation precision between fp32, fp16 and bf16 (bfloat16). Bf16 requires PyTorch >="
+ " 1.10.and an Nvidia Ampere GPU or Intel XPU. Default to fp16 if a GPU is available else fp32."
+ ),
+ )
+ parser.add_argument("--local_rank", type=int, default=-1, help="For distributed training: local_rank")
+ parser.add_argument(
+ "--enable_xformers_memory_efficient_attention", action="store_true", help="Whether or not to use xformers."
+ )
+
+ if input_args is not None:
+ args = parser.parse_args(input_args)
+ else:
+ args = parser.parse_args()
+
+ env_local_rank = int(os.environ.get("LOCAL_RANK", -1))
+ if env_local_rank != -1 and env_local_rank != args.local_rank:
+ args.local_rank = env_local_rank
+
+ if args.with_prior_preservation:
+ if args.class_data_dir is None:
+ raise ValueError("You must specify a data directory for class images.")
+ if args.class_prompt is None:
+ raise ValueError("You must specify prompt for class images.")
+ else:
+ # logger is not available yet
+ if args.class_data_dir is not None:
+ warnings.warn("You need not use --class_data_dir without --with_prior_preservation.")
+ if args.class_prompt is not None:
+ warnings.warn("You need not use --class_prompt without --with_prior_preservation.")
+
+ return args
+
+
+# Converting Bytes to Megabytes
+def b2mb(x):
+ return int(x / 2**20)
+
+
+# This context manager is used to track the peak memory usage of the process
+class TorchTracemalloc:
+ def __enter__(self):
+ gc.collect()
+ self.device_type = torch.accelerator.current_accelerator().type if hasattr(torch, "accelerator") else "cuda"
+ self.device_module = getattr(torch, self.device_type, torch.cuda)
+ self.device_module.empty_cache()
+ self.device_module.reset_peak_memory_stats() # reset the peak gauge to zero
+ self.begin = self.device_module.memory_allocated()
+ self.process = psutil.Process()
+
+ self.cpu_begin = self.cpu_mem_used()
+ self.peak_monitoring = True
+ peak_monitor_thread = threading.Thread(target=self.peak_monitor_func)
+ peak_monitor_thread.daemon = True
+ peak_monitor_thread.start()
+ return self
+
+ def cpu_mem_used(self):
+ """get resident set size memory for the current process"""
+ return self.process.memory_info().rss
+
+ def peak_monitor_func(self):
+ self.cpu_peak = -1
+
+ while True:
+ self.cpu_peak = max(self.cpu_mem_used(), self.cpu_peak)
+
+ # can't sleep or will not catch the peak right (this comment is here on purpose)
+ # time.sleep(0.001) # 1msec
+
+ if not self.peak_monitoring:
+ break
+
+ def __exit__(self, *exc):
+ self.peak_monitoring = False
+
+ gc.collect()
+ self.device_module.empty_cache()
+ self.end = self.device_module.memory_allocated()
+ self.peak = self.device_module.max_memory_allocated()
+ self.used = b2mb(self.end - self.begin)
+ self.peaked = b2mb(self.peak - self.begin)
+
+ self.cpu_end = self.cpu_mem_used()
+ self.cpu_used = b2mb(self.cpu_end - self.cpu_begin)
+ self.cpu_peaked = b2mb(self.cpu_peak - self.cpu_begin)
+ # print(f"delta used/peak {self.used:4d}/{self.peaked:4d}")
+
+
+class DreamBoothDataset(Dataset):
+ """
+ A dataset to prepare the instance and class images with the prompts for fine-tuning the model.
+ It pre-processes the images and the tokenizes prompts.
+ """
+
+ def __init__(
+ self,
+ instance_data_root,
+ instance_prompt,
+ tokenizer,
+ class_data_root=None,
+ class_prompt=None,
+ size=512,
+ center_crop=False,
+ ):
+ self.size = size
+ self.center_crop = center_crop
+ self.tokenizer = tokenizer
+
+ self.instance_data_root = Path(instance_data_root)
+ if not self.instance_data_root.exists():
+ raise ValueError("Instance images root doesn't exists.")
+
+ self.instance_images_path = list(Path(instance_data_root).iterdir())
+ self.num_instance_images = len(self.instance_images_path)
+ self.instance_prompt = instance_prompt
+ self._length = self.num_instance_images
+
+ if class_data_root is not None:
+ self.class_data_root = Path(class_data_root)
+ self.class_data_root.mkdir(parents=True, exist_ok=True)
+ self.class_images_path = list(self.class_data_root.iterdir())
+ self.num_class_images = len(self.class_images_path)
+ self._length = max(self.num_class_images, self.num_instance_images)
+ self.class_prompt = class_prompt
+ else:
+ self.class_data_root = None
+
+ self.image_transforms = transforms.Compose(
+ [
+ transforms.Resize(size, interpolation=transforms.InterpolationMode.BILINEAR),
+ transforms.CenterCrop(size) if center_crop else transforms.RandomCrop(size),
+ transforms.ToTensor(),
+ transforms.Normalize([0.5], [0.5]),
+ ]
+ )
+
+ def __len__(self):
+ return self._length
+
+ def __getitem__(self, index):
+ example = {}
+ instance_image = Image.open(self.instance_images_path[index % self.num_instance_images])
+ if not instance_image.mode == "RGB":
+ instance_image = instance_image.convert("RGB")
+ example["instance_images"] = self.image_transforms(instance_image)
+ example["instance_prompt_ids"] = self.tokenizer(
+ self.instance_prompt,
+ truncation=True,
+ padding="max_length",
+ max_length=self.tokenizer.model_max_length,
+ return_tensors="pt",
+ ).input_ids
+
+ if self.class_data_root:
+ class_image = Image.open(self.class_images_path[index % self.num_class_images])
+ if not class_image.mode == "RGB":
+ class_image = class_image.convert("RGB")
+ example["class_images"] = self.image_transforms(class_image)
+ example["class_prompt_ids"] = self.tokenizer(
+ self.class_prompt,
+ truncation=True,
+ padding="max_length",
+ max_length=self.tokenizer.model_max_length,
+ return_tensors="pt",
+ ).input_ids
+
+ return example
+
+
+def collate_fn(examples, with_prior_preservation=False):
+ input_ids = [example["instance_prompt_ids"] for example in examples]
+ pixel_values = [example["instance_images"] for example in examples]
+
+ # Concat class and instance examples for prior preservation.
+ # We do this to avoid doing two forward passes.
+ if with_prior_preservation:
+ input_ids += [example["class_prompt_ids"] for example in examples]
+ pixel_values += [example["class_images"] for example in examples]
+
+ pixel_values = torch.stack(pixel_values)
+ pixel_values = pixel_values.to(memory_format=torch.contiguous_format).float()
+
+ input_ids = torch.cat(input_ids, dim=0)
+
+ batch = {
+ "input_ids": input_ids,
+ "pixel_values": pixel_values,
+ }
+ return batch
+
+
+class PromptDataset(Dataset):
+ "A simple dataset to prepare the prompts to generate class images on multiple accelerators."
+
+ def __init__(self, prompt, num_samples):
+ self.prompt = prompt
+ self.num_samples = num_samples
+
+ def __len__(self):
+ return self.num_samples
+
+ def __getitem__(self, index):
+ example = {}
+ example["prompt"] = self.prompt
+ example["index"] = index
+ return example
+
+
+def main(args):
+ logging_dir = Path(args.output_dir, args.logging_dir)
+
+ accelerator = Accelerator(
+ gradient_accumulation_steps=args.gradient_accumulation_steps,
+ mixed_precision=args.mixed_precision,
+ log_with=args.report_to,
+ project_dir=logging_dir,
+ )
+ if args.report_to == "wandb":
+ import wandb
+
+ wandb.login(key=args.wandb_key)
+ wandb.init(project=args.wandb_project_name)
+ # Currently, it's not possible to do gradient accumulation when training two models with accelerate.accumulate
+ # This will be enabled soon in accelerate. For now, we don't allow gradient accumulation when training two models.
+ # TODO (patil-suraj): Remove this check when gradient accumulation with two models is enabled in accelerate.
+ if args.train_text_encoder and args.gradient_accumulation_steps > 1 and accelerator.num_processes > 1:
+ raise ValueError(
+ "Gradient accumulation is not supported when training the text encoder in distributed training. "
+ "Please set gradient_accumulation_steps to 1. This feature will be supported in the future."
+ )
+
+ # Make one log on every process with the configuration for debugging.
+ logging.basicConfig(
+ format="%(asctime)s - %(levelname)s - %(name)s - %(message)s",
+ datefmt="%m/%d/%Y %H:%M:%S",
+ level=logging.INFO,
+ )
+ logger.info(accelerator.state, main_process_only=False)
+ if accelerator.is_local_main_process:
+ datasets.utils.logging.set_verbosity_warning()
+ transformers.utils.logging.set_verbosity_warning()
+ diffusers.utils.logging.set_verbosity_info()
+ else:
+ datasets.utils.logging.set_verbosity_error()
+ transformers.utils.logging.set_verbosity_error()
+ diffusers.utils.logging.set_verbosity_error()
+
+ # If passed along, set the training seed now.
+ if args.seed is not None:
+ set_seed(args.seed)
+
+ # Generate class images if prior preservation is enabled.
+ if args.with_prior_preservation:
+ class_images_dir = Path(args.class_data_dir)
+ if not class_images_dir.exists():
+ class_images_dir.mkdir(parents=True)
+ cur_class_images = len(list(class_images_dir.iterdir()))
+
+ if cur_class_images < args.num_class_images:
+ torch_dtype = torch.float16 if accelerator.device.type in ["cuda", "xpu"] else torch.float32
+ if args.prior_generation_precision == "fp32":
+ torch_dtype = torch.float32
+ elif args.prior_generation_precision == "fp16":
+ torch_dtype = torch.float16
+ elif args.prior_generation_precision == "bf16":
+ torch_dtype = torch.bfloat16
+ pipeline = DiffusionPipeline.from_pretrained(
+ args.pretrained_model_name_or_path,
+ torch_dtype=torch_dtype,
+ safety_checker=None,
+ revision=args.revision,
+ )
+ pipeline.set_progress_bar_config(disable=True)
+
+ num_new_images = args.num_class_images - cur_class_images
+ logger.info(f"Number of class images to sample: {num_new_images}.")
+
+ sample_dataset = PromptDataset(args.class_prompt, num_new_images)
+ sample_dataloader = torch.utils.data.DataLoader(sample_dataset, batch_size=args.sample_batch_size)
+
+ sample_dataloader = accelerator.prepare(sample_dataloader)
+ pipeline.to(accelerator.device)
+
+ for example in tqdm(
+ sample_dataloader, desc="Generating class images", disable=not accelerator.is_local_main_process
+ ):
+ images = pipeline(example["prompt"]).images
+
+ for i, image in enumerate(images):
+ hash_image = hashlib.sha1(image.tobytes()).hexdigest()
+ image_filename = class_images_dir / f"{example['index'][i] + cur_class_images}-{hash_image}.jpg"
+ image.save(image_filename)
+
+ del pipeline
+ if torch.cuda.is_available():
+ torch.cuda.empty_cache()
+ elif torch.xpu.is_available():
+ torch.xpu.empty_cache()
+
+ # Handle the repository creation
+ if accelerator.is_main_process:
+ if args.push_to_hub:
+ api = HfApi(token=args.hub_token)
+
+ # Create repo (repo_name from args or inferred)
+ repo_name = args.hub_model_id
+ if repo_name is None:
+ repo_name = Path(args.output_dir).absolute().name
+ repo_id = api.create_repo(repo_name, exist_ok=True).repo_id
+
+ with open(os.path.join(args.output_dir, ".gitignore"), "w+") as gitignore:
+ if "step_*" not in gitignore:
+ gitignore.write("step_*\n")
+ if "epoch_*" not in gitignore:
+ gitignore.write("epoch_*\n")
+ elif args.output_dir is not None:
+ os.makedirs(args.output_dir, exist_ok=True)
+
+ # Load the tokenizer
+ if args.tokenizer_name:
+ tokenizer = AutoTokenizer.from_pretrained(args.tokenizer_name, revision=args.revision, use_fast=False)
+ elif args.pretrained_model_name_or_path:
+ tokenizer = AutoTokenizer.from_pretrained(
+ args.pretrained_model_name_or_path,
+ subfolder="tokenizer",
+ revision=args.revision,
+ use_fast=False,
+ )
+
+ # import correct text encoder class
+ text_encoder_cls = import_model_class_from_model_name_or_path(args.pretrained_model_name_or_path, args.revision)
+
+ # Load scheduler and models
+ noise_scheduler = DDPMScheduler(
+ beta_start=0.00085,
+ beta_end=0.012,
+ beta_schedule="scaled_linear",
+ num_train_timesteps=1000,
+ ) # DDPMScheduler.from_pretrained(args.pretrained_model_name_or_path, subfolder="scheduler")
+ text_encoder = text_encoder_cls.from_pretrained(
+ args.pretrained_model_name_or_path, subfolder="text_encoder", revision=args.revision
+ )
+ vae = AutoencoderKL.from_pretrained(args.pretrained_model_name_or_path, subfolder="vae", revision=args.revision)
+ unet = UNet2DConditionModel.from_pretrained(
+ args.pretrained_model_name_or_path, subfolder="unet", revision=args.revision
+ )
+
+ if args.use_lora:
+ config = LoraConfig(
+ r=args.lora_r,
+ lora_alpha=args.lora_alpha,
+ target_modules=UNET_TARGET_MODULES,
+ lora_dropout=args.lora_dropout,
+ bias=args.lora_bias,
+ )
+ unet = get_peft_model(unet, config)
+ unet.print_trainable_parameters()
+ print(unet)
+
+ vae.requires_grad_(False)
+ if not args.train_text_encoder:
+ text_encoder.requires_grad_(False)
+ elif args.train_text_encoder and args.use_lora:
+ config = LoraConfig(
+ r=args.lora_text_encoder_r,
+ lora_alpha=args.lora_text_encoder_alpha,
+ target_modules=TEXT_ENCODER_TARGET_MODULES,
+ lora_dropout=args.lora_text_encoder_dropout,
+ bias=args.lora_text_encoder_bias,
+ )
+ text_encoder = get_peft_model(text_encoder, config)
+ text_encoder.print_trainable_parameters()
+ print(text_encoder)
+
+ if args.enable_xformers_memory_efficient_attention:
+ if accelerator.device.type == "xpu":
+ logger.warn("XPU hasn't support xformers yet, ignore it.")
+ elif is_xformers_available():
+ unet.enable_xformers_memory_efficient_attention()
+ else:
+ raise ValueError("xformers is not available. Make sure it is installed correctly")
+
+ if args.gradient_checkpointing:
+ unet.enable_gradient_checkpointing()
+ # below fails when using lora so commenting it out
+ if args.train_text_encoder and not args.use_lora:
+ text_encoder.gradient_checkpointing_enable()
+
+ # Enable TF32 for faster training on Ampere GPUs,
+ # cf https://pytorch.org/docs/stable/notes/cuda.html#tensorfloat-32-tf32-on-ampere-devices
+ if args.allow_tf32 and torch.cuda.is_available():
+ torch.backends.cuda.matmul.allow_tf32 = True
+
+ if args.scale_lr:
+ args.learning_rate = (
+ args.learning_rate * args.gradient_accumulation_steps * args.train_batch_size * accelerator.num_processes
+ )
+
+ # Use 8-bit Adam for lower memory usage or to fine-tune the model in 16GB accelerators
+ if args.use_8bit_adam:
+ try:
+ import bitsandbytes as bnb
+ except ImportError:
+ raise ImportError(
+ "To use 8-bit Adam, please install the bitsandbytes library: `pip install bitsandbytes`."
+ )
+
+ optimizer_class = bnb.optim.AdamW8bit
+ else:
+ optimizer_class = torch.optim.AdamW
+
+ # Optimizer creation
+ params_to_optimize = (
+ itertools.chain(unet.parameters(), text_encoder.parameters()) if args.train_text_encoder else unet.parameters()
+ )
+ optimizer = optimizer_class(
+ params_to_optimize,
+ lr=args.learning_rate,
+ betas=(args.adam_beta1, args.adam_beta2),
+ weight_decay=args.adam_weight_decay,
+ eps=args.adam_epsilon,
+ )
+
+ # Dataset and DataLoaders creation:
+ train_dataset = DreamBoothDataset(
+ instance_data_root=args.instance_data_dir,
+ instance_prompt=args.instance_prompt,
+ class_data_root=args.class_data_dir if args.with_prior_preservation else None,
+ class_prompt=args.class_prompt,
+ tokenizer=tokenizer,
+ size=args.resolution,
+ center_crop=args.center_crop,
+ )
+
+ train_dataloader = torch.utils.data.DataLoader(
+ train_dataset,
+ batch_size=args.train_batch_size,
+ shuffle=True,
+ collate_fn=lambda examples: collate_fn(examples, args.with_prior_preservation),
+ num_workers=args.num_dataloader_workers,
+ )
+
+ # Scheduler and math around the number of training steps.
+ overrode_max_train_steps = False
+ num_update_steps_per_epoch = math.ceil(len(train_dataloader) / args.gradient_accumulation_steps)
+ if args.max_train_steps is None:
+ args.max_train_steps = args.num_train_epochs * num_update_steps_per_epoch
+ overrode_max_train_steps = True
+
+ lr_scheduler = get_scheduler(
+ args.lr_scheduler,
+ optimizer=optimizer,
+ num_warmup_steps=args.lr_warmup_steps * args.gradient_accumulation_steps,
+ num_training_steps=args.max_train_steps * args.gradient_accumulation_steps,
+ num_cycles=args.lr_num_cycles,
+ power=args.lr_power,
+ )
+
+ # Prepare everything with our `accelerator`.
+ if args.train_text_encoder:
+ unet, text_encoder, optimizer, train_dataloader, lr_scheduler = accelerator.prepare(
+ unet, text_encoder, optimizer, train_dataloader, lr_scheduler
+ )
+ else:
+ unet, optimizer, train_dataloader, lr_scheduler = accelerator.prepare(
+ unet, optimizer, train_dataloader, lr_scheduler
+ )
+
+ # For mixed precision training we cast the text_encoder and vae weights to half-precision
+ # as these models are only used for inference, keeping weights in full precision is not required.
+ weight_dtype = torch.float32
+ if accelerator.mixed_precision == "fp16":
+ weight_dtype = torch.float16
+ elif accelerator.mixed_precision == "bf16":
+ weight_dtype = torch.bfloat16
+
+ # Move vae and text_encoder to device and cast to weight_dtype
+ vae.to(accelerator.device, dtype=weight_dtype)
+ if not args.train_text_encoder:
+ text_encoder.to(accelerator.device, dtype=weight_dtype)
+
+ # We need to recalculate our total training steps as the size of the training dataloader may have changed.
+ num_update_steps_per_epoch = math.ceil(len(train_dataloader) / args.gradient_accumulation_steps)
+ if overrode_max_train_steps:
+ args.max_train_steps = args.num_train_epochs * num_update_steps_per_epoch
+ # Afterwards we recalculate our number of training epochs
+ args.num_train_epochs = math.ceil(args.max_train_steps / num_update_steps_per_epoch)
+
+ # We need to initialize the trackers we use, and also store our configuration.
+ # The trackers initializes automatically on the main process.
+ if accelerator.is_main_process:
+ accelerator.init_trackers("dreambooth", config=vars(args))
+
+ # Train!
+ total_batch_size = args.train_batch_size * accelerator.num_processes * args.gradient_accumulation_steps
+
+ logger.info("***** Running training *****")
+ logger.info(f" Num examples = {len(train_dataset)}")
+ logger.info(f" Num batches each epoch = {len(train_dataloader)}")
+ logger.info(f" Num Epochs = {args.num_train_epochs}")
+ logger.info(f" Instantaneous batch size per device = {args.train_batch_size}")
+ logger.info(f" Total train batch size (w. parallel, distributed & accumulation) = {total_batch_size}")
+ logger.info(f" Gradient Accumulation steps = {args.gradient_accumulation_steps}")
+ logger.info(f" Total optimization steps = {args.max_train_steps}")
+ global_step = 0
+ first_epoch = 0
+
+ # Potentially load in the weights and states from a previous save
+ if args.resume_from_checkpoint:
+ if args.resume_from_checkpoint != "latest":
+ path = os.path.basename(args.resume_from_checkpoint)
+ else:
+ # Get the mos recent checkpoint
+ dirs = os.listdir(args.output_dir)
+ dirs = [d for d in dirs if d.startswith("checkpoint")]
+ dirs = sorted(dirs, key=lambda x: int(x.split("-")[1]))
+ path = dirs[-1]
+ accelerator.print(f"Resuming from checkpoint {path}")
+ accelerator.load_state(os.path.join(args.output_dir, path))
+ global_step = int(path.split("-")[1])
+
+ resume_global_step = global_step * args.gradient_accumulation_steps
+ first_epoch = resume_global_step // num_update_steps_per_epoch
+ resume_step = resume_global_step % num_update_steps_per_epoch
+
+ # Only show the progress bar once on each machine.
+ progress_bar = tqdm(range(global_step, args.max_train_steps), disable=not accelerator.is_local_main_process)
+ progress_bar.set_description("Steps")
+
+ for epoch in range(first_epoch, args.num_train_epochs):
+ unet.train()
+ if args.train_text_encoder:
+ text_encoder.train()
+ with TorchTracemalloc() if not args.no_tracemalloc else nullcontext() as tracemalloc:
+ for step, batch in enumerate(train_dataloader):
+ # Skip steps until we reach the resumed step
+ if args.resume_from_checkpoint and epoch == first_epoch and step < resume_step:
+ if step % args.gradient_accumulation_steps == 0:
+ progress_bar.update(1)
+ if args.report_to == "wandb":
+ accelerator.print(progress_bar)
+ continue
+
+ with accelerator.accumulate(unet):
+ # Convert images to latent space
+ latents = vae.encode(batch["pixel_values"].to(dtype=weight_dtype)).latent_dist.sample()
+ latents = latents * 0.18215
+
+ # Sample noise that we'll add to the latents
+ noise = torch.randn_like(latents)
+ bsz = latents.shape[0]
+ # Sample a random timestep for each image
+ timesteps = torch.randint(
+ 0, noise_scheduler.config.num_train_timesteps, (bsz,), device=latents.device
+ )
+ timesteps = timesteps.long()
+
+ # Add noise to the latents according to the noise magnitude at each timestep
+ # (this is the forward diffusion process)
+ noisy_latents = noise_scheduler.add_noise(latents, noise, timesteps)
+
+ # Get the text embedding for conditioning
+ encoder_hidden_states = text_encoder(batch["input_ids"])[0]
+
+ # Predict the noise residual
+ model_pred = unet(noisy_latents, timesteps, encoder_hidden_states).sample
+
+ # Get the target for loss depending on the prediction type
+ if noise_scheduler.config.prediction_type == "epsilon":
+ target = noise
+ elif noise_scheduler.config.prediction_type == "v_prediction":
+ target = noise_scheduler.get_velocity(latents, noise, timesteps)
+ else:
+ raise ValueError(f"Unknown prediction type {noise_scheduler.config.prediction_type}")
+
+ if args.with_prior_preservation:
+ # Chunk the noise and model_pred into two parts and compute the loss on each part separately.
+ model_pred, model_pred_prior = torch.chunk(model_pred, 2, dim=0)
+ target, target_prior = torch.chunk(target, 2, dim=0)
+
+ # Compute instance loss
+ loss = F.mse_loss(model_pred.float(), target.float(), reduction="mean")
+
+ # Compute prior loss
+ prior_loss = F.mse_loss(model_pred_prior.float(), target_prior.float(), reduction="mean")
+
+ # Add the prior loss to the instance loss.
+ loss = loss + args.prior_loss_weight * prior_loss
+ else:
+ loss = F.mse_loss(model_pred.float(), target.float(), reduction="mean")
+
+ accelerator.backward(loss)
+ if accelerator.sync_gradients:
+ params_to_clip = (
+ itertools.chain(unet.parameters(), text_encoder.parameters())
+ if args.train_text_encoder
+ else unet.parameters()
+ )
+ accelerator.clip_grad_norm_(params_to_clip, args.max_grad_norm)
+ optimizer.step()
+ lr_scheduler.step()
+ optimizer.zero_grad()
+
+ # Checks if the accelerator has performed an optimization step behind the scenes
+ if accelerator.sync_gradients:
+ progress_bar.update(1)
+ if args.report_to == "wandb":
+ accelerator.print(progress_bar)
+ global_step += 1
+
+ # if global_step % args.checkpointing_steps == 0:
+ # if accelerator.is_main_process:
+ # save_path = os.path.join(args.output_dir, f"checkpoint-{global_step}")
+ # accelerator.save_state(save_path)
+ # logger.info(f"Saved state to {save_path}")
+
+ logs = {"loss": loss.detach().item(), "lr": lr_scheduler.get_last_lr()[0]}
+ progress_bar.set_postfix(**logs)
+ accelerator.log(logs, step=global_step)
+
+ if (
+ args.validation_prompt is not None
+ and (step + num_update_steps_per_epoch * epoch) % args.validation_steps == 0
+ ):
+ logger.info(
+ f"Running validation... \n Generating {args.num_validation_images} images with prompt:"
+ f" {args.validation_prompt}."
+ )
+ # create pipeline
+ pipeline = DiffusionPipeline.from_pretrained(
+ args.pretrained_model_name_or_path,
+ safety_checker=None,
+ revision=args.revision,
+ )
+ # set `keep_fp32_wrapper` to True because we do not want to remove
+ # mixed precision hooks while we are still training
+ pipeline.unet = accelerator.unwrap_model(unet, keep_fp32_wrapper=True)
+ pipeline.text_encoder = accelerator.unwrap_model(text_encoder, keep_fp32_wrapper=True)
+ pipeline.scheduler = DPMSolverMultistepScheduler.from_config(pipeline.scheduler.config)
+ pipeline = pipeline.to(accelerator.device)
+ pipeline.set_progress_bar_config(disable=True)
+
+ # run inference
+ if args.seed is not None:
+ generator = torch.Generator(device=accelerator.device).manual_seed(args.seed)
+ else:
+ generator = None
+ images = []
+ for _ in range(args.num_validation_images):
+ image = pipeline(args.validation_prompt, num_inference_steps=25, generator=generator).images[0]
+ images.append(image)
+
+ for tracker in accelerator.trackers:
+ if tracker.name == "tensorboard":
+ np_images = np.stack([np.asarray(img) for img in images])
+ tracker.writer.add_images("validation", np_images, epoch, dataformats="NHWC")
+ if tracker.name == "wandb":
+ import wandb
+
+ tracker.log(
+ {
+ "validation": [
+ wandb.Image(image, caption=f"{i}: {args.validation_prompt}")
+ for i, image in enumerate(images)
+ ]
+ }
+ )
+
+ del pipeline
+ if torch.cuda.is_available():
+ torch.cuda.empty_cache()
+ elif torch.xpu.is_available():
+ torch.xpu.empty_cache()
+
+ if global_step >= args.max_train_steps:
+ break
+
+ # Printing the accelerator memory usage details such as allocated memory, peak memory, and total memory usage
+ if not args.no_tracemalloc:
+ accelerator.print(
+ f"{accelerator.device.type.upper()} Memory before entering the train : {b2mb(tracemalloc.begin)}"
+ )
+ accelerator.print(
+ f"{accelerator.device.type.upper()} Memory consumed at the end of the train (end-begin): {tracemalloc.used}"
+ )
+ accelerator.print(
+ f"{accelerator.device.type.upper()} Peak Memory consumed during the train (max-begin): {tracemalloc.peaked}"
+ )
+ accelerator.print(
+ f"{accelerator.device.type.upper()} Total Peak Memory consumed during the train (max): {tracemalloc.peaked + b2mb(tracemalloc.begin)}"
+ )
+
+ accelerator.print(f"CPU Memory before entering the train : {b2mb(tracemalloc.cpu_begin)}")
+ accelerator.print(f"CPU Memory consumed at the end of the train (end-begin): {tracemalloc.cpu_used}")
+ accelerator.print(f"CPU Peak Memory consumed during the train (max-begin): {tracemalloc.cpu_peaked}")
+ accelerator.print(
+ f"CPU Total Peak Memory consumed during the train (max): {tracemalloc.cpu_peaked + b2mb(tracemalloc.cpu_begin)}"
+ )
+
+ # Create the pipeline using using the trained modules and save it.
+ accelerator.wait_for_everyone()
+ if accelerator.is_main_process:
+ if args.use_lora:
+ unwarpped_unet = accelerator.unwrap_model(unet)
+ unwarpped_unet.save_pretrained(
+ os.path.join(args.output_dir, "unet"), state_dict=accelerator.get_state_dict(unet)
+ )
+ if args.train_text_encoder:
+ unwarpped_text_encoder = accelerator.unwrap_model(text_encoder)
+ unwarpped_text_encoder.save_pretrained(
+ os.path.join(args.output_dir, "text_encoder"),
+ state_dict=accelerator.get_state_dict(text_encoder),
+ )
+ else:
+ pipeline = DiffusionPipeline.from_pretrained(
+ args.pretrained_model_name_or_path,
+ unet=accelerator.unwrap_model(unet),
+ text_encoder=accelerator.unwrap_model(text_encoder),
+ revision=args.revision,
+ )
+ pipeline.save_pretrained(args.output_dir)
+
+ if args.push_to_hub:
+ api.upload_folder(
+ repo_id=repo_id,
+ folder_path=args.output_dir,
+ commit_message="End of training",
+ run_as_future=True,
+ )
+
+ accelerator.end_training()
+
+
+if __name__ == "__main__":
+ args = parse_args()
+ main(args)
diff --git a/peft/examples/lorafa_finetune/README.md b/peft/examples/lorafa_finetune/README.md
new file mode 100644
index 0000000000000000000000000000000000000000..432c93ad837c90684c0c5e58b6149372b77c7712
--- /dev/null
+++ b/peft/examples/lorafa_finetune/README.md
@@ -0,0 +1,121 @@
+# LoRA-FA: Memory-efficient Low-rank Adaptation for Large Language Models Fine-tuning
+
+## Introduction
+
+[LoRA-FA](https://huggingface.co/papers/2308.03303) is a noval Parameter-efficient Fine-tuning method, which freezes the projection down layer (matrix A) during LoRA training process and thus lead to less accelerator memory consumption by eliminating the need for storing the activations of input tensors (X). Furthermore, LoRA-FA narrows the gap between the update amount of pre-trained weights when using the low-rank fine-tuning method and the full fine-tuning method. In conclusion, LoRA-FA reduces the memory consumption and leads to superior performance compared to vanilla LoRA.
+
+## Quick start
+
+```python
+import torch
+from peft import LoraConfig, get_peft_model
+from peft.optimizers import create_lorafa_optimizer
+from transformers import AutoTokenizer, AutoModelForCausalLM, Trainer
+from datasets import load_dataset
+
+model = AutoModelForCausalLM.from_pretrained("meta-llama/Meta-Llama-3-8B-Instruct")
+tokenizer = AutoTokenizer.from_pretrained("meta-llama/Meta-Llama-3-8B-Instruct")
+dataset = load_dataset("timdettmers/openassistant-guanaco", split="train")
+
+lora_rank = 16
+lora_alpha = 32
+
+lora_config = LoraConfig(
+ r=lora_rank,
+ lora_alpha=lora_alpha,
+ bias="none",
+)
+peft_model = get_peft_model(model, lora_config)
+optimizer = create_lorafa_optimizer(
+ model=peft_model,
+ r=lora_rank,
+ lora_alpha=lora_alpha,
+ lr=7e-5,
+)
+# you can also use scheduler, we recommend get_cosine_schedule_with_warmup from transformers
+# for better model performance
+scheduler = None
+
+trainer = transformers.Trainer(
+ model=peft_model,
+ train_dataset=dataset,
+ dataset_text_field="text",
+ max_seq_length=2048,
+ processing_class=tokenizer,
+ optimizers=(optimizer, None),
+)
+trainer.train()
+peft_model.save_pretrained("lorafa-llama-3-8b-inst")
+```
+
+The only change in your code is to pass the LoRA-FA optimizer to the trainer (if training with trainer). Do not forget `from peft.optimizers import create_lorafa_optimizer`!
+
+## Example
+
+In this dir, we also provide you a simple example for fine-tuning with LoRA-FA optimizer.
+
+### Run on CPU, single-accelerator or multi-accelerator
+
+This 👇 by default will load the model in peft set up with LoRA config, and train the model with LoRA-FA optimizer.
+
+0. CPU
+
+You can simply run LoRA-FA as below:
+
+```bash
+python lorafa_finetuning.py --base_model_name_or_path meta-llama/Meta-Llama-3-8B --dataset_name_or_path meta-math/MetaMathQA-40K --output_dir path/to/output --lorafa
+```
+
+1. Single-accelerator
+
+Run the finetuning script on 1 accelerator:
+
+```bash
+export CUDA_VISIBLE_DEVICES=0 # force to use CUDA GPU 0
+export ZE_AFFINITY_MASK=0 # force to use Intel XPU 0
+
+python lorafa_finetuning.py --base_model_name_or_path meta-llama/Meta-Llama-3-8B --dataset_name_or_path meta-math/MetaMathQA-40K --output_dir path/to/output --lorafa
+```
+
+2. Multi-accelerator
+
+LoRA-FA can also be run on multi-accelerator, with 🤗 Accelerate:
+
+```bash
+export CUDA_VISIBLE_DEVICES=0,1,2,3 # force to use CUDA GPU 0,1,2,3
+export ZE_AFFINITY_MASK=0,1,2,3 # force to use Intel XPU 0,1,2,3
+
+accelerate launch lorafa_finetuning.py --base_model_name_or_path meta-llama/Meta-Llama-3-8B --dataset_name_or_path meta-math/MetaMathQA-40K --output_dir path/to/output --lorafa
+```
+
+The `accelerate launch` will automatically configure multi-accelerator for you. You can also utilize `accelerate launch` in single-accelerator scenario.
+
+### Use the model from 🤗
+You can load and use the model as any other 🤗 models.
+```python
+from transformers import AutoModel
+model = AutoModel.from_pretrained("meta-llama/Llama-2-7b-chat-hf")
+```
+
+## Best practice in fine-tuning Llama using LoRA-FA: the hyper-params
+
+Sometimes, achieving optimal LoRA fine-tuning can be challenging due to the larger number of hyperparameters to consider compared to full fine-tuning. For instance, not only do we need to adjust the commonly used learning rate, but the ideal LoRA rank may also vary depending on the specific model and task. Additionally, there are other factors to consider, such as LoRA alpha and sequence length. To assist with this, we have created a repository of reproducible best practices in the [LoRA-FA examples](https://github.com/AaronZLT/lorafa) for reference. This resource showcases the optimal LoRA-FA fine-tuning hyperparameters for different models across various datasets. By doing so, we significantly reduce the time and effort spent on hyperparameter tuning, and it may also provide insights for tuning other training hyperparameters. We encourage you to experiment and fine-tune on your own downstream tasks as well.
+
+## LoRA-FA's advantages and limitations
+
+By eliminating the activation of adapter A, LoRA-FA uses less memory for fine-tuning compared to LoRA. For instance, when fine-tuning Llama-2-7b-chat-hf with a batch size of 8 and a sequence length of 1024, LoRA-FA requires 36GB of memory to store activations. This allows it to run successfully on an 80GB accelerator. In contrast, LoRA requires at least 60GB of memory for activations, leading to an Out of Memory (OOM) error. Additionally, the memory consumption of LoRA-FA is not sensitive to the rank, allowing for performance improvements by increasing the LoRA rank without additional memory usage. LoRA-FA further narrows the performance gap with Full-FT by minimizing the discrepancy between the low-rank gradient and the full gradient, enabling it to achieve performance that is on par with or even superior to vanilla LoRA.
+
+Despite its advantages, LoRA-FA is inherently limited by its low-rank approximation nature and potential issues with catastrophic forgetting. The gradient approximation can impact training throughput. Addressing these limitations, especially in terms of approximation accuracy and forgetting phenomena, presents a promising direction for future research.
+
+## Citation
+```
+@misc{zhang2023lorafamemoryefficientlowrankadaptation,
+ title={LoRA-FA: Memory-efficient Low-rank Adaptation for Large Language Models Fine-tuning},
+ author={Longteng Zhang and Lin Zhang and Shaohuai Shi and Xiaowen Chu and Bo Li},
+ year={2023},
+ eprint={2308.03303},
+ archivePrefix={arXiv},
+ primaryClass={cs.CL},
+ url={https://huggingface.co/papers/2308.03303},
+}
+```
diff --git a/peft/examples/lorafa_finetune/lorafa_finetuning.py b/peft/examples/lorafa_finetune/lorafa_finetuning.py
new file mode 100644
index 0000000000000000000000000000000000000000..19091df167e0f7c451eafe40cf9e4cca24685168
--- /dev/null
+++ b/peft/examples/lorafa_finetune/lorafa_finetuning.py
@@ -0,0 +1,221 @@
+# Copyright 2025-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+import os
+from typing import Optional
+
+import torch
+from datasets import load_dataset
+from transformers import (
+ AutoModelForCausalLM,
+ AutoTokenizer,
+ BitsAndBytesConfig,
+ DataCollatorForLanguageModeling,
+ Trainer,
+ TrainingArguments,
+)
+
+from peft import LoraConfig, get_peft_model, prepare_model_for_kbit_training
+from peft.optimizers import create_lorafa_optimizer
+
+
+def train_model(
+ base_model_name_or_path: str,
+ dataset_name_or_path: str,
+ output_dir: str,
+ batch_size: int,
+ num_epochs: int,
+ lr: float,
+ cutoff_len: int,
+ quantize: bool,
+ eval_step: int,
+ save_step: int,
+ lora_rank: int,
+ lora_alpha: int,
+ lora_dropout: float,
+ lora_target_modules: Optional[str],
+ lorafa: bool,
+):
+ os.environ["TOKENIZERS_PARALLELISM"] = "false"
+
+ is_bf16_supported = False
+ device_map = "cpu"
+ if torch.cuda.is_available():
+ is_bf16_supported = torch.cuda.is_bf16_supported()
+ device_map = "cuda"
+ elif torch.xpu.is_available():
+ is_bf16_supported = torch.xpu.is_bf16_supported()
+ device_map = "xpu"
+ compute_dtype = torch.bfloat16 if is_bf16_supported else torch.float16
+
+ # load tokenizer
+ tokenizer = AutoTokenizer.from_pretrained(base_model_name_or_path)
+
+ # load model
+ if quantize:
+ model = AutoModelForCausalLM.from_pretrained(
+ base_model_name_or_path,
+ quantization_config=BitsAndBytesConfig(
+ load_in_4bit=True,
+ bnb_4bit_compute_dtype=compute_dtype,
+ bnb_4bit_use_double_quant=False,
+ bnb_4bit_quant_type="nf4",
+ ),
+ torch_dtype=compute_dtype,
+ device_map=device_map,
+ )
+ # setup for quantized training
+ model = prepare_model_for_kbit_training(model, use_gradient_checkpointing=True)
+ else:
+ model = AutoModelForCausalLM.from_pretrained(
+ base_model_name_or_path, torch_dtype=compute_dtype, device_map=device_map
+ )
+
+ # LoRA config for the PEFT model
+ if lora_target_modules is not None:
+ if lora_target_modules == "all-linear":
+ target_modules = "all-linear"
+ else:
+ target_modules = lora_target_modules.split(",")
+ else:
+ target_modules = ["q_proj", "k_proj", "v_proj", "o_proj", "gate_proj", "up_proj", "down_proj"]
+
+ lora_config = LoraConfig(
+ r=lora_rank,
+ lora_alpha=lora_alpha,
+ target_modules=target_modules,
+ lora_dropout=lora_dropout,
+ bias="none",
+ )
+
+ # get the peft model with LoRA config
+ model = get_peft_model(model, lora_config)
+
+ tokenizer.pad_token = tokenizer.eos_token
+
+ # Load the dataset
+ dataset = load_dataset(dataset_name_or_path)
+
+ def tokenize_function(examples):
+ inputs = tokenizer(examples["query"], padding="max_length", truncation=True, max_length=cutoff_len)
+ outputs = tokenizer(examples["response"], padding="max_length", truncation=True, max_length=cutoff_len)
+ inputs["labels"] = outputs["input_ids"].copy()
+ return inputs
+
+ # Tokenize the dataset and prepare for training
+ tokenized_datasets = dataset.map(tokenize_function, batched=True, remove_columns=dataset["train"].column_names)
+ dataset = tokenized_datasets["train"].train_test_split(test_size=0.1, shuffle=True, seed=42)
+ train_dataset = dataset["train"]
+ eval_dataset = dataset["test"]
+
+ # Data collator to dynamically pad the batched examples
+ data_collator = DataCollatorForLanguageModeling(tokenizer, mlm=False)
+
+ # Define training arguments
+ training_args = TrainingArguments(
+ output_dir=output_dir,
+ num_train_epochs=num_epochs,
+ per_device_train_batch_size=batch_size,
+ per_device_eval_batch_size=batch_size,
+ warmup_steps=100,
+ weight_decay=0.01,
+ logging_dir="./logs",
+ logging_steps=eval_step,
+ save_steps=save_step,
+ save_total_limit=2,
+ gradient_accumulation_steps=1,
+ bf16=True if compute_dtype == torch.bfloat16 else False,
+ fp16=True if compute_dtype == torch.float16 else False,
+ learning_rate=lr,
+ )
+
+ # Here we initialize the LoRA-FA Optimizer
+ # After this, all adapter A will be fixed, only adapter B will be trainable
+ if lorafa:
+ optimizer = create_lorafa_optimizer(
+ model=model, r=lora_rank, lora_alpha=lora_alpha, lr=lr, weight_decay=training_args.weight_decay
+ )
+ trainer = Trainer(
+ model=model,
+ args=training_args,
+ train_dataset=train_dataset,
+ eval_dataset=eval_dataset,
+ data_collator=data_collator,
+ optimizers=(optimizer, None),
+ )
+ else:
+ trainer = Trainer(
+ model=model,
+ args=training_args,
+ train_dataset=train_dataset,
+ eval_dataset=eval_dataset,
+ data_collator=data_collator,
+ )
+
+ # Start model training
+ trainer.train()
+
+ # Save the model and tokenizer locally
+ model.save_pretrained(output_dir)
+ tokenizer.save_pretrained(output_dir)
+
+
+if __name__ == "__main__":
+ import argparse
+
+ parser = argparse.ArgumentParser(description="Fine-tune Meta-Llama-3-8B-Instruct with LoRA-FA and PEFT")
+ parser.add_argument(
+ "--base_model_name_or_path",
+ type=str,
+ default="meta-llama/Meta-Llama-3-8B-Instruct",
+ help="Base model name or path",
+ )
+ parser.add_argument(
+ "--dataset_name_or_path", type=str, default="meta-math/MetaMathQA-40K", help="Dataset name or path"
+ )
+ parser.add_argument("--output_dir", type=str, help="Output directory for the fine-tuned model")
+ parser.add_argument("--batch_size", type=int, default=1, help="Batch size")
+ parser.add_argument("--num_epochs", type=int, default=3, help="Number of training epochs")
+ parser.add_argument("--lr", type=float, default=7e-5, help="Learning rate")
+ parser.add_argument("--cutoff_len", type=int, default=1024, help="Cutoff length for tokenization")
+ parser.add_argument("--quantize", action="store_true", help="Use quantization")
+ parser.add_argument("--eval_step", type=int, default=10, help="Evaluation step interval")
+ parser.add_argument("--save_step", type=int, default=100, help="Save step interval")
+ parser.add_argument("--lora_rank", type=int, default=16, help="LoRA rank")
+ parser.add_argument("--lora_alpha", type=int, default=32, help="LoRA alpha")
+ parser.add_argument("--lora_dropout", type=float, default=0.05, help="LoRA dropout rate")
+ parser.add_argument(
+ "--lora_target_modules", type=str, default=None, help="Comma-separated list of target modules for LoRA"
+ )
+ parser.add_argument("--lorafa", action="store_true", help="Use LoRA-FA Optimizer")
+
+ args = parser.parse_args()
+
+ train_model(
+ base_model_name_or_path=args.base_model_name_or_path,
+ dataset_name_or_path=args.dataset_name_or_path,
+ output_dir=args.output_dir,
+ batch_size=args.batch_size,
+ num_epochs=args.num_epochs,
+ lr=args.lr,
+ cutoff_len=args.cutoff_len,
+ quantize=args.quantize,
+ eval_step=args.eval_step,
+ save_step=args.save_step,
+ lora_rank=args.lora_rank,
+ lora_alpha=args.lora_alpha,
+ lora_dropout=args.lora_dropout,
+ lora_target_modules=args.lora_target_modules,
+ lorafa=args.lorafa,
+ )
diff --git a/peft/examples/miss_finetuning/README.md b/peft/examples/miss_finetuning/README.md
new file mode 100644
index 0000000000000000000000000000000000000000..d08719ca8f0e575478c39a1f7a45f0f2d954f7fe
--- /dev/null
+++ b/peft/examples/miss_finetuning/README.md
@@ -0,0 +1,104 @@
+# MiSS: Balancing LoRA Performance and Efficiency with Simple Shard Sharing
+## Introduction ([Paper](https://huggingface.co/papers/2409.15371), [code](https://github.com/JL-er/MiSS))
+MiSS (Matrix Shard Sharing) is a novel PEFT method that adopts a low-rank structure, requires only a single trainable matrix, and introduces a new update mechanism distinct from LoRA, achieving an excellent balance between performance and efficiency.
+
+
+## Quick Start
+```python
+import torch
+from peft import MissConfig, get_peft_model
+from transformers import AutoTokenizer, AutoModelForCausalLM
+from trl import SFTConfig, SFTTrainer
+from datasets import load_dataset
+
+model = AutoModelForCausalLM.from_pretrained("meta-llama/Llama-2-7b-hf", torch_dtype=torch.bfloat16, device_map="auto")
+tokenizer = AutoTokenizer.from_pretrained("meta-llama/Llama-2-7b-hf")
+tokenizer.pad_token_id = tokenizer.eos_token_id
+
+miss_config = MissConfig(
+ r = 64
+)
+#bat: In this mode, you can enable nonlinear updates across different shards.
+# miss_config = MissConfig(
+# r = 64,
+# init_weights="bat"
+# )
+
+# mini: In this mode, you can set a smaller rank to use fewer trainable parameters, but it is recommended to keep `out_features % mini_r == 0`.
+# miss_config = MissConfig(
+# r = 64,
+# init_weights="mini",
+# mini_r = 8
+# )
+peft_model = get_peft_model(model, miss_config)
+
+peft_model.print_trainable_parameters()
+
+dataset = load_dataset("imdb", split="train[:1%]")
+
+training_args = SFTConfig(dataset_text_field="text", max_seq_length=128)
+trainer = SFTTrainer(
+ model=peft_model,
+ args=training_args,
+ train_dataset=dataset,
+ processing_class=tokenizer,
+)
+trainer.train()
+peft_model.save_pretrained("miss-llama-2-7b")
+```
+
+
+To utilize the fine-tuned MiSS modules, simply run the following command:
+```python
+import torch
+from peft import PeftModel
+from transformers import AutoModelForCausalLM
+
+model = AutoModelForCausalLM.from_pretrained(
+ "meta-llama/Llama-2-7b-hf", torch_dtype=torch.bfloat16, device_map="auto"
+)
+peft_model = PeftModel.from_pretrained(model, "miss-llama-2-7b")
+```
+
+## Advanced Usage
+
+### Fine-tune
+```shell
+#Bat performs better than MiSS, but it uses more memory and is twice as slow. If you want to use the Bat method, you only need to add the parameter init_weights="bat".
+python miss_finetuning.py \
+ --base_model_name_or_path meta-llama/Llama-2-7b-hf \
+ --output_dir output/miss-llama-2-7b-metamath-10k \
+ --miss_r 64 \
+ --init_weights True \
+ --bits bf16 \
+ --data_path meta-math/MetaMathQA \
+ --dataset_split train[:100000] \
+ --dataset_field query response \
+ --bf16 True \
+ --num_train_epochs 1 \
+ --per_device_train_batch_size 2 \
+ --gradient_accumulation_steps 8 \
+ --save_strategy "steps" \
+ --save_steps 1000 \
+ --save_total_limit 1 \
+ --logging_steps 1 \
+ --learning_rate 2e-5 \
+ --weight_decay 0. \
+ --warmup_ratio 0.03 \
+ --tf32 True \
+ --report_to none
+```
+
+
+
+# Citation
+```bib
+@misc{kang2025balancingloraperformanceefficiency,
+ title={Balancing LoRA Performance and Efficiency with Simple Shard Sharing},
+ author={Jiale Kang and Qingyu Yin},
+ year={2025},
+ eprint={2409.15371},
+ archivePrefix={arXiv},
+ primaryClass={cs.CL},
+ url={https://arxiv.org/abs/2409.15371},
+}
diff --git a/peft/examples/miss_finetuning/miss_finetuning.py b/peft/examples/miss_finetuning/miss_finetuning.py
new file mode 100644
index 0000000000000000000000000000000000000000..27d852d071495aa7022e2fe1c3bcaa7402b3a29d
--- /dev/null
+++ b/peft/examples/miss_finetuning/miss_finetuning.py
@@ -0,0 +1,107 @@
+# Copyright 2025-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+import os
+from dataclasses import dataclass, field
+from typing import Literal, Optional
+
+import torch
+from datasets import load_dataset
+from transformers import AutoModelForCausalLM, AutoTokenizer, HfArgumentParser
+from trl import SFTConfig, SFTTrainer
+
+from peft import MissConfig, get_peft_model
+
+
+@dataclass
+class ScriptArguments(SFTConfig):
+ # model configs
+ base_model_name_or_path: Optional[str] = field(
+ default=None, metadata={"help": "The name or path of the fp32/16 base model."}
+ )
+ bits: str = field(default="bf16", metadata={"help": "(`['bf16', 'fp16', fp32]`)"})
+ init_weights: Literal[True, "bat"] = field(
+ default=True,
+ metadata={
+ "help": (
+ "True -> MiSS efficience and balance; `bat` -> Bat, `mini` -> smaller MiSS efficience and balance"
+ ),
+ },
+ )
+ miss_r: int = field(default=16)
+ merge_and_save: bool = field(default=False)
+ # dataset configs
+ data_path: str = field(default="imdb", metadata={"help": "Path to the training data."})
+ dataset_split: str = field(default="train[:1%]", metadata={"help": "(`['train', 'test', 'eval']`):"})
+ dataset_field: list[str] = field(default=None, metadata={"help": "Fields of dataset input and output."})
+
+
+parser = HfArgumentParser(ScriptArguments)
+script_args = parser.parse_args_into_dataclasses()[0]
+print(script_args)
+
+print(f"Load pre-processed residual model in {script_args.bits} bits.")
+if script_args.bits in ["nf4", "fp4", "int8"]:
+ print("MiSS currently does not support quantization.")
+
+elif script_args.base_model_name_or_path is not None:
+ print(f"No available pre-processed model, manually initialize a MiSS using {script_args.base_model_name_or_path}.")
+ model = AutoModelForCausalLM.from_pretrained(
+ script_args.base_model_name_or_path,
+ torch_dtype=(
+ torch.float16
+ if script_args.bits == "fp16"
+ else (torch.bfloat16 if script_args.bits == "bf16" else torch.float32)
+ ),
+ device_map="auto",
+ )
+ tokenizer = AutoTokenizer.from_pretrained(script_args.base_model_name_or_path)
+ tokenizer.pad_token_id = tokenizer.eos_token_id
+ miss_config = MissConfig(
+ r=script_args.miss_r,
+ target_modules=["q_proj", "o_proj", "k_proj", "v_proj", "gate_proj", "up_proj", "down_proj"],
+ bias="none",
+ task_type="CAUSAL_LM",
+ init_weights=script_args.init_weights,
+ )
+ peft_model = get_peft_model(model, miss_config)
+
+print(peft_model)
+peft_model.print_trainable_parameters()
+
+print(f"Training MiSS with trl on the {script_args.data_path}[{script_args.dataset_split}] dataset.")
+dataset = load_dataset(script_args.data_path, split=script_args.dataset_split)
+dataset = dataset.map(
+ lambda example: {
+ "text": f"### USER: {example[script_args.dataset_field[0]]}\n### ASSISTANT: {example[script_args.dataset_field[1]]}"
+ }
+)
+
+trainer = SFTTrainer(
+ model=peft_model,
+ args=script_args,
+ train_dataset=dataset,
+ processing_class=tokenizer,
+)
+trainer.train()
+trainer.save_state()
+
+peft_model.save_pretrained(
+ os.path.join(script_args.output_dir, "miss_ft"),
+)
+
+if script_args.merge_and_save:
+ model = peft_model.merge_and_unload()
+ model.save_pretrained(os.path.join(script_args.output_dir, "miss_merged"))
+ tokenizer.save_pretrained(os.path.join(script_args.output_dir, "miss_merged"))
diff --git a/peft/examples/multi_adapter_examples/Lora_Merging.ipynb b/peft/examples/multi_adapter_examples/Lora_Merging.ipynb
new file mode 100644
index 0000000000000000000000000000000000000000..7778c1a21a6ec1ab4e7f4aa0a029eb591728054d
--- /dev/null
+++ b/peft/examples/multi_adapter_examples/Lora_Merging.ipynb
@@ -0,0 +1,194 @@
+{
+ "cells": [
+ {
+ "cell_type": "code",
+ "execution_count": 5,
+ "id": "db4208b9-5da4-46df-b77a-0f1836c9e4ec",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "import os\n",
+ "\n",
+ "os.environ[\"CUDA_VISIBLE_DEVICES\"] = \"1\" # force using CUDA device 1\n",
+ "os.environ[\"ZE_AFFINITY_MASK\"] = \"1\" # force using Intel XPU device 1\n",
+ "from peft import PeftConfig, PeftModel\n",
+ "from peft import PeftModel, PeftConfig\n",
+ "from transformers import AutoModelForCausalLM, AutoTokenizer, BitsAndBytesConfig\n",
+ "from datasets import load_dataset\n",
+ "import torch\n",
+ "import random\n",
+ "\n",
+ "peft_model_id = \"smangrul/tinyllama_lora_norobots\"\n",
+ "device = torch.accelerator.current_accelerator().type if hasattr(torch, \"accelerator\") else \"cuda\"\n",
+ "config = PeftConfig.from_pretrained(peft_model_id)\n",
+ "model_kwargs = {\"device_map\": \"auto\"}\n",
+ "model_kwargs[\"quantization_config\"] = BitsAndBytesConfig(load_in_4bit=True)\n",
+ "model = AutoModelForCausalLM.from_pretrained(config.base_model_name_or_path, **model_kwargs)\n",
+ "tokenizer = AutoTokenizer.from_pretrained(peft_model_id)\n",
+ "model.resize_token_embeddings(len(tokenizer))\n",
+ "model = PeftModel.from_pretrained(model, peft_model_id, adapter_name=\"norobots\")\n",
+ "_ = model.load_adapter(\"smangrul/tinyllama_lora_sql\", adapter_name=\"sql\")\n",
+ "_ = model.load_adapter(\"smangrul/tinyllama_lora_adcopy\", adapter_name=\"adcopy\")"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 6,
+ "id": "541dab43-9675-42a2-8d90-7437df9f0fa0",
+ "metadata": {},
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "CPU times: user 17.1 s, sys: 458 ms, total: 17.5 s\n",
+ "Wall time: 1.94 s\n"
+ ]
+ }
+ ],
+ "source": [
+ "%%time\n",
+ "# [0.8, 0.1, 0.1] linear #[1.0, 0.2] 0.7 density dare_linear #[1.5, 0.3] 0.5 density ties #[0.8, 0.5] cat\n",
+ "adapters = [\"norobots\", \"adcopy\", \"sql\"]\n",
+ "weights = [2.0, 0.3, 0.7]\n",
+ "adapter_name = \"merge\"\n",
+ "density = 0.2\n",
+ "combination_type = \"ties\"\n",
+ "if adapter_name in model.peft_config:\n",
+ " model.delete_adapter(adapter_name)\n",
+ "model.add_weighted_adapter(adapters, weights, adapter_name, combination_type=combination_type, density=density)"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 7,
+ "id": "76596671-3677-47f0-9d66-81f40bc4d726",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "model.eval()\n",
+ "model.set_adapter(\"merge\")"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "id": "9d59f9f3-6313-43d8-be36-4ca2bbb105b2",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "messages = [\n",
+ " {\"role\": \"user\", \"content\": \"Write an essay about Generative AI.\"},\n",
+ "]\n",
+ "text = tokenizer.apply_chat_template(messages, add_generation_prompt=True, tokenize=False)\n",
+ "inputs = tokenizer(text, return_tensors=\"pt\") # , add_special_tokens=False)\n",
+ "inputs = {k: v.to(device) for k, v in inputs.items()}\n",
+ "outputs = model.generate(\n",
+ " **inputs,\n",
+ " max_new_tokens=256,\n",
+ " do_sample=True,\n",
+ " top_p=0.95,\n",
+ " temperature=0.2,\n",
+ " repetition_penalty=1.2,\n",
+ " eos_token_id=tokenizer.eos_token_id,\n",
+ ")\n",
+ "print(tokenizer.decode(outputs[0]))"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "id": "e5c1daeb-59c8-41d7-bebb-7abd052ab917",
+ "metadata": {},
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "<|im_start|>system \n",
+ "Create a text ad given the following product and description.<|im_end|> \n",
+ "<|im_start|>user \n",
+ "Product: Sony PS5 PlayStation Console\n",
+ "Description: The PS5™ console unleashes new gaming possibilities that you never anticipated.<|im_end|> \n",
+ "<|im_start|>assistant \n",
+ "Ad Text: Experience the next-gen power of the all-new Sony PS5 with its stunning visuals, innovative gameplay features, and more! Get ready to play in style as you experience the future of gaming on your own terms.<|im_end|>\n"
+ ]
+ }
+ ],
+ "source": [
+ "messages = [\n",
+ " {\"role\": \"system\", \"content\": \"Create a text ad given the following product and description.\"},\n",
+ " {\n",
+ " \"role\": \"user\",\n",
+ " \"content\": \"Product: Sony PS5 PlayStation Console\\nDescription: The PS5™ console unleashes new gaming possibilities that you never anticipated.\",\n",
+ " },\n",
+ "]\n",
+ "text = tokenizer.apply_chat_template(messages, add_generation_prompt=True, tokenize=False)\n",
+ "inputs = tokenizer(text, return_tensors=\"pt\") # , add_special_tokens=False)\n",
+ "inputs = {k: v.to(device) for k, v in inputs.items()}\n",
+ "outputs = model.generate(\n",
+ " **inputs,\n",
+ " max_new_tokens=128,\n",
+ " do_sample=True,\n",
+ " top_p=0.95,\n",
+ " temperature=0.2,\n",
+ " repetition_penalty=1.2,\n",
+ " eos_token_id=tokenizer.eos_token_id,\n",
+ ")\n",
+ "print(tokenizer.decode(outputs[0]))"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "id": "5bb08b46-90ae-48a8-8783-ca74b3e26e42",
+ "metadata": {},
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ " Table: 2-11365528-2\n",
+ "Columns: ['Team', 'Head Coach', 'President', 'Home Ground', 'Location']\n",
+ "Natural Query: Who is the Head Coach of the team whose President is Mario Volarevic?\n",
+ "SQL Query: SELECT Head Coach FROM 2-11365528-2 WHERE President = Mario Volarevic\n"
+ ]
+ }
+ ],
+ "source": [
+ "text = \"\"\"Table: 2-11365528-2\n",
+ "Columns: ['Team', 'Head Coach', 'President', 'Home Ground', 'Location']\n",
+ "Natural Query: Who is the Head Coach of the team whose President is Mario Volarevic?\n",
+ "SQL Query:\"\"\"\n",
+ "\n",
+ "inputs = tokenizer(text, return_tensors=\"pt\") # , add_special_tokens=False)\n",
+ "inputs = {k: v.to(device) for k, v in inputs.items()}\n",
+ "outputs = model.generate(\n",
+ " **inputs, max_new_tokens=64, repetition_penalty=1.1, eos_token_id=tokenizer(\"\").input_ids[-1]\n",
+ ")\n",
+ "print(tokenizer.decode(outputs[0]))"
+ ]
+ }
+ ],
+ "metadata": {
+ "kernelspec": {
+ "display_name": "Python 3",
+ "language": "python",
+ "name": "python3"
+ },
+ "language_info": {
+ "codemirror_mode": {
+ "name": "ipython",
+ "version": 3
+ },
+ "file_extension": ".py",
+ "mimetype": "text/x-python",
+ "name": "python",
+ "nbconvert_exporter": "python",
+ "pygments_lexer": "ipython3",
+ "version": "3.11.13"
+ }
+ },
+ "nbformat": 4,
+ "nbformat_minor": 5
+}
diff --git a/peft/examples/multi_adapter_examples/PEFT_Multi_LoRA_Inference.ipynb b/peft/examples/multi_adapter_examples/PEFT_Multi_LoRA_Inference.ipynb
new file mode 100644
index 0000000000000000000000000000000000000000..3815a360a779206c18c810197c193523c0f8dcab
--- /dev/null
+++ b/peft/examples/multi_adapter_examples/PEFT_Multi_LoRA_Inference.ipynb
@@ -0,0 +1,367 @@
+{
+ "cells": [
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "id": "jONLwzXgLg-I",
+ "metadata": {
+ "id": "jONLwzXgLg-I"
+ },
+ "outputs": [],
+ "source": [
+ "!pip install -q git+https://github.com/huggingface/transformers.git\n",
+ "!pip install -q git+https://github.com/huggingface/peft.git\n",
+ "!pip install -q git+https://github.com/huggingface/accelerate.git@main\n",
+ "!pip install huggingface_hub\n",
+ "!pip install bitsandbytes\n",
+ "!pip install SentencePiece"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "id": "36460935",
+ "metadata": {
+ "id": "36460935"
+ },
+ "outputs": [],
+ "source": [
+ "import os\n",
+ "import torch\n",
+ "\n",
+ "os.environ[\"CUDA_VISIBLE_DEVICES\"] = \"0\" # force using CUDA device 0\n",
+ "os.environ[\"ZE_AFFINITY_MASK\"] = \"0\" # force using Intel XPU device 0"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "id": "1351e04c",
+ "metadata": {
+ "id": "1351e04c"
+ },
+ "outputs": [],
+ "source": [
+ "from huggingface_hub import notebook_login\n",
+ "\n",
+ "\n",
+ "notebook_login()"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "id": "d85af699",
+ "metadata": {
+ "id": "d85af699"
+ },
+ "outputs": [],
+ "source": [
+ "from peft import PeftModel\n",
+ "from transformers import LlamaTokenizer, LlamaForCausalLM, GenerationConfig, BitsAndBytesConfig\n",
+ "\n",
+ "model_name = \"meta-llama/Llama-2-7b-hf\"\n",
+ "tokenizer = LlamaTokenizer.from_pretrained(model_name)\n",
+ "model = LlamaForCausalLM.from_pretrained(model_name, quantization_config=BitsAndBytesConfig(load_in_8bit=True), device_map=\"auto\", use_auth_token=True)"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "id": "f0f515ed",
+ "metadata": {
+ "colab": {
+ "base_uri": "https://localhost:8080/"
+ },
+ "id": "f0f515ed",
+ "outputId": "312488a5-f4f8-48a4-8c63-7b4a59e80418"
+ },
+ "outputs": [],
+ "source": [
+ "%%time\n",
+ "model = PeftModel.from_pretrained(model, \"tloen/alpaca-lora-7b\", adapter_name=\"eng_alpaca\")"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "id": "67a0c121",
+ "metadata": {
+ "id": "67a0c121"
+ },
+ "outputs": [],
+ "source": [
+ "%%time\n",
+ "model.load_adapter(\"22h/cabrita-lora-v0-1\", adapter_name=\"portuguese_alpaca\")"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "id": "4b655fca",
+ "metadata": {
+ "id": "4b655fca"
+ },
+ "outputs": [],
+ "source": [
+ "model"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "id": "e9ebd572",
+ "metadata": {
+ "id": "e9ebd572"
+ },
+ "outputs": [],
+ "source": [
+ "device = torch.accelerator.current_accelerator().type if hasattr(torch, \"accelerator\") else \"cuda\"\n",
+ "\n",
+ "model.to(device)"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 8,
+ "id": "138805b3",
+ "metadata": {
+ "id": "138805b3"
+ },
+ "outputs": [],
+ "source": [
+ "def generate_prompt(instruction, input=None):\n",
+ " if input:\n",
+ " return f\"\"\"Below is an instruction that describes a task, paired with an input that provides further context. Write a response that appropriately completes the request.\n",
+ "### Instruction:\n",
+ "{instruction}\n",
+ "### Input:\n",
+ "{input}\n",
+ "### Response:\"\"\"\n",
+ " else:\n",
+ " return f\"\"\"Below is an instruction that describes a task. Write a response that appropriately completes the request.\n",
+ "### Instruction:\n",
+ "{instruction}\n",
+ "### Response:\"\"\"\n",
+ "\n",
+ "\n",
+ "def evaluate(\n",
+ " instruction,\n",
+ " input=None,\n",
+ " temperature=0.1,\n",
+ " top_p=0.75,\n",
+ " top_k=40,\n",
+ " num_beams=4,\n",
+ " max_new_tokens=256,\n",
+ " **kwargs,\n",
+ "):\n",
+ " prompt = generate_prompt(instruction, input)\n",
+ " inputs = tokenizer(prompt, return_tensors=\"pt\")\n",
+ " input_ids = inputs[\"input_ids\"].to(device)\n",
+ " generation_config = GenerationConfig(\n",
+ " temperature=temperature,\n",
+ " top_p=top_p,\n",
+ " top_k=top_k,\n",
+ " num_beams=num_beams,\n",
+ " no_repeat_ngram_size=3,\n",
+ " **kwargs,\n",
+ " )\n",
+ "\n",
+ " with torch.no_grad():\n",
+ " generation_output = model.generate(\n",
+ " input_ids=input_ids,\n",
+ " generation_config=generation_config,\n",
+ " return_dict_in_generate=True,\n",
+ " output_scores=True,\n",
+ " max_new_tokens=max_new_tokens,\n",
+ " )\n",
+ " s = generation_output.sequences[0]\n",
+ " output = tokenizer.decode(s)\n",
+ " return output.split(\"### Response:\")[1].strip()"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 9,
+ "id": "fd5e6b3b",
+ "metadata": {
+ "colab": {
+ "base_uri": "https://localhost:8080/"
+ },
+ "id": "fd5e6b3b",
+ "outputId": "ec72241b-c427-4258-b02f-2101df0d171a"
+ },
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "CPU times: user 5.16 ms, sys: 443 μs, total: 5.6 ms\n",
+ "Wall time: 5.58 ms\n"
+ ]
+ }
+ ],
+ "source": [
+ "%%time\n",
+ "model.set_adapter(\"eng_alpaca\")"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 10,
+ "id": "33650851",
+ "metadata": {
+ "colab": {
+ "base_uri": "https://localhost:8080/"
+ },
+ "id": "33650851",
+ "outputId": "aae24052-0f09-4812-88c3-6fb53dec656c"
+ },
+ "outputs": [
+ {
+ "name": "stderr",
+ "output_type": "stream",
+ "text": [
+ "The following generation flags are not valid and may be ignored: ['temperature', 'top_p', 'top_k']. Set `TRANSFORMERS_VERBOSITY=info` for more details.\n",
+ "The following generation flags are not valid and may be ignored: ['temperature', 'top_p', 'top_k']. Set `TRANSFORMERS_VERBOSITY=info` for more details.\n"
+ ]
+ },
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "The alpaca (Vicugna pacos) is a domesticated species of South American camelid. It resembles a small llama in appearance. It is kept in herds that graze on the level heights of the Andes of southern Peru, southern Bolivia, Ecuador, and northern Chile, at an altitude of about 3,800 m (12,500 ft) to 5,000 meters (16,404 ft). It is bred for its fiber, which is similar to sheep's wool but finer, silkier, and more durable. Alpaca fiber is used for making knitted and woven items, such as sweaters, hats, gloves, scarves, a variety of textiles, rugs, and blankets. The wool can be dyed, and is used to make ponchos, blankets, and sweaters in Peru and other Andean countries. The animals are also raised for meat and as a source of dairy products, including milk, butter, and cheese.\n",
+ "Alpaca fleece comes in 22 natural colors, the most\n"
+ ]
+ }
+ ],
+ "source": [
+ "instruction = \"Tell me about alpacas.\"\n",
+ "\n",
+ "print(evaluate(instruction))"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 13,
+ "id": "fdc7196e",
+ "metadata": {
+ "colab": {
+ "base_uri": "https://localhost:8080/"
+ },
+ "id": "fdc7196e",
+ "outputId": "44cb6742-066b-470e-f507-cbf21e5ae030"
+ },
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "CPU times: user 6 ms, sys: 0 ns, total: 6 ms\n",
+ "Wall time: 5.86 ms\n"
+ ]
+ }
+ ],
+ "source": [
+ "%%time\n",
+ "model.set_adapter(\"portuguese_alpaca\")"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 14,
+ "id": "31997da3",
+ "metadata": {
+ "colab": {
+ "base_uri": "https://localhost:8080/"
+ },
+ "id": "31997da3",
+ "outputId": "8071de75-dc9d-4e89-e85f-674f1de22658"
+ },
+ "outputs": [
+ {
+ "name": "stderr",
+ "output_type": "stream",
+ "text": [
+ "The following generation flags are not valid and may be ignored: ['temperature', 'top_p', 'top_k']. Set `TRANSFORMERS_VERBOSITY=info` for more details.\n",
+ "The following generation flags are not valid and may be ignored: ['temperature', 'top_p', 'top_k']. Set `TRANSFORMERS_VERBOSITY=info` for more details.\n"
+ ]
+ },
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "I'm sorry, but I can't make it to the party. I'm not feeling well. I have a headache and I don't think it's a good idea for me to go out tonight. I hope you understand and that you have a great time at the party!\n"
+ ]
+ }
+ ],
+ "source": [
+ "instruction = \"Invente uma desculpa criativa pra dizer que não preciso ir à festa.\"\n",
+ "\n",
+ "print(evaluate(instruction))"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 15,
+ "id": "8b8e4e9a",
+ "metadata": {
+ "colab": {
+ "base_uri": "https://localhost:8080/"
+ },
+ "id": "8b8e4e9a",
+ "outputId": "84226223-e018-4feb-e189-969c344fd940"
+ },
+ "outputs": [
+ {
+ "name": "stderr",
+ "output_type": "stream",
+ "text": [
+ "The following generation flags are not valid and may be ignored: ['temperature', 'top_p', 'top_k']. Set `TRANSFORMERS_VERBOSITY=info` for more details.\n",
+ "The following generation flags are not valid and may be ignored: ['temperature', 'top_p', 'top_k']. Set `TRANSFORMERS_VERBOSITY=info` for more details.\n"
+ ]
+ },
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "Eu não posso ir porque tenho que fazer uma tarefa para o meu professor.\n",
+ "\n"
+ ]
+ }
+ ],
+ "source": [
+ "with model.disable_adapter():\n",
+ " instruction = \"Invente uma desculpa criativa pra dizer que não preciso ir à festa.\"\n",
+ "\n",
+ " print(evaluate(instruction))"
+ ]
+ }
+ ],
+ "metadata": {
+ "accelerator": "GPU",
+ "colab": {
+ "provenance": []
+ },
+ "gpuClass": "standard",
+ "kernelspec": {
+ "display_name": "Python 3",
+ "language": "python",
+ "name": "python3"
+ },
+ "language_info": {
+ "codemirror_mode": {
+ "name": "ipython",
+ "version": 3
+ },
+ "file_extension": ".py",
+ "mimetype": "text/x-python",
+ "name": "python",
+ "nbconvert_exporter": "python",
+ "pygments_lexer": "ipython3",
+ "version": "3.11.13"
+ }
+ },
+ "nbformat": 4,
+ "nbformat_minor": 5
+}
diff --git a/peft/examples/multi_adapter_examples/multi_adapter_weighted_inference_diffusers.ipynb b/peft/examples/multi_adapter_examples/multi_adapter_weighted_inference_diffusers.ipynb
new file mode 100644
index 0000000000000000000000000000000000000000..fec4092f4e6d26a84f6bff0c9f0a736b54ff0614
--- /dev/null
+++ b/peft/examples/multi_adapter_examples/multi_adapter_weighted_inference_diffusers.ipynb
@@ -0,0 +1,12881 @@
+{
+ "cells": [
+ {
+ "cell_type": "markdown",
+ "metadata": {},
+ "source": [
+ "This notebook shows how to use the adapter merging methods from `peft` and apply them image generation models using `diffusers`."
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "QaEZ3dPgGtza"
+ },
+ "source": [
+ "## Turn `diffusers` LoRA checkpoints into `PeftModel`"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "colab": {
+ "base_uri": "https://localhost:8080/"
+ },
+ "id": "KwvBjN-e62ts",
+ "outputId": "19c58dc7-95db-49c6-beb8-3ade1a8fe284"
+ },
+ "outputs": [],
+ "source": [
+ "!pip install diffusers accelerate transformers -U -q\n",
+ "!pip install git+https://github.com/huggingface/peft -q"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "id": "5S64sUQhJqB3"
+ },
+ "outputs": [],
+ "source": [
+ "from google.colab import userdata\n",
+ "TOKEN = userdata.get(\"HF_TOKEN\")"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 150,
+ "referenced_widgets": [
+ "c9f764b5036042af9f1505e3729cbc32",
+ "b999b3e3af3744a79c0c90657ef37d4e",
+ "f3baef4fbf4b4ec08480522be921f841",
+ "bd2740e191a74558a77a965b4f2d7f28",
+ "6f6a6cfd50404f1ea09f83e95b04550a",
+ "713dec1904ce46f6b2d5a9b7e3e0373a",
+ "a6bb8206de044c74a03d1a64c801e742",
+ "f2c67c29e1224df3b2def5a87eb8d368",
+ "486282a4ead148868005c592d74a4ed4",
+ "48f51c96b7574946bf9542633eb39135",
+ "35c810f4bfe741f091f172cede413950",
+ "67567eea233b423c8acd62773a4adb30",
+ "5161248cd0384d5887ed231ecd48c82e",
+ "6f72ea2c284e4e40899375c7b07c517f",
+ "d99a364420454ba5bfd510d1226b94af",
+ "d33c90e8ea0945d397659f6a90cf51b6",
+ "097fa44254ea4ecda7c8db995f370afc",
+ "9fb982789fbc4582bceb356e351db438",
+ "0204153b17ca4bb0b21fc033393ce9bd",
+ "f02041b1d5e1485bb2ba02b00fc2c242",
+ "4d327c9e91b34c7b84cedd8f9660e9fd",
+ "b44f7154c55146a3bf5f4bd9e438086f",
+ "b27ac2aaff694dd5999ab2cba91195da",
+ "556730e12d5d4e0ea51a0dd1b5aac331",
+ "584dd148b2344bdc92f1d0850399aed7",
+ "ccc5bdc185a84901994577ff7f1bc962",
+ "2c75632d8fdc4458814055172d1d72c3",
+ "2f016774e7854ef589442734d0bb2f08",
+ "a15c3a32bfd347a98c2a50d27cd5b9f9",
+ "67ef71b6521b47dd90e3dc0fd03016f2",
+ "989c54778eb7469fb91e4337d6f49b0b",
+ "439cf6c6f9e845cea4008e3219454ff4",
+ "460c3c96d1724713b78bddcfc1f3eb97"
+ ]
+ },
+ "id": "1YH9xWDcyhaa",
+ "outputId": "8b7b32f4-4b77-411e-f499-7b2cf7650613"
+ },
+ "outputs": [],
+ "source": [
+ "from diffusers import UNet2DConditionModel\n",
+ "import torch\n",
+ "\n",
+ "device = torch.accelerator.current_accelerator().type if hasattr(torch, \"accelerator\") else \"cuda\"\n",
+ "\n",
+ "model_id = \"stabilityai/stable-diffusion-xl-base-1.0\"\n",
+ "unet = UNet2DConditionModel.from_pretrained(\n",
+ " model_id, subfolder=\"unet\", torch_dtype=torch.float16, use_safetensors=True, variant=\"fp16\"\n",
+ ").to(device)"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 3,
+ "metadata": {
+ "id": "-kfTBaLR1Mp-"
+ },
+ "outputs": [],
+ "source": [
+ "# So that we can populate it later.\n",
+ "import copy\n",
+ "\n",
+ "sdxl_unet = copy.deepcopy(unet)"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 4,
+ "metadata": {
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 593,
+ "referenced_widgets": [
+ "0b7ffee735044ece90f010c6771d2d69",
+ "27671f87d0f3400b89e34bc428daa53c",
+ "33a018bf2ed547caa69f8ca91dcbb112",
+ "a91df5ceea8647d98f4d49701bb00969",
+ "c8555cb30ade40b9bd9a3435d6deeb67",
+ "b28a2b59aab9478e9ac3ab24a1de6f9a",
+ "c08fca70486040069d4f8f1df46a1074",
+ "bab2458ba3f54b229828ad9c8706aba4",
+ "2a0f746d6eab4680b6c44ec5cdbd8fd9",
+ "5269d405725946b3a657d3a8d7b25885",
+ "b4a697d8335c435ab21219716a1da022",
+ "85f22e78d47641d19efb6e6d62f6a014",
+ "d8bbb7402f3e44b2899fc98f02cee87e",
+ "8b41763280a048d485f06682ddc12ca2",
+ "05791b70a24a42138755141602399c47",
+ "753f64d9069640d985f399a058fc9b5b",
+ "19679186751b42e3ad2c44ea46c82a9c",
+ "d4baf7891f854c9c9898314633f97356",
+ "9c6ab017f5fb46eda8e3c22e9dd2b838",
+ "10bc970e474a46249e2a5e9e43fec7be",
+ "5c838962c7854541b61877c6d42481c4",
+ "4d54c07dd8e94557b82521772c1a2825",
+ "efd33121bdfc4ce195a07c9ef523a477",
+ "d2cd2572973249baa8e130b5777f4147",
+ "4e77d8b6cdb94fc68974d27b24cfb3fd",
+ "c292a598350d4dd4bb9b70aab1320c29",
+ "c68a5ad3bb664e8785e724085d208e96",
+ "b27c74f0c7bf493fa8bcb4c5b9c9c100",
+ "09638c8da74f4dddaf1d5d94dd8ad885",
+ "6a8a634cd3844fa081a4622d224ec940",
+ "2460b9e05b58481e898b139b94532c14",
+ "cdd8f9b1592842b48e1ffa80f8ec8246",
+ "ba9b002888b448738ba4b127e1046f5d",
+ "54ab158c643540abb8b3a96c1ae3ecab",
+ "55130e37444844f88286a87c8d153eba",
+ "7e3048e0fac94dfdaca1bc862ecfce15",
+ "643ba607008547ba9572fa4880a7d0f2",
+ "5738e5d103254c5485856f97d82954ab",
+ "beedc3b275c24432a2e959dcf9dd418d",
+ "10690b309908402289e9891203714199",
+ "0c68c6c65fb94650b15069a25d9e1699",
+ "ad233dfd52034b9e8c6c2c5b86995717",
+ "2ef25bd6dd644347baac12366d7002fd",
+ "0918b23f41e0404e82fccd08cadc6ccf",
+ "b25e822b3f77431fb72b4780067c90d9",
+ "55177afb435f44898df300143703e4d8",
+ "b79d3f5bd8024451bc7148ba2a5029bd",
+ "eacd646e2b984e60ab603bfc6d631de8",
+ "d158a80f4186411a8a9c335a8d5a888e",
+ "7049676db714446b98bba16b5f1b049e",
+ "09172ff4be4e433483d27b576464d1df",
+ "ea257c1c73524141b87ab3c1ef85c908",
+ "c474ed5e340146baae6c38f62013afe3",
+ "2ece04bc10934b3cb9d383abfc5ccd6e",
+ "67a03631ebc54f99928f0feb18ab38af",
+ "40ff502d2d5c40378c25cf84dd3323c8",
+ "230bd59922e84b90b0a141b3ac1e681b",
+ "6d0f946764444df28cb0da0fd0a408eb",
+ "c995197e66e04874a9f5d34db98b8890",
+ "f2596717405c40e1a39b721386e7a972",
+ "f8e6babf4fdd4c8e80d6dd24ff22d464",
+ "5e030e8a026b4513aa954203169f0a27",
+ "f9ca5d4810b34938b6f997ff66a8d541",
+ "b418ff1733db4efbab1b00b632b894e2",
+ "83f2d1dfaba54da38f0421b69930c3c1",
+ "577cc4b4f27941189c62951046db24ec",
+ "a16016987b6145b69caaac6712d72835",
+ "c82cf8cf90ed4e93bccffcf75881a56d",
+ "5a4c6dc09a1049c0adfca9834b045a25",
+ "c4d83c2b37504473afe63209a178b4cd",
+ "fae9d16daace412492b048b012b8d6dc",
+ "421b59f4021d4c4d930c51b6b4c7071f",
+ "60cc7415644d4e16b88f8fc5896b4b3b",
+ "fd13a58d6b444a0f955832647f64df12",
+ "8d492d53eb7f4225b516a65ef80f24e5",
+ "70849993c0c94ecf87c56e430f06181d",
+ "e820c557697648378966ed0a073826c8",
+ "a9ac3b2188594c19885bcdb9a659ecde",
+ "a708db5805424449afa269b714ebb3b3",
+ "6d492ddabcbe4d65b5d311834865ab92",
+ "e17e3253c16743a29f09b82d23c3b26d",
+ "e67a69c294334b01974f8bef36f133a0",
+ "24cbd9338ad94801aa11f4dcb2a867cb",
+ "c88fcf0d20154b1fb9b7e8a00116b5e6",
+ "ee8407365f5d42d9b98536152c9efe92",
+ "5ceb5c369f974b84ba850c9e81730a0e",
+ "a7767d5a440f4c819cdb87414f2187ff",
+ "f0bc6b14a299445ca705b888b3047064",
+ "fd0ff16b68b2488d8c31ebe700dee9c9",
+ "0e49d820da754da785bec2e5940eb9f6",
+ "0b53b908088648e3b2beadaeba0f5da1",
+ "804e7ee768794bba88aec3137f418868",
+ "0d786d8386ba49d0b53a5452d52e722d",
+ "33d459c0fbfe45389abe7eb43d2710a1",
+ "dd42a2ff90854b74ba5fde1de26b4e15",
+ "a3ce5829f8a640e79a19d737663b8474",
+ "62afb52a01924566b52f6c2d9ffb76f4",
+ "7a52c380a91c4f49bbfde658550248d3",
+ "3e418e46c47841ac9d717a6981807f68",
+ "8840288388ae4162884feef9c8e776f7",
+ "67b7783351d340d99c44149635b9be84",
+ "0f60c0f123954744ad13b670ca6dce77",
+ "dfabe7aa70024d1aa868ef5e6650dc6d",
+ "7d282fda276343c3aff99b001253ecc1",
+ "4cae160456c74a5fa761f026d64b2e35",
+ "819a26acd18f443882feb129f2c576d6",
+ "d2ed1988cf8c4bcdb1793b3d5068efed",
+ "6f113303101b4f448380a878d8900bf6",
+ "60e8e9f8e6ce40dd910ce1a9410b5e24",
+ "6703a0417c474db5bf261fe8679051e9",
+ "cb89ecd5a8c14051985495da1797a202",
+ "61db57127c5845759360bdf8b29dac2d",
+ "ab9c869439a94bddbbc0c6098f4c5b2a",
+ "587bd0b90afa450ba82e49cf86ee135d",
+ "955ec2551f8b400dbbdba68d7449de76",
+ "f46df85f441e4ada831f0e2b142f296a",
+ "d4f1dbe4ce244abc987b1089876e080f",
+ "13ac509e0d5f42e9bbb6deda62f77923",
+ "4a4a50a17c014f189b52119901104d79",
+ "cf42fc299989442f94f4a9df63005ab4",
+ "90b9300ba00e41e58170ec5634622985",
+ "4fa4f545258b4d6ca014a4c84ec4b24a",
+ "993e5303f107468f83dbf51026e64301",
+ "1e6c1c848e364ce4841ddcaa1383cfba",
+ "d432098a941c463599648b156abea24b",
+ "917139ad07a64e0cae89f2beeffae956",
+ "83afce4becac4f37ba916bf1901346ff",
+ "071e40d45ad14fc19b1480927d15d2ae",
+ "fe19dcea6d9a44d28f077e065f1671c4",
+ "08fddacdff4b4ae09adb5440fd86ae86",
+ "d62465d39d7e4265832901e9b9707993",
+ "4f56214f69034077bafdfdabc1c2aebf",
+ "29b67774c6944bc7ab93e7ba0eaf867f",
+ "0805d34df44f451d9b9910dbe5999245",
+ "2f2c0ea0fc914e7981e34d01751f74d8",
+ "5f52ae61812544f29f774f80fcb7a09c",
+ "ca5dc8342ef946a49d9e67a21f1a67c8",
+ "babce0e85baf4279ae1d22d64006667f",
+ "5cf6cd09cda64d688f4a0f7c511533d0",
+ "f668dd13af6f41d8be358f7db5261c54",
+ "8a8ef60b3b72452fb9ccc31052ab3b4f",
+ "7d29b20296aa4e33837b8ad53fc4adba",
+ "6a94d1d176b844db96de0c0e3cd67701",
+ "c80901426c87439481078b9da2e0c772",
+ "416f31db79fd431fb8dc06e994421b70",
+ "1971fcd35a564c449b4f437dac46058f",
+ "76a474e4aab14a5987cf25d1391d578c",
+ "ff3bf3f1873c4b01b0a547dfe02923ce",
+ "a6295c7e7630444c9b7425b884ad9707",
+ "3ede828a0374453e9aac9a6695befae3",
+ "dc4391fe30694a788134fffdd2a23d1a",
+ "cfc6ec59d45d42d187f42061902abbfb",
+ "68822f8f861a48859df630fad63f51c1",
+ "2671327d35e64f0da670a3a611fd0886",
+ "aae194e7f71f4eba80ffd18f91f083a8",
+ "9ad4192f6f244264aede1b3c8ac3c57a",
+ "90558769855c4bb08ff2fe4af940c45b",
+ "75384779c5d540d28afb53a0e318b674",
+ "a287f197e4fe4f908e3ee0a0e6cb35cf",
+ "fdb799739700447d8a5198f1f4f9b17f",
+ "683db0ff105a47038c350cfc74b88345",
+ "b79d32186443469d94836b663bf156b5",
+ "86cb336c1f684867bd13dae0370b4d36",
+ "7f63b3d80ecb4c3eb837bd0e616e1623",
+ "4f6e7b21ba0747f19b9d63468861c988",
+ "766567be45eb4db6b8d7a3364566c1dc",
+ "3c222a56d4404863a1dac60f1d03835b",
+ "db862ffbb44d450db514173df4c7f301",
+ "ddbeb13bb8174fc0b7d5543108d1c4f5",
+ "5b3bbc663d504fb99318ba186e6b8499",
+ "30bfac68f4224152b048d6ccf6013c5c",
+ "971f59d5f3e04697b3ab3c39ec0fc667",
+ "fe958df746be4dc1871bd58628697c3c",
+ "54417d8b9c5249d0a028d9e831dd8be6",
+ "9a37ffb9810f482b80f245f64947c371",
+ "bdfe4e4109a14a41bcd2e1e4242d82bb",
+ "22e894ba852e4072a1f63a83b3a98b16",
+ "95e24bbc8397455fabb724ed3c330511",
+ "d35b3848508c4b6390c243866649439d",
+ "c7cf10df8d7944aeb93947d5f4156c92",
+ "8e3b0b9f26a34ab8a932756b32834fd0",
+ "b1d427082b9f452eb6546c7d55016b36",
+ "061fcc6e5f3c44c48cde212c1ba515e5",
+ "d70508c304794bc79e80aab136eaf65a",
+ "01b20535e40b47068723073ac6c819ee",
+ "de0b54a59d9f47408d92915ad746cd5e",
+ "eb9a5f255fa0447eba6a33e1c30ba166",
+ "d1e4d2fd70e644f986104c998db7e53b",
+ "f786a0f386f6486083c15e576f6eb3e7",
+ "6715d91c6b62426aa49c344b65bcd8a2",
+ "0b0a85e1133c4ca3ba716e2403511703",
+ "017dc44dbe1c4de491e003a1e279a218",
+ "e3a1a5e9f29d4d28b0b9496493dafa21",
+ "c008577d922e436aabb8680ca0d13117",
+ "bd176c410a4e48a382a1b688e77aafcb",
+ "6b586ad7a3054c83b14243d69484127f",
+ "34fcd527a59748cf832c9efdb954fc0e",
+ "fd672cd5ba0c4695be4240707dcf4bf3"
+ ]
+ },
+ "id": "EMTVH9cLEZYi",
+ "outputId": "7a24b4b0-71f6-4c65-a242-fb3d502da6a8"
+ },
+ "outputs": [
+ {
+ "name": "stderr",
+ "output_type": "stream",
+ "text": [
+ "Loading pipeline components...: 100%|██████████| 7/7 [00:00<00:00, 10.25it/s]\n"
+ ]
+ }
+ ],
+ "source": [
+ "# Load the pipeline too.\n",
+ "from diffusers import DiffusionPipeline\n",
+ "\n",
+ "pipe = DiffusionPipeline.from_pretrained(\n",
+ " model_id, variant=\"fp16\", torch_dtype=torch.float16, unet=unet\n",
+ ").to(device)"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 49,
+ "referenced_widgets": [
+ "5e677518051c43768dbf06243701c817",
+ "d727913663634e368ade4a7dc64fe74b",
+ "eb73095c804a4272856fe348fa3cb1e9",
+ "7e9b46b10fa24dfea489dfbc150d2a2e",
+ "c8156b0cc68e4b3693dcabc530a4ea9a",
+ "d987907f09084d44b452f939aadff65e",
+ "e976b994189343f5ba7d762ef92c79e2",
+ "9810873713024e79ae6d338dfeae5876",
+ "2e18ce21c01a4a3ca992622957e7d297",
+ "2db944a049a04426bba181fddb2801b1",
+ "683863a313034025ab99fab5810f39c7"
+ ]
+ },
+ "id": "D5hL5156zPis",
+ "outputId": "2510b8e7-c030-40f8-dcd2-ef76fc8529c6"
+ },
+ "outputs": [],
+ "source": [
+ "# Only UNet\n",
+ "pipe.load_lora_weights(\"CiroN2022/toy-face\", weight_name=\"toy_face_sdxl.safetensors\", adapter_name=\"toy\")"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 6,
+ "metadata": {
+ "id": "p-7YWoOs02La"
+ },
+ "outputs": [],
+ "source": [
+ "from peft import get_peft_model, LoraConfig\n",
+ "\n",
+ "toy_peft_model = get_peft_model(\n",
+ " sdxl_unet,\n",
+ " pipe.unet.peft_config[\"toy\"],\n",
+ " adapter_name=\"toy\"\n",
+ ")"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 101,
+ "referenced_widgets": [
+ "c6bdeef396174d51af9eee277752bec7",
+ "685797f8907c47ffab4fe7a81ca22e63",
+ "414f8301f76043758f69bbfb6960072d",
+ "23c0492f021a4b60b1d84b0b82d15378",
+ "550b3ad10fcb422eb66f71ad95988616",
+ "222da37b5af14d60814c65cdd1ea20be",
+ "6a2b5bbd4afe4e0cabe39e95ccf528be",
+ "7ba112dcece64386bdbac6837004891b",
+ "2ffbf400ff1f4cc9b358bb10c6b9d99f",
+ "5405d8a1aa1d411b895b0523fb8e4ce7",
+ "04846af1def142ffad328d434ba228fe"
+ ]
+ },
+ "id": "a_2n4Odz2a0c",
+ "outputId": "4b3b801b-649f-4c69-b75c-f800ac75c17f"
+ },
+ "outputs": [],
+ "source": [
+ "original_state_dict = {f\"base_model.model.{k}\": v for k, v in pipe.unet.state_dict().items()}\n",
+ "\n",
+ "toy_peft_model.load_state_dict(original_state_dict, strict=True)\n",
+ "toy_peft_model.push_to_hub(\"toy_peft_model-new\", token=TOKEN)"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 8,
+ "metadata": {
+ "id": "z1DWL0X12rxD"
+ },
+ "outputs": [],
+ "source": [
+ "pipe.delete_adapters(\"toy\")\n",
+ "sdxl_unet.delete_adapters(\"toy\")"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 49,
+ "referenced_widgets": [
+ "d18c97fe685e4be080125ae770526255",
+ "e44c018bc76c48cd8738fee5966767ce",
+ "57b491647f1e49cea7ce34774a963936",
+ "484f694f734b4a92a14ecc4d048db0af",
+ "bcb3ec98d25b4c138c5e8f84c1e937c6",
+ "b0abce2d8a2046dba320e788e33e9d66",
+ "aef81ec1a7e844f883beba8c5754a8af",
+ "c040aa1f65514be28f0ca8ecdd1f69e4",
+ "eec76868d92f45d7a6db2e232a45e0c2",
+ "157c0c1e85ef40fb99e6cfe0e176be38",
+ "99717def9b6b4afe8a411a3bb83320c9"
+ ]
+ },
+ "id": "9PW-SfwH5L7e",
+ "outputId": "90721ffa-faa5-4628-994a-7b719a4ef02c"
+ },
+ "outputs": [],
+ "source": [
+ "pipe.load_lora_weights(\"nerijs/pixel-art-xl\", weight_name=\"pixel-art-xl.safetensors\", adapter_name=\"pixel\")\n",
+ "pipe.set_adapters(adapter_names=\"pixel\")"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 101,
+ "referenced_widgets": [
+ "adb2daf9d62f49f8ab1f0144b717d41e",
+ "bba38c266ceb4f30bb4bc1eaf5e3aa96",
+ "6926c8dd4e4e46d089bb387333691df7",
+ "abf2248c725b4837b5c2babef7f4ff3e",
+ "39e4bdf8d621451f984f6e7302fd6961",
+ "4abac6a83641414499f9b6b1514d1695",
+ "bf6e103b43844f17968eadf223a42acb",
+ "adf53d97af214cceaae895c8abfbd909",
+ "9d74948f7bcb498c9295e41e690a0a8d",
+ "d872c3900b8b4275b2224c9ec5e7d78f",
+ "4fbaa1bd51bf4b1e90337a435604d2bd"
+ ]
+ },
+ "id": "jHSb-iIf7IEb",
+ "outputId": "29124d4c-b58f-4f0e-c59b-d79b44cb162f"
+ },
+ "outputs": [],
+ "source": [
+ "pixel_peft_model = get_peft_model(\n",
+ " sdxl_unet,\n",
+ " pipe.unet.peft_config[\"pixel\"],\n",
+ " adapter_name=\"pixel\"\n",
+ ")\n",
+ "\n",
+ "original_state_dict = {f\"base_model.model.{k}\": v for k, v in pipe.unet.state_dict().items()}\n",
+ "pixel_peft_model.load_state_dict(original_state_dict, strict=True)\n",
+ "pixel_peft_model.push_to_hub(\"pixel_peft_model-new\", token=TOKEN)"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 11,
+ "metadata": {
+ "id": "yoPzMtyqG2ZO"
+ },
+ "outputs": [],
+ "source": [
+ "del pipe, sdxl_unet, toy_peft_model, pixel_peft_model"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "Zis3zKZpGy8w"
+ },
+ "source": [
+ "## Weighted adapter inference"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 12,
+ "metadata": {
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 145,
+ "referenced_widgets": [
+ "d74b1c667d42472b865ee1cbefc33a60",
+ "1074a274530e46c5b5a3e43653da43d0",
+ "dfde3984062442869bc8091bb94f2c36",
+ "a6f2ce8830734be4b8efe5ca0e14e990",
+ "07da49088e8d480fad03a2e828357872",
+ "5dd09616ba6544c499271054e8d8d2c5",
+ "fdb1fd279a0241429e5721ae2e92d217",
+ "7c6c4dff0a814bc6a7ac677980b45add",
+ "9a9da0d0e3d84a19b5d188c9bd6a83bb",
+ "de31002ed7fc475c915b4a29253108af",
+ "fbf3d268f30344b7864ce691d5bcb1f3",
+ "153a93d930df4ee396e03f1aaa6f04f1",
+ "c8e40d44aeac47a78f6502771f1471b7",
+ "270ddad8d7704f929a28c9fbbdabfa26",
+ "e57d317b3dda43bba13ecd4514f776d3",
+ "22b55b5ee1af4ea7b1acfe511b194cd8",
+ "a48d3ad24e9744f7898d1f2c5a696ea2",
+ "f29673e57d174839a0bde70bfa165715",
+ "13f5160dd981465890ada8a2cef22d5e",
+ "cc06ed7338b74ae6a1c563212aeb9f94",
+ "3a017f1d0ebf4a4aab57ac3eb0788774",
+ "48643ea67f2f4762bcd27de1d4cf0fd2",
+ "5c3d142907404cef8fd624839a166530",
+ "abaecfe7f39a43bb8fbd655d1a3009f4",
+ "d488374da5e74ec3a5973003590a7d69",
+ "5d8ae9661dce4a1aac8d418d84f3a209",
+ "32132ecbe71a4c2c903932513c2a1aa0",
+ "05700817adac4fdda6c95dd00eaeae38",
+ "5a7d87338ddc45df84080e0096a31631",
+ "cb9a536bc56f4d0ebf285e7f73d4730e",
+ "49bb475a11104e9496f2623e3d5caebd",
+ "887c5eae5b154eccb4a1caa3deef6e94",
+ "e87dffe17f1948e9ba794eddb605a908",
+ "2c352a90375443da835eef55b3e63303",
+ "db8fd6b2687c449fa0600d3e87c96999",
+ "17691a346ca5407a99a5e385450c97eb",
+ "0bca833a6aa74ebaa8f69feb738806bf",
+ "6bdb9b0b68c24b84a748c18ed927a8d3",
+ "355efc45ddaf42498d72d6134a28c87b",
+ "8b6464ce614c4aa29ac66ecce29b6cbf",
+ "bc07cdaad5b64fb3b0e1f8c214bba813",
+ "9e2e87c131a140a2a37dfdf483d27ced",
+ "47468a75637d436f849283c295a74ab6",
+ "af5003cf40ae4dfaa0660f247598856e"
+ ]
+ },
+ "id": "gEqT1vFtG0_e",
+ "outputId": "282ce865-c653-4912-e497-ff825c896ae7"
+ },
+ "outputs": [],
+ "source": [
+ "from peft import PeftModel\n",
+ "\n",
+ "base_unet = UNet2DConditionModel.from_pretrained(\n",
+ " model_id, subfolder=\"unet\", torch_dtype=torch.float16, use_safetensors=True, variant=\"fp16\"\n",
+ ").to(device)\n",
+ "\n",
+ "toy_id = \"sayakpaul/toy_peft_model-new\"\n",
+ "model = PeftModel.from_pretrained(base_unet, toy_id, use_safetensors=True, subfolder=\"toy\", adapter_name=\"toy\")\n",
+ "model.load_adapter(\"sayakpaul/pixel_peft_model-new\", use_safetensors=True, subfolder=\"pixel\", adapter_name=\"pixel\")\n",
+ "\n",
+ "# https://huggingface.co/docs/peft/main/en/package_reference/lora#peft.LoraModel.add_weighted_adapter\n",
+ "model.add_weighted_adapter(\n",
+ " adapters=[\"toy\", \"pixel\"],\n",
+ " weights=[0.7, 0.3],\n",
+ " combination_type=\"linear\",\n",
+ " adapter_name=\"toy-pixel\"\n",
+ ")\n",
+ "model.set_adapters(\"toy-pixel\")"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 13,
+ "metadata": {
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 186
+ },
+ "id": "QStyurhKsP_g",
+ "outputId": "5e3a2627-27a2-4771-e62f-1b81ded2b87e"
+ },
+ "outputs": [
+ {
+ "data": {
+ "text/plain": [
+ "diffusers.models.unets.unet_2d_condition.UNet2DConditionModel"
+ ]
+ },
+ "execution_count": 13,
+ "metadata": {},
+ "output_type": "execute_result"
+ }
+ ],
+ "source": [
+ "type(model.base_model.model)"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 14,
+ "metadata": {
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 1000,
+ "referenced_widgets": [
+ "28a5059a2cc445d783e94ad5d83a0748",
+ "faddc146c69545cdaeb81edc8a0cda70",
+ "cd08b99de03c483a965248ff4df752ba",
+ "d37c6ac25fd34a65bf307896443a5063",
+ "66da596ae59d474f8a82a600174adff6",
+ "b600178b161d4a87a0b832a169d7caf2",
+ "b3eaa188cc2e48d081488eea4ed2971f",
+ "c05842ed12c848c68c4a69de9aa742a8",
+ "18e3ba4a61784f04b3238cf273c90c3e",
+ "42a623abc5d84c0eb7de4e5323bb6546",
+ "a65484354d254516936fcb425917a4b7",
+ "64029a1e70e040b49e38d38bd36823fd",
+ "3e1ec3a51e9b4fbbab489d34640cda90",
+ "ea0910fc31e44597968b2129272cc94d",
+ "3a0e9adc345f409cbcd79d1bd19219e6",
+ "3fe7e7f00ca746cc8cc762da6f365fde",
+ "6466eff2786241eeb142f17758894bb2",
+ "c181408b9b2b437ca11d584e3d1e94e7",
+ "0371aa5607604c06a868deb2a413cb31",
+ "c212598c5a8747f783a6efc18816e868",
+ "89ed71090d5c4366b21d25ad102e7da7",
+ "4ab21d7b956e46348ad6f6542fd92c2d"
+ ]
+ },
+ "id": "iHwVV8f6s1EC",
+ "outputId": "47cb80da-266e-40c2-cfc1-3f3e5421b50b"
+ },
+ "outputs": [
+ {
+ "name": "stderr",
+ "output_type": "stream",
+ "text": [
+ "Loading pipeline components...: 100%|██████████| 7/7 [00:00<00:00, 21.14it/s]\n",
+ "Expected types for unet: (,), got .\n",
+ "100%|██████████| 30/30 [00:09<00:00, 3.19it/s]\n"
+ ]
+ },
+ {
+ "data": {
+ "image/jpeg": "/9j/4AAQSkZJRgABAQAAAQABAAD/2wBDAAgGBgcGBQgHBwcJCQgKDBQNDAsLDBkSEw8UHRofHh0aHBwgJC4nICIsIxwcKDcpLDAxNDQ0Hyc5PTgyPC4zNDL/2wBDAQkJCQwLDBgNDRgyIRwhMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjL/wAARCAQABAADASIAAhEBAxEB/8QAHwAAAQUBAQEBAQEAAAAAAAAAAAECAwQFBgcICQoL/8QAtRAAAgEDAwIEAwUFBAQAAAF9AQIDAAQRBRIhMUEGE1FhByJxFDKBkaEII0KxwRVS0fAkM2JyggkKFhcYGRolJicoKSo0NTY3ODk6Q0RFRkdISUpTVFVWV1hZWmNkZWZnaGlqc3R1dnd4eXqDhIWGh4iJipKTlJWWl5iZmqKjpKWmp6ipqrKztLW2t7i5usLDxMXGx8jJytLT1NXW19jZ2uHi4+Tl5ufo6erx8vP09fb3+Pn6/8QAHwEAAwEBAQEBAQEBAQAAAAAAAAECAwQFBgcICQoL/8QAtREAAgECBAQDBAcFBAQAAQJ3AAECAxEEBSExBhJBUQdhcRMiMoEIFEKRobHBCSMzUvAVYnLRChYkNOEl8RcYGRomJygpKjU2Nzg5OkNERUZHSElKU1RVVldYWVpjZGVmZ2hpanN0dXZ3eHl6goOEhYaHiImKkpOUlZaXmJmaoqOkpaanqKmqsrO0tba3uLm6wsPExcbHyMnK0tPU1dbX2Nna4uPk5ebn6Onq8vP09fb3+Pn6/9oADAMBAAIRAxEAPwCeiiitGAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABikpaKAEpaKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACjFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABSUtFACUUtFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABSUtFACYpaKKACiiigAooooAKKKKACiiigAooooASloooAKKKKACiiigYUUUUAFFFFABRRRS6gFFFFABRRRT6AFFFFAgooooAKKKKBhRRRSAKKKKACiiigQUUUUwCiiii4BRRRQAUUUUAFFFFABRRRSAKKKKd+4BRRRRcAooopDCiiimAUUUUgCiiimxBRRRSGFFFFAgooopgFFFFABRRRSGFFFFHUAooooAKKKKYgooooAKKKKQBRRRTAKKKKACiiigAooooAKKKKACiiikMKKKKYBRRRSEFFFFMYUUUUgCiiimIKKKKACiiikAUUUUwCiiigAooopAFFFFMAooooAKKKKACiiil10GFFFFABRRRQIKKKKYBRRRQAUUUUgCiiigAooopgFFFFABRRRTAKKKKQBRRS0DEoopaAEopaKBCUUtJQMKKWkoAKKKWjyASiloxQAlFLSGgBaSiigAooopAFFFLTW4CUUtFAhKKWilYYlFFFMAooopAFFLSUxBRRRS6jCloooEJRQaKBhRRRQAUUUUXAKKKKYBRRRSAKKKWmAUUUUCEooopDCiiloEJRS0lAwoopaYhKWiigAooooASiiikxhRS0lPzAKKKKQBRRRQAUUtJQIKKWijcBKKKKYwooopAFFLRQIKSlpKeoBS0lLSGFJS0lAgooooGFFGKKACiiimIKKKKQwooooAKKKKACiiloASiiigAooooAKKBS0wEopaKQhKKWkoAKKWigBKKKKBhRRRQIKKKKBhS0lLTEFJS0lABRRRQAUUUUAAooFFDAKWkpaACiiigAooooAKSloo8wCiiigAooooAKKKKACkpaKAEopaSkMKKKKAClpKWgQUUUUwCiiigAooooASilpKBi0lLSUCClpKWgYUUUUCCkpaKAEopaSgYUUUUeoBRRRQAUUUtACUtFFAhKWiigBKKWkpDClpKWmhCUUGikMKKKKAFopKWmIKKKKAEopaSkwFooopgJRRRSGFFFFAC0UgpaYgooooAKSijFAwopcUlABS0lFIAooooAKKWkoAWikpaYgozRSUegC0UUUAFJilooASilooGJRRRSAKKWinpYQlLRRSAKSlpDTAKKKKQwpaKKYhM0tJRQMWkopaQgooopgFBoooASilopDEopaSiwC0UUUxBRRRQAUhpaQ0AFFFFABRRRQAUtJS0AFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUlLRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAJRS0UAJS0UUAJS0lLQAUUUUAFFFFABRRRQAUUUUAFJS0UAJRS0UAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABikpaSgApRSUtABQaKQ0AFLSUUDFooooEFFFFACUtJS0AFFFFABSUtJSYC0UUUwCiiigAooooASilooGFJS0Yo8hCUtFFABQaKKAEopaKQCUtFFNAFJS0UgEpaKKYBRSUtABRRRQAUlLSUAFFFFABRRRQAUtJS0AFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUlLR3oASloooASlpKWgAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKOoBRRRQAUlLRQAUUUUAFFFFACUtFFACUtFFABRRRQAUUUUAFFFFABSUtFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRSAKSiincYUtFFAgoooNACUUUUDCiiigQUUUUAFLSUtAwooooEFFFFABRRRQAUUUUAFFFFHoAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUdQCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACkpaKACiiigAooooAKKKKACiiigAooooAKKKKACiikoAWikpaACiiigAooooAKKKKPQAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiikAlFFLR1AKKKKYBRRRQAUlLRQAlFLSGgAooooAKKKKBi0UUUCCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKOugBRRRQAUUUUAFFFFABRRRQAUUUUdQCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiijqAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFACUtFFIAooopgFFFJQAtJRRQAUUUUAFFFFABRRRQMWiiigQUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAJRRRQMWiiigQUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUaAFFFFABRRRQAUUUlAC0UUUAJS0lKKNQCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigApKWkNABRRRQAUUUUAFFFFABRRRQMWiiigQUUUUAFFFFHmAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFJS0UAJS0UUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRR1AKKKKACiiigAooooAKKKKACiikNAC0lFFAxaKSloEFFFFABRRRQAUUUUAFFJS0AFFFFABRRRQAUUUUAFFFFABRRRQAUUlLQAUUUUAFFFFGlgCiiigAooooAKKKKACiiigAoooo6AFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFBoooASiiigAooooAKKKKACloooAKKKKACiiigAoooo8gCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKOoBRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAmKKWigBKKKKNgFopKWj1AKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiikoAKWiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACkpaKAEpaKKACiiigAooooAKKKKAEopaSgBaSiigYUUUUxBS0lFIBaKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooASiiloGJSiiigQUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRSUALRRRQAUUUUAFJS0lABRRRQAUUUUAFKKSloGFFFFAgooooAKKKKACiiigAoooo9ACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiijoAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFACUtFJQAtFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFJS0AFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUlLRQwCiiigAooooAKKKKACiiigAooooAKSlpKACiiigAoooFAC0UUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFGgBRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUlLRQAlLRRQAUUUUeYBRRRQAUUUUAFFFFABRRRR5AFFFFABRSUtABRRRQAlLRRSASlpKWmAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUlApALRRRTAKKKKACkpaSgAooooAKKKKACiiigBaKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooASloopAFFFFMAooooAKKKKACiiij1AKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAoopKAFopKWgAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooASlpKUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUdAEpRSUtIAooopgFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRRqAlKKKKACiiigAooooAKSlpDQAUUUUAFFFFABRRRQAtFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFACGiiigYUopKKAFooooEFFFFABRRRQAZopKKAFopKXNABRRRmgApKXNJQAUtJRQMM0UUUAFFFFABRRS0AFJS0lAhaKSloAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAopKKAFooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACkpaSgAooooAKKKKACigUUALRSUtABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUeoBRRRQAUlLSUALRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABiiiigAooooAKKKKACjNJRQAUUUUWAKKKSgBaKr387Wum3VwgBeKJnUHpkDjNednx7rJ6Laj/tkf8AGmlfYD0yivM/+E81n0tP+/P/ANej/hPNa9LX/vz/APXp2YHplFeZ/wDCea1/06/9+f8A69H/AAnetf8ATr/35/8Ar0rMZ6ZRXmn/AAnms9xan/tl/wDXr0HTZ5LvS7W4lADyxK7bemSO1FrCLVFFFIYUtJS0CCijNGaAEpaSloAKKKKACiiigAooooAKKKKACiiigAooooAKKKSjYBaKKKACiiigAooooASilpKQC0lFLTAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKSlpKACiiigBBS0lLQAUtJS0DCiiigQUUUUAFFFFABRRRR6gFFFFABRRRQAUUUUAFFFFHUAooooAKKKKACiiigAooooAKKKKOoBRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRSUALRRRQAUlFFABRRRTAKOtJQSF3HIG31xQBE11boSGuIV+sij+tQvqlgg+a+th/21X/ABrxyRC0rnGcse3vSCLPaq5RXPV9W1jTJdHvYY7+2eR4HAVZASTjpXmsemh1B3NUNpCv2hN2CMjiurjtIwBhf1otbYTkc7/ZY/vN+lL/AGUP77V0otI/SpBaR/3aNRc5zH9kr/faj+yV/vt+VdT9jj9KX7HF/do1DnOUfSgM4dvyFegaNrukJpFnC+o26SxwqjK7YIIGKyGsYccr+Rri5rWRZG+Q4zRZvcFK564Na0o9NStD/wBtlqWPUbGU4jvrZj6CZf8AGvGDA46p+lMMRAJ24/CjlKue5ZpaztF/5AtiCefITr9K0PapGFFFFIYUUUUALRRRQIKKKKACiiigAoooo9ACiiigAooooAKSlooASloooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKDQAUlFFABRRRQAlLQKKGAUtJS0AFFFFABRRRQAUUUUeYBRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUlFFAwooooQBRRRQIKKULkgetc9qHibSZtKvI4r5BM0MiqjAg7sEY6U0BuXYb+zrp4m+7BIwK84IB6Ee4rxMEnBZizEDkmpomk3BFdhu4wGIq7/Zc5X/V/hmqtYVy3ZQM0yfu22nH8PFb32Abv9Vx6baWz2pbxKWAIVQea1TPFn/WL+dIzbK9pZwhW8yBM9soKvBIwAAijAx0qITw95F/Ol+0Qf8APVPzpkku1P7i/lS4X+6PyqH7RB/z1T86X7TB/wA9k/OkBLtX+6Pyo2r/AHR+VR/aYP8Ansn50faYP+eyfnQIk2r/AHR+VRyQxlT+7TOP7oo+0wf89V/Oj7TB/wA9V/OmBUFujEZiXr/dFc5eWameVtuRuPGOK603EHaRaQ+WT0X8qQ0zzSRWSU4LDnHWvSvC97YxeHLKOW9t1lCEsrTAEHceuTXK3lukkkw2jJLYOPeuaeJ1JBQ/lTsapntaurqGR1dSMhlOQfoaWuR0LxNpNh4fs4Lm62zRxkMioxI5PtXWoweNXXlWUMPoeamxQtFFFJjAUtJS0CCiiigAozRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABQaKKAEooooAKKKKAAUUCigApaSlFAwooooEFFFJQAtFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRR5AFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFJS0UAJRRRTQBSgZoUFjgVzmveJdOXSL2G1v0N0YyiBM5DZx1xxRYDpwCBnB6ZrxAgtI3fJNWodV1bISPULwnHAEzdPzq1p1q6M7SIRkcZqthNkVjbo0qFl5HIrcA6VGqgYxSvKkQG91XPqanchskjOJM+9Sh6x5LmM5xOPwesNru43H9/J1/vGqUWwSudruJpcmuH+1XH/PeT/vo0farj/nvL/wB9Gq9mx8h3GTRk1w/2u5/5+Jf++jR9suf+fiX/AL6NPkYch3GTRmuH+2XX/PxL/wB9Gj7bdf8APzL/AN9Gj2bDkO4yaN1cP9tuv+fiX/vo0fa7j/nvJ/30aOQOU7pW5rUXtzXm6XshCgu+fXca0YWbcPnbr6moaE4nQSIDK5x/Ef51RuIAw4UE/wC7VpelSBQQKLiOPvUKTOuwjjpXsVjNA9ha4uYWbyUyBIMg7R715zqFokk7vg5x2+lc4VAJwBmjctM9wPXrSVymieKNItdFsbee7xMkQVlCE4bNdXUlBRRRSGFLSUUALRRRQIKKKKACiijNABRRRQAUUUUAFFFFABRRRR5AFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFACUtJS0AFFFFABRRRQAUUUUAFJS0hoAKKKKACiiigAooooAUUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUmaWkoAWiiigApKWkoGFHeijHX2Un9DTQiWNTnofXpXiEmXupB3Mjfzp1pqmopgJf3SDPG2Zh/WrEenziVXIz8wJOarYTLNpYtFMHZlOPStRQKYBinblAJLDA96lkjwQBknj3qjdXtk8DjzY2badv1p8uoWvlOBOhO04wa5fNXGNwSHZ+lAQk9KUQu38Jq15behrRysddKi5ashWBT2pwtl75q7HZXLqGS3lYHoQhNP/ALPvP+fSf/v2azc/M61Qj2KH2ZPej7MnvWh/Zt9/z5z/APfs0n9nX3/PnP8A9+zU8/mV7CHYofZk96T7Mnqav/2fe/8APpP/AN+zR9gvP+fWf/v2aOd9xexh2KH2VfU0026+prQNjd/8+03/AH7NNNldf8+03/fBo533JdGHRGYUKnHNJvYdGb86vNGwJBGCOoNVpI8Atn8K0TuctSjbVG5Fd2wUZmQHH96teJ1ZFwQeO1cRn6VrxTqpGJAPo1JxOSUToWUMTkCqklvDtJ8tM4P8NKl1EUGZVzj+9T8hlPI5FRsSclg+YOP4h/OvbTJEOsiDA/vCvLm0yJugIrElG2V19CRzRuWme25B5BBHtRVDQzu0DTm9bZP5VfpFBRRRSGFLSUUALRSZpaBBSUtFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUlAC0UUUAFFFFABRRRQAlLSUtHmAUUUUAFFFFABRRRQAUGikNABRRRQAUUUUAAooFFABRRRQMKKKKQC0UUUxCUtJS0AFFFFABRRRR0AKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiikoAWiiigApKWigAoopDQAUUUUwFHPSsi+8SaPZLMkt/CZFV1MaHc27BGMfU1NdeJtF0udob28Mc8ZG6NY2YgEZB4GK8quVE+p3E6R7opJmddwwcEkiqSBkVpaEKrnriulRfkH0ojiiEa7UUDHpS5+lS2Q2KRx9aozXtsI3AnjyVIABq006DP7xAf96uVJyxOO561UY3GkNB+lTCIHqKFjB6gVdWOrk7HVRpc17jYIywBq6I8g4FEUeQFFdxb2ypDGAq5CjtXNUqcp6tOGmo/Tl26fbAf881/lVsZ9TTUU4GP5Va+yT/88ZP++TXE2bkPPrRk+pqwLOc/8sJP++DR9jn/AOeEn/fBpXArc+po59as/Y7j/nhJ/wB8mk+x3H/PCT/vg0XC5VI+tJgmrX2O4/54S/8AfBpPsk46wyD6qadx3PNtTtZRfXLmJ9vmMc47ZrLK8c139/GGt7gf7Lf1riBbu52qpJx0Fd1GpzI5qlNIpSINpOBVatGaF40O9CPqKqFF/uiuhM4K1Hmd0XopIeMuvT1rah2lFIIIxwa5HHtW9azxLBGPMQYUcZqJROBo1wFz0HWudu4lM0uBg7jzWzEwddwIIPQ1IbeNwSVBz7VK0JOv8OOh8Oacu9dwgAxuGeCa1Ca8SdWS4faCCGNemeDpYU8OWyNKgkLOSpcZ+8abRpc6GijOenT2opAFFFFIYUUUUALRRRQIKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACkpaKAEpaKKACiiigAoopKAFopKWgAooooAKKKKACiiigApDRRQMKKKKACiiigQCiiigApaSigYtFFJSELRRRTAKSlooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigBKKKKBhRRS0CEqO5mW2tJp3DFYkZ2CjJwBzUoGSAK5/Vdc0+60C+FtewmRonQLvCtnODx1qkB55r1z/aut3V9CreXKw2BuuMAD+VW4rKRrdXxjC9DVOGIl0IBI3Lz+NdcDVN22JbKSYEa5PYVVkvrYE/6RH+dX7hgvzMVXnqTiuNk/1r9/mNKKuJK5GeWP1p6qD19KEXc2CKuxRjYvHark7HVRpc7Luk2RuwRsDkHvW9Do0qyK3kjgg9RR4egVY0bHJzk49662G1lPPlP/3ya4atRqR7NOmlFJkENtGAMxID/uitJLXI+5+lEdnMeBDIfoprsYl2xICOQoH6VyTnYpyscrDZM8iqsZzn0rr8nPWkpaxlJtmcpXDJ9aMn1ooqSQyfWjJ9aKKADJ9ahucm1lGf4G/lUxpKBnnc2kylCCoIYdKw59Mt4A7xxbWUHHJr11gCMYH5Vxt/pR8+WN14Oc4PY100qrTNNJ7nl165mjKsBjOeKzTCue/516LeeGbJLGaVFcMkbMPnzyBXFPEPSvRhVUtjN0rLYwWTDHANN6VpXKgM2Kqgd8VspXPLqULM3dNmgWyhVpYwwXkbhkVpIVYAhgR7VxVdPY3ltHaQo08YKoMjNS42ONor6jbFrrckZI2DotZUqGNmBUqcdCK7JMMoIOQRmsLVLaSS9dkRm4AyAcdKV+gJnpGmLjSLMnnECf8AoIq0a8x8MX8dhr6G8nMUKo6nzGOAcccV6TBcwXUXm28ySx5xuRsjNDRZJRRRSGLRQKKQC0UUUCCkzS0lABS0lFHqMWiiigQUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFJS0UAJS0UUAFFFFABRSUUALRRRQAUlLRQAlFFFABRRRQAUUUUAFFFFAwoopaQCUtFFAgooopgFFFFABRRRQAUUUUAFFFFABRRRR5AFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUlLRQAlFFFAwozxSmmMwRWZiAqgkk9gKEA4nCk+gJrwpcs2cck9a9ePibRJIX2apbZKNgFiCTjgdK8nW3lG390//fJq0I6HS1/0NPqa1Q3FZ+mxslkgZSDz1FGqMVsnIBzjqBU9TPdketuDp7AEZ3CuaxSli3Uk/jT403yKv94gVqlY0iug+yjWW9gRhlWcA128Wh2ZYDymAzj75rLttAjhuo5A75VwRz712tjYm4u0iG7LE8gVx16t3oz2cLRdOL50U7LToIfLWNWAzx8/vXqKjAH0rnbbTVhCo0JbaepSukrz6s+Y3m77Bz60tFFZGYUtFFABRRRQAUUUUAIaKKKQCGmlQew/Gn0GmMo39qLiwuIVRSzxMq8DqRXjV7pN3asBLFg5xwQf5V7jWJrekQ3Vm/kWyeduzlVANbUavI7Fxd9GeL3Niwy7RnH0rNljVc4GMV6Fq+hXlvpk80lsyIi5LHHHNcLMnJzzXoUqnMZ1qaa0Mil7VZljG0kKKrV13uePUpuDszurcjyYxuH3F/lVtAOK8+RsZwcfjXe2ZJtYv9xf5Vm1Y52rHFahkanc/wDXVv513PhC9tLfQI45ruCNzI52NKAevpmuP1C0nfUbh0gkYGQ4IQmsudGidkdCrgchhzTKR7apDAEEEEZBFLVbT+dMtCf+eEf/AKCKs1LKFooopDClpKBQAtJS0lAgooooGLRSUtAgooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiijoAUUUUAFJS0lABS0UUAFBoooASiiigAooooAKKKKACiiigYUtFFAgooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigApKU0lABS0UUABqrqHGmXZ9IX/wDQTVqqupnGk3p/6YSf+gmmgPFoh9wfT+ddeo4rkoBzF9RXWgCmyZEyniqmpH/QZh/sGntwhrlZJ5XZgZXIJPBY00rglci7V6BY6bZNZ20n2WLd5asTt5ziuCClugJr0jTedPtv+uS/yrPENpKx6OBScndFuCJXmRSOCwHv1rvrXRba0uVmjMm5c43H1rhrUf6TF/vr/MV6Zj5jXmVW+h6UmKKWgUVgZBS0UUAFFFFIAoopKYBRRRQAUUUUvIAooopgGKaRTqQ0DMnxDaPd6FdQRqCzgDB+orzmbw5aB8OhBzz83evVrgE28gHXaa4fUcxyYZSGb5hkVvRm1ojaFmtTze+tI45ZFAwoJXisi4gWIZUn8a7O901WZ3ZjhiTmsDU7JYbZnBJ6da9OnUucmJoppuxiCu/sZYVtYgZY87BkbxXAEUox2raSueNOJ6VLNHHHuyOvTNedX7tPezyMMlnJrdNx5qYV92Ou05rMnspNjzbeBzUIiKsej2mu6TFY20bahbqUhQEb+hCitSCeK5hWaCQSRMMq69D9K8Vr1jwsc+FtO458s85/2jQzQ16KKKkYUUUUALRRRQITFLRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRSAKKKKfkAUUUUAFFFFABRSUtABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUlLSUDCiiigQUUUUAFLSUCgYtFFFAgooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigANJS0lABRRRQADJOK5TV/GGlSabeW0EsrTvG8agxEDPTrXVd68Qm/wCPiT/fP8zVRSYF6ysi5jkZsDIOPpW8GyehrN03/VR1pUnuSzPuNTWLcphfgkZyKwD1OPWr99yGP+1VHFaQLSsXrGIyJwCeT0ru9NB+xwLtOdgGK5zw3HgRtgct/Wu3sIw+pQ4II80dPrXJXnrY9jC07Q5ia1srn7TETbygb1ydh9a9DPU00cU6vOlPmNZSuLRRRUMkWiiilYAooopAFFFFACUUtFMBKKKKQBRRRTAKKKDQA1hlSK5zUNCuLu4WQFAoXGCfeukppqoycdUUpWPPtY0yOCN40TEq4HBzXH6jY3IjbMDlRycr2r0XW1zfyn/aFZl8ubOYf7B/lXXTm1Y2eqPMmjXy2wo+6e1Y6mt+RcRv/un+VYAr0YO6PIxqs0buljbCT6mr92f9Ck+g/nVHTj+4H1q7eYFjJ9KT3PP6nMV6v4U/5FXT/wDcP/oRryivV/Cv/Iq6f/uN/wChGhlmvRRRUjCiiigBaKSigQtFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFHQBKWiigAooooAKKKKACiiigAooopAFFFFMAooooAKSlpKACiiigYUUUUCAUUUUAFKKSloGFFFFAgooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACkpaKACkpaKAEooooAQfeH1rxCb/j5k/wB9v5mvcB94fWvD5/8Aj5k/32/mauAG3pv+pj+laNZum/6tPpWlUvcTOevfun/eqlV68/1Z/wB6qNax2KOt8OJlLUerj+de02MaLEhCrnHXFeO+ElDXGnKehkH869riQKMDoK8nFP3j2afwIlpRUbusaM7sFRRliTgAetUf7e0kddTs/wDv+v8AjXMk3sU2luadLWYNe0g/8xSy/wC/6/408a1pZ6alZ/8Af9f8afLLsLmj3NGiqH9s6Z/0ErP/AL/r/jUkOpWM8gjhvLeRyMhUlVifwBpcst7Bddy3SUUVIxaKKKQBRQaSmAtJRmikAUUVXu761sIxJeXMNujHaGlcKCfTmmtdgLFJWZ/wkein/mL2P/gQv+NH/CQ6Mf8AmLWP/gQv+NVyS7C5o9zTpDWb/wAJDov/AEF7H/wIX/GkPiLRP+gxYf8AgQv+NHJLsHNHuP1Gxt5IxI0eXZuTmubv4kEcy442kV1ElxBd2UctvNHLE3KvGwYH6EVz2oAbZfoauLadmaQZ53d2cSW0zAHIRj19q4odq7++H+iT/wDXNv5VwFevQd0cOYr3omnZ3yxhYwjEk+uK6FDleRjPY81yNv8A6+P/AHhXVr0FVJHmHP34AlfA/ir0rwr/AMitp/8AuH/0I15rqH+sb/er0rwr/wAitp/+4f8A0I0uhRsUUUVIBRRRSAKWkpaYBRRRQAUUUUAFFFJQwFooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooASilpKACilopAFFFFMAooooAKKKQ0AFFFFAwooooEFFFFABS0lLQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFACUUtFACD7w+teHTf8fEn++38zXuI614dN/r5P8Afb+Zq4AbWm/cT6VpGs3Tf9Wn0rS7VL3Ezn7z/V/jVGr13/qvxqjWsdijuPCA/wBL0z/rov8AOvaxXivhH/j50v8A66J/Ova8V5OJ+I9in8CM7Xv+Re1L/r1l/wDQTXzeAuBwK+oHRJI2R0VkYYKkZBHpXz/4zhih1rbDEka7TwihR94+la4J7o5cZHZnP7V9B+VIFB6Ln8KbVq2JEUuD2r0DgCDTry4XdBY3Eo9Y4WYfoK6f4dxS2/j6zjlieNwsgZWUqR8h6g1698EnY+A3wT/x+Sd/pXHzDHx7vM9fNf8A9FCsasrwkvI0pfGvU9IFLQKK8ToewLSUtJTAKKKKACiiikAGvNvjC5Gj6YvGDcMTn/dr0iue8Z2tvc+HLhp4UkaIboyy52k8ZFb0HaomRUjzQaPnvaAe1Jgen6U+fBlb03HFNj+8fpXt2PGBUZiAqEk9ABk1O2mX6xmRrG5WNRksYGAA9c4rW8Jkjxfoxyc/bYv/AEIV9UeMgW8G62Mn/jyl/wDQTUuXK7AeWeCW/wCKH03/AHGH/jxqa/8AuyfQ1W8DHPgbTf8Adf8A9DNWb77sn0NeNJfvX6nu0PgXocNff8ek/wD1zb+VefV6Fe/8es//AFzb+VefV6tDY5My+KJLbf8AHzH/ALwrqxXK2v8Ax8x/7wrqhWkjzGYGof6x/rXpPhX/AJFbT/8Acb/0I15tqH32+tek+Ff+RW0//cb/ANCNT0GbAooFFSAUUUUDCloooEFFFFABRRRQAUUUlAC0UUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFHkAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUhpaSgAooooAKKKKACiiigAooooGLRRRQIKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACg0UUAIOteHS/65/8AeP8AOvce9eHS/wCuf/eP86uAG1pv+rT6VpHoazdN/wBWn0rRPQ1L3EzAu/8AU/iKomr11/qfxFUa1jsUd14R4uNL/wCuifzr2rPNeKeFTiTSz/00T/0Kvaj978a8jE/Ee1TXuI5i7+IXh2yupbea5m82FyjhYGPI4PNeQeKNStdU1BJ7VmZQhB3KV5zmofEI2+IdSB/5+ZOv+8ay8V3UKEYK6PMrVpTdmbWi+DPEXiK2NzpOly3UCsULqVAyOo5NbA+GfjO2tZpJdBnChSThlOAPxr1n4FqD4Nk4/wCXl69J1d1i0a+kOBtt5Dn/AICa0c3exznh3wu8feH/AAz4WmsNWu5IZzctIqrCz5Ugc8Vk2WsWmt/GttQsXZ7W4lYxsylSR5eOh+lebjBwcV03w948dabjP3n/APQDU1Y+5J+TLp/Gj3ukpaK8RHshRRRTADSUUUAFFAopMBGIVSScADJrzzxL8QdAu9JntLa4meZjjBhIHX1rvrs4s7gjqIn/AJGvl+TmV/Xcf5124SkpNt9DnxNV046dSzY2F1q+ow2NhCZrqdwkcYIBYntzxXYJ8HfHQO46MOn/AD8R/wCNUPhoqn4iaGG/5+Rj64NfXeBXoym4nlHyKdE1TwX4n0t9ds3tAk8c55D5RWGSMHnpXsPiT4veEL/w5qVpbXly889tJHGptHGWIIHJ6Vx3x8lB8XWEQx8lmCfxY15ORgZ6cU7c1mwPafAjZ8D6f7bx/wCPmrd70k+hqv4GTb4E00+oc/8Aj5qxe/df6GvInrVl6nv4de5H0OHvP+Pef/cb+Vef16Bef6if/cb+Vef16dDY48x+KJNaf8fUX+8K6oVytp/x9Rf7wrqa1keYzC1AfM31r0jwr/yKun/7jf8AoZrzfUDy3+9XpHhT/kVdP/3W/wDQzU9BmxRRS1ICUtFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUlAC0UmaWgAooooAKKKKACiiigApKWkNABRRRQAUUUUAFFFFABRRRQMWikpaQgooopgFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUhpaKAEooooAK8Nl/1z/7x/ma9yPQ14bJ/rm/3j/OrgBt6b/q0+laJ+6aztO/1afStE/dpPcl7mBd/wCq/EVRq9d/6r8RVCtI7Fnc+G3ES6bIxAVWRiT2G6vZ0mSVBJGQyNyCO4rw/S2xp9rz/wAsxXsWkHdpFqf+mYryMStbnuU17iOT174f6VcG91HzrtZWDzFQ427sE+nSvHh0H0r6P1ID+zbrP/PJ/wD0E184ce1dWEnKSd2cGMhGLXKjd8O+IdV0S7X+z9WubJGOXEcmFP4Hj9K6jUPHuv3thPbSeJZ3SVChQMo3AjkcKK86zTgfpXU0mcViSKPdKiZ6sFx+Ne96b4G0LSdSt7+zgmjuIM7SZSwJIwcg/WvCbNSbyE7ScSL0HvX0yDkZ9eRXFjJyikk9zswkU7toWiiivNO8KKKKACkpaSmAUUUUgGyIJInjJwGUqfxFeB+OfDFt4c1SKG2mlkWWMyEy44Ofavfa8d+LB3a7aAA8QH9TXXhJNTt0MMSk6bucFZXM9leRXNtPJBNGwZJI22sp9QRXZf8ACeeISmD4k1D/AMCGriQMGng+9eq9Tyi7q2p3mrXn2m9vJ7qYLtEkzlzgdsntXr1r8KvD72UEkj3u9olZsTDqQCe1eKZGa+oLd82EGOf3C49/lFcuLnKCjys6sLCMm+ZHO6NaQWHh2ytIN3lxr8u45PJJqjfSLtkAPIBrWjjkttNhWSJ1KKN2R05rFvSCshHQ5rzov3mz2KSSVkcZdnNvP/uN/I1wFegXX+pm/wBxv5GvP69ahsefmXxRJrT/AI+4v94V1I6Vy1n/AMfcX+8K6rtWkjzGYGo/eb/er0jwr/yKun/7jf8AoRrzbUPvf8Cr0rwt/wAitp/+43/oRpdBmxQKKKkBaKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiijyAKKKKAEpaKKACiiigAooooAKKKKACkpaSgAooooAKKKKACiiigAoooo6DClpKWkAUUUUxBRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFACUtFFADW+6fp/SvDX/1rf7x/nXuZ6H6V4Y/+sb/eP860gBuad9xPpWielZ2nfcT/AHa0e1T1Je5gXf8AqfxFUKvXZ/dfjVKtY7FHQaXdsttDGRwOM9+tex+H9TtZNItY/MVWEYGGcZ614ZYS7Qo9GrYi1J7aeIpLgAjof9quGvR52exQqLkVz3gxq6lXUMrcEEZzXJah4ZsnupPJ06ILnjbCP8K6y3kWREYHIZQasV50ZOJvddTz1fCg3Dbp68MP+WY9a2ofDEavu+xQDn+4tdRS03VkwU7bIht7WGCJFWGJSo/hQf4VPSUtQ22QFFFFSAUUUZpjCkoooEFFJRQAU1o0f7yI3+8oNPopoCF7O2kjZDBEAwIOI1/wrFfwlpToytagkjAOBXQ0lNTktgOTbwJYk5R9mR3QV1kaiOJIwchFC/kMUUU3Ny3Aqamf+JfL9P61xc7ZDfjXUapqFsbGZBMu/pj8a4u7u4ooJJXbCKCTxnirgjenojDu/wDUzc/wN/KvP66y412xeKRVkclkIHye1cnXq0YtLU8zMJxlKPKya0/4+4v94V1XauWs/wDj8i/3hXUnpWkjzWc/fdfxr0rwr/yK2n/7jf8AoRrzW+P869K8KHPhXT/9xv8A0I1L2KNiiiipGLRSUtAgooooAKKKKACiiigAooooAKKKKACiiigAoooo6AFFFFIAooopgFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFIaWigBKKKKACiiigAooFFABRRRQMKWkpaACiiigQUUUUAFFFFABRRRQAUUUUAFFFFABSUtFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAH7p+n9K8Lf8A1jf7x/nXunY/SvC3Hzt/vH+dXADb037if7taO5cHkdPWsO1dcKOM4rZtQvlLkChqwmjCucmL8ap11E6dcJn6CuacfOfqaqLGhFzVxUJwRVUCtK3QHBP+eKU9Dqw6u7HoNjqN3HbxbZ2ztX+I16evMak/3RXlqIkUEe3j5RXqKHMSH1UfyryK2569TZDqWkorDoZC0UUUgAkAZPQc1xjfFHw0hKmW6yCQR5BrsmGVI9q+f7jwV4gN1MV0i7KmRiCIzyM104enCbfOYV6k4W5D03/hafhn/npd/wDfg0f8LS8M/wDPS7/78H/GvLv+EJ8Rf9Ae7/79mj/hCvEP/QHu/wDv2a6fq1Hv+JzfWK3b8D1D/haXhr+/d/8Afg/40h+KXhv+/d/9+P8A69eYHwX4i/6A13/37oHgzxF/0B7sf9s6Pq1Dv+IfWK3b8D07/haXhv8Av3f/AH5/+vXY206XVtFcRZMcqK65HYjI/nXgH/CG+ITlRo92SR/cr3fR7eS20ayhlUrJHbxqynsQoyK58RShC3IzehVnNvnReooormOkWiiigBKQnAzSmuR1y8mh1eVFnkVFK8BiB0pxV3YqMbsyNUl2yvyTlzXP6xfwLp1whkUSNGQFzzmtHU7lXkOHXOckA9K4bVz5tw8wIIr0KVPmepdSbhTZjUlOoXlgPevQPBmyW04u4iem4V0xkQqcMv51Vj2KOAvSpjKhQ8r0qHqYtmLfHp9a9K8I8+E7A/7Lf+hGvL7hsn8a9P8ACP8AyKdh/ut/6GaT2LNqiiipYBQKKKQC0UUlAC0UUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAJS0UUAFFFFABRRRQAUUUUAFFFFACUUtJQAUUUUAFFFFABS0CigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAoooo6AFFFFABRRRQAUUUUAFFJS0gCiiimAUUUUAFFFFABRSUUAKDXN3nhHRIdPupUtGMixO4ZpWODgn1ro6r6iT/ZV5z/ywk/9BNNMDxaJiHXmtmyOSmfWsSPG5Tn0rXspFBTkdfWrkJmwTxXKOP3jfU103mKejA1zjwyB2Oxup7UogiIE1etp89OPaqR5waFJDD61Ulc2pTcWdjBq80oWM7QOBxXtMdxEsSZlThR/EPSvnOOcpIRuxmt2yuy6qGIzmuGtR5tj1oVFLRntz6jZxsqPdQhmICrvGTmrVeYW0ai9tmHaRf516eTyfrXDUgobGjQtLTc0orMkWlpKWiwgpcn1NJRQMXJ9TSc+tFFACfrS0UUCCikopgFIWABJOAOSaM1Dc820w/2G/kaQ0hn9o2X/AD+W/wD39H+NcL4svoVv53SRHU4wVOQeKy0AwOBXO6rdD7Q6K2QDziuynQVy4y5W2VJZcHcOtZt1JkEVNJcqe5x3NZrOTkZOK9KEbHFia3RDe9Oh5lQf7QplWI4HWRDjPINXc82TuboRQvQdKz5QApqfzGGQSe9UpXYxn5j0rMggtwsl5ArDcpkUEHuNw4r2eOCK1iEEESRRR5CIgwFHpXjFiP8AiYWv/XZP/QhXtcmd7f7xpyKG0UUVABRRS0AFFJRQAtFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFJS0lABRRRQAUUUUALRRSd6AFooooAKKKKACiiigAooooAKKKKACiiigAooooAKQUtJQAtFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUGiigBKKMUtABVXUf8AkF3g/wCmD/8AoJq1SEZGCMg8YNMDwpRnAHJ9BVqJtpAPHPPtXtUUUUZASKNOf4UArxO4OLubJ/5aN/6Eau9wNmGWPaMutLcFTE209qz7eZPlLHHPpW1HNG6grkg+1S7pknNFGH8J/Km1qzwSgMQBjnvWTVp3KQ9WO8Ek9a1LaVlfg4rIzgg+lWoJWOSexqZxujsw1RJ2Z6RBIQEfncOQf1rrdDvpri5QSys2QTya8nstUl28hTg47/41rW2v3UDgx7FI6fKf8a4J0m9D1otSVz2NnCg5NSCvOdP8SX800QaSPDMFP7sdCa9Ba7tlYg3EI/7aD/GuKUHHcmUbE1LUAu7YkAXERz6OKl3r/eX8xUkWHUUmaWgAoopKADNGaaxCgsSAB1JqtJf2kY+a6hH/AAMUJXCxPJMkS7nYKM4yaoXGv6bbsFkuOT/dUmqGrazp/krH9rj3Fs9eO9efXuo28czbmYjJ5UZHWtoUuY0jFdT0c+KdLH/LZ/8Av2ahm8U6Y0MiiWTJQj/Vn0rzVdTsn6TqD/tZFR3F3D5EhWdPunGHrVYfUpqJej1C2bGJRXG304+1TEHPznH506O5ZCCM/jWc7FpGY9zmvRp0+U4MRVUI6dRXfdj2pmaKTPFbHmyld3YoyTxWpFKvyja/TH3ap2qjOe9bZVVAOBUSZDKsskZU8MOP7prGyfetG4uUKkBgazSrYyEbp6GiIy1ZAm/tj/02T+Yr2uX/AFr/AO8f51TtoI1tIFMUfEa9UHoKs5z1zUydwCiiipAWiiigBKKWkxQMWiiigQUUUUAFFFFABRRRQAUUUUAFFFFHXQAooooAKKKKACiiigAooooAKKKKPUAooooAKKKKACiiigAooooAKKKKACiiigAooooADSUppKACiiigAooooAKBRQKBi0UUUCCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACkpaSgBaKSloAKSlpKAFU/MPrXjV9Y3cd9cA2s4/evj923PJ9q9ko3EAnJ4qk7AeHx8HB7GtyybMC1hO2ZnOf4z/OrMbkLwxA+tU9hM2pSNjdOhrm66mMwFVz5f3eelZ0iIZGIVcZ9KlMSZkZpyPszxmkYYdh7mkrS1y02ndFiO528Akc1Ok5c5zms+nwuFbk0OCsdFOvK9mdvojqLWHLAc9z71u+ZFn7yfmK84Eg8tCG7HvU0Ev71MkAbh3rjlh763PRjXWiPR7d4zcxfMg+cdxWo0sYJ/eJ/30K8+WaPzk/eJjd13CpzcQhsGVMk4+8KwdJnTp3PZbaeFbWEedH9wfxj0qbz4v8AnrH/AN9CvJGkhB/1sf8A30Kb5sX/AD0j/wC+hWHsWJwXc9e86L/nqn/fQo86L/nrH/32K8fNxAP+W0f/AH2KPtNv/wA9ov8AvoUexYci7nq9/NEbC5Hmx8xNxvHpXnEso28MPzrON3bD/l4i/wC+xUL39oP+XmL/AL6q402i4qMeo/UZQIwSe/rWFeTq0RwwPPY1Lq+oQNa4jlDnPRTXNF2JJBxzXdRp6XZyYnEqDstS3JJwSDzVYyuRyf0pu8lcZpua6bHm1K7b0ZJ5rDuKjoopmEpyluwoHWnoM10CIuxchenpUt2JuRxgBB8o6elJO52U2Y4VscHFZbSyHqzfnUpXCxC4zn8a9m0wbdFsRjpbRjp/sivHCcg/SvZdPLDS7QYx+4jBH/ARTnsFyeiloqGMKBRS0AFFFFIAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiikoAWiiigAooooAKKKKACiiigAooooAKKKKACiiikAUUUUwCiiigAooooAKSlpKACiiigAooooAKBRQKBi0UUUCCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigBKWkooGFFFFAgpOtLRQBl6zptncaVdf6HAZRC5RhEuQcHGDXkyMB1PI7Zr2w1n31jby2lwWt4S5jcgmJSc4PfFUmB5hBJhhnpWqI4jgkKT9a5mIspB9u9aMMmFA4zTaE0LewQqJHVQCCelZddKPLaLnaflqi6J5bHaudp7URlYEzIoopa1GJmjNFFFhhR+VWRGp7CrcMC+WpCj8qjnSOhYdvqZeDRg+hr07SYY/7JtiY4yRHySoqzDHGQxKIfmP8IrB4pLodKy+6XvfgeUc+lGD6V62YY/8Anmn/AHyKoz2ksnyiJeD1AHIoWLT6DeXf3vwPMiCKTPvXV6tbskbxsmG47VhyWhWMsUwAPSt4VVJHNUwsoPQo7iepNFIKWrOUKKKKACnpG7EEIxGewoCggVr6eNttjJ+8ahysI0UCKANqjj0FRTyDy25HT1qFl5JA61QnkCDaynJHpWa1YrDZpAQcEVVX5mH1pq43qPUj+devnw9pBIJ02245+5WrdijNj8GaOsany5y20ZPm85rohwAPQYoIorNgLRRRSYBS0lLSAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKPMAooooAKSlpKACiiigAooFFABRRRQMWiiigQUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAJRRRQMKKKKBBRRSgc0wG1FcA/Z5eD/q27exrgfGuqXUOsxCz1CRYWt1OIJvlLZIPQ9a5z+19TIIOo3RzwR5xq1G+oFbFC5DD6005JySTRzTGals+HxxV/apGMDGPTrXO7m9T+daWnPlSGGfrUtW1JaLEtvF5TEIudp6CsUqQK6NVBXkDv2qpexhSuABQpWCLMakqzMo2EkDPrVetU7lNWLAdeORXW6DYwXWmo7oGOTz+NcVXf+GFCaJbt3YHP51y4hcsbo9LB1OedmjZit44oljUYVRgCpQAowAAPambx60b64bnpj80VHvo30AZmsadLeDdDhmIAIJxXO3kBjs5c8EKQa7QvXJ6r/wAes/PY10UZO9jGqlyt+RyNLSCivQPnxaO9FW7GNH371DY9aT0A1Y1XYvAzj0pSSAcfpSjoO3FQXLlYHwcHHY1kSRzSMFb5jwKzGdn+8xOPWhpHOcsT+NNq0rFCr99R/tD+de5EY4rwsEhgR2INde3xE1EniytFGR/eP9aJJsD0Oimqdyq3qM06swCiiikwFooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiijqAUUUUAFFFFABRRRQAUUUUAFFFFABSUtFABRRRQAUUlLQAUUUUAFFFFABRRRQAUUUUAFBoooASiiigAooooAKKKWgYUUUUCCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiikoAKKKKACloooABVC91WygtbjF7beYIXIXzVzkKe2aral4msNGvTbXfn7yiyL5abgQc+/tXlDjMhbaOTnp6mrSuMhVcKOADindK1lKnstIUUnoPyquYRl0VovGu0/KvT0quqLjoKLgVaersvRiPoandV2HAHSq1NO4zT09znc7n05PFaQeM85WubDEdCRWpZuWt0ySTUuNtSJIlu4RKV2hSuOecViY5roB+lY5tJNxGxuvHFVBgmVu9dhpGq2lvpdtE9wiuq4IJ6cmuTaMjsfypp44IpVKaqKxvRrOk7o74a3Y/wDP0lL/AG3Y/wDP1HXn/FGB6Vh9Vj3Or+0J9kegf25Y/wDP3H+dNOuWP/P2lcDgelJR9Vj3H/aM+yO3m1q2YHbdr+BrHvL2GW2kAlUkqe9YGKMVcKCjsyZY6clZobUio3UKfypBG56Ix/Ct21GIIwRg7R1rVuxwhbxRtGhMa5x6VJtQDhF/AVIOlZ93MvlMFcZ9jWYiWWeONirHB9KyWOfegkk8k1ZjVTGuQOlVaxVrFOirJRRKeBinbFz90VVxFPGSKk8r8KtBFLLwOvpVwQqT90flRzCO38Oa0lzp0C3d4jT7TkSOoY4NdAGB6EH6HNeM3dq/nFlQkfSuk8NeJbPRdNkhniuJJnlLnYBjGAByT7VDXULnodLUdvKs9tFOgIWVFcA9gRmpKljCiiikAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAlLRRQAUUUUAFFFFABRRRQAUUUUAFJS0lABRRRQAUUUUAFKKSlFAwooooEFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFJS0lABRRQKNQAAk8VhyeMNDgkeKW5kWRGKOnksSCDg+1by8sOe9eG3bF764fu0rn9TVxVwNvxTqkGsaybm1EghESoN64Jxnt+NMjUeWuQPujtSW8QaBCQOVHaroRcdBQ+xNyig+cdOtXCi4Pyj8qeET+6Pyp2B6CgLlXYPQVA0Z/u/pWjsUAnaPyqGU/IRjGRSC5nuvyNx29KpMh2njH4VfccHmownmALnrTbsdFCHPdFErjvSK7L0Yj6Gr72RCsSp4B7Gs6ri+YdajKm0pI2LZiUUnJ4Gc1fReB9K5sOR0Yj8akimk3qBIwyR3pcpz8t2dEkK7BwPWsDUV238o4612S2KKuPMkwOOorh52Z53ZiSSx/nWdGrGpex0V8JUw9vadSOiiitzAKKKKACnxKCyk+tJGhklRBxuYCumTw1Goybl+OeFrKpWhTaUnudFHC1aybpq9iLpS55qJpUXOWH51UuL1VUhDkkdRSscxeJxWC3Ehz/AHqUyMc/M350icuo9TWkVYqK1JguT+NTKuD0qyLdM8VGB85HvUc6lsdWJpOCVyTZ0+UflUkcO7OFFKFGQDn86swqMH/GkcQyOEqWG0dasiI4HAqWKJWzkVMI19KCWyn5RPYVz1xEY5pF9Ca69YFI6UxrKOQkEDk45FCYky9p/jXSbbTba3l+0iSKFUbEWRkDHHNdRbXMd3axXERJjlQOpIxwa8dv0WO9dEGAD0Feo+Gc/wDCOWGf+eI5/Oho0TNalpKKmwxaKSigBaKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAoooo6AFFFFABRRRQAUUUUAFFFFABSUppKACiiigAooFFABQKKKBi0UUUCCiiigAooooAKKKKACiiijqAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFACZooooGBoAyQOOeOaWlX7w+tNCOWHjrS1kZHiulZXKnCAjg4z1rzmSFmldgpGWJH507GbxvXzT/wChV0djHiNtyEHP8S1WwnoLZ2yfZIdwOdgzzU32dff86m7UAUjMgMC+pqFhhiAeKmlYq5Garqxbk00NEgqNlBPIBqSkxSGUZ1UBuBmq8I/ep3ORVudfmcVXgGZk+opTeh24L4/uL9wGEMmRj5TXMV1V5HiF8An5T2rE8kd4/wBKnDvRnbm7tOKKNKnDqfcVakhUITswfXFMSP5hxxkdq6L6HlR3R1S37NgeSw/P/CuQlX9631NdYDzWI/JPSuLC2V7HsZvf3Lu+5l4o21olR6Ck2j0FdXMeKZ+2jFaBA9BRtHoKOYZUtzsuYmIyA4JA69a7T7duBxa3HI/uiuWCjcDgcGuiiuHMfJ5wa48Uk3F2PaylvknZ2OUkBDHnv61GQavleTkD8qYy/L0ruPFKWKmgxuUYHUU8rx0qSOPlOO4pS2NKUfeNDvQkalugqz9nAPU8VEg+auak73O/M048txzIOMAVas0G1sgHp1qDqelXY1CjitWzyGTqqgcKB+FKFDHmmp1qVOKCGXLdU2KDtz6VZ2oOcD8q5+IbrtW6DzAf1rWlk3ZwwNMDhtThkfUZWRCRnqB710ek+M7bTdPgsp7aUmFApKkVVls7hpXYRNgnNc5fxNHeSow2sDyDVWTNEz2KzukvbOG6jBCTIHUHqAfWp6ztBAHh7TgAB/o6fyrRqNygooopALRSUtABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFACUtFFABRRRQAUUUUAFFFFABRRRQAUUUUAJRRRQAUUUUAAooooAKKKKBi0UUUCCiiigApM0tJQAtFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFJRRQMKKKKBBWLN4u0a1upbea5ZJYZCjjy2PI9MVtDqK8a1QeZrd8QSSbl//QjVJXAbCA96CDkGTI/OutWuYsrZ1uIic/eHaunBoZEgooyKTIpElOc/v2+tU0uI9yjev51buDidx71z2cSE+9VFFpHRUtIOgpaCClPy71DBxMn1FaRAweB+VZ8QxMv+8Kmpsd+B1l9xtXWfKc+1ZnNaVycxsM9qzSjZyDWWH+FnZnX8WPoQ3IzCc+1VlHTrV5oiykH+dViuGHPetnseXS+JGvmqLKAucfpV8jrVWQfuyBmufDLc9fOXrBepBtHoKNo9B+VWIV+Tle/cVIUX+6K6TxCnsX+6PypNi+g/KruxP7opCq4+6KAuZ7gY6D8q04ThfwNZr/1rSj6D6GubEbo93KvgmQFAecCopEG5eKtDp0oKg9QK6jwEVSg2ngdKrY+dfqK0JFAjbjtVD+IfUVL2Omh8RslRz+NVVHzVdJHNJgVzYfqelnGjh8yr3q9ngVHgegpa6TxGP3YrLS8GeZeM+taDfdP0rmk+7QhpXOmRsYbt1q6DWbG/7lR3wKsi4P8AdH50rElvtXGauM6rckD+L+grqTcnHCisq4g8yZ3IySc8immNaHV6NrulwaPZQy6hbo6QKrKz4IIHSt+KVJ4klicPG4DKy9CPWvGriHyp3TI4Nes6GuNA071+zJ/Km1YtF+iiioGFLSUtABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFACUUtBoASiiigAFFAooAKKKKBi0UUUCCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKNdwCiiigAooooAKKKKACiiigAooooASiiigYUlOpr/AOrf2U/ypiKKazpsjjbqFqeRx5q15eyeZq0rgZBnYg/8CNZqYZ1zjr3rpLMcEdgeKu1hNlpRjHFSZpuKdUkEJPJpKD1NIaBleaRQ5ywH1NYWfnOPWtPUx/q/xrKX7xqkUjp1+6PpTqYv3R9KfSMxD0NUYx+/T6irzdCaqRLmdOe4rOo9D0sui3J/I05/9W1VMVclHyOcZ4qnWeG+FnTncWqsfQQ9DVHqw+tXm6GqP8Q+tby2PMoL3jYPeoR0qYnk/jUIrnw3U9TOfih8wooorpPGCg9KKD0oAzXrTQHHUdKzH6/jWsg+UfSuXEbo97K/4cyIdKWkpa6z58ZL/q2+lUB95fqKvy/6tvpVED5l+oqJM6sKryNo9/8ACkFDNy3NANc+H6npZ1vD5hS0lLXSeGNkYKhJOOD/ACrmkdNv3h+ddDc/6k/j/KuQXqKqKKidbH91foKlFV0Y7V47VJ5h9BUE2JakVBgZFRR/OMn1qdelMRzWrADUZcAdu3tXoukavpsejWETX9qHW3QMplUEHHeuKulU3MhIB59K52TiZ8YxuPaqSuaI9sjmjnjEkLrIjdGRgQafWN4VXHhfT+OsZP8A48a2qgYUUUUhi0UUUCCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKQ0AFFFFABRQKKACiiigYtFAooEFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUlGaKAADJxRKpEMvykYRj09jUN2StjcMDgiJyCP90142l/elRm8ueR/z2b/ABqkrgQQcyR/UV2CKoUYUflXOWloJAshYjB6CukXoKcmSxsjlSMAdKZ5x9BSzdR9KjosIXOc0hOBk9qB1pH+430NDAzb6VZdm05xmstfvH6mr0o+UVRHU/jTRaOnT7q/Sn1Gh+RfoKJWKwuQeQKkzH9cfUVqQxx7wSidfSuaLsccnr61etpn343E1y4mLlbU9/J5qEZJrqbeoCNbVtiDJzyB7VhCrc0jGNsscY9aqA1WFjyxaMs6d6kfQD0NUu4+tXD0NU+9by2POw/xGuec1D2qYng8c1COlYYbqennPxQ+YtFJRXSeKLSHpRQaAM1uv41tqv7sHP8ADWIfvj/erdX/AFK8fw/0rlxPxI+gypfuplSjNJmjNdZ86I3KkGrsOnQPtynU+vSqEhwhxSQzXAdcyPj61zYhN2sz2MpcVJ8yubL2UaBj3x61So86Q9XNNzUYaLV7s6M8afJZdx+aM0zNFdR4Ay6P7hvof5VyS9vSuquv+Pd/90/yrlVHSriOJ0iTptGA2MVMpyAR3qigwBV2ORQijI6etQBYj4X8af2qEE+tOzweaCSTJrj5x/pUv++f511meOtc5NZytPIQvBYkc1Udyken+GSp8Madz0i/9mNaxGK8fGuataRLaQ6jcxRR/KESTAH5V6F4OmmuPDkUs0ryuZHyzsWJ59TUtWKN6iiipGLRSUtAgooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAoooo8gCiiigAooooAKKKKACiiigAooooASilpKBi0lLSUCFpKWkoAKKKKACiiigAoooosMBS0UUCCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAoopKACiiigZBe/wDIOuv+uMn/AKCa8Uj+4PpXtV+caZeH0gk/9BNeLR/dX6VcANrThm3H1NaAdvU1n6af9Hx/tGrbMQ2BxR1IJCxJ5OaTNNUk9aWgAzjk1FJOPLOAelPf7p6VWf7ppMEU5fujmqI6mr0v3aoL1NUijpo/uL9BRKMwsB3FRxudi89hT9xPFSQUmUr971rRtDvcRxDexHRRk1QuF5LVreFMf20pJxiNqxrr3ebsevlc2p8vcLiCdY2YxyBQO6mqVd7qkinS7oL/AM8m5zXA1OFlzRegZwmqsb9hSeDVQ1aPSqrdK3mcOH3NjsfpVftVnbmPI6baqg8VhhtmennXxQ9BaKKK6TxBaDSUE0AZp++P96t1R+4U/wCx/SsL+Nf96t5f+Pcf7n9K5MT8SPocr/hTKIpaSiuw+dGSfcNRxSoJFAAOTzT5f9U30qpagfaIycYz3rKpFNXZ6OXTanZdWae4dQoxx3p9byW0IhDCJPu5+7WAT8x+tY4eSlex15zCUOS77jqKSiuk8Mhuz/o0n+6a5ZRxXQ3rsFlGTjHT8K58VcSoo1oGPlA5JNWRis2PcR17VoqSAB7VIMugjA+lOzTAeKWkSKWAHWqe3nNWW6GoDTQzCux+/f8A3jXpfggf8UvF7SyfzrzW6/17/wC9XpXgf/kV0/67Sfzpy2KOhooorMYtFFFAgooooAKKKKACiiigAooooAKKKKACiiikAUUUUwCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigApKWkoAKKKKACigUUAFFFAoGLRRRQIKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACkxS0UAFFFFAFbUf8AkFXv/XvJ/wCgmvFo+i/hXtGpcaRff9e8n/oJrxdBwKuIzTteM4Jx9avdx9Kz7QYFaHb8KHuSx1FJRSEMl4jY+1US+4AVdl/1T/SqIyD0pjQj/dqgO+KvyfcP0qhnGacRmxDJIYwcr0q0Ccc1Rt2Hlrk9quqeKRLI5wTGcUyzvJbOdZYWCvggkrng1Mw3KQapbcN+NHKpKzNqNWVN3ibT6vdzQvG7ptYFSAnaqlNFLUxgo6IK9edaSlMU9DVVulWgNzAepxW8mh2T4zvHH96sq9aNO1zsy/Czr3cehUGPK5H8P9Kog1tzWyJC2M4UYGawgazwkk02jqztWcPmPzSZpKM11nhjs0hpM0jNgZoAo/xr/vV0GcW4HA+T+lYUKiSRQ2cE9q7OHSI3gTLvkqM81xYuajJXPo8ppylSlY5jNLWlqFhHbQl0BGH25zWZmuunUVRcyPCxGHlh58k9xkp/dtn0qjGQrKc9DV2XJjYD0qiFOeh4qrJ6Co1XTd0a41e42BROdvQfLSBs81nxRttBFXQaiNOMPhNcViqmIac+hJniq7khiMnGfWpc1Xk++31q0cpTmdjuyTWXWjL/ABVnVSKRfh6fhV8HNZ8YGB9KuqeB9KkC0JOOlO8z2qHcABkgUoYUibExbI6VCTTyR6iqd25XGD27U0BmXX+uk+pr0nwN/wAiuv8A12f+YrzOQ5ya9L8Df8iwv/Xd/wCYpy2KOjFLSUtZgFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRR11AKKKKACiiigAooooAKKKKACkpaSgAooooAKKKKAClpKWgAooooAKKKKACkpaKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiij0AKKKKACiiigBKWkpaAKmp/8gi9/695P/QTXjCdvwr2bVTjR74/9O7/+gmvGV7VcBl9ePbirqKNoOT09az4sjuavIflH0oYmTZqKU9OaXNQSHk0CBzTDQD7CigZG/wDq2+lUDV+T/Vt9KoGqiM0oMeWv0q8GGBzWfCcIv0q2jZFSSyYEHpQVU9hSLxTqACiiigQyRiq5BwanS+uB0uH/AO+qp3JGBk0lsodwFwTn0rOrBNXPTy6pKL5Y9TY+1uY9rSE5HTNUxWq2iuFJE0eQM8gg1kjpWWG5bPlNc3cnKHN5js0ZpKSuk8cdmmOfkb6U6myf6tvpQBRR2RlZTgg9a6SLU7nyR/pDdMda5kDkc4981q6fbm5ZlDKMDOTmufExi1dnuZVVlG8Y9Se5nkkDbpGYFs4JqrVy5s3gh3FlIBGcA1Tq6NuTQ5MzUlX95dAo4opM1qecLRmkopAMbdngmonUknJNWCarTSAMRmmBVk7is+r7dDVCqRSLyfdH0p6tgdTTE+6PpS1IE4PSrCH5BVXeBinKdwNJgy22GAqpc44A9KcOlQv0poVig9el+Bv+RYX/AK7vXmj16X4H/wCRYT/rtJ/SnLYZ0dFFFZgLRSUtABRRRQAUUUUAFFFFABRRRQAUUUUdACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKSlooAKSlpKACiiigAooFFABS0lLQMKKKKBBRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUlLQAlFFFAynq3/IGvv+vd/wD0E140vQV7Nqozo99/17yf+gmvGlHA+lXECdHb2qymSvJqovUVaUjaOabAl8xvX9KaTk5NID2waWpEFFFITgE0ARykbGGRnFUKszZLE47VWq4oZfiI2L9KtR8CqkX3F+lWk6CpJZMKdmmA04UWAdmim5paBEFwmRu9BS2bgS9cc5p8n+rb6VSBwetElzRsdOGreykpHcG/hEZxIucHnPSubqkHLyjpg/7VXPasqVFUr2NcbjHiXG6tYWim5orU4R2cU2TBQgdSKKQ0AUChU8jGK2NHnW3kdjj7uOTisuYEk896jU8dcVFSmpqzOvC4mWHnzpHUX1/51o8YC8kchs1k1WtzknnP41Yop01TVkGMxUsVU9pJWFpKM0VZyBRRSGgBCaqzf6w0rE7jyetNI5oGQv3qhV9+pqh3qojLiuNo69KkGCKrr9wVOvAFSwFp6MAOaZRSAkLA9Dj6GoXJ55pSKa3SmgKr16X4H/5FhP8ArtJ/SvNHr0vwP/yLCf8AXaSqlsNnR0UUVkwCloxRQIKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigApKWkoAKKKKAEFLSCloYBRRRQMWiiigQUUUUAFFFFABRRRQAUUUUAFFFJQAtFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUlFgFpKKKaAr36mTTLtFBLNA4AHUkqa8bkglt5fKnieKQDlXXB/KvbK808dRlfERcZ+eCM5/AiqiM58DkVOBVVSSy5PerQpsBycE0/I9ajpKQEuRSMwAyelR0h+6aGBE7Ajr2qvVhvumq9XEC9D9xfpUhPP/ANeoI/8AVr9KeOtQBdAFPqKL/VrUlBI6ikpaAEYblI9ahNv/ALX6VPRQFyMQipu1IKWgApaSigQtIaKKBkJiLMScYoFrGO1TUU7gNRFT7oxmn0lLmkAUUUUABPFRsTsP0p5PFMf7h+lAFYkg5yaYznPFObOKiJ5oKEJzkmqXertU+9VECVXXaBnmpxIuBzVNRz0NWAQD1FJoCYEEcUtNXoMUMeKQCk0x2AHJqNmIHWo2JYYJzTSENYivUfB0EsHhuJJo3jfzHO11IPWvLSODXtlvzawEnJ8pOT/uiiQElFFFZgLRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAJS0lKKQBRRRTAKKKKACiiigAooooAKKKKOgBRRRQAUUUUAFFFFABRRSUALSUUUAFFFFABRQKKACiiijUBaKKKACiiigAooooAKKKKACiiijzAKSlooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigApKM0UIApMj1H50Gs26/4+H+tUlcDQLr/eX86q3XkyqFfY498HFUqKdgPOdXsnstVuECMsYkYoccYJ4qorsWAz3rt/E4Y6NJtUt8yg47DNcKVdTkqRj2q0MtZoz7VW81/7xo8xvWpsA4sd3U/nTWJx1P503NBORTAbk+poooqriLUf+rH0p9UwT6mlyfWosBdDsBgE1JG7FwCxNZ2T6mjJ9TQBs5pc1i5PqfzoyfU/nQFjbzRu96xMn1NHPqaLBY3N3vRurE59TR+JosKxt596M+9Yn4mjn1P50WCxt7vejNYnPqfzo/E0WCxuZozWH+Jo/E0WCxt5HrS5rDopBY3M0ZrDoz7mnYZtkkkimt9w/Ssfcf7x/OkyfU/nRYLFvvQetVMn1NJk+posMtGqdOpKaEPoptJmgZYVwAOtNMnp+tQ5oosBIXz2pYIjPcRQg4MjhQT2ycUxFZ22opZvRRk1bsre4S/t3NvNhZVJ/dn1FVYDfPgmYZBvI/wT/wCvXewuiW8aF1yqKp59Bis4nJNFZ7iNUSIejL+dPrIHUfWtfuaTAKKKKkYUUUUAFLSUUALRRRQIKKKKAENKKKKACiiigAooooASloooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigApDS0UAJRRRQMKKKKBBRRRQAUUUUAFLSUtABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUhoAWikpaACg0UlABUbyog5cD6081SvFYnIBPTtTQFj7RF/wA9FqhcMHmZlOQe9M2N/db8qNjf3W/KqtYBtFO2P/dP5Gjy3/ut+RpgNxWdrcYOjXfy8+We1anlv/cb8jTCARgjI9DTA8ozRn3r1T7PB/zxi/74FHkQ/wDPGL/vgUXGeV5FGR6ivVPIh/54xf8AfAo8iH/njF/3wKLiPKsj1FGR6ivVfIh/54xf98Cj7PD/AM8Yv++BQB5XuHqKNw9a9V+zw/8APGL/AL4FH2eH/njF/wB8CkB5VuHrRuHqK9V+zw/88Yv++BR9nh/54xf98CgDyrcPUUbh6ivVfs8P/PGL/vgUeRD/AM8Yv++BQB5XuHqKNw9R+deqeRF/zyj/AO+BR5EP/PGP/vgUAeV7h6ijcPUV6n5EP/PGL/vgUeRD/wA8Yv8AvgUwPLNw9R+dG8eo/OvU/s8P/PGL/vgUnkQ/88Yv++BQB5duHqPzo3L6j869R8iH/njF/wB8Cj7PD/zwi/74H+FAHl25fUfnRuX1H516j9nh/wCeMX/fAo+zw/8APGL/AL4FAHl25fUfnRuHqPzr1H7PD/zxi/74H+FH2eH/AJ4xf98CkB5duHqPzpN6+o/OvUvIh/54x/8AfApfIh/55R/98CgDy3cPUUm4eor1PyIf+eMf/fAo8iH/AJ4xf98Ci4zyzcPWkyPWvVfJi/55R/8AfAo8iL/nlH/3wKYjyrcPWjIr1TyIv+eUf/fAo8iH/njH/wB8Ci4HleRS5Fep+RD/AM8Y/wDvgUeRD/zxj/74FAzyvI9aMj1FeqeRD/zxi/74FHkQ/wDPGP8A74FFwOG8KH/ifRnP/LN/5V3uTnqaaqIpyqKp9lAp1DEFFGM9KXY39xvypAC/eH1rSNzFn/WCs3Y/9xvyNGx/7jfkaWjA0vtMX98U5JUkOFbJxmswI391vyq1ZqRI2QR8vcUNIC7RRRUDCiiigBaKBRQIKKKKACiiigAooooAKKKKACiiigAooooAKTNFFDAWiiigAooooAKKKKACiiigAooooAKKKKACiikoAKKKKACiiigAooooAKKKKBiiigUUCCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACkpaKAEoopaW4CUtFJT9QFooooAKKKKAEpaKKAEooooGFGT60UUCFyfU0ZPqaSloAMn1NGT6mkop3GIzNtOM5xWX5Eo/wCWT/lWrRTTsBk+RN/zyf8AKk8mb/nk/wCVa/40nNHMIyfJl/55P+VL5Mv/ADzf/vmtXmjmjmAyvJk/55v+VHlSf882/Ktbmk5o5gMvypP+ebflR5Un/PNvyrV5o59aOYDK8qT+435UeVJ/cb8q1efWjn1o5gMnypP+ebflR5Un/PN/++a1ufWjn1o5gMnypP8Anm35UeVJ/wA82/Ktbn1pOfWjmAyvKk/55v8AlR5Un/PN/wAq1efU0vPrRzAZPlSf883/ACo8qT/nm/8A3zWrz60ZPrRzDMryZP8Anm//AHzR5Un/ADzf8q1efWjn1NHMIyvKk/55v+VHkyf883/75NavNHPrRzAZXkyf883/AO+TSeTJ/wA83/Ktbn1NHPrRzAZXlSf882/75NHlSf8APN/++TWrz60c+tHMBleVJ/zzf/vk0eTJ/wA83/I1rc+tHPrRzAZPkyf883/75NHkyf8APN/++a1sn1o59aOYDJ8mT/nm/wCVHlSf883/ACrW59aOaOYDJ8qT/nm//fNHky/883/75Na3PrRk+tHMBkeVJ/zzf/vmjypP+eb/APfNa/PqaMn1NHMBkeTL/wA83/Kl8mX/AJ5v/wB81rc+tFHMBnW8UgnQlGAz1IrRyfU0UUm7gGT60ZPrRRSGGT60ZPeiimAUUUUgCiiigBaKSloEFFFFABRSUtABRRRQAUUUUAFFFFABRRRQAUmKWigAooooASlpKWgAoooo0AKKKSkAtFJS0wCiiigAooooASilpKACiiigAFFAooAKKKKBi0UUUCCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKSigBaKKKACiiigAooooAKKKKACiiigAooooAKSlooASiiigApaSigYtJS0UCEopaSgYUUUUCCiiigAooooAKKKKACiiigYUUUUAFFFFAgooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKBhRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRS0AJRS0UCEopaKAEpaKKACkpaKAEpaSloAKKKKACiiigApM0tJQwFooooAKKKKACiiigAooooAKKKKACkxS0UgCiiimAUUUUAFFFFABSUtJQAUUUUAAooooAKKKKBhS0UUCEpaSloAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAEopaKQBRRRTAKKKKACiiigAooooAKKKKACiiijqAUUUUAFJS0UAJRS0UAFFFFABRRRQAlFFFAwooooAKKKXFACUUUUgCiiimAUUUUAFFFFABRS0UCEopaKAEopaKAEpcUUUAFFFFACYopaKAEopaSgYUUUtACUUtFAgooooASiiloGJS0UUCEopaKBiUUUUAFLSUtAgooooAKKKKACiiigAooooAKKKKACiiigAooooAKSlooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKSiigAooooAKKKKAClFJS0DCiiigQUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRSUtABRRRR5gFFFFABSUtFACUUUtABRRRQAUlLSUDCilpKAClpKWgQlLRRR5gFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFACUtFFABRRRQAUUUUAFFFFACUUtJR5gLRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAJRRRQAUUUUAFFFFABRRRQMWiiigQUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUlIBaKKKYCUUtFIAooopgFFFFABRRRQAUUUUAFFFFABRRRQAUlLRQACiiigAooooAKKKKACiiigAooooAKKKKACiikpALRRRTAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAENLRRQAUUUUAFFFFABRRRR5gFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFJS0lABRRRQAUUUUAFFFFAwoopaQCUUtFOwgooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiikAUUUUwCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAEopaKPMAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKOgBRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUegBRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAlFFFABRRRQAUUUUAFFFFAwFLRRQIKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAoooo6AFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRR5AFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAJRRRQAUUUUAFFFFABRRRQMWiiigQUUUUAFFFFABRRRQAUUUUddACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKNACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKSgBaKKKACiiigAooooAKKKKACiiigAooooAKKKKAENFFFABRRRQACiiigAo70tFABRRRQAUUUUAFFFFABRRRQAUUUUAFFJRSuAtFFFMAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiijqAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUlLRQAlLSUtIAooopgFFFFABRRRQAUUUUAFFFFABRRRQAlFLSUAFFFFABRRRQAUtJRQAtFFFABRRRQAUUUUAFFFFABSUtFACUUtFACUtFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFGlgCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAoooo8gCiiigAooooAKKKKACiiigAooooAKKKKACiiijQAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAoooo8wCiiigAooooAKKKKACiiigAooooAKKKKACiiigApKWkoAKKKKACiiigAoopaBhRRRQIKKKKACiiij1AKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiijoAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFJS0lABRRRQAUUUUAFLSUtABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRR10AKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiij1AKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKSlpKACiiijoAUUCigAooooAWiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACijNJR5ALRSUUALRSZpc0AFFGaKACiiigAooooAKKSigBaKSigBaKTNLQAUUUUAFFFFABRRRQAUUZozQAUUZooAKKM0ZoAKKKM0AFFGaM0AFFJRmgBaKKM0AFFJS5oAKKM0maAClpKM0ALRRmkzQAtFGaKACijNGaPIAoozSZoAWikooAWikooAWikpaACiiigAoozRmgAopM0uaACiiigAopM0ZoAWijNFABRRRmgAooooAKKKKACiijNABRRmjNABRRRmgAooooAKKKTNAC0UmaM0ALRSZpaACijNFABRRRQAUUUUAFJS0lHUAooooASlpKKGAtFFFABRRRzQAZooooAKKKKACjNFFABmjNFFABRRRzQAUUlFAC0Uc0lAC0UlFAC0UlHNAC0UUUAFFFFABRRRzQAZpM0UUALmjNJRQAtFJRQAtFFFABRRRQAUUlFAC0UlFAC0UlFAC0UlLQAUUlFAC0UnNFHUBaKSloAKKKKACiiigAooooAKM0lFAC5opKKAFopKKAFzRmkooAWikooAWiiigAoopKAFopOaOaAFopKKAFopKWgAooooAKKKOaACij8KKACij8KOfegAooooAKM0lFAC0UlH4UALRSc0c0ALRRRzQAUUfhRzQAUUUUAFFJzRzQAtFHNFABRRSUALmikooAWiiigAooooAKKKOaACij8KKACikpaACiiigAooooAKKKKACiiigD//Z",
+ "image/png": "iVBORw0KGgoAAAANSUhEUgAABAAAAAQACAIAAADwf7zUAAEAAElEQVR4Aez92ZIlO7I2huXKzKo9dJ/Tfw/nt3+Q6VVkvBNfQHyeNjvdfaXWK6ifQNKNJJNIk55AxmtRMpIyyUj+p/c+U/feu6py0OdwwOEYHAHEsIZMrMpa4XC4fz4AgUAghnX6/e/+eHd3Oj3/6g6bx3+8e329O/EXGMnnFQKOQcTzr+8g9fD9CSyuwDdR7vP8m1fQD9/5YtwIQGQR9Xq6O7GuYDncp99Q7SNwmH939wS7wiHSORXskoOvd7lWwIx8wfmzQtCR3LsUCCzk2ROWd0r6q12L6PDhADWtETSdoN2HrIYoOEbfFA5Z0i4gMUvCYskXKacEx862OGpNp7JSenUyEhdZUBkTMSF0XJoWgYywZCy+zm1F5vT6+npCf0UPd/3z9Ph9cPgU+lXZvpAPbZe5h2JqhQSfXM+nHksfTivT8Vv7yVyfNm6jMoeK//wbKjz82be/gKaeODYb52/uz2IMQWGPQ5H7g5L0OLLHUUxixBO6d2lay+V8xpHvondV/NdwjtZ5a8u3a+/U3q0xg0HxUlozpmAB2UFYMp7vcqvpYLfYIkv4WG2Evpr1W9WOPkao11qQYMFX+JbPJCmfotV8TT+OgYCRhIYR/PkPO83f6KtE0O6Lbzcwu2/ikQ526jRKaVONAvq5GMPLqEtOcCluKzIqA15OfJLjkRtbKrqs4ORjrVJHKyd7a3TEU6T16o6SxJAsIV5o0lGYwHh/RxaKj2SJ+gNSrGRIC8rqqBE9LHCEYcqo/Y5twVzjo3E0XapYtRZfeohAOcnXhz9zB3MZcyMfOSgJ4lZGUTi61fyYL5B3NEfCWP2dw6Q8JrmNcqCk/zhAMo9PsOKjaI4b1UgDAPUgNCz3fz52VOXJqG4jKvuPJW/xg57bSnSBS/s76IV+xcdr2u19e4T8U5JCioimetq68SHY0EdnVLI8LLJClFKUjh22gIu/xkfHxfj8XWjlR8MUM9a6SKQy8gOr5PgaFVTA4C0lDzGzX07Y8xEatd3Lo6+lhGIsdclGHj1ushEmEZRsJ+Y0qKiVDATSSyBVwQOIEVXlSa2q6VJykSPqMCe00iKeUaWkukiBFwJqoBuBZrg0CmtlXy3+MRJDFnKBTSAZblFkZQ/nCgsqqTU2VaAexoBzwQFtOvCUXS/pdwMXFI8YQaai46t4vwhy7S1ni79J0nnlJi+hxZUd2mPST1RM+WkpqIUt1S5qemHRcQR1CWgKU9tJmIvwWrNKJ3BewjJdBWDmgAqL6u+IW3oDjhLlrHBvATtmiAq6zMUt36UrJRp71uaTDMspaZB8iOWqWMMDSiiHbWkh47CzEF/9aSBwEwRkNuL3He7gfEzR306YJBmWvwNCwtRVbIi/RXgjkaB159MZZWn97djscfhGX0xMlO46gQAIYUqLfAIMMZIKJ8Ec9kBUPMEzx5y7ssxusDLTpTMroUfVqtHSbuJTpzPmsLXvmTEzCOhwXdYcXp994G8NKXzNTGk3+0pZtRJbR03mQCOYRlXNguaJ3zkGl8UZ1ukIgacs/B1S6fYDbYBp980jtnYp0Khm8+xjYDe2DJv5nMkLKvF7FDJ9LrIi0217VXXHFONMKEiPqDiUCRS5Aosnv//7P9KyqOexIBdte6pGNMFjWPddTm+UzrWTkp6qoxIl1+oEZPKQ7PnobAuaWKlyemCPkGl7VdZqH7hWc26XlkjHQoBa8snLsRKtbn6oTnoFS72l3OqIJM9ZvGZumhUZWlN2ZWWr3VZC9qpl0Q15kum2TUpbsFZbmGsz/AwBtV0fmjOwKsQFg1W7fIFO+7PoZ2a1H60t2VNb9a1HsV+mMz8asPSqXVvKM6dHqyGjq0qaW435mi4lHcd5xBNUkNs/amIqGS6jbtth+R4tcZkjLb/ZkOZbpllG12pOG8GS1HyNXKMlaJ5burNRLQcs+vgNF/S3WaGFknmrnsMu0CnGNZRcy0vzVz3i7FNeXG6w4P/oZv8izAIEwlRWwUynG2p4NcmVmO++pc9LG2I1h5Yc6daga/8k8RXOqih9nSWv+TEPRYcDipbU+BZdOHUmhuWPxddusYzm3C6t4+Uoqu2bB5inIC9redRle0omrYua1iD70+KWZVISsc02w5ffy6jsof4OOowWSn6E04JMs4Dma46oZ4TWzarOU4QD+OjvaLcMJtblWoyQ1uelupVcKpa1vEVH6aLn+yp/UBEHhUC9pustq/Et2vKt5FsImq+1NL9CQ1Tv7VxMmRqNaeBowZJmQyKs7cpuqrW0QJUuoZijv7Wi5rfpHq22jK4tabYufBSzDEiV70vc2UjNCWbnA6Kv1FIyGoyUkqgyVX1OsnyPVltG15aYOifsgZYvOSUC90h/NVLtllqyxITd2kcp0cVAxg5XBGoKQYYk+z/KjFfs4fTj7yIJl4wsCTx1WZpfh22aBaqkCTjH5pToxstHbvO0qYgXrPktb/Q3A/FSv7MsjmiCpfy3U2daZDy+lN8okeTBxag5bzTodxSWbk1N11OgOj1Ilk8kweIdOeFeQUE8F6J0qlFVCu/OYev6OzWhW8eiWUPXak6KF0ssH8vXQ9nZuB4ftSfbM6nbbjua9u0QOttl+tqrjLHkWN6WkjeQJSuYQf5Q7LFlIhXmYpoDH9RaqJs/XT6jZaTtVGn5tqRZ63LCs8f++KuSQCK+Wzh2c1dvEw8DJTe1F65U0QqpK2U0nG9UhWDc9L6ck3tN2vDNhJzbFzDuE1Ql6Dp51sODGbdFnVQLkUi0CuMaLbRZNzNwSxlQO50iVQS8e8ydRKVkkjMDMwMzA2fIQDL6Yk7VOQ4nYvVx/QzOvzkTlNbQBvG6jA4zSbyuuEEasWR/I0GEXodtJSkEjJMnrkKBpPEgc1BCKVECn/9GPOiVZaPeieCD8iTBYb5Vm4jOwszATWQAvVn/wWfp30zQd7I/XmdY0dngn8QRGHM7MzAzMDNwMxnQYxqmnPQH3/k7jNNRRmoxswLXS99MsFfrKGc4d48yXOHlrJstc3D6G6EMzAN8fkKvpSLeRoU/nmujd4Jw/dSl6MRvO7LSVTHMBjIHLX3wRZ5VUskqjGaWShan1LI4qQuzNDNwBRmQzioEnMLeeqFP4oXzweJoB7W7Wl7LTLonA6OZ1NnWuj22psxlM+DbbjbhZZuhbZ0elaRJldvytxueXZn4bqLjvgE0d8F2NkdqKbd0KHTfI4rXIVt2BeZk3yjyH8XqPC+/uwNiVUbSNANQN45QeA2o+7jfAbh7+D7WECVO0CkDn0J4gedfUx3ecevK2YkCM72k3xAvXMghVlDJALiIb/4LUlRkWjge1/P9G1L5Pe5asqS9oiAKUE7od9xqOpe7XLntVVKr31nb7XCC0K2lBdsI7dr4dmT9Tl+NbvMTKSt2xV/wJIE7X4F2O+wKZZ9nF5T/W3wqYx/Ym8r9q+RscW6nGBMXRjGVfJmrBNkVKjIKoZRPOa7JY4uHtyZETirOY3Sec5HmUc4Y6wa8yowmxUq8Sf25C+f0Z7OtcEykFnNN77MltDSlels8ZHZqu3O3zZK9zfmsGDgCE2bQQm3kpHZLe3XoJrYqOTBYBfJKHA8vnRZl9FsUVe81XFjH3ubnss0t+Fo3OZKyWU6J+jbf7m+4aclb/PCrRCUcnAgnAGVl4EijChFqaAuIKl/LVGnR4kxoGFQx0xF0uuKKYVuFqzD5PIeeiIBm9VPlszw7UNV6M8zRhL6ZwGcge2Wg3IPOvOOUDnBot7sXlwnk/VQi5dDaLSjCECvp0kQbbdYelAHdNGIiY6I420uSM4nrzEDWaeEkc4Q/+/CVNtwffve/WfKM2o6HIWlOUYntGn73jqtKSVERIuoKq0FUzqUa0stVWURjzizDvzkJfV6rg7P4WuYm6WJ1ZGUUe+H0m9/V4kD7OrtPvyJHH8vfVDb8H8B3CKPyhtmEvXClJZHdqdBsIx2jpp1tGbgwZPEw64lUkplaBtqsWwkh1a0ILLIWEMp4S46ysYCmJPvJErPkJGjOw9H+7BGa0WmZp19RI9r7C1rwEh/L/5Jfcgx/OdtcacebKy+0US6+XxlxIfcXSr8VxvmzYVm0+Jbn5+d7D/muFv5JxNKJ7t5bqh6eARnpS9vMkdHdEljm4wpAG8XvABfaD9q+LYfXkOCI+JuPow3hWTUzMDMwM3ANGdADF9PsFehyHMs4Wv4aYpk+IAOzUa6xG8jLFK/RuenT286ADNtCVONt11ZVNJPUT0tXAJLRSRtMKjSso7VkUekZbYRCa1B84C7JDWeB7KU+F9R0EkO3la4z1wR6bQGtxA1lnR+vBX5feqplzda3MsL5H+3bFpriD3uidI8gj/bnaPwjcnIE5tNv0KVe3QorEetNqF69HmRvzdnK7Yx25ads2ZLTNnM9tas811nS9AXCWuV/l5/HIXeZj0I+w+2V+CiePFlxgWuzypMLkDxm86yAvzcM4d5/xtHBAJMNtZ4BSAyXGB5Aww7SjJmYKRCUFUUWYv0MQWHrhaI8cdn2q9C7SQb3g5t0/a04zd3wPXS2t9JiVxkHD2syppXE7GFX2W7TqZmBmQE7AzKQ2SJvqIaj3TfmDE2mfJ6oXgHguuSQkcFI0ktRS1JUqoTgBPXEelKo6i8xA+ySnKrfblSBTXJmYGZgZuCoDAyNb3NkO6oZVuGi7dAiVgty1WyyVamdSmfKAPde6avSmWe/3dwA7eGhB15aQ4SloSpXALjJlhuOMQQSRGlH11q0WHIvvMMCvDAsjTX80ttFFE78otgUmBmYGZgZuFQGZJjiIW5xoDtkeL1U8G/CLreIbhd9JNX0mwh3BvEGMyC9t+zMbzDaM4Uku74QuxiWJiLY8BrQ+DsA4Eprens1+/4lmxXpQScZHCbVr2gkDiSFvjv72avc7dG7/UblBwN/U+KbctVxt2IPfo9MkvQOu4m8UTjC7jCm8s3S1XxNK9VNpIm5U56XnOsei7Q/ml4yQPWj8h2YZt4WdDleN3KS5Mn5drpTz/OsRV4wfCXVw9HpttN0EU+JXHIKpU0Mh39aeDeO8rnHnx6ZTU4PKh/tzzC+yudgKNvEtV1N96D2yCuZ4Zz0+FCX0cMv05pT13lfXNUuPYHH9/rLGO/UIn8RBS2AX6v4FX0/8jMYoByTWDSz5hMAmWMLQfXyYa7oMb/KFJUNRO7DUDfKnNzgBqkOmd5oa6rPDMwMbM/Ae9hnZZQToj9v7yE//dm4FcmbaDXujTh+34S3t9L01+kntzX7xi2u/eQ5XD6T0xKTbmVAZxdyWbGlqeoaWtwyJFA+AyCtxvpUrCKhQiSIGDgvUU5WSEZV61ipjPin2VUPtUCkV50TV41GzOukOiJF3rgdpTURyk7BDp7vHpHDjgwcYbYP8wry0+foohT3oiWx/ePlvV53Xe3D2m68v5/aq3X0wPjWNhD2iI7kHJGHIzDbAR9WGzK50cC6luXm4/2uilC071GZr1pHTgoHQp52yluAu+LtW4zUau5GM6AnZFp9feOoHttwdZ+q3dodaSuTN+RjlvhMl8CRZWykRYTIRPNir1yud6vldiIvFZX2StP9/nA7Zq25Dqrf6JS8uQygS5R/iEK6ihDnD80yzQ6f359pcWZgMQPcOa2u26kOsdUIiyY2ClytYxvjOk79+jO2zsNSq+Qcl9UdkcVtIXYEN6C2mGroYsaHPxLgW4BEFITMBoWo+KblvPLjdxW5ZRZra1uaruhnCt56RdBgLdxnaWi5bC14xqq7nf+ZnqACUbMzEn7FNx9pfiYddImf3DGcGgxi4OYIyZt6Uy1VMq/hKJkmuT2T/W1dsVVE3XTWV1ZwLLXN+bGA1/JVizOEykCIC92sECNh5jPBysW3EW9ALuRbDPjQ+qzCDICGn6H6qK3t80KwQw6FPaLaiClSdx6055pO4VzJwlQ9rRxtKjhN1oIPTd3+ypDJukbFBx1jXWlHbtG+VuYNm6X/JadUTWUKH5xCO2/bWz/xajDnif+DuondnkijwtIOvtmTaAp3avyGSlYrtGs1ToU2/KxhUt8o+YlXgz1W+1Mi69qkj5U+lxxS5jaSlqr7z1aSKBLDgwU52IrZJsDAPTgRMHsGoGngmipjBGf0io1Wptp7+wBD0vgWtjjDhBRZXhAa6o1ANCYjNIQtE4t8tgKxI8AXrU8BzoC0ghS571Xzo4VB64ZjLWbqKk1XMTuZJXKP4l7WM1srYEdVIH/oh/F1Cx5qboJzBo5uVsnzaH8T93hH5o7BIPpbxMRQg1jnQwPwbVchXfy5wr1SfAs+bt1qwCuMV4enXRU+mAe4XZoqOeJCg2hrwXEvgGcA/uhguNyKKIOMGA03qGoZeQFgIc/1M7YlzA31T7+hNPnzvEHrC+emLlle5nsYedXv9FAun1IcaQsmpKg0EnJRIJFeKgCt/4PeUFofQui3JZJZ1xU+CHHmaB+00X3otA+sxmwkx8LkpOmMCYjOpzCBU6pY4IGf71kBLecH+YWt9nZBtKMazjAge5WCOw/9uxf+LGCsEqIQtsdBuawioZ1aOdpLqcTzg22llt9dqd6+R6YhaVxlKPMEYo5z74iXUEx6OGtLlQJbJqG1/rO5T+pg2f9N/iSRrByLBEP7JkwQ+3moUdfQ2UxjDUSHzkC8m/tDhztRxGqgKJFS3MGElxWFH4i8/7ze0ds1O7LBwA34Xsf5CgD86TAavOYtW2i4kIq/qZJkdzhrdhoEU4sI0zLEfBFj3ayoATsFSpUGR5uz/CzVISmKIPoVS6gGR0xYMiIgxEGeWA5cnK8boulMbCXOFX9zusqkST4Zs1Rp2oqVGU6sGKSAUzo5hMGeVNO1CM66/J0ZrTIzmUOLi84fav2dgF+klastW3oiHCayom4gqdLMRZq19N4HDu9HmrmIs0Igc5iLbH0F2r4qmW/7gm9HO6d7Yuvo/jCaFvZH3FtUzySzYlOdZFke33YedM0IfGIbIF5XTgCS+p4CY3S4oD3uAW7LqOT4c0F+9oAd2deW4Ulyj9fgnWqJbg++l8nzHHAyvvstBW6Z7Nuw1cXOz1MbSqp5QhcrpNnnwvNCLj3XX9G0mYnCgGIoW6y1wpyCuxmylSKVk/Y6dAuklgnIu/SqfqVteZUXA3Zwj6s5sIInzpQEozHf7XXk4evjn0VyhbmoEvb0yNmVYie988EWiiP9X7XjJt/2whl0otL3BhGWxPfpCaUVbqdmawURv7pfYhic/duCf6fiLlzT5pzwN3ww+1vok4af69nNtHXCrhyLJGrLjAiYabE0u/liItUo2v2w/Kd2fYm9akXt/IEYy0gULZWqpT6m4PeJj0rBa/wNGWFhVoQ50QUHbYfvno9oyQ+BdWixp/zdIW6IwDQ7KYEYgood3XXMUBQoJdokRYEROpOlIYNp4pG6lFdgCa6ACGeQAADs87d2KqMHUdeKbw6nbriE3ZJzZcMBF+iaIYY0kxF03hXmVhKGxOgiFgtnvrF6GydTMQxpKcaLqBy+odhiR4ialDZZqz+cp+McckaEhTjWV3FUm+nvOlprp9EshfQlcXOta1XU22CO9wTOVjM6AWWiQ6MJpyv3xNK4bfoIq5ybqt1GVVV+F+ZFjFY939kThttv3y7dKw80mYwu7uWIxqymcZBZxasy28ASH3SZBsE4w2h8BUCAtGHGEmPBQnjWODcV+BrC0QqHyUTTFU6vcb7z/BvSeoj3zhaAgfHg1v6ff+3k9XWAIBBBhQNCzAvBtTFSLa3oIM+RcoV/99Er6hb1nUZ+hh1AlR1PakhNczVzMu2sqDE1AvvAtT1rGFpGTCDcURztTwdtrT34FbvvnSt0x2r2ERczfq0YZLkv1STAC0Iu3vTebq7ib3gCQr7bq+ZVU6LOtVysSpJXKj/sgJbUnEDnfU/LF/TpTr/Xi2iOLBFkDwN+UhXTplKiJfAGqth2YV1HCQx5q/Rskr0N9XV8iYUJKQat7i3GMYSn2qhb0xbkAPhbpEoXMwGRzAmXAf8b8Ml4qyFjG+XqUnbjww7r6HqcqbeOmGRC+6mqSBdPT/WmwWojjohxLRlltSQN90pB4TgNOgK+3j1877hIf9ECCe4pjDP/UAoyrhO3rqeJaRBsC+L4K4xqQU33H6/92r/ZshwWDHvzm3sUQ2lnwzHL9zSxmMrsXwoJNWO3TJLi02/om3vgUk4W5SHQ/Oh90Am2LWo4st3EzitdNmrjjxL0V660HVVbJ1m45kuZ/5ITMWv9J9aOUM6jZKa6oE0Kz79+hQd8FE5m16jUrklRR+wsto24mQyfAGjNttK2WrZT+ra/fQuxtC0RcR6lmBFKUcjUiMHOcJKiqCTcWJB6SZw2KbVQ0DTraw7TmhNt9FGlbsnpQ9pbiv2QBI3AlyGAozMcwcAtpWO1o1hAi5lwSr4KAqbgVEGkNlMvi/2SqW4ZMSPleHnZo2TselYhVK9IXTlPKfN4B6PbEUsE5pT8zF0tsC3FjGRhiB0IgObvzBcusqSgCVEVXmSyekNMzFmeN3S3V8H6Srs+MImvDSNicJnptrwVmeAIwZIoLgGiPlOyjJyd3+8XSy6FOhYA5058EGIMZSm7JSxzhC9BCWfUgXr7VuGYKSaHLVUUqnYqcgVruy/jpqHRCL5dWwTgB9SSD07mWlasqtSZpz/89k9Uo1f76pK5TUNqiZ25inSBw0kTYgmjr15DQ4PRM/MZUqPxGCGT18VENyloKUUbrhhsUuSIFMQyqVWYFg6IFZ/SvUGcI1ZGdRztFQstWe/Rg+EkgElBEg3ua3j3MNIX+K21hwQo7B9gltlPJAdiX7ReNeWSgxcV0NJE8YnWVZReqiYfAEJCQnl5W+LTegnpLVw5pPUkuQuZSPWpBqzqFXl0H4apAW/YsVpOeGC1cs8aKqwG2cBoaJVVgqPjA7PDl9hjtW5pouRU3jheCm3mjHqVG4z6bv+qZkTL5PoYJiS7ri7uj6Voxom4WYUrOtj+lX72vOp/DT3jcWcAs9IruiNqx5NZzIppErPKgeKSD7E/t0F7/Fmy1bawqrbHZI/rq4wPKa32oidE5QmLwxqI0qYNRkeuU/XIVaIoc21SmfPXWPiKYq7FvTDnHljmmCQynSthbjUPIG1GciFE1cBG8wl4UqhaW8NcgapVmNacISegWNWtMoeQLydc8b3Cgn8rOocGAs1/gNL8xcjZrlZfVLkOAY5S74amX0MJcSiAVUqexIb/TEOoUGpRbFktyjpqRW/IEKyi+AcTYoVpLgozIoiOEFxXEY1KTEnkmWouR+UOkZpaymODGRQXuSoV36ck+PvA1VCyiGoiS7zYyq7h6K7S8mOFIm1d1SpxhKPkQfIfKjU92vLsi3gkpvoIcYgJ8ahP20vB+Fr7MXTxBKBCa680rWWGXF0UFtOZCfDlbxFkf4HV+d3flQVEncAF0U3VWUbELLdSA9pJirgIlhyp2o947Fn738+cQ0KiqrGBmeVwpWFGZzMKUZ9psS3NIZ8g3HtebrtGCAN3oGogv8rCzzPoCqYlLqlSHL8CaumqPIj2GMEIbFE0+2D16tHCGq0gryW67tZ1USStz+Yq4YAlWc6CH3GxuLcyvA2jAKn0QPZBPClUAqMrdhYu/QkgtC0DTYwnBdEj63JHstUPRdoTgMKntOery43sI1oHNMeeLYLm6uqpA1WVhNOzyljmGV4BhflwhqNSJlqkj4hXaF7y3vb0d6T7aN7h7ZBdLthzfpoFT1URkPPDVUYHVI1nskAQj5I5VemZuUhXuYXDvtTy1+6xTcNlezXF+ypbUSQI3C7Msjzh5HPwkCRCPRfHuswkmpuQubHONbjKnGVL60lPFdOozWiCrK9QJkhSgLryQthDRBkhqZcRlXtr4LAXOpReBzxC2B+VGqPRd7DClRRu8utAxJYcGD509WcBiYaYCvgGeBAqt/AcOhuPwlWrMlJFo24fOblIORIoZiFF4RVUsQ/qcXgFHqkUmCYOS3K1iopjjN94uT9k6H/9I72aRRwSvlyJt6FU169yHQpj+KeJqmLJc5x1iUO4cE/+xAD7LMX1RAdQXcRuJHKmrpO66RF4Y8FZ/BSqWQKEoAiRa8Bh9hnfLGSK5qpmWTC1xHZYjXYGmtMCQ46A+z6CSGknUmlds5HWedN0Dst1LYlcY0s5s8PRKyYPaAsWBnKmoBdAQzu5t90uyvYJjFhvIO4EwxY4efjOsohiYgeFpNzwL1aNa0TdNfa0di/NPmpPQctfL8rxcru5xC2rW5yd1ykAR/pDEppwM+lEyCisUDGQdmVnbqGo/zpNZSCdWlpMjGpmSW83VGIexYGv0l9W2+COOoTDORpSWe3exRTL8PhQ1ddBSm0/vPepJ1FDpUtLfgk40S4LLTCspML1hacIGKASIvlZYdvypXPg1Ne/gdtyvECq+OFkUpC6LQ2W42TlFI4VFW8RX8l6q5kB4oIFOf5mKRFivlcd3JS2BbwKK0whBg0eIh6iqDvlE6UzKLmDO6wUIMg/lsw9TVaJsnUFwWBgBtNGcjAp121JdSeR+KZ1dFiaLzTbF1c5ENRqAkUREMWCMH0oJBOG87DhJlnusJ5grir4lfvk/TmrgDh1HFex7mshkngjC5laNSHKLok7maqgB/N9WIv0e5A5NFqEUXYXiiuNFmu0VR8EHM/tOIvF24Rcv8U7uNilKsgwk61qRJ1lD+fyz+up1Rxkl7+69i8XItBo65yga0fFB8gsWNQERja+BXbPtsvPBKjmYiIgBReSlA4kuOm0YxtNa6jod5GrxEpRGxV3ocoRLzFf2kB1iCNsS6EzcNYZXwgu+s2CMMLxum9+Uo5+2Hfw43x1WLwrgmTkQRwSX7bO++0K6FRl2VAqv3+p6gEzXUalI7ZMQ57/MiFug4w5UKyCKn32UzFGyYoBxuRvzgALMQcGhBg1VpXP0KTIfRdF9qGqe2am8w1f7CMTTHtHkgJ4luvCzxVaAYksE/h2hLCX2iUKtqwcUSfhMrg4AoJpIY6wDsxOfPgp/uztCbvgHen0Z9EHTiy+u2f/S53ENsmZWV8PTYEQwobbrYZt4Xu90eZ1I8EXjzWH7epvnQdRWU/IviV9oYXFrhUSK2YbhNHMizeC55LDWqZhvPDmfTGyrKAoTfq+EuF3UMkHCEcLo0wHizQESpUr4ojfQsA57C/uu9NP2etDp9FYq8Y8AKQYhiddVwC6kAwDNptR6xFT+lAfKgkkO/sU7UwssSf6LMRnO8wU/aAQ191FK1TRlhFYy/GjvBYDDXUWzviNooJtSKEqE9Rn/ExX7u1jnSwoFNet2XBoDpNaJMDG9+hz+ByGpiWwoCKMUSLrCXm2G3Gl6eMS5e2Vrl95v8hnTMQ4zkXXUsRFcRZQSor0K3Dkx3KKyMu2Nd032pK+VuFR367e9cuOQVI8VFrExDMA7m08cl9jl+n8ntqaEhsN5nhbjdG75pzxQOKtBm70Ey0W6GDZlcUZZ4VWXpkThGnbjy9oWj34nPX2KAuq9qnmxAuynygwuENI5IPRsK0YSOQr9ZGVSPZnIwJ4ilfuucOX6+6wgjj0uMcpKmCEQcElvlENK7mMiOC+hJEBal/sa/8QXOA4g2lpiMQ/y83GCaRhnSOn6MOnfh0AyIyASwHBJ2zZq6B6pq2/klO5R790QAVWVhocv8d14RsQ29mt95Vp9JEAdR9gPf5GQ463JWepMs6LRwFTPxsAXvkRDa6qypRawslGSOGnxBBq5lGKFErernvaTc8GoSzGeoBkLBKtYKFguIrkNwGCaH27aN7v1XXts3KzWHUSox9KCKQqRZGEAspiChIFV6hqLRsLQCssBtXb2GYBtotlSJl8KbCCA8weWNWIibgreE5SscKVpgrAFb4iU61ULK3jkqlaE17ileYseIt/gFMVp9vWg4KX4o1q8VC/05bx3bdfefWGx/G1k6D5rwYDC1q2JtLkiYcghGYN22gT8TyV2t3Mb+VAqFlKUZAjVUZmjuYr2DOQ7gYbTKwbHiAo7mY8Qd/LKbLYsBrMaKOxp/AyZxdAANpn2+ExGeoU28engLLU+4LchbexFTc44jpAHrAgc/qlEUJvMe1B0v2tuJCV+1CxIX5U6jaxJN4CZchkRwiFgdUMMXY6/eHv/2jsKOw+iXYF0nceVne5NCAeVhUgDwH5hkxdXgsxXcAxSMFWiNpMRS5n+XNB685gfRbOqsDv/DhJWYCpKtXzkIk2heR8NFOKRb5hNJZHKDZtJn0ECrKn9NkPbmIrOp3nWia9HoE0rwAkLciRaOhmCEG8rRAjYEpb1HTT1Fhl2yHGoswQpVc76lZiAPX6ZS4MsUt4g0TNtxovQYULiZ/9LhkZrlgEK+SEV2X0OnTiTbvgLFKnY5/xG8x/dgNa4XP0IVIRennPjbIFxYGkFtNSobI7QzLPiV2Lz7k5p/ObMo8wQ2uWY7tEEURcUpJCuHdfvWulP3OElKKZusWgCD24x9+m1qoKO589BqNH7jd0/buDbMw1LvagtWSij4vWpQtUJQG09sM+iCdCjON5JwSBy0VbUSSyjysrJK5V0K/aQSvdBqnyL8/zNMSlil2RYh8BJfFZASiyhSOqqZDBToWkVLky0DZP8Pf63F6gzkewh1mgupiFgCJz9LeW73RdYFu6LCQSQvTYEAM9wrcmM5SJGByrITMr9SMSUUMZ7hD2Ih2S6/1QgSsyxdORDTuTQ+1ZHnYGIcofHGlEXLipZTVdCFoMcnbYYQuM+IkXQGZwMcEcKbaQ0jqlEkleEk4FDy8lER5urWVgsyebAVre7V/n7qspZ//aECLqCSp2Ia28jcZszFtnD4IN708objOyo3ZPnjrMcVz6G0rbgwWCYC6g+ax3+LpKJMtTVlwBWUUI8VYrfUYlD4HARYBArvCjVGEwfO+Kqu1weGst2G7ZNdr6KB29Pf3+t38iG813+Kx0AmpWq4vDi9BAEBlNC4IQiS0WLb9FepEQXZYUJxYVM4HErazOFRUykw0NJVuBaihullYAYedsm5N7BEUMzsczeyr48P1K7bp7LnVGACiwyl8itVioqvHIKcIg35x/tRWLAMDbKkwqokokTQbqLilBnx7iOEd0VdB3KOSh/O7EmDMRU1xqOFatYoOZh1QUVg90dMS3lGhzTbAyenU4wjCCWyVVxrpICcBLM1RNNXbvWq3Fo6DgaA2W/Mfs0AlgqSaZI9bkLRME4+QTBAce7cZkRZgaL9ZeJ1UmhqNwWTze5eURQ/nAPoUR1XcDlXRFRi0KUIKhgt/bICxsx219oVOhuzZ2qGg6Ugkg22pbVKuwie7aguFKHY5TU6/r5VaDbMdsQUOLPeIgmOYrnGZYqGgbYxTLZJMvqs4IHYX5WZSmklXpwbSzmnZq1ShJ0St7bOkzJM9Vq8ZtD1fZOEda+6l3SDwJGC5T1mDNQrIvBx3ZFmhSQ4j2p1lpq1FNmtiKLD0DAPwNJgR00ZZIMgH5HhUto+kMDcUEsC0aTCcqJSKDVvl7MZWfiiT0rNhjcEwF0mMK3gVRYgD9XXVSBHw34zJHCHrLB+rcdbMOzLDakLIilYrnyQSG5UqhUQ67sRda3XojprqCxcWEIHqapKOvt0DFawlMhmJZTvnQ1n9cKZCpbKPEGA2BWKXBNR0lHNWoYkmdwEw3LTKSn4FVYdPrADR39zqBSAGHSwI4rKkUqp6r+jOTljvCb0x5z+2q8wlftEVbGDsKC+jvip8EMf5pajUrE1viW8J1Ba4q+UucMhd2gkysEsQUrVRw/IKRBbkiMIFSu29Hb1RqFS83sBwwRcmRum/yJ4xgjoz4SsozRYCriCvOggU6VkScfkq0hejXbUoCj/+aUnklxybfEmpdLufaZRPIq4irkgYhbNB2DUyy1dPjXfN3wgAzZqxc97U8gQOArq9LpTpaRtOpVFpi9JSn7wnm8PmcrH7nrsRNXqZA7HngxXpWccKUh9c7ejeO4EC+5hXDaCmhQSSW+TEaNy0ozyYTSfFB3o8hoMHtuM3NxJo2VfqgjVjvB2AZ7a3vgczSEMLR0vI+KH76HnlGjPy7s6yrv1NFSOrKMjrU0iIuC5XVOacppytdk0VYw0TWt8kZZxF9CUQln+xP8uu22mrurlXmfZb3AvbBG2YP5Luqzy7qKvGbAtaholj7GOyaaORluYoVikr6J/sZfVNyocGjCCi9PiRxsESimhacpH+zQseqFYX+euffklE+NUTVwTmmpehqsq92TvK1f4FCUGIoDZBrUp6yWXVpQUept0mdfyWZtKniUx/GsxN4l07tk3jK8Rj40BZh0NXYLR+8ZlWn5hVfL0KrkUVtVWgeN1gXTEFmWsQUuIgoniNr8dYAEj1tM6lwBdOWEq0fW5WAQZauMafHJkMqhFrshl3FZlMKJmkj1OoqpWeSkFcNKvsjwxiBaRuGiGlvqQJP0PHR888UihxfyGQ4B9AOOzZhap9iMeNyBWcpOA6RQBJO/LBYKIsnYPgssT/uVrQgtWHb3R+0J2zP3PeVO3wtpdQtOaxkpsVj6pxRlt089hTeuxhrK88AOITnX9EmmedLY/GxSopOfvgL6owgONEpG0yEbZE1NR52CR31IiLECnusqxFAU1H6NOeCv7VcMFbjhTrlZGTVqDzh3gknqumart8p235UFceZYoSdWnBNS8OW6GR2Rczxk5IUQoKw5b8MIxZFhVhJIcp4KoAWFaQXLBGEg8Hxng/5C6glWp0j1ttO1pUr3AZMWoUS/wEkrXGo4heVKvVOaOyLUXbASnyLPjAb+GQCBxtlSZFR3qIIYUjBmbPQiG843FJZUQcr/FfoavsUnRNAjPTnisIsVA9hlObIJfrf8WFlnkw4cR+FHQtpFOA5Q8o6jcK0/YIIO2CKMIiGEloIU7lZ0a3eEESVrw1CYds0vbLS6KB1tD0cAUYDplFVd8nvL/VK7pMLmOIQy0mxDrnMDft2yywbEYMZaKbJgAGWZFNFXZMgZThJXSg4ZQjqv1C345bhOwHhkxmTWdGJHcUk4shSlO0waqyPOH7yzwC8Pn5niVt8j92upiywRJGPtqLleckv172iKVAwI2VlUpEEKSIlfpWTqZcybFkj6+sPLG+BVM8y7VAK58tgLEvid6kiVQVRHhEzEfafz1BlnSOTKYvsAjzlSFnA09mpfzMcRvD4GsuxWLVgJ+6Q/3z1BnJFdovWqXiDFLEJ/Z3Y6CuQff5Eql4Ochy9fAd251aHYrsu60ZAJZpzxSag1b2+4kcGyzfnzHL/YT8tkMBP8qdDC+pkjYUkeaKj0xIA21t/ptcUov0oWG8K7lNZ9NsE1teGFXQKvWjHmIZIJSCSMOImhURsrwJ5YXhCJtoOQFEELBARcB7TgSblOHb4cm8kQz1L+WfqGvKQtOwGyLFtNkg2lcV0efTM9WxYy30raB43GB+roZZY7oAvc2pR6NGzXKv06vZ+YXYwttBxlY/cd8LiE+ecw9LjGwW2HBzngb8ZY+23OhMWCDMb2mDmgq4SIE1AIHwYX18XorRIapyY6UMAybKk4OM1DZE1CInBqM98ykwmSqn3qHKMght+58fp6nYHQ4cg2Jgxgt98OldkqwB5YkXaE6T0COOGci4+VgZomQKBaFSJzA4Em+HvZpQQMeuLSHqcF5nMuPBNc7WwWVirsFP8nWvABotmtnM5Ve6WFP+V8j6kIAsBXE+7Db50BrRVUZG4vaRUBGktkFWiKuMEJWu7IO59sLQ7+DBggGSmtRRXZQIdxiCiYfo0cpUhszA3JF91aRSBY8y+1TuqGY9cE4oz022IsavOJsxeuURpz8KgA5QTmLfzIDUEjMIgfn9obTcIp2FavBTCMqwF3M0bHhV8wdcyITfEEwELfFf+qDXIp47b3mi5YAY8JhlHowWRAMiioiBFVy/sIH19W44HjlY/nQG0QQKyB1vAZFf4O2iu2+pmG0LIXFj0BQJ5txiyVwgLoBCFyBKjrcm1+B7/BKXV2dUmA5jm9dFtzdghT7/H7wDgUzsbZEttpIVxhLNQtv4CaF+MlpQ317RadQAa5Tp9ZqWqmMkcUSyjya20Jdhv/rYkdWzW2obdUXJ/di3TWSrcY8+1n85KxqjHx0KhLlPJnCUpLxkUogRUwWwChCyx3JJ0hNZUYjgpsNSrWynxUYX7C5teafQe2g5UzNT86oC2kUVZTAhnI0GuMqh2GjQ7k6In1pMCyVnrpgSswVPMskTAKfjy6leJsoUTwg9bwoJHVhClw5nxZIXPQsl0xouLbnjItgMcJ2HVP1lbEBj+s1am0YCyfZBl+AxsRdH7NqLZb90Cj0FXc8K9yI2EjACLIERLaPKaJNJ9ARx3DcrfwRyfkEn0sjZyKAzEYoGxcQun9SdxQVe06J6EA9h/IhU4q7ZGfjxWj0v9Zq1RkRBCOGEbHBD0LMOB38Jk2ND3MuQA0Ni2NTKHLOFMzJkLR/+G7bLKMlBK1jiGds27RH3jLwEv4sOY4VrixiEFOKf/OmxQOKzSIXxOkeUcNiQoqt0+dOmqYWs3OwWQ26lowGqGw641RTxyNYgq0yloSEih2JTl6+ZOhKWLeAYZ2r5XBUtzNQ0J2722ZQ3DGDUks6YmnBtkE9pQKoEauzIVRanHYlUKimYYNMWnP+B3u0LnqAxY+GgxSHxQxYJaw2fTwYGwbXrUnY01/nTr0LRA3K1qobYhAHUOZCQcUhItKqg/+MBVpTMWHw42PCxxbM46mHaGtDWKAMOvC0R/O7YTBJaECUL9gfSVTsB9eVmhQfDAzhwPKwVnQX2hQttjccJwMppQSttJ2JQPm5JiHwEAjVFVEu91Dn1kVYVbY9YzV+d2xMaK7nsEo9EUgGkglVVFkzqRgtsRyyaRwu2CkcBLAvAWIPPDwZahKD4quWSCHFbBpk0HSreDJ22H9d1prMF3Lo7fsxjsbd4moVQDTiQKe1zblmElyLBYliNp8YxfmNrCWFirEGh4WLghwaFGaGgk13N0hUPDAdgf0QN4ARwqElQwa04oWX+XPL+bSPiBWFjVCGI412pPdMKqPxTYce3+qZ3PYKTYFlkqJDyjW7AGwJ46iKSNarItHjvB3zr6VCe6Cgp/LFnc454oiY7Iq+rsDk7UlJM53wfiyqXSVyTBKxOqTZVQSrZbtl0bkSRAx0JKUkYUZKohoC2y/20o/3QB41pXGnP7SbnMf1KNgjt/o63gcwD8zf6Bbn4qbRHe4kIAOiNLUCTMMuIPmwZQocv57HyGCgB+D3I9TbdFMzjV3oUDmSJhvobf08Xb4uW+ZF7R52QqHfGBgZfgvWYmjCKNz85WsXNF2UobKU92IyVGIQpoibqoCYzicBMq8i3Frnkoc8RgZv0HnOY4tpAfNiPg2migl+MKknqvrGihtyRRBTVswTd80JisUEFWSICxjKRSbJV5rHQqxiVxK4MM8lW/WdYIR/lQIfucryhWWG032D2S4d5TAehiNcKUnDVkumwYQguwqM7+zD6WGGBYUdV1zNSca6HZ6R5vpFUsYQlSCJEUK4sgonIAgSk7O6K/2Q44ddfqXFKya0J3ITP4z9bEDhPN7+CN1mwqVCpJF/81hKZZo+RUkDawevBbeXSmASJ/G3zJVdk3Rs7rjDKE4e2iw6zN+AaSsKtgVaaoaILcwcmeu2rEWuaRUqttoQvnwOiLtcvqjlBVe4X7VamU6TOrmCtQODB8a6InWsOWwVZONslSvccXDQkEAimBtBBoHbJUYUbLiqjNCJHZQEgsfH2gA0k0OmRXi7CRVaZ22K9X2W3FujtgzdhC/9ruAxAYpAsK7kh/rbmbY1VB7Ziq4lU7a5k1C6k/kKgJeYOcAJLZ9gxAwwRbkjSLd5lKz2po+5yvzKHYyqpkLV/4i8iAyhwWXSYWETL5nqLG5PzEAVpia573m1Z0MAxl4ZT8MPM2wUNFT5sG2X22khXEJ3QVurrerLMCLcq//RaghR7hsBiQPfE089vOVT3miGqKvp+46wz+HcBL682GBZsNt2GaY6hJ6dVHEqv5WVFnwKqws7JkNrjCCLZ03YK2XpcI+C508z39QYowlnCCbMdWwnF+lmtgHRDdIs5tfLHNhhrnrNKUhk7MR6QMUc2OfrBTui6hSdCNUZyfhTFHIoz4rV6dWEoLgpSym6V2BrrH1cwGecK3GmYVq4o0yWY/QaSfem4lEYV8qr1HyV0L3THYlT6Vx8RxIMrWSMbqfafOHfYmOhKpYRBR0PMWYTKBMx90MPp2vSy3lpY1Tr3vZeihmFkJbGurezDTlqTmay3ND7SLJQ0oVHVsBR2yNF/Vb9hz6kBO8pNgQjv9NP14+hWEcQtQf+wpeE+JHRALhYM9GMMyMLqXoWYChx27vAK3hJUdaa2qo+5g4xNylXnpdaqQ43yAzemh6KMMU1bKVKaiisdRDCW2jiyx3GAqYKjvcFHEB4mYl6AYOGHr+NqD0uGgurhl1SoAD/E+v6m5xBPdlJY9rW7JgF/1Q+Q7QUS+hzgC07bLeVu0SQJrp6q28aIm94PLlTbIBQuknMEKWg10BTjXy8p0vgGtpi7XZ4pmkWe3ZnVSEd13DsRiIrWmgD0Ln/58YGbGp15x3OlXHnWQO56klQ25DFSGglHwUXl2owy2rzFYqtS2vJBYo0CfoShvU5zCgVa3odo1rXhbdW3UvJZOYgf68H6GgyPsQCht2nrnOiKCSKVHtIOLCo0rAAxBohUwucO1UrcpcFNZn/dooSpfAoR7mtaKizSfffIa58K9dAqr/5y1R1Kcj2EoW+cm95sBVFtNwmnXipgQyJI0dHWNXyQ9wUsRru9aHdhnno9yyZ2XhkYTLXdgsBy7QVuxlCtXrUpOG7MIN8lwaRFoUAFfvpv4CVoqWVj21TRZceBewDYUBFNcLrFy0rIVMZLyZiq1YFEC6P/6j4ylCYQLauiIwntN573j0kA0CqX+M4OD5gR6x5iVeEmFxjgZgSOl9MUSmyGZSCk5kLltX87ZqVJWEmzW4mKQWR5zgjpdESpW5gKMdzTICtuODCLOHwml0Y6Apc9r5X3ny/6zbvObfBA/mpJJZZpJXdVzjNPyTOtYNM1nKSQDJwujPJKgEjX9x2uNz9YHvrNc+eZZAPBKmS7cdhx/WqUw2ENi6F4XbNVHD6W+SFr+LCqOCtDyjbQbU4Dw5kfBonyeN5eZkJ4oZlAQDE7xkZHlrONC8+g5NFwb/qxh+2C563ChJ6skiXi89pjhuCs6vVUYYxbXSfdnYx3+cVp5Sq0WtfgHeZa7dZCZNbA+E9gs5iTILAo6LC2l6YqTB6Un+FuxeCBLrI5GBXnO00K2TN8tPXKk6oyhIF4Y9aYDsWK9ZsRYQ7kw8VUNdw2g1tGgjtZRgoEivlmKv5f3KY0faA1b6RJigO2RNFNB3956r2yBVg2U8Zc41xL3dSy/pMXYUKl4WGE5bIufOuWl+oRT1ZES8EdN1BqtDjOKnDpOEyz3R41QrkYR91wf9iSzVmVmMuPZLQB2gUhR+1KHWR//UQ/Z1pRevc9u6utSqa8VAgp7sNmPzQDBn7HtynZgNUpU4wpA4okZH1cAkM9E+8+8E/hdC9WeaQawq+ndwXwsKiQEokq7G7QBnWE+x83PuW2l89QgIdK+/ckRlaqThJNgSSHq6dUjvxLj7siPElXoDUxxooXRJdQC8HWNMNomoAiBhvqScQJw6ljU0EhktjBNgqkt3S5sKioJXGS1vCnBS2kcFLevw5WwwskWlsroRLKToByEPNBSDoLMvgMPgD4DaAi3+lWuULaNApg+3EBc8KzARC1zCP+18p6TqE+UfNpNsz1LYsgTrisSzbHoahVd44oWNGJtloRQzNpaGyGRIKb5a2g4XIPykZUBBhsDWQV+iVMyS06w1bNlbcEAQZ+8zNy9v8votAXvSnjPSrqiTKptdQ0VaIH0jLwc5Ma3VX94BOYei3ldtBaoJIKkkHigR3KOGu/mAkbVaKK5tkC9FFdLRp+Ig0MhtDHL6bmoxJuBlPtOyclUOovK60Cq5vC/pPF9AUay7gqAEi6ElhjB4JLc2euzoK7Wz57E+JUPFs0C69HfRQbX7y5lesn/Ub8g31ZBb1ECuu8otvbKYGuRfekFgwvVHb6sQxAtITpMZSKZqhR1M5AKKrhOJDIgVdSCHeKFpmLkZNpX8to9yrDAf3uAEQZlIGQBOzVILhGRPlsiYpEYdCLYKdRQwS2aJLAULzkeirUL3CXGSjV/RrqE7upNl4O2Dhm0uORyIqUgvWvrw4TtXmlafFggWBPfAuFeEsoMOsmUKk0A1HZmwaKrZu0cQ8ogMoms2GOjKhP2GrYgdqqyN8DktFQdde2FL/pI24WS25aFyNaUNqJpLbMbvcIAB7lCcTen9wAq/QfHMWMNtyPxT7//7f+Wqh+/i7WGFwsCqAasCAltnQ8ZVvZhc1MCi71iUPFtHxsHo3ACORBaB8WIw9+cZ1chYVZ98auSfOaXrkBU5XuY684B9jrTZQ8tNO5p6IW60X1Qkk3XCVig0R98YmN+U/0yUwFrEblUFY7335Xb66zRL1EuCXG5rGpwVAC09nMy1lEWPQgJgSnG4TUkhm/YR5VSJcHclIuL9gVIOlGrP2RWnJ4fo+KydyaUFr0nmUPpexiAmHvoQDq9Sg0ulNbtfRYo9zdaH0Ir/wN9I1DKEuc2ZD5GHykL0uTHFDHFljJxYr76N1PH8YpF67Z3SchyS1FS4jtMQpoy75tFhxAluGh9B7lKkqCy+gM4ziKDMB3zHHGphmsjz6Qq2XNx0S5W++TASKxjtUe8GlKdVzHr/Al7vguNOexKLQN1aM11OwszOANMV1fKtZ7QPg95OqS+QlRCg1Sd69UrrVMA0zwBM0BjvZzgmyZQnwSBAuQTVmHyPAxjZC5GmK3e7DIKbXEibR9XquWfWyYaIkF3Vdc1cAoSpVZSNQdWQq1TYwckqv39Eeh1/i1pJQ5zIbBoG+hICCCqpFaYuxAHwe7iWwCBj5WWYc+D/xAIZFBb3vYqjSMv284kYCL7ywSoyH6wXKW6xhIVruRiTTDySpnSYiqTlhKkUhXVzEyqMLKHcqWtI2RCQWP441YxF7TEvwW5Har7g20bA04Cxav+jotofBXnS6LjYht3sVasCpGoMJdNSgWYtm1U1qFEfU9ivSlEYClLcIVAwdgQi1jpwFhvF5pOGbN/y2AQCTt2hz9DImw3sS4F2AbN30OghbBAFjVdDFLH/0GUXMOlusveBqGeEzN2xLvTmd7zOD+c4xUKG5J7RlXua77HcfKpPz3ePXy/xgu8dxzq/MYJ1mfM8oyzpwOt8aCpk0RrS7bXHnQsmvZ4bMPo7hV52w2zBsOoW3nywxbai40GBa595rdS8Bm8eJW2jiAE1ZXbdXFZqwvrnLDQpKdJkvwgI23kCNQyv9H6XkZEF4fqYGJdfnQeJArNXKTzkDOFheogHaII5ZApfe8y10lmOJVRwVEljmOLF0KAbchmiKrolMk+a4bfKFUSnlxoi6rnGYqTKftJ1gO9M6luJpNWbiotxLWETTGF1MFzjOGUUbWiSUV8XOyxN25cqfWgHpYt5N8YziCWr8iKZi7OPlK1c5WqW7JUX/2MtlS8jz/AlZxQo7bsG3/D4dAE5LP4D3FNoygRsbzCW0OGeTkZyQwpuOwoo2oqZJI95y2D2/AEglqK221iH6vAe1ZPn5f9FMgsn9wFTvZU1Hhux/2qMcsMPcPjosx95TyInxQ+yxHV9RH/M2nNT8DEDw4tU3PFpHVqAuA9Gr9Yr8UX8wPHxJ3YtRxLcgJAiQVElNeWxmmNn2i75RtYIUMhcbSVEcZ5gO5HXoUAiCfrPkErgV0qlP6UnCWMgfpFHzm4BNEF7jjuCkAsJlJZITeUlftAMsxZbGbA5ZSHYyLxXyedM87fXKvpJvBwJZD322OHra9SiKmC87GgSRNXiZsySYVkHtxh5QRpY8E1lBvyLCCWkFrtuTB7CFbM7FloLifVxFgaVRcSYVcYmqwAs2e2EU0n9iK7QvVLVpTPyoKn9BfmglXHuaVQVW2y9e4OwHk3x2wN4I8DVzM1BhOkGYq9tXzW5tqSAbWyDVkMWy+isStalksV0ZwFVQ/OJvP6WN5gJIKsoZx/NG6wo/y9Bqilw/BiQYpMtDT765BBTuLaVCIJo+Nnwztxh2SW4vTjcL/n/ZLKRc6/9of84pmMq6MvFuJv0WVzYGZ8ERBCzhaEc14idzAtp6XgWWyq3rcAQbMOFSD9thSSc75McrR46FnUqDNnk1/Inuum+a4R2sCvcPAVHhbKRStxWOf6O44UiVW4FBxO+GsLkjGOFdh50O66yiJ81IqUrRRCCFtbcqlG/F8SXKjX+0sSAQqVpMRWqFaKsUptgp6Cq3RQb7TvNBX8NiG+K+C2Rl4rCL7XyWpQLkhlDran51MOsjzUADfyejxpm+DwxVkESL8hrdslJEhH47NtJJ17Gtu1VhwJTSPaXlrjj6URfWPPg5zu/4G3fpv4D5OprQSXHQrBpiUnyLrhO4+XwRPEDYXaqo2MMMHHommc0+z5OtuEHNENjM1WDNyEHdKcMGNorrruLd8dXRsfSD1CJMgLBfFmnXpAJ4flw5hcTCpEokJ4+51uWDfTV4CLxHSaqEFFHse1C1QE7aCc3YWk1naxDugoUh2pYBThiul26CIWQXFVg3QYQyNFTEcNXAFQ4DZZc8WWnjVbMsB9ZAgBPYG6xfBnlVKflWOgpR8KEb1xp+wVfpQgyvu1KMdanWKpiWspSRO4KNqhVGqhrv84d8zZO0LxFMAVT5bMQUUjLIkPSBPsMSEvOzkowXmLzmYZkaIQg/imeDRpiuQVHT74bsBN6ws5zD5l7YymDXQOFx6xa1EjUjXNLARGqQku85amJi1HRuZ8mScUL8ecVeiis42vLFwtsgsdY2RL+hsGghtRbBerFgib2WYsZixSq/LY6Ya2YsW1nd+2Alc7vd3uiUZgu23Tbc812ggNm2uBoUeXd1vqXEfRPZJTKFZiZFYLpiugsWvuNqS1tlRqVM+oSrEr5JSet7InbQZCN1NoTtzbJ+xEhAvGCkd+3yTSFAA9qYqrc1hGOgplIUjGtJuSB7EiyRMOiAqmyDEEp67KrO5EGr2PFv/7xE0pc38R54WA5zxeKI6J68Is8+nlOen6OwDp3hh4tK3k3FXLOqUWZprd7HPWazNa3B/ANmOIBhvPMkahkoJnAm7sZYmSk8HbeKBErabVtVwasJU3rVHSKQbVW/2E+yHHwd++ZxYQFkJpPaalUudZyfgDwyEb+Up5QGB36Nd5EQveZRQ+A14FlfY2OFKRkpSQv27qLBwhvBqnkguOTuIVaRZDkRCDRe5LXKqtTAc5v7WuufmWdbDsbTQBVTGdwXUXyWv2WTxnTCAIx6FxcNyTGX73VvNeh6u+5JhOqa92QXNV4MQ7xYUjRBqFsM9M+D3C3cGvaXIDMTZGniH/s7SMBlnLtsaoj2NBKx4FAkfrtuk6ctCJyIFjbdsJ2H5VNuvzCNR/uJncvZrtWIICD5ZBrd7TnayInFwv4aKgbCF2hNrixpvVjb3DNS/i5IxL3kEI7ciUERKjZAKrviVBJZwV6zrXwRWvdc7EtSpTakFAgBEEJ9aijv/AqlRHweul2O2QhbA1/YW4/LWCZlj9HSBhgtmBcYGtOCAOLg7flJnF7OwUinevak5c38nWAkxqLpYitQBQr15Sp3r81391IIO7hG+odbGpWQI+b8VN0Re+cMYIafpgyFuUYj8cO9ch38CGO+JRB1IUicYxfXEQ2NHoT7UtpBumI9YuFFtyc6nqLk/160Ldxb3dQRqZXboutKcvcKPhiU4408JhLSnCJ3B0cU8vO7A6o+hAWhQpTUncQgBE04JJTOgHiLCV+kCwMlXjdwD+RNztvwPA2KZJri6+y/OwklMoDTD2RdOGO8/JtEpG0y9rhvExq1ooov2Q6LQL+BLzXTNU2yIqRaqwFjT9liVRyFSYE4QFhTPDxezsVmQiAUwDp2y7dTlPvGZzznzheHRKKBEnEK2QgFoREEwZhYBvJDSypkvY1Fmq98+HlO9/UAHjSOnftJOGzvhsMe8Svk61qQDWQFh8xffqnsBtyAkR2q+DGn74Ztet7yQzH4CJrOKb3qrBBgzAnA3kDvnqxCWHqpXZT35jG8/GalIpL/jDW3aQElAkIVVrlQgqwFpykgkhLEnh5x7lZRH0RNZqebUql/uUZANSoJdMKaxA0g51ls9Qb0mcKgNzceqeozOj6TIyBuPv/syXOBs5dCkPUZShBdyhdhnLbZG9YHPlFkHQRzILmjsiV0iYWsBp8FfpvG7BehvV7geDJEzF61c4r0ivfUWb7F4sF+PAks9Q5Wg0xtDuJzHmOFKWdBXeUk7C7wqX1yHLfCZODhbgRfsj3onjkGetcEx3NX53pcy6M74InFI0B23fLtT2Z9ZuyEBsikEQ6QVMSJFhXDHjiYHIB8V/UqfV9ZmJ6KCniBYzpSoD6S9uR1iylVjgAjLfl3zRFaJizRr4KqKXYdWdD9ywdb6hEDLDs/+ktnC/Xlvj1ngF3MEM8QGEplHQnHVeMCB9hwT24kA+KhtKLGBU7s+GOfcnZj0xGpryTKAUL6bdWaMaHFDpmBpahIpKQWiWl6LTDGlU8ruTYlGIMRM9apBhMSZ6VFIndpiUbGho7YvEoZkXoEs/0gA7c9wpdmiA3gds0hDiviTmMwHhryCKyDWD6KotLdQw6nRxuKEt06kweJ1IqZ5ZckacKeCiwAaaZsp9Cqr7egV3+zErplk5dbQUI46EfDr94e//2BlGCVXJb5dQRe8oVv2M9ihrddxjfUBbuo/f4ngZ+rG2K2fAiXDQ9RCh8cLWs92O4vomy3N1sBKEVm55bYa/V0LU1HTsqM8CBSeP0YFkWhmw5FDQyky0ETLAjcVRW+J2ZhdR+CpsuFB8p6NKBhCLlgmW4HSJtOQTnJ5YtLyANIgezETdhU+nPe4jOaBS5jpLFN+k6kBCQguJKoPBnd1yhUk0SKrPDVE5DzGU57i/Z86loWVtTVohtZkeF/0zAMavmVZVVjN74hUZ7g7elmti0JU+4sIPa3g116DTuKtba6SnTLrGor1f3ATByUw4bZ+scudi1voJOucuYS0XOpVk328gUh7SXNCVfPDcUxnS7g0EXdWKVMuldNJEXIBLwuV+wkVhBgTvexpCqCy2UHfIBUyQVDhO0OUmk44VQQtbh8yjAXGVIYZMMELPV9YUVJ1bP6YEO2E8ScykmCzqeDJqeTUWHN/RlIFlkl3TwSmPfMIYRYKAsKNpuFSKge2kRdiJPmq5ZZ+mxNVlILQzb6l1A6fhqheOOiSLUuwcWlkqWJ6rNK2FB2k/s3RosL4Tau4Ew0p0co6Uy/WVgaZdPcjnPl+2SrHzHJHPvrAEe48I98AQh44hXBbQIamfhKvevs/wLQQ9ZlfH6ay3LKxGboGeu473d/qWvbHDBZavJ6DO7QA9i0jiHRdc4PSFIjaJxFl8KoywIwk7deziPrqceQePckbbSHJxIwVuRclO2oJJDCKTcNOCUs8TE9TZINQCwz/vUenYIqGNMG4YafWAkFt0WmyuiqRRu2g24LAyWxE/Uj6gHBmaSiav3VwusTWH6cwFioUq8J9PZv3RTPsidSxpXwEQC16byxqqQpdC685xS2icZxN4x9sPSt1RTvs8vl1r2erX6pe0bHXyy66f9ac6TpdQXXUXLueHoZafMUhNcm/EWFN21FTwkNJe+0LpXGefyVqccTgVSRUXUMFt7Yo8dYPKoq0cKlmNKH0/B2co8xR0OCzFfhIp77DGlH4V6rqD0tnnhGeqgUmCTngx/xnAlv0lg7p4MY+d+2efW7q9ejRyWz06ozKp/8mOY0E1hFz3cF9RuTPqBipjaVidGU1Hq3tRLj/48tdG3BUeGYjEyBYfEl2XhUYqfBJ0LsQJg+jMv6FdZ0cPI6Uk4R5+5xh3rvM9+q5IQweEeShmrRAFZ4D18+OpU6EvjIcOgZQCFKus+WYHnEfRzyZQcNYQWqjOtcg+qxTzSY+EjYsdgtKCwWuVyRz43GX2kR1T1w9bVwAoougmz6pjuUohGT4t1epl5jbtZfwpsUsGOqfF+7WmdEQhdoljEWS/CBZNXZcAAtexC53nP5NDEOMPCnlwsXFdmWh5A5cx6PM8I2YGVCzU1ZNYk0JNXgtYNPTEqJap4b1H3tvKCaIp/9CsMUrpDNXGbtdWVRwz18vLtubBNXCEVjLxxymIiTjY8HXDD6cBCtym/I1SCSFVQRY5IB7+u9UQnAOQEiuW6lnGAlrG9sVF9VStJY66VnUK1FFy4bqgG7CNqg4Tu4hIgoWgPMifb0QuFwY5SGKf/hDeAlQIRcZAuAOiDr/nTThHr/0nawAx6gVKzgsX5LZVl1bWeWt54QcC14labQeBVrUF7/llFFxBqDbyvpEuuDhYfYRvnCU+j89XYgbda4sj5XrdBQ0Ljv9wK7sy82MtDgBcG2RlK9ngxmQ0Q1aUNhFWj9oEuodyzCSjVTMi63P6LUwiGTJeSWCFRWa2ZEParhH9OnyNXCKUnIYDeRXnKucOlNdYt43qSBtOCEC/dajQzsldQn+Dfwrr4roXrRqnycrSx+h6S2qqXmdJ00okJ/k+hoxrjUKZmBQ521ykw83ih6/+hfvOtTglYXsiNOIGupocwmt4qMdw3a+UG5QhlyXkWUxQzlk+XAEee6uYwpeDDT23E96uo+szWlnOanxxxfM/Lj6nHikqii2KtUgjmGqV3ae5sycDvH+vd551fZGfvrm8Py4gOldz7icBBcHQAiSKXu40bGtFGgxRyPWKZggr1TIUu8gBLoRpq7+PmlYjHJY6Mtoy/D5Sf/YorZRnfDQ7OHIM4JZq9wVGwHcGdfYQDzDYjjwYlMA9gQ3nMQjQVoSYKcgsyUXIyB+LZVrMfJ/fF0nFZqMrAEiFj+WiLL2l1vQiVavs5rGJpqFurF0F9wlvyaVw9W9J7pL11DhWNrKG45V7iDOBWhZgdQUiNX7kCTheRElujRxQNhpXyncjUHLDxmk4yUo+IUqOI/bfIXyp16Y0LQLnJ+CGuCmEkRRVDxJ/FMPpD7/7Y9ttI1JmO0x2gtcUD125bDjae3blw24gva8qzodrRr8r9WYyrAToFpez4Uaa+/HfV0vsHa20RQM4afcwbDCTtTBEcntRMTSqMSJ4O14+HHU89/o27X7Yru2MBgnTK0akxTmU7yoQ5h98zR21kuuQ/KrGZL7hDKDl6ZP1GekYXBuu6enRONQsb70JQ9Bfk0yvMxiye7Lj0kOKWi7NpvV7lFxGsrRQyou072FsAUOPRQnt3CEnS0fBKVwFI2crRa5SDEEn9/pzvnzccTbYXOk72QoBFRGQJ+anQ1qyl4QJRCmHHPGBrwPSdKe/QrzKVDiTzGzv15n7HI9rMorn6df0Tb9OEz5enjZ8nStUvM0t4uSI8X2eJr2dPHI+8H2RxHCz3E623pqnutGF5s7A39ItqIj/3Q0G2fnJkkBFZrlvyicXw9ZXuiQTHWopk5qm8vy43tjdIS+Vr40OJupcQE/AX1Lhgis5u8Z8MHzu67HmGL1hg5PM37lr11LmXoBv+vgNF2KR2VllEEq2FRnkB9xKRaK4puBvUImqmZ2sGOWEyrzKiiJmEIKf64WOQdtG91ioNKyeie389oEZMYCNP8rCY9upPD9ROkWGXPscJSqOU/qcUtMaCWds5keCEMIU7arQPmi6S7lDqMTseVKiA7giUp59tjKZApQtXnLKWPrxS122b/FT7+qlLboacS8cjbkXPeTb4j4BgbhvOWkeOkpvh+yW6jtw2NHFkJyldj80n8Tg4K0UFDHodRdUZq5R0T1dzY4X2vszyv2938aldE0Ps2yacpWKI/pqNT+Zj6N2Rd33EJSZkoryKlMl3BZrse/x3d6AgKQy28KsCuv8aHoBaHN1JedFGLlMlhROe6G12bUEwMqJHouyUYv9olaRXhE8F2eFgDFNk20pyyXHxKNQELHAqG7zHFaFmOmcpFkNXHgh31lXflcYnAWbHCaEbNHSH86e5FlMMIz313GlyjPTDRvnbwohrbVKpT8smbWpqJezKamyCHEp9gcSjWyv6Dx+/hVKCycAXt7aAKfAtmQnf30GqL1uKteug7XiRbeBDMe0KNwCmnXHZyBroKy4YJ9bmr8XRLdVi6FtMAvaHPxYCrogWWhX4AW7s/psGUDf3PIhdfSMBsr2flPdfQpYluqJpVDtUYoymBU1wo1y6yiZ71rxsPfigRDrzB2nJf5LuoVIjRrsKASBJEpXXtSK+v1UAeoZ7rIA+1CIFOgiIUQhMsAACO5ZdWsxjlxQZZuSLk+kru/i14IfrsnqhurcgCeut94CRBCVl/+V7w9hW9b5TbBZbO+pw/Hv5xV1k2FngO/aKt5fayvsXyPn0Fug0/1lGGkXH6pWh3uyQ1mnVXWgytyCf1yuqq6iZeWJINrHq0LbmFeRDSO2Lb7prIy22jq7o1qjXumIND2KMyqvbZ2TrubT387unu4Y3R94nPQh6C6n6RCh7HeB0bWNJmqYGcTi7sxoi2IZbFYkkOiWqizuHlF1yyT3IvyakHfP8tLlgVoNAu6blmkt4WWzO0hU+5XgelfX+ShhOjiU8KFYQ+yOQV9tH0QMRGtv1ZkUOvjgGWyaEc+SdkogX5EAsfQJzqZyhaLPYSq1eyk1G0sN6yTkBXk2ubtTfYBnadk+V6bUuTLAHY+/Zwc4V9bPYQdtyn9kzFHcylw6hwfTxrvNgHS1a86Ac5KmGt3e1gXr3JWRJ2A8IoPFfzXIRL4mAIxDBvb9cN3zkc51DqYdkgumLVJLw3l57rxoZdqhFsLDFskhHMZaibgUezAXO0ow502zwEHWU++8LyO2oqwEkmJyCZXN+prOIK/AV65VVu8JnVRYjWQX3gIU4Ui1+KAaUAtCZ1mxLs9NS07hvmdoydaZq6Wf8gkBu1DPCv1ZMpN6d1SpP2+6y65brzoqhhpuf1w17TrvCMy6JZu7xQe9v2gLPBTQ/AYfHhTU6KBHibZ1C1/bOoJue7XFoo5I06OYo7oUUedYNOrKGeV720V1NvFuNGOiKMR2BILCPSdoC+Wh3h3EVpVgJXxnH8bTzNSCr+nJHoEr3yIme1nYprvST/6pvyw/VZgI2E15lzJ5Nzdli1yz4j5pVsQwFU8DxEoRacJwx2t9R77oVQn2c/378qugBpNsvd5lTxxlsl15U+3X03MyE2NFTq70WjatHBC00pOSI8L1nhyrc8qbDf2hhRxU2XEqRSrUFVveh/wBsajtZHDb6d5uWE7ZfC6X2iAJ/Oe0b3wLUGottRNKPTJB9q1s32PMvW3H+4PfK5zSzFZv7q5Yjuf9fvYPP9Go0q6OkNIVBxHOW67axUHnbiPvraD0WGHKIUx/SDNFLluBe0j80AeCG6WvaXRYoD1IOIhLUMyX4hBBuqyvHetzL+7mzuQWNxZ8rs1mFlSMakQWZ/8ScjVejgffBwZmeDnK3sXDXUDankueJaulUZFpQ1VrS7SqWMYc0vJ9Bpvw53fpDDQUh8CD0vgWzihL7f2FQzhtuwLALiqb4z5PjcMysG4FoucMeKPL3E/T3roRMqqX58qx7lopeR8CHDxD/qtp6Mxb2Wo8kmTzgNxEGCPCNq+3yv3Z6PTfMrTIr+D7yN2oy/RoeItWb0egkp+zOO97CF9xRf7LDjruxo6xSL8gv9x1gMU+wtb1yjGDIA6JT2DHg6toeHz2DAX8dVvKwmHVio0+lmTeuyRaDjezJZVDhFyijHM2wVVWFenh4znDkL0pbGXAtWms5KL+jnUHUnwtiL8XzSS9grsNWPhr3s3h+5d0s9SM9PmU3XriInFD1KhD474fVeksZmal/7tDNvstEJOYGThXBqRfqg57LttXZkdSQX4lhStztPDODTnByYbnb6yNEY5ExFHjuxF+yNDcHpUBTj43ijTNUcYGcKVfVHrHoJ+MgG/WE2LAG0N0u28MDMcqUIbRNjvihGgjp625WMtAATZ6zJygvpu5ADi3eQaqKWZmtSrX36nsbK09u0s7jeURTOwXUdNks1K7B0HyKrwG9Al39eGloPHXwsb8ZTSNn9PGGZJe+8xV7HJ5zlRybO1rrFnw38heOxJ9x1hbUtfGdZHAXfAtiPVvs76VFftxqpLrotZQOt7+FWiN0KbbmF1Pj7QNdNTqGFl8KG+yv3Pb4ZuCqg4+462rfSt7I3urZVb4X81Qu104P4ldjleiDpEmMspSG18JmqSFbCqcsaKSn52s66g1zfC+h3CPlO9tppf3BTY0aiW7KB86TBUGcUnPYoEYXLDeBKiimkyCEosaV9OZtqviBUWRCq5lor1FnXlgUgYEuoYxuk9R/3m9o6srBE1fBM8bb8/zaaM/TTe04P70qqN/6YbOlaZLyfNxfAM4gyMZLseBfp+z2MWs5uf4zs+4th67in91qHun/p38joF2RvA1U9O6z1t82OePjfbqfYhzeK/CulFRnKeK1hUAMeqBrE2v3FH6Fu7kzwzMDBySAR5NZMcnAv/jGNNrlBHwzUSv2pXIcbz45r8r8ep9uqH7nqZvORscB+8aSUxJYdcI7f1QbAqhDcsuzLU2jFZapoHGf8ui/RISgPZVAnA4FaN7hdTv5+6SOipN725oEVCyzU2wKH9xAX6jDieNfRbPhTCc3NJxOE8aQdOpwZofVWlhQsN+BiAsVoh0aq0s1eyXUufj6PO5tlX+nd3Rp/ut87a2rXPW5mexNdv9Wapp3xLvViLl3mitfB+X8Z7ekllvjQ2ow4jA30FNhoiGYpRx1PnzwM4u9xYdmqZDsHPbm8lzZWpFD4drVS2sBdI9A0e2O/fA8sx4u1ndt4XmUPCdfTJzOmIv7PZT7SczMpxrKTqns6jjykUaf1JCVC6w/hGJe45+luO4JFR76XHm3hcy+oHcWi+9vezlTizLTCmVCaDYaLukB5aaOacm7iby4pqXiOXWFYAcfpZnBmYGDs9AbS8+3Og2A5VhjlmVipolFTJIVaoJXwMPLurQNH0N7q3ygdN+A8lfFd2+SvGO4YOzpnsWaC5q5r5xlWhZf9CmxZ9FrVLgYhzntI/CbRAgxZjF6fzzYiHtF/N5Gr5sBrgf4LvdIaR2D2+L/lgwKlYKDwpGVOJOL88AxAqheiyK8PUR/WfqfNd1/4p+v+R5smKdQfb42Z8ljsWy1RMp67Jkj28WpvZB0ywvqzuZ+mikmboULXwR2EhYfg7Ydb+xzXcE9ue5XzLJuRti4s2RteDLUYg5PAR5jTDayNTKykPNQuQlvjn2QN4iTHhRo+LQFEFHwg5rjha+QRqhhEZwhAvNaoUyz1bEFsK6drGs9PD7e7hGW9DSWdNqjtYxaroQrDA4b9IikBA663SM3H8FW7eIpksnMkOlADiZn818VAFMJvcxrl5oBRPDrODQZLR5+juSTKyEdHNE7URVzSRoVYltTL0PHmdLW9nm77L2dlvbEepeojMUOwPvcXyFp9Tq3xGstnulPieXHkoLGSf0V81mXuG5F6GBY48rABa+9mTSMwMzA2fLwHl2yR4rDZn6MbU2jp0tby1DOhLQ/NdSuLE6d7TxPutYbyyMs7nLj8xy1g7LVwZ8UKfjfS7b8zLT7bwe5Fjb6BlqOQl0njCUjjN4Nk1cfQYO6DLZPqpTULNW9lsACIY7wfjD7/6oUTRdQwz1dPZzSp563utXXUdXSoJHl9yW553ESX+Z73riOtqTMhs9bXO0Vz0+bJFZF/UWixfXjSOJGlXYKx47dE6yPUJ043gk8YTnj4RxdQS8b42OY/5yz+9fwWV0ndu2PS/5vZOq/UI5R4PLOM9YBw2j1q4hth3cobY/G6Ux1h27V9t1X0oRukHI1BYfSq+E40xRab8eJ9ie8CZ4E8yEbe8vk4ifgi4IzOH8MG2teoruauKgVqj6s7Otnd72U3V1BXM0unb7Dh/frycbrmfH7p11a5fZkle8V3OsBYJNABMZrjaUdgQ2OigsJjBGoY41vVDcIMumYoZjFhtOmTrvoWLm5T208juOER1c+rjQQlQSI9JSF34eVRhMbB6TMrw9itqnMpA9LFwWw89lcUDA2ja3C0Lmv8t6doXWXQfwveAsneEsRtT+PJhzdBP2UPwUYhBpis8MXFcGaAhEb876t/OR2fWuLip7RgNfhj+JDgUTEMjD1i8B1+Py2lzpsEBi25QOJovt8HlhgXA9jHosq1NzWGDaT033GOxZFShlRq30eMIypa1+3WuWvIa4elqN/HRrxtzNhzo7hKFL6xNB2Y8hWwYU1ajXkEPljklej5/UIuqzbkhXAGNkT38bQ+yTXm93qbvv1bJLdvritKV8u3N7h06wuvUZYLW67eZCzZZsr9Nd33MWQumqXvcbSm3odXloY47WbvFhi270M+wCzEHJH6RQRremMtX4a7bFe/dZa+O3c4EtOZLg2DYTJbyI5VW0shM+Xog3dAvQHlcAAK5MBFPvcFvNQpX5DpMzQ36rGVA9XJHd0fJg5EemoLUGKOjO7doMcNb191qkqbdnBo7eG0r8ktMfD3S3qPcbeueSM8+HdAAcidrdl2uzA9YhrmSgi55l8rVAgBE9RySPdHXDiLdpz6FAUdDWnXuVDwJaZ9UWvwj6Yoz2b7iuy09PMKPIOueaZlvtPPfcu1nKaCsW/mgU7G1pqydj1y9jxbUuSzrefgTdapYWfvtQDwLa0CJNiu72RJKUccQYjBbRSgHO4RHrZKWtLRz208pwiewl7Xv6MxUL2eJLU2Q47aKF1tbStdzfrPFBS+5L634+gIw0LfVVvRefP66BWDgUo+G5ZRlNRzSEL8Lb+4lAZcQW39bpruw5md+ri+p5HupdmMgpzro8l3lYh7M6JiiWPvSj9ejynsiYSQtK/xdCDAvHEXRBAH5+F49aIriCsEcGOkJqwOdfU9E9rcR8FsjFokqi7diQxYf59H0vP//tKga/SvxBgCk+MzAzcJMZwL4fh5HluZAZIw3BB48jPOiZHtxsxRFpQ67472azchbHj0j9WRyfRt5mBt7qGHee1kp3Z56R8zkV20/r4/HqiKzDljKXWZCxWRPNHMkSm0gpdAz2v//7P+p7hESKicx8VuuLbSH7/KaOtp1rWWyfy26pLX1uo2n5fkn/zlZ1lq9xmB5AK5VvhNMTY4/M+cO1emZPy27x9rhsyGBC8/hiINDxajqLBarl/ZSWvMXPMBeLe+EsGhKB41pBTKwmtG+1llwN7BXPk+0kCtcbkxW+jiA0AouXHAumX3IUYV32tvtj+an557GiLa6j1+VQ2+pBWJkN/cYbTWvzh9HrfO7JBru8Dr8SrsrMbpgwE45hvMWwwQOgfJdHZy/jnl7Ts+e9vAoecQ50qTjE+jSRTHhTkGf5zemOfhHoRNcr8PFYERI5jYVU83ZLyJKVqNsNano+M3DNGVi1x2HseXvDzzW3Uo9vq1qyB/htycyOe1PtSRO12bNvqsnO5GzaK3i35tMbcxdPVXr89LB9x7sUHiVmpGx/5ASw6eayY6fT73/7J8Ll84NEgdjl9YNEhAuZXxWJ62Ptda52fZFNj3ozoNcwevpDW74HodezbXJn88QPPNhgCHDv8xl23OnSSyeL1ZRhqAMUdItrujTVri3lb4ujoztb7zJTFI53lV9vNXUOqGA3zn7wG82/brsDstAFOeozg7Ln/trgn7sM1YXUynFd4EjuNeT/yPjGsNf1hDEbo9JhPAnbqO8Oa7GYUaPHLO4JMl1fHDkoV698x39mWRdLr1WtssEkSScadAXAvfZZaU1yZmBmYGagnQEMI3544Y0aa9qKSS2vMCiEZHRKRGdhZsBlYF1P2zF56KOzm+6Yzwk1M3CRDIS9ePUOTZeV1n66jHbhLwihui5BFY93D98b1SE7KwK8xvO8NIyep8VTjeWSjprePYJ1zQ05rNjrWMnQPlQQ3gSrJ8YemdHW0fJl/yk5w8m+p3mFfpODhdCObgdPLMMpX/fu+hCTytdLjLJev466C1e3uKZL8HZtKb/Aae7puvU1vYDZrO7HWde7dl4Hdb2lx5P+uDg9XfLuahXJ470rHb23C9NonTJvPVEPxGLYtdg9sZQy/T5ru3rtv8TUkgt086m5Bd3B6tLPnUcGw5/SriF4CbYazTDbXP9ROOV9+WtgMYy4/ZcPPvpwxmieo+0GM2uOV6UBZ/8ZK/32u4+CjySjjdbASKb85L9JzIgeF7H1I5XYgbMHRsB6M1vdXG8mqBnIkRm4xS7DPq8eAbCIQtdSw+h2ixk4ske8Iew31LQIhf6413Jcq3eAN9TCM5SZgXYGeMdpy7zVWh4nEJ0QGW0FzknTWkrSYCsJZVBdsfBjF70FiB2qAlWZCTYXWnK186cKxJtnvYk8lCtSl2234/zpR9559aX7OkA788e9/57iDfcmYsfnmU9rBFCO9me1X1LBJ2TZLkfkpLSSOPFuCrebhxWey29Xc/Oq4+rVtff2/ejqQnIO9beal+S15zNeDViXt/641uGXWussrtMqrV8Fxx3DylN4fVDjCXPira5OKuoFylg4bkJiUDticubTX+ApfXfybmByhsR9Grr8h6idrgAEyLmdGTh7BlbvSWf3tMcg7ZVxH+3RuISMyzknHt+30gK34uclWnTa7M4A757pTqqOq904U3BmYGbgGjIQjmHlAYL2csfFF2g+nSZOKToYCKENqmjx1P6iQ1GcKL8qgCgeKZKhF3hU3zbKkUQj2tPmOfc51yf4zIld67krcWffmnkYPp8+7HpCO+otdzTqGDWtO8soTf6M7Eb9dvsj7elL/XH1PAPQg7YXTmkL8SLlemfXWdV0qduf1bZk2wrbrbTLS+J26d4KTsXKCpRjVI644mE93bQuD+3RhrNiyWi+pkdzOew5blrDqDMy7Iy61Cnfsxe09yNtiHPInH4tjaBpq0UsvtbtoftbrV+yx+52GZ0BotNf8O33tt367VodhWVR+6nlmba0Ssk2p9/PNk5ZayFzXCyv+zkd0cJTPXKAI2bY0zVNbCqHp4CIXPhIxhgP2gF4QTGrFhzwnQvAEX+1LFWygOYS7bj0+wDuCsA1X8DMPZ/lmYGZgYtnoD6sXNyt6UCWARwX1h1kMpxZLDLgd4FsT5jZLhI1xHiPHXb2maEuchbhbLcmm8yqVIw5hNZmjB2b3a1IsBvBP2wdWbcCrvMDS/87/A6AJCAYF8ZWQp/DaVrjWnwts50+j5XtfvYgWGfAPbqlzOh5cInAnLeUYR3LXvmx8qb52q7mt2n2UL9zoy2/b+06n/f1gdF0S5VelZxRHxiBtfQqzijOOnmKLl1rXIfz3rQa7U4XAdyVWKwjgqaFNHdY7UzRZftDp5NnFkP+5LP7dEKQNdFoXy0Gmvcgt256d/79N3PmbMX+/JzNpXMY0h2xtNfsmvo4UqoexCF/2SsalcJIpM4Mgl0S9MHRhp8B8Iwgs3a7E8xa81NvZmBmYGZgSwaaI/sW4Mvr8kHh8n68XQ/clfi3G94ZI8NMwiWTZhRzVnHGxE9TPgN8IDj+cLBX71aeOhKrEYqVN6s/R8GZwuPpiN8ByO2tLevzbKbL81Ets2DnsPvmF+xeWbW+7227a/1ouu00zT4MtKPhdIlZCh5xdt7G7M9P6e0oZ10O2cN1uqMelm10nN3S1rK3YTx++C6X3e7ndoTcp77yaB5G5S0vjsbR+Jreyx/erxutxkv+ocu4CyyW7Rqf+9iW8WHdMx7WeGXxa74fzOO5i8ssvihFjdnMki9W37D4Fh658brz2v8ROR+Ny4qX+Y3+31a82trenKPLuR5oBWLleWiPXtGv23a9y+3nesUqjyBWhCv4zYytwJsqMwMzAzMDMwMzA9ebgXnU26VtYhpBxQKRqrSLqQkyM9CRAZkod8hel0jbc9mjTqc//PZP5PljseIV4mkjBSm1FQU+U+HffjvunSTW+ZDy6BDyUna3B8Pv8eD7xIbOVrebbiD0npc3IFzVXjhLdt5OPfdkjmfLes/1Z36Lh9v3d28ds5lL3Iu/JfZNff1dXXfFkVWOf5uydvPKK/YXJC++Y7CY8l/8XSV6D1oR3c216F7HBZ+rXX+H4Yj86/b1jcW7c9EV2/v4Eb71dJ7ErjkKUTC4PBDOqfkZgB74KTMzcBMZMLv+TXg/nXy7GXA9kw8zbzfIK4sMx7vy+H2cj3Pw2SW3ZZPpxJa1uxidIDMDZQbeZGdzZwAu1sc78xmAMheDnHWriaP3Na6zwm9vuFPv5k/OnzoiXWm3A3lURHuuaQvHX43p7tk9mJatfr51LWLU+vZrTb0WkUB9WOoP1UlW1hsGEfYS36sn6xbszWEag9Y6Ij/aw9Tycml7lkb3O8snnSVNW/LM3xJ7G3mhVo2xC5K7V+NBUlxswX7a3FX7c8gOsjzT23vF7kEDcDSidT6099ChzEj7lM/eeN+4KbmwYdRtR9rOm96DhqKD0XauSq9G5UuE7ZzRGC2LO+AUVxHbmO12tPzk9l3WXep+bd8s69v5A3bpt7/oc/Lz4O3Gd0Tg8XpHwAk1MzAzMDMwM/D+MkAHa/xfOma/v8TsFPFOie2CkZcs8eRlpwhuD4YnSO88CbfXbOfyuGdfClcAsP3D3//RGB4ZiE9FC+effk2s6pMD0EPn7HEDCNdwplsEt4mxcAZZnMtqY6Xu6PUQjbYvXfpW4vfIlFqX5Cz11L36Zz9Ov2R5FUtz9mqLvXD2auVr86eMa52H67RK60dwMArReO7W8vf1k59H0muru/kfZkh+F+88IG02P7D/GrZ8hne9Z9owZbJHoxiVL3tRaC7lkms5/1TAnz3fN2NozVG7Cv1wsoxxi8kd0HjuwU5svi63gz8qHfuiKeANZKVHds9ra2atGC3+pr4ddpDCEYpKngHouQLAaagmowCfjJmB/gxgRQfd6rI9y9xP+sPok4Shs9nq82hKzQx0ZuCQCXqn7dVibnfDQZS2+H/ZcWZ1FO9GsT46rmi1FSrvJskz0IEMVHvk9feucHtPEmkWC84AXCB4qy22WWVQ9KFybS5TXftnzaEUHXJoaa6ys5PWWZfFD0lZ3rbvxHr6FSFYMszXPmy/o33B445cMYLls8bvkdHyROc9K68/f1nnf4t1jaPbUZ/Za5ptDewR5SqO4qxpi1q0/Tg63hpSL0/jlCvE/f702luS022k6VKPa9d52K+l86Ov+ZT+7MbBmI4/N1b0+9ljXe8XPfJJ7G0FdxzyexNojDP8XWi127QQX7jDfmD/LaE1R+3Lmt1PD+SqAO2JQuO35bVkYSpl8OHAtR1VnO7iUwG1nzaq2L2+AwriGO1jpXy+36kUpRm0S5t7FEMPtGbhi6WbR1conokRhgjOP68a7NWhrBhjD0+DrPTtVKAsUadwHSPEEUQcMxRotwoMnv/FGosK8rG+5MQ6UAvViewsvK8M0MJ/+Gg68OZ2ZsBnAIPvxV//NxvjJjNAXUf9IYa9juQ3mY4bcDppHxwjUJYjRW32fwMhHeEiciJpOQJ/Yt5gBspO0eojUfr0+7//o3GEpd0xninEnPBuShO3ZIctnwpIqqP+AlWe+y4oXFm1dY670s1ihX5n/JVurVHzZ9VOFWe30kHpTLfWVzhStmSdPff4cbsZa0f3VuNqR73X+LAXjuVtT+toGU1bmD38vXAsWzvgF2OaZeuc/C1xbdFdiHFzro7u5+z/7hmQo8Pzb8hC//i/Pd7dY6k28aifFXnOUe3QWbU4mQsZkD7n5HQp5jhSC2Dbq61+WPK1q95umFQV/pKsfwYA5Kn3CkAWjlgUIhOYxd0y8JZTjNjc+912S9YEmhmYGbj6DNzYmHZj7l5983csYWPiwn83EMxqF4vZWS+SO272Ck+5ngyk+7guoZViMVI9oJeXqfsLLv6o+y38ErDVQxnWqvVhc3XlzPXyadnkQXIGtnmFZpMr3cqbWsHF2H56oduRKKi75kJPikqXp5LWv7w7O3jw9iJqJ2XTvtCGnrWrMqBbRNOrwJJ79LejsQ/+cNlx3Dt6bzoOX+fqOCvr2tTSOqefnB/2ZMX92VYI6/m+U7YAevLTI9OysXed9+d7h9vx3MKo/7qfJ76rGYkivYifoqiZimXX4ie2diqUfgZ3Y+eAy7HgXrzi5v58D8a9uhVj2CfTOiMtVA+bmwpvKgNqV3pTcc1gZgZmBsYygLHguocDmvDJ8UzTY3FOaZ8ByeXMyJoMzB64Jmsrda52ZDJ2orxzVMRYhEbd0+9/98d2gFYtMKyqmOhFCfNsLGIk1Jb34p/zzCxx+uyFc0a6xZZ0zcV+UqZwk11n7ypWccrACs5opCzPMP33zhZm/Zsr+D3cW3D8m2rYQMeKTunJOs5o3tZZuV0tnR9Nr4toO8I6u2fT8oOVu3+WjGIM4WNg15Fw+D0wZ4vrnRiimQaeJD7j+HNUYuWoyQaKY+fonEr7uXIvLu6DWImjXdlA91ivZEklVpFxRyePimz3u1mx2FTmcYW/S0HtIdc+/5pkH75zNeSn99X/ksZ3HIirhSuY/RDZ9QwABJ1aXAMp/TkXhx05l7Vp59AMbNibDvVrgs8MzAzMDCQZwBGT/hLeLNxOBt5My+lANH07TXHVnrqU4otTG7+ZOovrPOGGQWu2W+Pz2KRHqJqU+I9KGOi4AgAN9iRLAAMIXp3IdOpCI9yec7u9ZEb8ehOyxXm8j8ri30jQPf1hNJQjMEd92Et+dGViL7vXgNMT+1Bb86BbHfeGcDYmp+tK6V77tcJZF2O7Fdq1GxPVUK/HIkfV6lExwNV1Q+3wVmV4WHezwtH5Pxp/cwI8wF5+mjgdrez71T8YkzLn6c59b6/0deMM+9+Rt27jQVB288AoT/3NdhSVbYS4kB1NhJ/Cp2yvk6i6EYvFHAn91/tEIkWUEnRKsZIj8pOYGZgZmBl4dxnwY/CW56r2yhlc8d7shXgkzk0cTG4rpUc218Q+KAO9uyz2F4jexF5zUKaOhkVuOb1MnCvVMsZkPYGLGbMvBzUl8Jh9erRBOOZCvXzfP0NY/NIAnzkxf/Q+7J57kVfKHHEe6YLsWo0r07QTZ+A81bo/UvHLX2bdyc0DYXR/GF5dMPzSmIaIyaYWGbkbdaAFTZutitF9sIXVqBvcv/baa9rZ64l9rK3dNdj483bqyDGG08hkR1VPXHdqv+6AtEUUzroY23dmd8Vieyc1o/t+Hos0pRwThSM2ApHrBv7KrcpwfxT9kuyVtcftlX8rdsbv97Zf0rK4jr9XHkycF5pztqPz/Yp7IL5rPXBL32uPluvyNqrl/e8/Xqi9o8uWQl6It5ZeMWG2o8IX4R5CxhUIw7IuinrB5E5QsEVBEVFI4uJ9XslM8pgMxNwfg39OVOk95zT6xmy9pf5wUNPcYIqwZ9CvKsqvls495aC+MWFnBt5zBnhgmcPLW+kDONbpw11ZRKBaII3brolyLBMksUDFJK4AmCv3QdiBoOC72+N3EVVTJd/qn+aZk4bbiW6fTydGRs8jE+VWob2+1dLM6ladWe6b7XYs7fPpgbbIAreLbYulXv/qyChyacvi6BbpsaLle3KoZXrwLT8Zh2vbedMWWb7kjK43U9TJEJS4WcFP6mNBZy9yt1HauqYjKsY+2/koNkhpW5oehLmc+KoRbC93dR8ezV4ibx3YBh1lTFbSvrVhtkhaa/xssT22t71K8uNER0eedXGVdtt+UgZwje6AfbNtt7+2Kw8d/o9mhj3ckhltcbT1K/nZMB/TnrSRt8RbQWaW4fmCVwUcv72H2Q/1WbfdD1Bzunv+FQk8fM8YSphHMGI0bgFiLf+905iXYM7CzMDMwHgG1I48rjw1zpWBOWSeK9PTTn8GZq80767oT+LFJa+/FeHhPE4d20+a+U16SCHJDJI5/eF3f+xxM8HrUSDsTrlUbPQ8KdU+R4k9ZEtd5+uFU3R+HO4C3yFet662+y/1Fl7vw7Ditfjaao+Mlu+nj0DeFzPus/1R3abkXnnbC+foLLKfvMZzyIpUdwA6Y9e8VqrXFzXdHegOgpeyu4PrO0Ho3rIT5A4w273qQShlSs4OwVQhcCTA/IG/qwKDzFHPR+XZnVvZX87pp2SSD+6D7QbxVI8n3JrXnIK7GSNfk12w3IQxdNfoGFCTPTPwbjPAuzO+sUPNferddoMZ+MzAzMDMAGVgHgaO7Af0ENdtfPRMf9BjqJI2/vfeApQbMJ8cyAWHy+vW1E0zh911uslP1ckGcIxYbn3tn9uuJw+ljJxDmx3gchWlt6Uv7fUG7KDoKbSrhm8uqu5TQiac0fyMyifGVGEUR8v35E3LK7MJ2YOTKAwWenzogbzU2v9xd4T3RL1FRl8n0fQWzH7dvdrd/wqnccdwvz+jkmh3GkCc3XYfaCOHe4tJqud60W55U26V4+f2vb4HoZQpOcrNTWSMkY8Hm8AqyqOej8qzyfPvp5VQmWXMo7y8exeTqbuhouz/HZnUUwA57POMoHDFYBdynuGe2l17AmCBXhufcyKZuxL3rs2fK0nLdKPMQLZTZ8VSfnJmBmYGZgYaGTjq6APcOTw18r69SrecprcjT4SLZoAbs7b36Gau1W9xG9ivpz/89k+EUb7Dx19pIqPaiS6DwwpdqPsIxfPpbXjl+dw6vL1w1lmfWlYGtveTLS27uK+7nZd8v6KVFSuVjj+ajb3yf6n19WYyKpWj+alA7Mrasja8qyNXAMZ7I+1y9YOhbrvt/fayAfes5V/Ww2uwrluc/Sk5l/Xz1vvh9uxdW4u0I6oc8XkaTRWveCMQXl71+F1FSmArd+VYE3EPg03XMwAtq2JeE8MKWnnSMwMzAzoDvDulO5WUhNAak44ZwCBojYNRaFJFBtCxZt9CViQJTEixSNgbYbz5AN9IO80w3lQG2ocpt1PuvWfSYfGxtvbPid1sjs/A+lfg2uesPedzPTJ7rZh23L/lO2jbq36cnv5esXXCdZ67vd7xXMHvcauQKXHarc8ApVYB7BlttHYtQ7T7SQ/CppblOSvvg0zzdwiYSmoP7fEnqMZtfz77JSN6So1mo53/FLteGrXIKOsyWfdghGt5uz3zI15E2XX53+ItZ57ffm1lI/q3B1V6m7e+3sWcxWS/C7uk9nZd3nQ0pVe6VtO5t0u/I6t1LXq7/xZyydeRarotWdZanDampWXy1b3jusVZvuSYOK5i+xW2dnT97Ti637XtWlGXfVVLVjBVthckdbWiR1tEqXaRFZ+79LqF/OBDm8odOgVMj0yiRMBdVwAgpwZCxtAMTQcLNV6oM7b8I5pG5WSvzAA1xIrGWGltqs0MzAzMDNxsBsKcngPgWYsMn6gEzX8kIBU3G+50fCgDs8GH0jWFN2dgW49ra9NY1/s7ACSaBANoHg6Fq+oVKdXdhHHm162/SfDws7pN3u2p3D4j77f0fjLWn5O2ZE/m23uu4G/a0QRlFdETxSrgsyrtG4XeF/ZFbidF2y0l27Wl/CinjY+VTuqlB7zrhu2yt+VqX9urxRj98Q033uIKKr5rs/2490VqEbhX4Jz9p9enW5br7w/9kuvyQS277Zq8Zfdozy27zGfrTJf7Y1v3KmrdzHP7OxVHWyGTTw/9aWlFmmTk0mOUR8Wm9wqAsiwuCcGVaTEtKfVJzgzMDDQz0L/vsGS/fNPsrJwZOCQDl+mf26zqw6WVlGghUpbs5M8MqAzMDqOSMckDM4Ce5k44ownpe8Rf8RpQGRpBaKxoYRt1wFpRv0O3eOaqzyA1raMu15P67xHU76su8W8rY2UeOEtlXDp7JT0qrxEWM693LCjyXdH8LI3GKflbvNLIbfo8Vto+9NRqP613myy2RcNQuZKn94UtyA2j1SpttxRo15byWzg654yz5emjtiftuIbviC2MIRas/X/4rqgoGXJMLKvWcnr6T5nttdbW6Gnrml6DtaQzil+O8+3eou2bkjvdm9DTstofi94So4W5hf/4vdNeNX8bbd8tfpq6znOz9U21vGIUIZPPjv45ul0u3wLkOdwupSLN3v0VAJnIl1KKA6lS8ICxT5mc5MzAzIDLQLnrzcRcNgNz6Lts/jusb9xppIUtHIvf4doUOTgD0nj72ZnN3c7lzE87Pz21KoeK7NEclMEJJO5t/P1v/4Qd5fXxu8XdJRUQ30jbXWVQ5jWvPE9Vgimp70dadR7p4XY6U9/rrHQvnDRZb6c00ENU0G8jq1bssnupiHOS9zLmpjtnLnlE2cq/FVHpA0v2v/WlH7m0ZXFKzJJj6fbwyyyVHAuHJbk2WyWyVIb4bU/2ykP/205GLfb4LytW63YQuvvfPQNQfwjApTsiR2qoHXJhjqv/7Xm5floezWqqfY6Sb0dep+w+7rdbv+L3vZundONXEBzLyucKfwhvsz+Wn9fAH86Jdrq7vdgKq64bJ6021e7006NRZ9bVoV+R/eYzSQxK2fw8omJ4w1wZ5chy2lnRI77mkjLeCZHZnsWZgevPQL23X7/f5CHveXP/u43Wml5eLgMr93JaJHMfQ9/vetjMnfByjdtj2WjAHtVUZjZ0mo83UnqrzYp+b4Tm9ojT7//+j7TGYUolzWsgJTJUgFwnYqFqM3Za17cNtGpGz+paWKFOY2ra11803uDjubeVPKxyYRnHdf+IfUiXjfBMZef6ebUqZ96pmkjy3mjtaMsZCEgsudeKY0A9amvdzX+UvRHca/Ctv91HIrte2Ua8fieSfQmvXlkVBxbKnn9Dmg9/TvUBaO1+SlB72D8CKIAzkXyt5vlXZG7dSuqZHL1dM2c5plt9jPshJ2+2r9WJrOxZ8gN8OWA3dTCihKf7ZORqKixWZqNeRHVXACqPpESJFBvy8lGk8CYxM3ADGUDXVb1XkQn/WgJh//S380x2aiGuxeGD/aB4rznma/bt4KZ5V/Bo58qh812lYAY7MzAz0J8BGjL6pL1Yp3QfJkup6Y4jH/EzsXzOo1DYLn8rBe+94RXOWiC7/d0Lyo+U3Hy33JYz4MoZ8+azeY2paR/25njT9OWl4850Oc/rVpTLPOj1szwGu1zikCw6qNF79SkBo27PT+l5/4wBbvo9z3BYQhEiS0Y9A5mQK/ZL1rTPznsx2/DsruQGj3vjTW6pWnYj0pbWLHts1c7ZmD374EK8fi9yLrtdpQczD/B059/BJbvl6a4/V9rD/hEg92Gk3O+bRuXeq73VtevodZ6ss7VO66we9h/TN8wurD422rI6M5q+gTw3XWyPAFb2tmeg83kPjDHhSqMevGJIYzPtbP4gI5ifCuFXWjgfEV+mHprl6Lo/XqxZWUBNxszANWXghnov79GyXwtxTemcvswMXEcG0t1j3W4ODIaR7xT1OiKdXswMzAy8nQysG6vS+DFOZTBZ8Y6uABQrajy85aJBLud7k+21f/NdEBvOdNNYe0uj58Embvts/pxxrbJlnema8XZXjK7963NrTbPB3dqL+63qvUIKoUPcnp9Rz7OVCd55y11YnCxzJVVjxKr+M2ZiSXq3WJYMoT7L87IG+oc0RlO6P4p+yabBpHL7b1gmcFdQaO+D7XaknbrYsenIVjCtQHUbEf3qrm8TBH1G927W0t8aX/O309t9s3zo8VnLbPFE41j+jPLLp3S2eDhqfUC+PbtoAum8abqpVKl8+D7uLFuyxPvpFoSKc4pVtqmqrJDtUYUVyrFlu/9WW5R8d7ThgaYyWvmrkWVkpQa0w3jlxR000+5XAugKQIFUcgqRYQYwa7A13jD2FSoY4V6hp+/RpXrrZLvKpRPDu0aygwQPw/bSLr4T+5LupDHeSfC3GiY1Gv5L222Pw0HtiLfdo4kwnAHswrMJQ9aQjIUh7RZyRT7egp8h68vbhUZZBggSy2k5/f53f1yWcngVMf3bY+HJ5WB7baOU50MRMaVYknmj52f9VlKb5yh533D+jc+GlYBz+LpkY3ueRxHq8q/xnl1r7/L9u9LNl4I8rL7qasNBHXu5hnGYmwmw9iGp2F5wVypua537wGy082lc1RldLWsbufLacvdp7DujsRyxf/X0lh6Z0VjOJM99ko11H9cuFa95z8KqZO2LtsqFihJ2kB33iIoBxTpif1HwR5F48Q3eknn+Txi7wnadB1XPIySoe3nRcYeFqFkRblZW5CdrZuCoDNh9sVqD3YT2FL85yqkVuLL/MnF9Dq6IaapcOgPSqy7tyKH2q3v6oRYn+MzAbWXgfYwE29pkZIK8zdJFtE9/+N0fDcPcO+I4OtxbhhUMR87JpvNUPOzQvT5xTt/6belVk/4zb5ZkK5Ubw/rNn1GyPzq+2Bm7s3IydlRHrcuewvPkFpwyLnge/SyN7crRnmu6NNKuLeU1p4xR156fvqw/lvUtGd6eQ8urNnLFZ+OKRBuHfqcSn8HRmH3m/T27Ln2RPWghRqN6XeY1GLfC6BNZGuFWaN3fNH0r/p/fzy1ZYl32efTOCyvS0p8t1yoraG7PH5vV4JdvoYUrAHD6bANHSFCYqIRt4I9tndv8yx70RId8PCo2+qqcVL9n4uwt/Z6TfdbYXctml/PAiw0eqbP61Wnsur3rDGKKzQzMDOyTgW1Tg318mCgzA0dl4OL9e+GtN0fFzbhbD/fQX4QggdMffvsnsth+h4/zaRHPSamvYQWle21keU5ZcoZ9XrW+NWzlAAU6M77R6yQ4rVcJybtoXlaigdyh3QPU3O6YgX3bpQetR2bHAK8EavvKtBnI5vFQ79qJFVSEXZt/03evlcvEyjkLbhxDTBRZCG3I/sAYfu+sDF6HGXLm4sJb9mXW5RBW9qtmz9e+afriSbtpB3rGMfnlW+xiagjxcXsE3gfNoWd9kvgJ24fvcujsqmbLgDUyeEhsBq4AQDp3pWV71r3tDNxoXwin9WicZO9AISm/7cab0c0MvIUM0DHJTYWZ8CFRIUQnRGDEKuHcFsERzcHqtlptenvLGcA+Z+1w5QCzW6CWyR4D0LXUxWMSePRr//p9Pj34O8s0z4B3tlXCGdb12XZ5Zl9ySuAFzsFrKtr/tifl2XBbt/9eujYOe9Uj0/Z/DAfnALIP1HC1P2Vm+tu9jVOznPNK67nEUln7sCR72/X97WLFqbPdg9YjY9nSfG1X80dpq60t/ij+qJ+JXWOMTXwYGQ/jHizHORCR62le7w+/rEnWzLdoJ66sKQzHu8ZIOK67W5MRrkRfgml/yrajMVCnq9QXzhX/9rb4mBE69qyqWty+L29CaPZ8jazpaiCdzLI/dCpCbDS3PchHYGq7ZbztOYDXlSGltqd1IWgnDNqKXY9aWjWMYOKcr0yuDPCuXR0dRI9kBq4AQLqKp32b9MzALWSAO/LszrfQVtPHt5GBztlmT7AExXD4lj/WTHdqrqSaSPkSix/3DYPHfTChYfxDrRzn//mQZ4LOl+s3Z4k7D4aUdFQ5T5zKpiKjbenZtVrwamzS1nqngbcAsWUL9S45/3CyLFqeezHQ/F73jotryJt1znoNvr1VH6z9yOJvzwO3MuP0rDyt82R7X9qOsD1X7wfhGrJNhzD8xwFGDmZDDcCK6m7AhvZe8a7bOxqOcRLi8ThSDaVYRf50PseFZwBwwWFdqqPBnamxfHJv2dmFBG6vfpKAXn2hHbWuHWsv7NmuP5+n1y3YMjqPju6IhmKvwhAXd78w00aCtGdRIDpjjQleFht/BaCmHGGEsvBEIBIDolHp9qnORN5+oDOCmYGZgZmBmYGLZECOM0JcxI1rNIqMcFLwcIjQ73Q6co3t0/Jp9uZWdqQTg2BaOIWaiBQ1kYFHm0+PsZhTzcYonxkIdyblMPuewx191pV7H8ql3ZJDsnaLBCS1Ne78S5CLe2eTWgV2TrK9HnwNHpbn9CXnnBmzbPV7Ze1HFt+yyPyeNmq3comvPenBZ4RRK6VdjVDa7c9wiaw5JXJ/rZZs06WVktNGWKgtxpMF+aJaZ7uoPBcjzPBW2/PvAvpuGWCvePXe0baqW7zsvcyhOS7+cLiRwzQX29CqlvwRXcWvkKueAdBRVDAVy5JkPguWrdDOJ12ycJqUFQ5THZq1RU0rp4bJ0sMBiM17ZZetbiv9OWlHrWvb7eX9V23k+6fikAw1p5OVNhWOh7A3OCHkx/8yTOkhSjXJQCHPgjo6pbobqTMWujPAT8ZMG15yUpwDPWkhcfQJbJSi4T7QjTTUFAZEa+qTNzMwMzAzMDMwM1BmgA5WGw8w4XjXdegrPbgCDiUgJIFOCQJ9Ba5diwuhka/Fn+nHcgZ4h8x2S2lIJrh2sM+TKu8jt72ndHi/GKbkkyRPv//dHztABweYHkSrN9AvwMEvY3Xc0tL85OyNK7rPfTXOOrpifR3QTlrlGtJOwAfC6D5wbfnUYd9ibrX/56TXteM1ZHgHH844/qxr03Wts85WqaUzvOgJ3dfhPizJ9MbVuOxV+tofb+wKN8gDHgV231sOuCsia+enXbvC3IBK6BthS6o+ORtytG9EOLqRL/0zHDV6lHtHyRlI13WKui69uCrNUojg6e9iGOY44DoE94psZ4/Km6l2W7Rr28YlWBbjQAoVxW739ih4794mIGNqAekYbbBEB6ID0onqLMwMhAzEDho4czszMDPw7jNAA0M4wOx4rLnJ8cblge7jffe9IktA2ZolJ1NpF2nKuGuWN/rT9vaGa5EXl5r2hJSkXIuQbF+78Clct/i1p7AVdKsujYty+Iibi/o1lD4rudZiLhiqpCQHSV77pzXgtW8eqJwF9p9tD3pbilesl0KOY50RWnwDZoGt7yRbEN2perv//v4/509/PrX7233QaBa9LrflelLJsSxuietoXY1fRrSuHddl2MreOv6oD5UVvub4o/Omae2txdcy/fReaHvh6Ay3+wkdZcJhxnpPdn8eoiRjhiMh+7NXdCVOuXdET9L3rLclvRacD55rnONo3V6llXZtKZ9w1Gp3wu8uhN7RUmhntWwvrNbvmOAtdzeUe0fJaUW+VFeJfUllz3rOsrrhvdqakMIgQN+w/Xq3nAEF2Oltu4dYIG1P2rUlptUWzDdHv2rKSnRwSNLNs/0rl6pCHT1/x30jutAfRtSZ1MzAzMB1ZACDwiHjwnVE1/TivcbdTMp+lfmC1U7pvuEDzk4Z2K+J1iOhFTY1RPV6yBvKz/rM3oSm0fZZA7KU/jaDYyHoZxCmwlVXGOlJfe6PlNLSeAaAgfhUKDWRlVjQOl/JhFcX9X3hq0F2VFx3jrjJgcH3MR/dIpti6VBm/1lw9Oy5A/5KRUZbbVT+UmFb+4vlvyU/6v+lcKy4Rv235K9tPNwr3p72sg6E/g3Zf7ZytsCnAxkfzJTgXnEpyDORe3m+DmedVpmaAZzQLcLWg/kmLVq2tNXmVK7sKYUBP5XW+cnb8DM0IbbcboFRSVi+IlARCSxGMXpCz8gTgNZv2Up5mms45Q1JHjLDaVpUaRHOA/krABmsFNswJLYsIWCTmBmYGZgZmBmYGTg0A3xMWjgyqYNlcIZYFXaontsrz0DR4gVjUwD7om1y5W0rq32wK+dKfjkxQBySX0bcRwJOyV+J2JUHVlsUlfBJsvFLwAS3CNYhwW6d89vdR/j0KzJprRyPngePynO467SOS5U+x9V02yJL8uqalc82Atf6c19X2HSfaI+xw2TabdquJaew+y3vVYd5XwNOfMZLAXAZvXnPeg3jkryj18L795RLZsG2nbSvLdaoOS4D65DLfSjjyDHO72tJf46V1V3RHRbtZGSWbMErqVmX4R7nuV+x5JbjQo+tZZlX9zYY3BH+nXtKxM0B+E07AyvEy2a8BGV17Ti5RTdxkGPkQ0rSwxOp3Qt+PPneARd2+0cbLalp77DeTZuT9mf3FiDugSXO0f2/7PmlD6EJOCQaYNLgQn3YQiIbZrJiEKStglIkGbE/URB9KBZshVkzMzAzsEsG2nvmLiY2gPBwuQHgAqrXndELJOTNmyxbPONkRToNiKxIVQ9+OB7yH9Iox0ZPYANt4b75RN9QgLpVz+D2tm5wZmfPkI+jTSBjnLTbTB2GDB41vPs9UYhO73gjCWqjCxyJnf7w2z9R2+G8ufZpIaEOUC0Jh9hzBtYjU3PvWJ59Jnes3Tb6dXrV9vmI2u15KHudxixrj4hiYu6bAd2Co8izxUcztk5+rzwvtrUc6ZIp+71jFyuX5qGMj3O62jjmLfqzLl0NrS0W92qFhnvVqi0+VwEjM7Z3nJnQFMVor6h4EUpdozjC/oF5PsLdEpNaTnHxO74uY7g6ze0c9ksnpSWV0sXJV7rV4XR6pbcWuTfuR0c5iqqHIsQ54O+qJJiC8/xrIh9wZSZVeP4VqRJfPqJDbwGan5mBmYGZgZmBmYG3lQEcR/2hlKl19x3Gg6U71gJKcd5Wwm45Gpn0uCanST8TtxzTu/bdNV/MgCqGtqUWJraqivLXQmnnNN3yGn2Z/xAEDzb8vRCTO8MgmcROoSRYEDs9Wmv/hVqNURoqzzt7Rt0emZr9Y3mP+pxp0NQh6yt4C5D9VEO/g4f41mG+7BsdShWRvXDKpxr0/Xxlnzw8b659L3D/vVqL2iu3lWZj1uCbrEwcVaF91i2oRLrIssVZTeNrugvUCa3T6sdfkFTtuyB5oer2nmXVdrY1DlJ8yPNEZe2fw4ZUeUCLGfHHzVRK+9bpT0QcpLStHlXd60pdq7f3ILOMxu/X2jlLvlWcfab1t2vydX62I9qCSW2x9vmBtldcu8W3y+K3Pfc9trWPJu630RLRwwphjrH1KpQOWselu3/llwGcWrL2j0jB9PsINvMKwGFtP4FnBkYzoPfzUd2bkX8XQd5Ma0xHhzJAh0591B1S3iiMHWfuO5JDtEKjISRX15mxhucS4CSsDLyV7PX3za6IGU6+q+gASrBWvQUIyACp4pdNVq49sIzFLxEmx8rA7eZQn8Va0bX51xn79risqPuR+yUtW5q/L5pGPoK+LW91BuQOV808lNZ7UE/eWJ4XkMr14x6EQ8Npg+Mm3Oe/w624p8fvcDexJbt8TIvHvmVZy8ob5Futr+cJur9pemU6NDRDlM0aW8v/2GnZb1daP0CNRgDcKl5GcYCt7ZBWi29HthDW9Zl1WpYPCd+4sjpqsbPBVV/2XuSK3HWY60YnvAkT2/wKQFB7omcGVl0BCAhJNmbhAhlwzXwBu9PkzMDMwL4ZwKh65oH1XY0eOwWLJvJIZ26sfTvbudB2yrrhLu8y0hDaGGguaqYBM9kzAysygDWF7R/G6OmkLIlv+VPWmecYKRZrRcm8PP4WoOffEBruN0oNRRO7U+c/12yHwP6wzM53NLYNH1A7eraauGCcAScy3YUjWnkUs1++X1In4PyrvNr6Oel1+dFam3rmOUN1trTn5zF+fovniavfCvcQll9cN8WBDwcsOmZDND8KapvLh7UoESmN0KLLVis5Lf0j647Y4zjfPXOFTXnwrZtmZ7x1Uv2x0ib/x0wNSF+nVwMBGKKH9FXXYfwyuqINF3ZgZ63TGpaCNfhVE6vxoFLdBaIsqL4rAFWc4NLczgzMDMwMzAzMDLyLDMQD6LsId1OQNF/h2cPuWRNAIcRTWJxTFsnGJG4kAz19tuzs9eCsXSDXbzwDwA8uOwWgsaK4iKLQdQ/25mZnSwJv8UVACJbk4jWs3GNkRI7bv1gszi8S/XloQ+1wbr3rlYG2t++hdnuLbEfoyfNePbDH1hYZzgYjLK4cbzHUqdvOW7u208QU4wzIFYAyq0+/oQNaeVyQK946h8mxLyloKU+XtipCV8naZdxAznGY2zhhKHNYchIbG+wx8oP7ZaTLjg86Rk1v6SwWzi5tLY6VaCVHhCeRZeDp18TgHphVFUWemBdsZpRDUyKOgnkFoFRNbCxUJ7KzYGRA3ttq1E/2zMDMwMzAzMBuGQjHrbC1gZsSyWHUxpg1lAGe/Z85Zc3mm+0yM3DVGThf732085DusedzqfCI75wu12ZY0OIXMJXVnVKmh2OdQ/foahl+43u//+1z6H4c7UNJ77DmYb5pu7Q2OcsZGG2Rsp+MIiz7VJPQbxvYso9s0a35lfPOk43cql1u77ntWht1uWb4rSNXfGWvp8+QzCvW1fhQpg9vxKE8c40c6kBAHvzi42rCNXAgiUohCcZxLViztidv3Z6SjT8+N7UU9bQax1PmsOS0W2E0L/2x90fR9iHLG4R1jJpu4yT+FPushdMfr2Vd2y3RSo6F08PXtnrkR2V68C2Z7XzdRnqcKqJoVhbSNYZ5BaAmfCEeho7a6HEhby5rdiZiNP/b95FRi1N+ZuBWMvB+xxM5qqgUZGNFVgxtCoWkRgEEkblNM5DkK62apZmBmQE7AzJO2SJbaurPALghjcc1t+v2DHHWec8W7yzd0lbJsXT34m+3yFc2nn9FHulzvr08bOOU6w1t+e212zM25gO6rnRcoYWwsc7tp+3JXm10PRHZsRY1h/0u8mhWR+WLSFYyuNVYed34cFvtznkOv525MmmLau6ApqS4jIFCHe9U9R37Q/fjppoytJBwUtDaii7WYlVdQvpW49+h77ma2o2cmOkucLuw+L7ruNqFvfrqXjjb93r2ZMuzBNqHveLSOT8PvT0PPX7ebn7a0em4ePKSjkNpqYqlR6dEHIX6FYAopXWr4JM5M3DVGYh92bk5O/RVt1Z0Du022yqm4z1QF2lvGO2xW3THOK70qL+H5psxzgzMDByZgWKkiYNQ3ezy4Fa/AgA0b6sw6Q3p85K67cBtv/tcn+MGjXNvtQ/9cZ3by5o97a2ma7KRp+ON3EtQ/T6zd1pe03Xfs72j6Mr75qHtD9nCS5961vPqwXjuvj43TfnKdlw9CCyzF05pUSNrupQsOVvyybYYs1yhH7jD/uAV3DLqkjOat1H5LXkuvWXOqA+CkwwMKBQjg0jmhNKktwOd7h7/wYn0I+SIh5R1ZtrH30PMK1DtiWJvIhlzy8r6JvNvQnlgdHoT8d5WEO3RMgxCYbsYG0YnGeUSJRTqVwA8JA9ricqisSkwM3BtGZDD8+zK19Y0b9if2dmutXFlPCAHk8Kgx2hiqG9BGDQ4xWcG9snAHJ32yeONoJhjlPlLwF7DVLz6wNtnUce5f8Sax3Helsj9/rMkI5QroCXyKGddC0YtPjyzVRnvBjt0RKt5366taTR5Z18Jbrd1u7YZyay8QAaup72uxxOrGWQ8iGtjqSjGiSiTVklFMpYkhVTh7Pt1ar5VMkcwPXi2AK64rhbC9ffMa0iozpKmj/CtH9/sq4NuMQ4rHfdMy6BTY+JuaMrHJ/71gEf3+xUVOB6gEiUU5hWASqom6yoyQD22cVjt9BGdnDv9dqhOi1NsZmBm4FYyYA8LlRoZTLKRqSJ6K/EbfiIiHjaN+htgv71GuYGkTxfPmYFtXRzap8c784yhO5C9zsxMg6tWUNad2/Wfj1reHrEWbtli/nafNf6o/6Py2hbT5v2I+AnJ8YNQVOG9Q+8jmi79CJz+fK57Y4l5V+7mJwRCBL3bdtvp2v6c9NreUU6ND6N+Hj527RjmEpRuryXZY+tLT47I82hbU8wYT/C7VO6bafrm/uOGGh4haC0N9/f/2a8/oCa+C4gz93qHiEjYaXkoriq/t+zXqm+XwBanPzNxtCyxaqNlPzLjjcqXXrRxRvHLnmlZ7Odbxy/t27r+X2qVnH4/+yV1ljTdj8CSOgMWZwv+qD9avtXztRzT2M1ru0MpmHHWtVeZtww2FHn08aXhmTxp8/gS8LItBBILWfUszgzMDMwMzAzMDNxKBvhXadnbxhE9rUpL/qBIEwg+OqI6l7iVdNh+SnS2yKyJGXh7HSDGNim3auB292uaD3f3ORasu24+A4CYnZ5T6zFlnbXQOZD9/pN1Z0g9XdLyp0dXyxyNs4yPJuhpAO10N13mv+R0g51VcDlvZ3VnGlvKwKq1zCXQy9db+0t//2RJjuRS62GXz+N5PHBjKV0B0B9ey9ecguYxmPQC9fx3JERvATpscC682IkRVv0olMWrExyvbbm/n9sYs+YcGRgdZ0blrZGwHdul+k+nt36X1zG4/f2yOz15VSzO7/4MgLMSIk8KpfEgNry9bCKH3b2EwkzRJbI+bc4MzAy8tQzw/T+ICoPqyLgKWX8ElLMFlPHHFdnR8Uay1kqARNQSupE4p5szA1sygF2A9wK1L8j+sQX4rLqlxxSX+TsA7JuPGButzkVfd9YgTGOd53Om/jVXIPWrMq7Prc+Zn73sjq5AWG3IOFf93ujm6rjOpxXjFv5l83N0dJyZLf1f62p6S87fkq5uQU2PxsjPxrDW8sr0KLqTp6OYDKcBgQ5kfQczPgjmsgwY0MptJSdqf6/UlhBn51ynV1vS0L/n6tjN57W2uGLo9ntoALxTNrcXB7/vFVTe3+PcN52G0XNB7kmhjXlf1+54CmnRbrwmIGNWooQCRqKEVcfMRLiYMeuak7s9A9x40oTbAd8twszhu236GfjtZOCo3RQvFaA1L5cIotRfd3JYm8TlKAjWPBZ2J/DGBGfL3liDHeAuDxRV4F26RwO/anQds+7q6fe/+2Mc0wrkRpWXXZYoQHdjqHWULZj6jH8LDj9R/fQrwtjrTDSeHaL9LpnrTYl5P8q79aVmytpWjlsRaTp1x3YfviepQ1Zwd9rf21FcZ227xb3PLj/944/G1LSZgRvJfxmLH0Vxv7t7CBjzdQylPKDStxTMyGPFlQzDZYzRxfNQ+yVCxxKPd9ui2Atnmxfn1n6fUR+XZfRx+vC8y40eftRgvqvRvTewj92yxYc/e+96jXEUiRIKGNPxnT0VFYUiZZlhiWU5S3/yOzPA7dcpPMVmBi6UgdlPL5R4MjvH4cXk09t7+DRARB1HSm1idm+fn5mIdkeZtTtm4ErGNXYD38Ef2gZ6x3DPCPUY3mesbQ7u25wB/h5Uvdtyj13/WpcOrqT3Wq3fyx/t4djbarXm5Wj9XuQt58dbdHX0e+FoTIse7ks9q6qFjFjBTlfucVJrOZnxd143eiGXDsn54htLssBUcUuMh8SifOshu9rUZb5L0pnUkpo2/dmQfxPzgIoyFj+Kul2Fe0Jutnb0Orrdt+CXMeYR3U6Zn85if9f9sgrr6nxuOW5qHCuLe8lY+Ov4W6JeZ/FwrdqOmRndMrZnUPWi7QNGlOG37xc2evqSVuJ9n53SfD8VUBWVZwCUgqu9x28tFY8TKIjkBAf8pEqBrSaPwFztzFTcKwPltHQv5ImjMrBPmoGyD5DybJIzA1eZAd3T49FMc6/S7enUzMD7yoCeGQod99hzJKM9KqD2vO4cEfLp93//Rz76F8Eyg0IMVRLu6S6eWxReBemioo8xej7EqOu0Eo/uqTm337u85ZpG4k9/oVgh1jm56rff9Md4s5Jn6A+8X1b3u8NXR0bbpeirO+y5oz5cmfxlM3BZ6xdrCrXq5Xec6v5zMf/Cb3QedtWlPS6Z4wYdI8PEx8jYtfUo9mceBy/Vl82+1OGQn3K6XkfXN4wu14G0ScS7oTDEkS3RKbxhUg1gHbriLmRjMKAeQzmT0MUO/CkSM3C5bhp9mNT1ZOD4/jB31utp7enJTWQgHgRvwt0jnFyXAh5r5ohzRItMzDID0kv5MMrfpdjkWBlY2FUf755/A5HX5E4m1pHUu5Vxdd5Apug+pAVo79HoGdK6uxvXaSVJc3fQJpxVBTpPjanLIUazQfL27yh7dGOVqCcnPf6wDNu6hrsM/YrO9+TRuis2/WtUPfnxrWBs2v3BUOpi90Sxpb0Yn13p6UtdThd9dTfkLvN7Co3mx2qv0QyUOCWnP84B68XVm34rl5I0M0MHveCUHO/6jmiM2V5RNu0Gm8vbYk/RKgP4Rqu1R4Z2LXti+TDQo3RIBm1ZMcQr7C3+6OfZKtCrWPqYoukesJ5saBlNW/hapt8frWUhM7/dlxZwZN/E/upe3tW2taVWx65pYCovyIIeJ9rRrfOnnROufcAMvOeDUU67CxUU/dAHCqMDPwMgoyEkNC02MhThF0RVu5CajL4MdKe9D+5tSR3f1fxbw99W2mY0MwPvPAMYVrFr0zcSgWHk+JHknSd8hj8zsDED/lh8uV2VhwsaMa7i0+dIKSUJpCp6BgCJBa8U1FGGWlZGqdB4/g3J83lJkNYIl6f5zIn96F8VaJ+NHRHV+S0eEUU/5rXFO+qPltd0fwa2SJ7f4hZvt+iWdy3r2DW9zkq26rMOZKNWGeNGQFLnNWAGaq4rr7RVrDGXbVHmFpHSYaL0p0AzvdoQF3n4eudX8U0D564o87bOg71w1lm3tMo+YEm+Z/61td2+/oz2AZbXowQNGn3zS/a8faVuXU/rj2Lf7Glv3Uycp+OaXaPLdEU9jKEoIKDIcpwaTjLpt0HLmirYZM4MzAzMDAxkQI9RA2ojopcevGD/0i6MpGuL7NhTbFssGbr6CgBE6DhoH/sMjMl+Cxk4w8DyFtJ06Rh4cHwv42NPtpdywRnLkKS3kzYeAi5Bck4o8zaUMlg+08qYFylaZ139q/7a7XVaGkH703PuqC2OrghqW9qHveij8Uf9PMIfnf8ef7S8pnt0t8hwX9rX4hH53BKj1qW7LWXwchUc+14+l/jaeklru5ouJQc45Yr4gLIhegSmNlXgl32yvFPWzHaBpk0ldL9kokYF7SH2IxzT+LsQrDB0W2u6ItpmFdc6tFdtVV3bc0zxV4E2ZExbXEeXfaDE2ZTPEs5xljGNKU2O1/GewGVb6Glu1ZWzUbbduj6gXdU+lPhakmkto3W5dl9/SuttDrIUh3yh+tpr1HOdh0Wv2gJSO+qDKK4g8GZOJMaah3POKIWgJJMYF8yBuHQhqpV1k9OXAWSfm6JPfErNDMwMzAzMDByXARmPcXx7q4e4Nxxa3jGODFW6Sm50pEwguwD1GD2boR5nVslIBPTQDgpSXoX2tpW6hi8tdDr94bd/opwkbwFKkjSW7zHpxNDxhVX3jJbnxPs6ejT+vt6eCa1YGzuTXWfGt8j3rnDRNbMtUe/Vr0ZxRuW3xNijm6/rYPjDIMXfPfqQwcofXkChx81OxW1i7Uy2a7Xlfkmt1U+vw7eubfajsST7uXGlTdp2tGv0Z+n6JfM9Zcljlmep8+wdum+Y3soOLv4XkxKNI1KeGBoZcuU3WG7lao9we/DXtUkPck8EjMOSW8YZ8WddOJmrAFGftCQVrufr7u/lori7GiXy24mIvB1rIswMzAzMDOyYgVXD0yqlHZ2eUIdnQI6RONPjT9gebnoaWJkBtJk0WwbBjWfVZsJZcZ1WBjKLu2YAbbJ9f9yOsEtM7Aa+t/izRTcapq5++sPv/mjExXuCPs1XguX9RtxIrKQE+8j2iq+qlbOoPtzDpa7Bn1EfdJOWKzejaKPyhzcJG1B95kwWnZlDstGMxVwJ6w77EJ+b1s9v0bujB85iqNqeyWbQSeU5bSWGudDsURX5N8fSPVB3Cgm06B1Ss0BsaVnt1WXv2t8ShZUgHZ2mLfmtfGnXZlvWPYFuU4t9q+tu9Tvq61Y42la0+hYpncmLx8cdE/1rdZtK1w6xFAyuCH04bMPkP4rzkSDAFFtRzGt0hdBC5NKzPDMwMzAzcD0ZsIYqi194HofQomoybigD9XZ0jx7SD+SkRFdc3V2oC20KjWYALaobdV1zrNMadfWm5XWSbySQ63EZ/UucEaIzi6PygE1UpECdvHEFgNwZ2A/4dwDKe6Su6tyLYjI+q8/GDLzJpgxsz+p2BLMl9loH7cfhX9xwe+Ct7Bdm9lzFvlHoth5F1rp1n5OBry7Sz2WwxfFxNIq2A8sxtvVrtQuYHW8+qaESj5HprRR4eu8KnqWpRiqdwh/rYlkdNuVw7d4XZMU7+VeRAd2C7NDiXlr6DZAVWiXOe+JU968dE2CNpUfbbYew2jp3MemtZXcr42Vb6W8AC0DNTQXKpJeOSgtXAGqgKQ+4/JeyZ2lmYGagyMDcVYqUnI8hyY/D30rjAiDESqBbUEPa3uNHN63QQrzHjNxCzNsbiBHeaae/hSZ+Kz6ii+nequkyRNSSgN+U9cscj68RqJPjdwDqn+U9IJMo1/4ZuLzLvG4Q3P6VVBOit6I8b7P870W8Drkyrsv6tT2r2xHMDOy1KtmP80Jny/o90KZvqsJqU83XtFLdRJYrECXcwN5dKqv9vfR/FLm3n2TDVulVwSnzQI0YxEBkkFp+NIqAWt9yjGWu6tJL3C6c/r5dmIstIskqZM7JiP4oq9x25GCPk1lLK5xdyK4W2cXSCMgRXh2BSTHF5qxHqPdNLeH9+QfHK3dpLappNYJp9gK9TqsAtWLRgkflWdsIdHX/CpU7bK2xtMeu5Kq/bcVj0RWOJth6T55LHPTWbNTR7km8IpO+41/Lao8UnYoQjjZJZe6LSmWSMwMzA4dm4OBZxKG+T/A8A7M184zcZjlpRzo01j76Z4lq9ZN34QxYDTfkVtIVhjSn8LVn4NraVvvDnRffmmj26GYlmkKjc8vkGvUrAKVe0q6oznGS+qRQnvck1brAq007nR9r4JLuOWssta6f81bjOi7zPefuO1t31wH6Ma021XxN9yOzpJUBXoGwai0rw/u7A9riv+XJXnxZiSkBqwOllu/JHssweE8eemRKV0uOxunxs0R4M5xqO66LbksmdYt468bRsLRSchL/DZxExiiwVwv4hq7FLiMdGDcsUPDLhuTJSuDrfdPDuKnMI6/9N5CrVer62EB+lFYVtZNZiaXQLPOsRbTPmtYy2+m9kDf1EPyQy9pItueZLffgiI/olc+/plJY9QdDIuiefbOg6Al6JOYVgJiLSc0MzAzMDCxnQA/Gy9JT4oozoI+lrQOlhKAVhDmJK8kAWidrIC5mzKq3Xc1f1ZzMG8hATxe4yjAOcxwdHr8EXPsdALcr8P5Qs46a8mxsr/O8gTbYsKrRY4UjYsn2mXQbbRRnayalybgF284VtWXLsshWrwpDkdHdjqUPJSfC7k51+9lj2fol1B7dHpnzZOY8Vjheq2fqbJzHn217mPZ3V9r1z6dfEeaW8crySffYMs8lx8KhX1bGoWfDOqi2pWnTYlFR9iXG8W/YkAYOivyOO16NWzWsBqDr2e46mllhrWsdC63kV/CLtiMtq82GhEvzu3K4TzLk0GqxeKH3UGFeIaFbTdPbXbXQpJ2zjlCOA20fLPy2VrvWt7u4SNJJoa0utfhtLnwe8da19OOvJHzvuDkwjwKpwizdcAZ0A2v6hkOars8MXFcGcBThv+ty62hvMJ7sNKRkh+GjHe/Fl+ia/olUL+yUO1sGqm2D1sz4XMyYZ3NyGjpXBsp2BueWm705MK3J6ukPv/0T6aXnDQtmFqrX+LGrzsErYdrX0TNIrTtKa1vmmWjZu8vWwtvowXSS61YaLM9Nr1ihuea0oGuZ7OBXkJuedEBWft+gYqUHaMoMZkDvBYOqyXXLvXBGfZjyPgPGPrilXXRuV+PQuLg0imL43GF/NzKgo7hFeofMNMNu4eMpbZdVf32Jj33cmnIcLBs3MyeSwn+jLSXxDRGcf381bDGZQ9CrhKv9AX6hGeU7Ay5bOBM4ZzF1cjmh1kr/gs8ccw7PPXtBNV5AA8hV5W7J8fdXnzVPVnT5oD6Q94P3l6gZ8czAzMDMQJGB2pA5B8wiTVfJiIc1bkWU8SctGquv0vvp1AEZiG3OnQEmru9dXtHJ2FkPyEUF8jFb+4eI7C4V8dWs1esxKyzqu2CrZ4crMC2VfVfQLSvM17a23OOrcdoWR2sXvGre9bugO+qKkq8gNz1RqgNkxUqHdrJe1SHfI6L7fM9+1yPTY/c8MmXv1fG2fdC6TK+LXeO0LZ6ztj8P271al7fErrEPbs9tj28LudLHQD44Kw6T6/b3ngwkMsba84L/CUSzYOA3dRYqdWZofMMLWNQEp6IstSrJFbE+Fmy9CiCrcFF/N6F2y23TSlnZ029LreM4lj+6fddZt5DbaJZW2x/0Kd8dpHc5QjPb/VPb1XTb27LW6lfRQ9LxfoHCSj+qwluAIl56t07kW1TyDEBqbP4OgJW0W+PHbqM8dx1dlSd5jRm4fCtd3oNrbJfpUysD6DNvrtvUB9ETXpVBmeBw31zQrUY+R1016dsMUxsttlNVoMrc5syA9mWtVx29QpeqfhZMcTz2L1CxUChcjtFwqqiSsNa6myNWngGo2AALipUK5YZ1fqNEEnLLuRQDjVpMzJ+l0BPjIVFIM1fbDG/h4Oasrc30+HxE8kbzcMTa+Za4Rv3fYusadM8f72jPXOfhqNao/DW03VX4cMDa88a4wqBIMNnAuXj422h6u7rVD69tnEz2YjlOcfzpPMOKyMoVyb/SHQ15Y0k5M2cBZW2fio16lWrfdknHrunLRqV7VOZVaHDehnYNXHIbp/fbvNfW1yGRz6+y0q+dW4dXaGURJhbqPwRWQBQDYkVisq4zA2jvtAf4K6RJP7hO15te3br/zeBm5czAzMA5MyDDSTpYeheqzHO69y5sSRusjta1U6WxgAxuVlGag0DJXO3MVLzCDBTty13jwp5mPfM4b/LwG78DoJw4m3uwmZ3DKS+unWx7vv1McRjh6K7Na3jcLMYdvXu1WTu3bSusyzLW/YJb8NvWh1fgjJXR4zws/X+rtob3oDI1itOfpX5JvCOfPgfvTW0rA96qbFwz2RMRHxl5BqiPd23d7T2qjX+LWR2IKJ+OuHB19tfGX/rgWwp7luBXrcOiCKy1fit6ZZa2e75ujzjCE8RSe9zXtW7R9Hyb3/bw1yEodxRpYOGefgiNPQmgu3RiQc/hDHuTfasZ0K1+qzHcvN9ohNkON9+KM4C3ngHZT+feeqamTiYiZ7KZjMXS5KXxi/hWujE5WzNQ25uzxq2JbDV7tfo6dgq8cQWA8+IUdIoOOlc7W8b6/ec3GPAz1NbK8dncFkPWGXYlLrSdbjmBuBDBHrLx68nnQDLOszo74NBlRCs9TTli1Vr9Vqm+U9LKGKejXduVss39dvgqlnOLPae3WOBG2+5rGlY/sfhdGegW2iHbhS3GZPYc92J63NSicow65zGLzTtPyDGYrjgUXW5QXT1ncE8sMXs4lpOlriX5lvhu3NBXAkL3kkZ30d7QFQCzdTiyNC4vHIKmYhBwvydQvwIQRExT76PiDaQBIbyBKK6ju81EXkc7TC+GMzC77nDKpkLIwKGdR89MgsEzbsW8njwh4ENjPmN801TIgLS0a1xpX8e+7Ow/eChb5arw9iIkcA9YvwKAysSJpLCXK02cdWtOTcjhyi1nzFt0LUfXrYGhxRvNtw7T8vA4/qZ86nUXTR/nrkPe5LPh25b2GvVnVN5wuYu9ztY6rS6HOoQua73DwTci0h7B2kHONmrnZ1NtMZZ2jU5qCqJIdZBqHK6a7vIVe36n+1i7cw+re9M0eZbKrqx2eIL8UGr1tbiiBTtgTJGxnJswwxWWXeHrhiX0rLmXXgQkOMOe9Skw/sOfWTpzrg9iUUrvU0k60AOSsiDVuVI9idvIgHvRJ177g+akv9mqt9Fs08uZgfeeAT9kuTQw/d4zcn3xrzmehLnIGt1mBgg4gDcFi8pSa3fnCpvnZ5RRnt+Hi1hE4EnsKEj7JhUX8c4bDY6E7UG+SOCEj4J5BQBVzhWncLBTK2PlMydW7rq3ctX57sL5H+Vwpf9b1Ba8UtC+xf2GKsjf8/qsvdW0cvNmyL3WY8yAV/VSE21WHJyBW+/Px6VnY2bUiOV9PO+gdcd7+g7PgPEezUHo9dfjUn8FyJXWT1tUl/KWzcuHxFP3kE3DuaYPFd1DfLw90CMys/2Yywhx3p/mtdnUXvSIuFIvMu/aXVDvPcHDXxNRfzuQRJjooWBeAQBUIuuNzE2WAclsxr/CYnDVt+ts3itso+nSzMDMwMzAm8xAOAAhOD74MEOxryBseDaPjFfQDu/ehV13C7NXP9I6R92U2g2Y1GJnOB9a7AFdq/4aRa++dK+zDlvRFlfRPbnt9wqtRs3nN94hvhdIN+iipz1eWSDaW00n8t0tkmipwhYP+3X5HlNldoTUMWpaY+heqvkGXbmz05DU7P54tdZt0ZtiPLmBsaMtzP58W8kyvKWVs6V3+Fh5rmTG6vOG9ePYls/aIu/plSicUA+CR+voRdruAo3fcUeb9GNaObf4C+Z7q5O8qbkE9FF6xq+fnu4e/iHOPZ7+jpAf/8EdqgwjAzk3EDQ78dBVeB/83dhaNqdL3VxCyoflmbPBdgb8EceWiHX4A56gJ7tblOFIu2U3HXNdmIyQdsOl+NP6/rh0LJpO8TpKPD/rdrq+9i926rO9+9f+5HZ7IjYncRUZqDS9ddZ3Ff5OJwYygMadO+ZAvvpEaeI708q52i8PQ0jlqDWk3tfONylVZuZWwkAL4s/7j8lf1e/ZzNW0vElmvQccFWrVWpV5lAdN3AM9MaFPf/jtn8gp4+wh18vLKh7rXKdnDYlhruHNPyqgBdKKd0FNV++6NtDwh0ZUbjlZN0IR42+tORs42vcGvR2hAX62Kuq3SNs8GhUZ5/al97v35YflGaZ/HeW4/DMy+3PO9tUjYc9YV+5HJYej4G+rVvO1D20tjXwcbbUy+xzejEH2ac0Yx6lidVZHRxK3//ERfe8ikRG7L64jsrHuGmPirxtFs6G0dvAJSq26IHPw1uqZPWbXtcIWiz1eTRnJgMyIzjn+i/UGke0jVUn3VNIrH3+rAjlT702JARTu+ScSErZa+kr5OXBfWZtvanQLNlFmZZGBmNhIkdAerVsYm4yZgaEMvKteKMEKMZSrXYQvaHoX/yfIeTOQHjR2sA3ABczZRXdI84SYGVAZKPcp2g8bbwHyusmuigJw6Nuxr+38SYVbIdedl1eArozVGZfvALzh5ruyQDa6U+ah5Gw0sVW9vOZTcrbaMPX3ysZeOHA0dkYeVkzf11Ts6Oca81Nncwb8kBVw3KAVCtu2dAUm3H+8Delg7TOOD1Ykm/Yj3q+zhsQ937jj/zW9nkOzCufCjs1shfQm+Lc4B7tU4q1cWXzLz559IZFx44zv2Aao9kHvKPz+MWOlXwt6XPfLvsa9PLJPJXooPOK/VBoOKnairviTvJkMhNbGdqztbybC6eiVZoD7WxxDAuW3bkPdM3TRKw1junWWDITeEY0xZ5/eASweASP8pA7IQCPJqNK10t7cNAf48gYhdQLfYHg3HxJ1ajxvKX17KaDu9oQgPt24LMhKiQ8LzwBAtqaUQPhCct5TE9iTt+u6yDrP9XnbnqEdhpV1lkq7lqZVnvuz5CVX3cNaunBOjo7x5tp3KFE6Uktxxwxkfc9bBBe9UL6DH7FnRirUXW67YzYuF8SZLHOTbjRW7TNlj+jpyRs9uQl1Mw9qDL9YINW2zLwpmzYTOFeRM9n/jNO5/GrZodFp6W1dlr7uOZq25Cf/6Ay0d5dwZaAtlfooO1eihAJfoUiFe0oJTo/ClJkZuEAGpONfwPY02coAjyD6O0iDx3+BMbc3lgHsddywu/s9O8buKT0HoDUMg89/cOKgHnOO8KaNmYHdMrC8H8gu02NTdr067uPdI6/U9mA1Zcr3MzTFlyrb6xbluxHa8k1rpef6PFjTGqb/sg4jsG5pS2PuS2vPef1SD7JdK5oqz/2e90v2x6tjWdJCl9edPS02+4n2vL99l/w5d31PrnSkln+jGbDs6sbwFxTB4oEpqSscEbGiZhND9wFNN0FHs9EEW3jvNeta+Wwj71OrdxpNL6G323NJm+rLkaqt1dOT2wi6dnvOBxBG3+ivHVX0gkU1hiulTeSCxSo27++o0l1E0yJQVd/A7HnjloYf7VGj+NqWpruOyFpB0TQ66WSGqp6W0vFqOmDUt1u8rSMGLvt8qSswx8UV4lvYLg634d1oi4LO0OsdrhigaxjzfD7+Lbg0q99IBniMxTcTbySqehg6RE3XpSf3oAzUjkrhWFWvi44s1UfJSe2WAd5XdOo1bZsppYizds9r6DWqbO9mzdVkAO3Hf2X3KPvQ1XjdcuRG3W6FNOsuloEjelN9zKTdsPEWIFbyCzJJOlADL+ugiWAsVM6Su9feIsr7oC57Bnz+HHPfeP4VWe5fgbD95O7J9Zq2NUZqrDUViz+CnctqTE3nctdUlhWUfCCTISOtwPvdwTDb3Y0SevWd8Nfe7dqTJ/G/R7gqUyLs1XZtHM5M/36Uo53u9HskqJWqeVbjvpZHK8IBf39qeFs/fmmEW5taMOyLzPHHD1/wJZ3PUON5/DsAvPqlXNAaCV22QlK9qqAzpulVYF5pL5wtPnjdnY7IHBFjJvu19AHuCaE/eOtFo3ILco9KcJzCprztdO3Fe25sSg/7+yRJVvc+w9Z52GVElt1SsuRYuqN8jazpUZwrkc/GvaZXI7K8f+UavM83jczKmYGbyoDu45q+qSBu39n8gC5ld2zT8UmNZk76YhnIdprF5gny+jyNnQ81rpQUfHDcF6oWqkyoWXyPODdXmwFuOWk/9AfQUjyj27WeeEbznaZuw8vOYKbYFWaA9sA//O6Pbc8qO2iF1cYYr73YmdxOqyDjEe+voXPYv/awrx/ah72Q98LUOJrey88dcM6yUrWDnwaEeQijkUfpmHIkU/29aqU8Tup9XNPjSOfW4KRZ6dIp1Z5xtpUWMSDMfC25gVbwFRS25i0GUctf6ItrQTbHbOjmotdavtIxpztdlv+a33XckcZOTWuctGZ9qXInwnqwqXl4Brr6j/LiiD6j4M9BWiOe2A5vAQJjUZaUvPz3ASAqgVq4AmAOsxEkwM7tzMDMwO4ZMPfA3S2dE1CiwjiCPyme04dbsYXk6PxUR95Mxg6N8u3QXt1PwFOx9lvwFYCqXSWnfVRsT8JKoAJhH74gCzTyLcpuonaE2uTHVK5moN11qiqTOTPw5jIwPtx17DmZSG6j8TsApBlu4UxzjRrgZMipSKuEs/Coe9g7CtiD8t7BlmfH1G1ZdRg9A+6P4Djkfh+m5NEZoFZeupeU+ufIr6JaqywlPx9tzGh5EorqODCQrCulLBPi7VdIIqy0ikA1F+4e/XxODZUwlLe1q5CaaTmlZTzNFoNCaTfUVFQ1q1TUtaBTO75yUSsDKYtlPy9l+jlb0ErdkjPH+f62uAbJsgXXebUXzjrrWuu2euAFve0c91RuUw0e2lIeCWdDXhBwT3AtXAFQtvYj4U/wYT/Q60bKmuC6nZ3eva0M9OxsB3TQitkKy6Wa+PCgcMLJW0pX1Uhwkv08xFvJjZjJgheBjM9F8UkIEROOEFKlCdQGAUWSRGBraUdnFVlRiTOg1AuhRHKy6Ci5gJRLtMycSE5iZmBmYGbgUhkoR6odPCkHysQMCvgdgO8MQ4loLlMi5xKN8kt5qG9Im1XWOe7oqr+FYxkelT9tuMpRPldXerXunLUH2ds6+D5pzifbGm07fw+byvBo65T5tDh8Jaf/LSsWjsnvyPNodD2tXPbPthWrjTSfEF7v+F3OMV5r1BA+xhzQPPIIM+qfj2pnIPNDRkom9nQ/S0JWzPywik6LRwlLBGlvuA1dtpxFymjCTMAzV3WRac0JEGRIrgYlcEmBxfGtMRKJUKD7X0934c3Zgeu2PeqJQij4fm7srUM9B5B6rwkWerelbsnpGQF67V1aTudW0/v6tRfyOpyyBa3o2vhbcNr3LLBd9qrHCvfAdbMUK3bmt/20dPVIWO4dJcfC8T5gDFq6xs6S7fbioSwMhG2bRm2pXHJgJjDdzP8SVwAM9yd7ZmBm4B1ngAemMDzJOHWjGZE41vtvTW93gDadArb8sRBbO8pmhuuKVtzi9KKASLZPEWAtsx8VJzUzIBmYvURScVXEqnah9x8MjCAdAa9yo4pr+7XKRgmXwyy8BagEuOP3MZdnfu3zm2q0N83cId5iDWkHzHPmVJ89qjX4c7pwPbYG2q5o9y1RDNjdYmZQNx9ngjoPKL7WFfiKSnKtgKslS2H5OWDQtifqHhmNOUoLPvxVb2bIYRClSOZ1rpzUQhp/2JtccuryWNXGyrG6cpu8jx910K01QI3nLWj/M8sNLa/sNhpB8ys0ENlD/R14PnA8lJIFwW6l3pCM45frdqlg9KLqJ2NHIUcl7ZLVXaJoRbqbL7LHBcR1K6xBe3l7RER7tpo8NsP9w33TeHUyrtvojm1Hr6PWtK3Rqtkz3padY+tuJYrt7VXmUceuR60wUjV6lRYvgQMnG92iEije54Pk3M4MzAzMDByXARl8skHJW5Rq8aAuJ9VXQ9h+ljG1nBacMbUW5Io6GJe/FeprVFzgEr0mhB6CXac1ZGIKv9kMhL0PvYg6Eu8MVrSuNr5WC3fT4cwhIFhKkz8zUGagGLXKbiQcIUoYm5MrjV8BAHbhpW1vsWbDm871mdOinZZAsfLREt6lbleLu+XBCO0I/CMwDfffLPuI1QidLKuNLL72h9ek47o+xh2MGljWdWNHKGlrLXrPAadlZ2VdPqgaMC4BfvDkDCSCujqp2LPQ4yo7wlY1vacfS1iwiw/NosJTAZIeSZ0QVTCuxXfnhy12ClfFrP2iKpwxe3T1/pWpxyIHvD2YDcfl6MwxVJKrXY+k7G/Ed1cAuONloSRMq5MVly67WjCzZBejn7bMlhoL3+JvsbVOd6Unqs/s2yLrohAtqx85AVTyXs1EU1YQmchGg6gK6tGd3WYSmX5aHJFNNY1SefXWEJzsmYGZgZgBTKZpX477c6y6IgruYcjgUcM5LAMICK6sRMAVIYy0FLi3tuUwK8FyIGbFbnF2WtBimt7NjyUg3UO4ewtHq1aZItCuFTEmhoQz3csXdSPtF8l+SJfP0GoPOAlZKpBvnXITnO8gCoOfKTYr3msGdC9CH8Of5oSslLySE2QXt1qVuvXgFYBsTyjNrTwnU0BXdU6m/LoNsif/nGGKp+/pdStytsW15TMhlpbJV+flpsy+Fbta7Mn8gvvsDwvd+DMVepyhgFBWYwfd3ejuo83F7AQpbVuos2bXdmeb/YFoHxGUT0ykdP0QHVLMmRKHGNkhsYTUDKEfKxx811YkDib8cw5/DhnTok26M1620kTqqzygd5WGz3+UPPp5gB3GzzJNqzm1DilgXBn7VaREJCWKSwFSvVc7Xlf2JLxuYrv/2xEsZzWypi15i9+jm3ctwpLupYZyy0bGrw5qgkfCes6RKc/im89A0hXefLQzwMtlQI1EitQnBQu+vaGuilBw3Kc/GtzdBVAf3cYgkVn8OVTKpk50LbtL9TWdQ3k6fI5CYtFV4z5wpFcX73ggl9SQtrikE+eyzX3F6HXSkTwh5XN59x7sGLl/a6FnYaIrZZzaOL6hw+XouAXI+rCVVAEl6y1ADLN9JXj7HUF8pvXwPXlUvuPcCrfkt8/YttSWtphTYo6uEPTkf3uG2dseWzrSMjpdS28+sT8LurZiq8awmNjCvbDpr+RaLTKQDWuN0PCnFUKos7wK9XGbRBfZh1EYMorxCs8GFLzoQHj7QeTsTG3Ic9WTYoxsBOdl/QaCdJ8A/ru32TiuvVx4l7/th7yBjtO/O/H7lNjDx+/DY4jekndclzQ9mHNW9WHCLrqffisRe+VN9mwYSaeNb28TXY3vkiY1FiH9vEdcWxZA3qc4MwN7t9W7rL1e7I0QlTEcbcKhVoMZAa/KVixW5WymtEhVZCDDVf0+ZtuHcvKlUXV/4F+WoN1A70Vauo8us7ruSktP9vQxQtN9ni5LLeS2CZD5L0nt9zNDaFobq9TImh5DMX7xAzsr5e3Vj58SOIHzjhwfJ08qS+uVowNr6AEBdALzhq8AJHGW6ZqcmYG+DOj9p09jSsUMpNnT4w920LexjyKoNEozrFTMJYnn+1zRmPvHhGqKDblXZlIu+Y8E+KhRMae196PVPIZd2skyg6V+KltpxbstuSz5VO2U+HebSwp8MYduh4MUCebCtS47ms09MCo2c1crIlfCuh1PNyUM7Sy7baQTSN0VVmUlU9J4ZOj0h9/+ibbp+g1x3CfTJl6FxbLGd/85nAFwFewtZ7dXEcA7cMK30Xe0U81Zgm7wi/TefKjRDjkaI8mijB9unByPPFYsFr8wazKskUrzLSvOQXxRTM+/Jk/jG5AkWO6UEjPHg8lEeDaarjUxk1ROlRUd4rM+GaJS+uFTAeHVhaR6E6HdiE4zpP9th+/XGCivRXh0GOR4dFSncFXkzwu2RNt76H5LQdooD2AB7Pqq3RWkLAqzr7pVP59L63pFd4i0d+DEdRWO5WG3cVNwGLmyMznwLKeFQdJzurgzAltzhdjhLIEV6DfO0K2gR9F2WEgjEsXfbclrqNUxbvfHdaUKzPOvKR8yXlUH/4oas3S3yw284SsAZj5mxVvOQN7DzxbrxQyfLcIxQ3rYqWoOJWwRrWpimLnWjNPDVzUmYiYVYgXccK8LCQif/AZD/2kMb4hU3EfkUpV48TgIrt06S7AaHETZk4GjkcUdIXTtCB0AsA0GgzobpoquT83PLsXbEBq+dpR2yNsI8ja9DD0vbG8zirN4LXsziPeQLoTJf8iuEEbgzIYUy7rt4heUDLigOvgWIFYDJhxZQA4Wzr+lu+iwFMa52mBen9tpegPkJtV1dweWJpM1Gz4DPM/6zRltbWmvNbpD+4POg6bLpurmrPG5GxyCq/E5MbIv8tDRtlyuAUP+akcbicXFyIHKAClxe6mkIuSCrgBA0BXVFQBSETixIgRrcF68OjDUswQiGZKnrzV4c17mdPf8S+LQc1NiMrjEjrkh1dWKn7zq7MTiqYYPgFGCC74EzfWfBeXUoGXGkloAt+BW8Hfa31dYFpW9jiMC2EmsHkM68TeJFT2DGdQxQuew1rBl5zUdcAgBxpTSFcNt1NGvjs6/lR8dVw8dM98jvU1mL5+3eUHaiFp6CGegehxUhlgqMsorxh4Bo7r+JHqNh4C1TkonCGnVNZQoj/h/5V5eNlMzOTvmn5OZpVT25h0N3TLUunys0zp/njAZLgbwrEOQU0lP4YKa/ZOAVnLBhy9dQVA00yZeQPFPEfMFBTB15njqz5ZIlfR52uJBiOE/JSfUYHs6xVMM0ODwE8xuvHWa2jLT7CCBCEWK/R/TI8Efw8stb9PO0Wb5xjIgvVJ1UAmBu5gU68RiB+I78xbFFPqIrFJ7E+T7jB1Rc0+M4UfqmHYl/Ld4BeCYbO2PymfkjGveO7i/2SXEjrUEDXH0uoK2pekz2e3JhhxCeCeWb+3uAXQ7A+3aA9xZAymZ08o6f9ezQqM9zGgXRTWUTLCnCBwamOmjE6FKPJ33pwpOlmm5eoCk0fVPVL3cYSnxRJN0lF5dMk90u3awEFCdOa/maPlyINETN5WhUAWBCDZGbDoNIWt0fkE1IuYqVZlkOz+CsSzvrZiC1foBfBN4VqzJQDJG9Yy0a4wEnQa+6xbVvgFl2a0CUL5NFFFAf9Istsu7g1J1OyPvK4p7LjLJvDNacvb1ZS/8vXD2je5oNN2twpUB3cls++XoJnrUUdE7pWyDZDWsMa6XwczizMDtZ0DvBnPHGGlPZItHJ/kGIbTO6wjqgbJW87LP6w1LzH4srocerGNC8qpn/xjBedlfHIj++DOBV1q4R25fnOQ9aPnD2QDOD4iPMwP6JsJ9Mw0t6IbpC5BRF6f1wRLgnCn6CrJKTDzzdqXMbkixTkAofriQsFxlF1J0PAJOamagnYGys6XyYSdwXC7ob8VO9WZpZiDJgB7DNK2FqGfhv9/omhU0hurHcHfvdwP6sF7uFD1nZsmdbY0z8povdOBB4KXhmjB4lj8W34AZZvfj77Xqry1qeth1VsCUYOSzKQrVB0Y9H7U72n98DgazMZK5XlkrM+0MtGstzF6fanIWJmeeNfT+63boZE6GnZuZAq/lmdluR8sHAdxIlMNPybFMhJWbUC/DaITAm38oB/6dbJHvBlzKBeucTvfPL8/3p/vX08uLn3BjV3oBP4zMEOTc4f7+X+AHH090fz9knl/xTW/poTfrn+j6ADiYt7+cXh/cFYMHcPAOI6KdNVfrrh7QlQQgkFdgOk/oC78/4Db/SOJUC7u81xDtxMiAqyNdR7gyG2BW+9vrMR5ECS39aI5IpyK+xJKFzF49Zy+cqu+7M9t7U2IOGUPq3HdXjCwPCEm1biMHnYxRxkjbtlWpRRfFp0QrOU6QvlxcHJzwIlG4Hasc5cc3F2bcx1nLnRZn8lwsR7aqWItpRdrS8XVJ5h2v5HTAdIlU2qhLry60xc+B3l43bnJ7Yly0rjuapmE19CZyABmQXcp0qKeCHPIDuiVeMSSeCWEpT/7MwMzAzEBPBvQAx/JXMrzICCgEu4ci//VEV5dhRMTJf1RklgP2i/xsBoXXVyzQ44Ml+teXl5eH+wcUMX+/wxnAsz9A4MoACWL6QxtH0jefCmAChBH/nubiWPF3f8R5fcVpBP4wvcecBHXg0TK+84Y45A0UnV0C55kL3UhE5pwkfZPM3cvzM6b8/HRAOGoF3wjRfwjNfZyZwG1voeGVGnIDeB5lGbNh7h1WdeaLG4K6zi3kKDjZGVx/SLsD9puekjMDPgOyM6IcujpV0Uh++v3v/oheSpSXlg0x6HiQf1jQ8auaNawco7NMxxT2s1PhsmIbzsgv6/i0PpqBeMYfdhDiYFX1HxQS7ymKcc3kje1rG1LJy9g8j2UYK3bftmrE82bjuMRT5eBNKRlq7O3rk/vdALfqTzPwOOTCLZqo07r+3fP9/ePzl7/FGvzr/Z8h9PDw8PQFi/evD4+4CnA6PTzfvX7AdU/M52n5k1RIHecH4OMUgUZlhEyzfXBOOA8g+u6JOi0t/z/6ZXu6/efB8SFC8KDptIHm//4wQVnhlX3cUnSPaw6n56enxw8f6MTk6ZcE/fCP5LkLJBxBODMeQcXohMiJpQ+vrcrv1VA8TqV89wUbQRz4VN9P75s1WGzbjnt6kOetxU+l1pRKZB+L87us3defOj6nDJmSvKeR5VohxYl4O9Ep4JlK7J/yFnbxRn98+Ld+iUJfps3yJ8D0yi8jXqVE3tZ7ONnG1P2/x1obrQdBy1jWt1uxkLX1Kh16WthWhYSZdd+oBApvAcJ3KZFxBKuD2KDagT5FZgauJANxR/KzmLAJ/pV7VqiZ20tmgNtFNV/VGVUvZDK2Cbeq3mICJirzXDoV51p3juKm4Zh9v9A/GqofHj9gpv3l6fnDB8zycQ0Ak/h7TL3pXIEm6hBxs26ayj/SF2xhiZ8M4AsnAPQNCVqnP2F+TxucY2B+T2cGrpZgX4EFZSjidiCexjtZmteDT3Wv93xicPrw+OiuAcC3R7o8AUfpDMR/YE/y5ojkpEmqgnjfltQ0MNPCEaKGBt1mfU3nPfN0snqaC/Iuw5wzV3I9QONcST45nBCUP2nNfAsnvp4dhDMpFO2aUnZyZga2ZwA9jnevbigtTtp0BYCVrd6b89kmnyXL/Vi779rbz644KgvH4vckUutqukf3EBk+1mJ20PehOQFGK90V+hQPkrpUDkft1vMW0sjbyt5SZI3WaJH/7vbSAD0+a5m6zxpxP1rb1fReFs4WS2hSdjwtrQiGR0z5FlTuK4CneQfN2v1oHg3yvPz+/h5L7Pi+v394en7iG2zc+cDz4/2Dm8t+odkHZvPoU3QRgfUcKt0Mjf4GTMzpcasQbvEHH6cNWPWnG4jIrddnnFYQ5VygLwhBiq4s0MkBaMz26YtEcJ5BVxuA6O4Awlz/AfZe8EwC8O7xoDGpEIYPigJ0DjBTjlgcstQ6jdEvD1lVs5FRoz8tEC33FulD9il0nSJXPslprve1vs+Yw92GOjf1W3+UhNtZSMxx4ZDdVzxRQzGP+jCagVF83Q6lbsnR8u+N5pbndk776bGZGG0FkseyjH9qN+uXhatlJFEDFF8BgJaWA18XU8yo7viZbFZMVWfpajKA9s0a8mpcuxlHir7OSbV3nZuJbDoaMrB2J5GusAjA3cV3GqfGuuyBu7v+BUvt97jnB1NvfD+/vDw+3H94+Orpy5cPX909nB5enlD7CCmae9OjwJiQQx3zsEe6BYhOAHBrED3X6ybn4BPtpul4rgDTdwhjpuPOHnjkJ7M8i4f/JE9XIO5fH+mU4SOeP0Y93fzzcvf8/EQPJDw+wqsvnz/TtAlGcDbhTht8DG4mxbT7LnYc4uqoWTZweEtOdn4EfzH5rQNdp7Ep1pUB3ybSNF1KlxBy/YzcdFe9fA9ym6QHciD8fQk3p83dMyDtC+LaG1Z8rYybKjFRLDBdTw4FbMevAChlb1zni/FLu1qLabf+RLerdn5Gz5M6YVti7pUawyu1bn23P66WAxepM/zfsm59kTgONRp7Y9ijmIM7R/POn5cP9WsNOK9C+Xus/7yMEGNflr09idCe7Hla6oxmtMVhJKo4i5FDs3m8l+cJ6+uYhb/eP+IU4OG7P3/30+cfPn9+fX59fv58en35y+n1Z693Pz6/fLw7fbq/w/eX0+tXd/ef7l+/wffp9ZuXux/u7755Pf30+vIVJO/wffp09/LR8b++O31+ff2K6dc7zOPBJ5zT6Qv4r68/3uH7Afaw8E84D484byCc+7vHDx/x/ACeUHj5D//h3+MFRrhryF8GwO1DeHA5RobscToTlsspx8u1YEDAcfylEallvtJwZPNLMJWU5gVTqjolr6G363Xio/3RttJMdJdqVwCgTM1O/2/qE2LJHed+w6EwnUvcVJjY4Zz//opH0/eje+DR+BxcO14ecppp6KrcEktDV41giqx6VHbLqAGq+gxAFajGjFCqtrSoKm+JrEZ3SwHs6+tMR0c+886flzsgpshNZ0BaHPsLaPfN20pYVOv2KxyOnKKXdLSXJ/rhHvfuY7Xk5fHxqx9/+un/8L//3/1P/+nPD6cPX15/en76cP/w0+uXr04PX15fPmBaj0X6u7tPd69fv97j5ODr19MPOAG4O/2EU4LTCZN7nBh8fn35+Hqi0wDQJ6J/cvI4VaCpP0nef8HpAU4ewIcMTgle7wkBJyP3Lx/u7r/gAYP7h5e7F0z9cRby+u233/wX/6v/4t//x3//5dNnREQPEOB0hZ494CUeH1iWA5cdzdNiYe6Fen//kUsVi1NW0k/EYkoJp4JJKWol7FnYPwOU6ptNt+5N1Pd0ef9UTcQLZ6AcXi7s0DrzZRhJv0X1Y7j7tDTAyolCKUQcFuHzlfjsfF02ckdX1uV5gwhxMDXqoXeneU2jPO9snOdl8flJQkeLZIq9RWPtn9V71ga8IYfz9CsqbWm1MjMlB9MmSksz594rY1PBNCQ1O4kLewruAXVr52iccqfTildIc8smETW97JdswvjKdfnvQbZkyn3QktzE537gVsDVVDaFJBk/9ecKv3PzhhFe8W7Nh4ePj4+YtuNU4PWnn3764adPuD8fmo/3f4MHgB9Ov8BbfLBaj9rT/be4W+d0/zN3lw5u0H/CW//JifsXWo9/+YUbr7+mJ3vvsPAPz36Fe/3pKgHd8vCNc+Zb8N0dPngq+Jeke/oWaHf339CTwdDDi4RO/0r852/dHUR46heXKL7gP3Ul2CF9IOGRhBfcNESPHYNHH4wMTLhSa18hO+GjMwR1egzBqSZQJMwM8oycpG/+cA8HzXqBTVtIlUwtcA29XfyHY/v6oyNlWtsqa7s4nHn+TkdmfwjrQtkk1DOqlOOA1vK1zgvqwKqz+m4mDnJZipcmdBT9vvS3u9UDE7u8pxeZKXPOHur0lvh09wENKvVoNGbigxPXtVrfQtP+WLpepjbCaBOgy1gygUbR0jXSYCLRr77gwPG9E+DxLspuuwIQcUCN+pUov5sCd5p1udqi+1YTrHbCy4SYOpCWLuPRtHqZDKDtK/s1s3ydiAiR6ripLjRQjQ/dSI87amjajMX/Vyy24ze8aGaN+4DuT1jOh9g9rbTT2QBsY75Oc3NSx8yfZsnuqAmCaKoAw/2jVwA5x9wt+8QnCRIjTDJLTwa7VXxXgWkc7od0gHS2DXR69pds4K2kJ7wn9O4RryP9iCcB8EoicoLFnYfA5bBIHf/JDceDK+HDPF8Ta8FgmajmNIgPV10tK0UoxWQxtiECQmR8Ls7vYzPA2ec2O9ZSBzp3oLag6mbScyp6VxJRO5Yz11bSZHqwmL9FARN6VcWZza3ycRelR//WW3m/ckT1/R2brmyEp5IJQOu0z6KiubVUec63FukceuVatXWeV3pT6pYymjOcmXS1RkON0Q6nPy4LvEQoOTQXSfVHo65gpoD7lPQuYSD6pyx499mrLQxb69kdgXSC88iwPf9li5cc7ZK19sP+qGkpQqVP/HVPLodv8CFBI6d0QUckKy5emKD493d5cFSjpVfGhubmsd1pio5/eOUOqkjo/vPTjx++/vb1+W9fnn7x/PIvHx7xHPBnPIBLbwnC24HwDh5aoHdAEKcHgX9GZxAUL1bNv6UN3UlEK+jOEObn+P1f3N/vpv2kQmcTbpEfIN+SuHsMih0joNMzri6QW88/xxetstP1icfn16f7u797vP87XCYgSDyucPcFFxHCI8iAJht8luFi8RxsCCe4TEVevyeCSsm3LnMjekWt77SA6VsN1+XSKwb5W96dPL7afSZIqS2dluG0SnEUaaH19HZLV8EvkBqBezWna0Gtu1rjazoBMDLjOmAiaBUYmWt78qZxeuTL46nW8hlzXYu7IvCZQO/CR/qt1Dp2/rUl/2ZucyNJWUeRVBxcSOward/oh5zPqo9lS2kxjZn44IR0rdbqodu67doe/FEZ7niFluuj4OreqYT82r/iMOl+QUXeAqSr86bIy1o2o9mH9i6RqczizMDbz0DHLgERYw+/pvR0BHJN7g77ElshUksgy83GWIKIWa5fDOdJPq2laxCeBYNF/zCwf3n68oiX7T9+/XD/9Qn36NPKP35468Tv3cfkmh4SwAfXANzrfZwaNAkTNKwBkdbjScghAsIVsPHr9E6WTgnILJ8T0IZA3YeqSBYouK/Hh0JMOhDSlQTcZPTwgC3uAXKvAYLf6qoDa3oo3rB/DEX+DH28A04HfjEWI7gAczAKz31qtVIZhOZ2awZcZ6uBuL6JCmpxbvVai9Q0L8Fj31z/EGe1HzEKzZ30zMD5MrBl9MLbHL4vPOWeXrB7GOW+vO95UnlOXJ7z9fipZegcHYdH45xVS16Ybq45lb4NZ0bhl3ku8S2O1tW0JW/ylT+mTFExHHWBsMbnDbuM2Pf7cXFNQwTeGNEYGcphpORINsoWLzkiLEQJGPyh8YDX7XiCEu+e1Mq4q7JY++f6yojqZuIP37sWjhNetuPMehIGMf92cyeatzsfsY7ubvk54d0+fznRjfj8hn7MqPEu/2+e6c37eGAXtkncPXfrJ1b0/C5F8sn7jfr7H+jHwl5wNYAskg59MYkN+YZrBWTi7kdXRTcLEZvOA35wSj/HnP/l5Rug4IFjXADArwjDyPPrP94//nD3+rfPX+6e7z49PLrHgF/un/HQMN0sRLcwERI9fIAIvUUw2D754PxX347X+iJnvbwPwzHIW24dFFlGSaprL046fPHTa1Bk2cC2t83jRU8PtKC36DImI6wZx4JP3P9144Qa2moPNS0yyCG1K6WS+rHwNUGpJiEz4xp5NJbd5J3v1Tfg1aPSEXJwHGPB72HoDPTI37RMZz7bMY62exutv/acdosr0sgcdTI8dQnKGt9iLCyOowr9kgDmWNDlvyjyzqhdut47y9kMdzkDPPTz97I07b0DPbEbtsPy1YlIHnaPUgBhQmgVP/GMGYuTqukQEmag/FdDpTqA0gTYze9pmR1KjkmoMkkCx5VpXR0y9FtdeMs+LfDj3vovp+ePuDMfj+ySJq3G33/+8uTm/DSTwi03XhkQvi+xIGoIFUwYwpa+yRB5hOcK3No8KNIhHJJ0H9Q80GI/PnQegKsMJAU5BEIP+5I0io8Egl8kw0UIugfp8e7DVx+e8EaiJ7oJyJ27kHlcNyBFN+cj792HN8owOe5c8AIs1vpmZafGyjXhbjQ2XoOYvLEMcItQu9On3gDMDZ1hDP980nXfXWQhyPM58xYtWQl+i7HuFFPS8Xz+wOvKJAvhGwqnxzvcCYTx/OE7OkDZ3rG4Xb93DR+D3dEigT7inHjd2v85z/l8Ctya04F21ZrWljxrXU0nDdlTUP70iHNm+Ay47Dk9CCyzyWdthvenxl6lhUFzvMZ1j/oegZmck++J98CekwWyX7E/ef029SjJtLfSY0xkhIBhmhDzCOnwaHLO7vCGGul0j5/KwvwX9/HgNT6Pjx8wV8ZPaGFhHLLgQx7TYhqDsbJOj9KChdnyl9fnrx4+4td/f/58+vEFM/z7H17uf3z98JcXrKwD4uGn+wcsyD/iRf54+yeM0I984alc+sbDA5AHB7V4ohccXDH4OXUzmuvj7hxni6438BO9tFTvng34fKLf+sWkH6caeAT52d1VhDcI4R2gON94xhMAd/d/cX5C8wVz/dfnn16f/iMeTrh/+IATFTwW8AHbV/z//EJOf8HPBZwenvEYM0Thkzv9QHjut8nc6QiFT8tRuLbgrjnQXUaUS8qJSw7lk1PMG6LdSj9CcYIoM6wrkrj6cDvwN9heRwmkpDeUMjeWqqvIGzHb6jyOWXYtPmP2jCe0eogPtR83FqvWvlXCs2cwqO3w4Y00kOPp8Wp0TN5XnrLhHaW+4z81n7lKe14ftwNGe7tFt418RK2OWtN72eJs8Pq31b4Wfy8fLJzz2OW+F9b40f+YgW/qi4Fv+Rj4XtwV6dgAAuqEFhDDNmjwts5NZWZpZmBmYGsGBvY0HgG2Grw6fWRAf/aKMoMVE8LXY6PUJoSIJlwUoiqtzTsGZqRu0k9Teboj5h6/m4up/4cPeE8/WCRF02yayNKP6+LNPsSlhXV6+pZ+f/fu+eEDvp+eX368/4hXfX5D8+G7H/G7vz/79tuPXz3+7O5vHx7oMdwTpub4tQA6ecC5xhMm3+C8uqk/+JisY3YNNFqGdxch8JCsOysBn08M3AkDnzbcYeIOBHqQFycspzu4hmeHcVKBHxsGBz814M5bcA6ByfoDQvzw8ukn+Isnkp8+4zIAThse4AN+MBi+4rKBSw2m/vAQHzr5QDroPATXMug8BBov+F0xOkfCDwrA6Q+PIOiKBpw93b+8PPufQSB15B/povzSh7f0DabjtL6cLgksi7ZgVtZdxOhKX0fUuA1q0fkabp4AKY0QGLT1zGqdlrsIzWGkYXpPmXkRr96W0ets+RvJMZLX9UFvJVEtjisAcoerawP3ZXZrV9tla6tQ1wqEYcSffX7vqnGM2eNTntFa53ylpLfP6yWFP6a84bZltxTXyNezlqC9Kn3ewunPzDorZQ41x4pLy3TZNZ4BSPYI3ofdt7mzFsZ0fixvtRLLMEfrapkeusdWhiNBcaBZ7bpiGwoTSAjgz4+Slg32zIn6ezF5nInDqpvYe5xAn758/vLh48cPj1//+Omnjx8/Ysb/hLfmY3ndvUwTE2A6CaA38NACOKbFmEvfY8kc9Y+fn5/xsO/Dy9P909O/3t1/e/eACwJ3X33z8auvPj7i93i/+vj05QvM4xeCcR8OvQ2Ift4Rk+xHiuj0iNk6nRpgDR4T92e6HYjn35ioY3KOe3eARoI4MaCrAhigMBn/4K4QYPaP+3vcY8DuFIJ+OoC08dr/V8zvQeMtpHj69/NPzz/9iIsS//h6/+/wWwQvz18ecTni4Qum+zgjcanEZQI36cfuQPc2IdXwAwiwhTucPoAJHn7aDA48P1M66Gzm6Vcw+/DxewrBXTfARQ/6lQO/4OzWnpN3LgEDH0STfEKZMgufXV3gRcGUTxlxdSt6b8RUVLL/Kn5JskVaz+PmKCVGONRwtY/Fr8kavIDMiTKEcnZ1JCGEAqUqmcNtKA+3rOoz2uESR3ve3+60ByAN2oqidaClRV1r0SW+JdnmW9Z11Jpuo0mt7HHCyQjOzArkDGe0yPGyVr91K0v91rP2WsxPBbmqg27G/Yq+9VuAZA+sqlXgJ2tmYGbgEhngfVh22Eu4cAabPEztZUjGvSqgm3ejZumGZBkbJfme4+DJYzftxm01jr57wbz8FbfM3N+/PD/dPdIt8c9PWCv/hEsBT09PqMU0CmvdmDTjlhhMafGNiSpm/Jh3Yy0cq+NffYUnbn+8f/zw49PHrz5884hbgJ5f7h8gBmHMl59oen8Hhpva46kBTOTJuFvtv8cVgQe8oAeSOD8gFUjxLINm/2BjdZ8m43RUoOsUuA2H5p1097/PBu7shwwEyAqJgQAgnZ3QXB5nMvidsges1L8+/c3f/PzTp8en508P9199wI8H4+PkcW5DJwKYvOM3w9wPGsAmMXGOQ+cfxAcODKH48vzy8auPL0/Pnz99+oAUUCju7ASBUFyw7Hwgfvg49zmIwKpsXVbcV6iEnvkpjJiSs6KRAW6ahsDNVHFn4f7T6jgbAno7yRpIgs7rgNr7E02GrvHwSV1DUN5Pv//7/3VAwrhPJK8H0ZY+WoHKJ/f2UH6CmMrZh5XKs5/sbIa0jBXxDPCCxTKKCzpzcdOXysZedis98OI5fVsOjGa4bNmMI2MPRhWieXgSbshepgV2xoFGMpglBUbx8BxCAG5vHSo7w4BOHHPiL/+Gpr33f76np2bvsfaPWT5m53TDzP09bgCi9f573OuCuS7m+d+83H16wd01Lz9hBRz3yWBx/eX58+dPzz/+8OHx4zfPL99//fFnTz/9y0+fsXr/5etv/vavP/74f/4//p+eX58fHj98+81HrOR+/IipOJbSMVMHDt1OhCn1/QNmzmQTC+2Ye9NKP1FPdM0Bt98gI/SbYbTAD2+IQz/ay48KQJ3uKXIL9QgK4PSqn5e7Lw/3eBPRE5b+cVcSXarAaQ6ebHh9wanF//Q//MMvf/mrf/vvf/Wzn/3ym2+//vnPf4GTl8f7rx8+vDzef4N48d5SrOkjAS+nT4/3XyFljw9f4yTo4eFr8v8OM37cP/Th0+cfPn1CQnDGco/TAJwj4RQIf7hzCrl++fQLGD09/BPlGhCcfipEytPqyoCuo19jQMSP3+ELkoyB7/rHrEjFdX9r31uf6u1TGt3v9rHahyKZiW0QKQ/hk7zQFLm9C0QNzwedzJ0+oCwZXo3NmWzfW78avKGoW1Ci4Bw3tLZXsV3G4ZWS7ZhbECT2Noj0viBWMEJFvi1HMaj6j1te8XTkhtrxLTs1rjc1ZgZmBmYGfAaOGEaK4U2M+JpCoNYcosRzAVoYlw8B0GSVbsPH628w0cS97A8fsez/4dOnz1i5/ubD1//D//g/fvdn3N3x5S9/+fTl6dPrM26W/+nz55cvX37EFJ9ugMHE+/nzl88vP/7w8fX04fPz//jy6fX+8fnTX58fv8ENMPcfv/kab9z58BGPEgAab3F4xk+B0Q39J9yF/0I35WCGTBxMV+DdCQ8MwCtcMMAbhOAgzfbJd5pIu9uO3OUA+oEwKNBTxnQbEs2RIUcXGHAagKk+HTTpXf+0jO/e9fNApwDwnkL98OXL85fXp//m//3/+n/+NwjzI04YPjx8jZ8nu7//+vX0+QEvMKVfMMaPBeMp4A93j7hLCd7jusXH+/vPHz98++23Xz2cvv7lr//m3/3dv/uf/c//4y9+8W/+8te/IgX3H/DUAV87gGmyTP/d8ZsiQYk+buPc43L27aUcV0sRQmAGcm6PzIDOPtuh/on2uZWmYD/F2yNz9e6ww246s1s2fchNGPGihNREVkKV2dQaVKtPAESahbSoQq38ZrCqZYzKnVJcoTFxLLE/tI6Cg5CWt4VnzWIG+Kx3Sz4rbbpodQ+Bvexuid2Ko/Pc3VJv8I9A3oLZozua4bJlhYPRQu/6TFv4oiX5LDlSRQTBMaT7lqGJCa4UmhTUx+KTCNXh7p0P/wxYN1UGg16x83L3TGvs2Dw9/Zf/l//qv/vv/9sPD199ecK9MD+DH6+nH+heGkyRcQs/tvd4rT7Nd1+ePmLVHkpYt8fzAFihv8dLgV7vPz0//5tf/PLxq6/oph88pPuAe/2x3I+nfl8+uNt76DFct+SP223wBO8HLP3TT3PhHAF2IP4Rt9tQPQ2x9GQwOXn64O75oWsT5DrdU0RTb9zrg3uL3IkBIL9yIUIAN/5/oV8io8sKj1++/PSIF39+/Prx8cf7+2/pDh88WIyTg2e8DBTnHB8+vdBDC693n5GD0wnvCMJEHjRdesDi/uvLv5w+/qt7p9G3D3cP/+E//uo//1/+53/37/7th49fff78E3z5gFMpnFK4RyZOj/9EOcZlCzoZ4IS7MxffnuB59t3DPyKEUFDV8sybE134IgA20xTU/W2He+sNW3oM1/ujtV8YMLuxtQ8WqGSG9xvqVnTiSe3BnLCxAEw+R93jgwlxcMXRvnF/kAyvjoYzuR1HO9ATu+637VmlRma6B7/UYo62q/cpS75HZos/VuYJE492YbWo8uGRKamo3JtTjl+870U9fQKgMeMOGmV7KFPPrDBQtTOGyGTPDMwMzAwMZqAYWQpG96TEz2GcAzSy0myeNpgYY5aL+fnDAybBWPC+x/O6uIn/8cODW9LGrUBYvMd6Ol7CRvf70wI73Yd/jxfoYA2flvPpBn2qfcA8GbVYwsdi/z2m3Q9f4/U/33yktwPRA7I058ckmhZM6G4ech3v3KQzCHqJDj3Ke/cRlul2HdScXp9wX9Erng+mW2zodT1Ym8dE3C3FQh0zdXDc9IzOGkC5m4XAIK9o1u1OGGjujnk+bl7CA8rwH/cB4bU9eOMRzipgh6BxnxBeGIT7nZAN+vEvunRAJyTuWQUY5+cUAEqP/j7gt43h2+n50+d/+qd/oduW7l9//MsPuI5BDzA4NygjoNzs0TnIbgYSJRiGZPz4QsJzUlGkh6K8zc9+GeB8zqzul9GJ9NYyUB+6dokyGw7zKwCo5nEU37yP5go2v+kfnXWVULaKPktjKTq0wngPCA6G+DSvMDiJhS8+M1t3bldqlZwF87tWd+XNsrhTPj18NxpnjLWss+TSZSvPVv+x5EvkkqO92oLTRi5r13G0t6MIW3RHbbG8Hn5A9+z3VUOsqNQNMGazVQaCji6W6AxKilgrx60wkMBE2N2IT8Lu3TUnvKIHxFdfff30+TNuwafpOu7Sx806QL/Hze5PdPM93XmD+TQ49JwuTbfx9n16CxDW02n2/PqK2+gxB37Au3e++fZv/uYX/+bj17gdH3NvvKjHTc7xhSkyTgQIH9NkgND6PCbwMAddCNM/1BEO/QMfc3SAY+ZNJxnuJABhUDiQpHMHuq2I3shDpyDEd8v25CbpOpln3AiE8J6e/vGf/pmuKeDVn6h9xq8cfPV69wMW+O/wyDI0X/ACU4rKtSMYOAXA+QxEKbqXl1/Sa0np8sTT13/zM5h9+vxMj/8+fvWMe4voJAbuuTjpy702lFsDXG4E+maKK/ANBXx4t3eUKxdfBF4wFYMrGUyxE1Lv+5pOhDYX9Bh+/v2xdN/yQWdA0yXCdo7lQxeyOxLh91Px2YRjGBvFjF0VnbfZJ9kgy7BWj7zh5gJ7XQuOxr7gRFG9F35P3limnYe9/NGBGmv/d8+/ps5R1nZdRdHDHcGUVwC45+G7PeZpTxW9Sknpt0ntfVty1s4MzAzccgZ4HOIIND0Ukyi69WwenIQXkGRUyQavrBjEsfUaJEDzWjd1xtQayB8+fIV3/NA6Nz0D8IongB8fsQJ/+ukH+vEvzKZ/+gG/2IXb8vGbvrgtHlN0zIABQFNuzMr5yVqaqWMWjGVwmsejmtbrMZN/xG9xfYUZP83JH7/Cz35hMox3CuGNPTTZpxv0IUpTYpqEAwFbuukHM2biuGk/5QGYDvYBpikWnty7OGCQZuUucqpFZOQETZE5ZsID/XCPxXk8doy5+cMH3CP08vL/+//+Dx8/InY87AtE3JUEFYJ0KcLZAiIgKIKBs3SW4s5O/HmFk7p7xiWCp5/wBqHTh4cHPBiBlOJCB8xTjMgHnKdbhug/3AAHRWehmMOzs8XMnsOAMfUBr+PDUuT8/MwMzAzMDFwmAzyC+eFt1AVS08MdlfUJAMPKN6/xlEY0RFnbz3Hn3/3r9HRI6zQNz2uf9jlcTYN4687tSq2SY1k0/dx1xWJg5aDIp+mhFZLmF2i6UtP9GWOttlfUf2qfUSs1DOIN4Az2fG2xHaOWXEdTr8BMq7uNtJW9fBMco8W0zV6a4iI4B4lJIw+EYPJHiMBob5VjtOrtZrv0+ko8v8u372BVn6aoD3cfcPs+zJ2wnP3Nt199wenAI5becX/QC278cQrAcnNZbN0E3k3W3U9fuVvn6YHiuw+nR9y1/4qzi0fcEvSCH8zCi0Bp8o15OF6dj3kwGo2eO8bvAtA5A84RfkZW7/9KK/W40QePANMdNDjD+JZm3/c/UAqwOu5m1ZCALCcF33dPP6dpOX7r17PDCcAJ7ynCvUVfYdL9+vw1Hml4ffkL/Z6Be8IB/uByhLvoAbs/0SUC+ikx/PuWfHInLWSI/KNZO37J2LlE/uEMBeK424deWHr/8PHj1/AUd0/RmQuEsW/h1in6STWK1L3/lM4V8GiEc5ralNzmDTcsaPpIs+Zlrg4ypOn0FbskBays0vu+prXkwHir1S5Eyz64wr7OgKYZykK28mPJm471j65ulCs9NJGLCsvnQrCLYR2h2srrtDQmZ5g5ZTZKjtbV9Gg2dMtqmjFH0bQnJb0drT8PpXUfkeuZ646tAZMGoXLtP9TWt/Q+NKwYfUcjZDLQUVmfAPAoKd+NAa9uaHJnBmYGZgaOygBGJp6n9Y9MLO8d4oksCm6KTExG9NVdG2+aJpysTtNZmsEDFG/D/Ii1aryxB/Nq/OgvlrMxM3/99IT7f77Ggv3p/p//5Z/xLs8PX32NSe6XL58fP3zEWz9phR530GPlnafhdIsO5sS0XI5JMU4w8PQATafpBADzffp9ALrjHsnAOQeeqH15/fgBt/XTSQ3dYcML9jTxJx8h4yfHdFpA82n6nNx9//ASTDcdp2kzWycdOhWBdUhTqqgKddjACOqgT2yEQzP+pye6ZIAXH1E68JwyfpcYDxLgGQASBBix6W6kE37eC/f0QxIgpI7TBKojq9jimgIemfj0+RPOij7/9NPzE04ziAl5rPjjXADpoh9Qo2MoGDDEdxORAYqTbAEobIhDVW5D9fwhoUCnWy+dMtOSrZzKzdLMwPvMAO9bHbvS+0zPtqj18LMmxaxfaOItcr+mQZHOKmRsFFnhRN+5LpaFovfIYk3qzxFGquqEO/+uVx3D5XO48lxzpTU6FtGhcvePea7pbJm1hR/tSLesHJQ+VGwdlp8iUM8ovbIkR/nb1w8Si9xnVuWnHWOlFRLD9YLWcvO8utgi1/JNZ0/TFiDjFEMVDS/E5CmpU26jUVzxLQo8O3RqcqACkY1nbLUy7rGzrkJq3S7EGPTU7evjA1a1sTj/SOvYjw+Yzn68/zeYHj8+/IRJK37P6+H0T1gyx8v+X54/0YttnjBjxe9/4X0+uGcIL+fBlQFMp3HWQM8Q0/SfFs4x68XMG70Fs3ZM+J8+fv0zzKe//gar4J8fHn4GIQQBDslTNLitHtcePoGg++xpJg82IdBCPB63hQWs+9C0m4ZqYpJRjs/NzB9/QAGQXsRtqPr0LTlFtyzhG/jY4AQF6/unp+eXb//m5zgfwLt68BtnmOC78x8IwPo9nltwaSVtoqmAExScveC0AU8+4CFpOiVwJx245+f18SvM/HGLFH6yAM8P411DuJ5wh9eeIqWff/wZrn683P/TN1/j8WJAQe2X5NDD92SMTksA5ayRx/zhItUHTrnFGduvHM6fXXhK8hm9CPGCv+1DbVP76L2vVr+GpzGtfcTisz1rX17jTapjIVv5seRTVFU64IjM6GXGLJ+VNzVy1chfA2rxdB9oyQ1du24Cja5t65bVNBtZmVunXMa+Ba0Z9ECllZ+yX9VAMX7Jpz2WiZgn/HvPcjaX1RUAsiCDlBC5mvYjr0N5obqiMVkzAzMDMwNJBszhJ5HqKAyNR7C6KM/zSxYjL/Efs9inV9yx/unh9Rc0mcaNlfQA6+Pn+8949f5f/+XH3/zs9Nd//Ste8/+P//xPuFUGv2kFsW++/fiKX8H68M0TvRrHLWq7mTVN9Wmhm16v45b4sb5OC/a07o3ZLaa9LzD25aefPn/8+gMmvJg3YzncL6vTaYAbxGnLrrpUQg9zcZoZP0PBnU54QWfMnVOBgg4U6RoCZlF+Jg3ardO7WpbAFNudkgDPzcEJHGc59x/du0TpZiRaucf8HE8H0yULTPdpHR8/ioCfBvuAixq4gvGKVxUhFJLB7Unk7qdPP334+quvv/0WKfqMz4+ffjw9ff31z/ALYDgvosed8UrRxw+f8DPDj6cv+FllvEQJv7IMTxCWixeuu2jJS04DOT38CRjDitepQKnZkI3rDGp6NTPwTjPgR7vR6HkYiDN81j+d3C8Bu0ov0XEMhG7lnaMOMYD0uueOl7RENfQpz/B61Ndp9SCfSUavHGjaMH/98e7rYd+ZdD1Z+3pStyHcjrYT2Yw4ws8tecvc26XYMxhgnOkeCDEr5FXwMC8cHaQoKodA8+PELOa2mLBjDkrL9pj3fsG97R8fv/mn7/7x//pf/d//0/f/6enLp7/+818/fA0h3MWPnwTG3Tpf4wdu6V72x7uPeH/+N3jRzQnPCdPr/O9woz9+cBc/tEszW7egTb+chUV2TPrxm714dhhr7R8//B1evf/zX3/85b/9FWbSmFnjF4dxCvD69LduUf5faQS/x7I6UoTXf8p038Vwwst2cNmSLhJwW7m5vytQ2l3qX36Butf7f6GoSd9Nq8E6wT1U+DUjOuWg23Ewf3/G3fv/8k+fkIjnT9/gGejT/V+gRDdA4YeCCRI+fkbh7gVx0nO7dKHg6emnH3/86w8/fPnyxZ0qQPITLhDcPX/18eMHXEDAbUq4QkA/GIbnKB4/fH76y29++W//s//Ff/a3f/sLnF/gFAjPCjv/4J57GICcw0kB4LGlCBwjfnHZNWBkGhRkKwjEG/owjFY5Yv/V+NdGrzu+X1sU6/y5xbYePRZsidGytQVTt9ReOBpzC235U/LzoSux+vr8axqbBp4ECMNWHNKiAR7NuRzk0mNcYtyNixlnWzG6sg1nas8MzAysywDv+De1J7Kz5biFBMgwBsrHJKFlRBRdShwmu9CluTDNiTH+0kkFOFjq5pf2P9FdK5hY35+++fZv/6v/8v/2X//X/4+P337zAa/4x893PT3hJf6fPz1/+ICXeGIxm34S4OXpyytueH/+8vGrn/38Fz//5hvc3IIXhtJNMXi6FUv1uMsdN73QIwA4OaCf/f3w7c/+DW4W+vrx3/7Lv/7j6eNPv/jVL758wXtFaYGd4n75BX37d/vQ+0ZPr/gJXp7EO+epgDcUQYGGfbDcSj4FRdUsAvL5b6gSD+a6dRmqI0WnSzQuXzgOGDivoRuNnnCK8u03v8TzzS+ff0734Nz9M12pwCuBcL8Tpv30mwC4zIFg8dsFdLng44fHH/76w//nv/vv8crUjx8pYLDxuqTPnz59+uvdd//4/csXPPzMZpErUvrxp78iJR+/+gDHIIXnAej5B0z9fRTORe8rKzrvxVfiYcbhQIm2PpwFq/YK+Ffv4BXkaLowM/DGM0DjXleIYcQLW6VHGDgSxJoAWHJCjdOm6vKdo3yvZHkvV1StUTxK12paPG2lPH+yNNdpWWgX4Ou7GzVtuKLjNUQuzNYe9rejJbmuL3EKtCeHJ0W33eDVgLafVmbaEVn3Jq5Da9tarO0b1RKYqEIjGk3zaGzkbz9Kuum7VqIxrOPjZowejFeW0V5uvkwbWoJ2L+K5+/GHjx++wkI8uuAjfr/205fP33zz9T1eY3P6BuvgeAL2q48/e3n9Z9zB8s03P//p00+4MR436LvfA7j7Bi++f3i8e3CnFi9PmAtjDk5L+nh3D04AYBZzZjxagBtfHp8fcSv8x3+9//TXx494zShAoEUv46R4H/6F3aV80Bo/NnTzPXzyZy+g6fX/4Lm1fLe8TxNynyyyBIk7/NouTZXppiHScHcOQeYOP1tGmZXeC3HgQObxy2da4/+C2f7zD3CcZvx4uAHP7X76hLt8yDzyQj/o+4SlfUSFaHHr/9MrzhDwCAQeA8CpEX7a+Cu8Kun19S/PL1+9fKC7ik4P+OXj54eXv8EdQx8e7r795m+w/I/TiNOHj3hmmH5JAY8U48VBOL2gcyZynh4bAMH/yWm4R0X3oYw4Dr4pMarK1cRaKW4j2KDGKPff0b2sxGT8URztlaap0ZEbSZquS2ltUdNaqhxb2vglTsnR+CVtyZ//WkTZ1qW3R3CsDPTY6ml3jVPG2G5frWvZKjG1Vj/NOG4Qo9Es+1j9od//DHCxaMVV8qsjU8A/hbX/plSQrmxZz2tjTJddHSz+8OAYSulWhFL2LM0MzAzMDGzLgDUr60XloUwGtEzND3kZt170spi60rw/4tLdJnTDPU2UMUell1fSvez0fC9euvnDD5jd/uJn3376678+fX792dff4r52/B7uHU2O8aofTNhxo8vz1998hVk4JrVf0U389KpLzO0xA8ZviD3gFZ94RvgZ02Wsp+NRgg84IcDkGi/IxO1CH7+hG2xwdvHha/wA8ANmvZhQAwke0m30bvaOcPgaBU9xg/PY0gcTccoxTeppVu5KVEQoro4qXbiQEHEn6NTdF8G7swg8HEDZoNV9vNXf/RAB3ZaDVaVH3JpP+nQnD66A0NUSBIhfMaOfJEMtvHWz9ftvf4bXktJjxLiI8eXTZ5dbRHaP26DoviHcX4Vno+k+IhTwi2A4L8JcH9m4h7mvf/7N5y+ffkLOkaqHh6cvOB3C8w0UE6yTl/7DEVFg6Yc8tD/tWltv1lxpBmaDXmnDHOyW3/0LK++hP/gxL6YgUj78xhUAVu5Ok/WehNEzqtHz1/L8qWjqCmOdFgNpDzXtzQyu6VacO4KFg7Zb1RNss13c+/XKM2ZRXCZUBir5MfT7W6RfUpvq90RraZoyluZQ167EL1YmNOYovS4zlpVRtJUZCOZ5pGmNN+0RiWsDGk1jaQ5Ik9XI66ZEx6Gi1fEPM3GaVhIirU8/3n+Fx3S/fP7L119/++Gr+8+fvnyD36/C7/Pe33385uvTA14GSvcF4Y2fj/ffYBJ7/4AVctz48/njw1evL7jNBh5+xqr4wz3e7vkRuydNW7Hqj5MKzGdxTvBAJwO4wkCXAdwLfuCAu+TwiJcN0WkBeUWnI0DCk7d0N447DaDi/5+9P+2ZZcn2+7DKqaZn2NMZ+nTfgfdekuIgQwRpeSBE0JZk+IVhw7ABGf44fuOPIcCGBQi2RQ8U/cKUYVuGSYkjYJKXbDZv9+17ezxnz89QQ07+/VdkZkVVZlZlPcPe+5yufPauioxYsWLFisis/4pYEWFyqrZe7UXIvcXU1XJwWfjfdth0w/1WeaMWB+v0Vmu9QZxiqoF2W+BLheXm42C+LYZQGfgQsa9nxNlnAHjqITclIuUalLJf6ojFEOyOmgcsGEBoW+KMNaP5AZkK1A3Qj2GFwCEzKclond5MWDvBDqZZkZiZsVgusRtUbXjLWBAt+qAQeKoks2aqGujLRbgamAK2Yoxw8yF2xsDR1wkuTsycCrdTa6oqa3O7J3DwKWtL4WRveB773O2XvGrhhnt/wJfcD/fnUMp+/m0+7Zg+/vv1sL9cn2cfH19vfTQ+n96w9wvr8+yl70nok8HXWB9ND8sHiB6u5wcobACLPiTTJ2dffEdRDue4hAf9HXcsta+m25/T3d/1073J7OfQ3v3iY29yvbvcDMDmjbIJDS/OFeA+h+f6rlK6X4S76PFRNUKL7/B3910/YLuUOxl/Y29Penm0pu/qhkcW5j94hBsAS6vxM+ve68e2oBvrtmcHjx+NVQtk4+u/XmdhwpAz21bGOOJTGPtfzibz8RTs6cyDWRhP2TMzywo2zVwtV8kUWM/aXm2Fma3YC4hzuwS44YqrD2gZOiH4GHzAsL55t2NxJLaDPmeKabbBHIJIZFVBkcuVpgb0cEVdcok3Ndj+oU1lpQ1D+pVG7WfAoIfc/GvlAKGF291FSFZEdeu+bE2AMRWSN5787DkLy4gLXIJyEDloXBAdpSBqJuUI/nOpsvJBoh5gdvgL/WMzsG54FE4nHJQWrNksacUOP2KCV1O+zkbhCuVQztnZOQshmAOh7vhbRcEIXytWUa9WKf5SNItZApoPqawZBdxVV8tpp4617yZpK7b3plFqL4UlDCTbz6RJ9WV8WM5NEafAB9NA85B9sBJPBX0rNcCj7j/5HXU4TEEmx8O9NzYZiFVUPKr2OX7VYn+g7BZ9T0T9I9KT3Ir27ddW4mNGeOPW+4vxJfTDLlefxdnmaT/BI2fntfm06e8V07JQe+VsUbpy5WpLqCd1SzaP5tHrtVWwbvrGPO4vidPY4/GvquKND7Uqd68I19+OfR79Ivvq7mj6NNzO1ZZk82ICyvaNfPS8kVr07t1Wamd3N4JypzqbBSHsb3yK8DVvUkaa83UxmeDlUqSLc470unx6dnu9mp6tb29eR3GaFJdstBnGjPbjF48DzIwMnPIVRBM2t2Q4X64/BZthXgGZUzbOyUez2QyszP6XoWA9Q+DaaR+3eE75lTEAFpbtAXIOM07dkq+LVgpzJrC5xjBdgIgio676z61Tr+5NE6qIQLi98c1rKcBQIEs1bA6hXRw3UOUknzK5T9L04FctpKBdKsv4WrHgeCLA6Tz7VhacdDIaJyNw7oGOMNO6Zxk1Yky8jBl8n2yyg909QfWrxYJUM4d01DEMyM0sCCchQBaPdTrCar3GUQqnI7yisLWiyZg9iDQrkOWrW05F0O6r5i9E3FOKCqI3Tkz7tI/8mb6qvbFdbUwzm95Csot39PRGLJH6fBujVUJfn3K9vaE3Hnf5qJtikxehKL199T13bUoX4yR3/Ptq0Zf3U44/Vg99denj4+uqj6aPpx/v8/HDPo0Lt9+cPs0QGdo0+3n6/Nvh++Rtc9sf09c/++L3c3uUVA/nPDh/HvZtnxr36HsvpqpIF2OpXrCWhyh2DeIu2Fq1a5T2xvPXANSZjv3ufCsdy+RE/4lrwPWuT1zIk3jfUg3c9x3S9E4YNWF04Yf3qkaotX6LOh4VCjbkDK5mq8tRmOZrxpoZNxEiPTtb3C7/+I9+8vWv3//1v/HnzuYz/H/OLtjlcxpOpmXI9vW4sgTj8fRm+esxbvtxwrA3NsMXX30vSiaAVnYCNWAcc1Lw2fnZas2+QKBWYf1qMJ5Nf2zyQnZI5SqDwz2Fg55B69W0ri0DEInQt2qh8fdGEaqA+NaGgVSihcOM0rsxfVi7SpoCQM0N/G8U6DSjnBWvSpfEiAkZ9WMIF01piAg/KHbyoTLxhK1INWkigVBcEmN3CP5jDEWxTBmbBJDTjuYLijUzBtECI3gyZ/hfhx7oVGXZTPG//uG/+Y+/+Y8B46ySGI8n0ThmNgBPqX/3r/613/uD32WOxBQi2HHWGwABAABJREFUNhKrktDEcmVXMY1iuG/CJvQmkx+/YbQh9+K6g17x3QR3iEWo03XSwEkDv6ka6HupdL0YoFV0k0Sgyq6UzR37Mbxu9NlXQEOwL9AU1RB9SHuxKfQuAX57uDx7br/kfqofPrZoZ/23bfRj+Qyib9VxK1crtaNenn628u696eCzl/7YxDb/R9SnaekR+bvKA5uO1cIw+v2jTW0eD6XbtsbakuitVEtQ73JQ3x/6jl41Weu3nBWwNcq7h0mj7jpQfcutBbf0UfCScWrzLy+T8Zw5AIb2cb/h1flf/N3/+49+8i+yNP2v/vGTCWPUZfb5l99jQ/8/+slPOdIKkyEI1mDZ+ZzFvmyYM+MogCIMZ+cXk/kEF3Wt9GUgP8uxAEJ2thH4F4AGHsuTvbjgkWNPfbodEhHWiL1cZoDT2t6HNG0kKpgNDCcnXkCqOJsINTVw/ji2TlfEkMFGC3OZY7AtR7EWhN7BzmSFNT8OLuz1QhJMBEPWshag15Y+HDqMmPI7UrGaiQjySyLC6Arp4oQzjNnxXxIbZ8kN6qca+E5Fk8lnX32Fa5BmA0IcpTBs2PozfPf2TZatXf1Y4svkQbZmM6HlaDRhlcUvf/415LbLEJVgFTR7i95enJ/93u//W6iMurEUmPrjUlVqLyNklT6lMf3m2RW9ta9KQ5uw9ztolbUUqqTe6Ij5NCZ8+LkdYfPZ7u1N0lEB68LKUQuuQpvwUax2iGUfUQVXF8K0zp3e7Vts7d3o/4ZupX7wm/a76/4i+HrzuQ0vy1mmw7V9t77ky9OW+W48XX3vlteXx/FpS+Xr04Wb/r+T1Be/Q/YBbtv1ethCBz/vNaH/dvDCjP17dxa2N4C98ZgBuPflyq+luDe7E4OTBk4a+E3SgP96uku92y8gONo7bgi3hrAJALSEdYVbGaE2zA2SBaiPkjnLdINsHTAgvbhd/fIXvwCeskX/61dfkyPN1j/75S9Yp8su9SxxhQ3ZowTQu14uV6BQOBpX0HLIXj8OD3CobZRnSGxqoEwcjfCAAdpKCI7NNfxNTYRhdY6WKgWZEDvADbgN4negXlDbpZJVnCCpkK9LcHohSoP1wv5VBjJJAJfsOBgj92th8wNKUy7ymZUA3pcIQGvHw+XXQgUjl8VS4ruvHU4Zw8+08SjYHYbaO2gU4s3PlIhZD2IsLF/mbpLk7OICudN1xioJzANcnt6+fbNepiyVkPWicxRsHgL7im1Ei7FNNJRyuQL6M6GAKYScWEc6Skz7DtU6QBCnZFe3PZ8bRRgRt6Ydl9+pck/uB08aLPedSrba3SnnKdNJAycNfAANHP+I7n9l2C+Aye0ZADsvvVa1jn7v+fZi9bPlVaQd0yrxQ0W0xj98ydtC+Kl+uE25P2a/Bvan7ufckdqq4xZNK/U+9fI5t/k8rN3c5v/AevMr09KSn/jdC7d1e7c6Hmzx/S+rw4WqycF8NWETqCN6v7tfaXoRCsUC0VmNyn4103SVsUm9QCqQGq/29DZgs54oS87S4CZcp+s4PtMUQbhMkik73FMgW1MyUxCNMiBwWZxFoxgHdcCo1vkyNYAvP+7r2BIM5YNY8ftnrFk7AFGswKskiK5UE87l5YsxdXnqyJXGhtoZcHVw3aFbcw8C8irZpIdSIZtNqjC7OeDLnIAAtE0sMwpiY1ow/Vk8UdJnPexPkD+nEAujEwQBxsvw0HJfzAizNMSKswisaCvGRLHsCdMicuehaGyildRINuTlaDDJqSJZJ8yiaCSjMJ2AwIxKMaYGaZyOb8ccroDu4MDep1HwxEZRbzS8X6QYV2z5gwzyZGJ2BsMqDkbpU9gGyTuVxX+1p4mi0prLdQAnQjvsYiAmYDSVrHVEk6MhbBiryObmfoGH4tNI4bqGu/XDDcFdAtbx7pLxcfK0310H30IHBenTVbusPlbi4PpQF4Ueu/rqK6tO3/fty9Pm40ppx+/juJ3mNOni/LK2qTZ3bZr9pd+/pVzZPp/713pTnzrk6uWXUqc8zHfVHzYdxr1U3GdHEVtr4Ta5mh6nqCp609M2BoAbx+ngezCqKWvD9mCeEwEaQF+N7k4KOWngN1IDD/AEuOeoefs0gT36tCwNITI0YWFFw4uA+GjM4lTwPXidoW3wdJ4vOfSKM3kZab69XV2/u8LvBrKiANTauzQooiBOhetLTraSB0wkmMrpt8D9eusbcLyGp9nhE9DK2V8GT5WKez+FFywjluySRL4rQGKQrxbYaotQAWSNcAvROiLQtFkGxAnsqzR9yC0IguqWNAev9a2t+4XF9Utc1dy+BN6J0mVJCovQbAUN3wP2c5XBN39WEDfwUHbldmzMrUhhq0K1faqkIQsWg2pq4sNJOhGddkBVaUB6M0+s4jIvtIMqomqrUQJss0pW5/hEJSQgHkJYEmwhKqsqiVKmQ1ganDL/oO1EyUZuFSBiZSbLkVcri4twn1bjXYauqp1Ju6SH7inlQfgcKueUftLASQOfpgZ2XifuleBePwh88PXQUNa127xT2AVIa4TN07FOrb4d21be7IUK7PTT3bDdYWUv3p04/Xx8d68hdqGNYlUqaNP36adN2afF4ZR9HPri25zbMX152+MBjlIevPSTe48k9emtT547xpu0oJIPfd2jXNdGTuC+VhhSneFt3VdWw6HzHdD7Rhoi3DCaBgdKAHttOacfACk4UZBXW+6A6LXvZL5OEkF2NuznX5Ev0mwZhHM26snZ91J7/oTpcoY7fxAsmDOABJTOCDkrWkOGonWwFQsEgM/yWBmFLHJl8/uZxrpLBuSFbuXzb1jWpAejVvIJzYfved3S6jZSD2kjuoXN576M3hvypjcK5jo0LqRr2N3XiKRxNSbgKJtfD5evVoBRkVazk3GRmrYSSZU/kVThtWkPIhVtP0TWovpwfKVb2Q9C4pBJTM4A0NSBYL8ukLkMCE74SjP2QXXrIsLyKZrJ8rf4WrFCGi+gm+sbPm12hRxpGa5sWTYMFogIf2YUxA2XK8pjkfbkSrqlOZHLgX+Vxp1nAVQybkQViS6x8i6XaSvrJrWhdWxcApH+7Ya6FWqehVaKIiSvvuxzMM+K+m5fsvO63sP3fvMMf+fs18n+1L5KDy+9j8Ox8cfKeewv17H8nfx9pQzn9tiabPN3T4GT3JfTPRZ9D5rPp11r8eTV0PML7peyv939UvZTHpuKzPVzr518uLOdfJC7jtY7hnB124nJuwttVFbyG9dw66Y9xZ40cNLASQMfVgPNG2pgsRppdtdxrzNlc1mNA0EwKiPlea6957XOFHjJgHL0o5/8tMyyv/iX/kJZTAGc5+cX+KJzCkBepozYJ+OYcWaNU+PNn0fzsxmrhIGdSTLWkleALYz5yVktcATCvYVbUgXvA1YHc6YY0wSSxP1O2bC5pNIt0ijawH2FB4lwYssGgAAkzr27bAKASI3Qy5jRj1yd5Ii5k7GheP1Z2GgrMrM26jBFi0AXatCXPH/gSlhrbCWRxDELxaiIJ8oK0D0lQMicBjGWxyqEovCwcgsDUBubfbLGwi5KA+a7CQ20CivG9eNxgrazJQctR7Z2AnspzMpUlgOisFAAbefxze3ierlcrm++/uWvf/cHv/3s+Qs2VlXxmnaQSK7e+jKpTD6TsAqJ0sg336Y8i28SKmLvy4i8+6rWKuVhLwR5cJ5tCT9AEe1CTzEnDdxBA/fqq+65vkOpj5+lFq164utbCvaCW+FjZHI80F2wtQvQNgu/IC9laz9RLx7yezWGx2onyA8KlxsXHGJvVdbba2PTY+HtFPHgt0Pk9AsdTv8YlL4kQ8JtGdoxQ/j4NPe3xX1ug8IGm7Lnoj1a/la/OjBm4CCan6sd0ye0T+lzGELv0RxdRy+vH+zj455TAa1Dl+PQR9g7kuHeL61stp9xubWLiwlQ7ez+ukOaigdf/jvLYg3yur0pcVcHpE5nc7b0+Rf/7F/8+Cc//md/+M+DUZKVqydnz3SGis73BU2yXT1rhFmFCk4v2bX+yZOn7PRDuaxX1YpeufcDfMPz24RtQPH5CUM2wjF9FWxrL5eWnPMFtOOQ3GNMJj4rwAzgdojVYW2hWHdJ1AWZYV3FKAnaoMwuBLS14421B+mWy9WQG1jZxkTkFKx3PM140Oi+uEXvoDB6pXuKuhV5eUVOvmrGysFV8anFsdJtHMvVgEJFIa6snJac8t0p2M1TZUkLnPGV6fCD0Y22Sc3lSqRB/ZhNg8bsDoSaOEqBfYBgmucJkwRB+OxXv1r87/7T/2S9WIP/sajYLOj2evHf//f+O//hv/8/4Mw11MlH7V9UVyh7JjHQj6wXRdb/Cbqrrhkz3ohd/epB5eJZ10w8WnqpGFXKtCUurvIK6XI5FLD4RqOWqI++p8kRtOn7+DQMm8CBN1JDtxPoe8P0xe9k77pt13G/bG16n2uV6r8V/eR7h/fLNpz9/loM59NH+bD8H5Zbn8x3i/efgkbO+gm7G8vNu60zf1NKZ+rdIl2/cnn3829XrQ91D5ekeRFVWar3m/mtEuXeWsPZ+ZSOVfPpJ33M8G6NP6Ysp7JPGjhpYEcD1StoJ/bhbtuv0V3e9taryRwo5lWoFbV6IzLMLIyLN3k6yhfLm8Vi8cMf/sjGntfyP7Gx6ShmcXAm/zXBWVA7eBwPHzYMHWt1LPYBjija6RKenB2AuRDf3i7LxRpIaE4sclUHATMi7gQRnDS8XwsLsiQvv4FaH+uu+rtGncLYAqD2Q6nEMudQLXbhAcTrcvZDRcQ9sVppnFoaPwHkVVCxhHLJNore695ICSjeaGqGolYy9xWEdhEG9xWEHklI1qdgtl3yydHuQNGcvVEnY1JB/ZJFywxGzAJIl2y6itvUmFF7KQNGyTg5v7iYX5wtl4uc44JL1k4wUVByG0VTGubtj3/KLA2qtzOVVbR2VuU4tiJDyQQQwvSLGJSjmRNjXMsn2VxdnZyVtPrivzTaXO5G/CyNeItp8rn03VxN9rsGdvjflc0p30kD3ykNNE/hd6NW7u0xoC6DCT1eW3kqxdUGgEc2LOheSFssh2U8nsp+1g6MlPhcN9bVBxHPL/rO4YcadfAF2OL5aOMlrsStsnwh+sID5DmaZ19ZffE2puV6y/3L2vS6zuLa42ftmM6MRHqUg+T06PtYPka8e06Hc3ZjmdvwSrl1NjkAdODZ5Axhv+4uM27Hb721ANoGTN0nSE99UljVUC0yAPKn8bQo13hKAlPB+mGAhznnfU0F/vBTYXiZzfA5fVb74eTClTisADlx/6lSwbckZmLKtAJpLARgWgEXI2Cuuf/LdYhxalYP6Igx8a3QY/5MMBUgzoICM0WUAsrPn2GaFALo1MCE1yED3DF0bm1AWdG1IlyNxFSreIkWnq7ZB9kLFWR79js+el3SKKw6oGAEcf9h4rgaQpYVIh5UnOF5C+tTZahA+xIbwW0zJ8RK9xJCLOmcCCOPIBOfJRCuxsqv0xUSPH7A90wFMJ+SyLupKHABunh6uVouWW7Bkl+mUGRrFcF0OgnmbBg6StnzhyhsAh2QwGrr5TiajoJZFF3BnXkDmKMUzSegbmrE2RHUQmJJbPs033erAqLZRRLM/F5kMS6xireYKtqFVbMtNhahKC+343Hcp3teTJ2DMh54Iw3isUs06P2zm6njfpBsPb8R95fhWE12VOATiPJr4Yf7RPP15of76IfEDyl3CB+fpi3b/lJ4vu75ZPmlu3BfiW3Z2nn7Ygb1eS+zzTEG9jtI/aq3iJc+NLhnJpzfjIFc9mnYiXZ3AQeKcCI7aeCkge+cBtybxb3Ej3iHbL0Sj8jn6c9KNkDsmBk0tnSlMJyMtz5j8+B2NqG/uV5ofJ+xaR1rqy18AKM1sBZyBfQLaLIANdFmn9q0BnStDS3lBQTMZSTaSgDUCwsLImsRsOFQIwa/AnmYNeBl75YBi1LrifVzJBk1eC2YK/EkjcmpdHkBwZGQA+Pcmk7IqIKUzXkc2S1pZgUoATQuLuzGowz8ty+o4S8iFWhAWaTkc2cHUAoI3YpHXIRRQcqrjYYswKciJSpBsRL651tfqBQVSZPajUgpgvu2EloVkKlkMyasoYYqTIwVkyrnbMyarlM5VSEfMwCcxbBcszoZFkRqO6YgX6eIVr5//zpdX0Mk5x82cSo4JU1zCywjhjWSoDObdpBuq8sJDi8Jpa+ey0R2glfiG6FU3pWpK66H8yn6pIGTBgZoQA9ofX0Hni+/OnW1/O9D6T7twbDPjDUAsg8aH0c/s9NrRc3Xtp59LpZL43aHPBp99seG3Yva/a7tzzuccj8fP7XD8usZn/BzDQ8fax0O4bzF036JD+S6R422yjpQjCUPkMfx7ND8EP5H0hwtv8ffSegiBvH5kHr25Hzs4LEt5T/L/stFftUHr9b752AOXmCUonzuy0FSi3XM+HQ4VeheniOMJxMVJzHAms1lNIIc4AEPfjwzRlrCW0ZLwOh4+hlD12WeTedTKNkAlMFmoKeD43BTuQLolK6ThG2uQNvWMGEgCwAUzc6cUPAlfC9kztizxt4N6BNPpH2AiN86McmNMFBil/DpIVlmUS6VEl6ZVlRT8tuHyIXSMWU0hyBDQfGC3YLykrO4II4zebVRfwC8ViUZM7dE1iyfiUV0rQkAWxGsnGIPz4qB2IortTbLBAZWIdXLVg47bUgfqnEF+YXHKRbDivO/gkkRcrgZddLuqMyW5EG+Wsm3KgjjUbHOtFiAMxbis3Odpnz9vlyVK/li5QjBOQDYExHbBy3XC7ZtxdjgFAY1IjZbOVlptUauhdPhWNsRYcmgaClB0jrdm97cB1XjorLN5WL8T0uSsI6GL6OXpppcPYHhT42amrOOH/l3dj//Qe+3ATXdX0rFoOc34v6/C06TPWIe4WvQx2F//EPhE78WfrivdL/t/HAf/ZD4IeX28enrA23Z2qX4s8Tu0RyOP/0XZZuzk7Yvvi1bX+3a8XvavX5hbGXy5sA707eI99xszWFC1zCT4twMgEL8P/iy2lPKAzDYy/2UeNLASQPfcQ24V1PzgjpQ22NfVw6N69Vu49BWjMWBBQWKcw7VtRD4WQdL4apTJKDLME6Xi0yO8TqXVu9KQjauT4gxfrAxuRmQZqx5NpuMp4nBcgFkQVxwpqCtoXvwp2L1yZi3IrlLIga2jZB4LkPSCKTxcQeCRY+1IVYgZO6YXBBIN4NCnB30FJUN9KsAMdR5AtpglKDC9gsEBbm1DY8E4Z0vmG+RkhZGiEbOSkrEVHkarxc+pkwK059cbSAVtcTgm7x8ECunHaiJlElhMopKY/rU2BgD7l12lUkOB7/F2siFx3HmgRmVJo9yoWpt9xNwtILG7pEKzykWaKyxCmT/yP2nyCZjllnEq0W+vL0B2lMY9hsM8LdKovGK2YNC7lJmrZXpeh0nCbfGX/JKuN1LVSKu+lKqC7Y+nQ4qAn3pgorLVcCCp4+TBk4aeAgN/IY+VJ0vqWP06V5J5JACj98FqK+oxl5xL8aGzH519APRebVTXfYdJuTt49BmO5yyndeP8S3UDsuPX5fjL5/ngdwaTrNxtQN0D5d8pxodUfydatSh+SOK/BCkR0vo6/lOOtlfK7+P+WE/V1+8T9MX7st7tB76CuiLd2/89qtBb7Ke90tHioFQipAPCQgV3x1AJIgSdGnws9C6Xm3hz+aSY8aZtTWNIDTQf82ZvoBOfHnIDxY3JD4BirJ9PYAeUAqqd9I7KWFqQJhI4XT+8QGKLbNnAPxR/FbURIOZM802YCkAQ0kRlIbUPOZFAu7WPSdb6VIVNIyvtyfHfTkyUYiM44cZu39rr3dehSB1Q+zcQ21qUgwhOPAHD3Eiyf5TdHAlT3mSUUc5Jh4/fRUhqQi+Z8UDNYVO/MSI88tgaAaKsqACbkkEwiunBJZS+HD/iEBmwlIhi6kJ1fXiBjuKxRcQyBWIVmLKg88oeMbOn0F4qy1VWV9t+7TSOFoVvF4jhbRaPmUlxWj0jn2DptNxrKmYMyrCDkvpmmPCcmwBbAAamiXGq3TFnI7kUhWkDYSWULr4Mk0RqD1oLaWOrGgcpW50ucSKRXXjUizVsTbFbGKPnzM/9ilr/8L6pbfDx/L3OfS9GRyNz9kP+xyGh+/PYXhZfZRt3e7XgOOjfvZtuFxdnKSPoe378GzPEg/n9tj67+sDfeW6XlS/Pg72jFL7kvHeeLVL2RFPT6veaB5x83JTP2QGoJPIoz822C7xKA6+ePdkdVS5J+KTBk4a+EQ00LwEmsBGsI6XQv8v6iZl+zXHy5iNOIG0AugMA8tZPI5w4ge/MpRMGJSaxGM26Wf0WNE4kHMMLePQuKBoSa2sOEaX+YQN4NOsAnhqXF8XoFKD2wKWupO3u4bvDckToW+mDRjWtuH8yuGeeQQJpb32tQZWoBRJ+YUw6Q2iKp9wtwwA0kHwDXy33xD53QvQ2o1DtipOiiSX2IG7xcLYm2juwwFgkvWjQZFISAZhc6O3Gpk5Y377cKN0FjeDoSOYmUxWguops8JkkByyJjS47/iJMYupIWIpMKmaHKmnCkwuszs0WyEZpT0zaxCd5dTYU0ThtKMJF/4za0OC20s0zcIyzWQ1cHzz0uZzWMC9JJUWTHD20dQBVhZHC4s1nkOoIF2lyZgqUCjCuJaThBJ+c6kWzZ2UWFESR7zL5aU3wSawyd1EnQInDZw0cNLAUA24F6r7HJpn99Xk8jUvIzFzLkCDGR4kdMz9V6J+cfovP7UidJn35urn153i22R+uJu6jh1uU9Y5ur/9Eo/g6Y8Ttxj7PFuJDxfhjU8/QIl7a3Ss0MPl2aL0anRsiebibKOtR+fsz9DSyZa0/fn2pPh9zA/7WfrifRob59Xw8M41KK+f5z46N3xVvQwEMw2JuS//3eEXV4ersds37r56JxmiFIbTGDM3wXqdcswUdQVUUgAD8bjhT6YxB9MuF1fsSgPE1Qm+I2YJ8jiesCxY2FcreotIO9GzWRDLfPmA3wQ7AkyrM8LMA0hYEq7mcBOyew/O6cHXMjGCb7QMFhyKs1HEwDaoVDMAQFoDxEB/kDFmgDI7IGwvcze/YHoQlgVUSxVC99KLgDf0hIhweN5yEUG8ak4O0RIrIteyijUyvpVoBIL+eO3oo04kQa45Kk/xyl4ioTEXOTyNHoSdnckmit8LKhuBvlRrVEeuSYEnFXMlSST25JJxQP4UXakKgvUEVBn7Y0kGxtZtMlrLB4stlRBCLTJKEiyvJBhlN8x5sFo6vw0TJhCmsI/G4XzGZk2XKHgUrCiFgxaoUV6s2EcoTdlNFN+hEF8gIX/kKJ5L1/EbakKpKkIXky6vLaAaNNEEAp0kgFQu1Ujch/NFbo9QOqbi/qGu/W+SqiM8qEBHvxkeQRV3qZf13oOytDm330D30YDP3w8fFOyRCO5Wl/297kFEfdA++yASbTE5Vm9NLxpYr/bYvyu+I76zY+tVZjn02awBqN94W1U5/qZhfnzW6qXboYXOatyhgFOWkwbup4HfqJ7Y8STeT3tDcjfvIf9N0kTyjqjiFeWTdPD2G2uLlF9XQ8rAbgC3+f1rJWhQzuYz2QPjMSlrAG1ZspyXXWg06g+CzIDYMMU/JZ9MWRQMLM1Z8huPdbgvg/v4oHNIcAmslasMqTIwnGAky6Pf8DwlMoMgj3aH+wG7gpaMU8sDiFLJpakC1c+h6qomFTchY2LkH0MmwKvhcrIRVpTQvfjUyF0guhLDfSlFgsFI0hldlSIOonZxEMLTiBwhWBkTQrQyM0RlMN1yKV62jnFXLtkukEoqrXumfjoODQ8eIDtoXfskSe2Uh1GAQSEfHriycRI0Tj6yWzXk3q8hf0SD53Q6LScJd/Bj89Usm69WTNUwc4NHq04Tm0xnf/qnv/g//Gd/izMZaLjLJ9PL86fT8Rg4P59PLs7PyYtIY+3dxL6inOogxde1UDVUTzNfXLSqaiLVunAatsStD9JVha245qbO3EScAh9EA07vPY0iCfYkfRABT4XcUwPfmQakIv1vieNr2c6xy90ZAG26uzaI7D/m1F/teQ0eYu2JSFCi7RGvojjA07fJ/PCBbPrp0lgX133s2iNKVFGDrrvx1BAd6rQadRTj1bdK9SjvVmJHKQ8UdUd5vBoNF0R64ydfbtAPfLVb5I71emC5xK63nxxZ1h3PWt773A8RIX7TUAEoBUgNw8llhYYE5gFZGQPm8N0yn4wnLPP94b/84Xo9ev7Zs/l8mq7ZuzM/P4/DGEcRWh+ADRPshBFb/Vw+fRLhCqRegU8/o/lAURJfsHIgjm4oiVs+BVnlNaTVBdHkPa4roEpcUOhJmjnArCgTtrKEZ1FwGi6gFt8V1hCvRgUH5bLkgHDqwgycB8SPJiWf5TQM9Uk4GM2DkGO/puWI/YiIwXKZiIPom/CUvJgzFj8bRcuwnBZG7yhH4ib6UeFopkHIqDncOGlY/INyXgYsq52TVzTQF1P7ZL+j27IAW0vacrQqC1xr3nESF5LnbLlJLTBwOPkYTyr27UEXcaSVu1zanVNHqmHt8AcWR4/jCWsqrKHMEEK9qFJmBjzMeZ9dgGgv1iVgJWA2YFgFUYKCseOYoqGZ1izGSIKf/+LXP/6jP2Y2AvVjasUB/lxS+3Qa/M2/8Tf/yl/5d+GMrbDmVGbaDhNl9Br+FI1thjCyDGluNa+kgcAuGsriuNnaWwMCNbQuxddhF7Pz6RIbljupR93u/1Xa/yZxxt9RxX0riDvq9SC6phfsbVannP0t4miqX5MWN5+/O2e6rwWHlPKxGqtP5rY8mPZcfq3bNAdi0GFX4+7XT5/+D5R17+T9Ut2bfRcD00+9iskIUNdWx3voGQAV4tq1S54hcb6ELmz8LGvd3vr2w0P4nmjQQK20kzI+FQ2cWmR4S2xeBC6P0x2fXZdP7IaW3XA15MoB6hRCB8/JlQUMOf7Fz3/xt/7W/2m1zqJ4EiU4lDM8PEriOeCSRb63twugKpQsAsYtaDofGwK1YXcDs/AKciIN+bsY+bhTqArSItcsozBWrC4WS2HVjIiVFq0yuF1EV1dv0gX7WmIcjAHWZZaUIUfejoPRGpNAQF/QfFkCuyOB7yDchMPIwiEQnOWx+jQTYlKB+HAdOOhfTMpwjZEgg0HwfUMv6E9ZMgCmZShDAv4Wpqx5EN3wObJ4PktnJIgDNEjrSgToC/SzqxGmC2d4cZgXy5z55JCE6XyCKw5e+CBoFCJDTOso3IlpGE0YYtr+czKZPn0aJSzJYOIAJyubQUCHojcfInkQaRqACz0zq6CpEjMbktUytlTwPjYSG7OSCzVDR16amLkDNcH7d1qtjcmQL/Gh0latXFqNgIEozrLWmEOge+CHRPk13pcU6i32qZDYN5dFK4KACzdJPYHt/D1Ep+gH0YCvaxf228hrxgcp7cTkCA24R2ZwBr/dqkx+4w7mUz2qw+k/COWH6Im7GtwzA+DE2c1wQBP4Pu5U4yg7z7Vm0yt2G9cTSXI52dwntzsFH5B0QLI3Wjzcrh3A96ORyGpq1NWWwqvvVqKbGXBRfTRbGT7EzfB+df+288fCH9aO72iR9jzMkep8WAmPLLyD/P7672CqqP4H3r1BqnSBRWit45tjPZtH5uE4HLPGF1fwNS74QPzyl1//YrFY4EHOQDUIUOgxyhblgpWj+LPH0VyO/4LaLB+d4M3PtCAIFexoxeBezo42L+X6E0R5wU5BDD7LuUWj/yBLjWcDccH9+J2zZZAE0R6dfLIIIM2us3GJk/oIFAuMxoxgHB0ZKIV/QFcmC/CfYYogHGUcjyVfGgHgFGJ87iFg1TJ4Fad88rpPbvG0AW1P4BCwPgERNDkA+J7aDv6saVY8ouFOTy621wEul6HG4C0eHWNL5OxWxKD+KPuStwcVV61GYHSKH6taSCionpjkYsVoPuXCVTv6xHmMpoMx7voZZyoXQcbmm9NpNF6iljBEq5oC0D9NnnCIGqyE7gXHaTJzikIOgXuK0Y6rRPOMAM3lVkTDcY/PDwsHVivmT1iYMVqvaCaW+aITGggBnpktdkPeUYkFwMSEDAcmBihutVphA8AJ045I7BKagQiJL8CvT0TSZ/FcJkA1s7TzIhVr65I78eqo3ZcjJN+dr74n6+O+AarSX1u17vF7cWwteul9FfvN5MffuQ22M/a1iE/l/5r48X54Px8/tbfWPjsLD6d0Wd0v7P65CL+QY/m3f/uO4NA8ZV2N6OvHl9CFK/33/M4OxxVtzvtj+qQ6otZWQMduP3sL7purtEzOAJA2ed/VbLhtwnXc8O/75G6KbQJb5TatvhWrFy9Xd5ZtytPdSQOfuAbu8/h84lW7l3j1493zDqh512Te6wDMRiYg5mq9xhEE/A7IBd+nqzVoVtAz4cTf8ubmhlHqMcPPDFFr/FdeKYz9Awe1pFULUTXinCRBMgFV49MC7HaD0MKstVxEOt93culPpWubGvagZO9KcKk2stE/+Q4B6NlnnwS1uvmeANldPrLKI0U421CwXnBQCBALAsu0MDwrGiFiRMNxhTQlChe75QFamwyBxAPTQimIL3sIkeFj8hm5YW0S4CQG2sTTuBhv1V2s9R+obAsARKfqW6RKNYyswoSgRckQO6xA2wVD72iYPXzkBIXfP7aIBNBwu3C+kwvhJSi5xZZixFNU4qLReVVShSiHoqUX3WnZQDDGi2vCDAxrLYLFzfWrxTsMuYC1wMw15Cw+xqGHeQlz+0lX4P7lcsmqgJBWoWVdU8oowELLJ7PxermyFicbNoeVoiamLC73qS8Jcbo+dQ24hqpazYRtwqc27G88HjE9XJ/g5Ut1asH9DbSjH191yogB0H6JuZhd0v3l9Kbq52Tw5aR1nzuZZCcxvLXnlNA6W59F5eId2z5rbKfQ+97q11e/1Vxtb2/F3m91gePw6J/7R3G8Ot5Hkr5WczzbqUf1qx3BfG5+eIes83Z4zzmWsytuyPhQp2BN5HAJmyxHBfx6+eGjmAwlbr2diOh6o9TRLk256hh+xYCWwugMCWugF79zje9G4NMkHK/XOI2vZuGZloXm+KYDLot0OQ44P0rAHD8W8C4H4gIEWQWMjw3Dw2OG8eVfDmMhWY1au4IdHlWEiUl55l7iNrYXjsxLHSXGsLSGuuUZlCEbkwygXitrxuj5KHor9aTPBZP1iuabUXZy61NJjMoTVh0NI2u6QMgZntBY0bbFUPxamHX9haS0bEbPQbmvdJd+adxEqekFoXptgYT3jnnJUl8D15SYf4+iEEL0moigtkLro/gb6g5/JSGhbAeTk3ppf9Ipe/NgR2Sr0U3O2Dz+VLYFZxSkWR7mc42yq4I5+kQPDmwQJW2qDBUmW8LuoBM1LYZGJb0maCQ4ED3EwX+iOQdMC4SImKNJbIUGqtSWn6MyxdtfhpYa/ioo6AfRZJJANZnOo4wOkOXrZywICCbs+6QJGUwKWCMKfYL8Vjb1fUuktK5LUjhJ6hjJN6rG516LpEm3m+4P9wS1Z859atOvFD7w6nsD+HxcuJHQ1amTv5+rk2Ansq/0HbKDtz6fIe+ZXnpXt6aGvhqJ5JZ9pEAXdOE96AJC4+BaYQj9wQruEPj8d5L23O6X2c/YpjxQCx69Qzrp4/+4dXGtRtnWIr4MR4R7UM3wp+yIsvaS7rRLU7m+TB27/ThSpw2/e7dZbHGHVL8uRuWr0h6Jdt79MVuc95Nup7rSnBQuxZdlQ2sULsknbgjoc90ZG4qPGviUZfuoijkVftLAERrYfvabuybQ/CpYDE+doTe2bZS7fcgGMtc37xjmB2/PZzOWhzLijrc9G/rf3izDED8ZUGMRT1jVymg1i24ZgMepnZ8FhqURk6Wo2hNIm9FrV8lqkAwgL5oKrepNpNLxAQptOyDtMUpW0rEAdPYWrEDLZpaQIDgdBYkNUbuRb7A+7MXSWMFdMRgtfMFY+eUiY3XTpy7FOUK7VVhiGRXfKoTxdTPXubXLKmQ3lCMaCWnsRAAHlV7R2u8lYdkhpEEvO8ZWUHDj8imZoHsPg6o0Rs/g/5qVE2gvXAPyGaLXbAxJ0rBcpYDlaBNNMVQPV62HRkHyjEIUV31pXpMGGsZX8XVVZSzIpuNPcSpN0y+6YfpGu/4zZSJbjHumGmTdYcil2WqZrd9dXd/eXM3O5uvlmsmDF0+f2eEPI7Z5JYtMKVVKrVP9SWPENZ8W3P5Q/U0BNeV28p47cn3cy9Xso4vxKEpQs1iLVG1jhTQx3806P4oiPyJT14a7AtS9tjt1l/rbfn/XWvr5nMY2mgj+1/+r/43u4lcHn4OKwPmENef+blhthw6ya8g3Ilme/T5n9c9Rk3sroLfvx7sO2NP3F6xnrF2/vwzevdDnjjWpqE/mauunHfPJCPtggrjWuf+4wgPoqqf/8OuoV4Q9hw9QymDNtefEdkunY0uyDcf6XeHHlrbLQbDxdBS9CPNnCkRv+AQA4tiPwwn+92Dv2XT2ox/9mx/98F+zPvX65vbq+j0D/d+8/dn19XUSPzX6kOUB6GQyw09ELuIMKgMv5b8fh9PZbDzFOR6wKY8RA5wCjbj+U662lrQtOnH74YgxbTWzwruf6YInmAxZ8ZpVBNrzp2TYeyUvlWBcZKOX3/xivWDjHVCvk54qgINpMofILZY0lKaWoo7Cw/JEkrsOr0UiZY5Uf0qGBiOhSjVgKs3oEmtHoNJ0Vd9iIkxfXTW9u4UF6a50vYctlQ/1cG5djGNtYTMEwuRryVk+GQUcrWxGS5iNp5P5+QzxqDywG1moKWyms8nlkxnNxOoCoqxY0L3SQfMEML6IlAGlSP6w33Rywrt371jMwUariMeUwtX11atfvpMBpEOLRaoD34oYm259G188OXv6RbxarG6Wt5gw2fr6937n9/5n//P/hciZoVFNtERDJpaqYFV1qrUamVRQ7btMU9sEmhlgImfvGLOr8Xa+R7zrq0SnGLvP5p3lUgvS9HfOf8eM6qWu9/Jl/bNi5IerqNPXJ6cB9VW/X5plLimtE1fvig8ltd+X/PBDlW91qhBdC2m7xAcoKnsBq2YGgHCjXz98TEEwODYr9Edc9gLel+XY4o8o+0R60sB3VAPuwd/3XH2kijuR3ENtyFLvqEpOT1xF1rf6KajDSG040aSPcTSZzDgEijUA42Ty4x//+O/9vf9vMmarnHFeLFmgy6IA7AN+WACU2rKeMf6SY2LDZy9eYAOAOAGBkAmpgmEYawbOizOlCe9pya9oiAu0r492rQFylqvl8vXrN1maluslfvAYANrbB0OARJbFCr6Owf3ZWmjVEC3H62JNiLcbbLcXM0UI+gvg655cjKk7nahciPlvQ/aiUN6q7twpi0hFwcC2vUUVdpmM2hArH8ZRGN8lO65G4SIsRfcC1RJJZdaZlKhiSeOfCERIjLQja4TaawokHbNHkOoiicy1SBkxrbTSQkultYaYIDxMA5op0Q2+UiYiqrXaUCPhAHhyMRfAImJKQpnM8yTj23WK4xYC2dwJZk2ZyXybxO+u3r++foMDEKWjyDxL3759s1wuiMETaDzmNDfyMHugmlQVUlW4cbCjUQKR7Wt/apu+jpE0H/C6q5gfUMTHLgoVoPRH0vuOfh+plMdW0afM39Nw9S75lKV9GNm8Oj8MQ05OeW2c/A7qh1vFOIvEnXe4M57hHqhWjn0RrqiqWvYFz95a2uufLL0E+4r6CGkPNmriZNevaMflfmh32qKD7q5Rfi38sM+vL96naUvYjvHpv43hth5c69y/Lkfoqm+Mraf/AGuaJ/6IUu5dpc1Ic82qo3QhOLsEKcFlNan33RojIU0Vit4Izyos1OvAZpLEy/X1uojWHAQLYkzYPp+B5XPRhNfQ4CmOC/gofE+2KJppb5yAbSOB7Awvw5PFwYgh9jIJwKsGTZUEHW4qNuwMuOUibBtfYk0kBMJksVpdr26A9sL9koyGUpuwi7+QNA70Dr9Cgee5oU8Hr/X7piJwAVKG3Aa+p1BxSLGqxneFp1WsALcYmttRkGFvWDEogekC5MTf6JWEy75w8dWnhMa4sWoinLz5ZdSY0sknj39xTsklaKwUtSDfTDNAiaOUOhIH+uJCVWLbSHXsqMkKBAbUWU5dogOVAc5eB7fvOWGASNbjTkuW5wZjFgKwzdF6lWKgUSV0y1SAGBIiP8u3pxOxF9YXNAemy0qyGjOTw1Jfq7m0wr6jT148YQ6HBcFad6zN/oN8fZ7naZH/esJhYcXMGoBJiYTT2xY3Zn1payd2Q1KHkNFgyqJA6mnVJOAuRdWX1LB9iZhYj8hoej1369w7nLz8NcVH/e54NgfI034fWo8fkPMOJNak6pNdl3XYOsEp91FVDPOdFq0L/4S++34pPoiIR42dq63sbV6J5tTrWnD7abu77PQfHv4BrebT+OG7F92Vs+93ra9jHbs7kL2RbAbAXnWeCEMU2qUm1xweo0FBV5pf5h4+LonPrvIHFXciOmngpIFviwaqx7x+Oxx+8EXpXhIVCuOVju8OcJjhd1a3xtEsOgPhsSMQO/oI8OPtrRH7Ih4T0I8SUwQaS9YFcARLk9sSNPSvAWv9EIF1dYAU5AAODULbXpaAZkjxccca0Ig9ak7GyfMXz/lpicrpn/zxn9xeLfEnsvFvDeNDAleJAVNtl6PNhUjFmGD9KSPiMEcMbe5JJcwQcKsUqBYZ2BNUuw7xOtS9vRX5UgTUMmpAyxTAvV0WsJ9RaUSC+/HGSFEEVJZoXFgqtWoT4woyGKdI/TM7AXpJaH8yBBypPo0X554RzFiiq0UBaclZYGZj4PXEfjuYO3FWrEcRKP/L83NQuOZPyKBTupg4MASPEBgFDP+jIVXM1AeypwC2ACIHwpDLdhSNcNNCBtrc5KZR8qj4bLG6/vmffmNH/3LYM7aBmphSkglzP7gXaYZBSxCkWVszoTZxDFSiU5b32Y6RxhyBfZmyZHt2UnqcPnxQzfHhSz2VeNLAA2qg6cE8svY2ekDenySrpsIPJR0esXqB6jW+ubZuiN69J6rLOtkwOCrk3kRNGe7nyn58utg4ui49NBza2XyefrhNeZ+Y9hhJO8bn7yT59H33/Vr4Yb8uffE+jRsNcjFD6P289wr3jXP0xd+jsHa9Hq+/9YoJpum6Okbjush24g7mcs+ie4pd3j1P4g7znVufVcWwiRqKV6pXg6FOXm4GXYHYQTKdcQP2ZMx+uVgvFwvGgx0EBFayM2WRzoX+gPvaEf4MVx/AZcQ+kREDz7HzQRc6hzN/sJaPCi9PQUM429JVhNSu9lzyIREJHumYEDmj2vkSB5ilDIQS7MsSVayLV4y5h/mXNROoU7B/XsbYJbMomOI3r7czS2bZpQcZOZMsQyzyZ7jShGlcjMOAY30BqsRN3PHA1C8oZjrPi1O9oM3jkpPFyhnni1n8Ksg/H3EWGKVxvhjx0WKUz0udDsZpX7fUXWHt6nMzys9LPguLyT5TmLpz1HFxNgqvR9LSLZ8Kc2BwwIHBHMK1NPNGp4mNwizNo2yUFpwnIJVxzgBVuUUxo/w59+zgz0QL1hl43nZMCrUxz/Sc5de0mdSP0z+6JZM2H8JCQ5u22Q/dQ91M/zV6LwKOX2DwXysK+HTNEZbyp1IGpgvG72ImHJgrWCVlzqoM/IGoIxsTsT5klKPOSZynHHxmFqNWK9Cq6j7yO5I1ohu1tRXqVpjU8+d+P5ZI6geOTGzUX7wLgq17L8kLKqN3+yDB5l20p/y+QuXuhUg975Y+8drvw4Pvkx1WR9DL7nywq9HVvTi6th4mlivRFdeLf+4lTStzqzWP0HaL2bERx9bR6ac61/ZV/Xj0d+Wj6/Kg/edYbdyf/uAcox6PXXUx6cyP2U4HHfbu2cl0nwo4wY5g6Ei3KzNM6vuIecp70sBJA1saaB7BJkDy3Z5En4NjUr2w6veCe0tsFb9zI4BWRznwxvg3m/sDtYHiGoclHVDJnQZ5Q7byZJy9AOIRZUPOwHKmB/RPhZNgw/8GAsUYIGjDJUqVWNxYieBCitBIvWFEqPgHwCYik2uKUH/JBESudahijhT2LiYL0JOfQnJo4F98BRhhg1tNErJXjg4SAwVjEkSActkaCd5LqWySchZMgM+RDvqlNJyCyDizER0OwoXXjOqMRjOUUuqTG/xtKA7XJuKmwnPwQAOAdWA0h/5KqrmJwwi6UpFbhoHqqnABTz7KuXnJi08ZTHU+MoeLqWAkQQiOHuNzmgUZh2wtsUWoDc5KqoZWOQudIx51YtGtuAmIMNBPM8AWR3zD9GgfS0i7mpJskyEaS4cv+pFZIDtDeiZALAEu+BDEGJAHFPWSLaatj/DsIlu2Zo+fFBkwfth/lYKxr2SscaO8YhUmupeW1PawVYtzT5+BworStwrqv+pkJw90LkJy2j9iDjPpZ9+V8tD8esroij7FdWug7gXdqafYkwY+sAbsdbQpU/1TMwCtd1HztoJgJ88m926oz97Sq54X4CE+zcOyn1Kl4I36qmLoc9W7uefyefrhHvIPFO0kaY+RHFu8r3k/7PjcbeTmWBmG0N+/pq4UV0cXHsSzNc5RSdsXv7cyBl2OGAm7T3/zy/LDewXsTRykq1buzlz+c7fJ4R7A7rQNVRPy+6qfaRMm1PFQb9IbVhYASwPhWL1LLvz4NXgfxyBs4OBytcQbHbcQxn/Bk6wpZUkoGBH2BiMBi8J6kzmrgoGweOVAR/fgzC/cdSCv4KYN6fMGckhTyFPAG3IRMJhvgymSmkJJIAlHeNwsJRiLjO1ggTUHEqg85Fh/LqBJSGKAhsmuRcaaG2AXTOFyQHnKYcFsnY97flSymT0ImXuKFItJsALps8GmFBAsDBbfKjxiMB6eSzgXCsPo1t7z+gwCfZZVzDU5g+BG6De8QZgyIIYpimsJxtC+qqeB/wIai5HorJGgmlX8NUEmB/QZLISWA/z7KXFJ3dCMVjwQkp8UaqJGX2AqWaGYOG+pTlB8Jj2y6kD/qCL/QOSG77GOpEjaCztFCtXqYCmb/1YtUzI2neC+JObiS4UR4tg39MDgPhuOkicaJ2HMGl95IhUhptk5lkZZLnD+Z+2vFCPLUCrWwW1s+6TJIFqOnNruiRQtS9CFHfnGAn0fTpRKICPyY5DNT+phohrsJdQ7AQJHp+DW5T9fLqGPcitbz82xY/89bA7sg9TO1fn+aZM9eMxwXR34PWo1dF+rDS+xr7LtFu+j7Isfou37l9JXuovv449+6Om9vietZ6qjLoPn/Ptk2C/h/nr1pbbLosvomXY9p+fp7uO2L77iW5OIMz9OdUF1tBXe6rWbVKN/QKl8zoPCTjavMnuFHcTyO0zk6ek7XMsPW7UP2fs/ZFkfVot+ae4R3tS165HepPo5CRvWA77ZH0fOgufw6dY7lEFkMKhwHf819g/wZCMYjIGc87gENAF9GnXWKHNYzM/mF5dPQJsgf5AzKBNACJSnDBjoxSfoL+gp/GlR4FSZAYrUegK+Aa6VxaDVA2BNVsIKRGrznxLXc2FhuEJLXhgbV8pHNECumIH7wbM2R8A2nxSo2QorGZQMhUqShYCvC5IigNOAzAVJAqVEk1bMUjFTxlBHrWW+JZHcXOxtzocl2eC6UUp3lioKMSWHUan+SGHJBJWmFMUaKUEMBkQB6EdayyxPI/7Jgwd5xaouAFagdgB4gP6RWpWnBozMA9bFV0p2mpeyaQg0CZgXrald37Ss8ZCwRm51pkggu+YA3DoKJVKATgTGFsu15ABiHfIFC9ZGV0okgs7DhUHBzBHyaFKHK8HkCukiah50ShyC7blaBBV5K34PD0vaX4yf21EeXYDP4hR+DA2cmuThtEonR52d1/AnpTP7dzyyVztxvX88PlXN1bxLmpgBgQ57y3J5vyMdXOzHgJdzR1Jn1KYUe642Gb0ati2qTlY7kX25+uJ3sj/47XDNbHQCumnvMz3Esw0kJJzx4JU4nqEwGdBkX8aOOu4jPyJtq617RgseSktD2tcvS+HHaSBXa6eme+nWE0+NWCt+S6t1JN9+WZusOM2/EFHvSI8Yb8ihzF4oJnqlFaJK1DJQYH26nC/WxXi6yFby+gDKvX/39uzsAgIgHBvU6FBgtoABNgNM5WPCwDvb/cOBsXxtzwnshrENzXNG8HOKCuO3hj3NiQUWZObBESIURocdJYflC1YYX938vMgEMbM1OwfhWJ9wIsFydVsUZ8LvykolmK0QP4bXEx3zqxWyrHINRwkeSRPhZvAon7JU2MYU1RiYZhegEfto8pSMzYNeEoiLMDagWqiZCGMtRXm9SLiaW2ItUpQ1KTHGhDgUQrKgrxE4mjqHe0CVUSVAY+8OJFNRUpfkoATURxzgfhWN1prNQNtoK6cKcaGTjLWjUchqBNt0n8wldWKZwg06yFlmgKcTDTTCIwcDLYiS5DJkmUHyjgN8ESVn2bbpfpRf8h3E7ygPUSR7jJ2gKnCRxDQKl8wsScW5y1qlQXOyxCBKOPotzm+jyZipH7V2HOFGhWB0GE0UMIOECcEJA+vbM0yaZHKNBQKdOOmfVVUBLsIuYHf20dwbvalsk1iHevfuMHop2HjX5Fvflc69OL8Q//nySLaDLkMtKXdD3ks+C1TLtf+N7dPvD/e9K/bn2p86/P12t9IP6NlvEhO03Wr75fdT90vYluTY1vTL6gu3S3GUw/Xcx9nF9/Ente6nHgN1Wd3y0dK0R+aCe3GFT71HBsj81P0tsj/Vlehz82Xoqq3S+X2ksoc9/hte+/RiMwC7JQ3SZcP+IwVcrfbV7SMJdir2pIHvtAbsfXughjyXR71FHL2YDuEuOkOyCtQXY+QEOXdL/jaM9kYJe75rd/94GnOc10rXcjodg0XZ5ieKJ+BMuXkwli7YCJjl54EAwFe7WnJPEcglHClYZAhSI93unWPjzhaP4UGUDUVr6J2lq6/fvP/Zz/+0AMyH7ESJb8lKu2RGuNnAZc55YVrOa4VSLOP74ON5EM61EIGyDWKWEl2D0xr7Bz0zb2DYWiwkgA33i4XiKV1xYlkFKEeXNKJ2ULn25Xgoglyid9XyaBU0YA+pYwKdFMqneDm9yFhQ3uoy/i7KPmVgaU6gKJMgoWocdpYHac4JaCWD8CB4jgKOUm3PyXg89g0VZNaA3Zjyd69fSv8hbkvoEptBq5+p1ovPfkDbBcVyebvAFIrlqzVmmJ8tRzlcodaJExLAj+XFP4b2ZQxgK3C2AFifoyDIIhcstSq7geqANgwGsP43v/4aQbKVWKXpAu5plt3eLDgz7rd/67cxwzAkYFCkWHxIS82byhNAF1KNf+3e+2lbuttK+Jg3TYU+phCnsj8FDfjP9qcgzwAZfgN6795XygAVdZFwDoA/9u9IvhW6dH20q6d21Kir6jtxfXZYX/xO9ge/5bfsDtcQi7ODrQDQp3EdKckd6+vqamNXAkH1tdXWXnyd/pDfd2vf+0iwX1dbdb9PMZbXfy4HcRa8ri43trG3+ztqcogqfsOHwkLwo3EyZtidEWJ28kzXq//X/+fvctLTX/pLf5GBZzaHOZ+v4nF0cf4UTyFAJxBYY+oRfvkMFs+wCnQiGI778lVxg+9ueW4YjN9QKFDSyqTn8E+rC4gR/mfzIECwxv8Zr34djt+PtPs+7C8RKRol5hYzlauRvIooGXiKVz/WBgA/Y5ueiyCYa8R8rSoVOoQY7CqAj4yqrYC9YWKBdxzbVRzIOUBySpdjuumPOPIT80Sf0VuLd9YLRg0kqEiqErFAekXOnaRVKQB4BFMWIV2VRgZRuo8a6ksmyaAEo5BGGAdWlJz1UaiG/3GeSVlTHTMLogKFxbXpUBQss9k1G/WjLzTn1j3YymsJAKuS3YFYKSB/H3C8xC2XV1ffrPMFHlyTaZysR9mKvZU4HeAbeLDHq6SQqaZ6oFwCWuotnSGNUHueL/LiFv7aEhQTENsjwTxYxaPxu+v3//v/4/91vV5nKZvDMr/AXFCUldwWF+fj/+V/9B999YPp4vY2Xz5VtePXZgNQEpcpxj5RnFOGZKiuKsLpqRVvRL0jeR65CzpmNet7fbcE3XAzFW5uD4YeauzfFRS/Pljg0QSD3j/G1VHuf092FG9zYMfqzefjOo7PoR3j6IfXxdH7PP0S+8KqO0+oYcK+/tannyqX12/7Stkf38efXIjk2O/OEvfJWpekeSqewnvLVvPbfO9vkf2pGy6DQlXtj8a31LrRT6NBSlS4cw3AljRN1q3Yj3/j5PpUpfv4+jlJcNLAI2hg4Cv06OfSf0nVb/mjxBfIMviqfV3YPTM7P3/y669/9Q/+6/96tV7+k3/8T0B3F5fnYGVA6mQ64SCwCet9NVgMWGTQnWCKjw0RRAHk5T0iAGogUgPg9uuhT8O+gs/mC8+vivCu1o2CuxlQjoKEoG34o3csQJZRbvRBAANBDPiTqWLyip3WqCachAUdhRuSFrZWklA1klnARFE+91smtAtgN8Rs4JMQSaTbl3FwWlVQCS6nhax05ZINAr1JxacoCdvPrIrm4k7/HYWSlU6Utt8hQdI4DnzCERZirn+WE13iQ29xtAzggpwM6ceF2ogMUCIBWVQX0Wo2QBrFMUubAkHAelzWcwfr9TIF6a+LbKUmRg6ODTi7mMxmc0qGUr455DdHLJTATAthW42NPYcPFVv9J2wyiksPLlS0V4l7EieBTWdpurq6em9LQeR2JActbQyFhUfjRmfnT6kjFmOWrmYTtjxSZfhv1bRvd2MxUJJmGuLefTtil+xiVF/L9FE/GkE/AVk+qiLuX3ijyvuz+hQ4WC/Va+FTEOagDEOkdM/dQVafBkGXsF1xA6X19bPFhgbuXAMwkO9DkLkfE5+TvV/tR8iPPSbc5nlM7o9Pu8cCPijcIIsTTMMlDPKtvwbVt6+W3wkN9FWuHd+nq774zifxzr90vHn8F9GWeI7pPoqa3FHaZw0/SQJ31oCTAWNctzkWqsyKb6L4HcP7cTIbBVNW3+KIz7gwB06VS1xr8CuPcULRGHQIHASosmB0LNiHe7q2fdTAPmyB7XprgmeB7RpIAvgyqA3arCYEAKMmuuCzcLHAYoofueA5+/TLnygWuBQ9biZ470teDZfDH4YFu30yDJ4YnmdM3IwRoWvVjGJJJautooWVXGXIq1S5q1MjxFLBQF7jTA4w9Fu9QnFbqfA9UpEoMnFVZqF16uIyWsi0qhQiCcPVxWAIWC7lRBUAZEwa4L/pQsLA1L70TTHiTpzgA7MYNo2gsXgVyMrrICuYGwGZcwRBFhZsiJTRFpAVyTVNEeUvpFshenkHYROId84nvjs48kgIFUEe1Ou2SmJGJNAMgFOr5hSYaJCNpdphx8EBHco449jh88mcpROcm8CGoIz+k1aW09k5lgU2gOYqaLD8DAYcp4BNqD2EZLHkWCOTi1Wes4pDLkCmGlMUoey5xIpe61MXqdKYVKPLD7sYiz72Q2zssrIr3nXcXb9rGe+Q3/+d8sP7WR2g/ATeyX3vw9568ZboTRuUsHm+avJ2TJ3yuN8RawibfuaeJwrcrl6ffpzMB9p3gPg+//ZvkOv8O6Pg2wJ2lNHWZ5tzR7YBUfev74BCGhLV/tg1ANXJCe7t5NTn+KmhO9cANMXttPwmvj/BozkFTxo4aeCkgUYDvHD2vanrtOYHqP4tqhNg1LDw4sTfACcYM9BpUAzuCtkTy3jxItMgcFKwjBQkp1W+EQPHeHivbOCZ7WIE9cGL7FbPwQD86BHGKhCYNqQp9kKJhvmBrgo7iIcwwk/sKSQBhAqF0pk/4ABalvUKyEMBlOTHRu4vzAMQ1C+P4XGKAEoDqTOMCdzacZAXO9LdVAKUArkqC77QWRnmlkOKpAKJqmQ2BTUhJY7AOrEEJJuRydTgnzK6QX0rxXIou0gtv2LcD6XYuDvubXhfd6q3boy5fShsZoXLL3ExOMhLbO06hew2UwKOVizrmgH72h01mdlRzGyTxJrfFLcnuBvWtjqrFFkwshU4rw3lcaKZ9vYHxEtrSKj9f2hpSkyrSQQpn8kcqTjThAy0kolpBzMJVL/pbArEZ0omztL5DEuvwO0Hm2u5XAfX1zoumhUZOc5FcZGvAP4cWnx1fTWbTDAsaWZkk0Fo7adKu4pLO/4llXoXRE1ME/DSP2KwW/6PKNCp6I+nAZ7v9kWcOkn11U4/xTy2BnZV39VKg2XYzdy5BsBxc++G3QxVSbtCDRbgICGv60e6nK3mmPtWpov5MJbckFJ82dxP+wPrxB9l4ZeUy49x6uj5HCL/EJot9p4MR+fdYrS5uQ+frbyebBvu/aGtvP1kTcp92vfYsppCBwbu3Osc4GmwhV9HwrDV57YQLsa9VeTfCWZzIxY+2XaenfeE2BKFe7d942Iy5eXGWlt8/Vm6uSBzHH0h3BiNGRTWQC8uKOA8Tsxl9D1cA6SJjMIxkFLigcI1LaCTBSSxsLQwqaFSzQnowF4dOKUBZkFrys4Yvwf3g3DBrAvtR4Pzi+Cu/uH2IixKCN4wi3DxZ6cfBrdx/sFXPuf0LLzdOeJXkN5IOBQgKM8oMgxuQJ3gTwCtxsSFqSmXiQXbYl8K5ZJG8GshAJWtOsC8QFTFB9lz5jZYFSDODsaToGxaBK1BfSqcPVElo7eukWCmESKxkpmCSw4BJRGTPxecp41kFSAJVLZyQOP3eMm/4fwzYhAXFjlNwEnAbAoKeicxZpufnEH7aUITkCvC3eamWL8vXmgY3xQacEYyPNUTqDEyoCGqLfDPUD5Fg8C1iIM2wo0IM8EUJjWTnTTEkYqVmygkVNPSNmM2W5LxRAzTREynYLyNJ3OkyjQRoWwkhfEtfYB5oaDA34iVxOH55dm7t++Y2BkntCl/xhw2hPnAc51Pd3neyVJmFevo3Y0XXaUe+eWYuk9PkH1crKUr824fHbMZeIFTI0aCD10+jR92+fr4tCkPlbNJ7+O5v0RXd0dD897hGq69OzA/KssQSdo0vt788NCij1FaX/vepVwerwFF+8/W0BoN49zWZJt/X33blEO4tXO1Y+JX3W+Qvv3Etn5Jd7MeXgPQFuAUc9LASQMPpIHdB/KB2H6qbFRdIajeq3rhtymcorz4CoSJk/uZEAa17NPJ/BoIh+8NyC+eMfYM/pX7CLtHpuzAE56f4wgyBRkCSQ2IM9yb5uwSDxy1yQBwLehVAFaD8bh/ALUlNbeMPlcVkBMK1MLkws+qF0tLgZxAXfxV2NSSFHmeGDw2biB3+eUAL5l0gKHMhmi0SoSVWU8srAk7QDx7E1EMBQIhIdLWNQKufLqhfIwagUsDrNKAKGWImIhUWzaHpHXqpEh0pIWxmjWQoGQnh9u704LC8zIWNOYugA095NxLTP4Eo2vThRAInNprcF9iSlKO1lKh7KIjk4PteUyRtMKUHZfwuIIWYyiJGLYPl+tlyS6sWR5TKWkkZu0zbjwap5ceyUtuLrHUjkGSX62JEDZnIvmttZERqwHHKrUK8wfWGJoPsPI15QCFmsGG7flMxhiImEnyLpK22P1Vx0ZgIMQsHLc5HFMTRhzbmEqDmiLgIheLyMlirkRqC9FxwaYKufvNZzvaYvRhGjPZNuR3CjVlEGiYNgXcieUp00kDXRpoelhX4geLazo8JboO/4hF9z/bj1eoX8G6lJ24nduaasj3blYzAIjsUOUuac3e/ar0pdZUfDub76HWhut3ATk7y+2ugCeKBffbavtTfV6VLfva4vhZOnT5tu/wUhzXdn19bodKHpDeI79WzaPtVuoQ+TtojFvvPINXSjvv3erb5jNAFxXJVl5PNp9Dn1Rbef0MLtzSQ1vDfZzbzNplDc/b5jYkxvGXn2jXpbFP8PTLXVyz04ebV83Oo6xbPchl9NI96l1l2JNec+BNZDwcGAP2ybNfILS4ZhUAjj6M39rYP0PxF/icCMTHWlrKOP/87IzxYC33FKwU0MO9JE4wIYD+lKwlpHgHERLOFZamJ+jVBwrmrACIyXFze5Mu5R8OpGTpQVEscegfxW9vbjgcF0BPtkyIVfzA7sK7MwbD2aJU+/oDv9dhkMaj6SRYT8DG2u8S6MyOQuRdRxByeHBxE0aEQZ83QXEZBFfR6LKIXgf5kzJ8Nyqea6okfx5wpG72pIzf8TmK3gXsjp+8K4tno/BNmT2N2GqGUXg2BRLN67J4zlalo/RZlLzWKQqE18/YWBqB4VZmz8r4VZl/xkB+mT0PyIsXKVMH+VMN+SsVPgj6ZgT/5HWQPRXn9DKK36OYMnpfFOch0uZneNbQNqtgWRZPwfFoEjOAw3nTFEVqooMBfGyuMGL5NR5ZYHpBcJk+5XMpzflQadMjpinmQTYZxe9tQTUzJdollfPQivVFvjwPJ+/ww8JakHkm1yDC2upHPYUmM0PP+gqmgewfNT2mBTKxF5P8/dm7lW4qUq2yYA5HF5nV3JDpEAYEcr3NLDMl1/1QAUtSBlRUXy69TuGbXgShPupIfiV5ahhxf1Vnar63czfRtAtX5zO4YWryOEr3lth5Bhtu7UD7rdKmGRLzUHz8svbz7EsdXne/LD98Nw7V29Ja9m4cfBlceAifNo2vGT/c5t8b43pjb/LhhDuW28XYnqLN0+dIHuO3z/91vj//drs4yfuQbfdcovI0jeE/8V3vEFeA/+l0t4mpZgD0ctpEDgvdJU+Ls2PyIKw27+Cjq9IS6xTxME1y0uOWBlAq17e9e+6+Q7aqOOim1bmaCIEws/K3lWR3+nDRVcip00okBnQljAaCXOMdwlhvkiwXi1Eey/UGHxaQH8ASPJfggqJBZbaC1ElcXNr3EwKNGsMGREgUdgKlaSCdRb1rrSowJoKYuIUwDs9w8te/+ubtq/fs+Mna1YKjvsp1wBrf+BpsOQouxFplOqG1w1BYrs+j8UU8iTBPdPAtXkqrcThDDjedwIb1OYZBkLB9PksDgKbROPm9P/O9F2cvqE00ehonVxHgmHOv8mdlWEH/EeH4bQCsH78P2AA0ehdiGADTC6D5G1JlBgDfw1dh8YI9/krlfRVmL8rwZQkAxeJKX4xCxRfML6fEA/pfcLYa0L8M+HxaxG8KoL/jg5GQwvOVYiKMBEwRynpWyMA4HwXv8+KsDG5G5bwcLZbr6R/+yY/e3WY4E3H+1wqf/ZAGENyW3tEwCtcsCuceYBKAyOXWr1RpzpCy/HSKd2/fMFxfBBwQxm+WLBWsBbbwSeL1+/dvo8m1NnPCpAD+m3vUZBafX9IECQP2oH5OVIa52kNUlAlz8/hRtA5yAORrB1gZbZiCmCJcLCjH0svW6QpJyGLWA7nhoD/rq7Ak0b927+s0q45u+ghqwtP3SQMfXgN7eiVJ9kB+eKE6StRj9JtySfFeXf3wTpJHtT/oNzP88CI9unE9Fl5wS1InwwPafDC0X4z9ldtWV4t2iA3XZ435zI6tl08/hL9fVnsk3ufmU7rwkDq2c7VjpG2/ddsU/TECUqTyI91cfriJHBbYX99hPI6j6tWhBiWreg2Rqs3HH1Hok2kIZ5e3zX943r7S98fv57+zM8MWK//dVT+mglB6rF0/83qbi269UXh2dtnQIupa5hbDMDy4O+a03bOz2WK1Xq3S5WqNU70gfR4B2sdT7eUSRs/5cHjOOZpoMFfOPxrsldRkAISCUbVLv9aJggIJWy7NBjB6nXByrAaG2U8GV3JcyM/wWmHkHmA6yoiECncUszp4kORJo1F/DgRIyjTKxuNgIUgKEGYyYrRgZkDeJXgB4RuE2z4sGC0PR+t1MB6v/uDL733/c878ZdNScOpZxKxCMMepqRydaevScMbRVUGJR9MSL5tgtNCum+WVIPLoCltiVL4HNJcjJiXgcI3VMRqxHf58VN6ORufKVV6wy344Aruvy/KCzTGD0YUOLyMVk0ZhHGaeaMlEQKrC8swJnkpVo6fa2UhhWucpCDzXYP9U5lA+CeOzNzfZT3/xZhWcAfxTOesw2I9q06iYCIyDshlvH6WTUX4RXWNd5aMLWhPFozXsCmymPH++DovVciUvH/5wHpLGaS1mVzhA4b1MujXdwCK1ToH1BbQjOZFSkyryrWK/JcF8a2BaXccPm/3BohG2iUqiMYfGTcJ89UyzDuFb+gmktlVosF5qATC7hjKlQMWptRmTdV9UDybs+i8BF7/pzk0aGdupTLY0sUbQfGw4NFEKdI79b1HUN1A6WeqIR/xuv4sesbAjWX8s2fa/LY+sxBb5sTVq07djtgp40Bs9HXR8689++NhCXF4eNPGrfzwaJvfX9hbW0mtgywPi/vwbUXcCTjM7kdxGrzofXxfZmdTmoZjdXYCIcu8WfTKaooqK7v7XcE5OAFeiC7vPowXxGcHujlzuX/XH4nC0Qh5LkBPfkwY2GqBb7jx5mzQLkbrpuptQQyXMbdE1Gz9DRV8neW8oF1XzszwaLRZY4xcGXx18bCbzOACCr8fa7of3OGBfqB3IqNFh+Zc4DIe/kLYAAtIZnIWNG/s1skRLiR1k1NAyZ28lAH1XNcb+BR7xLjJHf44WJgV8SxbbPQhZcCFRXC7kzAXKV+oCryHiQaWjKGGdMOuQyQpMZfCZI4k1S8FCWxYQsEs+CxeYIiA0TqPoVgg2SzUqHUEv04FKM6wtewNLQjga4yDSlpX6aaSCBnUrdbkvbUdqjYJ8LASwTU71mwcrLqFY5+Zkt1KxW22AehxsrhgDfiFWNjIjMY5MqB/e8oPSb5mQOSRapasB9fUsTC/UAFZzjmC2I9IEx9E7xPBHOedBNAkmyF0EMyqINslQEhMEqxBnJvZtRR4ZQLQhUzLYDegUetSWjInWD5lrL4pGYJx2SEJmc/K3EX1ZfbLhmRKAUsJLfVgL9ALc+yfjeLrW3q3wp16YbKpEXrBbqByZ1MWos/qOu9G3bipcYmG7r+IV1mX6dMHuzyZnd/Ip9qSBj64BPdf6/9EFeUQRqJz/rH6suu6IsVfpLdoh7dNUUjXkvamGPeLyPJO2cjku7tPJJf7b11ZJLrmO0u9DO8N29o47KwkeDTMFmvvtDM6G22/7DlGG4+B4H2sXDuG/JbX94PgxW3aqn2DhY+VpMXiACBDAt/rq1aHVa3//8Svey8cn8sLHjo7s538sN0+QQUF78gZRtokcECW+fvrrB5gox9c9z1VO7wYk5iLdg8Qgsk0CFLMgWmoRbzCaTefL1c1icQNAzfJRGDMJAHrnZNkxoBBHezYCBc2BlHEgEXK1UWhQoBAeO/prbFsTA8BTFgMQyWmziMmgNFvEy/WHweAM5xM8SOKM7YUAo5orkJe4jlVRjUCpvFiFiwGYsga08gBYPMVWCIpz8sThjcFXSAgjVTzWggQQZhqyooDtSxklJ4ktc8C25RnbWMp6oaCSCJyRWDacsZWRUDruQ0KmKESWgF7nDj27t6DUpZoJWuvL1CXoLjgtsC4y/pvfDPFYHYq3apiuBaNpKMWqnCpN1gKFwppIwmSHE7R44kMOYgZFpzJL4nejyfsgexazCEP7dgK712mxljho3yZdRFyU4/yCEhAIPrgBwYs1DOhLK5Ipg92VrEiTBG8rLCIVBZQHu2NnUCo2AjyJ0KcsBXSlaDUumXVjBoRt64QZIC8vVUEpcTKaa1UIlWHZ79l6tU6zDC3ni8+z9Ml4OluuFkilXJDKsEMacurbqkxBXEjEPdcm1t1LK5trK67Js0l/1BBiN5c1dHOngEttx28RtW72v4ta5A8WMeRt3Cebq6nDM300DybonRj11e5Yadv07ZiqK9tv3H5h+6Tqy+X3JT/cR98Xv5W3+QmpqY+Vqs7nffMyau5aerjbc9Hw2xMYJvlGtBYrkuz14ki23zRUqVmVVNG5r+rGzQDA0mXe5d3xbuqI2s21eSE6YRzvHcE2mYyj/1baJB0K8WPhriZwKMcp/aSBT1UD1TP5qYq3LVf95G3H1neb18kmVKfpZSPsuLlvQi7OTzHUSjpx1SuCzNyqeHiwgQxOLAzH40YfaRQ9uL69xqVjIsTP1o4472h4nWUACUAerIiruUhxvYFBBqwXL/AwEmn03FAdUQalKQS0D7RnPB7kKDeQnJXBgvd8gtUZrAeLy1Ygt208bytKOW24ZE9PnEpgbXoSSg6jjLctZTIzoCFnmQk2EI0tAbKnKrrknMIq5nCCpRLk6TpOlpN5ZpMbeNekSKah+8oRxakF40Bj3qYQw8+1ag2fOkWRSNXcr5pJZGP0BqZN24LvyGhJjhM5lEVfgv2C6Hyp3Vw7UGOzcdSQ0iLQXcaAePBHBk42wOwJR09YkcxUiHyaqJ6YYIWRhTsyIBKRKguMLj1CYMP2KBSVqCroR+WLijIJWjlErAXrJVQqvZEqe4DhfPejBlbPghx7T5rmRlIioCpl5al6xOFihNuVTBUt66DdERRLJc/XTAdILgw4nV+GIUI7aU6JitBj0AfyWv8x3VvxYukuFdF/kdpQ9lOdUk4a+HQ08En12e/w07P/zdHqD8drwhVQNadmAFo890Z07Fewlx7+KrFdrXaM8akEa/HstpMQvpNPH5dhOxy3Ct+K6LCet9If9+bDj6/zy8flwMHd6tbddl282pTtGD/f/WXzuQ0J36v1NSBpo7ZdJfkte596NRrrfDLaJftlNXnbZDsx7rVxoIjed0uVwNcBDlZqhbDohJbPZRaEZxB4OUq/wAm+yN+b136QcwhXuOBc2XgyZmvHoridTs6mc456fT8Kp1GSxyGO7wwwszSYsXYhSqFaEKAdDlDXksFpkoDtDlob6JSzCi3ISbFsPu9mDwiwk48wIytVccuR4wg4kZKCIk45/ZeDpeCCnDjosCYA2+GKIwqoQcy4P6PkGta36QTmCYSdrQBNTID2QyjH5UWRzYrpNcVqvUHI/MFYD6NG6w33C7oiFXpsPpEcTREjTQlQK+T6HkEXUDZ7qrlFTkesKIskkZ8GdthEyWKAhio2VRtApfkHqc76rZJtHS4mj8PybKuKfvHjD+PrOGJpMicccMbCEiWUAe5MsUb3De4D81Uhxu8B4IrDk0kTMvKHonj8caraUQgxrJR4CU4v0wsqRWOzhFtTGZJQtdCuTDLziNQ0jW65cdAeCtfcEtEZHkL8yklDstiX3sGCbuaSimA+ZwNZlpJcczBCHubM+8CVOYLl4gbHoTCc0OI0ntTFZTaQdOeULTVuXdRGlVFFuCo9W1gxkrv+tMjH/HCC9JWwP7UvV1+8dbKq6n0094m/z9vY1bSPQ5/kw9+QjnL4LojtEvtku4/G+vKiDTOM+9KrPktyW6rhOunlfmSCe2D8TG2p/FQ/3Nazn9oXvs9zsV8/O5K7FwFi+L42frhPwurd4ie794wfQ7h50+jNY4Ml9tLaoXrkW5VtV0vEVkRN2foWj4ZPnUqEODSVrONP3ycN/KZpwD1K7omonouHVkFThGM8+LFz4jjywzIZzBSZCwDWWNoLiC84n3XFcDKAkTH16WQK6n/y5OJXv/zpfH72zcuv//7f+wfjaDZLpmdTfDvOy2ICYAPwMSrMKK48UMBt+LAzriuXEYTSCwU4xxc0jA0Tw0jvZDJRpM7qlZsNQFV+IBwYheN6wKJb84TXGDfuOPjWgDhxM5K7PqsACnMLMpSJSeE2yGdcXEXiSiLsySQF1oBGwwW1oWSGAmOGowkoM4kWTAIQ6YrW0gBNKiC28iKe+6xehOYBZCDUNYy9C0Wq0Wpo9V9xTvHuEx4yCaiz2QxURuhYJeiXkhy6CFl2K7qKU5TK0q00Jklk0WCogKllLcm6KcZRNo9RSsqPDU5UhtdHcvdn9N/UYiXW4lEDLWYQP/iiDswCQjCFzMRBLMTjj21XEUutASOSLdLUQX3U0Jp/UZXl8c+RZJgWyqtZAIwNWl4TQUGUZsB9PKswGKfrFW2kVAS3WaJJHN2ubm/WtzoVuChXaZnG4XS9luWphdsc2sB0DYWqLaQCPgiY6AS4THOKVcL2tRXjbtyny7NNfLr78BqwNv3wxX60Epu+2iWBPV9dCae4j6+Bwz11953Cm0ZR7L32mcTvGNff2xvaVW7bKNX7rfpq57AYl1rTdHay/faT4+vvjgyz3dr2FP540frtRIy6XnsKGlK7PdnvkuSGAF1O/RAfuPxaDK+Xz3THxvWTCPsaaFO2Y/zsvmwu3ufmU7bDwynbee8YM0DbjnO7XsNLRGP0O7/r+eE2H7+s/dp2edt6o7NThL/vuF9Kz07nQkmd19auBWJs8EqD4qBwPMl5ujlJlrF0vMlt9Pw1u7jgMPKTf/OTt6+K+dOzf/mv/j77/7y6+uaXP305Ob8Yjy+B5RypW0YpyB3grX19WAmKy37Mqlwuee7IvwTWDAbj543/jVw9QKtMEjzDJ+fq9mdyXC84L4zBfvb7HwMor9/JKwgQyX7/oFJYMbAtXx6+y2LMWt5gBRjW0DFWAVYLbkMQleWYc2i1KT5SsbSAFcdaRgCNMDfkmmhgOJ27bJTNAvyJSg4E0JC58KtkRC3oT9SmRlVCB4gRzVm8UHAWr1HZ86peV7I9KBfb+ct2sEzISz6tJCZZnLiRncPBWyQUl0qN3inRKNycg04SgDp6byyUaEUQJVWNOFAZA4UCNUGRo0EOY3g6A4AzP3IdBfkyveZo3Zv0alS+MM8eNEDLamoFtgbRVZjMAPntULQVLhLQNtYX/v0Fm5AiH/CdHHm6XK/MIIAHETj8yHNonI+eJqNZMHsrZy+pC4bSnArCg8omc7ilGwTFZ1gpZfkrRvSxPXTaVzTFdkvTBZ0KE2E6nn352eeTeEpZUTxn+uIdBz6M8vF4suZEM6w/5guoDKVgnhXPpYjkjdQv9ehDV/Zcn5wZvLmMoIp/tYmuQpa6yV+n9zxNNl6I6eid0eEY1Pnu+91+6odwVKfavlx3accP5z+ccrvk4+4kYUt4WAx5Q7qShlM6+rZOjpO4pn4s/aCNni51bE1rSXe/h0veI8guw877h9JzJ3Mi2z38bvrxd9Xzwz3lopJWf62arCsJD1m9kWwGoIfjfaO7ijWeLTmbko5r134+bVU0RZwCJw2cNPDgGuh4cjui7lBsg6NgB3wT7mRlaTVzyZpdoF04nc3/9E9++p/8p//b1WLKqoBs9Au5p4/GSTyPWR48SdjGkdO2ytGY0W3cNQSw4STELKsCwC1ISISgsQ2AaxA8YB0oAFQ7ay5WP/vjP13d5iHLgAuW8rJFJpCREXwGismCf7nAqJAx+FPYXeP0rDnACsBJiDuEhoI/WxmMx5CAvMaj2cNSvvEq3V7gKteAKvMNGOphgh+KJhk0bm3OLfLJQRMQVaPOGuRGZiKsGIUbNcuGUHrzyy30r0sCqUS+LUJlOr7Q2wpXgXAligjGxpSwijUGDlSraJkNInI02hRUvJjrENROyvPf/cHvpkWc5TdFlqzT61X6+Y9+/pOFzRBAKq0pqwnjxFMB+o8qaCkmP3AFwiDDNDEiBvZZDkEmPJeC28X7m8VNSBuyGgQgHuElhQWWxOH1V9///tkEJx4WVMs40Lg+64LZMwhTzSw58VYLsFhcDl8E+EdjmR+XID1LPdIs/PEf//Qf/eN/RPz69uri4ot4kpw9fZblq7XNKcCE3kWDUmf8hLQAmQvrhXZTZ6MelWaktq5L2rL66tsuq2YX6SnupIHH04CeuaYPtopxqa3oDxrhng97YKon5oMW/3CFVQ+6MXxExe5hXUnA2NPrHlVWFHztYbNRyQAbpSZu+LkiuHWF6AdSV5PuMuzj7PLyQ+yNfJCrU2j9PsLcleFYP9rn8FLuZh3eS3CNCN7xGl6vOxZwZLb2mMFwfQ6nbAvFACed7GhtkIvrHvpvS9LEHOzX7Yeirb2G255An9624r1nuGN2cQ93nmWNkroHW7hQCBPsmyXaokdPNlMBcTkFDILq0oJFtSPW/H79+vrmJptMGClfjYOn63XBvjoQZ+sguWRv0HP57OAbL68NYegwGOP6IWjIMDC7BWmVJ9tryu8DSAdAFC2oElBYvp2el7PZk3TxLgo43ZYcMwpHEEAeY87kAlyC9mCtXS2RCyDJ4Ld26lzgRR/FKUVGwUQOQFnO4mBMDu1QyhpiwfBgXeRPLqIffPUDtv5nQfN0fD6eUACS6DgCHTysxi3Ip6kFNxwuywXFqFinLkwMIgLO/0JjFSwnHfVYX2XsWR0WanIoq9SqS6zFSTF8YS8gLPMrb8RElzERlQ20c7KYURm50sgtSC2LC1Q+RuXIFLD6ItPxuUH0cj6jjVKaLmPn1GK0Sm+nL1+tV8+JkUOTHiIxKSNG07FxzkyLc23eH65REI0Bmk6CDO5YDWbPyJUrTzOt4whesG0o+se2kkY1iaJWSJPXq3SerNhQFTtBWznRnhhqTBmoLP2jkazKwS/Y2Qfes9lETkVUpZjyKc+gIh/n8x/9+I/+xR/+Ie2ZsJKc5QXT+OLz5zfX74p1/u//zX/v3/7L/w3yqAIFZsc4y18K/qNQ6YTqYVFIdzYnY8rUjcUogCPTpre7iDp1Q2Px9Uff07TvV7LO2/ftGtp/m7Vj3NPdju/j2Y7f/7bZenu0M3sxwym9TIOC+yUcxMIjelhuHuMq2Mf/PvppeKr39fTAtiQfLgaR7O3lPvXYfXrX/n2l2kr1Y/QeOVSjtq/NoRxd6bwTNevISNqnc1lzHtem+7VF6nHsPh1dnCT5tDWwv+N9cNmHiONeLh/igThQxpawTqpGYd6tuNgTDISSf718S4DlIfv7gyRB1IwIx2PG4HHpCaazMJngDB4l0/lotCLL+eXl/GwyP589eXaBuwjcwIU28A4WFHoHvAP6KUE4EMwqMEpQuA2sye8MxYMyZSzIJZ9SyKiReLJiBognG85gNuBkIuDIUtOAQ4jhOoEuzIRcOZlLP1g5eNiQZcmOn1OgpDhSLpXCXkizfD09u3j64nyCy4ltmGNglUMABC2F34XQJbTWzsrpSNDS1OhEhQxkTNGmR/tdBOMaMOWDWPJSs0bLQHkp18i9aGg0Y4BuSVQWycwXGjBtOHqLJ9Xu+JAxbAUQQ24MtIJZDUwrnb6rBHn4cBAbo+Njzjso0heT8AU6dcWblHj7sCMTCiEabsqG8cBIP002LrPLIGH/IwTDBQr6vEjkDRbjq5StwPfISnlSnZpGazDUOgjN8W1M9citR9F4WAmOQ6+eYDBdqqGtmWTAsrp4cqlOxQQO3leqS5GuV2+y6/L6lnmDhFPAMv5ylkZ/84tfMS2DDcmaExaCsIoAcsxItp9iUkEVxh6xmvOhe2Kq+ypscZsPUutLQZeljjl9nzTwITXQdEa6oYXVHT+BLtnI9SGV8YHL+nB1pCS16R4DwDX5o0rU9Ko6UH9vqd0fmdhOsLseCVXBbXaOD+92rl6eWwWcbnY10IwQ7Cbc494fsWi3zv4S/bzHiqDB38Y3d3sG6SCrO/Yfg1YHmd+BgIq456AJdDKxvr9JuY/2Nlx2Qjtl7KRWYm5ivceX59Uh3TpOzzCU9hwL0OJrA5LEwWM6jW6vr+aTC+NTrNe3uOrIOADlCnI9efpsFgar8WR2ccnYP9vGA/Q1am9Dv+BCUB9kwvo4cLP9v3UFLSYG9gHuufDr0Bce4Th9s+ozX7HZPC4toMwYR39wuQwGwCXM5QOEoIydT9ne0wwABv8ZMOYEW530lTHCDCRVDVjBwCB5zFFgyu4gMptl4kIST/BsCjh5V1AVQbU9pTalgb1OLAD86jBa7d/P4D8b3dAFNeiu6qo34h+POQFDWQfEadshBuM1nK9LerQqu44ibcgkkFarVN3J7jE+xlQInSL4smix0WXNRJKiLVVaI55PMx7GYbRmT9RIK33RIWPm1FXJMWcyMOsRvwmiN1H4lOZgu3/t4sPhvsx14Livw7cwY2B+YwYOcxo5cyH8Ssk6GLHgVlM2ZATBZ5z6jJlRLtEIBVtdaAvZXvxj19conuHOxAVqt3PB5N/PMQ60mYwWiFjnjZMXzCwTJoRKhr1cg6gmzl8k3IDt+ab3RGOmIijrksxZeo6qZ/OL9UqNhZVBa8OQrkULpGt2JtUiY3oRksm3yDiLO7ykLhUlrW0upyTT1Cbyg4R84VyB7Zj98UPE9N82+9/qQ7jZw2wTXIeoh5flSwh/Xfd4YztualXrPvp60GtLWo9zVd/XFnWk/A3PqmviKf5C/bSJ98rZDQ7Xs8vZ1ky7lIbGe3zsubGnp/UI7Yr0Ue7btXBiSD+8szXuPuxybbBVc2U8gsPhcni1PoIWm5dYU4UmZiOSK/eepbe0s+Fv71gJ4ITwE07hkwZMA3u7z7dMR+4R+zbXyMEv1O6eWtCoUJ39/uArohNzGRLW1vz4+UyePnnO8P/yFhA4mU2T8/kZbiv4ywDp8NEHwk2m+fXV+4unExbjcqtNXGzc1zAiW+zn/MIrzOJZLpAer1bwteB+Cha0SQBGg8H28ASOw4ODBpRJgE6oHzwKOLchX00kgOjx9pHre5CmccIxXoB/phw0g6A9RwVhGdgGV8qAsKkESgWOMhpdTPFdZ02zRqOJE64eJxrjpxTbWVRwBBsCF5k8XzHwDGpl7YABS6jgyi89o93qs5gw4GY0Z+V4b78qKHArA4B8hnPdL4DAPyWLQdUABqlVW36FiTfrQHlUUzI6DgSRkRjjwh2VKfNEyBx/HcLoXHs0ETR3Hs4BDj8L0ychA/FwAdSjOnFDazH/Fc0fY/IgfPSpjYOwu7SVp+YHlEyjyXjSIQ46yFfu99gb3MkHSfCdeZtVkeC/w9HLzLVgkWltBrnS1UpTA1oCrjJw/aeuakBEtrPcuLUkKRIkn0TsAiS3H9pACzu0/WuwSpfhGCOn5OjgJ8+e4CeWLrH2RuPJZLnE3kMoLDFXOX2qdohll6mv6ebb0a5RLM5pucpz+urUQK3SzsRT5MNpgGfzY19bbb11Y2+djy3eUeXbi/OoHI74+HfCoIbjR6qPblvRB0Xe2YenoXc23Oal1yS4cvtKb8jqQKd9qV8O+yWrqbq+t1VnkKKLzOI6S9mhvhuN08P+0ncKeqxbgwnV2IYfHlBen3Xbl3WIrvy8bf0cW6LPbX/YuTocwX+Aro6t75aE8Kevtp47c7GoxroO9iJ7ILa43vmmry598X0Fde5bgpwuvjWe4Z5noUBDnqYRedinoOrJFCdvoFgyWz19/tU6Yx1mlkyiZy8+O/vlz4tiAbyTw0cYLJavg2A+Bvw70G9D44xGC8YK7Dmky6eQv8A4GJYErd4VNnQQk43hNbKr7fBBm3ior9kfiERSueiqgnfC9xgmbEtqCFVu7zpuGDTPyuAwWGs7IVGCgHEhEqIlDzeKtLZmjWtSTOb4/cfn4ehKgDFgt3/DpmLK5EEpTyIXZuqAaYRknDIYDieAsRixlw5MyQKVsWaCgckBrU8ww0ATBaBrM2rsVayuRrURgOoaSkcqiSNG3PPJrdLEUHeKl8TC2JYq0E8KmF9bJlkO7sZgaWIwgzgm2awqEaMaAevyKcIX49eT6bv4+oKcoOW6AsE6Z08nOJgFZUPqFMC9ypEnjymfGCRSYwnxIz0eOSzAdqrElFO7yiGIvZhoZSYEaFrqwIyEjBApiEyKQcaiXD9jNUYweodBQKchQXM+rh0pJdOsEZ1CldTUE5x1oFgxumFyCTN0nd3e3qwuL54wTcTy35TDDbQjKXMMjPorJwxQu5y6ZJyYBk28WoGmUGnOJaIo94Zx6lUL2MVtldvxqOO3v+UZvL0L0Hb6p3V3xFu3R3D39u5J3Iq+Y1l6AB/gsoenl4/6hTrlhkAxPFj3KH1/fdslbsruCu3n5ucYTuly+bX2+fhhRyP1uKfAT2PWkz7PdKqNqR/7q+Rz8n9h/XgXvg9nn1ujH/c0N0m9Pv1erzBid289psm8G/B41xrrzlARPuAMgInXXdiulLv3ntS7SXvum7IOZG/o9vA6JZ008Clo4EBXrqFAj6iup/v9vXlnuEBPvk8quhIfiGf40vApccF4PM0AlcU6jsZv3t2M41eff/n9X//61euf/XTxL/75P/qn/zyZnEfBmBWjjIuPo0nO1pns+KnxX3C93DwY+mXAWC4iQlqCjQZnNc+vkX6wp/boIVUgE9AHFgSNmhcNEBd3f/KyuT/buwhCwgPAJU91LAAMA9xZiNRAPxKyfz8+8OBRZgQYl7bJARYvyIXIqKgVy4fx46HEcMXaghkrhKN1WEaCmODiJJaF4bCqQ+J4yeBcH0eZvH5KACvQUQ5CVAMuItU/YL4D/fquGp1EaiEditbEps5SiLLS+FRIcwmmFo2kw0nEfBNbNYRsMCiUX+BWrM22cmw10E/Z4gXQZ04D1vjhjMcpMzLaoBRNY//gIcMA+dMkeQFEx64iGnWoplrynGhuB+nFHkcsJchmC1aqMZpHJEiRB3iPlNSJez4Z6xdCp7mE8NngBzswnGC7QcsUDNKwQkCVkeoFuGGEMw9tBB3tpHZ1tYUVMYgKEVZWtl7DFJGQQ/VS5WReUBQbuWq+KdLKZiZ6WGSMm9h4ksh7izqyC1EwWq3XrBxQRgSX9FXhChC0z/rbGo84l1YRSFJJLIHdVX9XtztfNcud6NPtt0wDp3b0GkzKcArx1eI9CER7d17O4UGf8/BcH47Sl29YdQ9qpGKz5xyAwdXbP/bAW9pd9fc2XxPUfk4OtGJjPzX5HUN/5sElwdIlVUrYumlydwfapbTpfJo+69CnqaTqrn+b/da++EIqXN54QF+JffEdBXjcfM6O8gg+HawV5XNo66En0wNHC+7wXhis80HF+3rryXCv+vbw90eD/HBbhHat3SPgt0g7V19MX1364qvSW+y8fUs27UHI4p2ADpRVL/LsOYmBdqEB/mgElzcDoIpRdpxugPhJMvl//p2/8/LrV6Pg/O3rq9vsG4ZjWQH82WefMR/Ato+z+ViD19qIM1mvVtPpjDF6uDEwDGMAHQtSAXmCn/jKcGhwBJwDOLJ4FNAJjAV8kn9aFks57Y8W2v2TkWb54sinh4FeN5kAzMNFhMW+sgx4lNTfUpYLhwXb12hdgXxWhGTJA1QHQzskLs93W+wLHyDtZBLhGHOOvFQQ6iDJSs7NDWZqbTCpRtDRKqcIcPIYI9IsN83CSZTmrEPFz37FUDdbWQZae2we51oNHAeswcX3SWiWdQeAVCAy3lHjIFjaZzpKf4f9h8rwPZSGTxWvjfzLaRmuOOiA1FE5ZUW1DjML03L922W4HLELULCChk8tdoAyPy9GbHZETZbQs3UPMRzGjGzs+C+kzvlpMioA4r9E6cXovIiuRsmlWjcHMsfr4np6dhbPJze3S8TNKVbzJzLYcg5fYE4A5K15BQejZR1Ahu7oPNRQDl7gfvqQOgx+WhO0VmZnxeqcnYVSMDytoJPZcPnBPEuRZDKVSVEGr20GwtC/rBTxVOuy0kBWmPU/LDudyEaTUwXWAlOmTa4U6yQ5n0xnkwnngmHzjGdztmzCMynFQQ1biDkB5qL0DpJgYqVebX/q0gornhi7w8ahc30GnfytFcV/dQ7ZRmatiYBUu1TV5sZFtWbSXPTWp5X0wG/Fh+LZ947qi9+q2J1uHorzffi0f6HaMXeqXG+mx+bvCr6PTnpF9xPU/7e84ft+lfxMLtzusft10sf5PnXU811LNuTJrWmrGthX9S5oknQCzLZO7BXBG0TXLnUlgZsBMIrH/qhK7ClmV74eMj96k4W3qI2x+KmEu2u+Q3S6PWngpIHBGmheWy7H5hkczKFFqDeU+AgRuUt3itQIvYZ45UwOCGLBZjCbz5er9Gc/+9OXL1+H2UUymwEYceQ4nz9j13/cNaIEqCdnCnZtFMACzwMObQwZpkBKBr2BkyrImDJUawhLZ2yxudDV+/fsLIM3EbtYpjkuQAlomEzpOmdImIFlvMEBgDIG2II0wywB+iJiBhPNEmSM+i/jXFAdqYjWxjWG9/mVoTrCwmQHksqcgCEVzSK2tUxweQebgvW1jz20EhwlqArgVpYfAAk1rA+cZXej7/+5f2uVXQPNdQYZEx6A7CwJIoPJ+KKMgPKMsDO1gG/SOT4wKLkcrVhoK0DPZp2YBGsMAM4puyYGrCkoX0xKDICRwD0GAKeY6QwyYmQMLEfpnxkFi5KjwcIlxgYTF6WZAUFxzkpc4HlW3OJ2xfrdYn2B1TSZXvzqZz95/+qXkXYIlWv8qCQXbv7P4vAFC541Ni/d5thK8fn07MXzMcWvb8HbjOJLuRwWcHW9Wi81WSNlGCbX8mn+1EWA6+weBGdcrjRML+XwX020Wt5+882vw+RqxA6i0TqK5iMZkAi5uLh8+uX8C3HE/FKXkJnFDISmAfAsMscfhveJg+X0bD6/OFsvMRSZ2GE+h/2cllrQUUS4+vzDf/QPn1w+ub25mk7nX/3gexiW88nki8+/YFqAVGwDWjNLpXyTjXLU7+yiqa0OTBlQOxaMuLsqtfoS/ocOUbfj3R1pnfFdtKe4kwa+hRpQ9/9Nv47RAe+D6sVySGvVy8POAThEeyAdC2Zgoe51tVUhu3HxB4rpSd6ML9pr0n7odkmrynrRfdZbX7yXdXuE+7WfsgkP4bOh3g5tWZz8OG1fW6leUl+8R1IHwSpcLc5utuEIPjW/+367kb2tbnEXlr7ODSAcwcTP25utT29ehkF8PPqtYA9/n6fCbKfyaitfc3NsrZuMdw40jcYj7EqvnrWOR7qhVWmk+/calQHwWi4b+xf6B/sa4MWRQ1vgB6y/XGdxsV4twei24FYOLOV6zFC/vK/NxwM8naVzhAHvgrenxQVj+aQCKlm0K36MLQP15AIEds/NQVugntFbwOivf/lydQsIZgwYDxLQM6O/7BzvhpuBkGsAY5xc48FSrs+wLCZxcBFPGGfHZacQYl0B1qdhNg8m4yhjWXEpWD8tRwtQ7pdfPLnETSRI42AexatkxI6gq7CcTqblk/PZmJMKyBDjOoQutNpgxJlmGAJML0S2ALpM2dqmiHCGmn/5e09wORlrC9TlKOS0M9baIgIj/UBJPnkZMtrO4Df4+I32CKLnsFIVsMxxBDpWC9x5paFx7dyPOoDCrJeAA1MEkBHGaiHA7AHnECPLBF95G2efYW/o4LOAyQF67FibEZVnND5eM8WIsxcSZigY/mdu5NUrjIdVjF4LfGSYA0kpNQjeRuO3Rfw0iN+H6dMiuS6KaRZxYEOcjfM0PCviNc78CWeIMZmwwHa7wV4q87k6gzoIVt4ZZkQx4jhe9RtZhjmfshXlcU9bYiqwZ9PyFhII0AVzDeypJLQ/KuZzWQv0D4b20bdWeVhXxB8LQuuZWjKuDokhNZt8/tUXt7ert69eok34JKMXGpoPr+Hxz/75H2I30LHoIKxFWS3TH3z/s//p//h/ErHzVKxpqDUTELqshLqDU0bT9821jEqRRnd8S0ithvxqFKgUNic0wqp8ndWFaWJFKX7ItSl2CPUwGsfTf0cNydem7/vd6YsfUoqjUR9p9OZls/NGvPtDwT4+95Gwj+chWfame78jbT3vzfmtTXRPR/2MqBp+eLtaD/UU+O1+Bz3vPLV6kDuunuiuZ749k0ARvFfqlRJ21xRR3bkZgB1ZGiIF9qW55EbGA6Q1W1e0+6zjHvG7Ee8RyzixvqcGPlhvuKecn0L2gY/ZI4i651Hyk6pftUoAP2UTRSVcPSB2jQ/2cqT61iAv46zyh2fUejxNV3iHF2y0EseT6+tvlgscO9jnJQNgMcyalmzUybgxG70nDCjrB1BQUXwZS9bkAWPu3MuTRmPwWtobhawqBtDJGd1sAxzCNcYPAobYMKN4OEHMUx4cx4i+MCTIrgjHGuSPOFe2SLNxmT9lhXIyCQC+cXTGpp5AYfYADdgnPucIMPAke8T/9mdPv3jyVRKuiAljRuwnYcToO77o2DMURmVhjXvPXPaM3HiQXHVBEu2IA+AHiidpEKfsSrMuVqxuGLHWlkPOGC/X6lssFjx/gNnUFDlBtPBZa1WAdtshnh8EoUbnls+Pg4CwXIagVC5bKMxsBnxQL2UzvUA8+VQSmpRpJM40C/EYUbj301Tkw3mK1uLAL+JRIXmidRrmMkKkRSQqM+YraNuL2fjZi4sXo+gmW81TTaZwQjOrH1hKy2oGnKZUYelYahcopwTYIABcKI5LEukL0yTWfIw1tZxpKJf60Xf0M09echLiXuc9a1mvTgkgXeqmG9D+ym39QH0GUaGuVc4qgtmMY6ans9n69uaa08XQA50Qtlm5SlcoVp5j8vxBTbmWpC9X2IcTWkdNpj7G8mKZciYvnxbUrTWCSmMZOqXKknXd3xIdgT7JQLzLZs+FxaElJWy4idS/+lN8qlP4pIFPXgM7j0Ujb7uLt2Ma4k8+gOytirYiqlrsrSdvk/pqXhx1RPU20W2VhgGwoW/I9gYcfS1b/Y3/onL5VpHj4l5Seh1vX1XENjdI+ui3c+tuh7KqR4thldGVVxF1yOnI2vJX2b2vLRr90HVcWzQd6Q8Z5axPx3FQuT0yd8wJ3EnMSgZvHOIAG5ynD1AMSh5U9x5Og/Ka3vbb+h18jtFDp3Q+Tz/siPfL42j8XEPoXa6d56tTtu5InjWheHfRtgrasKdjWSUYlRKrADTqB9zbpV1u8BJhLBbQDfBjfSbeGuN5cbu6YROWJJpmo7d2/tNz3EWwB3DELkep3DrwZoGNXG3AdoAzcdaYsEZVhQWFuAz2ab92Ew8+oMw0lfu5mIw03gzYg4m8gEgTIxx18BOPw+IFbiV4+hcr3I/eAQYn5cUZZw6Mcf1nB/rxVIeEgQwRBXMEeyPV2V84vIAYs3eCsZFc2wv50hDPQcSwAyYKhce4sDNtwGpmBvKBllTc1GdbYLLNKBsE4d7DqDzTCEkEQI8THJRUQ0ChBo8Nf7P4VSBXVS7z53wKFxNW9VAC1gIK+wYZyvyJAWVQM6UzdUAu+MQogdINTYunk83i8SySnPIvir4hHORPBNDhyZwJFgh2y/glQgsuj1aJHPIDbXCKiJRfcBrAu9/66uILjB8aOptkxXy5TrJ4wX4+b9dvr2/mDMzL9sCmKIpZhIU0xyazjVrVhvKPKm/NMGKGIsgiTcpgOGBpGH6nzghMA6vdy+i92i19LrOPSqsdMUJwDqOrqIdAxAIQ+pWWCZPRui1S0vHIh8WBmxJnCKxWC6oRMplD6ye3zBQxdcQeU9rmf8SMjR3LwPnUyMfM0DqjpvTJVZmezWcYA9g4ttpaDWk9XAKqObB91GRc9m5RS6HRN/pEvOpSD5X2LMZi+bA5BbPlHK+a+B7fw593k2arJP8Ns5XQc3MsfQ+bQdFt7OGy6enYXrG2n10fn+F6a/Nv8zyCm9dztjhbvVxMW8/D3/+Oso/PVomtm3a5LZLBEe4NXZNv1nxaL9RzxFV91d4ZvJfqGJf+2J8PUt/tiu4Ruf38ecQkculdWF3eWrvNS0XJorQZAP1CftRrb4WOlqxTjw9bxNEynTKcNPBt1oB7q2zXwD1SPQ/WJlq/aNwJcNlVfVVvIPu9cxTVW8iguZw5bESULS/ZXwVgWjD2v8iXuFqsliUDq3j9MAIP3wyPE4AUXiPgVfaZUUmgPn0B6mwHeoaTwY2CnwJ2Qtw6LAD+8t4H5IHyQGksMcDvRQtAcSoH+3ELDHXiAvO4BWVrg0+WxNquQEQChSkURusoWbP7fcICU7azkc8+h30hFd8C9xTHYlctEQ7nkAv7gZy1YkHeRdokhyF30CigE45AE3gjquioDEVz6DBhygKwFglePHZglqTJtTERDCAwRUvJYkNOlSRIqmCtXRNXNFY1sIIBSwERiWU2GNxUvorDg0gmgfhIRlqLPyXDkryC6QoYiiXWnPK1JQ+U42DGWWCsX3CLa8nAel2y0xTTaJokc7ztmVGZhOOz6ZM0mKyW5+9fv8mv3rGkuwDVYz4xbTIaXcasSeDc36pKgGlXKpM464izwdjtH2NO2J0q0Ko0ntWWHoCsUqB2B6IsVk7rcGD2JVoK2lNffMFY/W06hw96pgKoW+aiUpnsgTNTB2zdxOJfjDGMB5klMhgghQuFmqVFfJrRvtLhbD5DYFz/UYsahX6gKRMYG2ep1VoGIkTWwQk0gQNzijAm9r1949LIIEWoa/GlOn/oqy3jx5DiQ9f6VN6nqQHXG3d74O79pyn7naXaW706Ec3UwU1BxFTvkSp5zy5ALndFvmFRM/BiLBi97CiPFHvL7RI3kum3pJHJqDrpd/O3KN2r0OWVyExQvxARUrlLr81vyVXZ6K9NXM+a7xP/QazPbuatMYbh4wduTKub7bDY+4xA+CU4Ps7j0436+KnHho/W9oAWPFYGn/5YeYbT+0+i/5BWT9Yr90Rtnqs63qRT5irJe8Sr2PqlIkDZwBgHirgXThIsxq0HmIY3NRExDvK8K8ri6vrtz3/+0zjhkFe2YHyiFcDahmfN+l2ysLKUFw5D70A1YFq20tGzBgGdpwcuNZTH6Dib7Gjsn5F6jaXinJ7hucFgOT4irGfFb1uLatlFVJDNeXAjqswB2+sT00J4HGbMPFzKT0ZIbxaGKxYgIy4LBMCrDKCLAFhvA+R4B2l5awoqxNmILTEZPGcUHGybgQLDEb5D1BCPfLYZxaekjHEi18sWf3ThRxRDrFYDFDP2n+FY2jJnBS0gnAXH7DXJGgA6N0P1Dq9jmSAxzy/dz4Fj1xrOSLDnOv+8evPqoTCa+LVieF5oJ1rN3HoUFqRW+fYSdZzN8sm+gE4GhP0H9LJPKbnC8gmmDZCYI5jnczPStKL6VnsHaYUGK3fT8eiWKZ4sZjt9vPDf4mEUBu+j8jZmzyKaOZMjFmIxnJ/j46SA/mggdKBeAwCWb5W8stQwWsKNEMLngGOdhKbVC4D+5xwETBKWGoeJCauTCbPE2kbHjtGiZu/IUUdWBDqTomg0mQP8jGAGyMLRvqvsF0ofYzKCeJJpkyI7Q6RkoqPKdFvk6XK+XkyC5Ao1wG+9YjZDczJYc9Kp+h8Xn9waiFcbIbgUiR6UqAsZHKW79T7zZ0qo/NfREJdrWQs2HyqhuRkWQIY9157EnSQne/O5h+f+JDUzDfBcVMPfWvt5tlPvz9nX2xG/j21RLMbn1kNSR7vWr+8Gfg+v73DKgUU3ZL6W/HBDsAm4Tux6mIUbROf69466Kpmhdxk3jB4+dEDyVoHqz8i187To4d/EE2zS+T3lzRq/UkTnWTrK5l3bv7+HFFDpx2YAPCZ3DDqh3WfF+Y6cHiCbr8SGHbJ9dMEaYU6Bj6CBUw+4h9Ldo10zcKpsPoluni1Pyy6PUlyoCegBNavAZdMtIfuCE7gJ7McQPW4zuGvjCbJYLp+fPX/56vXf/tt/p0gZv+ecXSFuoJkOoRKuY8t5jv5l1/WxMrHiFM/+LC3f4pvBSLEG4LVXPhBRCEw54vFE47s6YgrMyLgxLv0YDYBcG+tl60pOcaolE97jP7JgkIAB8SCR4aDTbrXVI045rF8N0xnrQNlKEzE0AwCwkwUAeGaqQj4zGusFPbKgGQ6wFoik6uDOcYwjD04pzEHIZRzeWgNgFBTMBj2Q4VBOkN1u0mwRxmckUlFE0pb7EAAgBV/F1n5RxFlhXRJ9cydFu8sRWCUVUdMQbSQ1Hd/wVax9VpmNoX67jAuthEmArSU/G60GQC42bB3PJ2dshkMzTtf5LWPiGAnLBeuise3YJp9TzcrkPEnX4yLlFLB5FJ3T8u7QLmYBgM5uNoGWUuHSBOP/IGsguRlKrCwG2ssoU9UNRNt5DCat6mOOXk7PlMU2QCXLLVhdjBsXXUJMhfWRW5U1K4saMGukQ38hwtzCe0cpcHcTC5qKofOlK6up2inXYD8G3GRcrvKnT56Mk2kWXFNVmjnT4ouCWSzNMqEaE1yiqiwnr+nTgYBatZVSN7etkGw25JLUH+iSFoYV5cgGEh9g+TBcDhRySv7UNbDTz11fdD8hjeh+B92hb2i+DQGrB/2et1PfI2ep7bq4Wtd17yGqs1XJ2gXIXp11/OYbiuOvuvRBOe9UQjdn/Qra1ShNa6LrSKUQPko4x+4xP/ssyMezvI+uTWuM4UPK9lBlbfj4/eFoXZwyVBqIqrF/bhuFKlDHWyQfeibdI2fAsXpEmwdU3ASDROIibRSagdEnguTRG52wi293XrAQU2PkYfSzX/wJTt/nZxfz+ROGhrUljs6ZypKxJgrS9Wo6H8eMoWuEHrgGbgbm4dh/y/adySTBt8S8rjUif3N9tVqs5fgxSvLyHfs8ytc/j6BGKPZ8lG3AaL4Q9kvEi9LPZGgA3DiNDGA34mBaNghi/5loHJUxsH80mcXh2dns+YtkyrJeNsIXOLzQJ9vmsCMQY/xJMY6m2o+fcWsxUyyeP2DavFzriCm86LETpFcC+PozRM3gNoPcmAcIluCPMntydf4iKrLvSTTMJcOg7IxvDinmASV9OnArNlU7NG9I6d1d0jwUm1Zyo62O0pqlxqXQiNK+XNi1meNAEqVg4WCHYNogFzTYAKusWAXTYnw+K7OrGU5c7HuEFs5m0zR/9+aSyZZVxr5JWFPZdD66XdyU8TWGDvBeo+/ogoF9jhaOWKtNPTDiVvhRsYMRikKzDP8bxOcABFYYgLAF42V6aDEDn5ovIJvOW0A7DNuzZIBwxLEPzAow8M9wPv0Mfy7ecqwlpmmxFOh7Gomn81A6u/vIqUi2HIYZpcGOOR8mJbjVFFNRXAWaSoo1z0AES6DDN0XwGlXgUoaZaudLULiMTewB6Q7cIoaS3V18N3qsovZ8ubF/WXsQSdFqa66+MUI1ISStN/meIpok/xfKhTfjrw2RC7hKtKriR/jcdnJ33rp+uHl7dxJ5kcfy97I+WLAtrXuEOp6+Byvz4zC6T718LfnhjprQgdzl9yQX0zw0TZKLabI0BDWPipMXP6Rd+mp6QPLtQrnrK6sd797Z8Hc1473bt++fX0j0siJv3gl+6m4YJUhRzAA86OVEOIqlxHjQa9MNqkoOUsiDinBidtLAh9PAHR66o4RrPaGtiIqdi6+fP704LYY3nIZam0vvNxsErbBLlQp8g17e9xBznBMHqWqrnDhZrdbJePLlZ59/8eKLV7+6wtsHfM3obDKO19pHPnvy7PL8glOZkvOLywxXbLn+g7Lip0+fwk1+4Qy/stRWtAC44OZm9cuf/erm+kYjsVqGew0QxHEIl31Ekl8QiBDRefNKUAE2kDZIHRd/cDa8GGeGlHolDN8DNEe3ebBYl9HT2dl4rCmHaTwVlI9ZAwuKTLBlQlYHMPYsXCvfcKsokBMHGJxccg40GE8nAFelsIeQisdUAI0C3bBbqC0x2mty9iw/u5wjuEaT5b8kc8lGwGWeSNEbZTeDZNYONADffkuoSXbvm2ZSHv03gjZVneyorClx41EBWF0CuzoebZqchZPzM3RbZCutXdYJX+fxdHx7jdM/W/Tf4pIPmEfmSfQ0GS2CEcs8QMxonbF6ALU8aMylBwCuTXxYm6ydUTEDgNScLBCNL6Kco8sw7bRUXOspOEcNUw9cD7kzC2KtSpB5gO2Vvfz6169fvcEmxEkpjqby86K7JfnT58/Z9F8GVbqqnMlkNgisT6bTL778Hu3PbrTwwdQ063T0zTev371+TSvIgEDMiOICNgMC98uniMysGGFb09XKXIw0AUTPRXKnTtpLHUuaJEJfQ68hMwDwq1rtGM5DJWjoGuYu4D6rgqtq1XdNnlPgpIFBGnA9R31quw9VdyQQaoi2aQYV8K0g2q3X7r1XCffGdw8hb5Tmp8BpaovQ9FYZAHs4enmOCbYK3GSupHMRrmR7VzfCbkgHh9rWv2PMm/bh6+ZJ1S7XSzwQ7LMg78PzPnn5HdN1p7GiA1Xdm9wnc1/8XmYPkPhQ5T4Unz3t0jxKLnDnrt73tPbEU05TclvhliRRLNBFqIeSeBNXvISDRM8bgGD0TqPjBdvp4Asjd2sQOQ7aN7dXZJrMtNR2vcLFmxF9bReTZsvzyy+//1vfJ7e5/o81QCvsFZ6dn+MPtMKAYFxfSBJv+zJO2FZ0+vrlm+X1Le7gcgQpPmfOgF0rAdKCrzj/CPGzv6QsgNH6CS0AwMS9/Sxmm33mB0D8pfkMyU2fcd1ZMGNHUI3GM4rPcbkGTcH92ksHIyFm407iWRWKjNgP1JIhbLb0kaGC0CxIuPz82fd+50vt7VmuwM2aN4AJBgAb9bC+mWN0GWnGPtEg8nMONCCJCpbMc7K4tnwhLbrlCVvtYRr2Y0zNpvla/36qhf088nRvWmqHUkVWtJss8Ws14OiFWj0uvvytF2BdUDOVt936bZoij7J0meUvV9mvk+KcswPQBpyWi6soes3O+4E2RzrPxhxGNufQMZ1+rNUF+NdjdnG+rvnOByynoCdkT8MxLYc5lmVLzZUwbB+y8gMNJfB0vkPmKgXNjHXFHGWM0ZiOslRHnmFt4r2jHYaY4pnNL588vUUabjDLqAHiYrDRSNMJWzuN6afYcbRxlrLeg02iildvXmE/FGt5mtEOeKD9+pdf/5//s/8LvRSTNc1u/+DP/MFf+At/KWKWSDMjrCGgI9sUiRTkpgIUMHsPfVrYPRf1jYva/axnAKwpLbFzjFCNXDHd5TDk3v1CuVbuHft3ja+S6gpsusNWJfp+74ZI4tP0vVcfir9f1n3CfXLeh6eft49/X7yf9/7h4f3K9R+fvh3TJ09DuenF+vGou73X06qnpknq41jHO3ka/nV0x7cveUfy4Ci/XfxwJwNqlumtvnXacSdlHVlryH3XmuH17RTmyCoil6obtjWoGXR9703sykBcLUhPsvei2KK4S1FbDDpvHodrZ1GnyJMGPrQGmu598KHbL1nDp03WxbkrbidnBwmFeLF1kZsoi5ENANgz33o5h4ScqEoMA66/+NmfvH35jk3XcQoBk+GcDXzTeDpOQHLKl9uHNoiB2C4YE+YDxKahWQA1gDFlhJg1qCyoZTSa4Vw5lOB3DirD1GAoXUO2CWtquQXjSWRMCBWU5ZMwnJvFwEoBkjRSL/BP4en3n55/fsnSUtCqNs6XvaLtJqEC8mvFKR8yZmRYaAWCcLxutPuQHIs46ApvH3be188Yw/8wpmSIqYA+EV1HGGuknxrpU+PfGjs2gA5QNfgFtdJ3ripWurB0SFx4h6663TDZhFqU7SQVLM4uBfEYxJ/Nz7hVS1FXbBYOGWOxbAqaZrYjmyZXtDCHs6VLcjFfcJmlWhyNqYWGUbkgs8wlzANOOdP67pg5FZA21eYAYDnpq304tDjlyC22GwoD4PyqzOgU2kfUDcHTrNhfIU5gY7aPumEDKfSNpQgWN87M1/DNGP54jNM/vNUX6IE0oeaC1F1oHU218I8Lfx71qDBesw4AW1OTNlqn7tS6Xi9//JOfcCAEOl6sVrPJ2b/z7/yVNTaHTgbgIlp81MHUD2jHVpsdaB/XFujVKdzdPv5nr1ROEgRoRCIAtXe1Iry0U/CkgQEa2O5QAzLcg0Qd2XXmbSZ6BHjOeX7tc6eTb9M+xN2BR65HJV3R9gB6VXJBUXJ2ve2W0zF+4Bh5ue5QJ+U2Pr4VtcWyef9tZNot56C1pHrUu/3sZn7k+8cot+J5p/H4e8nTN/Z/J0mGtJprnD6Z++Lv1qT3l8eV+1B8jqhFX7u0XlPNk9X1EtBri8t/EvtkgE8nh5qexKaoOu7At2NZc9WdOLh7hfgPzNPJX2H+XMC5eGt4Satl2eUzngRv377HKwScBjX4X4O0uMXgHqkjV+WWLTZc4okxICsCDvj0A8AB24zRQsLxtFE8ztZ4/6ec3MQQuuYKxlqyGeSfMSyPDaH5BjaX4WgtTrsdjxPOybKVu2OOJAOcSo/CjzYqD7jN8As6j8ezkPOGgaRT9rphex+wvfyINJhsCJ8qcYFhsRqsphSLqKQr0k7dYkgbVyLVXQfYMmQuj5ZRiM8L5WNXyGzQo6gQcBqjAacY7RQh7UmdRHddWy0u/AnD7otfAVJzjd9DYux6SF00n5Da5bIU2WdVHPqURxKGgBpCR/lqOgUfGEyetwDuMroNYjbKn8mNh1MNaMfo+s/+/uXiC+2tygb66/KGxcGjeLG4evqzX/0wXT+Xr1PEoQeaD2EdBjxxvLHlABzClaJrfIWQBWsJrQqxS0uqL0P2zBKEgVZlkBdbhAsMHslBi8UA3FEofzFwnBs6AVYaTU/LaSm5bBgklsWFtYBZQgMoO1nYIpQOgsGQMgmg3ZySGCORXaQu0F84f3t58XQyHtMJ1WY4IKUs+lCfsxkDiSEogV7sT0qnMKlU/60RXMDu3Ed1VsBrkWy1rEfjBxtOfuRRYVdKS5Cah+sKTbIL8Onia6pWRJ1w/PfD/i4cX/7QHE7OvrduX/xQ7v2Y51PTT7uXtmP8Wvu/sPsp/VzDwz5PP7zFoXqNEaen0x423iwK2b09oNant7v5Fo+dG79d/PAOWXMLjXuYiHHv+Q6UXlE3hN6rQ0lefEVZf1UVdLsA9VbCqlhnOfa7r/CqaMfOFW1RVWH3KvNYGU/0Jw18izWw9ShtA4b7PEbuoTyklx2qrsd9S76KwL1ABXncBVS0gKAaYFhDrTZkHuVrNoRZxJPxLH6yWmVhPI6SKQPheJTgDsJoOJhMaBnMxmJcXpJgd8aHBfoE/fX2AxTiLYPTiA20A/X4M7asycTHA+9vNosEWGMn4B6ifSKB/WnBxpH27gTEa7N+gfSEIWrNF+CWpHJVAgPbGptmEKWYJhwXxWJQjvGiUMZ64Swe2gxUL2EbMmZlgMZ7DVhLPgFW9gNlWiKmUgmzGfIXknnAyleE0rre6hUO8uQP2dGVUbjKwbuqplPloE+n7T7SOrVqrD4y4lWtneSqJa1ttRIAPWmXJFpUBwmLparN+WW49YzL2eQ6j6PVYonamYQZh9Pz2Xh0cZlMr6Pi83V5WaTPovHN1av5zetXV0usHzjynwF88HqSmXsVDlaoiaPQUDoBbR2qUjS4D5AXwtZQvwb21fZ4DzGxQnk2w0JD0md0ELImVDgPWhv7YAJY+6LsDFIyskETtVjjnSW/LR0ZJhxv/jwaw2djIawCdp3KdTAz0D7BIM2h4YbFAgvMCQ6yYAqCRQGqqWlWmqMHOYUpoAUw9dWodRNVJ1XfNHxv2g7pQ90iVHeR3bEdxTrCpnIdFKeokwY+qgaqvtz0VL9vK+xeYpsnoXoXt9+ED1kL98T4osC9eRwPP0+10NsywU9ZmXF9vZ3Q3KnEXu5be45aFsUw8tIaifdebBXrraq4GyuHl6mupsxKxI7Rfd9GrJgO/rpP3sGFPASh/ZT1Mho+Kj+csq8wX5I2NxAbjebTGJ8hNm5fgfvj79aCd5SnVd878tlfpXukuseleaaap6cJNLzbT2KT1ATcM+c+nZ7bT7SNRrA/8U4m78mtUhBhRy7HuHrEKwkNBOnZRz5GYnmHvJfnO8OxUTlO5us0Xa7eJZPJ1c3LPF+Ok6c2dG5eNYLu5NTqXEPU2BJAKRi6PwFGeZ+D6MCfEa4aMeP6DNqLJuBMLhak4krEhpSXgGsiAfvVwDyWiMA6XBkGXoL7td98qW1JgZkQapIA9M2WnWziCQiN5mE8AwRKthJfIFAinPBi0dpQDUdjA8BQTkM2F4DVgjkRa2GvpgtCGJ6VxUwLALRWFTCKJkCfpOv9TSZDnJo9wO8fsdjhXjprPXbbreDUXym6aa/egJsN7k12CTXPmqvaT3ESXD+IjoqWsTi89gVWkVgVZxSdJR2Q4UWzGkWA+vl4gveTxuUF43VG8Su2z8FjKyq+CMa/mk7Ho8v3UfQ+HD1xtc3YCFaTLYzb0+4qlrkb2KMR865ijYDt10OrA9Yx/mRyMOgPxMcaAO5jbJALS8BJyFHNeIIhK95fMGSaCElJU/MWtANTQtoqlgF+rDkN3qsFaFEKxPcowdcfY2ayXmjFAhNROWYA7OJFka2Xt+n79zccMeFUkq4z2SK2KW3KYnS5t2EBycto86MnUqdC91lr2bEgSbvbGcVOSkXQ/jK63SLaZMNi2r/7lehIS0GdMndxriwfR28Ed3urd/EeGmfTaR2/XPvzHytn51tX2vLq7pd4LH8/7/5wm3M7Zj8Hl+pyufBj/BoO5+n3orvVZae+VRduHq0qwCukebFt5VAbWjuqQetcvlRb1Pe4safeSec+HS9XZFdPkkBb5e0SVWyqRcBbpN5Ni42X1hHcLaSDZDfKyWEZ9Wtn10byI8vfZX66f3wNqNU2Dfb45Z1K6NJA9Tjb68i1xt2axefTVY7iWpwFt+tOYC9KJwGEu6Qbuoq5lWe4UUzk5KEBWvb0vHp3c3X19rNnLybzOd7kEy42lMEmYHA11uGyeGpoz38NoONtomFbQflqS3gNPwP7KgCNGJoKACCKN74ieHVrRx/hah28peFX/EaQRUJYXkoCwpYsFtUINkt9wZfC9Cz0ZHdJ4U3z6NCIL+tOR9GYKYgl48CkcsLvmKOAbYyZ+QxQvuA7vK14REAp/IM7YmMZaDZDMQBHziADoQI+BUkpofnVEYEwHN8qGehJbgFHk7jSJeHNZUmb20cLoS+krEq2n0nBfEqvJFOIS6sXcNQBbbMQY0ydzy+e01w3b9M8TWgB2dks9U3xd8JPC91q6/ySo541un4RlJdkxGTCbktYA4IrmPYYEqoHsm+KB9lrSgb1aLkthh5yoWN32BswHA1yr0ZGAqmd+R/usQlH4+oICSVDh5oZ98daBOpbz5BTkTROx+LK87P5Odv/pytmokY521LFtPOYwf58nbPDLB2ZfDqUYhzOZjOAPtVhCiJlpiljU1fNVilHwrIPmQd0LcpEbyabFLYNOSSQiaWEOmBkwz8cj+H0O5RV9s7SSeNynzvZTrddGpAW7QnvSvyWxzXdgEp+2y4nu71mJTq39kAqWv+rzm/RSveuD1FZibD9mLkYT4wmeFCeqhIHDIBeNmaRNKUp0I5xyY22msAmW7/83TS1OMNtRMfHtw6H53U/a27MY3iujeR1aGukoTWiXFMd+d0x9NfDYThlD4Ot6BY3PS1D2nGLy71u2m2hluJJNdn8tr5XMS5zq74PwNPvA374SNb7R2LqZ+UwU9fP1Y7eRfb22L9L98b+6wzkZQCXOUBGKF/XkXybEIxVEySer61CuFFGA5ACVxozF7QHQE//yT/9B//8D//V//A/+A9+53d+73axSMJpPF4nUxAYg/AC31pVSoDRXxzvBfZfBBwZG72DIbgQuGlgTe4ZOgMWz21ZCTiac6YwQ++TyQy3jnGRLYUggYEAP5XPML1sEPjiaFSmOjZqzNg+OzmuxzzH8TRjR0mAaswINEBVPuWAfvaa5wyBRGfW5mccD7tKWZ6Qsg0OOL0I2WvojJ1+WBvA/jayJoIVu+GHMQBUJwOEwTlQU4uSVbAOPM5YlKwVsGiHthEkFXKlSk6B0jOR9MxdhTp9mv5JeqTL4+xaU1IYmtGtZHWXxLdLbYHAqgKfWGV6ps6fl5OzeZ5d3bxf6ERkTgQLpikzIdmsZIFH8h58z7nCjLdPZ4tofDvS2WdgcNpWPvts6MRYulo0XEVRPlrhfMUNTaR12cB7ScSu/1gbOG1RoOYc6Cc4lbGQ2OnSDlBWZ6IDYFmeXb8NVqtXWHO2woRNQqkB9uLT8ydPRsErdQyrKbAddK+jzLSut7BjzrAh1vIyY6kBKwLwKTJ7kvuf/vEv/vO//XeeXD77we98Dw4X0x9gD+Sj1yw0xxhAQ0n0OeJk2TdoyCyNRn3uzeBuG51DW+uVlCYahfau5asZQuNn8d+Z1kwHPlT3rnfCbrlecRuOTlBLcjJQi52r/VbfITh4237zt2N8Ju73wo9x4XYu/w15HzldpatW8xvPE+I+/D02HcE2Zz/Gr2NHZi/Kz+VF18GeetXJD/nt96IDUg0rVg9X/QazethrxL13Xb1a/bZibE+lSOwJHVbaQ1P5ErrHzEpoVg1tlcdk63MiDhgAW1nufOOEceLtMiG2T6f+C6s78y6zT/P+2yz7p6nRLqn6e1EX9XcwznWze3Y296jyeZw6Xaku865qeSMqaiNeI2IVpferkgHLcr1g/J8tdP70T/74lz//2d/+z/9v42QC0p9N56vsLYAaNL9apfOz+dnFVKPtbPnCcUvsxa8LPoL9Nt4s/CTO+o8XEOP3cvt4+fLV1buv2QtUh4JhbADLIeSYYLl2KIcZD0TpzS9rQw7nwPiMgeexfEQyLRRlKShzCeBE8D8AVEs68/FEg8mATIbvcem5/Or5+AIXn3kcrXUEGLC/nAWRoP8oYBd59q8HMGLVMMZ8GcV5MgdfMmQNR8kje8T9lEg5uvRdNQpf/KsTLLX+aCIr0jr+cb4pjR8+FeV+NVtSmRROFP20mg0j3xyysX0nltgYB5ppNJra+ggOVGBEnPbDV94MMVA74+TjL8vyKXsFqfHZ8VNTJyNcuQDolE8T4PPDKo+U7YRA3MzIsISDdsA44x/Ymr382XBV20Bp/geDUQJwthquSHBEFGZ0OJ5gefsnP/3jUXzFmg4algkAbEJ2DPrq+3+WUya0PoD2iZgo0HyOrUChlUfPP/+cfhWHE+YTmC6YTgmMfvgvV8sbtv2Rxfn69av/6u9/zYkVyZTdSW//+l/9H/3Nv/Hfg1G2ZlNXXfRaaswSAtC/FCUgoXrZ5TRX3eirSuCrleRRDQ4+BJNjZanrNljI7xChX3e1tn//nammq9e3tHbWIvaD5NpDQT2SW5fFdTZef8oWg2E3O6UOy1RTWUXqm67vivtdDQCNQnV5/HcVpThX3EGpXPam5hv67ai2je6X2069m3Xo7Mu75fXl0QBUc/nhJvJ+gXZ978dvN7fP3w/v0n2o+7YMrqXa8R9KonuUc4/+4PdMhxmcHo6VZidX86gN4rN5RN3Yf3MPG8Ji5uYGHVtZAy5F3F2cQsiA/wMzACydzC9XRby4xeN+fv1+mWc3AOzXozd4W3OaL1gZKP3k2dnZ+dxWbcbz0XQym+bhK20SqaW9NmpjpciTmwF9IBYokPW22sElv3rLMbAaSJbXt8iB3PgHYTYQxiYARI5AjRpDxiV/lIJFmUWIGbBnr/nwQq7qWBWsHSBnRCqbR8JirBWmZbRm05jbcp4kv/Pnvze7PI8BmvgRjTgJGBrGpmcabw5nmC6G8PlEPrahBwQiJ6VLeHa81LfUggobjepekZZXAV2Vjt2N9+lyGRP6Cd/5Z17qAwWNfUsEF6siKuGaL5qDKmkhA0PmOjn4+VeXl59PtY5a7jy4aU2KFCS8DqNpni4NZ6/y9Wpy+Sq8fobfP51DGwmh/bBgAyCdhaCzHTiUjYSUVdnsixSsn7FgowzfikoLNHjEAqZmioLT02g6dljCEsSPiLkIWr0Y4Y1PA7NTkFqceRgZFYLmsMa7LL4Jk4VmepASfzNtUcQwv2YVsBqff/kC5D8e0/rqP4zrr1freBJmV/LwYX4gCdl46pJKYzbqdOnRy/Hsdn1NZYvJ9IxDLFarb3AEoqOqxeXipEtdeKO/pomdlaVHSA3qsIkLQmzzcoq2nL0fDcXOU9+bwUtoBPHiWjP/neW76li2RgCfyYOE/fehY9iOObag+7xX/bJ2+EgJnYry8xwKH/17p7EFHrRuvsP7w4FyXb2OrN1+njva26nA/rw7xL23dRetBOfLeqqiKd7CFqX73qesP4VsDyNnVQHJtXv5cS5sldmak2/y8Dp7xc1dDYCGzx0DezXV8KyojuxMTfZT4KSBkwaGa8B/gQzKdfjB7KSoX04u0QCPXqkCSdrZkw3d89HNzYIh1+lkwoFOeOMIc+N3kaYalQeuCbzzYmbpKAOyBuDk8gFDoT2iVIQAlaEqjvmVcz7ADgSasM5UVErDU0Qmgg25gvc0jaB8OHNo0oCxebx9GE4uLsaMUOPQk2lTTsHMmM2F+AUH3gWjW/YZSovVaLUC3AM6J5MVw/3IiNuPNpmRYEBNQCcDzsqFOYIEBOTlo/FouaHIq4kvkwybScIjilVpuymc8pq4ndsmfjsgzo94wV2/0RtZqhv3w62CFUGy+099ZQlQRdbPMhPAhAzgXnuhsiY2YMEF57vhFT8rc7ZdXWaLr86nv/V6tKALoE0sAEwxZlWYBgCOM5cyDsuU4xzUIjEbM00SnaBcMMiOP752Y8W6w6jCr2i8zOWyJbMQFcONmQDC+jaDUNzUXHypg9DHcOnhFxLDg10+ObaNhen0iFyHSXNhUmh1OJt7clQF4ohLyW5SazoYnkC4nVEMuF8nNuAxtoDbeHa2XK8Xy8V0PFnc3mBIsM0sRUFjiBAVqbPoc3OpA210a2H7qNTtk/rhDYMPFNoR+wOV+q0s5qO20+NrzPXMb1cl29L6L1893e6CjqDr6+5zo0/d78ZtUo8NuZLqXO7OSUkZhy5HuIeqknOPAbC3rLbHP3MC8OzwD+4UwjE/KKXL29S3pt9v2e9P7RTnYOSDWm8HSzuOwNX3aAn3jgf4Evj69MM+zYcM98lQxQ+ul5P5aL3dv6o9YzDHMnbwyo3cuM9jOfga6PP47+VZP4wNQRNhz2tz16S7QPUwC/sK6gBNbdyTl4e2UGRd5Xhynaar9ZphYHwwANxAc6EoABhEDNozzkokLjyMIwvAAeGxHbAeYCGnHYaBQe4CVbUMoDWGexmMp8B1EN2C+YLsCbgMKnlyQGfCqGE0CCt3DG3hQ2QxejoP/upXf/7J7E0epZPwMhEcxFNnFcfnWvubMQGwfHb5mdaS5uV4wjFe88nsUktPRxxGe21rDBhJFlP2EdJ4v8FH7hESmwHHdJeoaYrxWwluZ0BC7qvO9GY1ctG0FwHXe3263TA4+bPduOreNcVWKT2U+6IF5Kt0WLkgn03YpdmvKeITrUUXqJm2YNCf6RHyYDvRZLfMgORs7okbf5DS0FnxjvbN41/Hk3cs6cXukgWG9RXkjK7H+M+rsbAcwpn2+Y+WTBDQHZJ3GtoPkjQcayPZsmATfiZ98uhtOFqFpdYV0E1wuLJfa2TSkg/Ol3OdUdYAi5Xlk4R8ysa2TqPRinhmBJgrIJJ1JBQM3DfgzgHAtl8Ta13owtGvmVNgkoHOEAZzjACMQK1ESdhedp2tsT84GACG+K3RBeh7EoYmx/qgynKAQkcSSP1ZnZMvp1SnSFPtToRLIROkh5vTOLgsD/HpChzM1M1E9b3DH0Kgbh7D3/O+bO336nA+vhxtPn7q3cK+nD6HXgn7fnfsF9M8wjt2XPQ5u7Art7cUiHae/TaLVkxfXRzhfu3tz+seiP0cVIrrwNvdeHd9i+ZRofBXx21n0HtNte+89su5k0XF7F59jCs6eeXU8+3VK2NPDiXxuthjAFRs7/Tl1OJ/GpuuWvV2l13hd+/vJNgp00kDJw3cUwOtJ3Englv3pO8EhGiVIKQCGCYE+BHsEggjBChkqB6wtLgFg5HOcgCcqnXcKtQMq+JeD04ClLFruxASswAaNw8Zj8cxW4xgLiPBCoEfw7y4e3PwL4P6ipxw2BaD8ioeWbAQ+BRr0iwvdoKlwZUywPQgtCh59+xy8f3Lr9LRKsKnIwRmMtK8GMcXkykIEbskm7Cyk/NmkQ77oLw9O2clALsOreROxN6T2t2I0hWSGQAC1ci/YnSLPqQHsz5AnVyqOpL1XKqk/ev4qXFpPRkfIXoLbyKVxK++ukpzUyw0lKpMU2ouhJByiZOb2zHDTfsFBRFzAnky+nwcfVGOOKQMmI8ix0BjHQkHNuf3LkxWWQqKHuMBRjOaExA9JmMqAEAd4pTl2FMMOF0+RBSP2ulXtK31ABGofyG6OoS7I5IeyScmivz11VLWUGz9SWuFiY6e5o8MfILyE5UNFauOJ8zgID4J65TpADb/ZG4LOYrl+jbLlzrWLeR8izHnCXAMwph1xEwX4AVkZoDK5I8uIg1Kqu2LGEvxYt29q4IX/SGDHVJ9yOJPZX0yGmh67LeoSzQy7zxZ3DZJUnA7eVvtHvq/T+23ytwuwe52xeogIWpH2B0iyYe4e04CPiTFDsOtOQG/bP3w7uhxJ2v37a4Gd+9bufoJ3M+UfuIRxGRz4RaL3oijrLdeLk2C00mPRb7Ptm44tAJHS9hTeovxHSPuVouqsL36OSDQkfU6oLd7SDJIA/fgf2wf7tNbowH3ANlT0ker+K2RBiPse/Icqw29nj2QjZASaAgcB0YXHAZ049dtcEsYCwd8llSyLSYkDImyLbyGXXkV88IigNtExF6Q2lOdZAF1gCOsTR9iqHFZiGFMony5WV3LiCz2warkX85ZrZJYBDa7oNKRLHonC2L9uXAdw81wYId+HIby52X6eV68WWWcTIvDChm1T38++joYzdJ1TJHxJE4xM4Ch4Zj96UvA52gasu1PsLBXH4CPwjBXalxHnSWurQGQChEYtjrZV68n1ylMtTsfTqNEBq53KVlKrcmU27t2br0UBfen+sSO/y69e5X6dDVPKMniPv10qdmKFXgOOFpNxxlrc1bMH/6Ux8A5+76y6jaK3pAhCd5PLq+jGeunl6P8Gcc2h+t5yNzLOgF2A7Px0hnj9FNmhGhouhH9IdfurHDUFqsYGjh/LTUTQPHqVDh0MeZP2FC9KGkN/mSEonx1GajA8GESfBGNXgTBr0hN4hgR6XGM1WtuChTP8mNx1JEORfGSbWkxLNSBmcmw31ezQTTQPwqejeP87PwZFgJGC6pbLrEYg/GETqL+yX9XOjLaK8x1Aqf5LR3qRt3dRUpnjsgidOv1Bz/jdtg1XpV1O6m5a9N08PYKbzIS2Dz1FltJi4+AnRTkxPTp7x/Ws8xDa/K0373NW+6eBQ3n05bBL7qtWz/1PuHhElalWHc7NlcvvWtp1yv2VuNhNdCn7f09vBKw6Z3bAjd1bGrTi3K3M3LXw7JFV8/iNmV1UGxFlTtPVpO4JRuxB58x1cq9ZRoeDxKAr/vnhHA8VVj/hba2FbYbsXvvsWrKgmZ/KV6mU/CkgZMGdjTgHkH/c4eg7/bAk1c/lfW34Iued97NVpg+ZAYAlDiMVXgoZXRWI8AFA6iGjcmhUX+gHDiP8V450mjwVS4ZpAm2aeN+4CPWA0AK5gA13YO8hfugoAhwIcCbe/O1EBqXTIzcI4CgJ9ARDxU2F2KIF3zHPbZB/Ksi+hW4rQwSfDnEBzdyAciAs4lhri1cdMATsFNu34BD3MLZ6icIMDYEB0Vqbv1CbaqsxCNE0D4RSDLpjspK+I5L6aKo/m1TuMTujFA6PTfJTWCbyUPcOUG2OHlRkl4aoMWkXOpK0DShtqP5USfD/OwDWq7lfYXctHV2/uzJ7zz77LeSyeU0mc+0c1DM6L/sKTRvrcHycOZcyGFYmy5B2zCZoxPGdF5AjNcQban5I8a8uJdZKMcfaBSypjA9oX0tEVbhdDB2iVKPkxWhVsH7X13PqRMzQ93DepAWjejMY80HULSmbyDUIgEqhc1AYL1erle3U7Y7YqUJRKxJwCTV2gCMSdajq+XHEy0mtg6gJ6T7ciVW/VYtqU5TfbqGdZ/duavYASTd+R8qY2/1uosdFntn4YaxP1EdoQHXwK5FvnvtoheZlKGPuo513BFK6iQdoK37FdUUIDacBPyqU4y7RjbcGwZmXzZ3m4CUV6uvia2rxgvYpeurVvEm7Ohdkk/Q8NkO2OuyivLDPlWfBenT7A87Do7mgD3XpxPLvJXXWWh76fdL5Y+L7Ke8f6qvw61a7GXt56oI71HfvUVVie7nta8nbHHokWQIh0Ea6OG/JQPIlUd1COVWtt2bDj3vkmx2Kmg/x83T5rzPOyFKk6t5KCnB24VAMMo9xYTyZ0JJyXsD33Lr4EnHZQb8JNzMEC4LLAWpibqNGIvPL4SuR0+CPNE2j8A4VuUabiQjXhjwFtznEuAF7D9jM5hRcqVte/AhAvSxxQzpOlEKYKahfC7wFpdC2TPAleCUZhm+xms7yF5wHHGcfS/KPwuDG60jBeXjihSN18V6HD2LcD6PWdzJSDDyYIQwNsyq04h9XaJgHpS2BY3mN2Rh2INIHbkMxEkVGvO1MoGM3Fu80VZkfLlelJnvqWpWXY5RpUwy6h+XMalImi+SlM99NaRN8m6AXwS1jr9ywDE3QpOn9N91Ln8tZ1VMJQ9pjciODvWia2KB/CShNwPXUpIWYdMM0HEGGAC9yJ9KP8nLv/Lf/jNffJa//vnLpFhc3Z7/8Oc3L6+u89V8nKw5P4B1AVE4Tot0ueaQhsV7GrzgULazVc6GP4B+rRpnnTA+Y+zWL9AeYlVOeaAo3vx8bCogudYi9OJSwD5gr1FKN8uAPVujtaaskEoyk4D42qtWloFWFZfJeKzRe6aqmBHQWc/qf/QwziGwLik7hp45GScXZ2eYuO50YRazUE9MSaq6XszZYSgIrqUj5VSHhofd6mNHiyKw6E2K+SuX8WtLQmu6oKmYbMgtQckNA4vp/PDfkI4lMQPyidnueGSrAMfHCdpKVET7fdWO8TP60g569/qZHyG8XwZfWr/wRs9+5LcovGmjpmmbwHY1+jSwTTX0br+2h3Dp1XzTUwlQl+YBsLC9y/QO52qvGRhSbq/kTm9NcRWvIHq1GzWklA1NUwX9Gj/SGoBNaV6I4lyVvLi+4IbQVXanyk0dyL+TdEwpfaV/p+J39POdqttvRGU+SgP6T5ivZQmzeTiV0qbcTvdzO+gntKRXJnQCFALOGokV0lcKJ2nZCCzeP3LTMLwIagNIA4sYnycTGMud9MpBTTFDvxovkJ8FnAGOEIIwYZWxqWi2AP1n+RpgB6ZK15zDCiHpEkEyAPMYilWkBNKIMZdcN7TpS5Ct4+h9NHkXR2d4HcW4fkPNeL7e+BgpDPDj/616aHgY2AOHcFXgrBKkGknGJCAOi0PsqQo/MirEXlrioLAr14U2ny7ViDeR1Q+N1yMI+jR+uMpmxKZnj8/eoNR3r8tl96SsuZGgWIA+YnPx7SFK1KQENSV2nwLunhUVkzJ9p3uNrUcXk+dy8kk5XXfJYWEc7zYqxuzTfzaej6LzdHEDMGdPTu34RIdRMwj1q4nzdYgRp6bHA40BfhoLnM2GTZIE1uUINvJNsokj+Rdl2eLd1UtW7xKTYGdwjDFdi42fYnB/grS0qDHSMD8dGMsgSiZluJIxaqVgDsghiPmDcvRf/D/+7n/5X/6/6THMZc3PzijmD37/D/6bf+2vYaHgU5QtV2wKZP2pamgpQarSt4X04ZrHKaiKdOk1TUXe5Nuk1iHHU7reQ1QTP8a3L8BHFOMxqnbiudGA38xNr9wkf9ohr19KdquL4uonT9L7Yd1/mItSnXB3Kq7JKjYf0gAwZW1EdnK4SC/MS3jrcpX187pw89mm38q/udnYppu4TajXDtuQVKE+PmxWruthR2rvzW1Xn1Uljvky8LK/Xn06GVKMr/n78BlS1kPRPIBWB4vSN/Z/rK58PfuF+3wamr6nSo+dpYGA+ebWfTqG7qH0me+G8YvAp1+vnXz0Rig60NGpYHVNcQi8MzQfsg0kQ8Cgcpxq1ineIAYF9clK3xUwPhhdCKcB76A0/eTaoYVFpQzijtIlMC6/vvrV4vY2xe1fe8fDEgf8NMdzW8aGML4AnywPTTpwEaUvOZLk7OiOU/ao4GQB7p6G2WdRdA2S03pQAXp2H8IbSFYCJ82SnZPItAZVQ7cMYHMAGGuFx0BLXrCMGNc6EvwXYLRyFKxgnt3LAmlU6WLs07VO9VMjCi6XbMF9H47YKMTZg9r7cm3vGtQq0ORBAI+5cavl3LCWlNZJqihy1JlM1c2N1Uej/xZw4+fkIQZfeazAqzLkoLTVaPLy7dssTVbh2WiS3qS3ONNjfmVs0zMqF+VyFYQpizHGk/VS6zFYpY2JxlZBtqsou/0HxTTCYGN4X/t0gtexGmXARe8yulJ+KeivEXsMPbaHzbEakOBnP/31n/7sGw54iAH/dEj7RNIvvv/Zb/3u72CWUgucwOgP6lEcQCC2qoo2OCo0xi8TVZZARNqb19cyC1ioAPfo5XKJXTH66//d/1ZZ3nLmhBkhjbJMR3xUarNyXKJTrIXNaDG1xa9Nn+7FRPnNZdHNXRPoiW7SNwH//UAsrIfndVw0m4RFxsyS3XvC7WPVvIsaUdoxTdInHnANMuRXYwjNgcoO+L32Ofjt64d9muHhrTZyLe23t8fo/mU5Zj4fP+wVNSi4q/lG7Gq0yPq9e0fx+DK/90JsfQ8aPzyoSCPa6RsUWz1f+x6zDVVTUN/agIagCjRZxf9hDYB9Eu+K4d83qt5EuigYOp7us4lsMty1xE1Bp9BJAycNtDSw84TxnG0eviateiUqc0PQcIKqejpdSJ/goJitXbQgFyCEezXIKJM7D0AJrxO+hcNZ3ClSfC2IlNONXs0OSvL+lZe05gNCjn9i7FbbLIqXDvli+F/j/9gYq9Xy9mb5/u1Vhr0AkmMvF5acMkKvsWUR4YvNXjFmBQisgd/IDoFQvqwP7Aj+2G4+L3BhSt6Mwilbfto6A202A/pHKHKI1Ti6fPGEXR0paISrCSPPc0jYP1JDy1qSICNDZobqoDrqqnTjbjYR0tImrg7VmZrcdUI7oknZhWpi2/DxqD5YsC588y2tV8XzTbz9Fgr5WrR8aLCpcPKJgu///u8//+oiWyZsAvTudfDrn/3kp3/0CywxWo12gAlzQaNyqh2fSm0LxEQBOfl50xQN4/UcLcYa4Tiah7NsxMoSPLVSDIA1kwJBuig5YILyaSdG/eGoroIYmIBFsQK7UxAEuWYgaF+QfHm5nNPElE3PY4hf/bnArZ/SaHMWLpvrms1jyBTUnJammSZTTjagkjaBJBujnIxn+AJdvX/FkRfJdLpeLjF6N02iAuhXiuCDf2YWWMCILKUiN7X5EVX8A38dKEEyOkm3yyXSrvp7O/V0993WgOsV39I6Nj2+7rs8wQrWtw9braa0h2W74bZVwJ5dgFz1tqiNSV88iSS16Tclb4UcbfMD0KRt2UOurCaNQFMEBbnUhqZJ8um98JZt6sUfG+zlc+/ReidJH3+nmcrutL0UjpX8jvQD6tUn87El9vFpW/btmL6y2pTtXtemAbGpiw2oe1+5ffHOHeT+nPt01VduX3wfH9ffmie6ebIFSuBVP3dNfB9/42AoTW45vDuB6YvlajKeCuDLpRoItWY8ncFebAPGRLP1LRBcZWhgFZeLc4Is4DSPbRAYPj+ksFRUR0EJg8sNQ3II3wcjoBR4izOlyMroPJyBgmA3yy6+chjiP2XjBy5Up5WerDyYBuFZvE6C27C8zMO3MJlMbudaACAnbwaG2RXG7BJqEMl+yFnpW1kjs/msZOkqxY2j6dkUe4DdHvFfV+EFHvwSz1Tm9IVs/rV951Jcu2SfbdI2IcfssOrRwGEiX5Dd8FaRO4mkHWa+S0SOiqfTiXhKRqOzD+NJw9EiYPBYg/Vg6vhVQhue/ypIRhfh0+Xtev5zRtI5JlgLh7ETmUli/QCdiKOXg2DJ2uCCSaEgYeIHAxNcPgaXj1gNnDIZhFHG6V3heLwORlfraRombPsk334mgCAWsufBZ+SevsNyDrKfyW6M4IwQKwpEIFbtcj6AfIm0LgBbYY2DGssAmPRBhpCiZehiFdzCLMtuOL8iKOYFx5PZ+XOYoHj7MBnG9j94EzH/oLXv6tvq8/WlUKUoU46Lb9KbwMj2cQ80C324TYyJy2q8N1zqYv3vuh8qru9dUdE3RW9zdKuGoNmOrjLd7avjje0xon24/Pd8O8Yjv1fQcd7/u+xL4gp7PHl4vXVefRrz29QPdzI5GNldSlfDH9GvXKn2k9CunS+zH65E7cnVrohrERe/aS/r0pX47ofPdWNeAA+EwTZlWdmU1TxGbSGJsZ5WttfYtGM6s7s3bZ308WYAXCX57OobtXid3y5Dk81n0UR2ZjxFnjRwjAYeqzftf76PkfAxaJ10++vuvysHyADKAD/BGHSErw7YaDqZgaoYE2Ur9jwHRbGQVh4WQlxhXKSgesA8GCkuVmApKw8uWrfJsb4M3Au4a6xU4J9LPhYahC1SBunBg+y5wlaebCUK1iNe1oWN9zMeDz3C5AzvyhRh6Ba4hinAYHT2+fn5X3jyxaR4X2aXRXAZB+fTeBnm1+OIlb4Xk3DCPv9IMdZZAOWTJ5fTGegwZIFyMgnSDPwHF5a1IgPmAYQUij2DCYDriVCivewkb0u71KsVZ4rdxG5ClqCPjqgmrR04jrqdvxXjekoruhXhCq6ot6XY1LtmVg+uySLT3A/D7cBofHWEyzVDU6Tj8Gw2fn4+XqxWt2zqg12XZToBLGCT1rg4G18uYhqDVQEksc2OOoAYaC5Azjda/43umJ/hoGDZlVr2USmTZeN48ODlRUPyRx51Gw3ta2KITYE00SRjM80W/IMCgwRMosXqzArJ2Yey8AqT+xACyQbALOVMOM4OowysQXaJWi9ZTMK6FCD/9fvrxeKWCs5mk5vrxWSiKQKnC9PERkFSq4yT6trWYx1r6YdoGuLjA06cpoBdBgjVk+aindAuzGdPHXa5nu5PGvhoGmi6dLsHP5pMTZn9JQwg6czsauGS9Pjt2QXIJ/V59cVDw5op5xf1EiKxry4vWEcpeZuopt3Dv8ncBLo4N4l3CHTbr3dgZFkelhs/Z1zD7U5XurMLXV6/HsJU/MT0jBb4lJ9CuF3rdkyfnEMoO2gGa8ZvZT/cJ0+7LfooP3x88/Dp2bSbJqYRxu0P4483dD6Fylj/V17CwlNAYTZ5xBmD8XHB/ZKBUsJaQct4Lgj6/ILx2bWomApgTBQwBpK28VktuwSPFXOZB4A2Bohz7AHwG2EiNGmD/cA2L3hl4+OhVbz45ptfNklMFgDGuUBmwoHClMA9w4cAySw/jy+/uijH+XmRL/EDmSXFOEhW6cUkmUUTMCSjvxoZxvDAM+TJ92bPnp+PMlb7LjmySg+TiqYQ9pCZytLAgim/J38R5JGwmEBmyVAsdx2X1NVc1U7/EO6QO09T96YVnybZBbaYwM2naJgr4HusVty20rtvYnu327zEbkndGepYV2OBWxey50smIBEO2Dp+Ji/IX90PcC3QL+Cskb8kZuclRtaT9YRGOgN1BwtOChtHdJM1S2hB1OUyTlZJshoV0xSoLhtA60uwLulaOHGZ0z5j7Np9B1cxvG1kQeBzpu4jGvUOnHOsO0lWBve1JxGtqL4kUTUzwB3797MVqYwBbeCjfqQZJiSgRHVD+jZzFTIwb5ltGBUTrA88xCg0mXIgNFScbqF+cXH+5NXi14vFMgH9w0IKEq9KcVBWGrPuQ4p32Y0ZK9UKNHqDKbDOU39v5TIGXgxBMu2/mjekl085hnoeWxE7Be3c7heAVP/t2sjTmWtbSyJpx3Rm7Ix0T20fBxe/X5422z5u+8tq8xkec6yEbc6+/tupTvLDpWy3+mH6pqT6iWgiBgUG5+prkfqBstKa3r9dCydJWz/3aU23csb/nXWltGP26yF/rvRqL77q5WA5VJeHnwHoUozT2vY7xsWZIKePR9SAflz7dN0X/4jinFh/azRA79h+ZI+TXHld36teOsCaLM+F10vmAXB+ACNpleTsbGZ7ICbr7DZOxp9/8dWo+P8J7gG08ZDQIL62ZRGqYr4g0pFhjOFiSOB6DQsKwQtDMwJgpiLVsOoaxFUub3WyqpCZRpBlIwicCV/JXxwbACgmg0DwjwBg8mYSL2bJPNJCXrb8DxK8sxmBZqNPHEm07QwDwCxLRRBgH5MU5Vq2xWi5Xk+nOok4ZuMZUCJwX/vHzynMaUzQUcBRRZtSO9WqVLtEWVG4r07ymrpupCb7JuH+IZN2h00lzV3L66zMDjPR6H8p3x+1O+mAeXZWStcG3CdrNv+ZjtdplI3B5liJbLxDI46n07PwzbssvaLDRPy6Bdqf1RpMDcB4v9rfFuFy6yaW5NVjzUYKRqHO5NK0At0Jw0ENqrkjSYMNIjuBfgsDlhYz60TPwZbQ2cCcF5eXHAKMsco5XzGWKvlTuQDBSVtBMTeRagbCPRN5mmtTIf7iYElPxRfIjFq6ijN9rfpIJDGtbGSsg3bPRxNlKRToxOSuylMTPug34qiEvstJW6c64iauCdTp35JvJ/e+an9LKvIpiPlt7QQfVHcDlATJ8T1yN8dDGQA13/ilJ7kLus+awNeiR+pHHw77dpUfPpyzi8K3246wR7tY7cT53PxSdsge6bYpvVPPvfbuYGmG18hvIz88uKhPmrDRM1L64eFC+6sChmu1j38fh774Pj7Edz21Izx6dwDG3v2P6X3GRr0QIIQPhJzpOTR3HP7kxz/5B//wH8/n8ydnvx3FnKL7nqWQl88vf/STH4UJO30yILtm7/ZSXtwMrkZZsdLIqp2lhDlBFEO8oCrVgJFWymGInsN+V+s0Ze0mPtYJQ7AcuiT4yOrM+I0OAcif4kYE0IqCsYZuUT67/oeTZHUxD1+cTxnZZdSZc4gBaCWrOQuwWjQVhANOYgoA/vBkmj6bfxadncU5IDRlxiJMs5sgnY1wE2dMOcIMKbQsVTMMiKdhWZOyDKrx+88kc9dVEXYlVXFbo/XGVc0hfagg93w50q25ghbHLT5KhVfdWBtiVwD3LomzERzlhmI3ZPu9EKn+5ufeobOx/yquVSwRKpHGlO1E42GOyR2niBmKH0XLixfj8eyr9eoiWwVZejOeX61S9tv5QTQL37y/+tXXVzQ9thv5NfaPqQdSxzyUJSEDzlzH5NXPmDz2KF5AfNBH5McDimb3Hqsutyw6d1k0JaDhfM6q09qTcv0kyD6Pp9+Qgx7I21QTUdiF2SrLF3nBHJfG8VkhzKoWMcXvLYzX16xR1pQCimFjKoTKl0/C4jNmvYhZrpb0LGC8m/5wujFNNGpEqzaeZ+P9KqBSYKUu764J+iRN5P0CfnNtjUe6skxkV0K7cPcW0jvELgg88iqySrIEv4p3e7tuMd170/eG/JDz5H59fWE/hd/N/frvk9yvxbcy3O7E/gPgVamtn/vopHlGvBLuEvTO4XGvNZ/JQxkA7iF2T3Pz6RfUFXaK7Xv+u3Kc4k4aOGngETXQ82bbV+Ke51cPuEu2T1AQBzJlKWCalCSZ/NGPf/RP/8k/BfSE5Q9ByqP4nUZUo/DJ08vf/f3f1QitEHjJ3p048+CqzR7r4wl7bMbJRKOn2nClGpsVatIF5ATGnV2wyfpold+8XWejFUSSg4sB2hyncN7KlK9FxCMdNIyHR8bG7gzl58lzcD8GADMDoGm5d2AhsGghYuvSWRmNkXyMA0iwnExnl5dn8/NZWE44dqpYnbGNo/aPp2Z4nEccBibXJcrkh1ty2btOAYVMG106hVYEveldeRS3jyfJA/lZ2X1FuBpUn71ESvBL28+yYWNVNhW5KKtPhW9lQLG8V7vo0IDYVHiOjWcX8fnFtCyfFjkrcZfh5E3BTqCr32U3/SD/eZBfMCeg8X5cVOScQ0atzRXM10IRWWXMQWFfcpYzB4mxgAOpsS1ZQyJPLU0TaOwep3/i5a6jZoxZN0KKlvVqSQcLCCyVHsfycc4H0Pr1kjPgvvqtH/zgt+mk2JYTd+ocR4DRM969efOv/9UPb95fYSdgSGjwH/oZp9oVy9sFnZrJMQq24pwa6n4jlZKye21HCWsgrK/93QwPeN8tEQW4hC4pfHGb7F2EDyjmidVJAw+qgQ/YX5tnpL8CA0h2MvsPoZIeygCA1RZrT09b8VvieERb8dz02eKOzrer/PAul2H3vt32KHa2jXX5pQyTa5fqWNn263CX+/H3tdfp4Zx+G/nhwzm7KB6qXvfh05e3L76rHps4f4Tp/v2kj0Nf/EaOnYfYT9gJ20Ot14+9ghgF7H2WoTQaMJRGYhn4HwOsQVIrTAE8+DlNdzqdjDkIif1AnxKf5uskmV4+uQCYAa0wD8DNQs44YuDv45ZXArWQCHyOZw6+F0BtfIEUpY19bPtN/EHehcn7bI3TDp5AoLksX10A+YPwHbAwSj87jxdRMsvin+brH0Tjl1F5MZuup0mCLDk2wWjJKbOTMTbCHJeOMf7eyAr+DIOswACZT4LLIGcOIQWPlnP8TxLMAw3uUpbMEGRBLlU/SF5J2OyFbrLPfVXuqu3uT8f22L8rY3uMX6X7ZVdv7E2c9Pcgl3sKxKpVJqVtinGp9afgbpVWy2TqEPgGncvYE6CXQw4dB7jNyoogD1YC+OvzaPSkKN8wph+E1/F0WRTzLOM8iCQLGJJnZS2nSdA6bNM0TbTuPCg4P5g1BjDI53L+Zxv+YF0EmBOc0qVyRgGnTyMs/ClAVqTalLBtIZoH7OF/qyW9+ADR6zSvAKjntIDwy+9/yZoQlgQTg+R0T7oDuxN9/c0vOZhCLDnXQFNXY1yKsvw6K6+mkzkmBevIYeEsDspT58EniRLVbvwz5TCLZVelKYVVir4gcC3ur+6wpMMfsHNc9pM27zeveC9HLUgT5fN04eYt5Cc19H6g71loZPCJd8JDaHaycNvItkmyt4r/ft4k9YfuVnofv4fl1ldKO97HG0Nk8Gn8vG3OfTE+B0fD9Kz6CQ/ensvNJe6n2ZP9YFLTU+n0rt8T00R62e9Wa4/BoGDvqhsnUveTWXOGpiawd8UDGgAe67q0A99I0qXGA7lOyScNnDTweBroe479eD22du8C+uy6RFKlgWPAcPhZ8NCzRWOGA0SZruWoQxTnbWn3lJw9fKKEQXk8c+QtrUkBhlf50IYqacYUAO7VDMAC8pUG8mH1sHufWRwj8AHu/wziahh+NGb3z4iFm4JQfPDJN2iJ8eT89y6f/bXfuZyPfpAmv8yyF+Pw1SRIXkxKlm2C4wv2bheCiwD1jPUyMJyyiLMoOAuKwd+sXORsOIOPScBqAQQx9CeAqKFlBKccA2USvTIDzIQxpXUpqoqTmEbj6rSH8i5JVUvcJeud8+wv06V6ny64qT1aVIep2g04DPqmXYi1gXy6gYC5rC6QfZlEzzEqx/HzSfS0COfTPIuzBOchloQz2L5OYzrQmrMBsCuj8YqpAlx+Apy92IlT9gWzQ8za0L60KzakppIoCZHoEtgeakkD5ZorYP6Jrf3XmCHj8YT5HmgQQAYCiAWfM00maLNPeqoWsgTR8mb16uUrejXj/FobgK3A3AMuTQl9WycXaBssmEom8smTreoy9CEKtv6k3qEetdscRAv9f8hrt6U+ZNmnsn6TNGCd+9OocOvBe2yxmgL7H+7+B7HJ7Eu5y2jPOQB+toPhdiuxyO6FXkrVOPFuwQc4dtjirRxte7FFciCizaFv1OEAo/3Jnm16HxvxWNl8HcrLXL9g+wU9MtWr15E570X+UPXy+RwrUF/evvhj+X8sel4ae/qIS61eLI6uoe543SgNBGVfhmCEynGhBsYJTI04tgnshB8Go6Qsp2Sc3s7LApBZd2WFr2CPwS9QGY5CoCY8+PHLDtmkH46GioBKwCwgGsCLAs3rmp4JjGN/IVz2U7LZMgEG5hUe5RfRen4Rrf7skz/z2dmr9SjJ17dTVvmOnuThLXsH2XaTS3HSno8a353OJ7Nn7COfjePz9egqL55P52z1ifMG4EzbvoAHoS+TX1PhYPQZH1S6wnCEeM9IPR0qqtqZFMiqx1P6evBL7HeZtiJ2CQ7eO1EbPr7k9T7Z1SxEVUPj2M7VpBorp4eKGfpUpFpZu+gICvOfCIA1I+hGBUCfAv2L8gpbYDq5/exZcDl/sshYOzJbjd6s109Go5s8nYTT9Sq7/NWbX7BJ7FkcL1jEHRRp+fqcsfw8wsOHkXzW7aaKZO8gFYv9h5kBCFcTqzDWnGg1ecyesGWikwLoa/SBZEIqFsB4zLpxdVos3BjzsQwWV1M8kG5vXt3eLDSeiT8ScxDkCm/L0WLMzlbjZL2OsYbpnFYzgXkZAzwpUNNjiZBXkpowcHt6bM2+uh8VpW/t7GQRdbNb9irmHl9Hvd+sMe9RWE9WX4b2L7jL5NP0sBkWreNCtq7uElGvR/dgpVvJjlt3uVuiPfBN9TryZNhfgF9rP+/+XH6qz8HFD5p7MRwyXD/3wWC+tO3w3Wrd5tMZo3eeJWytuqlILXHnGd/ukz6hC9s84YEZgE4eFautL6/3+/E90XpYBrP2+Z3Cd9XATue4K5tPLp/rRt/V2n0Mdbtns11y7wPbl2GHhZZygnsYHs3WnN3LxulYAyB9FksyYIqvvbx9gEDZilW/OuGLzd3BRuTSCaxspZ8z7Kshf9y48QMBbgEB1fAC6XLslhwyBvA0Yi0wntwMo8rzRyns/6ilw/yeyI+IvdnX0TcF/zLGXFNsEjbzBN9rWkH7sLObj5YF4LeB1wjxX3719M/+5b9cxjcjDnIaLTRmi11hqzxBeCqVitXjxBqQFgasR20Ra8g1kGwIqy6aR2bvitxfSJNKwH9gXXyTWktvWFg31sYALJC/3PSt6WlmsLfAsYbp8fVfcYRXVD4tWZS9ZFuf+OnZ+ZfzSfZ+XE7mWXmxzq9C/LSKm/eL2fvwPctvcf/H0sN1ZzyZQ7QoGKZntQluQPnNKH+X3gLP6bCC4Br8V9/SHq8EsVK1iBh7NYtZMIKEYbRmtiGIJmN6j00EsSMsR1jQ37MMZyDWIL99/SZdLYH4dGwtZpaBqn5pfYe+TGem24D76aU5dWQxjLq3GTywodAtiCm9fAKX1NIlhh8PgXT03b6++zX8DrWfa6zOjvup1tKJ/ACC79Z6zzkAx+pil/Woy1KpmIqWtx8frVzDi/XtxcP2nwrb5e1z2E3rv/fL8sP9OTYp7foey+Fu9mu73I1MO6F7eNS15xmOrd2OLAdvVa97dKGGf4ec99BDw5aA2gsUYaMUfnxH2Cvxbq3seHbUpaOw7ihfl/4+xM2jQ2DD34/t4Efyhh+YGdAG/tFQvUZaGdDFZ1kKkmOFufuIBHcNDtrSwAQASJoT8pMrBkCMRQF59IYEg12uRIEnsvEhIEgIbOeyJTej+G1ZzkBc+FuTRaVwCcHhe/0Znj/l+NdsDYPbEegQ4iCdIhYGACguiUFy4RjvJBZKhePJ2WLNetLinTBnONFSUZal2vvLZiokwqjQSD9fCGvt7iRUkU3ID1SxHYlbmvOzdIcbDht17xK6lIZwN/mO93v5uX5ib3ljjwhWLymHCF9Wi3epG13tEJAFKK7FHgyH27g4LUWARmAcn8F2rMIrXO6j8TKZ5av8XYQD2OwtpzgX5Q3LaxmFn47Cq+X7rHhXjqYcNscpbryx6FQXZTzBbAsDDo6bSIBwwcg9K4Btskmj/BqAZxELC0EkOPBe0xHyZ0uYAMIudTYf81hAfNLp0XRSZOHkgSz7mp60XHCyhLqGzWMgvvUfbFmtP8jT9Fx1C9+xxsSqpkkG99LQgmO2NBrriRCHeg2AqdR9uFbw1eUlbunZj+8Ki4dxG/574Qp3bd2c+CvedSs7gq7SqmdkeFltJnf7BXd81Jb0l+f6HM6ng1J9Q0wGXu7d7oiH172j3IHlHSLbvM8PUd4n/T6/aEPKHa4f/7f4saUaInmf/vvih/DspaGjbr0oeK0c2X17WTcJex+GJnFLjCbv4wWagh+viBNnNLDbw05KuZMGPoYadx9J783QBHdp9lUOCEMyCN3AgDkzCMPZ2K2WZBqkV5ognUZGSdIhrXhhKJPltm8D76As4wM3/jl/DA2746MhwK1S5AgEGgPB41HEAgD2c5Tfdko6YA4izTmwApNf/iD+JmQOFPwotLbGKRssSalYIGnIaG4CD879gi2AMsRbQ+Oy2vxFgFPHu2LMkJedSVPlkw1DXVWEUKkkVN3tagJbD4cT2dWxpuTbKqJKH3n15NiJbm49maqCmqQjCz5I3hRVB7ZKcvVtmNQ0G71ALaVW/QEtuwjlIKTmVIOUmeYDgvOyWD579uXZbD6ZTliPmy8mrARm4UCCHz4zTbhtTeej4DWnw9GZ6Dorzozg4AhWkkQx67i1LycGpOaPtI4EEpva0ayRGp4pIUrU4Q+M/V/QfTFnGcwHxqvBkYbEHO8h9gJiUS8bg4brZblesIy4yDjBgI7hhM5SnIKI5OQ71pdHIQvjrRbsQDUK2D9otUrPn84W17eUi8MRuwMxryU1NOppFFbpYev+jjdb7XInHm3x2jF3YvyJZbIuKJmawCcm4Emc77AG3EvkcAUHPXsYAH10Lr71VujdZ6CPj0lK4s7DwivzAa8h9t9DWVR+WX74btU5lsND6U0/RvrpbEndjmmR9EW0ue2vnd8ifriP/7Hxw3l2yHkPPfhyqr0GdnWvxLYmfZ7769VRF5fZQHObc98oiD+D1zzcBCr+TVQt2dabQan8V821a4GNXIKg5PvAmUdaLCsKvHpsBiAYXQCe8vKag8BwudH+6wzDstjSyaaBX8gZNAWRg8I1kApLpy+MB6hkCWgolVF6tlhh6082+VyM8PTRQgIKwbDQmCt0MhEoNH2hbXmSX9I+UXjGXjCj4CyKbwK29RwtRctZYCGgbVbk6yB/gm2i82QTpiw4M+AbZCjzL7SnECsYJIxhM1UJlGZfVaO7sOJ17XQElyhfTDh95lGQ0HSbbQ4QuT1eKt96y8QHVK693Iim01vTBDVV870jiMeTFFe6o22V3rAYFNjhZnmqN5iJUMkhcQ3ab5jWA8gmjh+tMK2jdJpO5pu7gUWSYqb9wV/+fPE2TlfTq9vrEet+pywfZ9X3Kmed7ZQFJxzEu1znM1vcndJYDNtjyNGLcs4NEMjWUm+2B8K5H9Y4p9HWZiVCstDiciw/LQ4/S4JLDqtQ5kCH1jEBIUMA+xJG2QpQz7KExeImy1JZBtbhZW9iaCawpyidQbxa3/zkj//N++trjpugvPFkgmPS7c0SuabJmM1wb69uzs4v2V2UQ9AkjKpt1sZGJ4T8JttK6L9xLVs1wIasap1NxKBQ+50zhI9Ps/+dNkiII4ncm7At+WE2TnXQNYHDeTYUfq03sXcNDddbH+VdNHC8tA9b6+PL784xRKr6XSoOQ+i7S/Jnzrcp+vTfF7+du7lrvQLcu5cfTJvj2joNoMmE46Tm4Xr7cW/ChsOhUCPXA/A6VNYp/aSBkwbupoEWErgbm55cgGIwNct/wS8Ae4EqUAwb/oDXtW+nXg6AaCLY81/zAKAssTJIVYFrQS+GTYXhdQHDbMxeNoTGgaECXWlImPFWaMfJDEDF+UvkwVhQqgwKPuHB8OzLKHnJcK0EQaSIE5oY/tcC5ajECGHgFZsgy0bpKLodxbfyR9IERZQx+g8Co0jZH7h/VFjU3qL2jtv8SLReeURA3opWTavLKCTSA1z34OLEeAAZVGFdPkMX9j8dxSamllz9hTAJ9ttbR9c6VJq1rFLteAeaZTI/z24XYYZbP05bLDMnO6d3rTRwX+COPy3WE1meoPh4Alq/KRZYiHidgcfpczIhaVl6EUBemw6xD6zuwfCyA+ijWYqZentz/eMf/9GIfUXVrTgEeoLvWRiPP/v8OccR4xd0c3ObZ6wkWLI2ABcfdTyWuORsEcXMQMTEA4Yqnerf/NGP/+jHf8zBddY1VYrZkqwaKP7tv/iX/uyf/3Pnl+TTydnmWobTkn6wpY5as7p5oA5jrE4fx2rA2mNQprovDyL+lInqJ9E9mp+ypL+hsvX1yabhpBeI2HCjD/9vkW7U6MafNveHQh+yz/fZuJKRMciXh2T9sOn6uaER3DjmByy6+gGhYXqa+J6y7GuFbdauRYbTb+c+fPeptfgBia0/VOPae0kP1KuPj7wIOi5hio7o/qhOLvXI9HY2kcavjL2kAs9rDScuGxqvH2slAE+A9vu/scHcMW73IDlMAsAaPjcamAXhAbEA2pAyTKv9QRm4ZRw+xpVHgEkD8CVbK+Yrxn8z3LBZEhoF05ub98TLsYgOb2fA8i349P9n789iZWm2/D4sxxr2cOZvuPe78+2+PbNBiwJNwZAFCRagF9uQJcACRPmBEPxowG/2q2FZgF4M+EUwbNAGbNgvsi2BpASDFm3SFptTk2p2375D9x2/+TvznqoqJ//+KzKzoioza2ftvc/5zvfdnWefrMiIFStWrIiMXCtixYqKkwGYo71T5G/F048xxGDS19mDsG4QhBgMSarUPoVwJsOPi2+ExdcsL2VM5PIle1s2H6wDUEDxjg2kjic2lrrWyZznn0128CQaNtth7SfHAYPKtYfD2cHQzv07wBbK+YfugI+K0PmyLaKWjDFZ/dr44Tavo9LVyEW2YZdEyRZTR+snrEcGOznBccPBONagpVmkVCm88oul9AEpfmEaTo7ii2dBwiR7ws5gbRBgF27Ijm1M8sNJmizSeJkHc9ZczKwmnyCO0+gR/mex3kEm17l0M21DOaMnlsVdVxQqpUrROxTlq/zTjx/nHz6pwmXCcQHsIMdmjDuOoX77e0d3jjNE/qWc+pN/yQNHUy9XaLlVjMZJD55rh4DUTnz/Y6FEAi8FKqV2FdAbtTgQLDgZ7PDw7suXL1eLDB2AyxRUMqrasEk/4qhYQ7h+UmDMZVmHACGJq+H5ENQ6fgz87nH+kjFtXdSNhXbTc2PF+IiMq37EGL758N3weL6Nh+yWssGrnT3nkrzd5M81Zgz//bdggw97Uj7E/+vgHCTBtZH1t425f2I2mu9V7AFoiOr09ibhc/l9s6gRC7bb4rWxxbFiox+8trJvC3rlHKBhb7azu466xukNLqMqg5xGZps+db2eCXoeMZ3GHIIkhB7i5dtnJZEOGR0jbG2ObDQWgQBhs+5M9RItk4qceVzkflyyZKviw/c/vDi5AK8OFpCP9hihX05GGeIlVFn5CP6SHDHkx8DncZB8piPEUEZSNAeQaiqXwmUx5Hz5a3af5Qnc/pwHEcdFcapAxLZOqzTVEdEsE4gyVwdLsBGW+tXNANS4BtmXq3Vhgz+u4MHkbsI4MrfzUUx7+WEX6WIGSRlMaFE23HPcIbrJ4jCr65DEn/YG2zHSzNpzdHS2NHGfXbhFzvERWmbSGXATVnQ4G1rKqK0EoW3SDdEaQcGxD+iPshEL2ROsbkT/1EqBOqsdAkxB2qwilZRlAVQCDMwwQkriiRYLmOnHXGy5WCxSdobgfQoRf7lcamVA5PEvpQDWqth/jOJqbn/UO0mRIRE1kYGQHs0LULFcLtiQQHdHE6CbKkkmRmRR3R1DjBvEOMbo5/Z6gzlAo7l++wbTuIs01+l2QdymfYE4QHPu2AOgigx22A173xutcj2aXamrDelYN0rgIDKnybnkUZQ08s0gxnEJ+5br1hzEZz4lr2D9wa/7GO3Wh+/WeAwGl2s8ZLeUUTESG2TwrQshEf7dLPduCNsQVb38oRa+tx+rm3+rRwD/s1XjwXJdVw3gHgbvQOnSvCWSF5KSPHUeB9mxJtuRlctjSVmiXHPw8vDIHL8c7RPD3Kp6KtKPUGg9gLUzgCWtS0/IjqNiFZWfhGwuiCZMowYljkQl14U6UkAlOhWAzEwUh8mJtl9m75b5O9H8I6FE/mLfJkbf5aSIlrZRAHkOLQORjNnjiyDmmFg5CUX2q8oJaw+IYVX2CJpc9Y2yhkfZWxIYKcgpBnrN7JJKwNWA2YN3G4r3QHYEW9yOIIOEChfd/OzIL4K9ZA+LF7sZdDDtfTNx/bSFuUmwfNx0wUwXaLmj74sY0jDFuoABWhdy0JL+EcntAbc8tPljukVV3mdfRqntH4jNCP4cFSenPWwYWHFWQLicTuWLFlt99NCURYM8AXyJe1kO9gonRXkaBHenwXJSHOas9ljP07KTlEJ1OdagYmyAYjaay9GsWxWgXO0loDvS6HLiKY2C2X9bsYIGAHN6XxTibYhejp2RIWYhrMBEDUiQM/F/FxUAX0a4rGXlirWm6XRGCexQOHlOpC2S6R2quQExVveGSS23NprS8ap7d7laxjcANcpuvMGvG6qBd79D8T7U0DjvxhMHOQTj47mpsCurd1S8qSJ68DSM5VdKX/PYAzku6vXQ398uev3W7+gQvf15h6D3jx/iwFC8X8IY/vt4XkVdhnDylnM5Cn0afPqvEnatVufUCoCNo+vB4yo4u3mM+G70bcwtB74MHLj2uP1lYEIjgFz2EWhGHIOTwUOAo33ka2Q2k/jlEAhbCUR6iU2E3QytBB3Jcy16RioEcG6SgJDtQCSJXvb/mEwg68szvzAgPCGlgQ4JnglcBKzaQhyDcBQIWSKV8Sdh/DHAUhhiOX5RkpsphkRpG6CSj8cwOQ/DC3kYQp1gWUEJVglJ+aJFNwsS0q+LVqyZc1u6ngS5TrMYdyNyDeTF7xNsEbtA+9iWQGBXIS5tF8QmNS1kWxIBIt29LZWYFnITQZtvM3rzyRrbonzwugzxH+SaFUdWVj9QW9NO00CnOUiNTEIO3WU7OHt0cfwa4pWfaf6joztlNi+xximmeTWb5+mqWixWWAsto/JwsZzknBiAMF++1AZvTfozDQ9yJH76g3mnpe/xbP2MjsvZFAmH0OGJiAUizP0X+IxCQ8SDD6pCgjaA6Y4m7lljwAyJU4OjiehFvdA51uwuR29Qz+RtMH7hl4jlDJYuKBAToVW5whGQvIVqoUkviH58hhiHyFozZpOH+z91UO+P4jaHz4HNpnFPSifE9cVlt6PfKnF7+8JwYKPVGOGG+p+L34Be13H3TgDNKfKVN5t7N1KN0bQc9t2Q19GEfEr88LpWfaHxJQ5pcn1Yt+PGl7Kds+FzN353jPg80Lg7Mu5L53V44sgYj6ELecO7LNxco5E1NMs+xLrrUKK8fPb3b6wtYnr4YxB47/YuiuHN11025czDb6QKcANPDesh6AZryjWg6L2TWT9zqWV0VsYv7GwulsKwlMCkP1VmJu8R6CVnIxAlCGISA5lCNR4i/OhRrlfkAFTo4qcVNhfM6peLkFUF9Aes/AWmbbtaajARUXVCwUBCLB5V+SrIZtXyrTD+COaG4XSJATfSmhkkUTJCmmQsE/Gr8qCqZmgimGZAYWlnF2gyWNoL5ABO2OQyY5urv8hvLkltgnRLGAo2V80Zi3LhdVoD0/kFBNheX0B9sMRZ8cb7tsAtSHeybL0ToAY3kC49LpXENskh7aLuxmyV6tW7SWnyOOS1jE9i5Xpd/nAdVWexV8N4G1X3seHB6r/AvWe5zLKLdDKtOOeNM4I5BTpbIknPJ8n9O8erJTP+qyKNVgXnBkQ0asoigbxPLdihe7Y8ncZsFbBjgiO2A9AtdOhw6Oblwwk9scCOh10G9FPtMpE+C4kRmCiJ6XwZuGlKH9c9CPHoClDJsgP7fumn7EnGr//56gKZnq0sWb6SAsCQEnHINOcBsyshXq3iPKsuzi/Yc5xl+Ww2MZsilSPG113KQnX71hwzrjRcbLjaNJYf74fXcIOh648/Q6g3xpMhoIH47nf8dX6hxpbVNo3xvH2q60Skixqo41D02NKb/F1eNSnr331xOsrH5BpTuqPDYXM+zcb0uqH+4+Kv//Ucwr/m2qsJ+XX3adjzxd1NHAqAwzfYBa/aPXeXe5t6y4FbDozkwI2+8SPL3AnWHTKaGDeM8MRfO6QQ0KNEaqFlij/GlyeivwwhNI0qIyBtvZQYXYs4JucJ3jY+ymsQElItVSOYSw8Alk2W7L/UKcK474wCZDXN8MvwAzGL4iiKgjTpz0Qx8GyjZKFB9tpB8lHFIgCly7RDe481F8u0boUMpyUCcshYQ8sCqyBaYJuE6A/NSHsYbqCbyIgcYiFdhtkilb9mON0MKclxSPEbvLEIu5Hbg1nH94WspL6E/jgH7u6dMjoRrh79mFysy8J9H5q3EY7Ja41cM3Y7vz2DxOGhEdUS2NlzcEOcTLNygaCNW57z09XyfCWLM07uSpm1T+JiOavmmbofB/li3S//PCidbAVGU6BPHc4fvFy8YE8KUjl9RbWVzqoVBkrTUXElmZilJ0wP0E4B6yh5irU+mwJYRwKPrNC0BSFJlQuL/+lBOEVjUE8DJVZw8cXZeWa7Dlx/phw6JP2c3kQMWfhXJmUiYE3/q7ep2zdVN9LcU3N3jdI8XeG3xn6FnLdZrsCBLwq79RJ41xeFbI/kL3pwqwU2q7Mz0QfdBmRssXm+nhn9NSihPRocUF9fYVjuvWphYCC1NwuRPuYhmKF4nxI/PAQ/Rq8dyrtvfE+9mJrk4svyeq/dte6h89WRd20OdOfpnZzmx++u7/jK7cbjlzgep4P0++rV3pp9SzT4Kn4iwdl7Qd040N6VUssjLk7P9X+NGE1kfl/43Amm1EWyFJ52kMuZ20d8RzxXJ5fIY/klVWu80RpBqUO7dC6vMCDDmfxjkKgNZMRG285e1d7fJWbf2H5gdwGsJHkjACVBTzgOQrQLsqlycTJwFazeKnDkHz2V98hghUOWoLwjMT56acUTKake84wQr6DFASVI+gqxKAExLmakjRBSYfoPwfwptHHVyVtJtfqymQtQwNoLFcXWXlqfP22KmxsjvgV3xbaPLaQL1OcDMM7r8kjxqNXcv0u03+1wG7kVMAz+t6NLbc2TLnFe6VtY14/WJ9yje78aDje1oMGQtSWFCwplTytKy2QWTR9+kl8sJtXvrJ5+8vwkmE61h7vM2I9bptIQXmCbs0JFkNTPjD1z8dqLq+aU+6dlnKzUS9H9giniPX/op+oSoA8zNMAwPEY1DULOiEDtoGdAScpOEqyMqjzlJApUh4g8OB8lT5mheAYlznxSc0vFydLTs9NFjM2RzpOWiyK0ELQCoVGArsWfLUihnKIG6K5uo4rrDVGJbWOKufL2jdLwxHGrTWoeAR53OazjYD8fKH+k1cu7ed3UF8rWG3nNN7FvPu0uy6dT7da0yQbNjn5L3cS9fqrzXrumG+Wu0TfTMoZ/d43WmVpijPIxuYZKX+NsQmOwNbCX/+5uwcvz7w/ht7ufeyjeh+kNt8zuTW0jkeSB9EfjNmkdoL020DHWcG1ErYH7QwDv7K/9ubqx26R0IW5jbjlwy4HXxoH+UcB719tgDel+dLeUVuQ3Eb4l24QVniTaSLJH5uEEVflElGQlWQb5XFPrSDbMcWrinVlURDl9+CJ5YQeISFJszwAJyD4EZTIEIikSkuDwlJIwM09GGVSrVEn+sgGSmXU5m0wTnEPqEAIsv7GpeFyUn2Q6+TXDi4uMjvALqbUD1YcbqwEk4RQyipZhvBBlWHFI/NcUsKGvIVV/MQCiak7wwGVMIY7fWlhz8RLtNi4HuBElbLuvNtNlgL1oRFOd4BDx1GLszUFkk2MovT/eK8oHcAWqjbfQdmPabHWe9nlNMyzVP4nI7B2P0+nB8f1gXkQXDyfz0yo9q5iax2YMJ5xZhmWYOgfdJZoVuASif8gLkFo4QW9EZs/YSj6J6RJFxow/4j0LBzmSPQI5fa6aLADBdRDdJceMiM0D4h1lY1n0yccfo2mwDXg6md19cPf48JD+uMoWeCCNk2o6mSCqTyZzaH1SPj04mJ6+YO1Cawn80fFNh9HSBRZ4dqhwiTlQli3ol7gBRcGBXdAJ9fRA61Yww7HFBVpmtgGPW2OC1OT2enUc0Lvv9/A3nN07etEbTvmra8LXiHkH+xsqXH9qni799TGqBZNgw0voYH6vGNfwbUQb8Dr2GF3naprZkDY8SPg1EvbVRPe1Nhvi0lD8NaqyR9Z9a70H6j1B3azkzdPjvwNXXVPqttEedNps5dXWdrZlx31Y2qX5ktwSNJy0usEy4cFkp51rrGECZn8RTIjX9KRQS7AnJnpiaCTCI7fwLN/s0RRzZywpEMk1oEjyZvoTAVuie5ym0gzsTzmwsNDkP9OuYEQIkzmGTP3l0xH1gM2XxOBClHPEtGeAiVAwkskm8EUEFh7zZDINC+Q7Norii2WqnQDHER5+mHENkxV44gVbNM1jJJ9oRC18scjEGw9FQXAANdqsid2I1Bt3ADAKiRQB1UtVcP/rStpoaPFtyPWQ/C1B1nKAAdTxzNAb1yQf2NUzm16n9P+43KQ1CGow/3wAUVenw14apym0H+VmrGXejFo/7aJ2iyDLZL2hJmGNhVBbDcXy4GVuCLBfu6ky7ZM1BM2B38w4Y4MHp30lZ1l+guyMw59ieTGjryxZwwmqjG2+LBldaKo+Zk8uegFoaPU84ODeKk+CiztJMWXFp6BH5DGOPlWSNhkH4f1P85NnxbkcVol/qAH0HnaHazPAaiH/npwkjKeg6ZT5frp0mM6PQE5foQNF4YRIKayondggcey0cNhbYGI9Hc16PkmyJqIbJ8kkW7EWYY2ll0tdkHtddcch9x13reC/m2Df63Ic3+T7GsHeY8g6642F/JH21dEzXj4Zkkl8OtfjtrqZXW2giRj6Xecdgrhe/CB+OkFzMWpxJZ/Zc4fyIQ40uX+1fv1292s+FO/D+GH3Lq/X9Pw0hdvmqQNDkBsnAdN2G/lYAXAfhE6jbhfnSmzzu8CYXD2IrhHVEnANHLdZbzlwy4E+Dox+uzZffDekcEfGwfeOzB0QxiQsM48uCR6pGakLc3ucLcby2IgkxvbI5YUsJYhnmpOzdzmM1STCHAlKXtKRkjTnCV7CXJK2SZAMHuDcPUFmFwju20t5Y5fJBRt1bdFespFVhqPB9IGL8LZYzthkXCDhyaI6OHweJE/LYCIzIqyMZNe/wC0kwpWMjuSYHfdAMg3HIKRCT4BkSX9YiUMGw2a9HGECas02SCVkrLGbcXgd6mE4lLXpLmAV7YEcxkW+rUw+1iFUdaZu5uEMStkXfjc2S6WnwFddDjn39bXxsI6uYes2ruPV+WwyneUltuCaoJwf5ssJ8/T0Dg7oxdlPOmWWP8pWGX2lrJDwmZ6X205tF0cBYCWAnyKZBvN3Z7O8XMmqh9OppTTQkeinbBW4e15kz/JzpHMEejbp0m2kKNL69FP6EZ6GEPpZnZKXWBkXgZ+OpHdCXaREYQC+DFGA1b2dZuxeFhLghaAkgKr7s1NBefWV1uoTdRVPgPC5ofC4Vt/O1Xke5HgH8jbiy8yBTv/6Mlf2DavbK+T9NmqmuPRZs0HlUi60YwOBbUQbmS/RdTSNZxej2k48G0jtYYxerq8wNdoTc7csFzN+jmEMbX4pQ1waivfz/iqEh/gwvkW6XOr2iqth69K2Bx4TUbu0veqYLs2XlGhymYSRTbhePMDoxF9gkWdqmZ7AAq+Kk4mThJj8lFqA+MwMaZqevDxdZTjs1+R/IMFaZhhI3qgBUgdkuwMBsgVCmmMyX3oEeznlhIfCpBIw9ZovMxOtEMs5/ItZXERzoDRTq829gCcvaPNJeDdlOlgAMqXAxmiSPqyK4zDCyCctS7b5QvQBBXOeMCqMaoHoX+bswaw4/beUYoB0iFIA8ZqvpQD+axmHEGsOukzE4yYFRXLdWiazdM2iudkWg1UOuzTTAwCZuDtMFu/mcf35ewffjWlzA+DQOMjuXZTVl2Xyni/J2WSrKfQy7pr7b3N1A+4tcKSTCt8cTotvNCmiGo54QTfXpXKVxbIBpWUiPUUl53iFJzpKIoyW04Nyns3RCXAONJ/N79w7mh1OMao5vzih950viovlCued2O3IL5C8fdKgF9VS3kDlTCpc0pzMw2MQBoFoDfHkcRQ+FrUUpw6J1soOk1QbELQKcMw+46pa0MVUJbYP8F1QHVBd0RPoMvQ+vQVRNKWDIeGTBCp1cPUlq4i4RTfj1SAr+gMrXSQC6TFBUaq6cOuy3+vM/Ts03I2h7dNGoPfd34AYfthjhBxGQoqPp0uPGChG7kThEm0l9vrrzGPK2qaqabQRVNYg2xjG59zk2Nh8UOjxsJ77d5mJ36Tf54DfOmPL6oO7Tn0dvn0pcSW6vH6N+qhT3Hj8V6vL4Iw+4x6u8rwV+CEKXQtu2PhsNisfbfvIbjansm3FuBK24vtg+uJ6yANMvav+6QG4jbrlwC0HPm8O1O+nXtXNIcHFeORJV0C4jZhPzRHucemzXKwQoifphFl/STeaK8XBOWHMKjLctXz8/ieL8wV+UzR5itkP07ZJMpsdMHuLk0RN0oNQZtnadSvbfh2nyilLcqOCICXzCLz6aGMwCkKcTmaL4FyOfIgQPkly2t5pawSaY2bPAE5hYhw+pqwCpCgGckI6w4u7TnKVDI82ggSHcC9LbKZ1iyiTcUe6jNJMNHBgAE5mpKdgrQQN8k0kKbPlDSGV1HJHzwOXaGyS2kATMf7XZW0LdAF372JtwXrwd6F7gNyo3Ztwpcim0PoXvvcpSGvU3QqQc/3dRmCm5SIOAShx2cREP0b/83IxwX3//GAe04605iSI8RcVTQ6CWTk9WGVVGuEUFoVwioXXAvehtCleX/lBLZTOSd+S1RgJKJfM6rPRvKzoNhfaaqK2pjOSovaUQmCnWEjEJxX53/a7QFbdK6giJJsnIDQSrSog6bsYbQBWokEaK6SVCjFYeH1AoTJ00cO9WnthS93/ZqUaYsvrCtkfzRcsh5ruC0by6yK3+6L5Jd9yzefGTYd3874prX1lm4je325L+diVyj6nR8q6MXPgsrn7OoN9jgE1vVkDH3+bBXQihLnnsjmezaxrKKZUuPadTV/nt+HRfyS8W1fbndqdY9hC3vu4G2dvlv5Ix23jmAMYj9lBOv3vOvzsJ2yfWPe1GqNVj8F6tRYZwjyEbd9+OIRnqNxu/PgSx/eBbindGDej7M0otO98G9h60bs4GA00vV9xoK5OXWVmEwlc2TFcSPHuH85nU5QAeWms4tXy7PD4YTT7s+VqlcQY588OjmU4jcA2O5gzGKEAgA08On7L7K4RuPGHrtN68+rs9MykoYptmRhOsFTAPVsxc4/7fs24SozkpvlaSn6LhQKOBEAfCCJO8wU9JuKcq3QvX5r8Z27dNQ+rCsjMn5xoAXhuQWHQU4TVyKFE/xVHv2LqDRQdWlsLyOGedLdLVVY7avK3RzBr4WrwJpseO2G3MnBTb01bQt2o67Y1WtyjT4NFb98A2MrYQLgvyKjVAFeKVxYo2yeNFe1Dg7z+Jd5K31gDccBCEaVPJP8jjie4/ERjLKvJi+MHy2pyZ3Z4zsJAMl3F8XERnkqqnyTL5WmcZJNpvMo4Mw4/P2Va4IBfZmna9m070TlmgoaWUjmtOJgrDjhGeBkkK46rpoOZG1D8gWrniZqb3h6jNqgKTPjLJEjbe3VCMD2LbqozrJHnpTei0aLZQqToB0wdpjyi05ThqfoY6kG4lJKJxik8PLLGQfV4rcQE5TC2qNT1paS9rzYTAScPcPqHj/VSjGNGJH+E7MKP/0b4eLqEjX9f3DdxCNv40bhLg4vx69iland9u6ldDEPldvMO1dGn04VrSNf2bbcYKqkvfndZfTn648bXtz8/47x3gk2XJ91c+5bo4/ex+e3u4ndj9mkbw3L7Uo8B9IlqwrRsm1UBpi74GfWubwJtPjXob+K3pe8mkN3i8Fv8lht7cOC2H3rMcswYfumdwKsMEmEklNs6QHpxsUCYmSazn/7kZ5998ul0Ogmi2dNnH+Ez8f0P3p9NDlerBasCs+mdySRlDjTPisPDOUbZOvZIUjwnJ7GpoJL/HVSEMFoszj9+/wPwoxlQDlYbmGYQRuzGkw9SFfOpCEkS2up5Uyb+S3zA4P8nCXHfiQd3bRooomdVfK+K5quMDZxpMsG7C2KWUS/JHouOImG5IEqWyItsA9Bsv6b+WQCQTsKGZMmJxiLd3SjKWN7IY25Yt/TN25h+Zdi239zt5zVal1KTYMM54bacNl8bWKe1OEh7Ddeago3CXLRI6CHDVcvg2yp5tWvqgiTNKg67M3LE5iSdHR5g3HMweesbdw6L6m6SnJUZSzrcZ/nFyfnLs2xRFCvm9g9idgiz/FROzs+WOphL8+4YDM2qakUv4gzhiL5YhKxl5Ww6Z7tJcFwUL5HgWWWSAC+DMboNH3nKR76nO+bosjbXL83B0a+KQaKia+Kdlb+m/13dgLWAsoIM5Pojf8lOFKyVZDck/FwAihUOs7vXSC356reGmL52uDrW25xfNA6od91er5sDr4Pr22UwWfJ0oJ7boO5Z0xB28dh86wYQXC16t7Z0NZxDuprD1k3t6nD7ltvFuS+GGr7m9jr3eMwtZDusr7G0IfdF8UrZPfOxmzNDqX6b6jNHx/FKbGm5QmCoRIdqd+ru4nyad0PeVOoQT7q1aFu2t+gufC9YG+nN/bdxPQHXi+y170m1RnVzkwhQEesAeFTJ8LDJrH84mYR/8Pf//h//yfdn+OHHPCM/QGBCaJ9O5tP0DqLVdIrlP17Ts3AapVOM8qVCsKMXkQcTHUlCEsqR0zjKKTqaH8jUgpGoiM/Lc6Q6TaOW90QgFOjPnPurjESSGVIdCgnyP+YgCS5fpmFwMamOmI5NA7SOBeoGJiOc+IuJUJi+YF+oZnKr80izxedh8Y2gfJu5XgpBOMtyTIYw+5ZluFHlxD/HHdMI3Bu0Fs88bol7DtKL3Ai2/HW85LG9XJjsfmSbCuYWwIsk6NrXzZrX8/QP1hDrM4CJ82hz2LbVmLaIDg2j5v43i1gTYaEOyia9lqGbx/UvOdw3CGZJVM7eQomDD6zcHBwfVPM0qs4xR6tCznngIDDOcUMNLF5+dvbsk1W5kjUaq1NsUTk8whT2fHKQFdn8fHGRstbE6Q/p5PT8xYqsoJSV/1TbwpmDj7MqXhYX9MSUPQaBjq9myzhKIYTJaY8OBJAyYCoA1ChBT076V7tK0yQWhTeTzom3H9EPjeeg4Fn9uf6jAVgEWFjj0gUr87XFrvWnQHqtpbItQgH+e0ku6AAMqr71xQPF2MJ9E4WfrT+8e0Tq5unCu/7Whfy8YoZG4/H0dOvo591d392pPp5ueN+8PXT29Y1uQdeMcd8ph6SHhtHYx3zv9uXJ6MJ7APety5Vo62mhzkq+vcYQ6GAdpYQ3hgIzXuypxI6oFt0Goh0ZbpO+aBy4bdkvWou9BnovlwnUbZBnEHUY07QOYBIzk+/EYdifRjPkLds2yXFdzMMjLJUTTm7Frr7A/j4HqMAz/6RKUtt+aWjAgz9OEOOsvVjhwR/JLNUWW+kGUbggI+UxPcpeSXYAaC+oDHPqqVZCCGdM5OuEsOP08PggPp7fybLTaZLfmWjJYMIsMCe2apWhePfr999+75shVhzVPMRDPMoCEl753vH9gzJ4LvK0YUDbPcVvDYTtYKiIzrX5Hu2GrTNvAm0+GcgmTpdrK27rsUNWX6aekvryObBxBfTkJ+NAQf2IHXybRqApWkH3KAm6bgxNl2N3E2ODhkKJvVbJ6k5M0xY4ncL/Jn2IrbdBNdOZXOwJ4Hiu1WqaTg7m96dTHPfkRfZwsTxZZmkZZ4uz2Y9/9qOPPn2mroV0zr47LgT2apoGh2FIJ+GfdgZLOqdo2avR0bHYYQWAJSn1Esn3Rp8L2OwHoBDMDT3X9otL+q+rZikS9LUegC0T7xDagoqXj1F17rqu+vWumhUuhoerX0btUCtdHe1tzlsO3HLgdXPg8pGAIWZwTN6i9nJkWxlGPWp+5cbmg0eVOAJoXx1uBMqrgjDoc9m4vy+KDc14CE8H8+6Zj92c6aZu0GAV0AfTfWT2rU8D7+McXL8y4C49DY5dvz7+XXA3nSbpwISJLcT71mIIfgi/V9w1GqbOKtMIGpg9mDJuQAKrLk6PMLpf4mwR+Wt1D/MekvDMyEFLUJQVF0ynM5ePZb6ZTDtZSxY20IXNj87/Vf/HjpoVAP5LypInRSx75JgFleCIREldlgNba4lKkrI4OImTX9EzMg5vOggmdyfl3fn03mF4//jdQyb/V3mAfxXcLGIZxPTr5Pz+o9lXvnWYl/LfgoYRp9hks02TU8Au2MAMDNKlLERq222qrCIR8YBfczH5VOH87XWMC8WfoprU+5H8NNdertfV8YatfhNbzC7AXmTz/+DbwZMi9mstQlf9aGFu/tx8feJvk6TUB/aACAsSV4SL8MI1eN3E9rRVRg1R7yXzS2xSGrJqpq2j/VBbZl1U+0zNVGL9rF8gHFATRwEaWyxavl05FIIVIHUDLHVoXXqj/POzlVu7TcJyKdefCNcc+EbfY99JlEyj6AIQ9q3Tzst4dTA9xzaI7laxUhTmsgjTXP1FEJ7r5LiILeJ0HYrQdmC396PCtT8njGmNKKFASNJMvwhjBKb5rVsTB9XZI84miMIPCUMId9KkwUgdoCD2EmihyzCDXEsK9Ds7t8dVfLP+xh8Bb1818HZ0nbsT7SJcuY6fAyBrBHULDMH1xY/B35dvV9xNjds3hcen9VXU18fvh/elf194NfwVmtwn0cJuHNvdxzqZeiKGvnc9oHtG7W613al7FiVwmDr0svrYemb6LblnJd+h22qsjWIYp3zcl4T9lt/45rX5fIg28jZwy4FbDryBHNgYCi4bf9xAMThckOCUSQL2pz24WEQwS885u3GZYSMxi3VIqkYlJUk+YnpzgYgWMjvLNkeEMaZOEb4YCRGSuPg8SNoGIRGoFdhxSFYCDtcu5OJAMTfHL2jkJ0OubwrykqwxkOIr5mTTKDtIi6n2IIfTMr8/SQ6mybI4w15bRGuzcBHF53F6HkQPVAwYtE8TITLXFmJ2A0j814Fi+DKS/GhEklWA/PRcnRTJfkRedjl024D9sWtcLRGDhXTpWefur8Q2KvfcluRn3xH2c+2bdxutUwNcrzCaXS+pwTQJTyMx7S+5WxzUggDdUluD8T2lWXVO/43CeVWeaXWAZlQ7InNzCIW6C9s76G6sVikS4R7PsGwP1jZcWemgirL5IygOq+IoiC4oST0NDUGlqjTduFBa6SHSR7X6pO7a9hF1Z9eV6PykQJFUBHVdMOuwDFbNWBYwX0REWrxpEaC3VCvS70iuUJWzeRlWK24z/lpPDikotku7FtbbzF8cDlz3Ff7i1PS1U3rz71RvY7XFkFolVf5QUBtegFzNXeYWWpEePjdqeRGtXkIOL9rhGr4z6g4n3mzK3pruzRZ/NWxOqPLzSjxqhC0/vhPe0Iy7eDrwtfW/De671wE6WQcjNmgwqOu3wgbOEfUaJG4gYQP/AMyriNanve9CCuAaSu3L0R/XiwHcDr//SW/fZRC1Yfdeu7tyeYUAwyN8U6olmPyF3IWUFaSfYjyBHXaA8bT6lSR5JC8bJpicxTaH7byI16gBjComTJlkJkQS6VALnJCkVJOTCDArC+rcDgMGlcQ4swvSuKRsCERyl8JiwFk6CWfJvUl8MI2Xqbw+huWKjZ8cw8QBT4k0CPZ84tSFPQDBccDBYQhlGH0oFlGM2VgkRdYdsFPikIKP8CNZ5e9QZH2pwPWTIrtz/w40e0u/4g/wRqaLd2+EC3NvU+r3kVrY5K8DIOxapIWv47ep2EpXMkX7hbcFAepq4O4uXmGDVi4/oU0m0gDWFG+uNtQUOPgOOXUuh7mb2hvjSmxZtIHZHgCgmkaWOhhSvFMmxXRpg+ib4SJMM2R0rRRRMYzGsB8zd1H0KDEIBBwpLfWA7nHGCcI84wUUUDRCbf3Fc4Ym/j/GoWy5YicJ5mqcL2GLAGTmuLlyjqKqpSt1WLoyvmilDejPEWKVQ9sM83MaRb2ZFP3pa8jGY1gMZzcAAQAASURBVCLp29p4oFwy/tE2d8WoGm39DY1uinY3vy0UyWWJe8S7XBu8NYZ6xZLoU+EeXb727vqM1beNWweG4tcQ+4d2j9u76fFLc3jqt++Gvi/d+o6nx6dtTHg3H7oY6vq6TuS3u+s5ZPAjexu7i3REjOPJ9eWBq3FyI5erYFvfhvhuqzUp+h1K3cDsZ7gs7Mr3md2bo2em38F18/c2FmAuXoRqSZPclxbaocTGonXs/gjWeW9DbxIHblvyTWqN10yLG0L2LrTpM2SXoxLEb+ywNXPP55NDeieIQ0z/BxVmGDbraoMHorzNrSKNcbYXog9TrYxECGQS92UJYXRoNtfJ/Zp/JcSIxR+CnXQG/dUiDoOYEOhRIPzXRGxZLuMwnyScPIC7H+x92FyMG8cLTgSQdoBGssIOqIgncXKQJzPN7itemwk4uKCAroSdAoR0pICQm+rSVNiiNh4s5rq3uuYNGh7FGYvd/Oqsi/azuHCTu/51GVswArCoffSBleSem+T1o0urn/1MnfB4yE5WInpKcHV1Cf69k90S6QpkMIHbGKcOoW4UVJwCMEOIxzyIvorlmRQ9PoPqddI75WxHvkTpB2wNPkRNgHNE4whIHRCjouIwLOe2SoTVP12cruuYSw+xYq3/slIgBcSs/E2KFAHqPcZ2+6GXq6qQQWe1SqvXQYR1ZEhViCMFbOsCQXpmp7IWYT1/I81/INz+9ecfim2xOH47MCLFSi+Pn+pFf7GDaq0vdg1ujnqfEX745kr43DC5fvxFrdRldO9Id68xw1n8lGGm7/Jf8b70rThfL3HItwBu/HFf3XFfzbjvi7urEhv08AlhBLmh+YONUl8FTitgDLVdnvht3U3doNwe9m2FLoZ9Y/wZ1ldR+ka7jyFuz76xKfONKWA/GPA373r967/Lfhi87VjhAi5DvX5IFCKW6wTMlPKHdM4kOg71ybjSNCoSkQBckQw8yEoYWuA1hQlORC9ELVlNNOWYYCPJzCrEj8xy6P8E+LMjgd0kvegiG7GSsaw6lIPABKvvQwZKiMSpaM6SZ6k5/wnZsfvGjShOivDqw2HAUXmUhsdkl3n3BI/yZZSxOooWo8N/pW+APn9nzSwjSiVTnupUP1/208JZRpe9vjdZXX3dk2Onw+7i23xWNlCqdZO187sj0dDVORvU7hcsLl53w0Dd6yS/qDXQMBU+vE/dULxh8gHrsAdfE9PS2oGWCO1SrYspvawSvnR0tKfB9IV6AgK6tE36GxeLANIppYgi07O4REpynkyXOhGCflvNkoQFIPag5GXycZh+EC3uh5wKgPyvfk7XpUQemalfolZQGIikO9ieZHHTOog6P6thRp3d8UcLIP8wMcLuB0skESHTOFbGQt4LqqE9zLxBNu6jwj5Q3Pbep4Y5tvuiatbzjQUbXOKhAd2IV6m9Vy+Ui2xPDHCP4CXQYLd3sRfj6Eh/XPXDYxB04TU27HW9su+so2JvevYivg+4yxMf6nJ62qb1s3nhGv9TixrNvet/kS+n3COyDvL5IOT6674do4ttM6ZLz27Ob+YWYY6idu19C8B73CR986kFY8Tg2jgPmGeWGBXPeDOQTZm2r03QyzrEdu5fsecvN3voCu7vV6xV3/Tqbr6io6jdK8tOYBIbSQfRRVOZ0nWYTMVVIpsj+atfCgk/FubOhksseZDD8KdOsiZjRbZmVQkSBrgepUyqc+MrAxc6A8qD/JhJIaBAZXJPZJQQpW2a1QIv6hMMNbizOROBLjpPYmJSM9SeTqYzHTyG49LJKk7ZYYCKkRUrWV+YWEYpRg8/IkPl1BSKSnfVADwA0t4tOPLm8nnALUoCm18UgVqqyGlK9HJasM5OeotI8crbm0uIjIMGsHlzGLi7v83E9dNGQevoK4QGy3Hk99PpFa/KNPV2FbO+ZNwqg2lZsAKAeG1nSUtGR1hhcQgEdevKwasm4g84JSBlbYhNvXTmAnVWe3ujch6FOrFLGVWOGKfLxVAUs/7aN4yqiuQuldfRRoI2HqgY6RjEonyyVob+ICkfPCiabCtA3heprJrxRugilY4ttcQyD3DUam1pLlcv2I6kXvjLIx1G/355nluILxwHbr7jvAIW8AoMXTuS2ixjYFrgVxkYzezRgD61rpp1ZbWAPrLegKk85+GhmWPwEfeH3eg3thDwPxKeMXqhgxkP30/fcImO5vH4N2jerQEjvnAZzHj8Q/S/znjHk6EeM76Vd9N8szzZaJfdBQ+kusnBoRWSLv5L6Jel7w1c3VK6MWOKgZihBh2T3YeRbCZczNTLpAehBQlfVtTE4M5/FSTLqlyF1X2BiAtMbB6zqxKXKJpAlRpApPszvIasZhfCFikS1wCR/oAPIeGsppaFgYZkFa8fiWUy5kHUi8rpNE2nMRYdeRrNMdiussMiWXHAgN5B9nUy2Y/It/x6lH81rJ5j7R+V77BVAOeRiGma/hfSFjGgIstdJo26AusYN+Dx0GSo4/t+VJ+aXiULbf2soF0KGP762S+8jVI25n0F5+Z7HDPW+AwdNyO3yWa/bmZIuSx5nWZZVLSLN+4j5Tpa2kqu4W80pML572hws1QWVr1cZE9xjlbHLtcuruWYpGeSvczfQmBHC2XPSRC/1My9dnkw129+e9AnNW1PD6TTIIKzHf3C3PyvMF/TbhMZhrEEFISTC20kgBFaJkBGZ1FJ+wR4FGXOYog7/ZRxg/l9VE51dHFO1GtHMuZnbHmvcumZvCZc6vxisTrbPcDC8MLslECEokostEqpCLfn/jf5YN/lQQZtwnaeyOdat5PSG8FpwVxXG3N6EW5F+uOqH94C633cF74XycjILge6MSNR9YI5bC7pOvW6Wt6eugz0k6vh760ykW6EGX7Zm3xtZ68Hpiaenml7rpLP6jevH2eb3eVzj/u8BevyhkO7OdPDYSN5a+19AD20btVhG7A79++GdBsr3Ni6nWXomZIuKezS9CHUt/FfMA6M6AtfsBr9qpJ72Su95guQ3bGxiXFokF+c8CNbCgsjV1VsBAgmHK1LBCMEEjcDiZt5RfQ3Yx52AmQYPONC0SQ8k/KFkf8Osagw9cDuQk0Emwr4g6gaRtj5Q5LSjel/PiMcRbxM4jyOV2Z/xPTseZAuXpyenF6c4IoFzQNZjNPJkhlSVkYR7PgVRuZqZSKiT1Aj9ooGjx4VWhdsCf6N+IYxTbT3bAS6eC+2yQHR+vy5lDbQoDF6Nsulsga8TtKjcUi5FNCfQ9jg2f51QAAS2EDvZZMGdrPXBkKVzFX/bCS5lIZDLql7r6Hcj9Agb1N9a0daElk8KKdVQZ/hZGlcSOHK06x3hIk2YYodUAR2zoXj4iwI9oXLfiwCkr2/yPgyyT8IgkMdVq3uRZ9CLpfEjjJJSVI2NFOAgqpmdJGcSyD80KHOZUb+vAJRmBfsOWEVy3obi2Wuy7HbXMhRQsBKDq0JaDGBIvqbkFJqlonqpuO4cPe+AVon98V1c27FOPZvRd4+fvk58OY0vN9v/XC3DTZT9bQZ083xBYm5ajXIRzvKSNeGqfp2eaXDS+b+O53jch1us9Dd2pIP26s5+QDbYbQdLhvb/aTdJe5O9fH44Uto82i4Gn6/rOuE+d7xJuzbRiqx09DXIWMr7w3zRHYofJi3CtnjsSfvQF9ySG+WfvfV77ZRd4bg+uVeanfoxo2Wd/SCZgRiCDFJiDTkIdznczG8IOmsOHSJCXZO2GX9sCpwcG421poYBRKpi2lUHb0aRkg5yEmI3dxdGVYAgpbQ8d/GKSWp01YB+wpW2HIwTW9RxCmnMgNYmpEP+zjBXKQc44WtRVEy6ToN0+P3vnZ3Mo2O78yY7o2TWTIL5odHB0cvsd5A0mKvsLaIOiehILPKMP9qM7lNlWuaLM0Ru/veMAoo8tiTi3IY6mSKb+quGP5by+vXod+CboCZQX7YlA8H7LImMcHRZa+jGzD7dSsGBIXXAOpyHJTL0kY5PC7pRu41SQ6val5HuBJtdKrLaRpBIAJylWsaY52tDlmjSeR2oPQKtSyxF2F8gdrJgb7sCi/jBWsDQbwIoyMWlIDXshW+azlMLKLHXqCSytNUyOlzRNMrWBnCLVRijoOw2MFdVGkOf7SsZ4VBM79M2kvSt44oCkQVB1JDRkF/m3Du9dtvv33vzp2L88XZ6elquUSRKLTVHDez59IeWFgI2XbAphf0ZVmu0cDWRoxmwrp58dzU2w9tAvU9kWsbVx/YZpwrzY1L1x9zNnGvny75hq4B65A/Tu6bt4Nsj4guB7oxe6DrgGoGlxZft28HYlyEzx+tSHGN+CZerS7X5//4+g4xRnP/7WWdfAvnFfr+mHp1YboxLV0ErsbhBoN7e8WDS7/dTZbmV58JvtCOf/4oMMgYH6jB0v46PDzuhGrBbwNvCAf0YW3bbhxNLkd7H5fp84T6VeuSQ+3Z22QuckzzdNnohoq6OCXLlSGPJSYNsu9BvNY2X+R7ncPKaGOXSWLI6pZhpUOazP2/LLOR0GqxtYaUtNNSiOhnl3np4es1kUWHrjpXIxoKhWVC0zivIp0LG0WrODxELSji51Xy8s69r83uzebzeTLB0QonBJTJRO4XmcUFGUYaOrCM6d76cvUUveuLEjYj1kkWcnk2IgXvotvMRqYQOVykCsb9WNhN+0okrB8bUD06ZOuUOtREQKHL5pBvpnafHM/WWZoi15Dj8Kzhx4Yk+sMB3ey+zrdZogEgk/PLX+9FBktyv/QD/iE+ixWI00F1WLED5B4T+UVyUWQZXvcXnE4RciC0WeyjD4SFhOyo0h6AJMkzVqfwBIWwj61+DrY7QXFWBc/o4FJVWVKqG9OIUheV/x+2DONEihn/VD5G1brquWWV4neIJo2iw6PZbDblZIws1yoUBmmcmBGUq8JM5mwFAMyiHzdZ6K5sH1Avd7jWNa/ZYAmKrZ/XAJeGXA7/3iLz8m7F8bh/SR662+A+HFiPgPvk2oZ1TfjlaraxtfHhtrryNpvelOdX/oqJD7YCsF1jxyB39xmnVz7c2APQpjrgBtHmUxN70797a04j9N3dutr4GuxN23jUNwrZM7d9o/h9ZDfFWx/nqLBr99HrAKPo3NmXNjCMnmsZqksr+m0BDMVLjGM+4IHuW6sE7fuqtOYStTpfVolb8A1I/av3fzNq65FErSkhc8maAXSS1Iq7QTTV8UYRztR19JYmWRH0KuQp8suVZ4iSgHqgGU/VCkHH7pLaGkEDfIBLIiJOk/EC0QoAqweOJlMCVCqpsvnGBIj1BXyPcvZTjEOVObZAWHQEwXEU3akQ7IJinqx0mJMkuCQvlohZZuMBiRK5QOVKVy0Q2mydwZWluwjQj929G9GduDpZOaxOawiHxFXKQUnkaxE4lcaUAEE20DU+/bgoAm2eJlaytJNNRSrJ/KlzuIc2n8Dd5WrkQOraNUk1dpe1jby5gKhxFFnlRYOR21TPka3yVKVLr5ptQfJMnSW/q1l52EEfC8/jefjo1x/F0+Di8dnipDi8mIZxxkaRs7Onq4sU8T2JUBezJMmO71UXJ1M6ShXMF+VZUB6ExSqePEnzX0QXKKusB7ChRedXIOmbP1Dt+UXJ0B9HyJGEDsA5eNi2qXh8BLEAwHoCCCum+m1TMNoCQK5+K1ttkDss3ggzOkKJhmy6M6VkDYv86ruMaBC2/nPJ+ryfsQ2vWVuzvE1pA70cX/cW8rm2azP0Bdyo6FLGfB8dzMZY2oe2jfNp6OIfj6dFeM3ATZV4U9/oDTw7v1/XrDjZu/y/HGe3C/V2uxZR8463EVsB8K0RuJBXhL5TvE9auNvjGlOvLkw3ZkyRbpyjV3tU78q3+9vdk1N4+Rw69BqBmosY76mJ7fvdYiuPlnc8gj6kt3FfAA64lh/ZTb4A9flVItG98a7GXgu6t/cSRux6tR0u7HmQ07UB19kxY9lvlhjMbk5q2ZYfjW5suETWQdRmZyXA/Jva1knJ25K29eNoFWm67FGiFBcpFecHaw+AsppoK0EKYUzpzmoIr4sLeXuJOA44wd8QBt1h8jKenmPNIcMkNBMuTRFTnrYtM3ErCV0FQYZoMGVEUIrgEnYCRsPQOGnpDk45lK17GTYXLaq9q85pcXZr0x2qJqEtwfISu1mSwOoYQW4mKsXweOW6OJewgc0BktDgaH67KHx0o8OGv8W5ziaanUKwjhsVMi1LWFEpQYAux/c+ZykIbVNy+MFBPEWqX1VLuYHVSlU5wz8s/QBRWqopbv+LaRreOZgtq5Q+djAr8RU7TaLyZXE3Kj+tKvQB9RMrSb1TMj+ue1hJ0FnCMWjlXrYIMOrBgkeHjXH6tTamIHOoD+lIaVXZqs1yE05/CttPXHczlAgqAH5oR1zTjnUu1xIufIX7ZdkvS79Cka8qC6Ra71jfX1VJt3hfCwdca1KUvRGXF9nCXwrqejXwYzCPgbm0xJsDuPobOVSRFqMA1isA7n0ywl3OFm6zMhtzDC6TwfszEENFb2J6VU9jNO8h2/eurjYG2941Me3TWeC9EvxGUA9mr9zxNPfgGZ/Zg+zy1kvsC3rU3gANo3X9Hjo9SvoI3Y7bwDB6rsVJaLXIu41yj2cw8F7umA/g9fTe9na2xgkelxREXr3pzE6aD5AWGjnF5BUZ/uiSy8JKO3oRvB9jQc1UfYSJv4wg3Cw/MIjcJpBh+YNNBDZCAdP5NlWqV8MkeEl/TjkAniSHHPJNLAyXQbAIAvz6a8Oxje/cKUQzqJKdwFrM4/iAY8g00YogGBWT8E4S3k3jeRrI7DuOEe9w3I68hT4g4yVWKrQiIalLfaZyBw6Yv1FDDmE2wKmopszuiNcQVMOoPlqRYIVELSwM/DkUSlNYeI2LhtgAFM9/g3TtWqdZahseCqgkl+bkVMPTRLmEtRcgnht62kw1VwfwN+A9ySK8J9pVpJNg0MYENVqTbG3sHjbq3o+4zkWiY6Nwhvkj2x+CZkf7ar+vtE36YHheYOXFkXBS9ZY6bTf5rIpPgug4LJM8OMdPUBA9r8LnLI3ZMtYZ8/gI87aF91mVPqPP0Osw2mc3MZ1PmgC9S302rPLJ8nxRZOHF2cVygdZZzSbz43vJwfxgNp/Fzq5MPn3wPYW2IC8/1h94IeihRIMECyW3PgYYCwX0RqojHcA45aqqUtdc3vgu17zY+UNeLpC4y6HivhXfRDRw27/qzeOurRFjXKbtcWady+h0hTuS10l9oauV3odJcWO+R65E9/qO59JQid14R4OLv9nadcu62Zh+nrQdqQ1Q6s6mJdGH7RJJqhA0SNpylbH5LtcwLnMD2UX16mKG+pIb80Sq1aCt6Vhb/42KeeQ7jEQIo60AMOBsXEM5Fb+ZtpnRPW3GbSB+gx5U+dvrlgNfcg7wMnZ7uovZfJO7UP2cqeE64E5SVx7mQUmV/YycIMoeGj8nSL2pLCLqwQFB2wl6iGcYNmAUgdN+EjF7cIOdUlEo2rFEz3oAq/QBl4BYH1a4AZWYbkK5S7CRnXl7zc6y9nCKfBVz/iuSXZwqLT6L2fQJSQEqBwManlgm2pWMpYUyYbENOiohisDIHzeFuBwdKgdq7Hvi4hVjAM1NyfoDxtXET1Zik0Ml1WzREofweBW3IgxVfWvw268rex0lXDxZUVaHOqkpuwO/jUWEKU7FGvd5Umb3Uz9YJrs14OuYNmRo2qfNgIdHQWOSIJSn5rNlUMmKdfDGF4sZuLVohYfLOMB6DvyU2b0UQNDL+ozWjHhCcJegL3MvvOwcxDqKWuXrADk00/I4Co7TeIUxP9op+8IR7TlZOg4eVtWDMDmhCPQBsDNFr/90edTcbJFlRXWGKnvOMZuI8ui9E1xQLVA1g3Q6saMAIAfdVJqIbRaQrb9OBEPJ1HKZtv5qqYANB3IHRN+EQkqmy26xp66pVXePW5tNnXPjIqXh+nbSBtzn/7B+SdrafP5E3VJwQxzY6pYDWN0wNZA4HL3ZYcYVNYzt1aR0X0ToXBN+KdE7ANZYID0J3Hl+zod0XRc/s4NuC68/SAboIhvgoRkIl8MfuIY45qyyXOqGvdpQhoH4MdrwGHoc+iFsQ3rbAFGb0Y32SewQfpehy73x5fZg9srdJGjXk4+nW3o3ZheuvrRBDB61Pg0Ox2CuviKuG+dRcl1Uw/nH98lhHNspGy+7l9i8tW2UixgCb8EU6H3TNRiQmz+kWWriOi6/sqzRkcCy81lWAS4UAYWfgCXIWyE7BIojPPNzUliUaj+lMKkYR4voIkq4CejOf/1QShjhvAWPLuBEAkNIsnSCJkjje1TzpuVhFNzBCCgMpghbcTRJijtJ9TbW2czA6pQAdhIHOS7htQIAHjYVKIBSgSgmOu2g4jJIPiEyzL+iqknbQLFBVYCSll6qbAKVvE8gv71NTi8VkjXbovpIL0KWM+SyIzFVRVzFhOSR8tQo+QHGLXpYPiFs+G/nOOqxvcxDvMsaml9/y+MyOiCX2GawQOsFSE+G35Fdw7rs/t1lN8h29YAn55/erQM7kPruquyQcgcUbHDA4aRMr1C4ET9TlL5KgrSOBAcQ1VlxoqFYfRK8p50IkeGglz1WGjCm+1lBiNQyordcyNy07dOI5q4OHQ1MwRfaoY4jqcyZgQlZhGZIi58F4alajW4iX1VqNfXY9AUrA/JXq84tdRHDffW5nP7M2sJFQLcM7orIokpSDp+bTmfHDx4cYH+G9C8K3V3trPa1Pk8l6KS4+8Ed7pHc5IYvtR8AR1RaH1uhw0Q4vBLXoEE4CNv90pvj8zawdU6HZAtAZV+K9PMG2K6OceOGyB78srg3Ef7QKeiN4y4bk0aBujdiPPx4GkYV7wENcsBgXKoDvxoNfh3rshgz7aJh1Yz1Tx1ZJ1n7uvnvutxON2DcIM6lbncHGzNqzC7c9w7trvsGQTf00MvDlvg2QGkuvGNtf4OiPh4KACxrvtnYas/rOC/ZoDcyWBEtUW2gKbkT0SSM//UIGZ/pFvKWA7cc6HJg6H3sfckAdn9dPKNiXGZQ80cYSQXHKYQYZHhE/sbgns8nuyUFabslkdzw48kfiwA6BwBPQYhSkpM0586fZHkjVmjloqcmUY9BOa/klJ2QQBCfEdTkMR3BTFK6ZvSZ769QEjCuiLK85G+RphgjXVQVc7Ts4kSwYw0hZeenrJWsVEOm0kxIhQ7J6GIAQS7NzjqyVCxRSpXeAj4RQZoSFLB8CtSZtXihsGAEourUD01ItUa3cMKAuKTcdjNQB+8wriPqkNDxZ3SsUXTAdkaQXxdlOjRWuLBa5JqSuhCLJuw9GmhzU0b+t/nr+Ba5nh1TDESNbrWwfMYeeCgaXLJlF08cX/yshkfYRIputIjQOdrQCAjTf7gUhmAT5ATFxl1pgzPzVWUKF5I43bQ6qjIsgoCk3ZC/zUIMZaC4F7KruCCWrlBwWhyz/xwUAEqpEPQ7tApTJigQG6FScjwOhijZ9RwCFKu+YHXVSWFQKVEf8zN2KRBdQCkvBT2QP2GQ/RgAqpeyATPMc0u87NZiabD5GRx+YtqAn/pmhMUzu9pAE/FF/v1SVeYqDSEG8H8cH3h5d0Nu91+eyeLFbpSz8XAV4m8wDzR6ZF4J8VB1WrwC4HTzp46HHrgX7KcCFK027AP30WljcF9CJ24969+S2IF5FRG+zueHd5fVq7ftznKF1C73bqDctu1GErQT/vr0XA3D1XKNrPE22E4ObAOPsxDt5rqpmLYP8xq5sDuzs8W/9cq28D7AXq+gIaxs1rn2JlS/y0yiI+fIqDnA0jriOFWVgeDEQIxDHuQweU/BQRBGGlWCF3Q9ki54TbPb8IOohOAjdUJCPYKbpQpTdIEoHybI91hn3DW3QqSy1ZgpWCyz58pRHEWTo7jCBzuYZyCYJlhicAxUlKQYYSdM4paYWMgaW8qKLMUjzMSZ31XhRKg0vLjk953Dd+1URqOQk5aCswtY2UCwk3Qp2yGjLX9LOo/UCe5Oi5AUS3VM8JMUCBkyP5G6QtdigwT2KfcjYaiZBaMqqJKTUyRQYSfJLmbBmR0XofbYxmvmW6RyuR/d6wiLdbc2hvKfKvPGCoBDDAwpDrOFoa/NJzTKq1+X14Fv4XFguutyWFzYMLs84FU9iaFlda4zi0LFPXFS+7HxsYNOiGAND+E/c/9cRhU3BHPTFoypxOs3YFWk6TTENKCS+GVmptn6SPgx39fWcSb+rdwwlR6n0+rOyxJXUdje0Ha0zPMoehFiPCYNYUnvwSKHXhLiRjZ+EnKaBHBs3mVfObRoXl4tXOXH0I4uCtFoAZLeOTyAbpjR2dTrwENpzPbjJdRtH9ArIg5TJOoC9kPEk+FOVaLc8gblEZ1NBaADUKZ1JftVrR1DiB28jA2DqULUQeLQNhn5dVCDSJpxZvyY3B1zdiAnaRS8I9ijVe3edIQe/J1R/ZJS1HSv8FKHbXg+qpgO/aNydYC6tXbt2I13Wce3cqeonnYUtnG1di/0Vum0sKPTfeP8Lx1Y1f5tf9gKtIW28UbuFv5uFW48ZncvdWRCo6sO91F7ABy00epGZjdiK8LhIiDU+s51Li+z0toMLWDLsjbQJt0Gbjlwy4E3gwP124l4sznG6sX3BkaPWJdD6VtZPJihoEQY5XTYJfpzGBKT+bY5ElmIcwB0FheY5RURorC+ltCEYYPEMbLJSkcXHzb71mpkBIR4R5HuyNTEIlGZuHWAAXcVYAVElBWulQSQI5xhzIMkh//EE5SMKLgHshhXQJQ9XR7eD6aHB+EUq+/MsLFLQRoJqVa6vqwKmrrBHXlQNGu0XEoYRbgzwRw5FUKQ9ExFkTNH0Jh1kEXXlRLZVFpLE1yqEAYnWKEgNhKvCJProBUtQYfQSrVAFEZPwuybYokRPne5X+5NhMNRp9oPKQ6jH1mH21w9aYpap0Na+yyiVc7QpSTXSg5ijaV5dvktXjf76ElBgidUkglv2siEaDgNP6U+1Ti1XCR42peQi7VVGHUSSzOEVmfRSSzQEqcVDyckitOstvBE21Go5txz/PwASQ4dV4F6wI5w3MVSjnqtpvKrozg+jRLaLWK6n5l49gFDosyrqoclSfQJDo220tDnRKH1QRGp/JL/KZ8W5XgvGoQOz9IW2gcrAUQJTDmUR+2LlqFGpxdALKRxKDWOROnDND+9Wv3B1b9pW/ekOl7jUuGd7ES2Vy9Am/pGBW6EIW9UjW6KGL9Bu819U6VcGY9ruPa+L56Bdr+koi4Zzrx5PdxvLpjhKF3fCW1BdDnmoLvxfoxg2ANgMysbdr3rogy8WxgxLtIrpt5LgD73Rbt8nc8Pv7p6DOnWr67EDcxuJkNSTi1pbaR2Hxy8xXf5cwN1sW8e3+m9rr3LvVIpNUl70tbl0kbVxnN+I9v2wxAH/NLbMG8qr2x793G1MG2kiWfNO97GNnMPG2OFlwoeE2aIMiGY8lADnBiEgMSBXzKVrmfHkfail8g9QfGW9gDg0R+T/Rihx+whakIR0Zw0Vkv3kuvMIId6SJcILtAfQuZ0JdyZwFVynDCSGIcqIQkys4vcfSeo7rGPEvlfQiHzsME8jR+kB3khk+tDsJg/FhoFIhHdJNIh1EXoD+SHBIRC2RLhAyYLy4MIm6JiEsTLitliSa6IqoKgJAlxysPUMs4ekQAz/Ldosp9yIVwT23QkVBekf6b2V8zsVuZI3irFMWScBat9CUxQr4rTKD6OVQqSn5l/kNEasOE4hHMRxx8Xjy5gTwo7APeouyUrss7ZM2fvgB0eH5uLX2dt1g2aItawdahJaDNaQHw1JBLKoQN5GJFbMjCNSQcotQFjhkmYllaCBec302dkoMX8PUyWRofWKB5SG/UNSdDqFHWqOJwHyQsmy/H/gzsnErV3F0la0/+s9qBZqF2CnG0heRJOczTAKtULGZ9pr23Eeb/y66MuVF0EyQL1lfggSvOSmXgm8KH4KQsgKJkigf6GXA+pIgO6VA8aULU1LQD60Ch0VDDxdHajXdRLY6BYxw5B2/YAerF84woTddF5ZAR1UIaokrLEfOcDcW7oHRTE1qUiRM325eK3YztztAamIjuQfkR3DPFTu+Hd8Ko1/PRG3R54KVybiLcexcRNgK0nD79L6SnFz6JuMuqLOTQy+8huIOzop5PQl3bX1DUeMATc3St+qNZD8S6r2uhSDnuluOBunJd0sg62Fmf93Wkr6BJcrQdy1dFjYHZjuHbqJW3XvLuu6SjNW+XYqrBHCilcVrv13L+XrqBg7Gu3PTq4zC30EI+G4tuMt4FbDozgwFZ3G5HjiiC3HRbGOSbs5Dkge7OqRigByEYWBhbEIARviuQ/Uh57GZHqZLehmU7N6/IBc7Obq1IWz8g3iD6S2vn2I0pJqrZZT0IiSKK0JsPtQSIUvtvtdGEX4+Rs5LZcU/U6ipgyyipGzXjJVs+iNH9BCF7Ri3j6QhY4yFUy4OZTBgawIkyqAAvzVWW+H1p1dhRGQhG2HhIeBSDpFQKhAIFOzmTkXl711tGw5CckOqU3SIEAPwGySqCLsCYXGJEqF2GxVg/IF7JhFDMRFhxCNo4i30q4ZNqYEijNGOdGbburPO/aevRSLNgk6xdam8dtsEueybeR1dDUuHaiJNFllMBuFBifkf5p1Ane8/MyzjDG0kQ9rcIdLqtdgVekzeGrB0jUMQZqer0NWw+DxTBWRmRYfLHIYg2hxRudBK1GRP1DlQI9eoLQaiOv1C188EMVxj8HRFkCaifNNQuLA8DMOxQgWKxBEE36MMLaShWhVuBUl3KkirNUTnBWXXoI/YU/6+p0F5UrHgqcjIChx1r3c32Q/m+lAKPXAe0Z7cHaX6qm0Nq1DjUxr+73dZbl12J3ucZi46I4zrUb3Ef8JQvvV/H9oF8jq6xBr1we75C79GvhJuLKKN/EjH2VGmhRQPugO7VKQixBtyHds8PMfTt5EwlDlQEM6XYausGhwW7UtS98F6mP4WZ1cR+b4xqfoEsvP5cDHuKVS+3C+2V1Uy8loB9gdIv0Z29ih+ri09zA9v+O7xt+/qFyB/mzs76DufwiB8J7591JyUAhPdFDHOgBtSj/PfbDXfitXu36OFl2zDvWCDVcENR8ue5MWyICSVgOKs7ZZQWA45eQyxHV2Dx5T4ITGwPY44iYLQMbsjMDymhBAlwiJFFIdhEkSeRC6hb3nBBVryrIxRCZJEpplp3UkJUEMHEGMLPGd6LqjlAhpyMgMhWb/3pc/GaSfoR4pZljRSEMmjCp9QoEOqTCVZlzpJO2E7BSwCNzvTYV/DIO5lWyYisBKGXVU01LziJAl4iXzFtHstlAZLOFAyT5YFKEnFSAu1JmkZ8FMTPOXynx7Rg/pthydR9AHiA2wgoFLsg6JVlWlHIcpB9mSzxHZuEkKbOHSL2OG1RQXizXbWT8Vg2by0UIwGTUNsEiGiD3W+etbfq7noV8aLK7ywWEFvw+0jZssfQWGq14INnWCLHcZEMmtrowfa5Z/AtNmbMnm3ly7XlYJSFncp0WmvPWLgjm75lHh2nqHeoPKHh0Clj2nPnwqmQFieZjlzfrKtI1y/wuapaMp7S0Axx+PNNIXUK9MS+XpkBkxQqfVKgF8rpJ85UYd8m+y7Z2gIw+G50l8TJOn9B0RXGP1l9lJXuBg+izUC6PgERPoFm1xOAUVcgj0vqqeiQd1phEZXlglwvbS6znujRQSY3VBxSOsOSEJRIrQvQZVArtLeGYizABgB4id0Mh5wQT8RS8BLiE/PLLwW7AqWBxs+8aM6qMGfHGwPSVr7h13x6CsHixownsBLyhRI08zWVSjcaovmsMD/vydeJ2luKg9/t6Wst3itkv4jotO6akq+FvXwZVsX1owiN7VEuew7A71xCdfvwYPG2hBAZeSoHsSPIx1GEH7fGhB0ZRmgLpXO2LRYpLdvdeEnry9yHsxL3aiF5SX22Rt9hvOfBl4gAv9n5vkaAR9ZBe+CdBXCKQk1UYB3XKL/YwJgwhJBEjYQgR3fz/MNRKPjPRx8qVzCi5ibsQGjFCZgiVTxOrMsNgYUEiFPK+Zm0Rp0GF6YiKFyFh/AJZLCzvihjEUYTF+FmYvkQcrNEhNTIRrQxA8wsC29bJ+QCI7yoG7BwatWAfqByGrohDJVnhGx4JVdP10TKOKBHlhCUC2ZiDksWBRJIrNeJspyLBjITIEhOSIrWSYYUUJJPrmUYGZxSlq+UpTEhn08WiiA+ksAShBE3xQhPJQMES6DRq7ce45aivn+tmsyq5hKZ2ynZjV4sfjJDkmqguuy7ECcCiui1VbaI/qlGUi7DEmEpedLC9wcQKpzkc7CCp3RQ/LOARuPFTAXc064+GqCPbrL31TB+TchiiNoVkZ4rfdhLEEzSJelqes3UBgw6WAViroRPgj4dtu+AjA8stYUIj0T+02VfyN/53oExLNJh4Vewjt08kiiVAUZSjq4UYzWI9JTedMicycqx6aiTVDRA9U0nTBejA6p7qWlrjIkXJBmm/9sQ+BO0z4LRsOQCSDZLOMKazShuVkkxF62YHT81BBa50GQqX0wsOogJGRL5xl3HOcVzcri8XIu1NJbsh9DX+ttxxgZZFr5GE11FU00ub39dR5o2X4XruddGOYYFKwr6w+3Z3M28BdQGG6b1EQ+3ouEPwGggh1fXd4eIE4+nlN6aLW4k+tjGUODL9XDsJrxO78H5Z3VSXzdc7x5TyqmF8mq9WlquRyztU6y7m8ZB+3qvl2pc2v8RuGKGEy++9DuZzb9mxr7u9mxL6aHveQd5YRDcuJBfMOBZVvKjCGYKMjLA17mARBGo24CLEIxzb1lhmwIXBUkxuNLFHmEFbi1ZKBiEy2gK0wiBDGsn5mmTV7HKGDxkJ3JRS3Amq+1INMPVG/sPEImbWNjMRD8lfYp2tAICTOVplNlE71UoDLoaISasXF2UwOQzzbxbhT8vF14LJ+9XyW1H6kyD7nWj+03j1F4Lpn5TnvxtOfxIvfz+cfj84/wvB7Mfp6veryZ+WxMz+PFr+hXj+o3Lx6+X0p+Hy14PZD4vT7wWzn1arb1bpz8PsW8HsZ1H+nfjgp8Xiq4vgl+erO8cYAa2iBGumHLsm9Q2jE1bAXnjbtooLGPNViafc5A9Hl4uEbyY91lwk3mVpMSBtPqhhLdvoW1OoBmfCNSXuYe2VSE2otrRkKiJFSq3G8ke8iqMjjP8/ezFdMOG9+o0g/UGS/0aR/KhafCec/TzKfj2a/mm4+IvB7Efh2feq6Q+Cxe9U8z+Ll78Bn6vlb1Szn0TLXw/TPy0Wv1nN/oxwNf1hsfiN1eTHUfFbZfTjOPudULl+Izn80/L8t6uD7yfn37g/+bBYpWGy0HlgIp3zqj8KJy+Cxdcx/dFeXXzv0F3is7I41qITVOOcR8tEGKm9xIoM8yFVgn4lRdaURPV5moUFBaJZIOLKpE5ofYM/oFE86KeOu/VP80C3Z46fZQqUnTnhqjzkCAtQSAPVq4HmoFW1Wqswoo2NDgEt/lChHWt0DeDmr8hw2ttmfOepaT8ljBktx8B0Ctkjoh4VP9tgwh75rwlqA9vVcDQ9wHrLbjy7U3cWv/HVcJ1NXfAGrt0tu1HulUpz+MUl3qYrccCnYUgOca0wlDoU71doiA9+/Bg8Pk7CbSuN8vbjZd6Ad1hcu3swG0HBaAUAqLZQA+BpK2f72IFtUzZQ3z7ccuCWA3tyoPNu7Zn/cwNvCLexwAQgZ0CPYIFcI/ttRltEonIq2VpCkIxeTPBg5EEZwLZBht8sEUSxrUkCgkAv+Z2xCBnKBEh7cGOVYpko5hAALQKYRCxY8iC9IWsiSyHZa7o3SF6WURpFR1WeIcIhhOHbMU5OSjabQhhSHrglq1l+oYU2Ss+YV0YODKOEufi//n//O3/+7E+C/NtF+otg9fV88rNy+e1w+ufl8tdKCZe/Fc/+NLj4zXD+w2j129H8h8HqN4P5D5P8t6PZn4fZb0YHP4qz3w6nPwouvofwGq2+F6Q/CrJfD6Y/CVffiSY/jVbfLic/j6vvHM4+CpZffbH4o9/7+r/4b/8bf4EVhnzJnlTI1kKDBEuxsuZdowPUg7eLt0RuPLlhXKmSQtvLRbePLlDj2Iod+egwNnRZpo3yYC6XNsI2n3N84LC7IWH2fRHH6R/9+Cf/0f/u7zypfhDk8O37cf6b4ewX4eLXytkPquVvRvMfhcvfkui/+s1o9qNoiaD/g2j1W9H0B+XyeyVcXXwvSn4Qrgj/oLr4Hnwuz7+7Sn8cFL9RBn8a5b9Vpd/Pl78TH36/OPlumP7xX/7Gv/Q/+av/2kEwrXIWcFgAsNN2+RSWuPnBRggi4Thi9yxkn7f2H7MuAQddNdgDcC8q7wXBC3os1WpqChPsj87k4oyllormoL3nqBna1OFag0K0pIOSAQhZkPsxWMJqSTiVVUcHmMqh9QNWyaTDWoLhBeDmrqYKOzBS6AioHQheVRJU9TKkN/JVEbEnXsfJ10nhG9t8e3LuSw8+1J1vsuJtx1NhWlVtI5pSXAdtnprf5nvTn9pAvbJfxuAbvHwdcTzaq+Uaj99BdkvpaqvdGF/v3LfEveH1ldJMXnt16WmTLg106+uyvNYaXUrlawBwM6Odgob4MMS3ofgO4jrCb7t9827gFCIJ0PzImzsSyxOcIDI5idN0mXqHiyrApgJp281lOvtD1gE4hwv5wiAZjcgIEMj41V0ZZM2tuXqzoRZmdnMCdF6F55wEbCoCUAhZ9ExZkIgQlzu/G5d3pCMIxwSfjCUTxtn3wvBDppekdahE6SWWifrYOGN40C44XZYdyt//6A//4E+qIv6hbMTLn4GsDH4q+S/8Kb4jq/In2O0E1c8qzWr/SDjDHyu1/L5oDP4IgqrqD7mFwR/qnan+keLDf2rTvf8Uq6GYE2flDvWp1fezqjw5+d7iv/evJHcnk8wdRqt9sMJlF5qPdq3aVf+4B92bs3LXMcoHM4BsUFgVfQA/7DDuBPHBXXgDvH5wp8vX/vshwqqOEGx2Ooi8JYZRHMM8Tz96WvzxJ/94Vf5WVj5Lkm9kq+dReCes2Jz2qAoeB+H9IPikCu9V1UchWyOC94PguKx+EekE6PeD8LAq3w/DoyD8oAofhMHHYXU3FCcfVdXTkB0C8dOC85XjT6PonSA4D/O3vnfnYZXNsTgy5RMZnH4wMf/9HADMRf/FXotfTpngtDgYT+/kwAec/stWKeR8AKzI1F21Mxc9tbb711IAmakmMfRPuK7eKOt/WS+hVKD7SpyX2ZIKIEYLTrSMlGQSKUhbYuh1EMIKA9ZfAIOBcwBYTIMYIiyra08haa695/6bjPo1nK7n+9HrsANYP+8KXWsM2YV4I209Khpta/GAR7jn7hs5bvLhOnVcz2rXL8olhF2trDV/QN/bfI5LlxTek7ybno1ye3KPjVKDjuNPF+MYGtYdppv/9cb4/PRrvHnib7e1fFhRPOjtZ6s67ashBFIA2ogGsFtWk7L163L29q4tyNvHWw7ccuCLxoHOyLC7AhoITACS6CNBRyO4jJj5YyNsxQqAlEZEc81pSzoCwPk4l0E8DhmZzlcsqZJ1JE5xMxEKUYl8zJJqhp+ZUSAwrT8KCmQ1SjH5Vl9Wy6qRjTjC2gNgTnfuSQVQsWyjfBFMnpm2AIHa8mtz68opUlUM6gDzwfjfXCKZhcXXk+q9JH6WTvEXqcKlNbCFQEXw390g0mGQHEdZxEtkt0vUKpFLafozmc8UIVYk2NWKNClTdbAsC3wOPT2ffFAkp2U0ZYY6lkqFEqHMFCKsuonWOmCodXOFEDCgNrpJaJMdhEPpQTVwbVQPRJu2HVAtrcVFhcpvfi2sZ1OZeILDiLhwsiyyPI8W5cnX4vxrySTBcSf7qlPOaZNg7FYMxCtQ01CgFU61strBoZf87TRGcypKu9gaEznEH1uAYqmB3bdY0WBLVZaTz8rpp1Vsxl3qrAjxqKOg0GYSa38aQfhDNgBUnBxHe9Mz1S3pCmh1QfmoLB8G4XNyQaZEfFdhbRwWFP8hjqCiFSIemuvOqYiGOwJUGN2VH/aWyOOnqRMgZtZfu59JrTCZA0AMEEoy6CKrKtlzOSAPtAeGKC9vg7MHsEHjQfdAvUFRri47avQG0foGkAKjvjBN+waw63Mm4Ua7tV5tKQCdy3UId7/REjsl2bDYE/vKo8boiF0iurl87a0LX8fok7BHTbuluC9Gjc1+ujGjKPFRdMPj6eRjtnl16dlM3/XUra+DdjVy4SGYLt7r8OE6ebuUuBgnJOjzf9PXEE+G4ofK99tud17xB2udJ11MGkv4J0nNehF4JJ0QbTGSgxZVdK4VAGydMW8ATJwhE0KPzuHCbX+YIOgwC2tSj4RhgmADTCsGJgwRo5l+Ny1ahachh/JqVUGXhioT5hwdyIKyP9KJqnchwxyMGp7oQpKTcEh+k38VkWfCm5pJM7uSMhHK8iRO8EbzaRl/FEbyXyStAHFQzmqwXGLwBB5VR+5AuTDzUIRsxg2fZnol0ZYFUr77ztrUb10aAh0T+WWxUjYS2KHM/lSkzHzx3XL11SLDGc40TdkVqn2x7HPVDLFqCdfIq5ln47CKri+XqAcxwy43jLuwki3kUlsYl6q7i2rz9ECsYTdCkO8Dg6Eyj/UNkFqaalrTiH5tsQ0ukjRNJsvz8EfL4IOwPMZChn3A6jJFUoa5tthqMp47dZWkbloBYUNlPCAFKV89BQj6lO3QtrLQ0KTdUZQcLmUXVcwZEbTe18sFRwTgbBUkKAS5VERZAb0lgVutD5MQ2Wm8hU57SJ6IWuv5ai+KS5+F0ZPm02kFU1tVuM7Lg1Fo3Qps9AIlCYj/CProe9YFeCRCPQZS1AflCTXD/h+q9VLIla0unRqhhTWcaNGb3Dv4VPGWWt+8PQBg43L3Bqp5qqH5oRXA4OIdpi6MQ7NRzhrBUMiNIaqDK2QI7qrx/ijth8UPq9NVEV+Wj/eUi/bi1X+s+96Xh8EUxRrbbjx+WRv13Z1tK7W3cYHZs3HJ4dOzVQiP12/3uo7q4aP4Y3Bv0G1fDvj8dF3YVWbDpl9RQ03Y1L2bvvt1EDw9sjdbg7P5HewmgwlNztvfWw78KnPgy/aC9NfHBhFLkuisJyfF2AcB0cZZVB9KMtOErQQgDe6SejCWwEaIP6RbJt2ddQQiHQCatRUmhikAbZrUuhJyHD5/8NV4zI5JIVSsTDUMreQqZDUZVZM5eRnEJ9roa1KdpnKjZ3HyDKRmvyGbDmCRhEwFYDxE4mTmVaJeHOOYnzPK3qsWX5MjH9GGgxZgAOeOeEnRKktbCfi1CyFVgp0qQBnIrdh9myxqPl3w8mJPSMByBwqryGfcg9oyY5s02sLkozL4SVWdJMmyzDO0DmA0UW1wxtK6KPczcIeemiSyONLsXmPpzeUy7ILozVZHtsV1gKw5iQVCu7115ZhjRTHWX7MXj+/nF19BTyrKDBdI7ANxbQIwYi/6Iu0jjout+mLBNGJoCO5aaZLqxY/6hzEfJUr/MD/Dqw8sNtk6QUtD34rTD6vgZ0VxnsjBJnqXGlIZcUTL7LuQUQqSNynsWsF/K8I3mh7dSRqFGowN01i42WWahrhFPpvmJ2woiHK9Uoh4IxD6SZL+KVQCIqsIUD79FwVad5LlDxVlEwuKkFQcHvSOqFuqjk1TGqYbu/U2uAq2v/q2f2lkv73eEA7ctsUb0hA7yeh9EXfm2Jm4u9H1djOh5QY9H4/LtqZlA82WXgKUS766buoXvRn2cfrhTajtJwfpYn3tahvusmeN4Ay5pvEPwY7C38XA5wTGrzk8hH6P+FGU7MbXR6dydON347mh1N01ct/XLg9359pN2iV59eWuuTGmN46B2aDHw1/Hd2M2Mlz+0HaxjXf48nz9EB3+gNWVoMDGyECfIQX6uUt4C4LTKOLAVKyA3JCjVIlrakdkL8FIXmZSFgAl6tfJ9jyZeI4oh8wEaQCwfwCB6SyIzk0HILvEo1pEY0wTMkmMYX4c4wNUlhxoExy1xZwvAtz9KuDkV1AlLEcwvw6g3L8grGm7JmIX20OLcPKUETKe/aSa/LSocMkyxw7b5Fem/4FFOhVpmtZWVZDpNaMvXGKf0CDOIziiROgsBGpHAk6ICmx+gEd8ZdIfytMYkRXIkp3HnIkVFcu3w+VXZShVHYTpz5CSy+VDZRcnhVXoFSJGdagvtzLDTLCKdzAuoFLJ2UY1GXp+x8D0ZKvLG8jtXlU1uwR/ScOqL4w6LKonQXhwUf60mn5YBr9NeiFHrXkcYQyGjkdzg1N7YVUD9mWL2QjHVBwZnW6AngaH1e7ws9CkvhVDo4CexRQO8wKkyqQw6FsX58t388XXS5zSFgdl9VJ05PeFI/1FmF8Ey69RlooSIvYALAOUTI4PMxqEmrToacgeANMK1FO1r9c1DcigxGjgViOBW1ItlFc0q3soDTDYIlMn1y6E0Ys4DIFak2BnTmAFBJwUQ3YRoH7g26qKpLuCvXP1rcsZUB+wElyrODzQ0wZcuMnVpuw7mtmr0aDd+esIcaNHZ4TpyenDrMOO0JbcnnyKcmXVb9AAzGA0rbzP1cMxH4MfHo12Xd/LsvSUDnOaZq1zu8cBpu3mVQ9+Q3pF3nrVGV9Hl8mnc4gqD/31+oCPaCB8HQ64pnDNsrkHYKCw60SrGKYcNCRvoiFhK2YzvU11hG4lfnkedzPhGvUUg0H+JWffNRh0m/ULwIHO62EREs4kjlMB+riEFQX5xas6uxsNBmEdoY1/GivxyImbcybmcXY5dSsA5Fay8cDdycYfyOpHwxmU7AFgVtUMY7SAoCINMbKUJCxl0h6AtCrvI3zFiOKIlcnTMnkeRRPczgsM5UQTtNCKpQgE4gyeyeYpaxJBYq7jF9+M8u+GyWfMM+crSGMtIMYuh7LAbnYpVpBRJqsVqzPqi1VVSw9muqMnCYisCUgUFTRKAHXSiQSyVYEPpM8LzFLCPysCzhf7bd0xhKEc7VeuL+UVL9yEeBPb/iqJBytckW2ghXjlgZZUryTiTNQVo2mEqErZ9IyBz3FV4e/yG0nxNU5Ls+WYBL9AAGObg+UNlUXihlOuVto/rCYjSZ1HvEXw1yS5Ki01TH0EhuM+NYVD5EX6T5K4zFAOmOCP4/lnq+DjAMley0ugkaZInymDlKZ0lFtnQOGaYl1mhjeUpEaEDsqJigeybgpPVLuGMAuLCiMFBOq9CutijQvdz6gWvFOL1RdEtTWmdQT2dmP2w1oZVFMlNAEUAEuWRyBZNxlhjkZDfKVbQ1U382bK5lMX+jbmC8gBGrXp46Le66RfwMo0JLueet33osH2ef/21aMv7sp0tsjUGZKg1pmeePi2X31yrKN8vUQYmnxDepsm/8h/bX13CH9T/vp3POQ6T1/oajT3YdqOe3WYt0uigazp9LG5wnWlVuuWM0Yv7+baHXO1Gl2LEo8bY/rYGJiNOnr46/huzEaGyx/cG+re3mv1hI2iHL6NKB5cfU3sMrlNw4bJL6QhuiwrjO85RpcoJ6zHzN8j57xd5UdBcKZjwrQHQJ4QJeiYyOsknkZUQqBDWrN5dHBgs6EVgAt2alonZz7e5oPxKYQ/dRGnw3qr7E4Q3JMMiXSFOT7FZ48qJn118m6ig8PKmUmYoCYN8xQ2g2KcI4/sSfmNosii2WfMT0fRAWVFCXI5awPIhcwun0Iex1GZMsAMtFVXRc5MkryQ0FZOWXEQLdozwA5S6ibpP1+BBLdIzOzmabIsqhVSfxJj/XMUz+J09Z0ieKvQGbr3wMoJVsyFu+UGcZQi+M8YogZ1TWGszlklgLk1gBXa3ojceW2cHrATcr9ERwzdWOy1uyRZM8pPUXww9imjVRl+GKefBeG9rDhnT0CWIZiztQPuHEqSlu5DY8mQSjW2qpjUfq49FMWRDGmic3nuD+6rmKLIVyvE57xcpMksSvI8nxTVSVjdZ1kpCd/Ny7sFOxA4u43W18nNzNATvBcVmVMiTYNjpYHzIpYUwMaESqcPi7MQE05Oqvg56oRIiU+omfoYCxoQp9YQfZVOFCaH8LH5xIhHo8CaifxAWB2K+6baLbQOIHVOKxumINguiPKg4k+o+I9qKjXV8klp3K8R9oM25K5b+Rn3Hs38zDvD4mszeuwEHJW4e4R3Ze1GtBvD7rx+6qvjmF+KH/YpHyzdvULwnIA1s5/Lx7abV4P4fRRe2A1Wr0Ly8XGOocrVS/TAgBGvUheyG+NVtCc4xOEeUGuT3URtrLT3otiMxGSRa+0jyHUA5iWI1zqm6wp+nm5MD5Cf4ZKwsfoSmNvkV8iBpslfYRG3qN9IDuweSkaQfGnX2X65NRwTp5FVQlNdBALbPEBuRqBTtIQYE+uRmpgJxssKs6QIeRMsKyQ2iWysg7gzHYqkK6txJzgxy6sIzY8ikR0h7dnkAlgRqwBmEpfsDGsqBuGpil+U8byMZMiBjCWk0TOWBcJwBp4oZXEA0U0XJcrmBKelWiuYIoNmSP+cyXrxteD0YbZ8hkrCObVmtiHpG7ETIyBpFKqTzdCTzkVQm3bddHSYJsi0acLsM7oNwmAyw/f817/2td/53e/dOXowm8WzOaJeRok//MGf/K2/+V9SepV+EqeH6RQTlDRfiRnMclMc2flv9YeBPAi2CfAgfq1ZrgeuNYCFXWT37sC68deIgQ0iWBQbafzAahqKSXe1GulFccAKUFw8ivN7Sxie5bO796KkOl+8hPM6hwGeYVxFw6rDcLFIIJlY3GVhR7PiiO8YxqRhNIkQtcvgeH743V/79jtvv3vn3mw2OYpYxonncbj47LPV3/gv/tbJ2Y/D+F4YnYfxpFwZTx1n5YEKJkCVVEzrbpOqYBtARnvRV5VINWiI4j7nAITVKTWz2Foj5Um1rbu8egVdwRiAGkBBJNE/CFCRifoJBakbKRegCiHlSxOgKflHLtmHsWqV51qakH5LD3SlCN1+lzg4JodRPAbwFuYLy4HbNt6r6Ry7Rr09e+H9nID9ijB6urmfy2jp7zItKgL9EMTb2HcZ/ptM9/UtEzXqoXnfMnw8++YdA38d2sbgdzD6YLTtND6bB7kvH7rwY/Ryr8BXGHydlHT5cMWKIe1xXek98t/Ka4gOFK8+lD8SvkEeWmH0an4pS5KN7ZuU7ILUcx4yn4rHHsn3TMYjBDJvikyOeQMT/6mmw0liz2x1hI0IAEi6Enrq18SQAy9xEgEbzAVuhcLkIlzOJC/ZDDFHCkjukvE0RWLCgRDFHoDjiAl0CV5Ij2G1/Ha1/E5VfIiECSVlwGSzvPiwRIBH/rLK7ICqVQhJGBhRi/Qnv/nd4EUwy4uTsnj4/pNfLLMixFIfCsoMcyGwiEzoQt4Tm5jhlhSJMIlsm07Sew/uYTVEAWenJ2V+fnF+/ru/81f+Z//z/+mDh8xea/0Af/iw9T/7T/9v//n/829G6SRaPQirt6r4VMsKGCNxZ90VzrBaYmqH6qWLwowtVluL4dFFtkkuxgBF28DVeusfSL9SdEMDcq9akxt2WIjsiLkxu6tZfKnCizievPfu6mvHL7L4aBGj78SL4nSSvkVNM+x2aBkA2b9rDJQ5DWoXpzmHzN8f0NRRgi4A+2gAhHPtr/j6e+/+h//Rf/hbv/uempVWUF8K8K70R3/88z/4o7/z8od38vxOWcw4lDpM/xyAKHxY6Cg6pHyULW1HEaniq/YAWCcklWOZ3TkA4Hoaps+1VKUlnWOqo03tgncWRBL66Tl0tirkzGAWKfAvxLIPRIIaYNIpi9wv1ZkR8nVJuWFVx4yb0Drorks0RhS/LIMqrSfI2AzVyb0Olmf3jSxtg9dl7M7w6lLHj4TjIR21xnferDXtg6OTgYzBvxvDuqS9QkNj+FD8APIx9A9kHYy+qfrupk1t5DXTIDX7J3TL7cZ0sfp9ppvqx3Ql2PF5HZ7xHIZD7l1VRhcS0/x32aHsuXt+wDZS13P/LrpBZruGNFXWd20Q0gfgxb2aZvUKuE7wDSZODdE0xnWqeJv3lgOvhQN01p2XdeZ6cETIk/ClLo7Mo1/EGvzoy5xZ4rpmSA1f7QVIcHLoSSbNwvJi8FgXyNyohGCwgccmTSVcUVBxiBdNRemyQiIZ6VOQ5QUPQtRLHGhGAaoLBWpSuQifVOlTwDFBwfYGM35kfU3bI6YxiQydojifTDRVn2f58eSr/96/9df+0i9XP/nZP3/84vhv/8Hf/eDJCSJ5HAernLOZOMiMZQDIosYS1KDE1dzqV64y/q1sa3F0cYGBf7FcoAK8yPLzkzNqhhiMtJcfTO6fnZRJcsDE9ir+ZZJir3KOnBylB9JCJJUy6S0tRiXocuwjIMqNncYfS9tI9D4kLvF13R2pkMfVhgmoeaUmojuVabWK/1u//6/Ow4NfPE7//vf/4aer+OefnmPFk+iqsAaS0ZTaSNUEkYT6kqUcNgQLLWIxbYo+YVxCZ8ien3708uTTVf72MmdlST5AOYe3iNlowYHQ8yJ+VsTPtQIgpTDFQKvmKEtPHAemXSCgRZ1ggp5HOgNivZ7Ue7TwAwX30QOr6Lk1Bh0G+KYRCFj9FEEW9Vl+pMNIqYiwd2LbCbNu2LmRTTlBbdgVkA7MJngA1ZIZ7l+1viScKAxa+HEYFUO06Nx1Wc5dALdptxy45cCvHgfagUEjyJACsD26jBhwOpys9TC+tYxW7iPtwbiZwvrj7cVfP+jrW/aVuCJKH88VUezO5taOd8O8Aak+H8bo1j68I39MrvEV9bH54fEYfMjrY/Cx+eEuH/zUPcLu3UGa4Oq8R108TqLp9vzr1dRGi8fd0rwYR5uT1OjbTIVqPhXRSeJ1uNQ2XyQh5oMJI8Mg2iHW5MeS44OFpPaECVdkd7vk9VzmEO6huWvbphN/sCQJQzz6L2TrL4EJWKZQObGVgORyCVTQwjkAiGtKYw6eRQNkT5YgTJ7C3L9cRcwEEynbCyaVYTKCVx6VE6R2RHyIXZU/uXsQp8XTMjsps2XMUgabU9kRGhQxB9lKm+HsAnYwS6bV5YQ2hUSSnTNACGGX2WsKZo8rBxfgDYk7fBGjqEkZnFbRCaI+OwHC5VtR8E65+HYZ3K3CFyKqvKc6boyi1KkuwjGktvJ0FqKWVt8cVX6MH9YKMOQ/9OOuEKYQRxB5Fbb2EM0eU2zvB7PmMuspS3m1T5KgyM7u3ol//3cfZX/08Tx4HFVHAZ1BOzEk3KvVIh0erPaRJom+J8FbDWpyMiFgkJ7lsDWKkgnO/jH3mttu4RxHrmYstorU1qhqLEC9XRZvVcFBKRefj6qM2X1QwGK5o9W8fkGvQ17Hf+iKowDK9AkLStXqbVVJ/1ATnwfJMxYx1L8gBTLkplNtLR6ICwLlwbyFQjoIWS5gVwkWY2gU6ABUQHTznx4gBUBcIwwBVATzJHQNHKSy7wM01J1yWB/DRg5ISCWfcmxc2gHC9/yJKNxIcE9WxJh4I1wa5Q1e/ki4exTyIR0B/fCOPN69djzcrPRQ3rH4b7DyDlVL5xbmofgtsOaxS3+Tot/dqT7kqwh/XqV3y+3GdHt1N+ZV8MTH2d+TfYit8PY7WL/J/i5cP0ePHzAwdN8LYhxm3RlNei/SHFBval/kEDjxXRocgqEsfehv4245cMuBN5sD9QBlc5XMoWKlY2+4bgh7iHScpSVBB5lJP6oMoowEL+Y7sa22mXukcCffCIY/HrgkMxGuRwxEbUJIUQd4areRyrIIHFGs3gNg4AjUL4L0BCGNfb1Ianj9DJkA5mQAZE8wQqN5/bejmvKqlBFIjLNQBDAKlLdKaJ1H5bxcRkU+j4K7eJY0Uw8ZnogsEKgmIlLlW5VBjLTKqV4iUmKrzEKY6Wf1AR+XyL5sMEB7MfFRE/uaww6P4/AwZgdznoTJ0yJ+iglQmGBobsgl7Bp6FaK6u/g24Mq1yPZmMIBzOfA2xZHsPd5I0BXVUleXaY0miV0BamHKlrhLveEyKuIkzOfVMi3PjtPorRJvUfgDkoWVxGS4ZsZdqjVqpLFbgjeZYbK6gEiXEyWWglwc+kOEZRHn/9KOUhODaTxF60rjoxjkEYx9UlVnUbwwAyFKsOl5qRwTsVGNSnHKhyMguyse6pn/JwU3smFxn2x1B5NOrlaBDOv5BHiyajvq6JCyCEKORxlAmQHMFrDqFnU/qo3iJRCatqM9AOo2aDK2dZhH90Z02lJF6xpMcMlj7laNMYBvBswN1PjNqMgtFbccuIQD7avZBi7JoORe2I23Jglt7ofzDjfR9eQkX0+sn20LoquH+cBr3d2Pfb1hDfQaq/crdYwmNwbGL3VfeD+vH74WHj4wXDvnJHa3qU+JH96dy9Hs9NoxbeFj88N+iYPhTh33xjCIekRCp/QReRqQne3SAOl3iIfdmnZ7SzfGx3xJ2N4jZDKbeIeMKn9XcpIrt1qG2OcE2F5LANJkPEKvZl6xtp8yFyzhHFFYU6LIMryYiHNaOBAyDTwIYATAbbIYAJrMx9MO+wqw+1es3UAiKU2TsjLIiXD4E5b3TaRCzNaqQZU9kP9QlYuqMAENk9LkQBuQuIiUjnN+Zltj/MqjN0DquYxDkkWVnhMRT85j2X9jW453F+S5OdKoJq2N7cYCOGCcEr1AQh0LreBHZESMm2AFFORU2WapZRJPPVGXFmwUTjFij9IwezssH4rI8rAsXjKLrWliiZQOscMuEowzKkuMkreHNok4wg7A7ty8a/0kXxA3cNUIrShRY2WLBjULD4ji/KMPUwU4Baex5EGFwmSLnQ4v4uQiCz4LUs6KTvMsYyZfyzLaoYFGR91MgVR1zAgHdllzi/HqQuy4JoLC1F5Vxl4O3DQByR8T52w1FhHJ9Gk6f1ZmD3F/UeYHVcQiwAuRrX7DNP1pELEfXcsyZBHN4RK/r0F2EBasJqkOqhy0x4+ZaNfShHoidJiKogxmuWP6gOik2TEz0uIXFAKq6XyUCKs+iIiDF4bSkomHI2CTuigK6CrsOHe92VbStH1CefivzFtX8wU3xH5aH7DSvXg/j0i67Kq74QjILqbuKNSF8WN64HvLJdKvhqHoyeujHg1TZ1I7XvJ9rCHfyB+/1fzwqyN236/JBvyNcrvbq7sx4/mwQadl68Z0sXV7o5+r7dRtoIuhiRkYAprk9a/D1Xkv1gA2NrnHEeV6+YaCN4NlCPuriN/FnVdR3i3OWw68wRy44gtcZ+MHwUWCNdYz2GTwjMRjohMydMlMqqQtqq9pXffmMf2P104EHkk87MGVbO1W9iXIC0iSVH03ecgWEIQF4Rs/mw6NpEriTMgWMid5Iy5pvv+pUDKVmkANk+0vo+Sl4USkw3QHeYuPDWsBzAhjUK65aQmsnAJQcioZUuoM6a0s7xTFcVAd4BkGECkGSJesFgBrsqeotOoZJSLPSe08Qg0EsBjBbk4Z/es/NujoDOKMTfriS5S9x4ikyJrIvhw19ZQ9AGxx1iliutycNzlUrosh0gLcLMaKrBObH0tqwWpwnrf+GjxX/G2xkd8VZgQpqP96QPRHUJYiBs8R63NzqLRkM3eE1dZhEBygqhWrRxnOV2USpU29VFan/dbEStiua1ozmhSwmdV+xWQ/vNUcPXI8hmHkZZ8AfccEalOf8oOAMweSZ1n1GVvSgxhlQyK1zIrUY7UCYEU57Ggs1rtCbIdM/mZBiMqAP78XlQ9rCYqeQ8jVWV29fSCKVpfCI11U3RI2qEpWLW78QTw/rlbWD9RTqLjyajFBr5KDRCO12juG1sXx0HMZ53vit6NaJG1gG+L2+ZYDtxx4XRzY8zUcBw7UFuD28IAXoK25/7bCLudGBh7cisFgrq3iWmTXCbixdvxJgePLYni1r9P4HILcrck5XF2Y3WWMgR/Dhy4el0s1vfTic/V5XF2ar0PFJfW9Th39OQk/PJ7c3aVfDef40juQXc4PjgadvL0RvP4IeQw6kuaZK31i3nAAlViGfxc8tyDRkKpxwukAEouZIEfgcVbOiEhY9eCcBYsgobOOq0ySn/QooQp4k6oXiNEVhvgiRvOvBme2/ipF/Kzyu2V1H/8p2ImzB9PikDXvVhUyolQUN3ssbPK1wpYA/IJq5hgCErlrlKk6hGTh6Yqzn2LOMWADA0Iarmmm2JxzojBiG2KgESrZ0ciDDWdGzAGkijCRmGNTji14FZ/nxZRZalENK7Bel/1KESZaRtBpCcU9fE2WxTzAz2nwVOsSms+27iFklMLl3mgLSl4ULoukTvgVeqoIN7vfvPsO1GVTag2tgMup0KWX6yHengGHts0n/GsYtRTlmD5Gw0lE1lZpzPppYZZT4EaBDsY239UyehHMT7PnS7ZekIR/V52sLOZm1hM0HV6XAlbxREIxu6QtEsWNvQWHsCkrWDfA2AxtwG0e0GQ8zp2C5DRKTjnDK6geleWBnFBVpnnWG+HIQTM6VkgS59RnehdIOBBAZwzQwXQcAO5GnwXsAK75iGiuCkoPIXtDoFirHqvWsu7N7l71Nf3pghVE2FsAgGBspl+WQjrrzGJ0DgAkgRomgKouR2VY1Q3R0K3mu3G/H6amvz/xktim8gK7ZLy9BNNVk8VzL+/Wo5dyk0FabfPyZ3BdSjdmM8eIJ3vN1UNu+vJbzQ8PlePq4lK7X4qhXH787lzdnrMB/wo44NM2Ptxt0w06DVE3Zgx+P5frzr0duTdyDP76HSF/e23j4qt5oxfobhjjjZJ3i+yWA7ccuEkObA0uSBwM3Pwhb8tGQiKQRBZ+Z+yAtJlzhCWJU4pFupEPUP5sFrZkRp09AIh+EomUUeOJydY2sBBtcrDkbUtg+++sEQsNQkWTHQArHSkueSELEzKwB1eHfyFjPY+iF2CXdQbQQi/lIdYN6uWwh+l/AUCuSk+DCLud4yS6x6lhUTBNgkmsrcOsF7g5WkMkgggog35kYF5XgIBkX2x7mE42IbBAPeAPyU4O7WUcEgUciMs5CdgBseP4RVE9roKTMDoD3hBBExU1nlCQEBIecXWg/Ag/PAJXD4jDYPQotWkLRyiJlq6bE4i1qxqLJ/hq+hiOTSc4Sk2Cozg4zlf30uRhzvIADYAGoEZBf5RQLtYi66v+YoK0JPUPmCZ9TbKzzLf4A4B+d1GgRCH0a2mHOHZ1cBYDrlYPw+KAM7yy4GkQnkbRqbWSVggQvLX/hJl+K0j9h7xsWdFG4UT2aYbHsb3K74XFXekXqlRdY1uVIt39GSsIuk0Gwo4+7GQu17PJi6riurfxSpVRLVQzq6O6MTD2NhmceoFSmiKMs4rzL8rsjfdh6jBw7q8n7Q2PGlvFN7wat+TdcqDmAO+tu9pAE6GXtBvZpl4S6L7h27j0netcLm4btAa72hyhxjVGHBvFOuX1RPjwbuSstaVXph/3EDEQNUYjHMi6Ed3F043xteQNPmxg2vXgcu2CaNNG8LZLocs9FN/i3iuwG9vu1D3quxdNAPu91w/vi2eIz9fB6dGwmz8e4E0EvVHCzTdjIS0xRXOZTAWblIFkgx0M214zvK+gG5i4TzLxCHLMsstFI/HyviL5WAKdjUESsESkcDlDHcZDcUmvBf85BpgVAGxmBO/mUDVbGsroguaaqYj8LuIapGCIL0GbmOwoLu8GwTkyNUYgxBfBEgMSJomhBw/xOoFKzn+KJMoln0fyKRShNmCQM5tOMRXR/oGA6eSywKTo2GS63BQa2aBLXCM1PEZEVIiSNamLfMfSAfPUOie4LNIiR3UhO5PTHAXAxC/z00w5n+fsFeag4hxlg2POjlFaEIZRDOw0WuNGzRSP8/aNsLQaYN2yG1Dr6G6InKNgvbl/NYQ1sCvV4VTY3C6Z/IpArWi1v4Z06+GVllZYQGEvdRyvlBKe0D3gcJyerzK28GIW9qLA92VwN5ID0FiMFCYaWc1uATHFytU5DOhitBR+e+xcZu2voBliDnGjCyZpVrBSxBHOZ2G6CNgpwUnArAuV94Pgl/QrugskSAuNLnDopH5pGlxAj40W0CKX/HZyhRqaZmb6n6MA1CfpclpeqCspckSkCASeX3n+4Y4uyotQ9wyVyKNwAUISAJL98S5kmjB7V5j7J17sIc0AeKQuWn9QhK6etiKtcq3TfKNbaJfnhu+7xhnXL/z7DRfuoXO1fLV1VXF0OPjvyzBOJvFlFX9O1yNxn+ANfQW6Rfrt5Ye7kC7mBuoyhNrieYG2rjFUbWW5wqPakZbslD6EaogPPrV+eAhPt9xuTG/etmtvkkz0ZkQ3M+ltZpe6nUlDZOe6DG0nQ09ED46eqJ6Mt1G3HLjlwBeSAzbWaGBlYNMeABt8JM2bDDQr5QMRwcfNfQrYxC+b/sc8hilPhCpJVS4fQxN/gEmg0oANJns0/cDgsJEwUU+YHD5WD3C1zrZgNAo3exo/D8IXNqPLHLzwB5OTMn3BV1sGJiAm2ub5S7wuIpohDaq8LM4DJn6RLvOceVmWL444yXiSHBeaGGZvcVhkCGQsAixL7RZFwsMciGlrFhCIJkhp0C8zJsmKqjdbEFBCpFPkxcsSM3RNciMiEkHsvKwQi6f4ni/DZ3nwLCvZvfACVMxzg0fLEnASbgqjGOJ+CG1eEK9q6RLYK7+awvyCjAYTkWuZVRGiBnkZN5sIubSOaoTpT8HfYV5gan9QVkc5OpWqK75ogcXanDDIFA8fuWzFxZgKY7Hz4a61BXURKRanecnqivFffYZWlCQdh0dRdRyz8FKe4MW/CrF9pYuo8SXly0/oTJxTp5A8HlSYYHGWHFsLtJtc+JWMvnYvKN+y2hhxlsH6n+homc+DYYFu1FG2IQOnoqxXW26hEwbl1Y0pf+bjKI5qAkY35s8QKsmUIPF4XYSemkvMXTe4+sjndIl6u9pAE/EKf19PWZ8fU18h625Rf3E4QAfcrw92obffFL5be1xdfGMz+3rzmDyD8K9AP3bam6NqSNvzaXYwNoZr4L70GtIOu2V1Y7r4h7BdSsblACN426XQoR2Kv7zQPojd2Han9uF7w+JG8LlL8fh2vw5/6M5XfslduRJp6LVIcODSBKdkKaQWnQNwjnQexllYHCHxIq2pMFlXIL1xR942B5vaJ6rsJq2bzA4sPDP5qxaJZOGD8GZ7AOITiYfOBw7xmj01e3F5HcWm525Y3qEIIXLuYIq7ZX6XzUwI7my6DYJlLDuiQvPwmKeUJ8h8aRKnHAxVYpCyCONHiONVeT6dnK0uplGahziHYWa6fICUxuQ+U7vuSGBqIfHUthqoaJE1LzEgEUlIr3IAWkmsDMBT5QTgABVjhzE40CIWVbnEk322vFss7zAvHsb3pU0wGGr62MaCtnV4IrfXWsZN1284XQHamrDBbewKaNJu5LelqMFmVTdB1VpMrY9iJGevIhkyJ+ygYOEjCS/SeFbA4SovVk/KHLOoUxnzkKM4ZqknZlmIDCzHIOYXWggwTY1kzHVSzpCmV8Fvm0eXUpCGk4QDwop5mbGrmC5RYfrDeQ5CqNY4L8MzzpkusjlrLOzlDasPg2oVkQ9EIe6kkLPtUrugSV7oHADEd3YVszmbFEigk8xYAXimBgWt+jq5ZfOlElUMIfZ1kARSNrUDRTW00k5/1V4OVcl0Re0BMBSCpZ1ZAVihj4TJud4GM5ICJ4mkCgD0wv1QMc0cv8I1kIU2471Ekb++wDr0/dp3nNmGF+p1QXVYzPEi9wlu42/z+gj9cAtw04EhmcSP71Lrrw9cQhGt3ED4OJu46/763wU/PAZvt15jcu0L41M11D/3xdmF13t0E5dPrR8ewt0ttxvTm9fR2/ZxNwKY10Ti9qzMdg4NVOOvPQsbj/iLCAkr2zb5ItJ/S/MtBzY5cKXXu5vJ3gq9Hc3rwSCDjDRnG4CkZWUwyVAyCAITRjiIt5oS1jwrog/gAkJo5k8QEqJAZhKQpD0ZTjAhCqoZs7ZWij4XViTrCczmmj23THAwL3pZxS9M8JLshdzJloAofobMxtZbDnNKmbxHepSJfpEhBaIDcMQv9h+LczYAs1s1qSaT6KBYzqvFdBoeBNkk5FxZvIQiJrJogUrDTG2BdMqRX/gyxZEoFKISYB/EBHYQ6RFQpFeOttUeAOhcrp4tq5duXtmkRtKn+ZKFi6RYxWX0PI9fVOmLKH2GoCmDJBAhwVod1Wawp66xnrxLzG0uwLn8mCbl5n5dGZv4qCHUqlxrM0mzMIVWI26CW58yx9gpnuAVKik4Vy0L4+XBxfNJlNzPLuS+0zW4fLbCUCbcc85nKGJs+I2xIOCABeb04YnKYEmFJHWPKCtzGmSRvzw7/5QjnO1vxX25XJ2dnS3OkjKbV+FZFZ9VydM4fcpKThyyg1yeRjXZj/ao+kilkC0+C1YFFkGYqOHv1RLUnNhk3YuKe6qfIt2svn1GrQ+rrwLE3bRBIUMfoKMIKx1Sui65rERqQGWF2Qzb2KLOWhOPbvWM98JykegwW3WtVMsuFPtfoFeBr/n6HIp8zTUcLk4dZTjVSxkH5WW4Df4KcKDtFW1AL3D9Qq3jxnJiO0fvCsCY19XBeOh860MveixhgrNhVFNi17vcCGtfoFGIxmhvXUQMyiOvq+EfQj4em9Pax/vXHyrxxuK99rUPqpMSbgC9Pz/hh28AtUfzEDZXoksd3zo92LyyurW4FmYrrIvT0dDG807v/+Z2Bot2ZNDkrDDq9FamQk9iJlPzI0RwjV+S30hFNLpTFUdsBVbJ0gvIpWTJTMKEbEeES9RsOKI/d5tHBWohnzkczKTpfZOlZKsNYlyLAoQwHgX5nbi4J1MSBDL5/cGmh10B94LgQqfuJhk7QBHbETOjij3KiKlRgaufeDI9+vVJ/EG5+Ep+8LjIvxnP/nwSP6iScjqfRJMiilkgqFbLDJGdLaZRtIRwbQkOszLCkSW7jdEvICkvirPFxXGalhlaRZSzsJDny/MLzhybzg/mOVbizGQX0wnORckVLgsdM/woz6bF+W9HF1+Pkj/h+GKOMqA+kiGpnv5zuaayB261dOgntQAE/DUBB9Nzd4hdtp7kviihZtaZn/UpBEKg/6KKf/RqGhGfS8Qh0NOeRZjNZrNpNPvGKn95Z/bfrOJfJB+9+6L4R0j6APCvhAslB/HCMWbEtRe7zLKiWnKgb17BInSrpRaRpIqlZbLklF8aAY0C4584eXD/3js003TGUkMwlx8mORo6efmzIkTpuoMpV5Ddw89SknxMQRLhWZxJPwqK82D5NfU99VgEdfYArIIUT1aLavWIShS5GjuMn0T4ltX3RWcZQAaw5LI6s1+cs+SUpqaSJ1wumYcZO4DKFIGITzJn/XLX3higUGiouvausFDFUXRI/1BFLr0PwsNKg0P2TGxtLhWicPPbxHu/a2BBtZdo7Lv2HWd64P1ivFLacYZi/XAfFeu4HvzrxD3weJleYbBL7RCfu0SMlyi6eV91TLdeGmHVPS8veXxb+7h2Y74aTh9/N+zXyA93IT+vGJgN19ll11w8Xd4AGpnJ9dQybeeQAtBB4cox+I2b4ofSNgBvH2450MuB297Ty5Y3LXKfZurAEsGlz4OEJMQXBBd+nYd7SUtINohIACDGI9hgLyETZ6bTcdmDvKPpV6Uw12rTqUQ44YqRSpcNYUIPTlYVMqkKVpjdkaGJ51gxptclPEXJc3yPRuU9JKoEZz5swI2e5gGROiKKzZoYo9j8NG57LhDlF0XwB3/y05Pgs8Pyq5Pkg+ePHy5nn55ePPrzD/98eTGLp3eenyPiM4uNeB9Hkzm7TilneZEzVT1Npsz3Y8MT4PDHyE7TKaJ/Es+LfJlVebZYYaIS4Ujy5Sf/8B/+fz578t7FGRPdi6JI4jj+J//0jxcXgU5FK59BeBV+UqQHOWsSbGZFzrSK1czUQ8MUMUJV5+q0hYuztFd3a0pvylcDWSOp/VpljCZOJ5ythoqVFmfT//qf/8mnL3/6PHy/XH3/fPnkg0+zP/7zX56UsOmiYIGnSiYJO0a0zJJnq9k0vXf3Id6CZgfHSMlRhYlWmE5mF4uXOA1aXJxenOerjK267K+YnF188rf/y7/x+NmP2HMSxhfM8a+y59Po3g//5IMPfvG8qF5kUjaf0D446VE/5AyBmM5Hf1PB6je6q28EEXsAaA/TH7V2RL/VOQAcWVCCQTonwOpmYj2GYeqp9HDQuEUJ9Vj1cGQ7kvTEIhEtZ11bAp+sPsQ/cNAbAWRbiG0bkbvYgIPzKFRaEP+FyjX/q2vKm8dMXW+vWw7ccmAnB2y43AnRJGqwuM61nT8J8ocqnaMN12hd0N23MzioetQiI2OSi+qxPlxjHBdiQLyJy9ekX4WmeBM0vg4cXa39iqXaJ+36KzNgaDuZFMmbu/ya+mG/BD68XGPK3egzI/rkUIl+6aPCXlk3htMreAhnG682keSj13r9YnsYXHCDP+sm9eBgNfmFyCQhRBekGuRmvKqz0VPivmUzMJ0Fu0TUk6KgDaKtjYRghEVyDz2Qu+s9Li8xGN1gLc1xTpwFRhLcQ4zSCgDrCUKNCQd6BS6AkP5ZC9BxThQShavvRotvJcGn6AJM4kfm8t/kdXkC/exJ9h//J/+Hn352OAnmK2adtVMYY3JcwbNVgA2aK4qPsOVhuwKTx5o/WWIs9Gvf/r3/4b/779y7Pz86TCfpnXTKlPOMU4p1iFhwEUXTPDs7Pw3+zt/9z//W3/i7yaR4/mn5v/oP/tdFsQK/+QBKiuosyLTqwXHAZTnPV4flEl9A93VEgHHG1U8cFV+k4Fgj6d00PvLbXo5Rxv86zg+3YF6gOTfgMjgviwVVkrNJXafgveYZZNqJMWbWxQpGJPeeufb9LmeTBx998vO//n/5r/7Z458/xR1TOFksT+WFSa58StZuOLIBnQehXGseZf4/+Df/7f/RX/t3vvre3QltG6Ji5QGe/qsLjHby8jzPo5cnjz/5aPG//+v/m3/89380nyXLxfH/9j/+P19kH8XJnMl+HepQruIcCpZZEpfxBP9L2eI4mN+NwiyvmLCnBSj4rSrT9DytrX5iwrj8VtGLJJvLmJ+dJAVNlLxkQ4V0VFqfPSTSCZaAoJZYJ7X2spUBtZQ6JXAI+nQkW+1hPUNbAkAJW2CIeqpTCgjzRBzVDorDSieXGWKqQL+FCuhyCoRC7lL+JnzZL4Ci6HO62nGG8v2wI2f8+OyT38WjsYLLG0t9eD+sEpk9eKC4Hjw+6JsW7taxG7MnzZuj+uWZx3xJHRbH233x76ag217Xx+/XyA/vpmSdeo23q/cN9mz914V0Qu6FFoIh+Hru3+XcHi70BetcO2qipJbaNtDBcBtxy4FbDnzROOAPDm5cGV0DP6skEvu4SmCRTKMp0hAXKzq1lw+zE3ckT2luX0YRzr8h8QxHKADIfWTU5KimTQVjqkBNjAsjfbOScBzg3Z8lBcFLbJIFDuOTnIpCAdG49TkpEry+3EGUxNbHYF7gZofsbAkGCNNyqEJR0GQwrnleHuVnD7AcKjjkaxpjY4LTGm0qkISH858ZthrIcUz8sjcAMxXOoWLC4b2vv/2v/xv/7ffe+8bsAOFuqoOumOvVWWZYqyPXY+yRszZwdH/2X/zNf4CAi+PRl6enViGMo3KWJqgjIm+Mu08qEJ8EyYzTALRXYcXeWfgkXLbJAI4gYlIxSGgvN2K78diLbtNHB8g8flQfLkk4YK1te0ULYlYbHzvmDIctDtGjk6cfnF4Ei/J4xex4iqULwr6kfbUPjEb6LfIVbImP6Q1vv3fwl//K7yAW01SwGhj1IEyDQAsoGlr09fy3w7/3X/3df/7P3ldavOJQ5cPpMUd25TnHOQcFZ69pq0ecxslF/jSZTcsEl6Oz7ELKgWv3KLfj2Oh76n/0Hf5oJzZw6+LJKGTnB7P5D6Lifhg+VZQ6HSqh+qg2sYg4xxV6L2G1nPq53ghn0oaVv1YHLC+lC7HLTHWciG/dnSf2l8NGjrIGADDYo2yEtxrI4TKEO29j4XYi+VIl3nLkS9Wcn3dlrtGdXNatF3t0ffbJ58Oq1N6TgHeQ01TSs/h3KJuETapJ60/YBKufPC32+vqcw9nVFHtLbiPdSM/Q3XNdVpmbormn6J1Ru2jemfE1J94Uf4bw2MdUMkLv1d+mfaD79pk+HFeK8/r/+HmsK5U0mElCiyXu6Ox9/Nl8YSQMmXCDz3xcGbLBFlnmLIoxaeCUX0lDCD0aGmgyzZsirwOAxEwszadEyTxqMoUlx4ssFaIoxfADu07D+CwI8OHjWhcxaSLFgb0BMFB7OuMqvxMVdzC8MMGdmWUMOvACdL+qPkZbALs5pcTzTMxsMN5Z8urTJH4cle+gLrC7dJVzRABS6hln93L6F25d8BbEzG22zOJwNZslRXGUxJOD+fFqWZ1dPC6C2TS+kMBHUWxOpRY4/qk4ABizFRYQMva/ZvgPlYmLLUtgOsQ+ZNn4IPqL89iyZxd3g+owDDkHgPsS4b+MXpaa+X4E6+CUXGgiXYsZrs84xii7RbpAe4dh7qqZ1zx6v43XICDGXw64xb7OaLOq6DxqRua/1ZSoebTSRRwdFsGH59mTIlwtsnPUq6JcFewOx8yJRRVNk0vfSZDWMaPifIYifPrZ2dl5MJuzxRfTLjw7oQ2xxYI+oKl61DiE8ufPz569/Oz04mW55ODecxSK1fld7IE4UBjlLsat0wQfrOJdmR+zhTcKHgTVwyj+ZRrhjulCSqnkbnSV1HqOqMUCR255cPjK1vByKr7zB2pscNkDoNqySxc/VHQ+2QaRZHfiJaqrexbuNACYwAN6Jt0WvYU7pXHHFxAZyQleZSEj2gqIqKGdjwEAHY5VCM5G1uvARWJfE4uYdbwLehEk3/zlj8N+eN+S6B5c7g3eN29PuQPjfxez+1L0jWZd2KvE9NB2FTR9ebp17Mb05dsRN54Pe9fLxqjx+HcQuSPp+vj9fuiHdxTak+Te0J6EXVEu09YL63Zv7spWp9X5RsHbu6YPB5fuvSsAltp/266eK9th7ckxmNAD+8ZHfakq88Zz+woE3jbQFZjWyXIlLpLJRBhuCCkMn0zdMlZISMUw25KwpdaJXZKN+GdDEHCSv/GiIx2AyVd21koQ0CgjEG7NBajKqGPkuh/kGJAwGx6wkVcF2VwrJvNgwrmnIEGGK/0wwlPQA6Zq2TCqKePwSRl/htyFTmAOdthuKZINd7S4eLC4eNskUQ4Fw18NEuRhhESqNQDNBeOyEpk2maXIhwWWPmRFxJyscrzLBwf4p2HzKdO96Ao20yv5MM8RUrVmcL7IV3Jbn0zTyXLBiVdkx8cQh3yxbZgZYsTfAIEvilkc4DiDz6qQTQ6IxmRhYyhaAiIm1dO2UTM/MiYah9aMqhnWRrQwLtA+Noy9xm9bhocD/ESbwQwCsdoQiVYn6aIBoTnB5yh4Z7X64OSCXc9H8nwqlUx2OlRT0/xUli2+qEXIxVGSzqYP3mVPBTJ6ymKKptFBb0s2BPiDYxhkhdXB+XnJNovZZFpUizzHVSuIlIRhD0J3hhjNZpMJm7efsxQTpqwCTbXwQ7cwoyNEbWRuUEKj+8eBDJxPRw/F749J5CgJUms5QYwNxFWorXhoLdZb7UZ5rvOKx3oN1EwSzFgikN0aVXI6BFK/45KBEaleL9RSEngFpH7ImRVLIyIamuChZSbevTlg3bqGUoi/vW45cMuBURwYeotGZTagK71vLtOrHptFn1+GKrtDAdgiys/JyMrwJ4B1rLcmYIy4ws3TYrv63N56p0fA+LwawTev8Xm7NG9iGvs0vkSH8Wo06yOkD9AIqly76OOsj9mVr5vizxAeN6PjyOvysBszpiK7udTF2Y0ZU0oN4/PWD++BYifoiBZ09Os0352Y+hOtLzlJXdbsCDaaTzVbcKQYfJzLmkWWFRJuSDYZHXMdPMJLzEL0cvId3ZJUxDYumxx1cg8Z6X4SrMic2sbYMyaV2aaJcGQNxQ8OQMnnvKnMkNZw+FPJOBI5Cifu7BNFzkOmh1TkOYhhA6hMjnDFg9N/PHiG88/y+c/K1fcwyME7UMmuBDzzYCQu3+3alZrMJraNGZscbHuKJJ2QK0kPAm3kZd4f1OQhIAFVxkmI6nGMTcskjZaLU2AkFrMUMj2kmqwGaFNBnMT4HHX8w26mPJRzpOwrYf7NIPxFmeMh/g6bWcEM62ROQ23TT3V3FswahrcazHAp0sW7x/5m24wFfjzwZtb6yRGjFrTSUwn3HLMlR0l3iuqkjF5chL/Mw9MqfclqjOmKGTKxCdcqGj+fsE5iOrcoPj58Kw3nccSJyEA5jgawFFB4Gyf0MCyIYGwhr0ortn/clb+pBGkeXLIQornZUgA16jv53TR8MEu+yhHOMas+qwU7uiPE7unPg3wVrL4BzdY5aRY2lBdV+klQrKrsoVqHHkiHRj2LntmsvzgluyypoSoNJVIVUN/G9Sddl6OdiZc6KkC1tBRW2fNwL+6rV1YcP6yM6oxYSUXqPOqc9Dec/0iFkOpAv7XN7mxBpjMzcfdE9/pShib+8Xbr2YshisZeI0YJh8ofh/2wSx1frqPtaiNnt9yx1Xz1cD5t47kxRNfV+DOE7Trxrl570OO+ZaP7lU+b3hN/QOJVsd6uN9kCPvA1w+qHzWuyx/vSLdUR3Ym/lGNthRoqOih6IjxYl99FuHuLsc24DeNapU0eE2hLJNCG+zLuTOzLcBt3y4FbDrwBHOiOG6OIsmxuGJWcjdhqQ4SkIv5NywK3jAhBiG38R6wxpCgDTHBKeZPdPKIYWJTGdLjGfsYYCWTSECxakZos1uQoc/Oc0WvTqzZ9LzgMNjJtu9Q5SuAE5XPOAUDIK5lYRcfgL3rCn4Q52X1g/J9prr6Q1ImBUFR9Oyy+DXVy5F9lS6Q/JDyJYtqHyeS0ZDMWCJiqxTU9vnsQPuVPfpVO8XSJMAoeTI8Q7CSeAuo4p/oG6WrBrgFqwjZf9rky2V8kuLMBs4mmqAEJfnJYDohPs+BFkX4Spo+VT8KhFCFNpSMXYniCUZIS2ssPE9k+jhqCHRD3UdBtmduBOjcNZCHqTpPBB61rWBiKV8zVR8WjYPkwrO6WeNPHMIt2pz3VwHBVuyu4I/8z6Y0KIR6G5ywUAAK7eFS01U+NJ/1M0vRyFZ08uzg7OV8tV9CFxU++0jkA2uehDsQFAoJYWr2skpfJ5GQyOQ3KlTgPSnqK9o2YX05oMeVPlmk6BGBSoseqQWkCYy2CO1qlI0SrQkRDCxcB/uhV1FSVVpwu+rx1bzYJCBI60GRQSFzBhlU8g062HDhMQOV0N/V1dXyHQdj9qynAj27iHNzmk5/3NnzLgS8AB+jA695tIb13TcBLe1Pqsqb2FVJEIe3f/sVskLhjBWADrvmobEVSOjE2zGzMSRhVbvRx46AGuOtdvj69LyY/76V62BZyP+9W0o7Hbq27MUPZ/RLH5/Kx+Rj8eD+8d4vwDXs1l2sRh3sM5WOo6OLpxnTxdPvGbi51cXZjXClXa8cuhdeKGdGCQ/SPKdfZkWv1AMmFOX4Gamx+tFqouVvsuTlRFbMKG75tihTZGShUBTuKFQlQcpI4ZVK+RgyJvm64Bw8JyEU29CFyS75n+h+cSN3IZ1zKihhHBEYUyF3EY/xxL8ZmA0x4aWS2Hy/yqwdMvmLYLyNySWN49VkFuSxt5Fvy4INo8nF48R10hlBn1nJaMEfJAoVPISfgI/Jpd4H2CDAPXTJ7z8nBh/lyphlqzEQ46IqC3MCokwd0KBgE4gUHP6BFfs56QZlNV2wgFj2QCjDkUT6QqcTm6kFRzOPia3gvrfIFfm/CcKK9pviYhxLxEHXpgejRZQxzwfruD7Z+eAOozUh+rgbLDviN7C6XF1WjMTy6QSh6FQEJzqFOXWBGPMa5zeSjIHoSsQIQnlTBPRQzJvrVanQA+5H6xCVRWaydpMcc9wajwEicthSDXOilg+EkVHyjWfPzqlhO5uzKwGg+iqdSDbDdyvD6SV/B2yv7uic0A2spd5PgfhQchtEJu72ZwpfUnr8T5ksVK0FcJUiZZAq/ONDJcCratgsDgfYYP3X9Ug2BPhadqV3wN8Vd/VnkmyYADXoQuTLfAtjqgJgv7lB9ByolggIrbUqRkkN0xd4RHGRJkUAL4jNNZq0e+HP/ZHb463hR01yAu0sk9V3qZ+TvjgndmL7sl8YNlTuU8TojzxDO68d3x+3uN2JMKWO44cpyvly63OjGDJU7ROHu+H3PCxpPT03nDfUrv9Z6AewlaCOH6tgCvNKAo4V2bN8+v7h9OTbk1cfHuREeeNM3YHiAOIO0tcQdCsB2vjrbZnRvTWuQzabZzHf7NJIDjsEjm3YkzluwWw7szYG2Cw6/8pbiRApEFkQdCTKSibnhFlN7ADT0MEWKHMZMLzTwiLkOIpqmzm3OlREdPBpElRkQJkI1ySps9owQKLygDas5ezQD3KWbqTWYTWwCDosakg0sfhZF86hE4MOSxqzz488Kfe0eYs7PbHoUpZjfM21flgv255Zn30wWX6sWS83/asoWr/Rzm/ZHiGdun40BIiPHQ2iOuREmROwU4PCAF1V4HgZvaQZXnmI0iy1qNT9t9ic4wEe+W+Hwh+OQEz6G2AhBnzn5hAZoFzeybMnscxRdRNUirD6p4gOZhct8BUt1MwshExtjbRQfI1SAdOclXoq5N3pZ1SXOqJn0C/1aHuEMLalV+TvV8q0wvxNk5808OMqNNZjLKSEZjug7mumkNLZ0oz+kTMzbXL0SaAOQ2z8WYVADtFd2EqVoE9oYTKfCPVNE69I9WFdCj+B8ZZ24FgbPp+lRHL0ocT4L10sOpqOJaUWUMdMeiRXNdFG6KycBC0gx+iflo2DhonhQhSwiEWtaKwlGlHHRsVNaDz3XuEvT2hQ+HZYKCo/6NF1DfV4XfVUAOhoZfYTq0zkKFjd4NUADZ+hzUnuMBMvRc3Pl9iTcRt1y4AvMAV6uHUOUer19MfR2ft7XmgTIWj/sTZaqXGdyvy5if4xdMhq8hh6EOgdA4e78fU3ApT/DtDl6b+IzdSkRGwC7tcB99bAN1KMfurXuxoxB1jNDMyabB8NXg+tqpXto9gnqG9Y3tzSA4/W0yEDhG9GvjpJXwf+hfj4Uv1FV72GohzSjR/OLrP5I2fq4pHFF8UgpkmkQWWxcxu8N2CXehpiAR4sgxAsQYgxGLIiFnHrFtOY7VXlUVefaMIDHFeZMJd4hA5nAo7LhnZGodwEDGdtQi1CkcR/vOguzz7HSJDVi/IPwzZw9Rj/s28X55H35bZS2wMT5OaZB5epBlT1Q0REz+TEW4HJCzzR/OZmkyWT28ZS/s7cllXNmwMpcCbFLIcaEHcqpENJ4wFEAFQfQIs8SmWTFcoYlkZjjFA/EOxEDKewJcMIfZ9nGL5/OC1zNMBusg3+pWhbgGQmXRFihUxd2EOvwYLYDsOH1XljirYilgA9lIlVxKhYZMu1kkP0RgrVYLmb2XkS7dAHUoQ7gQHxzJkAHfiOCzANlC0w2P8kTK+C+zHDYSM1cu7oGx+u+SNMnUfIsxJi+OkYollhv7S0O06pissyBwvDkYpmfvoDlcxZw4CRNJX4CrQDjjCypAD4/PX3y2bMY3oTW5RD9NV+OnM3Ba7QL8jY7rRdy9JTN0+BeHB3Lnip9H60vZEVImwSYbUfgNuet9DT2q6idmYbnkApWadhzwjYR7RYJp2xjeK7WELFqr5I9GwQlh1ht7FdkWXXUJVgWoD+4R3FNVaiVHIOjHjp4AMsuucQ9NPu046o8No1D+q+4QRay7uY7ACOv639ZRhZ0I2DDI8/l6Afz2ndq9zkAaubNq2/024S46pMr6/r4hzDsG3/Velw3n2uv2qeN478baVzXd2HeoO6l1eZu7HYMryFXt2W34S579vG04fb1VMARr8J24er2T5fPONDmbAO2pY2vJ3NY4y7Xw9cnAZPLCjCZnyG5pXIMupYMAdvDDu1sDMJbmC8jBza6yZexgr8yddLoINlmzEWrI6UgzCH6MJ8qgVhiC/8YHzlQqWBK1QbuEtNvE9wQqHTcKWKW1gEk98gvmSQp/dcIamKUJJ+6SzVik41bOGe0VQUrBBr5c3iwpUaktpj0aclmU3bh4tpf87UIpk/L+LFqJPtqpvhzHPsQwKCcaf2oeHcWfgM1A9KybCUpPo9zfJlCCVHY/TCNzaSzdqqqnkiKRbVarE4O7xzI/4+qrEu0IB4iMrK7eJUX/FsFjz97kS8QeLGER5VZLlmBqGbaRsDktJYvymiCShLn6ctwchKmL+P0aRrLEY1EQ3k+IiMiKhsAJEE2PFFVtq913Dq0DdM8i3vb1+W52hzboNZbLNK+ijKgx4MR2zyWrJVI0i3vh9g4VU7AFVtVPMKy62ZSnCQrQxV9ACt+TvPFC5DaQ5YyrlVdEF2AzdWyJlst84uLYsXhubLUgdmwM+RM5jRNsQISXC7VEdAqfppMn6cTXIWeo7+p6up18J/uipgurko30BIWKzz0RvZes5ddxECmpurZAFDebd4J9Qkj2BZ01Or8p+KuA5g6qDeCP1c/VdM1nOtPKk6oXYW1IZ5HoahQYlk1Ajn8IVUvAjkdYgU2roacjcjbh50ccG21E+Q28XPmgN45d1nnt/eridn6dQBbkUOPa7xDEFeJhwQQ8566gFDwrKirYNvMAwr3p+ir41vjcLQxj/V0NDMc4HZ9erKzzYtrjDYmuNd1tVraKyqwq8m5gobih8jYgNekmc0YDUFfFm8fnMuAbjTd2YK/aa1//SqO6T8bbecVOSavBz4qOMThofghpEM9xL3o3Ns3vA8zI4oDqWUQJDwiEOh1KSy5VuIcxi25iXDEYUeDTH5H8haiF6K//C1igCFxx4QtLDO0FmCoNIUOcukMWJHYhSSngVazsxhyIKUBi8oBLZr1J1634FCSVXE/5g/U0RIbjypalcvvlqtfq4KnCIQlp30x14sPmRALfkzwC7zrVBN23z6K0lW1PMAIJY4XaZjhDgYhjC27+PQkIHmUWeVUxU0m81/+8qP/79/5h3/xL/327/3evzDFQ6hkQgjQv/Y6P188O/shFZMORG2qdIqDHHQErH1CPNxj9PEiSu/k0cnq4n6ZsF7xVpB9Nah+EOUHJvUDqR3D2l2tizKaqztnX8c8NIihzwXEuSTXhg1YcyZAg33w12UI3VyUs1gFlkq73l5XnsUfJraR69Fl2FY9D6JPoslZOF3G2WkZPMTZPxyRUbxRI1VHKxwI7dSV03+Pzy6K85fp8V2UqQln+gbZpMQraDXnYOl8EWfFOQ/vf/TBydkLWcxTEDsHJvh7ZZuIZvbZxMt5wCleiMrjqDwtn92fRe+w5hMG0yA/DvM5JbLHt4w5zZduwwICWgGdik4HRZwDgCDOpgJa33RX7RN5XlJlLVlgoG99HDGdnkz/XDe4E/3hBhVzi0gujU7b7CVQHlUbEFUezajI2L4iqrUVnh5higdp0paVXcACFZPf3EsjABQau65GZXcU7Rt5xuIeyusoHEp12F1Prpk+tsA3Dm58Lbqcv35lNnCOlme2ed4OVjv61bi3QpjdW3S9uvkUboRB61Oit3ZXSd0eWNfV5apJXT+Mn/tXqQw/T73S12gcE9y3xAO4JOioqQlsYB3S5un295YDX04O1J/wL2fl2lq58aoedryhsnnLXXoL7o8oinTDK3P8epCULFEGGQhBjNl6jDIQtxBkkRL0LQAZ8rTJfNIZJpoqdeMl4g7SnGGx0dXhI4PN/mqeGEFqytYCJwobOFLUSsbSzlEmM+YUzB6A+CgqHzDBz55ds8p5Fkcv4wrNA4sjxHkkRU4phrQUW/Fp9Va4eFhkS6aMtXu35JCBqehNmHhHKcFYCKWF7QTM2iOOQ6QmaH/4w+//L/+D/8XDt45//y/+pd/7ve/9xnd/e36UsvEUMQgSFsuLs7PiBz/4/h/+4X+dRjMmrTlxGIei+BzVDDYYi+wgnnDq8Ozo+KTKl8WzKLwbTJ4UkwcoSmISU9FyC6PyqF7DmLopmhaBRQT9a+uRJAfTQhpXJV0Kcgjax9iG65yWy4XbJD8AC8RgptuDCVuc1W7V/ah6lBZ3k/w0r2yNBfsbmKCTDiAQZATYXS2BmHMT/q//p//jP/h7/+Tdr905OHhrMllW2bQMz1bFHLXt/CUHsp2fXVTPnpydvbxIsJpfZRyyoC2/mPuEWVROWB7AsgqFYnmxCtBA4o+Tw6/FU1ZtzugcctvKFgCT5bEZo1vSwWy/MosVcgEEYfIdpEUJ6KJFWWQyx7LhM5PbSaMfWhvVPJS0hZjPBSr+mebA4gP5kV1UO/sjnjgwW4XFMgpCb0EzAYJ/bH7A9Ij8PEuhFALC+uFSqOdyiT0JrzFqgLTXSMFtUV8uDtCjTEf+4tTKfw/3fx/83Netc7f0FrvYqr16A4OJy9lCO0JqdPaj/BbbQYEnkPYar322Wa4Z6GpUDqHJETXuLlUbeqpHwVC8B1IHh8odiu9icDEb8Dv03aH8n3f8Bv07idngrb7+9o3cmWVHosPm9GO/rXdk2StpzJzWUN1H0XNtDtTVkZDVvJt71bABbl765reJb35dfDtA1IOCS23n/wSEcQVz8Gy3RcLC/+UCDzYY3pgjS6SfuXIUczyyYxqOdX6QyAibuBq/ZpJNylIBvAiuXoxXPEtRKMmFab6yuO8DMqM8OXI4gCzpscxG7ssfRMVDs/XAJRFO35ESmV2WsoHBOM1im5GxGlmiEoRFcnTwy//GbwXzXx69zN4vlkcXi4/L6tsvqg+fnryTzrXIECbIrAnLBQQ5FTgNJ1EyjSWmT589Pf9//+1/9Pf+X39wn8OrZgihFLFKkoNVgcXR9PTl2fKi1LG/lMPWgijJVxAf4RroW/cf/dX//r/8lXvxLH3w6fk//+Gfh7ODl2/P3ivz86KYBik7Q6ktc9PImoiMaB82LIg9YiEegeCYEzjtGSH1gQVcshIbpjrW+ncHIwAXwkRKeXPhdHA1zs0fkoBXtnbufxMADGooTkug4YopllNsBoiCRR48jacf37vz8dvFz1+cfW0RPT0tHoQpSuChzKSEl5l1idBlluIG6MXL8o//9Mc/f3+ewsr5PC9tJQfUxYyFk1XwWSYTICyr4CiLSCK6yrOv3p//2teOD3EGNP00zN4O5x8X599M7rz84Y8PvvpgFmXaJo56xt4PFgiko7CiIo9Mc1u8QsViGzH9jw72ONDxEe9oSaLC3L+K5s/D+Lm4ZX0g0kEWyPfeG06Q9jFuiodUmq6FnRtx+uDSjU3NZYmDC9XT6qt4228QRRNJ/NoSQ39TdZSkPRGoATw0b4Fxm2cuFeVW3f0vryXVrepR56L3v1Mul3W8SzKPgdmJYmgUdZk2vho78YxJ3I2ty7fd8GNKvBrMdcr1a+Hecj/Gp2c3533I8eENnCP6RgtP57aXSL2+DrWluo7fPnYB/KRLw17fvhqflYt1uycqqebwpYU2AIMldutoWYa8A+29m1ejy74rAKLANYrRQnCASpKHUyzv7e2WA7cc8DjA++K9Wl7C/sEbRLVv4U5NQqCyAQABh1lVxPAKQZZtAIyOklqdOxej0qz/JdxgR8G6QSL5xgQoAkhgLoyM5eiQxASTZICDYIUKgXCmNE2NI5FVEUeDIbweEGdqBlMcj8P0bhXdscl4bSIOg5NcTnseINCRywyMmMzntGCM+S8epd/6H/+b//7JxYPT7P0ye+vi7Bd58Gv/j7//n/4nf+cfJ7OIVYAkYoIZcw0kMomOORPMCHByYsR+1DiN5m+/e+fRo/dSoIpplr9AMYgSvBVNz+6d//Lnv6iW7E8ophMc1bMlAQc1XKvjg+Jf/yv/0lffLquXj/Lo66e/n1aTpwdsm85Po3jOwbYsXajeYgKyoPFCn/C6uzS9hl9LEqtcXAvjsnjpaxiFNhME3CIi7OMV7O7Lz10XC+0xrNKahwy+Dr719d/8a//uv/iyePz48fRv///+s3/wZ4+XGFWxCIApDqWpCWEq27jRBcJkMrl7fOfeveOEw9hietERZ6ehLtBfpsns+dnpNE4WSfp8+RIHrGGSat1mcfbf/Vf+tX//r/530vOjIvhltXoUTB8Xq7eq6Mk/+Yd/NIkyrH/KYBliCIS5EQoknUKn0SH3c1G6ZH+6a8WfdgJoBQAhH+Mc0YZik98NqucGqi7khHIpYGIb2VUFovln3RUvrsju0mxJoW9LnSPZdFuCKlWGYSillMjEP4lgyNANgQROawguhzgD9O11y4FfAQ7Q2d01qte796LN0+R9Tb/eW3llEjQO3Pj77ZC2XPDoVGG7FAAftM3Px9XsStdegy6rrobFN+/qUtXqnVvEDsVvgY18ZGTn6pY+Mnsv2KAG2Qt9E5FXK7Gba4O3O+cGunm79djA1k22mBvjvzdnMFDU3tFOdN4j2xANEhf2uDq8HfQzsP3ubxUi6caEIe4mKkl2Ye7yU6Q13PVEeFlhBUAXqTQ38/0IOkg4MsaXViDrFm3flVBuuCQlYRoCJAgkBhEQLo2UEqGWzNSiCEgu0twkMrm24UaIzlwFs7mYUdyP8wcIX1ibcKQuxiZ5znmxSFraiYu/II72ijmNFXEzMwuQ8Kc4Ero3vThMLpL582CerZKPHkx+xKRxUM7z7CJKDpnNldUHBiH4lgynFMeJtqoLFtxFnhVTjDlWqzIr2GaQTKZMMHPoL5Rz0FdysQCYGLyPkgEjbwiflMWdvPj44tlBkf0YWTONjlfVaVY+n2E9xVpDMC2ZlUflKPCZQw9mbpiyYJ1q6V3GGD23CS7QPLbptRC5frYszaO1Mnl4djldgh92hTqABntLSIOnjtCJV4KRA6iFzP2Tp3cepL/5IK7S+eNPJj/4s2d/+NMzKUNhmtH8mP/QjNiJISjT8mwdzlHbco74wjgmDC5QmJJkiuN/PKZW+QvWT6q8TKK5jgQu02iSZBfLJJnfPyzvRkdZ9OO0WEXTc/aGlNEHNHLx/MXxg68E5XM8/IThfetU9DjWViRwm6zNdL4FqovIzgEIihQ7IaRwWoDGCKKn2JU13LcezvqP2GX9mcrCAPn4p2WPFI9qwUZkPBixDgUeabhSAcRfAdF7UQHAQPfm7GHtN6ALWP+U6yfTdXVIBR1aL4ZWAPqu7ty/g9r7WzM8qvQVOyquM8KMyjUE1B3nrX/t/VW9GlXd0ofo3De+WwstFvHi2Jdxd7nj67J3f9i3GleA5zVw70N795Aojv9celtYT9bdt4NXjRyAUi6/unzWt6O5rsbntTzc4Bn/25Y4shJ+3f1SRtEgbjaZFMC0tHkc97sneFPc3tnGUXMLdcuBWw68Ag7444SHfudrrClPxGDkPXLo0yVoSXSITgiusm82KdkmOPm2yVc/EQg97LOUK3YZt9iUrElXpgLYx885FJIAJJQM1kYGolc1DdmjWQtemnSt2B7K7C27ZoHRMxY7z6LocRS+JdokW2L0c1YUL6viAEMgNpUSFzs3jjGo2KIgMw/MgSbMR2eLIF8l5aM8/2YmkY4NoBzKBZ1UgdqiOiCTcb4BugQ+g9g0UM4PpoeHk8MZHkXZpZqV+K6ssE+hkGA6r6bTKRbrCPhsSY5TJrm1AFBVj+eHi3hyjod8Dp1NMWKSrc9hlT7OlpxqdYD9SIh/ey2HmIsY+Ft/88RoXfoVUTVnLM5uDUAdswVjbFQSYFuQim2TXTYHp4TdF40Kc+rcbhKcp0xG/qhmSVKUcVZehNVxsFrGF3eK8r2VWo0twmmxXEoToH4SlrnHuO9xFl7zGfwSZnqTjGSCaHKM5c/pdHb49LPPmGIvcxxoJmzRhnlJnB8dnkbhp9oVYGIzNlpxMDs7OX3y4qOHdzAGizJOIQiOJZeDlj6lmX52ZLAPHAEBRYHlhLTKU3QRd1gDVAFJQwdM/5cPquiZ64rqCVZZS9tgjZQDGGumOzaLj6BPyym2vlQjnlg/MpWYvSgVSpC0YQ5944/+S6e1BQT1aBWk0lr2Ko6HnmsN0pN4G/XF4MBg634xyB9NpXq2e4l2ZXFQPRAuYXyPb+F7cH3pora4tj1a7HcOgJCN0jM6bHTlbhHTQvmabj3D4elkLdhWYLzWu5Xxc3zU2H3Tl9Mgx3PD14D9sKNrDJ5WZ92rKlfL5Yq4Tl6fyC7/x9TXx1CHR/TPnlwjotQifOzH4B8D45U4VNMubwfnGLy9PV3JQ2YTxLYziDwhzKk6NjmaVfjhwfWKRCLeAkRDZ7E9YX+wPSLpsMnS7ackl94U7RVWiJpqi2RtLqE6GYC2/IJTttg28Ur6XFlCmZJXiFNMoGbsozXpvz6gCxc9x599eJ5W7z969O78rmCCCEHbxGukP6bzMblB1quwPWG2/s4y+aCc4vUFh/KLcnUnCxYTCe/yU6Pp6vAF0jy+QjnOFiMikOH185NPPmHRA89BSPjI+KgZzHwj4KbYrBzMl5j+q1qsFZyCtFgdTcK3Juk99hvjiyZjOjv4NKw4WvhRiACaMH+8CtnJIE7isIipYsnGEithpOODGAK7ANi62pg21cW4uzhsF49tuInb/G0RbUT7mWqINoqAohB84Ym21SJJs8aDsoTbpWISx58lq6M0fj9MP4NJqFy4CZKORy/Clkr0kG0Vs4EcXzz54smTp8jTHNSAKX4YnooJYkO4XJzTaegBHMiM11ZtvA4mSTifRffZrRskf6q93eW9GD0tWpSsBiRH8fTeYjnJsilGP1XBmWtHsreJF+eLz1YvZ7QjbaiOINOfM71j0mlRPrk0HR/Fz8PwOf3N3lJahX8rqCXFauwseo6JEIUin85Er1YXlfwujcHpAGTkzzBjC0blzfVnyD4EtbVeE6C15EXfZPMAqrLiSVGZ/Zfl60/ajqVAru4Y0o3Zzrn3c3eE8VEMjUs+zO6wxpPmGo9tN1UNvqv/OkrG70nza1GXqpXQUderrosjwuetHx5FYi8QDee6bFvPNuDB+5xB/nSZvHQF87d0H8OHUd9WIeu5xuB32bSOyozExhezB2Eb5XXhNs4PXJbuw/rhLWY5bq8B2AOwBbFO64QcDX0t1AHtjxhfVH/+29hbDvwqcMC9aJ9nTa9BgcRSk1okvBBmDtPs7Jmtn0rKoVqISk6mVzI7L20FAPlHfu4l/Mn1CiYdGpsQp6CFcD3sIP0pJNGIC69B7Co2AyEhBBuG3ZhrEykn75LFcIKWPKuqe4hTcvsTTuJw8dHP/2zxMjg6nB/cuYP5kXYMV3kcMkuMUxjcVXIiV5AVSR6vsMsO8l9Lynej4hkfDp0aFk0wPbGZ25XmatFeEMhkmU/W8vzi/Je/+CWUyNyD2nN4FCgkSwZJovWCAmLlT0hSJuqDvAAlLyaH2CCdmyyISoOMO8dgPo2RSpmItslwsY39o+ID0iAoHDsINcLg7haruUdtxNT68iMJt/FN+uYv1eESnMtnj9waLHr2HgVsXQEhBopxY6QNADjoZ/I9xm6Kkxk4O231rWn2lWD15/J7GWccyKCTj1VZsgqxasvyxwoNjZn4YCENgWUQmow5c1ZF2GmBWA3iXCZS8jdF3CkLL8nBSZA8R2PCzr9aTTkiIEpm6jLVaVE8wQ0ROwpi+MnBcOYZqtQpvGmS4vknWC7ZI4wyiW+oAy1PwW7VRL1SNBX3Qyy+queqsEQTUunPChCx5ocSZO4vCx+dcIcGZx3FQQjcbKMsnykGLCBNqkLLUMKkFQC6jmonhuhHhasU44yFBehi3WNNQv1w+3PLgStzYLtnXRnRzoyu8/pdeES5PvhO7J9r4p5UAk7Vh68W3U6o4fx1ynbupPb5cGlGDTQtDUC78Da6YTQNPDl8NC7Dhk42egZivHblSvF1Vj88TPTrS7kOPfvm9fVpP+xqu5ur+5a1wcHunFM3ZiPDq31wgszu+g5RcC0+DCB19HRbZAB8x7m8QzlGxvOCutd0/OvtYa7fdH4kF3NJXEOQQcbFpIHJfhOJKEEiDQnE2FKAlguYU2eSeyJOkEtUaPer5l+FFfmLVImTIkxiEJ6FsCCysIQwQOZYgOhUXaXKy1BUPIjy+9iNSAYHho2kxdvVWRrfRU84FAlI6vIEX+YY/0hARFFY2Xbkiyw7KMIX4fxDjgeOo+dJfLzE+aPWKHLs8cNC+oyokYyaINwjeyLwMbHPHQVEZFIHMGo7a5JjcQRDoESbSdmEymEGc1SOSXQQBW9F8Z08P03SA6lLcvpJ6lQ4tHkAfnAclbUJWeOn4kzte0d8MTHU2kwPl17MSz0RkNvRoZBrZ1C5gKLWl4pVPKziRyH99y4PW2jhqt5FoOqjNJnnIlVcCl6SybdmyKldB0XwMjz4JEw+CcuVeWhltwc7MmQnZgoOBdKUstDBSkts1MVGAgxm0NrUcHQwVgu0FGPtVnKsMusw1SEcDINHZXanyt+GX6wkmCQOhvNpdZQGHEvMotSU8wTQxTR/z/Zk+d6fsN6CHdCMYwTQ0thQrs0kOZqJrT5RcTCgNzwN0xdaItKpzOQFP9SQ6tqC7xf6DnvK+VlZ90JtkzZLdrGQyplRl+CFBPrtlDNpMKgpcmekNZD8HgsXtjGGnsULQldAfbVSyGNFgbL59ZpjbHD0d9ZH+CrGvauNwD5Vfng8trq9tnqzj+t64fGUXFKOeqvehR3Xzdflsp51Y7XbqtVwud06+r3xivSMkEC65W6R3Pt4RXp6cb3CSG1qGn29sldlNAW3gLccuOXAq+WAyd0Usf22bz8PUeHgGFcQZJzUaqYMlXyqmMACAFPibuBBJLaNjxLumfdlOHYjMoMuAWcKwsw6ugHinqQno45U+5W/f/QHEeviJT/pwC9WAGRrpOIZiOPHSI6EKZijyDDtX2UXWfkyCE/lDxSZU/K/dAHJlEjzlFzhYjJFDCdbFDwMyq9U4VQH8ZYTdAhmnGXSjVivmiFxQqcyyUJJaobVXe4d9dmWoT9yqqEX+awKyBKe9QDWGbS5Uz4lo6c6jCxZaao7x18k0RjMg1zSpFVN7BI1KsXd7Ffh618OlWu4DrbLyiGb5dRvEwYJYdcmVmkHYXd3rFWkXQHYRr0dl+8i4KLzTCIOipZ/VdDJCN5qKsmeSX6Z5GONj4WPwjCZrPDGgipIZbFlWLZDbJ9gl8WSvR9h+jQvL1bLizyLaGR8LxXYdsUnEutpSRQSpuWTROc50E5aNUrx68qCCzE0I16AQqzOEL65o8VAFItElIvT0uqtEtdWrONI+qdWVlOxgT5MWBKbSOKBJ60XgY4k/hRrvddqiOqiFrZIMsGHgi4tlBUubnUeGTgpmaUA1ACX2yEmPHwJ8va65cC1OeA60m13ujYjbxbBZUPyyNI0FNV7ANzMzWY+V0o96liSX+6+ncKDJ+hj2iz1FT75OpkffoVFGmpfTx0q6zr0XCdvlx6JLzSQ114+zLXK4lu3dXVjtgD6Hsfwsy/fdpyr49WwdflwNTw+TUM892H8cJcGP7UbHg1vUksn/6XvrJtRrvcPmJgijz0EVDGOWZV0HmgFQHIt2CQ5oQngsF9ePiVpaY6TuVK6IOJ0bvzQQSU1Agw25BmdWVgnXpHADCvm1+DStCoilbYFM9lrM6/adoyAlT8Ki7dwFKNpV876xVSE83c5ems5K1Yz22Ngcj8W6kzkMrOPxFYkZXCOKXkUX+RBHqdPy/QjUSuhX6bnZXmA408o1BkCzNBTugRG2IZUKJN3thuIfZJeEUmRFK3K4gbKjOkLMIC85RQ9oFrdQ8cosmkKhckneBkt86+WUQG0yXwgsuyGUY1QPFBQl/QJXe6ddWEx1oWauzdDX0et5/6Zm36iyKHTf2tUKmcLa41KeR96YWhzFNR3CcCa8Ma1DjYwK3Okg7FTitcdDurK42fL6P2sOg/DOa0icdh52hF7TZVCc4JResR/Tq4D3ThYoEIyFn5pXWp6MV98BgzBPrgrNSF/p8K4KLjgIGepf1UesQcgPDE7tDmOlfBJhVLBNuPsHEdTUuoi9idjnURFaTF6jnqjXANpRQh9UgY8WvxhD0AUP9GGbFUbhUWdTJ2UJyOAHw6cdgRKzJePICyc5AYK8iK6pSyToJcsEGZaAV2TjsVBGVJf74pnpJjCoFLUi+Ch1oKspip41yXe7Eq/etroMeTqRby2nHpR+y43ko+33e/DcaNxNlruxjhUl9259k3ttr4beV5P6d1SuvTsWyNp5pdd3XL9HNf/7u/JQ40z+11u0OgOHer/GkFHXwMvzCX5ydVmbALN7yVZb5NvOXDLgc+FAzZBuVGye2c339zNwYgnRVgk8ouFJb1JnpFRBCcBkx1ZiWEHAUdqAA+IWfwhBmGNYSI+4IpHWuLPJCsJVzVCw48cRgKXZm0tTQ8qB4kNuU2OMvExpFWGMH4WT16IACeJ40GS+VSkunhRhOfsvZQUxjgoZ6MAO89EzAFzXhdPcisZFN9Iy6+DEzEO433KUJ2ApiDNS2OywygqQVVimyonfYAwDmXMkEmirP5UFc0vq04AIgsToAKzk3j6Ikyx/TjhLGIM2UWKN2gSBq2yKNbuItmeNsFcZJNYP437qREOAW82ew+UmL+O9olUtKi2/9xVe3ZcxNNkkhSrB2HxlSDCY9IUCZ2dvLCR1RTDhjRvTSrH+fBqwi/WMtIRhMsYoaUbMRNQHRIQYIKFAomr1iyePomSj4IyU8MIjMyzID+SPU+yIJI207YE9gDkOINCl8M10ES+h6BUuGkgeiNbAmwFAP5TrtQ8Tja7H5UPtaeZNtYUPt3MVixEihQYdQay00+kGxCJ6kL3Rt4nimgCCPSiS9i4rHXRO6tcZ2VIF+AFYfqfbQDQKYbwaoBBcNxur1sOvCYO0Nnqt9p7uV9T2bfFvA4OsAfgyUA56yYn5A07m08Dmb1oL6uPxoNwg7mGe102Bo/RzCRGQJkNyvY5aDD4qEeHr6bJacqHIoyGoaKuo6dep15DNdqNs26Focq84vghmv1ir8NPH48LD2FzQoDrXd1c3ZghPF3IVx0zhoc+DT580zfUqU3Y8MW6zhkgPhbkqcd6RjpzP/W3w2Q5Te6e2zkAzZuCJKRJTSQhLiQt3mXCiF4IOojayoWsKJWAECB6rPPq0Qn3ASfp6oBVCUZWKjO1CjqfLciNUVQs77NrswoQBNEJ4mWIm53ZhEKKtMiw/0iykulk5Ef5nmf2XkKWOSOShIiqwDbf9Cdp9BnO/tkerCQT/5mhN5UAPrECACiinnjHjYluJEJKFFVmuYEMSBHYrTCPC5nM8yMBm5C3yJAYs4NydbziPLHFURUuZtN7K51LgEdIqDRZV3Vz1RMejZZ6SV3zGGrFNpelNA/268/QbyRspRryuqANOFf2RlTPg8teUyWypN5wU7OaWIygrGOYbT8DlVgURVzE75fhExoR90lROJOcLmapDhJ91epwEN//eEZiE/A0iF/W/URLLWorGdhwHANw6GbGc7aAK6V4pzx/K1s9jiPOYz5js3iSvsyrl1U4i6KZfImyw5q8zP6zC4Pj3Q5+ES1elMuvQBm7k1VsvKTR8SMayZ2riqLJoEn+i9gGoGeKpF+xC4F1LWMSFaaCCvKfPy1Y0b21P1k1Iko6rSLRDaTVWDp9g+6jvnLOa4IaijUT51eE1X17DcBkb4r6DN3tke6DX20lqmRjvd0J8UjUm3r5409N404ZwME7yO6oq7fwevXt4qypGvjxS+ypi5fLh/SiRwWVl27djJ+j8mwC7ebbJuy6CxEvjhpXt2AUfY1+5fPKD3dLGR/TxXMdnu8ut1vWbvih1JaH8NhnZ/fEAy9mC1a43Tjvjwx1zFMr2bXgRj4e+L52Lzd+rONdVnv2CVwD7Ax1sxi+nkIMcjt+J+4Nhu2GfGWp+xH8ysi4RXzzHLAOefNov1AYN0YMKF8PBuvQZoUshxJN5JGhNSYRbAAtcXJST25LQpMkpGlRZCv+EIyYUjVNoMaGuKSlArsArmdMwWn4SUCCYsYU8wz+3EuI6K25d+kVksQZHapo8jSIPovDhzigkVweh1l0EeJyvrzAwicI75okqVl5iWuy/RAqHDJGZq2Emcgk48yqr5XVzyBPx7XKpNsJdlJrKAV6RJJkddGc47Nfkq7qhoG5Uvhqix7EuEQTwMZDYNkIgG17kp5Ek+dZ9nw+Y3Mqh4hRQ7N0Uv3JZqi5b1ySJQevHUk9eRz0dgEO0ErvydMXJTyuagTExfoixJ+aW1ur4ReGLkxurziDLQmyR8XiURy9LOI0Q8KnhVLUP1ZVMOWnS0hAD3EFykFa2IahI6AlwkyQaekGjCKbux0qQaFq9ypYYCSUJR+Wk8fYgqFvId+rBwZHxep5GVycLp89Ow/PT9iInCVVmmc6y1nmP/ijEjK1pDUmuz7YBoDdmOjnv6bmudAnsZiKPiOOcq1iVkcJZxL0RZSaTtgomx6hxSJb1lAqF21P52i3totZ/Kk/c2qEYcC4jCOul4YE8HYDgOXW7bJLpRvWywBv0285MMgB1+HrZLrUxvNgrtuE18IBDTN7F7Sdo1cB2G5my6RvgfWAbRQ1DV39QwkAt3S6QHuv8+lHo2uDdg8d182sGR5huN41Ru/v6nzjqe3mHUPvdeo1VKMuzrptr83Dq9XR58MQzT7MUNiV7lKvg8dh6HJpqNwx8dfh8L5c3bfuPnxTa7qCve/r91K1HDofwHvJa2ZoKp28QmPiFK8q9vXnCMaasy/uSrS1adGguINj/qC6MHN5vP1oTQAZypwnggE0PCEuSa7ipnz6McJ0ghgWHc8kAeL03cWLcPBQLP5ksAF5UOQP1bPxBB8ucrSAfBIl83KFo5U7nDOF7YcEfk0e66jZCBMReZzEIITM05hFAFyLTp7HSVSk50k5j2Xnj6wGZUzl8/4jrEtwlUwXoSHIsgcxLmQbsciU/BfFWJKQa46jU5WlFQbo4yzbJdPMq+Xk2WfPV2fzg7cf5YvHZbaI0mmB6Cr+2CspRK5B7LGuu1CMulzuHlA/vwsDuob2k3tyb0eRcU2lw2IYdKMx1JQIstSlmMkkpmCTdZ6Vn5znH7AbGz4E5VtRwmoMQjzeovARdIpPJylpxbzEHgZROl7EFRsztCwjM3o5/WTFAFyoZHZ8r9aOFJ9XFxdn9LH7YfCsyLCl0VG+UXUym0e/+1u/M5PxURQexavFUqY2T7PFIg9O5vliyglu6rPqA6zV0PSsAzzFc1GYg41ty9IPy/h5RZfTBL5YII0jXLnqmarnqqq2o5vgUlZqD3sAyFk3KD3cvlzShuHTBUj0uhRsCkd1pB/aWRklvZEVJwBARR9DSbF1An+GT+U3V2ErA+48YMd9lzLYS4x6KNm69h1ttrLzuO847I8/NbYOVX4pPfBe8mB9PZibDfoljqeNFufy8+6mSpD2Pu0G25G6mzaXUW3HC9RrFWIE78C/xsDE8uNLATdgxsBfjrGv3PEcHoPfh9mX5n1bvPu17cZs0NNpNbXjVqv5Q4My9yoA9LOtbEC6nG0X7IXxyemGXd4rZOyiuo255cAtB14hB7rv/36F2WBnLzySj2ziEYjxaxlKrlWMDTDIUBKrpBJINMQEBzHaplklVSGguI8eD8hBiFjuIquJW9zYPSyZj0uQ9l+qApKWTcBqrj1KnuXxi4tivsyXs0SbEOLoghli9gCUxcsoeISoHekE1gSPoQhwnALMNDVlcKasZDa2C1/cq84PCuQ0ljJW7BhFlpeWghgncx/tS6ZQKQDQqQowd0vNSrz8sP2TAZYHJFSZ/0Mi09k8I3/GUTKdzA7nh8B/652jsniWZ2mxWk2mOAPC9aQxwma79d13oy931zDInEbBVQdTaxnDsHlbx69DmxDDT44WNZZkCGuxVmSRvieS1S4SZCPc7aRJMiuzPA2O7s2rRXLBRLwtE8VwC3lZ9i4xp6mpG2geHb1JGzAQwvM4YYdGhOm+ZtUbn6DqJCpEjTir8tXpz8LoqVafaMEcwRrgyeHB0be/c6S+JUeiFf6W1OYXH1xkC+mf2NzTbuqgOhzAehfKIQsRptpp/7a6QOXOAQgeq5eQwXojIToA7QuQha0zqgNhx8Wkfi62+N2e2tFLJOiSQ5j1JwO2pYyBQBqtygC9QqosSOCAzJwMaLgJmpT9G6/Jeft7ywE64u31ZeXA9tBQKwBuaGkq7feA7QwGswnusvVrjQ3K9a/GORvI1lGfW2jf2Y59dT6/YlfLq68p3OptBR97X3iodl2cV8PfLdPV0U103RTObilDMclTS7HZo6G6+3nHwPjwY8JDOK/Djd16/xiqdsN0+4MP795XP2b47dWLrQ6LCKRWkHwkyQ+7ee7YtedVfmx2M24G1FnLFzK1l/EGRh0gaCUoyyoTC4lHSD+2G5KbhD7zo4Kghq+VJfYYSNMOGjyy48d0hOLlCTTEC1CW30F6ZOYYm2+Ee+aCE0yAVmm2OijlKQglAekeMg9tvj8vixT/lHGUIq5m+OQJ3n/r7rN/4bvzcvJ0+fxeNPmkWL4Xpp9U2bsBRibZW1H6KQ5novlnYXYvTp9U51+7f/flLHgrifBw/3Y4f5FU7ybzT6bRVw7uvTw6+M7B22e63z05CB4dHFzEycNH94Kj2bzEXeWEXchxzBS2GILwZ3x3CpOYI2HQxdWSpj8wuBG4a/Hvwxg+tYwuP8HF1MmdVBfv4IcgXbzaXw1GIzih3xGqfkF2YUD2Z3EmSTjoavHe1+/9tX/vX/63lsdVcrI6O8zCD1ZnXynDn4XZe1Xyy6T8Rpi8H69+7We//INf/nQRzJ+fnDzKog+j4n5WfphdvFXEn6TBgyBmmv8oCJ/H5Z10guH+QVhefHX2oESzY4WHVsRlT5jmOSI1HWDCMb9R8nGcJmF+zMT76nxVZTmnN/D/HD9DHB6dLXQAm3rqOWeBhXI6BOla55EQHz+t4mfqh9gpoaDIMdSJOMpalqoujcDVViY9ZJJpmRxSWde10UlNKR0UJtmygBzK0ofZjiw/UtbsdsAcyxEYL6FCsJbldCAyGoNdg6zvUOXNufaCrIFdyCjZjuybQ+3C7I4Z9aUbWH/Yjfn1p+4eG69Gz3VwDn1fxlDSzduNuf63ZlTrd8jtUtIBefURQ32St97eayi4TtvZW/8qa8FrLxK9IlyMF9EZ+VEA3JjiAzkULnMXKZBEdnP5GPywTxDxW48+5G34lgO3HHjDOND3vvovvzfGtGNFnW4yn8zkNZ2PQxU2cTZDh4lJmqHHqYqcLWL1XgtYkp80SiCz1SExhBEYsdElSJtAxJKQhRcgZm0Rl/WMcKwJYE2/Iz3zqLnUKH5xvvo4y+7pjNWYKWVpAMvFxTQtguQsnMyrktlfUrH2x0uprPTBwPR8ymlQZTg/CCbhe//qX/7Xfv87907Pfvzsg3SZ/3R5/u4q+qhY3S2iz8qLd6r4w4ijgtNPw9W7Yfzh8sXRd78V3J1/t6o+KbIHUfJpVH51cvw0Lr+a3nkym3373neC+d1v5+HHHChbBpwqxRbSVZatEPzKgrlqpq0DjGNsCUAfHMn8Yq19QPQsLipC/HjjLqOupsqIFaVWCdqUNqMW2NxjC3bEsVzR5Oib736rCu6F8dOk+GaZvhvl3wyS9wLOB5h+PVh8p4o/qM4fPYqevVPk07vnq/N7y4CT3R5GyXvnL45Pzu+GxYMyvpejWFZ3k+IwSVfpZH6+OLmDdVZxRhdBgTNOoROytsPWgUI2Wqh2OarCg5K59YjzHggjpod5mWkRSBPuyP/Yq+FWiAAKKm1CQ5CEG9JHOuksekxVbA+AuqMu69PU1hpHax10ROR77QFgl7I2mAgvgOxwsCyOMoLwhW5JRjwOcRICWcCCgoR+q1UFmc/RpWvMdWkqcX31Rq6Tb0NvLgdoOprYXug3iEj31r5BBH2upDBuvZ7Rds9y9gR3PGzHCuVGAeCne7WRLfQWTAuwFd99bPUqlWfFDeHs5rUYpx26xCH9sqtBdmO66H1sGnTdq9iFu2ZMy4H98WhouNqFJZ83J+TjcDj3qq+jYmSb2+yvX+DrCntzWkN190m5BMbT+/1cu8OX4NydeSB13z4w1POHWryLfwiDETjcC9q+ynipmU+7EPaYvkeI4cxUHOkg7PI6MKnJHRDEJORsZ8aDHITIrpl+ZDRbQ7A5V7K7GVXtFeaPXBQkqSsM8JvOjlK2h+qfVAJWDGT/g9hEGDGLOt9flXeyKp7GD8P4NI6O8+w5TkDL1aTKjm1T8LzQDC4bA7DOKeLgoExPgxx7fc6EwgAlLaNfHh4k8/eenT2bRC8/LfOj5fxlXhxm+UVeHKymj8t8HgTP8S0zOTjJs8OL6nSSvndw8KxkG2f8MoqmcfJpkuDB5mPJi8lHy+W9Kv8Jc75Z+WMpJKuHOMWPgkPE0Dg6KAqOp5UfGGiHftWMoNWHKqlCVtdGaDA2EMPVnfu3Bth5QxLHTpS8D6w5amwqksuVpZC7LLJ5qH+Vw8W7xQm1gkLQDGZSwWwdT6K/pcQhW13RsU5ZXimQ7zNm2jHuZy79nwergyD4Z+XppIo+S1ZHYfCPo+Usrk6OpuG771ZH9947P3k+PfoWk/psmHj65PTZk8XqPMiLu6tVWWbTCh/6yPtlsSqXUTGj7bTxukT0ZwM6dcLyi6PETNbOvyLvn2Ehv692vJc4LBsjxhBprDp4LMhw8sq+F3Z2sKeYJJpPbZI85+A2lrWQySW2Ex0cU0X+qdbGF1M+WTCgu4Jwrk4tCGtMwQDFn0YYLtdR0Q+0oUWLV/IpVMkJKX/0ZcD0J9Mp1+vrQlwjte1Rt4KeHREuxZhvvaWFfBMC3ljtyNk55mxQ7CBd1HXGW8cZ51llCA9NduOXj9PRML6ILp3j+dbN243xaRtP1fUhu5Ts7re7U316xkOaQZ6ftQl7fbXLn/H4R7YU73FfpyOub/ytIy1HXzbq4M6NiZ821XEF1MX0rgAA6XAB5ArdQt2mNjhH/bpcW6hG5bwF2p8DruH2zzeYg8+W4bxxxIMlft4Jvzo1Hea0ZJqxr6yTBIHmD1mPwdJllaDDOQDaWVsPst44qrOWcL+inZEy82EiVsXR1ZitRyRC5pFkZWKmcKpN6nKYYGX+nk0FqBO1yMoKgCyAhI0ikLF5fnmSpZ/iaIe9p8n5LMkOw3J2eDS7s4inzEAfTOMpxvcy5CgxEXGnCKe4iGTOlkNfWQpYIQwGWRIflNE8mk5xCRlPUi1qYE6Sl+EEd6KaZYZMnSnLGbLhyWqyKlIZO2nCF3E1xTBJE83sCS0nZTzHAT1n05ZRmrArIswOi2BBconNigjXyoO0JjEJFtqkcdtAIHSvoYvRo/h1jUuNZX/gIKC7Wk7BSzG7vDWgy2wILKcIc3E1HjikKJZgsNNKcqzr4wqPnJjG4HMJ90eZeBVieTUpQ7xhosXNC6Cig/tf/0bycDmfHx8tj9gNO00Pk0kwf/CV47cfLk8xml8tF2G+uiiXnAVQVMXBxer5w3cOs+IMax9qwsy+cxskuVyeiCiRXgeDOROORq8yzeuzqYASddYwazC0Im2JblnKiSfaA9I3mMiIcvCwKh9U1afyY6vWsC6qihFwNSVaO0Xcfha+wHYOAKtS6prGEfig9wqU6vamLfNgpw5PrN1BwCYI6Q9oJXAMaoEj1m8UlSl2u8sV3Ty53w3wzaTbp8+XA35zbTbk50vXbelvPgdcf/F7UIdmb2DopFlE3ed2rAA4/L2lXIrdLxMMPpI2r82WeJKAn2cj3NUON5LtoQvTjenm8mPGUOLgfU3OD/vYNsKeBrkRj2DEED6UugG6fnCf//HUrnNuhsZjqAUOa7jxuTZLu8qTz1s/fBVc4/JslDLQLhsw49BuQd1UCw5RMtTzx7fdEAZ6a/v6blWKR3eaLFakApJIHOTvhthUVM8lUYYcyEoYKyCStB1WnR9WFHfxAlQFZzIT4mXATILcEqQkiClkJVoklv6IUIhCEsaUVyencn4WJhwGBA22/wSRj6BTA8LqXlHOLhb4B43PzyZHc6St1X02A5d3nj+On3yIj/kyiiV/47MzCu4mR+/HwVFQMsG/CKoDJnnRAaLJMsBGKH6ZTGcoCbapIWerapJwwvBBOTlj6QCpHUPvDMek5eEsTacTWSMh78XYHcnYW4jQEBD60XIoXiYh7E/ADSg7EKpJXpwj/2U6AQAJFWeXkhb5C5PHqmr+1prf4gp/VmV31/MVLsPgetF2bmud7cjOc126izey6oYwzPilgS7X0AJBQOaO2Iu2hdSNARW+knJ2YDtJOqwO5QST5aCIg7rusicDBkkr4ICu4+p4NgnjE5p6mV0kuPIP4+l8dReN4c5ROk2DeJWvDpcXbOldJck8mRzHxy/z+IMyf4j3HHkNwlEPR4lJJ9RJDjQWvGXVwM4loLJiNj2YJoiYhudZ0+0Y8eAO6DhkkQIf/LSZeQGKEvYAPHaGOsTQaVRF+5qp05FXP4ZQ3LAnzeJTD+MF9ADivn5WEmtWigBWtHEqmTaA615iBYcGAj1sigZU75SUKKHk/7hrCFKLbGDQm/LqL15trp1lDY852+SNh9zOufnsOHN9bP4bNBbb/5+9P/+VJcny/DBfI+Iub82XmbVXdTe7e3oWqiXNYAhRgBojghSEAQToH6D+GUG/6V8RMEMJFCBAoCQIIiAJEkVwunu6uqqrMrNyedvdYvFVn+8xdw+L8PC4Hnd5S+b1926EuS3Hjh0z9/ges2PHXH+7Pm2Uwk3mRt+NrXE0wRtnbH6PXhuBvX09poqhcevK7k/16Y/P6ZcaHx5Pf6inhn7HPa//jp3RzzzZXV494exZcsW9T4u3PEMrAF5me6lxr9dOE+0F/YwP4UMl0Ar00HKH5H/orEOk9ZC3J4H126KXtBlhGZsXIrOngBVwljP0Z96Uk1x1QpOQEAioeUEBnfDSaFqBUDul7LUky2myuv9uACvJLqUYGcpiXIGHdcCZZl8NYUCdKVRea1yGlCK5/lxy5hegfkpZJt6zN+ev5ss305Po+XefT2ePPvnkNJ3MltVVGGPMEzFznFRP2IoL1RjgWKXsD02qp3F5HIWLBCCfxjilkY04FiQcDlxwmhhN1Uw/Gx0m+SqdRunJMX7+mSImM9+c8As9rIziR0mEd0chTNoHftQhVngjpelqLQcbqylMRYOZ2BTg2k7K5mXt34y6yzt1kfXDgUS3+DQyDQmX1PU/sZyxhWKEAQ+dAkonCJyXwxu0OLQs6UGsGslvLHA4l/LI+VxVwh5uOrbI87CcYCsVsnIQyx9QNJsez4DvBd0jY/6Qw78QKhha1v8Y7lAIycpuX8NPlkBqojmeMh5ZeuLwAXpFh/yWaIW2FoHWqsl3VBatHWg1AUV3EnzKBg+GtgO2NlDFPyPSwtBzqI7+YxBqrBj6lw6A6mNVaxjbUwBP6m4+OXUYfVDNpXxUaNM8Goh0Dw4mI5K1IBOjk2Uj2OGva7NR/bV5hsk/pNxUAnSvPV7N0+3CNyX2UO77LgEbLtuN3BnpZdr/YLvSypMMnyzoXm5kXddFyBHuAqrStz0d6wuIYh/t28fX5PywZHHQxY9New1pgW36+ltvjYOu/UNhBClq7Orc6PgRZYfaNRTvk/Rl64f9PHcbHlPLmDz7uXI9KMDA49RJdn+ZXam352QX1R1x7TMfak6CScmBvSVNPLkBKvLGGKZvmBNn6lsPe5TV+HTnKAAmAmvMY6gHBKScQrqa/gcCY7ABYhNMFNZRyKEksBGITW55bCgSqSnVQIYitgeAGzFJAWLBUkyaonowlwyQ4gCwRZS8CMsUI58lfjbT42h2CqbDn+PJ8WdZlrz5+vzFi+crOJ2dTqc/zYDjaYGVOrXU9WkZvsUhfZ3+XR1flVjqTyDOi7OOsGDXTD0sJSknBkxxT3mKH6En4cXpo4unp78CxSbxEaY9UZzKqXz6FluXuvoxfutxTgOaBPpKgQk4iRZsyjqGhCKNSchQzVMzi2coEapxx2V5/MdTeYjkkjhGXEbB1dV8OgJd/F4aTXeQx1XqvtVxRqzjwaXqU3/qcW30wFifw5XNUJ5VGGTB9D9KF1ZYiAIRcP4X27KnRbCKg0k8WdIL8bSS1T6E0c0mOeeDsbADfAb/0xFhcAWEj+JpySgqfyRNEHFyTC8nOQRy8G+DBh74RxA7HEC2ExU0hMsr9vuKHBsDCHBaHAZmHCyANQ6rOwxOmSjV6esqPKNKymrDCYXI3zRY40/saWQTxbglgvGPNoMewdhnY4m0HMmhfGrp58YBwxstRht/w4CVENJZbkBtUFn2iMuPkSSGNsFaEOrMKwhsXP45AC5BdbjWufvNTxtsm1Huzg0277fJRQ+9sYfiN0j3qG2k3sPNKK7uqN6h9+Fu8q5XSHOPeHfbPSxesXfZCq/ajeB4Hg6TA5UMjLSN6m90M57nG5G/40J9udm7w52604wPfnkJ9Z/6QVZcuc1B5ciqiMXb3oBrVwDWhby6XKRR8WL3Bjs6uzjbW/Ih8XYSQOAH9dTe2u6O0t5qHhI/JAnYCLKe39/9pJIVIMZvG/OphkyFyYW7Qmbr8agYXALMmQ8VxBUEwckKrk44z4sfA7lFF3hEQTAyiEDTorqXVx9RVyl9qSw35bE8tEh/oC7my40IGWU7oTirPDPNIwP+4+qf+fgSOJieZPXZF9/9Ovr/fFcVkzQpP318yVbgH//4V9PH+P1JymCGh/gguJJNRlTFE/6Ojp6En0c/xjg7jqbY+muTsLaBsmMVfDbBCiUkPsyiySyKyyA/wbIliEjF3Tz5mOsXOgT72ZqIJKLpZ8Vp0lv9rcYRgHfFKh7RuZ9JF215lK6sbV7uJBO+2mvrto0e/hZFUVEtfk3DJVyKq3RdtSo2GsZeV9qRV2+0bSSXjsFyGIhIdlvQW9bRwHDlL9mgKwJump3JebZoC8GzW4Nu1FaRWD5zMN4XjABUA+e1IMB+6mzFgMA8C/sc7tAxBNMDFg5Uvbbaar1AVYKttStACzFa0mHiX/k0W3+EzyjNzJe45pQVG13GmoDZCBHz6SJjg8FliKNYyjJOxLG1zYF/u4EucaYlQBc+YU32Qhrn4plkOFYlWhVwBVnxkMGPloSwWWJPiLu1RQDKmUBU0F2uxvZO8cQ8XB+sBLqOMw5dX7mH4oNl+YGxD0cCt3y4XXE+NQzXQzEJzHv6JnF35zKts26KYrMEabu1E5fN//TIQNsno0kTYqxGP+yVaNcrBuYg/ZwfQRhgxI+HtbevBY7hf5Sm64t4L9EhmVMIGm4gjKrRq2WoXUPxXtHbBfVLa7+1h5M5tI2H1rBHzoeSOij/jdvlRhCf1/SaGyLgOmFwYA0TlYwcYI6wbzgPo3ldPLW5fPFts5tknGABr+ElsThDEJCxpmH1ZGiGVR5CQVK6E9IC6TGxamgxdl6AKE49bnmAzOSSSgBggmSUf4qd/mIVnU5mZbDACf3RZMahxKvVk7cXcfTVMsfQPF+dPTo9PT06mT7+EXbgwO5oaTO8M+PoGGbq6vNkUk0+oXbzzSJkB7fUYH7t49+DJiuOiNL+0WdAf5Y7hA6DpQBmBMRnE8ETA4QKU1iPPl5ihAWBkNKR7BJNMa97B/gU4r7N4AJUTNUum5WjFBEur0h1RFR016VMdnWBpgbTA9rEPd/rcmRytahSK24f+kVAL/ukoWHtUgfSroZTWoAEXIMp69ZA6DU0AWam6GXsYYhnX2xVYvwjlUsAnqUD6qmSryDPllyIyXsTxCJsvKRUGTesBYCv6SesaHAzxZKUbuVmh8/kuxLVsfyM/iorjgDIMCiSpQ3DVoeDXbJNmQPEOIEYCy92hAPB0VfUffRaelZP3qJD0DpOlkDq9q5RK4ghF0xJIPzD05Guz20BQXwzbq25eu3X2OYah1rxEO6Ht0UQ4JQWObDrAxdVT1huQ4I6rFroH2s3OH+joQN1u6xSq2zIg/s6rytx7efAbP3Qsz8Uf209d55B2rIEK8Lvi6t971jXZa7H2sY33Wi3jA0ux79Lv1kr9vHg6A5/9svu56Gff5h2L2VgpPXyfc8jxshw6Ok20TBuNkfVtQKzkWZ7A3j19C//neFG6DZ9F9sveVjM3VA5rM4PKLeEigi2ZfsBceiz8gPvLF8UP9Sw/17YlIEbxm6IaDpTaEZIjRJMt/Kbxi2zqjOMvQVfBOvJo0lSuQcNOWhJEM3hJH7DDSDrl1CYiTz6aXfPiUpBQaWhg2VOswIg4KkswDVKmQ2JckpbKASu5f6RTbggOEHnVVGms2K1uJgn6TyP0jT4evVd8PosSLNf5X+SRlOM8jmzV3biqBUoI7AM2APsy4wDICqUWRCjlhgjwmSG7MWHYB1QDfMUxyftEe4jj5iT6Y/hUYIUFm371VcDvMuE5+IkAv/iHipdjG6ddBRQaItUl7MLrAt3UQpYaePSz+BobmTsMlusGk9h2mi39in++K8wBF0Un5bVuo8kpSvFChoNlUceFCbOdR9Sl4SQmHQuIXobE0LzisU1JxP9WkNQNVADtss2X7KXFRfaGrBbk+9sKSadNQQtG2hOn7GB+Q4rAawkqLKCAYiLJ1YMzL1PJL2ULRmFdvDqJK+S84MpVBbPivxxVX2nHSDSGFSpNdZxT2cqRj1EEnQ1sKkaCkRoHzGjRkNYlZPMaDB9hrbpRGo0IviHt1UYryQEFdE+CT0FkhhUoKmQ6msuiWL35Vjz8+7O9/HHqo2utR9yW1xPtP211Y0fMuMPvH2oEmgH0/X8tY+HK6GhuFMBcGN0D7l1eWVyc/9uJ8DudYABUlujn1dbd/nhLpLA3eqjvs49Rg/zOemHD6WgH532OrSsK7dfGi3tsd9DMvfLj6nRb4sf9uncJuxoOgqD/HiyPbSuDZo2u2c/4w0Z+3U3dHIo3Tb/GDm3ee/ye6NdNyG8+V5oXyaipCe3vRcgEohjGh7fNRxuOrngLogXdbSo6yOddoTrT6FkAA2wGGA0lbtGTQwD8mS9A9gBHllAYFqgRzO/mhE31EcGTcBiL47JjS0RkAuoJIKGJul9viHAt+ZvS7ZX1rOiWjBBDHjHBj8NT/LlPDw+vrq8iOPjPMaPTPnttzmqwTTGC5D2KgiXqRptBoAf0CZWSnLRDyATZSw6QJqqMqqZ5dWXzfHiQNK4VkerpBs+0EIsZoNCYeiS6mCuzfSrd9hg2s6Xi3Vd0FBdG5cJmMzQbUajy2IErdkOJIpgc7mkHqUuWdhUddnlZNym9et3nHfpjaA3q4Ax2a2qga4brOdclzS1GHeOQ1exo2BScVWk35K1zj/tcpJDknXSKz8zcVtfk1+Im1EkQG55JHtGFCsFUg90Y3b84qeqFp/giZUOA4TjSRbTf1z9l2EeRzM0ziJ7LiUhfVtVV5BSn1U4Cb0KkxlORrPovAoXAvgMJozA1AUUEmv2WrAj7TBQ4ipP1Wo2D1cTBooGDcNBGoAZfbG+obEDhVxDSd5sl2HMsQgnEko1Kzh8AGZRXbQzWLuZVYUuPp3cOukRcJEug+VyH1slvJTvXZBebq/7+N1RRyP4noTbOvU99h3r+stRa/tuiPKYem/Cg1+mDff53y/JQ/O39dh377d1I/UWN32ubkHs3ovu5NYGxXqouXXUvesAzW9HH4HbsN1sRRelxccxlxuj65xw1tFYxz6EHiTwg5DA+sH8QTR3dyN9Iej94EAngMWwiAGgNVLBnuI4rI6ZrlVGkLIyYZYN6AfBZ5rc1c4AXkf6VZD+IPRGUJDRUD0l0BYcKwRASyCzaR3k2vJriSqnixLGhQjyD0MOjnRaFtiQBHkMnCrlEwYbc9lZ52FRxMviqsBrZ/SmSl7n1VWEk/kVigLeV1i10EkABuzFlRYRrBab4DVbJGt3A2ylz2BqYizAHZWbhgBPZOVObbHP5lv8ipKLdNwrh2uEFeuCBDYvVUOFytxcXdBxoFir0X17d0rZuBxnLqphYyN968ZV1NXiAk3tYt+gTMtN970GOIryqxT5NttGVUQ6cejbQLZLVqQE7PrZptO5NTINV6RIIVMkH+oGzbhjyeUExh4CI8EcPC5/RD2YSoHUGKvkmAj/pLjv5wwvFgaqjEPDcN7EoJNjoeBxmB+F9RzNkyah8qm96kTVJUyPxijO1P9awMLMCTMkPJhKWeReufiQmIwJa7kYlZssLV8wNDn+gJMKeC6MCplpiikQKqf/7jJqCrpAd9skb3y5xK7oRtrDzbuXAD1Bl7j+eOiVG8lf8utkeCMKH3YhN0RuyyMvGfeeXBPqhMZbaezM/cYY3bhxdPuax7q+4VDHyXCWA1J8Xcq96N0Ld4iEn+qXHcq/P36Iwn4d2tEcKru/xsFUxMplvTRGDn06Y3jul3Ixflv88FB+V5fTbv0eGco/huaOskKW/MbuSNkX1cs/hkNH8DYy3MfSrrSb9fIuStfHNe165eV0j7FkZSOPgQdaYWvlG60DuFmG6Io9AEzzY88gcC8gDQQCQmkPgMprgp9vTY4K1iJnfUJSf4JXoKiokA2PLn3iShIvQNprSxY2lbrMxoGQFnBPJEitVmWs8wJ0eGup87vQBpjIj8H55arCTH9Wlnm+fHJx/ijPMQh5XNZ43wcRXoIc6/IESs7mG4ICbQbvasYhDBafGQi0upXgDNk12W98K4txpDuu9avYIJ+LI40zASyHgoq0D0t1N01xi3FpkpJiTVZtGXFGnH02pJwQraBLWVfcRm58dzW5aiTEjfQm2uK6sKurLep1nBMDDPUu92R1CZDqwm1eN9LaO/smj3JqBDSCFYjWxWfyHam1eoRvFEhnc48lF/AZkaB84kuHlaJEGwB04FqOMyhMuThxAHdVZZnheJRNGGn8pioyloqm8SxLV2VxFKbzNPqkKC85oKCcrWp8BEEcPK8VACbmnXEOaN+Gp7ihdfxnlLNoxC5kFh+cPRh8OonSBCcBYmBPP9LaEM8egEoT/9gilTl8uh3zendJs3DyRgJrCVtboTHoJ8RJpynp9aXFtxTFsrugjCj91ek2Ze93I4G9eXqJ+9+Qfqof7pHZEdH/jRiiMBTfJ9qXlcsznoLLLwkjY3rEdY2LHf4cqne4xO4UVy9pGmrt2Nud1YvtS9JL3BE8IL/HQ1+GayntqERRbuBLiqMlOUDpHqP77bpZZXvn/ulOCWMEAm9f/d3AG7sCcDOuH0q9Lwk0Q+J9Vf9Q7/dXAut3h/2AuZevi3SfvLmBU9hXCA4TJdiC1UU5raupGVcrln/gZv0OMX+vRQDOW5X9j5A9shMlspjOpp8rgR+iICQUpxz6FcOyApqyzKeY0i26DWCh4SIx2c8x85DFNmoJjiI54JdZXwJxGeHwJ0XnwB4ki745X8ar4qdleMJZAdiOYIbBmbRyFYOpiDGkpQtiYMFmehVYQyqnk8CWMhhYc2jcWiPW1IDNy6JMhITayws2UV2M1eb/4LUEYcdJzpWw6O4nlIBRUOm2QFuZ/22MbObYKODSKQEHDZ2GslGhjiYHElCoheZN3lYOIqC8lO39IBmhhoqF9WGErUhTgQirRfpzqQq4izhXPbcaL7DK+pJ1GCtO6H9BlePZU+ZdicxuwNpqTT5nKKJDMsBybP2jZLpcVb9/ffWHs+/y1bRIlvP5m7y+CnALO330di6sr2FOUbq6UfesReLCBo3qp0LWIVik0giXGIxjDWxbiSDGJKkUUaomKCFlueTkiCjO0AdEWhoLOoypx644VJqACroLTiSh93WtGXlfHDzUO0YCDJHvRVc1jbDmKPx+R/8Yyd9xHteRY594RLSR1YmPKFYABvUGV6KR9C3Y30tng61bVNIvakCiH31wzO11uAN0Yo+77ufbi7s+uF7PaSW7lsP2KNhH7WY876M4nPaO6vLmG4Z5ucuUQ9s11ONj4te9fHgL+iO8H7OmivmMWau3WGadolA7xuBHUB1DCy7DedEK1zs1TjMVBaYhr1nKl0/q4lFdsziAhb18rRAQyhaGpMuErYhSKZlByxzbbg3za/oft/E2998CsfWrziBjmJyZw8fnZT0B8DH1T5mUPZ2c9wVjUT4PcuZ+UQJWi+dvL05fv4w/ffws5HTeZBLF87rEsyc7QTn+S7YeVAIv0kbgx0kJbmw5w/HIp/ErcKsU/xJs5bIPP34j7EqpFsvpE6Fuxct7DKnlJ2b7xIIDh4idgRGD4jPFK5UWs55gFCQWKvDpQMU6wXHC+59EszFtilhmx6WxbG1umJTwoRaaB4m6fE5rtaxiAmk1EMWJeVendb7j3MoaYUFni7Monz3FtkWbxIaQkdO4ctF8Qcp9ugCudPCR34S18YIqJt+p1/LP2WjOkcPg8dffvr3A/ZPOIOOMMQQVzd+sMO/niAgweYbP1lWWTtnpW/39N8v/07///349x33tURXlWZlwvlhcM4bPsf4J02MZBHF0sSps/hw/0g10+hhaR8ZGYbmfxQ2Rmiyt2HA6Rkc8Atph7mSlNmnJghUttsewBwB9uCqKVVGUWqqiMWooopT2aVf73bV38HdctHddA/Eat7uSpMwwHHYlQV0K8ua17x3S5tz/hvRT/XBb+rDvIQpD8eOpH0phSIb7axwjz/0U1j070In7i99ral+G+6XU2MTzS+Que6XZm66N2fzWE8oo9Rrej9kssb5bv+fH7fHwe6rfrjXda0PiuXsXeqyroLvdiryWYpuhe3vs3gTcZnsH37Rgzcw7qO97XwXS7MZGJ9kHKX/v+/1dNrAbV/1KNfwMNTror4dbr2WAC+cAlBzsqlsgo+wfBOXBjoCeGRsvBVTlrtF2Jem1Z+WEm4SaNKopI53AQUAHx4/sGGBsMNr5byXa+Bc1sqtuPrIwm5vdv4z4gWVBnLMtYL5K65NFUWfFSpuVgzcXWXS1+iqKPuekWYxEYjb8TvAOCUFYFQAyBOaeJtdMY83VaG8yq9t9OLbXIlIjdLniLtx+bscZhYasl2bRahKNUwMBmfoAjqLK2K+bWt/oJ8aaMquUycG+HAdNxa4e3VAQGSqf6EDbOsC+Gz4aEmRy+alHmLWJttooxb02TKt7LKNxp2raqtpvpTpSRk8fonXdBT1HAdZUxOUnKN6V5PrfjQfLIyM0kDbGP0z4Y9pTXL45t0OBGQMX7ApZzs8jFE88BpVVnOAbtCwvGKEc4faiyh7jIpStvs6TVaV1KtRUnUGgkwSkxmodANevEoYgMpfWFlBuCdmOdqrFXohzjBMKMI+vAawjBQTqudQ/ehAQFx3AFnk83mKRBI2cbQDUYjZLqom8znLOarEWK0Sg+ZIE2lsX6SX5EV64I+PFPQQfJPDBS2BrqLun4Ps8mt2brnnave4Zivey9F8KjoyK7tkE3K/Lpymiru6NWP9mzM5lSOwk5H5mmne9T9QLj8nja2Ne0cFgP/+tdLjBeq5P2N/2ofJrbp1kyed66ZreFD33A9afyxkj5yF+xsTfN/0xPFyTx/2092a5ril1YPJQjx8af2C1OzxXrEdRn9aeh94bY3hbF2gWDDJPiSDFRYTbfoyhFW+SFFDlH+CmsH0C2EjgLdFMHRgSTatlVG2To8QAreQK3QCTs/jHe3oZxG9EpnhOVQ51qghrCLLPJv050RhWo4LgxREXjxj+X4SrxxwMxmTr1bk2fAq/AQCfZav0m9+kX8bJJJ1X2P8c1ckRJZ6m6cnpj19FE/QT9AShNm1mkKVH1zdrjtsnzhcdJZTTAVI/YVfmzXTdWYVCiLQMXzWfyXeqzhAgATw5DctT2JdZCTHlY3izKWNhcdovGyZ9agy3hAi274f8EzUE7/KQkr8dukZg08Tu8qjHrZ3E0kzRDMQDDFA7Z2UdwYwspmr83Uw5OSvkHGUVoK9VI1Li28lKtBo2SCHNRkLz5mm6T/EbV8eGFRE1LiPcZrMquGm6Q5oESqZWRZ7jOT8Ir2SFL87gi/29Zb4kLcMsrVossznr4NKfdPxWMWHvL4A+jk/S6HKSroLFMSUwBkMxYHklThHmitGMJ6FYJmrsFGD0aJxLLFqwkl8giRQenLeoelazeoDqQH5pCawlcQIxRYTzTW1QmOKcGhFCvD5VE8unHJrBDzT6AT3oxO5E5rW9EYV9uTBsEHCCEk9cTaY24CLXnxuCXEdvh1xPbcfuuu//hu7KNSJOI9Yk06627XsvbeZBzGq2jS6jco8f9A9XM/QG6hmTZ6BoE72/7fvLutQ765cxld1znvjlbSvY318+9UMlf2h+vy4/DIfec+w/pv4Tvs6yH2/75VWLeyvsUwB8XnaEGwKbL+LNfD6fmynd3TZbXcKYwAj6Y8h8P/OsB4Z19ghBtz36/ZTHQ6vuQAL7hkiL8NxmRzCNGTzwfgD2UDUee6oJhtCyzDd4SBQ32LHUAXYUIBzwPwgbgEV2oJErZpiZnJpa5rKPduJUKwaaTCXZiLkcfBrSUnYVbPbvcuCXoB+J4eqSI14LjveFSbmNp9IEU41giTLw7Xf/7jdFfnKEN8ZZelxHs0dx8Ghy/OhXz6YnM3yJyo+MTdDCptVnjYOO2uhfLrGJ4WY73VKIbPO59PZuTYkaFUkyKgziowDyY/P0qirwDqntDFgowZJgp5C08jcwXaJv6jWpGhnxokj+EK4pVC4COTjJar4ZZCrkSS5Rs9zK69pJEtPifDINjoZGshSTKEylcyW4yuRg3rjCkp4xsGaAbLuloAQuY8gFe5+qYy0rF3ZxTfvWpZFOw66Y1a4PeAJ2E6Dn8rzOM7b9coxDxc5v+HZMcfgDznqqqI7TSVFmRZ5ly0fL5WMaD3a3rSdsFEGPZP+ASGr6HsdRajAciHUTF5w5JVRRGszaxJuD+TmFAvmy/mSZkZ1KuHIEeCBET06HkKP00VrmbUtTehE7ixjqf2ua1Lz2ckGNPU+39NJd20xwTihOZm3x7/W3CeWdtNCJ9p1U9VDJWgIb43wd/X0KeSPLPbnd8+sCTgRNrv3y6Eo28mkejz0rAH4Ve4S6TXiddUNLG0mtLa132nXXmDmJQ7Wxfv73pTfr19d+JK4Tw450CU+/4Uo6gM7AfMmYvtjBxOiou6V/L/3lSeZe6I+WlZ9xiJOheL/sYHj/c9q8NYZKt0MWoMJsPUIDyAggaixqDwAT9lNQI9PtwvvC9Lg8fMT/qF6EOcY2spzWiNUctIOeEFGlBuo0UQr01LAGWCkDG4jzgBN2pVE43pRoxj+CVSqbnOHApyqeiIVoJo7KI04Chpk0jpjVJZcAPaAuPM4WeXbx42z6JMnPUA84DaxYghi/rN9OfvJnf3bymOlYziyjCl6bxoU9XZR2ako7n21eiVoZOYHqebQibbT7bhO7WGNfd0rhRqVgvCmNBsMWgPRbWA6LZ1Wcx8GxTqrCySrnRgWcW5xV8ly0CvKfYHkiSenh4j/iQlsAjSJDZu6ZFM/r+Byj9zr/kVSMiplyTUY3WoSETCvIqfwVfmwoJbt56NBadCbsVNi0TXeVZfQ1e2ij4EcSc4T3JMzWf8Tcu87xZVJcvWmt6Npo87KQUYQ0Fv9yTfZjCBPJZfkt1PtwGVw+R5YsqjqsceVEUWTBCV+omGD+x1V5VQZv2Pkh5YeDgtEG6qQIF7aGQtOuqmIWpPMyXc2Tb4riU7C7FB6Gjzapl9jk29IPYwDh5m5oEtaYVZXqLI0qtZvT56j8FKlSEd5ocfRpG4I5lQyCcMbwls4mFiXqpc6X4wRrCJQTHW8spQXtg8UGPTVa8FFmrkYm3KhSo2DxfFhce+O+GwFZMVd+M/1O7/q/oTckT2PbawxNP08fG0jayKaTREv59t/9uvo0+/WO52d8zn69foyTz61+HXxy7zW8vQfAMTM8tG8j//fVUPVUO1w9L0Bt1JqtJmZoFxBr4LwToLAtHpVrFACC26lr+uvQmDzr3NeG7pjctfX9MDI0fdmMirbND7JuJfHwvU8CbtgwWrrx40ZOF7+vsKUJo+DK0GwwBIiIFAAC+lQT/aSLNiCJL6Fv7WTVIoChUiEZ/oNzZFZBDt0IcWrenS8hLKZjRVCYTGeKCcsyidu8vkiyS2hWxUQOlAWGAo8CCbHDwN8PYB/375ls/HVmMHjNqRNYwoTz7NusPkkK7EOKhFWDZZoFb48ePcILPDszIzQUCLlLfEhMItDgWUtQlYpuPixoN025XV+WaZ3Q3PJl5FvcwqkEyM7AZBhOAJFlnsUTIGQKSGUxhPxxmMTAXQmYjGg1IHUnBbFgapWoIiDmxvlZMACKNOgZJvNREiQM498JHxGiN6gbZcRCEWupAK1hVk2iY18/TdhSbXoIWgFJMwytjFU0FVWrdrQX+YmgeBvRfith56V4K7QrtUl0LGtsGKrmm4o1AhhMWAHh9ImWKpUs8ujPQc8x4itlsU8mIlgLysMSpaWaJAmCzounRf4C5O0GHUY7jFYpoFKORNf4tYl7o6vqJHbdSM3kXy0tUk6nmMJn37nqlh9bnUChbQUMXIaukxB04VRegPBjyiBFl5N2IaJIj8l/PrWkZsLckKfJRs1uryaVL7HycD1I4AchAT2S37sR757gjee9e6i7WGK68K6ubtO3M4lSowDsKradnTxEtS/uHam7iHRxu/IbuS7HHQTcfNIYjXx8Zf68wvhSfk6nc7uYMdQO1dF9+qy6uO7W75DJXL8c93P59Y5p16Fc+HLww/vp3Acnfo33Td+vy4WH2j7EyVB8n/IO+nop2NWOH90c8KBqCp9pSzku5FWByQrIGxcoEFlF7GtUmPMBLoBKuNsns3bxamUA70BkAo8KY9l7HLTEO93UCXgBWvEf+wvwPsckAYg4w4lTwHSEsGwjlMOtGiiLYFPTkuIZZChqPw6lwTdt6oxDTmnFpGeFVTeOH8U1kdoIelpGsyLi/KflpE6Z1a6L42wVymiIc8DYS6pJcBiY6BQCbS21SXHjuFFs1Nit16RgYpjipb61VFaou8RxK2QXth8zZnRoFzb6OjlBZ05pRrmaBOUTkGLOQkrw59Hx12Xxyzr9+yD/iyD9dbX843D6ZbD8k3ry98Hy5+H0d+Xql/XkN0H+q3ryD1H2R4rP/rie/iZY/tMg+fd19h8Qrpe/qCe/DfNf1OnvguznQfIPYUHM78L8V9Xkt8RUCeGfK0/2yyD+fbD44yr9fVT8qj76fbb8eZT+Q3n1q3r6u7h6Eulwt7CIrmSuhO9UNnfQE/zpLURj1MfWl1vtJZIU1/ZOLF1A8Vawi/EDlmoKCSED2RoNRDAgbHXH6TYgbCmAnBVQp68iFNSguLrK6gUOfjDKZ8ECHeE0id9W1ckqv6qCJ8vkmzx8U9efiRzaAfoqKhc0GRP6lCaqPlHbpHppe7mGoDil3pjBjJ/ZQjtbAvmSwv8ofoTUlTKDUxGZEcEnyykUYF8FHklZkGDuX+2tOT2AIzL0NOHeiAA0iWevi3QAvDDBlYnMl4Vq3hntZZK8vNsm+3aUl2Po/eNlGQzepuwg0Rsl7BlB0Ovz6d4f+0v1GenT6edxMeMp93PejDdX76G/DkP8u/g+J+MlMD5nnwdvRrxNbDTy9va6775Uh0q4Nro1hyHp3aYtQ89sV5feKPuu4XR71nfICmo88Cq3RwHYV+XdpO156dxNBT88Ko1Ih4fED08kDy0+RAJu5Lhh1D2fXeB6SsAaXq2y8xHg4xIQA1ubFxRNt9tFPLmE4IGMMuMRuhd+Al2BzgW0hHasPBDJgJUyAJGAcSKMQQdfSZykQcZxTq5SowElDC9McxAOFBnNhkNb5PDhgh0HewGkJLAaoKnYhOy8CvEQVFZRvIiTVYKPyGjKxgDMMaJwSXGdGRCVRZHH4cTgrHC/yDmBibRduuVPjWnvDSdyL8XGeHAp+twq3CUYBcsA864NmjWWsFAF0vk8/t/9X/4P37x9/PwnV8X856v6v62Xf1RN/iG/+ml49A8hasDR7+rFz6PZP4TZHwXT3xSrXwaz30RL4D5Kwp9Us78NF39aT/6uWv1xMPt1uEQ9+E21+kUw+W2c/3E0+U25+EUwRWGQ2hCsfhZMofYzFABUhSj9Ish+UUW/jur/oAh/nUR/cvTpy6svJ//hP3r8n/5H/4r5blhXq2rOfEZiYFnUM9cug8akIIam4QrZ5dqrcruuLaF1WVTKyrgAEiYCQxlbqVCfAa8B7kBsehM4nuT4ftI6iZ0Fwe5lZuCzVcykfBBdLd/OZuGUuf88zPG+k8TLy9M4e8K8v5Y+tGakM3od54xhawf1MdqE5EmiasYUN+KP2gH5/GMyH/OiiNUA6SgaAHSjNciWaGARJUn4XrsptFFBu9tRVgI2xmhvDKTZP6CHoRk+1KBmdkJoAm0c380lFtuw/+3iewT8LA/hBwl8+BLYGt0f74i2l4p7k92x1PfIpHlhjD8JuGNtS+5dfC/g3jS96DbiHpo9fu7/Vhpb24Ltb5AOl/0A+EmdJudH7gnfMr/65x5k22f4UD77swV9mn6MT98Puzx30INef90BNZ91C/dp+hLww72iGxH9tm8kj77p8+OKbtPnuXUvDsGOHdTdWRNN2VdbGeSxRBDG7E4Aqw0Fofw6WrIHQICpfES05uiF0XhiUqE28Aq2K2XBUb3cANMjWQGB5YW+yCmnnElzGIDZmVC4jNMqwsNKyVlLUAMeY3oEYTOrAP9YLcLrtjaolQBMuYX5qUFAEagFu7Lq5obEBASGu5hZFV3iCYbJ4bxKcHCTJFMs2+syjTX3v9KJZlq10HqFvQ1piXvZOXH5QmvCyoY1uZ8iwdm9k7+kSi5i2s/iE0OUGEfJ+5CaQr11lqRHV/Wrf/t//fK/+eq/SuIfVcVfI9C6/oqCYfCVtpwGX2pw1b+loXX9e3isg99LDbM8xAjIsrFBk9BfqL+Cr1Vp/ZIVhrqmQ9Gm3mgDQP2WZob1d4DqMMC4H3meU0kV/LfallD/Ozw7xfFfB/GyvAz/Z+cv/qd/+ZM0+XtO2WK/Rzp5XuSXVcqku54yex+pwc3VyUFtde11KYTdf2TbXcSA3mFAMuxiLUAcQq3wZEWHhqSKsv7g1vqW9SK9kFk7ovOYZS/k8LXMWJtgxj/E6yfgumLMJdXjMo8u82RxVZwt8jK5+urNazob8WCxw1DEEF9jmNEiGzLTSl09EosuiVnMK5Vc7I6QPJnRr47ZbxAlOY8E459dL9JPpeKaoqvTx9AfOPOLdPrOjSsIsSCADiDdFOXZGmXPY/TGGr7xQa3m7Qot9rXxoFRF6hKX6zu7sY/NeDG+TtsINePzhSIJt3QH8/uFt98tu+ba/fzvK9znU8Py8KtP53Aa15fwedOjboPu+mIH5tAbiTmWl+ti/V8QnxOXz8+/LrkrNJTTr2Vf62j4QB/5FHbVfFica+MQt47W/lSXh3emSPV5thfDHp4GGjoQ7ROiLhseflwTbkrzZukztCP7TaLugLAjMdSGmzD1/S+jnr0D0X//BfXQwt0S6B66w5675o3SvE8AcEBWgKPM0YmLOLIX/CpsRK2kEhAyM7MeNuVy3lGMWTbYXBPxRbFc5kG5IjNjmV8B/qVJmmV5gdW2osBM+igKiLBqEOPjEWUBBC/LIC6mU5WLtqAQgMasQrFC9doPUMj0iL2V9ko2qMiEPxg/SYG8izLDU4w2vYZTlgAy/Nuwj1RuTPEkRGH0BXGuCvhqxdR+q/odl5KV3U8SmfYiobslYFkxF9EJCYQTWZXXGaZIweJRtZpP4+cFu7vAh6B5/FgyeSz4SPs0v0wUf5q0thbzCduKV4oo0y+mqskoBpGjsNFGk4xm7kPpaZhsAXmFTjmkGSkiQrYNUJHMVzRvjTTZuZqU0SKYTK7CP5TpHzB8j6MJupSOTg6xvIcb1AlxsW5c22D7NtVALHF1mQj4l+Jdji7WxoXim6IEFMWfvqlPlvp0fBinEetOKJC2E0DT/4wQcgqD0zpGE66LWAcIo+nVsnr59tvvXl+9LfI3eXgRHRXJDNOgRoXRsWEqYgOA0oRhh1s+GQlizUgqWmIzeaO0crLvxRWHjcnNZxwjVXWCcjO5T+/mGJJREGEiWGzM2NqhRKleDFEpfhBEmNKjrAL71M3m1Qio+dpM276z6rcj1YTdCb2cZHP1jC/So/EQ8cFLYORoeF/taIe62PzAWW1FpDdTy3YbN+rbte/gojvF4qjwqdSEcyXd62gMH2t66xNnx5QjT68FThB6S5I41LKuwobdUZWN0f/GaGyjKvMyyRO5zZF4cTcJjuHfp9uXYdOjhwjNJ7gdtt+e/soGqEo1GN7aLrLrfrCXd2UmzpeDH3bZ76AHPc7vgFqvFX2ao8Z8j86hEX1Z7ZeY3krkcM+g/8QNVDzkbaDJTiMhyP5FSGHEjHG/YCje03UiEl6A5DgSZEhuxhXIaVrk0eJS+4BB3Phg5PxdGUxgMZ2kJydH4FnBdIiwt3Q2efH5c2wyiqyMsTEXgDvOF8cls81X382vLmuOGwNYWYWkCr1Si/CftSu+4K4qn2CorogoZZIVaw+5y9FELLiVTa2TIsPjv2w4knjGLoAwO4nT4yQ5DutZFZ6F0aSqVpi4GP8wtfWUuVv/sxWjGw+lzaS2cXoxNisqTv7u0wkHhAjkZh8FuH8Gf9hMpfFJHXwXJVdpirefV2H1UwOHjGSsXeCIbQq0LcGjPFDSVCzOn8pAlsYQPGPvgrelTMfTYn/FEWycZQvCVTKePSU7tjVoe4PqRqMQ4rWVExjV3LdwrW1FwC4FUFpV52n0k7w6W81fzC8+PzoCzq6S4GmenUVYZ+miIi6Y43Kg2YLug3GhFlNj13DrKS9Lk+RGdZNNeUzyfDNUMI3i3ct4oONRTpAGrIrm4nzBdm7OdchXLBadZas6X+SRvMdmbLdVZvwCsa0Ca/sgWpXzl1fl18viTV5fBjWnxOUopBUaAplYOUJ0CFZNkBQkM6qw/SdudLHZl1FyepSmCRcDKKofT9IkSleJTNVibUQ2ZaiiR7AK4qy5LCvY1oLD1GqJByWO/mUlSg+I1qSeBdUzOg7VBaUP3dTkoh5sxYXE7AlyskpemwRptr47aW4EXc7m08uyET9w40av/25xBPg0zgaKedEoOVz9t6KX5V6CPs8bFRg/O37XNjLd/Gaw3puT3FHS/absSLh1VL+n+jG3ruQaAntap+fbRl5/BL57Ph0ne7ilnUNIaWicDMV7IpMM2teBF90F+6IRH807AbzKAg9/5Bp57aQ3suxGNuu4jZjBmzurc7CG72HCuxLaAf34PZTy96dJ6/GyDt2odQwIg3pyXIg1jk1y4ltG85cTvADx6gHxAcwhLpAvcI+lOLgfR5PgMex8kskUwxEmmwvCs9lUUA5kLkBHqfpodoQDygJTDhAvpvx1MDk5xWv7anURhksmXAu0h+aXQdVYKVCsgJRaRJqm0p3RhWa4mQ/m7Fd2+waYgAAGk+XsKJ8AXnO5yeEg2CjI0Ciq6rIOMA0CocEdoFYT7W1FnaiQntWx8anGcrk0AnbfybmLtkz6IN3kBoDUnlGnAYE80zqGJ9DiMX7sAxSJ4pN4JgspWsdkPzuYZUEumxNgo1QcpCZ0zPqAfE6CNMmKHLWwgUUVOZRI72j/qpYWJBvYcXbopIBhoaI5dbPBUpNJBoOqp4Q+yaGjbRcyc4+/LJPfoEexehMEi8l0liE/EZE21rTeWt61U4FGDE4Izc1Ght03YpMLyvBnYT5YaqDFMb1rBl1plRW//uvfXr09B+dj8oMdzrNnnybxlD2/KVAeJRK3nBW4P9OJEKiOdTDPXnMw9YoFginbdqfSD0JUKbFpmo+qQkcCyqpeaS8SgtLRzti3m8aPnjyeTlOpnuhY4WNpqTwHOJ9KtXKCyom8uFUHzOLFfDGfX6J0luwQhpjOHGZKLrajgHEHtCCJvlE7tTFGHpasLj4deBU/m5di+rGbeR7uHiTwkUtAbxL33PXfKR950/aw79p6wOO9KRwT2NbrgZeT3mAjaa7pXTML2G/EZg3cOVr7dSaRcVyva+6T3o5x+t8I/Wm74C3vr9E73Svbm3Uequ4aOr1ifRmijypyr9DG6KxNVUM8u3hNhQ1qtz1mN+b1+6l+jC8HP+zyuPmkIa3ap/OhhV1/jZf/+JyupX1ZNRKz8dAfLRsxe8fMXknaE84HqEmwXhAISxK5ysGAgSn/FXOsYGhhe4EpkJNbB2BPLi8gwVCQEVC1wPKZiVe5kdeEM6kAfkM8Qq9AMs2IcgEvwVS4TQ9fUgh/PtilkEQDrGpBT4farKzqqovHetk5yMhe3mAWlpdA/Umaon9gZHM8nT05fT6ZPokxa4kLZnJRNRzujThwV8fBskABR3qWbaZZbd2QynYEqUTZ5d5IBFWiK9Va2TbrACSJhIAt8pGcFjpATbWB62d5naVxns4Ws9OLKH0TBsdgUMFUKQqgS4rI37+m+WWlwyw9BJ32RDbuQL9M/LPBgocXPzOaTgZi4g6VdQYta2iVhjxUjMUKSwOC+8YJxZWZHav0gmWI6nzGmgz7apd0Wf7jqPpFMvmiKIos/Ptk8ihafZ5XyzQ6pl4VhIwa515NhOzqxNDct7Lq5LMtT78chU1W+tQ6A19uHYTXUZyE5TzP51flalGr72hEWWeLk5NPL/Krunqt9RSZCIGr+QsXyzcLrHHiNJmy8iGyUUS2FRqCKOv8B75gnr6xgWogXq9ZfkDVMsWifxpGJ04qXBG+ITO8FFWWhDMpYvkjlM6yfsOwhhrKErWjUFBcyrLWG1hXoZtYmsIKaxZqnStKEtapNPbtt5ou6GToJGBNb9fkobV5ORH3ohsJ9+M3S2/d8W7pl3Axrp6t/P7tzd7Vt/8dH3ofalhurjP73N4+7Oq1sXHA7+Pt6x2icKgkxbkG5hC9W8cPIKK13HbV7rjSU0fqtWPu1jyOJHAbKQ2NTz9+uO/2ioC+66cTY31qGL55b45pZp/SmFK78xxGy3F8WJnd9f4QYptOfxDaD6Gz77yNO18ZI2sBmvDCwXYZ0xA8bLKn1vCn4Za6njkgKwRlY1OzpIBa6QvMaOucKXvfM5NNFqAQSIgk/UgLosoqArgGZpJ1N4iMD/CTIX5MTUhk2pX/5LTJWWUxsN/8SrgwqItYGSHhYgVwDcdpEE/A/gUbLStmxU8ehcePAGrYhVerAnDLLmHmYussvzgJT8GRVGCATXyJkVY265+ALqrJ0uZov8V6m9tE1iY03/CmGqztaBvM4ksQ0glQAWRY8gRn8ZPox2H1ezYqJ4iLxQHTFgQ3aRPZMXJCowE1SoDMNiNSLcjwhSmRWQQJgGqGPkiRIYBVYqeIWoR8+H1lbl+OdBRE9vrdhXGjLgr8KYbqkqSaHMXh8Zfh7MsCj6pRdHTy2TJf2nYOTl5DDTMeXOsotPuympW0maN3J1Eoj0logxQ9K0gh0dIG1B9cOhVJgilUEhWLRVRO6jy9uHrL4hLmNxx9UGYRPvfzFZP+KJls1UXLkvqibSSsY2AlZWoj6wqosOoASaCtH4zOWgqx/NdCC7Xrv0mJqXqWWVSGHqD70JcE79HHMB5D+xLbjH39h57GA6Jm2l8rC/Q93cE3KgfesXguaJSRlQ5YJHS11SEaqu7gizKbQj2Ygth5uB4k8B4lcNsR/B5Zf5dVb4qpeWw3nl7ecZ/ohbJjRt8V3sj9LnnfrGuzJZtpu+98/Wl3jmtj9Tq+C919QNO9tv4bZNA8UDunuP89f6Mfj10c6cdx1DWsxY4qvpVpaD7p0FoOzb/Fxo1vx8t/KOehnA/RGWpCO6c4lL4d7/bA4HVYTw2zxVyaWAfdgDQFuLEGid8KzVRPQU2K1DZTIpgEDcKJrLe141QwFMxJFIjsSAAIAK4koVkQJ/9B5kBRsKe8M0p50KS8sKrwv8z8udd0qmayKaABSq32qdluQ68zZvyT+I3UDGZ5meuOZmz4lel3cawtsAkU4SKvsuOMKWFcuZfHYfK3nAAQlc85SMpYhbRhv7Vs3QuzfSTsTpkkE+pvL6E4Yix5PfdPVFOcZEPbwEe0GtY3MNzPQ3y8MK2MYjVZPDpdTqdv4+SPOWSKVqKn2EIHNBHgRKYm2P2btiKjHSKZsZZAYIX8zCuzSUNrGWLDYL/1lMSgdQBdNaqFsC3HM4ds5GBtATrWWL0XiZfJDVoSODhMof4nYfVHRfk3YfUIoBrXn9fVWRSy5cMAslYPaJqjbI2zOryPpuGdBJokoo3HLqfducxKk/ybMhAHsLPoAau0Azf6OdtO6nJZ5cc0Mp6EWXVVcLxbweLGoyLI2CkBpAbslzJEW5KKiKZ42p9N59oGnqFuFbSSD2k+NoypXsMJwVGdjSwheIYdiJ4RiimZ2giIlzZCGelc8jekGClC7CJAYjbUpRghKqmjWtKiHkF/a7CULrwGsYEBGZOlTjVmtatCpxnAgLrSROI+4WjHL7hlaPK5sD5NgHy7kut4hTpqm9H3duf9Mg69zYZ+x4fyH8rrEP0hOofWq2d8l6iH6I+Pd5y4/GNa4ecZ04r1O23XOskYCrxOdOnFu+saire8fu1+4aH4/fz471uf2vjw7Sns53A/J37f6fWzP/f+1I3y/Dzrt+meL2poXzs3r+lOiNy8+o+k5JCcH6T3kXTgx84mBg6CrlNmNPErA77SNlZ552TvrM4Fw54cuA0Iw9RBmF1IRkVkvAPIAakKa4Km5E5S98olLzx665kmoRcYU7VYS1Q4dufIXjBrXTFb6hQJkjVfDaYyuGkTt4AnfjgEq6iEejGhr6+wryiZ6ceHJKYbmtDFCSnJV3VwiVLAHDF+iZhF5kxWAGVVYxQ0h09Nzxqb+oKi3p+iTcmu68ShmNUnl3IIqHZxXXqbz3JZCSvgcio7fwiB8uxVzVmoYGN0tXwU19Oj4Eez6hOag64D6qUJmreWBLlnxcTAOiyAX90ii8jABY5UpS3ZUc0IWE4wTWUSp+RA7rCrZmG5YiqFkmWUAs8k82WAFBFKFSEih+JqniXxV9HsTZpOi3lyPn97MmNR4Egum7CvsdapNa5xjVTcTRtneSzKj7GIVnzc0Dau9gOSRpsITQeo4eByKX5sbUun1Rw1iCGYsL7EoIqC47hKl6srOhdjfJRL9neXOTt0J5zytlwleSaFcsqxxukx5k1zVgYK/JxqmDIINfTUHe4GGSFNCYAkFA82r9BHIHnELFkpoxC9llC41Shm1wV4CEmSyD8GuvRe5dFCAEUkfTPoYigy2osJahWSZ1zmrKrZUICmUYW6VeBk4YTg4q7/JHdPxF6pfWmWzRrQFLg2s0f4IfgggQcJ3I0E/GfwYIobr4ukO1OwR2cjXy+1F+G8W3AS7Y5r6z2x9xU0pCc5D9C+JrSjohtFDdWo+cZduu/BlezVdAep7deeB4r15eP9Zg6UeVfRfd7uo+Yxtfg9PpS/kduIp8Cn5ofvo3U+zSHO/Tw3CbsmgxVfbZfevSbQvo00Pw2y0cQnM6raDFofgV6i+kUSzAGuYbysiyds3dX8LLPO2J0LGU3wr69jUEFBkTb+ymGKUNQRxwYLCTHzDApjS7FDe7KpsAeTT+bCMYnAv3uhKXp5FDV3LkK0UBBk0qsGdoBg+hDmw8wHBpl2neKwMmfnAGg+xMk/kFn7YjXNX52U1VsakjMLzB6DnHnXLCwAhU+ZUDa8BoPN4az4p9cUV/EjTT8buAbMaXZc7w4Df06IxBpDPvoyPClAB2suXkBQl0VIgYHCStnUnKTKn2DEEgaXYbT6R39aBE+er5Y/L5Nvi/x5MPk2XP0snvwhzH8Zpl8F+U/C6Vchdvnx13XGwcB/CLLPw/ibmun5yR/q/POI/MVP6slXZf4sTP8QZn8cTL6sVz+pky8qDgOefhVkPwmTr+L8J/XsizD7Z9Hs19CsJn9fcQxw8ptq+bMg+X1c/DSevTye/jSJXv3jX/zptLoIOditvpxOPi3DOY7zw8TOTFCD3KAi5AKumdy6dyO37r8kJnxs0lNm3UHThCq0jOSJIZfpLcqgP52UTBRT9dj0ICjGRvrbeHKZL6+qvGCLB2reYvEyjp8cTZ8uFitsx/K8yDWZ/ogqcAl0mZ3NV8D9GeOPzpMeqv3hDBuxIyMguAF968aYV73oi9ie0e1XjPigesS+Yd0KwJsSS2HMrtA42TqCYlmyKmGrT6ibsnBjwGnqn8UB2kgbpMCg6bHSw8Cvn9TFU4Y3tU6OptrcjdcgNIH6hapI3toZ2GKiGTIQupMLLrho6JiLXN3vvpUbU8jL4/0yHvo2OzS/V+u4IFLm8jh0xe6x3oEah35TbsPJoWX7+fsxTj4bnz3pbaTe6c1+fvaPZ3/M+2Gfwf0U/JxD4f0cDpU6IN49gb0nVx7SmA173VIi2zqP+1m9ybPbkuu+10S7qF0Bst1JdbtoP8Q9SOBBAncggRs8oSoiKAYy40/QiqliTZcDaFAmomiGY0oMJDQXj7EE86WYreAfkTlstkJW2GMIRE1nlMrxmaJNqBhGm5V0sVrhth+yKAIQxMp8dnQsaKWWAsrSLF9dnUEWu3MZVQBfhKBb4AhhQ4d675AurYNcmH9w8KuMkFBEAHiVHBFxIlR9mVcX2pUgQ3BgICsVOjJ2Vb6uwueatyUGMlaBEKm1Wi1v1rtVRdsD9qPBnb7FkH22ieLEz6x4a1GXgYpcHCRZ5phga4PlehScPppN/hf/6n/5n8X/47r4aZB+HWafB/Efovxn0ZRjen8WpF8C1gOUAdSS5Ktg9acBED//UR1/HdSPCdc58V8GKsvnp1X8RZj/SZD+vuaI3+T3YfnLYPKF4H78RVQA9AH9/xToH6x+rMOAV78KJr8T/eirKn8Rpy+T+NMofnlyNMkXZ9WKCXUgMlwKpkcs+2hu3m+5k8Nm3Ga7lQPRcG3+6Lo4kiQW/U5bRHNLmChtFtHij4ZeGmYT1DS2ItBrMgorZ6t5cDE/e/3mfJkVb8+voig/SpDl7GKxXGR0fpzlaAooEpwuzQKWFrMwIdKIZSzR9VRBte6/eJQyyL2wO6zW+PRczS/lYAk3oGSDNTC/sPuKzcS2+sRTwdOhtmHVM2EBS4MRPYMDFFh/wtLIFqOgW9bLOEVtCDn7Ag0hmuBBS1VJUYCwlEb0ItWu+LEXUnJyO6jUAHVHySXeBb2Bah6iHyTwIIE7lIB7jzYEUQCuf3Z35GAukFjsfbvLhV3WjSq6HC6wg9hGDqcn9fWw+9Of1rrRBiPNze3r3dDgB7T8HTXbz8SO+L1RG3VZzs0f0b2FBxL7NAcyfjTRY/p0vNx8an54vDj6o3182fvLuXu+v1+fe9qFLQz7ApUIsgETLBPn2TKZ4ICyiDjrNMhjnDFW8q/JXGiAV1BwDr73owzfnaAcSgRLnPkYbMQJ/Qrog38ZA3sApnR6enoqtAXuMfxNlWSOsNfHDj5cmv/GCXSx2jGMDh/AK15xqBEyBwKQoTTILAWG6pOqOmJzb8zWXxkiYXONs5jJqpiU+NHP5QoSu5q8iFkGYO9lGTwp8rQuMzQWHVmgfbeya6+KT7Q1F8SpXQlM6MIZgC6FHiwLQ9qMscmoe/VJVmLH/oTodHWp9l6lAZwEbFhPbeF8YmUD36JazSu14ddYrpTVm3jFPuC3bF4NozMdIxudYcoUhGfwGIbnwrDJ/xumwsm3ZhX0jSbRJ7/WrtP079CR6vi3LJiEk79FDwpnf80EejD572SylfyNJryTv2EBJpr9v7QjdvYGAYbHHABcBbP/Gmycz8+TFOOoFQpYHkyl2KVsozgpOAqAPd/T37PoU2efSR9TY7sGuoA+ndbUtp/W0lbdWX46170tiWjm3ulKy0EXu6z0P3pbFsSXHG4QMRsdspR0zAR/lD+ui1maflUsr0KdDrFIouTt22//8HV5hrU/QsTnPhtP4vnR0YLDp5ey/4pwXYp4liXN0S5g409HKEijoCNplEYc/W4suVYBxKunNAQNw/RbjrTTrmlExUClAbCKO1Ym76FNhPQAKbdsB14QySEY0GLwowIwXhm6KBVsT6a6p08/1eCRTVOVZQxylseSqnyFliOW+LOnQLxcf3XCJ2s/LHrthVTa4J5v8ogB1iJ2rvnvKeklvZtflhvWcqPfX69xu/zd7f/1H6hxvIRv2FKf6R9A2P+19cOu6c3b+B7kcJ+9o8eRmX4eyf66/Ta+dY9u00B+HfUU+y+AUU2nzNDlaLkMO+nuKTtE8yH+QQIPEvjwJSAwy1QnU+Y6qAs8k6a41J9xTG86mWnvZRjNTmaAIKytk+D55flrEBDolHICzrio1K5LdwYv+BOwXiccpcSeVjYQYJyBpTVUqcOmXykiLyvsOJVkMJYQ7JLpv1CyQ18OzNjOApn94OkHM2vBsgQvKyHQL0vrGWWoPsQtPHA9PM50chZnA6BUhPH0qMzmFQe4JkSywgCIo41Yf2jnMQ1kfhnop0/0AUc4XFI3/2iQXnXdLwo82711Y/NmVARBfXlXe2uZtOihi5rJyPyxZp1l14+o2BpBa3VagLx/YoCOSsWHEsWDCEuyUhgwZlQjiZWpuqC/jNuRBEnQADezGiO1QHPRygMNpI2vHGbyZdkDLIUq5AC8HEYQxDr3CuxKZ0wizlCme3PQKupCVV4W1SXnYZk+5GBN2yS1xF3izjhsI/h2uYjdvsSNSUofbS5WhRhRagNz+eYRVntwCWhXc4k7zyBNZmW6EvRmbSc7LlfTfHVhKJzGErdclkvEMkmOiyBGY4Mg+xYyhiC6H82hNdrGIhEZ2HacQViMC6zzIaiPeDBUq46P09kxBwhI56P7GeZM2CNE8uPcVo+GlrDoGrWlKkHzukhArhqYIlPm+fJXv/j5P/3v/ZNf/OKnzjUTtIsM7uQ2FPs4dWw3qCQMx9W2yHbdi23L70TYyzIQvZ3PZRuZebvww/2DBB4k8B4l4L8udArMjS5/7t8R8G0B/Sq2yI+sb/2C2yrv3d6VRuWWZD3CTdDRdzfjtfA+nY2yA1p+v9TNYjbquhmJXqn7oNmr5D1E9LX/2zBxm9E4ZrTv521MWw7jkKnzV9t19mM2chguMoQB7AGlFNlVlHAA6tfhtPgX//Ff/g/+5V88OX528mSGr3UMRfI8+S//9//mb/76yzSaapoUo26AOnAINK3tAUA6fCNiPcQ8uuY6dWvoiVcIt+gAwt1E6/nlP7uAyyhmHl8W4OQAEBsIBolTTEdlISSUCaasgWUJnm0K3AhNV8z8gmblAZ6livByXs6vcHqDGxiWLzBkz7Pi8nh6VBVpVD+v6peQp7SaKoN34DLokInat8CzMPg0YEK+OKojdIAJe0y1UADwpnnuvScAJgxtLKkVAn98Qcx/MW76BVIW03vC+DUFo/ITbVZOv+ZogqA61d5gDv8yw3emw4MUQ398uz21GhEA3opYHNC6haph269stARDDffTy2dSTMrnmL4LgXIgLUqVBiS6gmTMKo4WBOQj1XQvCpaYpD8pcKDJjoRkMpmhGnCaMocHM0+OYFdYK0UsPbjxhnAFeWFg62oi3G9FIwlxtc7YhoSXxb7JSwOBDlYD6DZ2IGdJMQuzZ7SkinRkm8A7ihpLPpzopdOO07I+y5dYnJ1zxBaLHWU5Z3cKygsdo4ujetkhUC4XYO8KNUASLXS0gpRIUzXVcNWLWyqNJScfrQOEAVvbERLbXdhKThvRUvWG1+lfJm6aTtextMUoxqhIiwp8yP4fisugWHIGnQkbTZJBQn1kKf7lv/wf/tV/8ldfffVFtmRdi/007FVeHZ+cooxpeIsZ9aDrJTVh++qE2iX4Ma1clejiu2w3DcARlxg65Or/shz2jhpXV7+W/eUcD0I49Lh684bXjnpvQW0MEztqHFPswDxOPq7QmBrvo0/7LI+vxR+lfrhP825jhmQ1hvN+Hh64raetj8l389+V1DOr99QdXbBjtLbYgnpX4x3V9EDmQQIPErhnCRz4XmieegOzYB7NygZZVmL1z15LTCD+yV/8s2QSlCswNjOqzKcCxU5sz66msAX/3e8tv7kymwH9AyuFizF/CNijK+wP9HHITz4+QbGUKwq8uwh38irDYkRGI3DS7K1UGSkDAkyoFfK9CAzE0wtkiC5xr0JxOY4UQC+DbFWFX7w9e7PIpsz3A3NjnELO4uiCA8GCYB4E52IBLMyUsAw5UEIopxqxQlG7OPtVk8jYMgEKseUApTm0bSw41G1Bvbxtjl1tF8fd545eVRZyCGMJ9cE7U8u01HgxUcusxGb3VR0GKKpD+hGttLIUEwnqFJbmz1VnBMhHnOFctUVdYQoUNapKFDk+kRbRXGTQ6goiruMJcmbhQFP/6oU6mZCZvapgVsxWZDTjOIcZ40IsNG21YPfhUltO13lddqklDf9wYqmmQqU69TnhrK4IU7GYuXEEz22QRvgcBfc/KbDkwZgmy9njC5wvVsfzqwtsuugmjQTJghaFK4YpyyNYK+lUAJyDonVy5DJnTaMhmKhUveptxEgPGKoXCnfS0/AiKzvRsRw7IpKD5UxuMg4D/WuPugaZfKfCi0ppANFVE6F+CYiDqBGstsugvJyxT+HVd4v5lSpmZ/HsEYtXVKAR314Kre/a2ObbT6Czmlu+1jd7Smwl/UBvfRn+QEXw0OzvowR4B6wvnQTcvh/WsRZyD8BG7q0cza3LuHN2cE3DQnerbw1pVLu5PDx2DP2+ZnZ4PdslBmnyI8u01yfKv4+3wR7lh0Zl76oXBvlUJfd4uXpdBfvkcB0LTg77WzFeYkOcjKdwHb/70sf06RCHuyUwPIr6fKxfEi4EzAFrxNj/xFFagvqxf0jecDaUZpfxq1hnzHQySRwkWFmkTDBzmCxvIdIoxuQ2ueXSR7iTGEXyX0gerA+SMuBGHEQ0oHWwl20lkIW/vIMyWy3cJKgMEscWXuoC5QBuMk/SRG59ucLUA6P+YFKnmIeU8nqJp6Lqan68yorZBDaySTJ9NE0nxTSuTtPoWVkeszUTBAx+A/IFEXOEJX5yoFdlz+PJEX5Cg0KwuGL7aXKpjQfaEUol8K/K9aolaEwLWxoZ+7J2qy1qpHeBEoUPTQJh7c5sUSamiT+rdWpvUrPEogz4h5GxiVmCgphBk8Lkykstqhb5mRIht/8wYYsY1FR+BjXgOvb+1CJkK/VJELkJ461SZekFNyk+k3N90aR2VDR6E32EdQXWQujRLI5ZFREyFs/6dN23bhMctUJoIhuRmCplaevMCqXfinONUkkeaxrZXQHOozOGU50/r+Mls/h41onx3xpqdzjVFsl/V0+Y6ac8J2rFS04rLqv56hJtxcYAWig4P9G5xfIJi/i4R5i0lGOltayj1ShaKdCNMqPRJ2II1SlYukMMqIII2DSBgH26E60toQxoiBCteC6TPN8iw536ncn+Eks5FDZ+giVOc0E1o0wWLl+/vCwyllySScr+GB6WBWzU4XSZrWbspdfDzih2nYI4xRdVtAHCLsaivXinxrjYwU+NJfE7mGFnwlD+3e+WnSQssv+OOpTCMG2ljKHW52E/zY8l9WY922/dofLp53cqvRszY3rE8SD+eXD0JO64+rXsyPRBRo3hfEyesY3rXhR6xnnp67KH3gVv9AkpR6IL+GS6Gv3Ih/BNJDCmo8bkuUndD2V+SBLJEU76AAEAAElEQVQYPYoM3nq5CfJqByyC0wgLBWoWVCbrMkBZLlZpivU4ezePcQAKWtOpqUAoB5sQsVYAZFNhyNXmnYVNpf1q0txwaaMNyNsimoEgmOaJIWRwTBwQIeAlcsLH4gKw5bAXWzDZbICp+2qKt3XsVSYgf5SSQpZJmBKhJOAgH4CGWciqrOI3V5wEFi0qvAPh3kZz4pqvRaHQsoGAPZPHMhkCd2MRs6ou5a5HCBuVIhWYlAJi8/9qlMlLbHEJDPLpvhSxfTWZiXY/3w7DuVhRQBCae7bJen1aRn0Cu1WFglKZ1HREhPisXiKhB7/cItBGUiKl32b+N/yJXZV0hDo7IiIKLG0sm32qIepxBGFtEgR3JCR672pJNZw5KbSR5FTQv7gXKffFGIGfUrtBKhz520IIljfaSI7GV7IfuULBFKhmwjw6xQ1pkL0OcfaJVlhP58tyvgDcx/ickiRsRLBRu6wzNqGzA0Iz8HiSkrk92yk4lMsUHvCGZvONB0F7CVwI3ub822ZAC6IZaxIBm6GbcWastx0onihp+zQYyLItYiECBVU6gXWRNFcejSnSf/rsdDpNL+fSVylYYP/PvzifzaY1KihardpmQ0fC2hbaZgzU/TyuJRbnPvqlvcSH4IMEPhQJ6KH7UHj5mPnwhcj0QzOjzGzW1tXkO+z9MJTbfpq2Kti+dT9xY3Jul9y8dzpl45XIb+1mtju5u0vNrGVokCa/PWCKl22+w7992d5e2kOc+Dq9Hx7i99D+GqrX0T+0Xfup+RIb4n9/jWMoDFFu4g2QaRa2vYTShEva+9t975CAe2qGHmarbjMLdy63RQMrASjYk8vchyNYwZ1JjGkEhiLBdIL9DxlQBko294YxMIt5V0CVpop1MZPLrDO+1QXROAGXKVUm+wXCzGaFO8i4W6u2esJsahB+Y/5DMfIHIyJ0CAp3A7YgQxj8Be4SZA8v8RyDm8eEuvOjKzA8dkEhJ0PhHGbCHsscBzA8Z2y3xO1KNKnyx8mjz3QIQPU4jN6E1eMowg/PY0zh6+JRnCzq+jEny+KmpSgvL78N5qv5Z89/dfz8HBMmwTv9bNFTgpxCyQrABuJpPlvJtVJtpG5NsDj7cLFqiwmaprHnGL0IyTHNj2BQfpq0jgA1CjhKXKqcbAgAKxRlEKQVtrUkPhWQrEQQ7lCsqEsZzP7HZRM1M9AiL5VCgS5DVvSXqlZDVUrUjaCjr5rdBZX1tXGzI73LGRY4wzHFQsb96IupDoFjuj59gfqmo3zLF/LMUzyOwvOgfFzh0Sc7Li7nVT4toz9UxfF8/vbNxeLiIljk5arSEhDsQgN1VAdQlI/U+pCNAFBhxwPqnw2YYGHj7kijTo2ycSeBqrhrpjVbPSsNj9PqWAEQ31JW0fpsKQKJUyP35NLiAyKsNKlPGVQYjIxokjYRIFI76wK7tDDP1GUpPn8QMroMOg50iWPrOQnaUEEHWUX2pY8hHyBNBjVATdD/zUvcezHq1l2XOCDnQOquEorb8W4ZyjoQfw0FhMKFNMdd11AbR4RcY37XriE2nnPL6c5Zvw3//b7r9+kdtOuaZivZ/+U6oEWGf94Nh64Rfl1+uN/E/an9/GNi+r0zptT1eXiQ3TPPpy37br4AriewztG9OLrAOu0h9CCBBwncnwQO/CU+jJG9z7Nfs+GaHm3NTsp7DN9aBACuhMsCSwwBCBlQVJy/i9cUJjuPsILApQwYCGTkIFPN7LwOcHUm5Py0k0M29QIfApok2JQ6MEz4C6JQhCfQsC0UCIwBvdh5iSU6yXIDbzPlyqnyckaE2RATxZxSVq1wS1qU1BdHK4FZQd9oWSyx54jKFVtj2QOQV8ev3n55sToPgrOkPq3rCyBmmMyrxVGRnyeTp8vy4ne/eXuVv7o6T+PJN/+T//g/efTic5QWgWJYA3Jr9trBQMSiINy0/JsQFWmtIUVB9/onYLfKboUQg/QgE0gLutu8bgWgzWdFrCpXWERFVvStpLtzsMC4E20xBj8us3Fp3LiyKmEh8aTu4NO1sIm11qpsy4oqU1pbrM1nMU0lXWo/kysJwqYyHLCyHRadCoMjLTvgG+rv/t0//Pu/+5u6fprHF2VxGsa4PX0WY/lTnOIcNkZDO39ZXpRXGU4/o6slpvgxBmHwTU0MAtRGBim2RJjeoxdmQcXBb8z9Sz1VE/CsB3S3gPWODThxq/LWSn2qF/UXp9iz5VE0tbIUpp9FQ022DwixYYIhphSpTthiccvYl6Jo6qp0AZScCS5VcZqbl+wpkZD5mYYNHhN2LpjyTOutj4gV+ebyw4pquLRUx27DSJPffW2X2kh8uHmQwIMEPnwJuBfMIXw2L4c9JwEfQu3avO4XhdfZnmt/6p6CW0ljdMq70tj2t+uuamkayEufHx6b7bgNZfHML/foWZMt8V5768vfDw8VHJPHL+u33Q+7PHc1ivwa94cPrXFwzNhMz47ZrF5P3azv+rJy7doR757T66HBrudZccBsZylNAL+KMtHQ1H9a1XMcRWKAgzvEul5EEa5jhJLUIFn+GKwUoOf/VJFa6xD+M7hJWENXbIFjIe2MNIKXWOMU7BXm2CftH8CaWzsMBMs0868aZCaEElCuMEuKg+fCa6IRlXE117ZkzLdLJvyP2LeQyDGjjioIq8lsWmBqkp18+d3i3/zb/2cUHnFOwSw51u5TEaxO4tNJukynuP2pr/AiE84i1gzyz+vyMa3S9mWYJSOaiRktEQlX3OsSD52Em0hqtebZg+6yuSwaYwjBysVvJQ16DQEhH5fkMjfl8EbzUhHkcYOtSeXLkbCA8qCbfWKcGANNqU/a7B17LsK7tUpNmYAGrRJ7kmrDPZjVMWxkrbRXePPeZSF5g1WL1UeXgHZHd6KfWatpaRGfv3759T+8jY/mq/C0DM/REBIOQEBDCM/YZF4uL9I8Xp7nVbJgsh18z/ENdTRjzzKsMt++YK0HPD2bL4P8IuPgCUyDEjbwcm4vdZTVY9aUDIA7ITsh0DLYaoC9oXaaz8DWkJdJmy52lEiG0fRCK1eot3ZIBMMRpbRRbLXIgk2c7JhQBlB2aZB2BTBQOESCfRpcGvhpIJOllaTHkpXkqyokBEXxWHGZrBpv34ptYiyHCdDi2tjmpvuy1nR3TaD/TlCPH3716RxOY2+J3rtxb257sZDj0FI9oof+ZvUIHMCDE/zta+z3hetTP/7QWgZ/y7wG+/T9sJflgOChHI4n3W+LX5cf7tPcn9rPPybGf+L6ctt8HPWWHKK5fRKwy9eUsF1iQyX9l8dwnoeUdycB93q/g/oGR8sd0H4gMSgBxD7cha5PhtMHqd59gr0deCH67yBq6Y0ay9dU79rmPtUIAXBZUWtTL+b5eNIB8IRAfzawMosN4sEzYoKtNQbbmvaUwQRYnbxM8+JhU5bOViUgV6mEgVqaSwcjYazBOgBuHWWuozJgXkwjyCVILLSvlQLcJ7KT0lYhHHFmVGkS1VBAnFFvyDYErQqUqxqnMaxUQB7jjGK1BI/lWTw7inQg62p5OZskk1nMNk/OyspxuxmdJ3H+6PSEyV+xkk4vlzJPD5PvivC7uvoZTUDzgDmxrl8XmKNwgx1NaqYOWJsbIVqDXdhJsov3UlwcBDcxs6KJdPjU5bn20wljq2PXNYvcLhoW6bKJDUnTvlyU2gonymTR4FilDlxKgw2+jOqOXOhwkEBRAx2nkh9T+awFxJOT49MkfsRhDdMk1f5doD8Cx/s+HjlB8Vk8n19kKzxKTS4XS/z/AKXpBRs/qAJafGLooRziy+iMfKwC4b4HPvDQH4LN8ewkntRJYsB98alOdDq4kzUUbThBZrlcwloR1QvyxeWcIY3Gm2c5CdIFGe5a7tISFqY+GPezCkEexiyLAzLsYXGDg+20sdume+SqlPCUTCg/4gRtFU6wWZOsTWLbkhsS4w7Jjo1SXWPzPuS7BwnctE+7cg/ddw+90pL8GB+PhmecIdt8zw4fPm7IdCOobWzzJujHdxl2BbaQxK4sNtvXJrj3a3t3k+++zuRTGa+x7aezv13ja/F5Gwzz69Vefcr7+WzL6dvn2X6rN2L8nB9m2G+7H/4wueU3e+MSkth93X7M76bbxg7Jake88dzws5vdrVapjvK5IvFV3+I+QWWQHRsvcaiSY7gs/Jvjggef8czVc5JtPQc5cQQwJ/IKAjIyATqYOMvEnLleuxXawm5aI9XwloC9w4uGqjEFkQk8wAifK8oizE0cN7L90bQqGIxbKID/DKlSTxW9IVyVTwzkRXlZLupkEcVsswTPZ6gBWGqwokAxDEWYGi5nqxhgh58WtjBjKM588kk5YXsDToTKCSdycShwRoY8KZ7WOSsA8ECuCYiPegTdtCqBDFBvGAL6Z5ea1cIri+rulCys16a6/GbtrcLe22BNweXBtOSFhVzZLQoStASlPCTZnyu3ef6AJRlLLnX701tnaJKU2SpzTRRxmKcN201o8ylduVwt7tNE1cS5gvQaPOMqinx0DOOBDmRqPAP0l/GbJDmtKtQA+ZblDGYm1AuWmHCzny3wAYqB2dlZtqjzFQtR7PoA2DMMtECEKsGIoHsz0PQkTRecZ5xjw4OGSR41QSCcSX2NW0YtMTLQEctSJOBWKgfKqdqg4aaj6Fg0kKFO9JqN4KUOGsANlEzR0DbUl5SgSqhzbhz7jaurOnjEuJQXIll1adza4lLCOhascaxDVU3NkRGNO8IXks67UN2YMrHCgwcnVgte6ZNbSXIj5O67Tyff7rYJ7Izt3gkNzY64VbRNYvi+ozOc5d2m+E/NgTUzBruL4XPzS0OovUbw0+iaVuqg34iGR77sERzqi6H4MYhijBx8+n64FcHAt5NSTz5DXA3FD1DfET2mLTuKEeUNjN0Z9sa6cbW/9gPk1qurOwkYNtfDtrlhXdXGR6/Ue4hY87dm8z2w8VDlgwTuUgI2rPWQD0P/u6zuDmnBs11jH8fmAW6LdaWF2HTDXGtUFCAuOUwEMaXa0EkSm0gxwSaXvYzA85pfNWlZlOEu6RLgJso6/IeBDSheM69YWfAKltrAdkkImuW9IJeQvLIJYNmvidQAOoJfQz4gTbzVIp8wIMIK7y+sIWDfo3g4YHsp+wM4CkwMc5KU7DFWjyZlmNXsz5ykbCRmUnY6nWqvMFPSj085mQtD8JfR5CoMX+AWRhbmwD6qF+KET33pgl8C2hig7y2JWQ59eEku6EV0mVSa+I3sEtmaakfeFRcLlupKrQmNDxnbkO0ob/PQZoARqHbZmhrEgCuxkdLy00a6e7Gq9rB/WrP1YG6clgqac6obdmI1sJjtsrgmtd6UXMHwQHqtLaF8XS3pkVnBVg/5CNKosbPNDI5H8TJbsvl3enSU4i2UWjgCDAIwoPGgrlG4bUQnUhLEESqtNEptFdfIZCuBFosm8AaSlyUZWgsKA4Afk7GySifoEhrFjG/xKuMwrHo0SFUnFZnmytFmspJjpAd4KJLSgzGaGqeHggEvRZaTBmwgGauNUNdfxvL6tgtRJUkb1/a9JYrL4WsHleHMDyl3JoH9vbKrGvegH15uF62HuA9aAod3cvMYJ0HyeqBlQzQH4m+vgeltOsDLzmj9qvMGHODnNjqT35bb0NnJ9j1F3ozPIendhklfemYBvTlb2SMNVuG6/nyDXsFrIzY4uTb3pm8Hx9V4+QzW5cbnwCgdwdSGx4l+Lf2YMTRH5dng2W7oKZ1EoQ7r5hWIcc9texKh5dSHJmp1CcsIIbHDkjOy0lkVrmTnU82Y9cRLEJBOuJxLO4a5zJunOX3n8RY4EhZjQlTHPGnCFXgl6CxNgP27cjlKIW2OZK4dz0JUyDQqNkLM1pNJM+6CWzBjaKyO3gpUFU9hSmBMiMxMt3VkLHZEUBYYU5WyGsdYCdMRbEtkipFxaECa4icIekmAJ8oEpUO8x6uoXuLvqMR+o/p5vfyxvPRIydHKRZ28RBQJzmo4Kyp+I92jeKE6hOfEu/gxGTp5Kaa5hAwt2ObjRvVxuU8LNncCyi2tfh6JgMJ8Wj4jCJZELNThirbE7FsUHJUeV0qB4VorBl1Rl9+V4FPtNjrWgoaE4o0siQTaLMaV1SZmvMve8Op1srMupLRaJxMDkFGxGD9zlndoA9oXIyoOT/D4X2gPAGRw5mPbO4IaLW6FIhdPctJkQqRdv0zyc9oX7pyYoj9JYo4OQ3WU8qhZ+IZLcRJpGch4U1uZw+cGLvHYg6ERI0hqnkYsZZn+l6Jpx46ppQwuk4KGL7zLXA3tVvqqLrQD0D9LSxqGYpjRkKAoROFM6xvaiwzlI+1QYSlKQphRyumyWglB8Mkbo2QfbvUmfuVE3AhaKQS5JLouyWKGP7zCuzO18tideo9vpN0V3kHsGJ7v4LfAcdoMgMPYHl/7mq49X02v7++zdZl1yEcUY+SzLnknoQEp+Vz59QzF+3ncm3O8JA/N7+oaktUQtSF+huhQi57mjUud7BBU+yu8kbzjpnnIWQH4qK9r31Ufdet+GMyrD/n7Xl69J1WtPPxd/O5l4xhfP14u1DSnbZVryO6+M2BIBhAmLxne5rjTwS5jDlDDzQkeduJoGgdHssNgthbUpQDwCL8sZAbvaI4WeCWPLwJPQCgsKwwnKwji05liCIYJWLQDnewKUZtDAPYLdfLHPK7xCqoTLeAd0XzAslIAc9I5pKhowjfDCyRoixisfpj2N2fr1RFIEjMlABpu5atVVs/MPCmc6iBhkBnuTWH4yAAxvilBbPO8OKurp+KbWiQe6jQ+aJsgptVhoNDywJP4bbGa3enWXU7IW4NGtYkhRXNZbhckhnhV10Z2YUfPylia4KkKS1T6blMaQoprK3Bh+7QyVsKFmooU00Z4uRUUvS6JgO7b3N23IhsemnSLoDUWTzF1nU4lw7yHPucM3SSuZ3HAqgt7MLS5G3Mv63opb3i3qAoG3nSVZ5fLTGtP7Ohl428hEx12A2cYonFGA4MonF3m1SLTMXUMGOmRAvlcGjv6E+9C8CZV+BGwTznljuPiAOmcH80w4r9OlG5QC6NYw7Kushz9gWEvuC4q/FnHaRBCF3MlrXzRMsaEdSdjKSzYKsy+BRYTOG8Citr4qyfIBkljBOJ+uEWvvfxwI2SXZDU3uZqwH9WWX3/7lNaxmyGXZz+dzRIPd+9BAuogDTR9PlzfXwnoceTvgE5uct+dAjBGA7vbDmhehR7R5gfNvZy8+EOD76YtTsNzvN1ZjYeNgl2CEagyxLYr0Y8b0lA32tL8IvrlemHhpDvwGN2jew3N/mjxORdsuu7yJeCX3SjHQ9mSulnn+JT9sKulH7NR+01vPK6NRNsEbpo5BveyGW6SUsjDf1YALCTzhUmFgUOUsfcxmizqEvcmTOjaRK8GgRA6kJmYOlwxLKpqpilaGQUhRXz9CPsD77RpEgsdML0spmPmXNkFKueJHAoF3NI0KyCNBYccXzEAbqrUYVAyI4GdxzBl7YEM+MzMcqi0Yuun3EFiS0RmHAZdFquY9Y56eoQCEWN/rUOl2CmMOhLpGF4Zd7PaoGOlJnlUJ2mScXjrapWDTOVJBjZVDTbpn6DWqHZMv6tnaESaHFZ7kQyLIEKHUgH0FLxWiRLvPbonuHUZHgYyGsonbTuPgUj7KXAErJnbmShn8e73QrW0NYmu3bl0Ve6SdO9Smi+iXQpiBcXSEDqRh911pWV2I1P+y8nZkVUp1UIn2wNosB5h2ItChi8mGJLIolIqaPBXaz9aQkHayR/qArx/pN3aYc4mchbv6iKtI1A9RmWrNJmVywJMf7nIr9gKXK3qWN45QfwLnQCXMSi0toMhVxTO61eol6uahSmD/iwTSW/Updq1mcQNX2swshRSr+OEDcPYm2lrslaDNCDJpksNxJ4sZ7ygdmpO3zRPkP6E/e9sFaCU6SvutDs5GmJNA+lxLDVlK+z+azuSzgaJBMBYk2TQPMmLhKkCcRkrSrYrfq2K7XLDw6THfZuhSbTSirbsENx5kbiVMrhXsFd+/BvJf3/2yGgswYPzYbKfpk9H8lFv7KC3J2o//T0FdybdLbWdVeyJ3N+zewruSXo3LfL7cQ8zN04aGu1DBP3843kbkpVPbahGP36Ijp+nDet53bGPt03e8d28LW6hADQUdtB+f1H999b74+Wd1uy/rQl/iH3zTuXxgVTGu7jpio9tZLoB5Q+rtUi70dUF1mmbIRuKABX9Jun9hzd3LPUBTEyoV+W0wO7CvPUIMYEHhVn4K+sFVhULTY4GCb5bmO0F+BRlxpQ75h1Yc2N9AdzG5Ed4U1d1dHI6mWIqjVUGioGss/HlMr+6YMaXZLpBpz7JUEQ8GzjmBp4AXgA6tl86tC43LKgV3CufEGG1qLIM941gT03O4u7zCrNudBJOMUjlrpFYgUJsQlYLlivQR+ZhulBbdbABCx2ANaaamZuGIHQxNVGdMCGhCOMYQ6pOsbrVZ5OiO0VrILWppIu77Ys45WiS9GUN97J5dakK+3PJyt0U9KPFhxUizQq0eVysykqgbaVNLp+ulTbuyStyjiDlwdsukd4gA+henam2Em05+RRF7tHUlIRaiArojsViwMyqYEaHyferzvOS51kMy5AxBZbL4LvXC/V/nbKxF/8/6FlLFDh6QD96DDIGQLIsyqs6z4DX4RSGbN2JasnreFZ7jWUxJfYUwacqiTlJrp7GHEBcsqOd88LK2dGUwydi1Av28uJilDHHOV6TtJgvC24xNGJrL2qgNFhtaYYnYK7GmlsKoFYGPksXNY8JB+Yx7ldypIXGiNgkGj0IJmXHhwnT7l2seOQSr8Yv35aqTxfnAna3+8OVa0v38nQJba3XEuyRuN8I4+t+q3ig/iCBj14CPMh6dG+kAFBwvD50f5Lq8+D0/n78DXmwuQTNtdzh5dE8RMM7hIPrXsn2Q9v8sO+gO7q9t+H/zvrIa4B+AxnV9hM1hn5/18GYUl6FI4LNY9aTdhs/goTNqpJvdL+MonmLTI1f4VdGwg02k3ljg/ha8a4r3JcS+QPs0EMzNyvOKU41ntmx53bgjhTBX13ymS5M9IiGCyjJ0L8qCi0EEEwF3zRDy6mw5AJLcZF/MgXCHckSKJwURY6CUK5O5Zo/eg0XrAUYsNQqAMdFUSSonlltID9oXQEzi3LKLk7WJ4gHMuYsCUR4aJEtEKb/U1AZpiP4jU/khoZZaCCpamN3gLNN0gpBwT6CsHxUV6esPeB6BgZzFi5Y7giT5Ok3AWYhxafQM7MozId4G2CNooOQDVZGQf4JjRRjTq76cpDPRJhK5qFZ3qsEiTG+/N3b2HK6/OR1SLWhYiNHdXG5Yk7S7lM1Gby154faoUnb4MQKeB/kV3E6CvpIhmwEyQA0hy3BU3Y7EFs8F3R3c8ZNeWpnMwZdmNX1rI6WKFCctxbg4kabNIDejIecRRjMrHCdZPPpUKYUsBwtke0YaH7ULS88UfZjfPvUHCIRZWThlDkMsbQsArCW5keJaMUpAPO3q+KUgZKVNXvPOSmCWX8ANrtzsR7CIGy+Wl2xmpOc0AdSJSVRyEBHjdBY4UsXjdQ/5Ih6x59rNJLS9pCymk5Tjo3mjC+NDwC8/BExeqxHoIPt0YrFiGoFtxTVJmYOiMDKn8Urhgv+fDT9LynqP9eM08g4JLio5lE0Ee6nsWqVqZrSgpDtM1gL4zfGnT6ah2dtBwwlctjgadIUsb66yHVUGzLG25v2u5lf3CChNKunzdT7hmuuobqu+QWhvfSUjfAe4Y0Il6d7e/s8buQbvunKDmcxzWu4LXsKvuOkIWkfyobfd2Pkcyj9fv4xfd0vNT7Gb1G/VD/Vj7lv3vr8DMXYO2JXohv3g8lekS6nTYZ4CQ/Bj04C/f7e/0p2DWQE9At+dG3/SBhWh2wJ3D2BHyr/vaHRi+g4dymudU0bd7StSeGFCu7SCb3Mv1Yl52ph6MyvvM5C0uldwCPJCuKakmfanGlSPCEyqcrBvaQBpJJUptoYYICxDCrLOkdF2Eup4pSvOHMANQLMR3H+O0DGDLGBFXIJJTrI5QAl5zaBywCdWZBfym2PDE0ymRcB77A6z0s7qQDol7DdAOeMoDwZvqBVyKAcRFgB6dAGKqZsJ3F09frlV3X1LVZACbPB0VEc5ccnT2ZPAHjmYwYER43gWf3AsAEahGfYUvFqv6F3koCQ+tc9qYa2NRVuMnKS7zrCBVr5OYzaxrVIsLlvy1hdEpvqNUxPnY4Z1SoQ335aEavRJqKNJxAxqFl6UEtXGSQ+XU1mQW6LowqxAVE1UuhYaoMWfsDcrI9AF0Kwop21spzB7gvHmo4OR0GTUS1PzQ4MVQF+McHnADccraZsIxc5ra7QgBDnTWWWsHDDtxzwMNxUNVpnlKFKSuIC6kss9FG+OAlCI0UakqRAtQwP14gGS8EsF5+0FCxO3STjS1RjRWcOwD3U5QuIZYGEWX4yT6Z2ci/7jmkJQ4NCOgcDB7gT1pgqvHmKZxaW1HS1W1TUDeaqaIWiychBwUBUYp4vW+4yThxzBFW6YdUSNj6UZONnX6aNEntvqNSvzIX5NAbse2/xh8QHCTxI4NYS6B79TUoD0ZuZ1ncuux7aG60AUM5midYECe3XEXkTcTXv041yN78Z0sm25gNuXkHzw3ZzAjtKjqdpU1L6ydl/IVj7ZXS/A2NexG6dZD/V+04d6rvb1OuPrjH0+3n6Mfv56eff+RQYULWfT0fuwKd1aAy4uhzJPid9zm/xDNogaynu8DNAi0BUbk2gASQbIxGgEmrmU4heiA+P6RjJMBmMATfSEXIC1YPWqAOgY2B0nk44IvUIvIZJPlhbSB9Lf1zsY/wTXAgQMgtsiwBytQ78MhgFKZlbUE34JkguhCflHYidAGZ2AZ/VqR4Z4JTgE88X9J9QbxllOJbPa00HG5cJgI3EKUbbuHMsnwEr6+TNHFOkoIyzGKcv1LtYLZJkigegSXgyna6kmZSnF68X+VmJJfrp6RFOQp1Rd5T/hNYHOvyYq2IxQx5mtENaaw3yGsREMO4d18NYiFQYzi59afWAy3rDDaomRhkVr3/d20B422L1JrEyfCugSynmv0iBpggN1x00Xe4mK1HucvdkhiCwFL3LwWYkDw2l1jnnExsV6wBiRFF/WOdD9Sqqp3V0FRRM/y+CglMUNP9doClFGeyyQ0Iwn8EAOdC/9ESEwjjBlkZSMwWFQQQtoLPGD8gYbz9lyPls2hzC7m2GAjWxOxdfUOplBOqoMm/O4cxWJbY57NQG/bM5GH1DVTsLMURhbRfXarRrMl9qVYjRERiexSES2IGOTT9n9MbsDCnoNsag8pPA1gIWi3ASSzezKWESxjpeDGmXUXBitJSTNApp33CIhQ8jVk8ClynCDNcVp9LhNUsDM9ZOGKTLRSZ9Jm+Qk3LbhwLucs+g8kpgkGwTXMDPrVFhKk2b5bDvVkKu1ObdmpINqPXtvYbGvAOHGBhT9tC2NL8Fr63Oa3/HycVQ5F31ifKP4cfo7vg49HdhBwmL8tt7G36G6POUqwpvTO789RwqfoN4v0X94v3Ufkz/N7Qf06d8s5id0tCjvUHOe/I2EzZybd10b4MbrwB0L5Ytyg+371QCXZe3AfetgfvQQ++0J3ZXtv4B9tM/sq5px5bfBA0vN8gMMa2TdrTNRiOZjY5QDsct6eUPtOZIXaZ6Mcdg2h7cFCXaM1kVHLUFIgbagYqAUnjdl8E2OJ4JasE1PuTcE6zlcLwBHSG0JEk40RVNAY0BXMUWAu3T5R/1MVUPdEVhALsCujCykKGRcJjN5sIlRjyyuJY5C/oGDAiRU5tsezQnTLXwFgHnAGxoA4t0ckxb0smkyLPpbBJkMcwncg8EeksBgHmp08PYgYxVEcDRJICswF5MHrNmIXOmOtDpw0nIaa9qtEPS9tPopEohCbX5aiQNV02cxbtEiYTYtguUQ0BTYFqxok2Ei7Y0AQ7Lrri15uEiVc7l2vx05fkEiBrklRLl5VQpkkSRgPCqhYCw6i4JHCEhHnqJeXFsarRGowOd2Sehs9yEmvHhr0IsmAglE5TiSFHRkrKE2ADOGF9Nw+DU1BAcy2rDBoNIlkZyr3lS1kdQpLexHyI/NVwVBQf1Mgjgew5IZ/JeNdLVDi6LaTFvjLftl1BNR6B6aRK0iPQY8zQsc5RoxTVaGW2MGLaa4FvIJKNlBpRYehk1NJHkqc1GkhQOd7KvpOwUFEhBi+GNgoGeQn7WFtAlJAOTITmRgJiEN2O19yHOu0huussIdHcHBxzRNWkjcEuaBzPxPS8g6fpd9j1vrpr3MILGd7KTlQZJc40Q3lAWR0WDbc9JwAOD0Q3RPuX9OqLeYJuXfjz0Zt+Mbe92aj9t4qjv/fyMItHL1OeqH9MrdEDEBrUByThy+g2y10Uj165H+x1zQP0HZrUe1M//XV++HFzY2TpTzwf+hryPUTck3UPr6j+DjnIzlnpPKL5oeEObZ3EybiW7W/vUB91iWMgobmVt+gzkJ6SIyUQV5SB1ADEQCgxuiEuQTxO4ZGBOFVRUnoKx0wnuFHGpQ9FqMsEgBFv6SzztWA0C90As5usF90kjJ+b4TE3L7JtzX4H5TOIXwmKaoGWBAcJkcKe3mqmJWFeiEWRKHsgFqnMR2lIqzI/9CbuWoze4j2eJIoYLNoxKOUCZkA4TR8eGGRN8vAD+0uBoWayA/eTPikkKzF1BBrSKmTuNxbsR/zijwMl9FVeTEtdIpEt4nCQlixStilCPpEo2S9E9ERbnfXJvV5Pc9IKjbQnK4ACuFXa53afguIiLpppgtJovd7Px6XI6dvTsq5ic39jMpXjjssbpi2Tpbwryrc4Bu8+smmNtkaUYCgQqQThj22wdnEbJilO95JWnOg5qgDqrBGhNuPq5xBkU23qD8qhk3aA+CoJlXbCSAOm0jL8JQzZdcCOLfJQuLdugCuTkvKjLx3mVl5AuC+guqX4iJ6J0bJWweVdamEmaUqxKgbTxCkVL1DfGulrIn3qEb3z46FMtwRhJGxhYbcor9gHLDk1rVOic6BoawPIRJDs3pWC3xrnFMhmTXolstG+EJJRe8D2rGREOZrXMRJKGcMwSGcoP1YkYbHFugRZb1LkmWpjYdbkOkuyNzy6LmO5d+9/broiRUsl2R4feOTup9cjfPqL/KzD+jeeXdZzsxxu357ZPYTy3rqzDQoeWun29fQrjY/py1tuAMbJ/dFkF/Twbbb83dDG+df2c/d/Qfky/1MgY9/h2mTek0cXuCHRP6Y40opo9e6+9N4c9wvhnY4Zsd5mtWPK7Srpnvwts5Xy4facS2Op6d7vVVe+UofuqzI3Ah1F3A/kyHA6Vnsvfq2sXmXWXKLR76LlyoBdwEZPvHNQ0Web50YRjUjlEdxpPJkA2UrH3AOxgRQPH4K5Y5wWrEKqB8KMMrDl3i8lXc9dIJubzyaIpe+b3+ckRdRQGYSowvAyN+BXBzoP5fBIVBYySrbhxCvZiKphYJyBwI+UBkEYYXUJYFhyoM6Pk/5NCNi1tqw9ZUE+ikn0CGHOXQm/YerPFk0wcUSC9gQawgwAbFe1eDpZVvQjjU80kUzvVSN0hnNIE+adnl8F0CoBUQ7TYAUsmSpOZMCiVSxIGrxV2lxM34XWUstq8tAhIp3BYtsvZFlUFSm3vDd+uc3VJLtDdOpquxjbSJGZ1NcQayrRexlTICIQL0hdbUr6w5ALac+4y9u35Uv8WZ1WGocwciF9VV3WBv8usLuj+Ba6i2KJdFkc1Rl/5MXstcPgURvOwPo4myXdfvVpc1dMZaF62QNqfy6jRUlJUF0ey9VK9aHDYWumEsKWUUOyA5DDIJvNleMYOc8qazOGfRmmkIBeFdGk80E0KWrRZlIWLxWWJOypWchiW8kmFi89gNp2xzCM9gvKMZ+1nT2QMpAUkBjAjlh9cKasaXHS0G5ckIRV0PtlkpXVyGeADF7UikSMg9imwIRjLMrRc40uM7Lpafh3vGjOug9r4rkG7Co+Oc4Lphs3ocu89o9ejo3lxAhyd/SHjgwRuIwH/qeoPvV0DuHu2D6x2XY6TgF8NFHbsrLMqW8dWF9hZ2BXy29PP1tf//DyjtR+/0KjwDp11VDll6nPVj9E7nbf/ptwUNeLqUxsq5Oj3K9Gs7S4+h+j48eKcnw1+yLrLfvYG5/j9nF0RAlZK/r9vyokvBz/sV3Lf4dv0Y5+3MdTG5OlTvn3M0FjtVl2sCvc0955p71H30za8hitPkyhLCU2mZsvl8REnuS4xpahr8NwJU6na+AssYk61BP5oXhXcpBumZ9NJnpXxoqxTt1NAc71FjuYAqjLABuUlGycF3J1FBSdAgc6xoQA6aZ5VriCZ4Nd+Uc2tlqBQSjNZyy3JNlEtBCb9QVYkQqzgfAE8TdniGUgxwtQAPGUvkyrl6NYUny0hGwK0kRWeytlxFGJfjvFPNMWyBS807AaW1Ts1gvh0siyzuoJ/UfKlnKJmz1giCI+hKlQq/0IsOZhc+TL8jhioHJ1BcNaeLyqDKzFjouXb2mE9RbxK2SVCRszuJSyX0Bb0izeF7WuDmjFjJQwN28+Ao6pVG/gB6ooBQXxV3vEiMZFKKYz1tWhy9Pr12XyxTKZPiuqyvMBDZ/bF3385v1rm7IyQQsCMONgXzJ6D5+V5VYf+ArIVlgd99majAKp5MY6fzufL7745iye1HfcwOz7RCQ1JisYVXVysliXeN6fM9F/VK7SKZTClH3SwLpqX5Ik+CHsC1SwVhQwPKoZbKVASlJoi/q1hWixQW8ioNPSLMiuXS53ai1vaFacBrAD3aIQQY24fAnipoig0o+pJRp/LVRSDhr2/ihQxul6aAhpjDseMT/QSMVOjAc8Y+wx0CpiSiypLElQ2LtGwCMcnQWNaPLs+sk/Y8DJa2ogPR8TLKJzQ0fHiZbNOb7zcmejl2wxqfG791mxm4M5/8/vhXsYdETvy08k7MvaiujY6CbhPr+Rt8EOvsoMj7qP229C8uZyvbfoAunBvtv5v1m1acS0vd5Khz2E/hoq6AdiF/RgibZdI3e64u4411vBf78rD5L+Q/7gVgI5A9yB0gS7JBTpehzJs5X+4vQ8JdL1wH8TfF813PaKoDzk+XPsl0EppRO8AU8A3ZMyy8Pj4MUbQIOblSrY6dXUF9p3gThHYn1QvXrwAIH/5xRc4WExTQ7pC9cVqOc84xClNsMOvl1kULUD0oF2s8DH7MUZlsgO2ADYlyeTk5DRN2F0A4kqKHAMQzeSG9STLFpmtGFCk6WPSTCGAmpYUtEogNGjTtcA7bVFtmggFjDa01EBVGdYsWO9g1cS2haoIEhqQpEt59sSQgyIgdeDgEgsUDiDjHjQrlkGCVbnkyDA0ElYMgJ3ya4QTG9YLhD8dNG1+Ddxvnj4Bnw7c26ZYY0ixbSPabyVsjl2HaHfEG2g0Qtv93EU6MOyqIdIR5lNscm+IWLeyixHfxrzxbDmU39ZahIHPXi/Orl4nk+Lq4tvFt/OfP/704psrNlKH2hPA9mum5qXnSC0DL2vLBmCe4cG+XugjIsz6ERDeWKOwSNk9Mb9YcNBWMqN8cMlEu84FqCbpdH4Z5+Esi4p5vlqFyQojG5nR0LfoZOpkiYhBxRC0CQ4EBON0rdNlXKpu1UjTmxQI05nMfWBrOtNW4ziW51lpLBq9s5Nj9NgFe9ApTib4F4pfsXzBgcFXEGODsNA/qbY3Rcqw6RQMGzSFVEZurChd0izxqJHIAAkgyC5p4008kKe9XLdKwhuXxpkNCmV2qb08GwVG3riqfQZcwXaEjCTTZLsTlg6r8rrcnaz8Nvrh6wg8pD9I4AYS2HoUumHoSPUG4Fb2vRX2Cje5oaGkPQrArlqaUntrdIkjc9qLeHPWeQTxA7I4WOBpkzt01gPIXZ9VP4Hv6qIHt2rrZm1Hyt/n1H68/Qhb/t6MGHVn0r5vOY/iZG8mh6uG+mtjJWQvnaFEX78fqsUv28+jp4Mf160+7sr0xnaX4geG3gBdHp/PLpJSLr4bUV3S2td4G9WvYr2u6NIMqQAD5cCHXY4rEE9UPv/zP/0fzU7/9sXjZy+ePCvj1fHJ8+m0StOfPn40/T//V//H3//u1yAg4XlsvrHUro5DTv9Kp2Bt/KzYjk+248pw5vjkhB0ChqmYPKaAuWQxsZ2fneUZJtQyIrIIcLlMxAXhGd/aWwym0qc9S4wJJ3PbsBtfCN6ujvFSX9R5XGPln+k8X7z7V4B6kH/08uXZcslkdXF0/ITNwOzeLOOvl4tlHjyanjDVPImKiH3JYbqMfwP4i6PZb5PkBEf4K3YFxPk0PDlK8fU4NWWBE6RYEdFyhUNuAlbW+wA6m36GZxYpOEYApYhZZKk/sG2Z1JwmqBDNcZJ37XJhJXC5KO/pdqlOCC6L/9lm9+Pgh+xaOZFGJcgvcyphdMhbmsSEmyNt6KVBdZFEU/ysaodrNc3Q5N7WF2/mv3v7dbZc4bmnxMiKaX6ZPwG5Uc6gDozWp7GlhtNy5u+hyGKIqomLN4uzrJyomgUuPoOStFJ7LmbRUVZezev8PAiX7AhnlYXc0uJQ6WQoJBMsCZBdGeJcYlZl8OkAtp4sxpBGLTBeSUpBL9Ewi9Et49kxGw9sY4DaSZrOeMbaP0hQNJCIm+NHuaAVZ5xBTIyq0GoGqxqX2iZQPOH2z/70T/75P//vs6DAEkdYPc+LxdnFq89/9Hy5nPOIaDd7wV5lRAsXGql+J1i/SzwWazkQHvcmuO28Kikim1fvHdLU4L76+TdLczd2JnKzoMbtIdfOd9Q2Aa8to/JvlzfJdZGNFJ0sFWv93KxL3JB+R3xcgBq5fFnd5le1T81xcRuat5FDn58x1Hxp+FK8TSt8OuPDPrd+eIhCn8OtGH/EicjmM9g92EP0d8e7YrvTiN2jAPTKOH560Q8R700C7hHafq3bOHrorPfWKx9kxXc5HmyANTCD11RH2gXcT3uXx0lDScAXwRm2yaZH84tleFT8h//sL//yn/8FwC3h7Nz8Kp2clPl5XT5NZ8nFBeAbqD/R/DjHcuVs4C0SNn0ydc6G4CmzqppnBZlBGoCUsizAHHIp9+maXgW4YUfCycEg/WpJ5ZrsleU9Nkgy17HDuTTNb8jM2mArAPba1UsTKKUkgB9W4hGmG7hjZI6b2WhMleRCqCznp5OjvEouLs/rALc/1cX5UkhPUFTGQWz6zLNsKSS8zLLzq7dvZseP0xO5i6RlHFiWTJ+eTF+kJ5OLOQsSqg6GxCaylVUKXHVidMDOYKVODaCBmAzplhzCtUKxoGT3unc6jN1J7m1AXcGNqrCgZdYNMjQyinUU3Gd3u6ZgxKy4sDJCBUkLmUtDExnZqZsNPLxh8qIL3hTC9r44KqI0p4PYLTtdMHfOek6i4nKIA75mvy6kWDFRd4kxIXIkjmQ0T89UvzbSwoyZ34ePzi4KfPmTBT1xRU/EssA5noHQIZieL6t5UnOuGEAdhY8KxAuNlQzEMY0Wh4bgxagJxz5hwE2iK90uWeewyCMCNmlP+uwYQx1abT3HUCnNnEz6J12JWOBF3o3oSdXFnxkF2ZCTTqStCFX+6acv/uIf/9n8akGTouAF60WTyXKZL1BcpV7V7HfXcOZUMKq1oSHu3SUJGaPu1hKscfCoqHVOSro89/gpXu6R/Psj7bXqe9vG9yJdJ9j7H5nvpXEHVeoNscFyLo998nELqW0U3acA3HC0b9AfbE6TcPt51mtqsImxjTzePMFGfO9mjFbXz9OP6RG+swgNhL64rd9u2Hm7WHMtcilbOuuu7HcW59SbIY2/X43jUxZv/AD2xdIrMJRnP53xa1ZOVoe2wmfzmqejP7b9wqPDQ33a8N+js7Em4OTsXk6+zF24jdE3CEozxKAhvHpis5OX3wJ7o/JoNb/CAoJDs1b5ZQSKSr7CYl4ue2Q0jXd3vDgeycpcE6t1Ek0AXEzqQ5LZctYCNI0vhKh5ZiFL88JuakZKcVCf+VrR8WOgSXz542E9jHFAxHw89pEXDJa6fmxACnlClVoImGzLp0RwhuylNp/qfADA41F8zKZeMHdQT+d5fDHPnz15gTFSwJQ/Gszp6SO81JTTmCOfqkmRyecPZkFvvi4u3v7/8GCTTjkf4DSKMRvn1LDl8eT1Msg++dnnf/qXv8hzTR5jLg9ipq2ETKyaTLYYnOLjHVUT4NiLGzTUpLJmysUw9QgfE6PTdivcE5nMFU8cGSyvNdDCxAOILZMi3aXmmxDaCHfbpSuNDLxCXXfInt2M1OM8+Tpis23xxKpB0cJLD6dZTQWFsXoKjlm4yINyFb4tAqxnKhwkYUWPGiQ7dw5eow1smQWlh5ylQJ8/BvFH2npBjWgInAlHZwP+8R5lM/3agY0fzzLXvogUxanCmz7DI0iXy/oMi39WaI5Yj0nQvyAq2M84QUKsM8A0fS4nRQpIYArpTWoxjJlzFSkeIwVEqmGCJVqKA1iEL2ucOkKJZd8v3v/l/ZMdHyh0yQSVJq+XEg5SsQatMBJjzFu/QJtapLPV1SP4oQiOf9BoFleL+eIME7Ai+Aou8zlOkTJ2ldDZSI/stF3on0vCdZ3RdZNj21L14VIJuAx8qkx7damKsARatOty78bdaV1+R7nN5NfTZbmrwNA7aoO+PbMupp//4N9l2uU3yQZ+J94+/Q1O7uhm6BfKkT/0d3mImnvNDKXub0pfDuPl3P9161PbX7ufOr5e115X9matdmV9bv2wz5UfHs9hU6p9sjoiLuJma24dkebNwL3IoQBsDfR1xnWo42RE3qaU/+ysCT2E3pUEfrjy7wbr7UWNEO+Q2u35eecUrm09CGjfJdDjlDHNMYNVAPUya7AZbO1v1NwwHvQBcEysYmBDKoYZbAaV8bfme4V+yY1tjM7lZYcwH/L3DyZjw6hO+8XmG9wPF/BCHVIEmCHHUIO6wNFMHIPRhO8052phMmkFQMyIfwFCYTM3NSxCxAnWClsBv+LqosriACc/5FqwuWCGG6KiRI2Zl9ny8uLb+SKJVk8nj48TjqWdTJIirqZhzFpAWoIH62kyXVXFbDJZxVIAsiTCYInKiAnYiUye55+d0uBVlYMxQf5qgNoiuAqwVbuArgYqEQb2P9IOxDbW5/CpHzFyynoehMrhuFAggmLi36C/eoEwlwp2Ny6q9+nyeNEbEdaLjjcxQw1g7JQNzpKpcDXz5DAmduXRCDnJZb7m+KNqEpezNOfQLvZCvGUlAIMcuoXOk2KjvtA+WGly/AeBq1+IgJwm/g09y0sriVh0VcFxVqZFuEICaAyoT2lcTplIx+1qXr0u8gUGQ+zWlQd+akAgAtRODhKMCYJPakVijaBgRG3SP0aJGic7HzGmTR6MV9QHmfejJGjUcKywth2wYMHIIr8GGiUYaFgj4S6KgmhZ+LHV0oEuauKChoYemm0xmdFDsogTzi9YOFImOcrCog3XuCx6GFGxQDyfurobooYua0KXUYXXl4veiFoneiFX3fX5vCLftyCNd1Jwn9+35j20x3uuur5+r1IZ97i5R/hGjHYViIYcEbSvlS1qbsR3uU1QfhZfXISd/5ludtBPpZTesDxKHjWf1PjwwVpUn7Q3T9BP9GPGaHX9PP0Yn6Yf1qo996P58ct2YX4Z9IvRu9Y98kppYySvPmIw9PgZ3yLHhesjFx4qO6Yfx/Dsatlfl59nTHiIZ1e2L5/9NPe34q6eC58Hn+YYOftlt8L+O4Cwe6j94aYYF7tV0m4bT1CvySNEp7EqN/zMmBKDrQ63+PzRoEvwpZOzpRLUhcE0fiKBP7xTdAhAzaFIKsofCAm6gPij4wnT6s5eJJ2ClZifTQCJ5OEgWOacgVfizFhlNUDPCNPItlaAL380AptSBVg+plXKppbyZQV044oC1dhuOsViKKhPSARKZsxts46QY8+uMnnxCDslXIE+Tk7kAIbJ4YJJanDkDMQLwIWlENQrGHyE2sKKB/5JyQH/k4QzhpkFB/U/wxklWgu3CKZOvtX0fP1MFMz827bGwpOms6v4a/FXPgNbhvErpsmD6kQaA9pENamTL8kRl5/J3Byoia6jpvIf0amcdYxrsAsToYbY5TJ0t10GZdFMveTC5leQOUAYITNDj2w12x1mn9urQ49HGBwxLV7hsJ9qmexnvzPRHHdQv1wts4ID1ELMdE7L1dt6pjkoNCUtaMR4AnpcMn0ffFInV0GJ7/9FqN0X+H6alNFL8tXFIwaQmAnTosJwiiMCZEMUBKl4kU0/ywR45SkvixXGP5zSAAf0IWkUtmbAExToX3pHctDjouRmHBNV28nQDFnt4w60llLLeSjaKooNFmW4kNLZFIWM0LA7YuduucpYkbDJfwaZtBV0VnSiJRZglEV0xEp6SARIz6pNkbFmwDiaJIyH4zz7Lk3ZB4Jg2fXLThH2uJCfJSydOmz+guhhccudyCjAZ3Ppfu13q81j49NKuWzrIuuSLYXrv9elu7yNNqV7/53TpX9Qgf1v9R2sOjHuSPhQog5u0QDjGld3d90VV0McDf2ija93u71dR3cBns8Xqn88zSFu/fjx1LpnreNIT7hPa1d4/QbYSnX92y+vePOusE17b20u0dGEwN68W4w83G5L4E6kp+Giv23iD/cPErgrCbi3R/cOccOtue1ihyqzkSm0pZwALUA6yMnNl9rkvZCtNrayt9amkwnrLCSQJfO9zGsDnrEP0QSuNAYmW8FPTJpiYw9UAuJcXV2tVjpWSYiNKeFYZzwRogh2GmwRpm6gcJEDsJicjbPVolhplhweyGMgCSYFV+1SGJgmpCkIrZcvWgfkimCFOpIn4E9N/JKtjDnWGFMV9ijIByQHj8UsDzBDrX2mmr1mnleXzWhjrzJDoZAt+gT3/xFmLWGwit5cBa/y6jnLGXi4kSG5RGV4WyCUe+kfCjIPjUbAUonm/i0pYQkEreEUdzE1axRkKmwDhBiGDhwJBRNY/4BwC0n3SQqXH95Oc1mVy8QkohQQfoZHugVGUTDgFiJC1OpaJrBRxOgNFBRhX/LjBQeIXMT5cjKZagY9mk0WzM8vVy9fn6+KRRAdBSlHdz2O46ujNEw54ItlBXkGQlrsu0XfmApxSyVMMi38ILtHmFrhPVbz5LHA+CrIcrYH06ezI/YACGzL86oYVv9rMl7rItZgtVl/uoVPtcn0AaUycvjSEXN8W7ScybLvA1TPwNS8jVIwNrNVKSlf+J+1XRwUY9pfbky1W1l6B2HgvpYR7CUtbhj/qWpkY0KIOyuUSub7GfmurxjkLPiIRonPUKlYrg3WTWLZ/ruAqI2+msyUd9dYEl2BtqBY+AFdTk4/oAb/wJra9W8XeH8C8J+srTDc3cG1TYWTgKXr1MkrrzoXVNbdIiG2728e/WaLuF94W+s6qCnuh9l+e8ZoUfehvTl+75ayJst2XU0try1tf56Xlqf5AbPu6giCSlxqF3NdQH201YXXFdmZPqbeMXkc8buV+U6G32PkrZ6LAb59muPlPEBM0d6rYX27jvSf800qnS8gsI/wj2FGoVJHFIDlHm2glqAqtwJWEWb6mFloO6lKGd6FB26LPI/CU6JxB1oBH2UPkmd4Yw+ZT32M8c300QqAaLbtsiShDHiT/9QsBUBu+YGL1fyiWly+hSCbh9sxT8V22BfYSw2W+QcBQobEdRAZ4Brbb3QTnklQL7gOamwKWOV5Gk85bxZNAKMe0L96gNZiw1HlYDwmoFnoACPSSBzFYCSjWWswfL6cJrOiOD06/vHpk0/mF4B3jIVQd2CYM8KWHHrFBuIgOAowKAqOwnCOKRFGNSHrDSmT32RjnWEaJPNQ5whM8FakgwWqOOdMBPCqVhwi2mtihSezKTKhIvC2Xx2v9pl+p0g3k6RXgbXefXInaaCe4KEfS/tvwPpV/lT2MPLTKcAaVscVjjnZv1GcFavJKrtczZHAHIazxdV3f3i9yPP5IktPmf4/Wi7eLss3i1Vwtrhi7/RlfpbpnObLiC0QxZtkksXJajrLj8NnJ8erND6Kk+OweJymV1H5uAwvoujxPLu4WrF7gNYJJUvZqrEIYhhxeHCahYtSWwtorUyKBL6tAQqhCzDSmo63BI1MdSo5CdIkaadEkDvK1DS0Ae3ZlSspKatonbgd4sQBnUCMIRBKqSjI5yd+bblh2zhDk5UIzgWLzghXwVHJoXBS4xg2cmQlOzQ6CQsxdJsKN0Ymb1ULz3xgncs4Qn3kpusscWkx4o6/9dU9a2oLbXQpXWZurYXrArp3sXxu0rKE/odf+Vaq/85xSfvf27dJ3ar6Tm4H+XFCulEdQzT1hnH9Qk+NEvyNqr91Ice/I3MnvyM34Kh5bj0pHcyJE/VQ3Y5yR7/NfHAtQ/RHxA+Nk62i7unzIrcj1m8AL9N2sFdIL7ztq5WCxW/cbOXsF/Uz3OLZ8ckovI+J7bw/0PumZ7sOvkPp/0Al+tDscRIYMdKE/t3ItIAQGLT59XORhldkosNhT2TA/oF45uBBSMItQC8m9WXMIqeMYG5SMZGwnaO65e1AFiAjvuCBaEww4zxUJkbkJL9qIiArcv0TXtQ0OisMgkrMJcs9DJfs7I0vFWAiWQX5kwIgNnAtwxoEBksoALJFsklcYT6mcpkJZqpfBkBsZ+ZL9NUSrI3IyQ06DXPHrB7gJ55NxCgSLHHMzO97nOR/+Op3i//7H/I5zbiscG8P6AfcBwt2P3MoLOA+iBdRgK3RvMyPyujsF7/885NTNsBiG3OJvQ0rJ0yLswLAuVRA3+PjR8BTWi8mtE7QLGLQFOsFw5gE1bhNANK0WMJYX4p0F0oRM/rCLwLKFNdUfpzNs9/9+y+L4pJzfLP8oig4ZuG8zjm4DeiPkJdVmUZV8vr1WxSAiyvOSMgLtmEnUZHVk/gkSY+Pw7QEFgdoUnhEXaFoLfGmzx6K1VlUXKbReVo/jYD+1aM4ugrD0yw4r4PHGNdc6lgw+WU1HYC+E1dy24SFFCzTbk7Ptd63hnawWEnkJkmtII1W6c+iGV0aYJKPTeFDT2sdJDJSKCClVWVx3VmwrmE0bKknwl1Uvpgv2d+sAYOtFNuVWdVJ8X3FKkj14rNPFK2tDWwqDldLTgguj0/c1hdxol3KOipYFksMNbLaqkHHp+O2+xSHqn3f5fKIbZfZFXD3rpza70JjPg/IOobcB57HyeYwCY1r0g9LjuNksjMXgnJjdmfqUOTIjttJ+T66e4jP4fhxA+Rw6Ww0mRvmiF73uBhReX8n8gblg14qvfq3I8zA1UXq10dvyO0s/v39aW99ymP48Xk7IHyDNrqOs88RfXgAL13WMdrqRh7rL/0eHn75dPzw4ZQOK7FR1y34P6zWu8u9wf8tyAoj8qxtPdhb9pGktkNt0AaRDI6I5VSwowwwAl4JwplNOWAIzIbBRAaUVhwzrsztgv4Br+bksSoXoM+alQBNwrIrALc+8WQ6LcKrjDOU6lMZp2s6WIbhoDYuGclId9AmVW0ypvJmipcWUodDyIA+/A6BBUFgsNuNWJD7JVwG5VM0CCbXMdXnWAFoQQ/dJC+xA2GqOWQD51W1Uh6M79ntSsYwxaHPfJ5P2OdQT8ClJYYtwfw4DH7xk+TxMX5ywMIYOB29ffnm9Ss5/5HbeO0/hvE5xAMmhrWN+cpUmUt0j7I6R2DH6dW3OM7PmFBmyhuGC/QZeZUpg/Qk+OM/eTRhnzKtZ1+xqCEqCDJJj70+jadHaZ11QdMvJia18ZNGUyNMnCyPKMsn1CiCSPlk/7Lm2S3MKkOKW9VvvvoqOy+T4JVO7ErOmImXO1f5y8H4hZ7CIGY1YQ49j5ecBbBKwc6iiaEMvpJ0JjP9PGcLNA5bw+iETRxV8CTAF071Aov6sH4u6538GbQQo07MrU9zFCtawLlabAJnUl6O9M1in3CwKEPWYdRLkdaINHQM04Pn1R5FCOJbq7Va49Q+i1O3M140cJQlCk4eH82m0xhtj7ZhdsZejmZJCmszVE6WXOI8W2HNj1tYOKQOnWnNGo6WYGzppXrEXvGnTx/95/+r//zoJF5ltJTlA60kZKurRyePlsuFuoeLVSY5A4Wmydw4Vd/BrwYyl/hyIfv0wxZRPlcG/Tp3SS7gPtXkdcgjdPfB/m+lX8dtUn06dxXezY8vuruqiQ7QIPtort2SuU/2/d+vG8rKddxOJv0niGx6InqXi9xDxEr4fPZI7IoYwBJ9LL2rcBPXY9lxKY4Hf39J69ril+etol87Xn9dsqvFl1FT78PXoAS2hDeY7/4TXOd+OPzcf4sfargDCXTvwJuMn/1lXCo88qqxt1BXF3F+WLfCZhhFBOEsCjlvyfx7cgtEkx09uc17jGZludHEthAY1jTMnGLbg6sZCAA2BfNwDxrJal/m1sBAgX4UC3daMNGyxBFLDluBZQX9eRmCuBxfAFwq0UQ+VRlRS9CULJmlWGhBASiIulFnVBlnb6tFWC9qmfqssO8JSvz/gL5B+ED1Cp0EVUYTLgEnU+EF/wl0VvISH51g8o7vF8zItewgyxDEAGWHHrW2AKumAyFN2TUluIaRXxzZ1wu7qr0SAiAYIyb53NSRugKYGBNZHoFeQ5NI07qBUu0lqTeRJtZ1vELKpxwqpwBmK5IKBvh4tqFbAPKT9BQLKLA7Fk/kyJmVR9grLNgF/lkOASmzTwKTFg5pyHIOU8OKik/tl4B5aigLFIYU5ul72oUiwqFg7JwV0mZHBbWiLNB0LH3w6Qo6riL0Bt1Qk04OhjKypqPU0ewCwEqJbcfyz6M9tTb2JCNrhNrh+pkQF9WQQakEsMiR9RkNlAkQ7FSzo+np6Ylm/dGlsP+nDnafyyEVow6bHnqH/cHaqsICkCrgJxUthZZBU/swHP0onVXTWcBJ15xLPJmxmMTKANZpbFbRgJWEVRjyyIP/NIYIk7wYs0Rx60Ldp6J2X2TZuNQ+d61DLbk25eH7QQLfGwkwzLefAWubi/Qfgp1N3ll2Z853GOmY4vNa9geZ2ijJeycJyxeK27AfGtP4DUKqzvcCNIbAIIt7E26oEe6lebAm51G7D34anXtAX/Qq3xG8P8m7ysbMB2zk4SfwppdPxw/flN7Ycht13YL/sfVt5rvNaHSUNvi3qP00uxeKe6b5dKPIh0k+jxv0vffAxjvEFehSDQYRp7oIW6rC/AGbyKZJTiyn5cOnXPI5ASPJ4pxNurzu+AOmgpWYOL6kcBQ9Bd/KtEWQTOCXSIpTAXAKD6FAJ/CcWcEQr0q5gwLW2rLhB0DakxtGc7KF1alNcgPmoABB5YeiQBwVl48hKvrGrikaxnENgp0UYFN5cD/GtIU9qaD3hFUI5n4jDPQxRQLTGx1oaUI4Yc9qjYMgzq+NOUYKZQTOpmF5wgFZ0JMFO8XYOwuKFwRGBOB8viUAaUNVEde4vQc/snhLnOzII214hUP53klwiBSdhsGlWC+nHHqAGHk70yCJ0dCuPg1cWq8QsleN6wv1DLVRHQRhRpJDq+AXAmjN5mztu8Dff/5jkCv+cPDZL8ebwudsQRbUB0BL6eBYLHYB482+fCyVRmMG06a5fPxnOmFX3ICzqUmNYrmDDa+0MEElYlWhqED4pFJxNA/Lt8V8ITTNWChSFhmUm86F4kTnstG3IHbwOTugA8pWLI1wWrIWkaCinqcONUo/nHDHpzoY8tpxbV2tJPrdAXBi6AI2bjAnTwYbD7RBvj7FtFRLGFed+tawZA84e35ZBULpYSwWUcSGDdpFKRiFX3QxDP3Zto7TUgqsGB5lfbVYLI/SY9zC4gpWWzWkQXGwsXRLY894pibjWN+6/E+LaKN0s72erwY3mRoiTXkbDESpBwav/e+NwWKWcJuy+ynfVarWteh1jYZ7uTbek34N7nGzGHsC/LSNsBu098fhRmW9G8f/7fvxUAq+3Pp9NJYajwk92zxBm2Fa2o93w8CP97P1hEOEz6efPsjhwLN2F/2r1u74/fXZcmFlbGM1vHhFdvdt/IbgusjRgU6Go0s8ZHyQwIME3psEdr4A4OYuH2SfFnhG0LbBZGo2N/rvHDVqDwBzxEK5cmVjdhTaPClkCHoKQFHC/sz2Mv8KuMMuQ3gShUBz4bxkmVUtgcGuFqE/kDXoTBcIVQFhU159RDIBwswuZcUgdATb9E/vRns12h0ATtXzpXngsgBQJpCFdoiHd1mZMOWMURDFNBfMP01aA3vlrkeG3WBBElcT1jCiTCdJcUQVedEeojDHB07MwWcw37gAEkHaYchRM+QCmkBPeGLiHCGQTF6m2KmcauAawUAHV6JwsqriBfUB+plJl8AEVNU8419NU1sMpgsdinnXIxoHpKkfaJpiVY0a7TKQrH5Dfpq3BqemnNMsySI3/JnKhIVVCDykRvUx51kxQ27iFEBm4UCdww5mrLTUUlS9CYe5adIfTz94+QxiztCiG3JNqNNe8UFHY+SDN8/LqkQNKHX+cjWRZNQAAfQaj7FynSoeJT02JrMCIo2EZRp6R+yrEdZM1w7i1VxuGmRMc6CltosKdcM190gC8ZKP0dSuHUmOIkVn2SgyCnywwwNlRstUUswoQh5kxT2EWLOgWB2h4dhBx1SvLSFVtQqXC0zcMuRn0J9RoYEt1sSM+OZDVBQBV3xbmu5cuInxE5TYlrCw+yBLc61DrpY2d5v+g/qWmN9Dg++gTkh0g+E9tOBjqNKXjx/eybsbCV3HXJt/J5F3FemYHVub35augU3hJExeb8fdbGANnQAwlsvNfHoL8kLmZX/Ta1AP6xEc0uR6GUdFjK/3GnK3aLtPufk96XWyn8eFB3O6X8o74qdf781i7kzON6veK+Vz4oe9LAcEx4/G8XXtp+mv3R3AaD8rY8x/13QZ3NhzLy33KYDEJbRtF3gL2GSW0czSH2fLmabPzaibaWYO1dK8cfhYqKzChF74UNBTk7zAJjBWXBa44T8yzCSECsS02VmgF9XwJhGiA8mxxCAfLcBx9mIC3XXaK1oEoE2A0t45zCyTG6rizfEHgUCnw+Ki5nQBlCvRHmyXsGbwQcPJDOPwchqVi6jAo6PODObdxTZjKRfC2lq/KIC3GM/jHZ8mRNM4melgXGHGVMqLGZ9wC2bEEFyT76BKTd4TJa2CdNpayM8miBULGZ2fQC18lMsnoN148h2F4wDz/zRIvpVsy0eY48tbEZn0Bzo9g5W4wNYfg3pbQVCCppz1so1f0d6w/NTajQzgGKDKFDumNRDhU/gYTUaOTyUhtsDCJJ9qCBUhD0kpXHLur9n+0KlnyKisUvYjY+vDnmDOSaBHypo+hfuCg9YI06fIqagoOENxacyM4MVUDaOJ8kY/aHKeOqm9rBMEjdk8w0Rs0QKmz5Ui0x8BcS2UaKzw/hLqj89oXFjR46YakF15WXYw709qswqTkQ6NsPpXCqw/lpfV5FwSxJaMUvSLtqSTqqUAW4Ohy1BHWQTA+IhFC0aUdv5aZoYqa0FM+c84Qc4MwLRLnQUDVheePOaIa0RAEdqGBJiP4zWr961TIERBFcNne3VnayjCUi2ly+EKeHFD723Fd6Usf++j/964q3fOeDqOqUPzD/6WeW3so4tDa/GIHRJExRyX3e/37RIjSXjFXOtcRL9nvYwbwfE5N4p5Nz6FQyXc7yOfmlfJYFBPv3uC9LD3svkxfnhn5l7pnRGHcriTCJE3668hak28a+P6uccmtX/dovF9YjeMgdE1lzek8VDsQQIPErixBNzz578VryE1lNU9y91bZZ3N4JaqcXAHlAyoB8nG0XQyY7unwLMm+OWKEe+ZOjUW7Ca4pwnzUn5+KCtjFOFP+U0HTrMpNZWRiatGnkPNMxBVyDqFuWcAIyhS1uHkASMygS3cKqAONU3aUlRTsXwSq0hDl2JSk8UYeZQZiFNVUz5nEWJVZmzkjIMVp/7OEixyBNNFQ8gzZDEDOlDjkFo8XcrVUXDCLlYOMJMqgxU7udUSgLLAKLBbOowxI/wq7YUbTlCm0SIn3A+gNR1Ek9SU1FIDu5+hNg9ZAYAweo6sSlAeqBUkC7DkA7bVNEL808U9AXCo1UflTnMiTr0NcSNvjYVXJvJRA4yOFSPEhtcaTA8SVm84dpC/9mZQB3VL6LLOUo+VZaK1EI4s1vIOPQncpl9wHzSncbKfUhzcq6MpBhNaLyAW0yu6W3Bb+oQAvS3oWKUwhLhoOwCdQhoQlKIOE7vrKvGmQny5S3qkJvLZXmECtBTLxYZqmqKmsg6lc9okJCOJ4gM/jD4dggY5W6RhmCJ3BAuslyjRTxA+aoKYUGE+0CgKPH9iIURhcYuyyREAiEAmZZS2NQoxIqque+BW/WMstUwPfpNLA6G5rO/amx/kt+Tx/W24BuT3t3X31LKREutk2wXuiZ/bkR07wLdavf1QSAHokXJl3Od2gQGurxOWeznpR2bX1Whp+k1trr7m16bs+/bp3F4P87VVP7yPgxtYhu0nNyK1z5sfMyTzPuHBnF6/9EsdHGMauX4vb3cN9a/f9n4N+8dhP/+YGJ8TP+zK7q9xf+r+2vt17c+/M5Unslu728rQey9spXu3/nPt3hteYvNL7MgBwUBEFrYPK8m9bhy0iqPXVXjBhl1OjCryBd77celpcNSc4QADmdlNsK6R/Q+oC5AkpJtgzY9D9iMZooCxbJKYnCBFoTlAmObNBfkMGQDQ8CJqJjQYloAV5ccTSCfI1mBfzcrSCuFkzX9rrQCcZyCSw1+lqsA08PpITUjezst5Uj7H/mZegJHtPCwdZ4Yjz0ka5igxMALejMJHdXiC3X+UniTTgrOxbFfxkzq5LHJM+RdRfRInuNQ8jeKrqpyF4RW7n6N4hfELk+0oCLihmcSPgupc24DlWXQazs4D3M6E1EPS8Sz5Gd6AKiaep0vYQyWoq5PAThUIwlPOFghTHI7ONE9fcSiX8ujMgXoasRuBgwUmzOjjfnQRBMc4IcUhKanshhUF5dG5BJVs7DmCAMejx4ginR5dVm8wbsL1fsDmhyjT3LlkPeMgZ9A66x8g4zJccogux3QtmfSOJqsKs/jzSfSoTFac6LaKz3BaVIan0uZ0EjAwnhOOwcaAb40ZEnUKF4iZlQH6Sd6WkD34W4oMIDosF8gXeK0hAgfqPRs41mtB+USdF59r9BWPLEHvIvhUb1IptOhSKWkoWDmdCthH/gwl1Eh8zJIxz1dpiuETmx9QNaVQCNFzfl3BStBJqK0dryGAIsNqgK3/QFg7Q9Rp4WSVozkWnAGdZ4uiXMkNaPJT8ck6vBQjStJiWEE/0MAmRWwpR3slr9tQ77vJ6b6srBXduO8VOiyi/87Z/74dot6n4+dUD3OPKNqrn39/vTfDD/1a2vr1rXHTXoO/lW2Ge/p2PPi192OGqt7fuqFSQ/Hj6/Up3C0PPmUX7o+Ktayax2OjUL8VDYbclXmj5P3fXCsrxmPzlHfffa74lftEsc3uIDeG22J6x+24Dmy8qHnPxg6C7zJq3bZ3WetDXR+JBLyH5iPh+H7Z3COPg5+kIVpefPNqMdLu5bsGOJow53AlYBPY78/+0Z+ePjm+PFut8qs85+SvOXgIh4x/+7d/9+WXXx4fM3/PcQFsR5WpEGAcnzOp9v7KREYzx+BNdAjDi8uVjgrjkmIgA48o49xepmSZjwV2ASA1DS3gL1GLQ5sjR3mAIQt2XUBLyIDCQTzGNhAULiXGsD2ahLCkDPPJBo7F4gdki0UIedgqLB2gqK/QPC45BZg5+xWO/CcRZ5Itqmi6KItZFM9DtgQEZ2F5EQSX0/h0givRCssWTGXYFi2z/2lWJpPjrLgo8agTZkEx5YAwoLZs5rWp4NW/+29YN7lgBzAQH6/5KABBdcqygIVxVaRTBTi0q44ISz2QVZI7cwAvnQH6DKcQcACZUglLhYmvwuCELbyiGSw4kgwrIOKLks0GMus/f32xWGRIP8dJKyeZoU9liAoMDSqXfPCDxJJLWXFcWn5VVi+v8kW8XBZT/PrjKhSRZhkUtaEiA/ZLxmwkoCCGPDp1gQ6SLifVDLm52XLBdC5u+S8Fkr5nRKEZgJ5JUBdYhyqoAAnqW60HKIYsdk6wxWrxQAdLMytP56NHqge12GCfAS2SNymWjlgQYAMJIw/uiFNO7fBAF4UcCweQtbUIkafntWdazMf8Yz0BBbLU9hO2cUecgcCxxehFgv1iXUjFBo6YFfvuorgirr9cLnHs2utKuNhxFK6v493lgOO1DN5dtR9PTQ8COrSvDhpPB2U+lJM7yn+Tp3q7TKMAbDbX3W1nvRXXaz1sF5m+vt7X5HaV247r09nOcci9r4H54UNoWF691gf3jB9MrVeAOSH3U9el3Irbjkob6GvJbcr2t3LaFNp2gn/vzev40XcV3t/2ux0hjuehsToU77d0/3Ph5+yHx9B3pa7pwb3Pu3sN+C+IoXobP8T4e+HyCjRWy68sWuTaN0v7bcOXApqLld/OKs/Lo6PJP/rzPwOjg/yAXcyzcngSwe9e/+GLr9hBOzHkhKoAyOYfWRKMrpcL+aKJElEgBvCkzcRMEfPBTC1+KFESANTT5Mnz0zxLSyZuBdhw+UJeYFy1vMRMRXY24lJ1QJynS6XAbYBCs8/Apz0+MGUAxLOtLOXnlptCAqTYBdmWVLalTrI6xinNhM2rIGXUlep0uUy+/m5R4AQerC9nQVD6hoNvI5uJx5doFDOXnqfRxY9Ojp4esbUXGyFO2K3jyRmOguLw0eV3fygroDZwF65oP63AH84SkP32u/S30XkQAPrNYF1sMU+ucYaQ3ASzIKVZmQBNLYbJZszmNZXOvXLySXsFvK39moJ3nQVNJqf51dA0vYFd4Lj2YaB5ZMx54+iGHQLFRN47K1YhmNGXL06AL0oJPn445+uqmL5ZZhfB5BzFDhUNf0ERcB9cjb6BNiA0j6W+TG5gnn0GIHK1AWLAfQzr1WIBbNPYjK/Wy496Cu5oPhU+pR0UJ0IBmuKu6qm+VYfQvDLWeG6dnD45SdgQZ56LmJgnlWSpbVprIjf2ZVAoMApi5r6gR4H2cvIKaxGHUcB5HbzRoCAvK041fk9hhhvqkhUUzQ+jWVWdcdQXLkERRhg+XlxdBOEblgskfERlI4rBJP4aztsvx/zOT/n+1wyfWkhz9XVvV//Z3/++vRkjY97S91Fvv3U+/7d5V/t0mjlm9zvI+4Nr/G+iG8+uo62zx3O1v3U+h2PC4+vVS6Vt40bbB6rx+VR+9/YayLwVfeio6LeiH7NVxfW3h/bp9RQ3cvjy2UgYuNnwDLZ+sbhzA3auAAwQGh9936+h8Zw85HynErjXH5932pLvV2XeY3/vDbtmDLS/YD4fKgJcYhZWqZoNDYH+WQagZK8kKoFMdBJ86ZfVxflCM6pyJylQaiiRuVUQOaAfiD1fLue6FeCDYvj06ZMnTx+THxWCiHSaMF1LOVSFy8sLFADwmVKYYNfULLYp9fxqrrJCjYJ+DaPGGeiUAjZZSzJomHzkcTiTeEsDqqIaAAzZa1DhFr/K2BqM0ZKce7Ljl5n+aoEKw+ZXYWxWLAC1NI21gimmJjiyDOslO0MrrPnB9GBq2GXFQpxy+Bdw2xwhsZeWsqqcWgWaMxB3UE7wfakZcV7sBpDhFRVKEEPKjBpEi2iLfpUBmtYAfUlN0jcBwRFlYw7bgL7FU7/2IlOPFDLtTgaN00ryy9UQNaoHWZLBQl+7BFj3YJs16yumWKAIyeJqNclX0/mcufYZzjTxmLkMV+xkkNLEmQHC+Uzhs96RsDSA9OhcqlxJITMRG9uOS2sDMqZO/otX8W79oF/wBu6LXePLsjuNReqQZXVNtjGEFoZP/tPTI8YavFAvUmAvCp3C4Mhy/P2jaSKuKpFrpXp+MRdr6HOc8SBlwSmKiFA8a01A9aI4mJM9MVjLZAiIz0YW9Q/nHkB5Li2rGakaVmqALmuLhbqPHVFdWpNfzW4prNMeQt8fCbjR4drTDAjX6R92E92o3DuCP+wGfJ+488eQ2pUMnx/meqz5WbitDBwZvZvHXYdqcuOo3mWuA/QwX7+/D+0QuLHZsgN42yy488712hhdfMzMze1526DQk+dG6s723HXk0Fj14w8d/2N49Onvz39Nv4x4Kl0WN8yG6t0RbwW2/RNDi3j3Cd9GGhgESBNUAiY+AS0lsyumV4kFS2IbMp1OMLfAz3qeLcFeJFFOxiJML8cYaDBtjwd6ZnTNMhsIhoVPAfausAuaTKY2m60KiKFy5p05ZwxABvCEPnXygdG45oTjXEcOY/diSN+xqjzM0XLjmBTcJV2z0S6DJaEvaMcnqw76lHEKmZhFlsNQ1hDggSUIjOnZIizYWVcrbGTCYhIei6w8wAB7H4Gw6/AJ7YiC5xjtROZPE/eYQOqw+nlZLGuOj0qmQQmipg3Sg1gbqTC7LybsiuYcADCrbZimUcwzGzY1/mgE2oAJmQZJSQCT0y61ifo0VS9dQjEgcW2oBfLakgBGWZIdUXynHGmMGRW9YuqBCyBDxCmnOahRzKlj7IK2xXkLUcmO7HlZPirDywp7oYjwaZJibLMoo8s8fIZ5TVmyT0CmP9QxgwWdDA2oRikQAEclYrYc1sQlVO2ykQKXJm/FKKBbehc/P6q9Q9Y2tsSfS9Z+EpqPVoniwT+sc+gXeAhk04USIj0HaePcH65o5WSCJhBXrBKZxlPlqCdJlV1SSosbUvecykQ/YyQk5tXn6mE7ygHpQTF4FlRPq+p1vsTP1RnKjnWoVEKR1QOhQSD+xeb2ZQ3bjmzu3Umieu8xIl6LyC4KvcK9N2cvx46IHc/4jlz7omgm1ygO95EZTLvN+//2rRtky0vYeBv72MDLszvYDgz3rUFzyPVuWreDIw+fbLR9R1ZF+XyOyd8fUf4Y6KcOVKsHkOsORuZBfTrEzXC8L5/hXOsUVggZMP29Q/a7fD8rAOvKH0LfGwm0b5/vTYMeGuIkIPAxThZkO/BHZ5uuKnIkOkJNwICpcGQ6AcLKXgegzlyq8DmWIRkbRDmpF6w/TRKs3i1WkIlywHpNuwqKGpyiuBGt8L0CatO5rQ4pow9g3JNOMKoR3jT1QkgR43p5qGSSHuzLEoFOm9X8t9rLD4IqkIw009s0CPoG2wTerEmwQsBhOEpoolxZtZsT0CwVgAahlsgyXrCSKXDyCBqSlGea4cfWB80HFQHTHjYNJ/E8D69QMtgGrVWQKGDTqLYTsHkhKDKIUAulWR3RdD56R67ThIMpDUaPAfq7TbIgSsxxnD0NTIlFiQljFczrdQG1KY7y4TY0CNlL2VELyWffEkESpjFHF2iyno5hnyvAXUZIwFwBXFhkbYJtsrTTcDD6kZnEHKMPiApWVfHjvJ4v8hBfqavqfJkXVzrmS2ob3QFvyJ32ImYYVh9o+wTyMh9CBoz10YhcFOEQLk3QapiK2pc6QJf7MVcPKr7NQgPVq0RSMZJC5lrZoRGYjcm4S1XYRUBtVOthggHJKhQjBb2kxsaMXCZP6JFH9kJaFmDFRtJxiyLSMSjNPWOSVG1ZETNInu5jjNEEq8s+HFuuaknf2uJurY1tyva3qCi/Mm2U2s74cP/RS4A+trHy0TfkoQHvSgLNeOm/GTSWks0zgH2eVG7ve8fPfF3YvYqvyzU23dfwXJkxMWOpt/maXxaTX5/+oXpYQ9X95rZVHPY9es5mgzd+Hfjpu029xuVd9eAGb7329+Xcy7IxQ6C5t81rP/3NvLq7psbRMu9T9mP60vNHl5/z9uFrWjSiAp0MwHz0q+2st3od2AtIFFp4preLPVzENZS5BTG9wia/yDgDSoYgAKSy0Fba2SyaX60wqimwI5kcFwWm2ymGQmF0yu5NzGKYmBUCZLIDh4uqBdMg5m7BarmwKTjMPDNySx5TANghkLCaAPDCqyNgTwh9gn02vmrc/LexA3ctxGq5F+fGMgyDnsU2/xGZ8Lxm0wXKBTiZNwZ/o87UnApARrY4g/WpQ1Y92koLbJcHGWFE/uBZMBgzEQoEM7bhRlEWTiDHVmBYxH0kp5/RTv6bE1Rh42mUMIPOtt237LJFtUBD0pw07naqZ/AUJm+ZlMcxEezYv7DOToV+0zdqmC1XAFulIhAJA+BXjgSQdkATtI5BSwlExTEeiiachcAbJTkvMhYlBFnNjsVWB/DOSTZaUc05EgAO1ZrgQueVhVdlwWlfF8uqPAsuL6pgXj8qahYH1FqWQUx7gxqykhNPBEHd6k1Yl3yl8Gm6Xs+7ydikrxTN66sv6IC2dyxkoFj9hgi0CUFwX2H0EnQLOYQCyKPTMEKQHhP+z8PqCWOP5qMIclG9bMmMqBqF6qPN34jmqo5xzcSmkiyIJgwl2/WNmOQbStJSN8EqKxcwjmLEPgK2RlxeLb6RPiilFCnZYgbUy+dizOx0XROs2dTatcmas+ujzUE55v5fNSU0GsdcvTfnmEJj8vjvH41pmuLVNcSeX2p/LftzHvr+319X/y29v/b9qfvrGpPavJlf7s5737W7Wl0tLny30t7dquti+yPK56qfOkSvn7Pf+0Nlx8QP9c5Q/BiaG3l4H3D1Hv/1CvxWkm7vZwXAcWLsfOQf7Tv2I27G96czPuJO+JBZ5z2wY5jvGjYu58Ft2Sym145fnwvr0/K5ejnJV9Af1CcMyJ5KLHxwQVPiPgV4P8EbDmCOuVgObEq1/Vd26OAoQTQANxs2NanPxDP/jkH1IgrWBTYbUWgC2pi5xtCFVJkPCfDKnIPzbTVRq0qVF3AGWcIWYVTsRqxSoTFryQAdA5nktpllAVNSmdrWbtEqR6cJykReMtmqALyfyY8M2BlHRIDrisUKGGZXAcsQNJoDslAWLvDYE9XJSgsWWNKgxOgAMGblJykaEpoDQljZ8VOLlKPFotXxJOH0BIAt3EWcFwBHqgWOBUYJiSW1yRgX1GfyWjPZUo60JKHmGkqWRRTSJEwWm7RWSXKgqpBDNWiPg+iggzDnL5sWGi6SkHNWTzQnpXK6TAyFk/mqfn1VnpXhOadksYnDNUl2UyJgskZ7kgZE70iawHLkiQipUPY/Yl5ybgLNrThzFynuRp9tSE0SLZ09IGEI00trAIIjSnKRwt5fND50LElEFmIInHs+qdrUIDQPt4bDeAHSI2+WC1Ipe4w6SZmhQ1dSGUEIEa0RAnkJFV+tUzJDIUMadIdUg4ZpL9gw7TewyTTw5XJKIqrpA7w+TK4+QEEdxJJGlEZxM14OKvuQ+UECngRupwA0fj9eiSBhnnY3a+jeSwc//PaG1xzPdZev4bm8Y2J8qmO0Ll7iesbs6tP3qd0mPIaThv4IyezgxGbwdsRblCEC/ULe+XVAu7y670/OXiUbs/7X1HgzmfuVDYSHZH77HrmmRT1++s/p0MkAvaLXRXQvAgJUY1i0/W4fLn/sWQaBGUUCCtlCS7bpbJJhAlQtrhavzs/PBbbieoYlj5z9yCMLUDQMH7EvIEpXiRyJ4jSTyWJtRgVdQ00oV2Y4xgGmJbjVNPUARAbkS1L5FJKlDJCN2XO2AWDwAuylcuFhpsXFP7TAywKTMAfKE2YUzlMm2fk0wlAetUM/0sBMEpbmMgi8KTP7YlbHJ4+xM8Khz4SCBhbZvgtY1tFeaAJpHV7FBW78nwf105IjdaNjPPfXwWkeXFXJ0xKlInqSxfkCUrKSOl7SoNU0qp9N0j8qOA8hOAnDNxxcwPkAHGRb4u6zehbEb+LyeR2/wRI9mJ6FhMNFXTwrI3J+wvxxVb6ok9dh9kkdf1eXn9bRyzh4Ucff1tXzKHkd559Wk2+Jr6KXUf5ZXl6G9Wd1+F2Yfxak3xTLT8vwD3X+0zL5olj8rEx+Vy5+XAW/q/NnWfJNmT/N6m/ycvp1+eYPWX2ZfLdC/tETlj5iNDoEILlLqI2SYvJFpDreAanFF0gTWSoP5/LaYomE7qTvsJCTvQrqcpifgDpcPav+MF+dKAJmZCR9jd5NtEtBigxdf4kW4PqQsQLIV0lQP8sTOeZhaEPURP9p34XdZgwI1AXlwnaKOpIzPsviKRqCaxBJ+kmri6v5eVB+hgehJGFVB61Bo0i6FT92yZmxae0R76qRmvR93UVOy+IGJEETyXap0b+q2wW7+wMpbLx/Rr8/N0p1Ve8KuJw3+30xUdE7u+juiuvn3M/n/tRdNVwf57cU+u7domLtcO9IjK/dp+mKj5fM+Fo6xj7SgN/74+Uz1NghuQ3F9/toiHITP3pUe3RupwB4hLZHY29w+nkfwg8SeJDABySBka+OQx9qyKpI+8U7lFfqYF0Ndb4cZBNEEvbQzDSgKo6O0nR+fHry6u2bbIkNBn5VjrCKl907RbCUx9tmAtLnHFZMSmSJzcz61dUl7loE/gH27Amwzb8sIniuHlEVBKUwKALLYQfkNAchNNjXDDhfQL2mFZqr1o+BouHNGaXoKDHXMGudMCeJ+tN9jp4hHQI4COIEa+LmB2N+QoKOWrXAGZDykiBD8zC5Ys/p27B8c5VPs0UQYt4zj8PHFVsCMoyWLv/hC/Shi6KeYVLPaVllhNf/o6D69tMgf44X//JRHV7knHWVvAlLoP/bujhHAQir8zA+q/PzKnkVFm8xdymz12X8ui7fAusrYpJvguzTOn5Z56/q9Luo/CSMXtbFizr9BtDPNrIif1OkXwerl0D/oHyZR3+oVi/C6Osq/0mZfFWs3pST39UZdH5XL9+GKamXxey7gtqj87hc4s8om02KalJwkrL6D30Hm3vWYWi82i8RSGwKWIx6DQlL1pIp+Yg3yG8fLpPlbFKacFO8vWNiH+0C/z2sn9BRKE2ss0AB0x+8FtnPvBZj5OnTlj3gLWExhjUoRaCDaF4f/U3DIKa3jBfMtLREwkhLWJBBW9EGD60eYNRU4gEJx6cambg0Sk8enX7648/oXW2+YFRqCDSNcS11g8mxS5Ut39d8k7PNKgE5Uk5C15R8SP4YJdCMEvqaYWWfH2MrHnj+kCQQ/m/+1//bPfzcapTdqvAepnYlHawt7SLyruPc797oORK3Bj5mhWR/Q/QjyxvEfjv88P5SD6kfjQQOHVdtw1o00d4PfI9/rh1B2a2yNghqbCDKAF1Fq4TWFZmJfwscx9qH8Gq1Aj1jeAF0+tu//c3VxTmef373xe8ur87evDnjoFxcAyUxR9VSHMAuQxWgESoDeA3oJuVBrurDRAoARinVlIMA0jhbsbEY/ImxB5gQWxhZgKwW2dXZWV1OynKls7fwo8M5uOC2/BkagQE4fnsd2qc9VqXYpULQmJN8I0dBvPgtCWHxzICl40tMgXwpxB9AUCt0KCdkZtIbTEqUDFZArLiZ1Fm/MF5qcyw2JIBPZqCXUTVhzwOF2GcbcBJwmIWsIURL1kXgVqf8cmov5/gSRjEIOWFA5/gGHJ4ANbYWhCv8KlGKk4DrSO5Daw4uYAUCU5yKjQYuzLQ3MSD1CT6IVGP6JWH512d5RPxAbRXpLOE8rDl0jFJsNCAeIIxWQwNYXUHidAEyABmzPnPGzo3V6pRmIkkTgFZRAMMmMmKQiKRCpL2ZBM61N0JT+BCw4SFiLksboVvCXI3kLZkP9Zhpd9SAVU+WpunT58dY46QxcBy7ryv0QZQBkLyO+pJHUimNhs7DbJlfXV3RF7YlISg4zIzOsfPCMrlxFWXGjyoWqIdBzmvjE30BH0NvcBIV189pEpvajybTf/2v/9VPfvqLy/OXs9mU3QSUsj0fFIUCjXT8uyYQ7hpCzOBlcpWwNq7t+43Ed3FjIqF576Ku+6jDxxIfe1vuQz4+TV9Wfvz7Ct8HP3dFc4jOULzem/r9GpSl94R5wX5290bYkYWou1sB2Kr3vb+Gtvh5uF1LYHBArLM8hH6AEmBc8Eq4k9HRe9soohe5U8aqHzwkXAT2cp5AdUIwQD1N4n/xL/4jJnIfP52+fnUG/rq4uPrq21f/5X/xb1erAneNmkLHTY7wP//ZnSm/PmangTGJc8kix6DpBGeVuHecampYOBzWNPvPvO/R5BElMibWK7ztABxxzZ8BzB1CQ12AOcF/sQebLXTjuxGchGiTyoboyWi8KFkoVLmskCzpZUFOZdIc9J8kmERI9p+5ZuFXZqsxsgdJAy2VjflobORlRE4RbVzmXnk07xzqxDC714qCTFagrv3FQFerBjQr7iR2w+WmalArPMGF2iV2pIGoFBS0BEMce3ORns5JsL6BGTuwSyKji7CtEWZGMpDObJMAhZEQuLhgmcOarA2yQXFJuAo4WhhxCm1LAroIWaMlZYlIlwTFPf8UaXHKZ2kOXrqWWFYXu/60nNYG6wuTXJWns/T5i0+Ojjgv4ZH0E232ZRFgQjIz+LSOPeXqI+ONGDaZoALCMflMSMSgvHBrIwydgQUnrM2kwiBpjgwr84yzjMuYtRn8B9UZxwtU+XIlt6n1RPUw2DgeDlUWKtxaw9Qr3eXCfNKEnZcTglKHcuws9g4jXRM+VO7eoSAeqnqQwM0l8E4e8btWAEpm73h/vlo3273d9H4feenHgx+fkbmbbEN2VINU7A1+AFeDhG6RYG0c1P/6hPfKZDwdX6e8DwmM56TfxHcU442xd8+t/3s/Xv4HPEcD48RvqR/2Zd5BkT0IpF+Wh7sr2IU7CgfuKKid1wJN4eMThv8rELsZ1mPyXy2X5xz1lRWnk1SWJEcn6aefPOF832zFDLQ8h2LwAx7V3l729cpJDrjZfDyCuGMWAeQGfrXMj45nRzN2CwhIg/mIVDrmREdhOnk6v8TwZia7jipbXE2X88tyBYbGGScgDvSn+d5mrtpeJAA794IDqJoA6FdbJSifGE6DDcgLOzKdby4lrTs1vWyQUIUEUgWIQc7AboC1/GOCsZn4l00Tlk1xxBlhoPwJsBEHR0KdhWbbmeAHntblCadUBfWpjjTmpC3igxnrKTWbp1X9VI718eKP00tN9kMfMxhKoBfpPAJs3WPmsHF2I52CRQaWFHLD9rgqwlJ/VS0+py5Dwku5MIqWCfsUOLEMaghVaBv5Q9+BdU2kM7L4MxCP+yYWMJgR11qLCUvLACZDjT/KA7IbTIsYLGgSMQC/HqIa25Ys4naZ4O3DbknkRuWFr6VCaAhAHOlxThrnMav5yUst/qC/4KaH1QwOY7NDJ4DlREsdEIt4jGVbAG3XsoDipSaZAsBOa3yxqtONbdXIpo6rJE1/+bNPX7z47NGjI9YZipyBSH9hh3aG3yo2gTNQzYtqh/uN764pbuyoGRZv7Wk/xI/Fu9wu3Cby7dbZdvwOeu86L/shQaPgOPJ/O4ZIDOXpvzeGKLzfeF+G/ffzu2+FvSpsVN+PXBx9h9z8to+p7dD8Y2jeJs998LOf5vjxMERnKL4/9vZLxt+Ru5Gz/zJZJ9+1AiDK6/fZup4PMdR7h36ITD7w9CCB9ySB/vPRj3Gsufgu1b1wNl87XeL+xpCNS9DNTYCDOLHeAWTbLCz+FDGpePT4+dXVOeAVcIYnRvCGmc5rblkmPmA9qAg7az4bYrZ/08xvgjrLmJRFCwBn4+JFWJX/0hNkys1cr/DdMlsJBQOMgcM4589DTukVLNQ8LnTBviLqajF2G3Ak5jUrrVuFrTHGi1hizpt2UdDxIzrUZgl8UJe40Y+x0x00Ic/8NNmB8nhrlnagSXYOyrVfBk6sAp4LdlMRN/CTwB2IH/yqOWbtVYWmDFicImTFxAKcQCMGF2N/TwXwbL4psYJCGGxBEBonVm3R0bjGlhYFkAHxqEva8yDCrrhiYV5oWO2Hb0nVeCdKWpm1BO7w9qPM8kmqLu5kREHdmMicACVD3WoouJB9beAgUlypLkAewiphCgWp1jpFUANeO9F82NPLTnG30lJxTBwCYChIGTC2OfZXJxpgIUSsjgXTaQp0mVsiYAVAJwPAu6mkqkc6jVY02JI+naV/9Vd/9atf/rLM0UdZjpHIU5YDsnnBfoirtxwAnMxmuLCiAjHFJSG3rbeg498lDn82pYcz3EfKe6n0PhrycdFkGD9I/uPqso+G2z0KQPduPaQx/ty/K9e+6EZQ2TtXMV7TGlGTVhhc+/Zk9mv0w3uK3CBpSP8bT+r+eOvzMKaufovGlOrXdY8xmkdsrj63bcq+7wZ4eXT25d5MO+CJ8ArerJRHYOP8hJGt3vrpcT9DlCXAf/8JUk53P/q3qrda6JGEFOdNAaswnUgAX1CXPXkQLi/jbBkfn07BZWW5mB5h5HP09NnzxeIPoFV8AsmmO5EbRzbegtJQCTCmAZwBBdk5UBLA+Q6WNsBaYBuT7LRDIAysj/tPoL0wIzZCgL4sX7HBczrV6cMUETvM+QqtGVY38xc5dSReFIQKjRpd5bJJSCLvBCNMbVAPUhKeQWZlUEMpakAZcElFBpK1GAAWBYTOmF92oBkVwOojL7gUNpjml79UQX30IXYL1Nj0MzGfxfIxJOt87QHA1F0mLkzPs89V0//azYC3H4B7/lzLJMLLGMTk+L8pA/IgGurVHgBkhGGPvGeyXGCaj16dca51lipKo5lOzFVzEIA4l/1MiBrFvDsWVLRUW2kF/TniTASRL7Wzf+Ec/SFgj7IKSkhGwwSmGCcyF6ksdhHZZtC9bi2Hy0wMnYEs3FMpNjnsQGobn1LfOABuEkdTtotUwcoJjU8ZTenUBPmNQslhvFBQoB9Gg4KyDB+JnZ6RokRdeHLFlSvEKWmdqH41WyaWPeroarFk3zPyxEUVimUWXZoQIqyDjo9O1KPlEvlICGqDa5Q1QePHNdlvJrksY/PZT7L0wXU2Jw3Lc8MPo2AM3pCAK+a/c27/i+BGyKFvxdvX67eiL47b0+/TtHHSjz4gZr+snAz3t+uAyrys+6Xhc9XP6ad6JN9zsM/nfchtfyM7Htzbosu89vffRV0f2KMAXF/4IceDBB4k8D2XwNZbhtY6BOIDAgdabi2IlqTe/WAtkBYgjE9Dh0A4ufg5Pp6uVjmAvsiYjI3RDlYZ//hfzo4mHJ+LW1CwKeVlYAIdpsAF+mWnzi5YrHgK7LxBx4Rsr4CQN1qGJnkFdCxSpdk4jENR5n9L5t81eQ8ttZPsmvUF+AH7ZDvE5LAxa2BOSQ16da1pf8esrESnHEBUUDLrE7IssfwAZRoHA3BuUJJ8GN5LMeD3mUgqojkyTKEIwFrGSzJfIZVDf/GASvVAXikNlAJ3AuXZ8sukPgmoQragISQOD9YEMoukCKuA3NxIXqLDpD38sLzAhD3CN/XAKqUxkquseziqmP+c+4tsISJrITVJAoEMuWEQobEPe0GGsJ6Y9FijcQyQy2ClquOPurtPC1q0i23u11+OS923xeDLItUENY4UQX8WWKwWWGGSXvu5U3QYDMkWMIS5F/k0s29dRDFUFv5pxp+z1jgMjBvwvPUWQ41+4zJdlLroOW0Qoba8QEkI4ukk5dwFMtQrDTZWVLTAVLNrhfWksmaDCjuQUZsYnawjkRMZ2vBWG7oW6WbXRTx53KfSN266Ah2ZLuYh8CCBBwk8SGC3BPS+SMznBt+venmGXkaWUV7/ee297JW6TUT7k7CTxh1oWvz4cO2txa/ar9EP+3lcuNPJuPXD/Zz3EbOft9vU2G/Lzerql+pTBk1oQI7oHVfWtatPuWnvgX29Q0p7KYyZlem3cUctI6JaDDki6x1l6XPeIY4OiqzRSItHACgu2y4udrxN+quFTUGNA7tsIlw0gZjAXLzW4Nv/cjLjfACgW4gxD9huNj1++uzpqzdvMY+vy6fpBOB7LuDGBeqPMecp4vA4neLsfwWhYhVz/iumLQ7/A/CsPoFXSgDJ0QSAjiXT4ZoexhQEhWM5TU+VWAjumqYgUG2YDDgH5DR4qNHbysUx4O6plXhAqdpioNvGOWUEVyM4l328chnTZIIXViy4FwxVSTAn1vbUhDIA7GeCXe6MBLRDDhdDQWHyfoLuEMppj8B3FV6G+A9N5lE9DTl4lz0AyQKnQFG8IKaWt9AXFa6BpEQsWWTg8AEcBEXJotb+AZ1BFiRMVM84xDcMjuQKib0H7A2ocfuTsbAQVUyis7tgUVfHmEphMK/9GiwCBBysC012EmgpQM6C4FPT/9YniEGqAO19QuPUYAlMmF0i2rwclld7iW+eOBOh1t9IlG4jZUOl7EO+iSQtQ/wKYyXFG5mlDIA6Cx1C5+gCWIlpRQKx0SMRO321XQQtSdof8sbSCezOylMRMYm/ggiVSF2jFVmG4yXWNMydLH2Ho6gJmga1s+gUnKSzo6NT5v7raiWnQinbSEqgvxQ4U0tKdpbX2P8gJdA/xlrWRD7xE8WVvNGnLlpsLXJ3unWR6wQX1aTf/GvvW+7mZK8r2X9v9985Po1+quS56+rn9HP16/VTbx8eQ5/u7q6hVnQZdgb8NvrhnZmJvFktPrUxtfj5XXi/NHyu+jn91D7lm/HjJO8o++E+/aGYPp9DOe8v/s540BN00xUAjeGBJ/D+Wv5A+UEC71ICDHDvXf0ua/5A63JPvPvckgy3A++Dw6WoEgK+IijACHgCahmsxPklKBzLCkFzTYLLMWP8y1/+6osvvr28PM+XZ7hZDGOcXWLTEcbsFGbvLNPV5Ur3ZQqGB33l+eryPJviqkXmHZqR5aI2DmoCYGtSGLypWvC9IzDJVAdxAH9Zbmg6WVO//OPe0KzJgijxTQbXe80XTdBsr8W1SboV+m/KQUe/0fZPpdR2KQtWoyoA8LJ1GICKHJiABz5yUTkukpjaZoPwNCjY1iCv9iRwDkIYTdwCCPhe7nt0ILH88MgtUg1gZQEBc6e0CNihShnOGI4po13SNI6zrqiCViMqJIBpkI5cwGodv59QnbLikUYTO12BNZnpogiRlBR3qSr6hjNY115bPh30F1amSW62vZMMTbInjCaaLNy3i1xn0iBgCLSZJHld6nsTo4UhTgVIRqW190PiK49OTp59cqrFCflFTVkEoEEUZOIfs3zrygRBYNKzmC9oAPvO0e7Iga0/e6PnVyum7AXoOVoO4UGdllFeO4FxCwpbOjKMpSLi8RuLr1E5bapwJaTMecaJZ/CF/FEPSOUkigR5mNLS6oo+HKSMLr/pulcz9a2rC7jbh8+PWQJ+x37M7Xjg/X1L4MYjid1l/bn/Ea0ZnL0bUfa9ZdGP0x1cfe3T18n88B1UNoJEn58RhTayDGnD/V6+fV2u4r6U9s+p+/X2y240xm6K5/q6JqdBzMF6ZUN8q+ua2kfT3j8XMprMxtqUL88+ha1+Rw4uv7/iJ6DVK9mDJztz9YptRQhI6r8a7sJYa4B9Zd/CRDgaAGlY+oPdQWJxXfyTf/rnn3322cXl+Te/WzJnuyq+vby4BM2dvX178eYCuyDyLeccGbaaJEfAOQxXFpcV87MxuFogWrUwqVukYNYwnWKqHmZZPcOHY12fPFklsxQQaTsE0jxfAp2xf8FifrWcr+Yzm8UFPQvhCh4a3wqrWboV+tWNe0uDTa01wpIKcyivNdZSgbCGnXUDHqeZcvTJ/DM4FCsUACpyYCYeCYA1y2mMXUnILI7AZZBPaE528he//PlPP5lFHEFQPeIzrj+PpxdV+WRZcXrX6XS2jLLTOD4vqydVfMbZulF0FhSPKozyq0dxdBVWj4Lwoq5OgmRVFWleXVXVNMsvsmyW1YuymNZxluUYsierLGV7wW+/TS6qxUqLAKag0C5tSNC5CvAsuEt7Qf4IAR5Z+rBWmzQaiTjJOAmZ0CQ1Xc0XWgdBPpoLcqYviKKLNkztXu9M3h+bCAXS00n55PEJKz/0apTglqdYLi7zLJeCYgZOmoxHrSlx3wnih5x2KaDhSAuoKrxFFRxBoU0ROl1OiwYIvWJhBOUyTiZhMplmxWpZLPPsMiwfVRWLJyw0kafA+Ed9KM6ls2nbdIG+Ke2BEWf7p2WDpHQuTmh2QbXStdTiFavLJMDnRqRLut3ngb+J+98bN2Plbmne1VvXtWXol3GopWPa4l4MosBgYCTQuwf2Qvy6GTaU3d/eMfyIg/Yayr+/lrb0zb+H6h2ieDN+1pJH5jd6lA7lc4j/MfFDdfnx7r2wHg1j6HZ59Na86QpAR+Qh8CCBBwk8SKAnge792gV6Wdq3lxL8cK8E6NHecQaA3LS0wUuAJoYgZcGs/y9/9Usmcf/xn34C3A+Tc3b0zqZH/8W//Tf/j//bf300O8ZvPSCM2XKrCvq4/uRHV9O3sg7Hn3sBLOM3gaMAkqOjIxSGo+MjiDOdezRj18Ei4zQwkHiVlOWMlQHyastsgJdQaMIeqFfojCL8d62BZ+IMuVqkWklc+1/JlkWGPSqqxEbhETFosmn3NEonshcyGxWm+JlAjnH3iSk5RibR0+NTVJa6sInlgNPQmNHPf/4s/he//JM4fF0unwacSFU9CSaXeXH6Fjug4vjpozKtnoXRWVg/CePHUfU0SM7q8jHKQJ2fhBgOVac6criYFMFVyam94eP5Mnp7wVEDsyqcLpdxGWEHk7D6UESnb8uLU9ZX8B3Eqgh/UcxmAFNsaEFylS+W2oPr2oU7IDUTDYb79eVkwL0SneS6RNIEwboCCtiNBTQstAjDAk3MLLtOHdAiDTFksqMLMLNZLi9YBOGwAoyA6F9cnUZTLblw7i8qm1gOE9JIEDW0KhYB2CKOTgCGZ0EIuzNbqyFeeiK2RKv8xYun/9n//F+zenR5dV6w0zo4zi7Pgnr25NGTo+OJFj1QL7QOg6kR3WOKq40MAT6YkGGSvrt2KtDJYSt+nVOCW+faKPxw83FK4KE7P85++1C43nyFHM6VJo+GLjc2+zUMxbd0bjumTSc2G9mW4gf23Wif++eP3yHPN9OGfQa3fpK7pH787evqiB8UOLTeUfkH5vidhq1ZFn5vARM3vRo6tsLWl+RNqd68nC8TP9yn2OeWuX+e6/7LoF/2gJiO3E7SpBKP/IFOTMi6KXVgO+Y9IKsjABxoGABXYYWywAJ+NZ/PZ5Ml87nAweVqNZ3OLhdzTFpyZl5xj4PVC8e4YsKNkQdgDqsW2fOE5uZR6F9+g9hWfCQHl+A3NAEmjIkXuMywdbnSdAnO8lMYYhWCaWkyMIXPbLRIGXyHZxmfIChurXl6SxAG9vJnMfaBhO1OqF9rB0hNqwRNIRWhYJ3UyXGMG390DG1CVV3kjc4xU2IymWpP4JNYzgbG1ieZAVtjzJ+WJ2HxXZVjIv8lSkQUvyK6rl+x+zUMwfpPwug7JrnD6MuwZIfEQub6Iab/KDULWl7XC2DqKpsvzIIF9QRSOLLk5GBWJMJyDuuwh41UUL0Jq0WalLM4S8Jjze1r9ls7ZXE7xHQ/LoQwujeZWKLGlZpqnyYHtRuiTjJKaGMVdrN0bZora58SFOLhQ6OCpR6zp0cEKBs4PmLdIQ9iKif9WQTiRyspUabwaYpPpBK/rlgHSbNQZWqTJMuKiurjnaBZeuSA3RR04B4t0ex/gPRYk4mrOEx/8fPP2VWyWF5wrsMEyRdZGp+wF3q1QnnkjGFnNURmSD+GXJSei1+0Ag1mTMusDXxq/Yc63ogZMujiS5y1Vxe2QPmJBkJ/3f7gcwAGfmf9+cWWg/X3/vfGOt8hoTE0x+Q5pM6xeTViNy97Vt3I3Eywu4P5vNHvy/hfpT4/h/bv/vw7RNCLchRcdJ+f/fE9YoqgT5onZWfyfUYO8X8fdQ7V5cdvvSquYWMrt8b2HgXgGmKDybfvnttTGGTuThPe1yi800Y8EBuQgB6Ph2stgXuXh/966sIEBOTAPDilMfNp28JZYV0NQ7LVMX8sGHtMMbAGFF9dXWEc//j0dDo5Yta65DAmpuxxBWoT+AU+2AFw2pcpjzRC8DIYB0PyJhQWB9m7uVtD/wEkZcVtR0MB3YBzTBGTAfUAUxxcaoL8KGcwXgQsIMgrvG4/UzAvbC/pNTGWqZWr4lWvvqjIYKHmyCGkbakgDfauSk0wpCDQKm4hyrIBmQDc4glLfdUBMK8mZ1nypkg+l8d6zgqm4TGz3WVW1EDTeFJVbJzGjgWxoGJYeSAwRYG8EhHmMNJ6WAKYX6wWpyesCTDhX0rnoibyya2nljuEjKPjmrPFqoWWUnCshFFWUaayj0LRKnGCWefYBVFErVIb3GWt6oIErPUW0TS/CUt+EowJ0gVMpBIYdKV6kSQFLEadY08wZxjQ08FEVlExUL6aMEAiO9ZLtlU0kX230l60/1talKK0isAGXumYCBNTHxQY2wSs3SJsk5A6aCJSFYgTJRBfq6tsgS4qR0lFfTm/4tDfGdWG7DhnEUksay+BTJ6MR0kOGRKtLQgWJSnw35rlQKWLcZ+i0F6d4IhQdv++zXOzb6v8ZkUfSj1I4L1IoBmz/cfkvXDzvittn+DuTXkoQzfwAtTWObKq/RrzDhu4gXnZprqBeYsxzPi6rB92Zfsx19Ac0N0PpnNNNR9H8t22ejy18TnHy9HXsMeX6ue8Kzr30cY+tzeIcW+CgXeP0E6D37zgRi1+vAvbZzMn+tryEgNk4qmnMm2gBNU52MQMrTzQyyUlKDfKMoy1mWedHJ+egGF12FMaP3qG85+pXPUHl+AxJr8BcExiQ6wOzH8lfmwKzhoDReooKBQF5+6RbKA9+c5ULVQIYeA+WgTFBRzl5zHPauabZU6iI8kgi/03qXj1UYHqmfikIof4OtRmTVS0WgRJa58ipWZIokLKLGvQZsCiHYIGptUZYKwyEAK6YoyOrQtm6Ji1Y9uumWrqU2GZwbzAFkUz1tKYUBayYoG5Dt5+jrTPGU9BNFRHVLH8gecfCgFSCzVNE98SM3Yv3Ji5S3G1mCfaNlslcZWkEwQLyMf0ZZlDi/ZCNktZpygRPhsQMP7RjuuiqCcsTLDIIk//kqHpC9ZetVCNbKzey6d2u/5QJsujD5eZzQxcXU7lMKnyyyIumZ4HbQPlacQCulIM6aXqSKockQyQWKf5Mm2uTpDmJ32GVhOl7lW76VAJl5Kgf7pQfou0O1yEoE9jlVlughgwi5B1FWQUY+0DkWQ65fO4DrESO2K/CUsjDAzOo0CFMz3pTAsLpqKZuySoUTufMGdz/wS5XLNduPm0aH1419b+HJcCocG3zcDvlDjbdQ3S2ZW5i7uPd5SwgRS9rpJrAo4HJ5/xpa4h2ku+A8rqfXsiesRvHLEDRw3QOrR/h/Lvx3V+5aJgD+3Gp5/jkLCeGa7my93s/ryPMbm7ps3Yg+u9o/HQO1dnk63dd/ewArC7oofYBwk8SOD7JQH3Eu7e7ZuNc7/bZBn9A96V91/uFtaPDW/JFrKAi9lmCd6Td3nwnSawZfqPq5fVcjKZ6MAv/URgu5PkixxHB3KTmRdHzPtre6rRZDaXKV3BOsFJ6gYvGiabgey4BfyZ9Tc2RIBCoG+Z4CzSjMRLEC5OOqNZEoP4c6NDkpoKIfLACYGGdVVnIJMIQw+Wq2HC2qwMLiB+LJlbTFA0/a9JaZs0RhlQssSgXwymq7XxN5AIcNpDbvnaxPbm/Ci+iusnWK8nAS47w3g6Q2nI8dxDmzhUGP+nQHidC2YrDmajTw1OBoZypfM8Pn2cV8WcE2xVBMepbDaOMY6fpWlWZUvbiS1PqpyuVgdT7XzlhAUdg0VbaDzLBHjdCUL8hBZE0RcOs1szd3/QssHLT0OKCE/yQ+1hzl5SDf//7P3ZryzLl+cJRbjHtIcz3nt/Q5KZv6zqqhYSUvMG4gGExCTUPAEvLf4exBv/QL/w0BJ0PyBBQ/OA1AWo1FnV1Q0SJVHdolRkZmX+fr87nHGfPcTg7nw+yzwiPMLDY0fs4dxz791+zo4wt2GtZcvMPb7LbJlZxhFf8ORUskglVq780SzskmTtKIVQGDMgdJSKYpgQoPbJ1gHuO39SLi4vrmjr2HtUYw78n9gxgo91tUCrWW88HIxZmVExNcJqbGyO/ig/YZ002/x75Bpiwdz5IvpkdAvbPeikThHNLdm4mpXb0sCepHXOgzKts/9kQtaLv/Ro/GSkfhJ0UwM+ChGT2vGpNTfV81nvdij/rrsAteVOPojNfUJSnv0W8+HebDXHJQhoC7CO4b3P1crZtGWb4VSwHZPij/3sonOIXdjOc7hl35azpvaGn54YN23neLiYrlpvcGi0y/56HUQtSB+ec0OSB71pt9rdyIvveFu2ntKuOia+iVdXnrtJslWqJVGdvopPgc0RiMZP9yrfHrrkSSVATW/qfKoi8BP3vCj09QDJ8QcyG4L68PwG1OlRLVAWdbEhI3idNbtA8N6k4EDf8SQfjdgT9AUe+yzexQAAxlE+75+XsbEPPuJFceMm8I57OwAMWHSc37NwWSfK+Lre8SBGoCKx+v8McTXBV4YzoBgCZ6JAlOJWm47E45nyNbK4XSf4UaTJHkQOsQeUEYNG7fhMgRSfwqne5PWJxaFFLO2CUfeVBz8GonVTScRjEoKzgcMJKfz4+yMloRA7/S++gu0Al3RWRHiu7YzSeK1YPZdB5zipO3AOQpUPI97g6CkaY1WDcoiSi1H21dfPxuX5NX7tSuKaaZyHFlfXmFT40V+VczbWZLx7PhmCsJmFqU7YFmfhQcLzAlMEP/hFNWOXoTMqkQ/foJAqnfuLlLBZjehv6KHuBRvqKF+g3Vp/isc/bt2vM8bskVcjBU+pcPJhwx12SYIAXKgezcYgl9tGUaklFRuTqSBpQshug0b5Zl8nOhmlhlgCnH5ADDNFejwFSxdlLKoFymNdQD6RBwtR0ChWzoLzFk44goLug63Ty6AQpMIIIUM813CUVPCMmhgKUbc/QzQ/Vqnk/4Kv9vvnAd6KrV/w/Qpoy9DMT6tyof+d1wNIu5Puzsgj6xX2/g4806R9NI5qFr5TuEuTG8SStts6X8VEo2wU2XXTbrtD2iv1h3bZXRyME5MsBTuodh2EjuXbRqodhHdHp5cEaavfza1869/lVdZ1jgecAVjqbk38KXR/DTxp9f46fKJwDw0c1wE3Xug73jc7BNkosk6voxMNQb9O3qI6P1wUK5Zy+JsfdT05SAC4A73j7FuwIWfBjkenrATAhwMUbh6Xb+roTSkGdHEQmS+u2RYGBw+Q/4izrXSUF985ruzePBXzCdzO2BOUMXMANlaBJ79CDtzH0Dy8cTYnzaF614+CtAGkujHyVft6WIwf8AT9U73UagoRaIb95YECyLDK2LYGTyRmG0AMZNYEYKhf7C/6x4cH4IuvD2YGA/T85zjeap6zAOCCXXqEsMACyvV7n67n0JqzDmDIWuiJhoxQKGYWKC95bkO3wRyBmA6B1xC3H/G1LkG4Ws0X5bPJs2fPztn1kr3zZwXnD2hNYXWNB4NznN9dJqthsuDQ28Uk710qg5w8tMEWsx51E0bFU92j0nFv/Zc4PbW1MH59ocrQI7GShLjLDPynFxA/4VRGcysoatpED6G83SOqqFUmPW65p0C4fmlYurdsNh6XN2wQFOsvEJV+4LwQflDk6zHbg4MUx4HNr64+jE/VJHrBMUqHMZs8Tc7AUx8s7xW2ZqxQMl1pIG6U1Kj4rD+WCtiRtM7W1Mo69in0pIGfhAbovht9/scX+miJkP/HfgiP479D4Xc1ADwJeNPmaNofidEhwu23z9p2XjtmR8c5wMI+iM4O0vui9tPcPz6R6Lbz1D8P+9jelubg1215Pk96o10+/4jF4VXc345tOu1Wa+dJMft7+7HNdDjfLnkeNr75BlhS5h3Q3fmaLwjDCbdZtE5JpYlmFBykxopOLuGx3vjiScAfMQQCbMmLVOC5I9kMyOOFrt9KwPXSE4Fx2gCpixsZFGYcmO85u7yD/UDb7KDjBALj9dd69eS4/IDutAUgzwpjxomhnuNtxPKCwaC4ORsBj/tvtDpYHQoExQsHuRan89kNO8sz9OyYsc4xGgYhpzMNSiyMtRohvmIjAbAxLAWw6FvYVvOvGOMmF6dYoQHSwKq48YhY2V4SUJr1h5x1lrPSmTH6d73qBbv4l4uXUF7M8vk1kwbMdMD+hpF7HrjJqDcaThz4DntJGcIGcHbFswUUQpn07MED/h3IXyPHkWzd4llpwFroLMfLZTgZsRigmFUcqoy9hM3D+HsxwFeoN8th2WNTIBYnfOxln3q9c0iWnHRLTaK6Npl177psykayGmpeLsBg7sJJFof3z188m4zHsYBB3SK4J/0C2j2/LOZt7B7oNqZP7CcyNx/GkRUnKwuZraZh9vREzS5tZrqA6R2aycF7QL8TJ+zLSh/IxxXrffNTZpDwAtJSzNkJlEw0sU94tGZwSvdR7UaNqE3kSuqghFVsVjOFmzGbpZvq+ELC7Xfmj/t2astDL9hz/bjS7hHMpMbv5i05I7ld90NK7cjjm2qD+9GU6cN71W5qs5/vEMKodtul9vJp25Vq7PJql12mbH+nt87h+bskP0SqJu8urXbFN8tuhJMmWwqvf5dbqWB4Jj83KBx102K0Lg2vPanrfCl0XO7t0k/3Txp40sDjaeDeT+cmgeZdekcQU1/e1+mrbCmPHuSBsQIiG4dJAEYWBfLzkHJHBsyCKGIcKBqXHlBuIaITl/FPUMsQsG4d4D7gsDiswq1fSwCKOsmAQJ0rIIFNgID7I3YNKlgFC6zVPrAIVsZ48ur1awwKnPRLcaAIkOHvcv78w/sfri/BqfyYxBg8v6KIpWBOEyxfjgTSpQCEAiCH+ERwy9g/kma4r7CclEMHuBOohgFBKki3en4yfj0BXz+7Bu9mL1nOPF3M2MgUUItFgqHjMtiqf8oBZ+MR+tIWknY9Q0GIivDJVWst5KOY2nNTID+DCnz5sVDnzJPoIFOw3c9JNgMUg/8Xpjlh0WM1NJhZv6nieVVcub2mioiJhlTj1ECJ647PzWTvolitJASLDIyxl7jfZJOTZ8+enykCRk6oHLMIjeCUxBwIfSNcuhAX6RATasSUbk6KYuxF7vnPib/MZ2QcFZwxnO/6CGqDkWkjIHstEapwrodmLjhKrLzKJ6cshFZTacmDmaM+NOS6lY0J3UZSypCiotVXEZG8rGzc7I7ZLLDO+BR60sAXp4F1xw/R6LsH9PAvrhZtgVItUu1+Kg/kVlvUldqzC1C72o2YHfsQf2XjtuP320PaW7slk1nbLm/HNIQ6IvhQdJosH4Nmk/6x4Vqelh1/LJ2Hyn+0RXsk4/09rU2sS57Ha8cjRhfa4rZiuuRvZbxXRPfTeTjZ9OKP/CtyO96bRgnS+RRDxZW+hH14aPNZejoWKexnCYolL6CLPKntKcwdfjE4uuiSwV6UK4JCWVx0wHWxo0ueXwajcywCoSC4lhFegeJzToYqqnecFzuesO8NLiZsbuMZAkGKQhlksRPy0QcPDp7hUoQXEG7unkysSIx8Dz6xJz2D4IB2LBfc4h22tj4OJzssD08jFGE5xkZ1YhKAQX5aNhKBiMwhxKJfqwOY112FNb8gUeB4mZ2fDv705a+Gw4t5/yUn01bVaVG8Pj1FA9XQ464mVGXgSlZME1c8aBNARlYoKsynkCFkU4coXpkQTtxLOXeqQXNE819LqWAXfdIX+YCZkwIFDW+ojEejjZn+YKlwrzedOhMCAXcBihaBW6gCxtJbVjxq7wcxXEkb6XYrvCpi+0GNiyZgFXSx4FzeMdQhDKBnvyI2PuKXoyxvnCmhGlhDpKi9ijW7WCMYJ8y1UBVStJJonumc3VyJ4U87SwbaFIpC1S0fHj6QkDGzAX7T6K6a0LSkNWNGiuCyLqsQMUrPmgeiBu8lxhVxUQ/vlpexm1cjohHczLP/ruv976yIkz8Pcj3GOzO935J4x9I/Nn9bCT4N6Ccaq536ADFd7bKX9CHv/FT3Q3LuZbV8LzUyHaLVDb2tumxTjc1wIr6KWeVvMN0TbLZOV3035NlDa1db7yu7knkVgHijz3TJ0xahS6td8R2UfcW2idcxK8U2sgRWv8cMwBazBuV1ys7IdfJT6EkDn0cDqSOuHoPPw/SJy0oDaH71LmiGVxnqwDJT5OEmveLDkYaRV4f043yuHjvk6MDhK1dXIGCbcFOPbCCujtqM/vZwjB9nwyFQF7AnWgPmC0UZ2VUaoBtR+u6ADoMSoBWyi9mcQeSAjGz1OWM5LdAZeE0psWO8ZnUHYoSZfe5dRSs6hKmJeAFRGIgPJmR3elEi/zAx9N4HeTOKHEgafBlVRgIuo2DNF8miVn59dStHCFc++FusnCYzEo8NlGOWgCD6+XU+nuL0MmEjHsbjcXoaTFiAyvZHnjnFljQO4zMGLwGMGSovNX8rAL9wCkUYFfF8GCMuDvHIX+eodciXUwK952evrxflh0uMslkPk0AbwWUCOCMhp2sB2B5o8axfPMv6n6QewstHRsErbtKH4siIP9kFS2+XORGTW6tvKmaJSJ3WpfHc0JP5F2y2gOp2g8icJnwooOWmd48Wgjt3guptgYxlu6lLEI3gdBKWTDjkHxg/mknjzeYjBzZTCARtLlaGZPSs9WxQyLoWW+1Zx2U9/TZVEsu4iIlyGx+RvFJ7kLToY1yweiTKjyHtE82ftAaaPW0VXj8Ly674U+mTVKEpPE2TYr5Y+ZO0K82v+9Kgyt+0hx3W6YeH1mP/SQtLXfhj9tO8fGEzXPha6bussa6axcu+hi9debrimxYev/j+BN1Hhw80xrNDWn64+UU8mH5Th8067qDciDo85y1aaj20TXkaDO8YPFzOLgbH9pmm/Pfh3uZ7H2o7apfeO34u2yDF7Mhq1OpsVMJ2fOCUCBsIzlaejLYz2gzUZgher3sPaYrLB4UN2Acs0hWw6yOOS4/7dwasH+K3gcO6jKszC5TPAYJBHszqEk+RHZ7u5TvcOjxHqpiPs+daFAXHfmEBuB0QwA4LxFFlXPNzdsVBODgIs4mKjfnZF6dkOxzxcO7IOC5DFXvhC0Fl6NizIFJdyJ7/ypQwLoYCcxDYCzixxDC3ZxWDQxFizu42qQwxxdx9iPC57xXsVHOSDa7y8bCYX3JmMPvUcN5XlZ3n1fOy9z3GCzCZ7Tj7xYlLoPN3ipE4C22DOxR9kJcI1TFv1x+jD+waMDS5rJ0GVkhXVcPJYjItP13PsuwddS36n7L+b1lHMRiMWbswGQxZYj3s/bGa/i07ZzqBUHytdqOqKp8rdL+MUAWIEsownO5T/hQOTeHi9AGhq/kLhKI5HJevQOKnWG1SrDgMDtOD8fmwmohhzgSHqPIlkWX2ve0mqCfG6SNqQ99Y4M7DPA76dePOMbYSL307g1YhjZEeD4WPlb5MdVATPkKfzEqRkf1a6xqEFFRj44p6pdMMIn5ZI763szbSVxSJi5zw4Ds8d5cz7Y3inc9s1/vZCm2IechNJ5dDCkceux8V6pKqQaf5fmtEf6bgHZRznGQHaKCt7cN1cnjO48S+LXeX3tITkjp1TSN6derb6weBabxvTG/KX5fd212b+ZsydsnTzNMVvqXsqjIrwRo16pKni9fh8cdSrncBeruTAwMnSL+qyc48x0Ymav5U/IKvpIQHUUHqVV+gLh+22zxeBVMrpM+VMn8qwj+eWj4P5VrPSe+3Pg+BMFMR8tYB0DTQjQFsMP/V1dXp2ekgHy6mOHRXwxFuNnhvMFLLklsHc8HlCdfinsF+jmBeABth0Ss7Woo7A0hF7ZVqebE9aAA7ioCNwN/D2XQ+HJeDge5GDPYLG5leUBQHhGM42SAmgaPfbLcZh5FxVpSnX3EoboznYxtwMC2GCNJZDpYIlJxJEr5MwM59jbhn9oCx/3CVYctJFgAzfg2EDk3ABEQ767OfKSsPMBXK0WQ6mtyA8XWLgtNo5Jm47sivE9QgH3OYFacjxMIIB74F+r6X02dgcGFwugLrmmIu/qGG1F5AFXNFhHsh4ekzPH/10j1zJuPB2Yilxx97i/GwnE9GY/XEVA1LKa6f9cvLXv6tpSlMcUful9zkmcRY/VCYbSlEnUy51ELc65KDyEqNOIB3HW+YIQH9i+SdKgHdO9yPJpwKghp5aSqiZY01FQJIQ/hFcZyB6DksF5efGcwa8BTtyggZ+QuhVQZFcYJyvYGrCzgpwZUQNC5J9AIOEIA/a0UgYsm6Zqle9X2j/hLsvkhd5U3hdkwqvWLUTewLStlf6y9I0CdRHlkDqSekz1UfXvX5R2Z+X/JJzq7O/FOpBb+L8bLfpY39NdwqgSLIv/yEZnptEpHitrI/0m3bYm4y2p/azJnCmkYswPuhnXJ7THuEQ52gJGjedjU5tum0S9uCEPcn7ehrv1SmQryLMjAFDe3P0yFRs47tLM2W2p9zf9l2qt0xXcf3y6aumhImesfKuZRj/d3sG01e6xzdoTb3wyk0+SYOTWo28SbfrhM/HGkAFzefFwqDmF5LI3+7SWV9V3MQp9nbHN1MAbM4Ak0CY/o31zfjyeTs2TmLOAXQZC2esw97Ub3R5wczAMQmeAWZCeOG2elsOiaTizrhASKcnwulU335DkRL7wYz2o8BtriCkAoKL2b9jAkHjhV7Dsz1uY1NgjQiBJ1qxBFoFw0LzvkM4MgNKH9WVVNsFmYAWHzMH5tk4itTFZ4W7AA8mNWlxsxXuK2QKFYdYzMgJiPZgFlKUg/2MurPqnPdWPoXHLfFaQD93oiKF/mE2iyKk1k5mc/OeUeN2J4GKKoQ7pWU5R/xSWedMPMWeOn7CLMyQbFVtir1f/qIO5Uc935iKqillMNPlvNSLr9wSUDxXKOkf5EV869ejF8+e1n8Op9Wp99/P3335luk1i7ql9Ni2htgeLzpz76RHgm+pJLqgxHbFiHM+jQAIlNqLWW800IEx84ZF3xJH6jK1zQ9za2mZhh70KZ5RvPFJYeVsXGqQ/gQyDALpxSy2XGayj8xSs9d6mIaD2hEfO+RbegnVhEgLTLQ7kpSa4AsIQK6oNnsXzMsQHTN1rEsEB8wubOY3wyHzHkMLi9uxpwQVr2Y3szz4QXtZ2eIii+VqzxBz4BcuNgfiWuw8XSQB10ZX18pe3zWM+0pNX0GyeYzuyx2l+/Qwrqhtkjch8vhY/9bTPfctt/DezJvJaWapvHRw+t1OMc6Z2pZXzFHX4dLdTjpw+U/hObh1FaPfk02PQcrHqvbXYhru+yq1CqQiqfHYRX5oIHO5wKmW9y5fUxJjq1W9y8vlFgD8CDipgp3VPtBOBxb7V9Q/g61fz4NpAfg8/G7Byd0dR9p71n8HoL/lIvu1/gqVWAW0CdiUq+uE4Fr48mYxJub2WA4dJzffSgHIG/QpWPhw9NoWdw/qsXC1QIn7NM+mgAWHU7n+KycrTMD+5Jf0M6vih7eCZcKTx1LDv8YICDeHgu2BcXfHgAd64OL+Wg0wfLglYmTDah9CCx3e058fBwAJqNHBOCb0xsOhuN8SHEsD6EqLkBICAPdlvqDRTGjOnAGywYYTT0y+ZG431H6+dCS6VWXHLuLhxL2A1lxdHF24Nq96MsPz3uzYtLvTy5z3IFynJ9c+cCeoOB+vXJYd+DaiTgNINVbPhBHQ/GLmn5WUzgUEQpc9nAwO3KYhz/+c+upuRCn+o6royzAcMGJyBxHxgqEYpifYKtQSWcuMoyos3L+MSwymzIoAIPE19CMT4jXV+KaYuuoZSIFiXFKASLpQgDw+IDzCRjCn/GfaR7Qua0X4N4Bfm0zZEbjYS06e0KUZ8YxXeLeRNZOoO/6AVdokAG5nAQgVgHReIgie6JEAAuWlfTYMYgD4JiLQc39DKN0erMgajwZuoPQbMasFDYcnl84bwWF9BnVWNZ8RTgC2x+J73asBLZS2jGtQl9QhIp8up40EBqgJzf7w9btsUpKxT/z49DFLgnD5xd27dIxBoCC7qpKs3nuVJMmgfQO9BX7mNd+i3l/aluutnXbjmmXasfcrVSbTldM5wh9V4FG/P4WMZWxt68tkLTXDCcy+yk0WHUGN2gGPji2pZqkbylLje7zfC478F6ruinOEeHmM3KIVpv5m+HE8hAKRwjXyLoxxt+Mf9O4abz+DtBV5K5fRMvfhaTqQF7ufKNnh2P0eGwMhhzB++Hjx8mIndpdzbmYgU2vw9XeFbmO7PaHl6N/dT19e3p6dn0znU3Z5BEiTBKwItalueRZMhBZgwXBa24a5MAw+A9ASXTJho/55RQ/dhz+h3i2Z0U+HDEt4Th3xRJhXMCB/sUML6S4AthPx2djfIeGwwG2AUtkCyYnND5w5YHxGU7nWCg6BXF+LYcN9z+B5/vFNwFe00ihvKVc9a4FmrOixxwC/8D7RJ6RWvXOx4PTqvequOEE3t6wOq+ya3L4H4xbehJCrCggBrOBGnkiATKmD3MtXnDbzz8kya016Q78awAFIb7JyNj/ezExogGm84/YFlhG7MBTVp+oVVmy5RHa4PRlNkc6cV/N+byXDRb5u97wQ3/20ryx85LbZUo5rsVrv4K8xKPykZBYp2wmZ+Vr7SVqTN1jZ0/bql8468In5w1o4+maxeRR6ZZNiInxZEVsRo51Ru2YRDNMNXqRTkyg8zC+uOWc5o+93g3KsX5KIgG4JXUpEhEQRBbMSCdYRpg3mJSLOf1jynpr0L7dM3TeH17EemvE8wms6xe1jnBUsf6ICGdCtq9lwa34FoFEvv5sZobAYdex7412/sP4mEt9PMTV/L245W2/l12S51gKh+c/POdeMZc2c3ozNLI29dCIviV4f6mafO9FLfXn1Cv29o3OXre31C2KOCC5WdPt3gvr1fO4ChxA8zGywB9x1if+7uJRy5iyrjM4A+Cb9SGvRO1haT6kfE+0fmEaSF2x+bIgpvkA/8L0cWx1k7aOKLV+9ptKv5VAM3N6KUEogDDgARCZzngqOJ33b/7mr/79/+2/Nx49cyQ6ZxSeRboFi35ZHyxULOf9nOkCHPdx/8FBPK0MhoI+MmBt0aYyOtobkwHRHdjBfw6ABJcz3Czk9JQwN4fBnBgsZh6uNRj2T/CsH405GiDOCQOFgiA5FYsXqReO4DDFOcTy+Jfg5FPMrz5MhaNgU7fn51gB3IfygnW95ZDZgFlxjXVAWfJbiK+AoamHJp2EsOBZWSgxObNLPGIG/fH1Nefx9id99gCta5XqlV7qAm7AaU0zivsh7fgIiqtgZEvsTY9c5uQvFbBWjnzHDIabC/Gz6Gpk2CxGrl1Gwa5lYGYA0+YltgGj4BhduuqsqATpXR/wSPIEMwvYBrBUBNrNi/XH6B79B28qPmH83jUAZMAicO6DKRsyMunCRAVdAV27DqR3fX3z8f0nzSIWBLMxK/MkmIJu9UMu5w749qqZKot3zAlYPTuKEyxzDl2jv80wBdkZClMO1jlbrhaeN8dhEhZHO+pFZ6KgsKuu67i6suuIe4Ueltq9RHkq/KSBYzSQXjzpDXBIuR+3qx8u5yF1eZA8SYFbpDbl9CW3kYHfrc0cG6l3u4FDiyaMt654rT/YqMAW8Qe5bVu37ZhDGKVSW/XdpaRDiO3Ik+zUlHA3CXcQbUQ1aTbDjSz3Cm7QvPc4x5ae15Jt9cmt23W+zlCzD7dnXZqjBZ0k9iY06e/NWCc28zfDKfn+8jRlQFutJ7iZ3ghvKPaQcgHGpb7MnJ6NuiGJJZ6h/9lsPuzlbNnee84WkDmrgdm73YHeykW6A1AoOJMlsnh06NvNgD4QD+QJzvPwXlCwuRnJBZjVgFjSoDsSgG1kJlqgzkeB6w53oEgwIg5FrpVyZNcpCI8XduMgRsPxAmccOIA57j2I4foEBsixAzhI9vo6Y4Af0Li4ZIMi9u1h8HjBMcMSWTCYnI08maq4egayhK1gkU/sEw8mYDwb1u6gw2cIJvZWciLIOT+bDF68GH1zymg0vicsMCivqSwQXX1FJnJLkdUF6pI/bolIaqZyH4hLTM1lWgyCmwexXhrZ2LsmiEimpqnmOAm5YMmFGsgWfU5LY1/UkHhezqvBTS//hNOWMtMbFZ4/qa+vuBEsExUfkeRdfU8Gmox64fZjZleDPOP8szGNhWpYXxF2HYsrsAOcBLBxyZiWW2d9jCM9u2gsdOwaBvcIIgPuUmJ+tIWjlMw8SpliZ1FNO4sChLLNXl+cAM1hwDcn42fDweloxP8BB4iNJr3LiykTTUMWkGMGzPQQgxrzErUVAK0lidZ3SoEFgdVnK9etEevdgVbS3loGnsdkht6x+Q8Q4egsG78XUbrznb+X9sO+IdusHox+6zcx8Wrq4SBePClcHdQSzUM+m3wPyX9LnlX/T10xPQKbZQ7tdasnaLP4ne+saZJnU6qmtpthGaXqpM87M75TQaRNKtxTOn4Imum8+1KhB5T4AUk1Rf15hZ+U9PNqz59/beix+94vuzv0vhKhsrpYQK2kQ3BiBNLPVbyxYkB1hHs9TvV4z7BmEx97Vr32JwPO6FWuUa8P2gZ1g+kAdoB+cB4phEF4ZGBcX4yv/w8QT2CXvqNWASD07yeW8BKJghrJxWpb4CSLeqFH6cV8OpsJWV2BGmCXzWDAk663dctRACpeSQtu8RdnjUIx48wscD9bx7gqFNPFAWLXnmIrOBfBOD585YlUIUJIgMu7Y96BR5HCAAaGBgH+KwP4fRgM88no6wkLTwfshz+l8lFTcDnURMFBTMri3PhUE17xSWR9G3H1b5c5I0fKSRYCKcqQtIljVgFHKqpknMcte2CZA/1Or2BmcYhx0X9WFZy2dqXWvBJBS8dt/SFpZKt5xE0tMpJo+oRuwqEffI9FNb+ezUdjTuEF8S+KwTD1kGjemiTCYAno8kS703z6XrGEAPW7ZywkdfSXIUGrJnv/KUrjIwWjvmEQkHdu7+sVP3z/7X/4f/jfX17Mi/719LocTvLLT1efPn74i9/9+f/gf/w/mozHoRB40OVWhGvhEosNFdQpKW5XylKsNYnOUEfxzvxPCU8a+HI0sP1yOFIyOn88w0cW25s9EXxwsnt53jUxSbn5CtjUCW+vzeQ9MwC7qO2RbD0CsSdTIwlR7nlt215Lcs14PQfoFR1Wb/zwf6ZRjbvVVwn54emQP9X4Phb5w2qgqflmeNkyd/k+tnaH6znV/dhdILrqcKycXXTa8Xdro4eVp/mw7tgFaO/7sd7X/+1WzaIMH0F69VFTEq6m/IB/Bnln85uz8Rke9aNxgEIwNKP75ZRDrxYzRnnZ8mXkyDmZRc4J/MXwq88P2E5H9BgJRpsYCcTaUSLJrxrmGgdsJl0q7K9PSn9+ZoZyjIUA8BW+a2Cw5f5ogUMIcgx6uvUIIAH9bEbzNWVKPOD7OS4iLvlluiDDEd8sesh4xSxFjBDjoe5mMdYWsoxzM4+BDOTRVon4Gq+KRZFd7yb8W55l1SsW4LL4tipvkKJ+tYfDOy7w8RzUdYQvoUSrVngkqwEZBBOC7qdJtpgxyN4bXb946gxBAmEil1tnhjNVGFecuhC7GyEbgJuNcrBDPmWDj9kNJwCAgrkNNxsoRWkk4rvH+hC+WA+Q4o0jtMzkpIE9IfC3S50x89zvVeiPgnCsWvQ9Gdodj1J7woUyOOckjao4QLibLekNxn7/eZ/NlEhEj6hdwaDm7E7xImqrhkMy28Pi0FVxSXlj5hEmwxfXV4v//J/9C+04lgX3RzgU9ViF0fv0r/7l7z++ezf5NRuZU4TmZB6grovyJRqq3NTNS2Usr7pI0lQdmeKWOVrfu/ZOqTMl62vvL0iL3B0jVEjdpWoKXb8C7fh2zOFCRCe+hWObWnpD3odvm2Yz5mHfwE3K7fBBvBp9YD8uatM/JOZemkz9/5ZevpRimW2bY/MhWuZ9yO8l36a2m+H9vLal3Z+bV0jjabq17LLqiLh5LRNSrDRXWUxKMwCbmTYJHHrXpLxV5iHIb5E89FapVhXeWWiP3Dvzf/7I/fJ/fnmeOP7yNJAe4R098ZZne+fT1YgMiuke6KVe19A/7kwLyD2YFpzwlQ3GA5Aca2zBaez9g4+HC2grknQCcYif5z3AluA+CVx/8gW0CyaQDhgbMctsdUoMvQsDI5OJCY6DK6E9pxxeH2y3X9xcT04meKbMF3Pcf9j7BfwOQRw/cAEC6JM9yyeYJZ4/q6cKiFPTwS1rCnyWnArA0mCtKhKDFvUDEsrAmUxyDw0YoWeLUBUBRJJQKfL3w9Gkn50Duz2ajGUFsXoX/vHCs7LKzj+DUBL1Bn1uVlg0kuQTvMydcKq3UV4RuCxTf/qtRgLcOm2ibPzn+AVAMBMf5F1wUENvetIrX+gaFGSjRtAJRtRhSTCoqtulDH6HCrSySAWpWwUcujRM3JqJAJg+JkL4/UJzYV6E1tAN+mcZgPMSLPnNWBOMjJyLDC2mUJygSZpUxfxHE0qkOElCaxtXagyDZgvxzI65tsDsYoZhlI+KcpZz7IInTwynLD3Iy9EJJ06kqZ2VtiGQ5hxs12CXOLQ/re9GbNLKZtxGhvom5duV8hT3pIG2BuxR9vsv7Fp1464ev5J5FVjWo65RV8EHqeijEn8QCW8j0nynR17OkvzawPoc3xUJVczf7kq3VxznzT1AVkSOD/iq9bV/e8ku22sjPgaPumjJ5QBGXcWJv9Uy21O2K6lJ8xA9dNHpim9q+GHpNzXfDHdJcp/4ppbuRifV/bHlTLI1dX6stA/bRm3ubU22Y5pPycYuQCTsfkPU9earvQtQ8ZVlmm+MmkZ8lV/5VDKCzsWpr7jT4CUzYPfJ+Wgw4RRa/O+//vqbFy9efLq4Yt9FVtVmGgCMPbPPD97/EAGeBj4NTCcKzj5Kuny2kjY44Qd/4QugPKcsSDBwNsAPjVvhqnwGNd18xIrs7g+UdB8cYCBIDvg+n+L+7qabIENWGwM8AcBl7y1iMBNANg4l44RZAKxi4RlujfSfAacmFrxBrCRLjVnQazLEI4Ig5VdBs0OCCL2EXOy6eJkVr7L+mZC0nBU5bklDDKFqwTC5Aq8xPrd47BC7IpDkqLOYFCmwQGmhmGAulZBGQQK68iURLSJqxKlXSoN5oyN+xoHInKfLkllnLpwoQR1uj6PBgzhEQixQttUixioWr5OcwnFig19UE0bojKpxnDOrJ5hqYF8j/LiGqtsj3iDKhBDQ/uuK0xvYR982CTUFYYhgKbDMgjxKjYj9k4zdVFE10VgJMQ8Ay2Rm1DVdShE0nFBKVpVmEQI7P0PrsQ8ts0/4HmGEOK/U96QFnMNOp2wndEWv4XBkz5ym8vYNlBqNpx2DJBBF5am2sC9eKnS9F5DsQw1qRxWlutQ1isQ63IwiPt1Ghu2PxGw79oj71CWQ8tarnafr7dqOb8fcym5nhmPp7M/frnv73bhTjD2R0uQ/+qTzHdc6qX+saB/QJKu8W4EW3/vXq63JNs32zMN2nqSZLWl33VL51S9RrZelVlP2bcqoPPKlXtoM7yK/jItmWt7c67utn0SuLWeKbz5NXWVbAt2iPmu96jUG0gxAi8xTxJMGnjTwpIGVBuLNuX51rOK3A833i2nb9xFT//iZuHH5ruXPL4sKEhm8dYMddtopJien8/nsH/3H//jy6urXv/0VwHnOFpqL8MEo2dfFlZeyi4Hu5WsuYBuxNeCEZvO1Kpj1En3GX9wgAP98OxLrX+AwASUnQLHtfW+EOQKQA0eSDAAHgTLu7SLgOXhQZ39KgIRBwGw2A2x08bG0cGmppSOAUwxi4z3PalRzeclWQYKEvGWfPkMo2Xr2gLj7Bzaf6WXnYHuGuwG0eKPo/g9KBmuHieKdGCMpFObrBgw9gN/JIFNEgTHpyQQimpCMVUNkW1osiiEudnFFkNMowgwDimObSUjPmAErtnuL8978tF9hYgUETgWgB2148h11jukEGTlsHpfK06QSJ5Mt5eVTm4vagbdZVl2w4oKLyRY23EQPKJ9xf2dYKALaZw6AnYg8moEVGjQhS5XZz0krgrXAiQ81jComWZaMahGUVj0aHaqQLOYZkzmShbqMWIjCeWyIYdshm/lnLNDAGOKe/9EVaAHMQFctL1tWe4LUoK+qN69gmtIiwfStPGZZRXHzdP20NFA38R2ETiV/wk2+6ra7K9+s3y1Z1wRqddZf6/gHCB0swwPwegASrY6xqZP0W9bgg/vq28btwcHm6N3BhQ7K6Hv1npeDTf5uHXh1WWCHFD/EMrsP/fTjsF8nbfrtmEPqcp88n5/jIZq/T42+zLKH6Lmdpx3TrF1bk+0Y8u9+LhvvR4ORqZGzEZRlQpWO7pOZtPSZUgRCZk/7sYClQJlgOnxKBkOx/mgw/Ou//qv/2z/6jwMEZ7i/YxswEszhTi7/ZZSYFZox1guRxFeJwEl8lc8Dx8mSiEjVFKiKF3GnHGDmAHWpBNFxKRXj0Ixsgx5BdpwRPJg7G4FDOfv/4NrDwt9ROb8CnOL4PhxPOAuMkvM520SKjLEYhs/P8dOHHbw5MkrpSvyIrmdXbmLDXvbwAp6yqjktWgVohpAASkoorIifYiBJ5CpZBsGw/1e98lesfp7N8Dy57PdO8968AIIz7hyb0Di2CM50AH5Kdo83TkrhS3Ux5xCj1/AmBlcZ2TCqnRYhWBKsHCCYWYpnrjDus6KXf8w+oMtLKlaVI9F/nHk1W0wpEZMCSHhT9maLwR/LwXfuqxOwO8TXLgqxkihifChyjK7zLK7opa0ZMmfmhN2EmM1wj392+vfoYcaq0Hb5a8yA4fAG0amEK5Hzi4IjCFxhoeuPXxy4MJ9/eHeh5YJVQSX4YutPkbtOYig1akeFuZQnhWz4OkbLTkL2CP4Rth1CWNUF1dL1xDj9DJgBsQtCujcfj05effXVeHw+LT9RLQ6DC8csJma0lzRqevkiPNkQAyL2xTTTJbvVlcRYCUMgqSsypOiVzMatciYKm/lTnMYM18G/iXWp+Ioe2Iy4Y3j/W2hFtNEgq7iNQJNOM7yRqXET7acZf4erXWrnu/E4ytFeR4z9b7RdauytJt/kv5F/ndTUVTOccjxAvTr4riWgq7Z64DbfVDPKrAIb5eNmV1Pe2m0k2SjYDDc5tMOH9J+2Ptt0up7BbQ0sS7ZptmOWeQ/9ti4NJcQMwKFl75hvZzvekdZTsScNPGngR9LA9qsDMeLZbsa33sKR6EcN/aPErgrEW8mPRI6RXDwlSs7UBbvpT5+x+/7o+up6kI/GJ+zVCNzm98ZR+MW8x6abDIFbpiZNQPAcd8q0jCcCcJ4yyaiWKl6KkcnIulRYDHEn5I3tXPBHms1nxc10nrHsuA+UB/+BPRneZSS/z/qE5y97J4PnjPZitkAQzMdnPkHUgM6eLMwYuQ5CHz++v7n6RAXJNRhM5smDqN4oM4CsAiRhkSoJxrG2BKka/j7f9wdnvd6Ynei1fcpFjEXzI+PWQqBLLBYBH0ulmSEQyopBBfS41oRfC0aHi3iJY2oCsVgS60QKguq+ErVncsJReewOLJlexmlnpLicdlHNFvMbdtjHHJjhpNXLb66hIa4mB5jbo7KKs0H/ZYmiPHYXG0Yf+bpCoeIwbhKoxmhBgGp8OmSeZzzOxqzsQIzyFLifQQqXHdf+Ymu9wtWqYnNSpC8xF5xCQSSBtjs1Aa+LAecS4BR1M6N+2C3abhpn1knboh7/p34aklGjplApRrWrgfQffZsbPsSjIRghF1zUpq0hVcyY8vrq4j/9y7/889/9g9/+5leDrBx4WIGLM2wEKTproalDcySwlPQQicGLTMtLdhG3KZ0dW6k2L+RKcSY2iGzm+tLv1jVbh750me8i3x0bqNnqX6KCHkamlXKOJBcP811a4+dRJtS20l2jTs1eQ/R2FobQjr1Wb5rNgu1VAaQfT70m6ut2813Wjqmztr9aVmY7SzOmywJLebqsrsPl2U+/KUkKN/Mf8jZv5m9TaNPfT/PwejUpt2Vopj5UuNkWzfB++ilnmrPaX/f9dJqpbe7tmGb+h+J7iJ7bedoxTdkOCW+/NyjTerbJk+L4bOSvIUsr+yZby4CRA/frsM3uOeA76CxmUwb63ci/Kt+8eYMlAGJmUBn/C32yE+rjgFiwrXA7ASvwUPATgDVVb+RSENktBVXcWmSxVIisQDwMEHSgNmAY1N2EqFfobNPPOBSWlaZEuLA0RHI7IKwRfHSEhMF6Pp87tA++xUzAl6lkxJ5DCTifas6W8ZSdnDqo/kmv9AWUgz9vMMRGoppxyGYYPhge6Kda/LoqfoW/eTG/ZAvOaXUxqM7QlssDEB/gC9XkXlOMUQKIFQ05wC9lNk1CeDhA06Os8CjCmAH6UyMFIAG3JeJDE1nvLXhXOwwLgYPNsGIW+NbPODeNUXVcngp2adI60FDCPYacFs0+Fb2LKvuENdCffx2U0InaDQ/+kKn/Tt2WryGJbKB2JgP6Jyf9/oilDL2B5gdaArijN6uekz+UoyZQg+YNg+9ccCcOCRiQB2YP2aMJVfeou+o1NXsHZGf3JEqig2jZ0HHchzasttIpI8S8E/GreGdp5GI+qsYpcFJwlYeJmEjMCZwNs/L/+c/+xf/vX7377//3/rsvzp9X2fzs2flw6ERWgTfSnM1hRxiGHBeGicJmT7UPmVSDcPpOn3WkgmhkhBCRgjSty7hmfDN/ykzN73qlN1sqfZ83SSq7/z1Zy9isS0vspgzNcCvjklityq707fiDJNwudMS9rRk9ik87861Xct5Lb7Y6/14FddBs6qoZvpX/gRnadWly2a/VdWq7ZqkzJyFSOPLUaoz4ulBq6CWFxN1XHHpOSYnIkZ+HlG3WtJN8R7v4E4N4LQnbNNsxnbxWCZBdKsQ4whuMeH09XU8aeNLAkwbuqoHm+ySFN144zZsWi5TfT1EnrydGsxnH5Y4P4DZ3YjfxH8Psw4/vr/CgAWNzFCtZdaoXrwHAhZ4BzyRjihSFaiZH2Cguk0iRXcTwdl8LEe9H0tOPRp3bzA6Ci4kDscU4MlkYW2aZqUs6OZ2qd/ZszB2FwXqgf93TAYdgPGGqG+SDc7kYJTcbeBTnpv6gWCzOJi8B/ld9/WcCdyr/qi6KpID+CgVmJeyIfjZ4V+XnZf9ZfzhlKyRmQkhniStzIfDQEx6hohAhgKznGWsRsCsOEBt/JPxPYhYliLqOQL8ghbQO/Ec/CBF2TPgFUU8nL0IK0XZRZhxyBj/Gt2fTchpD+FTJMkyMQL1i9mbSZzNQVEd0WvlsdQDpZlL/bo/EdIltDJAvC6YLhsV83uekX/z4FcYWJjOJSmUpTCtIqNT5dBq6wXxArz02X7KeGCALzBSnBFA1lSREPBid0lzi+JqWwWAgE7XMH2kG00Uo6Z8vZCQ/63q9RP1k1f0/6uwMwIA5FBh+/dU345PRrKBdMIZYFgINaFInJigQT45IZgdSn4mp7II7X+ZeyxD8ayHMtbxCtLiRuGJD14JISvS6DssCX/x3Xf8k/Prmi5f7bgKu2++Q8j97dXQroVl1wqljp8h4bOue3ozvJvaFpqzqdaR8dd27SjVVl/JsFxj0Ovfvt/CO907Xm6W9KiBx990EoW3GSZx4c+1Kbedvx9Qk9n6tLcu92fYkdlldd5Onyej+sjWpPVR4f70eW+b99Jtt0Qzvr/vhOdt0unpvm2Y7pk1tf0yb135t7Kd2eGoXl5U8W89ufQ7Am20OqzlA82++eojZjLAsMSk+0A6+/q6uXMw91wpwh6cJGBOolfXmsxlD6/jcz+ZXAafxvbiiMH7w/AJ40lO4VJAVSv6nnLMETgsEB8FWvGUc0Q2cFCgwcJyjxgEsk4CkWyrhQqMS2kMX3IiwwHsSB+iZlXzXgW1fc3gwnv/kZqYCnIgQGAbsU08hEDnTAv3q9byYD0eXvPRwBMcpHTf8wkPFPl7Or6YF/u7kPgl8m3AhVYBhagal8m3MXzES7c9YA/AKHQ3nkyz/UC7G/fwa4JsNRlpDuNEDf1nwKvRPgjNzAjGGzAH5CIMvylSHHfbViYOTiQ3qlIjK8+W3fjvqlIUFJhPJwQY41dwwoj4Z5lM25Ado9+dAfvxuQOnAd82ABSc03AyLqwG7FQ0GYHK1xiSIrQM1TB2mI2D/DfWjoVlgwZRCztnI4Hc21cE+ikUTnKWGEAiAnRALIdTsYkHdAt3bKDYNHUZFg7hZHWwbl2zChD3BhAarHbB5WBqBuhxwHXygTLl4rlq4+DQQlVPd0RfrlJSDWASQfLBCgbhIoWI3dqKr2twK4FoA9x0qsuvrm+++ffvrX38zmUyq3qxwjyC6BNMA+qoxb8LiAEhrOyyFkEOo2w8l8h8X0sR3fKSIiDW4viJ19VR6x1/qyOtMdw/tf7N1vT26+HVRqysa9U+V76Jwn/gVlz1EmhK287djmqQO14a99NA2inzOA7SvB21ppgO/lkVTA22Wd4vZT3N/6jbHVOll1Tf0klTaiFLPu6797birhHGPoh/f9o9zRd3rk47eBoul0pb8bpkBgEBDl8tC+7+PLrCf3FPqkwaeNPCT0kANaxoyt98Jvpp8u4B7RNS+Z3glD9hhEbjvMbpgJT3p+YeXuXvq5L3J9FIXF7Cr6DEto4z3EwQCS0lUGKhvBuEaPgXQ5M5XvvhOUCxPoKgSJNBHYghpHslAIJGMO7PFL4lILQbOHciPAjq2Ezlld8iczYCAoniHYIIgJyQUX3AJFYwbCOMRRJ7x8GQ0mYEAB+dneTWZ9E7ecJrA9KZiHyGMH5VRC6F8IXWSDsyc2A5G77Ph+SIb3Gha4AkFPsBwwtYAkWMfFAiA2wppiuwSZMb/ISZd6oJwgFiriISpurKBGfCcbYtI4VuNYZWRgkpRKtQRDfUzfZCaDiqD4Xi2EJ0wMyKkHQ0XtFUBos/Gxcknpk10d2EOBHqwIF/USVHQJGYDO/lQFiaUAa3juY+ITrOgKFKdBSIzvA07qcLib/F0YGqOXyCF9d8SJj97/7vSuvR4ZgD6cLxwCB4NILJ0A67X7WuLK5C3/qmbZT/gXhWYEk3BHVVOswhoVju0mC8wdWLuxTawInnGEpF3734Yjv7Nsrq5+OH69a9fcTgATG1RpiDIwvSIeal9nEpAghYE1OVV90LCcRm5vmpZjVhLbqnWtSOqlecp4iejgc1u8JMR+3EETcpoPgCPw+cLp9p6xFsRVGClq87KsAtQaySvzryLYCed7oT43exM3p/aWezghOMsy0ey8DqkPVa2DjIPEO0PvT+Ot5O6j8xySc+tP6W7ed2H/m6Kx8c2rfxDdHI8h90l2rw+jza6uCR52p1itfty/X5Z1qY5B0ip9PJZJm5/2xFEOzIR1LIrDkBuPjo5rXqvwP6jkZ4to0nvY5FfXFw+Gz2ble9nxcVwgllQDvpfO9zvtjniPIZ0hUHSAk+lPTeJF0T28wsh3OIlUFPcL8oDgTI0/NFw8Rzuge0QMIorFCWUPqSDywfjgk2P/LKJMubLqvkpeBBEKrPKtaeMNrNuFT97xrJ1Y8lxbgHVgvE4RAzUR99f3CyuAPqT0/GIzUMXiwEb3fQ/ZhkAkb164BWS+EkQbrL3BtQLmo1VrWDh99ez/9e/+pBdnJfDi37/N/3s22H5J1n++2rxm4q93Rbf9EZv+8WvesPvqvmve4Nv8xmff6iK35TD77LZrxjnKwtyftef/bY//H1v/pve8I/ZjJjflywwGHzbn/2mP/hDb/FbSvVmxHxXFb8ug3LJOcGzr8rB973iq7L3x2rxuuq/YUJmkb9jcL1XfRj2XrzvLaa9UZWxWjrEt15AYbCwvkeYOoJ8ghwhXHmYrrt5VnQCzlZzYgOIjbZS1bGi8JzJcyaHhjc3N1glbrxDO3AeGO1MJyjLy4srVOQcSHXGDkGUReXFYga+BqSTCYxOmLPJECKMilCtfcam7Zcj87jxEZ/R8shr70oHM7vAwPkEGjQammZhf1ptE808u5LrrqlgNsPZBztkPsU8yBeL0dkJoiI5VsqNOzS5EZBkMXEpQ/3pluX8OUJkw/cyqa9guLyJbwXy1GSu5rOWqkBMqFl1WIN2ccvtu2wgpDiyYNfbYx+nXWnH8t1F4/a4Y7m087djmlwfShtNmrZofdUtbId9nKstf/PX8HF4Hkq12T/XUq10cyiZOt/+duwi1tZPV85HjW9Vmoh+8ZXRzTdDkgGE38ofKXaiW2YAju5nRxdIMj59/gI0AA6oO+Lu/vgLUMFPrYqdDcVzThr/1w983CzjjV4n7ax2goWO9bKU1r1s2F//hN0zA8dkf/mf/Cd/86//jhWTH99dvb/47vz8BSev/uGPP2AaMHgK4tOZGgsgFmeKwgBr7n/JKC9yifYAhaamn0+TAGlAtIjgw1Wq4E+3+ERQbACSySv4EwQBzLh3zJgYcCikIp7yS3hFulAWXxoyYQDoSD+9mX769JEzeolHCgAr5oaY0Suh0gwMKFx0AWk2ZUKgGl7dTNlFMyZAWP0sPA6bxLol1ZFZblYNOXQ/LwdXf3v53XfXs0HxzWL4bVle94ffZtgV7Ly5uM6GfH5ip6De7LKPAVBcVsM/9mdX2fDbanFTDf7Ym1/12aYTiC64v+6N/kBMNfgDefojUq8xGHrzm/7wjyBZ4+c3Pcr6+T303YOomFbDN/jcVNlb9v1hiW0F2uZgtYI5iVl/MVtU42tq6jxDtIOmD7oEQwvOUdr5s1NiypIVyYMhiwV67KszH41Z+41CyWNPSL495J/P6SEM9DMHIRDQdNBDjCH4/oyFFDhXzdiOSWxPX0LVqso7OMZEhoVgjN8Ng/C0r5q1MyRyydCoY1A0xWwEWjBaAJqxe4+9IhpOU1LszzcNowsTDIPU6GQ4m03/8V/+P+iaVTF99fo3L785O3/++ne/++0kH3149/b1q29Ozs/ZOgnpBi5zx2sLqkyvLNsa1qnVtz/rDEaTwzv+lLSO4VbBO8ub9HT9ZDVQt3nIv+oKq8BPtlr3F7ypmBROz8X9Kf+UKOzqCbfrof+/+l/+r/fUMl4ne9IjaUv/t2V/9PS1dXiHEX1/52Pg59HFjB8yXta7Gu7xme/g4G/kbfIckmcH6YhqtktXnmb8sfmbZbvCj0Gzi9dG/JH9SpxHWzBSePz1IHVMr47dfTO9FUxbIo5AI8VrYtinRYkPeHEEygNf4SHB6bUD9lVhleSU3WTYKmUw/Hf/3f/Nv/7rvx4PThkxxjtGLJ4VpydnJ+cn+nsXpwwD48Wu1wnALsB/UbIklBENxtHRHufynuvQ4uaV4Q3OkDMb3bgukx0r2TbzueCt/0mgx7i+XtrIrVHhCDWwXS95qLEb/SmrSsMAIIuZtFmsIjhRoOogLofT5uPYr2aEHwo1cKefbHhyxvhxjgO6jjY8OzC0rKUozhEBnCfAJAD71n/7Nx/1nu/hNY5JoisNnGRgIbiBMykRGBrh0laSVIxFBlFJgSmymdMP5Uv5Cda2A0zDuDIBUwQzREGob9Qa4t7LrH4j6a8voESX4GA5kzlGvKkwnOMijwPY5nCDoPAnwqnftpVaAsmqzUpQdyseiz1Go+yrb15NJnEyF802BMt7fsKSDVUkMxM4QnwCNzc4WdEuSqmQvd70+pp1IgiAhcLIOm4/5AwxGMVnMmUhxaE1tRwVwObTj4j6YJudqDx2QEq1dvfV6I8F50kjIUvMEcR+FRyhcepSCDZ+peewUONk4jZAoZSSzklWmpWzotmFKXu5WNxcXFzTmmyeShJW52h0+uwFmzGdXV3c/E/+7X/7H/5X/yHHJmhBsE6FDu9Mhvysmg3OZQUbV/N2GeY7skbmOrQML/M0SGwE12U3ordv6ClcdX+IxAd5t2yzOfL+PjK0a7Sf+bH591Nrp97nPd+mlmLa+mnHNMvuT23m/Dzho+VJvZ2+utXtVw8FKa2enOrSFf95anpnLlsVbdW8QZjfSn+X6/O+6oLr8rfMADQI3RZsaPu2rE/pTxp40sBtGvgRH6j0fli/JTZEXUWDWUjgli/+g90iX0Sk2Ea5yLDKIcoJTCjiA6e5Cf58MRydM5jLTpqCOTxCxuCsE3dR95woh9JZEnp6esJtOWexLEdnAeYcBgaqMUTLQVLCWY+yAkqys865iFkDANgHiAQXugEOp2VdX13O8TBnFHfIkllyTUgNhM0SUpdsWjXNABZrsjZ1PJ1ek4H8xNY4W+ktwYWfEetf5xz+CkB0Yxx3e+QkLIiPJy/zEbiTbWoYeEZOTyvTNQkED2rm+NwB+BvnE+jiI8JWR/rICHmNSioS7oJEExIH54M2xdsKjCVAcSBtxZoJ8xgfqF0xBecOKytk4ErxMf+E6xHLp7CY5GBhEWkDSpZkjMcmCu6GrTEq4p98EUumNoNlJZTwa+hJG0dOQUupKM1eojYZgJqCzIgw2M8UAvvnaNSFyxYcrJ4UQ0ayOuqvKcFsAFQ4DZqBc7bUvL68KqauFNaWcXDfTWEZ3Je4alpwYsRoPKYdPQvMqYjEOp/PMTOB79pR6B+yWnfWmjmcCWYMlSAv9QpnJdOq8kR7hP2OwOv9Pqt7h6MRPj0IVlXRfNQzH7NXKbf0T2Z0aEhMWqapqsENy7unl3MsmKyajCdnHHCHm9Mw0+kItdAx1BvMQtfIunmpiR0XClNJfBlahlMgIvZ8pBJ7MjwlfSYNpBb8TMx+jmxWT8cqQC2f+nezqbe0sVKU8bfsAhSvlSat7nCX3fYYNm63FKY0/bSa4VSqS86aJr+Im9ct+TczH3UXv/IPtq78cDn9+ecZWfWDpdDtmGXK+rudp4vauswylNricDmbbXd4qSW33d9Nmrtz3BZ7uCQbOVv9aj8f0efmtUFtM2nr7p51bPULyG/G1XfCv+Wr1qjaC3nrdUNCHbNMWBMT7eXhXFEU1/Pr/gxAyyA9IBl0C4jjaFuYAJ9HoFKcPnCPwXecDTSr7IPxvltMZhqAwd2AbqLSHktygZ/5x8B8oR0ccoSq4Xe+EMwNh4K8jG00GaLljAFBHqPceu0LFL1HOEaIKXed4TbjYVb8X9oAPj+0kYPaUijx+eEaUgrxAPJIxKwFUjDxoIRAf0ApsjBUzIyA+9hg+bBmdD7Kn7MfaD565wi3unGMXINm8A45+sU3yAK8TPEWNg8glfFpsLkImL19CAu4TYYbUagR0wgmQEzrAo0aiVMvayEh8jF/4EA9AJpP86JUwkoKcT9kJzyXD/lZ0EtJXfm5D1QtmifsvcKQRwLWE4cb7rhQJWnqKmqHERZSUYVFPsSWUPcBgzlQjVZAbGdkEgyXADmQpsAGY6EzupQ2RxOw2RCakHW4C7nTP8zLZ1bLWFYMw5mJHMSg9ZNVYQWK8ob2Rg9Qk68Eo9IZ67BpafNGkVCzWa9saWwz1wCEPxiuXx6iY7eSC/jfNeADLARmRLApNDj7E+vhjkNDjEp672CyePnyfObZadqLnAfH0cd2mRl5WE/9cVlXqhuqrBtCrdqEfnMlfaQAn+RcpqxTV3msSd2UETriIzVns0D73XL4e6lJpx0+nE5bhja1rph2jbpypvh2/sPlPCSn9FNDL+U4pNQy7+7vtn7aMc2SderefnJ/qZoc94f3S7tdttnzt9PW9+12TGld8euSX2Ro9XAvpYuIpIrN7kSG7TUAq8LmfIgZgBbHpVTpm+Qk2Wb0092TBp408GVqYPWKCPFueb7XVQBFcRPP+/qJF701LnOAloyJD2AXtwwDMw/AiC0n7XqIrFA7B0mDCt0tUXQLChP/iZItCB3wkPAuMfBeDCv6JV1QG4KYU54WEbWC1WPolyyWjNFipgksoiBmj/wy1GoQNgOfkKeunbcK4L1YmxO1xNfBhwgxZeyc0y9Y5gkuB82ypjllYIQ5YL/GATHsWRlIEe7D4fCMresJQDFgLksD0AODziPos88N+2Nyy8VcgQtnrSEFkToQaKBlJKKCYtIkLLqSD8IHdhSnWtMQvv6IjGHLpGqTldqk30WyQhvKsuCqAfRSU9R1GW+qxNWMQBXLDL5MDbC6g/LS0+4gzkmJsFu0YfB+GVsjDKDhCI37j9QqY2hdSjZILNLQlMmdPAGEL5grQnXRdAWzP9gPEKemTkkgq0gdmprQsEDzWhTailaMyAHqZaMg8tN3KBjR8uNfeBkheJgfSKIBFcCIBGolfdQb5gyZnSvAIAgd2d2sHpacW9ly4BcD/NVQRyGbjnksul/57OWzs5dnbpPKTMFwODphkyImvWbWWVvEeC61HZqEIEGu9JW0srwzOlSLgp+uJw3cWwN0sqeedG8tfkkEojnrV8hKrtW9qcfvAuSuojiR/rCiZwBSXXabvyUrlhuFGjfxkk0DTo9ta3bJ2ZBmI7g/f1vaeHvXv6AbhDpu9tPvKOSbn0vdLq/D6TRLLUs3vhtt0YjtDN5CrVXucDmbRe9WqknhocKHS3J4TiEalyCm8zqCWieN3Qn2JcHPdmrsH1y1dxUgnn5X7x5mD2z0wkRDjNTxW0I8PQY4xEWtAWAOeE9vrkHGL85ff3h/wSDreHyOUw2O3PhVl9VsNJiD+sriJXhLZhLnSxYiPXiK+6ScxnKJBU7JwUyg0nCqsX5gQTIJv0W5pioG/jhkE6xrTwAJTUKeGGJ3m8cIeMhUkDQ1uCcwzVHAgtEYthatsp4ZLLeYn5RMCJSIoXuKVcbRBBko7KaReraEkAxec7wxsewK+mmYP2M5LKmIWrmrA/XDVQYByctgDf5IAE7Aq7UQzyvQqOpzfpYi+zl8i3DV4pVh4owEoRKCZtbLScWeepWgZMSqtcgTlQpCNg0QGUsjhtZBpyoPCuSVIEF4c4+KiFJMI6letKk650Zl850+QlK4017VS34/mPwA8EqDKpT4xCycjxHoWwuagQ+Qs2mYUWQCI4PypQ9MZ00I/1GrZ/1i9rggXHW8JqfKhAm7+rC5UPh9UXgpSL2wgXQ4ByMkMcA9eTQewg5xloEbGdtTGN4nk52DOioVguJtFq470SVNMqM+ZRoGeTkcs7cPPaoY9AcLVqd4pML8/MWfXF/Nh+Piu+/ejEaDt2/fTyajv//3/l45+hhyQJ/GgA6M/YNpfYUUEWuelEQ9GznI37xWKdF0zZSHDR/+XrJGoemdAhxOZ2dxIpu/xc1wV/67xR8uZzPn/ro3JWmWasY3w4fVbrMDNcvvDKeBlZ1J3eiuI/tmtA+Yl3141S1T1DGfTR02w8fQ+DHzHtZqawmb+ZvhdY51aPVOWEcZInrrtUDksl+wNiDWzG0WOeiu1Yo7GR1E6inTkwaeNPCja2D5Atl8XbSe85BzI3b5Nlm+aFKiZOqQX4FeUpywFfxHpMOgluKE1PHVzfX/5f/8H/35X/w98Nunqw/g/R/evBuPzoB3oDDG/UFZDACDyUCBCX7pwZGAZo1JoRU/C0IxQWdNnVguiGBYBP7HNygQqoIFOOU7hQLDBU1gt+gKl/JAgbiDi6Lj3RlloE1xoxTG0v7IIVqdSd5MNDCQzb41UTLhWlAeVgBj+ewPlOOYssBeGHIqwLDP9qeXn7BUGDIv8AvBNQgPE6hAEH8R6kR+UDIAFPEVStMCuEx2h8uR1lqkC+5coXgDtZ4NRg3ICShc5Tc3N9EWKU8UJ8JhdVsqxr4bZVO6hbCV6iuJqnnl0LjqETSbrBsQd2YQ4edicofYb1iNnVfnxMYJvjSQy4gZaTd7YG/RAjkLLKroBXjLMBdjMzs3gmJYsAFZB+cZ1Ndxh62h9CGCt5Mtsub8MnJSnmRsCIUQ63sro9S8ZCGHUvNn5wDZp3rZeyJbtG/kYMqBofrgxdSRpoDalyJ8NXuIcQ6HFeQs8KAn4e7lcmS8bXt//df/8n/3H/x7NOj15fVoMrr4ePEXv/vzf/gP/sGwx9wXa4hpf8RTAfEXzRKCQJ+4QPzxHZHmWl/r+HXcFxda1+iLE+1JoCcN/CI0sHxtxPfxLkDtEcGktXu9f3hnL68uC/g2G2hZ/vN+t6X1Rf1IV7KkQ1ePyKXRFo9Ujwck2x4JuH8/qSm8DTE/jzY+D5dG/2k2QVdf6nrSN04OSb09/a7XoAnavgyARQJv/LRfGc7fMXAquBKBuZCUXDhz4Pjj4V/z3rff/vDD92LZMuPwKI4AGAzGecUZYIz1Lp5n7BAvXQEwGJrxYBERWE/kCynXgQZNucobLE20OB4QRjFRGvBbjIUISwQcVgTZiCLd1BrwQRNhKZdgofRdn4tTB3gPWB8YWnAcxCFIRj5CwxocRJMHsB/2DjMMsOSQWkA8KU4XUC83thfJF9MpJYbF8PlwPDq5ufwwHKEEjsdiOWlZuIaZTS4Za7+CSS9jIxr5og29aVhAnDF2ngM8oyUQ7ZVSqQQ/kt+K4RRZvEyh5acNRTjKxpel0o9CKmMG6uCX+zsxe/DSzClcvlD9dWnd8IMUmBhpracWghMqob3erJo9r5Bf9bCm4nmvOEEt3MYmsCgaLQU1aunCbpojKlUNmRxYFBw67PFenjt282k+o+0/qPTq3LFz56+iAeq+wEwBVhZthYWAPGiDU5bRW+pEisoqYVaVw5BsLiDBbSrk10SzCDeIZCMGtI/6sIxD7eOcxiqPgPyWt79RCQwZbQGWEOT9EV23wmCj+9HmzGTh9c/aAGo6/v77D/bUbMBUAH5ArAbGASq5JIWqVRlqhJKdqJ5FUWfIR0J/wbyQ828hbDSwGekkX6v99u+Rsa1LEkFAkp/rkteSnVNM8LU5Huxq1r0Z3s/g/r8X++mn1IfV8+G1O0S2++e5RYfLVo4ed3duTR02w4niLTJssaUfIk363Epq35JzJfqyLu1c65j4FWj37a5W65K8mb8ZXjOqQ8uHqpVgRLuOqeL1HP4+A2BV6Z2EnyKfNPCkgZ+nBva+UTqqvHpbpPdLgBLem8AWQGNRuJOPcIXRWkAxu8EAm0qc/tkvZTZdsCU8ZsAoHzM0vujNBFlcAzdRYTf1gGMM24PbqoVOMKAjhucdC2fEFDQaWF+06PAw+Ak0nM635XUtghdcIjYgiq8wQ9y135ejwpoYOcD3vi/5YGAeFgHzsB9gLdwT5FEZMosOw1owCE9uJWCiOI1Raj5woSFeGBostVuAhlLW3PBEW27x+3cAu8fuMGf4wQ9GL8ZshN8fPn/1nD2IRqP+2x8+9ubF2dkZm5wy/O2ukUjBCHWF+/gNqpM75UWtkqTyNtCqBVMgfVpZMq+iFNvMXqtAuuWTbJEhZV9Fr0mbHLVGf/I2o1Xhw7LUm5vR2cSh8OzEbZF64+GYpDHePWzkMz7BmlJeAb8FJIg+uSwsTeC0GyWho4uPn6bXM0wFzk9jy0829sF0cu9QMDYkXa9B++NvQ0spwkI10VswtDQCo5FYUCGTEI4Ih/mRH/0rv/x0AeLbe74NRSQJTNqA2l3aSyZgOULj34+YOPzYfvREYpWemZpsiJUyHuOABBW2AxotCjYGvWH3ISYq8HVC8qgjVDm4jGUv1xwdgEMUkUgT0B/RKIt9I1FFS+g/hFQyryRzfEbuFHvQZ5A8KOcjZUKAp+uRNWDPeLp2ayD1v8N6IU/xYRl3s3r8WKTraOul3MvvkGWV19h9BsA+yRdfmboxFhhSbHDaR+DotL020NHU0lhd20o7ntBDluiyBds8Ds/ZLtsZ07BcH4V+g/F96DfL1mimQfnwfiJo4uc1AFODwKGjaM0iP41wq6ZdYvMUJwy0elc0c24/+1vPvFhQAMU/MDvuK9mbwWBwM52NhjhGcNTXnAFiMV41Zj9GsBKo9fLTNTi/zK8Y+i0LVvoW+WR4/vzcJZ/ul8NrytOSOF8VOOXQMmgaUJfcNjgXNgdKxo1j0mVv+BHsBN4GTgX+FskhT8JzvXx2gkdPwdafQL8bYvtAUrCme3CSrx5Lt8aiUZDeVc4RWjirAPYqdoHUgCk5nKA6BXZSVRxX0gyD2NLzv1ypzDHGbBx08eE6yzgZYJEPJkxbjEYnfcOjsrzhIFhO8xLw5biKMFDNUgdMguvJBOMF04jTZM/wfjk5Y7YgPzlBdyMq7Bj47Nwiw8XVRe/7P3wIBIusDjYrT6Vj+mpsNdBxNCdZaFNG7rlzHoCv5ZVamYg6LvoJWllekY7WX0kiXVIwbKb4tr9ohOjFk/VHNA1gfXxy9ps//QrVsha2qEYsUBjQ7u6kEzpU/+z+Q3nJGC8Yx0NKLC3ktW60ILVhs//F7GbaK8YLaomzEIZB7+Woj6e9dhoE9Qtilx4rT5FsoQMW//ECAkbPMAxyzc4+msbjSMquLwC3057PIZANruwtA2NpO/iHVEJ84mnfycl4kL2mP/YHnzioggRaMKpJNRSSGD4Q2IXdlC7xaIILbcs5D2wMyv5AVIt2ZGcoFgo7UYCOP12wg2w1PjnlWeCwMzo1dgAdXXsmdgiFOXS5s4Oja8b+pU4olIaSCBBT/xYbedDVfnM2i9UGZXBqxt8n3Hxvp/OMD39XH8K3632+v2ySoSnb/vyHpzZppqdpv84Pp/yl5Ty8HTv1QE+7ret2lW3q+TE000YIt3A5+Hf2FjoHJe99RFPilmK5XRe6qwHQJdsB7dhV9Cn+SQNPGvgxNZDeDPG5fkPcQSBwiiPheNFQGHIuizw9fQbSufj08fSMVa54PggKYwd08BioiKFT8B/4iTK8QAF5rKRkh3jWVEohBnH743w89XTZvP4tkA85hyenJzhZB07kgDBQHrjctxwAGiSlDGIkx4JBbGxOAzBjpxYNAjAjFFgwGhlAb6mgWA4CsqnAauVgnoHbmQlgJ3cWc2YjTJCbOa4dEhX3w8MSITtxXCDeouKwKva6YS7BHW/6xaf+FbvdnD3T8T2EAgoL7Kj+zU3hdviEBsS4glmSYMnhcJz3xxNGzVHpsAT3DjgKjYPTPBvL2Q/HMgSgrtyFqBUNARSCK4mVwgrZTFvG1t917pQn5VuVrjUe9MkX0q1oCU1RNq2Gu0648oNdGfzGl4kTvnSwYRmxQ9uoEt0PdbgBIOcs8wW6OxxOtP7yCqhmMAIcIw9G2JCg4uFgMoMSOSCTJjw4MoKt/tlfVYuQaSFyIZjTDyhiNBzcYCaoxJINeShHLs4FIxefaBIziJMk6JlZz0PBWIdMYTaKBc0PcrpoUgYxbskK18nJhGPa1I2bxvJV++tbEfPQD0O00J7GgEe/OdtDE9JraCnKICIrp2lKUuy7+IVVAP/ZQNuP7s2Ulyuf0/wAOtGshQqzSQik7rmLnmEIetRVSaG+vAgq+kNcm4QfguITjScNdGjgoTptB/mfWXTjgd9bs6VWN94KG4X3GQAbpbb4bI39k7pzd6CtUp23vLG57mQ53dH+a/E6nE7KmepyuO2b8u//vIVaQ+Z2zsPl75ThgegfIklb/hphbPTO3ZK2yzY5Hk6ny7Kvqb0N7g2d7JbmAWPv8RTcR4qV9pLu49Mf/66maD/76T2zyh+3ejeU4FSvq09X5fiSgduTszGVrHocgwrSwQOb5a2Ml/cvL2+mxXSUPQ/MBCGADhnBdrjAM7o7A/W5k6IO5OA9coGlRI2EQWAU0GMcPDT8QCLoCxTpwCz4OoTRR4gEcDV0XULKnVCPWYgAVAAyvmlrEJVl+FIGegiBYoSwecnZUYAtDygwuVrkHPsFgOwNQfpStQnc7Udw550GSV6eivowYsDuOMFTI9apzvPJGeAUoCf2Za0DQ79xGJZuTs454MAOnB9cECJqUHJYMMAYqF9Qvj+4Uj0aBBgVCK55VGE3cMvFuVRKb7+NWlgPa8EHFVq8pA4I6X19peQaR64Toj69/L25NlcOWNzB66AsKUCtxfMCYI1yGOJmjQfYdYQZwNptGgdjgEqBvbOYPKHWTgPoCUO9KIWNCDUls+UM4ACWrCDiQdJeAHbWYPBlVao+i0TA8zRCmHtsuERO2wtijLq7/w8mR1SaCsg6Y7YAPVIcYWkL+h3th7n4gapAn1aLZd/uToQMDr1bRwxRlnJjBs57g/fGaJGig5cu5RhexPFkWnFQDiJU1gxWxWXQ1iIfYqMOb67waLqhpWxL0kic98bMK6CZzKPNom9X+DfhCxbIn2mmmaayS4jZCYuHRRsjamo1FENJ7G31HVIceKUHo+4irTJd78ZWxiMimu/tZjiRWL2FjqC4mfU+Mrfl2aR9l7smzS49b9Cl53D55D7E9bDUHkIiaBykhw5eXWWTnu/ff9ps2zTbMe1Sx8Y0+8kxZeMNsL9AyhJjB+uM8fry1tR9BsC6yFPoSQOProH003VAr350SX6RDDYVv3l3gEJWBeL1IoYD2Q1ycNN0xoYnYlz2ugHHTG+ucvbAwQFGzA5sHZ1MnvEuEmgxaOpxuYWrRoXaDP2C+3WjF7y6FAA2Ai0ECrwuaIz/Yi8u2fqdfkV1j+B++f4zLWUPXM8wLMnmWH76HSWIARziwsHuQy5G8CY2rUwYg+kIbAtRvShcuEjOoEYMXjhS9l6xoQc+i1mCFMH5VTg9kUT1NVR6s+nVYCSuzRg9x3dFoOtyYZL0J4mRcaCp7u6IXxOBz4jtgqiBcJA9b6wEL3P0mCoVcBRlWWkrZYDgUhfeBE5dBqLicdP4iDIpn3QkI40U7W0CGTYNOxppsyGnzleyYwUzKB8gzaj2YDBisH/hvj14Mdk6Ym8IMDaOqYOGqZs1IUmdqc85cYqurYA1CZ7HrSfEcKSf/X0gWJVjZo6gE9qnds4tuGcqflphhqkNUvHYoQxWFRpHqbhdsbcoIc0n5xW8Ut0QjEuprKXdxd1IKcKnizuoc9ia6D1zcYjVsJ1DNeSmYGp8p3GiitEVNAfoSlikkTeqy/ZOOHTNBwB7FYmueB5YK4Osg2zGpkBFj1XiTAtBRl1rn6gORI0OblyIaBXveEHDej5dTxrYr4GnjrJfP58xlaY44tp8vLlbFzfpFgPgiGZf7RlyRJlVPeIHbHV3VOCu9tM2k8PpHJ4z8WhajfGzEj/S2/zve3+4VP5A894/UueH02/mbNZ9fw2PladJrckx/eQ3U48NN6ntKBvaE8NsXofXdLNc465Fs5H2iMFVfdevhhoVNCJu41+/WeoSDP8GynN4tyxeg+TzwcVodKovO+d84Q0/PGE572h0rld9b/jtd78HzfSzqfgLHwnhDgPDmAeMHDNiCkQTXApg4wIFCQ3BW9wK3YRNXFoFgmpfc4Ik0BaSeJEYGesXIOWgGTFKTh4gGkOyGBmsD0gQDmCnf3oqTVYBqn42sOFIsgS3uYMh2A1PcYampYhsAFNQPKjNumSseWAsv88eOLHJI9tfTvFwQcDFfI71gEICB7ucFxEwC9j3kuxUX2uiyIZj/IISZeSc611jKpMG7GNDUddFkB+Aq5+Jn1zkJyb+1NlSdaotUv3kQgfGpM8UFdogytpyYkAUVZtKYFTKC2cinPEAdVf9m17BGgkFcE9PlDgY9cp5np+4WHbghqcsBWbTG5sRxYNkPZAXGhSXIBWmNb3E8k6NJIkZzCeVG4l7ehc/WIvB4IQRecbuMQ4ZH8fbihF0iIKfY4NQFlFQ4nl0Bs6XUPeB/jEkhNisGEGNIb82JYBetvEPaVyLi61FVphGKkmMvoeykgaMr7KPzN1AZNkJ1Sx/kAll8YkCbR/mmujLnPQWzwIZsCYuYyriOTYB+Vnp7uF3QxYNz4aDcZa7VoAFHyzyxmCABDplBYEOYjhNFawTUPlKpwaVy48UTIG6VY3uvNRJo1Rnvu4EqsKV6HTnOjRl9RbaKvAA79UtisfcPmwdb+FMs68umpirGbNKOjBwSNnDuURb7+f847ZUV/9JMt+tHds02zH7dfIYqV3n82yvzatrXr8fVndrkXwD3GIArDKT94AuENkPzbei/RR40sCTBr5EDfAor3DFLvniUd943mtMAlZmkFN0muWj0RjQ9Xd//Kv/8r/4x//1f+u/Nh5Nrq4v8t7ow8f387L/w5vv/upv/va7b78bDScMeQKMGNsN3x3e2QwqiwdrSA/kASj6YWyYBAoFf/AY8TFQGi8qUwOMCcmEawGWrIrJ3guhAheuIklLaFTqZgGZxdgwOBLKLkyFDEPDADLhm9V2ESgfpKax5JADcQG4EpCbG3Q6YaD1oEZ6PbazZCnsEG6oIowOECEWhQXAs9o1wlKBVfiQYCxIRomxM7AYAnPl2QTfIa0jzxoObdccE98QJSQIpkuYxo3ZgsQaPxob0SZFfrN445UAbXylWAB5ba6z4Jdx8RNxhPpmnoRSmHwLDjXOc/a+RDCmJyAJ1HZTVFQqwA9rD/971Bh3QXfZHg6ZW3d3YlX5mlP0J/D2iI07IT2fcoQwCqEZMNEUBa5ge8b9aRH4Y40hiCuDnUvSfrS1SXHShaZRy1bTXmMNaQBbMnJxi/phbxL0he1lxrEMevSEVxKpUU6S+CAhtvLyXx1CJhY82AtCLqxDffo58Ovk5PQa2w6NjDAOqRcbHA2urm7+w//o/8TKEI28fvXs+QskvLi8ePXi1X/rv/HfxPUHLyDE06SxC9k3ZJbczKiNUso6WtS6GBGVi5unj3tqQG0+6fOeSnwq/uNpIDpwvCGWMnCTLl8dnE7ylXdtv954kZBjlb0udezX3WyvJpdEIeyeY3Zo8VfpfjZ0U4h7hJtW4/KH+B7k7l20/vG+N51DCDTrfkj+n0CejpGVI2p6SM/cn+dOqYeM0PhOWLZBPHH9/M0qYpmw+xswwssiESAooAKtGHo3nEzwbP7Lv/wn/+w/+89ZkTmdzhgOnd+wGRDD3FMglItdAXyAOj4cj2fVIzvzjNjW3sHcAGpinei6IivJk/hczJVzgBZ3/AdpOWAs2hOW0VJAJGWISD/4oyQIE44iUXkF3jQF3C6MBM8D64kQw8kL+RiAxuEjzpXqgwVx3O7PXTUKNsMR3zzaAZDCwcUlvOw+OaQ8g9Ngzf7sRYiU4NvzYf8FW9ewFtnR+hLndc4S1iQR1C039EcAPIXmrBMI+wfsymkAaIhqOeFAztF8MBplQ44Sm3rqrYoWfasGQaAuNbESl5uIoD6Ni2zkDbSY3vCqJt0mJcftMm71jQbMCIpl4Ww0hwcjXLOKmtOIYcn2reJ8qlXesN0nywBsBSQBqOvWha50rIJ16BnVpKrbxjjBi9HBv2ylTz3LHDvCoX32XyJ3flkVM3IDgNneR/FtMFcVUHEti6gOOVUEShrcsPkSQ+zkizUYlOM/xXXBF0DLOujZWcjjUgRaEMTPaL19zkbBAHCnJlphOGJX1pHUKEYqXQ0v/rhCmfBVJbYX8iMGdbAW0Imlx0zd2HunsMjKExoIQjh9zW7O/upf/mFRXkIPRye84+gui6I6OS3//u/+7M9/9/enUza5wmMuZx0C1AniUuWTklosaq0Uq99xWzXUk3LUwtW5Q97ND/Nvxhx4Z7+KDsdnCh9Y8KhsR7xXO+im915KPJZavHA26B7yFt0ocLeb1q/MIXwPybMhToNLV9l1fOoo3d0l6Xadf4NT582x+TsJ7U1o989bn4u99PYltmvUjtlXfpnWJeHK12aZsf7egeFJabcXT3s8ufF56AzAFq+fxm277j8NuZ+kfNLAF6GB9J7YL8rqdUI2gQfQxy/+AE+c38TFvi/V6ekI4DefsqMOw8JguDJjjxgQ4oRdWQbs1oM3B+OpYDq94cE7jIe6v4tQMZxvBGOAqxRRI5wAHsJu3+8xQh/ZlwBo+fIDh1EyRKN4TE04wAy4hECM/4rckJOjpgRsOh1hGBgJ9AMZ4pN90mPDGQaU2cGGFcmjGftBViAziBCLGaCkgEgYOVwP8GPgHzQsmtZzXCyoMcBAL+CdQ77AoFYCArG4AH7iSofJ+SMR2V0UwPD5HM9xFgRgJAUTITbaws2IZcwcZsX4MjFw0JzwUg9g4Hi9R4T3XZfibl5bmaUV/1EHtgyVwoMLblYXz59+j5W+LOYG44r6gxTt6zagiDiYTPBtcR4Fi2eBZw5uQNCJWmrvCbLRlO3F5jiOpicgjq8OJ/iSz/8O9DPyP5zk+dRFwGz2D7SP7T3RCjV3eoXl5kO2+gwZUTQbB7EN0KA3Y4Ew3KHtmWuyU1mZrkKpXsYkoxG5nBrwk7UrdYOGKkX6MdJPki2NrP5Tz9SEIB3bT6sjVbKZaleOCqakLJ+cnCxmbIyLc79tHJ2Lfa44zODUwmxaWtwgGL2PvkVhGpkFDnbDRMFP/jRxqHXqqZSTJR/w8yM1ZsR4n64Qa3mz/b3Otp3ydP+kgYYGnjpKQxk/arB+yg+Sod1qzdKMN+y2G6DdzHcQq92Z/G2+5xXvr2Nt9/RDeE/OX2zxu9mUqTpdlqWjof7MR64I+3t/z+uh6Bwgxn100iT/UHSaNDfCh2h1f547pd76BG29K/I38eBtiN64MbeIJxBKiudRB/3Eq0PoFhuY4EYPnOn98MMFbtvAL/sUSzBBt+yGz6lI+Zix1SE7x+gIzUi2yaBYgJEWRFoqWsNjyOssLcQyDzu/f3AotxoLlYBFNRILeApWE1QFYArMhkCBXzUiEFHkjr0R4BTcLtRky1CkAKVbqei3EGQ027F6YNqC3Rwdh3UAm5rMGfmGbeU+P8JFMRdrOgF/+TsGgfvF1+BSZBLt1s8RY+MZJxlcXyym15BlOYR7oVZsZMPOk0NOy0I/2gjjCYPfmCfXo/yM6gFQQa/9HF//sYPX+ML0p9ObwVTYG+7y2BQsHmbFMowcHSfADAMaSuM7m70lvY+to3+pseIz7nztp/iUtPpU37QI25/qYlPROnB7znIOdQz6Z9gdTAt6zTjamfUMeLTrwYXxQhYUiR4cAkf7qJTJGxA+eyuFU3uM2FO4mt1QCw7FouPgoy/WR4Vl8Z4asYhcdG69HIwntscKCr1tiFoM+7ZCMceHHl40E0AdzdGsc0bw8+oM0ZVfqwM+qItORM/EkgogTZ3tHpqFKWDbieM12iJzhOfPJMspExBBqWrgGbT67pWUlGY27TSklHv0yfkL5maq/vuzZ2fjSZxixhHAHBTnOW5X15eXLOcoXfE8H+avnA7CZazH/NLVm3eXf3J9Q3xWjtk6CulZEOHeURodywfNRkEcnox365aLHmxkCGKgfZGUrlWA20RqmXLL90O9J7vobPwe3SLLvuRb33t7CidN2jWW135qXXVZlr7Tt532IN+H/bI1ebfl7Cq7jrczNWnsDq/z707fjj02/3b5u9432/SuNA4td7c67pSQRii+ohmqrnmAbZnarWbpZa76F2J5+/T9S9ZAs2P8kvXwi6376rVwgAbqn4KN14t4J4oG2BI/sYFPrOUt+hcXn0BmjHFzohPbNwIMWR9QAOrG/RGH4LJdPNAbVOMcgAO5gjxXZ/KfPz9r0hMCBGPlJqtChVvkJC8TAcQD9hEj/gGhPfKJ1x1/QckfMMLxITbjNSo4JjfiBGaDHpieFICmg8sWqKbuZcmgMthaXxbwJZ43ZJ+mGCB6ApsKI6eTopjduP2lUFzJSZarvLB5pldXbF3JaWKsamX5MiP5rsXCKcilzOBYlMEgOubG7Pzk2fPXY5YcF70T0KpnBJQzB7IH5eXH67/7/dux0NLVxmq6rpYyaMCEmgxuXXXLEauwy8R2oE5Jmfx021MwPOcnoBnUAiMsD6jQrGB6slBbHHnQ0hwXKeYumKUoepPA0HwsRgVlYem8CcWx7/jk3s+iv5jN3r+7YPcbhsjRBrMKYcTlYF9XZsPJvV/NzplZSEIxbllLwQwNaB67bcxIvVvm607GRrOQtQwlDHOhR5yFotouBmB7H7qL7vU0OBFhEOoFRrfkn13KfoYwOvGT337hpIPxEFXjEaLmcSlcNENK4tN7FjRj59Brxv0xTls0MdywOXH4ub78ODntz2+urj/Np9eXVAf7EsNgNOYUOWI+TsYnrBVgKyCtKXsj7N0Uqx7+T4zVvA2iOH7H51Ki+F4KmCL53IpIFVmlPgWeNLBDA6mXPPWVHar5TFHLR3vr8d3Lfdley7KNh5+kfQZAKnkMr72C3D0xjUk7HuC7+O50fiola+v8bcgraNhxtW3Ktk2/o1hEderQH+Pl1eJ7OP0lifhu0dlIfdCbtk7uRv5udI7QT4zoBBy8m4CPVcoXwqG0gZfincbVLB3YCHA61KkeR4wsu+QoAAbA2TedM4+qV45kx/JNkDRcQUnguQD5LrclPzALN6AA9CTDKh5/ONJ7EyyXB3gIfxAhMaPMFBH8OsJPHjAbeNHJBAF9pEofpCfYF8UbiO6pxzzsBVIANrICKm+4KRcn8q5Ye8r48ELLhAF8OcxGPTzTTxATvxNkhyCGQ1bh5sQOPidVdjkFwzO6D970cYtCLpF1y3zlF/1jGCAe4BDHGNSBAcD8CKAaF3+nJ1hcMCjzr05vJuVFPnq2GH0czl6P+h+y6Yv55MOHyxfF4vvF7Lxf4HivbwzyqhB5oZl4lgmmaxUwA1eqdmq+9ElkKhjp9Yf6Wid4lC+0kVP/HGusVw0Ye4Eqe7gDVZeT3qtF/sf+4qts8Mds8XwymOX9rxZD1gNQVtd9TzLmAlID3RnqdtFHhucV2DccoDijC799wLz/ojaYXLgz0dCwkilzQB4x4WRExclZz21z6Ffz/qdBdZpxxEQPQ2DRH5zmTNHQgngfuWwDYelW4SYEZU4q0N+MkwswVehmwRw7QYchfdK0P6O7UFDAnbMGmVUZcdJCf6IaoGGOqUZJb4KaUv+ht9nzkjZDX73hNZHYmmzgw7kW9GwG9cnFaubJ5MVwOP/0wUOOsU8Wi49YggOo0R+K/vQKVyacrFAO9pVtoeaUymfFRua/7ZPY+ElCfPoRHW+Zqc4WqZG4LJtu7vTZfE+2337tmC4mTTrNPOl3vxmzP3w4x/10mqkqe/NC81zt+JSrqy4bNBrP4EZ81008rV2Jd4s/SM5jSTfqdf+22K/npmiJV4o5pF6Jcsrf1Y5N+seGaxka2jiWwv78t8zMtwoXr43K38a7ghAdOPVqP9McsRm+9EuxV6J/6cI+yfekgZ+HBnY9culR5HP5MjGY/vj0nQp2A3YDhGJ00tHT6xsWgALgHKjnHzBPiMeJV2yGAjwCegngA9SDcZg2EGAB+2MDHamIxEU/gUlJkgiAVx8UR5CNjnREgUFkJE84qAToJlaBIx9AindJkOLb8dQwEoIJeBOcX4EpcSIKOIg/j6tM3Tcenx24OR5cFM/x22EHHmwP8StVjJrDcDi8qpjjSL8tDpMDaX3XygR0aMX9Qyp48xVWC2kKB5Fwe4J33pv+Ku//D0/+5KvB2WL+/GKAvfHyxNOQ/+TD+OPb68VwPs16N/jIoAZc6MOeslrSgZAs41oFlhGb3ynZhmvGq6etS+iP3jFdHHpXs/xDJ1XxMq++Gb46HY6ejf4rzu8sXp8h7eL11WT6+ynrJgDZPVaBA2vRUuzBz7QF6y0ceWfIHtcrTmVjb5/CDTBRC7+dWBToBu0sxYreYJN4mjB655drMclmrwbnLBMuF+O5JmXOeQoYALhyzWkdDu61C0GSBkv0NMjcWtSeSSfBqQY60Xawk5dmZ0LwRNtkYY3ZcC6+kIdaUVvRWWWgB1iKpBe4xANu8AvtkI8SDOGbI9qGVGKYaGCJAt385hqWHBLn8gMo0v4IAknmiAYTj1FgmQzkU3cNbvZbM9GFtTSCtV9k8S9VQ3m4krQpTBZz1DfrwDLi6ftJA/fSQOpaG2+Re9F7KrxDA6vnd0faIVHN8r4O0qqsnSWbWXdmOCzS95KvwVZuX8z1WFQrbVdEjGm1Ezrpt7M+doy/KrtqeiTfQ6zYNsm7lWrT6Yp5WPqP3Wr3H4HYoYe9PfYI/bRHdPZS3iHJjxu1fJbTkx3ISTzhbYIffPq00sgOz1cM0uM7f9nLGP58gWcIcB3UGlTEZT02whf8JAqc48rwt8AnEJQZIo3UyFHfWpqIBGoIpH9BAnREfAikSPhyJNjqaLMFSMPsYM8ZBtxF+dzXo7ZmADxCq3rGs6wYEHD4GRIzfFfyjDFg4P4AMDgZ9k8YUC7GxXDGIDN7BOEcP8gns0H1Fi+WBa9WrQWXFIs1YQs1x5gDlcHR4f9AiopRe6l42BR+QW5jU80GZ/nrP83ef9Mblvn3V4xxV9nYMee/Hg3cTrPov3HyAOC4eOb6VZnxkUyPeFsieX3VzbPxvq3j4K4y4zPCUECgwVuj6jOAocwd8VSCPYvQ2AnTHtQJgMxGlf/W2W//O3+ClFdng+sF0xY4MBV9Nu386+Hl//G9hhonHWtXISuD/wU74eCkU8fAezq7XExLvPxplHx0Jd/FWXQnQtTIoXqH/qkjy0lQIvqn9JxVJCfj3iWLZ6HhmcDVCdMKGJuFZiMrNPCtGju7Qm/UuMR1ixXXaAY/e5qGymhLMC1gmL/orrQIoB/12jRqJioJPHdKwPqbzR6pRriIpZ/wnTJrbxDFF6auUxyaAwHMI4tJZrat6Pf5gEkBOLPFP6aDDJlPoWNi1zILxVrkRfHu3fuvXn2FBQJ9OgbPTUB/lKBL0vIJUJK6PQ2mK2RMbWti5KiTNr9aJTeTD7hrv/3aMQeQ6cxyyPu8i2P03ZoyXfee1/0p0BvvfqUnuotCK/UQvd1dmM2SzRmbrrbYLLH77liZj+V1bAum/nNsqcNbuYt+hx6O7sGM/a8vXzHLF4GUGM6JmKeP+2tAfaLNoxvo/pyfKDxp4AE00NFzN/t0uou3hhCKS4zmdummCEgEuropA8NAUQHtGQCegm3TfCNYJ9AXEIkQPxtAHzb9gQyGAj9hEgmgJChuvp/iHSxekmlCUYTglqIUYIXDAuf7Eo7fRCQlF6gOOCZ0Ds8kMRU5oBS4lDxI5iJT4WBAtCDIaDIGhE4Zji4PdH9xbxYcg0acfcUOmFMWpIbYCIBHv8sastMCjO5MRkKRIRp8ZIm2kBJnGCrJMHpoMsRWSEg7rKsC+ydvBhOB7tXlp14xqsbVYHAzZ1Vo+aoY5KhzUU77g+/ICFHHjPV3QuEgSuoV1ea7vhKX5R3fdYRqXMauJFlGRBpSmd2MgfjxNbIGSM6lmkb52z89Of2T7CvWKucz5cZDZ+xgyKuSDfvxXwfS4kHFMlZxMwmsZKA8/QHS1dXlNT7w7PCpzPQG941ySQWJAlgyRYicovLoaZDGYSrrX+JSNQK+i6E9MAxnrD5HT+slxJzDRBNLOu4aBFy2z6iaEFx1YX65ZJiLmjuajhJtNH32C5beguI10qhu2Kc2C/JrGJBCCDkhFuhfieo2TgzUpQje1mEOgWLUhEzYSyzhFrvThpgebjqKB5QVpTxqikxogk1BXfUxmMzmcydcUEk0M1LiP4SB6D+4pNosQ9ylVrRxuExNOeJ2z0dNZ0+Op6QnDTxp4MfXwOqhP0CUjZfBMn/zhcAbcOGa4u69gJal1t+JaJNKpKV9+ttrkzstJ39+H+Dqot9hP+3g2JWzGd8M7yARUf4QL692/nbMMu9P+/tu9Wq32uF0Dsm5Y1QgQaJGGx2t91bZQyQ5iEuLcrNUF5eHjc9/aPKM8OpJ33iP9H3SQU9vAvSQBBoKr4bFS2Ly0SXDqjHeyvmvQqsYZwUWM7LLlv8cDQteA1eJp/xfnmW9F30mBzwxCj2wjQwDulzp7FXOuK37CiBH/EYJUWCUNVvCPgl+CaIC/qZ8zwU//QszBTcIWYxM4jfGWRksdzWyPuUuAmZpKSDVvd5j0Nis1KgqhuxPg5sPmDNz85+cVbdg2GxxddIfDmY3gx7LG8a9ASd8Tdh5Usf+7G3v+oXrhQGZOHP0ZuJDeYJBFV05Ehy1QYbt+AABAABJREFUyt5G1Yhl6/pBGu7uz78ppq9ZCqxRcPIvJqOz3vzPOFQ2H14gw2iEU/n7QfEnnonbB3fDFU9xdAMXiKNDKm8F4wqFpGAoJVJDCG/TlfKgo4gpXhhrOG7jxgiH1TGCxjYBLd/LTornz27+dFz+Psfxafz/7blC+mu85mfl3xTDy/L6hTi4N0CBoF4G6IvFJ2Dz/IpRetTLWld846k9Pk8f9JUq4ettalh5U07uEbRjEaC/LfrFSd47K4srF1v0rlmAwRQBliQD/OzDv8AJyDXibkjqaLkTSoJrFktEQ4jdpWmz0DmA0y+pT5m9E9tTQjPMy+TgaF7uovWkY+VNSPKgykiK9pWCreAXAWwT5hOYyDATqlDt/DGJ4ySRzBfaMJgemI9aKhTCdGG1O4sZ+i9fvJIIa8bHo4KT1Zg94WTlxQuauj94D0WlRI769/ctEnhbx4YctqL+chuX9+RM0ekzinW9VTYKf/abHe/zg2WwlbqvL6K+qbPt/RWoa7A/Tyv1PnpLmkl870MnUThcz/fn1d3ad0lJ/edw+Y/l0dU/u/XA47qjT69OArlFgFVpn3rG5HaQuoVCZ3J6j3QmPyU8aeBJA1+oBlavhW354qFupKb3hRCI/5EI4GGsdLEANg1w5IiVtdVwMgTYzGYMdBcjHL3d4gbAA9R1WDQwDZiVe5xhOJbLMV8Rs5jQsVipg14ANjV2Fr6JgygS9oZlA3wZQIIokZAZxQNmxUeSUnHTRSm4kB08xicINIacoZyGmEWlcWGOMEqtLFbBAVyEAXpygCv7x7CFZdV/OR69OnnR67PRzWSeXc2z0ShfXGZf//UciIxHirtRUmHVhOBQVmbEII7/jvv637T6A/PA457YnpIS2R+qYXlTjcZ4g+BNpLvKDdvhz2fjYjqfXY7YPWY0dsYix5OTn37UIiMNJ6H/ssZUPWqaWMgvBIpcfhCzzLqKSwHlUl4JKDkCUwP2YXVkXeUzrk9o8q/L0+cMs1dzNrIcu4dnwUIA3Lq+7i/GbHh6meEEdrW4QUSG5zUAGBMnizRQKSPdoHE7Alpm235XGsQVQsg5XCtDFJA50tgTKJJdgKdRsGaDCydQuHRKuxnriAelkzUonVMF3HlUWJ7qE/mk45xTIk4VaX9Kqwq+HbZPpzpQzeCoEsP4VDpzQzAMLuWlBEUhLwPo+OUJwrqWQVKQT/NYEobM0fQHqKvAOuRZoAr4ONm8sUIcC8Ae4GppFg0XxRA/IdydtFE9qiJ8ijCJgldoKNqXUDSiDZTCKUNKrKMiT+oLSqiQQeHp40kDP4YGUif8MTj/5Hj6BN/74mlfvQmWxFiI9NZXwRFXhyztsf8jaD5C1m77aZtZV85mfDO8XX5537QR2/nbMcty299NOnrx+uO0nafrvlm2K8+Dxce4xeH12s/3cDqH5Nyhh9boyH55dqQ2xml20N9R4GGiuur7sPE7u1h6ZQRmIL1+gYRPIWG9Jnrsxo7POu7VILG34CBsADezBzVPccUAmoPJOOKUQ23xoacjk5mG4Ihfil9IgMHc7NrxTn2vdcuInXJMALqxbAAvmtJBdVGUICy+xVs1nFPuFewRmvFHMoA1/8hXfUUCGd1OBfQ1gKYrdwXoPlz+5w93DpKJ1OMclLVgPxYiWb4MzMQjm+FlYCzoFeznDvxsOzPJOIgX2+WSA1pPWCHLCVODN6PiXd4/Z8jbKnCJytgkSNCa5DYSdSSNKgB/IkVDDlWzyVBWTb++rl7i81PNPGD3Zvopm78ElE6LC3Y+rfofx8P3vcUrt44sR6DKYAPRrTUAMIz6yY4LDnAFohKdnghj4iKwCq9iCJhNGvEu6mfsj4RbzRkqKPOLqjftzf/eovzTee/tpD8rb77pl9enOV5A7PH/w6B3OZ2OP1U3ObMotDwF3beUWSA8vhj4j3pLPWnlRczDhKCaSAgTJk00jR4wdJFqjpcYK2ppncnifNw7wRkq7+M/NJj3ZkN2DsUhiL5GU+EQNJhn86/E3dknWlCmCF1fQHFspRfOM40+0Wuq3ntH3+teJU63xmavX780TvQ67lWUeSMJ0TUdkkaJjzXEo8mINQ8WCQK6EnF8AY9FPB6KAKOqz4kJs+sZvdHupBKIpuE57dcth/QQggh7GE2vIGUFhlh6GNXTzD09grYNGZXK30UjrSooDxmtr+ZtHYaEj5Q1iovvrrfKms5tocd4Nz4GzWREpfo+Bv0deoq3Qf3cNZMP/m06Vs5j8zeFun9PSNSaem7Sf6hwou/r4nGupvyPzatZg1XbbdZs865RYMeJXuTll/i1mdYrAdLzXj/1aQagfh00iD0FvxANdDb3FyLfL0uMeKB+nlVewYBmgKrGu8FeKK7erjpQOe21DzYajkaz6cy1AFV+efXh5ASMyOC1YJk5AcYyQSr4NLMgNKAcL+wY5oawuAfUzalY3PBbiCeEkCqgjUOtQi/xUmgfsI0oUUbgEnEYHgpHJDn1pXB1JzfhTwGuix8H8wbQjAzkgQzIDIgFVJQe3uQIsRjjE4TRwkxEsRhBrVfNAGWAV0vEsG/gSKA8wHHC7vOKCg9NGWwGTvX6ajH9JNalxnoWmaZUYbo0NUoWxQBYWzlDWj9UJgfDFsPs+xHbx7ALjI5E6IGVB4PLGe4y5xxFPGL0eMYuliNdSSgpJYTkyxFpEHI0VdJYaMbU9QWzdFHvZcIqbpmmhmzzkBzKU/4qjRMIYtNRb8auOZ7qX48HJ8NixMaWWTUZV0OOLfOQsulLVgIvbjgNAMnJTF7tL9q2LNmX09qnRrZlowK2bFzxZazoFp17zwKMHkfGjTkzTceZatx/M3btCJoo9LLnDF3kQgW9kT0sxzYYjfNRHCFwQvOxvQ/gHPvBHsVFt+yP0n7/lsK+wTaBY56dnJxgHmjNwj6aLzUjgNz+RVEFYhUHC4ilBFsaiZxMNVAXet1kPAGsWysxv85m9l/tGWtkzsg4ZOarB9hnbXKseSdSjXMiHTXsT2fT+YLtkYrRcOLJBFg50HTVMJ0WezOmTsgPzVTv6EIKtOMKxdTx0aQRjliLeTWzpJif+ue6oj/1mvxc5Y8nsa5c3Q1/rlW9Y72aGvJVc49rozA3PvBugibVHcpPURuFZN7laVR8beoOT2KjD7rSi2j1e3RQmUfN1LDXV9bYHoZdFvPyBWvRQ2rXpNPOv19LzbJ7RH2YpIPHLQ5ht1/D+1Pb9B9FD8CKJadHob8k/uN+t554xKnfBXw1UgExJOnkgO88nuhA1CH+3zp0jyfPQEk302uQDUPobnoIVKO0vulpAxww5DPATD44HeevJhNQN3ARtKWjBGjRlaACP46OspuBxmoYK0aCDjKB4DyZtYcrSJLL4XwNBiAROQD3ACqfYUHXunwiRFRQYWcfUR23zD4Iw3FdwQ8FfrT24EbbhW3umcSYvcSLvZd/Z40ZpQfEFc/wQa84ckrciEDMGmDCQO8D/7P5MySIV6vKi3qF1Mu37bI69fs39Coh7/PvmEepPv6qP/ptr7pczD0TjQ1y4Mlemv2haxUG2bzM/rAofgPxfjYNnx/aAQIA3KQPdQTYdiZE9KkYveTZX7enMXJMV6Qb9EgBAPRbw+W5BbXKEGsUIJYZD4asoQwKP+vj+lMMRou/P8n/Lp+fZMO/wsqbTn+Np3p//GE4+DBCJ/1PMVORKGMefsCtv1+8hmEcIbxqHOvuFZ9RmbiTFw2JuYUaX6J6wDnrRYbIxjHM2ZW+UayHRvdhcC3Ka9YhZPk1Wyb1qwtXINAJ7A9Ek4vWpHXtPr3sIx2X7qGmypf2k8EHou2Duu7E8x4/AoB0FIXDDs76yBSOQxwNR8ehl9LRfATsQG4waoSVTlNVNGb1Gh+oXvYepUU3Tln0PcNuwd0LzeoFp5wQIYjzkh0ShhxHRnPMZthLAxZ7cHIwm6xSaDGz52eD92YjCx241p0aszp+KiqB7ctfkEhf/xqZc9URtvMfe1+/Gxu/nsdSaOd/jPetzb682vT3/84uyx35fe9fzLacbQmav5WH5G9TeNiYpOdtfaYut3rKYZmaY0eHvUWcZju2s27zbee4LaZJvxm+rdyh6c32apbpwtKs9kFVO8b7k+oavTpRW439p4e+ZlHf1DMAFDpe8U1hCS8ZPwStLdJPt08aeNLAw2ggPaard8HqsV8+vju5NBNX72ywB1BnPp/jq8DptdPplC+g0jIDr15Mgnw6dfAbXDQYjPjPkU0MlDqc7t7qAh0w2ckp4+5AeW9xv8BnG69tcJhQ24uXS0AihFuJQnRxIk7H+8Us7DSvz7SQXTTGZTGETJcMyRTxfKRIh2wTGuIbFCchOIo4U+YogC+5J0ZhcAT207uE1Hx41c+vGIzHjAHs4E+O8eN6z+prnPUL/Ph5pyqDdVXuoBhoc1kH0hWIgWEub8DdSyFZWfBung0uR+VwPoYY+tBAQSPFhBOEx9WLfnGNQ42jxayvCHlF0AmsS8sbMKW6D97GJKUkLYRlFVxl71WrRT0EAUkY9uITrJyzqz/OLBw9hrlHCzEP0D/52+zk18WgRKYsw5Vr7HoP7JTq6/OSXWyAzGnzShQMOQb+IYa8qEVpuKWjKGLiRh4bQZbRTNyLnIklDqQPDEY4JhnK/gWraOmBtBYGAv3H9lZi8mP70dMoCj/WVbPwN+F+bUvpR1aaikLMCVDG/3xHCCrMBKV2IQf4nlF3VZjgv1sgOctkNUKTFI1WU39JZihAil6kARyVJRDgwepbFCltF6eIII786gHhbEg+qBPzDYPL64vZ1fz118+Go7H7qjqDUd18urTCMoMM+VPIuss3rhRIjJZxO79XJZapq4gDCi/LfKnfVIHq/Awq8qUq+O5y1d0snkOorNto1WCrwN2Z/JxK1gqjSuvQfepXq9cZgA6C29Hpvr/D8gg57r8GoClIl1V0eJW7KHTF76DcsNfvY0k367WDy5FRD0vtSObd2e893rNfw/tTu8V6SllrAJDBRf/hSW4+3Cl+66dy/UaOQolK/bq2sFCS2xhoh5ybfmIEjIZv37794+//+Od/9qfPX573h+P5DAeG4WRyzpA+g/osbcQbIs9HLvd0y5cyH90wWJtnL7QlPGcX2C+4qdisXcGUAzjEN1y9oaORGmCPZaCBKSlhogPBgi3GXF9YqsduMwA1XY96nDsbeEnRI01SQDx3BdXU8JYI4Jr2A9SlZkERNseA4Sf0MdgjSsA/V22ezNgDtDcriiklF/ri5GO2oBm8mfa+ZVcWfUyS8PIOjAiLRGVZHRhZF2oQA8ZKTcbFb11pUC4ubib/5d9dvOZU4cGny2HGxj/Pe6dF/+8u5+efPElq0euzCniBPUA9GE928kKHovCucbIljJbymd5IEQ8zU10iLP4Ga4ZEyIcE4GEVjwzqrXhmIPSl/qxJ+LQoIW5OI3dz6o/7HPAw/wdvb373++K7fPEVAHWefTPLP42Kl+Xgh+/mJ9XkbcYeSLQDo/4lJsKsVzyj9sxLyMcZCbqR6oeLUDZCdtJl2AjFe2FGHIFcm+sQ+bw8KarTRXlJNwrl0hc0FZi4mQH7OQzYvWVB2cwrURJ6TBE4G2C/soWtFR2AMjYPKwHMZ2QSwicl/kTbNEdYfSnN3pHa0fLOPKgd2FFJkLud0hogeZD/EII5h4D5FvXD0qUqrJonRTMXBsnmYeqiiG0/ofev//Zvb2ZzFgmcnZ2+ePFicjYen5xwytpvf/NNL/9AcymwLYge6eavpZy/jRaL5goJiWxcq0TiopbxiWDpppHTZtlBYCPH/hsEu+t1xG90g0Wz1Cq8o2KNInuCtv6ua0V5V2Idd0iePcVXSXejc/hv5bH0m/mb4ZXAewIrfdZ69ZGJHral52WDpedhVWoP5a6kYyXsonNsfHqYmpLvl+Tw9kqSdCHweOF0CrvU6zJDvTagngFYxj7Qd2rTbZYPRPyJzJMGnjRwZw1svW/Xt5uPK/GbEYlhwq+GBR2C14A4uH+Dt/LJ+OSf//N//n//R//X3/zmz4aD4fNXzz99vGLcf3Jy8v2bt5OTU93bGU130BVniZLd34FAACdgk0OzUjUkKgJExZs0Aan6x4IMXKCv+A4AJG4NTOcbVzwkGlOwuuCyJLGpTnxyKXwAJ4l4K2s5IlHc8kV6wGKQNCsZwiXJoWVXNeCnXWWX+HCfVCcOw+OQX80oy/B4Wf2a/RoF1NKRWkAhSaMzeQTKJtZ4sF8IQEgBE0wnCMYcfFgMisv84mQwZuj3I3vbZxyXld3MR9PBs8WY5aEfMKYkjzrZd9PzoyAdwN5VA9QrjToLOgNgUku9WzS9klCIp5KteqiAJLUPmchft4iyBVXyuQYgLW7maLRqgQYu8t//kzfZ3978YTz/psp/uBq8mWdvT4qvL4vrd4Ov/8D5BeP+kLW25dRlA+qAJQFYVuoimlhbS/ohyOorZA5FoEgKaU2Bn0HXOtRz0HQ/Y/rFgXWcxWJOBgMI9ds7+jDsDxh/Z7oEljk+S/SoaN3gKG0rZc7E2IoZRjVywOqjP3ouRXQC1YPkaldJwtwIhS3JoER7kVzYlBXxUKGqdraBjPbt6G9B2z2kiEFoE53tSJxr0eROyw2y775/8/0PP3DWHJMbPCTZcDGb34yz4f/sf/o//9VvvubgZE3XkDlUGTVCukYNFa++4HT8pezHl3oq8aSBPRpIParuj8tuue5pKWbV7dYJe0gen/RIZI8X5EcrEe98hoj06ecl0mlV3FXAVQsmAv7M8DZJrXsAzS6raL8t1UztotAVf4BQP5csAQgSAqir1Ixphg+vcYCc/dmbrdMM7y91ROqRkicZEv3H6BU76rhfwlbq/qdmB/2oTFf86unbfgpX98uHlm/itlf7iHwENIw1kjp4l6AWMaAZnaTL5/3qOQsX2SHz3du3rIb99tsfwJGLYnJ+/hz369OzMwbJmQrALygcNgBy5fgEu+AU0gKq+ACBCY+EoSKq8HaQoalJUgLkdyDXi3xaD47ci3iRsSw/ur+xoAushkdKXKlUVMI3kVdNcElHXAoiFgsC2mLKAqYCOkCzIoLf8AzhxlHeYXU6KM4Hgz8Ka8tXEGFFNJs7ZsM3Wfl9xjFYfaYDAJQWRHGCVxg6R4E88lbyUCJFGavGjcVs0gFmMg9wwjlas2o0L3Bw5/in66o6mZY3jBj3ij/2Fi97vTdleQ4lJNQsgY9GBywortOKyBOALwtUoX7Iq14MsKY2jAfVSowmAXlUH3nSp/FJAckaMifLEPTU6g1pSmw8eM4Xf3btkoVfnww+jKuvnw0uquq3wxGbor549vLj2/d/9r78kJeT0eB8UbIi2P1MJVq8hiPaZgCd1a20HwSJVgE2AbWhNT9wVy1e2qrRDFhiBHAqUgRcofLnzPMEOcfRC3Ya0n7B5wiVIzwWB4sB7AVUBGshOpXU7RnODmCmxSC9dl40bKhGzlCJNidWHdRi0TRMBr2CWi97x9wC+aSMfAzBM39VLTKWbacIe5K8uSgeHZ7aJcOwKthMtvcCOwABWINOEYb3yTcajnvl2CPGsqubm+vZjLMVmFyKVS7FCfnPTmael5wP5szDUA/UZO1owHd+QiKuaH3SI8Kb+oqY9W2kN2+X+WpC0V8Sza63yqrEoQF1rmm057rb27hZqhnew+gOSYdQPiTPDtat9/8d6ewgvTuqSZ+eaX/a2RmWpZv5m+Fl+kHfWxy21476sEjHHpJ6nt3lIMpbmfZJuIsgrxT5bsm3RfSA2zaFfZIcQPDhs0RNA/Onk4DvXee2iHdttTalp5gnDfxSNLD91KT31IM+nocQ25EnSbLxGdCIoVh2x8wdj1wsFiP+pqATvX4mo/lsBrgZVqOT00nBclF8hLJ8ejMDeToJALhfDMbjBNX98RMU4NgPnOc9DGCLW9BVtL4yEQp7QDDuZT6gpOWIEDYlXBGYy1e5GfgUJkUBkW9kBrILvkgAvMFMfGaa0JOB1cUcXxozk0+/Gv+HXw37s+NzTxHQe349HpyfDE8LnDaKMf7xc1SBwwk/aYuPrDilMIJIQwjO3EeSzgpCACKCTyEi5hDcgqaRcBTVjYbXzwaTv3jx7FczT7f9ejDnpK3TimUGv3o/uP4X/UmeTxFdryrOGkNAKEDDSlhHzAn9pQyn33X4R1L4v0TVyUCy6xnCSNBZP2RWFdKJTP4SoxSrHFEYKjDDQcvtaMDBvZP+5e/Ozv7bL/78Ve8jnj+z7ENRng5H11n+b/7N8Pf/nysslmHJmcBovOehC6x3hRj2JRQtb+Ulzp8SwlX1WBm0BohWSDVGgAUe4HL1SZ9b9C9ZYtDHaaZk7gXhMV/44N9gwaA/Tl8QZ30IMa7fgDz1hRfj7rQL9qp0iOay8a0eNzVve4dgP5paAZCUluLiBm1BjIkgiHAyBHnovbIB+RNgQfzFxwvCKpHdsYbD0/MzunGqCpGE2c8HqWczDs/wTOMTvHxOzmJyjDU0z1DTovp0cfGRC1OBPpoNPWdZK/Dm6uPF+2Lxa9YEQyQ1i5WIilgZxFtqkht1ShJCq+NGrhS7zEm2NQGJPF2/NA3YUz7HlfrZDm7RTesOmZJXmQg8YPdMZB+Q4OdQ24PyWGsgzgF4UNq7ifn6/qVeDzZ28ngK5KdxdTXDq8iHCDTt4Gb4ENoH6fBIyY+V4RA5m3l20N8vYQ1H1jTuNk62g++S5L6nsPVC3J4VpLA4ikuA5hdvazFOYJFhMfjABoyzGx208TkHrAHsGEbPhrN8NBsN2P2dqzo9ezEc5+PJEFrOBoxG+AhJmosC5GB3dq7sfUQ6LsVOKYI2fdAdhDc1RBGjxTA/2AxSIFw4E4VpITHoi+PgA7hU1pBbkWFDFNxC/qiTNoAgGhocWgAoFc2BTkGRjOu7yz77EQkPAZB9tzddLIrTaTm8WfRns5uCU8D65bRYjEcnP/R+/2mA8K8Y2+YKt3WAGhj2AwPzzKvkjneLTpFZ9J1fZmzvbg9HROTFioAvTu7D8eL01YvZGcuJM2yrOR73EsrfsDXP6WR+ziB3/wV+VNn8OXi66F06hwBUjWFy6DAszDg5tgqCq7CgGooRfHOCF7XRSIiWWn0yk4MY7K6DFEq0zBMQ2MaQB5sl4f7PbvtVNZqOz65fPn/2/qQYD/s/sA/UMBtX06w8+S9OGYEfVAOmTYohxtkIP3knf9g5CNDsQmG2WHUiAh2BeJlT4eLGdpFrr/c6fYvUAdrWp8AlxvF5sP3ivFfQEOyAxAZJ0TR2j7zgmAYxOT5pAHMG15mDYTCfFR3OC0R3sDfIqHwhJ1d3uFMnMe7nQ5TtQIL9B2GiXUKzuvujkHceNUbdUaU+SFhZtBb95GuAfVm9ff/u3Xw61TAwge1H+7/73V+cnr0sqrm9E4ttbvcqF3/H4RjFLJTtJkDUD8Ui9FS1xgp5Nv9EZb3eOadq0CWiR05Y38z2p1jZkKKeihvdXYVFM6c2g67dPvRpAt227gbexUVqulS2Tb28j7v1jWl73iqNjAcEqXt3roPe893FHynFPrBU6iOx2CbLU8lFt/9cV3rgurg9eLug0aTV+lcm9YlVz1h1RnvmRsdsS3gX2VaMGuT2a6CR8Y7Bu8i5i1V95vebXWm3xal28qyrf/QagFXL3MZq+41ye/6nHE8aeNLA42kgvUs76W8+2elNsX5RUIybxn2NOcAYTAJ4lC/u6SJNBmd1acjnc4ZIpQLkAbSPhvnlzfVkcnL+4mzCzp+iK4Ccg6wgmAB+MQkNzFmjLgBRgHLpithEXBgVYCHhkDmJJUrYx6Apw/YBd5DH+YPARQ1oFDUXFFEm8J/iWS9pELQIgA/LhDFXR4IZq7bK+Fr02AUI9Ak7BBdWWyzn/DIw6wQsBsZmJ3g2Mv1UAn1flaesc5jg6k454KmAmSpwi5fK/NTfdaApRhIrVefTRXUNZ3ZSQmbOEeCUWAeU2Uq1fzVip3qdmQCODAxLin2OqvLZlKHn8lzsCWwVjVKE8pRFM4gWZo/Qn5FvdMLYswA68IRhMgtzXchLolWPBqDugFqG6SdSwPEk8KJq96dabWLYoYGA4CPsvIF4txwN/ljNBx9uimKWn7PP04BdLKfET2/G7zBduO/NOc0AI8fSqlXpaSOZsB4AoAwz95GFI2yi8ukTrYVkmJhIMOyhYyuM5rTwsmuXPbDFkBAYglCmqiyeHlYl9gmbgFIb2lZtyzgqS4VVPm0Y1rUq1JhwSgrmGhlWk8raRaJnJBBGEXi4A79s7IpKJn/oSZBLpaIWjBml897qoHuyIAqzYyQiBY0IKTz6oYOHD//YPypUZePoesaOszxFPDMDzkumcjwloTTbjvXPdAMW06NPehXdVgng5KdSK7scieImBIumTOHOTwrsuFLs7rQd2X+SUUlLP+86foENUys8OmwtXrMl6r77oII3eT0o4S+UWFefXuuZX5euTEfWadtjeJNwsvZ8od7v2j8OsT/1bpwPt9u6ctZSpR+Jz2jTd9a3KUNLqq5adFKLhENKHZKni8shLVvTfxs0mnXsIvr541va/pwi8KDve/423wPbObmvy/fx/vem/if0wAUINKMlAAhmtB6I7hlJuPkIRRzqrubTcd5j/ahbdTpHMMRrhTCe0ENHhcX5jHnmZMzYJx6sFXgclB0oBmfrQGUM/YKAmHGYsxekEhgLQOqV+CABqxhGZZScSBCmcChdBgIRxTdhKxdTCY7c1vfgUoCj+AynkuUW76BEoBz2DLsWnePgPRj+QT8ZfU5YnDAZDl9MBvi2CB7ZDqjEs+MEMH89n3/I8kmPZbtQB1XTGQHR7GODAQBiDMkY683z4fR6Wk1fBijHiYUkSnCHnQHSfTWoni8WH3v5aQ8jgWkItAJiHtz0R/1idskRBMJ6VfUeRWk86EUfg9ZOWaB8dlWCoGGsGmstciU+VlYgFlHKo+kTipx5XnH/fWSMKEOILrhGrBDQY3erCuOHdQdjlzjMvy6L55eLD6P+6XXvctw7vVlcYR3QtDM2AOpzHkI5v2F9LjYD64Ax+pAqWhxnKtxatLJYUo25YhvZmIk9zFwkgL3HFkZgazbAGU76jI7TtGBqmv5kUD6bDK/oecwnlDneNDTEAhQ/za+K/gnmBXsxEVn2f/BACaWXKDwS+h+MLtWJMR4ThsrtsSgEGRekoDx0hcTqSLV6oc/lqgrxvoA74DVtf0GYfBiE7CKaFIvNEzS0WvlvA0YNKecsCl/VFVLJFwYFxiHc57jNOboP5/xKq4mzk7UIaLWSnbb+7M//YjweXV9eInA8AtGOisGlEcKnQRXrV9zaE+v4CEV8HYrcdXj7K6oXKopcQX07z4H3h7z/2+/5Q0odIsCtdFY1bVO7T63b1Dpjmr9ZzXAUuFX+TrK3JSRslsaV2/pPpdvxDyZPs/etwrwIDu5vbdmSzEnCtDtl3YLQTI/DbTp5jPQuObt4JWEbqXVE/mZVjdRnG1kODEIgXR4E5utweX/7976s+9Jup/yU40kDTxr4sTQAluHxrd8FEWpI4oO9fLhXYcEaJUAyoLQASYIMxyhBzPkwBjKL0WhUuMcLJ8SOrkHtHLQ71gFkPptyqCuwD47u3w9qAwoGHZ0fgKgCqISueD/F7wFRZAAY6//tkDDMawnEZA4wwzmk8pUmfuIzvdyW0lvEHwPBplkSiZQnEB6wKSoWFon4jJyE+T2OzX/AV4yzI4kADsA3yqtTxms5sZflDZ4/jH2zeFZVrxbsmg+2dezZTSoTM/gxUq1HO5n138CjBxSIhsSbCuPenYByhpZBhRdsnLlgETX77uPUbhqrP3H8mBBbLFhWgbu74B6/FesR/4Cb1AuMDK1EkVyk24ApiwpCjSgZPJmQvTqJ/DoVYRkRn9RosSgct5oaWic93FZG/HLAmepkgwva+qq4wiwosvlVeY1NMBLRvijnV4tZVgxHeT6bzxcckwWwDbcZQPkcTqFY4pCPxhIip0ZTUiW2NUnDnQzPfdarMTwebRcZs0tOSZ6wLmIMMyYG5h6fq+5ezPszjgpA8SzMhS4zFdIJHG+HiH6hsqMb8KmqcLOnTpqXMU9Bw8HJOgZ2IIedJLqG/STa0VaCHfE+OzqhcWIA18IZAKhSn5RIHngs1KqKJR5K9BStiiQYVqVPD9yYhNFGRkq4cwCwJhn2CegfA5fJtGz66dPb8xMYQXLOFIHdGPbKZjWkUl+rW+uxeW3ErPJt5mncbWRvxP/cgrdr4udW4y+9PqnnNXv1PSWG1E+ylZMKVopYBe6kjpVWeTOmVdjb/r6QTSxS1jWXWnnt8f4dFNal4ke3cXtr0DcqImxzX5er5VhHPFbocLvtlpwtm36/xLdqYH/xQ1NbUt1Siw66h5Rq53mwUYSQqk2/Q9hldPzkLl5721W2vTfC4e2yo3YtbS9FecjvnRJ2P0kr1imLD1bgL5/A+inzHkiS3gh8Rk4/iAOGkMhQLv7KgXs4tRRsojtKrle3uQCNFZv94/DtukljALLs2QKIAbtRCgcXcuJ9AgSKF08avFSCECMYJl7AOiWQaxKoxnNJGGGQaF1c5tsDbMQgNAKOa7FTGakG8hI1hdSUCnAG0Ar/HzIAdlmgCUwG67Ks9CPoDDSmkzn76+ec1/pi2H81GU5LBvLLgnOnng8A67189CHrfRr0X8dgv14uIFtk1enETYFgiXRwZQv9maCUo3Tx30FWkDeHVuHw4e46oLvXDHtnvY949wdwxgIZYmFkGesO8J5hTJiDik9YIKFBEaaReJoVFISRlpt6GkSgrypCbdG6mYPq3Ns0tq0MDKEuvkIh5lbDwNhoFNxQ0DwzIWcLuPRxW2LPzQHGS794XrlxTcUUzIiWpGHLIWV6/Q/X1cf+4BXgHGcq18Ri2jGZMLzUMII94+TzMwbttW1IUzU0lXMuqX0XImr+McRPddkKiSLKhA6IqXrPy97JKC9ycLDTR6SROCiHlx8Gc84o0Llo8EkzQ9sB9EzDRiub08YlJowCUDcRxFJ/jEhS0RxNFp5SAcRDVX6QB1Vz2f0oEv1TawolWpz4UCfxNPzQ+StI5WnXK5uAUXwsQyuv/pFKgwpbiCiG/GE65Qgyx/ohwKLv/DX6j42FeDiwbiG2mF7NRhieIUviKyWJS7Jxpdt4djaSUkydkUw2f6twg05K2yi1TvUNSYYD3mztd+yON+SacB1ql2plOSiii44y8NC+CSJbCjyI8DGZQle+n46/uuRvU2pq1aecrrGXo+/J7l/ANv0Uczd5UlmlQq7g25Q2pabPlBr5mtFHhDsl7GjlQ6Q6hH1XjbrKduVfydPx5CV6qTJmcT9P5q9TT+5gtiZFVm+cAaiDHUWeop808MvWwM/z+eDpTxVrVI9gXBGV3hXr9zBYJlCG8RYWxQCgkjeFMMZoRiiHDNdiEYCqAGBCT+56xdUVx3L1OMyUsf+TU4bLMRgYyseJ3HKBqGQghJJLohYs/KFIGcBYojKQG8lwB43FnyUYhicZ3yKgHWnCbABZGr41b5QNE0IOEo5aBB3DKWAC4kIhECwFFaXASmGfS5cHK4rYVdw++JTlJ5gWgrmcNQ/zAQPyoOPilQB3zLJTMpNTvIcwlJaJ3ibiXzSDY5OjxfqjO/SrUOTWc8P7/vgDG8pYgwpncSVRfKt+yj6g/T57p+rxxJJS3vrAQ1g42eARtmRVN/CiVJQ1insBrxEkhzRSJEUxTQiE7L05zZY+Ig+lFa7Xv3FouuRIB6wIFtoyCn9ZlTMY+1viOV2Uw21n0edYAHxZUASmIJtNUHWhL+PY+LAv6B8MXjvhYQ9DLjQqQ0JRRwUO2VMbUxEmB5Q/hEOHIPhrfKxOhyflXP0qPWoBn1fnGV5GTK0wQ0EpCgjX0agdg6pZC9QoTxIc7yeKPDYsCrGd4Kw+jPeiEOKRGUUJ+mm/MGhsVqG7FQjx+RWesRSGsNNVKrmsOB2PuiIBOa0e1qNaWLBz7pzl45xtLNrHIw7DksdHgWw4DBFnhux70qcurB3nvLI8e/bshBLspuXxwGF7KAFX1K0Op5jGJ3Wx9h0XpSJDR/K+6E6a+wo9pX0mDaSG/UzMHoFNV3d+BFZfJsm9j9fR2ll3h/px37ML0F7O+8f7kyoTgUNk9L3K+6nBsRne0zB1LbpztCm3Y7pKd1lmXfnvH9/kuF8DzZyJbzvm/vI0KTwG/aaNbrvwK7p3rKIpzwOEg1dThjbNtjz726VJYT/lZs46HD/1zfGh/aNrXT05SZgejcYjpT80V2OEoE5sx6eEOFu0yt8m6UAPghyAgoOTwh7xNkAKZKN/ArhT0C90DsDn8H5xDtYpe1eAF3G5cG+E6z8jr+ER7fA/QAowBKCx8QUhDo4HHz/qkPIEaocckRFbC0+Kp8lyfZdEQn95/wWQi113gFL42AiDA86J3wPsihdd5Mq3MwMBlrkT2QZLsl2J9rJTKgspspAHBMp8AjnAj24DszivemeLwRtWJMz7J5kH3o4W1eWcbY96vy/nf+KItVrTX4UAswcoB8ZuV88uSXh3gOn0FCIDSgM7A/BYw+BaBgrgWF+ycU5xQ3XBe3AH4CJUP79kxyEH00Hg/TPWJai3ElK4nwNOp8JS9YrCo0YIjhoEwXxGC4I3sXNsUEpGPDkUL8RECzZxZLVkRGsRSEIgzfi0w9V8MPbP57P+YtIfvmXdLfpZFE5fgKJH+Yf+8NOg92vIzV00gdAx1F2dg/wD4GI4MRlkO1g3Fo8oEjCfWY6RPleiazA9VcPAwEAKG4nJJFbOZoNqPhkVTMJcL9hmNPsEnu7rQ49ar8v+NW1H9niYBmzr1MeNytpzwQ06DMDjNcQagxELT9y+VSlQKSIY0hhYXTSLvV7zw5KLF/bF4Qf1bNeBlPYWqTwPWHToxNUEyMikCftcYSz4pEyrOXCf/seTwiIBgD/8FpOT7Kvhc0XCeII+cxnOsLCv0fjjx96bH77HKKjQW3g0LWZYT9PZFKeq0empTkTIEI1o20AuKkGPe6Xs+XurFDYlX1Gf+IgamqFxRVmb19b2Ugvra1l+HbMKHf4+XBVZBY5+Q65K7gy03p+H/GYhQ6or9d6s9E4evS6aXfEbVOIXZyPmEW6aWm3/fj0Cw1tINuVJWZt9pp16C7lHS94v1UHtG7IdW6Ou/Ct5DuiWdt7DMbli1t2dX5r63WDg6XrSwJMGvigNpJ/j3SLt/clKiRtZ1rSar5RGmOA6z9bP4QodgGcc19c48RWVxk1BjIx+shMP538BPQBpwCDgEAeYAm3PzsYvv/kKcMTaAPwiQGYQAO4IrMTVojIwlSz8a/wSJ8wpGDdrfAjRwFV8wlMubgAKCcgl1GYVgNcMi8egLRizprquHYTItWRlAe6kLpADoyOV6YIqBMPNhfrxD2tAPxW36XEI9wP+73jCjKwQpzjhEH82OB9/KH77DIeo0TABUDBlXHAAjwLyALzgAF1B8INiNXMxm+KsQqKAsc/WnAwce0wyi6EH5RTTwxUHIE+Gq0H8jCkXE3aB4Xi1iq2PMAlUfTJtkgEDNLdCgU2tV+gNEahX1CfqRa3IQWIgYgC/Mx6x+iIKRE6yQBGNoAW0G/nRDdQZN8etxy+U1mfRdv8GuRYeRkZrc+ADgJ59OHGCGi+qEQ5NVXkD9GV7UDeHFZIKmrEb0/i7urb+MEHfWiYk0h4IKN/IzHegdq1IVQrzwceCE3/paYydu7qArXRm9Ld+ecYyEdZR+58DmlkYgl7lBxtkl7/dr66+yiLW7ieah3moE32Rn2zBHRWEzQtxTBXzY7QSOXQnfrE3ROgZsxn2YY8NOl3RYjxeR+TOPnz4gM2F/aNdGrYT8uQcG80uQGfsuXSCEp26QacagSNOV8uy0+ubmSqx2mEksacqBy+zr2pvdvnpUo87eqPeRSG89fBKrU/ArruMjJQUtwwuv62yl981ibhff+yOXaf/5EOrCq4CP/kq/SwrED36Z1mz/ZWiWy6f0v0Zb09dk6qVqQFwFPHlM5K+jyraLd7K1unOsjtlKU2d6nuY11hDqmY4ZWrH1IVbX12WWSvjMoKXPdc9rPzDObZztmOWYu39PljmO9LfyzwlCiVpNfTWaLgDyt07y8F1vzenOxLYP36zPxVdbj0d+Q+IkaJJWevaOQEitnLjr/N2W2z9zdmYXLQt7Ab4ZgP2/8nG+vZwppEDmLpTMzEQ3u05azFRMvCG05Dy0q3/+Q/Qch9HsJrjjkwHBJuEokThxUvFY/xSlBdpMsRm8MkiDswvJOUflJg6yN6DJSsgqKDLY56q6oLRZCAzvvU16nXgX6oIk+ASrjsSzzhLi0fWLSMTzRjUBc2ekV0zQ3ds/DfmoEnxeW/KwgbgP376We9l1n81GFyzMw8rULPFzSBHEWwi9O3k/Gqc/Zp5Dp1W1CwYjmrqwg0flWAt0vJNDBWxpvAegfMZiLLHyk/R/inj6sPsin3tS4fAGc/33MYq44wtjgk7GXFobG9MBbFGEpgOZVFe6BnhqDMVQyUCW+vv/8UzRcguotFBnOQXYqoclUIePyVkJKUtChuiNH9Qd47B4DoOsuSfXmblaFF+ICZqh1MTaJlB7G/L4XQyebEA1M45Lm3Blp90AUkBnlGhtkTc3Uyh7tEQSmFFZYFUbK1EFXE34rQADiBGYfPnGI+D7BLLpyxfLvpn7Cw0YMv/3lhveqYO2Gkqvyxy9pKideDiKHyvYvspFKLpgPpQrcP2qoCLVFE2VeKcOrYCcskDOTC70IUTU8lu0DFJw5OlxuU7jAA8cDQ9OZ/LCRHNUfozbmCQtQB9lRkA3Xe05Ti8V43BEVXY/pDC9nEnq0VBHbUrw9vHhQAlHl9YNxwUVl5pqGiNQh6x1Fe5YNXH6WgymU+psXyjIlEXqKo0bI330Y6G+Ve3opVNVbZxN6863vIWaF0bRJB3SamV8dCIw8dTD6VIvrrPr0s87G9W+p3qotkVv5bmpxB6lHbpqHiTVzPckT2iu3peV/w+WvvSfOP5Hljn+eLbF4kb4q4Fr2f+0/zAdg53AfKtsB3fKH734GPRDYmige4u21PJL0cDj9pPvpxqfmZJVlpdBUKA9Nzc4XkXopbgknqx73DoTvCz6RR7AACjFwzwDQQBwHKIfAg8Ao04puugJq4vQD4XegJ8tBPi5QoKXgkVaFO5fOsmdBZgRPETLA3EJiaLGOYXAhWZ1+yBGsFxTEIAHhNo4tXmwHfgnviK2kMtSEW0IGmpIaSHtlBRE4WSlJEfoM21rjIG2bnZJiRwG3mLCzxeQGzRjtMTfyQv8G9iu89R3mNpgCPkbMXvkD48YgDYHV2QVqimshi+jfpRFEcUspQMmTOIjpcIKPUDmycxrO4SX/6RHzoOyZ+UjBHnZ2ywj0liTZkCQTi1ulSVotZXqitJoQfr2ytOvGXfzKih8aGY0ASloqLG1EUVkbtsRHZNBetPFDXwazi6wi2FWuLQgubx6kJdAt/F11XFeVijfIgdgxsL7GL9q6USQ20xnWbwZSkW+cjZIVKsEaxTpeFRjJlZcBCfci6StgqaB4NLjhfgTDnWY+NDJl/VwDLllzaSXUL0jeIdtF92E8tz53SDkaqTBnF6wVqyH1UowTkubCotPq0FR+YJOeZP69i7elefPnHQNY+DnllGe0QAF+faAfxF7NHEFIE2lGBGeZrY2ut6pOMXNgKlk1Xo1FJ9+YBwcoYTKrQMBgbrK3Bw0tLwBGQsBKYaUBoWS8iE5jVgJBy1hge0gpy6WtFFhCWLrW+LRlRHhgaJrZK/pNuVln5Jlf4S69puiJ97B937dHY00SE60b01XuM7Mu/n2XpT6EnMz5KjjBtXev/48j7s0s7m3Xlw/ibVu5VqUrhXWARwxHWo1XsYyTtSO1Lmw2Q5MpcT7T/G1VH3O2ry/jXokOduhFcP0CoQdDbvjiAdA/CBMwL+MXKJ90s2GIzGk5ubK9Ca46OLm5I98hmtdakrcMQTwcRMwGHHdYE9vCIEc+FTb6vXLR+Z6tvB+6VYAdJAMGJoBfcvedRoOYjw+BRD6auCQUA+ADX4GbyOCBSvUVXkNnuwi4KJMWPDSLY0PmCCkwemChEyJCNUhFXQoSL45+NKjunBol98wV+x4yRQkJrl2Q0+MR4CJhb7yKG8HNfqWbFiMQkFHjQRUeXBdImwkg1fuD+DWVZdo6V+HySN0ziFWCV91i/ZKfWGykROXcwp1R9MFxwg1j9lpUDeOwFUhmkGB4FgrzyHXZl9VDW+SMWvhDVqxIIBgDmz2biodqSlLAGxkSXpOkSGoIoK4OtWnFDgE0RKwJkYEivOIWYknFFnN0rFFgG8wg0s/L4aXJeYDcOqmD+z8R3DDorQxjiyNtQNc/EmSQo+jvRgSRoHDigkbIDjtAsLaD8AfymaD0e98llZvaqyT4UTIzcMwBPgmN1seN0fXlf9U0w5/YWYlHE9NrK5bRGzN9a8Vkp4ZMWvho402ljRYagb/xavkRVPelTF1Je4HwVp1oLF7et6n7ljDyKrM9rMVTB1X7ViHHMBL9F/cuMKRyVNpMhPp/GZsnd7wcnORvcpvlG9o0/0azLCd8BcGRcs8fmy2ThpYDyfXWMF0FVQNKLhfseqg5K2oC8NP+J9F4+ez8Cy3aMoH0Q0LnUdbbz83EitMxIX+Rrl7hd8jPHU9nvb7onku2p0B/Gl002qzf0OLB61yCESttvlkFJ3E7vJqxnupBat+XjyNPm2+8zhfA/PmTh29dImnRRuo+umzPGMNjoowdDY8tyAzbzcmfdh1wA0uG9xSymHvETI001mi+q+W4g0SR3Ceh+5p7QnDfyiNQAyof7s5u6T5KinIIl9SG7w3wjchge5+5bgNcMGLGzBrlMEjhC4KeO8wSi2MDVp0I1g6kFR8WXjMU3BxrNKqkPrgZIiK/ALLAg2jEx8g4sEOUR44//AlUJf3uLxKpHIZtslDulznUQJICqTFDUKtJycXaEJiowBdwZsRVpw7A/es8RhjoGwGDC1AaSHEmO3VfGC4VtoQd4/oKWBCLIwGkG8F66HjE6KQEwkRxEQam1xwBvnIo42A3c7NcDAr/Ji4bDEWRTLaQC4t6MKyEhcAygB7HjzBW+kl59DzwbxLJJzCEBCqC0izBVZ/VbAyAg17rlFC8Swjlb+OsdIhn/8F/R+jHXSuHWZM9pG+y5nG9MhK5jd+JWcSCBwVqWMf6udaDKo6SyTVCdNukuwlG0IQ14cuqynjUEjsPLC+lT5B1gyp8C0AV0O64BWHqmRcxcomBPramoDLuuB+BDRWHW6xg5jBYKNNSVNpuZPEtogEU0m4pGY8m7Gyeg9IrlA3HQLqiKUQ4IWqcDeh4KVA/jDceIdZ3upNsr4GKUWo2gwClK6BlEIudEwKdAOxaQJAvtVsOb3Gm805kyoN/pkygHmyd3IWlJXS3sSh3RkZKOkKlpD/rYuolIrR+oyuJVpK3rrdivz0+2TBh5dA6ue/Avpi8v6puou77rV3FBLes2vs24UDgOAmEb+Zc6NfMvI7u/G7iIbmXz57Hu3bGT2pmM82Bes72s/D7y28jYtqgMpkO3xSjWt3rtxadaiSa0ZvxEWw6nho66k+a6TAg+X3F+347l3iXo43y4KXfEHabKr8BcQnzTTHi2IEz/6y/h4OGgPvnc8/K1qAC0ARtlsPuUs0kAw4mEx64R3yAiX6MnJmLNaAToAFJYBuKm5FsH1sP/CUdj1wygCEkz5MEffElvFlcRZBpex9Tf8zQ8UC5AZ3Vj/6KrvXIR+2OCtQNNAH7APXvuM0DJH4V2gIwjLrx9+/2zfGVUXNQcSFHRBPrBo1Qd8A1oZkg/nb0EvRR1pFW/pTA7Sf8UMQG940cvBZP0MN/jFOBtiB3wsBxdV+Y1lFQ8GATMNhWmBCIEGkcYaDRz/7pWvlJGN8wPKgwML9vjvj+bzm7GLCXQzx+PFYd38glPG+gP2/0El4wG2hjUEejpxgUu+tUB41RZgGrEFpfDw8RfkCjVJFZhr8hAkmoTyOd/Z4FJUSa6EU20OlU4eh9KB2qpxHi43NDK+US+RjzUAHpoAKHUFw0inr+xtlV31yt/l7KEKG4FzEIn3gIZMXFAV3gq55STtWviwkcL6Q077CJiWlQVkZ6TfCZdXbtNUTfEuCoMM/I2dlpfZhbsG9c7Bx1gI4SfGJEM0H3qAA62h75aWgBUnQvIoyW/TdXZDEW9tEGOsPZM5KBH9p/IYsdqx+Ow7G0DF8I5jgQMrYTisV10nI9HOIiAvBizelQmSqm4ve5Q2g2qwdv7zGrxTrv6oKNn0hy7NhMcntJL3nkPV/uj0BDvEIv88G5wUxZRNlnwU+Tf8oG+RRnp0AvUCJ2+DZWKdwsZuXhHRPuGnWZQCW7ebJNZ3j/d+XvPYDLXf26k5N3M91l2b+4NxSg/Gkb/abe5tCQ9po3apNuXPGTP4PvozLFe9mh7Z6sukH1K7wyU/XA+H50zcu3ppk84KXdfPbqfcS6VsPKXLyJrf8hn29mFnADbFSjJ0tM5m1se/qxVXfz0+vycOuzTwhXSGXaL9HOIOUm96G6TPIx4HQBAIkf0HxT2glEH+//7n//zi44d/43e/m5yfYwCAVCYnE7DtaHIyGABe2Ztlxsg1ruF6cQilavko7is7vkLtSQwiuWrxBEd1dnETYf1OxEwUA4cFZiJ7QGxSWcMpVYuYxmCzOUWuUQr8G2XJYDavoJ5uUwwRcGGfGgAg/8zD8HZe6Mhu3YkE5wewAoKx5+Z7hq4H7CMJQusNBdsgdYIAU5z0wbs14FMksJlDuhJIXGCiFUEeR7MZVpeI1YI0cRbObhhKHoEbZ+G1glT61veK+fl8CKzUgLFR3CgTEO+Ir/veuzkMsteVtJ40BNzVnFXyoqb+IUJIE3GhK/NQgcggjeBg5kDnev9rNjiT4CC3INO6fQpCjuVrggFVHa1mR9AX+Yj9bVgr4si3oFicHbwFMzaMAJWswZHheps4eAvRtZFoaZjiCx+6pwqsdubTfVRxoL/I2UYzn7BaFnmwCNiSh8PlsvJZ1jthrTasXCJhi0XrC51VIHrXipMRKeqq7k6ptkRzT+WVjY8QKLqDEiMrEmP2WCtUhciaC/rzsPEUC2I0MdSLFbRFdIhKlbJhbSiFkWhUHuakS9ciElcq+Or0lHvQA43HLIrU3FmXiQSIYE70+ydsLYquT8Y6fUHs+upqNpuHCNn0ZopBDl1lCMpSjypHIISKUONjKUQjyuC6eCQ0bztKbBF4un3SwMNpYNX/6Hy/jKtZ0Z0P7oYaUo6VlkxrEtjIqwFQj+y+2Up4yNvEn88NqdoceLdx+eOw44pfjh3x7aguRmnss8su7Ipv2mFtXl0xx5Y6JH/8CKVf0Jptl8xdUnXptjN/JCTNd0nYFd+m6bT7YVezXs1ws/ThfLsoNKkdFI7+uf/k4CadxJd99O32B9e9SSGF2/K3Y1al6PzLMf5VXB2I+PQsLt8J8bKI/f57y/3+t0shfTxQYFP8jN3Np3rNhimD0fV/+k//s7/7u7/6J6cvcLpgc39OeGUGgBHr0XC8KG4UhJ12cMpwB0XclMFLLo4UvAcqz5aHbdmv488XRPpHRDAN1mRXaodySXUIFtwF/iMQELEC6rEK+Rochks2YLCYsp3LcDG6Ho4n4zNYB8ZKWBNopt9/8ImqIgtVExFCWgANa/DlGQf4CrqYzWDZq+fvDum/gDKKAvpcxQDQrF7jiKEUg+8HOaYRauCw3/dldt2vvqrZpuqC0KpnjBqD04gQr3npNsMt0vSyS7e50fRgwJzBciZRxiwCxvxgc5wsY2N4xOnPtTWuca+peuciSBCjLkOcyBv0nG/Q0QaU6X3UwJOnrK7AVU5+LDGhSg6wCiVB90clWVkFFkPtRkVDsDQZRSEaJge1xhf/XNnLE9ZA5/0PDMyzhgHdIJMD/PkPZcb+/89UK5rD7YYiMIEV1kA/3Nk1YzRgEIt40LO1STJpfKltsD22gfWhGH3GnfLBwzgGjdmFqV/e5Dlm57UTJ4voZtlVwTkAUHb9CcYDKg5zi1o7D2JDOxOAJGwfRB6G2Z3hiaqmJKRRn9EFkbQWSNTOSu689xXbLs2nv2fhe2/oSXYURrmLm9PFdHByejo+OanyN0SpWjE4e4amMXnqyLJvSKtSlMRHqm70cFuFIh4QAM2cT3JCGFvrbDTmrGX2BiVu9Ff/6s3F5YcF6i+L8eBkOObBpM/M/+LPfzcaj6bX2I2LyYT8zi34tCV+sExNaYW2L/LExXzUm0b+FBefMX/ou2WrcNe76PD3c+KcPu0FiLkUp5m0CndxXGU4MJB4dc1sH0jEbPGsHfSGb+V0VID67v916EhNZS1/K4WUqfV5tzZqkdnQwEO1TuJye39IXWW7z1q6q3aJZqK/v6elPA/1eXtddnHaehSatzwrzdvUk+u5gpSw9azuoM8MQJPGjhxbUeTepNqK2Cqwut0stop+lMDOOtUCHCzwo0j2RPQXpoHP1u139vmWsgUc9TOfCnTJR/zySUlZwO/uMwNwKeY35XTmLigAQTZOYY0nkIXPwOVgNEbCB7ikMPaPpcAmMOGsUhME6xAKUC7yDuDXkESUtbwMre/JDH1+DKHLMDlQ3DWeICUsgaI3vbq5usLjHHQDQsQtBvePyxcvX45PWbYrDEvViaokSWouSSG1JCA8lzFgDaQRa34f/PUFTrNNe4YBA6jq9XDFkWL+YZGNq+zr+PkW0hLl+ofqFQP3gk+dRhz8Br4K7Mnhv6iVIgAQAesgAEAaruFAWhG0klJHbrIrFoT6ug2QAJAVzIKi+y97xU3GimEdQi6FczHQ7Mg/pVUvBRo1hqM0ZakA4GFFVSHWmuiGkgOgrySESqQqs178kRcUymawVgq6UOjnFwy+Q5IhapY2x4anLqTolV8VBd5NQOQ4ikuprC5eNIJgpaK4tpyhwNB1KyRhaV4L6GFDXtShnHnGJkwGiBh9mlccAYb5Nyefw/K0EXv+915i4+GPJDLvsR2Q/8DRnFtMXxSXWyd6MTpgbsQkFxhbVVWEOEklqXK1nI7B6+2j+vB/ms4vP36kBMPtVII+jhFhp4FKVZ2cYraRq1av5qLCWHmig4vVigCfEUUXNWi75CwscVskJjN6wzEHzGUM/aMmMjIjwNzDP/0n/3Re/YBdRyZgzmDE3IMrE/4X/86/8/f+jb9ggyDmB5gLYglyNHawkvj6Cl5R2xAi3abkZnhdYBVS7Ma1ddtIuXcQQR6R+r3FeyLwI2pgZyf9ZXQYnolU+1Vg3Q7pedn71GyU8saTgHlD7NTomvK+0F5+zYK3N5C/tQddd7My95fqshfbAu2n087fGcPvE1ej1vsp+zO8eTlq24rczHKvu/gp9CfwQa6u2rXjm23RDN9NjPtTaPI9nNrhOZv02+E2nXZMu9SOGB94kYlJfKQnF1BFL9pxCRPNxCdFLAtWA7mU/fejk9HVtatO88GEBaBuw8jGLNmEcXfhGqPzHAoL1MsdYXXs3P34Xb4JThOPiIPSZEAExV5x1d9JMGLiXmwXz0iMeAWKAoWzww643KUF/jOv+/dgVwChcEMXFIOQOFuJomA2qgD2rAmbn78Vm/pWVw6mLfDhBpi/ktQAf3pB2YiJj5sZe7YzcgxkjKmH3qB8HcsA3jk6LZwUBLIvZZG9Xww/Vf2v4UBMyCYWzATrSGMTJJFTOHN5qNpCII6JxV0KA0bLgGPFqpOsf6NFklVzDiFGieg/ez8fsNcN8zDgynOdvxfnFC3y7wWvsGB4Hlti4F5CoY0EAZUkMDUqmlqrWNSrEsgnAFYl2iNIonKoOQDSk608Lzn6gi0ROvKwXgadhx+odVG9ZFi+qt575C0toOZjmmfwsTe4yrLXnNBrW0E6NaSGC/2B/ezJTYcAHusno0OUiFXR5O9/a2CXIcaqRQUwq7CumAxglx6nQWhr/gfcd13CqMjfcRbz5PRVOWZF8ASepKp/a8fyYcA5qJlFI3wrg41i9Ty9wsrSZogbzDFmUkt5YDMypPbM3hS9Kxb2htZ0s2EkXtr5J5C6nRQrBDoRRbXT6mz1S18MJZgSbUJMWMJUzT7gCmL0Pn9F1cv+xWCUnz8/Q5VleTWdXo+YldLrf0aVs8WZvkFjbAD8hFABDkM3LM5BdIyrcvoVB3Dkw/c+rUQhzfLaCoacVjrS64z2zlC5fWB1pXnF0BctVEfzfcd30YruZmBF2dbvuA7n2P5laZNM1A7J2S6bYppzwrfQifdYk44vhLte9yl7i5wtkW7J36jF4a3TYlJHNHmt+0Mzd3ffaOZq0mnG76bZzHHPsO/PDVyX6N15rik9pctnNd6LQTGpYfksbs78r8ok3luf65L8oGyl7b+Fm/o7rtB+kg+emuq+g+yXLvgOkX+SUalLftF95Cep1y6hk767UtfxO9tlZzOlt0L9bgAOQQOMEg4wBgBm11fT68sbcAqez2z96VrbtA+OA8UMqbobeqBKmAKo+ARLpd8Jbp1JgKpID3oBQAgmRiZFLDCkDkdAVAJrwJyQBpQiihIhAvACbcmEOKAcHwC9gr3S4yQp0WGSIRGM6iTSwZp7SonGEJpRVgDcYCL3AQ4tQFJOAsONheowBgzACzEK9qL5EEPArHr2KGJqP3DZMUj1ecVS1XQEGXDSU8vYOwZ3dKVj+3ZurSuAEB8Xh2mpDg5Hg145T2PE+JkAJ/Gt92SrjJOTnUSAhfqHwex1f8IIPFMNlNPgwQSAjkPpQVhuWYY3iI4u8qrVR1hDAzn0tgdSs7wAMK02CJAJ9VK3pWLiG6Tu5fldtBquLGV5TYuL81ENcknsk7MwWHfEsvDWaQ384gG+X+XVsx72DWtTgeZ2i+ASelCRtCNfLB3nRAPIiIGRBJrKbNWI0ABwjCSaPjTl1psOxpf9D8z1eHYypiUmgZViNTY6wzGJ49WcBXL1sZLKySrgIYZ5pFrUQvxIm8H/oQS//bNWESBVKZJu+NLEsn+hKOYxwOs0it0tJLNfBoVQS1CyfOoDFFRpUWfrFXRDDHRlH9E7zkM22O9pNGKldc48A71xPD6dzXm+TifD1/P59P07DgCLeSEUhIHjUmQsQ8gxDYR49GH8wTg3IFb3IUMIFIzrOitiVD7qaR9a3qXouEtNQI7mlQqus9d6a2Z5Cj9p4EkDD6mBxtMaL5eg7UO9vJoZjFvdNzMtM9ePevoyw6Bqr/qvM6fyq5dDimW05StD6VyxOmd8bXggNcRY5dklzypxO9BlvaV8+63MLZFXpNsyr5KOCuznfgSpht2cSu2nzLuaa+P926JwBPcDsjZ5tbl3EthqadojYrpq1xXfSf/HSnhkbXdVa7/mu3r7Dmq0QsqdPlMzLVunzm9SgjERsUoVQuiULRxkqBS8gQ93ACAAc8maS7y3b8BDDBGDr/oDUtlsZ0TYdZFQlCiQDjcWB9ADmAjfwWKBW8ni8CcXYCbhopRLCRyPFF1xgXXjP2O9EgUP90uOgyXX23D0EDIGMANuMR0BwhY4B8y1anEZENTV/ZJbgXKM7FM6UnHiD0KgMoQMUFrg8AEU905X/moxe170XyzKy4EuJAJDxqYZpy+H77PhVbV4gQQKJgDss6ELYBQXFGYYQN21EvsFizlVijvGIwDwGrisVsWri2cVGwEV1yy9zgYoEyGRgC12LnG86mWvAO9AcZ7RfnaB+41yIxxe+LDsPRMfikxT7RBY1Gsj+H/CnzXz3nL1xT1imDNiqXacNAy5yJYAPKnYfEGJXZJArcrObMN7VZDUakswEfB9McAD55mj0tmcM3argvOVySx9du5X9OqUP7QSLWhDszYg9DXyxvXNOTYmYUwf6wNdFQgx+J5Xvefl4ibjiGEiI7MZB1dFflNWX1EPmgvHrVAIAkGcCRaEpEmfG8maB9VuM/U5vs0O/UH1EBvdQH14o2L5ts4msCETtxSUBn5HeO2oOLQFmWhJ4hUW6w7SOjz5FCQCNG6UDdJJ4VoGXtaYI4F772lLzAAqNcfXi2Oe+zgCwQ7TuhiOGPWfMd2jRMGFPbiYGHLxN+dyMGs16A1H07K6ZKoDgbXWU124S1fc1uFU2+VNfFsVa7t9GW8VSFxS2s7ypd3v/2WJNq1FbudM6mrm6apds2wz3JW/GX84l2apZng/UmrmbIa75OySpyt/k+ZDhR+K10PRObpeHTjhDvLEA3f745YezcjHKynkTZ97HtS6zNFrAJI2kmD7NHN7jn2l75VWV61Box3TSPzpBFNzpqb98qVedcEk9pcv8Jcs4d17cONBTC2y1X9WrRO/62LC5sWdrCOS0euF+5Lo4cBwuKPloi7gC0PQIg1iADwxxhz+0KI9I8nq2KRAH9dkAJ9ISpJSTwP5gg6whbwS/ODLGwmY00hxOBBNdAIpQRuOJ+I58LQjs8AhKEZ9SUaSRbHAgwU8HYWpX1BqVi9kWGIaClFYlEtOxundlIYMMVsBEWoIA0CZqBtoneUf2YNegVwzwNlMDlRTqihfzBd4PYFJQan64SBfjBkjJVdUG+dL93OBG3slMdyLs4l7t/cBduBWdy5FV1e9BVu8C3f1aHf0egGOXCxeYTCwKSg5Hfi2clYtAXdQsoWRSDtNzSC4jFRV1NQC5CeSbHxy5wf/nDGIgB+KacZQiiGKKRW55MYNMYJZduNxfgKobl43yMF9HXGHxW+rBXt0on4H+1dsaFSEJSIkANxDR52HzDS3AptKA6YdbEJ+XFrIiO+QgpEdU4DtUD0jAbPKupfzOQDZyQSgPJ4/zl2gfJWB8mUWVhXdRlZcxPA/6hWfIaDgPFrXKPKpgKitYbITITWSqL7tLYlQMuwwV0Ij2D7QQSbwuBajbcMBGpa2VhJU/1bcgCTqD20GctJxbdx+dnb2QrLkcKifZcCswh/Pb+YzDk7GmimcKYoGpzUo5n6yemHBJexeFRgSwkHpuaxRfMadsteB1VcdkbIvY1dlQgvL2Kfvh9DASrcPQeyJxs9JA6lrbD6KO+rXeIZ9tdYP+TJjSuVzg4735HQNwGbCsphUdl3b4+hLwqudSncV2hJpZxZ+DI0XNNzbs3BV1VSJjqrI6Cd0Jc3sF7g9HtDU6v6y+1MPGQvZQaGp+lWr7Mi3I6pZl2Z4R9YfNaopWzN8rFDpp7qtZ2OaalzSTbzae/5szsWhdAqH6pP+009+HW68FQR1AQgCjBAsXskpf+8nCQ7tg/QZkeX8USAY6AIHFfBGwapQFgE4zB//qMeAjUCHI8f+NQAAbZzTpIuISFHoJD3+wEbuky5sCtQSogkqI427hKe4S7qRBZgK1uJOATabr/T67zRJHGZl5BR4FrRRmsPnnF1FTSFOqhyX9U3VNypCgcVqMLbKBlAbgbmBlYrNLihzlgB/F75NoEiw98ucM7ky3P2dlLB6glcofshGl/3qVzqqIyIZY4AfKEZVETrGbRGTddIhMKsO8hGzAPqZM4XAktEwonBw9/BaN3UPs4ApATQNNB59LIYse/3KrYLkioWiMYRt4nh874xbKswHgokw1bx5lrVVRnQeoFPbyEaz5ZQWXS21hPaB+tQ+bICAwSJLVQhd7imB3qj5GWPgZe+Tqz/c8klGGAP94ZuCmRCWLMua1atsvgR9mQX8PoGSC4mNkbrsbPJJCKBc6tjm8S/gNhKChrFsNFV6xYtFhYs/Lc8BzMwsMT3yCu1V+bsiZ3/Mr1CxuxVRfc0PtHgutPeMZDroxyBKPHz83x98rKuve1QkypmA4pnFP8MSC4MlEsNSo7p07cqNe0DeHNfLM4L3DqpIuJ9i11fs/gS9IGh9JLb6MFpuNkcs7bWTM68wVknMYuHQZkdiVyuWMQyG1fs3FyGI/lZssVVNF8x3DbIx9ib+Y7EtKrrFxKxFD+Hrj/pZ8i5qJGer17qQqRlfPyObka1Cd4hI2kbSA6/mO7YZPrD4gdkOl+cggumxCmzTzC+X7orvr93+1CaXFD4k/91q3aR8bGu25eyKeSjKbTqHxHRJdf/4pvba1OLN0I7eiEl54pXZ6EwEI6Fzlz/zxoDKvj64wWjXzSEC1pLsKt6MW0rcjLtnGOkaKrknsZ9m8UfQ6u2K+KUr/XYNfe4cPgnCoPpKvWJ1S2xqMmPqHuNXRPJ+DOzCjS7HjL1ymNaM7VhwCmLr9QCNeD6A93VR6Q+GOMw7nI2dwFi1jF3fSL4gJMoENQodGUU3DUxV3zv6m2QC1xECUCXwFVILOoOj3jbGOMSuZNYMwIMnRABeCwl9/R90NBgAf5bwVRQSrVWRov2UzDoVEnIUtMNItEuicTitC/X6b7FPSlY7xHzBTN9+FJAPF69G/bP5AGEcw6aMSDB8h0LaIbogoG9UsKS0e49iQbGmOca88ZXBwak/uBosRkNgnNsqCaLx7gYCZ4tfMQ1Bda2IeFPo7toAMqFITR3UGdKYI5RIveu6cWsVrRchPqx3/DNkBUlUeWrPHLYuZoDFAejaUaGkaCWMLvV75Slf4Gz2ZsUOcRDa3XWq2VfV4ixmf6gqS0SoICrxx1YKkJFGsMN+kXXQJGB4yScEpPLoysFzup62n7MNnJOA69AwG9snmTph+kmhy2r6vD+aOfyfTkQQsHPBAuUZiEbURIrIEGbJrc7oF9dSniRDHUU59ex8kD2D465taChbNVRFW6g/5ADDkwfVaXdAizLxwae1hl4tmEGbySLk5TnCutEudsVyUAD7s80Pqw4ok43HJ4OcwX4os/sQz51PHKfQsbDZp0M9uLQPQwIDXGawkXxiGjqIusRHo27eN2+b4VWSfSVkj9JPH08aeNLAj66BjSfVJz4k8rWyvCJcZ1vlNlIDYBWxzH37tz8N9WtgFegoFe/2+pemI0sd7Yv6DrJE6T1WVNLDTsLNUofL2VWLmtrbSOdV/WNcbT+zw7WqBvz1v4vc29rbqfTbusoW42ZdmuGtbNxuc9/M0WzlZjjlasdslr79rilbM9xVskvPCah0lWrHJ17tjr2ci1uqm7ZImQQgCXYtY1ZE6wyNe8aU09xgwioiHtA80J590PFDLxZ/XSzmIA9wBf9xDRJgMwQNzvIEI2L1jOGWQ8HCcQhnZrbYdPA2gA6gToScF68cTs3fOTjLaK3j7YE/hZvIa28EGcWcA7eRSY8j8bCgCzNBTIiQQF79kQRMUuYjvOErNkRhgD6NJad3Vqrsqq5RnI/sRjrlOBKgLU0wFtypRJV95yJfl96yjFcQ2S+eZ/1nfU5p7ec38xswrxBrsahG70owe/Xn3uYXyQ+E8XmaV1WWnOALn8vgCjWjsiFzKG6lKnrUQ4ZI6E+cxOhPcaoRlhPDjASZ2Kk9w1H+eVgnKEe0nywNNqupSvYGwigZoopgIfSLZucWKjEaTgLC0R2EcxoMKpYPA2DPZybknD5rPppA3v53NsBvasI9QRQrzVNXKXCGcQn6nLL/EEcVsEV+fvZ9OZjl5Qvc0sO8kRyV1ZEn+CiM/OQdgXRnjPfaEi43TvKLtXWEZ5sdJ400hQrOEDgrF1N936OWs+INlZ6rQbrfN6w9DoNqiEFlh8gugo9yLzlbmajc8jNVTRGWV/FCsbL3cU/X8g4wbTkaLqePzfp9DiRWYOPYE2bxusq+n9ugDMvT2PYXnwTKzF9oueXv0IIsLSVhBKNlUQvtSHp6ABzqZykA3Q8FmcO1EEyn0TZohaW/jPfT8EXBUXRYHuM8O+PJ0nqwpZK9AQP/YzYSu2y2CEZFavZ1WEH4i0vJ4hlY3q7OAagzLL+63p/WL2gsM3Z+p8bvotMu1nzHNsPtnF9QzJ1+VffXbn9qu+7H5m9T6IppUk6t2c55eH9ol00xTcr3odak06bcFdOUCu6+wu7Upk06KdzUXjO164loxyMLz2tc8SIklO7jGdze5W+Z292rcAGKh35ZPBE55FMtBvn4aJfoiG5n/EwxX5o8n6nax7ChTx/fD7oZtGk9tUG3tu6dkp7HttLTu6Dx2584bbUFt1tFeceZU+zg5iRsvaIHEP+n0xlnrrIViUgQYCGgN+NokJ+fnw5H4q3hKDaOBKq5pQmYJQHUoOmrUzAKMV4imglurg8MFbtbi4TmZA32CYwkmCUEEkqvXu4HOkUMMBggYUYSyW0X5gt0BVhUKt7ROqWnkQ5IQh4hTImr1sLmV+RJGEwBA+RiysRGN/AJ33o3iMw/Bhe3YgSYaZE4RI8fyGvBnxHQFaLBVgCHZeLrOZpCo0fABwWzLLSJGEEnE5HMi1ih7BIurABgXgDLCZUtCuA1ZX7T09ubCJA0vitUscyZdRH0wys84rWRbEDI1IaA9bU6qeLxCXHyYD8pU6grykRO4ygQuqpLLYvW6qOEekfcS7fXzBZOU2AKoi+tPkr+qjefsYMoeRQDWRNlPgn5skkU5a6ukFiWRppugBjKGQ9dquQQuG5DizmTJoMLlkKw3c+QbTGjFtNqhgmS9V7TqWh1zUYNjuhUaj4xoDPAAO1ZOaNrMYyOoGqLm/W3goSEqTWttZUSmJOAGiRm9ZGPhsTUdW0DZHhMeG7IF3WEqqqAiD3HO0sbkID3yhPMzYNaMbCdWbMzu/CDH+xsfHnxkcUA9HwECGsRu5ddqnge6RXnPq0y9x+lFFCqUvcyKoXSZ2K+GRcpG2rZKkihDSJNgk/hJw08aeDzamD1dPsiSVfX87lMX2bTANiKq5Nu/6IcbNLnZu4m9/Ta30zffcdblSvlb4Z3596M7bKiNnNt36VSTV5t62q7TPf93WRo07uPDG1qh8fYD+7aF3a0crMTHC5EI+fh7bKDe4NOs10GbxsJEWymbqc9zr3Sbuq5WdPbea4euk0ijYIpR0Qc2AorUgCU8KsByAArgaJgF5y7gXRAjLK6md702YJmsLieAlp72egGRJF5xq0Y9PTZ+ckpA8C6MQjcFi+tKbvp88XwP68L5weUi1JEcVeUPwCXY3cWEgIIJpASqCqgo+8EYA3Rksw5bFfIBS0kRLxyxt4yYC9algRwFaQDmQml+HfaY4i07iFqo8rYG5TqcVIsXw391GP/ZqFOAcWYN6DuriUlI1lZChBwkjz4ubwo+y96fdzcp3hhcLAxDjAz1kPk7wcjlmc6ui9G19qJQsJR9HgVlJKcikgGeKXP8FKhCeCHGXWOVQXY1Ylfa4IVAMLqavCmGNAKr1EApbQgmN9AQSB5xLDKMHwWtfiExkLXy/eqleCCKwESbQbFNN6wwfzCQOqT3hsiQVJxWcB7uJwT2S8us4IpjAtgKoPxrlV2DQJD2d8vhpxl9ixNKlLzWKQh56i1PIIKREMlftcx/RJ/fRgzuxKpMCQllI7KqvlX3LHqdtI/G+TzrMLhxyUoup6x9nj4sRoxLfB1n8OGmQ+p64hIAGjIMWwurTCW4GtHCtp88J8McWcO5h9g+UERjI1UpOKfpFA5XZhFJppwruDmnrqNrngSpMoNm8G6VIWCjNjbp/rD98u661QmWTWoVRBcbJcUgBohJ74oQDQTbPJzsfnkBKbQQ7wL3NHKOWtFeFpHCuNqY7yhhp5m3ecINnsIT0vQtBbQr3klPkYt62s4XSmGQqGpUMp63781rcjc9f5MSl1S3Pfd/L1rhveV+TLS9ku7P3V/DVJ3OFyH+6l9/tR23e9fl6ZO7rynPqpo0kmaace05W/q0Lq0n5pmjmPCXby6nqx2/OqRXAu1eoS3JPGhTlH8jhDgpcz9isBW7t23KffynV1T2yByNMkVo7V8q6inwOfTgL8Kdf/4fEz3cfrS5Nkn6z3Sjqrmrgai4eofa6VIOVZPKNRX167CJIpr/BArgPhjoDXBwxhjZzCSLUfAOeBMxrkBI4zBAmvID7DxPFTwEMsvgSns6QgJYhiAJbMOyXoHgWFCBqwJhj8dpxfZwJHySh4aMCpdpnIhC8BKJgyOO5iLP4qZjfRF7lhrVJMwcAojIeEpiADZEzHkrKkmCaxglJVvUzU162BAGBAXmA2k5TiyThqaRtbT+kHmDSsd8v4JamBvdpz/GZ8tKlYKv2S5ML5C1EzvpPoHxwByWF8oOywvFIMM6Ro0uNf7SazGEnzy/Ep0mwPs4AllgSKoMCu/zqspoiVP+JBN5GmruRrBaQRuVCn/fKIjXFe1VkU0t/IEVG3qoVbS+k2ghEHLMnVx2XGjSuBxSXPgCK/7P0JSqd5smOXz+W/y8qqnXaKFo3jWNmVacqkpKoiq2hLSvEJWctFlqKlMosM4TYRLDz5pGTNPpMClGjIFQo7im35146oBf9dRrp8SkjjSoo3ESP2YR/pblwnLKMvLMwrbJzXkYEedJIgkNBDfqQh2hU1p28qVGQDtALJiHRAhVVt4KRe3ERfkCUHFP3u6nYTt/FU1N7hVsRms+416mPFwNPE5ohtS/3wMn6q68RwwtqMa5qPhZDa9cRMoPeLsVmSDLNNxGilJ0DCnU1Ah+IsLbsvgKkBEXcgkopXy6XrSwGfWQOp2zW75mQX4gtltP5Vdj2hTe+bBAIhHvit/u8q7zwHYLJ/8BZOl4lsSJk3GbaIREy/6Ou2Q/E3LqRlOJI7juxSpbV0tU27/TjKkfPehc5+ybSnjV2r5s9dObsSkn8a2JhtZPmuw2R/26+QImdPP/8PWw5G8gFlLskfIE0VqULIsftC3KOLhfoljBDKeUZGM8MqdBHX6B3b0h/Ny/t27t1+/fAW6uLq+YoSR/dpx7R5mLwAnYA4PygqwL0ynrA4KlH0P5gvsA5rRmV4gAwpiuxgyJYceh00ZPX9OdfrDC0unihHpm8nBXZy5A8YxEg8dS9KfOXdMMcnCdpxcfYY8KUxbUI1wDTLAHZkhRMGUSkOxHQ3MIjVyUNhvZwYQbhLlSFYHQnQyiqIAl4TBUozNA7XB3y975csqew8c5OwllwXreQRkf88xCFnvVwjJgWkO9Ka5hSQ6EM6mk3ugcwR2ZBpmwDX3/PGC97BfnPSL06K6ysoRvubIR1U4c7dk5GaATl6SDfOKD7YqQgtqQ7vCCjPrEnWJ8WOyeAXHSETQVH1zotKVPARS3ihQfyRFWJw0FLAk5RD4pUYIqxo4dLf3ZlFwhvKsX46qkg4zKE/+lkapyhfMCrhXUwgQHNLsh+Ql5rXFFXDPGgllSRDWxqDzOHuEmqnlB3zhq+npgImOxadyjl3GPlQUwOceLPxtv5rnvVdssKoDjmA96ZsMZgqGdQxha7TmnySKT4wNE0zWCLFg6p1Aa5qMPkCCxLXKrATmcRpuR5BoCDXPX6IWXViKMLSp6srbggTDYoiW8jExGwlS9MnM3BaKC/YDZltGg8Gozw63VXnGspei58kJLHqeT3HNG326uJhflpwiDInBKMNsxw6HJG5mPKH2XXol/FO1lSMueVrTuI/USKhTa1lT1jrj8qbj+/B3YPPd3gx3EN6IXrXmRuznutkv7f7U/TL60vlcV9LhfcbU25K2637/lrL7L682/WXK7d9t3bZj7kP/dgk2czwIr/Sg8ll3nPSV7pcPsWzXOVJWDICI9Ougq0nsoAJPmX58DXzGt8mPX9lflATL57lu4fp2GbtDFeKRnd3BFzQJYI58NneHn/EQoIw/MYiWocOL1y/OWb04L2b49w8GYwAvgCzBKWgyIo6TDoPjgBbWJTJize4oWgFc7hoEPPUGgWDDJbBDEHAJoMzRWi7H2BGBWIeRJV3DE+ONSpALzx92vAHJYRqwCpMhYYjw566YCbmAcjBIrA7xgjb+wzZxDk5mXGGfdfwyG3IqKlz5QFIHZNP2nGw3AwZ30Ldg40h939nJH+SbjWYu+tQEYPvUijWwKC/2aAxGofWaZKIaNZaLVQNBImtoE5QH2GNImZHjCz3VIeNpy+4R6gC4viSvcJpKuwqhvFBOCGplFdiaAUopZ2EYpOpAPtKDoj958oyYWhMWa+qCjJEeP4/QEZhaEQnQPjQXIcLZ+7I/xqbDYIQr0Hjen1uJ8k8yVujqp079bLAQKWHpmk+iBhGJ1lfwJLNVIYpSdiHYqwzUi5LRQTXL+h+sAI5ReJdpHCFcwOjqJfYYK5JZmszUAJlNSsTNpf7rKiW2EbfMUQsRX3UhdRjy+amugNEQCGyuHmw/VRF9MgzeKlzaonjqElY9mAYpSkTd/I4+E99ml1wtLIkxfk8aZoblycpSmn7uYdLxBGB2uyCHxxKsP+Y8NRaEDMaT8dWH6emLExYQfHz3fjxmUTvm0Zytq3DS04Ci3VJ9UvWbNa7DIcUyPrXH8m75HQpR2KfrSQNPGvjRNZCe0vRUKszqyVwFkojrHOk+DIBUOEXc+lmfA5AIbVFfFmZv8lVKvGuXCQ/63bScmuHE5PH4dlWiLcNGzvSTn340NxL23fiLRWtuN1tnkfa4y+FlE9FbatHBuc23HdNR9AGi98tcw6gDNL8hcwJMB5QSX25e++VJcLddapNG467Zc+gPq84AJmjkMrh+KlfP31YOsqSk7aIB/kAHs/lsOBguXMYoJuWPBYcz/AtGgzk7nDMOXYJ1gbfu6siQLyOK4NOAWWPHr8exMSKALMd7QdAfqAzMAQpMuB7YFt26eBGyvQM69fMLcnobwiUZxYDVKIEk0W88BhgV5IGd1gdxYENuuPTDqL0eegXbpyPBlT4jULUajrITEkj5vdSCN8vLHehDMDPwj5spCLtfnoh72WMUbv1rd5wUcTEF8izvnfXLKwVhGoSdMLVB8uHobTac9/u/Bg33itPoRja2cE8hbE0BJHGcektMOabugcr8AkLHPqv48jzjyF4OhsLnXaFZ6orLBxUZvCtHHLr8knkTlkNojWBhsVahfK7c2aV1qIe61ZSgWb6ETCcoBvcKVfC5vgxX7gIUKwFIt7hKpqDFUicxv2q3GYGii1dIvSguJnQI5ChnbI2qy8ngbZVfcl5BlIONzvdJB0FWe0IZkmCGveRTR4mq7YBIoUBMpSgNrD3jmd2Oyle93lnRuxrnc3os+9/jB8NijHz4gVbLsq9oJJfDIhQdQO1HcXZP4jvNGgVHhFES/4L8WqTITy+laPYe8K2hRhhxtFWZhHGDViTEHpAN+xPZFYdlwbrwm/C6sS6mBwn5EApWFODbu8hCAOUEf/NaKnipMbRKBAEnwBy8V/WsnamY+ADkI0pq7BFWwNXV1fV0NjwdXF5eUW40mPB0YiO6NH9Rzq85T1p3oJgDgJ0VDLZKmSqfngCiU1T9lW5WeVbVICbaZpV/nfGWd+A6471CSznvRWSrcPNX4PDfji0ie26bNLu0t6f4KinJmW7vo+2kw8Mp3I3vY7TUShX/f/b+7EeSZMvTxEwXW3yJiNzuVnWrq6qrp7p7BnwgCMwjARID/rMEwccmyBeCAAkQJAcYDLhgpqerq7q66ubNzFh9M9ON33dEzVzNzdTcfIm8eW+6hoeaqMiRc44cEVH9yY5jmGtD/z9e91jZGEtpmpvT7wGYKu76ZXNrhORz+/zgEYB11LuM1v7rX98ta/fL7+MtkIy48x5+PMOfYcw/vbI4rFrh5pbeF+uf/dm8iXe3QAkxqLGBPYAg4q6qAlc53d/e/dPT65vVbIZ/dl017EbJYaSMCwAn7JbsmsXpCecCc7otIJgmgXU/Nom37zZwE1CGSwnxK25nmShi8ATYCGoSFlLxADyG+cBNIm6wFQ5JDCd8/C/2AOOxAzrKEG4sUCkoTWX5k4IYAbX8CuGXAvy9ewVHPZMKcrST2Wd48hN77KAF85XK92x203UAPg70coJ7PmG39qxZfdExhMLejIJ94miCJCdgn2MeWReLR+nWT1hKWtRmOIH2FUA/oB7Th5hhg/WZ7DSZhSaVs4/aP8sWK5KHOaYuEuXQV9j7P8FKmaXEm1yudaJVI+y18Y7gtXbpYftJxYM6ovKAXdAzZSPLQTh/Ns8/kfQFgyBOiGGeOsMiUDVZ9Yvp5BVWY7I660LQibaCMXt95LTWDa3iiaAtZc13p/67FBta/tP2YkNVygI7e35k/5+T2cmEc3GbivUYlDyOw22bNxm41/1bxc6QYs2kuAKTS246t37wkNCA9aXb0maHP6aOPOJGqrC+zQroGYJgA1SjWjhtrVlUoIphCRhAFcHhWnPWP8SFhwn14gdfDSw7YlIekiQDufCLtiJ9/TObQhhkmlUrGgNM+8lni1ldsyiCFsjk6uryZEGFLGpaZAxJ0aKksJaM6bkxURKFlF5wSI9M2PYK/z23YbQ9wX9KXs+e1Gdn+Kdk7Ze0PNwCfYHiZcTbI9Vo3XFtHOnxbtljyuTXhtw93xevFPNuBJ4jIL2aE1Pua++Nx5+MY6y99eAE7vQTH8PBXrD7rqGGx7fj7+N6f/hhuYc1Gca9X9LTKPyW3i3G+zlu6cx3dz/Vk32PyNMtGUP6lJC4DyuokMuaCXRU7UFycfbp2NT0FFugEWI4KRAH+yMBw+jUZyaBU6fZXvJrgM4//MN/P5+dnJ7QFU1344KNaKbFq0X5ZlUvnaY+4VRgRANE6swdH2EqxBP6whMBPPEYfwDhEMlT9IkWH1SZqURkkFSbCxS1cfdJ2YSDtvlnnzSXjQhAEb3mbJTjxo/RL8smKOQdIugCBuigCVAtEI9ydMB+LW792wsMwd5sMUy6eUw8cTcY+ndtXrDZpcgOOXRHV/TGugmqjQKSzVDJkj3hu/ID++Bn3TegNRoPAc2ViI1QG4cNFjaosdkTOxElderXAt3yHb3ToHpmsOSTudPrJ9ec/YuZUIHFn8Rupu/bYpVNvojUMdMpSUH+pYr31900dhnnIdAYYe98rKDJb6/k3ljCXYDWF7E0BHNpiEF7T7Zc/OBk+j893mXLPkuA8ivWQ3ftBV3g5Iapnv8OqrJc1EzGqc8tJqadPxzxay6EZ8r8jHMYEIOG+Iq2CYu5TMBqstL9/km9WdnVnDhctKdF+2XbfMI+bXfdrvJYWoJan0hsTunVMABmtqUCN7Ml7Rc8Z8UHZCv1yKv4YNrZ5AqBbXd1eTFbnKyWVxRCpp+ZDMqa082KpnLfJ4gZKoiUeY8WSKR4LZN04UmKiUs06cX7Bne3Z2+jskNOBIelIooL9jAsNncCEF37ViO6PjkUDsome/fDp6Jsr6+qenVyevZlvbrghOSi4FzgZjZlVUY9ndJOIS3Ubk8Q0LqhRbKGgtA0PayNo1Zrd/zuPG2VpC1SHxL5Ns8dogd6PPTbkeiTkK03/IjcIc0x398RNqPeQ4sN3aMRRgKGeo6QROWNfB4jeIT/MXKPZ/vQ3Bzj/Lxa7Uo5Xs8xyjH/XVnJZ6xsjKWUeTfrCnf7K6tUiVMlvFuheadsV+kke/99tzYnnxEOeD9vzd+v1YvviwV+PhbYrlGDmse33I5jqnNqDKxNsh0hfP3IG3ONQsIlBhfoRKV1TeXJbPbx08d/9+/+D8wznjHFeJItTungnhXl61ev3lwsvz07B9VNT045r0oYM53ROQsVQFn4J1QMsB0LJYHJrqK1O1YBoFWhjT7qF6+6AB/AI66g5FlthSzhCHVNW10xA555R82nT5/sEY9kXF+tbAjwIPhMwEZOrM5FiLaRC2EpKAygHe5c+EinkkbCIVOxL00MmOMFAMOLh/Kj0667X0oMNQel0U9Ns6P9ulot2zlEEUBwUhEH6udCeXfr1x8ffXU4qoCWZgCIDfFFzgm7YQlAJmMGSKaXVxz9DVufAq3VgwUXdHAz4SaYJpa6TcSacfoND5z+bugkWl949jRrnyDEL7yNGFnko/LIT1TWKhcceMUkoLa5Aem7IaoDA5OOkZBZI1YvCrqqyakwXxgWHolpME+m3ojHOmF7cjLKgBYTmgKUkRuzuoDjNEU/2PNeFu0Ka2AEMobtcTgT903ZsS4WvE7LjFRppkiK6ifDhAUiQeu0bj2sPUOlPodUhjlbrG6YTq6vq6vrm+kKJM3CceA0CyCu2nbG4MfrX5x4NLDtURqHFsRk1+CfirY6hbdiTGmSTVaHuhCZHKsIjR3a2DR3bRLjrw9rTihjyLCbvwXTM1LHIN3V9af/3f/+f9u1NyzCrpvZ6emXk/xdMZ3SVvkXv/3t/+p//b9ke666on2a0xiIYz2Q6tX/pAfuCEqe8aOqx1wpTh9zECElbeDx4nyxwIsFfiwLbCr3xnFboVPVLCfFW148t963qu36bbgkosQB9x3/Wxa3rvTejVffreczuj4f/9321jEtuWNojkp+IKnDdhtq+Gxyj1Lu8URDnR/P5fliPq/dnpfb3VSuK2Yv5YdUe4VUIoityiip3sMrPaU71MyeebcJFkdFT7e92rMf2vLdzVK8zX8Wnn684FWRV+23s9nszZevvvjy66x7dXZ+xq4sLMxly8Jy7k6EQpeQu9ZF8IZiQiGg2JY2eAFsgDgC2+iUVF8JvfDrr4AlQcv+OOx3OGmX7ZKZD8JKoSFBrlkggvNx2D+nJAFL8T7AUD2kSMA13ldJAveNBJz2QNPrv5bJb8VyzqJjRQEqeQQru9DIx1WtXbH667z9IltcuHeP06GYB9TSBsqZhTmjE/ovjcRe/splKrxcTU+cvainup7qmwOg6bf+gJq2YfBefQ227upV0Zx1DRCTLYAgb9hWXuRdft9OQXKvo3GQYCOStG6kR0nbCQvht6ccpHDuO9edaIRHLNZC4PSMYRs4/NmQkilJoGVXsw99XtXXwNCywHoYQ2c3+5RPl8XkF2Q5zT9V9zxm9NQKIVt5yaWPsvSJP1wQSo/FFCr6ZdpTmLD5JUMkE1akZOd1WxcZE2AWDJK4QS395jTMXC/xjSZsAMpwhgEhP6hxb/+Qv/eWVBgGoZFQnr8qnwLKa47j5fIoPE5nYCYbw0E6l7TuuslrSoHzuBiHcpF6pJ6EpXSjitP4Tef6MkVcVpzirfOVsADiaESEL/QE2armh9aujma+WFBP29WC4tZ27pi0LPLLjwy/sB0tGq2ur/55NmehQH2zevvq/Osi9zRuG2ExeMZIU+RhGDOMAnPlenHvtQufgaYRvP+2ibobnIJ2/e/1sdqiTigwfKM+9NvxUPp7FXsqAd900mX2OjRlOT/OyHfl+jJIdXErZGi3593bZ0vMMz08PXeGZWPoHlNwaJ8xml3/p+v5dA5Jq/E07hSj5HGoBvom24m2m/qND7Sy63/0Huc+HrJh9+K4xwLmDXZ8SBbdw/El+I/XAqlG7dSrTQHZKSY7pHfSvgnHoRucsZ4aQKemmERQzZY6dHKyB7lQRBx0enYym0+hFZVw2BJTCwALTNPgn/MhYBaoKyILu0MxBPArx5DV35yfQxQDI9SWggzEmtKDnJJcESHfyvhXshHpjJ7lku1NwFhKY8MiTodVJTmgiy7/Aj2qUwToHSy4hbwU0qsWXjJTJe4gfQBWxSpd+tvVEhjaeeIugexC45m9/OLm3gE2p+2qO+t+ddK+EhPGlz3MihImyv8mCxcRw2FC1SRutp1IcBi27cpP4aYlw1kH9qvTxtCiy2/yedXNHG0xtmZbs+odBIxdiXJPKAHG6n8GDmkjFiomB0+oSFHAlnavXwJGp0z88eAtBgKYbV6VTIxfft2xWz22YR6KU6mA4erq1eu34QjjjcprmpBl7mkx+tplhH3E2hYp6D+wCreYnhSszuW8tJrpRhkrgbP8NW0DygPzs8poeKq3xkpCiC7HjbxQaHC7DTCGxNwCggP4o4IwekP2MYsGtrZKQkNHgCiQJBVdjGhL2IiKdiQn5RW8DPSZ2DqwG+rbMEiKRbqVy3oGjzjAldrkEpP97LDF2pxyisUXp0zoZ8fPhh2o2m45W9EKZgIc5qHtQeWwxDT52elidjK9vrqGFVt7QVywW+ra4CqijPhRu9AwfFKhTeHS3LkIWNPeCXl5vMcCWzZ9gh0tJveIegn+GVvg/sIRXRkPsJAcB7V+IGD/+QBr1umzt356/t+n8x9vV93Vtm/JjbS/E/VztfZSP8FdDcafj5GbXv3JYkP3ONf9IUNZx1sv8drt+Xgoh/067fPtOb+NsOh32aUapmU39KE+j+OmTXihj2ho2Pb7fs+6HYn6VT39bgCDSD39oM7KksdUob2DRvzn9iaA6QXdhewhQrdh1rEGABzHKVfMogZ8LOiGX9V1Xn7Im+tm6RFF7vxCj5YITeQAY9BsQD5SJPwJ/vzqkEYniMZ+1MBQKUTSIIi5PcaMeIHZgkzm9mSKnCLQJgoOdsvBUxuyGb8n+EKhJqkpgA48RAe7DCPJxkpp14sdh+IHuZASnXbEHKAfrAC26OrEHRZCM9eHk1a77nySn7JYmlECWJOSGSg9y87m3xYlZ2P9uZNG8k+C1VspoY9izOWMTXK0g2nEIH1i6PylDxuxy3MOA84LzrSi650++BLI7YaX8+/Amln3xlQ7UmP/djAJXrjGr9hZCI0+haygizODGYW49Qlvs0++oR5rIeTNk2b0L/1rT5j5VbSXWcMigWu68MuSWUC0Bh2imc4+5DOWSXxhGjUeFgLmkltOnQ8+sNmIDf7KTHZISjB+EzROj6IpIQvOFMjy7wTF7WnendEDT4d4O7khTyiELpbI3rHEIs++phyY4R27Y1oCO/MXVUJ42H0jO4ShCux7xZJP5ExyUqoNDztQYslxmh3CcyYe0YIF4ts9TzuRFTU1Y2LvlGUD2iaDzRU0N7EUBotdSPJXm8LPUTPDacxyhZboTHKg8UJtGEkfJlBXfAtOlW5ZDVwUsxuG6liWw5HMOetPaHAxSc46SaasbpgHx8gAjbRYA4A62iAMLpehyfVEJe4EJCE4vFJfcswzTh7epfpsV/pCJfa7b9QHfC/6DghTOuQ5pnjinN6fx9Af5rOredT9PtLu2z4V/6Pk+qbacw3j7kp/gN328Nbrp8BhqNowjUP3kGboHtpn6E/dtOD7Zn7SNabDA3L2oPwx/n0NZZzzAddDGwC3rOMl0b8pbn2Ti3JJyMv1YoFDFngpJYessxO292W/pjrWlj2TNa/0m96IAUDgB3aLfVPoZXfWidiEU76mTKfopy9MauYYMKejqdmLhs0vaQywywugBYQCDIr5MQBogQSv1HgRrHEM3MV8+iE0vRHp/hxoRaChwCU901sksbAzNYF+2hhO+pG/GCUigJ1ciAyOIhrxRGpKEPyZvvDuWfLTUyWAxcOaIsnkKfWvizejy5lVrixuZXYOPFuAKHOaivzC0w1i6ScgDxac18Si03b1TX09bQGldpO7+UpAtyQBUekDY/Lw8hJVOrOdqKbbtJEozHiB+dhZKC32FP2bFnLnl5zQZtpjqMBmhsYKO0SyEte9d4h2/Hd8wmObE/zNrEAchohUuak7/dwXbTFrmASEren/j5hMUu/qb5gyT6MpYDBtNhts0STs2zpBuFFn85RKhYqGjRw6CGuA/3F72oSKuAsn5yQwO2haVauWA+OwYO0E96yZZ/aIMyJUul2mNoxSEYkPMaZwI2+jwTY6HIajCBPMNHKUQVA1WUrTBBugFPWCOU+cesGmriw8YAHINS0f8oRtc5kKRapNkvzUPAZOUkE2ifia3zTr5ovo6SeexcYLR2+GMH8UI6dFkdQ0ruC+sPny5gZwD+gvOY3BOEQ3YsvksZIzwybTBa0QylhS3jXmVFKLTDBXDOx7XczRkO1t47fx2XLcE7xF+9N4SEn+aejyosVP0AJWxz+267a+Pkb7Aw2AxO6W/bZhUuhA5LA/cizSNotjn/ovQpD7Lf8811i7alTak1uKo5w/c8DQhkN3Epusvet/WKmHWm+3nf1QDof1GYZ+Ps5DKU9379ok8dzqcRnUuDsSCUmVY9P3vyHAv4/Xu3rMnWB2/YWE7MkjB+EHMA2M301u2G4FHEGgJ/IyuQNwT68qqDdWYnIiGBCI1QGLkwW78NsBH5N5AhQCj9TGVgHDCcLHgNRJxVBVBIJIU03U14Gg6S9PisZdwCU+kSCIeUJzMZSKyj7uOCBz4axAB2xkxysJCSaoKPAyFVyRfhUL0XDdFHTUJQJahCT7qsVtpB74xGQKGLPzDGCUBRHMNmerxVlx7kT8/CPpo4ueQYm6vWTpbp7/07RkWva/CFYAYgFZSkUo0KcEP0QSxDPAOHIEE7GeFXwZSJf9+LsTJtSbTMYiWAEc96b8kBU3efZGfIi5+ulOcoGVp8Ny5RfeU3L9CUruccJuBPW3rKdckw7Dwh3G6qOruloDwG0JTbIrVpk2S85JWKyWH4vZlOW+WJ5y4gT58ttmtsyKuaelsZiBDIrMTdmyLSeEuKCW3OUkZgEsqWMUppi48w9rzdkFKLCvG4lGtjMCcN7li9qJNtfgXFpHxaSZlyeXjWsAojVInsyYGiZSV3RIcT8lnLQc+qK20ST5BNHGTyLyL4oxs5pA0rQlKGkWaYtVzE2itBk3KxkqY3SF1pD4XKkMCKAsq1LQ2rExJYeAsB5u0smNspA01HTRZiAeZ25gAwYBqHCkkSASBRd8GwF/HLpBA1OV8EY406AYk2OnTwzROFGIirK84XS2E/r+GRFg414PyKN+swsQ+ocmkafwNMla3Tqw7+L7nlQfBkLafKPH7jt26601iDPmPyA5yrkrcTRa3ygdDb8T8ADOd2JuPz6Oz+aFtM3s2Z4ep9VQ/OfjMCwb1Amuz22NYbp4q33WaywtT0zp+sU2uTM6d1xaDjQAjmPwQvVigRcL/EgWSB/rRwnjU70bO/nw0e+RCCQgFX2jFVCkiTA8sW0IsNqORvAPnf9TcAa7kQjFgb3EdvmlKEnkpqgEKPyFmwwDVURIqI9L8EOIQFgvwE08R7C3DUTZ+OgX6F8BiA7uxgppQihROtM+ghPxQziv9Whj3HJXn80VD8EgedEg8Y3M8lP4JfjOYtwaEEtzgGW47FI5BY3TFV18KMp5OWH7eyacYJh8teJI4GJR/Wq6uuxOVTEUgbkJj1Tq6JMu8FOndfoFjWF9kgPuA+5e0eoosxkYkmj8gSClX31RLFZM9mb9M4c/GU2zc/XMI0V9YpJveoh7ECYlBr53nInRmiGBoahRVTFYYG1aKcxEYmYYE1GYA1SVrAEINaNDmn0xf5M1N8TEciwfARSnHDAxXL2WiiJN4ZcsAxn5ZYvIDW/oaHcHKTaZjc8zz+JX54zl+TXHICymr1kLjPUJWXJCBVPUmtfTjl1WaTnAOUB2kpZEhfDNLemSHgd2wyOF4CcP/ywA3CgeYGixNSGkicQ6L07tmH1E27hqG44ko46AxGMhDfXCEYgoCyTsVin88Y6NnBSoiLiZfKiifBDNQu+PImiDspYXmSy5cJtQrUPaaX434P55V6pW42AMrFmtUk5WqyxnDhBFkVMqmJpFi57Bk6iqeEGkZv2FY2iQrVADdsI3MdccXn5fLPBigR/VAndq7ANlx5xFKvaw/75nMcbYF9jOi+KBYveSxyc33v7bwenrsO33mKfUvkwxn96KfYwGx82fG7aDD0s5nvIwn2Hoc1kbjEQJig/jkP0zuP8A+cjXlMsv8J7robkwVs73sA6v48vqzgd6D0vx4q03gIB9wKjOYCh7zrOiZvMZJnCwPRh7nTj/n65cOiiBHfRBMvODGQjuSllzPjCzqhdTVwgzSShnRhA9uABX3w2gM4GfWI/UAp7thPMfveW+VxwfSLhd7Mpf/rF/3QSZ9ElLMSXYJ/VToLfgnnxAdKB+QRmrYgMvoT88ADr8QpRaBQSz//00JqZTIFFDxdSK/tlbU/TC1V3GcgK0YQ96SvMqL5dtXjOpY+JOKhwP3M7ZFL6ovimzN8XsHTK61VcwP529pQEyLd8Wxaes+22oGnA1FLNH+NbyYLqwlPA3XD7j1tA0Y9S+PWna04797zlc1jODCw5zYi32ZPo9ZsyzL0k1+eCoBPC7Z0MfNacBaJXg6m3tWpt0HYC/hvCWnLs1P0VdE6hhoo9fLGGZ4f8r0Cc1vcjP2/aTS8exAhvgzP6ZI3Gz9l/Bl2LUQ1oVVWwwQ3ASHTq1MyjJGPhGPgK1wfbAXwoik9mZ9WSekV5+6RjPu9O2erWqV01FS2HVTacYZ7VkEtIVs9Umk2UUA4YOsChiolQoYNPnlbJ/nTokJWfo4i1OqmY9Rm9CWELD2Fd7zoansgvzkFrHZwgDVecc/8ZUNLC4ZVTQTYJIuUqjgcMBptj0s4QAUyHla/O7uLDAQmmTM8pJ6BkaIQcGbu5DRWMcgLn+Vc3oHOwxA1PzrKTs1dvU1xlnR8Df5nhms4RmFAd6MDJTeow3rTCsaRMCou3E8tRfrGFAxeIH2GyRpOc11e3v2Nvpof63HH/aLsog1+f4rv1h0/3Qr9hQW9+3Vo5bv1FuW2Xqlj65hmVmyO0u3Y/7nFL3+fZTGkvpqA23kz9WMTdU1mg+uW83HkNHehsOcm4YOOI+mIcjcY71fpgmx3J9oXuxwE/LAp+nnCeue98I8YrehIcxeLr15QFEwQ6aAgggcEvnJZOYo/OcVaigYQiYjgLcBJaBRIsFgAZgojSX5NILnE58BRje2loZAbRAJLgBPr1QEQgwHgSJL+LCW7k2FXpwlfiAj3ooEtg88D8IhvYIcDlAE7GCrfiQyAaqgXJt1RjDR3SEjn92r+ujJBVXAW+Egu+cqYHM0MjAorl+1VxPq25edkVdcKZqVjDVA9ksz3UYxBUJyMJGHM7K5JDqm7aaT9gQFd7YLXBokoNXiIqndAsfoG4oBiukKxzvLr+q6WMnDeSEqBdcHZtEtt9wSjOImhEZ9wUSM6K9mgP3Ip08yjfuurgkSc/huA2P9Ce/dbi06rO51FsWYRRDzU3EOVGqycorZp5MZsz3v2KbTtB+zTyeGUcA/Dpnp87IFEoJqJaZ+uYbqwISZ61uFvRycQiqXUrAyce4OXbNtiZpZIU3XfoYGALSHLNhCs4BAMpOz8zP2vQ3rgCG6SssmLczF18wnYpi5iBCb3PEJ/1DhVBAVzJPKIJz491rFhQUcLJScF4iSUGwDHao45oHxkMgyTggjBCz0XIHoUUMrZVLKkJSAvtmdGIkL8iZdwcXTvFFSVJvm8k4AHxIMQUDLjYiWPcwnzPjLJYATAoG5xgiWWGFT2plZz/DJGJ9y1G+LIu6ZIX+ygY8zympmyQiaZPKtWtYg8M26r6+EtGadO378/ndWO7nk+RnTCnl5k/9SpXljyGh6HjgHID9+ZRe2PvDnugbr+Z7eBzZKjrAZdjK3CXr38/DF94u0RN8DktPjI+heSjlYZWfOdXRR8LX74l1YCyvj7dPSvUYn8M22QoNBLnlM3h4qD7HlPMB+3XPMTpsf3t2993aGBzHnSIcjwAKfhPY4Id+SS49xTEgBvqfu+tVfeK6S7pwVzVb6XP2Kt3dwAqhORBTbAI4mc3n7IcTwNS53UwvdklqoO/QQnkhEy9+/R+3GCJQLFea0WKDIWtf89xln/D0N1jgnXbmERyF0kjGK25y95+tDybhqAJJ4IWWgJlMulOxN3PKWzexETkyQ1/KEK68cHDPl/q5SwwIk1n49tfSn9s2C7DotHr3q8npL8+qsrtqi+lyfplP3kzLq1ft2evF5axddNNld/K2mdAVzVrQop5928y/nbT/mvSJAGEd+99vAy2twQ76JpFzAGyjxLxuFl1gRpYSg16Zzd/OmXxVsKMRho4JSMyGXxbvuhLo+yWHRLntu+ceY0mlmTXKw1gy7hMY6dUApDH3SIFJS0Ml1NErWSGI9NtcuIMN9+QkxHDpxaPoL5RnjS8HAIN3GR1ZlCXTgcgBZprn7fTbrgS7vzKjgcw2hmixyCXEED29KBSgruSCucwcK3C9UHhSnZintjKwBzPgLYxsw8/+nm1+WbZntHkurrXxlI2fWHFct9M5khizok+dwwFoBjBbq6N1IJjG2lyseQgx2sdWyTqNm7SbvrjyD2rqI5al9FBQ+WPo521X/iDOdhNYlOuKGUe20Qh55dpaFz2THS6Cl7UDSZqrX1kfTZEeg3PuLxTlRxue62xb557FmgafZx6z2IFjxRiIo0hru/zk7PT0HJPaeLCcmDacP3z3HZmL6TQixqZJlDEU0H6Td98wJGG7AEvIgPUASXnko1oqGX2ih6eCrL2IFE7uqBAG8Tl5JqJneMcmRkfcHyrrGPpjaJJq5qomuP86nuf9vD4/xUO/YkONtMn2tbsObTv87tNPwlbpdRSvqLv6UU+/3/Xb7zOsF/sptn3H0n6kxB3bb3O/0/dvHR4SbMZDh57P5E6CHmqOZxL+wuaBFrhbMh4Y/YX8c1qAqvTQerTOzz5qPAqqAkaAHoD14hI99OJfPDVnJ1N2MwRG5cAqpzs7GhDdzQWTmwHRgDM3HDmd0QYgtqBIhAcr/NkFhRcou+OATNwOiGAwhmBIUUmnSEn4i2rxhKlohjihDz44IIgr/CKymCaQDQwDeUV4QCeehcjxBo9GCRziMnGSJWYByeI2VCVMIgfgkUycQI2+TiNxhKLs3n3RlX+zeAP6LNvzcrrIJ6/a6dXpbHFSLLN6zjpXVsHWk+XymhPTVifdXxZsRAP0Eg+yW44A2v/eEE5KuTCs05lMXSSH6TzIihOaEC+ELJjj7i6bJQ9M6ghDs7kN3ejfsL++yNv/jhhgDJ7RXDk8psRGuhUVV4jfetCI0PfUBgVN8tnyl8rLn8gmslVcy1b1DFF0LN4Vg6bJWuS9+/SQoV39a3bl7xagZPTqS5epUEFFKT9dFpBwaRGW9VIWnQ5kYxGPdnWWd19ks0W3Yr9RTljOsgUR8u7qy3rp2gwmt3BqgrOCiryiLJ4XLMCop2zbZGmFh7qiAXCfyJrKMivzMFdINnW9EvGc0romUi/tDBF32sPu++mzzL1w1C3qkWwGK8TZWkDtlRzMeSCvYlQikt/72ysvbA9eSrEuoKzPlkD6/SPcUTKZWUjkG/ULhm5IW1BlHTPBBEa0nkDlzDwq64pWn2kzjg14nNZ9mSnUFgpJi9SH0Nt8CZ3UY+tCQtBteb48vFjgT8ACfZ14YEoOVIf9VWgf/w2TFOVITTax9rHc5zeMoCQmC/p2ilfBPvpdv91+x0Sz63984odSxtpDiebIVtGQ4cad4h7mn168myg4DtMPKZN782nZDTrS58ESQS28v4dZe6SkNZlxt6PbObfN8wHpGmlDr6Ud+3tPXgfa8xt533UPn/ui34YfLfE2ynO46Hy8vVI2RdXas27nlk4XVPFdH/gSPcBP3/kKFGA5o1iF7Qpns6lLGGtm/zOrwE7XAB9IZxEnp71y9RjEPtrqTT7lwN33AishEB3Q0RXp9H5gKQuIY++TQCtgHaFQoMBAS7q9LFSgJWCIsxfgY4CPIJVl6GpfdfjhbzFVWTfJScUd5EJfpg0Nu2g590hbQQksBA7eEFewmM8yNqe3hMsjfrj10kKx6AcRIAqomFHuaAiT71EY1NaczZfnRfYds25m5fs5RwPn72smrBf/MWd69QJ9OI72l4vFbDqbfXp/kWf/sSm+79r/gvSE/VHGNIr/1C0pklJ94WOopXYowHJOGyFuxDpp2FvppOlWKMRq0lgbgLB6Ov+UlaDMV6QNRAcYDTWJxLnCxOZsAZMJ2zuXkqLvn1+CtSuU7blkBWMvKhveOKW9vSTtn7RPasNgauepc1+gBy2Waf46a94zOYlN5xk0msy/m0yvsuyvXAI8mdsaCvvCCDvwF0yDNSH60Z4UnUfb68bS0Ew9/LjLvp6e/tV0ecrai1m2yFkWzQy0SVl+9cXk6jQjlkW4LhgdOC3a+npSXc7Zh/W1jax6wWwilmh42Fzx3lSnHIiSt1ZgnVALjWpxRb6EjskVMU26NkMazR55MQknZL8i08gw2szMSZp4zi7TeKxAAbDNDOC7TVTLAJelf1J8VFr7xrDJpRaBMRnoWBV5axa4j5C/zg5CEYo6xZ85/5AA79HEcQLaYIwSZViMQRKmBlF4rBFuScS0NMxSMk7EkmhbA47hhZyymNZM0FKaAtDDRPfXxhHKrn2l4kp+6Q4hDu7sQLKJdEv/NNfYd3Dsff5QekoCV6opYzyfkoI9PJ/wBRlL3VM07OOmLDyaUdIkke9JYwTse/8cEjDG51CcZw+zM2rPldIyLC1DolQRhj5DdzLtYQOntG/4bBxDPs/mTilMMrzHl29vsveJvIfwnuB9HF/8froWIDs/b2H86Sb9T0YzIEbAunVGRp7iA3Z0K0dAByGpx5s082DPf8cOKvYMprnaQATnCjHBwtkXbPwPGo0zdwV//BeywsTWAtMj6HWEKfgKVEyUOPXJrlBghqIS/hKiEgccT2eqTBIK4f1LeIJZamiASqkS7RH/JT+Uj6aI8WAc//uXt2sUAqHaEEnxUzFWB1gnWtNqoOAnsQwsbLgdz6ArACshAa9m31Xz5TJ6V0mfawAAU2jdXGVTzmp9zRSQNp/TCGBudp3Nb+rfTopFNkMR0+OyihAV6SLlAmEN4BcFpXSpgvBfp2ljZo+JunJQgM5/GlPCM6iYEMLCjC/ZjNRXN2Ec2ca6X9MuD9MYrOJJF1f6fiW39xAWZBvqFJj8CE6O5Jkegzk3f2128GewW/ug6g19/qyI4DjgwnPSUIh58OxJ+WdFfS2mNYdBqyYvIaCeUy+pzwR5m/5K8czaom3DzrNds8jhv3xVzM+rySsmszPlq52fFNmcfViLRV5TVil6FE3yYuY2Tc2X5+2ncnKGIbUm66SV3CdK0BxGwvD4KjOpsU60aq4vgnkwV4LSHMSLYqsFIoSkkUKaBAB+duec0iwB56e+/+APGeKRRWvQqy/DuKLkC8jJ6WAWyoROkCKLzOVOWArQjlqS9rktKp5oMDDm4eiParjSHTnRgqDGmmgVZWPZbMmWVc5XYjSL8JhQJmcquHeqhfOIdCs3mQO1VHbrivAtn+FDH3Ho9RN3r3PkJ67mZ1cv7PDHl32f3S7PI+BOJdrL9BiavREf7DmUZL6zC9DXMrm3N3EjaYxy1z/JSrVsEx2H7xHeMhHcf0jixZZontIWPKaV/FD+h+l3JaZ0pbQcvg/tMKQck6itRAxDWt12GO27hrqNydoXT79dnrtyx+IO/Yc6DP2fwT2S6qdwvkfbEYn3xNpRyLwAZoxw2yF/sMdmLI6SkuAMAnUnGCO/gECT+XRWrSrWL4IO6upV7Yaey9mck6fYc90dcOhatC8TdMGZADlucSlLMengz8qLdnIdsA7MAKYCcwAxhEK4WEIsLKFTXjAEqqBzBZyh3B5LBdKINojmAFDhAY+1wjw6gSNAEgTM/BblIAUOyXBCnZ5n9LQGCIKhG67Y2bkGVc4pZ7fMvtZEJBsT9q6G5LCRSgU75APn6Da2+19Qx+Fiq180HOuVX0xZFMDJZ1lVdCcQ5Ms/yyan6Makl6vlTTebLZtLHKv5P9T5D5PsX7MzUt2sgFZiONMGxIJ/1GKlYZlopZgSwrBlQmORXmHkmYfXgvXDeOjJ8QxlNl0xvFCyt+MbGGo48oV4mujS3GZCDgxiXxq4mtljF4GYvmAUQm3WVBsHHr37lov5J36mCzwSJKoNc6FtyVBJOaFUoOgJNNn0P2ezVdb9LQl1sbJSLCG3fOMhmJsTQmKNY+MTXNxw2JyTWNh+aV43i4r1IRy1PGXwg62nlqx7KCbfz+ZvumJZ0tQE8ZMN2QxbL7tvbY1MXtnjPTnFri5jsfEHcnfGkFYihF8UUHwyhBpwpfKpK3YB6opPBGMfdLNpaWbRrHUel2ag5BeOwpDLNV3tcT4Eu+9AEFHMFZIFQTSSYWruW4iJHndGk3D7IY5HWapOeghtVBF6msH21luvyAItSUYw4y7WBxNOMXDhAX38mNsRMGJZ4OovVzdnNMXx4Pw+PKnstO2XS2o6Ws+urq9nzKsyMRFJZRS3vvvsU/yPh7iZgp0rRdrx3vLY/eJvBQ8exr6DA5It50PpH/oGtpAyzPOVQh8qq1f04Ds/VYKx3WYeJ/Hwt8n8WufZMEOTJgbtux6nyWGe++Tc+j0l7i2XjYs6yHUwLza0G8eYNVJd6cmSEffZLfkNjZyi7KPtmR3OO4juxh2RvrUL0ICmtiQzAgCbXb16HYY/RxENIxzlvpuIoyL96RBh1AdZ4KH0fzqW+tNKyYMy/bFJ3xSWwHebzzv1XRgBZmCyse/WQESAjpJdxOlrXjr7n37TrGQhMMUTUGmfNHvOOKvAMwGAC4EY4CKkS1dKUuqYNBz0BmQhtujHYm4s//VqpSe1SjEldBMZnkPVHgQF0NQC4JaGQ19X9GiCc3h/SwwvLu/EITHAC7XhBiP+h+dGgm0QaBijgIIeVAkCl4cucBXWssW+dCV0AKWavfbfnpanUxoVwjc2SK2AWOCpoli1xXzJDGwSiPL1pK6Kq1V1U/9Vd37elKiHDTXgWj+lxOQQxKYpSWF+9RBQmoSwEbqpCgsMWmA1+FK0qxUxNi2c+pcTzmC2E9ppISkWUcPGIQxfzXjfFSZKREhPMTaOYeTe0x+KCxK1G08oQB9yxgiAM36u9XO0RjBc02xs/ixf3dBgIso0nza10/PVj7zhJ+TBR+vImTsWk7OrMDr68jnX9ooM7Tjx13O+2PWGXYTK6YwRqLq6aSitrH9m2IFBkW5yCnPy3g34s6+LhiMUTnNWE9Azr9aR47Lmq4/R1ANdDeIf0rkiE/VRI8tohIeH0Nh2jclHTUoCxseFtinHTBFwvFmurj98eD+buSqdgQbyy6ZyxEPAbM55ZTZrjRRCLejRHNAAUScJMAwzUHK4jBtC3QA0lLfbHtRPzURBVkirGCnK2CSJ5o1LyT0ZQIYyRwl2/1xCRmt+ygiFTSGK9eR89oo1K8x1WyycxAabSEJw7bFRWCayKWkSeaTBeotpG0PWhlq7I2nx8HJ7qAV+XNspzZIyyNGHKvxCvzbhMZa4Y+lUfY6JuEuzE3fHYzdO8tkidBeg2/q8FSWVxVtqXM9TPP3wrK+he+33+N/HtU0fL+/RPQEh0rQPTHGvGg/tsRha43ntfK+qG4KhDsnz3nbtJu7Q8bhYQw7HSN/VdpfDrs9YrDGdx/JCTEUdO6ZIJJqR6jgciwNAJIX9gb5/AqMJaSbVdCZYw5eeSPrO62UBemDOAPgShL1aXdut6ERhcBya0QcuEBeUg4bjKCK6IYEb9nEqQeQBlOAO5IiOT1znxo2dxWOnHZBJQKBBrF6x8F9jMh7kZ9yYogD59fX11eUVEAcIFHJcdtBWzH1HILNiGKAQD9mbLmyKxKuQtPyGHyATGsKB4FyaGwfK0rlnBDCtXbriN+Bjwfyeyddl/TorvmOyDdvaVJOTrLhmYk7TnbL9JTvMsDsoPcAVhsxm2Gty8rti8S5r/udwbrOP7NvvlHG1UY2QiAHptufRRgWqgVyhAfOhFuiMFEezh51EF2wu5OxtQyGd2wlNeWN3newV1uHkYOhNbHCWP/ve6FYQEXYvxUYowUTsCXparbFzrf1Y5gvAzq454ouJOWRT2JkebibZs+cmpeTLbPIBzStKFKB78S3LMLLJa4tN5ykKgkyFhgRE6VBw+PDIeAhP3Am7ZnpY4S5JbIDv6AGNCuxssWKxNhbjxOXiTdadxynN0ynNNhpgbIlP3k2vmwlb/Vy7S1LGcmlgsda24RfFA3mRXO4W8kn9xrxhv3/10KlZUCF/rzqWpRgNUL3v1BAjkBxdZFM0LcJBveG4vNVNXeZzc5IZdtUXlqLyQs4MYbmw2wUb1gtZp+IdYgnTFMlCBMLe1p3aeOOHS7VcJULy21dwzAqsjQKUDYq0g3VuoipRjKQpxEEr90/CuKzc9yyB4vriiplbp6+nV1erclrMSnKHKULsb8tZYjEM5b5DYSJ4ba7h2yy8uSW1NiRbjmTj3QKlqn+cl2mJ2veZ1H8u/sOc2v02DUP7hOxk426uPT3JT+F5OG4qaWMjJ3s0f+4SeFtLbl39zJoDuyENaPfoiNdReTeMOsLx7gkAvg2su4ETeDkerMYD/jvFZBD24nyxwIsFfmwLHFF3QQMBVdaqbSqxc3WY4ANSoVeSazZj2kaWndec8FVVSzDGm/M3ZQ54BfG7UJgdgAAzYhQWIIr/eY3aiQ5WtqO/hyeBVUQs9gRzChQutIyWQKAJHtIFyAq3KIV/PnjAKSr4HO8kYDB8omcUXEsPawLmTDEKP8FRwkQRJRo0AdcASMEhcdI/REjuxA/2OMKVrJICSIR6J5BOy0A8JbBSLZa0Zt+tipqxAeDVcnLTZXO1ZMEDnf4AUdoNLqYocbOZ6NmrVzftv5w234GRA4cpJzRdy8yEY6Q1mSMS28M+QSOY2r5okCvDB9cVqXcDIO2MbVbNasrq1/oXHesx2PgFu5NGlIGhaeSXP/T2/1a2S7BziRTNHyP0V3IGv8Rjfe9lhAiyHLFoa9IZRRKso/flpDhh2g4wlHwHbXbtr9p6SYsBr8CTuvivSDQMUaFkEpcUJzU0eDCvO1BVsXi3yD/ZwuCw4UnOGltKAuNUUzZZ6qoYkiKH2CifAsqqE75q05pmA8av5xixndq7DapFUEg0+0OyJTiZTDPo1D+pEonFSbE2cKMqpUFc7rwsFmCA6Cnjm5RYVAqmKDEQAchncQsNOc0Vfe4hyeqT6DFB1CWaMdiG/FY/891/XGGo3tnrieKmXRVpRSCdPz1sJ1iWYmE8BdtxIZJC2UgrRijH7Bt1cfnp4mLZNDeL09fzszMOT6NB//UvzxnNu7nhWDH2r2VBexQ0G+7q4JUM4y9eGsice7leLPBigaEF0lvjmKqRKIl7DHGi2UQZSnySO/HlLutYBLyf3TE67o+55dsL2vL7wz/Eq/kZ3md72tORuDH/55J7jAXHdOArZKYcbAePxj1G8AjNU3jutoZHhNzjXb69h+AZg8d0HisDD/66UoHvq13x6V6nKdVoqz1feXoE7YrEMS2//fa7f/zHvwdPlgV7umfL1eV0evL1V//093/3n5hU4KY6bKPDjiwgPuZ2OMOejcXpQQcEij3o7UWTBFFgHiiG0sVfSCwucbM/iQBCfXqUAzf/rZUiVLTla8mZLl7ipORZwd2lyYgEcwGK+aFPGByMDKAnZE7zCNYRy5j4Ct4Cqab97+EAUUw1CUfKCQQDx+BPLzyQ0kkV7LQCttU+y9Wnq1e/X53M6g9Fe1aW9Sxnj8kPs+58XlzPKlZMsMPMtJmurlbTD8vLs9mrLvuHhk11GGFgsSbzxdmMqGGMQh3VNo08ZA4VdJxREMZQKV7FzsPwX7f6ldCwo6kwA+bCJnCeSzjdX798W5d0+tI7jsa0C7B/rMUwvekiT15pDCzDfeN5S4CXuWHIJhy3Rttcye0dUq6Mdc2AScZe7Au3RUIDCBTatCcT1kLQjdyd5Pk79M879uqkK//33YxdgF7HzJwKRWPeiqy4BpLWGuRMIkIC89EtF/Vk1bZfWlSb8wwbz66r6rzKr7rmrJq8WzZnNaMr1/NichnmveRA4qp7z6HI15P3S7KuuELNrDsTJKeU0XNPIoDOpKgveaFF8U4Kcj2e1Ma2DQ/Om6ct4wBO954EUxwA7i37Mk34I+lBadkjJ/iDM0WXakULgJIJ7SWMwp+ilGj0dcQnWrNhB6A48tGYdi25RhH/iL9Blkkbh5T1kMEjxic6erylIMRifapk2DaW67AHEdQQG9lROxZGlGW+eP3F119+NUOCa7a7+vp6efHhu//wH//u5OTs17/+M5lH+h1BYaafGqt3r0b6Kd7ilZxb/kOvofvBb7Nh5Gd1P+W7M1QkSs49380h/YPdlswoiA+OuRVh+N0hY7mGeTEM3Yr2hIfnsvCuCrv679Kk1H2OdCVZR6YuLH1bRfb2/ftCCaa+OtYpSWMXe+jvcByMCWzirnk85HcjWy4HGgAP4XmYdpPsw2QvoS8W+FlYYKdiPzjVmzqcWI3HT1Wvf18MYwE57MFm5/5iWvy3/+3/8//2f/2/88m3UzHmKdChOJvS31rM59zlksCByIXvVHrn0sNJBJCTwM0WQPyEMgIf/0KyYQbxcetRJ6II7j1xx2tRzCHoCfDVJ4nnRCtGAx2KyRPCYW6DZ2A1HC6bJMJDccKrhF1CqMjL9o5vXlipeihspCTO2GKs6qa6urhSGs2dlokcTNdu2fzopn37jmGA7iKvqvn0omirk9nVaVmeZNeLJr9ul029WmXL5WR2M7m6uly9n/x5/eU0n9uV78JU0LhMkeIsECaQCDUJSQqEWUg0SocaIrGO6UxsKen++pwDgGb2JnMKrD2/avJnTIJPU2XgiVFgZZqC1b77bZiunmzoCO9QaOMKR38jROXMRs0ouiQp5gYH/fLEZBt0+9TmHIc7JblMJTPC8q+7xTUH8kLJPChsGjxMX8phApS5uVIhgY4i1c3FxB7JMKmyD++6/H+4fL+oLk6rT0V9Vkw+zqvzr6eXl00zL2+YBMY2mjQZVtlVtfTQ4MtFuWoWtuHQEzTOfLHQguLKbxQTHSG9T1zMuU/ZJKkphU5qCwQpjryjHJEPLCtn/CUoovBBgCDqBXdPZ3asKEZ45I2VWINsxYIghIUBRPbyT+UdDrQ5O1rXmKZwehsO4gT7VMA7dv908IO8dpUxUXVbX3DR+mJpPjuQ2ipBCC0WwppquZrO29/97p/+3b/7P66ulp8uPyHh6urj+w9vlzeX9ar6b/6b/81v/+IvaJQyUFJV1bRkxM80JwuEsXAqJ/1E0MvtxQIvFthngVR19oXc+u2hoXI99drDVZZ47zLf0BpkA2DjYZTbK8UcCbwlO84Vr8t48x5H/xSq1GJLLar+HbbDbsx/h3CPx7BFONbuHPN/itw9qhz0GtOBL4d5G5BjbBxgNO5BiYcDE8+h9Q7Tf5bQQEpDzs+gz0jPzRjnMZsPtbrHnWol953qnfwS3E7BOzUYQAGQAUyA5RwCqL9YlL9mB8f59DTPTtgLaDpnQjCgM9D2xHNeJ5NPvCecZtFVpccw6Q4PRgPENiiyfl8IaiBGAmSmIymg3626CdQY2DBhg5m1FxLjG1zWKvfJoIsdsKQgLyIB5CJtNFPsVxaj9QHKo3g7WUiQCmcRDf/SolsFSmKrQk5CWE/gmsMEXMUxXs7SBkZZO4yXs79n9+a6XbArEKKa1RkdvPnkPKvrk/lXTHZPhx3kxbmLhumiXlb5q+8L576fIgXMRtd+nzQYqkkqLT74PvTF6D3MBSH+dcbpsKShcf+irrvpOqb+L20/MACAVafvJgVHHJwSNdA4GgkZt6zLebeaEm7B3zRzIZPH4TUIDcNIYK4NyfoAogV14Hj15Cm1A2jrLJh/03J0cU4LqplSipp6evKfsymDM/8mpTn44oxEpx+c8jYngl2sXsBH87tfjRuhMhWqffWpZjYQi35Xs8v5bLKcTuZnTTOtXp/mi6aduQ8tQxBZsUKuecpOqWB/WmQsy5gWngdGC4EpXG9cOsK5y6YvBGuQ+K8mtqMiiSqn75qGufZM6KLtaURRe+Wf+NuFucglWrRuLIoZuxgxAuDMqHRZMOMfrQBKAkwteLRSk/AYcKKsUtkoWB+i/Uc4ZZpJRJog6BSBhua+5dDIUEcoSyUkct6RQxyMeqC8u+syvb+YwqP58O7q//x/+r9wbl9V225smuV0unDXoHb+6uyL1Q2DXhUtVSYBwZVmBusBIqnK7BPR/yRltv3+UE+pHh3zLh37lqX3c9J/jGaYuqGs3Xf7rs8w7lHu4bcpvSWGPkexuEsUZfiu57M/H2O9xyHAz6j/0RY+JnXJpMP6Mdavn2iGd87Q2H/FK3YY9AxlDHYb2bI+dgSASC/Xn5QF/ML9SSXo55eY7fwbZmigLQxy5wNulutFfzdffWaxl9WynjCfhA9NPe3YUIUtVdxanjWOzAUwgEvkUszmi2nOLiJMf2YeOseugjIgoMsyMIr3ELaWDDphwgHIxtdNr2jgPZ/VLPwCGfXB/iREaDA0QRHIHtQDorEfn35WLqY9SI2noCjkEieupAaThNQw/aGCPbpyFGpLZpTNx9WGgoBKAvwd4nCXS/ZY7FZuRJ9drzpWSObgU1JJipzN0XbXy4/nJSf+OjPEI5U8AmoyP5ldN7/ImusMWG6rhc+MBgqpxgadhgKODAgi7UlWNI+uOZ6UdObGNAM8rmxxkXRnuNO9HpKnrDT9MmvYBQgloEwW60WYrEhbJKVPTwiPkHWov2qE58Y//JL32rn+jSxdE9oQS240EPFyJtclpYmF0Tlb3FQYmx5smlV5u/yzfHbRTQHkzs4ir9RSidg2XPLxUcvHBXPsQ2e6E2bQkLkx9GVzkG3OWud8wfnT8DBrhM3aLwOJc+4YOcZYBENC4Fiyh8ltDL/MW5ZQ0DTKaakqDgXAyX2SUzHQu78Q1ptED7XyppeP/KBygH4eWVjg4Jh+kZBUtvCIJzSuzUe75U2EeN08Jg8B6KmgEYLxbGaGFMbiMKALm6NA91KJSJzQNFRRFyNQDiwwIds6ASMMQEMgZ1ffrHDgzllFnhBg9cznc5D9Kdp4+Bcn2M2Y58NCbZb2lB6fkDcMYpVUbitsv4FQ5PHaIMjtTeHPy/VigRcLjFqgryyj4am+9/dxqj6ECmet376eWgtT/J71gQbAiJzNLuPbWk16/2FrZqi7r8Ktq38F70gZ89+KfPDh+BbbkM3xravH8R/KOuw+RpNjaA5LGfZnHKZ83tCnWy+lPWn1dG5P53ALJbct9QycE8NUc4Y1BR/xz+01JFn73/2lT4JI5TsxSMuen0zpbuwKnH6q82/BK0wOrlbuMzOds+klEqCmaxmQWp2cLs5enYH7QVQClYKVnh7iBSIB6fMDSy4hg9CEZ7ticej0rNmkH7DwEzrrKdZTffZZD/yEjzQwAdAYwBUQhx89DY/GBP4CHmd1yEcN+dUZfwnWg4fkhnqkQb3cICWAprTBT0UhIJ1QwJsRAGzQsukMIVpDAjeQYR652Eg4XpJcErZcrU5n5/T/MkzCjBUwJ33EMXWFiRjMsv6+Y6p691sHRuDhWALcAMHcSasSnaShGva5pgTHHYvStUxIYEnm1rf5asnUezpo7eKtaA4gtfiWU2+7yRkGY9qIsNGUROpwmB1mhEaUd0gb3NbG7X8Jx7W5R5StOBqQhblqFS0gTicAWTO7Xf7Osm9d4XBOEjkcuq7fFuV81dzQSMym/9hNL7L8r0GmQmIAcl9AiJiySXXhn7Qzk+UZg9JqDogVNZfZqYWMHn1m3zQ0DygHeFAKZhwzNlMHsmxGtzVZQ4lFcu08oKXLKNoT9g9Fhljbko91+CddyDLdmHGtQfK3IIYP2oWGvbbBRruyNoAGmLlJMYEj2/5E66KmSewmTsL0yAcNS/st3KmaMNAEAzLd/HZWVzI4flBSQrC1btsMrADhbj3Uw2AcMhb0e2kiaoLMHG+gSjv04PwxZvYxRylqBvrUKwzjAvtV9UPdLIvul45F0EzJLpdLED8FyBJEEIa1keBuuKjRW2ptjGSmJDrk771p27ie/oVac9r/+/Tv11Pez7txd3229PZVEA37Ld/xh76CjBNQDL8xNMkdug/F2Q6LmpBeFdsBT37a1cdy/XmuXVlHyTnCwkM+h6UMQ9PrY8+c/mC3qSCJeSIeCtq471DivyljT7JlEtkLPtAA2Cjy4nixwIsF/rAW2Lwnho7jVSIW3/E+buBqvvHC++ioZ4N9UMuMrk0QBUeZcmAQWIRJ8O5iDhhmErM7mvsFiyNF7VqUY2Angu0zT5BJqEIAuImmAtBESCbuDYhq/AAWUgQW1BG4IsCNbzV1S8rGOw4A6KN+CVRFIwDsR/d8oKWQJ5SOSEGYvGQbLLwHe5iEckjxShFoIaC/Qfw5qQnedj8DK41Xs9vPZHLFeUmEOw0EPyd9gOlW9vTSRHCqPxGcnl8W9N+3TfVVWy/cpUfOdEj3GFMOxPd4MVSz9RVGw0tdMEwkQzwH9DW1EzdjZVCGafB40tDAfwWYy3/D1JZuTvcwC7QZSQhgKBu43P6YPtObfCI0bn26w00Yf8ln4A9DYkbEyKbguqbyIdJheUJP9LpkY6am+FB3dD4XjJnYO0/YzW/a2U0T2LgAIoedb/XoFQgp275mHAgYREvJMjtu8vaG1dCLjoO+nK1uF3fMg4/SROGz69/Z+R4iRgbMyFUmszFOYGPADz2pCZ2NkK5NcvFZ+/VBg0ecjsA4vx/OmpM/8w6gz6QyC5SNE7OZZgHZBJaeO/hkyzhOxbb8oIH25D/J6mf2CPETw7VKyoKCWxiAOTq2LWGsSLTnv/JUxLQgiSBaDAzlUd2yfFrOT4xq1fK8Abb6URxtZY4BqyrsQitgvli0FY1VGwT0/HOjCcx6fvWLWmoTBA2QEKIQpsSQ2Xuk57G7qRgL+xn791b8GVvgJenJAncqSHp8UPHYJr7Db8fMu+Epfu9//0nAd6vzcJfxXlrw2rROdlQYUt0Grt97tz7JNeafQoctrbsxn/Z8r/5PY/+A2L0mgQH8eOy7/rDaDnNh6N6n6dF+B9M75HI47QkKHi5FQ25jbjrnBCKptowRPav/qObosFEjOeJOzfQ3KugmPGkUQSkgQuIWdrPT0VBwFchlFXNd6FmmU7OyMzmrQQwV/cogLRGqew4yqcOuRnqiXZ4o5gCYxfRvhQlG8Ehyk0b4aLcougSU9BarQMIwiaRP0CaaPGASzzIL+kCSSQYK4Aic0kOk6B9ld3mA33nAo/ciUiMCX07YADLLr+10tx1CXJRRgggqkYVO9KHjFVLF/RBHKNKcreGCTiZKdYuinU8LuptdJmDboyuXKxHYDJPYEwn8xJonHZ2ttI2mH9qME6zOw9vmQmB94boq9IZzX3zFbeCSKcYPmMw/JnmAfYH+bHzEsoRFy+77zCs3+iSfvc+Kmzx7AzXJp+0R5+yydPYr0xsn1xIEaW9PLbh10aOvcIBsXEoeXs0rDeJGRtoyDAKlDtRzln/BfBuYRwWh5dNyHPIpjaV8ej6bXa3am0W+YCfZbPaP2fS6aP9LZuJYfDRUiArNQqADGmvp698QBKWp81Zm7PlZs19SddLlrL3uOHEBG9PYsnbSZmOHKHZprQHclE+AbjnnHGtK6QVpqNyvkxOy0Bb9KfmUc/q8CH6lLsVH1bA8+CNVmqDVz4wNldA9NIkynpK8aNuTdvKJeiHKt6HHgAMMAP4MR7i3ruUObq7VTi1Gs4I5SsypMwuxP9N7bESH1rS5cfI/CSQPheDEoBUd3sFdF35clFhKQlA4EEGut0zoac5fL7JzVvEyf4+dbBtWzjBqxP3d2x8mVzQG4H+KNywsihN2oIIASkaj6AigRUCzFq48IdWRh5T3ISeEh3oqsHWFSkn1of/YW/rw92I3dNdnKOWPxW3hf+5raOGh+3g5u1+3jbVTySNb619YXrZQnyX4HiHH67OReA/H8eAka4xPqt27KR3ntz/kcIoOhw453rFceuS+v3INY97nHpubczdeEtaL5G14RHbeZbH7vFf9Z+G8K+vF58UCP44FnqVefg5VQzGrVw8a7sq4rY6ihviWcw9nT8pkbbCC33w6/gOJ8ipw8R+zX0QVQjZxlfjZKAwWOFsAF6uGQQtgF//iw7bm29d3HsU7QnYQHlCMj58eoa68xDbphdfrCdIA65EWsBRe4U4U4Y8fISCXQMDcjO5YBLsAAdFlHH8Os8NFPoCi+CEm0AdwDNDUJ+gIhjDFEw6aXqOqjeAKN9JYJ5FfA8NB8xzpxGpPWDA7Ys4yiUmzmM4XwDRSyLCAmjvHxROrmEHB0evtwiClsTAzdefjEUnyGCu2GWK3HJ9DcZz+JflabVIBtNvipqaDlskaTLeKrKGvtyzR4RvOHKY/18joImhjtkuytknDFWEK6K8Qvn6IrNg8DBxQhVZ66biNFXkTdte8lI4wbszFp4XDDjxdUV5l0yl97rReyHHnl9e/bZeXnYsaMKJlIdoAGk37a+mUIbpvhSkFUEuzk8SD15lyds05X7Oa8xcKZt/XrpSguxvEGy0lmhBclLKiZO4LBqmbksWubTtrmYivIeDPvCFRrhg9rKwCKtIL5sE0by4Tj5eaSs/NokUkspTyQeFnQpc6y0dikudYj2F0utMkIDKa1JwMYAvahnXDjvvXIZDbCuCfRpnYfd+2DFrGVCGjISiEwlf+ceFQm/4xPHlIieufmNRHU2fG4BD1IoxLSUVl2qs0N5ynxt62tmhZb0CZnDG+xJAFOpM7HPlt+QmOjmysxZrqpMDmt38c+9k25BjVi/9P3QJRO9avkTuZeufxp56UP4B+yULrqnOUApsoOIj4GW2c1OpleBJweg8fpeXDiD5DIjzV7EF2PULjYdtx6D4iaiAncosPwPNdD9XhofRiBa6k89B9dBKG7d2h+x4GQ1lDd4p2tA0Ppzc+8Pcockzw8+bpURKPL9iJMrDNMZyDRmCBwzc7iIDJEiInQRG93c5spy+8DqzuQmAqmfN8JDan6OxmkxAhvcAHTApeEHT6BAwRtWB3YA8R8TO6f6EgTAKzSxkoBn4q0ocrYv2igJFuOABB6CDlOcqJ4UQVzsA8tMDHeue7q3gLYxB4z4WMY8562vQdcOOsfFJKj3twlrv8I10phpzVzRNVmftEvzspggaodBYrA1wv3TYXbJR0vniV56uz7vwLdvmvz0GiWfG+YWOVNk7GbSvPBCjfciwAh/iK89e1DKHiWi72I/LX0RWxupKAqRjDdaE0LaThcGEDzuh9hjV9xWQASWBQw27d2e+zOcnx4DaxHUjS1aU8XRk3Zasp09hx8RumN52a3Uks+y6DuIqLcERsXJjD+OYNd5jKtznzBYICWMzd61/FibPnbDKJvqvqZkavffmP9fwim/xbjgqgBQUAZXWJJlEL886Swq/sTP/6olDxCNQGrZ62+bKYIItZNx8uVtecB4CZpp5U28zdascM8yC2jIYce48ihGh1TZd6aXnmaAKYRy6kxipKKM7xjWQJpYaPDgrdV/7GTvy32FcL+FqxtsCAdSwQhOoSoxEz6KIGYIRqSaOUmtJN8QtyGwwEOxBkEbZMs6qBWO4hRIPB4bUwpvI1EgWFRpOFIVmfO9PNCFrvZLU2liUHlhGbQQBoOH/Ajac4NTmnIbo0hxh1iHXT8COcqs2qG9pPrsxppg5R0D5lG9CwuPvqOiaYanGYRXNxrUXGw/ZtEJRot4PvPh3+XuyG7vrc5fgcz4e/KU+XkMxoITryIlO5jv4mHsl1QzaW3jvWJkPv+Gw4PJfj6fzH0pI0fIDNx5I0kheH5cJst+rcW0ESwS7ZUBahe8vR1ijNWFqSWim+d96bf1zX3qT/cSXhRdsXCzyXBagOu2+Lu8zXdSa9OUASgaQBB8a1tzU6qfGkT92XHWAg4Bq8JZBO8ABSANHE3GN7u+mCBtLIW6QS4AYwFCAGMqY/0B7o+zXFZfDgFtTxQ5gIsPcLAQEDAwMZtEmYrIFEAEYREx2lzOyWM2rGKkykJ3iWOBIvEhY8UKyOjmfTGVoE4lFqqBcKBNRTR/+Mxj/QvqhNNbKrKVsqcsYsZ3A5g9uJFO4zAyRvblh7Cgqv83Zl88fJ+dXki6ZZMfdEU6QEIi7QXCSfKSIEgWgxLMIiGeqGLbnTHQtKq8mGLuM8ZoY5sCkd4Q650Apgz/t89S+AmRkAE1+1YJBGAEeMMGyC1ckZ+qtIPK4p+oedH/XCk/+6Eh9c2kRv1CNB/pEq7gBZ/N3C1XbI9IJtZth7h+kvM/IH1F3/VVZ/ch4TzSR79CEisbKKC3/ibx7xS3JoQTBXZsE4Agk3C/LLOqtgQC+2e62y2Y94H+BMXPqwccKFYRKIOaMXKfPQbIENkacYZCuHpsVacnJEOnvnrZHWHkMazWBaKRPmqsmhGz28HEULDVj9UTUXFw2narPAfpKzWy7DIMy5Idn8YySKTERTMszdYTURuulF0ZZrqC1BL011SU5kYpSV5K/vOkcJpU5QKSxHqsfBHXT5u4Yndh2lAUvqgf0QWrohlBOtPM5ZhoxV75nLpt1sKU08ChuFVrqIA9vHXynuRu/HM3qJ+WKBP2YL/ISqwKY+W7fpVPB6iHqJdsPlTuyN/0NYhg5H3XwZPvc1bIMO3UnOsO21Kzl683a9n+TT6zDS7txlvavzLs2Wz7BfYejeInrYw2Er9byGsobuCD6KQ1A+OL0PS8ofAzWVa7ci4LNb6W7JBAhx+eNkHnGRzvZV13B+rUiBS0yPA9zFLBQ9YqAA2BCzUOjodN6zWK1zW3HASrQZdBg9dWYDRrwS6MCNaAI3qKVXEy56BsiIefxZ+UmAAlgxBKQPtIMLSCn6y6EV5XjngrkTP5wFzmxmQbMChfXO6gm3zO1rJ0Vqp7TUSaxyMgjx6oYTyASktIs6KNmsE7xIjzMA8xykzRSXXNRezydszsNui6dFcTMjOM84juqqra/b6+nk9fXkbTWddiX73/8GjnC1z1WEp/hQQOvZXc0d9VSCVIIrfbXRmYzDARbM7w73zH6/Yct7trnEKrmnKTOr5NvMWfgnMGBowlnkCOJiu0wTyFaZhLj1DVcI5R5PitOTVRPei4s77oihn1dYR8fal972eCQpDBld2LXsolu4ve6yc8BvVn5VlO/pj3eXKArP/B8nzAuacGIxaJ0JJ+jmycfqYMb4HKbYCLhRJtt3Iru4pjyylSYLALrqBMxfTz6w1f/rcsaELmTSAHs9vT5lPKSbl2V50763/79YxOSfypXZ7NoEu9yTrUNtmFJoFB9ZkYSqhqGb67bvv7eZGsFZujAy9/aU44o5GYOCagrIYiYrIYsGMjIYNSo4wOGK3UhdR0N54pwyEpQzaYmSsCQb82wR1sAA2PJNxmBG8Y5SzrwvWwthHwk0lQ8hHwH4DbQlDHHRxIGCohPNECsgJx44Qay44JA/qhH+ttrxyFkU0ZT5L1nLwsQ2C4wWZ2iCRjIMWHBi9z8ysrSLOX2KsE6WiD3EtueCb6x20IGEn/71ub8pqTY+wA6psB2OMIYQwr/+yshj6Rrz3xV4/HeZgsI1ltLj+ezqcNjn+LQc5jMaOpIXR8q9t/wftlvSalcWbAcvA6n2rwHYFb+JafznGgG4owucfY2o1sv1YoGfkAX+JIrlEAfc2na0um1qfKqS8UEHIcSXnkrKnGr3o/Qkoai2otX47INp8BMQOzHAzdwFHfHesRdRcv+DXtNbHwJHCIQpgUt4xC1M0cPXaIrlXVIRTJAAfiRTMQNSFHCLoXpCLwQLYUZwJAA45UCFzRI4KxNR0IVeIQAvdQWnMpsISJoufKBJL12C1dno3JCmmNAAqMjiWuZu0MIvLttiShcpxyIwj7pqlktOQ+uWeXc5n3CQMkcll+wIWkzqoi5nxSJvvpjUbFfjtCoRfeii1fq0AdFMaXgoPwyKA5GKxnzg+tDoxsPY8LV/GSOC9jxDoF5xzgB4Wh8end8iQOUyEU5212TrhETA7S0lNz3fcctscw3DMAk6Jh9FAjUxTKQC4bSALszi8tNkyrFl2pA2AD/V6jft9JouJhs1zHtyAk3PSiqZ+pzU7gVrpKXDTMBUCyQnejHxaVkWqy7GVOqKbVlp4nXVdfV6Wp0U0xXzjW6qm8n1x2o5Z13GdFp5PDFLJcC+LlpnnSt2iyKKLAoqwlNakszQohfvT+jGXVWi6GF7zY+RLaHmF+uedZgFkRA9cVmfLIA0fyg2DtdoJ+iMyOla3GnbUHbB11AmH3kqiZiQWm3M6JBOSEhUJOWb0CCWNl3hqRPU3v8pL+mkhaOprOaWEZm7bJlwagxLKBij8YC5nKGAyXSas96HmMrpVQpWUsvS61Zyet53l8c+/xe/Fwu8WOAZLbCulE9jyVDqpq1/l1Oqx7tydn1SzCH97jsgfHy53BXzU3/ebXs9VONh23fovofPSLvzcKwH8D/M6IjQoaynW+npHA6onD5LRxa/YboCtPQ9rGP8t+gHRGP+ozwFeiCEAYvDzlQT032sXqWvuDRQCCxEmMIBYbsQkonZ301mvydIUOPHnz5lO2Ght48TbUU6DBXSIcvy31CJiHHxAGJom1fSFADB5BGQITo0xShy5b/34Hr7DhAMeTknGwqeQEWwwoOuVIhZwqi++AAqOcQoZjqUKAiooxNTlBtNDeVGApOsll2AgI+coQsr5uLbc59QTVgANaTzLxRDGnqA1N14UgOkQJ45pZh1ETWzpbP8AoA3Zb950HlbVNmSnec5ZIk9giZ1eVr8fpG9zqdXN/QNF99xwFpdv2ZL1S77wH6RkUL4agn6y1U2zkPgF0kCrtRuMb2qxmQrLJ8z1Qi1PM7KJgDtNXZnsiO5/I4zhyecA4Da6g+yjP5+Ui2/yFxjhlFChhYePnpO8PoaujfEG3I1jhxU97n2yj7ByQahqJUgFiqfZcWiq76cVF8wAoDVGKkA/i7L37ez95PJf2XCG0886M2dCkFqt6g/lolM5JwBnixscI6Vqthjsiobxg0oflcTjkYuqsv2pq5OqjZ/V72urxkcuGxLlkSc1Pkpow5tw8m2FxMOKyCLmKiDnnC3ZHOLMaIo5bZ4N4kdWMbkro1lUUFlmiNkhz3tXGRP3mQf2T6IlMMpgvso4myMUiwLV5HE0luKKE5MR2z+CM8WbLbDwpGwaWRX+dH2lFaIimZ5SGy1TEgJsnDGo+LCC840Fe2zx7C2AByRIPeZinWNDZ1mhD4a161ZDUUBdini5LS2ySmHbpGEhVhjQiwWazvqxWUulG9hrpQkDJ8D+5qHaXrqPk6Kue8++lbcR/zT8rPttOdbQHZxWZIptt94P/5bNoxrzAdd6eW5GyX8j9dhl0HyeWhakgXGuB3WZ1fW4yxzPB/5UxvGbDiWjM/gP2a33bQMhaN+qncbz2PXAKQIKb7vQdhECd4wGjhGAwY0a+cdddbew9+HsBvGe3G/WOA5LPDTLn9HVCCNsEVGig7VX8iDYjvhwSHgC4iCF+GM05ZkDKJ2XSUIIOgFFlyCmNjIsnEeAfCCDUwC1XAjgiSqwMsUqGGHteTxt1FVPiDbjaaBrYyYLtBK9HpKZvd+U63YTpPJEuAuwTi7lwDAnLdQN5wwFSMUdGG6qpKtV9b7FDntBCnoEYqjKT32cIScM5XUHO5KEhvpENTxgARCDIpLFMVFGwgRdtZ2bCdasMzTlskqb89m9GY3AHy6+G9W7Ah6wuFhnK50Q2tgNqsZHbh+7a6YoEARFzssiaTiJa82ptB7pFUQrMnAcdpRfTA3qRK7TfIlU7qZ42L/Lf5pggjE1dcTmgKzOAfAYwZgEpvS9B8S4pJP2s1EDcQpduxKqqVQ4w3pIsybFkNFiwxKwpy+bcxWkHQKxXtbLe7IHwWAqSbLvywXryasjkYVsbip8NIAvWsgCX6Gsf29SLmdEYetNulN7/IbkD1TgZa26pxYT5d1NWku65tT2qVlTutsRQOBJp4rX1cc2bzKTpb5rHYbfezL2gDai2DkJFwjr6/QZKNOMtlauaCJsLURbaDKkAoSkD0sTKqNAU8BPFkIvGZPUpKCSEoah7XZUo1l3SmNWi+KOXnKSQUUM54ht1ZgR42gDSVCh/ivGpo1qe4TDHyM2mq2cEVRJvMjgRAnJrYNmPuTGj+yMAttu7J9akWNpmSVliWmlpUuIKbhGaxDtDkdaVOL/VcKkfHP4NLyP4Nk/iklkfyiFEc12k7WXs9tkp/y03iNPE7rviiXtPVHIijhiAK/JjncXkkZsKa9lWje+Drb9uGd85SWWbzpD8+Bu5X3+V3Dtu/Q/Tkkfw7+u3mUNP8csp5ik90SOPRJqQAt3fsK30rXEeVwi36QgDF/ddh3jZX5rVQMIqaxO3vmUvWJqkR42skkEbprVro2VUyy+MzjiP5zzkpyNxC2moEmtgR1ejczHT4JQZpvcPIA8KKDK+BOzGkQFdkQ8P1aSikutA0RAN19eAii7xYpEcRJrjr7/WcAJyokGIHQ/wF/AyHRAmDjS0GtMJYAtjB0M82+oztGLgJdAbYcGlAujMAu0AubPDVWNAQHESuIDRimdP9DvHEnFYwO8AIUzebuLw+dvfxONMIi+bI5u5ycvs+v8+Z03l2+redZ9/FX+Tfni6tJfbUsLz51l5Pi9WV+deUc98tswTaMN+yb1LIsIW2viAASmFKTX4rkVNi0hU5q1dVvhJXl98JqVtM6dZ2tQvPKIxqYWsM5xEC5qWuM5++bKRv+/LXYDFoNvqSHNlCpRDJuzk3ucD8fhemncP/HQ68CP+lZgqRVf4+fIEd/frEnjacUl/Jqq4kxlq47pW3WTb/o8g80AmowL+qf/qemuJp0r2yP0BNvHpsbAVFTNTSt4U2gs3WUzRlbIGnmT1Es2F8IGW153dbvm+XFinMXrlfNosnrk/K8YY4NPf0TTrNFpzMW3HJ2XaxkafNpNeVQtuKasYiMNRus5SAnKXscr5sWTJukSLL5EKk25V6kxx9M72oDYoXSDs0EWjacjVxZ0Ut0EgleT/lpJJJA6miuapaeLWRMH8NwFgYbD8kYBCPAhoKNBO1DVCQm8C2alwWXJUWDh1Y+WcIxC8EWbrJ6+YpMadp30Ro3EuQRI4Itxlbnnh/JiEBHaZwaN2M7KSZSNXXhWgX3yyVrzCNNYB6oQ9JE1+7VaxlEwzdVchff340x+lYMQusIrAZvyCHPIa8x/yFNcieesuX/gPMu5T0+6xbsHbJ4k/V+h1N3JyKPw7i7oX9Yn4emZVfb4/NoV9bjLLPLh2K8l9WwjO1q/hSfvuTzXX5a/u5Jy1qtTaVbe+z/ZVUAlLcYYEhFgK8Uv3ZPuXxJbMVPfGV9N2SL7PBDin6Y5iX0xQKPsEAqn9tl9hFs/iBR9lQLErI3LVuePAzegjh5+bHiFThCbO70j/Ld5VUgYgaORPOAQFAIEe0tpwsWvEH/JNISa4ITpAgoix+kCfek6GvE0htKZumNkzyMTgQe1CH8vPOgHxglvIMEShCxB251bKxu20CtIQxgQ4uDhgGwSRQVsEenHfbRlYmXEziCK7egEKWhNc2Y8MZXkMShu8zgR1TBNpK0EYBUQCLSWE9X79u8qi/Y5f68WImP2h/+/KvX/9Vf/u28rK9Xs0/NdTl/tcyuqoqFCav/7+Uv/rtP/xOgPdATrEV9GCUSaaoj3YHCxHKmVz1MEqrqJkHcmf3iEQZOXNGkJISrcH3rL7P6mtZBQtJwANRKQ07JK12JL+7g2JvY8P5/2CIFB03otX7ml0ultn+DqXmDzVEooCi5dW3rMP9QzAomm1B84M0Jxm3zW0ZDGJ9xygujRq5NCDPIV3FRlLRGlIVekg1RWg/O2uIfTTVWFCwvq2VVL5l8g4R87ny0+nJ11dUch8a2l4wWsRq7zViGPCPXmnrBUQBtzWjBOQ2JtmJ5BjCdGV4wtNyoh2UaHQZJJFCCNU5WHco8utjGiiEj58cw9GPxxOBmKn/yMw1GNKcoATHsoG1Y9ruqKs+HthBAAX2MPgn9LeEKhJFl1JplBioflyGpsPKsCK0dUYyRROKSkodoCZAjMGEqP2dFpxB4ERv2tKic4B8R5QSp42P8b1kD0KyWtWcRkEEMN7nWxxSpAyrEv3A/6hZJeVTM547009HkuVP2wu9nZ4FUO5+Q7Hj3WSWe2gDo31a8iW5nII1XtRTiC5g31EgixvyPT+2w7//4Nujx/H9UyvjGAAaOvD5Heo/JkcN5eqTyR5KNpXFslmpiSyr6EjdePo9U4EcmO9ATEAAi1BkmKtwDa0S6A0JIGlXWeT2O+4MQ2MSSCdOUMNoFomI8dNEZ+AovDl4VeriXC0giOAlJuEQh4JgEg/RiOoq7CgZyYUcRUcSZuMd+aOJE3z+R0isjIUDZyEvhzpdwHj5KSIW/kFb4JRFuABmdvgIvwm2m8Ah8YSccdBMsgsyRB2rhbFqOjO1uRNEZW5vb1AEewYN+fvaLhCTQUqSENKoDCoH7EQyPDLhZ1/QWv4H7annizIgJ56yyqhRg2i7aL8+yX/7mq/xker4SQ3EGcHuz5Ciq+es3X958/3H+j/9hufobATr2pO3kjBFkWItjQ0+sFSmKvkkTCs6ffhCjRsIB0aYaEOw+p3Esg+c0E5uG2qyb/lM7I1P+Sm5cJB2AK8tgG75pXDdr55EyM8fLBxPqLeWlPvE/ecZToopMx2kPtzUHp00w4+JhttqpTuMQ9wmHHrTsLMSyB87fDcgp2J39czN/P8n+LQamOAl50VDkrUwV8Jkn/uBr8rRY+JhxPrq8octOmYJVrU5mLOvN5st6Sf/+Gd39bNXKmoxJ/cVJO2MDUmZMMVTEOMDs5NNZ/Tt2u6dgMxqW32SxP0bGWHea8hoyQgmE+BvJC3eUBbSy/JlkteXRlb0ZmzJdW6Bsp3HqREpIZBiJcv4PucDFMARNxWp5s2zqkuZqzSgOgzizjDk2CKPkGdX/SqB6YMSwDwFKDJV6A8Vj75Nsr3n6jNYfLWUHuQqI6S3OscsTq1YiBI1Tw0KqSJWcLP9QM6nKJQg0qmRqF4BDTxYOOYefj/3Vq7B+HPxuSDZ+h95aG6Idx26/7BifMf8dllvjCbuhh33ibaPZDlzD79HQfSDKg4IeyvOh9GPKpBJxOO1jcZP/8Xl0mM/xoc+V9i2JvprS23vLe+whfXmT3T6LPr6S4t2hBoOal5yDsiomH4TfKpyUk/KeBsDe2Ld89rvgS7x0H1CM8krEA8oX54sFntcCqeyNlsDnFfZ5uA3q9VrAsamKCrZJfMIMsEs4gjvnAYlKgAIJg4Qo3xHEwRtETFPBN6CgAdBnz6ibmosSesAiof/dxp4LqCirJAF/ogXK7l9HPq99dPFMJF1cAY6Eh7gDNdKsQLqgBK5M1HHNou0M0Dqb7AB8jCw54kIJmeAJ/CYmk8LbioWPhcgM3W0jSC26SaJcYwDg5sqmGIELGrb356KpwAx/wClAiT73bkpPNgapvptmX3b14uaaxagFmzqysePJ1KUB1YcP06s/L5b/AltiLKeIoFhCYD2OMF0BrQTPJgu7i+wdYwlDaXM7irsVIwFTV94y14Q7wxP0d9eT6reT6oY1BjIWm/prmmK/JpjrHZeSvIIwOVMI1OnROzz6B7xx8if8tdsYPfq4QW+IssIPKwX0ZA3AJYmYsgR8Op9ULo1uJ9esnM5u/raYvpmwYaagXzvYrgwWISNE95KTBpEKm0E01ZIWKsr0FvrvLU7ahKGFoljVJ3X7xSz7s5PFL86+ePWanVUnFTtsTjhgi6ntX/7n8vLfV/NidYNitnEtw6qRpPljPqdc0A9xYZIQqoaJ1KLA4BP95FeXV2VZMdhAGqolQ0QaITIujYmFmWyJUWoqttPBxahUXTntjfJDi46ji0mC8Jyjo8loCphUVinzVi14sJCHJiqkXrfKhBMfYwn6fZbGdfNR4frcgHcKNcwLY9JaiQGyCHB2mxFJIz+4WbFg0xsb2ZwPBYKxwaFY+k1+wXL3tibdDfkj9zki7X/kKXxR/x4LpIIfNeEeyj44atFxpH8gqtskHWgApBQn0gfpmSLuGCxVJTjFu63nqHtbxNPbTMN259D9oET8GMTHtCx3+v7Tt2low6Gqny+9h+WO6TPU7bncY2nc1WGM8pGa7OTX48rqMb1KdzTcriJ94Nb82kF1G/T932Hj91zMyZVgHNADUAKyYa4LSClV0VtWCYsQB8QARABAAzyYJAMFcBlfjz5lwoyAJnWCCjEERqIOgPMFT3glpCKcwGVwr5fU9layUfkH3Um1FCg8gbEphzWKcsIse0sCwvERohPLSRdAQ+bK60dsMBawnXn7LYBQhAcAjDXAUNBYEP+nXeoJAI0aRQOITEmCqpEuhhpcDM2k6O4KhmA1hhmmdJaydYpjFEw0+eWi/EuaQPm0KV69X+bLsvxrFGmYT4Gg2d9n03/Om7/GKpwMxrQdkmHCTaB6RGdScuMRsFC0DdjGsIBHqjzpxYcjrohPACtf6VknhN7iNiu/zVl32/21aYCSGVyCZloCCUiGMdyovrdJWJXwlfJZXJv8h6ZWtYiFZ/rFI7aqZI1zr7UB8Ocuoo4MQEn3Auoqjtw6c6L7/Iu8eEvxyFu6wJvy5D/GMpJ/o5ZEN12WBIvDWopPG32ya50tie293KES8A81lqT4AWS7mv2YaInNmmzBjKB6dpZX5yw1mbwjm2P5xs2q6Kazy0l3zrZVyuRs5slHrU4PfQ5yJzsiH9ZCel3a1yaw+BCPa/20KMWmXl5Pa3A2Qwqswa445jmWkdj4SkYXPWsWSmnDkhp3AkVGxi5StI9KZipx2ddO+SMgKEm6GjCA4XFuxXulI5Yw7xFkgdRweOKwoKgX4QhN1QoHLYAPDF6x9pgmovlC6S0ukyD4RKMLoSlFwSrYq7j60DqhQtFSQntsBD81TFfSQmle6Z74pPC13yZw+L5NsUzMT/DaeZOP6aj+9yVhmOqhe4znQ/0fyvOh9GP6jOVd+uqlWM8la0yHh/rv0efovB6TtTsqNUaZ/If0e/Q5HHkQOkQXQ/eAZNu5U1APrwGImTIHGgAyh2X/FtgWte9pKH5fpH1++/i8+L1Y4MUCx1vgYL0icFgvdUedBkoIfKN2M5kCHGD3n52+CX5Z78EIgYwJEL2JCKEUkwhBPKbJ1bpMlSEY3ByzI8RZBregZmZEJKjXS1S4QEMEk5IHpczshnTigf7GBbcFPAn9EojDGxXEc7CMKDY4JgFPBcGEobBcIwFBY3SpQPMBnRNPIXpPBUFPGJJ4gjAlkARlUyZEQA3q5y2ZuGMJJuF3+T+301/n5Z9Pavqbna/jouFlQ+8zO6pU1W/qq++6OWlw1gssNXMyBXIAsyrKLeUNSQK0aTO38MeuTv4RJ9Lfz/ADs9hlYwY5v10Y2fxyUl2TaZgY8gCSZlGyvL+9tvglEcnPewjuH9fuXhl+LBJGIUPpbhfDWiIEjUlHfoC8gQtMg9kg3Mw59IrZUR/YjpPjoR1PIY3s41/9RV6xYyZxSQtNF/jEPCa5G1+2vUa61toqQLZgftublksUQhPygq5sMpODa92VloXmNARUn2EB+unZkBTfctmcsgaAjYBWDOwwI4hRFKFtLEHQ5reXSR5cyEKu/Pi3Lo0wp6gzjR99sDbFg2lGjCZhIAJMhwXUSIyS4ebwiOmMPfbxYbzI3KxdGlK6CkKDBXPyMPbbiVEifJMtU4kwC6AMHQwIGcaK2DAwDcltVep5BmPTEiU+fiXClpKnP4PlHE+GuYXUksPByDCKO2uXzRJ1TJcZDa3/dRFjHfLy+wwW2LWmxn65XizwY1qAA1O+Vt7tDP6NdAvoQ4rkXlrfHBuORznG2kxHtYGOkvAYos8i/bavZUulw7Li+7tFf8/D8S3g9LXffTGFgAfLHah1OEUDwgfvozyMe9h9vA6jfHbya6ysJg5jEoc9BKOyBgF+wrlG8qX3H9SyjZMYg0hrJ8HkZYAXKYEEnPBqfzmedpiL8hYSuUkIZDFHgVB2XWFBJg4gBJispkdZhzNd2tdS5mz5QlhCfKFyUjtGPICzUKf9RkUz/A+SrrhEh+h9xAe/jZoJcSgsUA430aeKBSBWotpyQMCprLqbSAtkoV+8d+DlNowsTXVyM8AxeKbWQthAapQOayQDgPB4YjI5cd360/3obfvQkb/qlky3cCpR/atZ9uty8V3DKb3XX4Ho2XAGK9bXl9Pzrp3+p2L6T137V9rKXn2aFGBXNFe1SDTJjwEHeojRML+MnmTXNwSMJAi0Sao9V4t55Fl+wuZCcsFMBJTfZVNm3fxL4zrcEas1EAYQD+5JRNxNUzKpy2p7L39QZp0Dg0ihXkzXwTNaZQ4vkACzBp1jvovxALqMVtAeIdeb7rzJTpFSdGdF9olVy6uqmLEIePqfm/JdPvkvI78oLbRhQhYq9cbHKPj4rE6e2KAkQXjGYmvup7HRE+8lYlD7gM3Os8fEAFZGYlbNlBGdaXle5sjlvOQ6+t7fTdyX9RfZ5LrxlGJGjaCOlgJS6i8sUfa4c4Xc9MPJDOoSGhlk0TDPaH1QYRmdwPSukmddAeMANnpRNFJkGiJGlHwbKRwPhzhzhPlKbAVLg66tz2gVsS9TKgemGQMyoET/fewtCodUKwjisuyEYskRNkpy4q5ikYOhYooS0XBiKNKLFW2FYLTwkZcc9cJ0NE14QANaMixruWHYhkcCzV0vM8LnzZXeZo4urn0T4YbgjmMr8p2w53gce7sm3odDNdGPdaUyv8caaztj6FTsNexhmz5c51077Po8lOvhr96QW2rvj33vkmX6c6i+H8bb75aeQpny7nhUczCvR3Nnvwo/qu/QzkP3thKHCk2P6u8UqlR/u4T56ds6xOFQ2LYe66cUYxNvLXv9uyZ7+f1pWoB8Iu9erj8iC4xXrRSyzs+UtTwBHfjzXUoq7SMERTHbRJwtyMEr5jbw/ff1GHCZ+cyCHvo0obAvk75Z58wzJz0sFXgkuAo8kgM4JMBLYtNdWoGVP7cfO2js8lYbkEkPMsVHQZhoo7cVQrCgrETy0otCfYASTGNHr/xhjm59up0Ebi+8EIcOXntwAzSFImtEjmA+VtC4JaqjGVM2tKEDHmpjYQQ6oJmDzz87fs9+Pym/xTAsEJ5wVO1sxhLdtloVLthdTKpf5NX3bFYDAHMtgYYmdeIvMZXTSHBrZxOonnSbY08e2fXH5hZ+oEimFDHlpSzB92hsSyslflb/ZtFcZsBdlm/S8+35TfAK86mrl/mhT7r3Ycl/TZlIUSVFTMQRWXikSWkJoLf2FJLjxwIP7AC25VwFI6Kz1mGRNy0kjzZjqx+sM5uVrKlgxtZf5tNXzp1yPxxBMDxoCglzdfnffFs/hB+M8eLPFAObVc+i5mPYAYvRXdXgZlCB/AC9lhOWX7Q0Tl3WTmD3DWcGTKpzcpxlt46qyDrKhtwUTGI2CU4OnpFMAUnZZHgaK6IJ1FTQSEYaLPCUbNLt1lP4haIYAraWYQoIO34ik+wieVFTTEI4rBv80bw0FGmJb9hCXmFVf71SqQ5H+OAbqhqKQwJu5k4YK/mFv969g1ShrWNx+KGHDv6STYzstLqo7s6Po4lvVG0TV8jrOfU+ar3lk/xf7g+2gBmnMc2RB0f+uUcI4/3cjbBOf6qR66c7v6kOb0rYkNaXwoFzAHpG+029O26w5bORd0ebJzyOt4GewDSi9m3it/HgS33PdYz0Ydu6f5MOzb2H636vY2Ttj7nXdyRFe2h7EHYbkj7VlpOnXcMUDa20y3VIuRv6FJ8xzof1+RwSx3hqbb7QO/nlB3ssDv6bsKh0e2senokqAEA8AC9EBAE6lx0dnBLwP0nnEC7QAbN6ACwnzInXzUwKMZk0wBfAmV3qAYQyTocFoqm8YCRgnW78QkjCXqxmtWtSwQgKkKGUEJsgnniJR7mA5uEfrKAOIC4x/AJHOjGEi3kldO7nl87JFo7xF82OUEbRcOrmzBsnCMAWEzxQml4P1UdI0oJ53eJKoJ4YCaFoSscyOyoK4pnEzdAHNBmzpelJ5l/7F/XqN+3NdEIDoLvGJJw0BSqeshcNm+AXv2+y77r2txiHfl806CaMckhld2y/I5AJzThiTAxdMrWdlAG4SYgQTJhIDGaStKuaHv55UbDC1W0liVVOf1fk11n3l2FDhm4w9AXUkXZEpBzEAQvuXsmlSH3iN2WADz6mfJiw7xNXnA1MDpO7DUjaJg/7ICEGWtJCXtM0YlCC9GG0YsJJwNkrkjDpvmgnb2khmCbaQvN/6Eo6vP+CzO2ahc0a8s6ChIZJIwSbKaF5H5T0cQekHqTSblM4iJ8FCUyoITsclmnZ6JOz4k66yVXWnRbZR6Su6JwnfdOrOrsA1DIVnjOqtSrrHzwQgFlAqPYJ6WvrhH0sWF6mPRTyZnaoHDPA4lfgzmWBobVDI4asoMjllxqS9QYWWcd6LJkTRwCIb3sR8XTwY6bpdeHKCE0t82ClK6LwI2Pkrw2ji2eVCsVCLrSpJUOQ6kVdUL7EPZkhcakql/7J4EkAmfYeZV2bnDFkh51ZQXFNfLSVXl5ByU/PKVToVxYlryDahBrt6MuEwjm0HUY6/B7eDR17nyeeh0OHcnfdu7J2aY732U1pimtFSHawRNya+njOx+i5a4ddn+MlPpRy91s25JAsc7w+0q+LzWHOQymH3WO5czhWCh0rycfEHdIck49D+oe51xbrY1H7Nj46+BYedUF7XH0/mvAosS9ELxb4+VjguBq23x6pYu/jMPDjdRe1H69o7IFnRKlTjgEFNwR0EDbgKZQBBAMDeQJKMXkhba0fU5/BNOJvQqLT0zrP5VfdL5n+AXPoU7TvPa4AT8rFy3eQckKXdIveVISCQtxxyIhrnOSgA0jfnuOgSuAjoovHEIow7wkxJhwTRMpn7gWomkfwGJYzjZvPbeitfJXhCpGQilMDmKGuxGyS5JaidDBP6QG3GfHP3eRXVfNFw+lX7h6ahkfyajVjBvjq6s2k/Zqe/ITx5GB66SNGAbBgAPReYrSbSK9d1/ylNAvPMAJntQaiZW0rOtvDDIErK6pvutV1Q287JEyrSQAa5thg/CLuMLB/xC+Srg3jUlkZKtFZStotglxc7Spag8C9hqAw67/ZQ/Y9hp6UNzUHb7FIgVXBk4a9etrVb9v8E8NLtgiMBe9Aotoh8k2Vwq3opABlxRlVMf0JH5ZYUCZsfDCm4EgJ4pjm4xT6yc3kYpm3V9llM33FMAnhRbso8sWSQ9BsH5xPVsx7cg8hp+yjQZTqMDyph7lp1dO9a1MaSbWa8GAPPeMPFKYc3uqnfeneN1OpLIzQULCNniwZ9UHsH+M5zBpyJMcY4mytCEO5kZiYOKW6CoswyCC1vKdIIU8t1Ka/dAZ98jYFfajRUv4RBf8odjhjlUGfmshThCElRCqMQs7TDQddhyWMSh0hj5QQvBOxCoRGoUmKH86X2zNYILJzaN6BrZ+B/QuLn7sFbstWWKJ/aYTbIHqu4oV30EzDSD3h7pqB/fONDvI9EOgLmvfOHskHIt0XxDuXKz7AQ9Lj26DDWLvuIZ+ntFA/S4twJO1bqdihOX5+3hafnYdhipKVhj5b5Ds6bIU+7gHQRikfKUvDXHsc+7FYo2kciXCgzFAbRtQPXqmyxH2Xd0QchMUnHORpFbMuiGAANgHOws3UBRb7Au3pYwUjXM5PTlhgeX25ZL4J6MfGAE0Dezc59JR+dXAoU6KBDsxZZ7TAYYFJfe6BXeC/0NsmQXrPNK+k8WSA9C+wBsGoQgTbGsw2am5ulhjD/WQCaULKUmPuTMBALp9IiJ3kA09lndIyyCbv5BIXSqOXBHbKQiZKs+9dhIR81zak7yxPmIdJ22Icogcu9EdFDCOUwQGWdjYtnfBsMMPW80W2+rq+Or2+KqoLTqGq0IyNgYr8dLX8Lmu+usyWN9kHTkHW8PknFASSQcLkH6UIf2WqXqGtLRObKMBKXBXJSzNfAMGlM11m7G7JGgCgf92s7HQvv5tMPxXZ38QoiboyFSt4yiESEnr7EBJI1Kbw4xFEEnLhTj6aEvGMJJBqwCnKOfiRZ5yemzq/tQ+cOHPXAxaaU7K/pfedtkr1VTc5V+cJ+NsOes4uIBGT2e8ms7d5928B2JzXi5GB5WGJSL06mR8oEVrIXweGZzxlwtJnclE+FAt6/7WNwJ9JViUGX3E+RXXeZl+0k5PV9S+nr//7igUDzatVldfzCyZFtZOPORvwtyfOuWrQkG2dLiw6YZIoCCbVYltzVjEN3Q8Ip5GDFrS+SA1IHQuh+2q5qlcruvVNLAVLBJ/uBH8FDYISV92WSJYvu7Eue5biE2IsUZRskxetBERb6s0X0om2NB5IfZAnFTWStul9DaGUqjJXGCrCffIxUVqsLE1nEevjmtBqnJKsAThzGramkKya5w1nOFyxSpkoFkmXmXNXjLJDnDL6KxgTetd/HX7vb3DeQ3X4PXw4dA+7z+z10Hf7rjq3dgiTSoBNN+7dCD8Zn6enPSXFl61l7jEJey4dHiN7Heehmo/p/HnL9p1ClQpYsrlBx44AkOg7nNZmePl9scBP3gL7PmU/eaWPVHD3mzGs5INvSqrAvHYFA1w+x5ccuD8FRm5IRSRghklVxvsB8E2PK7CAPemB/67mZUigZKFnWlcqWIQboEIsKpCBLRLwBEPANjnwTKMB7qaSVIxfQyEEgOACZNHyqKs6tMmYM0EzoGEWdsVSzgA54iUun2QP/yTCe/Tcmwz7YkWQlccE0BBomOGMZlNAD/5C2qRAACP54NAtX8I8c4yWDBv+uMEiyyTb9jQm5DMNikk/p7OLm+n7qpkCMLOceSmlK2yLM01TniwvzrLuawyLzOj+RRVaH7ACbJLwPr38qoNiaURhmX6bGhLGPCJnbXes/+2m5bUJdNsZ7tiQc6X+Ysra1qncONrADWeiUZFSFLaBt1Kgjis9JTcScax10LHWqPcLpcxN1j+gCob0JyLrIBhgK5zVWjFHKv/o+mA2uywZAQCgM0zBkAAY+K+wSceeneY22Qr2xfooQ1o2doCxEuOCKUR1mzHt6YQiCD6lAGghcLNkbFlPE9BVzzfLyWp2uZyUH5fv31TnN8uPWHG1mi+z5dUqf1tOrut5O2WajkMmpJLRDNMZaZSR8tKvTkoX84kQhdKxrML5/VBz5+a+n+x2xZ0WAlPOAPnxh1aErssyjQfarJYuTZcaOqQz5BCBFFOSHdiBAhsZVwHKMPt4hiTM2pdkGSeqJCIiqHe6UmhymwaCze+UMRQNCr7PkU3QhsSUYpyR59zb7IY/B6DU2SqC2fsMCRr133uNBuylfvE8bAEzMC5zcO3+k/9NxfFPPpmfMYGbcjMi43BZMtQGQOJymBaylF2jZFtrALb12RvH74fvq23S9dOYfwofa0utY4/8ps/YbiDvX75lX3l/SmvskVopduvqdeANznt8xD5bEeLhHuljaR8y2qEZWuMe/kM+O+4hnxS469NH2tFhh9nDPXZ4Hi57DxewP8ZoGveT88G2ktnZue8icE9ZWFet9W/E3KFLdXNzPoDEqWBJySbuXXMSHjymjkhWBbDveTFfAPnZx5CjgmwhFMUUPMWMFMGMUxooomgL9DAUwC0GMhX08X80JYFfQB/iPQMATh8D8ZjQ5CkS8hILwVfcBWpjz3Uws9PvWTxqYIAkN52xjzYuyAIvxfJTJ6AHFEMQBKwEAP0w9yOf1qv25qqyTxY27CHjL7LZLhI8RkoAtf6LSwVV1ATQAw0KZCUvu/i0eUXEa+bjZ+2CXukP9Rf/799n9c0/nVyeLk5Wb+uintUnk49tczE9++I/5L+vsmWHVcPG3ITo6AzckjuAlCupoYXQwbUBq1+atuI7p9OI0PBlATGQ9KwrXk+YeT+p5lPGVW7K+e/y6WWe/yvaDO3qjS0mZqL3wrRVnwh+NVyktk8WD+z4hHe/IxDPm3h6R5j5oou8oDC415OjOpomZQ4tIrrGXZPgEQRo27zK8zd2mrdfd9nvWAYNDG66WTH/+2zGkMK/hi5rZ2HPkAD34L8u6pgi3sAwRAfyiKfs2kzGYDYgGBXBFhXDAYTGSg2OQ26r6gvaRv/8u7Ord5er9k05W1zlV92Mg5mrf17kF198zYLkaBkx7+YHjWxSacBQLM2HZBdaGFnxiRlGtHXrjo58xlKIt7AJiNpujunyDOPy10KAkoxJEAQLeHo0mLnopd0sqgpyzytHlsT+5r93qgfiaP9qzL5cWIvMwiCRuTaAlRpqf/wDuycfvQ01kEaRjwhljbJDcMY296krnBqBmnCFX3xEbLtFRNTGKCpse3LS0dA6ySmuxvPPGMYxrunZc+313EP3eb1UWH2fX8ox7+1jaI7XLIx+m7NHRnykDuQ+dqPSPfZKcp+CB5Lkp+vw2BQ8Z7zj7fDI/HqKsql2RE3Zw8bQB4wAQD3GaQ/z+71g9hlq7/1y/0goXmzzR5JRz6fmfdVrU2N0DIgHzmOV4YPfz3IGarPPSdqiUUbiT9eqghfcGhy4ClLGW6jHGwBUABV/ethZGMLBKPjwJ2AJrEJwgN5QCNIgW1f4gBaQ85vIgxiWAVmQy37yCaUB3dl0KOaX0PQIiUZSE6UBr+i95JPGH13FeiYNmZsEMiXKzdIlwoxcsG1OvhKOQQT2YZoTmNQZ6wF0UMYpQ4KkOjZNYekwDOmVh021qhsg86ycsiVnMSmr8v3/dP277/757a+6L/Kr+u10Xl9ffcm8lza7/HD53etv2leueaWnGh+TCfwy6XToiw9DfW+CO5XpsZvJQBuToYE8oE3sXTWTS2aOI7vlbGCIql/lq0sxAzJAatEi6nkG7yQi7BMyNvKSzJRj4Za8j6JZQjQ+CVW5uRDNFZoBGsEMDg8bVyxACCPRZGGMoPhka6W8ZskvALeatFdMVcrKm+pf1OVH0xYWDkGJtdhZYaBNylfirLohIFuKTNsZjaEup5nRuAW/bc2cbxXrUNxhx0lcLpxgOKCZ1TdZVdEca6orWmnX9aQ8XZ3MWyYvkZcte/CTsQnKImOwsEFIHAZwYyj0x/Y2QokVxUB70MqlJDb0+tOaJBcRrY4UGtR22pXFP9Q2x2LYLMo/acYjRnEo0qmBEBmWKh2RLGyRzzQKYGC5sJzIXXthHf9T46LERJVSNk9OIpIuVA/ZPIRaxuWyTOhDpHULgQdKfi9HncX36uURYJ6vxz+MoSd/CvJKGaNrwB4Knri/XM9ngVv7JvM+H+ddTre5uhv24vMnZoHbgjVI2G3lJTgaAA8qdWM9/burAnqZ8eZJ35SBFs/QBk3cjm+BDaVvuaM1/PT22S6HoW7ptbprhy1NBg+H28dDzinSrvQBs2dwjvHf1eQZhB3B4ilyd3PhwdzStzpKzhHKbpGMlYSxHB/SW6OjQsXvFtsDD6lu3lZ8K7zIIuBnW3yfTX+I2D0F2CVAkz9lcQaWzgomeChbwMkkDGLbKcyPff6BMwSiAAswtRho+5USmGP45Ylg0qEOcYdX9IkKpGJSC1lkqPDYnnHmIE1LtnNJWKRnJUC375P2SSzzVcG4TJkjAOJNdomM88JKkoLOwioV5mwnRjPEaTJTLIciRYJmzjrPAUYAzVOQJZvwNEV7PVmW2el0xloEtgf6pesJypO6Omnn1+/LrqxpGLyZnVf16Tmb99h3DzCmA7pgGQV6zFCEDvvokRb2qgY4UwhvilxUOv2eBougS5Mgm+79wikjqxnDIAUHNnXFql5OC9Yh/+eGXYCyM1IR+9mT/OCxTv3aBuQM/mFqXThgH33/SCHES8+IrrNXK1Gyez1KeKYyFsZJihakoXXHT+bK2LohjYLN5k2Wn+b1rK3YC+jSs6GbyWLKBPhvs/L7bPJvQgJDNDMblqLSJBZ5QH1hNE0daTpWTfCPfWlgC+hmR9YvGTfIso+uxmWHVtZi2xSh9NEqyq676jQ776YY6ZSzLDyLYM6x1NPmhJXB9KnTq+1GoAwgdKTFQwzAuPBPZSjlumYIX8RTl1kxHicM8ESAJtOC5EZLh77msLBEqWPdi6uHe5P11rQRQIstTgAjAqWNDCXMMuwGQGyeZDEI1vySYpp0NzZREgObOZFL0JD/esZ0qb6awJyLgto3+ah7wd2WSVS6iJxuyg39zTrLG3FMjZ5ctEvLD11xg6oWCc7QYNtW2xUQmMReUiqq8aBg/blzpXs8hoX2fM0f/EbtxRz7Y6LGr13puz7jsQ2hcHKNvZMNu+/aldjbaqD5lk+y6n1s7w3fkhupsGyvr8N2W1P5u8VnGBDuMTywQ/hgj8NyH8zus0X4qek5hszvGiBV5N6Xr2O8Ku4SvTy/WODFAj8RCwxqLB+MzWdi8zk+Rk0/OpsIPQt48YnPPKjIaT187vABHoSvQlnyyK4rxBQbCJnk4mVgekysfAYtrrtOE24SagRbY6xjhhAfhSMGpEtnAA8ASkwU54kOXnvx/XHJL8pxD9SYYsIStQhwgCL+YtWm88XZ5JC5+Z5VDGSdzksgdDkrewms/ARPMp6AQL6MWoFU+40M5F2Bjgon/4A9aWHQ3mmLOXvN1Df11QfwL80hGgPMiTphjcSim59+zJrzolm2sx+uq3fV6iKfd3kJCkbmJF8F2oK5nfsmMn2ATY3DFijYZIBFCNCAjm1bBkwWISYbtHO4AEuAmfVC4AocC7aEYvXLYn7TMd7gCEjBx11e+IeJh7+prKwtn0K8Qx8XIb1LxfTyUSPojsk/bLFvfiSYHoCX2LEVEtgIsbQKOcisZiVwx4aYrAxxns6iZM5QNql+XeQnzh7CkvbZVyB3kH4ZYwruJare7s/jOXQbRVizS9qZMuTJcwwnEOwAFRP6WRgx9RRe2LDbZ/m2qG666n1xPbMhwZZIzdW0WWWLqsiuZtg9IwvId9cdkL22HGz/pUKGuSKpYQmSFYULIkpslCjanF4uQreQ8D/lHqpCwEeTRp2Zpel7I0rIn00kc9OA+G9Uhck81Qhnz9lwRiiFl/he4ZAi2BmHwRX8o8lAbH2MEcQpuxP6l3VvPRLJHKkYH5CPKlMVTLxMQ7r+xE7ekpAhDLPEGAelzkG2wANKk/H2FbJ6L8JCmbhtk708jVlgaMAxmhf/Fwsca4FU+e5W0z72UTWTg1K+tibv6b8fYb6HclxdeYyoNx7pYSGfryW6q8dD23xD3Y5vee/K3fUZct4N/TF9fhxNdi3/vHKP4sZnk8vP8voezofeHloShr1Qxk3g5WFSxQAJZAzjBSrIgHciPDjHZx98l5dMoRFlgD5LoFQCHqE38CCgiDd1SZAlQSiRBhAkqPu3DyT3vAGkSHrAT4559yp29/9ePu0iuv85eDZ1jgL1RFeJEM3BdpEXoCVQsoBb3COu4sa0ETAW4HLFROe2aqduIVO4jjPAkOgOTk5PihSCqWUdHapIAaF283LWcsIvs3uq69eMbXDaMKTOEc/p655+mJ0y4eWClQ3t+TVWO3112U5WrgXOWbzAhpWNPJkK4mQTralNRfYOSrifZT1hkx9omG7kjG2PhKWQoRLIPmcaPeDfKf5nwE0PGpgsajqSp79nMMCVGxjbJCdsSJLWxultjmmwFbfX3nN2XuLyFg5+o0zoubkixAUhUVaIjfVQyb08sRJZAIytVNKOeebj0AaZY6VJ9kZUOznt2newB6Yvb6p2/vdleTMt/+0K6E/Thc3mO/YOUk9Sk09m9FrTK45JSFfSywLAPj+w8Lg08vGKFLAE/YbFuUExa09onU2KK+YD/cCATI5ijP6Us+mXZTalPcDqE1uE+aJgqpZ5UNHXbVuFu2eCCe/lbMHlCmxPavFJtUyT4EmgNLY+XAwQWQdRWGzSsLcopgc3E6LxoZIiijztDqaJuZIBf7KOUSfsBTsePEmDOyGsJyZyWolhgbJJAFXzSk7FR2jSsRuR6OCuOrKkVKd2QygTbKAlc2wqWFNRHlKFM9JF09jVCFRPGm0cLfdBTZpzfLPmi0nzqWvIPkZmrshSZ1XJNNSFwvSoeSSLR5zDa+3dvw+HQeEee6Puvsl3om71PR9Dv8thV/quz26soU8qD0Ofh7p3Je7yTMVwyJnc49r1H9Icdm/Jtbw98triczSPx+XXkH2S+3Q7JE2Kt1GCd+0QH5TdHBlqktxjKXqcfY7hfzjtfbq+33CyovJwF5kP6u6GdMfBa5HrTt3eoXrxeLHAiwX4GgIFfkLXUTU86Zv0jhSkD0zAGfCCEIbdVngP4J+o8MFlkOC7rugtp7+SLnMJhB++OsUWkGsSaGNaBxiHTlPn2Yg/BDRQBEDCRzUS+96A64dgkl5BshLIBFPdaCLuFPkEFoGZNCIcXuh4xsaegC0i4WFsggGQwil0MFZAZzb0gRWNGnZ6oVXhQmZ3GDUCMaSUlhkmPK+ij5npKGBHttmZMvrgrqMAcldwEg3+Ts9oy2ZZ1AwssFAaHkB/mczo/XbXIlEasBNTofFGkoIAzfE14vRl+l+j6QWpke2+dTiDvvGajVcn18BCIHKTz5lk5JAFmlRNXX9TVzetKdI2qh4WR3Xke/GDtxeiUxbEw5ogkh1UQYQrjUvEDCUj65OztFRTmwXmBSkhPfg47cdTuSLVzpAvLjicrJjdFOVNsSqulrQYHSHJV3/WTd6vqmV+wmAMa8o7tAafu6cnyJi1G+YzxkQtk6JcNRbMkrMmwAJojzTIFAKMz+gMWYmD2UCc1IahKJl2uS8wIXNyBK/M+19MZmSURgB9M5AgtAUEK8CS4Q3uYSKRr5mEAPlGqZPMTE+a4IWdw0YWMi5KOLmULmjhw58xvWEZWys0ALho1KW2scTBnapkNfE5mhcqiUmDR6hGDGc8YWof06XKZoqXvv7DJ7IjPfhMIOIhZAkNpUUZcjB1kcA+GagRVjWCJwBmnvUWpCgEccjqhSnwvitZ4D6ql/AXC/xhLGDNjcqxLd6q8fO8thLOnt5vR8ywRefb5aHXY+KsZcQHwZfjj3CNtfB2RT9Xmy9xPl5uohd5+PG6q9dD+dyN/xzPn0OHIc/Dlh9S3pOaABxjvVaH42r5HeMfjvL8ocNKNXQPJI3MBVT1QD7xOiQu0DRiNUyh5kRVL7AdMCjcQgGWPwJm6Pl27STdrXRZimrACWAIbQGI49dyCcagZ1G4w6miGzP5lu2lhNMAhcaUDztlgzTADVoB1IQgQh1g3QneOdOUoa/ZZQjIFdCkh7Shuogdvq4EcOkBBL431NAmidiOgYNzp/KzTJSOeHirJxvqM4ebsLTluVg9pR1eTIjC3UxYeospmCStQoBuQRMzkWQQOImmxGpW21aYciwtvf/sT+NmnWLDik7srD7zBCsbTMTkGc2Ag/zQhz/P8xu3ta9fYYOAfySz7Ao2X5rVk+umnhclHe30dl9nk1fz/HWef1g1K9pi7F3Ult81M3YBOtcyAVtdBo1gN+cheZEWjKHlUSBdfcaTHK615/qJuPIiKkCQh0QUxiHjszKGJ0CWDKTQfmKXnmgPmkcE3dTdmyo7Ybn4qjrJ2SUVm+TlrJitJt+dzN6d5GfV/MPq5k2eXS+Kpp7Rm/8aA2MUQXdahNa/04ShNBFCV4JQQ5ALHLbxE7ukRpJA9JBYMpkPRJPTXG+mcVLEhH2rpuagk7ewCBan1aAUBovYPwieJg7BKY1abb0CYWoOY0rL+ivKddd+pI2DH/UgtQBSXJso/lnOwtrBRLuGZbszjyOOdwXrTChzbKKlVEowYr2CMhx99cCH8zFQuvxEmJGNgDXWV0SzqmkRx7WQjduCFew2iYGG6GakjVBaMO1qtaIlI0PL4huX8EQFNq8t99Rkh84onKw6gMroXum+/gmv57kdfpMnGUOaoft5NHgIF99tGGOQF8fHPuarhL3lHxmYOA/dx8vaohz5xh2jT+JzPOWW3Hh4en49RfquPlETd723bL4neOA1lqKhnkP3IOpRzl3+h8tAoh8UGaRQjLY9DkjeouUbTMS+th+I9BL007DAVub9NFR60eJHsMAz1NAoOtwGrPzcgzYYAWCHfC/Rv+j5liiBZlAzqE5i3xf9V0vgExc86YkGuqVQSEAbhOBIeCJwyd43DfArcRPRGCvYi0uGiio2fYMRnlC7mAbQYgzkOggQ89SJHnJJSIBfWyg0D4CQTLavKno/ReQin0g7SVZPWKlowPSkjntB8vEvnbzu6uFp9C6nrmL0xBq0D4BQdmUTnR1FsVsIS20PgCfykY0koJXKRoIQwhlWGOuEtbTuCy9Gb2ZNtRDFcyYzK2wnzaqalZwxwBShqjvhLAMaFJ7YOCnoXGcHnr/Im0tGAISUDEWYC3YpR6bFzeSEQPz6K+wUfikgZbfGI72aKCxg2n2ITEFt9CSEuLa+MF3DgpBkUe2I/RuWKGT5p8tqdZPXYP8V+/O3TVnOr+qbZfP166z5bfbq6oZDuxoPx2qn7+uinYLN4QJ7+9XD6km9lJu9lqriQAv2s7VgvppD0dikzIRuDkSknvUIgxlrNsgtabUEawcok8xiMnkplSZR1sEujANvPGDjnC0bj8Bx15xgBI/98iLUZPOjXHiKC8n30C+4JbN5p10C7qc1Rp7UZGJETJA+mOPDKJKR5BdXFBTV0kdTwMbUcqXMWYtOoWhAywMijbO+pEctipTn6F2rQE3zvWMbXFqctjYtElD1mSp7tSIvHIYydZEjtxUtmBtnLWLkN5Go+sv1k7DAEXn2k9DzRYlntQD19IhKOCQxRhr636tIqvhG2H4F3PrvjbbfM713hy3pw21r31b3Xem9fQzlYU6pRfWUNtxh/mOhuy2/McrkP7TekPKhfPq4I/0EQ87Hu8d02M33x/E8nDtj0vfIelRfzpDPYU2GlGPux5RbqsN2LRxjjv/duYBbpIEy/Pqjhd98+JY/dAUTCkOtqO65J8KCBF7Zl5tzlip9sCu6UYkh5lAR/HQJb3kA4wLZi/dO2QAoekHjf7FMckWsQDLAkCn+hsJHKMZ/8HIsgYVp8SnnqGAxDhAlZoeDtHpuBOOdFIcFCEx47URnuXFDAV2SJEL0o50AzqHHnx0lhW0unI3WSurBDQ1AgUlD4xIzpY8glo4umP/EamhTlX9ESLc6h1cknelRMRWHmfGagD5mwNYUDE+rI+CW65KJGZiNcQyUWTjZmr/iklGCGWtim+vftPO/XaxmU6AqWx19KKsvp8WHdvL1Tff7P+t+ezK9LiZzVh6z0Q1tg6L4vpx9yLO/BkaTP+DAYI7ZsRmtIF7p6SKRYS5OCeBy5jcqfgpDBUFAYh6TwW5zKrcfGiAMyGc/HzYzSobJWHXg8t9LmIqRW/vVvzw7p3//i/ZkUX/gHOCz15xPBoQuu/pmXn27mFffzH73dvLdbP7rsn1/UU7/H+V/+KH5Ww5VY1IO5jL/xfYIl2foYo++PmJT7iyPIG8woXRddqVqFDcewPihJ7lIrvOIomR0XblbVFm2WckCCYZumHnPIIAtB/n2qQ6jmRAi02CgAJJliIgRsOJC7Bw6aV0SjS254G8Gf2R/UrRVfipm4W02w4c6Q9ngXa0wwykY+rnVD4mluMKLjXdsYEjDE+C8/IQ4mRujN3jEj9Kd5KqefvyPyPGgPtITDY2ZF8bICGMO+DAIQBPAxTxyJAAai0Rn/hLtSwariBEbQ9FKIIh1HdTCr5SxnheguHuuRJLuJuCZr4e+by1IGIjkPMe1y+cwbhnK3PoqjXxtKQPPfu3qnERs6XNQ6i7lQ3PhIPt7Anel3xNhJDjxsTxY6keInuA91HPofijLMQ0faPPjUjisp8bga8FP8n2o4gfpn5Pl59HwoPovgS8W+GwWoG4cV1t7DZ6vLlmTbrnhEhjR79wyuUf/CNc7oR9oQRVgXCYKgA9iKgt+AfBFLykV0Ad6sYPTjm8gY7BK8FrqCJcqHgKC9VGTjxGFRMEwePkND42STlBLAKOYp86DvZpgGvQHbgZAA3BDpTSkwJD+W4CXarN8lsk5Ts+h4cEk8uAtXUBGVTCKGqkB7+PECH1hQOc3IwxIsw0BmjMRzAxRFEJo8thJ7DQVW0O1E9GBYS3wU+gvUKOJ4rSWJAAsyAajnHX7FStru4zFoMxD+vTrLP+vT37xarHImzddvsjrN1O2Lsp/c5Oddatp0VxUFfvidxy9zIm71c0vsiUnYbFQO6aohMKa2PkgpFejoF0YONTt3ZE80hep8x4UKmm606/JDw/sYZ/xdDZj9pQJ1ig2CUyrhQY7Ux4ms6b8TVn/z+bFN+X8F69nXyy+YoiDiT7T7jpv33xs391kv7zImF3zRbOsqum/+h+a5vvgxCKMkBtATZtGO8CgsJTZACa1VRUrWVEPEG0GRF5HxqYPp+qbgywcJ5I7pgbYdhlxNLRS0lA/6EyqrmQeci5F5ll/0TsOHtCOAQslqpJBGsbYUaqdtiUb/I0ZbKLSaLxoMrkIGDd81NuYqJsMuNbBYGmCJ8Xs9oIj/9QHWkU7KBfSFEUWEKYxlAHQp6RBJLFtXRTkjxBVJG5oIm/IJbEySwDcR3dOlqAAw5C7MSRTrXRP0Xy+71KTn8V1hC1+FnZ4SeRPzAKp0g6UGiupW1WVXYC+Mc6eXsMtugHfMf8Bya4zvphb3mPt1C2i9DCSkvhk9+TpYzD0eWD76UlnACcldnXYk5YRr4dqu8vmwRwO95GM9Fjsyj3ss5vvh+nHQp/Swh7j+Tj/p2vygJJ/UMWRuf6jcaQHLb+L6mQt5j+90d2EXcCZMxDf/YBhXXPmN186+s09RhcI6BQgYRqwUFRrn4rYBy4UJAChDLiywhO4hvOt9YVQiJJASohVOJeedj5G9Cgs+CMAOJJgE4AG6b02Qa9cJQp0I2Y0ToaIRT4ARVQEQrpFOpoD4pHFXCA66ZkhbUQmtsQElISx1FI1hEmRwFBEHXNWACMM09Cz/woSIB2xG7bwcUEqB3SxNBUzBNBnHSp7+7ARjhoiES50SLNpD0568UksZ1SBEd+xcWY2+TXkZXs1rV9Ps7eL5qQsfgCbFdMfWABRzv/hJK8+NQsmdXTZ5UwoyfQRes//qZi8nbCjTlHWFYMTc03ktBTQH4tjT8wWzxxAOtAwVWR+6fdNFxJUJNm8T3NKeYQHkCRNAn1+aC+1nO6lXTD8TVef2hBkvS9pbJf0N8+a1/Pqy9Pp6tX8zcnimvERevfnrrT+OM8nH69/qG8+fFpdn83Yef7/lxf/MKn/tXYx/cx4isJjvqIn8VAMzKp6dE7HqgPboByK7HapZCawFY2lEhYL9dmPSMuwoIMo+LHZ/mUPuy1anitslrrFKsUAN+WXHIDSUgKXZAc9UIaiF3O6aJKay/jSoMMUztrRaSybQFEeLCFmrGYjSaFS5DsK2WSMUIgMQxad8fAJVB9JwdeWb6Q3KpZJgj/kKCk6tzbyAzti+Qgz0hLIHT3gbIrRhUAe1MUY0OjrYmWiUAZ0G9PEYok31lmb6QRRHSg6uJGCiagr7xNnE2UUlDny0qj3kz70O/XQ920k/341pDB/wziMICYUxEDovRfGfMT1qFhWhMhT7kP3I+RvojwgpZs4FJMjLKOGlKmvjLZL/zi5AxV6C7hr5T7+Q8qh2/Iwfj2XVccl3B8ypuGuDROvZEkH7R93bdVT3okHDRT1/yFvgdApyu3jtNuONXwXPRvTbREvTy8W+Gla4HMU+C2egUV4Acw65nIHiAiogjPIeBDoYpw1ngCIpAcgA5CLzkPBOzRBb18lf4FSfG/4L71cgnnqj9QHdkYIRBUs8YosCDYGpPDwjhBnKAiC5J6I/Ond9HG61aZLL/knSIMd/8CpzLsA5dCcICWhnrhXvOgfCABSdQNomQqi+JvihjTezQJyoWZ4RyhEpoWeaWAhGFPWLjCNaT/4tU4E6j9XMRGI9kAkEG4owhoAJlqcsj2NOiN1+k9ds1zNGvaVNDbH27L1alGw738sPyhqT2QWsLF5ERO7i/o3RXHaTWZkAhOGVNpd8FnkuoiJ3qC68Iy5CmoSsuOHJ+T5z4TcXsnNXYIwAibxrC8SFmdpMZlkRU7HzcXUzMzhYAWaRZqTNCUAAQAASURBVAwNVMUPl9hofjNdXAFsGe5gxQTK5ZPFrOSkhOlVXTHSsWBcJP/bcsW8oZQJdNG70AJdA4RhRQEsbY6wrhg9Lch2Gk80D/pJYsQhv6I0gc0NIjPzfDaLUaz4mgZPZvFgCub/kKQe/lo0tEBYJJlhXZyEg7ihiMxWJ46As6UXJYRn9SEiz+hZR+FRSbhDgVc0EQlNzQOKloWGeCjjInJaeiUzf/iXJm7RxE0aqJHFQP460JGIsLTlYUrhHy4xPdDH8TgmYBFdIlQOBRTMYBTiVFG1o5vfSmBbzpgQQ9ojUZBalFgLLYWOZfHaxtw3/u1lsd/yuA266zL+y/XztUCU4Z9v8v/QKd+ufsM6fEezDSFvA9YArGf73aHaPB5b/9N5Ao9vl2wEDhwbVfUbPuwkzzft9jXWftqmetjT4VbsUIfDlLtSn67tKAe/TX0/x67cUZ/+O3Eb/tAU3ca843qcPneYPOTxoZrvoX+Uznv4HFQ7EJsAaOviA516p37Y8uZhOGq3qaUbx11q6RMOIGRNBUICGy3BWJIrmpQSaPimjgll0C36JOlqTQDK7lDICQNjtG47KEwAmrmj6AalyzQxEq0ISgK4SenVywBzINAL7CNGEU/Z+5nwTYLphAby62uZ2kU3J1yu2+yGDeklwM/uTaArAM5DtCbOrl51DVNO1ArEyDJNBDvXQwnBJG15OWE/+9BDf/iDqUyl64dB1uJMTJBKQuBCGgYBU4OuZg1EMCQioU5xD25Oc4+uVgzoegaHEWR0zQz1prmC4aL69aJ7k03e1UzpAY2R9LZcZihfFcuzJvtPbcn5tL9iSkyTg8CrbvZdN/khb0+Foch2aS6HCZywzU7MkHEPHBOmhfwf996+Aec2/uayNu/v2m6D91wyYac6q6Cj9UQyHNthWsw1eZ0xZ4yMbqtyMi1Xr6flGeuRp/krxhno+2bFRJ6tKBDN5Arw2eU3M3aQKufX839ouv+xW/5X7BjEFJ2CbTw5PJgIli7T7V9ysCqd7KIJAmbNl+WUtcVMgsJ0KI9/Pptjnwlb3ASKdgRGsE5KTHqkOjbIMVQehlhacPZZHEUOt4BbC8TU/LBMPCvGOKgEEVGjrCZOPMpEY6EVBB40gQw1p7a+ojHUZR9oY0ZyLGGW46CTGyWggV7z2DLhWd4sU3e3WZdWEE0/qpIB0RJghQncXNsg8A+FbSQwYQwt8ne0f2wrmBpiy8CMdI9/uF04pGFtMmHrxKHIpUN/7kLFaNW14drPiHHxwx8R4hevsfHGLX+o19fY22/sO0XauFLurHkc+h3jfyjOnTBN3V9jWq3D/zC/Q2sM3U/R5jOmNOw5xn/M//i0JAs8nc9Q4lFWtWJYNR5xHV+qNxUNKUP3rtCNBQa1Tao0NiKe3w5IYzK3OD/qtREkixGA9WtDz50r6uWO736PEPyQCPvZbHw3qm58jnKgxjMqcZTIF6IXCzyrBTYFeOMYZ//A8s63PjAGLz+ACasDZxn4WHCDf8JD8SXm6y9gZz0lG6sYaDAwhFnr6CI2iN52PfGmvxN/uycFL/yHVYCvFBpR6doU8PAfyCIDIYtkpk2kJCt4CXfAz168fIOVyEX8F/iH6QqyCRGEA2Kcpm/vpqxATvb4EpX5D24Cw0LS2i5bpNsyQCAQnIEP+vBxoEyIUhlV4ye0VFZgX3FjXsb6SjdUAZYK0PjX41GtIVMi+0u08PCGMoJyJ1pwaZlJvmRrGhsD7KZZ0E4AL//zjFlAbsQkUpNRBw60nxdk2TJ6wFx8zsFVL/YPZYfSX3OkE2MOYMg4+AwrxeFcHCyAdljm7vs8hKucaTM7QsPw3QSpnxp69Z6aAlWA8AUTgRjEsAmFQT26ADVQR5C6mmXvz8rupKzL7AaNaMNwArNzSpi3wzzzjOO4TlnuOy+Ks/pvvqmu/j2TdFgozZoMM8yFBGE3bJquZFvGRmhTQAJULmcLDnBzo89ec9eZYJ+iFCTTMiHVMGGQyJyM9GEDLp7IK4xMRqfsQQQOHpQCxSavMH7016sMjVzSTjknPNbuRlvOGIRyI5uiNQkDCyI+wUaUDQ2tMmtLYG5aJeG0D54qJpJYS3RoRU1sZIL7bYHDii38sUpQwiybTs19fZQY/Fk/4rITEjZZXcXy7oIz6CzwKWls3UvKVCT5UEqcBRSCk59uLW8lsHYwPEOUWP1MXhC1v9bU69+1f/ziuRFyh36L7uXhxQJ/5BZIRf3HScRGVqp0t5VxR3wi2PEOjwPRhhF8J8Y7aCN1GLp27w+k3U/sYtArOXSv4z7517f57bvsWHZHpn/N7vi+hE3bax119Pd4yl0Wx+uzG3ePT6CrPf7He0UL+HEp2pOWp+tzvOZB+TjNt4Q8WWfhIZ/MQ7U2yvmw6Kaax6xcatn+WijPxPIwY+mGV+KWqhbYZJkVcYAu8NmteKK7koqHtgAcwZV4ic1F2sIJFdVyKfARVoNUAq45/Zr+b6APyD760ZEAbpEBN4ANAAgwBIgxOpxoVAhoxGnMYJc6QSG0jBkLIYF4ETE6XOEiDhO64A0I87Kbl1OPWjbkj+dAZtgZhCSJWJo93Rs2MpLYxQCI0SUqj5dL9M4yY0XvdOGKRHk3/fGTk3SBFYAOhF6fMC2ezR6ZgiMcDDrjwN1bglG4uHo9caESwR27APmD7fjzvKq2/sVy+fX16tOq+Xo+/31RfZ1z1m/3ZpL9mnW0q+K/y6rT5vzv2gmHGX/DfZn/rmqXeb6MZhD4bkrGTDh9LHKJNQ+KNTWoy/pdJLL2AHPgxZ9aJc0k4+r90gNkeBAHZrLgwofJR9GmI4nRtLJVUDBxpGunV5P5Vf66yv68zd919S8ns9+13S+68u8n3Vd1e1E1rzjW4LqZXa3OrldfXrz6H13zUDICM68berUpKuYUC6yRSYsspEVWuD1d0g18z1wrbMZpYqGYmkU+cJvSslJfobV3wDTnPLsqgNOFU1c55YCmmieqYS/zhzTaWDSaE9hkF8luAd9cEHFoNGUTN1wE27YAo0MeXY1IHaHky6Rz9AwOF0js6jNVLljkHfzwNkeQhiJ5tWKrTSqOuRCWZTzHU5YtYRxVEG0bQ/VJRU7bqwyynMhEacYyeMCdxgMp0QF7ili1IqPhS+m0NMZf1CDrCk0LkulcsTByJAFB7ZcTDrnGzjTvGL6iJrk5FiddRPNe699ecORbr9q6tNntdTsOufENor1v3RT9NvKAlTVn/Nr9juzlP85gX8ht3VyPsn6/j+xPxW9ow6H7udL3OXgOdYuXuGWYa+ge0nwOt+/zh1xD3Q6XariSGupNKvvD+70CN7E2lD0C31TDdcBt3//ap/9VHjtiDCrhHYJ43OE34psU2k+9j+/D/B7Kd2jXjaSHMtlEfHG8WOBHsMCd8pkeh/dH65CYpBcMTAJnAJiEwUCEacf61IBBoH+IxArgBGa/cDgVUxM82okex7ZmI32mhMSqXPoc3e6GPnW6Y9k2nR0j22Y+c2JGv8RWYNQrnGB0wiuCFjB/RUelHZmiofABsDiJWYAVffXprdjHEYGBWQL7B1NBma/N6PIlFYGZ8PJlDY9pW6/Y9NO3ABcTmEhJCIML72Q9hUpipjRDWi2Ip5fx1crQMEW40LSYzjiGliRPmhM65rvsxj5igZlxwWZJZT9OEV39kqP/CSVdkMAz7QlmFgklV/nv/tPqpnn7/ay7WMx+n918nE3fZt0VwzJl+8XJ6fen7fm0ejcpq9WSCeBnb6/my5PZTYnVS4YCAJjMBXHTIQE0ZjEV/X/c4fIWLm5KjzTqx0WY2qOSMf3Fyxvp5Mk2nhBdWM6yBZ4YbKElRRsA0Hp9nXc/TL/9p6w8bz5dftu8OvvYrV6XJ78nvK7zZd1cTVb/8LF+33ycNJcXn1b/OC2rOe1FhorMERsXiqUfGmEaEinKV2joFupEGslk0bKagVVNGo0CGn74oKSNOqMEQx+jsJC9JtFiBiNnyVNco5hFiuFiqy4EWyjhQQc6hNotSOUYl/GDP08E82TGE6z+wHTLWjQUfLRtoJX5gwQVyaGmXS1XSQ3H0/CVo8zo5scJxCdUwSqLh9xMXDAI+tSiCbFQMEjmfxQxR9LcPHzDREaVtUxoFZl5qh8z1vAOF40ulMbyjA+QcGzI5DFjxR3NHnc9OuLjxL3EerHAH6EFrPhR/dH9QI1JZHvTtx0rnjYc90bY9bSm86L+2pB+fvAu0YjPbn9/av+xBiC9QEbiPcr7URzVhw/VEW36Y2gepXcfKWCWX4UjrzF9+GZx8VZ/2MUnguto6XuYPyHuWFr2SHmo19HpSiUzsT9Gn2NojlF2yOeYXNtfQsjuwJhjlQD/VCLGCFQVCrAINxGG0CMhguRVXE3YXj18pOhJeBYKiSeIQVyAiOCXDtkCcAXyZqtKARSdh+6FH53ycAfX2knJtIZhsVE5PJlLZK85SIZ57uIW+jfp3URWwL5gA3RbQxb8I23qtk6CeIUYTupwho/hQRPACagHWqVH2e35xUhQgbro5nDbScFRzB3BAAB5fCJVjgcEAJIcH3UNB3xNltM8mJ4fs5KUwqSdS+ZrE6IKAdxMiBdPMhDGKdqb3knD4oJkMx3FeTFolS/z9jzrVvXVrz7coPOXHCE8u3zDkWPl5AvsMZtcl8yRr+acHHxy/dd1wTEBlQL5pae24PBm4N2byt1APzkW4rJO8iFSgQpgd0Y2NiqstTBJYc+Ar4SHhmosTlZVTgwgYdlF8HI2jLNr/EMEK1PpbI7zAdgDqThZdsW311/9+4oJOovzZfblgjZJXc5+UUwWVXN9w8KG6cmHSfOpJZs/snyhKmjb/E1MylpZkLQMowInYSSVjfebMtducoY+aYwf+aK/ix5ou1pQLYaWUlxOGaJv3jznUDbI8ENzyHCnEmUDDE89IKOYpas6lzr/RChnAGvU8pIIjnsAnhk+so34yTqjeRKYDv4hVnPWZ4pVHjlMmaXFLNZOdYFYyKHkSdJxlgL8b3SqJYl4zUkF5KDFXlPb2KHMyS7EQWYyVDxMgIOAGJHh9AD3ACWfXYRjabZwRvXWgPmlp5Kx0oB4ekdxtYYkDgzZYS4qI/6MGpEVWsbAdNNxexF03LXmMUY9Fn64/3j4Lh3j/GD/VGcj2mfhP6ZQZK5v1+e4DtttKGGYxqF7SHOMe0xiz/NZUzfUJwpu7zF0D2k+n/t4FHdAN2pXKv9jteB4/fdwiLorhyTmXl7SM9K6iXZvhBECVNlcm+RtfF4ce7LqxShPtkAqtsOy92SWP0kGkcKEzPbqt6m+OA5bw1BBTkAEqSMGkyPYBYg1l2vuzjcOEB/9goGR6KgGk4GvOLEInMFy1LqclkxMB1WIOsTpa/QgrpEX0jYsFUx0ICpNB/7Bx05TEI8ILhHCwTZD6LSO2TMwbqgu2kuQDoCqRIB7gEWF91KBSoECQ6ZtCSbPp7njJgE0lbpF3fwQZEVqEiIiEjHgQXQRP24V878dqHajajBbRaYwMiQZMORFU0BfY4Y2Rt9cPW8xHGdI0QNenxDudkBL9sK8ZpHFFATPsEJWzJ3djkRmGK3o2W8YMYgFDqsa0O88mFV91tQrph+5DZH7/5Akp0Kx8WaAfxtIWgktkgrJigN1TCRXXxAkTFcfIdIW4WEOkg681c5QgiUd9QjbMbnEBkk5A+gXn5qr0/mMXUjZTwrODPEwvQRUWtflSVkuu+WCZuPN1/Mp034qSArmgLWez7C2PwJDq16bpHRogQU0aayxtrTpaZmjLIXuZqlwCrkYdJ3sIBP6E9l8Q1NBuVFjKpqRjYjlIt34ooGx1YDGiTnO1bJAHia4o4qsWSgudCFAwyiBf1pIzE25VrAtFPjEZbmy5WzDM+lgFQjefYYojkDLJL8+yBu2NndV3+dIi3o5gkSz1DpI+YGj6wconYqzgNL8QJYlwUjElCu/VCKXxpgLcIRSoTynv6CQ6tAluzsXXkdEvUNy5/EOy5fHFwv8hCywp9A/WLtU4If3VG/GeB+oIGNR1OlAtKHKksUuQEfSD+PuujdtymfhNtbK3JU75lN+txOSjL3jPeqx05Y9rNVoaLxk/ayQNYfybVSRFPDIuId7GnbSeI8SEfz0tBwj5TANn64jr03JPJJ+lMwP85NycJTz4YCRMpP232AsjpI1WrTv1MZEijgcgSkEKqxsFZKrhGUMhCw8pYva55btZQi6EYjQixl9k8CjjKOdOKNqegkliCP8A3nYJBB+QB0c5QfgEX7wDzDt/IfIO7AiyCSQUqKBTFgjOTekw5v9JHvVBIFOUGZOMyLdEQU+qiYXUG8qyXhyITIJwfOcGTux1gk+dCRTGWOgQa2gEwrpQDPwErDZ1BgbXyQD0AxWZDB1a8y+11nUhHfzyoQV2CGyKZiGDsNbClIxJlyxrWU3YVfNBdgduNd2Zy7wLZclU7CXK+AmYJchAmZg0U09q09WMZ+lnHdNVebTFaCv9UDcmbNnug+cz6A1bRclq9pPDDq2XRMdx6G+2ks1Yf8ZQtgfxufeL35C/5TKT4QQ26TY7EHpWqFMYg/jY5UsDo7oqjPErOrXdXbSsgQ5Z8CBOWLsvzlnn6CaLYPqbl62y0k9Z9FHU00Xv2eqWJHNERhQm4XF5KYZl/TBoa3VS03CzYMlhkk0hphfhK13OiJeZB8pNZpMIyaRIlFq7xW/pKkvSxATMbQA4BcXwcN8Zj2MJQG7Cbe9JtMbWmm0w5I+xFJVgbbRQ/mwN4LkyD/iwj8aGxbN0EOtdBTTOHDDQh96cePU7X42lKMEoaHSG86WdjEAzSQQvi0K65BsbJdQiNVTE5k0yy012ALJM4FxyY1UyCz19MmcOMSgatrCsK7hJMvIXpgT16GWtWpbv/0eIz/cem7RJTtvAjXX5mHLkXJVPba8jxqrH8YY+9qO+Q/jPtRtlSdO1K+Hxt1DP+Rjub2H81iKxvz3SDzaa5M7B2Lc8z0dpm6HyzH8dyI92OOwZZIOial1at+1q+cY5b7Yt357Nbkjc/Mdv432OFeqg4l7uO/u/zNky6mVX/GcRgBSzGHwce7HxjuO+/NSoesdwz8v/58VtxdjftbsfmC9SuWa+554d8p8/ygUCMQIUmApZzqjyiT54tOPG9ygAYXQjys4EOV7Txf7ljBpmGCmH1ga6G8UFYENPQmY+HjIZK1V4CV73J0XATQhVMDBt4+Q/nWrfJk42SYSs0ZPPHklLB6fzIgqnLNzmqD0hQ5hBiGYzzWTHyCO3U70CIBFCwOETCzTR1Q4pMj44GHaUVqkJHgixZEWRcR/brKXGXGTn6olz6FD380VogJ9sWjZOS3MEnEGO+2Zio01kVSv6D3X3qpN+0YYrxwWvrIIlgQyeILJKjaByU7pR3Z9Btac0JhQYbt12zLMBhIkASSG2JG80LJXJfw2ag0cpk426SfSY76EnTOnwxCiHvbEs0XR1KKAccj+Il9Fs4gtORkRIEUtp/G6dDbytenY7bRmulfWFE31uq1WzFgB8jqNR2HrVqJyvdbAkGLQa28jAT0CUSd9xLiEhspxtxxERDmuOYRTluisKMkho4AFjQzM/EihDIHLhuhHwXc8JkmhMOAfLPihfPcMcShO0TSDEn/vMbd+TWTMRJNc8CKvORaAWKEyDoF7nA2RWnCxhCZpqgkNsz6gOSysZmE3BDnsI4FrGmySRI6bIhMQP1ZBR8kipsHwQQGoEcqiEQwrT8iDv82C9aNRhpdxgnroOe6+G32c8iXkxQI/MwtY6eJKNU/nxiv8N7UwnvbcDlWvbVZ7IievngUNgLEIyf+QqFHm9wT4nVpfI+3Fw63M3XbVXZ9nUX5Ht8NaHQ7ltfu5rrBntOce3I/yuF6N9KVKyfHb5+fjMYm7m2vbPIahQ/c21Y/41OMjJX5efTbGHKubkei0/8aGdmOIfmfutxuP3iH40MktXAKB+PozSx400AMjCdifJAEOwvMrEYd4jq1UQNvCYkFLeeW4gbBMPuKPQNWT9rXoOX+vpIAewqMASfasCk7o0GZqC7OWYwcC6bzEt6gF8/aVIIp+2dA0KS0npAtsUFX5RKHHFhns9xJ7vNDNiTczTwgyqTG/GSp0TtOdmbdvuuzlZOYMp0tN6HmXI8Lln3s2L22hvk0CQHdxJh3r54SiT1hadSzsxgrV8otUA3j20n9zJTruEdVaQxph2rB1j4MA9avYv+iEVQXTxWp5zbyqS7ZnKcqPXXuWF9eTZr7Mq49NOS+vAXkNmzVNZlfdD6qSn4rhPDaAB+A5/+BPTpEgPGOcRG1C9FqjjEPfTOruZSOCK1k7JSMgKqxgQuc/KJSe8iV90uZmfQrsFbyz/JRtZNsFU9EvOk7jaststmKZQztvsquG+U35DdsVLdsVLYPJjNMPrvNsgRVoUpCGVG4iu5JKZCKz0s0U8jtsSaKYAKPpbOqgv4SRUjWOBEq3duvj1TWvuWfFx6Cn2Fpo+AFAk38YS4hvtjsIQyQ14b/Ws8ikWTJubKu5BOIqac5HKxR9ovaogGpKRMmVpHmdNYsuf2eQpVR567hunwQZzGhdqA4RXD8DA6QznZ82Nn5YhpEnpnhBKrU4Ht5Sq5qSzBuUMCGpKtisQnmjYxw5G4SWjO+poNpEGijJH2SUlc5Gs3awsJ3tolw6oxpj19heIv3bZjAyIAfTGL/pJ9zp1ttt7aMma/eDfse+tmP+D2J+h9jiN36lb0EKf7D0g5wP83ywrPEkbELInc967fL/HF/Sw5bZ1WE3ycfQ7Mba9blHEyvm1l6acEjVgfvQMkN3otmTUUOv4DJWZ9WTZXHW2XtGAO6pm0i8h0JRf9AL/TZ2+anr+gc11Ivw57DAH7xGbAp7n5qkUPiuiz8PQAH7LRMNJ9d6kC1XwkiincBBoHvRdDwCElJNAmQIa/zC49N7BtThQWQR4EPsIY+AGnoSwU7vCI1oYHAAT4CU2COFQH0CvQLMCBKx8BMsYReeYrQQwYcTZl5g02hZAICSR9JCztGogFclfg2OTF4iGFmmJxx429fLBedIpEgrQUGF2+WbwFPwF+4pei3LB8h6XVLYJjD5cg+7SKk7rGAroKousUqTLS+y8nfdTTXhsNyLU3YsypZszFRW13OQB5vqZzc37KkD/Ke5wJlt0zNne3j272SuwvynJUMCcfMHhlYpc5jf/n+SK4pMgRsVfdx7hXmwuvtCojb/SSa5yAAK3FHM/04wn5TLuuqqorqZ5N831yX7b7bLpr7G7EV2yjpmUHXlMEZxxXQm9myd2RYI2KvZQyU80AzDAKJDm3hQWZ49dwDZ7lFjhiSC9IN0fSN/dKVn78mlYxDHOV6RdUQAXkcDIGUdRM6owsqUGTMoBPPTGwyDC8OTbEBzsjbhkqQfYsW/WHcrKsffZJgCKBQcj/pGKgzAQVmzUZ0iy0FiBwXw7B8TG1WRl4winqQU0NRqITNsWFOtJVJbizO0NtrlmaIa3VaCOy8x+8x8rKC17NsYIACfoI4fI8YVaq0f7v+F/wNj3M/zheLFAn9aFjhQSwg6cB0OPRDxNqiXfWAE4Aghj6zj8T66VWWfK72W+xfuDsFuu2rXx0hJv0dquSP1Po87rbT7yJ8vPOy53wL3CuFDxXVEjoxxGsujMfqh/2Gdh6FD95DD0P257T8sk2P6fJaylpjeVx83om935sY6G9+hpfDFXyjET9ucci5VIMjAEuILNpQkHDggTkv7/QNHWAAMbmKRKoiBC5Ccyg2YKWasEJHVkx8EH04Lop/9NUp3+QdQELKEVsGUflAe2W3G6UPFJWICJtHreg55N73gluA+4I+odB3r7/8wgrqrJQ9yLi5hwhJYkbBeKhZLFSjbAjXn2yRKgligSd+n6nuBo9ixRRir1wJ2AjEnucge3qClNv9k7JT70WkNt74syCAqQMg1dUmDdXh6jLvSoDKCMHTJgQo1J/xyGu5qflnT/esEnqI7Z/LMtObkq/w8PyV/qhq7MwGHLSTFbawNmOaLDqNlkORVk0/B50zRsR7DfjlhBENHf4WdktvsDPv1KVEdbcuVfiINvYdqBsKn9x27Khrqji2A7I+nSMwYwGkm7F7U1d1ZNZl+aK4uaNMwP6mkzTBjQYBqZDVDAs4c4tDggnODP7rvPKtKBN/RBZ67JoE1J6oC0Fdxc0cL8wc81fKQRKe43mbJ4JKK4NQqtDCsry7/aKauTZ+8Q4rJUGgIoUkQorynMtejbkp0a8FnZS2wetP8DelO8gmGYUFzPY2NzVA2xpGSIsjHiEJ5S1LSlLEQLctZEDIgqr350uCNKmF0LGNjhAOD65trmnYoZrlMaYGaqNDDz5XKXDSbUUgP/dx+lVIa66GJmRIeoiIPCapfKxie7crj5DxH74psiWakCkRW31oy9Fyz2f1N+wEi+TZGShteI9ct5QjBT84b63NtjLmt39i3YJtq8DTkNnQPSMacY9+4Mf8xPk/xf6isIf3wG5p0eLD1nqL60XGHOh8d6cGEByoCQUPLDN1jYrbG4lLtOyAALtI4AnDnnTrG/8X/xQI/bwuk6jT+YfvDWueuXjvaQrD1QlhXfEYA4nyn6DEMZJLw1MTzc9trJgiJLxOUoZue/lheGuVMqBGjAUwqSH2K0MTGJoTbRBAAiV5idS0/VUVfo22AeOf4+pEnNOB0TzZyo33BVLESquhNJKc3pxeUmAivhCxxpdQkdOhRrwZK0bPlBzRDMD2aMImUQybCUXQA0ICBgC3xkwrroPfV+d/Q2dWd9EicjdhLSOwUlb5o8S7lluT3fqELNx8JMBUmpma2Rs6pXmwv0y3p/2fuh6sBpiWwGoWAgSX4epIviuyEe1kVvKXb4sQdgOZtu6y706rKardgcksmzoXV6kBQDnMwDZF5ylYZ0qHTy8f1g8kgOevLoLiSQ6uFzVMmQCoaVjPmxOh29rnnGThHpavz6yXd/3k752jbdnXdVidY0DUKM5YvVzknhrFm/JTpOFn2CtaYmhYXeq0VQA9HfkSioaSamDOQcA/kiw892b3CoSS3oJE4PNCI3DF38VgrDlEfjEOyIA0KgvCKYBLk5DRUiJUtOPVx+yjn5QQEhzGxjM8vpQi8LuxGkp4h1dzH9jZZncVEgALC0kGGujLUh4a1s4wElBbSECfGD3qshS9EPFEqbSFo5hCidzSNI1qoAQ+DtZ+M46BuHfxXM4zvuBoUaq58HnyEnKLC3B+KYVweBw7VbZtB8nSZlrX7iF/I00WkjXvtt/l9CMdNpBfHiwVeLHCcBe6tYBIcGAEYkdJ8YwD7/XOl2n2vIEnHrpEWsC/37WusTTbmvx37x3hKrbQfX58nSRzp1TjeXo+TflSskbIxptsxreRhXMfx+bIdbYHjKYdSjnfv0WenFgy5HQxcV85hhDtu6q1p74rvu+wtwDEerXiZe8VgHNE5O4iU9ECDMez8p/efKeBCH3oY6f0VvBDCn7ECzYc7eWXMj3fyDXjQPk5BvngOkTiQy97ntg/wgD1IpS0/MgOD2eH0y9LtagDbxwtdBD3iFuFtIBuBTECahHfpz5SzXFU7psEwdyW2RURF+jhByGiG5u6yifZiVECQEYllJ3f8coOxGgi0xHOEL73HnvrGCAMpx3gEoEly85NcGwpD0hXvM5OtViwBYOFvzioIesJRi1k+7pnJwbbt6pJd4U/z7KwpFqyfVVuM0BTslH96Nc3eNKvspv1BSF1wlADY2jk5pEdJ9KZDiMuWC8olayQd0l2tuSLJOiXmIe4REoG68I2uau1tkl1lwRgF0/1j9teUVb75FT39jOE0nFTA9KTsgtbi6+kcmzPLfzopZixRyOtlSxvHZeS52n5qy+tJ9yvYaTykdIvIsqQDIwB4x4ABYYq12OGjri2jQzgZHTKeCkIiDXoGJ4kEwYmhxEGopxRBFJ6kyBBpUSDKggNY/qOQUyZpkEBjbunmx4IXscJk5IWbULEeg9B0pUDPXTauagumZWHkUApiAjUgvom71DF2AH1i5u4/1AO293STfvZ5pXkVZRNWkPifGPwE66hVYHzbG7DGNzirjGInJ5bg7lO0ammbsYevpw1w8oDkNBhph9q2ZONWSriV2oj4GSxFLzA93XvfIqdh+rUxdt/Jd978kSQp7/jrNXL1lG8j2DfY578OSkn6JCV207tHuSG3oTuRkgFcu/7hPcZ/zD8iPfPtobKG9Bb57ev4fN+O95gnaw41I2wbFSoq7D5OQ533hT/e7/j0Jg37c7oCbx+WujXyD+lWhdyJGi+RNALwsHq+w+keQbv0Lz4vFjjSAofL8JFMxsj6KjAW/BPx33whd/UxAbu++iS78QYZvnCFJBHCZ77nKkKJTWmYd4FX/BFXcMxqRUA5UNPOf79HzJDmJGDgRwk0YaIGi1kBLlAnFB2yAtJIDwhRNcEZ/+DGg13rziKPZ/0iLgrQm+psCzC/Ha9ASrQSeMoBDZkZoRi44i+1OIULB3/8wJW2h+qHH3ebIqglegbZ2CkLKPYfMqoWJBpwHzakLvpzhYFE7j8NgXqV0GM3xfYWQxpaxRXqaWsIvUwZP/4fUMWTt9AO1W5w5C37ZlZMjnFH/7BSvVqVk5L5PFldMSJT0i1b34DSsPMkuymK86sqrwD/VXtTn3TnpdNtwKE0w2z53JghDuOoqcJCjY2m/fPmZw0n1VirqPr6h4eeg16a15v/TKdjPQqlWVeiGN3LBQuUWTddsJNkcInmQs1RYS54daIJGData11W2a84y3hywuCBPe5EV7jSQJ8SheSQHnmsvncuszmUVqOkZ5SE4DJIQx8tce/VDz+oLVHSAwQE+skEZLmtMwogakcbhJIYqaa3notBlrUMIDTJ74XLlMJBdH/km0YAXLGgPeAusdRRTMKeUWR8XDtICpJB8vb3Gwlh/NHscmTKU5PdylMOKowkbgTAmFj6WZs0hEESJB7cHTlROJdBBPIvqgPFh4rGwA4rZIIhtTNYQRgcZPLYqxf52Ogv8V4s8Jks8PMpmWP1N1kg1fFDIwAp/o69Ut//ndzpud3xPeYxPrnHEI61ycb8E0/fyb76jpHwPDQ/vj5DiXvalwd7FJ6e5qH047kdFYvx7zXHPelaBx36PZz2Af9DTO4Le2gZG6NPPRN3pY1XrU2pvlO6bx/92u9cePEXsFf7AgnYv9GjSa0mgRAAd2F5BUSvP2YUDGWTM2Z+5+U1hmsn7JiOFz2awBbQCXgJ3OQeoBAHzgiEAlvpvDmbwg7O6G2PE5DC31DQj42EHqnZqx84LaJFAsQ2QkuRiQiGm2UDD2KB5plJk3ZsCcwWUCe6NokX224C5vqJPcSlwUAv7YqmRtGeFvnM9oBXNAJ6HcJ04lT82TkHfUgOmEyQbZJCjgoAsPpL7UKlIOg9kw934OESbbqW5RY0g1Yg3nzC8V8gPs73yuaoAZhrWWgxnTVLJsWzT9DXp2f/8rev8tnqqvn0/c1kmp0V7acPq+LT2bdts4BD00xZMty0BYsJNDr7MtnEwtZfqTgnBK+vSDY3TRamS67eGb5Jd60bZLARU1oi+HHxtC1DZsWHJVe10LMA586y2UkxX7QXdb1qOVEOeF9Nvz6ZnnTLSbmq2vOb9kOef8Gyitns48nJu/ft3zDmwaFvpJTmjlODnJqFJmHA1NOfszxawcmmJoKVGOq1ToDU8SgZrkSZfEL9njLF6BNuWrgCKfOLxfpsDD9XpNDgtffdXY+wqKbQApo2pEX04iOz5xWIbzBwFEJGtGEo1qddt6DUhaLRklAkV1CnJCQPW27UGnv9kYs6OBBA/jG8Q4Ld3dPLRIXKKhFp0za2FpjBb8d+EFkMUTiGg9CLf/mVBY0cs1TEXN/2DUJCKJ74sAp/yjBO117FTr9yiPQip0+arI+/Bvru6ftPfMbe/GP+u9KPpxzGfeQXZMhixP04fUaYmYl/pNfjLHy89fqCngrZwEbHyx28TvoXxoDNUc7jZe2ye2jcpO3x9rkr0dfFXT+f4xWiQ4P6Xhihk+TlerHAiwU+gwU2lfAz8IblnYq/Jc0w4Eqgn3indlN6nAUwvAkC8RAuDuh7NOmFdHUmGIUFgzWLUidX2RScxHx9MKq99kSNiTUy4BLFKKJHxvICtySw5a8wzFhxESTWsPtdsb1n6BEe8RYUOxGS8BuK2H9vryXwOXqSbc9EohJdxE6ciOeuLGiPTNGd3b/MwHHGERgNXtEfLLE4L7AtvkkRwJnaMVcCYORySZsukTjkc3HrFfbp9kokhoXW0uDAwpGAmNTRzdqKGSNu3tjWYOmi7uqyIV0rkCcNFGZmZN01sH5xdj5dLE67119/Uy0mX5zMrq7qv7pZ/d3/51uWEU9m87KuK6LZpHF1AVbhVAdCVB25/A/RJq9XK2mzCcOR3IOfjUfo7xOxyTF5anZXRgMumeEDAG26S/YALcrpHPCPger2V/Pif/HLLxf1fDX51Navs8WvOtYndMu317++mP3zu1V+0VYkDZ2YegPeDdDDo661kgNt8U3XrV+fz3qTbuMNrzWPgX948Ry/8EnGiTt7T+FBeSAQYzLXiRTa4LFVqtmgsrim5pA2oLCB0C3BUWpTyPrBJg3thySbH2JHhqAgwk1CqGFMlcFiUJB9DIJZKc1H1LAtYa2hzKGJF4pskmrdkVNwNJBipESFJp11KgciFwqHMO5wxCnbsDk1F21tCVPo0shb36JQcRmnK2INPdYBe3/hPYi7l+TF88UCD7dAKlWW+5frsRYYWs8vL91HMaf/7vwh+A9JjxA31r5Jr8L4jh/B5blJjpKbkEogkt1U7Po8Rcdj9EkS0+4Kx9AP9dnTXuyR1pDqYe6hBYbuw1yOpzzMJ4XuSdcx0R6Y9sfpvJtHh/lI/8DKJf1DPqrb7DvPiACk/xAmExQYHgDE+Ql0/zMZIImItPTgAyLhMXKFKAAkdp0JUMLcYjxW+WQuoAjwGVgZpoFx4YwQgsBVds+LXZQWMnw2XJ/gxjO/pg6/cPgjvRShcrqv8Y8YyTTAyakjE+ZktxXjGFLxP8VUaRA+F521YCAWyCbcoxD5utNRAlKbXk90NVoIVZh7riNF4wD4YnOV+gsFlBcaMGmXMFUS7N7zLMO8MBAXRElzf1FrtvYiBXH68oS9MjEj+2Yyw4Se46LLWXddsmt+3ZWnk2KRn02qatWs5rMLDtmazP/96mbRlqtZ+908P70RGf75pLvOMnbgdO690t3SXbsn0eqZDOKcddzu79TrFWnQ8/aKEM5hgIRd/yWkTWS+mIlAfWZPlTkbANGccsRB3MiIzpvlZPFu9Xa+Iqji0N+suVl9Ksvi/8U0p/riv8Z4V93fczRwO3s3Lz7mk99wglxGGyfnzGDS4BJtp8K7VpvG1yVC96h2q+TaiqEsp0ZIPBjruCUMgqQ99o+TAcidj3CPkjZpqnPLW/4RiXb/owHDRW6qw9x7kneDDYtswYz8li5/DZrKp0gdmsjbKEs8RgGWghS1jGwsSU/SpC+PUWQTE/1NYqoYDOOw+PuVGnZqEsUKQWltbkGTwGECExmxIlGOOdgC44di4XSjzoO9KEbsAaUyqMNfaEm6+LVGWW1U0QKeYTFmo1kmFzktMkpPMaURkuSELIj85QqZyXnk/ZbNkRGejWzs3Xv8F2SMw7Op+Idi5OstvfS2NQj/R54jNOB0vIUHkR7gjEq3h34o93Pn3VDWHlXCa0yHY+KO8bzjby2+43XkY6rSKbJ35v7yOlhX9COZvJC9WODFAj+qBZ5YQ40OIBD3xNc/EHR46Qk+ZiQwiUiUCSkEEorJM8A8YEiPQoCSwmJOD4BYtMGUIWAUmA4K+4UDfaS+zDQ+gAyBDbg35jvgDqB/+xYjXmgY7YfN+wg+/WWo4IVfE4B6ToCnL1bG7lXqNywCva8vhXokFieeMsohW2Y74KU/iIf/vR0kS8KQCKHP/I9uVVjTsQ6gJr3BWMJw2X+t1XgIRdf+QdX7pjDJ+2gYSEjNJPlVt2qZ099MGzgXK7AygJrGWNPcZJfl4nzBTJr58uT81AOXq2b1qbquPs1PsODr7mZZ37hWNC9rdhPNWOQM3szoQ27y7szkrT+WKoi1zPbUqErKpYT06bj1WqckEqTScmLwBPuybIHxH7Cq22LSXYwnGV2v2Mt0ctVm1RmbybCV0TwHzdbTy2X39ixjVlN5snjd5FXezablSTv7l2+Kd9WKSedRDjEfAixLlCIzJowWcpPsZNfe7U+6IqsiXXdTsIkbhJErKS0pIGzgLUWmoHLRro3iJ7WFeM3Drnn9Aj3zG9y0reWN+WbRbkktARPCn4Hsr88Gr5qdSzk2oA1fp0WmvYgY+KIBxHp3173YmI25QNg8ossiFEQr40TUiMuAmxsyEYFTpWFPRBpUMYEnCUvKkPOuV8baMOQ/km0TWEkthwihLtNWYSlHDPKFkkm5jQIqccSVYh1B+ELyYoEXC/zBLDCsp9ZxNvh4u3417VEK8mPfBHvXBsDSl9Af7hprjW1p5Euxv3Zbabs+a9rP9ftQiWNpHPN/qN5DfYbuw3yOpxzjM9R/6B6jf4r/U/jvxn162rfSkmrQsRVxHRX6VH3Z1OatnrIJT6skvYZ2b4Me7E0s6PA0UKzQU4nsgSRiI+GCu0Byj25xNw2nx3TlygE4ADs5tpaYl2Dq+YwNYGgP9C+OhH/E7gFBmZiSUJIoBKiiCC54vPFefAqP5Bkh/S18AlUBO0Nz4I4d8zZKyu/okp9Ur4MRN3j0ySBNHT3EbDMPWjbtJAo/NjKKHnJglaQhQ72SbjwrTj1R0MSz3Bmz0O9LGj4YFtjJPlfTxbNm5F/q+9eDK7TQkfgjp3mlMPuqwW4cj7VqV1/aIposhfIcj9sui8nZSTY9Z7p8syiY27M8yVdX1U09O/mhpF/++r+YsWxgdv31yer1kq5spt3XxaykG5hEkaS8Pc04CsDlEPSsR3oiKdzYXEilQp24p9SpoFevZKQmHsMskT8gRXxIO/viN/TZs7pX8xGfYQqU5vyEJbPDVs1Jlq+arFpyOMGb2fzNafHdjAlJr/6Ots0pq5lneb34/dfzt2cfv3SIo1VnVqCGeSkwFDSVSDcE4/C2VoygWy2Hbk9p2ISk9OkxuHoWnAoMx8hjE6Qoy1u4I7OUxXOkTX8Ox7ASpH56vAX7dMbza2EIDtHwklX8S1ZkjIUCZp2RnX4hwjrAFfIZSSO4ddtWPKJlrZJ4xkga3jxGv350/jvNLqbMhZoRyfEXDkX2hLtQleoQYxQhg6JG5hPFdm6YMWkWJjbfkZQ1X06owR1ZxFZOHxnhoqhHblK/VGZ4Bdehx657SJJE3GWyG+ez+Dz93fsUDrvfgs+SyEcxHevjH/N/lJA+0nPZIT5H8dLep81zSdnH+5Dfrtyhz275sX+KevjAGjHkeUib+8Kar6ToTwVO9TRp4p0XxzNdwzfAM7F8YfNigRcL9ADieENQE/tXjXUyOXWlJ19GugQB4GRBARPOgSySAkSBHBErvXrZ8oVDAID+oG3gTKANlw/YeWlU+7ONxu46jZNtoGJekEGKSPeQBnPJ+RFq+JO84ylok1aBTnxOj+FKt9AXSA7mYfsWNAH9C34cCrjtnpdWGcjihUuoKN9ti4Ifnc02BEgj6bEfVCWCC4yStr0wn9VNzzQvAiMQlvQVGKakmCKvdWoiQp8oddWYIWYoAATJyuOG6d056385RbdjVUVJR3DbXBb5SZlVVdNdd9+5WqE9z11owdrrCb3oGLq7Ounys6yZluy0aWqYScP2nwVB/Adyp+aJ3dy2XpTPxS/P6c5jr2EE9bcIltzWE9pCxE3ACpTEfsQpyoKMlt5BB+RkJXvEdssYIiFREDZk/7R8v5idc+BvxkkRjk+gF7ueNvXlV4zHtFfdZLbIizQlySFoRQb/tbYK94oMjN94NAX9060rhfT3lD6Z3blSeqNYplIY4fGs9LATPEldgH7TDAUJjHzGGRrKHiqMQSsh7NBrnNRJVmPiGYsKjLiOBlEUtLC6TehgGgQW02hy+AR7F4CEIwlMTu+2nxEa+hCJhTkN52pUzH3jbDtm76AfsD/L7ck3DcRhaTUtS2u5T3IPSX371fEv5qGtOuaPhUija2Gp71xGveO1/3FDuIfJ/hgvvi8W+FlYYH/N+tGTPqyYvnPYTu5rldizBqDXbVOn79H1udor94jZCe5frcOEDWh2W2ODwD3OP1Qq9qgSXodTl2KNpbH399stFPiju4bpGro/R0Kewv8pcY9KSyrbx32CYZhqbF8hUgGKD7j+gA+AGuA1dRy6PYjzhum9TShVDCDmE6YEI7skjU2XI0iCbUBBbMSiARDbI4K93eb9PTg2b5kq3ayWS3qu7dUMTVQ6/ieQBX4RvZjqFMLdx6z82Ktt0PAysH9m43tdrDxm7g2YnpEHdkKBAbv0BJokcJ3cTTR6pUFVsd88omODUaevCNBQiS2ATC3U4UMyo9MUE7k8laYPDqBeAkaCL2eIEBvjEEIfNpzpqYXbFm5y0MSglNJoLRCefwojkAUIq9DfNcmhsROj0I2dfyaLDBjPqgDmBU1+UbVfLtktZ37WNWf04bBjS1YXbfa7VXt1U82YhJWVp+wWWsTUpnzypo1p67GwFkPQuc5mQmJH0ofCcec5/ZKAtWENJRHeNGfst0OcCE4lQazvgmsBqJ8NT8nqXTy6YpktfWhG4olN6+7Lpv41y0s5tngyvW66xaq5muev29Nvu2JZ5ic52Qc2ZVCBsldwenHKg6SE7Nc6qpKK9irfeq89eLExMoKxYxzgTooMiChQw9UEm0/8S7ozc0lhKQeDkgxXVnNuFpVXwQASrnRPxYvMhSj9RTsItzFNRxQhDEWGEiveukpLL2FdEpHPhnppTf4XlA294qaVIeVBhX2yoZdc+tHkzZnrbxOvZim7ffkc0fappnBG488gG8e01SiuRA1l8VXPYM6v/GltzLtm3nUXNN2m01gDAPHOtc9vh0iPtaS9gcnzp/aFPaDqI4I++7fgETqto4zplvyfN1/GZK11OfZ3U/P3RtiVsuuzN+ITPXel4GPVHakojh0+/NqV8nAexuj7/lPkpGF6+3hnBCA9pOD99/GU7ad/8X2xwOe3QCqVf3Jlc3+CRt4sWBn63euOp7H55gMYeEsFeA1o0lO5CWNs8hjYSArBDK9e8ES7WnmSq+hD7MBGOqDheNWBRIAZLAONY4CBL1xlQTe2R9MmnJGkOrMgABCwyGs7gUkHOaagO8Fbr9RIhvuW0GHLnP7AMLZPhJ6op1SjkwyvBEcA1gA6oJjpKlwCyygHiXNSO9M5mClDNJFREm9XsEMHcGHaEGCcYGImzROJlkEoEJEAsWBQExby+U0uQwnR7AHyZaEgvfF35yV6cbGsK2qBi3SUM/qSrTgOuOqYlt1O8ytXmzbzamkXep7PWOtMxLr9AtxadK+6etWUbOFSz7J5zWRudcEOlVsKtXMnPeEF86SRyvTJiB9vSTP8E5HZrpKRtJQs2jox3xxbmV4vDMhV8gw1eZpnNPgcJmIeufZss+vzTx8W7/PqejHjuanQe1Yv8urq+s2H6Yw+Z+YSzckF97avohkXTYtkyV7b0E63Wq5vg1/94rpN1tpn+IuKqikLVY+fJEdr6ceV+v8ThAfQ2zje0EeWBa2GCYhNZekrUVhUrtL3/DwHwHZm75G0H1jVUrLReV3UIvrtDcV4CHFo51QezR5eKS340R5zXy605WgFrc490mJdc1WAIwA22glUXi+Vumi9Jl+tv+z/m+VLlpLYYgmJlplnuWT3LIxemLxY4I/CAn8Uxd3XwfpSYYZn3z5PRR1rr/j+5V0wFLxWYO/vYfrd0OM574rbbfWOpWI37q4muzTJZ1fKGOWu/1NS13N7+gvdT8+eD0NKV5Kya7fD9jGUT+FTdHtyfTusYUpXuh9POYz1lHwf8tG973Oaztrs9/YZREhjerb715WOD30CAHgJ3C1VYhRAAXi6fD8p3wpyAYtB6A4wQLL6jK5HWg3AhWgTQA2sIGIPkJjrUbgcQERoZgZEoUGQ9E1k4g9CDU6oRrnhUrfeq9dd0kEydpygW0Gn86vdI4X1rrqcT88eOKmb3nCZpvSpcMa+8s2CveaF/QKjVJj5RRF87dKniaJWPEKgsqQKbEoQPsQDz4mnQj3uJiY0YSNUH0lHBmj3l35Zf8INHcywNwYBYia5zOkhVLyVl3SYY142VnJEoc5OOKGMk8HmmLFlNx0aKyeL6ReTJfPq82x203bTur6s63nzhvOhlp6bzMkBzYKWA7bADm126WCI+wGBrpfKoQRSwxhdQcOwbVI3Kal+KpvSo58tovDjHpfzwaJYwIViYIKS4eIMKR4CdE7mbFvJ8A8zhITSRff+5s1/WNVfu5KBVSLVii118rZsP9wUn/6uvF7O/4w+96q9mDpoUBQcaMBZDUk/Tev2ps5N71VTMdXuzwe48Dk8wkH/1qfecedHLnGl3OAeBRUNkyjzhhzQO/A8d6uG0HkykafFXi+eo1aYl3ijCbtOMc+HxhjPERo8IoutXq6Pj4LBKJkYm+zDfNy0DgSwXCvX/8oX0hQJmtCQEkUwFuZSNnswWVjNIAhYOuxAnK/Q/KNMBfD8h3XSCoxPg4yiy+wg+Ye2hEH/wXILoWsA5rHU4YK5aDb3Oe0ZpXv6iPTgW0pS6L437u6XYi/ZHc/dd+muz50oT3xMFXbPF8ryYY1+lksp2CplUHAclfss8saZHM6Xz2HtxDNpdFj6uNb3h1hXfHvdT/lEilTwH8HkoRomu+2uueW7TyrH5/KEami5MYUOeozuv45KGtyOortf3AvFz8ACTy8rqcA9nc9P0tjPU5swjpU8KmY4NmkFTDCzX2ABoACPevKX+GdThxP6kUxPexsF7gJEfWDsFCBnAQEXnHkALxcCC5siGG58IwM3A4KERfisxZtpa93WfuvXh2EjV3qLs1UObDlqFkDn4ATz59XfflsIkoyUkEiDGEjc1ENwUKw6ehE7BIFxAYJoKzwToMsjjBOIKtKE/sG71w5+6u+l3umfsiM83ZImxOIxCYKtgyaymjBYovpO/GFbnOomjAdtwwSllqPZSjYs+rjqPGl3Ms+XzKupWHQLesvb+tUkP0E1Jgm5G49zv1c0B9hph+7gPL82x9pFaOP4SGjjU1z+Dt08JgIdcQWZaRP6Oo/Ef/BlqKKcIWLFwQV9QWAqj3m/IsSNbIgE1M+zk5Pmurp4X1+elScMDVSs1Z7csGpj2Xxd5De5U24wwKxCgi0IV6yipvi3t6vhKLlRzOf+GvFeB8fvgGadVMuGAFfchp/ZjbRUVhGDO3KdG54aIqSvY6dIesbFRzMUpeCE0bwLMcTgMPDcDCbDNeyKJLntTH7MOtvPt6lKIg3b5FLQ86wyGkUnzTIKSapBGCnJ0lYQWTH1oSHp0QUUY/wsZAQzMmbLspeHb1QBKKKey9lhAxoJNCb//+z9y44ly5rnh8VaEZGZO/fl7Ms5xWaTQlNozdjQgGCzoReQAAGC9EoFdFWNWO9Qj6GRRppqIAEiB2KzBYLqYtfZl7NvmZERK0K///8zMzd3c/fl6xaXzOUZ6cvss+9uZu6fmZub84IGq4hgxUODUJHzTsd+VDuJ+FiRqcBdvf2xuuJs1wEeWNSIBkjMdU0euvyMNc0puHGjsObJpWr00KWMq1NT2kJq8vnSGjOl4d/qlPGWjDunxr7LNWmlTPEMveZLs+4H/6boZwGfidmO1q6a17x/RmZWauKtad/gJKKq3PBbkM7rFjjzGtYqLMesqaZ0aFt+C4FP9Azs69pDZSwIZaw/6EPtM4HwEmuFOdY/2WmKoZm3VpihtwLyHxPqCpO0laTnzJlsfqXwgrBPkYGiaJyhQYB4EvEzJKAhKRgXwHFRDp+Qw2vBAL2fCbJyWmr0jn499orqDCoRvRDycqC/Akdec2Q9upc7IwjJbhPsjVhCOG2DyB/zp3xwFZuxmnU9nIg/0f0zxbnyAMGanifAWqbxZiTHA1vzoLQhnHWgAB4okRx2s0KDqVntbC8KeVJBuaoPNpr+FzhbaBXQjWEJllzeoa421WQ29uJXzc6uVu/uVz9dXH2+/uz+4buLi6837z6sPnz5cLVZbb56fX11dfHNzze//M+8GbAm9tboZ73yd2dlI9J+Y8sjFuRcrN/JRTrbW6iw+UJKsBOOLEpA24YK+FH/ABNtWl0haOkJdHoIoGEA++Jf88xj9fr+7pqvmGkQxVw4zZO3FFboxyahb64uflxvvnp7+fr15Xe0tA8P312++vn+7uuff/ufX1386f6LXzeXn695UVV1eKkv7V689sMWhNpj0oCHGNJleOi7BBwjJUPMwJHu+VDbo8q0pz4g2eVmgkgOrFOdCtchN6rEIAAA6PIaZ5ULH6TLv2hjWXJmApwXr0VKxdM+bl8zbFtd/SZ8k1PD4DJSZczHd7VhZKHinY2RCo7tobA4sdNyNTAQ4xevxZ9iNzPJEXNLkCbmRWvW14tlIAV0Wt6NIcuuUML02X6++4Yhiejv3uv9HzYj4jsNeEcveLPFE62Oxzg/Gj+dRJy+Lf1DDVd6fI8Rnh/Ch2vUn3VedMzej1o+LaSW0s6jt5Aav7vGZujkHUoe3vdobGyltJAkrKGdUmLe0imqeXjrbfcId4GW0s0xNbkozS29xm151qXHSquTLjvCosBdTrWM9xzWrrLwW2VT+Fr8SzwwKyxfCgJJa0a3HGNVt4XkORXremt9Xrgdz8mnT62LK1T1+ULrNNSuOnHtUApHSwDuZm4tJTgawklxDktcEKSwRdPnCn+Jg3WPUUAkIEGGIhVlNMPIVYp/DjUSJTdCMzGFtOO/EPRbyTaVSLqD0lCoAy1LSRspvdbHsW6I4B1ts1hfu6HrkLLSUWcFVaDrCYD2N7HqCv1DFFH7pcN9Y8pSDWrSIWJnLFAY4pbiRngFBJgs1n0jyxWmBdmLcp89aLDGG9I+4cCacItPKl9d82YvYxi9sMlSGZZl/Hjxni313129/4/3P392/47tN28//Mh6n+v7dyyy+eXhwz898EzgNXPKrOBiGTjS7y/5gMCXK0Zuq3dawsS3qJDjT2tJhdDZCoTy0i+D7TBVNqprmCf8/knmKWZn+PT6Fe8b6KO1zBkzNKBh8DYzb5veXDOXfMciID5p/N/d//6aYcHqn1a3v13e/HrJ1P+rn69Xb+82Nz/wVgkbxTL1rG9QEpezZ6jkyt/WR7JD21BU2ThcLKSlR8UvqowqZhgQjV4m6WGM2z0Bs/LK6cAkqROtjbxkqi7zARN6Cu1fLSaBeZhAGxQHfCNbLq898W9CD6XcwFRidkYl5cEH0FxgGWKb5YGTlmYlYQB41ABBOC4wJVjM9ExDNUVNasBDa5OMsBocdXAP+Kl8bEDhG/3BA6g3BQ4+Zubk0pPEVLhkz8dTeWBQF4+sRlR93QDqhvHIynzi4tqWUNcLztGeHu64abz+feWwAWopmYIXhLEE1ysO3/xScZ0eo9gOa0ft4zS7t79a28PHqbpbcKmt/DbPc7503MY9oIfMZFhcPdNQe2wPXXYj0c2yd7sJ8l39trT97KZchz3Fv53jKW2jaiMdH1b70YRHi0CagncFuf1ffU9UoTUuCg4U7jhLwMDEs0IKeNEmKBGCVGJek8BAs/jM9SqqWb0n3nN4RJOGrUIIKBT4aEqxUuVe882rq18yCPZlrsH4oixWZQ07m8dTUjn0ZLJSc9IQEoQS0yi2U5ktYFbeHJlDFTrDA62QcGAUfLHhgUUyQDAYWi8fCo1gYms0/2of4QsEwEVECpSU/kp81r+SMYwMEhlEVUaZNZoJQdhMBH+hYn/plhx5TcTi/Ju39w+EwjfyPF/2Wl/8evHFu7v7/3j/9mJ99fri29Wrz37/wGabbBrKR3ivPqzf/84XebV65v7N6g+r+9/uGBpo+cZPrMS/2LyVX+MryGiLHHTAAMl1xlqS4s+qSTv7TVpyaCBkx5IUKUjhWDUL3izGz9jEgv/r+w1vJtzxEjCf+vr59g246/VX+Pl/uX39ZvXm/v7bNZW++Zbvgd2v/qh3iS9eMUrg1Wq9h41YHn1YoHZqUl4721gFDbUMiaxhqSjSi85qwtaf4RAEmEFcTyyu5S7xFIAmZO9gDoiooKEMx+YLpD2sfhaJ9r/SsEgIPvRauRSHO+BYMYZZYOqrFNjCuFLVmzBwpYYT0IMNQ8txlRih4+sCS0DxIu+DjfDTAOg5ZBEnnflLgqJIIKQwLLdEdkbiwx2854CyYg4S/RprzEaM0Ik9teiYUR8a1j1c/gCuCThborJMEfwQv8NzgpsolTm969UY3Y54jFxjj8p/6tpem9DD0dCLDluXz6V7tIG4mFbtvqq4OTEHlEnK1BGNAQQSM2hT5E8Kn7PrSRXbQ3iK6n+oSEvVBKy7K1c4H1symmBY/rHZ9ona8xFX5uQ1s7I5Lq1R91vwCRbAcxcg9hCyohFFtMo4KPETAC2sV0ygONebAplQFKJJzYwQQsSsEmL7GtL8EYZGWJM4BqYCnZAj4iAXZcfKjAJ54Rk+0nhNQBNxFBIUwxD5Krah0GGQxSosSyGSpv/ZHN3DHsK1ZE+2yPRJARG4XIXWNlSW/sDjFi5QQguBhBoeCQPM1pGQpkYUb6cKRH7z9C2rZrS4CpMIp22TjCEEveWd4DVvB2t2/BqUi7t3D7d8KPiapwJ635kVQtdaQ3/xgVcfrljwc/me2O5y87l08eMOSZU+PuSdktQqI2U4w7griKQ0r9Glu4Jm+GoCm8NrqVDWb33QXNiFiAgZahkFOpE9Dwc+vOfpwOUHN5L15hZ6nsPcvHp1+YrFQXw6wDsAMa6SJpByklbyhUE+qaw+pFud3542SzhiUbR6RNB0eedCy+ptv6fMxdYoIlAd+GAko3GdLCL2CunhMS+UVwOLShOj8Kco9fo4z3NwI66mHQZvyw/GaoEhRaolxlJAUlXoX+fEVnmwVJxg+lXe5MJP3IyAzmA7WFxp2BAKiLEykoxReMHDYca2d9pC18r6dQKKjSkZkRAdRy8ToMnzkHYS8VzwcXqgbgC7NJyP0xvPzSpqJw6qJgYAXDGuvm8qSgBdoQbHyLOCAcZYVtfIYx9TcwzD0XNj2VZFam2H3LYSNwjtbESDMgLQlZoKOIHfRoS1oAh3ZmcdartaPQ/3W6vUcSFT7edYUo7Cv6t/Urkl599pTQuGE76tx+IT3f4VnijO06w5E7KX7KJzo9lBPRwgqqDqmdFktQyhjPs/0DVz/5ovF7ukEkxY5KDJWrGDD48TdQhnffUbWKT552AIDZQxfdEtMZq2oldCaELARYRsMiI3ZqO1jc8DX8FiSlffKED/kB8h6Z0k+akFX6u1XZidpYsL1Baxei8PPWhFe+px9+y7z6zn7/ISOPKdUKw/5v0mq5Rh0vgrybz81bQ6hZElEdoqq73q7QRAvL2rJwbskPn6YfXLxfp3pqThyJujzKlvNmvF/atXevf28i0fCXu1+or3aO/1veTX6/XN5u7V5fVvq4vPN8zrb96wcBs+WCrjFONRmXxl1upJJCBrISWod/0ILARKwi6R5tJIUqzJb4g1ca7mwY4xaHXHO8pa4LMhdmQGnCcWfOdXrQAtWERO87lcvX64JMjWlkSE+rwHLFnx1TDCaQiRK5avtGURkh9eybv+L43cokhIo9DWGimTtFbJ9AFD/cOfYmUyXELCS3GoOezhSQXvgfCESoIV5YMcApn1f6WnJYxaQOFxCAM1M1KXkfy0C9DPFoHlMk5HfIuANfSXr+EsriLzP4xkgdaKYZvgxuZkeRaLhHwoxf+g01O4OGRHPpS0XTbKSUBJOXNVLbNTlh58qVNTprGKKh+3Q0plqZuzfIzhNK8K/E5lXAKQzdQQFGTiEGdSVinD6t+059j3HazTNNF2Rc821V6rc4cYV7nFb/F6OLN30i20Ll5+P12O2cpdAgn+gdmzMUBR/Woz0XKqBh8I287H1X++HmtdohMux69pD0kfbG/4Ovs551BJbwV0vTHrGL0y9U36Od29oslY59+zB84eeDIPtN227smD/gpy+ZPGLXFNkK5woHl2E2TWAerzsSBxKSBScHyg37j1R6zh+ELMyXouGArCC81yig8RQ8IXTHEswUaOYqyQT51DwR5AurIuJQ7pgMD6AVF8w640yLWSzMgmUf5xuCY9g1RPAGScUA3hJF46Ek/9FjmAUzoWxginKySocwbzOKwRcoSDAP8oWR1gV0aQCySF0jhaYyy7k7BZu7AQ9zMuIGrmxQW2k/Fc7s3Nh1um+DfXm/v3797/8rC6efPm+nr15ooAj2cbuOLhA/PrD+z+SSRNpO6oPQxGWKe76y6ppmIdZJ0Un8hmBPKqXzD0h7YcOrFoiZiSwSAxDUNIvzXOfDoghgrraz4dbaZa8cMyJdcCH65KNxqHoPeX+gyaqhEOEaEmofFjuBQPV/fKtmQkmgPn2uywXWctj0dB/ckOmg7ulmGyTqIAIs9rZ0ibifbtAS9YiUy4nKgnLZuJv5BjxlQmCLhFb3RIVnAR0PmIwt1YU6FQJDZQyTgBtVUjI30DaGbdyeqECkITkjQRvoxRkvVgDDJD+0SojhMiGMeIjI/rscaPetNyNHqJO3IX/ZujacV86xH6WJGtuGeEj9oD0RRSg/ioLX1xxvkCkC8qcSEbtSHwmqL5d42DaMnVIi7u3aWvEbQ3oB6VtqOrFjIvqObWYu7KreYQHogZlFbKEs/s4EOu7Bz1PEQLqZWrMWv44nRr0WLSat+bTNP6eYntLVXmN/e7hGoJzqSMCc+HRblnVtTc0cnxP/er/NvhlEKKog92ZaSCQGdiC9/mmSMnRchiIBOgrCfXdCOPAgjNHMMFkRCCUBwVdxAoaF70Dxo5vPqFKNFv2QrHgYfQJMVZfgrQfEI5CU+Ksp6enHanGTsiXjHRiuUKWsGsT1A5miPSNRs2vry6vd/oKwFZ0xwNwRL+zI7L5caWmk5r0JI8rrX01tfnKNUcsLmbpRUISzKXkE30LUwbY4ttrYOuJMl8ApmkGKmAmE/L0V8xW06UuWYPT0/WMv2vSd9LZvdf8W1W9trZ/PYbs+28PsteR+t4K+N3KH++esWU/7vLu2+Zpl9f8Klgvhbwwa9xsoO+90eymCSSHx04LhLDs1QXjHpLqTwHTAVQ2/InCISJbEyqJy1saqNvmd3ysjLPXthhiacWNAoRK9pnXp+A8g3jGL5OoJHA+gM7nrKDPpsIXTBcwfFaoEINwtom52aieFQH09IO4qWxZXeKuXxwCrusfleSgebgliQNaZr0AMZRKAuB5shJUg0sjEFTwnsambBksf6S10iGDmvaasT6gWCBYN/+Qd/kohaIvRkkeaGQmxVcyP+6Yg8nK5CrAeliKq785sOKBlji/b/7cQoUq5KpRGJbVGvq1GruGkLqoQzDAMSov4uXRmA/sSGRjL59z7ei7/kUwOp3qpRlWqDpShALn4RvdaWBxQnSHGXPscDtyof5ruQRUgddn62fqub0h1cPejC2Tdby++lyzJAZvlI9qjts04Or/pKdncJ7e7WBlr9au1vxduUajF3rcVf85bpNtcnW3saIIQB/jDTPFjTq/yDWGQIGAHNVRdkoj6FCJR/MS/acOHvg7IGlHpjvPLMdMRX6pyAOLwjRmzlr3Y6V8ozuyjPHq98VHmi6U7OGiiAcU5BPQYzCFv6Ziei0zIYlQAR3WlWg+IMVBESCvoUoyBK3NXuhk0BaHeNIelZOTHUUrZ2rTpYIK177vSMilkAt2JCeMNXKGZYxaHpXMj0cKbxBYsmKX3NkY9C42apQsvgBZN2sjQyQRTYki4+MKKxepaNg/BejsA9RkbfpBmcu+hWytJHzJUcXXswgDOM/ZezFzhMNltcQoLFC+5Y3ZdfEynxd+eL6iu+CaQkTs9ibu7vr6w+v3lyt12/BYv22FuVf3Wx4NUDvCzic9cS9jao1mEuH5sJQKkhlF3nMcYhMQShHZKtXKRQ1a/t/Bh1XG15YEGKZLGc8Y3/gc02ii+fVFav/SQHRVxeoTHyykh/0PMGC4ZjkJ1cmZQBHQT9BLjQVHWmwk5edN6tgpBJXYWDiVcHREE9ZaJgKmVa5AVdK7UGDEDUS2peeYXAInaEmvwqpzUaYQN2acBF2eYSsUkmRZIYXel4FmkAcItDh3yI9YAEXKegGKSF1IitxopOxwpCO1khwNSir7ScAYIi5NRS53mewGmHlA1/ufnh4RxWxdCvXsrQ1XxEWTbuUhFZHKCl9Boe1G8DO2U/FAyMN4lMx/dHtjC44Jna010bHjKJ4B6DX04d8An17fWomm5vyktGhRcTlayiNx6d/FGyPUVHLapTPsTiHuEO4hQcO5zBqOMCeJ9uRfQuZYnRUeE+rCc6tT1rIVPupWbZUdelUeoqK2yjH4bVGINUe6o9ED21BlkjnGhz12zjRnQOBWWGOeteOIE04RAjk0YE4QSuyea1Wy4WZedX7pdz+KSVqyDQRASqo0FS/SyPu+d2TnJrH9lp2IkJtKUYgiwDiO4eGUsQzw8yqvhfvtKYZRB3SyHP/FjmwUIUBikBKc/+SpRCNDXH0RS02MGLWluhFa+cZD/gQnaIimUBaYT8zr/hWeqGOoQBtrAQowgu7CgePA5QzM7lCCU6d/cY1lEJ+VR7oEfbZgSlko1iYcqACZqmC8gCZdVVIxn9CTbYAIiCmSljcj6GEZhoL3Govps0t2wTdXa6/vrp+9faz69dvvmCrz9ub9ebynR8a4AO7WR8HuzHn1wrBU4uydtY3nWKWXeuFxo54/8FPNnCX/eZ60Ny48FGXCz3cFRhvWDuu4J8/Qlzs0HslIPEQ4OIdM9AMzxgB3G9eaTN7XnXmYYYjUOJpfSOZ6Wo5JAJxucm71yNDOpMBicBU7mMvf4H6Oodl6Qwi4yEo+CYDcfiXcv7qFykDneDyCDz1ZxhoDnYFjxJLVdeQBtZBxso48RCRDoaU/JGFf0BsshwDTM9GeBygRWriQHNVy5QoTc+XPg6lNOJtBPHl67xCMgVs3IQ6gSpDYAgTug8rReqBZ1wI+QtvoniQJqli/fCaPnJxweoxtVtzM4u7r+UJvl2wYcyv7wA8PNxQMbGQjnYnZUUQ4rKw0bX+oUsPMeEnbe3DDPKv+iPs3ZJ6Bc60d4cWElRT8Chtr+HzcltNHgcy5YdTSJ/yWOer0rSOKj51DjOv08uFtK2opg2eUyspaszjpne1pfPzMj2m6ivgOdIe7XyzAqCgLvhSx7ekmIDhUN34IuHc2MkUYwU9mOsYyDLsHuk5c/bA2QMDD0RXLcCZbjV/GYh+6Vs6sQvRAuMDLeQgItVkOjPHfAyYQzO4nlN3DCAIIYlKHIQp8iYy0YuhrEpZr+5uWSzAsIFQTtwIb0SvJS2sPliz14tJfXFRFMVV3HrAQgWhk2Rw9DIZIsG5gLSICMU0oOBTV5fSAVlAecsU3iU4FYnuGNKVUn0HgOFNhB2YByQiPEgxXkKEJUnOOJFUUOAnzZWNc762mT/AhOiEBGeNHcI5n06WI43Enx/rozS70bMzpR6eaDNQ0aGenCjtyTK0ueF5AGMYBlE3t3f3v1/89OHd71evvmJSOfbiYUE9ewHxQTStzyekM1eYKApMKtaq7JK2C80QrYlpHWEqgkZbnKzhC6uANgxU0FPuZC0SS3qgkBXgsyMQOuhvvbresHRIRXBiBIdLtNaGIqWEJJIQhgnKBiQXBmBwzhQQyr2ZCqYIlf32IpWtoYkGW0mW4DxqkSkschKiattc+CGJbnrUJKD+i4OMohV7sZn1hCqpIzwZw1vRDIVwk4Y5Cjrd6hnPUTUgqGog4ceVk4ohdmUJl3/BM7sg0KEqCZFnHKnW8XQ/hRn1AkcvQpKkYCuR8FbOctHQGwDoE9NC4lEM5cEvEMw6TlYrl/ELutjMHgk9sGcxz4VnD5w9sJcH6IW5Wy6kj36bem8MAMxhd049gWUtYA+6LRMXO92v87HrOCnTzf22UgJ7Cj7H63hlp5Z+Ck8ebv3hWk2NjA/XLTgs4X/0ulvSiQc4U2/jXP0w9EQQ+onBin6qzWUIatjj5VazlasPrOJRWOAoxBOfxPSOenSTp3OWsEBLNyBVdB8RtdZqEzfc+n1VB1EXrO0geCLcWV3xRigRH4EPwSE72cDs/kvppt1XRo4ADqwUnhcX8cOHVP0BAL1AqvhKYShPAAheWDiuAQdmmNyrSoQCEp/E4t0Gh3qEYV6eTuTjCIfIG5lEPezdzhr1VwrEKOLf6gM1zByqvACKoNYuKSd6HSrqJ5wbORnTUvGyWKMp38KF8cPlu4urd5ebL3h4srmLbzMLrBrR3wcWB91f/M4jC54MANm8f8NWQA/3vL5JiS7gD5tvtIR7xd6bMGQ8QX3V0+qNOoN59EG55v6RWx2ynrl9PhoF2zcKo+/fWrlfgSCUJzB3fBwMZzy8FdnqN0YwPL7AUmylpWDwJQG4W92KTUuptgd9N8Dz+rwS8DoNGETsoFkVJ3bkU+g5pXPSVNiuaxPhvdVfgMgVCqjFiOhW69PUsBEspXzwOTjcBZYaFfbhQimhwSEWqZVT6vXxIvG8Pot88DZ64Qm6D/+AkAMTP7EgTa1ee2Tp8RiSZTZu0GhHMlyxEmLTvDeUmq05CENHnMOonDNO8oeRKBB7PevDf3xFQY0ASn/6muHL7w8sEpM0/qkihEzy8sf1NauwvmPcc8HyvxVd+L2qC8VcXZiVRGUp+q2/DQyfrUdY0F5LY6A+Rd7eHVpI0E7BpzjPy52imoK3dk1hzsNjiIjnDz0Kh/B7ZketcwT/KY8Jh+ZH6zzNUVtXp48l7fHn/kPzY9ky1ZamIuqox1LhO7uR6oaYjQy4blRPAOLSoYIo3pnvmeDsgbMHjuSB6N7up4s4bsM0v0DizLWe13x1AWMO//LiM1ZWKDJxiKC5Z+JoHbp5kNLcpwAqjl8ViglwIgzibEX5igs9J+yQT7gaLSjIMGswFGII0X9KxbUmwSTNIvUrIv+CrJhGjx3QAwkK53Q4tiKcIXBB+bSyQlQ5fMnKshiDpScKK/UOq4I9xTdg3fEIA/tZSsSuNEA297yxwCF7mcdFMDFcLGnSkwYBkmr+6Z+kZx/S5BSIcVg/ndFZakk3DaLwZ36KokGY/Idn4eq4+RWR9vrhld71fXXLXjtE3tZpre/x+vmBZnONHu7FFQt0KkoiKdCtY7JFafRQmZPB365gLp8PMMfeOrQQ3CadY2NWhn6a8McmdNdbzjiUM6G2auFej6DULDRcYUAR7QEUqkbqAEF3L0SRUB3hOVWuFFFdVd7OSA70QaapMCIRntynVmBCqnvz4cMHdFFQDpH+iJIj8NV4SRApSCmq4VMo1erISRwYHi+ym6caovA8fpODVGHRQLRMSi/FqPoylSqahzMaFEnZqBkl1BQFsTK2TqUJRII/HxHGJXiCxY+x8wkQ/CwDWteb25UcFu1XMFWN9QO6XrMfE72ApxZUB+TqrWhkjkV8iApFe9LPmWN4IJy9H6dSKWM1tpQltOfjY/VA9ObWugTvPQGIq0SLG5Boazs3lrh46WY0dkzBx3CHsBg5BXRqdBulU1JaeDsaayFDPfr55fit9D6nQ3NJkx/Mh6v71oO7Hwtcv9V53p/CGLxjEKCJc+2TOj2BvgW8RLctLGaLp/jX9VWnZ5mNFdrPCqAf63BnX139mOIPiyVqVDDA7Z69WR7eKnxhLURMFSqOUHRC8MnuQJ7CfAeR2CiQUOS51lIH0Jl3TIGKspRvPldodPkrgQgQAYWmKV9FpNpBRUGINTIp++hzCC7+1RE5RVJiHKL11IIJY4JLQJQIh2Xlnh0nJhZfX290Cgx2Otd+89qZUYMRJDmqdhCk2E7K6k1bDp5q8OLt69egPWjPe0eOykhZGSFhxHbCNXv/JjUT1KCJk1AQ5jNcSMgA1MM37Mj+mVZirLV+xs5S7YCD4MvLVw+XjFYeVld/uVC4do0d7AOqJUAbPsSLar96CEYwi7P0fTFrID87seQUZtTnQkXNwZlVJZ9R9czrK1a+vKEV4GsGJ5fXV5dXjKywhqlvgVcrfUVB4b5qTtWnXSaV89qY1WdCVvRMYV7Tb7cAZk28BK9/1VnVaU9bL2eAqj6CbVcLshRwYItSdY33UMjtUGkRKbJXS9h8rncS1r/y6AI1FNDrQZLieOJ+r2LS2AYangvE94I9nsBE6Hlhls7LHwTas0gMZAwcOGk4h1iNQ2LFkcqFJLURkNooOQ05AAuuZqsyJdPZyXQySg1wOkGj9abxhtkyjmFVmYSirfTUi9dSFxiLtL4Gqi/+so8sezHplQmcBbbA0l+ayp7mAGaZ8TuGMSSZeko5xJvOH36/mOY9V+LriBwyekzdIwK51jk6o2ph7JiCj+GOwaIOVLcu5dyvmyn9a17zOtS21FS7puf9uSu3Gj/qYkrP08mtdViSntJwqi0tqbslcsdxop3UTwAGTWecrECjqZVsk9hW3hCcAafxQFwZllysTyP/zHV/D+xWa9PY0dkdh+TmQHyjl2h942CljvbBdAykb1F55x60FqwwJeUAAjA3s5hZzNFVhAspkpG5is05mGsl5CNhXkrZF+nHdy3zd+QjpESbZGlWOOsLraZkFSJKKV3WiVS0goc12ZpJJeIiUIVFosmK6+VRlqFzUCRt+I0ywjfx8/ysLMgCCE0VCYboiPjDBNEFaZzFVEc/F7Dxs9QOi1BDSiNodXnFW70Pa73su7r03jjM9UOPAkwc691MTOOzYESzr1ntj6Vsp0OhhgRUmirBKhD4yyLcEoes05HVM8/ADISpc1JSP0GLczYSgyDHxwqjCReZaGc4xQoarfVSiI9ECQFdyJwZczGE5LFFqkoVawRGoSb/yYUEITNMyPIC7ngadmLZP4QsGRlqeWQE0Hgjio1ikB41eNSq6Bb1oLYW/AoblXLUKwv1B5mbb6DTrMgRUsvhemyj9uElT4oQ8b5NsRYeKRFki0QliHXTDIbhB6tvLSVISKE6qOTjjOD+IT0DLeAyrByW71IahjDdtUnTQbSqSSqLt3qQBgRa3HTPwO2S7aYYc3rwQA3egQ+9K6PwrhJyS+hRAeeTu1PM8zuX9jzQawUuOTu856AXn4n63L9Wp/pr4sjtpMbgotXLt+57uPtOBFMje9YZU1yvXhLLXY64Iyyhmho57SJtiNvybCFDmn5+C37tjdrzZjI1RuxLWJrboknLxrMUy6lqzHnNa8w63aqwvPZb2ikd6jmYQ/i3EuchU/oQOo0eoRt36ji61tGlRulMMYYTndn8VOwogRu8J2OZO1ZYpiUu139Zvf5Jc7ur23ttzMLE5edEIavVe4hWrPzO0RGBgsIIwlOQ+W6uwyFFghArdospdq3vV4gjWgc8pCU62xWFCiatlHYByoXdL4TWmBMSgTtklMJeWaK5U4VpknPPa82ePIeCoFQBVHcgxK8pX7zV7DUzshSyGkO6MH0NN5iIT8SknKWrIqAIwX01lJngi5JUVryTUVtWQUeT9o3slU95AQNfX16vXl0xEcvafab/+XquFo9LVR50OOKSct7lh3cGWLp1zycC8ALqULyRngoabZh0vP9CkZ6+JGCVKy0UkVKb4OuzwbZniGJsdgGC6eVvFm7H60VqwkiWurPan5CRVqKhFq//AqcFaZ2PHIfzrTuU6EMZVvGutqqJSWh01AsDWnOlIinSl2+Y5/5DO3ncGnUnv0Oyiu8uy4I4hCUZoKMGOVKSrwZrWcgDzH+hUL5a/axVV6KzctaXDF84xk4Nb6SgGkhQYQKJ0IonZgqkL/Ak9lKPOijTUFFZPMB3msn6aRVTbBAzABHKNa1VAbaGmNEAeHKCN6S3tZFF1ko8O/M1iIXoVbFYioclRrSSLkz6WlnUk63wRij9GhFKSZpq71ve3Fmv36z5modbONXqF+tZHCj7zdgMlOIQRLQcPqWz8gk9kv2z+fRBc7n2mjl1v6iv6nMc85PqwJni1nLAk3sftZT5+fVWhBuGm19b1kK6NqKyuz/pfPVPOkcNOnXQqbalZtTWVF3apqf8uSuflnNApvScktvywfNqrTT+/nFqDfvSxnPT3agr4V0I2uxUZD7km1oOA4DS0DtWQ+TJPLTBqKIt/CapPs2Cs1+eqN5TU38i6XuIjc4UfWvJddy35dIPo52Jh0Hc8KOLO5iRNg4WmQJNgdul1tArMvAGjYQvsNPiBQgJ7ERMyBJxQ4oUIu5BTsRNUIDGn2MXkTvOgkxpR01JqEukAkdWK5kpMcKSdrKACDjhGAx8Q5zPwcoNwi4iTr44q7lN6DSvTygvBmIsAunGgISDT87GmmyHNRTqn8VIOxbaSKilUqB1H/pBB/6bW5gjXLJRJvieh3naV6EkDD07DWtWjRCleXpcftXkOfJ8gkBfCLjXx9oAsXaF+mLPUC/B8R0r3KVSO0FinJCaIdMKkwScSlPNuKA+BaHjUBqFXKMNXj3/zafI+DrBdXIDSnqOObkITJoUmqiaLNQIdzQ0bRmkmXMVgRY6IB9GTruVBE3SREqEIrVqkZaRotBvNijjAlPQHy2tWE4pjsUQXBqYpEMX/Xi7TOCu/iAnwwF3BDm0T7wE80ImD3qlRgqXIcc0wnom3flgBdPq+twB/qFvaYdcrR1i/CbnS7CQ9WcXhUo2Tu6Reb1qU4lrKxDVNa19GpqbmU7hEBhEoE9ewwwOjEUVhsdQ0nFgxzIndv5i+v+eF+gtUQpKfzIUSE3+xeGMkq1aCeMJfp6TLk9gftTGqOBSXaOlZ+CUB55Ti8pdb1zX+dJxmgE0GXt1oTl7JnO+r8ppQBxxbkRdfV8uDMYIhDjzZnHNZ68Lhu4OL+3YPkYcNSo7rZg7NYoNBN1suHJ/p/M8pjAe9ziWPofU/qQO3NmyNw7hn3ks/Z3UZ4LBQLeis+7hviNP0AU4GpPP0VBMH0zgTEGA2bT/jh3lmecjIlBo8uH2l6/+8MWXX17f3t1uPjAJrelKPAappicVLogYajHXOm+GBcEXPM2XKLQQiOBPuSTYgQz5oAPJaefFzxcY4YCPfg7f+TWxIyRMpkRzppQzIrm9/U3x4z2z5gr84QYL3l982FxrylbDAA4WN1hx2MYk/ubri82blb5YRQnRGDEqCBaj6N9gqaiokQBIZ9h4RThQ4/lk7hebL/R7qa//poMZd45Ys56UcsnoXvvBya4wkiedPOPM9J0qWTqw6McgxW2eplYU6Y/vXvLNXWI5ngKgJ+9CMLvMrkFezSLRFq9dZYgOQ3PZbEGhEoz9zkYGZTRRJAyYaI8mlr4jWlEsKnn1i9b6gONlRkLXP2a2paEqg4EWlUPwq/BeU2kUQbC5XDPHpE0/7zY8pqHhoTnfc6DB2PMWbL7oqZYTioc2oWYGGibrwlDJ99EZ+MD7J0he/6zBozg7hI8zVmy+YEfV1Yqdi2RTlIYdcpLqix+tlRex0kWCcyow3fov0CuaFxO3f2kOUzWezeby5h3vlIPNy+U/E3GvH75iBLThS8CUr96CKCM1KjCTe16/WV2+esdZAkRp1worq6BtrCxNernS1EPAj15T8MRbDR218PD9G9635msMIGq5FiuxqBjI1he3tx9YTea+wlcaLq+ueMVEO7pCJwHqC2IidpICR4mPLqJklCqVDyHn9Pzv/L1y+TUTHaTigmMJz3mtFgg5Gsr8E4OenuHxcL1dobl/1VeujPDPwoppLOjJakqXeDWI9uPDpZFj3huNUgcBplpUa2lrUQs5SJU+8aAaQ1b+DgCoUd6P4QuH0hgKJBLRTvSAMnPo2skUzUCRLDg3t4GEczZ7IFVQzp5/zx7Y6gH3T8UV6t9d1xzSBRo9sNdnhxSKrGATOApUeGvzww3b+OsNSLZz+W/+zb/5r/7r/x27gv7f/q//93/3P/wP11qHwlYuHgfE/YTARAELkakWSXgRkYKYYAsP8fb/UNDBjKOQFD3YDsl3AKLpSEUaMs+2aQhhFAVAYqVICP7JPB5HCMQM8p3GGhxG1gY4SurLrBqrgC1uxk1zmYi781ZFlBRzYnxBlOPRRQwNSGMgERB71ROoyYP8E0riqN8Fh/HH8BQ/CR41he0CwN6/8gSl/GlwE+QUoqgVIKkJeF6Z1T5BrNsGXzdIFQJ1ZAaRPGeGYmAviqPSMidBSlGXF1JwAg9uOpsVi0JUL3KzVohJOQZa4hwu1BsBZKgZyHlkoXiU5hGGKZ6UI5XVWW8ne+iizU8t0TKcgs6NQczMUYl0VHkrKXBJVEjS3B5JLMLdICQGkmkhSnDwg3qe7w+AzyDzhxf1z5R4gF+FI26l/HpILPagqM3ov37EmCc2eizF4w7ngMkH8ggYSUN5g51UVb2UsA5HL3qYv7XKrATxfzFRKGQ+ohFUMIGjKtSScLwHjmvvd3THOwtUiSoERKqAPsq7AHpEgxoP/4f/4//+P/vmu8+/YjGYnqkBYqj/cAcDRviiUvOzIE4yRT8AbGvKWr9UFqDz+Uk8EE0iRKfmkStNdZ/TT6LbvkJD8X2pXzZdXZ8LLJl11aB/FtapVVz1vhiahAVNQS0qTMELQj/RMuiXHzWnC3TMR46wXT4+W4LZ4rRjxJ4SUxXUwFvONZ+4IG+RVRM0aQUN3KhOUDHzmjeKPBlAN8O4kz2ZCosF+xYvbccoUv/lZg5ayuRLvQmikqOJgaAsGd3WmXDUp3OZ3b1iJ0cis/WXb78g1v7s88/ffHa5eXh3zSIP5jJFYDIoCDu1gPsDsQ2TuMQUvPUpqRLlONXMraiDVoUpkk08/bBmx3oiLbYbjyDJdWDGKVQED5h5iU5NVBFLCIBKQnhUcfl6w4Q08adxNSKR8kTCvz9c3PLFXOOB61GBNZfZBJ2KO70aQt9HYiYUnNBZOtqDiqIYARD3vH/3HsafvdW8rPQC40LfME77Ha1/SwoqRKYI5/1qq/Mp7CZX9reJElsnpaylnaN6E7rGKhYlbZNMwkdpGVc1Wc9O+VDyj8jxa0Wi69+llLCkiSZ57UEY6Mhf81XW/zNczytWYYXUN1cYlMNCmAj3tVQrwCRDPxIkRSxIigC+/4Lzw/oXnR3UKsrXEAVldKkRXO1LT3GIm3Gs/c5cO3LZXUocfYR3UtrgEJeKO8QEyHSlPFS8+jW7F/WS7xy1w43g95fVpT4VzJ8HoPpFYb0Uo2bAfkSg0S/0A1IlQ+RJK5WRjjFMqpNooaYiynbkzN5T/N7/wfay1RO2f6EHAB5Hyb3Jq/y+09BT+yNJiyRcwiTfNQxjwdU+6RM4FLD6BlmUj3YqCM+F8LxfaNZORipl6ZHY0LDV9FUTFgb1V9ef/Zf/6l/98MN/eP/rex783d7eXb79TE95PKo381BIorOdkqxDPKtzKAgkSl04eTrk/jXJ9OCCx9GK+69cRA2WI1ppDSlFeNgOVV3nY0TP7PRUUaUWSiVlhMxDv0vu1yOyahaL03vy0bX9mR6tRS3kEVWv2sdWqeHT1Db4iXcAuDTUlMB7+Vw2J2iKJl0sRvllvkf4nRR/BN7HZDHU89R+Geg+V4MD1I80Gw5/nn5At2H7GNZCxAXun8kG3eFz/22NC6S4kXS8hHd9fc1UNzf+uw8f2Mfx9sOG0+dffH3BK4xXZPm2FztOMkgg1mfNBtOJWieAfE2Qc08SD4U3+lEEkwMCZfmvEzcwRR38M1bABDes+zGIiEsTyQrFHOLY0ixHgjyxCmMLlTjFPhz3DFc0a55EIhGlyITp/gwwVznHRysGPJRRwl9RPvSFAoipZJyAIAuao3CrGVwlwnxsROgfZ9tdA5yG73iBoBSGOzMHjI33qbMNmGO5rL+JSFRqZWyK9A+Q0GsxkTUlyF2J0DlcNx5mUQbMDMSGwSDDO8w2a6Hap2lkVfio8oXeHeZA1oJh4gQZuZG0PJwcITKARuzoBQxElbRHAxQgKxHawFOjjYJpR1HEP/9ZA1oLrSfMkybpcGu2Am64QMkkH7B4P5bHMGjVJw80324HhihzEal48AeUclwoRSDUdklyorKg6akTowFgBOkuYERhbI+XQirY8htUvOptvrZMtHDwECsGMuXsVsOiHpT2azJuRxBBoCpl9EESpiR/+v4//PjT//Lbb7+Qu7p6dekvysUAQc0+eiJyRCl5OmxkOgeknKOoZM+JUQ+0XnLNjOIaCEF2/jSSS9S7dLQiovZdeD49dw/MtIfpoulW0raGujnp6qJbY+0UZ3qQqhR4Td+VCJrGlP13AIQS3MYJOxYHptK8xQSXenw2P/atMSeYHW/9PT7pu3qJ9NBq3oopzXXjOs2xXPNWviIPPHGwbkt8Mt9OWt0eFYIf+Jv0Q12gNP9T89Fdfbumm2+Ec/mTwxACatFr+QG7fhJNXK0YEbx5w9uKH2LfxvsVM+v3m9svmEAHiyU2jjxAJlK5JDompFAgIjYwi2iINED+jBu2MLcKwBD9hoWU82QAWs+8CtsBmX4UN8FGIZIZKXACD2kKYBzv8YvuEitUllwTYzGrygQb3zYmzmH6E0YeqazeK5pj7bW+fZbCLEmDNfGOOOdjfaMZVL7tKpiHIfxKg9fCYk8kaPzdg7AiyoI+Q0A2OLPMv125GWawfplSZ+U6TvW+PfefS3O+xSv9UEJm4AnCQv/yVEaYOluS5uNV+a6FoAmTxC1qJBQMfDj/alqfeFO0U9Yaao8d3PaLsENljQ+oqRtJk+2FmznwtQfQhJEJXHfpe89ZT1tBXYJnldJcuzh4p6nkVXNErvYpGpEVxeVsoRYuj+qIkSEJacNIKSyQRM1/a3Me2eDGrwbmBD8Rf/O+Q9TCLyCFTWZrL4JtP6tOZGAKuEMuNQSSxetmqm9IiwMBuhVDPH1sfeWNRqlIPzqQUAXbnNabz/U07UJ7LgnmA93MXO0TBsjTEPeSL3av7u9e0eoDEwpm+RXgezTC4isErD9opMwaP3YNctktz4xQCdVlBbpe/Uyvvnx1zWekr9+8YUEWX8BA+ocb3tCIyN+GSh8rIr/J8nTOv6GqjXQh+fBIKljwAyuOXamC8ZKrfWBGm4z0kuv/cs7Bc4ezWkXvmNdnvrTHyJnwZ8CTVyece8j9upUbkGizai0lGvzzFO4x4VFfwfEUdsWzxF2/jxRv1YY3lltLddWVWBOWmgwbK7SUHNkFiJJCFrwiGxQ6c8VJ5GQGuLV0pzvMQdE2wgH6OXv2wNkDe3mg39Oqy8tk38xiHKV0WMQVigt0h3cAwxMApjbfvv1yvbrWjueKRtKHcQl4JIgYgT9dLrjSE2PorUFfMxS1gB/XD6tkMTop0OEwkTEUWui/kOFnjsZTmIYy0kel/EqU4h6iGIdBYuJIRiUupsA4RPaeyBBvxUCO/cRGaHwmjPGAFC5ws5Zu/i88CdHbDYoHsVofsg3lJVQKC1Up/5FQSid+hBEcBeKQboY6NzypkMMMwxPBP5iltDUPTHOztEQnYmuEp+IvuFFJyhqrQ1WZDs4dE0MCmEogU3GgyK3ZCPNLTCvemUOSJ+whe0CqHv5UtSgX95qOiUVkRgJ3RVU62JYzCaUzav6VwimtxqqAVnmJlXATydtR6QEQHx3CyBwh1T+hKlkdNkMtzr0BGYwxOPsAXanAV8sRx6hh8aGnaK99imGsoByY9Yo3agRJNSouLhE/s5MljMmUUxOWMX4El+BkjBi+lTJSUUNblJAV/DD+IMU/faeZVUF8ceJCK/30UbkNX/K+u71hGHHBZwHU7KWldei1JXGW2vpLJyUOObKF4mGu6XwIz0+RNnyXfRgecNNxMpd+ip55gTbPVBdF8YdZo2gjwK4dZF8UFgDU1bsnAOQorCgiWXMNlMyq+hVSt/9Pn00oO4AVWl2KkVpJaSEF+SiJk4wRrdmk5rZO41R2W+I9/V2OKZ6tFfvNW7T8W0jouyv/KT6t9XXt16W7Smx9UnObSm+Rwp2Uo5m5qblt4VCjzqdpJ2P9hH26ONy/HFl0TBQbLD0Ikn+qcZFEXEC0odf+FOw/vHrFtODq1StmBtlz88Pm5jXPBjTPrg1emEEnLOBFW61yJphbP7DfPEuXf1Xv1VaWihqIYyoRsoX/gmOXixTcKLrwlUQzwSy6/kJG5F10FLlwgK5v4hLuxNMD/G9K8yMUoiMFS3G9/OXi/sPF5g8Wwd6GsHfjgwka8KXhzSu9twkBgZS+aOv4LqIcRWoOl0T8hjXQvFisoYKQKJBpxmBkob3z8+HgyBZXQBXCDTJ+IHfa5fVOQYFQCrGIGffgTBp/ajqfPLEeSpMqUmO4Jc2IQg0PCVms5Yq96Z0otM4NTnZSB4NZzP0LRAbbo9C1YIVtMTxV6nMgOLpMFhnCOwZUQeIPH5wRyrv+5BxzkB14Vd52SzHPaBXBWOdQopwHFjGK1VsNrO8PCtWn5UonEQmf1gJU5iDYcbjX+itfqB4uWQyT60xcOBKCkMQTDoqzLZGiG+ssSEh8YEcmo+pyEW1MeTDB0ZeS49AYgAwnXjfnfZor3uUgEw+j1I3QyhwBirWCdz3PgOdnKkNHNUmxg4+Ojd6u4ckDEC3iF3MeZIWGNGaJC+kaikC++cPD5vfVxZd8//vi4b2uAjwFAF3bT/F5uW+kM9+chjL5J9zSb3EIiyPbpZyYJHD6SaXBKTLBzelUatxIR5uRNtuO5Vf7XefRl3OudTzaXaBm2qRb/3TPNyqnkUwVMaiPhuFCwBLr6lprfbiEw0JlBmitrBqh9VhduijNBYr77+KnGcsxF0nvI0V9xrmqcGvYrr4xbXp28YMzUBYyJRgAlLaS24wRx06Fcqww8Z1ocBPgUUYfHbA4feDAT9opH10tH8WgLU0irmbuatGookVto+q6uJRMrdDhhdIEuQqLrvwN4FdM/7Pun3nwK7acYTEQ8+IKKfj6LLOGDj6JVhTeGSxurGqQAtzkQdQ/5xzWOJaRTB0UKRBwuXUQHSDr4DLzcd74Qldh8BfIUpiCFTMHY4ps2A0zwnSVa7GMoxn7hNPqzhOozHp6HU1c5EQmBHHXSXEXbmCBBuToKUPkE2TATtYmRHPt6GxOKJm5iRNUWYIzARKLKFUqFNAZXMksjpD4bLKdLKFWLFxr9sIfHlZSwF4RrIHo/xB/Kh98giLSgSmbfASnxC+zdaGqTCg5+icpnzoINqkLsVD+1iDHlZWMAZiZiUXBHyQkSC3HLg7rjGFyFZo2EspYJxF4kxwGsQlD73ik6hHEDAEo8B0c4qx66nQCJf4C04XhZ+hDsfhBur+7yyDEOqutiREZknQkePM/IJQoryN+rTVpkGmKCShtpEwE92TWvPKrV6yFAhJoHm5JAoiSpOE56XgIo1VIKMOA4fbqSqxp9lLBQ1/1KrdHMZKNzobApJqE9A5hBTpckFgVkg4qMSsFdmThVhKFTsglc04s8UDfpR3F2ZWdLz6GVKnPttdMmVf6oBCGZFd5X/l29DBEzZ0yVIgOSjrQQkgRFThTGlVw3Zj6RwuJ8rgsT5X2eTxNrtWtG/USX/053eY65RZ4qeXZkfdT+407W/4tJOTsyn+KT1/ruVxI7Hw4hztXNs9hi10e/c9xn54bGJEbt+gpnqUr9eV1z9biLhulTOd9q9RljOwrkrTW/8cKFMkcXJBz09OJSfz7b+/u2DD8e74NxHMAXgbQfj+3TGeuLtm/nRhFu+d/YKUyO5srQNHaISYvWYmuDIGIGzbMcoiju3dEMg6dFcUoxCHSUNiujWKY2yYuZF6WWdBfXU6xuEnRiII0J+rriakNRw8gbHboKCpEi+SVIKm9QQWuwhAFQkozJ8pjBJREqKb/VSxGKhOmIhYBfUgNX+hkmZTWkg2XcvKvmSqqcljGow/tcaSvtHIUNsEkJIDZrbzPzENBERhJQTIa4hwh4OCUFkR+4eyQWq5W/KgXIuzMIA/Z+nIz2HxUOEGDVAytW8gW7pYD9FDMugk5ElnbLLTzm8pTBbiwcpmCTh8ulybGUCKcoLMRXBAyXJqA8ZOUDyH+GoPeZ8Ay+db0wuC/VAkdBBdQ7QkZq9XN5ZrPGBMwezdS3qhee92XapT/ahTylEdjtWy3FjjJKLlW7za4bYi74SHXFRM60GoYVLNzlT+lxwAV+e9YvKOmqN6vEB1uXk2kcam3WxLcGgRPtb9UyaKRJRroik4GiYNdu1q/pw/HozmpTTnfXVBCzwHE0BTyAPQyVe/MMGx+uL+6vXm4pr/r0BgBSy/WP4qBjvRrelZ111ebKJL5KX6IFc/yUP+w1vrWEIeutHzRrqT7mClnnnXJyFW0Lj5xOlov7ipH2BjtsABJbLmP1KgHpFu5pc0PuKavAi+etx6Qk609f7h1yzkkuT9Yo8rzrYZLIK3Hgkr1SNM+mP8SHeZxplpUfPGp94WueUYTpb0IAau7LkaKJwBdfoJBAYM56OGFNhIlO0ArHD7NhO8dam+6fZyPswemPbCt41DeNaFepscz4fQQdHdPxAoFFF74YF9MvQrMm4AXq8+/+Pzrb765ec97wHe3t+xQog8IOT5Q7KBQitiT4IKWDNRXUHhEuEpCPCWEq6oLQwB0ZBUeQUciIvvoDJp653D0oUANNM+QKsSJIkvXkCMgmrUVdxgplJMWGzS3CqyUcKileE+qSKDW/GjIIXFWDwKKJdPIwiKakrpwXK/usNdpMdFhO/kVM0BIjLSwRKsCUuVQ1oelk8q/CWx8pYUYyLCVUkIMdpJiliFMZ92ohKatXLRgw7VpGKfmEGYRZF/YMUmZoUYm7wNDscI3uNVAq1fKq4QLLF9GmaTWJTDlcYfAGNVxiqS9YbROJfjZMx2uTAFT/CFT60g6FGGBK24qEi8aDG0sprv91AtKyYz657cwEbb/TClJymYRIEpyQlIRR5xBZNhMgyTW1yfzXJE03ou7u1tw9IhJbdwcNAZmELJ5/YoPPOthG91QPpM09QtJcDtwyw/lTQ4faereCBLKWLoeYEmL1HbSyBVM4YCESmKvPHH75j0PAV6/0kbA+vYFg/cQKSRxicMmy4fhwQzWb5hviLFIdXQGB0SFxs1YKqvTyj/XI+ye0c6WzZQ/SlH2e3SSJDI0exb67eOEF6v4PsbuRINnth9TDbcmFo6/A5Dbzza2hSnXs3YcX0qXstsmrl/eXX778PlcPYqdwlyCM0Vbw1s+adSb7kH1JTPTbWvmurjrUp/xx36X4NR0LX4LqfGXpKc4tD5Zwi1wato6vZxDYC6fe9iV8zz+iNzD5xvyvZjGpJF9NIx+K7r8Mevle31qfbl7+j7ftafVxe3D99dXVwTPNx9u/pO/+qv/8//l//T+5sNffvzpx38iGP7w7/+//90//od/ZGdQIjYF3wqhCE+Y1OTNWsUrTMCv+aAYUwmaViTA0E7qKAaiZ/olXuGH/oNtHIoU7zoAAhWv8G0BBWZ8mOwSrmzVzyXGs+AbLeEhwL/XhokX95f3Dx+QpQBI/PhPBKMPgkkieLLYVmtIQRwGmEMrsJWWuwjMlNEkqH4UELlIOa36EWftuijckBGc0dYSxYYyha8goQLRm6QHWOfETknDM6LwMqbwS1rTtRymIw7r0ae4TMMV5KFBEJoghEaSc8wYxfz02k8D2NEouAonHGOhsAm7ZVLiWKTiekF7h61LkEjr7JRRbRh5dJdTzCA8aPkUAOV8pzO7CdmVZkABHPC7+GTJIJNNWgQ/GAeGtPCKf7lCT0ICucYXRTZcRKT1asfd1x/e/bbZ/Hap79jptVfozUIDR1QXiyQ0tDJpDE5BlG22ToE3eM4AVEP/WecNeygpkibuVy9BX1bnS+/3kD3c8WUJpIiRy8j4xYAHWr5TopExksGXg1lvpyGEPhygjqfnCeBv2OZHzpTYUEYDYjVHrQGSGcjb3N3pnR6Jkk0a3UuD+zX7/+Dq+2+QtLp4fbF5/fvvP3z22efXr1Ys9UumhwJRHVAHC37YPUzcBQk1nUCs1g4YLn2klbKyIx2UxRyklZn4XmlGLr+FQXsVzXoIt04X2gMTvXtNGqZ2LLG+HJEsgPBCKT1FoqfbmAB0CH34UqwcfoBOtee3ykWXJThjKg9htdxh2bJ8q4kvHmq55VC6yhb4lkRcq+luxzt6WlVKTc39b/4o2dWXgHOdR12HUZVpvZUCPRwyvkdWQmfNqpgmvCxa2bZ0ltknVJg9E84fGk7peMEQ8Wj5EJe1OhrbM6MDPRC9abwx6J4fXSzVW0EriZCu5pRu/UEQ+FxluAj6WqPS0l0fWANwzVKfm5sbtvm/vn711R/+8Hbz8ObN2//8n3/762+/vLv5yz/+4z+yVagi9/UG5vrIEBE6Qrg5rjYxJX7P8iAtF1IgJ4X06BwxUgYkq5iV0kIIvzSsF3kV3NzpmwPEH8RhCLnTB2Xv+SARIRqUHiQoeiHFsIBVQw4iEacVRPxL12IJQYKF2b5cFzwBEAnIPgh9UN1JaaWgSRDRSjx2rRhQ/Pbrb8zChstkqQhwn0I7p6FbX10zbrqixM9GVDc2k1Owt4z+yQwDVOOkdFJMOSyQ05zkFD7NP3CxFX3eyklRB7Z2hfUBErWQsEEIPTkrzZEEJSHJDBWEJjW9LVRRJgokfGNe2VNmW3CiKLUL0QZfLW9yURIDHJysU/4Vvg+wOukF5Klwhb8Uy3pLqfHgoypTVH796tWrze3tO7k2R/8w9WBOLUBpsTHz7I2koVQDLhz9gCe0ZK9gaoe0NJJ+mkVYbl46yS7q0xTE9mLg3iHs0BcrCMHvtAmnqBlLMAAg6udzYibU+JZhBgd9zE1D7GWDH2tokZqGtVkQxgLR5j+yG25wZJUR/1jzxEfJeGcAwpv11R39Grl0JcQFY5SiLJ/FU0KUl8nJDS4WJB/CCSLrkMHx6wJVLImE5ALSHYc+SUYcLS90NbMh/VPkQ9un0cqyh+4i/zTaPIX3t8os7WYr5stDaGybqffSSkQ08w5AsCjYJWHvtKO0dtQ178a4HJx6DVarZ6vVEpyWqoW0fGRj7oMp3Y4dm6qqPcl1c+uxBKdm0vp8CYek/4Q+Uxxan9SazKdr2jo9T3XC0h1H/3U9LtIK3zaNoSOMUodvqosaORf5V9EJh0+Zoe6+BDrEAbqNqzAgMEoBPeECgS/rfgg7VHax+fmX/+n6s6v//L/45//P/9f/g8+FEZooyCHS2Kxu7gmpSSqoAezBAC8PbK4ury/ZcYfRwv2tkCOGVmgQ4U8ETApVHC8Q/EcghlpMUoKn+c71w+fIWl3ewCHcQSy00YsIbFyIXl9KtEIoxUp2h3YE8lIf4OYNXL93AmvtNap8bpfZsmCqiEoRXOTAZwd6xK5Xb/ADEZiCJpkM7Vdiu+IbwI6ylGFC956vp4nB/Vspcfk7YMm0oyVXaQ6L5YzjvXKdFeQuzeVCkYPE0wzEhP/OSCkhShelXRQtIKSJNHPi6wEEtiLXChH27NdX26LUKBZLqdirbvwaKC6M7x4E3IVFZ5FDKukqzoKU1qEinVe8BYFrvF+TMdMIi/15sEj7RBFbOlLXMxkpaFvkE3aYkpLhOUuSYiSMpXLslu+kMIgqc6mRYKus4fChmRQEo8p60YsdmLxtwuMR1Rc1q713oj6pc3MpJ1GIhPalgzPxMqE4/tTnwBhMCqJCjGI9G8NGfUMANmG4OpryGMfcvxHFJbhl0yRd2roB2gmc5CaGAUiRxW4C0OEENuv0oiKqV5arWUAoZ8sMBfo08tQ9KTBzyOVb6QwGHO8u7r/mcx4IYeDKk6vry8+urq4x/45FgMFW/KRhcsHmPj4Son5KEYMJWhhLlRhCgJQsioRobGGMbUhmOJQc0rWQBGj2DG4cJUF2wKMuyuhH+D3wXrPUyh3vJmHYvG6ugKi8I/ihZjEvd163uHoEjrtjzXjndDe1NE3aaiu5R2ku6ghHPuo4YYmOWDeOVkMj7QbRewcA3aMXkRAO17WabMa0Qtbi+HrTgrdDForezujZY2CpK6NY7NyzV/us4HPzgOIGH9GASjMS1I0MiNIprNF92UXcsCkJdJcrZkjhkaIIFi571Q0T8qwZILi9YsL0yy+JbK6+/MPXv/1KkKfwODHh/q+wiciDGEgBg4Ie9ldZcz3hQQLT8w5nkJmiKGlk6dZA0QN/DlSQxpofxTvBy4yJsOITqaFwmjEVmZiguAMQsUxJQbN5WRTFgnlZEcURO6FPYWO9YWlIhNpMxGo5SqjNfKzCrpjYVdClSMtCCb/4TYcTUi2OSGVtyq+VMYbxuSNRpFIegvgWKTB5n1U1/MPdqfqKTSoWIbEuwxPADErkDNUmWUWIRHjEnpSHkyzEXMWbIysu3sFeNQEbu0bhoySIecjSj7QxVEAdKoU4bE/O8OjDpT6BIiwvnUoBvHlQ13pVG4aSxKF2gMCQKyKwczQtdWWZZYVixQLZJ/L1+m7DgjGMpwXSLM0u1AdqzgqnaWT8eLlYuMC7WpGsVJCCvp0JLOX5T2wtZ2i5kf6Zf3gjYjhpLkwicg6W3jj+z1UHvg5KIpFzMglWDCXtRdbUgaEPBgNnw36K9SBMT5zUQD5sbvlSn7qKLBA7aEUuwxIr4nLBMRB9/CDLQwTGLVo+JKACfRzLCHdzc/Pr/cMtz/1ev37FuB39Nf6/43PgxhT/Cy4C/o0mIavkRBkrze2cSBswd0raGiXSc9iTZVIKJXK5FMrpT/q374WP3C19Yz+yel9Sd2MOaGALOyYDAMYH48gNz0lf6yqx0qgLRi2vgDTc4gYzxbMeFU3h1PBd8WvaybSv78u/ANfyqW1M8+54o3ZF6y4iLjx52HEKb9S2HKbdqagjGomV0FM+PMgzigZ2OKZ04P6uo+U21hg6eYoMdAxaUB+k6MNxKot6Wdjj4NCRi2ICxwpuf1Rm/DOQIEJctG+JSu9v797f3jLlf/vbr78QOnzz7R9+++0fJRcehMRM8Jc3g1nl7IhAhatXl5dMPAfeRsErbNFAM98ENdo7RYGJJiNvKGIVslYeE9A83KE1+hCvKEp54PVE68G6IPD5+qljo4vNV8BDU6sibo6rYjoWC8JBsiUd4G++fthcX7wSR62jDt9LqPRWEA0RXIizmDUnE3pIMIGXYv8LrfBmrBNDAWIwVlB8jpaaEobNirl/rV/K0oFjh/9RxWGJFMMDzIVjCuMoqt56yACiYUXqrjhZK/nyofmYAxnXHBCltIkN2ioQxAatWZJHRSK2MNf7GPp0A2n7S+tBzM704iVsKv0N4vUHO5krORzamkk6aOG4NMlxedgiVFDkR2yUrdqFKetvNSi2RM39k9QcuQwVshqnRGhBl7ZnJXRXkb6+jDHZh9ImxjDihD5mK0UlDXKx4k+1rxrUnlXai4mAVcUMOawz+EpqnKTdfiTW9cU6LjHx5y9cI8U94g6ph6+sUqMuoNVXkJkl15IzFtPc844KT5ZckjwiIo9YMBPWHprZL+ZmbeUQqWFMwIgHEf+jHp2OyB5TaKN3KzbnoUnE0HqzvvsgSQwEWGq3UXuEyR2DDNlofaRC8oo9Qq/DjdggLS7+5f/mf/3td18zX79aX8uEB5atIfL64f7uT//J17/88perq1e0YL1xoPE2XZu3a+JqYC3cMuQiBgOXbJ2kJscIQXqoHiXxQnuO4fofbFWcgMdR2ZtB2QMFpysYTzUrnjs0VReezCy7gheRopaXHdvvWeHMcAc83daC93ba463dn7KGNrvHoUsIpjS0LWQP5kcnmdK2FjRVF1NxwswuQPimcUwtKhfP9jK/xxtXzD7t7rksB6VycsBkumSA+NFlB5aXettehx+dK84GzXhgouO0FKUFpSLlHcEpr9u/Dz4xpPDIQZLu7UQfRgoxul4RN+jM/V/3ctZPEDC+utZnwH766cebmw9vP3/DTOGXb796+/rzu5u7V6+ZnFQIp7hTMnl50XOqxAIqAURownS7Vi8TnQhmqOSqNK6RRBEpeIIP6glX60AUC4mvdGY2UjGQgVZbVxXuarqx6b84mHkkwBscohQhFHrxVFG+RgARfFLocmgclYKopDnyE7ZYFUAqqg9CSkJJXsW0RSECDyZPWh4lJsQgUcrNFIdIQRAa5bIG2Q61UFUVB0NJztool0ixW7SilHN0gMmwJFUxCkkMAa8j6SRRgwDYBU9xC9VABSZM8Cwg4bDyiWagjSElStrokFBlLTM1MHPV8xF4KEBEf0sxEspIc+DUruNRaQEH8OGMkkB161FjCO2yZuKEY2gCGjYoZaPzOexOTUVyL9d8ngKGeu+WdkgkK4vsK+EqIcW1lEW+FIrCWLcuSjg0tBOK/pKHQrGHD4jG1zRmj+QYTt/KEeFbN66km9wIvXzh2J2qJOGakXwO2ZG0SWUgCkB/uru/27Djlt/4Ve1qOT7b8up5BhP/arWskFvzFr72EcIEDZ/Ucqys+UqaDkjgLg9DzYv6//Jf/ov/1b/4F+9vfuFNH/wEs/u7m/Xlm/fv3q0uPrx798tnn315d7vhg8A88NM+RerK+ide4N7dEe7z9gQqccCTOQX7DFfLWpsSPpb4qQNE18NU+Rl+LA+4GXbMzl7vfHHi1MDzJ5Z2PPbLBwDpGlOLXmb0CGHNZDzdjoqmxk9B3+KP890J6hvtoZynOuEpr4qH6uy7CK6K29ZOPtsJeb5Od2JVtJ23vS09XIedOaQArm/flvZAVXQdqbfTvxqYwzxFHKQfbr8mdFqxn7eX8riMwIVww39MtzODqA/ikkUTgteYZmTVwYq1/h9ubgkyWBFEIE9QcvP+97/64x//41/906+//r65vWGp0P3da8IFZkb94q8aCWujCQhWChzheUWMpWiRQEmhBLHHr6E56gmmgPGNVNViCWKWOy2x0EYl1t+oxBwKb0Qgg4jCFNqgtpwQ3lM0B4VCECORUTr+RwQYpZqB1tJzh0s4RrZLZUFCQJYCsfiZswicFVBSLRe+QIldf+V3tf5MsSO8iCcl2f4kxkVdBYTyHqFYDg4FEY4+ROVF3lBuPsPVK31RAc6/+0sF15QSFgoTtyja43Ot4PxS+NuJyL/X3LHtwgAty5b25Y8kaVujX+um2kEz5rDRTTqQZn5dTwwe3spn65+ZHmZSV6wUqoeeWHojTRSyJxvNV4EpD4TkE3TyvDX8JZjXuClxw6C2obL3xdRaeYwFFXbpXQWpSQSf7BUKUjgjE7kQ8Y0FdNW+RjQmo4d/ZN7m/r0iUw1pVsSyl1c8TNDLAHoso+chimdBoDbEUBpImp4qqPop1CvneIg6RB5f29UuVjy7oB4FUgNe4xPVI2b8QWqtf+fFWbi4auVSFJNdIOpQUoZalM6uBzlBzke0eqcd9l6QBzoUY2cZvJFWBOlvpf7apez8g6IaIfOk6HcpzzswsMRd4gsinHAdB3oDQh/geobD57HXD9erB97Gub+89sL9+82r69egvvnsi2se1j2w6S28rgj1cQ9XC9X5+hbQevUK16htalGf9jNFzO3mbvPhK4ZSq/UP6GcP00Z+RKmxQ2bH0aUyJDmty8LsO2le7W2SCltIFEw9GZi6Gutyh2Vy4Z4HzuEIDiGl1m1K/5pqP8HtPavmM7QXJYuNdNk/17jj6cA5XM9x7sugsgJtv++wD6mpjstOKVoIhzpfPlpILhn8cn3Yeiypi2ASdTi1CxA4pYaN389t1SMj2NvLBwB1w8osRn5Rxv1kUDQGG6B81NnwXnihuKgkPmrTz8Yt9ICaQ7STmoBbeVyGaiDp0qMUXInOBzy0rkJb+18SB71//5sm8Ng6U8/5HUkQ4KQAiLBMMQwvvzKnyGIcELj8pf0HV5fv724IVjeXb/7T//Q/e/P27f/n3/373379/dX19T/+/35in0FiBG7XnB1cMT34cH2NIghnBx8HV0klhYG6qhIrO2XNFU4psOG4Z0UNM7hCIicjCJqUkE0OmMgQh2l8ouKEGRSwqU33hREybmYeajhBbHXFEgjHXSwWcpmEQSnHSk1JhIRUzkPpME0QK5UThE8gSzENZFBexUpjoHDkUE6mIUVCSZ8diJocZCBi5GcdDMmI6HwLIThUUC0WcppOwEElNITK/OUwZOawV4ryD5DiYHJOCCP+KXZUbGo1PCAhaWcKbofweqhXol/eOXRWZAwtfNBGwi89opPIcHeoJwwZIv4aACj6VFZa2wGKoC1L0TaoOkCW3SZ1WqoIihjrLBYUKy0TXaja0aACSs5hGUVqv4w8mbVmPybFxNqHSqMLMJm0thBh4QjSIuVHloEDb1qdDosTyHxZA6MegEqwBVsyaN2g4UfifinFGwfxhko4OHGAhD/Uk4JynHBlJ/IDkbNaCVDhqUqEIYuMgQR1HRPTA5DIgR9gIJdpYMmRzRKNjuAWGc7qZTzt8MDmjn1+oGJwiDeYzqfbyoCL68ur9Q2v6cPyV4ZQvLmjmhUn+eeWKwZjUbcBnjxomP769eu3n30GpeRRsF5rzyL5R7bJUpVMHvaCSvtoBVwIW0gpmk2EBnGeRNyX+SRD29Pj2stUdOGkCnCSZHg3vFDOJ5F0Gqb91nEaGS+A63xjKZVcWTJNEc2gQlWy10o9ABhFG1BNZ6t6q5IDfF0o6DA92YJEcHPc8ZP4LjsknQtupdVwPL2MzyKs4pw2MU0/5bdpCpW0VrSWznOofTKPuby01Wr5mHi5lF0xD9fhIA7RGNwDlayaYuQUJQDk3pyjVTK9WTfuyICIHhzMEARe/sD6G/69e3/zl5/+4gGAQx+zyTJCUJABsxSzgAsTuwozmDhnxfHmjiDgT3/6Z198xZsAv777/fcff/j+3e/vWSiiaFH7coKpaIz/zCU7RgPEYIIivQDqWXKeGMQqage70o4lxYKsWNigMIiGbsmQkvYKA5Qj+HAgwqprNktnppwA6EvFKW6ftgEcZpEhJ9ZRuQ+FM9riTGeGNKvbD1on4jlmUHnlACzhiCJWgNgMQ0iFNzj7H84LfhH+ojyx6v3F76yjUNBvfOnk4I4AE2xx8yE9o3rMU2lR2F7OP7gsYMY3JfwVqlq51cWPpEzmMrAUi8ouDR40nlFIG2dhKHgVV4e6wcVnw8xHqeBvnSjliLk3DyqgtU/ElbTKo2rkQSgTXFIpswfkete/65HKkobmE6LQ1lqJlaRZJhANP/lnKkPtL5Xy33Ik2tqKTLYLHjZKgnSgLdHgpbRiUqA84VkT69pG80relMsYJ4ChZwIQiJsjf8tSbT58rxLcoFsSpXKyYmQw+ffw3sLRJ5wgKNzwt3S6/ww4z8w0mrJu4ichbj3iporVSYe7s6j17MtPV+CC36hNpAhHThRfhPA0I6jMBRgl1sImMMQFZDettHaInZ0w9WL92Yfba17mub1hUh/phPI03TVjAR4J2AT7kskCLc2SGPikCr3ga8FRsx9i7PDZmzdcSVbrnzEGRPVQH+EBJ0PDYBKF6TxW0MBm5jth086v17PvtbSpq7Hq+nhHK2VKf8k9UHS4Wo4fubMPNcGxRVw4eZvVaoS0hEK1Db+9j89TTOHXcodWzHMc88M2igXl9nAPr4X0irvMlI0dxi6ppnOIOCqWWtKzL+6u1dOSSd6jDSAYiQZmHgCMok0y3bEgmC9uXTtyPxy9c8fhvJ4vB1n5aVj6fOtgSjP6RnSSBiFdlHUD8NWyutsKNyoUJE0RKqPImdhdh57eM7Onu7gi1hyTOqIQqUIMdUrFEqGAWZCHVvG3SjXVp1UCLDKAwf2r6zfvLm7Z5AeIsTRTbRYK71gRdPPhvWcMDVMoAyKxPpdRAn0CMs2naqaWoI1ZVoVhDmPz8ozELJmFRfxDAoh+bdPswDEU8nQo9rUpyQ5hKNDSHyDir83dDeuVNBiJlxdzOCUE8zMqEZcpBUFvuyN+fZbLeGNBOKaSCyzIELFKHhVLYQR3SkM98azgpAONs+GmCElZdYfyQlRZ6OOc0hoRcdawRgMAh8SZOmmQdADT+JLHIT5yXtZHyOLqQ3BlZYuOwItfUVCAEJWTxq7Oukxlb2Q6PCar1XYDHlw5WwcLCbuEBVf70FUb9ooRcq2/pMMHe8N2DyryExgEaXimdfRaQ+/HTXQEUUuH8FJYpdU20NoHpOApDfXP6cxftYZKnIGr+0ANP7FUj9IQQP/jcPCtMgEMlS3UDhBB7QX/qhUGD1E6FSxMiw2KxSUrlQaGSRKyrQoaJAg1lcotmrmPzkLveucdWlHELVAXB5C1sAdZOpBPn7zSaiLZBn+B0lmjFz16Wz/cafkQfzxAoL8y3KIX6J3gNLDJ6mdjgkGBHi+R7D8ewyNxCqcdidkx2KDQ+XjJHphp6alu967imrUa7tXD5jsxq1dfJdeFjJqAAtEU13apAppKxEWvLdVEyymPuEQvl77rSPSUuov3lObzckes4NYyT7Nv6fKx74hWewltJbaQJYzn28YSDkfAGetDwFJlxY/CCIUbDh1SyNL1RJsRtqhzRpAK8oZIydGMwgRxVGThJFgp4nFnFm0RKYma9FRww5vB2peQJEEVnxG6UxB/e3tL0RXz6ux+H1poIh9hdxcftPN+bLsJDmnYEDGIpdKKw1BQC0IUlVmqNHOAonUWwjc4NXsyxCnAvO/KwxfiYbYgySKlMeWdMykWFBOKxIFnC9qhX3gbvgPgmEdmKQzSKvAAiAUUmjzmJ4JFKw/WOwm8Z6U+0sSVueZAt39iBT/S8Y/WqbNum9I4zIGkoivrqXiLI+KsxF/6Y54CfcnVrKogUkiqwJ9w7neVAzcDZoUptQ2azXXMB8Hn0nP9TtQuFY/gox/YKpwLCGe4EfhZFjnLSvUhGy1K+sBRzkcaIMtPJ0mBixyusvvPJFV48pjKLEulYmu4pp8lK3Bs3ZtUAljkpiMVh7HBV2HwZ+d+aa717hebN9JEnpFmBKnsaMRqlYsLfb6NABUoAz49FmBGXsvo3YPsQFkLV79zQkKDVJ4goaj27E9KsMpfU/EPX6COJtQ1gpbmUEqh+zd6TwB8qGy4GGLMmr2tjIDOwgfdz8e0/xWMvhC960L+gUS7JAH/0llxSs/DeedBYpi2L4eTgRm0lIQQqyBPqnOhkczTcw5eXL57s7mjn+ppFRVD1M4LPOIICqgX79UJ76/1oTzQi+oyCjjclKBTUrEK9fnMwsWGh4GSi2/CULGLQxxlQjl63x8V1BgFIfAL9rbE1vnOwngbp/3L1Rrz0d5x2mcUGffgX3k/Hce6h2Z++p23q8aM9K46TOHXclspatJ93WqcKZ41TltHdemSdMuhhQSf4+rTdo5oegFHVtUSZ+0Ab8CLbCFWgicA6sqLjxFcQFlIlQyOuWAx/zPi2QOfjgeiN/Y7SfSwOOsSyf9A0LmP2ncUZaAT2REPQcRcoGbchcPd2rd13eeVhQ0F+leOYC6yAAlfSWkAkA+oXr9hx0B2EvlZcYFWCfMGIcMDYi/FA2JJil/FIBGxQi4WESsQhOWAVdGDYwphSxzKJPnKW6wAJvacewqbhOsjCq2aEPkTcoLaVtEGVPEQxQrjHPMinOjOtCII2QAUJUkxsVK8qF/+CdFZ0xhFjPGBXAhvPdMIXykfakhyhIzSQ/+FosI4IpXgOExQFSNdPyDrn2HkrYpCUSBhhOjRygCAClLBNwN5MLiIUfoHE6svlvonuH1OWqz8j0KRorfGf86ZKiqHfACllzOmDC5RIlVDE+NIbXSWJJmgrATFjxtJsASkdmcaQ4o/wRfU2tvf8JKlYitmhK5qS9qTyTEvob7We9kGqoZSj2BUs1Ki0g2u2AlMO1ZZDKVRD1LRfstOEGmyRCWR1Y/UFqpcbk2tLIvflKf3WVsKg1F1jjrK9OaEQmJlhiktWeOH6cO1Ul4HwmQOJjNWJ8nYZ335Yc0ogsoEojl8jwFCtpRxiK+sj3C6sirTP5x6oU+GxTvhlNMV9fE7PaOIZ2hF28Sj/9OWhqohsS3tU++XOw3XOV2y/4wTBs6hn8vOHljkgbqvQNBrZosYTCDVTVRM/R2AcdwaNTBqLdrSMS5g1URjKNthcW/QCBt9F7zVXnNMF/UadHA6RoHBZok+U6PG4DBfOqXsflRT3BKcAImDG+fYGrspiUs8II7TR8056nq+1lqJLaSWNsVzXkrNYT7t1flMls1jjZU23WPQq3RbN12Y4DjDAPD4i/oyQullCki4h+t+LZXIKBIBM615cIcMuQQtQs2KRQABowyBh8vJX7KNCAubH+6+//N/vNh43SA7gbDD5v0fWeGj+UXt6K/Zwfu7VwpStbJfEZjiCFvhlQmEK28Qt+I7AAEN88IkAo975mIpvuG/AxRwGc5AZSZSLOuWlA6zAx4RHaIJjRzqqxA2XypIAgxPEIWlTJqtv39jFsFH/rBXHUrJH8zBy0uK0R0vSrw8DCtWYWq+X96ldM23CxITgIJLRjCEpZ9RsJ/P4FjzDQH0/Tw85ELiK/ETRPvewEV7H8kQL1aXZvfs2BP6x1gHDW/kbeyymaaKOv9M+Ct/V8H6JL307QJahPRZPbDLkHAkVUeni8DOWf+YiZcHwzLjCp8vNKOz4MpFqeGA8ImMUYnpcCdR5VtzEY59hGk3JB7YFz9I/GMKEM2fjPiTNkU8Z4iPW6lSYYQH3OyTB+AsnTx6smauyMRFPOCnGrVX8bPxQ1VtC8T378RWOltHd6ggYwxG63VZ6jzkrJtg4mON9HwJ7mrG4sYRRMLEDAEy3MQuDbi2++yO4O58wXFdi6P5s3eTVth948hdi6AwyoPcN5tbrQNkOwBryImRgIpcLbyxYF3EWioAjHans2tUXpEbGUfBh32B4MOb0NotlNaAdGslcsw0FyChJBeDH7u08GylznGd7GgTmnclH1uJIOKxA1YcWdwYxglh7R2HNRToEkrVgt1+5KFHOHa9k7YqtXa1OKeA1JoH/8M9drgtLYcWstwbU7Rhe7zTUnrJoCFF0xptYHMKDLiAGgKCRm3yCO8A9IXsrOOc/ueyR/bAufYew+H9HlMkqj92R6oKBwuOoRwAlvLoyHV3pnMTrxCbcoclFuDGo0UBzS0yhR9m71AlswzxAuWoDRYSwFbg7BHO9qBXl1r8wGdKFWRcsrP4eqOt0okWWFqgqUb0dAwhpRWCxO3ZWlBC2BLT2IpbhDx2CO4QIRWDqVhB4ODjHwV7NXUqClBkdJYhRnRoF/qIjjLgitDstD4vJAru6MeJlI+0aPr4ipsMDDJzB8cwO1BpSRRH/+rcHZJXSHNJxpPighluPr4xipFobJ3BxjIgk5pnKJCEGVF0stzFiYO4KZ9gSVxgCT3KMkroInjia0IjVSCJkPKFp8gBCp7pSFC5Ep7UV0EpBSxk/ldEwcRIalAljhRdrFiSutCoEZHIngrGyWswtFCA4iQJJOxqL5VSVqIFVUoDmepAJTEqOgsvSSXBqJuMb6ygFErbUjFJSdNywhAnA6yxaqJMkqUOzOxRrPawGJRQ2qRq6vIB1wkT327e/+XXHzeb79j+B15s7Cseej4QjuU36ITPAbGLlJEYvAlM3ZjHXH6uYlWwAwwGGUEUyKLXYVj6SWkTmbuagjVMmMqnUhO/4FOY8ZEY84Lr4WWrPtOKSlHqVUcz1NepnTpiGql3M/Gh0iqN4b4/mmqFkS4U03P/7dixEJ4oMTWSmxLX4setY96uKW4Bb3nO4y8q1b0hHS3/FpJxD/2tOYdPDuXYp1/Os25LdR31+Q1zmuoeO2puvfLwcqEi6x6o364rZmi+qaYywPzlMKXClwTu2zrxmiPBQqzW5eYNBcvu11pL7Xu6GMQcsGhCjlI5nSCeuYSP1sEzr/nq9eury+tvvvnDv1/9e3YWubx7w5rgzeYDWwqyT4jDIYKYe8IMPsyK/CqmQYNsBXukxNFFRirKIqOUEAMA/uFMKRlpkA9xy0eQkgt8AiN7NVAcqShWywcpTVsKh9CJlesCRJQZ6YTYUYQOdoBaUbgvs4vfrnWhqT4C4LnnpKSVRwiyLMFGeYQjVoZjGsj8oVhSJnxjLVTqlkiOSgQVC3i5U7FesSx27oeh3GQ9zRAEdo6XjcmgcIh4sIY+y73U0wCrW2izstZZtFqFr1I7Mwk2z0oJEdWHWBa5lkAuagfb0Sl8ywajZOyfQm0yaZj+FOVjuqXLPB8hOpgIILi9EsbYD0A+U1atPevuvNADIK6hFfRUH/pYvFjKX/ZZyBLIhxGSn00rnhxBqCg9td7CSZD4j7xA5qygPzLWVkXOQqZfe0C+ikNQtQUkUqrcPf0OCj3J4X2HOy1nkr6MxNmuh894rH/+5debu1/4CvDF/WuvE0tjiOBNRpyzCk6HKJ8l5INelmA9EYurODTg0ktBsLJ+6I/AnpqC69Bv0VwAyVI9hncubr8jtbr8vuCvRt5CFN30kUkHGFNX3Sn4gJzscsyWtoWUBtsWAdFYjp9oRaMYuwC330lxWqmWOr2LlCncQ/xWaz7F/2hwtcN8HMnzmd3Ov1RCvZ9VXSf0dY7SfigaOzqKnZ+hiR0DAC5ypU2MSZiEQTWh1IAksPYTMmC1W7Y458k02E3fM/an5YGqS+g2TDZBor3ijJJwQZQK5hsvF6+Eb0RdKhRDxB1dlw+FNtzmDQ/cwi/BKgmd680gohFu9lo/4CsE4NXX33zzz/75P+fzAlfr14Sk79/f8DDg1hv537y/e/+OiFM77XjiUDOyHVPHvl0W9mSkZFYpa6QSCDNYGFGUIbYkKIM/IUiEbZkFnDHaHpBEYYnYoYqgkSeKTgmKfJ2NIpdzIpckB8TkSblKUhQKGYrQI2jNQHxNKN6SF6f4kUcLp26yPONn9GQLtJm9k+YV5GCE7pw94jN/g8TEjOJXD19IVUcQDoAgAUk8aUHOBCwwpXog8OP0kEMQR0XY6cHQ7bGrhKRPQpZaRUHwmc1WSRKZlA4+KhAc2fJP3NQTX6iCxNyy00plhjCx8WoYOAmb6Q8iXL+2q3w0QfHJ9El8/BQtCzSJDIrQJ/wm5uaYmmmIj7OpkyUyJWzKPKv+g7xwucN2vzHPa7n333377b/4F/8FhYrR9ciPL6Gt2O3/+lpT/t9+941f4tc1QVaEbuJuQXLI9CEL9eawVNd/+4ecBp9+80ekdkM2xZmOITQusVxapdbmoUIOv2SPOZgiI3fk59QJPBBVdXZ2tDl3uBN4eQeW7ogdfu5KHSRS7ipD4Fx+wHcUVTgMAKZkjtIwZIg5/gEV+4JMzP0X1SMxoJsQ0gPHVT2ur3U6kObGjiHs2M39kJFu6JzuFT0rd8scrkMrL920mjGx4HSVUpEt5WGQuk6X2HUsnFpuWBBtaQn/JRbPtUzo655Qp3usVZDbL+/esfu+JuK8hoaFuTGrx306NnXhBsyEEl/kdeCqm61jcW2L7hr8Pe77FhASU6VW4h1zOPh5WL8DTkihlRWKOMjdffvdt//Nv/mvNPXIvvx8keqONUEsMUDH+//x3/2P//3/+7+/uOBbrShidDQo89ee7yzW+O4Pw65RRW0YEtrqjAWKKiIQErrwB3FG9iT4cVT42RHGQYL+FZG+/JPLgYikZR769fhK+5XyLIXvZF3xICXS2duhv7UV18gGe2fFOLIUqVtliU5KGQRC7qUsChaNFkooGHXklDQm/MJu983ENuYOIQkZlqjoX2pIagRqYQVZa5iXbnuqGIjaSxC6WLTl6NLwdEOJVR8gdEVkbKFPhdSJBIqGIKMwR5tgupBqcHBPUCgdbKwKcqkwcThuJ65NGpowcAQxf+kfa38iLwYqBOqa1rsNPbYy2ZT2T3g4iLxDjvfEsSCHuXYObTs5SjUS6eCZtbVIN9UMEaH0oHJ5WSSUDTdauyyB8lDGP1gaStu68JQ1UIWCx/p9MOQr/l2ur+/vb/7wzVf/9b/+397xzO2eKwPbEFFHdFVs9Lvp+nYZhDQbtQuuBrjbMoO51Rg9SUt48IYMc/8fdMHxcwB2WGKwz4fF/Ak8OIVD4M/DE/PkFP+kMAgcMOKihO50YyAgEy38qAJVE7+GZH+J4pCD+dQQO2Cy5WpcYS/BDP+pcvrHrvcOavMJjuKgqKM4H6zHlN+mfFLD6/TBimxjkH1e3DBF0NbySfQMPfptSXVSQcZQprQ2vKKdxBMOF1mJmsTZoSBEHoXVDlKnUYs+qFTSxzJ2WuxHWBLeO51hO7fu06nyRJxL+5T82t1OR2CgpLPajkNBEx/9UcTAvZkbKyWs2vWcu2/FgU2BggXde8FwFNGzMFGK2HAlCpaCd4XenPxtVGYW9SXdq9eE+AQCFD5cv2FTcL4U9ooNQ1+/+ZxZxxgoQCN+ijqks2IDadgdKRdSOzCpoEimZl1CQdmRCnokziiUsBTJCfzMLIu2Y0KkGSe4kUUFnRUF3imsghTbWLyKMnsLKFaKQTEo+KGQ4hvzMJeQK0xxdQEpWPrAa9ZAGbneTDjxpyhKCcXTJFI6yOqziEJ/oA6vUqkoINWMrtgGNzFUhv9RYwm5/IhEGWFwctqnAgxVokRADpALjgHw1uxvcDEEBGMFVMrwlzJEk06nwaPxhWEKbt45gldBahFqi6k26QamSAKc5hQ+MRuDZHjw9C8aqo1LDSmiknRIqchKYbeE0DMjxK8K7WBlnUnlYpeSmXEUV9AO1bJUAllIdcc1a1Wcal8/8gEvK/PK7/3t3d37D+/WD9d0UzbmYod+fMR2SDwTsA/UkvJzgMSz6DOVKLqpVWCzfMtyI1xE+7lCLAMQXRV45iBfqb7k4NA5/RS7qUdr7NFHak8hWC2RPx1hbKTP51N6IDncLo80viexXw3sTXhKE18i74H762ypsQm7tpVPkLnGZ54AhAot8xrepX1tGpXU4YwWbwfmK7sw6/QWypA7QBoFDnC2ZadGutvouvLDx5GtDofznJqNCJ8v519jxq10vtZqua1dnddy6lg4U1ot4Z912es3z0CI2A1SXqKjRV+rmqhukGQF4QZLfM9MPLfzS93ZicABcj/VqmUm5Ag0dXfWvVoBACzZs9+73UOil3QT+05jiQuRKeFMuY8rAiVg5O7Ni4NiJ7neNlHTzCu+Ffrw+v7+w+X69e2Hd8ySK7hE/uUvhCfr+6+ESawCIRrZJv9IaWuo5wo2TeFBIIBlFRS3SH1J0dkq6+yUyIxoznId9gZO0JNObPSrEvEREYcg0sFXksCU6whiYnZcuumBCWd/vIyN0tmV5YExD29WXLH3qd/v5JGHVlyYe5Jh7nk+O4WwoSp87EBUkVzzV5tHOvO16JYWuiSj+FFUJS2Fr/84l9rW2cEWaTSkKOwKK6pzzOvrwYX0TGzDy64nLLW2MOEI/bNPLLHYJabZc1LJ6WxwJTH7VChJ97Ag2YGmjhQRF1SRsAUBSVqAZ5nSkwLVv0NLqMXXDgnaLD2pJ3qt4E9b39qc0nbkSYbMep4AsQ/IOaCiL6l2kkujbWgtDc4RvetOadFG3ZmbfRgK6ixlU0s15+Cj5xia/scGtXZ7xmm1gbDNnOEQ9hueOEWbRAkwo8aNK0TYvuYVfH/NQN/YBuP68hZMff83GsUauBbjyQoPvsLaMDvOcsDMocoGUe2TV/4xn5b/cMfXKrgIAX6/vn8lh8h7oOr5GA3VzxjiG2EQ60GBcaSInp65dSBzdfetjLn6oVg+o8h40V4rnsdZjUJ1EUDR6CkNhupr7Djk3qEmWni2cj3undKn0JFQF+ZS8Z3OQ31CbRCK/jWkEy/aOOq7eYZVvxVJyG09M9QhU9fwOh3lU9wy9QG/aouJvNW25qtS/iobWz1r/P3StQ5FGonZL/5SzlFpVtbmLFdCPPQScI/LcvIhZtF9WNDLL8PqkRwhg4kIlsFHM/cIWp1ZnD2AB0qXaDuiIApeuAUrRiEcJwzl1s+W/HcsAGAhztWa2DQ+fRqsuLgpEFccpuAGKu5kbv8+FY+ncCXnJUmxlw9E9n7TJ7+8IhhFuOUT1F5q+EEU/HB7efUKIddXfNqJEISARfQEDdovPFgGu8Q8SVbYoMPmk3aIJFUNtwoOrYSVSQq+EoBrvgGqzom9f2S7DpnYwe0eHGUlDY4yUBx2GpXFN7pE63/5cTwnUWFeolexkgVIQjdy14V+RKFz9q/yZsrJMshJGyO6jBzhmxhzCk3lWqXMWfTJOcLXEcgiciqA6RzOhdgSEsdQN5H20JPM4GMSipXL6R6RgFFgxolThoQUciSsmsvlDZUIy/8r1spzyAHd4fLwZOcpzFLI7jECFRdjHlEZGzC+QqZDKBLRCOTD3AYlm79QLekTP24xhsMuKRLIxlcyskXFMD5Kk7adpq6raA/iX46ASwF0Us26IaWhSa5gap6mSHfWOzZ84etyxT79DwzLP9xqiOBncde3Hzb+Ani8tqtLQT5IhuMEQDNUTFYrk210dah9u7NYGSogonzGn+gCTz5VpgRc+DaIxkjkzSS6P5L09TEcb+kwUTEUyocgC5cClue6cO4YJ/v+YEbH4bKbGjMyO4ftxtLYU3xdPblZL+Yb3GqFgs9iBosQo50sQt0NqVZ8O+UpTNsu1b0CtEnp4Z1tpkRNzYnTAGDimGLewqXl9C5ALX4r0KNt3yzbsi0QXbkQv0SK8LZw2zLenaDeTYd2XD7BdifwKcamtQLL+deYS+ullvSc0rvWbK37Dm0pWq/O+WbvJM1VU5HxBR+9LsncOl86vdu892Q/O+68YmaaRf+ejWZOmhlfoTH5fqnNv93eyUfEAXtVh7tACEzlFqPbQC51qCAU3bPFRgz4xzweWT1t4Nb+ioBjvdI++vcPHzQFeaUQ7P7+a7CY/hcOgOAtMqdQBrjmuoCo1ysksZWKDyRKJ8H4fipJff0UVvARps7rX4UhOAeREKgCrPyFAe0HLzxxTkboC7KQfSEI/xI++itCUlCo0ph7M5WFeNKd0mt09WJ0ztfynoNL+EiIpACRbPGQvQo9vU88FeLd+mVjKpV8jc0EkSnEeQqIVKrDHpZPKJQOnOw8HjVInmR7OlkFzqvUaeH6kP7hVcZ+YK+lrflwTvw1mBErOc1Sxs4h3nqIZ4VnK5VPMPuBdGQ7uM0K2615QqAexbVgo6e8EerYV1HJwrFv5B2eX2kMEPbyQ7qeKwUDiGaX8a0HC3aYa0Weyn4rnCGwDjRWgleiat5cJ5pVC3H9UjN8/wEhH6RouEvPavDoG+vOmnhy+moBOC6356kkxKlhQGbPp+9a8ARJuom91V9d0rbprF/KltT2SEoLe0aytPHmmrG0ABTQ4h36w2dDNH1x8VqnDVtuvdLCnM3D5nJ1dfl68+HVpb6I/I4HhPoEMsG6v0+c9psSfzEzQzGVVzlQXAfnKOEsCN9CJqD3rmLrO11YrjUBcZfezWD2YXXBhztYGnTNpkMrNiOi992/uWfvIF2XbjcblGHkwG4BH3TR8JA1qXD5U6ofSSzSkVmpJpWmj6l3DhO3xXymJFBBy5WZYrITPPwzRTJfWlNJ80GMER4Gmqv47k8VTu1/gdMxef8q+MXJTggckEDIfPb7XW5vy39Sc6MewrmV1ULmpbf4LQQv4kLiqOLgwImnOv4q9qCk5SFIekr2w3ipoTMDgBmqw4rCvMN47Ehd3BWJYzTQHTU4o794D0S7PUnrHWuQaqoO3bmgcyfnabqCfx7Ar66uWHXDd7m4xxNREcQonvZSAX4ZDCjOhHhzz6oAfhVb+BZPQjcHygT2kRMBFsgk6ZQCGpMkdCIQ37qZ1FOEoZXBCGKVAAVXfBBA93l9mxWlFP/BV8MRBx4epaCh7OGQFjkoU8p6yVQkZRxiNKsU+EiWFopJwkJpYtJAEhPhZxusqSUxIelQyqZLtDQQZhyAY5pZbkS6ilKoZDR5UCQwt3ZWPXwqBipUSAox2pizf6WPjtAjKB29Zbg4ki48SaUi/aokMzNOiMU5EpkRROxRHz9KCykfIs/+EW+VODy1D9UaLDDIMhG/kmzfQuxC+RkIJWJhAUWWvSI0g8VFRRk30DOfIA/6oFDLwJPWUhCk0NStptiojF9h4TkIQ33lKOVIvjUzmOgQjn+jwYXOYRNnJJiPC22+KJJDMk+yWmEv7gr9VWmo4IZHym1JGoMjWoSDbx9Zf89+S/vQX6KlVhxJUwgzyK1AYNmuBuwu4udoYbAV1HhAhwYt7lwodHV3xfM/kPxAcH2tvi/T3YA7ASHeemYtRJT0saLK6n9oDaq8JKP09oCmHZDhIYzMZTUastcMCjSGxT9AUJuaUi8AZC9LTVj6NeTN9TUjorARa+S03tHLCq1Xes48Kw+oOboTlYpK1XeutePV06l8WfNV/V3lUcL3B+r+cPV9agb7MOLyse+hi8zYMTcOC5Ksb41Zz16PcR2HTekQ2DX/cfo+NPA9ztOl9egHNxpdxg/w+Q4q9V29A+HuqLv6eYmE2v/qL2M0U3IXtaXgWPPNzZKLLPXE3fLuG+6rD5c/EovcvGN2bf3q+tXvv7+/2HzOgODikhluT2aDs/F8PDOafH6UlwNvWbNDZTONKFbMa0r79W++/SIxC7rne7Hcvf21WmGkY3X5Xrfq+F4p852ieB80utNzyxdbljjzD0T+eCXgFVuRaFQCLidFmFIA1RQO8ON7x8XlL7qB3H3lOV92KQebr59KgDW1Ag/MjwIAaFbWFhkrz+WbUGjGFyKzjFZD2qTD/C4umNl1FKcfgcSRhL7CS0znHe7JFsHaFx84O+UDEj7IhEA8kZAh+lqtg6GkgWzyYwR6k83kHF8Y0MQnD2/MDbUTPq7RQinDpUeGI+qNXSV8yZU+li59AQBBOjzJq8Yvrn4VH9WLHhF1fCTL+Dq/Vlo1Cyah4qW+IaBy40iK4UmfND2vmrW2fqCh9OoSWeErFoJfW2LFRxqiG/WIJsjqaQ6Zp8PNR2m4/mr+SrtNxhoSAsSEuV5p/bqkXPK0hwXw1BE+hz+NDf9kP1tPr9H36nxchmT+4yW0vfyzrNQe+ZpQl83Jn3gdbuFVK8vcP8V2uqqEY3Vj98swhdNq7aqR1aVbqUkvLm+ESZqDyXkHu86AGPzNx8Wizbj8rh54fgVfEPgv4eZjDTjRiYBy/Ydq85XSRpNYMdaYg3V31BZ1waY8OIoXf1V5WnGnb0SALuRQTi0WCulhDygRJRbsLPbq97WpVIjV5O8vfsPXNP2bDzc//yVGQUJRY6RV6IvOCPtNBsWXHPgeNmmoNeVPW6XfvONdpavrh6++esvHilGVCwp146cKyJQUDqfE2bkEdLrMYi6PT/rkicvYjypgaq38GP5+sJCipvRMDlu95N40gpOtcPPo7AEcVZdAw3yHeYpUe/8d0fwUgid4Tklf0hJwY/bxCPflc/9B3D0l61VP5ixJx3wC8LjVnq3Y83fUI3vyOpNt88CLahqjxtQWqOMMLnmjNLPAYFizHTANKZYTU4/clX///YY5wtfXdz///MvFhsU/DAB+5tmAww9ioc8V7hBeEzwp/Emhvy8qCjM4CCrM2JkkQmkFDTlAAIdIQ9TQ6LLlv6yqsESoAEMFxJDsCHq5vrq+/uzt299+/0BQErP+igYUD5iB8HXf8M9GKmmHwsxqdYtejonAACunQVAWGQIarolQyzYcRfJBXnDj6TcMTbB4AiCzVC69CeZIaqmGaOwA/a616eHq3hOWSSUFr1rsAQ8kKxqDAlYxBMIEoq88FSx3EZNBqb8VIZGFIVKhMM5ipthwKStfBJxQWDqtWERR9JH+/OefKk0cUAQafUyNGmaxk1e9i79wTMeZjHmCoxpF8/fSlkAMfG3tap6mgq+XsgC7kTCVhF04XJGlpwmQ6LA7pD+w+AS7GACojUkuZ1nikD0GANIldFDAl/gkzNAHGsHlT2si3bQFJ9Klg01lBQyakwSHVXAuVYArHD/vIt513Et9KazMtqMOOl0S1GI1YwPBQ0okjOk2IOkcIkhHcLFJhqtBqekJh7+Eb5ZWVSBYEdHqX1QTMAF1CN8ZJHX4KC9s40CkqpX+HMDJu2Xq43q4nwE/iKgFG1WAHwTqly7GGrybD+/u7hj60ujWPHdjHKBrRa6VUCCfpSplHEk/K0Fa3FSoooDBnckFtQdBLvgK+IcPasnCExRk6sU1woAZvfzQhskIwYWlDkugv756DxZNnsVZQqLetDZJGiHIki1UKY6kXU4E8Hw+hQdwdXL6Yu5ROxV6DQh+ieuunCuen3iyuHHCD7XLJ1CmwKluqmJdD64m9++vEBcmD6h2Lo4cusDteWwZBaJauG5Mx3rE5otSuv7vqUpDVvNvCicBvvhOlh5acEBDWiR6G/+2voLtFHyJ0MsflmBtx5nSYcqm/eoXPYJhanI5G/r5Tk057fV+jV3ERJc8jb9+dfX+5j2RM3DW2xj3GjgICtpZ70sQsWKuV31bZ5Xoj5O/Cxsgog2HILr5s3zH3wcQIVnhmYaIjpnXUI7Il/3UuX0rBoi1yGLkRQmi05r/hz/+8e2//tf/6uY9A4DN5g4d6M56hiDFFOjRx4EgRDoy88aZiUBeHvD2LGyww1JpnYndNAF8cUVE6ElfU5lWHAjZ48PGwhEmiyIE0T4krEciaiHSFQQ9Hy6IpdjGhzenr1baxgdZ3hhHk5FJ7sWadCxrjk1+gHvbH+tjfFZWfHh4eLVa6cznUZl5lbbsvM6mQMHfHLicrtZsE0QpOK9XLCIHf41FUN2C6U2EgNwRqpH28EP6SE84eKOh8IbS8gYWSXNdqMHffIk+es/BpcYMb8jqwLeleAB82c5SbLnl4uZi8w0zuQweiarRTR95pUJhtfmD7bLVmz8IfsHmUcUD4Q1zu5ddWtKtMdJGZ/DDRtWa7BUEuWIiD2d85OKBG0sE52s9buKJR2zSv75ZmU/CeXizRs/NG3+G4jNhMotPE334YsXDrgfS6P9GoyBsYeoazsi1bn5bA9/iN+mJXRfy/HvrjIayhWXrqzXWUZv4R/XiZyOCoDZ+c5uh7aktxUy27ArrwJdneODGGZ+kthTtLepRvhW+7dXWnFHLtOGIp93jPBFOn+YpmGLlaNVyO085okfIn7Qc8cHDFzwTkETCaFoRe2xdPHypF/xf3X71FY8vtC2/xiBUu7obIuhj+dmdBm/pUPSupAaG0cnJ6zLxwDsP6txxmQBgJi6KlDutiBiD6hpAq2MJopsBOZb/XTBU8wUBBfTxYHDfi8sKbXXVuN/QvDWAvuDqBBOpqWuSNXJCGnFE2sk4dbOYFfCIyf2u3lP3iBYeZh5R4a2sWh1GSMLbIwX7g6LqOMvkir8aVgCneS/SeYJ8vxoMZkt0mxC7M3h8X6Y+m8pt/YKUo7zpIQUxiKfKW9bq0NxdHvEI9R9VZLEuZJMtDnoaPYpCn0Ci+PxjtLV/ldvNwtIGReaM7thukGIbrAm1dbPVbZQfbugbDQP0nS8tyeWWDTjd0iEmCPBAwOx0oxdbqHRES4+0z5p/FdBMFBAoAEhomYLAHajZGEPSSEibpCIKajPSdBP//O0XX37xlYthz+CBRcO8RqlyK6OzBgOa7IQzChCzKEx0qHp1r2UDDnNZ6REBLmcNEoQPD8tXIEUAoYEBMaiCZqaBFfsQTpFOqwsUKmmA0QXKetQZIXXgmDaCM4fOKg2590kfQ9LggfDLQTwRTw4ZRasAnbDPQwsCR4X+jooc/LH0gglsBXAMFQg3NQiJMM67VcYAQIMcBY4arjiocljJ3k4EWFyc7Z8SaG4uNl+kyDv8I54aAJhWQyP42CeEtrJXgweF47j65mHztR4vOKBUQEz0RozLmYVYDoIV7DIYQFvYCqIBj4dMsjS84RCZIBha3P7hYSPaNBwK/Puv5BMhhMduHlgKQogviYxbaAvvL+7/oMcXvGhLcE+zTXw8WALHfiMk1QCAhSUK30n/7ndMGQYwJFBAn4J7BlfUF2cPdfQ2qjWXLBbSaMWaBgkeWuThkELzYpfrOlpgqvdokxoAYLv8w8ewVI+Jj4cN8rnqiFan9qmBqAerUb/oxgoiQnaGAeiD85kOF060ZC3U8c45jrjTgJZ2e6/Q3+3EtWaPMSCRDpalukaWWz596gv1KS32e7jlSSCPUhiFrBmZIA4v0/LTodzwiC6szqzrQ3Ty6KaBGf01LiB+sqVrg0YdFDBqpL2BDR1l+fpjZqIASpVaKgby3IazrzZozkHPlcCEEeLSudagV3DOvDQPuKpfmtLPQl91rFMcY3wNW/3d3/z9rgKp3jF+dOzRI8AhzZQTeKPE+wNHxpToELrvosGQTzDZXS9dPZE/6rkxbrvij/F4Uljxdmixi89rvYf+r8um0/tRtfyiFsbbu7Exaw9ZqRVA3PNS1zhySrfeFFPTdlfv3n/49bffX12/+eW3X7XPpm/1uken+Fh3dIVNnDzz5zu1ixGkeIsbOCv+kZsiaUUhChoU6xsuDhpIgGNi4cZBsdYTxzpyysWEtw5AWF8SqQjbN36CEI8SPM+XifnN5UJLYxtJdwQsfcww4iRH82iICJtoVqQ4sp7WC0uJ+2WplMnnNMbI0VKMBHASUZqtFqZGC7IlpQNS4OIAZ55sSB9JL/hBxTnFf5mP4BoJMCpIjxQ0Zevo0NwsC1cpGJJ0nb2og7Q8r7QW1eicJHKtUPOzB+y98GFN6/FZ2C4+eED8ExXtJrhFxJlGGkSfxeesRYl0jEMkPevW84zgHgN0oxQ9xBCtRyCaAnc03KOqLLVd4MeoRpp4jJF8iJ4xia6VV4q8/ejjXo9TYnyYI3vidX+HIeQSTcKH3aLQmbCes+0Nq4OPxi2ShZ48DPFIJvgnbfFYjDYVwauugQs/YRJ5O+KXXMFVim4RhRPaWqIfaukxlLQNWmF6LBo8ae3hZ86kmSBneGDN1f5pmWoJHhvD02MYjQD1OALNFdgr+Fab8eMCfeGL1L1E6OGf9rMiJOelfA8D1LtSa3F/iRaUuhI/ugP5MvFO1xUGVFrZpvFD9K5A8FmQaJrqd+ASvaOPtI1aoDBaHZjqvT7iOWJIRTUe9TxcXX75x+++85gNFI3YbUumkLYMdb8Tueb7k8bmNn3q8Ps42j2dmvyz2Cw59rh6L2FbcNQZ8Rs9aNmxXJ/lmMskb8NyCwEp/wq/eLsmTp7vV4D8gCdq4prmI0rvaumgHrd6aPOdOuvyJ2PRU8LBQQW5a0NsdnV8v1YTNcCtagt1EdKuGi3HDzVHLdiJyXLkAeZSPw3IXmA2avqJ6/sx/HaQibWXdNtO990+zwitKSSs5vueugHrbizj+CV0YmU3aQF0uyYYSrdz0NzgKHGbV2QAE9CQIw6+u4PkzTTNjaIoET9RQ6mEWAhNxI5bBUAuDyQ06Sj+Kf5QHLP2SwkhxSzETRGMdASZH00BajcVCLVEgAMxpO0B8VMilFEBkRNHCBKlWWE88ZYKpQ3/FGY5tlFAQ5owybSGW65pEzX4JpJ9dVpmcnDWbwrHofFfYCruSRDF9GGpTJTzpZIElzSY4Es3FJK6QSv+wgHdkIRv6UzlwidC+RAUOJzFByrHXqIstIJF1rYLR/ztB3FDT1pOBJFwIOQVH+tJFSht3aKaQqhkhXVqN4ovgYfOOEb4OQguaVVtsTenqaaou8AnLEZr4mDJMoeoO08dozNbRqqNIz30D48ZHytEDISmovugnoahioRyUn3xAjxWCUe2q2bDz4KproOb8MUp6kI+tXXCST4RLUIYFQgiDU3AWdXostDf0rT9lWgVjmsYIL/xDMeqYi9p4OAQ0FMIE9lo6U7LD2GyakIjkexbtBcnqQ2S5PIbCwIhd+APrc21NSStkGxTUmXSLPKRkTr86cA3OEqyA4EzWiYa2ekSdNI0QU4LBQKwgm0UBIMsC5YentiwDWM5XygkMVMlIUVuTgTPnJv67fSdwrCcJWjTDM4l+3rg7PfdPbes4e/Ot6Fw5fjqeTHzBCCqcKjU6u47gdrxx913ImjhtXQwIA7GNfzp06FWbexz1LLzk254eLJWuCvcMxU8g3gJ5zkdnmk17+uZWbqpljIY2Q94TFQd91x1EpfGvVu3d6XYi291c3P34cPt5fr6p7/85HiOJqDbPXdwxdMEDY5fqm4makWzYgiObseaplXsxZwh63SZbv6C+cRY8b++5C0C4Sg6DE3UyBR3kGWrcS9gCO1SMVppHZCiFIUmYaWDA2gkKyySbJUCIeZgxTAyP5cm2n+d9xDelVLhwE16Cl/SWTEizLeGSPPgo1jFEhW/bj4nMmPVjShtnSMZxhis9+A9xM8dTxOZEY2ZCp7ENHpa0lma+QsH/bzcgoU3X+KjNKGrl1yR7slg8UGrL3Xm6YpiXMMV5wH/SlPOrFfJ09WWC07o36ctsixXi8jFOey1H1S/Wc9Ih/fEv4Pb9s7n2UvhSUsM3UKHhB36JG8Xb2j/eHTYvO34R4UrKMcK10tAVF94svJJtlF1JxxZLW4JXumTSwOHs4NmJtrdAlR3cGa3GcY7LIUHTlrt3PjiozqSdPB5IBBw+19RuOA6s1QJWupO7UTvUcRuOUmf5IdUd+KjpVbqHdYHeLRhaiTaqlsjK4vgA6akxKjAcq2bawtN3cKj9Uof9E+6+eFStBN4oo/qEf3tJaVcd1iqlMyU292JOalL86cRmKoCo+XG8Gr0v/psuDq0x5+6VjBQ1TJ9vTmgfk4q9Xf7Vn5g3ZEfpFg3fIj/tVcS7Vw+6ddjSMYW6pja4WrzTpb4aiDYwz17gP7pT3/010LEyLrYrKRmnQ5bKsjUTH9t4lQaxfc+ZDXGVJrszWqU8NT8Q2h7D2ohtXpzWmVX5N+arpeW53Z1fc10R9opnWtLp3B6es9mDucwy16F+ADTa0+MkWwrH6MZg+lq4qvtWOEYrFRLJGo9Fqg9xvEZwYpxRaeBfQVeEvZfyZ0TQw9sdeCQYCL/7P28n4K9XlQykXDU5Nu988quV2y8vb7fsLW/pt6ZP9Sv4LpHyddkfb+Czndf4LpVgwOTnIaI2UVPA7OW95I1KookdCXg1QKliVlTtAFQUQMwChSSwE3ogCHgesjnh1QWkqPyNFCgBDKwAEkvcRU4cMnH6CAou4LAsTARCS0KjaisYOZKWkLMXudSRAIEC41S0YjI6CYJPoYbtwJacVGLB0TBCQRSmK/oMrEOHLEyjuWLpeASaPbOdNkA9s8JXxJVi0Wi6AMzEp3vXEIR2C4qWM5lmPQXg/BMYkU+jBWW08iLw0VJ+9BJ/FWaMCrEkBwaJ48FOcjhjZCutAQIp4PL0NAtJLvU1QMOQaQbmPTMpKRDCj/ipjKTZqFZR8NDVlfkQuOLmL/wpNFCAfFT+F54Fj4k1AqSP4LEhbUC5i3OUtg4xT/BXwgFSS5Oh3SJMsEyXCDS8pdB0d90ToOu8GVSi9iafIwB7GLxNnkS4p9gZCxdDNyNyal2dKhvA/UvP4LYkEipsnQN4YpRDpX4ghAcCPGjpkEQO0HFIq5MpOk3XLX442klOPq2gMql6egxBR9FngYi4XwczQOLK0WVv9MRnIOK9K7kIQuqxRrupN0jIw+MGDNrDLa/lqu/++t/EPX8zL35I3j02KHSQvcpRqPcAcZILkoPeeO75l+PDhM87BjUQE0T6WntW56+xOuu9ghHK/0RhBYRraUj+oQfph1YuG1JRE1tQRoWj+gzRBnPT9ZeVmNXg8JXulOOXLU6qOVy5yfeFiJ3z4eL335/f3v34fry9c+//MxyoDWLgb3cJl4YjTUGaxYeaK5RM46sRvBMHqGV0jrrk5yUxvJi7sSsJDa+XzllmOFl0Lp5+94PFTf4u8RzzRMA9utkd3lx0xN+bvNx+5e2ur/n63+ELmFgOCrOrY9TqQMHU8U9IEdejv9aqgSx73UKyoAaOEMS5dI79Ms3nZxNpCgWh4Or0McmJqpcXP0WEsFkkVFDXoW2IClOy6krWzqq5NjMJ4TaFt0si1KSpP8VqGQCnotCHxVOHQW/jwC40Pbk9tHqXOAXZIp6vHMzC5LEvMZ2Qcukz6VB6skI3ukcvF0e1gBXm+vgHhwIoHINmFM/T7ZLFyGbOlhwrg9hOJ94KqP3duD4Buap6QWDRCeObmbCzc8NUln60RvMEPPmj98YIADfsE0v/ZeDawc7CHE1gD1DoHhmwtmG6QrAtcLPN7hiaDlTPHvR/ki6hnTXGb+MYQ7V1Yb5Cvhe8kGSy6vrf/ZXf5IoDzY0DvAgwRcMuyfpWjzQN2G/XHhxP9ozVfFA777p9ulTKR8mktsXen+UV0OrZh5NdCjttHnJRfKokieQPJCTdg36Pknql/Zz+ygT15Md3gFAZFMzEjwK3Eejp6eZ8Wpt5ZQnnt6A56dBuBTv7eG0liQgdV08ocWVGq2mS/SCqjtqF5lzRJya44sbpZ7bf/nlVx9uP2gF8BU7oxOAbx42CugJ3Lm/MiTghu1FEXyk07dzvZnKRD2P9e+4wTtwJ4gnrVs/e9po7xrd+OMGH28uCpObdyxoYXgAphcnAL8mvV693mw+/PDDX9jvQ+t/uJCwhsCzetYbtqE/dV7XV9gTBisE6JpEJBO6MpjRc8x047ELe36EUPFL5h/xWMetvZx3oqDqCCuSco0LrQfiZEvm4QBHWI6hzM769JjVmUxYw5yOgrgDGTCQmlUNwsAuzEpiwLbAlQiGpEpCwHB9FlYIzChD+1yBFrTCrY8S5XEeZ1Lh18wqcD9ZC80WJEOMOKFIn0nkQqGtamXSXLc0rJxUkdsZoPxrV6KRHiHwD3A0HuGGLNspPcMWnV3g1pualM0wgyAKSqWzbNUXWRVEB0soqU4CM/RzT+Ut49evXr/mg32wvb/SM0A6rAb8fnUfHKX9TEYDAF0ltM9VCve9yIqtS6HiPeDYdYo3pPPSJr1nr6kH7V5F2svoNH1AkgtF0pNJh6ScL23FH3WC9Pl4bh6oWlZOjqm4vOvNcWk474TcUL8IgK8I7sqhbuTz9eLYJkQ9XfmLg4t4Z3WMfMjKvEXSKqRjzfpXLC9GeBb3h2fAjkTJFvrALNmcaHnGFT2X7/8bcUDNrTcuN+NW+q7yWinzHGod2j1ukz7FV8WNBdJybzt5QApJSbS0fUhry3L/1Hb1NArpPZCkBoDzQu3yfV60Obo3F+h7XMSPGXZBJYPvfb56pXsp4f7rNyxqt0AvU9DgADTf1H07F2vm8j3fzwaD3zF793D5F86UsnbHQT+U3Nrv+dKwJFz9LJzbr8X08i96AqAUknXWQ/97xiKaEbx8+O79+3fri58o8SsBekShuT1kSs9QKwKeZKoZqdhaRUIWpUMhUDlyuCN28BQHkyttpECOdKEaTURcPsDMsgQOv9a0QLPAEJuEghN87BWTikwwx3yy3h7r2IftHb3wM/dIV+dWrnHDgkhm7Kxf1kcSstSE03ILZBc7GUxydRk/nO0Kt0nF4GJCxUScklBDzaFjn8oE7UqCJPI9aN8r2b5kF5jBVwn9V3loWTADY3AOwkxOoVbk0/zZNWiPIxkLpaRGmC82hichpYmip4eCFEc3Sm3Bo3kzyCVd0xdL83HwTUacow8CDjcqIekqzAgAmAgg1s7kxUlqkFj92m5TF6YH8fGwt2/efPX1V3onfHNHgB/PDbwIirTDfS0XgtacrZJ7t/tiqk7xElBKE9BrdY97KtcTgb3IUGqtdF+453qyuWNTLO0QesnuR2GAvOeqjMTkOYyeLB4viN1p5q/59XV+nMvzgz6+zp0P3RTUKqJBjTknUKIdj5W7HZdKrxj2kBGRGCVw6j49pMfIPI7cuk7t3WQaO1lxZEjjlOUOKH4mkdlBbfDSJwD9Clkuu8E8GqOG89EA4aNwVqj7HJQOfY5m5IkZVe2sk7TQhECbQo6OEOeO9UlSo0bMSFqoVL6JilMXAARfrC5HSivwtTM2d5vf75hg00Q/t1WCfm2znaIR34u1OD8esEPhxTy6C7Nv4Z0e9PNVUfV6YgWY8N4hetD9eZHRX+G9Z6N0hgrsKc6tnwm82M4b/SRbsQN3du1BdH+13ry/ubvbbC4vr7iXs6RIhIEEy6S1JMl/9mGKTWSt4wqzFMfelT6hQpQOcTNQaKIxeiQyzthvUaErrEFik7ll/uaMFcBr1I7BMJWwQiUKpactzuT5t2CIQ3aE0nNHJg4c8e6OKItzVQIgRFWwRNTnZmACFS4ZJf92XsiQ/NtTZEJiV2+pAludJKCDdsxTKgagbtR9zKifqpl1+uyZ6ikyzmOIUhRPXRkqg6L557YqXpGm0Cyi2dnE6FdhTWoXwSx8B47RaJ+ejlfLyQBFUWq3AvnRnAfflBrHHUyis5KK/LXaJ14WVhslWt98eM9L1XobWL3a1wQv+KGnMwZgvh/5iNH7Qur9UoPBf3ReqQR7GaWLQgT9JtT1BAhDEgQKZ7X5wJXn8hXRv/r+9fUVFw4vHbR+RrGhWVkJHhwzRQPMc/YRPECdcbhSVH2VxMhGeQU+J3fzwMCrmfhgv44zuLoYrDTK8ga/VHSPQfvOwKmfCdTjpFq5KXiNs0O6tpL00O45TkfWpBIVl/sKMPYEoy7eKy0p+Y2Lbtw/zarG6dLZY3d/EmWCB9D845rRlWb87loSaK3cGl5XU4upu9cYdBms2BJCQkHxO4Bnjzpu/sHN9/KUjDtrUVJ3UmRGIY/RCckVbHP/1PQdyjEGEAA8zeQpZuderqftZqq0Cim+/F6Q+K9gnTs6dAQAxrn+MVvGp0h/DJngenU/ZExbClkv87HTOff81Y+b1S+X7HvIcflOa4A2fNSJrIYBDhJkIHIlUEgc8Stozskw8i7NJ6FLmHVTkdFtRS6AJYwVkQiz4DtRcmmuN74PABRcdi9BwTc6c8hlfYi0CdHBKqsRvyEslLdVZgqjokPIztgSITk+oigBKowoDQ4Fk4Qpg0i1PDzcShLcPyFJ59xYAgJghFzsSrkyPjoIJF0mF/NbA5kvZvckmiIeHjtqXJdnpqGPHB2+DGKXAoQsECRNqeBTn2tp0YqNm2nhmmqxUHcUzdy/5XZSK/FJcq7f0CD0yWnzDQ4FOxJ1LQhb/2k0rKML6zjTU+gvFCQG6jWOpm2NaBKT+zcKwflzOE5CTd/O0UlJmDo0dxaGkhFLeMRFE/Q8u9OsAO/xsG7Qned+c3/p2F6vACFYqwE9Lw/ze9YT+nmCdNM2RBYNlg0Xd0EsiLNmAJJQWaRlPq5d1IwHht8jhyeNohKypPDZcAsDlLBh6gMcS8l5/U7GFVJlBB8YJeUabqTxU+Cc7q49LvUw6BK75i2KRhi1eYgu4f44wyfqrWSnOG+Vq5Y1Qay7Hw2maSET6DuDwzPtWoYpRuHnKF1SL1N8atpiO4lsaP6ddExiPNlTCoMRDTRkHwH3QUWrPniX3BFY7CJuf1y88WJ03d/KE1IOvFdaV0kslF3jRzo4k+ZvIGUhzwVoNe8Qu4BoO8qAlbI2gVMKC9qOGHfSxJubuPbuiXduNX8fi3bhAovVxqG/IiIigrQ7j+/TFmThiij0z4d+8n8FGBySJm0IFTgCk6S46IdnDWAgiH2EeKpw5dnDK2l1T5SADdz7E0dzgZ8JBQyW3a/lCEsylcmHGPhAkm1Rxjg6SQ1+E5XJ0t0A9IKpRDoC6LMgYuoSM4q0AAVBcCMkfhZpgLEKVJwy2Co7pxDJuVBTwiKbcP3DCawEyTyULSxDiYQyQDRBwUy5zMVMeionbSqESBbNnA0Z+Zwkjgm2ABVIRSOYUdRHdl2oH3J6ZxNYI6OYD6cIAcOfRumIetlexhqEHqC7KE49rF6mYHf8lbIzk86lMQmuuoxKSChSXRwBZsbuGMrw33Vvr4RrgJYj+ENnPKFruJ4sJ+dysdVWn1DlEssyck0IIsIUmnM9UCfT4Qi+CLQ21p9iyb1kxoDrAt8Mhh2v8awvNlxCHLFrhj86KIposx9OcJMeoRg/zgR3krLYZQVMIuChOaLAYj2Rxgb829zeXl0p0ri9vdUQwEB7O1gl68wkpBxwDpYHMDiTLvBAqbKMu7/bG1ZuPLmZZf76peC4RzDcX/XjatPjVtnaOKiHeGCGdwB+SD16gtNS97TPBGqGqtQ6T20678tAv6DJBWY9TqpRpuA1TptupY+PmwdKt4wqSKvJOM+KhOQSnD7FwTku/BwR9zXMWisalAUAQkRWsEWtV225UF79U0ku7tiZT/f0oOJxrGRd4YN0lt+ICrymuNTssKTwTffoCCq4a5YCiwgAxIB1Z42AMt0/gXLzB88nJu3C245DIg0gaIkVmIHzzbirEd2F8zRkMUjBgvYiV+8QJ+tDJu7oup8j9X51d3fHaiLWD2xW91/xWVBSDh6CSlI5oEFDPay4Zw8TCNmFXeLF+Z4nBkA0By9hVloojg70RQJCkssfsekBzGCn4mi3tu7+rXRa8zVTFShtg6yo4RIV+sQ5z/2HCminbxhnHCTDJvDjzC7vUs3z3CritUa9dFFWkFuQCjIVCSIe9ko3jnzQr05pqyVY7OgiueFhsMHHD7DrZAlLaj68VWL1u3Dqg735Kdau9kYrRfHdAH2pQAcMfOBt8wm4LLazKNMOMywG+WPilvBVoKTryzP9ogFHTVBmWypaQZvaiSE8dcEuSUn4Kg0Py/b6eYsa1AW740PHMxmhmwOJ7jCEAkTG85wo0jOHzD/8mFf2C5qUCwM6XkplCfxG2sXWcBPvBuSnGehmBv76BC0QDRPEJEyay/8PtL2Utx/IlHqxhhnKgJm25JYMlX2i72+IxVsBJIyzANmfwEmijzpMzJrrPX4ic8HVrR5KW2LQID2i08rdOvx8hq9taL7fLOzt8CQjeD6KrLd4H+5Yka9ORmW4plwPmsjXIa66wkjjDEh+GHEzWDo4C0d0ViygrBV0mUY4F3ffCjiMOgIxqS9O5ZiMK8aQg02hXZKYut+FRdmjSzjtg3MKKVMWhX7LLSr3r2JYDRnehVXvBTElavxhWZ3vekA0O7eiGsHp5Zo3pO5ZKDhoMygMJDR3o4Zw3ns15+WYNdXytLVLGvu5xIOe5KcjVM85/072lII1RtTWWkE/J84eONgDgy5X+NVtsU4XhDYRaJzjiH6bc8f6neG6Vc2iWq3MlAOEY4K4B+TrT0BNFOzyWaGA7uZxVw40yhRB6IgfzrDTdU63bRVza9dzeacDk3PwDBIBS577feJUcJXnT2GBVwvw5GF9d8s2ghecgbHuSPTITMSyR6z1JMJjAL2oIHTpby6sVdIv6xGStqCLyOiitFViR8IDl8RS5Ea1AKUliLOtNUEUJ7jlGcP8IyUMa2vK5HfRStmEEmytBv420DcpQYwVJ1OZjfijKdE2CNJbMnLdIDFYGz/xTtIT77CEIgkTBr+BGNJFGUf+BdDDS3RGosg2mlvFS8orC2GwFTYZs4pWU8qMEMKUlIdtvdPCSofxYKti/xmgwi5BSh5PSIGZ6fUrr4ISBanYyOKSWQve6WNyQHEAL2klhJvLct5V0EGtjw3veCCgSCs+yaySf4QNls76z8k8U8ZZpzs0sqI1nglNB3/adqonyviHqWozakJagSfmAZEcFv8kLHOK0UDHAAL3FUshyBeS9vr0eh5opRg7ckr+w93m/o4Hd6zi0+A7acaPidQJzcQFWV9lytEHisr1Z1ZiwpFQAKlYjweRVHWwVF5YkgjyGrJ7OuTtTnemONgDIzW6mCfNx83EJ7WEQ5gtkZraZW620QtE+DwaUJiflOzsObZXxG/7l4APlmoGnYs7ex47FZft/TRZOpbdZtMhOmzjPSw/ls5DvkvypfFS+6Rnjozg9e2KVnc4+m1zV3v3rospg/rqdHZM4YNh63X9i9u9z7OXoZBR3AuLSEuamXVngUaOwoGySI8gCZTUFn/dwjkTmmhXotXNu3fv3ym8EBZxhxL88ZxBQwKdtVM4JI5i8LO+QsAkJQuOY6cR1gF4dlKvLEdgw0AlU6XtBRlyiIN5mlsMZgThmYbOHjAgO9NayUSFmmnwI1lKKwqJmU40DM7VWdunBk8tqwjaxF/tRE6oqARxqTxizoaoHhV0JYg9EFSGU5p1CBxprrjIZ3xlfRJOYOZzpxtWQyV4wm9tEQS+lXVdOurIGqb6qiEBHzvXWnXcCmZsNUvtZ91Uv8GZs7eRDZ0FB8eYxauChB+wS1+uACf7SlbQctwSet6IOgKOH9Qu1R4k3fUY9VWdc53K29K/alHFn0k3+5Z6TDWbLLLPo6Y4VxqGdEFCc/O3/mFF4pM9Q3vOcPsH6eiTdZAU6ZZx9NUOeUA+YXPeJDe37dTXs/dyvcgbwceL+BmiX15e0x5YCnR/f/fNH756+8XbDa/+04j5djbXHCGnyrCfu85PQ4orEyAO0m5anCOrvI70E5nhGUE64icwEygKODM/8J0y22cxC8lEYsh5Am1v8PK7TGDyrIPDHl4kU+3TPl6EvRCJNsahWj7xQe3uWAHJn//UNaHEYDGfqRoZhYeCdO7SrnsqLxa6hx9H9ZnhEy2h84tSrX4AFx9B3VGQ0rO5maOVN0Ae1WmAc85+eh4oDadrbRNO2IowQZfAx26AC/lhX6v4gLZF6JliF5mE4CRxSyTFez2CqvtLvG/G0Am5R+AoRaARBQriePFAnrPi4gGK1hkp8Lm8+vyLr774Qot6FUDo7WTFEJqrJ8TXC38EYZR24SAQh0EeAAiuEMf7hfMWMuFdfEjIA4A0eFAAlEL/CGscBkWopIcJCl4TzwjmCMeFH+FUCraEY9+UANSfRXNgZ3xK6/Aup+tAKkmRhbqL9wK1FLpJf7kbbg4rzT/kCpL1977p5hAeyFIcwuLkqBHz7Gml6uy0NZVD/+TD0MoBX9InQsbsH9uYZcUgp6+n/Ryfduqf2cOlBNmyotgueys9ZWMO0AXPg4FuAOCaTTUYPG2R3otNAa4ba+gfnkz88zDGbSZJwVcR4GYdsnWuTQfHgoQ/MzfXnYZhinizLfYz9dKr2eDmUDvVndqVvK02WbeBVI/RnqNmk7eTf9QXUmnU4NBv6jPaNV86gMln+LQBlyDx7Q71I9UC3+JAeuzHn1pUCvGtjwZIMcCWRQyp9YZv6iPodcFk/ytsIebhNQC9ve+NxPxUIdYO6VLhNkwXjqboru8T+XQp8fOCuOxEsYrCzZFvzhRyJI7UjNFFkoHBPNAEfUlHsuYlqXxyXfeuSV3l1D44kl8jszfDraaav+4akYiW7IFBUoKf00nfql5G8Pg7MlPaZBsyyfhvUIdXCz8+CDp51KgtUmI3pVNFMM+nQpxKqpKoi4P5HMLhkPVe9cjvEB2m/DMF31XnY/m5tnf+/pA0j/qNe/aUMRPweiXilL09fSo+o3Ux06CLfwKHczTJqT2nY3X15feVyEgGvYmzuOCUQfwW7mUfjB8UjsgW9uz/IabiSJtBwfdseuDEzFMtW+sIiSt+tN5ZMJC7b4V1BTwf8NPBD3/EC+jwDafV1U+Sq5eM1R+1tahGBgRUlN6v4+sBCsuFY9oIVpI1Vi7gRDkAiVGESVim7wcxnNj8QSHa5U8KVhxKOuGgTQFZml/XQwjFVZxpM5yxRVJtklS72Hyjy8X6J91SfElPV1HLMr6wTGl80hAHp3QLIO+4W3BMZKU0Z9j4LGrSBFuU+qyUIFKRlNZjkE5UDv7QCj/j/58uFBdSVCB/sSEOTM1ZX2YgsFv/RRJlCaE4tNpPXVIEUYHT+rHqstT68GMIGJtvFORdQZWPxPknc2WfFryqIo8o+AVCXX+txBU4MEYUcM560GMqncmV9MXdH7Jd/MJBZNCoFkjI3gSQIfgn8cGTwtIR3FIaBngSnTKZ4DRCsmvNE+MZtRDhJKzECAR40p6/yb6yGirNf/zGgfowED3S5QfVrPiZZPO1EnhAR0Jy2vngT18QN9n0sPlG4bhqJ6FTYlUs5u5raZq4hXXAkY434qx1+Gotm681pBYmETwotBM4OUZXx7BuKrDliNr8QR1N7YQyCjhxxhynsQJfr3+in6Ket/Z5ZTZUuvDSHmJqAkgxiQzA1aR9pPX6P1pi4KQSKCRElWAd4xoyuOa41K6ouXEdy28CXDkdnJTOco2+58la7UkbZPX9Qq3CDi8cu7uMiwSfFUnDmDla/nLr8Y7alkO4LuIz4Yd5WvmzMVmcint313teYuIHf8RYdMiPK4BE6/+IVvMVvVXNruVsRTVCbgnyRFazdkpouYxXwcq8BBBTTePZ2oJxTpw9cCwP1K2t5VmXlkZYgCVRCANSn9WCfRTyDHj831BhWpHxEqA6WmOn4BCIZpxbYhUMg8OgcyMoSpNgF09JD0xTcFEkNFHYQFChCI6QnciHW/zd3cPDrXYX8UdANU+paFwKRjgSgjjny6rijSiKUKOq0Du2GaWIs+YvPfsLIXfQGEgoepQOOqf4KrOyOGFSdn+xYYBB6OmzVDW+VHJ54uDZXIGAi79iZd2tQxYJqEJrfsr8bgp8NMOqwBGc4KNQTsETEJEF3HIVuUmHhzsWXQBBK3ETB/TUk5MPPRvRhK8mwefS+Mkif6UhvtWgEA31LDfNSYeNoU94xmfqRrJEK39iHZzR4ZL6KrrJUrCtNlDjqJTHLPIUYwPOlaUxUMk6gMO3IziDL6rwsIYIlnV/kXRGCmM213jgJD8Hn+APju1K1hVu2VLgG+t/jyzqK+uAXXnJjfQMP9/bz6nGo16qlpbszdIlMdqVfVhZ5MGbNO50o5UKH3NMxbm0W9KukfBnemKgUuBBBR81OamS6i7m4C397laN8P6DvBf+sa/8jMJBu56Z8EwAz1ApDAujNhmHC+IahE94gwoBLqBk0S83/L/VMjztHawRgExTDVuj/GMmAanOqFEO26acCV1zuSyxMg9JTTi52L8FJ5cbaxS1R7dD5qjMRuQm/kVMZdII9qcD2tsPQYg/qyO1zL15VqwGyZAD/+GRCjowgJ78XqZDe4SUJeuUtc6/kl2nt+lS42pkseUdAN2xZg+Kk1e2ruFLeLPsTloY48IQseto7BSKzeuj6zbO3eL/U+i1lOeicXYwm7ECM7tGNCH6QPIprvbwYN/frbrUzApyrWC08xpSkwzSyXoFibknLaTsMQqZCZR5ZscWzpQrbOhRjjq/p0LBz3wSQFldQhxMOAJ10hduhQXFJOHwH9E5oYwOc0pss2bGVAmxi8uDNqUDZhwHNsor+olzzTbzUWnmFAqAG9oMOSBRsZGxM88iF3VF7tKQWDBlSjkS945OFB03aSM+OuS9lDcVoBKPGcGnJDVpFbpzFq3HFUYil36bG5s1TsX8dFnRpIZXrvNWTd7MiIHuSpVylpq8lCteyE5bRUsSle2Ek9dfWWyMOhJceLDrqZvlqiwJLjjZ58Ip/kyaBsQyrYzoYaD65ajwnReksB+mg0DF+ciKJMwAVxyivOFjjGFZ5tn9hjdC0VorwweyyILIWC6jJysCjbg/SoQTtstyfCXH2GUahsovcipYKskynRycihjB6zn+XkEiCmY1h5DQ4SZndPiBEPmMFkgts5qx0/PxRmbXkB0GkF5mLXfKrc7GeYKzhqlgcW35uI7oXG5dlWGzrqjwlBzED70rAcVVMw/CcYlRtu1caFFQBz+uF91lxo66/aRuNddTxlg0sKJDUzIOqP1Tp5MJiSg83of1+aWe8kOG9nAPfQJQOyoLmPgNTScKz+C+B4qzIlGyfawXk6OZYMLUsbUR1QgDPoPslIjF8FrUVqKCTKIoUhJbyUEYQQ5eNcftjIJNd1cvig0FdAWZaYGExHLO5fqFfaA54cjeAGavLZnwQuWelWSmWZdynRQuijqiDkUjXbznonzNNxOJifjXN1cIRU8oIxa+H/icaILE54DoDD60mgKVXN2cOpaRdAwKqjGFFLIKH5ME3IUWDTDUNU+hGL8yxxjmqZN0CGoH1jnKFVVQmqtOgWluEqrycIHS4q9fS49UdRYnY2RZZmo9g6g7B0/hB475RsyfGMZP5hBKpiKzyWl+FUNy1wzN+SWbqQ3NUqwdxCCIn3D0ECkPHgwJC4vO4JW0xJpv8M8+jAGLpLs8zlAJyxbBUmVuesGPczDTb3jAtAEcnrt88FFeDDOTlkOU1HTGT2JlUNGjs84pUcpk6+xHDeIe4syVXMfdU/sqz653YbZXdBzycOAow596Jo7BbzzbCG4iiaT5C33xMYUc6iYB1gDZIQcLg6qidYm0AdaZk7Qwr8UajSMG6/GyY0BT7cLqGNoeQ6PnwaOq450UkhfdFgqVWmkAC+hxE9GESvVG9nFVOJq08WoRdPV3//bvU38dkzZOOIa5DWZOqVK34T7z8no0dlpV6zY4XRWPp88u1jou8b0tqEpPGjCZtmuAmLKlI7YMd2U1LuAg6KDGWh373JMx3Di3Yfbphrlk+SIHgOR7riI5d33VVCSHZ/DKPdo394yZBenXzNhVUEuKudWniDBjikM+qmS62gdWLl/2GwOJjFs42IdjUsFMVmRKsDr5mZF/VWJ0/86esmcchSvIspTaRMiDn/kEfnanQBmS1avQC5vEttKpQMy1OlWyEjRzyb8VspOFVYvQMgtiMGsqoQVqw6IBiEHQBqsBn+AcRXFuZQ0ghU+hqpmkC1Dyc2hZEEnUuDW8pIu0AhER0DCZm5mDazPK6codQ4njtpc2GejmIwkSoyN+g3aOY2D3PRzkYiVKBeLRSYJ5zTlTV79DYVXRaDIrPFqI9DIO6CGElKRhV1Ixm5/p70gmUkVAqbQJxEXgSi/h7+qjJTKG980lNM8Kp6nM7drZrZzibbrLP8uz+HYPTltlBc+tt9tUs/6pa0StMb5xNC1p13is5j/NtVdihwUkGdQrbjODltoReUHhSRpyq8QZstADVfWmG8BCwueMVjp0sW7QKBcqP0MVzXohn9OgFSthXwzdJmrr5WiKwdAXow7ogEaPrJO6yvZkF34p4egE4bHUB2QldVaC/1BTBLKjf+c1ozlueTBzaXAQPv/3OkJBXTrNQr+hWbqWRXlirZIAZENM1cPptMhGC1JQkKJ09leBB5BzQEIH0oFfmxcIFiO/18wTrcvCoAo5c3ZpMKxLE9HoT8bLvyNIUTSDMKAxZs/TRig+C05SMzAzeeeJWlak63PG128Nn0rX+IUkgEECm5yYxAUB/QKteDgC1nS2fWFVx03VmGGpSiXC3CQ0eJZzKRBNFhepHs8YYxgn0Ib4ucjCSybYd9lIiXPSTQN+LxpLdKHhkKAjGy+ZhHY29FHC/slaMHJFm9D7PI6XOwL7qI6iUqV7gX2iiUOcG27MztTv+IjxCK5NFYiMQVVm3pKeNcmw6neCqsJ4ZslRW8IK9h27+6PKJ/bfBWuUencLG6/tMe4ZSE03dUPLjMkA55Ds1EiufX9AmnCZ5fHrUQ64heMbp42yb/XpaT671m2UIcDDa2ekRopdEpBtHJNV61+np7Tt4OG3Lv8EqdJhwtxZDQruLNZk4SJrOxluTikbpIak62CkQ1as7ElyOwZK0c4rTG0fw6JkDgFdEKX1WcWpMOp9GB4FQn2GvIit04WPkUOTQMxaaUQDxAMRIfVKW63Mp3cKnAAN0zmffzvCgLTnDmNrCmIp6yczoX8rpuf8bFzmHKY6V7yQ/Z5xdvmt+A3JUlGFUSWtJPlK/VIasJLt8e1BS6YfECeCUtpjMJKpEZODG6zQqdI2ad7B+zoEH5/V6moR8O6oBmkXxIA7qGpMmEQ2tKvThWejeAIEbSEpiaJYgSCjpCNRskWuqGpocC+8ppSYgu9IWNBD7GRkMiUuV0e2gN/EMiBdfprDWEnm57KiZGDuy3NMzqCDdyjzd+T50o7LWKq+w9bpMdwFsIFz5imKW524/CdjR9XvxGdeSlUaXCWtiK5Ku2SUGjvfWVQ4ESd3dMLhCcYuR81/IV14aIDM24xovURDEQYLbQMKUXhlwO8E2UcUdQLtp1lOTTJNU2wrieqpz1A8H/eFJnvoU1paSWzzxMdejhMPOXaog7rSJLXEyK18GnTSq48EcMilmvtMJC27PiSqvj5bmd5VqG4edbrPaSyX+uJuRGOMHh2WVbYFysRd3XqQ9H0ivJ9VyxQ53/2WK1K//gqC+CnDqWZZKjeKOJc6HWCKePooigVVhVhKUnXX0iu0KmmK4NOeKzwlC8IAHllzGi3ZB3gsboVPKL+PKtC4faiyXLExzNiDVVGmoy0tYHtVdUTPJlUMSt4t+V00LC4QUXCwM3CzOtpePHeR/3Jww1N7OQSifFV6FJdK3qxj97JiluMxC7eqL2GjJoTVbsCMFy7Yu9d3+1FceCTEw3UfCNhj3DPQYbB/y6D08OzUSG5klHysuf9a6fBXe65xlqT30m1L7dRaLdFhFqeVVXu+TvfYoMOgA7eQHsH2zEjNVkQRj7Xa1lR1GtLwU+lCSd8MzQtKsowMV75O53J+x1bEin30hZFvDpi21jwYc4ZsoE8nxwX+jsGq5tmTnogLF3QT76vvVdDDLHwpCfEBCSWcTn77vqD2E0FVJPYLa1l1uoc1xWEKXhHXPOt0hTJhb43R98kUnx5FPLvDajZvZO2pfBvqdlhb+EQ0aPSakrilqwoX9PjUqOhQ3F7DQ4WAFIS+jamuA4dzhdYZUEoBtQhRWssKn9SQjpdTkARVxa1nXYU/32vq0h6HVqtaH8vt4VcSIwlnqiDtfB96wrMoHJeYGl4kAjRmj78wE/Hdt0rkPfXjxu5ZfwWqCadRZwkA2qJEwk/fD/lB2Tq9hN04Dlu4pu+cLFW2rqPEs7EyAA14XIXtUDPa/EkaMttKbuiX7Sz2wWjvOzWX+dIacz49ebedJ4vS/RwRDdO0wWBwD10ieR+crQ3i0ap2QvspP/ThndMHX+EQV5ugb8iwq7D7qVLF4fJAPAEIqAp9DC0f5jPe+ffsgWfmga47PCPFppTy7Kx64eHHrl204M+LV2mrfVxB9lD6iKz2kL6IpFYxnKRpqb6X+rkRtjUTirfij7DogQb8emULMpAfosKB5EXBY/EpDA9O4BW71qdJbof4bsC0uMBPaIJxEV4ScYsu2ZIIZnPqgDpgCk2hLwnjFNyBjuPZQjte/JyhYWgxt3XQbsqHJ4KLr+CJ/Jl4CMWeiSZL3BqqPrrCCNSkWFRiX89Oly7Vx/g4cqmdrP427wK01dytCHOOaYnrWUkoQ59SIy3+FPf+eKjDmoJ3GMdOPb7ERRbEnNlezwEW8X8UpC2+jXYz0Wi20D6K/iGkbt45nX93VQO6Yq9i1HH6CXCHvK/4jkM/dWx+fe4nzm31Vit/YO8MhwFmy+oMeWQPzFRWq8nh1Tcrrir0jN2DZuyQCXyR5Ew/xO8TR2nG7RlZZI2WJtS5sh63+UwtqyhYeBeImXQ7w8zzzKU1fs2SdDCORCnKdMPfOj4RIf8LZU4zjIsk5cvvMj3O8OTiffS7c1GraD60b5ivtRqWnTSPqhxb62OZDvO1UNsY6cF3AHpa5ExLNZgQWqbaJNa8zpNkuT0bIZw4gZsN6YrdPPzUrjwBoLDg1a2nI9ozVbjO0wca56MKn5d5Lm08EA1pYZ011E8GiHbzZOKXCi5qhptNVnxdwZbwC7ptvaUtL5Cl8kLpovoW3ZbibWEzLA5rh9DeNbAtXASZ4ryIuLpobsUvgpY6fivHM8JiDxTnL6YYIsJhp4pbLLFFlCiLa4uGWjkfcWgUDXUMFkPoCJuFskYoDwDVekX6cDVqnpVqgOE9UVjhTSWLYsFif0aNgCOygjfcQtWabQE2wp8eUBz71Kr0FOllnlqzMfl19Y6VZ9iUIYn+SnOHLBLsoUUmzhNyemsQLWtkNV7WYfS3HkUNhJDt6TNKn4FTq9am4JlOv+3Yqx7t1ZhL0iMSF8y+tzrUsg7RJ/GZnV0Y4V/qfawORvBrdZ0WzrFnNUZ8O5A7pm2gTNHOe37A/ljZ2rtVs6+SCyUFBewWkIJS3NMmtjCI4i1IofQipIX29dFqzrUL+1j75IJz8co+LEZpipajpWfgo3iASqB+d6jcIJjQbbZwgmYOHHoVBXPi0m/RiDAgtdg6LQyzSFs+KT9xGI07bjDkPHPMl4YCOrP8pZoAH2VYxHVUGa8vpZTXV7NA0a7wuxz1O0shP6hDxHJOdXzSUcGFI9ul3yxj6i7T0eZUzblO5/KDf1GJ2Ia3FFjiHfvqkDJQoDBBqd4xpcnUXXIK3mPqTB0z1OkWc1dIy22+FmobSavqJryR3OXSAdVAyVaHAULJTnlsXudCPkigWq7S/DvAiKyMHC2I/YLWuKGhbwDjDBZAJ0QPKUFbiDmkPOeP6IGo91L7JXFEEWdW9gCtHe9Wzb5KLnSROkxQKTV1UBaCphCAB5cZhMVFW/WZU3WblIGawWqrxHmuB5LPMcftEx1oYMgck3PZAR4oLWQHHhNVVnMItjVkkF5Wv2CFsMKvJNLNcGxdX0+/QlAS1qSf65RTqELI7nMH3T1V86/TNaeenrlgFOjrDxgtp4MV7XgG8yKiJLJmc78TWpskyjjPIc0xP3JZrUadPrKYj4TdXDOgbK746T1QVe8uikJWKEV3tdr8UYDe7qHBsOCNGdvDN0I98g4K2MAjMfNPPZYacA3MUZlTI6cBhz2y7dhrRsM9+A9WmMGhHS+2OtSCpE9xYl1Qpxc8Z6jR6/TQ3rhBUGt1fUQVmmyIX/PK6aRzzpbfqMfIzlsdOPP13nqyCFqYWKLDQlZ7oFVOLdTAmh6QKoJooEzgRV8yVaCP8aqZlvRMIngUfo0eM6SjRWO29KwbRSisSmnoVcNL+vBEMfdwVrtyKAbuSnjGX+KBQbNZQrIEZ57tfGmffzS9QTeLRqGeXvf3PmGXg3hM4oBn4CfO5QJTCEexOxkWUQlK6P7pSCuEQhql9TkXhS45t+U3FO1EbUFX8UKS+g4yc6/padsYmgAhcoFue6C0utWQOg3z0IczT04mlWqsmNFq6i45BW9Z1TFDnW4xpyB1TdU4u3Hbxeou6NpGtVyH5R6rbVyQRsXZY8oE0ekJQLkoZC7bGGa8Lb9TckfJSmMlUdKjmJ8EsK6CR3FHPAfqPQ0qOpAo6U/C+49qZL/B93MoErWfzvFj9aJGKsCo0kvqrcap+dXpUebTwCCdZ1CLbTmV0jbRIr84CEYVu16c8i9C4RO599QVl7eV2dKBKI6/xXUR/hjxyoBVEVzDA1jLGkAG2RpzJD3QInwa59ItapxIz8ugtPyFyFH8UeCIii1oXomkfUv22JAwMM61Dzs9gO7vhY7Ni0kVL+xkdUEuiedkcLHJSu2rosYu/g7A0LR9GQ755PEo8CXjpLCK80D+kpHTYBxcNJkaOxaEQWKKzwBtp+w+PAcusLxJW2ZX+S9VNSRyA+o3LlVGgUTdtDXUl1HbW6eX1GPNaR5/qGdNuSw95c9a5yWcaj670vb45ypQD5B5XmLb+TxW3FYtI578gMBfSfc4DrtSvzDlYt+M4u0iQLZUe10jxF8GuOg96+t07vHO7whRHAZQqsTdd5z9rUStvlS6dxg305aSjFbJAodcTxMBHhrazKSizSD/7gqviGtvLHoDqpOVV3f0Btwd69aKFtJhs943fSWghnXpkdJOk4Q2ghMlDWbHd0zufnxSM831jIgpPsvgoXSn6RRVYFAKQWpLs/YWfBLxDNycV+3z8E42qSmeLVweUBu2Pi7mOqCl9uGaIDDvltbgyXY4gR+9suJIspLigh30D3yzQOPCKNJhQ0YZ/00r1/vr/uEzc12tBY0znYDWd5By9RvFRYG4yHcXs4wnG1VcWZuLlvw+cN1u77l9yla3GlKnkyZWp/AYUW0EVND3T8zU0SjT+r45ilCAdU0V4NJEUzvL5c6L2NXeKW41n4W6hU2ZIdU5e6iN5qOmFN06BxkZQb9TDKfgNe0B6dCz1vAAZmfS3TzQNZLBWyGl0iNRzgW+m5wz9rgHOv+n8gyI38E5FwqXdJ3ts6eW4q8PnstFxQ5YHqm2M5v07lUR0iZCw4BzLghTmhfMKYQz/OyBcQ9sbVsV2QB3kK0Q90+KZ+4nhQvAZbKWYRW+TiAt/vrgLbkdJAVqfR7lXTg25o+iJ2ChmkM6rKzTpxGmoq54dzHQNjx355IpvJ4jZ/QbqnGOv7roI0+H5WHkET38PLxWG7dIo0JQEiLDL6u//et/ULL9xqSgvSN7ERY5WZfX++/W8MBtRzYtpKaq04EZcxu98W6NdLJ0PT47opDixcP5H86h2IVWvfngXnMRVjdDUwwoxI+VCHtD2unaw/L2eUS7G3/7yk0XCm/X55C6uBbGuuzOio+ot51HUbqPin8HEztCDFP7mOlys9jU3W7ItcSjOGmg/Hx2L4/Oszx6aV2BT+KhqKIium4IdbpneMHuQQ/ODOrrRFIOVnMJg9B9YNASwlGcaW6U1HeoOj3KaSFw6vq8nH+NWadHFZCfWhtjxVbAR8lOA5zUNrpDMwyotUjKPrrOtQ7HTYc3gmcvHsjeSOIwOSAT4qda1AT6DuDJ+tqBR4cazzPz0281TGJjfuaeQ9bVLYpy+AnU8I7ZwyioGVrzKoUkKM8oNficnvIAz3XlsHDa83EdmpS/SdWnCs7wgzww0rdGQJWI+dIKce/2tTdhFj6hosBRlM8TiFv45OLqF0ZbeFXI2Bf4y0kq6kOTTyJ0X6WfRNkQWoueSndm1Rgd9BgpONd/S1kuVih628F9bqlej4H3ERgzZYLmK/ibKn4M7/ZljK3n6GM8I2UHih0/W6qmdL+SOL6w03KMJpYaGlZ0hvQy40p0yG1b5UvA/63Y5UWp4xwqaM2sAk8ndyaYZnWiEq3DwwdHWUm/WEWt6gzXeJGn+iXZAlzMZwaxN+6MNeKzNsYIuL5CDKZoR2QdvXYX6DmixizodCP7WbGThfP6pE7eUtctpE63mBOQJXU13wAndZuQ2AcXpQM8UKeWHHIGCH1m23MLlT1QynY9tmHM64l68wjb2B9SjuRW/iM7bFSHgVGdSl1qgHLOPokHPo76qHtg/ZbF41g3f7+Iau3d67lk1Bo3FZ/UztoH/6kVFgPODbNxwH5UrS1LbB/X4Omgh9g+r/VErU6AC69c0QnQQ+dLwByABkgJ9wg/wXu5hKLeyTQ6glEHskg2FlMjUbIHcj+MHLdz+djufOEdJulTpt7De3WV1OnFbizVtZUazFEcgIXJYrEFMViOMgYneBecA+QkgcGwSG8TU5q0mCeFbFWjIES1HO6ZXcyppW31aI9xUbsHzTebxbYEmzjXyhSunZwuVQrPibMHDvdAr/XlVpZ/D2d/ZA7z0X8S9my1P64z4orxERmLKf2rYD+31XtDdAYAU94J+JBgcn+GGdHBI85T0gr5VoSCeazEseb+F478FF77UV2nPzbjnWNb3lsPNzv3H5p08/1ZPSAMwTt4p/FxUiMeW6DnrrJPp/+umgS+9InOMEYfbWGsxLDRRjLWeOqZqprbKIOCMF8K2gBh2o7Ccnmi8D4W12A44FakLFfsmWCG5q3+YSBwEnE+QOEZHlEE74LTyVz8CDm1oLAizlPaIiYfVVKg2so0SZgxn9lv0bQknpnK5m+QAAB+FElEQVSCJ1RnvnZPKPg0rMMc7qqlH8zLibtbrNU+5B60hLZ3rw+1pp+lp3t6rp7gP8LBfKbg87bvRxU8a9olts9pkm2cw+mXjcQkfYStuVr/rci7IgwuhIvI59orrYTipVx3d+ciBYdIRZ2SGGK86HzrxednpzpefkXBycbjz0/nRsWXCmgbyLglBa8kxvF60PHa7KHskEFy+duBbAtqsNyCtLi4KHhctovlnwSx7n5HtQtmcURikM2F+q0RClqNcGgapvGXf3Mu3bCK0JI4VOKp6FGQCnv2ap7K/I+M7zOvx+3q1RePj6xuPi5zTl9RM08AhsLTRWzuXeNl3q/XddXpQj3TgkfxC+HTJnYe+SWPnkrrXceynW898S+1qjZAcqZe9rNhZ49ZzK527afb4VSTek7PzYwKnZrLH0UGWOPXe9W3+JMaGrVrD/19PFo+WyDRbqIt1emGLPY3mLzC1LR1uuETgB63Bfg9NifGr+uoJ3eQmex1oV8fOzZXjWpLJXJ6LatO94lz7iHv2fJ9hiAKNlF9RZ/ICqWnSdoLDtqCmdl0v7Vv63SHUaXgw17VHCQKTwCRBR4cKorxZKElwRF9MNKjBA/aD43yaI15b/5R1LHvY1SItYKheCqMgkaHnqwJnKl6TP7v76MvcRN85jVJpTv+1DrMX2F2ZJzQa551ej9u81T1NXAesy3d7+7W8pnSoYbX6cTBz9Lruiicoy2UbOvDFlKQHyFxiPRDaMOHUWsj/lxs+a467Cprqu8vVrBG3OEJABeqQcupGR0zjaRyVSyJYwp4DrzimTkefX4Wps0Y+4o9Ut0/h6p5Bjrg7XC4ziWzh2L9SpxhEIhxDtEzyKNF+1GNsvrogUur5VCf7k5fU5R0SVAxRXUuE/qrWmqNVqcnqrNGqdM99LpgkCZbQ3pkTaZgLqQyfiFq2G0BhJCavKRLYguLF178iZj5HGvJ/XJGMfXgc/XMOOgZFJWrLLqQrrPdJXcnPXssCiW7AP29MhGOFvBY4jhNZgmXUBXMkhjT52XDMC0MXOKQY5m6fL+jGJVeVCvyNZewurj8J6ndHb1MAu86Au64HSN1uPTDOSyyY+2Xrce7ZY9BizIyBxDtqUc3lxmrtzn8JWXht8t29nEJ8ePjhAta505psiP+SB1NcTa897yiwdyVW8OgAKKhFLNLQxg0oIzQWH33nUC9pzSFZUaORxFF5CBRSyqkA5yjZbNKupdEOliT5aghAT/eufBuryensLqIK4aGiYcbFG0v+OTdx7dwLcq0eK03WpzjQnadYZ2Xvpzb41va0zxW8PZAXUYVNFNJHWJ+HnjAVX0/P0z5eT9ulUGPmpyyYqsS5RJRaim6c2Srrl0lp5gWGhI9dDIsAQpQkTPF5dHhPVUfXfqpBYa/n8Drh7jVtJyeQO1T18eT8MePC6ojvL0FcUGVFGkLcHd2xxb1dub3cggm+sME+Gh2LWoVk9LaJjCADLIdo5GCAJWCkuiIeqm6vCYNj52qIdVSUWeQ7Sn4GJlTmfnUluHX05n2GBXzEcmYqgu1/adu/x+Rmx/JlKna3C6+dMiS6GjyEwBaxLBJRL6j6ZcPS3srTTv+/VSfRb+syiETzE7ykzbXHUacC9Z2L+c2NXZczqHy6O7JeA2gqoO6Rrp67FILRBzVPwvkbUGZ8nBLVmM+kv9bJfo9YqQ8us1IwQhop3oboR8DVY1lrPhjhYXbyxkzT+Hcynst+2fi+VaxSus9kzOm7TEznZQYMEXvqL49dRwh2+qKgQojLBaDptQ/oojFughxq+07cTs18mNez+v7iNKsu6iesR/d0tH9QFPtHKuSFtzTj27Xp8CQzqs1Fw961hoXp+jOUW9V166SM34p1d1DJxPvADybTttTb8aec9GpPcC1qfkaQLSi0pZOrcKZ/8ADI56PDhPnkeIeg1JeEr3ic2ZvD+B/fLqsFvYW8mwJMT3+jqthuPO4PBO3om5JnETMHFMkH/E4LrcDFTthxR2o2XMjP7Gn2lbRQp6bS876DDxAGxnU2s6tJujHya48zhis6QwVxgmyek3p1tWBAzMyo+FvjJLT3dSFCwnBrUfYy0f2gRl6tG/ut5ChxiU/MZqvNWm51aWFE4mpHXBbDjXV0dM4v1R1JDh3NRKgLj8rP/wzO2ewn3VTPpzVZtLDLVVdF/tp2PI8DqT2fK9iJtnXFJNIexXAOZrDXtSnJsreGVVxP6dkllK9sK2BJ7BpVNMAFhUGYg+pl0I7Kncg6LjZkFjLHRi49Y4zrk9UUPAacDRBSIySIr1GBFiyJV0wx4U20MKhKdkNMC+3qLcb08Ow51Wa4l3fu6dwDoe3Uh7zel7fR+r04XY9GYeJmGeJPvvdtZdwrnHaGq9LD0mfWn9aJleJ6E2RmL9oTL1FtvlWVl7+MGpreQdgtPR5AONJVrNE6Xko9wloUS7oJfGyjS7d6AXag8pF/a4WwpAXaE5nwuOk0kPxylNVslYBcPFzna5xxtMTDMeRd4TO845S1C5oJV1DdpTZcduV8Oj4xQo4h2mljnaWBa8gjkRmnX+HVge89SdyC8lOOkC1v/KWtFVuIMT5QFnLTduq1XJWZ8xDPRBbu/ht4HO9HOrMx6Wv62v0srOzOoVLoZSMK0YGtaxSuCUxNdqYJ1syGmNkPLxaoeAQNC6nHlXvOrJP+OzNwjV9r3Ht1Ijwqh57NXu/7KrnuOWngJZ2MeP8grNcgVnfTvlwnv1uPtxD53nxE6VLbFnSI2qcwnOmTnrqhLHNaq6aZw9/QaboMMAt8KW6Deh3yc7vijNSKj+EXvkz1wAGLSH7KlCr3IRmhZwEvHN2RPoEgy3gvgaZ/SRR8X/BSAz8k66NOT1TR2XvcHAPaSdFjVMkim543jZJSG2UEGIdLbNf9R4mBbtN9BWd8mcfa3uu5RM0xc9kJ9tMKJkNC6OK4lOyRyT2+QwJDykd8qq7wpb2U7eu+t7dsJwEjFja4C7BaYhOAqjtPYmACaa9BtPLTBA8Cni3u/a+Ku3XrpZI21X/Xduh8P0OQKkxLgMl3WrY25mtKtbc/yilrir+xsoM04rPYyRHNEFLKapz/J5ajxEdjivy5AKOq+5Hyu1xGtNW5x2vMQQnzvVfyC9CSmKrXnsjPBO/NvrvbHoYspRsKV6j11MARusoLCh2lMRTKLiDTPQcNQcWMsFlJJaYswRnB812Qt0mu5iwDXG71OBQ+JTEdsoFGFEXUzWygMEZ5dgeKPVN4riVfWxNz/yGHujXV6nJIdrWPJTjfXL1t3/9D2I7MnoIaR1Z5CdFaQ6DfeLruZYKdwuxMWN8LD753efEAB0yvcZzOV2xT8l6jFWnW8znA5nSc3LP/tk19Ce3q2sPcxUxo8aUvTMkpyiabUfjAqNGYkXdDqP/U9bXwbUxbmlA96upWqXgk2Y34zlYWzylQnTzxfigL8AFxXzzr2jGridjsCX8p4zZGT4wZ1SfnZlOEEz4YBz78FnMwznUmhVuWDE4ig9LYoBQZ0/q4VrQIN2qPUAgW+u2X69seY5CligzSjgA1goPiqayU3ZNwaf47Ao/Nf/l+nTxD/HYRBy1nNtTYXKXVO3PPudPuh2w2uKprKvlRn0F5JDnDDMtsO6PeLXOZk3GYLksfqfuv3ffMadOdLKdA3yW9eg+q6DhvIy4r/Ug1+c8KDxnH88DUZ3HqdTH07qVtEeb3IOklXtcyDOsjcf3UjgBxxZvTDu50a4BBO3gekN2AOmJmCvrIS7MFKUiUbILyXdCC92PbcFOKhwHeeClOhvW1ZCByJmiAebjZx9NtyO2gSOyenyHnyUe4oFHa66HKPkSaU/Sp1b6DsCS12v3qdZ9aHLNTFlb85wZOWU2R/h9HClHULRhMal5NSdd5s8KdQspRSTa0hZS458iPWVXrckUTuhD6yoNaR7zFPqfgudzs2Kq/07ZnmYpvp8qH4eXShwt3lWHlknhHw1mb4bLrUNiyKqVCbmjRTXaS0zXffZA/UvtlFqDYQEOmNfr72v8Adpo9rh9bUrDWvSuGta0u6aX6LOkPT+mzrvaeAj+VO1PwQ+RdTjtEq0STjyhnZi5X8LncG1bDkuuD/M4h5S2+jwyZEFnXIASSkeH7KGTiec1k9fJmnQH2w/v/D0OWekecAd1zqhnD/Q8cG5IPXd8pJmltZwvL60b6pI63WJOQZIO/CzVZhIxFNhPjSn1PiZ48TEuGvXVaA2MAh/NLUtq82k13NsVS0zbm/mZ8OyBj94DR+5B4+z8JWBfYmauMzNF47UAAeJ2JuszG1X4QJ59CefcI3ngqeYPavMGOhzePmvm5/TAA6Odd4Czd3ani8AWTRa0g5gtjiva1DtOo7YUPWsd5mdPC0lhWLfb4NPiFOQnT9TaHq7M/OzdKP+2Povzw28twiifPYB7aIuUot6oxMev63l9WiXVnife/Xt85Vv19obsV5t7i9uDMPpaED7tOwPH7fX7cduPqnX7s6r30c7Yv4NUKOUC11oFZFgahFfAKam4jBI/BfBFXz6ewmFnmUs9kJo7P+dGttRnT4+3X11tv7ptbQZ7XR1rbbfrYO/WJDPuDnUWIs/w+SiLwi2lStuqO/ttvt7xT+u0eZIpglILW8jPxWcPPHMPRJd4PteOTpPF/XW8V/MhsC1HJ2oLootjtmy/8Wg99qrTU3KPNeZ7Kv5Tcl8KfLn/92sPU36YkjsFDz61DqlN79a0++pU71H0CxbkDqGt2C/pIxX6xbx/asxI74o/pU89Y1GnW4kBmcKpL8JLdCs4ukZGXbcXwQVtIH1DsaWdMmAMLh0MX/792qL/GL8jw6ZkTdXplPi6l03h1PB5/nvsrYGTcXV4OxKIC2Cca+lTVtc4bXqKKtrtcg/UbVL3zYeLQdtA/zhaL7WQjLv9N3b+mPFteK9jFHpE8+2gafZkoHNdPkjXfqvTA7St2V1pW/wW0gqd8U+LfCLIfE0tb2nL1VvimZbbcTXZldt+OrdWBGSk3kvL719Bjit3Sp8WPtnjip4tDZBhr46rYsQiowSHAcvF6zA2Z+qzB07igfnOchKRj8n0qc07RfeH5ynYHqFalnn7EOWRMBAyyB7Bio+CRXEyidpppEvRMzW00W9LFTf4O9i1gHaAQjYgkSilJTEqfYsJozRnYO2Bef/WmOf02QMzHhjrinxE8W//5u9pYjOXx2ED3PoN4CHBjE7HKzrdaGw558AMmxaNYj36uvtWFIvw93PX4vnmQ2aVlntpPyMOp5qy7vlrvsT2Keta2sPtXc5h7JrTajQBieuIWRzxkrK3SlPPJaauh63OUUfJ2jE9WhKQa2+3RDVJjTnh0xcJDrtC9SXXyRYfv9WOeoZemK/ZJQofXvvLryG1PoWqNaGgLXH+rvprdpxqndi1pojeIxGaxDzryHxww7Ftbw3KSQC7yq2vP0vsmlJ615qa4jMF7/FfHL1McdsV3pPeEp/gUjIjcaZPZdUWoGTU/m8Q+kvAR7w8LunqfT3OubMHHtUD0fD37jePqutZ2Ak88AjXqEcQcQLHfLQsX1x1vDiFP9qmczbs7IHwQEQMj9gzt4UolG9D2V53q7/7m7+fwdrH3FGaMk8wI+xc1PPAo499e9KPmmnHuC3k42ghrV3LHXmcGRquCaM9cLkeR8U8wiXqqPoEs8O1mldqvgampM9TIXFACD6QrVTRJpfPaM6b1pbWbb5Ot5jPH3Ksq9CufNqaff6+ajUcWFEjbG2lNfI5/bI88IJ7fd1kT9xG9/BSrV3TJIaFU8+iG8IABHlEmRMovr8MxUzingvOHjh74Dl4gC5b/p5aHy6qB15Xj3sBOi63x/fuwJlkX7pFj+/Ds8TH98C5lT6+z88St3ugvj+9jDYaWh5BV7O4upgcN8St5giCVAuHrDnbXosLMerRzgnWDi7UYinaYg3bkWULWSq0v+Z4OdU8Zrtyt4WcroUMZuNo0RE2RQOf1zxKl683be1awj9wDvXAQ4oFS8ddbuByJffAPPASclwr5rgVx+1h5KOQFOVJFK8W4JQKh7TJKZ41vOZfp2ucOj3oj3XRk6cP7YPZgF351BWaeZx/P1IPvKw4ZEEl1L1+MvZY65J1inc2phQMTaaefKarUB1lRSfcej2dkpfhUx6ovZRx535Dw3yhL2HLxeY7XfvbvYCuvm+4hS3lVtErX63Eum6LveJz5uyBj9MD0Sl26+bjXeiZ+acyCX2r3BPriSajyowCB7ouwRmQHCUbOpfzUXjOMAlBMwh1UfgkzjX8nH65Hqg77Mut2Zer+cttOWfNt3hgvlHWpXUn3ML08YtrRY8o/epiZNwQ/A8OeqZGQkdUfzdW9WhvN8reXhxLSJfY3uK0kDRCm9W8HVm2kCU6B84htMFhxIrl4k+AWc/G7Tf7KA4Hd4etlu2nW8c2axi/nE90zZiq3yl4byYjdMqqojyAKtdZE0WR388zo/pIVqNDT6ozrcQRPQuf8HWcW14NpGW1lXTUlobxOGAJ7RKcce79Z4ZL+NT9cYrnIfBah7Ye5znXtPOYbWlNW6dbzBYSTSngWxtDS35SyE62tG17RredOM/wiaLjcgueu7afrUp2CLP39A5t99QJdZ5XxrPJET+M1MX9qe5HU0rNRzLdVag02boTTjFdAJ+Xu4BBQgkNuRoMjnbuf4DQZQtxsXFYdn4C0HnknDp74GV6wIt/Smd/njZwCRpcYEPhUbUHmI9sUSu9hfRU6hf3cz3EkhngDLIF7Zz4BD3w0hvDS9f/xTe5cwXsVIVxB/q4nTZyl43xxerv/vof5K2R5wDhEVH2fdPBk5sBgBXnBjvhLBmVLsFJ7Kqf5VT1qLROV8w+xmSM8U4237DcZayk71pSo898jcyXLtfh+WNOWToFl0V59f/AuuTtzumD8qfJxrUiZI9cl7JSU1ov7++Z08jvlFyERtGk9BFmBgWBiSM5V19TTE4J31Wfo/h5YFDNs07XaFPwGifSu1oUVMv5H0tiy2dKB5rPVMNrmewN6b3RtHhl9k7eHu1fW0w70n1qyrd7u+tUhEeyd1f1dqrHXZk/Av5y/ZdjPoLae4go+vd7Uz+3B9+O5OFhwTsAW7ptcAskzouwOw3OqU/LA0dsvJ+W4/ay9nl6e8klYgnOXi5JRFP8n6fHDrH0TPuCPDDVLE9nwoka/H6GnEiZ03nvzPnsgRfrAaJ/ji3fARDGVgu3Y2xl8XEgPNGYPpxXxosH+vLFzKAstnOJZ6ZwDveG5tv44vaJbm6Zbf6VUzZ/1Pnyzzm9OuV3piXkoCM8H9oWRo9zSamdVkSTmJE+RbKQvEYr6fBAZJevHz28ZRYFzoln5YHUI7ynx5Lrxn7t53Qmhz605NJZ6FCkZ7rVjDKF2wzOR14UcUUY2Tw5n7f9WN47Fp9a21PwrPm36faa2UJaqinIlP5T8Ck+S3QoXSk/oh5h1u7n2UGiB/aIYgBw1YM1mf36bMPmDDh74JP1QNV3n8AHL6QHP4maI1fFJ6ihs8izBz5+DzxJB//43XqIhXuPyQ4ReqZtPRB9Y2mcsBt2kjbJfMsTgEXddgnSIY0tRkhhyZIZkdbDSyC7jtuW8HwcnGNpvmQkeixZp/DMU+lWy63Tp7CxxzP36vzbK2wz6qdjfTV0ntovueVzUsghF4qdFePdCRwSIivBY05KvIeurmkzhxnynTX8BAiy22xqL/MJGP/xmliuhMet0j25jZG197ui80y1iGo1uZ/9Eg4zzJ9V0VPZkuT+YGfs+MTjcAe2reJwnkv2cpyXQvstx+Y7kg877AVUKFMiOkM8AaifLg3xjpAvesd99ggczyzOHjh74OP1wKNGzyGsEVmuWtvdXHNo+GwnP2MMxqRnH350TeKIVZo65g79097cFX9rFRyd4VaJJ0X4yMw5qa+eiDmdqOtHSnW5QzRidfAh5ENaGtJArzpbp4eUs3mPeE6+jnn56ttZZZ+gcFfNp1alL3m6squs2h2nnlF4Kt1quXW6tn1Jup57qNMjtG1PG0EagnSd522Eph/uOve/pB7ncVrr5vGHlhyWr6WHM+SZkmJ6r7+3fS2tYAGM61J4r07X+JGet26+dJ7DEtpan9r2Gr4rn5r2kPSUPvvxbLlN2TUF309uULXSA17LqtOHyKppT8Gz5r9rutZnyie78uzw845n6W4VHbIrHkuVTrsNecnVe/4uuYTDmIpLYbVvl9JsxZtwy6ltmZoXP5bcnq8W73Y1X79bfSmE9l3QvZ5j9PSvBet2dciR6nvzLUyO9ATgUJUOMedMu4cHJvr8HpzOJE/ggX719XPb1Dn31cZDnQOdmvEQRV1pR2aOzg5gjagz4JQewPvnCjilg5+e96B+u944qZrWOixAm6Q/F5w98Gw8oOafrnKDnrC7iuJzjHcAQjLcSi87WLURYybHQyO4zwzUjghPoODh/tlvtmY/qhM4II9m9xptH0ufw2thSpMRzqW/5a5X7/8zxafAB48CRvgX1OeUWK7nPGav3RZPrtJFbOoKViEak3yg8mgFL02RLXDg1HO5BaQ9lJ5dvZLdMsfiE1LnuIUP6/MyTed4LuNQY823lhrz1OnQRE+WpteaT+lwiBW97wOEgOrOdQjnWttDak29T/936WvRrmoNxtLLrTsF5phGx4eF5sH3WLPsx9eycKzaXoGdKHFImzxcpeUtKmS5BzTJMT26XYBGSjUuXh3rCQD8K7WUrrMj0s+gswfOHjjQA1W4WSUPZPpJkuO+HPrX9peLWFzQShacOq0M5IfVgagP41Br/pLSYfWnaftLqqen1DU6YNFA2QBxnj/O7WreP+fSj8AD+zfymScAwbS5rWm16yrtMr7Eda1uNcsjrLiaVWLX0VW7fmtnDrP6HFLIDI2c6Rlu+XD3+aFdpUdNRR3V6V35zOM/lYefSu68N3YurW6BVXI7m8ETgO0Enw4GfqR/VeeSLD6I8pIlob75SR6HXhlKq33GHvxIrhUvvH2qpeTWosYy3WCeT33teqd+Ks0P7cX9pnUItyUe2NWrfe3mcodoPsd3+r2yearR0twJKKySo6iTwCDc4x2A6V43KetccAwP9BxPZu+qX6yMJPakLqY8Iz6aB6igXEdVckR8YNXnEaQzCA/UPiKdv+NGMkpAKZ2vhZxduJsHwq3Fj7sRn7E/FQ+ox5Ve5+TLWNxPw67U/lRq6xHs/FS92tjtbSv2dPjVxeQ6oUZOiBh8s7PIneRTMHLiuLP+8+PFJWvdehyaFeRTHHpU2bTdfj36uvtWRFNSegwr3VZVuodz3EwOfeB63Fqr1axtb73aQmra+fQ8bS13hA/7BlTmF4R5ngWtJE43o1BEpITvNBO9ViixxjeeIA1pj5Hf1TPzMh/Pb1N69F2pxoAPHafGPd3JdHNPvSNAUww/UvjUlWFpewg/j7nu6dtArrIt14qM9gx/n48Pd3VO3X4ifflPPR6DJlPjH15fx/Lbljt1s9L9cM1rP/T8NZuZ6sUtUcu/hSzn1vJf4oFD+LcSa8g850NaxRK7ak2m0jT7/q0p50cKpngAD2za35DZDM1cUa83Vjyr5Bz5uezsgefmgZe0SCZ3P35zcsKdUbwFaYL2kwL3HaXGwFSLhwG4Ie4TXNwCK24Mn5R79jcWr8VfsLBj9+d2pvxUPXAOLT7Vmj/bXXsg35OAxd2oLtySvrq4+mEepdzjRtDq3a97XyZr9Dhk5FQLbsea8+Oqet18zadO1x5o+deYdXpebo05kq7G/QfxGWG9P+hYdbSrBrXPW2+0kOX896Ot9WllLeFZc5ifUWj5CxJ9Lp/T7hxLbncpGhWPlOQnpq7Ztz6eNX0/8ikAERx81P3oEGa19w7hM0Urf+IT+3NLm7f3xKc4NhIw8HPXyCVYLpqRK5R4dlddAabwXzq87ik9P/t9a7nCe7oXt7XtfJ++89K9NlgrfEA7OXU/at+Xm/f9rvrU7SfS0YqQQsOIDhgSA17j7yqr1vwQ2prPovQJnuTXfpjUYfG++JMcqoJFEiv8w5OPWkeVus/hilRs7yICp9JaEnYPK0dcWzu8UlASVxSWK3CBHpwIkSdgfLBmZwbTHtjeXKZpzyX7eWDQ/+azC0VUawJVpa7WkljI4yNHwx1xjdpqZ41pTwZFldzKokMYVG9X8HGkwqXbXCOs/Dkn2R0e3kb1cXjobMUhHigtZWHfPUTWR0977nAvuoqP1AVWf/fX/yA/XNXjhqFjdmwqRbWKrkoOuQ/yvbmiQdlTZMt460TCT82/VTvNtC2eewgNg8+Ssf4hFrW1fwi3ZHvMokVmsdU9vx0wD9dapNCT/hDnSswkZoVTJ0fw6+KJ9HJ/7lrvIXA5/wkFE3jXVjrP7aDSQU3l7LEsPUi3g4kf2Yr0KkVfbd0dxu4QtW51uk89l9uPquY4ziG3gRrzeab3u0rsYMsB18Z5KeOen6c5dunJvdcofLjE5LcfzHq/+12j1ccEeEZ3ln3dyuUnH3ElqgC5YOQ3oo6uAKp1PRWTS5Zxy9j935o20jWkj3vOPY0HqJFzpTyJ64vnw/9ba2EsKnoSxT9poYNaGGQ/adfsbPzkezVb+8LOok5DUPQkUdKnEXXmevbA2QPH98AL77aN+g1gocu4ka1Wf/s3f7/1hrYVQQLTLkB/RpsKn2QGVNCFCgqtNm4/DjsI2wX1UecnqlmWR5W7i0NmcB9H58eRksysamTG8JGiukFHcekjpWj3hn74vNGIqs8S9Di1vKs/D9dqnkNb2kKiuqbge1bm3u18Rl4z6ZTa++7NfkbIVNH+/plSG0mPonlt0a7ts6adSotnNmTL3jVTLBbA9/P/flStOsfiU3OuedbpGudlpfezYgmVZt/z+1dTPkl8HuUJxuFPA5ZYPWVpwHflUMIEk/dzM5Kia/fQybg+elE2LHpII/kZKfkKMmSxIxepEH9Vak7suezsgRfggZFu0XY32zGK+QIsPKt49sDH6IGx/phgOWj+aMz+6Az6aGrm5Rsy1o+e2KpnqNIpPNKaqX6++tt/+/cTT2V7I4Zl1wRkpPfzmS2pSKqkZDbmDeYzOlW7VKapXnAM0K7jp8zoVL9Ppc9TyT2VHz8mvuoXtseTiDnZ7whAS2tve8jH4o3TtdLTcR73fanT8eKXAD3S7H7r+RbSc0fuBcP2fnCz3yK3p8T2zPCuVNTtk5bbZy19QAtFC+mzOec+ag9M9bUp+IQz6jY2gfLswI+j8+mktJxbyBKn70o1uGJMXH4mwAOF6ktrR0Fq7e3wOtCALrI19ShCBhbEAUOy8WfEkhtgUVhhZZ7Nb0vVoJwBZw88Jw9Ev3DDJRmNvPSVoaKTBUPEc/4pPXCupr29H67z+aV4ce6mM1e2t4/OhGcPnD1w9sAxPFBfZOuLlaYurhSOlDmMnrQatVewb6bWI/MIIbG76iKBiUD0MUJasi9Nljb8nR+TzZcOeeX8IfpkHtt/W90OlzsYcXZKHHXP4I7tdKq1bhq3K5mimoJ3lAtT1WzNbjxptFXjr5KVYKZFzf90Ow3XOtfpSomTJ5e00p5ulc/nlVvCeZ5DXTrZF2qkg9M9Sxdw2xV/C8slO4Qs8H/r+RayRZOJ4l1r4VhyQ51de2ItvaVtIRNGLwIfuSVYprzNA3a3ilPwrw1bwn/X2q/5T6X347mcatKuqb42BZ8woG5jEyhPBp5a37+rzpM+nLVsVymzzHqFx+K8K5/4ytZyqvQWbrWfZ4L8UJlDHy9xthI8AeBcQIHZy46HKxXLliboe1yEBKCB1cRDSRPIaDxVEtzO5/09MKyD/TmdKTsP4NWtTfbs+c5fXWqr2zrUc+oFeaC09kiU7LM04VNphM+7Fp5l0zgrVXngU+knlckvLlnXEf2dXYD+7X+7Gn8CkGxbeFWoGFdJ85jg0IJrSDAZsur5e1btHubhmf1GpftRHa7tmcPje2B7XbeNmQZfA+v2bwO28zyenctnuXaWWc0iT80SLec5v2/DY3psSucTerIWWXm1Br+INK1ebZ/9QKILNC3/hFYs9lvdllI3rXtrraLfTKvx63QgTrWKFrNmvDx9LD5TEpfzD8zgs3z+ckpuCz81/1bikSGLW+CR5b5Edo2vlrfDeXOn+mNLNY95uD7z/Is+ce2J62UB9gOIClwn26trdx0L/3Il7kCLeNb8cxo5WVT+7SAZaYffWqWG7DGj/0b4GXD2wO4e6DpFpi19uuo6uezj+cXKXldu/fDx2Jot+RRszLYe+Bv3vwOZnJp8S33275+nVubM/+yBswc+KQ+UG2hJ2Px+btQj7ZWrEFGkJwDaBQhYhRi5ACy9PAeNeVdJqbQ2I9a68TsoCo0ryUMTzG8IzPmpMcDCEVVm86i/h48XH1XdWWG1LXV6lmjPwiPzr+YVjsx5wr5emyy9oPSICarnCa49Vqefp7atVr26aItnIbvSPq1/lkhfgjPrkouWQwupORQf1v2gRjgwnaTHytcd11i3ooPb5Z9zycQtaepmlMnOv4/kgfknhFNKzLfYKaqD4NU96CA+i4lrG+v0YgZ7IoasID7FE6EptR7Txikdani57tXAhemJqw7U0yWFdRtgd0RX7AKUcy1eYbFTYopPliNmUzi1oBq/hi8kH5Ccs2cPPCsP0AVo4Us6wrNS+6zM2QNH8kC0/RfRA6KzHsnuM5sTeuBFNKcT2n9m/Ql5YCZEnvBCTaGusvrbv/4HXdyuvp/qOFNwC4hCMX24+06Zq+9rCRKwZYhSsSc5ILaMITTQRFfRJszq51HHf0cazfd0PoDnsfhU7jxCUiPgqDx+x2v6CFI+bha9mrWpLeTj9sBxretmZWiQs9eT48ptuT1OPT6OlNa6KUjn/ymMafgj25KuWBMXrlM9ATjgLlB77hA/13zO6dYDp/DtCM/5ljBf2iq9AFL3rzq9gPTZoYz489npOKdQfdWJ3YEuh5H2NHl7X+vY0W7IdHlzGWSnOU+UWGDNttYg0pzjr2FRylVSM6kwdbUNvAr48SXLs5mPz7RP2qJD+9cn7bzHM75cfM719XhOf76S0g2nve8E5NxInm/VnTU7e+AFe+CgS8vgelVuaviDotXV6kprJftY/dyc5zrVVlfV/qMiEZPMKNDI1eLn+KYyAn0oRBc/pHNiQN2OUGO1WQsfEB4nu3yl6exIvbdC7r64bwcdR+xdrtsOcoRaj6rr9BSbXfe1neJzCHzEP4ewm6WdlJW7xSz1eGHdQib5j5NOQuu6OxbPSWHPrGDuSVSpppLYXfnl/qxrdnc5SynmpSzXtidv9prWw4xMNes05/8Ryh5o3pYe6pEyuhPBKn7qcwAXS9nBz0e6eh/i58VmJcTausN3/Wql1/zrdIs5DznWde8Uvh3hOd8S5ksbRyzxmyPDhvIJAQd8j2jEn49uyBKfD5QajXYvB5H2gGaQHbCIe5muYhd333KKa/GA5ijZ6F6WlPhFGg1CiWkpUZ7Opuog22inuT6Lktofz0KhsxJnD7zwPnXMCjz3z2N6c5rXi21ySXF+oqlw9h6gKTtt8adb8mzrGsWerW6fbnM5W97zwKF3pLaF9ziu/u5v/r4nr8m0DBoUA5jfhbPfAeiTRC6kcu4XBi9gpWSPcdK4QieGnk7P4BzjvCOMXHednzux36bY7+rP484tLZe+HHPK0uPCl+uz3/4Yx9K2nm87hOdyew+RsoQ2NAnMx5+NXqJhjbOz/3e8buxXLztrVZt0pPQemqcn0v//9r4w23Hc5rJed62gO7PgnPMl+TU9a8j6vk6toDpvAF4SAgmCokTKlv3oUyWDIHABXFISJdt66aRVO6dNSk7DHBwR7Wrlc8yf4MqGvlRz/wwvLZ/AwQCi3P+4dDUbwD8328d9e6przFismmsgfo+xjr8Z+KE6Nm8cU1TXiFg5DkokCBULviKgzlrPSC7L990ZkKn17oWu+h7BwJpOj2DZxHjN4z59N5UTf83kzRgsxWJgMXA7BpwzkqPuTJ+8BYAOXx8f//r7v9m1/Ab/Btc6yKXfI2/WFYniNTBCV8997sZ1UiXoUvUxYO8Kj1wr98Vkq5HRPOp71L6/iqOWmlstezg9Np7vG+o77oDOHeu5aN6I6Cg84rS4PPiNXiBrHC/W++ntEWyEjR4OxUafSYVY6RVNv3DU96h9fyaZZcd+l9m/aUMfjY8yr3176LH4VtODc2cbzckV1fVg6hyOcqV9tXwUx7Pn/D+/pW/8y8HGM/f1dvm9gYV92xr4YEd6tjClVzjNta4LSofVXgx8TQau2jm/Jpur6rdjwD/LPKDUtXc+gOQbhVjjfaPBeOdUrjqqEa5A82Ru/AYAcx2XNqepRjCz2xjF6QBDjtk1Ysd9jsy+P3IHcj/YFdea/dG/juXi2RtrvRdoGfZW4+F4+nEEDxl6/euR+4/yOTbuX1d7jHSvrcVqtP0j5ftkgqrbs+UW2dKzXD67/g5Mu5ZHjnJPrAnZdjPTk8/jbSwDj5lvdDzn9eSpT00fz1JnRFmlJ/tN4X7vJq7Yk4e8F6vtDYkssDYV01kCxcC/WYALZzGwGFgMzGKgOCbOgl04i4HFwGLgFAO8MFvHpdPUnXL8ck569U+T7eO7z4A29a3qPS8yj7PfyF93BTmMzFfS6ZvBPb+XqA/KnbT2bkF/dod9Oz6BsZhX8HzujkiXV0eN/Qy3LfVeo2V4WU0bzfaOI1hMT3PFKHuxPL0eXzsPz7GBu0TnfL08td7miV5Pr32PynaMrOYopmevx8Kz0fq5mZxkT+377RE/l633KwvNQ48s1XWuDtq19EQ8ZyN5HnIfz/bcL3+QZDvno7P6UOEN43PzrQFY7frrN1aD/zYP1n2EGR1LyzbKCQ3tI4cX4D0O2PdgyVscO04k2HbZApR1hKVs23n1GgY6D5nGbykWA4uBgoHb7UzrmFiM0GouBhYDi4EvzIBazJOoWkc5Kc52Goy7Gk8BgicukTqi0j0nAvefJhQhJJ+j117eNZan70h5yORZcYeS7nB+Vl1H50NHKcvkCQxcMn/UPc65JfXMuh4bL6sRXw/zQfpZnM/CccoemW/nfLWXlpHgfUbc5uZQOKQ+Wu9IViO+Q0U2nZEVTEY+B9BMahnI96qdlnqykmuSc7rTMnAO6ijOLJ77cRqWYeEfNh3F//ydjcoVeHWYBPLjok8AOtJdJouBxcBi4AUYqB5DXyDvleJiYDGwGLiAgRc6JFKqL5RtZaymZk9L/231T8EaTwGKqUwN3z0WR6/bKrxZlb7aGf5evoX3NPEK70foN3Eb138eYFXfhUPPGaAhMDlUAU8ruzI5jZ4cJ0TpvjfZMxsn5JNK232f9a1cBNKZa3k3jdLgxZ9iUZaz1wZXsBq587cXZ05/zxyeE+ksijerX4vnnup7xqLHpidWZtN9xMu8nIY3Xo55l/rA8WdqLV3JLSPNAK8kdNuVD4ypi/FFO9JaPb2foKE6RhueXhOfQD/oUk3mIMYyP88A/wX79XoDBm47jmsPf4PZtUpYDPQwQEeh2x6IevJfNiMMrEP9CHvP8i332cZTgJwU+fkSH99+/dPp9tSYLt3Hi0t+P95x5/uKq9X23cF2r6XTy7AHh1lNQ8B3mNKThWyUHk1PJp5ND37bpqfeNkL/k4P1bPR4O5fPuft8ehy9GvuZ15lrGcj9OMTn7kmhjdbutZVqey1byys0lqsrolhMVAp9fw56DmvMx/Omo2vZ+2Syv0aNZuUbVZoOwjZJ0XjjJQZnBHUGHL9/f0WGB8Za1eJRoUdcy579jn7gM4dzx/mdfE5192cCxhAkjgvNWzrEy5b6do/46fk8XtwJ43KKh/s7gTH+qxmnX3Z0oNkgj18AnE5mOd6OgW0e3C61+yZEV033TW5lthhYDCwG9hmgg9g6/O/TtCw8BtZZ0GPmzvpyn3/gbwCePmFmXWsexbH2VvPIOeNdi8/KIavugu+Fa3wtH87/YG6at5G4GudoziNxj8Y6ap/lNnC37GjcZ9mPjONIzhnPB4FGfA+G8s075obH7R3y1zlo2S+43uPVWLc+rq3k1sF8fxyNr+V+hNeyHP/M5Fy9s+bJs8boWXHPsX2F1+kRTMv19H4iueqyG3jc9ZBPAKo5nKhluSwGnskA5vHAzvjM5FfsxcBiYDGwGDjNwDryn6ZuOZ5igFYc8yddhjjvEwD87clf/1MWGldN4a3nW4Onr5bKwC/Sftb18bN4flZcbzo8i3/kczc2IktT7xReXml4tpX+e5DeWF+t16N59bzSsUbqmpXnLJyRWt7D9z2YvLqKfvxZe8qNZtcFx+fD1dE6Emu7w57THPrnQH/I/tmC6EA+8NuV/lSCZViuZ2t2D8D+HQDS0BD9+sN4bHiYScZgKRYDi4HFwGJgMbAYWAwsBu7GwLaEe1Zmz179P6vuZ8SdynU2dRpfAULQzFrVbnrtvX+ylsTtvX/+Rt3nN6u3GkTtvzJTWe6Ik68gT12X9187EgMfH99+/sZF9Xt5FHg8e/az9F7cyWPRne44kzrU0So8NoB5FG3ES1fRfj7Suazaleroh/HD04fmjqPOp/+7v7rG8XzaPOhYOtuj8nieiDgL52j+72dfYTJ8xoWnJLVnxWE2zDlrFn6lisPJsYOXTz8+9pQr1g8o6BzyOa9IYcfz1qKlvNFCTlZjSelxi/52L2xqqAl97x34sOofTY1qvXpy1ghW7j+u2ugWrUfjzQSpRdbg3rdsEKX8G8C0SrT3/smUpgGGjXGx/7tpminjWl7fcadcrq+2FuHjgi+E1eIs3WJgMbAYWAzch4F19rvPWMzJ5MEjekE4WZjOIWShTGegOkJQYvvx8a+//5vD2quHlMz5iXPeM8Xuefeun3p8tY1cb2nly8mzqrCszkJ+PKWvm/lcrsADMGfdvZib4Q6auVu5Y+91h/upuJjuv9/jgR3VP342Touo+J+GqelT+Fp9VI654e5Xx9PicRds1ierNttLuLJhXlaj+bHnnceXpfMZiQ4cfDPiuuPMPmO01KOlGLYj9ZhPY3gNiUUefZVjDNnz3q/O82zo1dP/LsFvhD7VhbV6cFViD5Q3KpgMDLbzCUBPEHfsDybbFWsZLQYWAy/PAB0ann508A6OL0/uKmAxsBhYDCQGcKBbh7vEB73TV6m/xKt6koWStkzC98a9/xZF+ttI1Sgt56l949fWc6/4473Vg3ezenLgq9W9v907686uZXUW8tTBnwbWw78XTPtq2bN/ln5kBCfXde7423M3t4fcE9+g7YHtsxkZhb4IpdW0iIr/aZhlshPaOreeeXvdvX8Uo/PpKa+S88GzSU+U+9joXw/a887j85wwXiHpozjnKn0kY1tFYfnYGVrfZdfyuXrbXpV9xzqo41hnCRbjARqphc6WaY2txJ4MqudZwWDQGZ8AeJlUo3vGS7/PwCJ0n6Nl8SIMpEPai6S70lwMLAYWA4uBwACWIrIgWQfzi+eFMB3u26tWO251XETJMDt/B6A7kpMH+c+65pProWqodm/V5VWV6okQ7RLGOck+c+iO287qaO94FUcjvq39re4j0mFo9OhydqBuxUNRxGW5zToOx3wvy7Pg42HN/uMMLI9+t7sfv13yBBw9dlpGYKtxEtKZaBnmR+ebRXDCHlCPYB7N/0BaTdORnJvAN+38avWeHgZZt4dv33zqz81amB/f8Bdysr8GgJPvJ71hb3cBJKhrsToezMCjh0TFe9aC7cEMr3CLgcXAYmAxMIEBnD7USWQC5oJYDHwxBqbtQAQkuySv5xpPAQrd8uWjXcL1rwLE+FZLxva1pnfF3/aSSs8I3fdazoDXfGyNVlPz69Y1K7qQSSTYjG5raOczmRkbflij89dyF3AHV/2Y/ZZDrIbPoLy/+NufQ+Rn+BMtRATa9u3YGvs6Ny3XbM/rLkHumCdexiP59P/thaEZ5aU+VT/Cw9REng1GK48rFwR34xn5HP2kqD1IPTVqGy0D2Wq8iNizsK7zjm/9aF6Uo/oJ+zuOaWEljL+t0c4BEWFzxW8GOjnMrwHyVqOA6h4XvektceEgdIdx/Jd6MbAYWAxMYYA/sZx6QKoeG6ekukAWA4sBZkDvsGt/W3PiNgzoiXmbpPoTObsvlefQnd8AUEL7kcjCY3PfWZccrkaufiaDDrjkZzFgr3qt5lm5XRfX3te09zOs5rp8rkDuHEc6YngHh06EK5IvMO+TiU6sndX4/Gnj60wOyAOfJOgo49VptHeVLxnBJ5F1XS12Ll0Xy5Jno1ubpXlFBuzITplX+Ro7b4EmnFBtT3GiTQY/f//8hhXJIMsJsALT6KpYL9Vi4L0ZoP1h7RJhiIuD0nsP+6puMbAYuB0DdAxah6HbjcpKqIeB7olbGBbLj4/vPcEeZROez+p92wxJjFxL2SuzxxSW5TzpTlhP5llc5eDx4OmV65Co87GjbDU9wTRmj/1Rm7mc2G8Q9miO5uzZa6603GPv2Vj9uXHUOOMIGm1Evk8mPVX0jGkPzqyqs3zUs7d7csh8lYPdX1TnEiMDOyN4wTlo5DjpjTWK2allYMx7vv89AF9x1Sw9dCYP/96pUky3qj2+3TCZ4Qgm3/WmP10clsJ6RLIAqnE0lh3Zc3O4JzeV5rf43Zn/aF244aivASCH2r+zJY4FucvRlsYvfBtdheVqPo4BGpU1MI+je0VaDCwGFgOLgcXA0xi44oQvd5NFeFp5hwJTulfQcSiHg8YnGa6u9DKsnacA0QXEEFXkfPQ6Jl6THLxjdJDPzBwZer92P3r9l0F3NK7G70hhyOSF81d3wq6r4vD890YDh607H7wUn14RPfpzY3HOqyefozbPzWRadGc0T+JbNKvpJvpcDld7ncPvLnrH8LnRd5K7ZfcdGJt2duhnuHu/2+WHnsrwwSs8/lorhJdbWPfTtsvGLpSH4Ok1YLZo5w6j0NaFbJfw0ZveaDbsQO10F7F008bVva4c5pPbuzoWA1+WAdkXRfiyVKzCFwOLgcXAYuAZDMTzT1jhQeZHtNFrnZgeNBx9i2uyahhyb3wKEI1b27AsSz/1nzzJ/6+/8Zv++2QNxBJuuN1zFTUc5NkA4dr9MU9JegyfWZSnfk/x2UPbEV+OrdjfHrl3ffuWjVRHsjA556XhL7lD5t0Ds3qlGa9F19WWr4tl+bwuVrvGWb0j+Y/4Hs5fzaXDvnAYR+gJ3Ixi548HOc6tRtCyF/E99OcYfiQ/HOvzG32DnBf9OBkl6vmk1H1i8iqdVcssnFRc7/v0uHLmRwZp7V2oa+l5YxFd6Q17e813X1egd+Szj7ksvjADxYT6wkz4pS+OfG5Wzz4DNH/WFNqn6RKLdYa8hNYF+jwGimMJz/A1y6cOh09nwX13VEFkgLOfAPRE609Q/y67B/meNtOv/G5V5nOrOxy9eR9rGrFOlMPZhoRwRwS52ScJbAfWtF/ZOyhWM63SYaBznNiws3As8hUaOyJWc0XchXmYAWdfPowDhwG0rhk+gF+paC5aJcB8Vf9+1MVnR4I2okbWcgfYa5vg2/+0pe990HqyeMoN/x5g0styPgn4ZWBkuV7LuNkJh+pYRD96w55fw+7XVUP0u7NlRyHHAJf1YuDNGMBuNmFnezNeVjmLgcXAYmAx8EAG5DQkgg5Oy7m1otOEnJXns1gOzfcY4ufvnGN4Mmhfshh4lSApVKsPJFlV7nemrtY7fWs8Pc+1ZbbXN+vaXV8Hz8Lcy/0R/bgK19WdjOrdZ/L0Kszh6AefInVyvJwoh7MNlfbuBbSbhb3P2luNovC4qMblJD8q5jlOFEAUZ+FY5FnPH9OfZ9pni42P0fhYVGrvUan50GOe5XnQV+MfvQuYxdVARsbfwYzPg3f2ZePkKnTckV9qdc3wkWztWIyguXxwh+akaVjpzEbH9PfvR118Bvyj2epfPPZHMaVEhZ7n+hji2Wt9mytt2S97bLA+/AaAoH793348tvQwNUqPjba/m3w0fz3uRS3VRXX6DUBh6zTTaiF2b4hYrdOxgATIglA0RV8TwlKk7KgqS6MZ7YkfNs1I530xHjai70vhhMowCtge2UknhF4QhxhY+8shup5lbM99z8pkxTUM0D70dXejg4f3R3OFgWlHPViCGf+lKBfmhpG9/cMOUDkoH//8n/8bnuFq9zWA4/LERIZCx8d1z69/cg/pKZAG6L9eb1wPOVnMUR+9bpsT9TjKeJ5H7y4gx/G47Vrb+O1eD/mcl4f2GH1nzvgW5mNSqkbpzJN8Md8A0n8cqAS1dy4rRlNVj484kv6pbPvHcSS1cd+r8/TwPf14RTsIzdF8WlYm6aOZHLXXAbWvlrXNs+TH5MOro49vPX/D+AH50DkoLvUM6XFlGN9M90MUYACf0gyddx6SrRekXLGXdnv9dgiiB95+Ccv0AqRoliG3thiKgL6iuTks6Q4MrOG5wyiM5fBCn33xIYj+2yPRGAPLezHwxgysg/QbD+750m51FEUytZTW7D0/xAc8iWZivzYAALE9amCCSJ8A/AEAZQvYmIfSm8yKPgXOpkWv8WbFFff78X24v35j/PFv5jHKNS99ja7la6LVUcf5f1bmh+M276jV2cm1R+eVzdCybTV5zLJlMbVFu/ecpfa6nazGtL/221VxWUJfmZOje9Zlg5ADqxmbd4y2Joy1ym0C2mhB0/z1TNDytABNoMdHbKYzs5PXe1jkkYTFHzXTKnBb/m3SzOgvgTUy+tgH6Ts1ilRbdKLb9pCmynz0wBt9AkBCE6SK7IFr41OoGuCkTFVXCz8Jt9wWA4uBxcBiYDGwGFgMLAYsA7LUE+HkotJCf3VNc/UPco6sdssB+vjnP/4wKGQkmHQJI3I+FlW1wvf8cpQXbMUrs/9w6jvfLdNMnqr03Pf1Eeqd7uKcIm85RQbuPBMuz03d1xyaELNwTBKaAS0bwyHFLORZOJViLmO4EuuWqgu5nVrvq+Q5teg3BBsfx7jeU8s++ssA9JLfgmasVZeMmcV+YzxnLwbu1qN3Z10XjK7LpJqh4lj3Y4nJneWTPBPb8YlkP4LXhgLpu7pSIwfphkCahKJjLrnOgLBH3UKmKBeTddaWdjGwGFgMLAYWA4uBF2NAljkvlverpSuryFritU4MTHPNSW4f3+gCQBtBDj3xYgC/9NY2IQVc59lv2GsAnav3XShPr32PyvrKTMtHcTx7W3W0lOKpXRsUViome2rv+b3/4Tw9h4N6+nSCq8EzpF/k7t3IfMBvAPpHRMfyPsnpmQPesGh8zwZ6d8a23Sb1ZnmaeTKem8bXckx/+BnnFcxJzFiY77hPYztGNIHzcZ6RwiycSkHDI1XB7FBdPb79+HO57Y9rSfKOV7BEniP4NuJjNCPH2xHfx1R3NMq5+VaOuywXaTXw+Y2fulNd/FBy+frnaLbg/1zOOpY3jj13/TVOTyYlV9r/iCxLy8Cx9pSeb+W5Az3atiK3PwEghy6UEviUUwnyem1v3qOSdu/rVbsyPsLAGv0jbC3bxcBi4JkMYK22jlrPHIMXiR2+JL7NlE0aXPC/SPkPTJPW1YpdCVzTSWdToL+j+6/wGwCCUIt2tGRLXapTAAvdrGsdwS+Eq/GLcI0mMoFBeRVoxkJYLOiqUgpM4D/r+bXe9XGDkM6u+4ygTvieWekMj46IWxH95Wzaz8N91h5M4CCTcp7r/G4um88cbp7vVemN83Bw/mSFHI1+1D4LVm+4+0Xd/HLtm+xfR3nqHtm7jdfRQtv2PUfgNkK7t5+9fst6xLDEoW+K/PV/wicA+AxTfZrXv/Kp4z9KixFBtKOfBlyRY2NcasvMWgol9foC4jP8NoD2RgYzhhKBekynUdRifzUdMSakhdoLRd4ZjEvVV6Ns1ftoBrY9t7ZfPzqbFe+lGODD1TpkvdSQrWQXA5czgJPKdmrZAtZ0W++STjPQS2z7cE0oH/ETgDwTcuO+oGSIeri6Nkc60Wpc95xAa7tksbrvTLiYim4lZuYlaWU7M95vmJyzivb9n2bRk6e20fLTkg6B75PJu/IAhvkTsL6/eTmNB7M3tZHXTND8TGCjm/+r756iLlQE2X4C9pgcNMO9EXH61p6F3M1z4VdtThj3Km5NaWP1aGpIM3U2B6BDP/5JvsbXso5i5+d4hTTf+M9Nqnv5DUz8ZXpe9tSWPnGZk692eudzLar1tczU/N5Hl9Oct6TKnHBWb4aQcCwQhz6BYC1yn+v7Wm3MKpLzciukkRf+5ZartRhYDCwGFgOLgYyByikk6+dGj41xWorFQMnAkYmEv0wfPZIjveNfibzaN2AgrFg//vX3f3Mu38NT7Z2s0nimbmqTc6lNvV/xPXCJwvGsmPZ1c526uvYCOum7vCnhO3zXbVqF4Wo2PvX2z2moC2gxsMuAvf9kNbsgDQOLZjUN992uuWi74SYa2HuBE8FvCDVtpKZ+DmCJovMgn9D67h9b9ydqpjH8xBqeFDotK+KdZp4A9B9aCKzKXq/LNo48KGZkHXWUAdjjLy0kKjfikya9F4RvhpCqnwBsRgklf9/rz63fvnWKDnLCv42esr31zJeKaTE/wEJcDCwGFgPXM7AOZddzfCLCGpYTpL26Cw26/Iu1YHWE2bDmxLwB7uKyZYS+77V7/5lb1piX/5sgxau3/93KoaesYM5vKiO1DD6//aRf09NnMt33sI9eQdJdmdcY1KP3qMLdpsjbUV8zRo9R4POi/r8t8Jis7hOl/Tzy++Rp91arOZqt3q8tmtV4+BrHs+lHA0IPphdrrv7CfWfWMcTD8fQOQbjjeHSkHLDr781fdu//PnMP3Hr5aP3Q51Rmnmhkd3wf3pFlVX9yZCWnafO5gn1Mpccoq8WB+et37hjP/ygC7FtrSEmYjIqlHjUzT8wtcYCQWWSNwnA1RxgohmYEavm+KAM0B9Y0aI2dPYS1rFffYmAxsBhYDCwG3pyBrmWDNdLLeV580B8Csy/rZm0eo1HXvt41macfTxDIwCmv0hKP39W9f4lo+cMyBk7oTQDshF5xj5gWRSxyocwt781aik99vattPD49vfY9J7vII/eQRnxDGR4/52p0vYbzdJGdDpdtx/65av5upd5Vvn27MH99N6RjXLxMov5HYK4Dx2P4wH7tQQR9xFH7vjW3tbTnv5ebxbGxZmkQC2hePkOxBsYui+vhePrMeWvge8btcdms31eqjLWa2+MzEPj9PFfyCeRr/ch3xO3vKDTy1ePcz+cjsxqp2htZPUY9tWgby5LVeDn3WwJB7GmFmJ8bvQiOnp31OU/MStSyDUPS1jsE542F7tU5ONDmVdKqyiv4e1igK5JfmIuBxcBiYDGwGFgMLAYWA2MM0LK06ylAiKIXsd9+/s5fXYjPuHWywJXKrz+4u/JNTXXV7gDMVs+N2LOUDpzFK7b0WQH5kVpv63VmfNdN7qOVq1JJyWqk64mCd/X/xJSmh577u4LrxvE65IzSuXt9Bv24huXKah6XzWCk5ohcVxeQkbu+e3e0musyPJrJXHt9bNTy0Sjw7f+G9CP5fGSsNm+zjtL3qahdb3/v+1XUX3tm2TxOwjItQvmd9jh6y57nWV1DJp+AUP0KEFk0PKtdWeJ5I4uXd710CzzY6jx+RA96raNmQ4y1cslTGCBu2+RPifJEEEywJyawQi8GFgOLgcVAm4H3Pg21a1+9t2Cg+peAkRnWoHqO8sKisjKtqG5Rm5NEx3WV41lTY7EFlrCylK02TzTG6/5PejGV4l3h0Kro+f3Vz1J0ICW/65W0rkvLqvQD4jhC+47X0L20MFcrn56F+o4iH620y97sTV1eanyO2ivXijgXrRLgCpXh8IogL4D5gjxcMd9GMK3v0aOEN09m4Xj4NnPPcunPMcAjiDUHvacFiUBdwb/GnDB/Pr4RyF+/ccr2EzwdS4p6eyENY3ovCrZrSDLIbPs/AYAb/wWpyhOeBLMascjqrZooWMoumlKqGIiGBFIG4iqdFRV7OmoNuuT3YkB2rfcqa1UjDGCE164thCxhMbAYuISBFz+brINk76wgpqpjrZXMZroAoO/0cwt/Dxg0a1Pq8xDzQOQEb4ZTr2nP8x64S2SvEa1GpZyJ/ZaZW2hoX77yZo6qJCnXKo8Hnxqh4FzRuy6fNl5u5Dkd9k5APy4+jRlBQCzcTfFw7L0WL8P46ZAaZe/ev47roVm9l6G1hMba65kcvVS2npeHjycQ2Ciu/eM7Bo42OtkKb6q7PcrK8EKxneGFgTXDZi614z4r56vjHt0j2vn0H3/abM/CsVHa+Vt7T9OPc5+zG2XCS4GDM99joK1vj+DRWdeOhV5g9o/LDmZYNHl5enqL6a55An6bJaDZiqzGxj2qOYqJX93gd7n11T9lgIUnLS/pxdt0ARAUaWNXn3CI/Z8R3VnFii1iiVNC//LvihclKlrqWmXwGJHSkLF8TMTHR7lVgbdK5vFjsSIuBhYDi4GvxMBNTvWjlNOZ6zGVrFNkfaiOrNWEQx6y+BuA2gBiRMVaBMlgG3IO/9fv3I7XH8Fm6xeXGwtHr7fOlwKy9ZawCnpfi7sqF/reXtVgTOmNl6cfi7a86wxU2D447hWEeqilfSgD3n2yy5M4OH9sPtmMGkaz+K+l4XGkL+0+5B7zODMTZt0FIz6S1WHfC/K345LtI7b7qAarl+aiZVZED8fTHy3ltezVslGJUoM3ImQbu2i2WUerEUQtbGabVO/X2iV7o0LMUBf+LZYWA4uBxcBiYDEwzkD9/DyOuxAWA4EBLGnWNLvVdPDWmRimOFjfP9OlgMr91HDqe/8K64iIa194HL1jMXzd3P8dsiMl+bYf8W+awqIr+kCNh+9DmMQPX2EfHUETsa3wGPP0Hlp/XeCw//nWXsRZep25ljW+p9c2I3KF7YPjXkFoJ0TPgqDL5DucbPT+qOV2/qF3ZFzavu1enVrbcpzhNr7OJJMPzp/MNzSyGTWMZvF7NJXaD86Q8SM28hwfx556Z9lMyPaCER/J6rDvqfztbKnMQDVI2T6i9EOit+IMoLMiejiefqii4Gy5Hcd8BAKfJjkOnpuEv8fFbVKii8+hdFSiN5bUq2hSj9Uo8ySWRs35kJzW+2JgMbAY6GdgHVb6uVqWd2KgPEHeKbeVy2JgiIH3PizftTo3L7cjDTIdjMjm4+Of//i/uFBwPGBXPXSxf4CLvRWEiiol8PLvB5/Kf1297Wv96+ICeUJ0597YBOSri3fwdeb79w9kF3P2Fo3mBDygdtGcUTgAfbXprD0OlSLbU/fbrijUHZd2sCeN2slsUcuTcnaJNPkMVeeG6e14VnQcqfo/4dR5ahl1Wk1v/bndLJwctWxxlM/0FEQckEsTvx3mz8/f2OC6+9CV8GbeVmxOqdqc6979s9teAhptz/bF+zFeKGLgvFMwFlbfcQleEuSsKPiGPnWxE+cUPlPXrhrNg9D2UdZuvqri+KqqA9y8aokr7+sZwK64JtMu07WvK+46LYPFwGJgMbDPAI7AWBvtWy+LxcCTGagsuPszgvMHHgNaLD50sxGEuugfGfNlIJ2cgxs0KQ+NlHT++8AVbXFV5MeY1zNwDTcvCUY6etdh7lOQj0av1O4wOQG5EmyOyptvVr/zHVDZvyDUdhiPBxurpzYP7THPom5nuFMRUZTo2rFsh3HmW9vp6l53XNqBn1TLyWxRywNz7ponJp+h6trjdap3/D5rT1gcqc7Vbr2spicHazMLxyJrzUiUJ9z7R+pm3uqKRuQ2G7p35+xmkrAzWaMZ83so6JNnWt6mU8/5nGaPV22xUMmu/A0ATMiZz6dYcxe16SbZ4V8FOajI2CbC0NzLmyAE07W5BwPpYu0e2Xz5LIrdZ+0vX35GLAIWA4uBxcBi4C4MFOfou6R1anGNBQa26ROAvD60sNXWVDbd5icNXQ3RpVx0Chbmj4KJAtcYXddP4Qqp656NGYDHX0eey9Mk/gQFjwWG9XjwR/7lwuPZnfHoH0d998Kbb57ezczua3G32jx03E2bPvnpz1/7jstXxM3Ya34emFmGYq7IZ5ylfoT327Mqtesx1XLFdI7KzhMP9z7zx+asz55enp7eq9fqcZyBXke0ltDoPMeje1Gu0HtHVI5lDr+7CYCH+zAwIZPL9s2eebVL+HmDQ3XxQjeE+u+JSVHJccK4BFS931XCGBWe/8OfA3yEv9NFRcnyb/sEQFTkr2XAkQ+4iKSgIX0mpvlZgbFYildlwM6OV63kbnnLLna3xJ6RD02zrzbTvlq9z5hWK+ZiYDGwGOhgQC9yO8wfb3LyfJG50VOA/jCFkoXWbU2tLevF0wPkrwG0TEvXF2gPXb0duu58Chk6Qy33J3POq4lvOdea1l2cJuzX7fTGSOk1w7OIyjBVrFn4d8PJ6r0guVfHv4CSh0JG/v8TPgU33+u9enQeWuotg70ww3T0o9VUtgK7lmLLldWMZ6AxR87Ls3DGK3okgq76UFw1j5SoIbxVOJlTFzthRmofK3so1nJpFgOLgcXAYmAx8O4MOKfcdy971TfCABZeIwjLdzEQGBg9/sCf/g7A3//NC/zv/1G8FtN0a7Llz9/54kHu9Cu3TBy+atAA9WKPXjlpey3HvB9/bzJE3HmGQE9WPTjZ4DyiUWHYCdtv6QDsqC2+1exATOrWd0e0PAn+EphncTW5mO79CE9DslVbzdEMNYKWj+LAfgfB1Dv+GwOesemo/GHufNsqdjK0Dp7G1hLSwPeJx/ejaXl6+Tv6Z8XFOPaMoJP4cbUeQeeveRxlo9++x9LajM+rHZo0J46pzkrLjvmD1PfJJBYcmNxZR7W5Sb9sbVuVvRhBaDuOh6X7XnuX57AsVmtjHJyVQg7XZSiyIWO2pBq0gxhqZTroozNviUMm9NhkDpUGZSD/Kt1LtRhYDCwGFgO9DNCDG3pNb2f3upnfjkok9FRCZywPbsrrSuslGaAn2rzapFR7cG/qZLeZkj+3P/71jz/MkKHPqLV743OALUYFoVNVYKhiOwGqZh3X3FW/q5Qqn92rvatyAK7K5NpAC52ua8PsHn8ewiwcPfe0fIex8mq8JM9Je8Elud1hMFYOhoGrx9qb/yaRF1Nczdsj6bC1WM0j87k61t2qG8pn0jH/as6r+GpZzGLxK1x2UetoETcvkj5QfxW+VApCgVzazWhvSc5AWxiLgcXAYmAxsBhYDCwGFgOLgZdnIC2R6T2JfTXxOh5OLOEvATc8yTRb+UdT+xuAv/7GXb/+2cA61CVV1cIHpMNXft73tMJV0NHvkB2ObqtX+VSe7Xrw2nQoH5WJTROaIXwP9KX0uBuHlHvu33uM9fj2EDMLR889LSMHr4qeDMcRvBptnv35uJZ6Lzi492lMN7cBTI2PEYHGjaUdJsmY/7jP9Mi4XvrP4kHnczUP3vzXOYzI9hMGqxnB93yv4O1o5uNHNlRna7GajAccB6DSx5zM6ILGpOOPrs5yaDUXVJJB6nyyjp7GAP9XV9p9vKUVMq+W7Zqc1dXl86bUc7HK12Za7VZKCiaLdqUeFi8BHc5qASwGFgPvzMA67rzz6K7aFgOLgcXAjRnoX3q7RXgQuLZgt+pvAIAH5+w06OFtCexbbLZLmsPA1Veic7L0Udz8w9Wp98mM62UC8WxP89J79kU/moG/k0Ld47lzRTo3LV9IJebA3e73qPGaW/uDWJ2b9MVoHieenp6Q8fnJf/V+8NVzZ9rNoSO2hw9M3Bd8TBVI1suno5QbmbxHFS6h5sgzMgPdKM2OOzM8wsaIb5OwrDMdluidzm2plZmEBv2+OXSnd1bSUS25YB4UbnU096/7EhheLNR9k8V6Xww8hQGall9gZtJ6Zb2qDOBkU+1aysXAYmAxsBhYDLwbA2FpTsv9tERP79s64eNff/83V539HQBNA5kmr/CXD3VflKmf75TgWaqm/8B1nr4q1bLB1Iqrr7fO4Z/z0nXNkg/wr0Iezd/aW42CX2LOgJ7tk+475gHmt+i58nwnYTuUzA8xiPhaM/CR2epjwnVxI/KPMIz2sxc9581IX5eVCdWlGM9Hc94V8sWNxhkDAmg4+j3vc9HPeV0yUAf3jhtlfpAOL/Px/SUie8efg3mOm3uVevp2xPzEm7dyz7Qy53U6epQ15lnukMyCVrzgRFvlvfnJRcKmWtJiYDFwhgG5YD/j/Eiftdc/ku25sdbYzeVzoS0GFgOLgbsxsH1xRy3cN7HxGwBbCV2U1U4bpCNA2Vq/pbmUgXNXkJem9HLgD+WweXfn5ah7jYRvwPlD59hrjMpQlovPIfqWs2GgMqMGjhsVNBNxSEG50cJrW8wNgQ05D7A0FPcLO+fDnrcKWsyynb8qHFfyGLnCwW3W/5ikBK9dHbhYq2MxsBhYDCwGFgOLgcXAYuAMA2vJdYa1r+STzxBaq8flenxr/B0AeMrqnkjLsYRFUmsr0S+hn4GRuwX6+5EWh79LR5eA9ju4/cmds+y/K+BY6lq0fC6dtpfmsG1pew/n5o1F4MF76pGN+9U0+FYoqu757UE2Lh7n3STSbx74+DeA480x5IlEPJvuNO9n6OzdWaI9NpkDN+Zylc0WE2uWwn6z+bq4HrLNYbw6G8tqEMXT2xyuyNNG0ZrKjLL7e/dcraDpYOOyzW0As39cKkFUJv04/ZaViB2qCr4eOy230fot2zheL349e3ANna+681YeiE9b1RdHRG3V7opy+z5R0enGKOxW8ykMHJxbT8lxBV0MLAYWA4uBxUBkYK0q1lT4CgxcN88DMq3+sgWgNKj3Y/cpQOUAVJ71c13+ZfCiffDKrHJFWAB+8eZBPjVbj+f2MREffxdKs9oj9/PQb6njnvOKdxbUnSGNeVPZmf88B458hsbPRyKPy2o/NyL9XrCc9fz4k2NNz8I6wmF/dSfzCW46ipY1pqfXNneT9VGunX+79z516Yruk5WbiT7yaNl1aHaMIxj4R457jPXj2BHApHy5wuPE0/cn1IkgK/mA/Im/0V75e8BhgY5VOrtkbpgr/amR5dPW+4eyXMaLgRkMhMXfDKCFsRhYDPQykJ2kep2W3WJgMfAuDIS/VvUuxTypDrt6KQ+sB54ClBb+eFdAUHRetRAT2R0ye7VqNT3snfMKyDZzrdHyTiIqB+tlNTtoqvuh9zNUFSqFijhSUQVuksrL6jEcetEnFfftCnyL2cOV9Tpao44yjnY0+lvZm332kXzqWFq+HcPqUwU9926Xp5MQcsZ9vsu/X+7k8Fy1nl1aPpcV83nkk71zUSpeZm+t2ExVaa60PDXIg8BeMv+pI64ZUMtwJcpQhKX5X79x+/sP3rJRZojMuGvolWF2IOGaocNwmSwGFgOLgcXAYmAxsBhYDCwGFgORAbXqVqKlJ1zoRovCkH4D8I8/rEdVU1m0i4pgRa46L+ViYDEwzoC++h9He2+ExdV7j++q7rkMrP3rufwfjb7G6yhjc+3n8p+v5POWzvvjm/w2gJbobJfZDn8CkKHpwEteDCwGFgOLgcXAYmAxsBhYDCwGrmLAuf0ONa3RwzKdN+V6vfF3ALZcHfTNgCUgS8QunxxhtW7BwNTvq92iojsncZDtr/nd33MDGLk6yPC5WMtrMXA1A3f7DcA6Fl094nPx13jN5fMo2pX8l+v6mBupP779Gr79j18CmGcEDX8CULDgJFJYreZ9GVgjeN+xWZktBhYDi4HFwGJgMbAYmMBA4xOAeDO/dSsfi8ViyVg0JyR5CqL/G1f9lqcSmeY08uSKft8Dzy+/+N6qHhctTyN0GGhCVj1Pi6enl9Az0W6yXw2TVgWwTLZnrLWvwrKyh2HXudWhc9Byy8fva9fr+209WQ7evunpNxhXGs/QhX5Sh2ZMyyPpzMKxOeAIcOV9RBuzV3NF1SOYXb4D+0IvLzPsumo5GOgKzIMp9JnbMbKaPqR9KyDTeZbWvJedNWwajxkLfA5golPNb72wMAUvxWLgBRloXYa/YDkr5cXAYmAxsBhYDNyNgTc71e4s7/f/EnCLD/59MX3H6E8eQy1jTOG5c9/IXM/1Xw9pSy1Pm1Eht5+/MZ5336US11Tk5kMEfXxr43u+ltVKJp6z0RPaByUzctVrqvby8fQmqR2FZcA66FhatpbQZDamIs/L6jVOT54W4ZxGx7UIXibQ9z9fHFGAb/eLdg7w8jKxOT9UE/7KeT8PR3PTzGi5jdNv2cbxesfx7WhqTO7de9q6RtCyl7O26cEHjs7KQ27rM4SB44POB7Ldj9qZ9PTqbDVj8LUaD7Pf0kPQESGf+zxTV6Tldtz+3gqmGeWKjRPAtdSYWnZwrFoja9laHtA4mfTjR8sfIWbPWmI4olfdTs5OXA/N1Xs4nt4FqnegCvTZ40O+sA+tuODO0UTJK7zP4nb/xzfkmruoFryVoi2mpMjtoGcbd/Vey8AarGv5XeivwEA6er1CritHzcAaOc3GkhcDi4GvwsDesY/66R+v8HAhn/Hyufd3AE6uDMktBs3CrcZiYDGwGFgMLAa6GJCT28nzUFeQZbQYWAwsBu7EQPgsWn9KVnymgdW1HB7DcruWfzxuxvV4eAtOfC0A751PAGqgHTrk12G4TBYDi4HFwGJgMeAyEM9ibv/qWAwsBhYDb8QAfWeyWY3qVVcB1kV1wkU5ho8FPhpPAbJw3RoKs64Butl6B8PiCvXSkh4Z69JCFvhi4JkMTPqu6vQSwmlrO4HgLJaduqaHpBNWCKDvul0Q5GmQ712dpfUrnCO+Qo12ZL+ExvyCwv4GIPGwHRfx6zXzpP9kGN5xLOXlefSjc0DSZYaxQX34V+v0dS1I32v1LAYWA4uBxcCXZ6ByAqmoFk1fnoFFwGJgMdDHQHUlT58AbJcQDRxyJjtsxSxr0vUHtb//R3qjsHPvwd6FspoS8slte+WtNVreSTRcff2kJyn5TxnaQRjpnsqzf4W6pXiAmc2pIvXE0m6YgdAM3eEDYwAy1+g64ojc3l/avSNxZ/m2R7ndOysH4DwyVk/mtxu7y+ZwDxuODZ1D5AW56/wkPieEo/ME9gjUdSwy3+iFb3s+tHsJAewIXzg9k1744jw/4xl56LiHdIe3R3keCdg1Lk6ALE/nLJnZODhXq0dq7MnNqxF6IHg5eL49ccdtdqI7YzoeFwg9/OhYO9lq06Zcufcvx4KqIx879JqmarQp5VADFTVxzIl6tDfzJe0yUDC6a78M+hhYvPbxtKwWA7diwO647TPYrZJ/dDKWGqvZrgYend2KtxhYDFzIgD1W9gaDJ23pePHx8c+//5uPG/bOfTx2lHFwkPmM963j/f7KkYcw69reNPftdq60+q/zguW55/HvZznPAveE+p9T7l5Z9jMTkt/hebjALE+aNPTv4L1JRvj8Zq+A+2dglsOpivoRMI4IcsWdOXvvsJ0bepGP3NHB8UGYsAg2ihifFnQUD1/bHA3kYXp64FMvTSTvk7pz+bQjakwtt+uFJWxkHNsu1V4vInKecPwx+3hiI55s6E19nzXuxKz5cP8eiy7E5m812v4O8m6G2B+ZIPARqarkHvmq9EQVoNBIzG/WVrP1JcnaWE2yrb/v1ktuno3VS3RdWj1w0FqEhvHpLhtF8mRMsxfEQM7nRe00bKyKPSKi4+AZtoI2omquQLJajGXWO5IDfA2+hdQRtWwtH6lRBwAl2gzU4YDEaIr9hBtUP79FvXXv05D7IEJfnGX1FRgYmEpqtkemMDUHIK9i3KY6L5Ip+nD9OFXNy+iVkXikrhytV+bmktxzstXcVeIlgW8EWpYaloXbNMwpKvMunfP+tm9uu1qTGcjIb4/T5MjrIDad0JsAZnOqllPNgOYeqekTgH/8Qe9o1XwP6MowZfsA1JNMwcSTgq+wpxkIB9LG0ZRnIsb29ebkAVLAgJ3EsWhN0C4PZAygXcsDCS7TxUCLAT1Di1tKPA2/8lTMqGlyaFgyipb7a/fhqFXUkN13L/pWczHwdAbwKQTN3e6dnFJOtum9UUU6ANB7tMYb6+lHwJ/ySKAGRk8XoaZQPebLZjEwgQGey8W0i7N8A4+Kvafrbg4vKEnRIkgRtIfTKyOJNFlbbFlg88AVnTp9q8xlNe7JACbDSw4ikkYBYULek+G5WUm5Grbne4K8yiXn9kjvGuioryhXy68qX7G6lfO7MaCnZnXXdwpWtoBQCu2i8EmMRplt71OANGpDJuwYU4Vu2N+yC1RthN0yyZUUM5DNZaHEzj2yC6a8Cb3WRLxfUajz0FcJ+TbmOpDfjK4+Yl7Vyk4GrRkZSo0DdkbQCn4tOBtgauILMMFhYsQigac0UTWqLBOgvtARmdmt3DEQYj8cgzLuC7ZBVTXxz3DoR+mg4n1pqBKwlLdlAPNRdtDuPGkGKyclFgjoSfM9eokz9/InAHFNVPiebTJcingW47l+YA3b52ayog8zILNbpn2AbI/ua8/fgrNUanpP3cJMdjBJvbkSvm9Fy1boXSQZkBG24dsoSaI0bKpdVWStvGp65Li7+euUbCE5mO2/VuPlVuqlLcKMvAA2l4GjmO2CzuXWxiTmCFbbaBm8nos7Y0yeg0EMvETJdqR6+EJpnu9LFL5TpqoNQ6kU2pVqTT3xPTXZipmY/AlARKUoj6O5iCSxpVTFApddvAr3oknGglM4rubNGMBzWpCUPNVKxlOGUQRJX2yg+fk3vmkEhPD90Y+ez+AFrRAoXIFfGAw2UU41hK005LKpN0klSUpCK7aUZDXEYPKXuvc9sQGFUiIg44lV6tBarpOEdIu+fTd2yCrNGgVcbFZDbTMkOZHZFn+TYrhkhXfqZnPc2a/j5w66BXuOgJDYprq0ZZSTQSWVmEjF6bRKoh1AIJ/d1xncXdBRA/CH9CEDkUcnf8USm3ul4OSuOy0dl0xjoHQYEw3MCmOBPhda3F9OOFNvNnZ4foyQfYSADOeIY5+tnxPPSnwiRAI33uIV61VPTsvK+us3bv76IyhRNDx4SxcAk1+E+thPAFCM3q85BVUVDJQiEwtj3dd21JaPkJFoI91HJPHwGHoMZFArJGg7JAmNnhdnkxdsSUBH0KiIlpllDW07KoMEzk2HgJaUknQex1EHI+mDoLcBEL+mI1EHzOEvb0mOSIOaPcloL5ui7tUyQlj7qqZwtDaH8txF47LJiH6kISc0Cgm3nkjdtpVMQlwu0PRFRSsB5A1D/DjFUtWlYQgEwpbaXlyljxmmCHxpr3qT2lYmPV1CEaXLp8fIybbHVWyQW61oMdkXqgVqpZb34XIL7Ys8RSNpk6bogkYsCVLL0hQluYtsBbKXWJIdmUnQQhB8MdaChdK9l8pSWjVKu5dcdOZSPunli1UNBO1bjd5WNpDbjp29KEcXJY5e6MGKBP+84GVGiNVKsgFE2Azie3q+NT3Rn08lqkKImbXK2/TS/VfShWex88+KBQiQlXuo3vNuyZP+9TynFr+ehqXOEwiBj+3p3aR0NKgqWuq/ZEwu/vO/499Q68jTu94N+pATXYj9qbgN4megLOdNioTwYZGBGdBC9sWsADPIWfrLyKbNXp8/f6O3z+9/wq20sZnEmScplx6qXWbyqdGUrLG0zEXSK96zD7J0i+DlY+vRY+HwX3lGtWJ+ixlyoU0K8hF2DdsPu7BHeM9ZTzywcwKI73ijGBD0JyH2byOklLb3eOfgR9AkaOnW9xVSoPSOvSN/Onu+v5NlrD3XC3xFSJVyV/CiXUGK0/afBlPCcYZ6HLUbMoo14C3r1g3uzqI4R63MRgMEmUfkg/adrePn37girdn65JgTjkWV41IwRcTPfA0dudZYORp6UHQY2U/MEC+KILFLQI/3k/RxUoyy5/engVe9LBKQzhJNJFRY5sx7GRZ6Dc+oiKXxMw13oDPud6Yuxs9nuEkzKrSlnsPWHmNHgSkXHT3bW7M8IwZ0BWDBgPRCjzt/+XGMTPS+gywy7Fr+lCksK0c/CUoCfKGxM9xqtK/Zj0CPmHAz4vOhtNjHC2PxqgqagWiQV23QmKF0uQ1C2SQzyxEkbrTR1WlZ7IRh1RtHR2mUeU2srRzYzuamNXr2KtSsuu9/qiaLqql8Uix3taDngM4hYShYzEqlSDbbu828hhnsNc42mlqbYE3cgKmP2HFcclx2s9Fp7BAtobvv1ldXpxJVYgKTbz0kRRifj3Dvn8xR0dYHafsNAGa2a1g6mrbGxye7wUSrM59KBVl/R6MBwV1pXwUS70DQmJR00YXckcVBE5u01bQhxT6UY6pJzsosqXgW8IrB9dkMo5RA+D3JLHQh9NptUSXEpuqXzjnDq6ue/lRKS52aG5A6VBraJcHlMzpp43vNoTCZ00x5dgYUM1XcTiLiInZW43U1LMVlm8qbqk/qQu+CqiCRijiqdOSADQPdBShN+i5+YSC+GjbPZUZrBjow9PZcZoQgVW8I/RmKpQgbSkXqs9ocC/tKqpttvwRUi11oCNBq+qMcsKQwrdJ2ug8Emm86mptlGBrREzGIIZruIqwHkLoBjhsiZGMwJQObXHe0Bnw3RmFYyVsyjaYwKdIummQakyu9t3hw8Wsoe2yIDasiFfCFN/0dgP/5I+VIkbi7DFgB3VMZCEDHALm3sc27nVZeB75LyvDhs4dwb8A/WOFj844nHFKQaspOTk11nnDT9CGdPbS3c+5H6LQ8z3U70R4+Ebsn0R60IzZFzJ1SdrqPBB60LfI+gtZ2PVwiObQRj+T2fFupX4qSAqXr+Vl2ZyBVZB6kRVVOSVDXfTOgeJgHXt4z2tKYnkwxqknq+3Y2D6doa7ijqYZu+4D1ts1zey05R8u8f43PZfjh0WUAMTJ2hB+e0S0CEi0NKj74GBK/UyPpNuzFphS2T/gr9OvfAJwBL4OhjUCqD9DVAFDKFFFOdbEGwne1E5labiHAxVwGkFrnUotWR61oh5wreDNVNjcp23ZVA3eakW+nZadZlswZnwwgNoDTQBN2at4VHUGRi95WjFgFEwiOSVI30ksmj3uXZKTM7tji2u1hDAvWgHh0jAzqNIVUeCgl8ZI8RCOCdL2KgMxLHqB1qhIXEbxiBUAEz/KEXmN6MsFKV71GE1jsTc9hBUGVQWsYRcSi2YNQQ52pK1IqoNu9ZEwlkA228NUudyiwqEgnifSK/LW9rutoLYAlNBE0ckM+at+AUrsIEmnavkjnDH4Iw33lH/brKeC67HdUYMIFQPyKEgGgrFZi+1FOWSBkY3o3c9KFaXk3lfhNPnUZgBTq0Uir0UUWH9HsBnYN6pHzA71nA1Bk4wZwO9qorttTOh6f64mIcNFbzI9zA3QigccMjS6wiNi5P/QTQrEE0xICTT9ake1400uJkBtZWS9k4unH83w+gtChilQiJyhNErQ5ZOl9Ti3ISW/TyRP5VL6PqyqamLPwIBSBun6WgKDd+9OT6NaFAIUe9EJjLcc1SMNLRuuLHCTJ8RyAgFgEW33pTMRAlCJIFwSt13I1ijYo3G2XBCpoKRzRrIYThPcQNEUFJyhfG2iZyu/kh7/ln54xaEnTmOoXQVptnXY0Csdapk8A+L55WAbTr8rUctg69GoCXsUYeltQoM+qKwgVlfbTcsU0qGCzWeaXW54X6zcfJYtSBBdi38Jx7XdsWHbOUSeFJ6sbddUyq5o/mYBqTmoi1erY7a473ULr1FvmJmbe8IgBeWq5BAptMfDQrJe42C6taQDuIoiBgJCGZNHrQO8n6zKZgXTEBQO7PGh3LZ8nilA4j+6XjQpNrtetAl53dUc9YFjgF81dIM9eqvAMPGTYay8te15X64scbJJSbzsTOJIxCdhq+yIKujqRNU5brkZpu3i9PVCezfS6vCR79JRkZz5eORKlMCiaYiaCGCABaupM0MuaIImxuD9CoPBlYLoACGnGZyDwk0DCk0rSzD6dFoovwwW4hlK8IJA5GZMsLpClN6Yn2mAnxtQLS2iszO7aV8uAhgZy95bCWaRu7wsNNTM9YXQVJOOF6lIrGxpSSu1icEiQKPA6mnCK5flpvRSnQymlVFLklGKMvAN7F0Gnu2v8BgbT69VjCHAM5rlA4lXMCNH3DIE21nKPb9PGghVpNr2PddpY2n8nLpzJCM9l0J6Pk3dyrCXCGed6aBwosrUeuf8LtIqKr88YtF0fx4lQrVePszaArDUOKqs7zRoIh7riN7/NU60OgfQYU13OHtDjPdNGD4ekJOlBgM3MqAYLIar7PnU178cbrJoCvw2ofMaImhsVVrroAoC0yRPfn68FPayrxOrAEC8RyMnKWsOoaJfarYelZFXI9CUg8otPSbM4NUwg6K21skja/lVkXYWuUctSiyhFkK5+YcS3P0qwRKgUkN55l8WT+ZIyImL3OAjvm+vAVegivI+0eloMaJ6FUhFannt9U0D2gvT3e+mIvjrLgA8bnvrpNFCNi14BrNqIUpu5odkofQ6gHQTlWoFCuqmlyLCR5ERI/dl5J6Jpo3hWEfMl1BjQjKHfanaHqgY8T4eEbFrzIlyCNJow+RPx2xZLpaTZUs7m+ayh0sn3YGp7Sk03RRZhy/0y6ZGxeovAaGbW6StAfF2iaG5k711/uFecgLWInl7l52IGG/TCvH1d5eGIfssuZKVntFcv4lZ+qd2uy/S28eOgbPkpdkRsY5re6Ofp0W17rUYSKARjKTyToVevtinwqNnujfYxLpNlo1gNvKJePaM9otEbaMdlMcBTn0X7+TtbVK7L4WI4gTobWG2j5WBqIwLBbjNLg+PNqMzLgNpeq9FOlV6bCRVPSmyVc9u30qt8tRjnjPP3DbRllEOG7efcay/gQ9M+/sBmx97yo4NBDlwFBj71TNvjRCgmIX+B/zTRmzjGN0dq+qaTi8Zo12t7rSZPgFvRhsOYfNCXfFQLlujQrLLms/JU7wSB91QSvePv0iRFbhZbNAeov4ySTLOcnXozm+RYvMeZr+/+WjSrKVCkqSwtck8+EQk4aHTca1TIn0om/w0o1zO01SBg3KpaMr1qxBqbxw3LgwKI4g6Ok8lO/gHb2lhN+4hUyT/LJ0xiaMI2Pp8eMwqa8IyaMJMx42Gd/pSUArDMRA1w6O/U5n/PAXDaK2qCPdZm/OEh+aU7CNpY5B3+xY6BQiMLjAKog2IgmLVREAahwrAyHxG9o0c8ijegdYEf337+xsQHc3TEbnpDNdyVNRrQh7oQyFDGGFtkbsWMWHzoSxIsEqCmJFh0zcwPYYpgFFhr6vGqSUnK5BMg9nHq6Ke11bQsWsOs0ZVwOkzIlKyEScjJP862XZjCS9yjv7QRhpqaf+m9WpAsTT3S85TEEF1yQHa6eYItcc9IBbRWdUFbNw0xIgO5KwkdBtWxcwAAClqEJU2tSX+HhU+WsNG3NApw3Zwv6/wK9JhZoT3bbAQCpL5/iT/n5odiMOGOZAwaQmg5R4DHpoM93GOfqDarfqnE7/ecZjmUP2cxDOCCyLhAmFbyKaAbDFUzb2cYcrW0CkZtcazxrFt5RB9x7ZsfYi5CK0Z/H8FxpRoVsmgKIvqh72FJ6UspqBV/B2BbCXB3pciKalZFFDFPK4uP3lmx3h9HDa9bbHswhXERXKBbdvQw4Ccu3piTxVb8urgBz12mAjxPkErakO3J0Pad0Qt6kKzH9m6cOsdVBp5d724tVQMupVIO6uaHNuAuFdpASPItC7YjndKtln9YSWi7L4cYJLIB6MQ2bQu9BEYbvtJXwIpegLWBKN9A6ONwqFBL5hDcl3FWQyMicXlsJrbIr/ZJqHvwvJtOtYh75L6bBf29rHgeEeF7klB4au1CDRkUJNsm0qAt/aMXGUAYinor56JmnVv4Y71gAGXv195AS+yBQzY0xoi1bcP34DkjYylp8qJDGncQ/FSr2ZH5Vq+SxTjgxY+p0+8CKhUjbKUDQOhGMIGeKAgyAp1A1o5uGQpX2yt1ZJM0OQgS9LYAYMgAy5+0BiEC51BRmd40JnTQsKxBkn18l64meOH03GbtyxJSBgv6c3B0SHHhwkBaXh2CVhiQI3UV7tq4alCA1JrA0FuyKoBrfvs6DWKsqXMn4+AeMWBaJGYwrQJRNn2E2xS9kgCJ0Ot5sZ3kUy1NeCNBv6rGygCoeqs6j4hFIMlHMEQDQfJEbDG7jcAFoaiUKt6l0KSenzFCSHASKNbZuAKj89R4Wt+UkQdMdE6DREhhzeAv2plxI5V+l9VeOtLzgJAyfUgaLMGxLtx+58xqtH2cNTFuiMEJfWwfHIk1d6avXUmeNoP8236V6IyvJqvgW8FY0ve3KCC+a6Vl66o1NodcE4oJ1bFXqii3CR3IB0aw3zTiz914aYRNBn7Y8kZwqKFe2UpesOWbr+pbpBsyuW/DJj6sDTb07WQJhkhIRb6dyRkEy4/v/8mzgXltm0WvGSTMOGoxpLHc4kH6VL8u2PpKt2hLZdHLmgWNfOMQVsbOuiGK4krjaxmG2jxqHCNAaq8gaw61DMOfv1OGNCLUYiF5x7StfTLAu1SXf1sX04638RW/S0q/uGCPeKBJ8T6z3m2OJWfKimcme36PCIlmxMeWugMD8YnL9F3eFECA4q+9Yzulh3eAaHlzyyRwApX7vUztkeKwTlJNBiXDvO4nh81OpPq3S/OZTGjkjO8BiyOFaqYQU4m/gvgRY2t3spBektFFW4HlKugp1/j+dMRz3uBToEfbz7/4FzWf6XvMbFqvOtkH9jB7s3AZqyFi+jYzAnMUTp/POEUqRXODrWZCQFusALk5kBTj6Gs19CMKtiG/z7QXhD0xIaV3ZCuAWYyyseUTewCSzvjcCjebYm+IXmKENvekzFEIpxFfkJSzdIkQLXU+LH9++1X2TdjmcxikmeNqCqzedQ4bcjCgZxrGGwvhg7Iw+uH3M+QTR1znyXLI8+P7j1TyNrtVyE3Mj3ibXs2HTQn6IolBrZgLbYlK/KBP5ZfE8C7zkOrgnOWb9PF4C+OAsQUkZWhkQ5/yS53UJnHDl7mN8YJ5AA5c6d+0gI3Knphi8DsyQ3l0PKGmOX5Gk2gdYsGevrlOr3zlsBmHfOwKhF22F9A2J/QEunOlri7JZAH/DY+k1LsprWbry6VoiWNmnkBuGFsaWcsVY6k0pmzR8RQguG534MLqn5SwJ+dtVrJphQAgVLfBvXBKc5sjxP7CQmtt2tVA85RFwGP1umkwDG7nRX45DOqUbXLmLvofIwf65WIpKtlU+pMf3gEM0KhhVRpQqNIWPXL6i1GDlhdoyYzfSQnrqERn8WlAUm6OGYYkHfrzLsTGNoXKLTbQIIkDtcgwS67eABxsCzlzKAJ1NCU+JwXo6BWAWZNpN0il3ssB/eLAoUzhOQ1bGEgxQgoUENATUfMxl1Bkg8mbAyacTcuHkWBK74zO8zZGEeOIGqY0zGTwxCYIASwdjmKMgM+Fa1Rxy0lGoLDdrPPR2TK/j8TVxNRTYendT7KwiE3RJhJ8gPM9EgRjgiYKcEE3H5hk5qEz05BR6bFBiyUENVGDT3SkN+qHJkys0Cx8N9CatCHVelknFowbsdMEjn3aVaKLb9SQLSQRglvqDVCZs0atyzBP+0107sRIZqYE3pmMsh5/0yqHBCxDs1mRJL0piI6mZbItKaE21WoQyA7huSfYZBG3hvLclFbqMyMrRI0l8fnW8WQ1zKNH8gyx4ZR6gkqO2FQs40boKjyUYcvXAHk5sggADlkFA7GKwHCCVvq8avII1No80IVYpZlKXom5VZaO6oKD66YstQg2yuySxVG05Hf+vR0xz5NsQYZQIgInYKG4GweCf/7P/ws5kiZ7WZ8MZsOHVN0CEMmxHI3oDTlJ2uiLWu6NpkFMG7HeYtGuHNY/yaT3fUNIkaDp9U92oRJuVHIj5LBjVmMFgEMxN+ONz5RG7b0IWzMps4bNFqjqM67sy38/juYc1gpZyt/HucaCcqm8dM4iWzvJXmw8jfV1NAQgrwJV9FWBHREd01wyqVoHpYNPanlFFAanV8JHi7ZianqiiegjQlDruKWdwoxdzTfBL610DJbD8QfW3raEyNuFF3eSqv4qO7Rv3UNpi8zRcwhBgTVEijPjhXQ1kgZG3uiVGpSx6AIMrwJllRSspD/5mHBigZ6+rVgl2MF3k9WGF7p0v8SuZ65NN5S0W8BH6xsyGcdXDBUUFKA8o8TuTL85J5DD72HJiDGliHx/QRen5Ro0+jlbvKRdy1ZVhD2dphEWTnLUErcE2PMuTikPdc3a45/ZSAVKC51SkFjT5RZZCyMlTiR0v3JbQPRuhZo8GtS5bqdVjJQAcybFOKZ7VGIDaJuzDQkbq2cN9fW+duqzmShNPL7RxOSytr/lG8MTD1kqYa5FAr5/fv6X79HR52TBjNOlVLDBrvXB8EGlQlJp5BMLDA7xtKXl6JZ2FS5RiGZfTiRt2X2TeWcLvbBHI2YWUkFCtA3xgi8QQq4xYcTPtnywSC7JO2aO7AIZvJN7L4kV2KYEmJUAGXF65AQOBpB50ql3iRXSAbBkq+xqYvros3Jw5IzBtvAcxyLpuTfIzFeSoxdsaiH7dLGMhKaddL1W1pYkA0fQRJPMUk94T43YydU5dZEl9+YOgY1clcKQeTzQZFxlIwtMyRBAeruBhei62fByE0rcIq7ZIrdtW4SrNkOsGDC+Ve1YiX69DaaFW9GMswyzS7On5Tj3gitv4iyN9bIloos+BMamjqMsSdSvMr+IEt7Qx9twgArv3LHpUx4aRWJpZfRKOIwSXmSj7SGji+UIIVYbM5sXz3A6dMYphfrhF70lEuOl/UEcqJeP/eEPQxJoeMV4mX/oSAaJg2hfvCG3QklhNm/psyEyTThjhbT55BCyD7mhSkaBudpm/qk/xgsI0aVIIbih32IWmi0aKm1sJUpLKFLWpkhLabbYqbZM40GJfuOQigpHR2e0AJ/80ntgAo32llImg20lEKZnMf0Tb3yuTnIolRrkzoPMIPzGcyC8hZwp771XMo9e8I1Ouq+UU4qIh15yIwG1RIjuN41fODFmrKusB2zk9owEe/Tylkcz5KZMEZEUAV91JA30vA3FBgRmNOi5bpL1a7Mnm3D8iL3UoWzR4m2YWBqhLrMpvRCRc9HY6ArbnY0eKYKMqEkoejmedIEBqbwZUmBVNuApzZiCNWWXixqp14cQiBxYB6YAEt3Dop41IJ4kZhILlmD48f3bBz29+L8f+L4XvrtJODx6gXWWwyvF4I4Q8PPbL+Hkwu6wT9tgH/w4LF9dwBm4MdfAdRjXOLqEg7jkLjYhX8aLCAE6pBBtYPtLmiuwFxwyhyzbX8LcDgyQLr6SfQzCdX3wQ53FCxFhTTlTWYwTrowCiu5nK1aGDrgUDeQMH0QJ28wBKIILjsgCmmKbomTv0Te8FfaIFNFCQzQEUZFhg9EqcyDs9AoiYrEqHjGAFxSlLxw3hDijwo6jmFFjYXNQRzqKhOjZlmdpxl8YwYCZRtnGKkaESoEXIwcpIn58/BLQ2T6ifbImZELloTZsMYmjHEpntJRzJGjTMG+hV67AVXXcub00TpAplwwZ5tWttrTyFiNJsEmt+B7y3CKSTeUVDyGqCtSOIwknx37wxfmMmgdzRnY8S3hECJm2GK+EnvA5QchhrFlGLO6IPVGy1eHkESzTBljBU9sTkswX6JERR1PxyEi3JIMsW/ZIIxvD8RtHSBmLfYqFDqaejlmYqyyTOsYPX5FGeM4AWUTvkHlAR49UErJlHJiLHwl4IY+YFRqCmWwa78GD8QOCBNk80l4vKaAaWFbs2VOBplasN6Eh4hZlk4JvaDIHYDz16jy1jHmFM07aMmMBi3OUPLVX6KVk4ztZcS954ftycdRS7MQPmROa+KAbsYwHOtmWkbctmW9ZsSz5bdHqEnBCHxYXG7J2SPlUj708H2W+UeTIXigpbDjXmC2vJPgFfdrye7QMvbKJXqoXGtib3oiDUda9UaYy0gvS1o76gBAOYSSFXmOSEKrvoYqwz26jE6snoIS5uUKTttv8VEe2sMwLrP4Xq5eEE7x4jtGLt5ifaYZDn2Zy4j/5aj3O3XoEA3I+IuSQXtseIWON2YiQJH9yzlQvWZJTUif/8C5sSKwq0dyb1quQoz32GplXOhOcQaietGdVY+m4RrYjmCXPDeYZM5+JJ4TGC73lNszGUHUa95AzE8dVx+HUXqxPgf/7nYJyqWwQkglSpJt3Zu5grPifmthN/0td2EWCcQwACDKvvEJGSk/t4EUbRqUtQJQJicErbaJdsEgnMHiHbHBnIPkn/NQOYKRkfbCUcKHKwEk86EVXegtOcZuikxHOmoHdiCJgbEyNvBjuBajeRsvgwS5sI/2sDbrETuQiatkuTU12Ur0JJkyNiEEgnEOKwvZ4SZ6MFuag3sZ0gqlkFvKMWUWUkIBYcSR6EWKMGZODXm/JgJoRGXOV/MJ+DzOGCeWFZkxWEFjA3A2lsXHIJBgwKvmmJKiH3VFigKVN/mLfcLXKzJEf4gSJcbfolGEglx24O8DwluVfyA5ySDz0cVw+yAYv0ZQCgBIa3tkGUgjGaQCE0RJAYC5iJyX3iZxyjA78tsFHEYpiq6Jsvso1U2rf2MGqgCGpbB6lFOxEubEPFXoZL+QLkgk1aFir9+kYTfqSG+y5VyRMLwbgFxlKDzQw5i11KcCN0iCJF0zClude2KOBwQAp34AnaAGcNqSIOKE/qdM7B2If+s+WaSqzyrxKJc8OnsTAJ3PUwtOVdXE/wT6iwRgHWGkryOiibcAUNZJL2w1LGQQlMpF8NkMlSQhE2bKnnBIbxpysuCL7ihGzRHia8TilLbzEn/XSSIgMwDGYQtWZtwJr6djFHuCRD25BhkrcwwGGfaAnE+oKMm+wMwQpOKfeZBOGFpODvdTRis03a9jb7RYV9v3bwEKY5YQaXygBW46VzstbFbG0GBaWcUbGuhNaGMt48RMKJDkVmuLpd+rkQzhnRLCh0iAHHG2YyzEFUsILQkJIMySlnfuGMBvHESHkwYZ5tiEjPWviWSlSQTA8GyXbLa8YRYcWrC3PEC7o5fAgyEHgU8UGCklrUidhyAzcYgZ7ppjikBzdoQ1RoyZ4iBx61FjEUhCCrFgoX+GUJkoezTCiwXqbACkER+CEQkqxHPQFiOCVKkugW1aJ7eDB0wYvikiv1KwlGQ3dN+0DOWbCk4OR01EZXJNJrBK1pm2w3DIBYcFVsuMUyFwGHVlHThCa0ekfdg3Q+fHLL/8ffnWMbxR64FsAAAAASUVORK5CYII=",
+ "text/plain": [
+ ""
+ ]
+ },
+ "execution_count": 14,
+ "metadata": {},
+ "output_type": "execute_result"
+ }
+ ],
+ "source": [
+ "model = model.to(dtype=torch.float16, device=device)\n",
+ "\n",
+ "pipe = DiffusionPipeline.from_pretrained(\n",
+ " model_id, unet=model, variant=\"fp16\", torch_dtype=torch.float16,\n",
+ ").to(device)\n",
+ "\n",
+ "prompt = \"toy_face of a hacker with a hoodie, pixel art\"\n",
+ "image = pipe(prompt, num_inference_steps=30, generator=torch.manual_seed(0)).images[0]\n",
+ "image"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 15,
+ "metadata": {
+ "id": "adLnc7sMRZlq"
+ },
+ "outputs": [],
+ "source": [
+ "del pipe"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 16,
+ "metadata": {
+ "id": "nIwIQK5zRX25"
+ },
+ "outputs": [],
+ "source": [
+ "base_unet = UNet2DConditionModel.from_pretrained(\n",
+ " model_id, subfolder=\"unet\", torch_dtype=torch.float16, use_safetensors=True, variant=\"fp16\"\n",
+ ").to(device)\n",
+ "\n",
+ "toy_id = \"sayakpaul/toy_peft_model-new\"\n",
+ "model = PeftModel.from_pretrained(base_unet, toy_id, use_safetensors=True, subfolder=\"toy\", adapter_name=\"toy\")\n",
+ "model.load_adapter(\"sayakpaul/pixel_peft_model-new\", use_safetensors=True, subfolder=\"pixel\", adapter_name=\"pixel\")\n",
+ "\n",
+ "# https://huggingface.co/docs/peft/main/en/package_reference/lora#peft.LoraModel.add_weighted_adapter\n",
+ "model.add_weighted_adapter(\n",
+ " adapters=[\"toy\", \"pixel\"],\n",
+ " weights=[0.5, 0.5],\n",
+ " combination_type=\"cat\",\n",
+ " adapter_name=\"toy-pixel\"\n",
+ ")\n",
+ "model.set_adapters(\"toy-pixel\")"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 17,
+ "metadata": {
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 1000,
+ "referenced_widgets": [
+ "65bf3df199b44763aa223fee96889e17",
+ "a32666723b0e4b9883a78f56295c4356",
+ "c08373a044204308ac882dd8cf9cdd3e",
+ "fa7876ade8e240fc89a35a1f8c7c7d3c",
+ "de583920d3b54774a486aef4c052e50d",
+ "979c68bd2e224a40b939c27f32c25dac",
+ "0027f3aa006d4276983691ad985ce91b",
+ "a0f8a1a3512443ac84799b95da70ca26",
+ "e08d739f59874064994212363a307f6e",
+ "52c7e22284b0468c8bc0c3b1cad047fb",
+ "17c29bbcbc0c437c9c8bc83e0b085f1a",
+ "65b15618abfd4e6f9fafd64813e86ace",
+ "1e8747251a1f4cca970857911d1c4a98",
+ "caa46820018f47abab4a962afe51cc34",
+ "22a2ea45880f4b0da47f1b213882dcb0",
+ "0cf822f588244e54b5264176f9611164",
+ "dd9666d76af04b72b08f59023eb04ee3",
+ "2702528a2ca049fc800ad44c492690ae",
+ "aed53b6480de4dd4bc7463af04840952",
+ "447d29db05384c55a57c5fb1bd121af4",
+ "2d7e7e816a63428b8f30471a12b57bc4",
+ "e15aab8dd01f4d5582db80e6ad9931fc"
+ ]
+ },
+ "id": "29iGITdnRhFG",
+ "outputId": "dc6a1e54-3f76-457e-da1b-e8677be5c31f"
+ },
+ "outputs": [
+ {
+ "name": "stderr",
+ "output_type": "stream",
+ "text": [
+ "Loading pipeline components...: 100%|██████████| 7/7 [00:00<00:00, 19.85it/s]\n",
+ "Expected types for unet: (,), got .\n",
+ "100%|██████████| 30/30 [00:05<00:00, 5.35it/s]\n"
+ ]
+ },
+ {
+ "data": {
+ "image/jpeg": "/9j/4AAQSkZJRgABAQAAAQABAAD/2wBDAAgGBgcGBQgHBwcJCQgKDBQNDAsLDBkSEw8UHRofHh0aHBwgJC4nICIsIxwcKDcpLDAxNDQ0Hyc5PTgyPC4zNDL/2wBDAQkJCQwLDBgNDRgyIRwhMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjL/wAARCAQABAADASIAAhEBAxEB/8QAHwAAAQUBAQEBAQEAAAAAAAAAAAECAwQFBgcICQoL/8QAtRAAAgEDAwIEAwUFBAQAAAF9AQIDAAQRBRIhMUEGE1FhByJxFDKBkaEII0KxwRVS0fAkM2JyggkKFhcYGRolJicoKSo0NTY3ODk6Q0RFRkdISUpTVFVWV1hZWmNkZWZnaGlqc3R1dnd4eXqDhIWGh4iJipKTlJWWl5iZmqKjpKWmp6ipqrKztLW2t7i5usLDxMXGx8jJytLT1NXW19jZ2uHi4+Tl5ufo6erx8vP09fb3+Pn6/8QAHwEAAwEBAQEBAQEBAQAAAAAAAAECAwQFBgcICQoL/8QAtREAAgECBAQDBAcFBAQAAQJ3AAECAxEEBSExBhJBUQdhcRMiMoEIFEKRobHBCSMzUvAVYnLRChYkNOEl8RcYGRomJygpKjU2Nzg5OkNERUZHSElKU1RVVldYWVpjZGVmZ2hpanN0dXZ3eHl6goOEhYaHiImKkpOUlZaXmJmaoqOkpaanqKmqsrO0tba3uLm6wsPExcbHyMnK0tPU1dbX2Nna4uPk5ebn6Onq8vP09fb3+Pn6/9oADAMBAAIRAxEAPwDQoooq2AUUUUAFFFFABRRRQAUUUUAFFFFACUtFFACUUtFABRRRQAUUUUAFFFFABSUtFACUUtFABRRRQAlFLRQAlLRRQAlLRRQAlFLRQAlFLSUAFFFFABS0UUAJS0UUAFFFFABRRRQAlFLRQAUUUUAFJS0lABRS0UAFFFFABRRRQAUUUUeQBRRRQAUUUUAJS0UUAFJS0UAJRRRQAUUtFACUUUUAFFLRQAUUUUAFFFFACUUtFACUUtFABRRRQAUUUUAJS0UUAFFFFABRRRQAlFLSUAFFFFABS0UUAFJS0UAJRS0UAJRS0UAFFFFABRRRQAlFLSUAFLSUtABRRRQAUUUUAFFFFABRRRQAUUUUwCkpaKACiiikwCiiigAooooAKKKKACiiigAooooAKKKKOgBRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRR6AFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAlFLRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUDCiiigQUUUUAFFFFABRRRQAUUUUAFFFFABRRRQMKKKKACiiigQUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUwEpaSlpAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRR1AKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiijqAUUUUAFFFFABRRRQAUUUUAFFFFHmAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUDCiiigQUUUUeQBRRRQAUUUUAFFFFABRRRQMKKKKBBRRRQAUUUUAFFFFABRRRQAlLSUUALRRRQAUUUUAFFFFABRRRQAUUtFACUUUUAFFFLQAlFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRR6gFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUdACiiigAooooAKKKKAClpKKPIAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiijSwBRRRQAUUUUAFFFFABRRRQAUUUUegBRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFMBKWiikwCiiigAooooABS0lLQAlFLSUAFFFFABRRS0AJiloooAKSlooASilpKACiiigAooooAKKKKACiiijrqAUUUUdACiiij1AKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKWgBKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKOoBRRRQAUCiigAooooAKKKKACiiijyAKKKKACilpKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKYBRSUtIAooooAKKKKAClpKWgApKWigBBRS0UAJS0lLQAlLRRQAUUUUAFFFBoASiiigAoopaAEooooAKKKKACiiloASiiigAoopaAEooooAKWkpaAEooooAKKWg0AJRRRQAUUUUAFFFFABRRRQAUUUUAFFLSUAFFFFABRRRQAUUUYo6ALSUtFHQAooooASiiigAooooAKKKKAFpKKKPIAooooAKKKKACiiijrqAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRS0lABRRRQAUUUUAFLSUtABSUtFACUClxRQAUlLSUAFFFFABRS0lABRRS0AJRQaKACiiigAooooAKKKKACiiigAoooo9ACiiigBKWkpaACiiigAooooAWiiigAooooAKKKKAEoopaACiiigAooooAKSlpKACiiloASiiigAooooAKKKKACiiigAooooAKKKKACiilo9QEooooAKWkpaACkpaKAEoooo6AFFFFABRRRQAUUUUAFFFFAC0lFFABRRRQAUUUUdQFFFFFABRRRQAUUUlABRRS0AJS0UUAFJS0lABRRRQAUUUUAFFFFABRRRR5gFFFFABRRS4oASilpKACiiigAooooAKKKKACiiigAooooAWikpaAEopaSgBaSiigAooooAKWkoo8wFopKWgApKWkoAKKKWgAooooABRQKKACkpaSgAooooAKKKKACiiigAoooo1AKKKKACiiimAlLRRSAKKKKACiiigApaSloAKKKKACiiigAoooo6AFFFFABRRRQAUlLSUAFLSUtABRRSUAFFFFABRRRQAUUUUALSUUUAFFFFABS0lFHXQBaSiigAooooAWjNJRR0AKKKKACiiijroAtFGaKACikzS5oASiiigBaSiigAooooAKKKKAClpKKAFooooAKKSloASlopKAFooooAKDRSGgAooooAKKKKACiiigAooooAKKKKACloooAKSlpKOoBRS0UAJRS0lABRRRQAUUUUAFFFFABS0lLQAUlFFABRRRQAUUUtACUUUUAFFFFHQAooooAKWkpaACkoooAWikpaACiiigBKKWkoAKKKKACilpKACiiigAooooAKKKKYCUtJS0gCiiigApcUlLQAmKWiigAooooASlpKWgAooooAKKKKACiiigAoopKAClpKKAFpKWigBKKKKPMAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAFopKWgBKKKWgBKKKKAFoooo0AKSlpKACiiigAooooAKKKKACiiigAooooAM0tJRQAUUUUALRSUtACUClooAKKKKACkxS0UAJRS0lABS0lLQAlLSUtACUUUUAFLRRQAUlLSUAFFFFABRRRR5AFLSUUAFFFFAAKKKKAClpKKPMBaKSigAooooAWkpaKAEooooAKKKKACiiigBKWkpaACiiigApaSigBaKKKACiiijzAKKKKACiiigAopKWgAooooAKQ0tJQAUUUUAFFFFABRS0lABRRRQAUUUUddQCiiigAooooAKKKKACiiigAooooAKKKKAFoNFFACUUUUAFFFFABS0lFAC0lLSUAFFFFABRRRQAUUUUAFFFFABS0UUdQCiiigApKWkoAKWkooAWiikoAWkoooAKKKKACiiijqAUUUUAFFLSUAFFFFABRRRR1AKWkpaACkpaSgApaSloAKKKKACiikoAKKKKACiiigAooooAWikpaACkpaKACiiijXYBKKWigApKWijoAlFLSUAFFFFABRRRQAUUUUAFFFFABS0lFAC0lLmkoAKKKKACiiimAlLRRSAKKKKACiiigApaSloAKKKKACiiigBDRS0lABS0lKKACiiigAoooo8wEooooAKBS0UAFFFFACUUtJQAUUUUdACiiigAopaSgAooooAKWiigBKKWkoAKKKKAFooooASlpKWjqAUlLRQAlFFFABRRRQAUUUUAFFFFABS0lLQAUlLSUagLRSUUeoC0UUUAJRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRR11AU0lLRQAlFGKWgBKKWko9ACiiigAooooAKKKKACjNFFABRRRRruAUUUUAFFFFABRRRQAUtJRQAuaKSigBaKSloAKKSigBaKKKACkoooAKKKKACiiigAooooAKKKKAFpKWkoAKKKKACiiigAooopgFFFFIAooooAKKKWgAooooASiiigBaSlooAKKKKAEpaKKACiikoAWkpaKAEooooAKWkooAWkpaSgBaKKKAEopaSgAooooAKKKKACiiigBaKKKACkpaSgAooooAKKKKPMAooooAWiiigBKKKWgAoNFFACUUUUAFFFFABRRRQAUUUUdACiiigAoooo1AKWiigAoNFJQAUUUUAFFFFHUAoooo13AKKKKACiiigBaKSloAKKKKACiiigApKWkNABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRS0AJRRRQAUUUUAFLSUUAFFFFABS0lFHUAooooAKKKKACiilo8wEooooAKKKKACiiigAooooAKKKKACiiigBKWkpaACiiigApaSloAKKKKPMAooooAKKKKACikzRQAtFJS0AFFFJmgBaKTNFABRRRQAUUUUALSUtFGoBRRRQAUlLRR6gFFFFABSUtFACUUtJQAUtJRQAtJS0UAJRRRQAopKKKACiiigBaKSloASlpKKAFpKKKOgBRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABS0lFAC0hoooAKKKKACiiigAooooAKKKKACiiigApaSloAKKKKACikpaACkpaSgAooooAKKKKACiiigAopaQ0AFFFFABS0lAoAWiiigApKWkoAKKKKACiiijoAUUUUAFFFFABRRRQAUUUUAFFFFHqAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABS0lFAC0UUUAFFFFGgBRRRQAlFFFABRRRQAtJRRQAUUUUAFFFFABS0lLQAUUUUAFFFFABRRRQAUUUUAFFFFABRiiigBKKKWgApKWkoAKKKKACiiigAooooAKBRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRR0AKKKKACiiigBaSiigAooooAKKKKACiiigAooooAKKKKACiiigApaSloAKKKKAEpaMUUAFFFFABSUtFHkAlFLSUAFFFFAC0lLRQAlFFFABS0lLQAUUUUAFFFFACUUUUAFFFFHkAUUUUAFFFFHQAooooAKKKKACiiigAooooAKKKWgBKKKKACiiigAooooAKKKKAEpaSloAKKKKACloooAKKKKACiiigApKWkoAKKKKAClpKWgANJS0lABRRRQAUUUUAFLRRQAUUUUAFFFFABRRRQAUUUUAJRRRQAUtJRRqAtFFFABSUUUALRSUtACUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFHkAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUeYBS0lFAC0UlLQAUUGkoAWiiigAooooADSUppKNQCiiigBaKKKADFFFFACUUUUALRSUuaACkpaSgAooooAKKKWgAooooASiiigApaSigAooooAKKKKNQCiiigApaSloAKSlpKACiiigAooooAKKKKAEpaBRQAUUUUAKKKQUtABmikooAWiiigAooooASiilo6AFFFFABSUtJQAUUYooAKKKWgAooooAKKKKACiiigAopM0tABRRRQAUlLSUAFFFFAC0UlLQAUlLSUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUdQCiiigAooooAKKKKACiiigAooopgLSYozRSAWkoooYBRRRRYAooooAKKKKACiiigAoooo6gFFFLQAmKWiigBKKDRQAUUUUALRSCloAKKKM0AFJS0lABRS0UAFFFFABSUtIaACiiigAooooAKKKKACilpKOoBRS0UAJmlpKKACiiigAooooAKKKKAClpKKAFpKWkoAKKKKACiiigAooooAKKKKACiiigBKWkpaACiiigBRRSUtACUUUUAKKKKKAEpaSloAKKKKACiiigApKWkoAWkpaKAEpaSloAKKKKACiiigAooooAKSlooASlpKKAFoopKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAopKKLALSUUU0AUwyIrbWkQNjOCwBxUqIXPH51558QUB1K3JAJEQH4ZNAHfiVD0kQ/wDAhRvX+8v514gFH939KXB9KQHt29f7w/Ojev8AeX868SwfSjHtQB7bvX+8v50u4eo/OvEdvtRg0Ae3ZHqPzpc14hg+9KM+ppge3UZHqK8SG71b86vaZE6anaO2QomTJJ7ZFAHr+aWmqyvyrKw9VOacKQBRRRRYAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAFopKKAFzRSUtABRRRQAlFFFABRRRQAUUUUAFFFFAC0UUUAJRSmkoAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKYCUUUUmAtFFFABS0lLQAUUlLQAUUUUAGKKKKPUAooooAKKKKACiiigAooooASlFJRQAtJS0UAFFFFGoBRRRQMKKKQ0dRBRRRQAtJS0lABRRRQAUUUUABooooAKKKKACiiigAooooAKKKKACiiigAooooAKSg0UAFFFMEkZGRImP94UxCu6RqWkdUUdWYgD8zUX26yU831qMes6/41k+LHil8NXaCWNj8pADgnhhXmsNsrsRjt6UANYtJIx3McsT196fGhEqHDcMP51ct7cRyBgeavIuWAHc0JAWcDJ4FGB6D8qdtNLiqAbgegpMD0FPxRigBmB6UuB6CnYpcUAMwPQUY9qfikwaAG1VEYllCEgbmxk9smrm00FARyBQBvQ6Xp+koZ21q1Hl/MQrrzjt1q6vibR2kRFvo2Z2CgDJ5NcfJaxyKQUU/hWA8IRvlHIPGKNwPZaKgjuITGuZos4Gf3g/xp4miPAljJ9nFT1GPpc03NLQAtFFFFgCiiikAUUUUAFFFFHoAUUUUAFLSUtACUUtJQAUUUUAFLSUooAKKKKACkpaSgAooooAKKKKACiiigAooooAKKKKAClpKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAEooooYC0UUUAFFFFABS0lFAC0UUUAFFFFABRRSUALRSUtACUtJS0AFFFFHUAooooAKKKKACiiigAooooAKKKSgAooooAKKKWgBKKWkoAKWkpaAEopaMUAJRS0lABRRRQAUUUUAFFFFGgBRRRQAUUUU0AlIzKilmIVVGST0Apaq6hJGdMvNsiE+Q/AYf3TQIlS+sSVK39oc+k6/4145cRA3Ux25/eN29zTRGCuNmePSuhVm2jk9BTAz9PtITbqzRIWyeSozVpI1DcKo59KmySeaBHzTAsRopmUYGM9MVpiNB0RfyrPgOZQOM5rToAbsHoPyo2D0H5U786PzpiG7B6D8qNg/uj8qfRSAZsH90flS7B/dH5U/ijigYzYP7o/Kl2D0H5U7ijimAzYvoPyoMa/3R+VP4oyPWgDMLEVW49B+VbLYwelY1KwGM0K7j8g6+lNMYA4UflWycZ7VWdQZTx3pWGejxXVs8aYuYSSo6SD/ABqwDXjbqF3DA6ntXrVnPA1nBtmiP7pejj0FDQFulpuaWkAtFFFABRRRSAKKKKACiiigApaSloAKSlooASilooASiloo8wEpc0lFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRR1AKKKKAClpKWgAoopKOugBRRRQAUUUUAFFFFACUtJS0AFFFFABRRRQAUUUUAFLSUUALRRRR1AKKKKAEpRRRQAUUUUAFFFJR6ALRRRQAUUUUAFFFFABRRRQAlFFFABS0lLQAmaKKKACiiigApc0lFAC0UlLQAUlLRQAlFFFABRRRQAUUUUAFFFFABTHdY42kdgqKCzMegA6mn1T1X/kD33/AF7yf+gmmgGy6jaS6fPJb3lvJ+5YrslUk8H3ryNPl29QeKitlUOhwM8VreU/Pyn8qANA9TTaZHu8sbs575qSqEFSKjEA47VEcmrkYxGuT2osBFZ8apH/AL1dQjjqTge9YaPEF++gP+8K53UptzzAMMHPQ0MD0Lev94fnRvX+8PzryLzG/vH86PMf++351N0M9d3r/eH50b1/vD868h8xv7x/OjzG/vt+dHMFj13eP7w/OjePWvI/Nf8Avt+dJ50n/PRv++qLiPXgw9RRvHqK8h86T/no3/fRpfOk/wCejf8AfRp3A9d3qO4pwkX+8v515B50n/PRvzNAlcsPnbr60XA9RnYGVyCOv9K5xajt8YWtgYMB6fdP8qqwrmeMUYHoKQUtIZFLt2twOnpWAyLg/KPyrfkB57cVTx9KAPQ7fUrAW0QN7ajbGoI85eOB71fBBAIIIIyCO9eNXG0tJwO/avX7L/jwtv8Arin/AKCKTGT0tJRSYC0UUUmAUUUUAFFFFABRRRQAtFFFABRRRQAUUUUeQCUUUUAFFFFABRRRQAUUUUAFFFFABRRRR1AKKWkoAKKKKOoBRRRQAUUUUAFFFFABRS0UAJRRRQAuaSiigAooooAKKKKACiiimAlLSUtIAooooAKKKKACiiigAooooAKKKKAClooo8wCiikNABS0lFAC0UUUAFFFFABRSUUagLRRRQAUUUUABpKWkoAKWiigBKKWigBKKKKACiiigAooooAWikooAKKKKACiiigAooooAKSlpKYCE4BOM4rG1HWNNl0e82ahaMXt3AAmXJyp4xnrWy33G+hrwsAYBwOlNAWLc5ZAB6dq6OmRk+WvPYU6hALRRRmmI17YoLeLJX7vemvJCD/rIvxYVmK3FckcljwevpTAuSFQWPynk1SJyTT0jd2XCMeR2rphaLnmMf981lOSid+Ewjr3d7WMRUXH3R+Va0dnB5a5hjJwP4avLpjkAi2J/4BUosLj/AJ4Sf98msJVL6I9ilhowbcrMzvsdv/zwj/75pPsdv/zwj/75rSOn3P8Azwk/75pPsF1/zwk/75qObzN/ZU+yM77Hbf8APCP/AL5o+xW3/PCP/vmtD7Ddf88JP++aT7Fc/wDPCT8qfN5h7Kn2RnGxtf8AnhH+VNNjbf8APCP8q0TZXP8Azwk/Kmmzuf8AnjJ+VHN5i9lT7I5yS3CyMBHgZ44qCZQgX5QOfSup+yzDrGw+ooNtkfMv6VftDnlhYtWRy0cjA9T+ddPZ3sfygyp2H3hXPT2U6M5ML7QSc44xVVHIrphO54WIw7pvU9DimjcDDoc+4qgcAkelYFjdogXeRwemK6LCOoKunTP3hVSdzmSsRnnqKaUX+6Pyp5Uim0hnN3IxNL/vGvWbK4gFjbAzxZESZG8egrhSq5ztH5VzUoGZOB3pAe1ilqG0ObK3PrEn/oIqakMKWkpaQBRRRQAUUUUAFFFFABS0lFAC0UlLQAUUUUAJRRRQAUUUUAFFFFABRRRQAUUUUAFFFFAC0lFFABRRRQAUUUUAFFFFABRRRQAtFJS0AJRRRQAUUUUAFFFFABRRRQAUUUUAJS0lLQAUUUUAFFFFABRRRQAUUUUAFFFFAC0UUUdACkpaKAEpaSloASlpKBQAtFFFABSUtJQAUtJS0AFFFJRoAtJRRQAUUUUALRRRQAlFBooAKKWigBKKKKACiiigAooooAKKKKACiiigBKRmCKWYgKoySewp1QXgzYXQ/wCmL/8AoJpgRf2hZPCXW8tipUkETL0x9a8XCsQMK3TsKdb4V4jgcFT0rqCxJPNNAMQfIv0FOooNAhfLfGdpp6sAAMipWI8o8j7v9K45TkgYFUCF8xjNjcfvevvV4c0yKHcw47iukFqPMPHes51OQ78Ng/a31tYSJMAVcEEh/wCWb/8AfJqxHbNuA2nr6V2nkP2VvyrgnUt0PecuQx7dD5MfHO0VaWBj/Afyq9FBJ9ojJR/vj+E+tdr0JrnbOapV5eh5/wDZWP8AyzP/AHyaPsjH/lk3/fJr0CjNK5H1h9jz02b/APPJv++TTTZP/wA8X/75NeiZPrS5PrRzB9ZfY83NjJ/zxf8A75NRtYzdoX/75NemZPrRk+tLmD6y+x5XPZSKpYxOABySpxWa8HoM16/djfZzq3QxsP0ryzyHI4XP41pGRrTqc5jXlufs0mUByPSuNurSQyHbCyj0C16HdQyRRnejL9RWZIgJ6V0U6ltUOrSjVVpHBgsjFTkEHHNbNm6CFMhfyFVb2zH2mZxJ/ETjFUY3IIIrthNM8HEYeVKVmejZiZMbk5HYis5gM8Gucg4lj6feH867DcMnkVZzGYfrXOTId0nB6ntXQL3paAO2s9TsFsbZXvrZWWFMhpVBHyj3rRBBAI5B5Brxu8IMs3Tqa9ftObK3PrEn/oIqRk1LSUtABRRRSAKKKKACiiigAooooAKBRS0AFFFFACUUUtABikpaKAEoooo6gFFFFABS0lLQAUlLSGgAooooAKKKKACiiigAooooAKKKKAClpKWgAooooATFFLSUaAFFFFABRRRQAUUUUwEpaSlpAFFFFABRRRQAUUUUAFFFFABRRRQAUtJS0AJRS4ooAKKKKACiiigAooooAKSlooASloooAKSlooASiiigApaSigBaKSloAKKKKACiiigApKWko8gCiiigAooooAKKKKACiiigBOvHWsu81zSlsbjOo2uTE67RKC2cEYx1zmtT3rwhOSWPUkmmBPCDuj47ium7moo1BjU4HQVMKoQAVMoIxwfypojfDZjfp/dNYpPHP86AKE5/0iX/AHz/ADqRIJWXIjfBHYGquMk8V2enJm2hP+wP5VnUnyq534Kgq0mm9ifSYSbeHK87R1FdJFCSwAGeewqLTkxGp/Cui0yIi9tztP8ArAeledOTbPccuWNuw6xjP2iHOfvr/Ouw70dDRWDdzz6k+d3AcUtJS0iAooooEFFFFABRRRSGBGRg1BJbQeW3+jxE4P8AAKnopgea3cRETLJGevAZelZbQx/881/KvXGjSTh0Ug+ozXlt1D5dxIno5A/OtoyudtOpzmPqFjG1tIyWyMxU4wgzXENp0qAkwS5HtXpExxA/+6awniyrZ9DW8JuIVKMaq1OOgf5147iuphHzDjuK45ch+vet2GZQMeYP++q9BM+ckjpGUFW4HQ9qobasRYMCn/Zo49qbJOVuRmebH9416nZ6tpy2dtG99bK4iQFTKuQdo461wssLB2PlnqT92sOUgzEj1qbAe1dKKQdBS0mMWiiihgFFFFIAooooAKKKKPUAooooAWiiigBKWiigApKWkoAKKKKACiiigBaKSloAKSlpKACiiigAooooAKKKKACiiigAooooAKKKKACjNFFAC5pKKKACiiigAooooAKKKKYCUtJS0gCiiigAooooAKKKKACiiigAooooAKWkpaACiikoAWikooAKWkoo8gFopKWgAooooAKSlpKAClpKKACiiigAopaSgAooooAKKKKAFopKKAFpKKKACiiigAoooo0AKKKWgBKSlqOWVIYnllcJGilmZugA6mmA+vCE6V7KviHRmBK6rZnAz/rlFeNorbR8rflTA6mDmBP90fyqVeoqK3GII8/3R/KpWBVeQRgd6YjW8wA8Ouc+tecyMTLIcn7x7+9a0sqHOCuPrWOpyR0oGb0FtKyqRG/T+7XcafYQiygJQ7igzk1Fawv5UeFP3R29q17aJ3VQEYsR0ArzqlRs+opxUUSwWbqF2RSbc5HymvR8nFV7MFbOAYIxGowfpU9crZx1anOwopaKm5iFFFFAwooopAFFFFMAooopeQBRRRTAKhktbeX78ETZ9UFTUlAJnl2rRgX90FAC+awAA4HNZDxL6V6/eQo9nOpReY2/hHpXlLrzgCt4SudlOd0cPcWaq0h8npnnbWMvau+uo2MMnB+6f5VwK130Xfc8/MYpOLS7neJ9lYA74s7ezCjYBXORRrgYC10aH5Qc8Y4re55Yk2fLY/7P9K5Bjl/xrsZTm2+qf0rjyMMD70mB7SOg+lLWX/wkOj7cnU7YYH9+tNWDKGUgqRkEdxSYx1FFFABRRRSAKKKKACiiigAooooABS0lFAC5opKKAFooooASiiigAooooAKKKKAFoozSUAFFFFABRRRQAUUUUdQCiilFACUUtFHQBKKWkoAKKKKACiiigAooooAKKKKACiiimAlLSUtIAooooAKKKKACiiigAooooAKKKKAClpKKAFpKKWgBKKWkoAKKWkoAKWkooAWikooAWkoooAKKKWgBKKMUtACUtJRQAUtFFACUUppKAClpKWgBKKKKACiiigAooooAKWkoNMArM8R8eGtT/wCvZ/5VqVl+I/8AkWdT/wCvZ/5UAeMEfIfpXQxsQo5xXPnpit5RxQgNGPkCrb/cb6Go0OIh/u1j/aZskea2PrVgYjDB4r062sLdY0/cxg4H8ArzI8vx6167bp8ijHYVx4l2setldvfv5fqTW65ZQOOQK7PTtGexu1lMisoUjjrXJQL+8X6ivRa4JHZXm1ouolFLRUHIFFFFAgooopDCiiimAUUUUCCiiikAUUUUwCkpaSgCK5yLWYjrsbH5VwaeHLqVd5kjXPJBzmvQaZNtWF2IGApPT2qk7bGsKnLoeRXEO2NxnOAa5C5tAd2IAT/uV28oyDms6VRziuqEmjtlTU1ZnnaDB59a763ltiiZkiJ2gEbhXAsP3zf75/nVzKgcFc/WvRi9D5eSszsr14xEFQKD7elYJAz0FTfaUk6SKc+hzSmMCnuIwJz8zj617HYc6dak9fJT/wBBFeOT/ff6mvY9P/5Btp/1xT/0EVLBFmlpKWkMKKKKQBRRRQAUUUUAFFFFABRRRQAUCiloAKKKQ0AFFFFABRRRQAUUUUAFFFFHUAooooAKKKKACiiigAooooAWikpaACkoooAKKKKACilpDQAUUUUAFFFFABRRRTASiilpAFFFFAC0lFLQAlFLSUAFFFFABRRRRqAUtJRQAUUtJQAtFFFABRRRQAlFBooAKKKKACiiigApaSloAKKKKAEooNFABmlpKWgApKWigBKKWkoAKKKKACiiigAooooAKWkopoBay/En/Isan/17P/KtSsvxL/yLGp/9ez/yoA8ZreHSsEdR9a3R0oQGkJQI8YOAvXB9KxZyrIeh4NdCR/obf9c/6VzbfcP0qgKEYJdB1JIGK9mgifAG1s9MYrx224u4P+ui/wAxX0FpyEahG+0kB+TiuDFu1j1MufLGb9DMhglEiHy3xuH8JrvKGkCqWZgqgZJJwAKqHU7D/n/tf+/y/wCNcd7m1SfNuW6Kqf2nYH/l+tf+/wCv+NH9pWH/AD/Wv/f5f8aVnczuW6Kqf2pp4639p/3/AF/xpP7V07IH9oWmScAeevJ/OizC6LlFFFSAUUUUxhRRRQIKKKKQBRSVXk1CyhkaOW9tkdfvK0qgj6jNUBZoqqNSsD0vrX/v8v8AjS/2hZf8/tr/AN/l/wAaLMLosUEAjBGQeoNV/wC0LL/n9tv+/wAv+NIL+yPS9tj/ANtl/wAaLMLoqataQ/2TdCK2j3eU2NiDNeXz21wqktBKBj+4a9elkR7aRkdWG04KkGubmidoXGDyp/lVxnY66E7Jo8jkhQQuVRQdp6D2rk8cV2coxBJ/un+VcbXoUHe5xZmrSj8zbsyEiC1osOKy4D90V0TQoFPA6V0pnlnJTclvxr2PT/8AkG2n/XFP/QRXjkv8X417FYf8g20/64p/6CKTEizRRRUjFooooAKKKKACiiigAooooAKKKKACgUUUALRRRQAlFFFABRRRQAUUUUAFFFFABRRRQAUUUUALSUtJQAUUUUAFFFFABRRRQAUtIKWgApKWkoAKKKKACiiigAooopgJRRRSAWiiigApaSloASlpKKACiiigAooooAKKKKAFooooAKSiigApc0lFAC0lLRQAmKKWkoAKKKKAClpKKAFopKKAFpKWkNABS0lLQAUUUlAC0lLSUAFFFFABRRRQAUUUUAFFFFNALWV4m/5FfU/+vdq1ayvE3/Ir6n/17tQB40Oo+orcFYfcfUVuikhG24/0Nv8Armf5VzL/AHD9K6h/+PRv+uf9K5qT7p+lUMo23N3bj/pqn/oQr6nRAgwAAPavlmz/AOP+2/67J/6EK+qccmvPxe6O7C7Mz9dGfD2pg/8APpL/AOgGvl1VG0ZA6V9Sa0P+JBqX/XpL/wCgGvl2Lnb+FXhNmRit0LsX0FGwegq0PpS11nIVNg9B+VWNPULqdocDieP/ANCFPpbUf8TS1P8A03j/APQhQ1oNbn1IfvH60lK33j9aK8XoesFFFFIAooopiCiiikAlfOPj/D+PtaJ5xcY/8dFfR1fOHjvnx7rf/Xyf5CuzCfEznxXwo54IvoPyo2L/AHR+VWEHyjp0p2B6CvQscJV8tf7q/lTJEURtwOhq9geg/Kobhf3J6UW1EfTuhoItA01AAAtrEAB/uCrzjKMPY1V0r/kDWH/XtH/6CKtN90/Q14rep68dkeG3UKC1nOOQjH9K4CvRb0f6Jcf9c2/ka86r0sPsyc0+KJrQH50HuK6mThPzrlbf/WJ9RXVTfcP0rpPLRx038X417Dp//IMtP+uCf+givHpv4vxr2HT/APkGWn/XBP8A0EUmBZoopaQBRRRQAUUUUAFFFFABRRRQAUUUUAFAoooAWiiigApKWigBKKKKACloFFACUUUUALQaSigAoooo6AFFFFHqAUUUUAFFFFABRRRQAUtJS0AFJS0lABRRRQAUUUUAFFFFACUUUUALRRRQAClpKWgBKKKKACiiigAooooAKWikoAWiiigBKKKKACiiigBaKSloAKKKKAEopcUlABRRRQAUUUUAKKKSloAKKKKAEoooo6gLRRRQAlFLSUAFFFFABRRRQAUUUUALWV4n/wCRX1P/AK92rVFZXif/AJFbU/8Ar3amB4yPvD6itwGsMfeX6itwUkBvP/x5t/1zP8q5qQ/K30rpZP8Ajzf/AK5n+VczJ91vpVgVLP8A5CFr/wBdk/8AQhX1Uepr5Wsv+Qja/wDXZP8A0IV9VH7x+tefi90duF2ZQ1r/AJAGpf8AXpL/AOgGvl2Icp+FfUWtf8gDUv8Ar0l/9ANfLsfRfpVYTZk4rdFqlqIAVdBwvXtXYchX59D+VOtf+Qlbf9do/wD0IVr2Z/dDmqDf8h2P/r4j/mKJLQFufTbfeP1oob7x+tFeGeuFFFFMAooooEFBoopAJXzh46/5HvW/+vpv5Cvo+vnDxx/yPet/9fTfyFdmE+JnPivhRkJ90fSlqIdKtITsXntXonCRcnsaiuMiJuK2LNuV5p2vgf2Yv+//AENUkK59C6R/yBNP/wCvWL/0AVbP3T9KpaKc6Dp3/XrF/wCgCrjdD9K8F7s9dbI8Vvf+PS4/3G/ka859K9Gvf+Pa4/3H/ka869K9PD7MjNPiialv/rE+orqZj+7b6GuWtv8AWJ9RXTzH92/0NdJ5hyM38X417FYf8g20/wCuKf8AoIrx2Xo1exWP/IPtf+uKf+gikxFilpKWkMKKKKACiiigAooooAKKKKACiiigAooooAWiiigAooooAKKKKACiiigBKKWkoAKKKKACiiijyAKKKKAClpKWgBKKKKACiiigAooooAKKKKACiiigAooooAKKKKYCUUUUgFooooAKWkpaACiiigApKWkoAKKKKAClpKWgBKKKKACilpKACiiigAooooAWiiigApKWkoAKKKKOgBRRRQAUUUUAFLSUUAFLSUUALRSUUALRQaSgBaSlzSUAFFFFABRRRQACsvxN/wAivqf/AF7tWpWX4l/5FjU/+vdv5UAeMj7y/UVtisX+IfUVtChAb0n/AB5uf+mZ/lXMyfcb6V1Df8ebf9cz/Kubl/1bcdjViKVl/wAhC1/67J/6EK+qj1P1r5VsP+Qjaf8AXZP/AEIV9VNwzfWvPxm6O7C7MzteIXw9qZJwBaS/+gGvl5GAC/SvrHr1pNif3F/75FY0a/s1a25pVo+0adz5UAZuiOf+AmniKU9IZT/2zb/Cvqnj0H5UVv8AXPIx+qeZ8xQS3UChVhlx/wBcj/hToEnm1a3fyZMtPH/Af7wr6bpMD0FDxt1aw/qtuo4/eP1pKKK4DrCiiimIKKKKACiiikAlfOPjaOQ+OdbOxyDdNg7Tz0r6PorajV9m72M6tP2itc+VhHIR/qpP++T/AIU7ZLj7sv8A3ya+pxxRmun655GP1XzPltTMp480fgalu7iSawMTksQcjI5r6f8AwFJgf3R+VP67boL6p5lDQ/8AkX9N/wCvSL/0AVebofpTjTH+6evQ1wvVnWtNDxS8b/R7gf7D/wAjXnfpXoF437i4Gf4W/ka8/r0sPsyc0+KJq2/+sT6iumm/1b/Q1zVv/rE+orpZT8jfQ10rY8s5Kb7rV7FZf8eFt/1xT/0EV47L91voa9isv+PC2/64p/6CKQixS0lLQMKKKKQBRRRR1AKKKKACiiigAooooAWiiigBKKWkoAWiiigAopKKAFooooAKKKM0AJRRRQAUUUUAFFLSGgAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKYCUtJS0gCiiigApRSUUALRRRQAUUlLQAlFFFABS0UUAJRS0lHQBRRSUUAFFFFABRRRQAUtJRQAtJRmigBaSlzRQAlFLSUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAVl+Jf8AkWdT/wCvZ/5VqVl+JP8AkWtT/wCvZ/5UwPGf4h9a2xWJ/EPrW2KSA6E8WbE/88z/ACrmpSDEx/2a6dlzYt/1yP8AKuR529+laMRDZf8AH7b/APXVP5ivZU1CYEf6S+Cf75rxI8jrXo2jrmGyH+5/SuOstj1cu15ke19Biign5j9aK8wsKKSimIWikooAWiiigAoooo8wCiiihAFFFJRoAUUUUAFLSUtABRRRT0AD0NeY3l1c+ZKxuJccn75r0x5EVSC6g46FhXmd3EzLM2DgKc/rWtM68Ktzjbi4XyJQXGSjd/auN9K1LmMBZD6AmssmvQpKyPOzGblNGtb/AHl/Cukk+430Nc3bkErz6V0r/cP0rZHnnIzfdb8a9ks/+PG2/wCuKf8AoIrxqc/K/wBDXs1p/wAeVv8A9ck/9BFJiJqWkpaQwooooAKKKWgApKWigBKKWigBKKKKACiiigAooooAKU0lFABRRRQAtFJRQAUUUUAFFFFGoBRRRRoAtFFBo8gEooooAKKKKAClpKWgApKWkoAKKKKACiiigAooooAKKKKAEoopaACiiijQAooooAKWkooAKKKKACiiigBaKKKACiiigBKKKKACiiigAooooAKKKKACiiigAooooAKWkooAKKWigApKWkoAKKKKACiiigAooooAKKKKACiiigAooooAKzPEX/It6n/17P8AyrTrM8Rf8i3qX/XtJ/6DT1A8Y/iH1rbFYg+8K3AKSA6sRKbHPOfK/pXHMPlP0rs9wFjjP/LL+lcew+U/StGhGSBxXYWep26wQoLmIMqqCC3OcVyA7VVYkOx75JrGcOY6sPiHRbsr3Pf9MfN9a/MOZF4z713RFeP6RfyGK1eW5ccKWYMelev9QCM4xwfWvMqqx62I1swooorI5gooooAKWkpaWoBSUtJTGLj2owfSuJ1OC6/tG4KxzlDIduA2MVWiiu1kX5LgDcOzU0joWHur3On8TX0ljoVzJA5W44VNv3hk9ap+DNSudR0eRrqVpZY5ipZ+uOtdF3pEREzsVVycnAxmgy51yctvmOoopaDMKKKKQgpRSZrG13UJ7Tykgk2FgckCjVlRV2U9aulF1OqsMqcH8q8xW6maTaZnIJ5G41188IkEjtks2STnkmvM713hLkOwwCc5NddJJnbT9yLZVuwTHIfrWZgegoa4aTjeTntmkAbHf8q7oRaR4uLqKc00atuB8vA7V0b/AHTXOwDAX8K6J/umrRynIT9H+hr2W1/484P+uS/yFeNTn7/0NezWv/Hnb/8AXJP5CkwJaWiigAooopAFLSUUALRSUUAFLRRQAUlFLQAlFFFABRRRQAUUUUdACiiigAooooAKKKKACiiigApRSUtABSUtJQAUUUUAFFFFHqAUUUUALRSUtACUUtJQAUUUUAFFFFABRRRTASlpKWkAUUUUAFFFFABRRRQAtJS0lABRRS0AFFFFHUAooooAKSlpKACiiigAooooAWkopaAEooooAKKKKACiiigApaSloAKKSigBaSiijzAKKKKACiiigAooooAKKKKACiiigArM8Q/8i5qf/XtJ/wCgmtOquowi50y6gY4EkTLwM9RQB4cD8w+tbwK/3l/Ousj0WxAGbGHIH/PIVwuxB0VevpQB1agNH2zt9fasV4Xwflbp6VdgcZAP8q0Rg4PatBHE/Z5wMmCUf8ANUHPJ+tek5rjZYI/NfKKfmPb3qHoNam/p97H9miUypwgGN3tXoOgX10L+zhW7mMbyAFC5II+leKDg8V6Ra3ZCxFZ8EAHIbBBrkqwse7hKvtYuLWx7Lj2orzrTb+4N5bqbqVlMyZzIT1YV6GZEz99fzrhlFxJqUnB2HUU3en99fzp1T6mYUuaSikIWkopaYxKSlooEJS0UUAFLRRQAUUUYpgNqOWON0YvGjEKcbgD2qU59DXmviPVNQs9cvIob2eJA/CrIQACKqMbs0pU3Udkzm7qR1t5MOR8p7+1cjfXCNbSbZVZivZutdDd3AFvJ+8X7p4BHPFcPGMkZArvpRvqVjsQ6aUUr3Eh/1i5rRQE9Ac1FDEglU4HUVvW6/v0J7HPSupHhlKNG44augZ12/eHT1pGOEJ9jXOyMNtMCrORtf6GvZrT/AI8bf/rkn/oIrxR13htq547CvarQEWVuD2iQf+OikxInooopDCiiikAUUUUAFFFFAC0UCigBKKKKACiiigAopaKAEopaSgAoopcUAJRRRQAUUUUAFFFFABRRRQAtJS0UAJRS0lABRRRQAUUUUAFFFFAC0UlLQAlFLSUAFFFFABRRRT6AJS0lLSAKKKKACiiloASiiigAopaSgApaSloAKKKSgBaKKKACiiigBKKKKACilooAKKKKNQEopaSgAooooAKKKKOgBRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFBp3ARidpwe1eFIf3n/AAKvdDXhciMk7qQRhyOnvSYG8prUt3/cR89q5MnA6n860rc/uk/3a1jK5LRtFpMnDN1qIQoUJMa5wc5WtS2k/wBHiyf4R3qbdkYHelYVzzrjGKktpWSeP5yBuGee2a6G8QeRKSF+6ecVhskZH3R07CspLobQm73R19pfQhsfaIvb5xWolyG5Vtw9Qa8vxW3Y3UUdrGjOoIHf61zypW1R7NDH87tJW+Z3AnPTJFer2vFnAP8Apmv8hXzvd3sZt28uQbsjoea7i28V3sthbLHqT7l2hsNzgCuepTbSN52q6LoerZorzmPxJejGdRc/Vq9DjkWSNWV1YEA5BzWDi47nPOm47j6KM0VJnYKKKKBC0UfhSge1GoCUU7afSqGsXD2ekXk6sUZImIb0NA0ruxZuSVtZiCQRGxyO3Featq1woG6+kHHeU/41G3iC9lRlbUJCCMEeZ2rm9SuUaJ8OnQ4wRWtNdDvhS9km3ZnTJqjHJ+3n/v8Af/XrmPEN2JBcsZQ5KnJ3ZJ4rgl5NScZ/Gu6OHs73PNlmV01yfj/wBsGWcD2q7FGPNXgfeFThV2nG2uhW1s1AJhhBA9BXQkeWRrGM/dX8qtAgelN8y3Bzui/MVk3M0fnPh0xuPeq2EOuZo98uZEzk8bq50ONwG4dR3pbnDTOeOT2r13w7DGPDem5iTd9nU5KjPSpA1lwqKAAOB0FLSUooYxaKKKACiiikAUUUUAFFFFABS5pKKACiiigAooooAKKKKACiiij0AWiiigBKKKKACiiigAooooAKKKKAFpKKKAFooooASlpKWgBKKKKACiiigAooooAKKKKACiiigAooooASlpKWgAooooAKWkpaACiiigAooooAKKKKACkpaKACjNJS0AFJS0UAJRRRQAUUUUALRRSUALRRRQAlFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABQaKKYDTTdikjKqfqKfSUAeKarE8Wq3qsrDE79QR/EarwyHevzN1x1Ne4kA9VB+ozXmni2xY+ILp4oX2YXlYjt+6KVraoCkjYxzWlYSATxkngHPNcuS0UoDAj6jFXI5AF5xTTFY7XZbuDuWNgeoODTGsrIgk20PAP8ArnYZ4ljOWT8SPWunjniccSIR9RVrURxk1vb+UxAXcBxWVjAr0NrKL/ngnT+4KrSWcaxsTCnAz/qxU8o7nB9xXU6DPGoIZ1Ax3OKgv4ke0kEcI3cY2pz1rCkt5lXPlSAD1U1nOnzaHXhsT7F3tc9DW4gP/AC0j/wC+hVhLiIdJV/Bq8tw3vSEsO5rF4bzO5Zp/c/H/AIB6t52fuyE/RqPMf++3/fRrE0+5DeWBIOgBGa181zNW0PVTTV0S+a//AD0f/vo0ec4/5aP/AN9Gos0hpIdiQ3Eg/wCWr/8AfRppvGXrOwHu9U7iRUjYswAx1JxXLazOj2bhJFY5HAbNaQhzMyqyVOLkdqNSUf8AL6B/21/+vUd5qUclnMhvVbKH5TKDnj615Xg+lO2H0rf6vbqeW8yf8v4khPJ5J5pPrVqJmDKOnPatR4yWyq/kK6Ujy27kGnQKcblB+oqUxKJDhBjd6Vq6cu2E59auFgFJ46U0hAAvotRzSAQyEkAbT1NJ5icfMv5iueupFMTgMv5+9DYFrzIcZ3x/mKyrlgZ3IwRnt0qLj1FXLfTL6WSMpY3LgsD8sLEEZ+lLcRT8uRx8kTt9EJr2TQlK6BpykEEW6DB+laH6fSikMKKKXFABRRRQAUUUUgCiiigAooooAKKKKACiiigAooooAKKKKAClpKWjroAUZpKKACiiigAooooAKKKKAClpKWgBKKKKAFpKWkoAKKKKACiiigAoooxQAUUUUAFFFFABRRRQAUUUUwEpaSlpAFFFFABS0lLQAUUUUAFFFFACUUtJQAtFFFABRRRQAUUUUAJRS0mKACiiigBaSiigApaSloAKKKKAExRS0GgBKKKKACloooAKSloNACUUUUAFFFFABRS0lABRRRQAUUUUAFFFFACUUUUwEpCT60tJQgPMviAhGvo2DjyF5/E1yYfB6j8696ycY7ehrM1yNDol+fLTIt5CDsGfumlYDyUkbCeK6GzuYlQAvH+YrjhxV5JFGORTTsB6TFcwtGh86PlR/EKWVkaJwHU8Hoa4IXMYiUFlzt/rWpYXsAD5kQcdyKvmFY1LeP8AeDmi7Ba2mC5JKMMD6Usd1bllxPH+Dip0kTd/rVx/vUgOHa0uF6wSj/gBqBxla9JkMRt5MSKTsPG/2rk3ghMbHy0+6e1A0znohiePH98fzrvYLxD1bH1rhZIxsGODUMDsJ48M33h396wq0+c9HCYr2Pu2vc9JFxH/AM9E/wC+qPtMPeRP++hXPsRuHYA81DcufJc5x8prmUD3ZTSVzR1mSKTSrlkZT8nYg964qnox45q3AoaeIFVI3jOR71104cuh85isT7aSlaxSQZkUE9xW4sdaK2sSvkQR8H+4KsedAoJ8yL8xWtjkY0QqCeBWkkipCuSoCr3NUBeW/Xzov++xWRdzoxl2upznoaewjoTeQ44lj/76Fc87r5TncvQ96xsj2qMt9KTdxk3IGcVASPapAjMpwjHjsua9itNJ037DbFtPtNxhQkmBck7R7UrAeRWkcc13DEQp3yKuPqcV7cc5wOg4Aqsmn2UTBo7O3Qg5BWJQR+lWaAFooopMApaKKGAUUUUgCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKWkpaAEooNFABRRRQAUUUUAFFFFHmAUUtJQAtJRRQAUUUUAFFFFABS0lFAC0UlLQAUlLSUAFFFFABRRRTASloopAFFFFABS0lFAC0UUUAFFFFABRRRQAUlLRQAlLSUUALRRRQAlFFFAC0lLSUAFFFLQAlLRRQAUUlLQAUUUlAC0UlLmgAopKKAFzSUUUAFFFFABRRRQAUUUUAFFFFGgBRRRQAUUUlABRRRTASijpWZd6xpn2G4xqNnkwvgCdcn5T700BoeYn99fzrP1mVP7Ev/nX/AI9pO/8AsmvF1UbRlRnHpS7V9BRcRGOlSBfal7j61ZH1qRlQ8CgdRVvFFMCNHAYHjr61tGePJw6dfUVz54J+tOB5HTrQnYDtra7hEi5ljHI/iFahurcjiaI/8CFcIZU/vr19avrNGR95enrVJiOkvog1hMQo/wBWSCB7VwzRtj7pH4V6dYXERsoD5sf+rH8Q9KjdkZpASuCaGC0OAjkj8tfnUnGDk1mqzveBcscv0pssLK7ja2AT2r0W2VU0u0baA3kpzjn7oqI07M6a2JdSKVrWOSihUTJiMD5h/D7105wCeF/KrIkGc7gPxrAkkCh/mHGe9avQ5UbEkirE/wAw+6e/tXHO6+U2COVqgZM9zTahu4wzSZq0DkUKMMDSGVAKmtCovbctgKJUyT9RVmqzIxZvlPWkB7X/AGxpoJC6jafhMv8AjThqVi/S9tjn/psv+NeH+W39w/lR5bf3D+VVe4j3dWDAFSCD0IPBpayNBvLUaFYI11bh1gQFTKuQcdMZrWVlYAqQwPQg5FAx1FFFJgLRRRQwCiiikAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRS0AJRS0UAJRRRQAUUUUAFFFFABRRRQAUUUUAFFFFHmAUUUtACUUUUAFFFLR5gFJS0lABRRRQAUUUUAJS0lLQAUUUUAFFFFABS0lFAC0UUUAFJS0UAJS0UlABRS0lABS0lLQAUUUUAFJS0lAC0UUUAFFFJQAUtJS0AJRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABSUtFMBKOn0pQKrXs8X9l3bJNGSIJCNrg9FNAEVzfWj2EzR3lqd0LFcTLz8px3rxWJfu/Lz9KjjiGV+QHp2rSRACPlH5UwIth9P0o2H0/SreDRg0gKuz2/SjYfT9KtYpMGgBmKXHtTqMj1pgMKgjoPyqlKuEPH6VoZHrUZHNIDLrQtypdQcckUropHIFVY1w6n3oQG2FA7CggVnbvejd70wL5xg04Hjr+tZ273ozQBpYX0FUZsfN071HmonXLUAVlHI+taIA9KasMexTtGcVIBSATFLil/KiiwBioz941L+VO28U7AV6XFT4pcUAUmQbjx+leseGQo8M6cBj/U9PxNeZMucVBIjjON34UAe1UVnadfWjWFsv2uAuIUBHmrkHA960AQRkEEEZyKAFpaSlpMAooopAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABS0lGaOoBS0lFAC0UUUAFFFFACUCg0UALSUtFACUUtJQAUUUUAFFFFABRRRQAUUUUAFFFFHUBaSlpKACiiigAooooASloooYBRRRQAUUUtACUUUCgBaKKKACkpaKAEooooAKKKKACiiloASiiigAooooAKKWkoAWkpaKAEooooAKKKKACiiijyAKKKMUAFFFLQAlFLSUAFFFFABRRRRqAUUUUAFFGaM07AFFFNk/wBTJ/un+VKwES6hp7weZHqNoQV3KfPUdvrXiSqWbgZYmkjQfLwO1arQkNxGeDxhavYRDBA6MCVxVrBq4tSx43np0pDKKjilrTGPao2YAnkCmBnqOTQqsCMA/lV8uu3qKKLAN2j+6Pypdo9B+VLRTATaPQflRgeg/KlooATA9B+VYcicv9TW7SbR6Chq4HNeUaPLNdLtX0H5UbV/uj8qnlQHNeWaPLNdLsX+6Pyo2L/dH5UcoHNeWaURmuj2L/dH5UbF/ur+VPlAw0A2qK2wg9B+VLsX+6Pyp1CQCbV/uj8qNq/3R+VLRTATAHYflVEL83TvV+njikwKDDg0wLxV53AlAyOoqUFfVaLAZ2KQliTz1qy2DL2+9VvYv90flSEYjpjPFenabc20emWcTXMAdYUBXzFyDge9cTMi+S+FGcelYkqgZ4/SgD2AEHoQR7UtV7KLybC3ixjZEq8fQVYpMYtFJS0MAooopAFFFFABRRRR1AKKKKACiilo8gEooooAKKKKACiiigAooooAWiiigAooooGFJS0UCEpaSloAKKKSgAooooAKKKKACiiigApaBRQAUUUUAFJS0lABRRRQAUUUUwCikpaTAKKKKAFFFFFABSClpKAFopKKAFooooAKKKKAEooooAWiiigApKWigBKWkoFAC0lLRQAUUUUAFJRRQAUUUUAFFLRQAUUUUAJRRRQAtFJmigAooooAKKKKACiiigBKKKKYCEnBx17VmP4g0r7O5fULUNsOVEoPOOlaTfdP0NeEdeaALcaE7Bg9u1dFmooBmCM/7I/lUuKoREpJk696nWm7QOwoBwaAJhVK4x5r8Dr6VA00m4/O3X1qCSXOcv196TAah+df94fzrZrDQ/MuT/EP51udzTiMM0tJRTAWiiigAooooGFFFFAgooooGFFFFMQUUUUgCiiigApkv+qb6U+mS/6pvoaAKfW4X6iriqPQVlTy7ZMhgD65qeOckcSE8/3qkC6ARnFWx0H0oopiA1n3oZZAwXIA646VoUY4oApDxDqiLxezcD+9XpFmzSWVu7ks7RKWPqcCvP2jQfwL+VYcTN9sjAZhmVehI70Aex0tDcMfrSVIxaKKKQBRRRQAUUUUAFFFFABS0lFABRRRQAUUUUAFFFFABQKKWgAooooAKKKKACkpaDQAlLSUUdQFpKKKACiiigAoooo6AFGKKKAClpKKAFooooADSUtJQAUUUUAFFFFACUUUUALRRRQAUUUUAFFFFABRRRQAtFJRQAtFFFHUApKWigBKKKKAClpKKNQFooooAKKSigBaKKKAENFLSUAFLSUUALRRRQAUlLSUAFFFFABRRS0AJRRRQAUUUUAFFFJQkAUh4BJ6Dk0tNfHlt/un+VMDMPiLR3iYrqdqcqcfvAD0rx0K2Oh/KrCrjb+FdL3p2ERQjEMY/wBkfyp9LSVQxDWeT83OTz61oGsluh9KGIUuO+KyVPzZ96lLZpuzms2BrIgODgdfStTNQW//AB7x/wC6KmFWhjqKKKYxaKTNLQIKKKKYwooopAFFFFABRiijNAC0UUUCEooooAKa/KN9DTqa33T9KAOdvv8AWr9Ks6aB5ROB96q1/wD61fpUKSKo5NT1A7Dep6MPzpaxl2lQeOlbCEBF5HQd6dxDhTih9DWfMhe6JAJGRWw80YJ+cdexoAosR61hQL/p0X/XVf8A0IVoZO8nB6moGjTn5RQB6w8kfmN869f71LXlMMX7+M7ejA8/WvVj94/WkxhS0gpaQBRRRSAKKKKACiiigAooooAKKKKACiiigAooooAKWiigAooooAKTNLSUALmkoooAKKKKACiiigAooooAKKKKACiiigAooooAKWkooAKKKKACiiigAooopgJRRRSAWigUUAFFFFABRS0lABRRRQAUUUUALRRRQAUUUUABpKWkoAKKKKAFopKKACilpKAClzSUUALSUUUAFFFFABRRRQAtJRRQAUUUUAFFFFABRRRQAUUUUAFJSmkpgJVaW8thFKTcwjarA5kHUA5HWrS/eH1rw+8IbULlyASZ3P8A48aaAlRSSmAeoroD1NYdsn7xDjuO1bdNALRRQaYFSSVtzc8ZqizAA8j86sXHSTPvWEOlSwFHWtIBcdB0rOCt2U/lXRW6/uU4/hFJK4h9v/qE/wB0VMKQdKM81dhjqM1lvId7fMep7063c+eg3d/WlcDTooopgLRRRQAUUUUDCiiigAooooAWkpaSgQUmaRzhGI6gVmGWX/no350AalB5qNHUqMsOnrT6AKUkahyCo68ZFYDg+a+AfvH+ddb2rBliYSNhT1yOKTAYsgVeo6etaETqQvzDoO9YJ78VpR/cU+wqbgdAKWoxLHx86/nT81QhaoSf6xue5q9TSBg8CkBWjYK6k9Bg16lkHkdDXikrEo4JJ4PevZrf/j2h/wCua/yFD2GS0tJRSAWiiikAUUUUAFFFFABRRRQAUUUUAFFFFABS0lLQAUUhooAWiiigAopKKAFpKKKAClpKWgBKKKKACiiigAoooo6gFFFFABRRRQAtFFJQAUUUUAFFFFABRRRTASiiikAtFFFABRRRQAUUUUAFFFFABRRRQAtFFFABRRSUALRRRQAUlFFABRRRQAtJRRQAUUUtACUUtFACUUUUeYBRRRQAUUUUAFFFFABRRRQAUUUUAFFFFCAKSlpKYEYuIdwPnRdf74rxOXm6kIxzIx/WolAMpP8AtH+dbCkbDkDp6UwFjHzr9RWhVCM/Ov1FX6aEGaolmz1b86umqRX5jQxlSSQAOC4zg96yxT5Rm4f/AHjTRUXuBqQZ8tME9BWotZsX+rX6CtNegqkAp6VkznEvHpVue68psdecVUkG5ye9DYAiguOB1rXVFHRR+VUkiT5SV9O9XxTQC0tJS0wCiiigApaSloAKSlpKACilpKBhRRRQIa/3D9KzioxkCtJhkEVRdFCkjPFJgQYGa1FHA+lZeQSKuxzksAQOTikgJ2+6aojORV5/un6VQFNgYL/fb6mr8brsX5h09adIi5Y7RnntWZU9QOhj6p9RWlWdCh+Q7fStID2piExQRxTwpPagggUwOXlHD/jXsVtcQ/ZoR50eREuRvHoK8yKRkHKr+VYkuz5gAO9J9gPcc0tV7QYsrcf9Mk/9BFTikMWlpKWkAUUUUAFFFFABRRRQAUUUUAFFFFAC0UUUAFJS0UAJS0lKKAEopaSgAooooAKWkooAKKKKACiiigBaSig0AFFFLQAlFFFAC0lFFABRRRQAUUUUAFFFFMBKWkpaQBRRRQAUUUUAFFFFABRRRQAUUUUAFLSUtACUUUtACUtFFACUUUUAFLRRQAUlLRQAUUUUAFFFFABSUtJQAtFJS5oASiiigAooooAKKKKACiiigAooooASo2ngXOZoh7bxUg6ivCGALuSBnJpoBUPzjp96vSk0+12Lm3i6D+AVxEEKbUOxc4HYV6QsqFB8y9B3qokswNRtoo5E8uFFyMnCj1qjt9v0rqppU2DLL19agMsefvL+dVyhc58IP7v6VnMOfxrondQTgim7gR2pNDRwEv8Ar3/3jTKuSgb2+pqnUNDNeIfIv0q75yADmqafcX6U4mmBUupla4brgMatg5FZk5/fv9a0V6CjqBZHQfhV0U0dB9KcKpAFLSUtABRRRTAKKKKQwpaSloYgoopKACiiigBDVdkwDmrNNNFrgU9i+gpE/wBYv1FSyffP1qJP9av+8KVgL0n3G+lUBV+Qja3PaqNDApSfxfjWWK1ZejfjWbHyy/UVNtQOii6L07VpgVNHtwOnStcTRD+OP8xVpCMuzXMzf7tXzCxRvlJ49KsLPEP+WqfmKkF1EB/rk/76pgWDaxeRn7NCPk/55r6fSvHm++3Hc162bqDaf3qdPUV5u9qxkbCHqcVL7getWzILSAF0H7pP4h/dFWBXiM3BZSMEZHIr2bTv+QZZ/wDXCP8A9BFSMtCigUUAFFFFIAooooAKKKKACiiloASiiigApaSigBaSiloASloooAKSlpDQAUUUUAFFFFABRRRQAUUUUAFFLSUALRSUtACUUtJQAUUUUAFFFFABRRRQAUUUUAJS0lLQAUUUUAFFFFABRRRQAtFFFGgCUuKKKNQCiiigAooooAKKKDQAlFFLQAUUUUAJRRRQAUtJQKAFooooASiiigAooooAKKKKAFpKKKACiiigAooooAKDRRTAF+8PrXhDf6xx7n+de8L94fWvB3/1r/7x/nQBtW4+SMewrTFZ1uMLH9BWhvXP3l/OqQh1FJuHqPzo3D+8PzpgLmlyo64phKnqy/nWc+MN9DSYGc5BJwapijy2x90/lRUjNhPuD6UppqMu0cjp60/FMDLn/wBe/wBa0QeMVnzRuZ3wjHn0piDEi8dxSA20kfcBvbr61eFUEHzj61eFWgHUtJS0AFFFFABRRS0DEopaKBCUUtJQMKKKKBBTGJCkjsKfUcv+qf6GgCi8wZid4596U4zVFe1XO/41O4E2KSpcD1FQgj1FMCnN91voay4/vL9RWnKBsc+x71mRZJXANLqB1IyBVkAVzqykH7x6+tdAsiEcMp/GnuIfijApN6+o/OjcPUUABqpjmrRYetV/egDAuf8AWyfU17Lp/wDyDLP/AK4R/wDoIrxqf78h9zXstgMabaf9cE/9BFSxlkUtJS0AFFFFIAooooAKKKKACiiigAooooAKKKKACiiigBaKSloAKKKKACkpaSgAooooAKKKKACiiigBaSlooASloooAKKKSgAooooAKKKKACiiigAooopgJS0lLSAKKKKACiiigAooooABS0lLQAUUUUdACiiigAoopKAFopKWgBKWiigAooooAQ0UtJQAUUUUALRRRQAUlLSUALSUUtACUUUUAFFFFHXQAooooAKKKKACiiimgFH3h9a8Hk4lcZ/iP8zXu9VbuNDaTgqv+rb+EelAHi6v05rSUAOvTrWR5brwUYfgatKQSKYjV3D1FG4eorN49qTimM094z2rALsZj8x5b196tkiqqRs0y4UkFh0HvQI9sC/6ORgf6v+leHL90fSvdD/qm/wBw/wAq8KU/KPpU9RmkinjgVcqtH0FWhTAaay8ESg8j5q1jUcg+U8UAL5gGfmGfrU8T7nXDd/Wsx1+c/WrkeBIvHcUAagpaaG9x+dG73H51QD6KbuHqPzo3j1H50AOzS0zcPUfnRuHqPzoAfRTNw9R+dG4eo/OgB9JTdw9R+dG4eo/OmA6im7h6j86Mj1H50gFJqk8hIIL/AK1Zlb9030rLwMdKTArqfmHPetcChVGBwPyp1FgEqk3BNXTVJ+p+tAGRJ0b6GvZ9MQHR7MkDm3Tt/sivF5OjfSvadKI/sex/694//QRUgeMrkN+NbSPGCOVyB61Ul0rUYpX3WF0BuPPlN6/Sq0Z/ekHAx1zRsBsh09Vpd6+orMyv95fzpCR6j86dwNMuvtVXNVNw3dRVR2JDAZP0oAttDI+7ajHr0UmvYrIEafbAjBEKDH/ARS2mRZW46fuk/kKmpALS0lLQAUUUUgCiiigAooooAKWkpaAEooooAKKWigBKKWkoAKKKKAFopKWgBKKKKACiiigAooooAKKKKACiiigBaSiigBaSgUtACUUUUAFFFFABRRRQAUUUUAJS0CihgFFFFABS0lFABRRRQAUUUUALRRRQAUUUUAFIaWkoAKKKKAFooooAKKKKACkpaQ0AFFFFAC0UUUAJRRRQAUUtJQAUUUUAFFFFABRRRQAUUUUAFFFFABTTTqSmBGyg8ED8q8OlQpNIpzwxH617rSYz1A/KgDwjHvSYHqK942j+6v5U0op6op/AUAeEMBg817bZAfY7fGOIk6f7oqz5Uf8AzzT/AL5FOwKAGsP3b/7p/lXg46V7y33G+h/lXgw6UdANeP7oqxketR2o+aM47it35fQflTQGNkUHmtoY9B+VLx6D8qdgMB1yDUHOa6cY9P0pHxsbgdD2osI5reP7w/OjzB/eH51U2n+6fyo2t/dP5VIy35i/3h+dHmL/AHh+dVNp/un8qNp9D+VGoFzzF/vD86PMX+8PzqntP90/lRg/3T+VIC75i/3h+dL5qf3h+dUcH+6fyowf7p/KmBe81f7y/nS+av8AfH51Rwf7p/Kjaf7p/KjUC95q/wB8fnR5q/3x+dUcH+6fyowfQ/lQBeEgP8Q/Ol7Gq9mpN7B8p++O3vXVg+36U0gMwHgUZrUz7Ufh+lUFzKJ5qm/U/Wui/D9Kz52w8n1NJgcq/INez6Z/yCLH/r3j/wDQRXjDdDXtGmj/AIlNl/17x/8AoIqRFsHkV4pqEbLqV2oGQJn9P7xr2wCk8mMnJiQn/dFFxnhmx/7v8qNrD+Gvc/Ji/wCeUf8A3yKPJi/55R/98igDwxVYsBjvXuUcaLGgCLwo6AelOEUa8iNB9FFPouAlLRS0gCiiimAUUUUgCiiigAooooAKWko7UAFFFAoAWiiijoAUUUUAFFFFACUtFFACGilooASiiigAooooAKKKKACiiigAooooAKM0UUAFFFFABRRRQAUUUUAFFFFMAopKWkwCiiigAooooAKKKKACiiigBc0ZpKKAFpM0UUALSUtJQAUUUUAFLSUtABRRRQAUhpaKAEooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigApKWkpgFFFFABSUtFACUUtJQA1/uN9D/KvBu3WvejWNqOj6fHpd2yafZqywOVZYVBB2n2o6AeZxnG3n0q6G9/1rn1bpz+tTBj60Abgf3/WlD+9Ye4+po3n1NAG8H96cHHqK5/efU0u8+tFwOiWT3/WniUeo/Oua3n1o3e9O4HT+aPUUvmj+8Pzrl9x9aXefWi4HT+aP7y/nS+av95fzrl959aN5ouB1IlX1H50eaPVa5beaNxouB1HmL6j86QyL6iuZ3n1pNx9aLgdKZB6imlge4rnN59aN59aLgdAWHak3e9YO9vWjefU0XA3t59f1pN59T+dYe8/3jQWJ7mi4G2ZD/eP51Ru2PmoQTjHNUMnPWjJ9aLiIyODXs+l/8gmy/wCveP8A9BFeOGNyCQrdPQ17JpgxpNkD2t4//QRSGWxS0CigApcUlLQAUUUUAFLRRQAUUUUgCiiigAooooAKKKKACiiigAooooAWikooAWkpaSgBaKSjNAC0UlFAC0UlFABRRRQAUUUUAFFFFABRRRRqAUUUUAFFFFABRRRQAUUUUAFFFFABRRRTASiiikAtFJS0AFFFFABS0lFAC0UUUAFJS0lABS0lLQAlFFFABRRRQAUUUUALRSUUAGaKKKOoBRRRR0AKKKKACiiigAooooAKKKKACijFFABRRRQAUUUUWAKKKKLAFFFFMBKKKKLAFJmijNABRSZooAKawDAggEHgg96WmswVSzHCgZJPYUIDOudI0zyJW/s6z3BGIPkLwcfSvF1HAr2a41jTvs8v+m25yjYAkHPH1rxtQcDihgGyl8urygYp+BSAzvLpfL4rQwKCBii4zN2Gk2VdqM0AVcUojYjIViPpSn73416X4d/5AFkf+mf9TTSuI808p/7rfkaPLf8Aut+VewUox6Cq5APHvLf+635Gl8t/7r/98mvYc0bvejkA8d8t/wC4/wD3yabXsFy3+izc/wDLNv5V5CBwKTVgEx7mnCP3NH8Y+tWwB7VIFXy/c0vle9XFALDgdRWr9mi/55r+VOwHPCP3P50pTAJyfzrf+yxf881/KopreIQuQi5A9KAMDn1NNb7p5PStIxJt+6vT0qg4wDStqI91tSVtYBuPEa9/YVLUNtzbQf8AXNf5CpapjHUU3NGaQDqWkooYC0UlLQAtFJRQAtFFFFgCiiikAUUUUAFFFFABRRRQAUUUUAFFFFABRRS0AJRS0lABRRRQAUUUUAFFFFABRRRQAUtJS0AJRRRR0AKKKKAFpKWkoAKKKKACiiigAooooAKKKKAEooooABS0lLRqAUUUooASilpKAClpKKAFooooAKKKKPMBKKKKACiiigAoopaACiiigBKKKKACiiigAooooAKKKKACiiigAooooAWkoooAKKKKACiiigAooqNjgnmmBJSVHuPrUBds9T+dNIC1RUIkUKMsM0hmT++KfKBPz6UnPoayC7f3j+dN8xv7xp8gDmnlyf3jdfWm+dL/AM9G/Om0lUUP8+X/AJ6N+dQ3k0psbkeY2DE46+xp1Q3X/HnP/wBcm/kaQHmCgbR9KuqV46Vng4X8KsKBjoKzZKNZDHsHCdPanYj9E/SsoHHcUu/3FO4zTxH6LVafaH4wOKq7/cUbs+lDYix8vtVcuo7ijI9qr7AetK4ELMCx5rt9EuH/ALEtFDYATHH1NcQVG4gCuy0TjSLb/dP8zV09yobmluY/xH86Mn+8fzpKK1NBdx9T+dG4+p/OkooASVj5MnJ+6f5VwCEBRyK7yfi3l/3G/lXnwXgVnUImPGN/Uda0PlOelZoHI+tXQBWaINaMJhflXt2q3t9v0rBVtpBBqYTv/fb86YGoqHj5G/75re8mMDHlJ/3yK48XLj+NvzNAuJMZ81/++jQBeu0j8okRrknstc7Oq4ICitB5Dj7x/Oq0mM9BQwPWo9SsfsEam+tQ/kqMecuc7R71B5jEfeb868rjx5qcD7w/nXqVVEaHb2/vH86Xe394/nTKBVDNqP8A1S/QU6sXefU/nRuPrUuIrG1keopax4eZUz0zWr5iZ+8KloQ+imGRMfeFUt/v+tCjcDRpapQNmUc/rVzI9RQ1ZgLRRmikAUUUUAFFFFIAooooAKKKKACiiijQBRRSUtABSUtFACUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUtFFABRSUUAFFFFABRRRQAUUUUAFFFFMBKWkpaQBRRRQAUCilFABSUUUAFFFFABS0lFABRRRQAUtJS0AJRS0lABS0lFAC0UUlABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFJRTAPxqF/vmpKMCi4EPFRHvVvA9qrk8HpVJgQGmN0NSHp0phwQaq4iuabTytMpliUUUUAIaRgGUqRkEYIp1JikBh3eh6eLWZls0DCNiuAeuK4PypB1jf/vk160KdzUuNxWPI/Kf/nm//fJo8t/7jfka9cpaOQLHkWxv7jflRtb+6fyr1yijkCx5Htb+435Um1/7h/KvXaXj0FHKFjyKNH81MI33h29675Tnqea38U3avoPyq4+6OLsYv40Z962di/3V/KjYv91fyFVzFcxjZpMj1ra2L/dX8hRtX+6v5UcwcxiNgqQcEEYNUjp9kP8Al2i/KupwP7o/KjA9B+VJtMObyPMNVhWPUZFjQKmBgKOOlU8H0P5V63ijFZ8pB5Hhv7rflS7W/uN+Rr1yjmjlA8j2v/cb8jRh/wC635GvXaKOUDyLa/8Adb8jUkEbtcRAxOwLrkbTyM16zSc+tCiKxlroemK2RYQgg5HB/wAa0adikqygooooASilNJQBJEf3i/WrlU4/vj61cpMliE1BirIHIqbavoPyqeawFSH/AFgq0Pwp4AHYflTwB6D8qTlcBifeFTU0Aegp1K9wCiiikAUUUUAFFFFABRRRQAUUUUAFAoooAWkopaAEopaSgAooooAKKKKACiiigAooooAKKKKAFpKKKACiiigAooooAKKKKACiiigAooopgJS0lLSAKKKKACiiigAooooAKKKKACiilFACUUtFACUUtJQAUtJRQAtFJS0AFJS0lABRRRQAUUUUAFFFFABRRRR6gFFFFABRRRQAUUUUAFFFFABSUtFABSUtFMAoxRRRcCOToB71Fj2qzRRfQCr/AJ6Vl4OT8p/Kt2j8aakCMPafQ/lRtP8AdP5VuUfjT5h3MPY390/lRsb+635Vuc+tHPrRzhcxRG/9xvypfLf+435Vs80c+tLnC5jeW/8Acb8qPLf+435Vs8+tHPrT5wuY3lv/AHG/KjY/9xvyrY59aXn1o5xGN5b/ANxvypdj/wBxvyrY59aOfWjnHcx9jf3W/Kk2N/db8q2efWk59aOcLmPsb+635UbG/ut+VbHPrRz60cwXMfY391vyo2N/db8q2OfWjn1o5guY+xv7rflR5b/3W/Ktnn1pOfWjmC5j7H/ut+VGx/7jflWxz60c+tLmEY+x/wC435UbH/uN+VbGT60c+tPmAyNj/wBxvyo8t/7jflWxz60c+tLmAx9j/wBxvypPLf8AuN+VbOT60ZPrT5gMUo391vypNjf3W/Ktvn1o5o5x3MTY391vyo2t/db8q2+aOfWjmC5ibG/ut+VaCgeSvHO0dqt80ZpOVxMobfb9KUZq9k0Zp8wrFRPvD61booqW7jDAoxS0UAJS0UUAFFFFJgFFFFABRRRQAUUUUAFLSUUeoC0lFFABRRRQAtFJRQAUUtJQAUUUUAFFFFABRRRQAUUUUaAFFFFABRRRQAUUUUAFFFFABRRRR6AFFFFMBKWkpaQBRRRQAUUUUAFFFFABRRRQAUtFFABRRRQAUlLSUAFFFFAC0UUUAFJS0lABRRRQAUUUtGgCUtFFACUUppKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooASilxSYoAKKXFFABikpaKAEopaKAEoxS0UAJilxRRQAUlLRQAlFLRQAlFLRQAlFFFABRRRQAUUUUAFFFFABRRS0AJijFLRQAmKKWigAxRiiigApKWigBKKWigAooooAKKKKLgFFFFABRRRQAUUUUAFFFFHUAooooAKKKKACiil7UAJRRRQAUUUUAFFFFABRS0UAJRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFACUtJS0MAooooAKKKKACiiigAooooAWikpaAEpaSlo6gFJS0UAJS4oooAKKKKOoBSUtJQAUUUUAFLSUtABRRSUAFFFGKACiiigAoopaACiiijqAUlLRQAlFFFABRRRQAUUUUAFFLSUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFHUAooooAKKKKACiiijyAKKKKAClxSUtACUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUtJS0AFFFFABRRRQAlFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRTASloopMAooooAKKKKACiiigAoxRS0AJRS0lABRRS0AFFFFABRRRQAUUUUAFJS0lABRRRQAUUUUALSUtJQAUtIKWgBDRS0lABS0lFAC0ZpKKAFooooASiiigAoooo8wCiiijzAWkpaDQAlFFFABRRRQAUUUtACUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRS4pKACiiigAoopTQAlFFFABRRRQAUUUUALSUUUAFLigUUAFJS0UAJRS0lABS0lFAC0UlLmgAooooASloooAKSlooASiiigAooooAKKWigBKKKKACiiigAoNFIaAFopKWhgFFFFABRRRQAUUUUAFLSUUALRRRQAlKKKKACiiigAooooAKSlpKAFpKKKACilpKACiiigBaSiigBaKSlo6gFFFFACYopaKAEopaSgAooooAKKKKACiiigAooooAXNJRRQAUUUUAFFFFABS0lLQAlFFFABRRRQAUUUUAFFFFABRRRQAUUUYoAKKKKACiiigAooooAKKKKACiiloASiiigAoooo6gFFFFABRRS0AJRRRQAUUUUAFFLRQAlFFFABRRRR1AKKKKACiiigAooooAKKKKAFooFFABRSUtABRRRQAlFLSUAFFFFABS0lFAC0UlLQAlFFFHoAUUUUAFFFFABS0lFABRRRQAUUUUAFBoopgJS0lLSAKKKKACiiigAooooAKKKKAFoooo1AKKKKACiiigAoopKAFooooASilpKAFpKKKACiiigAoNFFABS0lFAC0UUUAFFFJQAtIaKKPUAooooAKKKWgBKKWko6gFFLSUAFFFFABRRRQAUUUUAFLSUUAFFFFABRRRQAUUUUAFLSUUALSUtJQAUUUUALRRRQAUlLRQAlFLSUAFFFFABRRRQAUUUUAFFFFHmAUUUUALRSUtACUUtJQAUUUUALRSUUALSUtFHQBKKKKACjFLRR0AKSlooASilpKACiiigBaKSloASlpKWgApKWkoAKKKKACiiij0AKKKKAClpKKACiiloASiiigAooooAKKKKACiiigAooooAKKKKYCUtJS0gCiiigAooooAKKKKACiiigBaKSigBaKKKACiiigAopKKAFozRSUALmkoooAKKKBQAUUtFACUUUUALRRRR0AKKKKAEooooAKKWkoAKKKKAClpKKAFooooAKSlooASiiloASiiigAooooAKKKKACiiigAooooAKKKKACiiloASiiijQAoxRS0AFFFFABRRRRrsAUlLRQAlFFFABRRS0agJRS0lABRRRQAUUUUAFFFFABS0lLQAUlLRQAlFFFABRRRQAUUUtABRRRQAGkpaSgApaSigAooooAKKKKAClpKWgApKKKACiiigAooooAKKKKACiiigAoopaAEooooAKKKKACiiigAooooAKKKKACiiigBKWkpaACiiigApaSigAoopaAEooooAKKKKAClpKWjroAUUUUAFFFFABSUtFACUUtJQAUtJS0AFFFFACUUtJQAUtJRQAtFFFACUUtFABRRQaAEooooAKKKKAClpKKAFopKWgBKWkpaAEooooAKKKKACiiigBaSiigAooooAKKKKAClpKKAFNJS0YoASiiigBaKKKACiiijqAUUUUAJRRRQAUUUUALSUUtACUUUUAFFFFABS0UUAFFFFABRRRQAlFFFABRRRQAUUUUAFFFFAC0UUUAJRRRQAUUUUAFFFFABRRS0AJRS0UAJiilooASilpKACiiigAooooAKWkooAWkpaSgAoopaAEooooAKKKKACiiigAooopgJS0lLSAKKKKACiiigApaSloASilooASilooASiiijoAUUUUALRSUtABRRRQAUlLSUAFLSUtABRRRQAUUUUAJSiiigAooooAKKKKACiikoAKKKKACiiigAooooAKUUlLQAUUUUAFJS0UAJQKKKAFpKWigApKWigBKKWigBKKKKNQClpKWgAooooAKSlooAKKSloAKKSlFABRRRQAlFLSUAFFFFABRRRQAUUUUALRRRQAlLSGigAoooo9QFooFFACUUUtACUtFFABRRSZoAKKKKACiiigAooooAKKKKACiiloASloooAKKSloAKKKKACkpaSjQAooooAWkoooAKKKKOoC0lFFABRRRQAUUUUAFFFFABRRRQAUhpaQ0wCiiikAtFFFABRRS0AFFFFABRRRQAUUUUAJRS0YoASilpKACgUUtABRRSUeoC0lLRQAlLRRQAUUUUAFFFFABRRRRpYAopKWgBKKWkoAKKKKAClpKKAA0UUUAFLSUtABRRRR6gFFFFGgBRRRQAUlLRQAlFFFAC0UUUAFFFFACUUtFACUtJS0AFFFFABRRRQAlFLSUALRSCloAKKKKACiiigAooooAKKKKACkpaKNACiiigApKKKACiiigApc0lFABRRRQAUUUUALSUUUdAFooooAKSlpKACiiigAoooo1AWikpaACiiigBKKKKAFooooAKSlpKOoBRRRQAUUUUAFFLRQAUlLSUAFFFFABRRS0AJRS0lABRRRQAUUUUAJRRS0AFFFFABS0lLQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUlLSUdAFooooAKKKKACiiigAooooAKKKSgApaSloASiiigAooooAKKKXFACUUUUAFLSUUALSUUUALmkoooAWiiigApKKKACiiloAKKSloAKKSloAKKKKACjNFJQAtFFFABRSUUALSUUUALRRRR1AKKKKACiikoAKWkpaACiiigBM0tJSigApKKKACiiigAooooAWkoooAKKKKACiiigAooooAKKKKOgBRRRQAUUUUAFFFFHkAUtFFABRRRQAUUUUAFFFFABSUtFACUUUUAFLSUUALRRRQAUUUUAJS0UUAFFFFAAaSiigAooooAKKKKAEpaSloAKKKKAClpKWgAooooAKKKKACiiigYUUUUCCiiigAoopKACiiigApaSloAKKKKACiiigAooooAKSlpKACiiigAopaKAEopaSgApaSjNABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABS0UUAFFFFACUtJRQAtFJRQAtJS0lABS0lLR5AJRS0UAJRS0lABS0lFAC0UUUAFFJS0AFFFFACUUUUAFLRRQAUlLSUAFFFFABRRRR1AKKKKACiiigAooooAKKKKACiiigAoooFABS0UUAJRRRQAtFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRR1AKKKKACiiigAooooAKSlNJQAUUUUAFFFFPoAUUlLSYBRRRQAUtJRQAtFFFABRRRQAUUUUAFFFFABRRSUAFFFFABRRRR1AWiiigApKWkoAWikpaACiiigBKKKKPIAooooAWikooAWkoooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAClpKKADNFFFABRRRQAtJRRQAUUUUAFGaKKACiiigBaKSijqAtJRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFAC0UlFAC0lFFABS0lFAC0UlFAC0UlFAC0UlFAC0UmaWgAooooAKKKDQAZopKKAFoopKACiiigBaKSigAooooAKKKKACiiigBKWkpaYBRRRQAUUUUgCiiigAozRRTAXNFJRQAZoooo0AKKKKQBRRRQAUUUUAFFGaKACiiigAooooAKKKKACiiigAopKKNAFopKKAFopKWgAooooAKKKKACijNJmgBaKM0UAFFFJmgBaKKKACiijNABRRRR1AKKKKACiiigAoooo6gFFFFABRSUU9AFopKKQC0UlLmgAopKWmAUUUUgCiiigAooooAKKKKOgBRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUlOwC0UlFGgC0UUUgCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKGAUUUUdQCiiigAooooAKKKKACiiigAooooAKKKKAP/9k=",
+ "image/png": "iVBORw0KGgoAAAANSUhEUgAABAAAAAQACAIAAADwf7zUAAEAAElEQVR4Aez9zbIkPZIliMWNuF9mVfVU93RlZnFJLjgPQhHy5XJkKntT/Q6TL8B5Aa4oFOGGQs5qNqRQJP+GNd3TXV1fRFwqcAxqCihUoYCZufu94R43zBX6c/SoAmbuZv738rvf/eOnT59fvv7606e3T69/fvmUbm+fPkGA/OntJY/pLpnSLfl/+vT6J9qwZ9Kk29unr79J969/zDgvbykegZ8z9Pdklbe3z2n08j1bRXqRZXPXGokDWftIDWqTmh0h295o+yXpiA/d4P/zr1OdqV6M6y3q/fLHTy8vnyi82lJEQauQCYFudfMSDs1C6mq5pY69vHyHNylLJ2HfrDQAIWjfEtsX6j+Gacsd3lVKgs+n7zlHmZEcnF1l5ixzXZS8kollrgutSNbMm6oj4adcnez/5kZJZBHVGtu4yqhNle8QZ9XIUdvUfPr07dcbEwqkG5HF/H75UzMhom9wzf68+Tmv85/+uBEnl2+5xtz5jVQ7ZRRM64GMai/4lHve0+fd71tKW/YsppCExP83abuvT9gzBdowMvlUtOQs5xDuFQDElkK3m+Qg5WJP91n/JlegtOqZ2vpPexD5FZbbfJUdCnvlp29pdW37o1jhHFWyV+t/zy7WKuEz5u6QJVDQ1ZGGTGlPL51sAmm4Rcm9ODvtveUjpPKRaHuX0vG37EVlv8BaFX2Az+a5748JcSdLmHSI+vSdNHQra6Hc78yLZg8VfdviKN5aP915YYS8kpEh09iOHjSzuDFd8km3bX8RnL4Q1ku1p+RjLCMgrtnus1kS0IyQyHtNWm85hjwpGa/e4r7Vve9rJYHuQ7KUCvd5L3O3H+G3mrZZ+/r3KWq3NvilP1BzO/a6ij/uK33pDwrcEcQD1rYv5OP/5mDNL9YtMaAbdwcxZo31Y0Tmkx5hATLCqWopibYO095k9G3vfG4WjicUhb2DVwtVkOf07csf0wNXZsS0OFk6iiYYddzuc0vHgdTsbRWV/gMOj48bf8oo+pyZiqS5n6Skx83teFgev3idJP55JeO4tAVjZnM54lEpGfn4ufmj5rISNlalS7LevZ8lR66djvOp0nRL7PO+uW/FvMOH6xXrudtDtIK2wP0k9/q6n+RRisg58iBh7s+Ckurtc278NoMFnu/FmtyPnzl9AuUE2j/npI2cx6JL96pv5TFCHidlQJYT//pooDUIknnBV0w+8d64C+GN5ofQ3t5e6UD6Ih5cUBwpthuqpkHSpAfMBJbM8MA2aZtbXgRJR0LeZrsfJK0I2jS4kwhCk9Vlk+luUUW3UdhKSPypjt2HJJ5aDskCyiWRnTcNj4sNijTKUrXNUGzCiJE36NonYeBJD+uLkPzzhFIRJOVsmw0W1lAKlvdoqeKpJbOUReDOk3xkrJClD8sdoQDABADtJrPsPoXeruGSisCMGLNYNsgtNheyyximlmY3UXtSlZvGLJZ0L9GYBuap3m5Bbxku55QwGw7tXpW2EGu1wokJbDwx5gDmRNVlZVIUOYs5B5lK+RtO1tDDxXYPJogtMjw5A5NCiQWvqMkPWFmxZRFGEsEt6TLohl8n4KSVOg8IPlVBB7V0txPfPJN5uzXZi7pYm7EYAkpuhTGJm2lLuRtliOVD3oIjo1VYPNj7kApltcyY+kCWZE8LK/nQfwhZzj0qKQGxIW2DjAYZotRLjXAU7tyObBY+JFZuu700sGjgVvaLxJXml7aFdfJDjUmK3EQJJMp6hWUHkkqWt6jdq+AQLXJicmUfgP8WjrsUmxdqBiHd5pMfkhlfIIlkJaRVjcZ7ZiDkMedKukKYkaQV4VLTzlauPsHITEKWein7OPCs/DM/NLtrhWlnoistFW5F5TkrTLnrcErqYiph2z3vTI2+HtbBeyFCn5SZ9KYDhTIdUKZt0TCh3SRJZq00MaGtXXkMwCTCXwXsVAs4aUp3ykMZogCY5VwHqslaihU+UEkFZKmpfZAwPeHZurJzKPj5fkPId8mZ/qc7bFMoRtkXSNzFgkMe5VZxhl5us1vy2ZC2MAFQaSpH7cRJWcg+7LixZ2sR+J49SVPa09aY1k55JEj+Ly+/+4d/T04kp4d53AC0abMteZbeJdcil4h8j7BK1RnEvDqBj6Uyu6BoSk8pK8euAq22TNA3qDS89tbkuzbZw6NzNzamGNOADby7kGb2JmNJLjdWF8Wl9yJxlUdWSAY5bOQqLDJo4gP1apINxpaWtREacZ8AwyCYLgSBkjiyVYBs7jFhHbw4cAuSsWyTAjnQzWImPRdkzo4UyLXhsK2pAPrJZEP+fraZnImuRFNMHS4yjmWvHwq8o+B8hChviWges4O0zsvAY9QWAPW0Wm8MXtwHpslIbGpQOhzYFTYJTcFk3W/suqtWpZwGuVYhqmPrEASFcI1cSlOvxJE+CCerzdm2ZNCMRusfzykbbPCSyTeZ8/Zt+cLz7uNSKEbk4m0HmKc9s/X3WR0OZK1nDacGcRoOb+xJgsSXsgvSxElfSSfJ6RUAupWLK5srWXCD0B2yMnvSKNOGlgkUdfKBnCcR4LyFOw0zBKs7QsGY2x06QErVUOZE5MimKog86JYbB9ocwv7QpMKzZ7stavjnkbkBBszaX2TYcpInlEwGsRJHJ2NnoDBC6wmDj9XGpDFge5bNBAcAExl9kwhSJk+O5Sq6SunWdeCk5IkbAMuoUiaS8GPvbUzrRhqkTDHd4mSGHW5LsJ+eFzfpUnS4J0vDGUO9Jf8ulRE2xaUkOG4UZwx5m7jAVByShm5MA8P+tkTSvWxkGiJ3Ae+HZy32zoJUAqVWYmnZgSaT9C/tIHXDEF6M1AxZHxG4EDhjuAfmcTMlu7W0q40qWKTfYrOGeW5VlgNdcpOgRWZYDiyW6n5DK7oNDcF5sGs2oHx5db9Kzv11L7sChbcl3fieQujmb4sL1wL3rN4XBXASBdE6Uvr9AYhcoUWD+4ImPWT6zcu90/5Zk6hydwtAhG3x3e+RgfNI2G1f3n03iZ2VpXKQbixD4KFEaJV5vM1IlmmzTxCtqfIsMOkTEO7LSELvMlnVjeOUpVHI4KpR2Y9htr5J7wZIDtkNgtiS2J+CsqKkA+IksC3Dt1SQHq3Sy1joImx6K9FSt+FRMGBNu/5uy05wgzmZyixBxAEjy9jIvEJdicmn+NE9lkTlYQ8QZ9sZ2HGpTAxYGGVrorVBVd55sLVh69XuXyQZkYGARJP+kk8A0rDuu4wIyJkA+JI3BLkFhNQgHelLVUJhJsxpklUimd4zBgkImaNpyHlZSYLUy3D26UaxlYUmHetZYAduEZkgK82WE9wQuKkYzhZkIukFNNKwIK0RmZFZ0PwbHHg25OVQyhQLQBIckjK7TAeoBhAODCv9/SybJydrIvurqTht+TQXE65EVmkb72YIV52jgeoNOQgCDyVko+zBrOq6WW2wPpNdi75YWxs3WWRU8ZQ6KRf7FsTDuwsgKWlQc6SS5L1dtcxRjT/rtQBPxpTIyTk/eLeNTTH5eRnDMQprtBDx0VFhDZi3/Es4kpdRuoeG/LVJuhV5B7b8d48Sc/C+4dYMGdzSs4MWrBKk5wKsDA/KTRYmRnq6pS1UacvGIsApOTY3NtDzKZYJoAQ27mWozdBofYk44V7w29EoI+lh6jrsrqbEcRKGlWYYDJVf24X8BJGfkm8dLk0q9/t0lVSEycai699LN8hS04+5SOsnNqyodO8hudGA68eLGlUsjrPkQ9pX0aYd46L6erCgK2arKJKzpM0V9VDO18nUXfTj3RqmaPJqf6lhmYVheOOAYRPOQwi0PV44JWI05iA1eq6R188eJ4ZcXK8MhIk10pOpksAOUnmC3MnXUVmJfFdtJc1VhVgUsz6eVHpq/m6SOxiJ7eOTjPRFVyEnQiOg8Hj5kwsPdORWU7ibhjsDfhhKmTVQLhC1GkuAMCHFAjKHMDcIcss+JLCbVE7JhNCw1ZopwLhzQ76hARwohSm/476JlCnBfnfYJeklZURIjZRF6rZR0u1EWWaUsKQfFyMDVmWnIZlbfnkigd+GzmoZx+NytWj73nz1mobOk+PEakl9Kk1tepZcN+z86gp9/BwetGVBZzhd09CSqfN0E7mkE/omIspIIERDlB9h4K9mJNntMZyQhd0mJLJi2oQuJPqwDMFuJOCPTQsC0CjQ4cw+5AYZeaX+SOrZWMrLbCWHXS4S3fMfshTLbM6IP7CDGciNixiABxEHKLkVVUqJC3l2W6eUeLXFHFHIQlQDdxyhAWyGp5BsMGeHazXKKCkjOzRyK1lJvY6Vnlomf/xp03vUYK/pNqGrrGqEh9wKM4eznQSWyRFD3opQT5z197BGNmZLXYLMEdBUxxy2XSBwdpRPGVjTy0ZPRLJdekuZopM9+/hIGZ38dAdkXmDL7QS6BOrJYNmzPKxukfJi2EIbZCYpA0prpB5W6VNWU9IVvXxhidTYU2iLP+CJbQkr8fQdRF9/XYIIi+z4SzH0FiAy0RhbCALsDJHRQUJBkp1u2MIoZWjgwFRZ2ehlKg3SWBktrAek3EoiWvY9YdVRm4bMzNB0EgbpL2Xhsk80I8MTPjJKygKB1M5NWjdZ4kjZQeG1QDtD5tlu3VhpTIfuplKpgavUQJYQhkyO3RuywUSycUO0hdEEDdw6ZlJ1q87A6Al3Zj+4iCi2JhzcYCUZ+fxtCapiJX7jcINh4Q/iXJaTWfCtvFhfaa0Be9szsoWyJ8Zdf/YJWjUrIGh9mdiepTPnXbcpJRHhG8uReeGooMA9gz+nsDuRHNnK3ILpEMvbfhRzwjzuTo0B738oZuZUFNb9LOdZfytvpVelwIpcOqPWVGhrA3DoxXI6CDwkX963RFyxl/tk2uVdEiGtyE4sdDya1UmuhU113G4j58YmgTmYrjdjF95dL6WUYcp4ngL9lHhSI2X4QONvpaeUJVqDwG4kkIm3Waw02tqL4FUj1qTE4gSA2xZVinp5fdneXlVMCWLHA0pna30jae0qQVO28n2le4KiKXEckdyLUsp7aLFCo7dkJyWBAIe2uw/eBYXv0yI5G3ar9Nzk7Ztc3e9tLYROupd8DMg0C/xNw9I/y5Lz9r22+OZdeDJm1ZmqdonA7nOCYhVZXUixrY3M2WJSdUAzy9kljnSRa8/Cl/4RGWsNniyjB9zmCM7mo77tWH5vPeO3gH7PlbXqobJW4LAmVUle7rd9Tc4uF+xjVgmODBoqlJUZlFWd4ZtvAdcpGQgCD9lTa9jUCrn2agXKbkjvxFcA77kBQa581Mo2ibPJCWIrFZptWJSEselT4uqYkBT3v6FowXGaEpcKKMRbsoUOEIay3Nb1qDBtM7X04dMi0z3rSYu38GLajvRFcL3RvO81VqtOELlezByq41sgZ56Sbc8JuJsuyEu/EkM36jlxeRHffN8Jk/Mrutc5eqjgeI2oDgB6JWy/cTH3PEdCMjNWQkjVR9ZByCn9xkJKxL/UQXKTj3lUguwwDFIj5Aof+sg2Y1bPJawoplvxmxsIvl5z5e9FUEjq8JadngDjFYC5vOSdQPaWd8L9+tgqS+igJBX7GnZPjdhULhI1WDxkgdLl70nd/D3sB7KhPrkNkcsX2Mta2CY0MCEh7Ad0Qn+ImJjtW9I8vbUEeItSwLvLXqaHnC4nZNeu//ntlgwYHcquiX08AdzX4z1s14YrEZUL9ZP+smprqc2LLMmHvSHY/lWiH2UQWZjwYU8SdBOhZB/tEGgoBxUhwRVZx5OF82nrQ2hA8cZEz0+HyT2loydCOXzusS54rh1e5IMbC0Vh3zPuPYqyaVkW0NVWSw9PWduoN1hCMkJmQx7LKj3hs3nSHUW+vPy7//b3SdrPpXzeEq+Wq3OmzWRVFmFbo/OvqXXPTR3OjqkiuUKppfguxmiInhksiOvb0FsnN2zceD1cSOb07uppPJ09zxcWyAAfhGbqpGtOdMN1sgF4NjOfiLPjM+R4aW/1tTdJNdVIx+Q/SB3LJq/0e6h0VSxFNcVRCDQsMNomnNXVFndpTFzjfFCS2ZQegaY7Zi7x+pvGb0C0Qy9zpStroJwz46l/g9tOZYVw+0HhfPvMKePS9el1qu1UzCMtrIr5JNdGmHtHlZYKpW455c71csrbygrmX/6SiA5ee6lqueug10jZ2anO6EoAL/Sv6dXH/X3AZFnOsBwo6CyK3dRYF11TlWbsUbl/mAHV3SyHH6ETqLEp/FZzenpazOFt6GN/GuT6QEvolr3tdNXsZGPAmuKVJWeJlRzCQifhg6gWKMqaI1VwXyLO8GFWMhfjQJCmOPL2iEsJ0ovPM3E/nu9qhyc6de4MAO0GtCcqvMQVhZ7WPOxQQaaU9X13uGHfDOvqYJxq9I5HUnnjDhDo2kP+JWC+BiFaLt8hLdRT4p5ahA3Im3kHcXuG6szve9a7sftVjRd15YkCc9d29CJZZ8aWfs9SEKx7iRCP2tGYsGw/CoGTkNtuu43iFJIhlBENh99N4IYEyox3XnrqPkgrCq+Si6uMa23hmjhcZ4RJc+MQEnyr9JSylSv5lHUIZETtrzRKlJ7sIff8tW5Y0T4RchaKrBtLKfxrkMOMmuRQM4GZGX/9Ter71ue9wmGe1iHef8lQyi0i0cq9xdU4KUtPn7LExwRFXkGyZs3PBVbIqF+h8vNa1clKN3y8biNf2TZoARNR1hVN2R+dS2s0T63RUVIT8ZespCxxIPtW7R/JrqNkFilLz20SytFAmli2YtmhewxhKwlx/sNcEnYKuQkMDuN8xCuTFbZVO+9ZaQrc/pN92OEqpRhY2YXLQLTqkmGRLm0+f5JxSZbPzbbPFRSf7hGi8ZFwW5foro3ELwG3Whm7LFtTA/18yg77GW5W+PbBu/RCSIariUE3k+dRfB3mcVPdjEcpbZaHrldqbl4jJT8lpyxitiXn+DMDFoCL8mh7VqlrdEfZwZrnQg4h67SWXnveVpN5oeEpcaGJ+1QhV3lbXvPZdsrzsVZEaYdlfzB9eiQqX1AxO3HvrNQH6/wZdH6UGbiszrz6vZlA5kc5ooFutxs+RSfQqz7ZECoFyMmmbokaBwhr/mwsXgHYHzGE/ZCYkgZudodsSwDWcTGIoUFspOxJfv+vyXJdnX5mGz3YJFPH7DTxaTqxA2g9L70G2ZkYK6RB+GGG3lr/QE3Q005rRCv9ip1l5QfezupQnK3WIu2k0CFYXqQ/K3tJAWAfNcKUCRbgO9w/AocLy+ZpkHX6M3chm4eAnqqe+/cQ1B+XBJZXoLWhhtKPfZXbS35HDKIyfH4FoFhvfG+QN9SHyaGpMzBXMZnhcNDXKyHbOl88cjDlM3zcAZ4W3sdZw8HD9YoQRuDApxDsADUQTW62HA4HHj6GoEl9wCWAtW01HNYjZfv4Oi9ycUYrnB00gq0BGEMuYSR0RrBTXW55BA7nFEmV8EzIqkhJQ6mRMqzEgGPPYfO4KFx9pGL4cIhZFXlwJ00nYYjkFu4PLHIlLPTIzvanwQB2/gLI0QmAfB+SRLH0xQdz7BaR95G3z8kT5yVbLAUhumDJ+/l3bu0cvv59kjvfrcEZua9Zs73Hi96dafOR3O4ld95nhop4S8xY7tQC2yH6HQ5hvMicWviWXiaXPpFcMjYiS/yIf8OBus83LEAa8vsg2URCZ+qkucgRPhGfghe9tzCbeqNwl/lJPpA/5e/nRnt5Cii/nBrQkbFHCFq9sjBrf8lxjzjOrc6yI58rHeEpGfa7YHOt8o7eW9zANPujXhiN/+wwPda8vbz+EWtQR6dDtORfv/84WcVq3UBkrzTimuYIZq5RfN/gGgM7apab7KdGlVMsZW60nCpMAECks4Yljcwr5a5zo4z4S59m3TZoB4aokpthIXGT2N/yrPTwHnayinn4gZwXKW/EqVruVlbJ9/SzXLuMaybUr3+X3F7/nJ1zT7ervukDwaMTgHGGvsfhuVPt6OfxtGEOZlOBYJq95Le06V5VlJW5VVTetyT+zEUd4O7TtNCfdWM3ODieFsIPoEdXaNt0q1+69Hs//Xw/TPtdj2rl7OiYD9iFVJJfFqy0tkngt6dC2QvMXrp112gaAr0dsKe7hszJqJI4NxUCDyll04KTSTwKnKxSyg4/NAnOkB3nvgmLvm/7kbTBjlNL0Gi5dFOfyjhZ07u/X373298n+ac/xZEj/Y6jYWYLL6KS3rH0Ir7lYDcFEo/z1tdOBGRqQ2kb1NAkeYqDwLxK1FzrTPljZOX7QPYyklNVCpm6t8qp6zFUds5xhzE/ksOP1p8L6rVWLy+j6WWMgCEuJ7iVcIiRPOIJedCcC+ZrulsOxUMdaY6CAV463RnXVjVqgMqEi9O/CRTX1S+hQ2D2Or2b/UJjZP2jPGoB1+m340K6N4I+qz5uWMVbro1I/xEsoyq4kweonZjLCe/kOMRnpsH9JmZGFUw1SGZ+3/fLp/L5AMJy4DpVeiqVMOSMKB1LGq30ECdswAY8199kS0P4TQAfcwWDhkcXEsQUPa5lb53h2UXdo/rmp/bH6wCvMRLey22aKhd5doWXAa8TnW7OeqrVSFDURLVmNcM4jnJ101n6MWLyOBYdy/EAXt3O3ZIXCFxFg2fxqgS3bNU414lVonMnAo7ZH/AAWwCAs9QcAJah881wSOxPAGUKksnANnoF4OX102v5btF5AhU2v0up0vYG/ucHXr4vEwkFVp8B4F4wT6mBjC1hF5M8w9PnqdLKqCz4143KNXty51pEYkZJAjuwVngmI72jdDeVnudvO02FvLx9yXf53c/sJwSgpe1sjQARr+EI1BnR7+QM0thX59JVj1Fmvk1/rT/++tEMdV3ax9LIDiSclzf1K7NiyVkoRW/VazGU2QuGvE9L3LqJ69yWy0A/yu6F92JpX/MIE5zVh2GgRyXb5BFPyhm5HNQUijVfynFjDr045mjHgQZ9gxNnR9ewzrAlB6ubdg/b1AzVGvKYcZC96+NXyggc21sVbLxI2KscZU+FZp+33PmXr7/JbxDu/xa1yba33+0cEOb3bcTTTN01ZDS8mwAzaa52PV+8Am3k6vdlkaDrfFB5bk80GVm7lLWnr7F49lZFQtJ6uTb8/ksmMgp6vwrJU8qIVRpzYjV/IFR8ONpceqIUdha6ochBeAb+JT+f35RsYxRoQGb7DEA6miZ1ume/FYGiI1V2oZHZyc8mKwU7dPFtJcVJSMB0e5G7lICqX062kactOTdnyZkyhixNctUJ6Bfd6nJaF5lCwhY/Dk8CHKRbyS51JXTmPqHXy60gz6AEfEdEE5G0Hxxc+gEmj++CSQFPyLTNt+2+DPcdppk1RFEIC5W4oR26AzIzGWKxZ0N1GOg7iAJ9x2RlDhAMJhUkh4zRD3tUiQ+jXQWAjpzYl2HZJ+YSTXFRG6OxUhIa2Ev/vjM8ujYZzASBizXLsVAW05aeQ5SAuF1NVxq7BHaPC6SWRE4B5e3JXFDfB4F88BnpriJufSFP97ymrAhLz2CHBaJQJakGAr2iuv0OwBZrhYhoR6RoYB+D0RmYcWXacqkztsppboAKuA4KZk0LlD+DJT1bh9kxYVW39bpapAo2DbifDn+AkCejcZTCy4qBuQQxXFFU90GQKsYd+OlK6OZFc0rS6RxKloe+Rwuo9l7H2q7ATTcKfjXUpuPPLC53oQCJX5OdwdJsZ6KTL+ryo/YGfv37JJfXTCKxPvKl1uPNuZTeVeDdsi+bqhgwvLrMZBsk2NA5BZITxWArgc6WmySc1svjFeBfzbVRZYMsLy+vFWPpZ1+brXHAlmfnTGJ1otnRi3WdexbI9X+ceiXNyBIq/n1fntDi1rk/uXbAJTp9SolBOh8na3KgbwFSJJUixZg3eKct/aebndaEGBkIkrPsvicl6oPnOryC8rV2ogUW8Ny5TUmjQsAwAjlC2jAkZymTGbkYhwWYGg7VpDRAjWs3XvvArcLtOgWUknrPvWPHnN7lelWP4R10naZsLDrTq1VqN2C8ZKGBcojWCCCGi4YJv+PZBVhIZLYshMJu57S3RDJcnqPbET8rkyz7LMweziiPtjcaOSeNifJBQz4kSM+KCpx0cHHqWky0EiXvGYEFskKWGlK2sGxuDRL+wWWqYZI9V91UNgnTRJ82nC9oPTW3Ilj7DbgxJbuqscvYo+whyELlT5QGb+ZX9c7JnP3o2Xr5HQDHlbEdAeEHQRz8xkSJSpe2c1O8010SqDrRxJeh9IdsbUtE776gpHb27GNdQYCnGG2/jSBZkQ9nIT36ME5heIhc26prcpW48vmBMqbM+bPjO0NmtR3vd08pBa4lSAbDaw971pJFllR03fvsKK8tSTm9I27D1p9/4BRN97eACqeb+jxlJFfgdSSuqGUm5yvlesufF0LdpT85poew9xCHuOyzvamsBItr+XYtLfjgvaHkvsG35UwdW+vjsoayNDvb+t32lv/Zeq/8nAsOebvvxVXHuIRK6xCVayytGVon+6ePnLjWJHFa28w4gnPsem2cDTfTDaFOC8fOvsBWZ07YhwTlNuhJDtl88FuhfIRXUP1KOHvfnCl9Sbyq3/xpnYFSpVxaS0M2KfHbl+T28q1K1zIKj2d4WvSgl9bETa4HKVvUIj7VghNA9TpJTK47ju3rbZ8Brp1UJDuPv0SNnfcCymPWjrjbiiRrlHKx4x4Eal09ouNnYlD2F5ZrrwtHbf34Rp/Mx8tKYXj2/534b68AtFBe/F1sIKi3mowz9RdWKaEdBg1dGdWY7CEHsWD7TlhsNG1pNRjH6x7SIkBG42Ss2cJNQx8emBzUd2q0tTcQ2uwyhF5DaFlKc1hmrhE0dpbwCKwYS3OWydq7NWoesrAHdVTJCLVhxJF9x+hIZmTrS45UaOOOYaRzLRyNG6yOh6kCGZgPcSgZJCDDNnXBB+nYpwDs97JLxbncl6Ib5K0VrXbHfM/SXvslVYThw44bzaE/HGgbnDf2VMi7gn2sXu2uxUOuN+iyz+aIuyDDAtm7J6DjKBupM6B6HJOOU1gOXf3x0rqwy3wstKLHbITnxG0KjI6LY9IFTnXSRSYjgWUX6Sfl0o6F+0WYwmgiI14BoHew/O4f/v2eFRLg9utDNaz1bT9Z//L6J4MMnZ0Quv7OGboKSBHirCV2/lpz6o2mcYLnT+WMHDnb836qJd22OwzkVpxx7m3fHIpimrlMYMh6NrXGCB2pP+c9QsxgWz3VpReF2aHR0fJt+/aAL/mX7bbrwaV1Ha6cyPHphGUVxwqHco1B8Oy5ccQ+4+VVt2SCXDqzzYXeO9pWMmq8GCIHZxYIBIxtENuSpzJfQCCfBCNhCz0nHC7Iv9EoUfXDpOhb4UuOW9IiiESDvWbLSBC7xImzILBqwz7jtb4zAr283aKaa+Fl9XauqyGWQHtEBtV1qCiVrLuXggL2LNI5IbXjgg7ScgsLNMVrnzbWDIR99j1Ho4wqxGJeOXUH6AZM7XG+CojQEAHcLaHriOHfKt5nTaJQ3c0kSCvkSeLdVdBf5zpXo8GjRueIt/uV/W44g7rO2cI46TDX5tnvudyDGDIJGx+5qqVc+baDyEQiBlnYP7VF8ZzuTJmFltY2bvA4+XD1lsCKYbT9BpmBOo5eyFmAI3s3rqq061Er0zdx4VV3Wle/Tjb+xs7aMY1QG/FioSw67bv5fPsVmXqfAUj2pQpzKjvS6r8d0eE+q0IthyqaTUn+KMkqWAGSe9hXBYcUl2bwJhA27cEanqBQHaW17Mw4rGmEoUPj7wwJqjtNlr6BwhtgNj74vEFdjqS6JYKq6ZH0q3OQpWXIzixQiJQVQq1oR22oGJPYZm+jtzE8t7cJNdWpENhZzQlZYFNIQBgTnUEhX8RJjAYAw0bJxFjPAkwEizKBD5mjThGajNOYFM8UJRZkuQW09CFNM5TpGVYqHdmBylFkRxtplGSM86tzrHfg50wjMhoN5Wr9uZohr6GD5lMauS8E7RPTbPPAHLx5QVbgIoC9GxM6y1aDigxqXYDP2hEUO1ZCA1LZ5gc+mrZCU7abHZ1RyXU0uXAXyWo1wDIBkLYsWAhdRhasIt5RINZDACeEWrSkTydJPp709GfqRGtGdJpirKpaduWzqzRP+CXg+tyCzPld0G12QaxF3MZthOF2vto8uxpzPp9M2W2s6aAu1bTu1rYLah9BdmZK9kn1ZoTX2jv4rUt4LInJID1flieitL9E68odQFK5QC/iCi5hdhD2TN71JyfJRgFvIdzR9qtEDYfdpZZcbpsraIyKrnFHo5y31J6gizwKhL10pr/GQDWnSO7FuYWGW6t9vDEXkqhxbVTVSgHhPldZZVMEgtVZ6V7J6RuZ6Ddv/miCV94Tg0kmi82bICRdt1VqfZf/JPf+mpf51uThnKBpGXw/zmxHN24oUCZLcggDqeJWDUToeUkFqBApL6fQHNgkIsLi1k/1KmUfgFKBi9z2XWutZk12h3jXv4ZsR+AG2Ilw7Rp7RHDIt8zGY3vP0vT6aPADqU1GQ7LqK13ppzf7l9/7IojNJ7/AgEklTfKVEJ3jPMx9Do+qvSfnqp11g+5Jq2byACNqBpYkuLyX3mw7TSbdlHC8qR1Aty/a2EFQVBElmx9nDnyZBWgRBBml/X2r9o9rKobVYIAR8WUfFgAq18kgzbswN+UVzqRGpWvLaYNh8C4KW0tSukdeKHr2HTh5Sm8BsotwwMsFWd4uhuGklysk09JtNW4p2XsI4oZ0JxwVwKdy4DCukTSYHdZMChbkBqPNk/jaHZBVXZYT9KiRZe18Q028H3HPKfoNbDMcQ3X7HlhC04nGVE7xaOthniyUNPigYn5HQvoMANTCK78CsB/NyYK2DJojEEqmB7+3z73Wiffez81Tw60U+H7b/E8miHfaXVGLYHmxKDt0caoQPC/4rnd3yriEJqTr3PjIoZxxC1P6Q+5miYc7IHuu/BwoJcKTod2wPQnrchBelehwIxyyGminrXMQQK6KmRoYTKTfzspmnvwdq9iXJXJc3jj8JUe4764OYYIqupQDyjV4roGFEF7HKdL8FMZUejPR01V95hK2D+HwuGEENgoO6s13L7l0owHpDHGdFQb3swSd2KMqq1bCVYUezYV4dIj7BALIxUqdCW6sR881w8aN3hu9v7azxYhXCRguIIhc2I+2z5jRZ9tU0hGcU+cotG/vMhCM+1H1ubH0sUJBnLcyhOUSux/x2DQUGLmA9CO65XZdcczEHDGmzGJCWQZG6ebLyoCLHRy0cA0hfxQDXojcwgyqW/HpjUD0bINHOQgnB6Tc1ICg7TZ2CI09nOAPY+r1nHT4oyp7dqd4jnN8PoDp0coczhItdvz5zR/iDMODCF0y3a5KQHZgweMjI8tCZh0LHoJtswhccVBBr0DYwj9YjixUpjgRVqa4QgZV2uJvT8E1sLDb+hIcpTtk6gwJ1h9hbSG42wb9FI1W+pKMP/hI0xbF5o4tucCejIbDhvN4d2B+S+JNh0AAe5zTnghPXi0NTpOxsa4Od9RdCmLFAsgLfx6q0zgyzd/8jCBO2y42rPM59wjG31U9aZhI48gQlrtVbAnZqSHgxTSujzNEMUQd7NOWVFaJZKWn/uRE7/N/oQ8Bb7fNHa+R7q+UArI4pQwK9+tvksq/tjH9nTOT18NWzkdHnLnoRhjkSt+uWrrUdK8BMoYVvn8lT1j9/hupbHVvom1v01LVYnoVg1paxXD5fcvTLx9W9iGhd6veYSmv6/ecd538PiVoqS1GimR3msYMd/QsyXfqWz5NCIZgQm+KkLd6JC2mjHI2tFIdmMDEkQr8hHUuMZkDZZSpJUMmUwtyzXisZLoaoRqJfbnShwcehzDI2BEdG/sJDzRTtxcupJezwHHcN7Y2nhKQo2xBPU4xbhuzXd0XV3/3uS4c0vfZQ6Zol8l+LZk86ThAadfmeu0xEZ8BkAxRd1v0p0+T+BUAxVIKPnZRCnlrhtJkfnNO7UQjgMhC6BH8D9Du2873aykkX8H70c66l9oHMa0ERSXs0GXxkzr3v/6dE5k4Re7rsIIwstFlXIkpkxoRSQ16ss8lUD6icZccpLhJ1JWDZN0ahRvI6405pybV7dXhScMB0lzqlLpGDrg0EcNhWzsH6O9XZFNPqKhRfXTLKnoyn+6hyept7SQtnpeQDWYpcEwFDADeejZ2+nGF99ue98v8lNU2LL/ZX5qkFK4RtKaJcoZHYh1YMs0iz/pTCvQKAmQCkTiQpcbnfJaVMjI3wqQhM2F5NhcQJOwswmP6l6+tSuy4OSi2S1ibtEYGWtauntpLf12TxOzLFIY/Mo8gtB0aue0yIQf+a2jceG2ARsPhiiF6chzZx+FyfLcIDUAx4DBEekp5GNg4UGxz89B4ubCA4GbYIB4YEhnG1lQPAK+Eys5AlhpGBE+5ZVNfgCvZtNAP2B0N+6nqzIqphaExb9vslfByv6Oky//F6Xf/8I9ognAjG43yuUF9Psqe8NgRV6TJ6w3medIwN5PVV2EFh3X8mkAHZ+t17Ucj0XJlm1DIjFLeIKhGIsDnygysu8GmmIBc8D33eoCfv1OjDLDqlT6Qxey3RqyZfeIwbr3SDO4+2QrN2sxqPnqOmnSU08hVdamJMkK4vCqWtVIw+kEubSw8+fvv6RsnZGyR2yjywvFHrVvtKXlNyLq33eDCsGtkZYdVEL9AdBCyydKXuP0enhjH98c4PpA7/k6LyJRv7ZVIvjap5ncLEHd+XR0+IrYvNqtRO412EIpYyasTLePoY0UPnHX73oTJcqbMQrb0nMMXsBLQ2CEHgrIZovPld2BsP58PrL2J3mb2z9lDrc923lHXaq4qrg/V15rHfVpR9Gvc6bWRCjsNdLE0pwSfa+zURf5k1VEZuPVX2VgR9+SQKaGPD+ZW86YSSGfRDZlXytL9mNxnP/xNgD2pYLsreVbT+/zxKEWJkEsKMuIKuV/dBZmMLlyQyYDUBLTGCH2qVzpwvL1AGOJgDTduzXClADdG4/POa8XpEMszqI8DwtPyt/SZhmsMEj3stkyCApdjD7O+KYBfpm+9KdGS7AEpFWqX36P2u3SAksoHfZ+Db93blP2iznvYaRKlxt9xxIuqcGDldDT8EeXENv4POHSqG7KlwuUf+WM4DLyBg81k+EQA7PAKQHqf/wt9CxBeAdjeKJQdCIZs/F1AsqTm7b/CdM05kEiwLKKc5fBwoNeBwmG/EhOG3R0PXoPZgTzJq8KLu4/tKrZlF9APWdW1zG7RtO9cdtvWj3wPMacra2xLTkN9y/s19u59q91czUTPmQPySljQbjhLh8PyBE+Z6yZ7mUx46L3XFdCDDXj2HV68eh2fG5iuXIc3oP/BUph7LqaJt7GycUUcvum6uDwWnbv8amL7lfhgFgr3bo05CCoQEQGSQn1Tka44Ew35+HVF+lzjtoryKyHjR+2GBpFEo/S28QwMzfU8iOXcAz+YO68MWGtkB+ZXAAiDtPiDzEktFHZ4cOER+IMDtfd5excdwHzRNv1hEOM94xtD7HkhC7ZYVLy05JAcGj7SSsCNtZdqXceUCELKEvFSAjLRU759B66bXGs5Ldd4HdVlSs9A3QFM09RkdZ1JiT+d4kE1Z6x4YHQb8qBVr9JqamyGQ1T4y+0w5BEcpsqkxZC+BSj9EnDi/vpH8SGvbKPH7A7g1JOhuzelFJIqgXx3Sk8CqgPb+fFfsuHqawMqe19RVs7bF5I+5U/CdPaGNjbg0oYsjAs3rOrt2oZ6r6r5nJsznrJTWN9UkNo2ut2mXWBx++v6o+rvab+sG51rXY+2Eu7Z9x8ud2c9OD2oj2y95x8leF9UkGYOJTO+JV/snvmze5NruN/tdSWI+ro1oxMoZE4TFg6EhnOc6jjsmJWNO6TbljWd19IlVG7U/q1HFIJbM6FFfeU9555PYrHlnqTPANAgpcjf/L/J0Fx8gXC+nOkI1C+30xDPgB+yA9WawSDtJN4NXp7HSbZhIuzFvptvnWHaR+prZ3Cfvj9IB55L5QeZ6GGZWAlya4Xsa4akfdBxZ7TGkQ/nLHSCJ1WcC3Eurz50Q7JyWoCr4n+sAXXLmVnHxFMg+81KNNEJP7/LnJsJsWAn4yDtAvL0fB+/A/D6p7IHMSx5kNwUmTTsoVE3zdwZPwVFzvCkj5RNFn2D5qY1/cigVnDzkX2rmS2Av4hspvQMZ+WKf2MJ2JyV16sNtvQiWP5lvOHiH+8Z42zWvuDXm76PvHtr9t/GR1grfLHGmoj+cC378XYFeFZ1zb6yFMDvN4S0k7EVTxM0YIjnne2Gm1zy7+zLmGux3naw4DLA+1TzSpO5dpyF79KJ90qmybLFQTk+koLqpSmw9tbLmHbWQzyXmHcZ1Pa/u7Q4gL9vitY8rTdeclooIS1+0c/t14RPxDgLQIL7HaLo0afjD1uDyxRHQk1JV6o1I8SL7Z0OeBkr/twqXgNY/1m/PW6SrNdP6VK7euXv59gsKg62226ZOBbxvLOws0953z6l5/N0g5q99mRpTb7BmrbDzwAQRBdFIj7lZwc+ZAf2lb9Lj1Wo5MWHAihpi79ZxowzG0j+HCuJNbIcLqR4hjw78OzAQgc+3n7HR5tuN1AvV81C1/kK5cGMFH4QQRd1OqBO8YAaXTVWDm3lEmI3FpxaZKDjdprJ4qT0UNBWWZjLZkx3+2cA0mDzoNpI7HwLkPicAIMNhYnzmyFWz+Fq/F7OS3XTZ5CXspkH3/j/JUdOnsHPZzs/ot//slPs3+0gM5ddR+ruKccPT/PMZX+kjHqr77nSNObTndPGc48SYTTdn3PKmUEBB0S017QKTodnuMaC4d7ffiWcy98tTho7nZTmR5Zzx77+XaKo18nxuiLrcLE9enUxUHPAMV5VYPeooFbXRH8Qi0yRx0eqjqpwaoySzjhx5ws8I12K+ESpoXXw5gY2S4Kx4GBZyQ1ocsuxEUGtGT/I6kNPz7XVkEYt2ysAaV94FQtrU+cgBpQQrKyzjEfLgWPop8ezAzfpgNwRmoSOqfG8zRC7G7G6437HHFAyDR+tS7eZiztlue/kd4rG7POquOPK7JD7uKoPvN/J0uRyl3JvYmVcz/54Ouw7Z/F6f/UfqFy2TsrUBH2TDtpKGjgM3bqxlyvzu5Uxuf4Ul2/3yT14+d1/94/50j93hF4HECjpHdB7wbt0eTl3StA7u7oTlevSyjNRKSOj1lzH5PbIy9XxDqI5R3aL5bw6XdFgrWKkr9hNPPuP8C9JJ+6bjhlZ7rbHXTAjE80xXA92g3vc9N7Idr66w/+sa67nk60QqXVN0zq1VBGPMvB4Ukm8Jm7F1+NzNocqF4ptZpEyYmpv3oezasVrqkDbP/HVlMk11vrO69XX9eGKI+oypuwDmsPzgQ5kh/17lliJjM6nZSgQgLxl5LsJstpCAhXR56N+nTTbZwOyEZf6M/3P+fggwyHnbUIoKClQumWg5+bZgR+9A3IHeae9OH2/BiB1Bs1h4Z325z3QbnrcDN9DBXfmePpO8Kzn1h3go41ODJPWN5pzF8FJaAPu2NU5l+/tW5tuvOuhrJSaw0MWutX51hTCjc7xY/9umiuU5f35oOQQy68AkD3/EvBrKmh3hgSV/obv3e9T9U7fK8q5E6a+klpdY7gTq5PTyvcdShlptObk9Aoun3Nb7z1V3h2FNUcd/XJ1aY/Ju0p9BKj3n43bmXk75W4qvValb+fajzRfKosDRTq4VIeYnFhcFTarWL72EyxteSUE8ZfczG4INL26ZL+F4x3EDn/nWhoTFOuBdTcTeIXyOsUu3qnF4KRnpOMYXs8bWvgzVJLnzkRWBTa3WiWST6cPp6raXJhCXSlP7anZB2CaxiDAMH8Xz9DYBeD0/TZ530mvDGDVskMW0i8fyxv7hLntK0ridGVxRJ2I6kKxUmCyrhHaXJjrZsuFsz6jbH2T3XCOV4iV6bVGWm8so0ZsRWp57T+pxbcAvdC3AMna0xpS8QLqKT47cGYHqrV3JvBlWB9177i0rvc3zZetn2uAL529ayiHUak2/IUjlh15nULg4TLgPQOxJnhlUDEs35PWxbmtObP0kg537JRGEQgDyiznyt26oJRbmZT03Sjp867lpnDMglSSRjYh3g3tqTX3aZ3gIcQ+l/IKQDoToG8BSp8BYMcklc8AdNbJ7sgRNxDaM7yZlEdiI3muwK8ww9eNImw7PlfgBzBpJWE3xJaI8bBD8jxV1VsD1vQhis0tvkMEetJgD4eSp5SrQM25MotBvBYRZOYVPh3xrld8577Pe+E75jsFX6typi4+/9dSPIiOo8NBECMca/inP7bmI61b3C9aCgfGkr2zPiIZJo9dV9d+IT43renYZAciTb3Qh6ugY9ffpzzt6wB1dWf18xKc5c5TE6hM3op27+/7J6X0qdsiIgRO0L8KXhxY/TT0YtZRl51WfQaAXQkEODUa25/CswMHO4C9zFpfzj54MO/RcIvxUdyL46mh3Z5CKbcXE3nC374D73TNVo3iGkhgufK4atDdb65Kdi6ubpTWnJvxidbtwF3aTgsXf0ypWcp3YcVkbi+gfNGWpMAQwpASIww97+4Aqi4NlJ4/A+C8AsDvLauwNnjjLKRyvWKg82rNaXnz2ef0e9Pj56xxT6uk4wga+QrMcqZN2WgB0fEHs0ZX3UjGkoKAQ9OROT0Sq5ux/VKe877ATswDqfZ3iIIU+rvtxOIZFWsC3M/t8LloAfrF5aR1fhp/4kOzs7TSMHs/0y9Bfvokr2RjtkvBl93nTk4fJ4d0iD0V1tQws1CHGciB8XT3yNokB+BpM+7zc9fngEPDm4v0M15hdauwEg6qM8IQBWP72QAjhNSdXFh4dshVFqNXHYZDBiihu0XsHZfEkPysg9G3CsaZUzYRDsl0o+ZYnz3g1645qkqTBxE+Ouq45nNmj0cQNb/yu4DoFQDY38zPAKARDqehgxP7NP0YHcAioy398XphgXogZT18uCYR3Ybxw1EcEcJksBeGcnrY9BRu3IELlhZN7Ee7nd0lH+9dNpBKYt4ksPzRlsLF9fgr4+LkR+G7ky4rkvLRZO8hvtsQEGdToCe7C0c9TvWgRNsRN9jxCsA//Hf/yL8AjMj9MwBUWvodgHSXt7XEKggr56kUea+zpUx6kXNT+dKQOrovpiWEewYFZg0F7gtH0eXy4UNDFpRvTBFgFQOKesn1I+VoPPndnDOd86dWL11pnqjruOuBzizOxXHOAsHn4Fl5TxBoUuzG8o7G73Dl/UvGHpIPzMj6OtdlUKmSiZRFed0uCfsucut2VZZ05sZhHxocdocixVmViNi9xdWqLYaqva7irzN9GE14bUQqnuv/wVWRmZ/wyp7sgJQjBS/5zHVpKcVC0PWs8nzTLk/3YseX1/432nCgr5DyXgHIaHSWkO6zvEm7vNCEHz2E5wVd/MDtoAK5WF2mLJ9kDFnQ/g+hYZYPweZJ4sN14MAOgLXJHWmGrH/3gnNMefe1LRXAM607ozVLGX70IO7wWiMo/CDCWl5EddfAfSkdKecZG+lAd9KbQHr2T24vL//w2/8+/YLA/p45/BJw7V0D4jeHy+8O1J6d0U3O+Tp5H1JFncTRgIXraG5nnH/JGaz3tF2XXiA3575O7Y6J8Ro01l8r0LSBHG0vvT3M/hLt86gzUZzVrl6Nr3ldmBHN1CkDmsi+U107z5gX1hLgXLnQysfBkbS3eoXK2ZuZS0Xy+sH0jBhEt2+Akd9uJI8tUr6+KC/DvZhgvfkrjXtrLxTMFwrcn0d5BZ9p81YLk28S2rU0js9h2wFqKY6z5/XQm8E2/XBcptynx1V8es2IJSoNpFzSsa6FBVBxe94PO8CdHHp+DId2weSqnCY4pjs3hCp5XHJ37Q3muDvTd+X1npLT0sICk8tsqaUS4D11AFxvzh6Nbxr1bnb0d0O0afDDDJ1d7AP0lquTtbByYRIIB3voEZCFvI8T8viFBxniFQA6AUi/E1bFYJKdlqe3DqWzFvm6geN+12vPDq9kcq89yDMzKQ8wXbPsNMlyx3TjPKPF7YqrEVYuix8KPJeJhTbLzZ/9rSJ5lUhOnlHwCRwecn+Zrkv0x5ov4XJItPCPcPYJIeOZ+FhacmszkHmljH1tcEhRq8vqnp1/yeIeaXdEYu9fkd1dr5KIAubB6qTsOUhojUku0IeJGSGiXZZZ38GRsy9lk+5NDAEmoQ6L3kb85bvbO/7NIkCfoex15YRjguBfZbD02akzy1VwXiFYJ9g21nrY6UN2qPR2E2qwbVTFurV0w4fKCn/o7TjEubkd0Hy0RrIYz6D0Hsj0lv28UiVDyM2BgpRJ/zkbG5ubA74zES7cD2l8du89TTv2n/fE+Mn1vXVAHhGkPFPHR1inj1EDzcDqJMxM2EFfn+VjdPJgiXcLR2/fwSIIdEiuBCkHQjsuvOq4OSx0vJ+qm3eApljPstZss/byu3/4xxxQzaJ2r8rI5vYzAOZZjnVeZemrVHmQPeX5unZZ06BOKp0LhsyaqitrOeooTgT1GD/epToRjcwZUZ5XK+7A5EDfru5GCP8w/zv03CjscZhsBNFbDAJXH42yPoj6rNk5C+ests7yoSMzH/wPcTi8505k7zJuHmM03C0Z6uzvRLP9gkpzfBj29p1Ut0iT1xvvLYtAz7C9A7NHqj2yL+UnlZGFmhzxuwY5pI/maNeiHMA7mWSvILOGBJZPYfdRenZKM54gzw48O/DswEN0AEfmd3N8JqKa8bmPVQ8xLU8SD9YBXnVYbO9mh3mwNl5HJ/KcNR898rcA4UPAFKMn0rhOYB1kzHcyNefQXLmlZwcWsqeJz25FqM6ojCrI1yqkwGz3ujGNgzOUTNBjP6n032DjXVI8to5ZHbD0AqfDR1jjop67s5BNDkt9u4RVoM+dKpb4Sxzdc2m9payZyD5LuWK11rcKwhgc7q2B21PzL0f2jJsu+3z9VRrpXjlxQZPZ4Rx/PKOPHyTZdZPIUtbO2jpbFx+fjxzwE7EDq0tXUVWKPQL85CclJGPxAGOiSYbX7WUVdW8AnvCYnTUP95gt/VKKbKyNhpVj2i/rsJxfKZtMLEOQIXWDd5IC1fmmqWI65z7IrZfsUE96gBfpIms+UkvlI44Dfdr5uzzpASdbq4U+DO0D3kYryVWsJ9NLHD8UnkdyAb+LQOBdvU/paX124NmBZweeHTixA3Qcjj8onJj3ENTzweNQ+9xgq7f1QsGa+SEex9/f7uHO70c1Bqdp+xagl9/99vepE+ksZFvFA4Bibu9v0M+Sck9l7aS7hyFpKMNxUyMRRWH3p211vuUHZyvHsu+Fv9nJOe4hzHbG5KjO/k9DNlMGDIpVIOYaF8lEyoFsJ3RyMmOA1ITLCfytbAfqGrDCscPKe7X+QF0bteMIV9cYwPfnCEfpd1bv1etKz7vUSNntv995N/TmRn6YbzKL5w36AR2+FPoQN3pdkSjKV3tOpHX2krt8bYRXqW6S5CZl7XmyZnEG8wIUC7XDal+jlIMGGO/aToipWosy4W5kWGO9FoWSZKyUyUqT5c/XjZryTPPswLMDj9OB5jDxOMQ+LpN31vJ3RvfCdXO7B1C3567xwvL70FewAebt2t2v7IfQrjWZooKByVN+CxCN0+x60bWt/SKgq2Yln729GOeyy4u8rmXAXWbZ+jSI2M181uhklPh75DGJ8yaYA2fAFosK33Ky9BfwkanWuK1FHc8rEeLycbZ3ziXWQKgW4R9hbmJO4kRyneVjcj4rwQU4l3CenKNLOBzo1RqfQdRkT0L0r8AMJXadJlnJB9bBI+kk8nZtlMnKTFmZngxkTDw/+Zl+H+maT/IwhbFAfKgL8lMi45hVj9l+ruVZyjLYm9aYPH7US/qdLvdZfLnin2rJnz/bVvlg12lKz7vCXEiDcM5Q7ZJRWOIO+nJrBS9nkYBOtwif/2TIU3524NmBZweeHXh24NmBbgeah+Zm2A2ZUMpH5ZOhJ1j8cK6R52TvoSlYMnJ7C9bBhUpu9SsApKDG02+JZZLirMsAjL0CIHAWijdSV0jdJ9Zr539Ih/P4n+hzEeLGWWaRHUwBv4ucaFc9JdEB9B+KyCfoReglr4RU+P7g2L7gY79rK+0jtOzl9h2UI2dTyqdSnz3a6OSH9hcNd1fNoW5MztGhXHftUpV8suoq1hjIzkjZcL9WTQeN5vF66gF0zB9weBRXpXTVFYEL+q9YdBTjuuqgWf86+uxR1cEM3m30kbTxeYl7Kj7EWpeivM5RbDP4p0DC7JJ/6WJ/BSA/76evBg2EZ76xZ//HSgtOetAtwoWq7zagq4wALvicWM5C9mfIswO374Dev557we1n4Znx2YFnB9oO0JFo5mCkD2Ut4HPsdKDbPu5/1+qg3dVErJkvV3AxI0o4lWr/FiDxhB4gvLUgX6YyqcID51UygXynncJKCu511+oo5bkvZQSOTI3YNXyN4zCBia9npIyqS5LtEGrsoPDHIQseS1lOrnSBdhMiqriE20n4EW6mj+DQVD8cbph/yY7GJ3aGIOSAfZD3xH7IAZ59wEZ7Ab7suZSbzCvDwhZHm6kjVYhJwZ/iViFrBK2ZQj/ofCB7VVemoTUDdgeyS+TpvDL45rJkK+WDRPQjbPdxczpLbI50dko0tQPuxGIZd/+bSyfOGnEHGoqoXsnn9uExgLdGveeyMpJsap1LayQCuG+ayfn1kWWWWs7t665L9uMOp88A8FV/0uKP/OBBWwLysRj0AYTjTFG3bABk1g+rZA7HO8dQw6QP5fBOaT9UD59k3tux5/4zRvtd/DB1f7pPBs8OnNGBZs03wzMyPDFu2wE8c8LTCBzUIN+WxSnZ7rAa0b0I+9RV+hagf696TKxzx+nzxP0bvVHoc44WnzRfPV/pZ4A2s/Ac2MavD1iU2TMucHYPU53VcVQ80dDTIzAMnnVQFcUBsAbosxM3JRzn9yN5XrE/fvD+HVj5j9AZPvI8975HmI4bc7huf78OOd4inwOvfAa85S4gs1+SVx6XpMzVzgh+J2eQ+r5H8amDaCgEHvazTWoPd28yX+VOZfWXh8tqvp85iViUX3+daLz+SZDZedAvAe+D3WN/6m+yJmeKFHn26A8i9RrjlXZdLxzkWZJeAU/bswPPDrzbDjSHAhy5seWamiHrn8KzAx+gA3hG0uwIV9fF6ZyH6as5fEB8dPMD9ZTXyZWTFUjCLqm3dAKgW0werGRvZp1NL9+lU7JV7+Ji5zMEek885QS+dT5k/UrAGflbDMnh698lK9eOprStaQEGY8InBPkdRPz6xiBywazPPg+8e5v7wERkr1gZFKxYSx+BPRIr8c/CkZiVrOelMnuDI9zuFevVczObWPlH+nCI74F5j+TFkWTx90GPcDsSGyls0ueS+Q3UeEXeKzBlO/VRXVonZNkfKQcgHA703EA+4JJMt9mezPp3KSN113REKZ9jSHkN0+lkC0jvD6fmiqNi61CPp3so1kAbK2e0zhIftZgUiVpE3jjacc8OH4C6HZ6YryBF7DC0j/yKAtJnAMofDXkJs0De+AM6ycduawBM51jyk6OtWix9PH0cgTzjznECT89nBx6qA89FPjUd1C59zHz2cKqHT+d30QGsc9rqBf8u+D9JPjtwUgcm94D0eJC+BSg9WLz+aXt0SIP8nDJ/S+in7cr6rt2eb6b3Fb28yLMT8/xGFLflCO+r7C8wBuJkD1o0FNpqe+MFbj2YaV331YCDVU+TcM+h4z2czisDXA7ScVaOrGSNqaPO7YPG1xxMzWW9sjIeYmuBCv0hfNGN+BzFM8Y9RUEniN28/mGKjhvdKI+N6J7jhrzecSmM44E4DO5kmu7nnXj+cGlj6+12bXH5NLvtg+wCE2vbrc5rMpXaFO95P22yA2qZWJ3cHfEKAIFk1ea/m/NkQFthie8MlQTOliWROHbFNBbGJQYzWikQTtsgTozd0+s9dYDWBi8PFt5TAU+u760D1jKz9DhAXXeMoryngIO/VcV7m6Un32cHoh04ZfeJJnsov+fefsp0UButTlZra/sWoC0nQsjBii3cRvbil+7FuSCHVRyks5I5RFkqRfXd+dkSP1utPAXbKkE9sFilugSC5Qaw7rX8Ok90hCnjrlYVRTHO8xMdOA/0TkhX1OJi0prhebywZpeDn/eE1eVmPwHfLyBb0We5lXtuAGDCRVYk5QmI7OrHdldOUuZudz8ldfpKA0N8D1iXT6RkDiSBbtXnFtyVo8H9jmn/967p1DvZsaoDRqzMIuUq9rIBMgJevgfhsoQF2OhGMbf3W2fmfxcFy76B83fVyCzcrW9NJQtD3XmtWYClEMKhzopvs7zuUWCNIKIC89tbIOOVJD8DUBD2rwA6QnkU2+WmgwopbeloppwpXnIgWQ476K6KUuvsXaULs2g8wnwx5TPsvA7I6dOr6Lw8T6S9A+gzban52O629yZh/cRXDnni76JC40w0gQ8wHbqop+bZgXgHuruPfIyIQz09xx34CJ1VS4aKitT1Uv8OAEIIzI11jW6/OTLxDZ/DcZSLvRlBXvWjH9pFXot1orpZ+oTO0LZMwn3eks/6T3IOnMtOItbuDj5NRNucOvZuo9xzvkZLJB+X6o17FF6Nzrx3KaPD2DfRcLix/KBLJbMEbUnYWjPSU/bh0uq4twtZuoQ9nPAKkeX7slxLUvajzrJuGeevHB8lcEEnZyndvtuPxrC7/omktwvM1vD0P6UDdPWcbnj1QMqT4Naat/Q9+Lw6Gg6hlSRfASjAVmCxr99jEc8uZfKfDVmmGE805Rl3FswxD9OzMR0gUn5scWkWrm1JM1nEECQfkOq1jbg5etNhdJ6b31hvzi6UEJzZVXL2jx3Sk8NPFI7gd2OpnGZPOZHtE+rZgQfpgLPIHdODkH/SuFMHeodMa7lIX/J5od8BoJvlfXZByEPbROPAd7LyO/6ZIDR4R6CskR2CwsYt4N30bBgIVk0U57HP9vZqnPfyMg6Eioz7LbNNYBoqf5vbHh3xgffV79rc8A9czapqOYCzd6eRBOY+u9mHJ46FJnRqiMVGKVjohlf1dj1uq6z4qNUILpVPVk2tK25I1X8xL1bFOq/27PgEkDWO1mBVgDysUpb+si59tASO9D9L7tQ+A90th/mTVR7nN2BjhcykbX3lWpJy63fp+IK6Bnxvn1ERmu725J51cH0S32mGqsZlxdHdVvZKysuE7hd4aB6t2oU+hC8+OZC/U39xbVgrytKrrm/rouLAj/rkjaMqHhLEGnp7e3tJvwNANxLIzA8aLGTjiZsjwPFY1LtGO56lwQ8Gum6SOMskyL8mrTdkCM/pB7BxH1h42KJ5ebBgUY3UQiDAYcFC+wH11JNIDx+tM5IzyZhZzHJDVXo2pocdPhfqw07NRcTe4yq9ohXUh2Erurv5LJlhllnAp/8jdiAwzS8v9GWe2+8A5HOX8t2eb2+k/7T9DoA4y8l1BoCbfojzKrIgfnkpD9MTMvkk/DpvQwrDjUz2jP/GHs4O5S/1Etqet5upKF3+G3HhC9Si2O9Tff6NPEJnsYEu+Yke3yrXA73Pfty7G5bUrIfELTYjzVqRlGFqkOHwULVLzh051odO4Cmq+2ZXJcjZ5Cvi0quZWekv3Vgmf6wT1pwubPjznfTJN5WGjnK5trinbMValERYlOf7tpLoeJYDCFgh53b4XLSqpWuVjqL81U4E5Cv/zeJnesOqu1ksNIZ9BAGLZMhk2IEhwr0czmBuzKQ762+f3/Kz/BSb42mT/7pRZ3UHSc5C6+LkYrqWC5XBprncXGPFPZitijllcLfEB9jH23ogyTmhw/aSA/66RXE4CexAAmTWnMP1iXKrDvC06oSY3Mec2cdkpXv41NylA1jVztq+C6sPmfT9Nvlc5uei3Wqp4Diqj6ak0cpCikqNVJu+Begf6co/nQokd7rwTze8AlCQ9H0EWEedo/FzUz/gYDemotFFW4jla3KR2G7SitY2IEcUhG3jsqdyziB3Jxk9uiYhfRsZufA9341pOEQs3MLvb+ugynql3HEVKm57vyfCcyAe6F6DzBPMeo9bnRexHAhhU2ZPvKLF38guPb0sws/qbaWn9xBSVvHu4coq0G4jdrLXfSMa3dbdht5aFiJs3aypdEIARYGDPqi+SQ6dPktzRFb4Q87MPAJ/ls+gS34aWaOU/ahZa0aOv4I9C3/cv7ta5HR3lzGikP3I40WEf5fhMHAtqoGVfWhMeigbFc/upBgeB+JZNNtZjczF+50UCFB2YBb/XH/J1keOe1Y4dIWeDtLfm4rRD+4KRUi5AkgWfdvxSNo+A1C8SLObi/Jh7rvlSHZ2J6TXQB5mofiITzfNfODifJw7k6DdkG+G3XpvqXT4OKYIw4PhTooGuRlagUE3CsfqwWLgrQW7oo9TWUE/MwZM5fZM9HeFhVXxaJR5rT4Uscfs1UO1aI2MbOz7OYqs1WpG3aBwP4VvNXlfbGBWEGgrNXJ4MZG7wnPNLQttUBql2DDEXpc/+du8AkBe9O7//BkA++pzwtbnNFrT0g6O3SslVl3ARnXkI8r0slpofng3ikKQF9tON0pd3fAeS4mng3yO0Q708nZ0Oj2cBiQ6SLaq9Mf26FjQIxikLF0b8gucgWzhI1dnxiWJntwQg0uQXkNJDjUsYcKhx+JGuoX+nMVMNocw0Z9gn8/i4OGMruDqCSU0/1XHbghFyV/VRVsksTvOkaQB2SxBux7TbFUf/t79h+pevyVLx9jOp5LWcPqcTjg0YSXr9WwkvES9MPvNCpfv9bcoLhy1mixx5NmK4A/8zis2sTXDbLvdwAMZUiy0wqr9UfUotyn0pcwLW92Fzw3lIgseve1HvQJATjADnIY6HkAFhWGvFiwiR/KuFUFROrBLr6sME0YSnSoMMOnYZdtVTgJf5Q5utMUf0mjCBzvIWU4vQxPTGispPNmfBItn42kBfjA9LwnZFsjvrlKe5ROZP34rqGr8UdW8hq9oxYldfULNdoDW4fE5JQRezyTgb5bJu/CfLY3b4ld3fAp8/Kf1vA7MzJWefhmdFhN+B0CyI63cn8hUDTfIL7heIgI753zCaor6vFC8n1hGSeZSL2Vdr7Rq2fIv51g6YtN0A+XVtU5krqsb2HGuVFtQ95yYHIdsKzAayJ5LufXbxpIzX3c0fA11IIt8H7mB0lEzn2qRlscDKCMrpwPdU1ErLLTF9d/LQrrgnDIfOUcNJJnQpWmGgVkL8iRK09mbMmaG6AavjZnQO/gO373dndzmW8iCvPFr01jDelXcco42woE1BrbWfhcs3HF7PXzt3wKP7x0WgqVfRDYeW7cs1lzoKK2xiNp6WtVnzSmg0JO1/WKxn6Jjx/cd/iV4u2ebZWudyD4McRzkcUD2QVYk9RaU9O/4BNYMDnRHjtsRnh1uYdXV+BEir3/k/YYFIw52tBUu29LJg6RPnwGoUTCSOhkPlIffgvJFxH1Y2Tn0yfcP9JIgNWogbtJlLcfh6iZZGu6goclQUY2yGRp4SU2e2llrHATfdAQKsbo6P+PTeqTn76h7a/vyOyrwHVH9QZbc7IxgicqFutwoCcIy0JYxZ8tZ8GeqC7HDuoYOC0n9EJlRyn7UlPUi2CkOD+DMbWDBIEX2xqVdc+kzANkJ3wJEOIPPADR4e+LLz43y+W78LHlnZj99NovJwW2vCqIfRV4USD7NFv1Zuz6RMyMtoxY2xr1F3nAX6vq6gl9sl81gJdT4nHgQxX5ZiLAiR9CTgpQjLeomigRmmoONBneQI/3RgGAgYSM4mvdalMa5WqM70H3dTDbkakpBfKfDTVHbFbt83br7uxbkTwVylIV8bhOsLMHy+27GsaLv/GBazMKDkVqhg5lF5OAqbwD+knVS8vKaL4rt/tyl3oAfGWrC3eOVk2IrTewpWHga2QGBaa5LIiPCkZdkpAYaK4fZOTDiST5zbDWo4q9dbqQxmHz9TSpR7nFq30F37R5jJpoySuPonn8JWLjAnI1J24UQ7u9CXCvCiioNXCz9WDiROgawyPr9hWEJ0xYCCkDvoByW1F0AQBjG3sXhkbndpiFHZvY2DI9n6S7L47BPhHM78NwZz+3nEA0Pjd22k+mj7jXdurrKYQPPdWAOLJyL/2OgdZvXVcb60e4eeAUgxW6g6TeA8S1AAKSAKl01COU0zm9CsXAqCJS7pdNDsc6h5XvdGMoHJKs669pSOo0AZrNFmI4Kv+NNUu6VnXWMRtmP3zTbBpNrbPSXDjEjzmspxErPGtcCzmAY6RIHxkPM8stKhgMjyxUbpAS3HaGkZE1RpPsIpvQ/TZb1Slkl0PNVfVJF+rs4cOw2QWKQjJ6bnzwJZGkAh8NOjTmG2DYTFOEv0+lw0gxBZJTFTWY5JF/QT82nqmIpY4WQE2iNztto5IRKuXHTQzPXkVou+4QD+JucdXkXa7jVzcrf9nRkD7wT3aSpZoET8a401Y09PCOvvbsBbLG/gwZg+ZmAWY4ycBXKElJwOdo7iOwgEKZ8lJTP5XS6kzVq3n18cw1M4pQsunnUJ55qbS1xdJ8b+vXXSfP6p6KvIvA7AMWU7mGmLQR/TmTg9XLFfDVdvCA/nWPVKUiDv1XWFOckbFEnXNvQahzH0SVXQLcaOITJhD9wkfKt2J2WB2VyzzEkdNaclukJdJMO4ODA29mcct5J5vXg48go3/NpneqA7L+Up0CezrMdiLT6ojW/ALsQ4jQEaLQ9F9bJOGV6TFbREiILK4p1rt88syaCfgn4t79PnPI7jfI00Sa/AvCWzw3SWWk1e9Xg3GoiaJldclzjQeUDAWdpdBUZGit10y7pNiTAuYaeEvYs2WEeTzFkzjXGMY97dlmtMBFn5NZZu8wlrxlrf60ZVirB2TkycRSIehHVhPDansJk548hdHsrS2uaJk19WayWjoNv7QRsB6Ihz17oabpoE0R1C+v8NLo10OMwqXm5I9FJ1+9DGRdnKvdq+B1Z3U4Nd6voyu+i955+mID2jA9JGsmvUpslxBJa5fBrEYTvrwQLQedfpGrPhU7xqBoqnfrUaUDq7Zu40k8FdBtahdKzfBoL1Qtk1kgIVt62N0SB/1AUDe/EZaJy2bmJsDNcb9kc5LplsZTxZgXeLBFP+7CTcJBuLJPAMgM+hW4H0Cvedn2uVl43WcF1ex2Bq1v3xH924I4d0PsXjiR3pPQBUuuuWkX9wAcut3TXmJopW5yW7Gt9xkAOpCWnl08v3+vmZyVMG5CdzD/Pq3HHI3BusjVDPsv04TgK1/59Z9+KfkifLgfOKD3lu9mk/rh87nvjdI2aIRVIbpgjbb1Cg9XVfAag6XNoBYr3g8rP2jec0YRhgQ5CAzgcohYrI+l1B7h8sjadGaaLOIT6GQF6GB+rvSZBsVo6Pr5VBfB8KUtS+McHeZyRsoTy8aUn5MH8orp8/WxxnYtrb8Rtuvmacf39GD170g3qyifM5x4zNZOKw+Q6MT8JU9I4zazyFv9T7jWy1shEa2tGXvv38WWuoIwdhNah00AHCuGNA6F1eM7OeAM6P7SOCRKpw1OaT5W339nIrWa5m6HbVfaUR0X5ajw7NEKnxrW5oGMXTW3zfLhJJofiWCfVltzhmV0tvYUT2st43RNKOgrrHwJL2nKElhNCMptIlqYcccXmoiRnwVI/zoK6onunYGLOCcqqlB1OSRcHQV5mdelcXFTjGmcuWfdqDVDjfADNsBXUxoumNdK9IT0HRC4AKXMIwFFd14E9rxO4vSBwx1b7NT4sMZ82W987fy7k7kJ8oZ6yT2EHaaD0bDYO13VJp57NRQg3YzvL7cP5o9P2pDkzwUHJZ/8WoDRIbaJN8xmApN300gee4zmfPB9CNmydKqTbEdlZtdwoH78hKc9T/cArrEHOa6lRqezYpelCJMvqYm6hKOE0e54tQk8QibbsJyHK9cPt1W7D3IzDIMOQWziU+RrninsaWJhZ6/WQu7cFK9bgfiP1ShOMeWn2o2bFUiLUC2El72Ut0RMBeqgIaUNX1y5j6ADLrpLbCY015tfhcBdTs94aDnJO4fml/G6G9KR2+TjSmWUJzkoIof6LDuvp6/JxMjYE1oYh2jX0QZ7djAtldnFqpo8y6nZsgVyNQw2gtqk2QGc1NAd9/RUl378FqPgCigFJjb8FpsdCCqFjKG507oPrETByqwK+17pczYTwkYKFa+sJo9NSubr2MJc5R4c2m7Aj3GB3mKP+Try5jQ3fj91Pqhp/TdXN8KIm6BV7UaKmnLWhtULW0G4ZxV2VgpSvI8NZrktxBFnOaWRHOJLrYCxTZUEDogTHQYfcXjO7JGb9b1/R+86493eXUkVYRrQlNX0GIN1Ioi//T3eQ03b7/h94J4dk/ESfEc6/GZzOQl4+vf4hK/2N/74rcTYsYTIVqfgUeWdbFaAGxBlFkIWvC5aylTcpBLf6rKvnXHRHvs23YIzv+fru2NXyENVVLpa+ckoDbqay9BWyh1Lue8e01O0pGjrvI1zbk4tQrx8uUO8U3SbJ9zRzbNfzLKXsqpQ7+P7RQAYEPP1cPLOyvZzhNp3hdFrostJua5rtgP0l7R16RTHmVBO25ZfnRQei21teThAUrGOOpQestEo5mFS4cTlyF+P1IxwfRUSf9WNimm6Ho98l3+rABk3Ah3Ng7/ZR47PDj/UakHoFKy8A7aM1gybrgEZT146pZAJ+XTK1nn2Zxz82Sk9TzvMlP4khPX2e0tOXD/LEaufu+bnkM7pKHoQZ5sn95ayOmTi4ms+fVZBrJVWAhbbfZxycAKT+oZPqaV1Rbz1Ints5wNwzry3+znelBxuNprg7kzuQvp3rA1DvKzStx7xmMZXN/L6jWlCIQ/jDrFWnxktNww5fmv3G4Dgg+CX7Vkk4uFvxPihjn/IVHbDmDjOFreVzkE9wMRzMcjycyseCHEKd1agFnOWQYGnD2uFwfE5n+cz6W4XEZ9lCeOd6u5Gtpay1ck+7B73Z/3e//e/TjvL6R7rmX55J4ZeA0Vp4w7S3qsauR7vXAQmQ/jnuAfgtFCVaONwoy0Hql3vQ1OhQcq76IypKePLMdSvTirL0sjsB+ZQrAZQn2oQApWWXqharP5ZeZaWl5awK5b4pJvqQmVhXeiz8s/RVr84CtXD8nhtWMASkvvoS5y9x6Loj5nRhZq3ipL6Z/bSEcnWzr5j5hzWdRXLoylx113p3Jept6vJYUVfJm6+6ea6tTa4Hva5ab2PcnSDwT5NuRB1U+126Lu8C7W5/ujjjXuU9CMfJ5lWFcaxOaRxttKOliZdmIbB+hT8HF2GKD2XU62QKoaRN91006fADyPUc7q18Eb8EXHzKffkMQBrTdf3cJbklBQHpiWoOLDvcOX3eyefk54D2UGSinn1CRz3A30RMz/VESj34D6vjNfjxGsilRSZvyjkC+PS5ogNXT5PcC6QcrwVRQZ7kvJYlzuc2nlRvsOTb8LGyoNtNzxvyKKTr2YVt0LQPOeAPJsv/oRp4HRnu9nUp9BRIzb3ySg4sW4uBHRoB/hxFAsuN53M414F4H1PT8S1AJNE7+zlSvwLQUmDXbKhHre/82MFrrpdPYfM1sGCU3MGs63xEldwk4WYYzLXshnS8XcZJgYevScSzW/2MIzSeNAVYG3QtDdNBPencrqjRwDy3RrnGOnUplS7/XD4qoamQeaVsBpxkmM4l51HKJ/GRMDybvOeyht2m+XOk2BegI3C9HoS7KWpWjSvDwjN4fOaoBo2Hkdqlj5QZ5NGF42ssI/BnPLCWqGoI3OR29q28ll70Ua4Hxmd7m4gNdxWwNppr9sSoWau6nFuwDvTcpyFnBJ5NXX44rAdr1xwiScmH81pzFMSZq+Jwz5HuXsccK+/X36R2bq8lVlPCg9Lvcq9eASADbOxBsRxuzQY7Ww7n6SN0zsuWkIbVO+lu0Jgj9FDd7VvqdOy4icqhtt+g88epziJMFfXBpnW2V4/vL1fpwb3YKhawF4Ej6Q1SWNX9sHrqOf50B3hRyWOFlGXI7MIgf+BzFonG8iwsB95XeKe0/bm4QUsfoW93b8IN+hxLIa7jpwB3cshIrwD89vfJMZ03vBRv/A4Avw6Q7N1b8SejENl1O1PJ37/7qf7kO/t0hR5Y1/FGSlpe+sbnrGSNE559FULn7Wq6DLueSSnOgLvM59DMNJMGwSoeqflzh+9SBfGR6+FEDrpS3SWunU0ggFiLDFYyQpbfi5zCl2aQqd5CuC9DZEed4njYrJlT+sCLcJ/0cO3yClNk1S0Q3lktBP+oIc5cnNJPrEPdXdaDQGdp5UdA6HkrV5HGlBrpKWXpc1B2WieRu6XtDnkPutdnpXYathQsUwNQ4fom50LKjecwKcUSPn4DmF+tYhBOPcRBSPf1DUwcQzH4nHDS/Dq9muOz6J3bsHWT7tAbYJUO5fu39K1B9J8G0ENgGSGEgL9FNh8hbGumXYruHLpoRzyExarL0j8E6ZpEs1ql8V5VyLwky6GkNysvr6izCMwSfvo7HWgmpRnagVHHqJ+d6Wl5qA44Exo8MhCCA0LFWjik50D40LZxlkMpP1QPh2SoTJTG9Q5DHsoB5G9G6ZQunQJCJb/fVXfyfHkNrW1ptH8GgORinngFgNrevOgwWY6+LpU1+kzRx50969LXSrtnlpw017ktMmoTrzYtlyZy6LTgM9Fw8Me1W78PcW5cIKUDJvIeukKsqQc0fkUMoEuTJbBbRAhm1FCaA3wSE2Od3+CVMcoOYhCW26LrvUiz9X/+lcMIH2oFOsBCJIp9ltcGIyAvZydh9iY5SFninDXXC/Qkja7Mx94bL0WrV5a+S56U8If1wuNhOWJEpqDp5GxFVqWNnhftpi8MG7eHHQ47KR95m5YGizI7P9urWf+a37BS6b5W6VQKmY7lJq8DyEcMjm2EBsqchSbsmiEV0vC5Jo+FmpNv3QQX2dpsTZ/4xbf+4LcDwJe2+KN7aCgFxcrwblIO71o/hFL2gHujK4Ob46BDbql5WGJHmhBZoUfw33usXLrvvZaL+N+yRbQPIt1S0mhQkyIadlF/n7CrHXioifsADx/xEh6q87PLJ1gmuQU9ZwlE/Jtj1B2ZRNjGfe5cSLVwGy5iSCJ5im8BSoOtSNjyuYF1Jb46x0qB+dfBCkC8Wb7n2Xh+trEV/QMrNEnHyKsI2jqrGZ77AhDEIuBTLY3DIrVcFVKOEDvo09SF2Znl3+EwcyWm4dCgRcnYGRv84NpgGugJDaNMcuSN5xFsUSnzpCHI0/YIn6aByMXIGM5uF/hwOZQLNXaJFSZwx0jKxe7eL1Qnc4CYXGl0fCPlKVe+U+32anfLusB4FpPDOFhR+ltrnJqxihyHadNsFbP+YUKD/WsmLxZzOHNyPL+xU+mF86APwlOKsmTsxbDied2R6hZWqSTWTS3ZSmdH7uI4/nc0WTNo6VePjbklWyvp7u3T5zzYfqskW2mTLfJbgNLPgm1/sknkl8OlrpUzZqs8Y3wZ8CI52YxhVxZzXBw221JZ8sXUFuG7EwFl17SY5gHCZueuS/kUkC7yESWWGW+PQFmx1mIg/S17AhqclARoLNo1uzmm5D2TyKYgLCO2wnUkngg1SvVu7As9mVsT76YT5xOlRv1ovXLqdUzD1i+s0gaTEI6DAPMsnIbhxxo2s52f7ac5eM1lkkQO3Ej6DAApvmdFE1i6csoVoALm3Utenp+wyetVQl2J1lnX8ev3/pUbK68kRz5UNXCsV2Ck/3HZ6hivCF4gxnLYKGBVRGo8zjmIAOZBZ7idxb9ZSzsTedVKykgvvh+moc3TAf3s2mjCG3BrGN/T0Tdat/4i4UR7Q1iVBe5bclD9Ab4VWyNFRwM0yUHKGX7rj9L7ublGPr6xYAcSzXST3/ds7bnwRMAWBlXe+vXq6duuF+Ya4+tBJKxE5pxKzqtdZ6wCxCCyb0Z8BGToVYgJTHv/rZLGBtwrx92azQnOGn22CtdfM9GajYLajwbrzc3blKV3hMbh3GFVo6prkEv5D/pgwMmSZx8vDMjtNVj/eY4VK4970kfylPqIHD96RNCu87FmEN+P1Mk7s7Y74ZvqJf9OORrMrcpC2tSfAaAPBtAfbtuU0B3+NrVxV6IM8yH1ldgtsUitbczMOFjL1vwZ5LhvkEMDCEqXEmsyxoc+K98az3J3z7WJuw1t2WTItJVKTYPKgY/vpgNJc7AVFI4/QB1E6zK0lE0u1A5lY1IIbB80jP1QncRBw0kzgMgxER8JPiszPguzCE//ZwfiHaD9Qu4aw8Ap5yHaXRy45EerRe/yawwJB1ASUMp3afudknZbCGXPlHq3fwtQ+jIfNI4+AUzv6s/fErpdoTHroQAgJ6HEm94xgzr3pTAQi8XDi5nNBD2er74CxOfQkmxveqW9lef7WSHMptuCaWYpErkDZ7fVFZQqf2fgVISOWeffHaxVlcOBIRdbx/Glf0IxJx4n0OSbqpqcmUAkkHNh4aTY3vGB3SyhySU5sGzFnq5HEyQl4oDVjutqNJTWWQJOuDSR3L1petKN9iZyOH1vssjI1JfKU0cbYjLrH1y3a/PudW9pf5lt9XQ3wgnORY60lx9hva6G+ZuO9bxgpzOdyVD7e56Gral9oboGwcgTUjfZDyITmmyglENsHCdA9xzOXZk6g8bXmjpKNHVrKDqh+rE71q8ApAfn3ZbBKRZ/daptxM4sdN0OKw/DUw3P22kdWO/meuSA/OEVMsA/kfhBqCOVHom1GhTBlCWTLIcW7Il6SmeRtPQnZp+CIj70d11/IsjoyaN1ZqqNT+e1DkSWxxryg0RNrepbdmOK2FozKYX8WwM5HmVVaukjGTFTtMUfhZw2d6cBReo43Uc1FSsAeVKz9l8Cbl8BaLnUUNWV6dyjr79OCKdfGWIakxNB7jVjBjosyGtgVR8y8ugs7XB6A8Cs1r5yEGwpasQvIMp3/pkZDYZH1JGuOuWcSNVn4nBA+VNMrFychdBYdtoLNyu1lcUBbEwRDk3I2tAqIYImSe449t4RwQz6NB0mJnJGMJRQkqrUB2UCR0b+vEQ3cG9C15yXFnga9tPUOMJsv4lxkxk5jboCauZa2QeK4dR38YdTOciaey4/j9HNMgC5h3mW57C9soi2q1iZ8Ai8gi2hLBn7vmSFPa5NbcWfoY/3UPIMZkY57Mx1oXDWS2Tw+ZJ/BybyuQV+xYbRGoGTbvqpI0xTQAP9QMO6StnQ9Bwhf66X2MJr96VXAGjA2ixXsVxhX5vNjMDOFwjgOA/s8J4HyxHnIy4SORT2MarwW7C6ZnzUo9bjnccOh+qGNQbdjlQ15HAE/HisbPgjUG1mRFPSmuNN0AjUFvxp0y01tyn2lhW901w0ET/yXDS101AeN66b0yYLDRsm16W+GpkLIQF/nJFN0MihlNn/iHDoKNdMzxEejxArpoHes+99BqBl252WbbXStX8yh1t15ExaXKtoGfbHoJi28TPdPtJja+X8BCsNT1i/cpmx73GlVteoywFDrICKy9Q1gCpyMNAcugEHW6drpyycGldEkBfXgLscxsrcJbzyM3xlj7Nr2O36bjZEruhoBNZM9a3TpcvmnRmeImDFOi31s1CXgMBuXSi+ckb+6FWzWrpRjNkIjNbog8OpmQ1itm7vYfanes4FHumezjhE6+xZTOWhBDnjRdb1gjKqZuuwCbpQimUQEnioPaWGM0olyQsENoRcafC43SQdzmyXrX4fBI4Gw0cNzt6FZeusYB2LqpaW9dCCk578tm/NL0ZMZxnpe/AHvtlDK6OGm9CAWcqc8r59ev1TDs6Evv46ya9/ogGoZRNt9tHwMwAlZHt+wRMlK06I+YtF2fmBBNS6V/xA1N4zlQdsKFHCH/VV0pPy3VvODK9goivVmivy3gyTDz8LGTmWhQWQhw3BRFvTTXr+0yU0DaEh/rTnFRoQuwL53WE2ExHnf/vAOLeH8hw2CnsQtrPMEcUpIiDs3OSKxDYhtxkSsYflxh2grlqNJR/HxAitMIq5a09Ecr9yqkrMX3rO7nwLUNsCiuQucEbSJH35WYE25uQx5z+Oa56lHYc+jCC56XNrC57nxHLQ+qafVi6tX8ilsy9osNxmA2U/Z2MtfwuzaSmHcw+jrbvkagHTqQUjl6xRynVwNbLKZyfuA2viAmLxTvEgnzG4UbsMPCvXAs6wn5Inyfvq6tXVoHXnghDIDVsGb4ashyBx+NqbH9JF2D4DAFuPfxN19XBhvpjSWmwzQYwmO8xKKVC3u7dmKnlSWJBRMgscNtgHmAvJc002e1s/r4HbVniTye0DWt1E9IcCp5mgxl/TWFtXDezxod/MavGEkzEmH0OCoXLd+iHo58RM+XB5Huk1bdTLvuBTHc3Ydr6g10jOwd3sZUzf87k9WKRXAMrFe4LCXy9me/bfOCA7tt2oU5W3ynMq6VuBuTPeJ/HsZ78vl2k/fMNvUODCOr9sPi8Hpn7ib5jprM7L9gZTd7lJnK7DU3liB/xuy7UB2fcnYkOHE8nfBko2gTOyshFQ/lQTCIH9WeBEjqCdQYYpObGPZuJaFsgvhMyWz/RmAx1/on0FrJNRmJZ6Vj4PnHjnbwGi+7fXP7bfArT9DkDzXqiSfHt30R8xTrET56Y4A0bo5KfpkUV+F01hdPQ+fh55NNNl8f3lIK43NJkXFm4/RYN72TCt1MvAzwLWXX18zmfVTji6/CE49WctaoicHOz1Hwp/JKdhl/yVNgynWjEXGicSi1YxAoVAHrZQpxuGLDhMPEItoB8OCXa4W0W3gRowOB1cSheWrecK3bq6KeKeOrzbE+nGDrJXkT6sseJ0xAHPQPjb9iJJJfNz5PDRUjJvUqN1s/wbwOuej1VX6MP1NjXKYcOcTLO1S7ShXFaam4Q4YRp6cPQKQLnhW4Aw2rXF2r0nN+2pNd3Yd6ykjuKPatAzPlfYRd1aoHURk7l2hL3fBdt3QTLc8mlHKh9/iNTdaDQ0pHULpTb56eMLnjzjzn7S+1qbFjEZS88OJJDP0M3qUiRW5orLQ0pxqPfrabV9rSJrtc9mmfVfY3uzKF2OXntacym9G6c7sRZirsl3lScmfUwoXbVeaYeZ62aPIC0S8hWAT6+fXv+cgZT3C1/7p9RsLXL6fDcrCWDqFwAmr/rLQmev/ZezJYnRlw9+PwmDRs5cZec48CrB7naZzNXMOHtGtJ2F0eNzwSHvTqCZbfbUZthWNHkFItLDymcSv6U3M5Z5WdZLvdGgY+yPNclNw5BYsNDIY4J5ZTLg2D/sAc5wj3/fRRi+4yjfHStlcm262gkO+KBLgMK8dHFmlTx3kWPjLHjc/8gc8fqMpxt6yvUTf1zrVoEp40UOAfgS+br+d/ozeeTp1tXtofTs5O3F8N7BHeA1qRHY1EMyddRn7r/p5BrwDETOl+tuGlERzLJXZoA0BB7H2Z27Cg0fkagP6PPs++Bl5/n5GJTSROmaIVOCoOdUOgCZENJN1zu5bgHTtIKUpNlSwKN801p8RqwqXv/YAJcE8j67bO/T+bM0JHmLT3evPLIfH2RxUt5gs4qwOqbN48S7W+Vhyk5VZNo6yd53F0D34WjdvS+3IoDOP/vP/aZWYD/hHWnYnMaBhxoKWR5xP+T6rxe4P8NU0pOnQ0bJTkpn6bMgd3Mt4DxDrA6cOFlWinetR394Hfrtghs7U+Ek+yHkM3ToNhDIMlfX7TGVVLLmv9YHNNDqAzAbZGR/nM40fBq2t+aJidFZJa3U7pff/cO/3ycRE1BVUg0KnkThJ/4ILi7L99Z5TyI7AuVz0JFj3N7JmRjS7x7kJsTP52RKvg4hlcsy0L79XWKE6wfV/Li4nfJcfzLGwR0kPctao8NNn8mzdo2jNcffO97B1CX9ABpaY1gzWGzH1w/jAJnxm16+l/5vPPMvX3auSImqULhQJHGtn10oPn4mzN4+1Y3SfDAjzbZx4+EKf8lNygwaEw6tkAN5iV2kk5EiqHvoM5yDPY8gk48/NYe6BwbHetitwmLVNLzpWxdKh7CblYUdgoIzX37zg/gRt9lapD/zp0SypdCb2Y1512iANXGO7UdXdJhKkDc/heykjBJyA+D1tf+p3YYQQW9PXT99/TWB8y8Bk8y5WCBvjoeDNAmaSXRMjed7GlpVUV/SR5/f+80qz6pr1t/Ceep/nA7wmiGB5SPlMw7QTsE8wucGsflw08lDta8dhLiHHdCn6soOWFN5Sk65R/wI+8UpTXscEDl9j8MqzoSXHAvxWPKkKBzNIARBgm6ayUV7IvHhP510RtNURnwbzQwYfFsAegsQ3dB1eDTDNmDj0J67NAgMNS8419SJi59n9v1zKM7HFMtSFEO/uLZ9A5JQ3kmka/90k3yoIj1vXXaj2tugOHIbWb8HTrKFp9ZoBO3TrkMd09NonI6Xfndgx8lTmVnk9Q8pe2CLttn+zPpXtEQtszhX+Jv9r0i7A1GR9pvlrBGgeQ1c+7disf9iG9zld6gv+SjxzTiorq7/2UPKzicuSW5SjiMc9zyc96zXgZ15J5OejrPybusWnXT3FLh09pfDPdSvU/l7PV7jgo/Tt+7qoE6in7T1s3TD48p2ygK9jYNrz9la2B88mS2EQVftWhgHDNFqzfa45qz17zDptkKvf+6kAyVMg9bun9rlmKanpBfM8m8Gp98ByOuawIHPQra4GwE/EeVCjozMceTYt3P4rfj2aTyOFg2J85n1jyM/PZ8deHZAd4AOsuI4q+3psH3waBZB8Dl0aD1VRgcOTpaBerKaSMZvzdrAkJUk4A+APJRCPNeaJ+WSNwwbpXSA3DQBw0apo87SDOmdlWgZ59xWaDTSaGXDdujQ+Osh9Vm2Wsrk3Ax1ODQShOTjrDJsMHlLystOtsr88rvf/j4RNn8HwDtHR6Uby69/n3hEzmlkWRWZtpBqjCjyR1aySZzK1R6kdL1z0BFUx57P56hvdrJ7W4K97dTmMg/CuhjvwdhbJ1O89Rn/VPgHc57uxln9P3B9/b5TcPWOKfH5uAqlPE6yRvoPOwNAuEm5CUyJ3v+tWtvhdRvp5/HWRbLIGcD1Uf+zKORvwYKwQ1vmauQrFoPFE6mZbcOEhxQua2GG1Yxnb61hEEdgejIL/DmXE+6ZwuvQA3FtTL7xWmbeAMZxmkDwWZsRxC5PR8MkXkLTwzT8TGvvrXNdv+OaVPjOny9/SjJobJ8KaEhsnwGANn0GoNjpHn8EUHQJzLs19XquXRvFDyEsB3CMMu2mL0quuygC9xatQOjT5dmBZweeHbhXB3Do4iOnPJCykrnh2HjkaOfH+lam8YEFv/93KdyfFLLqdQKeCPTDrYooCn+Ww6x+jcZsllP83xFVrtdaA+zwfgU9HVoTrG458JL2lk8AF/L0OwB0xlA4vpGAtCRY7w0toc29eS1cnYlShpJww9jSwhO68soDPGnL796TfZEyxfG3WDA3fr/XnrQgsw+EhlJj1cPXP2jdrlk7+1yL2rPWHUBXsZU+jYweOuUTK/LB5yt4FhjkCOcqVq0TTsFC5c/aruCj+VYAGuukk81AM/eIDoRSESY1nX+LQ9lbhcGhdavH8X7GPesM+2i6G/H+70kqaTpjFX3PAXeb9kp9TDvOrNnlm0MErM014CbE4kDMyZOOFc7xRMZWqfMaxi+h3m3ulvajim143eqWyqMrd2abjtI11ieFYssrp7hP39O3pFPGJqlGCc6vDpQaubalLH0gz9YF/9nPBOq8pOFK5XOJasZzmNZ00XalmrvdFJMGPQmvQ6yi+H43yJs7Nlw/TYl6voKvRDU4cjg9IyKY+PO8C3VScmmyD9B3Q2R4V5Y40iF+7R9R+T39Oz1SVggtOVDmzwAAg4tjQTLy5YUQAdjQoyH+hMsmsqfjo6MOa6bKY46H0x4GCPL23Zp6muFhjk+AXgeeXe515ak70gFaU/zHOP6+z24XCe9pmVOn8HdeL9B8PQVSc6RFEifIGisk6HzETSaSNULPVmk6kq4b6/Snm9fx7+J/YGW3P1TvcotuH9idHaJBpTEZEvAnlTqw2w0/RIPUGqZQq+0RB7CQfIlEl1y2/e4f/hHl5i+1rOK2KNKZ4dpiuzLtgAv79gWmGYdCFRzYxSU0/zpEjrJyRjJ003pKvurgOfVsOxvrSkOtt6rqYSed30kr6qlf7gC9ny/NUfw1geVMP1RgvRccLL26lnMScmTH5CvHcOZ9s+JTatOA7F9czHsdS67dLAwxPILtRyqOiQnIC199tc9nFcuQD3NU89un6hNuYByFWPU7af1Q+u6saVpypvwlEQTUKZY13HKfWIM/5AnYBlOunDz5bQMb/yapN6zn1KfX5eaBj/ZEP3bNKkvAUQg4en+M4Es08u/2Wc5Og9mEN9bhEOu/+0oIIXfJMKZMrZ9D+rEMooR+3Pb7vvm9/ipk5ykpJbdcQ4VIP2aVfgeAblALI4KFIrt1NuQS8KoDpwPqcIyIYVthz410wXRBtIzXQNIQmkZvELqJmsqZYsM1xNmFOxaHfHqaHXh222zN05A7gBXi7/UHV9HCUWI4OQcpDfEPOYAcU+T6WTiEfqNgf0l0SXDFXevtlcyHhbM4LDTnlNTDQuAwdDuFzIOAHJyLg+FOEyxkmh38ObG3MYGh5Cnl7blys5gSdf4dgPRR4N1eBQ8q2KMEwCBmaJZXI7SzSKmNrSbojPrn3zVY9W3yWXdLVYyJdZoEekfm8EbnxOQq36NPcgrGzUKw9CWO7+Vc6LNbdlsX6usi6ziRSCOXc13BQV2LcgDZ1EF+mGv/HW7MeygY/TfjZv0FUIenRgvvBQK4iAqtuu51BLlkoPvm+CIsu2gdtSo+xV0Dbsea4nDkXvfcP4LhMBU8RDfEutWxj29lN0fYa+FffVkj6uRwTIH1szMsOFpTLOP7ZqasVXHLHjBp+bgDAljGWD/stgtq39xNI0muHImPx8HmszEjsNqeP1cJ5rVhaaRqlMyXEKeDZC3yKCT7FgHldQtACbuH53pPqbFPL+9xU/iMI3cK2YedvCOpeXR8yYT3+msf+S1AZCVK+2sFTHQPw8eB5SsAu22XOoG7kSTKIlyEWHl9wAGXWnfghErlWpKyCc1U2AOaUDDHZIECNZp0YUwtSLen/OzAswNndWC4V8pEvGNKJWSYtAPha6UOv0JDeTk1C1ckOg0Tx0f/KHlastOAppYQZ+3OyIOUTtxuwISyNE1ohtyriIDYWQTynw2JkDnLB7PAc0ECy0dSrIEgO3NoQDBslEdIIvZxZscrrWWZ3/P/kn4HIFWRz3taF26Nadg8ir3cc2AS6vMbciGWXUd5pblCmBx0cbzWFHxiJa80FLW+l/RRDeBRHPmzkGL57FYDFY0ELLrtXuI3JnNYFVv334ypDQ4h6Vglkobr5UBXrydxPEN4dqx6Lf1xahGETvZwRRH8O/icyl/3R2usGuEJq7wuNdw3nUOGjJXHuqkdWYJY5FnfPRqzlYVEYLLzg04SGoE+zOtmXOlQ2Or6S3YMvA4wAFRdnZo+CY5FMgyX60qGW/JgHq2wrHfWLfGUhLvr0AlH2qbYob9DtoXK89K86uKEw3SEwBBcOnD3pHIgq5U28DfMs6mn1s8suMFxUzdzCq1e/6uzNh1HAU2BDUOBCDH9DkDZUfxaI1YBH3G/mQ94Nb04kJ1bRgJQabsMvxzYr+CUSTgFpM/vqX124NmBKztgHVAsPXFxTJrpiQcHgsLfFAFN6XaaE4u/Hekq0/uvoCrHGqDMI+vKiXVMFp+nPtiBS9fnueARtIhPsDOOG2dhQTr3lFjCL/wtQORvrmrTsCXJrybIhLY8gjIju2fwprcy9FqwOw1ZqbNMK8LPs2ckKWO+yGt76bsmyvtNS70ESLkmYCdcKzrVwCqvcpqi1UQaQ9XnyOsnFZZGqMz3HZx0jSReRKQbm89ZVxzj5JSnw3bfB87t4RloV3FT/WHFcPfEVSh5bKFYJ2r2oOFAMcmIMJtXYzprRjsva45kqWLPWG/LVTSBzSTiEQffgtJ9HzNNFmohK8lNeAN+ZFge+8YYw/Xjk/TDdezuPz+PhDZRV8bXrw/sBJzeGNwwd4hrjgwNGAoP5Woie8Nq/fccurrUrq7BUE5kMfqzvQIJ/PArb9wrCJrdXoWVV8WUWvZQ6bK/s19qs6wDGlbCAWL7GQDhUKObhtptOCKcs6CGuaQDNYL/WM/dmafEdSBUbhl+KPROnJjTMFo5cBUHMDZQhlJJnopnB27dAaxn2vLCZuHWVHr5br+zUMaFpAjpBsre9kpsdV2Q1uk5fnbg4g5g3TpHA2ehOqbTWTsMSy64DBwHZnGEJFhyxl9JMXd/MHwumfBGjbecHZF8WiSe9EecIeh4lKP1j6HBKwAVl0JYnK8UVfJrz2KTLf0vZy3JZ3iTgEPnsxxwVQxoOAMmGlhn83xe3r6keS/n6LwGImSnsoFgBHZfiFyXFybm13LrEmVCVpZtJTzAFWWrrpA+0B8fZ2qP8KFOt2LueH55Tk9PdByQSWqoR6at2Z6uaTrTHplzPtmixl/ygVu1Ykfr30GTyL4s6XU8Rxw6IUPVSZhVr4ZJH9Jhdga7k+WD6PdDn9sJxu9yQy6LYWfNF3J+CHmRQ5PRXw8GIGDYSJAauHAq903eou7cS/R4FAGBEPeWNJD91w06DITK749wDLRAet9Kdvjz/FlcppovQBbjZFjDTZgg4mtARc4fRMS+QT2QwkztaJ/oZ3tAmAEb+ILjwInMzWSPA0YesjyAS42UR0iH7Dr1IbhncH70kquF5ZvN6SmTQLSJMLanAH5sEO4VTzfXqzVsegoftQNYD/HqujsaHzFgfcCFxAxlpT5PhDQ+EkfKEnZebpKMAShAZ7dQpL4bOM6nPM7CUcCbQldneT6IngjLnsiegyE0si7pf1EVoxSwOycAxrugyjXvlvbg7FBcd0E72nha1tnHwtf+axp+dyPTYGEK0Odp1FKlMnw0C7lytLXTt0EAMIz57SQQpxZUAMBZ0P6vk9f+rXNr1ofK0TwiGoKu5iTFcN4IgOM/2CM0uthHtFFrZnkyQlOxXIfOtHL4aYKot1uLw5M5ND6s9wSRd/abZzzY0cqRNUrZx4xbu+/exoTyltCcjuG93UFuvV2nIiuvIMo1VjmpAahuav8YJedR4ZgKH1OEyT5IGS7Te7dAhqgxlcu6ArPsHzmdlWAl9jkDUM47P9pagAf1U/hpaZU1w52Jz2MKL3R1H+I4BUPf84TIVNptoJH9l/IgTJixa2+P41nPfeYOCPeRmHu+9af0fxQzY78Jpj+/kbZgzXAnMdkUqNfSTPG771t+P//L96QBOK+n3amV8BmAVhsfB1IosEizVNAPq6AOrzT53H7RlPEfkG8/iZd04QLQCyDPncz9Yexk3LPhbr/Gzq7gWrymP/7CgxV78Vm0GgKzsAiXtCHTVipnYZ/+1AGeGquTlv6ddi9SDvckWCP5yxApBxFctwjlDoCmEQGK+HSSKRVwzkJT8B9EoefIKow6eddmVt8CBJIdPh1V9v36G/oY69vrH8n+luTt9wSsYne9BUge8fMhOrtlHP/8bE9cpLUz4xK9fM98PYT0XUDUyT/AJ76WNszpgC1u7o4qiSSKz6ZOjxTyvPnqjJrD+9JU3R5dF7HWYqTJTlsqDo5fzKRJEj4x5OsogDnIOcblEb10f7aG5NnXr1KiUVbUWjN9tGHXiJKD8LgzO9q/hoWvOfj7F3VS95MnXTaz6xmhJEGkvzOJcNuuvueBXpkSSspTj9QWNwkYlcv8cl0HwRlHEOjptgn0srGtGy/wW5EDW4MaD5HjUAr7h1AMGyi7YDfTtsj4oUxsCClvBSKJ7bcADZEaB0abqjeROX5DUcdxnggLHThlBv28OsXcIvPRz7MSK/wBUsrnJbkd0kM1Wa8Brbldaz5EJppfp4eOyap+IQRQFEh/Ph/yfKgFaTXhQfTOXGjTuY3V+LfvCVV0blFUAtWFv4PlqP6cw1TBHqQZDUerz6khmrP1u2/2lo0Yn0TsjLnFPAlutei8AlDOgCnArOeFLMTStNfJqtFKTAVwySD+XtWl9LNFT68AGbBdK4q8I1/M9bnvil7qUhXUtEwWWPldNJCd6aVo6MEFJKtrdSOcFnvWv403x0QY9LrMEYarbnhVrapCofpW5b6ocKgC8darYrEON8yY8W6Hhw2xMlGjhrFVMw1WGn8Iq0OGGj4aV5SGYYJzt3tDgOMOa3mrKFHFAh+ajm0vzsd/uuLOPTw4U4yjWR1E1oBBDb9KQNyqHgbjb+CWZ1O97uE0zGyzNjgoTWUcO+ySg4luA5leiWXMJldwOGCytBd0MJdwgiV03ZwGan+7h7ZFo2iNJvEm54vAjVcAOJAEljX+p7d1fuuRHR4fT0XtefQOYW14y+OMaZFdIPnqdLOUJT2ORWd4+FBCl/BDMdRkIpwfbWHoKs7VRHpybkYf7To+08jTAX5lH8FKLTm+gxDII7f2kblhDcUYDrzkPEo5skzj/gMSIhlhxmFF3GnifbNbZcQbSAhGCVMYiogBuvslh5ff/fb3SSPeQ7/H7dIeVEvkQSTT6wArt8WwlVRHY/gaAwORhviLvrHFF4JFv/HVLx9OW4+tGo3X09Tn01TSclLEMgILyErD5tZPVPNpQjDsXBXo+k0qNUMApN3iQFsmWUy7W7QZ6AH5O5yJ7bnzG0GL+HA/TxGwopw+OFnix5P+LsbQ9r62RoyBHYYDSgwREO41awFqJ7tY07Ht2nke1TXpDgeely2w47KrrKS7R0DSj7aBoOSyvE6Or4o4gm7R25eky3PRqYCQSYtPPaEzzbMODei0q5PA8J6FJf84uJFzRb2Y1z6ORUkAAd697xabbWCTt6yo1NQkv316/VPjMhpmBl9/ldxe/7w580X7r7+mlwPoFQDCV/NGgSH2CFThI16FSidzMPQh3IZ1Dx0eooxjJGidHCmTYuVK00NiR0r+O0b2/Ggi1r1xUSx03R5W+U5pP2w/zyL2yPNi7QtW7bP+Fs670N944qx06Pl1nb8O2Zplruj2qS1KM3projwMjoEwVTjHegmy7SLYYd5Zhymes+BH/E8mFp85Ik3OXf+3Wv3SfgagCqoGTidWXwFIkOHrEE7+gya+wqFxaAqjTcjB8MfEU2AvPIgHDM1ooJFh5QxyEHLEzMXIvBIwwkH6AJD7xgIwrSywShzJ4ZA8uk7As9xQpaR8HSvRHuH0Sa5FCaxuT3jWhGNf9Bvej7lSazE/h+fhbi+WHshrFS4z8nqTSpJpDVB/mu9Nanzk0GxmgCdwsOqcjJQiUhGzMimxhyF017/he1Rd5cq9wjvvqdIg/wrhGB1KKtcDP8ah87P9BxeO9alNzawP5ViZTLe9J3bS4QCTzCVlJ1C1qFtEH4ALl2YFKI0dGevhU++6NbwdQLmuGFquKIchme5zCx+7zqXntJET0ZqhtjSv6rA1fPD49PXXKah6laCXnl8BoC/wHH8GQPDwxbvNrE/roLXXwD4k128JzalXH2XTMobrdT8jtQV/oEB0442SrCUIQ6F42rJAJh7K8EeQiRhqpy0IN6y6ysbnxsMHpBTsgMV8bfkFk97d7Xh1xxGuaII1m02uoFsTda+hbvUD8ieSxCpOjD1ZuFd7kZdooAQaPgilYw25TxF6rXIVDiGK0oFdDZTwJ0AHk/N+MOGmVaPRsum6m/JpaPKvPgOA0BJUrmGUsX3vvwIwOveqs9pZHslC89rQhsZa4uRcQvY4virTq8xC6vnWuvXIGscZoRxc7eDrfKXAif0cvUAgaAOZUrPg0Li7CfxBg/nTcKEV41pG+9EYIXs0s+ZE4UoPHOzrEwLgAMPglTMkk20nDXiGGAqy70tsSr6UPFbykRRDtjIFOct9R+bFfiSdpTUqAyXqLfzyesbvKw9XF6pA4UyblamEA3uH4BQVwQTe3IBEg2+Zz+xnADjaF2R233PBqqtwrmQv4N8g5Hh/MKdyO0UbgRRSNVNABBn6x21+rSBlmV3/s/6C/LS4lMuvXXIINrOdC2JFqu/0nwB2Yyivm7K8CECY9mcAZAGXyntll6Y5DN7wbIaT8MeijWQEegmuSkdZrAU2RUA7s4YFlfyBFA1J7km1vz4Q3w9CpWn7B6nKKIPWEq8rw+VM9Sm9JRD8MTMHlk3dELYy1ISA4JvvjTxfyH+ohIlqTVfwIRpMzHR9eMPdm/kgHcJU0nZtWnklkMCyLO3cPndTyHQfW6ZmDvvZd0iN85tHVvyVFvrukkryfK3fM1RAUlr7/WFk3c5CxKeSzfMSFwcJiZVPm3nxOSVrrhOoIiImP31PMlNFvdBEOIgCNwyrw/KXgPWrBE4HkILQj9/M2RTQfO0fOmSn7dQVWbBlzhQO+Wgt+pxea0QtZ4lEHiVwISHkCLfAfuTnAqVm1pwQePLUOJ4w4R3PkCPrRwIOr7BKZ9lhkvU+WGWP9Faia9lAkFmkrAHiGomDMp39PQ4b8cTSjXiSj+TZDQF5ibkvJKOfwNndurhBJSdmuKIZMt8z5D0uvjKpZHlDB0izCWv7r+6V1sisRUbdoCR7UOyf4lfNrcepHUpJlBF9jh9tFMb2OAI943BXN/+lrso1IGXN4SJNWYwbvH6Ul3l9K6ZY+luyg8NdnZ01f+/gWUv1il+isBhW+qWZrRDiA5Ursir82nVy3g31lLGpilKsYC15edJILQCEWKFhgNzweaMBfgeg4yghe+ZTdbKUU4FPBtv6dgjVnx8TOhgWdDPT3NWAxckU3kUtRJJ5skAlSJkrurvQdPhcPjcrGYloe2k55zaH0aY4TzlzigXh9LljQBJYjhM7WjjiaYs/JF7gEWassVnDQhjsdo5xbnFPyZ6i8CeVP6zMq5qFx2nFpTsKga+tn8fpz4lMeKdgIQbOq4bnSmoKBhuLorqXe2P6EDC+BWhzYThjXCFRLPkniEa9PASQc54aRNZnb8cxkZqqlTfUTxpuROPATHo96ul29AYp2ug2bAfMkr56pDVNiDH02SNoQMZATmrBinvouJ9lms4leJ7FYRrH5sDLchpTBMQnEelEaCVO9xbRdnWw8zqM86xo3WaQq2iupA4Jc2mnc9THQ36dgVj583g6mQQoZjm+TuAJPuWqWM2u22KUd01zJSonv0M/RRsi2eEjyQuAJHItm17MV+OZhmW1t1FlaTWJeO11oJRKYyqXWkEBTb7aHhr59QoIdFIoemLpT8820Oleac0A4h7m4azF93pNX8dqjY66QuPn9a0xPs5qrnss1/xLfvYo7OUzAJTTfgXAI5TQkUHm8SIiNmIoSEYi7uwDttQCEoaNOKW0U0Bu1jXqybAtNyPzAyY6ZbUEZxBuQecT54JqxN+JmCdCUUNmezLrfyLbjwbV7T72iuvXzYPMI8qNzGzccxlN9j4C0vicy7ABP2V4NcPuipbMicDVHGS6oDykHcT54d2cg0ox9XpdbPWDZfLcXwHYfbjLHVWyvdAXiL59TsaX7+x7moCk+hoVElj609K7QAd3rV4/O7r8GYC31z+QaUvoVM2Utr65/E80dngXdH1NgkkWl8vvzbPt8LWcCylqDlpjpDfrMvyhxmTpeXGDkpEnzsmLZUpbxk9R4YqGHHwHZPd9bm0VtaPzDgHqFXqLTzLoPgOBe+tAxU2MRtnRQJ03grYWFUE+zYdXcIOIst3pWahO4nHmDo5YIeDV8YFBeTZ1nD6UJTA418KaUwSdy3mkQ8aGidk35kcBOo3b1TEmg68KmpGDNOxJE8stoizd6ht/OeQjg1Qel5nScagbIbgr5DYcrHVo6cXDdbXm9e8DdF8BqOZoaoGe246Kx7nQd0WbbOnAnbsEP/YmAX93rbVNzvRagz1eCLHBfmjLDTrZpGiGl3afd4RLsyyAR5pA5NlNygvplkMetoHLFaVAror6yy2WiHCgLXtK66rMYCR0064C3y4OLWm2F6VHFgInYXhj56Hnj+wgOwlZau7VGewL73SPiDTtgUojKg4buRclt/0VgDTgUkmyzzvpFYC8y+7uKc4+L2HUCaHGngjsup7FrdqXJs8RwYE/F194+oVWCRGCc3R6zysi2aMBIv2g6kn+hfB236RrrHrIPLXJ0gz4W2HvXD9b9dB/dqZk//xZGyJX4cZ6M/kb/pJeSL4HzrAzDXNqFIVU7SoeFpR9fC6RgftuxkBcx8Wcx46vUsk5krJy9BUmh0idRqNNTEVFA0TSKpjTFBvzv2RA/Y0i4T7HOyCpz0bp7gGNr0kvNpPCLGhJ15UJIGWXHZNyjp2qd8joCGvdKJluiqfbld04PBaB0tbGPe6AdKRBVlo1p5Yj62VjSak7z567MJ9ljx1IOT+63DCrA7uvALgRe3zQbQ9YlqiaUEOXE9wjUFWkFDFWPA0QeBiLvoPX4zO8Q1PKYxM157r+LK6wM9pxXVFnsLsQY6Hn3RDZQHLAH/HuOl9Yz3uHln20ajncUw0QSWvR+dH0WNtND3nIwnRb3vkcTBUecSafiNt0n90AmoST5+FkOJe9YdQUtKYTet0EcHoWdHqZPbntvwRcBVWDCiVbbHPle9IA2Yh5MO3wfJR40XkwAarr8SZjvu5uevQM3bNtowqtJoLmDbZhZ1qItbPPHNX8Iqama3ItBszLNtJXpIrb8B5dhVv/2z+GEIcdujNLqJa+m5B6SBMkO4lhO2vd4BmlTKHjiDNlxL7A+86Qg4/JWS6qiPGTsLaqKwh3MI8fbA5ntbrNONxG1nDsULDWpJW0AzjfgQ4Iq85FY9iu8DnvYvisWi6YV3jXvdob+x6etpmdiQ57qA9qw7oCuSuOw9TMlQZes7oWyXSnLjNsvhOscaTCOWOzqNhTPp5KNBlLzlY448wK1vEEOPLRhDRMBjTkhEocKR/nU6Fdsx6IJLI0zyGpwCr7bDGH/HN3sW7cWa9fAaAoMS1uoDCKkEOcY8GUTeSOxbhet6XvUjGNXsVkYzMLJtLTMOrAjXvI09fkpeHpS31UeseOvaPhJv0cE7vdZReLEGOG70hAXbQ9q6tn4byjHqYj5r4+qAHX9uBa9PfU90Wu6w1cj+xT5VXDQt/vJC3ocxEk4I/h2cQaKYCk3Err1XLDjWhA05RwNY174d9mhfSr49wsaL92GvbPAKQgBJKPgVDUdG87tUkjZ2CuD7IxvRb/snFzJkcV48Z8imL6vvRRBvZ0gYeo4TwwbZnsFLnL2EF2mKCl2DoI15mQmmc8Dd01eZAJ4Ts3p1FO1NDkJ5XhIICeSD3LESgCAYLcMsJFAs/gCv5JM66bw+9jtlg5My7RmnmRJgvZ0jsZrZBH06/MdSq7Kd3ooqF2mgA+8oogZSKYJp+DMGta6cBsjrP93yNnrIWT5zEfbeSVe+q0v2B4SYIJDxFIW7nY9Go8eyZDeLJpkl4omJ1OOjIz3nFBNr9BkyWnV6dpfMG3ZTZJafj1N2+U6/XPZRlpD2iSV76lHwKb+x0AUZrTACvxMf366jmW9/Toczvno4kJO6cOSsd/s4igOgyH2yz4cX+Z9/S+zdKTZCKxs/4RzKfPWgdmF8+sP7Gi6aa/hcC1ij5KFDdM7i6srKskNf5q9XP0o3VA7mhy3VzRB5lL4zdLkhcuCZKYlDWI1MgF3oBLt2WZGQKhGS7DPkLgRC3x+TheGHI5GSVvcnt5pZx0L9UOCwd4i+qc3/vv9g6c24EcbcfpHe7zpi/4/oQSiOxEI9SsQF0FGPdcnwk/ePdqDYdRf2pnuDUIzLKXbaBrroNKZNQsK5fWBrezxhqP2JBxKBdu1dU7vW5n+lYgq3unKPLj+WU+VbA9CPpbc8d5KYP+rEuXswUlOfZZHe6hTAGZ55GGNINyFWlnT6NnPHtLfCl7UJfZMB28RZ5mz2qSy/mFab1FDfTaUK+BiEbl6rzvXOOoqPxw1zQAw/6CTQBkt42cQfNBECaL3ViYXkuR6hj9emGaf6aku3Q10zWekpWe/EOYZR41bLMuJYeujIXZLDD/aMA4nIsFmDAEpmZIPodq5/Q9wUQ2jsw9jF1nou0ul0hyOppPTp6Sz6pr27OcmaP0klx6XWJ7BaA70QbbGV8DYlHdrNRFlANhpxCwQchiGw/QPh5Kc85/x9EYobuU0IJbNuKWuah2qjqYsdsf7l4jYIKA35iuGAZLuCL1u8CM92dqlgmW/UnG32xDGGE28Ef0x0Ri69bPXWVfDoVJbl2kjpHBScBfx+mpurIDPAVnJeF1cgRQgpAsSUoTpyAl/ljTFRDbRej6a+WRWI32jjR3K5znngXdtZZc+gxA+V7/snrIp4dQdOVeg/c15Xy3b53UziafhB+7tw0cR3Q8zqpCX9tDsmYGMVxjfhZV7gJfYwayxaqbt3K+ybqqMnINtmCdnVPEXm9m3rz704JkAhZy0yjytzyZg5VL6gmHkKfQunkZR/OU6c6SuxyOgKMJDoKVsanXQqD++DcQYDT0k0IQCD0rfShpTeF5HU5co8IeBxRxTQ4MrT7IpPeV83tkX17/xO+Bbehwjxu9GPou4ojkOxIipgyTKBJ4ooU5ABGsPPRjttDs34TJsTo60d22D3regemrCHxfCUv9AQLQpcwamXiNdrcDElbP/loiidmRl/pz0XfEpVZnPvpxHPpP4gjZqeUK1ef07T7pjf3pLiX4+qu0TZ8K4Js4+H39NQ3wCkA9XcP5ZrQfTUBj32l/iDb+aNYiJbDzFbPMBCDwENxoiGXMqZsh608RZPYGkEyOtXH2h/VO5vsmK5fsECAT3Hg7xg17DAkzQ0A2QyhBvltCVxlmdyPHYRMsHsHAYRM0jtSQjCFvpdXidpZ+SP6sRCfh5Etds1iyyMnmOu4SdciInC1/SmGZhrBPh0gHupPozEgEk30A3k3BPr6gY5v1IB0ak48ct8oU8ah37fl4Jb+tHAhe0u8ApFWR3j+Ew6NZWV48L971xYtmFOeXeHfvkRWsz1PXCOMaNmKX39F4pBCfNk8gUtCwycUOO448ty5yE7U7F8k6Ay720D2TkbOjU7NbCLQ4Scyi69xzOuvdkzp7ELlJxokavTVEXorSBGRI49AMpSfkIY1gXgeN+kMg8jMVmgZpunVtvcUncGauowwL73K4Tjnss9UBSQlFAarbLnbm8od5CYedOXxZOBFqjkM5Uk1EpcrFRbA2UnWOa4Og7C1AGUt366hCvkQHq7376IbpllAFvn8P/74tol3oZwTW8REZ146oDnZrErla03BcYnn+dasv5z8k2XNoVpem3Qvq6Ljwjk2plrMoJFtRZsT2mLdITCn3kJyGxMs/dc2otD2K4hcAqCoKkd8CREMFkmonIP7r9eI2OqLWqyglB3He3obPkSxWIUcwuQ8aBLOKrbZ2NRcx7ObSSqbKwh35EIe17BSFPypwGUE3R2u4SzA1Q+0/1IBtEKfr1lUO8y47cJ+XEa4IHDZh6ECs2IcEfxVJTxmoSyMcdtbWj6zhDrKwV1urMOI2aWEPbCWE1nCtD8bSR8psjUNxCAkaCtbj21k+xzM+LMJ1Tb6i5Jux5R3liioeB5PLlALJPLwtVZXWmG+lps8A/PusJAR+gTTLeHdQeYcT225bl8gmqfM1FWLaPYuSzgIjieRPUXxtMtfauESHFDt9y2eWpaspmmohtsuvJDAB9KSLQ/igirYEaTs95KRdYeqVgQgZ5t9Nd4pyWGyEp2SiAQlBK2VIV055R1cjuoGVUiH4TGaLpVw+YEWmHizkqgHa1GNAdAMoM68wNHkjQ6ctzLNzBBPz1bFGEmcfyk5ZNAdOHUZqHRvk44BtgovGqR30CsDL179PrwOIoyVpUsrXP+R+ia4d7P9FdXRhwZq2RzhXyGIdQo95J5mFyv8mA1SHVGIGT8ttde+K/cgnLZlI2Y/SVt5bvbWh5rrB0eU3DjQk/M7thsfbTvabqM7dHWbmut/yrWg1Z71XAAghg2yfHgAgwxIE/m7Sx24SKz9z1FGOqXFGi+L+3fBGOTtczq4TyV6hNPJhfBZ0YKPh2EZ/xRC5ZEYpU8Y47SvozRIg8g1/sOoqLyI8hKWWntvVNcDjHKira6lTi46nHzbacLhNZs7CgkFnRS3XM8n8t4J1s5hEuhAv97uGacDU7VpXyYFFIIAdviivvkdGzsvCiXm5ehZOBH9wKFmylB+TNs0+/h6T3gdj9fjrAQ1Xx4T0OwDqWEXV0BV//HpZklUUwG6ypdz6ijKu36Pp1jWAXESHYuNvuXUii4rOzyiKOBA357p7ca/v1RVHfi2i9uuMdB/4lRDy1jjoD5lSDwseC0XRvye35VmXr29IdMmW9TKLlNlhURhdz5iCBbEbtK7LivoZTL2F69rVquNERyaaQThvQsu5unPd+ovxzDWPPQzz0iwbGg7aZXdjhz5P6nZYrqjmiJQyC4Yda4Cb7GeXQMIQ60T6d+FTV7O/tXd3o26mHPInJrWPnIFEc+sz1OCd5b3/6CPHSU/4iy1W4OZ7877xYwERABNBbUYU63AiTKwrP6qeEd+3te7z0louHPOuJCf/SBUVV9U3WaOUq6h6QMSq5yQKk9ZGf0mM5hq1cwfqtGlU5ZXmEbL0Dcqn9dzIdwW+han121zT3FG78Ty8z7M/k43vW16s6fp+52iAEwDgYFE3mHKlN8DhIWE0qJHQYeYhLCd1oNjU9ID1XaqNlYacq+vPyiaQ9acIsgQJGOQmQ24sN20hwvGW3oZqvIdNLUzPmh120AJC4qk1gq/R+I/Wdp//41v13GnNDaq4S9Ib1HU0BV3b4taQYO26nAbOQ7cAEkNeLTBZLvTqjD8CfmSx3KUPPMuY92Z4kBKjOTiUN+LmIDxNewd4791VUpputgoQvwOwX+inCaQDY/588Mv3AQWmo89jkIzjp5YFRzG+FMxzTemkZAdTc3OcFXBS5J6Nl76ExRU1fA83X7OR4MCUGkdurrmO+ahrA11wSbjrcIVST8cVWSSmLFN3kjzJIchKQlEgTyLCG6vkoGWsEHk9WPtENHLflHIkdtZnrkAHfbQ+nUSDmfKRfatD+BrTufNFTeN1OOhSLgf+Tqu7RQN5mnnufPx3CabxHa77413XaVqpOxZ//QR14XfoI6+3BJFpUsAqMu9VwdgjoLrgai6Az5nN9nWeqo65gX0c4J3C7+RW0fy3me08BYep/ujlB0ysAZ/2nt2QHPBuxGwfpirtZvyRlIHJxHotTREBJDa/AyCMHf+iuvreWmEH83aKKw+HGrnrrN1mNQQbRIZb3J+ZcEgwEQdeKsTJwPOiNWDVyE2TDlIZ5K9p896nTTKXIy8HOpjXmYKNAoFgaV23qUTX1fvukKmZ9BfsHrl1m+9XvRDiA15oRTsuTPAo0DwpLDwKs/fJI7gHvc/inqzfRQdGa5APbtjnO3u++Bag5hWA0oBOEJkmztLyWaz5PmZxjlsyTjzkcAOCfJpi8PAmr7MCB++Ta5yZXlfYoGobITBDssQBZRRDRsK7NBhhE3o9b33EOJJXuFeiLkSiNdfaKVLyJ08O1/OrNVVif2B0QHJryPh4ZG34AIr54/3W2AuaLA7yHs5OBnO2nyigIgAG34EKZ0xct8zujPucGQdrQztLTJY7rdORpDnQz0F/4sjZM37lu1vHrBJz5ETxJHbbzn3uInSaH+9GF/F+yma/ZiKWnh143bLmZoKcne7rA50JuobcsEvrae+6onj3YUEX4pi087kaf+2l2T/QPa7LynKz1bXYtAO1RzKeu+ZttMU2izAS6RUA2gpdpMLrfGhJWatKJ11gLUOk3IA7psaTh6DdkJc4jYkDtSCjtNXXUJYj4V1wAC7AdkO6Ss7LbZTtkjJ5NkOOPS4QN6YHgYdHwJkwobEcAZxyjgDexide5rC91IGhjy5qIUSDfEhNfEXxJMZDuGMLIRz7MYQH78CD03v8NcBHGBYen/NZDB+/5OfyruYa7eg3RfwS8P4KQCe6Us0OmtRYQKRsVlLjNszShLf+9nkeElE4Z2ygwI2tLbI7xtUXXDEFDrsHARsys+HkbyEwlCNYZ5yaPCoFlP4Mg89Bo2lK/MoMnAmQo3xwDTWloSw7vl5FWiPQq1ihb0QuROr1tbqdhvR7D3K3QE18WCD6GUST+ENk6fwxZGvP1dWhq1oPDVsX2s6YN+4/c2YCUYGIHqnTTnMNqp1v3pLmyD2azUM+ekR8H1mopFmEzXABcDnEX3vDfZO7RDjy+UzDx8oyxG9wosPRWpV8iANX0ccfofWjhHaALzyvEalEqnhv9tdfpzyvfxpk2wPSFwM1vwRMsaTcXQZYs2YJLGWqQ07eLOysP5coOcyC+P4oR+LHC4x7+hzOtXLTIrCycMs/4kOx3A1uKQWSjD/pYCWa1QeJdWGHsUy7G66VqFrr34Vm2I1IFcsdWA6MsHqnPugJ9iC/hCPdO2XefXqNdT3jkTobEu9quN6xd1XmLcm+o5YGV71fEay0ZTcp36zzqKWpqBnejMwjJOLp6JLZO0PSy6s4Y4BltyOc0FpVixs+l+pnaOHasb4y2nrQWHOwv6/AqQdndfp6diejoeJYZOHJgOCkZjwOYY0v6DNRyuKB6F6JBP67vQmWS+BKRXRUlPSs+e1+AwZ3FYKuPcrA9htg2uvKhtzXJwrnHsoQXa+uccBNwp0qr+XVZVpz3SXL4X6UtMrrVXKNdfGT0t0XzKiHNPh7Lijz8iMB7ZUa6aNLlH2G1VoVhNw2/4I+W9k1c09Dvwj8JbdCfd+2xJeyh3a2TfdcZ8Cal0djrZFRjJnmaPJoNtuHWX/JU8o+jm+VOJF9RPqH5LK2m2Uvj0WLx5mCvNPQmt22S7xT76paanfP2kpriRH8jrFbI9R4+yg+U3vMSLJq4SpaANlDKbd+g7HfmS14CT/cpar04bX/tp50xJOfASA0+de6nzkGcZkNmqkc/PxgKoqcdS6Cwh9DLYMzAguAigPGPTlFI+gCG4dLh8Hsx8uUVZyLJpHXZOZDgpQJjYdryB8s6opuXIH5YdqO5nCLSKA/uc+yaa1kgpJoayDPKHWcMKfFNIyauBw4Av4R7dRMLPvH6Sr2xGZ/DO6bVAUKiZTDmCzccgVEGN6Sz61y9euenALxGQDivX0MgDAq8GpglRc6a9HnQ0UTyqFyO9X6fOLp/KspilFfQTzBR16n6btmbVMXsW3nxAkupgakqOv70v9dqzXZpvtp9TCUt1lie/o5idsCIZh6Lsekt5yshh4hsWYSNbk/QnVB2tbaaMLRjW5dQYQGUA67sNLhHNnYX+Lg2LPgH7qqFIc2PI/3VgPzcfJGbdcMZjVMdKkd+njY5F9CBYYVyoybVCvD6nWAFYAtZtiHA9jjUOpUtCmH91PNBvNEBHjCpAz/KD2NfrYmfpxp6oqWcEGHIz3g5lvOUf5W/IPq27LwGYAv4jMAVme2yO0zABKHZAylMryLPWijerSq+noOH0BnTf9ZpfFikYDxxnbDJVRE5kMVOcdTR5CXfUADWz0FWhNMZAEGw9+X23KXZJmngEjADyPznqKFD1PjuBBaH1cuEe7tmEnrcSC0hfrg41t2KrJYuj5d5SNPDHUVjb1ley9qyAco4aLOpKPf9hmAdCpQr1IaQbdt39KrA8pLMotcu+J3ORPSdpt8D2IJ2+5BekcTZp9PXa0IU2Lwmj3F8TUVhZEUeEea28Ju3Lqyeg+iBaP7rzU51u+nhK+uCdlXBbDEZGAjgz8pydPK3p36Bmfjc+QXGRvEMqwqLUq659UVnG5/5QAY7YrUK4iExLP6Y3XDJ9FdpcG+Ocgtgr0OHZDNJGOlDLOxv8S7Ya3tMbGTPNpeLcHGj5MmPHoLs9FVM3bWgJppu3qLzxqt8O4RDHv9t79LDOJoq3zbOH4sbg15/I5Wb5d/RxleUVXten9X0Hy0V5ak8K3dkIuUU2sMtGn/mNhFVIerTrpVxT0tGDyO6KMQFTJRgoXe0x/nvKHmNYb98QhVfAaAEajwwfcCbZ8BoP5wENcJjbVlt0mB8HQqwrjxTnLjdLJJd0wtaZwo84Rak+vk8rtBVt/BQfZNPqxv9ZFhRSu4M5GQH9OHW80C+tAMF5pDCM/+O32TzUG3f6xFi5ppC8Hp1AETN5mFA2DP0Jt2QK8LnsSFVbMQctNqVTIuVlkeTkFUHbaWSc/vIxR2FSvgdtDpl4D/EYVvRrqjlqWtOC/JHiKanU7qmYCeQGwYWjPdRZQZrXPHbuBQ2T0v3FpaHm4wtKC2a6L5ijWdFzaxVlRXP9WTLkJQiRURdw56Dt0iBfJqbdqOWMlcysPUXQeefYKiW5Oxq8mOoQ3QQNsJAAc4+Fd9jtfbodEeNzoujYq7xKWhe43b1JChpqIe1pnXlccwdz74i8LUYRxnAIjXJ7EeDjb/7p3v9Io6Q7TSFa9ykywPFlwgu/dL2FaQJN3Ntqi8CjdGp5qvvIZnv5uok+cwDs2B0xZYrXnq8MkqE/Aw2y3jWTgZLv44YtV7G71cP5gR6jNPkNlzn1y4kzK7D+lbeS0NCZeMfUfWMqDOW3zoXv4OgHasNCWqUj7QgAp2ar4v0WViy01fDlxrVCSdbAL8I1EOn0g4ksqtBiQrHAgQMobaM67pcgN+HORqzwfh03S7GS40odv8BZwPHNK0CMMHWQ/cdqwEuWXTnNBUS8ESVFvn0J/eH6cDtC6wNLBG5BBFwvpoe8rHmYADlfDE8Uz5e3bjfyDzmaGnsOqAdFRE+9Wk3nuPYFn23NeiMFHYoM6oiE+CUXqOGAr07klCaN71tcG6wU0rGgQ31DOWM7O+D/esbxZaedU2Uk7zSohAurWIxoIPruLInsgOwLOZiIYuXaEkB3RD4jRu/pCSIlbPMoFLSsCBxifmZJRzp900bGTuIj4yl89Bem588j6I15pgXe52Cs/vBJ16VY16LueCJ0W3S5J3ZIm2uR04zhzqhsNyxhSa09z5kGdODc+mV5iLGWrX+Ob5essVYT1giyXBK6Sb+xWf9pE2ee2f9by8WGBTFuS8S7n2Wh/ZmFyfwWw9ZzjywP4SzrE5yvkKvn7VTVH1U70fvRvSKKnd1Hrg6McLOGNufB94ThwDl9g25NPwLJwMHT+SdJjcUCXXD6flXYg1WvB8wp083iW9lrAONWForIxv+Wr+izjW7Z8BAGKNS9YXcQJA3SD7zM3r3wAHmWo+g5CuucsYyi67rn8X+Y5K2ZZuFRFuj1xpcKkdLyGCADLNNtLhoQ/mDlt2jlBiZy00aNphWYMOLIdz4EKBFNKt6yxKzO0p6A7ozkOzMI8At2ZTp+5qkLfhwCRZ6MZ+UCUVvTwb45b8kC3tt8Vq9MEl3U/21J7dgedK9jraO4TQd/vwZwAodndJK75cF1SgyS2dtdDpwx9kkHLsKfYcPSvpJs6bBQLxoemXZ+3WziyCKtGut3JbHmB1DssHPi/lNBG5x9PllCsZ2/lx+Ix2uUBdGlehMbWz9hlqHHzEDrMAgZuMKLR6CD6ktzmU/YhzRQOV3wol+0qebg4Kp7QriTJbjdkUofcy7O/WVQ0KH2I2KTBELcuFdDEvUuIKkNOBi/IC1sq+1nZgTrW9mwjTR2jDeeTwqaR7SznTrjpTYnqzoHpPmUWw/IEMq3zdz/KP66u1ZB954oCneG6s8LrQ6HHQn69mjfnOXfINQtfnoZTVnK4xu8lKoLngXRnCjVp9RnV6IQXIB1x4vjhBDiqRdD/xGQAGq4UCVmv7I6bRNx/QahbX5VqmuUBJ1xXMvpAriDx0Y84Nh2Y4xPEdOIvvFrQSNwLEH+RgYNANbK9ADhLQbii20XeVjc8VQ2dtoHVTSRGyEDiV5el8XQd4PbDg53rYuX5YYn4/f1irPHRIuduQhckNruduuqfS6QBPFguO86OZiPPCWgpVQQvOW3Ov2zve9PWn3mcA9oyVP3H3cuxREUlexY/4w2ctSuL79UrPWXm74lK+zycSjnamNVHOLxcaTD0Zr6qC77GCDzyMKyiSnpQ1LFmZ1dqrPRumwRzZ/SXJeSVVEIMGckpkZNF1mRrRMS6cnH2GJpowhK7NiOwiNIl7jcWA2mkkefpZGuuwKL2XYZXKjIXOyv1ZOJHcqB2e1fEwEix8jsQCppkFgT0Wnexo5r4q8r6gZ3Ccw/Xorhk5j0xgh1F7pV7McB53poO+5/EkxUE6c95leL/PfASTSYOyjxwEITeukUOqtWQfedg/IugskSjpU7GSBkPmtZcWVT3LmE3eL9jTQDLUElPKhvusGh1DVKT2qsOKj4VQRfkU5UpQ+BM4fpbjVslNyj6yrM73dK3yQOG/Kj7XMVqjErrm8JJeASAPsZBt5zqUR9MBHPlBBDRPtPC0uo609go+BwvjRh2pK8hhLYWMIlkOg3ktNwlFfeBWTE2TBLESBfWA6gJOUQqmO+jGHXNwIj5O+NPUdICXwd0by0wahhj61m5IpeR4Firz0cE1qBsrAl/GXw482pF3Ei/7I2WiT4dN5/j5Tup70nysDtAaa5bZOfy6j/FYwC/0A8D7ZwCSI5yJhxEFSrWRRjkgcl5SR55TYBwFDOFvnddqtOG1FrRr1DTnMxVtzmHGNqA3ZlY94/k6Z2aJCW7wGTaquI/vGZnxTwGX/W9SdDnJlS/lrnNX6XSv8dd81jISLCXttgtKnahhYg3jtQBhIlG+KiOvX/JMEchyH/ZC4ld99hhTWuQT4DCNDEwwXb1e1Uyr/w51zEt1jNV1CU0DTkwnVoV4tIpHTffQnOexQVdnxUyx4mI1fgSHwy0yD66nqq8uQTe26QkRGPo0ITSM05bzKGWNKTXozA36I5NeJYujxGyKTscOoFXZwzgdDhVQO5icu8BS0gtU/PBvfgWg5fAcz3VAdjgwIRt43HOOTfGWrIruPvcNk2Z4hBNBAe1EzIYPp2j0s0OHIZmuXgyaLfh0WXWVGsHRTJUzm47AgT+VxWH7NEU6cGm3MafYEpnZXPCfjWqrPhrf4l03JqYN2WY4TD3rPwS8yIEODvzHKeQRQ8rscJaAPju9Wsu+FhUsCuCcgoVg+NPtvh3AYnOW3Bw9Pf0ZmtTJ8kKHkfoVgKxMBxcdKBLXxnok3DrijO8e7l9t2v2KxNcFi2LlftSEChMTRtV1o07hU+WzB5wLTEDMdg9Z5FmslGXw2swCgThTeHW9UEK7sq43yKQ7U26q9kHXd45brWXTRagmNHwdogsFJbKTjL7JfjpRvmm9Ih/3wazWvnCE5hWYR/joWKwTrZeaapVKgyHLBTMba0BeqNZzpDUyvdWx2cc1YFr9sbJIJixbIOxwL0F20qmI+POaGdYiMafrysdYetURGYfhkVzV5wrOOIYzK3SsOoZH8IVPhD+niwhECXy2x3eRKxJ+xGe6lhtyO1KXiK3W/v6t/+zR3YX4FYD0/v/6W4C6/oz2joSzCqEGVz0WLYBeO1j+IvRG4uMw8Qs+ZbIAEoeKezL5hRDEciALjEnCfafJyd5lK5lbMjBp64Bz7HIWRngKt+xAZE5n+UwtmFnwO/o/1/ZFzUdjb9ZeWp83y3WkY1fsm0f4UOwDUjpY0SOF16uyHvV55vkgx8335eV3v/198nz9Y9JA6y73LTDFCDENA7f5iB10+nxuD92k7cw7j+Q7iZVjUqAJbivMxT0s07/2s50x5+8tBs88a6nfPh8uBP48vIEwLHmKg9+fKagFZ1pp1ED8fkJ3nejpiDQc02fxmWpgJF1wf/FZEdsgDtel/f3SIrUw+H2Eh7wypPtsNSfuaSF09TytfMURbtEJNboaZwtPJF17/bBb1+lKbtRxZKe3OovfyQ6UMSMmbfjDvPrZEhPcfn7RPD52CnFAV026vatIe9wVzCVPwqfhwSz+KtqL6UkNmZ7L6PFldk12cxxT6g5oTSTDWtQI2Z1eOQEMJCLe8rcApbcCrdzmo+YjVnidFQO2tOU/QpZKK5H0Zx8E8nBZAHg3vJu363miktZYd5mdmOLRoLheEpxplW6+JxXo4FxX/pDVWanvsjLPIv+BcWgB8N9smZjT2agP6U89bG5a0zicPrzLAeT0KiRgvKLbd1vyPCKfy1yioXvxHh6pwoklAnfn4ND74UxiMt7SckmfAdiXDSTyIcG4Crs7Lz/vExBb/41cd5sd0aUBB/+sTlc6gFPmCBOfg4Is320Pw7ErN8cL7NA7QxVZUREfi8u2j5STH56m7lxQl9ifADHsInf72eUpARPUgSslXc5deseVKBDkq/eGHoA+jf+BHkr6p/GRoFk+DVlUCkz+HZV2XSkOjUKvWEJ4zJvsnpSPs+VVnaBEb4GsW2RllKysvX6LVVlI7yTSaINp6uFbtIN6WR1CtEZCOeVIt9kVK2NJ9jmws0OGjmNkXXgNasxczMIsz8H8cmFXCrJpd+YjOnllxXPYwTl1Qd2+yglgFBGRXwFgQ1zo4obDQUDQCEfeyvFYfTtLqvFImUdidxJP6YIOYIXQ1p/isxaSroAJaNODa56r+pEnaHbFYv37e8Ej1+txkytVyirmPZZPEz0716ruR1G4k3MCycdvFBhKnlI+oQVLELxfXD1BS+x+yCAxE1nEKwC0WDAa9ySvK/i/VGfP5tlM79zrEVZnU6t8Jyu6VLqyO5o17i59aaFeMVN9zLtrraLQSdDjK4vLbJd7vpxxNhBX1z7Zr6VgIaVt3hfwnRL6SiHltVpqUbrnIunt1xZP1qNAos2VyhKquZ7Er2I5HwuERpm+8/hWgq5Ca27FRefhWWhM+6Qssa3mYgmh4XOLIb4PQ66QZplazRqRW43r4O7z0jHu+1TPaOp8TDPsekOwbwv8q/UZKyRIJga2eWF9LfCfynIz54WuHuR2+4ya8IUc1JGzzhVYOFi12MI9b0sk3eOolxVXLHHdL2goYSFhuXwoPer9SFXfcrU88lI4dxnPotEsYCLey3TwLsCV3o757TI98oJ9cjM7wGsyeWDA6xWaysPEOd1wadr3vlu8d/7nrpZnN87t54dEo0WS1wltXnOBJOQvB81ap2Rhz6J835uUKwj7ymjlRhTyGU/3e1caz+PD+lwq4UWuVXdqVGdpQ250NBd9HLrPOei65uID3kPykU5aeTT/Ts+t4Iv13fWZupG/JdpJvj9+533Bf8Ugvjzka1aQT+6Vv7bD+7XVGdlPPe/OKypdwEHtR9j6feiyYaXOqzXsHBM6vYoFNl7AsfZWWthp3U6y7XCbRGhI3m74vT4sb/WL/MMDn/CVInb/SHSnexlIxmpeMpcly31N+zD+fqQSThYr4TItRjDjR8KJ9Hlf1scKhw83R2fxu6r9oeEoB9mKndU7dc1CDf11V4chcw7qODyRUcVOpHZjL+SgjpwTuVAediG1VxcF3U+8AlCWa7mf6OB7c726RGo8/t5bY+rHyHfH/jLC/oLxrQdJlZ35IMwz/B10gBYSryUIPJxl7weS9YdeV83RGb040BG/21Nzd4DFOA/xxN/Y9WKPEzt2MdMHgkfTnq17oCm5ikrsMEBLYeAoPgPwwguHYjqR2cw+8cLc8yeNx+fH8QxXePZ7cGomXXsDP5i7xvsmwyHnm7A4M4m8jn4EV+Jg4qhXWEWAZdmfVlyzsa7LMhQJmAsf7UhFiL3oGpJeSFcXcrwVCwiR7kV8dGpeXWt94/7LddtkWUNuQK4YrnVskQl1gXsdgGi4cZ8DoR2X5tGQZ6TJgsiDuTrpswpJuxmtkBV973lCsCJuy0peNyZIgDCc/cjNkIwV/14fdgTXCrYV2h7ZkS6f007Oj6a6roc2cnyGc7d5WZCQQ7f4F7p/zUYoNnWOkfKVU0Z5QO/KJO8S+1YzEG3Oc5qinSp+mEGex7L3FbN7H9kvGNlFeho/bAeWd8nlwA/byqYw7H68g7HQuD3YEKxPJzV14Dor+4Ms0YtaelaXGpx3sk4b1s+h3wGswQMr0QpN+9jLv/uHf5/Tv31qXgF4y+8OEu/Iz7tks1+K81H7fMUvb/0EoLk6wmksPTtEBGqarEjKkXDtYyE0HaVAXEuYfr+XTrmmEXMqAcDzyHUOibYmUw9pXnB1/L5MpvgT587N6DN56iXB4X0oNgvBWm/C5RrRrkvm0zWOSwsg361qWduSPMucGkgdw3ZLGOgPPHXzu5TbGRH4s2wrfOBApd7n2v12rCq8N5jmo77zp0JA5aJNlbVHwNcJJN9xYG1npHZfyBJ/rPRT10T20dV9u/qxcqGle/EzUmqv2L9mQs/xPThTDgmJLGWEaI0DNTRNo032fBp/yJgcBhyie97XX6dkr39qUyb9S/U7FQWR7ulDwGW0CxIh7QH0U8HsJG3nyAR9s90szvgGlG6QIl7vu/C8cBXm+hn/+NRgVTPgKe09F+0USmsgx9u7lvcjRWExXLQkLoJ9oP7TEnSKxAJ1HOYrIbB3vez9hnE/LugcYw+EIMMBytP87MD9O4CjxakHICqqs4e8/Lvf/j6VS9ebm1cAtiYkDtips0KIm8MZd1egnnWudmQShhz8wtvU4kxxiOxNC3Dgoa/AGZE+VQRZrOR1JikbqU5Wa1YOB/R8WKzGdEi38+i4ZpOVfRZnlGezT9XSYC7H6hpXqhN7REOsP5T+Uu57j7TyKrKUR3GX2uMzoqeAiK3MwqX1nAI+O9e6C6pZ8T5TBRztHHkihWpeHAU+/meH2HlNcLIDEGXya7ND/yEN7pv01J1HInJOwuxcS2glg8DBWVOoHcXxXhGoZDv7/V0dToZq6/9fsjn8/MEAO0Gt18MJoPeEGKyFVO9b50p/nHJJQPf4GlCEFvUGRENaUFhTpGqs8WwjT8qAVCPHj2bn1n60wt5zPViNd6zAWhWX7X93rHVP/bGr2+t8bOnDzsLCA8wP+7BkL1H/2GgduGy8h7bcuBxOd2QfPBL70JPxJNd0gJdLo58evoozCQbFOtqGrBUnA9NpBuflIscCdBsizwil3PrFxsSN+rGG47+Pv2pzTaa/J4uzbR+5BlMjgaNspoIoDafJYiU+SfJJymaymCFCiZA0K4dDv/MxPpYXllDfqq5XWUV5IDV0Z62qLPI6me5PjeeN1mKHC8lLKW15JXfqlT5SlitfytInLstfjZVyHOECz6kZwWK7Ys1fUJmA1OtZGOXa3tRqdgZrBgvUXaazfSYmhOcceWQFLEeuPaOWtWv/EXwmgxLiq4XqBf51V6Mlt00+vl9nIOs43Ml4kop7lfp2BPOkDlgUplZ+H8Tff/sxpvYQnwgT6SNlk9FBw2D+Z+vdPwNQA39LnxmgV65prfFyY0GXQMHX3Jyc1yScRr2o9Itgp8sLBzz+TIVLMR0xKVQp/ky/GUO8b5Sd/rr+XeUMi6fvswNVB7CinuuqaspzcFkHrnu8uw75smaYwNbx3wx4Gj5UB+h4fKNDMn3vD/397re/T7tPOqt46V7ije5cg2sqepLqc6loGoEznVHELogr01LXKJPyft5cv/Gy2GgSeSwDB376aoGbZWGaxnyyhz+b/L5SoKUuZZ50RY3kc1nJKYgjE38K1NfhJJrVimCWCBSlIDTyxNbKeFzvz5ePLxlO8HRXpp/xOuuRPlzH6on8aB2gdX7WrTkOWMjNMfOs7F0cHHAsE/Tbnh7ei7Fn6SOqleVbPgLPXh/d0VQN3cbepqvNFO8kRxI4L4eP4JMd8wLP9W5HMpFPZLUYPjc6MhvZg/WRW83zyqnb9kB5hoFXADLZ9LMAyL5z6O4C8dImPPecE0EfypXb/6GqurgYatqla3RqWXaZdJXcFd/KbiREmBBaHFCC31jmWogtyzfm8Ez37MCzA2d14F0cdgbFfoQa0uH0YY+o1OD33mNZwjurpaZbRuKXgGlyNi2toE0qboNd50zz1Hn/mYlHWMP9qj6TU3DiTFG3FS0fplCgN1fkKvx3ss6+r/RIDftStVEwL7DrKxbdKzrNROj5srO1Fn5nZ2soO1lTQrd7zMdfY12eHKsJWBo/ixV1RH+jjGIfPMIWsRHOEZ/jTI4gLDI8tZNH+EdiF2vM0IPYcB+6+yZl6B5/IkXd3SfIfOH4w6VZTWMHFnAUbXJVcxeeKcYkIU5ARh2XZSFVFS40s5XhTkSFLPpDOOgnYiUaTA6mc80e9IDWxan4eDlubQPzblbZnK7DpHKMt96l0nSRA98CBIVQF9KkcmovXs/7MzrQaf8ZsCdilPVzIuRRqItWZ1MpT83xdMcRui1rCHd9tHItSuM8Nc8OPDtwyw7ggfn58Mw9v+K4egUmE75C4Mepg+CMwwIDag2bLKFpYzO0oh5H7xNm60Jn7lwjUX+zXwHYfgn4Oxe4sV0//5gpt806E+v7xvnLa7HHZzd12z6dmsAXZ+qy0nhdMmpKXpgUukpEUfK6++k8na5OVUfOg1nInfdf/ZAZQUxjLrRRg8hEJK+tLo4a4st0kRns+BjrViKfK3c4yAQGn0GURDhJ3jKq79XG7OgkFkNLv12TA5D+zI9OoDVGr7Sj1HT4SBwpy7C7/qJCh7PkNikzGk1l8Hr5ZIaou3wsi8YUv4VYHPoAMHVsKTm3e+rb1G0qF/YvnqNuolkCANFzPdXDbhUWT61HXcSEBbDSnlwyl4nUCGzCpXOXITtIgZFZSbFQxkE4dl1YPapo/l0OVi1Oz7s4eA6Soua/6b88YzeAhVqwtV4B2F1ICjZBZPhA4t6Jw0U5fSTTiYkOMz0NwCn5rBw3SCGp8jRhypzsMA3dJPgReciEmR/J8ox9duDqDtBCrRZzO746/xN/vQN8kGFhHSs/JlYr4QjWUuxtll6TBSUfb6CFcLClFmywwZydhINQwYw3cDtryjLVmzWG2o9XAEqHth8DxrTwRNVH4+J78X2+PhS/2noWm865+xK0PvPb22kDDvYH65qZDXiuJVLCuRkZTc8Lm4ZC/OrLoP8iE1qRdiChbETJmT1ZaJydYcXKWAMODUYGH/lqDEVV4OyaBb2Ga/uZoyO5jsQeqeHqvP7sHGH+nmIXdhijvKvny0ib1JHd0wl/TJM+rkIjv/X/eM/jrZPZ/bzYs+L7l+Ygj+2nzI5c5u0x2TjmD/O2BRYcLkfPIGOCT8uEzT3B6jmn00FT+DocGitvpS+1WyCOHjiRb6NaK6fimR6Q23lzuK2ZCk+6xysjDEOaYtwFtl4p8Cph4cpsIWzZjFCA4UQVPU5RBsex+gOUMC4y7MFrAwIPLQDuHguWp9YvhGiQroZoP28P24Hn7OyPQe+5F9ftvw+7dE8kdvrMYzoeZFKoOvwRHymf0sBu6yKFI7AbLokNoYYOEu1yeVhPj8FUCeQ85d9LeIJuptDtFQAKSczBfhtgnAbHirLPvQh3zyVOPdCDY1k7fXTOdxtvYtXc6rO0xjgYThWiU3fRj/DpAvrKqRI0FLGlunAOLWXteUdNsPPWtxwcbJFTeITYVPYIoMPnaTq5A/YR8uREd4E7pTpaslNLfFRp6PhJzN8+ff1VwpKvm42wKzux3q5MZ/W5r2mf3ZWK+cLgogPL7MxbNBoc/YqoVXKaREyf5XFAb7E9AFmFgnxTe+XRG0RYcVt6ALvOT20mOuW4sbNYl8A//pqPWdEEhS7GoN/pF3/pSPWncZqCTvf4DMA45EwP1IG2Ygt0KZ+ZbwartGYmxvV9hKJcgrc2nt5htwBq/zjh2MPNAaMEOXfShzWcmy5Q69Pl2YFbdYD2K6xv7GA3Xus3TjfZVGLH7ZkMfU/uszU2kzYbrluDpaf1xzXXITO35fKxuhhnWVgmsJzxxMBmLUWQz+gb0qJzvEZYGLCYaXg6Adhxd4m0+QwsX7HoAIauoICn8b0TyLXQ30H1tllefRHV2QHCsnwFSGBExUhvb8MHTHDlPn4GrOuUbK330s3OiM7S65tc0Smim2VujzXWM4EDJ7iku0x0UW0B2mNeQwzjV7/m4R8lorceAtwOXHlazGivqADdscsiKwAb3ZjAPFgd71SdR6G99gk+OUgekXaURsrMQ55NoBgm1gc7INBYxNED77bHIUIfdrZ9PH+7VIRD8IjEHI4Ier60RuMHH4P4mIme6M5gKdEjEXtGsms+lkbydLrK2S0cXw/O8HFWqS7fh2WrfIzo9ifIH7H6cV+uYU66CxfsNTs4ScaRrfIRA81fGCtx2LfKuzco3+cj169sNunlcIPga/8zM958BqDH5nQdc58hejqLDiAT69hWVVdgrnL5weO85ebZwm3DXJ8144QTgSLmEbdwEU/HZwcerwO8xFl4PI63Z+QftcjqO9ye8G0yonCndsd0G4bIchsas3vMrH+wYxbsbZoQJKndLNra8zINU4i2igMClF5+99vfJ7fXPxI6BW452lSBjwF0zxF9Bk0W51y5i4MzLZj4/AzFN8jdcK2cadyneL1EZu+syOrUO8VEQFZixZDOdwn0e+XQDsQ58VoDAUjzQuHONYk274Xjpg6zr/KsfaMjujFLsMnK4c6Max+Ta3GlLMkn84xc4Stx6X4ILp0beVtX6nvrGzcewh/DxVVxYC6Yxi4ADeMHu860k/zUOcJUe7R0zbJvrdxFPyeiKoj+YBpNMNGIEm2T/8CPUdr9DhrJ0EpvHQ0sf338tI4bci+ezWJl13ore8dTq07SXFGd7F6HZm9lnkVjT93L0iFzQEWcKd0sc4TsPA8QkKFdGpQlsh9JnFvKXc5DAme3jifkJffqzXkkhSsxLK8k5OkXhDbxhe7pFQDaJsWm7Bf25lr7MZ6WerrWVg801wDYk+n6WcPWCKuITzjhfRxpCh6gCl5ixAV/t+vG8fIjCBGf29X8zPTswLMDSx147sjDtlGLPliXjj//iSPEPYcTcdDhHU3iwaYdDFd9ZjyvhaatayDIl/QtQPL8gNMkAvsgSfso2ejMgRTHrp/ViAl16uZfmaCSG3xc5eXXCnSubpe026yGaICMpmRBDZlcfcbctM7ieXd93QfudMXr69+nCchnzG/Omhn2vAK1B07rdPaOJq/bKTJORklTr/+pLBLqXcj12ngXlJ8k79GBi6/CBnfPbuX6+CDdmv33SCIJuyw3fByctX3z3AIl2zifUzhQasKRBJxemabRuj1ClbjJnkjZ5BM2NMSO9iGS1+qVpS8T1FDVj6E6OftE6zI4GD03UflbgMijod2stgJB9/gMQFFwMRTfQrAtLEgEKRPALL4iOCbRZFxIOs4x6aEpTQLcyP298CztAF+5LRa+30paryweubBWmSYJlGgWYdZfpnvKzw48O3BpB2j3tPZQmHh7kIaT6CDyVHj8UDkFe7rzGk9MJbZHKB1HsLKjrrXqLMxz9ViovD0X/KOj0cQac2uoU0PM1VZ9BqBt3Q6YpH3U+uWxPl+hAJ13gNKFvlg5fcYGPsZ5myaLPvBWO2iN7pv2uVSDaZLXn7hLw7zkSeHOe9SGCJMOIBsMotZiKpI/BiSguopzPb97TCzPFCcJuTb1s+k69UoSkOsOaPtT8+zA3TugH3c2Sg+5epv9VO7sjSnYWEaQfViDCma03JiJ5XBcf1Fdfeb2+iEaFHKETD/jkQYptnF6cuUwBRR4Pk9O8E6EeBt1QW331BzpkIjm628ScPVcJRJWfAQrEvfPABR7vqeyq8rJU8RVrs/Bh+tANfVL1b2HxTJXpaxoGEkO0n+phXNBa+mGhcyROOJNBei/I4DP2GcHHrID2FX1DovlP0VZg0yFn+t834PJQveWy3+otltVvAuSFvllPS1C/C0jyECC4nU1289Zf5nXlQn40K5WB7/mXw6rdSk9SscWQ5cUGf0zEsYbwWx2ee05EjLrLzH5UwFoAzVYnhNLWUbFP//A186BX4FcOaiY67NPrVFk5HfLcJeUV6uApz8jWMXxtcw9rJPxAq3V3qiaBB4QZyKD2wZqf76FPUtEex+vq408MOakRq8qaFkvGdCHti6jA9W6EqiWXriU9xzqb6Paml58m2FRn3MvV76Uz0GvUKyeWPoq+DkIdMB83DFWbwByc7lujnBs7D6C8F4c4Ym9RPOcAhkm0scTnXEIctwBx6guDuqlLf3RDZ7cBPlIJOUu1K4crR/kSv7iGILOOI+Ve9Se6QxJsUUT9NzpZN09yOn2hiCq1phrmmpdHcMn/outFnkZgYW1urYoNUdLaC/d+XKg+LMB8NlrSXNsfAZgax5813u5scJiwtYh+jS96w7sCytQBtbU4ZU1lRO0zBBen6ZHBmA3GklZD5EvuJVJCbZBXgAZhiAFJ5IEhrHnOzTpm+H5+Z6Izw7coQORdR3xAfW457ml3j4vH6aaQogJyEhKXWUTKIcWuPSZkiWZqcBTnE8v5xRWl4JQyfiTWbRGWtfk+MxePAvr8HtkatD+LUAv+5OON9KX7xCls5YtYg8M9o4C9n7l8yp5RXniXDyY71S3nfkBWO5A0zv/vBzW7TxPnI8eIDIX2rANBlPH4oFoL/yxEr7+XcrjXDsZ0YgnJySQTd9uS2GSOWuadIwuZwex8KyuXsy0AuHdvBJTyg23ZshUGz0nIoGrprwY0hZyVhzYTK7YrS76fnd940okppR1yHFNAH//fuVuOlxV0a9ydJ1tpZ7xSmPwrHxscLK0ni+ftmtFfxRhVAvNgrh21UYJXxY7Ppqt1uR4q7cdTM53WwFMkFNfjZvlafnz2neK83dYIMQfZ+OeFiXw8ftjxXb09QqhcuTjJstOEyI9RF4HpENsRkUcdvC6ohZGWqXc+kXH8fItxJ255WHo9arWGiN0Wg1kPHPgVcEoyyUwQiMEu3p63oaGXFbK5CkEMRLTYxU92c8B9Lw//6UBewXLzQDNhjEa/cceyoZRB3g42w0OfOR2oajZ0rgiClyOZZBJoUpoNVnrG6rkAB8WJA1SNv7SOpS7mMModkBqSUBqQJs0zU1rGoc7DB+Rk9UG2WPL57H1j9FtrM8LO4UyMV1I8xiFNyX7pCT9JpCHER92Pku4aPosWKrRMlFF6CG2ZxU4i3Ov7E5bZkt4TP9ggeQW9DyrTJrxe016pIS6G+kVALr2//bpLb0CABtdF91/+RelJEM+T6ijI/ngQ3GEFI+OnC9KHynHWWnP5irI2kTOFitpoEu8laZZuerJzBWF+DQNKREHquXAdf0tgz6zV6mnWKcGf/37N1rqxI0G6BVkhbwpnATOfDlRMhEh4Ab/bTgzawWgvSdAix6bEMMcWogbjHHQ0QyC7VtmeEaHc3LZ46avy+R6gYyte8Xu3DTHh50hcAgNZSk0RMbG/z0OZTdkvVzybYuqjs9G6oYmvGQdRtyuBkLzuLabD0jWMRn6469gy/50+wDufjcoUPJs+tCs9APN2EIl5+NoRP4gQ6dvEXp+byMIR33s4zM3R6aQcy3104W4eSWyJeuMZ62NgqMz9Llsr+v+OVtzUImk+9ddm9Ya31jGCuIhO8wLs2vxjJzzLM+IOMJ8tktn8G0xiP+lNLg/p2aZRy0RkgbkYqk6A6V0hrnrXEWOBhpZ0iD5SArEdhFIyeV0HUbET7SX1yEbSEmxMT3KkClyC6XADT5MVyJxBo0KN8ehG0L+Fv4UlAZ/EE1TBYZUclP4lWwXsjFrxC6wu66+ZUqzVVCi5Rs3kAUJdQRZ4lwhg9sRhohtCj8CeEWZy5hNXcCh6iw9OXRNswQA4rfxlEQjYlatdlyHVvodgAT0+sdcUX4RYLsYl9/Jur1rP7mUFwhsfN+SEySX5izcj1q2lvOkZYAU2OlYAI8rDfi2LpQxNZvV9pkouywKNvIR/j6Zva7sd12iQsPK0BAp7rnzVf+LhZVdRBMuVibCu8glv1gSrDpLsFdCN4O1Z1n6LkitpFcg8QQ0t5kONbiV+9r5oUb+zBPVk2qQMH5O8vQddP8QwikwF7MgGvZBNCjEaYs0cRNs8tU6D+87GvhmDdap7eJOs5xSXYQ5JSK3bromHJ6ywm6UdLi9XK2uA+mBs/yaNjKf05/wPrJQbjPFDsI5tYgEVurZRLEZJ9QmYZvH+vRUFZeDEPn113RPz/JpCwVlYLloUr3I22QXjQiKEnIYwkSGnlc7LNR9CvmFvFe34ji+LmpqVcwTkPCQB5MDhkOejCITTNEDAuMMYzWlYcg7cRAtTOIlhV4CysdNr9FynhvZC9tsa7zXoiQdMSdS/Y5lpyKYqGnH+2Y0qAvcVRoAh9RO6YdwHzu4aS+aQFv599gVnMCOim36IEHRCql5XzKVRiUEb04fggiWGzjIreV5a/245uZ3ABBApdDlfv7+H1Q2xopWN/wuICQkuEwkCtv46e9naBx46JyBdYt2/BmzG8hWR+DArQni+zfMqLUzbAv5S267ZTVJRA1UIKaVZxnv20P8kU8LGK8scR7KIOU+YcuD50W+wxXOVggngAMjQM99YFoGf4ZJQmTtVQGRgTHXVi5rz5J6K7ZHJ3cC3UlXIOjgc+jjRpwCHebhlODzL1bOwMJUEl4XLPTCc2f273KGr3RE8uy2q5vhbjAk6S9lcueM0PPQQHo4NdEWnL/+fSL4qr91inyawo1K5DqX348E97I20miIx9RklJF2oD6OMEjwAGZZo/Vub6LZbTuUYiEkNznk+mQWVt5MqFaXm9XnyTjdGiWwXPiQtxDjeQXyAoGzSMBWxuOLixbCaXG395LofVA57oo06WACnfHYtwfYkuzSW8bZNHZI1zKqvUHFsLPGX/T3zjWhdfrXP9FYfgaAhhwAgbZ6v6lRrh4xI0rUKfri9NyAqTy35zlF7+7Oj9wf5tYsPDlcaCDDIpbX1RRsA7JA4yFDZA+oxPx2oDOIoskS/SRUDVM4Z/qTxykmyEKZ53Jf5UOKSmUPuAUcBUzo7bjNYrkx2hDh7g7cVGaiNWwiwSpZ+gRktDngaD4NjcTGfU4qK57wkrr8KuI9Rxn+Qpgo9f27ylZI+V1UBsKR2Y/4PHDJcmakfITy9i1A21N/NIiwO50qXwxknXdaesmuA1vMwYIchIJ0/n2Xm1lvPr+Ur3JYhPQVX76q0c1o4ZyuDzZZnklH6mWeWGByy6bjAvdwDYpZyXBqSJoR4xoGPM31IIDQWJ73hClukbY3IRQ9yOtyFsnvIeZPGX39FaWmzyA1BF7MdzRmx0HVls+hbuje5zSkLjO3X6dvqgGfX6e7fN1lMyf/F/Eb6oSzLZHsIBOSfhvic1rw3HLnd3O+bMi5q5/01aAtp7hL6d4+fU/QgnlhkKyfslWEkFjsuzYTs2aE5jFFMB8aoJDP+ck26wucNe+WPr2LlTCtK3ngVl31R9OwLVn5HtXloVUR+2pBRGtjX4Nm9G2NVq3eWYY+PT4ucVqtYVNQGFSnKpKwPlv25OkkTSRkQIlxpSB4zvZcwmyyQOs+plAVEZJwW+OzFtWp5ZFUkdkH30h728rkrLW2S8Zljrpkg2skE5N9yWAFke7xaFEUnTooWMZ3PE5TRfIQU4fsaVQK0C1zlZz3vL/hbN+zTCc3FuGzD06LLjCh3+g97eEknLbnAbRAX8B9CjLIQx/m9n5kKeHsqvOO0ZIfvRGrDMFHJkTV0I86wDDJUYOMwsf2IWZyAFe4GgGl3HFG5UGhB6IV3IdQGF0+uTa0Pdj/dUrrkdP1IpWznHSxjvN0+ncbQH07fZYeqbGSy3yh/Qj9CgAd9ul3ADqL4Oi3ABGkhuVrDESPrH2SigxwDl7rZVTmwBoWmJXPTVrBjREcwc/rBDamcqbYqOeGKKFL/hT8hg3PHTrcWB9kGJz9OFu0F4ucG44hgXSb34Czc9JffE3CmndLL/mYPqIe5VMVF+uHgLtQbIidmqmZdUqlVwYSQp9kxGTXJjxKbbKi3b3kK/dVQpAnFQuVuR5smOyKcYPL1jp2dpSwgS8jm1zFZKiLub1ndz6mkYdzbG/j8xix6nWwru+iknlG4mf5W5i66Zan1luE6bhBsPi0GPMkjeXfIA8pqeNSA3D5kAtBURZh8MT3/CDE8jyX8RX9WcPUUdy6Ycm36dWQRsDhMFNqCmFgm/NtiOkTd/oVgObZP4XxX4Ds0MWqRtAbYnSO5eOYYx6adtOVZngs2+2iiTbfpMxKEnTt0vqBZWoIaj+xAwwlka3Od3s75dxFWFDeJKlIsrWJ7rhhC6yPh9yEAErkQpthWwRfiBHtSj4c3wZsY7quk3zwZ/gM1duntIufzEkyMWIN8mBL7qxv5ITETixzMGuS34Fb86gGJJm3YDdNLWrrftLdgrmFXs7ALfLVc35uRt12relmvH0TujQsJaqQJKUsa5Syj0bWiLMF8r701C78DWn/OD3ZW9HUTMMX/QrA7l4f0MtnAKRdyvpsTFpZbjiwfl/ogeuaFgijNcIOng3x8CZQwlog8jqQ9J+VndQOVGgW6g5TIZTLKmeYCw7Hr13xtRwn47mmYEY0Zzgdkc5zkxlTNh98UGPkMxVDSue2i9DA9nRYAciNgU62R3jdTry+x7wmZFHchqYBUr/5I37EE4EUAsduUkmgkfe8vUiJCZnCG0cgMGw6G6EzmfLhadabAsFZ0GaMMFiJapb1SIR7n7SxgyTAWObyxq7kUR/DSTF1/AmlqJ2CR8s6KI2cuuSkav5nNXaKkna+VqPmUVetG9j4kIPsnrQiljQa5Nq6bo4uO0DJZRMaLvJx1vzskIgBMl5pabIIr7E4Hbt9muv8qSuIdN98C5Cuwmmkdr6VphSQ8g0JSmcQhGYY6FQTjKVEQU+diwI1c+12UAN6yyQPZg+Gcx/QE+7Mg9P2q0NRXBoLfhSs5HyX2qdIRgrp+XBxJNwkYY/EzVPTM1T56d4+p6SVLUmtkmM7Sge6vpuR97Q9vKRLqRkiS8WStDDBR3ommZ+Ls8A4jiDRHTfbxJQqF0muMjwHsgPL3e8G7gtHrBSZjhy6gdLnoeUDy4oLb7rEehTezaD7Bk0T+9CtO4lctz9HsD9oD/EKQGlMWnNlEe1n/Jt2c5o+jyngfJ/werepFhea4mGoYG7vp/xLGtOVVAfWYgIk532ZFBi50r+2Chk5MVdXCMCNt9wH1kSFjBy50hwFHPktrxzqQzfWn74RHdMuc/FesK+i0YyYuOXRjhywMOTWidKmnQzbwqxkdRz9SMKbwTDPNloWo2vgRII7DY6Erfjsi1gsByGuYDYxjAb9+iGjwc3DDW0vI2tzSuiQHaEk47afBhRNfd9+P1JtFaMmr7DsImftPq8UCEJM0f73C+34nccgYdxEPpJoE2sEUdadKTT1BaHBimKZnsbpVsf+SIT90f+lF5lLZwkSdtycx3QnSpoWjyrh4zMe8fG8BR2gnsjmg8xsc1JjJQcpZ8TFukRrjiMIsCIqnsUQuve71KxPB5EnwvFZNo36lmiOfFJy8U1uigsWELb7jkzIeJVB+jdd2VrYaGXAnLzhzQV1vJkQCfjrOGWVn5FxrHDoCUT++c5s9VOzmyV0w6FkMojtelqwP5q+WSHBGb+iS01qOWuN6YrsRzAl1SM4o1hqg5vKNY7AI3YicPJUAI5BWdgOKIkU6XA5vGz5kJYtfd47UG2HXm579lo3P6KJqOaCiRYhPcUvcrqHzNtARvId3CoGtq9wE6LtXyxTziVo+X5c7jJ0CZxNgdlCtIyV+oJ9zj21HF2/be/PIX8uStMBOSRZTkckrwyP+H8Mn9kuWVVft+CtjEV/uAKaeG+5vPzut79PawPv4U6S9IactDBAOLzNZ3Xda8+Hy90fleJQW31GWYzDbnyF3ojY1YjlwN0Qkzi1dLfQus4ysCtbaF3neymt0hry29Wd/MpP894+8uS5IKEJ9OuCv8XBj+1bxVUNEONt379olzlErh+UJP17bmDffJq2bXb59vd9xo7XUl0JA/Pt3ZY06PXY+MZ664oL64GVv1Ytp8lZ6PcaUWRS5bLwLZnf/i4p6Lv8uQXpLUFlZeRfS/j0+ufks912lE+NlZ5sZw5vr38q8YihUcqYv/u/WL79KtnSbwhAkz0T88I2K8omhafbnjG5lluN8C3/7sEXIOfA/bcq4Vm+aDTpRWyBq+65q5X204u/HrIVvzKRE1BnxHfIJCj+2WnRzzrFeJSLa92AJ7ethxrLXipjfQW3Yw6rcPzJ7t1HYQANyCDcyGnFNo1yHknRNwM+qrbWhkVvgCuO29qzzXVGAbxPsIC8GPJWk7E0i4VbcDH91pne43IM4KgXNUrfrmhFuwZ01kXNItnt0RPRAgNibgt9BoBGskPCL7GVpkX2VRjhNRkq83kDJj5M1zSgoQDCjNZYh8PlQEJGLPMHEyujb+1GHeHWBbyx0pm4phvcwxszPDHdfUu4SXYk0akwmZeuVp10nzrPtnu1UolKl77lDcNNiTtRmXROLwfg22t2rXCVoJDf2lzlWFvi93R4qSHZoUvb4iWA0ycM6Fl6ORRtPrtjkTaPZsiQm1kAT4oFeDKscs8Yun+pZ7lEOB+myjBV8tIKnb9xu8uQi5ZChAn54ybrYmUx7vcwSefdVksRnzri44xk7ZCbljbDj1P5NZXwqmuEa7I9HiqVLZdUJkiK3I3tMwCbC77phw6Jva/8URhLlTYozXsHMUNLwCkI4A0m6YewDSsQkNcnpAzrbbaYmI1/vgLhX7MJnYOWKxlUte5VvK6Ui37H9A/xiEVPKt+qqztxznSnkvM6wbZLqJvLweyCeMoyjwlTyLO16BRd5tptQXMdsiaTc3V+G1h7nqc5c3qJVYEr92XJmYSxLsnMQnGtD8XCTNgY4SUGYSmhN7rP3+YjchVWm2rjmU9lkkzmdEtvEcqvcGCIbbJzXcJAOrptkULvqXc3RO/j7RBAipSrOsERTisiM1QpC1o59mLMrUpE9mVTnC+6FxxAGGyvJoBjiP8ZgKZitKVRnjI0J4jQrayib6dw8EDqx4UuW148iXLxdzC3V8jb31x3Ij6gqV3kt5zTyXbaj7nd5dD5DMD2qileN8aqzqElnu7x2jcfWkkDY3GZ5HyCOw5JC0BWYKSUiM8CpVNCGm40bDScxeoAO0hhylkGVrJFpXI6OohTdZoDEjfhu1JvvMYV9HcZQy1BV95jb/aVCPb9hScrI5n+yA9KenKM58d4hxDi923yphH+Ssx+f8MJT8/kt3SSESnlCxLpef8L3TbPEkMuXMXuXvDgLEdSXq+RWDAQC+twWySjBiHRC0Rx7GEWcwBEldmyMAcx6T2VBS2azHDAndsxxfJAwm6orLq7MKRDF+GptDpw14m1SM3qV+e/KZ5gyu8A0GE4gQKY3LYMdFcNPKL2+coWtWF6GPvByPXqG338pvYuhI/QDTmilK8qSJkxHc4WVSeEYUmwwskUuZYgoax5PwuHczWlcV6qBSYWOMQSnPKtkCa75ebrOS+jSc6QpY+0amTugDZ9GM3bZ2rVy/7e8fML46k4BzrDTWEKZ1zLJyKkE8+WcRDmhZGIlifQEdIJbNtHMu4WzU/GIxgzPiVZioFcUc9QqeisZYek2W+5E4lhrd4carx6tGNA6gIUJ7wGQS4+RnGP3FucI7Ef3gdt5n7Tox5p8PnD2ceLSK8kppQp1l0WxXzeqoiwZZ+mS6xnzuTAPWRrXKBY/dihNRLQt0pPSz6OYCFrfZXrga/xa+ZhDa+FUQSvYayYHLcF02MrPiVg7g2IGaV4EPtWlc2GW2G7PIQFhQzLeQiu9yaBOZ2d2dnezvpbXRniUCHkgz8CGfpbiT6QfnZu71Z6maxyHyGSLpnj2WcW8N7LXHF6Ywrp8Ec+Rd4umcuuSLlOShAZl7ESUDl32C+4Z2UdOTvqcmAlSDAmD8mh8CNjfpEgO6XipY2c8LdBMECBVIpkqEKKZ7nfIrhDhUmxL993qfho3Cff7QNY9ZQstOvyPhCnu06J7BL6IzWXl/9M8A46ML9AuxH0CsBvf5/Kff1jZd8GdFftDJXPSpdG71RDNiz6Fn90JteQa66pM3J1dljnaBBqY3/UXFcgJwe/D+Fq+62oD1C6UhcyGRcqHWIuO+geOlBoCPG3OoPYziyI9bNQfkonEByGQ9OQfIPQqaXx6A3XonpIUV2VUfcK7zak73u5+63l9kbvhKT5PfI6Q1mN5d6rMaVK9v29My+f0sWYt+9v+ar8y9sLfZz3e34JgHypb/k5e3pDUHpmnG8JY9NuKqBu27eEBJ/dvxzMd0/4kD6deeRlSZjIUxIhvGzl0k01EEA6j9jf2pNU6QZuxX3L+PLymepK7jkUfikgn/gQZ5KBCPbJob4BfNNVA8AkS8arw+wRnBNStXrtgKHlLJxhonMc2n0hhHqwxr3pgWx4dNu/pTCvYopLcxb7NZ7s2G5oSZ52Ez2c6IyIijBB0+CJ2iNRjs+ZHXDSnLdnuUnubAzN++SMuyWFZ4/XynYQTqglmO7zowsr2pSIabUrY6LBTPz4Qs73WrFeh7zCJhBjEQ52MpDhXbqg/Fs2wZqItfadi7bG4YeOognY52CXjvQkP5WOACBdZgAxP9nH1Xh62pv+0vPpz5D42Wx6zpxfLsiJcnjOJvLmi+bpuTxuNMxiGe/k9j2HThMYKvmlJPk5ODUoyemPhP0v61MI581sm36WM5Pc5ZQt/U/IaZPudk5pUE5Wqhp3lxRbbik15AxZ1OkeeqiVUTpWco7aICvDc3BdB9DvSNcbHxqyhoVlnvFVspzixEBZr+zDcor3Vf5ymR80cGb2eOmwgKYkjPQtQNyiGjSfr6TvnNnVSaJ3DaW7+St5Owwn7AkbyfmzpQh+04EmfwShCbl0aLEd8rQCme0QgT0fTaDSQB7CsFLNf632JpE+49canfpxNB2283vco5RjvLbQqbHDuJnYnkfG168PlN8ooBB+2p3DeYFWYG9ff0XPft/S9+LzLS/i/J36b1/S92R/+f7rz1++fP/yp8+fX1/evtFT4reff5XgP/85LfvkTs+u0y3vBnQQppcOvhMoxb4lhvie+7f8iwHklJ90p2zwp6AE+ekbfX8X+fwlPf//OX9bf5KTU/al++KfpCwnGz1Vf3vJ/m9f/kyx2ZBOYJJPGpTC9+/spzMFrCucnlCOHJRhk3uGRS3JkhSkpn9wy6qkpuuI4Jm6t+XJ6m2TrPSNZOIbTsTs7I4Jr6wWkE1hyLV7VVJsFaWQuGeVQA06OGLf7FgzgqVX8KYC07GGsxZFVMostKzEzLemZmwhNG7NEHPeZFmuogE3h2IeTZ+IIeM43wcYwSCfpvxglOl2oLpB5xXywN+kOGlQeWX8CRxcfJlLyiVvePbkHpKDSiTd0+8A7DfopftukxL5jZ1kwGPIpezHYLPK4j12frXWThyXD4G2N5jWG6TolPpUrXcgeIgaTyx7sNCsOKEXdKt1WVzyU+bt0AkduaW//PT508vnzz//y8//9//b//Wv/9V/+vv/zW9+/vlnelPQ29f/8OXLl88//c+fP6eL7bT9/OkzbV8+f+FnrjTIT6bzU+hvv0y5v/wHIkPPvinoLV3DoXSkTk+/0xP35PP29uWf0htyvr6m2C//cybyOb0inJ6rp8vyKYBu6fk4ZS267/85PYP+8s/Eg7DSU/Xv6d1K2eVzehcTccH7fFKJpE+IOEcgLxK+p6rS9SMafvv5W6KY9mGyfP7lTz9lfhRG4wxLfnzbCPF4UkAPEqvEi29Q8/Ap3LkDmKAgCTGPwYjkNpViAvfp+uzAO+pAOspWJwA192/yKLmbcCWsnIXs+qGkjrz9iMSKrqb8XbLKKzp976KNHAgkZykXjJTXx2nebU+BhENRU99tzOmkoJGlVcqapH4PPXoooyr5S66Unhc8xq07F3Fqg2LjQENPcb6uV6bWmHgCx/QxDJFeRXw6bE9dDxEORonz6vRssrml/bhTY+MVHCZ82u3UrZM3+5Dv7r5L6dd26das13y1Pj3p/vxCz/P/5n/9f/yP/5f/7//n/00IX799+/L5U/pcAF13pyfLeafNZwFf0pPsly9FnzBJTtjpFIBWFz11pufd3+mzDS/ppdoUS8/3X16+pffZJ6f8VBxM3ggr+6TTkBS1McwICTnl/UIfkEgnAumWfBKfZEFe0hDkl8/pG5vyqUg6l8kV5ZB8fgNP5E3+34kdnSh8y7Sp9C+vrz99+j/9H/6P/9v/3X/z9vZz5pkLzinTZuteZgfmSYu2CGtS5pt+xWYz5FmjtKgmKXdpc5F38VUU95T4Wu7giH2zY80Qll7jVxp1LFrDWYsiJpgIua3ojQZyHuOPoRbqWhXyWCflThYxj5tV9b8TpVUZh2qnm7t4q0irPwPOFYY70NW57tI46LxCHvhL6COyyivBTuCQ8U/rvyQXkdMCck4AIhCTPsHFGnSbTL7u3uxp8qAD0zq0HWkhP1pz7AqelmcHHrYDcic2SeZ90NoRzahi6Abm3Zc2yUhPgWmbnhrjqfrXb/R8/e9+9V//L/+/v3z99vUX6So8PSlPzoVIuoSOCNpmCHoi/j09vU9w6Wl5vnCenl7nUwLSJ/+cDk6JXM5K8enyfR7nJ/lJyowQgcAs5wv2dN2eAgEIVALMyJQqPaX/SmiJcuKTThaynDWJX8qVtEmfnGibiNALBnSS8uX79++ff/nLv/ryhV4BSE/QyZDomDe2QkCBpvdu4DhSJZn+J2K5Jdjuvk/pRh1IE4HpKNsbJA4vmRtwuVGKtNs/bz9UB8ZTvnoCsHb2g119zCpfU4dzcL4iR2/JWcpWCn1lnaIa8svX/hvCGocS6Q402cFcvheQziYpSqNVNbrntbpqxFr6CnlpEJkLHxht0e3qRjWd7/pI5Q7r9m3iPN7Fkam1HOlVxKdCzleh4q+5WZVK/TSHitCJAz3brNkntpsvP8vtWo4oC2pZsvS2+vSUmLh8/vbt5+/fvr99e/vFL3757Z+/0ZNienZMxnSKQCnzs/v01DnLpEmR+ckrvSCQlLmefAU+P9t+oRf66Kn2l/yE+0vOmy/Vb2+CT8/F0+X8jJC3+cNd9FweT81TFmAiffLEW4pS5kIqpc1P6JNrjqV34uewxI6u7GdS5LXXkfzpSX8uO50AZD50R69QfP5M/nQCkOFTFvUuoEwqwaVbKiDnyvfYUD6o0zAXQKzRGuFVxM01NwdxVXxxu/u9uE4s97ITeIljEU/VCbD3gBg86glK+woRymVRHuukHAIU/Q/595yCa1Zzw56x6cUa6yXZdXIFAqHp58GFJPH3rB9X0vOCWq0+WP6dDomVkT4lRa82y0+gpQB6SLBv+0Tuku0dtkTAIj4yYbMEpQlyBHAIQlCEE4HSBG6soVoi5dyYVS/dOTTjk3JOvl4l5+reC89zqz4PjVcEdlkeUgYpdxMipGvylZxLp8gamlR6Ik/Pf/Gsnp5b54vd6RWA9B4aencNveH/F798pTfHkCU90c5k07N0uqi/PaPNT8WTCQK9nyY9g02Y6ckuReS77JBPLdJz9PSkOv1lvGzK4axJUdmaYNONhikjYcKUvpsUPpSFleRIzMlEmpfsX+ILSYxxwpCJpU8xJLap4nSGk+JTQ1JOusvnNCllSpMrTiRYyG7ZmXzyX4rbRM6dhAyZBNZuYeIum2hDfLKn4yqinmK8Aw/cUay5eCkP63nHQmh6dXbSaOXDdu8jE2umoRmmyp1XAPiMMLYPW+crur8dGsqJfGJpt8juQpSoEcAGRF5ZJyjwacg3ITJjV8Z19E+z5/08F11QoZw4OxRREJ1r/Kn2zLnbhAZJ4gRWBVoI4ApJx5KG/OSVHs7F89IBqlD3ecR7ImGUmLV7dHSk890cw0K6UX2lv37yzMb5W56Wvk/J1lbzjisU+X3bdoS2UPP0Hr91tPv9MBIiPT2dO/zI6FYuVF6+/So9kX39CznQc+mUgp7ifv5E1/vp2f3Xn7/RZ3vpw7HpWW+6Gv76/dvPn77Qm+/pfUGkQQcSFoWk+HQjS3rumyLof1aSSB8STtfOUUR+s01SprBcFLJu3ik0O+bzEBplQNIlQLJl8umTvElOvkmgW6aTqdIgMcjp0wkM2emZfXHCtf4MRZtMPUflU5scll4EIPjvr/T2JzoXoHpSKgLJbzxKQWlMCtSZgDOF7AVKSZeJpm0WeZvGzi0jlZpKBkA5UQdM1dqO44jHi7P2skFy/4gxCM7mxT03At366BnTjxRtDK0TUWNnXoRVx05ozsIxUuYln2zbWp75bQSOTfFijaWhfZMrkJOSu/yMgeytjdS3SPzNw++hsJ48jwK5wxVWGIzudfh0gPqqTh/6jgOt+P601jO/XNsqq3G1a1WDym1qcBJMypkfBTbB51Ct9Z6rXMqNHVmwbcg7UQ2IHAJKarpy47aWq4tMyqYQy62rPxLbAxxOzh40bELTtD1SSEMQ4XtrMcL/1pzeZb6JRVXXtxDohZTFRj4kpme0+XkqPcF9pa/8/PLyE13z//L67es/k+HLK70lnh5X3j7/9PkrfVkOOaVn+Pk9M6TNX56zPdSnZ9wpLT1Bzk+ZaZDfMrS5UR6Ky8HbE1vISE+hmXLiBqD0PDtLKAU0ScaT+5SLbskJz8+LdyaX6spqOi3ILvTaAYUmXkSCbNtpDWElkU5P0keGv7x9o68A+vLT60/fPn1NmV4+09ueqBn0UeXEPOVK5xkJKrEkCWSTZbuxFtbstZtyYHG17pMTkiUPhGTWyGmFPfUP1AFeDw/E6eZU8t4xl5X6FtpH5lCf3u+mA/SeoPz9yvU3KG/0m3MaHCjlIbYu0zxf6Z1FJbCsb66y15CdUXNGRTjQHL+C20lWVNhJaIsdBkIxevd8fZqduN74MSt5NnPBcMeEphDmJlEbHzaRnm7dKiSOuSoYyBZ0rNbIXEDCdQjtqfP4awYF6iipaVajNK3IeY/Y8p474yeiWQtioWDjGmE1d7jy7YKrWXhTmire+n4Y65UB6wrK9q7KPxM4DgxbFvpef3qKyt/3n594pyfMr+RJl7l/Tc9oP7/+Jb/B/dNPP/3il7/85devX396pbf9vP2XT//lX/7lPxNO+urPz/QiwPeXb7+mZ8tvtFbT++Fz89MKSU+O6cJ8wqbL8z//XXonzusf0qV6epaennZ/TXq6UI9L8Nk/+ZAllUlR6bUF0rx9/bfElWLpWzjzB3BhJRzqfJbTe3KSTLj5oE1R9E79r/nHB/DMnqzpij7lJWTCSVnIO32q5HP+LiZa2PTln/Ten6THE3o61fnFL37x00+v5P397a+/fvsvKZKa9PlLev0jM/xGHyxO50CUMZ8JEYetC+l0IzUBz19yV4QiG5EmaZNTcsU8Zg3eCytA6OtW6bcRKD1+SSC1CSg5lBF+k5TV+gQcNYosxLM8HnV8sqelBwy2/uqVnpZcIfQef63AXZ9r2Ye1VOHXJhr5VjzuRx7RgAP4SN8kkYi/fOzo+LsdkLkG8gEc2UkpOxlprfuPa07sQZPMS70lJp3bBatRrqXFebRY+XPnW3PxHT6dpqyp6IhT9dh6/FLv++d0dJzFW4AqHDb3hHScz0fGnvFEnc9ogUHbrZrrEJDD4Un0ZEgzrLEPjWSWQ0DPYNGB6+ZLJDkq8pI7CnRu/DtYkYc65x95Si/zCkrPMfu5apD01pd8/Zw+5Pr1n79+//rtb/728+vrL768fvn689dPv0zHcbry/y/ffqY3An37/ukbfQCAkOnp/JfX9KyYnsWnd8mQDx2uc8J0bZ0+3Uts8ruIPv2U9K/0ywD0SJYv0qf47el7elq/+VMU/WoYQaXzhPR0Osm/SPJrRk6fG6bI9IQ+PddPz4LTaQax257WZzLpIYBCE2bOlZzTX25H0qYR8aL3L1GO15/yKwdUUfogctq+faOTnr/+q7/6+vXtb/7mr8n1OxH89NO3r1//p//pf/qP/+E/0EnRv/rbv/lX/+pvf/lXdDqQf6aAupc6T5kTqWoSsjJpKKlxg4XtiM9DhtqM6ewp4Se9cEu4NGQEI89T7XcAHcXW97ytFVP7eLymu9A0GGvZX7Xwmc70DLh/Bw4tWMw7HVB/99/9Y3Ng6yyYXZWkfXSkCREUXSLOg+W5ZpCDhmoCfT78/jbg+M6MzFGsOSLo1xOGaMOqCYFrkfjMnBDIwcLhWMlEXquQsvSpZQ2TEko+tf9gZLGVYTolW+OvIXDIOUK+DsHXTpy2n5PufaFgIZqcYcbMr3VuWzXbnZkIBvbq5Wp05Jsun9M18F/+4q/+h//h//w//r/+n3/9139FT6zpae3PP39NT/fT8+n0jp/vn75/+/r99afX9Ctgby//zX/zv//rv/pbOivIvvRM+Wt+e31+Qk/7ZCZBmxRNG0qbn5KXPRY0SJ+elOcn37TNXqmGhiSBkSY/3c84tPulVxwQkG0Uk+9T1px7R0gRyZ9OFbZbOkXIN0qdcIqemKafMUufUvj6pz/+mV4BICbUBPodgK/5/Ifivrz88m/+5l/99b/667/913/zt//Vv/m7f/u3v/l7+oFkOl+hf8Sw5AXolqck2DMVDdrEo9yKfZSlHWOXGpc0dI0d/7upYkddl551TdQNus5oVWRNCT9+BSkNjvmT3bDYBskkt8mMDjK1iHYKq1Gd/cXBUiYLlh0P4jNOUDih88FMtdst85Zcgdbq6clBtMGqcD8EXFe4jVIowrvmc5SC3zmAhIJWEHL3phvVdSNl3BMIs/5W3rvrqZCme1eWBuwm4d17cDsCutu3y/2YmcarjQ8b08smPztOZTOE0YMuMuaKtyW0KID5Pb2rh7725k9/+MN//I//8V/+Cz2/T++fyc70nJge7/OT7/ylOHQO8PmNfrXr0z//p3/+2//qv6Yn1t+//5yeGP9EV+7zdX06DAEeb87BCQCdYuSr+rgSj2M8PflP/8hbnC+kwfY8uJBE5eLQTiGZ+OaJFzES2xRB/5l8ljc2JBeXwi+N6byhnA/kXxOgrzj6/jOd53z5iT4EQWdHr/SqBL0l6Bu9K+nnzy/0vqCffvolvTry+evXf/6nf/r5X/75f/03/+Zf/81/9VfpFCnVhvcYZcxUFGnEDRSELhWw2eme4oWtxGWf4pjui1wcnvdtB1IvsRhaiz2mALqV2bD9npYzO4Cud1c0TMvJ/Jk8CL7M6hkY7QAd5uiXgOmdkTSR9vuEFFpaSt3lpDwvUNB7qvxlt5AzAqhfc4hcY9BRy1e1qS75nsVImXSmSPMUfxeaxGfmTnOsRSAzSllxdrCTb/r+k97DtcLZFNtVnL/kYeD9eRYO1U6l3eGWOWOFyPc1bkwOXxPClQOgufNyh9LHKTurTc+S1gyA+fkgR7JgRGLRspcQ0mpNb4zZroXjjTT0PDW9U5+eT9Oz3q//8jNZX19f6eltvviyXVJPl7fz83Ra9Pkd9OkNNJ++0osDX+kZ63f6sOy3/5pc317/iZ9Jf/r6rxPq6z8RzfSsON3y83zI3/5t0r7+Ux7tF/KJTXEm910uT/dxapBKBAydUWQxnz/g+PDt71KiL/9E+PSsPvcvPbtP/vQ/haZb/oRDHmSg1JfsnUz5gwPpFY/kmF40oPcJ0ecASKAn/b/45S/odCidG3z+/PWf//VPP718+uW3//Sff6YXBJCLtvRjCaVLKdOeFdkzbsJOtzQfuOVwEtmJBMQKBMQiiCMLwru5r/Zu67hh6VGle/zcOlN+Ub5quNOk3PBy/dLx65iqijr2VsWPX63BGLM/r4jK0e1G5ZkHFVu/zzoYmsmMFozUi2We1NFZkxCuLJ8RDV5RcXFMY+6k/3s1VedNoPMNt8wrcuEQtpWjP6u2Hcd6M5106T8+A7DSEIo+dIT04xO3+nYoWYECCFLzthif9zfugL8EQKZa4rfhp9febfI+s3gdqPb/yMrxwMoUl3vPl2zSTcoclpT0TJSeR6enuelKdXrXT3rKmZ6f0pbUZKJ3sdDnfcmXiqEBmdJz9rRN74shgd4CRN44CfhMV2foHfOkyk+1EUV4gkD6hGw+hyAEUCjG7JUS0K3aZresztRISnm3sPwcOZ0WgFRyk5Y8JEUqTOCQUxqlmCyVtFtoUScoakH6eDG1AoVnf3o2n5T04Qf6NbBfvNKHon/xV39Fb/9/+cUv/k161eTLf0zv/Pn88v0rvUiSOplYpfiNedakLOmWkmyEoFBbeEh1Zi4VkLWj9vkBNbpb0FC75m5n9PcMjDnW7917epree8Efmf/iZG47LN3RY8zEtf/zWqkPIsDG/swHlMSQDOIcGg4+EVxj+JKvBMur2hwF/AQukNkaFPiaQdAfbpqPPG+egiJn/2oKnSnuC+RApWClz+nRxgOc4wBproaJLr9yr3soNOZcCB+/BBSpV8gWFbkm5OYSVw58IpsVFWEwGysTnINT7fnVypGdl7Lk0Mg5Pj9tbQz94Wj5gQ4xTNez6aO7+Rly+u5O/JRt+hxt/hQt2ej3fdMX/NDz4Px0OPnj6XByIT+8XJAuXL99ou/D/Dl9LoDEL/8LPd/dnvSmTry9fPkP6Vp6CkZn0pP3/FQ4Jf//s/envbIsXX4fVjlU1Z7POXd4xubzdJPNFilaEi2RsgGaokC/FWCAgGHoQ9nv/A1sAgZEwC8EgTAMG6Jhgm1aJpuSusXm1P10P+O9555xTzWlf/+1MqMix8qqXfsM957c52RFRqxYU0Rl/VdkRGTCCL2UcsXDmegCueBvpuBz1vvDkslUm/zwKT5EIRU3eLmDTKq482OB3PyN9hu1ICDwdx2MxqilceAk6VJMoB+WkoVnKM8Z3lcmgjeM6ReT5W//zu/8tb/yV5kNxLZEab5Os/l0lq1Xk5evX9pKYX9MkieZMcF+HiZgkARzwBcC2MkE8oLZKqx0tU/unF8oS/sylUf1rMM4WR7Vdbg/PD3mLA8jhKY59Kj14cFv9CgJffeNvvxRTEXUe6ca4ECr+z5Lqj9Ap6KaH3bQ7i5ut2Mn/11KdQjq5LOlG+/nEW29Q9ZWandq27u7y0fl9ukQI6KQPorEUi3z5Lb/jFJ2HNGg591eZzReep+XxilkVINatfm0kbzuQl0duvwu6Ibc8QSg/U2RrGZu87qtT29Ol0olcVxEGiHx8QCZMZtP6b09ELcLldtNszdHVRjZnkeSdpCK77hS7OfvkNlDXq46SeyaIfqRZY1bS2etETQ2BC+kLCgrVGv3LEFqjWp7LjQbBvhBp4K/SbJeF+zuw0QXXVoVELHAuM2TEZ1pY+t92diHjXocTEtK+aURhcNzQd3GIU/p3q4CpbeH4eNSolGRNiWNrk6rfOehs9JWbsBaKTPWPo0KRhH5tmIQTqnN4YcBOxEJ8rP6Oc+nZNpTES2Jvrq4+NEPfwS+11sCeE1AkROqUPFXv/gFmwHNT04Xy4Uek0zWd3cLJF5dXJWesMhFDjR5yODTHcO5ygy6eMLL2+mSTBVjkkbtgUuXN0DwrSzCavf1YU47zCdB6M7q381G2emWhxB4Q/c59l12g4dY8V2p61/OmrXc1zsCgIokij+8LZ1DPbIJvwdVLfus01hWxM1JG7PhnbkLCl2qTFQxdMivCWtdjI/ShscwHjI231KqNyPEyr0U/QXjLe2YU16xdc9XV72f8fi6N1Mv6WBBpfPIxtw9DhR6zg6OrR44qGZXYdUPt2VRTmXXtrBMRTStsqGMQ5x8qKxOPXot6qQms8fD4/nU7xtxx7Q0GBEkarPFYxVi/nE6ponStrEm180xWngbVdvvjXwujYb9/jmy54YwpWCxZMpKdnJ5m2XTjDurprqIlv1/gN688gosL7Ar7Ay2BK+aTAb5bVK7OGCcpGkUe7O8hKE4cF2CcQfZku4Y10qNolRexJD72atWOaUwu3Qa2ssUqddN1k8kQKsLYCC7rFyPDkh7LFIxKT+dQkytWLVIra9UN4WPHxixkkp605k975ALAPS8DGEqL22Kp0+fnV+e3t+vZvNkvZzak5T8669/8c//4J/ns+nZydnd9RwP3S5/8eLVGwKHv/u3/86Pf/QfrlbLZPpcsRWT0uU/V1tCtyku1F6MQNNetbF/s5EsGd1xhDVyoVw29I9P947925OBVq/rkFjrw2O+0fiTYwxlh7T9stz2HXUiferf6B31GsU1PzTKuDQpekfE4GH9VxQhEch38A90uxLH4jOmBduyej0ctcIOC1qUvTyNUUMH/16EjhG+JjuEUhzJHZa4m9VeFJHcst5gL2rYO1LU+Fq9tvdqtYePt/0+tJAZIBY8yJ3k3QheNJDU61jF6jRQVJEc9gnjPsl9+YcJ+o7Ucn8OGzvSsY/W5oPajZaKFeMPJx7NezzjwylHtsLhAj6yms3G2at9u2wVgxaT8V4HXHJoIL9kXlUV5GQGC9vZZG/eXP8//9E/ZD47q1hvbhcaxl6tNps109zXxeL2dvHmLfvcszU+76Vi98/k5GQ+m52gFdP5FRFoFo6NOwNvs6ssn/tTAcpMtCuAFQFyl6r4h3vM1VKF7gOquHDr5jIl3lWmRRjGpqriOdVVW4LVLIfOSUPIPyVknAUGMpQtjvAk2cB+RQNsfET6n//zP/jX/+ZfLhf88q3ubtfr9QIfMv/n619/lbImQFHFU3lo+kIR06T42c/+9C/8+D+UDvDSXCC4IkNnPzy1vVYuV6ajPqHd2lrWaX9AaSx0GkHeZvDtyZHT+q0ZKOqv9KASJFrTdDMJRcNqh8ojyQL9p0TsgeDtOPNT+qgeOE4P9e+pjSYxTtX3reWO3HVsI5ttxeZ9dEsTOETRTGPsP5DEiUATLA6JmOxbkz7saUNv7Nj2SzvqbdO8u5xt19kpM//NTpJxBFEP9Ap7KNEjYQ//93AYk30sKQ/hM6puy8NjrItp6veNxg+KzYYf+rmPObXT4lZyrN3ZvBdYSUNg4BHlgzq5MuQ6yV7YSL3e0cX4Nchwdnrz9fNf/NN/+k+5tRIDcIBSAfTcYpn3T0XOvOUKsIpQTQZKMza8vLy8JEGQQCa8tUu+KqWbp7wQ4H4tHoY6qV+K7rxnq7YratSuvCoYV85+eMLPPiatfCMyYlLZayMVoHZTjS0nDHUmQQFtXeREhu+rUi9nlYKrrlF5Dih5YRmfvM2A+Twn09nMn3hQyoZHzOi/vrl+9eoV3lmv2SaVtyLf8V605eL25HTGgxPWBhTFteZSZSdMDyJE+rd/8ud//X/+82k+x9tym/zKYfpaKjrZ2D8NExfaT6BXCJZFVcz+aGataGStkdT7alyrJ13rdT007eye+3bt+/jg711bbGdOw0c1HeIKkT57eynmM5w2KcO/m66wt3houMA1YIyQExtIOu4qgWZ8otc/41kMU1rf6PVw1ArDbNpPHnp59jNq+GqU7eM1bMkdxb9Vq8xoy21/y9o5fdxa+fvqto+3h3plexeglmplhjeW7txaA8BH3PH7KsX5JX3U6OM4OFVULWbanQ6MSRygaTfTjzvXPTHKhuC9ndTv0LdjlNpDnTHsOs3fQ0Zn/UfI/ABVegQrR7Lco5+P5Ngiw9+jD9ClQ/DqQ5DWdDTcSWqzWrGDzcXFxf1yIWSst1ZpxSsQPst5p69t56P9/DXjn3k/wOMSN2vyure9xlL0J7UM+pOtUsuAyJ4IUKa6olEtU8LyogsVmsqqalQVmWqWdS0UEaUx9ISSdgShUqfMC1p6hvK9BE4lz/KDfNkiTv5ZhidcabIO9ZguxdJfAD1PAaba+Yhtf5gLhG+oovUC6805E3tu7+5vrq9vbm/JI06Azrwgz37z4uXt3c38CeuYPVwxvXVCrpQ2Q80LlS6lTyqlJCpU6kpQWpkuO3Rl8UzkEs8tKzs3rxI44qSpSgABAABJREFUBw5dEj6evNgXaN24DHY0jA/5j5fo08Qlfku8/3ju+8T54/BAuJ/sqa7Xi74G0Te0+wmAfaG4pULYipa2cfOW4zY1RrXhmfclB5Nbs3hUTIYmxVbDMdr00/js/OExhv7a2xIiwmBI34z/vvwtl20qMGNHheD5beaWME612jEu9DQsArt26bFyikxydvUBtePqe9tf5+EoOTa+N/7u6j8PNDnWqlfuLsfJVKPpc34sZRezofKH8HlI3SGdesviJo3TvRV2FnRxiV3eVa6msXzh23IgW9drzTcXeucmCQ0lWqwKaOUbpC1+9OqudZaybY5m/xsXYGgGExixzT1VoWH7f0Pv4kEmABcikjw6IHjgMp3PK2CtfPgI/kqe68WFW1DBUb8SPytwk6pC6lhtCr3AMLtVEVOrZRXNUF3z34G1ewFdSnmlVNmrpGXLTpJmrol0IsuEVelIVZgRAhAO4So+kEGWXoWGwT6TSmxsSpUejGwuzpn9Q5BAeMVaasbRiR6SVbFe8oJknhXcP003X64TnhMGwF+aYtpZWEIzoYxrJoG64qjoyrSZYgXRaWuEMssrr2iql6Qlq6pi47LKPuCz5759hO9j1/1wWMG6LyZ9v1n+i+kaHnxXHNYklPbpEAgGEvFvUFvPhzdhZxvhw17O+7ZIT98YMPmAorZnxjDptH2g4mPT94kum0N3Eh3bpmn5drwf9rWlT7d6/la1Pk2iZ5X1qlzVv7olL/14+ROAFkWLQSsjcFQChuG6RXnUDFe9X1goL208qvAPnBle+VisRs/+NpSbzRD7xd7p9Afa3FblffkxaPJAi3Z67GMgOG4jdHrU/R3Oba+oVtVNjYwFnkzUEdYHV0ZgGBir4XwwO6+wYp4PUJJlwGxlo2FqwGzKjJcZH4xnQ0PnFvZni3s7TIbEiIB3fikpXEygIFgsFow62wQSQLQArRGbusrQpeVwsmuVWLp5FtWWVmmYyUjVU4Hx0qVlGrlKTAGnqihUyfKVbYczsmwpSS1jKU7iwD+PJcTV2IuUKMhEK0/kkOlFAVxpAbVOvCqYV4HN5/KYfrCMT8GOpJlPslqu7srRBJMkV8ERPmInTpLHf7FHD504qpMKw1FaXctzSmMS6DxhLBp5Oy+9Ul3CzkofDAHaf2iqh1Z4oGKBz2M72334zsQ9tjkfO/+PpCEepmbru+EZxrT7CYA1a8+cRcXNLY4j+wEiQ9UwTh9ndvKhinS1mCxU76T0zEQrzDjKep7J2SMnvxwfpT1kjGFfWUHVzoR5jF87t85J+tI1Bk1HeOG+4w0Ry4c8FanGXdA8bszYkFJS/lVHZqRFmQzW9UXGJV0rpvf8WIk28/E543tUufuBs660itUIFrWl77CxXWFETo3nA3pFjc8IuX0kxqfYw599jHbku8tjx8cVyr6nbgqq5GxQ1efn6CmWF2grekOWBjjJZZ77bHa3WBAIeFQAHTP98+mcMX5BYEfLKQuGGfLn/VZMCNIfXwYugbnEB6n2yUGgBGure82ZsaF/uw+WavNhoYErUmru+LykiEpkwdYgS7tRZb3ad9GZQO/PG/xrKp4C1IaSS1YmQO6Rog6fxdrgt56YkLBaDsYpks8oN6Bvjx8oNmPFECZlFaY+6ckDWSn2Y/psNuf1yVT3gGHN+P+GzZQUKyT59WryyoQrstIfMvSyYBnIP12LlUmn2OdTSSWOstDS5QlW5po4r4vOy52NpyWm+5CYh78foJv3zty+b3R15+lk0Pld7jewxsN/Md0zw9/impQePWs0NTnlhbdxKAm4IuSMSRz4K9+jc5/E4MCGziV9u0X25B/vq9OnQzvfPez57fZq57Q5lDl7arujZffk1quVF4zj5g0Uf6kD2z38EOo0EuN0aFRqX+6rSXttQGmgfloOWAMQevFWtY6sbWE9pXthlOOqdHo8UA2XBjJLxLy9hByXuR3/qVf56K7aNmJCZWOPNe6FnsKPO3uf7tFhqTvOC+J0B+kjZHlbfotb5xF8ti/Lvg7ird1XqjbZljEazVdMiNbQLKAULbihs50/CSCzgVdQXpLYppaqyfC1qgjH2+Fb3sCGK6U1yM3DAY1WI8lqcMrYQFRpJrsTRHB/9nkyFZimxA7TTXR+ZaC9BLfkSPnqXBGQI2juFdy4slaV5WXGVBq6yLLQcXFZv2Jin656xdjBs53NTKrbjddQtT2/cMqq0NmbB+yBAKUVd5lgL1CQD1lE4Tuogvt5dqK3pNneQfd3N5vNUkJoIZg6JzGRBf7HSmKeH+BsFypvm1omKfaJK9N9tjpb3bqJPuW+Fw+EHnMU6d7SR2EVM4mVfCQRsbhP6Yd4wG4efgt5CJsPtK53ReuEeTkuPv16tK49d8Id8VzFPnwNfCQ4/ibE6Yq8+QlN4NAs03XMA0KnLc+2n0xM0MVgdN5hIw2j2XcQVmPncZH7w41qmrajRdrjDTHjKN22tD1ewjMBvBzHpu1aEUtPNhVuEYzKQK4ziqWPqlkRUd27iGfEc1hLkiPF7qWULs+7FfG50q72OWzjjhavcdpe1Hh26bYlHUzV+MSUNprLMLYOm+DRu1e6kfTx6R1DjfkbBz/ZyEfRMTPSm2GLb93rZSewIWoYCCWWBepemZapzgypC9AydKKBeUjYsoe5/gDSdTGd5/Pp6enJCZB+s15rhBoCkwMULdbPAKBp/pI8YVHrc1ovsPlcHVj5jpKFY23g+2myPjEm7B/0turlUAnXGilp0yVZitmGXupcla9jfamc9LWIlcaM15wEz22ajqg3lxoTz15WNc1mo4CwDCngz6FvtHukOm+c/yvlGx/eQCxnmX5KaMkyZcZbOvNnZRTILf4IQxW40Jtl+diwcEI5qptiEjQzID4VtMRCFYH+eChPNycns5Mf/fgHl5dX7BUkP9OvitkkWWw200lyh8Kohe82kxWziaBhs1F/LGMCXBO1t/TytzrYWwJMUyfhufEXSlW9SEbZ4TrWSr3MC+q1VMP6fFnLWfj5sO9szKGdrvE86Bvd9x1sy+rLwdTgrD6ampQePWs0XYxqrWW9qItqVF6HwsN3/h6dO4WJuXHzft4hq11tH/6qHdHX+kCbc5Sz08MR7WAykj5IVxbukLsnt1hih+0HcRvVRnbziinjLzn5fqnEevuNqH07Wn2sQ//YvD3T8nOsU1Xd8hhh6i6tqDo/u9h1ErYzg6f6eASCRl3ogzcbRa1Lp21lf3gZbtFou9oG9HmxTak+0Odbp96DVwf7Hcy7anxAecEzIfFelHPp71eH92J4JPSI1vexIr/n26BZLv49EQbmsJkqWT798z/72asXr3/45RegysV6nae8mnZyc83O/jebdTGbzhhmXqzuVqv125u3NtsnzXPd2SFj4kqWcDWl1EefmfFjeBZ0m64na9YNIJQiBrf5ECS1vXFgYdmwcZVt4yDqKtcW0WrhsQFfk6PIQPojEyagX0IURLHyQGmxEESWChaCaNXtZG2BmTYsgq3VBfZzJRplGEclyJaSJCRDn1YfVcmkinEwKVCEe4mmMElfMTCeXlSWi50XiL228hRrTd9RHTUBJw3c66Am3FCfnBQsxVLqJP1n/+wPmCDEFU9fWDGRJ2dJdpcUU5YLw48fXYUKOZzZYWh6fn529eRqzephC81khSkiY0o9yqTU6j9K7fsJ6iUWYJjH6vmfro7hgdAYo5ruGBIP4OFKoqEfIVFlfPr84DxAk3mP8sbyy4aWoe+FRKNlQ74n/NygafBsXcZatAofkGFqJP+H//3/UVoFRSuGrQwrCLlljKLnBiGvqrrXZyv6GVPbpbfHoau6qOReqzLsU7vKMJajfeX3bAKr/hinWI9OpbvG0eXwen7MZqtmO47sprMmpOhhDbmVOz6Fhsjtb8exnNp2tW0f5rUv/TC3vtKdHm4b0mD1KHoe9B1sKHa8S++JOz0xRmCNSXQRi/CvnXHzJNgQTExa6BncCRI9OT37b/7r//of/aN/dHlxuQKw22uotKZ3De4tlryJloF8zeHXXvVXVxez6QlbANky34lW+2YJiwDYvIYYgKXBjr615U2aTmdT5gLl+RQymFAKJjasq0kvvCQMTdBWkFxA22zgwxNSsrRK6LgqxxaDzoDnpUFx9tb0GgLWYjbRTvwTVtJyuC/Mfr27l3yeGJS5poqKeAJAgWbhU9/+6yPxJwPs6hMOe85Q6DmD6SbtJMAjgEpZEynPqdRMUUp66aiIlUQof7w+eXn99q32ReIfKyVwKMZNsnWx+uXPf75cLDeTpeZo8ViD7ZXwpFrOpEFEWMC6qYKAYHVyevFf/u/+y5OTE21FKv4mwTSUXdHhjhJF7XANy6xGWY2QCy+2GkpuqcnaXjRr7bh+SN0drEcV76W4bN91b4GhuUjS4/QobSIir7uXelHtMuma9N5jd9nSZtjIidULVjdoHnLZq/l4pnva+CCJPbIexDOydF8+cetEbMr+6R3M80O6r0pcPaQ7V07SDXbp2ewpoi/CM8nAvj8Ra9lkdtgTgH5Zj1oSGzIoqGllF3FoxK7C95HnSnPeZWZMEqd3Kz1g8y6hu5kfQOEmH1DxUau4Kx5Dt+HWOkyit+nj6fyoru5i7gZ1lYzN63BkLaspwZ0Hd0BleTC2LOxSVgOjA9bPTs9n8zmTS+y1U3xPNezMi37nxcmzp0+fPHliUYBG8RmhFhxVHMG8JQ338wd0PT09nZ/wcl/BXivWxPXsJOddYIoQkCm0b+oJe4NZuYxVV6lhU1PTaS1Z1qHUKpTnZGWFDvSVF/JVteA18OXhZcn6XNKyledb8CANQOBGZ6/xMv24FA35fHggoRRrdk9FmSrAKIVJqNjLIOURX4mln/ECCTzj7Iio7u7uzGqrYESU4ny9IoBKhGX2qMEigxzcf3Z2up4ya+hUTzvEnEXDWhtsk3/wpr9eTdsJEakRgy3Xy5OEVy9LB/GTXmKrw/Uq054fVCU30DnFiDO1OainRLjYn4+xsdND6m65HJjaV3hp+KA0d3AgGVMlEMcJ966f4/yROrcrxkyOko41eQfijqLzd4oJjRJ3P0+HVgulnhPyH+Ki0d3AdTlIVL+iujEXzGSt3/hGCrH5W2IQ6HfFMYGwnhg9Nys2JB4z7oyrTIY32VZc/Z2yW823FB9GKta7a94/WhY82t6pbOccO6p9OJaPa8edhpYEsWmdtg8wiukP889h/d+f5Ghf+QHloiLXM7Y01vYwHeKZo5GonSMTMe3D097rY2tiKx/OP+IgIUGQy3V4x3gx3ywerwEhBeIFTAW4GU1m5jlbUm7WzzTAnL3QULM32eYzgoAT3lXLK35TzYqxgfx8tWSf+uVk80SrBPJXbgtj3rCELceaRQLMyNGeXk8n6yeT6a3iAosZpB1yuUDw+lK32fSV0oKtXATdGT1izB7cy4i7LCApKO3lEqkVFz7tx00mzw771LQfAeAyC7rkpVCxTSpyLsYSsQBrDhs1t5TVQkXyVaHUjflFyWuuOaSqcdZJVunKSqQgjsJAH4Y3o3ghmIVIxWSxXBJfyeXVEw/QP3WZYWXi9NiAxpBiyT2WMzuL9wMotIC76y7+miykHDWS8WJBNl+yNF0uCE4IBvTrVypVukCeCmpKW6nkjUy+H56gcMQRqMwTiONTvtIRGO4e/4skBY5R9VB84Hc/1B+RQH4suf+Xt+Qlfdu/713jvsEr7fVX+9rVoG/oPMLK2kq2Gn3bllrxjougiRu7g/qg4vhX7CAGXe01yKhDYlf7dvPo8WcHz+76O3JLPn36tPLjvk06NFOcv0PkYHGMdmLCEfYGXVRvBH3Mvp6ODDPw3v0E4Fgm12V/QFeRGz4grbaqhJvFNquZ8j6xd0s55xH8m/I+XR/FA52e37c7hrb3hCsWp4+i6vtmcoBBvVUqD3cRCJnpdg/M5lMT0AVtAa2O/4Q7BRiZWKK9f0CJmsUjHK9d6vkRY4oPB/tUaugaJoLugHsiCG38z+G1xNWuwIJEEcyAESsmCmmHe7sZG3MpghByDJgaTrUC1BFwDocBSs+AEQVmm1IlkTgJojuqJdsIQn0KS8KyLjBfdZma5KZbsSoZR3dRVUNZlc5wLDkZoelhQRMpA9AG9+VVcXecDXR3pV09gi6/NBuhI3IhWRmyYfGuWPmDAqrgVpT1cuKIDbOpVF8UUoyEvzXALiWT0AoFWAW82hAHSBFT010m3jKTz2CKyu3PrDRFvI7rpLR5ZuvOXSmTVQmG2KvvycSFHFRpl367y9303XQVhTusuur4dILgCBKPcQS2++r/GMp84vnBeiD0EzT0dLvDtHMONicWt4uJf1F2UbXL2+o2pbamgW6ZtCKkbVFXqjcu2ZNPI4LvElXL64urakTNi5ob9pUYj3zEaRdSn53fFDz+GhXbzTe+eoMyaOU81aGsXdpPGPryGwwHLmMO4307vh3hiXOc3mX5OFOtUVv6jdekVbXKiHpym1tv/69q6zPi4Nnu/5rmLZqYQTutpqxyR+lQEe/8jLm17W1XH0PTrlUhoVASer3jsZCv8WwOoPdeB86JXVSrWxYIkwo8FryiN0/mkAhsaphZa3CBr6BJALmGyPO3QPbNRu/0tZkmRT5/axacC/ADUO3tXhKiAedJMn0Db+A+14K+8ALaatQfwMq6YNvbPn/LO4LpG9Khgr2ynUt0z99QU6n4dhCutcNPVWYJyBy5uk2Gt42RM9C16VthYISan6knqEuh2JT/yTDRVRb5/EHvYF7Z6OkkCjWcgedKfVlkJGJo0YuJV57zKSmYRKRmhStQnh17mFnEugK8KVlaKyA2GsDXN0gu4mdLWVijMCvTtCzlqEhyzXn+pERvbYNCPkx0s+BVazzCoan9aYtrIptcmjExFpTYYTaVJ+0URKd4XpWZpNjsqqD9qTZUcAUnPu3Dz/YtU27rkIUidHK7KmnidFUt/rZWeT2fe95herjU1m7x3UfTUffwaNzXjXP+bhMcGr4Yb9fO+0+Dc59dY/J3yupkUioQ+z9Od9bpzxyjwxiafgkHlUTte1D9Y1fq06cvP5Lv/dPPUXaZLLGHXbVxVJs+5Ozsh61W21kj8N6V8K/Zll/3E4BdXCjvugeNqPbuSTqbD+23PjiKTp1ijsJ5kMmRrRiUNVT4nsyvqeSNGjrmUVxz/I5S9bygZ82GfS7cwA/B8/toPYa2smkPH/W0dokzEbolUJsGzoZ6DdCC8Xlhl7aY0ZwV0DxAH1gJyOS1UowfM1tSQ/WsJ7XhZIAnBGuAPKXG3RCejeurkg6BPkkzYMo906qSL+kUrdcrFgwIFIKUHStbBavtGpKsiuBjegdDVEWgF2irD2MposCKTNSDQLpwiFz26sPEuQxlWzVORhN4mHO8psosJRaO/0vyypdOIPHINQtJwLCsSGVdmVzT1qSWhaa92VqR+bwhm8eDu2UDgYA7AIsc7uu9aXC0MEFO8AMOTLIyq8WdTM3fQq90sl6wfpssnvQwEYgEf7qGzE7oug0kynyKTEm1pejsQontYfnby56UVxRtB4uOOpU7yqK4EulxMjvYPk5WrF2Q0JkZSj3RNiW2bAyHBsNPl588cLAHvO/FvS5OH8w2rnh0hjHzUemggazlPQBf6GZS7XMccRiOkJwLNUm426KqteQwnxqpLjoj/mEJLR4ho0+54IOtxHjcOtTvTMTjHCEdNBwfC7rE1WdbHRri+rRvkI25bGvVznE+ffmxlLavgvmQxRw6WzNmdUA65omsWltG/RGV4qK41kihsVGqEvXkA7g1OITGjZVs0OhyxNHk0FflAaNNY+zto2mNZ2j+hg7AVnWIpvA9+92aDpv6xv5XX4h4Oy7LhdX2vdiz8g0n1pg6Aayqg5QhQKPnZVNfff3i86d/6cmTp8vJrwkHgIlaU5olZyfnbNfPMDMvoFWAQHTADH6bhgI/LfMVBzCnLNJEHR4W2KaWgp8lcGR7H036N3gssQQQVgVcqgoT37FHC2q5Mhiq4ujeKj7Sv0TUJM0QcbSkfYqzDj+bAK9UZsCi1MCohNU9oek/W47KtEjCSlUEwPZGMzFkmDKOip2ICn7pasKBBEUSiXUSUzBUX0Fuy2G/TuVDpKoAc56gzG2TTnkRJ8up8AXPb9h3FRqYcC2uWoQN9pfPcSxxFCW+TkCcJuunsE1nL0W6yYi1yGTi1Sz94nz2w7vsNzw6KFgWzKqPDasOsvXyjBcMJ9PnMoM6MtPFwEaHTFEfI98PaWAml3QldfsNAIEeCi/Vr0bgo+odh15iAJV/R5zYJUTnjm9WB6dWlt/H+u4GffktNnFG+B30TNcxJhhIB/u3Lhmg7i/qu/+UNQ6yq09an6xRLRL9jsS/KW1Zw9z6dIj5tGmGecZ12+mH1G1z25HT1159+TvYjSoOXbH9rL5dP8Y57dKH5LRbbQy3vifkzTsSXzP7ftqbT6q3rowR8B5pvGEOukGYrdt7uV++R1M+iT6yB7w/B6YHdZJQe5uovibRL7V9cZyiIXRbbZ+U9+p9avTSHkWfXu6PVVB3QNlyDzOlQodtlQXpDGyBNTlK8CZESi5ntpP/x//4H/78Z/+3Lz//fjH7OtmwvhRMyaj/Kp+dXl/fnJ9fajtJ3tCb82qqteF+GGm4WXv4CDQyv0dLfEHLLksAW1PrtdyWYuFYG53mUguBi42WG3PovV+mhKo56teNqoShfs/yM91RmkNHuf/XheBsmauS8rD61YV9qoqOUML4uDMqc9FcCsgayzF9XGh5rQ8OAXMncWP1IMKM2T6mcC2hkomlRFUrHV4WS7z+vOVoHCNxOgnCaRrpV6WyogRxhebJhF2VTGXQPIeWXpiDEZcTrokKOv4UlKVsw/r7/+T3/4f/4Y/S+SsacTqb5OnJfJZenD398vO/dH52zmaixIHSxcRV3uKq93Arwrm/ipM4H6j8sp+8VACyQEzdwGSoYq+uDyxwXcYwce1ixYdr9VkznsMw/0+lnzwQPNDoVI3LQBYndn9ZY+qudON73EXSlzdGwb66XfluTPllzifVCFkgRd64wwn7yd9pvDikcrDYifxyW6E9nt2e2b+lZlNsRiur+Y4hXfozptuV9tHrw6K9XbxVHvu/bWPMoV06bNf42Bcd8ExjfCgW/cB03JaePqAhOnVo8wleioV21h2ZGb46D2c4ikM88jRCxbj/jCDfg6R86+pXOMAVL6JvwShTYmHbsX+qBp8yXZzx2sDMQZ1gbQmUBdIBo0BJho2pBUxP7perr775V9+8/lOjA3nyma4YGS4mv/d7v/vX/v2/tlwtECFyUQjQC2BuErb8AcTDz7BpRSHpNrjPwwQ9EgCQLjbFTEGAjZXb/HXALWPbqEG0IX+UQNlgn2kvBIs8/m+xemSlFClNkl4iM/WUNAM8MzhMlyKww+pWEh15k49EZ1TR6NMwtxTZljobhChXUm0c3yqbykZcajSr4oJKu8mspLFmUGU1wYQo6+TEHqRIBXMwa7BXxd3iTuJMuJ8ktkhOT69O5loiLP+ritpVdEVxe3u/WMi3ZBDITYgRNtmf/fJ/XNwv9FiHJQEpbxIoitX5clX8p//Ln//dv/Ofr5esyvBBd/Hwo/x0tmWef8jZkhkfHc/SvdjYlKVepWQc1w6kWg6hw2l6KKNvjVccd47HUOO01+6/S/RooWrh3tjQgCp195Tl4+8tfRwaghqXHfz77WrU7b1s+8pIY1l7t0gPT9ehzS2W1adnjabFv82zj087/7C6NX3aTPty+tqrL7+PTyu/0SEblyV5XUpnJxxvl4voFtRSL8qgRqfkiCRKlneMKMeTzTuSs2QtE88hmQLEQc7wUVWpqLZa7axaVTnGp/vjGJwei0do43fql8eyRnwfbsjDOQzY58zd7aT3+8YM8B0scqFBtMsdrNFdGNR2Vk4UulB3na7cgxXoYvYu8w6wta1exMT8GJyphMBxfDhiF0y0nm0AGGgrKlb9ahnA7PTklH3iHf3rXV1AxMWSbWg294v71Xppu0lqYr0BX5NhONul6NoAp4NU2zjIacgAijIInQE8NSTNBS8AdhRcglRyS2XRsEopCiFtJzI9P+QAbUVopVZW1vNcFRkrlaMxML0sV0nFzNP+XadYvKuzPqniIUPA98p1tnxUzxDE2K0WD2Oi8EgEugjuEpnqVIoYb4nA50zrsR2Vyln7E+3XSXpDjAUTWFglfdglVQmweECgnHJKlWxEHv7lBW2r1coiMGILVgMn6YyXOax5GRuuRyNe9QCjdHJ5c3d/fn5q822sOs1bmowBZpach0xZpozyqEyorvlsUNRL/EraRfkdyQ6+JVVgHxId1T+srLatwTyKRtrhlB+WYZ+0+VZ4YGTXanfjMdaHrj6GuIdmpII9tdvZrpN98XifmMpHfgnbrIZzavFiKxIdM8uqzd+VP6wx2tw8pz2ePTxiHUpRxtOulZ+DFC6H9fRRk95ZgOYx20sksNwvEfu/bWPMq10abIzJDkjHOhxQfWQV/4r4U4v8G6tUj+BH8nEy59Zuu7aX9mLbJG5/I4wiyPX+E87N6vXruFa95PCrY7Vdm0+V454+XEOracCQVHBB4Ge+kwzHi8o3iY7+mZZTQn8IhMC1zpQtYpjAw0Y0wElwJOQCkIB2voi8j5b9KKHT/H/+Nk81qVyhAujztZOT1K6UBkKBlsyJsSUxLjZn0Fnagi5FZ0leKpwzP/5+svkS2Jmk154PA4FaMWqoX1pX5utK5sDP1ZXKdihTCV1LXchsmpClq3wvNDn6GYCFHU5vdcWjzLWEqbPNsZRzQZzqB+hsFcnj05h4YVW1Uo8iRQD6SHm6QuTFLkzuHYuybNGuW6dcUbq9DJCX4hSr6TGOJv+IrQUS2oFVQQFNxBeNNzarJE2Z8qowxjSysCGhjJ2a7td6tsNNQ8V0BHscIRFOitzSDn2EY1saZ4V0PRHVRN/oqk7WvKrThmohUdGPH4+s/eI84D5ZSdbnvvfGvX5f3NaWxZLr3uHcOKo7zDZ7D/9sK9VTPb5qy6pXG7xq8+z5XXAuY2TVaNr8B9UZU7ivJ2v6jBCwL/8+ljU+/V5td54+ho18t6smpUHxwEvteKbHzCPZNOf6h2r+zQlsuCTNjVyJcU8AAqttovPruC1+3JTpLxEh8bjyeri7JykMiUDo3n6/6gVlvguJRn9st8h4J3wgreYWNezCiti04dLxJr8/ytiaw7RwjNl1LwjeqRISZhBR47y6u5ZAnAufoM/bvsCJmswjAt1eNHFHb+0CYtrdJsBc1WV2EDozlu+ot2SvmtAyBm3rhQGgwv1UFyhlVFrced/YOmFHUc1uV8CAVJhQzawRA6WVQ4GeCyipK9e7igqUo/u4GECj/5pdRPAi1UtuXhnGYmWsja8nofFMd6M4SE7tUNUqw0plb5nhBdW1f1Lm+kAjfSpJZRURVdVNbVklww3xq65qWV0N/EOs0qqyhW3WTIGNE4vMs7T3EQroRAYwHn+ojeCsTV3tGY60Uj0kaekwREzQ0lQiqa7arkaQgXhyt2ooGZxSKcenU/SURNmq3sPCGDufiHEj2Vu3QfchXkZu6PThHjo7K867/LUHz0+knzzwYXgg/qKM0Gjk18C/Kn4DYUNl4gbubB1RWmfMlJT7GORf76lcOxJt54ywMZCEL7wnXJswcx2yvlmJgcMRE0GZwDPEhe7nkB8nGDUJFQN9IPAxlUAQ8tuUoeidJdo6xJ4fo0ab/rD2cve6l+I+3PZbW6u+78uYnr3j6U1bWD1HIqz/j9EzeEbEoEkAQvTd0WWded+Vt5qXxr7qo+/Lb7d+H+WI/A4H9I5kdLNLbEWB7SAkrLglImnO8Twr0AkESY7wpl8pR9ATapB+Mplqcjg4kYW5zNUBfcvlwotatMvYsDRW3SJ/LTQpzGgcjIqUwVGDsKKEp4NP3h9som3JAZWY6qJpQNpb9GSzznPeGCDySmkJEXtfamwiJFUs7ZAGklheVWgSPRUtGOq2tGwUoW7yXluWe0QhFsr3Q/n807WZoE9ZZvjZGZDvuZ5v+pT2e47pY9xVD/XFsGTvTLlyRbCOcs36KT02KeZylqRW6Nx8Lm2Z5LO6FPPstQ3PO3YuOW9NEEc8KGSPXMb+GfInwYJg3rsM4ySXUPMiHEyKjNVcIPYjYkWxKUOAZnGCytULZInUctZcuVuC80vT3UwRh1Qt0c6Octp9HqWkMZGJjkpkYB7VdYqHfKOdQ8c5xgCtO08HfU9W+27fQ1hmD9N7qT/pDXdC/IGPBo5H8c+AvPoavBph7NVagV1E9/Z24dFyWjqMv6vHnhxfq6Z5S3pcGvMv8yP68RJrfNpejXjG0j3tUnhO5V+8NkHIqUkJuUdJ6E0yZaceY3WvJo0vRvVVsXuL7wLUoDiK9p+YfPLA43ug6sz7SQq/np4I3f8wbvvJrgOEoMkYJp3qtTl0ko3h/6HQ7G1AaEBZEDvEbqAaI7fRXoE+s5Fr+7OTgVqAYZbmNnkH1MUYsYp4FmB1DVUKUmq9LzwgVsAgeErAYGDagCV0zl54kZeATWeGNSHQlBITDguWn0KoTYDgCC9NU2F8WsUGOcXDAGwZcnBtbKllcBkqyylleanZJ82N1ouMDxlcqUYUW5TlhmjLsMAwrqhCXZlSXYiFPYquMlQryNLmP6L22pUqoXZVp/p019sCX6slRuYSFUDkdPKSveFXGTafxxIqlJmmADv2sHKDDIFzVXDW0sb+A983BFo42zwsn2f5LEkXlKoReSsAZ7Yb1UvfCLhUz7wsfsR75rfyCQ9yTT13o87SRJnNg0yOdn4H3SBRENGsqOtOyV2E35E8d/p3xNhPZr4bD3in+lC+akfp4jET3TA7dgGqfFuPmcpbFTVqexhXxEf87InMhmMgtyueWRjGBo6oWpsVboldGgjiaMwJBu/1zScwgTgkOjmHzHeciK1z0bHnxyjToMdFfe013O5jZHXSqFGsp/l7GDzW76TszHRt46bfoWe9V8veiG/jMipRMvZMnG6Qhcu+pxPtVgtV9kr08qnbOI4nboi9qEp9/G1MFCDaZFzb5cBRqTl3/blxe274sqokeUz0YXRYI/CMbgvy2ii9YHrKrjBaccoKAD60/6TBUOoA0mkJA/TgQLiVaUPzQqACoPy3IlA9TDnbJYUa/Jc4Xctcw/zpbJojCVQKst+wmT3k9loxzprI7g8b1hdwT7K36jFC3dZXgstWF+QX2SvVhAf8dZYEk6RAYrK+VN30lYbyfUJMei+SYmaWOMwVg8n6XHXTt2IGH2PEWXOWyE8W0kA793MhNYqNSU9fh0cKygcbb87FAT7S+E6cebOvWFBT4F11MU98NDNKP0QU84Eum3N9ZDe6TnlGamCfqImxf69ZagUTxVTJ+gn+S/CAeJfugR+xGX5Pi2cpL/1NXyrNdkv5NE3u9Y5nHn1rSQDvbsZMLNrk0+n5KWrTBhmbNaWT6WZ9h26b1dVyufY3ANAk1rKmhz13SrY7ULlPzEQZaDRKhAPnc7R6r5fX+rBlWT9vc0ElFbe/Bc7nyOcYA2g88sCjcbffyWWYvrPUdevw105hLYIdd/IWfV9G332stgajr/Jj58cta7J6ta1rErq5Z4+sVedRPv1uZg5cR9oeKLHNPOLZLnQpbuzB3Z7eGLur3a/aOW1NPOdoVscK8bsychcglHBj+vT7QPLD9//gNhtvyL4Ocd1csb663jrvQPnxZr4bygGTQ5t2ajJc2lnFZbmrY4IBHWKykD5ANHU7pXRmBkGfEv0esG9S1JZCkVBbttUqXesIFlRKC7D543rzm5//YrVYAQpX6zVAfD6fXV4+3TD5Z8o0EQsPmKWTllNGcjaQz3k+UKI30KThVUOwEgcmA4t640qgXwjEOyaFEEhKObdcrRsu7m5vCEAWy0We5+fnF/A3GC5626BSk5TKvgJUFSDmPcSSJMhrVlgxo9d6hJukAuU8MDD860CTcqvAWS/MkjGGHY0vwYwcYkECkiofkSkZboFiAE8L/5tFZJBla25NHrxFT9qiBcP0XJFXWitiWQ7Wl/XULGG+KPhDBFhcXpVj9BgEHvwwpwXvSJbP5ELOoHmFSNLMlTIrjAP5apfUHs1YoRxFHCWxiuSMgTkNSvYB5Y0NqZ4JUChxSOBFYJvij//4j+8Wy9lJNp2e5NNiPj0nOuNdAU8uf3oyO2VDoUxNUFkn3Uyd8uT5Ko4PaKxKnLdH2n1LhZBQZflgDyafSD954Jge+K71vYd8gfH7B+euSCH9BHgAMKaDNBzxiOMQPZHZXjEQZjYUHmPjXjSBP4nIq6N4xHW9Qpj1GIpGMRokiuPLMI98sMbhhUH/kSyG9Ym5dY73jJQyTOaj6eP5e6fyczkPVTvplseO/ln16gf2zNgzleTmZ/vpRJPika4rG5vseTKA2cJ5taO6h4z9AkWjnjUvAvtqLLwQ0PwccY45hcBFxgAvODP55a9++X/5+39/OmNzeqFLzRIpipOz+Xw6+73f/Sv39/carBc+tjF1YHbBElHYclcRbOUsgeJoFwxmo5uAtMC65VLiU0ccKpJX6siAPxiXDYXYoRI0DPR/9uzpk6dPUtYbgHxRjzfg2pQVYeXqNlZMnnIp1mLjvKSCqQJAf2aBD6XAXu1wj9VOyNn+QMXfU44x0Ces9K5c7V8kXXU4c/L/opRO3mCUec+5IUWblgqHG5o3iQo7JhOetECDyxiwJ/ygGxByrCfr3xaf9A0cFSHIpTNNateseubkEPOgpWInmDAdh0AF25mOf3339hXv6cpzqWXRx2rFNj7+EAbbpb6M2jyhPJ2+TnI4EAJxyEFmjeIJODAR23IvTM8Vdefz07PzM5YEyCp5YUJ6sbj79Ve/+vOf/4xWtD1FWTlAKxX3m8nf+Tt/6z//W397sphByyHZpkHtzdNwoaA8pAJH+eEXOrf6/7bKlsj4l5cqr74jnmU1/AnPtsrxUq0nePEviJSp5rWPv2f2KTfmPtZXt6FVH9m3P7/VXsMmx36L08O1GqVxB90W7anJtmJXqqbbUTl3SevJM7maXmiHffGalGP6cOyuNkJo58QyzA9J/tX2TtJeKRTT96VrtUyhkqN+zGwXoL6acT51Si90OiMm/WDSW50/GJU+KfJAD2y/DQcx8i/kQBcORZ2dx6U3dGhcDuvl/IOUYeJvT2mXweRVrouSO20WrdNz5tBARomMYcc/z/azI1SK7VJkRT7N37x+CbzLwKncA9mc0yDd9dv77HIKEJ9Op0zIEfhXdCAV9d9Apxg4+lQOh9jy3/95huIG1SqL+PQUZ+VyqalHylPgATDUKLfGuAWDDbtzYU8VDBgrujAMj9GOx62umWyIVLONRG44nhwgswzS3Z1Pwgmz2rVWBekB0GbwXXse2Z44Vh9yzYw3mxGaoQMuMN8WeEV6iiN1pKRQu1ljSVUzQ5XHZkeKY2xzI2XLXvlYNVVFIZj+GSa2QgVOUECmmgQCVkkREfKYqrVeK1hCM3lYh5yIYM2kgtizpE+ZNE8rLThv5ptwC2iybDabkil32QlWr98Up6fEf7MUTRLe8awHMuj49ub2s6dPoMN2U914BjkyR9yVUX6IID56so2kq4y8+AiXLrOrRkz+UaW3bvyo1P6OK+tdMPTLb6U39LWODIsv9+20MZ+I5fjkgxk0RBk/t8Lu2KN3AdpaDgvuv+Fe3BDweJd7xoKmZt99eW8ta1Gp1R4ewx4Q4Io1CB4+ptJgyGUcX46fOz6Gsi1rX/2HpcTcQpxtXbct+aE5gX+bUWdLOVnsW89p95A2Q3JkhfVkDZc6duik68mMPdNDUmbHt61hykcvrcZRmoIOG8uUB/V/e/hVyBOs1WQaQUbdqcBzjPdyCQV4Dej/6uUboCObeIJDwYiOdJl7s2af/xXbfjLdeSlEumFnGKCjZqJX7tzeB12+cCSFTLMRc13pUodS/mmYGRq/pkCj5RQji6nnCLDFrMK4thgYrEmh1dZjCEULhq9RFjCv+MKt0fA5ORsigJWG5yVSw/8+rI4HhKC5T0uUYWtwrb53MCS8Aeu+hNYCBUUDkGeaVI+3XpqmrItleAh6wqQVj0lgb2jdOHD/V13OCqJs8bSiCMIPdEsnepHCJHtl6BhHoqWebWj4X9qocSbFvWQzqV5qLuUUZMlhBCaQr0S2JjBQLk0CY7NHBFDhalYF8Nowsxo1nyhhKwGoCGeulMMqbaTYoVUYZCmTaEurtze8YVhhzWa5sC6qNwmseISiRxlsHLSkIZLl/cr8qaiGcsVO4keTGH/xM1nbRldWfEBncj1Qqf9uUrb+QsTRGgBXsjzXf2c9M2Y+It0lt7uaOSEuat/lyDlICXGN75Dj72OxPp52rWJubZqH5LStfgi3jrrqtPbN6ijbJ8vbazS32K44vY9I0arjN45Wz2mUd172tWBNtx7OfXVd0HCp//6WKnXxl4FRfmwvafq/n/fuw6NbynUzP7i0UtnoLlHm7PgwRWu1jF9pkX5/v+27AB18t2p4tnRZI7e6rLVSldn5Ocyns8p3OTO4KyQe2xsIilvz8eS6IDcnTj+2gd8q/vHtLPqqCzCr5UD5QD0QnjlYYNmm2AMoFxA4TATNQcZNXci5fPWsELtY6xGwDyHTK4yHuNaOCtWTqRriaVkMr1PFdCohvMF41TcKZWa5Q9LNarXgnQCms4N28RFiNqhMFVWzkXzhTslAq5XDa4PF/LRIYR3YIWqM0rwmxRQKG+BArn3az5erSbE9MXAjtO+N2cBZqNHiDOqJDS7iqYiStrgZaUprEx0hWqQY9OcXBSnMvyffVJFsJcw3UqO0i7qswTWNxIY5QobOxZ0IBJANayioqgurTSij+TDGmBw31zmajl7izjdPQqv6JhxW0teuPVO4X9dqe3UKPErYYl7SmgXZp2XZRAIFQSE6yidUkFIyQ0ldc5h1ZdoyPNO13p6Nsiz3iqafMQrVnMgV98xWeUz7PtKuO5JjLd+HIp9kfvLAu/AA/Tz0eeT5F3L4axnTP0zFh3Fqf0WNn2eT1Bqy7Oueb3IUAz3IhuG4Z7g0Fry/Pu48b7/gioER31ga6ZiyHe1pLG3/w2PTNrc2p4OfMLRZjcw5zKKRzCE7wCJarTYeMELYQPTf6AnOLG4L7zB+9lKvUo4ZDLb4HnoanwbnhtARhvaS4AG4YRcivA+3dRvwUi/froJj8TE4UfpAPJmZ83WXPPLkuNJ5NYqytsE84V5HcwJ3GjbXpY2jM5w/vb29hwUoz6bCCK0CNzWaDubTqLjgr9A7YqingWDQpz+vYFAcQRToULk4G240vCpqaQewLEtLqCpGVkcJwUoQLsPNKKaRdxaYauIQOw/RNzT7fJPaxpQa7Re9lGUAvdCul4bOhZgNN4NKNfy/SRio1vQVvjD2yAJEvk7Wn/PmsSR9y9C79r0BQzMwLz011A0H3nlMLc7UYpifTsMGOMqhFlOjGIZfazg8YYPUgtcVY+0q3XwpRdPXCpoSYgzsBTvjIyiF2hk8yxg+L3i64trqEYG5kl03sRcd5DSmYrln0Up18ar7Vc5kGF5LdT2HbXmQpEJqkcVZDakBeWsHijaT/DVp+V19gxxrU11SbXuyGEDN4JuHsnKAHLWLOBMK2I5MKn5K/SR9wVOSbPWUjYb0jMLamQlKTk5bwVmCrKDUjboqdi24MNnluT72X2bi8r5+TvWuY+9vXENuF8+H543Rqn0X6pNrvxS2kLuPYv/fhTH38H5pPSUt9DLGD/Hocg/ffbIHf5X2YdSkdVs8d3zbNbn0Xz+E53Dd4dJ9/a8bRv3wHD/7Vzwu7/vN7ZWrO2ntmUPEzdm3VYhIqmRtrr9ntlWEn91pvTwZvwagklJ9wrptelX4oX0GLz6eyrGIUc31ofno266PN1CjA+xsqZ0EB7vt8TijUsPMg5V8hxXr/ug1ADJDeGjmNaAMVa2WMnzonBWfrDpNV8sFsJFFt6A3aoOkF/f3Cgk0G0jDvZlGoMF3qSaGKAdwKSYagxbu15g0sYHAug7RqFi8DBVarp8EIh0Fr1lbLHkGMA1hlpVUuxxrJymmoE1Av4adGbYnrfFodOUfZYQeQrROFmyXNJkj/CmthIalFWnYiH5bQ7TwgRTVVIcrU8wLjBCUqNDA4CzFIhA0Ln8rbKzcgC7eUXUrtOp2Yc6wfA2kyyfypyIm95AbZ7ZCb2wxkVIpphlQ4oLmJMxmt8VjFdHBzHVVBeNgZEprCo8KzSKMkO0V+rcmctaiIE7QYcKMkbqJHzyz8KTKtTcoPYOOw/pgniCZ/+UQXKSpSHwihkM83WpSrqFJ0IlLKy8zPB3OgcAqkq2j/uF5H/LZTXw0DRsOfTQ53xnGZf+yvvmdMfrRDY27qX+/9xYZGmbvmiMqNJibup5nSYaFjnT0xr7DEWq7tBVV761gnQN2xroRHTZ80sc/HhvuoxmTf5j04fF4eGLXsTTssyIes4+t6KMfzh+2qFEX62gm66ONkvKyT5++6D8wFFvrIegzLGIruN1Lt2UPS7U4u10PadnYA/Dp9GFM02tA/XsUyGLPj+ITao5L9PK0gXmzx9qNkx/kY6T9Ew4Gohp4Xn3+P/3hn0zyF3/5d397Pr8A6Wk+PSPb2dTeykt1gThNTddINhAOqLfSrBZRSYJNnsEJ7B5DBDCDsYNtFTq+FjLd+hdsqOcHPhKepGfn55slu/gz1+eV8KIgpHD1ar2UbEa4N5er+83t9e16NVndnxMVpPmLNJuenGhR7GSloXdmt4snOxqxnz0D+WxanzAYbyYbzFbaHg7YDHtU5xGHwWDyp9+QNoBsShmWrr5XRikjV0QcxEdQlGk9BtEUI1QEYEPCIwW5gxk4ik5eQGmXunJu5g8Bb0xXEbVUIsAt/8jx8pLSPAWQI6BU0OX+U3vJMcBrzTJSRdmsJMR6hsNQvRQQvWTBRxqKn1SxLJGqyK8kg0JRlsUqtQp24ikH7tZR1kBFPV0Ri81kyhsMcOMszZbT0+t8/mrNiwGk7oRdmza8VJi+sngqz2f+VhxJga9q+9sn1F5BI7ODotph6rhuroMq69DVwNH37Yi/lQPVj1skG41jn1aHidvrl6Ipoueu1Tv+2qzff93m3Lp7P8gPMf843a/RXiWhsbzJdvSzA56xmDbvpR/u5YfHI3aX7t0HWr3oMA17n5m32EVN/9AAIHSqlpAPMsMtd6UfVXW/vbd9UN3l2yX75bghjTqPalFD1mNfHstRQU9n2GDb6cZQ5VPio/FA2a4G6AxrTxj+n/+//tv/x89++Yff/97nn33xg4vzs7OT08vLq5PT2c3tNQ8HDNExbUU4FbzILx4YFyQKRhUKFN6Fn3AwH+DRIMNAz7YnCdoLbpZgFGTJiDehADA8n5+w5+ckmzKiDxNbfmrxiTa64S9N5+D92f3iPp2czE/n63TGJCBFIZPNzfW11sgC+dNpkd2QLmfsaH4OfwjlH7pKOmC0hN2CoUyekRTyFdv48w0qqIoAuuy1SMnroiY0BljJB3mYQ0RuXhG1/mShjNz+2RMSeQrrzXyh7goIW4jiWiiiEo2L09MPktIEGlWWnpw3eniC1zTMzhQl9v7UQLxG47ky5A0L/mSB7ANsa79U9MF2LJW9ChKMIaWyMToo41Ahta2NFLCpiWHG4hCriVKa7sVEH+1SmmfZH/yL//6f/cEfUA/KPNcLItDt7fX1f/wf/K//5t/4G3c0hVSSs81Z0s0OVTBNykvEVt6UBlWRp/0y1LVyc1aZ+vTxyQNH90DobqEPHl3Eh8nQv5fx+cPU81G1cvOZaWs3pgNEld2n/ICBxz1HiP8eHg+1OKCbG+yGutJb1XvMD+PElMfrAXrIlR1zDvxd+kCtA4oeMkLcJy62t02zd1zbYrFv34hvTO26I/WhFWI+pVLWQzryWzqXGY8wHtPHOdh16DezaYP3wz2MDQxa3yMvCRoGwoclxqnW3ZCSLHBZamBEgnm0+ib5Jp1eF+v7b775+sWL5+zunxkQPzk9/fzzz59cPWMTGKAuw8uMPwsDMgGIRcPFvbAuOBjov/6CcKBIXhj8BSzygqpLIb3stcSWgpEpFxuQFBoWqgSWarC7SKYvQbroI2gL6ATfZtnp+cXF5ZWPijO8nabTFy9eFZOXNzc337x4ASG78bAs4M3rV69fvUIml5p9wpD54gd6OW72QuhZ6Jbw5HvgZe1JzwpeqcH2Pozp0HCau89qB5tIDRSVofomwE5Yn7cSM+OfEIi0rRwQRify+L7ys+tE6wFwDCib6UgM1RMXyS7hbtQxdpyQqHzJtVJ9KmhI1p8JjufYzgGBzQZSoGUxBYwg59EE3HgIp9cemOaTZTabn5//aDbPNceG6VC8Hw15vJtrOju5+mI+O+GxiExh5D3hHW3rVy/erFY3wu6KE8RF4l2MyeZCfYECcw9NRgNhjtD8VIsQ1DZFcjI/seZQE8mG1VPV5rlNmizu765vrnlrg83SsmYsitdvrn/3L/67dPqX9JoBtbciGusPLIugLcSjEmzSxc4PI7QyuxZpSVF9VpQ1opDZmzj2t7JXUKMAtTmw44jH6kv55UCLeu5aR1BvBOf279QecmP+cXoPFr2k3tEobnUz66699fYu2KPVHu1XdbgVHOdw65NPHk2HtuP6tOrLb3M4JIen2qypA5/X1xr515bsrh4xRk67H42p9f5oHuM+NdKa494cO4VWzbn90XAy/9qHc2fdDzbT1X6gesEzD+TzjqsfV+3jcnvHrijFYUPti+QXtT6iC8AYH0KYrFvVro5JMpvPtcyWDTcTTlMGcYXVCBDAdwbKgbTirqkmE4KFOXjw5NxIlkBFDVRroFjgT5ylh6XgUqoEiCRbMhk8FqSsLqlEXRvU9io8CeBK76hStq709ivo7+5uGPMWB+2Dub67u1ssWKpwzYQT4W3B9FWyPCcA0GaX0kAqTVYzBQP5K+A7UNlAP5SoimqA+5mdpZt+6jSzwoD+Jtc+myy0FY0421qE9WQxnaTLTQp/OOANeOIACxgUIpkbtBWP+UBInBwu8BEfcgZGql20bT8Cv7FiZYDPVeYLMW1CkeQSFlkIIa2gYTjqZJnP7hMeeViQodjH1hnLnwkv8SWumtKU9kyDRwK866soFoQh+hUzHSSDA+kc3gqWqhqKT+shViRCSVVPmMCMGqToEVqTTdmUeUdrniOxzDm7u7NgQa3PFlKXmzPaTkykmJpP0sWufnhnKd3lToPAdXRKT/u5WdspunPrcr6VV2547KxvpZmPblToQJ4Il7Hg77ivMf9b288629tuVWYyt84eCr9ZazCp8+ip1RH/vcMYq1NTzzygjfV7WR2PMeJe8R769Ag11qRBTSv2NIUIvVvHZzL76NtS4pydmjQUa1929I02UT0ntFpH3XH9qtNYZxuY12V2XUU9oav4AXltzpFd3nDOvdOQTsHtEQWvG3PrrPjOM/fRaNh+OJVGAslAj1wl6y83i6eCfGyuo6FuMiUQ0M3ZULrJB/Mx0URJ4T9DgDQKk2/SYvoa4Ao4pNgRnva2Ny8JUXqKS0FATuXhm/aU6FgIU4WuHpgf3G8KAC9nDIDrFVfsObNm8Ps6WfCCYHabYdT5XsGABq1tox5t6Ak/liF8JWBtqhrLYjL9jQwsHwigNlqD2oHV1OUphK8WUF1QvqrAR2iXoEIxgOpq9r+8IQPmrBgx6K0L9UzWFSANmYZvZTkJk0iOtCq3+vEhcFnJfyS/NIfatXxjwYGUIK5AfznKxuJRTCn4WISgeGyaT+YzRvcpVzsRHWU8COBjk9kuQgiFnqAFIM5sHKIazf+RZuYXHCxjyNCbAXiA8VpnxNifyJRSqdyUvaSQGnSANQszZBH9BP98Q6xC6FXy5VEOmmptNoEN2xPNedHBmlcjQClqfCu+roaSVo3PMqEsjvLDElBw2Tg7WffZSbvLPLf9rR+ifswy10Q+xMr2/W2E6OpuHxw5ok71lN5JKw6jKh6R6N3LHd/uI2cxbL1hv0Srz5Qxxq7xmpQiWn1jbw5bXWupPm3Lr2Akt6N/Rr+/NabjL3o49GnVl98nsGO3nz5S8nv206u+Wgx17L63DLD/aIoqg79V5h7WdIfV+mhauq5on7Hh57hO/uFe9RkyUmOqf8RHf2sZuLaT460S/wmxgvzBZwb3U6a5g4AN7QEPcQZIWRWE7DRCz7U9DCh9ZKBQb6W124XIgv8ClHTApwqkiB2AdAZljVZb2wBGNTZsucz8gUyY0WIATTVBBpjesa+YFEL/7AbECoAVwJoQhLqamWTj+fyooAKa8ycxDrXJcc2Uq2LRYJG05WdOn6aARuudhE8Mp0wk9l+AXGntX4rDSOrKqI0P4gzc+sb9VlQSqJIcyIfc6E0BL7ldTERr/AT5IbEJ9lZkrSSuVMdUlUMNzGeJM3sxsTOqcLVVVoncCCPolTa+8jYP8avoBfGC1E6iDy6Itfjv5KronoJO+5PqTyESssVbZV7F+OB05oNJIZQxIzFQz3ZoEQIDtgZabwjVaAVkmnou3DzuecZPpXaYFkZtP7jkKad+tozWyemMZ6vsw8lw97k+rvGhusWWkn4Ys0OV+DbVi5tm2K7g7pAYpv+4SuOO9XFp3tT2sObp6AdkDTwBiOKkmgalIzv41cjCRR+fQDAuMT467KP0fJe274j+aGtrxsSj5nE6JhqOyzsi1Liy3SD36NkWm+7kWZdQXvXV6rOrk8lemb376TqXcf1qwDkx/74+M0bhvrpl/jfGY5y2Ih1P2aNc54iC+4FuvOPJXg/PODu2N07HNHG6nwalpNHIw1GlIbrJ6nNVyp9X1cP3M6BQpso8T9gGB4BpGBJyBpKZcgOe1gti9RJZxnoFrDUbB1xmE/8B/WBDqmgVgGQYhrXi8ssmT5riiBKas2smhBiUpC6o0SpSqCJOeoYAeNw8AXpvijeAx/n0VAiS+e16++5bweN7ppkoQBBOznjmAAalJstObWP+gjeXMWsInOrw3RRAviQgDVJ/TOGXAFvG+FUQhQpwAw4z8C177R0CECggUZ2CjYl0c7CthEomskIb46AhFoGT1/yHiXA4TBRUUMRZsRRGWr4yjQ91zT+a5o/5es+xsLs0VvSiS3seoKqC1pDzjELLl5N0MUnPtfmSDiRdKxJL2IUJz5gLVR9pDP/zjwvFECgoy9SO1NrYs5pKXdPMuEkMaz+S7C7RNB9ZBQclTG0zFsgP9jfl1Ffcjowc1lcUyYKtmbRyQzrJY3CUVHHwdrc8Z+rn0mrPFzdVKa+ULpN8iHJ7FacCUU/5uDFas1HO0eHBradjUe20mTl+JHjf31YT6HYFM12J7WX/PWSrrsvd1tmW7E6N4R/fOUfR7xZbpxj0c5/Ezrt9nW951W4XeOKudn7pQ/slGs+/RulfjT1/y2ocOm14zMzyu7inzh0aPZxDB9NtVp+XNLLDDWTgG93x3eBZKrm9d5Wt1E8pPPDRuars0x9z43X+MnzMBh2u+0fX/XaZ2nFD2lVF5aGagSnLCHcwAUBhuvJuqIn9ur3ZwLvQqgC61v1Si5FcwLqVGmgUvma2EKgcKthsnwBYMTWoVwoypIgerorBe1UEFdqEECCujfR7MEAtOIDuKUVltgQiDmBiiwa/mdS/Ar6jRcr+oFQGTq5RQvvQa4AZ/GkgXlZKHlqRtENSTQHjb1dcqhgaPT6QcjpXPwmk4K5soVobpzc0D5lDZOFSmELjCc8VQ7GyzJJSVcRHFIYoYYsYgXAYcwEXyvinD+kjBk5vPsQQSimiuawVwKN6ZEOYVqxR3mMwIgc8RG3eekZ8hl5yLyzRj0iNuEnmWjUUkVhpCo0pIp1kcNlq0k3a6j8n2SnlBOXpEvbmNQpKYjUEhfxXwCC3Sy2WhCsCMR6y0Bzl7HTmkD7bg9ohw8SqSImqIGRWdaqC6nqvz30qtyTvJamDeB/h7epe250VOHF5dDXbor/NOTs9GLqne8Hpd9b6Nrvs22db+D51mJbbGmFmhLKf8ZiDaZBfiC7/OnSVMdXG0QxGwGM17B8LiTkM+aRHWb8VhYohEcjb8XQ8ah6nQxUSxN+Bs+c3vpMxcWfax+B95LgxTuCcQ60+HQLBAYmH8Gxo25DeHploEIy87HvG4p73fhz3jZFsA1lf3b78UHGvRPDVvt0jSIn7ScjsTARZnaWxXXG6k5jMFo1/dVhgqhrtEYvqDrPlZxUEx8gScgMlPnc3WAe3k8E/h1vCaQA58QYDWhXGoUGHvDFXAJFRcIaSmW/Cf5AiJ+AmK0wZkkcl0GBuM0A4C4YCGw0UCj9KqClhmbogIb3AgrAB2YN/l+fwLyavyGH+Om+TMqyr+eiIQi41iDGQzT/U0UA2Y+T30NmsEoOXbH2zXqIzCJi7ImPSvvJVAUIpDu66UEgjIGqgX+pgcqmloVdPm+4GvHWtKvIPaSq4Af68QwDc0Ls+jdSBO2nR6YxtKsBSMnjOYGyU7RWgR0P50bzl+qCkR1riLzYqlats8bEtdrA9gQiOkslC3uONxRlb9TNUz2T/U/lB5LBx79xp7D890/sTNguWBXNJWxES+NoN3AWgVySiFpEiihtMJZqSdjLZClRwJoc+UF8kHHKygL8eTGhBh/YjXV5Z7MFOGshS1KGXL+B4M4azHfa5+kKZ7MsUH2Sty9/NUENk0LS/a17Q8+0oWvSl1vIoh5+rPMuKTu5/y6h977wW+Z0VbUSz9S2O2O6T9LtQ61fDBbvpHUocS3qpaWt8ehR/84NzGEXf55aW9JJw0M8PktijyWPwjG3pEXtoNn7zDsI56slj2HV0qTHV+mj6WrCP/qD81jd9B5faN7pBG77gUb79zjIFiKOrOKKMkk55ZHdG/N9hMhh9mDXtWoHhvkbAqlGXyzb/fdk26I/OsMH/US9d+YaXjiLxMXgeRbE+Jg/sG+3O1ifoMfPHe93wm6HN2rfEvRDYqH8I6IER+erYODGQcSVITTYwVLNQwGyUasx5kpydnQt2c9MEayoA0K6XxoQZPNVXBUgYAgDwoaTBzUoFSNFKh40fAwfBksK99tBBucwUZxqLZozbEDWlzIN/c/NmuVjqJcFGvFgumU6SzbLr67vbe60CZm/SjS0FXq8WmzWzgtjsfgVPMCkaaMwb9TKZxAi4THOci+HSAA2F0vlvusp66axPNKVYNmKt1DbPymkySQteKTfbS3pjBUoWnYiMgeC/6ijEgpWY+9C/XWmKkUjFS2GVvIQ/Qf+KdAScgc4C+JDACKCPPvZp0cBGq3unPB1hWa6xICwRqFdglrMGeMW+QFZDgRn52q0nm2LPdDrHcwQAmrIPuIQIKTgNsbCHl2wyKzjT2Fmq+IpMGYC0cq4PGlmm+Q8J1vpysfSxUA39NXdJCzMskhRf8bCT2OmgTL4sL4zC03Y2qdF1K+k8W9llRrPUNJZp0eEi6nlR8YeWDIqGhGu401MfmiEfnD7fMg963/fzI/maLvgtc9qgo/Lm/qCD1LqV+X6i+0Yn8fy5XhHtCPidRFre3o17T6xko0OEy4EqXr1v7Dlm7um42zl/zjv5e914duZxY/q2/u2cfS2NbR/WtmesKGawK23jmsd6krBLmMr3/l6MYWo0sa+Ge2Cf3wBGVAx1ByTHsgbIrGh8P21yMsDdzOQ62rFYKKtUmZQNK5cGgNT4fgjsGoFwqb5DfID5vAoYrGCCDbgVUna61LR/bfMyyTUDnpfswkq+EhiWGPgbBFb98hBXQ8vKMwmChibAPyT/8uqScAKczwVonmJU2KxnQHyxZm4JW9azqw+ANc3+9S9+dvP2RqJZ5KtnEQjgSQMIk7n+oFu9JBgdtY5gNZkVxVM48hJioCzImeFwzXz53nLDnvm/nqawYNrQzXpynqa36eZsnb1N1hdpcjPZnBfZ9WRzkaRveN/wJn+94Q0Gyetkc1lkbybri0l6k6zPi/RVwW45mfI3PKBYX06gX1+yE6h20cleTQrySV8l6VtqbdLXlCbJ24I0tVZX0Bfrq4LNdlTruijIf5WsniQJ+dLkZHI2Se6y1eUkW5iH2VA/ZxedVNuAsvEOWyHdbdLpcrMskrNsffPyq19pZs8m1dY/vMhA+6Xyo5N+9sVP5mfsAcoGoemU3Gm6ylbzi2fT2fcImVhjjSezKX4G9683d+s3L3+poXwcJkxvXUOhh8Ub6iYwmdKmNBCZ09k0ZfqV2oK2s7hKCF+tWUyWmw1rErSfrEIwHiwQfpGf8IDInit411CHsY7D2L99Ut3Eq1vq4P0AHE6szlsdHd819TGFamXNitI/o29HVSA6atTJ61cVaesz0qQsa3Ea9dttldtVW/I69wUaU6/NqZkT7nuw23EfNqTRrP/duw4e6zSdHoQn42OHV2PSMekWugt9tiG3ZGY795MOZGOEjKSRsS19euu+k/4T3RnaTdGhWvvJeQdRlGV3En8CEOXuk3yMhthH/lFpvc8dYBIVD6gVdO/u61XxYcy9vzxEq0r+p88P2gMHd9ojWeXy4y58rE7X6viBsXdu4e9YroE8kJOjLgE/Rsu1jTyAUStHBe0ZRhYXVdMEHGCmoXtwmrKE2KzU6pbf6TLT8gH4Jhsy6pVUgolpBoLU4mK9mBaBNtxdAFUTdossSAB4V6wcZRP7HPAIsmXxL2qgHVfsAcoY9oIpQABZj0CMOzHA+ST7QXZ2wlYNmiuUMWgPkEyLC5gm6eVPT/LP1qdFelsUZ9nkGoBeAOuzs4S0qvISNN4b8EagPH872VwlySsB/eTtJL8AxCcC968L8icEAFcFlNnFZPJmkl5tCBIK4Psram3ITy+K5PU6vVxlbzbUnTjcf5OkqjtJ4fMWKenkTbJ5ssrfrNPz9eTtJDtN0pu3q/Ovls+zIputpriKRwR6fgGe3nDJymDeRDlbrPOb9e0kvbhfL97e3d9N8WMiQE7DLRZJcsFTAZ6H8OYy/MmsKtxwf3N/csqreec0Cn4ktGVbVean0q7y8Vny9i14nzLNzFKf0PMW2s1nIgmZ2/sE1Oq4NGe6UdUBLEjgaYUyWBxwe3cHrZA/DOzxiToKpVJe1xzWE+kP1ifE0BG8lai0urbeo4CkOqyoutBnKPKOZiFnXN6RDlVcUKBo8Q4ltQSCOLZMpOw7P96DyHdu4/sUuLMvOEHoBZ4Il+9S9fci9F0a+IHJOiQA0Nc1ik5Ki3ZEh4fFTIfVavs4ju3idIuS/te4G/mYd9teqjpxoG+PNLdzYoE7I84xXwaku5RAHPRp2xJLH5Nu69/OcT59+bGUdg9p58T0rXmiceG4tPWfPj/s9P84GTWqjn4y2N9qlY900ee3gZ48ILnVRu7O0N0aVT0/9MFG6aGXzrWUWYpABikhfv2BygT01k+Bazbayj7ufJeZKQ48A3QykAypj7hTTWP0/k0HtRlAhJPDemdpmnpAUX3R/dNkUSp0aHN7qC0GKgUSsjV/9hkz1u/Xv1gyTUZhQMosIE37yVFpwQvJeH8VecxLTyZMX6Ee294nxf2X6+Uymdosc22AI5y4REsZqP+EFfZOXp4OfJUUq9Mk+TK7+jy/Y9oMl9lkXuSsYcgnxYIh9mICXJ5OsvuCfMawk/kkvUuKE97zNUnmCUPvk5Migf1pkt2Tn0zuJ6Kk7smEWfiJzklxZlvxMAUffc4RX0zOmGCTEl0wTwdczmZKExY8oN45pmabc/isk1Mh++KE/YPg8DWLGxaLzWZmAFxNh02aHAQNj0RwGNvxsAHqajXN3vBuAmph64o9f4jSeJOxnoVMJ2utx1gs7OvMhB/o+FYhAjnFcjY/UbS3Bv0zqM+W/vQAnhWwhAAN5EkOdRU1kXvTXvJAUhnKV3gQPRyQjtaDtUqD/kN6+UTBGe830EQvVbeIQjGKOp71LU7qQ6KuJlKpE3mOizfrQ1Kl8SF97DDZrkGV1f8JcajYoOqR1LO6oFE5utznV7hHZsTt0ZLhvodLOu7D+8p9vPt2nz9douvZR7OvFYP0wWNQeSdq3e1r9Y/g1ZhfZGPoxd73gz4xuZ5E8Vz0c+UdWRMTgzf6vkk1NT7Ui45ng8OqyteHBADDXD/60n1vYfvS7+ugYf6hNHxznH/jckBo4DBA84EUYRTa7nUcUGUv/h8C8bttwTE9a0CjUQ1oRC3Ksi39Q1DOxmRZjkmKP2ZtMNMGdK38YmOj/SzApYUE5Jmio8346UCgOgKDckIRhQbzSyrRGrlQXYXnPC0R1v9MmFC5YzvLB/tZDrx5DsC0fZuUol84VgKg12wGorU58Lx0ihnqwGHw71o/OUBYrRMG7mpyOZBWzxBUUaPl+ldOgodQllKB5a5YcD/N7tmfBn6MgIPESwUUV3AYvLWEHCBXksOf6IwJINUdLDuULudBySrcZ9ZbFVltLETDhUA0NQWFzVt+ifuZJUMJw+MKWBS4EA2Blmf5OifUUADgQNkG0sHQDL0b9WSdEamkC5imOq8INYTHMWQ1TTKcCasVsdvdHW7cpCvek5bnKct/T07nCopWtDVv7WXrT5FOCGZYTKyG11R9TLapWGombCvtlxE63ExL2olsspTv3pFO6gl+zVlbmsoLVpUPBRkIsjMJpfVkSY1Qdg9pwAVnF0lVEmT1HoHOle2kcxY7GHXW7Mp0bYLcLpLHzHPB5qVBxzymDt9d3u+t2SOXN3RoXEaE7yjpffEdCXtfYvStHwgA+I3kiKI0u/YTDeT3jG3egTHZkJQt85AajlADWTMRWxGnm3TldTCPBGPb7e7oxrfze/h1Z8cR54Bd3heb7q5YhnxXxvmMGY+vGJSfVA+sGkXHumz3kHbOsKzYxvF1++yK/T8st1a6Z4/t+QbVWPZexLLidG+F7gJv3D6PDfQ92LVqeSN0CIpGFnG5ZHZx9iJV33fOYvU9DApIBAhz9YQ5OMv1r9k4Jpm+FQa1WdyA4jSdMWEEKqFD/qGh5nFTT/P1pUP5djB8a71EQ7fQAxS1mNWG0rkySCiL9CcO9ljBKxgThQRCeDwUYLbP5iXzgNYbthWarpmzsloKtgr3GzrWZqDIYKwaDfRvDYaEKXPEbcha2J4MpvuA/lOFAQ7JsZTdQxFv2iQnxXm+YoT+NWPhDERLpeyN9GMevySJBQgbS+FmmFV2IUcKC+VSJZcPEibiM73ojfLXT0rIKTIEQSMNZZ4qMROJ5yvoCdpnUpAyjVBaFelrDZZvnphvmTND2GM6pEtWQWQMmutSy2oFzMVCzMHsy3R9s9nciIKJQptFSgw33fAUgmgALoorXmT5bMNeQDlOzKmf5syWwm2buQI5mLHa+077OG2y1WqTZXMm9SeT7ynQSr5ifyD274cXwYD5TvRygGoqKSdIH8vQWXbpUo+QcBoHPesbKLS2mHw0o4lWT7U10OTengJZ1IUvcAB0NDA81AgwlkwVlKyw3g4yTM7gbPVAVFbSR/Qtq1hYqb5rNOlvLFMm9R7VzKUWgSvUyu7IwO0cI35J23X7VpGpDXTEqst/bQ7vKGe0dfFdLk7vredoiX2cB6S7H3e2cOtu3yfqyPlxS4ce0mx7889DNBxe8xCbNOZp+YC3Y1Y70718/OZT3TECn71/N0PN2MtkinMzANjZQwKzb3PCHcXZ3eFnumNIuPFceh8NReOdMr6KU+6kd93GKzCSErnhcHsfSVCQ8i4ToQXfpdDHkDXQPbwF43Y8VIEBIQ2WnZSeWVekuzMZcmqwrC69vkCVo0/wVfKbX3x1enX32WefLzTbBKgHcmYMFuS3AIBvpmDQmc3aAI2RDZKeGjorZwEZa9eOpCFCwdNSN2qEwxCkrpQQjR/I0tC/VTFgaxiR3XvQRctYNdytSSYMZud5DkZ0UK6oQLdh+2ETlNa2OSiA3pYAYgHfhTkRZKBSJiOa1awX6XKWsfAXc1wNLRCQDeLAL4fsVJIMQVfTVITKKz+EyP3KTfH6CgcoECv+jIV8orSMdu8oTdWyVEkXwewY5cGJawsImJs0KebsWORTaURZ6iNuuMWeGGiWPROYmP9zT8wDkfFAiMRpVa8ajYlDDK6Dq1GC6VVTxQKb5WqZTQkICjA/C61phk2xIK7Qsl12DcLxbEyEKyz6ktKmsxliYsxW8txUdLJJPiZDpKImk0MfmvDDSkS0MnVMTWPJT6kiFaQ7PQTygclyMaXg6mL0p6k2ltrl1aSOrdqk20tuvfIDqjojOdH8dRRLnOenc9MD3kwfiIvbarRzmgY8zvX7kruHNf792KOCbm9+42tV8vcAbMf5ML9iX8Wj1bXX9at6XovrHhmVlJFVxsR/vRHVoIy4VvBCSPRVPcwR3sn87Jw77IpGWQLlTn3GjP3HcXBjHnwQhF0hHWz3nJ06BPpHSsS+ilutU9ywtg0ba9wi/9c479lja3Xjiz7+MU0sK07HNFV62NKKquMz9mdcXPNG2R0aDovJgUC1Sy7qnJt9qnPOIrjJd0zPmA3fdVRc9M0ToJtks7dPvrf+0z/55dWTMzZ3Ya4Nm36yfHS1BG8zy4Y5OKC7pYZmGWXWGlwK7ksIyHR5zQsx+AqBsJ3fAVmiKvbCcCYJ0GlERrNi/JtR4Td8SYg2gP7wZW6+vjNUAK6CBC1zzvYygqQM8xMJzM/PGJmGirXCGl9mMTCj3pPVbHW/1FQWDdirmJcYa/BHaulBALxIS0/yDFViy+nmJFtPsVKxhgUBxYa35zJCj1bs0smkfMhlTXUoWdpZJpdVBqiX5by64j9j9KrrAt1maUEJ9PjwyniKuYi8ErHL+kpJ35oUDM8OOULy6H6bZYzvszT5PttMWaXBIxA9HyDGSYXX0ZVNTXESD0JWvAOYZQmT5SRlSg9xElEDsRyhBI8pWLfA/H46WbFc8JoEPKjFD1Dw/rU164g5T9gvlWon01l+fj55/c0rlgboTXAEWcjRYY2KD82GMmfzRFbyZgmRsEDZ2lGENAdpcvEJipKgHt6Wa/LZm5Pz6+KOVQpk5uxZJJNQkfc+MIdJh/lO7aXwwOqWSlhpeSryryS24/DO0PrWt79lXrf+Xevg15lVe54QU/QoVZK0tCq7bpUfukUYzQ28h3+h7J6DTwJ5LVG/I9WKGhfydz1rTN2dNM7WfRP4x3ME+jSv63L41bCGNeld/cd1Ds4JJhyuUFTTdfOMmiYRzUDSvQqB95CH69b2FXeI4SO07Bj9naYtJRYxXOqUvbJqv6eh0Rq/qrG07nT5He92KE8AtgVbGd2cvku5W6+0rA49NS6BvjM/pnlgulOlo8sd2QmOLneMc0bqNoaV03iTdTo2ZhK37E7iuOK7TMdKutwPVtU+t1in6m8TSgQLdQiQcgiKMf+n2Fz/g//q/3p6xmrafDZjeJ2R2tVysXhz8zaz7XkAcEzbYBnuNJ+y5ct8zsJWcRKA1eHoOuBllUiYgWiT6HSeR6Hhc6vJzJP7O5afXlusoRF9Rp35e/nixXJ5z2aj7DfPzH4WAYPhAa9vb67B1zc3t0BmYghuGqvVKlls5opTNsQBrCwGY4Ir0Y39SjFJxpjdGl+2oWXWt55ocHuJ3qaF2SDASYAAEWBVI9rbMjfWMimFWv/9KD1ZXUKpqvpnUFeEcDJ1yDPmolWiLDGA6wKBu6ivIlODmifp+Y/PitsVO/vMeVaBK2xAnmcjtsE/r/hdJ/fr5XytCIqaQtI+uYRyGV5OYXrxy+cbNvnJTpm1lWUn+ZwR9/Ti6mq5ur+8epJns8vFxf3tgu2Y2BpocZcly7dMMgP4680EtIepK0v4c//ICm93Ci3XzqETWKmCQ7U21Wg9o2MuF1lfP//mn/z+7/OOMFhrvymmmum1A5vf/ulPn1w90esdFIsoJFAT6bFQ/Yiu3a314nBljRERVwVUah4dVE2Sd3g9aNWj69HhnmPIdLYN5o3LY8h5XB4fpsJoRQ9+JN2crfMf/p48kgIPbtFH0svfAyCXuFuGnfNgK9oMuuLUNtVeOfk3e5GXxL1xWMVs2DXDpRWP8hPi3e1p0aqzjbtvzKottD3iEtN7Oo6DSTc08ctGZoNJoGkr0KA87uWwVp2yBjQMT0Kgcc7tmL5dPRB3itsjc9doxB6sjBQTYm3bvuobjejLr38j9rU7qOOJcDlklqGd8j0Abf2pKRzlqJxPp+CDmSMMpN+xYaNW02ogVm+AAoDN5qc//elfvDy/0Fx/8KUGnAFmYDmGaQUDIwDtyNAzpSPXQtR+OHSWcAFbzXfXJ4cCi5vbm9u7W3GOyP/4j//o9vpWyE94Homl6jyAgBKlgbfMdiF+WSzv/8Jm/jeyq2V2fZOcs7UNM5RSrWSdrzNeDjDbTG/u1vNJzvaYJ1l6k24uLtPV0+TSX3MFJ4fbekKAb4pLaV5a49qrdxsq17C2/GZGiMoU3p6c3EaMILHoSE42u8TDuJY85aHSWzLQqGAtsIxRYHgtS2Bbomx1lp2sZ6BndhlCIvsU5UhG242eAzBTZ8ne/YvN/XKV3G8Wv7pbPl++WazOGf2/L5Y3Ga9DuyvmySq/41ZVZDe4j51M1wvaMX/z1Uv4pKtbXt58+yZnc1U2WWKm/vzk7GQ+o/V59GJNTFSFTqhnGIMsUjLMztkru6IL8UThSsbyGgQVYgUBSf7FF1/Sq6y26DGKLUR/89Wv/uUf/yHNTwdwvryn7P5+87/5L/6L//Rv/k1/KYQYqhO5WNW1AwFx8yAwaOMJJ+P+4PqV1eofXuScy7O1a8iBfKB6ndkRrrruZugS7iEj9coGf7sDt2GFkdU+xtQdQ+OcrQ3lYMl6OIZpc2jnmODxGpYz6dqOGMzp+y0YrFQWlrirqyeMqQ6NN9wYHcbQ1Hxl/tRLYCopx/py1KS07BwubZE/Skb5zLBtsO7Vvgag8xvzKMp8TEzbHjuW9nv5OxB7gvNxFXsIt6MrcywPBz4jNcQJ7t5QcSCxF/EAn4+taF+7g0c9ES477VapQ5hBOiczDqgj/M18nsWSNaDsrpn7FkCC6bbqUzNFmEEiiAbmJjwAhjIorJ8BQJsGdy0GqOCgwHEQLvQfDPZsgTnXXQDbLhwbgw+1MSW7/bD7pFCfuIgGlAoZlXivlWpWcJAs5sEQFvA/S5l/s/6r6eUyO71LJ6cZ+2yebgT952yKsylOF+nJOj/Ns+u84NVd10lxmqcLbtxazSA9TCf7kEpmgKmnpFvgWguI+uHqVdaE4Wmnl5aqpqttjXBVZVWfsor/8h0fOFjVAduai2Ny8YpmApnnmbejPfW5sBexMQdIU2544HG/mSb5NOO9yW9f367uWKJBYMOiYOKlRZ7erPRsJNG0H5jSktpHlIYl2MtYU8EwvF6toHd78WRhNj25eHKV660JesqAJqwAUARGXfeL6VU1vamjkEDqopnyMUJWWWSVTC7OtcmpZXE2fSfF69cv5/O5v2JCuUQLTBlizQkbM/Fwh8cT3gHoh85MZ/OHs/KkBFr5lkYpowz55uCS3kvjs5PpXLGKKsaEH066rWCvdR+O0nVNgtfRvG1OnfbT1ScPvFcPDPRRxmNWX6q8I1KxX6x4tLi6gR3VmHa82BP77iG1zXOPyltS/2K/+3tTHN123lxCZlu34RmWblsY+d6aWjXtQFeJieP0u/SS2xvMR42OfmvKtT0T6+zpet8uf50Dz2EObU3a/HtzHt7De1iHtohdFGj7fNWX3zOyhemd7JET+yymGagi7SpSVa/Sym8eBtGqTENzQuzZZLbevAHFatK2kB5oW2MbjAozDr24X6xPNHndDrCdYLOhPEE+e8MrtFCWgh3ImiGO+iqbKHczBF+NvCqBW5Hc2ezwOTxB9UznQQ29kWB5yYMH3qJlYLvkrRWpm0spwYt7FRNMN9nFcrogY6qnA+xjuiAqSCaMcm/yyTX7+acZDxOAuLfa83NyLzwtJCwZphQfmpdiIYHiD5kpzo7KUdeoQoYsdzMM46Mz5ThD5KSMuZQlfsGh5DD4bhQqZSwcN/q10g505Sw1gblJ4+6mjNYBM+WH5gCJI5G0ztZYzF8i/57pM5Pknun864Kp/7jglpF0betJOxIDMNyu1xCkd6hmkvEAIRzPUdb3Z3BeF7xxjElUekewUL4WE/NiNSZkMV9Iw1tFsbA4y1RV7CDPccg/OnPIiZ5i7N/7AS4kz+jEFmKRGZW2FvVKxHxoJX3MbYvvTVY3i+vLyfILvYxZlsodZdVSgssx/5VCS8niWZK6CnG+FXacxtB0VNtm9a0o2FL0p+LfqTjdruEG+bldGuc07slx0cj0GCkxq2HNY8rONOLQeV+hTVZtxNLOadZ5lOve34Ix0o6kc02Hnt/KGs1BujkK4s7W+A5xqTa18zDjuOfE6eFaDy+VLKaH9qyRa/Mv35zwvFXCT4x2AdKvQf/RcE8/4aeSd+8B76lHlzum9zeEHkuTRl88uPcdrM9eFQ9wVMNvj3HZ8OFRRfQ1SOwJl9/OGaPICN0rFYTlhLwAnawiNaxmMoU2YSPYuVwxv4ZXXNk9TpCVzVuA4ySoYBAWQgE9CJSpErv5m6p24SkBW6vHR3m/FLYDr3LJeC+LX9GEsW4gs0QLiYpUSWFhyGAkEEwOhy75L9SO9ve826rIn6WbNe8uIINp/ygvrbQ7jt4LAEamhBs23O2fNNXyYDOEUWkxN4MQYatYS+hpTEwcUg37msekg3RTdf0M+IFSpP2xggqlu+ksaRJolczTZo+UUhOIkoSuVAWlrERpVZF2Tsm5LJL3NUkrLZiKxX6pcJlJxGSWXxXJPb/ONtKu5zgZTmIeP9GJZgxJoCIrlvsqkGLpADIK1lGQe7e6y3kMwPama167pghE23+yGav2UtVycB42EBqUKprm0tAtMANgpQcFpq+KLNSRzmpczjLTjBWN5gUhhEzmdxGxKfos9KyCZGmo7EcxO0Ld8poStYUXlpzFtczY8RG4ic6UiCtUXOO870J6pPOO4oqW04/C9ROTD8ID77IjjTC4pc7RvuBaA8DNqkuA9jur7kdHkzfC2CPFkW1JHqV5fl8E2Yjkjm53mKPf8vhW35puPRHwlnr/VN8oS4iJB3QbkEYtd1ewcYA4LnK5Po4S+997X2cTeFHMpJF2PmOehzQqdopr0HDpxg47KralxiHu4Q9o35h/nK7JeshFrOcOPrEnosYBr3EAIsceqjuwC5Dc7qIqIYJYNkzMp0rBiQBGkgzc8iIAlv0yt5tL4Duf6KMkTAyhAcH0ujDxMJxmiMzwoHIcnYmXBp8rwSTERP/Zqx7UO2e0P92cggVtOjg7/DByDTglGGBf9rf+pdAkIaCxdiflbVWbxPbsl2wYLGenyekJ77plfHyiUWthW3aalyHYMc0yAOyMYXiFASyR9bfPSmFTnL1zeJkuhyzDao26S1lttqMUQigwE2SJAK8R8wl3sCplBm01ZR+W0pFrdFVNseCfiGFoaRGbN8kWM31/UVhzfow5mUy6Ulq10VbbMAnrK18I3jfTZL4WDjwtMrb3Aavfp7yEeLPMs0WR3ywnlwnv/wVg81pfRV4L3qmMbtIIHdjTiQXQwuTolILDmfu/XN2wMf/snFXCd3c365On+ISm52EMPYpHCLSOeiNzjtilxxtUTjMV4SOXyJ3KKq2UIB0SqXykE49wTSvgZ/MCmmMX+5MSjGQvJ9m1dhPKX/IaZWrT5orRysMT0dn6YL1Ugkx6lR0+Sy3CdcTHK6y+lPZ6DwCHkoF0v8T4O0n8OxWnXd54PvvquxdnKRPfY+O0KdrW3LLrp1Ytir1F4kS9zuNcdWnSlNSiiT0Wp5sV4+sHdKGYDemxEhvV/HL0b9DeUirObUP9q6P2bXky1jHuOXE6pqmlB7nVKGsXrqDU8aNPVt/7AfLnVc2OTz0kjfpyRWH3b7s49D5Scfq4P93rR/fBtjF73IPEnTRUPbpigecY6T26HzO7z8D3rt7IBjqmLz4sXp0O8GbxRlNaGFC9dKi5rCwQeK2hju2kwmllJaaUaJo5b/klC5SasrNnueSXPRkBauBZn3oCcpM6Oht8o4L+TEMy4KcLFRmZFZQnCoJAB4WyTSmIVVEo1cb9BcBBnQBFDQnbBCAQohA4FABdajgntOIyTTezm3wzz9Izm9JjKNuEgV/1Ci1BZlUBdfJCAQOV8MIomPGXM4AvHXgAwCi1cpCguTxkSqj+QMhKMdZPjg6oeGoiNUhTUyiVQnAsfyilOsqwRxeyzjR2+oorTASbTVXSDMWDxcVQzlCh1IZCsBsYrAlKOsScyUxYBUDHS9KM3ZDY7kihSJLnbOK5mgu0K2QqnwCwlHghuI9dWrvNPH+UzfR0BEtSAH3O/J8lm3HyeuDNanFzv1rPzp9MsxnC2fqJdQJIZzkvi0CWy8V6yQJrUxA78Rj/PZ6RelJan1aifHOZaMxgqSvriPU4CAvlOmykByKCShRbqAOV6IyjyZBDqkNiynT4VJtImypDCafj3HcEGgikn1XpI/6w892Ug3V8YPWD5b7Hit4vMPyxju+GT/u+XuS7b0Pisfy8m++4Rj5EUZslWVPAuOjW5bnBBxURvy4c7bmDvRHYgXFPJS98PphPX+QUJJAYponHtsO4tVcPX5aQCGzjWvGewYGg3XDbBq/i1EAc+7nVOIHqkIQ/GSj17/F2LL0tw+v2jbs3PBaqhycS+CH2j1vnEhs82x4L3DzRoG+Ujrns0zZuzWE+w32prDvYvuP5j5I1zG5E6XDrawSCMe9oD2+Btv7D7yQgwsZRzW5sNnLMyyZqgJbU45KpvegV4AYEA+oL/bPdZLr6kkk1fiMzbAY5INNvXwJa+tNN3sCg0RliVZ4goMAYhXz6HF/2sK8EkglcK9irnoXFS1aCMgDMjvM6wx/cDLzmFqk1x0LGjIIDU5m4wpQeZq1oxJjlwtoCaMZ0lwlv9AL3MtFH01MICThxwUqGN2iibXPmSGOW+22hvfbRH+bLgpcA5AtNcuE8OUvT+2z1gyJbTNgnZ3JXrM+SjGnoZ0Vys+KdAPkr3tHL5kXF6nIy9fSryfKKsepi/UwT31dXEzbDYWVCej1ZXUyy18XipzymYPguIb2+TLLrYnXOCHfBG3nTt4y1F/nrzYYVDm8nvJCYBcqbU5Y0TJZP9SIC8pO3xcopv18ktwQIk+yWBc1M3deIPh5anTDrR+LUBPfWCkzQKp6en/zVyTNWda8md2Dq1eZusZ6+OX3LG455PfAMnys8YX9Vech6hB6orJZviBaS+zvFLemsmLz54unFF88uFIcpHNJDEnZkta7Btku8uoHVFvhbT7nVzXCzPtTm3mHURmp7lUuAt/j6qUA6I/0KKnmOUc7T8vCL7qReBUvdOqjBH4zhwUF9sTAZ5am8Wn+uIr41Jt1o7OTMG98OaPz5WPkdcZ7Q1793YlAV+bes/XttQjpO8fe3o3h0Vh+f4XvIGPZ9nP3O3FEa32Pj9BhhTnNQrdLSb4zFQRw6FKz4VM2rdi77WKCuaEJG7JM4HQi6E846SKqI9m1Bl7hvrUra2M897KqzbHzv4sKATMjs8HNMOibdapeyErcLjqj0MF8d4AFuG6UO2w/rTT4YocxW828pP8JUaEU3q/nN6bFooIuEGsFPIRGKdiZcjaAb9DGToGRMEPMco15MP5yORQ9THr00GOKWDmgSfNLWoc9LbcpPOUf2QAmiBhpnL4E1PrULfvIcwfPBfZOX/fKeL/A0U2UE5gSbNXZsQ9/AMIadq+pAMq4JH9S5fMxU1PoRra4osNufUSpfJdYXLc1UcoFGxnlB6bLY4KyKlJR02E+WeiEZ+FJU3N8ZbhdiBcbP16t5BvycX6TFNDmdpsvptPjd7HRGDJDDI5MhDP1Tkckw6835k6cXPzqnKisaBPRZ57wB+i+TzXyS3GTJacL62M3JJr1LVt9nNe0kvU3Sm2RzkSRvJ7x+K32bAP0zgP4TkGuyeVak3xRrYPrLZPWsyF4onb6YrJ4W7H25Bri/TtdXSt//dpG90iJb0rz8i3XM66tN8qbQZKc3yerJJiV9WWTkX5JG1iR9PVk/A3zznuJJ8iZdX6yTt5vF94r0ttjcLYvr9ZqJTPfEPuv1QuEEfqKVKpBOmEQ09eTi8sn5WbLkjc6sqz5Ns+Wrt/Ovbv/k6yTn1QmassQDBB41EEOpmdTGtOZitZDL2AuIxz+A/WnyzfOveb0aE6lYNzCb6WcuZa3wsri4OJ3NaRomJm3Yskntxowrto+lG1jDl5jdWON2yKyV1V30+IVPgXL6DLGFHpKQY42uLkKaaIGnF5alblN2Let0sFftjsM6lvWgqlBaVemBT6lsxdIrXAxU+KCLPnoDHt+7nT3Ie97xhX832qPTpW1n6hv23o7jt7A4ajyrHQC4rOAVt7u8VI/oG0vojT+iyOZBDnwwH4+r4jFmt3WnVsEZ8bhyHB3CYeDLEjwjX7aivSA9eJpE4BbGob0U4sDNK440IUgZm+jx9s53LEhPs7HhH7LbOQ1lgp/j/NjncX5f2h3l506GfRVDft8Yv7dF3H9Clc5EZxwf2iskGnUb7dsojS87+ccER0+7bn1y86+C1z2xQ77dSQSYK7reWtsCUiIXAC8/wEmgaw3GkxAsY3hXI7NsrvMN8+2L9MyquLuBjIJkJQ+x0AFQsxzjUYIx4UtRKzpg7F9fSf7yfHo6nzIKb/PImZky/fWrP3/58pV2sEQ2YBHguJ6wH+X5ydXV6RXbQU7TebG5t/WiyeX95D8pVk95Gdk8PwWoTtbMeJnx8irGkzXjnUFxICaxgoBnkpxv0iKbL05PPwfl83IABv6xS8PieC1dmgvemifesmJgUvxcarqhxSuhz+I15yT5FX4p/Jub/FLp7LkeU0yfY1yBl0jPXsp72Wu4JeB+TJ/+O2jYdVQLkYuX4pu/tPhGGy6RZsYV+XImjwhITtAEdV+RUSTQ4Lq3vLBsMv81nAHYGXvzsK8Rs5rWm8WqWC2QxavQ2DU1ZedMgjcZnUzXq1tm8bAHUrGeb5jQwy5PZ2+v7q4vV1OeQiw3V4uM1wNYi+Dpgicg00Qh1hLfTwq0hR+BxOQ3N3dfTV/Mp1+yk+j0hCUETCdSwPb06Re8IQAor46iDPRZ3d7eLpcsRcBuOUBmlinWUeiJg5yDSdM3+s1Uw+kJALnWLazzwEm9SM+8YKykYgNjpLQ4GL2YlSm/pi10eJ4XitrCDPtsnKrnY5bttQI/r+gVKjl9v9cNtg+87LsntNmOv7+163pOpyx80HdnrtH3//72iTs4/+GWDtjb0KqzCwSamgcst50TiGuJqhfFmXvbZT4vaz3E/3HdOB0rt086OM0rBazFZZzm0injr9c+cnbRtrBWy8MuGS0aiV2crby2NqDiIUbc6vqeAGg0xM2uKvhdsH7vMvYf88ndudMCyLwHDFDGBM425LgLx8tCSqgbJHqOn2NWY3QLTMYn2oJG1qVirN7IWk52LFseosNeCh9A7M75kDUcYZT3jhGEDyZp9iUkx8IBWGQwimwvZAWrZsyxEQoXFQhMY7RciIsQmtCxJb2POpmRlkkjpQa0flBLRUJ/GpOfn5yQw6A1W3JqGmQyefP2zcuXX4PoVUfSwPDp06srFvPymAGUuSiWLPZlbHqzvl8zOWY6v0xmG2asmxQ0Ig3KZaYGc4DWelUNk4UYmZYcTXJJAf0LqWH0ppieEFCRiTRmjSwCL4Jly0uhV+3tI/gpPmYBr99yQiQx7iMUK5aAVFU1h3BtB+CYfB6nsBmRFswWvIgLUtGjLdemjsNbOUeVLV+1VV4yQh+y7QpQzMR/7IM04W1dYkbj4Cs+eEqihwGK2zhneJdB/QzAn0x5hTKLrH/n9Iuni7N1cf/NJP3Z5u0LPJYmCoAU4WkVMGzlGWsa+UYLHHgl9Pzq8oqFAens3gp5UUTG5v2aMEbzUQXhMNHzGesmZqCMke+MoTmQZzJmGFTWP8wogjQ78Lp4Y4V3LlpTDVcdlKnX2YeiCuegy3BU8ixDzlWiRhFIexKy4VtyuDO+JcYc24wxnQKaI3SHBotvY6uMceaxG/Awfq5p3CRxepBn20irWnLUXX/7BKDeyJDoFlmN2pYStzTtCLKdM6ia+OvY3it3kD+8mLgKs/rGd8fzdw5O3zk+jZTSYUYUp+OZXs6h7TdvHi9tj5p7bOp8giBEOJ9OfZzVYecgoqzeilYbbGUs02AbuftcPqSuywkOD4kgP5gzIKXPh94WvTNNg4wq0YrjVRDkeqKm4Z6jGp38K+FDz5q2NAelKrnBlwdxsUo18zvZlBSG8AxeC36mk9UzuTJ/rtFVpnKUw7EaEbbvHpkgONaR0hW5zzh2FQ4rsZiL8guKwWWGBMtswTQOYUDx8UqAdCaR3LHTP9Pyb5kIRLABwmdsO03I1GiyKLWs92pSMJn+nmHmtHhi+twBshlyZxB6BTzUmgGCAr5KEswfg8waUNeO+JTPkoRNLfViWrBlUpywxRBPALgQlOdEph2qTWgiuZx5BmJpVQO/A7G5taqIiUNmi0664QvUWjZUeHT6S41aL39kFstYYg67NfNMA2B9mWnfITLRUVBfIB20LjJKDTiLLcGW8qnLWD73dtyJoyQKezdsysl6XEb2WfNAXMG8IgFmzbuBHQrrUnvqcxBWWYuhvuYGpRmPWe6v0uwyW98tivv7N1fJzXI9XeRL4iSeNS6LfMOr0/SSMHA3S4QxjVYhFGQ7zmySvRU71icTZrCo2tC6gjFmi0l3QhAFJlomnLNiHJb4BHNkIIfm83BlVhq9mkxWiw/toSbxniKP8rQJ1/MkgyI0M+PRByqKRMd/p4fn9jAOfmnZ8pkIPD8kthW6UhA7pbEQRcS2q8KuPO5FsML8cUd1TxhH/TCqWBa/eqjZd8d2OTF9+/e3oUvweiM/XLZ/r0NRIzGeslGxcYn+D2zMmgeMeztHz+1Dize8UBe/t10xZojTDTt3XsZ147RV3FurlrgYa8VpJ4xxV6vqgzJ2aU6r1BugKY1SaHRv5ohGH0q65jND0erQ7TwKADyzOldE1XX1GZQJiarko/hsmFV67pFVfzwpbk7DqONa86jMG6oOd/MG8WGXwRwS70BcQ0nvCQ25ntmgPM5lsPY47Pbl4obuVGKIAMBUFhs49M3fAYYgKs16EVbin0b9S9go3OU1BCZB3NVQ7ba5HeXpuiIUxrNayjAYClfBPuMPpWiFxvkD5LLtvG0sI0rhXSCyhjM03i9Cm14CDIU9xdyQWXwKXpzxylptVz9lIayxFvolqBDOpJLt0QNWRAIQWaPU1NJ0k0XK0l4km4JmLtkEHKY+1xKDcA3XG2Jj4MZkkyt8Ksgps+yTNLJszFtQF9UUt7CoeE1MArAVvEeOlrIqJKEmNHy47ZSQr1nvJpVLV4IrPICJ7H8KV4bz1TLmPRAk4J8dPZkNtF4JISd6Va5UYzx+qgBND2qw36KB0vmSYHIxAOnJalHc3a+/Wd4ulslFOseJvN7tjJUQm/XbdHqrDYCYQKXAR3L1Gwi+Z3eghNfAYWA2tTUA7FPEYbBes6wQApEFbqwKWK0WhAsu3+E6LYtsYhX5EHIc5M2spsZXJkpulZtkMJbQeHocIVrSyvYy0hBYiXjVDulRyygvVLfjcPJmJSeWvIqX51RXHYx2Zj2k7k7m/QSRDf1Exy7B1iDXE+6/Y8t5F/zclmNKCq45JtOPklfs20afeTR7kMMRn13UQT00qsSNzV4E5tx0rrdz3ziuUSmCdJWq6h0xpRf1jWuOHl1wNrvipEqPwU9UZrQACyI/9Ffo0Xx4vAF2ztzPSByW1fYb9HXX1jQkNu1kuFOrGpe9Lnr8sBcPiA9rwd4nNg/WatjPfdZ5/+krHc5vjyLUGjoe1XiAdXv7OZK1Z91a77ZdgJKqP28t633XeI+zanMWBckcxxqaMiwGAM6Z329A074MyAJvaW9JigCjGwZ1bZwWXEb98H3hEoitDLv5mfbeCyoig3NiZqRibvSGLBVmMNOdifElUlQRwBNEm+Yr9v23AWM0fKstLpmbDtZM3wrz6uEBtOxVuWEvT7gQK+jVtRTwGIEtMLXql9nwy3TCZBtw6nSTLpinAh1PAJIN2++8FRamojTTJkEIQA/CB1mHssDc+a80dH3/Q11ApyE9biQkEW2oXdEFPkIVPomTeG7C6PhPVUvPUNwHoHpqcAWK1+MUYLEXwI0yghUNfqsY/sg2B8kg6msukR5laK0uuxQhGKPIz5Kc2IcZVEx8mibrO+SyJw+hiKFk1gLgguVmlaMTgFzPbfSkAX4WBcAxU9AA7Ee1eTK5mORnRc4WqQuG26fLJZ96yqG7Jv8mxAM6WBeuiCWdzqdTLfbNslnO8oDFuRZssLaBMAE/4D6iALxCw4DeeacwSZnP0yS1CnbBkSXUuCvNXpCkgnUf+ZL/JlIplOXZgimN9Z8hcZJ9Y+bIpQQ4ahM9GxEDNIULH5NtbyfXcpQrit4jULUo6tXqV1viEIFAEN9zthT9+THNmHR0bxkm3/POUzKr7jbDvEeV4ozab02P5uMllpQ9fEbpNEh0mMd6WbZ7Qug/IWGVYw8cWYde5XYXxFrtoD6oReJnAvjDv4PBMZ7o/2IOadSneezbOF3xCsLLDG5ou49IUe6OjQBgd3UzvLxzjaEWzWFeGcv9QDr8sJdeEDf9PU7yXlICywPEHVAliOtL7OulPj6H5R/musNkja91dK2c4ft19Xjzhyj1DQndMCQGLAOAdX0Nty4GLOkQmOL7p43xgVHMCwf+MkNEJRpsXS9X2gUIiMasIIEwA8Cqyxwcg1qlZmT4pi7kVoPXgmVcVodqIQ5hQmoqYEhXM/6FesUGDAqFSUABwDzIDsSqbM0xgUa7woNiga+2XxBRAAsCNAPmJk/W0+yc6MSoNPyMAZrAJNCJLJ5qSDTZJgdQyW/VXZqxt48gvSTLHEyUHEF7O6uSV4RzztyhMls3av0J4cp/wvSkJMgwvVgq2/6Ltfwp+12Y7BemV13yVQ2KnAktQsVopsgB9/OpSvrzKzA0eFtNI73JY6HtPWoDwdf3xGksy52s2O6U+VMJ824UWBHz8NRDb+2i1BxIddA7LPOMOVE8J4HhAsOkEHhbyy2Y+7PhRWLXeXajbVLV1kiUGQp6eNRAbZZrr24WKx4CJOwWxaQguRdukNkPoBuLWVnC2wOo5raYI2hG+Z0+o25j7jef6EmC13ZHm2OtOTy0UhJV3K9yG56wHHhwKS1R0D7NpcrisCJPlmlxca+X2dsPz4+rbMuqVF/dqrwmMWR+AImdivfp6A7rK23nq0N/8McBSu7rhw/eBx+Qgu7bzkYJRcPfy3dhTF8PiDTj5qUAwMbtmnvLuIqBuNPa7U1q2KAxcckgh67op1lhDA11gkUh0WQUX7dj4ri0Py3nHxRl9rMcVYJR3S1Vr13qZplxXFunKq/EsOeZQyf9QOaYSNerh5EYLOp9sjG6ddp9o50zoPYxi3p0VodpiOmhbFB1Xvb5uZNYmZGsvetGTFt1vT8WrfyyTjn+27o/RG8uNPCpkX4gFcDwmxcvAZ+/9eMfgI+ZhQ+u5Tg7P/v6N18LmQHSUgClsKoQ3vqJcJvmsGgCPpl42aGZviamnD7N8+rmei8VcHzOSt+NNqkEi16D2FZLdpjhQhIE8DVELWDLNVvQkKf3WCFHM+/RKNMbaEG2GtXmjQSM+k+W7IEjLD1bp2xvTxAD+lTksAKhMjlmesemnsnmSlP/WRuQst0lW2oyW/6CtxmstDkN4hjDXmqpM9HN9M+0Y87qJxhJfdRXGEHF5Q80Kq8nhMQbGkQXHBcRHiEqYPSd8XimFZHW2cXR+rzDFhroCaXETKPeWKczAmS2r4KVzwz9a3ieVuOMf8DlPCjASq2GMA+nxexngP7J/Q/EhJF0gPuGafdsxbOa5DfZ5lLrnvEYlTc/0fvQ5j/HhwnThGjD5eeKudLntBUIfrOklZlwxTnLeWcaGqS39t7l23XBJKDFWc4K35f3jLjz1EHKS2trVhZpTImG9IK4nABL3YNNmdLszXR+SgsSKpCHfzBQD1IWl8Xinncv8AyDgIU9QikkfjD7iV1ewxWPyNsWP6C8uoz1KQnVrymFk7vFDV1jPfnaorximk+JcMRk+TnRQZF9XWqn0MF/gZ9TyznpQxz9IMW/6Lvp2dsnBlwHapr0S675roWsqNRrhnPrGxdKBhIH3jNb+tuDqQ67GncJtcyANscoavOPf2sav4xq28OOtgdiPg/ACQ2PBa7jV6mFKgcn+nQ4jOGBfWxfYcMtMoJbu+eEShS1sd9hdsW+jdNB1lCir7+66laqN5CUawD6qLslQD3gge46vblHZdYr5d0W7OfOHt2+jY7pMdV/Ou2s709F5YlwWWUf8/MAJ8caHqBK+5vjDB/I9gBN3kmV4dYbKAUyGfxES0slycn89P/7//mH/+K//8O/+Ds/vXrylCcAIK0pg8lp8fXz57zw9YQtejSEnvLuV83eWD9jo/fTE4bixQxGQleGsMpxWOE5ATGTwYdQLyPRRAAr9u4URAU8Fuzof393/+bNGybq2Dg0/AQMNVANxgaiwY7BcBag8hSCffrZvn6y/lFxclcwpyefEUEoeoHdMiUpGiYpUYVwgUFxm3meTT//8Q/z6SpfsVP+UusbMsg/K7L79OTNZs7KYO1vzxi5mZcnpydZeomZ2EN8w/Y6lLF1EGTKUBShWEGKaUoO4J7pUWU+OfiNbUENxKvbYQqBAZ4wf4heIFUlQHym5pvTDODiR6MHT+ttaxO9cADUzsJiyYIPQYV4M+kfAL38IZ6SiwW30ZzXk7HR/9v7t7Nf/cnPmagDNSsDQOeb5MRkJKuN9glFCm/tRRANgFrT+fzZZ1+cn14+WV+xs/9a7xM4Wa6v18VsPl2xFuDFy8Ub1vxakGcNLaSOwZTd3NxNWd5LjMMsH9ZtTGe/ef716fUJm37ShoQUNKKeJ6Tpcn2CXB5BWLtLHUJI/i8XLObWTC25njLFovYvTU7PTnGHPMICY+I/Xmw2nSPxv/oH/+Dly5ci5xEG4cuKFQt3f/d/9ff+6l/99xc8uIADvuY/f9b3nAlnOJv+FhiYw727BoKehFrFD3Xl7/ihftvjAi8K5x6q7uwBtt0V3nfuR6fw+3bYRyG/ecuwzk5Tjz7i74a6CD8bX8eV2wLi0pCOyKJkKN4jMUL5eO/5vlhqVIT0gGh7D4uc9MFRJmwOcC1VOIad2hjbsBofxCmoPao1TeW+/hDb0+YW5xzgZDHfsy/pu2a1JK7VN0rD9+QZ21hLMw7KMWKcb4z3apx3XJRW7qCqijWNY+jHWnTiKMcJNoHpeX/Vy6//6I94fSwAjTIh3NXi6i//7u/+J//x/4Kp5FpKywiuceUFWACt5fo54JwBWEEukLE+8Iz4AnIF+u3CkBaDvo7LANu8/lZxg2A0c/NXq3/7b/+l3hsFa9Fofg8T20FsoMSzdM6gMDv7M2DPDvT3q/vvT+Z/e168SBZsonkB/MyF+zQBfZZ//yRnMopUB0ELZAL5LpN59lu/d5FN2Y3m5/Ce8E5fYUTmozO+/oyN6kGwBBEaMuaRwObHn/32737xez/Bcr2jIGPiCusN6FTTIuHdwNPJhHwCCUbcmTyzmExmRarJ97wmLOGtwuyfueEVvPfkW5pIABpK7flDwhMHpQ3Tk2bMfYXuIGHRKw209jS7l85Yo6wX+pJPDEBUgBS24in+SoIUSeScF+Rv2JWI95ph72p1W9z8w29e/gnzuBbJ9Fc8pSGUICRCB6KNIvkFUZGiHXmJUKRIp8vTdDaf350XKWh8vUGNnOH/NVHPJr++vz3lXchaZKxxdtykJqLHEEhsVtcv72klxT/MjUq+z1qCf/nyj8WahRb0JwVUPFi5+8lf+O0f/fC37bHAU2scnK9PesrtjXZ8gjXBGpxpMm+6q8tn/EOmX1tfJU4gFlr/6le/fPXmFW8e1uMPdb7izZu3t/d/lk5/UNyadsaEiq1DBcafk4zoOMLvtZerglXSPc07cxfjDkbtrPj+E6eNsrxntvLbbPpy9rrbYIRas49XT35nFWeydVc/WzSELH4O0CNnVPYoe1u/BQ3WAx7o4/8Q/ft4xlqNoYnpx6fj3+XxtQ6jjPvDYRz6aq0+U0lsi6eP4Td1h9WX6uYV/4EO0qVg9GUwDtoe4dBjT9GHivn46uEY714N1Rv5jcsGMZdtB6vl23StnJFkrXrvOaPTaY+t0xh/NnTY2XANer88rFYnqx2Z705SQ5HQ73ZrYKRDDQ4LdXb+AGL6PhXFioWaIPL56ZkVkif8nM6eXFxcFckds0OYVW5LSoXdJ7z3lZk2vBhg+6UxRuVXCB4AJgsGNPRKBWFHo7XoArCqyTOa/M3iUOmhKeGaAqRxE+bxMKyvNQeM6bP/5BrwL4gIxM4Z41+ezJ6eCVEzCYSRbg3AgzsBhRacaUILM4kYQtdWRrAFSOudu4aQ0YUwRkbbZBwUA78CJUt/AGxRFAiuzeyZM6+IREraML+4aXSZeTfoZbchLMMISqUzzinBvdCup5lsVKXxp+acwICAgflUuBHDAfSaQMNEIGC98pXmeQeD/arraeVr+ByEDNzHS4rG7OGDJjNZe5HPcw2MnZ89ufymeJVupmtf3lDwBAAxC4VEWkCNEYqDZBmKk8LaLKc9U9bvMpNH23rqcQwRU7aY67XHmvyEuvISwJ4z4mka+dhW3+JqLe1FJ9SRhUzVItDQ7LI04d0ONJA1ko3Ay9MiQRSWgODxD62vrkIaSopssF7NRzaXTi9VcRt7ivJASkynGMJrquezqV7eJmYibP48KPfQQwbLP3bItIr5Q5g6t/d6DjbtpYUbzdmrxz7wzDink/MAgXPorPV4mWrfQ7m/F4UPVfZTvfEe6OwR9dbuJEFC9L2yu4UHANu6Ub0HxPrjTRlFGUXJVdzTrDcquor4tEdwR3Foiu2+xsnOrR2Lu3+jVujm4LntL3/UPEMVh8v4IeRoj0MP1/LSMV7aV8lam7Z63bDEWt0xBsQ0Jmtp8Xq7pWLCjnTclzqKu7OGfU7pyI7RzT3kjtbtQd4L4mqJ0GfpBWOsaXeWQrOcmQXy3Pg6Dw2Va0waGAeQE1g3OMXkEaBe8vUtEGv9+Zp5HZIqyCyElr0yrCVqn+vIpRVxKbGitQQ1OATrjFSfFGgsGRTHka3wqObM8JczlLxhlg6SmY6vferB8oDRzxQSTK+Bn2xNk2cXydlmeicszxaY2h1TuFSLhOdaI8BBJleYNF1BkJ0yip8yZG4rsvSoQ1NKWFoMcP2FtgVafcGAt6II0LSgLVvs8FiA0IEgB82ZkANPBvLRmYF/LOAMDr4HkdvAP+k7y2EOEtN1rFSD/UobjhfKFwdWCKgfks/gvbxrvuQtvlgA+kezMp9antbTFUUOkutnDf8rhIEShaQVlOg+Ic0YeXJDUMS0fgAyzyhsRbFKpwVPJAhcmIaDMMznyYBG7qUCRk6YoG8twGMEHi2w59I6YYx9Pr1Jsjd5cT5Z3xbrfJlqNyFmQ/EKYuIb25afwI34DA6/SKYEBcDzOaayclydRH0DZC9FbaYQQZu1NV0NGhXjWD0osBQXgv82qYkMiq1LmccJqRQq8riApoId/pTXCAVkOOKo7Eys15E24c5GBfw/7NjWtO4dcd6PX3zfiNMxl778mKYnPfJus7Wmh49n626A0wb1cQeHX5CdnIc1rJprUC1rR6csuZmeiqsPOgZ07tMWe1GgnDexp9w+nrHufTTBzzHxUHqMZ8bQDMl4D2WOJdq9pc9vvSpqeMsmatYpuvi0uolq1qv5lWe6ckp7ANBWtqtuM69PRpPuO33dcFLs6Ti9l49ouOG6nU2/l4iDiQ8WPWzRwfo8UsWdTfBIcj8ktqHF3Bnh/EAdjQ8nDjubGBAVeIp/jsaEOAXe+A9OZvUmc28Axr7YV7XA5saBL4r+BNq211z5BXQq82LRKcJgng/ITZO9TYQgHtcaUgZuMPQObLUBZgnR0LzQqj0cAOGLF0PjvLsqzS5YIEwGGBbZxC2oAPYX9iSaEW7EIqIKnhqs84ztQTXj3URSpj1uxKrIwKCmrM9X0YCzXiNAHKD/RBHwkB84iGHkMaA4VV11kmWRSPQPg80RqqAL1bB8bEJNk29O8QKRGKHXlYesohi7Xv5RcjUmMIWnUYhKCYkCHuMDxRZswzmf89OjIIEwgnULij0UMQh96zELv/qqohhLTy0sW8EQjYDveFYCVwVUCkiSZ9Ps6smazYlYZwz8x4rZ3Xp9raceiDRFiZgmGRu18gCJvUDhouALfmoJBvj1IIXBe1vF7Bqr4cwKLu2fCJWUflamhwKVlpQwvm8NISJ1RJXyoZcc2wvNeD60Uhew1rHGl8vMT2Lsh8luZlaFA5/Uk7vsDJmzGaD/4IuCKQ/UNPZvnH4g2+HqR3T/w3X2fjGs8KfSx/DAsT3v34mBb0a93w10nRphcwpQJGAgduzi3hv/vZMYrisqGmzWlnU7OUSuGeRs92GiQPdzcFU8YhFYOc0Odq3inbUC/1ZVZbRHTWLdOquEzDFe8p7gcXBvrwgcq0T5hdm/XSoG+38yRLjPjM/YS31N0Glv6APDKvbxrD2teiffJtez0xaKovyy0Sq7/DKcy+yIvsxxS1dfyDFZbQ2SCMIsZ6EooLVAl6AXEA8MpYFVgWYAlIbQQW/Zasnor/o8MEzz8vUNrPCw6gtwlYfAW5WEp+Ubd6tPRS3z1NA7o9qUzw39MueE2AL4qNn7qzUz7LU1pLQCvTL1hGrpK8AdDwcYQM+Ls9nkkuklOWsDhOkh4Ar6bMYINPsCaWSZdmScmDn6y2wzm2azLGUFsyCtJpwwDQYcJ5sJPH5Lm9Ez+q2NfQx+a0aQZh7xl0x/rU9mhRrAhqes1XCjkCZnTQ1i5xku9GzBSpnWon4PN5whWE6+ebpKk+M+FAcOztBbrTKfTHI4XIrS+MRyqhJx5BDIlQ561KAIij9gMBvy8zRDU4M0+UfgWT5RO62Zi8On3KvKTDrSDQHQb/OAaA3iBNLafhQWRAqzk69/fHL7g+xzVVvzugEmJZ38KnnzL3hSwvQveLPDqJY0wJA1BprThfP5YD3ydKPZtJP0G1Mad+Bz1jCgozlf/YKETnwgzTymNjD18J6bbD2BaMYDCls6osUj6h0z9jtSvxAh/xUjSIhM5U+8lfBDjOVr/lVZZcmOD2NWfStb3yY9qIGj/PkBHe17givnlo+xv/0r1jYPV3KE3+I2wbFyUNhldTBs/aLVaNr383ZOrcLui52/0btZHESxt9yWZzp6RYsmVi2mj9MxzXB6zJct7Ek4zOrg0l7Nfcrglm/oYp1aD/XBLQ9SFaHdE5oBwJivnnHr1KEm59t2Mdo1peHD9A/xX9WCvR4eFt1b7RgF71H0vuo/RNVQN3wp95Xepg88vch7yBH5tyUemhM6b9CuoTuXoahDyKhiIzJQJpCkGRV8Ms8GoAQgA1YB79geBySsHXYAz7wOSuPgmhiDeCE2Qa1KfAnXPMPYUiII7CiMoWIBbmoxIK17pAAfEJ0Ek2LMGsFAoTaV6L9AKUXaxB9+RB6aU07+lI3peQJwMmXGewlTmcsCJ71rKs81uUVVCAs0Jk4eem+YCgRnmIqXaYLFSMNM9sLEHgs0ZA1qAU3NDsl3Zd2jCn7QqDzcdF1aSj7clsRUSvs1BKHAabmsapWV7aMktCKl/brM3daQTJwleziwzlLEbDz5mLJPqmb8MIOIEAe4DpzXC7MUEaiOvKS5/UwlsrbzqV+8PUA9gblZchfD+Jvps80Jrx0jPlutZyv5LEtWU3hDZmEGAH0ORxylef6a988K4Hw+O6F92Vp1wZZAxBtawKG1Coi23qHHEwobzGlKU2TdQfN/8LIU4JPeoN6GLBS2PLJ5KOT2mrmU6JPSkjUyLLgwIj+Zm81JuvaEM7FyMoxC5/2PgyrtL+bQGsGyYP+hnOQ45xZzcLZeFOfvlR7Wbbh0L0Ex8QN1dlZth8QiPqWP4uRONz6O572vtbX2/E5F6pkVoe6yrfcANPliw86jN4LxmoMxnEbCkPmBjU8MmxxHhHG6UavhynjEYrhnBH+KzMYD4rqxlEBJZpyOacakY/6dfIYVbohgJCB0m/GjAlW3bDA79HLXOErQcLyA2Et9tdr2HiDImXtFnTX0W/6wocMBjups0z4TQn7bFi9q5QuqckSjjDUdW/RG3DX27/wNw5rFwo+V5dyumE/BrQKPCJopBaIGwS/Z0IaDAuUbVlMtw8hGSQ0y+K8zjpRPjU40UJCn1Zspo/WM7bKtDaBzDpZfCxEK6ZtE0CAS9cChWD8jK03eAiinYHndvlikqsnpzOSZrC7I14t+mdbOjvtCoWds9rlO3rApaDJDYZ9GBLMV8/6z4klSXBXJCXEMM92ZigI/oWG9SkAOkDFk2T2SkWsWJBD5MFKuCUOb72mqixA2VLJGZspEEKYM0+GtXxrvLhBjx7Oqy+FnpaonMKvP/ap59uczvk5DnoSPCSrzqeU6uB5cWBM6fyCy+xvvnNydMlc/+aIocA6e0FD99eLNZPab9fKbdPnXlstbOj4LJCwMA4jb6yDoNXpIo0BQVtImq9lmdbJe3q5wCq9N0Bt317f5G+2GxPpvnggpwtOb43xt8GR9qj09rYX0fuXpenOfz6bsc6THBArLBO3Vnhhm/sQcskjjCXRkH6Mr+UQ9h1jjlbxOmXyg7oRyqyXGQM22Sr6WGkrwvzow2YpQRM0/tWiy5v0A+Py5eEaH9TpKvBXF3apwtu+a9wbL1UkcNPbvdCFbiehbWcs/2sWuO22noPieIMeySORLnf25sVLV0ZdflZef8ncjq3XZoIEzVWJNWjXqGZGlh91R6+zsqo2OopydFnUw3JkVWbGT9mCCw/yzR1uYZjF9nN6hduwBS3PL5ejzdrtPOv/DbGzrNkJz/4q0q9ZyevVxwwIPLi1t9+SHrAGoSX/ARZ/jH8DyQ6g6bJaXVm3RrW9oss7iwD9mEqc7ax2WOazJYTwbtR5J84YULoPf2kVHz3mXso6u/CDDgR4xUCSWFO9uaweVdqMSwjRIpqFW4BzzZwwUC2Rpn3UDstzHKAX8lTc3wU45v62LgDElInSYZoBMkBlwyVsFkowhYaA4EBEQDZ5jWghAlGtV0DB9tlgvZtqPhtk+mznYcrPO2OdFy2czrT6d3LOkd5afrbStKMgfxJqzBxDc2TYzvzhjX3qYAfLzGTt3zjbLi/SHT/NnGe+1TZkIpIFrAVB0FDQsz0BP4U0JWxcnV+esebAbuAjMWFmLudR1B+vS8rY+8Eun03nksa1WcaSiO9bPMZ8tsaXka9PI1URl5t6wNyuu5K3AhFpEXHiaKIqZ/XdPns7Pv/hpsflief1D3qh1xwb/z19qmYXxgKEQMUGEwLfSWEtDccUPOHERe5Qq7ilON2xyanOKeHxi7abF3AVbkdIiCFRl9lZdqYuwk2gyXd2v7m7ubhd34qzuJs5sE6S2QDU9CJIwSZcdpof1SaXU50wbilWTKE7xlfSUY9BHH/aCOpMsKqvkxSo0pnbpV5z9SrIsbQnyPMNy41OVjYLy93f5qLtx64mHeKWP55b7I6RQuL/BH0Hed55l3Mpjesu7ap1YrxGN5P1mgLDipxsXTwCYgzvG2i1D3eRqd6Ls+Z4ctrxsump8uVc6juT2qliNirVjr94oqufb2Bcdjh+3aCuOVqFFqsZqUyknlt6w5YDe6U8bGnxcMPoMa9Kt37hcl8tQ3wOPWtv1cAuObcga017x05hA7wzd25xdB9rlYP+3nzMEWegMfzh3tlHDoiNcjv5+7TXK6H2pv0dhX/VlE5oBYekSeqQwPUfYjwn1euGUTcmgjGkYTBZXNVEJcDEhXLc3sdKl2KjE+YiQg+cHAodZMtM+mOB0tvLPT169+upf//G/EvJDmAm3daST03Q6Rd5mxXvBGNnn3VvL6/x8M/nxJP3tq+89Ob+bg/wYSs6X8/x7F9n6+2D0y1Mm+CguAP0zEj05mZ/ML67OQZaT6ZSNb7L5+Txd399tnv71H199eZUtWXiASIUGskADxkxpoRUY47eZQqiUrrPZK7anXDPhyeCs7Bai1AMQ2Y9blCWjy0MJc8L27KPIFUHjU6P7/Uc89m/y3M22f5H8rUNqbD8l3xCyKUZLLK5+/Plk+h/xIINhd960RaOuCqy/Ka6zF7+54YFJPn07Ozm9yW5pHOD3ZgLNjPUQetbEgxk9BeLM0ulVynqLZ/niPrlb3SxZAzDhXVt3xeo6vZsSVqz07mCkr3gjcDG55QXEWgCsqEA7CslZuli8eM0Dla/VoXC7HUL+aXp+cX51xTMKrNGjCBpHucmEt32hN51EvVF8KOLTwgW2JtIjGsSyFytznXiSQ7sQjhCrYLu6p3o0XNxH2TdlwtiUTaQ0fdIpvICzS1J++/CyiqZd/ng5dqet3XtHyGrT+z2zXTX+jWuXjsrpuY/F7xcaxSciOtoduEc3F1U1aiR4RLL9O1XTtueXcQTjD46k3YtGqRh7IE5Hle32VV73tULcMw/UJJLYk4wV6SGp1My/6ib2Z7nblXXYY4T6TdSPXD/bssg/Gsy5HKjZz/PjLcHcg41257Ud5jwbPmmTNQi4bNDEl56Oc9rVHy+n0U3GC0Lhg+uOl3Isyk73xplx+oFCY8+8bxch/6GWuQmRITWeBvUlQyhJyElQnJ4hFMVYukb8la1cwXMOMnmEK3JVUi2LAUiZpspQmaP/aohUWcwHZ0Y+u0myK7/FDIwmgy01givAbvyEp23SBgCeXSrXTDFZLIqcsfqcoONuvXo9uZunJ59np7MJe82czFJigPyMT/CgDSELxktptixdzeHKXB4eKtzz0GBS3C3WvNJqTVABEGUwfK33mAErZS0POmSkJrDILrAyKUb9QZUsCZC9mlAvbEodQ5mytzRautcOs6aWs+9F4CCHVpWlW3SE/DKvIjX4b3lqtU367Hvf++z7v0UkgK0WqbHD6HQyXyxfLf/N//0Pbr95i7c2t4vp9Pyz789mp5vF6kaPW9bMp8JSHgKx/IKFAdoNlGcwXxRfbNbz5eZ6uZoW0K5O7n7+x69uX78hmWn2jzZPJdjgPV1zHgKwCBu38dSBP0zByTNe40ar+eQaeg8rNmgDlIeCtw3TBwrUk2tVkcZcLGAtL3hXI1t2qQZPGIAUpVvgUwZmFOhJhzUbjUoFOLlDnKlfPOAMu6b3H8DtI6ta+vJxtH5U5sMqf6cbddg177DUO8D7+HYNdD1Xp9FBdGfZfRuouOqmpSG1nXeOqkLN55E/fPyvNwYajHE1vsURx2HtnJrg6CKuFWWPSYaY2HymGp4I+W0mwQ1x5BdH23EVp+n0rfMJ/guJuHpIt8eDQ1FIxCPEcToQjEyMkTWGlVvU55k2h2PJ7Ws7b9m23DgnbtM4P07HejZkhUZs83m4H5AV972QjnUbTsfa9n5P2yya369SsjiwT39rv5E2g3ZOXflwZYktirLBVCATQBx8Vg5X2/Y4Hg9oRrgwmoFi7h6aFyRExUDtUwBakb40ZFay132uOsq+ySUpXbD6k9kZ7PYjaMf0mpVWnAL1WVcA5p7DVoRQFWzuyQb04HigZA4wZ0d/veWpOC2Y4q+3XwH2bpjZMimW69VMS0w1iAu+A/gxN0VIV1vCnPJhKwKY/c/Wn/a2gMnkAhoFO7w0l3UH7M3PBCR72xeTVVDM7pCsTMDwrFh8blCVYIBbpYaaZTv6y35pO3iUPhmkGS5sSfD56401A1CZKIPFitZ07WAXVMxAfIGv8CvORHVCr7vs7qJ4/dXyjolBTBHK16sF71MAgme8TwEnqjocWYFLwMOJNPN86Ck3rJ3I8jtm3E+KGxp/QXMuXjxbLk/yu8n6apW9XWdPivntspjeTK7vbFo+2y4RPEzWWvibTW+J1VDP3j9wSSNM0ju5QNpSfqFU+lYGaJEGZ5L2JjeaQY9r+MAkMnXoCUF1qNnJQkksVBJCwhgMURCQsm2pHZilzouPRH3gUYo/sPaDq8V3mDHM+ujdA/sas4Oeb1CXTn4/3+MXs3k/rJiORyxVje1nm2fErVPtULfvlyX+neL3qNGpxt//x1MGlUKir30DwVESsZSHaPtwZWJNAreG50P+MRJ9vHWv0RHdS3LbBW4rlF5lNEbSfAIw3OW2TL41qeDIkBg2DbIxPoq5hbQnKv9v5Yzkua3wnlJtzTsVOdickfw7hTYyj8iqwXnn5cHm7+T8Xgm886JCSOyhzqg6tJlQkM7CRKzUnLD/JuhXYB+AJTgm6dAIUxm0lD56LKDVwErbkLkVcqmcmr4GxYwKPlThRVL3YGoBM/9TTcAlqM7gGGWChUwTJzbQjkMgd8mbsLMk48+oV+TT13l+NZmcoRiT2Q378YorHiugOJBdlgsi6qRRfIli4omsYnpIvlnwLuHJFHt5zy3QUDGDiLEOSgt+SIqr8C+Z2k6Ug9F/IKXQpw7O5helJdAOL6quHuHTpY5nLGe4QwDD1tDyMu5WjEScwyrfe+38z0wv2c6OQJrqpJ5gDz0U82GzXIFkMTKwTbW1VhAri4BRL95NZ5uT7+fnSXo3W17C/H5yenvH1j/nf74p7iDUXkN6rZo8zerT+81KgZ78KjfDx5xoGpqzDfaTLyIOkeJ7pgNZy6glaG62oaKGWoyTaKigFRuG/Anj9Cpg9GeuGvx5JwAPMdSreWNw1e5UD40nOfHhBdT81h69po+zmOp93unLH8P4gVqNEfGoNB+7/o/qnL2Ytz35kH41WjRC2pK9drsIyqGbSCm04mdjFrm/ezKaVexsOdvc1ziatPoUdB+dMZBI2zFuzKBd2s6J6fvSUdzsJCMjwrYX+yR4fsP+ln+atStvb/M9x8/OrcFzjzEJ4xqPOsfprchDU/EYQ0PJTpbuc9dhp2c6OSAleMy5OVlv7+rkUu0pUatlPcTX+1NpjDk9vHdkNzgf5oeGjAbPRmm4HNPnaz4JNfdJ9HHwuePtJwMCZxzdc5crwbS6ABYAarN8xsjvYvNrzmAoWop3wwKY6BkZaMn4CHRp9xsAN+Pjwm0C7kDC/LUYkmF8hdhi16lrcdvT3BlDolSZkxDYdOkCodQBlM65/ykpBMg4MViecATwttTU8nKmDmt5yX2SrJ6wB2meTVnlC+TXuwEy1vKiDbKZYo4OjGSDZGfa05O5LEz3YcGv5FB/JeyICWz4ia7Tr9X/2RlGEJLqOE2TXvTqA2ay6HmpWySNNIBuaFNKqkdzsqNEseXV0T5Qp5JQ8TTnNsb+vcwUUtJ+ZkxtV5Aq9iMllZmQzy5KqGuLHNIFu4FOE4bkc3ZHKlase0jZpZPQCxpcgfdB1PyHq7qFNxzT6y2P1WzLZMGC3bS4YefQLLtTCDF5lSXTWXqfrvPF5s2c5dhz3tXAygx+ZZLlislUBFE8bNEcMp4dJemNofAZ3mVTIVP/hhY0odZrqEaj+eyuMpdex7Mg9UipptisAvLEJfRYbTGaq5yFBGopHvGIXj4hXlk+4yVh6eyV+cHyqE2JrKwdrYxa6bfqQs7hsDv26jMlH/K71uVM8fTjIZxLFhFiGXMHriT3fEbceijK7MN+Wfru3m1Z4ynbdYdzYi/F6Y5aY347rNrjaduhlWXti9O8P3fgYevn7Xx5pnrSHqcrffxb4r1bZ/NkYX6wO6zodEOq6KvPkKc7Sm0XILvFGL3fg1TD8tpMKmYf/Wfw30hL3J3ulZFVBshc+gDBd7Do6D3Om+zb4cmPyJZd35TKFD7LrxMYTPcr9sK8XSyT+4vPnt3fL4D+S7bZYX+c+cni9l7jrBoxzhKGiTkEHgFe2nAHPoAtThrc9UM4sWTud0KEGbzSaD3itrJLKu2zo+klAFA9CdDzB0bu+U0mvdRSVVAsGFP8IRHv7OUkf5akJ5o5IigvNMiWNml2CmwnOkl4p5iUVgRhLw3QjB5WomqfHwU4oEkK8rVtVUkgY95ACglsMn1R2QwB8cNSUZJFIDJVl4qStlaS3l64F450lkajD6lhhzSuooAqT2NLWhyN7mBixs4Jj0DIzODXKm/hckI9KvFWZgIlPCMXFTSARt7142bOMdwvF9H0PELA+bx/YbHkbQB3i/zN8vYW6gyUtGIcfpJMb4rN60l2D9ZnSyexvUuTE03qYpjD1pawveuEF4HxgAEBetSAI80MRS76w+9qRCSaNFmDIugjKtFTSiwhctXVcwItL9FDG4I39oTVi43Nko1iPpYmyGoPPDBPQawEcJhYJaLDREXXcdJ80FUpJvpOpg92yl69/eiuPVjto2vynhniiPfbErvsf1ztdvcDpwhu0t0xclmXdrU8tmJmLm9g4tZCAZ9GJFqqYmW7nPIeyhvavrOdUrpMrXm4i8DzPPZtj0C0c/p57C6JR/F3U9cpmn2g2uWmL9omv+wmdT4HXMEHP4z0ZJt/rCGsxKfeQ5zzsbRtK9CXg9zHExpb3afAQfmj2qE99o8s1ewb+68cIZ8YajKklc5fzi/yn//y9d2v3n7x7AcMpS8Wy/u75Z/9+c/+p//xD5kSrjgBvASEA6tzBkNttCQTLAhHuwOKAsF+LrVQoTBcUSy07ySzsaUbJNTUIVWVBUQTtAR85hOmhoDLCDGYk56fT3kl1XqSX08nT2bJ23x1Mpm+zTdXUBCBTGc2DYW3ARQ/5R684S0BU6IGRQW6EoadaQYPL/UVvmSwH+wrg7P5nyU5rw74HZ5bTdbfkzgzA1Wkv+Amg8qASKnqKhOgmFehU4YZImo7lBMulIzbZXiHH1FD/1xsY0oT69o6Sce5cyVAoPMGCfriML0j2R9o0IZqG+3Mmd7dr3+aJNdF8evNZMFOnasVuJ1ggADB3Ei0JOis4AwUjwflE4JBdlbCb7PzZP16ls1+8v2Ls5Mn95PbxWR9k1wvi5NVcvd0cplufv3y9umGRwVJPp2eEUfpnQ9acXGu1y/IkbwMgNYm4OQZjfmcXBJqBkftdBxFLMXySo2Xv7GeiDlqaH3w9GZ5y55CCvp8ubGCQB5mLNabu9vrxaZARHFykiuczCcnp1OMpHuwtyyPhqiDdPEpm9E/qrbF3r7nbMsvRBS3den8nvHF3vHI0GZdd3v/zTrsPrN3Xbtjj/w1xPYwIlv6zAwhTdE7Ozo80+f/QZ3esdqDumwLay14kF3OK/ZSnN5KCqn6r3bIflDCNXcWY/j3WLpD87aKfbJ68rf8uc981Wane2aVq4TRVDkDnb6qpwfI0ROA6pbjLJ1P4MJlxfmdfp8q+x71M1g2XgpVgm/atSoPt0u6c4a5ddf5IHMHfHKYvs7wgAaKxQ1U96Kjqx1Lj9NBExLeScaLDnVjhh9F2i3tUJVbTmWVIUC7Em6a57N/9vv/v3/y3/2/L88/y6c5w7rrpV7xBBU7acIJOA2KZmIN00S012JOVACoBNbbjcrdKxjFoRLlAtI1A4fK09l0xiJebeiocqAb00gYo+X1sFNksy6Vmf9MQWHwnunlIPfV/fKL6fRvPDldLi4n6XWeXMzzO3arXKdvsvXy2Tw5O0EXApAst+XEE5awaqqPsOkmY/tQ+K2n55fzHz7d3N/w9lsgq9Yg8ByDe/vp2Xq9nKEC9iuoAe5Ly1L98sarq8pZKuYw7ZXpiZBjheHUqBTy908ETuZOqx+yurmVhPaBpRqtL1uIlHLxGROc1O56djM7++yzL/69883i7d2r+9XiNi3mbwHYy1UCJBYu54mJWlOLH+gCTJ9aEk7xj+fY6hGsvJ7Psslq/r3V/eV8vt7c0Kzr4nq9PmWR8Wzy+b+6yX/OFp6K/WgQAD2BmFpNr2zD7wB2DvjyMIEXFRdLYg0Ms0c0CLZwzAR7sOh+t/BP7QZLiFdr1vaSR2ihp0hEGkR0pyfzr7568X/+P/3916/f8CBDwSCvd75PfvLjH/+9/+3fwzbCmflsRgSkSA9nBGGVX93RuGzgEI26eYOE7GZWg+Jhl65a4KFmPabEkcwaWsTqhPSnxCcPfJQe6P7+9nT5buLI7lBPlD4FqPGljb9zTu0E0KtOXBzxPSzZE13ty6wWm+5beX96ucGOMOrgl+4a91lJ0f/RFdX1U48rafuhPYrfx2nMswIfjxlpYJ+gRn7Dh6G0Lz8QHCvh5vS16cFS2vr718jFjfdhaJfxVQ7W+TEq9qpta1jLUvsQGpyw/cv9cvqrr3/Om5mSyRsQGZsxcmbjljzNvvzih6enZwapNU4vqMSsmykbc8KhjCiUX6JNPA6ic3wG0BMCnU5nb3Q8h0ozT/SfqdiMCjNgv3n99rWmbkzuWbUJZ4ZjwWZrXgWWJM+K75+fvkonp9N8wXSTWbaY55d601een55rdH86W83PnuZP/jBdn09Wn2fZmea58Pqv/HIJnP2t33z2t57k9/+zfAO0ZTNKgCJBB5OFfnejpcWauVRN6+dKMFC3W5llpqlp/NpTpJVjHxAwlea5zuvPdd4eyUSzqEvi6uZt9GXmlrRKeWl1xaciqOholavMVgI4Xcnd9NGbbikto5dSDT7MNm8kWgjYy/b+19Oz2Y/+OkA6u3/zOzykoWmuX764vV2tbt/82X/3y0KvfAaSM3fLVg5jerJKM6bx8HCA5QNUuMnSWZLf6YnQ5I2CRNzL6uLsBoKT/PmpNndaEjEq6GD993IKPucJze3d25cvT1iUzeuc9YqAyZoQEeW+WV7P56fTKeElzDXxjDPNzVvY8jkBIkYwZ0k/YfRPwX1FDLdXz+hHT0lTB2Lyadnl6v7Nqzf3vLBA7lSIQJf76utsuWARCE8vluq/im9wldo7OqxGuO4Y47cy8s2tgbBKKKLoOnrGHWPS8hcq+o3u+M1CKgcqu3hPxFyqdEfdqmj4s8GyfV+lOsLjJ8bdrqiLCffVerau6g3QLh+V0/4tHlVtNFEf/07/jOY6RFhrwRH9p+QV9Z/enD6x7bp9lPvmu/5j+I+3dFCHdnu1c2IGqy/11ar5PC4u062u6hmqGo46TfhuKDteAxCTkXYWfg5FZX4oDjK+W4kB+4Or+jwSPBoawikHePaxei/5fQa6XUdUKfgnJI7IPGb12Pwbsrj0tnZPjmz3PrfHzD+c9N7aqvdoiBV0lGZM+n/x8pVw/Yy59RqGJQgQIGb7nVl+enoCLrdRYMP5mllvIN/wE1hMoJjnAeYNg1OGpxUt4Hjjv1peX1/rgYAiCGoolnAhjDMrYtDEdM48XyABFt2k2ZtN+popIuQDLMnVNo5sIglblouyoVA+TU/uWa9K/MAkn5xZH3pbGauBwYUFoDFh388Vu9AjjndFMeCM3jKKKEBKIBcPaFZK5TuuzSF2BhSSXxXtaGjVtAN6T4eEXwaCirDjM1TpKBuT5fU56yg//KJ2ZWSaGY+q4Hr8x5OakycXWuC9SadXJ8+ml8ubF1//MdNnXmhUXc8RaBv8RKfQYxQm8RM4cWFlvEGANtMCESi0fRPtwxQs1eR9zKcrvZOXJd6qSEPyhGC9nty8uS2KF7MTlpnQb5iIw67/hBDM5Vmd3G+effbUnx3B2TqalnFTCgM1XGVTkhLUJevp9PTszCZoqU+iLb0HkbyomIiAjkr3YEYQqw3IwhB7i7FsklmcnKf6njlGzCXCxYxptlKdd/cR9HSRj6DjI7B8d+55j5K807xHBT6Jfg8e2PltqbqFDeuwCxBrjT3OsJqcdFPj3sUtlE+PfpSry/LnRCkjUqI8tnyqnPJzOMYaEV31co4E7YqTItJjJIOTGzMUPb/ycE1SqOK58qh5ZvmZMuDTIKhVHn3xED/0PStojJRI8xH6jB+HaPgw8I5tGdMHQsV9Ew1z+vRxtg+3a1/1vF0aSu7LRPTD38RDOPbW2dVJttYIJTkbg+dgtRXvdZos7jeMx2qsVxMzIACC54CkFbM6tDek3aIMCSbrK/B0nrOnJ2jrlWF6cJRRGGPFFYJqUAtwMTdnNj2f5rcanZ0sJL6YGZIDUdr7vxiRJk9njc5ONlcJ+31uTtP11Sy/zrP1DDLwKQO7DAmjIFNJ2KBnBrdz9neZLP9SGZKgeXafZKfM607Z/381SxY/SfKlVgRMfwke1Ki5pOjxgr7+7HrJMgBtvyb4igbSQoZwbB3m1x1n342nqmAEXtnu5LqGieeERAeb2jt9m7W4hoNX71Zpm+tj/6550GpbXIo2hdDQC2inBR5g2oymYGndTs7bFXjl73w+vebFvhtaWVjf/KVJrDZthrH5KduHaqdWraMgcljnrKvWtH7Ys7KYZlecNWclx4RHLsvNAnIaXrVEkJ3M56wuIVz4HnO50vytgggCi1w9AvRPS9NDlBCCZ8YOIJ5JXmTqO0VUoPUCeskwhNjiv54esykOsR5OPDul89KDsY43zfFWifVmxSwmdinS5H/4ygfmDz7pqGVSReTD1ErDuXTg9kPVS6Jt5hFSw7/RlcJlCx5BXpOFWxxy++7P4+/Mzqrv9y4IemCi/P3qu+v25Y+WGv8+xpWCf7zjxEXvJ93uP+2cSLPab/0gZVRpn2TMM07vw+MA2nZ7tXNitnGpfFLtCBTTdKTtLlDdOzrKVWQ03J/sCYACAcvQD2R1OBeuPCtcktgSVcTfpc/KWfvZ7LWGPfcRuTaYE3QOHWQ/v3yi/gg88BhtG32NDKxLBnmktTMOE6RB+Qyy+yxxDQ8LpoPDtR4XUA7yAnIZMGMvSchK9CRvWlQgbqa3huvJ1Pg6I7LCZHDz8WZRAu/J0j7uSGdomPiC6AJQiA6APn6kNY8ElJjNXmbTS4aWiTKokgn3a28iPT2YJMw7IQULIgnmnGSClVzae8MEJEGtSCC6cLtt8hL1NO0HS9hTxlU07Ci1sEK0fEqTrgOjegr8Nu6F5gIRhgS8PN3FVHkx40AZEqF6nLNl1Z0byruLgx0gYFdVJhD62fQsdl/NMgbnLy5A6ERUdAzFSIL7ei8yKwD0HIDGY8t9e/myFtmqURVDeX/K0jlPF/JidsF7mld6P7OeLoD/1KnEyrrEXLus0hXYDIhYjbcD0zeYmIM0tYUpafpZV6EqjQgb5WsVM0VqT0+QqV6HGnRRvctCJevV/YJaWupBXQIZXkSmiWs8akCuKKKmMQ+UUkv3UWxKcEmy/4CV0VXE/ZTHKWko45fvSvhxTPgguYT2DokPUs1PSr0DD/B18tv6OFnD377qC2u3iYFdgPgN46ioS8kVa+1FwHNurU0us+J4pST2jwfHWL2ca2LGXtTiy7GV9qazFit/ed1Blee2rHwEwuP1xpe8eWmjBeVIcJTe8upPNcbv+wl7S+KRkjY3z2nssQOvMA7Ry3efArg1euI+tUfRNnzuddr2HsWudmcYpeIDifb8JvZ9U/r2IYnz48aK8zssMKymGw23OJs1kb0QxjagBHLCVUJZQkwLFlZq8o+2SfFJGcAmgP0LcWX8lrOmdeiDAtJK6kAbv3/qbBu1I4CJ98lmxeaMguPQaxmwkQEEiTWsLmPzDAU/R956c55ufrgufjHNGCtGyjrP5mBEzQuHEasUGBwmPNBgMzdVgoYpI80Zm4EWq3QzL1K2mgEwohQSmfDO/ZMgghZxmA/8Y6aTogrpU2qL5pUFZkZ8qgpgViU9IeRZz5H5foQElyEdiJ2GS+cQCMrKh35E/KOkCamwaqkMHkKoe0Bj7qRRBocwy396gnwN9yvq04762vcpZwh/utaTEvoJsJ41FKB2YgE96MGNtCjYHg+v1E7JYqq3J9+uk1XGjkxqDUIEIDltcUKTKBLjCZKCselqvVS72uEziMTGF5FTR/0IDiqm5dCbUq0jp0BryhVWyjaWFPCsQJGIBR1MYyNIUYPPNqxSIFJU98Yeosol2TLD+ql1U2MPXx3x2TLe16njnuC6obsnRmrmvo3uSB2cR7KqyMKd+YHe8icJfahjbz0jGytN7bMnP+aPU/1w7+7r46p2+Rlz9qx2TqMKl300ffltDvvm9Hm+g0/Uix5Pnw65w1mRVsOE40rVnffwCdTeb/q+j/7jyPdVZH1rAJxL+CY5RzLjQ7/N360j+GPY7JhspI/aZMPf9uHSYfWOWIraoWt8ICod0bpPrKLm3c8Zccfoqln2Gu8zIhb0FwYC+zC4yxaJwhM+WM+m7XoRGABPaIsC1tVy+xJCdLzFAHuYKiMIpRhA/4SeuBQI001Pe634XY8nCRQSA4iWQXg9H9A4v2YXgcw0MC8RmttB4JFpIPh29vV6+g3RBvCTlaa692lyv3ClbqKgRuYBaSMgVGWPH2AfE0qE9QRYNeDMwDMf+WZyRyZyUQwNUQqYK7Qq66W2EjqkuyVqJy+LskKG05detOpQdXCI6pIM1aWN0XvOzop1NgdcSU6Q7vUtS4oYMvdyPbjBcfn09IItlsw3QH9+YmfZfJksAedEYyl4HTK19sZesaanQ0z8MfSvLqPXOHBJPJYkZ2zhyfC/nuwkU6IF9RBmBtEgIlSHUK+iHXi0RIvBlLoKLWz7UcA9/Y5mUol6Fz3TKioA9D5JHyKplQeajaTeS8dbspPVSjtZUU/NLgZqdgiZZwuBMxRP/nOI/cdyyF2m+Mek9A7nukE7iN5hsXcL9/Q7FPtJ1IfggfKesIcqA99E3b502MCJBwDciuKe5eICiy7pfXsR7KHiA0j3jfZi+j1iKYvk/E2Ee9Rq2dUeRW6RKCO4OXZ8mbbRgrKJqpGDRit18iQzHr/voxmfH7iVfYialT4kSw3HszsWZRRzx20ds+/Lj2naLi2fulS/x0cxMPQHfNj3/CTWqi/tFnnpQ/qnjXlqmLI6Sivzr4I/PFGW9333980vka7BrUg6DxZ1OzJMbwmBdUbiwdLM6gagCyTrAQF4TmhM0yhoJjwpLLXtl2grTOdYy+b3MELLHJ/bzR1M9BjBhz94psCrWAHhoDz2+08YUmYaOhOBqMqyUUAbc33YlP576ebpLP+auf/AOa0UFeJn7hCj/sB6UPxJsb5lcJfyzfKkyLRbKCzhlBQLdv4EZk5WizTnHcNoSw2+OIb2GXlWAggo6GkGqGdUfa5qlfDpfvbnKmWmW11V3YJHz5cnQu0oQWaQEkv0dET4qElJc4mmpCb2q7nlHLUdskkwu/+HWfI8nz4HyK+WK82uWZ9kE177hevZWJPZWGwA+oSak8kvaQCY8pIvJmdNtCOQtv3B1hW7ACU07n1SnBpz2G7S/Oskf5umP1Cbq1EIDHM9v9FstOVqpUlHKZsLUb+40vMn9hTSQwFCCHSzqAB17TmAO56165P1lQUHLwgLWLfAcmJb8itTMHbFYgXiE35ZeFUEa8Cy0zT9jfQrD0vgE3XmkKkyLlgho1T7uxbnVwwg9Oll5k/Vi47onhnl7ki27zPb+6rc0XPoqUp8hzE/12nbnONyWR5fj0vvuyrAuYYnCVshka+G9dxWOTS1k7/3iJHecDKv0uZcy4lsjHWv0UQFffkRyeMnI+zxiPp473VruC/tPCKtdtIekcAmknZ80+M7g8RxJ7MOYfvFPeQJwBF1/+BZjfy+PcSO+LtqzVRjRimt5t/kuICcd6BbLDFON3SOi46bbht+XP4xN5c14NX34nPvALGej5ZutOqBvg8Kh0SnwuIugSAofYKDWV4JaGP4VtcAc6CajaWDtgB5Gjp1WGOQCYCjeeE2nLEd2vBvChWLL774cqod1sHcticj6JxJH0Xx8tUr5nzoTmitydAxbEH2c00EYQq/HhAUwD5Avkbni6fZqzz/xib/SAHG89nmH21YuAtAZMpQNtfeP5sVE9IXU1aOfv40m865vbL7C8CeOSzZBe8Q0LY0RDEIlRFmoRwgo6SKHFHCPiUbR0dWTNFbbBJiyjJNhUiFMrOPuKP+EbJKFbbot4T8anqSdmZVBeXsscrCWSD/Anez6oNRdkA9rcm4+yzJQPkC4cRYTABKptPJii4kP+vhCtEhnt/M5rxZoDgnzKJ1cfhaDciznvlqk3/9zXOWDmudBk1OY6lxaazi+9//sfrDWitS6GZ0QVb7WkCixwvWZfV7qlDFeiobCZ2fXyzvTxn39zlE9N2319dv3r7CJpvlpUrEn/RtQkfCAb0AzsoEkcVTlvNnrfMgH4tH7+FN31v8qUBN8G6/DXv4/Iit9yGbuYdH3j3pEdvgXSpvfdpvDdyATLJ3Ac8jw3t947Ku4jbur+erbqjYKHp/lwdGhxbJed2GS/YyxUeRx1RxKU4ZJHoiLmqwOmyco8Fk4DJua9JoEo+RxHoOt3ygRFZIkxiu1VYs1qcstZbqyI8qH9gHKg6uMFeeCJfkoP8BVjjjMX2j7ylB/o3x8PGGnvEbl7LjXBvVcFOCfW7cDgbDxYFXRCa2grzuTyUMAQOqwHSc7SW6ytWaXwNagnE6qKFh9afQJ+mNTQdaUuSMxJDDGHNmVsZ0zqu5BPSobagqmbFR4/nFdJr+7E//lL2DKNNyAAUDvA6q+Olk+kUy5VpIT2PyCSP2PJKYr5/ljOtPbyBjYgiRiKIHkCJqTFa8NbhYvyV2yJO3i+s0OU9+6z/7u2w0pJH+hOndIFTN/WAzIUN+mipkStpZ/R+NQzfytOzoPmpj/3WSXVXr1FwdoXlbPPfPsMCnajbXSY2V5N+o0VefAcGf/vZ1fnaRrJ7evn2xXmV31y/Wd+ni/prHQG++/rq4vyAQWG5+SYsvmeHDjB7WYxMpKP4CgRMUECfe87DmJyzMWL++X1/wnGcz4f0OS3D9/fr19eJcz3M0J0y9Lp3MJ5t7dgf6rR//dLFcXt/ybAdY/oK+ROxHdMqWPsz2ounlQ7UgMqQzkQOvJd7MbpjXw35TmjhE11KwJ74KMzWNTPtZJdOvkvl8k14X2dJmglFO0Bs3YVfrtMf+3d9d+fDCFtPOieJz7VsfF+yTBkFoHeCu4xiyYsfskleWx79TI6tA1vg97WqE3pnxO6Q85C7dYt3Qs1W+zShN6JGuXsLhvyOefufn4d/ucjVOj4Y76j7clr7e2/PF6hP4AD1rfVD3f4agWt87PTUNhzeqadi8MxgzyrOvoe56AqBaUX3dubj0cylAQxjKaR+BrLO0Tf8pJ/JAcJ7nuQtjR3qzRDXef7Kh874KxdbtW/cDoQ+NEr40IfGBaLinGsEg6sXpPdn0ksNz2+xKcTtRNwIbaap2pu1RQHJcAJZKDYQENfOHqRTKEXIGVAG/RCVsr+qaNKKp2Ka2JfX0llFiRPAfLKY52evF3d0Ns8bv724K1pZSooenQHWtPZ5lF2fgfQaZIZ3k7Cc/S8GJydn0nvdJaapJpnWovOKXDd5Z5skuL4z8M8+/0L6QZ0zvkfzN3bS400sDNEUEI7R0WW8uQAmk6Ow3aynGRf1o59TLB646qroIiRw8nGAn2SCPIxXWVVFjcpxdPbt4ejnZ8AqIWxYALO/e8ljlfnO7ujv9o//mv+XSnsNoIj6bBc3mp+lssuTlbqgEpmfBLqHXmnk/m/9o/ls/uZ4D/e+LxT2LfdNFmp7/rHjzr5n3RUCnpzUC+PQpojne9nZ6djGbz+5W9wolMt7nkBN+MpnftFLrCdHzWfU9mKCJeYLOxvIBJokB75nGpocHPMJQVyAk0H5WOauUk4Thf3/Yhd1uOrR1H0SOpSA0cpyOSN5lMujyLoW+Q1nY503xDmUeX9S3wITjO+Vj4lhvwDFfuj6amJNoup4AlI8z9dtpM8i9DueIaTOqCKvFf2NksZhHcHQc/TwgrtpDM5dy2IjCHmJqPtatJ3J5Lxv3xvjxAGcUZqL38q0KYm+HdNDtsKaO7dpX86BDpWD5WcvvGe1oVOFyuP8EM9sVGznBD3EiNjPQjxn1D8QknD6w3RbFIyJxekvxPlMdCpfqgJoE4J3AXVRlCE0tv89rXcsfXisVYNLbVC0GEJQDqb00yKUcxq74T0UhdoFFu1AK1MX0awkVhNQDgYT3+4LaWZB5f7fk3cJ2q+MRgcA/88QJAITq2RdeEzPW08ma2f2M1QL31pvLz773F549oWyl+SPTTbpmF6BFUlyACyf5dbGeFfM/2hRnyeYHk2yeru95KsDkb+mmsMaWhUqVUiOydaEBWrvT6pJ/rcOoWrkyUtW9ikKKrrqq1l2/xXB0Rv5cpP7OgeFKHW8mtsZoqOqKq2Sb8nSy+swqyLzN5BbMPJkstPFScpNNeQLzq/n5dHL9Z6vZHxTF7xLlKT6knYHU2qWVV0Ok6xUdYKE3hU1oCB7bJGfZC940wQMB/vkcsCxfvp7cE8Vpyo6G7QHkhHk+cq/9Yc8vLqaLz1l9kmav2SFqmmeEFhxauqso07te6X/1M80luydfa0jWBIF0K0JaPQdQ2EcvVVRA52AFAltXEW+wWIGnWDJapmKH20+y49h6qRTZQfMOs/pmHvepMHy/7av18PzxvzKNX3l52QYdYh1qvzVxwXA6vkuP/oXqY4kOnT2gbWlJ1rKi5GyajF/r6C3odQ/0Q8ukHXxiv+1b9wF+bvfVdk5Lnd6MHTb21qOABtSNwY8+PrW5/k7uDe/nOCeki64nABITxJV9x0STub3cplyt7dnrBhnbgk+psR7AuaEFvE7N9/1sRpL1MxhbEpq/ndjJIpjWNnNn3XdJ4HoGbQ8Q7XWDiw7g8G6r7GXrw1oPsFNBHUnVBVDbEPnSYh5GWjXLxug0wioCgfxMQ6nC/RQBpFgkkGl3FT0/EHLS+L++PEApKmkcX7OxlZGwwzt1TAy/KIJqzPkAnTOoq9HaZM3Y/poB/oQpPXCRGMIO5o4ADGfzxcXTzdnl2YSpJ8VskyxyLefVEIr2j9eSAbb+mZLkTy8JZqknc5QkjRUFsPMHF1LHghaZU7WtNHadq5zos6JyoqrAr+xcL6gIwmdVP2R8mAmsaGlaZfDpY+JqYcWCtAyOZKnt+nb19qTgTW2EbWosVoVrAF5rAXiWQ+uzQRDxGvW1SniqrV6npwVLgbOM9eAQI5aX967W801yR8sJncuf9AY9ONKfJVhpriXCrCSYTvOcAJJ9oQT9oYSAP3VdTRtTr5ODqcUzJdC/+i2rRHSlZxB6DgSp+i0VtaaFGmLtQiuLddl3UE8HfEmYsD7KMn8k2Q4uH2lxcNZHqv+x1HY/HIvbJz7v1gPjWi++GcTp+E7R4MQI2TamCXUg4qeW30hyGhWw20qb9g/MBeykD/UfEJ85j754KEhQIpYSp2tEQxcuxZ0R/DRUYURZ3xi8R/ANiS7Uz+02QVrww4C/46J9x6EHDIKt9yLGTlxEyAlaBadRFA5PN0ZcKO3zTKg4kCgF9Y12tGoGDVsl1v0P6i0NVu6TRqZfPsTSToaPnIl3i9WX8nG1R9BeAt0TZRfwMafsG+NAHsDYStJX4CIQlIEngoCwCxDbpQMA2YFFiM6w2lQQH0rtxaLRVQ4hM835Z6XAVVqcaJRWuy0y0QKENqc+dYH7gmRwnpzanA+9lskGYpF8kjIsktwLPBIQ8L5WViSwcACQt/x8kryE/Sa7XQLs1jwiuNokr4lAtKsM61TX/57AHGhxrU2FEl4enL0B+dl2QzJdMYZNN5KigoZypBRTwtOWQdI8wUWU6xfIMZraqUZVKzn6Rf/Yv5uxFWi7TGwvlRrU0wtB8sLSXk8pXRvoFcqW07xBk9XiKYs10vXbjAUhjM5rUpam1szTuSI4DeEznWw1TU/WbArEy9jYewcMn6+z6VJbSRGcaSJWvk54M8DNZMMwPIEF/9WZ1ExIZi2AAfdkeptm7BylPT15RYT2n2K2kMxRx7NXvKmjKhBgwyJ2gC1YTkK8oMoa49cEIYWeiFTaZGMhEeiGb4HeFa3RXBUqU8ZLeXeIe2J7RkeOsrdvs2vjf9vs3tS+I/d9jOypRl9hmb/FGNHv1I46reJub0Rk8b00/g2FBI9yn9/JIWLWkbS26cjvy4qt7qAZHNXuoB+d1fF7OlhX0fI+7TLwizkop1V4jN/WwLTX2w/wc9vSdk5Q4OBEr+Z7cqzp5jdQ7/HcSgKruBPrHsLdxElJk/B/nvY6VAj/ypwtN2U0qjvNp/ODPdDwurs5OHsn+z768Rx2iggE9Q6h7HbOQ+SOrxvL9XScExQemRgvdydDWD2E20Pq7tStItgpJPYoxFzu5d0W/3pt4BFOEvBhhjX3Jp4A6ACIg5lspoRG4yEBnjGhQmW2A488C6YSrhJsUsI+bCa2ggiCBPExfQXvNGUIZCdcppFkUDmDxpr+I4CWJvdFca/t+yfpjFfQAvaQzcLf9FXCnBYQnWb2k8fyzVXKDHLgvWafkIV2K7hrlUCar3ghbXpncqQPY8lSOL4V69qPmh+40D9Dl4KAXhgSDZd7qfqWe6tiWX52ZjZoDr9scx+Tg7w22VYJWaQ2M7QsQv7LD5XhAtC29RKzgHKG5LPPJ9lnzLYiLiN/ueRRi/bv106vihwIA4C6MKCNaBxK5rzDTXhcCJieoECxKC59yJ7gjYo0FQP1oHy1mTqPBvaJKhFnvZFcqQP0F3O6BgGgsjTTZ7WEJ7ieQX2rLf1JkmYnIeb8YJrCSrK1NF073lJkK4nFgY5b+gYm6sX+T0XhKLNKupD9rU883GD33AF8vMoBFR+1UfSlOMbxodk13ib3wLH8MF7uO6fc30RqdFaKG1s08ZuAMcvrQESCc0ztRisn/Io5kZ+9sldwLlahzYHsOPJrx2dxqfE4wimWEqcj1uPjMGyKLNyyiDnE6S1FPdU3Bu/j6KXnDvJG7PUwLlLLNE06rajruPvK2daiT+s4jZzdjCKKPs9EJL1J9Al2hUSTerxXe3pLrQ83uUdP1epFsW5e8hBL67x3X/X1ySpf3lp9qfbsaTtv6iQq9ZxKtHD2zrFJu3tYPc0RJ1E2klL8Fwq3TXhAgIBrFQLSDL2RFsJiOF8wSpKY0WOFmlXBVj7MvBGCp0iXSf4qnTJS/7kN1Z4IeVHF9o2f5idAeKrm6gigOEIBRPDK3mSyAOiB6taTnO3er4rkNp1c5dPrPH+GMMbyeSkwwE2rStljPr0nBmHxr14JkDL0O1N3YbVowdqAU2E7ffuAd0iW7qa10n2Hm1uWss6Ka0Z2lRsOnrXit+ooR9mhcLaca9Si65i178QtSucKPeUd4/eVUPt0Fp7VTgeFQp1BkYGqTBixtVjJWmm1mKHi0kQe1GzYFfRlkbzJJlNG75frRT5d39/QB9jHn+UbdAKamCn7Ptu/YPP9Tf6iyF8m7L6f3iXFrJgsJrO7dfI8vb1Ux1HENuVZj0UNdCXtFpqzjkCPndTGal16MH1g84x15MmULZ+kk6TT/hJZME0oK8MAvVQOCwgU6LeECjYXyPNgRYiy5hUEvCVazQdd2SAeBfjFNrfyUZkjX1RZ+myvyvPSvpH+MSP3Jf/4bhmny+LdH9Edo5e4ugv1ElDQnt0eU8f30jES47rD6aavh6mr0gN12MfD3gPKblPJbX8epn+bz5icMe1Y8un7bd0lJrbX05zDc4/at2IXq1r5Pp6vVawu9rC9qsJnbz/p+T2NqvYn+3pG3BVEE68B4DI4LyTIdB/XODbZ9CtSlVDd+VQZH/XnY1vj/o29HNwVt0zI3Jlwhb2un4/VGg0+funnkaoO6zOSSfBAQ5+Q/4Ekgjlj9AzE71Z5VIsl+2XIpIg0/ziqzOqzR8+Y25Y3gBxQZ6I0KcISwtg2VVrz9nlxl8CW5GjkHVQP1NY8a4sUoIeamThC4Jq5wRA8MFBb/ksvoTWQ3+vXb0FfADg4qB6qpMnd7O7m/p6kxnDJEoBnXGI5WW5+9NnlXzk/WSVX7PiZF+en0/t88jRJr/PpXTYl9iDy0wIB9n+UqNV6enH2+e+wVTyj0bBi7hCwMMvP0VM7FJkmKIN4kiQg5Fz3h1OFPE9ANepwbqFyXKczMyboSe9Zr5M8zozTPSKb2W59t6+MVt2E5wDg8fXpcnGaTlf5PCcmIyaczifrhdZeC7XrzW+wYeWw/A/+Pjl78tmXyeb+6Sa9WzBFf8NTmh+eaonua9qWCTw0jj31oZ1SXkj9p//uT3/5y18ijm6X5TwQ4tkQT4ayq/MZqwHocysWGZi6otHzJS09mM4y5avL+eMD9To0ootuiEZsVYK6tx5zMcNNy4nNLA9yxK68tg7U9E67/7QovrsZY3obNNZk3wkvjXHIx+WI4eaLW/ZbZLubNdqg2Atx68YMoCkXASsVU9XTcZGn9QPMERf4ZQ8jCGOF4sivHXXFpSbmWKfh+Kw3DjPxw3Vdw3I2s10Mcxu2KIxzyG02P2+Yvq+0bJ7Kn52t1Vc3zg/PEOJM0kHPON2Q0qgycCljq+KYc5U36jMwiTn0dModDHcYUnm1k8vO1g+WdlYfmTmmT8asdmoFcReNe6Lhj8rTwZKWl0NGPGJt+pSwXuifQ2dP2R0Fxszs57Zg+2lqca3tzs5+nNYPqWTTaWxikGICRu9thNYU4gQIIwagGLh1d3v79a+fL3l3VHEvBMbiXaAeL+ZdLF9fvwHPERsgXC9jIlzYnEHy+dOznzz5wWp2sykuprwQNrtkYWmaXCTJGS+DnayYzMFDBCZtb1hGSslmfnL5H/zl6Zy5QOwofzIB97MUFWBpmI7JHzZuTU1U4wjnymLLJdtBZEnihesvvLB5ro3NO8M6t0aF9qx9f4NEO98r1vg3eOnSRXoBaZcdZ3bUKbNoeY4ObY2P86hKlaUQoPyxqTOVw2Z6UnH+7Oqv/We/p9eynfAE6Jvl+m7x+vN/9fv/+M1vNEEo2Zxo/x/iL1bbysf56cXF6dnZasHTGCb1E1jOppubz169Sd/QddjElb5HLlPAFFzw/8Wr5/ktj3oUxOUU8qxIu3nOTk5ms/m5ED7Um6dm1ismJBVMQgLX630AbBjE8mLt8U9SESwHQQkxBOsE9Eq4FZPF6L30I5jIrTIZ8xHrdusbQoH0qbwiJgNHeyWAtpl62FHbH2bwvvcQOV13niY/aBrGxPd5qM3HzVqd13J1Z8EjZbZxTp+g0R7uMzb+ve6jiYXHvyNxOqYZnx7Tjs5tvCxvqdiuWJ+4D8RpaKgYGnqMK2K2O9Nt/cfbXmPe1zd0HwhHsCPkDCbc2uEuLprGE4BOnqX7q7LANKjkwlTuqVBQVfn0GXkgeCs4Mio8ZhL+QVYn38dop0Zn6ZT7gWe633Z67yFWhHYJ7gqJh7B9nLqxP1xN5ARI4qWR5EBi3UvFliPULyqhGfpl8EB5k1YBEEzZmoABsjfgxwdoimwhPk2ld3QEDvO5FZp4L7RtBLAw2J3xJiZBTUNrXGg/TqZbUBvRqRbvTjVxG3bGlup69S+D9yk7v+dvkvSSWRoaNNbkbT07YMRXU4ZYOrqZ2bQQQB6Lg6cEA9Mp203e2RMGcCZLjanEgK5godlp8z3MWWa/m22OkDOqwzN6Ciuigc9QM3D2nIEqhxR1Mu3MHODubmkTwGervZpbJCEnoiePRqF7AG3Zqf/8i5/OcXqR8uSFV3mtN9c//NW/+jevf/OCqf/MzhdgZ8tWvVuiBNo8MiJGI4cOwHz/tHgyX17lk9cEd9rDCV78V2DIZDBt+zObzzWyb/uKIhfxeT6l26nHCusTHGiSD7uL0gPogCQ5LASlw/H4SY8IWF2urargonr859edNcLMJuMJAF1RJRBz0Gut91qPN2XK70vkC09GGZF7PGllQwStGh9HhvzkTRTpS+YBh7MaU/Ew/mM4f6J5bA98C78DY1w21mwPANpfKb5jFpdoXl2j+4fvTVetSrdAZBkD2rTj3b54qGJ98OeB8ZnJa9etWyiieA5ip5JtRzbI3E/ICq6Nq3iL1MZjGvXrl3Hdesn2qm3FtqxK9dkVZt1BGNJjGFaMez9jbk7UjrbbOTG7wCHO3KZbvS7m5n5zbzPl91GP0EYH+K3dJw9TtZePkI2wjX3EmlpGJzjzklAeVbW+rWs91ALqgIEc2ACWgdrgHsbQn9gw7CsQlMoAShDyIVCEMiU3DZdSWUhMTIXrVWpBAFmaLiQ8pshAMFw7/BerE0SIVPhMDLVXpJiYHKExDm3KPllfTpLzLLuXPGAge4TqXQLJcgXWv2QHSWIA9h3Vu4qhRkJ+mq5Ok+zG9AEAMtSMQizuRJwhROlohZX+ujbNLeFFnoyzq5zmp2m8zTTu28uuVHsNQN/Yf622e3sE/1qt4Qtxc74NOhOjdg2H2tiCQIosXyQ0mNxqHWay+p75mMc7avTJKluvLvT4ZX17kvHCLmA/S3ppL54Z0dh6SGBRmV4QDKDnSdFqtVCEMHmVTq4ll2UDqzWBH0+E6CF6BsVqbsD+NE/WT+iTSfEGsE5AoS2H6Ez0Jh4SqCe+gD0LklFwxasICAqkcrJm+F/LWPhFg5siBRSyIt5LAAHPqdT51cMppX+Kgs2KNjwegCtRhM0pIt9dYB82xl/kX3PRcYSVAJJv5XzROMoeHtXoy49IymTv/aFNGuXEd9Qo+whJ6w0ln17d2iiinWNe7fZjXU1zfD0rvjLOO36XH/l3JFan7/e6r0ViH8bpmOeo9Bg/RIxcVp9WEWGZ7LMr/q2P0w0OOxoR6j3b6EG+ipXbU25ctTftX5Lhzq3SMU8AGkJipt1ObeWGu1GD1XfpMr5t9dkdaELCKRuXfdUb+a1maJTrMm7MjuL9s5zhGNH7895do8+c96XPbo0jisNaOWLwSMngPPeuoWbHZBLoWgeamg5WwfCLZwsz28iCwDhZ4HqLLwThfPBTMJ2Z/2sQtg4VQAY1KQsBtHW6YRfVNamAOY2Y2rMAzRcyOoEzK4VMawoM+AuyMUSr8eMV27UIviNMNmQECcxpA/DNpndpfid1BcrE1OccaQdPvUAKJMk/dpnUMC5Ss+ltkt0iQKGLIhs7gfIkX1f+370ktpZhiSjFdUShUi5Vs/OgIFC36do5nUz2zgwi967ZVcG5xZbUqLxty2KaQP6tDvMLzcpjF3qJfMGZH1E9CIIsT5mfc5KzJyhInXk+mrWlmE8T7UHcGsgn0oMju/HMyEmWJ1lxuV5/w3MCmtTYguCtBdSZ6F90QK5VSO8zEvUvRZmKVPWMQTsBsS4EfC+NWCGuKJd3B1DfEL/FnXBjDYCS2vaHLqlOT8CgpegYATsCDhiY8eJKrmQr/pUK7gPOEjF0uPZDFJ/KzIvu0Y/dGSN6xEds4q7Ovodp36HvxRhT5dn4PQB1T/bFW3Zj9N/g2ph3FMm1vlZ7teFjxEN10wauIisGqMqikV88n5d2hHjRPDOeTyn3G9O27VWL1/mh2qtxdjulohjTAyva3Z9tq9s5w1yG9Wlz00D1MMeqNO4zcboq/xg/zVs+Lt50Q7H6Ql2mGmtU2o/m/OPKfQafjAsp+iGj4/x5qa2+NUzFD3KSvRRuT+bsrMP62ox5FiLVdG3GRh0LGe4SbEMmsMgoOIHs+dO/apIQuExJ4BZoTDhNc0CAWYaqtJoXFTQQC0YstQKIFdPT5DRLzieTa1sJKpwv2JYx+R9ISZJ55RwM/99vipkWgU5Os83FOnttBkodQxbI0/u/5BiAXTkG/4Uuq6MkLC+dkgtl65B/qrTnhLN7XqP4/3/2/qTXkmzL88OsOc293kSER/fiRbw282W+zKwsscAqEtBAIAhQJECAGmkgQTN9Ew30ETQTIIAjiYIgQCMC0kAUS2JVsTJZle3LrEzma6KPcA8Pb+89jZl+/7XM9tnWHjvN9fCI5+bX7Wxbe/V7Hztr9wMILjfgj/f3d8cHKsIdcy+qwO+MiRHOIcvDbwlVGVeXJfGRf1KuTM3SopEtyzlYHXBBt31yrThcR4Opl10nvFHxmL6v06AtcKey0FwE4yqffW0DfnCj2WcvRjgVbzOqQORNq5IzgNOZNgjyFibbxqptqCopfayfXqTUDyqZxhu2d6mJafLYBqaoN1QbbUhalkwSozIzTESzYq26t7mXztg86j5VB304g0J70kJrGxBZq1KGq6y9QDoraiqPtD4MGTr4tHKqxyF4P3Yf1N91ntN9f3YhjnnKG/IA2u7vXQcSKlOfcQ3YntFg4zxkb4PRlAerfnpPHnup1I22ZeDpGu7x/1F+OF2rg/yEZ/aUprM7qhR6/HMUH1ehw60qzw68ckDj9zcqe3//97w39GZgBCDUl4rP6R9ycsUlSp7O9xWH77YH6krT//6aYrtzCK8/TzhhYD6FDziH4k9k20Xzr8hL9kUZsT52amxNxwJHNE66KSb2btRQvoslezXiaoVxxGT6JNCepZvNNVMhCKeItW3XYO4WERNq2UVcwx+XhVniDoZ3yrpUxYK296N1uJp4GwRQy0FTdOg9ZttQmCqI1LwOydrwOixn1+Wc0FHdtzO4kEvwRtOA6Rzep1xumCkuhQjiChoIT8vkOc0S7equTmJrs8hYgjjk2ghD7KYqbd3WO3gd3sWQXbo35Yb2Zp0NKMfd6IWAcTuqXD6s8YYyqixc8pgcbAMvtBhVt+g/12adFEyyWbOhK0M2Gy3d1rHMVeuPWgGAqgUxBWt7Rt0t5m9vCESIDNj+lXUEHONFzVKvuySwkSicqV/cBbVQXnpR1GogWDXSdCNafDZihDw+rUGwYrVxpjMB1EZFstoX9PQbCaSsSp5l+RzmOlqMSjRnyYp2mxLv6+ecPkY1ksKtqwtpINRe3YPWoPmtfPjOOMi+ErsibD3uMr5tqe9MAZ3D8TjDv9kDxev5Lil2XJxu6+HnAFR825mDz7wYOy3UoZact7dO72+olOm2qLqQQb3bGd221JAVbcpDnn1e2tnGAUZFe1l7NUHuQE0xFp0SHGV8cGZDdFxGcbrD1etwg7aDMxHQqvbBM3vJXYe9aAEhrjNxOiDsEn22y1h+57lbiXTr5I58WmqIwxB8H1f3x86dspH4pHPZvORO0YFJKMRlnfaaYE1wTMidbtbFn//ln5O9vFjk2WKxyJeLC+KkfPHO48df05GqTRk1i1oRny3n1KzobXGdEqVpP37FRsrS5fGhQjZw7KClbLu6YJ/O1eorRWxE9ArxaRNobkbJFo0lvbmAbJgAeE7Yd5vVmmV6d17eW+dfsp+P+pU1L/xdBW6zh+zys2R3/3StZcpbgv+HWT5br99fPb+a377USIOUQTd4SiGxt3LVXv4GMZcRz5nzcIo+2TfyvsHtNrTzzw7DTgbQo5pOFv7ap24Vx0hWyBpO9I0PdApxmJyceAwhTo8S7TJd66D7LgP3UJ6uS9BIzjMoOYrOmaDFjQpALM06AIvYaZ7NsuKtnOOf86dFwhwtzvSaMdhEkeTJm2V2nefPimLNSWLs6JnRK589ZmufIl0lLPDQzCLt35+k92kizOfvUlmpiTQ84U/TggYGjUPWhMw4YBhBOQtF5nBjRe9sRjtxXRRIJMrf2CwwdFOML8lUQS1P17IA1T1aKZvNX/7Nf7u8vEX9ZsyCesmSY1oyn376xe//7Hdff+MNrVf2eq4hq11LoPaWf9ZPkes8OZjRwTwGsOddN8ByD1XfGzJw2kMb8KYl7FvYQG3tIRPyfDRY3+kAOj0xZKn9CuxhP0S7h+zU7PP6f4o2N1GDJ43tTymFjgE9/jmKjzNuctvV1iZ8p0QD7jXViOqx+gqzWYfpe7iJy78rO51vQsYrnj0e8C9M7H5P96DeJKhZyQ6QdDRhLMOd4JBWOkZrpVuOaj22kL/Tj61CaD163Np1QOzpZq7H557PXQmC8vXq+f/t//p/fn6lhZjWA0ov6Jwe9dli+ezZk3tvvsF26nTp0gAg+qcPVoFTlt29y/wci/hgQ0iknlV1mF5eXs5nTPjWUay0ApjlcXFx+eCrrz7/4gvaFgT24qNgKmFrz6vr58zloHlRMA+c7eSJ/tmVMXnOgt80e7K8fLZM7rARJB3/DEdk5ZvpbL3aXM0vygtCSSZplFfzN+7d/v77d+4uZ7fenV1yKrDtVWrLPbU9vdmKVXZ5TZK6Utw+7GbBbfRMgDjtMu492IHeZU1j9pJgue5uWa1SbUZdf+rnRr55lJJVj7st75D/ma6TXWo6ff50U9CzrpaBFTHraxklYB0A0TlLctVvP0tev5s8vL15tFITQXDGhqhrmiGWzlY6wPcK7TR0pBXAVB+ajewI5VtCZQXHgWk/IvryZ5sVh4uVbB6rwQC1N/TBHTKWDUtBAn9mtMFA7dBstVr9v/+b/8/19crqBZhaG4CEx08e/2f/6f/8P/mP/+Onz6QPJlorQO3LYHv8UAOjT/NkwI4yXiVHPfDKZaPueZX5jXug/RbsV4h6PIDYzPEGQA2zt0Y/w2nQiFFNoA6/Y6+ePstui6oLmSzO20wNKTfQtvYxkEb7bLKGDcSubl2Ix1dGFsYc6lJpMDv9oRrbmeL/GCdOn67ECRwa5V77zb81eIzL773foxZt0GIIXiG47d1Si3xyhnoStGkmJnOO64v7oMmo/zXRh+l03iGufPNlRsjO5pnPnj9dr0v2UyfW0owJwjS9K9Lnz58wm+LeG29d3LpFvEXww7QIxVw5E25oKywIiejoNSr16XoEyMQJIDMOZ1JH8F317c+ebVkD+strTfNQM4HYX9sK6fzWzeY/uPvmm5dfL/O3l7Ov2f1/sXxyO3/z9Yvrn919n4aEgjcEMvmDrtvlv5jPb+VPbi0Xt3MaCzQAksuL77/2zr9/b8a+n9tLojx4qzOeSUSakaJ4Tf+8HSAfNHxTuw8U84cQGP55yz8n3J1zQHR+4R7g7UQttw2PnyOFYvBoOh5DiNOjRFVmMMUEu5ssqZs5qIp5LV1pV3003aoRAUqAgmc4aXlncecvOP6h2Kxm6dImfTE+s9SEmuXn2YZjoYtszoHPqhJp8eStfPNPL/Kr9PHD9fJp+ug6vXOVPS22l5v04ZefcUaEAnTGj+j61z6hakBcXP7szuuLu0W53q4vy+Rqll+CU6S3i3y1KZbbkgGBRZJcZ6wzZtwgzd649y6jV2qs8t+PsIYPhxSs1k+yp0l5j9qySR5YMzW5WN5SC4PjhMM4h/zlIx7uOXdVfHd4fbccHOUYNfSsn0PvuiH4JOHRm3AIfwr/vTi9funuIdP9jYMw1L+uhnvl7kgmWOrIPTwn0+7EHZGKfqd6dOgwbOBEtB3EQUCDwyBWO6NbRm2MzvN4IQr9KP2PpOqoNwxQtd28owrY/TVnLiJXFW8P19GQY2sGvAEQYOJwjmu/g88h5VvF4wW7RDXFrr1yKfyAXBN96z+9RrfsCo+99d0dFXCCCxweHs+YaMnq1eqM4qaxainVRzSIstcCj+Y0A5uwaEvv6jqZLyyEB0Zwrlu6pZtdMy00bVvHuDKdgv5SnZq0StZLZknn/nZGNY+hoaN7lc5cuk8VjNNdul2zuHPFhB8aBCBpvoW6YAnLtDD0VrH9L97/3R++SYvi7Xn2VbG9l+Vfz9Jbs+VVOoeJZvSzkJP1opoZopOk1pz9pA5gzeMghltmS9aVMoOj1FJf2+8H2806zfCxvn1Tb8h9LRfqsQXqo6xCjxZmeNzj/oDXZS3lRwObLsnZIC7YlAsGuKr+aHcFwu4iR3fprjZp+taZKm+d9JwYxxwtevz5aWPeDp3xTNihXch6gCfpdlGuqAzMB7NJ/tqGn8p0663la//k9eX19vbzzeV1+WSVXDxLn14Xd+6nD35xfQ078Cl529CTT5qFi+WtWxcXt7bp9UJnh1Ep76jlWc7u3FvOF3e3xTpP5tfPtlfPrrQXkA6KZlSBikVzgpUmtIF9sTGLEDCL5ia0tGk1359pb9TWp8/ZWkqHV6j2qtyD3STM4h3cAAO34KKB/N9KsLvwONOtOh5H+orqGA+8qsGR1w5xxqRargbA6VU6vJyCqhLu7TlmuOrhqHGAbisnCAj8x3Fi/KF0g8MNtK0b6yWOa1m66l3duhDD9BJ1u6rSPUXugOMadjVxuhWimX++pwG7VOXsCgme4m8P8Ea5j34NnEn8PWnRVsI6PAO8kSBQbTxXDwBjEX0ok2BDuh3SP9Gr4Lj0Yd2NmXNUGCdEgilW+ar7nkt3wJrmoCZA8TZz9Nm5h3n5ST5TbE9ATnBE5zu02qd/luSP4cEjQwRwI35SqCQuwi6TxzodmO36GSzQokvaBtfsvWLnLjHL6Jq51rP1x/n2/ST/UquE0/tMEklzDiAjhuRUKeYcsVaUc4KZzz1Lrn+nXLCz/AoGeXaR5iutBmY96PpdxWvzT6UHo22yhi5lTIg9YcbG5e1+qCD2oL7/Cjru4QpttwuQTN9HUuU7HmJIdIV1IRPZTkALklu4ETxWS/rhyvrSI2nK1kZZNO/fsWsE+2RLT2blUNDM5io2t64frVfPrrMZr8dFvqDJp073RcpZwRz2sFScTakz/yddazpPdq22aPKYAL1MH1FLLtNnHM/7tHz0NFnRDkUeJe87+WgYQFv60NhgYIFxG50vwardGbvHlm+walyHBtAUKO7OqcjXq+fFNdPSqJLacEhL4An9VctlD9v8y1LllelD1VK2mdVst9mKCqtGCi835hdRZHUrgISPsbBGhYz4auwBssvQGmWuql9wB9dQlfQ46nfZ2Qy9Z4bg1fvHiQd+uWIFh9Ix/6E+4xhniM8UePc3bkiiczuX3Fi3m+AZ8x9MR2U0RYcGTkQ7yL+T0eAw8MveIarWo46XS0zlIwZ79lk6Sv89PGMljkzrSz/7wt4JHQ7t73L16uzg1QD7HfERgBrUeqfU4PHPPUR7ssd5v/S5OJlrio1eHI5/02ahz4sRdNOGHM0/mB8XTUgH/zikF/lo0eOEQYdxtJc39wgDzL9VV6bFb4Q/TOihN9Q6OHkgihJMETxJLZFUFKgmAX8Vkm3lqTW+tAlAtO5eWyGgaIwoR2szuRm23EeSbAFIa29HJgCxXpMBgM1z5u5cJvmSHlbY2CkAbABDeCiBDDyILTPANfGItgdRIGdEXTD/f8u08m1CaEfbgvEB1g5L26oBU70GzIRd8VWPHa/JQlONeydzR95NmTO74H0QFzaE5doM5d4s3GW7D9y4ykRXuXJOBatU2Vlj9UnlRg77f1qv+WqzvaLyMNjD7q3M4WcNLotCiK9zHerFql8KcUOTgb78Ys2A0bzML9c0OmHCVjxWFTVkxNDPWkVsLQ+m/dhEfgXumr9PsL5l/Eeb/TCrLOPQMcaL0IHVxttrNTizOUNYVwjS5CGqiM6r1lIBq7y1hYKrNcGzVSVtYaQdg3Ri2DXjGFCqgunuJBWhVZkmpPLMq49XHvjOeYCaXr0GvnOmHWuQ+6N+HfRyGXAZ4Iis2QCIMnpZ9gJD6bQFNtpzXdLJLbwuqUO6/Ke3Aod4ToHHUjzdnTvY5VP5faBlGfPs0p4B0pEb6kG72E4WFrewT7drD4eOXS31Q+1swd383gpfrZ14IIq4B8gd1UvSYj7+OKRS7LdDeuvHpUW5+3wVoQ4nh7THVW8rSqn6p3VWAOeVGh85Tn2dimSUtm5y9YiqY9MgCnGIpYmlRPU5+zem6R11TxIPEaArfIeKzdcJ49mRnU5csdNsHyNUiGWkYiG+4mZ9m4wQEMOzqafGAQjUEqb3J0umicwXd1gxgNJM1Zjn67RcZDOCxAvNy7YlCclsnXIkcLbeMuHn7p33/vEfrJ48Sa8eba7ypFhdzu7O1YW8TbbvyhyE6qPHOdKr53LwQGaFDzeuFo73AQN0WY5TEYx8xHhOaRwq/i0ZI3wGs3wvo56VDEO8a3gwpbLUNfVcVRBdgqkqRJeR6eZNABKM8dAqY1VuvlmXyyXrTC6Xb+Tr1WJx54LmnKL/pPzqw8fbFevOl5zkwEKAYraxw5uvWadLq5AawDIT4nTaBVv6/mfJYqsmgeb9cFzX9g1WBG/KB5oaxny0bF0mF/mcsaw7mxVLxuHE+MNaLYXZclustBEtA1kabjADqJbFXVXc7DEwqhlgDVhZLqMJmpzEpDgtTaAaM4bFDKWNuQCN1JIVF/r+cQopeSZ4h32P/LsWeahCGerjR4EG8s0/jL5/9rznB7TrxgADiD1gf9/6Cb5TfsGdxSkSKyU88vGHUZ/0KH0DoOM8f7Aih8Z7Tc9UFX5Y6vRy8d90fZe4DtXKqc56H/L/EHyq8AGXVYZXXJoNgKmsKzy9fjsk9Vul/uwgfAcBA65uWOo44d7IO/dDt1T2SphiwothslfKEMJodWwT9bpoihN6pbS5Dz/3yh1Gf/E5+3zQ8712ktgyR6pdZfmK1dU7r3eGPiywIRpyVPsQBv8UvgMlxiJgAlHLJtVNapuiGxdFQlVgxBZC6jVlCEBhkwgVYUmIxOkDFnzS0cq6T20MT9CfsT18xjbxTL0gDGIxqBaF2i6e9Opy2iv7wVyKlDlH6oHVRJLLdy5uvft6Wn4vKdnz5xkNHdugFHkyxkSCJ9mmWA2QKjd3mbQgvCOnmx3U8qxAEeAB8kITVR2Q7/z/zqZBzayAhWfEmiBkkbQagOwke/H6W+9cvv3Dy7dp/3FaMz/zJWM46+vHz77+9erhI1qWtAWZg5Ow5X/JgXMXWfZcG/so+iZAIOBmJChjMx/2lGJajuoSITsy2a6Tg4TZ0yddZOlCYbyGlyh36gmBPnoozE+LK1izFNjmvioLRQn0VUFhpTplFFQ81TBm/sz0/YCGpIazVOv1CTPDVRa0Xipew/VEXrg8XaEA3aUCyqvEcR6I3Xwch1dUp3uAUnhVpw9w44CzAEf1eegkYL0JJSvuAXXZUbsk4hP0arIP4J5Es4XXg3A4aLwVGGl+OOuIIpYS0ntr50BxVHwDn0jOzSZDf3Ncikpbm7hb7lO0cRvjFva4XXGJxOlY1jgHxwy+9YSXBXfn2erd8VwwZWznAtjC76AcDwh69rKI/TY+m3DIV71s9wPtm+6rdIxzabMMB+nYqx4vdXsc1TdZX41cM7sqGvO+0gRCzJ8grlGc77ENgRFREK8eC4EUyim2J/Ih9CLissgJ9G3Bma/02AKhixRiFnISqlv8x6QOTeT3EMntYjmvunWp2Iq0EiZtsx7ggjBrlhLJwRSOs4JBgPUPZyzPnH+uuHDOWtFlmbD9y0WSPc21r/xch7QiJntaQkpzQut/c2+iKKazwF/qygdmZusHy30yZad/ceByl3k6vjvc7yatsfu+QYw24DkoZkE6xJOCNzg44o6PPw/fDbOn73+Yop1TW9pRtM4QQTOTHAN4UVORKEn1qqebFbvnbG6/Mb94k9Uaq1uXr+fzL6hM2fz7LAJnr30F18k1S0TSGZ3uKbNt2BYqnz9OiqdZ8XqegATTzZL9QWfFrSJ/VDzNSzafpbZ+Tq2hypGdZxtEqXGpdSjsV0utpBJeJeWCtbv8ttGKYH9PBgGgY29bzvVSlc+fYIhqCnOGxEj7EglAY0ELFeDJYANViYpP7dW3g0wb/ZCx1dPuw5gJrFxDrfLs8bjbN9QnOuU9f5xBQ1T+vp3+tncfD3E7AH5C5NN983chQ5oMYb4gz59gtVsUvwuGbJwI3xXldK2mfS+CkjsRtU6H+n9CuYxIC2+LatWQv+HRpakYIwAVgA+x478ATazahFefgx4IRRFjVD6NQI5WOTmCh6QjvEj3uzLx3ZWJlY/1Ccq7qkHzbzYRa4smscItxYKlLbg/3qhRrmRL1V41XigwlGglddhDltPn2z6YuEWsSXIJ0UNlhexEUnqwLGNh2Qrg1R2qXlj1rxMSaZ0koT2zebLtnCOT6NgnTrdLUbl2+IECING/CAmpCLL4UBcs0Tl8FXJpJ8bt7Jp9WC4XbAyj6f4WwXHyq2ZkIFbHDag7lvlC7OjO0ANLleGysa5c4jL6bOHPzwaI6pVl/EHcrXnics1GswjhN3JhDPz93hXgooUwhNGl+eYgbkgk39VHdTOyMtTz27iUnSOpvMGkCmA1B+vefvdtpm5xWBxrNRLWc2uYh7IkqmfSP+0EFtoy0gPubKsVukwFW7xx+cbF8mK7uV2wN60ib4r41vX8+tdPnzzYsJvQRqvENYdIQTkrCj7+6LP7Xz1cr9lmqpgtbnF+V8q0o8uLe2+8QV3dbK/XHBXGagA0p8qxbMCKQ3XeFrSbfXYze0lRfYn+qcNWf9XmVcNXuUITgjuBe5XiwzgE+C4h9AbJLmtv6li6vYxfIbzywIkeCPV992U4keNZyWOtRr6dZ5U5wCxWpYnSVKw6CXiHsnPxQNtooF1iAl3qsOydmJCa1q4K6OOJoTaWU80eRG/MM8kNEntfm11PuHsr+Jl0cG6h4MZdpNxIbktDWdEs95ZdAZ+EZ7UQYB/OH9irSVyXQk8MDKdf7v9AGxOiYeAfeLraoAVIIAlZATKUmI7ZywHy3svHZPB/V7cWfrCrBa8eo/KNEUJdjYFKRyVe9/0P6ajoo9G7HytLZMxFr2jjqlkpSlZYbs90f1qfuaZBe3//LkeBO7lcMN8S0CvcV+c986mJ3S5v3boFtSJ2zcTQqQLgXF8/Z6mAoih28We1ZcYyTXGgk1UxvtYP0IDQsk8COyJFZnsbD+3PqLlFbDc0v8++/zohOAPbdyJlh0emcbO0FM6oRROBloB0xgoj96KyZ+oUOo2U3fbNyC/uJfdYBI6T7mff3SWGVwFg7ddGFg/Ad0pUmrVxOs89+/cP8e/Q5rxXqURv6T64EsBV6vJ0P9Tw+rMyMf9SLu3xgETpCvjYLFNVT6gAb/z4PXbdKViJm77PcbtZ+R6FVxbXFxcZyz84CZjGAW28zWalOTfJ9tZi9vr8DfbrUatyuyT43qgZsC2zxRvzZ8Xm62J7l2qi9iOrh5k1nmUPH3+ZPV0UTCfT6WAPVLeZV7a4WM7+EXqtt/T0c6IYw038UxMRzq6t7UrlTRWqrf7Qm4aBfQ2poDxouMq2HKWSkQJBowX637K5st+9EHs48otIDrq8RA4iAXngnROzid8/cTrGeZFp/53q/e1oqYE73bst+BkeJ/gtltJ983chMX6cno4ZU52ebpT1gfbG0s9VBEfyiX4lY61G0hOrTcM/I+wOyoreBv5+DtRN8ztrACYqHdg1EvA+5dXT4HUzDzesnjsguCEkgjFBfvCzJ8KjY7YeA3krAVq4JpIE/DgR06JzuLr6h1xPhEcn6eIHViOJ2ApHc31irUbIA0kLJ+gWEiCEdJd5yGrx6X3skveifQeBuAnjD7uMpor+3XPWj+5Bj0I3wif+KYhSPy2Ytuu6ZkJYMKQwHLGKBpntw/m8Cu0JOojcCfnZv3O1enD/KzZQJxMuagAIrIhJYwf05tKqYlKFjhujDjzjQDHODWYOD6dBEYExhYMwkB0akQwWsaI1OtSaAFt7R9IgYfxACgiJcE3hmOkgtQXRZR9VzWj4qIIZ0tluLjNm15ApfeLMlzG9xy+ysGtlnyE1FoVPOSXM07dio9mmc38zBnA00f/21fpLGpFr1v4SuNPXPmO6DsdBM3WH6Wgc7aDonkib6sHoAdWCGjXb3M22HBFNZdIuPprmr1Ui1C5mEFHbGHHSeXHUBS01Z9LYakXbkSXEqtZQ2JoAaiA1k/2IVEW08xRVSu0DTVpSNVLSfGE7F7H0QCuDabJSsyoXkLTq5pUsFGxt966o7bsk1IDT569XsIM8ENx8ENUr5JvzwMQK3otm37Tzq9b9wn2T1WbYyGZOpwEwUel2q6Vr/UQPd9tVJ7QR97RxY1lxeqKqfWhBojuA+wH9CrUOgTZImFgKjj9dYsW/lsvjXkF7EYLOJNwQ+lQCVbuexNh1uqW/MyHTe8R9l4bg55pIspACPOB7VhAdMBsJq129vewtPg0qewg99Dx5Ou477+IfCgljL27aoeQ7/Kh8d8BoPCQGku6UkbtwwB/sQvO2GDTHAYzlru8QDi1y7790y1J6i1l6q4kWFIcCfkXRVaVRAK91mHq22MgibIVrWq1LaKRIjBCJtoEm/0CXMYu7IFa7vr5OU2btwxYURUJs+sh8IdJlypJfOmKJqGgE0KN/QQ/vhrCO9gITfjJWf2ruBTRM3xAWk4qsIQEGAqUfQWGloc8sUr5ZXQVmHYstM77RBOFCYV2W9qTxrcA1RJ8jPd/KdgrztDArZQzew0wUe69G/70znMAqnv0fpxviWnzCY8MPDQosOWy9BAqrmYgrrLfd5voz40fPgK+Lck7Rrpmmb01BbeHKtDAm9azTxXyTrPVTOJstaAMQpsOFeTsQb3OWfDwty9eJ2gnvVYHyh2zyk2W3mENWbheK8qkL1k9vd0342W7gi1w7yUsVCd7gsK8s9MZJPfpE/e4HeLJhKYpKrphhBf80DiYMw+JmZV37yCid3EuqztCnw2NIJ13VRmnWvCgRyLvvkPHf5S5+kytP8Ts8Tjti5y3UoT8TIPjG+/5bvz5nEjKZzQS/jfN6MX47RUqjrE+2N3gjvJ+GSnAIHjhMTBxte6hprmrDD5HsIXg8qnawDtE7ofqdiiRGyUYDAKKgc/NtE1F4soE6COqQfXcBLYcE/7fgEx1AMQQOvSS7curNPg24V3qLfWzjuNotQh6PM8SpYlrXYaL0iWhdbU+HuJ7jfL5B9cYV6+S6pr31JTbUCqoqM08rvCHIUKC/sHBLwY76RwXmP93zLOu0CffWdBAVYHrerVnghwETZ0EAFQG/deQTWhH9K7TifFebIGRBlXXTEpfBRCF+xu7s5W2O/V2kOot4XVwwDkDIw5aLM7UBvE5q1YGiU/X4q9XA4IR0gIX+m+EkuBSj1Y0A94dBu1VbdEZR33jqwOq8/Z9O7TqA7Qm/e9aORYDuQN9YCl2aXpisySileKoq6K64WbVFJWWPghf5nMEAHQNB9/02VS+7RncodFqhKfuEajUw0bwN/lCLaACsVNc2l+l6mWQ6o4tqSXWAjOie+gVT1TWkcOKAhp1YYFKwBBlErV2xakE29tK41BiDNiMCRapRUzmlDqhlULVYUqJKxHQiDVh5jYKRvhugyDp9Vq5TaugybFEZzRDWOPwE0nHGL2fumDtfTo1faVV7YG9V7SKcvbjPzrA2bson9k2T34/YaAAgr8KS1xj0hPdAiy2aOWfim9wb7ZXxnoOujQMSu4g3DXErXMpgK62pBG7oYjZ90ySon7qtVdwKYe/VKvBWT8YQVZvVQLk0yq5N0+0trjDcxnAPdF1vhCwSbkhUl3bclGuz4cc5uMSYZyPdtXGgdrVc2mBSP8TfhZA+0ds178Znu+i7VjTQT31oeni/QVHfv2vaJWlYQP80z9677C8YVuPM6L+nhis0UpCk4EdhvE2wt8kPisQFBMFiIPXrKoCziFwSCZroOLUDYLUkWJuoWD6h/Pp2zlzv5Dkx3IbRAQIz2BDUKeLapMWdeTa/WrMidJbNt7QZEM5wgrpmtQZA/bmK0aiAZAGE2FojEpl/JtP8O2KaK0KDXlBR+IenuFeXsixHXBuX5wDyRCe/gVw9VGsD3rJH6JwoJADv1BBOzw4/Rtq9NfrvJ+nS5TEMCQxDYhjXcmKTGHHS48bOmujQucEWbZOn6BfkyuO0BlTCVlrs1m8jSEwloyaAw747SfpU4zzlosiurbwVpGu9MB38Okj6aT67SstbkOhsMDUBmAbGCBSH9eqYamJ0HTSmFQOsFy/Xm+v5nCEmMBhW4lyAdU7gr5UH6tmXLsgggZb6pHbdU0N4/hWVWQ1aDRb4qIiF/sJzd9m3QXZW3wblVH6oP6tHPnbRf4S2y1YKR/RfQ/CBN2c/k8OhzbfQ4fQ1xfjvV421++z++uzy9qUOlbWP32H5B0s/4XdkvHQO1mTU0IrbA0OaUOuGSrDSuWM1X4nd1cndZdWp2PbzWlpLGPiMbI91aGJ3v/zN/PDUj+jvmoDUSeCshr86CFW+ekJ68l6B3AOxb+L0uH8osm6pdSHjTF5MLlphl9+nSxxyBXzczFYiPAYRQIaYBJyhhIsgNySGMM8InyLraIvOpKfreIoWDdqGyfagbBKKmqRyhW2RDZEa87b5o79V7QJDVeSklAJzi+YIvkAgnwT0rBSYzVkRoEk+4M1mDCD4JG16VEFjWS/xPxEcMRx8n8zK5ywVZiv/682Ks1rV6kAdhWfqhkUK0RhBIbTWFgBkWbqjFEuBTX2BSVXaR4lmMTiyW9zM8SfyuQKWAwfuyAriQAnpkHC61uMAs28PGHvcJKsOPXrHBhsOVUM1QTeK30qVotRBX8mcXVyJ62fpkmpiTb45jUQ27qHOUQxqLKo0qCnUm7zI7ibFHQ1GKYZnS1lKnxXkOY1UzpSAJ/WBtcNaYcJWsdIDagX789mCsQam/s8X9LJRbbkU8IOhRqx2D1XN1LeAoF+itZoYbSVKQb8U1zcAdBB39x7zY5C5ovKHf1QPMdKr9HQPvHLfdF8FTFXzF3WFWh6XVJy+aUVepKyOLScK5xyAt/XO6mlhRO2PjtQ9gAa3E/jEYl5o28sEN6yIVRlIjxcFuf6t6P1udFuxPss89DS7zF5azwocwBnXpFJ/oFzGrR7KdYmT5A54rxfsTnOLgu0h0UvSAA7YGON4vQrei7Mmpl29PfWz1sQtmsi5Qqtp9Tihx+Iw5g3sRjFu3tFjvS9QA69+cPz6qf1Z2cr5AMRJCooUzlA7Fd7oIhrSAb325E5UTK99i+mXELGRKETStHvCIk2TUBcpZK+rKz956Bjq5WcxJyMAiqWI9B9xYCv7shPp6RQn4ipWaLKNP9O74VpezPK7mmWUXiwuNsRotnsQulxrlghzwyX7rrU4LCBTkIcuTBNiE6B3Bdd0cKyQsrosYNSHXZx/rFSYwS/ikOkoujtpSBiWOFZcdohxyjIrzs6Xe4tTwAfZsqodfio/B+yAd/OJUZtGxQdt1fc/hmnGxvsmzT9Tuay/x0Ci1To251+unj3JsqcE2NSjNJlzyDN1ioXgK032uSiL20XyJdtIMQlHe0nJYWwa+zyZswbgjSTndGACdqYMlRwFliU/JJ1lT5hsRsd9UTynp7+cMeK0SrfrzZrGxlWxvVitnrM1EFXs8vZCpbFlu1AqlcJ6bQ1KOvsqmXEwMAAdSqDtRzXPjUsNGBBkdFV07sauGwwS3j+t/MG5/mPefKnzKksHeoiHfqEONSn8/lrN6qcelxVKRMSnvLcHaMel92gc/47E2RH/hs4xzmi6V5MRv40y64tFxwmGX4GiG7LaeY7nduTGlrqB/qWMEbuzOeLc86XDF71KqOzo1YpO4+mVFcjsB8unAO1gvSSvgHs8EKoCjhyp97Gbu/VmSEZgeATJEM9vCzyYHBLn1fyG2J6iZFxJTuFzI7Rev3es8d+IvjvvEjNXRBb965FYR5vrVzG++NTtgkJhO+gWeDMR0SSoMUB8DA5ZzOAmWmIhsfpVFTpt2MzFd/1k8a6Cp8Vyqf1dCkKxa2bzE26xkbs29VEU/1xbxKgPl10grUHBJvEEgpwLsAEoJKmnvl6b/IPKolTLgCy7c9OnmW9qVm6ogEIcuMAwqoHsPWCnDkgSN3yN5w7TvZQ504ypsPhQL7wHzhpKolZoktizJ2z7zwR9sjkGms5+DR7RCOBECVHQesw4P0AtTEqf4tehEKtb6S09cu0AAQAASURBVGZeskZYvfzquV+kd5KcyJ55QZun14/Z8ofDKUDI8yVH/37y8UdFwjHAt2/dYgU63fw0TdW1T33SqgPqif+TDAmiAmqSmSbcogN66Ug7wCiob4fVK5njlYa7qg+XYJYYuPGt2SHvxR5g8gqMB6o69coXh3uAGvjd9t7oV/Bwf02lOMqp9RtjVyjSvnMOwJAONflQfo8rjmtNDgmo2l5Ra3UI81D4kJ5D8C5/d44Xi9+7ONMh3RZkj3MH2HVpBxBr8A34s2Z96udEW6Y7RwpF9npJHdf3H3QL0uO+gR7LO3IDYQsZ+FgVOrDHImY+oT678EqFIYu8BzrqaehVGaBfzJEwBKIZg1XW0WlKxOMLjQRSrENPJ5HO/COObUqS31XkT6BfXd4QIJhnZcg2yR4rVFJIpS5/RVGssSTgYuL/s6fqT03ZkPH59dW1JmEr+pppdj/omuVzmcxup7MlYRwrEYgUOVtY8d5mwbCAtpK33UdBTfIFncVqpBAgcpirpk0zXxtua7VDbGfQZmmZgY39/s0y192iOPBR0vDCCEJwlPwwehld3M89UFdqETEzo22GjXvlxfSNdGO/oEZO86ES2gS2nsDxWq0IePzqsqtNsE+v4bCgKmk9A0VlzceMHn5KbHV5b/72j3+QzzbzxZ3r7YMyvT2/tVk9ufj4z/6kvOY8aSoDW/tfaQkAzYRtztyeH6ZPLy+zi2J+K9/mya1Fur6cLf9q/sW/fvCVGoNaH0LFQn/qwxMkLuaL+ZLoP71zl22Cbmk6T3GXirO9pr6rfltYr6K3vWppPaAiq5ARqX/KpwlqrVA1CVCksqGqLbUH6k/5i7T3/Dm9u7BGqOf6x3mOcfx9wpukh/lxVF1GQ++lLuYpkDD2bt4d5RS922O8hp4nvLf39GHHIo9LR7o1dI647Sm7yAMtd7UeI5bfnmRk3RSlWxGFvZmm0E3EGeQ3WHa8CeuVYCR29OqA4GBze4EIZd/llPWLJWB3ACGnL+HYLnSnSh/mtwV2nEUDzpTRhzl0wE1Bq4H8lwXsNeEb1OYsCuDtIypzr+gj+JzJe73qdHj36NcDMn94Hayrsz4trZtIFJqw5SJTIywuIpNgXFk6wZVPIn8t87Vs66inF5cQjQnSNBsU99P9T98/CetGhQjqfLlkzxbGBNjofb5aE8wRTDHpgpkbitwJsvLsMafCat/F7VXBtitIQaw2f4c9cZh184KpAQDOHSbPZ4woUrNwTAqZBfqAqb1C/QP2AupygIzyB8EsxNNjnRDQLsfWPThTdHuugLsHr5UNmctrwc/9uNeCIS0c3sjd8fKUbPDQ2Eug6Qp5XXjWm463mdrP/8W7v/fT7/3sj8qcM+Ne227vF5vltvjq679Lvij+nUajqGTafV9VYrW5pjuf/Tx/dvudn6V3luslLcoypV26mpV3f/P8Wba94mgBTvWiohScLkctK2ZE8zQEFnOmlV3QkOWBmqlWJ7OG1NAEi6SqARVNO/2rkgOwJqYWIDAoQQtT+lYHToCBGTxa3bUCcktlXfRIMnjAEwGNhJADgZO9uh/gAfddcPABlL+VqL8NVW2ijS9hnUHzSCtG22+sjnZbJC7LZ9fRjafrwNbVpNbwgTy7erpLHD7S9o1dF6edvHVv8RnBH9KnxbD3sdX67MVpAKPWfwP+oh5G/DBkS8uTrukIn4YpHXud25CsBm300MXv1WpH0ZEbvoQhsUO+mdTB9cp7ZNVPUF94uT3L0EIUYpb2FRVI4OBo4BofTebhLyIleiZn87bH8nBUbEQUJRzN5FDMx5JL7dTOhI7rdLsEQitBkTvrOJn6QzBGB+92w3gAW7yn6XMmZzPNIymXfraAZvxv78y3d0u2cJkvFUOy1JN9G8t1Ulym6VpBPnJtLcAs3yTFnN5bGh0KzE1ro4C17N3F8TLCQIKGnmyHeF7sIkFEvbvakJrXDmOXCqsLXKFdxkCqswuQM+ceazBAPABu7Bc0gFOxHzEF+a6Fmnk1l1g7T/t3h2pglxWQUioS6O3DcuqbeNbsVHIee3MUAMBt+og6VTLXn/1n06c5J/kmX2s5AH1hOqvrGYNJTO6nyoIMo3nyRLP2syeqE1SVtLjOHl1nX5fpkuaCNUJRIVcHPnKKzYwzhRe3ddoYB0owiKDV5A+ppGVyW1qV14rvi6WaBdbNX25eTwuWqXyNLBiBSa1Folark7ZL3wrXhsfd+BuM/AtjeRG80h0fVAxqx5zr8+A3iQk+jqqrc/ymjdMV5r5f/+DJMMu/K6IXgjOh7bk67/YenH1a9ZC0QCdw6PFSi/m+xz1lV3sAF4WxcWfZ77F94nb5L9LqIVm1da6Vf6ewy73ajQTOY/jOBXFK7jygNM37/v4PXHYlIkvCb1XIf5U4xAM7bxqVVw6SITHErEU4hHajcJT0vxuV8iKZ73X7kDLfVHF8U3L7/DDBeb3qTqBTRRMa/x1b3e7qAlCPOxEP/0nYJ7+ypLUpiulooY+FTgQ7hDRZyrQc3tR05LPHorrsCZTY9gdywit14TImwKcW8xLcwV/992QqWNIdgscp8Rx9t5zxRbftnC2EFiz6ZNYIPbi2+Q9DCdsZK4iTjE5awrOUPynijGSDcTSDgEpRB1jS9K5MlRFuSE1RZTjS0feOuIhTpEQE7Uu6Zn05LwzmygaVrYwq4Z6usvjg2f+UT8quOsitnyswH8J1KB9WYmoianyH0SAWjayvtJHncrm4eCNLXqMmsGksm0tRYWgMaGYP7UIF7qpVbPSpRSfayYddhO5xkh368Acz68t3qVRa1Ur2AmVWjxYG6CAwLVfRbB8P960KKcbngoE2HaK6qkXCn2qzWhLoKa5IEKbVWlkDYPAKeaIyrABxmtbjIKNXGYMeeOXCQddYhn/ZWjgAe+EttJf80U2IDYnTL6/yaNlRdAdQLrsAsXZYe310rBhoD/W3m/ly7Bh3WBkg5IfZdfpGNVtXQuzIhfCw717Ec9A6U2nKrcczRubmBKMCK9fW28ExbZwOyHsTXW+3Wth7OXT9GUgO82ogOyIRl2mcPoJVb109io8ThXJpe8P0DHV1rwR6Atoc9tIcixDX6jh9HL8Oh9qOqufeH5s1HZhX9AqsD9+nxWaoN5GlFnGNtwFESbDjzlIY5C8OQRTzEAjNPuEI3yT5qRExPRpSQiuCIrEhYCJ229I1z2QJmhDa42V5fXVFXj6fbzdrgvVk/Vq5WRfZo7Kcp8lTJnYzbqCRBHXiEv/dTnNmgHjXP0JhzOlQF/TOsnkj1YuFoGzMvlX7YV4wB8hPBZYGRITRu8WUNZ1lDIYQxVmgSYYe/L/SlTv8w4wUVPiOU30YsOJUpYc+mhQVlouUFP0PV7ULUHi+mUTPqgBX0muR9TS5m3rkO6ZrHaW9zUboLMt0c4zqoeJDVzpeN4wK4mS25oTSFT/VISqA2pWsPMlZ/H1BXyWbR61p9ZVPyvI5yz/ylDidZgBVhZO+mELGmAN1RiNQCGa3HwX8ybyYPyjnWoKiekx9FG8VpS0RYeIYw0pzWp2MANCyhJwTAzQDiT/OHytv2TlfUPJtoIWRpbMn/Gl1ys5ufGWGSnUuywj26fvlcPeHZ/Tu4xe7zEmMn998nKpeIbDL6LwNdlkjqUOpJuEP/FKENzb6xOlKveY3dETn1nc5YFa/3Q8EGMIJyCOJho1drQasqxh2c7scYtld/Ci3x0tRruvpgHHMiKidDPWr2yMeqm6bZsrzuNWjHBq2jPqnYjMqKxgYZHYtDVlnSTTqT8SxYVcE70nWL4cqq1USejPzrgHayuhwGsivfeKfA0jOrEZtsO4FxvggOM4IZoPjC3wYcdvLo+3Lo8kLK5nfQpNfmG8rQVR99/KBvlac5JQQWheogvqKFfEZIDUIPI8PC4AUJds/TbewWJDOfab4E7mx3pKwnw7TnEXDBGO0B4jIONF3TV8qXNimXXOsySKUp7PDRg5Y8Pswyb5eLnmkwz9lF0gmC7FfEIMKeoWlG8JFdQBr03ctDka6cbFPbuilsE64rqES9g513f2x714FdI7MXYz78PbBTPQoEhj7kYzDUQr0yW4w8nYQKjSgracmlxizTuvT/nOrYU0qQxgw1ZwgSs9X5zo9/AUtRG24z9ycmbbwLLfXy2Sz1AgAbQGtI9G4UVbOOBmAygQOW0ZpNQg3LUJhKtnbyfZ1HMxvJ00K1VrN5sFkjpFbsCxF03cYJ2BlgI6gW2lOkTQAh7YlFc5WsGhnW8J+HUBgoxLCUL0CT7WdB2owjwbhkcTOAwLa1U3UOQGhQvH62sr9bX0MbvttdcAru2/WAzdWwfQ6O0D1FnoPqe8C1JPR6Jsn300SYredtMs7QLdB1Jp/r1KDVAMZB7SWBjhMAcf99O6Mc8nt9kAc3O6s/dk1pFGsdRGPjBjAYahV6swHc2MdovTpRTwo0RQaz+06pAExPSnN6Ur2+7PBdPRhoJeia0Vcu+L0KPfBzH0c+hzgtRyWbrOhRPsCtWUFLKNToCMKi6BU74iDA4Y3AuxRUbjFTlWdVEhEUPXkyaPVisWa5Xy1oL+WeG61vlZ0pv0duYi4HmiyNxE/cZmOFUOqemG19Be88vVl+ub11fYiXy0u2PqdE6A2+QLqW9t8nTJWoFZIzgFhTBOHmZ0lzL5DrBxe25cEbekUZvaHhNV6+6cg1RXt1ePmwtUNBzW+Us5J8FpGhmZyB9/GWHG6xSBkVZGuP/cj0U8vKW8FmuFzgl2NfjY78pDa8YTEylcM+M+jMwFoCcGszKtce3Q+ahC5XJ6r1qC1krotJdai3BeSCDk7QqcE1MT6rOARO0NlZfc1/cZqigqD8L5I59eriy/Xz28X6ZOkuFgXT5KU4yFYSDLbFE9twcA8mbPDD7N6Fjnbfc4eJcuvkqcL01Bi1cGPstt7tA8oZGumMjZFM5QGKppc0dbQdlLk6D/Vh1YrYwzsPKu9pLTkXfPU2MmKAYeqOQASnGmJgs5/vgY8uLWyWFdtrj8N3mlvgKuvhruoQuz2/XvGvrdBv5xDqSbh+9e5X+Cp0IYvmswO/oVtkoenPTaOWxflTirnCD8oMDGxR8+JXAbQ8PPQ5b9rnnuoDt3fxCEpFfwE/8Sc7bUSA3rS3dkf4zHVUG6fT0aqbbQ6KCjl3h9TmnmuXCOlFHjViD3cvIaO6dZ890Q8nVvQ03n0quNCItKXNBn802tFrLQbG0NuIh17uMU/aBgSLYRv6eMZq0oozYmuiPFD+tvm3mn+C+ZViTErPa/GIKCBhun6Fh7h2cCKNCGQ4ykYIrXjTpxFWLXIX3/9rjr41RPBaU3FLJ998eXn16vnNA4shFIelDxy0+x9wi5Wb8JIQQ+R1cMfvP/+T3/+k6tHD3WUAIMHdPvmxfLi3uw1ZgdxUBSdwK+xbwudtrTJNpsyv72g91jjCZDbfJKgF4A67kZAbaGlXPMA8vjNjdvZha4gV0b6Q8y7/8Wp+HWHZVSx7DabCkEfsaAIfM6k21lxNJ8ER8hsM70yuKNNBcDJojdOStlTrLsDPAeOVraGZvKMVjcuZ2UFp21+qAya1WM1i5n92iH2zR/83h/+T5+t71NDnrIv0Or6CaH/av08KRaf/uaXH/79P9CG1OiQBehsJpuWby5KKskj8aZCqURhQ4wObyoTCwCY/s9stCKZbzIWA7DVFL3/hsPIklxQ0s5UgC96DVtRrU17LGGIQIMDWgegUjaHmLZmTeMWnNCADj90vDiM+t3PqWrat8HQQ8v55bHp26v5y+PDpiZebf3e8S7gFmx/LfcGQJeyKTY8jTEcyxMDdBtEsb5PBQR2gXbwTPeK9Jv56PbTtwqiV61Bb0TY8dhCBJ6UbPhwoHe5h1FdCj1ZvXMuI7xum/XglnrEbSgZ88wf9GAF53f16cHugGL+Y5W2QzgEoKCDSkM4I/DjrBhh2M5SKGLzm6uMPcpW/qHfWt4JHqrOavVzcCtOzY9drCxKBU9E8EIhdBIzpRVec6l/3YCum7IUerNhSpZcXDBhA0yFRwroFK+Xm9UqZ1d/hVPAjYeY0MMKR1b7rjRp2yLtcnX7tfR7r91LtUwgZ5SAyURLZme88dM3Xv+999PkVlau6PvnaCcd+sQE7oyNgDbrFZNA0DnM1TaNTGkJU1yofClmyqbWI2426Xvu2CTqulCTAwJTgxQeFJtRNSPQRdy+XEolrGYYOLexG8+7fvoa3IVUOX2Sa6KxT1TeKWgphchwM4ZV6F9hqE3FdBsh+KVEcFoNdErlOKMKjuZ69uBeuVQHPmrxpMFX1dKHKoNBvJicKtV2P9n8/u17t644VRpNiqtbVLH5l4wHzcp3mDL00d/RhoTBwvvpNJss/yzdfsVKApOtaiojeJg9MAFvaC25NgbVyXQMAVAJy3JFRI8m1C5wCn4v9D5meQF3euj50G61aqHoIvynSoNoFpg/qeVkADBJyuEyDE/W9/jdVcGsdaG00BsOrBB6P6b/Xhh5j9xetgF4IP9A9wISjd/NSB7+UwlMvho+mWLvFJwB6Q1ZAzgx+FD8mLab7qmIhuTwIaed8rt2Cm1X/0GIlUg3unP83tgMY3t0G42peubUDCqkDCu7siulC/H6Wu0Pdr+X6SEjAD3FHH8nJr9behWJgUM1Zrw+xRxeWHrI6JdQ1Rfmk29cUFwrv3FlXIGXUKWdZxrKHVJzhev4gVnrcRju0Zq/GRWz8U1SBG0zE9RNC6W/B3YclY88onD16hsCdFrNC4TpPh6MWaCnGdsEVYRmfKb0yOrAE1vWmcwWv87SD7ebn2W2Dai2fSe2z5gbflurP7Ue0xiSSqr52UwUlzISLqm2vBS+IZgFbLGmaVBpLhjeEQX//UkQgxql2ezZjiN8Zdun4ZLbviwMjIBiaVdI8FSJq3JewIfMtMu0kG9qwA7uOGSQoPTVH69Mm95S4yvaVUQdyM0h5OpTmcoJjKqUuIigipEFNXqvYl5qFUORmgBD0q7/Ot53u2VB8IYYnRqmcSYOhCaIZ+14cskgkAXfaj/Q+KTsi+1bLEMvs4fquWdJsSqYSfR6SK2TdDUUWXAsR2ibWh1Ux6oD6iG488Ul9Y3p/9erlQayVEtNMA6Bm+ptbaTpG2qanqIL1BYkyuwm3QWHUHR5fGcgB/pOdrv/vjMeeGXIeT3gNYqv1wupJ/413idq/MsuXdkF6G29RnpaD832aD8rV8Dum3flzx4+E9zcamMhK8zDg3cQvc/cCZJuACXWsMVeHm6BDnxseQbq3nZnL9fgQ3Kdzx5lvMSd13ibtVdeH3C8Prg+oTciFHQfpx0s5tn1j+Md7XkIY/5B6kgpB5zxxH6Vhnze/CaOSzkmt0fuWFE0/ONWGbrNei+1iz8+1Lz2ocuKnWBHE6CT6r3xGciKCIl9qvCPwJ7OfQI+bprbY98lYvLXy+0byexri5WI1YWiiRPFG7Zg9yHxu3iIFL+hC6E/wZf3rLKxP/Mv3i1XP+CMMDhrByCWEC/zIptt2CdeE7JZDQyDFe/EkhN/NXqgHSBzZo8T7ynGVICKtgCRg1Z6pJtYHTkEs6ik3lsyeDRkRbpgWNrgeiLwhIlbJ9PFWBD4WEr0ZqJHyf4egW/fJahYVnn+WT9ZnnIcYL6v0hX+CR/wdIZ+d05xOuYdRKuYsZYS1R6r7Lmk5dfEzQC8QLlTdtbOqpiZIFWFnRWeqjIEF2r9SFpl65dRyemGICeqCCl5ACjCfv3Xaxqe9O5rOGjNxKB3VNLZc20eZet8IWC3KV9anrOvf/5FuV0Q0JcpR1LYuJOarFZhJYey3WTFLUwr2IeqWLOL6MVyPp8zcsWBwNv5bMmYkh9f4WVcFx5nXKhCohcVET1hqWJFZdVJ6Z+wBJnLvl9CaF2N72adJzNJV+jGRcYqe2glwKG9kj1yx99aPe+cWt0b+mzq0+O7Wm78u1nD9AmJ+y4GjqQbPpli7xScAXkNWQM4MbgHv+mfGHlienzkpMd7JnHzptj36DNRKmgnaz4oKoye9WG0Yg+vUaohN6ePqTH7or8a9nyjDbFxDkBcDMo9ZASgxwnOLmbag3QMyE2EMX9+ATmvnDNyc91qTdufQ4LGqdpcTn52l57M5reIgdc9LyZPn2j8UE04ke3NkHt9mWD3BBRpGKFVkRwxl8doBDvq9dV/0BTrgOwBCoQ8MzfDoivgYCpb3Oyum0Jmv6BXDuETP9b075ImguKPlzKylC5mn6/yz7L0p4rSiD8J49isna5cgiIaHTZTXM0NMDUTg9Of1BSh55cI1eQQCYIGK+Vx91BeoaTid/sgKU0snyix0tbaARKjcN81Q3VTEn6yjPhP1gkkKscy15lB0PgFtUwTlW6k/VFPL/Iy8ZLtiSHRQbmAhgdoo9GyokNdhtaFTRmRBE2YFv06rTxhXrEKgtNclLWqDFV+M3cZaUVU6UMxiJqCchT42igOZU+CCkAW+uhcLwqUdR8k1T65u5jd1QJflTzs6eynXhT5+u1kc1WkD+AOwCqDVDP97EMHTFzTksMWGjb6SNmwaiEz07mWHdBsKLfaJFS1DtvJUJ2gtamRB5YL0w5xg8GFXhcaqUr4w2H3ikh+qi+aKcfxqhm8+nzlgeCB8crk9S6ufYHwu5QYd8JZLfUv9ASPdl8XMRG5jAAM9tXtb4/qV06XvZ1nn+9/pRzko1j5QCida196z7E/TWlBBoaBA7Qxw5px/Rm15EIvdZ3X8xm3gEM/fRDaFRSyengNg1rtzmHERo47MDa8ke0P+0t8X+s28lgP/wEQPS57FBsgnAieXk+8ROJycb91BcVl3c3dAznUS1PKZY/II7JjNwyTe8lVuPpovU8AVYW7c6WFSx6008+uvn8uy3ZsdcYqXlfzgB3Z+ZIq4iMU0wtn9pA5FYq6PeDSmkkwCKMe0ktPgkAP1nolKZ6zXRfFnL19CLI4ITgtVu8WxVts6sPpYczvVwDOcs05+8EwU0hhOAE9/bBFYt3/BYsHFmlO16x2EypoOSBdpQ8dX0V2dtcUcYLPreZ8091bsDtNSa/2+v2MbtTFffHZvJ8UrPucSw02iASiPUaJAjmmYJ3kj5Jsla6/L37qeOY+J0pUY0AbSNJHwwQkAO4x+UqXjK4vT8v7vVecEacrZEAxs14Wo8A+6oipQlvRWwSrgBg3E1MzTZ5dN5ltpUKiDUa2DbJoog3Y+JPzm1ncoXdOyiiBvEd3O+vDqBV4Dw66G9zS9NHT/sJjVqL5Q/mN8aWM3ZzYBBZuaMFXSc2yjNW6isw1ssQzotUMUJ7WBbOzFK0/jguYLaiI+uOIaKs/c4Xh8/vb7edZurR1vFQhWaNagyVWSJQvZ/0mGtmg7GgCvJ6Ut1hwLP7MNmOfKdnKcuFr2p+qomKBYtReppxh18KWukAKmlmDP+w7I8ewZxREB10iDwR1Sr8jdTpkHpTY85t48lsr5h+nXckuJFa+J7epT8MnMWUzHX7HAxifQfttvHp8EpvR9E+cMzHtIye9HoNDj9NM4pTIbY8Cp2h+6G/xHlUse0CfPf7vcD4UXz+Xratby6Pqa6e5+whAi+zQx8DUC3n0tdJVaUiaY/p9lOUQg354UCDw78c7EzSIi/kFh8XAkTRMuALVEd4ItCNSvmNZ7iV33dGmHeHqcVnfkoIIbpvuAK/pft/5wBnJ6i4nXlj1O4s4RzREPNxJEu8TTBF7QabWQMhRfL+LXMBRdCYa3QiXlCAy45BXb0WIFxGldfCTJ/TF5/n8szT5A5uYrREANS6IPZ8yDwSYThggGqOFYLyJTWFsXcXFVk0MdodXBMdb3sJ0zo2iJztd2qlPag0oGEUg0agGE+j/930YUQLpUkXGgWVNF26Ca/kpwahN/9D8c4Ym2LdoSTwo68QEHcxEeWLgsgy5gav68Ic990GGe+j2ZUtn4WCeFLJ/AlAY6vJWpG62EyLTvpHPFU3jB40M0DSayX1muDwAqjETWmUfgGq2jAFsqEWtP+D4Sv+qtqIkUXK0G5nFQ3NCIy2akE+tUBalDhGBuHr+aUPMFtpvqkwvk/zOjPPBqtUB8JU+GZPctk/L9JEaElYoyoAB9QAySeW/2pDsJYsSZi7SmPsju3RIcPmUSmKNT20ZxMp1tWto/HHwHNVCjVU1QMXHyly2wzU0BpRzyCWNwmVFUj15upEd8L7jiaONjv33TflIleFY2U4bzD+aT0v+eFUi9xSdW7Je2GPw0kESX5SlE+R0DYjK25KHNwB62iUR0x5P9bWxnKKrXiB348YZT287us5hbh9sXbQnvDe3h1vUkuvJDbpaAlaBP4DQT9+yMbbL28o+By6mbTLefdWDNzzR4tyiaj0G2hb84MfIJz2047k9BAJ1dTupf70jZW/ZdSjagG6vxkh5QYz+lM6g3KO81Nap2g2gAg/K6vv2dVk1IaV9X9KhuYZNZJ4oQK+M3ZKscNsZ9mwBFcENOBbmKsCxBwAKf+wIXoVWlk8mMZzQPSoSZ6ETYtmfwBWCumQVOSqPUI+tGCGzWeagpOX1u8Xq+1s2dKdPWb3RnMaqDf4J3tZXV+nlA0jT8ntbjgPmWABuTATPF4sZxwa8leZ3Sr6wtz5P1t9LZx8V1z9OL36Tr383mf+q2Py4vPg0W3+/zH+zpTt/+WW2+lGSfVQAWXyerX+UzD4stz9I5p9lm/fL2Ufl5neS5cfJ6ufl/B/K1Y+Ty4/S1Q+zi18W6x9kl58Uq/eu81+un/1gfvERrQU/K6Ac3LFHzhje0d9yh24+Q7SHs4pCLmxfA/AuH0esmCiIVYwrhkqndN7nyzLPlpufZ4t/SK5/UODD9c+Siw9n6x+l819t1z8tlx/l6x+m81+W658k84/TzQ/SxW/K9U+T+Sfp6gel8N9P5p+mq/eSxSfl5j2NJq3fxaslQy6zj/LNB8nlJ+n6d7LFR+Xq++n8N9nVj9e3Plyv3t5yGBwtgeWHrNPdbu4RbleTgArN9aIByQgNDZDt/IpaQaOOMQTVOnTX5v2fl6svdZYwrRZGjdRoqWuujFOFpZefw6ShZYAhnX2VzalId5SW5dt0O2cYiTlHapBqOAsfsekszb+1WiWrt6mI1Ecoy+SaTAmW96wJ0C6Ovc/e/gzvHKloxer3veTDCIPvnGGSg3Ji/nHamXQhMfPx3BhzPB1+xx1NhWD+80e/90REcfbJaefvbNyu3TfrEObBJ25FIPUaER5biUOta3nMuY2LaEmsHo/55Wpw6tG8yzN8LxqkJz0MlU7wf4t7j56GMYRfkw/JqfP5dJS4vKOSsLH6wxsAEfsjk12tuoxi41r4kQlduj2QmK3ziSF7iPdlwyp29Qi6o00RPYLjWdMljrAaUfVV1tk94BXv7Gz7GR5T6q7gPkrH0j0YFBJ9usCPfC5P0FVLJ726SCuYJRQSiR/xEHG4+lgJxq1ZoABf3awKo3TV3IxMjQT9wY2YrBJB1GTy1OlOSCZydTans8+L5WfZ/A+TVTJf5vnFfHZxd3F7kV/e5WAoxKoLny5+0I18VeT/9//Xv7j/9Jfzq7eSxZfp+p0t4fvq/c38N+XmRyV7Cq1+nC8+TDcfFIuPs/UH6ezjZPv9Yv5Jvvlh6enFp/n6ByUNgNX3tvNPytUPFexe/3A7/1Vy9dNy9nfF1Q+3i18BT2a/LlcflPnfbZ//8OHzX/zn/+w//0/+Z/+YI6lkUWWMm3TOO668Ed4VX3h7youRJ0GyxfLfffT0v/yv/8tb2c8Wl58k+GTxmwSPLT6cFb+TL36dbn5cXHyYb3+azX+VCf5xSsMAb29Jf4TP0/mv0/V7pTWo0tknCQ2AOXzeK/IPaYCV89/QqKAZMNv+MJt/lCU/md/6eLn53dnl5z+695Pv3btNi25x65ptYLfrdbpc5Nqeh/aJAnHWJSSb7Wz59uK1leobAE3IorWoAKLYvrvdcOjE17ZaQK7DPGqnzwRSPVNDNOVcYaYTqdhsgYNGBFR97Wgwhgro9ddoAK1PTqEQLXgcaa2zKzSLycYatOxEl5U9MAQ5wKBH3sSnLnBPO6PTOTufV/eb9AClFBfaoaKcPC7qOH0oty4+uvUyPEXnrpSXHOJOfimU7BZGXBJSVLvj9ZdZy4CA1mmXhJwWRf043MYKynT1dEhAqHnp0+VxH2o5xciedp29H1dj981vUceiisF0/hVB9NHqw3Zz4ju43lYe6kvutT2ScHAS6T08u23igxmfjcBLFnZDPjlCkqw+2cZur0Z3TCDW7Yz6i+2A/rMHJnP4+6VsdaUffM2+8Ko6SuiVSfdQrUJilJA5Dm8l+ZIp0xYbGZFXTgv1CdItBnJ43WesaF4EopFyIlBAXz1YoCUKm4fNjRhMOPxZypPgk7h+v1i/d+eti8t788vX3s0uOEo4Y6Z9yioA4rjNOzZdhMaEyUoy+mD/L//8v/qTf8P0fCahs25UKpTpn8G8TP/Sor2/VHMl/XO4p8mfWVBnueW/Ncj/gCpl8icEfNJZzRAgzP4GB/if0YWcpH9lGX+NiCz9G2vdfHR9/fQHtzf/2X/E8MSVThVQ68YoKrvQg2fu1aXM/ZfjR7g9ff/OJcJpsB2AD/MxAisFNapQAHuzbLH4xaf/3f/hv/rF7cU/aDtN/MZZDMlfmFH/1ub6/6l8kvxLVlMk6d+XOvHjv6VbPUn+vzbz579JgSd/Xeb3tdqbARloZ1/aNrKM7LCJE/f/HwdyZdm/0DqB/F+uV0l5/V//o9/5wf/pf/+/eO+9p9vNVVn8AE3md5KLOz9Q1E0ErpalV7Rtvrgsbj+f0/VPb75antYIYDXA/MvV5rM0vUOJgI11ZfEWipYZmqiAVTHNSGux2oMcaMjM8oKEVoKqpehpW5DW+RUMBbB4gJrFu0W4jAXgLlUpPanZ5GXXKIwJD633g/StqeI0MOBApl8D76XpDMYx49/fON2gGtBhCH8I3uA54SH23FD8MIHNJJTe93yswCQuILXGgiKyUOyhaoTMI6yDifuZ38GJdaqnXFr1Nig0OdGj+VE8W7HckPzgQ8ePpfdYF3GJMSPwwclqv/+x/ffsCx7KWAl+96YJGkYjZ2IpNyS5GsNsG8jxwxEkMfl3LH2M619KF9x0sXo1fSlNf6mUOvB7Oa3YYuc7haIsXsfE9EQ2Ht0QD5knNJHeRyaJpgApAvKgxXQDQgSp2EjvLrur2xQY1Ar8NY+asAsUsuvYSRPHydWmj/OPy/kHl6+/nS1ZbDnXFH2hE/0bP8VvcOWJWRprxhMW2R+/lv5BXv7NYklMSXctgWAVk1lSC0/FW3EfSlhPsR4U4SkslI6WZr6LR3HEe9LLNPIPYYpGC3+lBQMfeZE/Xs8/tfgRbxAngg8fWVlf4vDyX6almi8qMkW4a/7nq/dWXy2XabZcLAngZZkVs8xXMK4pObbwuihXtzIWRufX9JhosQCtca2g3ZZrDtWi0/xaS6XXd1QKlgZUZsuysGZAQXuNmflsy7OhP/56ffWjn+Xvvs/Mewpgob2drAZJJpNvqAhWUtaLT8/8Yp7duVhelqzaJci3lQIIzMoPkvKqSB7MFFFRKooqsExNBBUObHjCRBhqfbE1ERXya6UBaEjOys1WRax8DIGHoNi20EQ0Tf4hB7a+jRXZ0jMueDmL/1Mu8OT2cMUP3bQUDKivEns80PbtHvRTs71kQvnchPTTebZq0OkMJ3ktSPVEeJxE/F1BCjUDg4b8jmfCJZyREYBm2zq4tNOaiVkG3vsTrmFgGxO0OPbaAvDgltOB7T/n3ys91jZOB3OO7gNu2R4zH0oHoUMIAd5jy4E+CayOSHRqzhE8jiHx/vvp4wBTWvzdMYFYMziE+jk+VhBTDaaHymgIPsioP6OvXCbXKQvqoqABu/dchEH5/WS2JAZT1FuFJwrULc34wJvJ5pbiKEWEBIYWi4NL2uIk7iaCcA2Yx/rqvZWnYa4eeC2nVTgnFMgVo5uiBFK5VjiU39/OCS+JC6WBIlNNt6B3WTvJ2I6f4l0WC30sfj2//FhYWplKfAaJTdxWHnGdMZZGdNQSxlnTRCH/zjNVkG+RIsQwsikfIoCbdNaHrEI9df+iCfPQn7MO4T06s+kY1v5CksB/sNScIGXPnrAn74NnDyIybIcHg7ZuYnGuK/CKlOjlLY1MZxzEbBr28CGeTq/ZAInzdtleKVllpTY8UvNN3tDdGlVsiYMzPrEcFahO7ZLbmBNFt/5nuMFcwsydT8mVOzV3a83MspwdddQEpAZo0j1LbnlE4J3Zjxj/KdO/sQqheT9iJWLNyjfhyNfKkSR5yuIQ5uHnVBSqlkpUK3nL/GHGCECyVEEpNOd0r/uWljDaB1W9TtcbxGpDH3SuvqrkmxAkyjJtPaoFKipxWYymQPJHaXaVFt9XXVWWG2GOdS/2+ngIKN87WffepQk4mM+lQhi+3KhmnDCMXfUKO8KU3+4YJ043RAy8A4fwh+Axz773YZxfpY8oix4uE0AjvzWH6TCwq/0ZfqGaVlDlQvyjL/OEa0q57GfjwiaKnFxvgy0tBYbiBB/3iJGPtG7Pd5DC58LaqhY0pAw5Ia4xwvFOC+M08dbH2VWZyGCH1kvW5Q+kF3PH6CZTXX3GpTn+oVSB53GWIs7/Ap+9ieME7WX7bUc4uuBahu/l823w/z4jsIHgQvFFsGYPieE5mXbOtE5hOEDlIZE+1StBZGZsgZJHlKVQ3mNDYm5x8bsS/qSEp/TetG5Xwhepo65kCagR51+k8085BjhJZ4o4JcEnXUiG+l71SRxHPMom8WzR+dNk9RPNAdeqTXqgobGQXTfjX0k2tRSySUPTX8GbX+KMfKnhVlh+lWfImmwuQlCYECLGs8+32adsV6OdRo3S0GWj1NRVc7cHvwHyvAh2U0kX7/dYLeTpsdLOveo6UOA4UC2YrHhvy36sCrTlVQiwX4TkqyqIXPG4MeERXxsL/4SH/4kbF/QQ1p7FXbQ0nJIEPfGIZc9Q2gn54vZn2eI3bDWkQjeeMDBslSYoitA1jEN75HLLSAIDB64djDIGBRZ5yRSyd+mh91ac2i1SRqdHK4i3uuos4CFbhaCBI2lIEhjZ4KGgB9iCQkjFy7VkHSbSDGLxMl8Kw7W1hEyeegVCM7ZiUqW7PNzJNVY3/7sBkU/OcZ2Lzzl0ORuPsxhFPfK/s6m1l1FddSvE1uNe8nMgIPMs3pumy6iF6NGrSkwkhJERgKht7VRu3lB76IiTgGNl0KXRR9tsn7lo4TTtwoSYycS2u/zb5C/IwHUAzwEOQ2C3t7ULUGzOEOEIPJDjmW4LNbT1A9oQq9ix5/JAo4UaCQ78VSGjK2gLrGtLFxKR9iSrcYCenB0It6BDt4bHmuywLeUkLWDMobf/pmVpRT65TrbEtR89srHgIvi2jRM9D5TLYB2peLbnGqorFP95fW6dBhB4KaCT8XwqScSlRgBRoUGs357FssnidpL82FQkvqKbXXeFWR4Iid7/Oys9WAwmZqAac8wnKCScIrgHYlNoNDbAGoB3su330lyHf8GP8E5cpQZvPEIz2zXI8OmchnG2/Heb5d8WrDHdXBbZJ9LYojpwpZpm5+fs7SMFNBfIYjbyxIFd5tWQQDxKoaviREW/dVyrZ7KrHKXAkzoWQK7fKViQoF5gOrwXbrMsbV7OIsDQR3wkaNrV3b1nGh1YsRD1gnPVKwHQQU6VMWaPPlHKomXLyW7/6Xr5r6ywfGYUrrPQGFdRSFQJxd3qX5cY5UAuCAE6vMXfeBpbwa0uUdYWwKstYVUBHNUtFWu5fnu7yQtWEm9/yuINNfEKbfWqBpeJUPUSO7A1xYiWX87x0GolXskW8WSL0jxdflqy9VByYY0P9OFStmmo4qUiwQJONDq0qoCVvYruleEuqwwxI2Ai4brIZPyCVrFMFk/nIpWM1olluC4J8FT/fSRTpNrZiKv37SS4vT36ObegUZzQymk9DrxnWlgv4nHcd1P0HP/1abx1T3urjxSj6+D+mqIzmMHwkADYrQOqkTdaDqf5pEc1d1OsdK/jYrmT622POAPFv/KOE2Qe5MBGbYmFDXwHa3yXFmTGlMPpWDO5S++aw67YyYdRNrEDn5Bo5vc8gXmotj1cbhgUPDzdrpvQaFx6y429jwD97ybU6/JE1rjOXZJDIVP4T8FxudMxe/U8kbyX58nAWKlzFr5HxVLPokJjTeBjU+35VKxjunuExGva1gBYdOa1UDETUYs9QAaJunx5VoDHJv2qqgR01lBQ0lJ88JZXbFUhKyBlrekX2ZLzuZjw49GX8ZUCZHNXM0YvRvXaMgVlk1z9TnH9uzYdQ8fEenwGqUVo6lqmE1stGAWsNmeDTymLFR5R8qlL71oECo12iC43yC2RhnKPofgUo/zzMv1EXea2etj8IwwLC3cFtUvVGC/s00VLbdTivz37o0BV8e1S5l7yWVS7ZcujzdUP1clN/GEFar7XKIh8RSe+fMgkfZUZWfAmxldYbF4FZP5XnveTi1wFaG6UeJ7lbhUM67tJFwTvs/nlh/nyN5qixTag6oGHMZhcpL11YVUUcLnk4N45k4fgoO05DQ8Jm/eL1ffQS208dSSJXFOa1Lyh9ai5TPZPojGFTn1aEaov+hOyil4/7qTRWE0Ia70oB4X5MK2YsAFPTyNVqWlXjSr2gUL21H8AVTb8/ZZeO7e0HeA+G85v41sZ1n524g7KSYCzF1Io+JA4Sb+Xh7jlqdbjC9fzgDp0pG5egAcWY9sts0Rrhxkb/SJoAcqg8n15FfLgScC8IrmmtLdinDhdq4Yk139Iv8iKmmbos49/L+4Qz7od1iZyF7mefe7a4XvLO7QjnWSX7amO94bktgltjUTLUUNtfRfdQg4M0TDo1pXehQTCiYng4ZYCsbbBS4FnFxKyzp6INTk78x3DyXVyR9KbivgE3/YidoCUgIrayrQ02laZiKLi2ciBStMYlNseGRDQXiliXv03iEJkwh1ICUcU4ln0wwdrQom8ARIAMUFcghQHKoJmjvQbaXkvyR8qhBEcDuCDaayZ70Fn6/YNxWvJ1xY3EbiJgy7t3gP7t2bb99ihUVuvaFcZLo/5QCPIpPcXWoWXmpLBisyLX6YX/8BhwGl+QTRHEGeBmrjxP8m+sBhVmqmhIVHA9Si2gblEGFd5SXDTTW6rglqR0ymt2erJ9k2Fp6unxJop9Xx7bSUCW6Er8tVl9ltKjO3PMwxWYbQgIWuXqPvsd5DBlEn0PUmaVJISQfQoXD7lb+4yVgWmeFdn+pKef1Rm/6P23NcQDesc8BxpnGDNJLeOtIJgnKkQ2dxWseajrjzib3G/mgdw0V3TgeCnONx6+tV2YPSmzJ4uyz/ONj8o8n+uirN+2/hKMZMuLcWNmy5O/1XHPczJ4MA4Cpse+mzxeZlzOMNdk6KgX7qp3aF3tRCoVDTbGIHQ5CZ4qZEjpqrDqiBiT4bJkSvUlgBszhE3/IAicLSWrVMIwdSqeu6pRcOXv5Pn9k3swTc++pa9ugY9EJxjzjK0MA5MXvhNJDugOjMeG2/d6G3cI63z+97CaTGPc8Mv4E7FOHtauqt/oBv6ZXe4ozUsDZR7E+M+6ZJHXurXys1gm7Z3RSytep1yoFznMVIEXU2PgBzqwxofvXqN7KjgBgRjKiLeO2Daj0qTzx57p8nsKDEAiHUbQKnAyA2iQzpAxmlf5fZ6IC7pON1FHs/t4h8BCWU6ndZLfzrhdCsOrVc3jT/dJ6dhdu1oQXisIdVngNTwrgY7TIsC9eZRUWjHG+IagjbFOPZDakFSqYWhZDvcwiRCJBHY3UI8C6QqbuLAewx8Z4KGiqroZlVwVpFZaKfe1m05v58vPrEJhxy05K9BsCTflFGKBBlptlUf9PXPZqvf1xagWqNJYGdy0MW0EXsTLQWVozDO+obJsX+VCLJAseDUWEhpGwlgjjmTy7M8n89nOp5WqtBQKZPF54XWts5ZNSvl/DI/GKsK5BkS7AJ2qIGmIr2JD5nk2tTc60cpWiulENcfzcO0u7bJ6kfFc/b35CeZP1efTzmeMuLQXM5blv+s0GnNmb/xq/5sSg0AdbU7X9Lk6CIPINsFMSXfZumrII2NBen57JI1AB+pFPXbR4aJtpKqWBnEFGEGj7aIteKSaqoS1DS2H+WIMaktinrMgqQqMyM/XrDoYu0ZgEBY01IpKxrT1D5swg8QWU2OmkN8iJIGIS1bWgHynWzQ/fjLuDY5jLIbzTxejZujPFXhugq2NQTef7Uy4sc43U98VugLFndW3c/E7LfRBUfV+B2RXlYsg+v22IGy3511a9gwue34dkp0uNXlYvqFRW2+DsdKvxGZXZIRSNymjNMjJGTV7bBBrH67DL13BmG/Fzve2yu3V6G6vHoyR/R0bKcdGsM5Tp8ePaZUu7qiBV+dqw7E+kzkGfstTsOqt3xjEUH/GHiudFyH4/QE/m6H9/0H9OAPciNDqyQfFcLgPsQRJmGULu5ENIqWLKxRrG8xEKERHdzXabrkC6a5IrY8gIS9rWyZ6OwhARVhHhAiLUQT+TEzJ5vNiKGLcqMO9vRr691ne38pBx4TwJmLTYwlqut3OFM24axWHj3CUjtBncbWhtCIgWFCi55ZsvxFfvl3ajCgW7lhQggsrYOW6T+K4XnSdB4bOkCKrJM9qKaE3SXXDDeFqrQZbfoT3Jlt6RVB36Yo518q0Hz6fr59PynYbx5XQC4mEl1dChh3D5YWUp09/fMwkqinv1eEVLKIlU9XT3pWmqlwcJ0kLn655dSzhMYeQa6Kk+CdXLbZXC4XWp6BqTTAGAKi+9w61NU1Tpe8urRVXnWaNyQ+N4jdS03cmm1L7tQuJvFzyNdqs0Im4wxlxmHMHLi2eag+eJW0NFJheU+5B/HoIviaFR6mm9QAwJadhPJF/pE2IEqXFLs1C1UBZOH6TQpNLUz+ZLzYqz5s71KI1qZFSSxRtoqb6ibbvW6oYJGlk4hV69SuANfroVUeuVCXRpb2XYzCVdgBPzw7LY/ScfDa9aQOojQyDnzPVDsC7fntiGKAMf4qKvtraGQPEYc4szLdcuvRXYfJTbJdEwVjCqVrzAY8+NW1aORNeej8vgeifUVkXRgDWgUmUxLdX6vKPwPEXc8MIPaAx8qxB70GRV7qSo95KtdLIhRMzePoz13NOJCFqzDuTLEcqKVD0mp791aQioG/sauR+ZhImvHTcuLlHN3WA1l5SQUi57HfX3URB8KXLeEm+H26Y6YY/g1a6uV8owrggZa7AsQTwUUhEfRxSIs85IbEFCum4ASGIeEahkcSQcm9WsVUL3c62ISablYMGdA9co3COvmXiw12CJUsqBUz9ZAqgCNwYgI4M38U7ilG5lIcJCqQLRgifKqEEzWCw6N11BLUzcpirZn6UNONrt19xIBwCiVA03SNOWsAPrHIsu5CNiQTAa6iQZNCmLYR+9Ufp5ufl+mf6qQqVnSaPipdtn/MCS799Q21dDavKKo0RmZTq057nqI/8dAT/60HG7VJyRHoQzQ8/ySbfZgl/6HSxld66XLSBl9jJohjGJrjdkG7TE85bRt64HNlVoMKWK1OnK3JJ6mOQ+Z05PS/ZxkARJSwYnoIGA2ZLagBCpUVf+MTJmUp6FeZ0kBQpA6JClNp5gj5XY1JNQaVlcyZ8L9lKElraucU4na7yrZaCZBffJjM/4HTvMBj0W1VwUxPSsPKXepIb5p8jAD4RDVYmkgV2fr9cvNpmT5gaS8/3jYOITAGWBtGgxFVSWoQCrjOtVD7UuZpOTC8hGmtDyRJabHnAp+7NYfEHPVA1T/7NC0Nb+BmWI46gFGDJWb4inNJw/Flvly9Q/QMFE2zhuwcQB8lnkTT5NB6OsSgFumpjygfV4FT2b0wend6cL0nXpj0jqCX0YexTvIPawDekeLddtV4u8Raw+Zgr6fx7KuOI4YAYwUUtfl6yWNDehGmA2Pb4/R0Dodihtl7gdBb4Tcnvdt7MTImELTyRKClvMLcxxbOSY/NFrCXrNeNkRoyWG9HVZlYbUbkOvtYySAQoBO2yjHAK1qzF69OVCbwn5iIpcfpieST0drqV30MxGfkxJmRNxXaEgmBAxA/EJcThZvbNLtdYTo9cJzrZKGenixEI9ojTTRGPA6ECMkjLsJ+hX2I8/jL4j/ymK5j0bi67Y27IihFjeK4fivb/FAdrJJMDwjwKuDfmS41UUGz1bNbf5su/1Znc+mwMIJXLvRHplQxwQYRAdLg6SLtwyCQKNN5OolxkTJcMs24aSGpuoRlIdf63dn6h2W2NgMxU2yEroSJCpI8Q1zqq2IdPZrE6plzGLgGzwqoqdqfxqK5208LpSNWfjet7SaP8cxADW+SD5PZL5OCVpNKUBNyVMa4s9gWGzsJTuWiElcWjn9TnskfmrvgAqY5dPumfJ5/7X6jDnkxQVzo/ASafgz1aFoOTHButv5huv5Jmfy5FaKVozFDLalmatoHKlLNOEzAtKiyVH/K5afp7KO0uE27UwpDIl1QmX53Hu/SFHQ+mo9EzcXbVJySc4st30jgo3aLiZPd2zcp8DT/CqFejbzlU5YcaSw6EC3Bt+NtAarvmpJ2VZnC5AKHT8eRFMD4I1zkyUt6Du/2kOkJrejjAtMYOnDkfuh7ZhJ+FAP048uL5sMhJSMOLeVFOpBb2b4jcDF7PLZDr0eA+3WO8U5Lu/5ejkPj81MkDOk5BK94Wv05VO4enlPU7eC0eXpxDVWJDvnNAULdRKOxa6AeDpG07R3Cq+GNd4Xr5Fl6J/g7aI+CNSf77HdsP7RB2H04RGyX+lsAOcor3wK7bk7FoSpxLk/CZ5zVeO4Uw3tNANiCtx6ncP6mcaaobDjDTlS2cvlP1KMYS4ExERChkz4V6Shk4RhX7zIlXCL01s7uipzlAWJ6i2mMj4WBglo7Aa4aECDMoxdWcZWaCmQaHYwVYdMjfH+2+LX4qF+ZLGHYRYJ8kv6fNNyK5PnvZ9d/KG2t69qZSZ54GbJHogoD4SdQuATinyluSnhOTQq2XWIEnfEEHycwxlEuPivy3+jAKanqJphAaVAxC8JEHaS2EpHgVo4/7svvJZoClEZirkK1S1ZgsoLzdP2D4ur7eNiaN6677gS+8oV71z0so2tWzqe6O5q5jZqjJ9UhEgT7OecuE1Frxo13w4u3KsTiV+X815k2VvIwvVLNP6SfZEkcbtdZAZokBj8nR3tOZnsvW0vzqlCUY+Wi0SIUoLNfK9etxDSKYbzspmogHfg0jqoZYm5AEwrYKUDz+iY9TDiKVaoKdNI1nY/54yRZLyXxgAMGwFVteCktOZ9SbvyQC84n5+Y52XftjGLgdwrLl8ulbW161gDUxp6rXTLQUqzFnLGkalaRxOP6iWtG/Z8NnpGsfuy6P6Db6x/j7+lZ70hp6BAzmpwe6v/Yy4CCi2vRoCYdnQc599U0RLiglrjAZKgd3J3RGEhI7O0vcbkxSZwOWjnQ/RCP3jgkJvF0bEXw/BByl7wXMuj5Xuxh4CAfm5CgcO2AS3OmRy7zA8GRYh+icUU/7gWLu5xw/mkyf5IkH1ikqHjIZnWDSTcq/wiMiKhtkghM9Keou9i+IczsPgHXFhQhib/6ZhUBUscIqgisk3L1dkHPugK0KrBTMKc0EP33171FcKrD5cVfZZd/qz5ptq9JVlq6KzT9gYo4kXCRkC5YBRWZyvFWjdCEZXSWobRBDMMe2PlH85Q+VsBpmBlbAG3eT2afpbNn5fpdvOESTZyTu+DdHWjP5X32cX9/nM7vi2r7VmVFD30TtG8NgLBdD3GM9KyT6pXHMymz8uUri4BVpuYQXMfozVwVBG8ZI7mO3NlXhuC+qXkhQXCAFcSQSQOxwQDkyJ8ULzOFWNGbl6vfLa9/XCZ/AXMvcuVWl2qMalRVXJQ1Az7eTKUekoeSWUL3/4KTgC9hWGqnIC1X4PJV53b6ABXVQPa2IYmlbo9DdQ8KW6OlzB/ARopq41oY4hnqm60BsIooLL8a/XkVzDxTIwADJzz1f3+xvu+tG/iNJwbfGB2y6Zgd0j2AHs74NZi9h7qbDaWVTjenhsQeGx8/Cb/1ezjWnMc/x2W5VicKio3f68Uez48bcGDumflPj0NiPSOq4JCQcMShSKMBj/jE7G887RWi+3WIS1pK8LPavpy0DT37c0uMP7aAZxf6whji567ze6V/Gw2faFqvvQcBg6CQGCefWH9GuI1kIbqV23oc1+3bk4tZR1jmJNNKwEM79XFKFDThj9BJ8RfvJcXu+Iw7mQRQ9ijVFFwpqNLljHiwMA+Y7dduqiiK83EAEQiRmJyJFsniy1JrADwEczbGq3Gz+F4ncG2S6z8qrv+oZCZJsg4vTLVK9Cd97M804lmjCn6ZnmRWEkynCtnoDMvzDYVQ1ZCFqBGAdPFxOfuNNTzoh5aJFWN9NNSGwv8ihAOS8GqwO4B0GFUcI64yqrqsiViwCxDLADSoomEWK3FiZBU1JSl77c9yBHV6L7QqS+yEppKNZVGBqDhipg151MDgKaCU81+mi19pp04ibJWgaWV3ZJsgHixop6FSzBh9ojS8nKUm/9ff54/t/tmoh1ECsC1birgeTO+v6yoJOcFUNPZCgYV0RCfoWQBAXTYEcbLjI8CgrPl2+PiVcVULQKz6LghNdshrPgVwnOjQxJnfrnRs7ZCL9lt0POUI71O8HJs1IuIsWRiPuOCCkDgL8+8Ak9ghcXrENNAmYo4wOT5rqObFOqmGMQzavsYqXk9eD6jJcainwafn1rnOhnusYZNR9DTerqp5QjDUTxzxOjjZ4BnJGmIU+gOGEPab3JHS0MH4nrndPKRrB97VpELp6Nwh3QPwlrQjDUrp8ABzpEqGXpyhmkZZuCfjUgt9MOR2K+qe0ZuOhoOAgVo9VLLTfTIo0TIG+YT4o0lf6dPe799qcXBQk6TxZIhANDdDO/OQqoI4hUIkiaCoPJJuqNoXxTpilWV/NAc0OqGQSyGjrjJ76L9hiqxE6LzIsFCwKjY9lOt7xYoJ2fS4EnriczgQeO3iK1PG2Gr7nSS9+HflxV8n24V25KRJYKwt6qtEm3zoCdrUTrERALg5B92r+qi+c3qyH0hbsBBJrz8fuUGY3Z7rDABMh1R/q/e2qx+U7CGzWaA1/OHlXJ0jLIA4c0tIVg2wTwfEffaVKoZo5IevBKho2x89awNcQddSXnPd1FjD/lv/Orn9r9Qrn7IR0EpFmSxY9StDRMd/BcpWNFYBzKNVaQvZLmE7/wACbn3/KieyxcGlsKMrye3zH2Srn5bJn1HkNA+tdQmW5IHqTJmLT3yflO+yEZD0JhDXG4AkWEVG9//s03J7acG/AngI2XaUI8BqiaplqkXcaRxova9z9rBeWD76QU8/BpgOahNYi4DiR5aPjZBwSoyX6RWbSs/wUSsOwPwYMoYTIhlm2KLrIA6+MVqEN/P760J2OgT1BtzTUWoEIL/U1xi78DtSIx/ySbGGK/qVRF4sPqAcJ2voVyOwbSV6Rbdw/HHn+b7sQ+V2eVT83UsT/NPl0NAh4tDA7PBv5A5R1Ui4K44QarBKsOGffXwCYTfRsKKRjZCeytJYHeTF2a3CMZ1weCUdecWcDmABmf/10rjavVnfSeBN2wv/GxJBIb601xSTA06ojeM1s2VsIHf4Xm+08CdStYS+wEf03WtTnzpTiIRDcMSWnYp2dRmVRBK7ExzRZcssagvxBfDASyQkLc7mrUV0KCoFX7qTwaP+hCYYn8rxD8cRGpMrZl9lnAOgXIH9o/9O/3S2La/+oLz+fYX+GhDw6E18JLr+U+uB32nF7/EbFeGVnjV/l1rJroD2JDuZp0ScBycmKnEtPt3OP2WyEwCTo/AzvmLVW1lCi7OdrAcp5nfWdCXLPnZySfEnX7ESt7j6MZO7aHArWlYorOEZlZgZKpf6nx7FovofYlwVrWAVT0vZg8fKqgk08mg28Szv6kqKxd+Xi781rxIBmCQjBMUZ+RPSaauV2r+f2kgWJa5/mvCz+X6yfc+qbv3rrthdBafGBnVAUT8yAeo0Aji7loT74EgJ6WMwKyNP86ymo44NNhW8DezJiqBRohVWhWDUpBsoVZ59eEYju8khRv52pYMdDesm2TBKEWfG6Umcj0Zya4JNU/i8OOWmaHNWHPxwkCvOKrzBbMTJnsV9BKfB65iHFu/Wo3Gc4qyYTp7tGQGYrt0xRYMCTubt2tC3Ol2qMOs372FUEfZw6ypC6iSPo+qw6QHs4dxtrXYgjXZnj4TzgAbLq6PP6fJu1KJW3W09tpTv9sGAH3+V4nSL9oDHgVo95Ic9dWayYHouZT7B1+4SYD9//zKHrzQ0cXrHbeer2lEKhOh/9+nyjiiXKmyySHrjfbLWUUrEhGfIpluUu++eRK+q4jwLrmysAALF36G3VdwK7dtDSE5COypqUxbOc129mWzeB1va8mGxmqlQRXqV3oRv9MojcfbX6eXfWmTvc74hsNkjUoY/j+8QTRoNwwVjCTCPGKb3kSvfY0I4P/AngaSJTf52xWDHGgCm/msvyHVS0jtuvjOmii2rEFIM6isSXoMan6ZKA9L7cNweQfE4A2xN2Yi9+xYoZWwjP4tfJstf2REHTPhhPQAOZNNPH5bBbWoCCRN7rVKIVcM+nGt1pILLO/K3bu5eybJSBgYT/AW/cnP1u+nV7yXJXzid6luV8lokZAOhyUoVR9mMADD4I0XEf/ZJOv80Sy7YaHZb7dSpspbNphR4qMC4g2qXNwhVD6xpZ5VCA1yqL8KXQ5AIgeo6jUzUkO1axmyNBGTKd/pqGLryhq+Gi2I0zwh3MyvOPyg9/mYYz+0RdK7fjkHje2QCGvJBpL+jVHzj374Ip595DHV6Lz9xHHjPu7CAFqxpzCmP+dZpMJ22Buhz6FcjxjkuPW772eRGXgquQOFeY1uGTNIh4t8i7z62FHCE2OdxWj9qXIfwd4ate58VXjtaiNWjv7f78wLULXF1dbd3TcgdT8ReqDCnlEbEFPQeJjVCw4k18Fv3OW5jbM4Ls/eGBI0UZWzmN5K+IZO7trgTvNCnF33gcwRJoD1XQibo/+GXU8W0So/5PuAqOuJAJBZZEg4C9aBHYRBxN3M2FHVVl8WAFgABIoYHBSrrLa6kaa4/dD6hQhyAK6gSf0mkqUFsreO6tEn74kG5+FRBFUGahhk8DquEmScUX1tgZr3+qz8sr/6QMwFSRag2p1w8uQIhIRwxorU1RO9/6COtKlzTyckqmMV83KqL+UhMO1GcCqGxWHxSzj5SH02h9kYszy2sKQc+a8HdbPdQkNxFuCGI+ZwbxVGUVz8pVz+2cRUPsj1W1p1Vwu41i5mtSmBLUNcT3M1AbnCsbPUP9dlzcdNcI3lTVcNHbNJy+Yt0+TcqGRVOYOrcRGe0IqFxkpUcHcBUVU30h4ffk833y5XWABCx0wYAaOG/fYpaPK1W07lmZclzBVeWl7jdyVVedeMbIMNtohf4agmoHmCbI0j6nqtC7cMyHs7J7v7ch9mCTRDbovhmHm9Ez3MydV7ce/9wWkAI6YmenFyWE/m9dGgtA91RL1hLdAhqhMQL0SFI80R4PFZ4YCA/jowARO0YMAOVxPqzl4Pfj1Um7lttSzmKp6vT0LaPT1/rqg+vCYOqZa63zh2O0FauU8c9BzG/2N49+nRbkx3IeLs8ljuUHtIzxo/Lq+Hkjj4x1XFpt8hp9/gnEhD8MFQcEW5/sndun6N2y9elhHsPx+h71JPb+mb1YgwAp/tkgEENDqF2DfDP2RdublzOqrP9cr02dx204yk+9l+hlBDxDOGOel51VWKIgDnN16IfgchTZKRuWWZHKEQGZrG9UkRpcCBOUoBs2P7JA0YpblMUTpDmIgm7WF27uZdU++szmMBi0Fo22CbPlIMPi37fUwh2+28LokbtAqRTacXS4nG3oQrQ+O6YMFHVV8VPainPeJNnnAFJKYspjZKQUVPVleYiRJ4lq+8n6w80DZ0RgGQhP1gzwBCqW2AaA3d5XSjOcgndrACJ9wgKwCMTbqyI0V3/ZL9aXcnyl8ni1/KqjgLAXjLxIe6luBlIocedEsQflcYW48t+qV9xJWlO5Nm8aY/cLNaPfG5hutiK89XP0tUfJMmfQVJF4ZCLofvFqsrmLaL7jOMKdOQ0RwHY5K7acToGePZJUixVYnInfECQMhrVEhp/TG3iPgdsZYooZFR6SxiZ9lzB8bkqJzsygaN2qjc1xcS0FPb45TOA518OYJk8qcSlu0ZX9LH3vY0+TiX06up/A7Ry9733avSD+0rDGx4OcXrH8LRUZN2uwGAZ+yrCOUBY/Asbp8Xc2HQ8LWj8e7R3NMDY3Oxtj+3Ty31AzapMH1h2p342imSAwxnBlAglpS9BR5NBKdMxB1kow/zgv7aTjNYLs3U5XatWySTD093eAi2q3scGk0n69LA5lq6H1YsH4QF3XfBebA7p4NjpujW8Op3scMxY1cOp+ylemPL94r8JaHCjJ7r3I5T69rixWcFjvT0nhnQdYbm6Kfa1qEgBmX1tFNgp1FYuXem8lHjnEk5Zb6gCIAuDAChiZh5OrrkViqGMJ7QWJNnsaUE8rlavvFoOisvAdDaIKdk4cvahAizLs7YD+TUrRCkKs0etASjKZ3+QXBEyMm2DIQv4KOwz80TvSkt9BDjY8qSGNGmDKiyZEvIMMdlaHGmcjLCcfZzOGQFYlGqlgIxnata11Pr5pf2svOresPJCdVpxrAH4aXn1I0YANMHJHSWjaKuxj36IzW3cR74175rv3Ae640DNsCeh+uEAPqpWlVImndYkh0OrPrFDVJYu/11y8Xcg61J+KDXHNmbKgT7f6ihpjUd5YVVVdPVesX7PrFBzVIK9FqjeMHEIABGAKrBEqMJoXr+LqhgDtpqkZqr0lCLSMNO0H6sXtCOEIbOVKQwJiq7WY5XTD43IDsAzpST9u3tNM26qU78pP02z4pvS7gxyg4EkQvoMfCewCGXvifA4gfQsKKeZ2+uvYINyR0YABtoxQ23uIfgpboh5xukhnu6t43aP6eHZacviulAgnohb53AIuTG3btux1fqPkY9O72mX60ekX70g8VA9Q0UKHM6b2GNRp3Rc+h6qE1T0Ulu/KRZDUqgAwS3dGrunCGKL4vSBOnflHsighR5sCpYZQvOpRdPzaMbXRPrUf82gqDIIceoYzDdftwiexgBBnkVY6hYlNNzyl2zfoDKX2SNRWyBNln16LwiRGf3Aal2URa6e2pJA0xBpU6zezLbvW9BFV6voQPMvbq2VxBg3C+OWf5Fd/FWps8kIxK9thS6EopQRoklKmwFfzu4bMzHUf/sj6TLAMjEK69Tzok9hKThUUot9C9Y+CI3lp5ty/UFx9V46Z8+Zp0nxfWssSVb8LXa1DbrvJo2kwj68kG/4sbCQ0070YjowQkVy5SwVepI9LdOnZckWQFR1dgHC41tFvVq2wWwoKwHtEQSuVlaoDshRlSyyKX4hmQdVWsKgtvCpcueyJhN+5h9S1ElPvSmvfp5e/16S/Fv5Qr7eaShWUFvZSUy6YdMgDiaucVBDP5fWMGMKGQe0qatesky4mgSVu6hkNBettAURkuqbmWHlLlVFZDVeZnEGsNK0Afi0eqLs6pJdleE1qPvp5wNE5nRRIgjKDPy+C8kVDejHvYtG+AfOUWL6Wyt+98bpiNlwsmmLFfkw8mk53d762OdxerqcVrzhhKGixHym+zOmaqSbvmpkjYy9DJX7KLeY+XiZ9hgbcZ5kdYQfyx1Kh5LqET1Ecw547YfWt/Fk1oGf7NEb89DL3mSHEhn+1NfTUcwhwqIbKiR3muvvUlzQDYk71gF76L5d2u4xZkL2zdk7VJPHJQ5RDcFjE6fgxPg3k460iJKS1Xrsio8RlLaoxuZOyGm8iBTg6a4RACItgh4FSxb2efyjAAm4RU3iT2DPu0hbecIBOqZ+EPQp7e8BhYc2+Z8ZJoC4SQBrAIq51gBY9GgFJnB1VckqVke9bao1AD/XOQDassaWZroIKSeqSh9PC7BjRxRHJ7X++aXoDmJuAWIPRJlEiZiT6ZgxQscszbPLj8rFR2xbY/OU2npKzoGXBLtqSh1IfDC6S9q5Agb2w8GNEKEoVz8pVhoBYFxF3d1yoq+vwHqLs4UuDyv89aKT7+o/dZ03XAl//GxVQLoarhKGV7D4m4lAWne++Jt0+QsrIrj7hZKVnrVjLIeWyUa7ABG+VwpITRp77zE3rPKggndKTnQ2fEHV5QkKai8l6dXIjBCiK+8pcVUdlKo7L1lbQdK9qppeQqkVFNHJl/jb5XLd/KBDANZYrz5fcg+EonvJ9TxOPav+FWmoucexOpHKvygvVofY+hPVN/KYn+rNLNHcQbo2vpjKffZF/9toCoehnm+06q3EMc843asrHJwPrWQSZ7iitmzM0FV1SK/ae0W/0Dblge3dWPmgZww8Ih23y+P0Eax2JFHp7IDNVLd0kE7B9fajNEl7ntwbXrvi+tCDaqBujR2pM6q9sUVxuv52xBVvSCjwrtwKWSG19VOOEFdZQrRkSHRo3BgHW7oqWc1CLm1Gcto4tZQwRwG7fzf55KWj+TwERSESg5LoaPtOwub3xEX2pINjpYo92awe8Mv8awBiojCeqG9bbu4S/iXat4fQCo4aLhAmIZUW/4qXxb9ptn5LG+wgSAj2r8pGCpdy9F96Me+fHev/Jln+bbr+XpJfprPPiAAt01ClFnjsNnTf+ItGa1jtshDP+YttsX6doDBhLyC4b15X2Dd7gG1MNKfMOFOWKecZMXAxL8s1B8KWzxkB+KDc3jFTzHvSU6zs3rn17MRvOJV7ZXBFKld0yNuAASltNJ47mL4fxebNWIwhyeW0ZygUzgEoL/8V7mAyPUMBdiADoTOeZ6U1CcZDTEfpKa8SXkOrgFk89OEWcHfD7NFMpTJoeYkQsxKf8/E16BzrpTGl5z9Nn/9xkv8/Rbd5w5R3Vm6F1Qvxhx5K9l9CJYnkP/VLY1OLz8vZpxwQbZKVpaYF+MKhKBHNwAVtmrTcvIEmaf61lGbMalsks4dUH0c2Achg6j83iAGrOnvTl9YDjKUCIOkgxyHEfq+pL925/iIXQuvy2qg6Vl1iXF3GUGwDJCRqFH0230VxzhnTg2+tE2T0/Na8EFtc5eN+ZSaaGwrNy9CpYnun+zOmakgf9dXBUdYot4bc6CFYFxJRZp2MOE+y2vGnxUXdLwQQj2Onfy8GPWwWjOfWRu4+hc8exd03wA6lkfL92ao96Nwe86bg/MLpGvNug1fjAaquexoYhz0cp0WQ4eRnVEolbSY652CrPwa5I4m9yriIEQ6vsk7xwF7/H8d8b6mFqgL/UHlC4lChMTdo90o/lH8ffkumoxwkucPB4h53QvXeoH9dszv8NaL4B2cp3iFe5+1MSOSxCjj2qHzQ1UXuRARGIuHO3GsnVa5iKmESVxGFWeRkzAFqahATdZLFZ2SYFqIDPTKtwjURbFKUls//IL3+eZL8farDgMXOFeZDKgOwYE/8bF6HxW0KFWezGW0TC+xog+Q5gS8oM92z2ZI1zeVsqYNmWWaqTY1ov2SbzbNM/d+0BPLs4jOdV1DOU5YBoGOll2tqWpgCVUpaTb6k9wu4XDUX5tqrJaaZOPSqr39UXP+4SP86yQiyPQT2PXVoE9Is0qat2KwJV+5hL1a/q4y5VIJ2dhoo5n0+aELp9C445JpPVcyI2inrQg/wWmzmvyiZ0HUtfDh46ce+AKJqI9/OWAKS5FQ2heDgqE5BtXmv3LI6/H6lgTDJAccAjEPQvGEiE61UiRA7fZLrf0IGqCfKVLlettyBaIkLDQWF/DRl+e9klqWH0y9nhVxXodaFR5N2uoBXHF6YB85YLY7Q2evLC9MhVNgjVL0Jkheiz4AQd/1Eq2LkVmnxYzO9JdEQV/1qNmD7H/jJt9dOrNJ+qkMwnP8hFIO48Q4/XaRgCC4N6RbauJmHtiNbzKc+Ru1jSFzbqbSGN9RCne7quF0epw9S4wjkrv9Pkd4YvyJu42r6NtYQPwe/uRoT3eXIoVLBsyE3lnFoWlHpxCvIb1EMGGFY8ZskTlciLUiq03wqTFK4o0v0irr0Vinn7LP+NEk+sLAJGD3jCsQVWAsPK9ia5Q3hZo/tmQQx5NdwUaCmuzhyJ4wqSvWql+zgqfW8TK2Zlat7afF9Ggo2W8N29JdkHnVzw+2BkA4ZaXrx19nl36T50yRfE9v5pHInWK1WTQroYKBw9uLi1p3bd0wHMZvlTEPfrDd0b98mHnzt9cucED97zSJXZDBFJf3660cff/gcLRQSEvytv8+Ok0l6rT/6m80J8JeFtZqmtfjrinfi9ww3xk8aZp8ZAQFJgu5D13HnAMTcrG+pklXBTSI3hbkK6tkCyM4BYIITXyXbrdVCbzA22xVBsuykrbDV4g1daXp5cbm8WG42tvlmRpNJ7TH1jmfZfLlg8tR8vuBvNr/A2+bYlATx+7Pnb/7ir39RbFdUhe3TPyqf/36afSRVqmJHlAToJv9QXZztSkpU7qb2UWPJzZL5J5zRlqRLVTu9AYQlamfAmAaNF1v4m+T3U8pdbGkRfEWxGjOaBgCgtWonEP6gblrMz9ECjFAVz6kRWGYa4QAlpApXzzdL4CDeH3b3qO/fgZWaeiBpPI2/5UozRzvnPbwJz8nUeY2+h7tv+64mN2Nx29BzvcO76wpiSW5v18YYp5vueqmL0wvxukOW16Ou3FC/eskPBQZxLcKuXEcYglfkw7/dMf/+6mG0Q/rE5J4e9/BgLq8ILvUCNEU1n1wE98ZJwAHKG+N+9BAxM7jLiBCmJv3lNBW7wkM6V6RDBT/jx4BzDpPgejpNr7YODFkIdRKXfpAOTniYfidgv2BxJ2h6HlLK4qDiOI/Uuj7ALVSSVrpXUKt0Wo8v1hCXNkFmS8vKsA5hjGZxlUIgRfZGwF1RF5dFhPXIpMDEU5q9LRqiJS0dqHqFobeQKtfMacK2gnclKwHkaMVYIiU65JnQivibEBFYkSy+YgTARhIs1PZ4T6zFxNThgwsItNvk+g/4Yw2AzgHQkgLlItjS6qbWFH9Wl6rLWvrorkiRjtxivVnbtVqtV+vNluB1Q0i7LdbrDT3TEG631ssLOmooltWEd2gxgC2A0vlv0mJuu0nKKi7T0pMT7m7HBMRzo3jhIz7WAAslh+JUKHz9k3T1EztsSycB64/9dojlVb72T2WossOf+nMvb8vtplitr+VLXIn7OONNjlfDCPfi160WVLhDk5wJOPMlzQE1BJhWRAfU8s/S5V9Y/K3Y0egqPaWdFy4lY65OC+qM2qhgwFKjSxCoYcZBco7tP6BVfQPkP9hQqHro0QN7C+KpnWKkeq96KJ48yzjhSwirWtTOIMu9JHy5TX4Qs7FrL4KI4de8OoBm9m/F0yTPvWSe8HLr3l+Ymjgt1J1xBwa0Q3UL1pEIfyNMHGcE4TuSNdFO0LrXrqj8B89/aLt445AdF3sx9UoKPaAPjFfdZgq43ibm99UhMctx4YfljvYQjLMKc/iCzi38oDMIpLuGBGCL0B99Tnlg0ovzMgDjFmq3B8KtDqMlvQrvaYv30gwDY25xuksx7v8u/jiksSJiQv9Bb/0ZqkuI9lrU1aGqJ9Nr8gDmuK/qKtytj11IU9PgZbOtmnHYnaFI7OTG0xX+dpnbJirqQ4VcEtTrrRtxFuEXW0Mq1iL4oe9UPcRgKloCRjDELjFfC90DKjIUmcGeflQCcf7xAK6iaMVYBGPkiB+76xDJv52uvme6ENsBMLYKtUwPseUSRwmF+PJvyuXfaD2AdgGys1qNhEg1ywCaYJEixRTcvi369Ck5rOXV9BaeGBbQMmJmvzClx3CFLt3UI25Rr61mJsh0ffJ080HGXpma0EJlYzNK01ReEAO/xLpOD35u35I3qms/elKdA+BEE/Br1tEnVJDvxBoXOQocFQqJxT9knARM86ZclMmVetbVGqT5o6aAs3JL0+09csuMfiwYWg0p7rE8N8keWB88TrZQW1t2ykl43bhpZMA4kE/zj6GGZ6w5Lp7/Qfn830uyPyXLaok0MnGmm1KSog952racotRQSYWO9CKl+3/+cVpeKsQXAnD676EgtyIH25JUOxlmJYhi4uwklo0MzU+qDJbVNhLCjkDZ8yz5oa2QcV9IesVTfPsu/3Z3zwGQNxCrRsWES2Z0roH3SYU3nmtI8S/IvrdQR/o4YPQ93JUVazLO+Ly5jd8OY33cmED4TQnqeYnF94BTVbKAetZEXFM83fWtK3CcGjH/WHHgMPRc5xzbG1M19OnW0i4kFjOajqWPIjYyu7Wxkd19GPjONuyKqNpjgy03Oaa7z9Pib2+HiMm0ZOzmOL2P+hDcfby+uXy3gnv4G6riL6G9Q6p+c+68WcnY+4JNPqXQQ41yJmje4nbDtkxkH6G5xj1l2FI8skQ5Fn7x422cLHpSyuK1lINvFW2DpnCQnl/2Ylf8I2ww1AdvZA4Joj28BCi4PrTAgD9wibz0olNPKlEYQdL8U/ItojMNRGGXQjT9iUrRJPF6WTz7g+L5z+lftiWhoJmWNT4UJtJZELuiqHTlrghSd8lX/zXreokHdVSU2KMIc70N1zuBlVckW7aqhBiqcv6bYv6htTr4rXLFXKrpUCfJ4PJ7BXNdqocX/iFVXJ1YD4qs8puaPBTE6qfF9Y/KbJWk/Kl0bETFkMgHW3e8YC0+OVEo/JcP+cdFwgSRNEwgzPWHFTma+c/kL2qYvK4/zlPjWq6Xf7W9/EsrNNuzXyxNlLi7hnAwzZnHL5KcQRiXL8E0IFffzxgEgGXViy8O1lZEH/C1gEGMbMKdaczNGJq2Eqao36SKVHni7GC0DPK9JnhWaK0Ib/gyNsPZr3IGPPCd9JtXugGLTwXjsdhpcfpU1hF91wQX1JIOBZAucsTp+GRXlos7nuPBlOezzN23U2DaLkBt54pLG7bjWae6LZVAI4Os7S5Oe68T2mouZVDCUZzjXvBgESJiW2KcQekRycGtwwGmE/nEagdOU/okQmvbqULFjOGxHxytWxOCUBKVzg8MNtqj0+U2zjmW8sLSvb516VM83NIzcCMYdcd23dsiGarzXV9FtaWHa5TbkNCGBxWNR7sfIpAGNE4fuZ8wAqBA2CqQYiKCJqIgPdLnTeyubn6FeaAo0FNa230q7iN0MgJQxULzP6AzbsAVWNHrqS5/UgRT9MDyD24mgGngm7dSDtklWtT3T3JFZZfjmDCD+R4Jy79IL/5SbRIdyMWkf9NZ+FIfptLDgCQlKtd54WVySf+x4lHSLERAT4WTjDlsmZZi0krm/YtLytkCWPyOQkYOG4YUY2jmXP84337AnO80f1Zu3tXCWWVJqPygD116srs/tu5kHXtV/PeTt9YMVApCp+KsFdCnectKB/Dif7STgBkBYEiEEpdJ8iY0apphPyUqHbL5V+RUFqsWECI/kscs39CEVRRbylaYxT1C9nwunprDM2MM5l6avJYkT6gG5dM/Tp/9UZL+Sclse9UuxIEoPe0GKy6gbB61svKBD5gML6iYGfVJZh9lLANIL6yHnm1MtY2TaKlXwtFCEWu70p3PecZkbtX4M0mwxUJVaPYk0rQmRrpkpSq1ajLk0LrXtBhaIkXokPAgQPvSt9swWxlR339fdgu797H7To5/N7u5vUxqYPctVOe0P/0949DpVDGXg6hqT8cMGukj3t4N+uZDd0ygmX+eJ4ocu6orLrU4Xecf/bkT0WTR/qVo5nafYvzp3g7SQ6LLuec38cB6C/PW9yfWNk73SDfQQbVxiMlhcPdIS+8GC34gucY8V6H3oPSAKuQpH6dRT5HwInAaX7COQGwcN3OsaDrczg4Y1+04cfD8Zo3qVdsLItx7cV5CYNeTXciZ1D6IcY3sn/XTdE007YF6QkBDuKM4TV+TUHMU9zACQAhoHBUf8ac4XnXLH424ygYiuPp9nUQoxs3CKVIEVgotFV+RMb9f5uyuA7X+i7a6rMkgqDFUjs37v/pH5fM/4lhYOweAcK26jE4RpGSJMV36RIoujsCf5gqxKhcd3FLbTJYtxKTa7l8xPmCLWZGlVQ6aHC+AMUyWtkyWRaXaFUeO2qkqsburSgeQm2X5AbbDfgGpSIEgzTXRXauZNQJQXv+ULYBSRgDkRPlJhctffeFRkprhT4KkEvhJLcPCoPK2yXJMOZyao3AcHCoMETWBNt7jJOANLQ3aCMnFnyUX/8YksjicOgEzhNRCqWa6FKJTG1h8ogO/CsoRINxhir7fZxtZSqtem06ewGImhcVOnwLygSbQUZ/JqOygiG1AiZlL1AHOGtNwhV3MBhOV1RoqgzUGoBS+HGS8eT7mkgWvrnEPVKU3jvQq9xvygL5T+64XU8unaLJP00Pz9X7ZvacmUu+nGNkFaKCN2GjruCcQQ4L7IZejh/uYT62t1pAbCRqCRyjDyYFW4JgyzV3k3e7uDPhDW3uD+J1SGLe3h0+HQ3BHq8TO0icRChQp424MavToHPKOSAzZa/DQj97LeNy3vSRdYMurDQRb8eJ1xu9x7pQ+j4kujdmOpAc8jwWSM5ALvNai/uz77pM36AmLcZkfr45etQEcUyG8Ap3tO8X2jiI70IidFSVLEAGQyTO4NFSc5MaRLjavaS549sBaDu5n8nXOgLZ/VA8Q9OLPqb2lDnIiZUzF1S32MQGQDSL2pLP08i+3jABU5wB87pIt4ANNvbium5TJ1G9tWvK0JXhkvS/xvrVDTLo2h2FSkVavzmbsFEmst81LlkMwbvCszDkZV8bKLcR86x+mq5+mxWslnKwv2rQUivT2vR2wJRjhvnjx92rNQCTY3Tl7oDLa7U2kJyy1Ofr4lV2VviqLhWbnpytMNgdxoz7o+AUwq5BXjQKrGqoKchAut5IHVb4yngr2dYYADLKnRTYrkiUVjC52VgQThSdaVQLKdfHsP0ye//vJ7F8Lonamis/KDD6WlGwBVSuyDS0VW/+NSkBUlHT/p/lnKWrbFq6ooIEFmgOcAy2k24xw0XRQzRUjKvmayWNmPOMHqEyVwQ86+QFuEGBn1RKGQjapFpldvLJUrfTEJUO4m56hbSBQ8wLL0JvQztNePh2KCDDwuxlhnCE59P6ZzlrVbRp2983fdWP397E7zt+FTJO/w5ryK7DDnpDyyiA/xKUWpweYuE8887iy6KEa+nU2MQ18e4fHqk0pzYnFHbPdmw51o1UlYm3j9F6GASFwDpAXnvC33pFi7X0M7Tm8Tun633RdvGZPxz8UE7P8b4Rwug6xkzy9l/mI3FOygiYhcQq3Edrpzhlhct6scc+fyyFDfNwh8X2idUMMJ5LvQ4P9FAlNtGBGfzH3Q6WJBTIKevgRIrQB0UI8BTsW2Kkfl7AJuGK7+juoOT2mpa34NBqoHVjRwVLcYZvZlB9iP1tVKSkaQPB95tP5/YKDnMQfhsRbInJ+VcLib83U0GSkTfH0j4urP9QCAJ0EDAoROlT6IJYznY3c1CNUt6WnaD4j+mdPGu36w2Y1dPRKkIJX4MK1xgDbkjJxBSp+nmkvEAXLbxYGZxoB+A0RpAJiXaI3n9inGUBK+PXlGA1QnfWiPisV0AHFuPHsf6YpSSJa5rts0tXvJle/wzQbO/kL84XLhy58qwKzcBoG8hVQvKQjn81eTZYixzJ9iEDlqNPT8CLhs90VazDRB29XZTfP0ovy1v9Q3voTLQ/RhC7pJtEeYXtSaZRUzWQakCZlFawhFoFUoTlH63Hzrnru2foJPAObuTCTIRQmtcBYU9rUxpnt7aPgXoaIP73+2vvIInuTra8DzDBQPhCatJCZzkdyTD1uR1zmtCPofitJVEZmuCfC42+lM75Jo70UggatxwB/lTjKA/5O8J+WXgbNNmJ4hfS0dUJeL58YqDe4tsLoveK2b5x2ZJ9l3oIjOZ59DubEWjLS9oJni0nrsUULftcnLZwWB3dYCwflu5Cuo7qyujgNyJC3DckVc31avm0wqR+GejiG4DXdOT/3eGnA3kb/h6mD7W54UK5VlwK8lWiVZpzrDFtsYyeDPOTnoe+F8w9MRqQ75h7/ROrWmFX5RzlxktyGzJrKcIJa1N63BRlcAyBnG3YdM3uYJzAdtAq5qmiccE0QiwYhUMwsBe0/UZRCIsCaBG7BlJ6gzR8TemufR+umFTqxlLbgUXAtNgA82l+9m8oE6gl/2rXdsrkraLP+Zfhp5KFk9ScnFSz/LFn+FZ3BHAyFdHXhW8wmETKFcM0DNTGyII+lqNunz54qlhNDsZXhaM6DHUg7Z+P65R2ZpjXB6hYmvOUcY7Uq7Cgo0NgosyRKtv5jtsqRnmInT6Abe/W4UcZautQZjieAhI5fYtHBaM3p7+SPAvCIXU3ZBhRIRab6nyW3/vn24l+knG8g0zjrANdJZYpPYybSi3DZIMTTaY7TrVaQwQEAb1lJP6pqDmSstuB7JR+m29WC4tvktKYorNyaWwwEzTnJgVOgiyf/tHz6T9P8v9eRW5pzpe52i7M9hjcl8/sq6JL6jLaU0CbhQDEVjfQqZ59ks8+ydIGqmtyvxgQWaQ2AnIktqma0PGnE8sfGU9Rn8s0oVQFprdroux6ppYOtMKE2sNDcqjMPGjgCSUWt1pCxMPl8NXov+NpVf8ZIxiQGyI3N58OfGu+BFnmPwBbGzT7iBFTgcm+EtCe6ssd/VStualE2opfemKTL/CDI+K/AQaxiZEzw32i3dKzsarJxn9RYB34O/DoP6RMK7kAxo+hWjt14YIgm9kNcf2Kd4/QQH70luCIPxJwHqdoZoWq3M3qeUde/ACGvTT3SAAg0luiyqlg7x5aYJu2LeXIN2wYeLjsu4y51MHS6oMAw+DBAuvy/EUhQ7BuR/g0K9YIIZTpRk5Gid0/G/ozTE/n3ogUlXfqIDr3ko8BxHcnl6ggMevSz7vJ0Po5NmtjG+kfhDCsPruxnWwth2RpS0Z9lVXfFToGFwkPRqBGhYErtBwJ2hdH0zJKjP/W/WkeyZSvgEX05/zxZfGKcJFTYJlwfit3q6BPUbKOe2ut/Mrv6ozT9UyYPqddWUi2Ok2Sfw8HePRBqwjmXaZ2rrUAHMSgKEIHaTdErm9MTOGoiCFG+zflWqIheGgfwtoQiS5bJfrxZfJKW/1QzVaQUjD0QlGtMTKW8iM07rpcQha2LhFH6U+ce8Do5xwECv2Zip4LgDKSUWXH1s83zn5bp35XZtceiFu67tip8Ck9mWalx8Bsl8/TJ0yS9YlJRtr7NPZ09o9OfuVDmc5oQuJ8oX66i/z1bru7eeu3evbcu7lxer64Wi2yzYknurLj1rzUIcE2nvorG5FGMXqxSzv7jTUC0OiyCV4tFtZFMzfgq30tWnyfpfWoLKz2qGrSrm8JQC4dqnFILWEbCjyxriK2+g2YlpfKtw/raV9BZk9FGr6zGyAUkVN+UHL/AME71Z8Cu+QfAb0eiZTaP+3044JmjCQf4vQIf5oFX/m/6a3Jdbn0H4NJ2ZU8DAJQuXVMBf6oQ7ccwzh9h0JnXFdPFbd84PYQTw0kHpae4p9v2mtSGM5HQSkSnPyDWp8s/5HoRwIH+A0+HrB6qqL0Y0G4oMeTzWNxQH/kQfEpZeMt486bk9HggFm/pKTgdojGAV9iRajtG3MzDXi6/e06criBHlWncf+N8WoIciBXT/TOOqXAEW6qewl1VbVA52Iq56vt3g3forpfdAVquMvnPN0ihlYWzPArKxT7rJScBlx8o6lGYpqiIPIJenqtAS7gWSulZ8VG5eU2xUvbIgniwLTjU/qHX6nIWA/vWcmPO+uoD0Yubae453BXm6R2ldQPEoNtLbfx/+Yti8dfsPqMAn+hSnbWuK9E/8RyNBFgD449P3TU6IaucoWWSu3kd4iR/RFT7/OmT7Xqd6TBgAti381kyX15cXzGtXNNHUFHKPfvhlgOnZl+k80ecPGXsJckFIYVLwuwi4e7g9FkAZXdefoU44ePYcwCkQ62MVPNvtCAhR2lbA0Dn+JM0eZSwBqDQGgDg6ue2xpLiXRpvml6lFpWYyjbRar+gbJYu/M1JJiQK1jn9CwTcS/y/KVijskm3i9X66aNnX9x789ZF9tOsnGcc5Ta72j79D5KrP07Sf6ujhLW6F+6o5HVBLPSPsSw+GJiBM8sGkmvNHaJBR3lTqqyBmX2q1Qs82AkVtskPbYEH0qG8DUNTlfOMF8afJimDAFLU6jAtBKq0tRNkFKLI0AiHGgx6BpNPcPQTI2fYBbHSPeNsxqX6/frSHFWR6KP5Ld5lDMF3GPtSjfdAC9lUEgyNQ7qF03q039O4f7SVf8qjq8C9duZRzAbe2/HvZvd3cDxOiPWIMeN0jHNK2nVzD4yVXZ+M6dFRH/V+WI8+N1cfBspxv5bNuhzrHKcH+QzJ1Y+gfrYmXmcti54GwEQ1App9uSZ/zycjBv4HJ7yKH0w2jaCrv0MmCo3R4vQ04TeF5W9Gf0seISN4oJePs315jO010NXrVTLoP+Qft7qX7dmBsaxefRzYa8hkZQ6hjhUaFxCpq9iYRzrsibEsRtIrUBGOPgumcPBeMi0USStMlxhhWGBNSGG4guqdrGkals0NZAgJp2DOC5dImkBKIG7GJ83m9/PZb+xdrn51YkxlirNewfTX8mxymEiuCR7ls3+cPPvDpPxTep0V1ptmCKUlIDJiUHp7ISY6ZPyBuI4sxTEWvJIkmhMVnc32ilcLIuFk4HXBHJUFncxJ+ZCGxXxxpU2EaG6JA3Etivwyv/hVWvxuWVxYZKyubXeLlAiXCeRmcuW1ONfgAfVmEy6rku4f0saiWftwmHl6m179JL/+UZr+S9YAqN1FnrIh4E/lwqwfTa1R6eIS8lS2OpkBL2kFLc4Ei3xNlfENQLXlJ5WKg381GrCgDTfLFldXq/zyqzR/ojZAOS8v/025/POSHT6pGFWFM9mqaLUeNvyA9K0aY/NM5wCofKmA8uDqe+n23TJ9oPqEdtJN6kl74wBXm+ZE1dPybe37GlZxqHpiECaQEjNdRsqn1qxrKpMND4CltrfyLAvmqhRnu87Iql8nNEfGjYvpET4i07Mqp/aQ7ge5WfvxXmF8Fz0QSv+UKnQOx1CRz6LCKQ2A6ntmPmGeJNNq2QmhewJo09yRL2cT8YSno9qOk9pwppQ7Pm73Az60QE4svSmtwArngSnNT87wZUU4nL0vJ9gejHKG8V08hsrFdJvu/646sTfidBfzCEjsnDgdWMV986eshYh7fWKeLij2z3FfokM9U/f9B0P7EniEK773YQlDgVIICOyRwNmrhHMw54KUrcpUG+NUVhIJVYTEQzvLFX2ZXMWCqJo/02m5zLoROqs3CaUIDZnnzbxqzfQgllN0xa6QV99LVz/QRBShwlOZuwhUcMBsTo+EDdtGbi//olz+lRoGapawDphsKOmsnVmohin0VeezGeZIEpcprzsQLkFgN3uoVgHthRyrFeZbZJvm+TOmrGAAW9bAk+yyWEmlzfdnqx+V20VS3EGiIkdZ4h6Q7XDQgwEwgEddjXN/HXTc3QV1aEdXCNQ0/sm9LnapyaNmQ9lc/Vl691+Wd/+EY5YpI45m0FlvQs60b5I1pbAX2QLamAiBeEpAnt62XfmJy+VA84qaYdoVFNM3mywngzO/KNa1LQko1tSnaxx7t0w/ljFP/zB9/j9JZn+q8Rzxl+egVQkpYTG8lEQXwLBdF+mqLJaUOcqDlOQf5vmX1lCkxK31Ir6yTh8qIopyw+Qummuq4fqlgBUIMkkstDOp6o55Q3D7q7WQGMTX+Mp1cqtH7V9Ycu1yeP1UAfmQK3qvAfihbwnn3UPVUSXGidOVdqO/ULEFMW2cjnHG0+7R+PfoOD7jUjy3FSeMkMSYcXqE5IisyvYDKeNfn4p06Ne8w/lI347WhyN5dnRrAKZZxHfxzNeopV1ZPWXRRYogvg+b7xpXvUx2uYc0APwttKNtP+9yRlJHEY3we6FZ/uVpvdlaj6codNyX8xSJgfbs5RIzJP2tvmL9Y7tio1rVoIXmHFo4MfmUtJOfyGSKoINx0MkNdjt76Vt6+6wH3n0VrQIjp2byND21NUcFSfrjv6ZJGA646r71GJjQWLl6tLuDibwzOnCZgW2ZlquedVgsP9su2AWIflnizprWOShC9bBeczZoJLCBT775Z+vnv19mf8Z874JznxTUKzbcsqs8KMTrihqRwrShGUx5hJY4H8UI8vRgMabpaZGrdqtR7za39WqzZRiE5gTKqxmAQzi8CoosWf4yufh4W/wTgl1YSEJ9uQgZHK7a9gB4CRJ1UF2popI0f6yI8MvVP9pe/6TIfpXmtwitreGkXfApD/ygFbQKgjUPS93n7KmKQ9jmZ0sbALfTlNNMLJpS8j+RdJbPKBMO3tKcnAWNqTxbUkopS3WZm7N4Vjy7UhOC8r388+Lyz8s14zxkbxkHAEkcrPqYpgj24JiVxuTMCpqRNASsBNQAK99N1swCfWBoXoFkl1UK1S+nlvEqcnIoaeqFFZfVBFjZtDFVDRNrj5gruOhMHdUKUXFVxP7QujuTFvC39bHy1wTzzfHCC4lA1IWELE+8cnnLIa8evwkP7Kun5IcrpKm7jYuTgOm5b8wbrnFH20NVb2XViyCuh7ZLGmqc9cFbz25px7qzSjJm/jpoO/b8chocp3h7Ck7M1A2JIZ6uynq0ndpbGds+GeXQlTsdElsapxscRutzjNmoM31ULbtcogN75oD673csYCAd9/rE8zWDuJCov6IDjPp+1UAd9Mwgm8kZrll876pouYqIxJVsQmCCMKs4BD2CEy9ZHMxMGA99FPOBqHiXmIhQzmfRQMMoAdtoZhewUkxGMChKZ6xnCSHqKogI2WiSFZ+WK0Y0Ct5ON++RsIjLJIOt8E58FXVJJymWlJz2WjxP/urB+i8ZT1hvnjPJXJP+wVSgR7SmGRvEkBpq8BZBdpUWt8rsSbm9lc6eZsXrCUcTFG8lbBK/fout4jmFIJ1/ka6/V84+S8p3svx+tn07mX+dFW9lrHzYvJ7OHiXr20yRf/Lk3TK7K90JkKUSrqA2yrL6rgfpyeUaWcKe69sOo4aEz9G+/IDVTkxfXeBBda2g+Gg6FlAF9OXsV2Xy9+v19mp9P8dj+XVS3i62VwUTwLLnWXk7zZ6VBacp43NynyXbyzR/nrHLfgbkQscnJ5dbTk7Y3Enyp0nxWpI9Lou7+exJXtwts2dJeZfpP3nyBucop8ndYvMwyTnE96pY/eNy/bMk/VsaEdLF3Of1TrVDFQCoGnhKaHrRlbZqYt12gdIM+2zzxYOCcwCkJ2gUiiqnqhH1Wa0WLgX+VmLWvijuJYVWLWsoQINIYky9QpbwWSlR0FK9r9poRNYylm5ZQu3FTLFXlZN63Qv4Wa/j3hJTqGKcOH2o+jFtnO7yGf/lCu9bXDjOp8v57BDKdnpJdu3qQg7VsPGrN4V48q+5+9b587vWW4unCIxxuuV1sP4xO0+7RX2/+F3cFwA51KL26qC6SlV9/65x/BpRheN9dEqBOG1Vc+sKXH8O+ahBNIT0ksGxachPbu4IwnRThkRM5/BNYcaax+lvSp8XINdL3Esfk0MF8DQKBD90E+Q64YiegSpwnkIVGMZUAfgiEm5Y5QX70E1QIpzKKR54EQPxZ+GSMiwiF5p6TBWyK66qgiuiIsIycK1zFCgPtAcIorgTloHK/xAoexarMJnDQ9oEixlxFTHYl9niE8lRxCUZwJTyCSqSAldmE3EI1IYg7/mTH2+fvJcmH6qnXjOM1EFNB/JyNk9mxTxjHj9H+y6yxWaRvZbPrubZa1n+bFa8Nssf5QnB/UOC+3z+kGZANv+S6eM5v17le+ns85Kp5MmXBP3b/GG5fj2dP9kSzs4epes3ivzRk+39n/+QNgwW4hApZXrKmTKleSm/ewm3C71BSEOg+1VF7JEtcpkrZbEvQynP3//Rm//eP/69xSK/TrcXm+J5ntxK06tZeoc5UWl6t8ieZaRZgJvcXqePUpoECb34F9v0WVleZMkzZkZtWPO9uZMmjwuOS8u/LpLXk/JxCjx5vCluF8ljchlgYWLVJrtgXhnnMizv/MNq/tFyK5cqfFfVMO8qobjdPOmNSk4RKwraj2z2Ayp7u2oDJy0RZhvZMvnKq5t505hYjZWBelJnvg1oUGOQpbhfVY0sFZ4vMkCUwnxvrkoJyYdQKYY+GA6SjipC7sdfzuJ4+m8Lpdx+7OW0J7n5KNGheE9R/ijJL4jou2rXC3LfmJhObZ3i65hI+CMnAfe18Ly+Qke/BeRqh7lU8bXMKUqYVYGVPekWt2IPbf0EJiTi+dPdlmKM2ZM+of13is6uCc6TI6dcJ+g5zr5bLuP4njtF89P947IG+Yz7pK8+95rWqDMRVato/JG769PbZ9/L34FdP8f139OaENKsEqesMRhR5qCsIf8LTqzlq4B27wE3VHePCD2HeEurMFVkHvC4ChaPbUptC0P/KOMAREKE9U5j8y/Ub0dPKls6AhRHMHMmgGT0K1tkZTv12/cISMYkDoJ5LjsXtgC1WL2XbX/MJjDoo5aEgnqToKYA/5GiDmBmlWhb/rK8e/fv/4//u//N9dXlBT3N6ZIAlBBzzuaVCf3N11mxmOWbPL1kQbP2ndeUa7aiIaojcMcQnV6lsQgtIJ5pXTLwlO1kNGKgySGMG0gKc1GQtlGarUtZPUo6u7ycbdfXrFdlTjlW03V+H2dFO/xITfcbHzy0ryrT8kI6IG3fDMkqsWdMwCU4ozjdZlM/O6bdDd28zCPuxVl/87/9X/1H/+v/5X86L+i/z9lstSyXOZ3sxZygP8kYP2F7pTk79+tHioCZkJ2tP5njT5ltaX9dmw8JkuGKb82TFC899WVepJvNhhpyZfVknWznRfJ8m8yv0+dpubyFGMoB32lMiWL5UlVA3oA1YJW+DwFRJPT9Jzm63clnlBTPbA36MZW8OgeAJiK1zp0BlWxVnQRAg1VNSmYlse2sThL7wBobSLSwHiyqmP495KwCo0CoFgcUm3spy76xWgMmXMYMbuLautzDLeCLeozfA3H6RcmXnHG5oY9/XKWuX8fxJ+a23tUq8IjSH1sQ8mNIhN5Idu3qQhoEEx4av3qj+OM+75L6b5n3/ce/a13MUyDT9R+Uoh8j/bjoitMGePG3UYt66qy/vQ/Qk3edRgAOvFr1ePfyo+pOqbyRuDarKOv0JLr0OOlYvmdkNaSCO8/vL0BcrxrflNxeZb5dQHddXOvidK8tkHhx9+YCdA5dPnsJnWGXcEDQuBYDRENgZ9aqSYTawCM5xFL08hOGWfxEhsIm2cV/1gDw/vX580CMUJG+Qitt3qK5FnVsBJShgTxbLNQkUEcts8aJsujbZYaO5ouLnHAfekI5oS8/LdhfX1JWCvkV/YProklJU6JsRGkVJ/Hl+u4PX8vT1y7T9JamozAphe1Bs+dFsSyzFcuFddKTtqERK5+oQxCvRoXsJYaEFYy8tWNny2qAAQj52gWJiFLzQ6AVPmhsBJTPU+1TI6De0rKRiSjWVyx7aucqPemaijeJ2bFI0pr/uEm7Ja3n5Xa9TFfMA2NAZaFOdvYDZZ4Mk/KZ+iLrdTG5i+LhziU6/MMvNH7hgC01ojQWY55UKwvvyUvzgiOcc879JWup45zVAKNG3Uln1xTLdrVChnf+Ux/EmdLQknFkmc9JUXmohFprkG+3s4QYXUWleUNp+b1k+2WZfkW9YZ8hKI1HxUnmAbA5/1KZOqhQ3uIJaap6rAsRqnZYQotFjRgHuzqymUCEBo/hCrvKrp7rD6CGUuPV8N+yT8zv9880PwTvncJkmqgGViwupEkEfRrY53s40V0TFela8WLkTlTv24YW14tQWYaN6Hq/i6vy8AZAb8mMtoG8vzPmqVFR3uSMCRx7xa3YJh9Z02x3jrmgq9sBGnn7LyJoyo0yOsmmzp3sUUAoLwybJLGjZ8x+EofR8o25eblUv2HDcnsrUcznFP9M4hPp1vVAFxLzHExP8JL3bbj58ehTxXMCB8eM63+cjuv6ST6crIl8FfryO64Z0sHhFe19/02uK4XiG3WJclkIRITFy0KBHKGNZYJJ1KN3SHGv3NwVXHEZiIp9iZBAMJ4EgwR5ZAmfGIxIjSTLQ20XSIvgCbkVMxGv0fV6DVx98z7Tgj7WNds4fmAT98VUPbWVckhAEIs+VxASEIo9GPOvtzwUDxFalk8UqpVPmJ+RJM9FyT4wXPTq0t+vfiMyBJG2ilvZlohqKUMs+CNXHcBaf8wlGYSLa5ClAzjKopObNgDhLiQGVOOFVFqu3zaISDUaADYrCuxJFrgh9jjt5qQR7p75/TF+nI44mA1VXjWe8KbMsgsrfJREmyzNWAo8ozDopKc7npYaOwBRZvIYHkrXOgmXLXx00b4y2yxbYyzs88OlwtJiD3XMC4NYGxoA8i0zdRTiM6Sg8hJCmf+dFv1u36FMESBIqeGFcvMuzuNwXyP9nppzHCcg9lZj8iualDQsaA9sGdHRGoD7ZfYJKxbUIFF/oWqo+FnhwVuNOxW9FiiTmW7vlbQb0UKVWZ+GTwoVINJ/mMg3Upt2zVc6JKH8mRo5zrf2YMfpEaA9A9i4cpOSsFd9bV5Db4MheJOap/g9EKcrxMl8TultDXIjT3QUPQRwLj7IDHGI6r95Q+N4x15H/n4dK26Ebveeb9aBIZL4t8zT9QthiOJFwyl0qUST2xN8X6ykzqvnOUpwTKPGd9wRu7U5WIi9wvG3zxjbdmE4zz6KrrQ2bfe5j88IFuj+N0kWSJPwugIHINO0HSAeBbtVoJxX4VGZrzLP5gFK7bi6Ecq9VxVye+vDRHHHqVRp0iu4V8sucKdfbQHBTtNFhDZyGXGJQiZjoTtxkHWXEjmJiWI1eu7pepUjyOKRV5YmacDA7qJXTKWbQjbr97VnupPVgQytci2g1mc6/yydfey8nVDSmX0h8YRlCGDOiUI4QlGCyG3B1pT05Fo87hGcCHS5GFdLDJFh6ihD6jqO20UMhp3gEB+isuagOw58CUXNKrqpDc6jtEGohhIImqW+Ycvm6JKPoseXJNlQqXqQ4SivARxmQOksBBI0z5gUhYHyrl3yHLbjSXOhnKjRHqshGhugRFXIVeHzSRgNUH7w6Fr+8D+cIZaqYrpoLVSqQE6xyqsaQxBLsdHQAyykChxBUA4lwzpyNSMTNoRSa4MCWb2Tbt9jo08KBwK1VyqZNFxIqzrwB73qA+VY0P5kTAOWdlmdF3eEcXPbYCx0yZQyUkfjV2YLeX5JTvPqAJrZr54O84BK/NwXRXQTbE9U8yVU6USLTiH3Mgo+6SZOYX4yLdr599zvp/Fr8xgZAehrrY64Ru3CkB0rOb0nIKbapWEqra3dGQvwdNugHZ2lPDtue8XpFnLvY+hj6M2NgQ2Fplkd7EHPkI57lI/rHZmkc1/5xua00nE7vpUVHjHBDdlTKoHAEl4iDpukeZO896nLpwvpEvbUjWleCvb2SJnAIS79llaBcwwPwBHCGL9KT9DEMXus6GHXD9rRem1wLAVfoYIDspCckIevicIaxT52KV6bfcpC2LL8viIiAiFCKGULwbpOsYLToO6qbz5/QixHEKXVlh5XE1FKDLvBE4rRgcoaAE0LgVDtADIJIq++l6+MuSlFIFjLV9SX5J8R9qXbN2FvMgkcNUWHflmFn8CFbnk8SwkLz+k2li0EhUSvhJyI0d16o4nw1c7h+FjNGfGeWuVWAsw6RZ6CEPYpRCYCJNf6lTVBCJMRK0tF5Jfv7rzjYsrWmWf9rPU8hKlKqz5R2FS24FUpSoxZO9xx0XNNj2EGvxlMnk3Ukdn4QT30GC1U4myBVBl851YB8ZjcIi8pi947QxIEhsixRiP+FISCIISnpx8nQoWHifZJUGQUug25bN5FJ7b8Byh5VjE1Qwt6toLNLgoGKEQw384+LljMrU1FWXCg2TvwVkuVKibVLQ0d7UfF/Xmy/LTMYfsBWVKMleMaeaDtgeZcokAZ2Swn2R/cmLZUtxJlWriGevrb5wPUBKpXvRfm915D8F7kEeB0PtMxB8Ths8hDA0iTwY1RXOoB12kaqtQP4SB8syheRbB7r1ruyC2mij0T4M4/cKh+9R4YYLKe4/ocWhw9v7xBv0MSx/GJtY3TLhlIy2OHaLTDHfLYkM41/FzyTZOIGbvP6edK11nsM06H3rru7nCI67BnBnU9McZjLK8j6cUDMCC2IRjmxfRNKR/UePEO+TZKvDl3jVcAlxukk2j9HejMcWkHMgM9aNZKV5y8Q9h/ugmXKnz1fxL9EFARUSl4c5uqflLQ1Fdsby2LutRbS3+tMKESPh2ntmTWoybOY1LXb8Z0I3vXkVUuPlvPP4K/x1sSSOCnuJ7XIWB+8jVsgELSwWJQZerSIyMFhk0QKRyRCy4L7G4zOYCYPerjhZtboWXCskP4bq2zVdhnjAyutFBMsIgh0iUuztMe/VbxiSA3kHQtxxm7jj047oA6w7wh6xS1y0YVNZncaee4gYhzj1Golqa05TSlobQHXCavVc6v/aaec646CxkVd4NIjP575UEs8qrisQ+m+1MTVJkYolBxKlJnnQoHDIiEw5o13YyG5fU7M44CkC7UK5HC1mqgmVIBVJHA57IJRVoTYBpLO7FTi0X6QyqVaxNknS5UA6E2V00FcPjrXgbszenifochZ/HAWZh0nexF2oWPQI4ggRv6BxNCOiRcHI/HMR/RtpV10/xb4k58HNHWnen3E6UcS94qvWPZBLrIGEv2nAMQcHcJfBQR7uBKKY/Xlb3LmjnV02ibErYjBWAcWvlBkW6iV7yAcdsrTg8SnJBR+apr9UBfQmxeTzqal3akUgNyj+TWIdu7NqBD0QbcdIm05Q0/n1eTUEGHBe5yHDmuAORN5NBCq3sOdsz3pCwkqvoj96Aem10ZVmtqYZDWACAaGIGOhcbizruEF4qCMQvPBLK4DA7E5dwUDKX5Ez1a5CSwluAyqYQJG7b6tmAJAUfrMowwL8urJFmwkpdpGNpXkfbD6oNi84F6mLWPO9Rs2qNOaE6ZyrJ5UrzhkokE4WsRpb3f7IRdf9PxtnOlK3VRifnuvALVO0vsqEEAiyCZ3oLa1asg3bwlk2QH5vPBk6xL5l/KIqMVXC0I+PuQghQ0PNPU0EVol1OTrJ5JBZBjVHfP789rILYfIOmRW2PFuUFEFx9roHCEgIaLNgr/cZ2NzchKuvzNLx4Tm7pA6aFXUsUBst42VADYOavAWT51z9rCNvevcAyvSujDA3SUohlnJITaStOu5L+mAzGCwKQkNmCl8Jn+v9mWa01UYlkIqsB4zhqAB0zWogZpipbmp3mAzliTdNegVcnJZczmYsRJI0/sSlRoWQvnCTyGkfW7mb6yX/YJJi42D436Q/NA7SHppJEt80BVuvmX/aWMaHMZJn7rr/gNFqePMyz0fAfyod8sd6CPwFfI3d/xwKXebzDM9Q85qmdWHJ7we8gdTHR+qbucB2mjjN5fMXQI8JY+AR7xeNHJHh063qh0Ao4Begn0XD18ulhDnLuYBqFWtDxWIcZ84vQAnyHwkM4G9yrZkK9vxPAKvYYU6Bg0fUuw7knAM4Yx9YsKUoN/g0P84LrEEKWn0bapDngO+sWS4vQeXv1q7yF6cdlu3pA935TyQ/q8OL/8VkryyvCdNr2u0XxaSKdXlHXey3ZdPNq2LVVAQ/QjiCJnAiWoZjYnh2fCIy7CZbJ4/5IloN5I1rGcpiuLGhXIMSygFoJw2BPyo236K/bWzLTvJOGbgrQ81aGypJm1TRzmTOzdJhL7Nhh/qcezqVQp6KVVxXP+gCFGJFyweHIOejbenmG5fgNgBgpb/KuskDDNLWA1TlW24e64WP7u8Swp18TNGWEo/S27jU8JVTlmmeHBbYdsEAudd2bXFPpUdNzwifGpVfEqEfvEc8RfFUZe1YfdrNSkDuLc27LLCoeaQk3Ik1mezRf8m89ns9k8vZXniyXjAMzuX6/ZpFXIxerN1eoNVobYJCKeaT1UQvgUNxS2/YLIU3lrJo9argh1eVY9aCioVpoelTbaG0q+MY8JXWcegyyeuvxuycZzG77D+K1KTXRDQCPh6XB3iD8e7boTyV2ua3K0Dr8VhOdwtL0aBr3lueeQMyjiyIyO3v1KBrSQiPEA0gk3NHfwQM0qCae31wfkuuKx+gOIdODQQorauzu8uJUWp3cYJ6W6PQ3OblCfSFoooAimZOirmGR5i9gfR/sweikADunTxdec2sjn0wkDqyn+CcjfZGJCnRm0ZQJtMO34sjYWQz0KgX8rUfUQsIbntEtRDjWHoKe66u+s4qNwGVARv0WGVeRnuUCI2Yh+GPXyfl+CIGB06ms6OEwUpimCZsI0s6vhRO8oUJs/wo4rIiY3K/KvSW/ZoBMU9t1X/AaPDTu4EKvl5fuz+298/t/97XWxKGfbxfy1fPE855yp9b1NeXHrp5/N5owY0AoQsfXymsqSTsK0MHVJcVV5zKfkQr7fZYiSfinidFpnoACwohOCz+omYUQYzKUYsOLAR4VsgaGz1N2F2bMjRDx3WKQiVRrw8QeX67R+95K1UnZS71UK+ruNyjJ8+qq5GPeojXEulguMrnGVCijBGxjgPrCSNbCK0NxKTF35wbDE2i4xdSL3mAmB1KLyCmP2hQpkzT51ukyucXXBZc4igM3Xq8eff3m1YbvPWbl6zvEO62L9/Mlq/eiKxmGRrBgN2rI9PxUx/yzjcDct70UxYn3mhHnEb/XXppDJZIYH+HnV1CaL9bOvrVarRWIOYXCJYSLaBlYltSABvTR8YG0GjIUtTVw1aqWwyTL1q6pUpV/Gj0PedXv1P+ht1qwaFW/vRw9ZeFPeri+vE/XTYZ/jPfQHc460QsnzX91y6UAGf78O0Sa42olinlPimRi/R2zw0tE+Chx6uB8CivnE6UN4jOH6m1ZvXdXZBmbzqZHVeaj6/h0ec9K7lamxuyvO3EE9tcfbhyjUZj31eUy9cR7HU/bxxdZxbxwhznmOcD6CZ5/uU2Ejmkxh4f6BydDVRXjBBg4p9gp+fg94PaCAQxnr1UMoxQwKYPSTEuQoGLNawSwdFsyaFoq/LfjhCWSl1RDQn/5ZhykPMz/uV00KdZlqTMB2zedxqyEBtQqItDixl0YA281/vkw//+wv7jxLFsXs6Ty5lc8ZK7ibXF+U89s/f//1hLOfJAFRMLfLLOAGZwdwd6t2n3FGMDQARegUOw67TM+zaI+k8CTMSWo5MbbSO4w6x6LE+uGEz6BhSExkFvD7dZbGNSePaOtHPisSFatwVJiNi2cVCldN1Mhugp1FBKtoqqaoeKlVAZSqQQhfZp/9m7/7/K9/s8nW6+ecSkCIOFttn5ebfPXVY7VWCc2zdLNdae0yR4at7iXpVxaTqxZTzyp1SYKp+FINVLURNEI144YoK14bslIRy5S6Kus33jgAUCtCmVRhWqGkgXm7QPa60rtPwcJVZwbAb2NiyAnu1SGPQHXQ5fjw7F7jgrr4Z4Ecqv9ZhA4x6XXLEPLLDH+pvNpw1ICLg8ID+fbiCIxUU/2HVinAgdxQOq3DQDiS6GmvH8WnT0RTvT4Mh/XooNdoo91fT8zdcdnT7twhilXvFfcHOI5r3KtPi4Pjdzl7/7ojkzvVBTH3s/k/ZtpOD9k45FUMwRy3CL/x6H0D3XJpSxp+rmQ9MIybaJFP4Dnkh1PsGrZ4IOfAEh/UeYD9EDjq+2+hWOymW3WpGvOf+Ii9UIDr2TIVQKWcKLLmJFTh2Bxp6wG1CMpmTVAK4BJmVS0HhUokN7c07yJ5Kl5gaIIQcOb9X2s5Jq0CAisFXCX78KSrtzbXS+D59g5ztTmNiqyifJYsV3n+rs4LKziDSYs/1ZywaUWlzb1m331j7zepnM6+lNI+AhDyZIbU14cndDcgHyT8Mo9Zw8aeleNequ81Yt+npBunwC4kmuhan6CeeIM6jmirq+rFj+0CJ0KoEa28dg9K7fr+m3DI4cEuQLVG9aeVtKDwt6i3ElTnw0b6qIyMY4Az5/W+HmznilqYKTn7XI+2w08N3306PTXKJJp3OZcXoZyo4KLhQUXZbLbPruc0F8tbm+R5vp1Td27nd65XV9oAlk76YsFSAE0BKrb5/NEqu689f7RSXDpYxG/KmGSNVWhtAAtZCmYUaUSLxSeqDTauxaPGPdRMVS0VB+onCOJkNzUnVC3166wmgTUFjfXIzT2m9SS7y5RTC1iDD6de098qE96T48qMv5GGflMCz6rU7Zm0l4wDAw4J5+OQcYldqhH8lvSYdk868nBQO5AMzS8AoWtaoGokuuXSgYzY1WB1yEPMc0o8E+MfIudUXI9ANm+KTxzLTeG7t06OMBmkbX9nqcgq6iH/+BugMaOnW40qHrU61j82vQbVZK8+93kAz0/9Whqrg5D3CT9P/o2q5C9lFPVEeHTVW4/nsecVlz0euLkCt3iwLlQX4zGQfg+AEwbxdTEEhUnEPczVUZdoFTaRIyrYaE6FbRRPJz0RlFoIiqKYa0EQRXipvlZQlZFk64RdHS3mZFNFhXHGIp09TGdPtO0iUZqmcidrNnXfXm+KZ+V8w7SgTV4UMx1EYDLkNBNuRnRc6HpFYAF0hQxZoShO6nsmCWMmuCP73RzQBMXZnm5QGMjJSIZEkwpwl6iJEj2BPcCnQprGq5+H0/bn1TpUTqofXR0j4VYJJxWYxOkdUZxSn7p8riKHgXhQtlYGekxzdv2hxZcl81xBQE4dyvOc5iTXpuAYiO16u6WNQH0g5l9v7q2L1xXNw0mNT7iJM9WYKqM/bsz8UQUCTtAPJ6VMCzRQ+8AIsFTUppE0q2qcQ/lOsPR4h+CYhj75JusmI58H0WwTK0+E+3m4H8IlGB8Sh1AfiYssTOY6XSgcplwT0aaweoWDB0IFbqVfAudMKmqveIOocYZM5bfWDY0z3Na6degV2mHc+9srLaSATaLmE8NG0mGW2AjOTWQNtauOkxX80fZr1Mp3zsGfYAaqg4QGDv1UB/q/n0kTukdijYw53rvvgHHrvG+g7a6a1RSJk0qw4/9awoGf5+JzoNgG+pAOR5Y45dNwf9yjEKcbOnQeuphVxSbcqWsAfcPZ3ObZYIJkVuG+iS8XHyVzTk5lq37FTHYRZhE2sYcPl9RUOKVMecD6Xzmj9ZlhA1SARcOgYA1AskwStmAHoDWeYDJZKN+8lm6Wa4VlBHFFkT2fJUu297QokL1fFmpVcL6vmhaEZYgg1GMvBesZkrzwPbWU2+tqkifV/G79N2rnmNmoQMLuShhKT596hS3kanVWg3+cbc4yxPrWhVhOZ9Sixo9za80aeb0P+zDdP36X6bFWMW2cjgS17VUBy4XAoWjxg87fDDWDSmz9aAR62CnhYwU8a3hH/5TgLILtGxoyyu7nM8p9BpCpO9fr65WdAq3jwLTpP6hZuXiQJo+0eqFkW1AtK1GdpEQ396zJeG11gG5+hKspgIo21Y3znq32gmkVAbNoudJOBYcMM40sEtwlXbOHlATbevFtqlxdZ9q9g71r+eTig/v+D3mreHGEu5S1S4Kjy3uvh97PU97tEbO+HtAhnWOyTnpInw5iAxBTWelUuW5yy/AG5d6H6L3tfOJYqLdPOihwqA/36vJyIUTlewZLI26xmR6BxOVLbvCwYw5Jb1HFbPemT6ENzKkw3vfvCsf1UL+YvAdCRjBJ7xB7s7StDFwtEfCb4PAUywrAAxL7+B/A6qVCxa4zmnZebhMddRahB9UPkPlDricm6vkK7RweOGNtbahThzECesmaJLrytYuiShq43QEo2KEz3yc/OAEYCtbU/W+/iARLeiJ2IrhhZo8OlGV+Nr20zNJQI4H+VzHRLkBEXURYcOdFp5hO6y5nz/L5VZFsOPWJGExbf3JmMJu5FJwvtskzojzuRGW8Mm3Wh2uouynpmlZA6d68TDkpWF3Ilratv4pJjXTY5475YXT92F1VjuHvNDLT+ekeOIdEvwZToZJR1ZcuiSsQJPljF62CmHpsHkV1o2bQ/CvKRZlcckw0T4rUOQwsnRHxz/iUSQT+GRvFUks2m9e3qzeA0H6kmjBIoKQieLjY1DRuTOBnYErDA3CjNmmqj1DkE4X7OjeAlH5+eRKaPaotQl2BVlVV1dtz+KkWse7RJcA3eLn4b1iJb9D+WnTXA11IjXvmzxcm6Mx6f3vYvUweHtPFXwzh9RASbU/HGeI37RyAmEt/e8X5jmkY82in45ZuPEusjVc/0w5DYG+buEY522e3zYfoKYY6jiO7e6RT1Mp3Ffv9Gam/o42AcdI5dPWMcQbTndbwFD57dUacqz3FUYO6RRlTJEbow8mO/x11itUNpgN8GjiHPnTKwnq4e+pMxfhAHQ61MZ5NGKfHzepi+ldAoY31QhAsMc87ZwSAYEuTfxQDeQCkmJsvF4+YVpEp9IKWiEhRlcEJm8o7RFlJ/pRcumZXq9VmvZpdcDgrU322tj6AaH7BLu4WXxHCKZbiWAAaAIviMt+8zhzuopyl+bMiWYgxu7yzdpNxiXm62bBzkNYM0Dyov+lEYJSOKVuZ7+rVSlZAqnuNY33/ssayamiFN+mj2xfuZMzpR0q86kAQqslb+9i6evEditgET7vK+5g18yuaqiB3bqgd0MQ+7CkoDJk5UoBYbbFzBSx79yh8ZVimKHZUBOGANUHHh4zyD9PlY6L8TK0/QvB0u35ebK9pPRbJPGNWWMF+oFdMNrvOn65nj5mKpvrMWRE0ZDlJgKqSP7BQ/nVam2KONFVaaiwnUqMID2CqqaDGpRTjQQpFqkvbcn2v3OiYYeFLX+FWOCBrPKp7iY1d7gYldynPad+7bxvHQOFpV6zVuDD/pQ46ttif4d0e6XzoW66lTPtxyEsRXteuMF9fWRM4RMyqpPu2NxbqioPmDD7sKtGBxL6N0zHieE2IMQ9IR+U7bumQVg1ZEbcGvO+h5e1x6TGDSZrEBPvTLV0aBO52v3vlqbL9BdjArR/Ej562Hdvjyq4hruZ9459Duo5rA9XO3GN1HBLd5eeyTpHo5pzCoavVoRDX4VCq2EuHuj3QhsQ364FDbf9W4Z/fta0KUxWixTqVZxykKQ6kbAaFMpzO5usrBpNi9X9LKORSly2BlcJrdaQqYCL+2qyFwExudb5q6o568LO1nfRlfaoaVSDwon2QLvKrT69+8+nz9PV0yRgCYV6ebTgKbPXs8eXlXCcwwR5m8OWTP7onECeVpawU3V1uSHiu37aOZeiKVD0ag1OVCvgHJWLRLbkH8QnIxzCJlQiMdgkLVvVotjvcky1hzqcF3PFppyj5mBn8g6QGaoOhHiIAJF5+1A3E80RCEIaNCKvnebZQv3yx8k7/LF3SOHx49ex6mz1Nnq+3i/XmimXl2+vvXW2YWsYBc+rCp9dfDVQxopKw9lelbFVIn9rSSnnq2hea9K50sgQ4dlFLNBLgRqkFzEoEjY+BxCV1916O2kCTBg3AmR5gegTrQOW0U2w6k743zqbXy6cY2Mvwxs14JaDjAa+0HfCLB+xRJHynvOb44x4txdLPARCRE/aQDGbEuHuRNNg50HuB7EPaZLAZaYeNKBK3yeK0aTZ468qa5FzjF5TZ+y5wfcKM+UAIm17arv5dPQdNijM6nu/lE0wOfRsxj2466IwhIR2P83RJhiAuOjgkcBvCPwAe9c30Wj3Cquv/EeTjszqlE7M6hw5T3em90d3e/VifkPbC8oID6DI0kcICGVUJgSxYtjkQevnYk4XI1v2v8FsBkCZp0OXpHImHAPNIv+tjOGietCCaYlFsrtYKv1KWa3KEE3M1RKTAjD4Opnmoo9caDMXT8s3/xy9/87dfPP4v3v+ju8v75YxzhBdMAmccYA4rosDtc+IvyVUzg0sbttSOElMDciPhihlATyHar+B8BALs35HWLPZ9uogg0dC7Pf1dyCBfV8zvIDVNiM1pcKjQmnpUGM6rkdV4qIyuClhBt8JsBcMTrwYipPVz/Sk2tcQoGygYMUBIiNdwkOaFicxidzrzeTfxXaPSLNI5zUYKcjtbLtfJ9WePV/fXTx+ls036nFGArHj+jMf5s2z2mo0RbQjwWTNOPbMZQVQYhKoBapw5W5rWIxUJ5jLcFFCgLzWgqKqV1KD+QUb1LmcPytnTjHUIGr+CTpzMaGk8/RLpGPbou2WIMPxOjbIeoq7gTsvdDQoJsj0dQ/bw6mQf8CaP3v8dNjVgmpeCr1u/jzJwGodaXvUZGPLc+t3sd84UW1oyDn903zZ+dzpyY80PlzBK0ZHV0MRIDyh9w2/5tl98R24/WhN6qCZN6u6T+1UV6rCrdRJwi7haBDzKdrRE69roHHgauEaZ2GtugHA6uGvEsDrTubYxD+LZVanNrvPsDj2CsMPpzIDxEhwSdrohscODDqezHVL4FfxED4Si8YLToxWbhTGBN7GPek+tn70CEgJZSrMpLDpUd2ndbDAWRFdQwJegS7GRJAhJTQLW8LKnj7Z0Z1efFfv/KOqfzfLNWqEVAf2GRb5qOTAtaPX1iqOentzdvnMrudwWbPiSp7Oc/t3Liw0/2Bb1E4iFsF8AD8NMQcS6pjyZXgZVU8Sv+pPMXXKXMiR3TkXQ+wGBIwXKXrTpwMAt6E/CgTGTIDcG7tACccjeEbimO9yAEieqUnbQJIqYujftXCyrFh7KLhCYmoBVZlarlKh77okDynm5IVynGKlbzPihTmnNCWuAtyVRvNqTK4qYQH9zi5XkW60VoYoxP00jTrCSFtQZi+6J+FVFNSFNQJHRprC4Hyx0oE1gbQaeSFqAz7NqNWk1OHlibptQRWDKW3Lg5ngDmecCny6kxSE8hgSqxulzaf6KzwvzwPTi0xfm1XWYB/DugW4bQVdRjawBqNs9+0t0P4b1242auvcV16UOrbcRG2OqsGYA/OPaZ6H/I2Y7lHat8M34HghO7vpMNASS4/QfUnUi3P02obT7+R06ztPl4qKn+LNL2wOxvpluL0IPZgd0I/4/sK/oUB06+Huqm/d/W7dl7x4jHac4wOJnhTUhP9QYhUMKvpRHlMMbxtISIRxFSQRGzG7fMsXCgGIisIVATM+BA4TEaFcWWoGmrld18+tTN7DFRgEUU7Q1twMAfbfa2ifhnFeCufwyX7xWLvLitub96w8pBduLzss7BTuDKjaz1gJvGGlk3MCRAB7FMLoMKm24QkYbaYcPCpme38aS9RLBpSxL7CjPknINg55dniNZDXXlZ7mGSwmR4f1BlZ2t3Qdxuso40xruMuIC6GEFkkN3Eg3kxNxtkpfqh2qGKkxWbkqaidd5vibipi1YFlo7Dny5mF/cenhx/Sxbv0mtWCQMETHf/3GWXSfrH8n8/CtMtpEliWW5CrJVH2nFWlGyOj1N2Y2KrzZNgnpYSfXZlJKmVsymHeuJqa82BY6xLzVg65qnbKHK1fqoTNRDffkYXfMcAPKQUBHXiEd+OpfwG3okl8lkQWkvzMl0hyAOvG+rX4QHxmoAp1cMqgb/nK52KLlJv5uH6Nmr/HRg43ekKTeU2nRuB2A2ZUHY0OQARjvU0317XPyw0+CYFG5u168Rz1cnAYf6FCTyAqSzTaza3AKKEqOZ5JvoEaR9/BvCDn8Yl3w4v0GKERf30oDPX0u9Q5n0cn45gS1Lu0oGhJAIOF1IyHqVuDEPnL8y7ilH4i2TqQhb3w3r6qf71NsMslNwrfpV24AMwiSP5c0HTJCAguUBIEDu6guNWCmn8z/npm4LdvaxlQBFPmcmtXiAlGcz+wOXQYBtuXyyWjzf+AuQKRwS+nWWPWPStt6LKFfZUqtsQLu5XH2z9af4b4/ZO1LxrRV3onCveMAuEkI6RqhwamCD796HmDik91I5guPL8JCS3ZZZuWMipz60Xm0qIOFxVc6BslKjSQXQ/3afgcAwjYoU2/5bHbIqodae5vUQWqSLLefAsY0UdqXzPF9kdP+ztKRgl6jljCpGNvNyVFVfW20vNGOMS5O+FMurllh91YM9FWwtpYlk1CtMoCVJgpSqrlNZ21Q1s6phqkcMbVGBAdJ8YGECp9FBJI6j1yDCFOJRznXmoIQa4eY+v0HRBxmFr8MVpwPw9ISzvSHmp6s3vaReWhNOd8LNc8DNPf5rgSaXxW4NQEfzTnurg2EAdWDwCrN7L8YUXfSzra44GWfpKS0zcHZmG9Vx8+1c65GWXLAgtO+DoXu1hbZLFcj3J06wa9CicZ7juX21T6VmluyKY8CwgOCJijCS2JpD2cvG/RlYBZxBewNGX2KwFyHSqo9uDHacJl2Ox/E5lGoI3/v+u1oNQbwPkhNzB6+6zBQq0cXOpQ4ID6G486CBg/knaX6RlB+ATUCk3lOiKusytXqmWTrs1i9iZlqrCmkNgDpzdTGhRxsB8bhlWj/8gRPza4K1Mgto1QRglxX2+7+bpM+zkiUDZK+T7WsZx7+mdvySJBJ9iY+FZXB25RXGVRcpl1kDmp+O2IexY2EU1aMCxeoKCZ7jk3oDs5CoKezTyfrzhhGg6iWJuYEgNArDAlwxc1DtFsqHyNb4RHbssEx8dKupDVRxj7JJGi8XGx4cwzQxfSolRF9bIbIGKXnWYuTuDU2idmq2LKH6qC6km/mMtiMVg5h+ucmeLrQogNqzmc3XeflGLgQGkWgtUtMw9FmRM0efrWbtVw++cESsPmDL34oDBQj+i2TFVlcGtKlrphcjDyC6Yaq35ma1V6mexTrJaSrQAoXIlp6bWY4NUE+++1PjW2ZIE9fnuAt1P+H9tmNyM6nxX1V/X7nknrf3yXY5z9rpEyyMJFpR7COJ8PehejW3SnIIVS/bofd8L/ILAMb6xOlTRPfwOdlvQzWhR9Ypqndou/wNUvbUeXvnxev0euohZvRcfhAY6EdeRtkjrcku8O9XYoccEHeg0dRQ2QQiZxjE7tU0EIZEoA2QUxKHGniKrBdGe7RRMeERRfPCDHwl6CweUHGHr5N6PusIqoKqsxccndqrhoFCKgVVXIrgTQWCthkTfmyCtaHAg3kXXIRVmucDDT0XisMYDNis1qXiNm0PqjYAQZ9QN8zJuEiv8+yJunTppaUJIT5fZ/MnampYLCtlpCKNCAVepoh7QWboskxPTrhDFWxvoVvWXm5OPcKmxbX/MebivIa0ailkj8JVwr1Rxb/A8Hdlnj4jSh5HrgrRacO9RSCZnldlCBCcSYnr2SJwg+9uFR4fFnGTocDbztfVeluqDcf8luwBNSueb7Itbc41wTmtyhkjABwIkF3m2a2UiT+yluZCzjETVJdFdidnnIBaaVUE8daWNUvBVGOAISgfXqfiUelsjXGsF5QK8h2keismulv9l6KwBgMpwjHWSlQUjVT7QXivrtM9EJx+KKujCbuCnNU4Q+rEOEKX7dkhL4MOxxmF63ZfqmEWL5OBrq8r3iz5SMspRpm53gAYtnxKjrfXt2/Kl3XrhF8EezPHDh5RKhptmNL336NVxKEntwaNqFBrXqPa5wi+4wVt4wLppYr7tpvlJk6QdIHKmGaXMDtXr0XC6vKMW8nd3A7nIUC3zTqE2YDXEvFA0Nn92UDb9+C0R+rQZV5r1c3ZCwlW7DBjD++ge1I9fPZQKPsQKlXVGr+/Ak4QWKHQBznOQtF5wCDSYpGlAn2iIYuT7DtASoEVzpdqSqsJoBDMHgERvBEY0SQATRETwT3LeJPi9WQ7S2cPLTiVImoNcAYTRznxQGynhsJakISQbpts7pbbu4mdBbZNnyOgWH+QFz8ngkuI9CSfnUOJD+caEtAIA+Gf5JmW8A/B2l4H1Sarj7ZOe29NRWos65wdO/X9Mw3k7QoCgnxQ8/B0lecfBho5E0AcIjHV3FCjDVLsyRgphMVM7vw3Mn2m6ntmHMVOYnEMFVKhXfDpQV+/K1y8aXPgjdnILVJGUiTNREuOpaonpb2HO9LTdCsruL9dvZJUAq1+SBnqmGJrAm1ytK8UdUKTw26liydlcjuZb4onyTp7lCbXLCTPWSFCA3HDRlKc+7VW648JY1uN/KTZjI7/bXq1La9Slouw0tf60Wl8qmKoumA6LVFVTlUZGgKQb+8lxWWSMZ8HM3gP6GtATTJtbEDJarng2I2Smzd1DoCawUKOXGDuqnv6a3hwrxRUOTUzNH4lsyWteQ28305/f8a/dC5yCiRWLvyqOrBpkd5XQNxSc0lM2vfr1sw//9OAJwcFOf6hvwhG1bW3CxmSW7/nd/ndsu5CdtjDqViHblkP0cX6xOkh/CnwHj6Hls4UMYbTI2ucdqjEB+Bd/jXE/R17XYLr3KYSrS9PI5O8yQ0ApA2zMlUa2f7+bhK5wg20hjr+MA2rInTkHi5N0ES0JtGIvS3ExiP2IW7cyjjXdTtOw4bg79ZD7KJgmXvJPRyArxKnecBr64uogCbDSo+bPqsoiGDRWgaAiIAUsbE9MV2pwhemInhLWoIAjlwLuBRIEWcl8/k8ZxYH0yfyXI0JoieGCnRyK/OFFKsTlNknwRBrfTfbdFPMV8nsMXHrarVlBkiaL4sZizsf5cm76VXG2WDMxrYFwYqgynkuLuiFGuKETPswvfbdZKnh1GboIQD3Ucf5ziCGTEybxpK5u8Z41XkVgT2qb1tNKimu8ZLaKPVlF5rgzjAKHiPPQm0tuQZNV8XFH3b3isNAbuWybkhb6+YahPh4x7cqHxMMsnNAilpvqnJ5cZ19/fDj5GpZsrNnudjy/LTMb90prxd5dpXOLu7cvb15ttpsWEnCCdPUJuoWKwGYks8mswwa3CqLayoD6wewWDG71y4bKdpQ59YbhJga6vsv1huaGHpUdWWGj9qm5j15jjlFuqQeGvvaFav4qnGKXdz5Zg233susdDeLyXf9+m2wcagMsd0qxFD+NwP/VpeIf3v2Ou5cnnc+p3HbQ0323qtmMbkB0M/RRNEnR7Vstz+6fp2iV7+Ym4Ie1949TpvelQD+ZXbH9H+xB1qHx+lQUXV5nqmVXNWBLv8D1Q1uOawSmVzXYUrJTsE5UPFkkOcpHj7Zn6NW0FnLj4qC5BE073mtex/7ER3HZyczUxl2LXy9JpyUD0sppiZgVxQFBC0UBxH3aB6+xW4KrXi92JYqCuGIwgm3tEcKiMZCN3p0Zxcc2rqiQ5hWgJiRqcn+TPIg5BeZuoHpUlXvPpOI0mI1S1avF/kTYn/6eovsSbF986O//s1281lZ3F1kz1gnkLPkc5Pnr128/8/+SXrnoTp6JVMam67Scd9lOjpS1HtdmV8RRzgxu81b8dPUdO+ZAMHz4VVDIuJf+bIhQ6h4P5BiNJB0+6atjLACUrxPvupPlr21Xd3W9jhFrrWsCrwpJuUEPjV7cfbLme+ehW9PNah6BLv2npwPll1S279xFb5p6IpSQ4Tmdy8yqgGRPKX9bHN/Qy0hm+Mjnl09zp4VX3/29fWD6+XtbfH1s+0zzgDO1pwup0MB2JmHs6HZHzTbbLZYts6uCs6Y43hg7dOpS5PI5ChaQfop5Mnu4FL5qJqPsgU7iP5IqNvXdc++1pgJY2BqVgjXqiwJ7VGltiek2owIx+IAq72yTP8Pvnr6/kd5tH/HR5F7M7u/dF3I7EFFik3YfcQF1VH+2C+q8Q6/iXfvCTy9f/24MmrYNeCGUC4D+fvB3bLeT8O3+x1hHWfXFP5TcIZWngzBbfTvkBGnOgZoV/gaPkVJw+mv+OqX4dvk7yTn1ZZUf9nqN6idkuOo+jZ10au8wY8pREFbTxwuZFD6y5RxilnBQy+TQd+8Lu6WUGvCY3A1CYDh0RGO09tZHUf7XaFyR57ixao4hlhYNOeZCmwUO1qrQ0GOBegKrBWmqx+ZdxQRkDr7oajKWAMFBJ16fWl8gDWZBFIKlsRM3A1XjI2vplbrhSjuisbozBdtuqLE0tmzLH2won83uV5mr3HQK7tAPn36ZP3V/OKCEC3TscLrVbbWPPA8u1bEZnogRvIrlRAwZO1NVovKH0eJqAqgplWoPng1smS0Ox+fmyeJYbfZ/V/9+pN/+8tby+LJ0+0P/oOfv/HTH+MrtrCx2S2Q4HIXEXxVA0zsTsQuRUbjIdbPnC+A2UHx9VxSU0E4SFYHKoFoQh24oBmQZVdUr03xfH11PS/Z8Gf9yd99+Pjh1eziKis4XW6WbOc5k79ml4vl7eQpdVLMZuqhZ3XwIp8bExoT6tTHRPrR+BWXKxeL5Xy5YNqYVglzugSNSF3apjZckJQ4SJWVGk4GTJSNYr4a2CryhsYWcJCsqUKu2VzZEpiFxGBGwHh5EyO6k8UVee/lteKVZns94KW5F+0FI4xUv1gT/wLGkOnpM1XgiZoO62UF4MrYG/IcIwD2XkJkU7na4l376RT/9VlktlQZ3RZkF9Ll0WhxntAuD5xrowNAiZ0HGmA97HfJwa3DjowuwHmew94ub0FuQOdQ1rGHmxXOR8wlH3ijZAXruVp9Fc45COohmACaIncCmybKgf5s1PwppWxBUi1yVyXFp55j3erLr5EbnzFOY5cSw6rdK/4enCnqUQetPdV+B1a8Va7Zoke9txZ2azaOOlM1X5G4Klkul4Rm5Nt6X2Is1mdm9PRnOcCNaCCGuagwf2YztLGRySnkMmlDpz2tt2+Vq3vJ7BG56+Krq3Ixz55e5ncu0h8tWSTA/pBqejAEQDf2rGDZsfYJRaZmGKm3V1etsz280BuSXYUpUmM1lRbxjlqO5qohGGfP8W2HbJgg4GzmqCdyT/bhv/pXn/7pL/P1/OnqKpknb/zOD2hdJZyexTCOImdRq9m1Y1zxkydroIRWtSLIb4q1Bhh1IlIsYAaYy7JHVRjngGmSbsLKZPFrtvnfrpjGs73elJwOd311vX34+GqjTv90fVvDT0z9Z6CJFb8F84A+zZZXydU9q1RUraLMGWii/UA/v1qtsgJLNQaSMpJkA1Y0gFR7OVaMFQDF+l6ZLamsUif/2pomlWKsM5H7pSA6m4Lc84dl9rVWIcvF0SXM6LGdtLwujuotEuJ+Qaec8maoZXTZ1jnHfnbeafHc8SCORPcKmO6wLsJUyIAHGu/wjp5TmY/gxTwHdBiibug2hDQA79J2IUf8do/VyQFNuuAeTcY9M54bC5iM2Vp5EnjE8GCsqqjvQjmNP/j+u9yKOoKU4UT4NjhK73dCWT3fcaPQSC8/YqzdEpJu/s5X38L0NQCi614t3doIwV2WMah5m4xnx23SN9AOYdYgnPIwIncK+Sucm/NAqBgkKCa/t8R58Y3XkJEidrYtnq8ep3ug1/9WHFWZWNBkUY9FRcRSRIjqTHUkAnf6TRXHq+9e3GymENEW8VWazRc0APTa1VwgYnx6WReE7NQHm4Cuzn9CKnJgwLRtPYmvjwSw6wuHo9OSWNx/Nv9yU2yYy8FeQemiWF9f5Rf5OnlerDasKSA0ZC5LsiqK1aN0dqVmhTQxrUmIo55f9HWITMc1n7qaWIArBDagHj2jCkHNpBZVRG5BLH41Fkxrx0H5dbF5yGAJferlnOK5/3Tz9Lq8pX4lIahrGwb8WRFULtOjSk/FxKW0/rsqR96NU0VrLTUBaludO9WD+lSy+PuJjo0mlmeRyHZ7zZR9SndDtD/jCGBm/NBjL/XUgsjW22Sl/WSlP9P/sVNxebmkBQREmHxadE3TQCJFJrPVOsA0EjJTAHXkSysbnpBfCARVKYPqGq4AropG1M7S8xC170rKfAmTcO2ozZMBXiXc9Db0W/EcVwjSwdBvhfKvlGx5IC7NVtbL8PgSV7BQ8Q9xYSDCuXGaR38L6S1FznlGAPpKsPao3mKeriEV9oSWk1OEFj+EcTqW2m1BdiExfk86apcjl6vlt0AS97DG6YDQSsQtyDjLRwYObnNP8FssZTAd2TuI4xku0dPTqfYw3Z8d+zZO76c0DIrPy7GLP1Syce0aIe8yPAxyJn8O+aRR808orwafQyyM3d50Y/3EO0jdJxZXGYy3hAVUBEnl7ONytiyTDxQZpdazzyb96vrVZB8LkLa5dgJVNmpZuEco9QbvszJ7BExQBhIYOaCzn3CK3lyB9MpTBCix9PbeK9d3iuTRmgXBNCKSdTK7eJw8WxXL28tZmmvBJ5uFruerLL1dbGh20HCQYSWYmvnuUZqxPeLm/TH1vPZ+Bh4zSyba8+E29OMGKIphXoxamW7KK46tfMFrWWGusVVTi6yUc20JSbXTPEzIBUcE3J2tnkBk6WuxzWdsr1RsHz9eP356tbpa5Bez+cXjL79+dP/Z3cu3bEEsBUD1w1fSX3ZUl2sUdFROMzdk1RT6VEA9fAUGotV/ACbYeFlufh8Li+17m/ViU36Z0P2/KdbrFaqxWmSTXm+Tq9X2kk1AwWb2GdWGTv3N9R2OAQDAI4tJ6E/flKsku8qSO3BWdZWF7lWTYkKRbS1XIAwjPShz6vNlrbyAUlC1SEZx14nUAjEkoLQ1HnhLqJGB6x1N2SNX9Tbwfr4dHrtbmQd2kDp14Juh0rqmPuizNQYe7AgJuPG2cUVjQXJxR1LchxojDL0POwxqwIEeqMnany7XoQe/M8+kg0s/2ANtU056RjqF5asIWjFPtxD3Sxr3zHhuzH06Zky1L737Uk3mP1Q3hkqthh/jvP8/e3/+K8uy5fdhVZk17eHM99439Gt29yObbNqUTFmiQAEmJNmCAAMGPMI2/UdJPxj6CywY1g+2YdOGpR8MmBIpAYLGJimyG+zu192v353PtIcaM9Of71qZUVE5Vdbe+5x77n0nzz5ZkRErVqxYEZX1XRErIsqvjUkZz8yrWuW7XC/z2gyAl7SvWk0JJNfTWqKqTHVSi++hr/IN+XRBh1B+hzQPVNfvsAYfbtHeAe6m4daO+eFW9buRDCXd/UtW07DzUqSNfRrOEeKUn7+NcaodlQya0mcBuJeNZKgUEAnQZJzCAD+x4BmWAeAcoXkDXr5kwP8HdkK0wnICTBr81wwApAAxvfGIUzRcBGLZ/CW5mhU3461YsTFQfruaz9nrZ5Itr5LZ5TS9SEZbjeLqOFhODNCmoBrchaWzQpIBV9xD4/CRrFJCIJFmrJohpi8ghB5dptqqZGQXW1UA/qYIaVlKJ8FKdPUYjUVYfomDtishaAFmTqbsnz+e37x9uXy7mbCHUjJab7J0q/I5AgvTwDTOvkDWxNJ+qJNz0p3/XJHEUdCSTrntSxBrVZJLJThTIXqix/Md2/Qwv5OZ3w6IGyL6UTFXF5LrD1noYezxQ78gGfSf6bQIPHzk3Zgl+UKOYXQNDfmjPPVjyvCSTAh1NxTK2dSWRAlEW4pV2eShpyo7f/oWSD2Q8Gg+RXC17W492r43IoHU6EQLqfMpPxXXflWU7aknxD4Yo8MynS13v0INCYSkEK6oPn7eSwNBn0Ht92JXZQ5tV0WUn63FtUbWMn7gj14FhAyBowJ7lz4py1GeLQS9ApGoSx+T7vXXPk7ZY9+UbGx/Bi+PGYWvjXXrraIvE3s4R9nRV2zxE37YLhsVNTQY1zEOD81f0bmV7NWprL0qreezV28n8OkpopbUW2KNtufRZXOCIXqLaeJwTxG1JO9xcYep9cEafWfvir4LD6DhB9Ln3XRSq3LHY6yzDpLB0c6Lu+2OUr0swUiMqQOeAqgxCt0E3I27hkiFTAFGgmVTJQGMiMvPgftJcm2O/rACqd1o03/ISPTxVCJxRtf7whw3AG3jWVZscRmSR+R2/odXs3nyJU7/54svss1vvBl/cbH87QQzIL3A70cnQI3W7MWecAzsFJcPzhJgdeiXMmJ2n1T9SOLWFcH6hypuvPsECi6P2FN3jf1D5xnIQ7XKy/LxpD3+8Q1hhL7tqs4MrrKJkcL6POAVhvZpEBKBvahUriu7Z5Rh+sfi0TJVjASH/laemJhXDyYZltM82yXXX3092uI6s863Z/BYra5YheHFJtMv5G+VMy6oFpQUrgYvU3tWWJyxthsZieF+0lV2lcAB5K9OYMKCmdXHrDsVuxecVDCa4JT/dswBcevJevc620wxUbBndvmtlpez248W6CJcMp+xGpjcbPYJ3OdoAOIzAf/xaqyDIy4NktNBvXcqC8oS9rdeLd1pn1DkMqtR8F0V5L+gvKSmH9OrLMK/GjDXtBVMMAPISe9dK49lJAPhsvUPRvVMaQcx0N35it51MQ9/78W/xZ465H0YfulUgbbLO0LoDqpzG1l/XPw+HCJVP7fhqXG5w3MNoTy1FsMlqSm8R5h+GeIG7So9NGUIxPvneOTdWrxL7H6Zu3IhSVydLrJmvAs/vAq1grr0ZvGlzk6uUZmvKew+xnaB8x/IfWR7qJNbXBXeXP1XTNxP2Ui9R9YGr8ER30mhg6X7SCgN0EZcPT3PG3F4U/awsqJ+HW7DX2WDtBGxs+YqwRmACqzjHAy0AZnUlBy6JBiqRrVUjbMyJyA0ak7+vLL40/irQS/cz6EUqLIXELMBYCuBS9kJY9sjSEYEoF8LNEFpEGMD/Hnx5Z9+e7sdf55k3ywWX4y2X4znX/ze2c3Pk3/xfLMcsQ5gtwT1JdlkNs/WN8vZLNPxrviQaLahlM3E9hpEd0+UUFX1okBE1xZ0fZRaCQTOy2NNZxYRkkNA0Hp/uRz7Zw95VnQlsIrO2IqSPWoEMuXaI0iqqRPD+WoM06OmSaBlXQSnpBXb5aZYr19/9WZ3M7ldXZ//5JO8eLK8ztavVuvx+u3Vq2fpM1bDyuVeihKkpX0QzUQnDNMgy16ZpiSXzlMH3T2/wWgrQSVymUFDUHaHRvqtezCMT4uef/kHr17+6eeLi8+20y2+TNgC2w10nATMxADIm47CeWDaOIotf5JknnNQADAfTY3z2Xx2tpmN2CEUQ0n2Jlel9VJ26qtSXRorGXmg8Q5KkkRWX9Zgv5QjMU1oMVC72KPmG1Cip0FmyiuLEHUUtMxlgR4+iGlQxjQnhr1WcSYXPY7pCTez14jL+kaxzj+UcpRDlPVj8IPQQLNNg1jeNWlTb9bQyoHgPQfu0Lu8Cn4/SdpQ2R79nMTwZGIJPbHVwQo1qtA7Tom3NBncdukbe3Cu8b1HzI6xh9hX3r20vVy4BiX2cH2QpJMssIHVjevVZQX2C9+U6m58ylI69B/L0CwxTu0Px7KdyqeH3rVdKzrWrXeS4d9tyoL4YKwr+i7EtagVOvRxgJ6HsjqFrkeHDTb6bp1C32BwGKE2EktDO2gX/fInDCU6YSJhJkvlhmEAWOdRcXZV+gcVCRjhoL+yFmaMX1zhYgO99sGgs7n/A/oTFnViAgDllAV/DO4TeAPltvmProvbdfYj3LyvVp8xvJ/mn/x5tsnXm7Onj/P0KtnO0rP1YvY8n9yu367PPn08WrJ5/LNE0wsOlCWkitR/ySGRibKRFaXosmp5sPU5SqoHqxF9xYcwJajAtqsqsp4m7Ki0UhSHknrGJX6UL3e/+uM/2F2zCU7O5jc6MlmbpVoGKW6mpdAgZ3x6ku38008++b3fxgkmnV9cfno2+mTy2e/+7Z/8a/8ySeu3m5e//AXraT/5zctk9Dl7aDK37OPaQrqxzBr794v+wGUguWz/urpKwvDhvzXx/EnJzSrv383dC5Ur1vnYPJKT4kd0kpT1INnk+vXnX/7JH25eT292f7gePS9mTP48my7fAvbX66tRMcME4pjo6XSULXfZcrrc3I7yGTvC3ubTNZbAdnLNMcDWb7EH6YtUzYybsiqSgxgS1C8xG+gttoeVJllYfM53X1W1rwBZ+NPKZLYNIqQ9QFlZQUbpyyYHVAD/CIuh7vv5JWjiq3qEpgyWH/uImLwzXH3XagThvVdjd/CerPLENB7mzoVEHgjhEFMKG4Q3+iZZFb3/9IxiG71Xg7R7uvcSOvmdGcncFPButRgiQ1B7rdBm3n4Z4lVzNVa1x30zkWB9zDuGk8WtH3pIjcPwR5e5WZchHGKphtDHNF1ajWkIe2UDcYxpDyn3muhvhcNcjScvb8+sJDCeGkuLvpRlUv0jyBoSnKcepbBmeiD8dQyEPuQ63+vq11EZ77zOoWM39dyMeefS/HAKeJgvddw6NmJv0Ex4H9hjfifchXgE9x0a8YIUqhMuNBlgoSFqz8DO6SwSAIBbmtywQfOGHjVq7aXpSFrNA7ChC24/DEST7hmYB+ABFw9zv8jyuX6Jck4C5oTXcXr1ZrP5/T//56Nrsl/tcPWereajby+myde/fPM7/9bPn/+lH+N1xNh2zjZCFGxCmoze6JWwB73u4MHpELIltqXjBN2RVmWqPlvI3WBqSSj5eKGG7YUrBf8Nfr7507/Yfs2u83I8kduK0LMUa1Iy92JuLygs3z5aF5O/+jsFS6bVRrQAp2VtptMFTTB5dHH5e9OULfC1bvtbEWj8Wu5Fkr3nUssHimGKKblBHDJalMtsHcdAudWyGO82G5buXl/f3tzcfPnHt8VmenH25Ka4mmTrYpuz7VN2vb15c3N7u1sVK+qOMYQSrjevr5OzNymofbFaXy9H02V+s9zc3LKKYIZFxEp0L0/9VFqltymjRYL7USM9RDYOslBJ7lrFLvXqQv+aS+JTOcuaQAOtk6M+eq/RmoLKYPlRxpPfQ/v78Yg97R1DZb2H5XZ5/O4ZQ/Y4qcYs0Nfiux6hlxY/Xqdo4L0pzVvTRYtbNvSE0HYhcEo9Hpg2SHUHvqGmAysS6NvKInEgm7bcR+NUthsApxdUWiRRRrO3OA9YXO94dYw9xPvkdHppW5F3s/l85GD3XCy6LK2u+LimlE5zISEq6Lbq9jmCZyRRd5N8iFT78o6GuvQfZTy1xK56ncqnSd/F2YV13UaCnxA8KKs5QtOMOYG3kQ7Q86ksh9Af1GtABvsu+8vw4DWk8df+1T6tzGMeNsapYVS8c4Sf7KVhpgGc8dVO2dZTcYbluNnKSCFKRqPtUUCKAXgbijXQZEDIkRgZxR9vFTlSC2T5AKpGZW3QVnMCgl8aIgajTbRhJYPc+WN8W/7gF9vfHKWPnpxN5mDisyLf5NufPH3+289/6wm7uef5SodcsSiZIwUoUnBPTiNmnFS19ooqGRnql4gHXvE4t+/l3J/RZh4qkmbJnqJ4B5hIjzam8/nF7HI1unZtCf0W+L6DeoH+ArNqHyFXVsUyhs6balewZY7pkskBpU//XAcrpM/HY4b9Ma9S+alTTw2Aa0ktRFbr6lN5YGpQ2XTomiqBcXOM3+jL214nrkjuztYkYW2GRdO0SKJCdj/iqK9f/rM/XAHub5bs/M9hXo+ezcZnfzjLp8ntzXTz6Xq6Wo1mX04Y3E937ArKnFGa5tt8Mr7M080168IzTo5b5PluNnrE9ABj9QD9XcHWUPIoY3GwbBw59ZOGk5RUoy5H3zMh1HuF6dnWE5GiyRAqTIT/KQvJ9EYMrufFjn6LjcH647VS1ASWzl1mZxWmgAGXFDGA7DQSmMYXBYQYLyx+jCUI8XH2rnBN7v68MroqRs1fh2ZMRTv4c8Cb/9R3bIxtOuUYUG6c9yQZ4oaDSTNvv95a539iYeJwaJ0y0upVrteK6R4o3KzLcMYuauh+PLqiQkwPqyHYL2SHc7ece4X1t0Lg1h7Ys6nSvTKKt7fJ/ntTEbR+tlS+zrqFpJXVHSK9qLjAOHwHhg+e5Q7y3CHLg4v9Q2Lo+uT+UbEP16zo8vB77a+PYQVAu8+8DxELAgQBOUYG+gDnuesP2ChQDYjnj1KgcgQP0OI3A1Q0sfa18VQNM1tjA/nlty1KuJinvvlg8IaT2eBFcwdiqX/YCgKxl/XBuU0QsOw12y1Hr7LRl8V2O9pmM/a5GbNU9C2nx4IH89FGhgXSSCPwMVymJxWqKQEK9q7npTU01BHdoOuPsOr2k0hph1eVSUJbGsJqJ3zNA7CHD1EG6slkyZApv34eCMjqsgtnFkFU0zStJzDMiL+0qUagMWVVEZZpgFqFhktO4dMZ6e5y2LPY7BMGhUqJ6tnUoRSHIOYJlu222+u31zdX1zvOdcbwo7VSNnnNcHfK5M/PrMWjZHZRJAsONptiB1prsjCYBQO3y1G20XFmmkza6QC5KdMfOioMIvUYq6x6LFUmTDfTeupSg6WEVhsUqT+LEtCHxKenSFXHca1pUQEPspo0y8T647JzUycS9nopo/cRPSFlO8jcQ3vnpEi2WE7xi5NO5V/L641NZC0+sHWC8Pgx8E41cKq2Q/MhVcgbAu9U1Lsx957mnS2+341byBWzDZFtgXemG6+M3lr32QXIRUZI2PFDqf1/FGqrycPEudg9vA5sqeF2s43IHuTtKaM7KbaGfabCddOdo1QW9bp/6Z2lDNdDxOI+Fmec993Vq8nZu0foJCHgPdJXBZw8M9AcrW/GRHqLg7Ee4vjO8J1aquR2j7y9coavcwgwy9dZg64EzywfnYqNBkoJlyCKF4cevMnYaWcyG49+IzDTAKoQouYBQJ38FewCpMg1EQ74RtkTXmfF+I3mFQCg7OZOgrxc9JozAORFg73AYQJZhtnkn82oLCPf4+RsPFqOZp/sRs/BfizxpBgh/vN8/uI6Gf3OLrvJ2QOeGIbANWAOXwpj0LeqhQmK2AJ0Kl8f/nYksqp5qNZJgUG5D4l4QgBGol9yG/sMp5VJgmCu7KoZnj2sdWaHTFSGSrIt0B1V2EFsGlGVChgQN0aEbczfao35xWtLdczw9Qfoo1UtirAGwSggFQ8W9G9KsHIPbmqUA52QgYsdlg7IOh8gFwMTzPhYc1Y65wGZtakOo/6M6TNmD/5mRmAyYT1zNl7/FlXOR4vx9HrM8t/kOp1uJ7PdaKPdPpcZrZvg77+bYT4YKmeuRDvzjDkTTIeByQoSOwrmn50GpigUZKWgCsRzo1N9y6aaJKumVvQx9RkDawXjIebomrbAHnszTt/g6qa9iMrObb3I6it7S8y7L2klTvWHgyglqxGhhFvtutub5FiuIBWCEPar34M8To3DVe72T+fffEc1Yzx/79vvsIiON/8gDsf0c1jS4VNHuYdEA55cBieseIa26MrfpTfoQ5t25W2NDx3AZ2xcgBYd3kdjzYKb3JoxzVx3igk4kKq11OtOPHtaIfDzN2ffitxA6gG9XOzXshbPY+N10RJT5ip7kH808zV5f59iysqdLrJnvHP20wv8mOPhNfBD680Pr6HTOAqdlV8JPmyoVPhDkcAoA0rgK719DFpVtKEQI2IQFg8ce3dBrDFssBlg3gAY0EwcyK5y+JETCgfwOYC1IgBpTkHraoGwioJc8BGMV2zyL3bTl2z4uV5nLPzM2e8FCJxd5bvrnH2B4KnlmvJfydg9UsLyQ0KMQUI+ufxuQRODZ0nzHq7DYg6fJINiDDKbWjQxgrCsiqYK1JE/fFrYJNUG/DOmNtQkqh7bWXIoFpAR3WmxsBxd0IA4lrqUZSdXGFQpXXK2mhYUCDarNXurrizlVZO4ij6SavkDE+OhLiCAi1mzYV6H9rVmRkKkQSbG71ntu8hHbAI6KRZptpjm0zSfpOMZg2IZB89R19F8O5qPJhxlQBiLT4fDKUA1veZuxEp++CrSVGIPKI5olUYsGeRqS0hkuiSk5zAVygIVrtdiYK0isObBC0s7qpb1UQZltEcCJ193znhyST0ZvPZ+7yHrSorrEIe76D/G92sAHdIWd26OfuZdqaHhQqCL8sOMHy72Qyj2FB6ntqVei/tdgKqOYPXTDZ9Fe/0ME6GTqnOk4V03b2Xj3qeczlodY+oZB/YViFso72Shtlicd9LDEIuzSwf3ySu8wXUnmbvkIR71njz238NuWNLJevBaD9dATHkPjZ0sZ0f14296czSi6uHAoFH2Qu4SeNpoe0kS1Dww9f8Cb4ZSDSyRZEOVViZYf8wW7uMV0E4OHnKzLnY7oCuY7q2MAKi19bq4JglD2uapL2QqQCZTQRiVRB3yqhgdB2XuQpqdYKPPUb57utu+2M7fTMezZIq/f3J7/fYX/0X6yd/YzeYccPtKwC15rfHu7VOmAvLktboro+D+JTZYZ8Ka25Lwn8q0mObNldKV2qSvYkqFVY/RZ5RSSjTaj/17cQjqEjGwz744v8wvvtxMi7mG79nqZ838iudETcV4g5ISEpVWzPItTjI7XNRlb6FS+W350PhBFfFfl7aldn3WL2L4I9Uvwgo26Sy5qoUTlVksshSzjFK/EicKFNoHnKu5MVZ2tzwk2DeAdx3nBv2EYf5xsRilm9H2rBhtknRqLjccfcAChmzMMXGcDTzafWVrfzkHLE2349GcxQBZMsm2zzmqLpm+VP9RkewZ+1TlTr5FY1ZffdIFzQdJIrGSxLoBlUQA9U91caikRD2YFllebo5F4sqFfphggaHpyW56Kq8QqCLib5yEqmirb2U9gyyO1qvrTRK/bZoZu3IZpf8qhZHRkLsZE5IIxKmEvVIxwYOE7//2G8ShVz9DKtLyyz4kW0zTkIE+YT0sJnqY8JAZGy/dy2vRYUNap7yjHprcmjEdVfcSYzmHK+1e/VYvCt4uHWI1olt02KCJI+z96YuA/bvldyMJb4t310ViUX6Q4UidP8j6/VpUKn5JPUyF6Rbh29XF8cPtOneX7ECTPIC4QZUMqjKirxed8BC4SVOSqKUcUjUF8aKyWAE6YNwkz9i0h9F3IB4Hzwo+bbfyzPFfM/ERe6YCcLegCIExUJRyw5lP+bQkW7b9ETLDatCwsMpkFDZJN+NvtsnLNTvd73brbTqZXEynmzdXr65ff/3jnz8pihl2Aj8dOJXY+Kyc4AGciKLymQ3w0ilQZYkp/8ugVeY7vUkYuySsBKf+o/THf+O/9+y3LsYbdr1XBHMbUhXqkXY2pvU5HlUZbXU+hcSqpBqaaUPTaPDaNCg9i7Fp2VZjuAK80PLuZVdKKUWS/tuvWooVjrYjYjVxdVm8RFME68mzbHm7ZSyd0+NosgkmHu49ODiNcR5jhgOEDbhPWQc+msyIxBJIJlSWnjO5KWZ/kb/OkxXnHI/GrB9gxgTnqGI2SSfzKesFrDt5gTMdNTeZMzMync45lE5nh9GfgPAwl8OPDF2eZTCZStCvlISi0Z56MjKrizIDQ6z69AhD18bgotpVtRzwGSvIyK1c9c5GygBuD0XilT+VW01iHuHTcx0l6Mn7a5XUr8Yhqggcam3Ukze0TsjbQ/zBJiH8wCqH+p5cl1JBXs7DaWvPibeBGwBBxhCIhPXyo4i2YJs+7mirOfv+8YbBNKfKUKN3XQ3SAG8lkzmMNLfpsk11XXGDLdSYwalWYJy3c/R9SFscMDrxIeZ/p1p3lXffJqjxjeWsJQ1/PNqZhmsgoqz12+HiQHlKXmm0iz4eU2T/9fCe8XdDeKRE/BQZp9fYpA6YMkykTy2g1I+7xjyElzTej84dKgm5gNCzYvn2+uV2q7qDtNh3RfGYCHJhJxePgmo2wgo/slOKoJa5/sNKgJUCzDuFQWr4UBRYELSbQrvcPFtmj+a77YzB2uR2vb0plgi6/pN/8Ce3X6aPfzR+/Onvgsym058V8z8rVi+0QZEsDgedqopqQIEG6TzWmry13VsjxaL9ik8DaKFwFUc8PcL2wo/mAaQLT9G5Zttnk/koPZtiRjGjwuwMGqugvQFTWQPYSJpv4dBcjlI2DTKrYoaTGQFUeV8qjVGqAa1U5Ugp1eW0+wxVfMtnTLRn4Hyl98alkr10knTwb7a4vPj0J59y1G+K18/V21/8J7+gsbW+Fg+gYrbbjKfzt69fvl2vMBSy23y7Ys+flJMOMB/xAFput5fa84n9oGDLSvDReDp7NWIlgRaIw0VddDx5S3iczKZ0SaYO3ONM3Yplw+yLilcPliil0iu1BqAopkxPWV4Y8kWwGQD1f9hwLsUjbS/EYnfuyqS+JKVaZWONHNS+5vsbdBN/KxHgIM9JD9Hbppmv653glP6rFERqZm+NiX9PfUR5IJ96QQ/y3m4V0SOH8B9C01PEQ68SrKuot+ijic1eFc/eUJYTeKH3LPqOCOce+m8tsVnlVi3dq7KDx/696HgOsFWYMrJ6P9ubIZ4BID2Sl+DASvYV9jHt+6aB+Lv6fZO9Lm/UnetJw5+PKgSCBylouEjfC8rw9giBUmy9gFCYRjztHQS6ETDRC0fIU0gJ7CSQWkZX2Ae3ISBRulmxebsIwKPkTNnGf8JejTv8J8gBTIMZiz4N5VIQ8Et2hXx8YIyTixAVMWozkCDEOi8M/M8oMYUnr3fJ69vVeJvMxpstxwzz0wHW++KP/+k3f/z5bHF9ef6bi6evz87/6qO/vPvsr/01tpRRVQx1Ok9xVXl2vxfk6mjmuj47yKx6perqJAEjWzNgEOU6M0FNggakQPCx1ujxgBp1FyM8ZECyJYi02QOJoroa/xDgWTHouXHtZd9TN4jKCGhjon1W0u0hEBwW5I2hO1M982c//pQ/skzOHq2++eK/+3/8/mQ8zTTfcZtlC5ZBX2Wvv/jy212G2cNmP4zVj7f4+iS7m2ye7s7pErjlC5rrUrmsgBhhLqEX9CYRZKpykd2v3U4on39b1lRvmDdJplOcyXIWpovM84gaowAdc5egGvnHvNJiZS4o6cDk9aeKtT0NvZFX+fjvXJTv4GEoow+VrrUyqvLH6xQN3F9jgcO+o0UClP0wivkBBL3KrfWNaxcTBC3FBKeEjykyLqyHr8khXqL3xUkNzqJhZIJXR6/dvy+lrewDy4khDa7hNk1vuS5vUzYJbOVYHRU6kMGS+m9Neh/biC3aLg5Neboom/E1/bn+RdarhyaflpjBtm8sv2u45HZ/GVrEiqIelH9zLCp0hqjIk4NqIJMz9m58EM4ni1JliGva7LcV1fHPlrx9fSbe76tbAfqmH3Si/YOwj1C4btpLB0cTR4zmpc1bxxAVSJM3FP9BnLw8jEZQlGHYGXBKvv5kA7BruSYIavSUnOPkShFgeVkIGkAF4pPHMKHWC3tBdndgq8kAA+7gMLaBZ3f3y+36bJ290YY3WXYxvpA3+Hg2HV+eTS+mowVEm6/Pd6M/y/OfffZXPhnNXpk3B4APDlOd/GojlwYHKTmoQR3otKu5I37Y6b+dmWIPUuwVb2P/8lBX6fv1AEarRqBXkwlts/0/qtD4vt+lpSoGk0n9H5ViZOWMfKMTZm+EgPlnGhYX+69ywhXkCYEyqTQPymg+XFlVRo+vZ6pSw+c+n/UN4q2pZbbQssLPagiWLYC1s3mxZNvPqYzAAtd/zjVYjzj5a8Ox0Ov1bjZLcQ2iU9KX2O0n24yvs/xmlFx4JP0IHyD4jtkhiZ7rvVZ2qH7aKIWQAurWBLnoVgqinsmUvipN4Q5Et6OjqALE0CG500+xAeCf8HOMj9ubUfKK4f/xiL2wOIIgaMqzKeugq1SopGq5qrUBLUl3iGp5hzS4qPqNyJ6I+Peo6Usd3n4d9YsY++9L3zstIr5D0Pn3Z2zSDJdnOGW/DJYa9Faj7YqvkZ36SIsfb6BTmZ42a23c763/1nOivD+/iwoidKNFjnx7hnwHpQv7HoqXXli1GQCl6zIaD36I9y5NhJbwQBfZe6tSkOe9lXifglxdQWYC37kC71Od95D311hFoZs01Ry00tV9BHrAX7icC/0LAwlKCq0KGvEnGCbgTiTvIvCRFyI7YLcD2IHQRKnjmOT7k0xngDKY2DuNO7hfvhhs2EhJAoIwkTUAG5AWN9CbyHj2yQHuRGhwu0iu19mrMQ7vWhKcLXdMAmyZAXgynY1nOUVhs6TjRcI+8dM3yeRavGVKkFVIULKrAB5DmFJUcvdltN3J9RQn72ApHYQMe8aqqlfYApag6RfkRGrV3SnUMBELx55EKR6/GaMkQPvQZEK3yia1xcVaEeWtMyEmqof3NainHDyr7JK/gpZLAb8QjmSMlhQwzeC+HJtyOfsjvbmK4QqmUfzxaLobsQMov4XqQTjwbOkgeOJsp8WO48LYI4n6SQNqVDSg2SLVuWxlWUE4+0wUKzoZoySqA/NftgALf7mrJ5pyxcdmqOSrRpGyEpIErzZWLKuzawYLVW/xYDLNqySvFqH7XHvd7LkQd0+ue15HQu+iKOnGauB1ez9ViUvxco/U/Nc4OdbVr7Ea7l91V+RDdDf9RukyXm4AEHHImafY/o7Fjz3zxEmkcXpHmB+bh76aJR/INqC4ho11kMcrN9SuOsh68OBjxh41ZCYh9nc8YNTx4LXwxBZpm7ZvB59mM3pM3DWaGmvGHLC/x+hFzDkOH/BvPLRooEFzn4haCzaVNpS5Bg6BvMfJu+o+vKZdHDrLHtpn/CsCGwUapYTUfTn2nTXnfuAWQMhQmkIClAApASL4ZAshdMEe+o/QlvqgxnS1+c9ux4FcGx3zO3kkJIo1gJPGZGkwXIfSypgQYBN8ApFp1Bo9GwYzPpTrzOEJ5CILOZQi8JWd7zazbLTdbNcs6Czy9RnnZCXrongxAhmmk9E02axWjJufFz8uRs/z/CuNjos5PLVFqL1KtQZUDA/ejR5DQR6wdN08xgTQI6kW4z6dijm8nDCQe2LEkqpQQ+chRaAKqncw9m+ZNQasapuhZSryoiW6eMAYZCsleitQT6mYFa67EX7x5dQBhDVRDqSN5DqIlxXRecGwkc97u/exskAv2FsOXiGXVUDVou4s5CAehM05X/TqYpsuMecYic8L2pSB+d12XKwnS/YLJcN29RQaTAR6WTbaZGM61SMb4ycvImlWig/UIMxue86yoJwkue4oxjoZvZZ+DaEKonc+4cgxNo0VPRaBlCjN8iHfKzb+xNq0tpA+JK7csZhNUr+SloxaaZZvqKevMpQXDLhqGjXvu0ZsmePgo/G9Pkjtf6jlVVX6MwxO9f7gVXO23P2xnUfvO60mpzi0/XI1hVdviMpr4ROlHgR75emkbJPqgPjYQ9evRlf8EX4d8oQWIXuXTk6NjyW5o7QxixP131MilfW61LBBXBrhWlfZp3boMC6x0lUnjz23OOTNEMcQDm93fhPLt7C6sP7HV/05TjsIN78UB8nv9AEhB8t5RJB3XQ34v+sijtRwQHKrMj98sQfU7B2StCrtHZb3YbEOvSMETL7Dp73IUhZABmzG10HjnQBMgJVAEZ8CTYAelkiWyYqyGH3y5gJq4/A/m83nOFZDqxHccTHFQ0essBAEkqBI2K6SnWtAWUAsOa+rCIwHPhRgBBjEZgjMEqDTPi3aZSjhGKgbFcbwq5zetes9m8PPEiyBdJbO8mV+Mbucj6dJ8WacvOaIKU4SU7nC2ZLVLqFOXZQvmKokj4gCVYTR2UOg4alkEBO1hD0HdyMPT6K0B0f/LRkV5UV4pr18IaHKJQJIrYLUBn2rJTwqpqnC5SfZStYHCdbCQU8HSTx4jlq+hiqq9OrTufhTSYy0Wsqg+muegtZkQJ5NTcf5ghPfhPzpJCz2VZlneX42TyezYoIX1BzfsoKJHjYOPRvtFvLpGmtluexTdT+1LHXgrlF82Z9qZEP/oiFIsmA/vUIPOiiOzYjMlEIUyaJYLmW18hWhPmkdkxieobNzAESjVOOphJMvGIif5+PBGfJYcT6Z4weZIVTrVOn2ygla6mBxF+13sPrBR6MrWuTXTWNHO6F3Nr/ftQ+cotQmLSIGKfWe6jkJuEPAg5mBwKuDuC+6w+7py3Is7UC2qv/1yBhsLFcU9x7iY4V3pvfbhc1sTj9cklCLJqtTY5odxjkEzTTLasYcFDrczj7IpoeYcxx2wsombmTriECftdrF80Wtsy5O38zYUUI9ukVCH/XUr77/9teztD43695K1hN5fw49zINeJ9/ojVJeIRBFGKgXzpFnBAiLfXsMDsrfGXcHASC+gXn65Sh9NJn8hKFR6Uv4TdwAWzhXzM/YPmWdjs4A7mItLwushTUc2HtRd9t0xejZrZ0iyI+psC5yjAS8LNKM84M1tqq8wvmwZ1BWSGsCZlvn06vldDpbJcXTZHI7Lp4ud28mu2e7fHd7O1ucb/IxHiMrzoydj1+MRufwBNIB12SfUH35b1CLbDy5UiB7Tjk2w1B1Js7lJbgf3bd42QmmvPJuwkmZpFo1JW7b5YnVPZCawqAnAg5WRBefyddK3r2wvAbro3ICQ1OWJUy+0kf2iYCsMy6F1EMZYYS26gAjCi1JBbrr5iL5XXHhItGK92+Hf1Ocn6X4t8mpAw9jKSGNpGQ+ZU7G5pGIpZ9Z94FG58fpUK+VGQaznCHeZDvOZpP57e4se706m2wux7OrJL9cbt+s80UxuUrpEeMp9VS7alBfXTRbPy7GpL5m4S792GafkJaaPpVr1Pi1hFZn1o1eUeDQP5lOJs+omOg8vgzQixnsVw1cRTq8It/I0pDRyv6hK7hJ0VKgkdV2+1FOuzpnBrCMYeFalWhciuCfrjLGwh03f3u0vM066OPo5psnXkMVU/aHrer9JPdKDb/Rrg8VN+yXqyZYs773EquZuSlVL466W6s1i/WYFm6H8rg2aj0r6JZUkoLGunR1EN9buxPk7CJ9oHiXuf/LFOONoASVf6jDVokOdNJK0RppGj94M1QNIAE0rKBVR61ZeyOdS8XL3ye9Gb6bxIE1C83WSh9q+Z7r8P7L9eoHbdTq6/I07zWyD/axq149AtcUwmMrE9dJD58fdFKkJA96bV1TUYxFGNQB5OoPYJKwjSdDs6B/Bkz1OjLgBJTKspubW0ZYHS2VHEFF6fjxY1kPm82Skf3JVOs2s90W2HV5eUGMmDDuy/wCI66T8QVbQP7oaTLGAWOZsB37aMvSTvZ0326yX/75n203a3EWIMNsoCjsh9Gb7Oq/e/2r6extuntydnY7SZ4mydWn483Fk+dnZwtg4CZb5dfJZrs9P1uxQDRbM8oMvgK5pXm+YZ/5QhMGWsKs8WfrM1ZfQmFawCtU3g2g2s0A5mEnkwJdlQd5+h4oM+QIgdYMZWrVSDx6G4jYHpq5iC5zoefoKh+suiG6YkwE6funQypLqTNzgyFwqgotIyLqwFUBk4lEzQrxkJgTPeaX5rrZmifhxK9ifDbmYIBxgRvZulhz3FueXPxy8s1/ufzT8W4xpznX5+Pidp4+Yf1vnmI62mSVloTr0Di4alaB6aWZjqOGb8rxwWxHWxTz2ezs7GykoI5TlkGowISOgWgvX76ezacYoHQGBGSlwXSa7HYcZCF7UXaC9JBpjQvdlxAzANoz1KrK9ICpzwr0YveqGRTynCIlxBVp0J5/HW89OoiTgtKbOupJahL/OsTEeqO+odeFAJHQ8PiDvLxeNSVQ07j6XvH3pIRWUUwCCaBUPwnYhbrD3evRLKbJykd0fBzCU93uuZOF12QfxwwfY6gJXnuMeQ4JDy+3n1vg49rtJ1bqg+qw2VkPLNcHLau/avF4Qxz2XKfaxM16xfNFPbMu4Vvd1T2coFmXAwmb/b+Z4YFimroqPf3ib19c1kO1aVBQ0MhBD1ay/gNvhHmAzLx/GFmfMZSKR7/G+lkvOQW9cSjTV19/w2SAu1gAw/CuTxniT6Zv33wzXyy0BZBA/lL7qxA7nV6eP2ZAlgFaABa4yuAfG7PPwVfJhIFcHQksSKYRV0ZYx2+vXm+WSzA5UAzIpt2I8ABJObL10TcMye7O2SkyXc/T0ZpRkm/ym//R9kePzlgSUMynZ5P59pasr0evfv+r8eR2c7NIJy9n539pNLlJd49XydXF899N2TyGkqdf43OUZ58I3/E7QJdj7JzpAgCdFh7gUqKJDIN3vI8xQFAMEUZO+KSruWuQsynBtHi3XLazkKFSyaefBd2spSSzXQ5D1WrUwOcKygQjJewZPLK6+8hTKDYElH5AHwq0nDZiXfE4/DzI5UkordQeXJj8oR13n7D7Z5bs3vzqm8nofHHxOJ3upsmTZJFvpgifZ1tAPFM0o1n6JB1n+WYzHW9e5Y/ohaP1z7LxLpm8ZOEw2waNJ8xSqdeo36Ac+wekv7g8P3+U0rA6UgwB8t16s33+JHn+4rIoLvHqL7eoQiK6dJoul8tf/sVf8KRlvnIikl8ZMB+sv1xtWB7AzqJ0OvVedWFNI2XMV+TqlVZN6U49tEUBlYa6Zgas1dSw5eWsqqdBn/Z+8LdZy7tlEAsjivgMzwSl6+CkLDFxl8zx71r4zY0zethVt1dgRNEaGdK7yg0EDxMYMH78MAUdzsl38Yy7aKyfZrzrvzn+fX+9Hfzydgn6sPHRb6h317juHo7xBoUT6ZRd9T01vqVCpvSDN0NVqorWf18E3JK1OyquGVS1x458XtVhtB0svrvo76nYd1aYdZuW3OjB27El7Z1FfSeFNmvzve7Azeo8UMxhdwg6KjHkQSGCvBrQlMO8bAAc98ef/ujFX/3d33v8+DEu+fhJT8BbjO9P56yh/Af/8D/b7jZTbZ2OowVQCaQMIJrOZ+f4U1CSgL8tupTPdi7jwYsjmjUAFCCgRUFyxgbhEwZBMd/A8C2U47Pz+aPHl3IZ0oirDA15ibMTS7Zm3B6vIYwGCtaZTpzxOmFd5pJDwYBtm3Uyn/E9SL/+oz/+8g+/ShZXo92zdP7ybPHT9Oz1OPvsanz1N/7tx4/OqenWRFDBVnuMQJcS3I+whrqFzmUDmHmCvGUtvC4Pc4elCji8QjkOcEViKlLALCX7PMxTPhm/GlOxCyz3uVqiPLGe4M8hNghjoruiXF/KbrWB1gX2uumxbGTZlzpFd/kHf/Gr3//lqJhl02+K7Gk+WRXri/EtjUKzT0ec+5VtGXHHGji/nc1wN9O2PbQ2bUQn4pBMWyQANleraAaAixXo2nQqnc1n6jhWGS0kYBFKOmETWOF3OiCy0qvonghFl9rtykXh6qvyczNliZK5BMplPYlmveCnKmmxAjLgVFb1W/vqeJ4ya6u2TZpjN1faMaoPKt2b+oMS6aMwrRro6ly0YNflSf4l7qL5nsZ3aSNU55137KbeTdFB51oDcPJ1tFptHEsfxGbSve3XZh19NNdt+nvagk3mzRqEmODrFmI8EI801JJaH7v4tBIr8m46jGzWJufwhUQDwXJVyzfL6uXT5Dw8Jm67OFxyeGflDpfwBErHCnGG4XMCJ9a0RVfN0mNJmm0ap7aHQweJkvVtsbeD4LfFR1QWIYgGkBLSGu82OSDn2cXvLmYcRSu/bRJYf8mxW0Cr6RSohIrwpYAp8B4nHTw6gFU6Zwn+cggCnLP/Z3FJxvGYzRsZYn0k9D6+oiABOknDni5pltyQMx2fYTZk+RqQlY7nePqnoD+OhWJ7HwZz02R6Nn39Cq8MgBjxCMJ5r5THuuD89U3xLFmki3WGqWAeJkX+GAtkPvrRiL0ik7+Ev3a6+skoX0+LixmSoQEKyZ4wCq/hXVkoWyYZcENi0fJYnvTTUfYYOiLNJKGe8v0wFZZ6FBNpdNi1X1dQ0QvQGg+/m1BVWiiipHCUbYXpVj26AMbH5pEMmpPuUnm/Kmlq7MsusC8vDtVp4zTCxlENSdBJvTxPIV5ieLGShH5iVHrTgtwTdvGfTs6nyfn29WtMty3bgGYvGXwv8muG1TnGIMto0nSTs/MPO+2nt/nVLs+0O9D0KwPfWIRC71iA9C8YKlIX2wPh0nOdzPDUX2ScR6eelE/SaTKeIrbmCZALPshGfu6K1XJhn90Z7R5rHcH4Nb2RvLqrzelQGAKyDwknxfNkdEPJWgWgqsloJUXsTBlWVeM86AYHrvAGKPU5KGtJFL0fWt4twzlFfFQ1a8yjue//O94lc/xbdvJvbiR31cpRlAXLchtvb++3ngvCoAoP1Lnc77mr7oO4NiQfkmt474z1H7RBEQcyR32mLP1OUg2R/F40TTmHdW8qTt9rbfoDPUTC+aqtquNECc1gszGs84Xi+I1qZjoW420Vt9ixHO80PVTmnZbyXTH/YNS8V0Cs8PcgXlzcXoiHDlHKkIKcLCYekqtdWHT3HtTXXvZ9YvtrbFUSaK9fyibwIzxsAcbgf/aXfgOfZ8ZHzVV6KpA8SWazBS49gvqMzAN7hPQEvpgEIDPHsjJW6hyEyHAaEt4SmetTJQhui5mcvylPMMvRk80GCMTlk/Eu38pm0CoENnpBYspiZSgcwWI6mJXzobStJ0BxOd7eFNfb0fVGm7Xnt8sNd1AkpYL8JDTAnlHcZAHcLMZvbE9JhGQEFwE4UVEWBTDOTBohMDMJtJkmkBMLRpIy0iyQJuH1V2pQtbrvFXg0WyUkHZQhCbmkeF0hG9EHGdQq1tTWAEYbbiFTiBkeUF7+l2Ionxdb8bQnpZa9wzgrEstSd830jNJpMZ8XY9llgGl1Cpou45TfzWaro3q3Cf0CzM9CgbNiN5dDD4PzGp6Hq4775UEj9PiP4eKzy+SbTwzOaswucO1ETP+jQExSZrBK6aw3wgzNKAN9z1REt+QRa0/9QLMMkkhwP00pC34Q0GORXszYWorUan2wbBGpwPoG5VWfBD9e370G1OeGXd5FoC/7irWqZx3OZFhR3yVVV1264muyBuXU4r9fj1TW/9692KcozNqADJ6ndxegjpOAD9YUv/vKHS2hq/ZddlU/w+ZofY93YD+rkBpbuh7ZLCUQNwNUcOA3h7xdfmNNtneYN3BV1+ShdgPFc9lcki7rtkXOrqg2mxvaHg0gZ7O33G2EKfCpaaNL2Jb4DvmHU/bUtIXJ6VEN/q36g29QRlyGRVbaiXoIYJFxTcDYxeXjv/xX/9pm9WoyXRBHLC77yiDwpCH0EiHJrUIIGqzOsCzDpvZ9ANgByfDcAXi9Zexe4+haVnxLqskJ0gKeQYyFAKeF8dN+7WC+gtHedJqmbPACpGM7IsAguA+OuGUA96iS1hLkmxdZMhtPP2ciIJ08mU0fjdNVnrGGGKciphamuyTfjle4jnM6GcuCp4tb5iWyfD5ir0mAHqaHgTyzR5CB0RY2IJrqjKfdZ+BDNqGnUNkjGmLGf50KoIADhdpzrNeusDTXldYe7wA7/Vap1RnDzoW6t/EKsniiMKxH1YlLQmcG9xAoM5o8cdgi/Ka8Kt94CAb7A17xlm6HbKmN5SeDAOjWKq4VFSY2nzuheu60jzbT2WS7mYwrmKW7VIt0Nxs2+RnLmUdVGL/ZjtRt6FvqNDSMd7cJXviwZIB/Ygt/1UomtPoMKwFSupZEhYNaW45nJju9FQsSOSjSZTJFqfNyzBz9S7IjymZddm2rGNTYGWaAXo3Sa6xK7V41WvFl0bFlXk2zJaxMyzPk1jb3bpLZ2F9b6hCuD0Mz5HfQx+al2cOr8XY6TO59Cv2xl6o9sYkHrKfSKB3fv+g936yF541LatLEqXHYNeAxp/6eDtJeJHmTvhkTZPNKqSI2Wh/wT7OyIUst0KlM6CKp4lw98ojsPvMGntcL6yg9lsTDXoW4ys2e08x1Sozz7u0vUfF73K6XZrhwAYqeQvTgQFTC4Dzvh/Be1Xo/In7fSkGltHe4B/EH9MRA+8MJuB5+OPU5UpOe75MNctbTK/V4j4E5mE1oDUwEfAab77ZrVlhqCJRxWHzqbZwTaoFmGw3VEUtKAbuRplFQkJZBZCPVkDtc8fQhXkaC5RO8EtRiNJgckkyozvutA2wWgILkgP2OpoBxxW41SWfArG1WbLEqhM9UqErT7w0nj2W70e0mXWlX0ck80Q4tDCcXl4/PRptigjcJu8bjlKTpATIu8+K6GJ9rABjMKYAKSCQoQeXuoRFgZCdGm8zgk6KhZcmLNzmkukQubNl9ub73FP7cRr+naUvdx0FXMunmBfVBwQMoQxYvyaWpy1SWHaJdY3EOCnbdoBmP1yNBGp5LTWVaJULNr2OgU9ZqAP1lG5CEnUerZ2zixFkSsskmOoYLQyG/3GbnnPgGHFUnpHFyHSdHTyTMhBC8NVFgl7owl+adMBq1QkQdjLbimX9mPPCs8yYsyfuYGlLdUH/Iyr5V4jtFGNmasGAQhWKYe6JQ+GBysEeQdgFS9ciiP5irrtaVxPDu15GedXfG7y6nN/VD8VcjPNx1Erf+hjuJ1cPV4J1wetgmeycivkumJzXl+9NVXaz9LkD1nhnstpqWDtYU21vXCY5YYDUuxx6b3Joxx3gMTY8ts2at7+Md2CVBs5QuyjJ+sP3aMhIwOG+rDN5hap0j9KIQaM1bi2yRrUbxEI9DSolbfAh9z/gBGoh7Zhx+iNr08RgkeR+DI2kV/7iRFd59qnuVKia7T4gZH74ZFO+Xjz2k3wi7+D8geDJdL9ebzWZi46yC5uZZ4W9CsI75+QCH3GZw0AcWB+jvthsmCeScA2La7QpcvUHk6fRCG/zIsiBeSMngltA82EvYkUhBMCwD9gNlaBhWAnwpuUZTGALrgPuCe1olCqwj6yude0sJSb7ezrYbFn6+nk0v1xuVihDLmxGTBykCLGBwmbCn0TZjp9FkxB5AcyyNCQtPOS1KBsyMJQJFcTFOmASYs5ZmzFHCo6UdO4twmEK4FQHyhPgEKQNydK02/fsr7R7/jNvP9Vvm4UFtZ08QxXRqT4sxmpLeP0KM01RpJic78JSCV9HGxx+c3tkSdhhKVVUSl7UQlScCI0mtI2CteCeZmE6UUa1rg+6EsbfUKdTOihcrW7rN7Ap7SeXMsXAmg/bygXDNeo9kvMh3LCPnSLD5dnszylgIwiESWxaHALdB9Fp0wvg8Jh1D/LAUxjergFZx+G3rQyjH+yZdRRRa+MsEkrzGuJL8KXnw9acbk6SuZyvRbeZI1iV7D8FNnj8cPSdsT2acilQShmi2YzNZwgzPuRWLJKYPKqy5Gm1M5UpDjPLaj/BVMf4Z9LuPtqwPNfZ/rzcevneVWPE7uYrbf1KL2hW/f2pJD/LYNTsR8ECsWGrRlLAZ6TGhyjU5vcTmCHeXhu+jgVPzNumbMaE6QRUxzonVFSgfMNAjj0rpH7nvx0j9eXvrENc69JzeHPdI5EeUd4PeiAfXwZvhsFPyIjkgPf5Q77z15+McHpSiq/jQBftLi5unn/Jjqqu0qVjvUX7/8LVUk7/2OFz+Lm0M5/C9oqw1b+3xWFWMXDcBKL2iwFX48Y9Hn3zyKXCnBOz6Dc21chd0LKdo3GrkCQ0aZ5xWiFDDquA0NusEdIHW2beFIC5AxQ7f/M3N2fnFdA64tzFTR27+u2ywULAOqCb7gBJxDgcYbnc5mN02c2TXFbCahus1Yg8wK0/4oqEpYDx6uXv15XKe37xMJ28Xi9mPZ+Nvr9er4tHFYsSKgBlzB6Pp5eMLPIay9XJ3c1W8vd0t11PciRA7wa44yxOMAXYP3YzG84It6UcLfFHw/xkVW2YVxufJ9PxMzicICAZVBzO9mQB1DXv3kzIHX4E4BJyJ/WiUZVmJVqoTBdLWUuqpCC4GB1d49mpwDwGrYiCGkO5RXjICnM4EE6a3TkKyGNL4EBOldjTojxOXVEaj0bdQ96SYLC7nT5+saHKQPT+KuRaJ/8nq+mp3O9ux3RTzT6PR9nZM0yWP33B0Q4JDjtYJyATRhAyXngTIAfUFlqCkEtwvRqv1ZjZfYLtWFdaPLisLsEexMbAqAfM49IDwWR6AhbvesvBgO8Hdn/6MZcmyD0w+BN7t1uuVwL72EEoX52eLORvXFsWTJ8+fPWH3IMJU2Pq/6mfGlcQIai0V1vNxQFpmPY1DD/P3lkQtEPpDu4JIIdCU0CUPrRACTcofTExrHVsj+6tMlh7F9uf9mNqugUOF9u0CBGVLm1WxZpWOY6srDreXfUrs5GWdupV/JU6d+KTnuKz+cYiT2Abi2ILvGlcIxK0Bt6QP266V8GA0uqS4h/3qHGL541JdV63tEpN9gGGXeYg+S+F7dRhrIA6fUPH+EYiY0XDKONd9wzVV+eP+/eyjvwLXXI0RiKpwYSrhe/bbnwLw55Pf+NlPfqtINDOgN305TK+9c4BL69Xtcr20/VXcHwfclSySsw1LZ9m9UeezUhybOc4YU8csAFsnnBIstGTw2Twm2P9HY8SkSirJaxAKHMbWixcXj38slxDMAUaKgZDZmlOC87dLFgcwPi/kyDllGpPNV2n2979++1+/YpB+jbnw4mz2k2+fJqN//vOXP/mNy6fj6fZsOxkX691yO8ECycf/5P/zDzWaD9LbPdao9PRKmFWjLdoNRhaBFpMiEGAOCPtiVxSf/I3xz//2vzxKl9IWMktScmIfvTCtli2gD0sCDNYaRRlrVzx7UG8z9CEIWr3lLbmkZ4w5XFZ4eOoJZDYLdEAQ5/VwiCGgcHhWvvKhijdwDehFC8ub2+3rHafpaq5mR+u8GudntPvmmuTlZm3Q2nZtZQ35OKOZkuLsq9d/+mWWTNhfdr3DJsi/2W3+3y//8I+uksfj8/GIBeAURBmr6WzDvkAc4mUzCTI4NWVDH8h2jwXEP2FVrhaKyC4T+pcDECtCHj9xPE63JcL8g0jHKilev3q1XH3N9v9azJuzwD15+fLlt998PZtNmQGAVH5fnEyx2z16dPm//V//758+f8QZYdDjtCQ+9Ga6SrFbrpYq0a0OU6waydvIHg9uXfHk2WvZQ2h0H2VMMHq5Or+5luq3BuUd33jGzX9ZfGT03Y2Pdv1+IcKBcqJaEqyNXh8mDnpq/j72//p3/coP13BPTQdJ/KBEQbchELNvjYwJaj00TjoaPqKH5m9o7+/70eL6CagpF9V5F9gy/nLvnqug5nvgIAY5XCDRcp06A+C5PqR70C9Cea86qOAxUZvE9+l5x0r7/qUHbYSe44E4/vtXq48Sn6aB0Phxtuiroy9e6BExTZXR0CwJgrTC+oCdnF0xGTG13Q6JVi5jwR6O19c3ogQkFazaLF2uxxzclOCpDwgDJNmQsHIwJktmPCmy1Xo1m7F9P6CRmQTFskUPHjkMvpLHsRRF4ykkf/vp6MWPPmEoFqqco8HG0/NFunz75svPPwcAgv0ZlGUEV+aD4aWbbLVkxyJG64vpzerln+fLafLVbz6+2HHCFFUBlgKfOENgywkCk/XVLSKyxjTfbKUZHJVsYkOWiOmAUX/f5wWpxqMr5gnS3RxHFI1Ul29oahFUUsYRpTg9VZ8iKS+1QRWuPkMEkM/hfkVk+jayZj6VUlFXnJqfzruZW5Sh3Ga2thgvzzKVOVVBXGM0II9z1xf//A8+/8//4DJ9pG2Vco6Ke5WOL3b51SS/yDbLouDo5RU+VxzIy0pyHQJBaFes3iyZD1qp5hnHSi9vF7MdpzNcb1MmA5g/Ug+bMffC6LtBbrTLCg61vTxuyDU+O7vgMGkkUZ/BKFAWrQYAq9NufJKF/sScFFUmTZMHnP6w3TLyzyOUcusvcg4JBtyrMupRchISXZ5w0sWPfvrZ8xfPNuslO4XabJgmoOj2GLKabdD3orxLcWUPaNNhV1ypUE9ub62urG3xsIPJg173F+pu4sT1cBlqksQEdyvi1Fzvv8RTJRxOHzpeCHjeuI4erhEML+J7RBnXuil2f2qTvj1miB7rJbkBQM56Qv87/GDs36U5YnW1i9wdO9gmi2vt4bbadBdEirwRyqs5DkG90E0zvspx9NN15frVXh/289hQ91E2w7INHy04WmBTJyHG86ITqnH3+hyV4NeHYHBvP+LL+K40FrqrvltVH1N4XyBB+ra6SNxNhGDKEQjR8t8wrKyAsWbehGhA585HHvpC26B3rb5kraYtttSgo2B/zsguG+awT7+XLAgnmAVSl03AcD8AEG9vSSCG4DllBI4ttdMOHHikCJCltloEwNlpYsA/EB64LUu2maYcoMIVh21nLH0Hzsu3HPIkEUCMKit/onplPx3NfiOZJ7dLAF8y49hf+aMgQc5JtAzhag5h8lbko535cwu+6h+8WQysqoMDiXvDJjNJ+vNk/GhUfGt1xd+dWQFJorpaJn0CBe3ZlOjMZJ5YCjyJsbDddav29nEOinEKhQRXLas9+M3oJaGueqKT1O+HVKpTXMaeupcniVKJ80IuhLPqaPMd+cykV9vz23QyWybFJM9ux9l8OuOk5vN0spuyv1OCYhds0T/KZ1qymwP70Wsymk+vrpfrPFvtiht2bprmk2w1yWZ0MqB8aodzcci0IDq6U+sirtoD7E2AhQKYgSYNybIU6d+Yowrgi6YkZaDjZdsLMweuheppfc6wkDuZzvyiGhgUmoTiyAlZk6obdoGmnViEnKRA//XtOUuRq2pjIFAObaOqSyVlA5cN0qvHvbr3IdPt/rEM1WL5Ugy8ut5UzVHVAQyrN8kA0nuQ1EqRSqveTSAOUwiPJZLh7cTVVV9L7L81MUM8q9Cf926ptZrejcnRXK4fJ4tLRLGtVzzyjXrDFcKhCUJSCHhjhcejAacPmg9FHGSM2/RO/faA2+AH11Wzss2ZoibLIeg6bosmhzImVig/Vpw3rquhJyfj/uFfLnsQtVGVB6hBYN7Kq9miEVlr1nchY1TmAwVb6+WRoVYEvDIh8ECFf2TzAWogNHurbNYRBNxCqsWExyogxE+v8X4DDPUA9xI66kPICbBkdIyYJnK2Bn0JExds3UgMMA0kheuO4zCQNPkEzgTxdZffOCzZ14eBWi5BMQ3xCnM78tVYLE5EisBVAwpNSYD9NbQrIMk4MTymWq4gGejqwHTWDGQ4lGAxjJO318Xrzeg5UxZ4JcETqnTOND9/OWs6WeOJ4AA5ZhRY9gmaY4ko9WSMWRMMTBwQS001KlBk6W2WvgYhWB0kjUFSA4xSaQVES+WKwP7sC0jVZRuUl4cqdVex0afpek9cUaqUkmfVOlGmKFhlqKI8ozRsMfXkKDLwr7KqSLVtlcdanEqjMjOArJ5zrCptlkTLyHsGuw91CGFzKsN0gi+VVKpI3xAKeK0zv9SJNL2DktltFRS+WeTZea4ztrTbEpe6hPIJlmvsX4vo2JJJSbInyavmUgejjaQSqyH+RtrtSbNYMh1kMUAPBwVJ0PIVCcglI0/dmJ1lFakmFQsdPWGU6or0DU10SHqZH2TUH5KrnoTVA8JFggkSIk4PuKpjpqfzePAcqnvV9ZrMPbUZPyTGuoUIQ6AnPIThR5ouDdBMruRwb1J2tUKT8p4xLsw9mbyH7Pfp23cR76A8XkYdLkAi09vtwBNO5dGA9l/hw6vT/njHNpZ3qbheQ6ylQ9n7nrrqFdu13fmlwu7U9pQuzu5BWHp6fd2e90jsKW3RKnczshlzRIZ7J3eNQNyN8ZHecorGggAHPO/EIbA6LdBb1oFUxrcZ01actzA92Tszjx29WilAFuMRqBq0JYVz9fIqGgCecBPYWJ705Rb+gt5CUoAz3dg/R5v022Cq8FEFfYXj1zmnAiOAhk4Z5sFgYK+f81HGjiu4fBvKs0FcSk3yjZ/4hcwcI2CzBUwvsHDTdyndaFqgWJuzEpBPSB2QDj5ki8Y1Y7TF6NH40Sx9LmQ/AS9qQ89iPONQ4R1OQGxzBChFFDCoML4dMKbKAe/Z9oVM8k0Hi7myhPZwJSqeZgXf67TQOcGTUfaM9EpNEMroUY3lIM5rxYK60+iyeWovGudcZefTI6TwKjKUToziKgrn5XfRh2vPpUSigVOZPTyXZYiHcbVbVfIhZ83TWEXVlHi/f6Et8LNP0T711VHMtPiMuRXWT891Qhbn/YzJAAEAAElEQVQQ3cwo5nakThqaGZYdsy6TyUzdBDQNDAeds+MnvlegbfEHnuc3m9GtQW1kApCzR5M2m2LOR3DfxKDNaGvaDmtAjcJ4v/VpWg4bADMD7dvxE8Rq+kadiizTW5pBpiPrRThVml1ikYNmNztVh3rRhykCerIRqTF+Zcd1aDL6bLS9HCWcQEwOWZnWFnDHA03ExAT9S6ueHkfukztCzkBto/x276BUdO87pDNfPKoaEQ17w0QZLBh+ARH2bhwCR6+ua4BI58YIsffUEB/oCfjMdhxzt7Az94KGcGgVZkjGPpoTW3OItrsQEWJ4FWoVCePxgcD7GNs/cIUSuxS1b6moLiGXWFSXUzbvpNdEqnLca4Znz+TEEMKEyhIY0t96dH5a4ZQXdMHrqGsNQEx2UED5+jmI+w4fXE7uXKFed5DHmyRumFOZdOR10U5l9t3Tf1/l/u411ybBfbpmG7/3G9fatdsiW6tZ60miMTqgk9C+xlaFliwA5FMqLyZcJLiDa8FqAD5hwjHTlWB1vOVJ0QCtoS/IlRmMzZixsJVyYAHA1wIwEfB3/ipK8piZokFYUTIeLGtD4E2IEysAlrZOlwkGRTHh4CsW8O4QIaIK/26Kl6P0zdno8Xqkkwz4g1rCadDZXD40zqxdgNgrVFgOuYQRbQAYS4NUcKpOPp5iT6TpdTG+gUijwjJgVAuKEeAjxD92LZKwsm0wTsTM6yLK/Q8K4XApZ9tFhlqS8d/HEVLRtcvMFUvy/CpeZVfcCO85K0FaqtKd0CqjKKuaAsaEFrRIq65jbiNQy+G5M0rwwxrhhMXBWOIACGdnH6nDOFnnYY7IWgZEgQLRT4b5N2EhgDrFWNbWLj/brHHNWkmn2nWHomls7R8kQ00aRwrcc9CwpKHh1CuIg5opG5tlIEXto/aVh4+6meppWeFCN9PqAMUJ6BOtjseNJqNXkI8w9dEnT2whizAcIqf6k6LqqHNLD8poYoSbJJEw1g7EWskhtSew56MS7HJe1dMH8hmkCzLeX7CgpFqNa49xQTUx4qR3F/5OCn131YFzTcO1x1rR3kz7jlpLHtDZe/J+mLr9bqSqlzrZW2DlC6VqinZ/tR41N9qsjOgYGyhTI6uui0FXfLACvVIuOMSltXRXznAbUsshdpt9C5BoCL99LWOLeR8LFztz9162YNwWd9VPLFJrOLQLqXG4lXhP89LSYwk7MhzRwPB6GeURbgPkaY6ZHfAcwqGjpmX08Br1lnUglbFuxsSC2H7/8QoWEuvvj5j+IOyE4ZsZ0gRt9HXwr4TAjD/r0/Y45/v7EngF3BV0N5wvZAcQ57hWOYZgDRABOhMCM68P2QmGouZAdJaEjpKlbwyvAVRhLDMHeDCMzwOwMhnNQFrGCXk00Cp8yTfMPDmMMR5BjIcyRjyxLSD9eCiNJGdyBcen5Ply84gjZbfZkzR5m+5+lM1fjfIfjZNXefZoN77OcFAfrabUBfEE//AMYpMf4UKqr39YHhQuVyNMgCejEUtUOfmVRaDPpRgBPWghAUNapdOvcEIqts+1dpkTfDW18Bmq2CvU9R3UW2odXXtC+R4S46oFSpKqPXgUShUBJVaXUDAJEnmUfiMIqtUCziSiCuSCuZhE9o3OnhtLJ3cKspCX1rVLMF4xhoo5JflTA9CUJXtKYQb12RM2Z95FIvnqXYbvd/kqmZ7JYto9Gs9eT9InRXLFAdNpukxHl0VxU+S2T2ey2G7fTkfzUbrKklU64jAHN6C4ywArtp9QSjp/SV8yTC+lIxHdRZ1N7loI+wTDYjzDQuMECbyPUCEdlHwEpK1qlTC+XzosjvXctJHaHAtQLDhxAi8mVgZLt3JXcyWTf3I9Tre0obgQzX8V79pXdRWju33qAwuhdhnBwW7fMYEcm8ycJlIFHLt63yHHMtfT+98wderqOc4Vh6v06HPAuzFokWzN31ZTbcTwWHDIL9oxHkr3+XxHWUdksDrecea/vzUb2jui7SEVi2i8XlX/9V5syZFUw0t0/OPsm7nUyaOiPdga2aDqjIjbOg43M/SnNumPtLhnaLROk4/FHGFmPw963+gKjWFPNgMQsnsgvjuR6zWQlTk/rI96vU6XLtSv2Y16mIVcHTQuV6AKgQ7yY9EfclN8yLId0+vH9LtpwLt3d95a94cQCGQ/BIZyeNY3Qm8o+2ZwUy8CDTNKCihi7az2/Bc44sYC3AwnDzyzlWp++QDN8E7DdQccDeiCmXwpYCDAONqxx6IGXY0S7xuK4JhYWW0MDjOjoOFc3o6Jzo0CfBEUMoeMsXhowKU4cQDicBcxpxCzJxjYv51e/YPbX/63mzc7sHv6zVn+xSh9eV589nS2vBg/OZ9vP5s8+mxxcTE/IzcD/ueMPidYHfAstqz5RATcWeBtZxDv2AsovdWpBjbyLCklPJ9aQGDrXHkGoSKppipMbMybCjfyLNGrS/KrxlzVJ8EqwuL9ZoTlc5QcsVI2w/4mjywRo+PJPpUUAhZnj7pZtPFGagPveiC/JyiOxjU/GsL61HpZqgStWl2pLJBIJmz7erPasKpitdu8WrIQY7W8ytej6+Xs/Nvdy0nxJEnezJPno8nNOHs00+FrZ2y68/btbpNvRtvp8vYaLX+1Tlfjecbqao3oj1n0PRlzVLDOlaBErQLhw7uJ5pdofmAKHURWAUncsAV5wtWIzsAqctWFPqFaaFZHG1sVo9vl7Vdffr5Zs6+UIjEMIGM/0BWLfVecErelJ5krEYdQbBeXrAzYzuU5xnyGCpPSxM+vSoGm6ypSxVa69UBFVubq/Ih6QifNDy2hqRtiUFukzXdbZS/u3ZbxAXMPXbVfxmYz9dM3U1sb1CP9fv8imoV+GDEDdWzCxlpQPj8J2DUEQVCV8/S7d+FAc/9Kx5ZNZAueytitwCCXC7tncjrnwGrP5DAUfBP30XFd9rFl6FS7sMHgICIeM7gX516ZKfKoHg7EOnyo5W1a6ofkehpCE+eK6x6HS5rh7T6cMi6+GT6VzzH910sYwL9FD3UuB7MxQ+gn33pj+n3/5ojy7iMpLYqvyg7pcbcA3zgEDIxFxv/CRpe1kf8YT/sZe7SDuswvWqsoR8lqs9u9eg0gw0F/zjg5+MzHWQHNrMzd5G+ub5dZzsGuQCntHkr6bLH4nd/5rdmEJaQSSkPTUDPgCmsVKhkYZxZ4Zqee6ePRbAav7W6dbdnbk0N9081q9fbVyyRbuf+PphPIJVfz51+Ps7/YXhQJW7o/noyXxXYxGr+dgv2yl+Ni85fn6b/6Ik+/uZnOtEXNfPZmolOinvIF49wyik0nb9jSaL2cpdnkcjX/7z/67Wz3J+N8UqR/WozORqNHxebReLrJRovx/I/H+XyU/QbHJ6CHbHQhG4gjESQ1TucGHKmJhocln2mTclzDSoiu0CgE1BbhCx9RG+Ivk9DNPmW8fbF/Pwis+pwAZ1p9YqVSjvbuiYpTMH6mPFktykrrspkOrTnVzM2YNgUsA683HJbMIo0E9x8mSdjEab3E3wdHHuB0MX17u12s8+t1Mf6nV7/8D3/F5MAVcwTJaMlQ+mj0hg23x8UMapZ2bHHHx4LS3MGKZdnp7PyCA7coQSbgbIJLkTaWvWKnWE3RsPKbDxl4LiCHRGCqadh+zMkDtCEKF8jHLp2C7N+8fs12n/Q0FIRtoL7FgH+2Xa+X7GMrFiwIlkFKX+Ez+Tf/x//mb/38twrz90Eq+ufZ2dliNiULMlImWlL3jJuk1ByRbkOhIC5pzwLcqsDkW4sRjyrJI9TPq6sirp47P1u+y5209YQ4bxyu0z3I87F3Y6wPKaZ698YqJDom65fr1F+rLpXHHhZDSj+13GYtWtrCtNcS38zcFVPpsysdPXfxj+OHaKCrCI+vNWiTuL2IXvljncfhJvP+1Cb9oJiob8e6GpQ3Ispe6J3Q8n5AI7YIuPo9Jo++InaFAET76+BhH/0QocA6lHwHrjC5c3bPG8QYUnoo7s6FDinloWhC1VzaIHzgHwhCzH0CTf734fYDyYvqH1bL70kvrR28NbJDIEdUVaIAouWu9GEGQXkDDGmMVCSAfjbE1D95V7Pek0Odbjas/mTcmFF1fs5BchqEBZZljwoOgE22QCmgpdAlzLV/z3a73uAaBBFYkgR50QtPOXpVgwD9gGOb3Xo6TS4uz3fb3ZxFuvLwJnuxXry5uR7PZ5fpOSDNuO6KzXbD7ARGSL4CrbIzkXYUFSsdIqtCtulqPeawWbxTcBZhv/kJZZOdBasFZx+QGTNhkl6v1l/frvBuefrP/uOffnLGSQTjYjFe/OLbl7vV9fni7NNs8nY8fjR/9OdJzk6XL8bZ5Wh8nVw+fvHzzwRktYhLtXHNlsi7eqrU3fiUbp026o2ey1rGYx3GWwQc/NNTKob+pHv1X+0KZ4OxEuyAUrGUwgi8llmomcz1hYBG3LN1/tV//Y+KV5vd9qpgvS8bd+7YO3OUb9jR/9vH09lot1kU5xcMlu9gM51mi8frzTR7swTeM/ejsjjFC1b49dPcthpElWKyRV2Lhdiz6fT88bkWC8tg4CRfyqeJNUL/2z/7y2dzdAuhwLimnuT3T08U9CaMxcicAK7/ZlpqKmZ5i7nJcl7VhEW+GYaBZhbUmWgasyhYfqCexur1zW7z2Wef/Qt/41/cLJn98Q2mBD6226X6tjRgVoKMDxTDxU3S+xUU6aquosMnlAf0SojyBDrj2Z4Q0fyAgkGFsYZCZKhoMyYkfQy8Bw0M1L/33IHEQWzof526fKh3FAj1N91FaozXAEAfUng380oiwq2QkJ8XiMfH4wpRQYOCkWWjIqo8PsJdPh3SVCT1z5C3ntBtdzYpPWZIL6l5EEqZvXJOvjZ9dxXZiG+ZYYho4jGDpsXZYyPWtBT70vmIiMe4rDXiqPyhwaAlWJ1W/2ElxHWPw8Nyf3dUrgvu3mf081+F7y3UED3ENHG4s/CO73hX3q54edHQERhaVYcwLbgq5PQRIRINRAgUMpacbaZTNujUE9KBqkU2zjgILMUfRO8M3kIcBgwDABNO8BRxO07ODGECyYTP5HltyEyDsMlKDMZnsISGaHfIJh/+RoztAghZZAzC267x1gGKqRANOGOFbFltMMNX/GyxYMSX3T2ZTphO2JtylG1tFSc+OWQw4IbAAuVFPt0+YpQ43SAYGJH5B8yWRwBDveRYXIzpwvlgq3MOOluuX2/GxTf/dPmHq3/+9CKbzBZFfvFPf/FHu1Hy6aebPGOM+c2cEW3WCoy/SsffYBztHl09+9lns/R8NLpmw3qWEIBuMSjK6qtBTXWIaIrjwQLlu1bGj3Qk1Tkhj2XrCEczhK/EykTwNhIHayEBfHsgu9HgnWz0poCysUWrkSddrhkjJpZ/tAeuPizW5UxfnLYWCZM2k/nm+vXX/8U/ueQQaDUJ7aE132oc/mO6bS9Go/k2f0lVaZcNG/8kN9e7twn7J40wCGZqWKxC9l+lBJ0El8rXXguFhcIx59A4TUrhTCe5AJzeQAVsS57xo4vn5xcXPpBvUgL0qQSTANoZVoYABzzQ08iA0rweoqAs+QjJXORAAHhJuXaAGb0SO0JLVliiLnsiy3fr5XazwhxlukDCaLZBM1x4F73QjFXyjb4B3ulFIeWpLPsWHIZVstJ1GY2f+aBxPmt1T1Fi7fc65AoUbYHmd7nn96XGIM4bh2tk7/9Riol+rw/1NEAcNXd1RXyqqJbPVmXHOCf8podGbuEyrKyWjIdRXW3RFT+oxQfI1sW/Fl/TlWsp6OewKi2zCi5twB41eh7bm3uA/E1WDxzj/apXkpquThKgfhIwqnBd8PLXAFKsmBAOgVqznFTyMeJ3wbvvi3RMnpPSg4ZCLmIepEZH+Qyv43DKUIuHDbgA37kYD1upO3L7NdaCYUO9ag6+NSiEq8Q7ClkEtwnoa8LQKZtysmRTdoCy6o/wBBgGWNJoPkPwxMhvA1h3UexmApZCYPzTyCtgSiaAgvbOsxvcGPGlOACXhqDlpg0K09ix3L61qBZgZqXJdACo4b+xBsTj2wHS25A714g+G39uhDCF/txrRGaJwzYwIah0tN3pPC+cWtKt4KDKwgFFqHuKCziwVRsG4WainSzX18n6djzH8wcYyRY1LGjewo5haiZBWPpgKhQOHY82OnBse1Oca9tLREUGnFdKTUqHpkc+LaAHqV2QU3FWJdlN/iidBHoPGaFFW9sotWokKcZSdCuzEQyXFK8H3SrOFjZyNYSR0jRa4EvNsm3GWb24M9Hay2y3Xu/ydT5max5OV0at7LWD9xe4m6MW+Nyw/Q9aZCB+lDL6P8rPst2ShdEozWsHOleLS1uC5rQvCla7aCpBImG9YA2YdaO6eN+YJBM2EkUUSjFDVb7+SKz+YPhZh3MpQv+pNiLQa7AGaVBzS9JPKb0CMXf8y3ACc91QkhRhmThj7kwGhp7pL3zi8s9Oo2IJhbY2lbmiMrg8vwXjm4js2aniJA87QVdqk/5jzIehgY8t5j33wVvj10Cxp1TRaMtXiF7qzTUAzo3XJ+9LLh4P30VlfKOhBtmLUa5DrkqIrb0jdTKbKaaPGJfB4TZT03bsH4lvlnW3GMqlmrHN6mGve0Px+0JaldNa31ZKGAXlo8NAEyL3Jd07VI529Fq3Pgtxx10OeiU86JMD7OwD+l7OnhjTx+F61qDiOKFfJxFlzDkORyQfdPDwjUEvq6vDo3TXstyCcVCWVI6ZAbBBXIZG9TICuCnA1B7GgUZicb1mcFd4DVgM8F/hrm+u847/GcZmixjGjpWVE6D0thMPeDP4Lmi/05btPtSNez82gCYBUpaE4pBOktAhw7rYIovJ9LzI8OfBJySfatB2wYh7UbChJCgWrCcrAMmBm+KcsYJhjpWRjhY6DCzfscnLbMzhAGTSImT8mJJCK3+h3+42zDBgIoyyS3xDkpvV2fQ8T1eb7GpbnFEz2IFJeVFTDjVh/JsdLFXxDAuBqQTqTr2kIds5nkMGXktb2QtALgoEl1LH6jVOZsfgIGO0x39wrcoGahdjxsWZVNHwuzhgXdnGo9pgSXhVjWaD38KuojfOihfOJtWihWUVJl6InDhd3uA8SFUmLVFUCleus5SVHgyTA51vk+XNMk0WnPq12+qlwCIJ7CgpLS+2+c06X61zTgLeTtjQh0UaxWo1usKVx0qmyfikZZH6uQqevgGd+/i3PHk4bavYso5C3kfwZoYBzaEt9aWdugVNKPT/CMHTlN1+JCg1o6dROy61c/YEqtHkGo3m60esCSjGbOvEF9m8y0Q33m2e5xtk/0Kg3xm4O9tok7ICXNwwSJCBxjTBTXXj9KVpSWKUmlSiXQhihOWjPnzFBYbyt06hezn2Ty7oo0uHZiiqYhclDQpWWXU2xV15DCroOyUa9F498Y0d/7LHlWvFLY12i3N0hONftDjcQX5qdIwoBunn1AJ66Vu15DnQVSybR6Ltw45fcnfFlknvQEvNSnTqqqv0jn7VyeegSP9+qn6d+4DF9KYOz4O+bAaA5FI9jQDU/JXXPlTFfKCfVsd3K1tQWLOYUrnNhEZMK5MQ2aPuh6pgTxENYR8g4qHEfgBR3j+LuPLDu8j7l/Ndlhj6dq0Qi3fkyBApYAzINGd4W/iW3drBrGQQqBOYl1uIwBoe2hqX1XiuFnqO2I8zl++NPFiEc9W58QERohJyJh4uhpYFFRUNkhWqE3OigPX4pBAEogGFgcEkA4UBiuxCj4EAQ+yBCRgc1D6azoCeOh0Mpg6AcQIH1su3HDchRve3+VizBexAn7EYgPypb/6vsuCglajjdAbczHazXXaecWIxTk5YH9tpwhFj57imMzAOvlVNhTEBxKoJOHS8ux1tMHi0KMEqoN5lPUwA2AOmNNMCaUHhFgGBEYlWGYDJMhcU4qLaJX0Z5fGqqBMIvAqfk5UkwhpVLzMbA0+oiCndU+GgHGWRWFlS+5b2HI8XlL9dLeXEhG8WC31lVNiYOviaU7tA1shoEyYs39WTUPRFttuk+Y3csNCOzBxUS4cgiew0DSH96MrWUrJK9vLNp5+1AnISw8zASqM1ktSWchBFN6GLyUi0y1RJCBLsAZtuEo3rFaY+cSTbgJXHKoLjKkr8YtaU1Ilhk47mno1eaeqSxFIgGRBY2qluCthVRonDgMuoVcU9fRU1IHcLifPZc/MqG6EzbsnzMeqjBk7TwPCuFPfEWhkk9fAhqSdvjdX37bGqWU/9Q5WMtiTUR8dJwIG+VNsA1k2bbM+kERrAr5Enjuiwmfr9xmIGcbgpeZftHnIhf6X1EKdAa+QBRfTQWkoP566kiOUdg7HYw3U4xEKNZxg6hbPWbLZCJ/3ghAOeHX0mZnZA7wldVrulxvRxeM8TzXpfj1XsMXuiI6GYcxw+ku37kwxeAdJZ9waiacd0tFUs8mw2lt81KBxEzp0R2x0ONCKUUcBcgY3PgqAYWOdgLgA3UNIYaSPQhKFl8DfHx5qTiFpAw+lc8r3hpCgWgVIsrv84mCh2rddhxr40bPOCx/Z6hGM5+Ay7YsunvFBAoWBloCuLf3fy7sb1BunldgL2Yw5TAVYaaGue3Zvx5IvNaredc64xLivTfDXenU0mb0bF+TRZT8eXbBy02c6uWdCaPvrFm+vp56+fXIyfnT9J0i90+MCkYMUznMbsVDOiLhrtR0qKlAgFJ4g93W6vNEaNfsydRq5AxSequ/An8pAmlAnEJiMwWZqTJrlPOG9YA/nZ06RgZQJhzl54hvoFlzVOropxRzGG4FVNlIVTkg0bEYYhKaXNpAJEqT9ClKEC93GErXTNY0CkuWfzuZoA4mmmaXK2W13d3GzwgSqKZ7vJ1Xz06Xr3bTJ6mo+usAd3BQtuz5PiNhmd5/n1OD9jzx/mfLCJ8KnHZMBpR0ssKD95iamkDe5UERvJV5dBFInKJ20kAcD40gt/zD/s2NtTbZ1cK150CCVD1CrBXSC9GDOrgJmH9tDx62L8ymw/Og//zFqAXfoyXbwt2MEIPyE6HE1TTJm1YGZrhrUnlUlzsgHkaSZVUR5Sqhll60pCCYnEXPbkUR5hd1rg2+iR9PgqsxK1D8XpZZjmIL3nrahiJW1LXo9qyNVJ2ZFw5BckevceoTT+Jc1Le+ipV5swD/tebf1lbyv2fnFxHePw/bi25n5Y/dSKCP3onp4X/j1o7a+e1NfbazLFj9YPh3sodOrqxDbq5BPLpjA1Vv0G0Zt29MaxL/cAAyBWZ2iougTfwXMsV2vxELi8Zdu3EpnyOlL6ons4HxWsi28sp/OPKe/MFibO+T4cYkk+hk/QgCvd76GBP7bHoQaFi3QZPip2O9wzxp/9+NPPv/pCg+aAf7zw2acRbxU86CdTfK8FhcFKAD99CKslCTtsLnhkmNYgFq84PD0AezBkGS8IzRCZoGmWMpauDVi0dwuLTQH2apJxNp2mqdYeA3yA2WmBJwrj/7slp4wBGomFDp9vyAFveb7VWoUptoRNMWijUiFD9pVn8J7Cv803v7+5GmXs3nOjQ76y2+noMtnejvKbGQ5Lu+tpgtf72e10/ZhVD6Pl7ld/fDHdfHL+ydnZ5PHlk9FmfXW7TSacFDBRaaBDZhdyCmSCIf3Ff/X7281uOgePT6dnSTKfMzKtwW/Nn+BbLxExALBkKgyHkiWe3v1Ol+mwXKZRVHlOSiCPjlwG80Fp+F7KVabqDSIHFU2KKEpKFqKW5UN+Ee4v4WYx0ptHRosALrlsmNueNLjOUD47eDIHgqWHLTdmSe+vrtcvs+t1yjKArxej9XhydZayPnj7ZpPerK9Wa5aAb5Ls5mp1s8oZrT//dpNik9kAvLz3JQ1AG9cc3IQYzqdU6yJC5+gBy4YlHNvNeIdppH6A0xZj/XQLKrFj09cMG4PlIfIOsuoUV1dXbCKlelkPpTZy8FJGOI+url5DTxF4/StehqFWB7CMGSbSoSpMOeSjwMUkvUQXplxyYwLIXEFP0p4ITIP2rBL9srjqgc/6c9U0YmJkBwTGNsp9EDygPEjZPxy0alWEJ3txvSXs+XwMDdBAaMMBtB8iyZ3lH9QTT6nxx17ZqS372rrC9Uo+MgPgX3KYeY6ooYZY5J1CDEgoRWxQhnJb29jnXYMdGaQO9ajxg6CVj5P1jIV7xhq3MlelrdbUOLLG36WFIBapS/KYzx3CXkQr83LuegDTQRZnpI3QLpQb2nFAOYNJohGjOE9XWc34Zkz/mEGTvh4TFB1aN5ZsYDiqV53/QA79ZIA5mglMVl39pQzyNaxY8Rno7VsTdToNhwoelfEl2kiKT4H7//rf+df/9r/6t+VvIUzFoUkyAJgc+MWv/vA//H/9R9MZGN53wARDCfrl2dXyFhAGqMJ9X97jSf6boMFV8vbPN9cGqxhUByyCiaezOf5CYE7hxSnYGynGIzaBuXzx4pykGWfHrsFzOQO5bLkzPZ+eP2GcmIxUhuNc2b4H8IuHz3gy086jYEQAH3sIAZtThnzZGBSVTsCAL4tZjo3BagQk3C3YSqjYzfHQZ0gbUyJliiPbno0X0zxZb6ccAnw+WWTb0dnj+eVsgecRCmJUWxhyBN4FxfLCzpJ8Dmr+5h9/+c0/+5pWm2L5TGZTxC7Y6UgLXMeM0QO4GWbe/QigO55+LugtGCqGxGiwmSCx8r+Bq6fKaHD8afmZVaBQKgEaRsOTcfYJxRfTX2m2gTZlpx44U2FrajWeMgONmQfhHNyp3HQ0X4JdNNXJW+BjNmlNZkn2YsLcyuxXaXox2j1O8OKZfLXabL/8/Ksvd9k//OfLX45erQtWUbwsEtZeo0ztF8RMCLYVnMfFLQpkpL0oXjMJI8tvOsWiwTtrynEPLOFgLoOWltXI2LyQOqKhRtyuzi8uf/YbPzXbQL5UEopUrcMdzee4HWnGhI5BPbAwAfevX71crVmjrHeyuqp7+5DTJi826zXHe/FEHVlCTOXJSsPLyJLjErJRCtwoZsqR0igeM0TKB/3TFnJ40qyImsa+I4WN66sgU2n1wadJEJ49tbyXtGWm7IWebT3Ans8BfXg4cTwy5DsIhNIPYqOH6N0VxZbBI78gkYRHKGPWUa44uj/c/8Yr8/bWpZ//Q6UOkvOhCovq21Ou903KpMOddkX8PaPPnASccBq3ijqIEQJVijku8nCnHnJCD9yXd69Qj85b+fr4Svw73kJmX1h/J+oXoWkAhOZU5trXmwy1mJYS3lPUSYJ4pcI9FvEkPnHGBw/H2o3DD1WQmju6ao9RyrsNflflvttadXH37hXfvf4fTrc7/uJGYsSt2u3wqavezfgqf8SqIhJLQ1j2egGD8QzAB5FryJWhb1JxoZ+w4jb9/KtfbNa3HBS1wcmeFaICUroYAAaPaWQ5ZXPHOeg9zR9dXi5mbO24MecQDQYLowMNE/bvYTd+5hey3TiZaw2xcjLDkJxf4GeSZhw5rCNiKX6U/viT7LcBctq7nfUGDBBrQoAx+8lotVz+8z/4Z+wBqjmBIl/hxc4JAKzrxfFfKFCCaajcMOVEAJOytbBU1WVAWlXFX2ezZgCZmQdLyPEeYrkqG6EyvSAG0hIyg1OZrNBKVj6pNFvhAIzlS7Ip1sVmya8aHlDGRApU6aMtVgEOPq8QQUlWqPEjiC2iYXiNkkvtFja4zNSI/GfYWV+qAqQyTg63lG34FT//AgRb7NakjmdfKqziZDJITIWgx+/FHKI0A0G5FqN4LJ9ZsXvJWQfF5M+S4nI8foIJU0y/Zl9PFkbPd/nbdXGdgsUxvXZbzslliUSxTnTuGzqnVnBAnTqcSys2ML+wZNLJ/GzBoVrzKU3G8V7JYnG23Wyvb24MfeNUpvbd7WZnl5dPnj7VvA/zStavBMFRMSqQIsDlVhEQunpKPptrd1G0LbVKiX7JQiAKgs0WU1CtOklm6oJYnPQGTbCowehr0BhXLJizHF8yqZpLDLlbs9ijIrkUoRSuqjCCtJsEU54o1qhqN0t2ymOktZx3fCyFPSrYHdl/v7IdaZzvV2XapPWeFap5vD+2MXnXcS6kyxa657su9Lvgfyf1m0a8Be2l4msAXGdWiVJlIaYsxbPsq9m0h061V/a8ekNBEKcK5fbUvtUDzyvAfbh92RwLD3lLLXVI3iNbnKPGP6g4BCD2cH9xMc8POUy7uGa4h3Z8SIE7LPuusprxzZh+8Zr09ZhQ4dCoBE5tzqhedf4nzaUInxnUO6xVc8xgX0osf4VO9qmHfLqefB/ilkob8ixzuVogsjMLhVUNWQr4+JAqm+fsJjjTT2bz+eP5HNzGAJKhaIOtuHLIp19AdgEPZE0n384vLyaTC0Z4tZskUJ75Afz7gZD8sZ8OIA1KPrUOlSfOhdK4NaEknctMwH0bK0GHQhmp/OPNUtCJBIBU4O0cM+HsguF8EnaXjy75XC3zN2++YdbCayaITC2sNiwJVqFYEnjpEGDpKQg0m2lEOE932stousvxccJKmIKcmaCQfOo71BRhmRTAvQebQTulytYBIsNCFgbnH8PTRqKh16h2Ppp9a3vOMHFB1h+JyeQrw540OapmZyGxFeYE2TvEVXihsWzb9t5GiFxB7Mj6BvyNSrAKRtNX0HguOczIBpADjCFVHKCoiA5t0PJdebuzIdIMX/8Zm/1nrH6+yovX89EjrakoXhueZ9d+tvjc3LIqAs/+8XoyeoRzDkYcw3VYMCpR5aJk057aT4PtrM+gZaBB+ZQlk0BzAawHoC9oSF6XZnJkjmF6kT9bcXIzLfcGxTqO96bhgC8gvxZsSx2G4NEXFSIjf/lTCh+nV+qYGkEUjWalRMjlGnD5KFZuV8SqWELZM2aw6DCsUxctWUnkjuTWKxRpY/88K13P9csZetspbb/rf0lZ5kq/refE7tIVvUNKiq74MtkEUS0GXK0ie75muQP4OcmpiOLU91IsyKC8HXXpqr2jhclLlVP7rY+LDmF6r66OUpxsiJyn6s05t9wjSSjXqxkqW8NCxA/sLPuCjH9gGOKb+O1kzh3fogPdDtB2KVKkh5Zv03A+oYbDAkPaOubU/B23F01MUupFr2uCursBECm4bMgQo/ZptpHyv4crFFxKFRUZkqK4703QtfsDq1S/9kN7hZ7l9B5fi+xn9X1K9eqFysd1fv/VQIxTFX0g+amZVUPyHPBoq7UIKt5CbZZBSM+hksEeJxFazbfZbbFhsFdD5IA2HL4B93LmBn5WoA9kjF+NtvVna50dSD1llB68KLwLXzlta8tP0CmlAcd5BAjaDjR6LzLILptAy2lFbiiWEFAYGniAXIHgbOCPh7rOigJvzmaz7TbTrv1F9vaK3IBUmFACRQLodckfRkPimjGAjQoRZGbkWNuDMlpOPJYLtsxOQNnmCiSF9sznogYw1Q8OjMyWkDM6pkM6lyZ2nHUFkiYZTcjPB3xqPGRCmE6V0xoEZmJissHBlE/JklnVq4iJMQEhl34lg/SlOkDHJ8nSuz51kWgxKFAuOkLrClJ/narmP1CwStE/zvNwwr7S1EuOFhOkZ0XANLnEHMPu4R+D5zbZQVnSPJVSnaRK+ErDjOXTB6BhI38iCOMkxiwAH+gQM4B2Fhdll3pNTlRnZgRcqCrmCy5d1qriqxrwaUFTII1PnO7UV3xIRzJ6AWyYKlE8UazRUFtCYuogUv1ERiyEik05AYIDo6mt6NUHymJUJpe0qf9V2FMP76q1EZuQHqooKJ0rsKii/fOQ9DCt8VRJoQSV2CBoRgQaE6KZ/oOMGaibH0zdvZGbLewx3mtCRxhea8/YRX83hnC7Q8YuGT7g+NNrWeVQ71XLlScBj4O1URIo3SrO3VuYpxBoU0ng0JZ4GKfXe3l1WcbBvoTOi/W7ixOyV2w6P5vWcNO+7MzcSAh5EcZlaPIPmVzU8OiBIHng4AGvXVzrWkY9xrZmHG4hvUuUj0B0tchdODbyeDWDEkiPw4E81mocDgTfv8A7aC9XwtDvHYqORzIGapBc3mZO39paFavg69+k7c2nTqCXUUlkeNTwlsEdMJSBLgCfENxifjmdnjOYyx/IESil8X32ghGoBnVl0wlLRfEXYtgYjsAwLeRFIseuxAAXVQT/hOG0KmCX34q4eMwYMv8MAmp0nG8cCHI8ekT2IlmSJj4gRraphEijv/idM14OZN+wvxDrCciiRQhy8b/G3QUK0C8OJwVe4HixawsdXy261VizcP0chDhmg8hcp0fhSc76BTalxP8+zx6B9rPxS+FL/qSfMJiNxxAjymiNFFxr2GaGVGwhgWxsHhsOd4/zsvmKyRemYcOy9AQpnFFzdKocml1QlQRQbbQSTcMQFfPMsLo2vwHk2oA7IcSQ85U5MaFdTUCgGQ62Bd6qTuhSlsxolrDggSO2iiluPrN0tV3REhx+IB8f9IdXzg6rZjtJ5mYRcGDCKklu2ZkI/yxaTmxQsmZaZEWAmVUlAX0kQp84ArF3D6ifeRgWcwD+meMRzjfB5MQvk4auwpnEVCV5Q22L9I1ak/9cqqQ6Ac/b9QV1HqVXekAZguiG4fWovGTi03oaTQxnFSyl0QZiJ+MEUvIw+2KOZm530IYvccYaT5ej5Nsi/4l6i1pcdSCbScJNCtR/fVhTe7iMcwJ9EywX9f5WWdX+xqAkJuIgs0XTXq1XV7xJsfcn5tGK2H0mLjoNoOsqxe9KPjk+frOd+itwKv2pwnldK9205w5ooT3ZYsuGdYpGi9ytFvfRW4+otcrWardv/BN/6fYZD8seMh8S5zhZVw1tx9w6w81czZjOzA+Y4F97b5PDV0B4j1SlabaQN8Y39uzq1ivOT2rnF8v74EFq+Z1XXNw+EaWRfwc3FycW6jsQwopEhgPFR3J0CRnTh/BRpQbKqITvcbBZHVdXM/57XMlW0b/bGt7lOyNU2FqVkyKpN1z6ag+OiQhE7xjISxeUtNyKnM1Y9AoqBfPi7sIwspKAbkB/XmkGGjfyotcm75PijLxgbtjL/UPTBBpFF6B0lpakwWzBMQNw5NTIcllvE0yYGHgH/MLqUD6hVziWW8UIJmpXIfNUYUcYkCiTExs2gpSLiwaqZTOohuB6yoWSsX9tuyPMrMoyTK2lrkxUYChsR7MVsrKUgGihac1NQAcLd1ORNILtGgqn6FI4DcNLDCuItREqWGysIkZmNRZeNHVyswhokJCgqsc/S9WHOIvEElCj3Fr4MIGtX5Bufzi9a4BbhhMklA9mJyRP+/V6wzwJswHbLd78Eho3feh1oBqKwtTJ8glrloWX+ZvjRcVepMX2lrFytvdx1ytkoZ0Z55dtppbhPzoXvKYgGgbAjfsTPG02QLXjAr1r0QgapJnk8KVZH6w9qiQV6Z8uGoMziCFQHh4M8wtFUyc3BayWUquUYsxNB+ieHuhFEY/bEwxgqBkFsZW5QqrFaJ6Ks+HUfIqV3OpF+vArBDojTIoqVXytXSUTl7Er72UTBtI7BpylMqsI/qObY6yMqiSKw8fyPXh6UOeBYh68GGMYyhrC3rUSFOl5w+MQDt8hzZAmdYWfKuQQzqfy/PWgb+87ffqMchiZnwQcvzWqL81+DCDo8qTOHnI1AwyfNCMPY2r25WHiCU+xNXxCtgGkruUafynP5jfCOLqTRWpvYe00JLTW2htE2WJbMw5HLFvs4OEWufEMwsA1nhOIw1GBLcGjlN76rpM4HHjFWo3DgeB9BIbrbYg0zfZ6WP5HZYjb9ShxIGjm8gYLBFGgHGOoYkLLdueoSL0U6NQnDNrEiEOI2SKVOsl/M1v+qJiw/8yMbeCBecKVuHKwJpf9b0DojGYzpo9/xnYjFyB9E4VQNeAtlwxc87USQBMG2pTHRphZNiz8yKLeq8vzR7jfyNFGg+na4qZImR9gIPtS0wlj5gG0ySfrftm8J9vuitULFTh7VWxZx6r1phuKJV4WiGCxzBPNjWB2fANwly+M6lGw8Xy+/UQ+KoKzKV4oGRsHMbA+myPhhoN+k9fj8bmAsZzyOXGWHfJXLJ8daS5ivkvW6YjtP9djFgOzc9BoIeNGNgOVnTF1wZJTGQ8sPJU9VI7xm4ZBngHOMcQ/EdBVZR3Wk53XsyYH0BjNwGi3QVXfUQdlIq6G/0uEKxcnWgfNSKHmTcOgErMcMwplZmNUrLPd+Xh+W+QXaXo9Lp4xBp/nz/Li23HxSTK5muRPtvmrSfK8GF8tdFQW+tFKBko2qwc7R/ad4DlwXy2CuaL1BsB0cLq2FbJhfjZ+UmOh94Tl1kiyFvZnrF2SvbQqY5+ou8AJjia2gD66IGM6vbFqatKDAL5V5FRby+pQUY7vbUqEYjKdHzalI5k3mYwodSQmX/AHY8KDMyVoCrKbiXrLaoHxmDXr2Dyyf0phpOEKylffhMYvo/qKvgzhIkJfBo/3WNquvEK7VhEnfu4Zm5Wi3IpS8V3v4f3MgKiqKw5L4io+fJ749usqPfDzAOVQGn/8ksYaUuqJJdY4h0f/hW39pQ40zUAQJgSaNM2YgbVuZgwxQzi0YIaQPwo02zBK3Ad5355UR3K2cu7k09GOQ2q6l/K7CDX13IwZItfRXAf6tDV1e7b+DbFnfq8ZHtsnlSFvvVPbsMGmP8LZHwjan6GRCof7ZG/wOzki0uQ+b6vaWiP3eb7risSSEB6o1fvo3/PGCvRCjyqqJurHxxM0MLBdaxwPclmLndjwbS1rfGoFqd8Z6GztBEoEKwG7nzy9+Bt/81/8Ery9Bvdsb69XwO2NtgkV1GNUHlwG7MX7Yz6f4QXOGPAONAsY09g1OEygXLhOQFbeNxw7AKIicr3aLq9vNkv8Uraz2XzLrjFzeMw2a0avC4ISAmqGroGgGpDONpv1ki2JgJHba4a0KVcID/awQwat8RW6ByQKe+Ysb9WoPbIxTkz5tnsQLvxbUPpKZ5yxN9Fuuy7eJPmvltdnC9s/lOPJ2EU0WU7GZwm74Odn6XiZYBJMOANrniabSc7+MxwevBhjEiSLOVvjbCfstVMk8+k85/hZpEZy/uwqNSnkqUvRQrf2YJEE7dE/lSAjRh+WRYhVueQ4Qx2Fq1Q/arhRHXH4QV2jzTK/fVXcLvPpbvd6u2Zn1Zub9dl49mazukznN9n28TilCR/nHK21vdiNXqfpi81o9M02f7PLWV2BKpnN0EZLVjCo3KYpVJQaETMA6wIbRD455h0kQ86WPvAhgxEoTs2h0XZSmmTQJABQXnk4P0G1YXoENvBJWXkwYU9PNRpNiU1mEwXL5erly5fEw6Ssvzir0rIZtCiCf8iZ0E/oDHQNbQY7TS8uHk0mj6aT+WIxZ3siOuFmvbm8uLhYnNPkpX4F4mPVS+zuS5lCqmwRnvgvs42QYL/zCzR3DKi5T7qCVCHg2QMjE+8klvchDsXeh0lP3loteyhrSWRsytaMqeX6+PhRA20aaOk4cRThfUfdh4xTTGfvjX/33/n3vHOWhPUH5arxaBPpTnEqy+y5MF5+JzZ9md45/8PCXXvEBZXFCo9pA2VMHBM0w12smpT3iQmSH2US5BmeBZ6ey7MEDu1lddj67cQfXuxRS/2+Ij+QfrrkrOLdsYO2Ev5B5t1nar1oxKVsxpY5w6iGlj/8ChofxsXh8431CVg6woR/iK86CxII78gLBSQnn/f1M8bp88k37MTO0U7r1ebq7dXN9dV/9p//p2+urkD9EIHyU3ZnnGmcXnBQgA9AyWaTc6G3ImXZLq7zUw5oZdjY3Ed27NYykfc52A0YyNaSnBiwur3m4ICf/87vubM7MtiIMHIk12+v/uRP/pCtJ3OOrtJQvVySqIccTnK28gF3ChSbwUE+AWkMCI3T82AD3QC3q29fAXhnOkl4Op5g12DFcPwZUxAbTo9NtTB4skt2eL1rG1ENq9tgMzMKOMqwXWa+SNg7Jz8vkjdnq8t/+0eXv3vx2fRsJVckztddnON4on2DtDWnCWcfAvFV+xKrBP+QxGrl8ju9+0SINVUbCfmTRD2EghWhqQPUvBmtVpsNUxgaa8co0nzEH92+/Advbl7JFMJ/ieFxYWraRSP5NIXwqiwkK0ZhicMWSJxnAG5mjycN+Y/OLhb499MoLOydTmcymOyastMnq57NpYoBffn+z9Inj5+cn58hOIAf2K9F0nQZIWMtDeATpL5acbCAxuxtmB9zjCd0ytLt6eef/4UsM0lIVnkwvXnzZrXCG0tVHWXPZUxMv6XuspckHfEYFOoLpgx2Bdo8ffr87/4f/u6Lp09ZjWGzDJqzkAMYfWU82rCvqaB7qVqVbVVXRGNXH2+N0A779ikTsCS5ynH60oArGZcUwz663iGy68zACGyoZXxRmDQQR0XhkOS5usiiHP3Bw77aQRvVxel9HiBIWqtBB5fu6Io/DI+s1mvwuGPRVYkNfneKuB+31jbs0sOg+po8MfYL3AZlv5MOHjBT3Cfj8AMW0cpq96nUE/3+HlCRVmup8nc56NReXcrDO0S7v/VcTWY9xKcnBZFOz9r38rkDtztn8ZeLZ3e9e8xRzXnd4+x3luH9Z7xPwyGt19rVFR7ffy0+ljhMAwGyGDmY5a5X1G2cSRXhT4dx1ktCWcggwMSdFbV4Z2AECPYB5s9AWvh1gAhvrq5+/7/7b5bLG2AkhMAtYW9wJQ/C3riSCwRraa6WA6gigBw2ixGU5BGIx6lSE/bOl5EArIQvMwCj7BJMyhHBQnr8A8HigQLPIluczX/vr/81Rp8B84J2Qos2NMzS4+2GGAFFICjj1XLNWePmjwxQ4T6uIXTc5PPtHy1vV7erDUiRta9a2Wp8cBAqOHEAgZnA0KQC65xVDfb6BNAX+O1weACmygponYw5XRipN4/TW2YBsuJ6t2IwGmMm2yw3jy8XtjeR9FDhSDWpJLMYZPYWBdJLUpO4ivFPRanuysYF8qQSbMnPygrAK4cWUCEGwOUGpCkSvPnz2Xa0ZHsmoWX25BF81uwHhgg8WIWNJFgoAHGeUR+sge0oGDXLUIAe42a9YcgevD6fLy4vLrEEcHaiRHYURQwaiwudc2lhiGw4vIBsuF7cZAbQRsiM7PCjSJx2NIGjw5sRzOKwT2juGYuIxyxUAKtLGfIS4pLNIH6Sjw9Kw+qwBjX4LUWYDWHKR3XJo8tHP/7sR8wgcfqbilAHo8figoVLk3FUp+NS/SWWPqs2sWDHzen2eSuyOL6Ke6hPL62TG0X3UzhBP00n9+9HwlEdfD+qMUzKd9TXfq10OEzTd6FyNXob9bWUp5Ul8P6SAVCLOyxeiXqHHsY+2FNs/w1nilADBWryf8A5AcSILT+Xyq1Y7DNprvsK8odAN+13nEIdqUvT6xHJvY5+H1iRgWSqc9NvPtJErPko+gGCJeeXxqopw+BxlNJGH0x/suhN2U5moQxdYwmH8dZu9h44jIeBN2m5zWOXCBDVvhH7NQMkRMn7+IoXCMzyglAFwsCAqb5foDsQsaFuNtHHf4ZnQLy2n7fRZcFKQnAB2AEvGeEVWpQhwbpMLQklHiLGqVlIAJQVZ5kJbC9zBu7ECYXhfoPfguzC89k5dkee3zKBQIDsoFLl1CJjiSiHH9zYd9l6y6FgAEi2A0IGJg2E/DdrILHkMdRKgHOFtSEMODMdz+wIMC1LYB0AyJFjDzRaLqBKKsYIcJbjqzS/wNlYoNeJPJpmwtajc9PDGUsP8s1Znp4Xk1u4ai3DhIOKbeqDE8RczeKIPkn6WmrlX/V+RxJk02U4lzYprK2lfKmJBG8HPbHkGHnGGSgeDybWLCMh6B9AT62Wu+yWo29J0rnEKkU4X5IStJFvcbOlA2oYFUlhwtDaX2c6Yj0FiJ4jlovRDWD+/MzODJAYstToskieby5R8HhyJYd9Q+dmvWg5iNGouqP8EQUVE/n30+LYhFYYFuBjSsxHb4kE3NOGZiOgbUwSyYpNaBUWD13pKwRkioNLKjCJVS2R4XXGpE2CWxmHQ3AanXyNYKCOqqUMsni4iLEpLEJESqGK1E2XnQPgwcN7KYAXGCWpMaL8dLJPFdH4bspHS1fXu2Jw/MHvZpDbeLfcAkGlrBaaU6Ja6tXMHtXF6UvlGWX4XW7mGxpT8Ydt89dwKJOT6KoSWzP575QnnaqfVoZ3iGzq4QQ9W+1CT6H0JrfhIr07PNAlQ6zzONxF/1ASTr5GZ3HXVoGuxpAQa1VvnvAcKMijd0j/DIA4R5n98UHvXo8g3kDep9IPZHsq2VExYm3HzI9mjInfc5gW6RKv1li1PtiTsVaFQNmlnxr9x8cfhgY6m7vscAAjYSr1v8O+pQFZiwF+GYzlDmoFkXEDCvImA9Gmk8XUTvXFXSTLQI+M7ea4iwCYhev40LDsCI8gUL4QNa41oPcJCcJ/ADUsCNvZJWUlJ77jwunMIhS4uCyxCpgdAFxCwyb7pAq42nAzjWOSCx0DEEmxpclKc7kpndFj0CPsGB7WnIOkAXsCeUGF2rRfu9mzfgAOBrRlpOgNrUWoPpK9lYGhijD1wbFepgcOChAAlYj6Y8PT8Sp/sx1fEANbqrRjpYFWPzOTwM+tfN6tK+luIQlomJgnqVIKVYrdjYKgR1kW/ZiQqnMIyIbUNBgPTLMoCvCebDS3Mc+KxSZn21OVKN3KAJKRIj1QgNdFe3aqLOlB4Njuu3yzxB0fNbAEQoPuFkYyedmz8yYi6kGmAFXUHZNDMqIHe0RaHilORp+1iOTXBdp3GWACsYw9PtQRtHKXrrD1SQHyY9dRHXIQAzcu8ag0o5KojFXNSnb+ojBnJ026m6qdSvkllF3VR/npkT33XjokUro1mLdWD6eHSuqVqF7IScT1zB/us2n8wxXv3Un2fipOr3lv3XmIruJe7Br4oMSjCkPbpS53hwEgsuChFfJEamhaM82YA812jENELA/Iux6Cl1ggGFrzKkNzTqBKuctnsFmDkogJ4RBoZX0wptJKcRh56reibJGXxqV3LCGU01pEbN32tHJoyriN4rCX4u0V4j2X3/vVFYT0QCxVLWn/2Ox1zZg9dRk6wnmYJvdc++n75elP3ZdxGIpy9bTXYZ53+BT59HeU4n2iwkjNbgAEMxuAFMNehns0yArKYkEnniTa6x0M98mnv3F1tV4spmwxz8oA3FHAb0nGNpTa2EfjshNcwAUryQTEg4PNG+CJYi7lFCOIrU2EcFBhADqdZuvsRi40wnuIfwMbgK+BXfMEGk9YUwCaB9mz8T9oljFvPNXTycUUfAseRGK9EVQuG1MKrgsuMhwM5gd54s7ES5jBfjYlmoF+p8mUZNKn2ac41WhsWBBdbjGqtuRj4gLvf/AxJoomQGQSYEoAaBEuudwWuMsvqe0EywJ/IW0QBIoVMRR2pyLhKwdYFWNVTgT6VEwFWJVoNTcMTC70w1pf5kY2o2wxGt9mxTQfb4pkpd1KNxc4MWm7y9EN23lylq+8TGGmqRtYagNX6UOlqNU0KC7Urp8hhXDYmQiUTxdzGgkDD2Q+naIhCTadsTxDRhGYH/MgnV8rl+w0qkUzU3dJrTkYqJCUJktv7MFKpY6qCf9A/Ve0FPMu1EQ2JcToid4gI01EZgkY41IjqoOE0IwBlpVqIyqbECAnNg79jAZNtcEr5paRIRCZyEp9aSzy62HQJZ7HL6OyWzH5piNL7/uHPAMlctNPam290AeXmYee/iG8eVwSr+CRt7qTnnJ3trE+iIkfA7OBGg70AwMPXqOB5faTxfinn/JuqV396gRtRL+PpQyNmFopcct6E3M/tVm7JKyVNUwtLeX776zWa5lsB10xrsBBAXsDoJPE6C21n+SA79CHu7G8W66hMj0cXa2VDprkTqXUGN6JR18mFNtz9cvf2ijNLHFMszivoN97JHlvSUEeSnRpPxzZ3psSHrCgdu0RW17CSKWmD0mBTqX+BUSrq4QdoGr2WWegX4txd6vV7TaZsKBWG8Qw1s6INIgc0KihcrmtsMBWI+6AeHPyMVCsNGKEDRkr19AvkuhOqVo2yhAxXvgGDMGROmZW4gBezbcFKoFBAL+QJw8aPgGQmieJD7Gzt01yy6zElmFmB8GGNRm3Z+B5KkcjVv5q0FmJwEazahj/prY6y8BwMYUIpFKyXJiEt+RsAiVWkBa+ZhsWDNxmYy0PwC8F1GneLJTIKLeJi6FgA+elAqVjJVSXSgvPZLf4UuEyMGCIScO8BPqWppBVk8isluAQA9ZJsMoVUfNsNsnmzAsAz2GBzgXqEdEmTDQ8Lr2ZAsHecuCRF5ZG97VCABCNOw1tpvKpJKrBpYrmYHsmHgXNkx1wW3M2UCCyqUgIXIBbIrvcpKk5mQbhGAEtjaAZfW2usTFTSjxkMqiN+MPi4AN5NJQvvyLjZiP9koY/K1gVUKmeCpn0hnC3y1sTUjuwGuqXVSG+ZDArw3KoQT+I6wMR44PQxV2FoFOgRu9wzsPDrltPvSvvDzRfqOz9+08rh8D/g6p/sylr7f5+pT2ipFbFtknIScCfqAubdXJYR22JEF8HqU1rphkTZ+70QTwgan+IR8prI+6HEpbZ72RRtRTd5BPGrZvUrZKEViI1hEPerrmIuNy47mQMTGKawLAWONIiTt2wfWtMao/Os706Jh5JoY3I2yVDHO/cWnnCYUhNa0LuH5ujX82YPfU+FAtD2K84soq792e/PP2pXYVHuWI9d5E/UHynepo+/VWJhrRq+QSlrZ+Hvl5SC5jpElqrupoN9ALKGJROv7y5fvsXf/YX2y2HAQs+ZnLjYF9GjecDI8GuLJMl6y5bpeliDOgGPGc4yGvsnMFpToNleHeH776KR4d4zgjp5ttJOgWi7jbZejZdMHDPkgFk8ZHjcfFonDN+/60QrmCuligkQvvIqSUBvEVJAZ4zMAz+32zY7lLoHXAJGgdx6lAw2RoCtKBhvpBmGQBAr2VBjO3UYXgKDVMqePaxlgykr8Q7f8TMwWj0kkLZdB+f+13GSoBHKafejh4l+L5zJrFMCpkHMEZR4oLCBEhJcN1abYSkMSSEi81k0bMr2mwEhcmGTlJOtUrWecYEx3KcPF6nb3fJ44zNV7cvdpOv2ON/lr6ZMTmQXosZbDAabPdVoWaxkRGCTHoQxIZG1hIPOFYx2G+60arcfPcUmyEvXplzlBscIocQHC5XK3PQErSWs5EmSbTNTnapRRXJFbJ6/VSaGpRHnQNgMgjJS6OiGXMmA5WWd5aOYdbSZUqXvcgFdzOeyKWJFBVGpsl2u/b13MwmMc2khN2zy9nvUB+kpTyyS9vVRS5d5Yc//JDupqu4Qv1vnv63en9qXMr9w/cvq/wSNURxtNCiB//NdfroXd1g8G4iBv/iu2ZciJZatEnXpYo22mHfhYa0AyVpLbGMbOq8EdMspfWb65En1bopWLOs8r3R+E5Feesl8xx+Z9vlIbalDj4DsM/RThUV/PBBL/LUgkNdQuDBJdtr5UTWiBTyBvFC4ERmB+Qx54OE9/IQKhUCtWJPqmOoi3Pr4lkr4v08ujDN6nhMiP+gZH4/mukuZZAyDomEjnX5fa90kByxNuZq6eEGiRCkXwQ8C3fgNidopf/a3/nby2tcz+WIvrpZ3lxfL9cr0OX1zZuX37zUybJ6qQovMqoM6GRhLkBf8wPaO1JwHP7mPpQVr4UN315N1ktg5jbbsufQeDo9Oz+f4zY+m7PUWCD20cWnl0/PJ/kZ+HSs42BBsswg4PtD2AaXmUBgcJ9DcFmZe3WtIvDhsdW97D4J6PzN3/5NCgb2snSBHWMwIrSweKTt6r/8+os1RwoDYIVhcZRhDBsAyokEGB3MEfDriGmSIBkmBbVm85k/2X29vGUM/Wae3D6b7y6L2SOekmfnDNNr0F1zAlTfNEgFDQyr4pQgfVsKOiqRq9VACvNcWCkYVjjn82+bpXm2YhHwP7r6/L95u9lNXu7WT7P0CvvkYry7Gk1WLOPFrkJ65gG02EHj+47JtV+PvKFUjuZW8GICNAtnQ8+iYQFqypJ8oPOZbKrNZnt2cUY6sQv44Ack3331IMA+YeA4iyBQA9HUZ72h3bUrvzZPYtqHhd0clMC+QpuN1m7L9qN85hTY+SeZzqdvr69Wy1vEANmri3DE2nqFOcUuUaYrtKNOJpMF2y7f/eXf/Su/93u/h2/YYs5O/+NztiCd/uzJkyej9Ft4UtfQO9Vfvc/C4oO6PjR5Pijl3E2YoNIQuBuf70Uur2Po2x7gPrDukHmW70tl7ybtcIXs9XCXPMrdp9J26cuTgPdFHw9ZIZrHpf36bJTjnGKKdvGMIh4pj0fEQz+r5W2xqOKSDsPOxBVe4xOPZHumWkyPumusDss88hTLH9fds7moMc0Rdv3JDdu3SR50TtFhDiQov0kfaEgKeWtkrp+gpVZNxmMzcbjG6rTHxohCM7uX5W3dJb/ncvk7R3qarO8dM0QPMU0cvnfhJYMOnmPtT4wPt/kgxmV1vyvQX9SPXJugMuYkAe3fxjwU1tgrdxuCNTvAUZbcSTSCXizmF//Sv/C3AMJ4/PDTAmdgN6O8QLY//sU//b/+B/93OdwzHF3sNqBYvIXWcqSx4XABO7AmVzJh43zctdm6Eb+RdLNdMZsAPr69vcpHZ1vGgGcaLy5WGqfGdHj0eF2kKzy/AbtMpPJOZHgYMZlWgJlZAPjia3Upsw3nF48hUjQEzEFMsCKKxfn5dMK2NhRofi8SCZCZ4LFys7ndvX5DDmUgC5tbQlVcyX+muBDP6UrQnGF+jj3eTXaT8T9epf+kwMEdfq/x/Z/mi+mvXv6di8W/9VcuQMOJThUAMANmeXXPbGybNwAD/+wrKp94E42bkXHffSqArTZFB2gULbEEebvezjfJ7Xj0OBvf/NF29E92XyZbTodAnZdwwysJbswT0AhkR58cnSynJnSvYfVkspg9efYcrG/u8qruVEfkaunF5SUcZItx58JGGo8/IYVDwX76s59pebccdmgGk9SMBB6Jk37QilpSLkdf/OLler0GoHuzQkAvefXq1fXVG4qjFWzOhCopN+aI4L5mYcTBqm+hcoKCGOKZRKA3yRjEAPg3/s6/8Ts//x1mdLTrKdrBuSh7jKWHaaKGgl4trFz71jMLhyS15dDLqmlm60GOtnU1+6IOSP2h470nSV3eljzvMKr/96s/9WHFep9loW1d6kfWR6q7R7fcO1qthXJ4lLrrCdcQ/YTqwJfwSZfnjbMc/L6cKG3M512HY5zTLKtsa0vwsGMJTUXWrmYrN2lqWcrHg69v2zuhPVsU6zMAUUQcbLaNUuOaxdSDwy51IC+1czrjewoSahfkifvuEOZDaEI1HzAQBH5AniexihUVZwwqjSP7wzVWtcf+vB9TPzgNnPaVaGttOJT923jZyLFXs+StVP0vB1nBcsaG4WBG1zcgVy7QKvhRvj2A+e2WkXO2e2c8l/WpAOaCEwLEgfFj3FHAvWA1HtjOkXFpuxy7wVre3VYaJwGfLc4ms9liOsP5hOPDQKeATRhKLlCnBkP4L7EEmstqyA+kQoKYBBrA1wIDw6q4tgNDGb1nfJpsOrAMkW1LyrXsB43qkxeJNUIvhqoXLJDKXFlAyKYaMxEQHfOAemMAiZTdLZPVegT4fruZveQIrDRjZS2OO1obgdRirOpJ/GK8VQB3JFkO+pPxZLUQT/7hw4PxQFI+pfhpMd/mG2QFuJ+NPp3mN+RU/SmfXDpdYaxti6gsRBoQN/clntQ2Oi8Z/vhoIYcqIHtsvNluJ9PZ2cUljGyZAUnsxwrjZMKpDELtOv1B8J4ZFTSjFMrCOUpNLftL+ldZagbmG6ySxAidkyoC6cdpFCF6a0JmZJDY8jIHgbGA6skuU4lfZ8q1PNBr6qZIXjx/+tmnn97c3tBwSlLTMMuADrGkaDI+pAj9V9gvnqyE8l5F3/Nzzz8qajhPiVhdLl319PHz3Wog1vy7Lekdc/eK3KE63nWjDvyOBX1n7MMXxwP9NfLUO6irQ/yoNC++lS6iOkxnDUDX/sFGiKBRXv0QKJp3p161B1c/nwPSw4eTdNEcEYfZoZCH3LufQr3uNoLbPzbcXezxlKYm311Zx6WhtSN7lHHxrvYK8fE8SZy3tazQCiE1xMRlDRmHCBz6AlFdushOkh8mTh+q38V2YHyz9eOMQ/QQ08ThmM99wl08W/cnpqD4XeGN29AV0fs4jTfbk26Gvktp9yTiWkYSMjpu/AkwapxZ6G773BDuNzibpOMzrRJOBRzlk6LcNmos33QhQwFKsLJtbgmo51FFQClfFNbUatCXNbb5ivN6FS0TI30LiJ5PfwwhvJRBbAUb5YgyupS7TXJDrIA87NklPmHQnQgApb0/ceRhZJs/juwSdrazvOQ48wqsCXCmIIbPxRQsLJ8Y8K6t58WDXywFyGGnWQ6zCIDCckACoZNAXbIL2IyzT883zyZyHJqPAfos08WBppjaUD0eRIBslkNsycX6iFE+tdkPg9Ts9E8dC02GyKupWOBoM55sMhbsJqvtbsopAEXGENK349F1UTyBA/VCO6ojaD17LCycvkZS6QSFY2tprS+7+nCy7xx/G2whUtlGXzg8zTm2mX9EpTrkGB5zefYLsRtAZ902/kKqstLS0SOCbDdE1Cg/R/fF+AbvKenGTCxTmx4c44uA/yaJefPLaBDQ18qBUb55oRmAyUs7s4u1H0x/8Mxqb6wmsaabMc+Do9gmy188/4QzxXAnUjMginogWxl9a4IRtvqjNQ8i/v5S83ddbWmN31nP7PNscYb+90bLuGNDCqStXUd41qi7H5t8mjHdud9ZSnPk9UGLqr0nQ2OVI8Felmx1vbjarwG/Vu0ZHyLW5X//LRV+f6WWd9xGJ+mp9nUOcjoTb1/uXTMDMRZy4rLdH6iVa/1tWNV4fXf2viYHF7sZ/zAxQb8hMJDv3cTqr3ecejf+A4X/AMl69B+r5T6Sv4ci7ixej2x35vkxY6wBvlDWkfyLRdCeahT7R+FzPVXZPMWf7E6qfQqPCTEJgQLigcWEtCMLy4J5MQvICY4DUkVpvuLyIoeaEkTMSDLZ2DWG8WONp4OiOcZLo+FAT8yDCfCfoWKzDIDiRmAYlmzCiBqvhlqoUN4kwGYFNW6ikWswPpyRhHL0DzYmkNhjAGw3bNm/1Z6ectQRrgSfwsUqByk7Au1Aq/woqiS7jL0XSDFyiJGsGhxnIx04UBbbjL7cpo9vd89SVjQDaoGx4sjUBHuEIjRzIFgaEgs8zEFcsivAxBo0hwfzEZDwMwESx2xAIOqYIqnmT1gQzNY92aNsd6HDCQS9uZOdP7OR4OEq1Z4+klp1goBy2TR0uwXfYzBJd1gK5YA9labhpB2pkIItRK21WsBqbqomBZuI4JZa2m6wePvjaiW0v9mxlAId8qemokKsEKD1M45n1tA+fM3fR5qyvqe6SCpOi6Bx4Erxmh2RRWOiq2DWUmAXjJlHYtWFMmiWRlozcw55dFnDuJhI7nHxXRWKn+NwyaKHIqbuZBMTfQx/MBroa3kT0hs0dIIPRvB3JcgQhXxftEHbHa3Ou9LjvfgeWwNw+JaJ6ugtE+qN7+/XvYI0LDnP6nm8FCxjFeA2sdHHNlMv95bELjvMSV18Dx+RvIW3oobIhvVMQTVLsYPfPropT7OsWHv7nK2hhuZbqRQ5nLKTxdCvgbd4KxuvmhP4PW6skOUdjUz0CBaKbg242PeXqtn6rcXdM7JTTg23GqC5ZwG92csGbS2LNFelIBcIzd+slQ0Q2Fq8Jxo9UE//RC0ELOA7uTKUpm120gk++oxzy9PGluGSoq4KpXCm/hBmBR4sCtb4IoJ28MTjxHbY1G7+YEGQKkVxwABgdZty8DCe6zr0V2hyfENSkl/Ks1yUwEO4yYOFcsD0ikeAZDZJ8R0yMZEYnAscn5rfkfxWMpbOIgprkkUhx/dZMroFwqpFRAB0J5699hnC/pYxc5a5gkN9ykL1x3LQ8caydCwT8xdsrP8sLZ6OkjnLjLNig2WA3zqWjAwcLApqjkpkE2mBhAazMTpkOQjhg/2p20QLBvRyRn4WTGND4PCO+/48mQuop2+L5M1o9NykVNFESZbJW7UMBPCSTxAh8UU6neBrsxumCnJgbjH9ggeUJgJoAxqAbDQcmYS0DbCrxWSCwFvpGYcEs5SXEX/imYJAR+aOjxWDjGzmY1YBvkYsppCxpikWhNDlVhI8APxYBOb5NHnl7VWKTJJsIs23aE0IYeWlJuwy9OTxo58qRQYKlUUuGgIxlDzavVAfnbwkrwL1yyP9jkAi4mNs/ru+l79iT7841/m0TF6w5+kqssmz873RW3iTTzOml8ERP4WWvEN+yxojr3erXUvpvVH0XDW5NbwTdoV72Zyc6LXzbMP1P5yyS6BYq3G4i/4gfnAbdXIe0hMOiux78IZrpaAR/RqO9+J2r3LvP+/WXvv8x0OU37sG4AgHr3Go9xHq9uRm7ljFcbg9/wcf26zgQ4kMZ/Tz7q7vRPlBXV41fwyRobLvouLNUkJxAwP35zCwoFYyL/1daKa1uHcV6dWoVMlnWaMqpvzlVGxVV/tUOshR0Fm/rkKJHPdLlICaYjVcLLwnBFkyg97zik5nAwidMswrRIxfDoARGEwk48IQAoWFNR2MwgUUPEqAw4BAkkGslKmCZUjDFgiuXfANNJIKrNUGoDrTChwLfLRL5QkZWwyeL0K9iA/ihj0bUu4kvgb1YSURrRRRYE9QG2A2HMzFXTLwx4C1AC6OLZTMPj3FaDp+u81eXq8e2R742fnsbD4DZk9UEjJzSaVSiYQ3dK2iNEWgVMVRQy2BZYHFaLthl8yMkXZWMAvmo9D1xTh7bNwoXmPnagnU4g2h2hhjikGVAGuMCTn0J6xollr0qMLl5a8/VwmQGmJVUtp13K49Op2rypBQutC/xBWuFx/al5kCmp4lHcQxnK8zyKgLOiNVDGVMqQ2oiPTJqnDNFVT1l+IE6iUuYes7yEBhJgcVmF+cP7F6qDmkK4r1ywJE2ZNxrFLiTwlvNJ4v5I54xOSHYaf2EqqUGocquvfzkEMv6cfEB9KA65zW4q+m/7gJm6kPVP5HNg+gARoubqwH4PhOWXTIWvWxHgPALCd+hlo4eOcNXbiFolGnhiUXKFyhYlaVFcIEPDUQ9wfcu87Hy/vtsKr+ffyCTYkMHu7n2eQVW89wgM+pHJo8mzFBzpB0ENOt+UBfBiJKRG29huhtSJPFLdVaEJE93YokNNkq5EHdu1i/s/gWqfpHIPpTh8kZN0oc7skd98wDMkDSvS5vtNaW2fMthayVFfebiEFJHKfCSeUY+CrD9qYwsE28EsVB8A4v9fQMFAtKBuppUSdAsGCp5hbkiU+840+gJ3iaDIwcA47NLR/4zNgwh+nilsO4PuPT2ie+4IBbbWcDJBRI3W0Zs18n+QXvCA0yJ6wKpXg55btvC3Iwvg7IZPMbAdLshQ37v0ZAoDtQmNFwMCTmQZavC1zzcbURfmUdKjmYhEAMsDjYm0vmhlYIIFYxUx150uQEpxrLO8j+PksZwp98C2nO4QNIvr1Ms8vbW4yFglN1b4r1cj29nawXk7PZdMSUxCJ9nCarbLfIx+wpxEQBK5BxcVkzaTBO8JmZ7kZMFLA2gEXC04zdetbJlE8WQ7OLJoqY3eQsFRg9l0mEXMwkGIrH+GBMnfXS4G0tNOCubz16E0J2OwG/LGHtnLkRLoFsrQew2QI1HzVj1iZb04yjfAFg53QAbABceKDacuJDthH61iP5KJ86Y/+kU/Y74nQFg/62ikBYnkfrNDp/QOulNZmACcOByhSrU+Gs18CNtkAm9R1EwJywPkM5siWIz5Kv0sUbtYb1M4lpsioPAa0EsJjyrsT4Is2aUnEqwNPMp78Mx9S1cKAIASPY86nR9z3e6c3TfG+8k/dtQ7aTy41+y/qUcJjWLOUg3aXyqDvxP+AW2r4W2//Y0Mzwefsjtesvt5nalKRJYzFxuXGYxKMdl34evi3OvsYhlNkVD6rsu5q1aMb05b9vWrOCgWNnjQJFd2Cv2LCr3ktR651mV/XZYwCUlLVG2nNWeo/4VfbWT39/Ne/O3ePvwb61zIPIqv4Hkd+7h7uqf2hF48b28HvTW+gDQ2S9vx5OKm6ISO+NxiUP8r+3Bnq4Clat53UIfS5UyQOOtuIXWCAoReFZcLDSgB6FkLnhxVJ88rNPVssbEONqdb1Zy/Zg1x28RLR1o+0gBEKcs89PCrDGO30L7CcnsBQnn902e/v65s3rt2kKVIVjMptPsu2IhayjbL6VZzmO9CsALpsEya5IRouzc2wPAVNWIeCAxBrRSZoJMXNiVJYmrKwF3Gux6Y7s2BCcNMAupUKqFCAb4fzi4uc//yuYJbADerLxPirAJuEwsl99/ssvP/9aw8/EgEohkA6wUgDHGt6WjcNZAgZdZ6Obs9mmwAWI8u3XEMRLoVfbLRuKTpJ1mrH//Xqcz/NkNSrOivw2GZ3nyTLbTpMpS59ZP7EZFbPJLH+d5V9trmbj+TzZnU/PL/P5c+p7O0+yS8oyhK1JDxSONIhnEoKhbWYEMd3TiP2YMG58MYCBaA2y01qqDs1n5pDN1OBmCZCHrQw7VKTJBzt+C91xHFtW/Omf/Smrfu0IB362sY1UOE0Gw5u3b23sXiLgtqSUhMMENtgm2gUJTXF6tHZVnXAyNPKgDJpbjp2SXWBeHQNWJpLNHmA2yDS53Y4Wi0eadkAmia0/bgcXz3Bru0xIz9ZK0Z2zjdvHuO+fBtTNvn9S311i79E/pH7tLfiDaMfxv/vv/HvetJ19spHQFnGKMhr5630LZs1xhaO56lyOPVPK8Os+pQ8Z7R4uSY3SFV+rS1N7tVynPnr1a6W0MKms5/uoC7ZeqRb+jaig2+OyNfLGEfcRuFXbyNMaHxf6IOEuyQ8UUrVLe4ngKy7DkO0Eh7Fd9YriDwpXfON8AFGU5VbEfFKZ5r0q3aCTPexpDLVVBA66xE7QjCR57zBqPMkfXV7u2P5/AybHrSbbbNZbTpba7lbr5Ya93Lfr5XLNtkF//z/+h998/TmD8uA/DQADxEGAEnN8fnYBY/jiss/YNg5CnOHFtvQkXj59wllSBZt4ArjTdL1aMa5/cXnJyH06mTEavZifT+eYBj/ebFbJDM91sWbvf7m7j5Kz+RS2291a5gbFCsCqRFjBx9Yi86hd8rEKpul0Np/+N//Vf/tnf/rnOjQYuEzD8R9szSQCm9mvGVO3C4wt9yGOtrp+Nn0MrGcQPUmWaXF5kd5OsydPZ1d/Nfn5i8U1podmJxBXy2VZa4zyGBq3jiUnInkfMZS/S27+29XV72/WyeR5yoFfxfn5bnO+OX9ztv2WZQuqFfCY2QNmVwS48auZL86phhYba/Uzu/5QNaZNxs+ePXv+7NlYkwNMmyQzHaJATSU4eqI4ufWovmhksiu2KWsPtqvr129lawlua8kCZL/8i1/RlILfZEVl+q/xey6TXpaGFkhgEzGDQu00RSNS9TPya5m4LCZmFdjX9ez8EuuO1p8Un2q5L3WkPei5wP50vODst9lksZAL1d/+V/4Wp5KZD5KbOjRQuKzx/MmECAmHAU0hWQxC8674RHfNHnBZDJ+Ssrr7o1Jbrr5yWsjvERV9x+/B5fSsp5Z7Kr1LdLdcJ9emehurfS3sPgs1PlUvOIg+VcJT6Q8Ke4iHUMdyJL6qe+Dd33ddP0dG8QOvOwQa8gzkoXrZd9PpD8LdbdrFvLWtu4jb2vSAgT/sFbsPle+WiLp3BiDO2CWN4p1fvdi+HP1poVwCcPW7lxOS+jn8mqRGDflua+ytMLCM71cbvQtp31u7DGyR904WvrJDSvYWMFRWI6+3TcXW4+2uAVrPFSnd6MpFmaDJrLhdXoP02LQGBCpMzhA2o9JyxBcmxBEF35PV9ur/9/f/Y0eHjs0M+pNsA8byG6GshP0fBUkBhdgCIFcdiAs6ZIdRIDjgFvzuL1VG8fEXKiYTPO4n8zl7aFK6UD0kGuXnRKkNTixg0zUEDE4zUVC97wCdk02xBpkCO0GKgGPG93HoYR6AMfnzi/Of/MZPRCwXeNAyVdB5v6++/eb1N68xLaBnemOXr5nguJ3sXhdXm/FtykTC6Joaz4s3gN7F8qtni/NPR1gvwGQGzrXBJYPsbHt5tpjZVMF4uV4y2M4SXkbxV6w7zidfJW9H+VUyXlLXZLKe4PCDTXK2YG/R1PyJsOu06Q7WRJb9/Hf+KpMfeD/hA8TOOTIR5P+Pi87cBJ7KQANp+0IA1GxrptUTUOaMo4vVRrZzKnsKaboEbyJ+D1AZsxxUnjaVuWS2CqrW5Iz6ggwRFCPW0MhWkN2hC3ONmQcU6iaDxYLjMYH+5r/yt/6X//P/xfr2Brsp2z5SxslbuMGHZqW3IDc9icJgj+kIeyu26n3Gvvqt8v7nvbRMaHwYTRwrchPfI+P0fk4xk4/hjxr4zjXgXbfWaeP+HEvoXb5G7ATRtyHO8UGEXbZYwp6KfCcSI89eqwcPsTg95wBo24fWvW46arovLS6An097tB+Uw4S+p6avfP+uPn28HiKtqcDh8rTa9w8h1N40qnG7j/dYV3sNssWrVRw1efofsWhRb9ziXV3J+cSab+q2zT5uL7+/lPY8bbFd2j6Iv9O3oK20g7j+KpDq39UjIyiDx/697IN6ReKcGl+fcwjfMRc6PIYiNMIbqhRiFVPVVKOqNsIrnAZCFHQGq3F0rVCi9sbc4SHPDjZARZjJbRwaHEDIdX3DWbCMUYPawYnyuQd/yukbCAhPOdbwStRgO5ARZvn6RVHMivGXOUdiFXM7ZtgQ5e4ZDiwZmwUJm4K5yYB/OYDxZTZajYsZXWG3vpA1kLB9PoPQ48X8jFpgOdhOOJKNSEwNFvAy7GwzAeUZBQxPM2SN/735FiEnIjKWLDisJcyQkknTEuyjv8630xHWxXgGvC+KM4biR5wfrAHx59kEL6AfbcePRrM3WkWQnwNuqdhmtJuOzyU0LFnOnC7wv1ntNst8uZtMsun1YvuEYftxcYGNgadQoemQYrvFp4pCt0xQWJdkHS4bLoHDWQPwKEsyHOelP1lULBS4TqdwvZA71GjJb8yO/YTUXpDILQdcnxVLaaA4B8TLcmMjHzoplsoI1ymcptSv0S7/+IVSWLshwUmWA7VgebYMI6Yl0Cr/pR5R2TSX7AyzNHCpgp5YOHEOAFYAMyhrWwnOIWbUCpGwZZ6ijSx9hRWD4QE9DUfBMivKIr1Phq+iAnQqddYQF3XWEBSNHoyuHPsPiUQjLRwGfzeHv/fKQu70Rur6jkeCv5PgqeUOom9oYFCu+9cv+pVs/n71sz9VwlPp+0u/W2qoo7q7OeM1+fAl4PI+HCOBI79czqjRjid8F07EpV5g653aeS1CfVvJ7h85sE3Dy8f3JfNy/fyQSgbkZbDKpa7iBn+SLRRhmcraD2YwgDCUcVjSgJwDSJynF+Gyk4nIEB7A4wMl+Q5r4do7qb1+AAqv9YP3pn9U16XqrviaqB/AY9X+LnGf3KRVxLHcIUtILE0FQ1iANUEteZ0zByAG0ENguNnYGNmY88LY5EYpAojEAQsFS4GPbi+A/4B+wFSGz3EM4bwAht3B6jA1kI8XDOPR2v/efP1Z4ItnjEark1mCfz++QJgiGv8X9Nfwyg7fG5xvptqq0kCllezMtJhVANemFBj/RxqCAp1UADtBnyrYQKqZUiJlmgBbA9cjWTWYMhny8fNoFgifwG7G8rFnIMTB/c16+hgUjLTUCE8p9ijC638+1alkwHpE3bERkSwgHXo8ys6z7Yz1EHDh4DDtv4+ImmdhagEQLf7y9xeolgCcmsD6BdA/CyoEmtE+AFqbfGLhmHZVBY3QqxF0Q7SCM5HRMU8C7ehvhxuVjg2WDbDdyllHChCIpyF0grLsFJlZjvJpLelEVOKuyqpFFSPLR2qRxaVNRKUVhcVvNJpzNBmOXBNt2Kr6yRqiHqBwLWCw5cNmKAi2S1al9l0q6zDdY+JcEASyOD7KF9KjuFqwVkwt9ePjh6gBb+0fcMt1Va2jm9fbaCBZPdt3+uwyfzgte1yHev/oHAB/RR4oT0mRnXqQtn+oKtvV2k55DxtLYlQvUrcLw+NeCgth85EU244DrcCa7F6lkrlZlvxUEFmzTWtl1YQZ+Ohj6sPtxZi+azw+VCcEmpSu1biOB3Z2V3t1xTdqG4pupLRHxK0Wj+63Ux+2cpNmiH0ca6C/xFjnzbJ6YuIiRNbUnvWulvgepsOS4hrVxTjGYeC35hibk9K9v+y/eaU/NOcBH14C7VB5lTyTCIQFy8weWUZUQE3gzUC97R8jrMwLjzNc2eiGHXt8nHUKVMTNW8AViGrHA2scmXFllSDQZ2WD+jQnILgpcPhNMZkz1q0BdAB1seWoAVaOZsnXyYwVAQsc3+GfMdS+28idnaNu8YZhUiDDbeYaLJrkKtcGqUmVFxC2AcXhXwRg1j6kgGWZIUghO8EwqfAuVdC0hComP3/Gv00LwNmFZAdhJxsh7YIlzYDj+Wq9HmkT0hSRyG52UJHuLpPdRb5jyB10LKAswI1wnPuVssIhW7NewiuvWRP8j2621EDO/g7nhag1rE+qIWYBZI1bm8kkBygUqFF21j9oQkHHsbHAWqYHglmTUCS7J1F3ZNUiAb4mlIueEm3cJLGogxhifXAQm2YIpppU0ZSHvZaRYKe9mOBqJoOaydqXNdDP5bHDOcToSk1JEqqGkokgCuIZ0WRTSYlwZFUxtpyp2iihMfL0DTxlMumROxaG+3opQrMcopIEh1cjptXLX3lMpsPMeuoa+298O8rih7z3DkppvpEOkqOHE99UB++QIXmNZvdcJZ5ci0jMk4NDNNCQ/6B2jSL7U2vk3vKNnlKjOvJ4UolHeA1L9hKdtqu9Wr8THT19X6pzO0q2z+ChRjt2SVXPePS50fpHczhBa8t2tZT/Xt9fZr0/o/eGXmz2ZopH/Q90qwfLowGZ6gqhEKhSOj79nduR+ODRXVIdVOzEUuO88A9/gU2z0GZMIH6fgVgMF3tI6XF9h9B/H2lizbTKf5SgNdfwyA9Hye+6psN10kE5XFXC8br2VSKk7Hzs4/RsKJkU/tgIUwhewFd5QYo63Ikko1GUwVZArECkshjGE+pzRoYSNWzM2xJAKj8QPEwYvAcssz9mqiAJihZ+ZoyZMW82EgIacgf+4xGPBABYNgEiHc4apxYABTOreIklS6AUUT4/42S70WC4Qc9SEIlDjDCrQgxzs6yACiIxbLVXENhUpgN/U7kDyZLAjlAc2FlQtXrTy8KY3BT4IClSopg6cCyaoi4473Ae4oTgCWBcLvQ2bH+x251RPG43SE4efnEEjEHBIGH+aUieI3iZR2CGA8lZ0sCCYNizfMHsGU2foLpSZpqMTOJl3ChUSwdQjVVNdcQWwjwhP/sjUQ4GgP3X+cyyAmRWk10BOIkJH1KNxCJWAZNMykbB0JSqBjLILpR9IbVjkWmlr4oyg0OZSYG4ym4FIwGaCN3Gi1Iph5cYe4xKC5e4hQcL1B4bic0chyQfn34IGujtBd/LClKj+nfC6tEa+b2s4TCha9/f2uMwHvelqvWuRhOU69XKd1Mj+UjxpU1jY3Vd9k2ThcvULOvOo60UEY8ie4n9FlUYJQ3CEEAkv8NBgciyrPGvETfrOCTG+QdJjmaJ5SGMDPEVJI8jCce5eKzlevAR6NCsw+sVC1zTc5zUE65XKqpmaNNYP7Fs/SXWtNcjw8lJUe86yNsx6jD8+9Vfo4OyGg/935oGeVdEs0HaKJ0qtFBFEo9YVHF8GrXgV8xc4XLs8GX5/Q1Z5PvIUs5XDLEDVn34thjNcMzRkLJZAmA/Rsu5A/zsAC+2l/+UUV3OVTWrQAygBP463ubrRFhuPUKUshRw6x/tJmB+thICcLPwVjCVlLV8TjZrPOfl8LM4m+NUvl7fTiZAYWJm4HgQpjYcwk+G7fDHuL8LJcPTJwA41lf7BAnPC2gLsmePQKmT+S2wHqyrGDAwXi7ZI9Kz7I12x2E9Lzei9U+iMEQvo4GjDzSgDoTVQbkwLHazUcbm+kwZmC8Nw/DoYqTjvjbFltycQMC5BEW+1G6cCQP3m2L8csSJB3wpcs4zwweIwwHMoUjKBZbLNkFeDbWjgu3lSAJjxuBlxDLrjGT0qBkDKis/IJTPzMiGrZWK3YpDF3Dx1wllnKA8xueILwgzMOxAOp1MyY0VsPRD1jRCL6MOywYxscHoG/QL2Mqu4x+nrRX5a7ZWso2QcBNCJLYQtY7DbAnzD9tHSLtNvsEUHCMhFV6tzWiAmdkKVKC6xFEXd+t7KL0EOArVr+y56NKXio/TdTZwfJG2LyJOqIfFzgu3lMa3Iy6knlfPHe+TNtKOuK43VQf5wTtkSF6jOcjVwTmOHv4+jHOdHG7I3y9nf+rw0uOu0V/Tu5XYwnNwP7lbicPr/sCUg+vVUm7c+nfl403Jt7Trd5n4uLmDGC1tFNLaAvGcYddLoVGQGwCN6Db+3XH2K9OdfK+Urprci2mVmXrX+IfHEKhoDz49tZ/mIMN7eWhWp1ksMt+ztZs8Q4wrZIgYIYsTn5Ql5K0F4qqFpvHK+r1G/+4e32dxXlao77ur1ENyRmgk3gs9QGHKEg++ujjGQreSA0GF7EPRbi14CEgvzG44WOPGGu3VsDmpwq2ClOBfmQrKaCPLRGnMmbH+1WoDtAdyMzKPAYBzPDCaU8PkwFOst7t8uWQ3fXnTWGb5vFzfaIUsGxCNRl/PZnPW57JnJQHK1bA80Ay3nikFp2fni4tHF4x/y/scgyTbTRdzuGNRsIkQJsFkyiJgsOoTkPHsfHl9c8MmpoLT2AYyGFQDjAUKZeCfje615AHbgDzUhkqw/GAj0A/o5olPipmkVGSZJWfs27lkq//JmP128INh5yC0dA7oZjscPHJggHMM6wm2uEidoQusCy2FlfaEuuUSw86ZsMTKMGjOSVwod7NGqnQ+TzdbPKCoPjUlBj/7+dXbN7/69nNMBJSPdw9Wmjzvk8nt7RUFYggxi2BbM8nFh5oRwx3zSeYBlUTHHPQ1na43VEFTL8xzqO7WvgiB0Ey2YKNRUWw1VUAnCOwuzs5Q72w2TUfnk3Q+O0vms3NyJaPJjz/7Mac9mLo0KUAe6yHqSfwR74/qGn4ptgrHn0TaRATpJYFC/uB59KzeZ7HHb2X244QfKb6vGrA+cyC895SDqO/hg9erWbvvYVXercgP1dxHVd0oyA0Avan0njmaP6ihtE7cT5d34+nee82y7jPaGo/pBiF7AsEai8WIw115nSamrMXESU0mzVmOIEmTuBbTzFsjGPoY27JxeGj+Tjqvu3pDt73bmfnhElyAWJga7/poXC35u32MRx0iSfrHXagsV1lxa1O+TR4Z8Xg/wQHFghwFTA8vnr0Ch9H7J6Ew8tUv20HlMKehq/QVlFaSF0WJgt285jQhINwvtC857AVm8J8Na74QnNXiUVGaRIBpdtVkOJnTvrghAX5A+P0AqkUGD61GhRiVw89y8oTrPyw2WzYXUikTHSIGPgeq0sTmI8NAPvgXYHp5+emnP9XmktgGtpoW3yDgOxj32ZOnlI4tAI6dTl5LR9vFz//y73I6GUVII5qeULHJ5McvfvxTDjgQB7YLFYxVH1jdXn/x+RdsvcmJB7g5aZQfh35ND8z+kPmRzZvnu0WWvcX4OB+l8yJd5xtG+PG2fymv/6txfpFnN9PJ+dv0q9fs678hP3ib8wQ+G6U3RbbgAOOf/dbPf/zjn6EiicdPgXY8neAOxB6mHJWwwNQB/SMh1WVtwAQban118y2Wj1RPCxFiKmSzfPv65U7rJTAuZMBYs8jKQX9YX05KVQ1gK6uWL+vIAhqAU9jQg5pMUzfMo6j6TElofkPlM1G0Xf31v/U//J/9T/9X+FaxtxIbFskeQjD2VWIygZkOTBbmEGxSAP2oZeGnm/WVSh6PKfuPPXiDi5ar+W5xpZTdwmm9F3uCFeJ5W++t6TV/39aMZWTH+6Qvy7tJO3VEs1+K8n34oL9fXuKBnO+Af2u94lauel5J2P/mb+V2NLKF5536yYGuGqWWnb36ksR1FO071m2/bA1hOyMehA91dz5NvOfYtdkizTdJp4iW0FgdVP0SMT7Ey0tv1OZVGgDlK6z8aJLVYgIdb8aWX+Qa9Qf9GKqClHG4S2iniSmbMTR2TACrZkwX/yHx9S/SkDw/aJqgbQ+4tkPkD7rqB5WrdTM08N67ytACRSf5DC8fzeQEbeh/X//Q3hALOloeRQojU5aCJR+BSI/V3SKVyXbat8zgVBzayaFskIJC5SnEuLMuZXDoKmIhWE0rGCFJ4sQddKlIvXxB5ABKHs23RwPhorE0o8H/nO1nGDUnljF0ufvwH2wLOGX0mweoZ3Lk0U+miseTSW4xWjmgiQKWC0vO/PzsbH42k5u6ALOMA4wKdildb9YaJJ/i/MRwO3nngPV8vPt8t3y5vfofjF48HU8Y/h6l/B9dpPP1uPiD3Zs/Kka3+ZvJaF1MsHTW+fj8+cWPH+Phks05TyDVAQIL7ARQ+MXl44vLc+YbcIViqB5kzn02k5sTqgBTIzM1Zd5ENglPOP9MqJDpSKJXCiUripO6rc2oE+aG/xcn/bfaYx/RQNxZ1myal+r4J4WLoBz9p9XUPtxtjmT2+PEzfLHQtvTjKwk2uDK5cUE+iSE25kellkDZ6jsmoKV6pGKs4xIX0pQeXcZOtwMCY2+VECnJB6lR9n3wOMWe9mPoowY+CA14z47viEVP1hfi4/WONNDQb+v75ZDKDQC9n/Weac3QKq3sFXIo08HVYi1123mtxd1tnLtpVx2I1XgIpQQZGlVp5IkiPBf3gVdg3pzlGD530czrAvi9pvlQYlPCwEcZ72T3N3l6jBc6vEbk6pGzq5RmvGsgsAqBJqXHBA3weJK0XQzjeBcmjqmHu78RdcrTn0ObNsWo9ZDTeR/N0SyzPYvoaCQnb949KW5FhQV87RIsa/8lgUL4TZcRGyND58QYejTYppuAnd56QngCnEBOPN1HbA0krAit+bFo1FloUv4tYq0EcjtKzD4TVy0RyJPpS/j4RZw520NnoigWUA8tLBwRi4mYAVDlOkNY2Bk+tlLXHVryzfJsPp9hOMipnvF8htX5tsIzv9ytZ6B05gQknjbhNMirSjFvsGNsm/MOkAzjQNCXvyTVUgE5BvEoBxnmJ3BoQrLL7OzJaIK3/gbPI3gRpdLyGfMB+bdZ8VjD9LjLj7IZO8alq8n4qbbw2f6Ub46OPGNmgk2FdOzBnCkLW18gpYHtkYTpDm1+CgNwOgpgCkanpKUcmmxuOVRAY/WUSQb5VdnqXhiqgVQB7ozuv1DW9BvYWKxalRwkWU60az9e1vIyMNSCqFT1hTnCEJBE2ZPx7mm2oa6ohdXPkKnppUSGx9TQPCOsJZCmttWlwhRWhxEvRZW3kkJPRqDA/jpMtfiqEzu1atl5WS2octuFwJ5zX0Tnt/v+b5v7c7A6NMc426pWj+uslxM+6O+XszyQs8H/iDx18e/yTNMe9KYH0n+nKMb/brswHegqKsD7ZXyPEqtgQ7dVwsN8dsl2KvcH4YMq4OMKqQkQsGv9ZXCifppylvo/fIccluIGQBXXKl9NXD06vb8W2yvVkqk1yjkNLbeVxf0i71Z0qdlKEzxWKiylCY93499Vp8C2i6ApSRcl8ScR9/C5TxI1Qoz7a+n+HIbUwqVtUh5tl2aWX+eYEsCr/+n/XhWhFUNgn2a6d/KuZlAuwLpArICa/sBYwuvlVRWFe7hQHWUDs4zSHGnM75zcgqyCasqt7fDBqMBowLtBe5JxWNd2m+RUihUGpX3yIdQqSTxIIQRyXIAcPAr6ipONQtttzAb3FCF/eznXU1yO8z3ngwlY77QmVUXgtc82mmOckRjUZwBDsiGTpMHPXW76qg9JHIOlDW0km1bvIqpGwsH+44Kjd01qqg0DdkFlW83tmPUFPLLqV5kA62BnFDRdsH+oFjlQc0Taprv5OFson6omiewkBLY6EgQnq/+v2lOSQGLxEox/MJKykDXj6DQEEd4mL/JZO8HYtUlApSibRJJUukw8GJk1RV7fr0iKqDRLSCVQ65K7tYHFwWmCj5WxkWDGWgaRu/xTb28+CWGlSr8qVYJYf5C4El/yhAIriiCkIrhMEA/qqeKkrGVs9RmIBgUknhGGwKBsH4m+XxrwNv5+yRxLG+Rv9vJfz44bFBJrKYRJbSoqpPYGWrL2s6r07xKVMwDlW6WFWWvhZQlOfpCpaYUMH2MOo/KtZT7sSG08BtxaHJFxiXE40LsKeQyBkORa7m8JJw72X8jbE3CGteLiMYlaUg+ruyXFZXVxaNYo1l4c7uJwh3gqPkTbTc5NaZs0tRgpORqVObnc2LKP+NRKefDHlu/mQ5UBjEL/hyMNgXfTNxF0xGXxxV4qIr37tinUkKGzdCILt9ErN+BNN3DlDnAsZC7YBmBWLuFBjf5K4vFG48r5HFwHALZDokCHhgXJbBIpu3bWUUZyibWSivGUFVAwBWMydKw5BJJVGIxtoF+5Rat8qjHIlwO8NGaOjz1QWOPzkkdk7JjJlvkokNF6wWkoOagL35589ETDvVgcYs5EAfD3Co8hskiIjP3y4XzDFkOYKuTDa8gGtSFgCYEWHLOQgOMAgMTpiFW+Gyq7y7UieJycFcmOgfekmOXpFyyXHWc/Yvf/NNVZxZN8mey2qA3u6CYFpSfLZHI5Ts81nzFlC1FKF6SnXlJOspIpIGrpXZWSZODwW0XmZ64FjBnmMrAxNFtgQN7WQcge055FKo3/3ITBBcT5SDmpBvV8ojZMmXk21uJOhJWkO3TKZpMqfNAkShITIXypO0m/Gk++SqbLrFjpaGbTtsSBQvXEd4hM1iacz8A2Sia3qmPCyEKwfiu1S55nkiR95RIoHF1wtyfl3Qc8WJGJPf98fqOxt4+K88voqkz6dKZewD5+/z3ax1koftvUkgY+xhwe6H015HfEpeus10DhK7LhJVY52j/75XmoUg7KjvV/kDD4ob/VjH9/vQaXdEDo2qj9wh5+C1roS0k6ZH4wDXfwPxCo8dAsvRnTyKSI+tf1kKg/NdAOLCvQtwYq/estqd8bXfu4tixN6aD3P5E3k9uY/BDjqLlXvqkC1+heSQ9a/WZxD8r+PTELygmBOxccGuLOHHoyhqZ0Gn+M6ZsxcerHcK8GDr9AfQ3p3cSUHb4AHgAHehnKXgJHIiAVOgOw6W4B+Y5risCQugF350cqCJGhbFzCbTgbiGpD5dW70ZmAAOUNVMFeSjAsqERx0GWIUzeCQq8qllJLAq1bZfwbKGkWAVJJXBUljxRtKMSHRNU8gLnE8MAn5cBis+ZkLgFlGIqFg0SRWyn6MAQsKbAYHGC7ckC7+YZjCQTaOWgMS4D3/5Y1wRzXlbIf5iYD87J7DtMd2nuUSYHdmMkHamCUTD4wgXFeZHNbzMBSATkMAeB9LTMaCQpACg8jnytKYrmMjqBH6Fk+QCauFAj6Z4/PsjmkMhUrLvpTlVQHwW5VWclGYUHxdUJlstY380nzDwbuzQUIHUppU6Y1UApB40G5hOQzBNa3enGDUH8Ig4TWF0gubRXPRWavkQtQylRKU3KWhPpzecvIksTiqoTqc599UCiodBD1R6KPGvgONUAfD3/foRjfi6LjN8s7EnhfBCE2RY6tivh1tB+Pj2NdqD2PhxSyf1S+ZkfeoeB9jYZljkuMw3Fu142ParvlGuszpnzAcK1BWm13pznaUBDUuMVyNuvSWlacpTUcay8Ox8SIEaRttlRz3iCOifM6zyaHuKwh4ZhDi4oGjMo0tddS7gA+5WyDZx5C31JMPWqIbDFNHK7z4hmE2hJbRml001vI7lKmBaK+pLiyIzIm+omeamOi4i9AZR3WsovIAtlzJU5eORSzuwHH7WPbFfNaLu/CgcKHoF4cYRhuFsrVrj0LFqQKADJmnGsrSSE/nuSqLvhnN5XLPwF5QXSQoZbSlqMnwp10XUliwFF70ZBug8oKIQNMyJuzrJdd+GU+aLqAT7IC7PHzYTAdF3X2vGf8XqiUdb3ThN04USxi4iBEbgSQ2ILm22LHfjUTdsYfJxvtkSNfHqwEnUOsWQ42GtIG/zC7wgufZ7YMytg1VPVlLgOsLZG0qmA8Wo3nX2+TZ9snF/mLdPZmm59tNqsiZ4XuhvkB9vt3bIyKJpPbSfqEXfkNWWuDI2YjQMvZjtUIOyolNWhQv7SSDL1zvvI5qYRRj6mWWmkNLnsE6QwEdmbF1MCO0PJfYXkYihhy6RndEiuYXiR40IqzlEaS1g8rmlkL8Z5+RaSpSDnROXMomg2Q+YJ2wfeQsy5iJ9ctbRMqWkghEY30j+1D01yqZdh1SRYg7c3+SNmWHV/XF5Cns7eSzK5x+krtzmXSejA8R3GSKno0epXsOfDr4ttx7NrTH6M8Of3UcdDm++dUDiZi9N1vEfnI26Ylxz6qK29/ifv89wsNKsU15gU19XkoAP2k7GdRfFcdnaQl9VgpEe96sIVbnaTzeZA2otwH9B0yH9BEeQcF477awb+fT7P0ZkwrB2/EgxdBK11v5MCyenlEiRoI4Xcu6l8uXxRh1K19UG9hXm28yaoX3P0qJ06RbN+XYKtuasJ/h1V7n0Wf1HwI9oDXSUUPKbdVvNbIIdx+DWi6dUMKzWMtJKJAWAbC81ElAf+MmBvc6vnAZ8QKwAu3aePI6Wz2+s2bl6/+9MnTR0BPmQFCyoBgBrsxCXCS0YFTWcbGlrIGVuvr9XoF/AQH6s0GDpRMINqcdBxpZObIbwQQSqQlgxytSM0rSCbBTZNO3vmATkVIXntVCgfi+sJWohpd1oFZAqH8S66urrM/+6Vcg7QEAHjM8lqQMcPzk9vrpWwSYwPryWyabfPPP/+LCS76WA4ceYVeAK86NHe+2WyevHj227/9O/l2jkXAmWGwPzu/ePrs2ZzFuKzU3bJEGNNCpxiAw7frzRdXb78pNovp60W2PEOA3Wy+XT6eXL4txovLp9fLWzY4nc05WCtdnD95/OwFS5K3a9yNNDPALAQbHGXZYjo9F2RWE2h+w0wowmP26V+t1nJhEtD3o7jyxWL+5vo1qrbmksHAH+sRGH23mksptAFmhmwlsVF+1GvGhZqEiwgdu0blNZdAK/laZYTCwiFHKotKi32hxQJSO82m83/8j//gF3/yf8T4UAGavlC70wcwTXCT4rQBBJnP59hMuGc9evoI1yl2aP3rf+2vT9Jzm/mx9RhqVXVFNQphicaD3VtuanURhySnLx8PHgLJQcDzR1FHCowoPwZ/CBpodIAfQqU+1qGmAf9WD3gf1PLtXyy1hGGP7OzACIQzCaxMCo3He0xTKGL8vSeCkG1Yid8dVf8Mw3C54rFnr39smcXh4TzvQ3kfG/2gbWP72ARq7kTbVdZJnUCFNsqKNTCkpVpnEtQxjZHvadBKEwqKx/g98kAbhh4OYkLOYYHOntBb9xbedxqraPLparsmpcfErd9Zl67MIZ728FYRPFSwujzWng57T9uYqIj9lSMO9hSY2X7/IFJgnE7LYjAZfJcks8XtP/pP/5O/9/f+b1NAszbFAV9y7iyu9oBOzwyaBxsyVE6LCL8K6Nv2lJQlaG4Sk67N7BfsiuNVsHgTWUaATA5oBQUxESybICgvSIyBErk6XNQAdgLw3Ww4UgDu5AHjcmnQ//b2Wlkc5IJeOfZ382S+4AIJMzkgliB9VgpvbhfZbnLxxMbgjY22DB0lW47tYtPP7fk5G13OHsGcjYwQEJj705/8xnq95Kiym9trAC6D8ZgCZHn79vV/9P/9ShB19BRhGSKfyBM+mW2WT5598rf+J//marO7vV5dXl6OdvliNksXUw4lY0xczGWmyPNH544Vxee//OV6tQREIy1Vwgpg/5/lcvVnf/oLfIqgl+GD/gXmCwwV7AUmAbTXqi61h80PFOfnl3qkslpDTKPLQiCsIXm1irJzAeA5YoCYPF9Zx3hUUlLA9gWp+eir5XJd5BsTb8xmqqyfePvm21fffimzgkv+TVKftSQV0epmCqHgcfZM7Td5Q6GPHl/85m/+xqc/Oke7ciPyBvKeoa5Y9pLqQzF+7XuJ1aaKPv3Tu6GV6JklsL7LxaDZgyMFnvhuaXmHnMihKU+TZ/Nt06Rp8vGYZt4uykHxJ76rB8kZa6yXv3VNiUnAOlspcvxmbtYi1sAQebpouuKbJd4/5j2V5ZqPdR6HB1TjbnJ684XWbC2n1sTQdJV1GF+9HlqZWmTrjLpSJJAvAvbOFXcxy1l2uqZotZjao+c95d4s+ZTcD0/rSvX7EO5HFXAqQy+0S4CjxQ2RGRr4fydXl/xd9e0SMtDHFQmRXbmOxgfxYrZHc/16EwSdtamBRC6gVV2h1XNfm3masdCtyqJAWaiAnMZnNawrDA3cZmwaqKZ98wGoF+esW2UoWQ4wAH0TBiRpzBxfEjSQLW8T8tjwtsC8ECd8VYCNT1OkgXsKdznKRLFCGIP7kkOCGcAnzuCmYvhTtF0ikIhGqykLWSyYIHpG7hRPGPAqVAgsiAw3pgZkFTB6jTUAkXkjqcI240H5RLGMmbF2DbfzX3k1GaLZAXb74fitlNNzsY+SCZMjszkJebG5mJ2vVivxETZnNJypkfRmm51PJ8+efsYP5u45syW73Zpyx5yVm0wExFmdzMRJqBJiU6Hddqt6Sg9ydaI60jJwf7uWAhlULzcMYvBebjpQSgFSHaJKsz57omMTDOJLSSrElK45ATnqwAmuyog6WCwRzWGr0vqPBNScVQ/M+cCDErD/qBjVo0tgj5SmJIlwEH+ycHgYLaIew/wQG50WCfueqjswx8JepXYumPcIcVR9PaPVWPm7L0kxgKyDQWfOzoQORh+jPwwNeLtZn+sTqNa8PB7N0sfuY5ppIKgxboUQ+e6U5MX18L9r4x5l3F2msroBEBTg3OL3FeFW0UTp1EZQBbtLG5rSHJcdmvPh6Lw2XXWKx5VdWgYXIXY9Hdpne5k8lXsX2z1pFeqnDCXGFn+VdS9PiGkNBCZKjUcmnDqKcUrKCllCoJVzT6RUEXHuoQxJsc5DJAKEy8NBya30gdgD8TxD3C7lio6XRnWinHERXT3h1LrHPO8TjvtJHO7kObTurvVONmVCF1Xcii08omTjwLMay2E5H0KSBpHziQ544oGxaQjkQsNQNcCXkVvWvuIaAnZUPn0FDbyJn3C6ujQ8DFIrIPCqKQNSVYAS7S7i0gJw8FemCRdqYbEBWeIcIBonMK1wvgFRKAhrga/sEmMKQyI1rE08dMQD/bWFPSbB7GUy5RTdx0RKDIfU5Ju+wRt9VDwG3HsZAFwTntEsUDLrmLNxyj73ygUGB/tqUSvlaPsdCsMNCaNiamPq6XS+wAAgNWGXf2YSdAgBw/2bvNjmxXWeL2Cx3TJlge3BsD0GwUJOShmYPmcEX/v6s+KB3AjM2WTSmOoIc/nRsNyZw8g2GAbkgVMmBK91EbKs3BSiaM5f4M6lGJtB4FO6UBXKMX+ngK1FQmko3yvoFVUFDeNPXoL9ca7neGHN7pAhwd1LDHWpoay9UIQaRmeWCfTLSBALXelb0yx2CH0HRyLMGLUNFofUqQXYEIlxdZGsR1V/90KJk5dRstqhojz49NiI8iA1PLQQDPr+OoMHHeM8odwg/rHAEJ5DaI6Vc6f0/ndgQ7fD5SwbNeIf+ghJIRwLHfqBfAWHXUPk6aLpih9W8p7Kfwf9uYtnV/yeywOFUGz8ux/CrttWtcclvzs5mwJ0ldUVH8sZh/cz6rWOpXdpPAPAY1CAB8jgcsVJzluKNPqYIISd5vt2D5UOahhYISfjHjL2VN0110MwMOloWS5Pf3FHmSBMUEKoYIiJUweK7VmGlDuQobOqMQyPsaj9DEOWfrKPqQ0NhH7RSIki6uoNDUOCMwgxUa7qFWO5jcD56K5HZQaXAY5xMQGvZdt0NHVGhtZ2XDpMS5BQl3CnZSKrgWIYiIfYabgaBMePqyglhMPWikDgj9wQi6zMJSbCj14H8QQAW6S4eEAlKkNpftij6EHjKgWASkHlkDn5PSNQmBOrGO22bX8M6ZICApZho3iNhCsjGLbQ4L6KEFz1dcf450CMbqyeVFumBW98TAC8d+Tow5IAluHiEXSbzgD5BnBlNXH6sKYXRvMin0Nsq5jlL7/NN8w/gKVlLEhLElXQmBIE0yGU/aA6axdTnTOm9bM7ljj7oLx7Z6nWAtVCxbDSf9k/rnDTBpoRTteFwOKHbNKgqYabMknlfBKwlpL+FYVkolR2JhyMvzU5/E0hBvrl7KWAEYgdAW2zpJBE1WWlIHjGagl1H0pXeWZ0KVVFh7IptJREVGJsDMSnvIx39XDqZ4PbqQw+0n9/NKAedOy6V286xvyHnT5Evd+JBviSv8PLe0xLGeUuQGNZFUE38QunlqeisZFv3G7t2SOrpHo1GlbyAUEjNdhkB2TVw33mB+IR2TjsvMtx36/18uaiNrWqO1ntHkvrajvVPqsxfJDH0BQhcCpbr/7A7FTc9Tlk3B1Jjiq2tsqiKbyrOpTbo/NQVk+NAo0X1MOtKUlPzEPxafbVnkLfQ1JDnpr+6iKYU0Y15+NdSjm8QarXTmdXixKsHM/mIEuQDAY4nafpdGIjzRrNLbaPNYKeMEStLARBvFomCs6jWPAZziQCjgzZA+0MNBpwtESHgHtkKVElhPC8Ediji6Foq4tR0LH5VIroxcfylM8ICQrlj2gTHJwq6SEDgepeAlZbjlBGagTdBq2Fb91HRtgd00ArmBUF0k1GcwC3OfuApQG+MopggDAM9+tYL5tXUEZ2nSc2xX0HJqwxPpfi0lm2fQb/dHwDNE+maGSG+ZCmmx3j/eMVS49vt1fZ6Dad8sJfsNhAklOeplyE3hF+tHuSb6fJ7AojhUqRpsF8hEFw5GbSQzhauUhDSNKs7jyb/SOBBNntgiFspT1xFgdhatdPGSh1B4EAPyxUayKlSKmSZrX6E+s6Np0YdwlEFv3zIgiZMLzMmWHQ2mbGxWRice02rBGnm7xQ0uQ1eZg5wHsKG8eKcTWrbFFzmX929eBRfifOhbNHr32cXg97P0SYPe86Sfzc+FZWiYNHiz3DQ721quLv8dnABv28Sg28NKoTa93PuTP11FJ6a9TWaTpLduJ9h+rl3MnlxISDPja4xA+oR51Y37uRH2ipfPn0cQpeJH1EA9JUbte6oH1HqTFyD0p//1VE6lseJhR6pcdwDzFOFj/WmH8/H6kQtWytbn+FXBOevZ/Smd9Zc569qwgXoJ95Pwc4Q9DPIS59OKXncvqjMsRF1MJwODV7oA9VCzE15h8fh2ngRP3Ve8nA7KG5WnqkQU8BTcAl2BJsbSPegLEJC2AnuKZs5QLPxfi6PmAmGKkRYgLCzyW60qAx2E640HAm0UKTysuzCBU0lGcBY0O8osXUEKWyWL8UnYesMM8H/iZdJH6JRoCVXFaK2FMM/y2SaiESv7JEaDjcyDRMzaPoQaplIXwyAs8QNs76NmgO1iXKTAAZNwL+ukQnbvzTXARTJihJm18a2MV7Jk3A6xgJSJCl+ZS5FDbTkdMNui3whxH3LGdXH+3AI0sG1qovfxpfR8ewltyqIIPl+iSDeRyZCHjSa0GwlvDCiZ2OxIAs8tknu0TlU7KiGgnmMwymbPFUKqVxs/9GLg4ikIaMnRNJXbI3eJJ8XCaVyaqHsnl4VqqXKBqfOnByzX7MZwtc9qztZIwpQeBfymA2AJ4wIJZCVHeSO6/ORMveme1jwvdDA9YVHkxU76x3Y/eAkrgYnT33bvJ9p7m8Ll3qfUDVhVq+1693V8WCNPVA1y5AvND0M1P5SwW+0pDedPZ7SmDPr2b37BP6reQoNfSziOuejYfiEfd6WvXcNUsQW6Jx2PMxeu0CBDGIV3XtXvEe9Om5aqRN/TQ5h5FvT5IkZmfXat3KPy7OFRj7sgcOzULjjCHsHMJjCNTiw2P/2H+tRXpkUJXxcrbzPkOhIeCpFOoB4pvtGIhbA54xZG+lOTWy2bKncijpO8ZUuuro5XreLpo7StKbrausrt0GNKQat1zASd57Go1Rno36rQvhRN7mZQZ9lBz1DWW3m8n0+ub66ZPHjLsDN7PxW8H98ePV7S0bajpi1EtLEI1/fJIugAyR/gvUKV6ocV8qDwKjZZwIVChvRtka4mYcxI38BjM9UmFRin+mEfdx+lK2gt6obOPzKatl6bfymlcmAXmntgywM0uGXMxOUJx5/ZBZzMzZnrF/Dvu1o2oZ5daiWPFhm9NixkkCWzYAHW3TCYsHtBuPqQpBKJqzC/Lx9M1kNvPBf5z8wfFTDgWjkPQNTvDrHYuD05zlvfItuhamT7YJJweP1ul4Pi4uhO3HGYeCSTDD/4acbVh/wi5Gr3P2/bfJB1cAKJlTC7T/j/nZKxLsXDoZ4fkvy8S0ZXJaowK6mT1AIogB3tTAdK4C+WdnRDDK9a30gXqkQGitbU1ZelaMsquRENPCyqvVFxMEoByerFegCYIoUGYiUyJSGosH3HaQ6jkvYvTo0eXZ5cYa6Uz7s2ojI45cWJG6XV7KPEi/leWgkiVSx+UJJZVoJDo1eqGPvZ9uyK3W5+rk58nh3vWtDAT1AOqHd/T7WycY9tz19uuKH8bVqE6U7YgGOt6uLs/9pY0atruKJ9bIGdV+PWPuoXPwXWm9IBgkWCNz4OwpzudAwx0lNjg9RERH28WtFoePFulfvSaZdNVRVpO4K6bU0mA+js3u1kyxDAetEycQ7uwH8RqAWIQQrnUE4vVGrt5eeqzCtSLv+lgr8K5s7pKvqaWghruwG5DH+XdVuSlPD8suJs0s77pSzRJrMcNFrWXk8T55m9w+xpyogdB3BrcDOaCNyT3GCyY+sAyixMT7yH2scuhJvj3s6j+dfv3NV//+/+n/fHFxhuc5e9vjJ6+NKIvi5vZmPme9rMauLY8h4hKcUrDBPyE7QUVc7oUMxZgnCylFApJdmTTqDuz1dMgUtGFuQuK/T1I5ltn4OTdjo60zdcqvpYstmeQMY0eHGY6lSkgiL/xixCb6LMAFaArSgkoZpWcjoGzEjp6rmw1uNZQvAyiZm8fO2TjdLZe7f/SP/snjR484AUzw3g72ZeMbNr/Zbjfr9Xa3wE4ApSfswnmzLqaLyeNnT1kVzGyJXNxTdhBaX1+v0tnjophnxQ2OO3jyc0oaVWdtNCP36+VOqjO5VTo6GucrNt1cb9hXHyjMSgwMHiyxm5trDZWjCpkOUilVpmxiNAdAtNC5ULiYoFcD68Zc9VWEN4AlmXpVGOSC8EZi8wQWp1b0OPSpGYmzi3OyiKcVrVj96VFNJeNBItlIl82xaEEzSbJg5AokrkTkf+//+fe0A+r8jL1Ep9PL+YLl0mfsovTTH//0R5/+HjMc2m1V7S1zRZyVzy5/Kh8aHxUVCVGePrJG2j0jKPbj9XAa6G/uUE5fYweiUwLOMNxDVpdnoFQhVzMQddRm4g8q5v66qqnjg1fd+N/9d/49fydKVH9/qScFwZvdSlUcM47FvWXcoqaAo49tdlIoPIyIBzbNmJB0UqDLXqRWzSvI00yKY2qytbKK6eNwrQjXekxQCzeZ1zhAX5PHOTjnZvaYf5NVnPqA4aYYFO0S9pRykKut//TkHZLU1TeG5D1CM1za4ZRHinyo5AOt34FplL8Kej+rnvp4lj1SpIJ+ZRZeXIxRz+bz/+K//C//g//Lv8/WlqQKvumSo/ZCe95rMFjP/nYrOcHDYq23EfIXHnSChTa072gOtEgasJZLOZQdTvLMJgCCBBcSUiRXCQGVRVIqgyCmUpRMDDflBfsqJDyt+45xcRbLut+8luqKnxybwKEQSib+24g3omxegNNn51dsug9LpNORupoGGc20axAOOmz2yRFdU61wEJxFI9gtWinBCDx3Y28Ca5CbAjgSTasmOBgAuZFaw/ZZ/uKzZ5vdirXVtkDWgbxG8MHEwHpV0atBJclCgiUhj60Vxt5Yrjbb29tbqcL0IBUiRz46m88uzh9LBUqR8k3HkgtiwopVQI+mAFWrcZVRFVVIVw4uxFDtxMKKMo666Z/F2C3nzBAkS19KjO1zicqp0sYMe4Ym4DCz1XqNeoiEJLcR2dX26l/6m//y/+5/83c5XUHmjTLrnyQOl4oOD3Egiq3oq8+YTGHFd6XVab+753f4zhxcqe9cBpopatgjcj94m1rvlACxHkIpwwVDbs/VnHlwRBGPNMdlHanwu0i+x69k0EyQy+t7xzmxDkmapYTiQqCp1ZB0SkD+juoD5czhYdYgh/WDqjPwGc8AkKVKMU7GwnNyD0lEB3ZeCkm1GI+/6/2h+Z0gR62ioX4E7lzFVp41mWpVPlqWE4Q2OUofVyTkqsngjwNZteYdGFmrbC3XexCgVuLHx2Ma6O8yx3IfvDwiVrR09LTn4j3Ae4nfyzRPAGQZIBZs4yKSwWbwLsdmGZ3QowbaU/az0dgsBABWJVmYLJZT2NpHoxUw9CagKJ4liuPDACRpSlDpbgWMfahY0muoWa8G4UbcQCwUsiuH5zQIShAsDrmGmsVQfJR7zUj/ju07lVtEY3bc10yGpjiMhzgyUq3KgMYtwDwCwF9D6Wy/yasfAyDBADD/GfxwWBk8kdj6VWP0XSPs5sCDC76VIiXZbpnmGWWpyGXu+5wprAmD9OrNG2hVPXnTCLwDzQnhSkMBkn9KPs1UQLPh1N/RpmAhsS4Vx26nnBZAksSW9pWd+jEBoLmJxUymkM18qD1JlLL+/+z92a8ty5beh63ZrWZ3p72XrCrKJYmkaYqCbEB6EQzZMCD5yS968IP1n/nVhjoQfrNEGrZfREKUSFMlA5RFEioVRBbJW/d0u99rrdn5930jMmZkO3M2a+19zt2598qMGDG6GDEy54gmI3UiRZ50IgsbAQBYQaWMUAWKErDVsjoMVQX5z7+EpAKTGQ3ewJVX/TS1opynI+Qu0kF9MCFhUlyLKQsbM9irM/XNV/TEEAsDn5NOIEAcylqd2slwSU5q1go7M7bGrg6dOJ+BH9ECZduUaVRyaz+SaiE6K5ATh4rfS5gRHrN2h9ZiL35Wnurk9F6qQxEy52y0QzmMx8+yOkgo665n2gWoWEsdeDx1eCJCxUqvtu6swvyuDuXjKb8WvnqHIUy5EcfgSrL2WvA2pC2jc+S7gVb2YsuiMGK3rYw3ULkxupWyIp370AOc21QZUm+GDFYi9Gn04wNf1ezpsx6nRk1wT4aawhytdjr0YPaBO3Qb9J8+PgHPlm+g9flGA+2Y7HhtR2D26X+MYg9K02i2nO0cq0CTjEA6bkUHQcop3HIQqJQiOeUn7969d2wZsZ5jcqI1rbvn7OU25ioCxWYuUBF/6OB4jWFuRXgB5QoSw+Pw5zFIoBpqiMQKkHfQCluCRELa1ddgXLDWn7NpuSSaxJK3br9W4exHyrdr4TPqDDvG04ULpXUjwaoa5CYRVdURKBEUz7+X+Mkz8FkOpIh/OwfAG8PzuT79a04LUB2sM8avDoOidAXjVsudCSCVTMLf1yJTv8mbBonhajq9xnr0HaCjkEkGE2NPTSooaFYeJtoWZzbnq2J8XViWgz1V1BvMbAWaelOqLtgYFQKubK8ZzWF7ApdqbgAlxDhVxOlUZIEuptTKSOlIRMpZQ8ywyuqK6Mg6IS35J6vyRoH4C+Vi8VJGs6XBJk3jzOaXfAohqKToilkCmuw76gGVXCI6gVRMVQNkQbAJdxFrsw8RypEFJxQQdOAIHgMIn0TRQzwz4/kW1RvDP3DO9lTs+X08yNx2hF3jl7SN3+WyaGSamuJH7aijDQl3g212wzEi8nuDGbnNGUiT5znsliXuSRS/kr3tvk+fnf4FtyR3H+1OvTbtrkyp3AR1sHJh1Z0abYxxkO6xf2jDCyNRE0OBJpFrsNSeGdYmrp7ViW/GHKflGKwss42MtIHSNv6hEJgjIqSUNQs45weVjrYPWsFci0PNchb8bM+caLDda9vQv0H1OfupWyDaVZ7tlh/TzFTJaGrxKqHgKwWNhFYE5xrbJp7UghTW0mg8mf9EY9xESurzV0EiLmKIfEPMXSGm4ZRZhLCJcY0Z4v2oE1CwHIklBIhFFzjKpHRKxkUY4FcXAwklHTsCtz4o4v8S4NVF1lxU6r24K0CRDi4eW1f9qD8heGCp1lU4jUH4lBiLfRSkSzZTBYEFKwtMQuGhoFZj/BrF95cSrBF79fDdXF4rZktQ6o4VtXNPpWsw0au0qjwaYG8W/6Cd9/FU0KwSCXEXQ1sDJatKd0Jq9atoVOksHWQ2nSDhojaqDmVV4LNwxDaOKqMrJaoKhQkHJP4bJXgjROwFclBe8SEfJOJs1khH72BnGOWYjzqCCooYqecp5oCpAsG/aMCTCEglXU1sfqBVrJ10lpPVyZAEDY1rUGeCU19pG/8z5PEssLdVdm7QpRSlezl00R0GyyJIDOsD3/EqZbaHafM7iT1sq72N8mA2i12AKva7tudxpmd6l7+Uyhbp+W8rLnHd8arDR+Qy12y1gOTsMI92P3UYvyzNopVw/48Vohx5BAL4GDXGryfLnJES0keKAH+MJo1+/I5kX59V1R48Dh3DKNuls7/eWfEx8zmDavYWlpbvRRpd0Fmj0dRGHD/eYPRS/5OkK7rROHfj6OPZB2+QN7PZ88LLKc6QBqoRcmQmRA2TK7KcEs4ulne8F3vBG5mMNCsc451axu8VpTlSFzMROxJTBBuCUpRZyaTUEpQXsqlMySIWXR3JiUhFCuh8FlcyQE0fGXLs/i5oeYhrUAWUleVOmPs85gpQDr4s5pmzYl3rjRS2A2LxvlefpHAYNhE0i4EnJhCvz3yRVehODSRppn1+2NBG22tiLW5wdkDi82isBeJFYWJ6PnZLAZ0HfRlXMTgdDKJ7UblO6m7wBxWvHYNzx2ofYa2BSB94YtDthK2B9NFfDfAjF1KYLr+erC+3U+rlEm3hQ3NoHkAVdghOHWw4KGJSQkL1pwokY5GHgU4yhgvSFUmiLw5nhC58DjHRJRNn3EARHIGBmpCTGOCoJGvwBnbgcIYMO4JiOvUtscV0/opekdcxUQKWWwzemgqa8s60a1CJlkLlEZoAUW3SIViV7rwaYQ9W710pJ+m4u9MMf+uu71TgowDL59t4BY6j6uA/7vdxT6tkp2wL0Ccy5AP85xhwgL6WHa7pw/1utqtSg/TZbfSvW0d9R9D2WqNPn5rSPZlTaOssaeWoVxkF1VEeKhf7jAX3hpU8NlPI3Xlh6Zg7aKCGx9pzm0U4clVasD06GVpkjpEI4NE8hwnbFSrxsyYl8CHSDyroQZnvtcaA9GHjw3mAdq/czwhDFthr+iHi/WVmX2+9HomA9T8IIkO7EyV6H3ptK6mNdBZsUh+ICi0JYtg2hxhZcwFEYQhysEh4ZpmcYWiWOx9yUUSf4sQ/DsI9oUGlXJCoRMJ0FiPnRFLVR1FgkVU6DrEJbglQXMQl/sMVXolGIHVpEo8kW0PbQuAPnhW6C5kAYcKAaJvQFFIqQJBqwSZwB0g0AXQsKy2wDw9/sOGp+NZH9JaA8F4yKH6dgCli+g8a5wYVcn2K2H0OdCL6J/o1dwJlsMQ5zoLqVWnxlsVk7apc9rIZ1UjpcNLVc1slPmYYGAWuCv2/PCU+icKiLMPwrFNlaIosWnxSm4IT/TX1BAAHgmsXXSw4iUYSZKjNlh1Uo9bGhY1qq9VAxomq1dW2MsEyknEWy31HttQ+xM/lPxsL5DYd4QDJq06v2whZu9tyjLis2RjOYxj+InE+mnFy89TNWukTLwFXZXiknpW6FKAqWb8aiUfeDtXlABoHIxBwO19fKti3BDekdmTH9Ilr6lvnRp8JvoGTLVRKCq2E0K7viF5sZtVgPjzWPlyaeeYEzGvVzAWtxDBnhhjhM4zTYpkAbauWmGVLHbpCrmP8oGR9SrpowbaU4RqNEtv2mVFkQuqQPv6+6xkF7OBpffrgfd8BMHw7+76qTDh33CoVbHdljfU3BIhe6S4c43HSODkrzb/74cd/5Q//cLL5ShHs5Ac6A09fPP/qq2+IUfFFn9eb5TcKw6Y/idzBczzVCPEUfPqJZSV0kiz+achcOa+68cY5ItQxWX8r8bPvFcgWD7zJ+mtF1ZdvA+goMCiErntMOdIBNCydSoh46pVSxuE1y+FbkxBbmogaEZIrbi7TSZvvSLRWPcFxyn70K7b+mX61XX11cfnDlHeLdW/OtxO+6TWnfEJaTyQ7sNiKm8N4zrqLNeEgmhU1ZydVdsTnc8qTDW8UQIVhpZDKpRV2Z5IEe3nNOyAtgtmuGPufvEVH9UDA5F0C1HSPSm8LxBoakQR+1FrKJ5Okiy0jJOXj5BjaFqhwIhOtIdsIMWisZqDxBYYVMx54nUrVwqq1/iV7KmFUMQJuC5uPkFUKgYipES9Vq4E8OcCX0mbYB1thBnfV6Er5PxUGzTx534PuKDsLsYAoJMcbIPpOcLANneM7ANy/P0AWpCSsV1imdW+2nzwW2PUEiIIWhwD3rhiO4jijA7rQ7tX4Zd+9XxL1puP5GcXm2Yv5cAXFMzyE9NmzT4Xx+PEr5i9Dd8UDhYBoeLd6Aa2Sx9m8b6Q5adXzpZ1Kpu+DnDlLYnSLd9R3NO1ZNO1m0vKcbrQeKE1MvfqauJOo9LQy3YnsGzU/QAqUvm8DJ5R6B0DAYMI5KxuJLuaVnFymB+zuOVYVd0By0QmJUscGmygaQGjgkw3ksq6dVSkJIeEIkhJeMinh49N9nMdzeBzMhon2Gjzq1dCtbcAGQidVA+dz9lO2QK0FI9Nq9ZovgaPwzBdCe5bEsN//1Z/+s3/6H/5f/9N/49/4a5fzX7Px/PrieyKum6fX/9Of/pP5gu83OWZStEk0r+8D3Nxc6y1fR36YR0GvOGppCretkjKa5DgoQyJpCCJGVJlw1pdKzThbI8eLSq4MmWibSx+mrlIhyQTChbYIZFU1aSOp4ore7LpDnOngUGP6hJiL7WK5XLHgx7trmlrYHPopgpZ3HMCEC/VdrbYoSB/JobyG3r3PvhAJQelaiICdQG0hZTlCbylBSp0K1OJTY/BkdZGEwERBMEuNkI5uWiGkiiiBmdRziEpxXq3u2QfUevEtNnTmRQJqlyoIYcINcTIwPQ1WywB2obUBitBKMZfoFFKkcuOgyIelKFUBAkxWlpaAXKI89QLVRUFCWnoJJrfQzIa5cVaEzzvNsgogfxeZ0HnKhktP7j4sX7/+6e72A30ttjWaz+Ry9FKpF/NUUXVZC35iJ/4+h3JZZ7KWFuDdOfB3eVKmcXVq4M+Zj2qBjoZq6VO2fKtwLyD7RyRK19lLezzCmHodz/13jzK3YqPqD9ucXVIzjGct3wEIfRKQixq+QGmo62xZnNOBaLdJXLpIzw1riC+U2D1yO3E6FQmnj3O7r9zuh5Wcy3FrmMMkjjZVVbLnWjLfg3pgcdatk64ht6xXme6kHQD2Cc32QW5jPiEaIp8HmFOU+QyjHV9ajgGU6eM51ikP5Vnik8ZMDuzqTM+S62u6UcxNvJ+DIzIzlP85HIWIJ5ED+8n05ubmv/hbf+s//Y//IyYC1sS7/l4ssRPR1pMnT66vr4E41NMcAkHq4ubtkyc38SRzVJmiwAjxHPBamjTL0kg6DUTCkwJGMQ93DyCwIJOLQuUcEUcmHRIHgV0YJ7m4UwEkzX+liRrRWcG+EVBbAA4pSuzNxvzKEFsTfWvE32LoAmjJ/4QN7y+uLudfff31an2lQD/pqcX9kLmLYT21LAdSjcQrspdopKICcOcMUdqKgaPwFTs4VE+hLGWrL6X07CV8oIAFupG6vfsgTOupDxOw6/+K74tFBFzpcjG5ur56cvNEFUOmz7aJDBhyI1ueJU69A2miNIcIUzIAuzNwaQYOBJV0soEfciU52hqw+4SmaJ2EDRsfF8wuUW2k4nXscgqQaQDaDAYsT5tNr/+1v/ZX/p3/9b+jiQA1X0hUfwnlfYRaVU4gF/SWBlV1TmiZrIIffT34TQD3IB/sOTOqHg/+nB+lRQ2paJcaPDL2t+SQHcUFqJMPLgaK5t92h9yozw598B21750y25fu1GeAf/LuPnYfHV7+Yg4qM1DHQbqhwk5jQnAuo+nbXO3xfqSG4BDTFNaeAYgqBF4m7lMzP1BVC8vJj94hU3xaZU2bVBYLLcN6pQGAZJKq2g9Sowdl/iAat5hGFbK5WuU7QLbzDlQ1RBi8NHuJ8zn9KVugavqh1vMzI7V/8nlFoxyM/TtGUzDFa6x8VWo+u3z64hmBHREz9Rbpdvvk5uby8hIOUGkR9vqGR+F0cR/3qeIwUtJA0SB/ISTBXQCc4ghHXR6cpYPRbGIHsmZmDuJirQWS7Ij4fHZOp1SiYuFIRDw+UglAmEkOYTTa8wVdLZwBrGkMB9OmZewZCjb4UUWWsyUfpwIeswZavaQI9vKWSRFtxq/Rd9G6RhaIrUJgjEwjTHUNya6gwvekmoSrMmiFmVn+4k8Rx+xK2EmIKk32VVqW4L9W/tDr0LA5ITC0/joBH2MmdNZr3MpTPeYU1AwOP80nXnoQW7j4ooQ1U1a6qzaqlKWG4YVusZSrPlErQ1CJDqGUFxNE2SBKB3dxtKSQmURaUsXHJBKrtiDWx0SozVTAVi82b6Z8HoxqyUZM2DDhcnF3d/fq5as/oJKb1b0aJc0kiAOVqURb6XzKkoWQjh7U0C5VoML9fP0ELNDbYJVuu7atIO3rzhPaZU3vCa+VY3fgjgBBP4YycNqK9dEGZqbqQxuh4O8Qysi2GGWRRlM1snUW/snbdQBoLKEb6mS03nAbJv+znBA2jF9qMLo3VhKNTJcV3+llifWetPhlBBKl+o1VdJQ2IKEMJMGhUZrZAhfbh6xvaDLynOrYo0+oXbIq61WmS5yBdGnSNlrDqu3WyfMwYecBbh1rB9vyToGUYzBl+hSeJe2hPEv8Ml3yPE+aVhow/B4ZFXF1baMrqHXzKiRzgnCTqGrBShQCN9ZbOxhdv379huhxtWJpuyNOYxME0zeYz/U5XG3BwrH4ERkKQ1G74qsQMN2oQql+OoWjEXGBiOV8tYKOJhU5ikqqV9RmHZmEr2hUYhJTcjrEsXqckiW6V54VORrMY2ceD8BDZrgYUJaywYwi1FHQSZ4+gULZiPXnCqN1GA4SXwJDI+0rsl09l7aTl/zBQBBZ11Jg4x36RReFCsQ9S6AOhNAFX32pM98ocKUcQIsilUonNsv5KbGVhYK5l/So2yIyYm91NWS92ZOnz5mbWS71UTAtUvL2rGqqKmSP6B+h5rQTJZNLK0XkWEnWlkF8CK4jsj6DbggXMdIUCuv1SUolQcQgOApPLGVT27Fip/5hFPpiTm4gNZ+3UVJQP6MHoI1W52sqQX9A2yhdbO5+f729m+Kr6hWoh+MGQq515h1tdBJ7sjonAXEJsOD7DmxRkVbXfSQD5aPeBCjp6QV97KPjOd/zWzas6UOM8pYSD50tbzlFYubfxI62bu67WMnusI+L8ux6n6CKwZ5rH/9MlnUlMcKjM92+xFGtXGM6+ldyuI6l55Tpmqx6JtukDj5nrlfnsg2KJvFjddcBSKoYWm+30L3kIlznVeTi8qHUxEycH+gS0kLHhoiseGdpRs76khjGDJKM3+DQR9vGz4R7EyNV2stnPEJo21eXQ/nsxT+ogqdYcq8mnxH6LXC84QtH6mBCqaCOkCRd2EGhYI9YdLPk61YgKZon/lrdkdAQMuGVgrlA1ooXbUWvYE5hn0I6dRsUhWk0PQk2dqQJBUkAsDDFavqTBolvdQ1lDI/SwAJsDoIpKBc3jpAaKGQFpMSRpsO+raJilA+xqqAZiVS0yQyCBSA4CC71qE2s/KEQBCpmLOlOqAtAH/9KMh3ZKucHs4BK64Ik8HUVT7/dK2vIaDIdGlllv3YBkgf+BXORysQgWCWTmVdoYflS16ZQjXh1VguEVDVJ4TUBx+UCqF5Bq7PlJt0ETzLA8dSHMYQl0UEnqlAkpdTWcUCFMBATSPXVQp0oDw5Jy0RrZNLVVZgYyuYTSlKPC3XCBTd6a5wEnKmVP7pMVp9mozGkfHibJ6TU4wFLr1KUqlfKmj1FtSPyJUqt2Jk6u3b5Z8gjWiA3YKPNMnxAF0iObcsgHeDdURQajqc8VjeJDlljjNCh6GfQQRYY06JFSzjZ6gDoiRcNnlFzImsTrarG1YPNrbxd/UrQXS8k4VQ07d7b6N5YxaJ5jb5Xe0y6s+ctdSyx3Q8OTXOlG4o3pUZtW9A+KuDJfsfVl3FNJA7Stuvb7pWWtU669/Psq0ur0k1A1gSd2zo0sZ1vyGq3Qm7fXNTJpxvY9roSz6WN7zyU5Z9KergWg1qObIVBHhTuvHgfZkd57A7ELjouoxnTEXmfA6hAmiht/S2R2mzxE6Eir1YKWZEVodyMUWTQFVqtvwQ8vXytBxDvvRJX6w1UlcCBEWUNRJMn/owQjrFnFwEBLClilFxKcaqWNSukSyGvaONBGDgwIyteClvBA5y6IIJFsXhIEFzMj6tDYJUaZbLhTWX05Kyaoqe4q0PAV7cAiCmaU6YUWWSpIxTxcyxEEbJeGFYFfRaWduqcbNkF6MYj96GSeJsLasNRFRKAAFUlkCmtfoVmJ3RGd8HnLynQDv6BT3WlWaiEHHpirqdYw8hKkpYGHJpSsBiq9KVgmklQl02TFtIBlDXrgZCedVJ1NTkQsxASK7bqe7gKiJeuhgtVsynk9C8fVbkB/moEb4rMZryrIFR24/EaJJUiyjUjEYZl6yTxjK80UKbaSk1hhoSclu1lI3jK9OiyRmeW/NDHuZjgsdo66c9D6PleejpMYEV/VCa2wpJKUieh8aP0tc6zH3SOo6hWBapfg1BszKxe2Mrx9IAAkw0cUqermCYA3v9L0aRp4fc9f9rwNqTJfCBfaDieT8Qq4/EH5JdF2Zb8clUtZX8AqdCzTZIJy6KehqmjjMuVUUTEA336tPnlinS6SeCXv/5tNCCZSZv/KEjLemdvu1FqlFFuPd1HHtbI9ulDa8Jbv/t76nuofblb9SXgxhFcSl65MXfAeIxByUMtoBnpjB7b0OykLFoWKooV2V2FzDuybcyG4AZVlO6lajA5KJuZ58RB5IciP46U0ApZHNE0kS7PgdNuqYB/Pj+uBfINFE10hPDc2gqxHIzBZNe8WhNOVOVCrd4mXlZA6VXjxG0X6xX72CgAczTLKKwItNKH0JKATNGbmOkiXfmTGMeMIUxQdFC4q61dIqeL4rq4OjQ3JAIskURWfQiTcwr+CpMjPE7VEWaEs4qTlePsuQz1RLzoxQE9UHiRtG5GgANxofJhGxMmHmYk4a5emMgaWNZMK5ig47Nc4goDD3ZLgNk7lCUDuYJzDmiTUZwNRZ20QMoc6gpHxFytmxgEYVBYmMQEqYwIZwJj+mOA/ctgNU2EMhKv1ormCSohQpKUNTeJzRa2oaRAkikMp0NJzCZ0KSEBqR0kQfE5BxXAN3h7GoCQVXXXTjqqdoEEB3HhcGV9tTlBSAKi2CVBhpm1AAgXtV39HvB0wt5QtAgzHfLDMALl4ECJVp6sQZRUliig+ahlBA3JubyRaNE3yiMruf1HKaFM91MMlbQqMIT8yy0bNnm73qeZDeqy5Q4V3lanFzJSzzZaQDL8AVXs1f2jFeRafzQNhgTPy5FauxH6+uoXtDz2HM2V29DZ1a+V343319MdElu9tw6cALX6PX2YId3K1lDymHFAGw2Q+8FBGJWr0R+baWtyHKdaP6+yW2aeE5l5o77Ay3YJtKj1Q1e21KStQ1a4LxGu11ea4SPRhF9ZL9PWEi49Qs8ak65MrQUDYbRXd/AbrkUHwQ40pnZtbduQFGOZcVepCyKGbo01zv0FAPttiuIi1lp9q5ac/xCRnAMkh2ezHwmdSF1dP7m5ulmu7tickuD+cn7JqLJiKv4vXip4i+3rI+InsoSGPy9l0XAyIRjRmUZsgXMoGqtCLt7a9AdfpRWYujHSzVFhmMQnQUybo1++AACv2Q/qdWy+llx2+1bIqqF0c6KipDX4CmVAPAooTcSNsxYoUR3UZp06cxpfAeFrA6KYahF5otVcB2PYP8DHNSajeko0SXESorpJsx+m82uqrPhY/yRIcacsCx5n8VRGJ/7EhveKXUqrkY2zUayHINKE6QksplLHusgFx4cVEL/iUEcMyvkrC0BT0NU7gyV1Y10+MbNZwFm10jlbRaq7EOTNlyrxHMLF+gtosbkgrlw676J5SVUkrm9EsB7qtWlfgq6IXy2la4izSAtGrmY8OChRrTKCUYGJDQzFfP0FAtaTn2RJtRqK6pMIGv4Xjjpgk/nqYnuvLy/7HWTeWVdlt5dbdki6X7InknZV1bYulQVTjawCp6i79TGoblmBZDS3lC5qRZhx9N6VWGTgCOJAKNMBGaZts209qfqeP214G9JmPwZyKJ8D8P0MP3LGuGWZ9juBbfOPqW+F03aUqqTr2o4Hev2nIA8ZfXqWv/5BtGfM+xR7WsBw2+2p0Sm/yIVNhpOlrdr2Ka3UUZeWz3TgDIsfLPX7P1pfm7GsbWR3wPT8y0hOlPUq03WsR8mNFN9GCwjnsq4nqhys2rJOZBvkWc8sJSfOwr9kAueBWgyXlnxGpqMifci5NCf6MD/DH8wC42zf7zRREuc6LwVejkYdyxB3Tdjy/4/+6P/z6seXf/gX/mVF8Rfbm+vrb779+t17XgnghVJiII/2a+OfC17/vb65qQTTd+D1TAJrDr2nSVSoCJQjhUoEXhqJJ3Qj2NKovAIoRWOVUoSJTipYdEJBoNfHg6lIlmUdLMKZX/A54smUfS/Xq9WUEV/UVLjMvxgAVyhKTswoidII+4hSNRuAVnAjauRBz4kgG2WgUlUs2ZpYGXFJf2DoZV+Uk16qIH+wosujXSm1GkozAD4sV/UTPzRArvi416G6iKX7C9bQksQau4iBSiGxFJqAfHDVWcZUNaiizaTqqTqYWy/EqtuF9eOfdjhVr4yx7xVtZ+VoE33eIDTJGpox0ukxIJcZHyyDZF6rpYPE2WG3VaMVQjcrKZ2tkmzCzqN+1VhfjJaiNhW687+CiIXs56uL5H+VvhS5RNqgoQhhS87KqJtxecnyoks2/VGREGQEqoeX/tmfff8f/kf/yXyxuFxcXl9fXV8/v3oyvV6wTe3VX/mf/1U6BWu2eXKjWbcQFNYrABYWJ+kowflQjXKGRDNflo1Kh4SWnFG0n5FOtkCtMTu4jWwY2ARmB4vzgkYqNCD08XQdUOIhi6KC+1r2ITUYwZsHrTaj0PhcaJr1pYVJ68vyZhPZ7F0CbuffZewRokAZ399q9Xt6BZgnI1gHqtLk1+gpwi3X+DjOQZ7FNPhn+KhEv91yg7T72W1ITVY/zxKtUYuyqG2WPRJL4hPS0TS54idweljS6Kmf1O49Co7hWeKU6R6WHfNFXSMN0eayfVepeRO09R+lOwWv2Q96BBHV8bhxyyp4ZJSXodTZ5G//F3/nz37zL/iyEkHgfMpSoMn8asabvjfXz7g/6QLM55eXCwXxl5fz6+sbRduO4AjFOMSTWNAQwj5BFKtZcJwdfUb4mAN9uDE+zV77Ig4a6Ubcyap1dSpUCcivbr3C/Bl7j66e8P4x2MxmaEd4HnSKs/W4cwgLRMttwfBaIUV+BMjExtEBQKD4YQTBVffnNgi0toiMQ+DLVkhPNcDMqDPnyZpx5R9++Bfv3r6fwlvqCZ/5hCVfDlsvFa0quOcMXE8zi4i6p2eb7CMESmHhtkkxtDKCaAELj2LH4orI6eF4EkD4Vi+ZEUaRcgM4p9rpA2UKnDktl7ds02QN4btBw+vL6y+/+DUyoHTwjCrYDVzqC2VoLsWs4p+HNpTcXvw5p1Eg2dOzfFKMWRhNEGH56WbGjrEfVnd3t3weDvugCZ0iNooiHpcQ7CXriCnHarW5v79HE3+4QFWrKqQa+eMSkmVNbsVo8+T65vqSTurlHUG/OhW2H0XsT7Vc3t/eftjcvpc51fGhF/MNS9eefPn2L/4r/+qTq2cXm3uLl3HM0wpVyugKQJq5Haxhzlhh6V+Bi2vvXVngdCfDDN1l54SOeRaNkVfyKdO9tDgSx/i4oo+RORxv58z2MH2YahRljNlnHgOJPvzSVqRxorIuZXqAOc7S5X2i6JPbyU18zmXPTgF7gSf7QzYFiYh/woZkOeJcatFnH2YGMGnmlknK9gpgG5KRBxLxDl7Mw5do+jVL7wBEk+ocmuiaKpDr0VawZFbRlbDHSWcFzyVuZ4ydOcQ74COlhD0e0yrDsg5SvqxjmzA7wtktX8rtTLeV6UT7DHwYC5zB/GJhByIycviTNSVngLZvf/PqNR/6vX7yTLstys1W/AoSNhF2cx8yxq+PADiCpyyiez+wFG/ZK4k+Cd4UWmmI3bGwwjoieIdbYO0ecNmNha2/UCnwuevpjaQYTRoqYkcHIr/NcktP4YsXXygYZVkLz1KFvRGYoqfmATy6r7Uvjp5ZNKLugQaAQxB8wUlCScdsQJQqFHaYSycHI/BzBZ85OBczySIA/cA4e7IZLEjNLlhh4jpAq06SKqO6Uqt0eNTeL/jS1VG4TbfBRaoUeKq8lEL5oKMU89EIhO7oAyfhuwMDZ4ETuSTZeJDHP9ip6giasG+p+UpN+i/T6eLpc3VpwmJYQ8oriLfd1BGivyHtIAcejCLtBkcq+GgCvnsmmoExZINR0PPilg05sUC0IlroBQm1HSqnioudfYMO2ZzOG31M4SebqfbqA6kxrHWqpj5uoOZfr4nq6ZvJatFFpCOor7TRIWCOShpjJFyCaQf4MG/1ZDa/hE7GpMjGDuPZcsmOqrLs2H2A1FEoc1vxbqLP0E/bAt2NmnTuaO5z1caeLmbZ9UZyhvBQkk7Owedc3DpFPAQQhcujoX+jtMQcTp/FpMMiGqWWqIEZw/WgJeEMJbkevXqVSAV+Q0jOxs9Mzp4lYZ51PcS3r6fVJ3O479vo2+3swW8PR3+9ApPzMP+2VjX8fv6ZMONnUwBJrWqk3JiJZJhnT71gkvnDp8Gzb31bVvIsibIHXKaHmSfMH401XPdhRkXpGOm5XUR3Jrk1noU+ZbLEKdMlzuOnI1bUU0Y3hsIm+ZCX8xATOXBSWCTgjHFsR1PL7eTe4/es/o8wiWBNI/GQcSYINz1kRFUOlwlwGRVXuEcYqFJ6Ag6jkSmXjaec0wzzKxq0JbR4RrEfSvHfmCQUMiotJgRywC00mDguRDKRp768S3xJYMmBAvditPpGeNP3ZgIcPPKK+3a9At1SrOhhTgMh70S7eYa8TaSlHvjITTjb6XtZbslQN6Eq8a52E/IIN+oJFSDvu4rn1kWSqBKbHBmkJckzFUyL6H4WB8PVHVAILoYRXjscN45mMObqnrjLoGqIjzQ1f6VNGPxV78QGsOJdvgAw1eIkKaP1SghdLTEIPRkibzWoXsmY3JvSTDZXKCMh4RGyrfXUKSy9utg8F8L0rSZJlkpvp29hLOFg4wNUJHoRMgGHrW87OS8PkaqixCRfiff8lTCVEpjE1vtNbXlPQI4BY9FgamL9lV5NAYq5lhhNdTbJzuv0/QqWib2jzza9eBaK2Q2kiUyGscOWWV5CCgUkUTxHHIEXWtfQZQG4hZ/XSg7LjHniDXOMZ9G5+ISsGD0dlnvos/d0DUfp0/M7W6elWblBBBuMaqLdk7sUcwU1Byp/C8p0XeJQLrtXTpTYhdwELqOCvjUC4bgPYfNUx1F2LuvRne6usnEpipoO36xt+4SkaNm2l7bbqA3p1rUObY/9R7lr5IGZhF+qz5Mvno1lvQOBM8BUXBf1MXKlgsfJV23GUY5EG8fsQbCicWBdqlqmD5JaEkY6zmGx0y1/kDKfkT+qBUpfOFqRynEcCRKd8eO24aNRDqYdD7Ggn6UaG9ZSrAjg5pOLFSGtQluiNw+vEvtGLBiPJ0e9wS2CKgIqYesRRcwjJHUVUpxneARqineNINYR3DmRqCXDbExPnGaOEbFJUcV7en0AZcQ9SnXV4aug1sSQ4CbCKHVRlQZDcHBEI7mRczoqZ1hV6FX2IpYGKiHN5ppshOpgWrmwEoXSTub1QZr6IQTtpaQMIBYSTYzI1IrgmtgAprTYCx8ocaRmVcRZtrOdtMheLM1cCMqGRoDFnBJmLfgNFg45cAn6MR+Ny7SGYnTTSDOlpXAgGT1OJX+zkBTLFHGV4mrR6oupklqbgxhVQiUoH0TiD8R/VjhxEh/r7EKwZJ1Q2wyiCuIGI9jpwHVNBTNbwWt+ZtOZdgfVq93YkJ6P7IsaWM8VFAWzBKwYwpgWyckY0qSygJJJY4H3HmIQzPaifkb4hVtAHlyvYhtSL3+snL30sYSdJkd39s/paLT4ftX9pNEuQHKOWi8hWimeTTwFI1vxTz1R4BTw4DvRTu3+WRvSX5dO4WVPa2TPUiawlJwgF+nevt3JY7ojdeuvfXdJ1VDdpfuhI+oVIvr69PtF9GMM26TsAZfpfn4qGY/ZwafHG0/i2SHGoELWsB36GBwH75Wl4MxRYv3nRPjsFv/9EdLkOH5mkCAQZCENq/xZHsFC/816NZstCK/YPmXF+P96PeMl24uFBt99dxIOEXL57U+9+DtnPZDiO08iCEXRlK+cFUoqABRY1IRtCtlJKaiKLkREV3NFx0ROGsoFQQ/FwBRpTiuMNCtjAXb8SyVgxf0izvrThas+yHUxY2Q64rqwnmscYaIAoCHYhzADh1CZeQAdKnb0mUoquMroN7EsSXv/M8xvgE2EZWbTy/X29mKLAivmQJJ4VR+Gto4sAQmdIjMKOa6Fo3q99wUmxVTUhokdRrWUhTozmu2FN/w0IDKKzBBs1YCg1m+4AtMBlFF25nBoKJbCSwXQmKshGNbLwLKcTZHaQK2PsmKV6k7anY5AU13zwXIqW1hVkLVdWVFLrNTlwEpSi4o4+DYmJXhCkoJCaOUWn7xUsUhl32Ag2exlJCZwo0hnvYhBnqVYWjdksF54ds3EaqbNamVtdyAmmxkutpxczSeX8jVxwe1nXtfkpCRagHiQSX4ROc5Sa9zRidw39n/ozEDfE6/36dGjcx+fHvT9YOwTttqPCkbxjO3Dr2nYxm9DCkYHWGPE72zB2Pddme9Ot51lv3kCo0/zEt7pYN2KtKC9cZQxazZv0Z4E6LPzYDsiMZxKxjFmRJXDMU/b+mM0D84H+PAYphmn0WaFO1jbmAEIqJ6domuqEtUqKBNSwLOkn3ki1yYqGtkG8GdexYPVD1McTOYfraYXHcHlM8lHtUA8DPItUNOlG1pDaWX0fIEnEQ6hETGkAsrJ7HJBxHa1mGuHRAdxihLZQ33K5IACWwI9ZghAJ9SKeIt40p8HpqugQDgF+iYWe8dkEuS0YjWPY5OIsFcFABWtaii9CrBEavmcFN8FkYurAFCVtkZJBPjg8fNgYS6K4h1EJCpF95Ti4nR1Vj4fQhK+rk7nklTgUkWW9GKkYXRW3NUhi9H8mgEmZNwda6dVN7CiThhcI+9KZvZRZcfNkkggC250uSIMhpUDWeDphwoEGV1nNyjRte0hpsT6YqMqRFcBHKZxeH8DMBqACERvNXj6x5YBXbxSrZXREUyUEIUOa+2U0wGMs0orJFXUWETv3n7I9FJVcOkQBhA+UXxGJxv+ASra+DCO2dlmKKLhfB/WUI4hM5ip6+CtkQJCW2wmdGWBE/Ffzi7lgJjNjaLGIvwXN0mVxmqe0FzqR3WUqh8SWIc0cnsRGvg/42xpCDXCz7YqoXlZnZOrclZmJ2tTMggH/Vk01qdrxNKgSvebs1GHAtENwS5AP5hZ4BXYu5EDI2YR+hkALR7YBX7ZU2yqN5Bv98/akAHyfUWH9ixzDy9XmioWRtsn75DyQ3U7hPeBuD294YGKY5Zyhd8oeSElUHtaudMmD9cEnWrXPLlHz07CU4GFrE47nMq/h75Lllp+9wSoE3bhC0N265wZIMwKbgqewImLIp/Z7B/8g//+3/xf/S+fv3iudfu8V7uZPrn5vbv3z69uru6WS2YDtGXO9pK5AAaXLy+vrq4c9kOrWBYeuvBAohfh0VXCLYIszv5aMJLm32skWADBuQrZ/zQcq3/A9cKu0po2WBE1g+c3ZQmFeeHYizg0+eCQWqURz97P2N/dcIlTHSlSsZISpsMhdYYIQ7atHQ1YJi2QjBInBdBe30JgOZ0sLCmWR/H5APbZVEwpIfzjO7jEmczVUC/tqT/bzthxAtt5/D51D7AfJlbgPtF3c6d8mcGxMN8iYK0OmH65GTjr9aU6sTArs74WvmaBbL0qdlZnQGlwpvgDmJPZdzYOTcCKFxt5ysp40qpdaixxTSZzHVWU8oJHWYURhY1zsFOdESLx2ED/ZR0sQntJz+R54igruQeoqxtb4/ngiCTwyKoC0bKwkWryEYXqetubNG8OCDx9KTxSyJFzmB9mmKy1GEjj/Osvv/niyy9e3N6/26xvyC6mN9vJ3cX2erO6vLtfb6e2pHqkYU+YxkGtu472zh4NSGbQRS1Y391de/r1EQOvmqPvaTBA2l3U8xvUjdyC9tiphVc8Y1tlXYA2fhtS0J1ijcqiBTsle8ANrP1Zue8AVp/mffABVgNFocSQHgPEhYeM9dIBboPtWNLFwEdADo55SkYPnB5lk9IL9LscMwChWX5mNFwu4CXlA9fkM/tOCzxmC5S+kL2jvG8bPhI4JTBzyEWdlRoDLOWOwf+Mc5oFjrV3D10TTKAk52DBz+vXr/5vf/2v/93/+u88ffKE0H+xIFS/2qyevHr3gXc8ibOWvCq6JFikcMbm69988wVDz2wG6iAMJlq2DiswYemeAKiKAQXkLNEKB/Xbp8iNRJw0DosAjZjDPUJDlRAUchah4zv6A7xru9FekFpvQ3CmSI9S0grvZmxoI6COncNbfCUoCjlbeDpn4NiEOjccrpOG0xXdShW0lNbKOThNdTeyih34KlLVfxlJyNaVUiBqCuqvAp2xBfVSjB//bbxQPKEI1UKEYDrLAt+dKA2p24QUypL0TAiIWRfE5qRek4SttUOorLsjD+mSIJ4lV6kdMMFdaDTlygNZwnSdHIZr2dHazSfTUSk6MPFlABkgdHcz0uK8Oh2xhfgHC6eU44+0gHHACadTH0NtYQurnjp8dT8UK6ycxzkItDdX15dv3n74m/+P//f72x+Z98Ig84vnl0+3z66/+PrF/+wPfv8v2APp1cGFxhW/aKssVvyrI8ShkBSrgOW1D17inJzulHwy1+MYZF3CNMcx+eVShXmGbLMf45drnYGaPcqNJPlDbTOg3xFFTUl0ANT4+Q4yy3ouSWlSNoWft6fY5N6V71QTxLInVKa7eDRhfNGzPEJEFrTPBiXpiHTRo+3DRjRC49yHcwZ49IYrfbJQODdFVzgUZcXAiSMnKkDy7IAf+g3Fsu2Cw5ntn7WsJ8Z4cqlbnTpZDIXDPpQ21S5s2KDdZcfg7LDPlWpqehDfvrcCmmONFiLjbN9/eH93f/fHf/w/sqEiERqD1RHRsvr/yc3NzbMnRFuEVQRb7LDIomuiyZurqy3f/5J5Fb3qIG6Cm4Knid4dWK2YJ5jPFyIT+Fdg5XoobtOsAQPSmw8fbrU9paJkpIgNoS000gFe1YkZAInSQhdhVLeEyx1IglxdQw44OnZSTRbAjvOGDTG1ir1ZxAgxx/bKcPGEocRvnqPP9WL162+eoBFj7GiOZRRE6uwNMYkjvcZERNunVkikFxdPtK2QZ3HV8WGMnx1+BKnqKJx/CRtE3vUCj+dDhLKYS1v3eFer+fbiDzTtIj6MorNVK78m7EMKvMLXtqfs4m98lv2w7l9B+JbvGGDn6LZYq3TKdXSVI9c4VyWN6xS5WOeSkxZ3TS5url/cXNNGthtX/8NZQhLdFT73oNrxT5v9s2LKo/eUq4NAmpqpblT7w90tXiUXARf4dDNfXGJ0G5Q2AkxDuOsjHUChF4r9SenAJW/v7n773W/+6T/9nyjDBKhBGVZf3m+evZj++/+Hf/+rL/8c8y9GzyfERXsHhFzwc3b+fZFJkMBLZytXg4zMjHn6jWR1GNroEdlgK+vUj6ZFqtLas3rEc/VQ/ErOUde6Pj2t1gPuEbj6tVylbEdDJoZ0GCmvepCLWR+eDx14cev0CB0PrjtyB13N/mV54SFl7UqU3nTdzr1oH6lgr03G6NVhEztOY24ws+JRpKWiu6aubqnqmjGdqOnYjVInGMoFsxrLIfSPUFbW0GZ8PB2yWUKHxrnzzjyjcqW4YJv1aUtpKBOGapirzbDNZy+kIWgv/sdCKCsbaTQZMODH0rNL7mE27sTOVe7gn0zjgJEYiaU7k+WKgf6Lq6c3GoomwNJBxHVxdXn17PlTMOMjW7xY6cie71zdbW+uADqeUziOFqwcwsREaxHmASEE9BcDwvSURSCoGJBChfectheL+YYBfCJ/+hcicgwIqgJTinUogJQOChwpRpyWiFgEaTFSGJ0Og6tM+yoBFhNFmSzgbXxrlMEZywmi59n0en6DPhqPV/BJTMmmOpqv0K+4zhgYkfzFmwAK6elQKZRXgMvZYTpKCV+fGDO2RsrDGj4bk4VA8S0CY2qPUQ3qm09ACPEVv/LysXjyMV7x1w+MV/5csIurXujQi7/046IGiqeRHSqGSWWffKjNynwu6EzYsmYIUzsSaFTXoTb20aFoX9G9kqQke0J0zoUX0ZNWamvWAkmwOgCy7MVkyVn9U81y6EdT+NdX+vi0WFqcbJXEy0vsL4ryaYPb+w/L1T3vtF9eXzGPxPahYYTt5Jau1Itnv/7qxbfavNWHbS4NOZJxECidJbd9BNR1KgrltiYqYA+ZfFxp1KRZYVcu2f8hK/qReOfqjjZ0pgiNEx2XA46wZ7Zqzh7AooV6mAYt8kcGNKz4yNLPIG6wAnpM0gFI/S3WINYP/R5wp/ED0DzMteWKvf22et8rqxSJnA1+4/0jEza1q+36Qq/3MMbleq+S83jFSqo9aX4m6/MVJX5fBYF3KtNr/5JppOstksv76g7CThnrnEmU4H0+EDxmEGg75IIQHNbPZc3HaNvRo60JfpBMn3kbwsbolkdWoK2xbduwwZ1sC2eMxdpsRkNyy3RQdJUBK9u5SdVRHKAU1BEGbTYL9vuHjUGEqxpSxbkVgROTzed81tZjyRqQJfYSGoWyJOX6D7Z1cMJBD8wU8+Fn/Fu/EML8jYZiHQgqwgXsTKCzNMWBKHsNgarlQwrvUwAoMVJJ+82HNK5vKQ0wJfCzzk6GLpFsna1nDZoh7F5fFAQ/F7IX/u6o5KDu7L1qpOF0m4MMUTWqbV6o2vqGAJrfK725Vo3j4Er9Lu7FenvN2ev+wXmuSvgLA/AUVVRWvBHA0h1Qr9zT4E4nKmbSgFVW7HzP0npG3KGQdIbRgTM7oXSqUYYryJbOay+xmt5Jhrpg2BYOSrjC5OOQdohSo6FGrkJVXGCZUowuU7eFJO3DsflC5/kb5YRgKZbEyc5klSjBT9Y3k9lrSdx+JU+YvTZfOk5Tun9WwnVBI9jxj55BzDvBWtKgBEFi6EfRtVVHB0h8AAELUVt1eEn5HQO6W5RurtbrDze8/764XK1vMae+7SBkUmIltr4oV1UjAPmcKpfzGd/EibxRely27/nTBz9Uyrn4tOXWntWt5+qh+GfWs6VP+atR6RbekFszZyMBVi4Sxfy3FV11rSzQ7S3luvZ2DBAyzlJrWHVrUOkZ10rbOvTEXMvOmpbkaMNPFPQRyfWM4tlWaODGq83MFw2w/obi9NiKh1dBOZAMZ4vzANqBRYfyC7/sEZKZBdYgbg+LEgy7zLGEnzEd/LOgYXEZ7YwKnMgKE+/V+UQRj0BOFXJFzm7kYDhspUeo46EiqpunutboAWZ4SgQoLAluLk7+QWxDGcGQxll5q1SxFH9Gi8hNNB7DV8iocCxYgKq8/EwARWFiqYgsZczE0MACPSGnUE8ABVewUVAHb3ECFs9MFwfInRJLo1RwaZGucRHo4ANV24f1d1XaZW2INXOFqbkOh4bgRVVg5p8B9WIAWqBOzkewmmqSapdqJQQL45wSOWVMmQ6cqvJqBDWezKn/FIusYmpW0ii0svydMtFowpEM1SEOt52TIbsSloqblyQzK6zyIBTDRLwDWJkEpafHlrJg+xr9S7uPyvnjn09MW7gKYijLStlwO+FR72RlsKKmBqtSAOReZkfPSP0BFg/J7ZAar0DYt6+f3GBIOp6mhyFyyp9wshYY5dKidoTUGuhRM1m+Kur/jyr+d1BYafEjqh+ePIowSzqAZh/jzHMf4idR/vPStsNktFyj8coqqaixC1DBo2Ps37xW38LD+z8UyOL0XT2fc0Ufq6FMRmEemSN6nyP7mn2sqhrn8rLGWWBKjJQFdnBp47chZc8SJYbEWwvsNgatqXrki15saf89DIsWabMt26Jd2gGpuMktWsUBbBeV2raIegHD1u4l6ykouWWLRRVyRSIRjZhx2vyiKFMFQjmy0iapQYp2rMGLzHEWKxh4KTb5qr12RVrn0Jrr62g5Rym7SoZVMhsVZJASETuZj08BctgUkRBx0nS7Yvz16WT6CnSN/BP+MDzrwIs3bNdr1vtTQhlvTibRjsEsQOEYhYZzjiDMBFJlBk/FbPDU4SAV1vCCH8jqUWjL/CiSXlFBn6FXtKtR69k7QjkP8bqCFT8RcsR3fNsr+HMp+LUx/ig45qw6p0MVUB2oXlXB8hsCFxdXKndMW5HIjumNgmiZKNUXBoSqM6eUVsIWYexfo9UCh32FQ1Kr7U2QaJMW5fcKjBiMOYtPmmGwbi5IEbQFBzqaWEKIKc5TvxGhGYPqqPCkmitQFfg6e2OuQqr0rHgrxCbkZjMeD9XP3mxnmggCdWsq9TXtLdhWEbsYyVUvVl/Kf6av5Q4Tv0LAWyvWl5M6isqIjWymeQBPKbGPlXnr6w0Q6dBaKJDAZGMrbWZrETJw4mB+IIqZEVMaf/tW/NPefeLFoTZor/S1xSmFxwFH38x/3/NH8KhUCJEuPeLKp1yZNnof//Ip3cM3gWPsvI/PMO340vH8a5q36tuWaMcZ2FtvZ+Ua5zajIciOyRCWy0IfktCMr3WbbUQUCd7+9WkT9EFKG5Zp4x9skxGa9Dlyn4LD8AENO1ulxC/TvVIaAwfgBd+yGrlRU5vGo71Tfq+c4HcYTS+zekGpar1kZO5kBj1y4HsE69JGw+RRWuL3KDIKfBCfqNqweiF1L05bbpDsJRxVqwdD2qvkefU/L7dzWKXdbsndFf0oADFCYGXcRjY9bHKxnz7Kubop4YXj7m+Ys1ZLzPheq4J4R9i+aD9GHXxQSUGVGDtiZZG7oybnjRFwFRtB0RdHLPNWgmw2T8RYQFUjqQMZ6QpBtMFH1Q25gikERNdQAJowRmhlJsEmJbsuIaurpAtWqNRVXCksptKuwAnKElIVdsGqMl8DoTiTdN3TOZrAsl2SRCesSifrE+VwJVEdSoaqDVvU9AepWVzjouKKqTm6NEjIR6Lk4LaudEhXheIOjNW784cmyEMEOMzp+ag4WZgLIoAXonqPxO/hYpVQXSU4COQz6jyCLc8RrZe3SSI/0frPjrZ8RVifVbv45quvRSp0MDlp3gAS6WSGKjX36mKAgGOPIDiAzPUYwb2P8QGiRkjpQnl4CV1SP2nYOU0ywGug6JM2z+HKjb0LDuf8qBSNahTt54cTLwE3MPZp195/YB/F/vJy5Vm5UrykHNUHqp6UFeGeuh3ar40x3cKGXT3jomfZEE+2pM1ZgKQbyFUVdtfG2Lzwe97W39F0pbLcTollW7SpM227CEgnQ+BR677STladwI72KqwdJOP8RLiZW9g/S0wjST8KkK0RyucqlO0IWiObWY1NtGoxlrCOt6fufVK0FsJHGKKqDNyIYZKVKiCoaawxZvxEmco8N8iu85F1+KLkdvmNkLy/lnb1AcKfx1YVc03fTOa8CqyYh4yDM2RocYajIpZgU6S9+L1ue7NZvmBwVTuvc8BXo/aM1zKuT7+BXKqJCpUk3IoxDsVtkiHR2m5lywvAAeEsqKYGtjQ372N6ksS4BGQas1W/hQsMzFTpJId5Br5B23/0zQz0UgQzuO9kdOHuqkmpsWuQBEuUwbNbzZDUFJGFp0Q0ZojIZSVRqIDNAhiYcRbExWVRpBP6Di+BaTSN9293b0EQO8ecgzGqmY0kzcYKUrGygsGzkitEtR1XWmw64XsTeNTikvdMeD2XIlo4Na37jTiV+BHoU4BPab0QTjJ7aacUM705rZBdaMqau/wo5BPbU7r5yi7zm3Abehya7wI+e8WqH14Gpmvw/OYvbJfPJ5M79QAgl9vxRQx9I0xvEQRD0fsVZLjPfqhk6Lo7ait9d+D0hkY1n28JLtWmrIjD6+tHhVmHduYq63YWdgDL50+Z7kDdgfJTegdyaleTqqAvcqjKH/ta03x0fcdoWeMsArtJSjQbdAzDBs5Aw3Zy73pvYccy/4ZmLXdlB6VKG5ZpM2nZ5CDWQ8jlDEauywBBI07LmH0a9s1clfhlOjN0Yp9RG/eJmzZgfop27QJUF1DkSl6RLiEFYmey03U6MQEOuGCU9hHW4eh3/mNYt5CXcUo7hTadRefXch/HUIPzWY5cqT5uWVBOPEjb9Invh+/VvE16uuZhhOwbbRGPCClqU7VNgIqCQp0SmtMVYYFX/ip56NbIBOuK0SNOV4gUQ55EPdzyxGSKNBm4n05vbp7c8HEAUMHyoUCfX7qVlg95aQWxmUdiiY4cwit04p1N9lshiF8vtYwoqDXD4EAHTPUy9E4qW44u+aDAfQSa7m2A5A1/6F+o26DOBBuPru9ul0+fPvM6DceFDiNdYU6+1mp9rsyJnHPTdOgDaxXLbG6JCjfDKd6lwQShpk4QBEousF06pInYBIHf5BUUwbFBHQQGhpQmVpZdJ5QIvViCG+AErqNdhM1kVzOWuGwn79+9A7xazdhYiqL370FXfxAPEqYCbrHwyL36nnFEFA530CiiALkO233FTCoLXeRnKvJLwfMZW1WxxS07iC7octjwONh6tpheXi7U/5azRV8DZ5W/sioIMHJT10JdWdVLknRJtQphFTDnuhOhWlLQKD0G7CbvggaDUKxkHJAuioeDlfIfTsqDcj65PR5UOzEPIx+nJ1S/gDZ6cBOfUUDb4m6AaD4eUYzLxTPlEJmwSAxMlbOjeZQ9pDI9zKC/DzRM1106Xm4nfduwDbQ+Rw/LgdxOABzuSZciMmbZFCXCmHTWYQxyxoGqXbs2JOOTaAgCec9YdUncSg/THuAn1TrChnoHrN2v60a9wjgNhnWs03KVzp1chus+bDcxdAXUlK6GxvKV8ZGrlL/1myEVSscYpPnMvmfffWIhgn1F8sRfinAUYJGUSO+akrZfBE2LILbT2ZytPB3mhHzCOZFtNh/u7pca14QTAZsUFAHRGIH7nM2D+JwYy4eojBQkDLMIRUyAhb3VLpbaMJPg7/07dvURTNML+n9xd/dBdhCGPzm22d6v7m+uf38+/VJrN4ztWomKP9VECXFpHX3wFmITIM7VkfnvuGVQhZOUyNm+RBBSqme/hdgkO3SBDdeZTBxK5HxFmSCY/pmwtPsQFiJNIOu08hyZS5Uuv2/g9DZ960DYIWa78qzR7t0J66RyH0aqg6oiyUMi+3vak+R0AWLP2bv3Hz4stPJmulqtPPbP9+UUgt/d34Mk38Rr8BipzEmUEf6zUh/nEYb6Cepo3t/fTqfaPDRww2hSAjK7mgrmr2Ex2y6ePn2+3jDvxBq2i7dvPtAFwGXx8JubF0+e0B94hWtrCouZLXiK/vJicruih7pezefzxNBVdG0sRoJrR1VUAF2DIl8kPdLfQZJQeM5QqB7OiCNU4QxJHC3lAJfPnzJd0Zx8HXw2DnN/CH1qPAd1Ky03rOdppbl59rAZi1exGfmLKbaDdqj49Vx7aEs7l+keLgeDx4z6l0z78Dt1wybDv9ol51Z6X0O1y0tX00160AwA+MEx8eXiG726tvSrAcZhicRMa7SfYCYrmYzRUjEQOJcIYYRM2yI6D6AhtGQ6UFSi9aXHN2IfB+APXf0B0Z1FZ6lUcD6IVdghzhB+/MOqcLIyLY1aAOEFdtShXgHCGK8y8FAqPL3XuTIi8ZA7w6hbfcVKay0cApkb8SOdAYCMvjvEh4sH81kZ4UCfMf4tK4MkDVaTq8sFHw5TrKL4LIAUpDSQ+JeKqzwCr64uN+tr8XAHwPMGvHdwT9gFBERiNGm44csD2llfA77Ey3QsRCIUZXVE3snaqQ9eQxqRCT47bmH3TBhKWI0qmcuKRI3LEGJFE2LSOaiDbKeJhZbZivaoayljjIIlPgLJQiVCHEVheuQEiPF4pnz4ADUNKS/gnVw+TaZe5fRyEe8W4zOi1MA/nVW9n8IU0IbugTwLV6A3AS39h+USnNkVvdAQqr6BxEToby1A5ZBSuBC+NeX7aFs+df3+w2xyv+FLF/RE5tOr/+b/+99e31zP6JPK78G6VMC/mb94/uQv/cW/vF0gks6C7iXXDMXFXZfW0QUzkjSzdXwdd7Lm41ALrKRdAXmsZNTxsaSdX05v4x0pqmy/SJ/NQkerGt5xZIUenSzsdXRlH13fHoGNCjS9YPwMQIcX1Xh39m9KpTJ22UMq0yXycDp0CZw8Fj5M0ihty92rf+YAZjYjfd9cr4xQqpcxy0SbJGiHe9Klzg1MGOaVZJk5iSw060YiI5TARrpt1Qzp5FmyzZgNniVO1n/Hrad/32bS12NOLfijKVprBNt8OvbDMVLwmZlPafMODl0gajTGwh2kYywwpl4drAXqsZvdJJT2WS2iPw9lis6HINVhNMchhlS1jeF8jSwqTCZIIXgiiOIjvoRHiwUDnHwFSaESy5+1xkb7jbAuAmmktORBKclW/E0nwCLNShACcPUdtssX2+VyO/vJVkYKJLFQ37pEUL7+QipWe8B7KmClEE2fqg0MYrklC4AU1GtVEjpvV+vNcrWkB2AtAJtCq7H5CiwKUyFkqbsiHdXGVrCWFpYRjCNRVe7Iaxe9R9zZa79ZxheFOWLUvD0S79332Xu+ocgkjd+/DXhUaYeTqyhQWUi6kr8bp6+k7+i7UsV4f/Wd44S2E1DyrMmtMdzhG6zsDkTzka+UFAJp/5fH0Ofz0hu+BOd9qLbzH42+CIdT48u35GCktDZMa4fwE1ioMzCd88dLWF8IZ/4aMOQ0uIN+CQNscZZFWt7E59D4ADHj/OK7Wq/uVu9e/pOf1KmgO6HBuOV0eon/r5bb3/8L3/7lv/iXzBFKJtDyHWF3loTmISEJVk82EcfkVdOjjkqFNnH5/CnTgTn+97fNGYisf/5nY6eoscBaHUfoduKqhMr35Xcc+i4HZklyE9Ale04ZNScaBMD7G7k2z1MSJqoRdiipauke2tLOZbpGOzojRzJyTpSkA7FNidaZ7tPtKM/va5yW5EZrFbXyHKB+fqv/mbaTeUGZEZOtKBpxdHIdQdeBMk5gB+HjgLpN9SiywzKNRs+SH06xU1rkFNpctaMTR7jlQyj8EDwPsInFK36BJqkyzjBg7RChZOQ0AOZErKN1zL/553/208tXmzUf//Kf1hZQ7k1+GPUkCNMSHg6FT3CIxT+aATAX1UNKUUre/0FzGQUKphRcOVwTqg5FaQ6/KRSqCTN1IiUv/orwdGFXSOeV5T8ardQxUEdF0RdRGyUi0BHXdAaHkiBzkTiTNf+KIugOPHcQhxjO+agEZwCJDsIozsg5UZIFsLPIaJRwwDwSzn2UU3f93OQ1fcDTfzU9B07mzp6dQ1VgLRAlxPJyIfmKD2MD0fQAbSi4fUSBP75qLuEaFX7lYDlutiaFkaDiBXPY4NVsZsXys3teP14tF1PWrN1cLjTZNGflv+YB6LsS8y/kPV53hN5oQjYcNbSMCoX8fC6AJIscGPVcF0mGPW6isNJhgntqdBiTz9gNC4xsjgHjDxQ1ZH06WWqdKx5pakGC88+xOr2GLSqj5KRzBiBbopdNFFTMuPJN4b7vAOxhMlQcDdBYN9bQLo8lDzEaUTZe/72YlV2S69R6eB7l1ddIR6h0EErYoRRdE1HJDZ5usSb7cgSibdUG/yZxkS9pD+gx9/TvC8Z7knvbpZO+ZiVjDPPJFu7kFsBO8w7gRxGjNTvmY2YD9nIchbCVf8bK/lLvCTuLS51kjWwmXsMFH/j3fjRmOCBHP4RMkIlSf4ycXs5/75uvv/xn//w3083lk+dpgQ1vBfDwYR9GAhsGITQESoSjHVfoCygG8tOX9yzxCoIfvtQrbor2p6+8a7tyPipJCtMgI0vw9FrREozFUwdfFgbgWQUgxtywa9DlZMrQPkxZUwTc/RCFcmLCV21FKXWWBIqwJkTUy5mqXlFrcmRjHH2350+BIC4+Jiw0h2Gxk33A+85pbL5cT28GHh3fCSAlHVDtrVSLo7YK36DW2D9Q1aQ21p6o4yIRtXmDkLmTXMN+mIwr51ODf7cWbjpjygHc/EGstotCeRgryPS0YQ0QiSnj9zPWmBF0A1NHQM6o/gCHIn9lKGOpkPoDHPIEMZQ3vkxEwhcxCJyFBEFqD4b3+aIF7oiTKdBf04uQw3G/z5h20qQTymzu9CXg2f32w5erzXJzL05iomZSH5QESQsHzMvNUqnn6CmwUolEt5349HAYBps27vdhxDGlUbO+p27t17POrlFLssGqjnVa7uGfw6E252q0fqdw+Ys8YIcdQZFqcysKU7Lkn0tH2rBhfMiHNWzjZ4mPkehvx1KxnI64JftkvnHK2OZ0tYc9v49/n53bXwLp4BA1tGAlPSdeoeXa5+pWJbqGsiXkwHRmP5KuD79Tu5E8HxNt2GAPWgtMB/9hBTDFEToE58c0489UVhg/zNXnyY2q7W2vBv75s1nRnEBGmW5k60WOgVLQk7oB2u2QgfT5bHHz5Jq3elkBwcu9y5XiaeKq5d2tELwEIgQRVsGBhUMJrkFTAIYKI0lUoJWqHxDlROsgDhYZgWKBHYolkmAobTXtIK7CkFyt8ZAyZIRkUk4swNDYLbFXQLh0H0lAFNYy3fjd0F723QVZTpVIWnYxzxwikbNduAk2wK1BFdxCi3a6RK40LWHdaTBzU+Ym70YF2uTrkL9QxXl19Ryrw5gyuQYOVkXtCuLVURTE3qS5KqGQw1sEEwYBOR5SqYYnUSQPKfhYnSCEAXMHpKWjvFlftNCEl9nSy7XEFTn6ovQTeEWZqQK6CtUmRvZFpPlwLaV7yge0dg5DdJVT0gWuUY/KnIfLKFEjkaLSI5E/HbSfr9oNF3i0iiA33DgkRva4Bm1UYYBJljieZIDbaUUnWLog9SNtHv227fz7Xb1iaKFvhKCv/7G3SmHBvWgdCB4bLuVGLXYad9Bon2aOMf3gLupzwnI/Ukxdl+B+vEH6tcMmsM32iURbLpAoKjH32grkhs1DXANYanfeHnPJ+aOle8YSSv/Muu3sn0FYvuWZHWiFnxSk45I9GraIU3vu/DMAoQ1DojwTFHlUR9XMHWP/RlGAnNAdPnHiNVr+fuC8mvz25dsfFrOryyeXHz7csvb/7bu3//Af/0PmAQjCCXV4P1MhlIKjF5PNl9qGJ3EjTpJoxU8qTiIAST3leGAZVdQszFZkFAGcLyCoa6CL0Ajo3KlIvmzO4Md2i6JVrA+iIjYtFyHNC8f6CjFlrJiXxN1Iv/lyinF00VWQ9rU99t89J1Ap2xrFpwAJzSMLrRJDKlQcglU3w1JAx7xBsA9h5TmqLkiEpsbrllBpWkrqTIvcTVzNsUzfJLzQgkwWKIihMXMiUhoT/KRkeJcbV5iUKwjnv6ac5C/yP889iQtpZflkwBfTzT3vk0S17OPqOUrWrhqBDRnH2t0CNvOBB2hsAKqOghmyO6129WEFEB63YlNQrTpjHsL+p7cK4Izfvb6YLheXv5ryZrC6A0xd2ffVx7CDw1o+LDWr2jH++q1yaScu5HGAkOqOGoYU4/1jx/6Dial3p4KPOCPllOfVjm9Havd06ijcgXJdd6AqFU/myI3kVpF21KvzOb/DP2uq/EUer/l4DUv+fXP1ndzC9Rp1bf/WZ98J/PDKBlUn/wbOQLaTZwd+2z97fiVD1U5rd9a6LevEGu0Y9mjYqRtUHbvwBa+wUW6Dqhp+gLAEiDwYcQ6CMr1TZ1/qOKp9XCkP7RqIYxu+QfY7kO0010C9x1uygRnZBnBA0KdW9Klpjj7cQ4971AWWFtHt7BinU6GM2bjr9VCpyhz/EC3P5qy0/hv/+d988/IHNkSZzGcsft6u+fgXG/Kvr66vry+9FQ/LI9gDERusn17fXEm4eRVLHRyYE6opzt89FUgGYgC1EikGLxTUQZL+SSv+vAKE8M9Q5RWm0fmgkDBMZ4WG4qm+hpYmaSNH9dnEQKKdIB0HeQ6VNY8KVl2b5R35IdTestAAbm6tnOtgX+gZ3Hp51okDrappNIwwgBfiUk6G1RHdgEgbUD8lJAMTZZMhZSVWiz5kIwctdO44QFGrqtnCOqSU4VitWImjjwGz1l6vqhNeK0jmTxjJcTzWT8hOlE4cr+U7OAhreHivXRsEZYs7ILYDWRDOI4WY21LPQGzpwEgNovvnz55P589YevT27e3r16+Qa+WZW5iupCYdBob/t2w8+uH29v5+NVcHYbNYLHg/mBmBJS8OrFYsGFIv1rUrmiDZq9YsGQZ2HDZKldl77TZsQbYXocA9YxKxuSJhgtIQZxT00KyiIg8t5ez8RzZ7biMUOGMDjZR+XK0/7RY5zYpN6rn7DdS4tKjTtRGCgqzof1SGCtqSw3GG76GKEdNC7k5Z9AqxORE8lG33+Xr4nxdcmGoU44bmo2iqPX/afe5MXrVNBhSJes8yK1COTJfpglLJg9p5gE+D7enZ4Z73kEHqsgf4qHF7/Kr0z5Jf21ydntlQb0CHknl3ukfDbuQCqtAOPXYaN5QyanaXINwhi072ifjKGQIZrfAh2Nq8fPnj7e2tBkTvFR15pFXB1LOnz3//z/+e1kPok7+8GMC2O18o/N6+9eYnhFZiZcbSjoIUy0GtHoEj9Vh/4Y8+CaI20usEbDykOkGicVgxQh1/JIB4bLq8v+NVTI2zenyUSGy9utegv4aE9V1hQn8t9pjc8j6EgPyf/wS3ycVuL50q3rU1pGU+kOcuRQa0EzEnsNuHp27bHRzJz1Q21VeHpVc+9MVcgsvdewWUSouSNiM3EmNw4A+73b49bghJfAazbRqPl8AQy7mpYSoqtG7t/W9y6nHnqHln2wSPGqd3FSo+kplFhT60su1TvNXg1hEaTeHYXdM7CsZxB7aiYp9P+GlB/8V8rh0/PRifmhTnZFpqcXPrt3Gvkad3AEwPtWXTdXwOZMo7JwCkPX9zuRp2kHuyUkiY0AnEZBi7By0Y6d9MF4v57PpqcXW/vEcuaOoHePeqzeQlQ/5/8sd/+o/+0f+FF1F4M3h+yX+aeP2X/+Av/9v/9r81n83jY9WVASS3Pv4HpHG4i9KAOdtG7cLqgp30jCoY9vKp/04VFEq6AXaJyHJuH31P5jZmB6SlwzC33rp0sN6B2m1wyu/msIYhta1njiXsTTvd+rhl++9Qe1KdjZJxg39bn4wwkAhV29YbINkV9fxKNqq/w69S4yteUfRe98jq1nCy+pUs2tcuHcLKBmiK1JCbbybO2ZDjq5jZjSexwPGnLKFBUlaqUZSzD6ZUltBMjNGqSfMw+U9Hk4ep3yiupUe3CY5wj2B4kG0HpERRcDuIZ7su54Fkew2wa+A0q0f0ZBBo7k9MNFC6Xi8FJfzxn9791ZCqgikORdSGI1W0hGNKKHInMncEpehNEJ57PqSfR1aViHhOXAjliLv00qZoifovLm7vbt+/fxsPN3EgOGPlBaXMP+g7A+vtUjL5Y2SVXRqhRU3FZOKvyIxugD8QHF8lU7BoRSx5+AQph9gP40XpHqQo7kIKMUlELTNG7Ggci97Jj2o1xO2Kd+oAa4G7QIHUYDio3RDbqsz8wh1oCYXZccBYHsULuO+W7+5u72cM87NNrL4+R99PvUoO0l9/8y1NaI+Cmp9kPExv5MoNxNZRv7xE/4ypoXkKoyIQChGn0nZYQvAmoNwB2iH36bMnN5vrhErZ+gWcJovLzcXqz/7Fb9+9e62espyVRWjzd+8/PF98ubhe0JGu5JaipHASqmT/UZkmMIKEdB3cT/7plGTVI5Gzn46GIzVB80/K+igzxpifgtpht5EKj2mOqNRw9c9V8WEpY7Q9GKcQ6R9Mz7nn51WqmI0a0+hpHqDbwOmZJ++NdjhYnVEEMWIafeIYf41ahFJJ55bLBk7GHJB0XO9zgOH4olCvgR/6DO9Dn/vrDdqczQ3SIaKrZyn8Ap5HqSEPVn1rBLPEzkTm0y7NnNtFx0EafeJsAbhFmvMYoQ0+pTIdxqyKB7yoIXTM6M6ADpXAT+NaWtl2Tibi2UCUpH11prMF9mfVhIIfwpmVNkVBeQIt4qC7u7utttnRSJtWQLM70PRlCq9UQ9hp1U5qQrGE1gOqPHQiCtMSHaF6wFWLqkVCkVSbrFb3d3f3HruFVoTqIxDDaThWL1nST8DzFdYp1mK3liVJGPrVTLRBH/Zv5FMA3B0sF2ckGBYSlw7Gs8l2rJUvwkDUK0kq0nTdjW3rkbwrNNw1Q3P6MF1HS27Q85WAOnZYsGBOcROnoihnBlr8E5K+QhCqSeOUqhi4tknxHSyndvMJGeRqA69M22K4wyxSYFU1yu8GFMVKhkUr/4h29yyQmpuE+oJ86GGNU+IT7vhhGO/SA3PtUKv5Ahzkudx59hqgfvUQa8l+N0Ce7kMXhesWGyB5cirF4dX1BO49qWCi2F4tjgh1MZH/UveA959iYury8gn4yJvMlpp+Wj29vlzAjjVCdIRFaQ4SURy1TAHfJVFhP9IOvTdVPqPaT782pI9RyaeGU/we1eA9mfESexh0gft0aM0MBHFvXUreFW1uhZzIWAO/mxnnlMQoPUcICN8O/fPvGsBD26JDn8pKbS1KoZRGZBJoHXza9AEp+DfuiODfR7cXfoAOe3l1IRzGv+1bPJ78BPDPqjoABpSSGvYoizrSXRI60M4DysLQMdSMxHm4fzwuh5m8S084xJHuRmeyuarCjuswznBpB7txoNC2PI+jG4v1EGpnC49VosCDtqHSw9W9EHt6Eq0PrPeunnrCKNBis0G2/NeAP+t7iHPgKLYaTCea4qwxVzDR1sH+TCLBZxUPwIhvhFZFPKqVCCPYMi+VOctJu6lKAiG+5gCIlMQHcoVTYqezKwWyDrOGRtEgh0mkjDZb1H6LLOrgPU31D9Q1MKVKfZALXhUgX6VhylTXXNaTsMHqZWNJC6pCQWlHiZlwStkC95SkGJpz8C9ZFSpIKEcgljhD6ayriCNTQ4+KjOAZKOKgPx/yDgbgHf3TKdV3KvhQrxDd5hIoH9G3t0iDFjWwi4pF6MMVlzYmBFFHUQrZovx1C5nc9HZOvDDeH5CMRG6GEPCdO/shFKQuLu6XS3oFmofiFuDFACYBJrwZzHsL/GTzCr3upYoWdrsjybcWO+jn1KdgATlGoUek5Xk//6Os1+PU5ozWO6IJkH4E1TkscwZLh+Z+JEYHAEDFVleXp7H/Ct6tujDBCIbdKMPQ3GtsoAXTfFap++INdZQtenINJmU2WJWQnD6sR5XJWolyjqJVOARo6DZGnwZJZDnnnvf4Jmmw6lN075xDH2E3fFyrddPug1L3vvmKMEuf1+1hbJ0Zm8Fi7WNvqwUVCnRwOMoaua3byoyAdFaiTdeBtvpGd3zecwCMZNWgThSODStqNjwhmNHiiFhbL7giKOKbOSdGYtmFnTPD7SzS5yVIIiWtmODtWyIdCahiY4ogJByPuEpt4cBps36mmGryFkoCIwsQL0ApiNJALpyIrxSmcSgGFLUUcdJdE70uAHDDdqVI0eeHZ/dcUQH96FOIIlU4+O3W3yu/O8Iou/y+lNQrOe/D7y1HsKtqfk46G/wBkgiUArGoUe/MQIfAkkNZ3AcvcQbT03uF0tsrMaoqUxAAJjZ/qnPaK8mQXG8VlIdLNQGlSJrJHFqYM5yZ04F9pDXYv9kyTk8cz7efaYsI+sVIMwxud0PBV0u5z6lIXOvcNJckK6o3KQvLB0mr4+iNgDRzpS6D/VOYwgUtmBDQqzioIGVCgPdP2EKL3gAfqZjyAjJ7B20nT/R+i53Q/h9K1QwEn1DE156TFGwWdcGaOL359tOvDeklrgpkgirduI551vVKjKdrcOwb0W/I25s9ik+qXUXbaoK9Ujt2kCtpyt+1MRYraU9Jl/WKdG9bjBdTWWkvBZFJn9sM0Zp/Sdjrfkf9OrdFl61TK+3hf64WbO4Pln45/ZOaBj3CDJw9vFEzJ1YZ8NNMWKvQGTLRGL1NcqCEspkPJH0k9BM1zOYKdcsWI11m++pzogJ9bDvhjymrU4FTgCcqD/mJHE5R/nDaLvep+1M9V1VOcbujG4Iovv67cnyU4i3iKT1oHBER3NCHV6hFaM/3mFgHwQAnvXrKtZhfMZSCJaIv/tt4jp1IZcEK8lWEbL11TMdBdAqV9EBTqI9gs1KsBwIH7DTqqx3+ORx4uWEQyn+GhCGhCDTeC9D3UpAhZYC0jy5YiVUZpYQ10j2cG1hjs1khJ6Q2RwWsrglWZo132Any4JDPORGMMsJhfBPb+EUaRdpp5VDG9O7pkRKIH0FF/rSsz1qdH2BcY7Veaj8eyrVuzdNCJgBXvsSfkGVUlOOsnis+Q6RvMUkNLsbnDCcnRadS/MiuJS3s5vZBEeCmRuAiJ/VYg+YAJEW7BOm+mUuWZPsOML7lppPofeREBahfRV+HVFRd4A7M84M+muDzV2WIoxvT7jaE9blslAXO6DNnZDVK9SOR4ilzJHHc88FCv5p8CXjXzzC4aYVmvuiDZk2c2PFp6Fbv38Av04E4vNatJbzB2tmenmKvPl08OmElhzLdiSxgoUkbvw1p8GlYplHazmbjYM+cPvM4fVtqC7K3Xi0KAwpbBcJ4PgOY2RTDdhj2uk6FZeETdO7kuQO2OO+K+lN9oyx99ing2V/EvTZCUIpzXEIg3Djy2D9wGGWbMzNAevYDUEc2jttB2GqfHbHxLooKxzWw6dF0hdSso+BRJAoHewjl3VwCrwURlQj9vADROocw0s7pEQZd7CtkGRGSEUkxlgsKzIjwFcxxIW4Cxpm4KoVuscKIkA/2ngQQFd9h4pVQlv/zVrDG/okD1x9QGF4K+NRxIKQLTUI9K2M9yVcHQKtf5S/W2jmn4xsCGUGJTlY1jJEZ6xc6iGddlRLQ0nOkgBpaiz2l5bsENeR9GZgV+xqFRTpoNPbfW1jhG2FyR7uxl6bbTwvM2NaJ4XWcxI63mczYZHNNz0+OwlefJ5catud7FFvcgBcDZCK1vHqaxOB4grJ4An0EudJUi/sNmlysnmNrvS0gjDgCOVQ1UIyiFGL1DcCzADFV4a69ciluOJ+zsdX6m+366mL+Y+iDLCkHm3V8t/v7Smhu8a67WHK64BAXT4nM6uMn+p51ozQbfLp+lPqGL6B88gLHSGN+lTKOWr1V+VxKyUkWM/Mj19a3tArAR7GzRNfjzx7tBsH2n7b+nU0wwKhsnRpaj38e2oIdv+N2kfL3Wk5TOB97CxT5XIB26RfcepY0peKBH6WWVBb2pccglor08TkCnvU9gvZxSNBw2D6B0LDPXqpQPhqqsyIjOXTSflLAh6hIw9qfVH3PrkyXkwwZoHJXR+R+aFQBCTGJRjQV3bBrOtuYkPLmP2Kn0X7GNdkeaMvwP280snBfERCj7hpONQ8IfDdUItI1mjgCKAVBwlVPQcIjpJNRHK9raJak3jkGgRhfsZsWYfB8u727v7tnW9LQhkkKvsOqbzLx1YLpXG8Vsz+M70bWi7ALkCcjYhXHzuaVZjtImRouLTHL9HFUJYdGWhWsjsw8jBjgDKywZJM2MJcOJI6jajEsVW4VVoBRSFVFrJj6eKu3bz/4jduLWzzg/h5uzk5uP2jfWHoEL148p6Mqb1pfE4pHvw80XELBujjiP6zqwXWdds9UnV0jEbxHmrO6tPxz3wBkeWmykC6BqfsjDiSFmo7pNczvMhdTADp70aqHYpXcSQhuoZk9OXFKHHeXQLS3O1nJPL6pd7w/p46yQNUkRxFXfn0k8S+CDANmN/5FVGhkJforPcYiTer8HQCkZ5fUY6uwbp1m14/J+E709lfq/RuYZbrOGteldaKMAvbqM4paSCWHMt3HoOwjtvHbkE4+Uf1sorxuLJslJ0ryTDW89r0kKdNZXAncmw7dRtarwa20VRSN59OLWfT1++zQUOOwbMG/rf9hrB4Su88+FbzpQbURglIxouc9B7FH+A6hzWb2g4c6sRJbHBIrKaZX1EPk4o1NSHiYHRodPAjoBiji1y77xOg8djxXoLeP6AOgpoMjiyDj6Em6R8zkMkdYq68pW1+8vL39wJ4/iGQBt1dqsIM6u/rQC1Aory8ssfGntluRAi9f/cj2QGih9ynNk/MVx9MXgCxFa5DoFFxdskWMwkSrQ5EGgPfYpbO4/f3gCq1gVzRO+k6w98U/ajQ94k0zD7a2ooQWAisdimtRqu8MUOP23vxGD8RC5YJJPTkl1Kb7VecDedYI9KhvMfZfZ+GcvyFQfJegAyVAoZQVZExfHsJXgadsGLVBk8mM62b14fbdTO/UMg8wZZkabkHUP7m4WcyfLNcrvgAwXzAt8MzTAhDZZ2U6XA8vcndBUXrSQbKAzt5w3a6/EOLstYh0L6T5ASXs6FbMJ1ObFgq7aogQBe6nj4LZbmKH3nyJYrJg6kMUiPZtZDOya1zix6XSScx1F1fWSBgCG+7E7iS06imxg34KqYd73kZ9H45/zXrFLwhwzB0Nsoupatgdmfy7lmk7kM4EOpsnuNZn41bVrvLptCYl5uc72rEef1bUh1z79X/QVuioy6DWoyxcPBz8lm+8BCxb8vNbPh4kKkxMolmgwqq4uywwmudgGOc2XRbXJPvZ5qkjlYrzQZUIqkwyhknbng3ynP3oiQFVP7pupQK/PIesbtqyls10tI5dThFGszjlq7hn56mKReTsghB/K3xR5EOOECaW/zD4zuA68RZj88A00KAV/2yz46haPQEvc85CFcKK2nGWoDngUonz8EDM5vXrl4r+ObR1o/bxZCn3ZLog0OPDSew3qthrerGYzUGHVJ980iY/IkCClWfpPxMAbAVPb4TughZ2I3uzZn3IQjVxT0Eg6aF6clg5p8pkAMpzgVeCeyhdtzbewZDQ8WCygiBXtICR7AHXkXpyZeXKdBd6TwV6wObQVRZ+uFlczbbThT45d7HyFp+aC8IP3AmEDt/hk7vX88UlfcfFHGfh3Q+1MS0fo2KpwVV9OY9oRB+ODtCBvp0JXeRccVEJXKKba482SwFFIuaM65ONtF5G5lUWSqGBiqknFv/gjizZtT5Smn+pa5IVNEwY3YfZdRcFdF9rDNF+LjvYAqeY+xTakYoioteVRrJ4eLSPruHem+qsNji5ugUD/QzycptWDjEJ/90ePXM96YNCKPy6Dx7aX8lj2wgutNqjxmMWlxqOqV28jZ5vm2ye4BM91PH6J5tU/dedieqjCA2GjbXvO6oGXpHNehawUcnx4xZtdmGrEj7GwiV+mU5VqGxFUcMOJTLpPI7SgO/JFvz33i97WP0ciu08nR7UABK4KLzRogXiKS3un6y/In8x+97LFVhOTdBPoYsULaVIyKsvmChgPJVQDDiBDv8UFkUsExloFUoB5R8HJ0KvnJ290WLuKfum32xZgU2cP3tJBEUoR+h/v7ljmXYM2WpiAep4sdPxldh55DdiPGARssE8VJJoFoWzCwvbEkkvyeeorimdHNBFx51UJ1M6Yfblfvl9e/a3hdXGyDPLwDtczd14fFawLbIHUuq849ODDDi+i1wvR2PbooJ24URZRquTGBw7BbGjFAuCl18SW29nP9JF1aocWV3NOpks4EOITSPjgETb0+0X6/sUaSuu37W+p4Dk7sJUidzGHiknNXD+WlrRA04CwoNFARRh0Q2WWzNXIMQfBY+Dclah8a6v1/wLFqLpCcBNnRW9e2CZ7oGIEtpIhwjRBLPynMtKoEkTINNUiiafrOGPzQz+To1lUuE99PO2g/9Z9U/1qH5Bjrbv8O9aSDny160ydb5mb8iQIxNR64ewZzw0uRcqzR6kHatWk5CuWmTp3TdYpVvjmqn6Ip96XUBP7IXf+PK3WcdbPWn3zhC2I6qEZ8+LB4beAeDIulRoo66JKv1UjyLpQjpOeBenTwIWNuccCQweFcyJh9AyuUaLdUNoIxvoWb0W9S8TEPX9ZdbtnLUasJP8KCIbRVEKSjSASUKbd+rFytV6zZeMFLdQrt0VFYQzMK/QR69UClslHBeXDD94X0UVugJcg63iKaFwuASZuhpgTPU8YK5Ne+hebNklHQWQzpoilktoLoClHSL2YzHCM/htWOC/5mtK4goQPTmLuUdhWTVEkKXlSeS5TqWh6iJsqxR01qCmTgU5+upa1qitYQ1ySKbN7xDqGu7O6DUwmVyyV1rGbLLozddZ1nMVUQOqbIAsTq3mQ590EER9POMkRDuyXhcxpnagIoGDTObadJ/295skgaweIinxkeup7vibGQpB3PWSOJ7vvqz83cJcKKeGJm6cZLXgEX4lJP3pHtKL5+qo2Ovk3cjl3ZgJu2PFTaLpNfhJE4FQU6qQEYt0HylXHtZi11y7IpHscjnVBcuFnxNHWaC0aZk+itl+omhy8EJWIwu80fRthP0yPjZG1vljK9I05oA+R+lcEJ3iOpmNHk1zRuk6b/5aXydIOCO32Qf1A5Gq1vsrA3WvityvyspU0I5rXw+pA7UA9VGN7x+XI9wja1e2C+mwWPA5bh6gqFCVLPujFYxryIpzBmdghpAolSzhp6TL2ZLj+AxbuK81j6gLJO35h+N0fnCqrvGGvUL7bKXVNbS+o4S9TOwmwu85kuEddSgAYSOUNZuVw12j+BfzlwTRRDAEJjAgChe+IhYgCoIUzrAcCGxts8OYPCvvGYB9A370JRpuSiCUFAmXTk6sSItl1/CTAqvVdPFGHYKllu8TiWkXRzEibiMqS1WCAQro9WMfwc+qkZTCccCT5UmKC7Xg27MIKeSr7rWkUL6oikNHSOrHSAqZfYUlmm66vrcCynmDZKWKWb6WXy/u45ORU6JbiyZW2CBqQrqRaGLvz4vH7j2EknsXrWY/aPdL19uyHXQHqpaecTA2T6C8uwloVFUtAnVt+uTHNV+B2E7esHBts71U13L1TJWJfYdAtROLm0JvlSju1/eDFfcnXpYGRHlzF5ZI1Quwf0LIL/AruZiUoAxNSHPXsxOR6NVlpgr6gz+0+KHgPseqNjm6yKiR7ispJSPosAWc6YVzPgABAABJREFU6jrpxtStF4dsoFRikKAjLn1Pm0NnvENUL7dBTdpUbUiNwZjnas/v7B7OFjMGB8TK5jXVTs/kCK1s/zIdIkJ62d4lTpnOKpX1KtMZYSjRY89ekjFtZGKq0Klt4nyo3F6FXLCPmzSx5mX0OBxzDkc+bXX68Dt+2d26zd2Bsr30yGFF7E5CmLEA7IpSCoxm8X6iFpffAUBYqWkrWy8Mdl4bRLsE57JB2mq0VTqvJuO5hSYPYY1hHcJWe+3w+IoNq/1opWGfPeIwX8YjsKJroXiZKHuxuCIK8aDpZLm8Z9SfF2sV72/X2veHYXWiGX1mlaBczxLWCTmIIoxBJHGQBt0zb8IgB0epMSIUMiYnARX+sMsQk8AaLt3e3y9hSijGAOqa9zgvF4qOHExVsZFiKSmvxyX/WRZiDAVfkg1PpPjEFfG8/8tcAl+k0r+khzVNiKRHHuJ96JFokHsM9U5ancExvOo0YYg6152KGbed2Kk0KhVyCtQaoJZJSIZxkhcpMq4sR4s7draTBS4YauHkIOCCwCcpNOqPM9DeeK18W8G1aqJB94q9XSgcQsLUv1RUbjR5l7xKFAJwEiW04c+S67KKOYoCMYUG/RVkgOkehe4Q7hF6JiDDwwzF3ty50GX1l7PVQ4htr5ISvoDVPKRuE+a8C8S3D8FFn09ns0B3M5yN/RCjaOY4D+H9HMo+zVoM3EiPpzCS2k6Wxesp4peK2jhq956+TifP/X4yuj/XZlX2eIb7nWVpSVXyDHg2QhRhgSPrVbIeTOceYcjKuKXOGXhEIuvfqFqGZ57t0foSktNtwsyhnci1axdlyCk17WvNzHxvIqoTximrNtw738t2AKG3vn33Qhvecw+G0D7+LVulqneMEJhRx9pBw9e8HUSE/L0zxakYUVDEo2hJz5n5xa/evH7zX/7d/+z3/+DPP7l5en1ztbpfXl5ePn/x4je/+RcMxs+0uELj6bygy2IGdu4hwCJqIdDZzN84XFOoZEkR3lcBl0GTCcE9fQt2c5dAxUxC1+IfvberWF1jpH7kES2xxygA1lEziKsxXOBaWsHMA1vAeKQfiEM9gHo/mOhfH10FR6tAWDDCvpCQTS9WTzfLm8kTwkHeYeAdA2zy1lLSQ0PaRF7fpiVOo7Q6yvF1qcBjlbHk4FDh9F6DMcWySVDvcEspO2hfKqxalZa78QzxCZmlGpUW8COpvX1I9H0LuRJ34rXUdphVbfbDaktPJTjJtTS/FME3MIf+BsttDMY7NTaviSV1RIGtN3f6IG98CRh/YR6BkX51Hel2gkZvgY4tLoRv6271gLx5SaoYSwyutPpSIudvBNBvKwPwWqgmh5ODqqvglNVWqQ7cksMfA4aVV6ZtvkLHyewlec9qqZxablZfycdnP6J/1WMJVtH0kRY3DjKaFmsfLjCGBZdPjNFPmzbXOqT9lCvKW8+uoqw/2aZqQ2rUg8/VGmYrs4ez8Ttx4pZp8dsB4pd3/bUgnRx2qEelyhYs04nZYLsETqlVmT5KnUTUoUmUjGujml+foge0IywwSkKheajXOSczitU5kJq7/FWOyHd7cLRzSIBHVDSeNWdi+ZhszulGI/SummAE6iEoZS1y+pQ2eehWzUoeUsuEe6gNSzuU6SNEn4XkUP1PE3qYpY29j0RGVHCl4EmD5/PF4t3bd3/7b/+tq6s5MQ3BNwiEO+Atrq6+/PLFWmEPwYm+s0vYT1jDnjs3109AduWEqcMBvoL7AFd66KpIKeHAOVJEYzBQEAUEpqzelhRGRllIvbxfLgGSZ0KAkAkW0/V0aaBCPQVPhGkaQ2VJEnzul6vr6bXmMgCrDvy7nM/YBWilGFLhY1LT0uPUhhSF50m6dudhNYZLQ5wMZbKipkVyDMdROCFkFKqRSjUzbSgWWZ1pSYXXuqoWakYlAdJhFBuicIXX4EwuFnqHRV1FVqepa/v6zVvK8Q53MOWU0WmdL7ZXV9cwI6/u5Ravi36DHElhvSH0DFb3a/qcz5/wVQFijDt3auk6QEqvdfr23Zvbuw98fkKdC/Hy/eQthiRTmqIw2vGRivn72w8/fP/9mzevNpOf1Dlg2d1qg4u/ePr8yy+/5nt2VhUC33WqWsdBlVX7fYeYGCcn9lF8Lv+ULDCmjT8lfX/5unwqLZL10P19rg5APCsGGrHoFQ1gnVh0rl5pqHGuseFhPufVGc3jAZ/PY0xajt/ndHCAvOYwY9j14LRrmr0mi+gh7QAfQQKXLDFzzL1zIMMtlUlGJtr1TYTVvRDK7CpSwU/lv6Pf8d7BWqlynK8qFGF77D9K04iCtFfQogiFY7vc/vby6dub60tWARGIUJwiqc32yc2TP/zDvxwDnAqpiWocfDF2ykodxe8eWZ/M34pZRGgKl8Qh/inHamzF3yqWPEBrxuO3E8bjScKH0H/zJfQbxkcZE91s+NgXHwcwtgb/Fb7p4CVgPvFLmCdmrgPBH2nsr2HRZ8+fXi4Y8NciDIkX4b1f9aT3wBbsHNYgXYUAROpO36WMcHy0x9f7vwZQ0TSuTZa14nKGoVZwSkZVcaU6zwCr6sfY/wFzGuI7dERdezFk57B2Uq9SJM2rYO0M2TFhc/9ntPpkTusQU6sTqCzhPT6hCSTYRr8O4vVPL7/DQ/CRyZR3CeS66q5uvoaIN0zMFbKLF8+/vLl6hudyC8RKWjGWWmL16vXL9+/e6RsDWxbC3b148cW333y7vGeb2oUcZUI3A+ErOsCr5erDhw9zNvxBGCL0tWx6EFIrdaClLu66ZZbrf/yTP/nTP/0/r5d8olozFdSBnsb96vZf/yt/7d/99769n9zp3pBKybGtbbSmk1XLdRgplasC4lE8EwJ5O/9uiCqTNxId47uDT7kO/AbHj5I9eWw4bDfGgvGrkefhT6ku4srGL3+PynQS8ZHapUOTA+t8Np8ZtEBbqfFyoxXG47dllZAD+HQ6XOUWsx/geq4OgB8bpZY/x3S0UzZaTpxYl04+ASzvzxOlZPLgeQrnU2izGiMTjykLlRDX2RwjtT0dbUA6Ree2xsFe5mhoQEcbYFdOqORoQ6ozRq7PbBmioUsCIg2rE9Yw1Lnwl3+ZGdBbjA7ERbFSzK2gRYG3uCbxYhshtQ1SnUIuUY/wQqRoPG7KVa92Mn5LD4OBe4ImL/ihEGRWbYiKJFmN93qCQluWKphDNuI0BcxIq95LZtsfPhTAhID+MbKrWkMHVuOAVgHd7qhldmDXrresxGund2Q51dKjTfWgkGR+1erBVMmVLWqShXUVFnhKyskC5BaClICZqSE1pM5qUZ/lafibx+/ttLjEwq2Pc04WM1ax8TWJKzxhOn8vtuDLSdg2lBF89SHwKlLipy6jxN3df1hvlxebuXoFW8J7XoOJvocmHVgCZ/F0HzRRwE3B7JRCf7kfDJlM4O0Vvj7h1WtSUrcJE2b0cVerJZjz6UIuK5lzpheYHMC/ce3wULtq2CpbbGcd2HVAc3lRBubn4zwW2GP08wipcaEdP7dfzSKfM2GBmlucqwPAZtnsTjqwdu3kPnQof3p/MfiMOYesPfUawSj4nKVPP0JaQime402iPMbfKAgN+WomR6edw3M6OY+xUidOcKv5ZF2tTqo6SsrF+P38R2U764iUUvl2i5SzAWAOaNWpwDBQDP26XkO3vRYYZruv9IBK7EctzSfBiuWJxRXlEOUTNxOLxOeTCGyITrRgmjBms11uVoQlxDEyqmIpYrE1K+YJYjRqu9U7AIqg+EcAZbbggUsu1CLe4Su/AAm8KjU09k9PgAgsaBiKfQm2VnGIFCF8YkwjstAJohhJBYqdWPDPKC8wae+RXMItQjr1RZbb7aVCMU9WiAIsoaXDKkWsZbaVOlW5hedMJMSkQE5f+R1cPV8b3ZfaBX0wRcG3VerYa03K4UzQq3vc/XBWoyjCji1UzwIJGnaKFokz7Td7ax8gXmY5v91KPgcyGEJyJK2rGGzp+N0LU5+UBknfg9tMXvqtcXmOhdCHxJl5ZQQAMwwvxGL2xt7FvrME8UTllwr56Q/MmV/Cf/R/O7mVlA3vpkOpdwvUG+WVEzkt/YIXyGKegQ9W8x0yOaOEUcCretuLBdNcvHCgDgbKq7ugDxpf3G3er9YoDBR8VNC94JPxONUPMwXElf84ef0QH5fUwe7nwLiFP7xyuvN3pMG5zLbxxz//Sz5nTuvBdfxRWXwPh/J3oUwH2QPawbHZwO8+CrTbZU9lHrG4T7dksR+typgWPDBG7ZPbV/VD8R+KD+7om9z38rk6ACgL05Ge3lezTwPeqEcje3Ydq+Y4J+Pg+UCt0WmQTuCYKh1NGMwhj2NMZQPnRImVwJ/FNZtnj7Z1vHpugNQGBdsERB76hK5CJP5pbxKG0TXcfjFjYoCMBtcpJj5ROKPgCiwSjsP07ICNOaq80qGC7bQwirlIkKiI49xtUMCkVykd5yvqIsq3XOYldhG8+yEAtOwn5PBOpTWR7toEho8Ta2wVbn4/OkL/KqSqFKnyoU4FzdfQu629KsmRqTowKh7NoqBs0FfIj33NyrgmbaWA5DqO1y34dOMHR5gmpBpuLdOgzyTE2gTTuJ2bVnwiWrY/pnrgJwTmc2aq+BQXg/JgKDTn8BwS/mGvA5tuJ0n5lcJ8eOifupOE7/QN7EwYAUzuAnuoxEoqByRE9ureQqPbg/5D1cO0JnJFWVC+LKHiQ4dDVqWTzZSB5tL4pDH32Zw9goyLijrot6hnq8P4keQsds6k0lzwsRJZoVCgkf0IWtXtdUYFHoxxr47R0r3Fnwt+fhY4x/1RuIUfR/ML7fXBTx5f9m0cPf2heHjUVksb1HzXuMFtTA+sJOmRXqK00+fqJZe3azkq3JZYQpAOYR9+u08PbRizZHKu9BGc0RD9OzxhhE59tS5J25xrXlSiFuk2VVFYS47RAYJsmc4WqXEk0/bDNqRJ053Xrcdbet2FgsaMRN/uW/10zZK+XX2aeEUeraTemCPwohoOpJQUUGPnDq5YwkyCCEXDnypYTWasZ5goLlLABLoWQmjEVKGY6RU9RX8gMRMWsZHYKtSWZlutzIkwTODqcCRuhhKmPw7FQbMZCyYQB4i+h1ZruETj+sJT1AZSiCCl4VWW/Vwsmbwg7FLYL/3QEAn0U56Dzip/Cwiu5jd42mnZQCu/jGsNGuXKlm8L1MbpZYbSAh20NfyO8h1oeA6BfX4QNbTPj+0hdjZ08C2lj98pKHPaKeeUuNFc8faFBbHbEsilfTJJr8XBoFdHwwmDsB4GNLotKcFuY6C6ux2d4wJrTRIR/m/xIm1fq1d11TMM5yPEp2egQH578Sb5o3izXogI3B7ojiXLz5gFszPTEb1SzxNeeitdnQgwJZr/m81s/sqimYLgQeH+gF1UIiwJpm53FNcbwNpCFyWW0nOy/mayuru4/NE1UyXElMM/8+5pKFeYh1IjCFw/CqRdQcfYfxQe+stuKkQgPM3ZVrFHpzrjn/87XdlgaXg9QoFaw+yseYFMsoZfLypzTU5dc78l/t70eDvkX1XZc8yvlVtwPP+2qsM26SgttOoobQs4CnJwjQpPPlSrQ/HLCvXS+gnQnqMract0sTtfCa6nwy99p/nHOWYAOu+8OmHkSrfepSHfZbrIfmdgh5rhgSwX7XmoMrQSJGN84Wj+nY4wRmIn4aFABEUFj7DMobIOwn80C+zTap8iYUFxqWypUFiRBlHRjMCHINoLcvjlmfGbp6U+hPtsrhKmJ4wB1bGNewK0h0UqtlZKkbYOMzVrPaWyV6owAprAU+REXpMJSQkEaBk23/litJTF1Suv5FHor5hMMwLIFUstpVAwSCgWvFCccpjx4+SJDKvBSaEYxNLCOV1NE4DQL8rqZ2lbHYm4yp52zYz7ZR8pIDHMApJpVOF09FSkB1xR7b9WAqrrfooODLSAvqGL2lgNJlcjFR4nz1TzK06Xs8EMz9RQv4J3AnWF/4LqZH+1i4o/ZATvU80UwcMhPCAz4Sz/FhucXN+9AEG9BjkXa4rkWjADsKW7KbVwXbD17q9lyYvDP+3Pdm/yCSpcNqf14dpM+ETFfMZOtzN+x107LiBHr0SgpjE6jNYG9ZP1l7S5/E5COj3wU7BEQ7FoSM6fj4ewQDyCTjVvtFlNv3YzFsUhNQMa2YAXOvmXdOBLwEV/KPMMvyFbG23tlJRpxiSKHmFC75K+l1NHn6/NuQ3Zy3ccQof0cYRgRcPW+oIj9Czxy/RosU3Ewj2aRZ38sz80scfl8aKdxBH1Hcd1D9Zh3tr2wzakR2CnxcBtGy1aP2ZgasyGbdJT2jdW1x4hCE2Ak5h/v2uK0MH7BF/Mf6hpRCatFo2xRsdWiqoJfhasRbhYfTO9vN5cMKqn2Mlx1XLCJIAQiIQAK3aJ8N+cpYTjJzeMgzUQHJ1RLh7K5SNsBSQkq1RBl5ho5oGISrzhqHFYOgGKtKARP9ZmKNhyhGWhQvTgaIR4KEzjMg+2IuQHwcP/DP3egnVxwXyFGMWKDEOEpCOCNqugrL4GQAfoR51rO9ML0H2ItrskQTvG6UN4nFvEbfzd93T7BEV7BcMKx2P/dVBVVLtmFGtSSocDhS0Fa9SRmbKJDda7ahaJW+bvwsw/wJn5kCD5HN64XX2pgHpq75WfUGvgnDQUz5sqt4yj4wQbbboP6Ob6ZnpxA8Sitmzao5du+Zsxrs/7uiwk8wvmMPF9B8l6hcOrG+oepV6Dmc2Z/rpdrW/VXd2u75kfY3NQOyYb+sA6LTNSCzAT5bcO5MjQco/L70jHlY4HymhGYTLXy7/zuT5soVmGHydz5IKVjKKEkpH1NRsKcO+hrgjN0Ft+loJQKj//3QLRDkeyF4fieTj8W1w+mYcx29r04Zc8UwuYmLTMPjj325ZyCiTHZrJJIVdqVEeZrmDHX/tsEhw7Sovf0I7SICta83jNjqXs1aqHYeDL4BVCTlSA3muvrMJKxRO00XSRlbQmn+R5FWkotEP3Dx9vFzX49ar5ueDnZoHsAOMVxxnCT8aTfCKYw5X91Co1rO1pJj2Yt43TYyE9HSIwrFyDqMISODvAUDTlQcrtdrlcL9moRDEysZEOD73rY0nsqCgIUY3jmMLNxIwScVV8rUMpQArPINsJjtI4B7a0lihFUDwuRQIhuxER/auzUbGSJgqOwCS0kVYK5sm476AUEvWKAigMsbKnikWLQN0JyqWmrj5LV6kRkwgSQ4GOUCAKA5LOqdzktYKjMqGGSa3HSCZZiQ78VBZ17CgfBepSptC1l0dWLCcS6gjiUmZOV3Rlddy7o+mZ3qG5cBCQ3G5uYZqO/qHXz0sJ2l8HNN5MFgBOTtRPF5Kd98ne3S0XC1aL4Vn6XLA8xN6uWPzi4umzp+BHj5QLvdDvf/sDMwsKUifcIOCQlm+zxRB9BbuZAnbJlMtpNyq+VkFaWfmulEKBOWG/1q3pBQBmsVQFkis6u+rwqg8ibaROiv9F6MMsqsyR13PwqJSRmasj0iWkKhl7PYV2rIwReNlAuUYZMoL6/ChZOvrkNGJyFuAnYrrzV/4ROWYzZiNnyENqkaW1hPSVFI3tBwXbC9Q9o8XpUQC1vs4JEtu9xjbnNuQEgSVpjECMWlluMsYMMD799WgszrU+3Ag9S/wyHVr1+UCpc07LMdrWy8UN3QzPvnSqCw3KLVTYkzxVjS722DBXs6t8CNZuEbBLbkoXdS+LEt9hH+guzc3e5Nf3lk4v/AdpIS78EU5UR+yzJK+N4DiiX4KW+H7ujxfze6ITohyGSMFiC6DJDFUdyjvwFqMq0DFT8Y8YJ2QhUNghshIMBKYmpcjRkkI5DYBqrb/WU2uJBKw08g8iKy1Y06+DYCsifb0cqWB/Orm6utK7CpoyiP4AizTE22N1cFNgpW+1aokHY9KSS9QoKYqwKBc2UF3yEfrFavWusf8aclABEu99B3vtg5lHvnfoQdzBeIcSK/IjX67O32GQkh7BRalc1NqtKKoc54xVJergQaUSyU6ShSbZmU+DRRQnJHFolAfTkmfSf+EmU/w8nb+mZacX82dPX9xcXRNns4kPb/0uV7cvX/401R5TONDXcvfJS9gvl/cf3k/Wyy/42vRk/hKJ6tzSidQ35m5xHrgxAg8EZPzt6ZNnZGcz3lehhI9UxCJbBey4uF5EQbg6mrpZkHV5yT6jVxerL+Q7s1fysXQnbN++Xcux6R+IFR0KhMZmnyhHYxHza6GdSvV+CwnPAIQRjj/rdlBjdNr2eLb11fON1f+nsN3Rls/D4rm6Q6hSnU/mqrD/egjPsF62YU70c3/YkoYCjWyWXc5jZOADJUpZZTqJK1vzgTQYYDvY1tBhwOI5I0Zh0vLGyZABOWcqkjq1Gf5QzhqkmfzvLarSSeVKHzgDIDlVVcVP+WCp3C/pqFXz51mxx6mCPKm4GQ71hvCocxk4lBnQIWyyFy30GeBzusKhw+l8Whyiii1wL2CEIk1DOG86xSUESxp9JK5mPYMX0xAK8ZIj4bKj5S3hF//rRxnip2dnQoj4J2m1U84hnMZGiXf45NcKn9PYK1ERsdhSb+4aA9FaekHEpP4CATu7kPK6JVm9JwwIEv5Ptbs7X3MVMxRn6FcjqzBcsUU727enDgNFIgjNvMCbZGTRLAmsV0w5l3WApVB6YEZ1Cpygifo2jVWgVckeEVXx/mspL2F3gPbzeQiMXP9sDtnN/xGnnlntSHk7W0ma0/IZNTVUi8u5vhXNF7kW7M1/rQ14Jku+U/H23ezlT68Qotb28n8G7P06CTG3+o30Iy82+nQXziP3pl+7JDpXN1dFmkvSYh/tHCQW6iWCSP9ALW2IdEYLnwHheTobkKsmBHskaNCK3N1ZweTUroXqRUeUlUKIwV8RzREBk0Tby4A47TIJwQgGBeDz+eNbILdHTjyyTnKkmpscKb9wtCM5/EzJwoCl8iXkcZvVD5OsSqlHBpJAJx9Vkw3MAHT1gZpVqtjBs6MPF6K6+ETJ+c8ftdc4fuw/Kn7kOESP1Xrt34PfAf5Y1ju33MIryx/BXY377o7AKHdRGMbccTw6de66j/mND/tE1UpbtSqhwupJkQoFcjQicpdpzYwiEwUlBCOMV2rxPAsbCLsZiifuvvfyaIc6iarFNnGHozAsRKfikAiFVNvNh/e3Ky3UFia4CPEoqcIgYn8iM6+pkHDSCs40hCpMoeus2YAQRM7hGhE/AZnCRLHjO00KGQn4NHIcgRPxFpTKutLipD3dkXIjiI6ooLHIOAwTOJVGSjroDwV02ZUZppMOYyiRy7t2vAHL5RkpU5YQqssa+uoo0wHbPNd1+iZywTPL79z/J0rjXJcEj2BQaB58O887MSqeePV/ASuSiS1GjQOxTlb5lLVNE4ouNF18aUHNzR8r5hfrBQtmFC7T0CxOg5JRf/b+Z/m/eOq0nf1EQmtxSBP9X9If/Im0XuDVzBUj8drxls4AK3kcruMVwqUO4qougFQheheF1EAXiwpvknfIkyQgqsLcgiU7Cwhi+W4AKQE5UYiRXF2kkjSfzNipiS6L6jeJbkCIk3jwLNraJUXE/WMc5e9dmT6XLrVfwPM/V6su1pnUpV3iyIkKsP966FqD4Jh/19oC7HFylXa71KxapwyqgGUOdZShXCmrTA/RDMSZw2SHlrb8Z8AODd7ZzqV9Gji1bE+EXEos0zXaIlOzYXiVNajN8APRg8aHZi31fDrgMHmBfxBxQTeQLFmW6QGSX3zRz8gO+FZyr9Gt8qC1aysTGrbhDX0DYS9ag+oTyI6s3/5m6mIUcQi1JODgQcKQ/5JoiBaMmYAJWxMyBkrEvXFILazthkHR2AVIkZAsCn5pWDjV8n4mIUnCSCucchRjAB/w2iwh0AIjh1kRDiFVChGuibnOKlT8TxRl/gYFq4juiLAcS0EgHKFq0JWlFLFsQ1MJ0Z7qDChUUzZ0FUtl+S9DpLP1NDDoyrOQyqLI1+td4o9Pwyn+Z5JGNsP3JKI+e5D2FMtEOlL1IrP/HOg+Z8qKlahl5+AiqFo6AwLscyZVLsgzCBL56WJxybIZl+ONCtvlJw7FswTQPI2kjqL8l/1rhabWZTaJZTnsMcUXeVnVY00kAjQG/yNQx09EZnHWc6cuwOApBaSieCZNnTVUMFSIAvoQeKnx1ImhzH0L6UM0NNmuFPNv8Vi6wfpOAGLBcrVVMXFyRgkf9VwF/Xw92gLRXJDnxEhW4NMYnA8lHMn/kdE+O1anwT9O4/Z5lRspF+oTgzoAtFuv1QcCUVjljrYFVa3/IabV0cWnKqtds6VCnZxNSD39pBqLVmZMz6lFVAPQn0OTntqFpjX8yBwnt48KM5fWKKy+E93WsCQJvL6Rg06GO9a2fN+XAjt1bjAMTfqkI6jXjjslmqlOuQ2kYFvDHOFFeReFRi0azD+xLMqmBnd9J/PvmurX1giO0L6rUcRz9TXBh0ZJiTW0faGGPQEz8rm81+p7IibFOWymqE+criifTnlv8v5CZ68FUjgFXqUDmfVzZfgyQAXjqu6CohwdjvjYPYUBfoJ01ujrE2MabQXEXAM7p6xeiOP0FfERvQBKpaTJVI+IxhIfeiwemBXz6DBox1LF9xOWMEHEV4s1OmK51gD8/ISkXAdi9F0CocGdeoOYipxeP0X4ZPY+0ylwg7SiMRNOCXTRuTq/KqyQW9cJNoFx44vCVj1zbhEZEDjEmW+6y/uhqnHUI3DqcwiJrmLfz6ZWora2BVUbpW3XOFXSsK64qp3SIbzGsQMFG4oFMkfF5VqmM59t7pn6JkkJ3quVNJILhWSQ8be0aFB5g1yaf7gAKbk6K+43ayYTpAm00lezA+wvRC+AKFzIVhF0x/EgiKkP105pidIR5yjlTFY6qJoi01mejNujeKq60RzkL/QpsO3z5f31dvUr7ruLGSt9pW1hpmAtQP1Q5dX1bRyHPiUa5B8x2/4F3KPMiN+CPRxcjLWbth1B5kYUXjhAUHTyaf9uHrrWIJjn37XIcs5j1RnSToy3aihfVqfN7XTIeH1qv/snC27L7Wws5GQ7h2PsN0hPhFxKLNMnVcVul1XyABj8MmA0bygOJ9rPPXhytp778R8UI1cwJ1ri+ktaqKcAGtZoeF4je4qgB6LFTHst9RC1QOhxbMco/EC2Oopttm47cRQ/E2VemYUXPxCfKHjhj+BIB8vxMTN7mRObr7SjCWWESQrP4zUAViZcOirRiWKOOGfGOUFzFS2Wk4rFgsxRvcVmjjDVUD18Fb2JdeIu6fznSNTCUVKRndd3E59RxlofjQUTZ2m/9vl0unAEV0WEFpzosqJKIAyZUizGXM0d3oLDEDGVNlIoKSVCIcZF8CqfoFGWz93QVNxfSIktlvk0EyD0UmfKnMjUQIKslzhQ9xRnfjkhUW6/gNi2kYQVtjNDndJfBUrqBGr7HDUwMW3CwH505dTWNJR7AKDQ1N5FKgsUyHNH4GlCi0NdRDqK2vRTzcrb5+pGJtea8aUwORAfvdZ8AWG1ImvH76qUGEiMLzqHQhVM+apqgaWpefGPzklafcSMg15Y0Z2Fx+qPnjDOe7Vm31pmA4gLk6CQAMskh3zrGCwVn8/Hw1sAO8f/hxe1X8JBjX4Q8n7ZP0OMgXsrahMmemxDjZAHSmBpBuDgflK1s2yt/mRGCB5u5ejpJrZVrwiuDcgwk0Zpu+fUV99OOKJzf67BeTjbljuMH6XDVHkkIIzNuVNnWO2MVpfaOXKQzFvHrOXcFn269cFrHJzplN5GA1LWq0yXyOPl0oK7OlZ+BaswY8kz0jvkRllrxKhPt6DrKG1xaEjozLb5tCDV7eyW77NMXgvYcI/eMT/iF4xUMwejkOw4jhjeoP1we3d1eXW5WKzun7O7ypMndzM20CTeITTiBcoZg/1bvlLK2L9CE1Z4azxULINjiumjyrPaOHRDQTcVQRRfUdX7v1uW5iumUsClsX7mG7jOXyvugjWxEPR6P1jjuHEzWGIVhqlK6p1ACgNHcIrjttreke1UeEPUmAruSMBLhzoSqoCyBpqloAkI8nZyq+IN28ZD+0YRprDMhwKxwxLPhJPW9FPsAnC8Oh8U869OXIeP2ti/VaoYtuiGS5vooRZQaesG8FWngORs7xwCOxdxRE1buwmpSIbRteuIAp+n9+rCrb8W8owvMZtKSsj6W311gYGst6FW1TSV+hIBmSPxwKAXwBIgLeBhi0/aesqZj2kp3lZzucUpIwBn+F+svf7G/sbUEDtwytsUf+NcdH0hEXdeCb6Y/jBd4JnPUHCy/lLcZi/Df0BWFrbhEaJAkp9Fet08mQFW1SG2dHMnU31Aw3MOdAZwH61Big6J9rai3nRIZn+2urhaT36aTed4PbefZUW9YVNwrbgDgmmVq1/zU6IOvtBTgsVx3zXAtWd1s+yI/IgnZOvpd4QYk9j+Z+BWrIloj6nnX+2GlmH+KE0vcDcwquzw72Yf/4p66HpcbANH3X3FUepwBnsWnMtd8krwmHTbVxNV+FhkinhgDM+M03P35PJaIj2NRvh2jey4zCGaebXrIQShUlBUTuCH5nG6DlJV/AeRflmFyVG6KlUWNSzTKDqoPQ9C7tLrAFiW1dA/sygrkoGnJEpBnczrnnyKqI9OG1XJNh7SZxRSm4EtqIUT/GfLlJd/42/853/pX/1LT58+ffvmcsNO5Isf/4c//mM+eEoYPiEQAms6ubmie/Dk6vKp4iaFPQ5IFBYpjSIGtWXtCneEjp+1daeiMZMHz9nF+n51d3+nNdnwZB7CZ6Td3QLUYp7AT2LYqZ1QbrUEUcEV/DTWSoAFT/6Yr+B/xIKiAFlnCQzsUDnOwKgobLQ9qL4vTN67i7IaRGUCiq3iUHoKYiV+FbGy/Pmc2PZGZsYbcQqGJc8gyjKlzwg+pZI79LryO/gxqUKLXrYuUEQrdWTFsKfFRToKkgnVCjrclsKX9aNMhqXTN9lcznnn+2p5z+cilvIlMBScr+eXzP/QlvIE+yr7e2qH2bfv3tkJISfG1lZXTBdA9Pr1G1hbLXcfLmZ39/SHb+gbE4OLJASKm1xOuNH4uY2trKsovSU0FFcHVn1Uac48FmRKbli8hHvL3cjRF9f39VDy8rvvXv72uz/7C3/wB5ulOSRhYPkQfhaSYOQ5xKjzyOg7jF2qk+IzcJQFsmFHYZ+GFG0Mj9z+p/HbUUctdvnPKVvgkzDL8H2afSIpPPAl4EdvVHq6Iy14XC9zmKqvv9hWaZjPeLOV/eagivGDhibRoFKj1VuNHdnrbVqT31a+Vjwyc6aea7bbXq1KC5Tpkfp2ovVZafh+qbFq2781Hlbid2je4lDi96XbfNoQ08Zzvo/NDl7gySp9Y37rr9VQsx/CcgpeHHkQN19eLb7/4fs/+m//m3/0j/8HRdxe8EPAv5jP2V7zfn0PQAOqrIjWn1YvO/6NwKeweMRD3PbmvNNQv1kJzaEYJVKaP8XqGrXnv/b3VGfjYvPm9cu3717z8jF4ipUc8UDIZ5uQrsF+04uDiojEOaZ0Xa6vbzbMVSjuw8kpla7s+E6VzUXoMJQFxGSnlABWksDx9j3dDO0ho5CNRVCsqmd0ee2NWbwtJFBkXF9qh/iLC6JJiTcvpyKns+U4i5ZJghL9R+ebAw303TeAGdi+V2H1ZYMG4pgsijWUrnim/XZSzfbwgkdlzIpddS0oJ3dgbdeXNMtk9padXqGKN0AYHtdqezqbGpKv3Cial5aQjua/fia2ml8KryBDC0+v54urK/g9F+30FZ/Xev/h/eXilk1CwcCj7SdsJzV7/+H+/pYXLbzgB89jxx11MHmZmEPzXZoqsFG2F0v2kJWfk52+FB8pgVdJnbAbZ6Xi8POfsihKMBGl45L3ladXsMcpzUvdl5evf7q745PJE3yfV5GRxC64v/3hx5c/vfmX/6XL5VbvhMQR0qs7qxRSYQxcs5IZp+eZ0zEnkEmOSYx4QvZp0haXf3HaRYL4d208t04mGGr5tUpiNL09pl7+aue22bEaUd8dcldqD3+ThNw4R8t2zFR0Mc+wtiWTexmj1OFEe8KvJusE+9T45JqQOIFnySbSNTtUxSUwp/veoqyIznRFHkdxA9dm+ANuHCcP/A7AmXTcwyabLPAKnfcQ/iKLwxpFg6bfCCDR1mWtOyEl7TByWfqg6dAzV6FPw1N0GMkzzJvPp0j82LTtxu/WaCxeilrMRNYk3IlghyDn9vYDeyoSoxA7E/UA5yDAZY0PQS9hDUH1bEGeDgAXrd5RKA0X8MxIbBVeB0/lFKwYxZndyTCIdXVHghThncZAHRghSas13BlQ2BcSwCHeFipl6jA4FtMiakVkvKh8efmEwVp9qmnKgC6j/lodQkQlIdIKBYj1CPBELV35n+AqF7vJ5P7+/uXLH1RNIXPoBWg6P6RRleDN0uiKrCcvrp4+febeiOopXPHQNV8iI1LJ178RRydS4lsnb2CG+DjXEffl+mksolN4VVXzNlrUH1s0jLGTrrYg/uWzD+/fv+ObXDietuenwTZ0tOC4fnLz9c31NdZSJJ24yjmcDAOSlDFpVHDgTav5rG4f3UjCfBbTsyxIw/SpyaSBXBl8kWkfK7WkXmqX67EvEN0ANa1YJGFmzKi81AI1mlCMWtYQX4C+WAZIvhaY5J8+vaFOLpHX4M2r+/u3b9/rOwbq67J8bcn3KzwngPZsjaUvB0uipjWSiymbjkpUka+So67Qfz5qFhhvkWjuIC5a+UhuJVnm3Me2RCad8Uv4SNqS5HO60wKd5u3EfCjgXqesGptniz4E1re277DVV5N6v+2oylWK6ZHX6KHmomB8XC/zOKp2Vc7Fp+w3h5Q8ftCoL6WCeMQiqDARkEi3kRs6C7MO2ktSQ48es6Wf0ntu263RyjWhj5gJa4SVDrPM4yg5ZPkH1Hf+Q6qeZCiosRMxGPr1xebyzZv3jqe8FNneOJ3PmQuI4XQFVgRQEWExTDvRcLgeOKaBk3IpRgm7W1SELzujmsCYXq4D18lm+ZzlRlP2C9IejIrD9Q9mPMdAX0hnwXVwjVjMy/RTLXTfSKQO4irifvKMg3BVx8TzA1m1HEZJE8p0SdewBy87vFDzTH6UGppbUL0VGhI2amJEgRtfa/WqcRacLPUJWElKDINl+0zxqKPa1188+wjSeL9RdukKO80hvKnyY687cZtyDyJZJ1Wn/HZBvKvQoWUV/od9d8JlH172oFa0wYf379++fYU76TUM+ZES+Brdqusr5jQIgmkEUOVUHKLRSHz1boD8gHL/4lmEAZS+EbL6a/TgFqylidZPnUB1KJng+dWUd22nzPWphaEBx0JEFJ0+F6jF7Ry4nJpdcnzTKCMpgPQvHU5WxlLvxU6ps3BxTXUnvaEVeYGo8JJuj0TTHREjrupXTydf8R4A7ySTFI1w1fGtJO2uUBmaiuICOgkRlUdCKcp6x1NLsk8s3f7FqSno37Xeeg09dWts8q92DVrPNO2bSwspHc2Q0foT3e3Xj08Jgkqdc1uLqNCn5LHHkiXqyelzyToXn4EKtZssGrps7px+cH14NHHE/HaW2p7hpyiaXM+I2Aa05gID9e0vOp1DwbvNLOtcYD1eEn0Kez6e3CypNEik2yqFiQYMFSQlq8y/nRjg00Y+EdKuy4kMjyYfaZyj+f8cCRXK2C4Ob4iVNMSv2Flb/mvpvNdAEI5pb0TvsB6D3DxdoOSPIJsF8Q5xxAd6R0eKRRwY9cQfIpbkwIkzeRJK60+sjAIna+iMQEKrQiDhAXEfQCXpL9b6k3VcFtDgJ3wpnwi5mL+vga66KMojQiQC5O0HbcJiIMyhpcAynSOv4X8pvrjQRwakTYrElMqH4YkwpXPZyQlrn7gEc1V5p2Yq6r2U9L1IqSBwLaUUEumE4wyncIZaUWAIRBPgS1gU11J3Uk0y04vdci3NzGhHf76ENV1gcltY7S4Di8otwdk/iIzLK/x1u+aIHAyV61Vgemn818IiSwEuJ1AdOEMlRNTwiL95i1ZYnnoQtpgDMLrodIQyAuqQbj4qOmWchlj/SKcjkCEg1BdTo1HmGkgdIVCkTo7Uog4sTmIT2+Revvd27CquFfvyGlicK+3Kwh3UpS2OddzPuV4L9Nq3l2JswYltciL5WC1/oXjd90xV2WzbYbQK/eQrYvb6WdYJacIfeAcgxn1bWvX1mM/Qv3Hv02/yqYcaqkaNGueWUr80QHhMrnVUj/H+sElkyzSQyJZvEZQIkS4he01WupMIe/xhL58BhOwz8I8ql8ilp5XpEmcg3ckzKjVANVTUMzpyhG5DUtplPZa33I79/tsM9kCyt7Xw1O76M4ZiDgUys++msyer5S3hyMXqCy2VWLwEgU+pEucSSGnJMiQaphTYryqyWJm9cWBF9CIu8fQxgplXgOQGIlTSBI51rIiyk1eT2RvFOYR0fMBVwbaYopXVY1xWZMJ0b0F8FF2Zn4ST0CmtICc8FIGLBZUAXQTgKj227GYDu9k7hV0CEvU/UwQ2+yBkRpFnbwlACVBdM5IUue5AFNYp8iNE26wZq76qxlzMP51CmGVqjT5hbzmmXmJ2p6VV99EoaWRNM/47AJ07+bTlxiizTIYRfA6cVMuUceuAZGgiUZvFn0zvlIqxoYjwJ7bgjOhfo++aBFDDM7nEtybiHYxrJgmi8Sxb6aAGz42n1pVMXTjBhBF09U7pTcxnlyuF0XgE+7ooqJYaC96BWQo7HWYZm92qbyEOouZPDiA6LQJafgFkM32tW0EYcqXkPpaN34qRKHU2hjD5U51CVuBIVavtVWpG0j1Et1Ng3I4WnL3eLr+9WP96u/0n5KWDpYiNZAe78pxBSVQvosmFnZ/VJZvzpP1cHb9COp63Ifp0rXo59Dx1c5WzCTOkkWjMb+8sXeINSmlwKOlIt3/rh3+JytJQhirwv6bYoD4NBRrZpM+PBp/Ap8F2ly1/f8v0DmNcqk07BtLF23dHs6D9bmfNwk30M6ydSSy1M0Elqs87KxTh6U8DI0celajE6UguXWSVkioL9Y5Wsov9zwZW2iErXRqE9IBlBooyt3ai5HkchzbPMRDcqfCoMRQH45yxOmdkdXA1TiOojFxd+7lVGKqr4jGiGyETn7IOm/XY2kSYSMgjowpwtO5AER3xB5h0AxScqB/ApitMArAhaHBU+OLGTiHRrt0rq8YV7CCJyEmRkrQgthFf4YiB37xNw7xSLlS0nlIFQGJCwh0TKaogibdHlac4WCbW5mHmqm8lWohWG5GQRJ+ESJ9yBaAK7wRWRIpuSqRd5Flbwrpwdo/hvMBiO2XMUuIf9aBmYaO61C5YHWN0zs0m7KhZrl9OqCQyGJ4GKgqUTqoIqqaJ5uIi82oMnte1w8KRZ92LmjI1m4jJlP+kSrASt+CvZrIgua9ajX7gRu+BC8HY1sp9DEp1UAK5ZapxgUgKobZmD2hceSdsaG/7mQSFU5ih2KlGEe5X4TlIVhzMJNgKOGuAZJgqTlIDtS3a9wBI8nD1A3g1YiplRBKVMKVO4hF8MqiRSKVchvEaZL/T2b2WKluhTA9Y7dEaIOuztxbD2g6U/i4UZTO2K1sadgCtTXgCxDKHhVVqCYu/CR9EdGK8VHrMEFZ8gk2RazNq967aOAGpeo2ZXdYtJ/pIy95tH04fPNGe3HMNPjPzaa/v75M+DI/WzAaJbJyDMBdFthzPSEXj7d+PWW/xLpX7abuwR8HKupTpRDxCYlgg+wbZnM4atCG5qJmo/DPDwyyh2wF82pq3IVlGf6LDJkauvfVfkEe8G7GywZXvcK2SETuQq3wsrhF5EFt4QBVtCbmWs+l6On/NuuQYcAwighOYsVsiY/8Os1gn/Wy7eTaZ8k1cGHhsW0hhO0XQxDTBWUoBZm8WWMx/slYLUSnSZ7RVMZH4smaDl261TpqIhzJKHS5FXSW1AoOOAMl1oIRi4MCLqYu1d0wkcJIA4iaCqHvF9Vt9s8wRGnIlcjN9C5IPQYQ/9WyAhnpVR9QAag2IyixLcSF9HlaMQMISIIWMk+3Ti80T14BOwjvVJB3B1nmt0a+OHQI2KfbUr8ob1+ACsKRr4KBMHZJFN+B1rMjVvjnQhVDC4Eer6tDZJtZZR9aPLDZXG9HKyTDGN0ZqNLcgDWYEmksxt9pcY99iMOWjvOyIc6lOgV7oxeo0MrdqrDoLiTSsO3viAikHiXSho8pLvZPlN9fTpxfzf7ZcaiENLSqd1X8VofxBbub3CqwKTORlKgnnlAj7grYJ3U6+Fz2aQoIXMCMU3zFYvBKJhEsLOd7mS3KT+SsZR7DqbPZyIVWZQ4V664C85MpJpU+IxaMnL5kHUJEZ2V5gKS+eOplFkmGgCuIIwUpXqTCXHFu0FVTZxtH73Bv/TPNzte9p1hBHdjxmm/aMkAGbhJRSzxgVPnQWvVypX2oerRelZUuWEkv8Dn0MKmnb+HshDQvkVRvdhOP9oZu+vgah9VvcR9QBb9OOgZSMXJe+GC9WamCcuHE4D9u5r9X67qw+eFIwCwvxpdpVOlDW3/CsOGoXoCyCB0M8ovZUsRJ86DV7WCTyeafAoRyPxe835rEcj6ILNaL6pYdlZgHM2TMmHo7zGZV8NFbRBHF+NKEtQeEOLXAF2FOsn/WqBiR9KHrgSGEDqcgbTDShOErfTJ2sl7zOqn1QiDD4eJaDKlKsBlrwIkBsfkm4ouVA29UlSw2JhhJrLkhTECfmCq2Uli6KhyI8A2QtFMFQqgF7qaJwbMaXeolOhMwLx+y2qRhLgTgRtsMjURpdJxhMnz97Dr8I09GM0JDszfVzvfQpkUhQBWJSIeXBCHIQxFCHgn1FXYC4qDpKaTSYpU8KmPQs5I91KpjICGh4wQ6hW/TkswMIYniYINLsipMAUkI8wiRFYZVsUVUFp18lePjYj1HSZ1VlMFd351DGcy19qrJcGzLkFTapCmRpLKOIFzsy4m6u04vZ7Yf7JV/12jDyjq/QLcQZ5ryksphfaZtOsVf76s9cwsCcFTNH0+MZLKGfXFxfX13Nvlzes52OA3211GTJ3kP37EZqXdQ26nPQpTNn9UHgJBAl8tLtTy9fypGkCfylP/vBfvHFFzeX8mGqIUtIsDxFirnepKUS1qoUVe9BmUpvXSlP/2FBWuuILJQ6r/kS2cWKmoBIf0O9JPB9cDEXMqLKmSgtUIRvDX3twitIPicfzAJFg/XKqFq0F+ERCsbo+QhqfGoidBtVN1+kH1XDfOPvcxHpxgzAoUfw91mPEz+iBqvZ7l31iezqI4p1q7+V65g59fWiMsJAInbTj955X+9qnzHF/hQdSvXyyj/qXtY0rFzaeoxWh446lJqU6YYyZRHp8Ss4G4RD2cIfOtpltF9Fu4Ql26MUp7Ra2ToH8Bmt+ZBx+ssa+/pHw4Hu9dMlWeFKOVlWCdwUv+GHjtcd72i5+2K1ZjNylr8sCYunDPgzjMqbmvPL6yc3ehVY+Ckg2y5+uljQXWAlPaHxM7k049/SR7GQtAsNQd88l8jpGwRsNnyDiW0NPwglRSUeSF9P1qvlZPMVEdz08g089WFXeCpyMkdCIsfaksD/KR2AZ4vLK0aJ3S+JlUmzxeJGdWZduwivRBl7zqCANDextFEChm/fvvG3xlabtT/OKix1SLQd++qeyQCFa3o1Wu+JsrvoYv6UK5s00vnZXKxm08X1k7d8KsozDHDvPMIQXUXljjpd5RlWY2179n6pN30TQDvtpIOEjNJxqGR6L0S/n7DdPFfa7w8EhbL5iHqs1ZpaoZ7LIhE2Z9QfG4qkITJjI0tStnrlg36U3IQuJe3tcFmxMs3EzvyrW4zOEL49tGL5xfOvL6+eqqdmHxaY/8EbUDmjohiaD0r8JH58wm6hSaqQRXi9WLyUaLe1qCMkRw0pT3PLB9wNkKYiZEJMK4IEDc9GX6v9Ci+CXr4sxHTwteAqSYG1Tb+pMAxhXN1bgKW61EwmIBtWFIcUgbe8Ho2DA4A88cdOshKYAHxxAaqLpSqgwsgkmoRs5ka2cpFSWfvofe6Nfsp1PNvbYh4Rcqg+/F5jmrYd4IPh0ij+aGtERdvryBO8ssOucSrI41+7HcJ6dNjwQAvk6iAlVXY4HsgEexMFn4TbgnToX7LVR7h7j53CvSi1gj5ZbY8Ksj54H5+asF1m6zjh8A4AHKoa8gDxUySY0koDVtkJPiD1KXj5g1Vuvx3CzpW1k9n7bJzR4JtxzmjAkv9+1T89jDDFGQ1CFc/L7XCb5XbuJUXDQIpEvRGLnJF2UVIi24U2ihUYxmbzdYUY1Jzwe0aAS/CteAT5DngmjMTG4gFCFtJEwwyXssDDSw0j2BCyUiEjXSW6UlRR3ebNm9fLJR/YcgBDIKQYSGsz1vf0OtYwJZzabu8oYUxfQXlwhY9io0ohM2VNxhoybZu4tPYM186eTq74/JMDNaNLPuzDJMEsZTTSirDNEvT1enJ7dw+9Qi44qn4zon0QtCON4lQYza5vXjDtgH14OZVXIPTyqmYntE17rqf1TSdZ1yorn4SX5QekO/nX6aOOJayAFMkSg3TWK6NkWbloR6LquBni0sRIpJnVjrCeksHUx9MqGhncfPAx2gT2lAHB4+wm8gXG7j3rMqGHh/OEBlhfdJQqMWHBj3IhSIpEs8inkeAWFD+tC9J8kZrZbiMmrpaueA6U9B3MyfpIGshopx5p3CcIcXfSpOgaddDVnKyDagGBFaoSdnvzEzxVHDTrgIdrx09lOUQCM15ESTMAun+sm2+aymqhaFQ6zhYYyZ0yEqaDQv6rx6Jcm1jQz8c+C2QT50Rp6X3Uyexh/DhnPiXtQTxLwhPToVLJBPXOrkybYacRSjUeOj2sQFvhh9bnBP6HdwDKd8/d2nrq6fnzKz2JOnonrd5Vr7p9fcSqv4Wc8DDOkcisOno/R8nt0D/L2JcIHQLrFD5pzMCMhl0tZDVwGtm+nX3L2oQxyzVteRaiRBtIn1LfXraFPwzz72j9XqYPUNDytIP1KWp6gH4EPkQBimZ6j9SyVfnQsymX6TbTTS0A9Er70BIYFrHoW0zc79p6hdCfGFoOx1lvZxLqcihO85oM0uvJZvVUS9gX94px2bdeKoValhCqmQkjypaqiAwkQmvjKfwmwW4tQLazu7XW1PwoDBY6aOYBbG/+ohXiUi34OtxyProi6OS9IvmKFAtz5nPCQXAZh+bCf/+ZUhmOxEYBFuHefPprBl/vLv65lvFoVk3RJBqo+8GaETIOljRWrRZZsoKDfeqphHoKfoBpG1Dw4KGjWOuvrPTcqZA0MKzvNOobwG86qN22gkfd1SqWnoWSCHUaxMXeRBrXT+qaU5HeERlnl3VKvNO7BHKmbcGzgamsvnKAKjTynG9MC8L6M3f2sKwdD/f/BptvZ9+7mya9cR6kyKFkdxqLFIeaMfxKsE3or5+sQA0qU+NpWq6jmWet7CIdYb7p5d1ySL5BpsF2dhCit7r8AkbTq1cM8YuAJscF7JK4iMTLyOLts3QhFS5PShVRkRETqhDteEoAU1oJVBIai+yYeYpuCV4vDvpYGRNZd+4aa7UZpRDkfshOhjgiUHzSxawtQSlJloL8N45BnJT3Ujd7eAU9/Tr8bD+d/6EcxuhTGqb8vS5ltfmEdUuc3nT1ixAk+VzK7aWNAryco+ITsO6zMQ+aw9+rRrvuY+KQbvUMlcSqLlgj2/wAk2buFZ8MyJwzpEP/XNa+M4oikof++g/LqvMeytX4hF2wGgnFCfH8qJPLpjFcV4cflKtcoboe0yB7BEYtMuOQlLN7iH8RxZVx0wM56p4tQCL+U9cy8Yuo+udK9FsguUX2jg7M7CRRVqEGuFFoFGEQOSioIOUoi/CC+ISn5nTOcn/CbV5q5b/xNDguCiIzbYbj8CQiEkgccBFo8AOjONvifEpqVNpYEq7rf4R4fj3X8R1KaFhWrBTLaG29QPoUq4IRKYaK/GdMFG3pJ1h33ycM2kOnMf4Z74PytVcUEJVidC3qELk0dz1UV0sJiLjpcP0tXp8OhiFMpYOqpj8AvPGJnED2ZbJdsOtRsOZMmdISmJiGacGV7N1R5arrruS8qUqLVMcym9MHShxQmSKZuajsAHJNLAZOeS38x6kY6WfGSaurWKZzudBAO83JSyB0tmhgOYabUGTyWMXgNDmeqoxaKxo5N0k0gNpPbaMOiZQND1IKD5F3eY5LnBEgFLNWKEzvQ71Pebjo/Rf09lU5i5AVhGu6QEpA7pO9W5l02EYApYYRrJJ5hk6eeaNcO8yiqJSVovRxVnQFmALbLFlpRgJR9Jbml3NvP+VFabpHzNTCKh1CkJUW3OCkTU4HjqBjWy1x+HzpscBD2PEhePaovwPvXGMHe8BUdklklPUlXWYfUIOfF+tsl+LOb9ZAOLELEKnSwE3EWj76Xm109T+y1JKi3d8qS0ek27Igaqhc6/0Ez5Pllqohbu/RoUNB07eqr0DpSDZ2D8AUbRtn3SiN3mfuH4vjUXaocWjpdWgfNxgcR9US3gEYtnxt7GFwXKSm4SBmTYmWhQ/Qp8aoJ9OniSLR3Pg72jxKR1nnvWMnCvxauXg5AiGk2mzn89hdUbEU77kSdhHurrQKSPA1X78Cn28PiZGCG5bBetiRIXCvT5B04h728/n+Ys6wNxvgECmLKEIoFflQCBVRl9ZqEHUxLSkI8RMRD/GZQnY04lVbIkH3PMxCMZLUJfxz/I8amxXjwcRj3zmaQ7zXTCM1JktYR6JQSMv0LVmdGKnjCyWhjs6RUYRHeEcBPF/BzNvEi4GiSYS7c8Oak6iJVoyg4+rLycUTXougPCpCbSTC4d1kuxv7VziZKEMJapOUsCaDp+obwA2kXvpS1o4G6z1Xblas1CcbXEK3HfKxqQYfG7QBa7NOjqgCLMcXoF+otWcvd3DHtZPL14795XIznpa0yJy1alp+Rmu4pdTmDsGDFNeyW+KlCt/lAz5HQp6Bbm47ib5Y/XrCW+yX39PYcgr3NCCjzFWQT/KtAJXYUxz6i5WQw315T4ZJIrqFFVR1CgFgWRdVjWId1cUM3HkQrl1dLz9ICn7OTTHhIxipP6yXW7a/Wi+/3G7f0k+FC1ulwol/MpJuJVM6GIAezeWM6UiAVCEBkw5FIioryRXVQ15rz+E+QX1PxT78Twdeal6mD9Rwzyx961epl70x9/xmFcTROgFoxwnhTQV6lRyvT0UxcJUH14tH+Uyd5OhcltXQAYYoNt6SexTo8Y0sfYg87m43RkPJfN97Jj92AdrBhnj2l1kOLQKfhrR+miNKgncIOVXlI8R/PJKwL/I7rds2yEMYpy3lIewRNc31fQgRvzs8sxvkRLhQkS0sXQwVOMBVFDWZssWKBs0Z3idB0MGSm+2KnVEYddT7AITUCk4UYdHVZIWCssToADRmSbxAoAwRzzKBIo4IVyrbARbORgylQE1xFSzh6zhOo7RiYEGCW5CoQPNIrWBE/CDEbaKATbK5xEpth24SzXIeD8o6lpJGBI8hC90jFXpKimQpTKQiBFWOFJNqhEKqoeRJeSXVF6E3gk3ow6h7BtgSdRKSAHHxmSqFJNWXEpc5VSAdlhyirqSl2pWaHCakwEbppHwBbCVD1E6gbYHBfG1h7wBJY/f6tLSGj1Arkk1WpD9KZMtaKwJi0Whyxuo4N9PmTDCIJnLSras+pNoq5ouUMjth+p9d0WDY4F3qhaplVOpoHa2VFV88Ax9QLxHV0I0PZKw37IPFfRJcUcxUvheSu0JsBbkqoQvMsKIlw8oFRqEoDsokz92bCYvpRIeredldYkfdcUmxAU9mcccIbnplgiI2Oqoki2eSHKl8VkmUuTyUkD4FvnKfj88WkAV2XvTw9sjOGEJL0fbQh9egJSGrFKZolX88QLZITnTrMr/QruH71u7DJKpaMik4l21Ropw/XXsD4fzsOzjm/lZR3w60vaByhf1e5IwQe8rmbG6FUCayoSF9cbJl7zMjZ/K+RMYkUVYz4EAikdFKKcEz4/SJAF5SZav24Y9h2EfbhJdjD2W6iVfT8LiZkxbLLsCgDh0E+/Fr1sqjdBkaifg+wOz7pgTBGaf/IZpeuGwPzObqrGyeL65vXimAUFChAIUlL6u7X13N2FTnXoOMhLssOlZsRoo/h8QwgosPxV3Shy4B0bjhUShPU2cBLLgWmkoKKIHFMgZibtL8EVqx+AhMhEEiNRV4ERmxwkeHQHO+B+xUpYCQxAGOYslZ70iKgACdiFJdBh06J8EOofSdswkr9YWpoWLNXkRfR50HAVmRJGZRh6DHEoAWv72YPd1svhbXhBwyxKF+hOIBCzM4Xe5RE4VjVvwbsykhyPM5ijlnyeUuPRltXAIeQ+IKKWr5LNHMRViHdMkUhhuLrtVPpHkc0osUM83AUGQEFURSTSrOGsf3xyIumLbiwP30PQqR6KsO9NMUoDtipo24EjLr+2IcagZAMNbgPPMIP13MX1ahv+srV0e6vJqeJCCk+Q11/FDS6GCwHj86wHR5icUty2zldVLCUg2Ok6okxWXR9Ze6aHegyr3Y4UhJ3imP/k+YBYbyzAnf/5quF9d310/u7zcLEEGmy81OvYhGGF13pgRQjPkv8d/ZPdLV2R6PaB9JmwofHNP5GhjVeWfJCuLr3id8DbueKX8p6iXKHco58IPPMOe2rNrscUfxYaCwXu03ff+zvSZCblkBytF3gHIKH4fap6Ibe802zJqUWmU1xrIr8EZqnsxYEJIMa5wivc5vKJctMITUKhtZux1dj2+Mkh6G6GyhnQBSjFRx7DPbvvJgkaWZ5wOcRqjxAFLN8sHrNlpxNMmNWxqkTI9mth9xZMXPKH2kxP2qH46RbXs46celaJqffFmXsjibtwTuflUi3gJJARtbGv73//i/+3D77vmzLwg1mA0g7GWxweXV5dt371h4QEyuwEIb4BA+8C1Sgg/FKAqkpIN3ARJzvbwouAWpRASVBgQpmC/KBHdoTlSleAWwZhq4wpnC1Wr16vVLXgUNBoRbBDvMSICr/oD2h1G4H7G2GSgWC1oVSVXt0khs5/9CRYaCH2FLlRSnpxwqIEsvD6g64EgXxYpGwxzT7ZL3oSli3NfxIzMA0/xlK3AhiL6PEnGYtwoqE1jTXFahHX11nQapsy45MYjeLLTqoXRVhSZKZUfBJcQkyvQSqNDFpU4YVo6gHS4926Smc9tphmqrzWfVeBV7KBVw04gbQl5F5CrSAWMtE7KHWIqEOJQXvd/eBSA+jv6VVAdPO0VpgkFayGP5p1H/KVtLvX37Ti5NATcCXdPtOxJff3U5YwZAnCnEk6FCY5Qxc3ma7gTUQCEBxRJsKQmGsfIlSIC70yMv1GwapHxbQPenKKarzT3A7777zd/7+//V+/fv4TNbzK6unyDg6urqm6++vrm+Zh8scMC2p5tStOkgKcv4Yp4Bj3yFxNWGKeiKos/JgyzQMq2oO4ENtn3WT37TwH7gbAgtVXoENRoiSukjbdi2yhjLt6kypKFShn/MRKNKDTPtNJtfMCLoR88OllI9/Q9q28WtgvUUD/ekK+Lq+dfSJQNG9X561k5lJgclkIh6e9bbtTge3NtrcQhA4x2AEitburTJKXLDjzPbpEApctzoC+YKVnXSWq7UORdkNwhIZPeyyuSnJE6xW1vuHm5n9U9Lr5k8fwk4GzCKG98HyGoX8EShDXPWs8tXxFz/z//X3/zuu+8uF1f6vCnrqwmg11/SAXjx5cWf+/XvaZH8ent5tWCjTUczOjm40UPF4RJngjCBgfBhJQXfRGYaYRRQ55CqOCzik4jXtQ8jITsIGyI9E3hlxfrDh3d8V8shOIXmrN6C+wkEf+qEiA8g/hGfE4P5CScMsImjONBKYtmmU8iMrZKLkVqpo91pkL+91U4y22shpj4MWLDWdIbYKya0/nCBDUWiXq9W93xaQKIEkz5SpTishupfHSKUCgFq7/rfs+K/Im9ek7BgWJPcxEx579mvNwHyEZpklYDnNIkCf6d2pu1MwDBrUtS8hZuRVFLZRY2qUJ8tgJh5YQcqmMn+2hnKDRLItAzkRLo0PK5Dx0ytvNF3ggG/Bpy5WwXmrmhP9+3UAIiTXwpJxTjq9JLvN9y84MUOj+Mr/BeTyeT9+w+3+hwY+OoTyw0o0XchvvCCe+TCVsjuOHB38IYMEPUNQpA0tpysEllJ5m0TuEmdFOQzPaeUIGyHtLi6ukHcZrXiZWjuu/X22fTi9o/+6I/+q7/zXzJHpl1QtaiNPsb67m79v/vf/G//9//ev/sBR/bn6uJOkGAdtoEScPahi0RXRQkchVESxQmiS7prCoiTnU/4JtJwvnhOlk/UQzkfil9TqicKquEcmInf9DQPUNRxDJvS+pkPhNFQ0Z7pu0ZmV9ptDP9D8bODhOgxIjpxgg8tReJQVmVsdsoKkSNEd9alz4Yn+WEhqY9/gVIZMUyZG6mG4eqmLwHvM/kI08CiW05NaE9mn/weskcBH1+rlnp91TxFRB/PlvADACfybJA3nKeRRa1Tqn9ArUaghm5tDUeQfooouSFyotSyqmZ1jTKCZRqE6JrnsMJbcuyXz392FSGyYaEzQQgvBF9d8Y0k78zIKOlM0RbLHm7vbr0e2qEP/BwdeeRVq3Qc1RA5K7LRE0oyFCNVDuAsVIhVlM3QfnqO6X0Dv74LmZTTdkDWUsG+1h8R3ikWQ1JEMuIJgsbjQZcahitKU0ICpIZ6BuLIwUWsrZa3NyWmI88/dTRWK154oFBaKbSCHDPwMrRkMijL1qgSaSVZwjHXN8WkjGjM1YyrlIA+kAeZFNApZczJxSecpA3k6XICo5I0uFnjEqy0hFX6O9k8BVUnbRM18glVTSM33DDJo0kAmkEAdeB8kFKSVgaH+pJViwkyZ4XOVmuG8Cu6hQqLQ035jK2jmF7E8jdxMyMnwiPI83mHiydPrti6VEzV3pqL4JNw7969Jy/XMVMuMEU/ZsNQl0N6IlCuphmn6CUI1/hxzQIlNOSbH/DI+uq0+Oj/1ZV2QIIzvogPUsa+SLd37378/reTyaWkgyQ3RTc6oh/oLSDSHWa9vcMuSgXnSpUsppkIRbqhe4mbZL+kPIY5vf5w6DbwCZZ6CJ4D6pxR/zDpoQwPxW/UJTdiTjQQfsbZMVVKuwDtq+UYK6tfwlP3tz28ztWTHtNjPkpWZ78q27Bcbxc1LPvf7To3envh3G20vRB+wBpHoy3QsIQ05DZoT8/28W9bLxQLA2Yz7hRwO5arIct+/A7ttFTIzZxLQzUYR70CYQCtQdWX7bNSwm+1aR+f4+B5RD+aoGRC1QLYLjJaVc6VKEKvEiriJYDQIDxhtxZFTFiNPb3arJ+vtc+9An6iY70zEOP1poxfRwXmeCcnNgtiVYziLY2mO47ylSIfEkawpPTupDcc9f6AQnCte5BKGsdkpf+UwV34KhJ3hSxEpWZIsCTRZF3oCE8lCqJg5whNUT6laU96ki4jUptsGdzV/o9IVM+BrgYLjpZsP08oieZ8YcoRpvHp9sz5yjCj/RKMUDFgo5+rS802sG5IUl2oMyTWT1qQSmVmlECqfUYp3wRovwPA93Q5sv5m0DzlHX4oKMbsm2jky7H/KI7vBJf8Q7E4t/F31ehg3waVFW2VRiGt5zpeXC7ml+vZr+kHTliOTwC+0BcVaJHlUt9WY8wbpdT9oh+q10LUCrMZPQGai713tHUm0bDDdVxgBZStWiGQD4STaJUO4lKQ76s4yn94eizvpovvKRehfYDwWsjyMTlVNC0qkeNOwb+sEkrIhbbrFxOMv3ivlrXXeR6AdHL5IBdzdVZlDPkGyDKDzS3HVULyAKnHiyYg8ykAFtetmBbALbkB5b6sjpOa3JpsR8uEm75ybDZolaN/SwufD4E6+0jvBMabQpZelZTX3oIS6dR08ZxsP1Hbvzi94iJmiOKCZy9+FIyJNAZZ9GkoH6gOeWCVTtdBuaXdSz5Bm0oL/m27NaQ1smPw++rVYLU328mHKjQNso9RGZvl9I7JoD1L3gOrLUq0veleG47WZFhEH3/Z03vuJXI9K3aceLpw7G75VBK7AO3Q9qeCZ8F5P8nPGqNuxgepSjhrn0mHFQjah1ALfY5jniuSEw31Ss59OJkkEI7TJDMhcTqHklsjXdaoUfQRs1S5VCxnw6S7okgJGiVcFcYS+WI2rZIgS9Ch4UYCE2YDCB9Y+sOXiBhxZE0DC4PgzXjjegWI4IPoQxESNvc/ohL+R6gEi9QSintSxC6+DqRU5JBMY/nuPxBGK6xR+6mTwAEOEU2oKhEKbjQDkNimWgAn0tcKInBEBiYCVS/4KdIiSfAkgfypjAieC+P9m/v5ZMFWQdSHIJD6rZb+TWVSQooQSMFvtrzXchTysgF4yFJHBUEwJwgUU04hWGRK7w5nBaj+jF3R7PBOTzUEj2GYSUg8zFGaoiWhUUina3bz5IZ+2HZ6zZoXfM9RMHTyDXmmza2BfrW0HPXDu1s1KR+r5h1ZkIDSMbsk7heObI2fsW4fN1Hk7RklyuSUUkdOqHcA4E4LCQSS/FWFcXXDpjKF2EjXMjjcQ/rYq9x5ZiUZSoV/QiNdxKviU9U1XBQJVtbkkoqCEsmB19EJ5bBg9byD03p1r16yPnehm1R35io6q1TqQn0kvcQC+3QXiYG5SIaTKBsKCZ6OKKswKmi+9hZkjF984qOY4KMIfYSmpF5HHw2bjGdV3VlHS/70CKkS/8MiowwR3wFoVwQueozys94uE6Q9/q1+yQNZtOw59ejTreUh0L5+VV+d2v3vQ6Q1caPVok+ce7GB1FAgMDN9I5vhQ4nSnoFXQqr0KP+pxPRZrypvXtvWa9S6SVDkO0cOivKUzHYLzufq37cFjdSnTdiEVJZvwkflOxyhDYo2bbYsP/88MwJKsEOWKIKYhgAjYuj0SPFGh4RNa8INsNesj2eYlfU/yy+596ezH3kAEMEosCLG4hqK8/UwQib4q0UUakiEgjAd22pk2hQC+E8xV4qSFFJDS9QUeopKWDyfJAJWjACnVdgO7cDzChGtGY9nknRWbTSmW+lImWY3JFb8UgFJugWLDRtMrier1e37D6z0UPQ0n12hOByYAHAVL1gIRZHDfbRVleFGWEYANmcXpc0LLSyZvHOtxcK1EAWHqpZbJ0b3WfcfkGQYRuXfBrLO7XcAyrH5HV5KJR7xLd7ItMfsW1Q1QHyjN1TKBcmeOT+YiPmH9veAY25h+BvAwXh7aYFSYjt9xRmrYfYVX5wDslHobndUpBuBPE1Kvw+05eqOBqYTJ0PTB6BZZ8ury2ezi2vH4uoZav8cNT7UTCl9qQjZe++kWsGG/zN2AaIvIc9SVsj68yX5DuS4hBQQt1iGRIYReXqRm8niNd+EnukzvXBgRoJ/6kLIowHBw94q50ydE/HWIYf3jSBCKiqQq0xlNQmA59INn00XuiXle3SD+Uw2PWZ1RqbaNQhHZFfSxVLfn/byKPcCpKbqogt/UiIf7AamIyAFPBBAr2Ap2ff0OxQe/MefD/jFOS5mOI6qqMBIDbGnGiEfJ8uFU5NnZj7uLb4CvSM5sl4dlHVQyScUHjNXX+ehXOWQqaRZ99H2jJik1hbB8qTf5aSVLn2anIl/ac+6S0m4n3RK1I++GYAOM9QJm7miFdKToYnxc8yHGYq6HVyJbIxhi/aVZvIsOEOyVk2Pz6iPm8j6PITYg+o4oEku6jN4qXwgj8HMVAfpmakeLjFOn6iiq+uTIhOiD0IJxSbEtZwVixC1eIPDGUHFbMaI/wX7AGl1EIsQ5iAzSClshTVVgrgDbt4DQAGL2CRWrnRgWghlkqBHlZWgPHiZTAopq0VB+m9lRCJcztJX+GgAHcudkUrIT+RHyENCa8Q9pUC5ug5iiiKJpwX6FPzZ2pRPrN7f339QB2B2fX3lfRQVhTGgSzXV7VGsD0+AGouVEpgLhiwv0btVqkWIkaBKVRKRtQLONU42UgN2UlY1TTKH+GS0SDRQk3Ea0COzWdQQvc1nsWpZVmHxFTrwiX1lV/yKNUAaEteEi8yutWGu5nrL27E0h62vUXzSRMR+lVwL2aAVvvyQDiFZ0vpfaSUuakwXya+EKUUqvwxbiIsw9d8KCUeMOeRvZiKYA3ecEXdJfBzLi0bhODUKCbzDQNXs2GKZhCol0VzhLbWV9R8wubhWxUnwynthgcBkgPojdIsn00u9FyCjIR0qO6RZhO+LmbgZ5Ex1MrCzJGG0SSrSz9dDLICN48iJCnD89YysjlfiQMoz+hOshi1wRlkH1vIh0ctql+khmfOL5bd6gtV6DxBA39dfMbv6CK6fa9nkR1u3ryc0qMlQ7eplMSYRsGZ965gPl+sbFwmJ7VHwsGU2baCRDXj0mA+uS9ueJaRII6Uherxl2nNE42k7MbMyUd9hS7Y51D22Xd4B2dW9zzNNRKtlzJzoYLcXVFi+xO2raR+8pCVd2W27+lZek98QIO39grYJEhEBEQJhLGuLiR5Y2aKQhDRhv8AOP1as/VlpUJ9XgwnGCINXF99ry8V7tsFnbkBBjAxCAKUwhFCKK4u5nwDVg4KiNBpBjkUbbxwi8QwSe2nIdo3CI24iJGJxkWBQOaQn2GNSAhG83CkCDsV3ogbNwbixRbP+lphncqUxeHRRSCcWYGuoFOIIpyRK3MXCpIRKBJcronqWUuhV5JlXC81m9Ae0DB0+6hjRE8AIeiVU/QrxUMVIeZU5BW8cDEor8a8dVU2lZX2kPyA15MMyIamDTVYhl0nfinkuzYmqJF0zck6UCJ1U7bH/IKnG/ptEjbca1KAyITaVx2g6B0u616VlNsS0hLa8mK51N8axvcFd84s2n1y+tDS5hBwRYfocL7eY523kMfQSqzuO0ukrdy0ky+2lfqMa1DMLdBvcxioSqRpURfCVdqa5WH+DCzFLxku6+vKdeg5SzwkNzoPlu8vYUSsgAosXUxdmzh31nA7kbP4K59UtoIVq8rqLiztuiun2K43kz19Lqmi5I3BXdvqHubmJCu/l28lfbJbX2vtnM7eJuBWtqbSA1jWydDNKlRDb6kh2jWzsLca7ENWRSPt+fQ6FV2w//nXPc7X4LUgmOE1lGgU+Iw+14GlHX7ucxLWwSfDZY8MeYWmuvl3a4l+ihPVKy4y3Z8mnN+2nxHE16uVZFlRPoRJG+mCJZbWLdN4VMPjX/S1mAArspEQb0tCukY3nWAChLVujgfnzzH6sOnXKDese2kRHGH68iJ9jg9fvhCPM0yTJ7XJ2zk1Jh+RbjRiArCy8pK9iJIJ8cSZ8UbSs1yUvCPcdPRHbOHwiOCcymrK2mF3/iVnYkORiMSPCYACSZTbEIgTHfgdSoZIjcsUbipF3ch3ZOKahB0DG8lOdpIYDP9Syjnq0VKEI+hEpXXjvTukdZaCLg7GrE9zRDgR00gBosLIOHpFVHKfQSofL9CtsJfVyqV6cJERi0Jh6b7bL+yXvoTLrQZZ5D7FWx0Y/S1zAIIqXkhLESDMQ7flo/VUd4dSOSskMtGzlciIXPXQCiX1HaM251KpRlaAN4ACruohgWYc1c7Krm13egAY0I3Mvak3MzMQLjriTh08IXSuCCIftxNBo7snD3kaMl1nMDRYg5t9d0hUraSZp6mm42twSNLdcw1D7KmlcS4pwBG9pqj+9DcJOO7Q4hHQO5TJTJsyu/OZMeATMdGuYVWIA/ka3z+zJ0+fLO96w3+oDBPJBxHDVGWZs589XvagX01N2bXoEmoJDf1zUW/HSQRJPBHh1r24B/Nc3tt1QDi2lQQCvcMyqPkB9OB8Vr0BcW4Ci7HPyswXOYQE8zzfVMbzCP4c5ND29kBPkR0svOH2MZFQ7n/erAGr5HYBsmDAD9JUlgmc/w0zAI6Ufq7Ok7NvlJ3KF2e4DtSEV7tjrnh5wqU/FsqheBRpxzVSVFUWzR3rrCRvmbBg1cy7HnkdotA/FdW+MlIessgptLk31uvi0qfZC8orAjImgrEmfJRvKQNvpM4FWMsxSaokuf6ghVJm23Krk1Gu5r3PJq88CJU6RnqTVvYAqB9LYv+Ic/ik8qsJoxUMaNlUIy3A/oRIDmQQyChcUWvB27IbNb7T3CCtuFAdrfcHiijdntTaIUtA0+g4+u2ISkHlJTPC3eEvS0gXFc25SJCpAIU1Kw7uMniblUyNRCNjhOprwrPAIrsxO5KVhYLRVTpGggXwVWEHeM/UZNIgPmhcIKfIiA3tGlTWA6jjIswIuIq8KsApIw802hraUkapa+TRHedFovZO6L8jUfqCQcpBdb1l9vpAKQiPgajwTAYhc5fnIufbeO4HDjkDgtN8E0PsDWPFN5rQ/EcKtnxQZPiYMLVM57/cayKGq4JRoN57dkWsBCOS8BxHpqfn0jf0Hi563GtQmmJioWtM4NAdtRg9zjpsRE1eWpyXoEuAGU63j13Y36qKhh5vUjbhlXJzxeFbhix+E6iKQVAorOsyXE1qGYCQJoGMxD3xwAONHNXEyUZhUGm4nlz+K9uLPa1LCcKQyd4ab8ZbuNbWT38iPfCO5VpBZQWmkj44tnj9/tnkitMnk1wIlX5YyiHv95u1k8ooPe11cPEc3eSQa8SW65fK3v/0z3gTAW0N/dVDpDvEaC51l7WH6gU6rrCDPjs6HGEqujrBxpNPZZb6hAhDzhMyucJSziAn9E750Pv8b+pY4e56rrSilwep3MduySd9vVp9x8m+9Pb2F1eLfwkiAuDfJ6I5sIeXSVokAvW8JOgbY4xWdHMcBS98rKQ6WGBUuz67w4N3q+dBkqtJgpCGurMhDqsOcO2Uth2xwqHK78p9/Kuyxtx6BFmbI9thLVSJkS+dEWRrpMHB5zhLbyG1Ig3Mj28APKQ1gmd2LUCKfng5xB9V3QOgwn4ZlGtnMNphwDt3inEs/emKntkMc3aRSUQHMrohgQHniJ6IEjxcSZIHKkgb2/NFQpog2eslVK+Cn0//FX/2rT58+I4RarcEhgCCS5jGt/UAZMyXSYjPN9+/eACOKZh99BG54GxgMxR0KnGFI9LIgYJvNiZkUjyjI0pWC+/s79jRHnMIlxVOKXvTH3qPSgkAHhckDZNEOdNr5BP6OzjUOLz56qEs5VVScSIEJGTQoTAQFTnmSiGrTT0VXksiKavSSdG0nr8CfUFKSgGttRlRHaaOxTIP4EkE2I4jSqjpCQ0MaJRVG97Xk0cRwFZrAwfxhFFjN3DgPEEZ14jwonMJhTjvqwAv5anGVyCXU7nqjg8U2rD3D9+jp0TgMm3thi4JgvEYdTzVfVpt2UcxsqHBQJCGkiuU6CMtSgOCVnNX+SXF47vDlUXavBJOOeJf341cXEeINXyTQ7BF9aYmUk0gr/4mX7ohQR6/dSF2cTOxg7f6jTrpfNvS5/7V/69/89ptv+SY34/3w4c7E0V69fPX/+4f/3fsP76JvgYvKcdWDxw/ZCXQZc1kylKqNW3N3oIFzYt1xSGYbHDZowz9DPh0LdLfcp6NfvyYneleHvxayOr28KK8lf742rFVjOKNKRgcgqpstFO2QW8MP4DAuKH39lRUjFiNGuJsqDfbt2n2gNqTJsD8ftH36J7p+fbIF+iWopLcfOUxWlSIlNIz1cNEyFOaERDgbFNJq9Ch1kJTnaPM4l299RC0YZ93JaklJVCU7pxtzCK3ysYCwQCe2rNHSpxMT4IDPRBVkw65DcPuDxPl/G6vPCGDu8bQ2rz5Iv0/WfQH60LSHkeJv19UnrTAgztB5Mrmazhg91R7iilAInrTGfsaKA2C8X6lgRDHFimiB8ASMxeLq+uqGKISAn/HYkKw4g5BDgcb89euX9/dL5BHGOJS2pRR4E/SEXCs74Qtj2jQzghFHPOpNSFUCKb06KW3hmWIkAj8N30JLBKP4yV0Cst7TEy1ZJq1YHD0IANmGRcP8WsOt0B8eCuQUzEsz4njW85DJA/Z8cepr7+b4G3gzBxCBJpvKWGVVwX0V6be++0KdmsVrTVaYn+uqSmEoCG1s1wTsdCiOq9KpMVI2wD2j4B1j/0HWnhOY3ltLj9nvJGEl76lfjcGXJd3ppE/PGH9j7B8WgR/nyDIvkbP6MlrtoMReWAAb7wCES0W5o1UaxDErIPkQL67hHu4KEtPOmIiSj9LsEooDE/jaZ9XSPuTw6rCBR8MFeychMA0eQtMFtrhU/+3A5pLK7H4AHPon5vI8bgxujtlsoWbWfxSj14smLAoiS2HSJUX8VjY8Uz0alEeF9VM4TeY/Ev5vN3zGCxrAeDUcZh/eLN5dcq++xg9xMe7Q6WL6+s0bsCC2V6MJd+/kYvET3wGYTq/0f3KrDpJ80iqqiyGNbBvVXXr5qnR1tAAe+wfaRj7bs66S3biO4d+HM/D8z1LG4GTkoxP5V7XkkDyiBD1kus9K42WO4jD0m9UhKtv/aGsME3a4ckuL3rgl6jI63mgx3gPIdd+Dd/Zimax8B6A0IemwWWG5SOaSpj5R0FvcRP/Z5QtLPKDuDSmYM46c6MxWWKOuv6QmwlydlmmYcYxd2qwyVUNEhpP42MZsVHRY00pxsAhM+U9AorXUrNNRcCELMMBOnbZTHgzaJJHxVqAKblxXDZ8TZzDu6IrrmwAE/RTxNVzNGDgyAnkxu1TIoo4DAQ1nG1exFQEW+ERCYmtRrFwQ0EjIQyveW3SRhv+to1YTxWgogsRShFy1rIHLQnGTumoK+FRHhflgkCWYV5DFyZprSbhiNKGhLlEpqybEyAxNIxS2mucNB7BQlU6IvoQsgaB5cFYdJA1Em0iM81SCwlG6LULTOiLx9R+XWqqWg5Hwznacgd9IffokyTQ+cqIC5Gt/SUZxQm0ja/LC+YRPbNl3HD0DxtoR8eIT6hvQHvqjV+ZQmFK1vawb3T63i1wCNHuKvYXmS9Vt6gRcDIQsHm5u+4E0o8SQxEi4cjPW17ijQh8VshUfLZvKzXS/oBgkkim+4kdKYLMQOs6jGQAXqzRQRcqtSKVwPCJ+3lDXJlVipOk4bjCi+RXvAZtYVNrdVMwQs9po8RU7JqEDBxC6FRJMZ4g32ulgS+ukjWQWh8UX+Zy06jn3OXGkBdQOn4+Ht8Dvhrse7k2yy7wap9y93Z+eO6ld9OjTkY3YNy6rfgxIGS/Rd10erC81pm96dH8rPw7zejXqVqaTlXg0d1W6BuuxQIgoV/ZjzuCmREWVgYln9FBrApSpWaOiDaxclxZRAuTe8K49e6T0cQh4wz4A25BhDn2lWUMQwiD53EeS4TXLVFBs0gmvyruvCG3XKJqs19PqbdHNdwS01NbpSSUx5PewcNsTnWrZjH79Ga0nwGJ5AoG6nEzj8SzboYgIHgz8WRmKwNxMluvlV+v7Kz8XqAhf/iIuYVUQyRdEHauLl4qtN8v54slk+pL1x1tGdidsVU6AAhoj7lo5Q/SCUMUecFagwoFcdt2J3oEDfzFVcKaYhW4ERZpKmOpdUNGgFwiGwW71rRjNfoCIcEZpoSieUl4RV0AsFeD2VmCPTEsOjKklSNOXy+13S31KCQKN5vp9AzcZ6OyP5MBKEuY/ALi44AusrLNm83kFXnQNhM/cgqJMH7Z35aNc4ZtAUX6RvwOQ8qdd+sb4e+HPJa98iyDpvU8NKtF3NDgMYJYcYvajNg+gxpIfRrxLg6mlMB9wLQOLThZRrgJsXr7WqyYg0BJciXPVs1SMqwP/fH6hjzPc4a/qpNF0tIX4wZRG+0JZ764TLYTryT1X3zDXczH73qoYXTrxp+6lku5tqoCUPMQdP51QifdY4iX66YbvAePBs7f4MrrZQ91vlXTlICa+pxe90W4/QJ7JP9VxYOie0B3e/HF6zdvC3r8ISvk1XJmo46c8ZiRULebI6MGLjPJL3Tnxog4K0ZWFu7pOyGKmYuX+kKoqeP1oAerFZa568pSwnvRRT78x/Mfg9Oi0D1zoXD51IcPwmCnOA1wSguZVdUS2TAOJmfzV10Jo1yXk9kVfouk6GtqC0ubcQVfUt13a5tCW0qaK2sWMekfpMGhQn2HSdmnnPEwbrQkZE//oXubuapIelx9l1YK1nyR+JBZAkjzBcLv0JkA4qxHWwLUnmlyvOju5y9pD06Mh0DJCZyL8urPoFwEcqF8UjTHSgCWideK5AFokAlhSnUVKyXAgPVDlAapclOuSIWdPZPuEWUrjjJc+HrOhfxYXiaxMA+3BsojNupfpLoFRzpmwgojDJ4dHGu1faxW+gAQHrC4gQNCqZX1ySdEHEQQj5nz61mSsvvb2JgRIDl8MJAKDDzEKYRe9iBWD5IppeL5o4FZBOwcREmBFM4QcgL2KwuoQ6Ek/DelzRZ6mJZQAF5DCaa0IUlRlfJe5BKY89oi8YCspVEBEnBXmqFSHamzBftYhm52L2MsfFaQ3rykIR+s31vd3dx9u31suGhACTpd3m8tL+jMSFMwVianHQk2BSgT48Y4xdQIsTAElujwcNRqs4rLkbOmH4dqvnprLx/kFizVxPPaS5+GS7Pup0XBal26gfYIembA0uI49SXugnWaiVYEDsm5ColGSf8g5wuvkIbi8frPVQYS5XBpmFECim8F+ITa0MGzQxYzlZMqGFJ3hPp3TyZWu+LHeUhAtC/X5ILG7hpQhwyTCDtXkV2ihSSecXivZQKBfrV4LMnxT6Y6R/2uB3XzBPIASAsVdRjE7I+HU3GiqBmprgRQ3Na8NiEr0/FONwOEzd5BSAKIY7w7VMnK71K7UqapA0ouiGpsC/mklQ+mG6qeoGNXeW/ksF1mVAXdiSzvuoG6KNnKJ8Dk9xgJh3r1t1GYVrdaGD0GOEDPE7txltkXSUdWbM45lGaXe4XTRm+EnMOw3UpOgHUb2D/swynGl7b7pcXz6qGQxhvyY66iOSB9kIZH2WKDkk9PRMsp6/IBEqFGp0HutWaNHYi/xmQpqOphnab3xQugNU/FO2myo8dzaWgVtH3yYc1urPQ1UtgVBCUcJGRam0nCB2ljOKM1DLcU2RB/mM1OwSpiwvbh68kSLeFZfash/8pJQgQ6AomIFvGQUKWynfE+U1cnfT+e3UwIMQhgxI/ZW9LyZvFJ29Uxr+jfvGM5nYHKyWDGNoDBGy+JhobXpis7IKBpj5P65prambxzPEJSBS+BEaM5sAGy1LFr7fhIhgc2A/uobhtc30z8zvnTSECmcL7+HswIp3x6SFfGVzlUo5ZqLcHJxv3q/ev/B2/pDwYiqNOJgPkPYYoKa+nwSoRX9Ib3tMJ07kDI7kJmKQFvv+6mgUQEpselsu765WD2ZbJ6Kz+ydtIKZGi2OYB5AQ1jHL4QzHMewKcf+Q4Ws6TC7XJoTnTXI3DpL28DiLQj5CHbDuGp99qHS9poTem7a0Z9molkYwGKJC11CfflLy+LVJLqnQITKvmEZZGc/bGe4zq+FM32nOFneRjPrdDF7LRIF43Fw1f/J4iUzAFEJdwaskv1MUoRjHbUUJ9pYa8hYrkRGs2zsxrl5Nlk9mT59y40mEYT46JU6xFZUPiwItwxOSzF9biS63w0BvuXej6tMf2TuN3+ttJx7tVnxQg7dUfGUcO4Z5qOkGLXCSy+vpovba1Slb86o/2az5KUA7lnesxfzRAUBpDKaaqT7rf8AUZX2xYKcFbCgQm1y7SdbGyLCY2ZfTXfYySpXJOOfvYXOjSdtMMzVbs8GV8J0zcjdCUuBf3DLOMGh/StTci7ToUPo2dC2RBtKF/UdQqvKRkk5kGfF29dh2qId+0bNcwPBrlo7ACxsLFiRTvYvSWrKDGQ0jpCOPk2q8v3XtlWHeXrWsYPtbvc/Cl0rfpi4mn+eAeggNCjMkA3Vh/a7AccM2CPO7RofaqQwLXxKwgwsBQUwo+VEW4dhSPAcxukrzfogPfTpw3wI+NFVHqPMWaoTGgarB9V20Pz7JPMDn1D0w02ScVKGLaeX/+yf/emrVz/N17+6Z+PAxU93b98vruZv797fre603H2zZO0NMQRLjafrxeqGhyijiI6bGZKfa12BuhSEKnMiDA2+Xl5ePnv+HCn3d0ttJUQYvSJ+1xIHx/SciVKmrBXSIiL9MbirzUYdfGiDl6WHM5X3l32hJ8pZ3t8jicFOugkKdrSm35JdLY/aIjyikmgMzg7tgDnGl/0c42spNR0gY4dViGm8Eoh6VL0AISsao0hcuKCN+gWENoyzYhOirljUpEgKlPnsajbVO69JidACPtUhuLWtAM7uynfgQ1PB9RycDpXcwm9UsF4+WLhDlbltec5YVnNT+umiwTTyTQeAmjK4rmA1+pQiJaWhdCXdWv5Nhg80APlPgoPOm5JqfKJoGJHCqyQga6c2J+h3786j68IzgZEI2M0taalCbhR6ITgHargMB0eoepcqNLnO5C1b8bd62tSHm5DeBr60uLxEE+Y6JIsAnltK22xBMLu8unzyZMEhz5V0OqaSKS/mPtFr0L6/SPsftHd397/57W9fv3qHCDqxs/kl3wygUk+un3z5xZfL5X26fWCiQ3Q+4B7+G9nG2ZXbITdKP9VsqprVIy37PeKRJYbcnA2t4lyq04aUpZ/TB1kgHLafZMgXckv1k3/0kiH9a8oZMVxLj00tAeJo+FpwiyfCaM47MUHS4LkrHpeKJ/hwz6/FabiHVEM/in/bFXKPn0qXpb2atOQGYU23KhMmHECoELuvNR1acrtpKmiuV18zHqFVTZ9K0Mjr+PGPzDCao09/0BQQ0GqFjwVJ5jAygSniCFn7mZRtUUiv2Bx6zfK7CXfFThUGYbwwfgUZsPy//2d//U/++E/ms0utWWZIFbQ1q+o308vJ1SX7jivkZu3BfH7NWv+rqy9evPj26dMvJtN7B+08K6bakERvQJIkIH5+83tPeZeW7sT97UorFzQ4qeBIwYkWWiCZiHnKXqF8YXcy/VLxhmMaakHH4MmT52AQsijeU7QDsWjf3f6Dy+XtdvuUeI2Qxit/EDlZLj8gAhKHa2IOH84C5kPlEm+AuhBKOOjTVS8MmEOiUzgIulg5LkIBi0ATDdl6M6Lt9dVzIjZrp64Aml/cPBWDan8eSzR7CeOo5EcuzllH9vvnmL0tC4fS8f7A9G1mMIRMWW2FfYEbe/Y3ZgMq1Qu8rmQbLSCsuedo8DQDtAWleXToZkTzIU7VV6HVFHTA5t7Nnw3z5Rz0CdkIn4Lg6hkANQTOQwOqyVSGzxE1r9lPSW6vngBHdCHdajDS7AFAwnHo+EfnTr07Jq8g14soOACp8FL1XymFtYhEsNncPH/y6z/3+5eX11od5hVAdAWFNZl88+XXk9mVZ4200CeF3dxm8lD3YvVuvUf/WbQjlrqnmJvSen7+cC71FG4Yv//p1XukUTOqhHJ0Ae6X28Xi6XyhL/HJslSLvilVnEz//t/7+3/vv/67fEEMMZzUQ5ncffiw/tf/2l/8D/6P/6eNFsLBQNVWo6UrOSe5dh/CS0e0dZUrrhE/FIDhZHu8cxh/fGnf7w5P/g4vHOBbPrfraGEEznt/p7BcCG2Lbv8e1YWMzWUdJKJf57HsRuD1WXgE6T6UMfqf4TfUjs/zBcevc6OgnFHZp+6ufLw/91qPuqNRcR+N57nTAx6+W7n1ddj/SHI1JDoAUVYjqjImHnGjBE9TWUZF/4u6FpVs1ivs1IT25zN+WCtng6LM5nRg9rN81JKs1aNKPURYOHXRZA9uv5B4iI4n4maBuWrRLBku/rmsSAFWBEH4YfsQH7Ds/fKS75VeMQhJ/EDQsV2yBeHm8sn6+bMXCzb71MIGuDEy+SuWHBAu6a0ARSYaCSeMUHSkaEgD4ZoDIPCZs5HoFlIv6uHDXYqZraEDGKgJr+asOyI4UYZHEn/qJRCK8dxi4kDRUxp6h6sGRheKnWbs+E6eQXhiJBbdMBshvuKBimKkivn5qQuHizViL8aqfSAYLisoKyWoUCohY0ydRV0dKKQ1JIraFPSp8pDAV4cyrJYygc9WQyUSGmoo97GOpOU48WWtByjaaG1InTwbpQ7uy8GuMLHsr0X7bgfsTpOqwcPmajEOtwkXCsPq4VCarhEvwmT9rIqpfDAxVySuhpR24uiJHzWnEcFDljuBaksR8admlxtEg89nbI57PVeHWcXcIHisW342v76Zz68mLFiyD0qE1FZdpLnUtOCLi/vlHSP3KKpeMl8QQNmV5r5UFe43XjrhHjF1vBPDqji6DNc3i9tbfs3REdfUYL+UhIZbjI7FnG+BbfkqGPN4dJa5Xl99OZkyWfdOd0RlPbQ67PgEPHqswpjjQY8BU5RFcq7qQKUyW4HPdn1o/mdT9FEYla1QCQynyI3wO2Aw1zVVW4+dPAOQzOOiSHt4LK/hS+VhuTDUzly1wuTUdViy+Jj+XKDW+2FVg+251npIw7IO55+rm0fH0Sb3tkMzm08GqGlSal3fB6CkKrH60lmHPoQSXurQ7tcOjzd01itqF+dS0Mh06NPb3x3JpUDrdLGiPCUrNK61o2ETyo7r65ejLKNqV/resJfW9B3I5KrlxA55B9qlfI8q2lHUsf4VQaxe99VSFoVGRCVaUbD4frVi5c81I5aOrFkHT/DCwvw/W1zpa6VaAEQcpZUYhB2MeRLcKKDxV4Mp1Ppjcg7G6CDwBVZCqluxAsTCCg1wMKp6o6mYyXsYhn7SCi1Y10AEI1SFZU4CVDeDwEW7DTmQ8mgt5cRtjqHEA23TqEkEc/6ZVSlqChO+kiSuCrEipavHg2MvBWVB5m4FA27Z6ZMgRfnUTowI4CBUeCgiEvP3Yi0hIAsisA4SgpPg4r/I+Ryn9tj/8JyA5xmyAPHoHMvPEvr2Auoap89EBydUvWrsn28AY41iZX8vtyZO2KriA0c1GCdYy9q2Mcy0Mggku4mKEWY8vFJRtNrAMDsDJWbLrIKidt48gUHYz++oEK8jwzjpogbXhI+aTl4LgRSwCuoFwh4EKUa57wh83u2Ob7NJVnRQeDmEpllupx+QNt08UVeUJWwS7T9z5ebScjz1KNibR1+d43Ua82AGTW/9QsANoJ188H+mochJE/AJ8i/pcE83z9FxMn1F0uvv4S+v5o0aFOCe0t24vd6s3vEehV79kc5SNmxA4uADHp1ko56EB0srCEY8OUMxfnc6NYynfXDk907GGD6K53a7diUEcaVZSumRLkuzzPL3aPjXOZPsTxQ670c+FqOMNI7l0UPXpX+2Z7vJhjWpm72kVklsg9fWI8dCJUEbrQEp/aFR1Mj26tyq+3ieSYQr7KdZJTP7HwA9s8oZgLJ+OV0SVEx23FMqt0gD4xeVzSYZrtUAWmmmMj3MsFEK4YCIBnJkgyQkHi235IwCZ+FT8nzQdMNiPy/leyzTqFMP1g6cAhoBKlKFUYpqNJavWF6Rj8IBhUzEtcRP+g86QMZNebmX4ILwhvCFqJiPAENC7BNhv0IJ2DgC05UI52LOqwJVbKHQyZEGgU+E2qD7GacATn8668JZenE4ggMkZUIrqeu3nVScHm3o59cFpL7qY4VdDaqiI63WloSy6VWpkMyVjMsE0gH7SFDF/z97f/cjybb++UGVmVXV3fv95ZzfCM+MPMbGLxJCaCwQNvbgkQEJX41tCWQugb8LLI18AVxzhwSSL5CQLFtYHmM0I2zZzPzO75z9vnd3V1dlFZ/P91kRuTIjIyuzqrp37312dFfEWs963tazVkR+14oVESUUVSZFXB7AZBxRbklVwunXUS66w1OakOW/5aVQajFv8sX5Huwf5tJY9zHx8KqUB2O0qmsaMgpsfRMbL03ThpIz8W+J/Sy3kEpJOjMdiVmtNIKtZlvApbtRa1fnn1psV5WEmQQcNHyNAZItWjqdQmoW9EdOSTZ7g2MQzheGKHBx8nAG0e1xHv7Y1An/EPXsQgYpzyu+vI37puKP5w1D5izSg1/w32ww2mYQ7S0LOiDPANdtBzxBpZ/z41Mb6Li5WS8vzvlEGoFwUZCDHTarmA0rqXHlfun71gLvQTVaeAdPyL4/vg1O/WKOfeg2XfeduP+OzR1XpxN7005fnNwBiNHSyUVqWmOuHL+Tx1HLprS0kr9vy+99YzpiBD9Vd8IYqLc1VTShHK95HBFOdAxX0knBGJpjmqs8WX2tln5WoLRWrI/0drQ7JkbXpprHorlEmZ4rPZI+O949Un6Ypy/2h2mba4WHaRvvkuHSyRqO6aUFFLY4bYqaqw4ano3dbpONeRPgJddSrP7Ig6v8+EPIBqL17SU1j56O46IWF94sL/PCHxYi8H4gXnUP4mDtNWr4fBhZXOHLR5e8tIcHA1i+A/Bw1fXd86xZeKMsInQ8l0jzmlDt3S1enS1Z04+SPJfpa8lBUQCW1666Zq0/UMmlzriDL2KsDAYEaX6mQNACSALxoCGwqkAdGdgRbT2fsqSC9YLtRFWRaaxk6p+hVasCiqGQlBnxZJQCBGHx/oDLts1Zrg/ZkR23GJY+bINHQ/6e4/SewERgqFsKnmouv6rQOz6xexRh8g1gpNDaRWhOzcjSJ4je0Eo2ZcaA9lrTKlK1To9NIAC3hOb6hO8AsMRGNt/OVBI2ZLasn3ExTBRJJMm04O/Obq4W51/ZQzlZhOdKshdv0yeYqbeLYIb+kLGHD/6irfoQr/V5rdTymodoFncfQrUH6LN+asXUC3nO6PMSHTuvXmHFc4T7AIsLv/zFw8R8WewMbby8/wNt6YL3G3IpYHHQ+eLcN0p5+nKeMfxm7RAn0+3qZv0TGlPEnT76sFsMV9oBNlXQNnI5hOWYXUbD06vQyVfCY2z1PFvXw77ANFVo9ala7Zabr1n/4txXfog2rV1PsWNkG32ou8Rc+jaUgWfv8Zhf5x4DkEbzAWSy10p/73o/w0OpvW8P1bFHzp452U6yNR9/Su7f+t7S2+3TpaXvD/frPY5jRudRnjcLXQVyzs7dARgdqpBX2Nj3tvq0/MU0Su4hdGW/zuQYrb56RSxKn+553lJ6bJIxcbyhsXnHSpF4gJ7jLR7DOXp1DPMBnp+9Igd82y3a7TTHxqDj65LRLmIS+YA9RNage/6LeYXUbA4MAp9dhcAzl0JwVtwDdvjd5dNClyy+XwNE7BEMRFTPn2jCWwds6lUB2nlm1p4j8klBULuF2AmfuKqBkvrpRqc6GFGIbko7FEwjw1INf0eRVd5C/nvjoZCLYk0bdZQtG4JWsctiG+vS3dzrctBiw2YUifkUU5Xc8BMYjxDIOEtLYDjGOgKjNtiSdqfwmPktUUHaF4edQFXjj6Frcq2tLbR/gXDTExLnUmCj0hY0lceCvLS/L6FyQ0qqzWIuezNpX4lVmr0LwFAvtUnk1EnHgehCNHsDf2Gn79ET7Q0hYoikfZPHX9QRLeJ2PrKh34iHCoUl/VBglo+7beH1NMurhFAEO0NeEL3/Sow97nBL4Zxz1CHyuUU530ysGIS7agj7DLi9OcBJytMEeusTBDpd/6y+htON49Evemfwhi21GjKT41hKaHqpCePJhNLW6+zTqCNbrXiy6qMFnrxSR1t+esa9sdpLPGD7VP6pqgrp4/VMNb8LStcFvSjxHmVn9LlujDP6Vb/Rl1FgSMyMQk5/j+/BEfxofycxZ32H7QHZJ9S8E8JTnTnGk2N4eruP7K/V+EMX2Pr2bf9ERG/x1PQxqx7LgXvqfsqdJRTONtYpek6t7Gn8u2dKNaYT7nu3top9p9Rv5crevghYiKWhE9atBwAgAkwpQZcV34C2ndeE2Wl49svl87u717z3MwuRmVP0I7i8WYXVPkxALe54/SWPBDjBz62A9fq1r/P3tYPge4BGoBMQh6X8giqACmiJLcseAuKxBQwBGuEoM6YpggRRHORYZf3FYv3sdvktVUE+zkYG5Q1MpeGIEfUVebm2G+vBPAagrZ2AEMRP3ngKhariYiI7mn8DHDICRVEZHlt6+5nhE91x14Lqk8ufqmDLl4bvnul8U1O9DbWgML+owCPWyfxCdgveuE9Uv3C/+sH9Q7cWyz3iNkU2o18RH/YhZEdTGtUbVtLzrpvVgo9Mn31dAmmPjABtBYAwbWpL2yLcUz1nqEkHTkPbijFBW2lWp4LUySqQA93w27M1Nw1s9TA13+2znBBK2gOk3ny6uP3UBUXgcB6bUX/WwdHKMvJyUhR4yvizu3hzx72RfDTPExkZ1/aUPr1aX8ODUc4vMo4B1l4hudPGKIEThPsAjlV1dLG6Xb/hIxU8xI8JcP6KN+uuEKCauvP1t1/zjWQHxX5O2wVFEK0gY4nExpqkwqmhOz1QuN/03nNndyOku6RD+elcaXGfSj9kY7ts6t5YN5utY67syN8XdVwPSnbX8FI7WnmQOoX638E+vaNwp459ad2R6CnVCv29kbl26aWm6QP+yNz9tj5Mf2+x7nvMNlZnCynYHh/50tDXsU/3vr2TdGvh7d/3wfJOhfve4OWD3y22Ct50Pyjh+Piodcp+wcmdeM7VpMJ1JPOckiekn+pJ9YWpA0d2g1PNTQ29A0rVca6m78CBh5p4kMu0XDVe65r89kcPVwGOvEAQNACHpRw9iG3Z5alEiOCUxRsGAqvFi9s3i2//+FcvXnycFTG8kud7XmHOg57LjD1U412FxfWbu6vXVwwQGAXwkLAv7XGFDwBMvdn4/un1zRs+FMBLG8EWIiCMBkMx7+7YgwzEuAODa5n1Dq5AEYAM2MW9+CSWqU0II1ZBuDBgKsdO6CSRKiKZTZ1VXOIok4FMHRIJMWXEdIqq4hdjDu6NBBvpuYMbp5mVRMRN190qN2YH8li4TSjykftHiE4soGv0m0TzelONicBAGDkHwiOO6Gp+JJWwN3U2fbxyaUxS9IPRdgg0Q8P9SqsoTUHjXF+DgBmOkm+dSq3mSoOB9K/pq25SN458NVY01QEW8bfqtUmj2xkY2PFgrWv8KaKXs9SNh3gXqzfr6z/85V/anxkkL675SAaL5RwG+BwwoxT6LbL0YTuS/Tkd2U4eRdWtHQDzTICjSQ07Mk+UqNd6fc1tsY8++gDnS6M907dwnTNa+O7772/u3kSMiBmPChkimrZaOCk9ig0AWztU5oj9qfxHqHw0i3GiWvsqM1f0zqqRwD+6hqcrGCv4czlwustKzLXjw7Q9iVS59CSqHq+kb83q2xudfb7n8+znS8B8QbM6xaRrtEvtRtMmNZ2vzRioNzWo3Qg9RWp7PDfV+IBW6cegfXqqHMoYpCqdxqGX2mHuiw6kD/swreBh/jLUe9L73KfnXOr7TKVp61HhzrrD6gFjaa+zt9Wnm4fdHEkvNU3fU9+j9Uw1b1GeSs+W0odk7qnvRKUTihOi5zp3+YZNGOFPowBG/MppJZJmH2hMqY/5sgWti5B49BbgAqq4u70C6P/lf/3f8DIe3lgOvuEBx6AxlhfX6elpAohhsQHTkIwYxEIF3ERLanXn5UU3hDsFpKDEIUn6x3DjDchrseD9iYAs3bhZf83HBxDyOQIXTaiYRQ1KqFf3leWfmIp8rmLqqxKyqq4tQq2oai5bnCmmphUbQXz4qavO7KL5T9R6df7XcIoAlpxTznypmIHK2m+vaqUZa4dm/f2c+7dmLTImyuVNwq+bzc7997KDjrnjaGSGYUsXbbhhC4ClgRxD6iDfzbpa3L48AwBnsxXSsWiedKLw2Quo2s1PL39YLvIt6qVvycyHhFEGJwzt/hF9rCi1og1RErD40h472xCWpNpQNv31bvH1q+sfvv76OatxELCD8DSub9DyjT4XfIHL6GbNj7Xgn8vxeZtugp7q6CVv6/zE4/J7hzH2Vs7DC2wP/lVFq33g48maz0D5lPvcDqMChw86x+IfqHyOmyVAmNA6ifgFq7XEtFXKwr8EU9UlvDk2c3FjTO9JIMeG3Xu2/irUszb65Pd9jr+XPZAut/YyVFHtd66xVGMU7NN79RxFnNTrsNT093HKfwxPSe1tFYjj3XsqW9Wsuf/e1iPj36vapLvf1sfrv+fdfZ2tcqBadm9MNh52qbk432O30/D45E7/3KtwuLc/OQn7qqaZW9/2ML0DMOrmCkaav5JvQmPxXGIU6GTneN8OffR3rHj5nrrPmjxcOiu2XdBVfrvgSXPl6pEOj+0G/5HbKLKX/7CesbRC8W4CstfPP0/ioYCPbdPOaYEOJzgDBmYWfVqQkAEQMk1IgbgoYMLveLlg2KlzYQ1fOrp49uzcB3q9OPCFpvrUKWc8/DC4sEdukQcYQ7X5gybE58rC6MDrg2kLq8dpAdhusUqUBXvxeAJjjHCBW1yt4LIIkVG8RwRt3DoI+1B9cvBEfx68i2tYk0u1FFcyYpmGlT6II5rNADUhKchkztanAqwoH2T94bsfua1BBJ32F/gxA3v7/MVzPm8gT6S0F39L6e6+2dol/wx549JtY3YMS1f4mGTVeFR/nyrYi9cmtY0Ip/2CRTJ+7op33vvae16iafdkIY0/+X6c2pjbaDRbOrL3asxo3nYtrels4Fva0C4nvW10Knu9N5sGWjo2rQ8HSQ9YscMrAt7nMd+6fZWPlmXhvT3F/3YGrPuaH3uVafcUmdR0M5L7AHZ8+rrdqYw4wmxbpSyA5Lj8fMUjxnwtwNtuLMhrnlGGp3wiA5RPAfGJGyTiDDfTODP1QG/GrUuOtHsScQS5BOEe3p+nuEJV/k0r2FMq3dekTz+59+XYk6v9VSrsm2laQUormEe211NFvuxO/fm5KFX92ViluEqd2nDpKltVYhSq2GQvrVSGcdzNP6U+ahl5nzQxGc+V9p0aQDzSD9j6MWi/+q0092Ovqc6dOEwZHlD58mdu3DnWt+pI4/T+7zW341Xvc5/eK7tD3FE1lu4dDe90nN5Wny4l42zEqHMucW995wTfBp2A5ETZe5Y8jcFT67sT9o0TY8HYinFdVARc4pQhCxpgL3Tn2V+nPgUrAIUseIEN2Hv7ycqX87ziI0WZZoXfb5ie3XwOVFqsXsojpmHncouzs2cov727ct5x7QWnFvVkplX8Ex6Y808nBD2gIDTc3j6LBwFuaOIOA545bcnaBr/P6satARykNDZNWT/veAjd7j7HkYxHWiBUM4ApjhiTQWIxqKhSHHTPQgVQ31y0ClphrcfVm59g4GVAPgkcASQuLy+Xy4+s+uJHGZs+jYzKy8Tj90334xUd1jBGZSdRdTos+8DSiibCo43BNu3Kdvft9e314s366oq3SDEKq55jj7Cl7kDMIH6Hf5JsU1bhO5CNuksPYt80qyJB/3FVBlR4Z2xxtv6cZwzuVl+ro5iRMuh2htrSGdDnijUGy9wW4msMwvfz7x1aBmezLp/37iPjaFpbatGI9xfsZFQzTt4uLr4vtbqNeE5CTgdHKPAzwIh90hlqnC0vfvAxaL4xALTnUQMCEfc0hEMoJUUcKAvBUgcEjFVSQW0nYs2qNduz7V9hHMbwW4Mn2GZ+359A83a98Hn0mMR4jR2JZbFne5QPJ9Zr+vs4tT7HU8ihntXZuT+/o2Qs3dviO8z3Z0+8y3G/wuM4xlocx77hqra+t+5zcX6w3Y0HlToibmP/3JUd8tSiztAVK3r6rXrwWMlkqbgErzdzdwCG88BLVqkbKL3yfemmfF/R26WNdZyaGYsqMVaFbLnLfvS7eKqoV1X0nvIzpke3p37uePW0bo9R2rFyIHuqSM9Pmu3eOh6wvlvUa98tuz+/N5hF7IvK7fvVvUuO3r/RbqCC0+fOERbCAYfUPDcQRcCwYNUyjwiDPKgVU4xMbfLoIl8EAJIUbhB5MA2bH1SnxpECmqTZ3INOosdRhU6gxviIbsIDrdwor8Tb5LO4QqCdVUXyAn58kejADpqRqC70k2QcwD+VsIsFqFZAQpFEWinRZETDH+4IyoxSecLauAFWgfcVBEosZxPvrRwFtZzS5ED/z4pH9ZaWmXAprRm3nlyUX9a+ajZE40l9r9CMARoiXC1L5Hxo5Ob165c2TeJIy9pKybTgW+LgkJ0N45ezWgu2FqBfqLj+Nj91rYnsNfawMNiz5FO/pOS0Xc0ZzgbW7bqMNvgSBphdBpcAsYyHsYfSdkFxvSC8VArzh7OP7o50+oxm7NkMYpNSVEVWUx3lMNY8v6CwkRDm65euyaolhRyzGgtuVnjaGgmRTUIVdsVh2+2uyP4qtmq8sSo72ZG+kziSbUfqpCwmbKD3YHtP3HhwJB7m/+Pjj9130E8Oh2XWgZ2CZFug9Ju3AP1ezeP6ITMwUcb0AMcauTYJKSdsvdQRo5wTND8Rax+c3tlSX5Qa5/WcpxonwoiXnv5+wmE9c+PO3jc8rLYa3Tte/2Hrx5T2c/aPj9I4nh4rNdZ0p47H+LbLM6qYNvMu63BG1Ir57X5bcd7xsI/D3jshuxa2dW5K5+gbDlJjU8dP5rl3RvzDTEBHbyLOEMD/lepuvvQcd16BH3zwAKYDowUvJArHM1kK4GC1NNih7gCATljn/+3ZxdXZgieAYRZLACzEFOffCUqcfyIHMIPKeuugE+z6gqAgI9KOHZQYa6OH8VJLt59YtGLunFEGPGRsNbAMwwKeFYauRX2rkgApLBd6sXrqcuZVOXxMnUzHXWn4o3TbXBwBkfzoVICRxVUXmXNrAgbnW7Hum1a4RgKoyMoYvMWRbyPwiKff6A2pDPXmVJtNsbixtzSFT7w7/J3ge42Vw7BNE1PZGVtV11HBRm6RN/Tv+R7w2E4bUTpDtvOz2w/5wNXt8jt9UqldwlakvdKqJNt6M17Pb9GF7SwzXPSM6jU8x1G97vsmK4tK7O2rOEa6eOMxpuiO7uRKJ6C5HeJyInCa/Ij5JWv3M01vX6Uv6H6stl4dd3GPrutyf91hizZyYbdCGNbPVE0npKkoSQpSAk2taqk8msJGZ/U/a+fKT0qd+Ncd3wKkACpVGn2L69/Bd7b6yn2/ddeTnvxLSx91jZ2p1JxsRz/59zeyPs9toz7NVshh/D19gNLqDf1v2VH1Kqz4AHtcLwuF1m/uVENGxbnDNi3bovQ+t4KudbZY5+hbTMdmaLsK2rECPd8kbvdEo5ft0uMZuuXJTq+KozBI5sT3XiS5zf/uUhDVXGa80jx+23Lq8erU8AC/5rx4gKrj6zBn9HgNezlHtST2+r+XuFdVTxzV9sQ+DcO9PD3/qelSPloZs6fq2eKvWDwsIl14UfA4TVtO/QyZMQJjNUAkANg1KxaciBRFiGpZxxAEQfQBCE6zumfmkhX5zGWy5ke04nykiEU4QTpwGPwhCBKGZBsT5DAq8OCfsMNuVKWFeywOh5brQiTSzhZmaIj4H3E8NK0twBOUeBEj6jUPQxyvKxhUBUqJliKR2xewpRT9jiw8hFd34nErLZ/Vg35BlTFpVvQoVhdnvBAJetVGQ5ut9OiG/zdbz7Ohvmep0eMx8SAHT6orYbQJ+RvjGaNg+8ys3zD6UmFccufyMHFt3j/L2LV1sDQNj48U3rIXoK+6FpmYiBbZ06ncmyCbvk1CkWGUqfmQ0vyOAiiyJ0C8XfOGH7nx0F7BuUJ3UDjqSizidm8UwVj/o6YqM6hXLN0RWf2N5qgwzUkX5yWYYM+4KAn5/Z/aSOOEcW2SPPz3ph/f9EC3HHWGqCU1SOK33W8R+IVGwBNh0pOLOFejdjbPFf9q6KlnFwreApQZQSs4kmEi7aUiF4scD+1g5hGkw2O40jbVMh2HTSlTqY4S410eX6Jh/YUXup1x8FjFXqrafiza0jVkDpcOXPuPvQ/3ruXar2IftXepqgDXE+rf2NzXIlgsWyT6YG6k3nlq2gM3FN31N9v1uPdttNcYT2Yd+q0q21NIn9y+2zo32uboG46NX9D2tjVtMc4EbOTSRNKrAnXfIGl//wEurBcGRhOcAAJQVJZKE68Gr51wpdBbAiwzxggAuN03QLd8TNIgbqckJ6oRVPMPAAONP8xpMYiZRBHZg2os9cCbVm55mvMHoTSwywJoyrF86HwFsPbrSZHRVfV5UCeco3mk+SxrkBOvUQynXPA2iKbH3SZklBKf27GYRVxeCXm804DQQCAm10HBzLwq3ixvVy5tEnRhAJClaXyp2iMc5c21wSZOfWR6+dNAGY7r0Puv/04pA6/H6az5zLx7E+q/E1xt0murdK9hyd0MAsDdG2vSwjYmpFL6sftes/ltSucnEUXBnm137n9gUZb2eRbzgtu0JUBfZL0++8a3+2eZmW1Fr9FL9pe0EBPw9EMMKsLMqGnk01Zp2tKpQ8vvUyqzJ8HgY3qAjZ5EChC3nLSQf8N/++ny7KOYo8hxSF6/gwPMvcOtAkpxQb/oivzZuWNWl1C6sUsV5ClSvLbacY0zD9OcGOzbILz4Vsuzm0/j1jdRiwk5URpJUnnW3268Pl/wFERGqigfzZJ2DXHZk6xo9rM77ivCkWvOFufm2rstOkff5trk5vjn6BvJMdX/ft1/jR3FJok52Y6+95o8UdQROtmxFbrinyFJK1bD93Xp08f71LdRn55quEd/F6WpbE8Zf4urL7rvZMeqQeZqUNXsxZ+kCVpNv47iznpv6HD6nmgcFu5K23M7X3WkhKCqGSzEMwBjGMYE/JWGO9dKFfSlo8I+oo0I6X3Zpq5QiSnxfXH3FD/2tsYpCvbzVnxOVX4q/37bA7Ua6Gl1brV6VXIwNz3uNX1kt4Ftr/jUylui7LPe+T4mh4STk2DlGwdIAA5wReCR09sBGHlPgLhZ/CJ0Yt0PKBekHkikGv4sCuZPOkingJgIZCgbzr0gkvjJxUUBrzFCf3GbWoQ3Iv1McPotMlcx8K3Tm9d8VuDNFR6DheAUg+emBGIQgsv0J0rqS6pM+ur86IL2RFEcioxJ0Dl+VAXjUHRHJM4rEFypH8jyLGnBSr+HhhOEkH9xR4iZaWY+yGo1NaNv6RRVZamxjp/FoCsP3ErRA4Xjj7KlZcxO1cEwlj7KZFM9KpuamqGU1eyNsA4Bnq/Xb777/jteu+mT4S42c3kW6Jrh2kcf8jSuDUle7xm2rsHr58sLxgR2MA2RTINZO4jSqvOUFyiNKeXLZe1Gmxooqz6HDAL0DUD5Od2UQSznkq18jlLHhA4AM5KNCYqsRLYy4At5chfALL3L9Mao3sE+dFF9p2KxWXqoZIYSnECWkC7HYyO7aPOdvLjBUB79DFT5Rp4DJLL01jii0i5RLlplTWZfpD7dmH47PEEEiCtbWuwJtP2mYhqBim3FuUI9pk/q1FPmOkWmFt8lpbw61H9S28bggV99tvJ9uCbtnOrTqkYmO9WV8DAf2VRtWPak+hH5tPjoMVPqMpU/Y+6frR9FjaNPqzyzHarmjMgDyIff7TNVOPKXe3NVngo+gFK2+hFzU3JMixxu0xO9mVZ2bMEDms5rzD3HATirogOdYFv2mL68LWGupKb0d0/Z9gRkERzjT30S5RBJIMpF5iwBt184mXr+NfAmG5OIgANghTCauUz+FHM6PAinrhU+QtDaLBBCwwIku2sZhR8QhJKtHixYiZPOaQZ7cQD6v3z98ur1K4Q1Le4Rw7H99PKn77775uLiIqMFIh1kBfKjBnzrNBZVVMuXgsuQj0lMowmso1b+2FUyeCeVE1hlo6jglXsjcbNe/+lPf0wVZKgYgLq++OLzD198hnupiPEped/FwiefqsOpddCcYm37hECpae40ln7uv5inlKYkEtNZ8+lM/MC/e0zkN65VFqZeg5PEnfs79SiNPf+ujSEfPxP3gXL88e4yrZF42SDCV/6408LrV9frK9ZccQsAHm9SUcAqNV7HCRiuMWpo6bG3dsYlb7+pWwG0LLVzDEnLxoQ9oLWaCSfpKV/zJk2sclvJz1q7sqz2slQHxgR96/Lb9dnr775jpHFD/+QBkdWqXPzy/OLi8nepcAuBfZLzB6st6kPfs+MxKnFzmJB+aFaLepbO7Lnn62jTNC5FoxBNrs7ju8WCfEWiBZ8zJlAhGvASMv9RwB0S3g5EWl/C3ZyTUNKRiuUtSl/q3H8shbfb9b+/HXnrd7mnz6WfQM8xv19z5o/4Xet/m/r0nMpT6dNnzMZ57r2qev69DMcSj6j7YVV92/Xpw1IHSumZezvbKPKYus9pHjHYaGUuUSdTwyHpdW+jP+y1rmkvf84B7G591OJiI3ie1wDAVC4EOW7ScPOfrRiSnOxyHWrU+s1PphmZsL81wgMMJhqj62/Ns6dQ3Lt6WF9xVrvV/jD/+1A6bbuisP+5tj6M+DD18IBjJXuA4UFFxwZj3nrADReIrlug1Gd5uVqBmqHzH5QU7EyR/wUeHEUPAh4FBBl5LksgRpFfBHAqMaVFE6+oTfiQP+TqMiI9PEoKcdSvWmA8eAvq3ep8xViDB35RoB5FYF1cXF7waSWJzOwrIXLhU0rAmXBgSX8s8CDYYWig/lDRrBeWKSwtauJDyJZSFC45YAmXO3QDsur2Q1lnyOHrU8t5lTXEBvrkf7CaCscNLaVZdWy7mUauwkP7oxnnlZSKHUU72ZLeyzmv+G2UpKlQnPZtASd49JWgXXqfmNgGsJVs+LyGP52KBkprIUwnAZbTYeiokm0utfEnE5st0jpLGnCxePPmDZ+qRrE+pHsJvhlasLgsP56tUyi9vLm++eqPf6Rz8gQN7KvVBX1j/ebHDz7gG70ZoEZN9VaU2W81r+c1BLHLpRJW1fMmvUhvZfKQLsytqKpcsp6inAjsOZP1P/0wCuybVsrTuFShC084K64XK96pZbH3A1DQNlUkErE5ULePxbNN+y33VBF4fHQPNN1TOflz6Xl8cHrP0Xb8NjW9QzlJ2/F2T+Xc8aouHk1JXKzukQtPDQB2TvhSUFeEvaPn4t/xq2ndoe7L9jr7dHhPHTONQS/76JiONaeU3q29tekZnjBdT+gfr7D4xzoqeHBcXtE7PEMwZ71WxW3Z6lkP2t1z32CQHdtlIOw5Tnl2KIdbsGmc9KWjpPa4I2knDnaSRKCiVO7tnW/YEdyj/nAk9wicQCrHdqLX5GtuoJVx0FMBEO/UxyVfH744/yPTqgEalGaqM0BDcAFyEDwJYcAS0YICcBdEIg8CycTq+uMAsB+BKHB6AyE2SmdLqst/yDc3kPGxY2DNHRD/2eULgBfojnEF/nHQEtaZzy/7ZyA8illpQ952ty666uYNA69eZEc/9cXNCniMb6lU+MIrMcV16YNPf2DGN4qqQqgsrHnHm7b99MFrtSofE4SGeWJPB9fND7iqlUa5Cg9t8h4qP1h4SNCyEr7Phfu0RM/jldxvZsPROp4VsMmd5xLl02B0Gzqqfc/ms9NVx0ttcVI/q9rIsPCXNlWY/7YupX4Fb7VY+13e2BMUK8COl9Cuzi8v1B1F6Q1IuDyOQjjSRT0FMErXvTy/oKvQQeww+TtbPv9peXm9OPtIT9SrWve6oJn0iphYf0L+bPW9ZSk3C5fW2SJG0t5mbalI4/SGwC0f7ljcfGrvX6JB7ohRWXxzpIwIX0lb+ckKBLn7wX0/dZd2jhoYt0F+JEwSA8dw3GaoYGL9PdyOvwJ7bbln639l+vQ9YkcX97/mfXpOwTE8c7LQN51gpu6FMUrD26jvAd/uLZrWffzV7mWrx0Op86SqXPuxaOTP70vLbYIzFg+JUdxfw2F7THx6JNynB9113PibNf0SR1J7GnDMD5Ll6vpL2npzB6AuS9ssvTLSY+3HxMDusSeSnljted9G+jE237mzbyMAT6CTOPTN+AQao/DU8L4NNx5WlzEaYxWKMtfZqvT98f+wJ3oLAGAaFWSdRfM+DdyuigEE7AQ09gqhrYAh6IhfdzAHa535gQdb+DMPqAgw0mSGBBxGECCo8powICiUhAIVjZYVGFMPCCYTuje5kuqj5XVFwUayiGXIAdQK/nNSNWAuvAXh1MufNzQUr2pFvlUxWqsgDPoCKxXNERpanVTNxiAAx1DtkwdFEbt53wM4hfvQmfolGitfOV9VNzJlveE8RFHRaNGyyTW1pfyp9+VFae3TD7aDklMcPoV3yyf7odPkmzBmLOaSF9rCFfM2fkrTgAT6lul5/tkh2kbSnP3B/9GmYlqLzb4nr3+DGXShOXcMVpwUMvCHLdJw5o+d2jgwlvC2ghriDDfJ6CVFOLvlPaVkmO9PNTSIBzAgYYeLXl2y27mHwBY/0xXl0YTuFYvJKoea8yVjVArxkbyroRQZuipkYuLJzBmjw2cLHgC41v1SlRqV0ranaGtTPNxjwZAYjlvsv2UeE4FqlHcZ2NYNHuP0u5J98uAQ51Enib1hn8anKCO9pMbsOwzGXn8H+1W3bZbBVZw9cAeAcUwJD6o2x1HpWN1tA4aT/yPbRvL+1OEx0/xI6H7Nj+HYO9f7GIUHZO+x1Y0vp0qI3m5TDPPWU+bTKAftHlbV1+hwC46cVYuxfx3Wf0zpYbv3arA7DxEYvRqjXZ19VFIMsxYHPSP/PYnC35O5tPaMP2/t2N56+ujqNkvrI0ECnKnCDjEWSawM8NcpTIlOlZp0kEBOXAPadRoVbiEH90acnge3kF7yZVxRLwXwxj7+i5wiChw3WCkNx/ojKQu/pysdLgCKJejmGKlG0YCb2mTgcVsSfmYJ+vp30O6yIrkwWjkg2qnlFUgzSQr+SQWbqugrb7QrIINB7WyB9RxjFVhlCWOlqgLPQv/BN8QvPo0hZ3uDDhd31x8t7j7i/TxqS01U1byxjvnTkjZO2RCIK6fIjLwleb/NbY7u7T27xjeulIjVGq11iaITCCq+kQkD/DuUTm5INil1N1VlCIicSXaew3ZaP60lj/w2elB5Rb7spH9WDz+7/YzwL5c/qAKw7hn5JkWtv2mLbwBTdvP87Obm7OKbnCNWIUA8tdEfR6R58z+nRpJxe73mvbra47EBRhG362sfwOXHdv0Z4gue69DDoW9nXKLby+/dGxJrirrcSqLf8jxJq7udiurQDXlWpwyuvyAU67tXdvPVd9wb42GAOgcVcijBMGmVMynCvv2TmwC8Behywfe8Yyb18bTN/zhQBlOdJCli6/chsBs4h2PRvT7s246ffd8nPdJmr67hOFx64H71qP/XkZjGYUo5taaHEdqWtsNtfbh0S1EyPX9WoI6/yFPekXKYZ+e5x+0ePOo4KoHs0259nPv0xMpBy2NhV7ei5f7A5g4AF546uQf9Y45ErkojwTOebdRIoigb0kTJQHiHx/jd7PXpdhF7h56cbGoT6qNFt2p4tNS7Z2w95TjDFYeTRI5T/BCuHTcqy35srErvsD3E0o6MsGM0slN2T7Z6Re0nrME0+M+zlMwF+ihAKgNwsQSbjQKikDKwM4nonGiUthEAwwHnUgUbTIcHZINU1Ca8CBqr4HSejHGCicGD+1QzEugBlDFpiYBqhF2CIDGVCzZqHTZplYO1vBVRzztmirNYSyHO41CBG/1Dln3hHrFRaqKRViV5NOpFDXgYp1IJjQfwpUYi/uLTLmOjxCTu8sLZZcZH1KfVK/qQ0CWY/WvSRiTehOW+XfTfxzRXfr/w/Rwb3cVL/do2JgbChm6cUvGdoorfDnGSrWDZ/k1JGogdi9ZYBuYdABrV4LYuRBJsXe05HiiDzhZOC20FPaAlqkFai0hNKSZo2cal/82DfI5uze0vJtrP8Ysi7xHYSZnW9x+e+HiITwOAVOhDHBmowJJ4qUfLsHrONKcg2t/8a6XI0e+RcoCCS3HGHUTdsu5Sr9c8ncwSJl46JNVAqNxlUcizh9wGJJBT4cWSBwDqDoAGEjG4Zjc0q8VocBxyxZ6CWcnfCh4cge0wP1jNr1bwqeKDHrbqxk+l830OequpJ/L4JeA/5qJRXlc8xhrsZEPfjCPREn1t3tFvi46ST584MBI61ezIT12oYj27PTdenK4tm9ZtnL0ei/auPxtL5xLH2JqTHSs1MszVaGTYm0CPzd6PuffyHUek1UbHDtduWoobzZnjbM1xzfWcTU+ek9xH712q86Pfl8ScxX36QpuLNj/k+2TaCr9JUdErbhSWbO3LySYhZAk28KFVsVMmubOCQG6gtkgDFL5gkh0K/4Umd7cfr6+er54x+Q2uEU8vF8Ag2D/Ke0h+gLLB7uohCwoHrq3uFq+FGnfMaELHG+YmX4qq7WmAIUYR/AM98x4VABPTE1YD5cJ6UApgi8GKb9//VNB9/g2LtCGAvharr/NEbjwX5GjBCq4YRfAieepYIwWrrLdodXzjYMXKBkuZuvl8eXu+XPxjDbvoSccuLp7drt/wcheHEgYl2hlx8MAEQNAQpO1UicVvFhe49ExGfEYgUT67/QCd2ajiT1WzRkjG9PIKs8zODvThyNcA0OS7g4Zt9u3722/ub+yEtb6zmzf6DzqGY8VgyPVfHtjyZJut2KGNdwmG6jVF7VsHP1L/QbVBPVtQR6JCHaF3MtwzafRWUMWLJXQiaTxjiyPfBGCjX2X6HzEb1CEZkV272CWtbNxpAK3zt7j9/OzmcvXiivHaYvltY5eFvnCbhtWgiJp/JPkeBfnzH+n/RYgDMC9416freeiw9CJEtM4ZhN41n/3K2zZd4QMyxwpn0I3d5A0vjV2cc3aIyT3L7PMIxp5xcCCTSuUOIbrxO2eEbGGQYCh0D7/tXQw5zr4+W63Pb33uXE88SX1KWSblKgItbYwMWo2KOb+q3jhZ28ZQI4yH/r5iQtpKin4xuQ85Cu4mUrtd4n3fgp1epQ9fXQ+XTq33lKmtvvRR6Vwl2v2HPj2vlAaxHzx0m8ZhShna/qE2DsgNbe2JNGUbSik5KuYd/3gP5zHx0atOZ6maRnuP51WX41pwWu8dylF135Fp2VnX9rMP1Ih5NcsSoKbEi9LAkOaqXO25mmzKJl0SDa04h1JIckPvhd9xuvxolXzHtt+luaeqYcXryT1/cF9Il3pydx6r8KmifaIfJzTOwbilNcY65CMArKMBwIjWnbDMxYEci3suLs6frYEjFATO3N5cCGiuXvHOk1w0eCnKzc2aSdD1i+cf3C1/yutWnAUN/AWOOBOZqwGafWQWRA3sEZ9gUoijJ3JwFN4ohwUsgqWCrTEsx+XF+aeffqobt19y22J1uQZHwb2+u/vhx+8z8MAUuDDoh/3t2aufXl9fAM5Y/IMCgwJG5AX+l5crbiRY00ClJkvpcvnRxx8+v/s0MAskRcnt5eXzlz/98MP3P6Bat1UkDuQ1L2UujkNyRpZRAkGDsQ0q4nmqH+PqlT0xgWLd66Bz5DjUPvS2i8WUFVNfti+tLrY6xFwRdveNb5f8pPmqUFTumGt1n1qrAveGy4AkAIQ0qQBd7+oQbNuPiqrZD2+Z8L+jNXqG+FYizZSW8msAfL8NkbSUvUfp1eL6+trBW7VsxnH0I+g3rP+hw6aZ4LVN6UnCek4NID1DX14tdHfBa6tWH3z4wUevrl6Kvm3e8panQux5f/zjny7OkeAZYXr86vwC9ODAmN7F6BdtweKcKRAZG+hUNmucDARQu2ljUZ2cyjNQjgUHojiDg6B766pK/MhIQBEVZfBhIV0fu0tvYkSjo+kk1A5pzBRxJztwDseheDgO9N+OTxKBodG3lE0baav4uExpPo73IVx0iDLxVg31ykeLuHtMdzyGv/T0Vh4Si7ci07t/n4GON0muIlwj+BIwY/eqYu3RQ10r3VW6kiOLUiNbqG0+cuRAT5++z73d8icaXQ1qdeUujznuzIhTMB0TD1KnHfvZ6+ndgMO6TuXfq20n3qeOLKf3K3jPCdvj41Oe7MTn+Mh33XBvve8jHuxLj6/dnPlT4z+nJ3ADrEPATojEeHZWYluy7ymsjM9cuzPZTmbKL0JiLABUeH119Vd/xQ0cIBDlQR53f0XZxcUL0YNTnoCNc/DTs2c/XV58cgOOqjNfd8Fe/APTNJoJgUhBHHPopIxNu+vPQCx3y+/5kNPV1csffvgO6LRY8i5F5mmWvBfoxbPn/+7f+3d/9+Xv7m6veOc5hfA/e3b+X/83//h///f/DxeXvNocGoFihTTumlnfXvO9I+aFIQvFBEhnz1xo8czJU66BxqIgvYWL1bfnKxDZc/ksEjqV1+zBW75jPtOm1A77lOcmgFUgbYzubt7cvDy7PfdrZnw0jDUg1u32/PzHy4uLu9sPrLaq1b67Mbdd4dgu2GZNzrsBA2tfzJv7dzWnWPp0GzT0IvNfHpjKSxnvEoxuVP36+xW9ZJu/3yJt6amSwbXbtcNF+uItq1zWv+fzVYvzn25vr4HyRJa1NcbcwNvNamME9vzZc+BvWlwWY/KMV/HcEDP6QTqdkjatyvn35vbaJTHqiRbs8T6n7777jiMUNaQ/o/blTz/9d/+l/96/9W/9L27Wr+mHrD7D5WfPz7/79sd//+//+5lJ0+F0K7Uz4GSQfA285ytyi+X1m1eMqrmLkC50CaOOcLqtP9PI6lsIKFRBDQYYMoxtXcHRcbnE92x3d69evWYRWovZIO99h2tuRjFETwR83xHbmheW+qXkO0YvFBAN7+zhp7W0nrWRGZIQ2u97K9sciq6HsA/n9ab46NTh6/Dh0qONtAq1MB0vNuF84LW9m28e57AnuvcTyuexQUg8CWbYbyzUB9ax03hPnLvf5VPb9/G+jW4SyfJzJ8Ijw2yib81ZpvsLTq17p/GeADfOvtNEoon548VNQLYi9NpII1aSPb2p3D54KSqBqKqIjla3ed9SbjC/o/7dOrFj/F1lK95YmwnCyX6MCk+W/E3gbURg0x6b1GE7dcrWHs4xsSNVKGLJ+geQQAMTgIBAdliFLiCDV69fel9AQAJ6EG9d8GWjC2AZvOBscAxjAEouxVZOjqLBiyNrfoZLSAEWKEIN/BG0KQ+vVw/pzleqii96MVdK0bff/uC6+qyUEKBd82JQ8PdidbG6u3muDKCe5RjPLp9/+IIZ33PQtXOerNNxyTUMqOc1jjirS/L7Bnf2TMBqV9iFdTatt2Rhvaqbrzly+hapmxuXc6Q64ELuTuChw4yYlBwTCIOBVt//8IPV8FmJCxZoU8iC7EsGKOfPwwg/7GwKbSeSK1qS7JLbJllUGgamreOotqgHOGGYat7S9ZAMKg/b3Cgtvr0C9hL00EwU0/rX1y9vb/jBYk3aD3xsy1n+mytHcaslD93S9WD2Hw3A3PzFZcCxd3DUDtnWa0g6Td+y9DhR93LJ47paClv6qGeCmP3GFnRLn8ECzf7m7vqDjz9k+Gm3sR/yutBzmtrBAs8Uc1J4XnCzCb/8HDXd8NnlM8ce9El6D6cQA03PAAaIzZ16boCvYFAFLGfTG3oaBP6qdpBI4A0k3p2builhfSmT31L+Vd3p8LwgNG9G4jkfC86XrEZiYOB3zfjHf3iUGc0268cd4tlxrD8310Or+HP7Pdi3d6eVKjGQTztWEB6j4TR775D78ZWq4Exd/gV18o3zOL1vKzI19TWgm7HUyN3HoIvoWI7cZhvSGz2UbVg3jJtUjfwqPzeKmqNHasvWRu9OaqxG82Zn7n/krplvvoGKQD9LPTI8IHGSnnvtUoEhzHt8GYt2on7qyLKPT6k6VcMe50IqPfg5enhSfEqqxMfKztnaQ5/2pW7u4bi+tEfrvaSTozf1s2yAJ/YZe/ysW8ALsBsgEXQLeMXSMI0HaiUv6gW1fE4PXJx/R3mh4Sy4AJg4Da9zgiiABLO0n9hZVz9A9x0mYpe0nLObAKVvYsJWjHqO6EcU3AQMoVQ1LCh6/ZqV31mbDZDC5pmjDoHS9Rdn158tVn/ikQFkwFk36xs+1iTKAoWxGgOz6swmPheTublAx4lQDUsV72jastBrPAItFaLSPlUppxguq30ATCXmQIJiZvh9zQvRu/3MGlx82xZy3N1d8pIVM/ITx6waoddxfK3Ju+eJSizpABuMZZmkjo2bsG75Y0dISf8MwDb/IDxSe1GIb3Mrm9tGtnN7rdsWvZcyEYxEO2MxPsj1IwvPzs7+4NCLdS8rWp4FOJfr2+8Nsd0PkUoRcNqlWh1cW+EcYrtRK4y2DNk2ao0L3gUDJ7PRY7iL8xcLbiKtvtIbHjoHKPu+/+X61ad3bz5fL/5AH3T0GDU3rFvLujJ6jAQGnNyvyKlBj0ReRvRa7CMEObt0UIjPHYfVN1ZcHC9zPMYsXtH99TR/EEhajaoi2mCm/6uF5xwQXH1LGnaH4xpydj+3UHTl7Ha1ZuC0Ps9g3lFKRKxsDGQuf7wITNtFF3c377b9Iraxk40J47S9HXPdPoZnW+vT5076DR3NF9rp176PRTuJuTrWL2Yxz/HsqNqfnfu928+9RT3GLi07tvKW8HwG/ml/mGe35O3hh8N2jyqtykyiMNaRq0NqXASvREMAOhajyOXpgEHL6gJ1gOmtF40ud5Z2aIcqkTp0om8/Wc6xv8et4zw5QskRLMfZ+lm4Ru9J9Ok5Z4pn5Jxj+wXSj63TvXyiCP7xy38DGhAoixA42QXvvthH8BEKvVScInguaA29LgpyyK1Y5CMityiqmsoE/1izIdbBTNCGpfyPZmcvwySFBADOWUkgjDDJrdqJuUyfO2bQ4rhFU9hlcU9GENzEwI2Q0cGUJ5ssAjy9FQ95ZObVNUBlOuVlQH1yxxWSykuQVySlO8FsLONWgg2VrFBigBK3qaESmKaODBKahiIazzy0qmb+lQOpr54kj/C+TXKKZsqreFNIapNJuig9cbQzMu8tHdkekhhVP0R4qEPrGHYDbzPZFsJrsj65yx2e1NV40mF81IMfNXuywS+76UGdC/aBEgqDeLpxItPSyiCCDl/UY2LI2lK2X0Po9kBMM/JkSQ2dM5oaNiettOXqSodAnCVtqCV7x0PkdFn/23dxxP/lXLpH9RxdV1WOesSppFy8M+89B3J0woHqWeAA9Sa3IjiRqw458EC8kWI8dfvmzWsGHqsLGWJQE92WynT5ueSxfHPy75i+r6rv2IVHmfuFhftRdX2U8EmBql7xS+8bW/GiMvvq05EPPwMQ8a0gsoryd5pozwA0a1x8FnNrBLccqswjRn6l4Jjx3x67M6Sa+X5anVNT4wp74jltlCLuLUJVa4KZeeuptnnrxdv0TdlGypwn0/HulDIq2Ukc42cvMkasJ+5UoGoy+kDp6PmYKGKvpF9/eXK7d62wpfOYzGNkm/5NFOdm3erOAHihgnPIL0GMwKm+/6VqQRWbojefCsEvfgjQ/QYEAfzixTfgDxF4hgsscnFSm0dseRkPIIL/zuJTClJGB/wsrAD9AOe/C4QB3ghYMqrI7GOkPCWQZgewgZ8Rieso0KNw7FGIZ6z3+MZ3Ljo0YX0Ob5JxDwpXL2JgICEgkgqpExngOBKIZNLV9xpRywXrgvBZXakxjMNmTDAtHYQvOMOYKL8YAHR4CNTyXexONqNu+Y20TAYTtEw/EypuDlABayDj8hrTC+b+rW1C7KGM6yfMLVvvz9ldiy/PKMY7apLd3hXLFg2/P5ZQbznjSQCRXupWbCVirELHi976+IafLZ3bmf6tQZSMPkTPYslbgLa39hagvMmn0z+wcUxMzMet208Cbfm2ND7yUIXxxF3uwXCniJblvo/oOULBxVFgbfKXHhSlg9oqot1d4WZnTBtVCMKjAibkFVoYN58DVogeZG+hgHvnf1o8+9Pi+tyuzVuw9OjufGXjwhv3cMnW14Sng857K8jTNktx4IIWjcgEgafOcQF6ncCeA3Enfbj8oLZDmFFCi2VC1+VFi2/JojU9UEdZv5ShMEHCGdcq0ZeB/qxiu+PzBoTu7u76zc0FDyS0Ta/KTPYtM5TuP7ao7S98q9Qjrqj161Be7J01N2JTJ4/QPBXqKeOv0oY41TmlbLjvT1VD7fDd82zAe4a+dpwn2+LGecf2aG/3hiiq225s+jEx15t3+sme9u31vvP0BpmPpqvymx+WFHit8irhZWX2GQA4i6suAmTnomLBGLrR8s+TGFzure+j9eXvPF3x6sNZLs45Cp3tHUf5bZibq+ADWqCP3o74WDQmdhh+FdmqXHWNR1QoM/G8t5BlAT7bCjoBJgCphSWgBwYDhS80BM7gY0biZYCEK+yDSyCL00XJ4U0jD96BXUg6s9n6L3wQAqADsCyN+9EBUoLAKqK8oEch7GMHAIV2HOL1KcH3FLFOGlwuHbzt+od4o1PZgIm5zjlbnDf0m9U0IMnhQAd3IDvoqctiqq2zocR7jGWmlkXnGkEDpRnCmFWb/5og9XCNCCs/XA+uTXYI4AZDDpaaxztobtD7LYwSdujhUaKkxiNsUIp5KNqRHckl3SkeJaM9qnvmCX+xHb0fdY2JfaL7Cm2lrS1jSIi+9d8CgiqkFs46DHPy286ILpqB0VcSIHvbBJpFLd4JVmfT8WKahwRsBiH9giQDiUSXQyXI2ZnLrsM5Bn2Li1tepe/UPzP6WELJ3flydX17g2v+Y3jpoiF18y9vx5IvWRWmxdEfXvtK1c/9uFndVkQirFVv/UHCgYKm1Jd9UnhoLPzP8xDn3KHwxPJxCYwvnz37kOdReAtQJFlKZR0irXCIca3pi3bTv8btbVcO/UNEnzh81WCl/IlV/9moqxjuVPdASKs1d/jf3+zQuYdj+mK7XNAtudb6vFG31WW0olK/Vbnmdhx5J8xG31AypQwlb/u4Mw6bNN5TeoYt9O+dRaCah0vrPkO5h08V49qPLu5kK3RVatEwGoZy6rx1rPfqRxdOa5+p3SnlNI3z3P0zCYdnNWgR6jaGcV7l40oeN1uj7aEFH+fHIWnbeHLOrn9nfKb36LgEgHnWf215+8GKxwIDj8EIQAnXKC+/CdJ6VhOYwi1nwUE5IB+eaWTccOMrcTAIlGBK0SUu6BughMpZAA0g4830vJ+EBfQiFpAFaVfvU84/CaXaFgRJoZ8dxVAtcf6VzwUQPKE8CEZ+GOFKKrP4Aj6rjlRQuiXXnztLfHaTAQAlAUR6kJfD2F0CzeJDINigAk0UShfdA6GEgde/W6yvz86/EiRCF0/ZmjxszDtQ9Um3fVqD2yE8n8oDqjX1DAg751FgHEOnX1QwzuVlwkVJbc19M/X+nI7QWLYPVV77sWRHiOyC791SfOu3BapalWjxahkO2Ygj9xbCF/fq3UGqGTm6dGjeqSBABV8HLo6bexRNXSvzLUAo1Kl6g1BSQ6G/SinRZpLLV8SWnna9vqL1BL2WCKw9rH9P/1z49AVUe5h3amgIxgYU335KIU+kjN7nfgiU7+W3IcoR5Gg7GjRftGjOUZbVRGlxrRKcbBzo1dWZVaI/FJ6jhOePr70rRSeBGO0OpOkF9JkMWtRi/14sLklah3R/D8M5YU2Mz+gcjMnKKY6P8hST5+RY8jvOl6eHEx9dQnp7Jtv1NU9I80IgziMcoftdv37109Xrq9y4I4uyrLOrurmvalqvql2zrcHBRMoO7XZ+l0fWOfrIQKLn6dM9T0sfcUXlF6qqskd8ICUKQ6aOR2jeFtjNjThhDGSuGNtsUyuP/pUZ7W5bGmYfphZ3+B6Xvae9jlD+VIiiefJ1zqRJrdtczIQ+dbDHHnVmFM/xfh6OyZ7Sg31gD38cmv6+p+bD6dxVbDi/6Zg7A4C+fp3AVnJzMo1njT/T7SQbE1sy71VmdPtkrw6H53BpGavg7XDuZOGEsgnzkC22oo+lU9njavVQueO0z3Ht1GuO7anoo7m9YX8qK++VHmp6StMKO5yU93edNSvX13yByzxKWNrAqGB9LYAmB34QKDgOgI2PcQk3SAE0fNcNXxblW1lvoMOGByAboD8sXMvAQyQgArhBa8arZs5DlE5CGdGNx7M1K5R5WaF5sEwD6iDxiwt24Q4KxxnV6og6+QfqkZgtCAxn4NAgTybrssisIFQRN9xytT8lqILRcZYY+kcfffDm6s313QUVz3vk0epSHzDW1RXYi3Ug3mQgKrhhDJ+dMyZimMI06/XiDWG5PP/gGa98RGNMwiyUTTrm2LVMI5PT9V2mgfnQUblh25vuiDoy8A7HsXhMxJXyKBDcS37kqAX1aCWdfK8TLcVQ5U3pRvcghs6Bz2O1HO3NUvWXr39iTAUjESS8HEiDblmLQy9h/GlzOb1t4169uXl+w+fbfGq8dI4WxkSUWwPqMQS+FaZmAdrWDDeLV9v0NdxCrQ3uCI9Xi9qvoca2qmBAxgdGeK4mDrPnoXaeVqcEII77z188Y3URIqhSQzwwi70NETqitY8N1Bd7+RROinmpaF6LBDWe+OpZg0F0eNfQ82cf+9qrxeI5M/8ffkB8CNi/9C/887xYKTVNDDYhSDY+xfokFYc2u5RbzQ3pfUrhVoXwsFNVgWM4D+v5WUrf3+j/LOE4wugxDf3rjmrOC6qYJ6g2526lKjzOfh3cNsVdrDbEedl+fNOne4k5es+T9H3jsM63JlvV2yiaG1FtOIbU3Ni6yg+XDjo8EqQdJ3YoO1FspUNM+ipR1I9Qeyunpveuud9RMherOfqO+IOzB2JLNKbWK4BjGCtihnGI4UM8OWK24CFq75OZ1q4kpPvszU5XOmO+n4335FjfsJJmm6wRBEsEq5y9ubr+d/7ev33rp5CYt15d8yL7jAT+4T/8R//3//A/5AU8wTeEDvyC0tur2/W3338LJGExMSgHOrB4cfvFjz/xHn2eGcBYoUQWwVPod3+haIuXD5pm/X01iWgnCB6cRTFYjvlMEd4Vr91kaXVWfQDdNc1bC5dveIFhgDN4K7CMAgYffugXROZwAX2Lmy9d2H3+lVYWH7lnFtY3vYDYcCTwEbMqiDsSddh/bQvQ0hIahImXL15ePGeM9FngP7gfeO8b1q9ZQA0yvbnm8VOYhf74400AIRjLmdbX4kWrf/byw7vn58sXsRC70La2ylpkyj+qpWiitMWaYjgt3imYyfaclZ5SRtHSPGZJSEGAjZZodhPABA3KQAxPGFoqhxLtyrYIG07CjSK2Vme0r2/5Btvr1z+Jp/MgOZXmH8bBuJ986jj17u5LBpwJs3vahZeuRtP3RmgYYao3dwNG4yYUo2PwU5jpMFWrwR5Bb4xsuihEbmhBUYCeStvAhh9sA2X57Pnl1fWbEtcTue1FL1/9RCfBnANn1LzR7Qx3Hc9m8p87EJ+r9vz71uq6bj/P7TJgO5ysg2LYqdfoYaUcBsgyRH/9mtsjEFnNxz0ozg3tvH519W/8nb/7P/m7f+fq6icEva2XcyR1Y5jEV/lyp4Aneax0hVzlac1xH0KcqdTWHnYqOd3mfpfn6E0DntAUf9zo69Mb6hEpm6TYGA7h5MGr91iFjdQg6/GgbDFO99Pf5bLSvCqB1HdL/4Ns9dbnfseP/6rP3C9Ob2Uu/eD2GhU+xvqohETvScV8q3GPjvMO9hgb8Xg/e096Dyu9pzS+zenv+LcqNNV8gDJ0Qt7i13MN5J72ltJjHJ9c/9jYg+YJYSj4uY7TMPeUve72Tb3VZCfXoTd1SLi3eIjv5y7bGw0quZdezlbRsYH4uSs4b38fLuy4rWDXil1yZAo2Zf70jhluwFGm6gOVfXP58p/84Q/MsZKoF2iiAMgSaCQGAlKwAKbQUhYQ8Sgk4FeQLbIV/jhPHxOgC5FQaxRKZeCvgJRpNZIF+wjjfaEnqxbQIMyqhyadc3UNM5toZYSKYLIFC/QZNqgSOn9oi3Z1mo1XgwweRqsqTG5v5FUhMUk1DTwgLW6CAO/95sD6/Jp1PmAosRVVo7baR4wlJr6uiCGHOaujOr67xCopEFc41C9VK1KSHHZFYJ8ESvVkCBFM8YgyxCKo2fBoO8oaKMX0qETlOhiZlOtWky+uKi3Fsg+blGxwg4DZBslkhmzZaqSdg9XG2tAu26yjtnJuEE0D3QLdlnd8/IEA57aSahxxcmSG+9nF82cvvNfkwi5rZYXsDNQlau2PIQ0+w1R5QgETWly75Rb+Cqn+oYI5dBXF7+I102IdkdY9XFeGJH1jRb/lM1/6vlgBw1l0k7tWcNsaGRrCadIxaS3W0UBovqLKGpjLYdgpQh2jtvpCUL6dC5eo7s3NG76Q4OPtPN1bHjOSv1utfU/SG0Q4P6ofOU6IOnbWJm2KmmY3cRjMvutjmuBJjNrIp28Pk+rtEMXDlSiGXuS39LuJwPGNO8dZp8i78fYJrBx2145YdwBalxwuAbkoMN9gP67LfeeL8xCNXlGSq107OrYDSS7om/jOjcPm6Af03lO0sbnDWCOqufFWz3wvT9k4HHYUtnj3qo9Iz81h7IxQj9C0n2VOf8/djT578tZoe6tgMsOR7rLFMp2xmMZ5OpvSq9jrVRmq/dgiVcdqpl7D8empb8fLPoxzb+1QNdB3e1O/FjBYp5mt+wBbPgTTXHwtfFovbpi5FF8Dba+BCizvf8nnRflcka8GYs8pyUS765s538Ud4gmxLwAKsLQ8/w7UPsBUifIn8hKBKVKyppznC4Ae5Vs0mebPdhGIgFUAT9yzEJpox/sOXDRWS174I5QRuLi5ymihThzjSiXssXT5Fawm3IoTKQCXfhd0LOao1SBcicWGP7K1wxNqWlDJCjkvzETs3Q215ntOvpKR760SB7G+l0diIn+qk1CV9EeLs0/uzl6pVCQWfpJ6rTvDZSFhsF64O1QhlUhB8anDugph9SY6o0fl8lAqPemEq6opP4Y1Hv0A1+A/PGZwl7QDLZxvPiXCNldaOxhyK10UrcYHpMofDKuhBVfXoItfh6rKnlqPtoqgYdkhp0ukGZd3zF9CXH3DPRbwNFtK/SnhdoySfIHZH43qaTmYHLdEGRkW7VDLfBc5HtPZmIxndIFw+mTMGzejgQA1aPHgVZ0JKZxO/6uMWJHgQWRvFOizT9zqBMHk1kVOHCpgM0G0uoakKSWthZAivfoGdQw4dAGpuE95zHPIUEQVVhrbiad7XbXroZnZbmKj9fhPmPwEmC2mHP6zDo5nlG1uGCQn3jEph7r3bpP7h40LOu7mPmQX7X13Zfeq3SXi4fb2BNdbn8x56GaX2t64GrANOokWyseYlaHa97/LO79xxaDUVH/Un7orB5ong287SvAHtmPiOfyy7Ch4R9kntj601wO8J1zVUlNZ6BXPadFTUY6OQ2v2o+z2vHaaugNQ3YfsmDhKWZjmInRQQy/Uu3RQ6LTCqkpv6LD8A6o+VXikuWNsner/1Jn3lkLVjgzUkVU4tQuN1o9piCN9+PnY9ldiP3XHy2DQcIKBWF/vmvYb3rTobCuTmc9fvGB5tWhL8NaAC3gnUANVICMhHeuaMw4gEQQspul+Fgfo1bdScAewREQFAgPqkFJM2TgkxhLlQODlPyRAKr6qCMWwZ940CAmtfhQ2UJgifRLSIBdoGkfS3hSk2wXQAYCszhAOGaAPXm3oYjBy6ByYEeRhiajVJzZYiJCcakjFLdAHRwVlVHN5BqGZbCbqwAhC6croBTcKxrxWhiK0yKhqEsGRTdFAlbMFQLYiy27SsshXdapUj/W7OTpIFKuhLouhsyMngb8IWJr0SDHB/+iECa7kxKkQ5Y01fWllxa5CNiIh/7ihAJQPxH8GGWeGUBNzltDAJo2dwUbY4SijszJMqWaiy75RaRmqBFJzgb4itSIhUDa6tDL1L/QcyE2f9FYSuFnXRdnCaBVzcugeD3zzQk0rWf3B+tK9U/VUTW794M8j/2M00rrZfKOgXMSCCejGhaQO2bMlymVCnQhys87TCJJnlWwOpOl0tyw94h/SuGKDWp7/6qnAeFR9kaN9a0fZvdus8L2Sb4/B+ByxHck2ahrDUYnaP0DJqSKjA3sTozYSo0ujq3tFfiM+JgJjkB+j5G3J7m34sYs0q3wJmBXDvA2IVXejQDF5EdyztUmprZKxv21R33qmH9v16RjuR7p7K7LjXj9e3ykas4fHZDXKH+cGRqljEr23x/BPeQ7PkU/5D1N2Zix2u81h4b50Zoaj7zHTOw/TON/bOjTxMU6W3eI8plf0Van01LcpzwMpkz58nJ4jqz6nTOwANAA+iDZWPDUoxCd1fv7sghl3VhSDv0FgjAoKUwNEhBe819KFxsQ9y9+BGCzQEYoEgMIS7ASbcCxOmi5zghhgEZo4BpgIffSEnQ3jLHtuOHgVCn7hgCIca1m5hTWYZzm0i+8V53+BMcu0pTKpIjrqxwE+rRfRgliQLUlNKKeARHek8Ip/FJFq089kUwUNaoZSwgXiS67Qf4QFbEzLfcNbI29veQYA3PiJRhY/GRuqDDJz3p1qf6gXvD/n1psbhsiBEO+i+QB0eZf36gxOWfOoHdz3nfp4+Yzd3e2H1sC3CYW9qkjhnXT1R7oqxCqV0ZYxxpY8P6Yhygct3S1eW0ne4aMeA+gWklbWeE4f+SkRh7vsGhgpA3+1gepsJuVEuH4ZAIeeK7N8zf5uXV8JUKUT1cQyX6FGXFk7QjA6YSLpRLY9S8fYshsOFBuJwR94eDK4ctjBtB5F0JQUJZIuKze/Y3x7t+JJm9iAGyHNqNjvUiPFfQnoDldpf26qF/r3FCnEHRu0MR3DRiuTmlGRPqjLZDwLNS5RRzjiVwY2ZTPVDxFt+Hv7Bc8ULO9eLVnJt/yqquToxVLqzv0xXgB1HVWMn1s4lixIMxmVqbPMelOUHIdZfzP9fUV5hg16eCufCCY5d5089ZduTs9g/+HH/jfueK/Ge8hdre/3YfobVzIoqZCl/Sd6+l+EPj1hnBJK7Y6TZB82b31UfOLh3JMGR2mYVqOnHNTfM26lZxBI4zkxqluaZzIn1/REH7b177Rw59PmXOyI1eE2hDz2lKsP154NmdS84i22Exgjt6N2J7uj+leZrXbZDvZRFd3boEdJPpppt9s8WiEKnrY6e+N5mLi39Clq9jPrOC6wHZet6yw/250fWuLIq0p4cwiwizsDTsULUgCrIiwuFExYI84aGBoRfsGIeBbUDh4RV7hlX2BJxCO4ocwNYvAaIoE4ATONHUO8Tx1QhzGg1C0XR3EVxvIuRRc3qEkvUOLMOZbxRGjlP+GbQC5bjGqs3GhUBZsnMIr1LMamLrdDY/WgOQs4mpDBaEAyI1Us6gYRLjCfeRIZZfjeRcnIUhcGUZapgANA0QQU3C4dkk3GJ61Ym5rxZa8UDGWITAnnKCdGLYKFg5JEUluVEyln9VK4FI26DOqUK33Zo0PIrnSUoBDliRTRkrNMR7EuEYTUliFiTEZbTMe4qpSQLwuNkkikUGFr0IhqwGqWp9sx7GdSb1mQlsl4lZQegyKg1lkCyjoXK22Qy6+2V0d8tTwpPaiEzg0uIdrS7Yh+ejZLfnDDDm2r8ReXNKMb2ew75jhzcmtCM7yQZ3njgyk8K2KtfajdlknY5Y4y2x5Z3IveSqY2KoZmic6b0WcXIFXb2hC2tRHHSz7lmxf5O07UG4cZRM0Hlq3B9dmKJxmUtGXKoEl0N/UklGM3GFTxoU3fDpW/b2VP7u9O7SuQVetTbe2oet9C95s/7yICfQd6EntzvWrX0NyXgHGiOnIJzKnrfN0el3QF28nSOtJ2siP9qEQ/tuvTEe5nDo6uxFFmp0ylv1/PN52PHynEsvF3inpvO/KGE6nDjTA3R97Pc/SaD6d3ZiymDh8WP6a04nC4UsfowbfDSiryRBi2MnpY7Z6efOIYvfRv6TlGw6QPH/azK92q1uFoDFIDV1ABXVJgDSINmufdQufnvhX06pWQkUdsb34vpLj4Pmyseeat/8/yUSExGioBYy59EJNkVWEASqCWrol0xBeFQ+xMjDQwKMrPWCJOUH3fN7q8/Rz2xfovScLouxNvX/sw5vru+vb63FeeN/giCBIcMZcp7rcS2QdPC92Gumpd+xKoJEXCJ+sCSRXjhgZ5+DPlMeBLMSiSYkasZNrxD894OttK7cOgPFsAXOmmnizPgPb6/PxDVptnuPJS5DYsFImh1OCcJwSIYYY9NbOd9OL8ZaqGF/odhhoVQDBKrI4XaaKIf2wr+PGQwYeLwFPKQhoo6Ief/1SkaqjO2LZG+f8KFTGRukd/Bm/cGbDcoFV0vFfAHaLvVXhxpT68lZ/GFTenM/DJWaqTSi1/qkXqzX8dBsPDDwP3N6zZ6kwrSAKkY2p5d61OPwdGW+mAtw7GeFfrSc+mb7e89wl9PyB+1740fKG/blqslDVpVKNxtv6UTyXcrb4jbV+xf0i/W33VFmrDzr9gfTVE9m71NeociKCAFTjL2y9//xffffcjXK/evLm9/owFdX47gg8V8NFdZvEjd07azXpAiR85E2Ja3TZV2UO9lWOAseKG2JLA+mBxxkx0KaToez/4HqTF97dLQu2j856G6kUNCU4yw5sOjCZq1srItK0iQbTMx6Mq2J31H4vCWDwkR3JRDu/nfukOS01Lt66u0+IJZerk+BtH0SO96uIxMXw0oZTgzGbzqjFsfXqgHT5Oqwz/lv7D8l3pUfGJh3N3GI7S0Fnck4z+Y/Sc0DeOiOq9CKpOgdHhLQ/rSj5ec0amPnGEDz37lv6uYLhf15GS3KL3vtrhNncAtrtGuwTV1WfQuLdDnXb6D6qGY3V6cr1jQ+ETH6vrjxafWPtbq0I5PJ63vf/7G+TJK9ZV7amaqWrR1+WA12M1xyDsMM/Re7ayVaqO4e9lfznp1j4nVzB4A0yDIFAbdM7kvsOA1T/1N/7m7c317ZvP3lzf+ApOgNgarL+6un7NRwPANN4BQGZxt75ZMUt/t/SN7HU6iytM15xxa2xI8Q4UvuI+AwhGtAkc1jo7Zi55uQ4oZr0SNC0uzj3w5TFQ1l/7i78W4IVSwFmwkUtnkMrbRavWDjcySR0vUF2GY4Vcrmx4lNljG1ZCeWwuASxFIrDaBpSpRtwMhsqML6DP5wFMM93LF5e4YZIhBXwKUUzCcY5Qbfn69frykpetOqYJrHTYUDaFkNZIIIjZZlusBmZtfkj3PZRqbRVx0MEDA073QrHmemwlKvLB1ryqyHFdnqtmGICDRKxAuRqlNBOxPMQNfeFUW3S6s/Zj8I3himU/BR3hpu/IpNu+shOYHv38yriE7GzFeJIVKdekA0NB9nwqjj1RYg9+VT9xIHbA3DLWwlVepJbYLx/1JAL2HZ2wOOEzrOOWTA3PxkIj6KZk6rQRQA9a2a/1YNxaMo2f5rXHyhgOzNKl1ou/+2/+3X/tX/vX1pwxnDavXlxf3Vyt/zEf0/hP/7P/9B/+f/4hTwjwmqDrN29+5KPaDmTYmrWqkRUbPEkc09IxwuKi3ARgREfecR3nC6cdr8ddn61er/lMxRWfPiAizy5cpkWf/OCjj7/4/BPdKj/pA/ZFTZTXg6k40pwZ02MC3tHVkdgltrWM3B3H+5GcqXOrXJUe9nS7pru8fc379C7fvnyvmfToTE/f0Tny7NPXaDsiUEeFo3hv7oCqP8+iMUoPr/4Y8YerOE7yGEN9feSvAUB1gVE+V7+WK4GxaPCkG1W0srlxySDx9Md+nNenD1uiQpPaHJZ4SGk/H18jyJ5yWGNfl9FVEtUUvf9j6ahwvM8wUsZ5jpFyaqL8Rw+my4fjNfR1mUr1dZmW9pQ5u30E5niqZ1Zpz9/rvyd94hj9Hm1zxWAytofb2lSOVMV2KybAI7YB+iQjo4CHzQOghBl/nrUF55+tP/8X/7l//Z//F/5FsBioZ+20P9DTGdurV1f/x//z/+mrr7/xnSfiFNHL3dlrAJ9oyuuH2prm0YDYDIdkGQtzNoaMBqEJ0PyH9dWbf/Vf/1f/zt/5N9Zv/Aosk5oMNPh2Ep9ZxQ2AD7xwIivucs/8N1sB2YBOs5sY6F8EihxR3pdS0XGfVCX0LWzDhWLIpZaUBKYyfPH7aERseXF5vjrn7MiLkxZ8fpWHks/4kgImAeuqsl74dvvt97whPm7rvyXZwQAZtQyKAoyrICHU83G7+dLucfEV0FNGxwGUOpQSNAcYMtmvWZExpgdsbaPrQLTBz0sqQedYBBoyeVyjAvA391KgFCe1QwMjFKzRyom6+yB1707ACZpndIEU+N7v4FLqkhl/HW7OVt8Wske/4xNl0fNDPEFzs5Xp6honFA/yDACokfGOD7w+lbX+xqFqbS3SCIJgKmrfY1etjzs/ImvbyoOHY3MaLf9Z3IUfpbTO6vvF+WtX6bvavkYgahj4VUcWT2jxCGPCSyL/0m/V67iKZXPPX9xdrj9C50dfQLy7+BBE/oc//uV//g/+Ac/TrPmM3M3ncN8tv44vti6q7f6OxKqN8I9TiZaijM0qWMfcoNN3/VI3KUbRz55d/s//Z//Tv/VP/zO8AZQzhQJKGWycn1++ePH86uqKLBrwO76qrbbcNSIZQxpLNYfStNTIG2r3u9+4SmJK3yh5itT0d+TxeGP8XcPB8S7xnLPG9L6t5+nT98ntKe/Fx9/0nogM2e3GOVYPfL1gn96jYkKatkWxFP14nDNRfB+BawJbrqhc2TbpJPvd4/tGrw2LO5HfKp1met/K2ynPW6DM1Xr3Pt5oWiRQA4DqAl1H8NLJJQaGvup9uhXtkEbdv+AEYTi1VvCPwbtXduQ8HKPSudeZvcTD2p6ktK/mUym8V8/hcB0uLeVHun1vw93r6ltiOM7/0f1KcPpu+uSMY9N+xEoDsEKm9Re3b/gWwJKHgln8wzqP5R0fVlUna14uL58xFiDtlL24JEs5BBlcU4QtXj8wuoWwBSzdJUVEDH81IBqijvsAACD/nr148eEHz16eXbPy53zFR53O+IAqNyaAMCKwOkVlVQm/ClAKh1ECC7qFSSiNAU1brGBZjH8VFxlHX+VUeeQgkyxFaij/m2by5ytGEWJGXpYK7r/0laCZ9obKOEVcJeQyPgI7p+HVoacFuQC7VRNLqiwONMcGk8WFEDgbSMyPCrzGL8GHjjZHZtbYEoYCVDbSJFI7IyUVe+Fva2+g2GQJCsUGX9tR5DHNkmAY02YRHrtJcuWDwLUkKWKeGrUMh9glW17JAWLGeVuPcR4ycY4EqiogpKs36RXC7hhLxI0afFpDnM77ptLQ+KpCiLpUmQjooG0ncfgvTXPYUzN+K0oPl2RLpVRtJGDBw/KBg0OsNKVlCppp6RwyvU5FIqEgfQCOm+srvldw+cy7RPm2HQnoZ7xgN5FQF9DfgKTy7dTVmiUW070dEclhLZvbOpkhB8S//rf+6b/xN/6pq9evDHP8VpqG9WEAylXkv1DV0jSrURuaYmuHygyUqm5Hm09uqZ1ne69L9tZhE6K37Pu0BR5s8AlVPdiHX4dgnQFz8Tzh/HgH4djbfWft8hag31vo6GGsHxeKMT0jmVHFFtNGz4zIAfKWogN820X9iKdPF9cBfw6fzA9zpqT2ytYcfD/fsF2P3VzVpe9VLd2PLPurdqdgOv4+3m6nZitZ/heJCvaObfHty0zbZR/XLO2Qre1oTFWUq+xrBqUYiM8hnWGqGN7LNrW4Q9mq+zEzATM8tiDe5Nd/x8Rp2Y2GsXImCvSQMMMf/4MZ+D6ACItF1VwPbgB09m5XZpwxp1ggPBDFnXOTt58rybyvaoTFYiYKRSkBHhYIdApFwQC7tBw0xAojrzwrISxvzLkGRjt17OQx1nXK7wSLYxRBdWmiiE8LQ1KbtoRAplAm0/gvpfBwhCb+1Ie2NVeivDmWCWBVya1nqQhAOdgsy9xjzSXamW6PpTNWw2MT+Fgexi1Bm0OXu+vP9MmV5Q3zwYtap231QAvgN8ZgVlPTrdUQYj16KkwEyEEvzQBtnpYQbuODU+Y65nT+MD0PJ1EM8tazlFbrCCvB64RbKdPAdhoo/sObOFoX/uJP0y+nd12uRbQuSUIPj+pGG7bO/2jrGziqdKN+bxRQ6mIkJsBjy96un/JUfW0P3/hprdmoa0JtE1n7BEqlroSBgAWGodmiULbIbXYJbYjSEl13buQsTQplMG2EKY3zkOHhL0MV26W6XypmSWKOX4PLtHD1akvu7i6+iVr6J2j/wrVzDoFoXX5tqbpdIm6gmVlGg17RCJEy2znaIduIUYoJnKug6B4qGH/evvzs9Q8f3/I8gM4WQ9xs9bQSo5tdyiHK3JY+tl04N5s4pdudiGnrvdtaTs9tXUtPF98r0f+u1e/CpiH3ChxHnI9nkz/1F3n6m16K+t+1vfEZ2r/Z7fU8pqZ7bWGjYli1a/P0zfITHfrfxz79ROrvUcNcD/35GLvH8Nxj7BHFeHlg2214fiRGgTGRa2GXO6DvKYt2fXtK3SfoouLlCfv3YdvbEEUsV09y8gEivf69zvQMx6TfTWDnXO27WZ/uIzMne0zt3grPySHrazb1aEddVd19cKe1F3u49sfLA8vaMxkqKpfiuvzzi0tQhqgEQCJsYTVygRGHCAEmyAygKvAFpaqLCbFdrjxBPHFQdCN6YT6dNf0sKOLtkFjIwCPsmBLGxFmwF5ICRChMuoPMwIPqEUknkV0lpSumQ1V1RNEwsDYJs1ZERZvCMJWyQZriVrVIjpqQZC7ZwYB6YEotUciYB5LxUjn/cFg7MCQk3kGRv+IVTweL8BlmC9seWXVZEQMgbHY+O/JyURZ2sV1kge9uqk/lWrm+KNtUV6gc30VXhmJ6F8OqlU9PNNiGE45yclM+zuCW/oBlw6uoYdzIVtVrbKQ2GcuzVKOioUONSmvyTirn0cMnmUiuDFZQMAoYgWRIk3C0ngcb/DEWV6JNz6BHefwjlUjJW27INxgnYW+3vvIhbcpNdqzb55pYKiIHiYSLtoDJE8M7FUHCz549O89j8um0xRZxe4CKmv44aMwMpe7qY4rNFi8J9DPo1BiZC56jOD/nltwVdeRpYZoJaTWqyK4oP1t3iMqBUKUl0NI7RQN1emw6NwUTwqbozyJV7fX+V7V6wBP62XrwE2p8/1SNdaxePmZ/Pk9P7G67Hu99C9B4NTpUrd3zfG5ceEjHfNmB+ft5oa2SA/6Mro+r67Ykh8x0pH7Yq8PanGMbNB9z3HN+diPLsQr3qxpWsO3tKdM6HlbYvGIyj63z57DUTunoyeGI7UjtZo+2vjO707dCn97VP813tT7cE6aij6LM1HTOh5vfW60D/X9wpq89UMLffA9uBR+EEaIHkVmmA/0isAuELi9fPOPDTAE6PIboBO7t4vxbsJjvcQHAq8ZFL04BIo06sSBk0IgAOQZcqkJCeBILZe6Md+Tf8rDkR3mlvYvm0QOjR30ET6mmbRTc/H7Jqpib3znHvPpKG7ihT+EP/AmRAudiSYucOKBHrbjlDHegloLwiCmDF4sYJ8F8mo2gauJQZrpJ478PIzMUYdWUHyWIRSts3TI4wVO25cU3Wo0ubaciMqO49Mer8g2+CI1MDpDQoVdGDH1x257AR2i/jt6MgFiLrr3Eyr2cItG0WLMTPYv1X6iLuA31U6fc5RoJPCPvn/JuxGCY7NeTPAcSK9ajnMXPQQFSNWMdFdbVEjRZ04onuq2X+RA9pshbK0QvK+9TG1oVSV5s6a0DheDgwdblmwjk6wElq33apKKpx9YB23efmFh8544/yutfeVLuq3rpYiVY1r+746GO8z9VUNCDUhqAWFJWoYlB/eWv6UwNU1WJOM0AgJOHbpHGcFRgDHTKYzRogU2CB080zaUK+EiV5eShd0qrr6Rp7m4+XKw/ePaC131+72op9Xml8mh7YDBDlRhT87Cpx786lA86VPnQD+6a7BZPk1cFbTO/Te8PzF3N5nVYMpWaUkYN+xweC01UDLZIlemu/HtKt0n3WulnkU/9/e1NjTP6s2733PPprYidUtP9Kmd+rRrz4/Xvt3oKtXwoiTlvp35ucz4g5ltx7vydo3csh5PNlz3n1JcK8hayzUbvHFxf/87CFBWJfXVeL9EbkUmq0zEp+0UTxgC8pVocCurE5NBMk4KhlfYUTEg7SqqCb7uaEy82hKeKwEbjwdRobkzATnonLL2OA0U92y8iXbWer9F2uTiI6ARUcLBQ/OAmIGIPhMhU8y0Y96NPPuIZw/PLS5f0+E6SwhcAk8DTwA4hbQFW96TFM4IuVWmMwYFQhgJnlfnnknrwEp8eO1teM6holuNCrkqxooRglkN884UqotLYiB7cdb2E5XqGaHCXFDjZSkCTsgmWw25FEcQb/ckGs7WPv3FTIeugAzl4pDgexXVXMvkmpRgrRpjZhH3YcgSUwuwpUWU5byIR0YQT7gZ+UBEnZFBYq8oP/CNXaMmlUK5ex1gSH3RLhez5H76mdeST2KxZ1Kk35gqqqdWhSSkzsJKOjOpHA4MWj/yJdB1xyTvUOHG2UChs6xI32i2mQMG4RHoV9qhtyq0GhflDQvnRE9WIS8uVwTGy1UnKmC2EIPeU7AjtWQ57LCND9gaT+xLsWNfDkgBbM+RmGPXpLakKGePKIAUa3wfAL7uFNTak/KdGMpUKo6h4OUKCQUoG0NXba9+YYTIsxoHlRTwkk7dL6WFqnEQ0DQHdxFX1bmXZVCNA2tCkP2TT/kPk3r7MnGcjPfF6+348tYU5t9/TZnjq6v+m74QIjGd6u8jUAEAFXjebohyn44nBTKdjIJ10rFFvifSj4V7JEfOXPfsD0+MYeq/81LfDXh3WViYeG7toGS9YTWdGqzveFs94adixO2rYkdobhz3EfjQ8HSvvEZA0dK9N8YGI4WE/Mu7TG/mZ1NRQMVY05krhqSgV2x7dXa0P94Q9sm+BNOfDHP0eF/ZU2ytC0JMQSVjDEazEXPvyzdX1q6tXvG6wTWqKsNOrFCHN46qsE/nMVme9O6Xip4ZgfJpXiCYcxqlEXTx0d3sNxlquvrk7fwO0eXZ++YqFQM6EwhhXGjvCWYykKMj7G6bVz1Zf89bShhVxUm81rs/aEkSGWHBtzVIdCxi66EpQVrAlwD2gLML4D5BafgNHwmAEncMlh6y1kyBM5zu1pHRPb1fny9vXH2CTWfnoJ2jYyCgIJ/znbLdR5WCidsgXPjXQ0oRzQ2AtEjbqdttHIXdaVn+lE3FM3bWpY0iHMsrqfFUBK6s/xD6V4rGBemtQs9iE40gpGLwqAzQB575eDXvoCLVgEqjBYvEP+6YlWdipDx+asFro0TH91vMqk80q0w4+Owskr6EdfDdw5j8WM/evkrDDffuxkn4NIFtcsR+sflCzlUpJdnaS9Sd364vF+fcUoC5bBGlB3kkbAcYAPvoS/3koPjcgamyCYhShVDkzTbfuwcHTv89f8E7Oz3iRvzeHWh+DyeaislG59Hwhff6VPYfBB53z9pq7M5xNdANralgIuC+wsgZ3t5fL87uLH589W13y2e4Vr5h9Y7WMZB7bMI6xkqqMO0huqGgpDpXp98X0dvbeH9i29bCr1lRqSrm3Bi0IAx9+7W658pe/u0X5nRqrcuAXbSoI5YG/v3t1PYhI3bci1v3GPUjffUIT/Sf9st+nfat8VvPEhy2xyhzDs0fsEGkrzh3jHL33v093oltd1XNq3FKyNfc/Fg2JPLezGQDkGpfLhdeWnXNikDlQsGH5LfWWIzDbOIPdsQGrg9S+Csf0yDMIvfXjSRbvreMBdw8YQu0YgTkN9zLMCb439Apeq8d9VW7lgpA6/UEvgRdVnQZmuCKI2MGxd9e84/LN8w+ff/HF5wB55jVBI06sOhYoIITKTOnnVx4SnqA7XC6Ew0Amwesd8CAadAO6sMeDBHwAgJdn3r7+6eUNr0+/vjp/9gxvWPVReqpqcnotQpNkUJn/tCC5UlDIMsMqcMy25CNivE3o5g0gjFeaao9nWJmdFXRaa1VK9EoqJqNWouosEGoW4SGLJXcVMUjmRV1RgBQ48xz05rDDyFh3yv338scfw491qtDKSkyVtemIf5pwDxvKY46DVdVh6WYoLSCeEEeqohFZNVq36Cx6VTZ7C5sbHHGyWSw/0CWh6ukxDjXfHIOV3fgWf0Su0dM8t0Y2RxNs6apUqNEJc6qjtQpjROw3tC6V/OCFL9WkvsJvRwIc/cwtT4vAT/2ZY4/niU7qynuC0N0eY41iO0OcY0GRPVXPWg8xhVLWGukAHyngixZWzdn99GxrziZSl8Ge7vPW8PBNA5W0cpu5IqZK06kaFn96+QMfPQD+Y4m32YLRISLLP9fVWWHSKOSDaGD9DHJIMablS7+8MhXTPB4tD09dG2T04D4AEp/R+Oqnnz548Zw4kMZvTde/8iz7RHXIb2WK2Gqhlb0b5GIZE3vZjiWWlRlbxyo5hW/O1FjvMXGK1qfhxXRFdc7Jw2ZKqvf/GD3H8By2+1vpzxoBGrBv8+ZL9SUzm9Q+N5WuAUDp8YKRLYf8Cu4TezxtWJW+o2mrKlwK2d7COGzH6BNmH7Wi/RQ/dpp1OovQ2nHmSl7i7Hf01J2ZqbZ7XDuxjXaMHlDOmuZxmxsljwwkxlHyWP2+9AnSP1efnLMLnWiKf7Y2XwJD04de7+de/WmLYSczvsM78CY6w3HzJVeEu/a+L8vO1l+KwC7/xOsv/52/9/du+DYY6B84xIx+sJoT6n4YC3gTGCQSFovkXS3NT9AXr0LnOwPAFOWYxwXiuL456ypYQ3P7e/R/+PErvmzEW8wFOsJo7AddCXjaxKauakegmL4OSNQKmXCj3MUcQV2iSWwJvs4vP//yi4vz57gRiOa8unjNSqOualIZDZ2d/XVLC9vJovoCV7liYorjx+71JRqaCwh9iT6dYDp3efb61Zv/93/x/2JA0nRoxLhu7ZsfFIwti36xfsZNZUCKYyzprdZ6Fb/wBJtRE+VksFB+qZNSowl/YLDoNQ/1qsfaWwRPDs09xEqheZthY1e9eCOdQKrbYpUO/tDIOB2e1joJsrt4rG9KZ6ONaPHk0OU/PgT3N/7GX3/2jC8Eq9n+oJdqlI3/KwhsGW81x6vOlD7XyMhcNlJDrRYzfjOiWJz98MPdmzefp78J8fmk2+vXV3/8E3dIWuyGqMBsB7ez6Qi1JZM4oCVetqpkzRL1pKP/M3/rn/33/lf/3g3f1FPId8UiFyncJoeri9vrL1R7zvMYpQc1tTiKbwcwyiV657wKlgCjk4/j8WVgPtV3cfn8g+fPn794Dg+vA1JGR1s844k7NdamckqLMCZicWBRh9vYA5NT5UDfqEvR3G68Jk8YbJf4mYacFL8NwljXk5XPXYGj6Jjfpt5i/zvbp3uew+lpVAt79J4cX9m+I9jE921T6/dJdOWTSPY+d3xPkHyM5kfVccb3U3X2/vfpGfX5+gpXiD/1p/ocb+g29t5nAA5KPUnh3t5JRzym/z3GgSMvW48x8Q5kH1mLivMjlbyDaj7YxN7eNWqr6o/ZX13iEedQ+kTgRaIiPtr8PIvX2MAAoHdBE2jj/MIlNGyAdBFYHlsUI4gE/YmPxhFnUuCEOlr87Qf0uz6C9RV8rUnt6gdy3P5eO6s/AhxXPgCKVAN88cfhTbzKkV0gcLCEGTYNeCnBEd3gA2b1fV4mVC1ZrC4vXjx/8UIr8aQholiJY3GfXeDOMO2ri4UEh1MnXmkwXSqALh6wCwUNAyuhwPjaxSQ8JlwjNKulA42ptJGJV1IVzjAgYFGVUsJuvQhl/ulYM6U08UI4huNN5s7hz6KpUUGUw4getMgvs8my0OxCw2xcizF8U38WmVQb0+bEGTWOERIxayUzukDyqaCs5A1glahWJJ8BSSpWHIqpP5wumhJDr54//4D3TuV1oizCOReey2i1ZdeeiVhn0GlXZB2WHcH6ZBe2KpIxXsTQoMla2hZCe2uJCjpOVtSkYpQaKrjSv+ld7a6UAdk0TPPIkGqyDiQ/+OD5Jx/9zYL+FrCpLO7JlTitv5S++pSM54cxC5jnjaELob+jSIcB3DFI8chDHPO5Xwy12KjITUr2lR32ca6VN9pIGngmx9I1IY+EGVtj+VaitcAQr62yd5MxvKds9wfoFG0HePc12AH2TdFJDbARS6pqV/ty4NT47Cj8Lfv2I7DdRNX8/Ql/uCfJv30H4BiPTx3HzOlsnSwjwpp13qrNZF75sN3DpeVDde45fx5Pr/V/b/s+wLQWD7A4VUL1T577T8iOifwY260mHqiz/k/6wCCx/3jMKHlLcjIbsVU6zcz5gx4qxg/zI7c5f+bs7qczO7sJ8/h+bkie7/s8HHl2Cl2LrFjgiOKLi6+SFvAJk/KdIxnEJpkNBXrdfGEgxtWHwU3wLG6+NCk9qEdP+IMG+xvUFgiKtn8SRCSC8mGBgEfBIjzaKnBZNRG9UVtAYqlrzNoDZKNZqfNL1uNcMFwBspHltUHr9au72+c+37nkfaMMSXiG0lNC7Xrlprk8scmiIazc3eabsuuPDOPSZTzYkmkDLwPYKF1/jPhi+YNKBq0qWPNlA8ZIvCMJauqSpRqlpqoPm7L8sWmDPV6XoqHIKX/ErTJHqTDWMEWJSBe1VJUTaNFSZqvVHFMJqEmn7avK7qNFKyqOq5rKv84upU5Yy+/muhw2halhTeJHFs0CWUvCYaNor40lQrf3VOiJemqGDIt9+OO1SnD6DTTHMJ94h2nFyn4rHhmHnQwU4phDylzHeHkodwwYBXwXf+wJg8US+pghK6W5jVJB4yHaa+vi8DG92cVo1AWf7TZqs15QrMfy7ovF+ou7s3+SKquTcVAFQs8raXVrfMRo9+567SutHAPAV5EYhHVO0l+iSITfb+G8vWMoglgWNnnKqAHnlWqqVHF7/aUmVn+q8wWuckmDxVb5Xv/+9I4TI5M39ea2Pbqn1+Tt34uNsm36nImOPne17FgOJ7G9x+O9MjNrFnpe/EfbMc8A9L+zfbq01T2Bw2sfplE9xm7v7eH0plX28U2t7+OaoU1+s05u9xnFR5H7PtOnJ8KPquNEWxFO1lnXwbkzUaVbXXiP/sMNqYL+DkC5+Q73/enXp9+SC5i4NyBvyfRTqf2l+19xeAcNMWfirXSzt6L0wV1mvzen9ZyGFuqESQb00WJa2cyy53wSkQWFBF7zo6oDDRRaEvCUIxqCXfClmGBs+CWISTjD/zqk/qIZgTh7di2dn+3UB+7Cm/5eqrWETLrl3UTyMBjI61yARcJU6sI6aV/iyI+A5cysRrhcRbKq2ow6Dz3ohj8QsTkD2ZrIHj1DdaxfnBAsymCW0Yw4tfg5bKR0FmMqgshmVTXV9smnBCtlMmy1i2REw6LJGAwvWkptKS42g25e9cOhjRpDIV0MKab24zgjImrkL2OJ0j8GTgHQsb0lcY4CzdT/hJlslZdj8UQvEyr4DBj5OOG9D15s790LxHzFvSW++TMKXaXPCEHwjRrSuK0mbzOxR6w6D/t4oCeVNLYMKxwoxj31p0/bBCzTkZ8Owq0u0tKMZrzMHhImITkk8CGR1FCO8CUx7Ep6oKOqXLSYP0elHBLkQYl50zJaA5Im3Elxr6imq6fEbKucBTJlt9mrA9LoBmzdprrDW3Ec5KMwVTms6Ocr3XH+eF93BJ+2Bq1dnkjp07r6vrfoEwXtz1SNfaW/A7AdBn8TuV7sjj/u+MrjNuOjcoyAjzwP94xvOsuzpcM47xinj+HpbO5PHhiLW9PBn/3CR1PrqlHsvcXpbPrDVhkecIQo9U02G/kDKraLev/Hkt4ExIfNE9xT92424mH6m7fdOXKUnrk+0PkzxuGURN8pTpGb8I4nQmsFIUowR4MVwUyFS0IufgAIOI23ptA/FIhQoVPyw/2EMibqKRgTrja9mknWSsegZUEstY915MuceykwoWpx84VzrXy92C3g0wI2oKATw8I9Lmk3ax8d9cFfoRcPNFAXUVTxqqj0ahq9Pk95x/0B+a3V8gcLmvdiMvkDJqMgdn3PTFyCzs0NmG8v2C1XF3kKmSGIzjTnU4OyXvtUTr2qkCRH7ULEvI7EzQKFRC1CXKsbMozvcSjy9s8xItV2kVC7ktZNZJlcOjMlyZcL2gpP4tYKbL8IoVD2OGRAcK5pR1XEUCyPkYg19/6yVFCbPmnpM8HycpOnzWwumBmEibTPvkN3XqhPuwCaeQNsbvU4sOLhgXM+WZ1r7M3ynLs0jtyC4NGlmwQhJmD5Tld5MT/3ZSjDzVteIcXiIsTjnnViSp9P4FG2vLv5HO67pc/SZATJu3m+vjVrGw/3LCJoNVL/JGqXvmOLG57Epw6WboQQsyGUNlBk3NwnFiSqPHda0gmqg5TOCmbdYRusRPvAHm3drhoqqjvq/mS5sreswwl9VfbySpz7vZijzyo68WpZV2Z+axLgWa0PLjjZ/8FSH1vTJ9ZrUPP0x96xY7RXhIvz+GgczzmHnY76zS23+tj26WOqN+E5we5Etgj3aMileEa0J9NQM6fe4b6u/n13AHL16Q3spA9r3WG+J1uOz7h/j+xJxcc7Xf3+1N5/rzPvoI73+vD+MFQ09gb5qQL1VHren6D9fJ6MDdUSASeBU2NJ4Ak58TSODvRkRKw0h6VVhxwGlg2zclAb38A+8o2JMRBSAiu9loGqyQfXhEFMygKac5b6BCnyxVTmikPjdSsOCNrHwgLHR6+BdOgBa7pXERLBr3ovhkxdhqpoLrUJEJTPbEIj2kOrOy+pPh7tl8JgyfS0qmWteEWSXNUxBikNrLbIRPyIP2GLRNhLVtcGaXiLsTlnDnXxzAgo0bKViQBCMVVVjkzpV9gaYEApZ9rRYpmKtEppWGCgIKqjayhwWU/IFHkkCtY7kWkYtISiseliihsjtWgKGzwJ65R3miZNFh9oeSfxteobl3RIzK6FhFkFpY99TJcJTbe1NFURbyxU3PAk7mXu3wq5vsdewZ0N6u5SH6SxLp/C2IijJM0VSXL9Fc2cZYZKOr5ka3kLKpaN3IrVEtG4rZ3kS5u5ga/Etvap+RZlzChYykbSXCKm5gp36Kfw7oj+ln2KCNAbfmuDpwjkL0jH5gpwqPX3l50Pc6vObQzXklwY+AWc2fZ3sNnRzNx854z2JyZnnLff48FSP088nUGfUga5Bx2PGHe2SH4d/YP/O803V6PpbPp0leGpfvcRqPQxo/bZ/tCZr5471mWnjh3j7LxRz7MnneiVFUpHQ1POY2o0lZpSjtJzRB+Yar6PUrUc63of+3HlY8S29Y7kumSIykiJEQdMIbqB2EAdpSPyieFOwYCDRHtBQCCh4DkO0TZoio5OI4puvuTpg7Ozn/Lmxq/5+m2MqqAciddrXvvDOvLBR3A/8WdQABx3LUlBVt2PZyzWxmr5XXiRxxqiFinwaBajMLHc6jNWWkRb0C/1JgfARc+5di1izvgC3Oxnk500DanV0IUoGFe+QOD6cyDngtlcblysP9UuX+plr91ESQ/jww2cTHzzbAZmAk59lzzfH/iTaNdruPzWKGnrWKMbUDOL0X2XpbdHqJfAdv0ZVu5WPPuBVOprVGJX/mi7+RQpzkdDVxQcd3JO+Mx9GPhZg+7eKqE5VtQTyE104KvmwavEySGFIzNqFD0u2cLLrLnXqw8Xt5/cLX+C1xsyAndVMJpSzfojRwirb89ueTSW7wnQoDw9XnZhAtajlqMCaWQU5HbQ+PuWEkspjn7X1uONYwhohJr65feRKlQ/QoSIts3OlIFlKNY61kgMae1LHbb0xXjVKGHAUPpdjuWvxSUnh1bJh+BuVJPoDtLFaH+AV/7ekMS2FceQe/Cxwwkx+WBFM4LH/I70onP8h6/Mc1JovrdWB2R7xw6nac97DR3WUKUHlPQ4p1dVdM/c455h6GX79OEI95wPTM/8bvZ2n6QtjnTv8XZ7DccY3Ve7avC6SOzvQnWiz3QM7gCU7NgBKzvDHi9H1mN8fi94fnaPK6gPjkWJ7yihiX72ej24Rr1gX68+3fM8SfqtKn8SDx+hZOtCMNVzsO73ye4Tru6XEgFZbUEi3SWFfOumgTZTtwrFCAqzmdgAk3JrW2hwFfBTtiHwRtHrAN0BElEWmBgOOIVULLxZnfsWIGGbT6yu1qJM/OOfWsfdoLfRxdySihdNVS5/EGDmn6OAfNSnznJRFShga7erq9e8Bujjjz8CMgWTIiPILkDrQZXW/279ofvzlwLoNW8rYjDwAgeE4EJbF8+g3OCe8yk2OPkM1kBfP1fnOXsrJLAGEBdsZgmUL80XXmfoET1qiw/w3+TB2YufnEPHFd64s9RD62z8AtN5uPZ2tbj4kPrFCXiCsRXg42gvrPLqRQYqGyuEOxl0UqLn6ST4bFr9+CWUZLwEAZ3UCq/MvHjxyXJ1uTi/Qhi2UoU8G7asuO/LX+GVUeGmDnLSw1DHhDhV0rK05YV7TaskDqTOEMnrVUYbDC+Nj1SbpvSSVUAyXsqup6kQjMVbVkyHrrFs2oeSfVGKPKaLs99vFW0Lxodm2JK4oUmSlJW7o/wmMbqzIU1TMG1bm7LsUIr9KOU7ku84e1K9YH4HVXoHJvYG+aRQ7NXwG/FnjcBW99zK3OuWZ/h51ubm2tb4j+uJ/A6xeckettnRzMy4bZB7u8dxzHQgNP0c+XQGfUo51eNTz7HZSM4Y7mfoe5Y5es9zTLqPQKWPqdGptTjGkyfm6e5Njf3kASZ62T79AFV7RY7TuWmT8b3+o7Yqm9JHhv2/9WIekQSXBGRJ9+8LUmeuFd0Fg2RMIRgpwLYmiqMlw7AxXGU7P7EiuYjtMDexlAph8Qf3zp4xB+6EsfTSJ34rV4CEfKoM+Mml6uaax3BBkLfffnd78fJlnAP2IYU4EiRxu3zWFEkdqOvDnW8BAiOnXGBaDOK/obYKOynOAW3wi57x0Alppttvv1iuPvmbf/OfxSXAGTzICtNuv1DD8jtyYGdpFOLV3ZdVrhd3v6/6SPeeACD5hyBzQd7i7q91dcc8vH+tmkIzptBcjlqGjjhtzd2KpqdavjuLNpC6dG4RFAImPMy4E0efZ9AfLv7U1XTqmFnzhAWDvIvGUFLGP+ynNbx5Ag0Yr7fFihbej2N6GC1kbT/h4Etc7M95rmNx9+PLf8TTGui8vf5EH1bfOWSJ+cXZtxp41SqYyfvUz0ihwWowZkgArDgexx1rGgacWTuIWS9evXp5c+2nLa6ursD0vLMVBpeQqYSKwA8zTRn/cQM6jlOnjDlSIQ30mzZidSAOmSjbLtLdKBx4Bpm5o6HNNgjEm5FWLxUd38fV6DuH/I4bye2N8x2l3kfaph/MDW4cZDq18NTfkcP8c9U5LHXY59XXm/Kn+s3daNxOzc3ib3Ptz83O8ecdR/2v/Cg/F66RYS5x3G/WnHRH736jO+pW8slsbWk9lJmzyAmwP2JH1GJqb2rl3l665wzkFu+X6q7rwJZ7ZsY7AKRHaQrGtLK/bY+KwGy3eJTW1tW2WvRxCo+Xfks1Ot6B3zifOgIHmzRXg+x2zUoskGfJVmfsMl2yFECIOqBfcFhR9+/LLvumJdDSHRSpPPfplLYEsmA1ZpiFUhQ5Gyz4FuX4IAB4duUrZYB5d2tBni9wUQf7iAdO6wZUYB5F6PS5UpKZ6V++iRUQZdAtKlKGJ6BM15aY1TYCijiZjSYcADC6HOX2De+CpFQ5RWAFaBZFp1HETqTMwTqRMJvRSZAnJIiWFRBVOOOJ0JUqWXW36Ko+bBrkv1VzX1uviAKhdJyLOPy8hTOMjnooIzs4bO3VpUlfxJNgEoSsrAIgY05cH4O2i4MEZ/axaII98aF6pLDKgMKxQerKnva649WZ1yS5iXFzw5iAZ3R9MT9fzLrO7Qn9Gv70GZ1i8nJXp8q1GNJJnU1VisOkZX7KmlU+AHra8+WPL1+9esWaMer67PkzKKzw0Qfyeqnn6rXv6WxUaKupVulmM2RhbKQyX5k+3ShTUhVEf1OxeyjXdKBVfJdhJz9nY4etZU/j3q/jz4h6bCNsh6S6Y4X6UFNvSz1h7mcx+oT+/6aqInBvO459bIjY9jMAjTr8Nhw4+fu5/5KajlcGGz/nsR8z3RsdHD1+BF9jcSb5xnN+LlzYffh239gRo9Rxr+k2Wx8N/V2OhzvzK5Ps7k31/aTV8r7Ij8HoZfv0yLCbOFpzCc7p7M64rS62M08/9o2evuvSXuwwwCWYXY++I4PeIKtGTta0aFsgPmxbcmRkDFoSdQ2gZXBy1DJIh6GVliZZRs9Ee7e8vGV55ntaeAvQt1y8BF2jIsGxyjAJ+he6OTDIQwF6Ac6TWewe9Ul7AXReWzF26CfBx5hIX4TfPEQIQMKShXTLi2iq+iDdM4A+AwA+N2xthZiLr1VOulbh8zzAGiMMUr6BE7zLZDPLbJiKdsk7elbfIsTcNDrFxq4zRw1ufQNOZo1MhYiBjRPcqHe5Dps3Q+7WH0tZfZd6Q6SOQGMxOqzWgzRWSJ9/n6dskYVKq6UG1o+peAG8S+jlVy74HETuGMC5duPCIqWPOfBeHSShhI4Uc+ofWc57mVjTf3vmwnyWCHG9FD37NAQ2GBKYhpBaotmX+txdZOb+HC3W15idn0OjShffIY82bhDAV+HEB4vsFmmSm88i4bysatkSd28l6JAOWJ2IO9rh4QE4bz6Bfn7x7WrlYxtSvQchMxuJEsSiIzQLeLZBO2W2pcIlc8xGRNJmi56xdEPfTQ0qqpWbNomD4s5Ihja61LZBts35RaLxyDEUF/fmPG3SdZheKw7ePxxlN8q7q9NY+utM9L+tc9fqAzUf2614xgbeK9Lb2stwgLh3jh/+aqm50gMKDxQ9IA77tXW/0fsZgn/GoiezO2rcl5haKcpOU25Ej6jFhnlITa0MJbPHvZ1n5zqw7eR4B2Bz5u5eInat9Zy7Ze97viq/N0y96ydVsXT24r/69HtR5Wqkk5rq19cwAp9D3flQ2VY0YLynVeXYq65EZ6W3NJeCtq/DlhuzWuQaNTVAFgqAjInbzB2DpgNv1BtESA54mYlnlokL3PwWrytCZEjsxIFslZHcZDEBtBeiQiiaOBBEibFgx2TlB52TFjsLD2GBFsClrKg4uDTOi6GdE2cyGydElggImuGkoD4RhYBGS+wmE+E6nIdbQd6OQzKzjhhUl68kahomoSxwW3jNACTg1WKx9NlNap4gUREeg07F725Z10QyRlJV4C1q8jw0GhJcoXD0EKnGjx6USkQaH/J09VhXiyIA8geGA7KVJ/aS0XlHzQymdxj40u1qRWTgs4EcElgPxa2Q0VA6/7CZVio9+Gxg4YFKFVIRy1VuCBuDrdn0peWj3JsWtelp3E1DoEitfumONWN4GyZ90gaMBJ0v1JFrBQ4CQ2+EJjEcGt8RBw2Uzh3mUKuolWxl0lMHka2S3oftgoH98HH06DDbUPoQE4Psn+Oxwjv0pKGHDr3gkRE5pu3mGuwY2Ue695v4E0Zg7Ej7G7RrThjIZSPpMwBDulHv631a6PQNUrPjlRPnOwd93bHX0Kc7lpOSo/fT+f6qRcXIih7YJqO6Iaz9NVf5R82FTKzseDQa3aGP2cfMGZSSnXWHo8W+Xn26mX6KlhprsUf/Pc0zij40cV/kH6oXFPpw0UhW/+WLHKVnbJA9ag+VDezHze3J3YdczeC1L6WvvnLftsC1IVPHXg5Kc6qGEyOOGkUGf8ImiothQWkkS1qVQFKAlyAPVHz+DZg6AFA3CXGm5rW2XDlDLLzkHS4AUMEws74CO/4EbsGEgFEyIEXAoQt3siod5twlEAc3T+KGXAw3sCH2ct0RknjC0qLxKdQgSlC069nBp9Fu5Z3kzqS1WH15w1gAbVQgXjO5fpO33a+XvJk+dUdF6Xdy3o8T47voVqCf1/gwTY5UNBgcfT7/gYSYv25KOF0N+Ac8I+dredjne7qJrehdDdxFAYsvzn/imsXjYS769xkAVkCdy69F5RMHlFNK8PHtG0wt7njJamC1L+HhOf3KQDYAAQAASURBVIEbfGBYdOfa/bQGLUCJ8aQW/GN5P/yk4AFPYxEHbUgbCCDOGISoVGxtPv5sMptYD6g71t3rVeJvCxhf/IFKzL2FQSmV5EvC8FDKzR8jFHK+AXDL2AM57pZQ6n0N2WVxBGLItKlBe4T/apjJCIZCOeG9+dIh3epPdqd+xa2FWvJYG7lD21axGewe2qK8nS+cg3uZG3FL9SGdQ1kJjGLTewIDY3/EWJMYrk59qek9V/Jdlq38HP8cfUv4iTJVq53fwcfrtmW8DrVfBBNsw+9mGS3akfvRw6ZqXmxUToK5f/a9yDS2U8q87mNLSmdxz/WWY3Ud4BvieYDlZy460cO9bcFZN/xuTmqTpvVK4tWx38iNdwCgj+d6/Sz2nH0aKThr39N/UentQOzEpWVHnjEwfRUrBj3lt/TPEIG9bfMz+PEOTI798VhbRwsczdhZ3tP/j1VzfJttNJqamIQoYFu7cgSULyKTTzxX6IwrmW9wl+Dcc0oBoGzhcwiRBJpNRVDvMqGMPvFmyMBnCvVBnjDX9TTIUwxLVm6pSNdgIj4HxUPmXZHsGR5oBn6vyK50D8JEqceQUgIiF7miExALK2XAZz1CCcA7IFoBjUFwnh4D4QA6i15jxDLUaCmgmUVQAltJvgY0QbUYVerSNozaQZUqrBm4d4DaZHSg9rC0d4mSykdzgSDqZpSiM+5dwwM7SlVl6Axh/Gy6dVYTDoQoIyF0t1mx2orKqFIllDz69CBNrEM67ZZmMB/eklBzSHoFvVoKERc5pQRj0eYII4K0ALFKRayCgXTwsGlAGxne/LOO2h1Cqi3TbsORZFnqCGHYs7uPhfLS1cveJ9Tz3ptG/Yn6pg7da+QXw/CO6/YYc70s6b2NeDzxF9NCf96O2ug0qhej+c3LZ8+AAAOAaV/woub8lr3HC/CwmR/Sxx+Z/tm7HT/u6TX06ana43VGtsadh0I2zFj0K+QO80+dqhH2lN6P5Pr0lPNtUMbZgnuVO4G3b+tH7X268c5IjTMc+1Ru0fqY7NG/xWum56/CKWUi9F4QBEk751rvl5Cmz5Pe7oPHn5jFuc1//qfSnmsDyZ5nm3PHCXjb/cPOIySO3Bokk3urenvnGvVro7r4dZhX3q8uy2WRJeBedQTM6fngR8CcGzcAmAMPUg8AVB3/oqmZF18G8NUeRWJuoCN/oETgHojWi6hXRRAqcBmszZp9wToyoZDUtFhaqOirNLFOaWFFeZwCt0kdDLgJu9VgN+BDxWltA8/f4GQ9iMxEOZu1RQvYGh36U+vpBaM6C0PimdnvSiqSmnhl19FAf03jGM6kvkjzzEDELfAmACXULqUwUpT7HXoWG0j4CxIR6qUqIgatDYigkHban3+SNV9Jq2Chdc8zBSTly9AF/dxA0ArXEPb+BsEVcypQNo2pAhWO2ghZGgxn5Kcs67OMJDplQ6cZdLgzhgjQWhBrYywJMRsuoSTLpuRE3mva7fXveQo5PaFxLS+/xYW4158Rqomh4Sh7CIMBCXzLAuLePm/x3FYupjX5RoFaS/Mc/4PoZeSw4tl5xxmLs1fymd/uOf45ejM7o23LqY7nmF+Kud/BLZ0HM+NvbgVW3umv5JRyUGdfiIcbzX3BTHqOeRrbKeX43/EZ4w/9ts+cujn68fGs/lB6jpeas3s8/URbk7awGTlJiz7Xpnt7hh8/3xSMJzo6xvRONWbV7/D9lt2KAOF8q5Er5XONtuXKb5lfRATaORi8U+3aKPu839fwh/rbPn71Fr0v7dP7LI80AJ68h6yOvGPioHYKO23qTzAGYcvAZGy3t3m4lzXtYLs1E9HgUBH7+pYX/yPmTQK4g8kjraLMl48GBHogRg3ICeozsTEZR4NVgxUpKBAvrEWAh1LVn5EAFgCLYHmAda7s7pQXspriHyTxriBVmwpTlA1vg3dlC38JwQALaRE+7N5igL88Zs+mmGVsGpGnod6yVTYswGqxDQePGIg/KLO4FMlW2LbsJZApM6byaYrlMMZY58ItVGa4ZBxkyGaRzkeiyZaX5bO6CCEZ6qGDhCG0StsYelj+qKUeYLDSYVXWtJ5Xq5h18NB8QYNthwYjbHU8xN8M12RmsRZfi8j3IhhZGWpa1prpj/UVIiQSNJP10Rp6qwoa18Fuq+wOsSs3ebh0h3k729Tfr+F+jm3FLfcgMSOyV9svnVj9a1q3h1UYPaXw/QnL++bP+xOZ99+T6oRjC1Z2y+2hww1HC/lQZXh6GgSybLm2JjXsil5GKj2U3H/sRtuN+cRxz9TEnlH7o3VOrdS4avq0wJRzjlLj/ulYvx/J9ek5PU9FH+chRoXHUEbmTWfp27RPj6x7E0e30akxmfJPKb1He/pPX/zo9Kz+PlaAP064PefacAqPJ93WGWcjbObeinfYl12/XTro0Abpsrtjq+jswUbyBz8J1GbXFGqXK8dXanX+krmHmoM0+VSb+Krf9KvPt4w+33zBuyIvLi8+uPjonFEAy7mp6d3Ns+fPf/zpx59++HHJ978UFk+KVxd+k4tPA5dCASap6Etpy5sOVUnTtclXlMGhsAnLSTCzngY1Q7QhiqrLerPirH8piRoYMozxtsBwyS3orrScabVmX72Lmy9Ve/4tpVlxzkMB3zTvrGT8kaOMo0IgW7cjUhV0RjcHtDn8oEvo1d36C4PCV3UHClrSOctnNWXOCPSrmexAv6Jqh13AZe2TF16frb/Qw/Pvoy0shogtI4czv6mrsDb0ZBgIYavrojiLUUuJw0hPLaOnrfO3lmlQOfmnH2rnjUDI8x3lBNMdWhyv1N0Jsfvi1j68WH2D3N3151Rkce41ar32ha2pHKOIrPbxGk7Dfr0454mC/1YeetY1B36oJjVuSfeEoSQeDBmP++b+9wn2MnvT0ey5P5ybA9eDtEW4nD0sP/H/MPvg1PR49O/CVHRKqXfeH77+97/I93B2BojJWMMxvTdQPWYYf2GLE31jotO9Sfa/HaO5TfG+1JzCkT6nZ2TYp3We9qTtNW/miUpyFe1bfFbve1Ovvg/MejsU0LheydmGiyTNuuaXuq4wFpve3iA5AMgFM0eLizWdJTtpbetVkN4tHth+O/6qI9D3gl91Rd9J5faeRC3EM5H21NsuKiXdXhZO7F55n+5rNko1ldv5bTu93FYaoeEqskV/eKYw98a8NRKObTQmyfpvvtz0/Pmz/+3/7n/z8Qef8DHYNWBszbOkvM5x+R/8B3//H/2j/9IveGW2l+c0TYqHh0X61lYM575qXhY0H+Bulr8q42i6yyvJ5rOztRCImJcinmrtNnFxywpwGzwttZZRyIUbEJl1Rmk4aW1wIJjXIfJsri6CnXLAK6qkjeA3gDWjDjkLajfuyJDWkfgIZFdJKJhWj+naj/QxW6JGUg3y6acVXvtAsLKppiotvWGSHsbr4ilqi43l/NAiogYyCQ/faWYExWPH+Q2LuSjMnQQGDPC32KtM8bJPEhFU60u0QrCz0Cx8QZmxw2tDZ8qY1E0GOWvz2wLcBHgj4YaXnBJ0FiDl4Yroy6DO1tG3uIwp1OmPrtO5WOjVPBuUekzhaKYr0ZVUvaM9IhmfWn0q/QhlO6L73N9h2ck+ceV2tL8P2apheTJNH47YWEqilz1QL9hGqQNs9yo80twBE78V/YIjsKd/QKo7AFWtsZdVIksht+YmQ2/zju0NJEcH5MRx1TGjn1pbj1M7PfsY2aP9boz3zhCUGxW5HeWnrsxr4sePWQd7x14pJm1RaxUGNR6nlLF0E/BeT58O69tohdGHJ0nc26aPtDKrv49Vn2720p03Uc7cZ7VIdS/3/jn3Vl2/MbfzoNkNUVTUyIIk+YtZBcPW+1DMken19FLNbvR4H2DUP+ge9D76WN6iJlCvM6RJAStuMYX99fnl+nfP/gXzyz+tWLSRtfJM9K5dgZ/3/QQdgv5Y4VFyLTrlu8FAGhjq6nwrH4Qptk4dyLUV9fJpWsiYlCiQjPP649x+K9C36FFd/uDjjUUb1zXTFqagL2lWMMU198zLo56BRNbUIxo91JGSUn179lfCU1956SS0bjm6IA0gzkgj64t00dbXIwEupTxlW/PZZ/m2sVYYH/0xQ4nyP4tnkJE/r9DxgVxyN1ho1apa6RZqw28BfqZH8VYc1CEEgwHQvi88iqN+36D8tLQ0X8uvABZ1GaRej0nEHHWsYGtA3B05o8KfMJx/xgG6brJn4yutkKyCMF2K5cZHTixQfPENvERa9bxLSo0Q8IRjIuYD4IiR02pzu4zoU1mKxSEjc4QrsbtX81NsQ1SbC6hs52P5oZmHmyodidAhXzf3ITdcB40SScr7a85G8MlSe669p/6enso/+D5GrH9ucPp7Wm03CO0ed/wfmQ9Gtil527+8pb+M7fi5W40H5d+K/8f0t+J5aLs/qK4KzdX31Ni2S23nx+bu3NiButJcNfoBQM/UdTTILbdJDWqmlKHk3RzLMfa97+/G9I6VcuDnjseOU79lf7ERmHbo7pS0u/ddf2SuM2E4HzYSm1QCMpcd9VTYBj0bW3PhLE4A1I6GOf7j6aUw+jvdyYvy2MBqNzfrly+/Jb+6fAXEW/lSIHE//1jswRU9flGOiuF/Zm7ZSR2WtMhXOgXCsjaAl7sGndMBqDHuQ6aC6uZJBUCdCssWUKsaFQp+haFBwsLoyGmJZxLUEsXRhrxT9lnZnvSoWrm6ARCdJtED/o5JBxQ+4wuS1jhIS3ay6suGW943GLIjXFaP4SgnLPZ+xFqHYUYkFqIMStXRSg3p8lVLocZi6oMmPXAfDJ6k44VoDl920PEebv8SmsHp5mwO3g5JxMk1tdLLeeUMvhvEbAQChapSP/QUZQxgEfw1QoAjda/mpFU1MMSjEqlDkitkfLybOwb2t2ZutFmJFuShFs2fuB1vRsKYmLCOJTOJjUB8MyK1bQoGyonHVoUTpSrQ9wiNTt7D94ssfnTgD9WayJX+MQH3rzqch6LxW9kYgb4/jMQjEvWRSxkHDeN1ZBwzjT0u+jajCrKP6ewHR1qnjn7KlzoTetnp6GpKSbWGFdJjrRt16zDESGLFqbT1Y/1eoOfv6S2dCMyuVjzoSa0Mns6j9Bb7NYh7rD+CVHU/rKBvhcOc09JpG00pcxHote2R6otn0sdIHcMzo/4AWWQzPaecPaqIt/2EBzobsp4AKEl2exfUtO+ErR6zIyIeC6lp3nagNJdI9gLHWN62eV8us6oNE3a8bU7xq8EBjl2yYxySi8tnlxcX13xD6m7Nl3p5ENj05eXF+bmveIdNwC1SB6j58KhIXKhLII1Lksae6Wk5xdP+UxTEeP2FGgqiDm9cCY4HA6pZHo7osVfwDn5mnbUR0/X6Ud81uWBFJvys19dksO/N70yef4MwOFIdZScM0Wy+uZtqwO5/7w0olKReOrOdnJmSUIlbskmVkzpBNKAXkTu9SIq51WPVq0Cc23QEc1MaKRcOyZktDKa14iy6NhlJhCEHC2KBPcqHeynyDWwpVlPxlqw3P6DVtH0wOnXMXQut2UZ66pY41yfGEGFgUbHBFv/jiwmpuoWYYyWMUcRzCPFJt7EXi/LqXITkZPMDxRCsOn8Oy3RXNhkZI4UhIu2tPl+lLMVDanPsvxWwPYNeKuHEixO3Em3el2ynZHquTSklNEPf9nPj2xYekNz8aPdMql9t2Gt01+ffVfrw72nnxTHX9gM8Yzt0KueTB1FQLzZaHLsIia3WHrhP/eVtmr+O/BFROlX/4Nexxz36j47SsTYO8B0RgSbde9WnZ5SPLbhTvqe+Oxyz2bEv3He9qI6yp7vwhZcd7RuddU1Mcd/XKl1SfXpHz9vM7vr8kOvlA/0bw9NXvU/3evcEvC9+O+k5Z57Q2hiEJ9T5m6pDEaiIj3Hv23g8GcZEYZrh16HI0vZuRW9MA0evH1rPM7C0Y2AaDCCit7iNzo9WoJjOX+DYHc8BX+IHL/85P+eyJmi7WF1EktVAgkIRvigWRFe/nSYDAQv0qK69NhKGMFW1tCKB4UHROVSyYKLlIktlRJmRbRGvbNxw5+s7FY7FUGXPv9BVorL4icfBt1L4C8Yvj+CVqdUE1CsMjsfWT4ir7vwZHbXg/GCPUYpgOgWmC0Nbg+iI+9GjGbbUzaM2zdacesjyoShDCN1GmfvRVukMrYTrnoZwvCmzavDTOjpqYNJU2jEW2fhmmF8ITlnsWSPdztId6KVE8/A0vsZYrkQ6zqB2xeeHFdJGDUtKyhqlQtDdcIbmYo+gcWRJGcnz84vbi4vLOKPBFoJmmIOKh61LDqTtY/nRaHDr/EO2XdF7DR9lZMu7+yWexuj9dt5vjmqKuVg8tIH31PkJVe3R/mdMqhb8BQWgztP9/aE64v7ueJ53fXBNc01/iXeMvb4+vS8wc+ObfbyhHT/S2lbR+bddsC83HV1NKU3udH8ICdoO+HNPzGJx1p991dnQjvB27r7ERsnPkTqmn0xjMqVM735Ma7NHaso0ocxKdaP8WZ6JtmMJ9JUDPanX0qBLIcXurFUDSAwt6XfV+Zy8LUKwaq9nJ6146Swlg+Ydtp1ss7JDnX2D0Bbf7uxg82DzXMEYkLJCVg+TKUrUhQuQtl776no3p4GZ8l2dX/B52nMn4SUoW6BSNMx7OYBuyjK5G3CcSAnoUCKkVocyeeahJMt04LtJGILRAZHAQ14/9FcSI6TiwG7zeT74bvmHtA+9CFkdcjX/0GLyO0ApIN0APKVVW8v0B4YCpJz+fum2jLTl/tgT1QOtbwG4OqLT8EQtM7Ie2aOcaEnPgwFyZql9tFFx7q1x00lobZoJbuTyLiC/CgzkjqSwVwF2FYWEN0nLA5wNXqKhC4mDFEutVyKtCiqW6JJkMt0stWOi3Tr6gDEWF9dntxe2ovKwWMdoiKQKbIK8elWTcpGLNYMqrUzUiGrQE2WyEYqC/sakDHBQEUV8Hnix/kIVq6/zsMB6fQ1tXe8MpeWVbRu/pF+TTCUH2vTYfzm73qY18MRiZdDJf13d2nZm4jeWSnSjYFOi/ETPHkrZmXKGPpnphzpWu2xtbFs2o6eMzO2nvw5TSsnO0ec0H08/5tp+mGcrEIcNH/E7XgoOWzxspErnIvZ4zfdY7343j7lvv0fbdpTodlsRjv7ZlRR71O0n7ardz9VRe6/6dMfSJ58qzl077nF5D6nOzt6VpHMlqWcAtsI5YQyhKdlwjlrHxH7BXxm1jy9ptqr/ThR2su84CD+v9Xdc2V+JuepMY2X6fjYS5xKjLA3v1gs30ubHulim+1LiflQ3JAcdU6EnpfRub5uORwe8ABVGmB3g0KUdEngn6O31DY+WMunsSn0RmytLfNe7jrNYyNfOZLGJwDNWPJ9jqXYBhGV+tI+2pMWMMBcURZ+AUcAdRQJV2PQoUBJ/ALUSwygEd+BBYXxXPKweslEcZRuC5QHjkHInQesoCT2OumDGOXGRNOLSlCESrl1RHQl+q5x/9+HyhtI0iUqeoQBYkwr0l5YlNze8yxNt3FsxUnjrHnzu6nmY4nVhZZIF7WUzY6m8/iPjuEZbMqld1G6FVJGNTHHIgCH31oNBGlWIzogyYHOryBpRfSpRKqvdMCtgJZI1DvLJkPEa9WQwgwOlqnyEW+kbPiKxWt1cX7948eLTFx/erT9jdLW4OFstXTT78uXLLz7/kjCqW0t8QIC0imLafTYoQ7JRhsM8eV5mkL3/+BQ67rey4ajazNRpw/bnleobodLsf9seHIGxe72lMPbt9WAnfw5BAnNESPZX7/ysrWo9wvE9GmyT1i4PHN/0o8MjfBg7wV7eKq2171v+zFmZo+/Vvk0cPRkTVb4nStuCm9wjrG+U7Evh0glu7NPw9mhb7fIgM90I+EHy9wkdpf+ttd0e78bm3DRqUtXz+v4nDioFm7JWDkox1Yr3WOlJTZrDwN8le8a59L75wjneosfQjhVoRdkUDv50yjL3szj/Ru7lot0HAMOuv/jv/Lf/hz/89N31FVO2V9c3zF7zglAw8poPhH3/3fcBbaLYQGUxNeJUWCQnLBVHChYp1pqQmXhQZoF/YMdhmpl0W6ET3uY2OkCvTEwDdNVrvul0xqgAtLgxVA+b+V1J2WL35vfovWvnThzBhG74nV19KR8lsSELDdsOMFJUdGhUskjWq6rB3srrjuOH+Gm9Uo42+F8qpYnsVRByTOtAC0v0WMQwQ3WkUuXKwgYFVs4ddaUaNRJrwYnesJQB/YGRPfn4rU/RbIJhngrrzzibcovR8MU5PRH011eZz9Y8JJ1bILwmqumzgeDPcMB4ewfl9np9/erVv/m//F//j/+Vf2V9e8MtIx7kcBRFe/LyWXrU9Q3Nqmr061e5mL05tsGhyvV7o9TnN+mBDEeUbkqSOurMGnTsyD5p9q3YmP46TClVizn6k9ZxVtlRvxFDAxKpMVgktlr13fyOxMpsxN62D/3seJ+eje6kIB46c5FtJ4b93P+R7TIx0AjVNNVYtd9qrDmxx9Fnfc61MVe/LQOz7dhxlfMdYU8y9x77twDt4WmkMQokVF35kQrlGIPz+o8seVojaOtrcKQPowiJ3p8+XTwj55Gan5DtZzT9hLX4TZU9rG/LMSsYmmxjqSWIdTwt2euaiO8hHMVfuo9i3TUxEZoQmsRW1UYtPTdwlg2kycQtDwPr1N3Zv/y3//a//D/6WzwSDJK85hNhvOzydvnsxcV//l/853//3//7l5cs445Q5uaBcWQUHP7IqiYHIR4M2ibfVtEAGIGVQk95wPhOccuiCr4M4PoZIXV7ttibBcLy1nrKJF0ias4LPUG8oNGYFkzqhFPWGnZ6PsrN+S+APjcSZIoUzgBKsYuoYxuI/inJsWmomsVk6IHaMaJprboGCl+jR2l/jcqZ6CHHhmw2a6723FJItSyJWYPmv2SKefSHLFFSi6X4mgNU6sXdGh+vLThdTeNwC7cYxnkv5+72JiY1hFzb5DRZQa4C9mkjjK2Z2g/Yr1ZALiNAAp77IS4jckzFvSEWQZE6e/Xq5dXV1Ztrug+4Xw946Y+O3jqebIYNlvEJxWawHtk3r+YOE6b4LvemRnOyPX1Xz26+532q9Luw8VS+/rx6+kiR/m17WATGk+rtxXB61pXRhzn8WKljbe+JR5Gm1dlyyeIMAOC+h3VLbsyU3H3Sh8eXw6huVDqXmHo4N3Las/bdd+Ft1ZGsWz5V09IhzOlM4dZu6k8VH6/hmFXsWyZPzJz6FiBn5ngr7RfuK4Y7QbMgv2yVOKGmJZD9w6Q6BfW8Sk944vTsCLvvq336Ke33nXHQW7StksoM2GlgbF3cwqF7chwEBXRjZhSZTUT5yD8o2ct+sHCvxD5iuTo6jNIuHRMTO+HpVlSTz2yzO1bYvwGW8jlXM4tzZvcXl6C61fLizWsWeFwsFufMedfyEvYDWBTABXXrY3BkkHqXxi9j6ZnCW+R5K3+BTmmW3HyhhtVXA9CnFhkkcE/ixocNaARR8aZhdE9jUJbfxA2cQac8Eink67MmGVGEKIkUelico30y3oIIkRSPuZLWSismRylZNDPd7WfLijd0kqyxQacPA2QYgywi6OEHgpTwHgrKavEQReW0g5yMFVhOpBP5QXGpE8y6ockcSRcDSow5ZhIfzahqiIi9TttYxBSfcB7TkVMHTrlwS8TuLRvdLOQNLwAdDrOqbMtyZEHdirtDNES1hSaxzCMiGW5hiJggFCjP3kU9PPFwdnF+sThfLV5/REDv7r6h21zfvDm/4Clz1pGtbm6vU1eMao89IVIxWXdsw7Fy/R5uttor+tBtS0+vhII41tMekO5dM2aH6vQA9feIPP734h4DDyqe/Y2Iti2f86s6zl7vWntbvyPbdg5bOVy6remxuUTjeOTTzp7Bw8pWJxw96duiTzeGEy2OasdEGe3PgrHoSRJ7fC69Q63nrWycwknuHpP39yhbub2R3c3nGlsDgGnRRmwmNVwFNh681QvDnIed+RlHB/KOhsqO++P1DPp+Mceq2k71H+D9rzhED4jG2xEpqHRMpIf2HI7Nn16Uoge0PSIbnYFfvc591S6J+7h6yRmJUjEq2rjRy/bpYEoIxVkIVvQnqC1IFm7eASS2IxqUAPTWzN26CIRl9Cz0UIk2+etQWEiluhUEkDefoqnZBWomFbvqCUR1KBAKpoXa3ijgQ1urpc7osIUD2A2D08m6SUFDkMMYIEYpABOnqqVZVs3FaRUKZKMidoXs/k9F1JBkVIqtIWxv5XWGT6gSxVZY1JMq6Fg0Ry7a4Fv6W57QSKZmWdOfGnpHhC2m4l8ipWZIIPfcqaihEfxUJ0yJDBFob+lZLZYZzFkxRg38yjEuuLtjNMfwwMrhUmRlSJpyxnXSdSi2DI6bL2OlAKKv/4cm0OexB237aWg8sFckFC4Gg/HinCa7YyCgDgYPtyJ+nhDgzZ8350vGkHLredmQh3wRWn0s290GFunqdutp+wmhnrKL6oneUzTs8g7O7tJ/y/8WgXcWgd864RDq7UvMdm73vN/N5yp1N7wFaM+s+WBk5zjqGRMykMnmGtb2TqFGOX601wSOHrHNjpwGyw84HqkzV/w96gnDkRr2CM9/E64xHx2Z4i9P5lydOuDt/m7uvxiGhp2yz9Z0a/5jIndPfE6sY6/+sN3G+Qj9va1j0lv+nGQXEFG4Scw3bP3pHXSTOzZZtz2wFPAg187NSduLdMZzdZDarDuH0ok0/5lRKHWTrjASxsSgcu4YRisyL1HVrH3UDKzDselOdlOZobTI7E0EyhW/uC6VI8GULs0hhHSm3MECKZeBEx5gpHwWsbnzj/nx9v4KeSTCz50HBJWOJQ3QaiDJb5R2Th1GEWGWl5AClOIRI4FCwC0KOqnBtLjiKlGZsoWtYyKuVSW4i1Gz8lgRcesTNwfwTSHbmL0x1rj+kk7K12ZaEgfDo2goilJHp8D5hpocaaRSADKWSf9lN0kAuNAzsOHgfQPff8/V76uKpumIKsc/J9b1h8p5wwBcT6yQxE7uF6jd6oZFwWwwYGOR29Q3X2r9/OsoRIm1ZiXQ3TV2YfqTXsXkcPcghKqperAejgwJnN534ykC73jECRVqgp0phi/L9XK9enaZpT9frYjw7TnjLdaYEfWzm7/QB74i3IxGnxbc2KNip6hxeBhrWLTUXmJJN8YdpkY9fKCmbE2yDlXzgXZY/FBpRSxXpAM1GzVsXf1G6nxijv+e34t5hWNJaa7sCdpOumKPxpLYsnL/PO628IPszkVvW/VT5h5ocRKNh+mha2+dKwdqNrE4y+u3I7N4cptjXEmxY/Fhnm/rfsocva73sF0ERgu7eSIIKdfWdokYWe9L9GbCmyvv1rXnPhW/lb+rCFRjTVt/zv6kcecYf6O/jQg8IPyTFi6At9+7B+gfAAV9KMC0+tKJijr2LrnHx/2lO9SWrUvOeNkbmfQQEOd1rTArF6jgcXLIsBikJnhTIS9eVg2BiAXoBG2HCNXStvc9OWJVCEipRkNRHzeEsRlSSNd+QK1H/phL5s5DCQUOO6lfZuVzWjpaVTLiR7W49HwIlbrEuNSDf+JolqQjGqhbnkZJ9MZXUvUPvTosZ5Cuxq1Lqt30V9ZZ9rBFkpqBkjWsH/iD23WPxXlzVeldPUibpTMqtW2alxbKAtn/6BkKGMnonbwaTrA4yiKJP2uQqkFxxAZJBt/mFJXQlGSrWimmzpSGmMJ4GBvSWqmVEuhjgX0Ntml9XydEoHjSIIvERucIMTXFmQsbxGGD0WseobL5UfaO2VvN8JXklnxlqvgYXQNP5Nht3Gol0gamJzg+sbon8OgXrIKGqXiy/207HIG33fHetv7DtXunpV4Pzpk7mTE6MxLtxz2bYA0995w3YT/yOjMZsT1S30z1Hk6uCPT3TMYx4sOVRnJr5mCqK5Hp4z9lmaNU+1Qka61/zffv8A/NuEM+LVu1eJifJ98v6lybjV7fkye9q1PwxMktf46w28/6A5Hu3dKCabF2hji/i5Tr2vdtNdPPW792trkrQE9v87u8t34QrkTrMDU7SGZPB7rb3GFAJgzta6kTT0p32RpW9u/TuIfWudVKBaZsgXNiPLO+nka4yhJ0JuKZWuaxYKtEkVUQJ8vqIdkcKE0+2DdaQFfCTsFi5pthC7YVoDbkxYEytsqDItEBYuxALFBSDcVGQtwaxE7C2xGUWhiAWsrINUDsVD2T73pGt7n7bHF3cXf+B9bGLNafuD//w9nZ5dniesE9Xl6iT/rsDW8RyhOuyLKG3lXv3ppgUc0dE9vsfc2/lPWn/C6gDVlHJU6T81wsrtKHl3fXH8vjdR5tLKbyzgOr4Zerv0rVMx5InXQ23pLwpf7eAnDAYyFJMbajiIyX7O3W2voZJ+pMwqijYf07SZfeb4lGOdjCvDy7+BqWiGChxjeWwoONcDriYhBxe/P52Q3fE+AGBDXwCwy0hpiePJXzpMEAnuAg8eEJYJ4YyFPIeA6nAkSc/Y3DrvNvo976lhmtsqGPrVwsH0PILrZMFVNo9HaY7e16GZ2yledD74JT97p9GeiuEv1ZNvJqqjRpcbRawjFfO+rP1mkrck6KgT4tDZORwd1JaXf1K7+bSv2k9/ndoa1tStkqnmb6q/q0tKMco3nPr9URV+zOyAOT1VJbwgft7vEzwsfUccvKEZmprZ5yvMVeamr2eD297NiVe+Jj0zOR75Feb6L3fFrHKaWXfUy60zwbhv4Mb7hiyiul7gA8xp1eFo295b7oEeny/C0ofoRP86J7Tul55ndcMu0D79iB38ydEIHubOqSuwqGs6OO2W+4d06a4tnVMJ8v8UhVcuzco+KNrQ5gbDRuWxxzo55wlo6xcJCeEJqFHXpJ7xMSRyojdhPiJScxKSALWLCTNgmY4/YAe1FlUJiukqUQSuadIaske653ABEK0Y+AkD04OKUjnivNkQZTBsaiwSlkEGXm0kXFhf80qqC3GvjHa0sB+u2yKsVSkfTd2eXlixcfvgCmL+8+FcSfX/PM6uL2Y76ZdXYB3L9cLK/vbi/uFm8Wtyyav7m9PT9b8uZKEBtvQwL0MwDA+M0C/iU/fq63P7u7WKhttbjATz6jBg/DAAYA+OMwYHH72e16RQkVBy5Dv7hcvfrp5dfffMVn15xKH53FV2oorC1axczQLZfnLsIh/OYc+ShmCGwCxwJJZlfpDBvkSFA8qnjg6lB40VWmIjbDObRX5aMFqkb4wzTNDgsusEnGI13jtaG+aVSVxAp7vvFplb5U/OkYqtneBkoZwhe49cKtGd8WGHIKyjZyl6ZBjy6E9aASddzDcE9xbNy/iy/ZNbdGkXK7zxbbQK/cWP5nnNiJxNjef8YhaVUnFDvBGWMyRx8ZHpMY+uhjdPz8soTo/op48c0AYL+/M+OhftyDYGdpSA7H/WofSj2s9cCsNga7MdM95o/n7BXNjRF7nmPSx1jfif8xajc8w6zJ3s5BhE/a5rydo28pHzzZIr6lTN+T36XdR1ana6SW5JBG2j0Xhnybh9sIbjVpzehvke73sLFv7gZslCvcYFhxjUVkW1r4p+xYRII55WHuf3RmTFCcuf9RYNvFAmlbtGhsgYmhwB8hIEpBdWBcMB5pEpnJDh6VDvDLOo5aXAL45c0uz57zxVkQqfaD/Mr1wZ0iVysMXhRvbEHCkHJVoYg1eMr89I2bK0ugizs3wJTZZtzij0GEMfN/Qd81r64BfUYTpYwxkF8u37x5/S/98//c/+Bv/+u8y9618LpZjmtZTMsSFmdnlXEEAZx1Dh4+9q41cl5bKb3QpcFEpn3JESDIKGPPYCAjKEc7N/W8QbmPlmfPz//j/+g/+b/+3/4v+gZ1o0nCarmkagxiLMKi1VrwMPTF6pl1TLUyvLK2EPinJ4lFVPFZ42+p73LxXDolanIQJW+qSlVgtyIlKzW61Y9Lrehu9d1ycUUs0ON4hjhQLx7kzXMMGS6ggWsFNSc+fECaNVttkRBDgtRsiJOOxl8SbCT7rfyS0pwsbvIR2vArt/0lYDnwTlk2E+RH9QMdYlWq2FLe9BRv9hHWhX1bUQfNaNu7zdEbs0omc/+Dzo3CcqTlN1eSDcODUv1VfargxOv8o35Vp9bnKNte7URqxDDQW6Nt86P1qfw85jd6amtKmatoT3+Y1Fan6dRtgtMR302y2qs1zbbJaR2nlG2Jp89t7gFu6565AlQn4zbuNvejcuriovuUKnt/5vpEz7M3vbfNek48vpen+O+t25F6euvvPl1OjnX5Rfj87qP0c1isNkmDsBtbCFcGGknImybreBpgGPzeUTDoGIqf4lgmNs5sdAafdb61kgbbzE2kekKf3ijdl+o4SYIQxY/R7hHI1pbHY1lWwDAjgfMlC2FYK1VP3MbNSDrpy4a4wMsrWXSSicOl2pyp8VIXnvgGwi2cWrXbaIge59iDtuFlkXkDneJfxyI4L/pnK+WICFXDZdhEj3jPmhiR/vKSZ1LBxbxZFE3kWU5vbUXq+MDKnMxeAwBdKubLOkllCJDawRgQiQ0TmpWkI3n7vrUTrmMQNOz6GOGw4cg3iE0zF879ibur5eub9WuEDSC0yBk7ZAyMdZJmPRJHTRrllDrsUjbG0c/muMEt4eVuxe36gw8+/PCjDyXF3fCyM2Sg98ZsHTDhhuPYG7Kxe3bGd7t+/OlHSrEtgGZBDzX1bUB311TgDR/7IlDGiEBFS+C+/uAvVlINuw+zZvGjWZN32EajRdhwDJ6FrjRGoBV5kCInka32SZqxoGU89OmRvMMzwzWyJzGa2atxm/fY3I7Oyta+6ll71D2h0WOde3/4+lhMA1GUMZTvj9vvzJMxPjsWiUkV7dCfKlv692o7ULSX/10THxIXP2y+cyIOhMnoc299qqdStDWm7FrPGTiyh8fre1XvI+Ic22h08NVbtAe242fojxm3Ha/tgEt7i46xXoJb0d6ray/xYJT2Shwgznnb6If7z5N6Uk4eFZO3YPdAiE4q6ubScv542qS/11H8kS14oGkezoRWtJON/KDlJF9G5m3p8XwbyreLR+CCi3EFwFbb7nGQ9zjgG0Qa/OlLky59o7ahvI9Eiw7YSvAnDi6bvoGb0DkTLAj1bgBgjmls3sgZFC7+xln+gzvTaYWZul8o0pKoGkGqBCkwVRka9NB8/lQwmI/aTO2HK7qUUhZXKdmYU0qQPtwK4Ajcjy/urBQH1t+4RoWnF64Xqytebr88+0Bv+Qes5Q8vltzrgMlJ/rO7Z5SeLd6Qurt9BmGxuBIfqwoh1u3A/zqDCx3KPQgMJ718Bc/iDvBNiQ7rhUZc+g8WdrRx8+zu7hmrehwSyMAye3wTmjM+4f6FcVTO+wPeENAE5aqMNlLYsoIhJCVHKNhkWy54H79BhA6rYVBF2riUWHupeIBfVibv9Y/ORJWG5x4IXI6TatzHV+FocPTdugIKuI8BR0kOKlDlnRLkHR/ZMRwEmbLiGUSSHre4hsOaHjYrJMEj6iqdDNkiecqTRnWNeaIAQqcnGiX1W3RJSBzK6C5P0zEh93qiYYdwSraU53Tpa14q5igjnQQKan+K1fDec7WfXucP/x519u/R3HGemtxBKRW9zX7q85RyqskZ/rnf7hn248hHRxh1Q885pLl4djggjh2oiqq9Kv026lV3ZvrvI+24tJNt/efrkN9CC87VsafvDd2On2mDPXcAjpIdde2evmP7nKZm1HdUYjT6No3s96Q637u3u9+bx1F3TqTHKftzkR47+FuucHWxAAcsJddM16Fl7vfiKVs5bvQmd5Xrleg3WK5n3JtGWo11ENQ0QpgHalDn5qoPedhGjkEFWDMQ2YJClGfMUYMKxWfgNiavRahCf2Z/wVy3LEcvo/gBF88E3/G8LF5ZBfaZjNbHUDgGuwUtmuEvW03nVhJysKQaolsuBwYt3wIEiiy/SjN78DosAcsecNG9uFkW/gETU3rrOOX28vaWVf6rW5/5FuinSNNRIrMmkKudVbDEnZi6uFQbLyGXOUsCtaXIRbYqIkF+9UAhcvLh9jUfX1aI//kucnG4J37g7TRLrGpCsGubjHbLm8BuDbhZFwxXgoOOyI8yEnGqHatIjyxSCm5E0w/ktPbViu7jGtpzVwhDyqXYOzDm3CLGkdsmiZcUSoPRjV8c1MggUT2+jMEJ2Q5hV5O5lITH+NsgKZGTRNVO1mQr0e/l6fN9mgqnTJdn2eZLUEXhzjZrbIeP7FDxpiWNMVU4ypXmHYbB3EEvRxW/9MSfRy3vb6WdTrAjMPSJHbLZw4J7BJ6U9PNaP7kqB+KILktPfwagd6LXP4w/epq83bxmLzqkp6PGKWXgfcLjg9/bs1u9zqcaKc7d63jgvMJMNIZob8yfqp+K2Jun+qeUjZFTUo8e+55ao8fHpKq3ZXc7Gntbf4v/lAg9nLf82OvNw5UeJUmfaT3nAPvkMrlNSG4kicKCkRrwW6y/ELV1a5q3DFalB+ngRDwqNMmq7TWT08Fcru4Rn1DCW2xu1yJRXuDOnws/xGcAP7EiR88E/ofCzgdwg6xiq5TjoRqsvJv28VLfY7pSUeSDVdBvvrDw/K+sGvRihnL9e1D74uKvvBVRtYhK7IVTvIq46JphSkzFlii/LebHd+qxfHN39nJ59vHqjOU3qPD51Piiv/FL3M376ln47kt+zi7vfCnQG+a78wqgm1QTE1c8GcyDFxWRejWQ1bemaHhRIeIWK1pxzNqkOg6ntLNe3V3yfv6z9V+4nv78T2kRRzLwyZj5eNcjRZEv4bEkbQOJ/waSv/aIgjljEWmdqMhmeMSEPewhsfMfvMSZ1PlXldOuIoYIyi0PLGsiocWSyghj4ityzheRrSxty2uRfK+S6Ly4rr9Y3vKaowxt7DbWOJGBVnP2qvUJE6+iPC2dPWkfUUg3iwm/q+DtGinZE3N8M82dHIh6Xq5RkRYOfa4cJRJntvBZZhD2bqhmq30xzDDGEGVpsMNWS0/2veIdOx1XS8q8vVK5xOPRrFtTPVKmV/v9fCP16N+jkzXHxJG/AifWcvR+SGz/HkmdUgbeJzweVbsuwlP+KeWAe3SLuUBB3+lz97TXKfGZKsfJum8zrvvYsT6txT3+TAUys+B0wJNv8bWdcV9NtGvxwABgwn8EoYIz13ZHKDia5ckt7W37qTvYfRfVmxp+akoF8Km1/jr17bT4TvZd1vnIXvp0Lu12k3scELlNrtA5ZaJos8NDMoGSSQi4xY6i2yrLIQLGe6O1FYcGNVKWczk7B/bpATrIo4yFIGtW+4BqgHar9Y1psN71FSte8mRt7hgIzuERw9W1WBcC96XiqJCxXBVnhVeqZRYMm2LJCSNb1ZQNucqUFgLL4NaioDKnjGFSA/LWQsFhK6pP8fIILPPsd+uLs/VlnClkzWiGXMw3gwW1jS6bumXMltnuGMNuxZxoEUB+LOOEGvhvHXxWtskmK0K0fuqUCaOMJXgS2YeRwfvEzaFXWtPbBC5DIpNKu+bGKjj0YgzgGEj5uM2YrBSiGCr/W4Ucrfks8SqrevQ/FdUZPDZdrsQfpCAbhnKOUpb0Q6BhDXd0OjRQz9InJVhQ5K0Xg427hsPvBOuvQYYLJ4H7bvCoWUWplB1DSSOnJGqzJ10Gsq9QOXxqxBAYn3iHBpIBGbYxaUG3jfSibbJJbVirYJPvVLTkobIt7vtVdezNoXYYKtoxENaqEfZHrrG8pxzt4Cj9601ULPro/HrremzN3mo0jlH+PjXK3rOpi+T9J9PwJeCTRy2Hx1UVyPvN+6O7u00puxybUe/xdnZ0jOO5kX58248iOwlGijtK+lHvyREu7cdEI5xPpv9oizvVf/Js1aiP4akmHhaTLakhGrTsXHeuvrTT9Lg667nTn/fdGeuquj1n1txAw/p3MtUbdSrNGzamboyadvTcRxeD6Oe2Ru1+KX377SUyjd8KGDWTsKAPnPm2FbkVApACswCF7a1B4UxpUg0rNtmQ8jiqkEzwKnZnnhU4xdswmYPn2dcvvv/hh/XZ9+dOjS/XayDqG16Mc/bmmx9+/JF5WRaWC159PtZq+uIXlPFxgNwBCOwTKQrVU2Et1TmuV/AL9GDgH87pRejehSBPr5CqTGKIFnEwc+TCRIiweyx0zYzwl0BNS5uUxUjEChpgE6EKHnkvPpPNi3/C3YRM2Oe+B+Yz2Y4AjLyt01BQOyeeb+AnLCz3j/95+41T/sw9Ey56OOkKXfFDoYtKt5fy2lBrzQU//LdrHzkm4Kw9Wl+g/+yCV4vyePM3iwtWT+Ef4PgGBM1C+7gHJa2ViFEuVPbzCxe+3tSNOtnJ5PPAEY7UIxGIOMa+4E3+i9W3CMDhFvTN+/iVyNInhSzNKM6hYObpbb+KNWXeJzH02HSIkhFECzLeNqDfHhGwh1/fvfnsbP35YvGXiW5sOiQgGJ/j/nL1jUO5RANSfpi8B3W2/sQ05yavZ10m/n5pgVey8gJWe510qkOsUI7D3jlJnRIGK1F5DkNtE4cwtZ3VlrOdd18pcfOl7FvnZsk3dU1t07mlrUx2X+2wNAbCNnf1KB39taiUF7/fW+gcJ/Ce3fu2tryLFtneZq+i22xvN9ejnT7dWd361ejoT5ykj+1sU0rHcEz0+gbqRLd+v06t3ZR/Sult9enRZx1LtGsOvuc5IT0Xn33tOBeKE8w9gHXS50vHGId5lcNZvc1BLdqW8q2rwVAyHOsOwH49A88DjhsXHiB8ssjmKnWy6EagXD4QiZ5hWr8n8WHjzW+p9ywC0xbfcbDvHjtFx2VP6EFjLx0TZWIne5zdKVdTs6MtqIlabpPJTWjbGjt+kkOu5MIpCUgVAIKuPeqAcNJBbIM4eTdl5JdMOf+Y4vXtN+SfX37w//wH/9E/+C/+Hx88++j67PXNDe+jfM3znmerNz+9fLW6ZHZ6gKDgOueBFQQ11lMDqA5sBLTzskgAseiQRTiaFYbDy08LKLPlPVgGmw+WBiSabRWzGIgpOMZYkCrsGEFVJqgjrFEEnEFXHf9alSHLqVUK2G5vL9a+v59X+4PIHUWAwWO9gVR8UyB1UBEmqULB2OgmLQLHKeiOL1wET7npeI2dmtzWh1Rfw0mb8JHaGGCdDIEVW6e41kqxYIoBgJpi2frgmPbiVR4ORtUA/fVOFuuWmJjjDaAQbniM2Iqn7kbOiEpRXe7gSFK4gkO7YpXPeFG/VNR6MNzjceRbVNFFaE2HVkYZMWSd8NdqDkUilNBY95TWz1PNGoR5tfJHk+p7e2PF8BE6gcU4dVWzDQ2chcIY0+ET7tI0VkhBd1bDWxMMQlIXJNN81mLcVDlmUsFNbpNqIqPkmBhYttV0GgeGOhqKOLlFnmXf4hrk4N4xvyO/k91WUqIHWbYF3nFuWrt348DbtrvTZO+mUg+z8rZdLf3s399euBW4+7rG/dWoLwHfz7dllszxz0TvSj5Jfm5Ud1D53Lr/nl6RqH7QR3eM0JiYmio9/Ui3T0/5j6LsG6fuCh7DM8hYqYF/U8GBMnA98fGIsewei71Un97D+t6QNiFlHm7ytcvmpiiktp2ONmb7+jgr3P+w1uWJ/c7sWskMmnsNLT039zZHB+wCHoLEYr8AnnYHIxzFdLJx7P0RBolfUiMBXOOB0ACJcAtcJrAUyF7xVCtvqrm7ZUE5c9VMwztjTZrPUZGGzmr1O57QXfKJqwumZn1at0/7vdtnd8s3izteGH99vny+Wnz7p6//y//fP/6vLp89Z17f+d1gMTHo3d3nH392ce6HsVhOw0iA6X9uCDgjKz6Ejm9YZwG939BduMz9jV/Yde7WNJ/f8nNa+MYXdl1IyQIY5suZ3125pD6f3ArPm5trXjbEWnPm4Jknf7a6wBlGKcQhvUAkKBg9v3zFJwIWiw/Ju9a/WpmIXF+fLV67gEa0fubbMxfPb9Y3q3OA8Q9rXl4p+GZ9/+3t9TUT62uU8JGvszesfr+7I3pW3Nlon292hEA6dwZYLoX/8Vke56Tbl4PHmWyn1QkaNcI+l4j67i9xJg1mxmvb8qfV2dVPqOb7CRfUEmp1FFfHAIp5JdCaL4exCYTZHDrwEMSlXw0TGUdRwDW8dxcX55fPXgiQHbqwMUq7ffbi+eLi+9WKEwf+UoQyBzDAenlF3IJsBAgd9OfPXpyfX/DBgbJ7vjq//ujNZ5998dPLl9dXjFioC5y8GvSG+APk0QUlDqotXZZFYuuz5Ter82+WV4k+pnnv6vX1q5cvV3f0RiLDno+i5cNq3jMhhonk2V86x++DE96ByciC0hv8pbvnuwpwYpPnJv7yxYuPCFQ7X2x33eAvp1a5VPvqE3aDdJ3h4PlbDP3cP5Rwyj0mdpNG2a2Y9YJ7EaGMu0FPb2UsbIKDFMpgry166jIwcmltMDXwDccaWk/vM8xeRSN48u/CEb90e3T2eKNPD86/s+Me3w7aPhy9g6Jbv1/H2D2G57DFKh197rqtJTvZA6r2eDJt9we1Y2GnR92ROOD3dtEYh21yn9sKiZd3zq9cujZMXH6yUmDmPsDT3wHIFaBO9I0Xv7DUcNHbXM4OV+CXWN26Utd+qx8druqfX2l1hgrUMbUv/mM4h1/D48Ov7vJk9GdMYLFPH+dAcc06UApT3PMEuxYh+8C14WceyoArhFRgALSwC6cZgJcXqdCXP/zww9VPN8vza6a0FwwA1iyT8Pu1vrayAX2GB28cJAjBSddSls0euA//YnXNyygXALLby5WU8+fPli9ffrdcPju/fB5zgk0TArfF5TO+RgsIcyoX6Mh9gcWCT1Odrc7Pnz9/sWQwojY1L/HqjGEAqBF+9bPqYsHghMdw/ZAinjgwYOkS39zFZ9JYyDBmtb67evXqtbcUgN3MHa+Wq3OwePMDGy7/yEKUoE4eD8ZBwgU2BAcSJW9MuBlUIkdRgC4v/z97dn52gcnXL1mU88M14wTQJkB0TcIBAIhc6KnPDk7U5i8EP3vUniU90PWctLcsCrYGyJoOxC/Qz76+B6xUybqnDg4PgM5nq9eXy2tHWHop1RroKP66np6qUQOHBUaffwTh/NnzF4Q+pdZRScYyd7cvXnzw8SefOsBwKGFtSRg4eETzbhUOBmrX12/e3BpWI4kF1TvkeHH57K//jX/qfEUE1OMXEvAnnyT74x+/evnTS4Z+jDuIz48//Pjq6tWbFU3MEyKg/Nv1GoXeLqAWRBVq5uatlj+udt7VN3/68XzJE9jPHLjaSwX9AfqJpN9JzqIp+ImQ7eiCK+NvDOktaQuMrBeXH9w9f/Ecb4xRGtkoJb7srVAOUqyEBQlvMimVurWVVNSEXhJNrlogPYlCmWQnbCospRHa2e3qHIo3VqQU15gY1RVXz0t6LB101bG4Zgq3Wf98cmNg/3yq/PZqWsE8ENJjOl/x9F367Tk8r/lAJQaheyrDMwC/l3XPaGM6Zhp07uWf1dNJbSW39Y8BHRNbzE+Rma77L6176ffEbdufYnbV7zbd31G2Gmv26R22A9mSPcAw6j/Mk9Ly0x+h7a0ou85v8zwmt6d3HaGul+rTR4i+FZYa/d9772sM49wZ0Y3UR94jHd7PD7WftyO7/ySCyv9+hkBKZog7+4J2AEoxQxdyRHCv3sL6FkUPEE32hgElRrrpFMCF9Zy3cAaw3bx5ffv61dX58iMncQHJYBFRKSiRudWrxd1Hury+FB+DtExnzuL2Y51ivl5HLyxdoxMc9glpFoyDHK/egDM/BFKj0eUuoK0lgBmos2IpSL0m3oljjGXCnWGGGMxnAEBrl6LMNZCTaeIvg44Ek8yVq6CeNHWUggPgPxDgF3iyXP2QIpe+5AYCoJZbHPxnlY5ceLlibIDQ+nPzrCCXblhA/C6rd5BizKwutSXhzDTe02r4gwiQ+E9nF+v19dX1zdWrH7+9/pHKMPPPK0FvlneX4HF08tXbs7NXPAXhm2bqTQ+6pEljuPqeFKvPrYrXKMy8SF0cXTDawUGYjIC3WUoKRqXO1p+xIwhI+RIbByof3q4/YqocgeXtX+gxzwNoa4Fntg/hAttHBIhv/dhTo9RNRxiDWKqIgwDRN3mny2+9FbNerBiGef1MexkhtgRGNwqsZzSSmw7eCji7vfpkfX5+u/wWPWB6KGk4ML03TRZ8JRkKY8drbC+4V/Ds8jmT+z5gvWJ5EuvFGDvdPbt9Rv8ocxiyLrf48eHF6sPV6gdicUc/VC93M4iGkV/c8U0GAndFBHJbggNekfNf2hpPn+vQ3RvLFher5Yvbu58g2KET0KRrZ2RyZpUf1hc3cigGK+tGW7Odf+1+siVgSLKVaHQK+xnQ4HWrXBrLwAz5EOL3RGVPGNwpM9HWdFSavTbUWk60dBFT0nZ136CnzF1Fi+fk34XJb19v67DOuv63X/Op2H2Unco+bC755Pre59WR5cfYneUp5FOWjoj/lkvhH/uVRaXtoJ49nszwV8/daZotB7YzU+y0Xf6Q3LSHTynH6HWiYd+2NfdfFd6w8Wu6Fd1NyZEppPeEbw/pkL6RvU+c5Fcxj+KHjL21spMcfmteHFJ8OEpE7/2vwqHqvZ2yk2JyCvMpvJOqjcK0WnV7KNWC474JVUEatzg3ymQtdmnBL9EGrciNIRKkawM9UAwiIcsfEESMJDUYqfbBO5KFGMqVuHgFfC0mXvvQLRPVK+aPSx+MsopJ0CaEEiYq3DZKxCuwhRoEYxHcTMPXDL/6rUnm5q+Y2g/+Yu7d1djQs3BFA/jgkg5oLsVAB9P2eV2QXghZCw4DCgWvlFnsu4MYnSRTzliveJO9jvlfHRxYzANiiNkaeZXjuIEw6uDImEHEq8/ByWDgYoBHmIwqjAK16837+sO/Zzc3z65+vLp5hTsgV8YtML7JTDUBMCYxMXqnQ/jaHDRiEIxmGqb8xR34w1QtYJgStpBLujjw2xIyy5e3yx/z4AXPv4aWMU4FIK76y1QGmO2n0szsZwwQB6y4VcOdqCMBHX5HiFBoCBqmiGl62BOL5my7gaA/CDmT7jDAiHlzJ5EQZ4v4UYV/TT0m8qky5/1ZEsQCrGuSjhUYLCLmMwSuX+JgwNMiN9yjubt9zpfX7m6/N1bw2zkSJe5RaCA/w7b7sGmvcgiwJS3NWrmEbHE1srZaVKuk2dNoJVhc1q0NCXSgRW2Q0KmDW3nSVKVedGZ9NlL9piJJzUBftJvekUzxDm0nO2qAPvF4H20U+MUmfp21+sU2B473He9hrVMakP3FbLu+HngGYGbMNFfVPaOuYuX6Qpym2qaUTvV0PX1XuCdZY6a9c/l7uE8h9U8IHJbb0xv6Ovbpg4oeNv7rVc5p6Ht8zz+m91RhLOsT/Si8T/c8T5HGn90ee0BtPKkZ+rneOBeZA1o3RSA5JnznVvaHr3d4zoe5kfrGELUWKAvphm2jeCcgfZb0yLehQ8rmLzwKyY5MTb95YR7wJSsWmNkd14S4XgYAJErIHGctcWY1M4iTt9Aw/826F1bMvD67e97W6mRtyZ1rdbIuQp5r1vC4VscXoXgiAO5cJGPrElVmeV8xaw0cKTQI7OPrs4I1Wa1VkIrceGll7l6FMxhKKv9xgwKAFzgYfMnaED5PC9RkkTeAFDlWdjgnvb5dngOw5av1Gay8v2BOmFUmxmdxvr5lWT/T2dwnYPUHK0h+gJcZaDFrbLOeXi+wYtwCnpwdT1Jv2VgP8inRPDv7k2ML4aOuSifB7vyr1E6/QY1gWEzAQJxLC2MAIWx0sWMBDC3AaEhwe8f7cwjaq/XZdzfX5yxUQd1iSX2BvtjMHL/z9AlUM4oHehzPiPfnpquclIn0hKLgBYkyXmm5abdP4SslmLEhVt875rr74uyW9Twg6wu/e4AX3GNxQbxAHJOoYw9/qRfrk8rUui0c8OwoSxdB0NTDFoSOT4TD9Us6RPylxrdKL7k/YKPamcqCkTKwdOPz71JlPU547RoYwF0w/HJ1yfDv1u8ZL9eMnuiAt7xbiWb9E5rIJwS0C/8UiVWjj/K78786u/jT7euPfGjcKFu/VE4hOnlCRJEupfb6kA2K2x2IX042HOXuFovKCFfGeKUyfZh2So0547iyoZY7Tkl7BiFPlNCgqwgteAIn1FiY7sqZomdY5Dkeo9Hp3RbP6Fob5muLci7AT93pwLVVpYbcoWMinRAc4mrxOMSyb23CQf4qfNR1fk4/4XrEZvDyC5ULYBaDHadtRCDHhGtH5TFxOIZnR+1p2cfFbdfWU2jzLBu2SveUoeSo455GSStPEe9cnKc4YUrpXZnT0/O0dH/WF6nqGad5mxy/HCHvqcQebVPSthzqQjglloPMVPdDKOXPKfYfYuWXKPO0cX5nEdjuYO/M7B5D5cm9HezdOHygNQ86AGpI+ZQJKNF+5gXGgVyiNKGFAEdoQSJ4DtBhfAKKXASCUtVmTQVJ4W4EUalWZRUsTCVYyugCGpPWTrL62sQ1j5kGg8KoNDBLG2VWcxqpq0vI5oZssIa4TqagoXpDy/Ic6O/aG6EleBODDmSwwGO51AxwLztiAjHUWQiJFeUuG8owQqdIYMxlRXCZ5I/K8i9ZKyd4Z98CQ4H+h8GHaAFtSspCQg+LsWokXCUOVdWoZ6cyJcreAPwhMhl9vuSjZkxZvzi7eZ457bphQGEUpiqKl/pNuCSwZa+dzRarlmixuFp0t/la/a1G4DiI1WquuANwBbZxYY1DLjaRadn3aPSjtzoD1Ykt58uJP32E+qib4Rn3a7KSCMMZjBJI5+EZ4RgEjKFOm2qt4YLrexjPsaEpeoHJPnUtfMaQAgyxrBDPE/tyIP7TmjdO87MK32U/sUYZNkDA8mdZEXtuADgi0TlN2BeWtx/woLn1Ub0748b/cJgbyEkqtrtFRsfsUjx+wJfa9FVgHlMYa8pKP7Ww31qbLVXS5FU2vXPwc5ttUDbIUkrk+WPcwwCSLJYdTsgQE+hBX3lhzcq4HuxsiEyJ8Owl7sgOWXhjech7LPkJuWf580tXOE4J7Z9fjP68anxfX5ieQJ1EkjUAgI9c7U+J4H6JUjXq4XJ/+lbr6Xu/Do97+jHTWEfEH7PVeP3wjO+O/tH0Dv2kbF+XkwRH5tKwv3VGpsOJmVFsE+pH4X36sM5J6eE2nbDfR4gnh6M3LX2AD9XK1buqs/eU+7wcy3fbp5/15/d4e9v0rLFX9+/e3mZuOcHEVoE5/trPuUVDOT/xWQpx/ZmL4C/+cSbsQUR5qJHHQNefObV88QffgeMEfx7G5c08Nx+f3X15dvlPlncfrFnHfPf87vajs9tnd+d/6WOyPCy7hp+5+Wd3i1e8Nr7enyM48z05rM95xhJ7Xz7DK/n1ReeChZpv8XR0cuNuKmH8Rv9JFxR3JODjwuA/+jCPV6LZhfM+lymMQhumBTUZJ/DAqw/v+tjuHbc1QP9OqPMUqPXljf6Lc9esOKwBIYXiowg3vt4R67aF8KsiKu5P6xj35XcOqWBD8+0bHz/wnTx4UhLax9VMPssHDI0Jag+HS0lUKhLlPUUUWQoUpVrr9bkoe8WU//eQavofeyU+xAjlccW4tPZWY2I5wMsheAZbb5qA2a3N6qSaVpTNSMO8PLv5jHEUNVnfnN+xqt5bOEJVn+bFUzxCiiORdk0T4NvlOqBsFUJ27IVGIskNAyekYfbdRL6ih/Zyup0YEyLbWd850CKk/DMYkGrsJQBmoIAI93iuefqXgcTdmsa1xqknFTSAlCJze/MB3yq4XX6DShpF33haYHWdt3b61LBjQwcjqw8+ev7BR6hmuEj1bl1JRm/+6frltd8x0A+riUNtTKi1KJVqvAxspSvrXuXWQuduPveGzOobuawxnbam+dnTMxmlcHuNmHAG8e6p9L27Z74vi/sGrJ3jU823H/IA/e3qD7aI1w0tmt7Y3TgQo/Qlq8xj7txYYCWet/K4QedjD+gvKwx8fRx/4ePvnh32LmubSqh5+P5ASFtfHqjeYe3421zHeida1LrSUhOfy8pAeNhxep1/mJ45qemvxpQyla25/yn9MOUwAjls95g4bPEc/t0/7OgjSg/X4hGKTxC1k9NlOTu2tzn6NleXm2iosq04d+zHJXPKhfUEPRuhwUiuOZXJ8zb9HYDtM3SQOOl48rk79XC017k60k5LHFB+mqKjuR/v89GmjmV8D1061vX3m288XaaJxzl+VLcdz7Q97VsOyQEQ8F9BAcgNjITM73lKgDUUAMtYRuAjs850A85qShFYA5IA+ILZAQogrk4t4A80lOU0a96U7moMQIMY6Q4IxrBBGAKwAN7xfCSwGyzOBQc9DAlYJUI5aS67YigxXvkT0DSEcAs/DcSAi6rUBmHBibx1Sc3wGPzHq3uAMqmc/EwMUzVh4NWb9Ur/We5DBYSYCAusl6uXr64WvhZG/320QPDtXYslYMhVT1D8moCGDCSwtU1gE0lFEnDLHOe8ubnhqVM++QReZR2ReEhE23jCrczt1esrAWyGP8BgYD4a2HjaF7ha/C34aStW3dyuP6bclgkQTfgGxi5SGVBVGDXXOEYGq6E3VZZcV7ZJygWPXsHLwQrWnoenX9+teWGOcWb8ZLlcRNOa2sEMBhrOWVMPYufR29evXxEM7o+wWAfYyu0g1w0hQKDB/wyHAOPUTWWLi3NvC5Qv6bXYBZ4vV89XPLwLB4uOXCXlfDambngvEJK85pWWhkoxzYtTLHPRRW4yeNPhbHX57PLqikbnVaJ02ttrfIPfk8Fl//i0Wv0n//F/8g/+0//Mt4Vi0g9H4P2zTz/++G//9/+Vi3PgcuIB0S7AIZtet6Rx2tqMy0gjMlmPRFXRZKDwG11tTGLAi5n42Pjxiv52Qx1zV8Nlb3fXuEmdMG/3Ky9U1m04ZCBtOxuEc4Ae5ruvSNRADUuazgEHPEeKZORKM6J6v625Kfaw2eJsbG5oB1O4pVpESqrSxukULQdN/JoKCQqh+W17QATm+tPD4vkwqQe4vX0i1Hkxa7yK91vZEiLzuDsA+23spc6NLL3bvmfUNdVxwrhnKjxDmY7txvV2SEzHgjNq3jtyjaf7mYOqaW5w339N9foyM4o9taqHR/Zvo02bh3P9ra9AeN6iD72t/emtK3k361+naV2stk7ZXk1W/c7+EjQ8wm880MBXnQAv/PlGg4CVn3cQleeeyAKkzPvjXRTzygn0G6YGwQO8XacB6uXyRxHB9bP8tPuWmExGkvvp7OzHu+tLS32D5/q7779yGYiwGKgFDuEBRy8yIifANnV0vh9AA4C54z3trMTGNyY4BQDL17qpP1a6sE/LkK9NZwEiklMZs6EVo9PJZ+sXlrlQHiDjBDIoKXoxv9bP2+vbK4CPi7wzdQs3KBbgdXt1DSZDCUoNEZAdNKasK75/yNSpoFbrvF8Z3effI7xxmeT6d/DfMadrLTBPRf0AsRp5NIH3dZbD6jAqOswfb565uV5wvtBwF18BQSlnPUqwFx3V8xEugaujFfS/dO2Nr8bEOLwpp07BeOWh+wqkhcXjnspUQWTYhSuVMpOtuIdcjqiCCnrURvTwtS/acn25vgaF06SGlxLKAvzpdWzlkFXNkAxbxGH95vqGWWirz4dyoXHBoYqL5cubl69fvQLbo9mv5DJGfP7jBfc8qLibiiFmTwIu8rYXKRI4tLz7kpsj/9X3/18GBQyfish3ABzTni1efv99WvaCx36Xl9/f8FKgNaMt1qFxY8UXSeES7xzyq3HMjV9c/PGv/rFVVpgXErla6Hb9ZrX8675D1ql6XPE/nvUxOltyXhCFD0Pc7IrpbPljYvQJQje3P/34E2+s+tGvRrhaLI9P2KSoJDB0AYYGaCO8vM3W2I+WoMO3Xj/78JOPP77kbPWZhrSugdWEemyBOuJH3D2/eXP904/XftCMprA7oZZzgXK7mW+5DeiHTH/64ENGaJDxzXPBvuK5ykD4T9FXlmAYNsQshrmsD3SOOlNZ2nFnU2rYWronDUU/4/Hgb8rb+x3pUcoWPkkwn8BuX68jfvcP/6ZP22eWv7N7ai1mdU7NH02Zw3u8X4tO26OpUtl68kT/2/CtN3Lze8+LUyPWNHgB6ZXVAKBIWwU904nppztt0fRIp0r86Ty6JxSP9PYe7fcVV7gOV/ZwaVmYq0Xph6eUzLHd5+YvoZy6HROpt16VR8SYpxuBK8x5o0MYwbmU6Xwu8WA4Nn6D+fFnMOC8uC9U944/nCkSJIrO1rfXwKDzS18HSUmghFhuOz5wA96eAaWu3vBJLwpZYJBnNwECokXg05XoQXiSFRe3LLK5vl4Bv26YvAVatDlLmVulgzJbehNoCalM6lN0aKlRHZtvfN7LtTpZkECBr3Xh1fjGgFdWMj18wUuIoBMLJovFK27kxKX8F1q6fMjV5AmUak0qRSzkJ12xVAcotMJCgdEAT6HeuWVsilzr9oqewhcaRiwAemGZyV9fjWodxJviXVWERf3YhQIyXi6uuSdw/RFvnASRUhKAhw7MyKcG4zImKkhjqEwUD/skPRzcyucmpYNaaNVanF+dLV8B/cXXVRIHEl3VQ8seobBA4Ftr5+cOQwW4djUDL5+InrEC9waMJfcUbJirb7/51u7ROY23mIfFCkehpklAZHm/H/r6KwdR1ePCl8qWxBmdmnen8qAw2B8f1MFP/MU5Emw+AIA1Gtn1S6xSCxhnKJJhwJqPlV1+mG5CDYawkRgcHEhbx5Ex1PRx+thq+ebqNS90ZTRJLi2YESwdzE4SivWjE9KV6CnpOPCl1prE7fPVhx88v7ggWlVFysr7mCJM7YhQZahmVmm94QkZ4g9S54zWVsa6Xh+aBu568X0HjOo9HZLYsEvOXdNc+stItcdQ0iKi1ZF9THRipbEn/ArTFYRfYcV+RVUaO6odftim3XwoeX+Ps52tr4ynIt8B+J1n557xRDc+e4KKzo0s5+hPYPJ+FdMx33Scd7+WjqP6TR/krvDtJst07cdaVBbDXuhjf7ZndN6NUn1FRuKYKInD4909/aoz9LDk1OKUkqms+9Qf6Hs7lbxP09sp78OvhWq7Xeoe24Iuf3X5XWfGTrEIiWnrTRS3rN6mYPUtP//ygspXS6ag75izRHj1SqAs/kRUMKpc/jHhCzIJfoGAVlF0ISRQFbP72LhlGcgNc5HgETQwGsireFyJw/Qq2au7M946j+blm+urJZOqYFzeAqThVDJDAZNQJtsdb6xnW7wcS4oJbwQ+Qh/M8o4gyLxfhW974RVDEQD1M25hLF105Boa6gBE9zEA7TYISD7VpEauClksXlpx40CaiWrAWcEj0vz7gx7zUiEmnTEqunXoA13tQbBkU6vQAbtuOJbGsbY4QjSdwE5IuQ5/ZSOl9Xj6gCKCJhBEHY7gdtqDD+niGx/h9c0wTBtrxPsMJlTL5r5Sye7Zwbq7hYQUoWyxbypUO/AnLQ4sPvZ8B4DJaeFxdTuxuAMkh4y2iKw4XjrJmjb4a9YvsQ5LbvU7vFGUNDtSi2ffM0SA247GWnkCtfqqKbKYVnHUVbxRCivHbxzG+aQEtixd3n6hBnq7lvy3ePadk+U8/sEw0al3NlExEfYJYTRzb8p7MCRLSY1mbcHF3ce313TCG1qDnq0afWYz2fYzc/8wGpLbD92nJsvFRxlP8/5WT1drFXVYjS7sw8v5YnxMK0WijH1Ak7PujkGSHzuw9/L9Cs4yZOnSjn7iEkf1GgQ2fgt4D5LfnENTvse84mPSaMArNjqbV4AwfpzG0SVmByJSEYaR/6rMXrFsUEKrXPZxuZm2uHk+SBcnasAhFPffM5lo77SentzzG3Gqku73Yvq7dq/+xOZUk/L3KGX8ZX+IojmZrl731gId07rPKS76LH9n97CGaemszinrERS6H9t0D5FW62Pe34GJ0J7d0/o2NTDorw5VXk+59lN2uVl/6bZL3i98LBVtD+7sx9o4ja/q9545dVoVnor7AUFA5Gk7yFPV5c9KTzXB2JP3tQi0oa1IsqDnnJU4BGn4E2GQbV2gAAilggrQBa9xsQhIGqgBn8wpB1uAcQFETopGAVADAAHuMJ8lRvyws6aGJ0Bd4BM3NADwCLQCkmSNAU8VqyRyTs8LE+NPPFO3uZKP9SN35SquCF/YBIeOQBxzuDZFTMTCcCfjs76bpx4vpVFHMTgSqR0KHOEgDyPIG2hIbIhLRY4CoDzlVhvng9J8+FRUk3AJzmIewbjCEe1RzlE+pYmKihxYBEEaIx8AgG48PES35qLZ8KQUq64Ex9pHy7MPXVTjI8JWoHYWmdlsRbGJd0vgqUL2m6SZEBq7LIPK1JMMrqQW7u8YiiwZKWUun8ZNUMsLxaotmwJCQkCdSw4De6NvPKixdtOfTEGsuGrKL4WxSsce6N2qaJU1UYoPUYFp4om0jccXkWlyF+poE2XczcKIGN+KGVBLfCYgLR6f0snpIVGewIKULbEDpBPRj9cMlaOz9R21RVkURjECGtm3FZm2jnFUq9j+QCdSUaoVleYNC13Bf+bc1ZZkJOjnPlTjoykos686yEdj6kj4VBYFGiLBo9K8dcuTXTI6EDQsiUyi2fq7z823tuec9dxBFyLbbsSz3rXBxfS3uDhSinfI3nvsDN3L+94zJNDvvZe/Cgft8ZOKPKwzVavttN1U+cTauyHc48iO2/i0FRkjUt8B2OvtyeOzwdzpkR4k9/pRc5b51ubpo89eY0XrdO96HaZrFFjUfnQIpUxU0bg/PKo+XDoqMQF4Yku77Eg9vlIonq41HMaa9puq9UiJK+6mlLHoyMRWXbo6zolPLU4pc7JvhX6Ez73dAqn8TmcjtK3XbNM3EtNO1SgFdpueog28/3/2/mVXkiXJFsRiR8Q5+apnVmb2vQ2wQYBgj3hHHJAAh5zx0wpg5aj6H7o+iOCQDYIgUZmV1XVvPTLPiYjNtWSpionpy9Qe7tt3xPbYYS4qKrJkiaiauZq5uTtf0zFVbO1ik0Mv7PkI8ITfoEUA/ueygatlXNF8wl06+GerAr7Sc+lgL/e4Wgo0LFWxhU4LAS5DeUVc6wGQ53V33DDAZXe2xLKJ9GwNwpvXcU8Ol20IQUcuKYwnEhEsbBOexWaA5QF8C2lGi9okMrWHOTB3LKns13xxGw9vRsIyDvd5IwVbLn/+7t2HT8/8ULKStCJYMFpyQeZXfLFUA0/Coi48eyFT2cPGwik/dsiGBkYIS0Z4wsZWXriYTTXriyh424PnDYbMVRquU7/7xBtjeE0aLoZMe/5ArS1bzZaRGRe/TvDu6c9BR8tUwJoLHRjPaqFnJ2k667GgZoSh4HhwHWieK3cBZax3H/+ZCJ/+mrBCwIkNHs8/+/LpO/yiPM6X0tEASiXABT9OaWzo4Wt+GAL78DjfWSIg7lz/mCus+ap3nOysCmc7vBiPFSs+U0F3PHh+ycrhjBI1szWtvQnDQf/8jLtWBMtTCHywAB8Ifv7wB97ArwwxWJjthKGGH15H/igj34zBA6MDgbxgaFUBD/Rz/mAm8FQSv6yJHyZmFL5lQSpExkN7gslSmFabtSINAJg8vcPnXmQCGEhgw17lyPlGWM0Z2pknRwwie9DPxOw8B5R4osIPqdveaolxlhHWIDH/oeR9cfhOKhK3z7d8+YxfL7ag3DLal8+/YE04dAjAc1SceBKG/wlugGJArT1opUDqxdb7aGCdMMoPGeeWrv0LI+vYWr065I4Dz7d+jeji73x1mEltXaXFY1WrQ3G7WSxBGtIqbqN/W9VAOMRfkTTJIqZPzG0qlYXQoIaA9Z43K8ODisjzEMR6RzIIqPDQ1sS0WZHHjsw9eXnU9kvfDmkVZMqvFxhIva4p3BNG+5M4Eez1uGo4UJy3+lw0aKNCep137wV4cceuzQuBRpPbJNouZa/9JnEFx1d3uz8e98xkc1hg6YD1AO+kh9KWRgLhVUlKWG5ggzUM1hMA4de5wBSXtImo0Fy7KAxX3rwPjesJKilgrYZ4WO9ypaDI2jJe+o+nyYctjcwWN8OQOe+CwLf6YwlDDhYVAl5X8N0pSArLaHRYEiDEK/Fgw5UW1FgH4gnJw4ACM2K2JM4QfOISkveqc8FIJReverCaUGLV7ipzIzgt4c3VP1uGy3dmIGEdjM+twoAFNbqkACZcrkHQauzp/XdYjiKdv/z85WeoIkPYCBCXD46GBLqvH5mh2Vqn2QI82coBW+izszs5rAUFMi+ogx7uRPojq4zANhtQJwICwdLl+x9ETCGsiZRQHi61UWFe6ueDKdLLmlx1Yz2rsybUEwtw3q8PIwBBD1fcp4VvFcJZLkeBbK2+UAIa3kBEeVloA4SaN/dDrbdQQNcIkgf87fPinCUAsnv74c71OecAnSCSIt8L+2A/YUElwaGkD+Pzodwlh200SqYWnnqbJopCD9YE2ExUI28hoGZ4W3/bs8xQig+f8LEWrNTRzapgVGyycyjIXmOiZ5yxYIe1j1Tz4xEcM2OMZ4uvhmhzZvD2vC/8Ni0UiMxsi0LQGA+W11QkzUfcmiJskuGiyYoEZh1RXiy/FilnfDYfVAlQV6GdZfNK/HtTa7KMMps0vldJejl141cOugUo2Xez04STVe98ZdFXQbp0cgcC95zYhXVD/0rzEjejpefOGeQgVgHQaxZX/aNZLJTrG2fVgVuj1z0LIbwnE716pSu81RykH+81BH6Ri2ftCBAuecRceIH25R6ruRTGaINRh/MKLUDka/9SafRYy7U+OGAtgxbP19cPW5qvRoEv41RwyYC9Bnc0/5IuuALKtZC9zPMV217tTWXrF6xjsBTAr5PCBa/uSByLdVtHYg3y+S/wrSfPH/EtQIbNLVY9WKfmC+pcymNFgt9w+g9+ESTuZGEILL4TF+MMN/v+EI4v+tFLWuSKj+QmSwTLOZKj+cUNfm42m0Z1JVuG9McaB18uxDUfr6rzdn8kCKo/wWVzrdtykoinooCn0kEbV3uhNqqQeG2YtLhuBDhwUEX89BVPdQCGcFieWgh+LoIlgp6WGFZ+Iyo1cOP3ugACpHjWhEUbeonGBT+XvBDt0wcsN68746qzgXBVDyt8LuD9p998+RFfXvOPP/zIIQAHwrKfS0DSNAcOyvJA+f8JfJ8//RJEuXS0/0yCZzhMZLGVBK2ZWhZQ4U6Tv8JmDcvmE38G+GdP3/0L3v7hlXhOD8Jaoehoq1KEwCVl3FWF9T9OCHj2hXMGpk9Q/HGFbeCoJgw4wQDDZS2u4xMM3TDGQHKWGrhVzzT8xHk+WbBTBlvzIxSZMIidD3Di4S0Bjhsrj/ECV7wDwLrZiSyqwm9/ZXEwi/UTY8gKn2+2oQESefLesD/x6/nR4kfbuewGpJFnvvi/fqwGwmaRIcGItqSIkiW31E09OxgDSWBUMyyfEQ0xOcEY98tHfJD+T+/wdbF8p85GDUt23NGHz/PgbOV/xSkCP+zLU19sgfpvfDOMcxVYHBzudwmfJzqWJSqCquPdl6ePH7C/IFPcbMapzs8N8pQA7/XBC8XE9CM+hgxoloehff4bcHvmsV1ZMDILwc8cwvv3UU+NHkqXLnzwafXqYFptyB8WYNZ/9I7AfQ/2HPPqYq73LJ8LSjG+695FqDocpOhZ1Wodt7C8trmKewi6gXCaf40Zqx3lQ5R3O/XmVc0zQdsM576XHtw5soznchYse1Y2SvtIaZi7+bw6AYjo0WiRty0W22ukyyMCsCjkgOi8pUBGpR6EuXHX4RqqVgW7prKw+Uqajzmcobh4TeVLti36oCZfWxzwGesDXUzVyyRuw+Aay9aqHMI0tblgxJIUtwV/h1WU6blKsEHmsgOLgz/96dOXH/8DL/C29rJlBE8A+DKPLVe6vKiLFe6/89LqF34wkRRJxqLwhR8aHMhsaZV3P67GsMaA2pY67CNg8jR3NuqHcavV0Ji39QgHi2dbWYOlLmFyXYoGburBmQoWz6wGgxpBLAsJ7QdcYFgixOVnFcSPiduC1JLGWhVm+OMNPLwTg6siFpBmXJ+BgdUTBeJwMJSVgdC2MtVilFXApWs6oQM3m7AXF6xx0RorVAycvRjAG+d0Xz7/2S/+8rs//vBXP/mL5x//xF9fwBBw2WZsE2uTGWx5pJ4lfk4PZsGQoeGUnqxBOvYwM8Ph6g5G7Hn/w5d3/4qVNVV4JFSWlXdTscBIi9SZhU0Ufvb3Pb+jE8YAsKHXGt0waYraMBh8iYnKGCGeBzAuluzYxj/MQz6IjzFAC34oKZFsvAgGTyUCQ7vuTx0Ka0rzTm4Es6/UMTsY2JLWyCAqVsDv8L23ZMcgqThsVw8oFVFbNhIHU1gzOQFJcVi4rLNndpiKAgBsxpIH62bV/QFfvfUjbhRDXbk/8myTkxufYIHmT9xy0uL0gMt0/AYGMD79iNU8csc8tcmj0SEqCeIffijNbt364fs/4U45WMKXPwLIowRP4YBhlxioxx7FczaODia8vQUICELxoa2J2Fjips56VcG3i0V2+SqfNZhfZWqPlpRPuZpYnoN1zwNqPI+CNZv8r11oQLzwo/3qBKDlitd7PPAalh+6Egwop6OedB5TaLPXsWeB6Vwtcaj4dM+fAucYvShC7IoyixPaMd+ZT4IH1/KKApPK3GKI6LIp984mB44qprZNMz8nFivn5vqmV1QeYEX3MKY9hJ4+Ro/ylH2IK1/NpSnfGKwj92Zm79pVoff6f/olA6y/H4MaLD9sjtqWiwGoTKe5i5d8fPXkP2MNg6UqV/l4UccLdJjX8rBrnlh4wgCfm8TJAGx/astcvp4/v/sP3C7PJSb8+ZtN6P0LYDzxjnyEo97OAZ4/fPrNE74I6N0f/aXfFkcw+VdG/fLniSfZgRue4GsmBNJ3++BTBNS1H4hIHFgC02W3ZRBzhoC1JhZBHz5+/A5LQHw/IteT+KZ/fmeOrbNxCRO/BcCltVUkYSAwuBOHizC2DIrKZGG00WfLfnLFn/XJhN9lhAqlMyC6p0xhp3UitywbngxezmSXVFz32nsoiQBiodMa8MRK6/1//PH/+6vffPy//l/+b+///Y+4SosxBltDZDxGQgqGnzDV4BVZPJgVn/mQoNxcRnZ4IKCbRScoDZ3P+ONK+fOX7z68/wt8r+f7p794//5fMNAY8feffv7+45/wMYz3uOHq3Xd//IzvCcX6nwtHhP306U//9q9YODKzdNeNVwDduT5WQERQuWy2MCoQzCaXlJrASoWztxdQB0S069ZmBKvkmnAsTybEfDnomJMkxXcB8MMWCPwJZzdfvnv/XtfX+VnbL8//8eXpP7//+ANOITmc8MHKFyTTg3XJtYUKqDZj+Q6bWTAd45++awv33+MFAd/zAy9+HsCssHFEyjAxjtiqDhYTQDiRwlcW4eT06eNnJJuqyV+4y+9bYJ/FPxzrkCfnP2/rJwecmhpPvjdlsZ7+G6vz5c9YQBDEHy77f376I/YbY/WEjxp//mt44fMn/Ig8Hpyt9Hn35S+Zxft/xncL/eQnPCa846+UGD4boR4f/kkKqpiSkstb9iUvVSsbV888Xm2YdN89qMBWit5xe2UUG+F1ZNdrBxLFYXkriRhpLYe4647jrV38D4Tp4ff0B0IMXDhn8gMy67/zcYZnd17Z/sJT9OKx0qS9wkzSEaEwr/F5SBk/0rcAjY2stzdNS71CltqNAD3zmPQGxNXdm6UrAk7aF5miOelYhDvWVKyCwzwU3K8lfC3afCKPbzlT6lw9eyFNr4YaW76+8wWcG3bwBZ3rBkO1F3MtvqFOJvj2Hi4O+EY/rbkSoLX9Dy+0gi/KR1QHSkE0UdBj8e0JL/aA07VUIQtYRmaCzbqVtcWzhStN5Zn9EenL5//8m9/8H//Lf8H3k75//vinH//46RMvqH/87vv/5f/9//r3f/+39999NEqMysWM6NizysZcVAhuocMfrGyBjzcEdB0UrqwuvmEGODDAyowKyxQKNKhnIenNZwo0sQTYtjWZNeGVSo8nW1XCkLd34zQA5nb5+7uPP+V51r//8d2PH/ipZi7+EJQ4wDVgyIMHQ9ojCYkJVUSxpmiblTbJliEWLay4av7Tf/rlX3//s//x6fOfff+TP+L9ic88Dfizd/h5YBT7O3wfz/f/z//l//Gv//FvuuSMxSjLg1LAlQiYEnoJVAZQ5lSsalZChUdyJrAWomHu5sDx4WV5WJjIgmmMNIp5qFNmAjRzFJErAy6RyYfvNgDhCb9s/L/57/93f/PLv8B7MPiW/een73H31ftnfAHru7/5q/9ODMAdy2mja1UhQVFUDqxWGnKqjTM3jJ7mgohYj+mTBAMbSrMktkFTwINVM1xg4+97nIqAB2SrJIBzLAjA4/nlcuoDd1pCawEMjS1MXQZLBwSEQBNvReGhn2Tml6XSA//wjgJB0EUcqvBMj8Qsk1xyMQPYWk/aGAtGzPpkHryi+UoWkLYz9ivnV9xgnV8x/TfqhyuwMeze7XuGa5aQUOmAIBUt9A6AdSx2UarOUFfX46Oly+vI6XrY6mzGTTcEIa3O1cI53IbzsHvz0KGSrFNJiH43vEfQbilMV7pQn5nF9xAUyI0nhYip6BFzEqQw0/lxIwuree9bgCJIZJX0W1cpWGE7F1cdGggG1NPH6FGesu/MpSnfGKwj964WtO5bZfau1xD4QNTX/lcBOfz8VVo89NvA6TXCVqYsr60M+NJs6wa+gPM4QDdt+CqOy4i4QokreXa1EispvTrTCP/TUYNX1SF++HetXQwHvXjYyus9vg4SF9VNgSVHemAVgbUg1qn/yqUeZNLVYMvStvY7AGAm7+SanqBjGsYt9zzji+ftsSBREoIccD/Sr/76V7/6q19++RF3/PPrQL/w53+x2nv3r//yr//B9SiJ0I13TRBtKU1a3/DGBlvREZgLctnxGQWiT0rFjoq8FMozK16zRwdviKfEZSi/Q521gwv7jKruRqI9l6q8mApINBFLYWhud7OIGuxFEF/7+AW/HvUdjM1HJy+WASCYiK3nTJALNWpiy+gWRc+U00xYuCWw7AMbEDOIdNHXInBFiHumv/+zn3z35z/7P6A8+NZV/KDZl+f/jAzwqwv8aaqnT9h+9/57/Czvu2fUH3XA+yd2GwlvWOFX63DisYCCEzdsGU41Y0e6zwl1N/4cCeND8pw2qLRd/mbTEoIOJrg9HRqOo1nBknMYBpYhBtH0xIcNRhjHBCLQ5/npf/gf/4f/83/5P/3Xf/6vHz7ip+J40Z2zx+L/8AMJ830wBBEREU6syJ1I2PLdKobk2R23lgzfRPo5Scte72jBilBGLRFkamBDtUIbFFqmRsa67x835+Cj7ZpLcLc59v6/mRk2iTT3aZDSd//bmYoxz+HAR6EZjPPWTtXAg1+WZZXBvo9r/+i2EkJr+bH5/l9Axe4hhFbvMGieG7gsscXj899wm94HYCTi7XjAGph4F+nXdPr4j+afo5Q4GCM8Osf50rhoz/sG/DOvHWllZTT0WlwwQjMVXEKIu7I05ul9Y3wGY8/jDP/4Tn4vZg+/oZ+vfy+YVanujHXeOzcaPOsAezXYU1qP1vphtK/ENUDaIbSzCDzLCwTj6gSAusY+pNmWHVccG9ar/lWjibCyGDYWxkOzA51jYkWOPWPRmyFZADph1dmbB4RB9IK2cyj0CDoAcUrnqUYoyYo7E919vzohZX+kCHkhlMcvQ9nCBCur3E6LV5iZxpY7kNDkogAfJcRnNLVMYj+XQFqQYci1kIGaw28O6XBhRtYvVKw0zCBzyePEVRtiEIcPcaKtIKnT2ohS+UhOQU2CSwjhcJUDHaJknryHHp8g/dFuceBdTFh94gL7x4+fPn4Pf+VHp8TM/OjP9ZJlmRZeCmbI6dQHTrQmD/7HlgsmS1A6FsZWmooDGQZ0gd6c7FSKkNDzQAwwYZMW2zSHgI3lb6cSsCCl918+4ZOpH3nekBayMqehFUGjR2V6MDKxDMoSzobZAs8prJkGtVkurKyHkwAw0uLEijeB8ztnMY3wff2AwtIYMr+HFt/xw3MGnApg9Q8VF+Skw2iU8ZEG4PBUxvJmEVB+Z8O2QtEe/0MeFh5oTpwYaKBi/JAAYGGB8OaJ84OEQHYaB5AgdioXlFSoCyif3//z/+8Pv/vN7/GTwbj7BT+VZ4Akwc8wvOMpKD1SeBt8apgHQ0Gyh7OztJKWsUjU1sqLnVzgkSpLGPwHYT6Lq1tjCc9Zhw78PAJzspSZEsrJh+HI3GRC8T+HAekZZjYyXpaKnSxxKMHO3o/SBRrLh2NKOgRlIEuaLfLFMytvp05QkZgZ0pgSQ8fH0hm1W7JQjvluYb9If6MyHR5KOhZAJda24/Sm/joqMD9NmG+cKt38OW+WzwB0XTThHKV3bto6X6GTX9d0hFrQOVkPeWN+X3Gm6JTidXSVXHWRgTRuvAg7OdTvIWzkuETqSo5ZkBSyD2KdlCPKJubrXRB07tvrjZYruXeVIrwknM+9N/dWTPY2do5pDb/nakGqAZ/i+KncGpgygL1k42qrvUiHb9E2a76452+Ih2irMYIZuF7s0YJAha1GcMczd1WtNLisgWSLCXoZD9MJI72e24t+4owO7exsG7I5UQkBFxBxfZGrB+OQn2IMYtYPKQ1ztYIAZ7FyF7t3gWsv0uYS7wsi4gtk/o3Lui8/4W3R/FVgrEbxLT0/Q+p2hR5pctmCBzdWfNobDEzIllXClkzwpMubtuDhWtFqi0kOS6yo7HZzcuB/5Kte4pBU0rAb/bzkbPjo4yVwgJE3/vGkAKKCqWYcwfwPt19/+Q98YSgBkSYjoQvPEChTYizI9pDM1PAQNcRFL7cWzEKzk73JzwRVwi6TMwjRtYFxSojfxk83LhlhaE88rcGSFN/Aig+j/itOLD9++NnT84+4bIuPNyAu3hVKt9zg1hVo+MUytkC3j6ImNsDgmwO0txcR1soIoG7YN7HFP7L06qHfMjdL5sL5bGWChhWWfcqAcfGfENQQjfAsO5NDTHx89k/vn37BC+v4pTPawASnATqX+BON5YlQRMFD+wjUZk1N8mMfY2Q7c8z9VkpFNVWylUfSgIN97sWuoD/zt3sBgbdTsJ/bryhYQNJAR8rBEG1AaAtqKbiOyZY/y5NmGOKQq96xf/6pUf0jfiqYrFElDgf/MUOu7e1hkIDFFKBouTIIaeDEi47JUk9o8do/u1d6a5Oeqcu+wpRNfN4e1/5lODBXpg3/CdUZ3wn42qS3/iksWd/hAziwmXn12fu6uWF/bcVOoN2VZzUWG9Er+56iGsHnMbKvARwwfS/QP5mi3k04k3BsSw/01yYtVXZoPW9OzpbTlu4moDkowPUHhQeqNTJHgXpdGe/gs4c+6B/IA8HRItuoVBTXeNBa413XCsVUK5rXxnoNaKnw6yfbI4vSLCNkEhcx7fy4GMKrO9c/9iUqAIMKaylbCdhaAC/nXEBSARtcTcbRAE3q8N9WJXpNZwizTKFySOhM5NKKJvl4YkpDMQc08Se8oKBoPEwwG+tNmyVTUxhm6pKs2NnFIhgNRdPaBLc2sYlFm+5hgDW+EpQ/LQU+cAFGvokbSfDPKCk2ZLjhvijcrsESscuescUz4ztJYgHcOjQm8GE3LRidF6JxrkY0LrlUavTi4jkd4c0Rk8jvpMTSlQdnClASi0WG9Tv8wBm+3pQ6bDioQBOIZcA24cLD9KKSe5SQmBKdDrYWNjerDciRPxPQNiVEZQInOTuFSA6kyE5lhw/R0hs0P7/DDWb4o5kByozZmAvrg/+WKgzSbfh0Z93MgwtVWlgk2LKJOrLg4sle6unCP6pFlfrkbrbGnn1WWVpRQw8bJUgExq0vz7h36cN3yMbuU+LPl1mNuGvIR1U2JJVddUzVWT9xtPSQL2RoqFSPsUoWplY1sgufFxPGB02cZeFdLnyZkv3AAfoTHMgIm2052myhk40OumWDJ3uYp42GuXBjZ608TYVLmqRJcB6WtDK3o4dZWkRPLrX8KU0yh0gdbCeybjoplFCTbg9kxrLtpOO1kuDNnTDfnPneOj9GgbZZawqN7Oo+TpqP+V6636H/1CzK5ys4MtnRZ0/lJs9925CdM8Xx2VKEipY5i9i/yF5DCd7kBa1zD5Te0RKfPxjiHmRHEJeiuRA8fW17gToqFdyK5l7U8ajtRUv205WP8+dgrNotVsQnh3ZQXEj9GzrwjB8v3mnZBAVfieFnayzekotlDNpywm75+a/Y/vAv9orOHl2tfWf6d0//wuvlMOf1XKBwOYotxXxkEJLhs4sd6uVaF9Gx43OZGx5qccsFS3rtBy2spLAlCIKoO2El58XRFGjmiGxzBZYM9SRmvlXnh3/Dqg/fUs88cNEZ3LjgxOT/+Pzl46cf+fWHX55/wFc64iMUvNL5hIUUbu0AMdjocr7JvC8c75TiUwT8IkV+RQyvseHiNPSwhC8uYEeN6T//JW14nRK+0FjKuDEG9+birAwzlu++4ptDGQtxgYyrmrhVhr+mzIj42OmfPX/57vnDP+Lti3fvcDUat6Hje3W+w60p3z/9FZKyK+9Wlo//jObT51+xljz6qlwgjwc0IAyNreFwiZ6lAxlYLetFs+SGJaQ3GP0z0TjT2FZpbehlAyVN+cQr5ERlEPC3H5c1JkgNa+8/5xX6p59+/vLDe/7UNGr1I7LgKdmX7yHjy5ps4rEaeHPGfqbtO3xNpUbEqoSPPH/37vOf8/s3UU+OFHpRf/veVdWW1WYv68mxQCV/pAaWqj/s+QF3RjE9xxff80MNf2n5e7P/Hpf8gc9fyX3++Mc/ffj8wy+++x4Mf+AVbn7nz0cUDQVm+exhxaRkOwAFJK7SMHeWKm5pgEfx+ojiJpf1k2lT4a2SP2cDn5axQnNMsEdhVEEIPz2BOgQgDYyCw9x4YiM0hrEpAa4KCT36OHOITT5/Ahg+LWBUYcs3bbTE12EBCNnTTIDH6CgMAICGP5t+8bvJDRmO+cGgWYYD7tqCH8431o/to2vpsfYftDDxMB1+ye1NXkEIbIcIbDHTzj1UPS9YFA4XYG/We+23x+5cTeRdR+nxLGo4Cm5z49io9aLzUI/HiZnQQ/bJUGSEzwSmuZGnyMqSDRwQVZW1K+xXpuvejVYOtmH21r2uwKmar6HQ2hw+D7dpWWHfROF8boL+SkFVlLCHUrRXWGywVsWdFriFGqtuGlLFF3tzwqs1rqnyq+XTgysYmNlFTlokDypw8R8v8ICxtT9d0ImHLQ8kGrwpuQQyAZuMozbV1Gi7WFmvLUFkh+2CsNbLwHvdProkWZGiRUJFB/7swbUJV6f4ZCpulviAYy8v5r///J/+82++fPe/f/704cuXH77gm13e/RHLa5xX8YOeWLjgngp+mhlLSSxSscVSkotULkBNttMAnD7gK0aBjhqbDbeQqedK6PNf4oTh3Ud8KSpxDM1OEr78BTCfvvuBvybLpedHfLeMLUlx0Rpf6Q8OuLkfyPhIBm6b+enzB1j+5OkjLHEzxp/eff7u4/u//Ou/+jVC29Ciflhk8zb6J7v7HgI1qAWLwF4u6SCRA2TQS318lt7rRQc1AAFWSA6L5qwzGPTTTcs7YuGsCsg0gg++J55P/BJKfDAAL3WYgZ//+PnHn/3Z+0/PP2P8z7j/6rsv+DWu9z/ypydQb363LHLHD0t9wonR03v8wBZPyXABnpVB1u9tof/5L7ge/R6f5aClFveoLc85cU/X81+ywh9535GNkZ1OoM785DEXr/y2e8rQoGz4xlLc8MafsuIovMe9STjFQg1/8vQB33OP6D+8f4eviPrN//Df/2/xU8P2QQtb9yJvvjfDB8vMLYth2UthbTNIhUzlkpNqy266cUMvlCChCU5WZkEre3Am45FgpGPTPLBo5mfcMRTGEka0w36a+i0EymQ6qDFh+D5UMuYhw/nAVYcQbHEgwIkQ3izjKPGLhoDjBEiaDYw+o+Bww1O6zx/wIW+dH1nwTDQ/r5PKWj57DwQPEg1aspy0nXZqAb0CHfLzGjndWKymgVt+m4LqEydIXcOvuzJegcb+wRnz9Nu/+3uvQGlTtt1wLCxHibFd6LVzI16PaT1mxqw+C2whTehOn6WNY4xLqkwvy6VHJeTIOdAzu1of85JcfG4BTKLN7vghr92+weEUh4CzR+Qg8PoZHp29gC+LuEz5az5//D3nEV5x8ZHLz1i44NXaVgL2Wo7dj6/xXHngH5cFXFniBngu/rBWs4t5utTNr6nBJWesLD99+sRziXef/pq3nnz4r/CH3+cv+Glf4PBhDKnmN4XjGfd2i5KtHhjp088//4iLtfh9AKwLfmoLkD/Snly5UBBE8qIODx4rDMBacDRjszRNuYFFerhkCFmbn60CGY4rFKz/eIcTYuETnHjwnQ4G1ikSFjH8rh4t9CkjHTgxdRaNpcsa5MPPEaCwPCVgsUEa9qaSDD28gMCtpYRvmsTX0aBszFcrJ3SgRIzCxTSXWBYXdcJSCgtf8MGWS1VeUwc3Lo65Fn3GGwL4yeVPfwQCB9cKza85+vxTnpPwNMbWwRDwvUxYx2NMuZrH3pHWzfgtWJ6lfP5rXjbmTIAX12/4QV/7SVfMKMBSwxU2ZNx9zu+V/0t68XyGl9Ixo0zGpyx+wFsiz5//nPovf863R57+RML4mAIL84GX2hEEjvzZXS7ZEQ9ZI5f3H/CuC2bUT1kTVh1B0aW6oeasCbO0VFm8D5hR2EV+wqvRdipqBYYPYbg1iXWlL8eARacPK2eiMLkjYN2s3QHc+MFYYmKXAGHgYI7wg80//vgjwQDPwWZIfnsP2viSU5sStrXAjMJYcLaI1ram9KkdnqKlqCNFJpswKJF5BknwNgc4nZ/+HfsqvgfoZz//hc4H5c6tOfIdME1mauwSgNXjA8aOpcYbMj+1czZ7wwRjzTMuzCK8LYazMpwF/QyD+/2Hn/NsTWe/y1son54+/yfOt/f/jPHghMfbVp9/g099fPfT/wa+qVbk3nxgWPEATeVoLdjaOwZPG997ZsYXbG78erH3dUTDXBfMKyQDJe7G6C1cZr6v74LqGcTeHHtxr8Lp4atEXsnF7KI5sABC6mCey7HB3YOmPu1TOCy3Hq0KwA9XSpYH2sVc4u5Zqhb7e0gpt3uEevkY9y/1y5Y3zq6XZfLyYz/HIO3GeDWHxOWnrYTY4PI27atosrJYHeJghNUCXuztvAIrBn4qgIscu4+Fq6sk44OaeMn+Dl+Rw3HA+hjoWHvi549wTdu+YpyRuQDSM0ApMCLx1SALybaIMUt2Y20MOFIyF9+Q9rICYGC1ZKk2VLAqNGbZ2pANAtldEfSxOpEzMHDN01aTOK/hjdO2QGcBtdzk8g4eWAUyBVu5kh3/Mz97sq1hcXXMMAYIKxZGnsRFAwU3zly4o5g4i+LWGIkNe3lllS3oMRBcRdn6F8t92OLIDCrYAgq+wjcMeD19h1vTEQo2NrJcpvMHpwiFFHi3EgCf3uPCNk7s/tovmdsBH9/1hC97pR6WFsLOMXA/En+yCst3rO9FG3qj9/QTLv2//AV6031KXFbaXVKw5xfIfn76/AueePBrZIGAXlVbS31NP1QJP7yALUEtKcBj2qHXdBg5KzSWrWkYUR6qQMPqCVKU7fSEaQoHZYARzGijEwbDRwgbS2xsLPjMuPaHDU8QcDLCMTAl3PGmGS5041QH77d84cksB5X9+i9/bDUYFiVxgFIPMJFeoFIycuuRqOUuC2WkhcF5wCQsO8iATA+F4CAgeVwHwIKeNynBhBOYdrAgAySVU4AGZwucZk8/+cnHD5wDOBr8BD/rhZ/45Z1XmGx4MwRfsIs7nSA/4eQTNviEMQ4A0ODOK5QBxwdUDJYf3v2AN2dwYxXu40IpOd+eP/3ECFiBGLabd86DlWXBrMRZOfmsaqgsvUCTUI9t5slxQANVyVFTGATbb13UZPk2q4AZovRtW8yR278DwNdCTFwevLuPOImj0Vc1bFxU8XV05lEmbr588Tv68EkAgCgfxbvGz8e9zDfAz5w31xnNeIUgffF05fvQsScVgE/4X+ezvPizz0xM+MKlLCT8Ci+2H/BJHqodmcsRLgJsCcFlC2TsidpyjcBlMP9/+OO//0DU97wiwMvKgHl69+OPnz5zCcddWBDCtgDY0ANb8sEDF69/xHVoU1MnJjIAJFYJQLIruFwm6pERvJU7MvjSNk1sigsOLT9nfF7txnruZ4wnmQt/PMAEy2vKWLnwCjQ+GwANOSBveIE5runiwW5usHbR7yG8xyVSaGxFRaaJra6qGgKw+d0stvDFrRL41pTEilCGJYHQ/mvHORZWSBygZJbCWzSGzd4kwCTQwULThc8pDoePePYwdWriialkOz4vhllvGZsVrQOS6di2cmRPA7ANZ5vDeZysNEd2s+p4ywkF07jju2XgJrOQuqWIWNYhWJ5CaDX//J6/LW3VBqJ8rSRp8ydC4r2LVEm4IzxBPFaq8PMvaGlRbLaQnxmqrDwFhMo0rDe5p7YNR5LxZMOh7+ThzBFhs1WAQmU9CSxZ6ckIRg3pcD4YrdgLWbut8WePzR3kgtX7h6ef/uLndqGfvpY3jAWDEuI8Bt54lw97N0cCN/b85OPP3uO9FJ4lpkKhl6HthMESxPsz/MngRMco2bdm4QTDPntixxAbICPG4tmoew1BhGRYHfJVA208Vm0SsAe1aaSyis+XHckj6D3l6VcQlUX5+nvjkemqiPjd9l+zs2kJvdc1IryMPF2Bl6H30lHnZrgGn6NKe9wo+vuF98xYf/4V7fMvBckXfny91wPTr/FQ2EZHT6UDQK+3pa8Dz+TTQnrFOtXZt7fIpK7zLaLswtRAnyd207q1M1LIdt8BLWqgYphvECss67NNWpYs5eM6ii3TaLUIGWsZKNgBr+RoNtTgdZsnATDGnQRc9ZgbzaBjN+GIYY5p7SacvFJNSgSBIZbaxliLVXlxYWFnGhbe+g0tmYbEycgTFpA3jdPSqqVkHwFYEEsVoXAhU3czcaXCDnVxsaW1EmJTZawyiCVgG7NJCbAaXO3YH01z1axeqgeQgGxoToympjc65kcJgulxW4Z0cKVZYmnh1aIhMXmFnQNkZlTiYXo8c1j4L+VibGz9psWV8qVDYpLY0cdKQhyh0Sg9pGGH8LMFFXKgIWuSIqf40pob8LmepHl6iL2mkXnqtnTjL0e3tKaFgiH8kD/+aXpmvtadPfgsfBXAKsAgxpwgZmk0WWcWFH/WaxueMwrBCylE8zOd2XMTk2Ku1aOpZEALtZizabsRUPFIBaJhGk7E5STNOVlkzAPexKU3NNKskbu2RpMnwDaF2cKbAHj3Ju2TCctsVQKyRRCcTWOfwSkBL95RxzSh1gSjjUYAXTRGHw3wZArBmijouJWRkjQgS1VRot3rlpG8pziTSc+YQ6Y5kAHRfHt8exXoTZC9lcBeyt3f3JYTgAoFt2xi5nWuOtdnLYtmPT3H1/4RVfO7Cv9YiiW7w7xyJZv5qmZxq8qkaNl3CV6dVTcZrodi8ZZeU2DRClPtOuJil6WKQ+7Y91zSWHv3Pvm+tipbx7xKFLSbdRDj5kAGiOaIhP6GiHHRq/6qD3WGVgtBey3gCy7+YUGLl2MwfP/03e+5jMleXBrhlds80gs2ZVudEx+WXIzx9Z1A0uOwAAhe7M+vW2TDdwNs4cYG3xuw13ea4VogiGFxYObmyl+BhT0VuEyILt74zguN5PYjTXmfutNkKBizbbU0voC06/G8ig8YXl/XtXYytVDUxAdtzB/bJKMbGm3lxTJwFQT955+bjCogO9w2Q7tACm3cUIEr1rbuIX9EFjWVOG9TLFbn6b3d9c6L3baM52jZyom8gMDr2bhrnDim19LdaimSpGB/JAPR2GvMebcRQopmyisNohmnslg//WSIrTCMPw0Tn4ADTNnT0sorEG1r8IQpBLOnjTWBgFFmxQyT77XgodrZM25G8iyk1xTi6xB9ODaqs0XhrSwGQdufEoGGNhICpob2vImFevYmF8aBkeEQlBHopBlFO4tFFR7sxaiooVayN/ikT5ah9QXfySNkoKWHUKSFKgn5MwNUYG7D+unfxS774dnYsg123D6bzdPzL4wbdyMqYcdgFpALcUgoI27+wZ74C/a9/2+mttqik/9w+5ZcMaNxyR8y7vtHENt5rYulpKXNZM5PKOyX1HSixdsI0U8GKTQtYcXjks0r2/IEj5TwB1T84QFZDzVNVv9qy+C9R+9I3ju69vQ9/K49ssOjefzvYVV6pMW3RK0cXotk1cH3fFUhh1SFYp161/7dBUKdXa2J9pwVeJzLegVYoN0Cv4O5yrRjU1IdtM8jdMB9xIv+Ff/Q17MPJg1xde1/mUaDEwAD0axd7BvIa9UO0+S432Md8VW1yqPAkLwqs8tFeN9USZXygSoNa7/ViRJfGbLCEr5HgcBLfDkoVgW2JoCblh9cF3Ddw3UuX89jUaxlemhTT0ovrXyIbEt/g0juVL3Hl7fgfmjdPGOuwMEa19bGXNTywdBcUoAR04AfFzE8A2EPjPDzT1gB04IaPpSuVjCmyOsLNszLtHFTaNlMYEtSUnBry6hcBj7jP4JCgJeZ2ZNUmVVingi4FT3ZsG57Ji9o8JcSyVo1UyQozdGUik+7FNMHKRNBnz0sbpZTCNpQ5NaWgTkySVjVkwOfFoAcKnT2xBRo3b0gmd4CEdNrqcJw4bgQoimaeLDu+ZFli8MGXG1reRnnxRppqo8ghmDu2DCgaUxmF9vSZf/8bI5mIbulvVgom8QXpCwOmzBhEpIWf+qWh3CSqavLNjtMhw3+1PKtBOKyT//tbAg/ooZL8EbA5gx37cQpsbKPjECN3dB4YUdNPdYEHDt08mAN5ofdEuf9OEHnD2XjtA0Z4599Rp9f94P9FU0y5T5LHPsPxwRtIZLesqEMIU1Li5NNLR1Fjlt62MPGzVtZ+/qfrS4pDZdZo+nUZImtu0d5GubN8K0CdQV8TqHr6bd/+w+0+Pi7qE0+DVXq6TzBIb++diza6hio3kl0JiTPY2c/9blUrWkz26NtYHbOGpXv5C5dF2SGVCzp2P4YfonZybQ0e7l2Y3QOk8FXrfyGzpyNk6MYYuFKGR582V4eeRD4el2/UChG3PKVAcshfg0Q7tbFx/Tw4TxhyIrIWj3wxTz3mVPqyusJThTIf/x3fAs7vvEQX4JOHPbiWvmXTz/+oM90YuEKBa5f82OguKxlJyDc2eXPGHhDAt8aCXNGYFS8GcAPIvPEAF+2Y28mmDmNzYCG4aEEUh4EyFaGSENaJKvg56LbZTMqFNIkGuamL2iiEw3wyCp7xsZCio0MfCsyWoRnQ3pR1urYTXuCfd4AF1LtLnldpeY1YxsAQuHBhW+KlEKp5cxyc1QcQ6IhBi3DWcs6cq+SUFxHXSzgbfMDXYlb6jNeUZUsTKVSOBx0LsudE2mtkk2aLjG+x2soG6qF0iLRLHBITFGTNQfd34/v3U+PnHhuhyTW3N3AhVVsxUtRM7Y9Y9yxn9hnHtCNeLgLn3uQnYDTgji24+rz4/wEAD+i+93PfwIFz8t5GR9fb4ovPJUpOKKGpAc3NgCIXzr4gK9YxS9L8HZ+pk1c9iczPkNlXVTifIEIRKKxndizTRtZESBFMhR1MkXjYcbNjSGKQLP/1Sq9DEUGVshCN9vsYfb8z8RqYo5eQznYTacrlC+1unipuI2ajQZTfdyXGo7vqrv/NVSyxTsATacMJNvc2nw+MgXkE0lthvk6DI4Uq5W5Bv4A2nDkW5HedKrAgVpPlq6NbFq9kMsAI8c1HBaJthLg52+hsVdjBoIRu+2RLiJS5ms9/vtChh/M5YV/rOnwYWJ0AM76iWbwT++/+x7XCHk/AC8Zfnn3w48/2J0eROHShMtULu8QEdF5+w8EgxECFg88PcGthJ/xTYLsMnbWSdvVw2hbv7grV21lmGQ9MR3S5MM0q5Zs5OZbrlhIgwpn4r1RsF7DtmWh0DyWhITCJ/YvSmrSA8omk9zffKaTjxIsHAS1Zgp8JJ2ZmWJqk5ZyNmC1g5Cdrwsht6QLXYJJRV0wkwUGqaoANOWjoQo1XUVbNUqcQXvNIwWk0gAr/kAqSNn6NyrhWJiE8I4cdCbSK+ZgMpXaf7EQ59jj1P7DR/xOhfEiFuctjPhuC425hQ4rFHyn1Ud8We8H7KTY0ew4YPY2h+BOv3RLli3p7bZeGBPN8PikBiC5N9uApcB8l8E0yJ5MNYGgYcPcrH7JybTo0EMFy63WM4IRZ/qhuCn6tNcjGdrY3Y/QncPdL7G3SFUFuA9OPeIuh19PxKeJo2YN0e9Z26El0x0OCUG7M/x6CRy76h/51Qi1Jtr35NEZsK4HF56te+lUIU92qmDVmWhk4lBF8M1mWfMqyhghcrj17ynGWGNWqbfKZX7Eu7F49cyu3OMz+BPX/ns4ZdlzPnpnINxXkztiLlo7SMNLg/iudZrxLnOQw4I+OdlrORc3uGJnXeH3g/WCn97+h/7XeFX/xc//wO+S5+8MfHr38b/a70B9wLejv8dXN/KqPr48/+nT5y///u/4okB8o4gtCkgVKxScOkCDmwS4OMFJAeARFrzsfABfqvhXwPmXf/n/fPrTD/xJV/TyH0knruEp0dcyw/TSuCmaJmPDFPNhRxBSBrjUnVDNlRXBw86comW20bMtr5J9tFpkUMTqBdako5VV314843YBwhVfIkiR7hG3RmbEhlZKBNDgKXd0iEFEdtlAMrAadEiSmGvrlvJV03FoY1WDhg/JlnxawBlKskkLR5kmYw1ZjBjjGmS2z88pljVhvHpOzdGT4aM2BsOGKbi1h6avA3hisk96ff4kEkG3Lc8XnQAdl54OZiFZb2hsK5H149tiOTrtraTY/BtPmLlTPX/87sNf/PVf4Yc/Pn/GV7Xi6/5xSoAd8Ef85lsG09m0DQEu5PPuHrjincD07UlMmruk3TqIcCkgDmIfP3z4yXfffYezfuzWiGXHNHRzatnpvFEz1nRLPdrbhJOwjHnOg2ca1HPfTv24++9X7I7fWCLzqOfxYvFRf2cr3CV6x6x173tt2js+15ZjTcTZpMbRjsfzMfS6V/PIdeNvAYLZJhmHmhRGr6H9YLE+B3NvraMmOZ8yu0vcVX0adDllxg/UXnMDu2A96h/+MPDWZwA6IVpoA6z+FBg4WVcn/pbbw/RrAHbRcRfP3TUSsNXD9Wi60ruS0dvTXSqQ6l8MA0Lv2lXwAumj3qTt+C7UZkAgiAVOgLS2RQ+V9ppKCz6sx7a2hMnziNca+ZqP1fr7D/jmb5h9R4PvuMTHCxW/LYQLXb6ic2X//J39JAAWFlSmJQcvL+JL6bmQYF787kCcGHA1wg8Fwu39d7g9wT5KjHuHrCOtx0QsczSiviHj8IhNyYub4hobkOKyZ7HOEp6RRXisGklPchQFmIukTuqY3hI29jOufTIyIYUnEgpNK+yqXTYsUql0CI5F5JDfE2D1i4f7SC/cHrrc5dK0KcBT0xxoXwTL1lALucCUMltZxc0UOKkrOxTAWe2uQ8HDq2aCJiIncPLMz9Z0B4fNGgWmLx9Zu2rJxHp9piSdzQFGsvFa/A2PU8TsuD+iD/MQ1/Y/f8BPEr//yQf8njHv1MebAR/e/fgei3Zg2SrfdnGI9ozdz0tnM0QZamfQnGEshOINQgD9yC/4x57KCwj8NL9P7VwYKsiYlQrQtEzpG3la4GHhoJDP4mEIMmlsDYowEaphl1VNtEnfjPGyz1ai4xRUgF0Zy9gqrfE8Hv3N8+4VaM74Ngua7pgZmon7PwPQO1+xu6KfRueIbdpJKzptEztj7l1j7vFpQ91GK/LzTEbJGkMY3OdRz6/5LMYMxziN3qPXRcY0btjrx1QN59kxW4YiATt+zKGYOgyK11yu0Pmgi70Ey2xRWm/aWJ9c8os9l+W2hIA/b/jhewv24UI7QyA4g+AjAT/8iJ98+jWvUfIXQKlPF/6Bp5cXC48NP/iLnxYGn6cv7999+Jc//K+f/wThz+hl33ACrnjY0oLLH3uQv7LIetfIIEdJ9rKVDU5Q8CUnZG5nIHpnBPamwbNBZz9rB5UVkCsdW8iow0hlw+xoJVadLSz7LXdao6En09qwGIhstMij1t4qobVfrKUm+xPFlmykQz6ptkKvt0QPySUcywU1ycg5OqzDgxyyb4VsLFICROUcWLbKVpo8aso/80lMYl4hdOzVqEWNDKHJ/K2y1IJmeBjpkrlGM5gmHCuo14Qo0Igzn1KdhZ4x4Wrl5ZqbBnxYIaTW8lhKbpNF7oSCZ8rqx1gsowAdz4rxxLQttA0ZWviEzZf333/+61/9CuNv77BRiRr9+APeAcAkJwo40NGGxE6/7L0DTBZb8+cKaAZxWtPWtPh8wC9+/pOf8Jzdhz7xQz9gjZBo2VZZIZg9GNR2EsM0HoROTsmIbQMz29BvlBdbAzVuT/E9gYTSfMo8lk76X/NovCrtBJ7hUmewMwjLvffhhT94DX5vvFvY33qFsBNfs0WJHl73Duu0Y6bAFPf6Y1u/2+YhMG3WiDQvdW69W1hj73U/57032s3tq1ozopRx2+OBarhZz+ZN/4gV0MgdYYYBx2NrP2j028v6orcmkHytIWBDt42Z8pUeHVphcP3BVuq2F3isJNILja0pvuADg+8+/QQ3DOHWHnbQyBYigmNUnkMAAphcIbBBEDyw0MA3FaJhiwsYQKtwScixl/TNz/ikDUygk1oyOmy1Y8sRCwuNITG+rUBoj0Z80HetymikTQS399Wh+WczkoBNsiaHCE+ZQfnMTQbLz9AEe8jooCJGhc5taLDgCCVuc4i03kJTeMJ1kqZPG0XUFioILkczU3NjvbE2UFDJh88amGXOqSvbqBmUMIQpFNoShle+cwUseZq7i1mkTfRMckSCCg8Wg+6xx0tqPeiiqeinQE4gjqgpYQzStny3mIRQcMSgN2ebEBkeDwWxFNHSopx0Vg+16UgQViVVAR+bwU/zPj3hN7z0oXz8XjHOx+3F2kxhHsAAADbcTQXPzPhITbgav8T4/RO+lQs740c4AJauZgjKNEODeIaRgcDLH7S1WWtKmbMzBVvZeaMQYJujMljtXNh7M/Bw3UMJM7ko+zO0VYay4kNEGRehi+YQ4K3z/hW4w/joMwB1av3QvXMd6uWF7cxj/nzL7sQaxZ0JV9hU0c+f/dcMhYnv69UeW28LUrEpY2ggTFY0ukPu3SPIT44Bs3N/W51FATvZHOM0ejt8ZsKdH7uZKCsb/zzASnt0qNYg5XBrt5JNlBHNXrI1RUJPnDtr6NiyMHwtx2oDDy4AdCXSLv/7tMNFSlyq5DeIPz/9CcuPpw//YlcuEZurYL1dYCsGAhKPP0pk3/z5/AHfJIS3CHATA+42wB3BT/bd+brwaeH95d/Yf/kF27wnHth26fe9/c6rfR+LeeFzy7/gCUW2sZBcQvFSN2+tBs/P7z7/OeSnJ/jicudHfnORfUYC3PHgbwVgfYPvcccd0u//zQjjO91tEYUE8D08gPuM3wnm6ghbQLM8fJASlzx4QPeM77YHGn6nNin0fT7Pdu84M86QyUX3lOu7ZbhWQ2TliHzxDS5/bus0hrP1H+oKDrg764dilJ+/8Dv13z1hgQg/fAs+ckKmOdiXn5INNIhKslYZ2H/4D/Jk9TwpjCwXgTbutrplRBSSv3/8/PQfNrZ4x4aMiJkSp02of8Z/Rg01LtmSdrDEt+iw2hYXOBwryFx8Krrxwe70jIywFX/Vx+YD6kk9L5bnK9b8TV8g2y9FiL+4ffkzomt8qUEkbTk3nj7jm/JRLau27PlBFY016gw9Hjar8fvQcOUvTHNe2/BZCfg70/D4D2WQsOGh7FhznBvj1x4wmr8gZX1CHzOBca03158jjrvlbMbirTXY8iTgy08hqLbvv/z06fPP333ER25QKd7Zb+A4SHJP5IM/OoHaYsf6/h0/qPOJ0wYgLBbHHVac7k9/AjaQWRika5SeP//k6cMnyEyE04jPFBM0RKsMg1qHnkiORvrPWUE5+bJr9VA3eoVfbOmZHlby7pXLfGxnhbLHrZ5Xr0rVCmEmqmc5MF4V7FAUgQtnb1H0ur/i0OGaK8/uKMu81nRgrlOfWCFMkajwxzmuZstEgDFaBTAzRCsnXPsf+DTmCVX6DMAKhw3skwuWJnW0qTXmFHyi9dcvL7UKuTYqnnvb9cu98VnI2A7Qon0hb3rNMymQv/XmXQrHIMUQtqZah4vU8o9uBaKPpK0Z1JI5F/fJmCsVrCw+8pfAsPCAFRYsOgniSjdfR+RiBasKWGJZgf8wtEWIrWtsVaFXe4vCIPjPdSZd2EITRx5uuYTJsmlsoaJN2hmMBW1oi48zCijtKgABKNdDBkMtG1CaB0XAMhR87dk4iQW0eEhLmf/NnmqWSe7MRWzBAf/Ek/jmYVvLy5rsVYsoRkiCehkuxbVgRj45Jgs6WV6GY+ZiYDkW4BbO8qUbRyLZkoONoEVnBx6JGK1MNAfXmrext9yJxNytClorckFLgxSHOAbKMSjwFWypIPtpb8+cLWhjCUvqJgcq6II6I3PipRUqVEKx5xRb8rJdmOSyaJzMggiGDJ2NpCARMNXZ+KGTWdKGNO0hQ+oNTltCCRACcsXWeqmmRplZ0mniADXVExY8Nf3h3QecMPMLuKwDC3181PcjF+ZIm6RozjgA528Cvuf6H/9wZoDCsHaULRRF+tn2y7sfcZIMP97zRyKGYbQInWmQKVnmpNhM/82WDaaCh4mWljWXjbqXtkmyljLKhVmjGaM1us+oIpEm60lw+WIbASd9j5kdi3U3eseSevO6RwU4CTonADza6eUdZ0X1DlFrAMWDXGNe2WGJR+ryUZ1vlQaXt+PZdhV97/ncDDv/rT7VhWUzDvp1QCHsPC+cCZtsPHrh07v2X5i9oubBsYvzYW+2+GKcer67RoI394JH+z5IY2ezPZBLg+S1zLvU09pDU7QcyHy4vuBK13ZrPHMZ8Pzp0w/4rYB3uDrO8wEcIXA9ntdWeazgtXbWEwb4BkP6cWWBFQf8+OGBP/74x+cvP3x+/gk/bPAO312ECHaJnYsQMcBiDlffeZUXrnbCgaefEiav82D4/P5f8/oDDIwec4I9r5WaO2z+Gz/AwGvMcAYsLEEF11k/Pr3/hKvm7/D7ZrilG/Iz8PETxZB/fP7yPS63P+O6Pm+9wMVsfG/pd7wN4xkfj4bvh3fv+X4Ce/GtR/iuJDSJBg1weAmWbzPQBnX4jA9J8L0IviNhvfBC3CdgYlUHhO/fIy7wIeO6LzE/mwxkwyc3scoaj4vUnj6BD38EmjI44+Oi8CITe8slseIPxJIDuH3G7Vsm44xOfMQNWxtBWn5i1tgyo8/PuN2LWeM6sezdC5rP9puyOTurwPMzlpX4FYiPYPL8TnVjlZ4/kdVTiYM6ICLGiLVKVfr8kePy5dMTI1rW6EqxPLplDT3ro8rnHOHFP6BJry2YeK3+K/NC3TgTgAO98YQLx8Xtf/yCmQAomEH/BRlBBp8f8GmWpw9/wjyBnOYAZhQw3/23p/ecb5yZn9GL+YZpbBrmyOnH2UU9oLBHWC9mHWc+dxbbFzBn/h154SP1X97hTZjvP33hMh2n3KCLic7f/HgGHzCHDln/yPepMO44McCeyNn++ctnvo/EXxLg7Xh2g8/n70mbe9kn3ET0/O4HfIWZAqcdHNDckfRAIO7ZloI0tgt7J1PIjyhDF1CsFduSoyaDmB+PLoV/7n+2Y3v2R8hMgDMHTtXreHbc99yIfwJZdOt34DP3wK2OYnnZrAhme8RG3EO1iq+qURaXWrOH42J7fv3TQ1jpm1VtjPpCDNJVOQp0JxreQ7b5gmNF6x0YYfq2vW95d1MgMk8A4FvOzGVHc2A3qc2liQYhngME3dcpqgyDfGVwLHlVdwB+DPbN63gFmoNx+TjZVTtHhcCwYSbxZdhspFY6XEKnnbowRz8dAoA8hEvZYtnSBA1bfnP1TJfvvvsZViF4D8CuG1pgfMEnFzgwwzoSW0bDHT92bRE9MLQfG/jw4c/+8i+/fP7xyRaaXMTw4IaDMl7/IMENODgehS10+ic9evhIyVoPfLkYghdvDuFtzVzy2CoWizmiqhdrJ/seFS0rscDSAi4t4564gMYpwQ9Pz9RgMY1FFb/qFIu8d1g8YfGaloZcbGlhalvYcIEImZ+LQC7opb3lZctTaLhwpJct0L/nZd2EjwMvfBnLvLSgVFxqbIn5PW4Ef/7yHU5F3mEbomMZR2RGNJ7JXjbCNHzagA9kbfEVkrbQZ0a4LYpL53QiweUU68N8YW+LZtowL/NdFtb0gg2+oRLIPAkhGphoa3xQN5yPGUMsNw3ZbbjAlS/HhRysVjq5ShlZXoZvJw+ss+EzLrM2hIzPJX5a9JMPs1CtOBZYoBt/fK2tcc7VsBHh2HlVcRqTTuc0pjb6rD+Y/2C32eCXszguOgHguBAf/DUKqKTNQ54FaumvExvInJNY4mNOYt7aCQOy4GznvOWdPJz/0H/58vEDToEwCpiiUMCP5+Fw5i92gT/Om7/olIPjhdOA77kj2BjZPMSZDPL98u4DeqE3fPTyFrgPeFvA9jsgfP5ob+JhvyU126W0dy0HgdxePYsQVXBbHmqsYJbOoWQ7KRwLwNrHbMBUz3X/aU1MSDU5A3mkFifi3TncCaYP5hpH/cGo2X65g9PROYAjUWevwqULPupdzjQ8AGG31fmrbHrVFA7Njz4s1plz4hS4PtseMooJxRTrkghGemyjI7r8jJwGFYdd54U1+DCDqU6wFXO+kOBRMZxCCUarM++gv4V4KtbeTFEfVGpzPi8FNftiNqAKnTpzDY3ejM+X2ziXuKZfvlcbvZwM/E+z+NAv/338PTtNfuI3A9BSPtzylT8/Vt+/oYV25kATW2MwCq5a/wZfIPjuw++wtrAFDZRc69tSmxceueImMn+TiEv8dHUZS6jnP/szWPFGBS5QUAEeXvAxRLuXARot1j/9hounj//E9wd4PZXLIy6YuFDDYKE+WFRhCz2WerwuatOVeZGP3dRAX3wjGZL/8E9cO8meuWM1jJMErOEQmrdEv3vS1m5qpwYItjJ7wk32eGALDdPhxRgyxLoWbazLgf69Xb2GAR7wghn1Jicv3uJPr9zk7y2A+D8RFjJ4fvgnfgMj00AsBkrb3Pv0ZDeFm54cMNuxfnv/h3dPP7FqE9+yQD2RGiBsXAyK8o+ow+d3H/8Zss06bO2PNVnL0nCLWvqWNhnTxhS9QkhbRMd3UzKXdx/+8Mxvk4QFt2jbr2XjGyf/YKFRBww37DEKeCBraJA6NtSzN/uaPXLAB0jMnvXh61SuM/GFYNUzDtIAATiJj9UZCmNl0wnpZF/ao6ktlPiCWswgbKH5qL3sGXsQJww0xhnMuQKFDM74bC7iYg6g93vUme8AfPiDrruneY6R+vTfcX5mvc1bm//cNzS3kRtkzGpSV30sKNbxGAX8xhdnvtWBn6XJnFEZ2P+cXqwSZHKz+uC8BadX/4lb7vWWr5AZAengG4ZwyoRvAMLbABgmPfIzKwIlTp1+zY6Pv7cO5KgHWpCTMb63h21968inX9FIcrbefmb1WMdty9oirT3qjnkNioMHzposJ2eh1+v0upxt5lFlmYq0dlOIVVeNv/dVyUJwJHKs+p1/1crXIdmQz8o9aprymdfZse+u9U+T25TyUFWnkG9m9OlvODiqj7aDSvroN+m0e6nlgZVh3G3VUKf63KQGk8/AwNFfg1DnF8sg2XONCTUdC4OmY7TZlB1hM9wm1JvB7grURXeND4wLjg6Nm0FZG7hlLZgvvLm+y6+VAuM2wla+sRO+fCxb4KldkKMWD2lhTjtbYPPGA6xUcG8MNFhDm5KdXBbxH/rwQV8uH+GDC//20o6VPL9tkA3z4g1C+lCj+ROHy3RusRDCYRqvx3jiNXsujLhKs2vV73EagCULCHy0K7sohT6fAATYIC6WT9Dw5AC3QsALT7gpAst06C2KJQW75Gi8laoWIVx/IQssSYABJDa5UOMfF0XKlCWEzHh4wjsPykscmLvZpzqYV5Y/4fIzcHCbCq5H4zI2sHHbDNwRBzi8QksZmk9YxqHfbNhmlbklAu7++NFucNJJlOnZj1opexIgc1ynx3fHQ29Vlb+tCGGJ22BwaoSg4IPagyFkbIGJiuGkC714dwXjotxReZYi1YeFVZqW72fLixfaxRMu0GP5izcBoLG7rThGjEQcLPc54ohiJSQH5cikU51NMjmjsv5gaPVRHMp5XHKVmLjios4cHSLzHCbVFp42UrTPD3aheJgvwsUlG9ymBba4GQkMsz0MNL/SfGOtkBFLh3veeFcn1uhgiHhosmKqPOch66kxshqyElZYMOT+AlkV0CzKY8E62yhzlADCEgIm2eJJBYCC2QiBW+yprBptLSOLTV5Y/VPDjdVR/YQ0dz5Zg3B6LBLbbNE1W697abHvsSBt+okkzSCdjVtEux6xCBCaSx5BeYko5AOlgcvtWF2S2jcJcmAk23WKQJLTcLPx9Nu/+3u5WctEdOOIwgMfBBzX+BTmSJStU5t8dpKOLKHnUUQxFJvBeScLMf2Ie86MY7Tf4FNfG6hYzUSsnBqKyKrRHVR5lIPq9YpW4d7vS8ymxb0lvypJdk8v645xcp+MKTS+fJ973Ys8w97sZGuhSMsWbvbyH6EoY3Viaz6sMHg5064ZYwmi1Qxp27oPyxr02v0OtjZBQEuJq6GlQMxfihzFIuT0jRMw0OYxypY2dKaeC3JbHti6XLGMA9di/GceiGnIdNVDXlGGja01mQJkrOfM1aIolllnhlHP9RyImZf0lAvL7K2YHpn2esjeW0ZVCdeYxM/VJmHWxvhzHY/DOE94cBb0+a85Ijju5V47UTF7YH76GwbjFdzka7GRC3NXVZcsVHuziIyTGYcAYvZiAzIY4mF5sUd+Ym49yittpclblfTTXxOnPG4TK4wILGysbQygtxMYXHTHA/MBC/qUL2tkNOPUS0g5rD2rMozLaWoWnMGsIeMqtjhY3YGPTI2VVvbJUnpshZFsDMkw0hV0jo6dMODQxLuzUH87E8b5AzHJnyOV6qA9x/zLOnilnRu9WQjg8zyGAjypwP+chymSLsvVc2lcGZhi9b5iMHE94zJ4gkvrDc2TxZ7veuGRxp2Mzc+fazJ2VOe1g+lHRlw5MNS5RxMWkOeRZ3j1ojd9j1DaX+ci9Gpki76vsnm8YrPj43YYfcnNaZDN8Ky3VutyZxPf3dKuKkvBxyBuX0O9Kk2zXoMMZI/sZxwfs0iPyWpQ88fq0sD71qsJjZSu2cmbS4fgEuWgnhbln1HwvMlLBlo3w1rLaLrhT+sYC84eNrEAt/UWV0WpA08MaOt0XoVVQmaoDkKZgT0tG65NUleKRSv+N+IEEihVpk/dMkraDGIW0OGtiJQEzAzeFnMUbW1kStFnOiGcyWgrim1VyQwtOBnAONtbmUhV1tkd/bSwhyXEfNAyT6WYesEMtinp7GW+imxLfOOq4gaEdHsVM+G4cGWFZzzhrQbF0lYabMFBsoGQAM4fLJY5RDkV36pGQ0+MLsoo6NhPfMsEvX5yBYXFpYH180kRl2dKoCEmaUuy+ZHZ4jkpiQAHbhkTPqTE/3RPhcpjQrPlsbRozr8UkZwJgQeh+U8GgrOOpDVZvlk06wRFncIYdMYnjuoPO74lZr4oFt9MQEuZJD62eDeLREPGgqVM9mpx3+R/tBJtNrDLIkSOkUJlx9BsiQ2vlllHJ++AEcSOy6KGrecYhT0YC1pfcuy+yXaPQET5aoKz0WF3/9Db5N4s9lWgHsPuDNV887k3jAPb9TsAsJZ/HXAIZJ306fvZxY9d5+XbEW9j0c8hxUv3CP6BTb1DgnJvejnZ7tC5xR4BcZv39s1jXMtniTt/vltZXnVt4CqcJaks1ci1JtvuerbR0HzCJct0J6697M3PsD0Be6O/GY3ccJ8xPg9gr8lcYHCdwUut6fJ5ziLRwYojrfa0msksEYkkLGCSrauWpTHD7Jwrw1hY39g5U5KBqhUO0fkfj4gpzeaWaJtGtYFzdf9EoTZta9yv3d3QNj16UWNOKxuhBCy3dDPlVjCQmU0D61lwtFi2/uyZn1NpOW5rdFuua0yBRt9ytRoYWjzDz+OcXOTKeZE4GNDac90yqLBRbzrfMVRoth8+D9P81NwkO2Uqso4TMElU01gCXjdRU9ibks8m2Rb+Acj6zHLNE3pe8jcPoqEXcn6HH01jlbkEwKy66rkF3dI14oUC5ZQvOt4uwQoqMeRitF8CrAo8C1i9Gu6PWXoUqcXufdyi5w3k1ZjeoA78SAweencIMpLHS9LmI3itGHYcZ2xWrgF/pR81NJs0uUo7jalr/T23dHCwvHNv7x2A3N94jjM6ygxrR5nmdGsqG+gvrDpGc95L43ZhkicBT7pfmMgb1FIBzac4q6K82F0gCXjHNIApfLCj52UJFyTQ2eLfOnhc5cPMJKY2NLS1o0Rh4MY0CIeoQm+dq43subVVlz0rtrmKi939kMSVNxvKSGrJcSt84x1oVSAFDu3lmfxz0x3FZglesJA3nJOdUgoo0V6giiR7j+rxIES0Qs+mEN3ThWwaFVHO/XzmMt2ZyahYuUNpNuqUb2ECg6RJRtHWPKAIOoopaNAKGlvOizw3qFzbpJYZCCRukznoQGsP2adwpjE5KhZLDwV4pmT7DLpNtK2Ualt/rkW6Y2fxwV5jJEJpGkEZ28mi3x5QxAJkJV6u+UDwez88/12BM9FO2ruwauOImgtXW+3W9KDykO8GPOAQOeQi+oQ+gPfm8uIV2D99fOAX7rxE9tu//QcqPv5u1b9qLA7xyJVl9DqZfPCKHl35yHnPGkwI0u2552+Nsmrp7K3+HP3K6Fwj7o3nkJJ3PVjxPYHV9zWt420zOT9G64gHWrvPpw/EeBAXjIdekynYClt7VjHA1vuSlH3e+I7PZUrWRnpZF9had1p60C08ijxDT0+MHgnK8Fk8LWzMgpus6EFdrBezxClxWTi4/mhUAcT0C6ScLg2DMTzUiubOlcPimCazjnpET8n1mjLbKlG/bu5qE7Jz0iqAR01aN7LumsRiv0jrMKuWjNqhVoazjcgo+ljOFm1QHTjAPxMPYkSCiQXxSKFzIsBiLfwYhe7430JunCgsSPNSzq3nsdXf83sE/bnXRNY9I3TGoJNk9mp3j3vXPqq+D3/9Cltr1gBfVyvuGq8vMx/G5RsCyyTi3mbm7oMPE7WPAyuIOE/dVRbexRgxzgrgraEKFMV72bI8FJmXLcWjRPcdyITV2TRGC0pt3WyTt+w3zeYNikljTQuySA0ws6CezJ29rlOa46JseC+JtzoXXQLWE29xXjt63MVjkZzhotopRQTK+O8PDw0h6t1gv+CQ0TVyiHrI2d7Di4rUVJqvvZeTOWYXn4fqlaMAhYZck2PGYXD2ZQi24yPriUV44UQLabI+29MiyrkhiGIrOEC4hwsxUpIHfZmFe0WFZPe26/xu2BVU08htbUpUYS5DYu1ls3bYbDlDWDKueFdu0azqnFc4+kV485Ef3dIrA6JRvifvl4p7zxx3xMIc9Yq86vkaE1H+/XRoy1fgj/7dvajBYq6CpLZXJxZ1sYV21YhWI/n0Nfuz39/SIjdz7T9eX29h3E83U/f0PU5rUs0hXZtY6/QYNTB3qsrv/djpPmk+dc2jc5Ul+ka5Gxo4GIDq7sPlezDQi6HVFs+4cxeKwj5+QiD8PkAKmn0XDlilGX/htDFrnMXfJJtwyz2FZo9QaYw0HeOkVBa68xgAMS/I/Ap8flNN8Yj4qStiFta9Zk2mZwn9FL6MwLv1WBDGl36HIAWwfVq3rk9h5U38+gEeq7HQPArjLmOMPociVx6c6KtvjofFkstatnmIeRv7CRgyTvMf3yZkjzTgXjNYSpX6DZ+TIM8N10PIlnGuRjnaJk5iFvlFeeUw2UgkPv2aORS1nYTIZpYkUtW7Ktp/c83tNyLstZhxlvMp5ZXvHKoqb9Bxf2H9E2bOPD/Tludq9lWw2DJQHl/JphhvYqyBZYy5Nuv3mF3v+NnTr8Fv3ArH/1N88quq12Kq/NmrneS4t+3T0lqO93nNjeFP1TMCzcjIERXPRz96aCSmhmEmwDU2vZpUerAndfyqTPmA2r/hbd1LB/4/8BkABTFoij6Lpf8Gtgcy9mp9A+U5nmKvsJyo3+BjUA509Xp7hdpr38Np6rmsQUdroDzuSkgN161QoW0hrWz2NgDYDtYEigwKt6IpolLOx4ggfS9+S2STnisHcTc8HSIJO81L905b/HS9O5nE1KVKRhVEbVmZbCkAMU5sM4YbbEJtcRGT5Z4qswcqgTM4yULGxjSZu6nMvrkpuoumXAyP4OwVrqmSvol7REn49qPf07b/yrUq/FtRHmiYX+VgnCBtF2P8dwA0ECVc2XYrHENWx/X94xjOp/c7Lx7V+VDq6ukXz5bUzrdluUvHauXj7i7HgfEk1eIzAPk1ZQD8Al2DXNJ3LvHbZg4+js2Eg8FOumF9MDNRvF6aWCeDnnQ3Dnlhs/7e7k3kffw97YRrpWrM6NWIr692l4zSVW0VvcSPOFGOID19tJGcLHF1fP3uzWLZSAWdrJFdgX6yK3O7StZGXCKWkupQaltt1ipcj+8GCjYtGNPN2HSd8/sSweDIOAb3saj6t/INTFqzQqzkjhBCWFNdtezOKl2z7zKCQwRc+Y+clj53z6qQRVaNnov3BJxBHlNXJJCsH2HO9LUqTL+efgbzjM2OuHHlE+Uz4b9u3+kq7RsFzP34PkCvhjF6lHv2O/U7OLeRdSRp91Fb7IL2LiDU/CXv5+E7AIVjI0J19GjYvDbV15jTMgYY0635shi/SXevQB6f/Hx3Ah7Q9/6t+eKGdN3Je+VbhPa4bSNZ+yXN/nsQxQFwjba0Fsl5HBaIlfF4apTlBFg0PQz0SlpCaspa24DrXiPBvWAUoeUTex1Fykg6ym5GQdepTQUvmSnKYqaOpX2l1OR/ZYAWloK2Qrd0RLAbn3IR068JcN7aCp8GuW8R5EYLSq0HgqnPo7rQMpeuYVKpuhH7sLmnwsodb8/DCqBuJ6o+hH7rHFTga5ivWxOnyDGbJzW+Bejv/r6oUOFRvnjRGvcV/YpP/OXI/Oiex9zgnCnHPPvc4Gxsm/fNbwar0fzqO8veqUPtlQJ17NVbDtImuWyQJ0BuD6NkI3s+ZAmeHjHKEXkyF8eJvmfkbuXPgJ7xXTJcpG28dvlCsQHWthlg1w5blKw/GAWxHacOITs4drrCDMTYwai+VzVEldiBalMqtYszpIjXWZjJavECnjtKzhECz6zy51GfGx0WgC6CLjhUrfGuA8JN01jVeJNcYT3Ic/PzXcoqjmoRPcWKFkV4m0quE5lusewHrfFrYOso7r1WD1ri0/BT/MzJ2XTtuzECdhC75t96R1FgL/xVdbn21a1GqzVd5uG43VsFdX3HHRF5bHm73mkOOyq2g21xZGh5xt3RzPNkw/PwHQCByboF/Ip12v1ecQKHqNvoH/I84RSnn+RII/aOg3z9Q7ZUJ18z7FXELcvyxXY2iroeYNIPTIuuOIZ09tuYc4TCniZ56ZlN2s+148pO3SsjNDKdtbhyPNjwSFlQqBBoBZytQq6LKllmsivHpVHYj+MtbpOSo7vgjrXGuw4IQgN7CHXGTWURRTZuCeHgQyTcWUCFUr0ezI0LwQ0cxA2kYVPS0naTJMQet61rZNZ6i8u2HYsVuuCiJTRqxqiLT9bqObfYH+XFfpE6/R314vcmsQIYE6+UxicO2luN3ipw0wpwsmH+PS+/A+Dh8rQMZzZZ5TYSdGwqlNc3b3PmlHa/Yq/rZHo2KURhtc/CLP6Rp7/PsHR3pCkCYdw7MLPqSBI+urom55lvW8K4g3BhuaRwHc/ZfG5tt+SGSKtGFXk9m3ArBj88IGWsuoNkeyhiP3HLdhWrqRCQ4XsQM1y3mr4NpfiJil1eL1mVbceQpzdNOMYhYqzCKUS9jQ4DeYWV7MBQeAO/1RTYth4hPUyf8nY6xUB5kq2SudNOIWHpqQi4E2rKfMC9yB5wQaM9WIo2zbZ2ihRmmxfAheQ5CBlyCeIg4pzVAOCeXeEV5EZrjM1syrFoOdTcoibKLe833dddgbmDgu+XZp598Ix3AHJrX52ASEf8d+x9AC9rXe94rzKN/UVM47bfca/HN1LPvWXp2mtPWnZGr59UasbdLRvoOX0iPytTmNg0OSq6VGY6AhDEhfaMb9vGYFKyglQM5Ry39FcfhH5ogbSDDbWOvVhJFbfqk6bJoYHSxoNW2UkojbwvxirAZRNpwCA2HbSnd4O9wj7AgnfTubDZS2hl7wG2vk8pe7lDVux43vStM4sa+xRLVDRCz4RojbvDurCAb2IupmOpgT12eOt9q8BbBV6sAtzxl98BqGiMv1nWjzIQZnb8cLZdRdpQ1Hf61g7d8+B13IKpNz2bzXtA69Cu6XGAHvjFlWz3Oi/Mf2LB8x0FHY/7yDP1qQ7KN9ZzbwXiuEecFOYYz/V8mMhmwqTC7M2EEVZ3bJ7COzwro0WPpYN9d4d/s3s3UGtv7bGN+igv4EQDpbT3iM87G5e2/eJZSgnCDiWOKKXnHPEVM0Wx79WJiHJBLxDSLKrGKNl39Km2+I6IzIz2kJ2Nf98IoqfPRPlvqqy9MrM4RpLjd1AIe/lOFbXzdskUaCpQk4nb8zNaOXe3R68eVdZT4xW9ImaUc4TyOfqu+kIasMGdZPa9HD0+e/U6bqQ5IJ4WvYeTxmh4bIm+UV6lFRr1uJf7aR41ncVrDnzQ5+vid/IE/s17qdH/o407jrQ+1CASSkxa5dyLpoG2mVpbY8dxeXrGZxKwz5efSZg+/mT8mbpl2/L5jO8KK4xyfK1Z2dyiEfYFP4YPBqHmFjVRvgVZYc7UfMamOW9vR7uNHOrfNpjTTuU7AXUCZzBr1oG51641aNF74jMA8msiELXGrQI9iKLHVFXsJPgg3N9ovFUgVwDzWFNWit60zuar513GK89WI73tYAeXQOlkkIDEoEUz8ahjRE3bp5XCpi7C9uQIgtDRLHa1ZNnKaYr1GLzoxeE531BF8Kq3U9wW0UInrlOMC89hs2A4tJ3s3IaUxeW5TPLDDNerqNHYYAGbyiIlaE8u23d8m3FSlWykzt/eW/amNn/Y2E3kUcAVzQ7Om7pVAdSuGsyW3cPoeoP9urJ4mHLei0hrnmUdPgPwP/OFIZxHNkZZ1lXHavV/4jxmqxB2xnbJ7/5WKZShMZU3bUqf6Tb3k+rs81jdTpIc7LHH+KgGJ1lNFnJAfhJhbJYq8AezCleJxl6X9U6mt1XrM+M4mwuoggYJl6SXniFW8jYbT2h11dYjrIUU1308XkQMoUt+oUuiI616IprkpkY+zsERpVkhTjXI1tECsyCucGgb7V2WlXHmKjPr9YntmMoKbqYhZ9tqpsmJ3wuHKA/wALXlcSrVBWZD8pps2JXd6e5/+xRPHqLSJrVbtU2ZevQCInWXgMv7AC1MWXP935yIJVi3PX8UmrdMwapXUunncaJllLvJ3KCjGJz+UKxi34GtBh5RC4YrHuvGJPm10wUtVUNAYR27H7kzo/YDlR67xwtMUE17L7TE8nee+ctI0yXHKGogDTO74VnvMGZFHSxq5qyix2PJM1N5xuZYVpdX7zDgQceDbseq1fV6DBZdehd0+L56AdaNIbS3nCbsO10cXKw9pIcyRTCNG6fc5BO1yTof8swu9kMhEyndfFWs6OByFFyGW+QtdGFFmxX6RgN+Sp8LMMiGPwBjl7qLbfAJYrLNTxtk2t1Fyk2jGLJpcAMlYupvlV3N9lpujubCntQ0ytFDKfg2dhUyA3pQCb51fZ1+RnGTrOg9Txv2AN70VQWKmmKUCk3lcSeFaGC7i88u4ztl8hZGFWgfATjCv/2//30xzDaO2ASfztDml+gzVb7ZWVdNqpPFO78Pr3aBpnH3edNuSxnKuWU61+/p9BhGfZHjcTLw9MAVz35PZWqK+sy44Fm7HWdeY91fE2d7lAsmM0mi1sOxKCBv2ySTeK/JKpqy8bnhyblmZT1uKGvZDPw9pAcbwzZ7YyyPeABwwLMZF8oYRTQOgPTApbcQMc7Y/FX0Xl6kqax9gFDNWQbyWcNvubM/D1hpOxs3RHSIjBn6TEyYB6BLpK+kbUfsS+5EUEGalW2MxuCVIle2fiXNPRPPFb7Q9n5mD5Gc/Bk+K9+K20Q+L2yy4n9bLl5vhlk+P1YEjfPMPNztCe8AxN7F0U0W1Zv0WBXAEB0YpWNejKRg7elyp8ocyPc+zK6vChD9DzkoQNy68j4ZbkQZTQ7l4QAxLVd2BaWMbhcKuenpIaNX03KsPInj7uModa8c3R3C5Q8D9wi74W9BaT3IuykVDrsY7jIuAo2OSnsKvMWB/dkmPxuVVaMgt25Gqk0vV1LAf2+vcd5aV1Qgjgbw0Cw0VwS5K4ZmzNukuWvRN4ONZtVHzrnVgKEhle4Oqu6BXs5v6FZ6b5IpDSr80uCi9irHNWbzW3Q8sQPnwWv4c63OGbBGSdA9hlEfc4y+K3KdWLTB95z8ms8f/7GYLlQeftR37EWeY9hlHhZ2gywKy4uamlo+wTBzug+b7an+g5kvrAgk2TUeTJGgLzRNBpNmTd+xMt3E4Pwa1ng/ChzrEW+YRlUB6SmM85VZ4RthZ+ToLjlq5hHGVGscRIFLEWsvCGCFU+O7pgjh+o4gCnLSpWiP4ELHdYfaE93JrtoDdvnvMvZsNEzaTiHI1P0vEhDaq5amjtoVp8UshI6k3EMCh9mhms4B56sX7Yg9fwTrvkKtC+UlXqtDa/BKka0arOL3R2Wz9nPA1xjHlUPbZUsLPj5dfE5tOaX+VS6B26T7SbPJURtEWfEf2F3dxc9ftR7pW8jaw/BxGafkK7u2dYTX+Poox65HlJXQi9MFge3STtTvDMhuXzh44VyYIPnVm9TFUKnqCheWaNY2ZbkKn7I7rPBk6cMk6OjuwVwQg2hT4+/TKLwHKJ37oUSltE/t2NmHKJ1l6fZdUqXf0pZvdIRmI8XFe5Gcw6LakuRywLEAdgTRLnpD0w2DjmLTLxq77EKBcKYpTOcAoXjAwHuLrps3FVthVsy8wwUYRaZRf45miYS2Hi6g6bJKteKazAtd8nDHGjP5vT1dUoGi0JdgEgS4xchqClwWYAQUkxIRaQpGI4i3vo0KXFDLZ3wN6GpW+ChBwOeFWyHS+Q1v+T36GYB4jTbKGwlb9177jKnMcusFnkGgVc4tJp0zYB+ogX/8DIDMjhCApwVL476aLoPg13c5+Y1z9E7FrifUQtS4aFvXP3rAxjOK+h2yIBQMbhKe3336DTHK6xBFPI/dswdE2Nc2as6A+WhQBGIXHyUfaSe3hpk+H7J8N0KIpGnpW4ONnDc/W9IgskZLo+V1w/BZfTbeswr26SXZWCdu+s4c5RG3YhM18sLI4phdeGXq8fvms84mWcCJNVls1hJswBpXAeF35hFjzdSqaUPu/TqfZDjOLvKPchzHStZX+WCbPxLTiCHW+k79d/VvAqRYdj2vMaaes89PvP8mOcfKbN00fE9/+jaobIpnWYGv6myv+59+TcTeNcXg3BBzdHZFuWF6SHULzC6RcAzs2nQ6No94y/AYApooeuPR4xD1URaEvQ6ualXEy5GijebR+JUr+80+70WLfGZjZLszvnq9S6NW1zOH2HzezQGxUPfldW0zwj4DHmE0t8oJgKjFZwCgwR8eLuSX9TKmzDoztjR+gHbiu5PJMa9mkKugMIg+ji40I9bKvfYJQdS3EjgIXrNsabaCt3xurLtpvse592jds4LgIBo9Mkt60SK7Fb7RJDlGVZDdEYKrXViCdqSepfS93g7Yiule30n7GbMZmyqFQ04Vyten6NbFO0zgHXF44XTlnkLMONX78ozXwsLocQ/RHzrEVigmJ/LSLJ5v0oUV8GGU4M0LQzwalE+4RyP2wnyO7Gf7fRozTN8CBCj1ETNfToAGh4KGj9cK3S4/urCXqWXPquh8DtfDpDmQJxDg6wiQdz32Mh+Dz0avzkrTeW3/MwDOc+8Z/5iwemdp5/HavPoyCDpzBu/JDnB6XbrSpl5cP55Mrc0KzqLiKD1msnQzJ+fuPUe33BIyQ0ayXwy1q5t1xBWORxU/9LUcYOX95m5XRvWLpN4ni7X7uhUjr64rE8MOdjnKcuXVURUnQgR5hRb0i1j/WrD6Mn6u3uKxSAjNhzOoBRlw2/0uiMXEJK+MgxUGsrIrYfFdjhHPFsK1ujp6qcnpbI8IxrzKbootQvA4w0gff2cNd8vzxxVmyVbriJTHIM+BNMJryAhFNP3GM98F0oy1V+FW3MJxqtnHKes8BdcwugqH1Q+7RCPSjVQ2Z/R75+MIM5kqC+BozJHRyz7qqfdir+adOs9U9WVruIreyWJlc7wxN1+quZXd8Kx3ALKCu5TkvE2Kel4cJ/0ynp7ZsfC5Hqk8u0Dcd5fXLYzFZBb59Q/6bKav187HCILLzXR6vZoTvd4m1IZSWNi6UDsU8foTsw3j7hDg680o56DqdJOsXj/rWkbeRuYbjmuYutWM7um6UDtK41eRaansHNGFtfMk4cIsNmvg2LuOtt2KvlHe9hxaAEp/hdVmSQt7NkXLtz4NGqZUKUQKtI4njI5fV+2RuxbeAdP8Ry95Ls9ud1DIeAfdb+8mgsXWWbtweyLXRPDZA8Hla6DfUL7yCkzPl9Hcevrt3/29HT6Exh0ovwMQvgWo3q/StZMv6IEn+x//zKzOop4hfr6rrFSVwqzGmbySBLQdVepcnXKGBavJZjOjSd9Ns7oy0WWmSr363JR2JFnK1Rm8GJ7/ngQPdNPUGvVEPIxTvXVCZ4WQUBADqk8TkQg9FCsfZ5sM5V754vdUkZjuvS4gp5oGW8Za86moTQE3jRSo2RWVOAFQolW62eoQp3knL3aOd/D5KhyEF1TNYz6p0leD4RSLZmltbZ0krEdFrbWu6ZyVa8beaiQoSvDLfTui5GgP/lwdaZt8c/6ps3419Co23Wtl4whZG12liTlG+Sr8czhFbc+Btb01Xq13w9r236Z2PCdD7/Rk9+PH6vUV7h+two7jghdek6LWu4EfkhbNg0qexOREd3vPJ5TRda9M2B7PcUIoymT5xjj93rrsfdu3nj0V8Mq6oKG8eEANTvMkLceh8ZAgLNmjxi4oXW+WakXdCiqk73ct7zsHyND5eRWf8OgwhpFmCDsrZpiRfbShjP/5EcSs0nPREVkSYm281SrA3Fz6LljPDf74OKxYmM0KB3Cpz+OMBPkOLPaAZZgK1GcRLEjQTsBoreTNfgmU3ZWKWlmXQwyeFyAabTiuu9etQYxvrWtd028t++P53nNCKZb2qOOM3zwnKzAa2qff/u0/EIb3MrqdDmd+6O4emoLLJJUZM5wZg8Cxz0SHs+pwnlRG9UTVAUsELK7pbs5OgKhOJXq/3cRs8iwY9iF395BDqNJu/y2HTeYz7wPUQZqlc7NmDb13JZzLfTO7Vay5xjg1YOzIbiYi4vnclTzjtc9mnZO1OuP+ZN83YsefUYgAuCIfBkQmSaGQOdMRMvoCiIOvXHL0/LzqnGwI2Y2LpuuTEChB02ZV+lh7QDGEbFvF43nbIoVMnWuSTTpQLlZwU8MEvWOTFtY956BfcIKyJw7pV05j6EAbhrzzvgI4pRC+vlUvb0vAi0OW8K+nPVmI1fjHY36UX0/Wd2A6WdiCSeeoXli1m6sxaptcp71o3C9+LT6b36qEy6eD1rCLHmNsX05m/ba+5zsACQRPfrUjKVfwa9BX3bJUlwx6aVq5FjNJUmpv0ba06LebgE3zgmHT5phynsMx/K/Sa+9Av5oi3C4xzeDteWw7H2m4A+SaFjRumfv99hiVu++0NRxrljWO+3uXcXF1V8isk4Hce77RmN+94MHMe93qRiy88sE928cY0kkzv6g1Hk6mzsW7csjw7H0CUVMvOjVQ9nOnrNh+Fpgc+8AjHPjCMYX2u7AOUBkFKfsSvDMWCVjdOG7J4639VoF7VMDn9z2CfQsx6oIWGj+0sBo45qP98d3Hf7La6CCjF57l2Jdedi+r3sx52Invcf/0SzLVHWbj+8xiinV2KpS2RW/RpbLJpr4fUfrVWXJVgTHPIvolzflvnjkQLhbWZRcAGL9RpMbv1bC2jJodNTwxu2LEGbl3tWA1HyaAdmRXo9W/B5n29Np0VtPLa+Ufo0DG5Qb7fvHS5vnp4+9sdvDIA7O4P61s2Wn7zhM/d8QWN4bcWiCpIxvQdPAYBYWbfd+Lf4uLxR2A+Ts29j3uDW69aAl4WYsv30Q0DOedcVyyb12gEF6doqjo1mk4GBcCZxwPshYCWOoIOGvTTgv2pBGA2MwDZ+oWB1rYN03pm6Ba4MaEv4mBX06wXFpG0IXQapkj1LGe9JXh2pz6rUeJU9pnRGW99IrH0t4rreLWx4F5uPc2IMfek49Rqte+Y+9Fx9eIKHuoonBxVeA2LynEOkT5BKfVWJ/A2es6fjXfRMPULwardLmoPjPf2lSGbrWHR5KWQ9DtHaO99g1uVlyu8FXlVbmf7S4bHBfQl/7s/UeZOm/45AOU65LQ05d2V7QLVjeGHGfmvS5cQWeFcTvkVZibNTRcnoULg4A3GOFBtB1dM+R3wN3ZFOxfNoE4rpGJZKeXloCyjj6xXu4Pgyzn52hncu7Iz5XBMQXgLkIsYPCGxnXY27kpunO4KvReHNiHwUy0xUrbdibRArL/mXVs9aYSDWWXA6ClhwtZsXoeAa4MdzfacdvaI+AXIe0OfV+H243PffO4XzTMi29jatyvpA8XSQO82jek8s8A8HpVngawg+jXDHD1Ds2Vsxlnc2W793ylUSM727vqfH2GzzqDBqMyaTORl7o2ERqgWSUE51lA9a4T9/QZdeq5mdeU54QREgF+kY77zVyzEYJcouwgdxNiFqq85mfxiZEzfFSr0YhcdRVkmqXPSXh4BUYMG8iLudA+2DuNvGLkiJCUPN1NSveFBxuHWbwawfoq96+PYO4UoIPo3S3BrpVUx8TFssRR28mgaflie/095QuLKLWuo1u/iETTseyvC2Ozfm+XSd9l0LNG8wqbR65xcreqh7m9HiQfk1aw4NXqPqSLmPwkDN4N+73zx/sbBC1/J9jfXxq9p7Gfzekx3R/yiMd6wNoIXsF2d6WNo1B1voDi/nxmqtp81W5WZ7w+afbuHbJm3BdQ6nVZgfOdBTqK7CJzYsSnKpc+A2Cvv3zByeQ+/QoN7PlQ6E8d3p/twgt2VmnK1Ja5/7U8H8vgmFddE1TR9z0XYHYVfh3xPhrxx1Z/m0HrfKMmymOoWMOx5UxvHJ0Z+6/SJpY0ylvJ9geNKCqt4S2gualOBXCYxWwr8qC/C+JhBs5F13KjTtHB5ipQzEfyqntt3AC7uWpN5+bhivJcHK9V4XaIKm2fBS60HW+k9RlVEbtRwAL2hcIWLMbNlxmZMafX3Ku95WUzwJi+hqk3VSQk8rhTFMxW5Kzx5L8DwATzQKAri/TBoSl42vmK3SHqNlPFOWt04jxpI3QzD2Y8/Y5EE2Ej6u27e2ftOgtPd8XVV5drTY9q6wy4tp0pTphfNUCpiTPBwX28lFe0Kf3X7YElwAHrIdZ+F7d2VUCxI/MoTzGbGOVe4nNU+1ata967+Ycke76m12+1BjJBzBjrRNetbNN8tuv368Mq7RLCAhQZRrkJWij32hfuD97sXec+QXs9wKmFsYC0jEjClxqNqucEgTOuLZJn8K72vfVs3MQfD9R67K9O3o6ZvTsUNplfzWYKb5MV6hnXCc0r9FORThhp0h8fu/Fr2ZneE0ndxXVVs+1jKd5xX3vk+3ygVYcLoC+Ndjhs6z0vGt8l3XsGqdO9Z/SvJtZmGc9Mogge5QurdyPYCxm+DigdTMR1VNNoZ9aVYme+CjYKmY90O4FpXsEmBZ6qrgPwby5HKqDiq/79UZCVxlBWmmln59sRxsGnTzgYvYkPUgGN1guO2cnQJ90vGYUX3uGuyAFl1N8VYLfE0Dd/pggqvL8DgCang00JybbFtX9esJPxws3M1Azi0v+qJGSQss+0y3Szvvf8GmuwN8de7mO9KhOvMTTt95Kph0ywA5zNayE1sXsOK5mPr1XU/G6pGeTeK3KoMEw0RGuKi6fg9emiaCPHqLlI5jeZPC93VKNh1c7fYhHSDWKMHbJzNVBcDgI/MvWNPlpVeqlS2NisBiiMSxAv43fB/nuz+X9ZkiXQnUe8N24q3Gq0S6ZXtps07hZdmZyvfDOLA2XafH0fYxZjp7zwKbtd9TxfjUTy0F6MSioLgOyiPa5MszdkujtUcJCoT/9IxlZ/ISwUnCXNmdJUBt/XIip7Z1s0XT8QDrgM0A53PQiNXfzB+Rjt5uyDsqnfRcmNjxFz99crjGs47rWs1yZeR33RTTw38C66qbFSXVhDv8mamGuCOfSBaCVQDX0A9M3ldAXswhWGmeOzHiO01orTsS4EeFxmFyZ5Bqp5dLjtgWOa7qsbvGYxp9O9zPDV1S1m7uRdiL2PK6exxw+B4ZG45xTU5y+Y5TRZm61TDGcn646ZVjz3ivKM72kbZInEYq7zucgx1+U0laMARwgcqvN8ZZTK4DtziprPpK7oNebqOkSVV+NbcmeCdWzW1487Rh111zd/k0DHr1LHHKNcGUoxP2raC3p1Blpz1D7+Yb3/vMOv/MK2ugvf/Yniux0aCXWG51EbhCAlxHr6Eq/fS28UzKLedOaPvauajhr2VmmSVwDbd2euzFNjJseW3xFdN9bO74fpVKlL6VhlBBc5R9l686uXDw20aX4tZCqvpWsg9bx6d4d3oUJte5jJN1gmzcT+3o2713cYfe+I91hVg9MzbOh9r270tb43aaPaTZQJZWvXn3AbmAxHSq+ACrq3eqpYHXn1Glp3dzT1a3HHcKUG80jbZUcrSHp5ZaleKC8ezelX4SKu01slOdEocDY98h53OKBFQPlYQe3bgNL3cFNgt4qbpGTKVuNxjkYD8OVUh1NxRwj6e7kkXl/kZbK9Pu5XMv4a6tDIQSpss5Cf0zEnlVD7kPqurGoLKzPgM/7bYvGayHnduY5qMdaqt9Z9KuCl1/heM8r3ob6O8oLMvYZrRudbAvbMXOghD4j4S3DP9w76Ab3bRVfQvem/1CpFPD16pC15MAfUFbeoamFfNG9X9iYyor8sgSarSmlXvlBu0l19BoDk8T9dlbNzg+V7u/NYrX8X08DvkvT4PKnROzx7rorSVTSQO7ayVKefxXZs76fuXm9O53rXMNms0niO5Mk1RWYM5RAl5qH5MBnLgx4WyPYQw70RN0fKAXu5x6tEZZHdeVPQ9xGUMdAGJLVnrg1vBl8ZpIArXWysmdDaaoh3NsxqKUEmXyYVwXbnNT9e85YrQg/fOJbXbq/6OvfDVyYS3J1vdJZ87PjT8ZrhU+8o2he1S2l3ijSlEbK/wkaXaHxYTszxfiYenevBkTns/RiQr862g7vXJZzFU5FQDefQju3a9Xg5Je/fFFJ9Dv0SxWbi4BNfXzbJ1Aazdag9T2hA+y5xzwYxf2yML591CxDVnAn8byZLPlTFx7q9bkW7b1xWjV+kCJOhbZzvRPDCaXIh1OXJe0kfmeTlWR8EXD4pW5RtKd4iHYwx53anMIkMonnCc/zerN4q8K1UYH5fjDsR5BfcrSKTyXFSmjPJToJPmtX0VLpafyPNOOVx740oXQvrKRwekQ6fHQO1ZWq/v4kw5Ip3AP4ni2hfzi32uDa3vDo7nZSQJ+gdAgrNprg+72yaXKsEURUiEb/6GJFqlUl7XWK43Nl+rq/Nx3PfureN0tIq8VbPSudUV9obNHTNwK/ZIELMFE0ymZshXudNmpdkNx8uZRFo7fWF/SWcA4VT4jz/o7TtvUgP0/p9gFMJ3NY5J52fedDUm6ee0W0JzKKnK3b6Jcgvs17zdvGKYJTnEb5Cy1f+fsJ9RqR+XVBc7VI6Hmq7wWfutWMDZLrbiRUefiQo9GhGF72yyyZ/C9niAZBo7B01eGHmju5CYaIywDn5KF7NB2htksHhPBmA1bUKEabEA8exYjgUJjI5gBm4blbuXfrF39+ndW/wXTTGJ0LhOIWmqd2hMQaLwSIl+4a1I72YEAcDsv7AJsonyakQjux1gUaBTuKfcReHMYITHpu99c5UoFnMpnIG7UFsJvlPmrWT4pWGPFurLxtuuzyKNtOOfEI2Uf0mf3MVaM2Ob64IRxN+8OI1j3hNpRdg3OtmEJR7swKFEpi1JkJNysCZpzeJ2TOL2UGOTbgU6fRANvVCvgptM5wzryPWmhm0js2OUfIxdR8XWGbvfvcRn6EGyeePv1+q374SRyv4mnOSOzyb6s69dE3bS5S90vuV9VCRswGLWEWzh16f/cdr5HVvD6c+/5YG9yP2mAxyP3ee2uZYM4mZygf5Dlglmzb8Ke1Mvj5nBpEieceEsjcEA6ila+L6zWJ8G2kzBSQYc59h4fWxQ4oi2Pc2nirWTOSRDe71Z/x918j1zT/4VABr8PH3L5pAJ7nxfckdpx3qiB/lHsT6MxU9q1euv/vr3YPWa3j4iK8C9atYzGjjIPMS1faD3gY3SyMeF+Zf2YsKoFnEEgcHL3rpvrMyw+GKdFZyHMfYEcc0ve9hfJyw+HtQFyII5JnX38IFTV8Fsat+Ja01AWLmOBbMKTr5mDX0Pii7McEQoNXr0fLquWaANXzx0JHWEQCWHj4A/BYgqZfO+me/zKsyS1jBMcO/8POS3ZCIm7kwNG90Pl7qK5K9vF6ENoKej3seYVWg2zd6Q3D7yJdFuG0KRFcE+/6cS2bJZanvAfIyvbo5uifLN9u3CuyoAPYF3y92uK1MtT+99r3qQv6xopBjc1W4nQ0wvJBkL3hNWPwV+qpcetFvpBftAflB1+WUeoO44rAM9sd3H/8JHFbfXle+AwBreCdgNcK8WwGv0umdqayMbtAYny/G8+8+95LWLXIpzhQREhpQimeK41zEsj7/rjVlPv12jN63GvUcqNXkQEyaiZyM07R1vtV5/zhfucc540gDwTHz3jKwHXbtvH4zxDrYWafQG9+VvqpzDG/HnKiAbHF6AzxEK4C8Oc9HLr3g6buSqysxz+/poV8X5ogzg7paTueUsMqlhxSqNGUfcPbaB9fV93DP4Cy/xxxRBnK4n34Gf2UTfAcRvGvl69o5IfpGec77uNVlscL8Oc4menb3qGQUXwHPvGYJ7qo6rHAmaoJ9fvIx82o+A4W6joJOcB5EOXwIi9nFkVWswWvo1jR5N/AdJKIZlQpVv5LWmgHWnq7zMzlF6zD01cU2qfVrlk0bq4d/xvcZ3wLkUymPQ37O+Kv2qpEtvtHn11gLH+37j9kl5QL/S3B2pX/ToDcF35Vm07hZ7RvMomacJqPHUT740D1Ood6YvFVgRwV0eLnBQWYHhwc3rQ+X0mB7vm5jhDr0gVo52wO+D+UyX41Lhmacez1wkZ71GgvZQcTvAPztP9AmfgZAMZY7NWFtXtTTlv93P2bOSmds5gI3KeLMHqno/Kw+Q1VN5uBp1Qwx7/6CljpTb9wdeF3929kJ3/rqc3qNSO/sNl6V2VX5vcPaZi7Onb5BiCbVeKUEkHCHGUFuXf8O/4G6yb+2H1SgNj6rGVYpVdJLejbYtv/zew6g/a5wvovJqhZn7DbK7S1288G1cyTSuQp1jO/ymoIJb9fmd78bcCxw9BrOn2jYk3dXsgY6zaGG3KEZRtceZFOYkJjcylf4vePzjujB1KMwkLGKrwsHjyrD7ELwo+JR/JhsM9+jhEq/cd1Ozt4iizL27dv1yq0Xc7yi6Hnt0s9Xgy8SepWfDrAeqfGoJtApo2ibPiUw5hSzxO1Be4KMgd963yqgCszPqTgZ71w9kHSekqPmDBmHPQPy5qsKYIbsPdSeK12eknrOrXOYD+D91STyALV8FRQw4PjDsSiOfJTvmcXbIfFwtW86ZM1xaSoP87/W8abVmKd6axrTQwBD+/ZtUecvAf9PiVuXIlzURyFZvdj1m7mSd3Ppu09XcAURA8VrGDh7A+Bld4PlmD4UWbE8z58Zb2R69ArHQqUjxVo1TTaImc8miJCL+m8ir8+2A7tz1ZhhO+AWWUU58GuIslTHySt2M/wVaJBFg2Klms+ucl0UNduTrBbosYQwuPtfn52iPLZmb51vrdlGebP4GiuQZsIfLLfpd2DOz5/NaTu5N+1i0gwaA+1Ce+Tp0Mx0hnB6x95M4zskY1/V8Fj1aq9Cg1x0nIvbMZ+6d37FUvsqbq1valQKdtWv5rWmCdFSqib1Gq+oVXRdmETtDg4EaOKrIAX+518xzIfVtwMFE85IvA8Ljf5obI9gw7bPXBdk9sDbIoMXYXptteIQPUJ215Y0ZtdDVj1fV+6vi61XXqXeNYF3GXugWwt3YsUw+XsU7hTy1pV7w3+rQFmBW0zt+ghZa0oeb+2XroDGyLeYGJDjHwiq90ZMPeKN8Odhb5rmPI19lhoq3s0T3gEARNrD0R339VWK1hF790U+ZK0zJLlOXxFZ0pmLueuOMS9AUaq5UAetYqzDZ8+rwdxPpHn2OQnjRavtZ1gN3AU44DaDX7Oa1NRxo2aT9k258TC8xSCxDVcc4THht5TntikscTakZqK35aYy1dsNpm/doQJevaDjpJU+Kt/kW1agufvUATEsM494DBzbF3En8ceYU707rrxO4cGol3WR4yzcObv7VXLIcyb3ej0T76eI8IOkBoEGXhGc8s5ZMQhaIKd3cvasYAsEa7ZTgRbX+7Gtfw1gDbJ255080NhfNxN0eF+U18BfR8sTHaeTa0ardUXHfgd7Fc5jnYk4meBBoo/q9mjTthjQG5ZN460ZMz1vpg1vSPx1QKu89fZ1sH8klr6LRuGRCH71XMZ7/bj3THEicpTPYD6a70vlpSOTqhHlC+uzCYvcPX0XjhGA+yDcSfDDlI45vqQXKqViPeFrQHNF28WN2vwBgDtT//RLBjx5N/OAc7z2r7IMjOuuXL+65zINQkRiaJ6qxs5z3JjGmbj1WX5EHsszRT7DrXflZsxKvXVcaEQ4jppDudKF1HViXBy8LWgCdYr4MVz7b7tvaQfJjlxDvmfqrxCd5FrxQ9xWN3UzfKJNlGvMM71C6yH09DWHpOnkvhunG2Bfx/JZMt8ZJOwYzipiyLGXV09fYe1RhLjRLcaKcrQ5I98C86X4YNh9Ipzh8Gi+Z6ZzzGXXWHsxXYhQ5+VdSdXD2rvGL2L1px2EUOP0EumuN+J+GmUB7b9CD0qxFL28kNE8eXDpjXVPj2v/BX7rMwCWpOiSd/wdgFhIz2kxxa6JW4ZiptHh1csxsaKOm7l5tTYtb2QwT2Bvajci7LCPxseJnREwl3xEJMTtGeSDvgWbORR3mjN/YaseW43FC5N7C79ZgXj83TR+M7hNBbAT6dEcDe/NVhc/3xr/Yrp74HpHpz0YR2xvevQ7MF7NeXUksY5Ps84HeHbgH0HtJTyRllyJhM8A/H3++Fo+j0nrfNXSo5i1F6B3FuIGlwvHInq19vIpsh+7j6P0zgjHmHWvKBV6V8bzXQ0aWHlv7VVojjfrc+gOVrNKotrxWNRN36XbpMk6T0YswCebPksHhHcTsArPvA/m0Uu2CjmYEK3rDYMUSnxr786ribKl7OaYD18OUO8R3nW94BU+DD29H21EeDQc0cW9pphPzatrKJ3PTMmDDK/KrgoxmFeV7W0Vicmh9+VOZRFqqwHR/dC6Fqu9qX63c6MWATNZ1poNiHt0N+rW4dmwnCM4eThFnWG5u85bHLBjfbZvJrwceSvyqn+yCCuf3NAhNrdGz80os+6dcR/Fs75m0MKryeHojFqBoQECK1UROzXXJul3AKAMf8xEZtrOZNYO9uq1M6nP2FxSiBhIwyXYpgzjOIZOQEpvfoMCKhMreYsKOH5R7ThSt4jbxXRCsihoddzmrNKRo4PxbahRqTvMqm+jlm9ZPkIFin2/aD4Cw6+Yw42qfSPYXQMhDgeY7HKpo0BTvAbuoj1jvIvhDOAOm725gavoxl8CRjzh6B2AdHfm6prN8l7BDnK1aTzHinJteVqjs6v6u1p7wPVV5M0rH3uL3wu9qY/cXNbM3px8ILlp0/j8exydKG9y7RuISZppZhbPgKMsjL0j2I+cerwOdaxN37GBF1nZubFHdM0rEjwpcC7yUhbKDl2be8qts27S86DtUbhoVnuUN2F3BYqBGY/ibvSzDpcfJc4Surs/BqQYortT2B3wgUYtHGFecGpjBOM4NuoTeO4ud+3QQTtQgfbc6+DXRJR1zL22uUozzu4Gr49LbYrx7WckF6+HPgOgX7GJTgty1E7ITmRcjAmkxzd5kBTnx0rD7oP/IhXWBPHQ969hEbFoOjEI84WVl9t7jq6JsK9LjilEWVkMqnf/NL3s9w/9FvF4BTSH3gbveAVv61nv9beN9/Wiv+Ac106G7bc2msr3Plkrygu8Ju4YVzMF0cQy/Q6A/YwldrwMlHobu6L1tLrTOeU/ZpCWTQPvtKpxLhswL2GhchVzKMbdG8Wv34NpxAnEp8SC0qaP85x0hL3nLnkzxKaBc5DlJBMYF46bgWCgc+76/R8lNUbwMSoYjscrVinJ09cqxnwO9uLeazy+5IHcjzLOt8bba18jJM2huo0nSTGU3dBvHbsq0Bmp2ZmgUWmOHJDRi9n79jhcgc7oHMa7m2OcP1HuEZix6fneTV9M8/gqU3QdpjSuw/ljYI1fa8bkd2VKwo8zhyeY1Nmdr3mnngswJX+t71hnNWzB8fkTfifYfgcAq//QlcXOM74IqNPzNaq9MEquTr3W3LMMe6MjHf1tknRkCd7cdLydQTEWZwLtSgfG80W4kOSZBBdfT9WFpe9K6cbws1QH9R90zaK/2V1SAYyE/oSGqTOYPYOunWSuQ9oZ+Cs1f6vnhQOrYsbdAuCHD1kDRwV6qbGLaSrZAVWV96WoHh7cIq/NBA8HWhz31ShY4zMAf/f3Oh8I2gzcULHL1J0+zll0aZtx+Dxx5hTNL5Mtbv2dshHfz8KhbJ7LxpzicPZqEMGbcozYNNiljJR2OZbGYYx6qV0Vy+cIAJs1L7kNFwm18RnNgM9k+gOEM8RK3zBeZVerPcNqxqaFbbqdfHo4Zzj05q1ipeGLPKPcIxT0Z7jVx0BnOzmvApEN8RTPDexD3agzkiyu5RdpaywKm0PRmk6qid4PLCKX9jtnRel+rr0aO2Oy9xvEG/EPZaT5uapVwImzF/LKrMGgrTrsuIILrKRf1XBlut044ztG94rVZqjeoBQDxxpqRuMrkAOjdr4+nmmRl4rQ5F/wPM+hEaWaRQ2bE6qrOAecpSqQNn8J2Muek4CT3jVYcHLX4Bkw+MxA/YBO6ritzV6NhpOzlefoctWDJ6f9TdsB1Z5BsxoDnF5XpNGL1fN9WT3Y6u9laTxg9AcZx9d17Llqh3rA+bBBCZl78po6N961ivmpaBskX7S7YFg070lNoZsEfBh9MA8QG+AfQHtdLirgmeqdzLc5rJOYhwfO81X6CCcNAHuPQVfP5U0fK9Ap4NNv//YfaPbxd5WBnQ/1r53zG4F4F9GTvrNW9xEBBEMZoIIY2Yzk4XlYOPsZYRR9B1hEBKVUbGVwEhkgxzKK9CBr/ymU3eawwnVGupNeaOe/RbjGX5GvuHl9asdugusOXe2Qrj+f1z7rll8vWavZWpGvu6GpMmpafTVKH6+zGZ2oW2+qbA/WWdKz/mAoMk4VTVfOolxht2O8ToxIybQeCS9EMI3cohxMtsUWcPKqWdRw7bgardr6Cs1JwldQIMaARgzhx8aZYkZHyTFKgdCufA3xSjQx04JyeoXSNy629rKBbwGFZvq2mT+wZ+b1rih7DVhrmnwO4BTITdhocz5ERHv98lIPSKje0lZu4VMBqu3KgNfxYYHtSj1ZFvMhatO5qZxEvt5sjk0x/Ypmg9W2RcPpJqqrmFyFM0hSYzE3IisYuBzwWkHcoIGK3aFoNyD+1UL2huOhJo/IFFQfiuFXOz/eEpurwN7ZWEzmmSBwiVEOIMxEeRCbmGmT0kulj7h7QyMX/SER5bWZXTPlQnkJSIH51owVWA00B16fAaDJqiv6dPrwDoCNFzZP8A2fJE6nIgEwiAXy3Zp9CrGnOwNxNQJ9uH+U6Rrp3jfM3C4jv9aCEM5H4bq8d7KJtahdD0fpXctRuAgLjSqsrXMobFwfBYwI3M+/RxExe3IcC7eJJF15J6F13agZujcWTWNXbnpp4Ny+FjYRapempocTCUBuPnYM0HQ9FajHqkmDyowvqiAmBB1hel4xSpR79o+rb45Eb9hOpFFD+nG7SWEjVOFTo2/4T3UPUJf4ef5MIU4aCVPGn4cLghbgwq3V67rmvPWUeyBNL8ecF3bjVHUeI/R6kSBS8zQLwr2s3azn6Abnhcihl0UdJeaV3nn4XW0VNFU9Q18SU/TWOxiRpDuKgzdfUJivWyTZ9dqu1VIPSIM6+PxZHMgALb1HkBqR1aacV/zEDrAeahPgvgaBYgxc0EWz0ETjx5Ij0at4d6qUEo8Rr6qFR/QUILhSgjcVFE39XcXhKpxb1OcqbvfBecEKaJL4LKrzLWZRbfAiGqft0W9UQ8HG+swHkte8veeyQ7gt+g4iI9OC5A2mVBFhROaWfQdoHHDxDLyQZ0Ac7TGFO6fmJYXg8rWV8YxuF+Jawm9oGDIfNZOWdwBQnKWrqFS3I9iF8xiYY0r4dgCc/bfPdbJl9RziVn1rRSeLqN7eU5QYgF1YBymvzRe9t2tOnX9vhY+1qG2b1Zmvfw0YNZou0IiDyuvbaBnlMeFoeR+5WaLt0HH+R3nb84EsfATvxkkRfYu4fn235nBwaGqgqzW9OXwh4WaI1Z3H66RiSWNPk1J9BKg1EYRyE6jJsvQctYu4Y7wmhRH6Fu1V9HovrjVVsDHhXnzBrKJXyAcUm2R6mCrsMT4IemRcelQeR2+j37sjfyZlDcfg+KZcASXLJuZgTJv2m/XTeGnbM947E2ZI7og4sd/1mEtf85dm/G7tGPOK3tWIadxXqhAjlTRXLZvheXkHIJhPiYaJTcLOPmxm/KyjotJ550sLkVmRTIOaW7jQMHo51UlWLztQII+/feOxtn+5wqfISuHFadyTgE+5OHC3JuB1VnTn0It7T249Dk39gLly9G3TfUY5CDFwb3qJzMBrR5cCxO0O5ynThx30KfYvZ3RylDWkx+i/DVmsm1fShdg7kFHGpgv0vQrDXn8D2LpLaD3M2n6g2UXgkogDMg/fNVuA1ZgWTuh79/FwputfBEvfBRTRimixq5L1+fdKvaGwc7sz93zncztRRT1WnHNvyQJGLF3ncYZPB7Khrrnp+61h6txWyTQwKlXnXLl5v7s73y7fGf4zNnWtnPwuIdZhgDlDqYzb//6H0vJEO3KO8gnIxVU7T9wufZ15tRispRW3jq+K7FPdAXwvcM1BoRP3IJrtlfXE8EzrROpAsDn2Lh/iNvFxPbKmVFjGOe+UYBMd6yNArXHffcJwFLx6A8xe7gOXw12rrOtXtFoTIhVlDz1tsc59Fb3ttKXN1UbRhH9gb/KCj/nU/BvkMp9G12HVMcxjXoFk79q/TDT6cZ+SvtbMjIi8al+ng6443waW7tIVJiozngmO7Kw23+Vwl56wijjc73oIUb9CCx2xblPzOfiuxE4N92LyOznx4bLfL9j4ZQA8PgbN0ifpSd8CVKo325g/cQqtXxBW3qFKQVyZ3KtxVfx15leyv4qhOB3m2aNxGHBcowIWzR6BJs5e+ybIhcoinQuRHxkKQ6bE4/aRCd+Z264pfTk3RBeBggYGq/i7PHQbULOk3XexVrl7+rG5O9JtaN8GdXdy7nCGzxlfJ3CJ8LqYFDtmUYFxb2E8k7jvBRF5xrGI9dZ8TRUoBhjN8C1ASKToX1IrO9jG/zx58KxW0C3ODkuv4UNnQjAB4G1+D3KTwpDf6A7jseNkrwo5abzLLA/VrFOvUBFn7xlqL3YdS1Em8Wv3XqD76GOJloids/zFoCVNVqDl+gI6DARy9+FQHaQkm0MVaKQRcDxWwyyo2iMSDC4WA8NNZK/PZC4OOLiD322i4PhxjKLBAblX2Nl5KyoXEprJYXp0lIUgV1cBPW0NXq5szDrKiVQnrixnrux6ch7fNRAaEWP3tJyzmXaoDHUFV+pV3SrLsULVrW2UaQ+/4N+sVY15U01JyWZC8Z6AdoIe2wJhk20PZ+yoKMd8x8iTvXWaxTuQ4HbVPJ+kRLPOnrsD4XrT9igV2qWeLplFNsPz6h2ArJ+hG23X6F1vuESv2k4GTZumskZ4/ZrbJeqj9GhF0rCfYXW7op1h9e34amphFCBoLHxEXLhRNWbwH3bmoyYz/K8qHWJ5OBeuAj+Co4F55OEZZ/UQRRxT3N37ODmBCaaG/ibTeL1TCQkOKj/oKiozb1k4qnRyf6kyIvox/i9FuKjh4zablWXVVt8CJP65mPm8J7fX2bW1jQF8/mBxcCdWz2UNfEHLmH/6JZGKKxB3o7ArC9/rXNjlXhvXd9EBWbkrRO1SaGDsLrGr537mvLyOVUcZ4B8Y03hdAcgIt+sKXCxILdfka5tXrYljEWUl5cOhOhTNzcQ1GTbNCgOPUujVLEckH9maxhvKnb51fQr8MfPCuGiWeRXdc1fLxPDY/BeBXo7doUQN4Yn3eLE9k3+V70qxc6RWvndsHCvA5tCfyUADd4yY4l5FzzlsAi6WNu719fVxQXpzeOy1q9cZphKteWpXaKZZODaDxlc0GDRxYo5RdkAEchoK2sRx+0lBsWRcrMdqhHGyu/ikHO33BN7VnwS4//HhyojdSsSOpZhxaJfpAdvVOwD1cFATEZOF4JrmS8yquwFU2XyrCpUN20H95mtT40TYKM9j3s7yzLx4tFxuV6UaWaP8aBWIoylu0ERlnUjUzFsWXsccI8iLyK+UtmqlGXikbpoZjzZ3JzN51WM2kaPn58KE08rk+MRYwaTjxoCGAr2KeTTIYp102TrsWAJttRXobuGadBC9JjAg9oomQDPfa5V16RI+Oto7ydNv//YfaBPOzErDsg3rrHrG+QNadr++PoPMTxyXLLI1bc23y0YWN9yuqVwWqDj/Bm59Db4OJhtVXsSiV41ZI8xoCpxycDoQ4NMcpUn3Nmo8A46yWfvQTIbQ+f2xK5dteldoI/nmVZaTQSKmxihqToFXI3IYTcTg7sJhqHlHnw/1vI2DUgJel3WJPN2O44j5XPPvIY3yqnzG8wQcTj42abfZPkD9jye+mfMW9GbZi6O347WL6d21sKfOA1bxFaoO4prd9NxzLRRMBCvlgdpfxWrNMd0j3rzjwC3BeUy45LYeL7qbpnhnw/FroQSsLToapxrXJ+OjRwfpuFpD7P6DXKLlwMyhXrnAFMdjEYuwFMcl6842eMbXgOZWrzTod/eezaxeQJfBzYZ9ZDsUYzAC3hXNztTPfR25WZxxb9PlpPL+EU8Srt3vloIPYs3hETReBwhx3t6Bm0Jre+fQh7PzcglBtGeG+KoEZ2JtZncJyGaUxzI4nbN2kMdKKr8eaXY1U9ykLa9iYh9IMyIUTIrmJniE2jS+3GAz+qBiezO9nPz9Ab1cyN3lmoZ6v8H61KWQplsrdTQq9XH4LaGG2vACnGl17V+xO982uvaWY3bvpXFA3zsr6ukPhBi46Lw8xpq5Mq2rfQ6LqkQvYMZqQZ55RA6yr68ZTEGtr0C0Q0ebKLet362ukdT35HW8eurwnlXPpKGv61MbxbLXvU3NVEmbnjuVnjUiKhfNGee8E8/MJ8buCKz53L8yTnUq9Ol56OGawsx8k6OPLJrrg2YTeLcy4hfOmjxQTl7fLd1t/sTjTBNHSXFQ4ny7cf0Lqg/S3JwVPiKxqpH8UsyoHcj76xx3H+cTX6F60VajH8e65zCh9z0CQsSPcoSp9Y2KBW6bIxLBS9lqO9i/3N7L6BoXWO3AJ96zLq/eTHCEQkC+xOw8ZvL9qLvnOwj3Ua9SiPVphW8MsZtt+bphQzjjG+B6Ne/pg+tKnJlpKwc0VJq1FvfsPM38EvBqDITVglvAV72lN81WBovfraUXCjtKK1KKcuFTF7HWFC6DJgLpb2DzWrrO1GEzR4DfFH+TQNNA86SYLWiCaqHsuc+YNX2ljO5RHri8dc1XQLPunhMvDmKU5znPW94af57J41gWY100X5Znk0xTWfP0sZbgzdpyUzMZsYkDX/9zAycDwWXvvb8w4DDouj/Ph4ros0KCtl9puTSFu+Xf7m654td8f/t3f297wLPqBpyygGVbQJV2+QwADDQUtHwq712rHIV3n+2LBp9KEZVLZ4S9T69nmMlcyvpndzwvoxSUhVhHmfGqQQ54FSBlszovr6mWLv22XzFaeK7xC3DZHzkX73OY6SlowMWZu/uSgqskWEa6kiQboEHQtrDtNUWgG6Lndp2+d72kp78ucomkiNLeYibUY10yyO2p4VjP5+yanutYg+NG4XuguRAesjqA/BpdiuKnXTLsrZtJLfXcNHWD6cqDXqKUFwdqOtKM4Agzxk2bokpNm56yqE8PqjDroZ3R90IDcxB94FWTwXEJUMX9BbXZWBMjAg3NAb0x1K17xS0S9ogPy9kZTguzqbjdqiDesO5sg2d+ivepN7butWIJbbvDrDK2NSq7SrFCvnHjRYNv54bKrYq35bHLuAk2UxBnJeF80CaTB1EOsvP0JbwIYYzXgKEozRvMjH6d5q70j4Wog75pBhXYHPGBr7rehmmzRDc10D7lW8TyMZVyM/pNR1BksFUU57bJKhrclGEMdEYWyZtSHVSvjnsHPr1yRZ6gEZs9lxfU16V7QTIPEno1ZKtGJPgxX2/+nbShkh846o07z6hNEPGqf/oMQDVZFoTsFePXcu9KXk9fI7xSjSqH7clz9yL9pf5Fh5pz14E05nEWVePcRE/K6ChVPZq1pofYs1SUepb17CO+39u6UB3eNXvwim+sdpQjlShnG0/KBbdy5tLIYMnC7Wxfhl4G0aw27lWspw9BVmKNvLrPdWU70bBq9Crf00/gdk3G+R6LiMoXZVlFySPunOp3eLyrEMY48a7iwrHZ3DhuNH2mlUsRhnvZNN76/mlzW1VjGmjGa2wz7h0TcV/unvYZsLG9ejVDJMfXDhV5KXWBNV/5PCcxb50hZJKcfrh9l88QalesiFTsa7GrlmXccMkVcBevg2s2hIDgpdhwyQcK2c8fB+rj0m62Owd3M5G2QajJAYaOOajn9mQLHBxwVoi+UZ7137DLNWnMx6anvpOTv69ij9Uuo0KsVLKy7/E0kWHcwAVZrbaxD3Jsdu1WHW+NXgW6tew53F3vDGdn5d0ZniF2xvemiYrYSXpw9+ETWzUL5U0T2Qv+yNz25iL7XYO4y/gYH1T4DlFqbl/fyNY5HtZgRIpBKZpj5FjbXY7zsLCsSQ7cI6WBWbPrjG8T8MWV9aDUGif5IulrcH3rZB5W6BXwRar3CFVaFWTViOz4GYAnrgtggefndNzJimia5c2KpmCVXaXIiI3rN0vXRVIzeD7HYoyZe16j/TwvIct+8rpad7yAEs41kZSN2zyX0nIUqLR94baSBQkN5YB5c6xn2A8wZ9xvarMrqWYiTQRYQt+0n0+n3i9qzRm0ed8py7AHrex7+pXRvRvNUStInBk+jf5MlCLoyWaX88wozNhM8DszSxM8mCCTfNVtIuYRk8NjBGryXdhCmr/2X5GNaC5DmHxw0KfHzkdnHr+mUU+zMVpZsRpxQuPMB7aRhkhCU7AVTvEe7wCz6CrQit7Lm42sp8f6FJkcBQVsvk9y5zqcyqXhXNLnfTdP8Ze7Sh85+ASL9+nINCPiWe8ASJHVJd6u9gKySLsA3ox3Fc6H+VuoW0w2ylflfgvMq7gBZ35iIJHJXCbNLsziDWqyAj40vXGHXn+TgA9l5tk9FKvHJOMTwIWX4hkJuAxBctxexfDMPHGGTgZotdJ7IRTh1IzKKEfHY3IkE+VjaN+411sBMQG6RcDEbcxd/BAYHuiAn3X7mwDW0d00zvZK2xAtiKWV2vU1iXxW17a/SBvvlpu5Np+LtC/8DHJE1GhEzeqqSa6VinqM0gr8JRoT86dNC1nrLF9j16hV5Tfz3g6cuntOBXhccWJWjwe6yDEaa56MORdlrEen1kTAuB9JX2ui/Vg+4ztG3ujNe9aG2eXdYVbUdY7TUsMaNT0uNU7P8rwe+yPmj0ZtPm43i5lRqGx6cXt6Zd2YaWEsepVZYVZMel4z+hVy5aCKaRt36mLfj34y05aOx9hO1CTyiXIkg+zAIX5KIfbWcmN0aqOhBkxULrdSU9sez/j64o6CqrduEIV55j0OQgPO2MCDjmfOav3gPncQjs23ncRWvy9U+RYToOyfmNulS/gkTN0FzcZYNH32KjeyWsHx07k+cVc9aOgEIO4WpUWnvYdBB+KuavCd3JfuSqsTTONVdDb5N5WF4y2aTYa3CATMZo6XE7gc8PJqzM/hWLFiT41dlzN8A7ywAsXAqVkoLwl3ckocc4fXLXK5pCAPDvKABfehdAE1LHgWXbHZK3iB0DPr6QchmsiFvWzcsmj2gk7qi1hNL0SEmRNo2kg5gzZw/1q7vrWyjPJtTyN9BiCP/5PNOM257nWFNpCd9zzHO5PMrmPMgIfOvTLT5XnyfGtAZMHaI03G3QPZsNVYNDouUtUz5j55Neh35sPMwBVZzLg0CJgqTf6qG5hFlMrkZopQmV2pibBclNcMxeNpGs/x9ZgZAg2bUIFG77SqMYgzyDM2PQ4nfBtse1HO6ZuTqnv8PxfLvY9PM4c4LZw/1jUQToz4roSaoxYRwA1FjneQ37nmTYbN6+uRdpSbCI2aR58gj/NtggfvkQhkuAtffGQ9f+2/gR5nTpadZHyfreFbqca5V+aPp8gV2MVMg+JDQ99DOJtBVyE2rYcGW/N530i6tc8cBl/XJdngbp/8S8DZKz93Ca9Q11ZN36Zy7Xef1sMQ2ZfuoN6TQEhcufcqcD7EJJMDZjPcYl4z9gMaEaowi10noxTIu5qgEZmMfcHzBamOuR3oVS7HMpLXfOkO0HuNLijLsXqeT/ZGoV8qnfMF2YswM5lfthp+sKqpzhCbsdlbtGgf6YmhNC5H40K+NbciHJr3j1hzeNN4BTRJvPkgQmQV5fYSEFPqKX0LEL79hxNMkwyeELQtE5NFqQ3W7gyMnnHtfh+NzgUt1t778s8Q1BneB/tl3zqurojE6zSK1a7/kAdc4iOeWWpAdTYMDg5euET3GVkjLDSHSrHMP3KYASxsBjMo1s3TKdzHTV3j3HHFOsyfg3fTjgnN9xqTei7VAMXQwKAuqVeyNq4BX1CjeXVgdnnKPkUvyUJzW1Cnrvy12FzOOdUtXA+TRlnUx58WqbO6+l2F1YgEbvVxo9YM2KRk1xZSNrvWhrdvhUy7wSZskAse2m27OKFD9b/s2BUZRjlEhOhll3o14mvL2IKXH5ei3uV6LnlXFCbDRZcoq8JRE+WT4BFqII85NB3vQ6wZOip37bPR8QXlSc5xVm9WexKzyhrAilP1VAo3LRzS5HG6xjUTxnP8FqA1aPJcK7stWQtYW4XsOrx1bFcgj9MFlk2opnI7WLbwGSIBW9fApCdn7+ufT6ZzPaHbIMbCbkaQsbu40HR0Ywj6a5q9rBKjvJfb408MrzxqW2SnrvM1j0VwTBfO4z8IgmcEIf6JnnqlfxDCkdheShjTOKx73e9jL4Zxi7gaiPsQOBPrVVT4PmV8ixIr4PNZQuy6Tj4ycyOfCf+n3/7tP8Ds+ePvaCwHQGx4DrrlzO3aSGcap78v+ei5FAdlTag9TOOrDm2f+2qbDL3qO7j0r9nMgKCYNZNC46xgDPnAY2bIHFbhvDkj7GXlfGrHgzNz/yiomM6kl2Y9FrDc9CrQ6jQLg73NcZXGvUq8F3HgW2R9eVI9Snv1BU93LwgrU/XOv/PQA/coLyIUqV3FQVNFKSNEbHqIqL8RDY91B2HX+DLf/Ueek1loFGZAduUyBkSmx/aXCCs+xXsO++bMiWrPV2OK0jST83WLNezNt8Fxe+X+SA0fkamCH2b+3t7c+zIVBEaff0X7734f1lq26n7CqhuM0aftshiDChbYzj8A4dkXXo5DoWdU+Ny16QTvGvVQMFB9RWwnUzwwJ3YV4QD+JPPaDLHuGS4SUE12Vcbd3csF73p8QZwPlB2Onq8LD5Xv7aaTynWgaPepz+2IOXKvAj39fRJvRnHOzd6xctfEPhNoTGPQu4vhAGdX1yWZ1sxrzS5WlxuDz6NRujzHxwFUtW9e8ENzd8Sq0YfPAPxPiLN8BkA23dC9DrgVl/yL4Zo+7yz8rm326NdRmFCtNQ2uraJr/tpbfY5bazxUMUY9Dm4vofAqem/RHBBDduCju4r9qonquZdnM0q8th3lXWmSyd45afb1nfd7k9rFszAuZk6zPoWLN50nvCCPfWXgWweJgnCkgayxSPvF3tpG3C05xt2yZX/M1Isw47hhc12OkWERNA5BMfqFZbPptVKI3v4CPQzmj2nNWJNKPya4fWNQOrWdrMCgnh40Cg0CsXstRw5RXlvdu1WnXI/pVOWnicfcozwN0DWsc+maTnfsGuI2aj7+D6CurUOikeO2WQXtgBisbsItRO+Jd46LyYM6aNujdG9952g2ppHrNh7VhOEpe+Krnci1Zp4Q07cAoTUVIrqOmT9urxIdpBuLITlqPLEBgtvsFe4WaC+xF7S/RZ2Vzmr3OJfhhVDniGx4i2dkOyivmw1s1AVLN95gcK5bgTyWC5uonoILmy53M1BSvXAgDIMztOW7WatNgx7Dr0P/OOmDyTEyGug4VY7hvPiAPjjtWOF71moQF136uyefh42lQg3K9bDMLyHmibtAWDWKXQvN/C1AyQKapuXCrIBYOnB+yb77XEMKYXeI+YyKLsrUs0HW0vTg3LJncFjv1+RWA7aG24w+8F0jWUvno+o4+lt9m5SKuEuFd54N7w1UxB03wSrOirGxept89tU/htlZjegKuUmmsGk2NRzNLih1pXD8bSEK3cRpV+PSTBU3BTLk8bc5gW2bVa8Ex/Qhx8l5NT+CJf8Qa5PsfJRNqBsZlNkdDXMs06uiH2W98pucOSuf0HiQChzOYpK/v26G1NvizNGs7XkbLRLEfNN2VwSvTPFOzo1m7+ER3JXUGeOaode2gN1Rounjah29CHpRc4o7jPAZADw+4Hd/80Oa1S8BG1hGxHP6FqCsyZ67n08D7I54zsH5QpDsmnPAB71fNvpe0n4kmnF8XanNZFTb7CpI7X5Yc7i2NeEaqrapedY2NU7tdUADWP+T+65AMK6pHqDx5nKLCuwayjEBTZKxTd37NjdQga+7CA+V3TEymtsX7iz1jvDaNV9jcXZMlm763Y717wD48CNmcZaZutjBQ8Wzf77Yfc4cQKbPulK0aB/lhcz10uY4tCs2R6ScMJoeAABrR0lEQVQ7QNndR0RXOovv7d50zzCXPW9Woxlpk2fzrPpYrCaBQrnJp7BHsyaja1F676vJvwaZ1Myg1Xzghbw0Q+avk0VKKguQm/URq/QZj1ZBml4Rfyz3slamAO8RG8BGlyg3XO51PFFokOmNURxHGJ+pKqLc/9EbxyaTM9kVgIeTvYTDrqwL5nUzzdUwJ2fw5ysQX7OU/gx+zfNaTeTf2zv2RlSm43c192Im+zA6Gwhmqd/h2e2boWNxMGRphuTeXc8vO9aKLsJX3TkizGJ1hBAnC7VZ1VOV3J4/6cj0ya7x84p+9WgmuEwVlwwpwREkvQNQ4Q0UjjWw+Rq7QtUeK737EzswBe5P8kaD9GiJ1Hxqzd5SaHzHOOjFX3MmQNnU76VR2yvimFjt9dVoDlf1m6oYkn3V+fruo+E+POh7p/3dAu0l9pXZY3KeKXUxvV/1VL/byN55V7pVXkjj2NQpJo3zw2cA4u8AuF5CN9b+jgJ5u7l9VrSNsWkRz9ui3HPs5t1zmNbP7MbN6IXjTBZTpKr6O3KTxhSmGRWEJx3PBHXmdawLyXShqkrWNE5qdhVn84paN5GK5SDuPEiF2ldcVckap9b0WVzbgxqiVoNKxnDHqhrn/2SgGNTleLU4YrrBGYGpXTEKSFAz/GPnl9drkspr/BmS2mu3Zk92vVmhqTKeBmeGGEmNwXdnPXRYzaKqPs1ERK9Xn2G0UWorJmOU073Kq66zkpqHT/ZV3eYR9lo2qnTr6DvxVdtxXqv3gnbij5Fv2VvPl1U0dGs+xFmUquEd8DCYjIXnvb8DAIiEugr/jTRy4V4m3To6NHcejcPhRP7+hO82VIcrczeG9wz0aNV4ND73HItvKlZ9kET6TeWDl6U5Y6X0rrrpXceye6hCgYz4SPDm4QE9WZxjJa29YiKxV8lGzZs8X4EHGdx5wjeybMwiqRodoPDxXfOOok1yg7uRNn1rAwxeSW/47TSNM9EadEKz977t8STrsYpXznqker4r+w+sUvwe+prPVffS1fdKnkR2quVArzK8d8Mn3lT9O+ziNfUGznAmdyBvqK7vjyyCeU2ivpFX7K7kdBX2d1XHCym44/hBph6RWnN3nmI4DrukMLZb98Y9V3sfcA484pEnYh6AuqkLuKlQnqYLzbj1p6pucoyanmPa1+J+Wr+CeEYuNFPbqwTaTXLv8FjNok59xnzQqwq40AmV1G5cmK2YFH1bzb3Hxi28UX8da/WJgpHrqq/GWXV3Go0qdUZtBRCvskd5ZdRpzOCbq+ZJfC3uIHIFtUyqafwe2u30vTFqrr255+bP5S7ZOTnNe28ugj4DsLRfQBI3bF0AiSi/AKdOyEZlO5aXq1WQy2HvD3gsEVRef/cnPB/xWGrz+D3Ll5qWLxW3V4eB3o8nEF5qmJr0VMM7V/LO4ZqJ31RZVBXNrzvlC2f1Q+0d40kSx/QV0R4ntbc3FmGv79dkv2sC7DJ+jCqBcmYdxDG3ZW5Ayo38LFd+C5CD5ABZUbaTS+5uPLc8hud8LQdS7Z39NGKaqravNT3fvfom570gPfv18HDMoYkR66tBcpGlYCUfrEBvvEwfrwL2UtjUFzmO7YssYinGjvO9u/gIdkBD43UAc55w03JASfb1zGniQKkUJPRspB8EvX8FBlQjT9Whfo9r4H6/rq297HhVq/061mRvgvNzaRfy8eyqMDpuxOvolclKEa8djmmkI5J9xuDyWbQ5KJHnKoHpRhy7KAtgfu+IR+YoJyLVfBsTbCAMHVAoDZMqBrku3bhWvVG+6fgOc2LnfB28ApuYj2ywke/0LFI1fLuZchr9afxNwLsY9ObsKriMVqXIjecVABrLOwAwueKxCrANuNN8G/AbtMDI+eC58LXWARPG/67KMRbwPCbQwPBazPOsdiEohV0uj2yMdN4eRyugifxaS/j2+nJ03B/dz0fWhXnGcDngNY9/H8tLUnitO/bpEn+tibdnRVPLEvBbgFhLu7trXRM7N2pc8V1b+UDkXwJGqI6FmwZhYNrkHFyvFjvngs0z1AHtMa36ikvTXkX0CkyGcy/Yu7zCr3OsNSuHsjHDpJcjKglWuCbneZXoe9ozTMZ4cWQblIaVGUcXmts0wMfM5nojf5cRFOE8dA+pN0ay9ytnm8wVyO09XNdxWFV3nxQ8a9hHuXBvVmP+SmeB5k1FVLNxd6zbZWGXfZtzhmo+DyrQtJeyGcjtnz+w314FfFp1x9a9JBzjA18GmJ8nE5bjHAvaas4m2XReK2Mdory2YusAzxrkvObC3KfITIzgGEd1q49CA699c2wA1O9KY32bd4oQFlkjC20jizjHohxtJPt8a4+4jUvv27HGyHWsyzRhtoi/igB8z8LzagbdfeRXRGHd4DMDeyrpKTYzS0oZaWIUpVj7o6VvAVqrR9ijviMo8DniNqJxj75bc9bgIZNi/O6R211iKK8z2V07BGCyi8w4ukPBbGx5ebEvD+e51FQHXbXxm2a+Ao9UWJ9QTgqCy/M5zVp6vFmHCTtg6m/C9s3kVVZg77S54Qy+b/3mE1fK2nuL9F1Z6O+byu5o2qkj5yjvhvsaHdL0UF1W1VHPxZ8BUAlXcTar6tb1Vcn5yb0Z5XIDp3058mFAlAusiu1htKbjyaydm856/d0AwOr6zcyV1ETMzssb71A1ec8pd823cSmUaRF2de0hXMlYmfX0K6OpxpjhDISPV9N4jL+rmBF/zxWR6NeVezw3GV7OpEux1VHQdrYbrHbOnyIKiFT4MPHgMvdmi3dLVx/bW1bUdaF35tXDl97TqNOXQZfGGPdcb4/MXtRd18IL8BdJvOAQm9VsjJ0reW/1HiLTE7Ma+SIFbVeFCA2viSxDT1d8iLJ02a06YgWa8so6H1vGFStcjjQ7Yzo/k/tBpwZHRp7mZ//94Kd34TMAz5/+BnGWzwCgAccyQNnuUzvcU4eoNYfB3xxVAcyGR3g4jSi4/AgMr+KgpDST4/Yq/BkcxD25Kx0empNxZ7L71mwOj8VFhYrxo7wPfjwxxr37Ig2tB4EGXUPIs53Ha3o28sr/QWisOE00dtHGEL/UKE+kssMkZi3ZtxDq3hloOcbtjNeL2GgQsY2ZikmtgV7Kr2PoZwquQVwsU+a5AOz+uPTWUjase67XIBau5saI1FQ76qmzqM6Z2bFkRG/sW1+Jmb8SNkZWb1ENzW937F5T79Whp3dEG44iSujcEMEWRcNVfyDUV/r93YANFO+2u/E0YQ5TcjAJwhFm6urUZDOiTw+hJcx4B2GUI4+ePtrskZ1JnI1R7oFt2jhyjYD6pJTrvi1NPTe2PG7V/zhMYoY9VsXRILrskjv4Gk+NeRxbH2rfJ1Jv5LP3nbrom8hful8416Iyq/foir7DzXgMiXIA7PEJJlPi5j4LlGtfgxKtTl4zpBtjHdw6szFY+MLOOMzMNJ+yK5TcWPE5kVfGC8812rlZrT1tMHkuGWvhI9aqMiGtsXjMaxcmuHkRXKgRGnt3PSKV217+vU9NzMzkVXBwQ2JfVrpBo/n7ALDnL32pKNhyxqQK2S+Ard4BGIDftous8oqhlm8b+wS6qJ4AuJOrj/75eGnuHAU66X407D6/TZJjA8yKR5sYN6LUq8MDpr9vBjyMtSr50vUcxNcUwDbOBTWjZiloW7v030lCSo9R2zvl+xamqMCDzMOC1Uyz2LvQ9Mks99eb2kz6PRvfnYtq1PaH6+OVl1AjX685ynXlFxpBFNnVtwAlVUojnBut3FaNZspri4DTtC6VLfs14uKhUUcbBi4v3ful+myv1kTUHrFoM5ZnrtmMEZq9qEasSZSb9pPKOt9xfSZh3ezYIIrV3kqOr470mNQVcPIS3PHayhRRDjQ1Bzb518ieUd0V0WI9By41SKE5VrexV+Tp4c6QdJBaGDPpfb9NzysyB2E1nXnRBJkeTs1Tmohf28QxVW+FDwDxcnYydI5s1ji1hmZybW2ruC2joa6H0KyAp9TzqkPNW9a+TQ612X00g1G4D4G9UQ5UDzmeGa+9DM/bz+SoSTuO1dzvmi6oDwDxzrw/NDHARILrrxUuGZdxuXbxr6F8pbELp5dXT19VdVe0tXfOIX4GwF5LrvwWIATJcWL0E7QF0wKNAV5SPpDcAZfDGcbSRfkwYO14bTogeYzntTSQZo/GZqCeY126O2vEHFsXThLoZbpZopNxD7g/IKX5LHzIUHCX4e71h6C/eczbWzq724d6nRHeCnTVuMWd4irMh8KZnCqTZvOpFYBFcx5nbCnYC8HHUCdfC6L7ONA46zv1gmJgGUS9Zqy+BUiUVjZt1dO7+n4jO495+vg71KeBcDLbHqIPxvRZVItI6z2Hll1b1+PWtj6hnT93j0HieEh2jVcv2ktu1vPyTBEFHHSNochuwK1mC424eWpNm02ln9m7pWgAfBfyBvk436LsUe8ozIwp0unNh15ZVIGm177kLq1PmiSGWXziiKzqWEFzQS77MueULspbz88aUpWv9UkTMpJGecXrfF3fHR3ivsNBphvkW3hnxmWQuyo/yafYiXq+sShRRloFQivRxrsoTbOTSh2Hu79wXM2fXrj5cVEp4laYESHKvYgzNXTfyZF1+3sIqq0ihc8GeGXuwWErRm9ub/m1+i1ffWbjStgcarB3w2RyAsxMqkmozOvk8zPzerY7+yeRQg72DkAs9pWfAVCcEG2S34TZfUs8QSiYPDI30IzjAVlssX0Q2pFeKOpB8Vo0kRDmLZAPJnmp28w0aOb+GssSk43ypRW9DEwM9/JsDtZlnG4JtDfTq7ggbgztzajsxWpW23eN2At5DDju7RF47XqvFRKJ5TqQ12QBJ80OELiRy+MQvgUTYfrQu3CymGOc+URgOW98kvPQfU2kn97abnOnOvoOQOYqIipRn1S27j5PXFfooT/C8IAbaIzPOIvcYd/LqLC8RVPRd5VuV3aXcI70FH3zc/Re0uL9hEv41CC9KJF57bWhGe8LZ3r7gb1uPZM6o7FLbT85gj0Crr8KxwEHgudYpzPwWnWNx2tl2m6Ag6KLDGRn1XbI2nnOk4AZ+FbP84RvwcCL4DSgcbkX0b16Bk09YAvwvUfX3pGnGW5TWaBtZr0JOGnQq94ZAjVm8b6ZF78YgknO0Swei6Icbc7LdUbCjHlF+XzEAYJXjzbP7z79hs+br8s06jxiditw2R89fkbYOvKxCTbAPAZYE5vQbIdSGR3q2a7yP5nfc/oQAFIRzql3ABzFY91Q2M77hsEvhn7ZXBR9F4fB1L+4NAHuRYKG+N+QiMkwng9xLCTP27/GOiJHT3Oc6R2yi2TE6sKglwNeyO2eUNoF4lhHucdkxqb2Vc2/8coP0keX/urSndEUg1U0zyB/O76rUVs1dtdA3jcahRvBNpO8V6ypODLCdmjtnfl3APaev6azii8+BVxolmhLGe542zJd+nXdIt2tePRMEXB7c18YrKV4Hrx5Rn6uXuvAO1sI7eM/5fqB9ifuEt4IWFx/KijJOda2MECzLubMt0FHnM3xisYu743ijiPB9oXunBzvKePeUVT2YZRjJeO4eH00czZGtAhk++Z4BAuPXhNxgeMk901jAyVz47P5GQBVI8aSvB00HIt63wndS1D6GFQaJwNBc2Nzf3QQIGxzHhOyXq/bhC1N4hye8QXhNs9Qz17oGKtn09BPIDe8OirfR9Af5Y75Sq29Q+nHgYtGsYYzRx6g9aAiLOQZtMJlV7MYnUlWyrf7aYQOg7qGvqdsxi14lhGq2fLxD4vJBce3iB/l6sisqJ4XmlFeOJ2TNqph4HuzrjHjoEiubY7lsXcfPBClebzq8l+P6RKup18sJKVSdfHNCkbFjq9r/yVYavs7AM1UOk45kHfHQXTlNyTE4kH2pgTf1l0vUiOnd6/oxwNOTqzjAe5VgtcSZ7OSPiIu9FKDwaZNz7fQC0po2G6S7Lmf4eO+LhRRLmx6gkUs6AvNfFA4ytcRXJgHebN8tApoqviEgaA/8Syaj0B+76yD/V4XpBmLoGatPAD7IgVELremihCqT5Gg9IWy29xnvfsw3o17r45mfrcemr3J+VBCaBJeAw4+AxDOS9ZJPr3jOcVat77es4qBcwzYzl+bDHFXONYoo04lWcM0NOPzqobDOVWdSIEXr/fErvM8j11Z2SQcSVYyvDdm4yCvDU8L1qQ3wKwYXqzY5jyc5zNsbpdds5gFpcnrKzpSsBpH8xUZR/CrlZsV3sxihJDZLtGL/G/T9HAFeVAtNHX8+ohReClfDyGETdg60O00gxG53WxXOofxzxfQxyWmP4CFWc0W9tBri4xc8MEaALqNhEij6IpNhaiZRBvJCi16de+MRpRirCj3EOoi9CzP62f4nIwyGMF638fxGfYzV+iL4R5Ecf6Fi+t3Cb1Al4CLyS1CRMwLqU6XbjsmLCJJNOgj1ZfCHavzQjNN5EEMV6k+CKc3GqsKaIhuOFA3hF4lMtXA/vTKd6mpNCeNzg+NilnjQKO/HpPNUXBMF2qoGH0zYu1+TFPzcQ34bOblQd1LGjU9o6LXvb4+4aaZzg9Hr7DFuMhsL6zsB16Drh6xXfpY5Cg7SFPpvWPhmO+tUx5zvrwX6egPyDOpjW0iWqQ69poMHQF7sgjUgMfGuhllM5em11gpTCc/Nr5BL8ozqlCkJ5LSlEySdvAOQPAoA7Jd6oL5HjFfaZvxGYSsk7zDGfkM54GNGOruvcnrqQO0XV1Luebqj8rDBdsez7ra62sSAtjFcWWsuPF6Row4mBiOsubj6h2CEHRXd++eS6/PUuEdEY6bxmrMoIztZ+o5E8VtNHkO12TMJ45LnCFjL3GLlGAfmzIYgNTGnu8uQWOBGQXAQbhdmDL22ei+HkKCb52DW76IAD6XPeaObLvCDfaayYHrHYV8IMBH89C3zjDauNKFATe3gTDg6dwQaAZNDCO45EGI2nhec3xuxJkQ5fnYfcteERaPqyMC+ZIKj+s5CLFyvCK7OtYqxFLKI1INDpTD+DP7xRGWLZ9+rA366kbiyU5Sahe+R94BwDsKzaq2krhUV3CP2CCkv6jclJXGyySzSe6RDFD5E1WKrlF+pAwv5aKJ+k2kOlc3leJuBUGgk7E23QfHormSNKw2g8IHcU+Gju6KOBO3QddUjuZCz3JGf4bJDP7tbC5JX/QA1RuXk1FmyjsTAjjOUHLcziDcbiDug+z5XhsuwkLWw4WsuMfzPQdRsbD1vwszrBOpNReGuwvU/hnR9TjyDgDAnt89dSFvV4JdITXMxpVHKzTjViSbGnSNp0g6M9M3AMx/tqFVFxC43QM8kUh9rXqcXY/POaqqdA97St+jfY7YVOgDRmDbyPmK6yUHyPSvJbTBblrSYhzH3FTDGT4OO2Ncp12Ml+KuzMLYNXpXpvsaQhPt+pr9JpaYb5o5shcKLkUikUkPMOIU7gLsOW7qdQV6x6fFNhHvbqBBPBw21hYgXl7BxoHbHcJmr39+ZuA+jiImzrOJowmpbW0w9q3to2bMLVreVNa4xO0l4epRVogV+PootOqaa8Qabh57m5AawfheazQbY0bLKHumdRGiGeTD+I7TPc6otrI7t67zWLcR4hguET79ivLH36e1Lg4fsvv8N9R/+D231dr2yDsAdmQS2h23mhnzAWEvl+a27nUNQshlPtZhy/ZIHoZbO/bA75ad0Yl1XfPb2WoC3TeXnYxz/kfcXtSnN3MuIbVryMAE9jN8BLsLvJmOEGJEaBw2yk33vUohR/wxAoiJmwSXx16x1yNCgDu2/rcXTfYR/LwseudxXgQBBbmwJg51LeygMh6xaTMzNELAVsZjwGaUV6GcKcXeRFQrIOsP7r3qeXQZ9MyaBBy82ftSSk8BgsuXk7kp+OVs+4A+/g0TVY/36EzVEb8DMEJrBKDqwC/AhTPXFWhPvzLa14jXGKK8C2W7gA99jshc62v/qsDUxFgXqzlH/J5R2EY5u3oJEbAJkA3v+IzrB2DTq8yACItmc7V3FU1JxlQbc+/SOROvhUS5ziJdrZne164drcgtzhOWdOt7KsRkzMfrDDOX6yKMNR5CrKKxMFFDt4m95+XI+UP4ZvEmcuQQ5aaxlKp5nPPRUfnGMYJXnMYFsuMApK5VYdxsxjkQDXp7VrS5hVzkfj5EUb04vmNwr+3YbLJ3ldfeI0/rWOF5iec4LxnHmSbaZ3I8POWWirXyWnrHUuVbZxcBVvWPHWtZSUUo362kVDPJn5ejkA9H9F1jb7R6V/E33EJ3neN5zAC/Fq3+h/G9qmvQ0Nq7jwTXnljXp7bs2fT0hoAxLxNavXZ45/O7D/9U2zqLg+8AHJ5yHviGwlXkhHMVWi9hH6meweX6AxntJFlEKJqXJXQM90ZegFWVsI3livJlmX8VQDMD4SW9dcY+TDOsQGbSbED7DALYwh3bY/WRo3wP5+LuMcemMhrMyEgt/s24XGujoYnbvfhFHQS1CQIv/RWWXo1Cf+fmTBZniraZTlHVTfv7GGh0LoxVDLfje/oSoG/Oll1MAPItPLx0X1G+w1T0QV2kLauu7cHPANicWYMOz1dOzTHFGV9vOBVgy9lnTzTs5ltdJ4hePRk5+mApU/3K4I2uijUz6nGDfj3UA0N1eTbKyTPbG7YRyCF2UmpA3ULl9ACuKjSiHJohDZw9qpJMn4MXVvNQzcPXXWY4xqL17J1Vz2BG37v2XPuCUqxYM/oM7Ro5apqw0WBSFtuxcS/3IlMHqbk5AhOfmD8OdVhQxKs+FdA9Ylf8GrlXNpuKGqRwAR9UMl4RZ2FbD0D1ulrmXZ0o+Tg27QaBNjNyQIE07ZvRYV8b16/4A24e+g5CTfUIsfUeVGOOE1HFPG7tXlevBpR7b7+oMQuEgkPqRV7o+FLYvnwT6bQJOzWNiJo3eDfA41wktLOBdvUo0y768Q7AYz82Z+Ed6N+Bgw+LC3fIaz7ETlYyj1uE2onRJ3e34QDj+NdjVCTm9KLelT2QW+sjmUGsgmfRHDie6ZqJMsn/DI3oC0qIGIk5AQnejF4vJUeeBzjUuThg3VVriogw2LQpXMZNkHE+Y8vb9R7gMFOEybxmoG6XuyPP0zhQLkQBvv48oislRP0LyvN1uB3J5sypqzcgoCyaOPDq6QvARyhFQanXFNVXRLiXSNZjiCaygcnIEJ8B6D3WZ6g9K9dfe41QZ6Xx6kiUPehJIZ4lN69MCL9Z5m6+J84dFUjIo1HLadece2fz2cOmzJ3OdIsMnj79mvkpu02esIw2caQ8l8uFGEVjoRxiJtFGBNAbH83ZslLGGTLey8a9MWpHFjdEdyEZRg7Zt0hkvMfVdcgwZ5/TuFffsuVZHA4wfj8t7k0+XkVNENo1cX4epjTpeL7azdw9zR4NT5aJ5zlDryy7Y6xG9HKDA4JHhC8wF7Zxv4jyMEb3iB28InPVXJ3dfaEfPUKFCIsY+ShW1Cx2LvVjucmMEKs6Y+82mxm55UBoRi+QNdCq+TLo61eEOoRmoPQblaydd2rmWXXfK6v2oB6FuO9HGfaom88cr6G4jSsAG9jLEnWO6YgGNTbfmuMlG0dQM22n8xK+fldnzHaFr8bEvhCPSHJSiepkdzNvELqfKuSlEWiPQyL09G79LUAFz4d/B6Dge20TldOcuBb2EjRNU2y78/VQmGP5HvIqiFvzENChRHc7OV0XACE5anbj2hzzvCHo7wDOXpcYVL53C32AqrMd+J4ciAFy0eVkmhGbygLh2qbzuRB2kAW6er09/YXEelCavbcoRS9ioReBQtlrvmChzlAalPd2GQG5Bo/KutdzfPFZ4UwOC4Oa9zCLggBBmgJKNVRXdJFZNHYZgv56oV+jPmbkmb7GRFqc48Cu+4tUl6ZLT7/92/+ZAx7OwLxvwVqrcis/L3bXSbfE3s0SBQaffpn3AE6cudZwl1djlEuL4WkCRf3ULJR13g2Nj0VNSVdwP/+SXmE+N0CaqlFNzKGOWOBsIsj+SNpFpLlmj3CTZ894LtQ1Vk1iNfQmVeBs2tSwtUZ8BFVj9tjOX4k8RlJxFaV7ZbpOpqXppQBb51YkPnDxCO7rmrEQ33sZW8beGSbRfkaeYT4fdwYtsppBDtf/ouuUHPkMat6jEd09XnFN2vUDfLeRgHBA7gUtjItmk1K0OQB7psIx9Ly8mcUAalf1zgRqcjhQ3ibOHZQx92toa6Uk6vPve1ycaiOVUmWZ5/cB1AmVBL0DUHqMOWbr/Dy23tsLanGo9rq/2c9U4O4Vvs1cmUn1OhvkMEhj0FVQkOUdhqBHKYaGrL+C5Is0H4qMKhBrFWvSq220uZF81XghhQEUej1HyVFzo9TmYZ3bvMumZW+sC8dJM3jdgmRBZr45Q3tM+EYTAMTGcedz/AYtZ4bVy1KPoCr/1dffq1RXwIvzagUm1x7Hp8219Ef+ctjBh4qKyF7dg0AbbvPXEjaAjnYP8tt9tWDvmaKdZT6Hb/+tk9jNIU+XGoqavQzbKFGL+pWzJHBWb7RP8t5x192KB679N2L3VdrT1O+JKb3Y1QdI91ZiTPmw8QXziNCtyAh0Xx9C3O0Rxnp/zNb7UarVfqzdHseqdNUMjNdWo6w05q/9R99in9qcsT2D3pgeq9jgPuNizDwXD9RjWDgeaBa12ouwMMz7eIGwG99wrppdzZo754LqoFnMQx+OJv4AZ77L594MW9g4pfkQuyydT+HV0xdmm816nvhesOm7aTBTw00QGVyV72S4SbMiQTXbUyK81kzlcv1KaTKnhpnyKpLF1Ocvgpn24z/R67lcrB/8DEAoYBmzQW5SlalOmt/PDNmGhO8X1yNdV2OHvKeA4nkGuZAPM9ga3ExrX1nkFbfz/l4RuajpVXFhHrC2LELUBg+r2WSuURN/yXELvQbl8gSvhZ1H2yzIgUyFeQbZESCcwTlA3l2cg2tc8C7R86YbuKAub36VgnaQzdQ256RwZObGUekhvNc1TWHSrBi++SGbt2zSO6lE9JclUPPXYEk/WfwaBJozvk3A16v0IXbhRXKJI0Imo3cAxPTI7wAotRH2seTHteudk/X0xzhELyB7Qa+67hLxJU/yHxenhm1q/FqC51V/R0HBx+OeuOrgGJEUKEDv29i1LbtbExr+nukYa6lDbReuB9SdV2m8BE3AEb2mQ6Ws63NiHCv0WYWy3LYuuDXTL+bnALTOfWCMLs0Z2cxcvxTb+siQGFbfYtSMvpekgxS1cv0uwfejhtfW/G8y32KlmaBtI+YB1VbEBmQ9r5q5NDyzqkbIPcvzXkx4zsDWR+wl5IQ0ZjVFYB1lcywVEciD0IO4Ay8nEo/22PuA1ntfwl22ha3530Sok01HFbtajN4l04A/k2MznCsXWFf1hV3hxsfbXXH7jG7V08w0jshVgesq1ZperHlLIaztMQKraQUbqVK4XAK+FQDTL2EGUjz4DoBFeX7w0U8VeHuqK5BnRd1zueaGoc5AP8jcXe2r69pfwvASkDWvO7VuxzwiQ47N+dyOedX4V+HUyDOaM3vQDP5j2iBr/YHeLSrg4A+VvjK9fL5tAm4aHKvSALYe01pzLOimF1jhD+EkOElonIMLm2g3MhC38+Ce3XmoOyC8LrZ3KIiF0DsAmrApZmN+NlQwptfyPsD6vCTwD2e6QbsS2/grkwsae6/wKeT5edOuDHBZwHBgGKZ4bYkmkzoWVPkqm3B9tACbpDAsyv7OePav8gtDctTsxz7lUVQHWMcLZHucf79yjXyKaMd5OJHbdW3vFxn/ePoZQYlrxGeu6Ge/fc81T2VblL02K8IU9kXvrZuiNx6RgsMhwnSyEXl++gy5UZVdHApKsdl7Z8D1ii0Su3KJCO4ONJcjjb1yoyJ7IYb2zUxT0PhKHeUhYKNzffwpDGoCqqfMwuvF4le7LH3TknK8anZthu1x9nkChJ7NJnhtoBo2q1cbS3M++o3m6swYgfxM9F6OcRR69dnUR57iM8lqEzkZTO2DSyqffkW/1Wd66/zxqYAlPMTpbwEKbhmAqoY6d88+1yRnPV+1ndJ+ieQnx+w6akCqwWrNCw/nwxG6qB6Tw31RtAHM7gLvdlgHLxIvmm7b07vBQDjjG2FPZhqh7ibvz73OstbcjT4PSQp/mETtWGsO5HMJSC8uRq3+6xm/lF4ViNvzTG5a1Zqe9o56H7kzjZrYVZo6tauQezgonf/BxivpgjvWGnT5tJfZtfyFdi2mpzMUQq5BHLgEK4j4HYB/oHE4d8wG4fwDKuUGAeea2AZ7DUX2GkRudlmU212fa8bcpbx4UJEvEL/YVmWdq9yc1Sozv1IVtfPpHIgYA2W5CTPPIsOE55hXlINJQ6xDghmUOo+P94zWlg24qLI57FfcY88uWZXyK9bbNMIeOg7UHIOxC3rjFQ4Z15rIth9Fld4M2DDYLkJ2qrkpqlgJJ2qyXzqyoSlL108KNcMBDo2rURvYT3K4xKxOZAB7lLP7IRpk3zKUz6VB3Ft0icQxZD/+eCae4S7AGmeXuxvXe0E932Cs0rvXlFDN2ymvllFdIlQvPoqZUdtH43m5iDLveMyySTty8DSP4UevCBv1K1kjKFX+TIIb+Ax0zaawGVSzEa+ttDwxf1QoIeh1Vq/XIqDexszP81wD4cbgssl8M/cHM+gkpMwjVzMM1ngHAK2giMYub/Sze8PEod6EtNDQ2NQj9AAFAqmH5HW8NMXs9OxccOjC0vW3FmomtebWHG6Gf7yoKMKBOtQu0kQekrGtjefrEAHnvQpLgFyCU8DetLmfMMocKy05am7KdwR+IYkLoUaMX3nf5uQpDIrm4ewxOvccINAumKMpAs7knnwGdSt4Diy964CL+14lbFZPJLGVAPtHoH1V+iOczdLAmTaD3wHofMtpvFa6ZoDa9sO2zv9o3YmyRl5aZ64S1eeItWaJlCWQRGIzltmjfF755jPvl5qISmeh2BqX4UAurnOSElXYMvgcwsiqPxsXr7rU0mguFQhHKNqYrt4TW4LPSqQUxkLXYzYwq31nNdNyZGR07LER3UDxu8tgXtTwWLjaqx642sY1NVt3h6Ai+OB6lxdHXWq6/ebRxu2dRiE0rqtVo6bQheMdmnG2OE+vzNUEvKgCVvPZKvz09Jlh974PHPkL1LO4mvwK7xZR6tm7Cjls1HVYmVfzDb1HRrmFswq0pxFng+p5pgKKDBzsSlM44Ui7h/VuWx0f3M2bMX3vPSNMHUPCCDoTBUVz1zF8cv5oLOL4TvEcFqLgqUSwVawxvmjrqN5YeU7PinqPqzUxCZF0jUbft64vhDFmYYzm6jMAvRGKBaLNxxpnpBFskQ8dYrxGdxsTTtO2bYT7aA+QhEssScFz0FVYqnmAQBMHypnQF4bLI/xahrpXtlepv3QcNypwi1jA1LyZmbSRn+zl7jNPzaYZlG4G+VguNX6MNZaPRRxjHujdVedYsf2xlLHnfbB4uwjvJ7nDwzPZ4RNMlf/jpBOovZh4oBoHXG6aXuQTp/jJ2VJzjoHq3sfRvBaeV1WsOdCuvLgajgv2kJvoppShfTHo3GcAinLEQEWXNe2rgRBpy048WwgvoBufbzWLGVmOc910j1CFPEYujGeaPTKXB8pkAMyYm9dTs/3Uc/M6HMLEcVRGyjeRMGzJ6q2D9epTW05ppq8rRLSC4TFKvQRjoMvlq0YZKasIlzAs6umYHuVMrQQCTBccvxBg0Hycid4EPKxcGE7M2520NQgb1C6bP8Z/77sKG+Ru373U/9JYU6W/NOIMmM+fJevhrHP7Afjm/FliDVCKriGrwrZsrn0HKYi53HfN28mM6lfGkup0ezJijRc51L09jWavStd83Yejv88g4wjlGiF4F7KQ5lg6DuuAtVBELAyOxS1ArNlBaoa3LwIieX4DEN4B6Pi2wkzqgNiMXLpPGZVOL9M+SZXlPkR8b1xFUTjfHop8odOx1I8QKMoVA0d5DK26jW1u3Qu2MZcDlKL7rdneAl/8PYv54WuSKerpNkUU1+8SnKQLPXcYNBPp0evhHNL3gh8CO+LUTP0I0Nfnc4fS+OS8Q6zJAdrFxPlPgj+g2S1S2FXDB6zJAUqDMqJLBZFNLE7tVdtskhG+O7rQdFRvs0tKoQ0MTnU1w1tFQs/+zwCIE3ACSsHzqf0qV1hVzcNnwEDaPO+vopWKqXsHS6cdbZUrzkidDQtiJvp8jjEK8Nncuh7WHM0YsXfmPVcCwOObv+ds56yKewHlhExnKgnjZr5+FaFNwWq4+9t+jmatQWzyFL3B1RT3Ojdq7TKMtdeOsmKt5vP6ipqTGVQDNpx/2dSLAwWUsZlNpp7j3hHlGecx2zHC2Lff6wUYw+fe4bz1KIPquU1GnHq+av5chTNFujKq97vNGRKn6ILXme2LwR5p5wzYA32VbX/WTe6qNxn3PqvtvIOvUuglcox5mjYT88RfGX2frWfpdjrnLJzDYZjm6z7QXK/s6iJDg4fnbq25TaitQAQeA0kvuF0hHGSOyh4rsSw+GxDi4VeBd38GwOMPk8yR3fqsgGixwmfhvlb/okbe9PJpYOLYSTNZkOg46ZLNnEtW3OB5HMOLcIPIt4Lcy3mv/a14X417SV4AqR9NZW32pulVYNcBpAfyrenjkcrndlReUhBH9kku4fJAl7A9DPI2Aw+XrnD8aioZE9Gc912gSHlv8yocjxupuvICIRKNMSDnR/oMwN/9fVak5+hadC0W9fWM9fWeABLEGm7YWZs/kKauwDy5MApdp/nK+Hn8JqwwZTaP36VoHetxH9u2e3uV3IXcy91ThgCbYtsk1INqGjeVu5g3EaSMbAdmbrxpAwOfLYVxbxQKswubdcQeNwWVfePbGyY4aRqscKxx7KrbRMCRSXOCac74dayRf+iraxg6j4hNbmOgWNuxpXov5zwTdGBT88FYoA57x2IQIiWejz9jy2uPHojlA7SxB9mVzvl3OCPPKCu7WjPOutcbcTwRGWOMpNGkLXp7gM0ZHqP0HLv6cIVYNgM0kHTaXcC5jjhvm0n1YDYLFY/DUXbAMlxVAbfcFAa1ct8DRVOR49bRCqHMpeheN3uliyBdG1XJAPW6Iy9lt44zarUqFuMH3y4Vt9EvAXvzFkKHG0L16FUs3NCFyuQVKgbJDLqOJRoBIcfmMcBH82pmBCVmn09A2cTto2VR8BFz51/09pp77Xs4L65vJtIc6Ben+jUReL0Vbk6Yhxqa+zO852jeOpaqh60EhIvyzEDLccbyRjY3IjBf+XnLG1XgPrBKM27ruD556q5aA6hx6caxakBoxoBNl1L5tHNChZzp+bTza0A9fH3lbH13F8B3ZxfPaHOgCAK5m23rrChjXP18PlbMSuxqzTxrXKnyuvRq5AaAbdV5PlppuR73snemXc8leZ1H9ugq78ykjIVy93nh/NyYj1VYenbjudS7rtkbhSLKhc1xRE/HI8LeR0d1jjPfzTaFcdxNdzdoXhvz3oHQ3El74zLAQddVuYyjxN4m+WiwKV/O2WcFQkv2XWBmjGo+Fx55NI0jw836NKIfusKqoCKgoJ5pm4/drd6IPmSs+QCvYmLsxekFKXDE3MfXBaXpeUlfNHshoC+iDCzrrvo9kzNoNX5P46PpBsUQuH6vEI9FUXacorw73pWtZvK4Vp6RIjqBKMT1TLG/a1ZE4yiXWcS+wFMcZqAGJIFdj5cC+iyN8WflCefV7wOEnCnym4AmICKbcZLR8pyMOHWoWnMuyEt7K8kLsxoM5oVRXrps++LPJz6o3r6QL2eNFL6CLFA/jFovkTigUb6w6grdI3BhoAeE6mXtpZaArf7unwIYxr+CgPMs9C/SfCgyXoFrWfk0EOy14M7ZBeDH0ZeMXgj+iLJ3FUo3/joEL3scBVciR8ixeTLr+xQTUcD5cKwL8z1Zrqb74byaaKWymTxC5qj2GQC8A9C0A1g4B3Lonq0blAIccI6BbfgsfGmT20+fCf/pN2x//MesTc/oAnEaNB/j88imy2GlYvWu9cbz0cMhDjjq3LdZh6JqvTPRmaB1drVmBueeNsVVgSL0uHdl3NojVgbnriQVUEtzGDfOw7xrL667JLlrT3PHYvK4PtZttGe6w4TgV5sKQDVdCcEtHTXWwZVRcPeoHMu93OVVcxijxV4hg5I/Hnk/8jrUgvOfEWKOUZ7xnbEBPZQ0DvT8GMX5PBPrrjbh1bM3z3v6Hk/VatWr44xUIeLKJjT8tQYFj9HjrA7mG2JEGJtqpGSD8e2FK/RFk+7D4+qYQ+wdrweipcsg47uSKy8RAFvP5L2xZvbNxvyZSWBiXkUYMR/zj+uZ+f3dowi8nB4VzzEHRxsI9QwHZhk3+w+6fL/Ltp3nPMk+/p4G8X2A52ebfoy95zMA0yWAYbbt5dfhPFQPajL0e+vsz7OvqTZh2i1p5YlITZQXi69OOraf+J7qggpTNO9QLUX0rQsILXk+wW9kxC8cFFSsWTRV/sJAt4Byki5cFQWAwozbq8BvjVNXw9M5H7oG72E251XPeFI/H30S8D5mtyhFwdwrc7tYt0P2XDwL11wubIbYNJinVEAVzYgz6IpmI7k5PMDV6j95Pv3276a/BagJ6AzClftsmJ/dJgqtzpZu8QF3GByvTH0GtmC/hKTz7M+/ZOzZs7ohz7pAXlB19bxnzvh7vrfTY7xAO57Tx2sbNec6fXHzIoypwn3m8WizqMe5zrqumHxdjwpsZifYZq3qiD1uRdzCbAWer9IBHHqP7rGkXLnkw0S0UQjXFBGLpqNN2hfumzWM9jEp14/jCl/Glxw3PK4Sb/IfU3KEOwg+OuNYlxDW6BQRVR9de1YU34NAKR6j0GwijJk36z922extVqPIaxPkpAE4XBjxWrSTqe11bw7HXpAZ+2I2wqXWzOD0bOKApnn7B7OtrqD3EKJ+NfPtyB+v7kfLeTnumwOvmEhhppl2iyFT0FXWReztJjD6u0KT9CrVuXcAmjgNbrir6Cnb5ueG2UEVEFfcj8Bcz+oIi7v5nK7X3ZieCoQ0lemxfN39FIkHc95birG99hvtgT3Lnn5XYXog0mPrBlEGMWeocKIKWfbq3cVExh7ugO+kS0zEg94h7iQ9mB2u3nyIyy1PFtDdXSgY9vQyQ6/+Cq8Xb4r2nblp/ij0+QpEtNc4M1+WM6K/LIFdE0AT9aqZMwg9KMsdog+IXdwVkjHx6bd/+w8MEa4kNaYHVLBWx/B8Ze27bsVMOj0ddfD89GvSDmxD35xI/k/1Zwwu/m6cOS7bVjPnr27jg4s6St4u6DaFg5UZzpNV1HnLlVtueNZZUT7XRSiugmwilIiH2/l6NgGifAhws2514oM4vSJsRomYzYhFtaN9LfdoFJYIBEvfqlcalyGIDzGH15N8D3JfZR2v8qrrzDZW0mviWfSQmyXtGbu+yAj6WrMY50q6phBSGTVjrW/mylzMtwDc1YzMOZR4xH0nyurN28nS+VjIz0cE7ilcBuw9NwNt+l5Vnx6rrr5fsa7LyY4YMconYefcx3Xu9t6Cp2Fq34mzupdHnJlR7tnfR4+KYW77O/Ob8/wSVs1d7BJkgGgsNj+nWnBIXkZi5nhYsN2sW3dmroAWGH6jD47k/H3f/CgYS714oA0ftFeq7Bye0d+ECiYQJ0zWDlVriweD4E2Gym+X4qT7KpawrkRcwe9sgIeoeB1rYSfkg5p7Xg/K7zFo3b9KJyPOuzct435Y7wsYE3g1HQfDFTEHZnu7HNaFJsK4t+kyVqoCXgQviGua7m7W7H1Y5TipAe3Djo55HsGh3oRmBbRrXL6DNGO9Kb+FCozn0rj34erToxsPTLB50mcAIC0dDdeGChlL645+8w+6oGz7pEJ1OjvqsroesuxotQtMMfNty6OlmzgbQ6BdxFbX5CbwW7RauoJEkX/LY8WkafBoyiLHGXqDOhxAm4nYtbnq2tIWziDlyE3XlvSu2vl5OBk0EpC8axTEc+YKvWDFCvKAnl+Tk1nc1mwHmgM1FMkmZk14F76n7EIRZRC6sESzJlPb3FSzi+0xwiqUb8fp+DyszfZSrRFeq2bruIS8ds3hog5e81dX4RfffYpK1s2ZcYENKu/vAADkDgNxo9L5Md9LMcil4HDyPZlxoEGvUzVhMYzf85NsdIf/YpJdF41+CGxpZ4v1M/qL5Nm/eFWdlWKN12sJ8aBzC7SGksa3Sw4t91epQ24xK8h1FV5lYuu8kEKR6SCpr6YCgxzrLt+dBnMgTpUa4T6a8xwGCSqFTYNepi87c85Hjwgn6xyheuV6NL2nDPI+B6QcpONex9I56X4s6ON7aQgu5KkRfC3VHsy3C2tyH6giF42stvchcLso81kURZintDljNw3asfYSon3jHQBqiwBle9Vt9+Q85+/v/92qr9fYAOy54coBfiXg+Xn6MwDDOIzCUtdngf34S8/MufJi3ZZArzvWx1gpjkAdfbMKbXZBC0ChnYcKqLtFp7HLc5NzdwyKMLqyJeXEtxxcMUMKBkeaGjh4RkFAx+o5JlFXe/NKyaj+w6uJyqiOGBkW4GNjL4t/ZkAlioCH5cEeXZD0EDNs3bgpDJB7XU0cKm0s9Lun8fpf1/6ijjh/ImftXwrSe0WYmSEFTQ8h36K32ayHyUGa9lPK4cyfQpgxuk+UzGS+pNmj+5ygTvC/8/HZJ4mOA0rswL3jXpG4X7jyzoI4xL3vRlX16tUJXh4RO289UQcEakpjzezBIRxvY4XX4EOwMWm6Nt4jGDutoyfbQEJiUKwd2NoKAOex/xbAEnKIM46ygHQksJgnUmIMPAddJcqg7SgQxlUYgMQugDhm1N9TviqXyPmS4kTAsYwUVEYJkscuJ3s9wVoAsitPRnH3ywEduRYUaz4iqj1vXId7XRpkOkh20PW60hyzRZp7d7G99jWBb6S2deKbmqsq87p2ZLA9P6l6tb2qpD38B9EjzbtlWs+uC4fvblmMBk7V5LxsvAOQkw3n1lm1YIazrvQOAPtqu8Vjkc5Z7SrgTKhdgEsWlm30RazYjJa1LGPRm/eqcdoaIUZCitS23tLW/DT6V10FDHNpRUVXSuorjuLT81pBqKGZbHLzigsAd6A1AuxWxeGHs18bZmphv9uNG3xvkdEKM8QqeG5ONr92dUnlx+E0W7yqY2MlklxyVnJxzll96tlHvBnRoREaZGY4u4uE+spcYXC4uZdMkenhuHIshmYTLbKNI6iqahv1AFxC9Gd4ETdG8a5JnNU+5c67hA7PC5BFQ/iSJ9753MW9aTzPHJVf6tzEOqzsVHWMVzNvzo0xyI16454Y5avC7R6IPRW+cxmLY8KuEtVzoHDfXajCf9XcAhsUjl2NdwBW8GooSCMUIBRAW1g0jErACZPSxdpH/ZpgFygP84klAw819xFCbP9zTxHSNoJG2Y13CecRdoUbGCu7gcHeLgC+SHbNoE3l3oxe3B4l1d+YyVVDeRWO2F6LNq7AjXpvmsJNwS8vSJOtlHEb434d+2DM6E1+q8AdKvC249yhyPtC9IYEx75nvUZP/w5APzDeAQBY/32A6jyvy8osq2/JlbkO15AltOnEc698jtuL5ggrwIjgFgeELRwlErc7gqwY56vX8tf3oqywQlVX+mFjfAWxrml9xlxrhgFnO4vcZ906q/zDaPNxa8u6eoXNi7AqOFzSbGZ6o+zqWL05XFvGZJv04AL92DGC7JUBPjhibMaFLxDiO3LNLBZW4Zg8iLvYd6QxsTFyPj53oDvqjbwqrwFDh5qxEXCdEXyB00PwEHQPNa9o3ldxFyZ1re6Z5LHoM14zNkWmvelRmMXm3r3jRq+2kdKmvJrtm9bZoFvPapbuLaN9XnT1m1F7q5o5XvPsY1QUqluBqbAFWMunLhycoKSrfgeg5VXrtkJZfx2sBtqnAaxHdmEeYuwy7p2PUlnO1iGNQ+V/UBHzmaWwM9SNYHeyOGIeiwP/onkE8ZDPS8U9RPaU090ynZyTMNu0bBrcLZFmuRF9F4Fdxs2Ik8q7BQIfj+UD5MIkW5kBR3/uVTQ9lkd0y1qATY/GjHsN+Kb5miqAudGbHl9TmsrlZKZj93Fvt5gH3bp4l3TclVQdTAcmHbnKzwDAGtfyq4dUnYNdvvZP36n53ghQRbxUMRNQVTkQNqY9DyKv3eHmAxTQMyUoXLxZBz2D5rA2V2rs0N8SdzusQQrmQNNInDsLX8fYbNm1jeanEdx1b5p35e8st4Si2jLfm9pWkNTfjOW+89d+BvTGITxWTxiM0SCoo01Gn4FyzEuESWKXxIogvXd4og24oSCR4aA+MhsYRGTJEbnu3QVVu79p7lyBxh5aXYeepyS0+L7cvO+M5fwxbQbtvI3zmZz2Xu16JyoQYABNbdbhLPNO52OoiwRPkFJhhnh14Rbz4ncAlo4JSqyzrf5hqxh1pApmwqTyeVAF8z9K7bDjjoDid77g5xH6pB0bBRHfvq31TBltYKyOJgq85XHvftXlHrPkvpl9fRndrX6TE3VmB9HsAvOTwxFnqWPerSAKFOMqHWhcgE00GHOL1XCQTZcB/iTIOMRb74tXwIc4zpAXZ/WwBMbT3osp/kUTFS40TbNO7s3ITWUH4F7qO3GqSxlnMHs/ru89lYOMwrmvRqVEo5mZ+mnAFeXz88gAhsjiJF3RDIZtUb7yKpMIHrtghRO3QNqFkCL7eXBgsk+MCC5HKshfRPfh3sv6+QMH6OlzHOIydu/+udJuTzvG63/P7jai13zbVBaf28Ohmf/5l5zrjc9yDNHP8B8CNzrj1Gp0D1VnfNNd1MKf+DYSnzPwGL/fEimfYhiBKrk3RuIp856NejExmjty65hZhQ8KzXxAnUxWfJqUEA15oevDHxh4XP+9/JVKfW3VmTTzUtbyrbfFXjw2dneP6JooaGTHY1rEje4n5S5yeGWfCdHFCc4zNjKft7z/pyZ8pJb5k48zy3yYrh7QxtMj1O+ION6n9iLGo+VeX9mLT8RZitZCrPdfWJ2r2Cpg/gzAoozHmSi32C26ecvFZ0Ja5tj0jOqgpgS5Zz2/+/j7YIWeoqBqmofd66PPAHiJILgccAqQ1AMtO/KbAMF+ILbgB+bqcqdAf9PpiEE70SNIL+3jJZOArf5emtfZ+CdHqCjLMTYnOYyDOsOx2Qv2nmF4xneQMkbkRsiDoC/StZnm2MCnbhRc3puRyo6ICurCXpxb2DeTaipvEf0N8/VWQJME2zhbiubrze61MG+Owhz58SFwDuP2VhexXE/MOGWRQtGEpjxGF78DAAd9BoDCUoMah33S7r/830ZbotWS2KR4FpjkZs7MwvWGCFKHiJqUuXzV4dcGsl0jCePzrPNgnn3i/ZV/zObpN4xXn0lf+uYk5fsuX5OYcyq/faLBOwMlfGvuvboQz/uFNzM6PpSZwtSzhieM7JRXYeSzAWiSC4PUbJ2dD+xnWA2GoOCQJmLQzuAH85V4zPeYl67eYRapvM6jzsi7zgvzhW3G6u5fmgPmM94vUnZmP7YsCMyXBTnW+9ouNM3eulYaKWzTiNuV+82jTeSjLGrkgt5MM47FPGCsTO/4M1/qmme9L0RuMXr0XUVsHU+i8cvI06zqCswTPuM7HyVZzmRU2cTRbEZcDWXTIiiBBvsas56ZURPlALZDjAioOTg0r7XvQJw45vTQVLG6CD176MX548Q7hwOQO3T15nNP36TUnFF7EDTFmjDNyVewKH4HIOPgiz312B65bYsi5IGm2GRO8dRkFmyepUdplW82XMsuALe676QDC/+7MCTqO1/iEHd3UXY7hGBRFI5v58nLMm4j7Ix8VQozsV7WxjP1Or8sn5tG92QVpWheFXoGdjCZ0QWEpoG69vJ0PrWwF+q126OAzcK+9ry+Hf6Ywz6NPWtpar0b9ITDjj3AY/oXnJOowIGd4kCpj1Xmq/BCgQ8WzNyKdwBYEpswa1hTpXIt55dJm552nLXYmbeukC1o+0ZjzQ81CJgdJLkkttGmulq/WdAGSAbc9M2G+58vhx6kMcMOV7yAUL03MuM6ZdOcUZtFaHoxXnW9x0moDo6Mpstu40Is2sDM7ZtCBGkaSHkYf4BZdzUq1q+Vuze8vG9SCFEuQLto+TWo+XjUasexfSxS7Rt7C3kG1q9GO7JXeOwOexi4VxG6aA4sx1EKnLoZCSjKSUAPkZDD3POueWEvmZjOfJTFMrD1cVx6vxkp5h7lqwrQHFYfO83DA7GasAdwLnHxI8MlaJsgqN616d961bGZ0QGDwerUZ9c87HrmDwGs9J9+Rez02YBgbkPDdwCe8vE+jFS2C6oew2za679ALxbOBcIdgg54j6M7zwHC7q5xyN1w5nAS8yZ5bmVyu6BCjtstLuy/HZ+TozND/s2mqMC45ujVX+01dizs79nE/NSfgmq6Dtjums/A6dkPQmymf8Z3E/yMgZLtpXwG+c33ZSuAMdWwxrkHGX9vw31maC6v3uWAZ7J7AN9z9Vj/DgCx8F+TfjT1y6DuNFuQEmDkN7B1piP/0DeAClZZtPO2dE9/1ul5gLOX0hq43wLuLR7IZDTQtwh5Bea11egNZz2WA8tdafVwCpA6zfXZf2H+rTcnqzouU13z2h6BNDfUNXCZpDRAaEavlSc1xXXBST6eXbRXccTHDSbpRZymyxhwcKUtom1GicZR1t7Xu6M6Ri/208MRY/RHk4scH43eJJ/xjIoghwexCBHnifBrTYy7V47jEuW9ONG+OD7ErstlcEape3vZ5eHuBtgci8OTKtMeAtjMG74DsP4dgDhTo5yD2XOjY0hi5cxGA6CymVbsCg3jreBb/UZMOBNo02m8lOHXkMPNaqe5gC2qhMfU1JgjMwMomzm8b85Kg6IRmSnmtQVSxBcZoAsnYVGTAlkVLmwGTbf3shSAA99H7vo6snjkCr8ItwPD6jP8RQh/U0EPjM7rrc+5eaVS+UF3bxl0AkAK65rjtiD7fPDEd1msHScIgOy0z9gQvYczr4hWYE9fvCx1FNe44IC1xruOCBfDbVG49mrEVrTj/dVwHYd6Qc+91b7dJy5esAjHQvuhwYUmznyF77yjNdmOlZrz43yFgFxmzDxccb1tl6/qVldvLwcnMxYGsBOvVrMvGM0KFFUqeMboxX4KtLo+hft20z4J8OmXNCzwt31vYPEIHG6Q1gLpM80FnxVnRjPOEwWrNQuJ/VIclyjvR1o8xjN/sbtCGnOeP55fweVKjHFeRyP53GwBWKfu/k/vA/yOZsFn9RmAAOETHFPeZz36o7yYw9odFu0V0iRsm1aLQB/Qe1yQ/wi7MG0FfHjd68pBbEdjcpuC3yJis/JQNvW3SesVo15epbsNcVH0yxMB/iW5AGQGp2fT0xfp72qer5WSGnMb9+4i7Ma3wHTwN2G+ApoA8/awfBu7XeV6M75vBXYfFMN8Xt4BCNMcgPh1L3zfPAy3wbctTpQjUB2hNDg077gyDDdO4KtvAVKntuqnvEgjFlf3OdEEHL4L4sJQyA2BUi0gTP/OwK3PxeO9gLoHEefQzvPCChyGuuDOSKt2OdAFoduMexHkZZv9vbXNa77y8/M5Rprns2kZd64YQvIy9KdHOTLp7Zs9fU0MmoVb3W1sn6tjxYpD9prcZ8UtOVXIGYzP45JGy6bseUW2UT4foo7rQeuuWY3VZP464iqj07NrTHIVa2w63XsGc+Drk2dzX+Aro9Vt/hjSjOsRp1NfGc4f61Zuw0aT59Dj+s5xbXu9J8eiSKOOUmsKlwubOib42uZC5AUqT77VLwQv3XafTzrSw1R/6BY12Y2O36O+JcpxKfIoUJxroZ9vOkI/ypJf32Y+4INZIjnlt2T5SAzrijvPuuumxD3uTaNE8DsnGEO/yZdX4G6jqUBXhcO0v//Mv7z4NaDyGqc27q0xNzWXA25GfDN4q8BbBd4qMKzA02//9h9waHr++Dtc80+H++fnd086XDVfScKRLJ5Hfvo1O6auT4Sz6vp8K2IOX4CeeeU+M5yKO6xE7gzpZZWHWXNjd62pM1pg1pIsdU+n7rFTNmCQ01o7xFZ1RadmEs0b34IfRmFleagxk7UYCn5+vFAKH5JVfaoK1MRjTaJcWDq+9PGKi+cVaRTuasYha8SaYNuE3aVsxI3+PQ6mn7+3WFEEXI/jBge59ZjMsM02xahl9fIcx9G1vXHk8A1ZTeXlYVqCELSnz1/1iXF1ZPBtKwh1cSqiuVmobZxhZXruSW++m9ftCs4zmPiV4l2p1fOhF3QX7AbV3F3H0siqv96Pst/Nnntj2tOfJyJk4Qzf4emFivtClHv2Pf14fIGMwdq86x028xzGEXs8e/p6Jvcs5/X+SjfvUljW1TiPWYS4pDnJCuOLUdO2GbeH09MXIEAeP1RP2XSODyuM9KldfHK1eCiNQpmaeAeAIDY/M1qarGhC0p87pz5vRyH7R91ZeQuzZngqIuBiRMg4GQqaUfqnAkfnEC+qX162ctybhpfcy+LCPak4jWZQUBobNL3elIcr4NUuJkPRjPjoUq/b1JpofzvZCewNUfCfdD8W7pjXJKXC7HCsYwXx6D6LoImyG7wJbxVoVgATb9eEOTzDm9HflHeogMZ31yjfgdWREJqsyKROxn4HIF/5zwbL5PZpC0/JJYR3gFjZt8l1zqFp5cw2g7wCg5dKplnZul41PThCOeleA85rFKUmMI8waTnORQSUNQCj8R24TabwjZvFQYml+FoHSLOxyHqQbGEZS9STB2g9l55+HP2qQM2a9ChB34w7pjpAG3Q1Aw3s37puXYG9o4wRjC57BzT67k3NYwGkoLEX6s1+VwW88tHrzFA6ThPZe+v3out3V8xYMJoXi/dKqumuYq9/B0BzPF3ylqe2K5+I3+2IRjeQhznfIN5XA1nPh83UVOtYcYz6AZzNQLWBotSxrp12NX7BxA1ccANpVJBrWXmIN2GyAqp/MUbe/MpGR1MuVubaBK9FizyvlTG+kaoP90wUN1YxtZ1x3GujQJHnXoQ3+5etgE8V0fDmHcbUYyF0lF+2IN9sdI34AwyETz0XJsYk2jIHnADw6Zm/AxBzggxTbQUb5VagT7+mQ+depZbDrM4pOyd4unIWZYfdVqY7oB7JFGkdftS+mh0O2DlD9f5rhFuO+jUM31BeqgI+N4qZCT615mVIXn13tad8yRErVsmRX6ZQe6KK6vkKCCcWYQ+Lh7e9eu49fMIjgvXL2ch62Dc58W43r+7zyjusgXWqEJPl2IZ7eQsdEHo8Tg7oRp2qT8h01tUrmNUv/vZ4Bw/76S99BsBzrYUe0BV6jzYHJnNsd/rNoS9WN4ZfAt1R0rgfzqxZ9Kg8jDxfgzuEmCcDy4JP0dwF9WZ8bQUwFhqOKFwb4qHQJueeV6MgH92jXJidafZCA/OSiBFEsYqI0eBMIod9X5zAYeZfn+OFYzEPNW+5q+CAvRHyLA2sLfzxwlScxz2EM5W/qE5rmDgQvQKsPfwdgGxuELDBtwDxu4Cyms/y1HbVkYw65ygRoiHXn5iuNQ23O6iQY1msqai7zsgPRZiiURsVg7arzvIdsN38zoSaz6SmDrqrwoyy9e0TCFEUJ3JTL2kEHP9Wk7FvxLlGfuVX8naP3YmqzX/Tzokge1yr6zp7nM/acgJvPWRz57odPdA2kqlzjBrIilUczYo5GV0Gh4VG+L4qYi5W1b68YlL1Lo4HpBedewf43s7F55vmQx1oNQqhO75i+vfwOFrPKwA0FhTnJ9jtXnl7GUmvvPjt8prcrSneQ4g1OSZ7NBWwaI4x4zg2LYE2Py4yFgF5YW64e29VDAPnfLRKCuIwjW/gxPcC0WgxyYmZ5onfF8R3AHD/T2GVfeTp2ahaRVPKZRujLdpbSSKzQelQ8PvmcYjirNNV5bkKZ5a32SHofeIWA+5NRIdcc5Ambnfl9Wb8VoF7VsAnsCa2T++ieVNKHvSmUc6D+079WgifT/nbQbhkwhd70+HqgcwmnzgJo3w46GWOvp+cR/SC7oEqnIrmHqRTthiUIjQ0+hvjFl5j43XvZIQ0u+gLD20lQMZVfnwL0N/+A/Xhd8KgtoTsN8KWK534jIA8jXXnfiP0yZmYjUfrqsbhKixnTgq7/l7ezfM8pyfLz7+kYjlj81S8XtlhidvX5J7yuWBVYNfI058HLwOhHdFU5CJ6w6el0tUO9Sz1qSyb4xg5VB4rhup1hj6NJBSFKqDGUQrjZnMXQp5uK6QdCPVeEDVRXkWYaNg++86+CXieT7SMci9ewyZwbvT2gDr6hPAH6x5eudwdK/BcBe/pZWS9vd9J2M0hYOKb7JuPiBnlprErZanmYD+lgWWEY/t4t3LkJAzrUBr78acax+JAQQ5V/eusa00dUZrastb0fGeY1L7KyK8Kw8CPY5Rrh6s0oW47cuxFF5p6OzMzuYa4XU0VJTKMcmXYeF2INg3fik/DJkDE3mI2BqttcffIRp5RrkMNe8W/uPYPMv//9q41vXEkR5ar6wSz04eeHzM/9w57tvl69gDbXVoAASAjX2SSoizbJXZXEgkEAo9MUrQty8MXJih1BKfFyue6PvI7aPjq6MPx6iQyW83W3heaYX+G4ORPawYSTR+r16RjCrs7ikOk13HhCA3nVPnpTwDi/0kK9rsC9CVO5d/4bNka6JXTR4QF5yOYo/JHckcMO/PqV4ZLJ1LOhRXpDcv+h3BppheQvU9LzyZ64TqcTeHl9+E78Kxdgus6x499KS2tImoBdCYvEb1A796B3IfvHnkccP1yyJ0mAo4UQuFfEqxzpuN7Cw9Ise/GSlH3JALfJi5PWV5JZo45wsQlsZ/o7e8A2FeOJRTDXSsq/HlgcR+Yiy+kBQi5HEOTYxGTgssr5mWJeUS+k20S9jGsk2ChzspCceaMzLcbc0kgJCfhtmOdqeHl8+rAqwMfowOvq/tjrMMrC+/A+ovXU17EZ+u0eB2tVzcLdKV+MekIea7hCLJe+LkokePZxxXkdyz2EXRTf7jevouE9wyIYFpHBiILU8F+LfhBz8RVoKOTM+2bxxjWPocftTyYfpxOswHGoAWt8Mj/2yWINf9foNyBbMfacf51zViBX7f+V+WfogOvq/tTLNPnS/KOjQXXOwie0K2rshWeLP8qzmk7+gCbjymbxp0gfajGQQD4v9EfnfaBdtJOc++5Ezs9d3CtuQ30Qz7rp3C5tShq99ALLMQa4LM9+9DptPKh0aROb8rp/L6a43ZLNjfGQ1uxu07PS+2hdTt5Xz4uDIzvkcErxqsD6x3Iq7HfuOskL+SrA4MO5N4a2LZU2IpfdUPilaCpDq1qlOgRlGd7udXnsW2YxBj6EK1UekkKzLNNKL9Vq4Bt0LjWMz7JJM66rD/l0V/+EBiobJ059USLwNHcmc33yRcQIj/O8kRK1gH1Yx6WT3DWLpeS1dTzWZY1hxyzbFfRWC+PfizXCp2pfaSkqgxPT7K0hgF6jF+v6qbY1/STdSD35Wz7frJ6npyudDGv8Wztk3N6r/Bc+zUxv+Se7Iva1QCQG+ua5jYswt7nUWP27DXaZos5n2AeBCPVOqEjF8oneohnfJLEO6McP6o/ALydesZMmBMl8VkhCYXgMCfSyuTSX0gb0yy9dGnCQ8/JNQzgb5Sj6QbHCH6lLkNzldsB0LkeI/qV34Jnx4wuyvUEBMyOTLgrL2SY3OOMnOEPy3j70zB2s3kBXh14RgcWroLD1/KVdeANpcaYV+OV/L8EFzqHmxjkT9DLlZ15fPXGd3LnoU+/mX3u1vGIv5ZHv7E2O77QHPEXUowL8HMQRNjw5bpY3nC53nQm8MBn8smc3yo9Ndw+1RM/AVhezFy1vS5IfsukwUW5hWrljFZkQyD0wU+wJ+csjV3AHQ+ys5in9bPGgFCsTYegOR2ud8xu9YvTgBPZ6K+eDuNEGzTL3UyvzugAH9ZnWMKQBUhUFzVWa57KoftHbsUw4UUl2rgI/kSwXO5H5NzvuoPboyd4RJqfkvNoazbwMB1cmoc3bSNhxD6RsHA2XtBkrMb68CK/fIC+42dKzvVpnGW5ZqYGOZ/uEuwC5tzPtRxJHJ3M7U+uIspbgG5//l1/CEB/B6CujT5ZPH1VML39LTHH69cZwvPv2j1ns8+1JT34M4q6kpU/uzrLSXq+/OXvn8mBT7r17zfI36tTlQ7+9ZDkWbNUXycpMACS0Bt5wYRRGCzd/tNk8ZnQ026Y++x7IX/+riF/6Odn3+I7FoikGc+8kBHGASY6adVY1qFJRyslZ0Xg6rYr2o0OQAby/lkm+FTyv37X3DjKoJaSWkpKuY30XWGfkZ9uI+FG0TnTCtvH6jWVA0+6zvM+n/HUeklMN8PwABImqgUKVJR1qeDMf5iy60/ETZcqblgpEbn6BNL/5GSmJ1eIA86+Y4DalY6/e9DRRF3ljoQS3r79ZgIy1KzyKiMOZ66KVfNGJqOqB7VQEIg9hjUsV66ln1IO8sw1yisoSq48fdLtjbpjbaWFXPy7rNxKeklJlJmYCckpM3S43yecauIHERnnMkWH5uZRdFdzPuFbehgaOoMNir5XBHSRo7PcI0e7qLS38vV9OOAQVYUkSKXXz/qQ9/vKP6xF4Ki3oRqfKzaD9Bpaa88KXNY33ga5M8exbL1udEXXOZfofJdGRNbUXmWPZSbj6FVds/7M9CW3eY3sy/I4nfndBngwQC41zrgGu4XrZXlGwRhcTvlU1rgwsjHlFBhMdZ+AEWNcDXj2GLyaJMvoKuDozmS9yr9+oMrt/ndW5qTglTjFdGzu1umnDOZgVt7nVfTxM/xt8GyPnthFIj8BkCPa7ROZ0m8Gm7IMvvBFMZMoygwy18+iZKaaI7tj3moVkS7l9Ui0cO7xrEnPFDhiRV0ZZvAKRHnVeszw6yFpAWVDnA0QfcriAhhrkkeFhqWyxaTH9JrAnj/3nL3mPPuVnpzXtLEWUJACyBFJpAv092SWmaTQsd0fpKMkBcdt6kJg2bqpJz8R2bW2nJ1FxAP+dmVxgltZdTYE1HBMIbONTGrkfqpd0JlLARZphN22opbEIFtbRE88TSPuqQ5e6QshWpHqqftpQ0ddVZHWKLNZRw/bwzifqKIFNxghaZAMgJyBetPlGsSKlFay20+B82e58dwwNchmes4RXuybMoRoQhPto00l2YdkCl5mb9rCpnFT4ABbj4Y19SkULiDKPKSZPuz3nB/JfU9ej/fNXWQtwEzEt7e3f/3zv4cP++kxTm7H3DodhMM9nTTT7pkqQqglraFsznv2Bh7TJm7DklaDy2zhWEMtEBlEEuKjTkgtmTFMDF6SEeDapJcCHwM9K0G0V3Jd7FMux7HyDP2sGrdTReENZpjqENk4Lk6H/Iu+z4KtlP8Z6zrUT2qCiMfKFTS5V2FhOkZHBIdTqX0x243Oye+CKcL1IurlfI7GeG7+R7Md4nPR7+nDkPlBSul55iwhGnk3KC8ZfJNBBDkYMGMDElbgWeNerOpJxSpKxTBOptDmWBJiDng3zgzwHOzUBGDTrrzByaZ7QuzmMARw9CFgoPT3tvwx6Gl8CtCRQnIRBqGmqmHee1HZCTJrIpbqUi/CiLWxM4rloOzO6Z+x6ihsr51BP7fX6IOznrbRYJpjnfRCMKITccV9EbYQewlCCS7hrwVl9BS2+QGTcaWToAJ4kX87+oOsi7kxbL38bMKDkn83WpQ/LJw78275PCWQVBodWC2aXMozApIXqmRJ4URd7+OLQu6JdaK0oQtywBjLMQS68iPkvJXfKVsWlYLQrHRjFi37mYSn2YQBextjRkxm0czkBDe+qU/fZEiBMUO5R/Ya+83SobcpxaH0Bd6Yh1b+4GwAe5YmXDNt8MzemLanG7SNqZlGDdv0Y2tmy5xMyPoxxZY2m9zSyFuA5AMZeFWcZqQzExim5q0sGhuYRMl1NpjOyIFZht8mE+LxCCdoxBV8ZZpdi6QUQx+b5Hh4BobOYMJI6qeJfSaoEHrIklwPQ8aNnvHcgga2US17CYynDfmQZD3Q0P2JSvvjG5k+14o2yBg3wvlyPDH/DJ01pGZFYK8sfujIyCHgcym/WDkHm6/Xt+x829G57PstYcRMPpjJc+Cc/HMy6KJ+wJS6HN9P0XeDN6tYd3ctM6TMJFIMeHIclgffZBhitpX3+G4zb1s5brarcikIswMkSm2TTpo3P1e+MSkcoZmdgUSQHrPO0/v2mp6Ni2N8j4S10TdTZjggj383wAm2PgUI4We9O5DBHnRYp8Q1fW9kDWR5E5MI8Cj5pqqJbzg8yANidjBhFIUKOQkCKIsae7XMgZN5JB+OH/XMqbO8ki/jWV7xBabx4ulMXif/2MjyfI9tRhuGS//YRVyR3a9V7RUd+7QcWGoeP20pr8R/jQ40m/Xczaohkc71mi/ZTm5XeSxrSk2QPkzlpAHdO30U715eGTeFPY+H2ukpI+LYTwBkIgm2S6SfP/BGv48fLu90rlvGqUPmsd04ZtOSahLP3JQwDX/9QWDqa2iOwnKhAq4J1Ewd/To9sQO8JFizJyZThdZ9Rd8Zxd7jdCv0/mTweVb7Ti/EqwOvDnykDny3V6H+U7n+rkluflfvI1XxyuVX68Dm51ZpM/Ac5W3Bq51M7AVv+DDlyC946j/zp9f0Zevr++jzNvc/57B+qPhL7yTyBUAuQRNK0TNbA338lFOfyZkFHqdymgJXA7k8eA1/hgBP+cLU9izicnS1t/OM9hI+QgdseZo1GnxdWN2ULO/U4Kb0wFqQHefI8gMDv6hfHTjTgdyeD780zmT3RXyyyV+knlcZv3QHcjvjniHTvHmk6QM9b37NtZKWW7PjLFX+0E+4l4ff3/7Qp6JcE63f3pDVN2L2/cWZXj7ZV5m772SAef+rlu3PeZ19Qn/mbVVxbix7wSgbn8n60zqk7t6l8tmrUPAYUaZft21/NUzWKiujXekM4jPyKp6ozM7IE6rJOg7whOz7s6Jhzh7PVsjcB6yifY17+w1/BcJA1p+bff8Mq/7NMN8Yg6vEvicvPvTVpH2i9ttPdez73GuQ1WCkdafPKTeg5M1Wcl7n5+8Ock9A1mugX+GfYXp9r5nFpRJd7H0587/+ppfm0uey43ul/9m6/3B0ZKj8e99h1QwjB5aZrZexh6Ffyf9YPpazbvvR/vG9Xue0zQ+r/AS48bUrSwZR327f1Sj3dpnjOuK9x9HAVr0KjPJUl6N6DgPZGP78m05m+bAT9hs063hGDqozun5vIBb7ciaQtzE7vr8rx/bu4mxZ7jNxzeQV/GjfZrFIb5sr8uA+kOz7MTXYi+E0uDOnSQSKxepK9tca+dQUOehVrALRJDMRHcsOmXRvJRMw9JysUTnuRZTUQJwhXf/H1n2SIzL1QL/bMV0wW8ThdVptgdHdQLzE++jfPbBY26vJK8Ky17vAwMg//0tn21dib+01zkmn2R2gursSvojUW2mh8fhPAHRByAoXKGypCofd+G0q5tZGsBQ72rRcITA75H7MOGLKjCGX0d5/hi44BkTpHA2CujMS7oCI+AccngTNcrN/9yZytPKjeM1Ps87Mu4TdsgtoOOiNipc1o8vtV1XIYqw0db5mfeOOYHvvuYZ5WZ572AvshnnJJKGkQzmaD8LLd3Bc6Ilg6PWp2QBMTFDrSAD/2drKGmboLy5Qd96j0geEewBl04kSoUgBYY3JRSESJvHNmvC58yyktoPjfBcdMryLYtf5/hhx79gNdTdgkutEPQ53CDymOKxFzAN3NnE4gD6czxkHyYdbp+nZ3wHAS0qXbafoYu4jOpcLFBIVzd0YEeYd8sscLijsRXFNB3iTG2On8DjN/pjBZlm5e8MyQ1+rR64SWoTFBI6Wlwkv8if+kJCFHPL6pcB7C5ctTOHR7WkyGm+QsfbRqb34P1UHbCc12+lcAYPtNlCd4355XdOBWJDBm3ApgGwHAV6yKYj1M4vo2319UY5oK5i0Iz+M2npdlN6qTuH6Z58sW98fvSzZZbsOZbpdLqz9eCjEu4M53ya4mPJAw3L6qQWua+8uUmMPlw338l1Pmb9zJ5HBSlwgD5cYFWUICNts601gtgxxIsmv6jLvMyzS6YT0AnclkVicBAsmNRDYayizLwDQVO7VZEjzmZVSsBTYNOJrl3z5ckX34nx5gFig17pc0lrs+UuoXiR3dKC/8SyQNddAmf6wZQUnj8IpU/m/e0dXvmdajHwM3g1m5sG7qeLKhHvyAOnKLq7HSnT9frtBdLxna3Z7AQ9Z/Z1/9H5xj2inygpfGisru4l8+6bW2+DdqKUz8psMeMeYRM8CmwyRqigpZ4Ti2iHzO9pv+s71t9usn0bhnbf3+zJbU4pMt62ez6Tema93D++5lGS7Aps0wANl83642jVm2Alw2OzDLENPQHgyvfKOQER5+z/9XZryuwRYKKyhuJe1dq7qxFaR1StyL4J5MBIUCMR0jBGaBODKBZJ3CDSz2sHA/IbU36PQHEsfvNa8P8DFteGfUZJWSeQH0IYTq0yxpnBMmKIsFt6jn/kLTBniumE8Yv32H7NurrsROD/k/fdTxrUAfLMPoWxG5L/Nn/0RGOoCnvVkYUh1bdZ4JqMO+dopieHxuzEys96XlUUKGD1ix19FFyhwWESdGlvV1TG/3S1H7531u8S/OZkiz6x9nsUnJGB4n1CPHJQaEXiHiywarL4IOIZVDzoQ+Obc59MAmilfF7N92EfvNQ1tTmdI1rOcjo2QaxGN8nPqh3goZ3W5i+wl+V0t5Xvr2RAmVy1XpwmX06P9d7w9OSCKZCtBEWjWmZkeacysfXXAz/Qztp5/yOArFK3hSkUnBfZevSa85Szv1UJXbPQ7gAYpXmhcjsDINDSzK52iuFg4h/efzoF7wr4A9hom6K29hvEsa0W3b3z/YWvsI9GhdXKHFOGG3xbIKGhPcVRI3HXF5keRQiO/AyAH9Dyq1uPpmRxTTEGxcaQSTkHBBAGNc7qEQs+iTF/WV0Tw7EfzhDpI5AyFkKmMdw2GtYqwMxGagZuRZ8gMNedKiAo5IRmPRO3PyhhZk8MSdjlTlqGtPQYzAQLLHtqvim7gWKnYuTJMJoaHU1uveWzwbZgi5Y23N1KLPLVNPjayHK1mHWTWSARMd/spsGEfsn1MC5k1gKWmF5JnUWhCNFPrcwap9rLwF4MF63yrFBwsJ/tQLtiGDOmW1g1BwGlNx0ZotsIQv71wcAGmIZdpw98DRAMGGYfRyaUh24OTZ7VY7jcva0B8rL6GQKaZOkw5LTk2PsWwKe15bdjZlHIKGTU1KYiJ5R4JDWNYTvyG0OObBRg0cIPOEm4YGN6HS+vMxHqW07HJkDCwkCJ9zghNnJYiw6TACPRkRjF0SXe2QuYRMMakowgz/cyrZ2YkrLO29rFSky6p4SRTbqwyhSb1owbWOoHWinYOq47KCmb3yDCZ0IKw4sQYyDwuBLkPwuErprZTZJS/R2tuApFzjPpcC1mgLvUk9kQU1n/943/U377CVmgPt6gTtQenxKZiXaU83koBOk4dYBA7CtzB3W/OSHWm9xOPGLBSMpaj60SnKNhKIhK0yhQpoq7KY2OCdSlbyrr/ppttNZ0N8gtMVtucR/PE/o590/QB3eBxRsZ9Y/xQnpFgh5fulfSZntqtRGLaPrTCcu0Uzm2vsdX7Y1eiy5ROq1ns7f51LRXILUgvAKwXkqubUhIe9lx9jWJqne8Bp85ORz/beisGjlNy67oFE5hSZjzkZGOTeNEx6TYQ8O9l8tedlIwZjzNj8LYMr9UR6yIhy1FNivr9Jb33WtRsDVbZvujkLiG1fJ3S2icrwl4DOXfp+CpDBLvTVt1AlqJC12FjOTUiICwE6NOaGbE+rb3ynKaJgjxz9BrQ+9SmT2oQO4uRaY9Z1dBdCPxdYcK0coh35H8wH2L3miwTlh2SHeDqik3itvszHuFGuZnOv8+pzOkbt903eU2/yWvIVl2I7rlSJawvzNoZ2cllvTqPVjFkBgOgNVtvaQnvnnvAiCQJyhGzVXYnkU7Eq8qu59EQTJjhoMymavKYuJRO4oGqJD95C9DNHu+Uxv8BqF6leESBomgNEkqNlsfejVK7KofB0inTpcemwCXIvDwWjByXYS43ZvgMcPaykI/kjdcAf1BVlyrOGcqJusQ6Ba1nvQYNEn2M/CLwWkWBBqWPlmoTJOgtKbv0BaD3JDpUg2k4Fw30bpZTIMhdxHzBKOqMFT0AZzKDCHWErN4ha8iQC2tIYvFkgEEFIQeqPs+sJZLhaVfrxldrHkmhQjygRCaJUsE83deK9HQJBM3KCCcE3xrRzbpvK/j65UHbnllZJSiopA7OMg+JY0HnGjuxleUKaZPWirlkJWk1R5hEHaJeBvYs1+BNLy+nygMMKnW5IY4pWJ3bmM0rWh0wj16hzWYa+GWGYnANIPACFWTsLchYC1hpZIayXuiQjeptDPqKISJzmsbvbVp/HN63mIpFo9MjWljyjIA5hUCMjaWeOr8ozUNjBUDlmHgONoUSlrCrj8qxKGw9IBt0zgOL5ZcParnTPHPFRBVFhkZGR1WCT9B5APSRRNV6eO1ikPXTC8DTKBhiB978qiE7GQkkvfCrMa4Iv8LsWcOeNIwG6cAnwquhsIRse0wzDatHLr6O9PQVGcXm1U3ZWvgqDjTdqAH96GKFQc4Ra45B7uriWIMCr1pep6ha9XEgeeKfdaCqyvkplvPYqUTPKCawnuVA6Rn6klX02/UEtX2EHUZXfDTWrLquoDK1iIIHU+Bs6YMVTtnKWg1j+oWxOQdFVOJmL9dOLjuCCDOCIFy2RbXrSHGWv2cslgHeSEnfYiydtDe581TDxZde0rfM2TFqllhICDpjhdv3H99+/K+90d/mZonMFIxLB1W6s2Lsvq2j16/OcvhMJSCsOzJVu+1/5Cc40aFjKtqB2Fh28LmGeFNTfFziE7xVo3jKxPKLnD0fdoSHazyWbcNSaVQkoKj25rcc9bPKjEA7bgK02kidpw424xCo681dW5Aa92ZmBFFEtdrmC7iNMocKIQUrQt8Ny8PjKWesqekXBu8PmLM6jWxsNlZ5hl7XJfECZ1kfprwNUUVJJdi0lpSNwKM6VFuuGjpYo7JlUPIUjTZJDhu1K8KgKvDkKBp5T7nqDWgu4UUxE688NrFBd6BqwECjuxZOAGtk5CxaNWOzGKHmQ2xw3h7Nz3JBJSV0WHCGHlxkQURStKJXHTm3GSqtPiGUFrcEPMcjtlVtamNlgMvYOf23uFooZ2WlzXqljtFnx3StQP9EnTWak1ZoR+vASNjKCCfMQRcs3bnnb5wrD5DVI5aogtk+4sF3u4IyoL02WI7J15CUqSK02+RsxjK3VRW25NLrzq490qQ1dSVEXqdh06tM5TffXKRHZ8Vqds9tcO04u8NLLJfEv8oQM/CEPH6VEQJve9WTvJdWfaiqjioG2aIcXiEJI3irz/CSrU790BUJjdaRtRBRjQnPPAu7BWiyYnvc9yQyBwfEnL0+00CR/iqwSmX5J0SWe8pJzSGKHDkkL3OmEqH8VaNGKAHiKtqJ9QQRv19kLuHHPQzfwpAxAy4KXwvSAIVV6kfnyMzU0f9B54A4gVhG5Aw133pZH06zM0XQSiX3shaWRTgGKdqK52PkwPm4rPsfO05+tUy/lZIYpbPbv5zji1UzanQ/zFf99UhtzCJDTcSOsqZ4vXC1nKiiouwkjiOy5m299Zez0mfNyKJXXYpKi9UiaxgwN6cufiisw8ImfiZGtNBodckZTkb+9v3nz58/5PX3zX+TT6zy0wCEJxp7JfXbvafrlSadC+aKRVZNhtb05DcspEWeDK5IywLJ6Qhvo8ropvNWhExrrqXhgEfM+DyCpE6AEUv7gBDpHRGhKE4iVchoGqu9j+aqYH968cUAgz74iM3cTRNbRFtutalnaYxmYIHNKU0iqFqteViHWWN+njbL5uHJdno1ai6+Xsk+EOAbBiLUVVcKMck/gWEMpJ9TbzmLg+qdpYEGiQOshc6MLxsU70HqrLz85DOrbmnvXaD1HBlAJ6P871FMTpIiAFqC+LwAUkI3rC0JAn9CWAgMLnO1WHZyMfnKzHyhD3em9BqiIuUL2SsFmplVxsrUG6LyjYmxyaQcmPSjIHQNYaiZi7NK39/w+9G1lmYS0x6s9EyHNys1GkOiyahAjVviJygEq0PXSz14R9rcUOItVFYBcMoIctj1rlc6HMx61gveqPWEQ/OxoxdwEwl7nm1NEt04Ux5gVaB1JOLWiVtC1hTrSgYpAhgrHPCAGF2DRnIywqtYi2RpZUpKgv8Uke4mKwf1E0ZDV0gLpQvtzMSjmsgkrMAlQ5gF6eFV0kOA2VPvoyrVwVIRncjw1ytc1KY35zKQEncDNTkQJ0G40HgpZTGJaDDd1KbW0AbRHS4q7YF5mFlzd6tkZ/tP61FZcOqLQXxEI7JcdBDVlAciGRw670AhcKhds5agKyy4lWwKmHQkMkBTwe5qsrndt60uaERp5droHq0jeJvREtLoeHSzNqBnEsjWzxuIuB5eSSwkQJmrkWt58KSc3MMA3SCR0G6zKLExgtaaLQYtB3JodK6x6kIxU711NY1ggx4ZWFD1ln8WERAYeRQjB0lKx/BcoRI3ElWEsGZsxDEyzoRkbFE4ZA62QcEion1Zr1Ekju1n64uQcpLpqwIypDwd6Xoy4CUICmSlUXw9mz5UIXxiPW0MfmVp/h7J22NZ6FYph2LwD2iMxT6UEpqNBrOAxWRHPtv7XMJ8//79/wGRj2TcDPLakQAAAABJRU5ErkJggg==",
+ "text/plain": [
+ ""
+ ]
+ },
+ "execution_count": 17,
+ "metadata": {},
+ "output_type": "execute_result"
+ }
+ ],
+ "source": [
+ "model = model.to(dtype=torch.float16, device=device)\n",
+ "\n",
+ "pipe = DiffusionPipeline.from_pretrained(\n",
+ " model_id, unet=model, variant=\"fp16\", torch_dtype=torch.float16,\n",
+ ").to(device)\n",
+ "\n",
+ "prompt = \"toy_face of a hacker with a hoodie, pixel art\"\n",
+ "image = pipe(prompt, num_inference_steps=30, generator=torch.manual_seed(0)).images[0]\n",
+ "image"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 18,
+ "metadata": {
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 1000,
+ "referenced_widgets": [
+ "8b88a1a63cf242de8a68962f50498c72",
+ "777c5583820248838f0c39e82362d9e3",
+ "491da86a94c44b7c87366b4bb72a3bd1",
+ "31c3a375a2964a06a2473925fe9b197b",
+ "0ba0a0fca31c482bb628a6739d341601",
+ "734e9a834ff74b64b17453013208a116",
+ "9784d9210d6e4214b78ab5f8c33e8044",
+ "490be826ebc14d5ab4e9f0e10ec79d5f",
+ "64ea3c5cc12841f59d1acba12deb6a88",
+ "fc1391aaeaad4eecad967e800a669ec1",
+ "272fceb4e9484b389067080872b1abf9",
+ "5ab5097f19cf4474945f96741c444d71",
+ "6d8fdd0303774305ae20dd39e2a1706c",
+ "031a326124f1496abe1f3bf8de720029",
+ "b9feee6f48bd49209e72e5c5e3136f67",
+ "a2d497a2ddb04d8fac8a4c0f8aa7f5dc",
+ "7bb3f4cda33947138c61aac74d952289",
+ "d3b73a841e68425994632d0f05cf4f16",
+ "71ad1e3dbe44437d8df985cfae207dcd",
+ "598fa824f517445394d08c37393f9f3d",
+ "daad0d12aff8470d990fbbbbe19d5891",
+ "16e18e872ab64b3f8bfb32f580c3371b"
+ ]
+ },
+ "id": "sQOnSrteuS-S",
+ "outputId": "44c5e61a-370b-44bf-a5e5-80b7787088e5"
+ },
+ "outputs": [
+ {
+ "name": "stderr",
+ "output_type": "stream",
+ "text": [
+ "Loading pipeline components...: 100%|██████████| 7/7 [00:00<00:00, 14.10it/s]\n",
+ "100%|██████████| 30/30 [00:03<00:00, 9.26it/s]\n"
+ ]
+ },
+ {
+ "data": {
+ "image/jpeg": "/9j/4AAQSkZJRgABAQAAAQABAAD/2wBDAAgGBgcGBQgHBwcJCQgKDBQNDAsLDBkSEw8UHRofHh0aHBwgJC4nICIsIxwcKDcpLDAxNDQ0Hyc5PTgyPC4zNDL/2wBDAQkJCQwLDBgNDRgyIRwhMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjL/wAARCAQABAADASIAAhEBAxEB/8QAHwAAAQUBAQEBAQEAAAAAAAAAAAECAwQFBgcICQoL/8QAtRAAAgEDAwIEAwUFBAQAAAF9AQIDAAQRBRIhMUEGE1FhByJxFDKBkaEII0KxwRVS0fAkM2JyggkKFhcYGRolJicoKSo0NTY3ODk6Q0RFRkdISUpTVFVWV1hZWmNkZWZnaGlqc3R1dnd4eXqDhIWGh4iJipKTlJWWl5iZmqKjpKWmp6ipqrKztLW2t7i5usLDxMXGx8jJytLT1NXW19jZ2uHi4+Tl5ufo6erx8vP09fb3+Pn6/8QAHwEAAwEBAQEBAQEBAQAAAAAAAAECAwQFBgcICQoL/8QAtREAAgECBAQDBAcFBAQAAQJ3AAECAxEEBSExBhJBUQdhcRMiMoEIFEKRobHBCSMzUvAVYnLRChYkNOEl8RcYGRomJygpKjU2Nzg5OkNERUZHSElKU1RVVldYWVpjZGVmZ2hpanN0dXZ3eHl6goOEhYaHiImKkpOUlZaXmJmaoqOkpaanqKmqsrO0tba3uLm6wsPExcbHyMnK0tPU1dbX2Nna4uPk5ebn6Onq8vP09fb3+Pn6/9oADAMBAAIRAxEAPwCzRRRQ2IKKKKLgFFJRQMWiiijcAooooAKKKKTYBSUUUvIAooopgFFFFCAWikop3AWiiigAooooSAKKKKYgoopKVwFopKWmMKKKKACkoooEFFFFJjCiiikIKKKKBhS0lFABRRRSAWikpaaAKKKSmwFpKKKVwCiiikAUUUlMBaKSlpAFFFFHTQAooopgFFFFLcApaSimIKKKKQwoooo6ALSUUUwCiiinYAooopagFFFFMQUUUUXAKKKKTGFFFFABRRRSAKKKKYBRRRQAUUUUAFFFFIAoooosAUUUUAFJS0lMApaSlpa3EFFFFVcYUUUUX6gFFGaKLgFFFFK4gooopDCiiimAUUUUAFFFFIBaSiimwClpKKNAClpKKNAFopKKdwFopKWlbUBKKWkppALRSUUtQClpKWmkAlLSUtABSUUUkMWiikpaCFopKKdgCiiiq1sAUUUUgCiiihWAWikpadgCikopALSUUUmAUUUUAFFFFIAooooAKKWijyAKSlpKYBRRRVALSUtFIBKKKKYBRRS1PUAooop2AKSlopWASiiimAUUUUgCiiilqAUUUUwCiiigAooopdACiiiiwBRRRRpsAUUUUwCiiihAFFFFFgFopKKYBRRRSAKKKKACkpaKL9ACiiil5gFFFFHQAooop63AKKKKQBRRRTAKKKKACiiikgCiiimAUUUUuoBRRRTAKKKKACiiihdxBRRRQMKKKKACiiikAUUUUa3AKKKKACiiin5AFFFFAC0UlLTS0ASiiigAooopAFFFFABRRS0LUBKWkoo1AWkpaSmgCiiilYAooparXYBKKKKQBRRS0gEoooo0AKKKKVwCiiigAopaKdgCiiimkAUUUlPWwBRRS0gEooopAFLSUUtbgFFFFMApaSlpa3ASlpKKYBRRRQAUUUUK4C0UlFAC0lLSUwCiiii4C0UlFF2AtJRRSuAUUUUwCiiikAUUUUgCiiimAUUUUAFFFFFgCiilpruAlFLRQ0AlFFFSAUUUU9bgFFFFJAFFFFO4BRRRQ7gFFFFLqAUUUU9QCiiil5AFFFFMApaKTNIBaSiij0AKWkopgLSUUUWYBRRRQtwCiiiiwBRRRTAKKKKQBRRRRYAooop+QBRRRQAUUUUgCiiigAooootcAoopaLAFJilozTsAlFLRSsAlFFFNXsAUUUUgCiiikAUtJS00AUUUlMAoooqeoC0lLSVSAKWiigAooooVgEopaKTAKKKKQBRRRTQBRRRTtcAooop2AKKKKTAKKKKSAKKKKauAUUUUAFFFFJoApKWkpAFLSUUa3AWiiiqaASiiilZAFFFFFrALSUUVQBS0lLSADSUtJQAUUUUWAKKKKLAFFFFFgCiiinbQAooopAFFFFFkAUUUUAFFFFMAoopKAFooopWAWikop+YgooopDCiiii1gCiiimAUUUUgCiiiiwBRRRStqAUUUUJdwCiilp2AKSlpKACiiigAooooAKKWigBKKKKACiiii3UAooootqAUUUUuoBRRRSAKKKKaAKKKWqtoAlLRRSAKSiiiwBRRRR5AFFFFFgClpKKfQBaSiikAtFJRTELSUUtAwpKM0UgFpKKKLAFLSUUW6gLSUUUXAWiiipAKKKDVoAooopMAooooVtgCiiigAooopIAoooqkAUUUUdQCik3Ck3D1o0AdRSBge9GRQAtFFFABRRTc0AOopuaNw9RSAdSUm4eo/OjcB1NAC0U3zF/vD86TzF/vD86AH0UwyIP4l/OjzE/vL+dOyAfkeooOKrrNGG+8PzoklTIwfyobC2pPketGRVbzo/emiQAdTS6jcdNy5+B/Kj8/yrPMrH+I49KCx/vN+dPUVjQz9fypM1SjyxI3Gpo02ZJzg0pXSGlrqT7hRmqsjgjAH507ado+lC13BpJ6FjIo3D1H51S2t5lIsTFgeKb0Qkrl7cPUUHjrVGWM56094SVQFuw7Ur6bDUU+pbyPWjNUTaZJw5pUtyjbg5/Kpc7dC1TT6lzcPWlyPWqU5b5QG79ahld0CAHtV9LkW1saRYDvRuX1FZHnvmnidsAZI4osFl3NXINBYAc1nI5fGCe9KUcjvRYm5f3D1FG4eo/OqLQuRThbsVH0ot1Au7h6ikyPWqiQMDTjC2Rx3oGWS6jqw/Ojev94fnVN4WyeM9Kgm226eZK6xxr1ZsACiwGkZE/vL+dG9P7y/nWFLr2jISDfQ9s7ST/Kq1z4jtXeG30srd3MrhETkcngdaaQWOkM0YODIgPuwoaaNVLM6gAZJJHApf+FUaQ2bnUdQ1GS4IywhKKu49ccdM+9bFh8NvCz2KR6hcX11KUCvJJcsmQOgwOMCiyCxkJLHKAUdWB/unNPrTu/g1octmDot/e2lwOQxm8xSM9MY9K4/UE8Q+F2MGqWU09tCADewKShz0ycdc8c0WvsBu0Vg2uvW16VEVyuW/gY4b8q0C7bOGJ/GkFi9RWfubb1aow0p/vUDasalHNZu6X/aqZWbYMk9KLCsXOaMGs5i5PBNKN+eppDsaGD6UYPoarqrFMZqOcvGBj+dJTTdjeWGnGPP0LmD6UVnLLJn71T8kdarqYculy1miqy9KcB86/WnZEk9A5rOv964ZQcd8fWn2hZ4zgHg1Mmky4wb2L1FZEqTB2wG60qefgAg8Ub7Csappc1nDf5ZyDmoCZM96Nwsa5bFGRWMTJnvS7n96dtRWNnNJmsfL/7X5UmX9/yoCxs5ozWN8+f4qsuzK6jmjSwGhkUZFZLb9x603D5/iosBsbh60bh6isld+OjUxjLkgKaLAbAYHvS7h61kIZO4NOO4etHUdjV3D1FJuHqKysvjvSZfPf8AKloFjXzSZFZW5sdTQGPqaNAsa2aN1UIiQ3en5PvVW0EW96+o/Ol3j1H51RBb1P50oyR1P51BXKXdw7UhYDrVQA+ppHJGME01qJqxb3A9KUnHaqIYjvVlCSBVWJH+atAmU9M1G8Q5NQRZ8wDPHpS0uO2hcMgHrS7hUTAA9BURmIHBodrCWpa3UbqpPcOBwaVrhxt6c0htWLm72o3e1RRSF42OORT42JBzRdA4sfuozUIckmoTcOJdvGPpVWEtS5mjPtUSuSgNKrkrzSWoPQk3UZqr5jlsZ4xTJZnQDDdadgLuaWslriU/xmtC3dnhVj1IpNDJqWkpaVnYAooopWYBQaKKpAFFFFSAUUUULUAooopgFFFFABRRRmmAUGjNJRYQwgk0hVqkpaAINr5pwDjtUo60tAxoBx0pcGnUUAMIOOlQNG/pVqmmgZTdHxjFM8p/Q1balApXAo+WwccGrEikr0qQj56kccU7iMtoznoakSFyvCmrJHNTxfcoY2Zr28hP3TSiB8fdP5VqUUCuZQt5A33TU/2diPu1epaAuZ5t3B+6akFsxHYVbooC5TFpg9aebYGrFFAXK6wbDnNEpCL1NTnpUMgyOaTdtSlqVCwzVoOuwVBtXfjAq3hdvAFLmG4FcsokpPNVcZzUzovXHNN8tSASKTloJLUjaZD61K8iDYM/wimtEuOlE0S5U8/dFJy0LjTcnZB50YPWkM8frVd1w3+NMPSsnPXQ7YYbTUfNIpxz3pHCui98Cope1SQjMQ/GrhNvQ569JQ2IXT5jj1pCuAKsSKN5+tDKuytVI5rXGRMUOQM1YEwPUGo4UDKc+tTCIVdyLDxKpx1qYEYFVxFU+0460mykhwIzQSKaBzWJruvJYI9tanzb08BFG7b9QO/tSuFixq+uWekgCdyZGUlUUZJrB0jw7q3iuM3WpX9xBZsQVRR/rB6gdAPfmtzRfAz3gTUPEErz3LYZYdxGznPP19OK7yO1ChVChVA4AFMNjjbL4Z6CiES/aZmPVmk2/oBXYWOg+FvDdlb2UVtZpqdxmaASDfMdvdSeRgfrTLy5jtYycgAda47wtet4m8e32rs37q1hFvbKTnjvj8Nx/GjVj6XPQvPm2YzyO+M1XAmY5O4+xq+IG/OpViwOtUrIi7CCR4CpQnjt61fbUYpFZZrcOrD5lwCD+dUQp5HpQB7Un3BGBqHww8K65G0lpHJplwx3Mbc8An/ZORj6Y61yuufDnxJ4fszLod9LrEZPzRtEBIgA6gZOR7D24r01HKdOBVmPUJY+MhhS13KPAbTxQyzLa31pJbzj5X3/AC4PuDjFb1pfw3W4Rtlk+8O4r0rXvCfh3xdaTLeW6w38mNt0nEmQMDnnI7YNeQ2Nle+EL5tC1u3EUkj7oZE5WTPGQR24pNJ7FXN/cKUODxmk8viiKI7gTjFS01oCaJFRTg08KvpQV4qsS3qaLXFctYGOKZKqFQGquAzD7+KVVIbBfNRGm1K50VcanT5LEgt1wCBUoi+WnL0FOyBWxz30IvJPt+dOETBgfeph0paZJTvUItjn1FM01gu4EjmpNR/49x/vCqlpkPWdRJmtKo4bF5hmRsetKBQvNO2mhbEyd2Nx1qCbCmrIWoZY8sAab0JRWLDAoDVOYBxSi3FLmdy+VEGflpuateQAMdqPs4oTE0iuBnpTpAC4qdYQCRTjCM027CsVWdQeaUOmKma3BOaT7OMc0xCQ+W2c0x1G7ipRCVzjpSmPJpJW1KcrpKxWAwaeQPWniFhIDjipSQBjZ+OKmUnfYqME1dsqn2pvIariJ0JXj6UrIC2QmMUru5Xs42+IrGMkdKZ5Rz0q7j2pwSrMrFRYXyOKXyX9DV8CjFO4jPET+lPWN8dKtgc0o6VJpcqCNvSmSxtx8pq9xQTQnYGrmb5behqeNDxxVvAxS7wo6U3K+guRoryqfLPFU4lPmDg1oyTrsPBqpHdI0gAU00DHSDmqrAkcA1dklAbpTEOQeKU20iaauyk0bn+E0rxt8nBrTAG0UkhCrk9KI3BlaAERNUkfQ0qzxYxuFAmjx94UrWY3sRr1NV2U/aPxq350X94UCWInqM1fQhKzEUYQUR9Pxpn2uIkgAn8Kje+gjOGJH4UloEtQH3/wFR3HRaUX1sckZ/KpoxFcIGUZGe9O4Lco7Sa0rUYt0+lKsKqOBUijAwKm9ymOoopaYhKKWijQApDS0UgCiiilYAooooWjAKKKKYBVa5JDLg9qs1FJEJCCTjFNWuCKe9vU0b29TVj7KP7x/Kj7J/t/pTuhlfe3qaQyv/eP51YNoP7/AOlNNkcZDjH0qXJLcpRctiv5r/3j+dSfaHB60z7O2eoqQWcrMSGHWk6kVq2NU5SdkiW3kaRyM9qtbTVOGGaNjgr0qyPN284NYTq66M6aeH095D9retGD60zdL6LSFpc/dFZqrJvc0dCK6Dzkd6gaRtxGe9O3SE42iqkgcSNle9awbfUxqQitkWVYluTUoNUQz+hpwMhHetTnaLRb5qV5OKpfvM9DSMkmOhqhWROX5qxC2UrKIkz0NTRtMiZGetPUGjTzRmsr7XNmlN1NnrTsTY1M+9GazftM1SwXEjvg0h8rLtGaqTzsmOKZHclyRyMUCs9y7nmlzWW0km4kE9aHkkMecnNNoDRJBpj/AHc1liSX1NTr5rx8561LV9xp2JD/AKzNWQwx1rPZXB704LJjvS5RuZdYgrQp4FUtkmOhoVJcD71TKF0XTmk9S454p0/ylef4RVJ0kA6NUtxGzOpwfuCocGkdEKi5tERSZL8Gozn1pzIRjIpu046Vm4HXGtcY+eKniGIRz61CUywq6ijyxVwVmc+IakiB1yzfWo3jbaa0NnJ+tShBnp2FdStY86W5nWqlVb61Z5qyqAnpSsg2nikwRVVyCae0oC5JAGOSaqySpCjySPtRRkk9q5qe5vvFt6NL0WJmUcuxO3I6ZPovNK2hbRe1PX5pLxdM0qJprqU+WGQZ+buAPXFdZ4O8B/2XJ/aOqnzdSJP8e4KPXoDmtrwr4OsfDVqTEPMuZMedK/OSOm0dutdIQKLhcqG3QMCF5FQXrpb27SMQvYZ9a0CQoJYgAckmuX1jUDcTtEjkRJxgEHcfWi73Elc4rxvrcsVitpasRPdt5a46kHr/ADx+Ndt4P8L2+gaVbYXNyY8ysR1Y9fyyRXAaZaQeIfif5UsSyW9nEd6OMhiB/i36V7IowAB0AxT2Q2OHvT1QGmipU6UiQEag5xTtoHaloPSjUZARSEAKeBS0jfdNAhIjtlVvTmq3i3wxb+MtJVFYR3ts3mW8pyNrY6HHJH/1j2qxH96rEUjRuCCfcetP0A8htLmVLiayvomgu4XKFZOC2PrWkikCuj8f+BIvE9p/a2m5i1i3XKbMDzcdm45PpzXCaFq8l0rWV7FLFewZWRZV2kkcGjRjtc2mB2mqRBzVzzFPGaqFeaQWHKmV60bfmoQcGmP96rWxxSu6ti2vApSc1R3H1NG8+tTbqdSkaSnCinAj1rK3+9Ojf94vPencLljUf+Pcf7wqlAcHOauagf3C/wC9VKI81Ety4l+E5zViqkBGDVgMPWhWQnuP71DKcNUynJ4qG5haTGKHYaDPT6VIMVSaKSMfQetCPJxyai9mauDaui/RiqLzSq5ADEfSnRzysDlT+VPmRPJIucZpDVQzSB+nH0pfPbByD+VNSQuRpFvFNPFQmfjoelV5rht2ADVJ3JsXSwxURmQfxCoDIdp69KpuWY9DRcVjTFyn94UvnRtn5hWQA2ec1Lhs96Gx2NWOdGHDZxTjID3rMtyQTVxTmpb1HYnBpQagKv2ppEoHei7EXAaN1ZTtP5rjc+Oaj3XHlv8AM+eO5qrMDaVhS5Fc+rXAblpMfjQJJv77/maTQ0joCRScGuekkk+X526etR+bKP8Alo350kro1cLOx0xIC0MFZRxXPwTSbxl2PPrW8pygPtQ42JehDMoEZrOthmetGcnYazrcMJsmqRDehal+/Sx/dNI5DNzyadGox6Up7DprUsgcCo5sbKduAA5qC5zt4NGorakKxKcml8pfWkjB29aXmp1NLoTyV9aVYlDUc0DOaNRNxBYUBNVbm2jZhnNWgSKr3BO7rVK5noQJboBj3rStEVY8DpmqMalgea0LZcJg0+tgLGKQ9aWmjqaAY6ikpaBBRRRQAUGiihMAoooqbAFFFFMAooooQBRRSZxQAUtJuo3Uxi03Jx0NLu+lPUZ7VhW2OnCq87FXacjjirSK2W+XHNAiPHFWkQ7yMCuOdS6sd9OjyO5SwVbOO1OB+XpipJIzzgdKRY2KipumrmlmnuM5JAAoZTu6VIiEMKeyc9KE1cmTfcqkNj5QKqyh1c5FaWzGDisy7ZhOwFdlFpnnYi6dhoPtU8YyvSqe9qmjmYDtW7RgtyyFGaSQDBFQ+ewPSo2nYk0RCSHlVzUqqPLqp5pqVWcpVeZICNd3SpGjTPSqxds9aTzHz1NG472LXlrjoKfAqh+lUTM+OtSQytu60W1G56FucAmo4gA9QyTNv60iStvH1oStoTz6F4AGnFRs7UiudtVbh2ByCaZJYCL6CpAFCdutZi3DZx3qQzOUpNrYuMXctOFz2qVAuwdKy3uGU4IzUy3DeUDU3K9m2XXKhD0qsLhdq8Gq7XfYjmmRzR7VznOKpakSXKWZJwexqSeQK6g/3RVN5ouvzVLeTIJVHP3BSkuhUWhZGB2mmkApTGmjwnXpTlljZMYPWhLQHLsLtyeKsRj5fxqEsi8nOKkilXjrUuPvFKp7tmWAvWnHIPAyMCmecoYinNOnH0rRGDauPXr6cVBqF/Bpto89y+1FHAHJY+grP1DxDZaarGZxvAwEHUnGap+HvDd7441ZdS1MTQaWgBjjDcSj0HtnqabGl3KWnaTqvju/P2Z5LbSkfDuwwF+n94+3vXrmgeHdP8OaeLSwiwCcvI3LOfUn/IrRhggs7dYokWKGNcKqjAApBP5y7oj8ucZxS1KuTdqQmonLdc8AetUrmb0OKVgF1W7EFqQj4duOK4+c4jdzyAMmtK6l81s5OK53xHc/ZNFnYZLOPLAxnOf/AK2ai+ti4qyKHwwuEju9X1G5UoJXAEjZxj5mIz06gV6raXtte2yXFvMskTjKsOhrlLbTYtH8EfZWBKrbNv4zy2SfTuau+ErIr4ZsiGGSGbAPTLGtHYlrS51CkHoalQYqvFD5WDnJqyvSkSOoPSig9KBkFIehpaQ9DR10ENj+9UtRR/eqWgCaCYwuD27iuI+IHgS51W5PiHRJFjmiizNDGh3zEHqD644x7V2Qq1aXBifax+Q9aOoHiGiasl/EFYFZU4Oe5FbXBp3j/wADDQ7ybxFo/mJZyMGuYIh8sfUlvoT+XNY9hq0c1oJFy46cVMlfY0jK5r44pFHzdKrWt/FdKSgK4OMGphKN5xnIrOUJPQnmjGV2T4HpSEcdBSBsqCeCaXNcrpyRsqkHsOwPQflUTovUAA+uKlzTGI5rSne5NVaGZPJM0hSQgqDxgYpigg1YlUNMc1ILdcDg/nXVJmUdSsrsOjEUu9z/ABH86tLbp6U4W6f3anmQ+ULPcWOSTV7HFQRRqh4GKnPSqWuotmVbn7pqvErMRgZNWLj7pptmm9gM4rnqOzud1FXgPMTbjlTR5RH8LVd8nOOTTvIUDrXNznWij5X+yaa0R2nA5q46he9RmuulDqcWIqyvylQo2ORUEqNu6VoYqN1BPSt0rHI5NlUDimhRmrRTiqrZDGgkXaKeAKgBOamzTugHqopDlTUW7ml38VDZpFFtWyoPtTqpCQ9jUiM2Ryaq5LiPYfvW+lM6K34UkkpErcjpUTSnynOR27VXQixNEQXwe5rRFqnvWFDMxlXn+IV0oxtP0rhxk3Fqx6OCpqSdzHuAF29OlQEj/ZqzdfMVxiq4Qn0rnUzu5ESQAbWyB+VWkz5YqCGM7TVgcJiu+j8Nzy8U/fsQyg7TzVGMOHzgj8KtSgqCc5qvHNKWznArZWOboGGLHg0/DLH3pPPlB6g/UU8zO0OSB1okjSM2iLcxYDmn3ALEDJpqFiw4pZ9+/g0mJO7HQw/J1pTD70kRkC9qQtJnrU63NGkO+zknrT0tsZJNJD5jvgnirYjI/ioV7mckik1ueeazrqJg3BrcMR9aqT2xY5yKsz9DHHmKOprZ04E2YJ65NVTaHnkVfs08u2Cn1NK6uXZ2JqKWin0IEpaKKOoBRRRRoAUUUGiwBRRRSYBRRRSuAUUUUAJUbnBqWmlAfWmBAxOKgZmB61cMQPc0026nuafqO5mfaJskBhVpbiYBcN29Km+wR+tPFsFAAPShqL3HGbi7pkSXFxx8/wClWhcT5HzdRTEQK4FXyq4U4HSuOsoqVrHfQ55xvcqLJM4Ylv0p6PLt6n8qmXGWqdF46VheKvoazUtFcpb5d+MnGfSnyGUP1PT0qZxh/wAadL98/StE10Ri076sp5lyMk4qvMitISetWrhituSOvFZkkzdTXRT2OeroyXyUx0pUjTHFVPtB9P1oM5FauLZlGaTLvloT0pjQoM8VXjuTuAqVpxzk0o3iVJ8w0xqD3qdNojAxVYyqe9OLMoHPBq76WM7DmVPQU3aueBTdxPpRvOe1MGIVX+7T0UA8Coi59Kj851J5o66D0Lu0HkgZpQqjsKrCc4B3Un2gjvU63CxoL92oZ1yKZHKSKSR2xmqMyNYeetPaP5etIkhpskrAdKLK5SbIHiJfrirIixCBntVZpXB6VL577BwOlJq5Sk0wNuuCc9qrhFG3BPSpvOc54FMi3uoPtTSsKTvqI0akdTVi8gXz0OT90VEY3AJqa5nP2lFK9AOaNbiWxE0I+Xk9KFiC4wTUzsG28Y4pMgUajuWGt1ZT1qLCxbetWDMoBB4qo8owp7AUtQ0HnJYnOOM1k6vrcWkqAx8yaRfkQHv7/mKqTajqOrX6adoCCeWUYLJyVIIz9BjueOtd54Z8B2WkSLe3wF5q7Nv81uUjPogP8z+GKOYOVLU5XwZ4Pj8T3Z1LWpUcq3y2R67ecFx2HXHrXpDaZc2EEVtZssUCYCqh4Ueg9vwrYhiWEHaoyevH6U+TEi4IwPancCkTIbbDHJx2pmngi2/E1cEWBgfrUFqhSNlPUOaOoiRvun6VhXs3Gwde9bcj4VgOWxXMnLOamRUSCRea5zVov7R8S6PpYIKNKJJBkdBz/IGumkXby3GB3rkPDLSap8VLqdifKtUcIPTA2j9STSS1KZ3WtW5ureOxRyrTuFznpzU9laajpttFbwrGYo12qPQVsbfl9COmO1OA+UfMxPvTJvoUE1GeGUC7iABHGwf/AF61LeeOdC0bZHf2qBokfllBPuKjicxFtqFc+gp2uJmjSHoaqC6IONr/AJVJ5rEfdOKLMVxaQ9DTTKq9c044K5BosxXQ2P79S1Ap2tmniTnpTYyWlBpKKALsEiTxNazqrxuNpDAEEehrx3xr4Xn8JaoL6yiZ9Hm4HOfJY/wn+n416sCQcjrVm5tLPXdLl0+/hE0Ugw6H9CPQ0g2PFtNWN7bepcBjkVZVQHJBaoNe0a/8B6j5N0zXOmXDf6POF+76g+4H51LG+8bh0PNXG9zDEJON7akjMA333poYZH7x6RuWoA5HBqpPQ44R95IuCRf74oLIc/OtQbW/un8qNrE/dP5V5aqOOp9U8JCS3K1xcrFcnjdxng1YjulZQQtUrpJPP4QgYq3DC3lrlecV0TnomctChFya6E4nH92lE4/u0wRMP4aPLPpWUZ3OqeHglcm87AyFo+0MR90UzB203GPWupbaHlPcc8rH+EUiTSIcqozS7eM5pyx571m2upvFSS0F+1XHtSfabk/xCn7FUcn9KAYR1Y/lUuMexrFye7Gq8jN85BqYdKb8n8OfxpdwHetYarQ5qqalqOppoDA96CueatGIEDHSqjqN3QVc28VGUU9qGNFTaP7oqXaMdKl8tfSl2Ck0O5D5a+gpDGMdKsbRSYFKyHcq7AD0qZFHHFOKAmnhQBTsK5Rn2iZsnHFRbVaF8HuKlukUSks+M1HGqeS/z5GR0FO+gWIYI8Sp8w+8P511AXg89jXPQLGZ1AJyWFdL5Zwea83HPVHr5fH3WYs0QyPm/So1jwetXJouAcioghz2rmTO1wEQFe9P2nbzShcU/HFetRX7tHh4l2qsqyISDUaQ4HWn3M4hI4zmoxdcD5eozVOJmpNIPJyetK8REQ571Gbkgn5aDc5iGR3p8thOdxY0O8c96S4Uh+tNjny447024lLSdKdncSZLGDt+9SFGz940kbNs/wDrUu45qVe5bkrEsCsH+9VoZ9apo5BoN0VODVpMzk7suEH1pjD3qobz2ppud1BNrErdTzU8H+q/GqDSg96u2hBgB96Tjrcvm0sT0UUU7aEBRRRQAUd6KShCCiilNAwoooqboAooopaAFFFFMAoooquugBRRQQaAFpabijFArkUsgjkU1P8Aao2Aw1ULvqOaiiAGcvisqlJS1OijiJU1yo0Bewq7Dfye1aEcgK9a5sIN+Sw61tRyrtHNQ6Mdi3WmyaRvmzTZZiW4HajKsM5qrdy+WRjvVRpozdSTYspLoQTxVSSHIpPtZ9KDeDH3a1SSId2ReQfSlaA+lL9u5A2D86WS7IbG0U7k8rGpCdw4pGiOT9adHdMX+6KGnJJ4HWk2NIj8rnpVhlAUZHaoxN/s0TS84x2oT1FJEkaKQcgVIYlz0qvBNweP1p8lzhsAVV9SUhxhTPSo2gTnimG6/wBmozd8nigfKS+QKQwCiObcOlP8yi4WJIowAKn8tCORmqwlwOKQ3DCk73GkWhCnpQYU/uioUmJUGmvd7ByKTbWo0kyV4E/uilEKFBwKrNer61OkylF9xTTJYNAgBOO1NgRREOKe0i7Tk9qijZVUDeKOoWdiV0UqeBSyQo0gYgZphZSPv1OwBI5xTJadhnlL6CjyUPX0qRguPvfrSIoB6/rTFZlaUASHiufukvPEeoJomkKszOdtwRkGIBgCT6Adau+I9RitIktBzPdkxx4GcZ4z+td/4C8IJ4T0Q3F3CP7VuR+/bO7bzwoP86T2NEGh+GtI8B6Z/ozrcXzD99OQN75/hA7Lx0rX02ZrmN7hwAzMePQU2eGNnIKg49RU1oFjBQAAelK1kFy1RSUUALWPeTzx3LiMsFz2Fa9U5kJlY0dARlsbts8yc+9VQCJCD171rS5VCQMnryayA7vKzKu7J5zUstFXUFLR98VyXgEbfGutsOq5/wDQ67uSMbTkZrivBC48ceIwOzf+zmmr2Ez0v7SwGcCgXTEcAVF7VJFEWOFFHkLQlWZ24wM1aijcNl8dOlLFCqAcc+tTUCExRilpcU9REckQkXB/CoER4yQQdp71bpDyOaEyXHqVGGGpKlldNvLDNQBweRTsw5l3LIORTqrK53dDUokX1FDVgUrklS28jRzKy9c4qDNOSTY4bGcUijQ1rRrPxBo02nXqFoZhtyOqHsw9wa8JtIrnRNUuvD2oHN1asdrAcPHxgj8CD9D7V7hFqUiMdwBU9q8s+LNpP/amm+ILKGXciFLgopICryNx6AYJH+RVR0JnHmi0Unb94eabvwap292l3GsyHKsAc9Km381pY8p3Ui8JjinCU56VB5y+h/KlWQMehqOWPY6FVqLqwmIaQZ9KtxgYqjI/71eO1XUPFY1Vqehh23AeRSYozRms0katsCOKikO1am6imSJuWtYvQya1IRKNmPerMZBFZ0gw1X4BhB9Knl1uXzaWJXwVxjNRrGrNytSmozKiNyabWgQl7w8wqBkVVdPn6mrH2hGBwc1VeUBulRCLRpWmpaEsKYbOas1XibIzikknKSKuM5rZHP1J2PFUy754Jq0GyKNo9BRoBVDvnkmrKnilwPSopX2ijqA8mm9aq+YfWpI2JIotcCyAaXmhegpT0oAo3UZeQdMVCISluwJHLA064ZhK3J4pGy1sQpJORS0GrjY0/eoQeQa1vNl/56N+dYqpIrAhec1cxdddmPyrKcFLc6aNZwTHStIVX963X1qDdLvUCRsZ9aRluNqj5unrTAk/mAYbrTjSilsKVebe5oI7LgMSeO9T9qzmEyzpuDdO9X1ztrRKysYSbbuyle7CQGpB5IC5PalvEJbOKrmNt68fwijVjSViZlgJzmleOHyBhu9QvGwUcVJ5bfZV4709R2VhIUi8wfNRMsXmfepIUPmLxUc6kStn1oRDLMfk7fvUP5AP3qpBsYpJjyKOpTehowCGRiA46VXlRPMOGqKyJMpGf4aryFt5603otCVqy35KnvS+SAud1UxIRjrUquc45qbsqyBlx3rRsRi3H1rNYGr9iSIOvemTYuYoqMsccGiJiyZPWn0ESUUUUtQCiiigAooooEFFLSVNhhRRRQAUUUU7AFISB1NLUFySAuPWnYCcGlqrE5UYNWFbPejQB1FFFAihfcbTVQOa0rmLzQMEDFVfsbZ+8KGgK2TVyObA60wWhx94U5bVh/EKEi+ZF1JMpmq12wfbzUqx7Y8FhTGg387xTtoTfUpFB60mwYq59m/2hSfZh/eFS7j5iiVAYVJL9+pzajP3hSy22XzuoHcrRD5qcRyfrU0dthuW/Sla35PzfpSbGiADmpJIwWGCfu04QAH71Ssygj5RwtK4Mrxx4zzUjW+45zUiSRg8qKVrlASAtO7uTYrGz5+9+lRG15PPerTXS9lqH7QuTxTTZSTFityMgHNS/Z3PTFNiuFL9O1W45VJAp67kS0ZCLN8dRUbWzhgOK06jdeRxTsY+1Xcqx27CMA4qKa3LjCn860McUzZzUuL3CNddTLWxlz0zV5bVxGoI6Cp9yqcE4qTzPlGD2oWhqpXKTW7gdKg8th/Ca0HmABqibqP3p3saJXW4wq2CNp/KrR3ZOQetQfaYj61NNcxo43E8+1DbaugtFPUcM4pJHWGJ5XOERSzH2FM+2QkdT+Vc/rE83iDVbTw5pjSC4mkUO6qcDPrjsOppK9tROMehreAbWDxT4tuNZvYLh9PslH2cSRAx7+wJPQ/xY9a9ZnmMj8MSo6VR0/TIfDOhWmgRSmVoE3SSFQN7Ekk/59qmBzTZIrrkk4FN2hWBHFSVBKMGkNEhnYdhUiOWHIxVGlyfWi47GhVedljJLMAPU1X3N6n86Qknqc/WlfULFHULzGFidSCOcGmxx+XGFxg9T9aLuy3EPCuHznA70yK8EmRKAre3rQV0HSfdNcP4K/5HjxIf9v8A9nNdxIflNcN4Lz/wmXiVh18z/wBnNNCPSooXkIwDj1rRjjEagAD61kxXU6RKN/OOeKV7644+fH4UaCsa+9Q4Qn5jyBTsisB7mR2DM5LDofSgXc4/5an8aV0HKas9+sDMuwttAPWp4ZhLEr4xu7Vz7SvIzFjkkc1Ol5NGgRWAC9OKLhY3aa6llIDFSe4psTF4UY9SoNSVRJQm09pUIW4ZcrjOMmobfSZLZy32ppM/3hWrRT5mT7OPYqi3fuwprxspxketXKhmjLAsD0FK9x2sVkDhuuR9asKjEZ4xVPeVJqxDNjaCeM0XGTiJvalk02DVLO40+8Ba2uYzHIFYgkH3FPBzUsTlHDDtQI8S1TR38G+JZdGKStYSkvazspwQecFuhI6H/wCvUxI+lereNvC0Xi7w29vkJdRfvbeXHRh26Zwf8PSvGrG5+12Z4bzIyY3BGPmHWri76HLXp68yNIsPUU5GHqKo+W/90/lTljfP3T+VVYi9y3Icyrj0q+n3RWMA6zDKnpWrGxx1rCotTtoO0SeikXmnVnZm7Y4UuM0AU15AnWtI7GMiJrYM2c1Mg2jFAcFcgVAZWLYAqmgLOaqyxFpCaGmdOWHFJ9oTPJFTa407CJGUzSrGGbJHSnlgcY70zftPShWQfEyYHFUrmT98uO1SPN8pABqsSpbJBqr6BytPUnF2R2p32tvSoQEPapRGp7Ubg1YX7UxpHcsOaDGAOlJigQwAmrUSkAVEgGamMqoOaAJc4FNMoHvUBuI8daQSJtGaegiGeUs7YPFMEjCAn/aodoi7Ek0o8n7KT8x+akURiZgR0/KtA3B2ZFZpeEdmqyZY9n8VD1GhrzuNvI6f1NKk7eYBx+VI/lYjJ3dP60i+V5gOW/KnZWJJp52LqfapEuW2cgVBKY2KnLDj0qRUXZkE4+lJWBsbLck/wimmUBxkdqY5i7sfyp0nlbxkt0HajQpajXuASBipjKfsynHeq7eRn+IfQVOWh+yry2M+lGhT0RHFKfNXFQzMzSsT6mpoWh85cFs/ShzAZWUlup7UaEFMk0MWOM+lWP3G3lm/KnOtvx8xHA7UXQ7EdmzLMT7UrSK33l/SprdYPMO1z09KjaOHccTfpQ2rAtyMNHn7oqT92G+7SeXCD/rv0pxWIsf3p/75qepVtBhePP3avWYVocgYGapGOH/nr/47Vy1ZEi2q2eaolqyLO0elIBjpTDKKcrbhR0IHUtFFAwooopXAKKKKdxC0lFFTcYtJRRVdACiiikAVWvDtVT71aqOWJZQA3amgM8SmpopjUn2RBThbqDT0AlR8inHkU1UAFOxR10EVLkhSKrFx6mpb3+GqoNI0WxKSck5NOt2Jbqaa3SiD71FtLjTJ7hsQmq0T8Dk1Lcn9yaqw/doWwnuXeSKilyAKnA+QfSq9xwB9aVtSrojzUr53nrUAappJMMRj0p2Ib1FQHd3pSpJPWkjlJJ4FO87BPA60mhqTGbD6mnFW9T92l8/2oaX2/hqbDdwWIk9aVoGJPNLDNluRT3uADjFNk3ZXa2b1qE275PSrZuh/dqA3I3HinqyohDE6OSe4q3CGDjIpLOQSs3HQVdAA7UJu9jOpbUlprUtNatDx76i0mKWigaKF0SJDzxT0yYx9KfNErPncM1Yh2LEAcVDPUh8KKcgOKz2jOe1bsnllD0rJaGTJxj86EXexWMT+lT3kbF1OO1MMExYYBPPrVm7glZxhD09aoV1cybu4Wxs5biTgIPzPYV1/wc8MvHBP4nvlDTTkrbFhyF/ib+lcZZWMnijxlZ6AiSG2Rw92ynGFHJ556dvc171cJHp2kpaWkYjiRRFGi8BVA7VLfQoxLqc3GoTTYxk8fSohexrJt+Y9uBVW8eSNxGo++OtFvGFUMw+b3qNbDsaazq5wM/lTZOQahRypHpUjSKVOKaYWI6KKKOgwooopO3UBpGRWNcwGGYjseRWyahngWdRuyCOhFPYEzN88eXtbjA61yHgvjxd4l95Bj/vpq6y+iSPbEmd3U85rkvCREXi7xGHJB3r2/wBpqaGzv1OVyKY55piTpjBcUFgxyDmkJBmkzSZozSGBbbzUWXZhgn6U8qXG0dT0q1a27R/M2Oe1KzuFwtHuQcJKwA7E8VuWyukCLIcsOpzmqMX3xxxmtKqRDFpaSlqgCkYZFLVTU5WhsmkU4IYc596OoEE6hZmwKjFNSTzY1cnOR1p1SMt2jjJUnk9KuislWKkEcEVoW8vmL1+YdapMTRsWLlkKk/dr5/mWOz8Y+IdPjHC3kjrgYGC3T9a92gkKOCDjPWvL/iboT6VrieK7WFntplEd2AScHs2Ow4A+v1pp2ZnOPNFoxutPXgdKqWV5Hd2Ud0gISRc4PUVYWXJGOlW2jjVOS6CSDMo+lXI0OKrHDyrV+NcCsp7ndSVoiohqQKaVRUlCiU5MYFpHiDjmpKU/dptWFuRKgC4pgVQc089KjIrOU7GsKblsJdKpgIBFZRUhq1pYiEORxVVolPeoVaJq8JU7DkYYH0prsCTRtwKYVy3WrU4sxdOcHsNIzTCnPWpim3qaYw6c1ordCG5N6jkQetTqKhSMnBzUm1geBTQmx5XNJ5dKCcc04EYpPcEM2YqCdGIGCKW5kK42/pVfzXOMk0DFWBiOoqbyWwBkdKjBfbxmnMX7BqethEZtnJPIp627fZmUsPvZpgDnPytTgrmBxtI5FLzHcha2b+8KlMRC9RULJJ6GnNHKc4U0CLDQ5WP5hwtJ9n+cHd+lQukuE+U9P60iLJu+63SqCxcMIO35u1SiIiPGe1UZC6eWOR8tPWWTyj8x70kJitbE9+aWSEtKDzjAqqZX/vGp/NfzgMnGBSLV0MMbE4wfyqZoW+yrwfvVUNzITxxUwmkMHX+KgbuOhjYTodvekaF/Pc7TjJ5psUr+cozxmmyTOtw43HGafQm2oeS5HCmnPA5YYBPFQebJyN7VJJJIHPzMKSVinqT29vIJD8p6Go2tpM/dp1vLIZOXPSmmSTP3j1pu9gjuJ9mkP8BqWa3ZZDhTiovNdf4jUss0hc/NUMtK70ITEw7VPbghDxVcySHufyqzalipznrQnqE46EuOnWp4uQaYBT4+AapmNrElFFFABRRRQAUUUUgCiiikAUUUU3cAooopWAKazbSPenUYB61SsAA5oApcUoIFMQYwKShmxUZkx3oArXkTPtwKrLA/pU1zdqrAbqiW8BPBpa7miuStA5ApYbZw3Sm/ajxViKclc5oexNxk1s7RkcVBHauo7dalluyqmohfYX8aa2Bt3LnlHYBVe4t2ZRinC9GzOKjkv0xzmjUd2Q/ZnxUsluxft0qP7ah6Zp0lyQ+PajUl7j47dgeopDbMc8iljuTS+eeaNRoZ9mb1pTAc4z/DS/aKDPhv+A0tSmEUDBqke1LHOcUsMoJp8k4U1OoktSubT/a/SoDafNkN+lWGuvRahFzl+lVqO1izZReUzc5zV4VUtWDkmrgFT1MKt7j6aaN46Ubs1rdHneykndoXFIaXNITTRJm3hYXBxnHFWoslB9KdIAWNJACmcioZ6lN+4hWU4qnJHIBkKa0iRigEbfelF2HLVGOpcSrkEcjtTtbvzYWjyJzIRhB6t2q5eXENpBJcTuEjQZZjUXg7Qj4y8SPq15kaZZOCiMpAkPJAz+AJ/KqbJjE6D4PaBLaaXc65eBhc3p2oWH8HUkfVj+ldtqk5eURBshev1ouNUC4S3AAHfHH4VnNKXcuxyScmodmalO8/4+ovp/WgU27YC5jPOAKTzVzxk1JS2JaWqNxqcVsfnVsevGKdb6hDdQmWKSHYGKndJggjrTsBcpazL+6RbVj9rt1xz8swBrm/7RndyiXxJB/57f8A16LOwHb0ma4ibWL+2IQ3UnPIxz/jUB8T3gBBu249R/8AWp8rsFjvc1BPAJusjj2B4rif+EmvM5+1k+xQf4VYTxfNEB5kSyDP8KkGjlY7HTx6dEk3mF2bHIBxisfVbjStK1tC/kx3mobEAUAO2M8k+nQfhWlZarBqEPmQt9Vbgj8K8u8d3B/4WXpx/uRRAfmxoirvUTPShxTgcVGrBlDDoRmnA0mMkBPqacM+ppihmYBQSfar0Fttwz8n0pBcW0hORI34VboAxS0CFU4ORVkXhH8A/OqtLTEWxeDuh/OpBdRepH4VQpKLsDXBBAIOQazdeJGltgkfOtPguTENpGV/lTdbQy6WxB+6Q1UrAtzCsb4xHy5SSp6E9q1Y5EkGUYEeorncZq1b3Rt02kZGcjnpUsto26lilMTbhVSGZJUBUg8cgdqk3UXJNmGYOgbpVi4tLbWdMmsbyISwSLtdW7/lWFHcmI5zx3rQ07UY/tKxlj8/AyKrSxNjxE2c3hjxBd+Hbsh0R/3DhcBgeR+ea1YlHTArT+M2iC31DTfEcGQdwhlwT1XJU4+mRWJbXiSwpKvKuAwIp3IkXkQeaOBV0DFULeUSTAYNXxUSeupcNh4p9MBp1NMGhaRjxSimSnahNPQRHvHSkY8Z61SZ2Lk89auJkoOKzkka0ptPQSa5doyNo5qm87DsKuShvLOBzUSxuy52H8q5vdj0PV5ZzV0yv5zHsKbvbOcc1cMBP8Ipoi2uMjvVRnHojCphqnVlVTLK2OmKcYpOuaveWAelIy8V0w1Wh5tT3W1cqp5gp6tKTjFTYFOQfNWjVkYxldjNjlenNVJTOh6HFafaqd0+KylLS5vFXZR3zO2AD+VEnngjAPT0qe1OZfwq4T7CuSeJ5ZWOyNC6KEMs6ggg9fSrCtK/UfkKn4J6VPCBu6VVPEc7SMqlDlTZm7LpWPDY7cUqrPsIZW6+lbBAyOKQ4rsdzliYTJID90/lSuzjsfyraKg1FPHwOcUrlIxXd8Lwenp701WfPetNlxj5x+dNGP7/AOtPoK4wsmyHdjO2nZjMZP1psqKShMijikCLsI8xaaB7Ef7s+lTOYlfnGcDtUPkj++v50+SItLncuMDvQGhWUwBicLn6VY3w+RwBjNVfs7b/AOHH1qYW7eRjKdf71GpWgsTxbwAOfpSSLF5xYjvzmnQ27iVTlMfWkuIWErElRz60ai0GjyD24oleHfyOaVLZum5fzps1q28/MnX1palaD4JIPM4XnFKzQsSAmDTYLRhKDvTp61G8Lh2G5eDjrTtoS7XJFeAHGwE1M7KTwgHFVRA2R86fnVhs56j86TQ4vuMJAHQVNbkEdBUJQn0/OpIg0Y7VKKlboWwKeMY4qt5p9qmiOUz71XS5BJRSUtLUQtJRRTAKKKKACiiipt1AKKKKdwCiiigApaSlzTQC0baMilyKYhhTNNMWe9SF19RTd6+oo6gZt3Z5YENUAtCO9XLqZQR8wquJxn71LXY0Ww77IxAO6rEcLIvJpY5F2gk1KJUI4NO+hNtSrJb7gctiq/2VNoG88GrksihTzVPzeM+9JXsU7Ev2dRFjeelQSW6MAC5/Kp/MzH+FVXmAxTuJWJo7OP8AvmpJ4IxJw56VWS5FTSyhn/Ci5LWo6ONM/eqVYYypO+qyvzU68o1JtotJAY4/71O8mNm5Y/dqM49afuAY/wC7UalaIWOMKxANPeNWwSe1NjcEk4p0koHbtTTa1Fu9CFoV9TSJbK2SDQ84H8IoS5x/CKfMws76lu3i8snnOasiqcMxd8YFXM0LUiS1E70o600tQGGapIxmtCWkNLuHqKQkVZ5gxgM0CoppcSYFSckVDPTpL3UKTxUZfHelbIFYPii+FnoVx8+ySVfLjx1JP/1s0kzWw4WN1418TwaDp7YtrdhLeS9UC8cZHfB49/pXsFzbWelWkGm2EawwxjHlIAB+IHc1zXwk0SHRvBK3p4uNQzNI2OQoyFHT2z9TWqx5JH50N9EO1h9Mdwi5yPzodwi5NZ81zgM7PhRycnAAqRpD7mYMwPt0rE1nxDY6JB5l3OFLfcQcsx9hXPar4xmvbo6Z4Zt2vbtsqZlXKKfb1+vSreh/DkPO2oeJpvt12/JiLZQfU9/oKrQd7HPiDxD8QruOW1iNjpqEr5zsQD6n/aPsK6GD4SacseJ9WvHfuURVH5HNd7GkUUSxxKsaKMBUAAH0p4PFFxXOAm+E2lKoKajeD/eVDUafB/TZkITW542/24lI/nXoMh+UZ9ahNF2Fzz+T4LXfItvESEdt8LD+TGoT8FdXZgf7atSO+Vkr0bcR0JFOWaRTkSMPxouwPOD8FdU2EjV7TcOgCyYrPuPhp4u0pjJbbLtVH/LGfk/RTg16ybqbdu818/Wnrf3CnPmZ+oouwueEJqF/a3JjlM9vcx8OpBVlPv3rI1PUJbzxRaXd1M8hUIC7cnANfRLXEbyM8tpbyM42sxQZI9CcVxV54U8KeLteN3Bc/Z5bf5bq2tgFDkEj0+U56kdad0Ddyvb+OdDiiVX81yBjJQ8/rUy+P9CAOEb/AL9Zq8Phr4YXoty3ubk/4Uf8K38Ndluf/Ag/4UrId0SWnjPSrqIvHcRIAcESYQ/kam/4SrT9wC3UTHsFkB/lUMPw48LiZTIlyV6f8fRFS3Xwk0CaMva3d/AccEShx+opO3QLo1rDUFu49xHB+6Rk5FX8e1eaN8LPESzBNJ1YtCO80hiI/AZFTR/Dz4kWyKIdVjx0x9tbjn3H40W13B2PRaSvL7/TPid4fiaV3luIkUyu8UizADOOR17jt/KrehfE2GVY7XWUNvcr8rSEYVjnr7fSnyi0PRc0maggvILhAyOORnrU9JWDYXNJNK7WzRE/KRSZpDyDQBi7OelBtiw3b/wxUzDDEVDPI8dtIyEbgpIpMsfAWgcbW4PUetaqtuUH1rjE1mXzgXChO4UVv2N8rqpDZjPQ+lK3cGjUODT4jscMOoPFMByMjpS0El7xfpsnibwTqFpahhO0e+LHBLLzj8eRXh/h69DaaltMGEkbmJcjrgZr3bSL/wCzSiKQny3OAMdCa8x8f+D28J6k2u2HmTWF1OxljI/1DtzwfQ5bHHGBVx1ViGirZuPO6HitHzVrLsW8xEnAO2RAwz15FXBn0qZ7lQ2LSyA1IHqvGCe1TBT6VzylJPQ7qVOm43kSBhQwBFIBxTsVXM7GbpwvoRCNc1MBgUzHNS4+WiMm9zOcVHVDQARTyo2HAqq2QTz3qZZP3R65rnr07ansYHEqp7rWwhFRMvz5p+/2pC2T0qIRdzbEVIODswpr/dNPNMkI2HmvUikkfLVNWyJnUdSKfFIhbgg1mTjLZ3d6ns+HpSnfQIUramj2qvPAZORVkdKUdKm1zROzMu3QpMQatE0HAkOeKMr615Vde+evRTcLiirEP3qrKwzxU8R5ooXU0Z1/hZYY9KYWHrSN92oiDXZPENOxy08PGSJdw9aZMwZRzTKawyMZqViZdi/q0V1IZCihcn9ahLxf3wPxpbmIvtAbFQpZknG/r7V2xd0cckkySaMsI9oyNvWmrC+xhjqKknZofLVTwFpizvg57D0o8w6FfyZOMoakkhczHCnqKDPJuHTGfSpnuHE2OMA9MU2OxQMbeYeG6+lTNEywjg/e9KRrqTecY4PpVlrqU2w5H3sdKWoNFWFCZl4PWo50Pmv161ahupBKuSMZ9KW4uHZ2AIxn0p3CxVSPDDrTplJlbJ5zUkV1L5qjjH0pHupWY/d6+goQMjhGJl5NPkOGb61JBcymZQduD7U95nMjA7cDPamQ7FRT8wyatkfMarPOwbgD8qnEpY9qTQ0PxmpQPlFNU5H/ANaplBIwBU9SnsQnrVmD/V1EUb0qaIEIAetPoIfS0UUdBBRRRS0AKKKKEwCiiimAUUUtS99AEooopgFV3Ztx571YqFkJY00BXeV0NSCXIpWtywpwtyO9MCozHPehWPOTVk2ue4pv2QgdRRoFihcAsR0/Ooghz2/OrMsDE8Colt5Ac4oGrFhEPk4qSKMheTSojCLGOacisFxUttFxSIpoyykVXEJ24yOtW5A2OlQfMOw61StYmW5KkBMeM9qrTWZGPmFXkkwnSoJnPpS6i6FP7Pj+KrDW5JBB7U3cT2qUyHpimIRYG65FTiP5PrSRvlDxipGYiPIFJvUpbFZkPQYpxiOT/u1GXJY1ZLHsP4aV9RyWgyOJhnNJLE5PAqaMn0qQn2ob7iiZ5gf0oW2YnirjtxipLc/OaatYG2R28DI2TVog46VMAMU4gYoJepnOXzwpqMtJn7p/Krveg9DTFoZytLk/eqQPJjnNXEUYNRseTRdk+zi+gsUQdQ7dan24qNWGwc01pVVSSeBUlJW0Eup4rWB5pnCRqMkmuW0PQbz4k+KSVDxaVakeZJ02qfT/AGjiqsiX3jfxPBo+ns4gL7Sw+6o7ufoM17jpumWfgjw3Do9kzNNjc0xUAuxPLH+QHpT2KNG4ih0zSltIFWNFQIi98VhlsCo2nkkwWcsR6muS1rxmqXH9m6DEdS1N8qUjBKxEHBJ9cen61HoOxq+IfEdjokQlvptueI4l5Z/oK5ODStf8dMJ71n0zRMgrDjDyD+vPrxzxmtnRPBSwXX9reI5RqGqMchDzHEfQDof5CureUufb0q1puFyppWk6doVoLbTrdY1wAz9WfHqe9XDISajzUc9xDawPPcSpFEgyzucACgRY3E1l33inRNLu/st7qcEM+MlGPT646V534s+KDOJLHQCVX7r3ZHJ/3B2+teYvI8rs8js7sclmOST71Sj3A+kV8V6DMPl1myP/AG2AqRdd0h/u6pZn6Tr/AI180UYHoKfIhH02NU09ul/an6TL/jUi3tq33bqA/SQGvmDA9BSg46GjkC59RrKrjKsrD2OaC1fPHhfxLP4d1dbpSzxFSkiHng9wMjmu/k+Lljt+Sxnc+hAX+tTysLno27mvPvALbvF/iT/fb/0Yaot8Xk3caQSPebH9KrfDzXbFPEGsXd5cQWi3PzKJZAvJcnAJ60WaHc9czRWcmvaQ/wB3VbE/S4T/ABqVdW01umoWh+k6/wCNIC5WnuP9nKM8YrDGoWZ6XlsfpMv+NbcQE1ghjIcFeCpyKBoqLLJG2UkZT7HFWE1K7QAeaSB6jNVnUqcEEU2osM001ZpCy3SB42GCAtY+s+AvC/icSzPbeTdSHc08LYfPqQcg/lUtPSRkbcpIPtVXfQR45q3h3xN4Pu51sjdXWnRtxMkTGMjHcduvUce9bmg/EazdUhvE+yuONx5Q/j1FeqR6i5wJFDe9cv4g+HWleJpxcpKLS5OS7wRgb+BgFeBx69TVNpjL1rqdtdIhWRSWGRg9auGvHr/TNa8CajJCtwl1bryTESygHpuH8BrodC8dQzzpbNvV2/gk6fgaTXYLX2O1uY+N4/GqMi7o2X1GKvG7gaLcZAAexqo2M8dKQI42QbGIPaprW9ltWyhyvdT0NS6nbiG7OM4bmqdM1O103UIrhdgkDHt7VpdK89t7h7aQMjEeoB6iuusNViuEG9lUtwoLgmpt1IkjVBwc9DWvdWdt4t8OXOmahjEo2kpwVI5Vh6YNYe7HWrGk6gLXVVzja/yE+maS0ZDR5WqXPh3Wn0HU3ZpkbbEQnykdsH0Pb61sLXS/Fjw60tra+ILGJjfQyLFIsUe5pAfunPseP+BVylrcJdQLKhHI5APQ+lOavqOJfg71OcVXgIAOTUxIqErlXsL2pe1ReYvqfypfNXH/ANak4sqM1bVi5w1SE/LVcuuetShgR1pwhLsTVqw7jCuSaeFwhApF4zTi3BrKtFtnfgakIxbI9pzSbWzTwwzTq1jTuclStK5WuJJET5BzWRM9wzHJatidCcnPHpWe4+bFaXs7HOovdFIJITyDV+zBD8g0Io71ZhUZocUJNlpegpQaQdKjeVU6mhgI6Bjk9ahZKXzoy3LDH1ppKsh2Nz25rjrUryuerha0Yws2VncpIOTirEUzNu+Y9KqPGzPw3f1qSBGV2BYdK6oQ0R59ad5uzJvNfYf3h6etQebJn/WfrTwjYOfTHWozAT3qnFPoZqWhPcSYK4kxx2NV/Nb/AJ6n/vqnXEBOzDDpUX2Vv7y01FBzFpipVCzZ47mpEKE/w1XltTtjwy8DFNS2YEfMvWmIt3DohX5AeKhEyYOYxUk8W4r8yjjvTRakj7y/nSBCAxHGYx16U6SSESkFOQetBt2AHzL19abLaM05YMuCfWkti9CsZbcMfk7+lWPOg+zg7P4vSqps5Mn5k6+tTG1k+zquUznPWnoJtCLPbb1/d9/Spbia28z/AFZ3ZyagW0l3A5j6+tOubOQTHlBntup2FoCSW5lGE5prNBuPyHrRDbOsyksmPrQ1q5Y/cxn1oEOga3EgOCMd6fIY95+U1GlrIGH3P++qmktZAxOBj60+uomiq7R/3KsELu4GBgVE0DnPy/rU7I4P3ewpXG07DoiBnNWoyDmqqK3dTU6Zz0IoaTEm0TbcikAxSEsBSr0pWsVe4tFFFAgooooAKKKKQgooopajCilpKWoBRRRVIAoopaYBRRRQAtIaKWgRlPO3mEYHWhpmBPSrxtIi2cUG2jOTin6juioJW2ZwKfHIx7VZFum3GKcsCr0FIfMijNIy9qqGYlula8kMbdRUP2SIn7tPQGyokpxUMspyK1BaJ2FVbi1QYo0EmUllNPMjbqngt0MgBqae1VWyB2oArJIcVbGTCPpUKxDFaEcS+So9qVtbDuZRZt1TPIwx9KsvbKGpJIAcUJajb0G27Fgc0XEpRanhh2jrUVzECOeaGJblE3THPAqSC6IfpTDEvpTo4Vzmgplo3+0DirCXe9elUvJU4yKswoFyBSuwSQpmGaaZxg8U5ogajMVPUlxsPinABqF7hcmkQHcwqo2ctVELcuJNuQVieItQlSGOxtSxurlgiKoySDx/WtOA/uxVn4cWz6x8QrzUCkclpp0RjDOoO1z0256Hhjn0+tSkUd74D8Gw+ENDxPsbUJhuuJR29FB9Bn86h8QalBE8t5cSiK3jAyzdBVvxr4otPDmmr58rCWfIjVBljj+X1ryrT7HU/G9+bzVJJYdJikzHFjb5nPT8j978qCkiabVdU8cXT6doqtbaWrBbm7cYJGc8emfTqfauv0TQdN8O23lWEOZSAJZ3HzSfX0+gq1bwQWdulvaQrDCgwqIMD/6596dmgGPLEnk5pM1XuruCzt3nuZUiiQZZ2OAK8v8AE/xNknV7TQ90aHhrph8x/wB0dvrTSvsI7XxL4003w3GUkYT3hHy26Hn/AIEewrxvxB4p1PxHPvvJyIgcpAnCL+Hc+5rIkkeWRpJHZ3Y5ZmOST7mmVaSQmwpKKKYgpaSloAKKKKYBRRRSAKKKKADA9BRgegoooAWul8I+NtT8H3pmtGEsLjElvITsb39j71zVKATRZPcZ9EaR8XPDeuxRwX8UlhdPhfmG5M+zf411K2ouIVntJUniboysDXyfyOtdn4R+JGreFLcWcSxz2RkDGOQcqM/NtPuKlw7Bc94kglhP7yNl9yKjrmbX40+Hbq323kV3bOQcr5e9fzFaWl+JdG1ttunX8Uz4z5fKtj6HBqGmhpmpmnJKyHINMNFHqMvJeK6lJlVlYYORkH6+tcVr/wAL7O+Y3mk3n2e4wSIVQbHbk8DPy+nFdPUkUzwuHjYqw70bbAeQjUPEfhS8S31e3lERyF8wZDe6t3/Ouu0fX7fV4QU4k7iuwvo7TV7M2WoW0ckDHLbs5z656g+9eZ6x4NvvCj/2jpE73dpjLgD94gz3A6j3o0ZSdzotUtzPbbkGXTnHtXPGtPSNejvisbEiXbn0zV6502G5Bkjwj98dDS23GnY5wk0LNJESUdlOOxxV2azMLbXBBqq8OKaKumdNpepG6gwOSo59variuVcMOuc1zeiyCO5MZ4LDjj866EUpE2PR9MnS805SeTjB55rwjTLJNP13XrCMYit711QBs4GTjnvxivZvCkoa3MZ64/ka8asXeXxl4lLE5+2yZGf9tqcdUzJ6M2lQAU7HFPA4owK56tRwN6dNSK0isOQKiJf+7VxhxUezNZRxEm9Df6vC12VS0n92nB5P7v61YKCgIBW6qVDnlSoDFyRzQQcVJwKOKbi27s1hiIwjZIjUHNTgcVEWVeTSiZD0YVrHQ55y5ncSVciqRhYtirckigfe/Woo2BcYodmTGTWxXaBwelWLVSpOamkFEfU0dBEvaqN9EzAEVfpCAeozRoBhiCT3qYIVTBrU2L6Cqc4wTSlsVF6lDkMetKrsHOCelP8ANVWP+FT2zCZjgDA9qpbEy3K5dvKJyaj8xu+avXm6KIFcdcdKzzPIPT8qYiWZmBTr92otzepqxcXDp5eAOV7ikiunJ6L+VAAzHC5z0p8Qye9Syzl0QEL09KWI4PQVN9TRbDLsfMv0qPftj+pFW7mYIV+QHimC4QxHMK0n5gk7FNmO78afIT5h5PWnNcpkDyV606W4jWT/AFI+tO+grO5RLNk8nrUrki3XnvSmaHJzAOvrU7SQG3XMPf1p3QOLKcbEyrz3qW9LC5bmniW3VgfI5+tSXk0Im5gBOAc5p3RNmUonbzV5oMrbjyetTxXEHmri3Gc+tOme3Wdx5A4PrQ5IfK2VRI+epq88r7iM9hUAltc5+z5/GrNxPCrj911X1oug5WVsykE7jins8gbG49BSrcwjA8nP41PLMgIHl9qzcjRRZEjuVHzGp4ZG3jLGmJOu0fKOlSLKh4xSTE35FneKUdKiC+hqROnNUkQ2h1FFFMQUUUUCCiiigApaSil5gLRSUUJDCiiigApCwHU0tRuhbvTAXzVzin7hjrVF1ZDzQ0hCU+ugy4HBNSA1lrKc1dhYutBLJ80hYVGwYVWkdg+M0WEXNwxS7h61QEjY604SHHJoGPuJgjDntUAuhmmTDewJqLYKXUpbGskoaMGqVxMuamiB8ofSqVzG3pT0FYdBMpmX61enZdozWNCSs659a05QXUY5oAaHSrKXKhAKpGNqrsxBwaQ9zSe6QtQbhOOtU4ojIM5qRoCCOaZJfjkUrkVBdSgLRFkLimTxlx1pMpblQzL706OYZpDB70iw88Gki21YsiQHFTRyDJxVYIRU0S4zmm0SmSmUUnmqc9aYRTFAGaS0G5XGJIC74FUpH+ZvrVqDl3qpIMOfrV+pl1K95e/Y9IuJgfnVCF+p4Fdv4SFj8Pvh2NQvriOSe8AuAuzYzlgNsfIye/X1rgluba1voLrUU3abazo86g4ZiQ2wKB945AOOnHPFbkUd9471lNd1iJodOiObCzJBGMjJPHIyM89c+gpPYtK5VstP1Dxvq7a/rYeK0YgxWwJwQOg5/h68967tQFUKoCqBgAdqYgCqFUAKowABgCm3FzDaQPPcSLHEgJZ2OAAKSGTVzfiTxnpnhxDHI3n3eMrBGefxPauM8VfEuSfzLLQyUjPDXR+8f90dvrXnUkjzSNJK7O7HLMxySfeqUe4m7Gtr/ifUfEV0ZLuUrEPuQISEX8O596xqWkqvIm9woopKYBRRS0gCpreDzt3PSoa0NPA2N9aHsVBXYJZBehNNksXJ/drkfWtZNOu7uAtbRM6hsEhgK1NP0KZomN7vibOFAI6Vm6iR0KlfRHJfYZ/7n60n2Ocf8sz+ddNPZxw3TQrMSAwXJIz/ACqWfTEjjcrM7FRwBjmj2ovYnJtA8eN64z60m36VrXtq5hD/ADsQcY21SggEkm1wwFWpJq5DhZ2K2yk2ewrVWwiZsAP0zTv7MGOkg/CjnQezZkbcHgc00MQfX1rrNM8OW13bO8xl3B9owccYFc5qFutpqFxAuSI3KjPWhST0RMotDSqsM547VWPBNTgvGQGBHsRUTKSxIqkJ6iLjPNTwzvbTpPbyvHNGQyOpwQfaq/Q0rEHtzQI9L8NfFSaKVbbXh5sJGBcovzr/ALwHX69a9PsdSs9Tt1nsrmOeNgCCjc49x2r5jq9pWtahol19o0+5eBzw23ow9CO9S4iPpiivK9F+LbGSKHWLMbDgNcQdQfUr/hXptneW+oWkd1ayrLBINyuvcVLTQyxTlfajJ1VuCPWmUVIGFeeCLSe5kutNuXt3PzCAYKE89PTr+FUI1uLY+VOWWVDh/XNdaCVOVODSXmmxalbPJGALtcHPTdihlXOHuSyylWZm7gk561VYk54H51rajaTKCrx7ZEPI9qxWfnpTWpaC0uD9vh+Up84Bwa69ea4e5T/loM1v+HbtpbV0eQsytxuOSBQ11Bno3hOXBZPrXG6z4MPh/wAQajq6XXnQ6nMX2bcGJiSxBPfqcfSuk8O3Hk3BGetcf8WdZvU8SaBp0MpW2klEzbeN3zbefwz+dTr0M+pFIwyBmpARsH0qm7AtU642D6VhPVnVHSJITxTWbGMUw9KCORV04q5jWk+VklFFGK60jxHNjJDhDSIf3Yom4iJFRRuSprGpJRZ34WnOqtCvcyl/lj5NQRRypyzGnIriVxkYzxU6qxj681ySrSvoe3TwdPl1vcp3MrqOtNsZ2MvzHoaW6jYnGRioIF8tzXVB3jdnBWgoSsjodwI5pRgVki5bHDVLHMxx81V0MDR3gdTTwciqGS3c1cj+4KYD6qzIGJqyagdSc0gMmeIqSc5qxp3y78kUlwh9KpkkH0pga10A8QHvVPyVqspcjGSaXDn1pgXbi3MuwhhgLio47R1PY1HcFldev3RSRu24ZJpArltrcgLyOlSRxkHmqDGTPU9KkgdxIBzzSt1Ku7F64h3lTnHFRfZv3f3qbdsxdfpUak+WeaTiNPQRrbkfMKWaDMmdwpponGXzQk7DuRG3JJ+YVYNq32WPkdTVTaas7T9lT6mmkxuoxptWyORT762ZpVORyBUJHNPvyd68np/hVWM3MiitXEycj7wqa5tmM8h3DrVaFj9oj5/iFS3JP2mT/epOIKbQ37K395asXFuWdTuA+UVSJNWrv/ln/uiny6Bzu40W2P41qaaP5h8w6VRyasTj5hz/AAip5CvaMciFuMip0jIPWqURIOOlWoidwFLlE5alwHipFORSBRSqMUJJCHUUUUwCiiii4BRRRRuAlLRRSYgooooVgCiiloGJRRRQgGPEHHNRNagjGTVqjFMCqLNR3NTxxiNcCpMUYp6iE4qNoUZsnNS4pDxRrYCH7Mnv+dH2ZPQ/nUw5pcUgK5tEJzz+dILNPerNFA7jVjCjFQTw5UnNWqim+4aLILsxXhPm9R1rUgXKDJqhIDvqeOVgMZoAu+UDVGS0LOTuq5G5Yc1BIzBzg0aDTZJBBsXlqlMYP8VVgzY+8aildww+Y/nRoOxdWEBs7jStCD3qkkjHBJPWrPmfe570m0FtRskIA6k1FtK9j+dPkmwp5piTBh1zRFpsclZDSWB/+vU6qdoOTUTOOtPE6hQKdiExTGfX9KiKHdjNS+etMZ1JyKLMd0FvDhmJNVJ4/nP1q7DKATWLr9+bDT5Zl/1h+VP9409RI53TtHbxH4wmikLvZxS/vCoJAUcAe2cY/M17LHCIo0jX7qKFH0AxXMfDzS1s/DKXJwZbtjISRzjoB+hP410Gr6jDpGlXF/Pny4V3HAyT6frSe5SIdX1ez0Swe8vZNka9B1LH0Arw7xL4qvvEV87ySuloD+6gBwqj39TUfiPxFdeItSe5nYrEOI4geFH+NY1XGPcTYUUUVRItJRRSAKSlopgFFFGD6GgArQ0+N5I2CKWOewrPwfQ/lW1oMqxCXeQpOAM96mbsro1pL3jsfC9u402QSIVPmk8+mBWvcWjPAwjXLe1UtAnj8loWkAcv8oPeugVB+dcMnrc7VocnNbPC+JVKk8jIqPGP4q3dXsZZZ0ZCuNvc1SXRrp+hj/FqpSRRlS8IWGSR2FVlmheNlc4zkYI5xXQHw5eH/lpAP+BH/CopPClyxyZoB75P+FUpRJcWc/B5VvMrCcEKPQ1fN7bkf6zn6GrQ8JzNu23duccHAPFNXwu7My/bItyHBAU0OUW9yUpLoUpruFlO2Ug+2RXL3ttLJdSuql1JyGz1rtm8LOOt0n/fJrKuLEWk7Qs6sQcEgVcJpbMmpBvciuktZLZQwBbaB05HFY/9moX4cgH19a6uTR1AOw5+tZl5aNbJvHPOMZq4z6JkSh3OcurJ7cbiQRnHFVDW3fRPJbjYCxyOAKoJpt27geQ+M89K1T0MZR10KqfepzxbeR0q/qOmCylykn7snADDkVAgzlSc0xcvQpdK6Pwt4xv/AAtM/kgTWshy8DnAz6j0NYc8W1gVHHtUGKNyGrHuOnfFLw9d7VuGntHPXzEyo/EZrsbS7t762S4tZ45oXGVeNsg18u1teH/FGp+HbkSWU58okGSFuUcfTsfeocR3Po6q8920DoIjhtwyfasLw74ysvEtqTb/ALm4QDzInPI+nqPetCYNJMiKCSe9Q9NBpG9dxWl/EUkXD9nHUGvPtc05tNvghYFZF3jpxzXbrwoyearX1jb6jEEuEyR91l4ZfxpoIux543zrtx14zS6BdtBqvkOcCTKnjv2q1qOm3Ol3GyQBkblZB0P/ANesK4fyNTjkHB3K/HrVGh6fZ3Bt5ldTjnn6VueJ9OtdU8DXFwIBJPBGJ4yF3P8AIwcqPrtP51y8bhgCD712fha8NxbzWUo3KoyM9MHqKkzZ5asqzKsiEFGGQRVrOIx9Kw9XUeEPEN9o5iJt0uN0OGziNzlevoD+larSAJWNSPKdNNuSJQxxyaeTyKq+YMU9ZAWAopyVya0G4suUUgNLXYj55kVx/qWqCLhOTU8/MLVXUHb1H5VjVjc9PL6nKmUxLmZ/TmrML7kqLyAXJz19qtW0SocZyKxVNM9N4qUVcqXKuBnGcVnuH3H5TXRSKmOnFMSKPJ+UVvGNkcVSq5u7Od/eDsalimZByD1rfEERP3BRPaRCEkIKUpKKuKnFzkorqVLWTzeMcirucCqkYER+UVK0h4FYLE02djy+sT7qUIWGQOKr7qeshCgZpvEQ6AsvrdRk1s7A/LWVJAwJ4rY81sYzVQjdUPEK9kaLANJuTFs4QIvmFWhEtNhGFqZT71vzM4XFEE8anFVDGAw4qxd/eFVCxyKOhpTsW8DA47UADIqlJI4fhj0FNikczKCx6+tNJmctzRlSM4LEUzbFtI3D86q34Jljz/dqBlPlj61ViVsX9kX94fnRIkZbluazlHzDPrUlx/rTSs7lIs+XF/e/Wp/Li8hQXwM8c1lY6cVPKB9mjp6oTSLJjg/56D86LuFHZSZB0x1rNZanuR9zPpVE8pLFbxiZD5i8H1qSeKIzOTKMk+tUI1zPH/vCnXEWZn+tFw5SfyYT/wAtV/OrFwkR2ZkXhfWskqoOMVbuFwsX+7RcOUkEUOf9YPzqxKkOR8wPHrWZjmrcq5UY54FSxqI4CLPBH51PEqFhg8/Ws9FO4/SrdspDD60alcpo0UtApXJCiiikAUUUUwCiiihAFFFFAgooooGFFFFIAooooQEczMoUr61IJMKCaQjNNdcriq0sApuEHegTqelVWh560ixNnANCHYu+YKiluFVeeKT7O394VVuYWBX5hQItxTh14qTzBVK3UqDk1PjPekAS3axkAimfb19KSW3EmDmmCzBXqaAJRfKe1RveKWwelKlkATyaU2Cls7jT0ERNNEe1KrxnmnmwXP3jTxYAdGNAXGi4VOBVaW4XeTzVlrJQ33jTHsEPJY0AiAXAxQ8qnH0qUWMf940r2ceR8x6UtClqVxMoI61ZZ1yajNogPDGrDwoTk59KLK4MruykU2PAzzUxgT1NOSBe2adkS2yJuRTCDVloQKetsrAEk0NqwimFNSBDVoWq+pp3kBe5pXQitHEcmuX8a/JpaAnrKv8AI12CKMmuR8fqq6VCe5mx+hprfQtHf+EQE8IaWAhXEC/e/n+PWub+KmqyW2hw2UajbduVcnqAuDj867HRBt8PacMAf6LF/wCgCvP/AIuj/RNMP/TV/wCQoW5TPKjRRRWhAUUUUAFFFFABRRRQAVpTzSR2UBRyp6HH0rNq1O+beBe2KTRUdmTwaiEhKyq7vnht3QVGmoTCRSZG2ZyR7VUoo5EPnl3PRdLCi8t3JAXcDk/Tj+ldhaXFvcSbY5kcg8hTk145p2sXNhNHiRmhDhnT+8PTNelaPrWnXrxvbTqXYcx4ww9ciuOrTcTsp1IyO8l8MJPtIuCAPVef50L4VVGytz/44f8AGtNdWsF2J9qj3HjaDk1oVxXkatmB/wAI1/08j/vj/wCvQfDIPW4H/fH/ANeugopXYuZnNR+Eo0eRvOQbyDhYsdsetY934Zjgv2xM+WIzjIBJ/Gu971Wls4ZnLupLHHOfSmpNaoafc5KXwxKLhYjcZLKWBz0wRx0qNvBMbuXfy2Y/xd/5V2bRpvDH7w6UhGOtP2kkK5yI8HqTgyHHrmqmp+CoPsOZJHK+Yo+Vuck4/rXcSSJFGXkdEQDJZzgD8TXkPxA8carY+Ins9Lv4/sYhjYBAjgseSc4PPStKXtJysmTOaitSjrPh630+0nbE6yKOCTgD9KxbTS4bt8faLjeqZbElZ974w1zULaW3uL0vFKu112KMj8BWIskifcdl+jEV6MIyS1ZzTqRb0R0mraUbWIeRNO/PzCR8jFYW/bJypX2zUf2y6PBuZSPdyajaR5Dl2LH1NWlYzcl0LTuHGM5FV3XHQUI+DzT2ww4xmqE3cjAz25ppBHWnp98VI8YK5zyPakJK6Fsr66065FxZzvDMAQHQ4ODXdeEfiNPY3Zi1uR7iCQj9+eXj/wAR+tee4J4AopNJiufUNtcw3ltFcwSLJDIoZHXoQalNeEeCfGtx4cuRbTZl0+VhuQn/AFZJGWX/AAr3RJEljWSNgyMMqynII+tQ1YZHNBHcQtFKodGGCDXl3i+w/sq/jQPuRgWXscc16o7BFZj0AyawvEulReINAliQKZgN8DE4w3+eDQhp2K+l3Kz2MEiHIKDmuv8ACUxXV9nHzxsMZ/GvIPBeqS2076XeK0bAkqrggg9xzXqXhqQrrtrzjJIP4g0mOSOa+Odi0V/pWpKMJJG0LdOqncP0Y1mbw0SkHqAa7H432Mlx4Nt7pHI+y3QLrnhgwK/zxXGWiB7KBu5jU/pWVVXSNKDabHZ+WnowDCneUNtKYh5ZOO1ZxWptNuUWmWRMvrT/ADU/vCsnJxTmJ2V2ps8meFja9y/NIpjIBBqIB9vSqsYO41poAUH0qZjoR5NCkN24jFWYFJbpT9o3dKmQAGsk3c7HblEZARSKoGalxRtrS7MbIgZxGuSDxUE+ox+SVCtmruwVG9vGATsX8qzqtcjuaYe7qKxkfbADnYfzpHvQBnafzrV8mM5+RfyqKS3j2n5F/KuJOm+h7TlWXUzhqA/uH86X7f8A7Bq0ttEc5Rfyoe2iGMIKTdNO1hxnXkr3II7vewG08+9SF8dqesCDBCgUjooBzmkuVyVipOaptzYi3YVfu/rUiXeT939arKITx81SBYgf4q9JKJ4DbCa43yAbe3rULOqsPlz+NPbyvMzz0pr+WWHejQabGSSDf9wdB3pY5B5i/IOvrSuYwwyOcCpIjEXUYGfpVLYTYl5JmRPlHAqNnAjB2irFzCWkGBwBTTbkxgAd6L6ElfzgMHy1NOe5UtkwqTT5LZto4qNrZye1Lc0Vuo7z1+U+SvSnPcr5S5hXANIbWTC4HanPaymAYXnNFg0IftUf/PutSz3MXy5gz+NV/ss2SNhqxcWkmEI545p2JuRx3MJlTFvzn1pbieITMPI7+tENrIJkJxjIPWi5tZPPYgcE+tFhXIDNDn/j3z/wKrUssJWPdD/D/eqsbWX+6PzqxNbSER8fw+tFkMbvtx/yx/8AHqlkuUjwPJB47moBay54X9aluLZ8jjtSsgYxbxc4ECfnVmCQOQdgB9qqLasOoq3AhWjQbbLpzSinYGKbU8tg5r6C0UlFMQUUUUvQAooopoBKWiigQUUUUtdgCiiikMKKKKYBSYpaKasBGUJoCEHtUtFMLic1HJF5gwalooJIEg2cdacI6lpM0rlEbHaKb5uKS4fGKrF6lvUaRZE/zYqu98yykY4pEbLiq8qZkJzVRfcOW+xM2oNnpVyCdpEyeKyvKz3/AErRtFwnWmKSsLIzeaOailkdQcGrLqNwprwhhyaBIz/tEmetSmSRsc9qkFoufvGphbrgcnpSNEVd0lNmmkXIz3q95C+tQzQAnINHURnm5lB5b9KntLl3uEUng02S2HXNLbRBLhDu6GmiJOyNYxg04JgYpA4p28VVjidSQwY8wr6U8qDUAcee3FTZNOyM3OXcqyy+XLsA61yfjx92jwn/AKb/APsprpbrP2n8K5vxsmdGiJ7TDn04NQviPQp6xR6Ro88f9g6d86j/AEWLv/sCuE+LMiPp2nbWBPnt0Of4a37OKNLC3RB8qxqBkewrjviQqizsCBz5jfyoS1NGed0UUVoQFFFFABRRRQAUUUUAFS7ZJIxgZCj8qiAyQPU4ruLzw3H4a0xbu9n81JCFURoM5I9CaTdioq5SsfAmpX2mw3qzW6xzRiRAz4OD68VRsPCup32oPZIipIgJLMcjj6V0Nl8Qrew063s49MkcQxiMMZQMgfhWLL4uvRqpvbVpIgekbSEjpg+lZxdR3ujVqmkrMg1PwvqekQtPcRoYQwUMj5yT0461mxS3Wn3KyxmSCZc7Tggiuqi+IV2IUSawt5toHLM3J9ayvEPiRtfFvvs4oDCWOYyTnOP8KqLm9JIh8u6ZreHPENxNdv8Ab7kERoGVmwO/f1r3TQdXg1rTFuYXR8Eo2055FfOFra6O+mebPqE0d5g/uhHke3NT6B4z1jw0JF06ZFSTG5JEDAkd6xq0Of4TWFZrSR9OUZrxW1+NOprEouNLtJXHVlZlz+HNdv4S8f2niK0uJLz7NYSxSBQjzj5gR1GcVxzw9SCu0axqwk7I7LNIfrXAeNvGS6bJapp91uIUyO0DBh6AH9TXHH4s3+Pv3B/BRRGhOauN1Ip2Z3Xje/u7PUNPFteTQK0blhG2N2CK811Tx54kstRngg1SQxZBG9VY9PcVDqvjy41aaGWdXZoVKpnHc89B7Cua1C5a8u2uHiKb+xrro0bL3kZTqX+FnRXXjXxDr+lyaZP5c8DldxWHDZByOR9Ky7LQLi9uNk4eBcZ3EZzVS31FrGPEATzD1brS/wBtX8rhWuXA5xt4xW6p8qtFWMnK/wAR1lr8P7S5AJvp19flFWIPhlaSqxOpTghiABGvY1yD6xqcceU1G5B9pDSQ+JNahyU1S6Xv/rDU8tTuO8ex0eq/DtLCKOSLUWYNIEIeMcZ+hpj/AA6KwPJ/aX3VJx5P/wBeufuvEutXCLHNqM0ihgw3EdR+FO/4S7XdpU6g5B65Vf8ACnyztuS3G+xjOpR2U9jigMR3pZZGmlaRzlmOSQMc0ytCCVCA2TUwZSOo/Oqo5p20+lAJ2HKPnOKSRcHPrQqkMKkkXKHjpQPdEFeg+A/Hp0ll0zVZC1geIpDz5J/+J/lXntFJq5J9PTkXFi7ROrKyZVgcgj8Kz7SZlATqO1eMeHPG+p6BE1ssnnWjDiOTnZ7r/hXrunz+fFDMOjgMPoRUNNFx1RzHjrRZVni121Vt8RHnBABgDkMe/oK6fwrrEV6bG/U4wyl1H8J7ird1ax31lNazDdHKpRh7GuC8EySaT4nu9DlB+YsQcfxL3/EUboa2PWfi0Fm+HV4QcjzYmH/fQrzrTjnTbb/rkv8AKuv8d3/m/DS6hdvmEkaDPf5ga4nTnP8AZttz/wAsl/lWNX4Ua0FqzSz8v4VNGAV/CqQkO3qOlTxS4AyazizWS0JzGg/hH5Um1f7opjSj1/WkWYE9a7U0ePOEhZlAToOtSxHMY+lV55F8vr3pi3sSAAk/lUzKpaFiWdYSC2efSiK+jaQLg88VUuJUnClT061HCmJ0Of4hWcbXOqTly3RubhRuFRig9K1sjzvrMiXcKRwSmQCaRRzVhWVVJbpWFf4HY9HBSvVjcqqpycqfyqG4YJEzEED6VbaeMtwe1Vbt0kt2UNXnRabWh9BKEtdTPju4y2ATknjipZJRj3qmsIDgjPBqd1LVdRK+gUFLl94esuR3pGy4OKakZqVAQKqnFc1zPEytB2KwgkyOn51L5Lk9vzp0kjRrng/hUQvmB5UV3LXU8KzEa3k3dqcto7dSAKlju1OSy083aDjBqhorS2jlxjBGAKdDbSLIpIGAfWrAmRuc4zT1lXPWnrYVwkByKrzBw/BPTtVtnU4waftBAJpoRQkL+WOTUJLeprSljUp0qsY1NFxorGR+PmPSlMj+V949fWnvGuRz2pNi+XjPejQCuZZN4+c/nU08khAG44ppiXdmpmRTjNS5WLjBsrxlzIvzHGfWi/kdHG1iKsoihh9ag1CMswIpc19QcbFAXEuf9Y351oPJIAnznpWesZ3dDWx5Csqc9qbloKO5DFJIW++aluJXGPmqSOAA9adNb7x96pTLdrlJZ3IOSPyqSOVy3WmiEKSN460+OMZ+8KWtx3iXQeKVelJjilXpV9DEdRRRS1AKKKKNACiiimkIKKKKTuMKKKKYBRRRSAKKKKACiilFNCGZb+7Rlv7tSUUAR/N/dNHzelSUUAR/N6UfN6U+kNDGU7pJGC7VNV/Im/uGtPqwp+B6VPK3qZTq8rsZaQShxlTipWtZc/d/Wr5A5+lKcU7WRVOrzGcLWT0H51PBEydRVmgUGjdyrOSrjrTlOVFRXxwykGoBKdnWqWxNrF9MZ5qQYzWakrFupqbe2e9DRSLkhAFQuDnpVOaVsjk9abczOJiNxpWHexOyE02OEiRTjvVd53ULzVi2lLgZP8QqkrES1NAR0uynBuKC1HMc7o2IFT98amC0xTmU1NVM5Jbmbdr+/rm/GoH9hpn/AJ7D+Rrpb2RUm+Y4rl/GM6SaKqqefNBPHbBqF8R6NL4UdlbWV59khHlLkRr/ABj0riviXBPDZWBlQKDK2MNntXptnFIbKA5HMSH9BXCfFiFl0jT3bHFwRx/u/wD1qFuaM8npKU0lWSFFFFMAooooAKKKKAHxRSTPsijZ2xnaoyaluLu5uMLcTyybOAJGJx+da/g5d2u4/wCmL/0rP1pSus3YJz+8pX1H0KNPiiknfZFG7segUZNR10Gl6uttaJAFkLdOMU23bQqCTersUF0fUC8atbPH5jbVL8DPv6U2/wBMudN2faNg3HA2tmuguUvbyB41heMrgglsHNLbeGPFb6cl3DFE9vMA6FnjdiPX5skc1KlJ6lzjGJyfI9qaRW3HfeIZFMUP2lkztwkIKn24GKyZ5Z3cpOzlgeVbjB+lNNtmbWhDzVuxglupxHGAxAzyccVVrV0EgahycfIadxLVm9YWeIRHcoAF7gA5/Wn3nhixMUlzFPk/eKmVFP8A3zuJqYtgZFcxfQOkjlgfmYkEg9KnVltWK1ykMLDymLH+VV3dnPzMTUsULyyIpVsE4zipbuxeBQ6qSnc+lO62DlbVyooGD2rb8N6Q+oX6ynyzBEwMiseWHoKZ4a0J9f1VbUMUjA3SSY+6P8a7i40Ky8MW6JJNNJ9oJB8tRzj3z2z2rOpVS91PU1oU7vnlsRtoNgwKm3THuK5zSvDsBvrlLlvOSP5VUcc5PJx9K7SP4dTXFuk6Lc7ZFDAG5HQjPemR/DO4jBZknTk4xcKCfxArJcyT1Z1SqUnJPlWnn/wDnr/w7YPbfJD5ZBHKHmsG78OBNzW8px1Cv2/Gu3uPDFzokXnTtMYmbYN04fk5/wAK5rxJN5Gn5hlZX8wDtnHNVCNRdRVauHle8dfI5W5tJbUr5mOemDVenPK8gAd2YDpk5xTa6En1PPla+gVYWZmIXanPH3ar1LDzNGP9oUBFs0L+GG3iQxoAx61nmT5SD1rU1j7sJGO/9KxzQrFTeolFFFBmFez+DdWtr7RLRfPUzwxiORCw3AjjpXjFT2l1JZ3cNzESHicOCPY5pNXGnY+jVPFcj4jgGk+JdM8QIMJ5giuCCenTP5Z/Kurt5EuLeGeM5SVA6n2IzVLxBpw1PQrq225cpuQf7Q5H+H41ktHqWh/jhA/gq9KsMB43z6/MP8a5TToydMt2B48sfyrSGoDU/hTMJW3SQqsEmOoKsMZ/DH51V0xEGkWoGceUKxru0UdOEgpTaYuwhacEbAqbau3rSjFYqR0zoRIdjURxOWNTDGKdGQCa052kcMqSIZIXOBj9aryWkpP3auSzbW4GaaLnkcVvF3RxySUiKK2kXhlxmrEcDiRTjvTHvApXIp0V6jzIoB5NUoluT5DQG7+7Snd6UuaNwrWx5ALuH8NEu94mULyfeori48hQfWqo1EnjFJo66KnZNCeRNz/jURglOR/WpRebg3FM+189Kz5F2O5VJlZ7aXB5/WkEEuV+b9ae13ntSm4PHFPkXYFOXccIpAvX9aEjlVsk5/Gj7QRjilNx04pcth8zYSB2GMCqzRuD2qx53OCKY8mTwKIoY1EYqcnHNL5R9aWMk5qQA07CuQGKTPB4+tSQxyBuf51Jg1PAvNHQVxCGGARzUwlIUA9abKuCOKguCVK0C6klxMwjPSs/7Q/rT7hz5XWqO85qXE0UrIuh9y5yaBgr1NQxnKGpQeDQ0CDJXpk07zmwDtpARzQxG0fWpUb7mim4rQkjmO4cU28m5HBpIz0qO7OSKfKloS5OW5CJfm4WtOKQlQMVlpjNaER4FPl6EvQto3PSnSOMcVEhyanEYI5pktlErlifenInzVc8haaUVCMU9LCJMcUAYpaKTAKKKKXkgCiiinsAUUUUAFFFFGoBRRRQAUUUYpAFRPMiHk4qSqV5Cz4K801uBKbuP+8Kclwjd6ymikHarNsj7SMUwLpu4wfvUn2yPsf0qoYHJ6Chbd9w4/WkFi39sjpPtiehqD7M+TwKa1u4PSmBY+2R+hpPtqehqsYH9KTyW9KQFtLtWkAANWBL7VnxW8hmAGBwetXBBIO4p2ZzVZQ5tRWnAJ4oNwnPOKhktpDk5FVmilDkbCeewoadh0XG7sXvtEf94Uv2hP7wrP8ALkz9xvyqUQOR900rG/MF1KshAByBVcFcUk8TrztNQEN6Gmkx3TNC2Kb+gq5lfQVjQBvMAwa0ArY6GnZiuLLsJ5AqK4ERlySM/Wqswfd0NJdIySDIPSlYdyw4gKjJ/WnK8caFk7HNZzbsU+IMUce1FtR83kaQ1AEdDQb8E4CmszB9KfHkyD60WVxNtmslwm7JOKsC4Q/xVmMu1sGpVibaD2ptnH7FPUh1FhJMCK5nxQudJ+kg/rXT3ETbhhSaw/EMLHRpvlPy4bGPepT1OmCskj0vTW36XZtjGbeM/wDjorh/i4AdCsf+vk/+gmuz0Sf7RoWnynAZ7eMkDp90VynxQtJ73Q7OO3jMsn2nhV6n5TTW5oeLmkrd1fwrf6LpyXl40QDuECK2SCQT9O1YVWmmJhRSUtMQUUUUAFFFFAG34VkEeuxksFzG4578VV11t2tXLDu39Kh0y6Wz1K3uJAWjRwzqOpHcVveNL/T9SubSbTypAQhiqY78f1pdRrY5atCzjChHJPXPSqAUmt6HTrlraMIm4kA9RQ2ktS4Rbeh2UGmajqVnK1lYzzIQU3pjCkj61av18R2tkLKx0y8+y7ceX5IYrnr8wOcZrb8Ka/Z6PYyx3glBcggIm7+oral8Y6VMP9XMfrGB/WvPdepGVkro9KdFT3OK0OC9t9MkW7tXtX85mEbDHGB2/OuR8SaVbpLPcoGWViWbngnua9KvNRs73/j3E3T+JMD+dcrq2mrchlZ3APotFOb5+Z6DqU4+z5TzeREVlCMxOPmz61s6baKt4oj3/dyc+lWNR0CKPzJ42cdCc4xXXaNp8UUUZaIDAGT3Ix612891dHnqnyt3KmkbYNXs2dAEWVSc9OverHxGlt7zU7doGR0WI/c6A5rVe0t5ZScY9MGqV7pkJYMcsR6mna+pLtc5SxTCKuO1N1k+XZbQoO84z6VtG2jjk4Wn3+lwTWOWjyev0rKS5Xdm8XzpxRS+H8y29zeMTtJRep612GtXUF0lsvytsy+Rzg/WvPkjbT5JGgZkUr8wB616Dofh57zwzb6iJ1MZjZ2GORgnj9KagpT9oTOryUvZs9HsHX+z7baQR5a9PoKluiDGPY1yPhfVtPhtmtfMcMB1IPNbF5qlobKT9+QSCAQpBBqpQlGVmjmUk1e5jeM1P9iIw7Tr/I1x/iXQLBbay8mDAntg8mWJ+bA5GelWb9b6a0CvetIrPkK8jEVJOkjQ2f2hw58njnPtVV4uEE7l4ZxnNnAnQEsp0kAeVS20hwMAHitKbRozp13MsCBUjYghfaupmtILqNVkUgIcjacYPrUGowpY+Fb5UJI8p8M3Uk//AK65fat2Ot01FM8jxg1NbDNxH/vCmMBjPfNT6fE09/DGv3i3eu04luX9YPywj2NY5rb1uEwXMSPgjZwfXmsaQAHI/Kki6i1GUUUUzIKKKKAPZ/htrS6poI092JubL5TnPKE/Kc/p+ArthGc9K8F8C6pLpXi6xZD+7nkEEq+qscfocGvoTbjisprUpM8+8S6Tc6Ha6pcQAHTL0K7BR/qpQwOMeh5pNIaObRreRf7pHX3Ndf4wgE/gXVUP8MBcf8BIP9K4vwYrXHheE4Bw7ryff/69Y1/gudmEa53fsXzGpWnJEpFW2ixGRjkUxYzjpXFzu7PQnCPLdEIhTHehIk5qfyzjtSLGeafPZanE6WpA0SZ5AqN40DDgVaMRJqN4TmuyDdjjnFKRWeJDj5QadBGgmXCjOaeY8U6JcSr9a6InPNWiy5S0UVoeWQzqrINwzg1VQQEkbOavSLuXFUxbsrsc1Ero78NbkEXyArYX61GptySAtOELDcD3pi27A5yKnmOrlQ3dbY+7UxEAAJWq/wBlfHUZqVoWIUccCi4+VEjrCNvGKSUQrt470rws23npTJoWJXnvSuCSHZiEo4FIzxbzxSGA+aDnikNsSx5709bjdiQyRJ6c05Jo26c1BLaM5GCOBT7ezZHJLDGKCLof5qZqeF1PQVD9l5+9U8cJQdafQSYshHFVLvB2VbkTJHNVrtPuc0tQ6lOVQYu9Uiqg9T+VaDJuTBqrJAQ2BQNCRFNpHNSqV2nk1EsRWnbTtNTK5SHhk5+Y05vL2L85qtg05gfLWmFydPL4+c9fSm3XlnHzn8qiUEYplx2o1uHMKmzP3j+VaERTA5/SspOtX42wKTuh3L8ZUtwatDpVG2B3Z7VeB4oRLCo5PvipM1G/3xTEOoooosAUUUUuoBRRRRoAUUUU0AUUtJQAUUUUAFFFFIAqnLdx+Zsw2QcVcrJmjb7Rkg/epoCWWVOmDTY51jB96Y6Ev0pjxNgdaB6Fn7Wvoacl0pcDFVBC3+RT4om80cUagWmvFVyKT7YhqvJbuZWOKT7O+OlGgWLIu0pRcRkgZqmbeT+7TvJcAcGmKxpQOrTjac8GrRIrMs9yXGCCMqavZ96tPQ86vH3xzHANQtMqnFONV5Au/kmlJmmGVmyX7SgPIqQXCY6GqckYLDk1YWFSBU3Oyw24uYwvQ1VNwnoatS2qsB7VVdI0baR0ouFh0VwgccGrn2mPH/1qz1eIMPlp8ksZUgDFFx8pKbiIuPr6VLO6lgazg0e9cjvVy4MSlRg80bMLA0kYXJ/lRDJEwbA6VAzxAZIzRFLHhiqduaAtYmWWNjjH5imiePeMDv6VCk8W77mDUa3EQkH7vvRbUDZBDN0qyQMDiq67Tg4qR5Dt6UmQmKPvH6Vz3iM77S7T1iP8q27eUuzZrD1MGQXIz1Vh+lSlqaJ6HSeGH3+F9MPf7OoqxqA8yS3VhkAsent/9eofA8wm8IacSAdqFDkejEVfvh/paIFAXYTx68U29xo88+Jf/ICtx/08D/0E15XXs/jjTkvfDdzJI7Ri2/fKQOpAxj9a8YqqXwhPcKKKK0ICiiigAooooAK6HwrpNprNxLBdSSKY13KFOMjv/Sueq3pt69hfx3COy4OGwcZB60mnbQqLSepY1nS20i88gyBwclT7ZwM1a03XLmBYreOKJwPlXeDV/wAZRoyWFyjbg6MM/kf61U0bTYpY4blpHDBs4AGOD/8AWqG043kbJSU7QNNNY1eVFWO1hXJHzYOf1NdkmlXGSViX/gSmuo0zSLbUbG2uJkJJw2AcDg5H8q6dooS2SoFebOunpFHYnKD1dzy+R5tPxE0MZJG7uK5/XPEs9sESK3hDOfvMCcCvUNd0L+0r8yrKkSCJVHyZJPP6dK4XxP4F27Zzfbkzjb5WMZ98+1b0p03bm3M6jqNOxymkT3mvaits+1oyQzgDAxnmug8VaqmnSR2ekiLzkz54AD7M9AMg81nRiLwvokuXSS5uCVQYwe4z9BgVD4V0n+0ZpbqcmTa6glskknJyT+H610Npe8tjCN2+U9G8DaJHqeifadV8ySctwQ5UAY4GBitzVPC+mw2MksET7x6ysf61oeFYI10t16AOBj8K1b2FDakDua43WlzGvJG9jyaa1sYJP36Kqg/xMf8AGrWpRWselgJbLu4Ax9ateL9AbUbB7e1EaSsQQ54I9f0ritN8TtC8uk6mqjZmOKRk2kY4wfr61vzc6BR5GOksoriE5jAOe1df4Y1L+zdF/s24jXyHcleSRgjkH0qhp9l5cTxzJE6t8wOzBH5GtM2qBVVcALwBTlVUVyoXsvaPmmakNxa2TB7OwtoWUYDIpz+ZNPu9YnvIDFMsZQkEjb6VlJCUXAbjPSnNkcUKpfW5lKjy6dCWNow4JgjIHYrWsI4L63QPBGUTopHT/CsmDYNxfHtTrdh9pLbsKB64rHExdSN77GuGtCWw+7hgt5HSOJQPpXGeM7gR+GZlVh+8kROPrn+ldPe3druZGlUnuOtcF46khFlaRQqMPIzMw9hx/M0qMXdXKqy0djhvLZkyCMZ5pDmNgUJB9QanQjyyNtRKQxwcfjXpHHYjeR3xudmx0yaYWJ6mrs6LHCSFAPSqNCCcXF2YUUUUEBRRRSAmtXMd5A44KyKf1FfUee+a+afD+lTa1rltYQMiySHOZDgYXk/oK+lhzUysNFXXV8zwlqy8c2sv/oJry/wFqJi0O4hK7jHOW69iB/ga9B8Y3t5YeF5fsgh/fboZDICSAynpjjP1ryXwdIYTeQ46le31FTyqStLYuLlHVHfve/uidvX3pkV7u4xiqhyYaSIfN1rH2EL2sa/WKltzQa5AHSnRTZGcVQcErxSIxXjNW8NCwo4ibepqhwaRiDVaKQetTZzVQikRVepG5qISbGBx0qSU4qs5q1oZNXRcFyD/AA/rSm4/2f1rPJyc08y7Vq+ZHE8PLoi4052jC/rVT7Q/mkZ49KcHBxSiFC27vUSZ0UabirMg85yH5pizSc/OelWxAgzx1pBAgzx1qbI6LlHz5f75qd5nVFIY/lTmt417Vc/s5XRMyAfhUynGO5pCE6j91FN55F2YJ5FRzzyAqN3etCTT1Yp+8HHtUVzpwVfM8zOO2KlVqb0uU8PVSvYqrM5mAzxTTPJu+8etWktU3B9xz6UhtEJzuNacyOezI5Lh1YAHsKkgumZsNjFQ3QVZQCf4RTY2RW6/pTuiVFtl5bkZ6VKs4I6VnbxmrEbccVCmnobSpWVyZ5TkcVHOwO0Y5pwG6iWPcQc1oYsgP3elRDDE5FaARdmPaqToUcgdKGtBJlaSTa2NopvnDB+WpZEyc1EUGOlQ3bc0Q1ZAT9ypyV2D5RUSoM9KnZB5Y60rlxSaIjIi4JSoZpVb+GpjGHx1pj24Hc1VyWtSJHUfwVejkUqDtqqIF45NWVj24AP6UaXE9idLgJ0T9af9uI/gH51EsG4df0qGRNpxmjQksnUD/wA8x+dKt7uYDYPzqjgmlUEMOKLjNgHIpajU8CnigBaKKKACiiik0AUd6KKFuAUUUUgCiiimm9gCiiigQlV5UYnORViqF9v8xdoPTtTRSArJu6ipUidwfmFUCspI4apYPNAf73SiyC7JzGw6sKdEv7wZZfzrPKyE5KtT4Uk81flP5U7ILs0mxvOWX86cEHqPzrNkV/Nfg9afE0qpgqanlHzOxoKgBOSPzp21fUfnWcxlbd8p6elVmE2ejUrKwXbNgJ/pCkYI2nvUpU/5NYimZSCC4P41IJJy4G5+T71aeljnqUuZ3NYqfSqcqSeYcAYz61Tk88SsMvRibP8AFTYUqfK7llxLx0z9asRO6r82PzrOdZcLnNK0cuBhWNTY32NUsxHGPzqlNGDISZFB7imW6ShGBUjmopYpDIx2GhIY/wAlSw/er1okiQZHnLnNQpDJ5i/IetJLDKXPyNT2ESCNMj98tWbkKdmXHSs8QS5H7tvyqzdRSfJ8jdPSgVhropH+sFSwqmGwwORzVXyJCPuGp7aF03ZHUcU0DSHCKIc7gfxqJYk353jg+tSiBtv4VD9nfnAH50gNpXAQGldgV/8Ar0Io8lQf7oprADIpNpCUbkdt8pbJFZdyNzScjnNasQ+dvpWXKvLfWjpcEtTS+HEwPh6W2LAtBcOPoDgj+tdHef8AHwnH8J/mK4f4f3fk67qmmYOGPmqPocH9GH5V3V6pEyHj7p/pSluWct45OPBmo4z9xR/48K8Mr6A1+xXU9Du7R3KJIuWYdQAQf6V4AwAdgpyATg1cNhSEoooqyQpKWigAooooAKKKKLgdJp8/9s2MNhcLu+y52k9Np/8A1Uy2v103dB5Rfy2Izvxnk9sVQ0O/j07UPNlZhGY2UhR1OOB+db0GuW1zkixfkkZ+U1nJfcbQemj1O88J+NLSXSSJ0MTwybNmd2VwMHPHvWgfHFkxJ8uYc8dP8a4yyRprJ7mOxcJkg8KCce1VpdVs4SFktZUbGcMgH9a51Qp81zZznbU72PxlaSKUCy5PHT/69cRqvjJI4zbie5upCmMO2FB4IJ5P5VWi1ixZvliky3oP/r1BDpFvq175NnaO0rbjgA5OB/8AWq1ShAnmk0ZWjW7a34hs4LppJBLKFcluSvXr+FevaZo1lpUDQ2sJRWbcQXLc/jVPw54Hj0qeC9mhCTxjOCTkEjHr710PlsWJHOT2rnrVeZ2jsdFGnyq73Nzw1CUhnwBtJHfvg1sPGXXawHJ9azrC7srSHyzMqsQCfrippNVtRjE6nqK5m2D1ZheJohCIQo6g5rx3xzY4vLaeFCdyHOBx1r2XW7mG6kjMbBwFOaw7iCGSFhsAOOK2pT5bNjceaNjzfw/r8kVqkdxOWlSTaFlbOV4wB+tdjb61Zzw5NzCjjhlMg+U+lc1qHhzbcs/2WSZcjle//wCqq9pZLZlmFlIEPqpPOa6rRkc7Ukdg+r2EeC11Efoc02PWbG4kKxSlyBzhTXLy6lbQlS8LqD3KUlvr9hDMzt5gBXGFQetNUo7iU5o6l9Ut4iC+8KeAdlQXeoxOiMm/qe2KwpvE1hIipiXhg3Kf/XpjeJtPKkMJicYHyD/Gl7NIOeQ/U75vsVwYkk3lCVYdQe1cRcz3lyqi5lkkCdAxzit2XWZXGAsYB9qym/nWkFYbRQHETEiqWcGr93IFQr/E1Z1ao55bksk7OgU44qKiiqJbb1YUlLSUhBS0UUAdN8Ps/wDCc6YAcfM//oDV9BKMjFfP3w8G7x1pvsXP/jjV9Ap2qJboaOL1zU5r7R3sWRf3cu4tjlsZHNee+HnaPVryMZBLjj6E16Lo9impLqBlLFYy5G04wSTivNbOf7N4sniAGGuChPcYJpLsXdJHd4byuQabGG3dDSsf3R5amwKS/VqTTvcE1Ym2moyh3Hg9atqmB608IPSqTRPUqxhlPIq2ppNg9Keo4oQpalec8iq7HNWLiQKwGM8VXMv+zQJCZpGPy0GbH8NI03y/dosFyVTyKnGPSqRuBuX5alF0f7v60mNXLfGOlJkelV/tRx90fnTTdf7P607BYlkIx0rSG3CcVim43EfL+tbinO04NcWM6Ho4BPUY4BZeKjuh/o74Bq0eo4NR3LD7O3FckJao7Zp2ZQjUkDg9KTafT9KmjcYp6sCMivRutzwJylczLz/Xj/dFQAc1enAafkDoKj2LnoKJVEtDqpYdzipXK2TmrEPI696eETPanKoUHGOtR7VG7wk31Hq20AE96dIx3rzxUfGalwCRWsZ3OepRcCfK7aq3ABORU5xio2CmtDmKTYNQkVdZFzxThGuKXqO5mElT3p5clAOautEhNN8paOUak0VEJ96l2F/WrSQKT0qdYVA4otYHIrx2y5GRUkkAB4FWUQAinuoNHUm5TVcCq0gO7NX2hOM5qm6kMaGhXIulA5dfrSsvGabGCZV+tLl1A0BnFSLmgDApRTKsLRRRR1AKKKKOgBRRRQIKKKKWgwooooVrgFFFFABVC4n/AHnB6cVfqhPbpvJ3kE80xp2IROfanxzkxydOBxTPIT/nrTkijCOPM6ijSwNkP2hvb8qlguC0wBxUTRIP46kt44xMuH5pqwaiSXLCVsAdakF0dnTmo3iQyMd/egRpjG+jQLMnjuSY2JAzUJuCf4RUqxIqHDdRUXkKT97NToNJjvtGADtz+NAuT5i/L3pfs4IHzUv2Ybgd1VoS7iXF0RN92mG75Py0+a3LSE7hULW5HcUaDsyR7klAcd6d9sKoPl5pgtyYhlgOaU2uQPnWiwieG6Z0OQBiqpu3LHOKsQW+1SC6moDaDJ/fJ+dKw0LFcuZFGR1pJriQSEAjA9qWO1AlU+cnWiW3UyE+ctP1DS5ElzJvHI/KrN3PJ8vI6elQrbKGH75as3MCMV/egYFGgNoqC4cDqPyqeCdmJzjpTPsseP8AXD8qlht0DNiUHj0o6idrDI7glgCBR5/JBA60scEQcHzu9IbdCxxL39KNBE63rYC7auFt2e1UFt03D9539K0iqDOWFDsBHFwW57VmuMs1akaqS2GzxWa23Lc0MFuZFpcLoHjS0vpX2210vlOey54yf/HTXpeoLgxHOc5/pXmfia3EmlCbq0LgjHoeK7zT7r7d4b0u6LlmeIbj/tAYP6ipequWiDUlDaXdg94X/wDQTXzuOgr6QkQPE6HkMCp/GvJviB4esNFWwksIPJEu5HAYkEgDB5qoPoDOIooorQgKKKKACiiigAooooAK3dDxsUk9H71hVs6UcWpP+0amexrR+I9M0R5ZbR2QgAMPu4xWu+kPdDdNDFLxgblB/nXnlhdXkYItpZlAPIQnFd/4Pvry6Nyl3I77ApXcPrXDUTj7yO1O6sWdH8M28OrwyTadbmLDbv3a46Gu6t7K0tf+Pe1gi/65xhf5VnwsQAR2q19pf1H5Vg5SluDS6EeqlVBYnHy9a4fSPEVja3L27CYyzS70GzIHA759q6HXriZigDADHpXmt9ZyrO5TIfJwRxVwgmmmO9kdtHfJLlgT15zSvdRq4DSKP+BCvIk1a9mZo1dgxJwATmmtqeoowjeaUemCQa29gyXWh2Z6811EspUypkgEDcOlVtLvDq2ptZIoXAbDk9SP6V5fbXeoO5Cyynd3bPSvTPh1Gz6jczSoCwhwDt4B3DpUThyK5UakZLQ7eHRrRIEV1LOB8xz3pw0awwAYcgdieKvZozXLzMLs8y8U+E3vr6X7HZy+QrfKFXgHAyapW/hFbbTFN7pYV06u6evTNesk8Vm60wbS5U3AtxxW3tm9CVFXueUpotiJ5CbeMgnIG3pWXqcdnp90w+zDDYxhRgcV0tzZ3omYwlQD64rA8VxSIiOy/JuHzccnmt4Nt6j0sYt1eW8sLIkJUnGDtArNNOPzMDggVUurtUVo0OW6fSuqKtsYSdtWVL1g0/BBGO1VqM5orQ5W7sKKKKBBRRRQAUUUUAet/DjwjBDDZeIXnkad0YpFgBVzlfx4r01ATWToltBZ6HZQWqskKwqUUtkjIz1/GoPEV69npDyxytGc43A44rJu7KsQxXtto/gprqOMPcXM0iMc46sw5+gFeRyOB4xlfH3p1YfiKvQeJb+/hg0klXgjJKsc7gMk/wBa1fE+ix6V4a0fVFUie+vWdyfRVwAPbgmrW4M3HGIiTTYHG/qfyqEXMhjyVXpSJcSdlFS1qCZqqwIHNPH1rOW5kxnAoF3IOMLS1HoaR+tIAKz/ALXKewpBcy+1PUWhdkhVznPaozarnrUH2qQelIbqTOeKLsFYn+xoeppWtEx1qv8AapPaj7TIR2o1D3SwbCMkc9Kf9hX1qt9qkz1o+1y+tGo1YsG0CjqKia25OCKjNxKR979KYbmX+8Pyo1HeI/7PhhnHWugXbhenauZ86UuPm7+ldArjC/Ka4cZfQ9HA21sWH27hUV1tNs3IHFNkfkcGoLlg0DDBrhij0Coo/dg571YhH7o+uaq7gEAHFSwt8p571pdvqY1IR5b2K1wQLhqbnJqC/Li4yhPQVEjy5GWP413xjeKPMjVUHYvKaVeh+tV0d8H5qFd8n5u9P2bsarFRTLDcVIv3qgYSYFPYOMEGnGDTM6mIjJaImkOF61XLH1psrPjliarNK3941vbQ4myd5cHFIju5+UZ+lVC7E5zW1o8IkhZm9azq1FTjdm1Gk6suVFHbN/dbrRtmx0atqWMA4AqORcIa5PrieyO3+z31ZmoJh2apY/OOeDVtBlTzSIMZ+Y0fW/If1DzI4zKSOKJnmUjginpwfvVDeMy7SOa2p1uZ2MKuE5I81xvnSYPJqpJK248mpEkYnGaZIDknIroOPlGqzsO9SwBvNXOetRIxA61PGSSDuo6hYv5pRSBeOtLjBo1AdSUUUagLRSUtACUUUUIQUUUUmMKKKKFpqAUtJS0AJVC8R2lG1SeOorQqJ/vUN23Kim3oZZhf+61SLAwXODV00/jbSUinFoy3hbIwpNPt4mE6kqatSyiNwPUU0T/MOKaYmmQuh3twevpTCrAdD+VSm6OT8tJ9q/2f1oV9yvkIN2O/SmBuQMVcSQOp47VEHO4U0ybXYik4FObOOlKZypxgUSXbYxiqvoQ07jJFJc8Go5EYL0NWXvNrYIP4UjXO9OOnvSC7Khjfy0+Vup7UjRvj7rflVqS7aONcAcnvUf25/QUCG26OA/B/KoCrehq7FduwOQOKrm/kz90GgaZFGreavB60jA7j161Yjv2MqgqOTTmvCT9wUBcqrnNW5wQy/Soxecj92PzqxNdrlcxA8etOwFdvu0sOQ5+lSG6jwCYRz70sdxCzYEWOKQFfkOp9xQj/ADt+NT74GIG1gc0zbBubDt+VGtwHIwJX8KuP1P1qlGiM67ZO47VomIEn5u9J3HohsHAk+lZzx9ea04o8B+c8VTePGaCVuVJoVuLeSB/uyKVNS+B9Vja2bw8+VubaR3QjkMO/P1pwT0xXPai0uia/Z6rb8KzBJDk49847Y/lQuxoz0po2ViCK4D4qQM2l6c4UkrOw4Hqv/wBavRUlWaJZEIZXAYH2IrkvHtu91pdvFGjk+cSdqk8bTSjoxbniRBBwevpRV/UdMu7W4kZ4JCg+beFOBWfW17oloWikpaBBRRRQAUUUUgCrNteNbKVChgTnrVaii1xptao6qyvWtpYpSxVSQWUd/au5sNYMaNNZupD8EkZryuzmeR1jZuE5Wu48OENHKjgMoxjPasKkbbnZTlzLQ9V0a4kutMhmlYM7ZyR9TWkDWVogCaVCF6YP86t3V9DZRpJMSEZtuR2/ziuJrU0IdTtZJ1VkXOAa5650O5lkH7sksOABmute/s1t2Y3cG0dT5q8frWPqfiGKNUSznRmXOWVgeMUotpmsI82hyQ8GujGaGxCvuyCqc0h8LziVd8LiTGQCpBro7HxU0U+Ln5oiOSBzU0nim0kuROCyqgwpPBP4VfPMfsdbWMvTfCBknjaeFlVWGQ3ygiu7s9PtLEubaCOIv1KrjNcvceNbeIo0EfmZ+8G4IpY/iBZq6LJbSFT95l7fhUSVSWonG2iR2VJWYmv6dJ9ycN9MH+tQy+KtGgcJNeCMk4G5T/hWVmQ01ubJqhrCL/ZbPtG7I5qzHPHPEksTh43AZWHQisfUL2SWPyQwMec9KqKdxGDIvNcp4xX/AIl6f7/9K7CQVy3i9QdNUn+//Suin8SEecTzvApbANZbuZHZz1JycVo33KNWbg16COOq3ew2ilII6ikpmQUUUUAFFFFABUkUUkh+SN3x1CgmltYGurqKBAS0jqgA9zivo+00u20nRksrZAqRRbAccn3JpN2GkN0u5hk0238ticRqCD1Hyjg1keM5YzobxuASckA/59xV3To/JhYdOa5vxlqNunl2zSDf5i5X0AIc/oB+dZ6X0LOO8PWKpcTzEZCsY1z9ea7v4mx7Phz4Vf8A6a5x9UNc1pkflWsa45b5j9TXYfFONv8AhWnhghSQsi5OOB+7NW97EMp29nG9sjHuoqUWEYFVtLmdtPjLEnjjIq8ZDt61DauCiyD7PGBjFRtCm7pSSPJuPJqIu/qaXN5j5WWFtoyKcLSPNVPOcZGTQJpC33jRcLMttaJ2NH2RcdarmWT+8aC823hmo5h8pZFmnrS/Y0x1NUi1x6vS7p/V6rmRPKy3JaoDwTTPs6+pqDMpPJenDfj+Kk5K5SjpqSeQtRmBaTcwPUimEnb1NX0M3uPESKynnrWys6kDisRASRkmtKKTkZFcmJpqVrnbhKvI7dy1JKpx1qGeRTCetK21gKSZF8vH0rzlFJnrc11cps42CpYGBU/WkMQKjmnRxhVOCetWkZ1KicbFa6wX6dqiRV4yBT7vIk4Paq5LKFxXak7HmtrmLqRqc8DrQI1B6d6ZCzEHrQ6y7jgcU0wcU0Tui7RxUbqBwc1G/mhRnOKDvJHU1pGWtjOdP3bjJFG04zVKQEHpWmY2I6GqslvIeimtfI5ijznpXQ6LGxtW+tYbwSIclTW3orstswz3rlxf8M7sA/3qLk0RqKWFtnappnbA+aoZXbZ1rzIp2Pak1cYkR2nkUxY2IPIp6s2080xHbHWmk7iugWM46/rUd3CSq7m4+tOVzg/N3qC9kJjAByc9BXTQcudHJibezaIlhUHtQFXJ+YVBGWyev5VEA5J+U16KZ47TLoRSPvipogoTqKoLDMRwjVaW3mKjtxTv0CzL6kYFJuG7GajRGCAegqNI3+07iDtHenoSWqKKKQBRRRQrAFFFFFuwgooopMYUUUVIBS0lLVIBKrXMvlnOM1ZqneKGYAsB9aHsVF2ZEbz/AGame5EYT5fvDNU/KX++KnnRG8sFwMCkrFNsbJdISCUzSxXUZkUeX1qNoojjL06KKEOCG5ougtoEk8RY/u8dqb50Ax8lOeGLcfmPWm+TCMEk07oaRYiljKsQuMVH50YI+Q06NYQj4z71GwhHrT0J6jnlj3D5aY8kZONtKRFnqelNZYt3OafQNLhK6b/u0JImw/L0pJvL30kZjKHjvS1sOyLDojwKcYANRbE9Km82NbcccZqMSxelF2HLElgiTa2M1XMMWe9W7eaPYcCoPPiz939KHJgoRGJHEJFODmkxHnpUizxeYBt7003MP9ylzMfJEYEj/u/rU8iRkoSv8PrUYuYf7lSzXMaqnydqd20PkimROkW1flPX1p0SRebwCOKY13EQMR96WK4j80fJQm9xOMRzRLkFc5FRbcuQKma5iXqhpguIy7YQ4x60XYuWNhYIz5i8dDWkeBVCCdTKPkPPvV53UDvT66mU1YIvuyVVBBPNTwtuSSs5ycnmm9iEtS5+6A6Vm6xax3umyxYBOMr7MOlPJb+8fzpjRs3GamxqjX8Fah9t0JIXYmW1xE2c9un6Vr6gu5UH1rgdMvj4d8VIJCVs7wbTxxvJ6/n/ADr0h0D9QDx3FNrqM828SD/iWaggJHyNXl1etazGJZ7qBxlHLKQPSvONbsI9PvRHEGCFcgE5qosJLqZlLSUtUQFFFFAAKKKKACiiigC3pxH2r/gJrrNK1BbNiChYNjOO1cVG7RtuU4PSun06a3lKMUWQFCMHsaznG6OijK2h65pt3KNOh2SfKVyMCm6k8tzalJG3KDuwa5Lwxe3j60ttJdlrYRttiOMe2K7R1BUg88VxyXKzpjqec+JLN4bdTDb5LkrwnfHFctY3OpwXi4EpYcbXU4r0/XbNmsS8YJeJg4x196oWRtvMVlYs2QxAY9fpW0Zq2qJlCUpJxZgpNqsuCsJOT0CVamg1NcBIZGHU/ujxXe22p20bxnKrhsn5cVtzahbyJujkVhxyB71g6lnsdKjK27PIvsurM2BbyZzj/VmoTZ6zuI+yy8dD5Zr2GOcTIkqP8wJwSD9KqXWrW8Fw0TsVk4w2OP0p+07ITpt7tnlqW12AonmMR7hlxisMa5eXUogBRWQMVfnsCf6V6LqWtCe7chWaNlAKkDk9/wAKyrbSbC9mZzYW8ZBwCiAHH4VopLdoynSl0keo6M4XRLLcwJFumT/wEZqjezWzInkupOTnFS2o+z6VFEOiQhR9AK5a4ujawySlSQo6ZwTXLFXbBmlK4AJJ471yfiy5iewCKwJ3dj7VebUY7uyd8lFIwQxrzvXrlxqckcMxMfH06dq6KULshuxQuiCGz0qiNvapZZSRz3qNR8ldy2Od6sbIcqKiqby2ccYqNlKHBoMpIbRRRQSFFFKil3VB1YgCgDpPAWnyah4x08RoGWGQTyZ7Kv8A9fFe+3bYhIPBINZ+mWFrpVjb29vBGhihWPcFGT65PfmppJCytwenes27lEOxUg3ZOOprxyWdtY8QySyBmiMjyDPQAnIH5BR+Fep+Ib/+zfDd3cgZYJtQZxy3A/nmvL9MWQW5dyxaRtxJNEe5RqzXf2WNCiB2Occ8DFe1a7Ak3wnuI5oxtXTVk2sOQwUEfqK8KkmnhlgaGR1YSDo2O9e9ePJ0tPh3q/z43WvlKTzkthQP1psl6HmdlcRXFhFLCcxsvFWuMVz2jO6aTAN38Of1rQE8mPvVyOi7noLFxSs0W360zZmoPNc96ckzCn7ORnLERZKU5pAtRNMxNN8184zVcjI9tEsbSSKtovyDiqEDN5mM1oxPwAaU00ghNNg0Zx0NN2njrVsj5fwqHuK5XUb2OtQSIyD60qKalxTVOGqqXNImo4xRXnXAyar5GOat3YzHxxWWoO012xvY86VuYvR42A1chwTWSjkIOau2shJPNZyhzFKXKaiqpApJUXZ0psb5WnFuKx+rq9zo+tO1iBlAHpTOAKmbBphA9K0VFLYzdeTM+6UGQH2pkcSvjPark6ZcYHamxpgnitlFWMefUIkUcVZ8tcdKai4NSPxS5ClVa0K9woEdVkIBBzTr4nyTWWCcd6XJ1NYVdLG4jqVpQARWRDuIPNaFtkKa0S0MaiW42ePJOBVP9/ESI2IHsa0tuWNQyR9aUkTCVndGe010cgyH86jkkudv3z+dWymTTJIzisnFLZHTGbe7KqG6OcM3/fVOVLzH3j/31VuGMirAjIAqeXyNlNLdmWyXSr8zH/vqpbWJt5z6etW5kJUcUW8Z3+nFUk7WMqkldNMdBDneT60qW4HOasxoVzk9aUKQDUuMhqpDqxsKbVIp+OB9KcvFGOKcIy5rszqyjy2ixMUUtFbnMJRRRQMWkooo66gFFFFAgooooGFFFFJgFFFFABVW4VGcbuoHrVqql6fu0blR3IfLj9T+dPmiUkHkcetVASRytS3RxIuf7tDT2L0FMS8DJqSKFd45NVeqA+9TWv8ArxSsK67EjxoGPzd/WmNGhH3sfjTJPvt9TUbUWdx38i5FEmx8P1FMeFePnFRwHiT6U2Q9Koh2JGiTP+sA4pXRGOfMUVWbn8qGB3Cn8waSJJUUyf6xfzpEjAU/OvX1qCQHzKUghaAuWzEDbj94vWoxD/00X86jIP2cYz1pgB9DSC5ftoflYb1qv9l5/wBalSWgI3cdqgIJPSi2o0yVLYeYp81ODTPsi/8APZKRFPmrx3pmDStcOYk+ygf8tVqea3UrHl16VTwammB2x8HpVW0DmdwNso2/vFpyQKJVw461WKsGWpIwfNX60LYTepNLbAn74oSAbz8w6VHICGPXrSxkh/wodwUkWYIVWVeRV+RE29qzoWzIo96uSBtvejUio10HxBAsnSqbmPnOKmhBKSZ61TaJz0BpsmJOJYABnFPWWDGQFI+lU/s0mPumnm2KRDnkmpLKPiHT4tS0xvKwJov3iEDnjt+NbXg3XE1fRkjdy11ahY5c9T6H8QPzBqkIjnrmsa2u/wDhGPE6SBf9Evjtc84DE9fwPP0Jp+Q+hr61YyQ3kkpH7uRyVOevr/OvO/F4UXduc/NsOR+Neu6yRJZoQQcNnI54rL0u2ivrC4jmhjkUTMo3KDjgev1oT6lbo8Rpa2fFOlDR9emth9xvnTjHBrGrQzCiiigAooooAKKKKACp7W6ktZQ6H8PWoKKPUadjpdD1Nk1a2uE5dZR8tezZVsEEcjOK+era4e1uEmTqhBx6123h3WVk1KC7upJHcSFfnywRSCOPTmuetTvqjppVOjPR5VBBX1BFcMrQ2d+8iSLgErgtwRXbCRZBvVww9jmuE8T6cyyMYIZPLK5ZsZUnP6VhTV9GdEpOOqNB9Xt4F+eaEEjOPM/+tSR+KYrVGC3MG0+uSK4d9PuHiTLZxwFz0FPe0kNk6bcMAD19609lFdRPEzfQ7dfGqxrhLi3/AABqnd+KIbqXebmEucZC5Ga5PT7Nl3+Yo5xiiGymj1ZHMf7vzRzntmmqUUR7epZaHRNqkO75p4wT65FdD4euFuI5GDAqxG0gmufvdKjuIztDeuSK7Hw/aiDS7ZCn3Uxyfc1EuXl0NIylfU25bphZEK+4hPug89K4X+37TVElt4kmL7Cw3gAYH41avdWn0l5yYo44jIwDeWc8se+PpXAnUGhaSWPYuQRtVccU6dK6uZynqXNVvZIvMijfbHtyw9a52a4MpJ5yepNJc3MlzJuc1HHE0jBUGSe1dUYqKMJVHJ2Q5I2ODtOPWp2XYAWU89Mite3h2RKGXnGDVXUI9zRgcYB60ubWxXJZALLdCpiHJwetZdypSZkIwVOK6aBdqIvoAK53UcjUZweu6lB3YqsbIq0UUVoc4Vv+DrCa78Q28qxlobdhJK2MgDpz9ScVm6Pp0mraxaWEfBnlVCT2BPX2r6Om02w0bw7Ja2dvHDHHGFAVeT9T3pN2GJnIBppGQRTYHEtvG/qtK7rGjO7BVUZJPYVjsUcb4+vtljb6cjDzJm3EZxgDp/X8q5uKMRxqnHAptxeHWtcuNQbPlK22LB7Dp+lTDpWi0KJbO2a51GzhVSzSTogHrlgK9I+NN+IPCdrYIpLXd2MAHBwgJ/mRXK+CLQXfjHToyCdkjSkAZ+6pI/XFTeOtc/4SHxi1igP2HSgUORw0uRu/kB+B9aLkvczrKFYrSKI5+VAP0qysa1FGfkzU6KzJuHSk9CbjRGOaXywFzzTfMC5FOEgZMUuoEZUUm3mpF2k89KflB2/SpbKirksVuD8yk8VY24K80y2lXY1R3ExVQVNRvoyn7uqNEMPLzntUORnrWcLlzH1700XLis1hkbfWma3HrTcfNVBbp+44qxHMWGcVcaapkynKroh1wfkA75rP2EA1ekBcDFRiJjnJFV7SAlh6j6FZYmKjg1atUIJyDVyG3zECcU+KMfNUe2guoOhUfQWMfLTzSKPmYelOJA4PWmqsW7XF7CaGEUhqQBWbGaRlFPniHsJ9iFvvD6UgHNOODLj0FOVAZFGepxVe1gkS8PU7DOQac3IqZoVDY3Gl8oGpeIp9wWHqLoZV2C8e0dazjGwHNbstuCwBPeo5rJAvBqo1YNC9lUXQy4EPPNXoQRnnNRhI4SctT1miB+9Wm+xm27WZYTqaHUEGoFuoQzZehr63GQZB+VDRKGhBuokjBHSnxTwSDKNnHtTJLyBW2lsEe1S1qXexJAgB5FTOFAFVo72DPDfpT3u4mGMn8qTVik2x52nrinBFHOOarG5h9/yqQ3UW0fN+lJWvqNpk9Gar/a4vU/lTvPTGc1RFibNFVhdxk4zzU3mLsDUPTcLD6SkDjGaXORTEFFFFJjCiiigAooop30EwooopMYUUUULUAooooAKr3P3h9KsVXuEyRyOnrTHG99CuMY6CkumG5flB4p2z/bX86S5UZX5h0o9S7MgWT5fuipIZf3o+UVFsGPvCpIIx5o+YUaCakK043H92p5pHnUAfu1NKYhk/MOtI8IIGWpaXLUHa5JbzBt/7tRgUx7heB5KU+CIDf83ammBSR83T2p6IhxdxfPUKCIkphuvnx5a0/wAlSPvdKYYE3Z3U9BOLIpbjLjCLSmXjhRRJEm/73elKxDGWNFxWJDcFLdcKOtRC6Ydl/Knv5RiA3HrUYSE/xmkFi5aXLSZBAAA9Kg+0vuxgdfSprUQoeGJJqNo4N2QzUtLjSbBLkmVRgdaYbs/3Vp6JB5gIZs5phigz99qd0OzGfa2B+6tWZ7pgkfyjlag8q3z95qnuY4dqYZsgU9BcrIRcsSp2iljuSZB8o61GEjyOTUsaQCQfMaE0DTHT3BDngVClyS33R0qeZYC5+Y1DGkW/l+1F0JJ2Jorg+avyjrWm0qFcYrLRYhKuHOc+lXyAWxmnoZzuLE6sr4HSqb3AjOWHFWoUKCTNZ9wAVOaHa4RJxqEJPRqlb96qsOnWsYgA1eSdltgR1HHNQ/I0Ra8v3rO1nS49S06SBlBcAtGT2arC3DsTULzyE4zQk7jbE8PTtLoAtJ3Z7i2JRww5x2/Lp+FaXh1QbS6K8f6U/wDSuUupJtM1iLU4lLQv+6nXPr3x68Z/D3rqPCM6XWmXMsf3Tdyc/lVML6HOfE/S3msbXUIosmAssrjspxjP4/zry6vffE2myat4dvbOL/WSR5T3IOR/KvCbu0msbqS2nXbJGcHFOL0sSyGikpasQUUUUgEopaKYBSUtFABV6w1GWxmDozbcgsoPWqNSeU3lBx0NJjV90ej6L4x0y2jW3kRxvIYskZOWI5z368Vq3XiDSbuwnjE8isQRzCwwfyryW3lMFxHKpIZGDAj1Br1Pw3fW+q2s7uqlBLgGRR83HP8An3rlqwUNUdlGbn7o3TvD0+r2iXNlEZYnYqGHHIxnrV2T4f6wZFX7MACDk71r0nQ4bS00q2W1ijiQqGKoMAsep/StCadIkDNwCcZrldd3sjZLoeSTeCNRsY/Mmt1C9OHBqCPw/fR3C77RgoYEnK9M17A5iuIyj4dT71Sv7WD7FOwQblQsD70vrEhqK6nLDw7I4KFPvcHAqvcIuh6S9xckxxwcNk5PJwP512sl3bwwO7ug2qT94ZNeReMtVll0eYO7FeAFz3J7+tFFynKzHNq1znvE/iFNah+Q+RbJhkjbl5H5547VyDyuwxnA9BTWYt1OaERnYKoyT2r1YxUVZHnym5AqM7YAzWlaWrxTqSMjIyaLSFoQxcYJq7GcleDUykXCHVlwLT9uRggGpltJT2HT1pkyG3xvxz6c1jfU6CC5kaGLKqMk4z6VzF0zNcuWJLE8k10dxMrwlRnNc1cH9+/1rWBhW2I6s6dYXGq6jBY2qbppmCqPT3PsKqmvbfh/4Rg0jT4NUmZZbq4jWRQUB8sEZGCRkHB57VbdjnDwD4IufDOq3l1fNG8hAihaMnBXqT+YH5V2Ovv/AMSS7P8Asf1FTGbbIGYnaPU8VQ16ZH0S6CsCdnQH3FRfuCKWiyE2Wxjyv8jXJ+OPEUjXH9h2EjLKeLk7f4SBx9MHPFdGl6ul6DPfuqkRRbgpYLuIGcD3rzKyEl3dTajMzs0zsUDsSVXOcZPp0oS1uWX7eNYLdIkxgDqPWps+1MXk5BP41d0y0+26pb2x6SOFP4mmyjqfBKva2GvazGUWS0s2EXmnC7yCfvdug/OuftIbu4gFzckPc3DGWZ8AbnbknirnxFk/sS8t/DunlYbeWESXCxSH96xfgOMnoFGOnWs/Q9Tk5tboKpTAjbP3vb9KOl0Ra5rR2Mvl9BT4YJNpUY4q6k6mPg02GRcmspTkWoIz/sUsjHGKcljKMjA4NXoZVDGnrKPm+tYurM2VGDKCWkvOEU4OOad9hmPIUfSr1vKNp+pqdJQVrOVaaNoYem9zPt7WUKfl701rKaROAPzrSikG0/WlRxtqfb1OiL+rUnuzHOn3AHQfnTRYzHoBW00gIpiMNpqlXqW1QnhaPRmWLV9ucVJHGVFPW+T5l2nIqH7QhPetfflo0YRdKErpk/encVX+0xqmTnr6UiXcTZxnisnTkdMcRT6s1oP9QKbF0b61Uj1KCOLB3dewpsep26g53dfSsvY1OxSxFLuXV/1jVDM3znNQrqdvvJO7n2qGS/iZyy5xVRpVObVGc61NrRmjHkP07U5jzVFdVh44bgUf2nC3Y0lSqX2NHWpW3Jsj7SfpUyH96n1rMbUI/PLAHpUkepxeYpII5rRUp9jJ1qd9zUYYnJ7U8dKoSapAWyM0v9qW+O/5Vk6FTsJ14PqTzdRTZcsnFUpdTgYjBbr6U8ajDjG4/lW0KclbQylVjrZlO8EgcYGaqb3H8P6VoT3MbkkdKqCVM9a7Yt2ORpFYu+7pTfInncbEJPpVnzE3g1KlyiuCMincViW006WOL53UE84FV7nT7hZCyrvB9K21bcob1FDuqDLHApX1CxgRRSxsd8bD3xTi4BPFW7m7jYlQciqBlUk1MldlRdkO3+1SYZlGFqHzVFTLONvFTylKY6NCx5GMetSnG2oVmUmr8MG+MNnrTSaE3cohcyA4NWzxAKbKohbBNRyXCeXgmh3Yk0lYtJ9wVIv3aqJcIE61YhkWRfl7VTRBLRRRS9RhRRRSQBRRRVIAooopNgFFFFJWAKKKKYBVG8/1qVeqpdmNWXcpJpjW5RJ5qW4/5Z/7tIXhz9w/nT5niJX5DwB3oKRWHepIc+ZSh4s/cP51LEYi3CH86F5iZATzTSxqyTAD9xvzpMwY+6350utyubSwluT830pm81YgaHcwCt09ajL24P3G/OmSMDHBpm75qsI8GDhD+dRtLAHH7s/nQFyBzzSP1FSPLFkYjPX1oaSIOMoetMBjD5B9aAKmaSLyc+WfvU0TRdfK/WkJklsPm/Chh7U+CaPccR449ajN0gb/AFI/Ok07DW4qAbx9aYy8U9LmMuP3I6+tNa5TP+pH500tAYgUD8qlueifSozdRj/lgv51NPOhjQ+UPzo3EVe4pRxIPrSi4QH/AFI/OpDNGZB+5XPHejW5Vxko/eGoTw1XJJE3n90PzqMPFu/1I/OgV9CKM5lT6itIA+bmqiNGZF/cjr61fYgdqpESJV+41Zk0TMTjFX45Mh8jpWXPJhzxQxIQWbk8sv51ZjtU8rY0g654NUGmOegpRKdp4FSUaS28a9HFJ9ljOfnqkSSO1ABJosAt/py3FlPbiTHmrtBHY9j+dYfgW6u9J1l9IuzIolUkRkjaGxnP1x6etbQX96hJ6HNYfiywkRodXtsiSBhv2+x4NUtNGNanpG9hxxXjPxDQL4slwm0mJCffjrXrOh6hBrelw3sDAFhh0zyjdwazfGnhaDWNFnnhtvM1KJAYmX7xAP3f50lowPDqWnSRvDK8UiMjoSrKwwQfSmVoSLRRRQAUUUUAFFFJQAtaFmwlj8n+IA1n1b01sXyDPUEfpSexcH7xHcQm3l2E54zU+n6nc6bMJIH+qnoafqq/6SCP7tZ9Kya1CXuy0PVPD/ji3s7C1M2pmM78SxHJwN3p6YP6V6rBqGiapaZGsWYQ/dP2mPP1xmvlaj8P0rH6vB6mjryZ9G6h4itdMvRaQzLclnCRmCRWLE46AZ9RWl4i1GHSfDlxc3UoSTyhmFuHJPGBnr+FfMSuykFSVI7g05pnc5Z2Y+pOaX1aA3Xkel6l4+iWzdreyd2JwDI+APwFcHqeu3uqDbMyrHnOxBgVmlyepJptaQowhsiJ1pS3ZJEnmSKpOMnGa2obSKE7lBJ9Sag021823LhRu34zjnFaDjYVDcE9Kc5a2Lpx0uyMRguARwSK3l060XP7s8H+8agtLKFokkcEseetX88fiaxlI6Ix7jXYIpPYDNZN3OJivBAGau3z4s5sE52Hp9K56zkkeJt5yBwM0Qj1By1sFw+yEkZrDY5Yn3rSv7go4jUDPU1mnrXRE5KruxMcV9MabAttpFlAi4VIEGPT5RXh3hLwbd+KHkkjljhtoXUSM2STnsB9K99CBI1UDhQAKH2MypenFnMfRDWY8Bns5YyCd6Yq/qc0cNlMZHVcoepxnisDWtYXSNEedGUzSDy4UY4yx/oOTUNO40cj4u1AatqsOjwBfIsjmRg/3mIGQMenT65qoAFAjXdtA4wKq6Tpc2x7hmInk5JJznPPP41rx2hiH7x8seavZFpEaA7RXVeELS3jvhqd9KkFpaZeSRx8uQCQM9BwM8/1rnre3ee4SGMbndgqj1Jrb8cagmhaAvhPTxG1xdor3k0UnUA8qy44bI9egqW9bAzjLvUG8Q+J73VmiCfaJS4UA8KOB19sU/UwY7eOdRho2BDAc/56VpeGraGSWZJrVCqooQkfma9DbwPp2raEnlK0FxJHwwbKk54yDVbCTSOYspfPs4pVOQyA1NBnJrnduoeDNRmsNWgnFsW+STaSoPfaehHI6V1FsBIm5WBUrkEVlNWNI2ZBGDuqZQdp+tPiiy3WpUh+U896wbNEiGDIU/Wp0Py0QRZUn3q0lvlM5qJbmkblaJvlP1pVJxwKsQQZXOaljtxszWfOkaKLKOWI6Ug3BDwaveQAKjZAITVRknsJppXMJIHyxx1o8iT+6a0o1Gw0bRXc9GectTIe2lKfd701IJFDZU1sbMj8ajZQAam7uOxlNHIFxtNNWJyM7a0nAOMU1BtGCKpSJsUfIkP8JoEEh/hrQBFIrChyCxQSCTGAtOW2lyRtq4jDcadvAY0uYLGcYHEhBFOEDgjip2cGZjSlwD1o5iuVsjaFyOlIYnx92re8HvSnpRzj9m0ZjRtnp3pdjEjipJD+8PPenICx4ppktCSxuqciquGB7fnV+5BMfFURG2elMaBQS1PMbj+E0kcbBwcVoBMqMgUXAvWp/wBHT6VX1MEwcdjUWWQYBpjEsMFs0gsZ6RsW6UeS/pV1UANIR82OaLj5Sl5T56U9Y3CkYNW2XDcCjHtS5kHKyssb+hratGAgUHNZ4GO1X7fiICndCsyG+BcjbWebaZhwhNaU/wAzirEYxGKadiWZQtpcAbTV22iMaHI71YxRihu4kFFFFQxhRRRTQBRRRTEFFFFKzGFFFFGnUAooooAKo3w+ZT3q9VW5lZGULjHvTQ0rszTnNPmzuHB6CpfPl7MPyp89xIGHPajUZTUHPQ/lViDO8cH8qZ9qlzjdUsM8hfBPFANMaVbP3T+VJsbH3T+VSG6lDHkflSC5lK5yPyo8xC26tvb5T09KiZHz9xvyqaCeRpGBIwB6UxriUHG4flRqAiI+D8p/Ko2jYyfdP5VPHcSsDlvpxTBNIZfvfpTBbkDxvuHynr6UkkbeZ909allmfcOaY0z7zyKPUB3luYMbT970pvlPj7rflTzPIsIOe/pQs8mPvfpSCzY6CNgx+U9PSofLYn7rflVqKaQt979Ki+0ybsE0C2YyONg6/K3X0oaJ8/db8qkS7csM4/KmNdyZ7flT0GMMT/3W/KrE0beUnyn8qg+2Seq/lVua4cQoeMn2o1ApmNv7p/Kpdjeap2nqKYbmQ+n5VK9y6svT8qNQJJY23n5TVi3s0eMMwOT601ZiVY8e1OW4YAcjpS5kg5JS2Jls41IIH60siHJAI/OoluCTjNSOck8UKSfUhwmtxsaMA/I/A1Ua3ViSziraD5XrOk+9RzDSZKLKI8l/1p4s4cY3/rVAn3oyccGgZp/ZYcD5v1o+zRA53frWdzxRtJ6UXHyvcvyQRBc5/WlaGKaAxuAyOpBB6EGs11b3pAX2jrQCRlaWv/CK+MYMXBi0+4yHGTtPHf3Br1Ue1eXa1pralYOg/wBYnzp9fSus8Daz/a2gRxSH/SLTEUgJ5OOh/wA+lPdA0ecfEnSHsfE012FPk3WJFOOM45H6frXGCvpPVtItNasHs72JXRgdpPVTjqPevnzW9Kl0TV7nT5TuMLbQ+0gMOxGatO6sIoUUUUxBRRRQAUlLRQAlTWkohuo3bOAe1Q0tA07O50csCv8AeVWz+NYt9CILkqvQjOK09LdpLTkklWIFWLvRGuWEgmAOMYIrNSs7M6ZR543RzdGauXtg1ntJYMCccVTrTQ5mmnZhRRRQIKfGAWGaZVi3hd/mUcUPRDirs3dJGLRsdN5/lVqa0e6khWMgMW2jJqHTEeOxIIwdx/lWzp1n9qZSXK7GBGB1rmlLW52wXu2Bc2yJDIpDgDIxTjIojznHJ61Pq2La4QAPIzLkk9uayLmULGjNxknrxUJXL2ItTvxb2zYGWbKj0rnEuSkRQMRznrW7K67CzYK4zz0rn7yQSXLMowvQcVvTS2Oeo3uQu7O5ZiST3NaWh+H7/wAQ3MsFgiFok3sXbAAzisyvVvhDautnqd00ZCyOiI/Y4ySP1FaN2RznVeB9Dn8P+HltLoRi4aRncocg+nNdLTQMdKhvZmgs3kT7wxUAYuvxea7d+AAK85a5l1vVw7E/ZrMBQGVT8/cH8f5Cui8WeJltLA28QBvJhsAP8IP8VZXh7TvJtVDoC7fO5KDdz2J7/wD16aXVlosiPyIxweeRUG5mHOOKuajIPMCgfdFVY4yxHPX1NDKNvQEtrGG81u/UmzsYjnacHeR8vfIzjGRnkiuOiuZtX1G61i6Z2nuZCxLDt2+uBx+FJ4i1VbuWPR9OlZoOGnZk2FnBPyn1C9s9zVmFDHEqgAcfwrj9KEurF1NnRR+9k2j+EdB7161pL+Xp9rkZxGvHSvJtFXM7nPYcV6taLtsoBnjy1/lRIlm/q+iab4j0o2eo2yzQuMjsye4YcivINX8Ka34QvbmS0imn0NACkhIcqDjqAMjB9eOK9atdVjjgWORWyowCvNXIdQtbmPiRQTwVbioV+ok7HillfrcDcjZGOhHIq6kpKdu9b/jvwVMzDVvDkQE6Za4tUOPNHH3B0Brj7G9SaHDq0cynEkbdVbuCKXs09RyqtGlBLhSKnFwQmM1QikQKeaeXQjrR7NEPENbFuGchOtSpcMF61QEiKuKja8VTgColRi0aU8TJsvNdkZwwqF7hin3qpGcHJx+tSoS68YqoU4pl1KraCKRih5pxZiOtPt4cR5bvUhQVpJpPQxjsRxE4OabcEiP8aUyBDjFQS3G5cH1pq1gd7jN5zTA5pC9QeZyaiXkUicOc0gc1AJeaQTcmo1uXoTqx3mn5O41WWX5jxTxNh/wo1sDtcbISkpzQXyKikk3yE4pu407DuWwx4xUzXG1OnIqosnApHkyDVcqI5mIW3Pn1NTw8Z4qoG5H1qxFIAaEtAZYuFOzPFV0+90qaWUGM1UWUbutOwk9CdQN/Sry42is1X+arYlwtFiSZsVGwG01CZs03zc0ITJo8U1yA9RLLio5JfmpSWpcGWC/NKDmqXnHNPWYisnE39poW2PFWrdv3YrMMxIqSO4ZVxWkVYybbZq4B6jmnZqilwxGacJmLde9XYzZcopKKWqELSUtJRoMKKKKWgBRRS0egCUUUUxBRRRQAUUUUhhVa4iLspBX8TVmqFxnzvwoehUNxn2WT+8n/AH1S3Fs+5fmToO9R96fOP3v4CocjdU22RfZmHdfzqWGFg/ao8ewqSEfP+FT7Q0WHbFa1k3Hp19aT7NJ7U2TPmNyetMBbjk/nWqd0c8oWdixBbyB2JA6etNa1kLH5R+dLbZ3tknpUTk7jyetNMhqxMls4ByKj+zyCTO3imqTg8mmMTvHJ/OnqFh0tvIWHFMMD7jxTCTuHzHr6052YZ+Y/nQIkaF/IHHehYWx0phkcW6nc3X1pqSv/AHm/OkBahhbd0qL7M+7P1p0Er7uXP50gmfd95utHQfUals4YZHeo2tZMnj9akFw/mKNzdabJK/PzHr60X7g0M+yS+n61cnt3MKAAcdap+dIP42/Ork8jrDH8x596dxWKxtZPb86lktXJBAFRGZ/7xqw878HJ60XHZkghcBuOopBE20etOSdyD83amiZ8DJqJK5cG0OVWVuex9KsNyTVYzMO9StOcnpU8pftGSxg7X4rNlXJPBrQSVijEYqhM0vPH6U1Al1HqVihLdDk05kKNgrg4pVlcOMjj6VZuJFdgWU9PWqMrlcPx0FSrORn5RTAYzxtP51II196dluAG6OcbQaRrrbjKA0jogbkNRJGnGd1FkK4/7UucbK5/StRtvDXjV5ZCBDefIxJIEYYg5wM9xVzVr+HT7YkZ8xhhc8gHsT7ZrjtYiub+BZ5CNyjIAX86qKRVj31NrqGUgqRkEc5Fc74s8HWXieDzHLx3kSFYpVP6EdxXH/DnxbKskeiX1wixDi2Zxzn+5n+VerUmuViPlyeF7a4kglG2SNirA9iOKZXqnxJ8HW0FnPrtmNshlDTr0GDgZA+v868rq90IKKKKYgooooAKKWkpAaOnSssTog5zmugsJz9nJkBGDjOK5zTpY4vM3sFzjFdFZ3EU+mzopBwDzWczqpPSxma68UkaYbcQ3asKtiW3SQAMTxzVG5t0iXK5zmri1axnOLvcq0UtORNzqvqcVRiNFXrW4iij2ndnPXFaI0q1/usfq1L/AGZa/wBw/wDfRqHJPQ3jTlHUtWEqT2x2ZPzY5rq9LtyAijqetc7pNlCriMBlXOevWuz0tFUMR24rlmdUb21LrKFXGB+FcB40Ym7gHOMEmu/lPFef+MmT7Zbgk52H+dFL4iaj905xPMlXysnbnJ5qxJGvlMMD7pp8UCxLkE8jnNSwW73lxHawbTLM2xAWwMn3rpvqYEnhHwrN4nvnQP5dvDhpHxnv0/LP5V7ppmlWWj2f2WxgWGHcW2juT3P6flWV4O8MR+GdI8jeJbiZt80gGBnsB7D/ABroqJO5iJVHWLmG10qee4cJEi7mb0Aq8a8u8e+IE1a/TQLKUbI2zcSc43D+H8P50kI5u2aTXNZmvZlPl7sIPQdhx6cfjXaQj7LbMwzuNZ2j6fHbxrtAwowDVi+cGQBSflrQ0SsV7o7pc+oz071mavqX9nWDeUw8+QbEAwccdSPSrt1MkcLTOQFVSTk46CuajL6nfG8lz5SnEKtyVH9am12Mdo1i0f76T77cnNbqp04qGEDgkcVpWvlB/nI/+vTvbYLF3SZVtTIzq2GA6CuztfEBWKJCyMNoA45rkVkXAwyn8anEsQj6qTjpSeoHbJqwb76AfQ1dgjSeISqSM1wNpI8jqm45OAAD3rr9MD2cIEs8ykg/u2TofxpeRDRrxTzQ30cJdyjjs3H5VxnjvwYNOtZvEOkLskiJluoURiZQSMnqQMdeBXUrdqZ4pWZSyH0xVjV9cjGiXqeQ7O1tJjADj7p7d/XHoKqLM3c8p0+6S+s0uY3OG6qeqnuDVtfQvzXN+CbpXsrqEnLrIH4bsRj+ldMWHbP5muapOcZWR2UqFKUU2Lt4+8fyqq5w5+ap2Ynru/M1X8pSScH8zShOb+IdSjCPwgjCtC3ZSvUVQESg9P1NWoFUZwtbrc5prQvxuojHzClLqe9Mt1BhHApe3TFDRMWUpnG881Xbaf4u9TSIrOSetRtEnvU83Q05SP5c/eFKLcnnI/OjyU963EChBx2pp3JasYYtSe4oWzJPBFbaFdp4qjP/AK5qom5VWxcE8r+dBsmLfeT86VjzSxDOaWuw/MiFk5cjcv5042D4++n51YRAGJxSSjigdyD7Cw6yJ+dI1kQDmRfzqUDpSsowadmTcp/ZxkDzFqRYAP4xQAN44qcjijUdyCWMCM/OKqJGC4+f9KvS/wCrNQQqpnUYHWmrkuwqwHd979KnMJAxu/SrXlJjOKjl4xQ07ExkmyuLfP8AH+lOFrg/f/Snp1qfjPSpXdFysVltAf4/0qOa0Cclz+VXlxjpTJwPL6UMSaMoxrn736U9Ys85qdVBccVZEY9KmWmxotSl5QP8VTpagqDvqfYM9BUuAKEROVhsUSpGAWBp26NTyy0jfdNUJfvmruQveNUSIejD86eCCMiqCAACrkX3BU3RRJRRSUxhRRRSa0AKKKKYgooopDCiiijVgFFFLQAVVmkRZMMuTVqqF0p80EA0mtNS6baloN86NTkpnmn3VzH533Owqqytn7pp10rGY4B6Dt7VNonRedxwuI/7lWLWaJpSNp6elZ2x/wC6fyqe0DCY5B+76UrRY+aaLM0kHmsNvf0pge367T+VQz7vtD8HrR5MhGdprSOxzyepbt2hLHCnpTJHtw5+U/lRbRujNuGBimSQs0jHjmnbUWncerwYPyH8qaWty/3DQtu23tSeQ2/t09aBaDcwM4GxuvrULNHuIKnrUwhKyjJHWmNbYkP7xeTRqK6FIi+zD5TUaGLPTjFWvs262A3r9ahS0JP3xS1AfCIs55HNJ+6z1qxFZsoXLDpUP2Nt33h1pq5V1cYqw+YPXNMk8oORg1ZSycOp3CmzWTFzyKOgmyruh/u/pVm4kQQodvHbimfYX9RUl1ATCgyOKPUVysJUz9wGrDMCudo4xVUQsO4q55ZMZ/Cn2Exglx2qPz+eBTxETUXlsDzS6gOM59BUryfMeBVdoz2FTt8pJxT9ALEL4iII71FIyjqQPrSxSMUOfWqly5Y4PagCXdGT99c/Wrq28ckYLAMfWsPvV6CaSO2AVsc0gLwsosj5envSyQoiltucVUW7nzjf+lXtzFeaAKMjjcP3RqO7u4re1M8gwAMgZ6n0pdR1ODTxmR8uR8qDGSawrawvPEl39pnHl2kbYB6EEc4x/WnoCRnxxzardvfSnEYOEGMZXrgj2zT5QCxyvtWuY1jJRFCqOAo6Cs+7j8ts9jVLQ1toclqFvJY3qzwkr829GH8JFeyeCvFa+I9OZZgEvIABKOAG/wBoD0ry/Vk8212D72c1jafqF5o9+l3ZymKdOhAzx6EdxTaujN6H0LrGnjVtIubAybBOhXdjOK8Y1/4capo8Fzdxsk9pCu7cD82PpXq+h+IbXVtFt7xZw8hUCVUXlX7ggZxVnU421TQ761hU75oGRd42gkjioTa0EfNlLU9/Y3GmX01ldJsnhba65zzVetBC0UUUAFFFFIBR1rrdFig/4R8SyjH7xlLZx6Dn865GugsWY6FsJ+XeTioqK6N6HxE95aNHcMsQ/d8Yy1U5bKSYbCVH41uXkZCqx78fpVNfvis07I2ktbHMSIUkZD1U4rZs7G3MUMhQl9obr3rO1Bdt/MPVs1r2X3Y1/wCmY/pWknpcxpxXM7luilxU9mkT3aLLgoeuTisrnQaPht1XU1VkDblPBrsSygfLFj6YrC0/T7WK4S4hPK5HD5FbO5eec/jWE3dlohW7hnaRFB3IcMD2rgvFIjudRCgMNi46+9dtKsMYd4/lZhyQetcLrQ235ySSVBJJzV0lqZz2sUQyhApIyB0NeleAPDAtYP7Xu1JmnXESMAQqcHP1P6Vyvgzw1B4lv5nuw4tbXGQpwWYngfTANeyqqogVQFUDAA7V07I5pS6CjqfQ0GmrIj52sDglTg9COoqC/vrfTbGa8unCQxIWZvapIOe8c+JP7B0YpbuPt1z8kIHJX1bHt/WvMNNhCKTMqySykFy67ifzqK71S48R+IJdSuiQAcRL2RQeAPpWlAFLhgeB3rRaIqK6nS21xbQ26KJIxgdBxVKSTcSxPFZ6tulC9j1qtrVywRbKDPmzfeP91ehz/KmhvQp31ydVvGt4n/0SMjfgfeYZ6e1WkUBlRBjGOM9BVYCLTbFV5JzhR3ZqtWMckcJlnwZJPmOR09B+FJjRopgtjPA6ZqRGVs7TnBwapvMEZVXG5jgf40uNqbEH196EBsRnABNIJPmxkE+lc/qGv/ZD5Ua7pM88/drS8OLE+kXWs63ey28KH/RioBBfJ5x35HTFDQr2O+0DTTpqSarqTC2SJSQJhgYx1Of0rkfEPxLvNUv1tvD0TCNc/vHjDvL9FPRf1/lXJeIfF2r+KJVt5rh/sUbfJGF2r/vMBx/hmuu8E6LIkWCAzyMDnbghfSpfcS1dzLOo+OHiZ2W6VyQo2wBevfgda5/U38Wxq4vZtS8thghnYrg9uO1fRenJ5eT128Cti60myuxunhZyRjuaFo9ROVz5Dsb+40y5E0EjRuOD/gRXpWkeI9L1ILGJfLmJ2qknBavQNR+HehasJxcWRSST/lsgw649D/iDXn/iD4S3Olutx4fuZ5nUFxG4AZQMchxjnnpinoxXN8QoR1FAtV9R+Vec2XiHVdB1LyNVFwyou1oJBtK+hGa7fSdestWiV4JQrtn905Afj2pcthO5o/ZV9R+VKsKpnpTwTSHOD9KES9hkDgQijIIqKFGMQ4qQI2OlD3GlZFF2+c/Wmlqc8L7z8h603yZOPlNS12KuNBzW0DhPwrFeORFLBTwM9KuQTySRZalKagrs0p05VZcsSZH61XlP71qeDtzzULMfMpQqxnsVVwtSnHmkQk5NPt+9TWylw+7BIOOlTqoXPyj8qbkk9TNQlJaESjmmSjAqyGAboKZNIAv3RTUkyXCS6FbHSnEcH6U5ptqAhAaabpsH92vSquibMrj74qYjioTO5YYVc59Kd50w/gH5UrlcrFlH7s1BAP8ASF+tXHnZYc+WufpUNvcs9wqGNBnviqViHdou5qGftVo/RfyqC5kZAuEU59qctjKnfmIIzzU+earx3D+YAY0x9Ktmf/pklZxvbU3lqxE6U2cfu6njmyB+7T8qWeXbETsX8quzMuZXM2MfvBVoCoBdNvx5aflUnnk/wL+VZzTudMI3Wg49akqAyE/wrU6jcueKcUY1lYRvumqMgO41o7OM1We4UEDyh19aJaBR1TsRoDV6L/VimKVIB21MvSkuxQtFFFUAUUUUr2AWiiigQlFFFIYUUUUKwC0UlLTAKzrmV1lIB4rQqncQM8mQBj601bqNEEdwxIBPOa1ZIQz7vb0rLS1dT0/WtFrjnGK5sTey5T0MDKPM+YUQL3H6U6KFdx4qLz+elLFKzuwHBrlXtGz0ZSpJEVy0STEEYqCS8CghVzS3UMzzs23I9artbSn+D9a9OL91I8CqrzbRKLpnjY+gqsZznv8AnU6W8ixOCME+9RG0lznb+tHUm2gqykr3pobJPWpktZNmMD86RbWTJ+X9aYKxAG/er9ajcneee9WRayiVfl4z61G9tJvPHf1oW4aAxPkDmokY7utW2tpBbjjn61EsDhhwPzpAiymfl69Kg3Hd1q9Gu0LnHAqu8kak/Ic0wIo2benJ/Oidm3nk1LHdoGUeV+tOuLtVcAxfrTFYphmz1P51NelhDGcmhb2MH/VGpbyfbAhaIjPTNLzCxmbznqfzq8dxjOM9qrrcqp/1WauRXa5PyHkUO9r2HYjh3BzimpuZiOakjvFD/cPSmx3gLE7Km+o2tBCr5/iqcqS3TrTDef7FTNc4/gFO7JsSLEipwetV5beN+/NS/aDsyFGaqve/7Io1YEbWvPDfnUqwAIBuqB77GMJTmvFjgMjABQM9evtRqMmCFCCMH61n3evTysbawt5JHbKB1Gfm54x68Uyzj1LxTcNHZZgs0YB5TlWU/wCe1dzo+gWmixOsKl5HILyvgsaA2OT0rwY9w4n1iR2mXloN2Vf0J7//AKq6iSFUjCqMAACtZwGHv61n3MZGeKNWJs4uZMSuB6n+dULzIj4BJ7YrQuRtnkH+0apyMD3qkap6HM3SHlT1Gc1k3FsWBdRyB0rqrq0jkYsDgnrVdbGMADOefSq5hNFbwDqk+n+IkRCxt5QfPUcjaB978K9wQgqCpBBGQa8h+G1jE/ifUGcZWCFlAxwctj+QruV8T2Ok63BoM+8FgPLnZhtAP3QT+n5VMtXoZs4T4j+GtRbxBdapb2cklm0au8iAEKQMHI69q8+r6av7cXGn3MR6SROvPuK+ZmXaxXrjimndCEpaKKoAooopAFdXpkDSaLFtXJIJP51yldxoHzaLER/CCP1rOq7I3ofEy1e28jW8eEJOeg+lZ4tZvMH7tx9RXUtazlfux/8AfR/wqtcwTwwvKyIQo5w3P8qwUtDqcbu5wetW0kN6XdcK6jB+nWtix0+fajkKFMYxzWmtt/apMJto5Ao3YdulXVsbuMBRBGoAwB5n/wBarc9LERp2k2ZosGzy4rQtdIt2VWeRyx7DFRHzfOMQjy+cY3d60YWeFAZINu0ZJ3Cs22a2NKxsYbSJlQFgxz8wBqZ4YiDmNMf7oqpHq1qV++PyNQN4gsGyDOB2+6f8KlJshnG3DAyvtLfePeqkiNJMkafeYhVye5OKsOQWJHrWh4b0qfVvEUCpCssELB5wcEBM9weua6YmVR6HpfhDSBomgwxtGq3Mv7yYju3b9O3bJrdeUJG7scBQST6YqvcTLaWsk8nCRIWP0Aryvxn49Gp2b6XYRSRIxxNI5AJH90e1Va7OYsWHxG2+MJ3IK6XdsqlSPuNgLvH9R6Y9KX4p+IDLPFosDgogEk4HXd/CPy5/EV5sjeXKrEZ2kHGetOnuJrm5kuJpGeV3Ls5OSSarl1uK5t2aNDaAbcdyas/2lHbBvMPPGB3rEbUn2qQDvwdx/vVDJK93MoxjsPpVWL5l0OusbqN3eRjtVQeD1qo0qRTzXlxkF++e3YVUstyqdp5B/P3qlfXBvrtYI/uKcfU0WC5btGfUL03Mq/u0PyKe1ajXZM4gQ5IG5+eg9PxrOd0sbL5e3A9zWYl6Y45GBJlfjPoO9K1wvY3bW7FzqrKFXZEpyeOTx/8AXqLUNb8tngt8M3Qydh9Kw0uWjtzGhI3csc1r6VpEYiF7f7ViAyqtwD+P9KLCvcXS9HWcfbdQfZAnzlXz+8H17f5+tQarqEmsXpWBSlugwkY6AAYyR26fhRqWqPqk/lRAR24PQA/N7mtrQPD3nMjuPkJB3dM0mw3F8P6MsvzyRHy1OSTyHP8An+Veo+GIlzNIOq4UVmQWyIqRog7ACul0Syeyhl8yIRs7dPYDFJJtinNRibluVVSNwyegro0lQxqd69PWuWj/ANYv1rTSiasZQnzI0IjnPPelFsjDvzVZW+WlL+9QWcV428HQ63cJEYoEhbbuk2AODnnB69PrXl+sfDnU9IuZLjRJ2uUjJA25SXn07Nx6H8K9/keNiA6bsc5NZ99aW8pBWBAMcjHWrT6DueEaL4weyVLHVUl3ISplbO4f7wrsrW+t721E9u4eNxkMK7DUvB3hvWrRVv7QPKFwsy5WRO/B+vrmvMNW8Aa54duRcaHLLfwZYgRLl0X/AG16HjuPQ9KN2GjOmtyDCtSCuS03xWqkWt9C9vKoyWZSB+R5roluwVVgVKnkEHrSa7lKLLVIR0rNfUyjEbRxxQNRZl3bRQRys0JBmN/92qsRCR4PFQ/b2cMu0DIpouDsxtFZVY80bHRhansql2WPNVuhqPcDKKqi4Yn7uKkics+SMVlRpODOzF4uNWnypGjbdH+tOZgvBNUEu2idlwCM003Rkl5FbTjc4acrFh5R5nFRyvkCoGcCSkaQEdKlRZbkidz+6FN/hP0pkkgEQ4qPzxsPHaqtoZ3RJH/rV+tTnpVKObDg471O0vHShIG0Tz/8e5/Cqdp/x+p/ntT5rgmPbjrVeGQpOrgcitDLobuaiuMYWqjXrDHApst0zheBQ2uUUItSuP8A4x9amzVESEnNL9pbdgis0mbOSbNGPtTrn/UmqaXOAOKWa63R421vdWOVwfNcrr/rBU9U/MxJnFP+0+1ZT30OqlJRWpaJ4q3CQY/xrK+08dKnjvwiY2042RjXTnsaJ+6azn+9+NPW/wBw+7UBcsaJatWCinFO5ej+6KsL90VnCZgOKvwMXiDHrR10KJKKKKACiiip3AKKKKYBRRRSuAUUUtNagFFFFACVVnbB+8QatYpCik5IFNWAzt7Z+8350rO+T8xrQ8tP7o/Kq0iLuPArKtsdWFV5MrqzFgMn86VHcScMRzTwqg5HagKN4x61nT+I3rxag2PLSf3jTQzkH5jmpDgE81GHXkZFdVlY89Sdx0m/y+Cc1BmXH3mq87IFGSKiLIFPIpCuQKZfLPzNQDKT95qsIybO1JvTI5FMLldPMMi5Y9agff5jcnrV5Cm8DIzmo5CgkPTrTQEcu8RA/TrUIlbPRfyq5KyeTyQRUAaIHtSGWFJ3KM8YqsWYk5Jq6sqZA/2arNcLk/KaLiEhDM6Djr6CtB7WKTBZQT61Xtp14LDAq00o2gpzn1o32FciWxgB4T9aSazS5m2yM2AOMGpBK3oKkVv9IHHWsq7lCDaOnCRVSqosrHR7cHIZ/wA6PsEayDDt0rQaom+/XnU8TUe7PXq4SlFaIzX01FfIkaki0xeT5jVff73Q0+Ie1dtGbaVzy68IxvZFD+zV5/eH8qmaxUj7xq9sNKUNdGpxlAWI243kfhVaTTF67zz7VqMMVkatqq2MYVNrzuQsaZHU9KeoGZqxj02FXDeZIThUPGfxqXRPCN1rzLfX8jQ224FYyDlwDyMdvrW34d8KPI51LWVLyycpbvyFB7Mp7g+9dlgDAAwB0pXKK9taRWkMcFunlxLhQuc8fjzV37MCPvH8qjAyy/WrYx60Illb7IP7x/KmPZphQxJBNXaimIVQx4ANNEs841eGOPUrlVJwJCBXNq4XINdPrp26nckq2C5I4rmmhOeops2jsMJU0mBSNGRkEimfdUAnt1pFFjwCwi8Q6xgg5UDGOo3VjePblv8AhLTKoAaNEIx6jmrnhGTy/FWoKDgtETn/AIEKxvGZz4hlP+yv8qa3IZ7vpl5HqelW15HhkniD/mORXi3jfwafDgjvUuRLFcTMuzZtKHk4+mOK6z4Say09vdaRM7N5I82EEcBScEZ+pFaHxag3+FoGOPlulP5q1C0lYmx4jRS0VYgopwAIpuKACuw0K5WLSUQ4ySev1/8Ar1x9dppDY0uEccAYNZVXodGHXvM7KKWOUAI6tx0BqPUEJ0+YH+7VG4mjjQspxIv3SOKgOtR3enSxSErOF49GrkUW9UduzJPD64lmPfaB+ta8n36ydOEcaFw8ilgM4zzTJ1uGlZkumCk8AseBRuxyg3qiVFI1TcRhd+c1fm2tG6lhgqQeaQR2siRqwUksMnaefWn3EGnxW7O6oidzg0uYrkMkw26c+cgx/tiuZuF2SsAytz1U5rq0stFnUsoTGcEhmFcnfxpBdTBAfLVjtPtW1N6mdSFlcgkmWJCzdK7H4USNLqmpyN3hT/0I15zcTmV+Cdg6V6Z8I4yU1SQf9M1/9CNdFrI4akrs77XwG8OajlsAW0h/8dNfODh5pGPU9TXt3xJ1ltL8NGCNzHLeN5QI5+XGWH0I4/GvFop4422om9mwATwB+FOGxmQTD5jk9OOKZ/D1q1ersIPGSc8VUJ5qhMKVWKNuUkH1ptFAi19tm8tlz97v6CpLFo4VaWT6D3qlS5JxntQO5Nc3DXEzPyF7DPSohUlvbS3UoSJSSe/YVvwabZ6XD9ovmDSDPHUe2Pei9gs2V9N05I0+2XZCqo3KrdPY5qC/1KTUpfKj+WFeg6Fvc1Xvb6XUJgoyIwfkT+p9619G0QyMHmHHY9aPUe+iLOgaJ50iyurBFOSMda9I06yUorj5UHAAHXtWRbIsChcEjpgdq6mxQeThc7QcDNOCTd5bGGInKKUYbs0rCC2TaBHl853Nzj0rSNVIINmxsbu/TpV4IxUHaau8fsnK4zt72rFi/wBYv1rSSs6JSJVyO9aK1lU3OmgvdJ1PyikBDA00H5aSI5B+tZGwkgw4+lIuO4FLJ94fSmL0qgH/AC5+6Pyo8pSD057YpKf2paoDldf8G6Jru57m1Mdy2M3EBCSHHQE4IIrzW/8ACviXwfFNcRRC704MW3oS21exYdV/Divam61Ye4jW1ZDGDxznv9aq7Gm0eC2Wr2WoFQTsmbqhPf2NbsMETQg4PX1rpdd+Hll4qu2ubN49OulTlo4xsc+rDIx9RXmtwdX8L6gmm6xE+GOUkJzuXd94H+IdaGuxd7nTi3RVYgdqaqDYKoWt3FdIWhk3DkcHpVyJiYgc9qhpoaWo6KJSTxTvL2zEAdqS3Y/NQ0jCY88YFCViZETRuZGwp601Y3EnINBuHyeaj+0Pv5NVZiTJSjM5wKXyn/u1Glw4PWpPtUnrU2KuEsL+X0qIRNsPFSyXEjR9agE7gHmnrsJqwqxMHHFWPKY1WFy+Rz3qxHcMxIosF0JNAQoNRJExcVLcTNtFQJOwan0EStE2Rx3p7wvheKZ57ZHNK9w+Bz+lJrQa0YLC/pQYH3dKRJ39f0pXnfd17UdLA/iHrE/TFK8T4+7TIp5CeTTpp3Cjmgl7kZt3J+72pn2aQn7pp32iTP3u1OWeQ55pdStLDDbSY+6aUW0hX7pqUzyAfeqL7bKF60JCdhyQSc/KaesLg9DTYrqRs80NcyA4z+lPUCYRN6VfgG2FQayPtcv979K07OQyQBm5NHQRYooooAKKWkpAFFFFPQAoopaAEpaKKACiiikAE460mR6ikbkDPrSgLjtTEG5fUVC0TsxIHBqUop5qRR8o+lDSZSm47FPyZPQ0hhcEEjvV7FV70skIKcHdS5EP2snoyE27nPNQPaSAEg8U0zzj+JqBNOynLHFVqhWJJYJHiXHaoxaybeozTmeYRDkiohNNj7xoAnjt3ETA4yaalq4IORSJLKYH+Y5qMPPn77Ua7ATLbOJ1ORwaJLZ/MY5HJzUMby+cu5jjNLK7s7cnrT1sHUmkt3MQHGeKj+yye1McyCLOWqPfIP4m/OlqMvrCQy9Pu4qs0WD1FSrvLr1+6Kiwc9DRruSiWNdqgVaT/Viqi7gF4PSpjKY4VO3PNNJ3uJ6lgDmpF4nWqH2zB+5TmvSrq2zt61nXi5waR0YOSp1VKRqmomOHFRG7XHIxVWe/CygBM8etedDCVInq1MbSkrJlxyN9PRwpqit8j4LAg+lSLdxn1rppUpRaucNatCUWkXvNHrSNOqjJOKpi6jPQNXPa1rj/AGiOw04eddyHBRV3bcjj8a6rHDYdqfiGVbhoLAebLJIEVVG488D/AD7iun8LeEzpryX+pFZr2U5AByEBwcEf3s5/Kp/C3hK28Po0znzr6UYeY+nXAH5fXFdJR5ALSUUUgFXhhmpmuERgKgJABJp5hEnzZpq3Umd7aDvtcfvTWuUkfYASPXFQtCynjmmojBxkGtVGJzSnNOzOX8Uvi9ZMZzGOa5cwH1FdH4p3HVAM8eUOe3esM5HY1D0O2nqjNmQo5B61Ver9zsL8tzjFU5QiqMk89KW5djJ0WcW3i6YgnLoygY6ng/0qv40hEepRuM5dSWPqc1BNP9g8QJdDO0Pzz2Iwa0PFy+bbW9xuyckfnTW5DNL4Qt/xVdwufvWjf+hLXsOpW9vNZsLm3injBB2SoGGc4zg/WvF/hM+zxqq5+/bSD+R/pXt2psItNmkPRVB/UUpbiR8x6t5J1i9+zxiOHz32IOiruOBVOnyMZJGc9WYn86bWghV6UpGeaQcUtAxtdbpolOmx7EBUKOc81yqpuBxndXX6dIItNjDA8qOlY1djfDqzLbzTEsrxgH61nSxTQsXMbKM960Hk3TbhnrmujubGa5QZ8ohucE//AFqxvY7HG5hWesCKIIbdifXNWBq6uOYGGT61Hd2z2N/GrsOdrcdMVK9wryxEN0fNJ2KXN3Lh8QxIob7O5CnpuFU9U8Rpd2EkIt2XcRyW96kubgtDgP8AxCs+4kLRgM2eaSS3E79yKy1MQQlBb7yWzndWZqt75/m4j25B4z0rudBRW0pCVU/O3OKxtZWP7TdfKvQjp7U4yXNsRK9rHnw54Ar234e+HbzQLC5e7eMtdbGCLnMeAchvfntXjEyqjMU4AORX0J4Xa7bwrpzX7h7poQztnJOeQT74xmuqT0PPasedfF+7le/02024gSNpAc9WJwfyAH515zb/APHxHjnBzXdfFqUP4itI8jKW+SAeRlu/5VxFuNgaQ9BxVx2JHX77pgM9BVSnOxdyx7mm0CYUUUUCFAycDrWhZ6aJsNM+1Seg6n/Cq6ukK/Lhm9amsYZNQuhD5hT5S2etBSNt9UstNj8u2jU8EYQ5596w3e51G4yxJx0Xso9BSwafLLcNGQQEJDNXQ2mnFQFjTA/vUFbkOmaOkUiFwS7dB612UFqI8Buo4C+lQ6Xa+SIxtLbsBnrsdM0eLUmJlDKkfOV7n0qG7jdloQ2Hh4SW6zmYlmGQoHHsK6XT7YrGUlVC2c4ByBmpbbTorVNsWQvHBPtirMcbCc4x0pXZm0r3J4oVX+EVJsX0FKgPenYpXCw0KM9KfnFJilBxQMUHim5KdD1paheXnGOhoEybcTgn0qJidxoaTCKR3ojbcpJ9aaEAJz1NWD0qLNMZjtPPah2Ghz4xTZh+5b6VDu5qSckQmi4FJGaKQOhww6ZGauXVjpviDS3ttZMcofHysuGGO4IHH4VXwTCSQc59aWIL5i7jgd6YzynX/hxrWgXdxe+HUuLuxTGN2PNAxk5UD5h7j8qxtM8RwMqW94pikAOWIIBNfQcV8igxH5V6kp8v681h614I0LxUjz3VoUumj2x3MR2uuOR7H8RR01KUjzq1IaMuhVlPIIOcilZGaY8HpWRq3hbxB4Fvo2us3Gn9TPADsPseMrye/XtWra3iXMYljbKsO9S9CviIfJk3H5aYIH3/AHTWgjMTzSFjk96XNYfsyisLluhpWhcdqtxMd1OkYnFUZ2KpiYx9KiFu5B+WtAFtlC5ApbFbmcLaTcPlPWp44GVuRU3mNuFL5jljR1JcdCGaJio4NQiBs/dNTzPJgcmlVn2Dk9KauK5D5bbgMUPG2BxUil9w5NNldxjk0n2H1Ejjb0oeJt3SmiWQHG40rSybj8xo1G9x0UbA8ilmjYgYFLA7seTTp2cYwaNREAhbPTtT0iIHNSwb2zuOB9Kk2kE80m7MLNkPlEiozZS7elW+mOatK4KjpRcOUzIbZ1yDSSwMHq4zMGOOmabknO6jme41EoGJhWrYxtHDhu9RqAe1XI/9Wv0oTuhNWHUUUtDaEJS0UlDAKKKKAClpKWgBKKKKEtQFopKKAI5/uD61EDheSKllBZcDrVYAk4IqkCLCONuKd9oQcEmo9qgVFgfN060BuWvtUY7mo5LmMoOvWq5ClTwOlPKqI14HUUBZDjcRBc4NAuI9uQppriMqBgUbVCY2ijQB8lzGIxlTioPtcQH3TT3CbBkCoSE/uikFidLuPyidhpFu0P8AyzNNR4hCRtHX0pokTstGgEi3CtIBsPJp0kqhyCpqJJU8xfl71JJIm8/LVXAVrlPJ5BxUH2mPj5TUjyL5H3ah8xcrx2pDRbEw3AYPSq5mXJ4NT7l3L/u1XLDceO9MRMbgALwelONwDEGwcZxULNwv0pWP7gH/AGqEAvnpnpTpJFBH0qtn5l+tSTk5FDGTzsMCqzEnd/hU9wTsWqe5txGaTvYEKxYHv+VPi3ll6457UkuRt57U6Enb170rj6GJ4j1K6sPIhgKgXIaMEjlT65/Gu38NeF7bQrBPMVJbsKC82MkcdFPXHX86888Xc3+lA95D/Na9icYhf/dNPoJkisGRSO4p1Q2zboFODxxz7VLSAWiiikIcse8MPap0XagBPIqOHvUp6UARecv901Ab1MZ8tvzpyjJq4Io8D5F/KmmS0cP4jcSzs2Nv7voa54ngV0viqIm7bYh27QDgcDiucIo1ubw2M65hKksDnJqnNGSE/HitG5DjnAK1X+VlXcOeaethnLa3bkAnHvVNr03OjfZpDl4iCDnkius1K1SS1bC/N0zXCSxmKZ4zkEHFUiJHT/DN/L8eaccgBvMTr6oa941mLzNDvhnpA7fkM/0r528JpcL4ksLqGOQrb3EbyMo+6u4Zz+Ga+i9adRoGosGGBaynOf8AYNTPclHysO1XLSLeSxHAqoBgCrNrP5T4b7p61qhEk9kwy0fI7j0qnXQJhgCOc1DLYxTElgVbHUUWKsZtqwW4TdwM4zXV2ltNLbJ5cbMvsOlcrNaS25O5cr0DDpXfeERPcaQHYE4coG65xXPXfKuY6cMuaXKaWmeG2vbTz2m8o7ypUr6V0f8AZ0aKih2+UAVFp95DaWrQykiQOTtA7YFPOqwn+GTH0rj5nI73G25R1XSopFM5Ll1XjHtXKfaVWRSUPytzXci8jmBChs+hFczqNqxuZSY8AsSMiiM9bMcqbtcoy3iPEV8sgk9eKNPjhvbkxSKdoUng49KingKRO20HA45p+k7oHF1IyCN4icDORnFa9NDFrWxttG9tarBZkKvJy5zg1xOtQyJNNJNc+Y5OTxitu/8AEUNucRlHPfnpXJarqX21nbGAW3VdKEr6mFWpG2hRkIK/hX0H4UEq+E9MWddsgt1BHtjj9MV89WdtNeTeRBG0jkE4FfQ2kSi08M2klw20w2iGXcfu4Xn+VdEzjbvqeNfEVpX8bXxlIIGwJg5wu0Y/rXM7sRYz3rU8UahHqniK9vYm3RyyEocdsDFY9WtiQooooEFFFFACjmtDTZHtL5JcHoePUYqXSdKkumErjEYPHH3q2bTSVvtdt7NW2hlbnGcYBNFylHqV9Ol8yeYjgM5OD2retF/djFY5szpuuXdnu3eW2N2OuQDW5YgtCvfj0qWWjotGhF1cW8GQCTjOOvNej28EdvEI40CqOwHU+tcp4Zt1tw0giDSALhjnjNdMly+7DKMY60KDeqMKlWKdmW6WP/Xn/dqsbk9gKfbymS5yeOO1HI0Z+2i3ZF4U6mZFLuFRY3HUU3cKAQaPMAqs/wB8/WrJqlI2JG+tAEz/AOqWmL0pJGYooxxUZmEakt0600SyfNOb7n4VTS9EjALE+CcbuMCp3fEZOe1DsCQxmxSNNmMqCTVZpWPU1GXAPPel11KsWjJ+7wWPJ6UmT6VEBnGKmxTv2GAOO360fbJLJWmjjMhUfdB5NNlkjt4mkmkWNFGWZjgAVwl18UdMFxLFbWtzOo4SRcYY/Q80AkdvL4jivbeW3uLKOSKQYeOY7gR6EEV5Tq2lyeF9Qe9tQ8mlyPgK3zMCc8HHQD1xzVg6/qd1eSz2ek3O6Rt2CWIwBk8Y68Z/pVm21vW7tHtL7QxLC0ZEnmI6q4HUdMZINLXZlaFqyu7a8gWaHDKw64q2EQjoPyrjb2U+G9TiWBZvsMqbhG/JTkjAJA9PTviumtL9Li2jmDKVYZBz2pSXYZI8sUUhUrz9Kja5i3YxUM/765Pl4Y46A0xrS48wfuj+lMjqXhcRhelOE8ZHSoBazMvCE1ItjchOYiKTki1BsYk8btwOhpzyoG+7TY7KVWJ2Yz70slpMx+VCaOZX0DkdivPcrxhaI5wU6VFPbTIQDGajRXVTlSKq9yLW3LiTLxx3ps8qEgAVDCrn+E0+SGQsPkNQ33LSGB1DdKWSRQ33aUW0pYYjNE1pMW4jNNWB7jYJhvxipLiUBhxUUFrMHyUwPrTponZhgZ49aehLEW5C9jUkdwGByOaqmF88rU0Nu+DkYodhK4+S5UY4NTrMu0fSq8tm5xjH51IttIFAODgUug9RrXcYJ61G9xu5Tt1oNi5JORzUsNkwzuIwaegveIRcuDWtbsWt0J6kVQFmBnp+daECFIVXPQUXXQGmtySiiik7CCiiikAUUtJTAKKKKNACiiin0AKKWikBG4JAApnlt6VKeo+tOqgINj+lRmJuSRjnuauUgHJoAzN65296mfhBx3FWzChOdopHjVgBRcDMM3H3aX7SSuMVcNlHiojaKOBRpYZCJQY8sOhqNnUjvVv7JlCM9ajNkeORS0AYmzyc89aaCmeM1YFowixkdajNpJntQAxCnmL1606Zl8w9aVbWQSA8daSeBxIaaFYTcjQ4560n7vK8HpSrC3l44604wEOOnagehLlMqcH7tQM6Bz8nerbRHC5I+7VZkw5GR+VF2LQkZkAX5KNy+UPk4yeKc0XA57+lOWL92Bn+KmLQgyuR+7pZHUkfJnipfKGfpSFBnkZ4o1BWFkYbR8oqoXXcfkq+yrsGfSqhMW7lTmjoCBpBx8valjkXGdvGaV9nBI7URhCCMGptoO5y/ioiTU9JAGP3v9Vr2OQfun+hryPVbWfVPFml2NjbS3E0R8x0iXcQu4c/pXsE6GMSKwIYAgg0dAK1nn7OPqamQsRlqgs+LcfWrND6jCiiikBND3qQ9Kih6NU1MRDDGSCcVaA+UVGg2jAp27ApLcGczr6k3LAjhgAa5C5iNuwQjr0NejXtjDdnMgO71Brh9VtmjaVG+8hOPzqW7O5pAxZRuXGaqFCMA1YLkDoDUZO7BxxnmtLjsLNHm3OfauE1tAuoybfb+VdxfXSrMbeIBs9CPSuLvx5mp4bks4BH44qo9yWbXhm+tLG2n025RvOupkXO3cpB4Kkfj+tevaxJJF8P9T82No3jsZVKsQSOCByOvGK8V1ZPs2swTR4C71YH3BzXsfjq78jwPq7j5t9vsxj+8QM/rSl0JsfP9lGJZSpAPy9xUkli4b92M+1Q20mM4xkGty2kWYBuN46j0rRDMyzuTC/kzZA7Z7VqD6027sEuhu+7J2Pr9azYriazk8mdWIH5igNjWBrTsNevtOiEUJjMY6IyDj8qyI5UlXchyKfmlKMZKzKjOUXeLOlTxnOuWk0+1dzj5ssP60w+MJd2Rp1qPxb/ABrnKQ1HsKfRF+3qdzpE8a3sZJjsrRc+zH+tQ3PjDULpNjwWgHtHz+prn6Sl7Cne/KHt6v8AMWpdRuHRlLgKRggAVUku5zCIvNbYBgLnjFI3SqrzxgHnpV8sV0IdST3ZDKcmqkjZ+UfjUzFpW+VSB6mmtEFFUQdz8N9LjlS6vJFyxIjTjt1P+fauw8a3DWHge8C8eaFiH/AjzT/AULS+DtPfaBgMo+gc1i/Fm5eHSbCz6CWVnPP90Y/rWX2ht6WPJTzSUtJWhAUAEnAGTVq1sLi6dQkbbT/FjjH1rq7DTYbVAAmT1JIoGlc5220K+uAT5YQf7ZxWjB4Y/eL5kwKY5wuea6QKAv0qYkbEwTnHNFy+UplEhiVABkYHpU+gQP8A8JTBIVOwI4BHrj/69PjtTcTqTnYOGNdB4JVI/GcyGULut2Cox+/nGcDv93moY5PQ5HXFA8aXeBwwQ/8Ajorc0W1DwkOpG0AYJxU/xEt0g8c2rquPMs0JA9QzD/Ct202qhOBknPAoXYlysjV0UBUmC9BsH6VqZrP0tSBM5BCsw2578VoV0x2PIqu82wqa1YLPknAxUNPi+/8AhRJaCg7STNMOjcBgTTuKrQDEn4VNIcJXNJWZ6UJXV2P4o6U1TkCl7UmWgVtyAnrVCeNhKzep4q3kKPYVny3MolbpjORkUhlqd/LiDYz2qoZxI2xlwp96ku2LWqnucVRycg55ouFi6ECA44xVYXErtgt8vpikaeQqQSPypkY5zmjUZNUbqTjFPooYEkWdgzSXl9b6faPc3UqxQoMszGq17qNrpdo91eTCKFOrH+g6muItLfUfiprJhhlltdEtiDICOSc9jjBbHOD0p9ASIlt9b+Kmq+XYF7XR4GAkZz8o9Tx949OO1ep+GvAGieGYikVmtxKSHNzOFZgeOBxwO/8AWtvRdE0/QrIWunWyW8QxuCjG44xk+/vWjSBsZEUL4H3gA3IwcVDqlit7ZuqoPOAJQ45z6VYCgPvx82MZ9qlVjt6c0hHk17bRXlvNaXMYeOQFWU/0Nebz6c+g65Fpv2ljbTruiZx39Dj3/mK9i8S2qWOqyEbVjlHmDn16/rmvNvH1uxs7C+iwJIJ8Kw9CM/zUVXmVEi039zq0kLN8yLzjPfmuiaVOSScfSuZ0aY3GrPM2MvboxwO5H/166ow7o8ipnJLcqnBzdkMhmDOu3JAPpWg0mQarWwMeelWvMNcNSquY9ehhpcl7lYZyODRkjPB/KrAalLn0qHVTNI4N33My5RnI+Q1RmtZCuVU8e1bkjk1CzNtNaRxFkY1cBeW5nW8TBQDUxgcsORTkPJ+tTZ5HFONbmnylVMJGnR5xiwsD1FVtQla3WPod2avg1l63nEH1NdCPOeoy2cshJNNKEng0ll/qakAq1Y53oyHDZ6ipYnKjmkVc5pMYNXo2K7JXl4FCzH0qJhwKco4qWNNkqyZFP/hqONam2/LUM1g9SHGTV1OEH0qqV5q0v3RShuXX+FC0UUtW+5yiUUUULuAUUtIaoBaSiiluAUUUUMBaKSloAa3b60u6o5JVj27s80xruMdQaYWZY3UgPJqt9six0NC3aHJANAWZbFB6iq8d0rDoacLgFwNpo9AJsU3FRPeRocEGm/bUK7sHrigLE56UxmC9aiF2rfdU8c1Xa8DH7nSgLF7dmPIpm456GoEugU+73pDdAHGKAsycOdw+U1BPvaU46UiXe5wAvU+tE0hEpx0p63GkwXeqc+tDeZv4B7U0O7qMAdalIcN2pAK2/Izn7tVWLeYetXn3lvbbVVlO/oaYIlYNgdetC7vKHJ+8akdWwOO/rTQG8scfxHvS12DQQbju57GmZPGT3pwDbm9Oe9NIO0cjr60a2ESH7pquxXeeDmrAB2np+dQiB3fkcHvT6EiOMqKWAZzVowrtxis+8ulsdkajfPO6xRRg8licCkh2Ok+E9sLnxd4h1NhlVRLdD+POP++a63xGUt9QZSQGmXKj8Oak+HmiXfh/wjHaaipS7aaSWRSwbblvUfn+Nc5491SBNY026V0xFN5EhLDgNkZHPv8AoaHuNFq14gA9zU9UoZQkeMA80kN8XmVGAwaLajsXqWkqOaTyoi+M4pAWoejVNVLTbpbuF3UEANjmrtMQUUUUgGP1rC1nTDcgzwjMowCueCK25DioCwoauhp2PMr63WJwUHBHI96qJgnac49q7jW9LW4DTR72J6qOQD64ri5YmgmZGBBHrUrTRmqd9SKzVRrMTEcgn+RrF8YRR2+tQzZGXVTj6HrWxC2zUEfI4Oa5zxhcPcayys+UjjUKPTPJrVXJkN8RTBvLZASoY4Ner6xIdY8BzgnmexD9M5O0N3968h1Bg+mRt6BTXpPh+7N14U09G5DW/lnn0yv9KHsJnisbFG3VpWs/lsHzwetaHivwu/hu4gxKZYbgMUYjBGD0/IisS3YZKMOtWmSjpEcOoZWyOxFNlhjmTbKgYe9ZUNxJaOABuQ+9aUV3HNwjZ9j1oKKMmnTW7iS0O71U+n9afDdrIoDHD45B4rQ3gEc1BPYW142/JST+IjvQFiIzJj7y/mKie8hQ4L5P+zzSnSIh/wAtmP8AwEVKmnWqYyGYj1b/AApisyp9u3nEcLuaejXUh/49mUHue351qhyowAAPbimlvegdimNP3MDLMSPQVIbK12D90CR3Y1MWFMaRQDxQPQoOo9KqSgCp55kQ8n8KpPNvPA4oIZ754DAHgrTAP+eZz/30a4X4v3QfVtOtgwJihZ2HoWP+Ar0LwbC8fg/SVbj/AEdT+fP9a8U8aaidU8V39wM7RIY1B7Bfl/pWf2hHP1o6Xp4upkaT7mfu4+9UNnp894QY1+TOCx6V1ljYpaIOhbGM4qmxpEsUKxoqIMKvQCrCLQFqzbxB5EXP3iB9KVy0jQttFaa3WR5Nm7kDbnip59PihWFQScE5J78Vpr+6iRAxO0AZNQXJHl7z82DU3YXKJHlRHAHsKj0n9z8SNFGMExtn8Q1W49kq5IIAPr3qlaH/AIudonH8P/xdAnsXfiYMeK9MfPW1x9fnNdZpGkxXGnQzNIwaRAeAOK5P4pELr+jv6wOPycf413mh4XQ7Bv70Cn9KNWZy2IrdNkWwHIViufoampkHMZb1Yn9akrrWx5Mt2JT4iFck+lNqSGPezZ9KUthwTbsiVZdpyOtSPMHQeveonj24xmm96zsmb80o6MtQsSSD0xU1QW/8VT9qyktbHXSd4orSt27VQuc+YMelWpnCAsTwKpPIJHyKg1RLM4NmozzxVahxuQjPNAzTAKevSmUoNHmBJWdrWtW2h6c93cnpwiDq7Y4Apmt63baFpz3VwcnkRxg8u2OlctoXhi+8cagmsazK8VorkrAARlM5TacbSOoPfj3o8xog0bS9X+JWseZcGSLSonyeNoReMhTjk+/fHOK9x0nRbDQ9PistPgSCKMAcAAtx1Y9z70mn2tpZ2nl28CW8K/wRIFX64FZ2reIPJ3QWTK2RgyY6fSgTdyvN4rnWdwlrFtBxyxJpn/CW3X/PrD+Zrn+popDsdEvi6fvaxf8AfRrX0XWv7UeWNohGyAMMNnIrhqt6dqEunXQniwTjBB6EUBY3/GVh59lFcqDuiYqcZ+63/wBcCvOtY05dS0eazDbSVBQnnBHI/lXqV/J/afhOaYrtZ4C+FPQjnj8q85Dbl/Smr2BHBeFnT7XIqnJjiAPHT5v8K71OYPwrgfD0SW2talEuSqnHTH8RFdXDMSMZrOpHmRtSnySbNNByafkeorMaYrik+0H2rmlh7noU8coxtY1Nw9R+dG4eo/OsyOclsHGKn8wUvq3mV/aVtkWJGHHIqJiNp5FQs4pjONtH1bzIeYX1sCHnrVpSpx0rMDcnmjzdvOacaHLO9xVMbz0XGxrZHtWfqcBuBEFYDbknNQvOWAwarSuSRya6VFnnKXQtW1q0aYJB+lPELZ6iqkbsO5/OmmRtx+Y9fWrsQ7tl5YCM5xSG3OTyKrwMzA5J/OldWLEg/rQndiaaJmt22jkUqwkDqPzqugcr+PrUikqMUpMcVcmxs4OKlUqV5YVVOWpyo3oaEk0Dbi9CfYpP3xUoGBjrVZUb0NWV6CjlSCU3LcWkpaSqJCiiigBaSiigQUUUUhhRRRQ+wBS0lFJARyxhyCegqjKo349DWi3SsyUt554PX0ql5giNhhjT4xlW/CmSZ3ng1JDkhhg0dCgEojGMd6kSUeZ0qu6MWHyn8qeiN5g+U/lRYQ24YNJmiPmMjB606WFy5+VvyqSOFhGcqevpRoUtggxh+O3rUDFRn5e3rVqGNgHyp6elQNEx/hPShiW4Rsuz7nf1pC6hvufrTo0by+h600xMX6GjUbsLEU3jCc59almYCQgrk+tRxRuHHynr6VJOh804Bo13F1GoxwML39KfIW3nrRECFXg9fSnSAiQ4BoEOk3eZ0P3arMD5h4P5Vcbdv7/dqq+/zDw2KGBO4OF4NNCnyhwfvGnSF/lxmgF/JHXO40AN2Nubg0wo2wfKfvelTAvubOcVGZG2A+9PUByg4bjFSxgBxUIdtjc06GQlxk5pa2JLfasjwtaz6p8W7OK4XfHZs8wXaCAgGVz+JH6Vr9RVf4ZlpPi1qhODttHH6pQhnsupNs0+UBgCylRmvD/HNm1xpM8jA+ZEd+WxkY65/D+Qr1/xDdtDNaQhsLKHJyeuMY/z9a43WbM3EUjKVyy4O44A681N7M0gtDF0PUv7T0S1uedxUB88fMOD+oq2XKNuHUHIrjfClyulald6JLcecC++KQDAf1Iyc8jBrrHbKnFX5oRuWF0Lm0WTIJ6HnPNSXoY2cpGMhc8+3NYGmX62kv2eRsJJkjOevH+NdDdf8ec3/XNv5UhNWZX8OZGmtjn94f5CtYs47fpWZ4ZH/Euf/rof5CtmhuzE0Vyz+9MJb3qzkeoprOFGev0pcxPKVWDnoDTCj+lTSTgDAHJ6U3JIpqQcpA0BdSrLlWGDXKa7pQgZQAcH+PZ+nFdlk1Vv7T7ZCIyQMHOT9KUtdSoOzPLGDR3ijv3rn/EdrNJezTiF/LAXL7TjHQc/Wur1y2a11kxu2T3NL4lCr4aMS/e+zqSNp4/eH/HNXHZFTOO8kS6Sg7mOur8D3wl0wWc0kMZt2IXe4UsCcjqfXNc1bHOmw5/u4/U1Wt0T+0LWJgCGnQHjsWFNgel+OtKi1LwjK/Cy2g89C3HTgr+I/XFeKR53jFe/eKIjL4V1SPGP9GkP5DP9K8Dj4lH1ojsQy/HiRdrAH61DLBJEcxlj9OwpyOVORVsFXQdxVFblKK+kQ/P8w/WtK3vIpTw2G9DwapTWyuTx+NQfZGbBV8/hRcNUb26mlh3IFYRju8/dl+nJpRaXT/wP/wACNMLmu91Cn3pFH41Wk1OFfu7m/Cqf9nvkb2Cn0HNSrZRqOdxoC7GPqcjcIgH1qEyXM5+82PbgVfESqOFUfQVE5RT1yaLgZjgq5BOSKtaXYyanqdrYx8PPKsYPpk4qvKwaUkDivTPhNpVrOb3Upole4gdUhY/wZByR+lS9ESd7rd3B4b8Izun3be38qLPdsbV6e+K8CsbUXl0fN3FR1PrXq/xX1EwaFa2IOGuZdx5/hUf4kV5zpMDLEH/vH0pLa41qzbs4I4Y1iiXoMACryW8p/wCWbZ9xVe0cwSByuewBNaA1F8j92tJmg2OynkBwvQ9zitSy03y3EkjfMpyAKbZNM058zCqecYrSJCKWJ6UgY8c574qC7/492/Cordj9owAPmarN5Hi3b6igRTteYz7GqNvz8UNE+g/k1adrFiHOeprOth/xdHRhjoB/JqOpLLvxX+XVNEbp+6l/mtegaEn/ABT+nZ5/0aP/ANBFcB8WSBe6KTj7k3H4rXomjgLodgOn+jx/+gijoQycQRKuFQACl8iPH3RUlLketHM+5HJHsQ+THnG0ZpwRU6DFNH/H4fZaeWXONwzS5mUoJdBmMvjHT1qGUYk/CplB81j2xSSRlmyMdKuMjKrC60Gwf6wVaPSoIo2VwTipqU3djopqOpj6i/Pl+hqpCxLY7Yq5dqGvGBGR9faoTGqHKjGam6saWd7i0lLSUigqG7u4bG0lubhwkUalmJqVmCqWY4UDJJ7CvPtRnm8a6ybKAt/Y1tIA7Kdpkb1BwenX6fWmNINE0i5+IWuNquooRo8LlEiJZd688AjuOM17DEiQQrFGMKoA9z9aoaRYQ6bpsMEKKu1FBYKAWwMDOOvFPvLsRIUUgN6+lHUbI77UX3NbREhcfMR39qyNwkQMjBlPIKnINcF4w8VTzXo0nSp/3rkpKw6gnjAP+cV22gadHp+kW9svIRAMnue/607DasiQ0UOuyaVR/epKTQhc0maTNFIZ3ejL5/hmOMn70bp+przgIUBU9VJFejeGWzocXs7D9a43WbP7Jqc8ajC7tw/HmmluJHmulxM3ivV48jIJ/wDQv/r10sNsyJyRWJaw/ZvGuo8582Pf06ciuiVxigG9SN7ZmGQRTPsrDuKuKw29aazr6ijQLlMwMvPFKPlHJqWVwRwahIzQrADZqu0lXnUbKoPE2eBTsLmEzyaa5GBzSNkMRio3LYHFQ46lxl7th4IIHNMkxkc/pQudo4pJQcjg9KpolPUdERzTWYZPJoiByeDTCDuPBpaDvqWIGHNSswyapKSPWpVPy0mraj3LCOBkZ5pSarA/vBU9NK5EnYkRtpzmpxMKq7ScU3awobtuOKcy6Jh61MDkVmhTWgn3F+lJNMJQcdx1FFFO5IUUUUa3AKKKKaEFFFFDAKKKKl3uMKKKKaAKoXEpW4xz1q/VC75nFUkOO5BNcN5nAohuH5qKcfvDRCOtCSG2PN25I6/nT0u380Z9fWqu05FSKpEw+tOyFcuPcvuqxFI7RZJqkyky4FX1G1MUralNqwiMxV8selVS7kH5j0qyrERuSB0qqJuD8o6UnvoSh0bOY/vH71G59+Cx60qS4j+6v3qQSguPlHJoAI5HLD5j1pZmfzSNx70kcg3D5R1p00gEh+Qd6OgdRkbthcsetLK7CQ/MeKSKQEL8g6/4UsjjefkGc0B1HsxMp+Y9BUEjHeeTVgyYkxtXoKgeT5j8q/lQBJI5+X5j0pAxMQ5P3j39qV5CCvC9PSkWZhGOF6ntRqIcCSzDJ6etMbPlgn+8alEx3ngdKaZ2EYOBncaeuwDVyVf6URffFOWdir8DgU1JmLgccn0o12EXQai+Fv8AyVXWf+vVv/QkqQVH8Ljj4rayPW0b/wBCShbAdT8TNWk0m/02dWcqnVFxg5PTJ9cU1rqK7tQ8bLJG65BU5H51V+MFoLyO2jA+fYSp9Dk8/wCfSua8Gak0+lG0b79uduPbB49OoPA9qTjpc1jsZvizTbi31C31axEhmTCP5abiq8nI7Lxx+NbFlfx31nHcKpUSKDtJBKkjocVoX9vHfWcttOm9JAQyk4/l74ridDkbTr+50hjuEblkO3aMfjz6UR1VimifxTfTWMFpPbnDeYy59Mqa9HM4l0lpDnLRDJ+qg/1ry3xbJ/xKoPVJx3IPRq9BsrgS+GoSAcmOIN/3wtBMtjc8J2jS2E4DD5Hzz9P/AK1XHkBUgA0eDUJsrwjuwA/I0yWN0JDqyn3FHUgjVskilb7prLv9Qlsru0jVAyTMQ5xyBx/jWmfumk1oMrTMQBj9anB4FVpTlh9KsA8ChdhMdSHgUUyY7YnOMnBwB3piPOvEzxtrpMbKfl/hOecmtfxpBE2hzttG4W7Kvt3/AKVxviO0vLPxBaGZZI1mfCDcORu9j713PjIY0ScgDhX7exoj0LnseV6fltPjx2yP1qtehoNlwhw6OCD6Ecip9Hbda7So4Y1eW0ivC8MqMVZWICnBzjirY+h6Zot3/bfhe0uLkBzcw7ZRjgnJVuPfBrwu/CJrF0sShYxO4UAcAbjgV7N4BuIp/C0EUYANvM8R5/2s/wAiK8a1TjV7zHa4k/8AQjRHczYU9ZNnOTTByM0oRmOApNUAM8khwpP0pYRIjjBK8881IiyIOUP1psgJOSMUDNLzE4/eKPxoLqejKfoaycDBpmxuwzQO5pySIDlnXj3qFruMDgk/hVTyW9QKY0RLY3c0CuSveZ6fpVWWRnAJHFSCIAc81E7AjA6UegEthYXWp3iWllA8875IRBya9v8Ah3od9omgSwX8RimkuC4QsDgYAzx9DXF/CbT5n1ufUDbsbdIWjEuOA5I4+uK9iyFHPAqJPoI8a+JF3Lq3i37DbAyCyiCEDsx5P8xVO0gMMCIwxgc0qTQXviLWL+NtwmuGKnH8OSR+f9KucelFzSKD8qmtgGuEB5GaZsOOnH0qayX/AEpc9qLjN23JMi+4qeUksiAHk81FBtB3EgACtCwhS6uDJ1CY4IqQuTW9tGiFyi5yOcUl+ENqwGM5FXbhNkP4is24bKEUIi5HAoEKjFZFkhb4p6XgfdQk+3ytW3EuYQc9Kr6FbxP43a9MoDQwlEQfxZGCfwB/WmIrfFsHz9Gb/YmH6rXoenYOiWfHS3T/ANBFcT8TrWO60mzu2uEjltpGVI2/5abgMgH1GM12WjyeZoVixGCbZD/46KOgmTyT7RweTUQmOck1HL1qMVLEaDgqgkB5C4qFfm5FJJMxtgv51CszKMDFAmy8hIXFSjpWekrs4BP5VfU/KPpT6AOpGIUEk8CimyOoGCetGozIkcvOZPU0jHNTT7AAQoznqBWZcapY2+7zbuBCv3lMgBH4ZpFFyisCDxZY3GofZo9zJ/z0A6n6elWta1620exM5PmSsdsUS9XbsPpVWCxgeK9Wub2+i0DTHO6Qj7TInIVTwQcdOxNbuh6Pb6RYxwQIM4G5sDLemcdaz/DeifZBLqF1Ev2+6YySHb9zJ6A10i8VLWpaNVbuOO0BZvmA5FeaeOvGElmTaWsmyaTkurcqPp/KtLxp4nh0PTQgAe4l5jRhkNg9fwryjSNOudf1E+Y7tli7M38XrVRS3BKxu+DdKa6vBqMyswU5BPdj/k167pxzFtweOlc9o9gtvEiIoEcQ29PvEV0VlII5xnoeKTeopdiGcYuZPqP5VHVq/wAfazj+6KqmgQUUUlAztfCbZ0hx/dlP8hR4h0uCW0kusESqBzniovBzZsLlfSUfyra1GPzNPmX2pdSGfPt0WHi+dh3gx+q1oRlz0DflVDVD9g8dXkWd+1T2xjO0iriakBwUP51Q2i9GHKjhvypXVvQ0tteCSPOCPamXF2iY3A0tbgmIQRThVaS8UoNuDzTBdHcBxTSBs0XPyVH2qGSc7aYJmxTsYSlYV1+c0jQsR0qFpW8w1oA5QfSny3JlXcUUSNg5FRvICas3KnYTWcyOW6HpUyRrTq8yLMci5qNmBJqNEbOMU4Iam2hpfUbvGetSK4x1qEoc9DTlVhS5SuclL4I5qTzDVcjpU4QlaLESdx6zc804yqe9QmNh2NHlSH+E0ONxwlykyyCtBOUU+1ZYglx9w1qR8RqD6ClGNjSpU50h1LSUVV+hkFFFFGgBRRRTQBRRRQIKKKKl7jCiiihAFVboKmJDyatGqNz8zYPSquCK0kkbsCUP50+ExjJ2H86hZcVJCBtNCY2LuiyP3Z6+tPLReaP3Zzn1qIlQehp6lGlHB/Oq0DcnHlmUfKc59atcYquBHuzmp96Y+8am6KcWMBXy347VTwoBxnpVgSRGOTDHp6VWLx46t09KHvoSiSMKY+h+9RhVkH1oieMpxu+96U4lRJyGzQMbEE39D1/rTptnmHg02MoG6N1p0rJ5hyrfnQ0HUSAJgcHhqdIY95+U9fWmRMgH3W4I70sjR72+VuvrQHUkyvmkbTnjmq7ldzfL+tTkqJT8pzx3qBym5vlPX1piJXI+X5e1Iu0xj5f4jSsU+X5T09aVGQRj5T971o1AOA547UwkGEYGBuqQshc/KenrSDYYRwwG6kBGuNj8dqbH99frUyiPY/3ulMQR+YOW6+lO4i6KrfDNtvxc1Qetq/8ANKsiqHw5kx8YbwDndbyj6YA/wpdBHYfEtPM1GxUdRGSfpk15vZSf2P4lDMAsFwMMxIHueT6Hk+vAr1Dx+pfU7Pj/AJYH/wBCrzjXrQm3juEHzRuOR+nr3I/Kn0NY7HUs/wAx7VxfiiJ7PWLPUYlbaTh9vA49cDvmtzRb5rzTYzI2ZY/kbJyfYn6jBqHxHaC90p1H3k+dcLkkgdP8+lJaMswfE7K+is4wfnRxjnv/APXrt9GYt4YtTnOVXn/gC15jdXqyeH5baR8yqy7c9wCK9J0CVZPClmV7gf8AoIpkSO98HYWxuf8AroP5Vf1U5dRn8KpeDx/xL5z/ANNP6Vd1RMSq3qtS9GQclqto899buEyE6n8asOjAgjPvipriTM+zHAxSwsTOqkDGapeZLIUi3fMw4p+SDVifAbAGBVYnmh2sCHISTUu31qvG3zCrIPvS6jZ5t8RB/wAVHoQx1Yf+hit3xl/yA7n/AHX/AJGsP4h8+J9AH+2v/owVueMv+QDd/wC4/wD6CacdxvY888IxCTSpye0v9Ku6hbj7OxUlW6ZXrVbwWCdLucH/AJbD+VbM0O9SDn8KHuaLYzPhnfvba5d2DsQs0e/H+0p/wJ/KuO16FrfXr+Nu1xJgg543E1p3GdL8URydEYgn6EYP9aj8U2iwzQyqAN+7P51a3uZtFDTwsgIPUCtARgdqo6amFL54xjFaNMECoCwGBjNR3qhQuB+VSI3zL7mnXEYlIBJGKCuhlMils45oxV/7Ig7mj7PGv8OfrRcRQph65q/LGmw/KOlUDgc5oAQjiqDDDEe9WpJQAcHmqh5OaCWe2/Cok+ECCMAXD4Pr0rrNVuRaaRe3DfdigdufZTWN8P4RF4H0wAY3IzHjuWNVPiTqQsfCksCuBLdsIgP9nq36DH41m9WB5h4cUeXMep3AfpW8EPtXP6BMIZDAVOZTkflXTKOKbNVsKSSoGKlshi5GeODUoCl4mGDwKsW1u092qRDO44qOboMt2tq13drGobBPzEDoK7CC1jtoljRfujHuah03TRpyOPMLliCeOMjP+NXjQjOTuVLxMwYHqKypLZpOMgfhWxeMEgLEEgHtWZ9rjGfkf8xSc7GkKTkrojW2KRbSQazLGP7F4pgYtnzty/iV/wDrVqG9jUHKPj6ise+ugmraXcopAN0i4Pvkf1oU7sJUZRV2SfEps6Haf9fQ/wDQWrttBO7w7YH/AKdk/wDQRXC/Etv+JHaDP/LyP/QTXc+Gvm8NaaT/AM+0f/oIq+hiPbmm4q+qKBwozVeZf3pqWr6ksif/AFQ+tQ1ZlA8riq9BLJIf9ataK/dH0qhbR73znG3mtAdMUykIzqiFmOAOprOur1HYGNshRzkd6n1KYR220/x/0rh/EOrSaTol3exOiypgR713AsTjGKdi0jB8b+OpQt1o1pCY5AxjkmJzx7cd/XtWF4Z8NS3/APpt0JFRiMbhywzyT3qt4X05te1ma8vAJkVvMcN/GzHP+J/CvTnaC0ttzFUijXvjAAp7FGHdPp/h2AXEqqMkqgXBLHBOKPDWlT6xcjXNVG4Ej7NEc4QA9cH6Ag/jWDZ2j+N/FDyEyDTLc/e6ELzgfU816kiLGgVBhQMACkwHdBis7WdXg0bTpruc/LGucepPQcc81fkdY42duijJ+leN+NdffXtVWztiTBAxAw2Q7dMj27Ukruw0ZElxd+JtbeSZmLSv0B+4v/1q9E8P6KLa3S3gUvKxyzAcgVj+HdJWwgEzE+Y45yK7rRCbfM6jO/j8B/8AXrOvVVKN2b0qUqjsjRhtHjjWNY3CqMDipVglBB8tuvpT/wC0nBxtHFOGoykfcX8qdOcZxvExqU5U3aQlxFNLOXETYwB0qL7NP/zyb8qlGqS7mXYvHtS/2lL/AHV/Kr0I1Ifss/8Azyb8qT7JP/zyapv7Sm/up+VH9pTeiflRoLU2/Ci3cN3LGYyIGXLZ9e1dTcjNtIMdVNcVo2r3CalDGFTbIwRuO1dxKMwuP9k0nuI8A12yjbx/esxYgqeh6Hav+NPjsYHz97j3pmtuX+Jl6m7K7enodi1dQrHkE09RtlJXjicoofg461eXTo7mNWYsM81QKb5yVPGc1u25CxL9Kzm5W0NaXK37xlz2EVuVUZOeeai8tQ4OO/rV69nV7gLzlRzxVN3UHH9K1pt8upnVS5nYt4Qryo/KjEfoKq+c2cc/lTgWPY1ZxVYtMlZU3jgdas5XHQVQO7eOD1HarOD6Gmc0yQlfQVBLJGhwQPypWyBVSVv3mD6d6mRpQXvkolj/ALtNM0e7pTFx2qKUgMKjQ9AtLJHjkUrSwquSKqg5FTIisnIpoA+0RMen6VdR4/KziqqW656CrbRBYTx2pAQvPCCKcJ4R1P6Vmyn94KbKxD/hTuFjV+0wqOv6VMOgrBLHFbqcqPpSuFrDqKKKQBS0lFGtgCkpaKYBRRRSAKKKKTaAKKKKaADWZcyBXrTNZ9xavI/FPyGii0uc1JC2Uantp0uKlhs2jjff3pqyBlZjzUsY/ej6U4xR/wB79amSNA+QT0FROaUWzWjBymkIBg0p6VJsXPel2p3ri9qnI9T2Xu2KqD5ZfpUJUnirqiM7wB2qFyi/wfrXapHkuDC3QKp3Z6+tSSOolUYPPekhePacx9/WlmaLzFOz9asjqMiYEjg4z606Yr5hG3P41HDJHuPyYxz1p8siCQ/ID+NAdQiK4PyDqO9OlKiQ/IPzpsbptJCAcjvT5HXzD8gP40AObb5x+UdRUDbdx+Xue9Tkgy/dHUd6hZ13H5B1oAfJj5eO3rRHjyun8Xr7UskgGz5F6URyDyidq/e/pQAOB5nTtTQMwDAP3qkZ/m+6vT0pok2wjCr96jqAiA+XJx2pij94v1qVJTsc4XgelRiZt4GF6+lGoi6Ola/wmEbP4hl8tDKNQ2+ZgbgpUcZ9OKxtxAq98HZibzxTGW5F4j4+oYf0pX0A2vGd0kviBLcdYYAD9SSf5YrmLu0juIHjI4YV0vi3T3OqPqELFw4AkH90jgEVgB2dSFUk+gplrY4rS7h9J1h4Xz5cx2uAP4uQOTzj8s/hXUSSqRzgqfXpXN69YSsHmCNvXLEEY+Xv+X+etWdKvxdWQVid6AKeew/yf0osaHNeILFIJZpY2ypO7GMYyegru/DDKPDlqiHjAJ+uBXK+J0ZrVSB1yCcfQ/410PhF2/sGOJkZWjIyT3yP/wBVBMj1bwdzps5/6a/0q1q0rC5SPHG3Oah8HROmju7KQryZUnvgYq1qsS+bHJ/ERioe5mYslurSGTJ3GkSII+7PNOnlMbYAFQCds9qrULEknzyjJPpWcblS7Lg5GalEjPcsN3Gf6VmqcTyD/eqWyki9azCWXbz0rQUVk6eP9IP0rWWiLFJWZ5r4/Zh4x0BFieQ5VgqkZb950GfpT/FviGOXSprZ7O7hlkVgPMVcdPUE1Z8aD/iufDH/AF0H/oYpvjp1GlRoTjfIQPc7T/8AWq0D2ML4biN7S/R0Bw6kZHTg12V5aQJZTMkK7thIIHeuH+Gk228voMD5o1b8j/8AXr0S5UG0kB5+U9aUtxo8e8So0jLKw+ZCVOPT/P8AOqWpX5v9Itt+DJE21vy611Wq2HnCRVUEMDXDTQtAbiJ+qOAfzrSNmgkrMtaYT5TD3q9nFZ+nH5HqW4P7wfSmJFwMPMT/AHqt4B6is6M/Ov1rSFAyKXCRM4HIGazxeHcQyj8K0Ln/AI95PpWKfvUwJ5LkFSADyKpmnseKYaQipL97FTadp93ql6lnZQtNO+dqL+pqGY5c11/wuXd43g9oJf8A0Gh7EHr3h60/svQLHT5MeZDCqt257/rXl3i/Uv8AhJPFhgjy1ra5iQqeDg8t+J/TFeheN9aXQ9Akkjfbdzfu4PXPc/gP6V5X4etxuaZshnxjB7ZNQu5aG+QLfxFBGuANvA/A10QQ1iyR/wDFVwZB2nA65J611lvCpkHyg/WhlkUcB324PAYjpXfxWkMW3aigryCBj27VyohAvbPgbd3Qdua7DvWcXqwqK0U+4tFJS0zIhuYxLCVJwPWsl7QDox/OtG/Mv2YiFsPmsZl1DPMh/wC+q5q0kna56uCp3jdtD3tgRgk1ha6oifTwDjF3Cef96tVkv/8Anof++qwtdZ0NobkE/v057cMOP1pUpPmve5rioQ9npa5d+JZU6HakMMi66A/7JruPCDiXwlpTg5Btk5HsMf0rj/FFvFP4fuxIgbaNyk/wt6iuk+HsYTwVZAMTkueTn+I12dDxWjpAOKYyKzcgVJ0pMc5pCI3RRH90VXaDPIFXCARg03gcUARW8fl7uMZp07lFUg45pWYjpWffzui5z0BNA0U9Tu0dljYklPU14x41v3vvEj2cM7vDFtVY93yh++B+NelajfLZ2k93KeI1LH3ryzw9D/aevtdTJlQ5lbjI3E/41UTRq2h6F4a0pdJ0tIuDI3LnaBk9+e9YfirVX1HU08O2aKzyOqyMwIw2cgZ9OhJrS17XU0fSWaEgzt8kS47+v0FQ/DrTD9km1W4cPNOxVMnJUA8n6ml5iOt0PSodF0uKzh/hGXbuzHqa0qYDisHxd4hj0DR2kxvnmzHGmcduTwcjj9ancDnfiF4o8hf7KtGG9wGeRW+7yRj2PH5E1y/hbSN5F1Mny9VBH61j2FtNrGolpWZ2Zt8rdzXolvEsEKxJ0HAwK02Vho0LG1e7uBGA2wcsQOgro7a3EFukQLfJwCTk0/StPFrpg3jEr4Z8/oKsSxFAD614WOqyqTSjsj2cJFQhruyv5Yz95vzqVBgdT+dM71IuPWu3B3UDixnxkGR9okAPTGaWmAD7XOR/s/yp9dpwoKSlpKBlzSn2arbN/tivSiNyEeorypWKMGU4I5BruvC93Nd6dI08jSMsmAWPbFJrQTPFtXiK/E68BVwSOcj/AKZrWhJA5IwDxU/xCby/ilCQfmMEfHtsakSV+SRTVyZMzkgm358tsZ9K148rGMjnFNWQkg4/WnyBmA2tik1cOYoPbu0xc9zVOdSshFak0cxACPzmqcljK75Ljk1SukDkpO5Agy4q6ox3qL+z5lIIahkkQ4PWqTRjWiS5+br3qUsPWs4bvN79assTinocrhcn3D1qhdY87OR0pWZveq0yMXBwahs6aNHldyeJhzkiiXaSORUCI2ehp2xs9DUvY6V8RKoAFSxuAvUVX2tjoaaqv6GiN7DktTSicE9auMuYT9KxIjIrdDVwXEoTGDTJsVpIH80fKcZqOaFw/Q1rQksgJHNSFQaBGF5L+hraXhR9KGUAdKKPUYuaWkpaWggooopXVwCiiimmAUUtJRrsAUUUUNMAooopIANVjM4fHBqw3SoCi5zkfnVJAOjkZiQcU6XPkNyOlNiHzEVJKm63YD0rCc2pWOylSjKF2ZvlAj/Wp+dW44Oc716CqgtGPAIyfWr8MTx5BIzSry9xhhY/vUBh/wBoUeRnuKmwf71IQeea89PU9h3sVkgwXy3WmSRpjnJpzIdr4z0quyNgcGvTj0PFa3JYkiGflb86dOIQwyrdKbbo4z8pouEbcPl7Vqc73GRCEscKf1p03lCTlTSQIysSRx9adMhaThR09aeohEMWwnYcZFOdot5Hl5pqxN5ZBx1HcU5oiWzuX8xSAduj87GznNQs8WT8lTeUfPzlcZ9agaIg/eT/AL6pgSSNHlcp2pY2i8onZxu/pSSRZI+ZP++qVIyIWG5OvrSEKXiyfl7U0tH5Q+U43U4RHJ5Xp601oj5K9PvetHmAqtHsfCnGOajDRBgdpp6RN5cn0qERPuHH60XEXiAR3qj8MtVj0jxX4kguw6+dteNMY3YZuefY1fHQVzl/+68e6FJnAZlRvcFsY+nNNWGj07V9QNzGVVNqN1yc1jQkRTb+nrV3Un8uBSozk4rLWZmfG0Uuha2Jr6yjvIW2Nhj0I6H2NeaXUUmg6wQyEROfu9gvoMnJHv3xXfz6odPYB4t0Zx0PNVtZsLfxDpRkh4kAJRzxtJ6g98Y4xTKOR1tg+mF1wRjcOPw/rXSfDywm1dZbWEoChVnJ4wOh+tcdHK5srvTrhGWWFSNrDkD0Ppj0r0D4JSb9X1VM9IFOP+BUBJ6HsNraxWVnFbQ8RxrtGep+tc9rN7I188SkBY+ARWzrM8lvpzPGxViwXI965BmLMSTknkk1CXUzBmJOSabRRVAQwn/SG+v+FUB/x8Sf8Cq/DzcH6/4VRH/HzJ/wKoZZY0//AI+D9K1QayrD/j4P+7Vu/uHtdPnnjUF40LAGnHUUtzivGTZ8feGk7hgf/H//AK1VfHZaSfSoUQszz5CjnPI/xqnc3FxqfivSdSuio8qdVHbjd2H41a8Y3Cx6zo4OWw5YBfqKpaCMLQZV0bxuY3wscjtGMLxhun9K9JuJUELBj1U15n4oXyLy1vk4IOOvcHNeiwyJeWKXC42yxhh+IpvYZzlwmZMj1rz3xFGYtWvegBYH9BXrEmnhsEP+YrzHxhB5OsXYz/cP6CiG45NMzNKXf5gz0GasXETecAPSqOmuVnIB4I5rbR94561oSirGMOuWHXtWkKyZI3Eh+VuvFT2xdZsSFvzoAtXP/HtJ9KxT96ti6P8Aosh/2axN4J6j0pgJI2MU0nApJTwahaQ4xSFcic5bNemfCTSo3uLnV2dhJCTAqY4IIBJzXEaD4d1DxHdvb2CoWjUM7O2AozivbvB/hw+FtHa0knSaR5DK7quB0A4/KlJ6CPPviTdSah4vWzDkrBGsaD0J5P8AMflU+nWflRZ5x0AP0rODLrPje+1EMPJ81inU+wx/Ouw2xtFgE+lS2WtDjXw3i20Ucncue/rXd2tuPNB7AVxGnWsa+PbUF2ZHmLkEYxweOtenmBAzbflAAxxSlJKyLSbuZ6IGv7cehX+ddN3rn7ePOpx4OSGBroK5qDvzPzNcXpyLshaKKK3OQguVBgZjn5RkYNYr3JBGBwfetq7/AOPSXH901zjHJFYVYx36np4FTmuVK6JGvNuTsz+NYvieQ/YInHH71D/48K0thZsZrJ8VfJo+c/ddf51dO1ycXGUfdasbHigsvhu+ZDg+Xn9RWv8ADCVpfBsascmOZ1/DOazNfXzPDN6fWAmrnwhYy+GbpcjC3B/UVvpZnnHaHpUW5vWnyE8gYz71W3P/ABYqbCJQ53HJ4xVMsScnNE8rLjBpIZdyncR1oHYmR8IBmsvVpDjAPXFaW4Y6isLUnJlf5jtB49qCorU8/wDH+peVYx2CnmZtzf7o/wDr4/KqfhuAWlmpYESSfNnoRnpWRq9yda8UyYJMMbbBx/CvX9f51a1G9NrbsiMVlcbExxj1P5cVaWlinqxfK/4SjxQtuHcWcPBdeyjqfqTXW6J4f1bw9fPLADeWTggBGAbr3B6/hVTwloy2enLK+RLN8xwf4f4f6mu5tJDsCyN0HYUmIHnWK1a4nVoURC77v4QOTXh/iPWJfEWuyTgfLnyolXONoPHX16/jXc/EfxOsVudGs3BlcAzsD91T0X3znn2rkNA03Di6lU7jyo/rRFW1A29D00WFsMjMjcscd66bTtPN25d9yxqcZHGTVXSbNruYHGEXiuriiEMaxr0AxRJj2JhPJtC54FK0rsOTVS7n+zw7u54FOgk823Rz1IrD2MN7Gvtqlr3JSTTGG7gk4paKuMIx2M5TlLcrWHElyOeJKuVTsP8AW3X/AF0q5VPczjsFJS0lHQoSu08Gn/iXz/8AXX+lcWa7LwYf9BuB/wBNB/KgTPMviavl/FOyckgNBER/48KWKQMpyfarvxlUw+I9CuFUZeNl3Z7hv/sq5ayuJGEmXJxg1LTcdCoW5ldHRB1x1/WnhhjrWUjsUB9qtwZZD9axg5c2rOitCChoi4CG6HNBWo7cFZDn0qya6U7HA4jSOKqSEebirTuFXJrONzG1yRg0JhJXQ5gOeBSk8U1po/LY7elKLmHbkqad0ZcjISfn6UyaQhQcd6mM8HmfdNNlkt2UAqevpUuxukyGKXJPFOaT5ugp8RtxnCmh2g3A7TQ7DW4KcjpTl6UCWEKflNKksXPymkrIppiKOalBxSCWENytDTQ56cUXFysnQ/LUvUVXS4h2DAP5U/7ZEo6GmJoew4poppv4QOh/Knb1dQy9DR1HYWiiipd+ghcUlFFCAKKKKrQAoNFBpAFFFFDYBRRRSQCHpULRKRUtNz8uaoBExHwKsqcqKqMcGrCH5BRYLsfgegpM5Y0ZpoPzGk0nuOMmndMf1pKWkqeSPY09tU7jAPlaq04yhq0B8rfWqtycIauxndiW6n5uDTZ4SzA4otycNyetJKxDdTTDqLFAQG460rQtu6fpTY3PPJpHdt/U/nQBIIT5ZGD19KQwNu+6fypN7CMncevrSea5f7x/OkA4xv5+dpxmoDC5P3TUwkYyHLHr61C0jZPzN19aYErxOXHymlSJ/KcbTyRTTI3mfebr60quxhc7j270dQJBG3PynoKZsfyh8p+96UgdsN8x7d6QSMYc7mzu9aW4D0Vgj5BHFRgHPSnLKwV/mJwPWozO/Zmo1sKxeA4rm/ErLBqui3RC5S4BJPoGU10KOxQHJ6Vz3jAEafBKWIEchIA7nacfyo6geh6ov+jjjo9Y4U7xtGTWnJMt3pFvcqcrKiOPxGapxDEqmjUtGXrkTC08wj7nJx2rEsr+WylBRyYc5aPHWtzxFdrbQGBlJMiHBHSuUgZWdlJ7cUJaFrYd4ssdsaazaDgrtk2jgg5HT8xmug+Bk+fE2ox/37PP5OP8aymkUadcQOvmRyDlQuSPXFM+Dl2lj8QI4pZAizQSQjccZbggfpQTI978QD/iVn/fWuT712WsQtNpzqoyR8x/CuNNLoQgpCeKKRvu0xkeVizIFGeP51UV0Vy3lLk5q1Kh8ktnuKhEGRndSuA+CcCTiJRx1FRa1dMNEvSFGRCxGT7VIsO05zVLWxjQ73JA/ct/KncLI88tNQN9qGmRmMJ5VyOQc7uRWl4pXzPE2lIMZAB/8eql4V0SfU5nuoZoUFpcLlJM5bv2FTa7JI/juztWVA0SqCykkHOT6e9F9RtaieKbYyaMxXrG4c/y/rVnwNrc1/bPYzeXi1jUJgHcRnHJz9BWhqtiJtMniLfeQg8VyHgl/wCzvFT2jEkyq0eTxyOR/L9afQD0xhjFee+PrPO+7jXJ2hXAzkYPWvRsc1wHjaYC1uBu++CoFEdwOA08n7UvTkGtyMbc471gWTbbpPrW+nWtBIc4JXiqlwWVkbIBHpVztVS76J9TTGQy3MrQOpIORjpWSPvjJ79avyf6tvpWcetBLJ5j8tV6cz7gKaBk0hHqHwhTjVXHBzGM/wDfVdR4718aP4feOCYC6uT5SYIJUY+Y4+nH41y3w0h8jSb+63ffkC/TA/8Ar1x3iicz+I7wknAfaPwAqPtWZSjob/hWAMpckZYBjwPVgB+n611vlYjPNVNAtI7XS4F2fPsG445q7fN5dlO65BWNiPypPVg2cfpUoPjmy4BJfHJ6fKa9QQs0jDqeP5V434cefUPFunrE6xzNJgOw3AHB7V6jdJf6bIpkuQ7SDIZF24A4pyhdq4pVVGLZqQQTpeI7BREo5OR1q88qBThgT9aztJjkvLaR3uXL7tvXtiro01VXAkP5VEYKGhMqsqlpE8LrIDuIH41Ntj/vfrVEWKqceYcn2p32H/pofyp6C1JrlIRbSFnIG0965xoc/MrqR2rZm0/zIWUSHJHpUdvpypAqyE7h1waiUIy3OrD4qpQvyGR5L4DDB9hXO+Lt39jyqVKkLu59q7G4jWOUqvQHFc14ktjc2Uka9SjUlFR2NKuInXd5lq1tU1bw7bLdtLMJYFJy57itT4QK0eg6qo5CXZUfgKo+Fv3nhuw+bjyQKb8JZnUa/CGxsmDYx7sP6Vrfc42d607Engc1GWJqJjk9aXOBQFiO45IpMDB47mh13NnNB6Uhkb8LXK+LdRTT9FupiBvI2oGXOSeAK6pyApJOB3J7V434616bU7tLFT+6EmVVRjOOAf1ppDRj6LHshe4Y4J4yfT1rU0a0Gr6z5jHdBEcoR3//AF4/Ws67nFlpqWyH5pRt45+UdfzzV/Tlns4IUheRGxuYjjn/ADxVWGj0XzEjOWIUe9YPiXxeNMt2hsyrSsNu7r29K5y+1GSOPNxcOwHRWcn9K5oCTVL75i2389opJAT6XZNezedMWKqc8nqa7KzgMjKiDqQKq6fYF2S3t04HXA/Wuxs7W20q2NxcOFCrlnJ4FNspI0tOsVs7ZVH3m5NW2+VCx6CsO21drqed4r23lgB2pHEOV/3m7n6VDqF7MRHh2HJzg1NtSWbNwqXMW1twAORT4lWOJUXoBXNm9nd4o1kfLHHXrWgsGpLxuIH+8KGilqjWzRWUYtQwTubj/aFW7ETbX80sTnjJqZyUFdvQXL2HWH+suj/00/xq4ar2dvJEZt4HzvkVZKmsHiqKfxIuNGpbYbSGlINRrKjOUB+YdquFanP4WmKVOUd0OrsfBZ/0O6H/AE0H8q4012Hgr/j1u/8AfH8q113M3scz8aISbDQZgOEvipP1XP8ASuLkjRHbaoGRzivRfi8o/wCETtZCM+XfxkZ9wwrgpEBc8dRQtib2syGPOwVetT8h+tMghQoeKsKipwuKwj8R11HeBLEf3n4VPmq0ZHmCrHatjjGSrvXGcVm+QvmlgxzWi/3T9KxF4dqTvuUi0Yl8thk4xSCOML8zHrVZmODzUi/6uqu7EqNmEgTzDjNMbaMUMfmqN26Vm73Oi6sWEZabIy5FRK+O1NdsmqVzJ7koIxTo2FV88U5KY76FksMjpSMVz2qu3UUpFArlpMbBjFDKDTIvujmpaG7MpK6IzGD61ei/1aj2qr+NW4/uL9KL3JkrD6KKKZIUUUUnqAUUUUIAoNFFABRRRSYBRRQaaAaelV9kjqOcCpXYg1HBKSMEH64pgNkjbbwalhRtgyak4NSL0o1sA0IcfepFBDnJqSm8bz9KAH0lJRR5AIPun61BcDERweanU8H61XuvmgYAZoAbbF8HLcfUUkxff9/9aht432n5T+VJLC5f7h/KgfUnQsEOX7j+Kkdn38SDH+9UKRuI2+U5yKDGxcfKfypgT7mERy4zn1pQ4L53Db9RVcxt5fQ9aAhyODSAnTdvO5xjPrUbE7j8wxn+9SBT5pyD1qJlO7v1p2GWn3FgQRj6ikVX2OMZ6Y5qB1O7oetPQELJ+FIRJtfaeD0pAGEXIP3vSjPB+lMz+66/xUaDFHO8be3pURxjpTxyHG7tTBgYDFc0dBFyLmNT7VT1jTl1KzETSMm19+V78EEfkauI6LGvzDpSSyIY2wwzg0CJ/C92t34OtVAIa2/cPn1Xp+hFXV++K5rwVMtvPq2lk5d2E6Z9B15/EV0w+8KCjm/FqF7qIrzhRXLlSD0Fdjq8RuL51z93ABP0/wDr1y8sRjkYMuMe1NGiZWW6W1yzsADxz2rKl8zTNZh1CA58u4WVeO4IarWoRNKh28Drg+tVPPEukybmPmRkA/SmJn1u0qTaU84+5JAXH0K5/rXBGtTwdqP9qfDCwnJ+YWXlt9U+X+lZZqTNCUN0opGPFIYt4qjTEcfeLYJFRJ/q1+lR3Tk25GeARiiNjsX6UJaAyaqt/aLe2M1szsglQqWXqKl3mml29qfoI5Pw3YtpWq6tYxXMhjjZGzgAnIPWsLVJtnxFRjufaUU9M/dFdTZAjxLrHuIj+hrmvJS6+JU6yDcq5OPogqIavU1mkmdPeHZauSCe3Feca0smn6xbXkXDh9y4PdT1P6V6fdRhrdwMcc81wniTTXlspJmYExndgDt3rRMlbHoxObcyg9U3D8q8v8ZBpPso3ZGJDyO+2u/8PXiX/ha3lXGUg8twOxUY5/L9a4fxfCZNLSQH7sn9DQtJCWzODgOJkPuK6GM1zqnaQw7c1p2t0Zd2QFI9K0JRpg5HWqt59xfrRHL+/b/a9qS8P7tf96mUU5OY2+lZrda0yaz5v9YaCGR0Ckq/pej6hrE/lWFrJO2cEqOF+p6CkI7zwJI0fh+fIOHuCB78CuSdP7Q8USA/dkuWz9Nx/oK9ZstEi0DwwsDSqxtYmkdwuNxGWP615r4XtmuNSkuDt+Ufqf8AJqFuzRPQ7+wOYAB2pmqt/wASu6xj/VN/KrVhaStlN6jv0qprkEsVpcx7wR5bdvar9m46s51VjKTitzgvA4P/AAm+lY/56/8Aspr13xAuZLc5/gIP515R8P4PP8daWgJ++xOPZGr2HX7QRSQebkrg4wcU5StIVSLlGyKehXEdr5iSttDEY4710JIrn4LSH92/lkjvhqvfbo5AQrNgccA1lUlHc0o0ptWsW5V+cNnpT949aofak24LH8qabqMdD+OKjmXc39hU/lZobwTjIyKSqtrIJHdh0q3TWuxnJOLszIuGDXjoOufT2rD1Q/K6lscEH2rbf/kLH/e/pVTW1UsTjquaTSuaRm7WOU0DUdcg0pILTSjcJB8ofHrzzzWn8KI7n+39YikUpn/XK3BVt3T+daHhJt1rcHIwXU4H071m+DNSTTvibrcDqSZTJtA9iDVa6mZ384MJZehDYFMSUucHFQs7OSxOSTzTkY7h70eYE5NMYgDJIFOrN1VsCIdsk0AtSLXbkW2lzHdgsMV4kv8ApPiCV9ykREkFjxxwP1r1TxXdiDRvMdhxzg98DpXkEMpFldzEZZ+Off8A/XVRQ9i6XGra5LdIoWFWB2joBj247VumRY1dyT06gVg+H4/3cjnPLAf5/OtW9xwM9qfWw1sYF/JLdXjOQdoJC/Strw7pjyvsUfO3U+lVkh3PgDmu40O2jsbATSOqFxlmJAAH1obGlqX4xZ6NZCSZxGnALHufT3+lYMu/xLILiV5Y7NcBYg5Cvn7wYYBBBAqldXsniDVzCrsllCAdjIMN6kgng59uhrVuXRINsK+WAfuoMD8KSQ0JapY2MpEEMcbH65q9eA+UhyCcnisqEs94jE8M6jpx1rurhQ1vMAoHynHFFxSOTiLrPE6gkqwPIrshzzUFiP8AQofZMVYqZMkMUoFFFZyjzJplRdmPXr3pTSR9Tmg18zWoctRxSPaozTgm2NYVSiUC8c/WrhqBUxMzGvQyym4ybfY58bNOKsPNdd4JdWgvQOqyBT9cVyJrsfBcKpY3UozmSUZH0XFe0eWzL+Ly7vAxP927iP6muERVZUPPKg/pXf8AxZGfAVwfSeI/+PVwFqwNrEeTmNf5UuhD2L0MCBDyfzqRrdevtTIpV2gYP5VOzrtB/nXnzdRSPVpqlKNirt2yDFT9qiJBbipe1dtNtxTPOqpKbSI25BHtWWLZt7HitR8gGs5GfceTiqb7kxITbthulP8ALIjI70ze2X5PSgyHZ170X0HYa0bbuFNMeJ/7pp/mtnrS+YxB5pFkQjb0NDxsCMqalVzT3Yk0XsLluVwnHSnrH7GpMZpSSCeapNMTi0RNGcjinGM+lLuIPWnFj1p3JaEAKryCKPMA45pSSRzUbJmjRgm0PMgzgVfj/wBWv0qh5Dkjp09avxghAD1xS9Ak29x9FLRTYgooopLsAUUUhprYBaKKKm4BRRRRuAUGiimIglYq3FQR3DMCD61bZQaRYEA6CmMqNJJ5hwTirMErGPnrUhjXPShUAHAoADJxTBKd56dKkKio2AV847UAKZiPSkEze1KApHQUuxfQUANWRmB+tQ3LuIWI61YiAwfrRMAENAFO2ln2HAJGfSleW4yOD+VWYtuORUU5XcPlFPQCJZZtp9cj0pRJMSvBx9BT0kUIQUzyO9AdMqSnr1NAxokl8vJ45Hal82QGgOmw/J39aUum4fJ+tIBPMPmEY4BqNnJP41KChk+539ajZkJHyd/WncAkc7v/AK1OVjtf2x/OmyOm4/L+tOUph+OMetIBAx2/hTQ2Yeg+9ShlweDSKV2Y28ZoGNVuW+XqDUbkZHy9vWphsyeOxqNnHp29BR0AerL5afKeh7+9NZl8tuD09aeCuxMnsew9aRyqxNhv/HRSTuM5+3u10vxtZ3JDGORArgdwSV/HtXfXnmRykrEyZGRlTivOtTuxZ67pN2GGYpQxyvYMDXs/iSBCY5k6OCRjp6/1p9EJnA3TObpnGSGqhc2X2jdIitk9cLWytjLcQyyooKR9cmo9gjtZu3yt/Kq9B3OaazSNFDR856kda428Rra/uIUyEfIwfQ8iuzmk/djuBXM+IIhGYrhAQxOGb+X9aEVJaHtHwiuzL8MbiInJilmGPQcH+tXi1cZ8ELx59O13SSTjZ5qD0JUr/MLXWbD13Gk9zNE26mscimAH+8ajuCVh4J60uoxt2SLZsHuKqrJcbRg8Y9qfLn7IcknpREo8pfpSGM8y49f5UxnuyeGQD3xU+BSYphc5u0k1E+J9TjjFuzmOJmLkgd8Yx9axdAke58eX0swUSASbgucZBA4rTj1aG08aap+5uJR5UcZ8iMuQR1yB9ay/B487xPqN0DhW8zCn7wy4PI7UJWHJtndFQylSOD1rB1K1WSOWAr8rAr1rfqrcwIyPJyWxSEmcp4CvVtLnUdGlO0szOg9xw3P0xWh4g01F07ZIAw3ciuSMr6J44S7mB2GYv8ndW4PX613Wry/aLOUMjK65OD0q3umC3PMtS0y3gtJJI0IZRkc1jWr7ZSM9RXU6rGTYzd+PSuQjO2RT71aE9zTD7WB96ddTI8AweQ3SoSeKrTHigCR5MR5zjiqROTk0pOaSgliV658Jk2aHfyZ+/cAY+ij/ABrzzwxpEWt65HZTmQRFGZihweBXsnh3Srbw/YPa2xkaNpDITIQTkgDt9KmT6Ail4+v1tPDcqb8PcMIl+h5P6D9a5vwZpqtp/nK2WduRjGOcf5+tN+I9wLnVdPsQ4wqbz6AscfyFdPoemrpVj9nEnmAMTuxg0RshyT5dDTtYzE7Mccj1rO1pfMWQHgMpH6VohiKzNVkYE9M4rSdTmOajRcJuTKXw807RdH1iK7vLhftc0I+zeacYYlg2APYDr713viER30EH2dg7Kxzg+teE+EpJ7rxzYQmR2zI6qOuBtboK9UGpPZJLYyN5l3b8FexHXrWE2+Y7FFNXHm1uIjsKkY96mtI5IEYFTyeuapPdXF5HFPgoxwSM9sUkb3bnhmPPZqrlUlZoz5pU5XTNJzI5xj68UwRynjbioFW6Gcl+n96mmK9JOHbH+/Ueyj2NVjKqW5p2m6Mt5nGelXa53yrsOu/dgn+9W0m4AfP+dVypLQylNzfMyi//ACFv+Bf0qvrQ2tncAQvHFPnbZqWc87hUeuqfJ8ztjFIqJn+DyDb3Izk7wc/nXPWL/Z/i9dgjh2f9YwavaJp+tgu1hdwxwvyQwBzj8DVbTNMn/wCFrtDfSJLObfzmZBgE+WPpTejEz0MdKeo5FO8vHFKFxRcQPPFH9+QL7Vk393DcNH5UisADk0y+OLtznGP8Kw7e3kaNWJHI9aRaRlePbgHTY0Qg4QljXnJkEemFMAl3rt/GKFLN0OOEzXAlt0MaA/NuPFaR2CRv6UEhtYjnk8nFXJJBIxAyeO9UoQUiRT2FSiQKcE4zRbqCfQv6dAGnBYgAHJJ6VJql9PrBNpasVtFwGdejnuD/AD75rJa6kmuY7aBmCHiY9OK37W2jtIVjjwyjByB1NIe+hYtYorCzEUX3Mkiq8srT4weRnIzikmnZpDuwFHT0otVy7u3OegA6c0DNDT1Mmp28YxjeMg+xrttwJ2+vFcroyKdSVgMEA1045cfWkyGPsxi0QemR+pqemxpsTABxkmn4Pofyqd2AlB4FLtb+6fypksTyRMiqwLDAODxRYaIRMWmdc9Kdu96fb2kTDfJMQ7dRkVP9kt/+e5/MUWEypuozVv7Lbgf64/mKYYLdefNY/iKYWICwA612vgts6dcYOQJv/ZRXJGCyI+a6C8d2Arr/AAcsC2FyIJxKPO5ORx8opdBMzviou7wDe+0kR/8AHxXnWnnOnwH/AKZL/KvTfiX/AMiBqhA5Coen+2K8x0NvM0O2YjnZgk1nOooK7NKdB1tEy2jcjpVgsGTrkVAuNnbNDPyQB2rnnVjLRbnVRw04PcgBfeeTipVaTYOTUW/5sZ5p8bjI+YZrpg7xOatDkm0TIzbDuJzVFZV3HJ/Sr2QV61SFuu7iTNVa+5krkZ25c57GondQg571O0IG75+xqB4Bs+/39KVuhSGh1J60u5cHkUkdsGYAP+lK1thiPM/Siw2xVZfUU9pEz1qNbcZ+/wDpTntOnz9vSkxxuPWZOmaa0q7qatrhh84/KiW22v8AfFJaBK7YeapPWpC3FQiDn7wqZUJcAng1WhLTDdxRuqSS32Dg1FtIpqxOo37TL5wUMMdOlakZJRSeuKylUecDWsoAUAUNoLNjqKSlpiCiiikgCkoopgLRRRSAKKKKFuAUUUUCEpwpppN2KaAeaUdKhaUhsbf1p4bIFADzUExAI+lPZyBnioJQ0o6dKNBoergjrTgwqGOFh1FTBCKHYqxTupXjcBWIB5qKOV3R9zsePWpLwxmUAtggVHF5IV/nPTnihAT27EqdxNLKUJUEkfhTYDFg4Zj+FLIYSwJLU9BAmza3zHqO1Kvl5HJ79qRDDtb73alUw/7XA9aABfLMZ5OMjtS/u9wOT19KQNCEPDYyKN0RI4bt3pDHfIJM5bOfSoyELjr19Kednmnr19aZ8m4YB6ijzAGVGOfmpV2BXAzjHNISmB/jS5Ta3XpzRcQg2Y5JpF2lOpxn0pV2MD1NPSMGPA9aOoEalS2AT0Pamny/f8qmW3YHOexqL7O/ocUAO+TYn3vao5PLaFh84yD2FTBNqICnP40whQhzH0B70uo0cnr9orQRT7mJjJ4I45IFeuWV2dX8A6Vfn75iCOf9pcqf/Qa801XbLp0qiLHytznOMc16t8NrK01D4aWUJ3MpeYsV4O7e2ad9AkY2nQk6Ret1A/wrGm4tZz/sN/Ku/h0e3ttMv0BbBkYAnsOBXO3eiQizuAk5LeWxwcc8U0xI83Z8jo1ZuqxefYSIVyQNw+o/ya1byJLZwBvwfXFZVxNkEHIHTpQjV6nSfAqVo/Fl/CDhWtd31w4/xr0S7QRXk0Y6K5A/OvLPgxOsPxBETEfvbaVBn1GD/SvWtbVU1efb0JDH6kU5GRSqC6P7n8afz2qK5/1PPrU9RoZtL2x9Kh8/y/k29KsQ82rfSqU67ZDzWM5NbHq5fh6VV2mh/wBqB7U37Uf7v61XX/WY9qUjBrP2kj1ZZfhov4TL0M58T62443Oh/nWH4MyfE2rk+rf+h1r+H2z4i1k/7YH6msjwZ/yMmsfVv/QzXVHY+aqpKbSO77U09KKO1BkefeNrbzI4rpQcoxQjHTPr/nvW7pF9HreiQlpcTKnlyheoIGOfqBn8aTXIN2nXMZ5yp6+vaue8D3Dia7tiSBw2PfpVborqbVxpSRrjzCc+wryuZfLuZFH8LkfrXs14MoDXjuoLs1G5HpK38zTixS2JwcrVWY0+NyYx+VRStk1SJbI6KSigk774Zab5l7damXwIV8kLjqWGc5/D9a9NdWMD7SA2OM+vauL+GtlcQaFcTyQsqXEoaJiPvKBgkfjW54p1SfSPD81zA22U4ROAeTnsazfxFo88u7i413xdLc2sPmBZVwvXhSFH4dTXqogUIBz065rzvwJYSR3E8s0bKSy4yPYn+telcUPuBCIgB1NZGrjYxG7qvetw4rF1oAOpI/h9aF2BHEeAljHxJssIPvNjnvsbmvTfFdvbpfedDAoneAlmQY3nJxmvM/AuF+I9kegBPX/rma9V8TY+1xMpVh5J5B9zRLWQJ2MK0EpSNWyCQMjOauRaRGGY+ZJn61BG7jDA88Y/KrX2y4U9R+K1zJyTfKz1KyhOEOZa2IbpbbT1Ecs8oMgyAKsW09rcx7lmkwOOcisTU77z71Fn5KLgbV9TUtrewQqchvyr0IxTpqXU8WrdVXFbGxLBCyMEmfdjj5qbbFkVVbJIpljdwXkrRx7t6jJBHatfyVHauerdOx1Uo8sOaXUwL2VxeOA5AGMc9OKs+IWK6OGBOSR+oqrqY26hKPYfyFWvEJ2aGp9duM/Spjcupa0TEsL67tIEWGQKuOm0GsQapeL8TrS4EgErxrEzBRypUjFdBFYTC1ifggoDx9K5SdTH8RbD3Mf9a10sYWPXIpi67mPJ60STrGm5skZxhRk1BEf3S/Sm3KrJbMrAEHHB+tToI53UNat3upMSAZyACpz0qumpWscar5nQc/KapfZo21FzsUqSf51NLawhGxGmME8CixVzm/FF3HdwXBjO5dnB6Vw8I3Txj/aFdhqYVdMusY/1RwK5C1GbqIf7Qq1sKW5vZxVO9uAuYwTvI6+n+cVNcy+TAz5GR0+tVNMtzf6ku7cUU7m56Cn5gdDodukdoS5Bd8sce/FXr6VoJBGoATAIqvcXQt0GFy5wOPzqnNdecy7Q2CeSamxS0Jd7SyxoDgE461ubEijX5dpNO0nTooYhLOiNKTwSc9e1WLqYTXKbcYUdVAwc0r3dirWVzR0pI0nL9CBjmtJdYjguQFQuy89eKzLRH8v5cZbuamFi0ULySDnHAHajYmybNaTxbKCAlpHz3Zqkj8VuzEG3QDHGCetc4wVvug8etOClSMgj8KjmY+RHRnxRL0W3TrjqasNq05ycKMj0rlwORWuelVd2JaRKDkA0Ui/dFLS8xiYpCODTqMcUeQjmdYAa8I74Ar0r4bGRLC4RhiJiGXPUnAzx6V5jq5/4mB57j+Qrt/AeuCPU7TTFGfNDbiwPBwen5Cqt7op7nW/EFN/gPWB/0wz+RFeT+HBnQYAfcfqa9e8bpv8ABGsj/p1evHvDRP8AYcXszfzrkxP8P5nZgX+8foaOBt6UxhkmnbuOtREnJ5rlitdT03oVV/17U5f9YKZlhKcA/lSh3D8D9K9KOx4lX4mX1zsFVlRt4+U9amjkcxg/0quJZPMPJxn0prcxEZHLN8p+6ahaOQp91utS+bJk/MfumozPL5Z56Y7UDQxIpd4O1qGilJ+435UsdzNu6n8qc1xLnqfyosO7GLFLn7jflUjxSZ+63T0oSeXcMlvyqaSZs87vypNDuyuEkDD5W6+lEqyF/ut+VSCYlgMN+VLI53D735VOmw7shQSD+E/lU8W7zRkHrQpb0b8qcpPmDIPWqsLUuhEZeRk1VulRMYGPpVpOhqneg7lpJX3FfUgXbvzzWkhyPwzWSud1asf+rX1xQ1qNuyJKKKKZAUUUUKwBSUtFMAooopaAFFFFC3AKKKKBEc7FIiw6iqa3L7lBPWrlwhkiKhgvuazmjAKjzFOKatcpFsEy5Ge1IYiFPNRLEAGxKOlIEG0/vFoAcsbE4/rViBCobdUEaAH/AFi/nU0SgA/Op+ho3EyfI9RSFh6ikVBjrmgqKfkIzrqLMmdw/Gkigyr/ADDkVJcgF+GX86SOLKN868+9Fiug6GHAI3DrSyQZYHzFH1pYotuSWX86JI9zDDL09aOoAlv8rfvF6UqwcE+YnSliiwH+dfu+tKsQCt+8TpijqAwQfI37xKDFgj50/OlWL5G+dO3egxdPnT86QDyn70/MvX1qJkxjG3A96kaLMpIdPzqMxkKfmXp60NgkM2njp+dKEYqw25z2Bo2Hb95fzqa3UCT7w56c1m6llc0VO+hEkcgU5Q1KA6j7pq6Yxt60rRjbWX1iPc0+ryKgkcfw/pSGZv7pq0IwR1o8oHvT+sRvuS8PLsUzOcfdNRmcY6GruxcMDVRo48HHFbp3MbWKlxKgtpcR5IRuD9Ki+HHifVLTTrjS7e6ZIYW85FCg8seeSOme1XPJVl69etcO6XWh65cJZ3DxJjhozg7TyBVIOh9HzMf+EVvHbl2DFye5zXCMcj8K2vD2o3F/8MhPdymSd1cOx6kh8fyxWETxQtyomHrCRw2c8mOAvTNcVcPmFnOT36c13OtIG02cHnI/qK4u7iUW2AMcHpTLI/AN6LD4k6TKThWuvKP0fK/1r6G8TQoDHKFAYggkDrz/APXr5bE7WOrwXiffjkWUfVTn+lfU3iGZbjSrW5T7smGB9mGRQzI5wVHMnmJtzjmn1HKcbf8AeqNWxixQFYihPX0pTZ7sEntT34jNWB90fSuijCMtWrnJicTWpNezlYp/YFzkmlGnR1cpRW3sqfY5vr+Le9RnA+HrO/fW9beFYPln2nzCR3bGMVjeFILlPEutIpQSIxD46Z3npW34Tv5IdV1uKOFHxcFsltufmasnwdK0vivX3IALOxIz0+c1yPRtHqJtq7Or8q9x99f0pDFeY++M/UVepam4zkdUklaOVHc9eR+Nc54anFv4jubY8eYdy+nGTj8ia6bWF2S3C5/irhGuHtPE8MyN92RCcdx0IrRaobPTJFDJgjNebeIrYRvO4AGXJ6V6U2cH2rhdbt3uoLhlAyWLAd8VCH0OKDEdCRTaXGODxSVpcxCgUUqgk4HU0Ae9+FSieD9KjyAwtlJB9+f61w/xE1n7XqEOkxA7IG3ye7EcD8Af1r0GxjS10m2jxhYoFH5KK8o0mKPxB4lvrq5B8sh5RtOCCTx+lZre5R2PhmNRE8qqwYt3PFdVFKssYdTkHg/UcGsvSrSK0tFjj3FeuW61dggEBba74Yk7ScgZOePzodimWep6VR1LTjdoWRsOqkAHoaurnIq+YUwSeOKEiW7HjGih9K+IVoLpTEUmVWDdsrgfzr1XUpRLJC4YFGjIG05715n4uiR/H0aH7khhB98nFd7DZ29rEFhBGCU5YngHjrRO61RvhowqVIxl1ZZtx867iSBjNO1HxJpGmzrDcGTzCA2BHniqUt/9jmWJYg5dd2ScY5qhfaPBrd6LqdpEbYE2xkYwPqK56cednoZilRUbLyMzVtd0+71Hz4BJs2gcpjn86LXVrDP76ORx6Dj+taK+DLAfekuP++h/hUi+EdNTo1x/32P8K6oqyseJLERvc1/Ds2nXQmktrdkdQASzZP8AM1uHpXO6fp8OipNJamQllyVdsg4zWUvjq5IA+wxf99mlKF3oXCvzq19jY1G1nn1KYwwyOOOVU46Cuit7O2vNPjju7ZJV2LlJF6HFYGl61NcXUoMKIGj3cMevFXfDeozXJnSdlO0AjAx7VLVi3JyXoZJtHvNRubaKfyljYhUYHhc44/KuM12xk03x1phaQOz+WwOMY+YivWtYnEGnmaMDeHUZHvXlHjWaU61pV6zLlU4K9flfP9aqLJPUYViRAssnIHYVz/iKW8N/BFZTiK2EeZDuwWbP9KtgyTKG3sc881VubVMF5GwAOSaQ0YywTb8/aDn1zUV1FOsMh+0HhefmNW4Gje4whDJzg+tP1FVWxlOB92jW4zh9YdYtPlVjjem0fWuSjfy5Uf8AunNdL4kJ+xxj1f8ApXMVa2JnuWLi6M+ARgDOK67Q7D7HYKzhlll5cHHHpXN6FYfb9RUMFMUfzuD39sV1mp3/ANhEKR7S7sAAew9ab7Au5S1ecO6QxgDHOcd+RVnR7IrKkz7g/oOMdf8A61V4LdEczOAZOualnvDbkeWQH9fSpLWm5u3F9HDcpECd7EHO3PSiKPfeKg5OccVgW7yTXCvK7MzsMlv611GngLq6Lnd/+qlsNu50FvAsMQXvUkib4mXJGe4pwPNOFS7sSMzybeNyS5JB70efbSEgyAg9sU65t5C7so4JzWXFFKspLRsB9KjlZpzo11htiwG7n61b4PeszLJIDgnpV5JQ/Qj86EmTJosjgUtNzRmtLEC0h6H6UZopActqyg6oeOh/wrS8H3wg8babGyOS0uwEN/eGKo3uG1GQkdqboLbPHGltjpdRj9RV/ZCS1PbfF/8AyJ2sf9ekn8q8Y8Mt/wASRP8Afb+dezeLz/xR+sf9ekn/AKDXjPhjH9hp/vtXLX/h/M6cF/E+RpZ4poyc1MAMdKQKOeK5FLU9OSuUJJHV8DpTleTeR2qwYVJyRzS7Vz0r0INWPGqpqTFR22Amq5uDvII71Z+VRgkCoSsGeq/nTVjIg+05z8vY1GLr923y+lT7LfnkdD3qLbaiLquc9M09LgNhuiZQMCmy3TCTFSQ/ZvM4C/maR2tfMOQv5mjQZEl028VJJcOT1ojNrvHC/rUsjWpY4A/WhsaZXWd93WpHlbIpym2z0H61KUgODgVOg7k0QygzUmBuHGaVQqqMdKD94VRFyXco6CopZEUDK5pSagm5FK2g0HnJg/JUo5Aqpira/dFT1HLYdRRRVXICiiij1AKKSlpgFFFFIApKWkprYBaKSlpCIrj/AFLVmFTkcGtO4YrESOtUWmYY6U1YpCKpG/j+GmKreW3B6DtUyzs27p0qPzpNp+b9KegCIrE9D09KsICEbII5qGOd843dvSl899p5/Si4F2Jvk+lKxyKoid9vXv6VIkrFDz3o9BWIJEJcnFTRrhDUDSPnrUgZ/Lbmi+o2Sqm8EDPXtUcsTK+MEjHWkjZ/U9aWVn8w8nFD3Cw6JDsk4PSgRny24P5UsRbZJknpSBm2N8xFLW4CIjeW3B7UhiPofypyMdjfNTS7/wB40APMZ81uDio/LODwelSbn8w8moy7kNyelIaAA7e9S2+ROvFQgt5ZyTT7dj9oXk4zWcr2ZpB+8jVb7tK33aax+WlY/LXlX1PVsIPumnL0NMB+U0+PvTvqTYrn77VUNWz99qokPXqweh5Mlqx6fdrlNcUHWVUcl1XiupQOUNYWrbbe+W6dAxjTJHqB2rRPUSPUdGiit/hzEkQwGgEhBOeWYE1hMazfh9fzS+F9bt55HJR0ZVZs7QQOB6DirzvxT6lw2ZQ1UbtOm/3a4q+O22HP+f8AIruL9S9jMoBJKHArir+CU2+NhGPX8aZXQ4yeRnlO7oCR0r6X0W5GqfC3RrkE5SBFOfVPkP8AKvmy+gaGdlPTORXu3wmulvfhjeWhwXtZ5BgdcEBh/Wm9jE0x0qK4OPL/AN6lgfzI93vUdyceX/vVC31Bkl05SEY7sAfpV1fuL9BWben9yv8AvCtJfuL9BXTQ2OHGLYdilA5pBT16itjhsec+ERnXddPbzz/6G1ZngjnxTrx/22/9GGtbwcP+Jprx/wCnoj/x5qx/Ahz4l109csf/AEM1wPdnvL4EegUYoopa7AYOs2it50hBBIBGD+FeXauNus4B6FK9e1Zc20hB52j+dePaxltZl2nJBA/QVpBg9j177FMFblWODzmuTu7Oazfy5du4jOQciu7Q5Ue6iue8RQFXif1BH+fzqRpnkmoQNb3sit3Yn9aq10mv2QIEqDLFua5yrWqM2rCV2/w58OWOvXd619G8iW4QoFcrySev5VxFew/D2yTQNNuXmcSSXDgnaOFAyMfmTQ9ECR2OohLTTbqdl+SKFmPPYA15T4G02a4Mt0rAR79jc8njP9a7Lx34hWLw3PBDkNc4iBPoeT+g/WsvwHatbaQS45l/eDjsf/1VK0RS3OrVQqhQMADinUUUhig8itbGY+vasmpL15UswVkdTkchsVUSJnmvjKML8QLQdCTAcf8AAq75ofLADNnLHGK818VF/wDhKoJNzMw8sjJyfvV1shuZp4iFYv5mQuc/lTlFuMma4efLWgvNG4LG2nl8yUNuVcDB7daiW7s4Jtm5uOOmaqfZtQL4Kzrk8/N/9ekbSLwyKdmce9c+HWjPQzhe9Fc1yxf+I9MsXVJpJAzLuG2Mniqn/CYaP/fn/wC/RrB8S6RqUl5C0NpLIojwSi5AOTWGui6u7BRYT5PqmK3uzxXRi9TvI/FOk3Mq26PNulOxcx9zxWePCN2p/wBfEfz/AMKwdO0PV11G2kksZwqSoxO3tkZr09CTnIIwSOaXMy4U4w2MjT9MuLS48xmTbt2nDc9vb2pNLWW3vMDKhgQcd+9bJqpZcXi/j/I0rtmsR+qmSTTHT5jll4/GvOfGCyKumykECNnAyO/Br1S6XdDj3FcJ8QIP+JFFIB9y4H5EEUReoPY7SGSKSJJArkMoI49awfEMrxhmBQRuu0Lz6VL4Xl3+GtP+bOIQp/Dis7xA4lu9hOQq4wDSSs7AhmmKwSIsc/J1qxqWPsMvPaq1lxIoz0GKm1I4sZfpVPcOp594kBFvCSer/wBK5zk9OtdJ4nJ+zW47bz/KsnSIBNqCbsYX5sGqWxMtzpdNEWj6QrSvgyYZj1yT0rPluReX7zDJUHYvHYf5/WqWs3n2i6Man5Yjt4PB/wA4qSzIECYNPzGjXnnFvAzN1x05qhbFrmYyN0HX61FqMmRGh789K0LeEQxKgPPfnvUj3ZatlxPH0+8P51tmRorxnVipHf0rJgCJIG3gleQKtQlrm9VWJAkcD6ZNK5RuDUZWQReaST+dbFgZyj+cGAGAu79apxaRbxtkvIQDwMitXPFS32JuOIBHNQvAO3FPZwBzUXnFjxwM1EpqOhtToSmnJbDWi4xVeO2kjcHgjNXs0CtPIwsN88f3T+dHnj+6fzqQgZPAo2j0H5UD1IvtH+z+tNNzwRt7etT7R6CoZmjjQs+0ADOTQLUwpnWS+mIA/P3pmiEHxlpx6YvIv/QhQuwzTuCCC2Acdak8NRlvGWn/ACn/AI/EPI/2qp7DPZ/GTbfBmskDP+iScZx2rxnwxn+xEyP+WjdK9n8YnHg3WT/06Sfyrxbwy4XR1Gf+WjVzVleFjfCO07mwucHg9aATzwaVJBt609GBB+tcaiz0JVURckd6Y4IIqxww4NQzcYrthsjy6zvJjGhVuS3NR/Zowf8AWVIUOKiMTbifb1rTWxkM+zQjcTL2NRfZIDF/ru/XipJIWy3Toe9QCF/KI4/OhDTJIbSHzBifsaRrK23nN1j8BTYIZPMB46HvSSW8hkbgfnS1GSx2VtvGLsdfQf4097KEMcXAP4VXitJTIvA6+tTPZyhyNo/76ppCbAWkQ6T/AKVObdTjEn6VXFpL/d/WpfIdVXg5+tCFctg4AAoJyRVOVZFHAP5063LeawOfuimItVDJ1NTYpjoSTSuNEFWl+6PpUPl461MvQUtLjew6iiin1JCiikp6gLRSUUALRRRSYBSUtFNbAJS0lLQBDcFfLwTiq5hjxkkfnTrzoPrUcoO0ChDEEagth16cc00QnafmWmFSHz/s0qZOfpQA5Iju+8OlHlHB+YUkat5nQ96csb4b5T0o8wGiLC8t3qSNAFOWqJkcj7p60+JGCtkGhAxhjH96pRGPKb5h0qJldf4Tj6U9VYwEBTnNHUGCIvHzjrSyopkPzimLG+V470jxvvPHGfWgLE8cY2P846UojGwjzBUcMTeW+QOfel8ltp+7+dMCZYhsPzg++ahaM8YcfnUgTERGR+dV2iPqv50gJih3n5h+dR+W+1uR09acU+cnI/Oo1Q+W/TpTAVY22feH50sMbiZTkdfWmxodh470+OM+YtZz2aLh8SLxD7PvD86c4fb94VG8fy09ozsFeVa/U9e6XQUBgnJFKpcKSCKiaM7KRYz5f40KPW4m1tYUKzMTnrVJrSTJ/enr61bWNsVXeF9x5/Wu2jJvqcNaEUrpDFtZdmPM555rldfSRbuWNnZiYsAZrrRDIR/9esKyiW58f2ds4yWu4hg+xBrpjfqc50Ph+FdMuNdsV5AtbZh2/hAP86naQe9a/im18jxheTxxhY5dPjBIGBu8w/0FYhq00XGLtcTzFkVgM5HXIrntYUIjA9wP5mt2EfvH/wA96wtfysqjjBAz+ZpvcDidbC7xj054rv8A4J63DaajqGk3HCXyKVYtgBl3evqDj8q4TWVz83+z/WquhOY9TQq21iOD79RVdDGW57yjtGGUKpAYjOajuJWJQFAOc9ag0648+zRySWI+Yk9T3p9yeY/96pW4Mnu8mIAhfvDvUovJgo/drx/tVBe/6pf98U8GkpNLQHCMt0Tw6kEkHnw5Tvg8itAyIw3Rge1ZHWnec6c/ex2Bxmnzy7k+yg+hw/hK4lhvNbDQyTym6ORCoIzls89qyvAsrRa/q5MZ3MeQTjb854NbXgObzLvWnAxvud+M9MlqwvCTM3iXWCuOZGP/AI+anqzXoj0VZs/eUj8c0/zF9arr90UtD3ERX2JIJcegxXkGqbYNcuSQrKWHDDI7H/GvYJRlGXGQa8w8TaekczXOSGYevfI/pmqh2DoenaZcpd6ZbTxn5XjXHGO1N1q0N1p7eWu51+YD1rA8D3yT6AsAcF7dypHORklhnP1NdRJIqqSTgUnuCPOp4PNDK4+XB4riLyMRXkyDoHNegznEj9O9cPrC7dSk98GqQS2KtpF597BD/fkVfzOK9jt1McQAzjn+deV+G7drnxNpkKY3Ncp1Poc/0r6EtbFI7ZEmALKpHbFTJiieSeNmlubmys05LEkDPOchR/Wu30mEWunQxjoqgD+X9K4fX5RL8QXigJZLZ/LGRuwRyf1Jrr4575EUCLIGOqYpvYZsbqXNVI57gn5kUCrHmEgZx+VLyFckzTrsbrTH0qHzPeqjTvI7R73bDfdPQCqiTI4DxGyy+IlMbK20ICQc45rrTOYJ4XC7j5gGM4rivFNvPb+I92zYJsGPYevbt710x1OG2MLzK/BBIIxWlk4yQoy5akJdmdRDqcjzopiA3MBnd0rZ25HHNY/nqAD9gDchgc//AFqs/wBuXAG1bKNRXJSTUbM9DH1KdSadNF0x57URoHZgBkqcHAqkNaugMC3jA9qbFq1xEzMsKgucnmtDgszQkjKIWKnj2qMgk55/Kqz6zcyIUaFcHrTW1WZlK+SBkYo12HqWcc96qwo0c6OUbG7GcU2DUpII9rRb/cmnPrGUGYhjcp4PuKdugal6TcyYCMefSuU8bwSSeGLrMTgIUfOOOGH+NdJb+JoXJBg2kHaMv1P5Vn+Kbj7V4c1NNmN0DHk9Mc/0pJDuzk/Dl9ep4ft47dYtilhlmOep7Ul8twx3sybjyfeq3hOZW0d4i4BWVupA4wP/AK9SJq9tfXMtvEWLICSWXg9uKvqUXIRcgqysgz7UXz3IgKyOhVuDgc1ZgyY4iF4wO/TioNVJEC8d6nqJbnG+J022duf+mh5/CsKyuPszyN0JQgcZ5rofEQeeyj2qSVfJA9MGuVq1sKW48irNnKY5lUn5WPSl09y92kbAFTxzVjVbZYWSZFxuJB+tP1ETupk1K3Ugbev65rWHWsbS38673NnKR/8A1q2allIdApNxyDjPBrRQtBP5g6ocj61RtuZVIPvV5+WPvSZRefxDeqCQ0ePTZT/7Yu5trM4BXkbVHcVmirCRseFUn6UJIDTt7u7kHLM69D0yPpVqC4nB3SISM8AUaLA0fml1A6DBHIrX2j0FQ4Rbu0Wq1SMeVPQo/bm/54n86ct8Syjym5OOtXMD0pDgc46VRjYkPU0VBbMWto2JySOpqbNAxapaoqLp88jKCdh5q7WP4hnCWPlhsFgT+FAGJb3cUcZVic59K1/C8iv4o0w7sH7SmPzFc5DEdpkLAhugH+fetzwr/wAjRpf/AF9R/wA6bsVe57P4z48Faz/16P8Ayrw3RAf7MU8ffavcvGn/ACJWs/8AXo/8q8P0OCR9JVgON7d6zfwipl9M7PxqaEN5bc9/Wqy28uzoOvrT4YZRGc+vrSsmDLkCkcn+dSyLvqgm9F5/nTxOwmAJPNURYtGFvUVE8L5yMYxVnNVrnduXbn8KaQrkTwyZc8cg96hEMvlsMc8d6lPmbn5boag3TbGxv7UdRofBbzeZ07HvTXtZt547/wB6iAz7/wCPp70x/tG88ydfekUOjtZw447/AN6pmt7gMev/AH1VeMXO8f6z86lZbncf9Z+tMl7jxDcDuf8AvqnyRz4XBP8A31VcC5/6afrU0hlG379MQySO4IGGP/fVPtQ6zNuPOPWoWeX1an2hYztuz070AXtxGOacCTnmmkGnAUtAAj1pR0oIpR0o6AKKKKKSASloop9AEpaKDSASlpKKYC0UUUAJS0UlACMoYjIBpJEBXgCnDrTm6UJiIFjAPIGKeFUdhQozmnAU2xjCACMAU9elLgUnSkAbR6UmB6U0yoO1N85PQ09AJsVBKQG5qYuMZwarSkM3cUAVuARzxQ+C3UUDYSPmP5UrKuep/KkWOiTMb8jrS+X8pG5fzpYdoicbu47UYUofn/ShCFEf7sjIqAxc4yKsAL5ZG/8ASoGVSfvj8qAHmMmQkEUxY8RvyOnrUuwebneM59KjCLtfEgNADoozs7danSPAU1BEilfv/pVuFAExuzzUtdCr21Hls4GBVhxhQMVDtXcvPerZZcDpXFOlaS5Ud0a143bK7j5OhpqD5TwetWGKFccUi7QuDio9m1HYPaq+5Bj2NQkfMatnb7VWkxv61vRi0zKrJNC4ArkrGbHxTscHaFvUyfpXW4zXDWVtd6rrupTW1ssjxylS5xleSOMn2rqSOW56t4nu4rzUC8D70Ear7evB9K51gRTbC3uLTT44bkBZRkkDHc01uWxzWSk1Kx7tKhB0YvyCJWEjEjANYniNcCNsdv6mulERrD8SR4tkJ7ZroR47OLu1EkMgIz8pArE0uTydSjOQM5GT64roJV3RNz1NcvIDHOcdVbiqMpHsmkXYVEI5UgdK2Lk8xfWuQ0K6WWxiYEkAY9fQ/wBa6hmJhhLetT1EzQvf9Un+8KWmXjAInP8AEKeOlT0GLmj0pKQmgDh/A52alrC7uPNH/oTVmeCRv1zVTnuT/wCPmr2l6dcW/iLVoLK9WPYw3M6bicnP6VleDY5F1DVHEmDGpzg/eOT/AIU7asOiPRxRVexfzLNHwBuyePrVikwGsMnI6iuO1+2Er+W0e3IbJIHHv/Ouy/jHpis7V7dZrdz/ABFSBzQtwPN/COqvpWqtBgstx8mM8BgeD/OvQZL55gEKgA9a8x1O3fS9YWRVwgZZBjp/nOa9IO14VkTgEZBHoatgjPurdAjtg5+tcJrwH21T6g/zrv7uKRlOCSuD3rg/EQ23MY9j/ShBLY6X4c6HFc6gurGUg2jkCMD7zFeDn8TXofirV20fwzc3UbeXPgJER13k8f1NcT8MpmFnqCDpujb9CP6Vm+PdWvNQ1qPTWl/0eMqVQDHzEdT+dLXmEHhOE3eoXF9MTJI74JbuTlif5V6EvIrmdLt1tI/3I2qDjHuOM10du26PnrQ3djJcUUUtLW4hKhxi5yP7tTVBK6xMXdgqgck8U0JnB+OJNuvWbD+CMH/x41euXS9iXIBViCDjpWN4sk/tLxBElqRKWjVECnOSc8Vsw2N3HaQq0LBhgH61tFNmcmlbU7dfN2L864x/dppEn94flUMF4joMqw7c1YJ7VxqUW7JnZOnOKvJbkeKMU6itDIbzRz60tFMQxlLKRnqKr/ZmRctLkKM4Aq3TH+42fSgDEWTDsfWQn9a2dUTzdKvE/vQOP/HTWLBEJgSWIfcTgelb7L5tuyn+NCPzFPqDPOvCdvb3MF0JoUkYMuCw7EH/AApdNt0g8S30USbUAICjsMijweCJ7yPpgL0+pFW7YCPxTd9AGX+gNPqHQ37cYt4x/siqmr8QL9avRn5QBxVDWDi3T60uo1ucvqU8aIqswB9K5JvvH6mtnWvmv41B6gCsq4h8mTbnI9atEyJdN/5CEP8Avf0rW1of6Gp9JB/I1kaccahB/vVta3/x4D/roP60nuC2KmiD97Mf9kfzrWllEUTO3QCsjRPvzf7o/nVzUnxa7T/EaGNbGjpjCSNHGSMYrQbtVHTYvItY0IxgZq6TzSKJIBuuIgMcsBz06120cEUP3I1UnkkDrXG2Qzdw/wDXQfzrtj1NS99BMOBRRRSEFNf7hPsadTH5RvoaYENk3+hRH/ZqZpCuABkn3FU7JWNnD8xAB5GevJqpqF6f7RtbGGXa5cSS+0Yz/PFO2oGqZJeyL+LVi69DI1uZ3YcDaFFbBzszmsrXsjT/APgVLqBgwtJ5IUkbOoGO/wDkCtjworN4q0oKCf8ASkOB9ayIv9Uv0rc8Gj/ir9K/6+V/rRLRD6HsnjIFvBmsBQSTaPgD6V4boqTf2OuFcfO3H417p4vz/wAIbrOCVIs5DkHn7teFaJIf7BQhifnY5J96noTHsXo1n8vkP1p8Qm8s8P1qON22HnvU1s7GFsk9fWnp1BpkOJcchqQCTzU4bt2qQOx/iP501Jn8xRk9fWn1E7mkC2OcUyQvuGOlSryKkoI6lBmfL8dj2qISSeU3HP0q47EBz7GqwnbyySB2qehoiOCaYSj5e392myPMXJwevpU8Vw2/7o6VFJcNuPApIbeoyN5w44P5VK7z7v4vypsdywcfKKkluWL9BVEjBJP6t+VLI8nGS1C3DZHApZZCxHHajqBHub1NW4IhkSZOcYqqT0q/BzEtIch+KXFFFMgKKXFJR0GLRSUtJAFFFJT6ALRRRQAlFLRSuAUUUUdACiiigBOlKTRTadtLgC06kWihgLSGlpDQBVbGTSIFJPNDum45B60sTRkkYbpTsMm42io3Cmnh1YcZprFS3ekIqKF3Dg/nTnK7uc0790COtNfyycktQyxY9rRP1xkUo2FD8x6+lLGI/KflsZFAEWw8nrTQgABQjd+lQHGQN36VZQptPJ61AVQ/xGkBJ/y1J39/SmYGH+cf5NP2L5hO/vTTGuH+agB0QBRvmHarMXTkg1TRAAfnq1boCvDZ5oB7E/GRUjcrURXkU4nNQ1rcV9LBRRRVMQlMI5zT6aaEuoCr1H1qj8MtNe8m1mVcAfa9v6tV9fvD61d+Dm2XRdWkXHN+efX5c/1qugy3rdobXUTExB+RTkfSswwoTyoNbvif/kLZzk+WtYtZxgr3Z3/Wp8iinayDFc/4pGLNTuxg88V0JrK1hBJFsPIIxWiORnCqm+3z1ya5jUYmjuWyOD0xXUWTEpJE2Dsc85rI1mH9yHC/cPYdqvqS9jY8I3RNuYyc7Tge3eu+gkL20YPbgV5R4YuPJv2BHBGa9QsJN1kvBGDSYi7vYxgMSf3pwT25rRQ5FZ8Yzb/9tD/OrqnipdrjSJM0hPFNJ96Qnil0HY86vb+6sPFmpm1m8suRuIAOemOtR+CkeW41bB5defqSaj1wEeLL3nOSP5CpvA6zjUrl1U+Q2Q7Y4yORz+NU9iep29jGYrRIyCMZ6/WrGaQUVPmMKhuYvNj9xU1IaFuBwXi2yK2BdUGMbScdO4/lS+Gtba/s/ssqBZII1UNn7w6Diuk16wN7p8kIIAIz/WvOdFf+z/EQgbJBkMX68H+VUtUHU9Acbkx/smvPPE4xeRj2NehvJ5aqecE4rz/xYu2/jHoDTsD2Op+FmXbUow2P3cbfq1Y/iq2mi8bIJl2mRo3Az1G4gfyrZ+E3Ooaiv/Tsh/8AHqi8djPxBsx38qH/ANCNHXQnoa2mjKkA5+Y1twjGw+oqnpCj7K2VBO7qR7VohQMcdKllj6KSigQtRSIkgZHVWVlwVYZB/CpKYRlvwoQmeaiKOHxwscKCONLoBVHavQTHnYpxjPbivP5ePHZPpdZrvoZhJKgx3qa06kF7jsdOFp4eo/3yvqPEewj0zVwD1NRSIQRgZ+lPVmzgoR9a8/Cybk2z2MyUfZxUEONFFJmvRPnxaSijNMApDyMUZpCaAOd2bZyo55I/Wuit2/0ePPYCufvk3PIMDkmp9G1FWA09k2SRKTnsR/jzTsDOa8Or5PiDU4s9Cwx9HqecGPxOGyRuUd/bFJpy+V4x1RcdS5/Ngf607UiV16BgeqgdPrT6jR0ERGwHFZ+tEfZk/wB7+lTWlxui+fAIJHWoNVbdAmPWl1BHE6rBI16kgQlFAyfTFUL875ARnHrW7qR/dScfw1iyKPs2eMgVYmVrA41CA/7Yroddi/4lwOM/OveuctTi8hP+2P510+uEnTev8Yoe6EtjJ0XiSb/dH86suPtmoxwqcpHy/OPyqlpbiMzMWC8Dqeta+lWrwGZ5WUyO3brikNGmnBNMkuNnYH8aljVncIoyzHAHvWj/AMIvcSMC80SjHI5JpFFrR7ZJreK453bgRzXTMcc1gRxSaeEiKqU7MpODj61fid7pW2kjB5BNT5iZdWVWfaPTrT6gghMZ3EjOMYqegQUEZGKKWjYCAiO0tidwCIONxx+tcz4eSW+1G61WdMeYcRZ6qvXH9PzpnjLUftLQaJbMd8rhpWBGNoJ4+oIz+FbGipHHarGjAlABjPQf5FPoM0ioK4PSsrxAALAH/b/pWuTWJ4mcrpi4GcyD+RpIRkpGyxKccFcjkVY0fUjo+sWd+IxIYZgQhOAT06/jWkmjj7FBtOG2DcT9K5644kiXPWZev1oeuhR9FeJgH8KasOxs5f8A0A14HoQzoI5HDt/OvfteGfDOpjPWzl/9ANeAeHhu0E4Y8SPUPYiG5oRD92frUtr/AKhvqaSGEmFm31JbwN5TfNRdFtNkK9KYn+tX609h5fBJ/A01P+PgDPGapaktGsg4qSmKOKfjimyCuZFIf5egqsZU2HCfpVgRj5xu6ioRbAoRv/Ss7jEt5EMnKDpTZXjDn5KlitQjg+YfypklqpckzEfgKa0H1I45E3j5BT5ZF3n5RSpaoGH78/pTpLVC+TMf0qtBMiVxn7tSPJn+GgWkYPE38qfJACB+8ouBDnocVbgz5Yqs0W3GHBqzCMR4pCaJKWkpaACiiihsBKWkpaE1cBKKWihKwCUUUU9AFoopamwCUUUUwCiiigBD0oqObdtG31qAu/vVJaAW1papK7989auDpQ0AtIelLSGkBSdG3E4ohjcMeO1K2cnmliJ38mm7DHIrAYxQVbd0pUPB601icjrR6C6kZjbP3DSPGxA+U8UjZz3pG3cYzSLHojeU42ntSCN9h+U9aVN/lN97ORQpfYfvdaYgVGwcqajMbf3T+VTKW5OWqEmTJ+9SAdsbzOh605kYB8g0i7/NH3scUXBfe/3scYo0uIjw2PumrdoCFbIxzVJS3fNXrbOw5zQDLBpKKKGSFLSUtT0GJSGlpDTAMgVb+CHPhnUmzyb8/wDoC1i6rqMWnWnmSNgu3lr7k1vfCaN9A8CXF3qS/Z47i6MsRfjePLXBH1waroBH41uZU1/ZHKQBGOAfcj+lc6L663Aec36VJf3M+oXLTzSZY8DP+fer9hpr2zmWWQFiMBRzQtjfZEqNcFxuB2+uKoXjFpZQTwGGPbitg1jXRzPP9R/Kgg4mD5L68TPRz29zVDVZQLaRMkls9ulXLthb6teEnALZxWNd30bs6YyD6VYMpadJ5d9Ec7QTjOOma9P8L6iL/T5vlwIpdnueAcmvKBlSCDyK9B+HjM9lqGTn96hyfoaGQd1bDdC24fxt/OnxlznnoabbnETf77U6LofrUPcpbDvm9aPmx1paM0rdBnm/iIEeKrrnGQp/QVd8HSva6ZKypuEspbJP4VT8TeaviK6laP5QnGDnIHet3waVbw9DjGdzZ9uap7E9TUGosT/qh+dSC+P/ADz/AFqxtHoKNo9BS0GSKdw+lLUtpAJQ+TjBqx9jX+8a4auNp058rOunhJzipIyLxS1vIBxlTXk16TB4n3Z6To38q9mu7ItA4V+cGvGvEcTW3iCZSSWUqf0FdGHxEKyfKZVqE6VuY9BugAqf71cH4xz/AGin0P8ASu7uPmhibs2CK4Xxj/yEE+n+NdRgzpfhM3/E51BfW0U/+PCm+OMn4j2wz0jhx+tL8Jv+Q9f/APXmP/Q1o8bZPxKg9o4f5Goe4uh0Wj8wufcfyrTrP0gf6MT7j+VaFJlBRRRQMKT+L8KWgfe/CgTPNJhu8buAQCbo8npXbwAxSI7HIB7VxW3zPHTLnrdt/Wu5ZPlC56VnXnFe7J7nThaNSS54K9mXFl3bZMY7gVI11Hkg5yPaoI/9Wv0xTwoOcjvXnYaPNUa6H0GYVPZ4aEktSFr3DEBAR9ab9tb/AJ5j86s7F9BRtHoK9VHyz1ZW+2t/zzH50n21v7g/OrW1fQflRtX0H5U9BFX7Y39wfnTTduf4V/Ormwego2D0FF0Bh3BLuxI75rISRbfXEmLbVjUu3GeO/H0Nb16AxYAEHdgYrD/sxtQ1C4SOXZIiDG4cEHg0yiOJ1PjO8dTkOm4H8Fp+qj/T7eYfw4z+dUb77RoviDz7iBtrx7VKnIfjqD+HSr1xMlzEkgwQy5o8wTIxd7J3VG+XPb/PtVmYSSxAhWbntWEknmOxON2OfqCRW1bXyw2qKwJKnOaGBhakrYkjx83Qg1lTLttiOmBW7fMJrt5FyAxyKyb+PYh9+RxTQmZFucXUX+8P510uutt04jOSZPp6muYiOLhD/tD+db/iOX93BEMjJLH+VN7krYZ4b0s3s5uHA8mJv72CW6/lXYzP5UbNjoD2rntAme20wKoHznccjnNXZDJcTbi2CT0FT1NFsdDoVgjRC6kXJJyuc8cn/wCtW6RTIEEcEaD+FQP0qQ0mSV7lQYHyM8VHp8q5aPB3Zz0qyy7lKnuKbHAkcpdRgnrzS6AWKWmg0FgoJPAFFgKd7e+RMkY74YnPbNN1XU00vSpr1gXVBwAwBOfSqGqSh3J3YUfyrgtRv7jXdSitI5Ge1jc7M449T7jjvQk2Bc0OFrm6l1CfLvKThiOc9zXoGmRhLQMRhnOTXOWlsIkWGIEIoAArq4ozHCiBT8qgVT2GPzWJ4n/5Bin/AKaD+Rraw3oaztatZrqyEcUbO28HAqRGnbsHs42HeNT+lcJdTRpe26M2C0644967izR1sIkdSHEYBB7cV5/qEDPqUBHVZM4HfkUKw0fTetLu8PaiPW0l/wDQDXgnhKMHQ23Acyv/AEr33U/m0O9Hrayf+gGvBvCQH9if9tW/pWVT4SqCvM3UhTyThR+VJHEApG3FWUH7uhR8przPayue37ONiqYEPVRVOVAk4ArTZazbsfvxiuvDzbepx4iCUbjxJID94VIHf+8KopuJPHepQH9K7LHlkqgtvyw5FRCMbT836U6NWAfOBx61HtbafmH51K3AekQLj5+3pUEsI3n5x19KngRhKMsKa6Eu3I609UBHDEA4+cVM6Dd98U2OI7gSVqSSM7h8y0xDRGP74p7KNo+YULH/ALa0MgwPmFJgiKQBcYNWbb/VD61C6Agc1PAAseBR0GS0tJS0X7iCkpaKGAUUUUJdQCiikp67oAopaSgQtLSUUmMKKKKfQAooopAIaTFLRTENxzT6bTqACjFFLQBEy57mmomG+8aloFO4yJEJLfMetK0Z/vGpAMZxTJGIXjNICm6sDwzfnQwbAwzfnTjI2epoLtgcmgoRd4jb5mPI70gLlW5btTw7eW3zHtTfMcA/MadgEG/1aoyGJPJqZJGPVqjMrZPzUgFQN5o5PakuAxkbGaekz+aPm9KZNK3mN83ai2oEKq+e9X7UEIc5696orMQRzV62cupJNO1hPYs0UlLSYgooooASmSyJFG0jsFVRkk0+uduluvF2pjw9pMWZ0kLvJI21AF65I6daFqwJ/DuiN8Q/FJZnddIsCjuQB8xznbj1PzDPbFep+OdP8/QbWGApGIZRtjHAK7cYx7cVf8MaDb+GdBttOhCF0X97KqgGRupJ9euOe1UfFbnzrZc/LsJx75psa3PP7fSJknVpAm1SCfmz/KtZlqY81WuLiODhic4yABQim7kEk8SEguMjqKxp5A9zOVPHH8qq6nqLLLIYxn58ckDFclfeLJlaWKBVLE4Mm4kfhTSDYp+JLkDUriJOS2AT+FY6WsrKG4GRkVNbb7m78yXLkkkk+vvWiyEkHbjjHFPYLXMKRGQ4YYNd38Ojm21Ec/fQ8fQ1xd8P3in2rtfhucQ6kP8Aaj/k1Mmx22nOxhk3kkiQjmrgNQQBVD4AGWzxUmaljQ/NGaZRmpGcD4wP2fUZmYEq8YPHXGMf41p+B0K6GzEHaZTj8AK2dY0yz1G1Y3UO9kU7GBwR+IpdLt4rTT4oIUCRpnA/Gqe1w6l2jFApakZbsBtV/c1cJqnZjKt9asHI7181jVevI9zDfwoiScqRXk3jvS5l1ea+VQYSq7ueVNerseOtcD47kC2l0pzz5YH51vlsnGrZdTLHRUqeoafOZtBsnbOQqjJ9jiuR8WtuvFIOeP8AGus07DeE7FjnIAHHpk1yfihQbgMD3/oK+iPGex03wm/5D99/15j/ANDWk8a/8lLhz2SL/wBBrU+F1nDFNfThT5vlImSexOf6Csnxqf8Ai5UR/wBiL/0E1PUR1WkEGyH1/pV41k6W+IYyOCeK1qTKCiiigYUD734UUA/N+FIR5vCf+K8Y/wDT0/8AWu5LA9xXM2+hagni43rQj7MZ2ffuHQ57V1/lj0H5Vw4xSlNWVz28rnCNKXM0tRkRynHODU685pgjHGABTxxV4Wk43b6kZnio1FGnHoLRSUtdZ44lLRRTAKKKO9AGZdgC4J7bqxJLsabqv2oj5XXy25Hc8H8DW5Pj7bg9N1Z2p2iOHwcdQG9M/SqAq64ovdKkUA5C+bG2cjI/yfzrmNLuSVMWTj+tVZNYvrJ5rdWBTJC7xkqO2PbmnaIuWdz6etCBE9rIBqUkLMfvcduuK1ZECKuDke9YGqgw3kcyEqSAQRxyDWtatI0IZ5GfIBBJyaBoc1Vr+DfahhywGKtlTUF3IEtHJ/hU0wOTztfPoc1au5/tdwhzn5QKqNU1ku69hX/bFUZnW2yCJNg4A4q3D/rk/wB4fzqrERlsev8ATNWrc/6RH/vD+dQandihuVIHpQKXtSJEUYUZ64paO1ApAOFUtSuRFAyK2HYYwOuKuZrlPFWppZPuUhn2gKue9NIaMDxPq5Kmyhc7sfvCPT0/GrHhvS/KgMx/1zYXp0HXFYGmWzX979pkDFVO457nvXofh+zZBJMw+QnCgjnNVokBch00xqGLDeeelXoPNSILK4dgTyBTqKm4h281mXerTW+oQ2qIhDqSWbqMZrRrn79v+Kht16/uj/WhAaX9pTjsn5Vy0z41OJ+uGB/Wt9+FPauecFrjgZPQfWjoB9M3vz6Vc+8D/wDoJr5+8KTD+xTkf8tm/pXvMbGbRASc77X+aV89+FMpo7jjiZx/KspK8R0pcsrnWQXgkQ4XGPepUlGDxVCxRhGTkcmrGSueRXmyoTvoj1I4qNtWTGUYzVcsrzYx0pT93qOahjyLk5I5HQV1Yem4vU5cTXU1ZMlESDOEH5UGNNp+UU+jrXUcJSjRAJev3ahG3a2AelXpiU+6OoqujuytkdBxxSVrlEUW1pVABpjKQx4PWrEUsnmjK8fSmPO+48Hr6U9BEUYO7oafKpyOtPhmkLfd4+lPlmcEcfpTaAgVfr+VSbAAO3NLHO5Jz/KmSyyBlJpW10AdIDgYBqzbjEX41W8xyBxUiSvtPTigGW6Kq+eSAMdasik7iHUUlFG4BRRRVAFFLRRcAooooEJS0UUrajCkpaKdgEoopalAJRRRT6gFLSUtMQUUmKWjqMSiloo66gFMbkU6omViTijqBCYpO2fzprJMMcNUhSTsf1pkiOAOT19aY7iqJvLbh88YpuJcHhvypFDiJuT0HekUthuWpMY4Cb0b8qjZZtx4P5U5S2eWbFNdmyeT+dAEkayeYpwfypkySGXrjjvimo7Bx8xps0jeaeTSAQRPkc1etkKoc96z/MYHOTV+0cvEc+tNO4mWKWkpaHsSFJS1FcTxWttJPM4SKNdzMewo1GUtdvPsWj3Ev7wEqVDIOVJ4B/Ou2+GegW2m+F7XUmCyX98hlkuDgttY8KCOcYAOD3zXnIsT4uxM07xaSjEIE4eVsdeegB49665bt4NKg06ORxb26LHGueijpT0Q7M6/VvFCafdvaxQrIygZYtgA+mK5y+1p9QkSSbaCq7QFP/16xHfJ5JqGa4jhjaSRwiKMktwBSKUTUe9hjGWJArkPEviKKOQrbsTMFwExnNUtW8Rl0ngtgCPuiTOPx6VzlrbPNubqc43GqS7j2M+4l1PUHzI0rnPQHAH4VZsdEaZRJM2MHG2uht41t4FQKc9SfepVAA9zTuFjKGneUN5PA9v/AK9DRpFC0uMggqKvXcrRqoXHJ7is6WRpOp49KFruM52+JMxBHSuz+HB+XUR7x/8As1c1qMKiFnxzxzXRfDtsf2gM9fL/APZqbIe56DF0b6/0oB5qKI4STB7n+VLEdy5NSwRNmjNJRS8hkV1/x6y/7pqK1/491/H+dSXX/HrL/umorX/j2T8aOgupZFFJRQUT29zHCdruAzHgetWjMvrWJcf8fVt/vGru7iuCvgYTlzvqddPFyjHltsWjKvrXmvju68ySWMcjev6Cu/J4rzjxqjCaRsceYOfwp4fCxpTuhVsTKpGzNOwfb4OsfqOn+8a5rxEN0inqCW/nXS6epbwZaexB/wDHjXN6992JscEtwfrXodTkex33w5+SS9U9fLQ/qa57xoT/AMLIjP8AsR/+gmtvwTIbeaaR/uvCDjHXkf41z/i6RZPiFG3X92n/AKCaST5hHQac5MMRHr/Wt6ua05sWkZ/GukByM0MY6im0uaQC00nAJ9qM0jH5T9KAGQtviVj1IqSq9q2bZD7VMjbhmk3rYtRlyuS2Q+iiimRcKKSlpAFFJmjNAC0UmaKYGXck/wBogf7Qpl0Mlgehpbg/8TMf7wougfMP0qkM4XxLpXkj7VGPl6N+NZ+jzEXDrnjb+tdnq0CzaZMhHUZrgIc2l2M5+VsdO1MT0dzV1YboQy5yp7VcsH32UfqBg+1QyYlQgdCOM1Dpb+U0luxyQ2QcYo6B1NfO0ZzxWRqkhNvIFbg1oytmMjpXPyTsTNDIc9QDTQMzX61b0uMyXybe2T1qrIMNWxoKrmQ4GfWhkrc11Owsc8E8VatZM3EfB+8P51XPWp7barq5zkEEUitTv88VXl3hyQCc1mWmrNJcbZMlW6ADpV9ruNQSc4HGcVLASQzSxBSpUg9Qayb+4msWUK58xxnB9K0LjUYIACzHkZAA61Vd7XUhv2sTHxzxihDMl9WvHXaZdv04rm3snvb0tPdvKATkk9M9qvayklrIYS3MmAuPSrmjabmWNVycDc3+170/MDV0bR0VERRhQQT9K6pVVECqMAdBUdvAII8YG49SO9Smk3dgJSUtJmkIQ1zkn77xKz4yI4yufy/xrfmkEcbMTjisOwtdka3TPkzLnGOmTmmgLFydtvIe4U1zxz5qYPJcVvX522je+BXPXEixmNnOBuGPrTQH0N4U1BdT0CEOQZo18uUfT/61eGWdo9lDq9lg7re/mj6c8EV6Z4JufsbMC2BIoJrk/GFn/Y3iy8vF3Gw1Qhi4HEU4ByD7EAH61CWpLK1msnkLkN0p7KwPQ1Ys8+QM1I4yKlx1BFTY+OAadbqRPyCOKtjiouftA+lNJITJqKKKfUCKfdxtqsrSYOc1amOMVR38NhjSt1GiWF5DIODj6U2TeWOQetMtpGFwMscc1HJIxdvmPWhPUdi3bsQMEH606Yk44NVYWO/qelLOxyOTTe4rE0QOTwaZcA5UkGktyTmifJZcmgOpGxIWlRj5Z6/lTXHyVLGP3R47UgkrMYjHcPwrSrKXmQD3rVFDBi0UUUCClpKKAFoopKGAtFFFNbCCiiipuMKSlpKroAUUtFIApKWikAlFFFUIWikpaNACiiigYUUUUaiEprIG606igYwRKARzzSCJRnrzUlFF/MCPyh6mmNb7jncanopAVhajP3qRrNWbO41apaLId2U/sC/3jU8UQiTaDnvUtFFkhNhRRRQAVk+Jjjw1f8/8ssfqK1qyvEoLeG78D/nkT+opqwEvhQBPCtiFyMqx/wDHjV6Q4J4NUvCIebwtY7FzhWXj2Y1R1hJo7ySNyykdBntTe5pEdc67ZQSMjOQynGDx/OszUNejnRoISfmAycg8Vg6nays4ZFY+uKp2QKXJzgHHeqUVYLmu1vEYs+WuSM9KbAzW53Ko+npVtOY1PtQQDSv0GWDfF4wNpHA/iqpPO0pBPGKazHjb+tQOWHBY/hSSAq3ZbdnnoKrbznqadcMxmA3HbjpUDnANWhEN9IWt2U8810Pw9+/f/RP61zF6+YSPeu78FwpFoUTqih5CSzY5PPFD2Je51MZ/dv8Aj/Klh+5TV4jbPr/SnRcIKlgiSlpKKQyO5/49ZP8AdNR2v/Hun40+5/49pP8AdNR2p/0dfx/nR0DqWKKKKAKtz/x9W3+8at5qnc/8fdr/ALxq3RuCYZrifHWI7NcYzJIufwBrtTXD/EA/urUHux/lStqDZa0o58Fw/wC7/wCzmuX1z/VRc92/nXUaNz4LT/cb/wBCNcvrf+ri/wB5v51aF0Oq0ZsWUJHH7pTn8BXNaxJnxfG3TAUfpXQ6K3/EuhP/AExT+QrmNZcjxUjE/wB3+VNbgdjpxH2VPpXSJ9xfpXL6W2bWMe1dQvCj6VLGOpM0ZpKQC5pG+630ozSN900eYEFr/wAeq/j/ADqWL7tQ2v8Ax6r+P86mi+6Kyl8aOukv3E/kTUUhOKK0T6HK0FFFJTJFpKKKfUAoopM0aDMqf/kKj/eH9KluQDJz6VDOf+Jsv+8tSXrFZRjuKYFO7jDWkg/2a8+1SEmRmx90kHAr0STLW757qa4e8jLXcqkdTTWgFbT598OzncnH4VOsEhvEliC5A+YFsZrLhJs7vaxO37p9xWtuYHHIosJF35goJAzjmuevv3d8xHrmtyGXK7G5Pasy+tN7tMTjgcUDaMmb7wrW0LrJ/ntWVOMMK1NB6v8AX+lPoStzbALMAO9WBHsjHr60qIEHbPrTm5X8alstD4pZIHDI3zDjkVctLuRnYyyn7vy/XNUxETySAKeiCM53HP5VLsA+6bc/DEqB8uTnAqASMhIViv0NLNIqLkH9ay7i9USNlyOaaQGrBBHeakkk255CAoz2FdbZW8UKjaoyOB9K4aHVrIEfvXQgDop61qQ+KIEOBcbh2JU/4U3cDsqK5P8A4S5UUD5TjueM0R+LLidNyWq+/WpsB1OajklSPG91XPTccVzUetancZ2WvU8fI1U9VW9u4gLoeWFbIYqfSiwGhreqsjMkTxmMJknAPOKswuwsbXBGPLXnHtXFS2JSAkzls9MDArV0/UpzAI2bPlgKGI56VVtBGxfSMYgGPBPpWFfgt5QCb/mzjn+lWJ7x5MBiDiqF1L5nlg84b0poEemaFcykWxDsu/aDg44pPiFCZ/Bl02eYpI5Bz/tAH+dYnhLVvtGo2uneRL5ijcW+XAA/Gum8ZJ/xR2qhgD+5zySOjCo6iMPRpRLo9rIP4o1z9cVerC8Is7aDHv6B2C/St2k9yQoxzmiigAoooo0AimGcVUhTBbPNXyoNN8pewovpYEVejDA7+lMIOTwOvpV3y1znFBiU9qNB3KEbsH7flSyucjgflVwQpnO2gwIeoo0C5Tic7gOBn2p1wWG0gD8qtCBByBStCj43DpRoF9TMeVtg6dfSpoZGMXOPyq01tERgrSi2RVwBx9aSBu5nLI3mqML1Hateqws4twbacg561Zoeogooop6gLRRRUsBO9LSUtUAUGkooAWiiilYApKWin1ASlpKKQC0lFFJ3AKKKKEwCiiincApaSihMBaSiilcBaSiincAoooobVgCiiikAUtJRRcBaKSlp7bgFFFFMAqC8tkvbOa1kJCSoUYjqAfSp6SgDnfD2pHwbfPpmpH/iWzMWiuSuArH1x27fhmuw8QaU2oWyXEOXlRcBAAd4PQVjajptvqdq0E6Bu6noQfUGsDw/r2oaHrH9g6pO720gMUDs33cnhvXHamtRojlhzuDcEetUJIGH3h34OK63xFbxK6yxKygfK2Rnd/tZrAYq64OCPWmmXuQwQyzZSPHA707+z5txBZM+5qzZARJKwUk8DgVkX2vtBI6FTHg8AryaWrdkUXTZSKy5defaqd8I7UMXmUHOAMdaw7rxHcTAhMjIxk//AFqypbqeVizOck5OKaT6kuSNie+t423Alj61Sk1JZDyTj6Vmc5pKojmLd1KrxqFPU16R4Uf/AIkloiqSQuOPxNeW16j4UaNdPtFUNyO/rigFqdKgYp9wg56GnhWA6VFLdeVcRx7c7++as7hU27lIZg+lLg+lLuo3UtAIbr/j2k/3TUNr/wAe6/jU11zbSf7pqO1XEC/jR0AlBxS5NFFFwKd7FPLNbGBSSrckdqeyXy5wpIz14qO8up4Z4orf77c425phbVmH3wPwWnrYCcQ3zLnGPqRXIeObS6W2tppQCu8rnPcjP9DXUBdUxjz1/T/CsPxXb6hNpYMkiOkb7+vTAPtQguGkK0Xg4qw5CP0+prldbYlI+P4jxXS+DpmvtHuIrh8pE4QDGMLjNZvjWO3Q2htipHzBto4PSqQuhr6DbvLpFu6xuVMajIFcr4giaLxRGCjKcLwetdj4UdG8PWweWRcbhhQOME1yPi5QniKNo5GcMikFsZGCfSjqDOgsrg20UClM5H94e9dZ577QRHx67hXJWum3dysGJEKY9cdc+1dOttMqBQ6YApMZOpnb7sII/wB6lK3H/PIf99VGq3S8LKop3+mEf6xf8/hSAXFwP+WI/wC+hTDM4JVomBHoeKdsued04/AU4ggfez+FICO1jk+yodh5qYAxIC/FRQ3UghQbV4GKkMhdfmArKWjuzpoqUoyjEmKFuAfzpsgdWCrGXJ54ppnYcBuB6Uv2hy4fdlgMCmm76sc1Dksou4n7/wD59no/ff8APu9L5lwc5m6+1N3z4wJv/Ha0OUY8zRgl4XAqL7dH6NUrrPICDPweD8tVvsH/AE0H5UASfb4vRqQ38fo35VH/AGf/ANNB+VH9n/8ATQflT0AptKJdVjZehZau3YwC/XavSqBj8nVo485ww5rUkUOCD3GKYGO16uCDGefeuVvVxqIYd8j+ddXJps3YqfxrmdbhaG5CsPmHPHNPQZjara/MJh06H/GnWU3mw7TncnU+vpWmIxcwgEna457fhWHPE2m3vGSvY+ooT6EvR3NVDhsg027x5B96SN1dQy8gjINMu3zGoz3oGYlzw4rU0Dq5/wBoVmXf31+lXtHbCyY9RTJW50j3SLwATUT3eVxt4+tVj8y9SaaxCjngepNTYssPqLoo5AAqGS9mPG41RmvYRwrbj6KKgEt3crmCE49cU7IVy1NcEcyP27ms953nkCxK27nGByav2+jSTnfcuc46A5INbVnp8NuxEcajPfvQBlWmiK6q9w7kkfdHFXo9ItI8fuc45+Zia1PLApSlIdinHZwRnK20I/4AK6DT72eTbEIIysagcccDiszbxUsEsluxaNsEjBoeoHQKvyqSpU88Z6ZrK1w/uVX5eTnkmon1C5IAEmMegFU5nln+8Wc9s80WGUJ4/wB0AccVVClBhGxn0rQltJcZdGVc9xTxbiPPToeaYGVslkPQ+g5qxDYuTvfhfU9B3rQhheeVYoEaRyeB/niur0TwuY5Eub0HKj/VH16e+RjHvR0Fc1PBmki0tvtLwkSPkKd38Oewxx78ntWJ8RfEgmRNC0x4Z2n4n2HLA7gAg98g5rW8WeLo/DlgYIfnvpoz5CgcDnG4n29K5Lwrozos2o38Za5nk3r5gB99wPqcmo8yWzc0qwTTdPitkLHaMksecnrV2iik2SFFFFK4BRRS0eYCUUtJQAUUUUrgFFFFF7gFFFFF7AGKKWimgEopaKGAlFLSUIBaKKKT8wCkpaSq0AKKKKEwClooqbAFFFFUAUlLRSEJRS0U7aDEopaMVACUUUtHUBKKWkoAKKKKdgCiiigBaKSlpW0ASiiimAUUUUAFLRRSAKSloqkAUUUU+gBXNeNba3fRWuHAEyMNh4BPt9K6WuW8SNFcazpdjdOi20sq79/AUbhls/TNNbgjP0jxE93YQ2N9lZgdsUj/AMadAB7g/nTL+/gsdxeRdwzhVPer3jbxloWrwTWtlpSzsmQl5LhCnP3kxz/KsXQvAmpay0ck4e2t2+bzJRksOowOuD69KrzLTKZ8T3Cb1ggGW6bs8f41S+w6vrP7/wApnjXgEnCjPpmvWofBmj6dAdtkrOrZ8xxuJ/Os2Z2BKWsGwDtjP6UrroO19zzSXQruFcnY3srUyPSZcnzSqAehya9B+xyH/lnyf9g1A1nGufOVfbCc07hyo4n7BEg6biOpJqrcqqowVAM4PTpXW6jaQlmWBRwRuwvNc1qbRrF5atkg9PaqJZlY5Ar07wvxZWnGOT/M15on+sT6ivTtAQxWtop6gDNJhE2Lo/8AEytR/nrWjVC5x9vtf896v1LBBRRRSGMmGYXHqKSFdsQBqSjtQAlFFBoApyY/tOP/AHf8atGqsn/ISi/3f8atGmAVm67H5mmSLjrx+hFaVUdVGbF/bn9DQByXgaYpa6jGcdUP6N/hVTxUv+iW7Dsx/kKj8LOYr+6jHQkA/gf/AK9WPE2W02IjHDf0NMOho+GHzoSjPSRx+tc94xXbqdu2esX9TXQeEEMujyAdBM3f6VneOLGRTa3QUeWuUYg9CTkfyp9RHSaGwksoGHdQf5VvVx3hO4D2cW5ySMrgnpj/AOsa7EEFQQeDUvcYUtJS0gCmN0p9NboaLgVYv9Sn0qcxKwyarwENBGR3FWx0FTJJmkKkqbvF2I/s6+9OWBVIOTxT6WkqcS3iar0bA0lLRVmAmKKWikAlFLSUwMa5/wCQ5F9V/lWk1Zlyf+J9F9R/KtM9aoBtcf4r/d3cDf3hXY4rkPGY2tan3NCEZVpIQdmOpyPYVHrVqZLQSKBuTkn2qFWPy4PtWtHm5tMkckYIPSjzK8jmbGcq3lE8fw1Pc8DcDnvVG6ia0u2X0OVNXY5RLGD1z1+tUxLsZtwSz89qfa3HkBu2eemaLxAsgIHBFQKrOdqjJPQUyOpet729uJvKiflyMcdP8K1ofD1xcYa6nbIPQc/rW/o9hHbaXErKvzrk4x/Or07LBEuwfKcjBJPSouaWMa28P28JU+TuYfxPzWvaaFPcxlotiqpxgnFQteDP3Rk1oWWrNBAQsWcnPX2obYDR4dnRzmSP9f8ACpl0KQHmZB9AaSTW5e0a/r6VC2uz4zhB+FL3gLJ0YgczD8Fo/slBjMp/KsqbXp1ODIg/SqUmuzH/AJeEwSR1FCTA6L+zYFzulf8AQUhtLZT0LfVq5U68+MtcgcdqRtcH/P0x69B7Z/nVWfcDqwkKniKP64z/ADpjzrGMF1XnAGcVyTa27sVhEkjZ4G0+o/8Ar1Yh0/Wb0jzEe3TAIL/L3JHv3pWFc0brVrfGAWkyQMKM9Qcfyq3pWkXGp4kkXZCwDAlTzkdO3uKv6b4a06wQPIn2iUqpzIOPqB610DTpEoBKoBwN2AM+3+FDfYB9paW9lGywxhAFC59QOmT+Peub8UeOF0zfaWQD3BX7+7OxuCOCOay/FHjRbdTa6e4MoJDt1C9QQQeh9CDXOeFbBtT1i0luPmTzAFDc8Dn8uKVuoBbw3V14hS41hpI5iRMRMh5B6cema9PjAESADA2jAxiqnjLS1v8ASbdowiXS3Mccc5HMe5sHkc46fpWHp93rGk6ymma1OjI6/upNmRJ6YYY/Wk9SWdTRRRSEJRS0lSwCiilpW1uAlFLSUwCiiigAooooAKKKKaAWikooAWkpaSgBaKSigBaKKKTtuAUlLSGmAUhpaDTELRRRSGFFFJRoAtFFFJgFFFFABRRRQAUUUUumgCUUUUAFFFFABRRRTAWikooTAKKKKACiiikAtFFFCAKKSimAtFFNc7VJ9BmqEQXt7b2Ns89zIEjUZJNecD+1fGOtyCxt5HUHgBciJTgZYgen9a29I0WXx74kurl3ki0qBlSUB8MeDgAcjPrXq1nY6doFgLSztlhhTCvsA3ezt3J96d7FJHHeG/AFppKJd6gVubrbyPvRrg9U4Bz9fyror3VLbT7NpJJFijj4VSQOfRTwOR07VX1DVDGGaSQBQSNx6HHc46H3rynxH4iudbvHtoZJPso4ZSRgkHPbqO9Fr6lnQ3fxNjF2ywWSvbAnEm8q7+hweB9Kg/4WPAXLfZ5BnqCB/SuUjswikEArjJLLzn/Cqd3FbRgdQ2P4TVKKFqjuX8bW87ZV8cA8cYJ60kerJdRuwlVxnbwQea84z3HWnI8u7Kls9cjrRYXMdxc3JKsse07uvauT1OHyHC+vvS/2hdRIEM4k74POD9arXNy9wwL4z7U0DaGQLvuYlHdgPzNeo6fgbPZhXmmmpv1O3H+2D+XNekWJOzPoaOoI17j/AI/rX8f5ir+eaz7g4vLU+5/pV/Oal9AQ6ikzRmkMKKiuJPLtmYUsTboUPqKOgElJRSUAVJjjU4Oeqn+tW6ozf8hS2/3T/WrtMQtZ2tsyaZMynDBWI/75NaFVdQtxc2ckZYgbT/I0hnn3hoA6vOp54J5+oq/4lT/iVcdnA/nVDw/8niW4QdMOPy5rU8RLnSn9A4/nVIQvgSQvZXS55Dg/zq54xi8zQJmz91lb9f8A69ZXw/bJvE9lP6muk8RQeb4fvFA58sn8uf6U+oHHeE7wRTNEc88rj6YP9K9Htzm3jPqo615DYTmzu4pDuUIfmHTg9a9YsJkls4irA/KOlKSGi3RRRU+QwoIyKKWgCtDbeUgXPC9KsUUUhC0UCin5AFFFFIAooooQBRRSUwMS7/5D8P1X+VahrKuz/wAT6H/gP8q1TVAFc14xiVtO34+ZRuB9MEf410tY3idQdGkJ9GH5g/4ULcRw0Z+QEVqabJ8pQ8DrmseBswip45CMrnhuDim0UM1+2A2zLjjg/Ssq0l2vsJ4PSt+7xPYAbs4+U/lXMfMj46EGmtiXuW7/AJ8v8aueGrUXeptGW2gRkk4HqPWs2eXzdp9BV7w/O1vqYZHKEoRkGjoK+p1s2oGENbqo+TgGqEmoTsMFhgd8VFeSW0Rd5Lht7ZY55JPWuflupJ3G3O0jG31pJGjZsSauFyPNOR02iqza3cBgFkkK88bsVFFaX0wBSxcj1IxV+z8O+bHvuvMjfd91fSndInVlBtXuW7scerE02KLUrvHlq+1uNx4H510yaZawR/JDggde9WYFREwB3zzzS5kOxgQeFtYvWLRoWXOCRkge3StS2+HeqyYMkiR/ma37XV7qxiMUEgRC24jaDz+NWU8RX5bBnGD/ALI/wpXYWM2x+G8fm/6Tcu68ZVRt/WuitfBOj2xB+wo59Xctn9cVRTVp0Z2SV1LnLEdzSHWLhutxIfq5oBpnTwaXaWwxFbxxj0RQv8qztaSNZ4tm37nOPrWDJqDHlpAc+r1Vl1CJOXmhA92FCDlNr7dHBbFpWRVjUkk9gK4XxP4pe9ZrS1YeTgq5U5Dg4xwe49az9Z164nvZFgmHkrlFCjgjHJ/nWNbqrzKGPFOxLZZs7F7lfNfcE7e9eiaNAltrFoiKAqnAAHTg1ykfEIA9OAK6dhILhJ0HKnI496T2GkdR4jyNJUghD9qgIIXnPmr3zVrxBo8Wr6ZJA5CSjLwyd0cdCK8+17xVfSSxWLRxIqyxzFhnJ2nI/UV6L9q+1QhkP3xwfrUpCZznhzUZdR0wmfmaFzC7ZzuIxzWvXNeDMrp10rEE/aWOfXgV0tJ7khRRRSAKWkopeYC0lFFCAWikpabQgpKKKQwooopAFFFFMAooopAFFFFVcApaKKVwCkooqgCiiigQUtJ2opMYtFFFT01AKKKKACiiijqAUUUUdQCiiimAUUUUgCiiimAUlLSUAFFFFIApaSlpgJRRRQAUUUCkAUUtJT33AKx/FeR4avMMV+VeQcfxCtisfxVg+GL/AD08sfzFUt9QLfw3EVp4WaWNsvNM5b5OTg4wfXgfrWtrV66RptIMnO1iB9z0Peuf+H9wv/CJxRrjf5zh8fXIz69qv+I7sx2i5KKA3Ufe71fUtHEeKNTeOJbO3ch5j85HcVk2lssEGCQWPJx3qtPP9r1iWQsSinClh0xUF7cyzOYEwy5wpXktTAfean/BB/31/hVWCxaWPzpZFijP8THr9BV3TtMeTEhQ7h0LD5Qf6mtmKwRAWmkZnIweMDn2oC1zEjs4zExht3lGcb8ZqlPbzRfeikVfdcV1zyQ22R0JwM4yaJEWSIoVypHIxigLHGRpvYjdiozwcVsapAsDxtGApOegxWMx5+vNBL0NDQ13arFxnAJ/SvQrA/um6da4Lw8pOosf7sZrurJv3LfWhjRrXjbRbyehpBqSrkeWT+NMvObGFvp/KqGaWgI0/wC1B/zzP50v9pj/AJ5n86y80uaLIZrzzCXSy4GM9s+9TW5/0aP/AHRVEn/iTnnv/Wrlsf8ARov90UnsJbk+aM03NGaRRTmOdWtx/sn+tXqz5DnWYR6Rk/zq9mmIWmy8xP8A7ppabL/qn/3TSA8400iPxpcLzjc4/TNbGujdpMuAT8w6fWsWB/L8dN/tSlfzWuouAWtpfXbnrVAjn/ALYvbtCf4B/Ou/aNJY2jflWGCPavLNHuW07xEI97IrzeW+D1Gf8cV6ijZAOe1D3A4PxNoVxHfyT20TujYJ2qePWofDmvnTpZLedSXJCgnt04PsBmvQJ8NGynkEY6V5Heg2+qnOOoP6CqWugj2RWDDI6HkU7NUbCfzNPgkz96NTn8KJr4I21QG465qLalF3NGayGvZz0bH0FMN1Of8Alq350WEbWaM1ifaJv+er/nR9om/56v8AnRYDczRmsT7RN/z1f86PtE3/AD1f86LCNzNJWJ9om/56v+dH2ib/AJ6t+dKwG3mjNYf2ib/nq350n2ib/nq/50WGbmaTNYn2mf8A56v+dJ9qn/57P+dOwC3Z/wCJ/D9V/lVx71I85RsA4zWWJC+qQMxJfIyxNa0saSjDqCPQ0xEI1WHpsf8ASqmp3kN7YSwBXBZTg8cHFWzY25/5ZD8zR9gtv+ef6mnoB5rEdrSIOzGkln8hlIHX24q3rFsLHxBPCoIRjuUex5qldJvhJHVeRxTG9hbe9Yu0cgyW5FZ90QblyPWlyxiLg/dPXuKgJyck80ENi5p8MrwyB42IbGM1HUsIjJJkbAHYd6BGhYQC9lMtwWfBA5PUd63reaytSNkIGARwnP51zZ1BUXZDEAPeoGvJ2yN5APXFKxd0jt11eJc4jLDp2pV1xFU4h6+p/wDrVwnnzdpG596el1KrAl2YDtupcocx3P8AwkBwQIV/E1A2sOwVRGmB7muVS9ywUQ/eP96tGEnZ8w59Ac0WHcvXF7LKMkhfccVWeZyAN7EfWopbuBDhj0qu+oQYOM57cUx3LRkYnqTUUsjohwRn3NUzqHH3P1qCe8aVdu0CmTzGgLqAr+9kXoOBzVG5vC8r+ScIeB8ozVSnLE7/AHVJosK7Y33pUYo4YHGKtx6dK+MlVFLc2BhgV1yxz8x9qBWZqwNuiHPau0025t1ZVuBjHGTjFef2dyHTbkBh1xXTlwLQkn+DNS10Lubmu+GbXUV+0wwv5mxsMgJ3YHAGOOtWPC+oFoBp90nlXcKgbD1CjGP51v8Ahu4FxocLFycZU5+vvWN4q8PkI+r6YGivIstKytjKgdfqMCkuwFPQFRL7W0jOUW9bH9f1zW7XOeDLcxaK07Nue4lZ2Ocnjjn3ro6T3IYUUUtSAUUUUeYBSUtJQ3YAooopXAKKKKNACilopAJRS0lMApaSii4C0UUU+uoBRRRR6AJRRRQ9ACiiii4BRRRQwFoopKQC0UUUAFFFFFgCiiiloAUUUU7AFFFFFgCiiiiwBSUppKACiiil1AWikopgFFFFABS0UUAFJS0lGoBVDWrQ32jXdsqb3eM7V9W6j9av0hpoDkPBUl1pZm0y9iaFnBmjV8Ln+Fj+g/WtDxpMq6G2WBcNnj1pfE1gklqt/EfLv7cgwyA8k54Xrg81yGt+I21LRIbWWPbdK+JflOOO+fc1otS0zDido7UuGAJz15zVzQ9J/tCXe7FYlPTn5vxra8OeCZ9UhW71DdHCy/u06bx656j+tdG9la6TbrEqMBGAoz1NNhuZ8iLDEFC9OmKxrq6kY7VVlwTzWjI5Z2w7FMkjd2FIqkigqxn2VuXPmSnP15rQK+v4UuOM9KrXUhA2cYNICjqyoyR/dOD0rn7pQBkdyPwrauuVB96x70YQfWmiJF/w0CbyXjjZ19Oa7y0tHFvncp3HIrhfDRIe4I/2f611a6jLbwCOLacd2GaGC2N+WF5dPREG5xjjNVPsFz/zz/Uf40mj6hNcyTecy/KBtAGMdabNqtzHM6qUwCQPlpWewIf9huf+ef8A48P8aPsNx/zz/wDHhUI1a6I6x/8AfNB1W69U/wC+aeo9S9KjRaUyuMEH+tWrc/6NF/uis1rtrjTJN7L5gboOOMjtUcWozRxhAUwBgZFJoRt5paxv7Un/AOmf5Uf2nN6p+VKw7lthnW4/aE/1q9iskXT/AGZrzCmVSVBx2yKjOr3BH3Yx+FOwkbfNMmV2hYIMtjisVNUuEYn5TnsaVtXuD/Cg/ClYZxWorJZeMRLNG6AzK4yOo4GR+td5dxQW9mj4lLsCCpA6/nXEeLGknure6fG4ApwPQ5/rXSWtxLd6VBLI25mjDcj2p2BHC6o4TWJJUyCGVh9cCvVrTfNawzKPkdAw5HQ8ivNvE6RrdQBF2kodxx15rtvCGoCXw3boyktESmc9geP0NN7CNl4nKnivKfEFu1vqOWRhkkc9/mP+NeqT3qxQs+wnA9a878SuLhS2za6tvP4//rFCuBvaJcmTSbcg8hdvFaPlyYzsbHrisrwXqcMOlS2874KSZXIJ4IrpG1GzYcSpn1Kml1AzaK0o7rTxnDR578U9ntLhfKVky/A24yKAMqlzWubSzjUb8dOrNjNRhdP/ALyf99//AF6GBmUVq7NP/vJ/38/+vR5dgQfnT/v5RoFzMVWYEgZx1qdbKd1BAXB9607WG1RvMiO7PGd2RWfqGqOlwFtZAFAwwK9/xoAb/Z1x/dX/AL6o/s65/ur/AN9VX/ta8/56r/3wKP7Wvf8Ansv/AHwKALH9m3Pov/fVH9m3Gei/99VX/ta+/wCey/8AfApP7Wvv+ey/98CizCxEY2h1mKJ8blIzj6ZrY71hrLJJqUdzM4JLDJxj2rXSeN5WjV1LAZwDTYE1FFFIDjPHFqUltb5f+ubfzH9awhhl45yK7bxVafa9BnwgLxYkHHPHX9K4K0ffbgd14p9ARVP7mdlf7jdeO1QzRGJ8ZBXsRVu+hwBIB061FE/nReU/Ufd4pk+RUpc0MCrFT2pKPQQtTwW0lwflHH949Kr1Yju5Yo9iEAfSgEXU05Bguxb6cVDcpbRoVTG/2OarPcSycM7EfWmrFI/RTimVcQMQcjrTzPKesjfnU0VhLJ7CrsOkqeqsx9KQWZk5OaUKzdEJ/Culj0WUY2WrnPcLVuHRZyw32x255BIFFw5TkfJl/wCebflR5bDqjV2r6bHGHQ24DEfKS+cfhgVfS30IQ4msBkDkgE/1o5kPlPPAGH/LP8xUyXMqHhR+Ir0e10nw7eZ8uAbuu0SMDj86sHwlorj/AFEg/wC2ppcyFY85hv1z+9XGe47Voq0c0eVIKsPWusk8EaS+4gzAnOP3nSuW1fw5faC7y2wee0CgtIB932YUXQzEuoWspw8YynXn+VbFlqIuLB4nIV1XGCeTWYbtbmIxyfKT6VBYBheKqguSCBinoGx7T4LctoIAIwJGHUVuXlv9ssrq2LY81GTPBxkYrl/BE00GnNHJE+wyEhj0/lXT3N9BY2k93cMEijUsSf5dKze4M4rwjxoKL/dkYfrW/WF4TUjQ1YrjdK5/Wt2iW5AtFFFL1GFJS0lSwCiiilcAoopaYCUUtFABRRRSAKKKKYBSUtFABRSUUXAWkoooutgCiiimwCiilo6AJRRRSuAUUUU1uAUtJSigQUUUUAFFFFAwoooo6AFFFFGgBRRRRZAJRSmkoYBRRS0kr7AFFFFMBDRS0UrdQEpaKKAEopaKLAJTZHWKJ5HOFVSxPoBT6ZIiyRtG4yrAqR6g01bqBx1/quoeJFlsNCtJpIztJnxtHUHnPTnHf8Ku6N4BSzmNxq8kd1IxDGMBioB5JPGSc/hWNdapq3ge7FlY3fm2kgMkcUy7guTz+PHb1o/4Wbqj7fOt4OMAmLK5GRnIOR6j8a0t2GeqZiCbc+wGMVymu6ddXFy08YUxgAAAjJrB0/4hTyTKk0SSA4G0/Kc4wcY9+eldhBfQX1qk0RV0YccY+vFTZrUpM4+WxuYw2+FhtGTxmqjXDQfKynOOh4rsbsMwBijiJJ53E/0rmNeSdriP5Ds2dU7HP0qkx3KBu3bIwBULsWOScmtHStKN6spkLLsIClj161oS6HbxW5J3bwOu6gLnJ3XCD61jXhyn411Op2ccdpvXghgOtctdj93+NNCkbXhARk3gdQ3C4z+Na946JKAAqLjgCsbwmwQ3eRnhf61Y1y4eJ4iqDawIzk0+okdD4elDSzEHjaD+tQ6nMILmTjPzdM1B4XmEnmNjrGD1zjmptcbzE2bATnOaT3GtyG3uBNx36irFYFpM8U/lyKFj524PStxHDrkUAPopKKLgLRRRSCxeB/4kr4/v/wBRVLNWx/yBpP8Af/wqpTELmkoopDMbxHCZLASf883B/PitXRH36BbH0TH5E1T1ld2mTAVL4Zl3aAgP8Lsv65/rTDqZXimI/uJcZwSv6Z/pWv4HctpU65+7L/MCqnidA2nA4PyyA5P4/wCNTeAz/od4P9tf5Gl0A6icAwsCMgiuS1i0LtIoTO5SAfTt/hXYOpZSAeorMn0kzZzIBnsBmhAcX4dlKXjwkEbk6e4//XXUcYrlZsWPiIZyi7vnOfwP9a6WN96Kw5yM0xEuatab/wAhCH6n+RqpmremH/iYw/U/yNAEmrD/AE85/uiqWBV3Vv8Aj+P+4Ko0DFwKKSjNAHRaSc2Cf7x/nWJc83Mv+8f51taOf9AX/fNYtyf9Kl/3z/OgS3IqKKKXUoMUmBS0UXEJVWSZrWbz4zho+cDvjsatGqM7bmOR14/WgZu2uvW13EHRWGRyCRxVuK9SViqDnGcZrgo5PsWobuFic8k4A9+O9dLZSgTod20d+abSFY153823kiZCQ6lTz6jFeYWoMM80DjDA/wAq9RxivPNbtzYeIWbJ2SnfnHrQhEMhQho2I6cisl1MUuAeQetWNQRluN/8LCqZNMljpDuw3c9aZS5+UikoEFT29tJcvtjUse+KgP516P4Ut9P022W4LOXmjUuWwe3YfjSbsOKucpbaNcAhpbaRUAyXKHite30UtEHXG0nAJ6/lXWXV3ZtavGGZs8KTkke3NYz31vZDe+dmcAKM80k7mlirHpRWZQOQeMYrch0e4DqRCqqCDnOBj+dZY8T2URVkgcsOclR/jT28cEHHkMc+uKeojqPscZPMSE/SmLaBXcsibTjArlm8cvgH7OuD6k1LH4vllGRDFj8aLCOgl06CXG5MY9DWXcaC4RvJnBwM4YYqKPxNI45hjP0Y1cttejnR90JBAIO0g0WYanK2rmWQsoYEdTWpDf3MLL++kYDsWJHrUHh/BinJGeV5/OrF4gE4wAOOwoZRs2+rQ3C/NiBu+Twf8+9XlmAIAwwPeuPBKHGeCfz5qylzJCf3bFeenY0mhGjqWkabdRyj7NEHZtzFUAb8/wAf0rGXT7e2basYXaNuQvJHvV19QmaFgwVgR1HBqhPcmZliUfOxwMUIZuafrNlpUH+ky7PTC8n04FQNcXfjG9SZg8GmQnhT/wAtDxn+X4VBqHg7UptIa+JjDRRl9gHLKOTz9P610GiXkV/o9tPEAo2BSoGArDgikRIt21tDaQJBBGEjQYCipqSlqSRaKSik2MWiiii6AKKKKTQBRRRTsAUUUUgCikpaSAKKKKYCUUUUvIApaSijpoAUUUUwCiiimndAFLSUtACUUc+lLg+lDQCUtGD6UYPpTVwEpaTB9KKQhaKTmlp27AFFJS0DCiijFK1xBRRR+BpjCijn0pPwpAFFGD6Gjn0NKzAKWkwfSl59KetgCkzR+FFIAoo5ooAKKKKNwCiiigAooopoDjfHtoot7PUfLRxBKFkB6sp5A+mR+tco2lPfK11biMJIxOFJwPbpXWfEGVjYWdsrYEspLDHXHT+dQ21tHbWyQxrhVH5mtoK6C5w1zazWcm2VSp7Hsa09F8QTadcJuYlN2W5+9xwCeePpW7qdmt3ashHzdQa4uaF4JCjrhhRJWGj1bTdbttWVvIDBlGWBHT8e9JfgyHaCRxXmOnX8un3McqMSobJXPH68Zrp4vE/myAySrhxwNvKH3NTbXQdzo9KXZLLCWCsRuHHXHWr1wBFC+9xgDuelc+l9LHKk6bCQOMjjmr5vWvYTlUw3UYoAzNQlSS2dA6kjB4PvXF3Q/dfjXR38m268tDhcZOK526/1f40xvYueHZCt1LHnh0z19D/9etTWF3ac57qQf1/+vWBpcvk6jCxOATtP48V1Fym+2lT1UimEdiLwhJkyqW5CdPbNauqDPOBXL6DqAsb0ll3CQBTz05HNdVqGTECB+NJgjnbxeQQcHb+tT6Reb4jG7ZYHP50TJlAcZOP61jxTmx1M8jaThuexoT6CkdhmlqCCUSJ1Bx6VNQxoWikpakZdX/kDS/73+FVKtpzo8/8AvH+lU6roSLRSUtIZU1IZ06f/AHc1F4VOdKlX+7Ow/QVZvBuspx/sN/KqPhNgYb2POcShvzH/ANajqBP4mBGivjrvX+dN8CE/Z7wZ/iX+RqfxEnmaPIP9tP51B4KURm7UE/wn9WpsOp1/ammlzSE0gOI8ZWTLcpdgDy2AUktznnjFWdNk8zT4Gzn5Bk+9aniaLzdFmPPyYb8jXN+Hps20kPXy2z+B/wD1U1sLqbmat6Yf+JjD+P8AI1SFXNM/5CMX4/yNAE2rf8f5/wBwVSq7q3/H8f8AcFUaGCDNFFJQM6DSH/0ID/aNY1wf9Km/3z/OtnRVzZHj+M/0rGuf+Pqb/fP86BdSOiiikMWikooADVG6QpyW6jqBV6oblcxZ7g0AjAvwTCHDHKMG4AzWhpl009spbcHXhvXP51DMm5WQ9GyKpaTIYWlhJGQ27PFMOp6DbzpcIWTPB71zfjWxEljFdjAaNtp47Hp+v86ksr57RyyhTuGCDTdXvJL3TZoSF2sM4A545FHXQRykZF3beW/Lis2RDG5UjpViCbyZt3QHgjNWL+3EiiVf59aYmrq5mUoBJwBQVwcZrofD2jwXatc3RLRg4VB3PqaLolK5zort9Iffpdu4OcR4PtgkVja7p9rbPm2XYOcjcSP1rV0csuhxnIChW5yfU0m7ouOjJIp9yMCw49/eqmoyxG3VWkVW3A/MaoFrme+kgil8uIMcspxuGasRabZQpunbewPc46Ukupd7mb50RfCl5D6KKeY7mQgx2MhH+1n/AOtWylxBET9ntx6/KuKjk1O5/hhA/AmqJMw2uo4GLMf98/8A16NmqRg4tTj2jqzLqd/245/uj/Go/wC0tR55z/wCjQRX+1ahDy9uVHvGRU1nrstszBolKtwRkjtTl1XUCdu1GPuhpX1GViWntIn9yP8AGgRteHrhTaSOARl+/wBKt3MvmuWwAcY4rk49Sjiz5SSW5brsIK/ka1bbUVmKqzKxYcMOhP8ASpe5SaL5HzgluB71ZlKsoZQoA4BHpUcIUyjcOO4FWbmLbErgqd3p179aBmfcOY7fOe4qtoBe58SFWOVjTd9CSB/WjUdxt/l9c1P4PhddXnkKZB2qPz/+sKfkJnr2oDy/DF2No2i0fOf9w1xnhaEQeGrMAYLAufxJrsfE05t/CGpO2F22zgHqDkYHH1Ncn4ecyeH7JsH/AFePyJrPoTI06KKKCRaKKKTGFFFFKwBS0lFPUBaKKKACiijmjoAlFLikxSswFpKMH0ooAKKMUU7AFFFFIAooopq6AKKKKYBS0lFID//Z",
+ "image/png": "iVBORw0KGgoAAAANSUhEUgAABAAAAAQACAIAAADwf7zUAAEAAElEQVR4AdT93bYtS3KlC60518/eOwXnVKmqpEpJxbnmAi54Cq7goWgNpXgMXoML7ngALoBTcAGNlFLi0FRVUJV77/U36V/vZuYeMWLMOdfOlNoh1poe7mbdupmbe3jEiDFGjIff/G9+8/T08ObTX7x58+bh/d+p1Pb0RqKHJ0loqVCVzRLLVrPFUTYyltMy3ERPKr+X/OnxZ7l48+brzl8eglaJZxk8VImawCxdlEgMe3JJA6MH70JpAIRNdaA1a/GpHlu1q9fRdJl4JuoNQ1yOcLy43dElkmOHkubqU3ugg9oUaiRpltRDYO+FcTwTDjYauK+OJeYSdPdbsPZP38P+8BMS2cVjOTTK/pQt3E9pzZsnjePDm8cfN11MvtfuCc6Hh0+/hpJ5hX1xMDSKMCP5JnPv6cPfSe8+VxweQTNlKM0tBBlkU00OPHb0T8ailYwo7ejpzae/BPb+b+PpqzGCmuPp4fExRJBV37RzECjMb0URtgsU4GfDIxIUyE1SOd9xY1D4tIV4dL/JT/oOm2MeKng7XxvNqerIBG2eqGv4O0QzwdcbVo5WwPe/RUPe9m2LR0l4fCTd0JBnhsP79LuXjXiBJCOkcmc81h2aRUPmg1dReX3AjbbFqcaycWYckKWGOle1tsSMKOllRr/twwK/MzA+Wp54KqrpAfhAY9Xo2h/iNLQK6yscjxHyGKVSuCXOIjaQiW+A3bnFI7C2HA5ETK8t6mofXyaTDgOGByobh7Pa5wwkljgpWpy4mgRXa4NgMzHYbUmCicrGOMXe8Mwvz4HHBGsvVTw8/p7Yv2q16ZFlOQAIOzvvK7aDabFlfXj3W0dsvM6DmiAfJMmWAFWfY1N09iIbx2qPiYGVUGsvluXZiGp3VCgxXdQh9/IClhwIEEj8LlsDKj+uU8TbNG8qu14r9u8JgLz1tusly0iQvdvtELg7IgkbHFlpP/1FRNJWnrVzdqdEM1vOPjqbmCRi3Czrgpr24eH936r99PEvhqTIcvVi70NfHosgjC5x4OgGCqm92iYLxciKQDZeaDpDB+MMINaZrYBil1rng8FnCT32sNChdyhEWOsVNJsvzVuZ64x52tbsNRgXYuqj4/Nf0tYYPWV2hdJzCfhkZEgreuOmjhbWQ0Bjcqg4S3PgOKSD/tA4ESp2bcXgM7vqST5Sz5mHp+93q66XI0/OijQjAaBSWhlws/tToxVzu18BNufjT5Bw5WMrAzKSU1pWeLLvg/041jHr86znc7nanavuKAhSao9mufVynXE1M4l5FK4yxExj5jRDWyMP54T/Tm3bpT8lN1DywPHurazHGMPTFsiuKCN7GSdYDe1OgaX5rQ0kVWaEeTl+iM1LZNvaSw1nZEFhRVYKV81qVUy9M9KFfdnZipImac1oqCHOQDBhs5M6aTkeS2MTbepdyiCkB5o04mUfQZNdFYY6KcQAZ1M4IjWm+x1xp+PYATpEbOkIrkLkMItjLPEF5GpzECiW4+alRxKHeBiSCDTt01G7hSV4vJVZ7dTE0wgdj48KQQctqRV0rmjQtZl0TSdx9x2p6p3Vjsv9oWiTqarSYdpLkAtIPNkSg/COK0Q7pW2gK/x1bZSHSvHYeSuUJFVzLMf30tA/JzEiu3Ri+tBPxwnSgZLt4Pc0pw/TnW7CqUjSTG9UTyX+2mTizdSdJm53tr2eyCuupsNZHDB4JQ2Fm9LZbvCDtgJdWTULzfQhklhOfQ8VJAyFN2P1vvyhrS5aQrS2KH3voK9jhGpl0ch7JjYl2O6ABUTDptHK7Cyp82RqCepMQWCwN2RsgZhnVPiYxsLDlFYrZ18W2Enm19hGepgSI5rKRpn5xY89ew5LWshx0nHIEpn9t4z2WOx+ogBfnRhW4c2zVGqjLYQSVBAzu5Au2tKooRpFjUQLHJ1kdLNs2AN22yxLt7zivhMTlwnKjsxkhzgdXzS8ReLJfzxjlusOVmBLOvYyx3FiznpIHVXioOKwCz31qQQNtY1SqlqVwakCb3aUaCSJn61Ebmlll6Y3wOAoeku1Z4WkgFrZ1U2ACvubTvX8sncT2Krnu/B1ppCEvgoPzVB3BUkG8yuU9SKdo1N1t/XSYdtsR9F2Rjaz2MgCdpQ9NoDTjFZxhKdK7wSZzhC7x7U6YXPLVGPDUWqUqW6CRCDBwcY9QlYvN8rgiNl4d8LlTHDnNued5G/8iLvDSWCJASG1TekcWeaxtSEmyQw0/jNfsya7RIjapeqOeARWIE2GIrdw8JbFoao+Eg6wobDFHnS6YXEFipeaayZqBHui0IbaAVmgmp0uoGtzAabWb/7mb2RWKFO8uhj2WE9pgoon4SMZQfgrvfGsbhPv6d2A8AcOgY+tspYzU3pvWdCbl9w8WwHYYlDL0NY5gndt6o4vpLaowvORkKQPkzB9B8KElj78jPu8Xnz8CXnuu4TwnJLYqZe6M02ZKRx6+epj1K/oHZddJ86Mu+OBNpnUKlOeRL1q9nNVyFXYWsndfZH9kPZ0tENqGPsDPURh8nJXugNkt3V9kcYSSk+LrF9Q8g+Y6+68LRt/pAw2uniOh2JwfKImRQ968RxljaYbGMWwiH1g3XiXcosHHv0d34ERZB990z3oXoKwdd9LJsNeIeM6765k/tjqheID98YePtb9+4R1MpFwbRPV9HNTZ45XRrAhMI9B5n1GZ5E5D4EtYfjcpYQz5cLEZvOMp7xds3k/4MfEzAwh3sOd+hnutvIpjO4b1cTyQVVWHX6oDdc7opDu74fkbs1B8nfyHcww2fq6OGBu2a6NjtJbK4/7m4+6w8cskovZiE1b1o7OTABB0sevTw9+B9hDHIOy2hq31XFVTELgbtwnqj1XcBS4RjYz/Kvu5GlIHnOoH0g815BcbJ6N+AunEDURjNVZ7o7dBVVEhXe2SjK9uTUqNIgxVDQc1oq6fbtZCO6/wtM5Eab4j3Iw+8ZxqkVF67DgJl74IjC8+XZZx1Z8gbAsL5DWIrRPtc4XUrvj+r/kqa0Y0h5CR1i23Ne/2oyp7oxhA+tMqnVsVB03kBE2ft8fzsK7QvWQaJ/+zn3cGRc+ByF2TaOnh9+zf3HtbUqnOZ1aTk2VZqkG7mhY9l3ZTHhnw/fpo3BfDYNhd7CRi+XQ8mFQIqnSlLnJiiR1O7at10TmBaI6sna8kS7uZfgoJ1Sf43Kffpmfakerk1JNx2VxRk1XUD4+91SUlfLmF2DusmS8muL87oF08nzly8KQmwuR5SzAAetEGK4jQo59dlb7mHgLpphz6EhcgQovJtf76gpD5+UEHTdJ7mbl8B2bhGgPCE7HiJ7qOlPzRFsIqaXa/cI2HWqNMS5sk3F+8+bdkp9roThLn23LpK20XxvCUkTuvmRsjDovl6YZIRB6nteSq89nH3GItP9cidhluk0sK9LUW4QiGULuzUbSS5xS+xDZqGHWdiOahHpCCVKSBh1gDs4hdH7w276VhBMdzRy3TpG1HCGqDC/WZivbKDwoYmYZcklkrVr2K17VJnbXXexeFiBhFpt28uyYTnYAKqjRVNsMnYMoERVlVYg9uvhoErq0g1ve6SNjXCDwT1hdbgox1HD69WZxSzcjsKXIocdIQNt0t22IZBx3nCUI0Ealscl4Kn2N5OZpEd7W2utojhGM+KbSvndFX40lRc4UkSpbWljJtpekyb9nGItUfMKowXPbTM6E/aw5hjvDzZKxlMkcXUoC/ywCaw7tYGVmSFm0qmVZNyMhu9IWxnuiN0nyW1l2WFhk62a8E2G2cu+Gw0bFPHIvEmiU4QUf3W4JIpQtrSgqajNMIR3dtUnjq2mM4yAXgcDMuJTYflw02Ptq+GxRWghsdNwv+LFW8E1IJzjkvDWTGhYlola11G0hnMAwququNNQ9CW7j7Eg3d2Bk6VRCsqkWYYi2EoutWfVNlGpgU9qCgZH1fsvWIoSyKvWQS5S+qMIn/iAejGxmM3BaUzHeLWq1DUG3W8G+cWS3tw7BSx/T25t2jrqOoMw3NFEE1GXLynb5aUBJdj3D7+PVQvgTOSaDW/Zdq3XA8QDrw731r97Lm7f2RUa690Wc0Uwi0Emc2+2xIeSDO/QS1Jol7erf4OLGuLJerwu3CAYvpP5VcLjTX/xQErCPlHhGBUZbBecuqGmgFQUYYIS4CDbzMOa4xTQjU7ftbTATyBAwPkgTWVEG2KHASAYdX4+iIJuntiu2jYxqmi2EitNNt7GtMMPJ8e78o8BrIvVsd8otjBJVB5f+y8BCKczrVONy2yoHlnqEWpf4T+goEzarGxHpz9iEtxmk6lAmNhF0FzLusXXdXfdMcaAdyOzVGy9KOJVP/qxrQlo9/FLnHYDNOp5jPWJX8nood7UrPss//do7e8rrubKL42rEv7tfoaD++p2j+dkXE9s7AHm1lHsMIfik+1u+y44fdaD4eF2lTXebyDczofsMLqarlva5tD73Px5+bN4dFH+wmfElvjIt7zvRVT1sLuvV8F8Sw1M+oW75k7KkHn9E7Aud4rFct3ynp0+ffk1i3v9um/G+r5NXz2UGjf7w8ortpW6caU74qCUc3NSDHLliefr0FzTf/84RctC88ex6es99ViPH+kCYfggQTqVJM6rq0anMDImKIwgqeQSmzJu9MFbZLhzWMVffPHz+VzghwtMGOxtYfw7YrRcKQhiIamkfpBLWJd0AX1EJV4DLg9s++ivYI9NuJA1NH1GghoQKK+gjotzL1F1kfVifmfdUxyPjdejLE6uHjH62YwoTZv2En41j/Gm+iSRBwOY1YCv6UJ9RLmKvJK5v4K5mBmyD3ApF43hc4LcXTjHFfTRpjhWVUpflpkoQt/IN8vpqeXFKQgn9OZwLZ4lCHb/VmVN6zlG32i22k/Ls1UgSdrOdeBOLw5bDobFYAT5+zVeD1M4n+3MX+Yb1VmDfPikMqUFmvoWP5CpmlGWX8O+RYFzHUvFo5/VEn8/2nX7ztI/sIWNpukeK94stx8lW3mLaz65ZXlSbAHpU6tJMClSQ11lVzWW58/0BdQfANHQYU7lmjPcKI7nq2GLw2vDsdfk4NaWYgaiukwpQnZtle665H3P4n7Q5TcedSsbcCa5BOKKLaQnLriZXySuwgDVY5kSXelvv8pYZpVF2JBgUSfrsc67OsO54QVzHLF5Tof1PscVnYrJjnK6ZUuegGiCDZ8FSq+2IrJp9HUV79DuusIGfSpvU9QP2vRFU2FJr+b39wu8ID5ZiOkcjTKbccZ5b3PZlQyKgYRlBpRrvaPHNBLfEzayOf2krG37HwO+KSOYN0LsgIxhp+rkJT9VEcjIt1oYyy8AdpqcNYzcD3EuCDU8kIYs71+ny7l3NzUSaOg/VbIm9TJKTbh72GBVnQt4IC7jmnsG7ecCnkG5Qu8W5HgaHUKH43Lhgki5Ch5LlJQiZTwxZwTX6EcrKSu+Hz62IYjia68pYvwq9x7rVh0Q+lm9q7gue1bi8iACjjPRsEq4CqVmObW17hCQhV86Swq0S0we9Pn7gIzq+e4fFcgyjt5jYxu1MgD7ebCJ5o2MjHjHpY1ds8N8ALDsWxnHM5+jfjIiqeEJ2NHypNWGcgpRdmDeCEZywNFukvqvqFzZPb+npCgqI2vukhDw5Y0gFCHochbgp2oeA8AausYAB3eih7c3x0BhSR7X8XVmR6AQ7pMcFN0aCERvM9UbQIrO79K1DMXgaU4HiF26XpvYMobtwYC6JJ1FlzRReVciUW5esTkeTjQt3PtJ0fSWgsBEM5VSkXqobqxiPm00PgWdRxeoUh3VDlfPLXYew3F/C7KeHfyIJtJtQpU7tepMbKW/1NQNl1LreJzOEV2MUgdQv9jATElzVEtNiNoebs4hxfbAOBwzQB1Pmbc+xtt2dfjGcmH9TaVdz3EzlmkPgZ2J4RnWmi9dh6/5yhXTrw9lNjs0z6LCe3KaZdZEzwwHtVUWdZDBawcjZaQTRhMUOqDIQ3sUlZRm5KogNyko7oQXIQFdrers4EJWNQaPpUKQcvZRMm9n2+gj/mJWjg/R3JghNJqfDU9HghNutCsfN6kjm8w4rxepprE+lULVe3vSRoKwmima7QS1BmGnv+CUtZARfj2ci6eKBWRSg06CB9CRhyi3aisw20KW9eXVWTYSdGVw5vwMQT10KMtFOHdYMkmGRV+nM9Qq4uRfSRN2XZgUv00w4d4lmDBuTdphXOB3i2sOztjOHfPQnLwHV692Fn5oDivXIHCNWh09wLvVF7RjNBeAZEaOnlJhi+lF5WZlHo5aPfbALaUMXOGEC9YBD/K3bUN8xLL/j7xZWEbTihhBBIgtJR0nfmCDcoazuiaP66m9T+FlDpas4lBUcZYqm85n8ds9zEjL6ISSB8WK107ll0tTRaDzy3Qyiq1mLhuDZ9zsVbt18BwDEnY2xcU9Lv/qRuO0gXtrXa+bh9vldxzfed18jpNLsB2E3HJX9PtRxlHGQnIVrvX5pA/hqJfAsdVZ9FEvBC4mKqnpmjOdz91oKQgLJsxfyGWi3VXQGTEKPYgVYyPd/iyFxFru9hawZfNdEz0KBgfOLXiyWu0Z4H4IRdVNW7svyO5CtAjoWRDj3pTbEqm7j1UI76T608HbPuTHpO+k4qKTMuy71/m0+/cx7WdocHyii3DZaku6bRPm0a4R+/sbozXAyGOVGRc51HP3AIUe2ZWLHZco4SkWL0ZitwjF0hKdKMCZMnO/+UYjDmn+yuNM0hYsCpD6l5hX30h7e1ZPNjJI2W8dIQrveOu0RqYN75zbtTVXw8Tts4yvwxmR25dk4yqMs5SVTw604dgQOIsx7JGG6CaIE+Cf01j+PbtTL+/CcyjJjMqQTdIfeLP8vMx8Rx3h35uCan0l4eTQd6bZWMo9A3xf6K8o1apVvZ61Tl+8BPv6MxdfvkPKJc1qe+tqtYVsy1EW98S9fNea2jVUobdczQc42qVVewer4X2zgElXWDUO/qUhvz97otVZy3avGV1J9QRuzShhB19A33b1lF9Kmy3cp33z9Fb70uZXqY6sf9R2PvNOoHS5aUfuZA63LfsoT/PnmWNW828LEEN8f/0IH7MOHv/v6dX8l0DOeGaHJTx/MxWhzLGTWwjEdCGQXIRHWm2aCSbT3tZDeAbiXTHnCKgD892a5BJsnqwZTlZrG6Mr9ICSao8y6aDpK09nO3sdM+qkPpitj3JARjP+Gat+gTZTqrtgYbnCXgmcDvLS4Ej7HwshXf1Q5TWppJNx70Jk/Se9kZBx/Y8f3MIjq3ClN1k206qp1sL1HmT5uFqoiN/zAVfM/sszXcs+M76MGpmUmxTq4cVtI7ZRPGuC9WUSNDlrsg4d6QAKA2TZd2p4km/KyeoaLGVH3JnQBnaGXfC0UOEGyW5bd6H3Ddwzwoz4LSLHoLRRp+9mlyrJaMlCKlxvTpjkAj8n4Kwe+Tqn4yt50IdA61UzBt1VoKknaJWJHjddqBtXsbjWNY8O5t1SqUVZR7A3xln9JQ3BUn1pAwjmjeUJszd35oe4cjGQCUCVb9x1fwGqJSJVybFVNQk/SPgdMbjrtzqe9mGOIboNIKOeyDXpfwTiKTdZmOWBpRTldNGA36EgLWXev1X8OYLajaWQpe8h32aF+XAOWavy7Qq552Tj6qfkMe+sfff95HAwZK3SWqGghs00tbc7MuNorwY6FK54H1Ogre3OazfrOThrN5pZNOZTLqJS9wjZ2xbgk31pz56bby3pCrKPTA0YP7oxceMb+FLnkJwDIUG2EOC3hpB+gN5w3TaJrjRWjjG4vhYvlyQxXZm15700c7SlsLDI6wZxKq5ANxpTFu15Ql+cgzbGKgGOnMkzFUPEm6puUDmiRXdemU7HY1tMdf6DDBIHzFdSu38SGNQ/H5uByJJVqYmjoTXesKFij2YtvXUiM9XOViSCgnmJHE0DWaEF51NPJ19HOGmMsEJabECADlfSlBYz4qtfmJFzb54hGKwJzQYDFb37zN0mTWnkWhD8NJpkNQ2piqBGmxJ2bqWxlp70iN7tligXXtZmGbNbYlDv7XTD85Sk0vkPWMTmKZqr96OpzyX4iyglziBju1c0b5C4Y7l14pw7twc8d3EFcdwfzOa3V/QPm9Y2+PyqLcCnPiemVkbXVmN/zHWD3OC1/P13P9Wdg81RmnvG/QikupT7fZPfn+yvDut+geZO7IzUxHDJqVVzvWOLNLU8t4ceLpGbsk0YOgCfNJaDi98FEPSw55jId6pPo+R5CO5PvPIWjvgMz8s1lBfCUbyzwCvt126FXlaetc68jeQZ1y+VM1Tsh253yuxxbJ1NVqW8a6V6O76/kXlFl8kSSqSehTGpL7RDVUoLxJVSj2QsrxJS7qtQWNcvxbugZvYciUuI4xHLEexmL81YYTZEJ94xxW7xiX8umyJYzZq0OE0LAietFlYXrqZ7/k2eiVyCg9cfmHc8yqvvWFpb84fEj8fMeyNObd/5OCzO2LBuZvaOqe5Y8haPeQfWRUi8FfSTtxnpeO/xejes5M17JhTHdnA3GqA9gzgoX26Wwz3cEzlDWzI75E78uQgxzX3anJZ1J7C5d9e28s4RlcmXIt9HyiVutYD9iUndP091D+FqXsuRszFU94CLz08e5b9oTot6Nyb3kYJbZPNPG3yWztlKcqKthRaweHK36u0hC6jLvqGy+/I5c3T29sLjB5/06vRsj8O68fGxnq7uSLZx69y/njshvPUY+wcVrmrdJcFQ5uK7HBf7jO5B7PHsdF+N1V1BvhfZbGiJNVEF5yVG1owbf+tieSsyuthhRZqXaMOFOuYldTURnqdrbVUqoD5hNa7khCvzD7wj/83Y25Bwq2XeGtTcdvx/0XbLjU9eCmPk/Bi8cutCzvsBtfmJBYlk8+uOsJnx9EcZkTSxJQpqvJ9lic3Bbr0XFEwnPjEc/XlcfWNO8GZzr+jb0RTULcgkcNiQNCCFj8M4h0E5WphtHkVreCpW+D7YrQSXzvYi3pTCbhybo/YaCTM0N3PRDAfpksWHuVIvTHoefhFx72li+wRXsnmib+bdUX4zldWTuZKATfCopNz2o8TrgcXMrsWonEMSHoxQbWlnIBnnqLSlFz5AFq1rC0dB4AmftqoNZuzuTA6M5PI2i6JMs2toAKRIk8QBn5aDoD0RldrODfgxH625vqniacnDXlTGsAA+oIWmU+3CAPNOQtTaZskG1dVsS4i6lKoc1iCz1CpJKgJQmUUV6E1iGh7WVyIj4LF0iWkDVwGrbNRKdmsHsZTA7zNqwpZRyY4pMEk0yr4k3tju96mVgqUzYj4kJrLlb9OK605zBB9oiZ9fVzQ00B3j4Lbp0EWGYVPeRN8eGA+Eos6bSNAPeYXYXPNARCo9UtJkijgqVhMTHDoxbKrJJXAeJFA4JQDZ7zUyxndRLaXD6YHQ0BA6KgtHsOhDTIU/DVhQNs9zFqFIpp1EdANJ02/laSYPXdq0/cR6a+s4848lp+7x5nMMxzraxBz5GqQS83Kp7bvDF/NoMzBiPsVXjyP1yMiUSZtHlqkHTZXlrflEsXPsa7yMIt+S3YJxtbG2C+BIPgPugBibM1CWYCsroDDupjpoJqaJIh46Yir/Jntu7P6dQgj9Et1OsCOI7eU4ElJ6t07mgx+Yuq2NebupQaEHs46Nl7A0b8qPG0SmYcdnDeSITIBDTZ6iuBkywgyeMDoJxX9J2fA0a9KrsJ3oZy2Hi2Akc5DJ5obZbpr5LXjBe6s5QOlx5TN4e9gcSciL2DNAxQubrF+bUj3r4GDmkWyaqVdgRVVgoPX84yATjH1jJKXm1wTsA2pAfN0wS06GP5mnJ6TWfxNyR4neFi8/OzZvU18G+eaOqG7PGQGuVCtU3FKCzwCaHAvvDho1ngaW5T0BVS+MP2h0dGHOnuGGG5IIgjIW+MrrDb/ExnNyVuX02885we+9k16Z+/dniA06O05mJ+NCPA/YbGnt/hnm3H0C8E0VmJvOe6czqV6PEkeDZjJRGttxlP/wmYkzWzANoT7bCPG3NOtNkZiKjaVG4u4yoDGGSoGkaTtze0B19l+KZXZMJ0jTPoM+qRHOW7m1IO1CqblvQfQe9eBIPst4M1n1iPStJz4z3/VTWhixJgHxyjx2lB6+StHHcEkeJXH+1ZVZ/+VOa233HcDbosMc2HVwzowF5/tXpk6zfOkIhS/gONNX2MXvrqnX0oUzXfdbvvayT7Zygjjhmj6diUeHIkn0El87SdL1jDIFbMZzoqBy4wnzI2fRgJ90YapxsSQfgG5sNd1O9AuW9vr63Grbd77JRzYpdez5aFAsGywgb4juIhLBsBXjkXPJTbeeNis5ns4s1QdXMRwGdHkOkzAJzDLAJ7u3jggwT9FyFd0fTk9MMigdnM0OTMMNxz9Ft745IfDD2cM3rFuKhW3HQfo1JceRYrTZAUn1rpVQT6R4U8r3d+PNe1yQKK+87hf2EaAd7DIGYX0eDEdOpk/k0Jxiugkymws8qbI32rJIZOw+ZYes65LC+idhqrMPgJv7SpHbYmtl2At+BjU3wE+vIXTleyzVV72NUPVmGiXBAS/FcLWGU0bGPPo3csy2LmA8oC1J0QxZthLpWtgkJ4g8d+3l1PFSrEsvVpnaQhUjlH23TdZpmnt6PZRYyCbdl6+SnI/Hqkkmr6J5+5j0WvYtCSJIml7oJwDWkXjLwPRPC5u6eX0L7/ZC8A3DqxfJnk+TvhEnTyMAJe2EcmyUZIHcp6g2lKsa1s717vgJYjKp5hV26jQiYl1jvafW24JaoKbOyjC7eb8ia4LDf2WIRwgaRLzAntlY/vz9SPY/9Bu0ey15fFOlVykj3+sK5Nt0+yiXGaHfgVEQ+ZYyEBMiIeZ31C92YBimAJ8LywTw/RyWRpbNs9DFjoFT2IUzJQ+Fjw/4bLmY7XN4OtRBJNBWHsrXwczpmAWcuHLjuNAArhBsbfPBXWxJgVLCUow+BoFNZZgPKIugjaZDg4x5qssl+0iY+5Yx//Nq4/knLUoo9ZuOQevXZHNZBBR/bBnY1UsvDFL8NKwOsh6JN9n30B8ZdveqvgCzwbW3M08nqlHGlGoQyRKr2jZb+yB61UV7h0mVwYgw0JwSaxbtOYE1V+24CTcrtkIItQ6aKtM1lhYutB0t4W6trQF/+WRunz1ifVDpBnVgrLvXWk6e0dFvIBq++SXbyueuGGyGHZgSBqGy+wVVSV/vFWqbk7nR48bfdpYDKuB38Cv4ys5UCzmCFg6b7MKO581Xv9hwT0A4510O25UVoyxgPBzLm1mQ6SsFgBdsWoc6sHTfEuWDuSiRQSDFb6pSBb2M1fd3xY7gqmpWDcB82z0ZZ2PTLzvwxSLlUF7UFcU2FGOuAsHsmSOJIuQwu2BAFtpQxn8krRSgaN4QIWhjzUZWN2wnIfEf0culalGUiyZBZMa2x2iV3iXfQWHbYKGXpQ0r1IvFKsLBMEyEWkWEWAord0va0yqzxfK2JFkzKcrW8uFYz7aDcmMFkUTkgTiSvboq5DlVPXHrUvFaFKFWiSJo0O0AhUOFdJ65OyxBZVIeDLLQq1Rtojl/q+Q4APPvm+6OmKNoEsEOoj2MqAw+WpEc/Y1oRmSWgqfb7AGKhY+etic7yvY23PYZdd12fGHb63f0m72q94jeqPucdp+UinI2+7MwpmIn5JP+naL7g69CT+L/5TkV1bZPvgYohm2GThpZe7ceE6cSrgXVx0zOHuHTDEGu9v6Sq71gM+2IIf+745u6vJBwBYJlasWHvQ6GO9Zi9XOKovDK7Xa32wTgBSeMD7aByowLqegA6Hld8Y1Pv4ejJCb9w65i1x21e/idoVGuzVt9DysriO/H9zJ90urtLHllKTJi0pp/h03uAv9anGZ8+/JaljKPydlP6d+fgOrOhPVi5sePPhJ23s/zc3li36hl13X7O/1jcBaV7Ucv1ERfBXvYsM/HYgtDfbMfGiA+VYT1IaXhwdrobxAgcgUesAs9OUyBTlia3lF7Hduw+NgkSd/a0Sj0fw5+tr3f5wOV0Z4+HNPq+rz4B79/ddP76uIdXG/EnwKxd9bT+KG/KFdJRVe+7zmeaCYTNzN3I7IZiJEG9ukyggocg0VhIkcNq5w5AYXhIBEnl9Pl+E1zEME5Gt3OP8BdUWCV+yXZpdh2UpN37qkzzec/2cenoxs4J9wFTU2hHnLO3AloBU0tYt2VxTSTDNxUQsVtYKRdVkKX0Djb/ZQpqWqS9Y16ut9NvMr4NxpHI24Vmi6FCnmOG9tpiW7LniObdDM7x/F7NblmG6x2A7uFy9MracyG8kuIKNrR7YMdM7GnMabhe87I2ZqaKWTJ91LDWClaFYdZEqFVU7wDsbohHp9J4C3yMpnIRdIc3mCG1BB/eRpymlJEoulGpov/ahizgLiMeSCqt/Nb9RCDD8XeH++T41lWR5Vpk2G5xV5KX4IrpJcgVbckSWQOuiXZMEHsedm3zXO8n0m8yWYH2UnFkr/nR5AlQKbETzWzmbB3oiHypcpzyZeI0hubiorFB5Vy488Y6qmCkQWn3237Q8TDNlyswha356dWM+qptVEQwiE2+V+lRshEpScoBHv4dC99jPl8o2KZHMSuIGB3sg58D5MDQ4yhJoWU8aXKqorMYBfEcRBI2z0keprL84+zkIRH+ceiGhcgn+lsPnRV1HpSbGZgYtb75RqrKmW0IChxsW97b3xKdee9ZVgRc4NsVM5N+1BT1+i6uXP/jRg3ptFEp60VuzTRNso7FxBQ7Y3K0FXyZxoU83fKPw5roCWOZtuu46tZhL/AtfvXmQncwNzIDfZS/vhUXCjGpSFOlOwzNKYZurry3ZHyG6bLXUQ3Sfs4eRqvK4DMAz0GdhnJ66XvnXfU9+pfNBp3KNBffVc2wnFoOAUpO+4YlgpQCnPQ0R5RhGKe36KgGT1MNVlmq7Z59iaR2C0kc9QQ7kESd0m+tA+Yq0UepXeyQVY8qXCvc4mZX1Tp9LMN7NeNVEHX6teJvLpSpt45WCcvW/GOAcBqb69g0C6y+XegCmCNArQpFkKpekW28x+o3gY+m91uOZ9QTmCRTj9+JmsXXixudedS9Ng1KHYndNZkKpBkAxOYmSxE6lQ9//Zu/8QKM+0grkPUKqQT5vbF+skELPbfsgHh0fvCc6yemd8CF5nvfAvxM8+k7KVWnJ+lnfSa7w20bg7Fb2YgqvwGc+zEr+LrBWdb3duqqM3FPj1z3nNSnetIFBg6VLGUudXnJQTLKR16Pfv5TcKfPIiMS7M42HDDF2z14fGUcnKq+BHYMcZEOZ7krj/VdiMcfS9foNPewLqM0rF0fE2rpLc3KSpOXeUa3DXpPPACY5MmAzSTCW3WF2ha46nrZq+Ne8pRmCErIzFPmnhAzhlBuW9B6I0IMKoefGS7mp6dfwa93GHpWtu1tMBhgkmFR1Z8BNYvEfg69jStA113YbjWHuUX5LCmfkoespeF/8G9s89wGWPSMYRCdjawJZbAM46COxzRM3fzmWKenGPqsIsSi2RtaRFBw3ag7MROkjlmRfdRTQdrNin5qUR14zUCHaqt7sf4t8CFv5Xk/fJ4C+W0BPxVqjW6cuZ+bdfK8Hbn9RH/fA567TRVchTdUG9Ft1ajbbykU5/ZUmXnmw8bhOONnkx6q6crWoefhB9vrRmYzC83M6FmZd4tKw4gqhpu0rCngs4D0Z8uafv2L790Dn9q8OmTkicLH2HlOmZKzI6ceMDXeE9pUtjwxmIuxZ+4AiLoC8ZpbgD10Jcp9E3vMTqXEeVIQ30Y7bOd3GKS8sT0YTGP61rmIQPoK1siQjZEqTa8sOUeW7IC9bs5C7vJvqE/y7thUPBmtO5hnxDLXNn3fkXO0jnYdazuuE3bKW5GO8cFkGvGfZroyqqvKNVuT7N+TYYKvsUzkYcwnEYiWeXs9OnqWjrsDhVezdgGFNbBnS0y7MHVpE0HKNMtm7XTksJVJsxDWWB/O3cvyuKrUMehJ2WwbFg8if/+3+OMXMCYoQHVgvnkLqJ/olQgc3leWMtZe6bdjcGbIwdHhCUho5Ncs+5ORWmTLw7npxPVys4MnuKHVV1eR9/i6t6V1vaI6LXNeKL3u6eh+5Nyvjdg9B97VWFVIVo7L5brU7AJRJenmQpO1LmMVNnx48UuKNmOZC2h9MJ4R/YWM6QVD4yDjzNkYv2E/kFaDZMER0jPCDlvYbAdhK5uuQE66aAnKPZUfdRtvIBBDo1YHyuwWRtmoWIpJ0tsN21vpUfIioB0kOZSOLUVCR1I8Qauh/1OPxyAKdwgisoGrMtbtbcMnN5ugqyGo1vhRxDtz1PAbocKpxWMuxwUwvvJrPPVEZXy5qB2D0UNo2yA9bIFgDkYtJi+DmaZKZGVADGzBpd6CUm3CRjtZkpvRhapcFi/sjXF0AQe2oSVYLWrTyuQ7svXFt6WDbN9Iu+t6z9A/k0ybzeBYpKpS/8kQQ+J/KPaeYCdzxP36yc0uUM5msj5OosDQ21Rum6PyxNkJy/Zmd4FpkfbD11UlQDMioUbf6GFWnzM/JQFCMnpbtZawx4s9Xat36F4/oisqovuGjejadRgi2VnkJ82pyMGx3ixjJvWO6ESOvkJ0W0BvNGYxUnW6wqwL216WFTuOUdJeRuuYZbSS/xy6AUOG1JpzSBttqgdAHxB2il5U27ZaB6tBWKqCfri+DpBlOuirygmW5kl4stswOX4HnkpCTbmbklCyx6UDOeYfdaf3fDVpqiB3jhfqpAJaFpoaKFuQnD24CA30tJAuiMGdHQUhaWhGfWqO/Loi+myYZcTcHueSehYVbN+5XyPIukE4pkJONq0fLxt6df8UcffYRn2MNEOSOblBHDwkdq1Kg+NtjjipjxqbFHo0oVOZyh5c6rskHrrskUvX4oxz3R27SjdR4yvTJNGrzRZCqwUhmQCh01+mrd647hc+yRU3vGDOulBEZnNRKcB+CV9XI3+Yy/CG9nUML6JmSqkHvuDXr2Gqv/RIqkRs35ltvi3pTPjRX3RKQEIESh2PNHxYJ58OPr8E3N+a59VPoC73MCHDNcuvex5+aM3qK+LOZY2UHBpcZEqan8KedwAyOL5EyCB1Ngm5tnJVLSsyeVVduqJfNtQyTUp23DmD6UymyFIPaRy4cx0X3XzU77TpibZE8v535Zcd3uhsegyfB87PdJqMIb677T1yneUmSw5B8eKP8SMIZT4IhydtXd4ZEJ6jmwo0Qtjcpb0MAznZtPa2eq+mY6Jn1b/mObp7RWv3Lbia5cevv49P0EdJLuyXklf8edJUB/zCq+14w8e+TQwIn2XYkzKd36meqbtrow/T/g2HURno14z7EHhi5ZCXrbZjLNtQytTDhyhctbdVjM2A0ixGFaE11NuDBZ7UFgqbSSf51JFoS0qWV8uiAgqKfUqzxZGNjVtqQBd3QA21q66Vu9V8sVYBrGB8iOZAdTkMXlQ5lMk+ZRKaKIWaSizchTG+qYzfWEZ/7z7TPe0tvqO68fesYA9mgJN+SQTQNj1c7zJZHlVXa3+IjXx5QpC6jYj6sDZBOU6OLUTiECbQMZqKgRkbqj469G0TBe1f0/TyKLCds6stFgkuvWzNtj/aEYqXnkJY+8T87CfdaS3C71/m0AusAq2dZTbsWpwv0Rwb54jLa3ZJSIueXa8a1Pu9t3J7887Dg94BFuZwH9S/eV93VZvnD9+/agzaze3ca03tk+EpJZ3UprIz7LATTww1C5uhp+4BF8qD6CaTu5ZMz4pckY1eytkm6Ei8qvqXanSPVg+FZIJhvpuM7VGs/gq4vVdZuMMRumwvemRl/A0Ox8MwNgElw7ceMb4M2PbDdheGwtv4a0Fng7R8+C1LTX0PU0hi4ngVtv86jIRbJL6wyqfjmfiNKe0rd/M+sBnuGV0m4R74KBfvsk7NvfNBpLbnhjC9rgbvctk1pdLCrb16kKivIX0l+U6AdMA2qaZs0+yb0gkzwEcJ5rqwl4DJXhPe1wptFjKZpxIkSo+UhV7CpW8fMTXEVeQ5PPGGCX85bURnWMnRvGJjAt1sEXU5ALByrE2fkK6LtEm8UPqfQ/2rpNXDBNwUUvtqgsgjm0pBjvGkFRXlurin6xbgUyqHgzBgD4URFI4qipEdK6OceKQfIeFumw8tKxPPUbsBqUa5qHZ1dGM+lR2z15NdpprS2pQ3VhJIlzLWae5Mh3ozlfDWflgOZhqN7t5Rfr9FrBpT7XxBTB8QWZo91VM81qbrGO7jYpuRmIoJFokPkWK1ymnJ/IvYV/aqHhkM29cTTfjCE0XNNDkZMygS9FXo3UdMqftfuQ6+6NfOR81OH/941LbyfuuugPd3Y1Le6G1tLal9dluZvDYKI9mmuUia7LwP4mXc2e6F9rcSKtxLkxFO9ySZ+gtB3KjxUox2GKJnGAEbmWllPO0iaQfNMHwobNeIBB29esrMpRGM5p8dWeJlM2bRBmYJANu5Rcr6ECgFREyHYncta5KrrSg9Tbboqq8R7WU6m3Lky8aik3Zgz1YmpkFJEqZNNV3U8e5EjQ7oWAzHt1f2JcPk4+HbuZbFTjJ1haz6nq2pT0UUO16tUWWiSEJSJJ0ybj34NZs6kEF6ecpJGV2Rlqfs2k9oAW2xiqgoZtYRDjabHdTHrTyYTJppBoXp7qVsT6iSeveMqgJ5DhGmDvjg7SQ8NbcQiNc+qNyEX2eybdrKlOQFWWctD5UUSql0K+LcLfeDRuTjfgxbOJfVxXhWhzOhn3Xf0F6hpWOek6p6bSzvXQdrVXqamSTlV17m6L0D4LlmUyZcqUD0DsBvigsGV0E7aWYHaAEU/P0E6OuH0FHnT5sSLn01jM0rAytHbJxFb/ioQVacx98T1dcPKp4efoJ5e/431DK/eZ69KWuUh54I84n2rz9Qz3a4X8K8edCv0ylUngVBi/K9JfqkqVuWhkB3x536iJwTqtBoZzQtzSh9w+HNm3zWP79+V0pw/uxKfyCCz7HwjhX4WifwtZZJO0AjDHWj+g0BLoPXLXt0JoqUhoLyZaYS/Pbot7jCmHJEDmaKcklQcu/+7Trq/CIdTz4eed+7PX0mm671Fm/dOuwhO27E4CCP4rSuNBgcxvrK8Cg7BXdUnlsDVo5vwz2j3S6TzGe998UxFtNFUBi9ujxR5N7Gul/iX2zFs4DLfIx4AX7c0vZ8QNH8vUdWEKraPNSpShE3QdP0qlCoqwBiuJUJqOaxZ7PfyKolGuCEYne0lJ8RDhXa0/2txDeIZypCzibqvenWuAvlEFM54Qe6CPUpUrG84hlNaxzH+J+xMn2Lz+lXnq7DvV4rBHtxu02CTFbvNOhGZFna2OLT7wMrs85ba5las+Yrhre6l7mFEktGrjhWtHZ1GtNmXfuZuku0apujJVQt1NotwD41Pbmz2lZYWPf7AwemNIavmvt3AKZr0hXuguE1IvJmBhU76wu2MWvXvZdR01Glty4O4rvMNoXYW41Bwrpr882K6eYzlh1CjdOYpG8p3aVwWO+CpesZ3qOqV3aYdBHThwHDwfcbWUu2La32vRR9xpdkV6p+2vb3N6JyyKuPJ/zGljGMIMQxHZqTaTWXQcPH4xisdWBEqQh6tb1wvk50NmT917H4nbPLt0yVIKs9RgWszKt1G5pYkHMjS0x+H/72+1e3kquoX5YVz/btgns2N1e2RyCXw8cTZlpc79GRyoGvx9U5fUQlVafJGUrmuYYbTWXrzRu9A9D1fZ1TmvbpGgackT9yi1a19s6nUNKwtk7hZsapL0fR4MNSOITSlb64JIOuHz9y7P8KcJcXSdOZmBDA9EGLw92m6wLbqeGDCNpN4nJX2yLZMIL48cIfO/YYWQozBz4R8OfuxgOZInXZSgZLXKnWMsPciASFcHZckqS6G+ibGo/ZoA691C1cqhDGqbXxUsbejaRGeXRHthFfVjrIS+UmHGeb7OxnuKKIyRhGO03xRCLwLhz+aKd5rxJbl3bLl1mb+p7NhdwEHpA1RAtGLPyxTee6GjEak1Rz6sFL2gSDP4ichvTALnyAW1j4ANZUgc7HbvQ0be5m1djFrQWqLgg4t0pUM1ytWJhnLHSsFH7TGjLFkXpnGchFJf7GdioN3d2lPhIqO34Uke/NZvtn2MftHtdrnd7aTBemEi41b8G7G2lPJtEyRU+b1sGsfD43S+nl9dbcljpCPE/wvgXBrBxmV0YA8hXbXdilYnyJ+RJQch9ERmzB3jHxQg+xCHf+Cv5AgCx+L5BlcG+3jiQj7oV/Nu/1QPKjz61l6vCfQGe2tG1a+EGk+68Na8wuK+FCtfPJ7akZ460nyyTIlDtAEkW+S0LyTLngfTrGXvM5XCdLhBZNpQC26S5I+fxW6OdB1sZbqltdgrRSPusw5y5B5iBtv+dOtDwZKA8S3sWNQVdWIFPLtZWDiEwjlKXB64Ytk/q9R03I3osRNjHsru+Q/57V18WX+qTVkdB9rDoNdTFCd3nip/ZZkoQjQ1yEsks/+0hMszKodwACVMmGkj/oB8hrTd3hzq+UWVGXo3odVk6f9DlINfrJykQCm69ZCGO47MVKFR4tFXrVgqhdTiBwSJyd61WI7rRxWimkEuH7FBsi7pfAztTU9yryZhChNKkTaQskROboktQz03AWJSYE4GB41RWGJo8qRmavpy0JPxCN6oqP82W9eBNeKn30S+8e6PEqJe/c9rsKTnkz9DyHW194+OBgfO+NmYTThNr4BEYs7rI4iYRA/zibmOz0yGZf5eQFX1HfcNwIjg4mty0OPtGklOYF1xW6TPWdmb8CnLsdz9p1YFhtSU6TaMq7RoMnFfDMh6VDP5ujK7QhVR+AxkxzWLn0TGh3NgsmY5q6GLYthpgcNoOuwzG05lDMGqe9Z3/PYUia+Onhy00SMgvHb0NbsLehyp2VekelQbf73exW+62S7ht2BPH/b9u9bNzryz28+n3PJClh8dFoc0CfgeI8iy7S6LWmJmqvyKdojixqnfTy08telGNwA3SwF1FINEarNrdZsKCTNdGvaC9Jm7P3AengM52kqrl1af288HQnNYfmKyNLPDjfknkM8nnnz2onCDPSimR39izBL1CGe+/CrBsRTggJZ0fanfU30ldHIvMHnnKWd4QY1SzNZ4KL+8Se9ZeeE/OZYmvLCsddbhqqUbGf42vN7RP22WaC2z09E9llT56lj9LH1xxxdgCVjmyOEJ80Rpg+y4Kr1sMkvnLkc8fDw49eq/w+wN2UXZmfZNfvePzSXu/khyNahHRXy6p7DU7XlnW1v1l55QPsCKpgMVj36BHm2lEzgXcAYDQrWeVF1rY5qdbLJOmVXyaQL51j9tY/NwBKBDVwzmnOAn72ULOGBA+w5dI/7mXY3qx1IVFbYpMtEnfuIKlu+Gg7abfzkS9BeLmg/w6BTEI5GNvqkD1w6NNUToGE2F1GhQHdCrPN3V8M6Id9Mhr+8vFDf6+XTjgA7i5jZShSm3lMVZWdJNG3ezO3QQttGahC1nssjx0uxmwEyI5UVT+zk5z3ZFBWEItU0mnEfprgX96KcQNC43nQTESUPhaqFW0Ux2odYa0+WE2QqozdjoxwVKmcPS4DXFo7Fvexy+pUk62sliFczMbnN+FtuHDJ1MGKswwwMuoO97C7XcNqhc0KRN0HrgFtYm+ecYJpw3FNxDQsTDgpJa4KFtMlyThw/FG0ZA/L3qSYMOKoNRf7QV7oLmjwfIX8BbI/Fs8vcP1HMUkqVGp7Novl7ZenDh/8VcbsLH5TloO7OybEc9k+smzMR0UtwRXMtbdn3ECmP0dfsDM66rP02pOlDjBWJ9QI7e9VA3RiuGja3YW8ReNUgr0XL9m1/ev3GyOOppO719ezvQI5XYuHNBPFxDKVhLNYg9bog/jFIco4DExn++rld3m6WzP+rvZ5xTO2rZpIWvA84649WSQ995J0Au88L9W5hOKKiQKanFl6qCxB6xPecG3+Gjm6Q8VArotEvxkdMH9I41s5hb/IYVZCD5ZWRHqrqWRcgZOUU6AkjLwQA1bs8tHiMraz0qjOl4CdiFhYC7E9WgcDr5nwrRDyPkNGRB8x5/rRzw184DP0uWHMeIH2FbPMfQjASTgu1FDNDb+HoZHwcFruIuPu4Wkh1tkKQTwjybXFaCQfZTB2jnR5dJz2XGCZcGfdl3mkkRjZsecHkkrSybF8dxlPktiZRmGUqjCUqCT89G+Jj+8JqPnFYgccVx//Ch7yaf8qeAmlzH0gSQ8f0X7+NeX7f1BI4eUdGJF9+HtnWzon1N0hXDZJfO9ftae6tf+gkdUA6q5zgu6vGYhzXnzPty/CMl0y5ysLmSrx5R0bP5dX0+ls35GOXIHdgKxMHI0LZmJLb6I8APV5O0H35100w739ouLbL4qGY6G+7cB4arPzO7+LvNGGacJZxJlX9Rn3IhxY8+9pYM6WW56BoLqe968o8tUQDuWvTz4eH3h+PIfcTtchtcyRP+h+Q00lzDHSkyjk9CtP7pIJ4/Dhdyqf+Lz408O7v2eG5OnsFbOJeXtKBJpXAjHiavUMZPoapEKzzvPBa0sHaGwswC1w1XXw+NP2zji8F9sY5d5MPt0e5PKo43m8HznuyYMacjXr7p3mwz/jpo44BhV772nu8dzel8pn/TNbFG/zXIS+8+7qve+7/FC/5e3pMy6veGKWtbj5mMfEkl3eW9ZcjShC6rXBUAaWqH7YNJ814vro768c0Ka2vJ4UXia41jFOWd9xosrkL0AGAZ8teHHPggzoaHFsWa8jUZ70XTLpODpubCw6FxXnWXy3PT05IUbuyFYP637k/P6xzISoX2Tfvk3XdCf80KI/NPi9HW06Tl+5hZnw5gkwbRniI315O31LJxiRuJttr333qH635xWf4bYRDM7HIuQXqUXHwpnvJWbtAjlbRTXRzErZiIS36VvR+zjtFr4kidUIFUZmX7SbnGq9j21pPVHnhJjmxCHJyfFgphLwNFOJ1U18F6jCcF7LjMnJo7qgnXLlcw2Apzef/c3D6ouu8Wx2og0Tn7nn9GYHA6sW1xuSvRTgIr7IWDivKA7MAhza5uw1TFdlnFu57itfCquOKZ3T8yb/V4/d08Pnv+orOmGhTS8cQR8j7/6DJwHfQsxVnq65NSlyNSyDlWcnIME4wg7AWUPOnBZJy3m1UeZciwbhIIDR5BAgJnCMYkCUdDcbGMWwtV1nJba5vMVhKu28zVGawL3ExtTAmjImTijhqKkP0ziw+FDVcBmmh1hS93/vMLaN3YLuzVAaS0hPa0Oohndx4lIffBIbUohh1jsDGZHwSOic2K/regFmAxOXsS1JbaGta3c0iKPa0XkIkK5NXXbHSUI6mRBACLnAhPsN28CncmN8XwPUo0oW/P/G+CAQU8hUTsQjoeJGJAfL+40FJg3h8KCUydLf55BGsCCv8JnlQlXQp9g34liPnpD4AzFCDWHVs9PAUrlyPHYCgPF0z7uiqFpYuogsZA3JZpMgTeKjp8K03+DRkb38B99JbCLoYpeStrZRTyXyi3K4dwKZ7c0Ls28RxcUfkfBbnHPY5t9Nn+5GdBtwoJPNW0up5v8e3i1y155t4liI9qTJENqDVTUalCbI9tZ7NJaGp4HFOcypqDzbxYMPYGx3dbiqNEHAu1zz/WhCy9gd9Vz9TBDskdSyg/NvctHuL0hblX1cHBxZIcNdxetttXe6W5sjM60dr6ZNVLAazP/d6oTfVffrMvKpCm/z/z78gBHeQQGP7X3DAd6HdLeECFqcbN3wpKu1MJqlTVvIgFM2qAmGqRXbPr5OBBXAgpX3I/1Sf3PtxsFrGb7JcIHpn1ol8OVS7uRKwoKwKYlkGd7G1TTrOsoGNUhY/qFZmsE4OfcCeJLRnGhx7L5xNUbHriMJfqz6MtBGMuGwyCVA0qKbeGBzxg4YJ/RfJvkOQM8wk/oV+cOnvwjR46NeZvG8gjylQSFhiRsuLGwgMt9Yt0g4qeXHr85kl802ru6dYlmFwpR6Sea6Fh13Iwq7SbcI+LA5o5I5KII56OPIIvlJqJjj5olvL3hD1fQRmBBKExds2qQZR4qrVEfgErbT4VEv8RRaM3C17+utCFN+1OfLnx7e/710Emiz7zKrhphIV/Qh7CZhyTV2xEl3yaFGpKnoMKpNjomecMrYOR32TBj2ZzfTXaj/KJsjdfDdjwNt7vmte8z9DRM/qenSYsx/QawiLKv1dKPI1r3wbU54HPGnDNUX2bsnxaQh8kCENeUeNVqZJMkaHqe6erDjLDoKcrfMx2kUFQ1O6g7W06dfh9CAKBJDzds2LI9B0EhNaoXmLhTCO8J02NJuszlkAebui301wTq+6hsvhY9+vDzld4v3eyp251/trbuhcV8hKQOi2PH37iY+f19/7+GLdfesUN2BF40A3N6Vv5XsRPsd/V1+p37ITDCV5huDQPeO3EC+QbDHWe9e+p7uUIy7pCtRjXBgrqDkyKnQN4uuylAeVebXPdv8Dl+pfUasY42l72aT+f2tlVlEfQApQo4Pb9t7WZccbR7lsSUZgjqYfEj5Pt/Nb6Gk+5f8N0ICy9EZqxtbuTxp9uaCG6emtumtWzdFGMFZFZsNNfwlG/yG+cOr43wqO2d8XnoOfjsemYOVo53i5XqYwO05YLXkXUeyWHf9A8zy7ykZh+Ph1Bz5qRJYyKQS/74GnrQBDDhUW69f967m2O89PIV12RzDS+1R6AFokRy17cxDcua7pXVCC/b5kKLlYBM6jNtqECJfj+W3qk7vGslmC6Rju7fvgO/pl/yIdIsQ855e7vpnMtU7ADfvlXF20/N0vstlnkvYVVFZvV3fAfDlnzrySZ8i8XcAHIndqiA3fM4nK6YfNCTZod+mrcv7mNV1It7sVxyhAorI1w32kzbV5oRCODkBLMvlTi8ruCqFIVvR0Whm6gra84LCdBJRDaFZgbERGXyG4YqKsfZrASJtvXM8NpREjWK2VZDXZdkvpRM3tP6ypoIh+Bbm4sm+HOWK13FCRfBl4X6YIfbwe/qmR8TZBsWGMyndBXioiEyTh5ojQRaUARQ3HUH42g1/psDV7RbugG61VxJ4dq7XRReLYFWPw72502x1e9vdOaTMtvXiDcJ9jgOyi2G6oShIgDRe2kJlHgZ6I8yMLvv2mCMCoY8K4K0ycm8UlyeClcLiYnwYjCSVkauyObcS+00WKK+WfRtiC7s04IevakWEuOY9vp3RBcXw1KeI/rlKhTI9/ufy+Yyfc2YEfSa8Z1TP+HhGtQ/UCZbI9lKArKq90mh+MNs8zCpVT4D3wmSxDr6NurX5vhBtU20DvlRtIvWRgNzU9f9E+YK98NrudcV0VpoecAxs9QsKW4tQ+5RxHtKRjJvA4sdhUA2Y2m5A+6VtWR6QMA97NNO8Y3Kwf11jmFQZ+jGNdjAj3ypH5S3FBr1TxfNMTTAI7mAjPvoc6B3x6M+V+Dm5ijBUUZ0AZ5bXtL81stdwPo/Zg453Pd88Gyr38vmogDQibGmpvjNE1dwYdX15O0quWyeza9ANu2GOa7NPnCnv8Vi+zvgiZg31dZ56QK5UlyyvDTQ987l9+vebv/lr1HKoNdelXVGw2iWQLHws2bNGWREt9u4L8952xRX7CK1RAVIkWTvLTDjHmrcAcpslLolYNkE3BRL7g44zhUeW6LQRkuldMxIEqtoMe3rrviBKO4/Wdw9w7QSaDbX+hkHRxyJ0EwyY6ZdjipXjkia/EsAv/AkYVUh5AtLa5LzaMNNi2xEVcctNVXolyhZuxgkJIodsHnWLNz5n3upN6DYWdq2STzFK3+8CLah1Db/ZB1eYei1rkF/dLhbJnifamBeQgM652YCruoC+u6/X1q+zS1iE2U41wtAeX50zPAFobkwd3BpKt4amVBjpTyYalZ6lFvYTgWLmMh42wS4lRpGYzCNch4PoCcjqCoa7Js3FHr1K30fPrxu2Fs7egKgeIvl5+uz7EPmcdHVis+OTbGXiOw0Pb979I1QPv4+/6GLAwcI7AwnEKIoJm5rb/8TFK98lSAoUS+6cJaj9XYgKc3XnD427E2meu7T3Fbo/1NvtPa3W/HH2/QnGX8LmDjwlwvzG6n0WYWu+ULu/9QzzwqgDQ0dCyvOUuktT91P1eVyGgcPKyynH2mFcOob9fmrJjtzHViBZVswnNYdxm3rsLkYNmFcMgam3gfeXMcDavseiBQfzY4OMyZTfWj6+23aEvaKV06N93x2HjWaCTOo3jaqrMwXb0FIzav6GksSDjs1YroptPaySaRuuWFuWFI9NZPdLj8pSk8IiYxc3o64nwX8/gkMlMzCi139TYn8fQLarJ6q92Istvou5dIjuWxoJ4kXvUHISO8SZkHz4jsunt/qyWo5Hy2CuM3S3B3staHXY9SOvvi0rqQVqatsTtr/bWbbTqWrXrvKW30Q6qs6tMJylx3YCTDmaiUxyZ4aAwXA1y8Wgg68ESRVHlvN6gBzzJWAMYseaFvta39SKkcU4MRhLTMDuW9EExedJbJzFV2EwNphih6mvTNH6xYkEEsaBrjfhlc5Y98cCIJhqy0h7UUlTihr9xClpEdqk6nVpYgLL7bEjVzD+aI0vpCsZ8WdO9zhErBcFwH266lx3zoJoZoO6kFD/vzSSeZcOSRJHkEtWtNPpJsg+gBoG9V0JzYWU1ZUM6rn0p5bU1EB7AJBGrkFX3/hrBQ6slFj1OiCSAJXPbGX5DGJUzxMNDP8rHyV+tZsBpjLNoX++4vVo/Md6j1sSZX6Pb/ewI3c/g9kBt+RDK9WOhKpEHrSh9ry0FQd5Ri3YgrTj8tXNG3bg5T27aozf4gtM5TDNRBuhTJc+k1ylX05bdXBuHoocYpj+92WbFNwNSHELlE7dBb1OAVUORtMNbVwcOF7l7x6IVP9h28yyX0aTANwtCs4VxMoams0TgdZITvXCHXdwIYmhX55Tv5eGo3FaJ+zm3tUbNuE3DBxhOAmvXAE9uVuwto/Du7BlMLV72GYcYFUWHsQzIZ0NK7XhXSwHGGIDasKobmT2e2kz6Yy+yYvPblEd+KvRduZGlsq9ZhP1/jyEtpey5uPQXLm2zPN32Bomu+2sjPRlprZ93V4uLynt+RUUO+4el2hGNZVXcBOZ8Pr/yi3kwacuBv3X9jbrw/NssbRBrE5+JQxEclYcq1OO3LJja2OR4pJ5gzxXvcu7GU1Ut+BRAffJVOEEltVzo6Hq6zvhdFXAUc31Xr0DIGuJyoN2ddDXucekcmY9l6jYT8rq04p6xYlUSq45APMZI33I6O+alwAwm5TZUYjkwpcCuDbeAbnKtQJIAiypbLwRUNHBbFjMhbeNYdb4Eq77yDesxZpf/7VPME1PXjjSCSW7JoWuPXGpbecwEwkb1ZhPGUVh0wja/eEVp0N18FE0mV8tVaeKZXOFt+/w+PCp/BKQcq+O6VPpquhjWiLXy1oGpDsHEb2SjYeDGpuZkVdCLaTotgBqUHYWEfxxNjPaAd3dtxGmguqE2NHH+gm4GBp2AkR8CyM3bMAvTZRxz3nh0GdXR2Ibsm/NThOw7Js5ztRiwtukdzaL2mxVjMTHid1sUdhof+TZ0u0kcXSU3LRyn1v3NjJzYLrdqkPGGDGwtpp5NxrPq+QQwshD1MmXOILp7q3rXyAZV6+zFbzCeh3+OVS4hEgMgb7QO880kDoqX4CG75+zJCDfuPllTrc0wNR/RbZpk7hN8Kw/8ZAslnRKH6phkNkrSM4Q4pphwDOC4xb6cSJlk4zmaLDNqls2jN2JtvEan0b76H1D1j58ReFZk9V/IW5rQq+N9Z+z8+E9uqW+qJWzi8yszt1gdkHu3+td4vTUnefMY8zTB57OpLVRZX3/x5cONNkal1bK6C40bbTDdsM7dTEdNk8rv7zUUdmTo5ZvuyD62rZqJEvVkD/2XiGk7xAfGi95SmxjslhsmGYwt0yx2uWSfMPWiRovJhwO3OpzHL56Ciu55zJn6yMg/g5bCWCiih9fNH1PLe/GtO+z3XhHcWgYWcyb1Q3G75k/HZ7ZdYPZ7Lsa5p3/bJX2hpDAx4/mY4eKVn9oalffhfW0bV/a24JCiSlK+PXnZTQ0THDpvXmv5EsiLpvgwniVWX9JNRRI9Z9GVcQDOmS++MbRo7TeZA6bi4ZZ5zXdfQIXj6IhBP+3NRayXsHCHXOLpUrTHNTltrkIq+Kipo3wu5IqcEvcIyBpUis6W8Qy6Hh2uvwtbQAyd4LM5SLS1T5GIrkzKC97IFqpawQ6kvQoxhkxxijZhwS9C0Xl0PFryq2S0PBU3gwIzPBDEcxmjvfbJsLuc7RhSSCOBcFUprGDY/Jiia/+L/A9hsFUpROV5qUXhzcxKj+qTzMWp+YlTYQTVyqUNsb/fRa0TVoHoJuy0H9rMS7MQBvTpq/YL9vraEbvigsDg87ES0CbM47Wig8LY7feqh3zzeS2Op5vVXclr2Me80RxioWmx3xK8Irm+YDC8jzGjjd3rlJsMmO+qZDxbr/Xv4lnB7OuvKIvu8nUb0wRZEnqkoB1JFbk7ejVkXsFlD8MY4yLCeCiMqizDgV+4ztlyFKeVEfzOwF7KR7Do8nmaVwmuM3gDq8QBDWBmfk+1upwn0GWnoXG3xaB3YLNcQpmBqHg8d59Vuw+O9RSIIwy1Sa1zPUlSMcBg4DwqRq+ai/aBv/CfYir5O2qtTTHYZybXfGdQ9y8EuY/01aufoHHk0mae3nZAwGSIWknK5fIK+HJ52KQQiOvGw11r6Goc8G2lzlCe/44lLVIYYUL9lZVDPqsNmN58r4393oZ3e68ekFc6LjA2Z3tktVCFfN/aIbpwi66HCbE4T4mkLR8TPl6781DfQRoj0o5HPruQNzkxj/Xl767rDQx9fV5O91YIfP67yvarLYPvCdQBA9vvn/zlacJEQEfDXp889W/Svv4k078+YQPF/MyoOCGA164E/D1zad/JzEYPmWB3K+fnnhvoa/T9dllnOtzyaHQTxP4U1C+x5/7BDI0J7x8ftfAFtktap56rq8e/+hFEwgIMoKyWh9/baEPaz+tH8JstlD1wZ/4f9J3yfndBNlyJ74IdHte32yuvqifPECJj0sJl3WOrK4Vz8T2XL/jq6ezm5CE6KmuIEnX5z+H6t3fG68fO0MqFVjV9A1x/RwY+XcYelvg63sdQg95vRu0S/Ddi69PspKHfIY4P14mUIJxt0KPIRtPspf25ukc0drM4aTtMkJVCdXbVFpwtU+EdK3C0Z7f9lN5+4z/+u784XP/MbX9a4oJardTfeR4hmjukaseGU/y1sg4h55FNBsuFGbMFo0hmNE1dY4EWbRAILaiKDVNjiToKAVPnRfRtlXxQ3FI4qccOOJhS+VuCaOOGs8p+B34XfR4qsoAy+fRXi0msuOP5lD2geFOx29oEsxwQ/P6rSjckTuWrD8e04Rz4j4IjwyojpKTbTW3EbiQFEPNmgI81bOS3NS7r6LAW3JTmJd27Rare5/xvfi067O06W+HvKD1mX7P/yWVYx0XitvyWHVUO2p6Nkkwqmf9pUm+P5DvnOhOWzC1hpMqp0vSirV/08Ou1jPHojVWSI4i6mk7wvAW+43k2IlpbW7jl6ftQRt3Ue/lWN4Mscw8P/0O/LVJGydqYbytNV85ODzn3iwGs4b7PCiLJDvrySStuPqbMPMdmEnQxfxxHzU6clO/b2DJUFGxRGzw9Do28ug/KmMeLDACrshswLuddLUWFIxr6wTUrDv8AokJG3i9T97e/iPawx1cw/nFFWXjb904FuN3E0vmrkbnKtoWb8g/dvUqmud8TEgTZNA3kR+fUWO1F+jMhBgx3zxsz3jM98r4tsPRdb6j9fQ99nXE2AnXNg9Pn/8lpWJgOviiMqU+JcHlpH7/JwF7btx6h5Rni/FkITraR+QtcknAxarnc/oGizYofXlGXRd1uR7z9w9R12aokHT2ctvlBTauujM2o3MlCdJ15lOuSfh2nxQR+9DgOlw/52OaaERFJcROgOpIbOfkqEpPIg0wAQhmU/XD7HJkAQYwiI4cUCLPamoC99xokLlcjpWgwG2BDXr/0VCzfGBiajzSJyLUZS6RxBOmQiEqArG6GwkJQ2H3TY71XYBIa+ZgbRA7Odnh0CKJXt3Ldb8CFpTeBu1ugqSn7hcVXguAU9UlKlnQBSvS5zBE5lI82vuPQtf3dApTWi7su1xL2xZ+deQO27qw2uHWaY1NYgqZOgEtm5XHcNTavAa2SqkCH4rSPWOzrLu2uR1CdB3JQdhG2T+jOgLdjSZE5QhraC6gEgnN6Aaopn21WUlb2ftiypykEZdSx3zY0B2N0hI+JqNvSaGtpe42M6Pqy6d1zaJ9WQq3bRKWZaZmuz1PB6wr9rZeHpHUAdhK7zePgDkit34FAqamtAVVbKZIMDxuJ8BR6ZYQMXsZWtZjkfY4Tdh0f98kPUl2repjf5K/0NzNUt8l4X3e8TjIUjHNP6hSB0FiOWXqdcQHo6xVNmT9zErspmEHyavoCSxzuGbyrdXdrGW2n9I89qyZahyt05mbkoybp9Het7Aoo2vE+KmKzMHvJ6yIziEsfGonL8RxFnWK6mzpdaMw5+l9Duvs7Y7+SuyEVP66K8HJ975NxJEzLNhSmoNZoXZgnA1345v689ob+EuCyWUFXdPijln3rPcFOzXvGH+zWPkJs/tcB48kL6ZAgAlp6rGK+V2GMbsJ9q7JDbKum45TLysDV0euodzORoRrBxxpxni3FQ3YRIdq7A6i5xpytiyqa+wq5ZqDqDUZFupAJywU0pbxQYupBSnvQMqEa1qnLGQxWXQ1ITkqmk1B/uZv/tdx4hXFCoChWK5t5UDlodw88nu0GoR3f/foi2W6obvj6smH3339qqvMLVy9btNd+bf+tLqd6LmTWDGGDkxa/dytVXLvELX/ImXJDAPuKPgdN72RoC+92tAJTNz6Ndzf0SNFIsHbn6R6ePqVBNwC53e0fC550KORIGNTWf1tBsUVlTS+puZmOTJnZsNXUJIXby794WTkGym/PM+07/rbK8khRWM4UfR7Ww4hOYSIT/wD/pi4Zeont+hV7+8UvkLH6WfdHdGT4H/LpTwICfHh98vMJwp6Gbe8MwCC33z1lmAInlcSfu3Ifd/oCmNHVdfOAYY6QguW/rK24wtwIbLm5C7oCI+ejq2DW6enx7hCPgBWQ2GQL+8kPUSF1+R042hkU3SbAWi8Xpa+9WRWmXexguq4eHco8mbJni6tCJoZ2oNijJgE3griwamx1hGhu6G6f6yjo76fk1+bbhvT872dB9/HaoohVwUqwcZNqhhmksWmLU1oc2r627alS6pXWgZ0JEMsySs3Ozt6tOVwXvFAf7SZKKcSSGhUf31Ey+GzMRTsGEbbbt4qgty/zxOcdNQ6/lK10fEe7cV92QV8rrZn4Ba34t1iXPGUQT/hJ+90eeDnfYDdTvDcieeXQBb17jYL1S451hPuTdC1vl1zHhnUmnze0WTq9uFwzD8r6M5wCmXXHaMZzXKq92CR9rOAVt89mpXVBX+2pih9J1VWXsoATwDbIEzfZ706IJ/1caUcH1IOdxaSNBPFFkH7O4luxKRmMFpRfeIjRx3G/h7XXq+jZXCNv7fPOwB5PttiF8uRgdbqLdGZEBFBqSUDSofoB6UUfAEPIexPJzvGf4DdNnDS2Y42Hqiv2q1dvY9xfpdjunJhgej4DoAl/Q7qWFysP46y+sUzc+ZMQVbShZi73kOdUxEifgdXgD0zqceK0ufzlYuQHqhzxufMr//SZIO3t80oJ7sth4vKZ3Q+K9FnxLrcapbTXg7G2Uk1zWASSsq7JiuOAy34ttEVwBzRuurgdwDoNKUmZOGSL2SWcF2umrOjUt3Py69wVld1dUufBePakR3/IeBPWz6TkzoNtMo166SrgM2oQv+lm0siUyHhUIOOu+P80phKm9idncYSRmD6l8tujJlZcudLW3zDZ2DAJk7PAfcGCpjREqJLv9izjQAr+mA+7WhXHWl99KkO/7QFgsSR8CLKG/5MZA9mtcp8ZlKhFzOAGU5XUj49fZFOW3EBIk0A61NGaTk6RejLVOkcbs9aw8Vg4jDFR9l6V8WmOEgqgLYIm0tZDOeIjUuraHo3DmLU4u7htCsNap+AlizZqi1TauNnCAj0Bp20W5yOeJhDRT490G6WabEEHNxW4kCq8blUlq6mazg4RLr0N4Eu1ao5uHa5mJhvjoL5YDSl/o6kni4I08+m7RwZ3Mcjpm3N4dPg3h8F7pZY722Znve0yE/Bit6dQsWx7mDCf/QMQJtVt/rBTkXY1HeJKVxIuvtaijaL5Np4R1/WHaByqf4k1kIdGrNIXlL8YuHdkN3l0rJsnTYJ7pnek28MobOLTarq7Yw66d1sD0oYVTdvIrwxTMj3cNbWYVKml1BDDhoaHZGqGcSZpj1zrCnitdvsItQJSct1zbZrm2W91W6GKMfeAdEHjEJKB+LddVUPndoM71dlEbvVDc/iUA3f0pqq1pJIB3T0Ekz4owF+DxzaYTj5G/mLlTGcSndQpnsww7QN8zYJTnFeWg5FKq/BGJnQVJ4ttphP3C80v80wnu9RHrUXzCs1UabNrKHGiaw2X22qkwGsUrXtPAU8JmMYiQ3Aqgl1qVNTw/pyVTvBpCigZTsol1sd6K45sMTBQXS/IbB9ztn1DnTzdh16uogO/ySNdwA2M4h1x5fOfflTOulPJzsNkqlXMvrCpbw+aFf371cssyhnkEpxJxJpiWFZ10meT6trePNLbLq/T3C0eYFRBtyTln99Dg9zetGJyYoYYvv11T7200cg0zB1zDcZpGNimj3OFbGdH5o0EqQTLE+8rfGO+1gPX/6V06J3QogHRpDeSTKvTIhYwqRGFswnhRxi5Gxa+iVX4P5cfrgw0vDwioIxQkhP46HoeNNEYv3Rab+qUbMlYOWI90mki4IS53pXh+dAP+mXPnsYLI8OvWqJE5h9qLJvEdpA4t6rmtfrnzXf/NlQR5cYVVYcNSBHXfkZ4i1muBTEj5Tnzx2eYJgrHcAnLFMiQpi9G+cCC+fYBh0PI6z8Ona+ZcGQ6J2Wk98T15qiJ4WDSmi3pbBNO2G2QOGkmlAc4vRGGr3A1iziSO5HfOjF5PbkqIpj6JwIeutsUa7JJRD8eMqn8DLBfKzt34u46VsLHP3kQK3+xOf0sHvTFqd93X+a5y6bMJhVXX05WdPMHb6+z3oBWKJ0d7U9CnJTaXAydq3qozrJn29qvEJ7AyNX4tQgzqbmaVs9Pyn++M0cxdy5d2CeHr1WJNR75R8pltCL7PZO5HiYEEbySyqa5HWKI+OT9XUPUm68HX5PdHCl3HbBC9CGm26vhmJbcSrLMXzBeIg4hH3ZhEOfBqyq73qxUh22otXxqNqrjo6D+blBlvTeso9TEU5WVvbaQouJtvxmS8Z0NKpYSZH4vLCpqYGxxgBUyLYyFJYULpLXljGKT7uW4CC7IRrv0oDkD5n/WC3H4nmegX1LZX/3QHbyUPfg9Vn8f7pNbqbXN3XOETmDXAXQq3xlhZRwKlkrCbN3N9TRoE9z9JmLHh5dq7+SrfdtjtrGJ6A5O+4ODnXPUn9vR+LEEY9pOnpdg801XCAHCjcy/4+z+hZVEkJ2PvZz3F6/sExUvko8Jcxg1pCn71QKsW924xRKxyJHStKdMPquvLMFgJGprdaUEHCNoC1Kl8dBk04AFGUvN5kUFmAsR/np0GA3vpoLM1jMDjNJYlhIqdODxAmLtSrZ5B84989VlzMDp+QTCUj8NgTRUB2tKvVfqmyRUE/XtVdQ1buKkHVXf/IsuQyiZwk2sz+ehJtw4x5cemU4JrEk6LjEhZXVdJ8URABEgEMXwwGvrOgTVjGnbkEGHY0GIHkwOMA2wcqG5LH+JZRI8dDbUTKGrT7tg56y4PHbPk8miN0n69tBKAIt7Y1dBIVkN0QFTXZu7GLhkvyqskuAyyMiNGTo5f/jI0zT7Eo5aaoVWOO7j90mBA9+wqgI1IDJAbKT2JRjZeFlUQ7kmc7RWkaaxWtKyANTvdXEcSJchgVKEht1hDu+Vn3zfpaHI+k389hgxT2deob2pJrmYrkfRYMT/sKx0Ern/8NT4OyqsUz+eWusbjdbIj2XV8gb09cKimxycsfuJf2N2TFIWlBoGOjoUbnZXilkt47ajGAIfLBgfGVVY710TvAxy9/SKcctX7ZZNHJ9PAa3zvzC6h4Vfd9o9vom7qqCqVQEOPBUUO+rrsyUWC9k2M3CE5/FlN0QWDe87fiZvViLySAvogjEcYfG4oJoF2uXJUzE8RntM/7/YJU83An0D6b+doKXulv6OV4my7shF43dq5zUEsihm7vB3TgF2mZND2qcHtjEoJg8F0o+aleqFad1ar3wOkYXuhsRZN90bIZ9dVxtX8A2s/VJLb8DQC0+DKhqlhkkEqgnRUcNge4UWhUuhH7dY51M+jsAilvJUpl71XbgwnYso2iJD758tMenPAu4Drfeg1MRCOamZzOhxDVS4owLCXUnWw3+9HEjdtrwobvCemfDz6AI9ptKO4GnCFXTlvyMD+lVl1PfSudCnofx6wo/kbvXZeMnHfGZ7AixSjx24fS1K+RInSp6HYW6Sde3DQY6bIgbm0fxE5WtwrZ6IzslX6924DOnrPUhqldsom1cBwN7W6a+S6wZvaE3agkOmwEKbpNTFctIwtjNXRMmaSJslQ1cmMXJNdRTxhOn2Q6xcEQwVhDqkox/DsVUUsWR1WVXkiNLWpi+Zit/N9A4j1jTIrAdlZlnN5lTycLwScP31js5Y3oM7LOezK0HB/iTndwLlAWfTtbWuJ2QOu8tZMBIT7R+ro5s8uQum1uVXxvVseDfGC75add+TuIXmxPX80joBf2l2+Eu5vQ3hGmG+fletFZ3iWQaztgpM1Im/ww5x7Jzzzq5BiHgVf4BPQrJawk68uV6aqKQNkQbLLJNMAbfVjkQu3EYiyNZwEcZrYQx2sR2glWol7oT9NjMUbDJ9NQyWvtzeOqu3sz/572w+nA8ciLg2J3ANye31epA1v8sYQGVghl12F5HezCphiyLdIJTOzM2Opfux9E+eIzbe2Y7LUlbWEZBZ4HJqdD5uOQ9+hm6ivNGuzxAz7a594KZZxJ2R5+/p+urjn6qHp3QWQPG+XaBmu3nppf2/nyRp5Y992vBE717U116nvT12qZzn14wA0MGMpYTVqxCxBXF9j7wLaFhYTkRBGv+ZRbMVmZO7SN6acc3kfzcp/QrJSLNO02BOtNXBGvnrumMqe35WQHiasvTFDM3SJOoc+xs4HJnSS0EWQxQcNkpTZ6SpCdA1sdGlrnCf+er5BLJiK36qR0foNcaId/a6gqvJqiujCTnkzhOAZgMJvIHPUIn1419HWTii0IheBMOe7XCr+sGPJYuR3Utc7wxUHMH75JiVdhYALDU+paBdZ2rOqJ02xwb5Nkqdv4rK5bRMpgAqLgxEjX1zyt1RYCNZ06MRSNwcpCoFJwdhcq2i9Of5q88xT0X9H4zUSB/XdnkSQKukh+9CHPySJlDkgq/UJmdaNTqyNDZukcCvUWuHIrEgchMlRYMl6YMdm+L41q69GPcfMugJQtM79rxUevoBtgtcyVLi9aoU3Mshz4SiOJSR52qHk+GUFF0AOWsdouA8xfnkkOWN0dbtak2EdURw22fJwCIyolry6KAxOttqKayyQNSnIUuDDv9xXGV6U4ZZPqFaC/Hh16R+2w6gh019ee1A/vFlYT+rPkrIJ2LS5504RmWrY+dvM52ExpyxFVLu1DHVAaRtOUfsB/qCw4mcM3ecj9RjJkq2abSgj/KPn7i9nlCYe5tY34dYy/JHKfPsPQYtBctqKCvOYsoGRyL5s8q0mL26Wdx0ahT49npbnNbt32RwLEGb2GTjGf7ucD3a+4ZaoI1LH7H+5XpVb5m0YnB0KlJqOqDamH1Yjot8KCDcAwJBIW3WHXruMcSCXlus7A1blM0oFXbXqic8blkpO410ba71eVQbDQvVEUF+f3tRcB909drEkJcXTuUNBv9rfMe40OVqzM2pvbggj6XUZPEBlbv1UwNnesNKAoLC2zRWJyAKHdc2dfOQ+l6RyDzujnedheER5JXtcJyE8lO7ouOBINvT3inVEWu6YzumZyIH37zm79mSnKjzpf7+tA6KeNakdJDIGb/JhdjZS/i1m+wqeQTRH1hMUeoRo77/RVbDUEmvALrSrrNk23k56Pg0nDl6UtqrHVRyzsAkvBigD2UpEAtFWr61r4nip1hTUAFc/DAoEWD2Tds+6esVJd17smJQvXR2jW0dkKgzokrrSMGPlsfDF1LVO6mY4OAjNLAFLJYeSSV3OqHgXa1dynJZ8z1Byuw5MkGuffw+LNY+ggDbCfJD7BkruS2UyFGs7kvqdozVLM5ICmR5RVzVPmsG3UpDIrTrV4cG1kkdlpK4Nr2u3p7HV2R39Cgy7bc+1X1Q15hO+cGzLNxuMOtrmjyvXn7eyYi2VvWVU/+gOrXFfR1+n+kWndf8urXQDpem2Daqs29DU1wfxbTMVQgh9f9ZTjZI5hiUIA6djSt9EsaGiN/cvfhZ7uQB1DZFUWb0dTs60M7WnEVzLu9kcnAjBWGEGH1OONqY3U68LlzHZnKB4ZCFXMJs7N96c1+0Kqx6/S0qzxlYj73f0IT6vY9kMR+iO9kQLNOR5smn5rNc+U1vvQeXNEN3t6cnt02d3nn/cZjPBvwWE03I2tHRR03AycUvWnnKLBye7SpXMkKcku+HWWym88QG8hCWused6nh1R+qq8EsF8/uCPl126y3l/B0sdjSuMQdezeQCeP2KSWZYzmu5+Cr0Y89/R+my4oR42NBIkoKl/QX1JqC56Bre+k9tIlYwzahd3wse7yzJ53PGuEeGNrnt/14USTY61PaThkst3yWrEAmnQlTipjE9ujbQdfydTt26sPz26X+/kxruOMhLAlU12p/31MgLjlIqiuFV4vE5LuOkwFLnw/8tdpEvAgJ4ZdsL+eEnnn7Vge2U8HBxXa092yMwkpPhgWzsSywn9J3vo+GxhUNDo5OZC7AvNuwg8tmo7e1T1QS+kwotne/fXh8fONnYDb5ycUQfXNFvuTGD8lUp+7SenGqS3SuzN0Lrdi5cKScBKnKZEP1rhLaaKciufOA2MjvHSjuut9PD7goDCEt8uDIqJjKBTEUzFKaUWBUJpin6Y7GRldG7ZTLUz6UwsknL0gMRyJfbCYwd6pm6wKYt9q1/Nv3Itf/w0a31XkvUZPIAs1MrYyw0z+6wCW1w0kZAyeKF1SMi5NDB5fPMoEiCvxWEioEsktS1HRIjjXsThP5QqYC96LSTljjmBOpSQMQeQShsGUIXFUh9XC1bIEdffSZHahIwuV2dlXMg47+0lSBGPYsxKE6gOKgh6s7aBIlLKTGBwwJPtAmnkrVwIpSgfDS160CjmYqB7ohr+NkUKdKjGaonER70GgbSpnpKLErB4YkyIrNf1cz2DbECrD/1nDZVw1JZ1LIiO3JHprwpBqc9eUn049gUW9MpkO8tmBor9oRsbCrtlGUz6W7ri2Lo5+JLgeF+hrCw/wxZRjQjk1cbYQSMNeWs+tg9r7e5qds7KXDkWwn3cR3PBRtQj0FvHFBmvgvMbvPe47+ieWJTk4U4CvDCWzv+q3hdJfBUmPa7o5au8mpufX4aLYUt3JLTuOGa/uh2J0A9l+0tbov+qnB0COIECPvzBuV2zXKwptykIar4CRxpGrNvb3PaFLKDMp4Lv9XNqYv7wVrpwc4XaoYi7RbO6y7BnqXu35lcAM6CSD0Qa8JgX9OGfC4Gm9XjtwFgwIPvrhl4PN4NY04kBwap4BeaMpUoTm644ITxQvWd9QH22ps65kk37glvjaaE+jtaWwbRXs5GkIgibZDhAgiLlUAB+kGANQZ26ZN94p9jgGcR8os4PYu41hX3mZ5ZXET7dHOJ4rydNvhwToUqKqvQKnmAs81zV0fv5pivvYR9OGvf/PXnZ6nhzxXR58xJfXiqshqSoquLyz9Gqu0BTNI/nztiMw+tnlhVaMctrzw+SS99tKdab/qsFqG/gqBMVW4YwStyjArzJIwYO7GtghKtEcYPbB/6q0dr7XS3UowTo+j7XtpuX9JcjNgzKbkGVlbETSLDv0Hh0KbfbB80NfeTOV2h7IyUUBynITFSGiwMfIUykosrSaN40VnfbvpvbXd0P7D3wLLXSjVKmpNGX6p9/gLoHNn9A71xgqNg9xkqk4Pr2M7gs+tuo5fYgLU5vQ6WNK8u6VOfz1cGkFA/BorYSh7/ZYUvzKBCuPs3bgqig3kRffaQkoPdbKpESEwnVz9DB+VH//d1zdf9OlwPXRKb1v4EzW81KxR0GdDQ1Dpal8S1oa6673X+yQSX3xGOTP2iFfLvz7xJr+I2RzD4N9pzhiOriobkV/O7O/tzF29LCRKu2O/CRY5B87dzV0dNsEygojHCu+eZUcW3RkiD5mrfoGXnITtiF2tGi77XdLUxuNl84y+0w6J+R9/r17k18fTnfZKh7peNOO75ewlrKZ2t79/rEnsGWdbp1mwHI/1QvlOjH+gOGFN+Vq26sor4aaPj+39gd3YnUUQ4sYWRM3XbJlvjXyFkZ2N6zVLm+Jm3waXvUjQt26XxBe2PV+8suX3JeIn5K2+8T2CBLzKnLL8eQGe59O/KpOzQ4702M48tafhWxUzsfhuAK5nels9kSTHpt5NDf5UtskL++Iu45nvBJAFuE6/ehdXS//Pll+v94JLa6KaBytujLO65cbrGumFoYbX/rbAdt58oQ8eMczl3IVpQoZEzfmMO+3Zdhz2xTD6VHyOeHj6IYtvcMvX+jWPk9lNM94sJtBet/wdJ9+bF2B/ApVnTn4HKVzt2j2KaJsbEVDiaMbBg+XWAuw15yxzSb/CAfr971QenwK0GyjLsZHQFd7P728yHIDT2Hpespbk8yb5LZQOm2D1box2k1up+nMWmmY8N5OPxvjsTxB1WA93zpLMR/ee3wEQJ/OZdia57r5LmJcyTF3pKwAjSaK7h8YNc4iA48L1CCjZrNF+6brqMOzVXAC4eNFHZSBzS8Z9F8H8us7iUsuWiloOeX9AM2ZdAWDo7bbSmj9wH+LpMFmogEmJt9rdOEqGNnEMw0gpgEWZS3l70XU6LUDhVQOIKEJM688sNTTITFqBkbAgO1QIjcosAC6RtxhX496u7Num94I7NO9F6SG6x3GMaEd1CKHdyBdIkEv5QlzXepIdtO2P3IpVzUi2Os6Y0y7RKtXs/Od3rlCq857JqtYWojRsrmrMLdvVZTE7U1ckOcgiAUCYducv0evD9NV2xkOaaBNve67phG3CSG0rZdvgTbpVpQ3/Ana7LIcCb0YNYHjsI/qR3VRyUMS4DSwDacEtcUisPPAJeeXuTGDYMpS3W6qlPtZk6w8uHqXdEk+cnV024PX7hFRsr4jPS+fNsGKYoE4RlRApi6ynOcEh0J+nWCxpofmGbTeB8GqL/J72bPGtEWDPqOYQOrN1G+/6y5xxpTU1jNVMskZ3rHQXen/UHhjqCIYctP7u9ssujb/LO+Z3EeU8J57yBfi2P3fjKIoEvJfigSpngmMEx9bOUNPs6O18yN627ck8HXktzNWn8A1r/Dd0/FMxZk6sYyGFZgrXHNm896pQuStHaGUd7zjIURejzWFXj9MvUpVs7CJopxa/onAA4JL7tgjNkE2l9Vf750DFtyCrdkX1sswd1wxIXhsv1spIS5bAeSaHOSHcgUZMaSJGZ1FRG4DqJjMg08zXnGqrJVhBMbrZYulIQJ58DDwwNeN15GpixlambtK7jWqrBp5rgurZzE9PvO5MSGsycAltS94BwAP5VtK5vwUXNxi/2CI5DdhfEuBynM8u83SPh4/FisswJoYk18IVjaNeoXuCAvSjckIwkchKTCV0sPWaxqIKPs7luVzPtTOK5ahhv2x//9Nv4Vv9i1MC7M4kebVgbAEd4m8w3VU9TxXQa82/d8dai4ZR8deyqeuPjZlhoF8mWRp2D8TmyLb2oN92EK5+acHmlSxDPMUjFUoO+UZ3+2DvzaoJoqWt84CEA+rq1xG1tQq5JLy+z7OibR0OlfyKbckfeC2e30KWnSMnnOAX08s1O6+5CFNlNIZP+Q5+PRvbacDZXAipoyXEFCr/wp2u/jiOIuODc3ayQVsSL3hl83QxSxlEXfZ2xWxUBv5q6ylDlMPFaUiyQ8gR7ZsoOgNxPYqDur9+73PzcfliufdpOucX5vE8HYxSfHXXnM/EN8QHymoWVDsD4oJ0DJ5K5jW16nQIDUvuJDhtoToI42wGEh3WER+Q1ShN7qxMRJdI35/LPciKqLzBX/nXZ+iLxAfcFc89We73hCcB8w2u6iO/261hzv0htJGXdvN+y25MLAiUyZIZmZ0MnC5/kWm3xvUfsMW6/b6K6O6a7DwnM/ldkf2uYaj3d4HaWWen2y/uL6J1qtYRaMQafR2VfFPo8H7aPS/VOz8LaDlKjElWWbq3nrYiLk0MptSY/QS68nBBYi7kLBwwMh/rzmvrLA1n9AZa+1IhThnyHYDe8HG13ZNfYd2Pg4ElKir+vDJVj+5txi/lEehxG5GWNX9T6+GnZUSNjPHkjV7o+1hrVt7l6F9V9xkkv26ksBdPf3fLkeYdAHer+pbFnD71tmotubOvJwL1Oj+9uQO/FsvbGHqCbLAVyeoO6jbYbTez66qz2IzNANl65MvZEPRCxna1UXJmZIgEqydufU8mBUIerUoT75aRLIZggrB9DhTbHYpe2z1sO+MB5UbiiDz1KQc8DFK9tOFSZ/nkUe+zbU8uQiMqSKSGiKruA3/QLtd2tLk88F6/Aaarf0MTgUnROW1y4nNwkyHPFmLYuSJJEuIYEX+FgKtbvnhxy7zKtVBsPTJqhivGLTYCRm2l72gPborNuH+SQvHmf4IhfA1EraXaJa1Il3tk00yESf/IC+G2uyeeNSSjLVuPI4BKyHgaJ5bQioXi65oqIo4Y1JrckokzVzzoHUwgq6R23hbfhLz4GzxsLSCiiYM528ZBdrlyJ8lsnm1q7bJR3qsEjCmzihZ/Haoe2iphLhElL3BQ3WZosK+DB0fKJjf+U2szmsXgKoX8tCumiyg3SRzgbKG6FmRK2/g9nUw5aGqbmshxRG7bIZC9Xiav3+3GcjS+FgPSHbU09zwXycZFdWuKrueE2YZ+KpuTVMf6PgQgzD6Oh0CGYztUkgh5ko/JVAKAs0WSxLYFRYI86FF8YyVeFgdt3GY+D5lEC+P63nSkNsMAipM2x6IooD5umvwnX0f9iy3cGXTLfSu5yzYsdxG7It3jyPX2zR04pod0dcbQ8Of1uuI/oePzpfLUd6anWC1NQZP/2b9E93wMMPb4n/m6XQzPE92EIfh6A98R30BGIOwzTkarCvGCBc4fux4Dy+qoMi76U3nS7M1VT62IM/ndcNJreasoDF2W8VahqYGGU0kQTJay8+6wNNcJJScWj+5OG8oybpYITz3s5mBb8M37md4KhFj2eCA7tMF4KU1QB90znsEduwGR/h2FaoUxV5iceXeEbTqkALtVvkN3JD1BPDrtuPBjpgr1tItz7TDtpaDds8+EiUSlmxxvThTmUVHrTUy3wlbOfroPk/F9LW6ISMITj55/jnHIH/76r/9aGOLOMZOOc/WldwCgh5YJymFsFyLwM4FQVYjCqZ6roGBwjxQj7GHAgbRzFJg3HzdSNSFJvV7HxAQqbbYGF6dEzIZfCUPtkABq27y7/U9VVOBDP22H4f4QXbpH/Ndbpg5X2/ORp2GKsZrOYj7Ao3w28tOvSa7+KRW6R44Hjze7ysLuV2Aw/MazRvVnSl4lCwq9hwyZNrFo5OBjQykUQteeKcqFETEb8MH2pCsQwTlEqVXfyjhfpX6MwuF4kpb1vPYdl89X9vttQXaXic53ILQjD8TS4Xtf4fc0R2YbYvIbVp6XvJNmpIo2jyPKCCM3ET26AXLUhNsvLS54ysciDnUoVc9EJP4b9tugdpbbOlRlI65t68jbQ47UDXAV9zPew84UDqOz7/dkfE9uOU+v7Gino96xoEx8pgtsvZWD2kcBlXsbo6B3VL59K+Y9tp3knnzH3NZ3q8wKYSTcA0zv9xzc8sRikCEplvbBtYtEvpTTC+N8yjzvxY1TT7Ur+j+CLHFMjB3Wxjy6TXavygSmgzo8OYVdsN2zvCPnLonoIHr6+GuOelYVNeVEe5du06zWtJFpczybduGsbrIVbQxgs4P0QmMD0rpeG20/6OAs2wsfW6KqoyP3TSuoss0uU0H16ddOc1PPrHB+SofpS9sdzCRhswfq98T03pf1tqWXLMMFzP6W1QZgGiiI0tatG3XRLeIWeL/xN4Pl5JTzx6Y/2CmljtRn4Z4IQhzwh8bB/LWNQ0xmP0mGaPI2kq6QkXtWwdSiv4Gmqi5g32VzRuijZ7pcuLx9XQfr4F1hdstyyD/9BccynxHIpjCj87XEukLoQ39cQTPvkmFCgNXJiVUT2DxNboi0563Cid0K7gw7tseLrIezmBp5ifGJmG5n7bFJ5b/t2JPa5vUk9BWOz4Zv3vGt5ZwYe44q6c5d5quyk2MYhnzHWXRf/ZtWntLR4icx0uuKqGwtB5YxFg1oPiNLDXq4VfEoATOnn5vpwwZG/oBJDVhbS5ov7CmVlHRnwWMQ061storekWzqb6hORzrCnXp4nIxqMUczDAquFcvKsUxTFQQMN98L0Fs3dNXZ0uzcaYSKlccZGyfadHguysKoGdcZBWfZcYmfrOv/XF5grS341FcpYFxMZena5ybpatB7KY2a+u9KMoTemBJnVxDjyrlF31x4CVYON1rx0apTl52r3UkkBQ020IoCZAJ7xhNJ2zS+oovYwvhVTwM5A9PmpXIjiuLANDLBOxoMPE2gqDiO7MfWcLxUYRoetuGJvANIS8oT/GB7boyRFGt2Tu8XlWr22wYcRHiaoVnMkSZKqxntCfo8w5fd1A5zY6QvVjJi4+iE796dxN/QTNdlUJ2hn2tVuSWy/iQmOkdykq+mEOOIitsqdvm5taxva7ud6tqGPuAdEMkEHnyEv7xsltqPv6k8Sz3BCNUTI5Z18qr+GNdg7bXhkL/bTUMQSBvskGgiGf3uGoBDaGGHYHTNjlvHu4R6TiQm2t1T91nEQp8Y9og26NF0ginEHaOwujTiSILnzfCgTMdQU/PR1lC1j6m2oNJiX6semwDqXCxRMwVc+d0TgaJAR2xa20HV1IPvAFBsvWPBturAd2jE8lQKUS5OikNzR92Dv+irSHau5cSnG5pRH04T43F3UcJhGxAc3eh9EUdjYTvICUkiT2DtXa2cxF8kUHCgqWWw99R7IFtTtrOaLiDg1VKQGj9KU1hB0QicO4DoRzM9luSwDS4I2wIog+aVxNXJuBC66HUYKauTcb+sdd7LUY6BfgisnLMvkC4wCSKe6B5Lk+5y/Mqvgn7SrbL8DrD7FRuz8MmHekYlKa5v+v+OwwCnzjohfuc49WlgBZLXVQTkdwl0dat70mr8KtE4PIe2HyS2//r4Ix+47mcV042g9dQOhf71+8wJnOyfHU8g3CmvT5Mnjw/z7Av3na7Ngixm8oEHNteTnDSrrteRJEvfFlfpcOfTuhbZ+LbIwuWRSx+pkg5KbeqUPsGJj5/hR6oxzyULL0z1rfBCg6zlI9lzzA5XbGpIWZNCedarXodFMr3hVKHzMsyf/JFnPaNJXeFz228+/JZSny022kYOr4xRorLMjb16qEfrrrha/mWcDoexS+6u9UikXmR1+x8ebRSeS36S1RaFXZyK/fk29Qwf+qk/9YscQZc9U0qvez15VZCiR39uToiTF4+CXzDod53l8d3vzGciPa1fPF9/SIoxzXsv+X2GTFz3AdXOK6JPvyZ8fb7QFO4K9Gs7tpCXRDvZDN0tzhzQLrKqRXip6tEQcqFUu9lOMs1a8jsw86xmyz1NqyEtJDOraWyf45TSo8a88fGr55ghkAWTeOeeuqBhxX2DPGoPepaOLP0JfmrbRtQY4r86vWkvq/Ock7G7gREBcTm2Wiu2O8c3+CsBnXRUHL3qOlx4HHnz1xjbVyyKDjRVCCLKLshIWG30rA8AWnVV6qgpcJvlaRVZHwjE4TiUqrdB3W+rQJJt47dxoSu1KUkZcT+TasSt7v1dRQMOe7pKX0SOXMaH/S6znQFKKauBjsQ4o84vuNcoFjDnGu6hrZCm68YkMwXHsYEVCi3ampkVlIEUeU65fo9CJpldo6oKEbVV1ZstiAjDvPH7+NJqD8jfDevDlEgqPvFqUuX3EHh/Q62wAXA2IeQvd+IdYWUsfQIeQlXUAKsam6r9+yeFYApxgD58/iuSXr8t46yMybBZC0z4ti/e9tDPz/Gn+cMwZZlU+4kzglZvf4p6qeg9C4Y297bQvRtgO2Rf9RilTMyDToLc2cAfeIdTn+n8fiB4SOPKb/nP3PDZpBN7ICjY7U5R3QJ1N11iraiOOUZCVSsrVY3IgXFn2utYrvXtYIIK6MDrfUW+y8ThNvKxsoSiJ501Dx9+Bzz1jtQh7wyZs564gFklOQWwsu0wWMwlobyo5Hh2zRJF9RSJar5wqDhPJO4bspZrrzGSWKPcM7VcnRnsP1G4Uy4iHGliQ6i/9kHStlClsid32kCOKv7Ub/2AgQ2NWR7VtA/EnVSRIuaYpENkDqf6cmG+RgBdAiFh/OM/m9xYZxkHqB+P4YSrtbk2mIRCrzIBlRRnErZ3OgA18QRnbyqWlcOtLsNiTaGzVI0lzqJu3LYfWyraBugejSSdVlNRURqYThM7+XKMKPetInIIvqi1MhGZBNP4JDl+c3ZRhbKiT0BqSLr76rpZqgN4kdzj4OEOZwVsiZTltwlkURwjcbSr5ZpIIyHgtjAwhZT0qKzYTTWVKu1rl4x5V6SECKB9IbdVAC+XYReDu0/cnlnFqV2lQKw4KrijT55x7K1V3WdNdOUh3c8icYymwrRZ2RZgWjuk4hpd9zMCYtvoy7B2m6KrAkd5Mmz9nb3NNtb43D2P4YZqWYvGZ6JIhrf4g+OinFpAcGiIev41VSAhzEFCxhNQpBhqmwa6DHZSZgUvHQdh/BjE/a4Me1AvljWbhLPj7MaK2ZZGdqYuyYCerXgm5gBoD8Y379l4J8/cFELCvVM1IJtppx2Rl2/h22LVENq2VWB2hzdt+21E9tiassStje3CqDZuZDIwQnzNprOJYew24wgl2GRp9IlGVpV05J2rWSdQJ7Qw1GTcQtrCLsimjC8LJguHUKTaCA6W9xs9ubXfyTSs1fuWDnUEaaquSv7HByub2lE0JyZdn1C29MZgBRAXRtoUtsjaFU4KhXJIqZTcsgylQ7JCUezgG9sD0YmqdHTQLmxMbRv/1feNqboXx5xNkuxuG+lGJLG0iz0C3PWxa9ezQmyuflm1fNnbHoPY7CnutoEWaNn4/LjalyGAjoVN6wi7hJ6FOI+LaG4m0hjEgT+4IllaqtTUqVkC3VhsMOAgpWRq0azJYk3raGwba8UeHA1L7OPgaLMaT5k5wFZGYpRIpIhDCU+eD3RpjE03sdJsC6PraEwUQiwcfpMbyiEi6V//5jfAEcFC/bAZFcnXH1jlcj+Y9OlM4GEgF86IYLgQ6EDVTS7+u4OOCTufTvy5Xl4b1eYwTrFgIXNeTegejHLK3T6vxAD1elQA3XWoPAD1IahTu64kfG8YWRykhl0JRF1RW+A7xDzdtuKxZ+qeMtjtlm62rHPI/Hjizr0C/uj8DNnCp0Y07/+Wsu7rJDDK1PSbr3Tj4aNeH/C4d2168rc8fNGIyM8kfDINRPlh51fSyZ3vsugn5X5eoXCnQW/u8K4LE6I3V4WCmedXyM3X75ZV50MwQG011Q25dMcaRjHcGDScGqwIKJ1uJJuLosGFB00ggNqYRXpLSfd4ELlU7fD+Tz4j6Mz0KjvQIj7tzFyf/N7jJdU113aLmfhKW+R5jkF+AyF3uVZ4QPjTC62uJuydMsfFg36bE7QmAjuXLhLgand/NgjKW9huovqOn+9RyGqXj8mLbEYOikTtVK3o/fAud+U2GfPzN6CAh7IMs1PyVNHahCp2qxwXRZjA2t5Ha0OyCvU7ABnAzCyHhY8t0NdXxWQXzI32VdYiHFp3AnmEL/JfBIMlKyS2cbmxtJR9hWHfPsg2XKqTyk1jBgfcIxBJW4hXnUiHLg7ZZsJIfxxBPsS3MhmGoSJsm+XiKNkDkObS6mhh1By6151vC0dZjZOnSMufl4InzVWlPp8n7h52NtQxY2Fxx9vF1T6utr4g0J8kKW3U+t5fMZ1kIa4nomz3wj3X+1k3Ohcct35nAPe5O671ASqe0OItvNXo37fhGTg5NP3so7zn2dMDbPIwE61nDG5yp8+0zA6v1bTiUDXZ1qcQ4pVpr2ejqeRXaDqu6BxrVV/cmVso+17ocbxEd2tFsQcRtnRVck2TAyEizl/s8928IofKVkFU6XRcuo8f8VfOoMVIf9pKuywjbo3ZE1mNGwY75pbGNovwWCvn7kM5H7YdWbjsoqDTYHt2LDtJgETgaN2O2dKs9kW/bY+ZXbIM+VHyXH/q6qjJdwosJgZb7dmMIPgb5YnmVc1xdUaL/bjdCNInl2KJ2jnbOZU3X+898Q5AFEJmmpCOzcduJjEqn2N0+HGLrsapz7vZ53LGWooKQ8elyJxGHwBmtluO8YERj/6fDpHiWDs88V+/fCTKCl0kzBgkXp4SYQVgjAq7ohN2qR9wRuSIbnyC8GYr+j65SU/DhTxsDqQSKLiEOcmBuLvZNOdtu8AHlhjwoRdtnLAsclelz3dMJXWHbGYr1+hN7LsZ1DFm49vN9MvukptwyKNcE0zIaHfdlfBEKcEz2xkp0pNZz4SQHOM9EsPlDFmcy2JVh690HosSLnhy24SbHFaLVelL7ZyY+pKBAeCHNmqQm+O4L8bsyt4ISWxYAMmILSltgPcpCpb4T4nvSIVs/ep9JBsTVQmX36PuEh+TI/A1LXeygPFZx9rR+7QyzDEYIaGiILKObo5dd6WU1ufIbfxYLLYK57RrYjuLrkyyCtIQJrIBn0ieb04IM2HC035wsNYdSzNhnqe9rzV9Z2pgHbwXQUlXlybAwdLl6nabLZ1MSfNljLGLTUqRA97NU78RLTyThZb2mRndbpZqB9XC1+4JR/mG3IHF7x3rPcq9bviEoZbWhBMFbXFrEUnKNSI9A9pl7zdLRPvYFQRRAu6wN5vXVsedKudoe1o8x7WZ+TaEOYY0lpKNhArTpHx1zeKCUT9tI/IpT93FnAtaEam1WAYIgVfnSIS0yYn3brMZN0BNu/Dh2LqDww3dXRbqwNUNxt3DtmxCuNrupLM1TlbFtWnGSM2NY5Qt64sbgTfP0e6mGEo69mpaPRhVUleZ7dRs8eW+w5Hy5KXhYXOLg7LFcjr1qZQyufKjyX1QHOyGYFUm8iU6kjs0ndBzBXZIbJkYcZOmKz7JEm/K8p1ZG9Fm9UuqB94zwZZNq+w+wnG+MJ6WTw9//Td/7dEZBZVeqo4esJBWd6C5KbtNjdQDFqCToEq3GFBiAJnBzcR8ykM1doLtE4RQnbasARD5rimcxw36luZALj39SjWvfehjwqu7GvrMGaQqEeMg8L2U1jx1l831sDQqiMDKnxpIp9XQZ/fd0UT9kE+c+R2Az17u/C1skugX6wfug6eLTux+MwySnE9hROxcUtktUkekzx2iNOB430Kii23uK9uMZDt8DjyRlB++4DyptywvgS4oY2H/aPXhKPdcoel/4wGZ0Lglt5Qg+9m9Wzdtq8/Ciib90jSlwwnZYXe4G+EA6hO6D/pFbds4f7lbFhaLKWjqr2MtH6OuSqtpuocLQO9WawW1yaq6k0hUd7u3u4DBBZaYduYD4XaIHeTVmKBSGcoz9pqf07yQGcqGhCPJ8uEtxbAHdDGOlaxbLHTQHBaIjAOqGBDuCYDoGze8+GN7GahFDU/F/JcOJkshYjrE3/NbqDYc69jD03t/V+fWlI6dNmKr2TfvoAJZnEG0Gcv/TEBAvEeqozf3jLNi9eJ74a5pyuW4IYasZHLtM4Xc6AHrszYlJDNmzal3aVacTb31qEXX+wGeONYsKjt9FhnH15+5b+4sCf3AAEtxsI4TWrMKxYpet/1h391GywoZ2DX2YPhyg86GsGnHJt5oAnp+q37xMuAWvDNbm8iZN7vq1oMv8gNhEtQGBaYRULbK5KBQr3IfwVq1BwP6vGHalPkeEd9zgNykVJZPN45FANeY5h2LYfPAxs0ou2d7f6IsCXSpLputBnku/XNC7ckjOZY1A6k1yRoU22a582RunjLFaN/Sj13y+rpjKXhCK7Zp8KmQQnWkB/o+QsgfAGPL4ACkcRPqJZCMFe2VXrKOKMkL6Mg98d8qsb+J7BlB8OEp2OvsT6hpKvpm632mAfe/vY04lWkurcjEoiwtLmeFw8dwiq7HLHLOG0tuKPlwvufYUwWM/6p+jGsYA8R1d6/HJtSU0vS52wEnkCjQcG1b1sG5c0KxZGwdDCOuU7PNWYh62xLN4MvNBrisLtJWOwu8IimG9p1sKn/NfDBFqL/532y3e5u7OOlWRop5d4B3GylXktdgNEPcduu1+/B7kjjy6TG/TEfm9wAWaWJ3NJkxmmgk3/8JLluaqnfEhWl99nsi3AujmCn1wCUAVogo3OGzOYKVGDzZnXU6TcqgTC2ZIjy2BWCjUa5KbM9ajGMUpNqnpuS7kbSnLVqINuQOiypW1KXb1VEcyhPZTgAu1tD4FafU+b84pGNIyXwJzZFBq1tbVkTdoCYYKQZnpUAmc7krj0HMIbcH0A6+fR+X8Uy92kOe7m68t6BNeVsdPvXI9REEe2qeCaTeZvJZu9rQ9F+qJibP3iDpeomudsHXMAm/THIkI+HXrH0M+VALKLiF7s4WwSimcuXcMnyXf/ap3kO/TIelj/1ZFhQSZm6PvSX28ozDUnk389/8akk6pYm+rdj5KmlDAHX/H+EzFXVG/2fod+R0eBdmmG9VdlrznxHvUbdt4GVkbWiaWMbnbTyIc+pb7YyXCliYVNKw3RSquH5jacEegup7E31Elu4q1+Mh/jfyOJtSlambcSPbKdGB1YXNYZwtLHofX67LMqyx6ngYgEjKgt3Zy6ZSdWiOYlqE04CpX+NPg3W8GRmTYSiXCstWCe+a1jGN+W2EPUAVbZhvqZyUwjTbVVZ2y5Peg3KSXcWzyXa2TXy/mouf1svZ7i/HWPKMnNXE15b8EjA2CHQ847XthNDnxWmRAe3Z1S9Z8vl7ztO5Owvk8LYAn88zWY2R5mSe92Om9gPd5RoibzgXbUWD8wnMNZR8YNxhBVlgAt62jkMi3+nPMwrq6iIs1WM3Ek8Ii2mcS+p6fmUzdxriKfeHNklMQyNIMdGJ1266CCFpPmhV116h4f6B7wCQHjcyalQXcXtbkudqQdu8OIatVTgXhdSWZF/gK+o7g1rQMR8/6qo65I/c+HNlNfT9yft2euVqcSo4M09cOiCIOW1Vt/tVQe45u+AuInfmLcGZDtKVCtXmapHhmm3GCywa9y75C1HVY2HSMm6W3g9nKmFm9LvHFcPgT2Sn5onu+ebYilz1lKr1CN1aTxStKgp2wxbdRtLrwEIw48vfDWVR74BjfdFoWvE8jafHnzSOIWKu4RpQA8cF2NXVm+O6PH/Dzsw+o3kixWHNGe08aezUH/bb41i9vHDXPNODhamFd/Ujqtw1n7v1jXcAlZmW3dn376Fu6qvlR+rjEz+SUImrd4lEn7XdJgD9yBOxHvQNJY29RyhXAlzV9LA0xyGGakzyNuWhCksiXkMcQEKM8mSSIMeUQEE7yIaWZy9jAUSywm5k78tizcBWvLivs4+fUXORjfv2WbmipweNXAdaS163z+MoMn/aYkhbMP2U4EZpUEIxrlZsZ7DBPmoE9LFS3zoonXYbfTF4ZOI9+oB1rfAT0voWlgkzUl4OJrhMgXJQA41dS6jvW8LaJcd6BegDXvWNpuOSTFVWpH2AjizV2np71t+sVPUso+2axOdH27UrffOQtp/5Ux82Pq4SntB4vfW89cScKkZ0i27I7AXR8xKx+fwv6fi7v81B7kT53fJkQ+OlzGTsSJO9dDbV8Gki59bhPlYmqk2cAJ14pCTfDwQDy3v+urD19zFiUt2pXWSCJJZqHjp/5ZJYtZwdSWR8ZOEpi9rqCUsH8DVpuUcZ9A5znvjeDio9k1ABCLWxqvFOkVsMwxg7VvLQAQup7cEPQLTBucP0zaPhN7JDpNLOssJYxkXY4qzoE/w4X9I6NhOZzGhbq3AYPahk5qmSTjhimHa2vd7kHgorRhtqNZO3Rp73AoCJ2ZbMA67lO6plB+AzjYknmBo+fCPIrXFVTrQk4ySK/d1S6Hp9sSCJu9vV2oTf5qF5TnuRZEwzKRnBceHBZYxf1xv60Nbm6ACLMJNn89/6TXSueto+1Y/YZ+o1W6ZcDA7umiPAOElZpkdAt2r/TFAyL63SpC0ltRxOCAczlZaN802D7TPbmATjppxkSJ6xG3jCPDlMsBYmYvWjnpjoqdCdTG+ddDyH5cR1HQTwsKzJFKTNrVa794MORqU7OS1XLkRHwKHljo8Dt7iyibiRRRmtwtnjARM00t3ugCqKZhQyKbQgVrtt4W6sLBfxBXZRHxwvMTWriD9H8TG1pt2NjTOBp0KrcmpE2YuAfvWCnHnVM37NeDcphiydCtltPy7lDZOL9L0EpqI+5K5n4uK0tpCq4UoOi/TCjEf1ObmvPIocy9m2/Fe4Hc69/fSiJ+AIQkCcr6TaXSzjTTp9tkyQCHbxsutxriNDIHTRhzMi0yhfvClkpp1unBsl61JmF+GQDXiXBNmc+zByTF7MuSML83628dqSvTeSWb8bSLSGBQWz7AhoKuFObK25tz9QbQ1X4VqE6YUDKDYOvDUgScvGsXxC5G3CHklrqkeRB3aLAYzU/QxIpXHad3VLTn8wuIcoNrCcHO2+CpT+booZBsLQtlKT5r1RsTbFeJ1ANmWzXIiu4WLrWM82t+1bpMzJjxQ5JFwhm4wkvedq3kQPD3/9v/rfMtH9FJpYpOR4c6IMVb1v9nOhbwr54Da0T+EPb3Mix6Nkej0qiF99fv36nfAPb37C88MT37aulwAhEZBYaKSg9PSzo3WhXh0PVk74J6gNq9xaQQNm2XBnFUBxXO0K5c81Gn4ElVtRZCFSO5fgizOQsW238ADKM47y2esj91VLOUn2w893AHhphVul0DnEAamlWV2EyfVYXRHfyOoIcseiPBmnX1ZNVZVnNgjuIyDB22D41oejVvn518gzFZ7eMr1u7m1cOS62RB4uwTz2y08Myz07rO5vpTXqrfKvjfrnvyD2/GpEGWtKuE9qlpEF1nq2t9T69e5Ymfd9qdznOFEwttkWiT+RnF8bbaU///3m/W8BYaH9GJaoZiBPKdmommDtY1cEagz44U0+HcunzH2Mq9w+cb7hlk0j39RnqXGjpcLfPdAT5ZWd9WRxDXa8wnSIAivp7MFHPYLZ7s2QxB6iBue4yqqSSdia3hPClSXej/Kj31F7dNKVlZ9omyE9GTamudwLU79CsD1J5nQ3vaP0HiNttTOBOVco1tddPd8BbZAVKQY9PJITS2+7fMnGzPna8UfrttB+M1lBR297p0HnC4n4TRXt9W5nzQnONZot58BCuflQlePo6c3bf0SaMVoDV4eT3ge21vfb1iGG7Lh5ThKcgnGMqF337CHU1Tbg8JT0WLmcO/exseEq5s5fOqRyH7XQVP5iNMEsjnONSDIDM7/O+tU+kJWz7nKaCfqAy7t2UTTVbtuy7Mc0/eI8OMzSuT4DEU0yyfUEa52VuoEocF+KHD1ct5obrWi1TSRulTB1l1iAiaVFvV4F5WyWFqB/eSYq4ixDA+Qx533mc0Fud6OB7XabmSPV8b21DnLsxDT1U3et4sTLTdhaTXE8zqWSLR+qYA98xmMjJQZ9R6K3de5uyb6vsa6Vp1jsNBctvhDIlQ6+OvQ4TmCOJrqFYEoA5t1d/Qu/rWNExvxZlTT3kGylwk8+rM73kKVJ76WX40y9CQsxDd4fUKGnfi36rDlf69erCmaD1EF++it9sSnrGL8yIZE9xWuIy2IZVm05kmB9l/IIz/VDPUsz7PleWc5nWj7bo/bq5ad/K/96CpA2TqqSBBBnvuJ3FipAYDUvkBhVhXYZElwwqN5BrIZlUithJNo/A2CqsCBZF+m2UeHMhIwyEtdchAiCjFbwQU2J1bYVzyaZanjWaNAepb2ohT1S7al6q8qApzIIwfZ62b28c9aAeaKLo69ZCAJZu04C1KpMrK8SvuxkWCCb2M92HAlsAuHmrP6G9hb2mS606mSu71YvGGr7zay68bY4l6osJNCLJdnze3GJPG5MWdVltWrL/o3fAWD2aotFlAusWoe2KOXPDV7rLqmhQ3SgcONIjdM43pHpyMjTPEUg4QDK1tPnRroTpz52VXHwx7i2lrU3JCPlyG7tVEoQ/pLSqCludTn3rg2197wH16RYCRR4SutU1d5VgdMam6RCTWl6bo9yD1kAljUThXxgF5UgxpfnTE0coZsnhoMqnnZUMVeHugdjU2g8xVsJenemtfwCmfxtigiahsSFaoOMsivRuTyZN+JmP3RTiacFDBNSnStBpcgYerwSnGaCQFIOUzjGflGeakG08Gb8zYl/JhvYzGBbyVesq4x3R5DiFIysd7x9DkdHcNgbnhnb8oiGOYSt/AP3IjvEk8a4mErcBE3dh+BJi+2ISCuD49IGoVjlQCM6hNFpI3tS6L8K7sB4AmRAFtMLNVuvboYyNonhFImHjFnHnJMut/nOTobG9LT0xw4bn2x6btYUTRhnmmoP21kvxXm7FUXiiAlhbWpsbjM69KqEDnNDS2wNZhk8BGtQF/RQ8xjbZo5H0eyBpF5eIdQL+XZuXXzEKrCIXW+7OEUR8bq7xzTrkFQpg6Nd672Xanhi0GDzcJ+BrTIFIvr2g72kKFIUoa1uC2nDiP2aDzjhj7QVlxkBSbK2Q2OJn6/FaDfl2gobnCgSd0bR+HcAHh50X1Nb7ov0eGg/Pbfl9yp5ijwALuwN7N/T5RcQ2ZDPvbH0SEIp5JE8qMoTbPI2QH737sl3faTz5ihVkCwb6dOiGPELak8feF6+PikFVa4Vy2rtUDjjxcEOo2wWOp6W4CSuJAmQUKglJI8ZmPUux+A32OJTbT1ZKORDdkC9ouF4ecCN1kB/mvnh96T+w29Jft0jOdA47jo60puo05cDdDppnPImbU1pcGPhGFaXTxwvNMUyYQxjbMKrWQfAc+aJJ74rBL1rpNnFnR7PAu1MM0RHn4lcsrNe464bHvns8v76OHVmY02NmpgTX0VWhHqtTxi+01AuAjiViUokM/9B647LbDFIE11vO1HLCGbkEUo0Vuo0x2N+ubNHzUck72Kh0F86NDaWt7Qa2cVRizCIhGGoVWCchxTsqrVl7dsvR+kWc1WhNkKjDEsd6WVrGWKhe8VovkA0rGS4vo8kWZsUQ6EOrdVocDiX3DUp8etyVNMs0yBGvYNNektiw/2ebozrXcG+Q7YxPl+tOEhfEnz0uHoW+QVZIMVzoX+d6Bn7FcPrqIw6R8VJ4tCFcdjIaFe5oQUZeWLAqACHdwDmvdyYDFhYbXEV4VZGCZ8h1dwAVZ0w3N7JZDLNvX7LgeTIc425kbKM3jk8BvuLiLH2Kfy237VeuGvL+aGD1jkAXwhsK8xE1SPVJ18v1Po1eplenfU2uzvVhHJ593TC4VlYup75K1FwDcEONv2Cu3fc962NkHPS8FlEq7z21ibgWt8a/ofuJ8ILoud0hk/Q6o0mRL8DsFOtC6R0OpdWTB6vLzt01eV4qFWhWbvK24KeamO2xY4sV4XOqDXK5YX/sfb3FoaiK6OWYOoVwLndcTFc0vmyyUO3PeEqQ9lI7X31ygR55JqaPq8o7aAjEVbttMSi3vh4VJfKDlU8mz5gU7i9iivZ0pZxoqAsOF+SZZNXS9u7RLobnwnMl3w5ySs+OkpE7hJ7/aVkEGiBBZEq5drQuoemMmbrmtur8MKOO/7gmZjjtJF2indA5QGbNLJHV6LalRz8Tu3G6FIZC3fQzlcNCMPrDSQ9nEZqXTas24e9bMfRQfGahuLpkODJIPJibkIrlrhQIBPmSo10VqxyuSZ0hj+S2nXTwpYtm2+oiV72+X8yG15rZ2DVqmD9mrVNe+odSdBO11BZQMYQa6/ydhOoN+eXxiZzHSIOIb0OMV0MypkaId7LnaEY74luoxpJV7Sn2s24J7JwWt70BMimB6hJxIQZnKSpr9K5UUdsdeK3Q0HHygnEVnjL0bHROv1Hal0VcJt/nNgAS0tUGU4J8n/nQDKMqWRYj34Gcna+t6kDtE+5rRRJZPOVsRwLLS+rihiSyrWrKdyZjjuGW88auDG26N7eEV0p46lceNk2SoKKwdN+LJ/jaQO6fxc3TK+shOiKbjSqjD71XeIBV2iGWDFxTmViMWhvIWBe16ZKjEayZhMQ5nT7WiYDXkSlvN0JO05utUjCv8U+1eVny4i0A8B8B9H+lu1AdNcwqPh9weIEornHN3Uqgw2nRAtuUS8sCSyoPcgiQaQzmla2vCl0C9yN7tdv7SbcXZXzBadQloHDWfYAK0fmUME08nRSGcP7kXyTBu5vMrgF7/apZ4Uzc1c9PLLFnzuaYrc9M2/5cJ9fHyhOzmzIWJV3+Qpuk8ZYJ2VBw+K1/GAouK+C0FsBePBDFqqQuN/hZFIPnXli0TIbZOYjIuxKGhoa/m8jAPpDwl+xbVclTRpL25yKDXHSpBm92DtqBPqb/6pKGxgqFLT895vf/I2q1JN9JTMrKIQx20pglvuHqNyfaFsuomQeNhzUhlV59D1RqbhPyUu+JgCQBHUMmz1KbeXcFWtVRIa28c2IMuOUV0LNDva0hWdKaff6gPGlzZ2Ll5IgtCpmqqribWCjKcXrd8oH4Ox832XzdkFz9jQhDNZ8Lkrk4AuXARysfYWyiev+2fauUe55bzZTNXNcTRxHtoG6ss0+P+SpXsUGZLLCdzA0d+bVdEd82tAs4NjWlpKapkbolggxmwx77WEC6SEFappgeAIs9NbYYklUmYCN8GzPPJTo1nPjss+vEOj9CnynjwPYu3xU8YW5E/OAY95aiXuLaBNcRJekjPEOlnB8pC5ibiV0HsuPjbvwsd8BzN7aaXUl00ItvI6H6ieu81wyz8w9sLbf94k0kltsyCn7QCCiEw7RvtW8AHUfOcy75bfV41cuTpVebO38FEFC8vsP+j3p+LuBID5zfltoL6MvnV6aJRKpNJM18m0osaqaVn3W0BDlvdb8jkEPmDlBBt8uWpK9qVB5nHN49yyLYdtpP+/pbTLT2+UuvK6369FK8KrttbhrspzLJ5vXoJZ+qysnC+77htJcOY/YJZm2fY3zLVwKfHDrK3evn/HXXfm2vf0/Y3KOKQuDDOoT+X+nTtYJ4mblne87PcN/rZokXaslHYQCnPoteoXfHZ1podTHVlYZALLsxYx94285r4+IcE15ZbbJgtsEVPFfm72fQlBzRwjcLHPGXgTQmQurZr3YM3b6sJee9w0wZ0+/TwKWa4GcqMaTs83bhujMd2AvmZ1OVMxfGiDzRocqhkAwFRrn7UB+Vqod/VN9LzHvjWeK5veLOHLsWvteOL/qHYA336m1/RJweHoJtKOsbreKPvTbNTFkXJIPNQ48IRMItY3I+GpXIxrANfUImNZa8oFING/aAtZmy1RXKdvpADRYegAWZGrRq7kz7fUgI5mjPFYSjjm1G7NoF2a8vqJisgynuGmF58aJBO0nnVyI1FYbt0rOItpUqVasagyoRBXyZlGS2gm26xQyM2GXjpowj6zEZZ5gMocm2+ModmM6lWGmexxu7OWFA3tAyGAq8GYT/pq5equU2P2Lg46q5o5sMdHfMEY0zdBUaWkACYbDJP8ljU24Lkt7ynBWwGMybiJJk/o5X5IN9x73btehNGlsutX7WGQ0RbnxJqXVnyL2rupmSBQC3WjagfcxMX/LGcp9QSnW1S3HfzBp0/v7IkkvspRXhE71zmb31bsQjqRMMtnuOmtiMxtl7xrZ3c3Bg1AH3fg9O2FGTV9UPTaP6D3so6ZaIQpsAKfmyP+4lY6792bPqEvUmwNkivfLd/o+c8NLfkMrLefot+Nj8g9r/dkX9UwMV+4UQd1R3oiNVnHo3w1qCb6Nfdm55l54Up4U95rfEFhTbIls0Xm/DVxUcTPiWlTR0d2Rq3Lqfqb1AML2RyqH9eCTNa2PzyBaneVoQp40t/6PE9ZEdaSLkyvlPfeSF7ytgqTUkTPDaGmt5OpcQEfn91rCijtlYWLeHq8MLx2MkI/jTGbHHC9241u65dMCQQ7OojPd4hyeTLzuuteBZgn6wGWzkp+iusHh11A06gD1ufrXffPKa50F1wWpcIsLksS6ZGlflIXcNDKK3SyMpXSHFQHX53GtFwCGIhQIcY0jUyOJ2fEFNy4G9XFz83lZhiBseDWyrwL5zKtUPyO39cObL4TvRkMdCKazBaoSMlOzHHi77bw+GaxvI+iTfPpdTG1G9qelz/kojvVZ6gj6E8Z/X81tp675uTTxsimILY+KGSHRdmOvt+xVe+aL0uMsmS+5urX1uAnnL7wGOd5v0ZXyViQ8lf6PS2mYAa7R6b77YrnvfETqXElrJHhV0ywyJKbr0gJLEnIAbQOD5T7QaPEJHNiFYN8l1WD8WB0rLHIQHHk5+oTRy91Ws4eITXG2V7XgskXN3fwigSTldQUrkcVw1Db8Q0jFjpJDl7gwnxUyRWAGHAftpoWC9v3a8rJ2sVLZTE9+enE95T13L6AsdWLHwwjEpToMJfr0a+jz3k7DKt/Lb2oxKTtEx6dk7PD4iISgE/iOuKnvJmWYjsThMGR6Js1KVT7de8N2JdgiR73i2rglZ2w8Qt5X6JUukL4rXM+TccY6cvAdXRzsg4uktjWNbAqqfc4QNHbt2+/Wjak2Q6EJ0/cp1/clorGC6liOJACVuyT1E/sgX6zsVPfAwpg/udpQ6+67IPVebiVKMeqXejVIwOMkNGptwUZTfc2lw/GAK9dxOoahcnnzzpI9dpArwpac9+G0tII5IrYxjddWx09sdp9BPVfGpjp97wgt0P3AOo7LfdyfVTnbfv5T5LWeDKS7UBnTc+hXBK2b7xDmtw6E0FhyFmAb0GY47M9Vxs9iuIFLZZiLboAa4zKhrYP3g575Q23Oz6Xed6997t/uzvWzT5Ou7xbid/fjpmzCcyqPwGrpHpfOGjqkfj76o5WrrEuzEh5GVibHzeOrJ78dpS+03ON0oVMOsaNbpvFlWGbRu3ipVaCA6G1oUtNllKIPCYu09V5znnRHXEZ8C9EnzGBsyhLjtx25rci1JSzvfxfuxoWZ2Yrjlsqg7l+b4endb1HrCordacPOogr6pL7TjFU/oy+xiwcOonh6+p6qfl8lfYXFw/tG363le5ZquG0DtB2Y4iapKmKaqMzSedM+ubMxLRNgFkuaDqVJEVuINBdmaoe6ciKS+S9oEmWJ+cscsYML25SShS29oix2WE9bcW1Ss3Y8m7yqE/3E3Pm64S6SWxe3rM9IEs8B8DxjdXI6fTC9ajhwZ7IyLVC8xpHrujbW/E3ONeKyyQy/E0vEoBq4cm9/DgQUU4+jSoMjWqfXDgGkEgrmBHPAJt6BiAOXVW92vy51GC0RIEnZBIdq2CG1Z+lQZ+dS5mZESH9Qs7Ev43QzgbpXBqiw4TZ7LC+C6VbBYqNk1xxvjsO+IjnIiGSCCgCJw57m0cIGMZuyEM10MhBRkJZfhlGaDXbieK45blOh1Np7M3TT0VQW+Dnuky7Bq0xl56h6ds5hbNe4l6oRUu/Vqaei8vi/eCzsHGZ+qcQm8FPAt02DM99kgqG22Krc+xVVQ6q1oC24hkUa+r0cq12o+un/wJ6pdBZ2iGSITT4zYA1B9Y8ZHv/YVq1MdzbVJbV+wQewDFqJa28IWgjFKEp/sRv4he5WJPQYbORTvfUZ1V7esr4mzld15oL6KJrgj+KJ/yhefT3Ik4RLqh7fQA5W39BIOONgKjcUAvp/xX8GlljdSO2sv+H7RsFhOp9t5ez0vxE3YXTWBDjpdgYpW7t3p2XN/ux+B+/1ZXQtXXpqffY/Si9iV8iEujjVSuwHU+kjvdDZugD4zeXM4rw0kTD/D262xrJiLW9Os9bFle+9G3YxyqtD4Vx0m4+bavdiQqPSFw9XedkZHn7zm9/QJry4rwo7JgYBa0/p3lPXRyq4XNOzGjHZLdVsmG3GxCTxkoXcTpV2ftc2F37ioWqTqeGI2BKDg2K0klrkiNonVtqC8tWep5REFarVDRGwotq8mritBp4KnXV47j7O9Uou9015zyH3jy12UMSxbfUuxI+byFV+9e3pzUeePHB/y0WBE0EI/rtBE5teWSqQD8Sz6fVa3+9y5Ok3m8Iw4gTtpwzVr+4FU89o5xV2dya0DK6eiZRcG+su97AQSf/KINSA2Y07maQdPx5QMO7hgGuaCVrDEq5Pf+4bgSaoewyq632ALx44osIdNpKvzQ3G3Oal235nYPCm4TtnIkhPIeEulAS5a9K/qCqoPVVpg+qnTeAY3n5uz08+qOC0RI87+sngBsbG+nMhFRtIRabSDXnvBlofetKftrpvwWj6OV0P213zEJwM3FxWHZ77pEbHMNMggCnDlif2pH64I2icBmlSxz11gvaY+nci1SsyA6i6bJ6bnkkar3vF0GOhY1C2fRSMSYFyjKTRmKO9WpWos61xyirqei8iUQp4uS0e1DVXlSutJzz1nPKeafh0bApQv6B56eIsTEBnadprlI/647qRXq/y1upWUuse43h3q1/fLEzGehvSsnPKSMrTWnVpoeZkOxOpO8oefG31ie26r3zL79OTx+LpPV/9X8+ql4+Zg83G3plYq7IFtT7kdwwCduCZOTkqb3LSERe+g+59ib/H2j5nDkcDrjKfmRO+RJYEBXhTDqE0N1EVOnIAysrdcTzGeuPoKHB8FLZKl6Y8QlcLLAcKHdrjzhGtJ+X9sLCp1Tkov/bQShiaoGWTIwY6p4hRVZDVFqDGgOyy8GpbM7bnv3RGltULu1DOs4ZOaOffz8frMD2LCFMr/XFWh0kErhBXZhyUT3mKoEfQ8ZEJnw7RduTVO0YmZCqP20JKTsKcBvCrZpaj2U3rPN+y+r15yvMk9SRAGBVtWA/mdExbHCbMrIfzngOpSd+mFzbB6jts6wxOVZuZAnB/19EkpeR1UdGhgGw6zA9b1vBkL/EQLquTYDyFaR+UsiwyR0wd6OPvscpVWcG8W7P6FIJdWFYK9Qoq3+XfGZDWvMjvABhWiJq32DLFHUpfbeSaA1PGXRwcLVB1CYeltZjGPANRQTlzYuBBS9osdVERbdlZugIGgrFtKSpcqhL6LQVHmXYjyWdt8eUG0jAtvoZd7AHdACUQja+B7ETFDeZKdsF/KQo/nm9oT/jRTwWrE+iqSXjP4tyxokpfKusMexhrx6w4Ck4h4McIFUDVFsUjn7fJk55bD0qPqDKe6HgOajNXxUy1BjiSJg7uXMJiRJt7H8lBxHS1+MCw0BbfAhBLapx8dWaKBImr0sdbmsC8OmCdBqPBkQWFoOEE3abY02/rKAIUIFhTAUJnFEULik+7QRt6KGyFrbc2bYj7kpEWRxMN3cTW9rZDrVAto7BlyoVTbZPbztCrEWmt97EyNkU4cbpwAzqaLMB1LSRHqh0ZWvzQO/rIZz3pyPI9HCMGWgO3YAfa8I6oUWuUUR28DPZU0WTK7BDc9Z4ynmQGn5yFYJ+EQxnkJX4w31bBTTkkKap6/ke0O9rrntnqjmT0LqrDPJHY8z88NyWODOlhwtgyD6NVagbFTvUcqvhjM4MVTSGhlUmyQSUxPoJiNHVBahcNDI4k1GqZc8zavQkCxl41Q8YK4R9nO6T1mjJeV2jXqPRroY5WS969CcvIc3xFeO6m2oMbs+Ff6AsR8Ax9nWVEtAyiCqXr1tainZnb4AmgBNqNqAiaeeSBTs9MHuxYp1Jl8DXvaZSg+Vuv2Zlhqz5VN2h5HWaKgl0O1dJ/Dihte2lBioinXr1YHKFQmYWm4doXdLhoW7xhhhcVKdGWeI4EHHhsuemqkgB8rKtmM1+RhsAqSRcF1s5BZQKmTW1mF05V6/Cx9cIhJA405RezbO1cLciF5NIfxx19AdmFJ7vmnAxsOFd3VwKPo0pYkdlXTFVtUirTlLbfAfj8l+Dn9RN2MTnWaLE5BPrhFwDNyBD0tBqH9ieTcYyj3vSyvRdVRIlsBxgYcdskMobiBliQuFp4ESccRPeMDC9lZfIEXRzVGUw2YV7S9CiYrwsxJagN3rrZ76BTfTCrcpfPr8r6AFz4X1jLUVXG6RtpkXd+FUGHWS7Nq1/1rhetSTkMDvZRn67rO+grGl5DiKcWUuaUwYyunrMrHE/b9TxDwfClg/QwzNJnLkgAxCjcE2hvVmAssXd6ycHvjFr/8LDfeU3oeQdAakLbyczUtMc9xH1opJ6A7LD8hmonlNYvIC9XBhw47ZVEgb0VATv9ebMX/Fe4ZA1mfqVb9+4e9G4b0BCpxosu/WKq3jl50u+doX37kOOx0hg06bIPFbku83ddWHXF8OnRDxLgNoPegUHIcGhe8I+wVFTM7ka5l9yKqFTqOdqKQfGobrtoXHXvHLjV1bzdLVfR7e29bu3OPFRxems9gO5MWXuXIdcoqZWFnikjEw+A+pnZaUHlwGt7nKW/t2WsQmGv5XJCURsGD0+maBI3GRwkFaZFJqfdepA8BgfUCw3GlXH7ZRtZ8QAm8o2nP4sMr5WksuPdcPbrGU5XHjl3rE5FvodGssHpSGee5yirJNlNnFWJpXODVWg8mk7xOYiA8W514FVWSGqZLjPdQgBhWj7K6LS78gckjAfwiAjloNkaowjIZQZDoPQiaAHv+Tb9Zn8BTNchmDkPCu/JVZycSkbuJEqzIrRyHCtA41HmMs+l1h+vIRpr5np57d5c8UtGpGzOAJVEQrNVSC1HlBkst7MozjRldrkb9lz+c6qaWEw1hTvgGNQBOqWZIhf5tkPcT9hQPL3RW9x+9nzSZaPuRHzEKh6iaX1M0JC29M4HJMmiOa4qvjFMaEdAQsfb+DXPCM4k1dYufsYhOWWDC6W9eRSGnUgQk/MGBrzaYJw6rNwv7RJ5XDW/J0+coDgsSSaBs7cMR8WkHxVNH8Vrb4QTWvAOzgUtmt01tQJD4EGUMkijqr6oTJCCALfmverOE2YhI0xFZXiSFC/j9N2/tRRW6ZUX4yhTi2ooaZbSCHAyAiwMI7Tq3cdQbOGo6tTYA5b6qw0ib723uwq9VNoxP+TLnB0b/hdi1S6FS73XgGqM8X3JNsKdM0LZ6L/rEZzKUE6pSm3CaUtZouNuqVZOjBhLVRZo6s7PkeoXtja/GSqGPGOYbmeQ7NkzKOMV3TL2PJkBTiwseg4UsGkrjQLrzS+NBXNK91Mz4tQxSN+qtEByKJKKZMNY3BBCxRuvuiDIMMd74FGlXpNgTyvOdmDglNGorIo1hrKsyxcqFTo/ECIWaul05XCNtiwZXT5cA25kHSRmUAGlcuPjqExgRQGP2FV5DOJrXkj5NYYBKgLTMqAXB4lSYGJlEJxGqOGQf5zawiFLq48APj7ywk+DpNOVMKprffToOjpbicJBiUabXhAYqr3jzs8zyzbj3skBuWUmtggJGZ5ntqVXEN6IKHXrRizlAhf2LAmgTQoUPqXIqccEWF1vqGM1Jg43MXsG23rzuFVDTM6zpULylYfKzgTR7gcK2jj2xTFo6wgwbBip4QNRVY8WstdvGeHX4xtZgblJdAohKsemKnvX1zDvNl3P3qUGAB5v3fG0KJlr1arpNW2PlXXDpkp5LxtH6CCZtWwpR42gRNq1q1FbiaJzXQQO2qgyWbvmqBkL+biwhSSHfoLoTcZJ6SS2o7PjHeo6zjyBF76ptN/h3dplCbUDLsM0J2T1tAHx6NbOYrvCNHQLwtWZDQKEWgxbpdYu9yUjDpOzHFc78apXrliwPEJMF7mC2yD0dgSZ/7PSUa22fPEfNGLvGgkoMKlmxOIcYMNRthMvuabi09WQFof33fBcJE4CMcQxD37ADhQ66aVtLxbH3BRMT0WDw2qbt5jZlaMmwAEm4FPaBbgQAHBM3oP0f5QFEWv/Z8/RpWyzI5/Yt1/q1lqiKqMCcP4DxlsGDXyCM9ItZLXBHUt2WLWGPa6Jw1IiMBcVvOqRmSRJjqKC52AefPulpTqbogbsf8S5hsPiQIwE1f+F7/hCU4hndwkopYAy1P9ymYb5pWoM3A/vqunPFUmDUHEywNhHsBlJBsQgZx+dRJlG1F3t+A2dInT+FLVeevDdc1zgp149O1v+jNp87hCQgRXPkMlMn+zXhv3E6Xbw6MwOYm1pLMjSqKaRdv8E0n+ufrwdCFCdzY2s6SGLxJOyKLy7lYcon5Puz/6WRVTLXL8ErMbTlz9V+cA30BXV5mI+mddzM+plf1V7DeZoV8NfzolAEq8HCiiz5iY7jlOhE/9ho4sOgULXkCLTTNA1Je8tiCZHDENCyjPfgOrPm6cZkw8Wix0OVTLjeMCr7TFTqdcSn3Wr246EyWUxz3Qyh/PpQnyMp3umyF3/uaJNzCrrmQz6xgXufR2sOenb2NzM1nW444gXd00gk7CLB36Kr/pDzV2KFkaHrSaDqrpKO4qBk6I2LanUg2SK3LnDOiq5qc8N/kc/bgtzcEqy8E9v9AlA3UblLQKZWELM0AHrzTXeRhBG9XotwzCp8fTwGTbl2q8gsOHOLIn7atp0wvERI12gk2bCSVwRoV8gsJJ4RRElWhkao9JxuO2xkeS4mYyRYmMX47TG7umN5qF8/MzYZLMhMmLxLM1nTxEJEUoPjXoApoJu+zjyGigRvdTGaxs33IKFShjTo+HOiDB+TrBhGKiikLpHaUjmoNAoQcLoP0wbjla20dkYrE1abVv81nAgb5PCpOng7SXdd/WAqMalTBzaVGpI42pCJ+UP65PlQdIhJYpU0zUlIKU+8exfgH73Dzl+PV7Oc0alrX1cd/7ruMubS56azlTmmKMiNpvaoec5fpl+Fa4ajaQnnigRVIiNtxI7/sUKhDYGkp3Nmq11RqhQR0sUBls5NKtSM1gHuGJmwnBnUlbwpzRKRTzS2uxirLJDsK6dLuiSGBoDyp4t9DAbfhxCtaHWn4/eJhSGrftXQSEMy8xxZ8lgFdGVqVab9ChtvMiFifkc/JPOiWWBZQXH3quAp1B12uPieNr/6kw7LXuangO0k2cM8cA8YRVFr1JFkJZ47BFlq8DdOazFxuLpxdZ9cOeEImmQ2TR1jhnoWGynX0lFx6bAbIaBatVXH7OKMGeizHzCobO+ayMwdZsIDIn74qQZR0QmBCMJDiqMkiONzqrgEmfIRdAupNRtPXpXibCJrHNl7Xg5++MGT6B0FIdNFXdEJWdxfGaBII2MjFNnOxd0B0v31mQquuGuOG7xAHEXhK+tMsgASSLX2ojGnKqLFpeYSj5mxuEFSM4jHy0Lv0/KeSrU+fsqB4rYw2wHYjiozXgsbGF8Y1n9enCDrWE4GnIFcLDDE3/0TGUch740kraTlrMnHdlmwKudfNBoxFQl0FHdNI0fdQtuHXpatHqLCFGGxZWFeE2t4lBQ9HuCvQ0PxJFwItxVJ8zRYvGP/Hn8wKoynqZyQkj+ym2ifyVe3c8RkohXAEV02xEf00wSeVjwzC+3NWj5hJwAMs/4clQX3kugw0OCSTvh+NOHWBK6FE6sJy4NlgGgHOP6hyQBqGpL2IAAri0IH+CR2AwSHK+tJy6LQRYJedJ/VvYOL3sI4sbWeq9aOFzqTwuzYzaGmBD7X3vyugMDAltpRziIxGQxINcwVwSif9S1AUK9nJKAVTYrJkYsnsD1Zyt2koiF6E0MkZOHX7sRJK8P9HkiYSzN1+tlaCZ2qqivUNlR9dSU0uEXQpEDTBQJAof2WTqZq+2N+YOapLUQXentCL4WxAp81RxQ6i0sytgSWXXSgQMVIL1xI8b24PitIih6ITfUOL25RzTczQkAnF1UjHTEgkoY4g7Wkdk7GE/EVtmNU2dQWGWJw6vtIPf0dco3OldVWMne7NhVZEWhHZGkQwwEBghtU75NRh2FS/OkYODsxR1VjZFItmkUUpbenJ/QRyOHeLSeCd4JTphJjMJjqhfKPB2IQhdleamxLsC2Qy/i7IhpXKpiKaXvPDkTIIjIUVH07JLETfioLTk5LKbawwELTf1hpw1ql2hHVK6kZc3J0QdKnKZAQTLtpcxi7BLHGTvS1v8IoNWpVRiWOtzEkMgxY2MOsCmt9EliekDHbZedqlZIY6uYGtZdtZEZDXHTBbbtrDsezzX4Jo8lXghJFp4CjqFikYLNGuKtFjuaxO60WV7qhEsYmg2OBlxMVFOXITJYF6bewNGn9EtRZLoJGABLPUeqNFpH8YsTvZmq0gtvaMyABCts58yotmz8qgMTvMdjIYRVZPIRqYMrGH4xqZxXC4agLBeAPY5hUNWFW04lMSdXTkXykVLcbDKoDV4IiMmT82vOS5Dr3MQJBHYDkktVY+CYJgqBlLG3UpIzso4hnGrpt65oWURO2dwD8wLDh62Yo3yYwHBhqckgjFhVjmyOApGJ4VUr7DZHQAAWWRLWGjSUCYWxcCftK9FZ81Jhl+F4CUrstU0F9+5IazbQEukpEtUHerpc2hhRNljTjbTVObJnZzbyFM9A7DkBbRCVYasnGMzzJUhjDlnj9/vECQqxtmFS1b7rW/M/Ra1S35imfvPkXcfY33MP+sPhCbUBpLTPBDseiyCmdOUQmI7o+NUdYrygzDfZ2yByyvqWxTA34ow/eTTM98keHlfkGoMJtJ9HvuX5kLJ2dLMPw414EzAiGnH3rsS1ZnlUmeF6ri07nmgE1KhFrFodPKgtB1J99Kt8WfE63sdPphCIOraxEf1Oo7vvv5bk4f3fm1ofSPGbBqwRiJdvk8LIPy5f+7D1FawDNbEs9F8xCIZ1rbI+9B8eP2oVTlgAENqN3jfgzQphHSzX/VqKKbn01nU+gciRl3tTuyvJUQWJM3sUry4ften2hlPD1aR0RGKn9I1FVEICUMtpgZ1+uefIUakQUBrumpA6sX7+NXzvfoea8LmMyemET/UQhY8rhfHlve6zPDx+yuolhTb8YoZ7/eeIlUAq0Xz6C3r47u9N8p5ePHzkVg8YdtywkW/cy0jafIJI7xuIxnmol3A6LRCt4uG0p/i5H2QajNKrBEKXicOZcqLAueNOhxrbM7MBEpwtdO9fFXqjkvd2Hh99n4YUyvNHhQ+V342HPqsNntCjo9/JsMNQKF817u6Io7cru7CjBGk7+DD3jldqpNi5FLcYCCtB0uRuFxv98xssMWO0Eh4dEQUdcX/wMVu8eKks0qjogfDwY0aLOhuS1OUTmSHhllxw1T0OWQFin5JIZGCmHhvMLfcxohB9gIgXk7hM3UnGn0noE4nBFVGCITz/mkFqKitb5dJHHKxlQOyEL6oxf+D7MLzRxHfPmFvMJVk4FIeAF8vFHgyhisET1R3VQDh2B8ks1ZcRdAf68evb35JIQoaBjj/xLSOPFCsC8dMW25svX768e/v28fHx6eOv8alfMyDzqL8aKl1Ck0RJS4jMtu6N++kjHK9wmF+1uP6aa6xoMgnErpge3vzg9P6oJn1o41CkrNlF1g2gL9BqE9yBsWJwnPrdWgXv+M1lRHssPoYg5ljh163RUgkDsVnptQFwQOkdAXcSHAbZeXj3Ww8eS0dMYcMwLolK8nisjsAKd4eltuPS6AsIlBJL58wiL5J031PAvSAcIViv9AH9zK7wSBgWfNu1DvQfiJ3VhgXjET7HDINYqYvN4WryKeEKRhPP7+JyLEgvF2L7DuCTPkNBrkMuCkdir/RFAPry9MC3Xxh2NBOnrPDDuUP/1RBI355QSE4wyUeq8VWbt4hrkuk8wpxXMFrxxKy30+lv8xNDqDPhOYzRMoscqPyw6WtnLScsJhLnzCz3zGoCIm7ZsUi6dIY+/Rk87/+BgxdDab++fSQtaorVYLrtFr20TFr8KIXqNtwdDQcw3acXruIMtXxjY2lqssJQyK+PekHi3EAPsRSYoVdbFLlaM7HF4vH2lafyBxmBWzcyeQZVRo28tw8s+J275Ltoo1DA65eAJX/WWTjctfTU3bV0ispAuQjdTqp6sF1Rk3kwMcXJNI95ilHAmigLNTWZ34jPlAUO2Vi6stmerDZNTKK/IjlSnlrhSXnpYoQ3HotJgHgFwGjc9njzOZ5is2kOdKbalI32yCSkCawNcRx6S04NZLBIXIdbDb12UCHnuGEcw9JzpxwVdeab8SbwQsK00Ct/Wzz4m4A63HRJacZia9cczBax4MBd/ASYEKXm2Pcy42gEb6SC06aFhrO6DVCq4pO0QpBbrVweB4nlQleN4BwO69ebL3pl4l4QiLmklkMsZYuxvXrBtT9WsAjjVL6IiCBBWqjcYcqKqcBJI9nUGipOLkWVlq9f9NvmyTK2Wim/fmEF5WP7hAqFuq1AvESKTJ+L0sscesWVSXrNImjP+BBYhmp/eeLywreuyL/7T5L08kQYelpXLAqQIRaHPyQkqK8ZxMSJTQMGPQkVqTY6oeBtrBFRhF9Up9caBAKWgWIw2nW/IrJTzlwCkCvniCDIkBgQ5BujpsIhIRF18F85ebOQc/5TJISh0yGnYHVKzc8+GZAUuZBKfVUgjBLBMDCUoiQ5rsIWL/THhNIqGrwoKW81QMoWftUQzZfPtLFmOJhzGgRFqjwzNApDKVM2JHl8y8tAvOFDUaGzJS7lz4FQd/gJKXjTgwakuFUjdjW0Fyca2uTBrRi7pTby9FV7RuRJHfEgWsqL346E0CAkXl5Kwc81A8xqQp9rXAVLKgWHiNlnz55XTghzhI2Y6XGazhKjE1sFg1x/jJkYResmIntTiRPmDyKxqftMTrUgyYS0lTCYEDO0tbJosH2dwcBJ9fTlra7guQZ6+PpZqK8PupkmPE6YJtozsuxtyaFDjFoQ5OT9+/dp4kKbVgmF/pVLGZXERlTqTPZSJrGSevPc/vzxk8AaAmmVZMUTlGyYOs6Xpoo5BBEJAaitTVEznYTzYUx2vM6IQQMWSAXvZMkrKcsEkPcveh31JIdf6jhxYsledTMzlLCxZJdOMbVxD5CCyaCKlP5DoiAJlVhZP794yugoYFlwn0JIvTYMlLEQhiyhhIgMYKs8AYLXeJpEhZ17zBW3WpWzOGAw7YmU259D5aikhdJrFIufJBI7mgT6lcPTDg1NUlivtNi+/frZRzGBJ69afN1reCXpWLWEYZKF1CsV189C6M9QoncH6i6V3Dh3KnPI4FfxyVYjqxelesOcKBUjk43J0tnTKYKE0AvtHx71CRF3Kv2SnBXoy+PjO62FKh0A6OSPgckyIiP6pNJZMQ5qxRMbZ48e5ihzZjhwMCwdfXNVeXXn37FgSSIM0wi1/ugqMOmyHNuBfaMyBqzcu+mRtoCxy+Jsr5z84Hp40CsuAlVfdHSIAZ/qOTmR0HOEUBwqpvCSNuGEkKkl+LCcnb2XAIU2HPQG2c0Wqx12AzkLTjyO94w5tB/+5m/+5hiK1BP+VGzzoHsGGq5fOSPKRSaNJpGfL/v5T5H4udRKRDzTA5ueKs5TOpYMcQixDY5GvE+J6LB5CA4SCEJb4qKtHmpspGeEjo5Wh2OWwa1n/CPSp/PXffeivrOL+/Fr1C5LD2/LO3QlDoMaEzoMp85W14+++92J9T4JlBww3jJO8xzuFneC8NJ1arqrqsLvNmjgpBVRTthGBYo8VjUch4gYAf295ZTp4zp3Yd98+VNgH/4+h5viYhnjfIP46fOf4+j97zDxAkHfidZHnaCsnObzbxf4lxCgYE7S2YSkS6gP5E2/9ic500HLSGFA1LRN+DC6Rkk8doekKxJG7hVQa4Vjk5br4zdvP/xO6+Wbz/8jv0jxTRT6LvtfCfnly++5fPnywWvqx3cP7/ybGEqmlul8RcE3e+T106858XJl/u7p/f9TC5BXPyFJkOuqeDIIIud6opE68v53uiDQ+vbZp2pdH3z+oss12ejy8fObT3/FuL3/f9EtbrMoLgX/Rav6l68fNcAPT7pN9a5ua/k1xmddrX78t+RM71bpoSq6+PEZ1elVirRWcmHKpbLwutj78uXxrRdFnVFVf/pBvX73/pPTJI9ZebV/UIAyJ92f/4yTyvu/Z+iZRfLD1ZIwupb69PHNp0+ff/WrH758+fr2ne7TY1VrvqJnJPhHBiSVvQ07PKU9Glkxnp44hEEOdZGhE1rO77wo+Kreff6iQfRYg9V1qa7C9ebGZ+a95iIn6A9MH//CooCy5jsVD0rCj2/7rtvbr7q/qx79LVd9T5w4v3799FW3XR4+PT6+f/Pp37x9+P7hu//Hzz99ffde2dSIa7gUkv7ef/35Xz7oVt/Dx8c3Pzx8/1vNigd9keOr+D+9+apr3C++gFYwBKFQv37V3FaNdzPoNcEzGG8+/Vuy6foT3/VSrzNtmDMCaFtZUl3vrclavyUitY4gAbiC14uxD0C//ivl5827v8voO5lQCvn27Tsmk2y/aAY+Pr3XHXFi0cR4+qon62tW/xffTdR4M3u5PmbcSVxOtIwng6PQGULkXLi8V0PHrC8DyGN1Ieyf/xxmvsNDDiQToSfBB9k+vv3MBYhSxAt1X0XRJ/lwZPb15quGQ+P5SbZOow7Bf0OSPvyDXgM+ffo3zL7v/sGXeY7ZfRRpVhC/vNF1nkL2MahSHsn5o7KkyJkz6sjTd5pjGp3Pn/Wdmad37/QCgN7SVQbKAyFFlpK37758+dw6JUnHozL3Mzn//G9ZOL/7O5WfPv2sSfvuvdIrrPKsYWUElD/50nsLyoDfleXgxhd/XNAkcxbQjyjeMH/E8qNf1agPDIACf5BHXziSeI599HhU3t+++/rx3+i169vv/56xouceO7xp09z7c46dD3/nCMypPPKmIXOAS20F+1nHiK4c/t/kXO8zQ8DCmciePmnN0cr/W8Xja2nWWGLGFgzvEvp5brLgqCRoXaJpzrx9euBJ6kISizLDzpsn/NOX72HkTi1WMH3+M03tR35FRz6Y+RhJlY13whWL8c7M09d3vljUgvnwpDmjo/L933Jtz90TUX7RP5/mEkOmtTrJEORAUPfpAu6VEK0tn998+UG/CuRof37z9Vc64yrpfMZVs/StLty1BH368vWdyofHvIZktJUI7URDBh4/kIHHj5pjn7581r83X/5M788+vf1bsvrxX3+Bhj4yZxTgw9PnT4Jx84hMaKeKJsrnP9fx8/Dhv8sLXr3Qe/r0r5mnj/8g5ndv9Q7W+4eHH/HFrzmpI9qIgfqnf0vq3vOeMGu4vEgtJWOt2a9ZpDx4RBgvyZignmmcX8QFjcdXVqiYgbpmUIR65anJp7nEpkkvR3hVtIr53T+QUP8jImsgV8pDKWdfdV5T6yNseBc/L+OVdv2JXGNad8YflHzPAnr0Z7C9/wehHZHnriaJEi62+mUS5jkvtIJgqkrJX204WK2WtpIYtu0D66d/5wGSpVi/A5BxzFWZAMrhlOUFM1+z5TMpYYFOefAvH+cV3iJ3DdhARxKQ5B4wdyQgwmQitVFJg59S0gRltVsicspFoCSt3hfUQIfqfEZqoebcYUMVxUG8GnTZrYSwFKlFN1L3Z5ft9UHdrWzOZHjrcdhuVbecwzCsC3MhkhL6sTrV2zaelfQaS8Ooh7LUHXyaQypY/kuOKmpNeg8jLlRJHDSoaQAlyRY4EMmLagZYxzabqXRHWXepdLNDp7QvWhy1OOWkCBerlG99CaTZI5wC0CTSMiVSrQ+EI3ZpuQ3jBislh6Rto37QLTetGzlipecKViYkpqODl0MrqaqIhZGXMuNySnai5VKSmazQv7z55AtuIRUTq7yWmne6vvvy5RP9ftRnAHTRp7VW5++PusvjS1A5VXd1iaurBM4e6oPU8v3586dHrUdff9YbtWSISxpWViVBPWVFVAZY7x6fPv+sWzyPX3/67k/+B1J8ePvw84/KnnKk68ovOr+xgH6SRBfpn0ghx557rVs7D+/VGRZBzkwif6v8//7jz99//6vv33348kmvW74qX9o413O+UEa5KvqqAfqsS2SuUk2A/Tuuhlki9cdgS6HLH52Q5FKnR70WefuWk8PD+7ff+U6qeqDB0Oks04X0PurMJEP17uuTbo46NTpbfdbF0INyotuejLI3nZM00ELiK9esqjBgXINS+pJFZEwD341XP3Qy+/hRl+PqK3f1Ht49/vyTfjUdhz98//3Hj59/+vn3OtVxx1cX6Xq54gss5efxDRdMutx/1GXQ1y+fPn16+/YHXWRy2v2kq+GHn3/++vbpg0J5+8N/1An4y5eP6unnjz+9fS+PH3/8/376/PE/6Nru/Q//8Ks/+a/U0e++03h9/PnHL++/1yT67sf//OW//T/+3x6+e/qrf/fffPjhv/vuw69+9asP7x6/++FX7x81Srpi/fRZ8ZMkdUdjyGsA7dmUBwnc+Zx+01Iob9U1JomBzFqBYWBKKlNU0JpW+VKqGBGGTq9tNM3lRRnTkKsihY9X3yfTRw00/IJpcZaVLvoZSKLSaZnPIfCmkU43MhSnLwGJ0a+7RMvNdW5mK+/vhCfIdEoBv1NLCdXGoaC5zoQSCVPoK5fvb99+x1gQvxYDuqTXnBpx03vqyYBDwOPOFajsee9C3dTFmjqjiftW90Z174+on94qt+/1co35qQCYHITEuxZ6Sc3R9/adZhrTzmmGwLOWtUiRKEwun8kmxoyLDyjF9/a9Xsp+1ITRFNVaIHPWDfHwPg+v8BAyybR66IpHOZJnaI1iNYNNf/SUNUe7jByxqD9ckMiEkUADmpen0ljkDEILiFgJXdevOhDh1P0BiRQeiwDDrsNM/SRaMzAsknK9yIcgmEE6op/0XyRcD8GsaNUfZUmHKFdXlLKXoRyIjUXDM1DJenz65MssvazlgoyXYfwjrSwebz5/4p711585BllbxRAEGGYoN7YJUxafuLaVjVdGrZ9vuchTsLglTWAUhMLQgD3oBoeuKa1jgmtT2rVaf9YyS0ocA2VqWrGgf/yoAUUoqbzyxgseGRCtwKxnilHZV+SfWa0+KQZSQpDCq+G5wiHgW/IkW8nhrrwO5y86CHSvRlfXPrtpbisi3cdRFt872HdCiOEzpwW6LWYNMaNCja6aVq/NHt6+0+sE+dDUkQUzXEnQG40SkgzPV40584njiGkiHmKXSoQYwa/jmvexGR3SxOIjHr2ZqRsaug3hldXZ8PHFqCv/YtRKIC7YPEsdnwU6vuVWjq1lWjr8GkY0KMImLlZr/WNhEZdmJuGp10mnUuCYCduD61kDhklB/C5QUYfLg61+Wc1EYJLg6Ism0Bd65Ne42DpIzGSudso4wsxUpqUgsfaaYcFXQrVrWPZNYSE/CncA8WZbtZbM/lI1nKlME2cng3kH4FYFVD2k0zkfPP4oiX6hU03iTl5BjRtpyEmcSKEtugFN4F3JHGYwV2gVCwMoGFlFWf7asPdxI1h7KmvrU18SExHT3YDQMduEyCf7uSfRvnofa9LgV7S+M30Tvvt+5UeybBPHFapBvR9MKkOCviZS7dqi9mMI8KSb5g4aYSqbTdInMWPi6a1R0XhXhvAvF57YHk5hxie1tEEIpuNZCw8izv3m4I4RFX0iVjuvuL7+mzz/PYcr/+VIqwrnea2zusutiLSWs/LofKOTK7cbs7DaqU7WWiAQ6D6KXuFzEcsSIgPdDhdVnWu1xn/lshIHWp/UNS3KWoBosF7JTBZaL75+ZiHheld0Tx91u1hawb9+eff1zZ98ePxeryx0Gfj489eH79680b0cncs/fnr4k99//enHnz+wpunu2fsP9ENmPpeTFE662r/56Se9SKjPV7z7oEuVxx9//OndO110fPr48086HHWt9f133+mFkc4TX54+6SKZS3Bd9DAsupTRKvbuX/yLP9Flqe4b/fzjz18//vju8ftPT/qB0vdPehXxkdvJjw/f6fRO2vxpIZ0+fJvzk25+fvdByf3+uz958+Xtn/z09PHh3f9Qa+PPP+m66DP5e/OoE8n7795/9+7tp59/TyKUXNZ8XcnpIk+nQhYCjRRJVEX5+vL03XfvP+gaWg3OWHotoXvYDx91AaFXTTpX6W7Sxy9yLLyyqe6QbK3VvAJUqLwfolcP371/rzHKFenHT7pwf5A5s+npSSoNI5+L8GcbZK5zgSaJ0qu06FSnM5lOimpKqFETj3L8/Xcffv8T7wjp+pLxfffw6aNu2X79+aePf/Inv9KtsR9//FEf2JAvlZonPr8w6WUCuSbeu3d6zfDp08f/6l/8C6arQvqo24TvZc41gfr4SXf9vyoFMvhP/+E//ft//+//83/5z//xP/5/fv8ffvXu7cMPP/wnvbz6F//mz//n/8v/xf/9//p//t//7/4P/9P/2f9EZ9ff/e0//Lf/l//Tm8f3/+pf/9ffvdO0+/Kv/uv/8ffv3//pnynSh1//u7/4l//iTx/fcfHEtSyhM5uUK00Bddf/mffqpQRccbLp9FnTTHnQKynMOI54UWRDmITRp1qUhDpGOKg9ijpi2HTRrFFRRaPMdbaGXpNHYeifjBl0HYWSeqg5urmI1whzdavXNrrS1WtQpQ4mj42uVnT55UCfPnC5/UVET4/v9F6VXgB8/qpF+E8e3ir4d0+Peu2qz9EKrFHn9Zgcyq3i08W5glZoj+901SqVRuGDXjbqlTgK3ajmIlhDwTUN/UkfFK2WFIL7+o53scjAx08ff3j/3+gVwJeHf3Dkbz79l9/r4NOdT00wvUv29t13X58+vn3/7vtf6VDh7Tsukh/ffNTRor+v32nCassweOnQ9NP2Tr40W5iq3ObXxPALAK0bGlQsvJjpI2G6IhedYlHeuPL1cqOuUmFo6CizSxhxyBHLFIPOwHFIg1Xi1UsNjieIqvKOJSLZqdPh85BBa7Aqmg/OqKHwfv/DrxQxRro+5uD9rEXz/Yf3OiR/+ulHsB0beWVBY8+ST8BMGyRKviJ0tjHQwOkA0stkHeS87Sm89PikJgM6pSqzV6sfb3nBgsgIJk+6IK6Hz/ptbF3V872sN3r3Qw50L1lR0DmuX7nKVQuB0qOzyw8yfnjrV9H6DpsSo6dL2a9eVChKeODFgmj9DoC+3aTjzU4Vx19qIr37/j+oX1rxOMToHi5ErDXqnfKuVQ5r5rZC0B+chM88tFyZ5kWRksAqx+LnDgoPFeue8yBmRlHTQusdL31lrfzQNRKshnc4pq53LPVCnc/161Wr3kOQqbC6daJ7UPrgvloIHN4bznmfvnz3/XcadU6K6qAOP70SJ+Gfeb3D2VQnWs+xr3+mI+XD9//IK2RWDaaKFgTfWWdhJ55MAtaALBkSZpraq6PVWPhbB/InuNJCjitOVm4doooyqfiBN1KePvNClhfJvA6TzlMUXz5mgdJzlgZPcfdYr/R0KChpNQRMsO/kWisPbj0MxKwRdVrUTXJHKIwURLwATZAYyAUJlpzzTsaUqfv/Y+xPgDbLzvs+7N3fb+l9prune3pmMACxkCAAkdgocMEiSpBjkdZikrEd26XEUWzLlbgSV9mplFSsVJJyypYtWZZtRXFkWalE5bhcURLJcmJrIyFKtAgBEAACHAxmBtPdM70v3/ru+f3+z3nf75sBKPv21/e995znPPt5znrvxYJoW/qyR/uO2mknIWulw2OCTEz8r8O0lmoJLkFn75PfyC4ZITxtfupmfT7BdjqlHLaltPdDsnvCY41MigixWQFo6a2MP8IjVlI8r69llHtczx8tjcGDOBRSQgmSVhknQqdEYyJ51uGitQGtiziROV5E7/JQoOEpl5GUVG6QpqWf/FRK5Zt66r7dgjtl/fE4wZGcJCmody0FlkxWQqA3YAVAygmKgOW0ATydefr6BPS3udrQacQLDKE3GZuCpYkNm0lvVsq1qjpVikvt9X2M/wCNWkxYEKRIsFRJzobF5HldiiFBQGtcUTgpoaN4F2YsWQdJSdG/qJdWdZEY64zJIhpQq4k3hEERTxd0tal2TorSkbV6EhDIWQ6sgKlQALMXgLhFytj+RMD1vczHEyN68xnbVLT0nIluN+QYPJEm7kckozkQPvGNak1Yt3IDSa/HKWQ3jRARZqMFD9nRWg3GdHqccrcDy0oqU+9HixG9MLq9LPQiGmEDdJyqKdDNDV3gNIc/G3ByE3bhhIBIAToKMD9ETuekI3SX/RXuHCJbdRuO6fbMWW5w5WQ622Lmfkrx+QDNRBRunZ13n49PcaXnBCdoEtrGteECPY27x4TDGSLSHjK1zfxces19Ngoxfe1+FuRSNWBdMBrCInatEcLVgHQTAaFvpwyd5XTOhHrU6IwvDdOU2dTBgP7xqDdk2o3OKprUW5DWsGuvymbSsE85Dpoj2to5nSUloR3EBWgC9Ud+MT99PNyE/9GdC7KKFz0buWnb4iLWXbPcjUBHC73xZ5RHFhr19OrRpF3R8XhMFx/78ofRJJVepz02W5fucDjaPXPu7r07OAjtK2cm8GhR9w8O8EB8CNTAjXe2l1OADw/29+68/eTgcG85mY9Gg8Xy4Oh48vjwyX/8H/1HWHF//+jX/s7fc0VhvmRVAas9vD8dD4aL1fThXRdKhq89Hm0Nn79/49Of/olz57dZvp8dTWls6DhEZh0AcugKtUwmPL8O5/35YjJ028ncXlSe9kN+uEVqUoC0iQqvqhRDYg4rKBO9Tn6TlQMn4Z+TZTgJJtAr8VB7DR26g0zeYy0kds8CqdQTDYSZ2KyCh9ojQMVS7FMHxR/70F4y6LKqUh4TstFBRIPe3AqESzKby9gVmRiRzxz0OwhMQ4x4OD1VioLZLcG6E8wMspYFcZiIVclHDniDaCqKXEaaOjcvQAk6Rjh3UxMOpR50cAbARwxHmCbsMQ/LBm63ZMAQstgP0w3ZRTJdHR3yBDwDKPVgb0AxxTDsD7Z3eADXgSw+v72zw/YMq056NuiI6g9LzkGgJeok9ZeSQJBkzdJXrWumgUV1WkAIAK0v+j530FDZgmlV8/UKc6xdMMq1UlpPSAIGbxFV2dJcSXsEirrKUBMwDOrOdaoqAwCVyRgyK1FalvQgCw/WE1jUOCLmkJYcyKxhmmTijSoEq1EEplOTucfjVCgCybnPRZBiqBKVIuVUZUkhYdll5ZO80QSEjv8UlwkC7xBfCS0mrHTVKF09bMG6HFGQMyTBALhKMKtcE5ywYXtQk0HMmAADYygLo4RPi3GhSSRlBcJoToOsZtm4RX0iU1ksmOuqU0qXIIzSsCCRH6dKLYsbmxj2I4431k19RjWErHj5Q6NkqiBiLQzG6qGFIO7GjOiOQjUeq9AcimyTqN0YUtQyDuI7r0TIY5CKbzN4gCaDVTiVsRVjVXvPqJw4Ah/8KpQOJVtzwGyJ7R87rInaM2UVDoipalRnACPqoBaLJf+VhPpqzYGWVrAhtjetWVz0IJZR2/HOmDNmUp0wTRvhGQQEwzgPlMlzKEy6nMuAeCitr8bnZVWLq3UqGDI5vFPDyiOfRg3MGTI03CBCafKvAhz5A5V1MvsSknIti7mure1tUANelFUE2Zxgsa60lneKLePe5MdLNddyva3LVpK7ZAfzpoRAJaNXoUFe6CVhczJJfYNzwPtbvKh9RV5tjhNUiGcqe/29IL3uufO6sYydzPBsIjmOPOrd9t696yiuEyDIoVSxJH7rEfxAxP3cBVixg6RQbPiaRteYizkxBFdBVuamlLnBGdclkzuPk/R1LjgMKDmIc9e4YO+a3KRIK8duNnhCoWYEteg1XRJacm5biTUt4XOsYdf3P+B3xSwy5Tb8rEHQVMh4n3rWzJr8aGcNGYg1pfK101nvut5I2dCvUSlCFNeolhOZmzoDixYobTRxAzK9YbI7+DlympHCTmJ3IpogsO604q0+HtREmJQU0YLQzg42huwGBDzGiEAlNqQRXw03TA8RWztH5NAFpE8CxhWzE4QLOgqp0pM5a7EgGNijNOwYeQhQ1Ofsk6R9JyyW59j/7tOBoOdj913WCEcnUQRWnCFiA6gP7UHNviB/dq362TnA5daqx/MMLH+fWfZ2F72p/arehDYhoQO8iGswBD9T92gBbmzlSEA1qi1UwARi6oSxid2LNj8rpCJc9d/uDpmG5F09TI48azRCMrik82H73Jm4MDInHPVXh3TYBt2J45A+T7QOpnTrV1zRqKPmrBKneWXmNdsrpsvpYNp5c8ADP0Q4+iZ9dn3QiWStg0jJJf3RRX/eH/XpyUyXdIkYJfTYcYqBaEoHXLlRhCjKniMm97EkPC6ZMaJbQzw1cLOjSWQ2HA4niKzz6bOosje8T+hVC/Jmp6c0r3CYGnguYhQaBtQCFJ7i+g+60pkC41wb1wDSLOhOepQTzgngievqWeG1Q/hgqYVF84lWmF5dziaL8RM6mvDrsIcTGrbRYqzobtFl9wam3DpzwErObDIZDfpXLl98/OTx8fEULrbGO7aeLhEhdX9y5JbcR48ff/UrX7l//xHTpoh75uJ898zgzM51un43bz8Y74z/sZ//vT/8wQ+cYe3gzPjOW3dG48733nj71s3Xrl27du/enVd+87Wbt9442AfZ8ez1m6vlP/jQB18+e+6Z1erIweAIEfujUQ/bH88P0SMKoAl3WKpDjLp9tsXbH6efTg/Uxgl55kvaKqa/0lbpd9iGUdrcOoiuScgfysMYNod4Pme3tTjtZzZ1lDZx0XcMiEYBrFoDP1qDnzS29uK0VydLRottSrHWZa4xwGGuxmN4QEvDFLoE6GscTxke8lhF78L2kF7KbNKfHs236ILjRgxgmGaNPzgQga5DcmSkYesdkzQbdNhtQ6CxjnBB9bIlQS/oJE0VDitZb+WERJnBI9jhdW/Fo7q6KD4k/lQxFHTcW2LMrB8RcQDg+QHWlxj1LJZDxh99JvYZz4DWvoOuJ29U89l8kmlshuU8C3J06KqdEi9dD4Dk1lt0GtnlDzn3j6AtIhbshCPrUmIHnq0qFYdxAvJAo6AS0qryJB3KmgDy2NBDSErq/pTA+nZhQkItjK11TrCKAlwBoRR0iWNXGfHQAkZgtvwwP4xkHqAHCZgjZzgJMblSA+gV6sQ6/MNZUhQTBsCPvYordKiw9m0xFd7gncz25tflPi2FVEKNFGC4lOb6X57TCyMU67+pxCqp5BUeqsrbhjpwtsfglgwl6L+p4+rt4VWjBK93kCntlf7p2hJuPPX6b9uzZhMaXk50dtlEzqN0CNqtXC13dKfOkSohmhFs4oLQJE857DLplE4TcVCzQg5unM6isB5IRROSAjGYtY8nVdTA8J7xa3nJQDd4YDVNjGLmgyYOFkKXGSeuvR8secKHJuEWMYGAADCiGAHADSX0n+1grLoNt3EutlUyGEeH6E1uYaU7vA8NltWIjAyBGPPP5zwJoDQUloatit6T1QbWHBzNjsZj5xgcOvPkOuFCB3OnE5zBOoxxTVm2fJk/Z/QPIxiGMOaWwLgYzuMcErrSgVUaEQl1wTg3LMwxgSQqn6dCcUw0wIVaZkeiSWqQFthn9n0ygqemRmNG+XMM79DCWHV8dDwaDsllrRsO4RFFo3z+oUlcHigmZjSkFbTOerRGAreGpAItR3PeCdAfb7Fr1BLyoAMIGGC8S2nVZ6U3H+OmQapsYEivs+U5kutvCp+kBDLZMpoy/lK89e0jQJI8BZwTvvvbHUUp2AKC+vjNuRKtIUGkH54cJyVO0iyYu+/LNOGd5QNa0qmiVuxE3nVK/cqDRwGe8LEuSjaJLbduJHhykLW59aJgmn3WeQLBZdCcBhI+BRIoWk6hqPQNHfNybOzW7lpysLTrf/TPKUzFkOKFPuU2me/CUVIGTk1umGtOWCnRkxiCRWH1QXGnzFqN9QtMeahMhLwhKj5Rt8FjfdG8RMKw0HBRwvCekhte5MqaRnGaYYp5SNs6RGYlUOWoUHaCY1VWOpkPN7CnB2NDbTqTRgLanySQ0KgZdpnE4Nkwo43tDv194oONjk0NlIwOzuhCzgkTAqgNrY1/tFBakQnDjXScyDRE8QZAYpj9vRWPXpFD17rHXhkDB/MRrMXSxtJnZH5zOqdfyUIEBIwpRIymMbEXHYWrK2lFG4l3tiYEGJt9By50c5kepgcc/RqazIf3VhguWR8gptEVYaPHkJ0TDIZgl2hqQ4xCBp1RwhF8IohTqnQeq7lHHnolZDBug+DR8YLd7OzPZQYU7ROTCbgoAukQgbBs0HYO0sCY7oux0A4iAw/XRtW6K8bZPwqjiEXrTN8a3UFXrMZosNpgQxXZ0V0OpJeaiQRjysZvWqb60ZG0uWLY5w0bSNqnBbLRwX1ULkT1JcCCQYKxD5xZ2hvLwz4IdANL6hBsUEJMQTSd+9QdfNJAgxBZcBtA2SD05MlTxGbaeMhGJrt0ncXU5u3+nbtHh5NHj58+fbrPcsH/6J/9p65cvXH5mQtXr17b2R3ujM/ee3T/L/0//vIHPvThX/pnfqE7PxwN9Q6avvH2YHKAfJOd3TOz6fHek6Nf/ZW//Sf+7X/n+nteeuWV79x9cH/y9Sfve9/7WWk6c/5ibzSeTdDocjzexhsn04k+we3WrmsaeIr7KKyKGIUxLmMbXBf3dGpTP6fGKDL53NE1w6JUDqxIzdCTrQq28FoTqQCLSUigGClWIGyhNTQJF+lveV9HwABuFgeLZlOvFPcKetRSevSjyeLMaj7onaGJnk6HdFLwvBFPUcxGzAnyxIyPSeLarGDY8YFxBhLUeZyOyb8F+2y0G26qZZCSnRXky6SSrPnRn/QL6xkM6CHklfORpnjmGKuUHjjiCLWIhSs0aATj4dwh1KiGc3zP/iQDAZYf7GPpdOBz8AgLujtdo+lkaleDonR8DC8UAiuqwuAgoYbjgUxOUyosqUpSIc8v2OAGo6FofVbWyDARpBCUSIxiZ05xoJT+fSIGJ4VVKMqlstQtqLQmplEJsQU/UDSdi1KYuWuHBxjdD5yal5CsACSToCbBNB0AnGYUyTCX2geUYA42UZtWAQ8OySSH1TAIzUaEOauUWIUVHsiz7IBTA6L4hgUc1eU48SM+PxaRCz0gCMwqpVhMzIArkDzKvJDwwBE0ZJQYUQNwElbZkPFacVI85LwmPZEjvydoSNXj8D5ZciIrYVxS0gaH7sYdKsI/FRoRRC3DyXbaCfQU4JAyFnRKAkF0gU2OdTZYDVLgNvREvPzIIAB4HQ4KUTdT9XlQWAXDAY6sWwzoCvLjIIh0PRYXxbtiYbxUEuLhh/Bnt1j1OW+m02E68VEWKSWoNZJNr5g8Nvcy/0YL0KWlmLKxcsbwg9Vs/gbggt8h1dWlU2IsKqHsTPPBIUsQokZZhjHWoLmzPhgzVLm1QqqcWKNjYqUzm7jGSAztMBy3umWkI1NUTOf4jfGECTTJYrKtpJohiXGuLGYwSg2kYaCNR5zYvywDrIKxDVCFw2BUouIcXkY9MNbpTCcTyI63eOAYd1K12j3eoy0trJrMyakwIETUjL5yWQVIy0EhNdnKyU9z5cKgi3z/QdoPSk4RsnxDxfcXSkqjKjm4DRPwrYhelwiwIBiGkOVQSrGcfNI8FyL4gQe5KqLr0wUoaktESXFdgvT0ZqQkIiFJ8uzvWkHfj3i95yk5hTGX9aR2wctbHaHYriGEHEWAS83bAkubvS49RJoooQkYuIajfirFt+vAeN5ssLkG4EQdBcd9ktqz5N/H2zvm/oGsUnEW77ZM8NulrL+xZkK397bnoAwsvOpRZaIUDpIAGIoKss6WbMfG6MFPNspMcFxzsLZCo6VvBFQ1WSXAQ0ii9yk/8RR+1Wov32HgCpDmO2EUCnpC/KAS0ogIE9igkQzbAeknWPH5Y1GaRpe2iZmi+BM7L6DL4JvYM5wsjh0C2FW2H0DLxRQ1k4VMXdh40GVb98LdIA4/s6t0g/vj+9pfd1BKY7mtAMFESRaT54gN3d5dAseQfRkEt8jlPCD96t6IxrG3fI5JHSaT2S7LNgF3KjFDYe9LY4CbwGNs6vWnC4IF8YE/iYUU4xsCEMuvhMg0P8DaY2WIkmUH2Fm9p7dkTpduOWMM5hThxQ302Cgjmf5oi62TW5POcXcxNmSzeuCUCyrjBn1gnzS36tYmJaOaqlZqtts9b1xm7X853e4P0Tg7rWzNbMxghmkWYiwC0hQwcc4vvX9k8h9DK6acbMYMq3QtGXrYsWblxAkh7ME2IvKIuCzHgxF4NMLbnVVCeMDe6L4cCo2tKz4NBv0+dQUrdGPVoh1U8LPrCvp2rmyt4IXYjsPIK+Lwi+VGdIHTB45LuacAEgoiIG0S91wi1t1uh4cuduQFIPr32NPdWRjBJmF6PGGHMdNaIrQHh8RMXtFZ0S2cFKcdG9B0MY2kk377lW89ujc8Pj7+w//Cz/387/85eqTzyYT5oSF4eYR19/K/+C//c1v04A8esY48G9KlZ2/U6ngyooVlk8/U7Q20J93f9Xs/f+GZi08On/6f/v2/9vDpvbfffu3p028cPn384ssvv+8DH2SS+dxZdp/3jg4PZsczHuTIcv/T8fYWrT5TX7VHCvdAKbTaqGU5uYYHdwbfQz9s9tE30+bTEaU6sV/WWqADUkIdoQ56dTZmXPvHKbVm+uyKp6J5l4sWUbHgQRlVf6NzbYau7VdQqHds3LF+YQDuIUL9Y+/ZiuHLme7sDFmzR7CxxdtOeHXSfDoazI+n/ePJXqd/adKdLHrbegu1ClI6kv7m5J6+gofBMGNPJga4kgKm00N5ygiKwwdKEB8r+BInZ5nRN/EbOwoUdbhMtcXPA+CML4LHBfEtF7/gEZ2gUuohL2g3qAYBnRJVKlcQ4xe8xCuqMOELfosCrIAMbyV6M3QwHoU7d7TpugvaEWqN25woIX/z5zRe3z3ukUKD6KiUI4VrOFiIrdt/GAhoUoz/aEefJrEMm7CTG3e3Y52Ul11AmCHmnq5Yp8t7kPpsISQhfU8DPMwQAXB+/4k3xUVvzVeG7JNMFVIjOhBQnsTIn+SIVjIONadishIlbUAM8OzLd0RHeAcrJFnNsZeGX1GGKyaK2fwWJQsPC8Y3kHtTxOCkpHaSm0tuVAldvuTDvIgtAFlzQBIIWQwuAAIbRAEKwoZLLBj1KqFtNbyHKcG1RgXIkWYWFHpRHwgSZfiBTcqyzU8B8GGLyYvq8CxVwo4UIhXRjZXDDg+pudPmPnhRECrsDB4IjdOLwkjLm3/c3TO6V9yRpz0QhzfzuHZluHe4rVrtvjvhLX86TqKy3VimMjgTFwzvlA5bFKXccnqN1xGttt6i04sCbUfpEsuxUCve98VQfsmWV2afaAo0GUM8XmPHret2hhD4oBZMnTSCKGuXo7eIrp3OeZq5JBGjQM6h/qEQNaifpiJo6L5Ucx6+ucjTYJ3Vq4GmlbRRIdw5c2CDg8PAGdpzFGxAQ+Oq1Kk7fh22IDec0D3AUKof09BYwKcHIoWoE42oC2kZRQlV4ur0uSk0KIT2mzin0qHnZKUaV04lawUtQgFkhIya17+5bPIFrAGHuDTKxOUPRT3IZEOvK9SVtNaTZHKcyiQtvc3/HisArZRKAH+dYJnLCB0ByFGKDUXBwk39FnmLbyCSxG0cK2oo5mWW5BJE9XnjUQpeZ9ddZTTg3Kyhc/PbpJzkeXW6hNgVTN69ML+u9cJKI9GrnGA+CvH+Bx5ANgmCy2uTwHVS7hQDldhwpqw8NFkLQ/hoRRoOjQGQh16Um5STpSJPDTKlOE9y3QUcr5OfxhxmxLDCApJfi4K4AqvYzWqUChTqFdooqmsCtOatsVqo2o1YRe6tmJIpeS/5L3qZ9IAqRxpL0lKC3HQ0DTs0+XaRjhnDE0aJKRRgAZHGkrfhMAHI0jVT/WDMvIkdQaKO/XCLcm5L0txApYSRgTV/JJYOZEWx0lQkLTqzHFwYp6BPBKF68oAsvV9nfnDuDs8H85AuAGx34Tlau5BDOxBIwoQGoZMCdM5KYnCBBd6Ig2wjoMmApiGISR3GK0RiNEB3w7aEAFcThuqcPTmsPmBIJKQzRBHAIWEXhi6/tYw0gyDdcUWBe2OekVD1GxIVrwYEGiJtA9Iy3OBFKzyrWHuDiOMIRrc1cz7ESGIs06zIiPYItBneGNrF6jYIm5nSF0GZpXl6SGko3EIAOCUJ2wR3SCM4vXjFgVmiL/mollLRLoSZq5ItNGLwBQoihm8eU6Pt5LlnZGWfATAJ9+jKXVzOc8OP4KgXpFzgBEjC6EXBw7cmkZ+4WLRFOk0Wm5lYRnBo4wCAKSO8jJHFzu4Oj0DDJ0MAuvXurO0P2LlzdHDMAjE94BFvfcTPfIb4+OGj/UeP9h8+7ly7+uxHPvIjTx4/5M1CbJjfmo1xx/t3H9x++82rz7147fo1psH2D/Z2z+2Mt3Z45JjJKnji4WlEgJY7x1erT3ziMw8f3/vf/Zs/tbd48sv/q3/pje+9yYLBrZu39/cOUceFC9vXr99gA+/zN27MJkc+tE1HmHsQYPD4Bz5IrUEvBgyeT3cCLKNGWiqXyHEYp/kBp7o4F6hx44pwkwZKI7Qqk6tcUzuEcpcaXk3LmtrTuneWFI/6FllVcjWeZtc8qgh2X02H3f7WYIl397vjOY+q25LDEXywgnHhuD/YW26jPLyVvqctiJ3whB1qgO7txCUtvtHQJW7a6ZiVTKjDBoXqCCvem08OF6qJ4qIF0hMZYJLTBBt8kPrdm04WQ3oedLKiWyoE74Ckgvd5he4CezmrQPcEx4vLUThMQtFRfHfA+5xckszkAwSIQ/a+sIsqgnC4yS9sWzUNbBgu3ANTyvQnAlHF06nUZMoTdVv1qgSGhfvghOXgse5bgWIUcizCtYkeCh7M5Fh/PYk5o0P80lsWCCserqHd6WAHPExW3AJp0JDGSDgbpUCChRATzcQtqZ6gTu+cHr1VEhD+wwu2t4sWeZCAS5MB5TcciUd1eMi2Y70N+4Ik1TG/JvTQQxTXViVywgM6ETu36kQ+IzSsGzlllVR1K75oSmpQpiAxJaQpRKnCQyny1QT1CQEYe8uyNlBk0nUpPdeAj4vG0VyRTkH1yf9EeRhpJlBw15pLCwR5EesX9nAJdAKW23qJRLZGVCnHFSREfFUAA6kUkCKs65AZQen7sOyiDSri2kKKrAshlnQ5xIBsgtqvVUQFjQDRfOmJhtjo7Y2tWKDVinyBJ/WpHmFXU67wMPK120yW+tTIjuJAItGcad2KB0p4kCrPsUqQWNRE+LWhB8Q1bORFsUig2is/62xOEMgQNE2XNW1YekRd1YhwoYiggR+kat6j8gOrgkAgz/wDej0SUp+yjut4CYDmVwIlSiHLtAtTtJBcBo2sJbdAEFMPTZoY+Bf4wlTpJ6hIjUSVIhsnB7Cnjn/EAKABFh9rVkEbRQZFaDABwjuYiduZb0jwQh2RMqKHB9mlCHvZwdrzMZ01s2HO5+s9Uir4i+dGOze8uZx81ytOS3D6eo3jZHa/Utbn9Sz++p7fdxWXXlEWRnXHz3ENa3o03kCqoACBXEtjhTiN4cjKZtTAS46EjISaGLAcSZCYuUPeI+tR2It+WGqWX+cEqCCtWbyEYc2H7+cGh2jiSCHtPVqNh1mb2QdjnZaF3pGBiZGvRWBLJyNVMSySWOA8ELlUcXDzCppUMptVt474fmJTDnUMK0qKhpSOTBiIM5REwQN0mEu27FvlW7wpbSSnAbHiaa9LlaCE8DDwBRRcqWre+sJyOTHFnS5QZSu0+30Xx88zG9rps/LAW9sMOURplUI8Vq5M1x3zLWHCN2+wBhF5QUgV7fMOIqqxBZJBWIrTu9cTeXhJDmHgNoGVLRVmID+RqSalumyqIerYCi4mXi5XY7bau2NSQJ2BEMT/fm+n39np9PEQJsOJ7OQZZl3mjKtRkleGUIYmED7YxZNI5uIHjSwYfN9zzIb26GbTQceyqEkEduSJYGyFQJQBd/gfRvatcoRCOcgrrJHG2R7nftLjo8vu8i6BDk6gp0Z4lIAdv1xb2uTe4hrzl7Rp6qd/jwEJuzbYF8lahU1OSDEtSC/dNyaqm+ec2uvdYyVIykZCg7Y9/lI6jsST0U7Xsw3Wvi7a4xkM5Or0fS0gSkZEaiD8kN1znUOhGU/BQ4cnTOyywd+gP7rjjCRSQpamDK0EoVM73HV4vyY6YSHD9hKRgAOV3XfbccYRvtBzNPTjDPzb4g1Bw1EGAI0rXt/Je4poWyZHR7ffvr1z5sxsfnywf3Rw8PTunfvjrS187fjRNq8EWg7fxnCHk0NkOTp26WRrp/sLv/RPvfTyC3tPnzLzj+2mswnz9Bjn+edusDbz6N7d+eHRcGt8fDA9OvA9p8i7vcvbP3eYusIV+YxChi3HFy7uLhb7o8nhP/mH/uCXv/Lrr337zSf7D+68fQ+ZwHHze3eu33huOmXHzHSHN4yeZxcyDx9n17xug+mQTtVDoDe+x7KZDSJu67O9NMVMtaENdCaQFcehF06UZhQ1pzLqMZSqgIljjO+ztwB85ZIJDgggzuY2tKf0yo2iGJqS/Iv7SUXTQ9PKhx/gSjoc/R+eZGGUtt1f7aR/fKY7fsrz1UO2rnWoXahF/LhR8cEvtZt2HfzVsUrgZaTvO8KXPZ7XYo3Qp4zW2dZd4wYp/Fnb4zywqPJhj+dIrxALusO7rJ2Nhrx9iNGdPQqqjWPb6Wo4WpzdOucAdHbAYzaD8aNZ90nn+EYGurqNTh7c9gLmz8MJ78W3T0JVzby2mfq8KlETHFRbiOOzeKimoh7R85ApDuMIfp5hirUtPmxiZStMKhZtgdAwUB1mkq0vwZFopNC5hQFZkLYR3OACQaoqtS/sy6KaiZosKxdwCbDywGgBBmLOyifbMh/S1etmPziwWIUykdcbIhWvxPV5IRWJ0buL6fUMx2/CQKaBI84JwygCVqm8rpwkfuhXAEGZIvoPurO5Br9SxfQCyqIcFJPx+7orheOpahj8NkXpc6p9rCwGBQUzV0DT566AwVIMsdfmL7VGETr9O9SIspCcGjuVGY92GtkoqaLAxykadGIGR0ftvf4RGKnrkPRJBtTqd+7xM+qMDFhGGUmCWbvd/NnOKFTSk41LKb1EmFWiPtLQV0FgJK6TAJB8Ts3mqAyxMp9trRcDTYjhHIgynBQtoFdwhTOuend88l79Up7GijOII6Ixf8vK42YlmzMROtQABcrkjwbFb86Ah7UH7M8fEzWdxbMGfhpP7aa7+wPVdjTeZSBq1PWQxgBCz/CeFmGxX7c0LIDIxUme6ZL7/LMuqTpL22TCQ6bekFZiZUByiyhInI4qodJBMQIqhK6CxLlEtDV/XqgF3rXA+zWe6QxYgT+WoID8OgiHsYDLxPqrSjwbCXz6zzwDGaCIKDaIaeucKau5/cI91nkYSx3Hi0Gr9k8fMXyoQHl9iEtIYfNczX/3MwBVK0RUzOTHm2AN0aqbsUUjZB/P/FA6IV9lhAkDAW6IAr8RgQv+ZJXCsizTDU8cGUzmBMO7Tj8w8V0w3Ba2UDnJbCRCrgRF8yjdKtL4qQuLhC3OhaOKCteQwGfCgCKckGvctTQrBmLoIKZEUu+bkpNiacS3MuSy7tdUvAtOKIc1/WDDQ8srCnqPrwGjY0SfB3dMgOaRTeMmZYssV2kJkBnEcgc+2x7G8dYo+gEk+t4wOuYaaE7cBsdRlQ+T4cTxtP02J25BQZ0q8RKnycsCmfWRf4BRMHG/MZ8U+OVtKPbwKxTIqfWUmDq0Y0JlcwdA6hVM0IjSA3Ct23ACNkIKxyZ+0xhTXpE8wxFnPRR5KVIaSAw1jDdmEjCkqXaMEooZDGJJxIeptG9m0ZIFj2umSIgxiCKogdsiReeKBse+FD1AWwDkDQ0qN0EYbfWGPCyIJHQ97bTDmL1YH2ZAYi4QR8rRRVTnNKT89gc+WuiUR/r/bPmIG4E94Lia3IOOHwRRFuK2yAxm8SM3M8gnUbiU69vrnUAa9lnM5cI3ZLMHmuksmibKZPkZTD47wcILZo0zyEWCLcpIixFuoRrl05Wni8eYLQ9q25EkHU7MRkr+bFjlAS6J4Lq07GE/xRZGcszuBsR2ji6aDWkgHDVZUgYNRB5UYDdd+EAZcDacJIJZzwxCcJJCssMtflddpvYBhTFensNDcmzMYeKfPineyMtMedfLP/za157sPdnf36ciccAfI1V2bXUXz2jV4e3hkKcqnQOmuQPJ89cvf+j97z0+OsSU4/HArahdlnl4oaSss88Hlo/YxMpbfR490TAYLL2QZy9f2WK9YTDiCwBbg22UixTnzu329uZ/4A/+ws987rPPXrzyta9/5U//yf/w9p23jw95cHl6+9atN7/3PXacP//8tfe8/NLO1s65C2epiSL1ZZc6QJRjc6krcNhRwcbUInay8/Qsc9r4QilGv4NL/QSVOg4EFa6tf8ZG+IL1zOrjBcrUpeIMWoYqUOnWc9lXNGAUUGyY3nlC1DvsHDK4t2dvtUilkaj+iM/N8xGfbmebNAequjQMxHT24BhHau1AcwEEIzpcMIgUE9+GzdQIrjE0SblNtTVJUJkkD1wwFf9zh8LozNbF2eHRPqs3VDfw8HGvYffsqvPMgr13sHd21hvtU7G3WKA6Z6C0diEHgqgncc52KdYbnRE9MuDnRSzrVARZmMWX2eeGA5ALBOPP1IeSQTXY1YqivaTycA0J+5tqV43IfpMOEACCDLDwgg9oHPlTfPLktBXIFenYOloiTxV1eK7F2MCsBA8RcS8h07nd2mqznqTIxiDWGR7FVaYiNt7ZdY1KYRjnhy53busGjHCx7DE5iFuhTh3JMAW9BA/SdTvNYQ/bMB45ISeT4T7Trjq1gYQCFWqU0XvAuBSLo0prd/GvIJDWmbSmhLJDnNLBrHkCIkfghHQUbKum8JhSIbh0Gg0Uogk/yZS8ebBAEI/OpY5cqAnR4IbtS1qNJWOYo0JRH/SIBAexYqd4P4xI2XokYTCQc4pS0ZPbkgmu4ERmLGeu0OaGxQal4AECTr5NVkKu7BysY68cqaa4K8qk5w469oSqUGZDrMUcUgRdDBCda0gutL6eLAsQjEqs/urFkUNqMtHQ0QLJNHfgwkhh2KTGmByKnANXVxtwYsiBjMCRQB02MwQFVEJI19ebRJxCuJI8RCcgJHnJYinagc+wCtdatmHnQtLKKSmIUr6YIZkr/UAVwKNF8p/UqmgmJWZWxkm5hlUUFgK3P3VUxVtf80ubmrtIXOly2LCty54gOMlL4TVkA4hw/6gBwJqYBJCkCLZfDWSqMBm7aK41FDl4hirxokq4vx/Fsu9zc9Rl2LB0GQPXoqAYioJAlVDvBSIbzCBF28XgBp8XlaSeThF6B8T6hvxWvpWxhLjLjF43AOnYTrYU+QJOp4fO9Jrl1t8JbiZriOVHlxNP2Sw4ch3+g1iKa2aFyrUpKcW5dK3I8i43AHH2pJbYG0csyYnhLu9Chp9blpbNQGkJ/JOY3p1Mj3lBCzdOZSmi2METeGngv6KnYLLE0jlkwtIN5eROn3PcPLxHtWd3BIEqnR9k0O/zPyWka32jz8GBotSY/iBJZaO3uODFOBEq1YYC9rmtVWkn/BWOA9lgnpJIoXQaoLEIYl6gYT+WR3mMWjQbxuZu77EqgqbyUTplshyv4tIqd8dvSYPmh5fX8OwE8Zc3KkCD4v6luyMlSpji1h7afeoy6NzzbXsQcPrIQNHiQ04/ASnqmfsuamL82+QAhvJjSzpYY+I3rSjv6bGczIyjcZ7igGkmg5BcTYAEiniaxV3RIJX5TcS3MEJ6kkORIGzPRyDoVrOHwqlTu1nOyqsEihKCuRQx91EgXyLTLuKPURjP0LFTQJ2AA7kYRvHgcsxLr51hFasuD2i3NYzF6AslKINRu/FNL6aTfQ9aZAECoWntq167LcL3x8yuMYDrDNhnX+mc0QcjmUvL2bg3eEg6wpQesJ+s5Fib1JGT3hhF+eQATRW36ok51QigZmzsFZUDk4Cnz7ttVEzURkJhhsWotO6iy7QUMi8GR6GIwHMTbNznfT/T3nD62quvP7z/8Ng71k/Y/Y/jLXe2d9kFtP+QfU48fMwLUtXG5StXrl67/vTu3Q+9/MlnLl2hjvDsMw8JszmHaovPnzlL13w48fmB/pRXEK2Yd/Vx1gU3vlG0++DR0+3JmM7S9u7Wmd3liKUReuvD7mhrNJk8vPzcOfbHf/yTH/1X/5VffuPN7/zZ/+DffrT3sDN7lmoz3n589+69e/fvnz1z7sWXX7xw8eKZM1v4EbuPRmO+dUWHW3O5FQp/1jtcQGOQ78cafKxVLetk+Ji10uky+E/LZ/eFShjfc3VKlaYzKjjXmBDjtiGhCARxmMRITEdEDYGqdlh3o5uLm/Wy3uhTBGTbBhMj9txlhk6o2bi0D/Ye+iqh1dmYDbxxafAxb0qdZO0FM7PpQpuz0anT2bpHjVpOnlOK0V39GzHiF659eCvTETNk47t0L6yww7v6KDZm+QUxeEewez4YxE2Qia7r1mR1ZvyYz4tQVeBytdrZgyEmUtGeM9aU8Y9+ETLmDSpcIAg8qz77nFb3dDcSWSjRXzCDIIsA+CAL3qtHygc+Tw4fh+ZcX6EOdzGA1MGqXklUEo8kUaSCELQEcwUMUBBbpuA8yyMYwF29MJOCMbHDIsRznBZ+cu3WMrC5h6QIch7dCx8U1YiyFxyIGD2jF4ZyCOWrk5m14EkDHzPoP+QVT3bO2BeO7ezagTiv+03kD1sGBmdZQMhFgoTC2iVleoLLyKzwqrx4pwHBBbjnXIFNedUe0xdixQAUDW+2N2jGa6N4Q2JBBTH6Gjza6NeyYNCpJEspep+CJdyQxMYuDOafhYDs1VMWVC8CLR1jK7IVjHVDJ9gM2J3FdTVGGJOcFGScX6/0pigeiq5NmclMf/K8nj8rG4MHciZHEc8zeZTwFwlpIdEY13Blm6lL0ZDDNfxrTy0lfRn0t/0nTaXwvWT4X61u1Z5WMdvNZYkOQpFeQwDIXfroZRr0HWWpXTYyASyDJvKPngI7lkgLFNMohQcU1iLFUIckUwJaYNCPzQ1zZSiJA+UNZ1HJRF2TiNfIADDDNAdITDXgnhSxOgdhN4NKnEYEa6YGklN4Ulh3lxuPwieKulFp5LowwntA73aHPEJ2DpraTMcNLU6bq3W/0Yw8ixv21mClBO4gGIqU5IbeZig3LKrPVA5F1sxe11HXKaV2PAKEmO02o/kgruxTZzDHDYI9SINIg5ATS4lfZuTBX8mHgahdEilXPwEs/JWaBBE13oQHNESDaCMLBAo1+WY3zK1Ainkq+Te3//0uGocRINSbMCQoF/xFV+1HyYu+RoeBK+gtowABAABJREFU3GySZMJDbpMp3yCKH1cmKdT75NIl04M9hErZ9aXlOBQxdHLXTiQKH+uCKN4hIwGGaRsOnC6hzPhiZDLKUH2DEI9U0uCNb1NjNILlRc1vcHGjLIQ95w7TceLkZgwixdpuRdW2MqU4h59g0WwK27DKoin1E5qClaSRycsTnURvRlPZEZN1WF4tIh6T5FAsSGA0TZCUO4kCC+OiIaNCAz+UBoxidLPoJdhNLl7AVtA0McZ6b0SUhjLBQFPaJ3c+Q4LS4XAuG1DvE07JEQEULQ0mo7aQhkSy6EcYMSFdwkdFsK+c9B3qtSHStYmIAUlXFsCN3RGzKjc9BDUUK6AVNWSGcmszykVBKkzmpQcXXMm5GiTNwxt/xOCl1Kv4iHA4oQBmoLekoemBmUfjP7QnNOiN3HaF39FD5gNJbJJi7SUNtbPc9C0lJGfSI4VFELqZjW1bPm2ABK5gcBMOAQ5DFIkSSUXq+EFyTOUvQOo52KVgwaSGxxDUBKRXbgAkEfTrtPIWywYwp5ZGElY9Ojp88PDBm69/7+atm0+fPj7cd8mLb/pubW0xR8u7UDH3Md//omUfncmnzfoXL5x/6er1P/qv/asf+vBnnj56e3q0//Tw6exg5rOuvJGVN+HPFgysx1sjPj3GR9aOjw5YQqDWujDuUgQvmxwxAAA5O++ohGw3Oj48ZGXi6hXeFNnd2dlmfUyCIxaLOp/6nR/9xE989BMf/8B/8hf+0y//t68wbFv1JsPR+OmTx48fP3n41d+ga3z2zO7Vy1c/8/mffMLo5fBoe/sM6/h0Z6nRo5Ffk2DcisfBgx3uuIlVJ7WlFKMRvGoqBob7clFUZ/05pVKrgLYVBCUmMhGK9BndNpgopVvYdKdK8S52On/2cPAFN+n6qSZ0UvVvyVe32G9/jgcwjnHFbDGAiI03GnEthReL4GEMM6h29BXZZwKHrGY4fHDG0Lojj6CEfnFbwrRrs/X+EjHSWMeFIfIxKmcum60tjJzs4DNuw9/p/bt1DpD+yjl+u/gU0ee5QRZKBIE/SK4fW5dQODdwlCgnAq6EjybpZlOBAks6qlBlYBKt+rTak1skSptB7aV4HCtYoIoGs1uzTaMwYUROSbZONzxclDUtq+ENTcLoBrBsy6ElAw8Sxo3VhVCfgMENhuJCrvynAbUExaPvSsJyvDqBhQ5G7v3OmIHClA89wAZRplgKNNcSimEip9hZQxUfnIWNWEuByn0iubBVTL/JRkH4AMLHL0SKZDCngbSrXupv6LBERnyDRKJx0iKOWpesAZXCQSMR70Jd1UnWo86oUOXnPtrminsSChTtuZCghjGBDlO6BqhR8CLCOnamHH6F4bGCpggTAIiT/3F0GJRolJLq5qgaDyu+MSEY3UzpXJiJefOS/FLeqoEk8qz8cQAY9Q4MXqEC6aJrbEyjp/PqwhKELjdcNUa5AVSmk6GTQRFOTIJ/IGkExe2eLusUHukiJIdCwWp4ojQlcD8MKXTkTDlvQlGpQBJFFkXKqnl4C7JSvvjgUQtacM2nBEEDZwLrqJABSkPDpIXi+imspigdsTjl0q0UiBaOrZTmBogrq5GuSq6CrLnnUuHecQhCQqDMOJ1duqyUohoOZTSA8hnR3oFxfVMoC784lDbckJGGOFRP0ys2gr0hCY5C1Bh4B7fkmMxPscRlkiytBvmS6ZrXpDSsFCiy6ks40lM5xeThj5oqfouhGCV52lKo9VH5PN1sEUdX+AX71zHlqTfo+zaeTUojY0odJMiR3qxnQkseckd6gWMNgSJj9twnmyqKQzcgUkwEUtuDDe8UbVBQf80zIQiJUV3ei0+BEbvBNCQ57eCVGBz1hp+g7PKOI1A6CgQMVFZC+fEf+xVua1vxk+nBHd5pqA6UVP1AehRODeX9EjrnND01PdVyVIXjy9bx0R3xgDjyOFfQfxvsFHeXCQxQLQ2eaaoRnzcDQG54h+DCu3S0zeCuG7UNPHISWrJMrzBNXJD7NDoS8SQJ9vLBSlaKZCJqi44IVMymY+3oR6OQywFeMVs/wQQeskZ8CRLWiHF57ioWpA+SUE/jq/LJjrbYMEAlTxVFUqUBGd1aYoFzneJm+g10TujxLNe26mEdIDGCQVFedeMsFW1GtEFxS2ludMu7mGBLcR0vgV4Y4lz/gEumcGGNIzqZaATKestZCTzouGgwZZCos2I0Trb92imVV/8E2PgIlFGWAG+9UCWc6X0zzUELq3S6AusRbOxhyo1QTWgLIYikKyIlUCSYA65ueW0KdmVd3367zQAFXJTw0WoSaFCBc1ONu8bZHkMD5bvNK9I7ZKHQXZDjHZl2RLnL3uihIBrPfMpigzzm8KDT50Pjtllkw3KkWwMCSvr8ikOb4V1uUjq5APIWDjhxfjflhA2SiieigwvqPvCZsW4qlop6VnS1VIftDdqUL9aWhrzT7W/9jV+5/+DB3t5j9MOTAHiSXZEpO4OOzp45++KLL9548YWrz13d3t6GLi/uuXD24rWrVz78gfd98GMfXPYPr52/8M2v3OUBX6Tb3u4f7B+cPXuBxXMeIH7w+JAPTLFglNBXMeQSsqw6T63c7HfZ4Y3cYLUW831iug18amC3v03H/dzZs5MJr91m5p5X4T5kfHD9hat//Jf/9Ztv3Dx75dx/8Cf/zFe//tW3b9/mYQM0t1pO9548ffjg0d7+we727rlz5x7d+60rV6689PJ7+Sb1/v5kZ4evLCM4Hs43rvyCmLPPblKws6AuVBVvnuF5e+cp9THUSXourU0YX+ckRf3hLgB7r2fbsmJ+u8qgK2vGLNxoDTI5894h+9PTbPcgDrhgxGPofHyL74GIw8etj4e8fHy5mw9s0ycCASiog4995ciSd17BFD1zJprlEOflp9e/XwaVF1KzkSE1TiHK7lzYltuFtYpZ12wFFAOv5N2ffMqCj0dT1dzbxVt9edK9v8OAzbe3ywj9Kj4+xU45V1nlgoijZMYI8UkGXviVI36rolrnyFFxFop6uE4Ntro7wMt8v0WjblcL6Q4STqI8rjGGtSh4rKeuagLUf4tzDo3IExQOshkJGcukGJLi7NrWID2xSLb0OOCcpKINBTmEVI/13ee+4NTto6t6U1BaWMoBR0nhhBA8Z3XBUoYuZA9fQXnO5pnu5HxeCnYw2HvaubTo8473sRrJG/HBJf5Fax3kwUlZdUmoCSXxSCPsRyGKFMZLLntjhjy0kVROUZKb1zU0g7jFDdLS+si22JBcuJT0MubndsWHNQiDeaef5mDdgjUlVHm/lCkjOQzC7UIjCYvgXKErPYqDa/RIMmUIkhZFJPOysb72kYPcwmFGP+Gf0vn1PssP7opSCIXy3H8gV6SazwCG/jRvnxY5MoWMI2D8iQqWhtCQjIfjYvinLKYoBjC+Fc8W4E+XVxn88dwXArIenB49dcoswiJQGTWEA3KpRbgnFqcS4Ces9cECtQCj0AZlwZwyFHanawkCTS0FRaJsEnlqS3l0v5BRARHPH9YiOEYP4Aza8AMksFxVEX+8Qa+qDsYQYVnPKzrfH2jSwkaUhO+Cyz/54ggmIShJclKiBxKqiuiRZhd6ioUY7dFqRltmy54c9yYIJkL+h7b0k1AE1nf53ZzMA0M4iPBVHJ3LORnqJ4j55S9txqY0F0vr9ap3KI/CcViCSItItnzr+yR6KqDCHOwtB7aR/bROClGyVU0QmxZSFm2oAqcqGqYqsc4WOpAnBbzlrsFLtaEnIOll3jVOQq5haBUv2GLY0/Q26MT6fbmNVKm42FZdEipw02SkOAMZWVznr1yCFKBjGa3TeI6dKEuW8cg+UyEloXyM0gVcrWyuM0YXgiIWyo9XdQeMqR6GMbr3aacM2AWcEhACgEkrqmE8264W2iNgFca0QSURwpTrkAVutes9l0kwiauoJ2QbY1bPKEJRqIAkW8STZ45UfjNjOPKZ/rM1DD7PKQUOw2hIh6rSFQqHE+GDdNK4DJy4TQ4KlGBEDUl4sCRdUbiNbzVOgkQ+yJXTwBM2mcOqLBs5mchmb9uYyKHuHEAt80wVWilRKZSmjmbfAQO2i9LkgekIop4JdskTWWh1AYGvcKcAsOdGYkiTbJlk2oWgCx89IC3X4ABEfhNwvCCReCK2pnMKu9FKeUsWetnZpQTi4AeUXDsLQKpq+ZAZGDBNqPyKE803HVsM+dh8zcZd9sTnTT5Ge4r4HjR/3QoERsZDjE54zG/ox3r1MWas6QyBFtw22djR9Q1SohSwRL1KBWPQxTf59i3w7htzgz9ZujeZEBIiTKo5mZZfdS918sgNhJBRDUkCIZuuJCOyUqnBFIuImcRSuEQ8Qgfw4KIVnczeun2TJstXaA+dKX/m8uUbN2586tOfojfLIsAzV57ZPbvLQ8CUZWfPzs6W3bbZ8sX3vwSKo6MJ34fjDdaoB6kOjg7x6IPDfWzIV2PdwIZufKf6ianxLaoJgrEGkJ0SdMTtV/DNNZYL7t69e+HC2Z3ts7MZHUGGKLzWm3dJjfn6mK9qHXReeN/zx5Pp/+aP/zG+T/y1L//Dr3/jq69/9w329L7+2s27b/FRgqMnj5+88sqrfFD34f6DM8+c42PHW8Odp/t7586e45tsxCh9wF6rGkM7mEY1qTETygM0kJqOnZyf07aCaFl0R/3Aghg/vR3LI0Hr/ZetAhUKwa7e6aH6BA9TlBDR9enHcE3QZFmdr3NRW7rdM07Bj0Y4tIDkOESHPKZhoL6gE2UfxrhBM69nQDfur0d4x0kIf2NuqPBras6IkltS+BULnOpIWojBUfRAD4uPeq86x/3uNptg0BaI+8td6l46kUDj8SAwMDRM3PqvCBWR1NoCCJ+pXOFCatAU3Glso024AgwCFdQrZXNWAFkXMojcXm5axsGoC3xuwE+mcOC0ehg/AcJw9FKEEQlcUn/DMTiKOJJb52JdAkM0CTZ7gVWCHzEVrwoEaFBJRbPUpq/Zdmd1ada7SNVa7vS3t447fEnPfeWwbiiUMZDT4aYwGMDphQwJIm/8j1NyA0uc5VcxhFZxhHaIKi+XoE3jiDhitrSyaEmLWrYsARFvQzU/aiiYI7gSCQ0MpCzNJefQrUtLWyhYkkGmAYFUEoVEKbQIwKhofl1cPaFqaUTxv4LYg6UCVFkXu6QLBlEW+/IhS/yqe2mjm7RIDVdYtSCYJaWs0FZmkW0Y12kUV0wlFmyhXDQNuaQpmCyr5FwKRyHS+JWQ0ORwaUl9AYkVyMbHouwRFQEYBbMIHYLaDJaSSQ0MZfRIQNjTWClBrRymc4ij2G0ckBNGk05WqEcii6BAoAOirqI4IGEzgxMUou9QCBjdJ3QoKCTOlIKwhPKUOByEo1gKKBNTxkxH4hQNnNoTUjxy1cpW4cLTADY3gvCfQlWSm1ZK2jK4ASUjlNYAm4xQFC7wFAeHaRqJbXB1t4GGzmp4SyL1heB1hggg4E+dKyPJkqwLEsXtwc/wpmSYsd5kerUWoMDqnC/d8jEX73hagIOHSj1OSrbb0qxIwPy8v4NbnKNQwJWJ0XwKRj3OTDQ7NcKZqyi8pJwQ0HIaPHoCC5nWPY7Y0F8SS+lrFZhCujrUpgWzhoervGmVOWlKZa4dAOa0wpDxiGJE50wls15Buv0gRPAcQkBEJyZJiKPeqR9K0ks8JP7BAPGtorB+SlLFcJsKi8ed4d/e9ManQcBsQnxRAon90fBqdMfGgHzp1m84indbFazZgBJLiQL8Mp/WXY3uRokJr+O7YS84pSkumLEnkeuoIdXJt0jFgLT7ffovyGk7ZauEFOwLYWOENo1BIWVYpCtFt8c+Qg6K8OL0O9YsqGR2A/a5cb7RBo/9DHN2HtgPVRVODa7wNKTo8qlQar6zdyxH2y1gb4uTTGoxoVc9OHyHBFe+aYdNihw8BkD1kR/jAjQIY8gRctge8lgk0lS0NxICmTgIB4I60SLTJLIDnpUZFMn3j/zQJrCMI8IwVBy3CajW4AcidD7SOhqIWNhnXwSdBDL1H2bTlQIeocALhPTkE78ikmIsEPGfLiWMAKSwptPrdEnT531dbjYssh7ELl3f9dlhmpm917xUnp49Kj30mwS+FsnRh/rOqq7k0KwRN1Q8oXQ7iPoNOonWLEIh/NSXSKBuVMWkOjOU+AmjCzZvUJ6dG4zE4JDJSyeKlv07bBxWebLtwbU3gzuhBxMiIknLyJJkwB7YvNEc9OAhn2IyAACT6FqUU4rBCDYRYsDXNe8+ODg6Yop9ejRBxXjfH/qlX3jve19+5soVlIA1sTJvYaUq+i5tcPd7PBvAmvbISuJSz/TpHoNwdvA/fvRgMu2cObOLW/IEDWZjRjlcsrcc02FTlMMwaQ/b+DFnPjCxeLG7GC17j1BNpKE6L6fT2aNHh0+fHPEVgfg7gfxw58wOD/jw4O+lZy5t7+RNSYPVpWcvffH3/Z5/7Od+d7S3+uY3vv29N1//S3/xP//yl7+Moy+70zt3Hv/1v/6lq1cv7m5tj8dbly89g/c9c/mqHwDla3Zs1M5+ZNTP1CM7angKCB01bWk7zGilQV2YAj3b7fc9WoBfU/Vq26EfZ6sJ9mAnNHd5p5YmUvEUQhC7BXy4TPQ8x4K7ZKpQnwHDgJlXKq/v9Fj2DqzQ+pjvOuSf5H1xqPbFbyGlLu39s0DHNRg4ILUmx50sttT8NttDtyKUG3yo4OKkFmNniGB/qjdsgJCEIQ9KTAbnns5n290LW8Oj3mJ3PnhEz5zF3MyyUBGkAhtaWWdsROuaHBABkMAooEwF0mRYgbATOMy113vERAgSGEutR2w7hnhLkqEZfGLg3fC3+KXikUS04ZtlTh4vmBLO5zKkZehOZUEyIsWkWhOMAAX+oVmrMq9LtpqwNksIgCsGCQRA6EIVnllcAp4ruKg0AEnAUP5YIKJ0Z89xyxMa6AehBn6c5AGfTOn19wxWg0MaB+IYwFGvGjMWDe8Hv3FbPal5sBhEocZSoJWYLAMwFM3SFQVWCVyc0r2YRU9323TXMXqDW4KKDgoWsYVUGxliBVqkNjbUbqXObhPg+cYMTzFBy+XiFasBLIqyMgkqMYKteGZtiPhTzBE9MAXZ1IUoUIaZVyJcywQNkH1y5REmwysNrRykwGWkB5frpX7oBpF9VBee5WGNFujA27vwQtyyZYMa3AUuGMn2EMQfK6tZVQYoK0i8cG3rTmgXpMikEuy5UFFUiqXjTGM+cAYCeLGY/qfyaKo8EJ8kH5/ziQEgnDjjR52w6NHlqwVAzZ+V6yVzGiCzlNTABagpWJeUyDXgzXIkSiWSiksHsAhXhIU2/regSEiEH3imiCFJEspdpWhoMIHql3GQzC+7Q210P8UpS741AiexxCLPYLi+HdQGGQq7KU4HG97vDHgM7FxxrZuAMwwC1n6D912nMBU+5Q/cIPec3+K/ODEhh7zWRdCW5lsSP76gZXMIG22ZwVNnPotIkhg5KqcpupI2VHLb+Kofs+qqGFB3CJmb4EwmpwYVeG9zVMl20xC0OzVVRwGhQs0SD/CsnxVaKcr/5ngH1tOpm2vgw7YJ65Ii4y4mWutCXUZbRNLYsFBHRUU81on/NQZxbh1ovbpKvvUtTgP6IGl8h570Q5NStRcleIRrLEonN+GlaSV6UBvmQDFnKgRX1mQx2sk2hX4Mh1xEaRIEiXJVS6we0YEorPZect3Y4qo8QREkV8o20bADRoqEPEHZ1p/rmpRqqKyEpNHXKT1zTUJt/mWvCGSMRwBHSE6+ESIVO8l2LihB8ZKLwmozBiCxarZbb2XMeAoe2z9+aDLttlLAa/DQO+Y5Sw6nVUnkABUP0lEWBpwZ4uCOPMJT9TgtHJ0ElitADRoyFUc3mkMY0kQwcqFMX4T935CfTxDRHQsO84gZvE1foxA4HKlhEmaOjYV8uQj+3HXKD3PHwDB88UugMO7cMF8DMOTx8pkZ04sm8joa8XaYaDeeGuboQYMBPhjJ6ICQdCsVu6DmPCBKv6p8kjNTaryCgxYlj0gqidDwVP3vGi2gOphRw354sT+CL3YG8PYYyoUfXnjuIMpHl9nS4VcC7GG7JcmnbG3k1ChXcRvQEBa9LXvTUQM5PQjE0QlwRg7I6bIIgCZ6SzvTpFCQd0ApZneOJ5jNpgMK+EsiwxBwAMnoLpbXICSRr6FIqt4JlLSgkJQiB2sBhOxQK7Ti1kPhh4FgbzadPrh/n7bt9Vdf/c53Xz/Y3+dxXj4U/+GPfvSTn/wUD/9iI0e9IPGVRF6Cym3NPhgpGx/48AfoQPPp5yuXLz892OusDmnwdnZ5bFqrox8GeWyyQQ4cAIbwCdWAmjLxGcHwsKaU4k4ZtBdvv+XL92DwVXsOBzu9+/fv873hw8O9D/7wjyx5MHU8zoCQr0+4Ws/Ty1SRF15474svvHj98gt/9F/+nz852vPduV2+VTC59RYvpuwMe/1vLbu/46MfXNzHq3gd6vbZs7usWbi4wzv61FQ6P9GsnKRjjSRWMuuZLotG6Z2jR1CjB/upKphUTlpYG5PUrMNFKlpMFtPwACgSZglCSMrAJf4CGA5Ib4l3Po35zDY9/FhR9IYOkfOUt6/UB9RUDDFwxYBaqa/IJC6kgmHVdyTqE54dftQ1t1YKeiRUFmfHCDX2rlQ5vC86IzoEjNXdyUbZ1Xh12O884btlw8EMw895pvX8asan92BXQzbk8Trh8UZYKR6Uzf/80xUDkyQSgZVLtIM34liEFKzccsFDkp1U/WyTiAooZwy2dyXD1hONxLBeJ+MVVYArcxXSeVVMiEMHbkhKLTMeMbgQtphkYK4CSNA6/jlLguroCBmnCEHVpQNHJKSg9V8e8Qynb3nPlW7AlBwm59PibOya7jsxsHPM8M49QcYd6Ykdyhgd5pBaTchsBCSX+4QEUmRQxjdRnBSbPfrHosATnEHQ9LY2ZibGZuAkJguX5vkVVchHUG5jQgphb/zX4qSkRbMJUFuiwEPQsnHY0AdQOIU+v3gStksl9i6Ni0KGDCyhTZjkGRUSiN5oxmVV6z4ZEmywMqkejJlcAAY2BVd20vOr6slTUIrmXOUQLFwhiH1uwOBfg8eY2Af28zUGVaAccT1wSl8lSoPkRiUUKYV/QI+YEIsrE3T9y0ISEzmWThIANtrEkbyvCUkVw9LGZyoFKZngED4h0aJykj/SwKWbRVIAsIRVPvZwc15MbIxJwBevHMuRhUQWfLABz/kLphQQUk2AJRxbDrsZ0bVXdAFMfvUJGROzTGFS0iGHaQn/GoZ2zRbIz8WTL9kA+xNGLClFUzcHNyT9dgfymFsQMB5UJ8CtsBJ5WXKvsyux3SG7MNpLKMJgw+W1acjSmV4nO5jIJCP4yGZnNsl8WZBs31oaBN54gBlYRS7+SOLN/e8gvgYNPKcqKd1gbsmnr80DX35KBXVO0RUrDLIm68pVQpkVeM91UYi5rizYfEdG3RWmMizXyu3aBc9cM3+fpUTQMKNPDu9qlSWRxydE6LX/CncuSRrcs0uasAvjcZStE2AYKm8CAf+MvGLAh8SDJSwbGsWQNx7klacXKpNkx2ocVa1/TUuX3HiiRARqGkpg+LOrodKIQLTQhLXop6GmgXPe3DKghiMnOr3OmQQjJUENPHaWjBkybTDzID3NJ3qjO8SWiciuuIolr+Dz9ZIUoEQwK4JECkOEVAk2KrR86RKV88qokcTd+TIWDYPUiExho4LtDbuZ7QxoCV5iSQ7lsvuYImgqbDKzlbAuYZlLchQRdciE8gOc8rAOblO1lG0QBYIpQNE/M8TOYoNZ5LDfWjW7QdCiIFEMbCueGxU9M3mkLHqz5QRjIYRKdc6PiXDL6wXM7asJOt/0iX0Ba6oaTe4E94nK0BDPcoiA20gHp90tp4OPJ8f70LFvydciwb541u3mfDtLpmkmYeup83mLc+yjz6wVrx10DoN3GKti2zT6q/Qe/AJlf37EA7FwNJ9v0QHmAx7dkV6q19L7gjbtCJHU3Rfw7j1k8GT4Ivqne6sG1H+UGNXpf2BA64DIEXeYEvI0ChhEabrMXtLIOnqZtkqC7n0iQ0hAGQJQVokAjlm0jhbTsu1wRjWTTwKImKwyEezJKjrEp4B++PDeX/9rf7M7HqLEyTHdl8uzw4sf/R3PffGLX2S4NeTDazi9C9qSR0mwSEHY3aLjuOps7QLRObd7cXIw+8/+7/+XR4+ffPLTn/UlSUNfdsHggZpIY+wygN+64ikgQjFVDiWQ7nCunmjtDx6wOwga1lcO9an99Sd6uowhUongHPXyDqLz5849gdijB7zz58Kzl3gkdsaigzWeV5HyzV9WDxbPXX/uL/zf/tyX/t7f+2/+v3/tS//Na4xlhtt7nDtbKvpgb/bsM2fv3727v//04sXx8dHkAx/84O7uFi/9oJeHPrEqThnl4rHszkFb9jvxCYRiirzXe0aT0E/GIdSq/RwkCBeUZnZf5TdLWavKFlRpNO+gxIfqCZtdH11gbzrhJG/PHRI41Ff/aOor+NMh9qEd7C523DBmMFrhSCjG9Undz84+1VZCpMVMRZOzb1Mhc5CnR8RhmofXEHafMc8PICTG4Rl33ks8svr77d9l59wBe96OhruL1e6IL3vA9gz3tAsH59pMZRUuKijEDUSFfcVXBajqz3Ja+u12ADWT2sSPqhqTJzwqxkmics7oksooZko4+DOJ/3DeiEEdPNQFvQlP4R9fg+t0CAXUqC3p+Oonu/iUAjlaRj/QxKl0M2sUiooQAuhxaaE42zsVngCrvRj14RYMA7yVrPk0INZZDREHkJ/umxjAz9Ma8kZHne2HXPNg1eDosDs6YHxAeJxfhmFWkFhNjtMoEkygUUfLaBLCDoTwAj7jSLxiMxiaYRbc0YWyOPpj7cwwn6fP5iu/Tk0u9Yn1muu+o4w2izkIX+vLf1ca4dkuoMQoDhrqbhwKyc3jxVvRAbWS+Sx71uTCW2TUn1i6uC9jQEY75Mg46mRJ2+YnKou6yUHJnbyBLYN+myyqj96iZsDrFVESGaIrEYVY/MOZI94VoBpp0nQWX8GcO4nQuhEbHHIQbLUgAKZrCyUlD2yGEH0TgOXcPRfL5RHsV0DTZEg9frs7drZC3PaP8V7k0IfjwnJEil3kwRvOSC2e0wqjR/r79HkzyaUocVG6GKCexad1c3UFvcAkw3OxWlP4HMlVnQf+5doj9QhW9SrZNg2ITFdxW0ZSJOrpNd7F1um+hhpVG6rxZQMJC4ChY9WsJpsuwErVwU8VgzoCclQKShoC2wtOveEjsJgt/wCWFVAcl4SoOyBdzZ41nbZVvHamsAARiSpHOaUwmlnYImKQIOlhhlTW9uopFyIAaT5vk29GSSPggeVtk2RkH4T35HDPQR+Vo33hSiIc7aduTp0tFNaJlqrZWwYAXFSR+vVW7I1Gbhs1rlM+MmwINXjllF9vOeWas5pTbZZMViHPWcgfcEi8QaWgHKY0Cm4oCtWGVJBIn0OhNkddtgSZ8uB8CmQDSzr/SkQAgCpwf5BYycuJvIKT5OIZJ8goWxWOoviTQTOg1oIgsVyjJ0ChTYq3LY97qqwMbMpUoTUAGYDKaEAlBlIrbXpWVl09r1K5gpGkpEevwzMl5NCWDgduABe+Q1HhEAodUsHpd7mqRxdQHuzdEPaYRZclvZhBL/nWSabWCJVek0EUigwqxwaAY+gbB3krJVEJWhDxPxwQAK3basymrmSowhJRM/4Tjy5afFq8MQpqa67FJWooa0qzmssLKRVLxWfbCVVhnTRNSd3FKipHCJVfUnIj5nCTcqaZIYpiFQwUtWU1TudITmp23aKbcIVODfehomKgLgM1ESPeElRge/8I5PjEX1pcacYxCE5MLMhtKZa+FS0xB0VoA+y8GvfDohqgVAJltKEaocRGAkIbk77pLbFCQrSagZFuDAOAvl9bM7irL+AVjJEAjSszc2BmK8tyOONLvkw8Q9LpYFjsj/u+IMgOim9koYy9LtsvdEVMl0lfPKKuSIHBoI+K9FKbE1UZrSfb4E6OWAKNY6u2MoHCQsEiIOK/ZscoaMsWxcEDZIJMGC/5ReeawAPqFFA/njmppboODK7S6x4f8mXfwSu/9d29o73Rcutgb3/37NnVqP97fu/v/tiP38CzcDofUxjw8hyHHVrIplY50uasDp/uXTh7dXZ4uBpv/bk/9+//mT/7Zz/0wz/8sR//yXMXzx37zqA5w2IK0THVvemTdVd+XJnVFtiKzRBIpMwo+V9J7CGQa+sGeYg6nk8fqDwZF3HgweCEgyb30cNHyLa7c4YpfLnrdQ4PeWa1s3tm98KlM5efu/hDP/SRf+Ln/+Bv/Np3//x//Bduv/0Pnjx5CrrVbPra6999/PTptavXYfDNW7fptLz03pd2ulsoCt7dHqdBMLVLWRoXAZzOdS1LzdKAe6EPwiC7yvB1m0N6cDEkVgADQsQlVH6zWWzBRgtGFYveYiJizMbaDu7HNhRX8RgVPeks9xaDSb/DQlhQMAKNgsAkMlIpFPzk44q6BKj4b5ziWn3F6nEArttduxWJqNA/Yga4YEDMPpwpcxrh1KrM+I2+OKOR0Wp+5KeLJW1VwaYuSVEazeveqoHfOF0JbGRVIcDQVwCbhENZfpqqIog5eq4a4Vr349eiaijS6S2tCMySrjDyn+DJTWr60q9PmGphPb/wWOtTL/W04LEccsQXVW54FBvyrRuJ4gK3A0m01HiX/uawPw1y4gNlWcohLLpaxdbWwz4fKJzQSSPg4fdzn2Tp0y33iwilJbWumApKOQ1C1JJn++d4CYwZfvmP/6VPbCwEAJ0Y6ez0iwOW4Y0Ia8yjv4kOCJysj7BXjFvfSQWPQcxpbQXUGX8RfxBQBGapZfgUmtEcOnKCktpO2FQJeg48uD7GeMdhWAlCe5g5ghiTsiGpwgmShq8oEl0hgvs7tbX4+QEEkhDBv0HJMBM7QCF+A6DxOpqRUhRDCfUTzuEjMQAB1rT0SQcYYGNVYchi7mLBM14RGRraM91zWIvijVNucNV0JiXbLvaKuj0Y8EAHYm4zSl8O9nvMcfBkfPwjojqkRAd8rp7CBDRfIj1CKlXPtBavhDYfzOLGTWCWqsVwBD6ShpiaG6rcy6UF9Nh4ullRNTq3qPVCJoFXAWXYOLvqolTikqOkEG6Gr+RSI6YkoBnXGDVyQCjlg42rHPIqP+A0P6q14cOPwUXHyIkJ7qNpTSQi7oEN97ni2sLrI4SSv4ZLKbJLmIKDoFhEs9YBBVNpCrLA2jmg6+vUVCsPR4q7ysm15f3NXX1td8o3C3G6ieLVu2g4A7d8vuAjPJem5fBX3beDC1DyT0+ArlbbwAamQCW9LsMvGLg1RuRmnRkrhLtoW0OqOulZumhzcRqVGEhoBII1SevTu1IsGiVUPts48xaXRiGI897WYqBA18yLKg4hjuAxhbqVfkFxa0pJtyYQ0KA4KVv+EBqArfGfLlFaMM9/HK7Y0IO4DQGDulgtb59bbjhzdxgTsL82qsW/CblkGkMguXEI6ldqrgN0y4FLJPHuKDzg+h8xC69HYXgjdRJqqcFCk0tN4JfY6J9RI3EsyNSBwxI05mVRgFRVjsY/IEqxZkAJTg6LtTsurNWmKHOklZb9WPKSJB6Vxj/0E+WYpaZFE/ZPccLbM4Rtb9stOiEXDCmUYuYomAowOhNRQGlnhYpPu0aPyM6dVV+iQKJ1Ixmxwi8QotQ8tWhcBTWjckIGLOZd+zaDdAjVL/9hPy0vVwQXJhkwIv2wbbXnv3DPbudYwOaWEYHJBEPbemhi1N78KuWYcLHRBAeBO5slegu+S8DOBubvgbK1Y0jg8Gnp143sPPp93iPaVraBSK3HNVtv93iLfKezWwaOHY3LNrN+wNWBDDN0qMKJJWXXJ5AJ2kRVWFSsHIbv+WU+c7vsvMW1IocDNakfoGJbPPhwZoXJCyDY+1suWvbRvhz4oaMgtI33ZDtTtANt9j1z7jEXbm6sUZdcxzRKLQhvw3x47/5kdnTnzs3pdNIf9Xi5/7mL5z/5xZ/4HZ9+DyNhxhLQQTvoKNPM9EtZYnIcgBiYcH//iMbjydPJeHv+3e++9f/5L/9rPqJ09Zmr26Pd46Mp+2wyOelqMR0J/jrLK2p9+CCaRAg4iSGzuRbJ4j1wS7L6U1aT6L5AhxkjFkFsrF1MwIuc1OSbvLSyvJ21f7y/R9s84pvGW2M3wI2G7CFjqHnse0UnW8POT/3kyz/xqf/1v/G/+DO/8dW/u3V2//69vcVs/Nbdt9966958Or3x/I2f/dkvdkfHdJwWPN7M8vBiPvTTZVYBDJVeDuxbxbz267Mo/ioC4eEAyBlsJ8LANel8TTydtLGWsGYik/1NQ761Z7DvUJKXz7LTazrv7HRXR53p1nxwxLZgOuD7/T69f2R2X4uWNKDpuTGjnaQZbyjiRTI+hyCEh+FAdlVbEYOs/EnencfeBhK4XJmASBiD+WNUeJmMVffto6NZ5ru1QDAxZKO+sS5BJaO916XdnYdirOoKSgJiitTqr7vhjeLsHKir3k0rKXpBOdFOdNKYsQgI4pzWYW90VIOD2F0AcvxegU3s0EVM5/JhDyjwIjX+ycuseJrdbYN5/IKRm5VEtqJGoyC3MilB36/EImuSjCH0aKIrkNLVtlZSUkc1DjGJyUKwG0FjTnbDc4x5Ikt9Y1zAiDRREmlIQIldnn6Z9s+RRbc4PUvwMZP6iPDFdDrD21R8hAbeAgwTmMHnm3/bfR4TYcjAKIsH6ghBbEzY6Q5xDV5u5kZFnTJrGm4b5HVn82e4YMM+KwAMLKfLKQzBFZRZpKLLCC1EwY2UW5XpLIoHZc1UapJvUu1DO0HOiit64k1TiAp3Fg2S6FvjC6Ux0iyqQECcvrFcoVdbmJJ0REU+CBooWWHANhZwRMBPgjfFrEpkO5vGKpl0gQQl3iMv5WcoS0n8owjcyp657YdkKIpeBH5BkQlAHprvL7IeJWfk6gMsGfFHSTEmVKEtr8XklA90+Oohu8p2ujzdMV8QWijZfd4GbJvKGwLqEjFlJyQZu/VHuK5TMqSRaVeBTyO6Nxg3RsMD201GOXKCjDiiTQd0HayMgEP9NacQfdmSoaLRvSFPqM13aKfWBsNksGoXl3pc5JtFeXUQ37KHRa3qTgHZgx/aPCZiaOaIxa7UhkP5tHGHW1NiRE2WwnxXhBaZyDoc8rV1iDPjwbZD5tn4XCRsq0xcIbJQXDLggRuxiZkQ7upf2ENcNsjVwZj9ui4x4OlHcv2zlPps2sQC7EYxMcfapII2OussfluKvXGQqIbCScuqZHpqCDQ44BWVjDXPpMCAJjmF3xTRFXrNJV6R5X/C+jsKJNvTO47CGJ5M31ycsB3mRC475oeb/HK74ZEEsxtDLcNip1AGJicSC5sQ66MltgKVX2lACHgaeHMTUmXWyk95LtVfKxGuuLXmnHYF9XxKAqCLeBXLubTe2FChDWWpWZxNHykMXDy1xAs5+cbJrRrUsWIO1jwCRWJY5Qfc8oPjrqlIrLFknkRzC4B3xUuFHIil+gVBcuAWoDTAohF1kClFEkLGa+Fy8AsaWeIoLiwUmDXDsEfool2pWlrIhI4mol4pcOc5iFSixQsXackLEdmtC86R3YInScmr25w5KSnnWLc45+wfeqaWsduCXCq++2SI6cLaz0H/RvIBayNjXvCSyRxaBVpXpm6JFPbegWNSQ03auMKP3/RlSoG9DvSniZU+IED0Ralr56KM3QwCKCSqdXYCkksbAAZrYKVBoe+iF9CU1jMA9h3AY+DlVCqBfYqEcNNAeKDNhKsFiwJ2gCVFdBvQriIQk8586bZEZ88J4kmMXjKdAiOsM09wKP80tC5+9Gc82a2qaL3kD+TO+xH8aWkAtUngQJGUJRM5ygPs/TTNa4likx+DsTZBL3S6ANFkmqk5a+7JJ6fBxljAlIsATT+H1/Xceuvt11/9zvdee+P4+GhrPIbdw8nRT3zoM5/93Gd5mSZQIzYFMRGOfe1GIKBC0uFmAwy9XZ4cmDHB3+s8efIQC/zNv/HX37731nCw9dzVGzzVjCfotekj2lR0xwyEIKwSYcyGS2dlOhDeUQgqgE1+nSDUDIpoM2gR+vOkOVmInpCDbr+3Godc0PABgXxrqTvgmXLeXcqaBcTAhqSawm7XEpno6P8L/9P/yT89+ScPZrf/vT/97775vTvxRaYr+9tnR4NRtn/NKU4Rum04c+M1fSOYzohUfcI31R+1wCrL/eiDry9jPriSoRjRzo2PTzCWjLU0gWLVL10qpnJ7+x1elESncUqXj+cXeBZxzlOwfC/ZNQe8i7eCIivKwd/dHaKZsXUGipqdQ+NwlF9E6YElQz3W4VXcCH3BdOV41dLDlumyJz4qEO8McA8KqarBLpTEFzMsCwgiWnMBJd8T6IX1x1TOyQ2ApJW9APRc3VvJhCQnF0KRZhVVgU6b6hZUHIIBvFKmeA9VByTgsLqIA9b0HFDSTVQBdivpWsl74LUB9Q6mkkBRcMKTpUzzB5bAJWeU0jXjrjKeXHpoBCj6ik4J0V3lSvBo3iGPkxV4ifyK0T+yGevBpbdpHahD8VsBXTUUBIkV2rdCEWgIVr0Fde98t3eR/uFiNKOL1tnSkTtbrGvS5cIEvjIWB2I05jwM66YQYJCMVw6RadEdHTmDMp7TfAzGVMY8iSSt8ItMWkOlIBoXGk6G/WcmPBt2xW1UUqrKk18lBkjesZjCqiKTRMaZCqHGUkbkmC5KEIc2LtJkMIihmgsrHx4NlUjF7uRB5nco6WxLrAONdFSrCRap0VPW5SZCWToDCYrb/8UmOoZGFgLLck1JPYjDK04UoW5rZa6TwFnReEgMkcCRwk7TMFlDFLcHDcIT4BDACQVAUTJM+yHpMGsDiP9LUodhXVX/lpJNIEDgI1n1udqNNTPswVepiwwRBImR2Y+qXNCgtL0O0dm+hRdYts542EAR0FxSjmLUkqCjER7FgL+7tbWjRbOoJyfSJ5hF1cMR4zCEtuZZZZ1vo01Xn3CM06lXz6WDkFMfYQI8xZ8/6wPsEljftl+FQCEmRxZ+ZaRBokaKyIIFK5HzDz4KovQBJ6o21NoKQBUCNbi62d8fpES8zBlri3KP+EqKKhDFQj5MiAPAJHFeOjMNEPuWInhIFH+Wq6sfeBHGAl6ndg8HQZ7ETRr8NtD8hkuvAsBdY7PB+FPwnAFpaNa53FZuiVEwOScHA691DUCVjTko753i+lv/vQPMpHUGWafgilRUZpG6tbiFUOn6aBJiNHAJ3iAbxMqdYUvfiQRzeSdS6QRnDSec8H9W8EVqRecwJHALvu2g46tGYTIkQWMVtSKFLUBTn8lck4xg1sliiF/xFXORGzJiJsBGvuARnBTR+58CdRRpakmyweLTFxxtZ5toffoiKQGS8VQ2+CJ1g0gQj0JseC0NrAlVrgBJqeQSSYQ4WG6Krm+jIt5nzrjSq7ilACw9gh9BqOjOwlA31C8/ECaY6SxO8TqxpxYq+mXbFK9TYSenw3FnO9EcakkrnM41TRadRR/0pG/tS+ujNKab05L2FrawTnuANJzJDN0lmrNRnn5j/o8eKtPAtnVbPGZqP5C2gBkanrAEmWvhg/l0i7GFg4FwQjoROHMtoDYIgtb93DTMPCGAOMzMkUorahcOgNnyeLXaDRc0EM4Auu7JHL0PvSm/gVfPsKUi8o7cvArDM4YyvI+E6TlWPfjEAEj7/Ye+1snprVTzKDJl4ybMDalM54G4R9LBgC5xfSZZrwFFf3FdBbuXGvbQGf81FdbAXl2fLFJhNN+2Fl7r45iGvcs0p7zB8/69+7/1W6/+/b/36yNeiuma/PLTP/lxPjt19dpLP/7xj/EQwND3yxvUaSR4IAEFYY+tna3haDA9OHZ3Orqc8iljNXn23O5yevwrv/orNJyjUf8DH/rhw+NjJufdJIQMTvIZ1eFz2X0Iw7SAqBrGyJV/RCqfVBJE0dFJtpQC+wIQXcQhXNBZGe02aaw4A43YscMGmnvdY3XMQyaU7Gxv77AYQPNW6YMBD1cPPvTjozNnn+sNPnz12vk/9sv/+9/81leXky2a8ocPj/qjnRFzaywbDPg2MRvgcQX7iFCFPnpE99rEhh+a17OxQmeSsMM9a6oNr7aQ+25nh3V/jaH7wjZIsmmINp9unJ0b2nWiB9q9MKPc7PwA/DwnCjn0pl4ApDfIoNFehIhteq0UUPJNLFzDHOei6Ms6rdwmSTD/VFb+NQ3Lnn63PkdGiqnTTh+cKBjyjq/wHRPBgwBW3GCn90UOHOEHjn9S0GISyH+Jp5Pgu+TDXoNSL8DJnoYOVctzLwMoMb0KeReG32wYHLytZRdX5JEvjkNk/hwnL3Aoi1maw643LOm/6AWtceI967QMY/DFqTjLJb4FMvuU6yOdaPxRTE65IEkfutjlOdjiWSVAR0M6ZPSPgOB70ffknKc4cDgpsmz0vG45YLbSoSc2Z9SE5PpD/F3MaA+5+EYN3MCIbEYSClLAMApCPGXc7z8a+/6BB3oIkQSfGRzzsoNef4K4PPLOR7gZCBiLlhPejcsCXa/Ps0pQ4NVMEwbuhEdevou1juGEL3bHEhCBcrSr63DwYw7XPIUii8fqBqr2+1h8AKWV1BxPdVhGQSoRQBOUSJ3onjYO0U+D0GewiMt5QKISFK1xDYSUMliBzXAKHjv9TL4TNNxyY5cT2PSk0RgwMAcQolLKGCIvspBqJh7+LNxYKPdgxYyWpv8mWfgMRcHjEf3LOEVAgpndnRQcCoQUpBO0YWNKIVZ4xLf1dodPCi5vgEV+QSisdHX9yIRoQkYV2oGyQUtCcBoV/MsqkDL6/QT8juLVVqrKIKmRuArhENDJiCLCtSm6bGH3urj3imQhrKrKG3qwZAMhKp6Xd4hFcsIdSfbsI8ZyxacYwUSK7Rq/mtSDL//oLnwBgCzCleBUQ7mAJ89hMQncJr2dhcj/8Cwo/Z9bnEwF6Yhrsiwif/yE4/T6WD2m7m8Qmnf6qIxGWQ20ogmbBIWQCDfCFA1JCqmRSmkxA1AekT0kSgTZoqCaWxcHhkRNEbjN6V23J7RDbAPWLgp9qqMm0hzyBZLgCTVO3gW0Lteo2t27STboSk6xE7LKKh2lrWODsm5DrQFE1mKqwUYB4EdHpGzU9C4cyYrOpCPFDbWWmoSWJ0UhmmbfJewGNdC5RgLrPmC51Vm4Co5UM67sq1rTUgchb6zlHPhAyv5aiKBqp8LijeApAOo0mSadLiKeAocAf1ZsFCsNwAJ88qOiVIPJZJ8cDdb0JFowWCNUks1IGdnJ4V05icW8WRc3O/cla5FqueEhKNZ4hC7zvBMHdzkUPQwaFL0ygNuHIIMISxz1r5rScJT47DS/HWJbRtDIgwhtPeXEc3p+oWL/hhCVxlJs0TqgNs7O+lZ9AB5CzMzCLuEGJBTqj7pDenCEZF6zRwvI8iwzEjOmP9SNb/ihjWFFwLWJYsJZ9pgJbgyzOlI6qEZKOzbsV3IuOGMB2tYuT0POCNF07G3TmzT0Adg5MJiveNsgMsK/8R2mGB+4LkCX37aNDknmeOzF2XGGggMi+oxKny3jFDPGl2OKnQnM5MM4nUtn/ygARv9JhfIGYkY5moD/sSmqTYMNTCqGwnoUw9AbEgP5TuHB0d/9tV+7dfut4djtM/PJ9Nz5c5/45GduPP98f7g1mflUAJWGPjrKn0x5rw6fAe6PtlDJcnJ4zGw8GpvxOd/J0Swr4Tw6/PTxwzdu3mSy+9rzL3EcTybjLWbp2Xhl5zgIey6EyDnaqh5UpGK4Jo+euM8yl9FVrlUQ/YOI2JpVTWXXOBVaXYMQk2C2IOGRANOiE5RweHjIZ4sPjyY++IFs48H2zg6Y9/f3B8PtD3/ko3/+L/7F//yv/sX/7f/yT4xXo/v33/zyl3/9Rz/y/tFojG/yZWL259tPUr/wHD8p1cIgFMOXpORTg8iEfIZ9+Ukeny3jIXiOatNNxAU4AUd8YgxDWfD1jhaAsTtBz8wz+3i3mN3tZneJuTfGQuZaOP7vBSo2SdpeqAhThQI4PhDlVKlKiEDCiSgFuIgDZpAhMh6+zAuOAiIg2RqOS8Vn5jYlnJj3As/jF68pPGFjjZikdq8u4RkF4Y0yUS4KcdRH9bBLArRj63BGVdLR7cfyIKmsZO7RryJAjIVHaRZCrqwewGd2lU450DqKP/JKrxoVlDsZOyBOz0gLW4rqBSFYwx0VpXGs9nVQqj7z6u7cQ7MuwwSEYvEEzUlZQBmusk+E7WHw5uKJRamw8RDZty9JUQmSY88MTcZnuIW4HDhURw0Tfal7PJnPhr0t9t90fe6zM1swmmGehXUCZiaYGMhAjRkLmOKJcdlMrxZZWURa9F3+pOOaQSl56h7OYFG9GOzUURjSjaL8sEnEjNuRaDHT4EZQYHKAKMnewG+QeJ2qov5kP8BcKxCkiJHAEaZCveiRnrLlDGakrqlpGxlVz4hBxsFHRcElggMtgzNBEaJ6QbhTPvQNvHgCmuhAaZsjtZ9uePNDCyk1uIENe80rw72Mo26DNl3/NFDOOvhPqXB+Na7TyWIwAV90wUdRBSpmZMwbBEkWqdCTrTSRtoZyGh6sv6JRocL761lspDdCpCCpBIU1EqJYjGt2AL0QgWeuUVKuC3POdRmNWR28pdGhgVQksLiCT4hh6Jsqp7eEaV1aXI6wbZQCXHQkpYJyCOJF8RTGW077KbBA1KXSAk1245srZSRV/LpU/ZVzebNBVReCCRQ8Wj1kiR3BugFfA4e1hnlDNBgkWvjrt9AGVFdS8cnnnF3Ufn2TpJNv8Z4UsxD/18c7MpIoLlKZi+Xs7ijuRZ/UU9eFJU5WJar05nyS2ORSBo+mLvmOdQJIXkkR51rTEjyuQELU3jQYaPlLpIW9yk1KoWksi+AUMkhJxxTOa1JJTXqzD9cB1KHqsn5TCo6kUybMO5EAWXOgjNQYLF1IzVGABDfyEJi/1bEAQpQGirahwzojW6RsES+7vCuDg6cgimnglRQ8xZcMAn1Kj8yR0A2m0dJTw2dcNqJa1qPO77iSF9c0ONa5/LYUU0ucIlxfuzyVK0Ph4gRyDW9KoVxLUClNlcmVItzKHh4rXB3hP3eeIg4gShyVoquok/hO+LN22c/QFNiAAGYKgBS0man0dKSMlTbwzqKRRYHV8A5c9haXAXeFlJkP8sADR+DsztlrSFuX4TZpBDAQ2y9nX0XADMWsG/jCGXecuGW3v5yO2Bvrl8x4+7xPxrFfhbfq5OWAILMPauugJQ1cbNGBJfknLe9Bl7INJMRouTt8pnXOFypWUGHGlu+esv/HuOg0jfNwkKSH6wYtemiKYJdhan+etlldLOh98DIO1UZgVacQdpkCOclGRSpQosioajUIzR5rvr4NiFwci7T4f7I6vduOgYBvYRpM8UyKZSDh+IxcGoTQs7D65YEE9sAuv/nNr92/94B29HBvvtpZ/fwf+P0/9rGPM1fO9Od0fjxgY6jG9h1MPMhIR3Nre8Qf+8GhyXagOe8JmrCtwFdB8qrQydFk+njx//5//ZXD/Skf6HrvS+89e+Hik8N9+Lcbp0J8cpUtq/AESxGZHTcMPeBeY6N/3omBOIv+PRYp0BR+1V9dRY+z5X1VigeQ7T9KOHpq2rTRjRuj/PkVzMAuVUgAmD6UYAihISjmph7gRlvj5fbOOevrYnX+zPiTH/zk5WcuHc/2J4f977zyKjN/H/vYxxhTuv2seygzujfKjIHcNOLmIGyoYzJ5RqOL7ZBK7jz0bJlSrjBcZtXl7HtQJ0CVDgpYUIe4R/1ZvTjQHT+gZY+NPTfK0yfEUnbGVAJH6hpcgcpVHZjTkfQv1Kg+UQ8YC7hUZTFS/KFH7U36MF743zIi8Qr+rcXiU5DCnTvy0hsnBy/myycsujn/hwl43jFUMRW/QRqecgVeD5NDRZJ1qKukVb8f5h1wo8nqyQBk5bKiqMflddHZ3YLD52HOEbeISA1NWYe6RyZLNYNGUilu2BA15Ixa/ILSHB/SVM6UFcCKWAiEImt5QxyMiJsC9UaiGGX44yR6qgmaLvfusy4XqehCw6ExBYmYw2a3tOAqCXuqXeuo/dtiGuGYpCeEgZEU14UAurTosen/YLbY7vaJQjvHbP1nF5ARLXszFjz8YlBiNDTv786Yi/UT4Id8iocPDfISKj821xv6xTj9wlYScv6DfgkQi6FT6CpV3kzI8z9UFtszvMYyzayW1sMtHC7FZqmg41LlqB0yOaORQ6XgQQZ8UwfEW9V3t+czIbxgDDgMbv+yjAmEbu/Ca5cvZFtbiNwUZXAIHuuEuy6Z1rExyFyA/NE7zeRLTCFL7E6nMATLtFZ8CBJKvsc76Hg5WCSyDpOOjMPxNoR5ezZuwbZGeLSFklHFc2wFT7xtD/ngyjRdssN61Jy1JmtddfQFD83Si9UwmMohtLMVE+r4sUL7trGkOFfG1j+1C1fGX0T38Xq8HNyqH0xk69E5RCaVKuAZfmIrUSs2jDO+NcSgPto93dQ9QdjIpq1oSUlFJrDBLVXH5azy6F6XkTbf5TAGsWRtRYSQJiP0XNfuqpkk59a0XOQsxGv28lusnpw3iVyUIPVb2EDmhX/JVN+gZrcCGVyZvi7Fzex507KGcAodQJpID4qM3NGwAfCuQ5BGB1wBQL6Q8Taqr9RGuZJiBssVyiJVuICrxHdR+m1vq0AhS8lWNasArIQPdcLxTtSVWYB1Psn3ypL8hILay2UhUdYSc40zRU0Wih8BLLI+cp/sSoldgqaguMRVE0cSbEKMxEaFQtGmwKewhExQr+nwW/lx1gQSEwom52KKaiLCdqwJiR1dYne4oZBIVGEBFmPeBK4lFsWWIsoiIKYSMjiLUEg2soIFWorQTEHDqHXBlDWmzUXhSOVcl62kd5/XHBRe2BbjO4+iuCaRvHfSObmLSxdKzqJSLeL0WgudwIqw4JMmgLDGFsqiU5rAwFCYZNMwuzPWCTsFT4voHhcxJwyxfGoPyb/8T6UMVcNSRaDwQ5xnWytDNddYy76EIzp9G0VgWPtkpDCTxEN1MFYzXCzIsymXr/ay54cJC7ppTPoRaWHA8O9OHiMyJfWIFkfJjAwaD4HoQis90axahyFtBrGTYTnRgweIaVzBBW1lSeBDkYhv2eA1i+KKnd4KNFEZ5AWx85coDgUCO0nMTYY5taY+q1VFE2o7Mzp0DI3aFkY3OhnGUEtcZKE22Mm2NQup6BEmEEbCQctQajaZv3Xz1q23337je98bMZ+6WH7owx+8du3apz796Z3tXZjlpUf06WXBVQtqspM7Azb9DHsLutGQY3jFdiC6M7MZDxA/fvx4PuUbEPM3vvvad1//LhPnrBx/+Ec/DMTOzo6dHB7H5H2c/T4vA+LhYNUqM7aYXCIJlPQB23dkZHzCZxMcAkDZloiu5QDSvJadDqvApKgIpdSxcA8VqyW5tNWy7wF/ym6Pgj+bMr7z42eXF5PJ/t7eAcOq56+/wLYlntNYTRcf+ZGP/Ik/8W/9qT/1p1759qsUfnrw+PU3Xz97ZufSs1f6vtQrplTHGbyBEVdg8GJ3DoVkNyxJUVvcUrbrgA2SGdAoZtpk4RTBf2VrPZ82nm+rjXkAgAd+UTtvoGW2iqUhhYxh8QYWtawN6FarkqrkG1JwwGGXiH5bUw7OsmDS2i10eiQlmjOkPCfV6REi3ooSNyvgqM80bz0l08pih9YfymU4IRsaUvSBJkfcwS9UIZRjLQbBNWVB7OFERejKHpHjH1jQqFwgdbl9q2PoL/wFp0RFqFKlUaJwCW/ASQ/sxCUDBQCGI1lLCEs2yUKThhtBDafhnzcm2mU1UDBqIwkgwHU6TIRZ7TGLFfmYLoCNtH1RhGkmW9v5cB6xgwCWjr4l5FibONRJvzdIIAkDcsIg3bdkTXl486A7m7rdkViGbXkDU49xuHZmEx4RgG9ld5dMfqRzj6PPed+pqnPtAVg1k56lzxngnLpHlJ/oUnZRBnUNrIrlL9rglpEXYpMHS+FQxtsVPxp8c48s8Wl1ST3BBzN4AAqdW4jcUEkQExikDJAwr0jQpCYTXdBqdFJVkq9pBqcdWPiLHeg4h7r8Re/kmikSIyCoOOIwhVKu4IJE5oQmvOuXoZGakLRWdozJzIa7SEljyqB1l0VF9XQOKeKx0cWH8XMt5xicIA8hA5KHZFBo0TI74R6hDM3G+TK6JZx3ogQMCoSZ7Ov7DjEiltoRFTk2uLnnF+hWJEWN92mPgUSTIDs65pPoPLcjExaVoXT00S9zCgjv6pIvRIlciSikAcNAGMl8fpzpEkKe7zMbjwa0C+W2IIvfxqCyIiNwGfNRMBVFxUg2kOaiAS0WTnKy0Pr4voSWobRBE2RKitbA5IUZjUgDIZWD9EB73lxI2iNpXrtRL1ylQPLqVHAFW6hSrGjHAyAvEHywN05meCeJhPgfrtSo172JYF6982BXOsf6S7dcngaJEhs8+/bUmsBhlkveR+T8AjvXIYeOo+tSKiDudydVunyLF2XzhpzCJSez59Rmvc+nPMgKaTEIkEtJ1y4kGKKmSrjdkjtnPzrTpI/kij3iydKyBS9FR2ab0rJI6XlGh6O3QMet0aGqP8ilmz3uPg9eRywu1WhCXWHyo+QF3lLkWTE2fEZLEk9h080kwYAVsNwX1hiPZLmLP4qPIsQgEYqCFOOf+x2p5P071hChUBY/gSBFHL3u9Kopg7ctFG9I6AQPlRCEGooCjYu6Egd9R/JY24FX7j2CwPPJUUkneZIWFcdmZWBTwHeA5OsNBbA5Swvh8AoFAMR/jW5DVj9yWcxscAbJhkNp+6YLmiW+ERHB9EBCAFE4TRooyBjd87x8lpiUyRiw2HzziQDCGx3yTDClMYAlm4LYYs6OXggTFrULROlx5m2D/NJ0YwJjqCX6j9C0zEJufgFIpztIWuKTfCuAhzfpuatrDBd0T4f2kKPzGh5Uv93RS0wSfSiXB8guejV4kGxLKhaNGA2RaB/R9ep1LhBHmSeKxDY4TKlHe2na1A6MUk1oEmhJePcbiwZ04+CVLzmBRTehx+ibVUBfwjC6oH2xJ0WKiXYmYCj1VJgc3sqS3lXs8yOT8BB5uEspGGwShcnqR1lkPls+efj09q173/zG10bj7eP9yZNHTz7zE5/57Oc/d2b3HN0uaeNibGkFGobojdIfR4lqnVwQ8/QnW/0ny+liOp1P6JpM5o8ePllMFl//5ncOjpk2e/balRtnzpx79ODRmXPneETNfRDqkp49tYu2H6z8b4JAhrxIxBse7lVPwaYXAEzWu099sutGt1DeVDI/FLCFVXRTTIc5uO+zG5veL5TwWOoFw8K7zt3Z92NbvGVcsud9UMPRvQcPHz54uD3e2t0e75w9+zM/85n3vffGX/2v/vaf/z//uVtv3rn5vbcvnH3mi//4F7uL54g6fgNV36Qzav+UtRecDZpsRmEAgKfCE9wAo9qALDb5kS8yNY3+FA5KCL/MbRk2FbAGZEM+ZcHF9+3DIH07nwLmS8dA9OeXXfIYPcB/wAFOnJ5fe+HciTamB8YISVbUGlp4qxoiqR3gWPd7SKEgxXnnD4d72VWu/yxBQZxHm0SeIpF0O/+D1ewyLzjpsVsXLubPA2x9DQaEVlxRyyanoKQP4tdmZJfdwxKRY8h4mTMX4RQxmZD009C8MwcRlEFHjrBWIVXMncla23yxeca7ytCmCGa/05onCv8HGK0WZZXIAy/PWyFH7NqXI9kujiEEXQaVeGM8AP2mgkmbN7YAnjZJUS1SLBgDsEJ8HQchHMAGXEiFQrZ6Ke9SkpJIFZKp900hdvi7g0tUwdlqm+VMHmbxzUMLvnaX5zp53SYf02amlpHFYGvVx4tQ1BCtyaGvKNji1UE852/tGdNDgBni42A1eQ51Lgc3UZwWkmy4gQ+V7m0pSyZVsv/lL5rkIqpZ29Sn13hVje2CGXnAKh4Iat6VwBiAUVIGyupNyzMykaxVmAcbSKkqbBLvYCQ9DzF7J2M8s8EKF2akvtkFIjTIB/MhmC+PeFHHCTs8ePQIjDwTAjpwEUMcgigTPmcRKPm0ro9YiJD3O4QT7cIkCrS7s6t+rKD3AHfu8IZ+vtPA121FBh9yj0VZAVDnYOCwkjLsErq8rnSHxlKrtL7iQkBuVrOjZ/lESZ4pwqpvj/q8HBl1ZgeYZTJs77IKyFLxVnzCVQhoOk4h0DEy5J4Mnntx/p4BCcsWt5CS1oYgxDif7P2DQz7aiLguMPfsA9DycA7P/Rl5rH2gBVdZrQgogh9jWJdnt7ZYdjmeH3Hr6jbfdRm/d6v3TH9sP0eR0RL2UJk1k65m1JApnryJvpKgEO2Nmqf6vQK2g+xgODkXnmSjPe42uAHVCTmSSrqa5wjlzP3nqsqEtFkFg4ik0BSxluRVcDXeGxB4U5RcDShmU+QgXEjdgmZYXD4cbspUIKt4OZtgSS0suS1OqnyQ1GmTUPkn5VK05eqSuW9I6l6OpEoZ0+VIBZlYXtuYEad/HBbhr0ECCybEa/IIr4ZNEzSXIhWfyfoR4IESW3CSEXWIVhghNoyIPwTNEgG/JnjNKedgaadGRDT5E9TyhIoGLDMbBAm+5vMv4+aU557fSOZlMMC0pYRMiiyDqKXlQkEFMJCIU61YhDtbEAoKZrzixoKhIZ4IzKmygWAYwLWl/V9UuDh1SCC3m4uWWdjqRiKtuCTDecs5jb4xE9hYp2DCoMK24xQlS8u90CldEgN4Ar4uxi/QshL6CKs3cMtkML9eaXEAYNDIiClqEiYB34CcWKwFLJiQueHF4rJCQhokW2XnrFZdNkMThbK/WC9yYEBjG/x2rlNNKU1TS9tOz4OGkVyaizlTyfS7ae/onxWEsZ7ikLd5lOnIUlx4T7QmpaQwZiOSPZ+0uTRr9IPYGMaHBbpjmrta5wCTPWL++7gBZe3nyhVcMp+U1VwwMcWMiKCYEVIdodjMghlm6BnAvbLT5MqcOjTZg1IWVDcctgT2dUxMf1YQdSGnsk1ysrghDTDgsQJ/Pplg5O4/un////mX/wtK0yXmmdgXX375/T/7vp/63E9t7YwWfD2X7U2uRWM02tdBj/fD+UU7+7sYgiYibWrZEBCaz/nB4b76XPXu3Hn729/5LRoNtto/d/XK06ePwPmel9/zdO8pbYmrQDKr4tkFJMsMeDCRk61kmAnDaCDY7L9m45ByIZhvHGJS2+8uwQdJIKAPQ46FgbCzVaZTO9ZQwH3OD3TMpokeJtWT/8COaeY8POm3pY4Pj54+Wl5/4YXt7QvXbrz4cz/3c6/85rf/zt/5El+U48UrNvA8QIB/uaFKZqDOAkk+LgExZ1gzqyfvrJCb38SRLAf3siljEsdGgQgmEpDBZpx0NYEK4Bx5cG/49mkRem2AWJo/9zTIgVJyoiA9PClIKP+4wtRgUD1oXelVarxL1xPS8tJeHxbnELdnToCk02CH0EKKpyenm6CDMixwmKXAkJFZxIQk7IQUlsJCJnGIIINASZigVkIqN6UjCqLKygNpIOjwWximUilgAu4UtHFsuvcmQE0u1gTJ8pocYOm6wa2QjbSYxGFJ5mF5d1NTbUOgR4kXDSp4aitlS3/pzMsIosqJfSVAYMEhvBUVuVGVeXJMbCKMCR4zuPcH6t5G/HCiIPxzFlxRoQVpsBFwZIMOoyuaRDjXhOj0ZzXIXYGDVX/eG7I5SZR5YRSJMMDDEkCx8Z8uIMrnsSPsAudERSa56RwqRVORjEYZ2bgjwdzrC5G/4o6ayGFBBVPDuVZLrUTKILxDPeUNW+lds0gIPuo13VKbCZ0Hk3mAykQJRA+5gAtJ8KdXbDSmdkWuq7n8gnI1O76jMGg/1uJkm1POCEBS4VFaVA7VAAbZgAKsg8lHyqBizFBoUz0C6K+1T9X4ND8YuIYuFLjUIgIWrKS51IX40RaBJIwyXuENDDwLRKnBZNaZQhPbyJ7KsM5jaMa9pXgm79SxsQAmYUt9e73gc4H4CYMtGJ6AHV/zUwkMwwmUeVs5agIcIeCTw/UNyKgQvMhBCGzYtsli4i0caA2HBSICqQXJVisaU7WANWxQSBiVFPVJIipa6y1EkwhIO07S1inr38qpszg5uGklGw0SAiBHHCqV//DlXYC52pRNmuZopchBfWHWMVeyK9PrymjOzG0Acpb4Bjma6Q5u64C8NchysXRRrbe48EaOE9ztsnjyfOqLv6egZKNgvHrH0ZJ5ad1scuiEBcVSKwJFbjFOZYijYArT3lBFvPpL+nV+Q5FpEWHdgJ7qWjnC3BTeD1CSbltmqRI+FZzcVedNsDHkBtAgK1ods45u3j9NSxv3ggc93Tkx3uea6uV8rr04ukBpKnQolqV5a7U1V5asTXosLkp9yHu+yQKebjQzu3RDjrvMlqnA0TqF9okdijwKxRq+9VGH0L+t0LLvr74MVvmGZ9Nl2fqWIy1UrnF9wCOYZyduGSxa1SN+YYLKKNUg8/c14mw0KCu5YCXuKw43puZPPkjiuo2D5aOgT1+kuEBh8wSgYEjcFDElslnEtZ2NNUgvrZKW2RQh1oc6bjjWpfMrd5scrprQVSwFPCGgUS/xUZCwQEHMism5QJ8uTduF5N5pHmF9qg8LMHEi09qlLgq7aGSYqCcrosUYzHjQILPwSDM1JXThIcjVm53jOU4X8ewUEecoQcTBZ2acB8sxbzoWgb0yojUbVba1BPsXpaKFlIDmYH5JioOHER5YsvPHGpcIjQT8J1GOEQYsCz7TShvDDpYZcvJZAIWIMAR1wmbN6FMGaZCYxxOsaXlxCwQxT6K/TspmFvQEESZ6fWdkmIMIRbmJz6OQcAzDUkEo/tBq8UmrymOI+L/dMib8CkhADz2B/2qa1Sj6qlao3tHR0eNH+9/6zW9RT2nrjo/3z18a/r5/4n/wgfd/aL6YUjup+BhxNbti+f7drR22w2IqG1FQRNOd+eFltuwvlm/OJwdsq8fI26MBT/peuPTsf/03/9bhsTuCLl/rn71wuLW9k2de51vbfgHMpmVyFcy90R33WzuXx/w5tVsLEhSwrRonw5iAqGnN0ffsKtnDnYdOArqURI/GB0DZv2OnKG+vYt7MVmuBaSh8hE5QpW3+iDe3iB72OaKPsTLSoHIHNknBBf03nkbgz923589u/ZH/2T/7+MnDL33pSzs7o7ffuvnSewbsB8AVMTFL5IYENc8v4OgIs9mE04nUw+I5WoJ0foDxh/RYJ6xAF0HIsYEHh3ybQGVBTNChBysOuiA9HZvV8KEpvL7cjjmw+BgUEFX3jGzChzfhwFLCmYYZy4pQJDM8tKtKIXFwLzmgTNyUcazDDwuhvFKGpscxEEZKraSTwmsLaRHw8uVicslOR563x8BiDi66JaCXmv+LHfgihL+FAuDaHh8HZ7i11llSbVACuW0rtvFd5nmxYTKtBWjKGk+6R5w/TYgILMsfNPifyiQJYTEfP17lNmdvJR4c3dFte3/hNXwRxhBOtoktYRa0wdkwKCS8iEWF+08z+z8QMpgWCZ2ZgtfRlN2lgEQ9gxxBUxYrWpAEcpQKZJHGdxLyDv4ItyUmPYSwOOL1WscHvJTseNjfxYNZHkKrNp1g1lDA8QgL9eIssZSXV1olKEr5cXtLoYhCL8xImAR7VOtk9QB3Kt+s0p1g3HHrOd8OChL5VCCjpWqhGYzycAKHA7iY72izSDxXOtTaBCd31KgT7boNRfbCoGoStI0ssDqGD1jXSMdtfLdYrrPvYNWZXhEV8/fMqG/dVunTqzbokpWi2K0nnhVElZPFH3Pj2fkObgBYlWKno5Gent69WiijrJDyx0ovWuUR/IHIYYx6i4fQ0tnk0cbhMNCCZ4OzpYBR3jIlleMhzRlPRKQ64JB8vpB5K0NH6ihNJAXB6lxVQhjhxoqeaI8ZCBrsI6Niuc4pVhhxrxjXIaa4iOP3x+DUVlfeUMMO/jHjO/fOUzkYCMsqOrpIdcMPfScdL3eeIQvKiN14D8aTMiXCUDR+qGiRjOJMyrQ6SIWJC6sw/4shB32eXJlWKe84q99TOWBLYc/JKN0HQk1CuqFxyi/JjVArUMVMO00thWj3GavJXctqP/BdpUJbd9FrWhKm8QaJOfJjHAAAqwdKL2vAjbVThElZI9pArWmtS23uc7FhrVigQ8BsE0MAjCZbsA5GcSKiGkfOtTFSQr0XDs6loABxkmFs7rAZ9g1AwoIDlzUCcx2xOYtTzI1p2rj+kK9ki6OSSiMqATfiZ9XjgzlEnyXfyHNQy5tBEgqYF6sqH+S+rAA3osE0KkkU0hAClrMdRzVbgUTmcXqGuUxvwCpeTg69ST0i0RMPkEGbS+p8laUJdV6EBI6SUGHQVxOmbigoEojmTD5lIvzaCOAOSqlWRoKRRWCMQwySj6KE8IY8ZHQMID11WxkW2+gXvIEuLGblyG+d5PckzauUqTTOJ+U3SZBDtSkojkCs0YQzcYQdMmPgKlpchp+mqLUaLLVG1TApH3rGDrpLcYX51YGdDJ8YMwgSe5hjJWpjP3IIc+TpFjhLOCtOyDKbmziHYz8cAf2KkJIz6ipL2nJBMj0OjC8H6t82UlyGV2Yy3GljuwdXc3a6OJcIbSGqa6lDLGYT+r5aVYSSiQaiKRVWduZW3OSz69zIWz1g2F+NCak+zcsTwLgjO2/lxpbDqhmNyKscWZ4c0uAWDSM4D/KyokEyShEiJQigdjKaT0K3NEG2sZmf8nZn0ixrFZWCSkKKcAwFQcVoToNBBlVIFbQSDfrf+sZvffM3f/OYd/YcH/Mw70s/9N7f9/v+8YvnzqNE+vqMEwCeTI5X/W2MONzZ2d4Zs+1eIukDsSEWC7JFlMmICS8M4nthbD1mQ/1i+ejh09dufeeVV14FCZx85nf+zmvXr/Hx3cvPXjI4hC0bXm5kUE7lXpbFTgZXllQCVeWF259JYR1Ioul+5nML0ZRK6A7RW+GxDD0dNUTH1EGFUD55gnkIMqZInJ/VkNk3HEHSJCaSoGHy5rMpD1La6esMXn75vb/4i7/wV//yX3n22fPf+uZvbo3GZ89d2Ob7b2AgvPhZIlULTpLoHIvZ8YwAWNY4pJVI1tM4vE9ZTcY/+ROZPGgxMrnRVXipC37C4JmWX+frsRsAE7nnQzgcxx4w4FwUBTGDj5tCmXMSSZGuDNADKyrCKntlkWlpDplMyUrxGnpwkPGS3S8oNKyKyC3rK1g3XWQUQjnrArXMTUDkACEcuMNDuJMSNbgUQrJ/cKAgYdUuB0jkZ5Ob/OgIvKKVsTDOlTeK7lE3pnjDv1g8FqAUJeHOjJSOuoSEGRJlHmuaVYS5KxrcYlZyA9IypdAgSVdS7aGKuJIR/ivmhkrg5acdEUGsudc/pOydCCzGOX5rcJO6ApkvICfUTjr6ZXiNaFpK+dwVQ/YGlywkAIJcvYLK8oWJO9WZo5RIXu7XpzK5PmeGuaAry8qtCQ2BWKt0wiE6I5gTOtk/KDkRySUwzYRNItHBVCpReIu41OPQFKuELIuvgURdhAFqAr1hHJvcREed3Fq/dDxPJWWXDiVYpYztuXH4wD/xqIjiuH44E4esWZG8yQIgLEk9f9ywr4aDlVLNQDw0AkCRx99Zl8ECMqOxwqOl+O8hwYiBoBROxDBRdw+Iwd7Gyxig7AhauIQCHwGwcSKeSFBcJRvOSNV7kTJDdkszaNfjrPq8gpu+GcMBtOunzvq8XYDNYMwiBcY+IdorS4mXnWSUln+HHHFBGtiSj3ySOLQgJJUAhkwFMiQwBGIoRdj3NxcpZsY7j01ywVcxtcPRkiRpClSQkSsDO7RMaZAbYGE8Tp+5jcUD+44VgIDWHCqWZTcbR3lYBHKsBgneCbM+Ztc0AdqQCc6IjFuze/WtQAiY9Ea/3axLk138bi7WOevfcjmoFpy4aFrSLTpNVq4gHcUgmkqRGYwia2RG4LAdRKlmhinLCWvg5pr2zCxezW4ZqUKPBoi8sBoMSMhQ1dcZRO4KpEJ351ft7LIqQj+DiT0+bs7gmSfiV4f4HmMtJkCZJky7hTcyBUJV4ZUp9BTYDTFmipprNmzQzWN/BLXIByRYsmTbOrssGLIyDc/ebl/BgpJ5Dh32ZrTVwPAcFPOnrH/xOT7HzW6R1OsMdC6cIyUOnXhjq+6DH+sKWpKpcBI1tpdpb1VVajxLDe4/yaIaiUmP4khngDFOvGf2xSbPIsGxmrpLfumeY5BYRjBYLluqWtUsLUtxSF5ztIO8dm0caGytMwO+uREPsIUtu/N96iNFNuikZwFOaw6hVeSALNLW3FbCKy/rVgKbDK9dZ0hDI20CDJk2OSDK7ElmVadXIzlxTAESENMWYBR9lckMZmqYQQlnqqFpH+sy70J/DU5Z70xY5BOWvq2GeS6CGf0ifMzVAGdEtIvDTvSLD/C8ll/EZCqiHl3CpZjFgR+HzHl6jE6fSxL0bAniFOc99IZrmEwfUkxeYShGbnAKt9BELA3MC4Xo+i+XM74NjHa6nYsE2wR9oOmvEFgd8HHNHwWIqfa6qzVw5Iq8NhQgzNZ2KrOLGwZjqrZtK7KA1gvHCtyiqrVVbGUkahRmnMuOa1jiPRjil1EJkemBRSDPcAU+zENnSz7V+Pjxk9965fXHj57u7R3x0p2dnTOw8/73vu9973vPxWefcWlY8fl824L5+97WY2kzm0j/jnRzJDga9idobnjz+GhvOpmMxqPjvX3m+A/2Dw/39/723/xbU4wwufjcCy987vOfhXe+MHDh4kuM+5j+10zYl2eBXOjX4TNZlo5gvMxWS/MheHrg0qQpA4DZSvlBSG2TJirqoerfjFqwKdwRYZjj9Qvu4lNbOXzbEtdQh3Jass5xWnE0Zgnh+UdUGg9ZEp8eH4+3+PT7MVsVPvhDH/gX/+j/+Ctf/wZfk2VP7fbOmX5311Js9uJBOhSjj6gpkSgAK5xalaQKd56t34oC9URa2JAxb2VVPskUSVRDt4URroNXvzGFqoAglh4jnxWE5trusxaLs9lr8C9msr+gz+gQKiSUQyI6cdzifGAZtDN7FlY7g7sFRkkcJqzJELcyikxix2A06A7BGBGTLKCcZY4DtkhnLZfUxfUs3KFzSiIfkEEVlsKdiEEdueEEDcpvSENczqsGCKymoGKnCBtxIDlqT1l+0lcHSgw6e8pC0bgUAsEhOX2rnrXwjsNl5MZabAcVIITHKhGZK3bMQzatv4yJpRgSg0wUSb8CYUJ9R0XANd1IZlTTzuLPhkbzhSgFRWZ4aJgpoqcAgU/T/3JulQSAKQJvdsmAifcQV+C1P2LVnSfGp2wCcvgtLVUScH7E2OkeKRZ4ROV9Z3rNjHr6jgTZCQ1+1EhENQlw1h/oFz1jbBu+FU6jjkDmqQ8qjz2fsNbKdPmGAOzyMbs4jbSs2DBlgNd3ZAPkVElqjQZOiBBCclJQcBnR66xH7CeQureeA2eHdclbv7gl2tlVxUvZD/Q8dc0n+IBkPYpizt1QCrT+hRbycg8/3JLmnSYyMEQVJKDg0kRgEMGvPIKGLzHThLF2l8gceJdzFTE+ghhKB+gatU7MH1NHPT7kwsfcjIe6vw2FL6WgwhKsbeacsIArOmAwRS+GvQ9MveB9NG1+GSB1kGv6M7yXmSVkQh8dMPtH9aAJTsJ0Kdt7rDDMivBjDZjyytzZVPzKx0wHk6YGIQIJQtKvc22N9pUnmwja6p8caxOby+CZt3HwEjsUFItGnYqPvmSSi+gqSTZ/6JK+NIT5RlPTRlSiWk4fJ4k6hSqrFB1e5am3OrxIYjzHa6yPuqkjXKv3XHhG1YagdoiSwsGLr75Nvi8DTm4RK8A1Ie/0tCLNr0AkaPhCtHGLKkgu5M1c38vQ5trsUzdcvuu2Uk4KiweQRjlFcSykzcZZeSEtlUN+rBu5tz+TUimMO6hDc5oE1hg5NyW9BAAiJ0hEgQX9UdLmuBbg/1oYaLlpTMwU1Ws4G6m4J+ZbGaZ0wHh81gk76pa1Ugbpu2VFjGoDZnsV8XxqLb5rZaSuJxbgSXTiOdItc0hhPdn8yZadbzw89daWP1WfGTNclhZO5DCMThJWrPeW4BBN2JZ/tyNLUqkll7hfN6apAzKhRFdT+BTlDD1vocqf9ZeDXFW6dgCSube81EQTjGJtRxip1JgD2B94FGensiSzxmGF47pZkMvQSXbKbQqT5LUa2Bx1k0JyiioaFBDBU7Ak1pELxeUWqYhWXFLGpjaRjZjikN/lQ8KTXJKvc8VDKGJCnMELM4SBqeBDqeGRNIdtcQ/iD6+0AC0fw6RTRT7FKcyLfday6AvyTjGN4DO0eS8cI1WnUjATnSn8gt4UD4qBgOJsb6cHo/yxYhAQrWJO1kvlLC4TCUjFqXkGcZmVdd66TWTj2z/00Ma8RNIKoDLoldkn8y11xuhC7g/iKKJ/egM4myZyDSl0B8ncqRfAFdGToIiljtutK+D6aQYNxGl755SPNeKXXKasPT8XLlAbg16SHt1/fO/hg6995R/0eLCXF/RsbX360x///Oc/y2t/kBitukcou0dZhLbqqVHVIycoKpHGrijtDE1Jf8RLhHhOdX9ywGaUYz70dTh/9TuvP3jwgE0029tbv+t3ff7iMxfPnz/73ve9DHZepUeVoVxVFNHkMHRApzQCJaYKnK8iLTZQf1KEJpByhB51KSCx30ZN4gI5JMo9uZVtS3JBgbpMUmWJxOpfOKRv18DyB/v740uXaIZF2e8+e/Xqv/Zv/Ot//I/98pe+9GvPXnrm5pu3kOHM+fNk8SgCyFP9efKDcCQy2XJdkz4qV4pWrGzqjeygXa3q/0gHJKUoELtiUdbfXUWBCBB6Jj7iG8/p8mdWA9rYRLvZ8EtH0hLTeXOfXyUmUR6KXjQaBVqAYlVWkDDKbXCRkXJKYJ23EsQrrP4ahdzyWrIVSBfFT8FpCVRgUyUNz+Lij2syC2/OwprvISPWSQuA3kUb62oVtVdX6fyY5k+VKXx6RVC1zpcYw2eRrMIQqFLJzaU0hZTnzRGixrVQMR8gfnKVFi7KVZdJLCFFU0VKKvLIAJdS2hkKflONMQQwcxs/qq0ASPHP+iZo1UR1Q2BVxzRjeFdzOzlA00CmTEIofmHfjnoPRiuuXJHNSQ644l87QiSESwECFoyCBNDCJsIM/+GZO+h7EZXBphCAOLJV5R7cURopuLLGkmKaGaKputdExN3lOaXMF1kKiCEISDMAykbMDAdkUAxA/+Fu4MRhVGkA9UcKi4FEojIl0URGvugQVoGnkLOKHjKlisRIMn1erS/yaEFMXpsgT0zd2FlhY3BKGS0hAQD1lUgFkP8tG6YFMkw7Qk0O1+k101DiB/TTE6XRAl15J5jcSYt4dFBho7YDsc5KMhOp9PVZAWc6lQkvwCrs1HXj0fjM3BZbNJmhoAHFdejQM/1k68m34Jx4YxGayMFrzRgf0abYaVK3nIgnjGqILTa4NJ5GI32MT5wxFataopgoHcahCReqB5AcqrwOtS9wDEEx7wrmHWfSyOFYIzh9s7ZK0gqsQAHOn290qBR4aQD5adiS6Um+cgNzMqZ+da8N3WTObuSH/JInYcUS28LVXRUpWiAIXk/kilhvWx/iyXUoemWBSuKmcATg+0583RbojM6jOzDQa6GEflp4PJukjvOP0cFzZg6YezZBxtkPRxm+X6gHNvrWH68ZOJnbGfCWm5ZnKpcUqXPxSPbMby6KmTPlU2OtdPzDaVa3YYKej77AJIQ1fDgm0PmufT7KucMkSp99nLxIu7PT6R0yr89bqphP5EV3TM3y2qIOHzbvHLENods7crzLKIJ99lgXSNYBmLL1ORjetnTMLA7w7IZcukqwzRhz3pnyNt8eNlI3dPVQASGA6l5v+me6Fx1xsvapk+5RZhwoizDxm2ZtW1p6AUAGVu3a+BFSDUWgqCwqEhfAsXO3vF/9oQfASe/2b0nOdQmSDZfq0xP/BQSVFESSI4i5MduEwFZW5efcoE/9iD6F9AAueRPRGj5Q4glEcQ6MLlEwFrAUEUgNmGU1V0pRbXjwDkjDrcJxhHdLK6ToAIirEWuU1n4AvRN7eyjESEKqytEI9Gv4gBSFiDKyRg72INSYiSNpNcIzbDClQBxmnz2O72IdYAR1I5Uxad/JIIKcgz3eeoHR5NzFIt6YgS+5R3ub12OYxmLR4gzYe8yBQdkZFFa6WMYlzMmzXNgBo2VFB5AFUnqEUV6+4BYSHHLBO5R4ryXuAV1fEZ0BBX47NirantgjcgDEepe9n2iGiR2zWP9yQQA4J6Od11GUwYp1M2S869tK4YAFjaZRS6sVlZ5ADAEgbFEdu9iqz3nfn/XMxYT5Nd4Y0b6eqCU1CJirv350cPjGa6995zuvs9zg1P6gt/fkYDo7oLZevnyFFCVFSKa6xMufdOhMc6AF1ePBGe2w/X3Oav6jxw/mkyMAjvYPRk7K8Vah469+86u85ZNPpH3sEzd+5gsfGfOWVMpiXx0sG3/DG3jCYBRPUfJ0LKBs9KRCgmfrsdf8Uw+YVXTyIQKLeTJBjzx9tHKVeTrD62DTT/mDMbbEXjF5cMcBFWQ6HR5m2NreXfWP6eEPRovpfPqLv/BLuPPN128zpvrmw/3f8YmP81Gl3d0zkxkhCwuiAmjCpDyidxanoKO95Q4f9yfVRGegPXU+QTmQRGVYivuoP5vTQOS7/8MhAYVSLKxkv3NQiYMLy+PAaIa6Zg1i0Md1o2eAIjxJSlU2TYdGGJM8bzTyJyfP4YrTPDoxC3F465F+z1ViBMiwqRLzY6W0S8oVX92+QoqTi+pBwTiA1vzQ0LQqIdf+iKTMGpvgAcWBJUXA/1IBBdkwjXEYg0PRJ2tQteOixKWYkhL2vSTqSeQRyMviRXZ4t4zJ0uEshTqkKLlIXLmkYEKWf0lTggD4E/ZOSgYR8Yy3Bp0cmiYFgphrGjIVmJgTbDIa2+dCcKsfN+QSIWjH6end92lQVtfhdHif4Tg59j7n15wWGdxBRne9Igl6IGbNbhBll6O7TEIYEOUUPtGb53BkNEonDyp8FYB5WUsrd7hBBzBS1+vk3LsGQoPGO9yUo0ElSiqEa8LgV6OIIEGxOa8HD0QRR8uAwYe+oAwi0RcoYkxezVlpoZRT3BpO60oQkSlAlzWNAjR4fxyOz+Dc2Vtc3YaDmmKzEKRViMkf8qHLZxmdE6JI6aBsDGprDLsW7dv6PTjIGl5gNOKBjahIJwTkUQ2n6EWOvXYyk3bEqffBW6hhNbuA81qtwWOfG/6BQFIIa5m61hJIbKJyAaPZ8p1K3jqlGVzH4MfKlhaKBoX6BSon11ATmc5eKTtP7jLV5sw3nTPZEzU3gMk1EaLImcTBWUXbk+GOIQ5PoMkCpqgZU1WiiezAEaHQj5UXcYLUKRjwYjYH9tEDPDpRSznQkJhDBmnpvMd6EPU5n/iehcKa2vj+oyU2ROyvAbNrSieoLZO9OZs3WwqjD4ARWh7qNmVCimpX63L2i5Ij64HzhOG5D5Ik5nRyq5CWsgSnMNhkaOAnsFU0zl0ySqhEakAxTlGXasPwzp9GicToqBRFfUjN4Q5HsoIUR5G18Fh1Tg59L37WyJirXkr7kQDBVIh00G+yiyWcJKiSWAJoAK0aFHoDZahR1DlAK/hoJOpP5NWv8Vbedjwf9hfj+ajjk5fUK/Y9sByHU6pN23qiIYluDXKKlv39fkFelIS79IRwL4nQuALs1g76fK5meUvOkIc7ERR43sri2yXVjHUtlQd+0y5GCcYU7hVt/V99lXGjjLUKkUGBVZkQHLixQcEEgFSDSHBqiFNPDXMklcKAQQTLW1Jc9eOdKEEdVQaPeXUkqxBbMOhSlJtWzNtKryKiKSoNxUmp0N4ANypqQGz5QxJvIr5KQxCDQlkwIK3nBzQFi5amUPxIaygBJrKKOKzlguLRv8S0JNvITIjYeI9F6HZT9cTHvVKUJOGJbMyLgYVLIEQBtIdu1xYTNGZufKBgVpbUqLw4bnBChp4K9ylvZ706J+nYGuURUfz03/Edn2d0N41JpMMhjEViORExkdGLjESQgbqHH+KCjl4g298qMC5TN1EILS/l+Ausod8XhPeHI/thdp3ZfzGAKq+go9tk08ZwBZfBCGovhNVVGAANBOoubpD86EMlZXip6WCTeogujbtoVQSuFao+FuvYmv+Vr3zt6d7RYDRk087zL17/uZ//g+97D/vzb/A9L57nyWt/9Fv3lLhdCFk9RKhGvCCJLfj0+MeD0dPHT86fOz87ON7be3rpmYtvvPrdxdHk1q377CxCD9tbWz/8I+9lc2mWGUCuL8EmAxWwGcGgBM7mWt6UmNKhYbL+qgxAqwFGmsBzi6X0QDJt0NSWZmuJZgZXoKMrAfjPYeG6kjJXKt9kMjxChBOxa7F4+PAhBHa2t3jlwjbLJaOtH/uxH3/5h97zb/2b/85v/Ld/ny8tvXnr1WeeOb+1Pc5LjWwj9Wz5EgXNK1NqotQTTeWfvMEsLgHrAppN4rpcOadDCcIkMH5RAAdmid6unHald0HPQkF0MM1OlTAwqQjxeEiEe5LVc5KiMCmGrrVcuvq1bBUQtypZBERJM3Itx6RzJgWKIZgsTiBUIJzPWECCBfGTcuwAkIqEIC5Smmpd2vwoBRgjSUDBKV6BEqxx5gBR8akwsMYz3uGZG/UBMJGLVsRPywW1PAASfKJHeI4iC+5QlYb05D3ie10sJL8UugYKJOktC4OmekTf4NeaIaoFpBPEBZx+JzBhw1gni+hdBHDAFTLJZQ7L06wwo4GNTEZ6B/s8M2TgYxFS16LftvCVVOAMSDEAIGKyHrjke3x8G4B3ytjiKim4E1ChXbqz4bJXLqNUpOit2SVJiANgaZEfhBPEzmErUj/kwCGGlwIHI0//URVM0SGEg1swkESLzwEiraaTyT08w4NqIjmGs7GHX6nKJrwDmQI4n7ZmMyNBVGWW8SgrHtXOX+QII3JLcf8XX3ZD6ZgUFGl5sUSexhIg79d0WzyBk6oH7+oz6DjlVzbCCzgjLFuRyUkeM1JWeTmXInAyI7SdNhNyD2c8JR90Io3Eduzl32ZAqPy3qByYAyJF5VoD8BfmBcsdVBPKgJMbC4QiqQLyIx7KN0MXzoL0HER4ShGXUOBNqEM2aTHRuZNNtX8wQ1m5kQheC2tec4BG00hdBFxpxwSf3MvLuw4wCLiR4lS2GaFRlFpZaImLNBO4zF0RrMvK9Vz5plbOCfk8BEz6BmlBFL1KxDIBaDxwp3Pz0/CRG+1E65wUtcQobVI4+EkUlHM+y5dk7k+9C6glNRZCdnS7ypRcKQ2GmBsefPe8sw6cYjOjqMUGd0yHQ2DJMaXmeLRLMiqfPCoDucxbUDHio5awdlaKuUERyOwTBYF4dXTnHW1QIE4S4dfKbJMAKtKppTw1Pt/mO/bd5dnugJmMWd9ZSoawjDt51/IOE7SdwUPGznyIx6fXeWLApo55Lzpmx2EIldLpT89vdrnXO6sCV7urwX0DS/dp1jpZGWBvAa8uOlgtLrPFiDZT99NGPGOZiVUNA01m6pznxEB8cTBOjrD2CZXCdH6Rwl1EJujWJOrZ1ZuyTRItVZh5YVVmtoAVqsi1EqORVGUKV0yDilEsviGVUBK1BGsXZlVOxrvA8T90vQTWLC4Dzu/8OZnoPzTTb0SQ0/KBKJz8ggA+4CsVG6HkiLdui9wdnJb24LsQCMKbfZ37JKgxuAeOwluC5LsBICLMZw+GiB34xWGATK+T3+INVqN3FQgWdI7UgMAfnXIl8YZU5h7YTCgMmiIXCCD1RufjNTwpEQxSvqqMWXzcy9ccuN7JhA0aZ959Cc8sH9FnZR6C9smWhn/k8UKHbFU8Zo6rx7hxyVLPnu/toQXi9Smsec7puh0x8mQI6vQUb1tDDLsUKEHS4ENpM3xG4UapEZCy8YEob1nmyRUXqeCJBQ08wgrBPhCe0Ec4EKI2Sy4Xl21aho9pVtinKwncldDD53XJXT1GN+wtwsH6A9YlSLNpUQ60wXuuTJmpaE2qUWlO6BFy7kx408Vw1b+ladhVT2COxSmAFyMhhdjM/torv/XGrbf0gw5T87Pr16998uM/9tM/+fGLl86JjBkeXvoJavLT9/VXE1idqdW02SKMMNJlangyZa//00dPDp/u3b9//8yZXb4Oc7hYvfL6q3RC5rPz73vpgy89/77hcDQej3nBZjCoTNAqBNj47yEpK6aC4Qf+k1TLMh0OSYnsKRE266pBteJyzBGcQSDyzWGKtaZRLgAoY0EcyllwyWqveCNBcTh6/OTJ0ydPL1w4bxjBG3rT8aj7hc9+4cu//nen0xXfO370cO/M2YvbW7xxyO8p0zwuJlckMrpLDwJy8EOxiIwUCBlZfCcjSzdDugvM8FWICOcpgNop4SQJV3Ocm6A57y1GyzFOxpt2WP6HRb2Wnqc1h3fC8MvIN5yrXm4RqRagYMD+IVWLGX3VP7pDaMvQGygVEtWUhsmPmsoZ+neSD7ZAihSfBsI/3INzlI4SGbMxKWNS9AxOLq2MCmFNEBC5wCS5UOEbNQUtSeePiwwMFRPCWpNjJVC775kz3TP+D9+ip9uZPqtu0TUMDG7ScLRd+KCisC4lxbpTPdQnsKvfJJtjan644LLESnF1Cw5ALRiuuPPGApRkDp4bvlzOGZY5RNbyKyHk1AqVkQmxBVs7mPjQPlZh1SwrjKpmtifoKoqlLZHs8rve8XQbKlgdcN3lhezgVetAvkpN7BMAVXUQBdd8tsfj+CNGjcM8CIBuKEPE0GUyuwG4okkqrQP1X97hUf34xmX1I//+VysqhRTxwEnMmvKA5bDfa6cexlQo/0BMIVeACZVxi7QtysOHQ3hmqcgjho6XOohpjASAaM3hmyLwi0NGdWw8c6MO7LEYgkfj7WwauEVJvjxtGQpDEoIEWXvytBoKh/PBrmMnVSt+oiyYSfBInelNb7AjvrN6hZE3KKSi7/Dnu5Js92N7KKT+0v4+C4Ie7wViOoMVAB5QnF8KJjo2SMbXmQjsu8qKcLpciKlFmEAcDSAHapwLWxF5ge78WS751wiqGTPLpcjgQkLRU6k+KVRuNEMWlO+qC7/GbQ54Qq4ycTuMhHGTpTpo8oADHRiCiWvpJ7kQqiZhHL6BiwmswTjAQFVry+uwCVnyKbdVGLFSz0Sk3kRiFtx7Fc64zw6XDl8OyREBoS8rcrGe+09K0gSz9yKCQsczouTkexFRqcySUEe7TmzRnlLOKdopwKwAFLg8F/ENCu81hgXyr3RRuIqOIpGnWCSU5UDkPxPWGItwsRByGy6L+LvO2oiiDUNhTgkrJ9H2FO6UVLjSyQaRrPBPN0wa9SouGZyBJhtfr0xSw7u+Ktk4LkUpbHtRSbEjOEkzrjgcNM/2RRqCNefK4yD0FZ4SAbqLs8xLWBftfFG5OXgPMQSBd+aSJhD3UdPl2iU7uUQQvYearCgAEOzosUEVZ+RhYfd1QxBdy8eINz2yliBamBMhnNlQogN6g/DGMIJ0e3haZ6PheLf3SbRSMrlCOAkKoBJ1qRp0+rmjbMIbVJUWwBT1rNqUJHGWrhAKEshqT71bd5ojKMrWNBalEP9ae6AmxJp/0DGrrK0pSOX/nB4VPgCTkMqjDuCHBoD6hf/bYacSVYEibXBlSFcIGciP+nNOAqgyPsleA+6/hE3Ysg3jfqMXC8BrjCaUj56ha+XRwMxrY3KlsRBhPVtHim5adSOQVBxbpM9t6wKZxgfXbKqOZ/hQFB9ojWlJYCrCbriKJeSjEIvBSoKQ/qohyeMftuYF77XL04hLJl/K9LHbKXv4bSbYB8SvrQ5IKOe4gXbLRqPmePR0MuCSB4bpfYDZ9VfmHJGszxLXwDaGMnmqDZXaQ1HHSC5F+DKF3vloOJwe8/A6bqlR+LMGwXjZlH4MPUheLkk7BGPG29JWcOlJkUBf15UYyeobcKb51Bpw5ZngA8lkPr/z1r3huP/a9249fPTozNmz2zu77G7/wuc/9z/8Z35pMkF6HtydT2fT7e0zsINWfZdR2j94qf4JHFrtkCL41Q3CDgb379yfsy1mOr106eLhwT6zQvce7r1x+y1SGGV8+CM/+tL7XsAd3BdjYf5ztEt+IjQ4VQJHcKsSa0qgyCpnC2TKk2/q5ij9WFpIy0JL9/eSC//q+P4L8VhjIOcRz/JClwYvBeykqfHl0eRo99xZ8no9nppY/fTnPrt1duv/+p/+Bb4divwH3/zWhQu7L77nZT6/ZDxy50/MnsnXCg56qszLWiqTDuOLlDgYGUpHiuUuFaUZStr3YDoSJ9RfeXrKD79ian3eWzc4wK3+L9+6vfj5Hy1FiIS7JACDuFIUTEcJWfWQo/TnpTqMFsG9/iyrWgkY1S55BRMH1HbqTLFFFwIO67NPQOKkR6uy6GHF9CceZtiyXIi28uEYR3DwUn7NFfoP4/SU8UI7dwY/VkoMkmCmTtoZtrcBgOikJL3glruisSYfKgIkPZoRUn75ldeYyHbLBP88coW0EZY8SotEUk25AVIo7qksXglhJeXH5sC4JDOKpWvwMYw5T6+lb82XMdRQzWWk6qUC6hcUJqyyBRxkvMtlTpBK5Al1JjHwCHpoyxl1kOedeB/BaEhTxLP+MYAWRzsIiv4iFMlGGXvI+JFqiwiKWK3VmnPbTfxOSZXY3AArNbjiWMRJiqEOoEgNGaIFq2nJJ1NTRwNEGqNK2lXwkCo/RZ4W3we30kFQtSIEHwc0rbHy3qJ15cqDqZ7TjqBR3ACmbIAQiQw5KxPJmVdqXjEZGlE7XV626siHrCuMwdmQn808AuppHGTn7L7zZYcwmv2gBi5ZSCBuUQWEIkO9qlmtUFoUHLYntLou46BbzKo32DkCixTCBnBeq+8qqybEI/PBVAEgXuTCqbIFvZQlRnGTdDIVjtSmASki8BpPiil1Um7QqAZMJUGxnjJYY9ON3PiT7p/2AhQXIsUDfCpbIyhj+M09tGxcCiDArUSKAUJWLN6SSaE4ibL47gOYoK70NUCQnCQhU6h52qRuYFSmUbQduVWKcphNshe+B4YQw3I/mESKt57gjJKjcEAN6FyLDYM2eDRNWbz02FJscDf9JNcipw+Mzz54QYBcH9EdKqk2I9rWE064Lb7gjfEfObVTn3wPQgYZ7hKz62K3CVf3ToUzCWrdtg4wvIVN92/hYMYgkVIW59B3lJvpX0M7WHj5W3X4jGmZaEIkXU2+EJlnN3eWi4tL3y+B7zETMPLhYLf+M1tPZHrLIC8J/ny8HYqg6a4O6EzREUvAZ4Y7dRUSw1sECrhwpnrBjsCRXwqET18BBEfsYhjOF8cdXgREfxH18gCMG45Ab/UNHbZMpK65o0MFxxmUETTKoNsiYQIikLo/udzq8zUAiHEN4NZKCkXBBQloHXblyMEBeNIfr7cfBDQ7TnjZloHDyIuGrCIQ4GkBphKSiJjw4H8UAe+lUTmUvVTH3tj1HBNIaoHPyiYFpQWx+XQlSQshreseP1jv3ZTDQKJ8is87t2l9Zse0JT586RZDox+P/9sXZC8gH0jCEDgHc+Hwg43ScCMEQuoQKlQ6lLN/wNQ4/kXvyLpvG0oipfAozStrsoOX8t+XqEDRe3niT3W6t0wuYZrgrDvywfsZ4au/tWQSbLHb6x34KEiP+fvtVedwsNxddQ8WPiLCB9vxIDa9dMYLJu+7s1nv6eEMLL0+68aP5Gh+Bl5H3V3yWIzCsD1WOQz7owSoeOaSJ0n4B282fDBPWEf6VXdfAZh1Q1vM+A7dRamReROoQwf65Pn+Ol1FhgED3tj7LFL3th666jTY2mKvvW+IY3FeU65mzl+yx1dbO/eDOR7z6UlsTsPgGE9lxBN4IJ43h7LiJYyVj8kTZqvYmc30JyDsF0F7VAuy6NHzJvsnB09u3r71za9/g73stsHz4X5v8Yv/9B96/8sfgI39w+PhaMCXQ8ExGhrWNAsGsy3yjgNhYkF8CuTYwhyNx1uWBv2Ll87fu3Nna4sax3ze6sGDR7/y97+0d8jTGv0rz29/81u/+ruPP/rslStUGdjCrTjUo1HEK8SRtmRBTQIn/lm79aRoP1kGuOTJgVfqRFh/kyYAR5It1+4bQPJCZQNR0NCqlovXjoGn9rvnS942/HZ2Qqfb4wvH+zwTPB6z4EItgNMPvP/Ge26857/4y//Zdv89e0+eXL7c3R7uPP+e5xWn/za7ynR15qftEkOVSME5joNr22jO+YD6YlWtAPzqagqOVGDH6VEZAZHnmHjnPk/pzS7Zueg+oXrwBitwo3TQUOswzKynr6jS0kNkjdakrSH55fDnNWllEsOUwJOdC6mXyJTikn8cuzs7Qze5mYYA9rrtJgVr+UOYB5g0YEKwwMFgQoKSZlWdyhdcnLnMGibrKuZOr1ueL8hGUVoY6VCk1Fbz6XAxmVlPeQaCedIB70U6yzUfYBeiN1oynp9dIXJTzZU0q4gRbeNMRv6ER2MSZQiQCYt4PEfqY5iLpmRPBcEwmTaN6F42I3kl80qUW3GHtidLaGWAcZJh3pLWKe8IfeCgFTKSJpKYpnzqnxIEIvu8S1aQaOB7twA2vHKEbtogSot/NmeXHcshifm0fHqBaPhKLuGBTwGA0aoNXUZE1DnehQ8E6xVkKAE3BlikhllCBleGI7XgUJN8fJdUrQRaju6R8yK8BWjBm2H49pj1AAnBF5n1WCBJVZG2I8DwXmA+JEhzr2cb23G9Ps9c6RdWMbQvQzY36KG46bBxab4cu89w+3B+NO0+SQNI9zMY5F2KqQ5IvRP6h4QqfUVs9jPssfNUVn9oxz727/JdZPL8qgA6d5rffrfxFb0vl1tvLXn+0PaIBDKI83RHCPC2G9xHlTYdMOxhhCbNHDohhDe+EIz2FtML1BIbBtcL0StqQR/qVTfK2Fyh/cN2cMfZppVSuK6zXb4/ikVn1j3sjwDm7lEU7+Nhakhtp0ZJOaMFmFkO75PuN4/BDLwcSgMnxwfoqHBFabXNPxCgRiMGT6ToI1BKTTAyK5T+qpVUnYPs6B654iAwoZFVFHhcyeHVi+L3f/mn+qEwOPlnewUtyzo6VShdK/xQIl9PCm/KQ0mjJKVLzCVPe1LiuMEnXQ1YoM6U8nkeE5IoSMBM8JoDxdPh5Bffg8VcekJDY07sJQCLyQ0+WRY7fahgWKniG2FTYp0YALGmrOrOxQnWYKzbQn6SdZpUXTdKchU3U7fFJ27LXx5L2tCQtuUAFpDCFvJfOyrBWmZCWnSNgWEQDEumoDXaBFsgkk0EgWGBiyTpH+5/oDtF9ZOeFSgVJ0NEmj4pWJ15fx0Pkg8POoNx3jKrK+F0cWH6xIlMUpA+JShW6xoGM58WAJBOPN0/Eug/UA0IFQplA6pc1iwmjsMeEQkv2yLk+AUmOLLrooDUAFcDUw0pofcahe2PoCdOkTEyKw4Mmma4L06pnBJVWJKI3bLqkimRI1qTiFLUP4F1bwo7MgJZb8H8C4+hMmZiGoadvczzOHggLMOGL/lIeSJ2l+d5NDLEVYpDFzATINABkqKPmia3hDdqWQJhTzXER9U+qRyKOpvauQGbUqk/Lng9Dt1W/MPHC8E+n7OZ4Ui1gSzW4wJ4lM6WFCAzAACMJfdqFxwBwlmmBeBPGbSXfPFoKF9FxSc6k2mrmRqCYEchh53AKo0FkNPxTQJMUsQpr+TzD6Sw4X9u6GWuFgfHc3bz0OmnaTzktfSDAZvEkOc4KztT8KMreER0Np2yS2xMJwqfoI0jHBFk6TqA0C3beOsxD74m/jrwlGxMiRqRG9ZQKIvmZlgbyNQuskSLQIPDqyK3z8ATFoWenWWWg50qsjWgyKA/CqGhYxlenubQSLo8UIiOMAF6Yy0Tz+Q5eUp1+2P8wr0MsR8f9lFwzaHxDNT4rYj57CMvgnQsggfakFMWTnE5l3qwBYjp2S9//df+/qO9x2wG4IM7DFQePzp84dyVT3z8E1cvX93d3ZrwYjheGzjiC2YgSKRW6VG2dEv3+ICG4b54sZlnFmE6v/XmraO9A1W0nB0eHA0Ho93tS7du8q0cvh4//r1f/N0vvefG+UvnUt309Ni8vEtplKsMK14uN5QVWWqnjnfeUozswlfXLaGVqLLrHKkEfI2P+/WBXNb3iM1lMVLgqcNSsTBvOVo+evCQ0dflK5d54elwMD5/6dk//Ef+SHfc+0v/yf9vcjx5uLf39W/9wyk7Wq5d39ll45zrAOiNGoNmiZhW1KpaYKZ2G9GoKOnLh6PIAy2rlcFKO8OaPkU+RXVIVod0AgfqzPPqrkCzQ4SPzLVaRXFZVgfRqfVSwdS/OWtjesOxzlJDgSc92hYB/908CfvGH5GQ5GDGP8GJN8GeuEOCMCL1UkhxiNCVz6rRFRrFBEz4lMEAhl4Yt5CIDIv8WPeCB1uJh+rErih4QKMuWlKhQst+5JTKlEkfd10lxPLlO7qGjpTt4oBX1VJNKGm3064ieQQUWAuz3AqEugmIlKA+ORvGbyDFgSymA2PXufGKHYguWM1mA4bAo9bknx4Y4ZI5JSxlbKJOEUwiq6AEAmQUii6n9pR4JTjFFPmjr/BP+aZ3XADYcC4ptWor6Nl/FOUN73BJMb5bp7QmnnJ3HVL8QPgv8qNsPU/tc1VWrFvWLRHCZoNX+e7tP6VvbwRjDO1cV99XAqIyn2XSumfOnOXT2nv7ByCm9qd/aac4hu0NhwQdJiWsHU4I6Fn80zh4/HA2PTcaM3f3dHZw1J3g82EFptQe5XRMRQYbbEqeyRV+lREkvS6zEuPxaDAmhGJKegYxrcFIqaIdhYyVVBW2AR2E0u47ra2T8GAi7yFhv1CMLLx1WQtpXZWnEZd+ycv3i4BWV7FS49XQdVIUeshl20GpchVdAtfhIDy4GYqJHV2FLU4gBaWBHw6MTZLWFBLPtS1pgrOeA8upSTKlNnAc4YuiJRxrkmcBuxEUKDbgh4ffQAAHqIhmBMqggK+0wIhChOLa6boqgngQAFDVKBfODucuiYQxLAGw3SSAikUvo2awJQcYiJRKwqfQ4Mt1PKNSQz5gayh+I7CJ6N5k4C2rGYLFxGSYJ4BuJYTXcOv9+rbByQrIsjoWKO5k3esqVqk5s4HY30a8fpU9SNqbN+SJrZjZY10IClw+cG3m/htlnDDIGlDIkbUhygXsZtyTEtwHNQj849PN3EttxMy6WM3l3oMMHPKOqfBmDSmJaCSwg5jaf5sWUzS9r97H0JgW9aYPwoXLBShnyq5mXIUBnJ0Ox8ZUA7ozS+eifCZpyEwm/ksdonFiYhJnI5dHfxerycHhmScLRuL6EU3ekA/rsXdutdMb7i07fE5hMlzwnbD97nJ76Zwub5hicnWLUR2TXI7DSeeFP3zUkxWY5c5syCtHdnrdfV7Bx5Dd1zkT6Dtjq5HiMITmO8FEJETkP3VYraYvrjvj3jxxoWZYiDCCGy8A0IndOUQsQhzKkGpk5IccFGHoSXCxw0wfkspjtcKrjHdWMcyA/jzUKNdEQ3GjWUZqNEbMSKEwDqt5OMFSnTnzV/KYUr7kGzSdCfaQqaTDIn8A8I4Xk939phcY50AMQd76Twzcusszpmz6pKDQ6c3TRSbQwE9xYpU1JplL1MdhiHhITSTKn6ElVJUGKiiANoZpaFsaZXJammsulV0hjIBxMRJQhWMFJix5fSHpxB4rE7T5UelGNdIjF3f0HUmwb6QgMi20cOFRCnIhfrtKNBasiTlxfkbFd3Z9+8KKSVlEOodvMk8aoTO/4yYBZBvgwbwmA7/oLdkehkM8U8oDQ7e7zboHIwLckgYLl1ZqiDo7n9hbelPXxEpYIbhr2EUeBmBoZJefDF8lhC1ogZhUMiDSbUM51ikGbIN7tE2UzmAOolkBsZ/OQT19pOAlJt9eRQDcLxrQD5MBahK8hWm+0cudVZBSGpehBQ9u4OhR7HI+mfFmz/l8evvm7SdP7k/9yHxvZ5dHHfqf/dwXPvvZnz6zc551CbYGYUMH3HjvzNmRfJEaOkaRYscfDGGeyiKLwKMJu4tXv/Ptx/eesNmLRJ4nvnDx/OHh4b3Hb7o5l5d/bu/85E995sZLz+/tHbNM57BT/WDcINbvxJpbfcPLpV/tdQ0EFQ+cVY1+pF1scJXDgqcu1rdBTPqGc0g0/EWnlXrnjySP84KXUOP9LSmPQ6ZTqTOC0jSwEVwGfWY0R1tbSydfVhcubX/x93zua7/x1a9+7dcODre+/a1X793sfvYLz19/0dkNpqQZRtr5ATc7+K0Ojn6bQp1QRkYtbJ8CUurB/5gaPSM2jo1edChvHqE/FGcAAycDRc6WrioFIhUMq6CwE7We5E84iFS6kOMH4FRTSJlRTpY0L0UKoBDJpTJrcgs1hSIEoQfEZMSU4cMgZfGorJAaS/BMn9LJ+nlQKGDRDz53S1OIUtQQnn1SHQXCpcxQIQDAAQczviXJlKVhmGaCXXcqlWUxx7E8h2N10Kmz1sQXRBaM4VEg3RLWBHg0Z+aHjwhLzKpIH4zkglLsdm1Qq2M2iKMiPiDOvAGGM7R3neCEIptqYJMCvPbXeJ7o52eU1ERaF+o//4RSA8bBVFJCRo3ZsJtd3sw8q0WwE7lh0DkqD2dkV9038T/mWrjUCLAJQg3MhT9OCaEE9SIdT1qofg7KhLKg+uwSAslXt1mYtMNKYvoe9BDIWPK2QJJ4Hgxd0W8x/ktkQ08nwAZSQuGE1MyhdqZsHGSXEXwQD4cDO8kMj5UA8WaS5LEf7v10oB32YsYLdKyj4Docc3YlQBEfQB5bCyI07/3Qxwlsi2OCM9Vu7XvY1iaPFJVAY6OAeDWtEjjzriwcwcfY6JrY2zCcpkGEIT75UrtroKyDqTbdI6xgPBRg08efmfwXN0MC6x+PbZAB7q7fWHPBszt8ilg8yYmhcEEetugsriRwY3DcB41hJJ9kg0npaC7kkkb+pKbCwOEqJJEU4YnkvBniqpXG0StNRfjx7f7oRg+FBQC1htUSZqJZEhfXuBIIzXAtmKKAKD02PAtCXCIEIADRG9EMyEc5nNKZBZmCBNpQvxBkMsdmtAZ1ErBZkxfmLgCBwOw5uXKHPSJQW0wVLhosbu2fQJKeaszWClq6OFHhwVUXlJdASW6vj8KVEoqUsqBYyAkGtMGvz4qwnmDvqLAVRG5RBGutHElrSfxgHOco7XUlL0YK7wWrFKeOMFCUZUGjtnKURpvKZ3od3nEUjnVipXgX+3jLUbmnYUha366vIjOJejVzwwO39hUSKIPEs6rC6CWO1i2+OKtDGSTFDoV9Y84pyBVBji0NxFOGre6X5409fh2JdCChQo/G1TEcEg8gTto1kzgVi3GifUQLksogoQhJQ/pU5KfHzMB2J7gO3ULmYgfdg/Q4qKOwcsQLrFa9Q6rZqsf7QKnKRyD3/Z4g77OUCQbe+AlsbQpikICvTXkb47J3bBeT9UKqd5TIrCjv++Q1jUhLI6nQspn45ZWU7KcjClhw5XTxoyOoAOawxgEFYlm6pDddoYwcTkZ4BXYrCkio7vZ0BdEZtJI6qx5kjJiNHIzxXZywM8QuGcoBnOqCEcGgkeHJ8EjjfQSRIJID65pexfKHztplRVUrGPg8QLSgfaLHMc2Yxs6WFtT0xHdmyyouoxDqMy5PNxghB0QeZqJiQjxKHWkutZQrDMEdFQSTh9vCRmA1xCM1QiKo0MYh7ugXA0xnmql3GnxSKJo6JhxIYL3gORt6yBQ7bJkLV3AcIBCjfU1EijzxK0LS1JZoKa6JoVo4hAQJeXSyLIJtcqEhKUzRBFDQpXuFz5PMa87c6gUr0XFEKlXo3iiZsgpYDDACKzHobxASfeGILfeyvz0ygth68essIM0cBOEADhkiRKu29lx6oGR9JOoJeohshEU0OutIp15MVXgucufgA9CKjg5rlZfDjh3/WFYg5Xgye/2V17793VcnE4buqzPndi9duvSzX/j87/8Dv3B4dDBfTO7duXfp0nmWpViIMLhDYK2/cKceYh4pkwPjMYPm4+rg8Gh//4BXCVERlrMJ3wiGIsI+uPeUV/+zW+YDH/yhg/3HT5/ubG2dxxKRDv8CmdgQQBmCmZtSSumZuzqK7vqO3yrFBWUtdPpoWiVJ/OUvhTV0ToO+4xqlW0ZTpOAGbyOWfK/1lfxfdfb39yixvbtjzeiNPvThH/0//qk/+Td+9a/86f/Df0gHiE+gvX3n9oXLl87unF1Mp4PRmJ4RozRqAbO8NpCoga45SDG+4aOMbGpEk1hIyZX7PzCnkcwedxzecnQ8eSU4AdceiXoEWJVy1vfSRBsBIk8WPyETA+LVERhiXFjfEaydKd1UhwcmuESvrtqLnxuK8EtnyDAIf5AQAYnRj1HC/6TUQVVz9GPJDV0KrbODsDgxSUFIEqcYU6wSKSJm8pAJ+Rs9mCBGEYjcEeR2jXo6K1v2WLExw9W99KryoW4+58Z857JDtxUq/CcEyiFXPJePm1prdYYKcWyjo/fJi4fzkSS2QfKs2RKfZwhC6KQ9gi6mYOrEPTEc7MGDT7CpJgOaqDlTMXlUxi2JxJ7Iplq0CDe+2ifGgdmM54EgYAcFWDAoYNGGPyLnTBI8ciPH8SVt5PyLQU6IkOFceOJqxkyLiKQ5Bz96djRrIaFVtZzBQnGoAKD0nkubSdY2FbAOrihQCHMBQNynEMssuc5l6GocZOqmysQdF7CghU2LNwpDG8e1EcY4iZ281VkBwqUgQQmEMVenq12Q4LBiICAqR4/M08kxpTBN0ZQwLNnMo3Fv8FIgwKZEOXHLlRN26gyrwDEXsqwwhFlKOCzB7chyEymzSIyv4NxdzLTFdM7o16hfZVTLhlmsozLhSMzWFzoEYCUBEKO4owz1Uvr0EiS55QIR6ib8hZfGcCghtbdCy6b85TY2VanybrK9gLpXJjjUMajSRhvNLBFuZJQnKlMAOI6gkCUaG9ScegQC//GnVgsokF7XIbY4gJ2CzUGR9SEbOVqaXIZTQMKi1b7Iy5gEVStZ/vd4B666UeAchfQEIig5yUzBVIyLKloZf9blT5KS0vBGgYEqPFPGH2QZn8IO50IAlQ2hSiEn6jKZ/99/iEHTV8F1oRISufG40faYN5IgGW4kIa/W8PCA7QwEMWbUBAxAgdaZzQXGMGJV0nMcvdl36s2mfOO039nn9eLTzj6bGdgeMp2dOeozLb3Fu1hggEZtzlorb6Xo87vPTGpveOT7fPp3e93Ly+7bvAdj2b87WF1f8nqfyYXx4HC02ln2nvT4AkD/wWB6aTQ+8nu9g6fL2dllf6+zcFK/N2e/12FntbvoHS551qJ/2F2eWfX2F/Nzy94RDxL4sb35JWbsVstzC17Ovdx18WrBtwVYD8Eb2ezNAGO6cMQ8H1BtEdLgovSE8nwClmtyTaJfbqfJHpTrE1nstntIIEaj7gycvqChhm8ZV1EeNWXyPIucq9EdyqFc2mjQUNZW146OtR09c9KuMUucNeGNXDrkx1d48cui6zPvq+PLwC579ylOW6Id3IwDZvBa2WGFIJHXIbmmsUwpp5UjETXWaiGx2wIveEEIcc1OoQcpCMHygL1A2krGXAQpQ0R3xbLJvMvmt4gNDCK7HDm9DAer4T1xKjAZdGD8YojtppME6gFRI6MdO9ik+4kSowUEz75JHgCgNcRL2IpqmE7lFzUM43y8xwNfdc99+JRXhe7wcAiwBG4O/BMGyDJdRlSETuvyeRTPjU9/MxxyAoWuOelRCFGIxtmRJ3PjPJWJ8bDNkKUhn7HIq4RwBoWnSI2uGMS1lgYRycEBDG4yi33IZKzAuncGKkxFpvM/JcobJP2Uo/0IlE+74CgorHPNMMFn9bQjEoAWPDwM52S9GFMBFVnFSFZF4IZ26B1XkFKxWJjoSr2n9qaVYxDCYI8Uw7dWZTFuyp7ZyZtvvfm1r/6DKT0W5+GWB0/2//Af/uc//KMffrL3iDlsGrYrVy9jHbDp6hwMs1G6V/zWSeOE6c1Z6/Clhf2nT27dfAPl4y7j4TB7ksLysP/d734HdY4G13qzyy+850W44pMdFgrzwR5ZFXl9KCRScYs/IO8tgSm4ZoeMdel1qbwB2jmndULxrJKAnt3Al7u9N5Vjep1TvVvGCw9AmqC5oExRN1FGlFqwBrc2TLLiE8wvTKaocTgc84g1Q6jz54af+uiP/ezv+sKX/s6vHh88vnv3G9uvvPj+9/8Qih7xXMZwRmXw82d6HB4EYo2Lh2MIdzDrtUfUQC1rZaEKRGKmS7iwtdYLuOKnt7xED6O7umch3EgVuykSVD4djMtYs+Jes+eMISUwX3fRnWh+paarzXhDCJrJ20IUOFVEIjgTnJUSRAVSZgf6PKki/AO4U18WNg5oKFXKf86Q4ytBzMDhdtelo24Js1MHAgogaWOaJUr9kkC66DxIUQH8q4BUu0KBn+ee/giSWqtTzge99JQZ0/oO5h2WwDBj4XrHDt+NcXKa+t8fTO1cU0fDu3jA4LCf7t3Udz7y8BCVXU7QESGI6s5bhtNhWbL+TPidsLhM/SbfuVmF5IbuHq+ltpvpNh6qxJz97lR9st3Ooz7B5eO4i+XkOVxixvNXdBDZgelhfMdjHSDybBv6af+NFyHBKYn5aew5QaC+qXVKUzYg6Ku06NgGQCWrbYvDKGbAOuitzJVfvgsEpxQicfZcMzxBU50LHAsilboGEbCyl+kjMasuitvcMB2ZaxzUkUHEj0cgP+EuoczWlnfuqTfiMC0vxTGA4dIdOkRZWgmJW9B5JN8AfgQXBm+F4Yz+SvcaqT9/ngKd0e1QhE1DmVLOroFs0Xs4t+WEIaKpZGETW+iV/F/tOGfX3TcB/vizTpKkyUDDmR9U0+M7DNyO7nMiWpLIUpK2YSaMASRVWCfwHXPcGrtZDmJDD+zS5qIiBUBCyOMJ8GDXwnaE6M+gccEjBvTjyJjoQbRnfSbxFESBFc9ZVLKzrIC2aZ54EkDdCSMfdaAh3DI6R0vQswEFCrvIg2Lyj8MdSlgIhKmtRBSxBcbWgMt0hhcXsRNfnMBqaW9dioCL9JTQBCp3mUM5RqwjiRdCq7yviXhb7MG8WTDAOyq9CGbh4qoSRcrif31WZA7K1AWEcieo6WUWBbUV4IlQVh7qYLTIsxMNNUmpQOs8QYNJNAWjC3EXSsrcKEgjoC3lXfwltVzDEql7YrGQLJu15t2Aa9q7jkAIFIneldluhQlv3PvLIS09VISpK6QYnUMbeMAkLQdSbbcyln9BxxV1M/cyqmsY0+QEQL2VSZHRfHqux4ym7xBe9LfZgTPtLQ/pLdIzG+qdS7qRQPL84GCx29+ddGbj7s7ukL3M54ZdBgzP8FaU4/mlmU9inZtTFwZbu3SZ/HTLqLvYperwhChfoSbkLoyevteOp0bxLYMMT2E6CMYiW9Y1H3UbgWK65JEgHA8m8TxjgWWpKYanmS8PpWI4hBlM5+wu5DlQFiJqBw4ghFm61+zPoKxOqzaogScVHmdAD7YOaBhN029Ez4CBvaqgdZ9pbQI3q8nZzBHdG0CJ9EJF1ZbmRvPCpkMCEFMjmQDMcoe7+sm0pgUKAoQOLEzlI1ARTbkJimYgWmMaHxoi7jWenCMC0YR2J1GTBDBCEnKkiM8A0DwBgVgwIpvmD7q25mgNZL7HPu2y66T275XeHP9VcYAYNCjMumNCuJARopnNnLrCJhSAQZJQQ+mBInEr0l1yFKOB3Fka1JVlcmmRIwSgYkDQyCETOfi1mZQAsoMoveLchCRAIIUFBVE3abdocpGEO6M5GCHJg+jRlPN2onMBmWhLpHbLLYJDu9iBfde/VJ49CfBTwghMtOPBBu5ZFjNVwfFaRuKQRrAyjlL7NCackWI5/lJfUWHqGqLSElCB1VSoRutqQ6ZL8saLt/zXYXOIyWEN1OAB9tCp8016khRR0d7+0a/86q8+2n9MSXqoZ86wG+fc53/6pz/16U8h7mBEnaXjrgmddfIsxYYd/5cjb/lJwyAE9yTqVyh7ubz12htP9h9BFL7cD8ZyOJt/F2wK+t69x3vTyfL8ma3PfeFnKBabFPJQKHGkWLeRuQkep2tQ0EM3ilUlct5cb4DWF+S044SWznZyt873t/BUGYiW05IOdPysldN2gq9PdZvCbHWYPX08vXDxIo860DzypbAPfPBHfumXfvEbX//mzSevfe+N1++89faTR49vvHD15ZffR4BDaYwXeBbHWUlDAX4UGekGssWBp7pTDexPI7U/KAD1Qhsd80f80MCkZ7ZYF2VhDz/H9q4G4JDpwFAM21JW+2FA/J18PM8WH8lb9aoLbK2LesBUqi5wFoYFBecfFNVRDrURMM6pIZKB8bU1wQ7CxnrU7C0oqIgVQgMZjEJKSPj1katGDXeDE24Me8ZPo3Hf/hw1j9pjZ0fcdgipCn4d0A3N7Ppz5wRBKnOxFY580hrwbd4OwXYU/LpM6XZ7dq/RHxLhbKvz/2ftT2B1y7LDvu/e7873jTV0dVXP3SQ1mINIUfJAS9FEarAoURJtybYMyYNsww6MOJJjy46BAEZgxbARC4jjARFgB0ECG0mc2JmgIIABRQNETRYpiaRINptdXXPVq3rTnYf8/ut899WrZlOWgZz37vnO2cPaa9prrz0eC8bV2QYNcGzLScGJyKohOFr/ataa3Pl1deFyQiuhnbcqgBrgyN8mWtXHi3P2KKe47gDJtnFTUZe2wkqDrvnwB3HFywZ9YneCYYQ1ieuxJyEFj21JK2JO7cliuuMC7GDiWnKPrGJlwk2O/VEH/8tJKXphmrKonqWSd/gfrJJkxza2dIPSgZJNQvyXOD0hamUlAnqVox+NCcgFFmsYOuxKupvqZuTS7UIHFigQoJR1yrZWzMYEJzTJ/QwmY5fMAGRC+QzTUirJOF1UhDPBAd7amVCBB0XQk5jy47wEUhvAaxmQ7qDpbgjUKiiACDA/tigTsWiqysSZFnfBNWyHfQuLpIszC9P8IG4QmU4YAumBz+tqnSI79OJfbUCvC4NKT5nCcz1+haNV6nCfSrYWR3V25JqaDiMBUdVx0lWJEg4RDAXeFg4yQvIHFlmEa5ivVQA2ZYoncxM9MiLHIlq7Mf3qtKk4P5C3DksyaSiszWs4oKnUsI5d8trwXjSWIWWqzC7P6Jq3wa2AicCZjBOFX95jlLImdkIEDCcGipBgF1ERH/94Gojr0IhbRy6ZAVyCJn8Z51oDmoI+DkvhltQdDhAy55+t1PWu5KX8m+Qf/2J4qSppfU2ZS9hN0PAlJaMLH4f1tOSK+UCkAa45HahVksVGkesZnb0Pp+d3HZvuyk5moYGQKWtJOuoqv9jnLDu4S9G0fwG+vi+0ZB88tf7+1t7mB9av7m19wPpdbX5kfMA5tzxzNUr1sjiH2V3tPNzZ3jrcPt86O9tfnd3b3NvfecPa2M39v0JTTi6PDUxdXr9l19Pm9skBf+vga1C9PnMeuGHYo50cyyc2vc7mG12Kh3l/q6dTo5ti3tz7uStjq9cvO9CM3Tq+PuVsMBoqROevXD52XIIu6nZwti/sVaCQOxunG445efL09OXwNNvASdU9yHdJlxeNgwU7xmTEkZSSwmMnbtRnsLgoRvnHwOy+mzdt7WMmcDoFq/eST6ta0SEQwwznYGmQSCHzefpqjKdFSx0JvhMRjBAlsNX2h5Je6lRpNvbel0kDpLpDoeN3qmOY6FJuRDCr5Ak7L0JG/Olfr+GdKUtwjZlozUrkL/Xy1MPsf3NWho8rl270fGPOs7KeXm7dg0Khdg2fHgHFlfQbiEtEKIl5H7sZnpnAnPmbGg4XV59R1Fa+pJTVwQMET4crDNHPT82Mssm53ibWFcq+h83Cl/Jm8Qqf4XmkDGF4hnhjR07cd8zH2bWBV4YnCWm/z9tebWEZlsUM3GMK8438MujGgPauVvvnJq929H90EVuvpo8FQGqx2ndEBr3P823Uhn0mD803s14X2DjS1ha/Ta1omT9JKMjIz2pzb9uC4E1nEOELEWm0YleCmmaKJ1BLEzmCZ9mYJw5bR4iiWBUhnxjpVvb0E0XKX8uPfHuedxoeezoySfkA8/qKLkXNz2p7Z//o0e2f+G9/4mu/8I2PjlaX26f7ewd7h5vf8/3f+zt+22//ype+dHJ+qkBeiGaVU5LqApE+Lpwc9rtpJOlx4oTOGh+/uHN19dQi6q2zz++tHm9tPsJsbs1UzfhOQz746L0PHnxgX/ST4zfu3FNZ5Ur4AUsTh54Q7i28MWAd2S/1WkgiWRGiy1SE9P3NfTI06jOxE7rcnhFiTMjw4vp8hMainhWyTjg/NwXHgSX8pojBcDR/wif/xPUUVte+UE7hzxwKZAxERbQkhmB/+Xf9sj/+P/2X/4M/+Z/8pb/yF21wfP2tr9+6ffuLX26s9+L04uz4SeN7l0f8GCfB7u5sMWpNr1+dbq1aMa3+jEnXijcIQKmYAjrAIli3bl7TJw5brrr60HoDPpR1XnUM+gAIHPCy6r4Iaii2GO0dqKXMefmi1Ca6l1NRz33nnUqh1iM7Cj6OTbY0py3rUk1M3wyFgG13CgjJmYJUXgW6ZQFHTLFRjPU1nyWLKoFkIVClrkue0aBsmpSuRcrD0UQXrDhf57kaVDd3asCIB7+rOIaA9pGDVY0DgaHu6YOa620RqB2qArc/vLCTctOnIS3hNz3VXIBTVDtcbXPjEISNEyP+DoRxBtjG1vGlDWaM4eX+3urkkDVYnV5d7o3GHBl+3r6+d7X92KHnm07Puj40SdXJ7lwhaNKwBnrV3D0NHZPCnFnOyjyYl77azJUcNiHfv+GMHQ7MaPUO7pm+Id9Xct6CenwqDyKmIqBOIYWofAbNX6vXQbclmJqF1nhAEZQdc+cd55vSzBfHoqyaXy9hJ32KpeTauvKS7yiHhPjOjiiNNUzEa/ACykg+shEJG28mBRKKNOZz9ZrHq623M2kguC5fY6s3d95mVesHKU3Zu47ECUQitd9hDLDU9AE/9MrCOr4AalDDCCBDZ0hdBw++xxsX+6s4byL6jDwdGLV9TbIn1801nY1soTutNoI5/Ctj0rbZ7ZtzcUwctEGJ62GAYOjDxiODHwNgAjnIIkIrw+sIUSljnkb/be2L0RIWsIGXhYPxQ3+PQzKf6mMzzRHpbySQ+J5kKyu2+cJP7dH+G9lJ9K8NrG8UG7SsFzOmr9aQZU688b7cI42qhgSxv44nyBWi6CrIklodHhBSDpV+E3cj7iUZI6wGty0hrjsbqYQtowBUCrxPD2rQ6y6ZwsIOllMhlMmeBGTkWtR7m1FDCaHoZECvZDbFFnLti9ShHvGJNxrmr1DtVNThLb5mKgZdRa2v5WsAy4j+YCn8WeQCagmIIcBa6x9PpqSelv9ypOFdU8ykWN+WqPDqqlYsD+4s4wRNwH/X7RlWS8IB121d7E32uPgs7ibw2S+KEALUN0HzKtMS+MmogQVp5JH3QsbzNJSpNDeQn+VOYdblDpllHWCCRwhFSmGclHI9bnCj6iSEeqrOqkYc95fcsyd13zljNHlz4zY/eqsjFA1t63VrPpgGzp0tmfRVNhViapqKZ7RGPekcUCeH2j+sYeOS1TOmwLwgE7phCoiiNBpZol3G7PTMuoKcMQiod7mG1mL6G+eYooehpu5cNd0/pJqbGmm+/GjbYlmqWuAhPJe7EZqFnJpb/zR7NLLGB50x6GrvWmsx9U2gLNjijS0IRTWm3RD5fcY/KwHmMsmeaKz6wBS7maVNQY3FDsdgYEOaFHndnsOIO23FfJPNcZzRrI+c4VFmzAB5J8Sm3vhJMLWCmr4RSgmrTEkmj2Cy9gqT5dZyfFyTteBwoj/qctTAusEDB+rtqN/sQFhVCPZn5yWfrotAw+9jOrN5RtTHiR54U4oECmfHdSp8GLfpIdZC4ywCmaRcKRvbncc/9gMeWa1adqiM4asXJJ2Yaf6LZV4hOP0ibHQC6M7O/p71S/kUorQrtVoJFn9gmB27vOxY2LZrtRZMk2LL7tbqcLf9ZJW6rXXgjaVynKkzw4bnMSOVqBkE2IjORZXXwJ4lWaMpPvOySKAewzFKjfddbpxuXd1Owvp9OYL5U4xxfMj40kEh4TcOC3TDMhSjvfjRG8mmZUjuidx/efqZZPF4/qu1LixyAg/k1UzJ6v9cbR49OfnGm6c///obT04eK5zZvrg4vXv7hd/123/bF7/8FQRKRrOUX7lL/yOVVUKlgjVRi383TBpNkGSUyDBnQ5Zf/dpXN46OPnrwYLV/eXlm1qj1r7VHRHu5+uijx/b+0oKvfNuX7t69hSqjifEbg1LXFNrDchWo7AleQkKksEqfHAUPdh/nWlLOXd6b3PPobSBIPOkLXOCX8Ftdko0lfA78gpPEa5CTZPKG64T3kO5tXp6fXT786CNevhEystjevv9r/4Ff92+98vk/8e/82299wwfXrt9+/62vvX7vlRfvv3T/xfMz1HWUkI2TlpI7HY0Y4o+h5TFFGKKKuqcTpOHXD6Nq62KmJgeJkplfYma3DFN0OlVD0PUqaxFUgtRjhEFsVd5FqtwdGtISttSLwxqQJFu9BzWvgtaqa2LGXgUHRUNxUABPWNWpOLP4G2UdPo3ASgt+prK2ou6lEoKZxzPPGRdMKHYxs5PFa5ckEVIBKOIrNDqTKVr4DrQ45FJVwBNxfRkzKkyASUphsM9Nu+KsObvRvEtfZdPBMjS7z0m8cgzd1a7v5VXbqgwrS0xjipMkHLaleTnd484ZW3JcYC61iT6IH1xdn9rvKa/TNqYZ2LdASB9O3vOr3ROtjH7dLNZiQJVphsApZeFZX6qycpjro+EftSFJlaZ64Q4ZMGNuoGsJ7MrJDiWZWJUPPUyzvqFRqO2WqiZsBjCeoCTQw9oEJX28qRBjGEprbNhiTIXL5xrVjZdVyxQuNMIq77fgiamHkZjmVt4ZAoOQ0mu0adTm7u3b12dbtyB5vX04m4DZVPb0MH3Zvu3uexlb24b22HbAkBleUbWgqAUhJtZXLsVDjWmd6k+5HatpU8bFhQ7fxQzwoDHCpyIkQvRENZUJmrjmhxtK0+xjSdpSK4fCdL2iIYqgiOit8buEhGAYKVtYrMA/7QKMcc9rvIGbjHY2n8/kdXGg6d9onEIiUCxhbpN0bT5pTr3WLofeg/V/Up2dJBBzH+4wx6CaU7xUAZcGnLgTbya+1gjsxYMawSAarEVG6VX1NpxlSHnY3eGEIERNSNiMekkFIZQjaTyPyUdtshodD5UC9QqlxqSmQVCc0gTZ8YKSeVVETQV7pJ0MuCRgzdUDaJUVVbDoBj1qUZ+vxCP8xY4UOf88LFfl3TzP7xIw9wH8XODyCLjYwMxtclfsgoY0nue2hjtiXYfexC5ZrTar9Bm1Lc/f+Zq0klRO/we8m7JTsLSvorGslEWUjLn0U1qhy5UilEVaY//LNSHrJAFYoBdX1gUEtlL0hZtrmAvcNWQvazAxKAMSIIE9DZgFasnDdymuzi0TeG+mlgwviXCcDm/viNSde2D5OAW0im8xP6vzF9oEucM8qGLO4tXdZ1Ivti5esS+KeuortkFKZbg0cKOCtAjbtOiW3sXqo5h09UpnXCt3tXpiTGrG31W3XCMl9aU97QdE+Pc5G61BqkbSYV1tSukoBsuvDe6wBrjNvWt5hiEca6GrxKgxgK1b0bp0WimBYV8x+1MZxraOCo3HCfbCidYpguAlE53MZMEDzial9xrnWQclTZ2vmg6Li4quvXfUpvLF67Q0E8Kwq1hVQQgbb3gK/hhWiU7RhkiHCwZBo553P5JhHLmpNRBdkAhm1Uosklt67ilxMjadSjNNQmEhIuUZJI2CNdJy02CvGwx9L82gfYx3soObZ9g2Q0tyjVEMJFIRGg8yXlpam7khmDFh2IbqiZuixtxsPMGq7c0DY5zwudg80mzXd6g1BPhKm3x50Zr++RoGQkJiZ3W7RsWBPZUN+1q1yosw2oCUGGD/R0GY6Q1F4lLNUIwnzfaQOzqJJZHh99Vq1/hSvkED9xwIDdg7Wojri1ccGQTQ+Q6d2B/GKhR3NT0Yg62k4JO8sDWWD/ldXRmXXilV5cLtbH7UkgMhuhimAmQYKaWhlQgBaIU/mvzXWGfw5ZendQB1exP3mMsx1NMgYYAX4cXKjzwgls5egjCbxDk8aj0zRPF45+zs9G/8jb/5/sP3T68fnF3YqHNxuP2V3/4P/c4f/r3fd//e3dPzs5ZBq0K5SgnSuL0CQjJBLjweRAbbCcc6heCAmgUdk/VO/d/41Esvv/Hk57Z2j/G4FiWTdnV0duSgoWMfknjzLd84MNj9q77ve7745W9/evTALumR46hRxAw3ZOoCeCGxlxHl8puWLFdMWMKezzdg0u/lWh4W9NPHoSEdrbT1603aT/4inyQ0gK/pUfUlV6U8B2A4/6yYsoosiWH47sOWi8vj45PDzQNLGje2Wk/8hW/77I/86A//qf/kP3v8+KMP3n3/9gv3dG6tmdxrBmlr79Aoia04uSXUw8IBqxXJwXGKjb1ZA0m/KrNBioSudnL2N45mMYNRbucobO/Z28Sz3jllYLd8KP3ywPmuq417l7sfbpzfNcG4cfHC5tYHG5cvbmx9uHnl/tH1xd3rzY82r+5frz7avLx37WD1q/udznx5V8ft+uKF0ly+cL31wA6rs9UHJycvOYDx+uJ+J6OnyE+vru8Yl70+/TSyL6+PMCdvZSgZziysb2wm7MfVSHPzwvRPOBa4N+q+6FuqE52f4G8mi6oZLik/4vJyc42GJWuwBEau/tf7ZSqziDmvzMhHNViNGvHkzXYaaml4iS3Ys1zVivCrIyPHtQW8V1jZNtau4ceqqv4+k2A722Fnz7+TJ5QMWK2stBGL8uhF18EYAzALS06z6dqJQ2MN05XjtH6AIm1k7inoTZPqLKxsAFGTri8+D/mr7TfSfZVKC3L52dKbAWBdNYSbu83RCcoNZdYazxGRddp9MLppWSzVqOtTBKIxSSmYAMLNPdshMGueUcoMxbYgipDBTxagWp75hE1vmVnBEI/HnkcgYeNPaIyWNPM/A007WvwHIHh1qKeITP32+0AwTApp5kXpsAg4RoaVwpJsKyk3nHlsan/z+mhrw3HNrIqW4nz76v7q+uHO0e3D3RNjzPc3zs9PZHh8dXH/cuvp1eWB80I2LuwAPL6+3F+tPuzcsG26uucj6xdnL28dPt7eunOxOrvY3D1rtzflc+rB51t5s/ONOtGJFdk4EqHIGmOB3nAkp6zahOtgy83d0GyY/OTLMPjYhU0unU88jyBZLDfiPG6bsJDwEpsudAU7B7v1TteXX6+5dGSJ/gXe19cxgHJ+fmoM3hkKS5mxSPO9srOMF9DpcuGlg+u+iCekMXGww9QGu+CadyI+ASJmMdoSRmLuSo3FImdGhvhGBrWzCJlN84QbOhTPOk6yrU6lEwGgrVwtLh3EK1DSEmzcun3I11BsbUoyTuYp2BSW2ngNncRd/Vo6gYsWVMtFTYJ1usG9LwFHw/PXkijgroEWhkkAcskhhixSXLIlVomHzCVkCuvx3K4kzfvUvht+hQhimdPJti5iINygtoay/AS6p/KVqquHUFtIek5EJUb95Pjkz5JRREWvQa7DFvhLARO1CHzSTZJKDdk1A6d0jPWL9nVxU/JCQEnjezE3UMN+efUUZEpJV4efPnLUdjJW0hk85jF5W5dVdJHqfvNgZs8MceSJn3Eqtjf3x7k4GxeX5hAPxVDbcmED3qgHPTVQMrISATzVkSqTAQH+qY8x6EqoaOVhtAbpeo3XnHXZSRuAiFXR9uSPOoVNSslodE1MM+K7p3oL+YKBlwapeV9hNWTAXB8DnqETfkVB2uVtMaMeoBFP5e3/XDeGrBfmrU7KGOI6N2NWBGSPp8RJM9oY+CpUJWjwjXvI1UhP2Zk8Jtpetk6jnqV2SlZ6oxmh5wX2MT+Euvcv8ueqqgJTOk+GeauoZQdjEhVhqELxl1rH3tTpNrOWvZrrqVYmS1L2MqpjA7LkAyvMJSJyfxfnF411ZPcZt8iSxuU2RXo1O9MR9lqnJkyWsYlKMEauUTCuzizSt9baNqjFh+Vd1vGLQHiFZmh4GHyoCLUz5EI1+bHKUdZIRZa4FJoCwEs1PBjX7MD/Bc2IyeZDdkkL7/yEODtDpaNFtEP5yZ+5r+UChcm2270BQ9tWRh5WIZPaWQNzVm7wN67u5ZEjPp2ndWESbrQPorEm3RvguMbti1O1oaEQ84eA8oTbkDXKCb1BV4rR3miZigBLMVLu7O1enl1++OC9n/gbP/nWW28hF6hb9+4A/v3f9/3/6D/2o3u3PzL6aNYllBY4MW6KqcAeFoa7J4sCFnQIIu5RHe+W+sD36dET69rPzvQANT2YU/1ysgl27e0d/O2f/ZmnT57SbUMC1jqfnD3S6ZAqTF0LW6fApeDoHf6EW5eXsIwBN8It5uZt0YhJ6TbYl2yR54AcOHNbp1r42ctNqnXEzQ+8nj32EFOfwZRnsrmVagHR0zNMpgZcn55YXXV89/59s1MqEP/tN/7G3/L06fn/9b/6L99bvfvW22+9/fo3vu1LX3nhzuFnPvN5J/5WQTuwlvfAhjRlVK0y+MEmrsehaozYKI5XqwuVqNdcL1GClrcZ57Y3q93tzc0ynjNNxi7OhpfxOAylMDL0seEZFqZng98NP0i+Yz2gD3vZROmjSLP/+2Bj+9hRsRtWu23cPuUIb90739o9u3BILpfUyHd9Y4jggpqohznzA1qD0blnmjuWTZVO3HSd1pjwoCG2d8NhFGzUa4B1S+hyJ4epj7Emldvl13pmmheppPjBXEtELtQyIdUIVXvWezW5sTzwj5vzUJSbZkct1UVftYktd6UKvFPnQI2O0yAYnk1LoTyaLWvw422dnJYNhnwYqbQ9s12Sb2m16gtbE7Srr9swRw2DzFCZdiU3TleZ1OAqZZYgIwF8Y45xDjFxMUcxHowFDpf4okFUqnLHtOU2K0yqpaEUKc4/KEXgKCp8GYCKqMHDNJkBK7SmpjSwrNibm4Cs0ZReKCln2Euy1NEEFIjQC2Plzg01/U5U9RyefqQI/pQwpc+LhP7hhBYyPQ6zk3175JmYc9MvW5erPYusxKFN86F/YKWns7+vN47P+oST/jF5WYncdowtatnKNKsDfD5Fm6spoeo2DPANbq+2nBVuafLto8uTM2axXps2R/lRTgrjW/c8GjJUGBFiK4mWK2xIPuzRpWVOP7HBKKYljx1v10RDsomeUcucAP1545pnk7M1oh2/0Nl7nH8SnJLp5/TXkkGl6BTaoQCDNjKOlIjWGECWV6sUD3ukbGEgFyguz4Nw0wcgq+lkDSkem+oNF3QJqnGB12TD7yWMjOvLDaRIDz/n23KqLvRHTIX3Lql/lTzejCamU04zR3WL22lgT+/uzq3bsOP0LfCkTSlG6MB79a8a02NqJ9P8FaqMFGqCJlmBKdu8eP5W1w3ewM1j/J9Chh1rPGQUOaAX+EH23s+C4uQtcLnWrw0Q3lCwRuNZwgXQTYY11hK5SjolrBGvoIiIKUv4GsfJ/RzEZbzfd0Ylv7KyEKeezQBM2mc3X0GTyF74j681nCmg20Keh9jazyTFnL5wNpBDx18//iXe9XWDaMwcvXL3OdVW+j9mii/1yE1p7mbBjP63diN7NBaEYhuE397ZtTgvO8rY3L7c+MDYimN82D5dh/RDjaL4Dd7f4fddnanaj2zA37x6xeLLC8d6tvTOzN/uXt92PdS0XKxarO1Am63dN43uzxkLKsphs73J3t4ELghCDnTGdXA7EI/9tserffSH59tvsuUXZy/CQU+Fm+RTsGGYTTS3YXFOfgnRpZa1MiGKP3m3yGebGolRUdRz3NN6IbhqE/tQlLEeZ2+RfX5VB95UPSZGuqmD1L7aG8eXEnJ5OzxN62/TmI75lMfCGGDYqxW3qi0kSo7L/OyEkqRQ8kzTBu2CGv+thoeeTBGUBQ6AJ4MJ30hQp59J4CMh2IMFZIhluhrCg4NOEys3mqolfaU0W52GPsY8GPkshCRodIQ33DNzU60Jemo3f94quoExBoiLYutI5r7GOLupnLaQGxjinjMkcb9JDG52Z8XgvTtgc9V4e8DVwDKaTI+4KTLaU4J5jXapwKcefBquD6IN+eegAEFaxvBNiMevLOXLKBxIoQUJGGQ1EyUIETfFsW4J+mr71hk/YEnD0te+76QSvrnIzO+9h4qrVgZjWZwZdQrSwosAJk8oqQZV0WqFHLQkMoBDUpcfImTBtU87GrWwix/xKBhQJly0hfytw9unxyc/9mN/7c233nr40aNGoGn92fGLL+3//t//+3/HD//w9aYhz9QvIBEVnAGipCCHcIWWBi6iw2cdvKAzRdcL2j56cvT6V78x7aM9jgbCOBywutQSaF6NVx3ePaz5W61eeuVTv+W3/hZ7Ve2p1LbRnVCYWhQmUzRMFqQq4LkrHJJ1rOiSq3Zo3m+41Ns6qCRrlehpnSlql2fpPgG+RJ+8ZCFM66qpTXnm3eNkW15uIPTmeUD3myopKYLw7vT03Lr/NotY63u4+/v/wI/+N//Nn/6Jv/be9r5Pu33+p37m0Xf9yl0r09OdC87Kyd6ub5v0sZTrbdaM0JtVABXk9uqEgeq/OCBGp/CYIdLXciZXelyaRlQe7ZiY2T5aXfjk9AMGaHP3J2ZwhKDMSHzAomzYwcUKbr0xisNxp+EP+EKbmx/m326aKLC9T2mvbFpRnRv5niq6tWn3F4pNevFEzk9OjVPq25Dq25iQXatLQQOGJ7FrYRZdwpQEMItzEkDOlpAk2yXp3Ba2PQsAC0rB66ekkxC3vcpcNVaHApUTvqhJmqUyKdw5KgA2zDGdAUbQlz34LNz0jHX1dOdkhg/6cJVtrm0GAggz0nklZo0ttqr8jHBu6NDW2FdrftT3lV1DuzYYXG355PCWKRujTlYYXp/WOszgKQxfVQcW73/RlJxeRIDoffeNmIO8aJLJpwXeWExUBOfvzrKdoX2pCw0oDe9W55+PZXYRhKtenuz15yYBY9PoCSCSIBwFznwTstnGiDSi4m8qW4/YGoMzQdkbYstSghBnh3J5JOgqKXslwn+NWOZHKAtf3JKC6RuixI3Bnm7R0CgBADMWsIa8mDazgzuHFzv3t76+fX1yfn1yvPF44/qlrc2nllbtGu9HZWu0HugZXG34RsHtjdU7PIStzbfp8PbqPaZlc/OtLdthNt5t/mbzLcP9l5tfv3TKyPZDoqkutlLAQrvdjT3jI7RjamtmLiQZPbehixfOu8UIQSOXOAFCwpumr/cUPw5HcZen0kjUYgfD3M6JUgF0NqcAOqPWvoyztadesvv1EjOTSQWfawVmMC2ek2XDAaSn4PhaGn5+jMf/MFpqCRw1vtLlf2e64ZDPIl2mYYkKY8bXqS0GYtqDjl+wa/WBoasBRvYznDZlK7nKMAoQzAirNhPTfFTeYwyDDE5wCPw3IYIIl1C0TgwIyTv4a17BfIjxmtLGx9g+gfNSDuG/5LWc+bZt39dyxasAdflNKJXeNYUKDMfhVky+uXa/MQnKGmk3pQ7yvK9gFRjya/B+QvZbXUEf0Asy68d1yrLcFBGMgVNcoMNufXmdjDfv3/L3Wep17De/Cw7+JwEN9ROeUgyqa3yDEhoDLdUaC7uQPVEOxmoMpl0yKjWnnW7RwqaF6Itr9ISSWTQixPJp1vJ08xGP1sp+9YBO2mR1Yg14c0m+3kWFnmoIzq9ONSqj3EbzjYXW8nEucmWpUuv/ZDbbpEnMYbv0cfhOfehoINV4opjslBgSzlVrN4GRg83989XxkSMP21GnCdZRUK1auWayOoaHNPVVm8YG9NqF+H5ixaLF41unOiSWpquNI0VJMpjxDa7TiMe3dWBeWSmGhQV6zpbGYTV6YBc3jBNb6uLrXutVVY2Bxk+GoOBqdcDs62SPKhXXSz6yknseQjpUR/sXlRoolZppKc6zCjp4CFLtiTLZD3ginkpYBRHgKrhfT/5rx5fHiays4UrkjcoMQwos3fwt+IhPjhpYC7DCQrZYz8PyyyVniMecsVQEv+QFYmHJwIv3AQ21+DyNs4BBdcqP21SvchcqGlj3VFCkoxYWCqjljWOKCtSY65JWXBaLHc3WEWvlR0ZFa3oMzcquYcWkBt5wugEVqAR6K1932+qqKLNeAb8JMdenTO7NDinZm+BQqPDlCvfBprJizwQPkp6jIjVd3se6R6nMlaJtPD03OcyBAfGdd9596523j45P6Im98PdfePGzn33lD/2hf/pLX/6C0wg1Jk28DkFTOBjKWtBARMX6CeEKm3e/PTzDdXkKw+NjH6bgAdqKWitQ1bDqur2XuuXbVkJ99atfxzhfH9uzwVWLKxEwgOUnDtR+oNBrj/3EljgQIwqTIRbI6H1wKnR9eQTuWcAa5cKW6xMPk+ybctwk/EW/ozITGjJBzCAMTgGNHQMvvHqdn0KWxIKujo+O2Mzbd+7qBjBn7NStvXvW/lud5SOhd+/fe/OdN2/fvX3ncO9TL75iuKLecQ0q+wfeVMtYsejggB1xDy6DGZ1cypVeR6C6bGnKGbctk8tnkBc+JmebMg33wDXqAXjKnfbkX0eOF1IUP8xeUyVq3hcnZJ+S7uwcWMfgfDZUnB2fHZ8ejxuhTtmYxaUe16Vy40QMCzy5pCFhMyEmFccKL9ZVjOT9z0kdHLxQeDByvOP8WMSeokLE3MrT8wQHoXK0NU3IcfqD29dRtDCNjKqVeTsh6J9FcZbwxW65Zhhdx4YZmsOI5a8ESTMDWXcoZDeGY94ypyqsI4iEtMSUKdOu+aTYtaMkOwTLeQ4zHhb5bbSEOWz8zkPmYBkcGoYUPbREVkVJOZTCeq7hxTo8UhA9QssK9A6ZAe4x4gb7fopsrKbIrl4HcqxOGxoOmPAgjDYN3IlpwVB+K/OmuBAcgANLgpjpGpYUA3AFlW5JOHAjd2QPRM+BAiEvobQyeVFK60EUtfNo52LvhdXBjmPGr+6e2ay1xb/3iXQHgu8+MgTpw+nE2fAN37m+szcbDM+MGjbZEhlGzZq3mZK5FGa2Lsw5b+/14dLZiSc+ssLeQy1Eihg248yIHdnEqKE8gko0UvAc5nWCxwpXTCQjrSTN59Z6NISpSQGSdWzYH3O1vApqnEg5TSABxFUCZjb0VSlbvYWilD5eIirpeTVKmpeljyp+1l1P7Q6bCk9dyznIdQvXxSajbOpZNY4nMSdxoyZn3bq0PZMklhrAuYbFtBVOOHrRI2QMyAk88zmXkWpM4zFoWqKm5KpEZcrd0StVLWjcIASpME7hRso3jApbf+WbJwIdThfUtWbn8jIhf8dbsBb8Pk6GNwNmjd2kGOktheJPeaptqeCNYAetdfFlaT1Gv66PkbkJeS5oiVeZkhh4zUBRqfX4/WQYJoh16btI4jSYNaSlfPy0ks/llZj60NUvvtY51l8vu4m/SbkuaP06b243sT0lRUs+ekrguRxxYQDFmeQgycKXQhdGqSJ3GurfPKS38x1iy1JTJw7OpKU0NBy7KLudlTHh3J7IjbuNq2zeZmmt7TZjbFSJE25q9GTz9OTyNoibl3eVu20jls99+epnp8ufOqZ5qx391mNeHdff3qnBvDhoFej5Fyw8nu3FFkz70pWJBB0GiJ+1LJapuNL+3T/bfHhyefd0ZU/igfrjK3rw17q229YoFdQ1itUwdrveA6Jxonn4mhpMaGgAVbl2Cz86P3TYE39Qqt1cYkaBUiJ1qD6GqhW0s1fr1ey8Wf8+W1ENyYaITA2CMkKI373E2Jr/4TjYcdZzpcAoxLQiy07nBBaS/pXRIOBn/WxYRSo8Hz4MCidiQQxlRUfZxsVnSN3bFDcWowF7/7KWI+0KJcfpo8g7NO++JzJ3NnhlRW6qkzGFhXULJfQ8zbcCyhZAqF+9omEsG9PRub/wmwLbjwEPBc8YvbDBNS6MOOJGre9iTeLcxMezRDPIItVrCxXPHAcEmnEUWeqoZtBSuyzlxunLUNrYdILBDJhaaDHM47PPMMYyBTrIA1vppY47SvKWRx+9LV/dsmSiXqTxpmjXMSumZtIJs16vnC/BDYI2xayOwGdZ804LAWwZguq9FBBXwMcwBVSsh9kc2UzuiOj6U/U3tt/VEMAj1pF7SllsAUaWtrduHRw4bOu9N998/Re+8bd/5udeePWlw5Pzt37hjePTp7/l1/ymf/IP/1MHh+bBTeENw0ZzRz5KBQXnk48HV2BhVUiBPeB22lFM2PpVc6xgPja54FvCdx6857iPKnY7V9NLDcfOyZNHKP2FX3h9a3vXFyfg/97bb9+9c+vFT728a+l1QIYEqRMYLgFf2ZV4I+k1UoNIyJx9hjBXB+96DonwXZIuD2X/776WHM/y/ZIZ4DdsCAmpPwZewd4KKOrjCAHnrwmbEdlQRNTp6enKIWYZKLrx9H/2b/2b//V/9f96+4M3/9Jf/MvnF+8/fvD0vfff23rpMw9XJ/sH2+enl05aVneYvCb/fOgw9lCYqchekkjFViqOC87q0LNRCscohM2tFltv+obAgqMdP1+mRKvG+Rj/NHaJ2bCCP/0cJXRPY/daxFzF6XR/EcwO6SjWxn0KxLPeuLaaUvzl7o5vHt++fHB2bII2/ylLt0zQxTEQ1njnUgyzKojOTpXJoo3ax9zs7Fqeo2noRJ8rWqOaUeitNBkEz+7z6z4sCFeNULMVBhnwJnc/DAwVlbP/7HB+GUNG/XftjtIwyDzLQcSz6hKb2AMHPpDOkmJRMwOc+QzTDFRXFj/PYGcr6i19vdo0LG2O+tLZdsawBGagO1ZALvagnhiHdDR7iMqC9eo3I5jZl4zUomkYN/RGo5gJ6w5ZkEq06jhsJL5T8kIW/o2+lAvl0b3AAiIeKmer4bm4OV7e0IGztYOM243Xm1Uuax4h43qyZWIqS8sBHciZ9uYWal5GDGvZKWBUZV36og6pLjMI3Mihuzdq4I4HKeNkp8J7UDm/uOdwhtXOByCtVg+cIr6z9b55ls3t91WKNJOA+McbD9sbsPne9fmdjdXjDHLM0bjYLKGsc5M9Dv2uU5DO71xsnGSOteoWaEZ/iYYn6k5MSwDhDwWE1XlOpYXKxPrJhGTlzpEJiwzwOGWDDQJmZDC7Hgey0Rx8OpIfUY0DqUqkSA9XvvngwYhN3DBDlVMeF+rERwfGWKaXYieGFs3utPwtsS3DdRqhliY5tweElHPpisXlmE9l43jeOXDFKQd4oFFlneCO89NrDHb0JLRIDcFBrLHH9mTuNpfbBqSOrLNSeHvaJAps9TWmLE0ypa6zixolInuskVimoyA4LBydWNHel+ZmmNcAGQy1Cy4I4tKEpxCTOZ1MUUM9+EtEkcvl5Kt5CK7LM1ZN5kl6/rkks/O6kJHzTcykXIOonAkfJKaQSkkrElX45BtN7Me3yAqfSpz7GkSVoqCR3hK1SGOBWdKEMFkm4cfPUivnBt5NonXumwzL73P5F/4qlFwH9hrE4N/zDe6fhOANHnOr0FGwSTFvQ12vsSad6LHe3uaZgaXTa99MtGKlg/6sNKWmuARPCExK2kViTkzjdx1iBWfGUMg5N16F45efb+5eHAxq+86740Ts4PCm4xTMonLGU++Z7uK0+ViA4xQV7rQE+rRHv3IylMWEda6QcRomuPpQVTZPRtMZ9abdOGO36kL4doZBynCaeqD5mhOuvKFKVXBjIBghP9mAmrCkqyrSvindTzGVK6B0MSS9rNReiotdXniiOLJIo5hRpBgzdRuOw6SlC7Ie0V+qxABJFtmNpTqkzIACV2SgaKT8g+AUVo2eOjPxU2yp55J+SdnbEAWrAbiGKXgdkLr1f8k6tAzqU4aCM4hDY3T5PwiULK5qtnnvmtNFDUYTQ3VKCQkvcdpdijJrN5jtsFnQCVAXs5ghBkHacrn1W0MxGScwpAIvdp5YDrrYvqmzE3E6P420eGLTmNC6J3Mq5ckR62l/GFAZLGfM7jsMsLUoJkEDVU80QxlJ9ikTFX9ZbF3AhL1gUkiY5x1o2ikPrFn/zCprYzxF7VdZpBNJdbnxbRIYWipmAGU3sy7zUrnRg+LMtTamb5LOGfCFXV2eWFAHdyyt+4WT7iNs7GWDLfSW4/zi7MnT4//nf/3/ubg6ef+dB3fu30LiF77tK7/lN/yDv+UHf/P+7V3NOMzaW5oDZh6DEPJJu4ZhcXz0OuhZ3kWIksRudWrNi17Fw/3a8P/Rk8dHxx9CKmlGEkJazeXn9u17X3/99aPj49lqsvHo4Yf3XniBqLDz6aMnhwa993gVGOVjHnWnE03/RrawWf7NW4yIQ1099xbL0tuPr0L/DtdkmHgJl5fnc38yZzERtcCce7dIn8xTdroapOVakpZoMJ2IyGMz7IKQ8t79+6fH54d37vyj/9g/bFvPf/6f/5/+V3/yT75474Wvff3rH7734Atf+NJLL9555eWXZ0iCXrXwtmoxDM8sLJwPrx7DIFbkP5KgesibyCoV7Cw1DxZlJeLRF2Mg5F4zT/UG1SLCtR8BCJMY3DUMAd5K2c2j5YyMlc6A9l0adnaXmtNID+2E57yaypU0UNWjwT/AWctwjVXFdfNa0o//ikj+E7j+kbCnmpn8gMkb+AAWPrh7Wlcw8bUBuBFP0mNrROFqYQPElgqXvz5Uy+/0YE5Q6ey8r2OAYw0f2N8PwrLGolLYC2aojo1hnIZ3+weOI+gsIec16QnYT1Cc88240dPl2NjRpjXISgoZDXZSRZ8rxHOOIQmmWYQeauWAbQ0V6iKwCwimhSYCMUDWtCfXov0PWEnjcPJ8njMChk+C/btJF/P9z7R2RTJhZRG0gIbwQmhga1ohnM0Z/ZvUS1kT7X3gTrklSVXGXq5ZXNqlLBC04BKwElnLkULwSFMQplocf3HSCMvqESfS4jNdzfM2bPnfeM1mi6JbwlM5mYzzvWvHeZ8adWniJZ7qpyFAdMZekjDv0zwKPrAj6bihErYXbzF6wfOGgjjObWhnNrY8q26gYgURqTylaEVTBPHIQ0lqvTqRylDKOKwcZviFR3AIJMm3dLidMHZNJYQYH2/UR2OOwPklHQqg4uJFCaozpVk4KF/9U7wY3ySYtToG4BoEGIqUJAP0ainqc+A2eBRnKvw4N0qK90nNyVcavzHsjedX99KWaYyiUG+WVlg9AarJmWIVkG7iyHw3I5ZXXByTIyWBYJaooqUvtH8IqdLNNSnd5jfNTWckKbqnYhZCyr48TmBRz1/FlkX+gTJyWSeozHX8AnOBPRiti5nwtDvsoj1M18kWhg0ndTfXkNbYSbM7PY8ZxZ/yIGylMlD78SjCcYirsaZtSF2wWReyYd3SEluRN4QMrG4VeJP3WeBAuUk8v2vKluwLdoK8zj0YRgj8mAD95is748sGhLnz+qRZ8in0BsM1VHw0rmGlHQv56rgbxyoIcHqK9py1eo1NNBlsb+fmqV5CH9lg/7ZW+ztW2Ivb3dvjATlwTQ+36mBngBm5i9WJY9Sdq7Kz+XR1ffvJxqOLawc5asOMUTnBWvNxtLrav7xuAnCOZVCnGfG7RlI2t27pOGzZndYCNkZB9d7B8fSPbkLHyr+dBxZDqAMdzbF1a+dwTx3WLF4en/CWGsmWQWnD6toqaj/8HIVO/8SnziqSIqWodcx+pS1VgoqtClZiUVipOhE9u1J1YObim0W8znNQ274hb92DtBWinMImJtO/dcnVeennIocKSExAa8/dT1/lil6bT0CU2NS1qj+YapffKKHefKZ0eupNXldymjQIr87CxOrSsSUVNdkXiQMZL9w8AcpxsfBX89UCqpZrFDtt0JAe1By+2Mvhza8IK5mJ3HMlxiiJ2eq3ETxUdi6OCPHZyuJn7CKqPY7nTkmIMZk2UD6jC6HEQsoShjNIlSMCJ7YGyLOXrUa+uv6q/DImDpAx7/y1LOGu0WKjqtZz51nlpow7C73aGr1ZefoYggubrcd9jyuwcf5FxhoCVADYsI0eTg/V3jY4koGvUylz8hTVmOFYz63NfZZ+ZcdL4ye+NpBuoV8j0HRAg+TcO69pGGSAkL2n0qVvO77Ltcso60dY+PbY5gqjMsMK40NxDT4qQOiRiXOpLq8evP/gx/7iX3rw4ANjOc7C+ujBwy9+8Ut/5J/8g9/93d81haZ4AJIYokccFVyJ5is8bh7HsVHO2jOlFAmfGsXhJ9SdkUUux+qFCRfdEqfXHz190FCRiYCatwZfkWHE6PQsk2gDgqMwT85Obh0e3L99+xs//zXn3u/vb739+ls/85NPvu07vv27f81rMDMp49QiAgc5VrguPgOnxdJ6CxPaD/P9d+JXqHfNw/IWDUtg86uuj78EiRKYq7W6iDP7usT28q2vYAHWT7V7fZf2/FWGz3kmw5uWM3EiB0RJ17CcQn1zVUIqnEofPTFKvmEChAI7/lz67/vu7/7+v+9X/9W/8Jf393Y/fLxx8OA94/iHtw7v3j2kWyqgoXdrdDuHVyk4n4JBqopAdUZloKcMQ27Ypvu8rlN5ClX/ZZHkCdVzMAMj2TxBA7dZjcFxuQdp8CeKsXODt1R5pFQiw6Jn7MPqULIdCU3rSsxlIjIfkTu9tDMzozq9/RgG5OStulG9NGvbqfbVX/k3L7Q+i7AVdsM6OeqiU2otqdCSB7YnOmsByJubu/sbl58TMlVqwKoyzpoLV/Pt6xpVxU+HO4OHL9jCUjSjGuImie0m3jFh5oyBevodDbq9P47XPnu32rbYlbF+yVzd5tlr7U5adYo5JKam5ycDzUrwJw2bX6x2DTycs/8yNd04fQzC0zNfbHro4zDu4ca4QnjaWnW9KX0H3poU9kdp4PCf0dVgEvHClmx3VSILRfTxxRUCG6coErDU1gFSpv6Jjfy5YH3+mZitPUpPuoWQ39Q7qohaP2ZorEkaa4C35jSMp3C+m/Ms/cWracjOW9AocdfsJ+zcJIC9PgufF285opo9Iyyfgv3mbntF1Hcpl8qeTS+ZOBbURzzpmW3o97f61ix9vaVbubq4k9ex/aS9e2P8OK5Xl/vnmx+tTjkR9qo5lc22LKNLTPLYbeg4rkpZF1/ONu++jVhNP4o4cEycJwHO1Ulj40N4jG5HBUUJzcTGin9udXmyufl1a8kApYaCDcVtX72iwfUpD+fk+aItkqrn9Em2dNbyBIdq0F/fMz11PrOGuT5lZaSNcxB2xyEBpdsTvg2yDIXTOmz6ioJe6MXnqm35XubPP0i2Z+aEtZtOXaQk6Ql03MmHJPEhJYhya6/VuGxpomWXlHz+OQmrBsQsQTnqUAlwTfuKK8BRTA2XAXB9DsdlW8CYHJvCogCiWOyKYk9QYxoMnGh3tgd0xMQGmNOKPasScDIZm79150+Waxn7rwUV5b5cKVbX9YGnjnUqapR2iQc7SX2cA7bUV8j8eWEsXyvN7ltpXYm7PAX45m/CCgavq3zuN4kxxltbzJtveha6RqZ0k22dWSql9jJoxQYX3jaKNrDnvuTpvgAUOQxfwpewgRz0dZkBurkGai/r7BPuOcq71oAVKWQw/KaES5pJO3QrjK5OaOUO/Cm5pxsSaYkwdtK5Dbs2pfpmr9mira3z1cp5+Jwvot7YUrHMV9HrDCqncG/bZN6es4lztjvs6XKPgjiMmJLVI2/RG3err/zmBbP3RlOYVaqui2zRzqG36UT51rqTQvk6OjNKae2Ozmi7VTKkfGi1foQL9CLjaMF7RwfRbIeQ6cNSXobZOdnsbw14qju2eSFUfhVI9rQ7UcY4LPKiSnvAglGmYfbCKLJdC6IE0pdqWAiw32TQxdCQsuKkjpWiqlpZiKALH8ll5NOrCva/ulx4ZahJk4QtVt8yXAJzBZbGQLUrQ/IqpzwNSdAt1WcJg9b8D+LyHDKSuglq5AnAAPR/oiAAnCvXHksUUfqhMBiBmmGW0By0C83DVGiyXbDzMyCNqLF+AFWiiR1wz09OUpwxmXGpofiMo2QNk+BhQPzFSE8i3SYwlTHV3mCczmR9ruiFRVyI94Pr/IQzJSlSuAyTwqNOaNwXOvZ6CpGKL0ufWF1KFd9bsFmvlgBjopvCrP+JX8SRCsaMWp0RZefLetDnhBg1pbk6tAxpdEXCls+KHqC0UR9ZIJkVWAMfHqYWLkUAnNV3kKC8dq11Pky0jbJGmOe97d2To+OvffXn33v3nTffeMs3vo6eHu8d7H/7V77yR//YH/vUa586v8TtNr0jFxZA4TEEEkY6vVy1PcPDJBE5EEi9koKoFIRF0xu8vDo709fy7drL89OHjz58iGPJsS4NzUT7DKFdr/b3932ajde77YNrl6ff/iu/4+//e3/NF7/9y1//2Z//mZ/6+td/7md/6m9+9PU33vzSr/gdO3t7DpTACCg0rlaJSmIPhPgOgw4RLsSVEV8iWzOtJxfc/M7jQs23vsevv8sL4EkdLmTzDHg8D425ArdWzgkdNG6eSGmwG42nbrXo1tGeXB7u7+5jSAsJftX3fve/+q/9T/71P/pv/sxP/+0X7u3ffunuk9PHHz78EI9fuPcCCSg8v2cOjJlSB6mRyfQB4gOLRi0X0lIdA9gVPePaHVgcP6fmjrKv0SfilCJSUBgVHvT0FhWQgeSjsaxip5sbBcDPCTn1oEUJb1/jxvYektLihv5yCSQMeuoWqGAQk9LWcINdpQdyCip4ISG0oAGC0p7dPVX4gq+k/R+GrAmXN/X2Fl1Zq3ytvCJzIFDRWPFfnRsjkRFQc8sm/zb3LKluS08fYHfOMpvUShUDN5u3KbKjlxu03TLAdHG1s187ZkIvd6maojbkIOW8G5Fq+kNa9OiOTxvSVhwIhFRNBwQbe44DIdgftZ5gKSi45XN1zDAxEzjkxNA10Yl8YVQ8wKF5hRLGFDES6yGICyvmt5u/+RmRlDaeyeeu/S1nE+/rNotdy1qq0GPeyp1bl2SDO+ArHBYUp7JFhaegaCxDNOsjNQ5V+BrvxC+DVP7Ta7qj2NAFI80zz89bsODN+pP3zebbqWSccL8RGl2q6RptHnCp+xxn/IOyQWm4Z6pjpe+PsCMtva5JCEMHSCjN8h/lGCjsA0FMGTQ4dVl1TnUsQ15MCcGMfoyRO9SUU/OtsK0tX09cbRwKnWSVsXHhAHTa02ie3QWoYKgSEBbotaaBeNFQkV0zlcD/oVORDWEVl1dT1bLUhxJRS8UqqhL8C6v5jYbhZPUNisOtTEroSgLF0I0LoSxVIEoVd4QhrX/oSxMBm/dRNim9rKWfRzVNEpIBd/RoUCNeDyCRzWRm+o1ONR/3B8V6wtX6Wo2wqVlM/VNg4GPkQsGgGZ8hDOPUaomjLUK9FyNorvKmMoUNGotMnk+yTinIP1fguryWW7ab8DhV+FzLT4nnL7RLPvHhIN2CdRkaqinXFDHBehifXdKu7+He/qpkABLWV/ASUNaNM6tC9aJbn72AHohDXkTl4A2opZBQCbG5ZlcAli9nQQgqQ4Ws40FaI78OmNGvpY9lJX1IZQ8HsVJMPudbu/TDnnGoSg7uIv4SBXdNhtb+sww7YXvqgOomhWoIDAuoUoYbKcf55okpOVqp1nK721q1eWKZ/qVvLjZZPDKkElZonGvUadRuXYqro1qQxpZUHl8YcOCXY4Ws9mGLIaD3eds3gHWkNzefwlhpqtiWLw400GLXI/PrGxyWkVnfjIAWn2FWy7EjBRFPVX3Tf+vZ8NmqmHZnzlJPebqPKi4Si0V5HqNDU8GqNvFYSKN9IVPu3B0/89jufdwqk3/C/KmAUwFWvn04QemGOjiD5QUkxcmmJWlEOI+doyfFiKHaAb1AXbzWsEBj2MFXUGU1rIhc7K6iZW7SXTaCgcq8SdPJRBjCoQIErN23lnfCMVdhvBWWMJouyhQEgPLCU3ZbqluY6G3GIKuLYV2SkAIwRbfVDYNxJYMjn8mKRDH8GRonA1pCDssMckjnm4LOEAuGXIbJp9WUGTEG10cejUtYUz87uwb8MByYhnGais+zRwJ33LcJd86utQvQ1nSJAQK+xv4BCVmmEproMi6IgwJxwj1SIxYGuZ3aCqBfXXZEeZxOZehk3EKWhGxeN+8FZ+LHWAUYZ4Wb1H0s0c/F9jus/sbGYR9r2nnHEO5W68I5azkfU2bSLks1LoMau/MJBlHHK6sEODiI+m4XPRcLwMJyVUtmux7ogK+nvfH6N/7iX/ixHX1uq2evrr/0HV/44d/1w9/7q7738GDfyqCRILWqI6fRqn+efbacZ5z+yPe1WpJELgrhNChlvms5O+CFhPXI4LllNfupd3w4evSIP3N24mMOfaJIpR62U0rTIzXA52fnDiD6yZ/6aRpx63Dnj/zT/zhMOPLf9h1ffuP1N7/xjV/Y2H76+On7Jyc/5MzrRjwxDmH5+1W/1ebX3AhEyykjTqUqWG4koUbtdNgXzqKWn4/vz4/9L6HGhmXAQGnFug+9H2f55NMSmUj6H/zri09XIptJSDkQ3nIvbvKVLFF274Lr/Cy/S7KoevLkMTyclo0abP38K69+33d+11/9K3/p1uHeT/z1//YrX/ry9u7+04cnq6snhjl8hHZr14fRaVl6Jf94I0SZxqbhgac/VZkpLjX2ZDjGmPbW1Yt5eObfKBsrUYpy2Zsk/fX26+IMDOb7rTryb+iVpoq2ruutqCaOavSYKnaIKxZTIKTwC0O0DZFQkNyP6n2+Fy9FEnAzUkwDlGLOxWuK9yQI0kIoorsANX9wk9/QT8ylsdJUpeMkE6U7bT74M52w6QAuhIgZ7irpcvOoSrEwQamRSkZgGiUF6/5GVqW5BVV1TAcbPma2puBEtaOynBilaaLU500jXY5BlH31MwY6dJghKVQ7aBFrcjds1YeaWDO7q2cHsCNZx45FWoXMFTKDaro7HIJ05Uxs9S11vp4Frj4xORLVyoive4GoHrErewN6MycxzBqEDBgz0jLweJpPsnwP2E/maMtBeQqfMVcjwXqCWc1sNjpcwC7rxJKVUGNkCpIodFIXzw0bOOU+P9WWbxRvvp6D2eAvmwE7hNhWV8nhACU9qoG3cfGppLh6dyQbxCuj1yz38CWhS7e4jZkWAb5IaFeh4fzN8/NPX5ztG1OvEwLXjlV4Mqpi9vXUhqK4YtTfTndF2xPs9LhKJxKWEuSRfKK+Jd3F7jcCsnlwdu1LzPcMWloF3GSWBZt4cPaZXNtd+/TgG1aE2ky+VoqAW0JGnr+gPmgEmSJnOsXbNror/KMUqrkmlcKum+QV9epTNiqGOZaURbu8PMbP2kgJ1A/MVh6gBkzjGrmYCyI2Rjkt5jsl+rNX6uCnxikBLV+dvaTA1dY7IXH5Qs5EH8aBd7UezkxoVQcOo299eUnufIWtzctPK8KKD2b1+txOKgu468Ynr6CHOJZF7+ikculXa/+hS6qI2rSMwoyXFru+zdCactd4tmQsjksWtgPL6WGAlaBQ6qR0Mq0YML1BeZJPFu8CBfXH53lJlNUK3lwBWaee916swf1M0LP29H+Z9TW34KS8PKXglAusUFxUdF2qmN5DeKTkdfhMLiE35bk7UIZgBpT0E3xTesAH3/BC7xR3EzlhZRusK2rBf51DQCnDpYcltJDAFBZqCzOKnYRF31xx11Upz65eFmAFLVHePQwPCpxMA0/oIFxhw3PEeZ6S1sixVmWPc7UhEWASefY4+fo5N4PWOphWY8iNk5LfTy9oq+N4ufJnhtx32kymYcdBNdsXPTB0ly01/j4UGADpcHobe4HXZ7AzmC+izjyjZGUTm707SyPUBwZCPBPZt+79VsvmPFD3nPIsLz2Hh/DWxpkmtDDpypGkowU5yQuHaSsOzF1xN7JNW+O+P0CCUVSsUXVVm0oYPk2GiZG0HDnR3vm+vapEKoKHqpPw/NQBBl6MWpgt2pekUIERTqGGdRUrF65TTKdYv8nj+qLxPLY8A9MgnH8tI+HFhaYUBQ92Od/eYKHKmvgmRo/4NH2lCAZzbFirp+BLfCz6lFPG/mcDCNiKraHM3DQsFBBBywVmpcKxxfe+PltrXWBfHHMfdpUFwl4HrKcSNMDMl4m1HE+cCU7jN7XBWk2xMwatsRoB+V5kDOSDiCWWMFVEPsoaIpgt468lb54hD3/AQWKkxvDE8PFiokiV9pdPJLyJlPByiwkJKoeGi+IOjGQeFBWInOdmbmDTo4StpilNAOAJEPwBOWMmjSPKTyen6EQ3OsWohg8mM/3Bkke+8qbU8OADy1d9GcPRaIvS2PrEJ2Ey1gLhii+0/I2f/Jt//v/7Z4+e8hetzbh69bVP/77f93t+4Af+QQkZ62BEhTajLrnXFFG13NrFMw/xWllb9p46EeX6/My4uwarTCUvax9rPD5psQG96JMwMzav6LMTp0AeQ0cuKbkrxMOpTdyq+s7eRx9yu1vNdLBj2Nuoal7R/t7hV770lRfv37MTb/dw/8MP3rv38kvjlOXiorp1QMofQ4AnevrxaJBZOIKKRWTdi/u7vmLyf48rOtb/+3EJWYMYrq7DBptwWaea4OVWtvUf3e7DmpcXhOU0pD6Dkax3/sg/989+8OThn/2zf+bhR4/feOPN85PL+7cPnj59fPf+bSdv3LlvI1Nrq2h9svNv4SOznGVuzd+wasSTGo028UqzPj4d1JmPo9WjmwQO0SSZ6vWz6EeCjrShLrUsU1V+oUoJKV3vemSp9TKi49sOVRY1uNzC0VoNGpIHiAwjoqkHAw5ohdPlzBJfBOQqbVDjSFU1XZoMOce9TSi9HP9OUUEIDIQnPZ5MtaiGFFnN0d/XU2qwwDJxjnrrgKJmbI8V//qprcirLOBVJ3lxhEHm0HeUxFY7TWNX+ZCk2JakGOr37rkD6gSqdRnbNcLSwyrmZrIU7iHOjGDCWnT/BlFxilGUQrARyVEU2pNvkhUg2UwvECGR6bszeXFL6R6S/xRQQXlgXMyxLEpfLhH5tMNg/EaIDDKSacTMpAa9yeKyDgAr0SXRhJgbaS2i2fYan6zxGKekqVlshAhWXvRdDYdjlWFxohLCssTe+gWpu+Uk+JXJEYht3uCrWa4n4IBWzA+lje13tnfvUo9cAzMAyMGE+sG309welCwQ5wye880TujB542i+yyhvomRIGxKy5cvMvy9utct9BhT6hIt0gS5v9DI+fZD76lwisOJYnu7STHMe1LxTZ72qVHv6KvUh6F0lDRVoMgAEDtNfNdO/Mq2kc6DSSeMTkTiYutdiaEgMdhkYLW/rlrTl5JL861ZO84cDkTsqixKWcIdHkwCxC/9wsoGdEWFiT1qmouI37GUN1LSTYlIOb1UseZTWmqMqTQ2+jANAGpxT5ORWO01zpX4uqYfDGDbyq2JKBw/vGgxJgldeMVPBuyVPoCNNksQWm0fPQxgIuA2geQnAZB9y1nnFLGUn62fXgtWz1zWgj989LQWUZ13Ekj181ukG13XCgiZHsdjcG3RmsGcylPjm8jR0SbNGip0aVyAGV8A67fx02s/CwSV07muWep6KOmGJaRgQwktZTs65KXT9GyOlG14tQctuhJ03y66vX96hJHGUoqLWjxO+84bgKX/KyQoEMKSXAHnShMXCVVwGls/pa+pXzugxYfmk1fvXvnc+n0HPD/LBL0Bt21XtrHpjFI9krCOgk9Ap1bz/p3qUalHjWasnC4oaqDNbCVyNyLDxVQS+ScP/14cZoMYgDLEQiSoGzWkTmhNArrOr+pBHQ1EJC+DGY2geVDmEu1a+rk7OfLY9c5yHxCir3jMYPG2GrLESTJUK0Z5g6JHh0WLogGwb181XqtisWPUIVriVNsdIHWQcYmKzsg01q5Sj9LE9KvOPQ09i9gghJvsEVLQ4zJhtf2BjVYRkUDnV8b0slxtfLyuKGmGuAZBVbGjUiGeD1pjQpbRJtV8KVi5SasIAi6xYCMYGO4cNgC4DelM5kVgKWSS+YPPPPu3gxu1bD3wSPHMMbGZ7SAn9EjdYHgot2slkMi4XryUbff1MY8pTslRprhqzELJrl72shd94Oml8jQcYrxSAROXug+ptNpKbNITEvHyobGCugyER2qWvopkwHsWe5iyN2VocdcZQ5jgQ1n1XITKGc4s4mCiOAd2QzqB76+7NOtV4FUgDlOUlJySpVI2hnCrgog+oIWA7/wy0hSMUn/p+ifDOrDiHxeWry+o4rPNP7nQ90y5PByl6a/oncUUogTbKotsqQEdAgFEcEVvvZq0V4qaLyHm5PLet9sd//Me13Nt7O0ePjz7/hc/9kX/qn/81f//3115LTcsH3TFINC70hef1n584v/HizMp7l4+t4aeWqmZYRzdXgB7lpGlil+YBOo6AabedI0Gc4QPPiwsH88Ez5kpL7fXhp6MprkmDDx68e35Byp/60he+4twYvoLvAV+cO9xs69at2+9/Y3v/9r07h3cMkfk+Do6iHo7xnjbboaQndPjudLyTGGRQY513VWsaeW/JdX4+8eTlF12jB5NclEztj5LVqvFffFXWgC1dj27b71RO9XounLVbycXiTYRHqQQ/d338gnuZK6xfbZ44EOnRwzsdDJrlevkzL/+P/uj/8Gd/9mefPHpo0dS7777zwXtb3/e9340TZHV6Ys2YIztANbVyurfLJJqB9R0qw5l02eZUPqQx4xjEUI3/Kp96YUPVk1M7xDd2L33U2jcBBC5zmDvvh46MVK9eW/wcylIOL9SdjpEDnYfhmgUOX85WWbkud6aREjcGmWdkXCPH2opho7zTg+3Db3nsbICkEo/FrD5WkZQiOu2caqU7QcdLC3/3MciTRnM67F2bDZHFLvatAuN6+E9Wv57n/4I8JiBEPe5gn8W8DYvaS2nNfSxgR1gkLtGAULX7ht+BE6c37XhpT2+unpQoVfOnG8HyzMrW+hhG/T3vt4x1VgGNyONYyEWdf1EQ2UoYJUlVABxWMErRnlFANPMjfEk4DZ5cvcFSPUSCxs13G6apyqustKwuhuy8XolesW3KgrH4zb23glG6sWGxxzuKBr8Jb0eigHMr2uFa6uGYpEStK/92zc7Fq+EbyNqspTlgw+ZdSgZAgTVarkzP1RuUA6asoRBtiV8tJNOqldzVqNrwe3QEexlrOZucNAWRHDeuDs5uvXi59wH9CQGHNV3djStbZs9ObUEYxGwUtP3gkVUI04ROT1LeaSlMlGRtwapDQPrCjzY6cOROrWDn7bTkIPk4lU7CeJa5W55C6vJzjXPvvimJmUzYwhIuaDpzOM6ZTxBvz+ofhDgDt/YIZJDq+tCieKyNtUhhY9+XL7UyBvZs6MmnwijYaTvs8NGiaa+sT2vquzahwT0nlytI50AdRIEOjj6Ytmj7XC78OHtJQZcbTxvB60tnmqqlHzAKkGZBoN4P+bHvccVeA3LDzbNX63CoudythJYiuI/QE936Wvz+xfbXzZMGXBxgaojJ7EHXdMAadxsdTLfUA+NXzRGnEwGcIhCWvc3+BKc/r10V764Aj72gt4cZ108ui0YWtc7iZ3kx0l/euTZnfY3Hj9OVoeInZIC2v1TY2TqkjJV7M3vwds/i/MWQnqRuhqVr8FrgfxIRtJYDe9MbAP0uWSZ8SVwiVxVsudbBC8AiPg5/9rwO+qafckYXjFD1XD6vA26dvqhnpYT/knR+PPbf80Cr4ufUBI4JCnp/5a8SMfFBbm8uC/CUe2JxgOlOYchV3Wl3jpj/Jmo7TezJzvXO9sUuhddDzmfbtdTHkQhZkmE66LVptTa6E6WijmeqwnCeog5pOUYNDs0465hT1Ye+81fCrswKr2Co4DuUpKacGpbFDl7sNHGX41h1UOmNCHUwRC1ZJst/JKSu+cXpa6HKWHfIe87ajb9TSWuGD29CYQpvMs1okhUY69XhYIThpOoOrSBCtNEI79X4+gE1sKiuUnnMDGYEIIS0qdXLYGyCYSXRVQ5YDiv7CfcpJ87GDv96ACUgrUmVQyOX498ezYWExiry8UirJkex5QK9hjlyCzFamQlWroCYk4bE69CIitiYm7Zthl2jWLmaDkxIMThG3oMlEDwAcgdaAkSdtq6P2eihpXYUsjM6JFEy0X6YnGUeL3NagsKwxJ/pfQkhEwSXSl4GfdTMTl/L5Rk95m66GSKlYwqRrVOqW2rBeqKGnhiY229r2nnLKrZ0ZuikXpqKxtihP4eeDSHgWnJKWNl31LRpdepGPMscLm04v0EidG11ZK52bvgWu+LgkBdc8U0AjEoUp2S3xI/4akhQh8Uk1MS5dvPs9HRnt4kfPsOTR4/t933w/nvHR0/39vevjk++8u3f/sf/tT/6xS9+2aIgGiWddkPDCmGcGhWuVcC0o75LKVWdut29fa3Z1vYeh91MTmo3dSEh+F+laqooWWtG4WKPBDAXZ6dPn/L4qztFadCy9jU2c7WjcePqrXffPT2/uH/v/o/83t+z59OxuJaer6wjOjk63T84NNh2986h7j88cFDhNIRYCM/OAX3P1f4edk/GFF2DLdHyGqbQipf/f74S1fpKUD0qzKU8Uhrpz2ty62FBZJ6WNOv78jOav04Ud5O5jwM4G2F75xbNNFzw6quf+eP/+r/x7/17//bm+YEpkRdfuH10cuJoq1dfeeX4+IlPqmUcdH+3thypZPE6JScCy4OqOdUCiNXaq99VCC9t1qBdlw5fOz17erB9xwIxPbbMW25710Jbhn4q9UIn8rAXism+KtfvQuTM9ar+ztGPDWWbg4KrN/qJ8yeb/Va0FFJ673qW0vWvazEdPautEtJQ/omhjKmOjJsah54MRjVgep6VlPLKXBHD8PnBAxBDYqxcU3kfx08KeANsDHm8/yzuHlgy5FReX+1tbRwYnap5b2mH6ugrbNwUJ4Ourm45kKbqiKcNDqg02MfH2rnoGzW7kHHu50WjAweODeIiYuk0YfLgf6VAp8q8fvE2ZaNj+YfPOctDwhK5sGmpUZN4st7ExUP0+I9RwJea+a06jK/mLkhUzIp3GbApVBmLcR95AuItJJMtwlKE5IzcRuDCTshgtq536AN3kV6kzVtjy4u5TPY0QmJ+sMEQDR3SmBfAPI5cd/gAolv0xk4UUbKMNs810lyNtKpbWvjt7Xf3dppZqAgWoYPD9R5E2v8NfQ24hiFvelH4OAlKeu13kJ/7MGbwjQe3Wr25sW/QvRJqr2laRn6UqDpB7+NDZ8epWcsXOeKEEGeynZ5x0CkJdB2Qg3eGuhj43Bj9npaDDSG1DeiIOdUTexA7bXZjdXxyggGtXlMMfOjjtJL4cblxup3940OZFFf9KFarqVm7WK99XGRF4TTkUYjuFjIpcsYcF22oo7VQS8b+QzVVNyneZhaFyRy5cdzvusWRAiLrnNW7lEUzF1vqQqLFBeV4qG7oOwG4o8VPz6okLQ93IgVM1EElpYrmN0gvzQj1rtGfhUVhuSh+D3MVFBrpURn8D6UlaxR/fMXfSf1x0PPRz6ImMDhT1vKAhueAgfSLr7KlzKEidRZqKX5J3Eo7dmDWGLUtFeccdhFzZCgr4zZsK9lSl54rUeD6Wq/Udyq5K+W7uQoI5Zv3b/6diME8LEvsNj2hhS+yjimYqEkylKxpGorW7kXMKBWBL0SvE2o4akPGiExM46aq6+Zqn8W5vjpIR7XjDYPQK/nNw0nDVVUJTPrz9427XG7uiT1RU3UWrs73LnwNYOejhmd9FkxF0v2drT2GSvl57Ozq8k76ih5eqy5v5+5yI85WFwfWAqk6YVnzIIUzv4z0ck915jQhTRhAWMws2UoRjWM2drz9uK7yhsPCzFo8uDYHeH2r/gxsSQdqcjhBIhGcqhFVgDi4ln2PPLhUQNsp9UTHt+GV3xrL8WoydowA3mNnMll4mxJ4qUkdyChXYRrQU0HTFeE151VyhGdVAimVxkstqrZKOqSPkkFBgspA8eVrcl1vv500zj6d7+t8BhnCUMHQXreL6YQItjRXuHiiMl6zBjkElY+8Jc3ix8qt1dtXDX7w8Ok1Yx3EVGIhvLIB5ecSH4+elXTpCbwu1GeZB0O6oo7Eryq0txpbFoVxYsPHX2FNpTDsIWtjHkqnS+HGY7cjzNSnzie0rDMPCgOehTvwTCFNJ5G3zFMEAwXPmbukscBOI9DOMf3QmqRkWIO17iw697oOi1O7G8j3JWaj2qBmKvenw2HAiV5k/4ZaHFAF0JNhHPc68wjl4VwsHi7u8TJ41ELhwomgRBje7Jdy83fa9aIBGzlKIV3oO7hz2wd0Z4mShiFFTRPezDs/vnRWjIznvmx3fPrVv/23f/KnfvL49PT4qbNlzn/jD/3Qb/x1v/Gzn/syDzoJq8Op/dp6j9BMOcDXyHx0QGR77wA7LOjhiZ41NjUnIFlx53BUX4js8Jl8FB0FpSdwGn55bCLPOeehXsOgltteOUY+jozOWC6qiM2rx08f2ZzA4X/xU2c7h++vVi9qVC4vT50XtHuw98v+nl/+5//Mn721f+f27cNzTpWNRU1JxQW7h3Wu9vYeEW4sWuxT7EnvRkdTgp6H7SnMMH3uc1uvB/14fOgmCkvn6vdbjv0XK3KBuOEUiDCyxUhZHiYyFY4dRHGTsoj15XHOjriZGZBPclfe0lQgb2zSZ54+ZLgeHxwcchH08L7v+7/7j/3RP/rjf/2v/+n/x5+++8Ktj558ePfwjv3c+7t7jz882b+7fXVGeqe7q73Li53Tuk+723t3rnee6J1loNrhamqFcbMoa4+xdnzK2ebTo9XhkTObV/c3rj7cud5f+fqvD8E6f9nxOCxekxi+s6J28Gv1wxiFGYWFb/ZqcA75NfGMw9BF4WVEGR1djECqlq5mneqnj2Vjx+pA453/Rd5wThIsHEbkh7B+C7Q69WpCYp0HHMO97fdj/cWLa/5XacY+6HKPTBbZuAMyd5UwiTXbws5n9e7p/VhXzSWh+dx+bcleowUWs7NBVnVghdNmzJlY6qb/bDyAIT5UxRVG0KrtynmhY1FmzATVixlwOIxa3/JUjc0gjyyRMW04t9xRVDAuRV6kD0vhH40lnBT46aUTkHwFaNEbz4oKoqRrescGDcvLNg3LQnppS1lBHzfgylqMQgXF2Ek0OYKqcXt1lFpNq7SKqRnI1PV48XJOaVKVNFsnxhMgGQGcLqmrcm8gZNNq+TXl4VfXItrlDnbSAcNQtwwNRQWCtDiXhgA1xZ/e2H/5+vrD1OCC4/54y2c0tjla+zubR/urYwDOL+5cbh+Bdb2JUfbKcKgz8mNiFxQNMPFDGnQM252TMzO1LbbhWhBriyJN+g4+I5w42ZvGrl7H6n1lNJcPz1wJVk3bhApWHDhl+a+Ha6OFQR98ap2AgkfPF4aMo9EQnAauvQSA5HrURqA3p4r30oqmTo7Y5Vo7FaUxL31RZ2rFpBYD6ZR6JoaRP1SrmO7zAEoqqjyxtRUxPkut9fWGjMZUTNj6tEgrS8EsZdfSQcE/5UEsHnQjw81LI+WkZA+MZJ0T6njr/BVVqj5bmpV+sWhDiFudEc1wTXGNQkObKnPLBWNIGLchO5VZyhks5nUwKqpa655+hOIEhVIYL/wcDG/yF3VzlWSel4dnrzfBlaYEO2kHUMA/cW2//a2gSlJCavItrgG0DkdH9SrBeEq0lfYMpeeTFuh95NBTfJ/3byrimzH85ug1CZ9MVpmFLLcly1LS3AcpyCmVwpL7mq3QCMWUbKTjhpIFfRVcXLWEtFen07/rLCBQWsBWnesYxT19zHxVGTt5l1NoW2AHg2JFReHiqSTbu5Z5bF+fH2jpG4suB7/x6vDqwHpmQ8CcTOoamIwpBtWRsMqj74ux3Rg9CtTu/zZqNZZME8MmzOff9OmRynGg8A6TSg+vzbXVia16NPPbIIr/IzLWIfLHTmWKcC+GxETS8RvschaU+xZea5tXPVJ52AZpspJVktBg0QYqAAHD85G1FClJyz/iUgM4aIEfDMY1VwzEp1RJPYVG2RdBTNmZSy1sxUCjSwbZKrTaWQWdQksw/9wCEk+WDkZoR0yBjWNXgoBRCXhUpiSV5idMQVXsBMbakneVZbly1sKrydAJbZQmQYYAC8LpX7CN1gbbsp5NhKRqU3ArGpsDlWNEKgZX3azWbYo8tFghOrNlLpwz6zhZrKN/+hHOV7wywKKJNvpogVeY0aFsNEXq489QwSfq7MD8yDm/tDJ9dXZ6fHry0cPHHUm2ST03HdO+t7Pf3tM9nze14fUoBkQRNBvGMoTDY8YWJ0rq13Y6Gj0bruOilAbJNTNHZ3SsJZ8r/RdDR1iTg3BtbAkvmhs+t08YVSCmerVbaLe6dMuStcv5PBFYCVTr4yDd0+OTp2fnZz67e3Hx6MNHP/9zX/3wgwd7e/terar/Db/hN/3KX/ErtHdaKa3XkD+yQ7AGAmL60MfHjx89VAkPb99KZbXPbL/9+AamNEQ+DaMJakcPRE4kcM4PaRJOfTiho7tYeXL0+Pzcip0qzihiugxNhTYkhd2RtKX13D3ce+ftt3/4h3/Xa599tdnwre36V1u7773zzl/5S39lf/fgy1/+0v0X73/05CF264Apjvj299mHOiqYrNLDNF3HH1goYy74+DdvS+g6fIn9pe8RUuzcfulkz8egkkYS7PqqvArGGTHPgnsq5pOQ4TyaWHj1Zp3GixMFL46fPjXLQbeM8TtU6df82l/7jdffMP3/wYcfnB5bMnGNGXduXx4e3jYPYHPQGRU/fWBc4Pjp2f7Bxac++8X9+1zxndkLOSIwLndxinU7u/psZ2db1l1d+RLi1sphyn2s2fAnrRw1rZKpE1Vzvlo0RQv7WIc2MzikRdU8oK81maKc25ZbJ9xeEgqHKLwANRIRFgsmeqn+WacJUY3U54GWxjegE0tAL2IpxPPC03IUHsRMoxxanRBMl3NyRslvksVP0CpW/mojVwv0FmBHjPP+sziSa/vUtC0b9becY6uuyNcWXt+WYSdUxGypg+6wROmhC2nrb9gwsLVyFaMqS6teWGEzDNqrLVMDxpoVHKo31+DdbRCY0Aka0tZPqBxF8brOGzHRXoKpv3HDM+yqZdJBuurpke2d5APDbWFCjJJmmDx8Dtrwpp+Bnk2siS4PtzEXcvrvRDxFDFvnKSnKK76SK3559ahoLB6cFoQnl8TcZwUY+eiEH5zl/AKzvskunftyNTQVYIhdXe++frmtfy7HidbfPsG2/ucD7HeozvkTQnRCAZNKCeo24EC9jUVYcKkbIPvoMqaTMZHd31rt2aag3eFmGLPPdtUJiAC4+B2meA0xma2ek2Qa9wXVkVCMC1NK6AZKy19iTKjEmBLM1fd901SMZc+qJHVH/S6aqVdAG302WpdjQWEArPbygSz2IbKrXZoJKDUcWpInXHEEcZOA6KaZzYlIBZpWA7caoig8Nbm7s32wT/tTh+5hH1Jxe3QqGdSECcOHSdfOCnhanJn4pmVvgLNRorQc65sBKDfCUyDY4Ei0E/MAAQAASURBVPrF+eneyqHFoVkFim2G8PIXMxOfuNair8SFa6lqOHWVM+SGmXIuoZ/I/00vz4FfJ55skXsT9c1AbsK/CVKsef666QDILsJY+/IA7JYRF9RPEQpyzYsEYT5QiivGyyQo0Tw40QXpoXcTsXwzuFkFlwgcoDxLxkl383zDpEk4iYOJX1KPIZAH7KCsc6/fpuDhapBLTlPUt2DYT03NWguYje/5whnqRoi+DkEui7p7nTNN5T8wRLK7xeU62r7+jhz03Z+pE7l1nioP0I3txxy+ze2n8YbCmC+dvrLlcIxMKrqyfkBVtCpf2XtOUTs10FhSSy84hfiot82oqQYg45URnE+nK5hSpZ8eKho4hg0Gjd+sDsjJp1xGhjbPlj5J6zE2biF0+/rFM18uzWMUsnAgK9+W4hDNohEXnzreJABBDMn0FzR5BSlA3TLmzebaY6CdQUS103IIq0lUDxt1BucZXxwpJgYpYiCwWQp8CvjVp4Vfb75vr/umryNoXppqK7U74wKpsmTJEqj3bMhcouLD3vtTLdPx1c0aZUmWVDmaWZ2qHwIjcfn23uUriLy6ft1fSpjIhrXusWWSK4c09ObiCCJ3OgE6AG+HUMC6wm79WEA5y4AsSjSuATRRIia2xoGtg1Z1XzsTGgnaYaMFYMg1cpW5ShHcmhol17cyzeqg7rDs3BXrm/GH2WWGeNkZpAbsDcwpoXlI9goAKxCuz142Uu3FMMjl1jvUBLjmGJjgtoJA0WvlGdXmCV9d0Csut9FQzbtTvWmp4unhMBBKmGK0jBrjttJokjGa8PVvbsOT0xPOlnFE0oWGowNRjxEgW7jdiRVtv67ZNgT2klHJjd13cQkBeSmW5reAf2lUdW2w3zrvyze/9gvbO1t7u/s/9uf/4umZ8yRP9/Z2P/P5z37mM5/5nu/+3q985UuHdw5ifeyA5rARzJNPx/XNtx49/eijR49OL07v3X2BOFjpZmguPlX7sXqbKOQVAEdyMedz0TKhoKjgMEBfEuRZbm19eIw/qK4JTa7qxPZ7cQwfiOnklWI3rn/iJ378gwcfnB8fjad7vLu/i1laBseSmrXY3d05OXZUwJ6CtFIkYsWCzgm7AZQZgLjpf322qY0E/wldS5tLsijiPK0fife5taFpkuv8M6Xetj9qUrnJ+0teN3FOUWvR/KQePQ9IAG4SBGF5hs36pW+X3zz7lSXTgTmTdY339hu45yDc7Sdbt27fHkU2/3Px237H72Ap/7f/2X9mtcR7Dz545423v/e7f83BnokIak2N9O623n/v4d7O3snprcdH2yc+ZOd7PTqZK4cjmbvaNYlkbdf+/t6lExt07tyvuRF3L8yaOirr6tHmxmFno13Zk/3YWpfNjUebl7c2Nx/5GMtq68nqcm+rD7NowxP6Um/TTUqUx2vqwDCtJ0MzaGNs/ap+7O6rdHVj9QYfmjKrMRz86n6PMvsf50g3sN5svckyjC3ZfhBveHW09/KltXXh8sRq6vip2AmMAjOB/eZwO10iaPuB6JQnZUwHtGQizFoy9UYZqKnjKPqSF4eU3dZZ2eMFbt5e7X51y0kVzaHQf4vNCMkXjvetIO+oePXVopHOekLSWWv1jTipWhe+XEES74Low5YWWc2eSqkyD880AwZz+t+ijYasX4uKOQE9AkVHR+kZqnSkx1Ey7UuwSj488zMp5mWY4H1pv9zLpAaBOLkXZUOJgHo9ayBZhEJ6LWF2fgoHr6xKGzkGb5IIGnwmKnMpldpbQk+BiIraFzrgaQ97BxYOl7b/i94EkBfpBKdP+93Y9UWFkJniOY3mUY3ngIDnwDuuw7qBz21tvba5/zd9ouRqdXR1bkvG083Lve3t4+Cs7vEttndOty8OrvecXrU9x/Ltb+68F9WXLw/naBLl5etbhPOew9I2rm77bN1q64XLNglYl+OCJ6G2sDNaoaQ9mXEr7/EZFy0kSCtT81qxIcqYEqHNmjGl+AjAp/v20faDThqstdUXTus3fIkWcrsPAbIM06xTXoxlkx1sRt8EQ8A2IL1QD7wiFthLyLQ3rGGvqUXWGbUhkoGEAp2UKDk0tl8zsYjL8iFPYzwbToK+NykuWlgkn8L135PI0BB5/VHYEscyf5Mt3TkrElI0b3pTqVvCLrFiVD/NGRqSsp58QwyeL3d9vlmJTsFuO145lCYm9mZP+gvQdKztFexx22oazOqxQl3hNQ9uPQiGuaeJBmvQvEnxzb+x5rnrudcbCMUOkEk40J+PEldEf9XZZ6cAlW2uqFnil9ebeygWhztwnUQ36XpRpNtCbHwrbKQ3+T9xm7zPmFG6Z9Gihp0fg1vYEe+mVg4KKpgcmdkl4/xMiiXV4Jg9bHx+kuYKSZ1zlMjVHf4R9KZjnWGVe8f53xTU2lMTTLebCbMBho2hYY1/NHM2K6YMzxtr0nM/KPHM8VmkraYpvKO7HPXF5qVCrR7Pkl0ezO6gE8tbNWPNSLcCEEGaPUXumtKibQ0iCIRvQ/jlhu00PoioHvD6VAO9guidbqlWbev6YschrZ0m0MI/tTwHNG0MBjGgo7wiYmX/Eg4uYIh/QV5CQ5WDAgmcxeyGi/LTPLPATaKDNPUiLneF6jq3hylnalKjX9Vm5ajv6jGLVtWWvKKNhOYCjmTQP1krcuL1b+pg4yfyq2BZk0SPM6GabCWVZnAI4MQFWkjUDshigziv4RYLivIrJTZGGmteXw6+xnzXaaSQURrJla78GqQ1o6asEJhCYIjbAVxsQQNuUURrGtenNPafNrJAD5Msn3MA9pyVyDoCVl8ic03zbAxgRpnZlDQfmm1q+2l81Q1zA4xZ1/kBLu7gZ0a8ASOwMdZrycMwrVdWoxzxrIKYaGsDsuS4XGPGiMfxkQ+6JYQtL0hG/4Zx2V7Q2FPDJBnpYmMSNCHkJS5BOAzAFBkSIRiQSoo8KAXg/Mx+dewWZna4fs6Tp0/Pzi6++jM/h9L333vfZ4KtFHp8fPRdL33P7/k9v/e1z35Gj0Lx0Ew2oRpiSKeOWOSkJmvKz85PuN1mDKZjwtsfHOcWFeXzgutlnfdYGKwB6MEXAComrCOzWqnE0qvMGxf28sPAiparq6Onls1wQ2+99OlXfsV3/nIaGi7tRtjc3t+psx9HNk5Onup1+YTz7pYuOg7VeYNYUONnOLmnPq6EsLxOdDgq/O/qmmSVuGRQOsrC6VvnL6FrzcSpJYpe2LJEPVfqGsongK0TraFP3shYyh0T4DFTcXJ8fHBw0PGoTN6OLyGufusP/TafV/53/8T/4u7hy/pIj48e+ozaq6+9SPR2TTgX6Nbh7SO7J3d3nl6eWGpGYG2mMcXPAXdGSWYF4CsLHs7MwFtQYl/u9YV+mFU/DVtb7sUWmtnf9ma0sXzVRP0ufsfl+d4009XT0PeX+OPVJYcb4xrgI9yJkKml1MRrtIUnRfPbBT76IJiSeR5FHG7Gw4X1mayGLsd24Q9owZzUU2g2rhofJwudfO5j22VNNYJWxrJP1gzgUhwWVL/oaANAHKimrakQazvAdk6strtadajjauO+GmGQP1cmBw7OEqHJUbN2XjaUWV+Y5VAbaLypy8zjrhp8drljxZVVRIZ/GJ2Q7YIwaL0pVLYlIiL7Kzi+9DqJllv6sY4tusDIEogYhjibHq03EVFfngE3kCtyyIwP8iF7CpuSiDhsApwRG+Dgl0BSSZjhgQZufknhBZZyUmcsK20hh11KZ6kCEUo2Uhc9CVDPIpnPze4u2lGJrRERkOTQw2i7JaVmILXdteobZmIthn8jt1w3DBd1Mg0cWBaZpHYMGB2dOxaFv+E77M4ohiBsa3uz7V7sRsMxjWoFA8LANOOzcXXHWhuuePra8YVmIzUUdG7mUyK1NmghWanpd5SzwS0ewNac2xp8B5XaPcVpH05UutAledKJvYroSZUWU/cSLpjsT02nwwGedW8tbNDI1bmUTJPDdqZkbXsYDZn9clgDpv/1QmCJy71ANjkhPLp5+4lLGYUscq7dDv6EBlyxEysj8JG5FljEgtkN89K20bjoT3JKW2Ama/hxUsJFyShXem0B+sTaZ604FkV1ERWeo0yDEegCBvfumXmR5Q8ZIesrYYbq4Iq9z18RJ8vf1TXJJrkCAFsXLa+SRU4Jy8/z8J4rQC70fIzZJPum16BUMQueMsijh8pcZ13nmJ+zzxZojErsN0NeY1HergEEP7hGtf8TviA/z5UxIi3OVdTSZNM2jBPrmkRJ0LTwZ6nv5vY7Xqo6rGMHeIv4WrHkNpwHbWPzF0i5lXUE3YeN7GfcPT83ZXXH6okNX+C7uufrtqvVgYUXq8u7u3tPNpzS5Xuil7dAWl3eatBl4872zsPrU1/QON2yW3/7TWf8G3jcXll/bPn+fqP7PiV4cQf/1MvV9b1rC/42bq02LHUwm2QszQfhXnBA8vXBL2xd3964vH99feu69ZG3M9BGCHwfwCL+IBxu7P18I1vWrl3Jtbu6PtjcOtqwFmlStlSEMmWSxlylynikilUDoZwTlripfMyoooUVK8fvp/FNEPNzZpMx84exlFz9mjrboHL2MKpVTHlHXMPJKuhSgRJjhnzpaL1nMBgrjFUrKfNTlcl5nYLVMpJJiOkBPJJktq3J0DEqbtn7GaBVAGTqYVWvGHPVM2kKrcRqLCXiESvy/fBr/T1iQYOpOCLPMLUCNWxb95yZA8w7j3mZYZjql2audTLFhFqzN6Hkn7LHnR6LJzdyMiY1sfAxhet0l1jdsFlTuZkHwKx8aDsyBmu6wYcQjow7w7jkgQuuO0FgDJ0EQOJO0/eKjYaWlY2xGAiVtvWev3RZcxJvLeGRTki6jzA/WhK29ury1RyA7QdGahoW4lddGfkrNfLiXAyqgcLmcO7LDZ7kLslwBQs0aJ+pe7D5OuaOwhBlY0p2rWCPdpx0PdQbIRl3ilA+Hohdw8y+tXHKOd3c/EKN3PW7jlk4O33iwM3D/e1333p9Z8e3BRjnzUdPnt6998oP/MAPvvzyK8ns8MCCJcXv7u7PDMaGNTW4cb71huM6zZrrqNuf0c5gbEAFbrm2zcYMmrBY1jH7Bh9+kU/dNsiVCoXpYr7dxpOnj4vjKiaUdvwBd3XqzO+0ni5gMhfw6dHDd957z+Ghn/vcZ+/duYuSFqBcWXJ1pk388M2tw60vvv/0J+68+LJ9g9bI+qiY00IhDBxlUT9TmUTkty17N3oXt5PGco1UPBbWzTVR33oPQAmA717KZz/Lyzfdl4R7yXdOzgG5qoIP64Q3OHwy3y8KHVxvQunbTX7aI6eI1cOHj+7cvb/nQ7QZm+uDW/s/+IO/VWfvL/+lv7y/+/LOrb2nj48+/HDrcN9WqMu21W5e7u/T65WAre1DXs3F5UvWtbWGLmfHyd38rx1L2U54qg0f7j+5XD12Ni2lbOhU9/aeojc3D+dMz0NHkTokcdvnq6927l/sHZjlU7fmvA4ooXqG0tkCo625a/VpeRvhT2Ut705zN3fej6TZPSNixgzSB+oKxBgjfk12QyA+VlNHfCrflW/uyusfe5C2zaMa38Sf+jDssxNAlLPMS6kD4yfD0tj/XCMXgeRkuErS+GmwKQ/Ngmqdnw0byZp+4wgaMLi4un158stXmwdXW++rNzPPe3h9ft/zau/nyaGaeLW3sWMHwp3Zs3NwvTr19dmLza9dXJuB2T/fcFSQA0bpPJPAUEAbSbD1SkJmEd4aeQ9tz2alJiiUh6zwxZNSU85CxTNs+JPrNQSJE5VVx6zoin/TfKfP8+q2APG6eIGVIHoBXKS6aW6HPC5bGZ/8g6skTuKbvTgfpixMBHb5hr3BfbPuMMg0TjOIqxkf1TkjQJohtVtbOPVU2uZdq8BQZS3EgzatT0OJ7zpDibAV1Q6omokaAAAjoaoPPvU28f/i1uWL11ePG1+3E4PDAJusPEU7Hz/eYhR2UB8DLq5x0s5ewJzsWc37MRpq0drT8oJ25HL1UUszr++aQ1jpDNCcRhGzWrEOjBkVKrxxp5pP8PUsjFTVqCg3gWWfLG/kD1giv6oGnV7tfOP86ikjZsS4rTg1nTk5zrBXWXxQYvhsnOtUi1dFSBDVqmrA+eei+uDNbB6tbF+e0SjbrlrwhJU1e1aw6bjMuKjZqyrkGr0mXaXxNmNdxBZI8lFOY/+xhaHeM5zEN5juWIIbXRm5RlGKFP8Jq9ceSSCfgmxhJagmofRzSUNBMQeniaQiN7Y/lG3r4kX9OXPjLbK6/rT08SrhTxcLJjIiewIrac6ijM8VXBkFBl2iFLMiBzNhEzm/S5rlcVkvs6ydWUcGxLVGdglcvzyDNTSuE34y5aTHQQX3uPMWaJj4i6+JXuMr1mtatJQ7GCwJlpBn96FiooMYRyfZJ8FP6nWi5afKuRZSslnEJf860bPsKTOjMVWKjjSKLG4QqywUEwcHagjU1z47MyRehdSc1zRNxmr1CJ7icW8Sfk9TrU8vt/aOVg+3t+86+KrtuR2oo0t9su2jv3ybfN9mfwxs7W/5gi9YmnsjTts7l1en16dXW6qlAyKYBi6jU+WMEZyYKSDsE52I7ad720awGl7leNIuY1O+MkbL+BpVYfWYaVFJVAMda+0OZ8dwokrahDIzBVs12VJwMwt2qZsg3zhyDqhFSGlZLeT03dXDrTYYG7RSsZGfBcAbQ1yRDz1M5ltzDMHU8YeiV7ruYaQROzMUzuYLmR3pMHPTrqb5qGMWHMhsy1QDLA2zj5U62dFwKyp8qCDTBv1QJAsfSbPklIEc6RUY0aJG8Lm+4LhUvSSawFUxzBkLWXUd45zEMjKBh46V6izUUipar1Y2BlnpJ9cgNtqYTzufdq+0HmUd5iyoeB8IbsOFUa+StLmTsKOjMmGFYVPPYZP+cSYLC11PAW4LcB48W0Io0xQI67CFaI15/mZcBwFS+jQWFso5zb4NIDPmP6UBPKvqQSFhZM4wem4+BKlVaC2oM0f19MBRV8FajF/bZVEOTS1WXYThqZHVJqyxX2jaEaoSJSU6fep7NAryEpybqw5Tg4VZc9moMS4aho0JFRr+8xAXGltK6Ax8bRHnxoK3WX5zdLF/q7EpK2Iu7UR48uTBuw/ee+ddKmbA+PDg1sv3X/zNP/ib7969e+/+7aPTp+2Tf3DukArL9m/dunP7rjHlw5PjI4d1qj/IqTbx/jH05Oxg71bDbjMWR9fQkj5XfLj5pU8NiJKFHjrOR3OcsUDl/MyWaNVs+KjxHmomO59LzZJK/jpqDz54tL2zd/X0+Du+4zusbi+qymRiePfdN9547933COverduffe21xuYufOCiz/uUk7KMosTW/qDXzzwtKj3PiTSeSl+eCJiA+fmWt5s0RaJpDfRbJgVxATkSCw3glxKK+tZ5luAl7aRYo7RUlWc4LqELVepIjD0/Pz452j+4ryJQVabg7t3b/+K/9C/9if/5n/jpn/qZ9x882N3efXL0RD/uc5/9vAOUdnwezEIVmn18zhfheOjN81Wut80cqYjVHL6LDSN1YflVOpTnRnJORGe/kEZY7biyEFrrZpKWIfChoqOd7Y8sEHplw+perhLiVZ3UHe3h1SF6cGQ3SbOeZAtslKb2qXLExFD5T+dR1WADHOPWYkqycPApOlsqgdgiswL5lGpaNXVB0EafdT2lca7SQ4QhQwRrJpkAmKiDCBoFExa2AV1wHqSntdMWFTjEUC9bbVjti+NNPAFRfbhw7ufKcuXLU6vzrNRbXZyudo7l9cXyzo+O4Gih50aEcfKoesK4tEQd7P6Pzqj76BhkFyy6Z4fDq1tsLf2QXhsRnb3Hmni6zj8Qhxb2w3RNQ9oiq8suC1BryxZx5vEx4EmtAsJTMlXYxRqBNF01BdcEdAdJKunQqm5u6XtPbCIBq3Nw1NCcn7i7YBfCM3oy9KGoiplmKCrSxI7N1exybBFcB4oiOnvqqvaXRujXT4MUqilIV/jFhT5IBxXLa41FvNl+7Pp31hcxEDE16TX6bo1Qy2WVXoPIv/dCvNQK12MkzwRPUcoHoOEoskBO2K1r/QjU2rpI29CFAWiNn8APtKD6z3GCD/tvWqyCuSTUMT+bS9RhPaCBqkyNV+V3egXshq1M61wSJQhI1ax6xAL1u1owzUHfKQITKuQLZ19IlcMSU+2C8i1K7Yxf026GcSArUnPU0BZ+jZKAQu5ya/fY4laQVs5oAebpgaSiqqvVRHXMx6OBmixV1GkWQZt/MB81FD0UL93uiU0+QsNZIQiaBG4AiktblkxxApKKyf7g2dRmaQK+zkzHA7CU4SmgixqUJnWaexELXvP+3+u2hv2L8kwtWEKV8kul+uZs0t10AD6RZRANy2ewCrkpY2IDhSeen7/zB96Y4p9lvClyvfr/Y9TiQixfoK316RnqS4zYhC4vXPSE1lBveNzrPC+1DMdXr7fq2hKvaUEpkG15KqZ2I9Ucm6JbfWoFs7XLvHuOQqbdJLOh7tX14dbp2d29S+dLOO//cOOM73afy7uy8G71zvb1Sxniy1s7R992cH13f++hIaXdnVvO4e8TIA4R2vQVQ/t4ji5N4hmCXt3aXL1sfR/35KnDQfT1L3fO9Z45cTy5FO/WLH7jBVni8O1XLf1npsUA6+teSts+PTtA0PXqw9X1042Lvn14ZbogW2IQsSph+NM330eBCeLKfkpVXry2Ku9/lHA8/lRTbfUfKy1MnHYMByxmamtkofmIzIFfpVDw9LdhUtsC6oHw2i20BaRjbeygXF0ZQTH8bL34UnmCnzW7sPpf+LtWt7MJXMmZqazZEJl9baXqGKaqiAC3vE2+12J3q3ogsydjJjNx9bVoa02ji23K/qRCiJN0xmPOX53nD2V3cE5ggasmBx+vcMARDJ7L7hrlWh7cAyyp4ErygG6tZw1FQ8K5L7Uj0yKjSvwCsYafTHMIylRrbYyAeXUKpMdYQx21NbQwgwaNBlgEdcixwuoK+sZ72DYgYkhGu7O1z3KIMEbIrdTVM/hE+wx42k/SQgUWsKwbDuOxtkK5zoXCoExsJtd96MsEX6x23kXappNvMKi1qnYdvD88GYZFNDTphz6bkc6xc3UOwzZCM+06KhYXv6fpvDrftUifXK3n1ncxCFPptJawrK+37NgWKouHWxPfiljLMdqJS7M0gyvrdR5uHhqB27w82jg/9n37zb/51//G/i37h7V/T17+1N3f/ft+9Nf+wN/34YdPnz55/MH7HzpM327gp8cn3/j6N+7dv/fi2Quf/8KttKwVUTHdOZ76u1VnE9+QHFtSs20/QzrTfobMFHrY+bmQOmrhDimcuDp+6vhQM2+YlsYAkr/lJX3QB4wrRNvGisvLn/vq145V2vPrT738ioraMutFHy1H8u/iZ31C4Xt/5S87fvLhz/7UTzvT5pZpgnt3Dw9MDNqLTZMJrkN1+8jCjhXw4YI9SYRCp33ewyXer69C1o/PRltv4rgUA2KdoDzPZ32W7NlDFUGKE15y1C90FhvzPi6zkAWBj0v/+KlY14L18lzqAEymTd/jBHrnw+MnmPbB3Xv3mFKCYEmYqX/5f/wv/6n/9H/zF/7Mj+3vbH3j0cPv/GXftbN78OFHjyRhpbhqLFkDjUz05ofbpgEudk8d6aPu2Lw4TtDq+k4mg6PQmKsRQU5Zo+NTOaki6wqXh1TENhRm9fz6vv2vm/X8hFPSZJxrUndRqRbMqJ/zpYvFQWfNVOsMZjPFCpKtQZ/USL2Oc8TeNFtsE5DlzCJRQniMVZSFcpgGki6rCnuQuAWV7Q+KWQP7VWhAVbCMejkKVVwGBzuz5dXHkUa8BRsn5bZ6Qt0zwJ/hmO1DjA7vlu+/37KljQNdIG3W9ZmN774x/OHG5q2N8zur8z2t5NX5/tXWSxdautVxi6RcF3apOa/K+UFPffm3GQVUZnn0r2GGaxBmlsyWjMTDqb/2Kgjpqz7zOpExTK5CRq/OX6tu7byd2XJFWleNL5Zdvmat+ebqDcm1u7iUKsoowbqfNlyu4B4M+QRZm65Nq/oNT5RWL4DjNuwioMTxxfhq5Gn5BkjFfj6kTMDUkkZjoysorDEqQ6Y+yhtZUsrEhUe1k0lm8VFMWRg0TX/l9fVZDWY1ccIlADkfk+S7GqpIQwjTjp2zz21u/KzjaOy+kDB1aijHzE8mqH5mTRwcZnyQHQUAKcIbrxNrgEhnzdSP0hoJvd5+uuF7oEYdEbaMHtnHIhs7u5iUCC5lRMZVzQd5xyW7ery7Q3xr92221ExCR+BvHEl6sfm6XuDmxotBskvNR49aPKbX81bttbncnIH6HKJdmIWBekZgXq/e1iXJJHM0OCz5I6pGA2I8DiOfkllwjX5Mj9xawUjN8+5ZhVEDoU1hqloiVGMFycHnbz+lQ9YvCVJU7XD/S+X30jnD3pwiWPKugkcgWknPhl3xovY9fSqobHXCgyJhLCYYX5AIQGg7++6ljYv9PuyUtiTRigt4sCVaSloDKHBUfcKXFAG+uaYUr/2G9034+veTY/+fjJyszwVhFntbwOzDuYlZgN+8/aJfUG46AJ+Ie4bJs4clesChUb713/NIfzNOnwD5zS+BiluBev4ani7FLuUUqZS1eg33klSMHw+AFkvRre7qePmj2trpVHFyTwWaLBLoebJwTLLapNb1rclpNjbPTi8PLrbOntSTptBEopKw6VxJJ6xJeWpY33dntjePfULDzps9+26cS6feUEVj+Y3Z6yE3XGUZj+1mzfr3fpDLTXkk0mflKw2r0K8SmEn1WqzKrDGKow2+jMVVTbYuWlI84U0FqHj5JfDLULVhVDVJy6DKwMluZLTGgB6jMPurS497mgrBFezu40i1fxzKlucXR+vtOBbN5IHPrFaFOu3aYLb1gcL0FJS/9IApjkyGK9BgbCPWLxpRw2VXAwZ0CAVjAt2UuzrWQwJMlmWAdZ6Tfy0NGSsLlH+T3JAqCSaHYWKBnsWWO3PDIILmIcPoLulAR2gmp6rsp4KAkGnigcDzURlZGB2yH7xKMFfKNgkKwVOrO5BTyGACI8GVC6Z/GqIxw0klDAnDrvBZWa+9YV6AycMYxC00O+sosdpTDN7VcMx0UKNKREy+mRaxrR8DKp+WpXJyP9dTQ+9YtoNDQAzqA5LXogUynmVsbPt6p+UxdAdeHPBdZ+Dv2xyydeIzt1C+vHYSjSIuziyz2d6yzEI/ZY/rEBczH+Ogb6729FV3LL7m4POG8tX2cAkZDawTBcr29k+dlEwbMuGkjDYoW4O9fabv21BQJ9/mOY1SpoMERxT0abvz4dHZQPvG1us/9/Wf/9rPOf396OTh3sHBr/q1v/q3/+APfs/3/gPXe1t7xxe7u9vc6YcfPXzw/lf1AYz+47C+hMk9/lC9eue/nJ5ZXGOMs3NO8QSvMRxsF2nAG+3ztrTEi1IkYkjNhGKpGhelMw17pX/xa3IxAaKEa6RGlzjsDx8//OjJIwP/X/ji537ZL/92sPcP94JkOsLGgN3dz3/xS4jfO7hlVuHBg48gdHx2/P7774OPqaoFnXEqkQ7M7Xu3P//5L4CJt6nTgjbMPFOzUbpBJIQWIkLsF19FT54F80H/F6d6LkRilQahscfVEwLT7flbbt9cZsVM/LP7ZA5R8JbnuS8cFAyfuHx9cnLeYMntO96Zhb3t/c9+7v4/+Yf/mQ/ee/STf+Mnbt+5++jpwzff+QZl0hHEJp2Be/dur/ZunW/7gJD+La3aPjk/NQlrvMUYvqU+NgAq2QIqkt1eWbOenaCVut6sn55Harm1592pNwY8fKjRnFGn+A3tIRwPMsE5keYrraIwGKJq5rtRHZAbllRH1VeE82H8t2CD46bhVA9VAzUiUPJKETunUwJm7QJgqWC1f3R+jF8mKBOj+mT5k51Sao9mSoKJaGZjDAq1xFCGcsxHmWhJxdRcYK9JZkrroF9UcBaZG2vH1YujBlqvHnIKNjeP7N/ySbiq5RWXTnfodMu6udUTVfXi8ilA2jVlz4GPQBtwoo+kBllLqiCnn4HuEIpcxceNZ9doxaIaN2ExC1mRvejFEoAPn1SUdboxdWMiIQl+k6ajkMmz1zHyrNDHcKeeZ29DZ8rwoPgCQnOuVA8a2ecwE1VEpXnwp3mOzZjflq2qZ5ZumD1jNwNswAECl7wLbIj+JsTxagpj0ZlHnAdD16VGwwVuSHhKbEuB42bqJLBWLBkULDAbX3nw8N3Cy4YT5LLhXC6Hj9NneMMqBQq5NqabrXKL+pShQbHr6zt9SLcFBmDSA3qj9WyFEmVG8ZANJw2zRyQWGAF4QdyKAcY75Ya3WBNfRihs4u3zMupf7ZMEkTrdTqvtDAHRPjZN1vpjQIGKv5L5iEfJo1x0B9OCS01r24DzSQrJNFtWKNNwjE3PE00rXWewT1EhGgvRiqsMLGbKJ6RC8GR6SSPbhcFpQpEzWRPJwezycHOXcYb2pkZFTlKonMgP6vAhzVUs9oSo/+3P9osqyWG+RA5+N5DLUDGJYJ6XsgtyJbb1U/istTZmT+xzUZ/AeQl/7g7oGs5N4FLMs8LizRqEFN+UNiQ+EbQ93wnTehu5f3Y9gwXL55LL+CymYOXcML+sy/MC/RNlPIP7LR4MS8SwTjkY2OuMfnpdmNZRuOtwqRLSIp3h3WCYScXKYBj1gAkjvtjsxrynphYvWxXYd4KMxNUPbbCV3Bd3xHCsUu5dWMlzfWdlDdzVvc3rJ1dnL/Dmt5y17NAMITnTL/EaLeLP9F4atNcrkN4gzIFe8/bG3cuto6uLuyrevmlXvr+v+RpD37xlYPjy6lBLU62E1tV+HrccW7rU46Zv6ipQQ+f66+hjC71vjmzVAWHQ9McO6Nlbt6fScZq1UZYZ2zYwhI1zDGSkqgh7xj6tMPxUbE8nsg6gODwFoZLxw9R3fpPzHtTFGr92uTwAwGyIHOm6vA2DoRUpGhWIm3cbGWy/g5968fIvUsiiAG2dnKznn5b4auuD8Paa2MJCelVp4/zlArffD7WMfpVGuihsoiY6e0unGuPQNE7caxWw6gR0aKQfykjuCmGL3h48AlPXIvo4wOHS//nLwY4/NMjFBMtdMkH9M3fhWp+bu+QBEvyo1jwohqULniKndeEpM/j4xSqgj1zqQYUYImtcUCOmFg0cJzp0FEwzNgSzubPPb2eOWgapHGNLZkucs17rAVSj2twSqDryc6dzULjUmhmtA3nICaXoqZlodKWrYmBUo9CwCMTC1JshUbkw1jkVegI+gOCU6kZmlqalvFUVE0AInG0JPopVvuwp2Iye/H6nQKchUP240SpUS4uMhBkEE39xcUqNzL0pC2kHe4dG1jUxTv/k+ytNL8aBnUdPjh89evyTf/Ovm8Y2I3Z6svmDv/63/ugf+F0vvvipJ0+fjNdN5ji6ef/+Cz4r69NgTx8/PTw83N747Efv7dy6f75/sD893m2HnVr0cL18mVsQnPCN1m2/twgdxh7A6pfs+20remkSzdXTJ0+5QjU44znWIk3nhTsyc/pVI8Q4F1Xlff+jd8jVkqQXX3jh9t27jv2Rz3/lHj1++uY33jo4vHXnrqNvzMyY7uPvb5xiAGdxz9ZWXQUTOHqGOn72P1w+eXJ0eH1oHiD8Go+EUY8VGNsHXT8hXUAk/OKLoAn7WbhUH788C+1hQJR4SRHBNxkrtmsp4vmCnoF7Pmqp1aVfwE3ebkEcvI1Fje5QvQJt7SUbXoMzlO2IOL84/vQrL/0Tf/Af/Tf++F+1Mf0bb7/9/oMPvu3L38Zj2u7jpFSLQI5T25zkTLfdGNTXVsnV9oGPrVxcPdWbqrCYtnM8Xq2e8u5WK+NtYaXsPq50tWWzwHIU4aZerxGbvIjQdlepYFxbwC/hkO+trOgyt6lGt6TI8UFnl7dWm04p3T05feJ0TZNxZ1enB6puVd3YzZkR0Zz9/H5GmVGiOk1JzfiRDoK+pQqhgutQswmcG62HJoCCtMn5asvBiIZ1+gKRJkQK52Qp2VNmpYk+SpH37iVjOPcMxLSCrBAvjDZnv/MOlU6lbRKjTLfQsbF5YFG8rWtswdWVEB32AwxbXd7mdW5eHuaxtrabwdLoGI+1qtvbNJ/cNX0jm2FaJILOQWWkuajCjdBVm/VehSUEZ2lT5mK0uBchxv79jOKIGAu/KC2SsORNLd2smJjKm92qNlId/2jFjX7WKAhO7CxM4zfSAKA6E0OvotZa2L58bIwn/pc+Kyb/MHoKy0E3MNEwdGWlGCzXVJBoByqEZQRz39NqdUpGsKvXWEZLbl5Jefbeh6IGVOYaBOrb7jdTtGmvfAzpGGb6+4Wt1cvG/m1OkQpCW5cvKHC18/iQY7+PDrtWEmzfna75M3GLMjKnp8YIm7Wjq8pa2nnTX+erkyvTOJu3YoLCyKujRb21iAUVriiAMTUvXCehT9zO/iPDje0ttgpic/M1rZTDSXFcY6Thubp8DbjG+gBKEDFTy7lafQ4WoyA2ANTZyMev4Qa96kDpY2RDG5oqj3USOF+qYpNRRqRsgwSMyqmBzIKehJyqAZLTSdLAXFRTvKbUrbqsI2LLS9xIIXFUm7h5+TkG2RqNZFKbEZlUbrX77ghqdEg4pIQG1I0HpRzuvKowyuKWzcUjsdXTUoMU81Ll3kQiI/mWU+uH17WtXaWQtNuSyQ4TMTNbe5MiQGAEqV+wE06Ql78eep1kAf1W1wKsGPndlzy9f2Lsf4AOuD4RODSW5ebL7utS8z67Pgb63GvQF4SWp6VAirJQMQhMTIQGe8B8E6hivtUFyvOwvd2gdAOgoP5iasq3FLUmRQwlqGCKSZ3zcarqbvV+qwY0P/UzHK+G5ytTd055nfftPTRkCVWyxm0af9U2Tb2nenTCkIfx+qlguWXAqxx9qCg72KfqFXmdKjtejT7x4QJWpWzNCBdv16fpG+mTwvm+/uhXpTvipeU0iCoizk/DwCZ5lSUbVfVKzUQ3hJ5Hlzms5PQ1sqcxgIIWSMXTWgTJFUOClVs8YomDEzoVWLaxvBVchehXVkAb/4TCsDtKZoGhBJopWYQDWLsEDXBDRxQIFRjKkvQ4AcuPmjwN7QjiJrx0WZ/sixxTNyUvehQLVmOfRFZSJMWngIetIkMo9CYgLo1uLNHAcRYEIjofcNAd8HGhf34lDVQg/VUFQ2W55ldx8bjC5w4OqZDdoJPDvEDmoBBQTMvrj5HxZ5Etj6PWPuzTRwBaw5MJAj3XJl9Bw6SdpafhQKsazqM8FVeja8yz4X/dtuvzE4ueLXPnKvtEkQJhRxuoJl1LqHkZGAffwT2W1XIrh8rgG7hVDBZWywQ+NvRNsebQpIrsksCjGQS5guIlohEVPp5ER/owvMBpO5WxeXruewPHTHnDt31wwIb4GhhD4IAa9ZdGh8UpPVwUY0offPDB67/wtTfeeAf7zx36eXn5I//I7/vH/8A/vuNA592tFw8+hc7GvzauHnzw0CbRjd3LkydPv/TlLxzeOrg4vmv0d/8WXEzl9cVfDdl8SaAWllL7r6Klm6iMVTGrn+HOPHGuRLMNnCprqM7tKEiWBSI1DWw0P++iTk5CRTex7Vkesfn+ex/Byde+PveFz0hjMs3SrnPbfFdbjx8/cYQw5H7l936vw39OTFX4Mtjl5d7ZhsOA5ps+mEsIvglgM3Gt8ZtvvLm7v+MAnFu3Du7cubOz7UjHFLj76GGyWdRw5J70h6ihqEhXuA6R85aSzcO3uE1EN+kXBn2cr+Rx6SbbLwVnCZ/sS0E4PEhNxmIF+Ad9Ch1D8w82TaSZzHn55Zeyk3Y2Odp3Z+dX/+pf/Uf/lX/13/t3/l0Hntgf/NGjhydHRy/cvbc6Pt8/NdXFRVY9WFgKnk9s5a9v5pG6xQje+hxF6osYJyqc8qEIjdSaIWTR+dL6p2raVUsjDswAbGzfohyJtQUS1bTqEZGrvB3kyik3k6tLamDFwqFrizYvDn325fTq7JE9CZdHHTJlAaWNtqbcdh05mgqRFDidj6wFyKLIq9ppejDDJLG7yscwNVpSApMKNN+D1sd6fXXPNbJRufoPt8wNLezBY0VUDxVEVetsjKtUfTaUvHQRNDh4hSpKXasnee6Rv+nGGulQLaokCMaBFtqXWBmxUSPWYIk8yvCjTLvbsLca1Wr1qkgRizoOVd0i0gXK8jBvoT0PmZRoXkJ7mre54VwIhEGlSYI8eiW8meHlXeBY39z0eIE77tP4Cwj4DeumoDh1o5pLodHX3/K/HNm7/tLMpRAKVoX3EhBFB3XBqITPLuyODxkG/2MyllJESJkpT8+zkrVAKNmzppGB50Y71i3maqpzE/Z3HjhnnOPVHAKl7T7uKacUFqmCEpgoApApNNDbHZTwck1vYmk++yKphuKFiOFvENh8iLOP2oJn/n7YqhBtCbQCAy33BubnIK0MJo8GOygHztRAaIdmsA5MyJNH6xUjPSV3k8C/jGLYuKtW9K3aTq2HAcO1csmHDlH11jSVaubIbLtdN82vTaOHzohcdBCbYwWEDM8NN8MpbcfzOAZPLAfJE4TjbBpTKX6kLHUZR/AJE3pUSKDQ4aEmEDRu3gh6KpSswFU9NxwTmZJM0pC3qyb4gdEDC4N0Bz+itacKGlwL9DKCGi7F2ikx+iah3wlYXm/uzxBbJ7sJ/+TvTd60d132DaybfEvZH2eL/OUtfJ67RGxPv+ETocMyRma/XHMKwTraz8g9CDtvRPrF524oSXFvIC8oPn+/ifn4d8QjcyccC+1v7gF5Bqjgilmz2GNp1LFTqwl5CN8YaRLM/KYdSIeiNPM/WKJwqj7jdqMyzOJxrr5eaZW1BRgykWtWNY+MWdbhZhEdJX5SO5Kseflsd2Y2cz9qRvNcs6HKejVDg2pe9c+UQN2Bq4M9xdnQ49qyMlLLpbyW/7TVXTWo/wo9k2Jq/9Mth/84ntYX3FuKx6e70NuAuGqIyzy/Zmm9SONTl31fQ2ZTYgZpz0+u95hnFFUlqTObD32P1q6hSmsnKPRyE4c7mjrKY1AqbV9aSoVa1NRKoU4cUpyWjA+3uEQJ5KpzjXJLUrq6+FhLIPMW+xepqfujbDDZfstok3HPdZWUcgie9s14z9sj5SWfO+ZgPoisKSHZ7aoLrqUGkAwGhjZ2691WP6mxI7RMFcYmYrYu6MDUUxvcSLOufPiIWlcVBIRp+NawjZnBEi1curOx1SjCqNlgVOKuBQbOj8oEqiVhUd04LjhsRQIZPsSe3B1O36vyrrbeGs5bFNPcbhKqf0WYZn52kgDsODmgMNmI7Q0qYSxyrGlsEMjfZX20M3oKEmgErPjRM7ArFnMxmFjqIrZ5HY3SYFzcidKARThIFRFl8KLT2TUXlCTKlZADaNyfilVUaI8MkiFnGCGTK3Oehiknj3bbzvurnT08x0xi4noE4/TsWA3USFyeWYhBS6//wp/7C6u9vYdPPrAsnq/16isvfOkL/4MHD7Zf+NTlydnp7YPV4eEdrIDja6+9enr/8dGTM997QUFLfQ4/1OfpqNQYbeGrBaDXvMb6+BoCTSF64axJCDHP6Enk/tKD+Ye7+g6O8Lcu1X6GFKHRnOORoWXTKqqRu2l+2mxg/6hB5Pd9oODpo/unFycvv/bi0UfH3/Xdvwq/Ly6tsMI2fQNLac2DWAS0ffv+bYd8HNy9PWJACt5H0FJfcMAmzPfef+/07IkwkyGnR2dHT548fPDRncNfYbfA/t0PFyLSLNh3RQFhDv5LyBKaIAftamOaKkOJnl26j1nLZSzqWehAA7X0AR9dbe6r1650pZ/pcN6c/V+uTo/G97cm1U3C9G0JmJ+b4pewmdOvhgo2D6Cfk/rkpsePX/fr//433/on/vxf/HPvvPnB6++8e7i9/8orr7Xy5NpXgR2d7Pwg85OYd24PAPtrDPDcjn9ueuOuWN5wQt91a0rKREtswgCpqOWV1ZtMqWKw0vdwnxqRfbDrnNDrXUdcmmu1HqbD1nwb7/wVzcL11rsXPidw5dsEtmORwsXZ6sHjq4uDyxcPrZipU2FFtNktfYXlhAVaqd1h/2nQE0zoRKwcJN9pUQVn6GfrYTXr6g6srrYeJSSGlS6arai+m/ET3UCUOo3sFBgcK7xr0Mx+q6etVp9gadOjilPfKNYMR2C9/FXdKq6JuOldblgTyEBpToyKOKcL52bTDiOQe5UQRkAMT5ZnDAAcVCQMNB+uSi0iMoKb9KbSS1DN8/MJSYf8zVUcAgpZko04yjc1seyT1MTn6FJn5THaBiNcJcm8TPYlmex9c0B19n2hgiQIRHd//Xab8rpRihl8WSK9Dc+wh+0CCs/jFvFggI0BinLREZz7TNZ4c5lhBrXEA35KaBq/xJx4VthSRJB8v27j6mu1xcd8DB6uThMT5JClDi1gt8fiAj3WRLls4/EXtzY+tXH7J4gxXmL06p1h1W6yu9KrFP6E0GvNi2DhjAQ+CM3Le0Gwe6d9wNMD2fkG9Tf2n9tvBoCRZG0JyMkjKJ/WcKiovRNST2SkQi9agFYZ+bLZsKw1LmnTKlvVcsKJBDwnRNdRjmmxfhowDYwx0FagGv/Q1TQOEuK4k7qUKuo0SH3trMZmqAEYl0QYYzlWMtaEFTqXBgkPt7XyKtmLPvxh+XNI8WEkCinQhixcCWXuFI6/qfUeaSYdBSsKGQPSbWkGgsL/WwqqMxmG0gtaMqFsDIcyitNbjhAvvLUxw4FEeF535CyVT3ESueq4WPUQ1B3SZG9nvquaMvBKNRq13OcrAdIUGUdFLSgNsF7nD4bBev5KS3tfLPACsndoLcAQlJQ+vtrR6m2CbsCtf1mEdRHlFrjkm9h1+p6HNfguOnriWWHL68cFYeSELSFLEcv94zTzFK5TltgK7i0pTEkpx+Byc1/igxxdayyHran0pC6GhReYzNK8Bkjm3hjnOMFsNogclY7XYrwzklSKY9MgB1XOmu5s71rDwMuKOlqoh2nAnkJRqvq5fbDG8nkWUb9eI2V8Zc8bS13VoelqUwMp25tP1RqfRR1+7Z1dnt7ZPsg6t1Of4k53tS6B1wPY7Fjz3WDwjr64M9z0Aw4sxObomw7cudxpyhhZjLJBAQ2MPUeg6Ije5VWdV0Gr60g3SKaCpaF4k08kn5xxYl0/1ejGqofn0L/itVRnRiQ9qVQ4lbLr4+ICx6jBav0V/rR01LRkAKYQixhiev9F5SB6KMazFCECljgIcaoGF0mKCVSpw9NklOS54QO22kCOQExHacpbakgwsRkHiW2UcfIUOe9QB6JBvlEXqExB65/AehSEuCB5kp6G5A7HtyUoWEuWCYlJkyt21i/igS4zOjBYeAwXKhfMLm1qB8gCz17XiviHgUFJ4cDr9AMuRWgK98vIxSkAxVLhafalSya5+zNII6/dFyazYhUV3rLnnS/C4U4D8EV5CrQOWKaYDFj9UXaVvtukogRRTCGhVUUWMhMF1KI4FG/+PPYysTLCK0aUcvRFT8Zx476DZ30YB90mGVB1tsGdbKqPdnJ3e+fxRw+dCCX3k6OHP/7XfuLo4mn7ybY2X3jp/nd86Vd85/d851/9sT/3p//f/8U/88/+gU9/+rX9F3fx2NJvI616FHrXdg2YPej7AKqnseImPxSAUqdz6Xj42tQt4/g6SIpXlys+vkrS4zRE1fMFbe2cWYmD/T0N+IcfPFatVd8B2CweaYAxIqUQmQxrlrBAZbKc6fHZ5dd/9o3T+vNWq+d71pG3jm57x/qfjz56AHarYa0N2DUdYqQfPMKAAvLDARO4vnbV2NKwOkZNmxnirI89+8Ta6UdnF2dfuKdXMyxMnWJ4jM8FA6eI0i9ymJf1c5SvoxfKE1SSEjgy63W0bYHQY+CX2Hks/8jbm6sEC5Bnv4u+fFPgknruNznAWZKOxaD1wBLA00eP3G/rA2QCWz+8devWH/6n/5Dx9//yv/i/+7TC4e29Dx5++IXPvdgRata/2c7evk6UkZIdRbKl0uTEXghO2fIfjTXgbt3WddXmm9lKGtMGDzVt+5HezK0zIygnpHa57ewtx7YacNlulaZD4JzkZiURz8m+eb1s3SKnvKzunO22qf30qGX30/7XuZWipdPVVvU6Y3LD/Uyc+ixK8YsOSuDVvXod2oY2/BrYgX/jLdXEwv1L1B5RORzzFmD6mfIkhjGSAUpAlLmKyXyNCxKMqfDpsMWnuslajzazDdBWNkjMaxpWKYt2MDHpSOJgWFnWQb9tcHlz2UawVKLq72A2JSfsMLhRDIjD7ub+7GFJUkGeugVhtOcmI7rEjL0vYlggbq6oTX7YvhZuBVaPpnXpsaYj2AtUdMWChdqhLJsaZfgy0OJjmJZqWNkCFcycCjd4ln6uUJBu/q/hCo8Z3CYC9Kjtqq4DlsHSMtSMGWpmloQ06iE/6Pkes3onwBzcvrKaBMfCrPmCLHokOGk2XO01SoY5+JP9akI5+GpEJrzhoHZqcx3uVyU6Cs/vUkWiUpbwD0isipS8Hdwc+lPV/lEjsUiZIZu8cq+JZNVJhZMrQK7EEX0IlYSHUO8k6wng/JM16YzUYDppJB5JyVWJCuRc68tnaccwQMtV7Zh0yiWt9eNoZrjPeymlC39BU8vyZib5BIa610EnCsAqq3/lj/bojR/9+e8X9j3UjeM/pauRVa7wzW0pJBXMtcpHWPwEKITGwM/KBLdL4k9eMeD5sJvnwiv7JrWHtF30s6CbqGe/67wlmNKfpUXAlH8DvBzPPw+EXwRaB2Cus8/Gg+d3AuifPbsWTvVaubHq4oWbp0rJIrNka/onVc+SzL2kcy0qsjou4uqgoFGzecC1Z1mwYT+ZNf5RZFJL8bKqBe886M6ICe9pON99kmd4ySktnTVkao56xeN6KSfPFhxStW6PYqwelIH/gu3xT+XR/bV8wZiZcasH1aYZs3R2Azdhp7NBt/d9f8v3+jY3blkScHV9vHpycX3H1613Nu9sd5TE1tnl8fa1qeb2+7aG1XilCUPtVQYfYghp3dvwR5nmQM4cf5Bnrh0aMTRvZispctgv+fpggXbCCKUQgwTqJFIAOjKUadfQaK1tcLR2nqWIU9UVN7pbPuWlx71TZjxoOLb6sXVmjC2PWpB0ufyrrRPbnSGLX/yVFiKpdZkyIEhhLEBgWT6Qta6BXzkFH4z2BihI7WShwl8VqlZN2xKICvW+4MOGGs+DUWfzFwfO5WcSyNa78tSQZcQDOEZzGkym1u5/Ix+BIkPUrJvCyBt1CcKEC4BViIOhXBikKtX6cAx97BziJUoNKsoVC+cfLOZBmFjuGkpfa7xk1y6LXOqJnV8yzHbLcbW5+557Rg1+wuskxvBAdncWQX5eOBW2WNVW/CfZOmkwTInThU1Kedpv3cuWAUljWLrJHUf7ozedR0h3JRoVSRCe/RlIaUnCbGfUi5AIkPk3/BlSISR5RSZoHIVVK9rcuoYpPYzhm15Ee0+Md698drVzsLjiq1ZnGqfX8plqokZVzzq8trDs7p0/efpTP/mTX3/zrafnp4+Pzy2A/5Ef/uEf/T2/z5ZeH8/6Zd/5Ev/ilc+uXvrUC+dnJ098qNeuZV+O2q23BVnd3NOn55Zgp3+qUfUog59IPTU/UF3toNXeR72QFOoRmJEfAuN9gto4PTqxrwAnwC8gX0zHI93xMhJPUWoYK4ogXrNl6INHX3166jtgl6++8trBrbuE3ICf2cXtO7uv3Hnp5ZdOjp7eumP7r5m9hqMJP9hT6Mbl58Bf7b5NamfHTxzZYfvvzt7e9ekrpdp9R/NzdfW2VSoX1o8yT0vLNQBwfowcAElV+jEUI5kKSIHWlSSFm350hUbQ5u7MtuFbxHfJFpxqh990r7OSCirDRMkX5c5WLaDEcxP28dh/YZOpQpaKM+mW8Gf3gVqtS2Z6SqcnJ7Z0H97etw2DNoOgc/v93/2r/o//u/8Lw3J1ffjhoycvHb20t31Ll9I6nLNzmj+ftdI8ExPhKNDiyrNbRtlXO0eNAl7eWV2frlZPTY8RFoKqa60uMEF3brhEKZtX91i27c0Pdh1evnrSlDDjrSewekyNV3u+XWPtPo3FqeMI4v1cbOxsn17sXB1sbxxaAupDFLl+qnUfFDMus9s60XSrUqzmYZwzhucGbFnL1dYDngRrgcnXqw8SUjUKem4qm5E5gp1hDghLBcdqX8jarh8R8q51SIYxNdmJ0diAUc9AyTB12X1W9c3Adn1OedkSm/lDoxGAWf/XNmGGxpZTW90UMWWMx1P7Bb2OX2itudGomt32AIzqJOVRq1HC0a4JqE6u5V1L7VmqyQGtbHgMCssStS+mRyFbb7mPOLOQ8yRbmjrp/dL6Mm/ukk6tWFBHATxLF+wqwcKQgEUOC9yG0UpL1UswBU87MYjFstyJRtOrN9KUevfNChuBlsE1QhHb89wwR2oLR5glPcQZQjU5X2WFYNgp2JVvDPcZg1OaI8NkSGAqMsW+vdr8EFpoaCTecfsZGkM81oU+Vn1B18ts013csGIeZbfSBISqRh1la8GQzwSx7S+oVhtbDwNjN2Ai32c7JFuoSn0W1MNnUZb6dQML1zXrRveHG2MR4nHsBAEAHGhAB14Z/5gTR2lRwmpGDOINo+I6AuN/nBwQ7Q+QQd3SM1LBmL0QQZWWRaog4KGsdUtx1TiLopTYnwErDIviWFDOkKpBJNm63DkflDNlSUnBqV1IW6Q2Jhb7R254OBR1N+UbNmE46eSqhZYCw/P+PdVUVlyPpVbwMELKNnS0kC7cRY9yVCLEArLZDKoI4TEiUD2FYu8ChhLh5lonW4/Zh36Wv8S1TlvoL3mVfH3BYBFgIJ8rA6iKTJRT/jrqBplJnQv4DCnJF7ALoHkbNoxQAzJiG/SGtxFG6pWa2fIvvwfDMkzL5XeB2sOg83GEp+fK8/jc25KtHF1TvZSP7xi9cP8maklRebqwdUfXlxoJt3UqEGp7ZB17lwMxghtgDTKFnAbbaCBvo2MWsSUbHUmIYVKQqC5wrHZXp3c3d++YVb0+u7V9/8C+scvDPhejJ6G81e6psV9KZuqg0Vizq3ldDQaoN0alWrlCjaqwHIQtx/ZwmXpVhbhf1oyavJYlk5JeRcNUBL2J5XHkAf/r631NosP5m6kzXXdu8heHMrmZhtoSFUMySulfTkSklJNO5CdWxYpsUe6YR8NoLIsRBeTojWjDphJLQ4ytfYsLsBDaviGwi4/59bXg27iYChSmcXDqaTQMw1OCqRKLmHA3YbVySrWGGzIDR7lQwDlYMpUoWuTO53MFZBEuiqKx0YuV2QzojvWHHeYPzSFXrQJjilNMzzirgW8ZeARls4ecFIFFqIRKipmgePAjZjJX7xNONIpb4MktEqTMZawwSgjnSbY0ooEtv1xTezIt9FLIAmmApeoDXHgYyFBnAP3whUb0cphCmf+k12a35JQ8JjFsFFry8RPAXtl4qkd1dd4KUzrYd0zoeJ+KNJQehkF0z4i4UjpygwV7GFsiYSpgsdHaXz8LOawhPwv7G4G0VWvhwMnRic4B/9aWwrffeufhhw9OT47+2t/88d3tw829ze/8ru/9vu/6nn/sD//Iwf7B8eNjSri/uvfKZ1692nrDqT4m6fZ9GKwFUTnQDXoZveX72xqXlsJukXMMgqtaqa3Z3d11ivyirrHU/zCUlmQWyqb2IzmxXtq04ISfjL1mDIltjsOK4R641cSIrLyln7na9+Wvn/7bX7W0//jYAJ60Ru/PHdLKoUkiElqwsn/foL7DQBOTtRdRgIW0wjLamr32XVjL4HClfd/hSq+uTl+Oyzu+RNCJ26Tr28b6BhWeVPWmrLI1fjAGoX4kYMLG6AubTeEJfqxfxCbR0bO1wqdESvDTtWZGTx6HwuFXJK1j1++lnqAApgZpx4SVs+tZ0PJW5EBdokRXQij5TcewOeN09NRqmSvduxyerW0rCL7z7/nuf+Vf+Vf/1//hf3B09GRv9+CNt79uv4c6sO8gqs16gVdW7VfHRjfzveL3dHOrcezT9JgTw+jlFJnbwsAK4ofpFH9wvrNnyVxKX3vN9QHP2IRdjHSl7m7Sol05PPA2jyfroTGOThzaaN22EVH6ABGdxb3lnheTUPJ3lFXJFCq7+axph/1UX45ji7J5EWNWmkKuo1JJWYzhXZz1J0Gxi9CyQlHPZMSCIMfhHpHCnUoSOUOZ9CVJ2RnnXDVpRLOStT8I6xs3nHqfk8x7k6XZg+YQNEBlYGRYCY++qVlt8X99wWjsW4ETuhZ48PtX8Dr1M2VLNjE18XdJOyRE4KAt5cDTMZjB+MRThkhGFLVn7fB20U+laGoWSJMtyLVIfnF/XmJnMAIjSIOb282mpYvFlVA0kt1reDFHWa4FfamCWaEeE0RxuDOml+FNHqph5sLjYONnoHrr/xAnVTgkcmLQK+wDAg6roAX0ow7/TBrwB8BiQ/DdqiL5VYtmuKy1VAqZxeAhp3VcxE37aJRM+gxTCa7uWxDk7LHKi9Z16mpMSrlwOsTED1fT+GFaqMatoZgalnXY6VcBvZdQ3p7nQTWGTsyK9tq7yd/a41LFNa2wh0kWAegtWJnjjguPP/LJGSiRVZHMKA5MDGeKqRQ9xZehpFPS+idCWAbmOY0FfYitZoNHyoNtJcQ9ZIZ7cdgrV4gnuyRZxLj/aEpFBiW5kFN9QsCgNCo7pYBKoCG+vhYsb94CODmieK6QeZZ4CVpCFizjsVbeff3+i9M+y/TsAeJIi/VKHxonann3uIB6dg/kGuzIrdf2ACBXGivJFmWNHYsGFL+UUcKPL7kZyBmhX9JW4kR7GH7HwfVV8f0Nr9ahy9j/JHiW7pvfbGlfXwN9gfgMuNHQBbDwkc1NdqFqC9kAnF2YokUmqdW+/pnzih1jSBc72dNbdU36pW4bBq/z3djz+MrpZdPLGRRzAMxlmxO3L51B4ezB4z07/lYfZVi3HKbGhjpAVPlPtzat/oMrB+CcF6SgthCkWSa89d3ZlaLVbXFuhk63TVjjq/E2jl3VC4Z0lALK5q6/wAzIVS2a2JaY+lzflYXMHaJp3DXML1avt0Tk/JVSjzByN6aiKhE1+aJp9Og5gsbv1sTi1bDSF/YQ0v8xSS085zAaI9jefzuH7OTTOuf4yfpknAEdhWmRhK7L1hsy1HgOkvw1JXms6LWCSp1SLfKpriWao+REDn7UOaRugkPHGEkja59W7HrPwPTgiRNQrhXPJ0eo9kERcQYE3TdmhFHkTw33sovV43ioOKKs8NCoI8YLaMO3U/XmxOFXo2hnOT0GZWPnJ5fG9+ryJDjMZeW9lVonxsoPJcmyE/HEGTidfD8t8hrGqFUmaqE8lZSNjDKZY+I1wZWkubNELeCFxzqlAAe2xnnz8tV2FzjXn4hkIN1UN85BYqZr5eTg9+1h+xytMpJqd9Mw5ixI0vK0I5PTxZ1yDFBaOJIhs4pUc/B2DIp2ccZRQlWLGyYYKEsU1tkWgnvaMOinqIO7NT+RYcm+xR77B3ceHn345/7Mn3n40aO7L93+wnd8x9/6b//Wj/zu3/XP/gt/0KmeDx49tcQHtKNHT/d2Ty4uTyiJuTJLa5RdU4gN2hAfjry60JXY2T48OTn25Rfr9FqHDQl/uNxBdf7NzEYjm7arvCZuvlCBP9EY53Gw5joaa6i8rOvFpJkKr1jyWsBOVakAX+scsh0W9OQnfvyvG+MF41OffuXuC/dGa0leP9KIcm23vCrk06MnauWdu3edfUlVKzkUXk+rxweAHfiprX97zZiRtQ1zHgjx+PTMt4UaHU+jVTeVfRqS9MXrYFVOsPmvAxvqAqSPsgwaxnAvGnXARz7AjWFcqicQpRlt7Obt47vXYFZMD27uEyLMbgFY7r49BRW5BtLDqHcMl+5jCKNTAyeqJV859vXs7OL+iy/WtBqe5optX/+mH/yBlz518Cf//T/1Uz/5t6zC/uDDp9/3Pd9569oX0zGnpfIGJerXyp8d0O17ov6p7HC/3PzIV8PMjdHE+NB/FXCuOKNU9fvlGZH5EN3TTUAHxWaODRY0YD9jkG3Nhc9MNTRw7khNWyXtEzg7dyKctZhmfEyozWgON7oRUND0rtU5zhl221uFRiHCmz/hhtM4q+r1w4dJ+RT1Wluwod5ZnY9fyyjsSLlEjWNTimTQ31xFpseoARzR0uBtb9jCGkMgQUvj4JhqT3W5+4zayDa6nQVLnfYum1iu1jrC0mkvuxe3dvWFto+wWfl9WiGLg1kOmI8hsTV+xddBaHlNovO6xIdk70UWM+YyQRQ2OTJPEIWmkKrA1DjwQ6/hsbmGkjKVt9riHoSKA2zUXfIGcKgEooVLRdqjIqKwRRnt9m5OrBl12wBF4poxdWFOwxuYw8BGD89fq8Dtt/L8iURbMhin0QER6qnhZ9Rl8DNSgklKSQxPgoDdVSes5c5CtEG0GaFwfP58Gsj+0td2tn2a/Rdq/3MP8Bke/feAHfgzGk/TeCnOgtMVSBeyXn2uThqf8NVZopepGRQ2V4+a0Nq+jS/XpqaSEQ7EYDj3M1zqIf1RVBS6gjrYb9rVKfbis6WIRw2nhow6IMsUMg2UeCBjtl9qkfmHbutQo6ABlQLBZbuTSB0bXxRlIysgR6W2I8ZFavrrh0vEyqvHEly8HJpG56ZFa25B2lQ4HUqo8Im1lLQ5LjcOAjQgbntxCo1RsMf8RGbuC6r+L5XFQ6xpFidMGl4ZcsJ20uALasnU/4gjeyi2aNw9NlLQqaeTs7TD5GHRgiDmpJ5z+akAf+uAJfi5uImKmEkxkL9F2ueydbJQwELLT+ChF5OevXu8uQSXIs/XZcav5+VGOnPkaknQEZ0DdeDAaJSooJKvr9KVX+LuhVa2t2HHRE0B60wlClTX83Am4L/j9on0oedKCwZaaHQJA2YCp6xatUosKvhL7KKVNbNNxDX+QpCUw3/PqCEwIzgDJv2QP0IHFKM+Opdhmfq2+bgvYGfo4WBEhzvBosGsb51WWVRP6mVhMJiKMQPLVlvx4SeZLfj78TZVcVHQ2ESP+5seghouQf+r1C0hbJsCf46Ha31rVcVGbSeMOonQu32Fhm0cXOHEBn5fFaB6FjHZs2x6b4BWX1mu5iKwCuQqZOmqsDGmvdGR7hQX57moTqqZbw+rLKUIw/oSsbg6Fj2NHlXrY8Tir6gqIGO3m+ixD1KWJToxN/Z2RbX7CFcGSZZGgD9V6nOuHrvCKS5j1RuPA9qxTlopuMCm9htIRTnIwxZCokRkzSoPNRy1weUDqdtaBJFfPa++pgOhm6ewFKXwtAzqLpjhGwulhGVgojIqeskVxBxhcsm/tHY59YgwF+TSPWSXLKCVc9VZ8AFVQA7v2rdLJJIX4snakN3t89NTZ6ADu2PN/4hUIxMk/wdyNtFVYbqSjSt12uLl5eNHT58eP3UwIhXZsvChxRLYtMhubI1MI0o8Ai4gI9s1pnF7EmefomNeZay3whDaeYmEtDRqlc6G6/3oCe88ePfDt976G4+ePH73rbdffumFoycPj8/O/8U/9s//C//MP/fmW2/4jNZ+XxjQed69/4IV/vbLNP5jm40B9AsnrsQ8UOMWobus2t/b3a9nxcFpkQL9j41o972/KrZlc8LpqxypRVGRA10y18hQTU729ZVPDpsvQ0Qo13NQxsg6fvd/yg0C8F5H4tvvvvv+0YlPqDrc4/K1z7yyu+fMbvtBx3VUmSFvU4DiW9heF8bDjg8mkLw6i31aoloOaEwxIR/69Ub4btNkSVaKIUFPj9VYnJAmKwSPfxBHlJKWaBx7Rl2CL7RUC9zCGwWoPFF+18z02Kvwzr6RRfgkAUOmoMyTQFccXnKIuYG8/r1JsCSbt/WtHEspC4Rhb/zPgEwQ+2Qt0P0X78X/TiPZPD3Z+K7v+lX/8O/7A3/y3/+TZ+ePnAr6+jvf+OLBl/vYpw6fY7BacmG0dtwmiI3BUWvGWBGvwenWtgwzilXQcEQvIbPASUpnwFgwKFbfjHEPLdURvBYjZiMZPcxNTNeXd3QHnFW4e33gWNLKTERoaMh8oU7i2CZnNJO0BPOsEucjxdYsE5BNKrha7eAT8jmTHKTFpkqXLORhp3uEreIilJybKUiVzQIrIJwlXyolsWVCYJEyDphnCj0yC9HyGupgEBMxI5j8LVE1duSQxYZadi8P9tQrC2DNSl8ddsSA0y90MR1wgxvBSDGGr37jcJeH+Vn4Pc/rW2mgU3nwgeQwN0RcI5l+h4ULEAnJNzs5+SRMs6tZfpYM7gEqfcX3Or8hEXKDxVijhFep3cvb/HkduymzALwt+/BLCrWXAymk9a5BH/b3PuVNxgqJIm2Ekb2kDDc2T0NDW+iLWKca0Ofdlu2QlsydttQisj1DHLqOq+2998cv0MiyWbkMwKZTKNUmW7xU75NAbdAT5oGRQVu60rw7TcJDn4vX9yFSnbiwfgEFVxahkWswh+8QjXO9VISb/xWkydKOVKLqA0UW9Lr5c+00xyHfovOoWT2tpnG2Tkymdo2tgEgreQzoYnItImOTpZQPFDyDqBKVXLPG+c4sD2OsulSDFWzq2ULNaWopYM1pPk2dJ5a9+pJZa2AJmcx61nG8isw63qc+Ja8ux11DoJXH2FFoTDN1QukTqzIWZcFCeVj7lAXTwMYIBZUu5sSC0pTQqkdFU5Zc/6XBq8kEILYnArm9xszyFOIxRVoCJ2SeP45a0hW4RJRyybnk7o2phu7z8YX+na616nwMIjSm0IIC5dd/gc9fU8jwTGjmKNrT8yVxSTEimhc6CxhgmDwQBQ+71iVMZPn7twY2rCn7UnSwf6nrWaINFtY15w59MjGpryGvUYrxg+JzGNL8EKQGi5qk/NWuJe3U7KCH/LhcJt2f5WZz5BxxSsP6R7si6QgAoGxennWAJx1sJOS2xaBzoipPVdZjp0SoMr7jTXM2ro7g4WRrXd8qdGp9arnn1fULWeANR1HoEbxdzTx/VZ3dXB37QvtMkIEe0i2cbqfxSzldm+8Sn8XiI7SlNaeAaB+CchENNjDbNeXq1fXlKyNN2+ebqAQw+ccXoCMbUQ5kLoC3Uv1QwdVqxcZj/6rGgipDGNOPnyXYPHk1Ha+Se4lXCSAywFZLG2ifcK8y1ehmYENgMPIw3JMsfMLo4ysQLVYvDmgYjJQkmrH/TEnlDKgpSNYKl7QZ/nL1HlRBeDUSlqgJR7CfFSY8BCQNsZzGHAL9hKyayYDlFKCxC6O6ERf+8mFUD1EpbN1QRZrh9Gx06RARnsMI6SclLsW3Yv0Ckp0N+IBsC1rQJR34WThx7Gn2fID2sflkBJCvfL6fGWY2l9Nn4cHhKWHF1nKB1P7F67PT5hHowdnxmbEOp91cnX9pe+ve5dbrbHBRMuFbJedzDG+7+5eBDA1F1ZmJYVnbGxtHpfUwsb/po2XlDCJcG2PZ8VQLcfJzP/fTTx8+0Xd86e6ti9PjT3/m87/3R3/PD/3w7/qFN9/SD9m+3veNpqPjI4dl7Tovv+Lg1axVhFYWNsTpfmOe8o65w3oKqLPOVeBMlZRQM1HfZmZO6N7W3vtUaNgSuLiHhCjzoq98fWI1z/EZLOpKJ1YCQqO15hS8hj2uagZnpBe3Ot9rtfHTP/vTNqTKbv3Oa5/5Ysxr4VBoKrQWqT4bPrUeaRYjxTnkQKaypx6t78L1ERpqbjRLZtOENWWNvtrWx3SxQlK0p+KKR9bicqZhDphPu+scB3E211S3FtGRlRqZVmgzQTWw7UkDph9Rkz98XTSyZDKmekLPnWWu4Lfr0C0d0eDHjSD3PalwBHaL7eqKsEVA67cJHTJHdAEv0ZIGVyb9EjJJrzceP36MkhdfeikykKpzu3H9O3/nbzg8PP0//O//66/9wlffffdDroHtAq+89hpGIYWc6ieP9qkG2BuvWEy+CPlGTj1AkuAwrVFMP+bx8u5442pfFEe7r+Tm3B7Yt3V9fYjMPBYfDTMrwV3YfsuRbhfnX/RtLVMp15e+A9OHXWYYR92wKosbqL1pEoDi5F4n/NPGB9SpStC8MtQnqVjfR79Wf+lbTkh24xQq7Zwhr9ZySMUhCtW0KcYNlmtGesZFnZxz40qrS5+pkVct5DVpPVjBxLrwO5utavaZx3o7FLVt7xqk+sgOvtK67K12npp2kRICm/aSXe47xnabB7l9pN+JDnTlSdVA7KJeA4ePG+efrRrNPpCqzVKi32FprZeQlH65Knu5loRR4OQfCXwxd3At6YL3lTE1ec9UnOCVQVYyaTZvY9uo53JVURPf+gp8SW8yLPpP4YVO0bQjzkwCnuUUNns8JpNiMBWsoca8VqGpeiLDhN7LkkYtqaovW9Yu+tIicxc8X2LWeJ193p60zd23jLzgPiSdAqDiGc6guGcXx9tcZWMEtg5ufGXHpOzlcdv8NJOZHpLXHjtOZOtqL7fkyvcrNmxV371cHV2d33FYYq1HX282A6A/Got8N90C470dH6a1V+Yhu+XLDyRQNybmhLpkyIn4KFwYijzVjrW59JFynxmleBq3zY371khvbJs5NqtoHpNbveRRll6g4s2wxQ+h4Kpprl2zDbM8wfLLmpIZQ4vtFVu1a7e8RZ+d3TWO/6UBPaAw2DjpK/i6sXqvlihzZ8AkMSAM5ungmu1JUsB6j5Y6W3oykc489tAV1ZqqrKFTMcZLUWbz+Rtb7wUTuu4xpdKnrilWyGBCA0T04R0dff03jHIALi7JAxirJwEwDiH+zMbOrY29N1IOwGE1BhRL4szFMoPUSpNKi/GQT4+WgDB/7pJlUs2YAMOTgIZ42MwVxutrSetlCStfsNUOj7vr04TWJFZybAFuKSAYy9j/PK2BSKNiBXhdXDCjMj15FlQOSSSdbEuKdWxFCF7eMg8LG0p6c30TnJvg534H8nPvv8QjDMCCnitMbhB6lnyN9JigKB90ZYj7xQkh8mk868QuACQqfFrrlGAILa9LRsASSa306Ly6Rwk2n2xt+SaIjbPkum+4iEtdS9lBmeWgVSN1RROnnLcbV/fBbckrvz5KzUOnW0CJtWf3eRyVS59aBFR3cEdDpxORntLFxi70+oOgonmYBsa2M3zPOUBflqEWaSqY8EDJsKY0tg35i3XjNFHfKr9kajhMeR/ZI+5K/BiUOuGF89AHaxVsvDMY848XGERQFhoW4Q8JbgBaausDgEaPxPMoC6uyYQf8/B/uLq7ngiHG1lLBhHBKOkxE61AQ6WLETRlDd0WP2g2/p1TNPmNlgr7GaCqTzUcLgO7rf7ECi/lyWtEWDOFeC0FDK0xHfUpTBlBCv3KpROoXDUtQTUXpw3KATpMBqoyLQBNVbxklaaJqQIUJsTU3MpZyUcgZu5rMFbdQThh41cBIh5JYosVtLWj6gItFBnRBnYCwbiYTaicbejH3Ou351olG6NyiZt/B1r/QMBE3TzeEKFxIhkMLipqKzaOYlUx41OytcUDImljQ5TVEn5sIBAwXl7HW4OL81uEtUxUs8dGjRz7v++jhR5///GsfvPfR9/3qv+cf+YP/3Je/44sfvPeOgyDv3r+DmOPj44Nbt439M6+Y01BuC3hCZZiZKGJCqEWeN9WgyARUzAy0J5TEZ5D4wjFB6lHZUFVG/Gw7ICq3jk/0hC46Adiim/29bZ/pBtTgFo4JrG4GyoRGi+gSsHqqRyV3PezT0+t333mgymjgfYLscC+c5YONfIPpgnbtkGE0RPkvKqe5BptOeAv36nhZ0gjYiNdxt23Af5N76srx5XF+JF9WB0AN1XpOBxteDddqNDmfCN7hK0gwtSA0ordON4HOwe1iILNxfWbhyr4uidkPfaFs32h4DCr1sLxfb7nXc02ElGvGS8kcKQ/Jw/xFLsmoK1DPrgElqBb84wIifxLWli7ZtF/mtizr4vufnfgUNIS3Nu7+9t/+u/f3Xv6P/9R/5GSnn/rJnz64fWvv0I7re/WYsOyMQ0U0GNW0iL6LczShXmVPuBUcs0ktHcBqDMvEbaw+9GicpBR1HvLd+SXKbNC1ZdpsT40xNKqIylLM1T2y8eVc8AEC3p2abvd5R5ygNwofFo50e/KKc4taVExufe4301rHTAJTlH6M10rVEqj6mriVQa5c70sViJbMT5pC+cm8I0cdU9q08pqUyho2ywWfkOKTNfYBZUauEWlwhzNCs+scyZy6tODUKRI2Q1k2en153FfPT60/k8xa1eszA0+KjTlghFLXKEVlzjXIg+2C+fS0l5ciPPUjk4dBIOQS0SjDkm1JVKjggbrke5ZMVMmTpsL7t062gFwDW4or6TpFyVC4VNFUEfxwryJOMTfQKleuEsoaOH+5CJVTGaKWEgMgMkDFlieOl7QWx2SOZTtq5862cW6Buu8Yl/loTIe+dSDj9s77+/sOOBCzm16WvY4ipTM/7Usv5OrUB7ap+azVnn3oLdU2uV/rQ7K4bN6Gwmj9MdwHgFnyF1ulxW1NS2ukFoMGL/+yPkkOWW4N20hqDd6xD3Sf6yKy3VoNnyCjX7q8TQooSsZJ6Fldw7XgBGI63v0gylWLzeAUJ5NryJ1iOSM2s19YCF3NbGK87u9izCepcqtrcbTcHJ1p/YPF4+gSzkPJ3AU6yYRYqWTyMxvKA1piVaR2cmGC9mhyNDlcUC1j078NCwpYX9WBoIFX7cr8jllu08bAhBdjGtJY1JJXdqXstR5UhgIMLMnLENS0pecBOsqzhK9LXP8s9EiajMq04NTzQJnQiZvXJazA9ZNHJSwvsSRkF1BTALz8xpibEib4Y4C9SqOpm99nyYaeMi/4rHPNj0/hupxtvA4s0fqxxBjU6aTh4fsAi6iKXpLdZFpn+FY/63OHnoF9Lku8DtQNxePYBmOdBvf7f2UkniBt0bvJm2ENzbAaJWqVwVyCVQ0gh0nekruwEWQpGqGNqEAay7EYmWfJHTZZ6uAadXPTRycN3FmtRqXUv0urOVlcmxr1djXRzu98s5nC1uVoQO42IKQNzUX/NPhNcClUVbdYXXH1LrCQ/w6pnUv7xFfbl2eMgpDGYmKxuqqI5rlgrsJYNs1KaJppo0N7tG1QlhAow8AzVZdmrWlayNMXHJKq7tVH1mnadZpey5wyySFbtZ5V8VEcpV6sVxM08V3XGL8qikcG67ws75UcXdPcOCG4js5gwbxx8ixKT2HscwhHtq+USzcktreopcJrpCVTjlQd9VNLnee3hCMiKvN1IFBxKtpA9N2D6JFs73L19qyRkS6DlwBFDcIxZ16d1iyoj35sqe24VOY4MbwOpGxe0gACVC5y0yTB/nVhUxwL7gSUVTa0iPMN5hpO6/XRgmMDXkTPETAFAJCWyVPtCcysgNzcfHuRCfYI9g9X+mZKo328Pvvl7NIbdHxTGZbb72di21KZx4h2DM9d1vRrgZBZno9Wu7NujSxAqR7Aw0gJPJuVUjiWRvL4lxtWBWu1zj/lEMTrnbf0lqCkdYB9Vv/sMz5ws7X3NiQqWtzWtlXyD97/4Gd/+mf291e/6Yd+6P/2X/6fD2/f/fW//tf+7h/5fXdfedXnfzm5dxySc7Fx/Pipz+WaPl7UExZp49ozXngZf/A6hEJz8bR6nhqZslXbaFg7BKy6WX30YRzsr/TDOHmN2Tfo32y6xlP1p51W5jR2jy01ltX8m868oagSZfJxw7m8Oyq+mnn+6PGHjvzf7aCgy1c+9flPv/o5vSJ7sPPunilEa0qGTXYxDKYkDx0CCZtpaf0uLXSohiQsqkP1XMY/5xjgZRn7LjVajd1qkt81cmuN4eWGjoHYE+vdLSrY3TVwi4V5h1UJLmbKliWBNfGf6rWf3G+SanP/YOtgtfmNBiM6bryiIUPo4bDzDiyxqKJHh4srNj8m+kIF/FIjeAKLcEW/kM50z/7fBHgpJiqlJsrlyU8rsDHZrML1+dnFg/c/vHv3ThtAoarjtP8EHr/5h37g+OLBv/vv/C8Fnx2f/uW/+GO/+tf8A7fu3XMSTzbDwh0OAvORq1snSS83tMMNmnjXMEbGMlWYo28Iy0DMOZv70fb13tbGY1s7oubqhevNp9fX+h6GMGmjYdd9BzFvXN8y7LF5sXe9c7Kxf3iwc7j7UT2EHTvbLy/2rzZvbfui0/721qn1MjZ9jd7oNi9emnXn9G3nylm3iE3F7M580ICpKeO+MEOOzh5V6eV+q6/HXn0u3MeVVDOnXcA8YYfD+uNMU5bLrVmd7Kru4e77Y0tuKyArWZXm3FCIOUZi+yPtSBPO1ztaKHOKLIYmR/PBzrQxs6/A7606zvrSaBN0HSPvgxfar8sdnVE8dLRR2mFCETvVgr69oyeQxRrhJldowmpRmgQ7Y/Y6qm9mOmlT+SUh7E9Hi1PSJ330zj+ByOrc+hyxgRetaQ7xdP7PBBZWSHe/2Zwexxg4v19Eq9hV2vZU+N7zOtGU9XxO7BjI4Ge8pyCsm0aitwmSgTLQo2W8+VnwQgm1w35DXOeXJw4e0I4xopfvYqzRZ7N/FitenJ74pgkwwBkysUz30paDi3P6tHX5+dWLX9zY/lvV+90PGGt1vK8gbx1cnT+9PL/frNQ2naS+qNi5uj5iqIYdjnM4qjRgM3HnfBl12fOWmWF7tuc7AB1RDqfmQKjFp6WzG4qFz4xNHWnIiS5leD7jpGV8q71CA4Lj7dgsKcDI5E8zM4K8Ovt0bN9+C//xmaNvZyRtyuhp3RSQXgAhY/NTNCGGHTzQouDBiGpMCFyk2bW6ATh/UZRWRycBwBIgQxUNsogQPhLnJ0Fd7IJhlqrSLl+eTE7kyzKsURAz3wam52PY8uFN5Am+kfm4H9CbgaCw8AkmBNhx15DZWNUA6g2plnyG9iRcGmvfuQ1hZWVpoTZ8Wn7p9lQD6KhgLcfCgnCLC93XulX4kk1uBNVRuT6z+0LteKNcXRO1PM59CK/Um6uS+5LAXBMR+Pnz6ZQ8zM4awgaS7SUXGiKuQJWulwaQnl0T29tNumcxy8OzeHk8z+vcPkGdYr4p3/NlfHPU8r4AfA7sTRaQn11J++PruYghSUzR/iaV2zrF+ingyWHMh9uYJkH4siSMTfO08GlevZeP2tWWMAeNyW08dkK5NasCty4PnBi9eXnAhFxuPYn01W4+0paeNcXBZxmN9NvRqkqYomp5TDo9tq2BOgXAwPbiyuafWZijMaP9Mz5U6f2rSRiFy3utIa4rulrt+RBUNYUDoLrw/ii5IpsEhNHwKy9f3rlSwep96qgbwsKnH+MDATAuQHVL2sU/MGjFjABuYLBxjKpApejuaFBiZzWSn2R8C+3D27UuMEA6STt7zWMYA2g90qAB8eGpW2R3i8EppPZLsSPlEcXAH1UN7XCWEi8Kl0BfjA+QiSqzrBr+fCyGmcfnGPneSp5pKkWUjYsUgKVcSEPcW5VEooJLOjc2YFRBP2opvbdh/hJcdOkHtltcHv1qMtMCqysytWRCKyvOLEPjKPE67LU3DWBrePLGR7LlBQsV4oCgEGJLMLu/HfJs8Nkne8okisVmM704ipBvC34iNeZfNi/BgpukeZPDQZzPfW/CQ5vf8ijONIHHAThI2mi0UcCUsPXRYVa3g0Iip8GRUVhqo0y0UJkRXJa6/uLx8elP//RPP3j7veurx08fPXnl0y/8ul/39/7BP/gHDu7d/fpb75nAuHvvhbOzEx/3vX//nmEwaBDK3EasvQymIyu3RDaXdMvVezxcX5QBJrKh6/DWbRSHMnyKF8lH1z/eOH7i6GGfIp4v2qvDvri7v+PrvDnMwyYhCpbeaUM6V8dPtcS0nrg2Hz1+eGxYtMNjaETfu7n3wu3Dg21fEDvYP0yao5DAYFhOGFYNQ6WOrwuyw7ESVwhkxYhYo6sC7O8fmgyZ9fC+IOGcGA3t7TJJxV6sLHmyLFdvwKtTh0jKJDUotYL2UWjqvVjpRVc9yUV4amhtfp/1uX58+tQ83q1949ZGE1P2INeSeZl/4Sm8WjxP3V3ztjwZNOaspHhl8BSEohYq53FSfvJWQZFaiWuJFxIXYM8G2u1gToYq+qKzFBTx9PTid/6Of+jxR8f/0X/8H65WzjrbcGbry6++8vT01KKHli86GJTu1cdpHYzRDoYoDybslVMDbmKB2W3AX71wtNnG0c6tXas3WiqNgktrTpgDX4Vn0BzDsAyyunPZfX4iV76VGDt39C83Dw77CuCJrwSoIX1Pa88ZOm0f3iGyztTR1VZK6isXeemmpC25NO7j00+1AnYXwly8/mPDzl5+e/jiEWvbYrbsNGrwNYdnBBJ16QzBUq+8cT38KimrXSVUT8eUMa+LRWccMjO8/vpBYZgZMUmt55uHY2wliJdMlWqcuZr9O/bluMxOgDx72NoEkEOZWrEwtUQh4BcVEI3fIeaP6BiQHNcYED25cZSs7Rmjc6VVqp/JJg+Y1Z/e18GBWpKkHgNa9OSaNHFmEqwzLAXJtUCu0DWAQWCAd1s0I2tTYf1RQUn8qGHzM2/rQvqpnEm3Tnbz0g4rBxJo1s5PTa/Z4dowcz2rja3DvYO6plZfjVmHDYZw8DX81zunrOtq7+t7zkLbOTizxn+0XVXX50IqxJ3pF7ODRst9gWIGn+hAPBcxcVTOOEbpwdYGOOjtld3zU2MCEUUDbVaMCTUlw8HJOMLSPoAkrnJM/UzLPVRKjt7uQzrTV30KwFxemRPRCysTq/8TOXPoVcEkMJKqyvmLg1ghh4xa92gcVibYYY+3FGmNwMTOs6JpbMTKMk07KKVcRLAIEW5QrkDQpo0L50kjL0xkTu4uqCx5QYdZUEroFsmTegk0wiXjBKSyZZIhi86hSrdkm4j4O0AiebDqfcqb357XV4UNqJuAKerjF0+gfVOK9fsS+gzis0QU4XmoXm6ihn/i/MaYyB8SQ21wneLWqVm95VoAfAym+P6MprtsNgXxudN7git+5w05Ns4+W22agmTqce5l8W+NWAl/6auivmXKgTZxJXn2Vsg3XYi0ivcGyNC+Tr88S77gMJzTis3rwi1wA7++i4mCFDyr4UmNFkkPjAoYqbp1uWFwVOOye7nx9qalw5oQk0Mmc+vBPr7Y2D+75K3per5aJz4F5m3tG0x3FuB84sD5A3urzu41YrPHNBhrSUkrTi3SCFnFAV9fWTqs67zxkXEuNoClmIWDO5eXe1ca9p3zDjJwxhYd5qLnj0FgqFEzDG2rh2DBPTksdTs2RWAWoFk2fn11QOvV4WIjxkz20B7hWqe+wKOY8yulte8+P3IsEjjxp7RT+VEwrQ2wO2YWtDMZmxKPn4vGdHH4zORCXRvmbdALh2xFZk7blQ0Mr7AN+6n8tXQxe13jImPJnV3c2P0woYIax3cHjk5AvBn8BkKVggMMTfw1SjdMrfNSk50BpPKMd8UIlAVSdRGwz9eda0kbuWw0C0arvXea3JQ5XBuDVTSYFCVJ6gFhoxYxtoSV5SMsliM6jB5h+O4eHSHKWkdZWxoml69P4LjP94SkLkRHR135opSFIHUXNvcOTaRE5+blpxsB3zaOMjKAdCs7++Z0jAnVmY3etWxUY89lFEIth0Boj+SUtdp+gED+0qA4Ws9e1//I3F/uvWs4syGeRXbJQylXtrKV11imLb9b22dHxz/5E3/L7t7HHz3mYOzs3HvzvQ++//t+4A/+oX/JaOLjy+vDF17QJTjl/D954gjMg4O6IbF1qY7DYrcbpMTMxeaEnG8zTQXtlmT6mZA0at7dHblz8vCF69Xt3TsfCneJsRuhpSIWB+0Y17dR3qb5ts2oGiz9aFe600y9b0Ex9hdNOqUF27tnfPzj4w8fP7GTAktOT051LJl/x38ZDD1+cnS4bwWgap6mDh49LPgABUeSX/DOgMyTMNwbSuWptkdM/qMhO6sF9lXIna0zPefV4YMoiz/+Gk8CuUat76+b/3+rQk8/K/bq+g0xSKueVuMM5vI/ro5OrF6xAanjey+ud4596vhs80DflFIR8Ox/GGwXhVpkETpdC7bL803AIp01HX5S/a7u5n4L+MVXWD+DllAqLf2tYhPQ1caTo6Pt3b07+3dEQXjbDoqWYm3/6O/93WbE/qP/5D/lNv3cT/3Uy6+8bFRl/5DH5fST6ozu1vbedqzOyQA3pfc4kPXHOHYcJLY0o7V7/eLR9sGHrPTl7c2th1tbdzY3Hq0u7mxsfbRxeW+16fneavVo4+qe7/WuLu9tbn90dnXnaO/s4c7esY+ldOiOGq0bZq3a9qldWhs7F3POG2Ybr+lQUBPF/z/O/ixY1yxN7Pr2vPcZcqiszMrKrOquntTV6lbLjWYhZAvZRtiAZVlMQi2Bg8lIBCCmIDwQGIII7owvfOEgwoHDvvKFwyawISzCMiDZEoKgQWpLPamlrqzMynk4w5739u//rO/b52RWdUvye/Z5v/dd61nPtJ71rHm9e580D7D/KTduV5g1olZzmfSw+F3v8vbgEzPJN7cPmwporR0mv4xn0xME4FHokIpy0KmHhI0glrAebk4wKRuN1J7iF16ahuLHFHqzO3igyovp1dDxm2mowx44AhWQhqWDJMyy6DIZ/6U3907zU15bnDS9FGuG9HEduuAjbD6bpqxbvOKctMv5lvAlSHXWGDfc2bGfYRhnezdfb1ma0/byoPWopxeSddRUbHaoBPPux3OP5O1JKaogztsIO4VnslWqggd+BPMWpv4ywd12FEDS+631/YtMOAf/3MVFKopgFKNBOkG0nU5FevV/vrSqfGF6EsQe9EEEk3e3a4U31dsOnobLuBZoqW80zu2IMyjOV8Crx1QlWBqLLi0VNm3w+unpm6cP/vPrG583Nu78Q3v4v/rRnaNvXV3+yM3RL99cvbl78Cs3V68pyBeXL+4dfmxr3+XB+7vXr+04+eritduDXz64evP28P2b69eu9z7a33vt6ujbVyYQdl/SZsBCzqgqcwwJ8cTMNaWrmq9yNl3tH7+/c/WUYXjRjeAiQWJYHe4CW21FZOgmB/zIeZNC4A2A5kH37rXz7Py126uznb23C5fn0ubitPk/TD31jVu5tKkH0yKcTGSxRG14RjkiVYWwYN5DJSDCBVCgBo+e6JSI3CZznvC9w4/ywCCVCUgJR60gzaXDevjBYqbykzSpgVnSUvoZJ6R8oCo8tBEaBkF2Zi/61DEMyGnRAxtjMZxVRNrwAguZ8f4BRqNx/V/16kvA6nqzYWguBJvSsfSwEi7k7kNu5VoxCV5gMvezXhpohqy1Cs9dYZ/0bv1O7DKQwBtQChrYutZvrxM+aTYEJ2CYFbpi52ebdIENQMnvgjcMbwj8Gj8rxcL8XOpnKVbg94zKxJ8BrifCCsuUt1cwGfewlL3heWKfgYzgy/SDUgT4xExfon2u3GjoUw0023lb9iM1U6+DpKX5qW/4Xu2Zb7U+9KlNLjc79/jOTEapgYYp1U43l8RZGGDUkKogqLrrseffq6ha4Qew8iFEy4+bzirjlo/FX3u7MlatkVPD+PokybUKKuHy9+VCpXX4qjMPWXpbuhM8pl8hbBHdSJ9eyrT6AyBzG1gzxpRfw04DBqssiUyYEoAMOAT96iD0oErDhVhzAFaN+KKnoaHqlxgZ2LhseJtgkzRi2iQi3fVJxNYN4KvyCKETtWrB/MKUVy2pqSXLX4wnf5xUK1Ear9PIxPAcr9Ep72PSv/rzI+TyT1qyjds0DifZsBRDkQ65zMXMFDDqr43RrI7mNFUHPmKF8Y4Atn3JCFUtg+ANNRoiN5Ni/FD1bDzRykijb4bMqvyRqQYcPDGaNslUN4A+tFc1Jnxc1nE5jpYhPZYaNQTXmHC8UE/VbSvTmvzZP7C2fv/k+Oj+Qw6MGh3N6UPXrUolk+XymsvL/ZVdEG7y06CqcW9tRFWCpm0LLfRhpp9ESr48DQo0sCp52pmREaTf+pVfefToMycOMR2NjD/xJ/7Z3/5bf9vl3vnJg5PTCx0EH1fafdwB8DsPHzygZrqgrcmgyZvybgnez+ZC7ItXdrBg8ZOW6Ejjo5W3h6e+H6udfv2JkOLMrJ46fEKrUkvQ9gkr8/bOT88rhZo1a7BnqrvqJ+0h2STCKpvG8veM+7tanaKlfWFxBW4dNHRrs5wDcR/e+5JWKnVGqCzMWLLnSlr/BA6vsSvDsipleMh5WD3HQoIKYNA7QvjWtgjAUIAmxljqJC6fp4ykqqTO2plYRc1rQ7JSlcGaqkRxaNKNzpOPfODdCO/V0ysHB183mg1fNeVochS4ngvH07zM4+a2wp8PWc+TvseFaOXNRN3FJJ0rZoPyV0AWWWkZsNvbJ0+e+HCyfqF8dDpQczWaULd7f/Dv/fv+/H/+s/+PP/kffvmVr/ziz//83/LbfrPFKCZCMv9GD8LmqiXGSDc6idBgz29O46C1cKe3jz7Sutu3xH2OuuE9NEs0jIkvuZIxRzqlFpNeUjhHS6dw78ET6/0B9cU3Sy4Rb87Coh9ZysFImhwyqRzPmTNGRTEHLcoldrjBNzbQm5FQFcpqg0zI2MhIE54p3pu00nsaIoVoR86PpqaXknkvNjpZaK7AnVdKH3E2/Yri/HE56g1cVKrrFeBTk1VVpparydW8VxXNUcMkaabRa4JYflG1VCs2i83OTAdkmgJjwH/B5FbV1Z1ewpdP8y+mAS+dSJ2xg3EB4XO0i+ctz15g4hAAPGbSyCSPjms5ag5qWX4lyBWtHiIzLFW9FRKtCegmYAI9dm2AgxoMK2gSbeOiP2noc1FIR/k+Ra9Z9/SEJazmHRPDmMOIMwRrIEhZA1iL+fazg7/yy6f7p5+9t3PlOPHv3F74LPiHuzqiRx/snh9+dvGhlTU71x9p/Z9d3D45U8A/1Dy4PvzwRv/h9mMfs9u9/nTn0mTmhw5tdUzt0e5T/bXHu0cW11qXiIU6JCSeIk5z/o0yE13+pJbJI0ZLu1oQDJlDVFY8gOzosQx1KaWgvKePYjdrFKq6TDUUcmrqP73RaJZj6VlcgWl+7MN7GVEspaFZS2ABKwKtdwjPQBGnSiFNsiPIUWmxpt8KWJzHPGBGLjuYM7U3xidJf0VNHvUTDT+i2ZBQqQIk88TGXFBDulRhLpWfLaJBG1hIJZaL0Y0JD1iaKLHzsACTLQSh2gTPU0mCcFvoh9K8F7oB3fwMjNDwbK4RZvu8TbaN7LekU1QoaZQASZSewzHgw8gmVOthKLoB+xzkhN+Y4767QrZ9mYdL4093F5oavUIWzB0kgOcT3sF/9wM1gd0m3P7+qomjpSXWGsHN9d0hIdzG9suEBGh+WyNlcrwvEY7ql8YWyRII3tDlzbhBlt9+TeO1Ct6LNzv3b20pM1xnNMeA7p4FP2pcuyNUTQeWy18r2zf3Tq8/Od59WcWi7BhiyT32tdHpyKLOguoYqEKMG7UdEc0WpMeyb99oYhr6Pb3q0wE2+mh0CT84v/aV1ANHumBb2bgwcKu7UdVS+cVzSvRb251vmuYw3rdDkWOyygBNQDCVhGKUvLW+R/djvGGQujKryObQ24o4mZMdrgKfncV0BQOOUeQ0R0K/2sW1alN6iMyHVHe/uyC5Tk5zOKiqzDMoqMhqdPqwa915OENfHR5rhjFfhW33yNgzCjuaZ4MKTO2JJu9chk/wY3REg4f4/FqVs+TdRyq1fqtRdw8/4NByScSLfTzHRZwDXK/5SJCyqbAU10iYbaSfcEFWC1BaqGKIa/AUEY4rV3T0nmzZ67wacbU2eeUOhtd/0wC1Oc/Iufq4BkG6nbZKCiAoV+ZHa4NgVGQtg6NJGOIoKX0WffIhbihWWkgmIaYF4EWljpGmijujwuYwXba6Q421gJjvAKS2cma0CfWYTrKwd+NBDe2vfpGO74W5tTQ44NGrwotJ+r159zvfPt7fe+GlB1eXZ+eXv/Lghb2/7w/88z/90//gZ4+vnlrs/+ET228fvPDlTz/69ONPHn39zW+YAUBL03n06RYbi4tQP389OxMMt3cw5Y4rZRe4eNZxvr64/OWnp31GeMVlTO2cvmxFluJxs3d5ngMXJG1TKzohujeRJ869eJB9qbccarCr1nQdynb3ySKjSgZDm7K3d1NfAWZj89Ovg3iUfnvxVankVc2Evg1J3bI/i+AIMNbSFDouIItaXYIr54zJt+tT7zVQDxwOU6FIznUlaNeub9ZmZeVFz/MyZjhqHCV1EjmvsXd7T3fs6vDi5lwDeXYxHV/ov6T8k30Lu9sHOu0351dollY2J30Zg8f4SzfpfsLHvjwFNj/g1sME2Xn0RpFzSkwPX7wSeZ1HEdopF9Gw5sYOaCMFsxHc+L+tF4I1OhjqP/fP/PG33/4rP/sXf+Hx6eOf+9n7P/IbfjxftGvtDYXTrHJhOZBxX42JuKoIdS8r/VXd5wl1hF789ODe+dE9eWfpvUmVW+OXtSDu7RxaNv1wqPpKq/EU806807F28NXuWT62A0Zkm9lafeMOSUDcDPD5jv2aihVf1Zhixwrt3Msf7r46LTBl1z/rmvBh7Jz4xulZ3rDGQipzY3NxjW/ZrUzVpnTmiZDmG4OdHBhp6Iop6ar4/tzt7TnpbndelObG/Gcd05c8K5xMafCI9cwhHZd1bFt1peBVM0iDXJl7cHtff+ve7T4gO4QRtECw0wLqyTCLGv97e98xTKXeJLd+DyNdbTCIYjpjLN93j3Uu80ix0TU5vh69JMoCLaI//4nOiTQzYdCcm6rgTIplI6UC5WW9I4SrtrWkz8nohT8Nbsbvdw6+7WWjsCnxURvDWFCeJ2s2ZiydcBqJjnXVxQ5EaYT34gq6SpN/7eDhuFQ5Hty79vnC23Phceo/7ayCg71hfNHuA+0mDG+/dnHorKVfZ3/D7flvUEXsXb5Y3l/8mD0EH9/+QAuDrn/T7d7x5e7l02NUXjIYc7vz0lj7Q2u2rq9/kJUeXz88Prh/e/vC7sWxoSEfxZgBKg0FA0z4nkrT3p4sYWVG2eKPU+G5Gy85+757J2e3+++wXM54X6ePEeulKDCNC7IXRUpumkVTcVwdHX9sANRuQ+28Psxh4qrvM5pNfP9y5wmvNbUVeHZr+kshbXDI5F5Ho1YnUi/VmThhuqzoqK8rXX2dbAcH7zdWpymkE+qXa81tanLNiGsb9ciApYrbCsKnssh5kzNGNaGCVzouGq8jh3ZCFSh8ADrzwZBoZmsSj/Nt+otelTJXvTVkw5K4ckPjIbQg6WQpbmw68LGG+gDP9EohY0LFrlAtTAB2vJRM5BpXXWmsBeG3N8/RZy6XX6vd4hsUha9rJcz4Y6awufVwB7MJ8dO+o7ureidOJqHIsnXD2IbDihE5tT8WH3dJ7x5W+PP3iG2h/T5/DaXi+//sZ71sAzdvv+rPc7I/B7PB+FzIc4/fHSnEH9Ge8Trw690jKp7vBMl4BC4F30EyqsnnYkFr52ma29R1cWsZwZPTa42FJzb28KGXN1rofbe97wCoWfQNFIWjj9UPGnlan5pfPIUKAy7VSh1u1RYGa+I2Km4JkRLD9KYJaPxfoWOOKLb36nzGp2qO+G+HCmPd8c0b/FdYOCCtuVosCnreUOJIqo6SJToVKY9LuUlVSVK4ApxEjANTEFZpDuSkxRTYKXaVilY/Q+dhSIUGBvRqaZasq8YzxBDhKwFzH4p1C4nSeFc//scarirssPTIA0zbFdGYw8SAFj4MoTYVV0PmyanWDgcEfgwHqf9oKTeoO1Mjp0ZYzE0NJcVAB6575qUaNDbTBYLxkupwkxjD2zwHsqQMQRRxmPxe6sClahJXbSdF0hhDscCihkH6w53/FFi1WUieqqpB7VG21IYIqwpZ2rG1GuqZpYl++K4v97l4qHUYZDdfklzpILal6Rod9avmRz4XrDIwmGw1aewaOErZ+ElQrnkYTqTSLHRJpDuUSvZP7tlhYna7OoBrSbC5QoEGZ9kQ/s6nn3365/+z/+Li7OzhycGXvvzi0f3v+/v/wP/gp//ov/jE2Sk3nz1++tnDB1/22a+33vrlv/yzv/D933idterwYC+O808pMx7uBJiX77rdwWzEXQBC00N3jd4OSNFqrAIWNCaNxJFJ6rB3PlQaY8RDEXFqaq6+M3a042EWVTo4/Y1ZaARp79tNK4ulq2xZhaLiePrkqYHqs9NLB1gOQjfdNJPqj8rgsZjdoyeyxyihs7RxsHombSxmp4pHw4dqxKJYBUvCOf0bX753777KrSpzcjn5tg9ASYPBCRxZCilwHFly4HM8gL2r8mr3yWVffdP5NrnTnqFrHgvpmlwoSx2uhWI9LIQraMIFu1a5ECzNSjXMbCDiYBP6LOTzT3fRY7T4nP71QvLk0SN7uQ/u3aOWTQbo5J+d/8AP/eC/+C/9y//oP/LHLKx466/+8g/+yPdf7z+soq550LiI/Ujl1nA0DjCaFBfE6IJexasCTx07VM/OWKbdXByqBV28gCWUqUKr46CKnCVcW6zXJsspLLDL4enwKtINkFu+Kfm4DRldmamvls+QMRkYNpbGRk9usYflVf7zorU2JAK7nFuFcXI4vx+esmCj5VRfaav3aFv2uEyJVQSAGvXJlXAcUPo1mts93+fqtuSvvS/UatUaN6jBLsafhhdxeU8rVAKwY2nvxNjI9c2RlS6WhqpCDveta72w3Bw+swR1cZfAgyTGxvuP3eNq4R7aYkYwQkwxAauYRlf0RktjT/LDpRcwithGDgiEy+AndFTEpVY8KtGx0LUQzlOP/hc+wg7Id4MVOenLO/8Hz0q77gJW+k1c+FxVxfiMK3nqcBAsK/M0l25ppn6lVcIjq+AaWrL/9lJDwcdAL53BM4YDIDplX70Jo3pOBHc3OKSX2XH5TRTxkQwMYYODjSRY5clEKQBJhB88OLE0S7Pa3jflui1jzDRtQ5nOUUkZzKQfjiFnmT+zecWHSnxkkYtTaxgmyUJANyiWxNoqdbOUsgNziggb35wTinTVrzXrD53iAImiY3ShORzOTG+BqFbwm77W3tn11XNU5BVWtYhVjojnou2H5pmzN2NTVZl1MzCVWauf0MeTrgRW8ZBeRRDIyAYn3DSg9PMnQ2aCQkXXVuiErhYFTeS0YDdFxtLaTnjoEjPRaqdlCpqjj0Z1ypgQ7NEDHpl/4PES0lgahLCsnOu1+M3V4/BaaBDlQlbt8TmwLfiz36BHQXeAW3C/d2HBD70vhKzw4IbMinUf6u6FP7tifpAKmmrY7yR9BtLTSvX8fRM/6O8wSLqelwAj+POI2kXAhO4/H/Y39RxrQ/KLTD7bMb3F9ywki4+t5+UyNixE/54d6CGtQhFUztfPlkxJy+iilqqyJlvIry7vGTs8Pnjx9PrIQMql9Z03T2wOtGSAdWp6nu6eXFuXb7jk9v7hzgv2XN3svqhzfGm0SVHqTImG9ncPfFPWQLLPoFrK73s/LQ+ymmAa93YU4ezABkVlwZzDuUq7YqVE8QeO1rF1jCEyXExhewwRgopulovrDfeXX+UfbvamDyomAScKK3nvTcXTupqa7FNnJbE+MUxo+YVNu1r7RglU+nW3m+W4sddC5yc8MRE5p2i79p2/BBksilZerdaHV1AiDt8lxu7lV9PrwXfcAsxeyli1Sa8SaRP7keIK/4Ym9OOn/ICyDhKpSiSySnekB1qKstrf7tH7foYrGAfT/AgKdmHaey9NkVzX5OqNpjBPPqSQYWYw8jw5pnSW5qYEr3ZvlPwXTkb4MzOeSdrl4opUJZSC/Fp1CwyaUTgNJE5E2vU41S3b0gCN0mhqm4PNJ5cr+OINddF4N7VOi2s3nC3B5p5kw9MU7XTRoJ12zaXNovpfZaaKqS5ZmssRx8W0IZZpXH+FNLsHH6T54UV9gNsccqpaBErp1Z7uZGffZ1ePP/v07OzxxdnFxx8++jv/+//df/KP/5Pf/JFff9aZ/NpWxq/2Pvzgg/c//vDTx5rL1uG/uL/7wk1LKdhm/QdchHTW3X5uNq/Q777wNkrfxvQeEiLWaTbMVH1kNK7B1SrCVJWJr2dGW0p5wXqFQ1YPRCW3RTSIh6mWP7Tau/Ppa29a533tCwO3+0aYftJ3yYzWq8mSY827VwLHZva/XU2oPKtGNaBcmpApOZ3R5dWFSgrVMtw1kGoi5bGuGxiL4CdcQ44NxPLA9pMVJ0D/BmNvYZ7g9SxGJpbPcz8xwqg3as23DpvW7b7ZQ2ulZpGY3ayO1aSbg+/I5sEUp/M4r2X3mNSwwBqu+xwKvqYxmgaH+BDudrBWsi6u7kK9LmyLxDaWOJ0jTgNnitvp6dnR8alBwXtHTZo1Tu3D61c3FxdPfvNP/eQ/9o/+kf/9/+HffXh0/9233n7jmz92fU4IK9qtTcBvLZbJwZXbqYzyIyZOXuTbyOG0f77zUEXPwcqcaZbNp+eSLheqIZXS5HT1/bEu0t7NyzU5dj/S1ziYU88drGlPbcOi5Y3GjyKdEsqVxcTkDsuryTMawkVhaXJUEdg0Z4Q066JV/+aYJhjevyZRJ/l48zQKxv0gFzAzAK1/0qCUyVajOpFCz+VLMjcDrC5CmXRaQRv7l2UQCM2mtVHz/VadJgAYNlgRuDKma4P1hxny3svNUh5+yv/n+Y2M3rzko1NzsHMT4nVb5v8wOPKN68ZUfi85s6OJTfieR3QhyeJe3ORdIZvAggpMc/m9Kri5rt7owUllA7HuJV+UF8zcb/tiwKAbImi5MDAZMYTXE+DSohX0Srqh1cvg9Y7zTa55Rs5V+uaHXK2U5HMaTN+12caqHYss+1AgtIoWi6qsJP/kq9ngKmkGv3+sCVLi2rm1UjNF2cBjV5VzOw95s9sjXyaxHEgelOqaY7N1UP5fNnTQxpbjk4Odw/pjZrOsCL51qoEI5xg01BjdESl1JKU/5Pj8ioSREmfkWzI5w99r6/lW3TOXRpwysjXPqrH2PHSQydRuENR2T3f+j/1wCRhzZ8dja1WIuhV9Rntz0RlXCCLl8nP8DiPdfx+X+hW2wzUEqsRheyrUlNLwFy4wLJFa0jMeZOj0ZqWuB0A5/CZfYQXkuY76cNU2tvIBrN9WcI/DX+8QCR+zpGAn9jgejCSGu7qq7zgWbrEqMxHLQEs82GR56ZrEJsw8zLg7jU1wpEfre0fmXrKWudbPr3E3RfHWMroQZHVJGf9lAbbYlHviDMIYGrZi7e6a5yDArXh8LqorapuktwmpA+Da4JrnX/U2eD9Hb5AsjsK2KH0xfbgXrS/G/HXev8DU98b+q+FIeeJWJg/Q4tB9aWQAAlp5JPyOXkoT2r9NR1IUs6L8c6XuYvf06e7Np7ePLhS1mxujIjYPRsuI/8GOLYd9DkDjXj1//Zgfvt4zP3hjsLChT1tDxGqOaM3zo1qKbclinnrXglic5/rAuZqpuZqlZ4UVHgboyOpNbZYkYxOt6lQopjWsvY+VfBKd40arO2egnmCglYbEr2TUwK3gSln5QLCy7bLmM80VMtB+gOWjVi5KVCkw0hDRwqbQrD563i3hjY5pU8S3gh73Uc8HdkVlOCm1BMu0IxOtAqb4L7vyCjjO/Z88KmkUKhaFlUrQ3DmhCl3koHMD5rm8Dl0YgnOTv1zGNLf4pbhcjKFX2iDwNeBpoodiNjykszzSFMeJDT0UsTrs5Wzuyt6zdGHZMhtCMYmWlxnUyREI1GRp0gcfg1FQIAsnMpLE1QbZcJ3oFKDeGRRcmKTeMwn4lusc69iwnObjp9RTMy3imKp9r6kAg0naMZK84oBG9NjmV+ttTi9ef/21v/izf/H46OjFFx+cnu//oT/0h3/DT/7UuY+OXRkgP7Xu/8GLL//yz/3yu+++s3fYGYPWy7SLK3HvDDKEf8PXcP4c9Ag+mqjVcOOkfy/EJrSLoVtdTEBR9JUm0VfEVDMrgwSltKW/pTfc0QYWGfqOhTmG/y9vbSI+8ikf24gb7+0ooNbqVMxob+hXKpQULW2Nf0ShRKizvOEbFZd7lR4AxbIh7bHVT3CqiFPBfRpZxb5ZAlduAoN8bskM0Ub+oQhZ5jOZPbHKTRGBlelaEr0ZzX3xZP/oas/5mmdKsibG7pV1HhZ5ZGO1UiIVJejXo4fF9ZJtOKjEVS+yDYTKvk0BlGR4iJ/SD3NDe92Gy837hv8tNeiX/cugTriiUiSs/LEESGti//DJ46f37h1pG/z0T//h/+v/+f9ydvrkr/7SX7k9evilb3xNA96yEcvUpOVMh4eY9k9eLDawMlLNGE+TYOmlbhsv0zgqvysvshd9ZY5MHk55AVIzRftFGQiZNfIWP9ToqqVclueQKhIoaD2Xn2Neo8IRdlzCPCGxkXv9bLNxzIEWy0UY5ES+tNzbqmnzW0H2nyUjlul69nm/PXWRTX9sjBKMqmaCuvpJ3GMMxF0s5a16lRAGgRPmRz5SSUe4SN4fvY+/1g2FVyZIQKNqEtAeYPKwWERpvL8FrkumKUh0O0Uvc0JTyZvfbY6sDIm15C7jNlVPISjIoym9SCiAEMe/qDpsoxq857YKn2j66C1xe4gaflyLyeLCe3eVLGVM9IKJplwWseSI0sDHThHh9jOvgupF3viUiBKwMOkMTIubKVSxGvowPa2ExctgOmzC6PaSO5U1dulXM0JI3zVMPWnkV558B6AT4zqaSXOBVxi5UNf8t8K/LDAm0bxwtXgdsXLcUhwnNUwDtqG75o03ugr1En5JXIcZ/O7+5fX51bnVys5yTjhcpF8PLGGTYRkNNTH9YU2orqXCpS1UHa3QZT1gSAR0m20Ux7GIS1LEJvtSI0YyMHTGhqrC0gLbEqIox6saTyqFr1KXHWfYsKOigGGAzPVTUpxAvthVbtWmivcpQgkv+xNnZmYGIDVEmTO3QAB2cTgdRMYDWKEStor8JEQl+Mw9WqOLSmsPw8OERiKYYbLH1JA6whG17HBAuhX8Pa+79ANA9lWkMsuBX0rcJh/kEdgE9LCFG/ACFlXUPxdzF92DLtq8f56rtbL/2Wj6gAy1eQpd+HsZLfbmsQBERxHR7L2Y1vv+DV23DfzsXH25+6K+Ej7jboM1gL/+NYk3pKFwZoNR54wqnzRDoT1v8mfgNhkN9TjPTnIFbEmef4qVXFdFmU/fPbvc//Ti5PDWUR1P9/fuHxxcOAl07+Tw4urk7ObJxdX+xcU9BmmQSuGxWsBM1ZfuWQp3rzWuczazWT40NJTpSC1kYEptXFulrWi0p1Szd6XGVKD6pqLojA8P2h/4WD5vDGxkGPWzPB0EexvLCw7CHn9NEUeWMfKc7Ig+P3q3Tebm9kxs6IcQHzFEzd+h7tXWAo6gFk6FOTdX73z2tk/xi2WhqWwSG/vHpGewlYGpWuJN+DwHGZJZnSa6v0KUWJkiVaMcekruqwLabf0ceWvK+QEAf3kDUTkYCuljYCIGnyfBw7CoRFnJ4kpEQ0qeFvxg37VulXsbFyd8OUMPAyR9WVKFkkNaFdVwy3EMM6EfywcmEYpx5z489TY8pN7hnErN3WPVUYcy1whi6UJZ6o04zzhMxVUkSZlXTWvFlsjltsnUeXZCfa2I/XepB3sx3hardCVB2CPA3hKHzIXgHlawRmJC3chHsnLFnjqHqEHFdAtHQ3KG17/i0y5PHz/9T/6TP3/ywkcvvPCyMz1/3a//9b/7b/tbf/THf/KDjz62sNLCUIMyL7z80i/+pZ//8JN3zs6emDm6b6r6HFvsffI8cjGGq9vZyZOQ63V42/Jc6PYC/IVrVk/i7OBtSmW/RthVh2wXKnPoB4e+22tMblo+DMYMV+vLTeddffbpZ8Sn1Y2hbMwFjGVDb1PB7t5LBx2LasL+0jyYISjHN6Wz6053ObQ+vBwffjKXGv6jYGzU+G6HKI3VshpLDzKoraEmuH97118/cbTTvferL10tWBrVzG3sD1Swc/mZhN0DXKHznMhh7PJclvWye4b8PcveHxw4yP3i1mp7UNcXZ44PsD7KIEbz95mx0ld2b64COnkDcKNcTM+9DxqyGMiVjRoAlfYKaHQXYyVfL+thuBxui4Fz85xBOSEnzFOp0//U9XZtdxilRcGKx4EDaE739o/tMPlf/Ov/yr/xr/6bj06v/sJ/8Z//zq883Dt6QLvXO47tn3GUuicVIlmfv7h5iNLO/mNMxXftm4rq8iVFjcMxvL1z/Yp45wKR5ebqxTg8+LSmWeKZ1v0Ug2x2MGsl8GFUlBMeQ25yJ7LLT0wOJt7YQz8rI/pJ2u7xE/nUyRtdvjY5RQixLYwIVlxY5nF+3QZX8YB0MzucU/XNspXozgmqo1kbKfMJcy5vKCbX4Os2Rob3Rme38b4RoXNkXs5RdtZ2g7/d/9iQzrVv25v5aijbLJeeEJ9A1VpkeXQXZWrrgo9T6GTY1tKnAKb28Y9jiH2pBtzwZZ3LiDQ+VXLH4L1JsN39twp3xRyLSxsMcO/4PQ9orJjKZhC9rhDkdp2kDvjg7QyTfL2MvruPNsP57OoL0Ey5gz0mMMZkQs8LbsCRwsfkhvNhveS3CclALWshhRw0p11uEnLv6J0Ml0VowtKFB9zEait/d27vzekUVq/c78skxtrSg+k+XqWP27XpQodO42TPEtaG/ojAl6sAOoQvK6vEOQZrxgZjXD7kzSdc3V3D2CxdQ5E8rniiuI+Egy1bUGocdHD5xGhFx4g7aVSDft9Qh/7kPV82UOl3skj2xOAZl97NoWw32klJhKeH4QpH9w0xKoRX50+JlhTmFxv+S6ut109yB+821OGbf/UZLMKbYm7Yvu4LjJrdbWc2JdJWZM0V2i1DE+3g/Mr4KVFGiiph9k5LZdbRyX3zLQnHSi2yDE7lwpLtx6AMBZjqFV2GZNKqLj2BTBGjsGZaKCzU9VXwRDQjNtP+4rOLgADv4kqV3KiPdWQbHQSfavu3+aObUXVJy3UqnNgVLmpZlmRfuEq1iSvb5rVEiT2ZnEJ2Lt7ICc/p/uEfrAOAViUifrOAemlT9srZxfCWsUVk7rNfi1QwfJGtsH+Bw83rYqiXlQzYwC42hnHs3yXu4e5lg+JX/dkwskH1vcD+hlGVeAGvTPDcK9bYFW3J1cpWDdKpuhZswm2zrBwGLTZzZfsaNA5sJOwV89o5OC37tfmbFT60LtPq0sunduPannv69LwPBbBztS3bur482b86vbXSx+eHnB3U+XCN02aw4zlYX4O9Gm+5Gw85cpPUDhK11Sh16rEz/XYKzzxVMiTM5MLKEuMONQ8zVlGdN5mzr7feOAWnkFmMdHV+tDJaSJeaouaGESURqOQTpuyIhVWXhTJ4gdb6jTmlD4Bxnz9Jqz0hIylUOaEoh7mKMpz0TUg/o9ghIT5KJem+4absCUllfBCACQD3AxnKwmNpEi6EhXmXcEFV9HGLpwmYJMmwUi3MCPRAgHCOEIMxB1NAMYN3cA+1DYnJpCJX8YJlCRDXgyzMcgK90kaG8EiMW4pj/E3lwIFHIzYxC32RGWcVhpRlA1Spkf5yiyxikm6Ao+Axkxpr9tTsJ5zTlLest5gkYcw1DlTYcRmZ+Ru1pQoEBhZkjanqeeDx57ZYYYbmnJ1OrZIy6X35rXd+6eELL3zp1ft/7x/8A7/pN/1mg/6PP3vskM8P3vrg7bfeubi4Pj97yv1+6eWXDg8fOuZFMWHANVKW1kfwEb8nl+cRqOclWU/f69qoahBVik1WHBy8+PKLwd7enDmy0xyulTr377Wai3Dl3zIZWiWgY0MP+sYZdgi/oeonVdQQ0GO59+D85qklfl965cWnT827q/JJo++sj1GlrHzNEP5KTEmylM0Zlyq8Lb9gvD+Hny4zwvSa4i16Pzl2MqfVtA1KLf7Q2Dxkk2Mf8TV5towlITcc93j3sux12U0yTWVQnR3Z1tTs2oTus08c0Xy70JSkZX1TVpYsGcmU38ilWxiHAfTTHkM0FDtkxraHqewk8MXHZOF6K01sbt4GIs1O+qDXQ9HAfJnv/j0kyp6hmyaNdhLDwMb1we/8nb/71S+/9uEv/dLTp9dnn52+9OUvKQydUBubrmr6iLcvEBIX9MNbzzhX+srtcV2sMFnqNEqOEQ+YpYVhq9yJo2GlcVZvchZijts3m4oXOS2RiE6J2uRIWUa0lcvjtgbbcBQnLhCpNsC5TdaqlQKs2C32h4c0mxSj4PQFo2eCW++hcVZ61YQzI9qYDnLAM98GvbKfAsqCPEoUpjiMfyFsowFLLm17FdBBB70oTC03LycQm0lnXWuJB03MpzoEmALWEqJXMm9+e46xAiZvSsjO1FFCXAIL2mgBC5MePhPLoR6g8t1DJTdHPnIsWkszUwBhgnOlCCPgzS3kxZay/wGF1/8JK6TnCZ/cj8qA1qQuQsLMfNKGaXJmpQ+RkiK35tJw7EA2cRL427eczCgAc5PYYD3TE3faMPXuBRPSVDD2NjpGJigDQ44veJrXvjzUgGdsFu85fKwPXcyouaQazc0xsnnLvlghe9WcxUELWVyJ+Mx7UMamfkF2oxhmT6NVKILWegKvjVTUjea0HJLWWTwyq5xIdZXDji81OkugEYnUeQHfU8nQmYyGypWhAe1JA/nVfJKZX8BnXyp2aJaeTSvtZUijkl4jqpGOUEWTCWhkSym0fC/jWi206wvpgccHVUw+43xyypIf/sGCyQveTG305Mzu5IYpTed1SoomVKOcmlRQ8Q0V/UpIrSjzeVic1RM8gT7DGvZKrjTZXmfUystle1mK2b+C4iy04gV2UUGef2glIP+QekUP3wAGbAM9z9/zBr5ko/MkjQc6ykDXv+yzEg7Iv7ufTEtghliMv0KG6qQtwYLv4XOXDAv0jtde5nT/SRPShfq5RAM/yAdmxSx+7lA9T25BrVSAF87n8N09rm8ObE/1+dXh7hL8Wg9sJqlin8LyKjrc9HlrQ2P21PKYGW0H0PtoAEKaK02q902+fLxVrb1nmj77qwzcnujx7u08rHw78bxvIzvVXGl4crv/6Orxq1e3T+rWN7x/rwa5w4K4gP372gV9S6F8lZFy2m59fofxqpo+rDq6eHXiyr9aDbMeriajwqmdXdFYZbexrgAwmdWNtqcPWzdACLwgLt/MKJ0TH63quZqrpeE41sQYwR1krsur6GZ7bqNTMMDx82bO5WDGJoueGjayRY6nSV8ep1yJHgSIZLVR9QduxrCV382++DJGplSS6gcpnJWZIRzq4QH+UpMvGeTe5AhcIiZ9gCXuPIFoTLISLexxUqkfZIu/oCLSPaApbL331y3UAxEXoeWdAAPE6zAjIYXkPgtNuHwXDU06DYvwu/fPUEQzNg1YFB7Chi56qtkgi8jsYwDjyhphlb/Dh6gNliETB5zrWKBl/WuEPiwUtyilRkC89/6HQhoC6QQPvTnTC+7s9itV7gcfTH9FTc7+6p4Na7DU+7zy6bRkqWlTU9HmLYvfueoyAYXWWBJBu/bi/K/83M///Hvvv//08oMHDx6en1/+tt/ye9548wdPz43B7H788eOdncfn50/vP7h/dHx1fHRwfj4n29id4ZzHE1subZG3FSyNj2ZG2o3IflYOrMCVI0JS2xfuZaOgtDVlYfJlFni3TMUZOkyQAmtSdG1bEcosVZCnXbCJXr67cfR7Z1ODWqdLzi/XHTIg/NLDU9Ww9SJzgIcSKKv3Hb6xo73errfoj4+ORfzGEqRZ7OUcBG5cq8KwLsqdSz6yTqHejh68r6vPHraiGxD8WtI6ySTBE73XcPT/e14DN7eVZANZyBREHFQHO7x4tpMIbQnM08uz/d37WhfHBye4bq93Pk2qKey1HqhGZ9/yg9XSYey1C5jBuJGEUYWMslMG/obFDZ/D8xf5LdPT+GQuvjwP46SkloqeeUZzKb0699ZnuebsyU6nuf7H/ol/7V/4E//c668++dbP/eX7r7xy8MqD3aMTH2S69f31sjhc+O2+Z+wfk7V6KXrcTQWWZS/Fp9ulsN3PRGtqlE2Hnyrd41wBE9bAYa3qaT5olTTK7sNkisk0R3ILOQJy+iN0cuV0RoOoec3Xo1SQxPHSr3fhlJ3ySppHjJ90iL5n8Qpo64w5uoL7l9N0aWLY0S5eMmO3Ib+6cbrTwdEHCvztzfcpr5JwgINUyqgFllAuD0QQImfxfyy/nSZkhMAUgCfL/+Xvzd4T/Ml6rVuia8g1fDBidpOFWIMlvjckpF2v1UzVbrKgnIlma/9GvvhYqad4omAs+N57nKUtn6NN/K5SGQ1YFpmhFT2hMquMxKzm8BC53fsWWnP+5sDntaWuMCMYwvGvki3TYzNwjBdvCXmo4rn9SKn4qPUCkUoz0XckrADspdIetIUNoc8BgTz9/tvazdqNQTYonjVCx5zGzzt8doY/9Lh9lWRv5/E0oEGzV83PlvR3wo0Z/IzWFj8jJSY+7Pze96VoUzF9NQznZg9q61vFJgGKkKcMZUTb/cICg32jkrn3zgFzcfZLCOK17yszk95iwCEtoRczDn251sFTQsMe4txqB9Y1Im7tpmV41+1HlKyyWaWcdhsjtJwuF0DANFil409aDXcy3Fx+dd8+ct8PblBJ2vhJN2OTLalrg6MP22N1OzuQ1stZLQeQLB3j1FIhiG+0RDk77LXby5ev9z7w5vwonaVZ0aCSorzKc5PtUrS8sI+HUCZdtYqBUVgH5JtKVXCEdaivMOtaVYVr4iXOo5EbaMJUlUoaI18pR+ORiGJCnjbyA1MdZ61aa5yiH0cluTjP5vADGjOSqt+5/IZne21igkR6MnYEjxD+7JHr9fJNTsR5QYBGI2L7hxeRU+nN8zOkpQ6ga0vZ45zVhlGB0m+tPMJlzaBO189d4lb650J79H8TPqUI45XeGHqe3gbRcxw8h3o9LkTr/mvBfVfCzwdQ1gSwnfIvfOXlPC1mi19DPoH2V/xW2sXAcwnCNhjcmZNH6soTTAupySdH3Rtrvb7wqL6kt+VlauQpApynUlVN2gJU9tGqNTFDdN2rGBroQrVVpzmk2Jmcj3sVVFqVx5EXDqhcytDS88icvSqi3kWtammqAW0gEjBRNu2hZSetIBx/tzJJuBzPe23Y6gz4eRteV8aPu5IMW2SItwxnsZkUwVdGJ1gFJiofSKDR12iODFEo0TA9MEkUPwlTaK4aBI+QfEm1GBgQ6RqpHiYUSWoBjEjGP6GpUmxZGjtApwqZSG/eNwYy+hO8klW9+YeP1C2d4OivBD2iyl1pq3EJeRYeZtImr0hcVgYL5KBK3RxruRQT3lXKugV8CBgZ1QkI8RpDIGIfon49LR0Ci5AKyrkSI9zgX3xRy0bVdDTkshJPVJECpXMQhSAkWEMzTqyyyZ+oNvpU5c5qa+q6VBjeTDx1woM+gGYIkFYJ9jkH1mvY2JYSZzW8+513P/zwI8TVMD/+Yz/2h/7wP/T6G19x2mYHs9rXeewTBA/m9P2Lk6OTF194iKBD38iEdiNcuBj2EpNev9dFEwGlm0AmRYJ8AVb45JEaTFO/uoTKwWBMmjKYXF3ywfBNa+JIKty5kz4PALJXBa85E8ERiCOtB12gQ3v0b52GdH3qwBhTfUd0FWpNI4NT8qaldNCOOOWiXCtTLGFPUrlA00WWoxmJN3+1QRu6ck3GdorGVrARer1NwiXvxG6orJBf8w4yla1Un0sWCxlDNrZ78ML9B3jEUd6KTzo48JU0FsQGMR7DLCamlwhGTRg2n1bPm+u7ur083jvMVw10sq0ckt7DyDxpv5vZYWr461ZPo/7hxo4djHZ2dvDwoaNBdY0Uk7LxysdTT77+xiscF8N8+61vHf3Fn//B3/obL27PuVeWrCFb+5gmw0iEnIag9T58idB8qgk7IlVWCF0zBXj6SuLaQqlnScNuA9bcojVDtnLOWXCWdTZyuQUMeZSie5eTaWDRhylxJzuGhNewbkKKVjp7n4xwk/AuwCMA13L8sKIzrSBPnWLM5MQyyxiCDMdVNJDdIVlcVRwi07WMg5EPl/xGoxJalXA7dVoTU8eA69GSNPdC4cx6hs9GkrxIuIfWkjqMqd9bD5U4VMZPL8hUIRzASNZPBuIq3liFNvRchQ8Ot+IWwDZyg2wDmkqyPSVtirmyXBMzFBHIGVtht743kmo27MXh0GbxHpRBXOcAYz6FDMAwttQz4gAoktKN05uEqo9aUbk4O8XDrfUzdqVrTMuRq6uzp098J5hcaTEoieWOpqRdJbE1o5GJUbhOQRXflW+YPDo/UytcHz54fPrEB9r0bWHIlxjbHokMg2vtp7O+XDETkZ4NOvrs3xW/feB8Xwfk2aYwmZ0G/S2TmsdqgqWAVEek9Ze3R2a5olGUZLxd/UC/7B2Hokc5oiTDOcDS6ItkwoN5fmdtOcQpFBmQJU/esYxc8SgPwCpT9aVa7583hiecYfZEex6mwJSzBEoPsdLOHONWHSDbmeA+16ivOkZX5aZjNbmZ4+e+dQqkg5DWrGuFs+mMadzv3J5h0l+xVs12wAlQz0sfNbVIhbbmHQMzHBe89wRyyaPuOOMfPFz5bjyHpbqzkjpxqmIWBMgBLgHI9fO5+5QeIZItLYV/nNN6WAhAlWpwZa7zgo/nMQoebd/BPUdQigFVAFaS5VIyiJAtJY8fjMgG64bOEFtIKWLRBpG/KbSfKdvY2SAXvEERxPe4FpJF2to1WJwdtL1+7aRbqOd+cb/EKGxSjwY7vHYL1bI6l4D+gZmYdctPpLjOAx5UATIYV2MJmWXNipIIUEaMB93sn9zcfsVX2G6vz/Z02hX24j3VV3Ok9L6vP7bhD8k+B1isQoE+O85fvxqRjsNirwqMctdJJlbw8zcVgCkK5EIPXP1vPXPFEr5w1vQhRiv3IJo6Y//47abDFp8J2myEOL1/FmO+eJpiJjSUGc4/mfPgtVGTEZ7dvbdqrPQBrF4bLRnNFEUZVl2jZe1mL1W/6VGH+ODdKuPbb4icoEqrP6vttSDnI1M8bjjyCdMVmiLeYXqVnjx4CDGWHFObDZ7R2JaBnFPp4dFrkpvgK7cpI1dbgy/F9UowaNZiQXYFcgikko16CqmEJrh7KTwG2jDA9Y5t3tNYt3eqdZC13FMWB1gzftUdZlFl73r2kS8UZyyksRTa24xZ1CCHutlfwxVOHz9L1aQQCmYyNOasLGsEa1hBjyR9ENqJh078EJFrQ1qitTZxqrbySFWIMQYad3LZABVSu+9Z3cuEaqqVzQiM7776Cn53dz/QqHe+rT26N5df1hLc33sHK0x5DlhwMKWs0kjVyz3UJmv0k3AaZEcnP/Lrv/+P/EM//cZXv8JDnpycPD19ev/415lM2Nn9lkEXtVE1M7tHk2hl1p1ISbsuQeXDs0sAOHIWOLd+J35gN9YwAW7W66c/AzyK55R0P2FsPAwmFVDjU6HKsvlie+uuHVKKL0oZI0PObJhcm5aEwJP23/m0tx0y+866Y75njsvLXLMQ4yZOt9BUcmjf12pGzbzlkB3mieqImnra5QLS0kwtkuUcOeXGYtuTVv6gREGgRs646IJtPWB4kk/os5tI6lj3Z6HztNJNqg3IqCT99K4BwrQY4dI41xNpeqiar8/eskNVpej8Sk2CFM8naBfDndkYClOMG8419eWjyHQ2LeloVNgk6H85KGgc0obXYS6F995F+g0ko1ZV0qmVlKenVk/5Cpvs+/Krr8Ga8nRmr2/f+NoL/8Q//ff/r//tf1th+//+zH/50tdefvC177e68ur6nrR7jmFDFHEpKifQPyDA/v5Tr2WlPIgpsla2ysrhuef8pxfluqQTn4PauXqp592PRnYNNSbgGy96xUYT9ZI/RGvP13wrR2l4/pCYsttrRW70Gb2lDUaX2tM88IqaF3wyp9HWuOli+TbeRsMo3fAnxpwjio5ITtOoZgP56QfnbGvn9g0DTa3nH0GSa82rt78OuiEVUSQh7ldwo7C14YzvCrB/BtbH/DjWcybUoBLwKYncqq3AK/Eouu3UOh6SJS8kwxmANXZAhuwnGllSKzFuL7/qZcd3rPObw4l4ia/fxI29QBslhl7AcL2hWLpgva5cXvF5XLDqSe2ybDl6gqLcksuFB8g0xwdUZwf5KuNJkKnQRYHJdmScVX4o9IjZ2yYIwIadEhhJoeUKrga9QvCt2ORlOQcZ0WKp1rM3+DP4GjGitWpfR/wBuH56yZ+2WS9kIC3DVwDrevFLDMtMjiarrUdOATpmv+emv0Z4fEqUxSQgv3HZLHPrDZwtqionUAv1ETZPEFdjTwni4uO9X99T/Vijb+Sij3A1Jpj/kWMtAxptJdSqeVXJFXkkzFGAyiVEz7WsEMFaDjOcZfZIL0J1E4OAauXT+d7hd6a8lUBdinFpBgUkWKzjEQFp4BmPk3TDSbYpLrB4n9f1Vo5cqdf2zWFudkSUqFJcVlY8DFNMllJH32vCSxN4BPUpJ565w5NoXxn2uY/mMzU/mjPHTRUey1kZOHRxkNhpQ0ZXentJ0uGzN3Ecq9mKq69yX1c77xLz0B60lmPHyeRZegPc/+95iQjPXZwXz+kmzUPiebNG5g5oAkcraKyUGXDpJomErgW1oovaPLGfYoZ55WbRW+BTbIXcwW753qQtyjVJSr8lGb5B9VzCgfzVbrG6LhjXy93DNuZv8DfaW9AwLR6z7kTbqDAaMdjVc8RSUo9ye4tiI9+Es61VVQ328lxl6VmDT0rH+1SO7LCrfucxBy2kdFK9qZkYsiqFimXk01bksyCDUpXYKWl1HKgv8wdmeo0d7nEENW5yzArYMkQmBZ2SrLDxvgL96QDz/eCGcMbK8JN+K4RxfX2CxtScJj9LFHYcqBcrCsgQqGB5HFVg0w5is3NLXPMb8ZZYAZlkxJ29DwXgIGm6WjweLpUDIR04oqRJpgGZDdeWzaX4vTw0WRlrWhA7xpib/cQfP76SikkJ6T5t5SOSMRokBytZb1ozM0webLoTLQu0/cDXQNeSlTjPCXyYGnlHjuATie+uIsEj3tOs+8DTuMyb7pE2iHnYtN2JD6LVINhyxGLzzir1qgA1Jgz7FsbEBbWMAcBNIXIr/U2dhGZuMj1mDTjLRnpCOWVyMimtGL0wY0BGjavkMw4Na9mvt9gl3lsysL2cmEnb2UgKNVaNxjcDxUCbmlap0wv11GVshM+/akI0HQJYPlajkIR0YS4od9jKTksqjz769KO/9HN/6YP33j/QLL53+A//9B/9Xb/7d53a3aXF5jNgp+eHx19ysGQnsy8N1qiL9jR/y0ctbMY8YXjP3JbUKTTpS7iepeyt0MmMFbmBuovZpmboM64OO5xDNQtIiP5NNYcZOdcqpvOak4PZjSl99uiRsWZfKGvAJrOvcyWiWQXvFKGlSy/p2gv+TXg4Gki1OOxuGQS6BGdxsU9zU/inEE5SU/Qntv2ZVGleLgXDn0mw9SV4/G6uUHyPK95chAzlPBe0fdkkWj/JPnHsy1PDBnJWXHPVLYvXDhOOeksU1aZnjFnHcYMMY+ylpjPrk5gZKs/OOnOEeKn0S5kTA9pMhgwX8USgRXeEGh4jsmSs4Azn6bZ8IMq5MtMndt0U1ZszS68ctXx5ef/+fV+/sHzs8aMnL774+tWTnYcvPLi4uji8OT795PHe/Uf7L7WbUwnzf9PlC+moZzxEhZ+kyCsR9VcSPrLDIeEpZLE7zFQwK3nlCKjK9RgFoMqrToqm02Z4oQZwQCmU+0jCUpc4vYeh1k6Po4Lug3boSRVoXmselpZSx+bfIPbiM8Q+MD8DAbQ9hoKPPGKFVTGvB+ZvijCPpVG+QRgDPW6uyA1zhYZnKpU6R7C0+mTWVbZqzvgoiyAHS0Aym9B0zYTS2vD7HFocwJhQo9Oesqpxezy/wQ78UZrU+TRkx7kl90ZLk56XCMsgW89lqwvFaaoGv1QLCaJlSAG1hhsC0OoWFCteExD/tXeTu4zJHY060IiHQJ+/VpJNyETCIM2gG6yQCCBFg1meYlcECBKquPjbNpmuPt7Scehy6Uv48+vzT59+0kG/5Zal5zXEazqHaFupyexLFZv6BP+XVvRImzBDaX6HGVTWEfv1psqUVGyxSgsOcAF8DLR0MKUieYKIlw3fw9vkh5IhbKw3RHnstF0nitbAKUaIbtgYieO2TivHWwdyJAjS1YmhWVcc+59FoZ6ni4GK3+RDNUvVWqgnZQT9w0oliUo8DyrJu5hoFdPoE+pV6hOOUBEYOiLCLpe4K5rBJBJVPUgJM2w5RqFPVgsqGqjJiLEJ0mqDjJNMacm+uA9qw+Zom+DrVeZOuwK3sV5SDyzxQG9OjswbfnL2CfGrXWVAwvUf4GgsbWyIJtOKD0Gx/X7xutPAcHsXG5a7a6XtXkui4FhMvl56TCWfQ0CjCzKy81z0pC35BN3xQ6Ob6zmYbdB3/QKelHMKkJG2hWYb+l3gdwGdHW7VppWy61rp1l0IBHJoBEscUlVcMw23KbrbHNkIJHzJHMSAlh0T1M2/66/yMc7Mjq6GEkfbJ+YOnd53cnRs6kgTTJE0CRCGClDGsLP3wzZO6lY21M6lsrSa5JUEy+YqJHrOtVUiKdDOlUZ6dtotMJxa35ZfAzGDHHjPJbExCSqC51+FcU7Wh8PwXAW9eW4DFH33ZupAMSmkOsOjpdJOcpzBWZvzLdvgmCuBcPa74SVV6d3YCiCVEm7QFJ2usbHdna+UYhYrVh7opz/78b+sNjk47syyitqZ6TCf5Ttq7gwzl6/Sy82B/nEdJ96lroIKWhXUufKGLwQML301mTTOE9C56usBN/ute8MiOoSZEd90FttdcdNCRi1vE60HfVG4+ovPSLmnMS5p72k/RHXn829yVWzuKkgcdM9TCVK4oa6vBSnHgMq1TzDKWV+DRJGbkpJ94buehoe9vwbz7vWbuv/1KbAnnh+vkY+7ugnmTK92jo8atBs2VhMZA0hlIqMHBibashwbUo/N6ibhGDGolRXIZgyAXGDB+3CD+hz3vDn3WieNpo1Zd8IrZLygLmCK2LM/JAlL3tA22zv4sAnxJk/HeMtAFyfm/eCzTz776ONP7p0c/ug3f+QXf/6XvvED3/fjP/HjFola6A/oydNH9r7vmze7Oavvw9hSqNRsPt6oqgxqJSgjZ1BJutsMklK8RvFH/G6T0O9o4+4FkhUgYZi7VpIqoUrB5Rvo7j0bjyeTITQInCTThLGi9PjRIx0AH6FBfkpVJZBWLnzu+OLypZdfxro8bIRM3k2hq2KgsVEGZLOatnF0pHaO2eTmipWxq03BL19kjrD5v+MgVFyo+m0HOq9DKjOTZymnXFjyLpm2WL/Hb+iW/JN6AyHwe11b7bETFGZAV/rKkEEHIwLi2dkBg3TSOMfUog9t/JvLepjOfjeg2VlSR1etgm2u34DB+bVunkUIn1ow5hvGsqvGp7Y1u6sllEhleAqJag/zOoEVld4ELyli8dY3zgVmjzQsK5WYq2tfWzs7O7UE+eL8O3Yc6qH9lr/1x/7rX/ip//hP/acvvHjw7V/8uZ98/Q0DqJdXvizBRx07B9Z4CiRDV7PqcXk57VaGIb8q8tN6mPbO6L4N0fjMa258QPMduUTBtzsfGi3Z1WA4b70nHfMVmYWRGavyrl5gKCGmzwo3QadWGElG6CRNxUsfo4xU0T/QBnvn9K3r171HzW2ysSdXygiDjo3eTU/xn71itXZVIFoYUrrXFpMr+avR/WC4h47X4cFj9V9/WTltNxOOY+z7BkLD0W12YRf8nYEfuU1PtZv082wSatRa+bUftMGFYRTBSl7Tw7wE+sMSpZOw1uvZ09OrJ6+04ProPVs69p13DjqGmUowownjD87vdy2+3VOZd7g9JmUC5EcnpqAexlqKq5we+sKb9sOCLCsZQWU5WClxRF+DLE9cXOQC71ri+BmxNue7F7xxRkVUN7QsRtrrLID2IGk+zfk/R/ceXp69Bp86tb6SpgAq06QWRlBQSb1neH8Jol8NFV116CfchDWnQNvw13y/NWOwGqCOvH211vn+O6tCa+BBtKWL0ks6+ry5+Epfbdv/yFgNV6cgwB5gtpIRVLx2zpuzKaPRznTVRcUUreBSEp/8NXl5O7M0zjiKhZN3QbbvAOOhSWv659a4yNmL89dvL02+vTWqWhVTuOsEqetq7BAe4hTdTzUBDZU3u1fNCN0eqokmJrw9Ah2eoahSa6xKQGxvrVsq2Br0mX3r1191FJF9IKUcm6kKJmo066lVduDJcvuUCRusa66VoFmGZJ8HV79b0fU6ivsH367zULdqrbJLhyEoaxSVr/baV5Y3/+Bf5l64L3uY/nn6pRg8elrxRCLbWRyPGqAafoJ/dsVr/Bc7Fwzh7bm7/z0LGiV67CQfteeqg1ayycxSuILrvlH+Hd4VFURNAj/pckEnyMAt0YJZyYLYvkySwTpBSQa8G+iVfEN7kyqwTcg8rlvsLeTr/t0QzwF/TjHPh3/Xc2gncGxc1qTGzCjF+YdPTMbm6GXpeHEg3UotFhQsirEgJU9ZCwucbICDdNUq8q8KItt0+P/0HPetwBvUtUjkmc0/HO2lU5X3TQ1NjxDe2vw8KoOenU9hFui+1KgNxwc0ozSaNcbcKI1YNgr5PCxYi8rja6cJPtwwdb5HmcWTcdlapMuCyFaeFqXx4+NGzJ+MtWsAjaiiB3ZI4kYZoYSKR83WSv9SCrhRo/c7dYUrJG4Vp0boIR6J0ljhMS8oNtRmGPRFUq1DOqyxiAfBtdiHHRQrrI1IwVKETkaDu0QYtTZKSSmTHbE/WcezwEQPVfRtzh3hl2bhicPFfMQ2UgiWfbE37k97ISOIHR2UmI2JGf4tM4ye5No8+J+G/PbC3dSctL8r2TF2e3GhOcIszKKwIJ03GZgt7R10XH3zCEcySJtJcm6UujLYZI0ZZhWrkwlVg3abY8jYP0eczEulIcxwGmaGp3zCkRyW0PC0b3nKZXrnCKu5qrXUVyNqqiir8E2CNJPeohm+7CDUWQ35TGrv7//SL/3Cn/1z/9mXXnnhG9/4/m9+80f/0D/wDzx8eJ+UlgbpGn326SM7YUJamlIPhtFfoSuk3s6VIS2CqKCnAkRAZFRIEumxwWSXZD1P8g3OLSZczmMJIyIhJdQKYQReKwtMATrWQC91NnWEdh+88IJwnw2m/EU3xHJl38eP+wwtm5kcSPzRLqZUVr44o9Ffn6Exu9b/CFd6IurJf8DuuYcSLvZHj4IaJNu3MVqNWdVTVmb2w7jXRB/Qonr51a5oTOxzIDLvmZoS5rnE5eZcK1t7Q340toHyeTM9vpqPmv2njx3Vd8VkjcK3n6nDTWC01t85kz5RzFpvTmnv5vo4UzRpd6XxopApCTOOgZMyEu4l2iaX7rgaymlstLZYYN0VJoyXhxAU3F1itOq2+c9unr733sdvfO37Pv7oY42PFx6++MmTx3/lL/zcN//Wn7rvYCatVd6SLBwFnzG7dAaHzFAoIHROyaVxSpkNIidVMY1I6q/F2sZL8frttXsrtXGg4LbjowLUt4Hd2Rad56qG58k8bOeXynmhYVyKn9LFUWTJ/pV7iRbMAITCw2gsdyVqcriHhab8kpLIRJz5rUkRkSBEEYnrGYc0I8lCcyHRGVxDceBXSBppjXKmMAomuGIz6qvzJ5PJPNlabkK81ycXaIs34dMoUTWiYUdHrrYI7fnaK+TAN1THyph9xaE2MetQBB2kh3mum2oHIsE3RX5UsDhe5rxRwRIz9l1LiZQZmVFbIaPkFOGavB7ICAe2hC4IZFTW/+5FrqBNtk3YBi+4LZEFCIFyfOlDiCrm6qOsQHoYaKPV6HmEBg+4a1XsEs5PcPRZB3JSzeB8abWzi+NPFAFChUuAEUXTAo4Dko9UmEnouifpogZe9ShuAnL5mpkGVoRCorW87O2ZkpNx9FOLHD8kabtCnSKFHaoclPORVRbaOd4O1Ud1qdv4rjqZWYA5BIUHzMUhrOgYz2j7lDa4munAoedLLbiNnhxWgHjd1jioeoAcGB/0uXSeeStKOalbyQnV2sZnDQBSRnbjt9NxGpgsZ4zldgx4EEE/U4zFBqQqD+W0EUpQldrywbI5FfrJkg985o/S078mRMt0ZVYkky1K44jq4VSsumo/TiFLth4XjaJKImC51oEWsFRuD0dFcLiXaKD6cS206/kL921UOMAtbW4QLdAJHITPkko18CPks+DF7byL3qLe/Mry0gyhfgNbo3EXja/Pe2Fda13+wUe0dHvxxiYqPKOwevCOevp6kOlvw02vm2tLeq1KvFnfB1hgE/X8uv9J8nkUn+Ol+M1aqIV9Yt2kueyLv3exVJ8c/q189VBu1C4uajLac25uYpKOdhXHQTzAUla0d/be8Rmjxos8A24CTxG68I3I88Y5Ff3VOKxNJZbDg54/NYGrDqs3r5g6WrwCXzNxmYWa1A5JHOKBPesVTMKwjV1hdTEQS7yvfkcBXaP7g7fwooC5dKij2JS3ShWdrLeyVomZf5MxQmtmV5ZVKDP6LamUU3EsyRWXwT4lLf2QuwNkcJ6eJJUeywgo5RNEIwXV9tK6WWVWQlxwibNckl58zVG5W70nyObIGklIvcU7b0mTKw8/zRy8TZRhpTwbO6UedfHrcXHwnhtQtY1zTjxNL6eSP43p4sROzqazcjgh3aHA4PTpcX30Ts+BaMg2LChZ2iuBRp/VsaHU0tmKjEOisA3VJ42Cz4/fXL/iQIbrax9ZdPaDQWcqABCDqtZ8fbruKMadq7aOI8k4OgZC6xNUnBFXj6BXiMzkyLG6jq3CyK1yfdYie+5sDXULq8HtmFzTUGYbDu/Fd3GdjOHXoJUGS+cOtass56/3wV6Tj7waTDk/9Q0C5gvGXMYE3eD55NOP/+pfO3v08fHV9Yff/NEf++f/p//sN77/B6zjcp61dOenZwRR76WqDL/uTMaRMueyxtfjkdmzfuXLtIDXisagMh0xkxtxVMKCelhfCJn1uCv5ABctLmVky3F+/MKH1JXQZXH7Nq53fHWbwhr7g7SabO/o8ujosyfNCEGQCh0p7StcJ+Zj2vs+JGGuUqwg1xbMUjVfbs1fxb0+vdNprA+O82ET7uHdK1FGloqD4Prb7fk9Ygu6Y1VaYCozCzKEkZyUc19yF3p3LYHzyePZJjF6O1dfSz/LE3pd4XepPGDgojOFdoMZ7Nk8y9JCdgKYbLj+jIFmUnYcOqCQNl+1C+Bq933LB80TYl9z5GknHl2mEEeTdFTLZ3Y6Hu35EArFsDdLxF+rSXj4rnznGlzMCbJROBtEu6Lm6pNSPcSucVY/AY+1xO0q9AM6M4HWQlQT7bWTav/i8sm9eyevfflVd1l2/ckHH73z1nt/7aXPdo9e+eprO/emYUFXBGbAaR9hCp8Q+1gZuo+6mbzAdVsXWL/x/Fe87e8/yp9QBOjFHnsJIjEGjl/lFpS0QxOa1pHVzqtJ4U+DroF5cBiXbugv/9Fz0mYeMRKEsM2D4m3/AKWOdopObQMbroFPel2VnE6re/DAxktP90B7CqS+NzsnGuxzWzrdAAQT/GLES3p3PqNVV+nILEr9f61/GXXJFxhE3juaOYep0yhrKTLPtJEmlJ5josu98uAAnSAdKbV0I3zfin8TZsbJRiApxClaKTaB46uaajgMURRwG96LN/L8m3k2aCKYDP6POIynlKU6lafzHJWQzHVz/gY/4JSelFIMwiQ1Sutbcoc3+3+tUDqPK5FR2Ig1GCIivFqumLxcwsRzDJQZ8N3unn71+kJFfgmnpf6t2bqXfLO+BXLlbYSKrfMH95xg3/cWDCpAYelAU8LlrWyQB9f7R/snjlvuXBorbIvd3XnEbh1vxgtZdjCfZ7k+sY8oR2LO5/D80ATeh1gyx6geSeQ4z6RjMxYpvaqrpg9PZ/mt40YBJJhYKtJkyOJ3jPf7bKniwq59I1x12JeznITWKTu0lSyY5+wbOLDD8Z296yeREqVrl+VWViaL6r/4Hy+Vk9ipyESxgmkGbGkXG1NZsfRpJlXFDefltqSqOSv1eyyLOJ3cPoBGZhWM/aOPzEJYhyiDaDWblTwrL42MKKU+DQ4sm6rkltyG4LjZNbJh8XTbAfb2v5NTzPqoXRUdOcBlXgUEWU7knXBiww8KExmvhMKeV2mOPlS+4nnZVXDLPwxL+TQ+2cj9YPKyqeO0XsIxoRX/Ebno/i+ThwrS+LCoV326mAif//2Uep6DIIQtZwIuVuzAB4U3PyaJtuH9LrrJsaE2v3EkcrQycSLjYKXsZ8pEEP4PaGgXG4NyQX6v+0KyoDfxdylW3DbVCv582DYuYotwykm6uTZoC5tMGZ0V52GFBBbi/gub17LcdedXihIz1YOfjeyTwi0vV6PcArLQGiRRNTKNyp9Godae6i9Th751D7yZshZAxlSbtXa6csUykemp8hFLGFl1qaZ8VHKf/nmI12DmB+Dw1nv5IgaSClIRoZEu5N7Gc1UaDN9NYVeA2zsVKldK4SIW8UmkWolo5S1XE4vYjZI3gSWaxEtjwTSYgd36GDUVctBaTyI8dMGPE6x4Tmlc0sxEJwzo/ClkUCPTFSJBHuZOeYA4mCCVSYVzEgQZuiVuPMfoWOYCcHeldDz0H0NIkDaVAnRPeJ4nAP+KhZEmRy+RERNrC0WqnUwqEwk7EeVSvTjc9R2uxAFjpKHMXOlGluFW2KI1QDVHKDiFZw2t+JJWosnLLLDexxjTdJhwbigaJIKpVTvVk21kt5cP7p8YpnI2granTmNZlI1p/cQI26vKCZiFjsYQHem082iSVtvLK4ZCwe8c/+Iv/JV33n5Xq+vs4r0f/nU/9Oabb1oTolvLLI4ODz/ybbyZcYZeLmQF8wfpaKx8LCjFlS2aHZbcZzr+j0InutiUs0xrnoqUsuyYawLhHCgvYQSTzrqq2spNbNNbLf4OihWPal3wKtRseSIpXzV7cP9Bi3NgaoQzc4Jm8EmfWlVlQvHAUKvv2gpuJ33UAFSmFtsCJu3wOjwlyP5efQuLHzrHKYW6z/8UG9r1bytfpJ9dnsf0SlCqflcaT2OGi42JmdvzqTcBg2SE8lQBRljpYbK7e76zc+rApvr2MtwiKMuA7ltyaAGIwnP+5LOTw3v26mgcKIacojFBJ853vEUVpBpzcnjKbY7v9rwCM8xqhaiJ2xE1BS7KCA/P+BoVePUXx3KCGgKY1HMfoGKXPpUkzReTqDd/9B/5H/+Df+SP/pk/+2f/3X/n33nwcP+jd95/7Ue/qcEiSm5W8MYkYE1eWMeVcL7Q64zLGebhd1XnM2gaPxoFhYASH4tledSDz5F4HmZ1woermhCNoRYRxoFIzv5N6Lopt8W7wjdgE7FS5H9STFNJKMXuFnALP8gyvJgOwqAnoNzTMMTGSjPPkZh0iwWEJiDXI2JsVc5SKefXGtErJ3dlh2wiBAWz6RmvUCYa1iIjUAAo55LBpmLwk8EcTP+orj4QIgQgDrCRNnQQFlMRg2m0n9SLN2ESrdeYHTaHivD+JdoCyDMPkyvFJBzslVylflDJtYjd/VuZnaYSj57DVvtYQ5rg7GPDQYQnWVy4ghtNIgGs2mGuZdfNoxIiWoTqv3aldiSsDp93OD0aRVXj5JijCwwWC0N0nY99nwRPjQYW22I87qUp4UYLDo5t+vA94U65UQ73TLFYONQIlLyQAU4A0kQ/6qQF27JVPfeE20ODnRr/jTiUc3fyYtwzisu6cpKmlJVVDWWS2C/QoULoHOi6GLPfP9baDgF7YxMYMvfTCE/mh986K1L55COpTRmqF1Q3QfMQ+X/rmWb4CtK4qUWOpZbQ2j1DB9nCFJNN5k/9JRnLZl2ruGFZ3lR4p9My4qRv9jp2yKfSagNkjXXW7u+4Txnbt7HrAAWW5JOrZbMRr9np3oBXkrAaP6gRUH6pX73k5Ksu2uWfmEKqGmgDQz3ScShTLvAqGj/RKEAQ2cBM7moSsK+JVEBKtL1K8j2ugYiSawMSkaG04rwtNOguBgaNsA389mF0J/GCDigGB/hZCnXS89dEG1VyDRNh7aHw2xtdWq2SNzcqLSiwMsQ1fZoe5pXdr3Gp1pN94dIj+eK1UGxCEXMKRy9fnBO4437B373Og7Al7NrFX/oJmoeNSlPApF0I5vn26o1+9caWLN030Z5ScphGm8zANGlWwnb7v+s7x9Uw5xp6+gCKp0LMgioEU+qzCs2dm6vDwxPnwjNAg6tjFABrOmgZcgv1tjnQVhpkeqhVlCKr7VavG7oIxUu2HzteLt+IUbsg5nWswTsBlPORTUMHuRbEzGummauPhfBxqIZL89ch7pdLmH/Xzqcn4XkNd3VclU7pBnuziHESnoUvldU0Gmsbr9pyecUn4TMg/WjVrzQNUJWML0s/yjqWalnwLOHTkEbD6TQaVXvfwVAerz8kx1kPF1zZ8MPGvlMZt44QWvsKatdOTNhz+SNo6MOUxMka9+Br7mMm3vf66rAETQhqHMVSBT1WgNR8r7ZtuREn0kjn7v0a45MY0zmkxPRghTedGjPJDLS2uUkUtReHrtjUKh5o3pSb5lrKLxjwQ0spF61h1IM6WD51vhmXxqsUhOUMpWFAY5eBL5c0QlKWEf/8NfpkJA1tQCeXcvYp4qa9IuVqEhdfvTCqwzZ5MDQVJuwNYu2fnByeXZ4e3f/owQv7p+cv/sgP/DB3Zj2bONb65MljO9XybxlJyvXlWU97e+dVV72WU92drRH9lnTY36lZXI6k6ZjznBnES0Bl+7rCm0N1n4hC4zsddSFQmYl+hWejYapKSFs1hARrkU+d7Zud06dPMKD5Y7+EFUFqqLU8K1bTg4wI58b2aKlyo+4yJvpRxdbYye3x5eUT39WSXZNhw7GkYYizUlejqvssCVQtxc2oYvEbr+t1QONwI0yCQCDANc9CenUMqVF8VwSmTBhnejuQgZqooexJyELguV1SdxCRpUkLDHf3Xrm4vnl6/Wj33oPH2h0XFz6uazDs7PbK9wEMSTtYb2/39PTi7Pj8/kv3Xzi0Svb25thKj/qlLXXDiMt6CILsHn6ghT7lgOWUWYg2d3V+bnHI1KPxNCLbdDTspWrlYEknLCYJOuJC7G1EtaZ5gbPiPQvrzt5847UvvfLyZx/vXz39Pz25ff/Dn3v73osvfv1LP/h0ENzevhDGvceTG+EZ71dm4sy3c5v1NqFZh6bp2b2dDyt/jVzKpGbWMI6JSv1itIo7SSubJT1mCsZ6FZV8fp5hGfAyhODyCXHfzZ2NlG4kmqC7DAJR2gRzhQCFrG0DttAsRYnMujQwKmkpo1pjAJUab/mlIDZp/WyioyxGohIugHAqnUla0UswTqTRqCQlmShNU63Y3I+HZACUtBFq/kMry7L+nIsqJrKTvY6smWfEbi5fv/UNzNtfjnpVEQx1pxGO3XgYZYU9BQgcPkcNQ4/Nxw+49X89b/ErzSJwHNPBbcUHUBKXFdLNOYcs/iuQKlXUzIkZwE6bqW6TeJtqo6QQQDr/4C5Xc4e3x/cesm1xLnOwVsKpWh0dYNz/8KjP+3BuQEtCCQnptzqIdJrXPnV9cdQCVTWsDrdaY79JAC7UobpMsQrfyVa+tQhDzYcGEfXT3MeDC909sC3F4KLVlylRWtWT3IPSRdVqVot58uNDN/GrsqpDys3qMl1lcxAd61VLBBrKvCVByktbrjQjv71h+9onDNCqkLeVCHaZqqWPNJIln4wYo8sNp269ER6otk1cpuVBgXp5V1iEVOha/fGekfgIncoN9hWvd2ICRKFQq0nfxgbdBPkGM3F0lY72Dp6cnsHka2AaJ/oBGO/beBbfq4kxWVZAymCHmP5Pkyp1wTBYNRlf8Zys7Yz1jHrWtbGMaUGQSUT+oCsFZQC9pib5HrivORmq0HqhNd96aoxywYDzEMxO36suS+Y+v7sz9j94C91euOkxGpgZyBRb/uSNaruuunWiFvAm7SSEar50vvYJDNCCHBr1JMsSmAd6k3J+Ru7kyTZWbI9l8R38Cn4u6YIEEN8r1SZ2C1TiitRcd4Eeho0RMfR37wuw+wZ4g3zDtuCl/2dwz0ALG/Bt2nlfbG3IBSIW7oV+SuwErhjA6b06sz0AjDLXMeByH/o0EkAyjRUJGo5qSWWfKzJsVY95XG2mjJd961MHMw7dM9vKvIYHA+gKaglYTXnRHeIld9xnoJv3u1BWMkU2PouGexxzWhIAF0aF8de8xRDLAWbnWw1s/F3CYWT+mCxkocBzaDdXRXYjXqmGwwlJNEklFo4oYiFCploAU1KJ1/2YGdIMzCVN8KL4ykpKbA21iXVbKCYMmKIrRQm1uOElXlJ2pbPQ0b9EhSR3pXUDIC5+8bYRYJtOUtXZAo0XTiZWBq4UERnGGk0BXHOwSeEOcvLG7WJI4Ljimu6rRSoOIYKTVRUCBwuYHPFesfIMd5oawKHbpqt5rR2ZC0N4JCzHKK9GpSsBJRtuklsUslqs3KU6PQ1VrY+/q0qQCbTRfMESCM55AJ291gqqC9NVu+j28vzsv/qv/8Jbv/ItezB/6Ae/8Xf/PX/X3/l3/T76Lv9ubh59+tnZxRl5NvrNfrMpFFMypINng672g4Sb4TrjLlUQIEbMBQtAscA0qbepV6HYIIMqtZRkcyuvB0uphE4yz0tAhjKmVWZZ/vnpZ5+KR8Mo3X3fCW7FFHJ1yAfvQsts5Wiy1DdIDm0FM+aJpaLxt3gAMXa24WkoZ0IOXDo6OT5SNzGU5oYqC89fW1Mt4RhnbA9tgm1Al4iIigLV72Rnr3J8QmIjqndJAksv6x7Goia6AqBAEEE9Z1nZk7PLT86fOstfwCePTvdfaPHXk0en7737wdX1x3a9Hh6enewfPjh4cPzlq/snJ/Rx6vCTbLepJFotjzLaWs0kPTK5HuYWwOFKLOWcnZ0FlmUZKazL5+p1OI1B1x23IroSIBVtCmzwJM2ykJoBvEfvfyKv69bd3Jx99Ojy0cXufdakkZItopVWa7wYQElD1jfIavmhYIzSxcM4PeB5j4fIoEsIUTVKgWgsxH0liJqldYSifoSGSrY2rJYuZH7i2t+ExN660ju+t9d6LGTUkAHk7HgHpHiD0k3kJPAK6wZXuOcxhdSKyqPkAAp25Vyfv4SMtu/I52awN2V82I1HiUvefQj4oRnKGyoL9VBFh45zYLrTGrwaW+kleZeJhgSK+ZkcWLgX/uq4qRvWWq1MIJik3/LJYJYSc0+R3LyHoJfcSsZf5uS+RTM29w3o8BoLg7DoGAvXXKPL0QVAf1PMAae1IAvrFmODUjiRBwksG4CNhWOPdfFWrmryDvRDyX4IOwWMMKDjH2bjlkG6qf69qFWqWNBAJYMDxN9xNTrHnF9WOzOZ1tRbJVSNlCogUr6Ae5SLhtWsKYW3vYWrbuHKakjUecs+WXK0IZjU8SZgmiY5Xrkw43Q4Z37sqGI6HnTs3y3FJUWZppinhwQosK6MhxQKzYQXkai95BVHr+qw8/kSMCadviAq5zBZEGtgQ4fdxFqXAPwoZRBwNBMxWONeUG2a1DirlPJn+kMmRPZ2HLBmo48ywZlf2gC3Yx5D5Vd1Vt3q0orTc5NXnN5kJ0y1xaJeNqSbynrbyWWJhLSJ2/bFY4vI5UYcJWXyTgZXHYJOUzKuOY+9+2imqvG3CIQ/6FS2LggEb7jYhD0XXQiE4iWAd0ncy1yDrRfh8QrZJmbzU6ptyOZhm/YuuE9+DAv430CvZN3jOfrqTbehQeiyo+ctjs/9blRSmHXVz4/9wzDX59LdBY4qtm/Bbc8CWonmLnolDq6XZ29bnW5lGHjRd0meQ7PU+XyAb6qNnY9wId/QGaUyFczVvqjyT1crHwaNcvmk/KtB5aouHAWZQn0n67/sbIfqwexcPx6KCmUFj7/wwOCkZMC5NZbIcMvvwcby4qj3AY2tSgHlxy+axv+mWKzwgMBIO5bYcxrIKjPh/Mw216KJpV4hmGSjq9IOjBWcgy23lKJZ9ZAO5US4LdQpZBQFKCKDoMLfnHBvBjgq7w0BiDYuYq+YEbSco6Wd6SwJaSb3Eiat3qPvTCgipBSeCgKLmGV77Moq3Pc05mKuZJ2kYT1btyAta3pDP37HOrxhqcwLi/wLontKsQQFGxfj9ARiN4CKUkQruKHDJ3KlNSsFT+4AifxbXRkIg81DapILNCEaE+1vlky6PMrtcRh1d7IF0StLhyaTcMSkzHY+Q9khbdnrHXOqiYRaPmf4jhRo0pGb4YSKBJkgSM2VeLu27sXwLr8+iq2RoKFTm834SNwBXHJVRUAT3bjpLtJwVDJWX9R+2vuzf+b//dlnn6ruf+SHfuD3/u2/V/DjTz4hkY7F0zObQn2FNMW66rga854TLSwm9R5v0KCSHua2Y2q7IaiuCo17sVMGCtMox4WAYQZfVRtZ8TCe+hJ2KA5c4QBcQ8Iv3EmZcuiw4nV5cWHF+L3791RCnjVc7tuT++Ae5oOslKbGqKK7Jy/k53GoJtztxiAcjmQo9TYA6gXRDRvzMzRJGuEd3xHTARAftxANtPDh3HsPQ81DDAxMT8UVMEYLbISFZKIGdilzG1DK+T+pghtSoYjcJFtpo0TcMO98+vTn3/3sw9PL/a/eP9o9uzi8ffL4E7uVbp5+8vjpJ79yuPvC7s3Z7enha2++8uSzp8b4tO3zdDe+HUEH70PSF52RMJSmceAUDnZ3+L4MbxHO5O+ijIkq0cl8TRyNJOypu5N4s1NyI4mflNLP3a9Ho5tCmQRFpBWfCjg7Pfg9f8dP/Jv3/vh//Kf/zH/0J/+jg9vLJx+9f//o6+YjDg6eIBa8hkCIWFi9kZl8rHM7CqkRUOmYazS+Uey4B86KeU45jm9ACjZ2GYFnlebJjm8LNAYK2wyiDdej9rI0A1zaXwS2ebDeNnkBIGGhTBGpxMukKjMnSQ8ZT2CDMsOuuNTWbPtQGIquvKxS5n3ESYPDydAcbgCOMMLhHKeRdevMWM+GUs5s9/h90XvXr0Pr4rHK7U2BQq0Z27b6xIjRcPMDEa5sliD1YGAkEmZr6ts3h6c+SgvVTK2u1qEMAY0JqyxSsuIJIIzDZzFddBFKTysZGLBj6p5ck8kdPDUvojcix7qk/ZSYnx8/nTTT90MJ3dAiUhU86lvYpYpEnjWfmkB4j7P0qrnfeLG2bL0OsVZ5OhNpvFz+8MphOOVmJ3cLh552quVnHBihJmPx4BMr5YUovgYl8wmWCUBzeq79arXMnq9hmF1BxOcKW86TaMjVz8CAWtVqHUvudjqtS5/B5oFWzoiFxQkH+w0P1VG1XSQdJ2rZ3nxdWY/JQmW/XMIczFKPVFLGHInHGnEnD0jfuA3NZTvgUUHpuLny6QClTfjg7MO+1r72qqiqqXx0l8NMZYMUahXpZN7G3AuYR1yp8aBG6FwipObrqpgfN11loWEhXs3TJJ4TqHVkzs4ur6gruRpaovUsilOar2dWS1d6W/VYfmugq+EMBtQxUI2Wt1U9KuJDswGOOzOzPXvgobFQP37HUtA+PJI1ej6NgcRynHdhbH6g2j34gA5SGIimINbzvIFJJpfbJFnpsNV5PhpHzfEKG5h5XAA9lqTURIneFLWjdyYro1U6eDYIB0u3vr90hyOoOwhftk7+Ctnz15b09re4VCQPVhD45+OeT/vc8x3aLyT63qkD+t4xS4bR5pb1YQjfaWNJLPmkvsuRGP61LtDPX8PsJmcK30T3E56Ez1+IiIICOs6TsqcykbDKie2rHvk5RWqzfqcytvA1UQ5OwWKhFZQOayPBdTNutfudLrrO/HKClAI1km34qPWN/LgpeZ9DhFTlUzwmIjHmuOVWEPgq+XxZrHmJvWmyqDTGfIUsu5lkIRkJl71yENNmi3sXjtlblZp/6oAmx3Mo6QyVueEPPiD4m+UWjZn6IMkclj79bbONmgJlWf6nuqRHT7ChzxsqVn1+yW2KUAVZPJeCxnzLatyMdJ2hs8bXox3h1IlyqolhBdt9vUUhMv65UBrWpQkA+pqivQwjFa+giELeGgl4SFc956+Dm7dBb1rRFGWVslN68C/za+40YVo2FlZKf2woOykoPnvLr4tLtarSlpiDGx1SP/EyKlQxExKPK8u5pVQ7Xidu4Ui+mM5jcQ4tP3VoiHZPMZ3rwqXSshxIdoBYyx1P0qBCEqbki+1eF5c75+enr7z26vHJ8Q/+wA/8sX/qn3rpSy9bLG7TrJHdDsPXDVOnNQkOc22FVUFC0SgjCsMY1XhKlxhqmaZKZ/f05hR0bOhmVD1UIVUd1U3O5U8+87odvxNUrJeBg3L99uh/dFnb4aH2fUi6hNLftPC90PPN1ePHj7Zn4/pc5vj27CvLCcnGDjxCV/pRAp3Ao1NylBRtjTPDqw6SMewimAGPDa+0gQ1LAbQVjN9N7EKDB8QCC/X6XYRLWOpNTLk5IGUn3qLSOOcswjW6bvSOjLFs9kuNPlXS4Bvs8d7bulb4qAJ4ZGt23F5/+YVX7h/fdzjZ/XvHx1cX9/f2z55oN9wc7j944ZXvuzzfObSWgaFd3n7pSy8cneybCHJSXrND2HNMDl/Gp6ntrSKAFUU9pPMz1WvM14urqzmOI61giqy6Xlm/t3kdgGesbnSw5Xx04GUpuNCp3Y0pKGu7D1986Q/+fX//7/nbf9/TR2d/+Rd++ZNHv/S1q8Mv/dDX2VAlJjfFAi3hw21tpgbv8VPTJSufNl3qWBmR9+ppKS5uuwrKCqtvqUwPvyZcp9xixayfqLif3FrS0jMpSup3kAWA3oAlUeLMa8/KPm3Ehd/cdprZXBMvWCx8JaJSQtkFlO9ET/2zsLPLBoplLCQDKs0QQ274gXPUqLQNNxOaTTNjz5j1y6aUyjwgb6FA01voFo64yhF1Gf4v01HKQUtQiYuC/3dJVso6g+MHygJHxypsYawWqzTNNZj5Dhe9jjKW3DEfB/2LYy9UH63sqsgGQ+DbYE3ksC9W+gUqXUnXr9cFMHdYcpT88MS7T2cxaHlbkklZcK/ML8LuKw8HR0oDwHvZYHR9ZTWPJSS+mdMYXyMwtf9oneZkm9UtBz5441BVH5MnS/Vivbg6AJc+tVZ3AjZ54Uhi35PFLh35anlLddLtuHQt2UqZb+ycHzu6h4N3rrBjzZKGa8Cjhn6t+YbhjOY4drsmeNha/pSVaNZzHT7/KKxUCrqBa9pKnVkAiRrKKTcZv4v7gaIlsWkDDTbT93Xz6bjXbF7rbVoZNY1z3FIiJLt7x50X5kMfTU1UbalwioUmPctHwqEpPxssRKoRAxypBcvAsp511FXDiySxwA7EzlSkFtWASFVng+BaR4eHTtubYSYKqldAGeYUGE99CCVNzWWkX0OisorSAXirRSkB16RAJ8SsoPIGBusVb3/Vw8x3xMlYloWJwdjmikVZH/fFx3ICrsfC50oMSbavAxHJuZZaPG4DCh29ud2lXBTW+yTrFvqARnVD4y5qxabwEM8MwIbChqdZLeTw9zeHkcV+qe2yH04mr1qjPwiex/s8o8/zDLJX/4fE8yv77XNfuLt/Lk0B2yuYlbQSBduSvmjBo81BfnuvoIV/o5GJL/SL1yI2WBd7Gwplh4vyrbD3ePAd+G8vXtu5MOn/ZLAwIRzUoF+ANB0T5ReLVAx9HutNKBoKYROxltnhXK+8Qkqp5aDy79OSVait5uSLw1CuSbr4ruBt+ZpG3yotw8WIno1uzE5gfIw2lBJDXrNi+OpLBTcKEt6YibiaQ/Uu6Gkp+CKRGMtNhWDMHWhBWX4w43BVEJgVGrEKQw+LHQH5BBLUFqwqaUfO/tW5k8ROVTXVlsphxRAGCWshaMrAURRHZWjQWTsNDcK1qoMopzho3ed3b+8TNK+unLNmRBY2uBo2gHPqrur9a+t6cwoNupfIT4x2GxXnBizULBOwMCsDp5G3GuCj+zw6+CqEckOKRvuoilcyryG/yt/q606+B0LPeP8Ao/u3L9n0tG9kFFeaitNiG1ciPb9RIlnPvWoniq8Oyxuq3g0ZvElSZ2aDyVvK/9TtDwn5prvoxI7XuaLbw4+SB2Oj9DR24wxjOv7o2scTGtk6PbSquzNPPF86tblGq2xrZT/HSjHTiwwLKqOiWgLpMz/bXMHeo6ef/rk/++cff/aIV/79f+D3/22/+7/56aNP1W02zjqgHTYt3UbLsJhwW/H0AB0kJ7czzjKOsNhEiXTuhq9AT/dhMpq5lBfVo5PN2WFJxsAKp59B71x/WJz2LXB7yZ50EPZRbBaeSaW9KjpFYW//yWePTp+eebD7ANi+7aIHBrArPrOGTNhwEA7BlZfsNJ1fZz6GMfskBaWpQfVRpypZiZDLQLJkD3LV3IIlQBS9mEo3CReFVITR8/zD7dG3qz43jC9rA5SkS5kjV1I8efLk448/fvHer7eE5r0P/0v8qORe0yu7Z9WLQibTpUiFg30RG4oR9X+pFylMDsH6kDeH9zQryHbx4KUjhWH3ZaP8mgUEfNXIl7UvFzYBOcxq78QIm+0wRr9ubj/p5Gzt/z7iJ5e0LTo+6PboA722i3ON4sornbK1DhHNDmfkgWlfttmOCmWyNRJYHUZT+6huY+Pl4+gkWRbINiTxpkCxnH17la9vX375/t/zd/++X/7f/G9PDo6+/Yu/8OU3X7GJ2Ujehe8K5I+OZQwG0jzXpbBscE/3oOwa3QBidxnR/BPoOc0Jk4R9Z7WJxahuT7gETS7qDqOoJpnG+nC3/3GJb74kFqvLbjfsb3InxEM3Yjv777eU4uq1ilC+avgb4ksHYzpjpFIBmfUFvv2Sbg7fGkRDXFaELjE8juVs76UbufoB4y/uEloDIIo4xnnod27eYCvTE8iwkiEPHBcwj3HygV/T+d07ek9UGJGLb1g3N6gJPqVBIua0KHLaFt8nI9T1ZKYXNooqYZQ2hhp8ISHfYMVI1FPS12M0ca20e7tsG0MaRcVOMDG2gTHHK63EeV7d9xIWtQG8Y74ULsEUIb0Ml/XQd0WdXU9nyfp+ve7xY8JH4xk9xmJRrQYeKS36xljqMXIyx/Dl6jX37ROsWxr8OnEBw5kfT1Ba/XnVWSymkfxeq9h9vzadRC9Q6veZMKUpHUpgHZz9ajZ28U4HTp7pQjfbLXPLQYKOO5Ra+1jBdcKQkGS1NufwWK+lXFOyDNsfHhkf4SrBdhSExL6DcXFxaiWM06txLyv1MDrs6Egfho+0Zaj5ATVyeVj95N8aKORhchRkoo00Wf55Hi9dGXHNq3rNGIfdRMuBZMn6QKuhRWHNXWQ/9VLTNAWxMuv+Edb9caQdyjjpB5lZ8e9kgqk6cNTYazv4dk9FOZahtsnldKMrx9kHC7FikQf0GovVDmox4zj6RZ12x4Bsdw5WZOzlT8jhPgLJhJhCfOIrgOrQMeax92Dn9MsZfS/pXNL2DWzPJQvVIERhZgaE2Os1hjqWPsUuHkBFv/8YKlmPczHvjVLF3YVuEBcw8Jvyv00zv6lioud3E1XA9iLehuY25O53EZrou8e7yOEzRj9/DfQXA4fBDdzidLEFhzxYmBaFLbLnUgwy8F9EugVdv8+SDwcCN6yNXsvegciRQTXGkdKUpTIpa1acCiiXoMgkZbK7oMpedW2uZDkmsOJmUFgA22HLlhdziLPUjXFDNjNvK8WYzvifinudBC85LQS8VMhGJXG7IZFcMVRUvNfk9F8C3GI6NivL2adCmBgR6Mdz5GvPci2Chgoc1SUIJN9QqWR7GC62hFDc5EnU/ZG7iUh+yCZAjU7FJLVVq1TfDHMtyBsmBVQfxFkRpS1DVlEafJo4VRq1jhOKExcfslEyTkcAqQAYoqtRq5GuOZwfdkbB4o/fQCnmIjhKTuW1/jU0J0MSPumSGCpmBkVrCfkWwjY9kf9Baf/YfCN1yrUCGyDQCABtOEFz4OjkqPZvjSsj41N91kiOuMTT+GYerYdGO7FxPpmbc/ecJ8LFANfByU3Xq8oKI894Zo4p9YyqamHJaDg4d4Mu15fHjhhlXE3G2mZmxFZ9o0lfVgwbmXEub+l88rQArIxdLC19+ulnf/pP/6l333nn/NySsNv/4P/+7/+O3/ZbX331VZ9nQs0IytnpmQme1JPrLD9TngY3PawLgTIPlzMQmGIJE7xmK/rqyxnabjta40sDmzFUn3H9t8fHWrdjLTAPW2GLUlfyu094bjqiZr0vVUzYyKZ39i+u2od6cnxirmbOPKkgzEeRU8Iws1UDxgZV6o5n/3HqMFF5edguu2KZHjqaNaWFqmzJGxhtEpU9pmFmtSy80hWHEZo0+JyQdOKprGy0sPql4ggbFCQfAd0x4zSns/OzncvPjo+O9LuSzL63p0/tOAyzSo+dNRm1VsFlw1vdRDs+hyZkgxuhyjBCWQSifbSSVTkT0/y9xgSF64zdnuyfOICEl7p/8mDULZn+uTq10jbNqRojQSufmtvYO/UJ34aqZetqiUyvM3X6nhdrMbaE5/J++Qox60F6QYvReE7REcUprcatgmAHQqPgra46nk+83Rz8/j/wB//TP/3n/r3/27//0suv/eLP/OxrP/QDL33fGy2IsM1RNjGB8X/TVNKizSvI2WjiaTKRfuhlXT1Ki8Oyb2ky4piT75LMB5EbnSzSKwuZlMNrIfO/vGbo4oOKiqeNOOV6793EVR68lHBzL3jwAFlkRIhNY+KUmsbmOZK8BEgRfovB5fJzgyHwLQAEPY7QIaeXTiCg2saWSYW4F4U6BLGv5VqaXC2/VxEAE0fZTG3URWo4HdkikAQ4mZYlXKoBn0KZWiNk4wqZWxsyJlOC3xQ6zEJZYYfMpd6rBE1sBj8cZret4Z7uNvFjCEv9JH/IugtfP72Xcf4qnAO0mKz2GaCNijapRE4MugoVeIzWY93mQy1fo91tI04X4e9hmKhUTED3Mj+KaVM2FUQmdwlg9UkKNgSiiFX3GVq4gLZ2BbjcQpinM6CwVbt0UBdBGl+vXwH3vu+v66aZxPAaF83kNLk1mRgtPEBvvCDqICYTqt3K51TB+aRuQ6tKfNPXlMujlHPDqE5A9Z6muB6brs/K+uy/YlE2FVjPtK1E4cBrZEYJ0KZCzqD6dLkdXEhMHnlCXsF8iURpKyl6WH+jBp2cRCUUerWE8lNAmcTqYLR0iYptzDApYtFTAu8Yt7gAD8/ih/CZbaWVxhAxV3zhYCVcOLAW3KXvt1JjrX9ypAhYUmhcU1CnMxnSoJp0Or5qGQXWAit/yoF1lc8xuXmbx+AK2cJMXBCTchuzUkoaggU9WLKfkqelnjclZYvkjtZkfloNenGxmNjeR+Ojd3gtARJemuHL3emwztF/jtM7SfRdNsHPxW7Yvku+qAyCQb2lOlRChbzZg89d0H0BtpDPXcnuSnJM+Lqn/Ox7AhyE4ZhK0bg+IfAPbGoyeWYt+FpZ9V0on8O/FJ0m5hrlS9X31VIMAoe+XHu+1+pukf2x16E1CYYtryoohpy3qmyk/RKHneEqEHarvd6klHPrW5MKRqA2m9JjUHngYT7/CoLXe+9X8BxbXeNzg2vZGLQVsVFlRpbIy9hGN2VkgbdXXxsGFhPLmERwHBO8z+yd+aEcN9sVtkRdLOkWKzULJ4MbEmp4UAffxsvuBcwbGSl+AacQHQhSOZnHN35vvm7JeW63sX/jqSGpBNS3GN4JmdupDLtaWlc0l5gK6WiprxQV2hgabwmk5nbLWpa44yxogOspPZUKn6ga94eaDhrl2peBT0aDWe2JvnXiwGOvtxdzjlBfGh4+Q8BrkUnvRVO3wBTRPDue20UNUEC+4fYb8sWcrUS3V69kdX20N4iqssQp+8mpWcRncYjSOr6t4f/I1Vbmd1IFYz75pOy8PeEzKXF0k+9urIjmBOxdHRx+zOvStTWWGvSGcjVI64bsf8C4dAB05Q73To8OLJ6+OLFU4fbdEx+nvPq+8+Mnt3tPDb5eXX//5cHp9c0Do/CzZJMx6ytwozXvmD5OrPD+L/78f/Izf+6dl19+eLX77htf/crv+C2/g5t79zvfid6VL4Hc3ztqHSEZ85iEXYbaBMk4FgymBHqkNKLSBkVWqdNsFbJ2RdYsg4u8ufh+XUbrIClFHAdcQzItw4NDgJrdlTu6z94q/uhmMBlXZ5eQ50p/TP16/UQ52jm4X1l79JF9aD50c3h5fjHLKHZf+fIrMrjsGxXHvJ0GVdvmJGN7qPgd3Jhs66hjOiRh+QpIEzElkrK/e4zt8PhGp+7oeO1zJSocqSfGYbj8Wm/27bgfflvz/dFnnz148ODFl14mBDLT4KjA3FzSrUW+b+UZ8Kcy0pljRLvf2t0/biSr0kd3l6a5q96urRVWS57qdGQkrrX/ar6SvlSDh7yHglUBpHylWYhxRLsd6PjCN9JgagbcmRsZfU2uTq+yYWflTkVYjjG5uB3Rpik2ZVsm0AYSsn5V+Smw7K68JH4FCE6ct3qEXKZMmj7aIKvFA3pyfkR4/pbK+q8O9lA52tuxmstMSztndg9/5Id+xLm3Tx998vj80xdefvkr3/jKpRlOZFLeiCWjUVAECZZWcdPgX62DzBBysCl1ejKrzL6yQjOw/Y/qUNAOB1cLSQWkteFLyR9lAjcgFdJczO31S9BSxWK4Z2TzE2Ev44qJsfnVdnkFABy1cgQXigc//Z/3hU1w9SYrjdPDd8KTIxSWWe1dGRe3M2qdEzVBpNtci1z4grl1ZGRNRw4/51EzmrzFMgucA/FCroLWv5EIrTijLNR55CqLMnZEcSuSSc13UmnqOzTW6KlqgHcQUGNPyEZ68LvNdtrJ5ryUZmnS/vDswznyab7Fm61Gc9xp7ABSvwDDamYAJzeZrSbagI5OygH/0u2GpJf2ZgaSxefJxVY1SCs06uNb+saRTaBvT5vVabhINN4/+lDDnagPjBMzhsjFW+MzOXYWstBiD1tOQALS+XIw2AaRPxtHWAJb8LFDOtTpCQNTERiTz7Xk2KiGSqKxqkhIQNUr0MqwPEf9MEWG8SwAXKxeafMLSST11Rv2Yez6zm4mnpLDPwwl7+VXydUah3I2x+pKYRev552P3wdIwRezty0dRcDxV28Ivd77jjSR4VKk1Sy+saISSbpQWX3Fw25fuYZg9J2exJdggNQ2r3u8GTxTIDR3wMedzWZa8/OhG69S+NwIe6AcxFzm19HgS17bvX5x/+Tj+ivnb/QNhSOnAqY1yagDgy0pUkDtmG60TvbUGrHu8YzRXDvAKnIZaGAwZ2xlFBdba2JKa0zf3px91WDh7sEn3FcFA4lY8zQKXY/JDxjC0AZRx8aTjHbPTJz7NKkFbK95vwvERBH9wKSh4Ay3XtMrFBtTFzW2WojwobVQDFvlTNk5UaX/3DUsgS4jtH62cRPci9QpsBiY5//2fYUG9IUL3Epfwu11h1rAhD8fsAGaoA21bbr5fQ5RjK5LJsHk00odUXdw4ViS0bU8GCVT7yYPhxsZgf3vhRw2OBeJeSglpU3ISD9vQgdRwFPTlwfSMalFwL0M9x7gQuG3pwDHviBtAIFpawIKUwx86YPpT44ONsWyshmSMq5qSaUPC8Ocv2XMcbdhbtGPhKdGZoQPxQSDZCMP8DtIDCwSK9HcAac74Cy1cU0g8Zub9M898eIez0hkyINw9LcUVuLIuYlS1OJeA7IJxen8c538dyMWLo4lYUcOphu1mFSiKyr588VzGi52UMOcyl2CFPYGGfxTGODLjaKf4mpC9LSp1/3GWIPlnromNgdhyAExLYkZ7yphqSbb5iEuVI0cBmeLkugw1JlJ3f48ICVF7kBOeZMI7lQWWB5FfSOVfNehIWH+Rx10tPyNRxS07czq52koKF9ay8yPj7POIv7UaZ2T0+S1QbnCC1862zvWwh8+nWmQppb90SvlHh3e2zs5uOdDMwe3R5d7J9aJXtuVq36yVMOvIywvz64Mexwne2eu2fEETUZkhTuRZurWotJbi1BfffUVU8I/+qM//Mf+2B//O/97f8fTp0/ffvvbJoPtHEyhZXDqJ+bkSPm1uZYVy08RrWpNNWjUGOiigw7KoNi0Xje4QRdOOFT909SackWz0//rrWy/ix9KgDcUhDOu3bOQNMD49re/DcvFzl812H9zfmhb3jFF7O+fnZ374u/wUBYvfqAZ3HAtATLIyoZLNcrgagbrHbEuWU52LRsT5ZmIbDw+ugen8/0kBzfXiF3RmSRxicOME0Igp6cO1LmmT3PoEmuP4qQxUxPzRvWyzkqM0zkpYKqjxvnwWX639E1L+6ie2Cik4lMbaNheGh+KQhZRNEe0KSTSgBno7JbEJRafSQ+eyvAyKgJW1DJnCWq+ucrHMC9Kk1tRrhHW2GHQkUirmOcToqi1WbNOkKaVhQY2ZKd81ktlGUYIgWeIw3YouobMojVGUHV/dv7w4UNIqMkg6B/5R376J37Tj/9b/+b/6vbQnsOdD7713v2vfkWTGkIyEQa7ZiPPLLiURdnoKmzRGYhhdJik17rWaaFVUflFXzOBAqM8ZBVQO8hz6rm01LaYpt+xFzm3NIfv/qW0fAGhKjJBpx4PgtyXgNVsPOyoTOT8bbUYwwH2fzgujdd4k2T9FRNEOAZsQFLo0MyFzfMgmiB+zfiIkiJ3MbayiYJjfxgY5Fv7iaPFLgoIhGfgoF2El3Wkqbkq3najxlD8VIJ6qgbIzuJ3QHugmeHTU6hjz5XKJ8RjhjdNu4JWbAArj3tagaXaqiv2EEOqQoqqPPCXHUd4EHrK2rY2AA9tZMMXcj8fLKMHj6a1uEypCtlzwaNQWoyPFT+FZFxASozPlXfJNK7GLzmmRDPJ8Azj6yegqYlsIdhQ0LNrFYttqZtW/iBUojjv6NaPYab12VZbMwLQa6emyBhuICk9DMbn1LQyaomVgqFrGwEhR59rlsN7hrEZyGdvZG/We7AlBr3u7xz5NMrsRUJ4aab8nJyoxDRbUOVprglPBIFEEIXwCbnZYS7pRdGwKI5a/04lkJWOKik4UVu0pmLss3Xx2eh/1Z7WhlKb6G2lS7RKXMY9wqBQn6EFCfowSZgIdINY1V6Z2YShhIKFzhmMvXVBEoi3OMo3TK6l39HWABUZjzyZd4DP3Sp8K2hA122CBs57L5v/8zJcL5qDiEAIbIyKplJG/nbQls8Lh9cSlSSD3GKf6LvbgI8sjWHEMbiY9y+EV18P9PDbYV9n9u86xTy4wDaizNvhW0FuvgCwiC2AgVqjESs2llwLZjG4+Izoiov0etrErNcV5p4Ksu4aE6cXl08P7dc2mqMeNoZ5aD7TCnL800uEiN/PfP9y5+JrIZ6T/v1GiDxFz294tySTuZj0O/TTUwkKm8o3M534MXXhue5x7YOTp6kIFT7WkUYDcLV21reEJ/0UNxjAuTtDhQOegUUM7L+XBQ+PlrTowi4jS/TYk+sscJrK8QhDqMOaOEzNA6ue0tUgcSvnjB6OVSJYTkoj/aAdXhWNipOhB69qFdTHcUJ4a1vgNCum3N725YEoRisEnmF011+OAUL0lWgeV9vIdxYNx85Yo6E7MSFW8GYQDQJ6UQT5Jr4ZW0q8BlC8sezsLTIkkjBCIz3vkMwBIRjIaMNvdCrNuChpLZTNE3W1fKjA0MxLWVK0dT3uNG+0I0zlLA0EisCAU2i5I61wHYd0HZeNyGKhEVK60JcWNrYAGmIpYruc4s5a/JRC3MxdlBijkNkGUfbx4+MFl6TSUXl06jCiIIU+rxQ7tzZZWuJiG6JGe4uMaD7GcG5YxCILQxnnjQ1dvXj/4vYY0NWliQCSHN0eqtIsRX24u/vl3ZML3vLEZ8CMTelQO/DxRF7gXEPdw81njx7/hb/8s2dPH71msfrN7p/4F/6Z3/t7fq/yZSlK2UXCg7eIIDkOGJ2QMqhcGz3Hd2Y3gem0zK/dRyuylKopNI2nucHhZ2fvVxDf2zO6uXt9+Sar0Bb27FKDA/UbHf9LWsKe17uNE7pzqrqMWc7cvvrGuVSffPRA0//gkKTtVNPwFKjpaZz+7NykTRVYQ2ghf9CBcRWQztcqxHfNtbDVL9V35sQvdi6/XEmysqp6qKl2XTqnfZ7cUw1qF+qV3dys7/Ua6Y/PrDZ9Qdv3SdIPg9DM58VqGl9dPfrkk3uvH5n9r0uRVpjLt2IJNx1YWf9nFh0wfUtWD31NOcXefk0zJUUgUJ+wcoFnOwdbZmPcKJ2nn/RER0vJt3o+mHDqS8HurKgM28wYmJ3Iyu7AQz8lAWTFnEEOutvbFsLaypC6Aq8Gt5LYlJsmuSZSuYObljG4qkihdaCHHubOjXa/0nmedDMAhUswZlFC5cvWC6Gf8jdXIKC3bnCV4e6yexp2LaR8+OL9n/qJH//Jn/zm/+c/+zPvvfVXj99/6cde+m85g3tn3x6YdJ6WbvdOzy7MF/SaJQ22jD4pmU3hZboQJYZdvBtIg52dH3J5eqFMNge4o945MYRzdW0v8stN3VbWrQnMk5s/SdaDD+P86kspLdHTXTrc/yDhrr681Nxz5BOnnB9ORqVENhBQUCz1AM3MtvEaSYRlMHw1qOkyHX479wBRUZPSfWku6FRMZmmNQdbGyq3yXTQDSdOvFIqrAGJk8ozKNihqqpVH1JI4w1JOsdzIGoW4R5BNK+cqDR1Bw8JJIDy/3eHrmGhGOyJuR+/kKWM4RcwtVOx5MkRAXjiDzYsGi618gKs6AuhUlTFBq1wVN3z3dVUw/e1dfo2j3d1/b5ztpM2vSh1X/YM/NgpJfHapWdF0KJ4giHrA3KqrY2bt4Y3b+RcQm4gZjgLDomBTkg++I9XQ01MEj5umeQIss/tcWFPDk6EAq+k2hc9Suntnexe+x9dg3M1rDh/Y2flk6KS9m4vX+Ifdo8fyYuZv0IxLM1FpZ9+cJ8z1t9Pc5PxwG6dsdXjE794NXaHgcYZ+GnAhEyX3RWFy+xs9mQZv7hqx8o+yLVuuS6FSb5ufr0m+unt9urv3K4tKaWZ/Gtnlm1Ka8Err0ayd7ITNiO/sfWavNHqKlwyCtu/5qApbbSFjaduPhWoGYOSXXCIgxVkYxn/AitqHuwdne+ox6rz3/g271r6fZcaKz0z9WFjQ9E0nXdGzPjsLr9I3fqLvKx08e8bV6ghUmyqJ5Q7OUylJFIFcE8B3Z+LhFRhGTHH488bXxakcngoUn3ZrUCs/pupuFtoXirKXnvx297K9PK8QFAfKa4yYQfpabFhz4YVt08VxtVLClgJXlaPyLOexcHqOlV1zO54qC0UU+vkrBHPuEO26JvHwVgSsUEyYh16fcSYaCNKxsa6SbJ/ndwLo5HPXc69QL0kHIGJbyFjfItsE+lmhQ0NxV+NmWBTv09hpuWp9tuU1nVnuDOQW0ejoDskdqxvsi/El65h2vAw0yOi6JqMFsjhyVxAmuwNfyQeuTBtNZaTypnYlVC5AE5cmVXwQSTfVUvjQgS5EOE+tXO20q3J1crkZgJXpg6cU448W0ZyXVIrYMBMaGIVVocRmXEIvt/C9SAgKbhOg5Ul7SIQnmDEwj7n2kPBKKoZ4BAKIAuYBYsoW3gKPfGiRlQj3jm0xXKnwtUUQ8jm3pHVNFWPcloclGf5SLUdWA7pJ3fG2mGkOJN7TCwYijyu/Ndpq96IxbqIRfle2kW4hV4bxEYO9wJsyGl2m9sGfc+MMViEvbfrz328KA+1KI0IJfMWbVK1X5lQ8eJ+KUmzIo7R0MQUF6OQKbnPBG3NNl62qNBwzieKJ52vQoWVjECTfkJXzaSlBPFFOVnRM2elC+4TC7flKITn98oyPA6orZZVoWOXohR221kSqJ9qMUKer5T0kqKWI0LiNMr6hJFURYktibbgnTy/+5H/wH/7yd96yrOXk3oMf++aP/o7f/ru43NNTC7zPVYTpcCmqNJOPuE83Y8QbOSJTJtSqUF9oF5ZH6Ywykoyiknzo9iOTscLgS9KUwYoV387b+RmUJZ237sN4b7FROyUM9eucU8QCX33t1U8//vij9z8Ya7jd9zGrKX1ZRraRCuv0FChnRp3YLS/gmSHbsc/Z4WbJlpWwKg0AVtVqeWZGhjotJXUAjvUs8OufxcZ8akchmEF9GwIvbZdDIt52fYnstHrGi/7y9fV7776LlKW0x/eOp1KnSe1b+UW83YvTi+YBNKjSIVuPW22rBJEse9Puv1Do4JdqNLp01GPaywPdPae8sZrKehbuZcDDuK6ysSBKCGIePT0D2MT7mTwI2uKf/YuLC1oJIS6xhT9KrTykUQ3NDbUU27omUgIibHgm1XPMrAC0Iz9iDD+4SeKZQzg2wDHWcXnz8KWX/uV/5V/6h//wz3z63qPzDz95+tGj41dfDJIPSkeyWoZXiOBFDE+QjsXCEa0RM8ECQTTXjffMUP7pql31hSJF6fTM0HnOQOnRoJWjlQhebkkK/YgC/2RgRc1F1yNjZF1J1G34nzBwmdoYcuHDQpytBBMQQ5M2XKRbYMhM4LrFdeFJVMz8E0IDNXwppOdhDoDYXBTvFplKIOXGGeRDZNjg+0TyL41al4I0yTVYxi+O7PDTcMNyjq+c3G/fjMJYt6GS2jIcj8BicURFqWZsrmCpQ8TkC17GdVDAYnMxX5bx5JkQrv2XbiUcDB5DPbiWHnBeirKTM+8pyoF5SNYeJ03p5mnCkj/Yge8ncpXZ4Wbr/1IoORrdE+mpWS4Mp/z10FOLf6DGSrWaGCN7uWqEWGLH6dCX8UzXgWqM/4jOMBOb5QrzDXq4KMfSQSQake7OHiPEPTsJl+tIadDlECSsAJaFk7tB4iTC1fO8ZRPptJ1LZOOxSvv5RkeRtrGOzrPuxsURgxkq735GHfY0VD9CNXYDw1SQCZp6qmpnaAWfmcKt4yh84bgVmy3KSzqshBERL8zn+PCoI5svd65Oc/04K2+qwbOW6VlOnabqOty75J3RKW8TJUz+VKx1j7S5CK2npU7Nz8ChXqg3uLffwtDpA7AMHJZ1DcbFN2ZCxOUaw4w6BVXkR6BiKgoYkwkb2HKLvG5LPSk5PU1wv711W08JNNEF9uI+ChyIAQ3DYN08rMCgg5wU3bbXQrLeFo1tzBd+MUjzoai3NNm9fgauHcfrQn73lHSBDCubcCGL4znrZsPKYmgD4UcXaHrk8zjBG/7KYslDuLjcChNQUo1k87IoPwsKA4OrYil7MnaIMtVzX0Q77NuxDZwkHfzUVOnydND3MjcSFPfsGlWulkaCDukA/GcpHoRl8bn6uBkk406CbeCQDYw+2Y4toBa/cwSMWkp2M2lYDeMcdG65I8UAz3GWBxt+Ay1bo1yZTEFTwQ8jZA2OhYodmOFs5FCiii2Ve3AV40alKptt16rQZLI0526c2N7YYHReaz8w6/aKkkpviqFDF7+5aCVU0uSNKyW1xupiIF+gHdKSuORYah+hlHJpDIceHXX2WFx02ilo/q7VdZBVplrZohzuHn8gQJDPylw+eQUADYFrVCDVSKMOf1vR9oVgm/jbyNPmVkcA4Tgg6ykwuOvkFq38DmJS4wjHqH+Vz7Q/8o93KOeSdek0lfXut+IOobhe+lvmIVRM2VlNMrCDklxeAhvspZq3sTpJRPB3aGMHNwkSpqkvSaieLGEZnd8bmok718xUNuQ4jbzIpXqZOhZ+4YEslQHq6nBrSuGnfbNdj8Jg5OXu1QuaozVTd2ycTI1VFB4aL0w2Oa33nLeDCZmylfe/cnDQxx999OTiKWPG7OPbc1jaAAEAAElEQVSPHxzefp9xT61d208dsik/F4vD+Twu1nscy80gJzx1+J+Geqh+wUiumVKIvWReGbDFxhK/T1TKApC6pS5y/W7fhoAbyP3GSKAqq2/f9DDgqdugtJcXXrJa5IEG9Ifvf/zkiaPMrp4+eaKpag9GQ0bcw6FJE/2Oo8lArM5oYqqW33pWNWUENQNw8O5Ye9UN2/VF4adPPnjllVftM0bt+uYz5nx7866ChgvPdh2cnZ86WIPL2j32peqd69PXByZ++QFMq7A/efyIcmC01TerGWlH8vqruSdDz1Sn++fwjRkZotGL86d6NprdJnDOL89tsSXOw4cvvvjSS5Xe1DsZkxxdqaXvG9xdogvufrTGTXtMs1nanM9mZ8t6dxeJg82D/RLh31BZQJXsKmBzgNldc8iuyn9WkFSzxHnnCdkhq6vgYX9P5wYqW+JRNhHof6cwdc0B8lEVlDToDP2q3adPnLnusL9q7XLacrWXX/x9/53/9v/u3/0/Pnz4yoff+db3ffnH5Bv/hnROtzaAf8v8lzTQ8mHmxPDxyCMaS3X5uCglIP0r9jntWZBwu/OizDdZE0Na/nHVAOPCPL7LOfBfKnFtjrINEqzCt3P1arwISqged1onrXDbgzT046FgV/DBPbt6xsiE4Wsi8csJsFA+RJopnUW5kBXEgFcFB9zCkvQ4S5jCP0mG4Eg62sUBIjaaTy4ICkjaAjA3GmlIWP6RP+8hKD2zZfN1zPo717uy1Ho5Kqp1TOVHB6aMxmD6gW75CLsaxF7kGGARlWjIwZanVaKaYAHC1dV6U1iIFj9T+5Spg236A0eNuMdhAsXmYFUtfEctU0ZA2eisJA08g4XZvyIWbyO/FfPWRc5GGLrlTslIOEyUpG+v2v6x91eGUoF4MNK7e91YOJ5VeyoyhyavaaS4jd8pw/MlQTmQ8ydO074UN+P0ezf7V84BPzdJ3DdVbDc8tJMJh76b8aF6QBE1VG0Fp7K+f/gJktXU6b1hAoWJn/AVDiF5lbQSO3uHH07JW0aY64rcaikYxOdXqumBko8y+KxG3G0wM59JeIw2giRrTFW08B6rN7uoDPaqeQ0Eyjt+d//mVCJWKI8yEQNQU6EsDLwR2jUU2leN1Dmv5WCKSzMADfqhDiNUH9ZggNf0iflyK4YuHU/UKrUKKH2lTJEXKik7srDdylbl22eLcHdzqkK+2T9zcsT17dNOANu70I5o8VQLIlpV5esM946O+iiM2Ye6IIqKgZcpVVpB2LsyqADZeW22FEtmDDPji1Rbi4JOxnDKRsWNf2EhBADjHAvKNSlBBQlq1ckY2rLqsAnt2v6ut2f3VCFHJktrh491i3Ze3PaapGH/wsVnRottD93uXYsPBMUtBqaQeZ52fgszQC2fMgme3WImbobium8ihcjp56+BGVTPh87ziuq+OJrA5x43wQAK3ET4EVAYXSyOs9T1RulyxD82nncLI8OREarxxhqzykpIKJjTQjuS5hcmfHMbAoPA00ZU4NuQxU0OSMXG0+VFdCYr8jWousaXVYwAQNF4UO4mJwrl/JO8Qic2ddbinrIlLRMCuXxfNMuHmooqKzVo4caamJZCKTJao4sNe9RRAgjExX3uNmHjaighibXsVw9mwiZDQVKS0fmGfzlXPIfC/9VyHiS5PUE17V11uEar6bY+D2wUUlGIdqyMUJXGBp+V6lbnaX2adQ8RHw1RrNZ/ax9VuRmWFl6E24igjfklnAF8Tg0I8cLPCWhE+aBg092NsCrPO43KGnFpbEF7v4qIT5uKWW4AotqGWDKUpaiMGFGt8kpulMqU5BsZex1XIGzGDapxSlLDmXzpNH3T2Gh6JYWK6LBVUQCWBwODTFKnRmjSJHRGWqqYYJkSpEJLGM/STNa2RmJUY0ilfmf8X91oQTYpDeRKTRH6CPnnQDezAblQzHPpliDQaJyaaUXaqqrLDo6APfUMA9UmOW9trbI9upFJrfSmIfWtb3/r8ZNTEwi+Zfvbf8fv+Mf/8X/83v37Bq0/+/TROhljwCdzEoq5ZSHzRNgekm8ius/j5j3Repz4HnvYAG9BVpYk0IAKXnBRXdeiMc8bRMVFmlWP5xbH6uNr8KyjTiy7d3ilYSxe4q1vvaVT+sKLD00UGK23d/eMxjfoJc5iaAyOtJOumbqTcmjNhnVUl9vJ1K+uLw5UjxklG5YBZY4/38O92DW+XzUuzEIr7MhxvWbuJOmyjihpMmS64MRmDTWaJcK9CnMyW0IcGYWOgRF236qhzy4eZfawS3nBY9x+dvPowcMXhsMFiNVRgzTIl/TumihvhT2LwL2Q3ulu4iaHhp+BLWM2at+gWomlmDMCj5+ednBq7E9DZPq3dXFpiCkDDgFvSR7fBVOa9AzU9EcncnD4Q7bU85wSXG6xs7lr7tqR3VINywfy+UfK9N7Fxc7/5I/9M99+54M/9af/06cfPL48Pd87EEHLIHSTmyaji8w/sxgJuaJ5wAMHXyZGuiaRTB8o7zFSWVt1y86ZQqdDvZQDW4KCH36Bqix6pqNhGsIlAsAkT4S7/2AGTFhAm7unKVOlcEkSknlIRcPhwG9ji+8ARxiK5VCrRVaSLTzRkLAndE73p66A80IBZJlasTJFtmSVkER2azJhhTOPWgIlpihTK+o7kJ4LbQ0pL91I9uovIQKZT7bUlrya0QZ+KEnYf6TXX0VmbAUioXMNyhaxAAk1BqI73IWh4H7W3XwZwF5BDdvQk1FscoIaWkk6YAt0CT73JfHKw8G5aCRaDLMIkqUCiw2aU+28rblENfNmjVhTdtaHHdlztH/vHq+yDCLljCdKhfTfYfSzrXVOStA+Zf95DHOTZpqbuzTuvn90/94DS+SqiHxLJG/hvx6X+fTjOTHCdwbbTI+oBg7vdNyBYGbaGQKBO4ObMBrR7JYe8vN1ufuMt1QqhtTSp+SwZuDSttvd5u0bu1RKqrKmI6HcHDoBk7+aLw+04S55q+VunLDnJIvo12moMoE5LUWq/KVYYUcGWsxIeL93osnPFFDGkFHIm5uT8/OshRTJXfbaeKaHQ0W6qfv37x/JcMeSIqh+4jU7UJUctRp0OJztduRYUrXS7r1jA186BTe31jfiWV0WnzUL8tWg2s8tCr+HlzvHRyzmynx6BsEL8RMUKxsqvdiwQZjDz0e1Ly6lot6XwkY6ypMvZOpvcrXaZ+U4DazAtKBAZeeuAe+hZGno7nr+ZaVcpjys3aECPjYcgh7ngis7XfB3CFdAZMYCA46l5+mAXWiaKpoSA2pgxveKXdC9DfYpDhN2BxfZLVT4/P88CW/QxMMmvIAgO81gcxlh6ir4c1cpFnhS0633FCu0coXrThvIvnxr0OXkEEbKO8kqJl3Tp/wYylMiYjssC9XQahd8VPSEBrHAOz6ibUrB+6xJ3fFlRGMaR9/C+rXlnpINnQDixk98dbCXD3PM6rtpfFYWKxGMEf+91RDjEitHxWi7WRleEcJ/2srTvB7/jRe6jqpMOvJFx2PK1jKk+IPRhk5O0Vg4Fjz5GU2JKiIgzQp/gJf2JiInY5RCCrwcHNxTYeSBdk8byL/R4aDcWBGbM3NiNz3fHF5zKfahhrq1NwHPDEBN0RSQVlShblOQ9Kx9iKMx6GYhQDZdE8wgr0l8vWPR8OHN1Zc8K/uQ2KjH+4RwlRp+osps9/b0tWaVm2aVwQnrL5esXF4o1rilJ+t7V88EEY2Dm/JCbaee0kqQbIYLanvFJTGw3XRHah4VpdKkGzUincnFLiJJl5uWBwFNVeiXj1ArHWp5jVhW1EwlOv2q1ONzb7xIhw+gnotIdh5Wbppw7HDOjCKUYeWvVKzW+NSgiwnBdYJ4OqZBSUzLrmHjab9ibGfn6rUOh745c+Dq3p5vrBxd6/VYGKUN75BupEltGGrv4c71oxza3tPrPQd5Of2JMepO8XfWAFuYiTbPyssf86Tvv//ut99966Uvvfjiyy9+44e+8U//8T/4O/+2b55fWGW+w0uemQDAlyT+lZ3xvblisqo6jW7D/I42Ky4VA3VhjbGS3aXcaHSSpCJXLK1r+3BHDPlnsaOmdvhEekjlwFceVSAHdSVL3bq/9/Uf+L6zs6effPSpdrRv64j8+MNP1D33Hpy89NJDlpRt1OXTChHpD6eQrVpNTrQhAVvtvgVhAdDe7j0n8ds22togVaYum5aRugGLMpbUlaxMEYPXb6htVbT5q/231ZfXVmFGRizeO1iwHlnNAXalxjsb0qbg0SRXa4usCx5xOhk6mc+/mrWobVNsq05Z9VhuSQgwbs/jUo/4AuaK5HoqVRDr6rnXzlhzrdceFkD3LbKV20GtK3paRvsPv/RIcXv6pIqXZrAtRgjvvJ4D01rhUfczP/GaKQ3RgXeYINFpzcUQqHg9JUpMYg59JYrmHj9+8vC+HdT3Gw6wMG4aZX/g9/+9b33722+99/7lZ59aRWCAEXjROy/YWXJ78AR1eMaIYnh3/wkKezcvybebvUco5IxSeP2B3ZuXJfX1A0ZteEczoGLKbzTwuin1gNN1DMdcqereREGxZxy5LCqd9s0oL8AJURC/klRb7YZmCTwcZgD+alUt7ABTyDTjtIy+yuRu9r/tdMJpduzcnr8OeNeMN5YQCe089ELL0b2+cPpwn0ni+2/6DkzUZyVAre2gmVD7MSqGGXH8VDK48uYa+RhFQSj5NDHZKo3UHcZC85CUaPdD7c6hGdKwwAkfFagOFMyUNyc4RZNIlZh8eOJ5kgCJKUcj+pUTY4ynOnlmmEqJElTXjIYGNhVJKyr2MBjZwoLuKpc6qy2SS18eISxWXtdHTSyY5ypJPGxSR9Dj4XdUI46DacdhreRqV5azt8+1qh7f2L+5v+M72VoCyQJV3chkRWVjWRkQ/evOa4YjbF4sFhpfj3St1VrivDqW4BHL8wOuEeELXzL4qEPkYpcgHo0FHPlGbb3gxnEQ4JTc23XWF0vGkmuPKmxN9ZObNJodDYuzIJ0SXajayuaR9TF4LV0EokXAZAhj0Y1gQNrpEuSLPMIuoh62oe9wyCI1CAHYBaj0WVtIy7nGhu/3aVyMxrSUMmGrBJC8PLvo4LSoVyE66Ax3pDYsorxBULteCis82OFUIDXD9+5BwRXj6GjnQYh9oCMHaSomf9DZR3R6+zVZLWEtAdapFq0BSiK9oZ17908MrZUtDrNup4HM9D0EZG1hzKyNNJClsTfSJohMaUcQuLK09n3LKCoS+X3tHV2qGiSuyf1w46zszQL8jLllNL194dqGBT/XQD8HTJ9DeINtcA0qMHt26g562TA2Xi4HHbbypLs494W7+6wP24TccSh8y8nzT8EPic1DP+saAT0OuQla9j6Pz1B9DmLitrcF032xWPhieSEdruNvAGW+nKVg/DACCnaxMNnVywYYCk+rJhl8Gw303LVBNiVuhczd+8SCXvww76ZQkTChPyMN41iY1ZTrUclS65DTSF0p03gh9dM32o9khaJuqcuQYwAqM1YyWVfLIxIi5gOzfJwgvfBVkw7ixd4IV2MdQq42XUibWHFd7PqHGPKujT9cVQnrrIoSQRZeu/h6zEmkUzGSa/7EpbNPWDnDw3q9Caj5hPybFm7wQuJ++a5KfrT8Ve154COWimGtddSYpp7axjlX/GJf7dIktm+sDKX4aeAwacIXR/nsKrGwlYL/VEKHdz9BpcY4Ska+c6pOXa2MXsOuE8RB81FEb2gEEQeXrfUv1WDjtbQEYKs/nwzt1FK4oW3khqKtr6kSRH5YIDTNC+61xkGmUloOI03kKuvomDTW3Mk0cQXZjB/Kr2w21iUvM6rSRlk4QByrw3wTk2cXT/kijnff6T07j3Vbdy/vzTcN6dN0raEMPk8b65DntgjUwRENCNpO53M0Z4+O9+7v7Dy5dIBJGzH0DhA2XtsUQzNaN45SeWLn2Xvvvfun/uT/6/Lq7OjevTfefONf+9f/lz/yIz96dnlh7f9f/Jm/YGDm5KR6btl+yidq/1zYT2M9D+u9zrVy0CO9TM6xRHrILEfk5+FDkuYH3fz27ALrtZAtukBTXT/zfwGI7qGQjFXua7DIO2XKkNXh1ZNsKus3cdLIkzv7C5p/11mtsC97C9Pkl+S2F1+wC5WE8SosSIihQ1uzDfhpfvlurgosC2Rbk2xppgZUyxigrDioK5MiD1CbTdMY7+O1pGac2Xe8jDX6oTEOTR7FdOExNGqcgCkIcTsPSGc9BGjGPCO8S7NaKdL6J9i/UeeQCm0shburt/nZqHGwTMznb5NkwUYnrPMrPdeFhXsP7nfS0dg2y4xtBXrUH/6qyRpd/U1BdkbPyT0dWm6HO+BcqWO4Cu383zKgyIhTHm2pwWUqUvOWMeXm7/rdv9tnOv6Nf+Nf/4Wf+dnv/8m9L32j9UhGGI15XM7GDMilpSO5A+9ie0OM+hjpRgPpOoZTjEr/qjUMfnYvOGdFu/5CjZ+MGpxsoEOp+fNJgk7DouMbl3bTbcg2V3LN43pYzxEUCCfIlINy7ZBpc0SIYpAIcTXTeBzziAPXHvdyUJMtDCltMnok4k1Yd/RyP5K0FM01Iy4OSYQxX5RbqNx0mNM0ZYAgmn+TErCsDQ2pebzGqNNj0menXAmH3iHzSRp6aWcUqBmu2oyxJU3DrPFIw7QKDDdKwBo88ip8aXHpaJ5TSC4ksQoOeTh6Fi7a89y9V+rzOYpUF1WtUe90RVtea+CKoNvsIDSRLUPt21HaYzYtgGkQvfgo7Vwatb48hy7dR/HAaVRS0sre9dPaCHsXTx4/PrvQgQfSegHONtEiW93f7qH7J6q8I4f6YlxaEDv7RiVqlRuKPz589PiRWYW0U4/KV03UMjDt9YELX+WaxvOYyM3xyYlwZQ2j5Z0ksm9q1SYU6k3guiu5Li3OoRarPWnP/GQWRD8OVDw+PjRpef70aXKlSyXGVpcb8jqu15AJFqeGPZKmars69AUOUNX22aefKsajz3JF2wCX+InQzoMWpTq398kTh3Bp6evMwOSbIVnY5QW9ECTV2wYlN1o5cGMPgNEBE4NihE3nxURA3Y+ySYdEF7PaMB27yR5SeCQuYHrYO9KRsKC0uQWshfeq3RHZuaaD1GVs7fV0Xh+4GoEmcd+m4WmX1E3OgGMQXcUwuza4ljEAYY8hyI+Da5yvy7OcBiOllbS6KbBkOv0vdp7XrbfnrjGxBTl4Rqpk26YdOw3H4Nn8TKHAIkD/Sr6hVFZ0bYDn+e6lwHr+K/S77ivN0H4G4kn4s/fNa8FTACdqQ22FbF6eQ/+5r3g+C38eaaGJEjrfJehpnZ/tNQWP/q3V2/gIpKu2i2t8seLPGzXX5rvcmYawdLMtCLDnrtslPRq643Grr8jszsnucrTyc/Adbo2Jgp9mDxth2SzZHAIP0L71glr9Mg1rdhSxycPWHYpjXXwBGEVUwYgHBQlMJlU3N+PTVb89eI8Ylv0wu3rlWqv4r7Kqh1oB2Gq6tYxMNh+RNUbQaR5oOvuoIhED/vzC2vOQKltSRd4fRe0Wb5Lv7JjeSEuj9VFM/l5Zn+5HzErDYAYoNgrZ2TFSKFWrYEenEaMHaJSt2zRsWu4NzOR1ybjXKswEmY0HdciVn047kacaVCkZV2Wyf6R29VgZ9DdsFyJ/ya4SJsnARh1AjQlB41Rqp6qtTl/PGI7frxw7ZyDf817OO8omTfugwGBBoIfb69fB+KJnmpgaxyjMuMvENaDXoAk3gQsnGUux/wHCnWosHzwHBaJmP692ZGjEMq7bx7lMWi6m/gcdGIbmeJI7k5Dz1nCnmKHbmnKv/qsf7Dw9s5A/+axC4cS/zu20JrOaRV/EUaXzBTJ6MSFy8ZXLw737DysLR7cPnp5/evbY5x4eU035l5OyeFqN8gTDMOI98tdfeXR6+TM/+19/8MkHJTw/96FZZ+WIk5nWWz95/OTBw/u+tN7kslTnTumxpPYdeTlXQqeTlbtz72vigg6/PTl0r3zd13VhN9WqZCs3R+aFQqJkBLGSb0N923sshn1uro2Stq/rd/Q2t3mXM7KvcpOKpnzsPn3hZZ/pfU3oB+9+aBuAMqmu8IVgVa9KWVXqqshXnUNVWZGcnimBUTFsBWa3T96oihz7YyTwhKIV6ur20eSwv5KORpaMU53IHi3VGLt8kwhUkKSrsKQ5V/fsNrs4rBR1jfR+kWcwGJFD53PKOAD0WEANi3K8QbRmKrAnrvp699qh9YCU00p9+BLKLeqboOHUi8DFQ2Chnt9f7baJHXTlndIdaz3Ia3K51JH6NvbusLZcHPSki9Mhf4FfCZSAm2vnAmlUEKSzrEJSEg/gJ9mWm15j04bpnbMzpx5dnvgcafw2Q3h1+3R/5/Tm/PTs8Yd/7S/+7Cuvv3Bw8jDww8e39zteZiqIMA77sjgxbczOIHUDwy5bN6T3jp4K2bk82jnojCMiOZA3VzdNqFAEPhfdQcXWxvUKRRRcFlg25JdisgSpe5KOwt1iIJlKUKxHhROREvBp02TNc+7Z3jOVRxF2bgDc5B2F8akdfStQxtO/Q1qmXY4ioyo8X6sT7Kyja8vWancKqzMkNxJE502FYN1FXIxFYyi2cxXDeqwmlVaQk6aahRDDt8TPZkgLSJooj2mph0ZQpxyE17/8M3wkiSvqUYI42ZUuAhnuNcwclhrERPi70aePKsGaW6OipfeMXxr/5+o5kqGpSCIzJsTA1DJZqZI+z/WI8CEk5KMDz5Dirf48B28T6vQB8EOFSW5w2TdGHJDsa1SAQ3iuh6kDU0tw75dPbl/euTqEXytzqKfIUNXUNDKUMijWSDWc58qFIkMgoZ0PocFtJhCROga1NhOpMZsYM3BWfok3KIBldaWScnlzdnt82ORtNBu7T/vYsf6tr7G3xKYMJkDznvoYLixBef56ejx4Cz90VSG6PPP1by0bZDSU06D6tBT6zhrmJJKho0cELs8OzxWOE93OiydPy9GUTpkQVOxDC09nHNbsPj0H5xC5SpGs1xOTm4bsKfL87FNNHWRowhoAGX15ZJ/GnlOS1d3TzSS15hO3pnPbjGfNoYPd+w/0f44JdX76mfN/rq7UFFykdpEewAk17O19mrW2+NBI/kkV7u5nyNAMtV9dP947OiQi/TTFEBG6yR4yJ3U2oSgub2bj8vXh8cnRvWNT4Yp4388RQ9Z+yuOcO+Gncs8cRyFFQJb9ZGqd5+OqhTYketlck9dzG5RRLSadLvyeoxWzEHYf37JC3KGfFAXEE+gFJaCwYXQLMZg4OskG44LpeRhbYHMPx7NrhHr22tOG3XkEu2VxcfB50N4WuqC6Ngk8bUMm+BnWsMdC4ozECdL7hLJrr8vyEtqjf0oS88j3Nboni8zulIcVjqGvIG/FKtWWacBDaEKgGmUwngrEkFdQM5KIQ2tVaLaeZ99g0JnM61TeYnuYdl8hYxOA/fGGUWKN0YNzmmJY4Z6t966kzRZZp72L6SOdZfWS2E85Dbb6dCgTh9D9v8x+iypBQRNfmRwO492/RFYAxLpZljeDj/hKgXG+kuVDER4kdXyZvKglFBEIFXSFS8U5ilV0c+r219TMsbTZGJPREd7uUIXKx+nbNzqVg5ih2XprBp9KjwmIXBiYqdXYiNeI9r9wmSgo+etNNYSqrVOVu2LydgHNTmxKwX2Q1YfCaTlWG6lFMhmRt+dAE71U0k0m115BbNYYCMdDapZj01aHqpSTcZvyVqtgrABoSVeWLHKQ3hy1hr9tuwH5ZxS53YQO7Lcsp6GGyc349MfMRq11H6qex5YERRBAsx6RJYNkZtOrU+Ruk7ApZmTOfatlxuK1hxgU57fiKKwFWgd6TilB83dMQg1xe/vppx9/+umnDx7cl/CHf/SH/uf/s3/1za9/ffav7j15/KhxFCTlXOMxw2Yay5i9xd5cye9ldLAN66X6H+MyAqkN5JRBb+u9H0rufQV8DscW1+Y3GtvH7cMy3MisED8xAxKbUyQnka/nGut6/OnTTu+h7brlO6dnzldtt5nXTDG5JIesB3VVCGZORyDNqf4stAoz9UciKcrHhFsmIJdGDWM2aWjpTHQZKM2kiswmtV8gMb9F6CFpytS6f96WdDJigMGxqWyGRWhzYKHxzatb2+9lEyhqn8GG7Dc6k7DEi7e5w7F9Gy4nNp78JcQC2oR+189IATbBS0HhY25cWtXvPGv2zMjZkCd4SiVLiLFNupYDcXtXT544OeDYbraWAlm9MKy5pwR21mtyTKZ6E8Zf8iq7J8bY6p01K7lz8BM/+Rt/6jf9pnf+5HeOLc87vT64XwOzEnfvxJrDKcoVu8mC+VXY4mjWcJqDVdtPc2RKX156z+FGnc+iyWLqzYhODtngKsYmz+t75SqFj2hxWgs87fV/ybHsYr1MqMdyNZsfTU+B6BbepBynUJ75T5MpueUZNKz8Igj5qKRSPMWdSBWxm5Zma9HY5m5SMPowWQVnjcKlAd3WGbZYMZa5mZCMNoyPwq7RKPUkipfkSOuVIbUqY2TzufzFFtyL3dQ6oMNrSTKBnEYgI1QSLTsp+8ULFRNYYqQqfx6nNhm+S9fDugaVx4EaxqI9yVZC9yI3V+ynsvArJhNBDMW8sXBXVU444ZjcMnC46tmka0Fv1Q1kEnF6Lr9JgKnUIa6cCnF4PC1etdBraFYQwMRBSlsaLFFCuSc33RrRyWg2hpjhNDyF2NLh8C69FrJF7cp4kzPlXTVKvQj4Gyc0AYj31CqCCqOo/IuYLIhi3AiMJeQ8qzpia8LkbgacICWq29tyHjYCwO4yB5qlHEyRbYRFGOp0MyObZsLVxWWHMTIqwYAOueTaxE3IY0zyYPJZ+SV+lqK9wtRDfLmalbBOJ3b0PNpDRdp0shoHYRSnCW6au6O5MGaq4KJjlG3VbVeFpj0VqSvzGeWjurKMtY9ag+GcFeOgAqU3U89AydYIaSZ/MoK7khx1TQNaxRTaOj/NGLCcyatZKUCgig/AdBpAt/4qDZKtfCQ4PsKdpjdXaX+1qzg62V4QTsjmffRSzkHYPcwLWYS2yUTFSNyI/QKtCSzpZgbAmaPe1lfHtozdJSl9Op+AJUvAXYIKHVEX4W3qxZC4LT+Br2t90bBvC4jttIfd75oTiGTAg7wTKuZaSsg+l+k3hTRixl+ygqqhk+1Ohgyz5Y3SUlkAkGtZ0szPUCidC4rhPuIhu3xjTNsIhMw1V2WVrwxtJk5I0GX7L2QNZtXKaalsxm9LitSRxCkzutU5bgx6aAljhi0nUqKiCUoLtr3bsO3bOXj+5KJjR+JCx5nTbr5r1szlsOOeWMm6yVthwrNStG5+CQ8+7jmd9Yogd7FApch/lzJebx8+xJPuPlAYWqc0vSWFbekiwNkDMAW3xAoYkXOKyT7xU39Usnacw+M+Uh+0Ovnm+g1t/uvLVx2PaA2+sQtlubm/hk4da//1kh68U1uyYXxFtI7B6N9t7BqfU+csr7eypqHBBO9CgyQ5Oi+TI6mmVr4ACoRW/8n6qfdwlnM0cHDwXsgDywkp5f7k2RJnMgsvHyVJ19RDwHJeXtOIK/2vt4OPkOpFoLOTV1568YB47bZGe3gYi6uwWkM8E/Kn9tXGsQn73gwbnEkDOxLleyKeCDBJ4N0/4xdLokYxcJ+bdamLyqxYmkTI+gquU3Hi8OZNSr06+5JJ1+vbR5NiaXUWkbMKaUYVg8FY1Fu/9O3/6urq/P69+3qhP/xDP/QbfvInZLW+Ief4yccfRarhETMRBgj7fmcIEnlop4b0nuMrMONp1i7OXMKaofbE79+cf01+7O59iyjhBBy0v1AEPtezp14//7YgFpgZBgzNiWTAgguTXo6V0IzujU2gmBoc/P71o88caGTHC/L3xnebb5HSQFTHAfk6r+qO1kOWJePQi40VZarLRy60FTkImTV8y4uKJskoBs1Bho1xI0D259DP/F7cDYuZ0jD6vMTPtDVmsCClGdCcUDZdqebljJ/lSJSCGNSPr17WNbk6+/STD1WHGnNGAC0e4F1J8uTJmY3OrccbpuOynBqO/Cyt9b69CLIJ34Z88fcuGuSkzz9lp7X7Pdivd2xVbt/cpAJGzAiHZlpT2EcXa9isdOOed6+sr+j7DHv3HzzQVVOZU1exqC+G/ZbSeOYrQszsNWByfWxc0QXWV2Is7f3hH/6Bi3/v/PjwyfmjT1786qvnCsGSMnz1R+X7NLymNA3OrEO5rWSy1ClDc5enBGP+yoLGmSZDzS8VgeI9JPMIkU58fJGzfGmMwzwb1CuYzP7W+Gtb7yYiRXgengKdcL/LEw5+DAUjkFr85JSaGVafIRNvMRueapg6QFot1n1r94QlcFjtwW1G3Hec8x5VZYLolTngtrLdcyPPNQFFlwaOVedEIPb9jkCN69/0LXCJkhistPWB1psI0GXcRPomPd93+K4yv8EjuboouhqHGFxugxYxBxu+h073eDNzG/G9WgLDRkL1EArlou+B2rUSyQL7iVCPrcuPi4OZq0ze+CLf9AAwLXIVpFLIxNuL17K6w/fUHRxW8SP1HWNJet1yviEgyTSLVSJTshCMM395pL4GMMJM/3D3pL6TTAM5yDFhhcj0q+hGS5fwtowxHaVjtRmAj20Zq63JWk678ZrtoGltyWWrGavmW+6zctPod5Vy6dQHqSMT6R/brundiL4sOPxAzbJnKaOjC/g0zXTaKh2AJGdlGOoYNHOe1KOhH2Yu3Evuxz2zbzwrLbG6lChmilHDcUJuvrZ782Bn9zuE47/8GxbkeSdvTpuExzBSWxMGlkbR4FI3kjfeMVSW6XpDV+OlctfjUELs4FojxpB/xMDU2mJJDXo1D6/TLqaGQnMOiZNQRoF4xienTzkiAgaasaGDULkznADGVRZCxkSMPOQCIwYZUijWcoi3gpPAJbry6Vap2CAR05epnl0CpPyel2/SFzVtYwhSgHvXpIhKD4tfCnE6XHoxLydC1ktRu0UEplbCQbBhME69rxmAQRzMCNDbIjaUBjBEXVtEG4DF1kbklewO18D/WreF8TmIxRMiG0xFfREoYTIj5WM65Sx+oBd/CobMY0z+1UEe12aoRqMT1oGUPJtabxsxIrRER24jYoQBymPmM+DcUMWOCaRVcbjIRP0FViOgAm+FRvt04r1WnwcWtlZfxkV2MevUanZis4I4hgNYlxUFE0kQI16/WevUhvdsLkiENzkR/mEaZc8Q+8FWt2YC9XRzcxJU81U5uDrKENrMQU8WrB5tQ8Um96RrpYuwmoaRgQvihti1LKSdLS6jww1Q5ABxpOmiREZGa39fevWxznwN69d3tmAhfddl5w8Q13yJ6w7Yb5KaTNyComyaEZq4miVDnsmSh5FmdfZCU2nCDmWnjFTFaeRzpme/3rFG6jk+yRN5aA9YHDOdulZlXhkkLDT9G8kHqBwtoFYgehEZJYzLEpNqhgTA0C5lIQK0iFzOYMsHUKmZWsubIKOsNU3hi0GmAuhqI1H0eix1TIJsDoByIk9YqGFNixSF2zE5EZOi1oZEmihxQij3qhnJa355n7uHnrslwTC+BPvgow8+/uRDm33v3d/99b/+x/7wH/rp+y88PDMu7nAVOzMuOqovX8lE0ZKxGQUe+kfsPOC04ETFeCQH/4g1UEQiFCbjZKwFxEBiesNUib7XNRx/r4gVFhP9zbVIexwyfqHHYJrfwFjbenT/4cPHjx7JimoHTlqc+Np1ysvoXnrKdC20KqldW9UM103DwDx4pSvBXaC0uybvhwbx6KGU8pDNr+wI40A+0/7CvbkvQ4rfJc36haVU8Ka6PNrMpDUMiF/2dXt2qonv9EBba7ztv/+d93VipXrppZfuP7yn1jt+cP/dt9+5f/LgjTe/whlmpCkj/v1kYNtrPUVynp7FFLQFevb0LEjccJngnjHMaoxyPLh//7NHj4ZOJMuIUQ7NZM1Trrd4p0U6nlI4oXQAaC/MG+I9R6fXuc2vo8MuLXbwVXjOzCA9j3mw981v/qgqXrenQzwCQ43CyonRWeJXQQ/K8IdVdB4rDvM5S3pamthyjpqRb3wHKITTDKqjX8gqYoNrGkkoghgkS5uDSOAwAy5k/kdAaBywp1ia5+7w18Lyv+bf+MGCAiOmO/1o7gNRGWp+ZcEAGnAxvlC8vuFAyvRMlm6seXOY7KhiJF08LGOtDb94iInJr94R1OYthIxiYnqMZ5M7kPXqkqToTJ6Y69mDBAITN+mTuDXi/k2Wx+fgGwsKe0pZyvEY9tJN2jCMVgfR4BzCE+22SIUBQIlgXtnVfb2qX/wpAjlj7lGpFzdeTQAYgcUVSZ8rYbkkN0MRWg89k6W0Aqa9ObYJfpLE9zBRAatkag1WAbMwptj6q2rlIKIUmxrcquV8vsA1PsjJ1LGn0PEnkS6LaVp+Lo2XYSx+/4DrQhg/2hejMhFbDeQ61kllaRaYu+TGHIkKvpVf9WqwlTjyPM+VLcE0Xky60Bfmv7dVwWGXB2FVohhKxbrY7gwvGpl0DfrJ+byN4XzK9iRaS2UpAeJpaSAPfa2QrjhR4BjKBgqQpGM8UidLaKMy2eY8n1LHMFks0Gh2H7zZO+XBzrgGSwyT6QFYV0HYDiY2pgkJvASEKKRe8xZNG9aGnxhUmrUw+VsG+18XcmmRDlfyUpK1FHHqpb+YTN6RzNvmEhGp73mNFBMTVJiegW3ThXRCEz7+h9SCGyEW9g2QcO8TNLIF3M6HFTTf9E2G4TmCPT9H9POvAFgHeNcGqNXn1ll+W0hpn+NlcfTs/vx4//PP0jwjuHkc7HGzvYKQOUhVSlEqc/BRyR22J7NGM7LLgGn/s2P3Wrl5uNGWunODs/cRZlBvCemrfYdGO2Ox5Bq69hOwRFdFY/goQU+oK3j60Une0sqKG27CKix7K0ljM9jjn1u87icTrrUUX9NZ04yb3gtv5KSBpdyO0MlMY4P/LvXQHa57mpwYc87IlByCRV2nF93RSo473kIZ+Mqf4dBb82sZ8HLxpRj7DkUS0CB8iW1Ifb5vev1my25G2pkw9+gFj7XCbxsZKltCLIlRA99gNlZhZCUywOarqJX/abDUs29iAbR1fzjmvobJlLNaDLcXX43e4TsIQU6ccQgj++hhWSF4JThNM3GV4TiI5hyIUstt2PRMsEquoxWqFyHYAI7ZiE00FzIJMPoacb0AHywrYsAKBVwCKoKrbPXe9z45mU8Eafo31VjTYTx0GZTp3N6eDp0yZqil8cF1unCk/ZRBrjQcIVbD2dYf6FwDgfXcghbXSTIe05I4194Hu4ePfLCVBgSHe3I3VIlVEbi5fJXafu4v/dxnn7xwcv/83smLv/N3/Y4f/4lvnp+fNnm6Y/PWY/Ul14dkDjWtYB45Q0KjkNRYM6OQSC9Oo6mQTT+dcCNZarMx4h0TqQ3901ep4utO656/eN06k+RXv9bs5SZ+RFzPs3eo9wzCLwon8R2bDoiyOkJjcSwu3aW3jZKSbbmJ8fGdjtVuDR+vvbn8Mgw6xYZOVASq6lE7OaTPVkevWYHwVFxLiHzH6yXC69rkhReAcxLazIVuIv0Mk/OrEE/GpaBpqpTxxiJ0VTpmy9oZpYF4mg0ZnnkPi4ovvqadZ2feo0dPDqzEe/ppbRmZeXvPsua9A0vhx0WknVQjIg3Ezfo/D2lqIgVu+fH4va4gF2iZPot/9q6/pjVz/PBD5xU+vTiDqbKcpYc0w3ZLpFE1pGMgk3rajyLZDEd2/TX+dO/IPF4mDCACZJ3V4bXf9nbPzy3Qb7sdNOJ9Dvknf+o3vvzSlz785FPrdGw0tOY3aqID2QoVHi8h9g9D06HKCsDgcD0EBY6v6kOGgFWalS59LmMJsng8Y6eOlO76K7HXWsAoSpoIybh4t3tkRI/RrCQOhoW5Yw7+ISeqSNLVuop+pZ346hCObdLdGCOE3rH0VXNqDldkQgI0ZYWgxlmsrSIaN/1vwduAx4SEAuOlIAEboxsyCVl4SCdtb/Cfa7Bqv3kbRBF1haVWYSCbNL6J2wxMOR4Sf36bZpm2lF0EStfJ+5WlKS5ByI/Dd0M3/KznPGv5UjFbyhux5FwfJ1nsDwvIbhPiw9i/0FFLvfbJucQrJPn6B6xuBfJqGXvw+Cs731RM09nbYCtYGcr9IVxmxEy/tQCm4s4tc5RK4Ox/CwhmdGo0OoGtZgjcLHsmyuKrP4gDxFxTO3XZJqgRefgYD/yKB/lfA3R9azYDjLFGHI/9CdUugALs1VdbknP03iZbBGKXhmMD2q3Qo+RphNy3ksbApnrl5vopMPs60sTxOxaC5TntVNYIyoNgphKEBdsPLCfNprDnY59oiw43cqOTOO9v7+h9Z6PSmojqiMRpptQhngUUpOy0T+zm6mtFNtauWFu6SvnkG4QK3gY5ljKDlWn9TMzeta8Ia0W8TXMVvKTtMCDlhZ+kUd9Z2Lu6ZwxSaXAq6cGDm7Mr/6zBFTeNLwzUMm7avb5zxYfS4cEBiWqoNV4eOyNIOTq03YYjb9QAXplL1cWKgnJyc5jyjRSvzQN47el7X6J8r33iehw6aqG1Tqc5BEErdpBgqp2fG14n8dYwQzSQle9hOfaF9LbdA/A5ZlJd1yIRsude12NKKHhwzEPhpVtpJ35A/+ZuizAs3yNZjEQ2nWbmldf+UfkYdWyUsKXhi40BISouba43/VlaWFYrPBLeJhvK5SXQs5/iy7ccuGPNsjRUh2SUxtgXRxvCcE3RFljzOLrLV0SmV2UYu6wbTwpRph76uPJSWoM4LG41opJTofW1i/EIMwXFUqVrZlc6t/ASYNj3VNohDFMlKLqBigloiV+CKXO9YjHOKnGUm64WggIhZMeqPQXEO/dSkCOQIxE4YPIszcUHDzJUWtlSRVlbEGRKKJFdDbCHt+N01u6JHF1zBtVtU9Lrfk/TNaEaWCh/E2N0P4KntLIGhBqlqqfyFwPJsuRwV+8F0HB/OSlVLI68abRA5bvUFfI0ofTnZsaccAnZKGfhHdZDPnJLV8poQpMW4RgKE9Fto+0W6swfYyiH4xa8XxmuBtRQiNC6nj3fhUGdoSO1xrAbr6jyjDZmaKC1iZQ9+UKWhWmZHgXQQHnRtQQZvscGBYE29nPw9tvffvz0s6dPHl3dfvpbf+vf8j/8A/8jpyY79cE0joWnvgvWPEw2n4lMTqV9+W3cSDNi0Hfq0Ga8BWQWhvJwOQImGhXlRWPFlSrntpV1y5/4/z+vLaYvJB/+0PWvfC8Hbh88fHB6/vT08akBVKNQ7qmTJR7sNXRtYmoyC6ZVQ9mi7Vv2ektUKrJlrgmeF5q6olE35KvEo97ziDmlpoKZPshdcGDbWw/bS+gmfoAFZ1nFSjm8109WW1ebI9Q4LmdgYAJTKLa+Lnel3+ajxJUqfsV2hZOLi8um2q6s+Du/9+De9FrGzrf4nyO8ZSZ1LeLbkH7v+Hs+8HPP6WRyXBdL1Uu3Pm/sbG87BRlEJTiJFm5GMS+jFs+xk6oqSs0bXt/0dTNTlZX0/g1Ho9uAh5m52QkAur1SQPXMrq+fPjk7OTo5PDr/6N2PX//K1zUKBnEIoAkTMlNmmfFC3GAhtLmkuQLFSP5qzMYtDvMTXaKadpMmFlLXsBKO8AHIS9QUGMMo81lLaYNeJAGVrmsRLZ1UEz0VTsu7E587l8T/Sc8GSxbtUeii2L3o6ib/xp03pptImJwUnoFsuEq4wmMm3ONNExPfxRVEGveYwsGwLnLcuoimj0HWvF1awk+5H22iT8UhGafVgY+1jGPK5eT4ckSp4zOO8NS5WrllcgYRhi3ZRBwGRzaqaJZ4BUU1BUwWBDOcDvR6857JVbK7pFvG2XviLcRRqsmXMjhM901ubADuiLGEip0ynlUEXMrMA3JPRJ0Jbd+0g23DTISqOzm/1O3F0HEI6ptmQpVeyjA+5GPfrWRpsagIAPGetDQzuaZMmyb3KV3H06hFNcPtaWm/SgisCHIEkZo/nvijatfRULmxAHh12z+mm1Gb3hjGHLozk+75CxjnoHwIfJnP5zVaFdkIoDaCdpBxIBJCVpdSnjaiaS7d1mOHUKx1P2JdMyRRp0jtTth8Ql0g1p8BTBMGcwFoYpA+/zW8lpgLY2K6vXbqWspQBYipqWg2JSiMpMwKeDXdutYF1TvnEOmsJUChsZHIpKACcGEGwDdD7AU1QkKB1gXtPDg5OT5/PEuXy/vx0WVCM2lT4GPFMqHkDR+M5cG8zEBMrwWLEFW+JoKnihvGqiBBe7yDKj+C6O+vdw3igd9ArzTuK3CTvpf+x8vzQcNNpuwadtJVkIFNom6ELWAe79Jv0PQ+YZM1BQ5YoWNQbudvBrFWNd2tbRotoEv0Ev1NXXc0pVqphdzM6R/buYIEYzmyfJ3ib2VhGnalAYkqauNnR/IKugytY1A2B+FGJxW6L1xYDsEiDK5rxzeGJdx/qzKC8FRhdTLz/ilPQR73AhdGOneoPDdWxIiWBYRwDdCMu4+ohJ3Z18PGULgIsab1rWh9dcYPjH8A4SYpuqoEtJ8ybHJyMq70IZvYuavylyv2pZzvS1bf4yw2NeSm16wWRrFdyLQoKpB8Wbttwi4q1lmypTXOivasSGjqcVjWNVofCQhvaVABqdmMQoVy9V0UXr7d3gUDA4q3rtc3rNW9sa+/YzUhzjVJ22hIIvIiGmDnMDgqGKdKc9Mu2M53gHLS/XujLbs+6uCVDx14t+mpL5WQcDSO6Wn9DxQn17LGCWM0IMvTwWzH9PgJ4xAyDoRrVLsKTK9BY6Ibk1tYhrG4Bzy2RPJJC3iqjgkVv3vwkVs89dO2wtx6RhTaVunqosh2WixDt+T6BZK5DQnPRYa8Rp/vQkhj/ykNAmCExxbpI5baUO0+UpY9noRlWGP6oV75K0h6mDWV9g7e/eTpL17uvP0D3/zyp59c/sbf+N944803zy7OD5wsvb/36LOPP/3kAwPNDWuRZWMh6Ji6NdBFt62JSEJGdQgrj6+sccxbr0kWyouLBEk2mcIrW7C0Jq3paNiKvb/ZK5Hv0nhZ1xBK9u0lYOkCE/nDJtaPjw6f7tif0z5yWEZbqd1w8un5uZ3CxEnkK2fVW1BvFu5y9/ADcloLZPJgQ3eyPwNBoLyy8v2tZLx4k9KrjP1nscuJjvDDcZkeS+7G/teDR69gm+lq90LBmY8fNpaWVHV0fnF+vWttcVX4q1WdWlqB9j2KPadR1U1QcLUlnFqN0LXPEjlkU+vq8ASiU0VTWdiYxHerfstMdO842zxPmFs7K5Tm7e6sbfD6RbTO7sHb+4eWnTTrsr//RCsh9xLCrluzOiTzxdl5mbClkpGXsPRcTXq96/T3pJA/6SKbds1P+WiFNx+0956Clc8JqubEq6+98lO/5af+5H/0/3z06cevs0VlpURZPYD5Nyjya+WN8tOGoeILQHgB5uU5gDHwCUxtm/I0RgytRLmpq68Mf966qhcip9GEfYOSCr5fIk0zVxNqQmryDuQYYRSWyvOtm0spTO62IYrOVlHw4O8scSSJ5oIuvKde538Rw722D54sE2vuyom3wAALzM8E0x4VHikHNfaWHHn1dRUa6hQzmt7ZPVYbyoB6mnWfxY4PGv2DE6KalER5N0AxCkFxskiONSFVL2DmdtDSpgRdSSyFW+wn11DucaOdbFpcbtm/WFcE0sw21UpSupTF0MlEFoRbBJUxuaIytR48EvBvE5iPJQDeOFLr4xMsYy7zRjDfbbjVnvy21/iYxJZ48mbeImmYWOP52FFR3qhT/kJRDQSH4ut22Bn3h7MSmEHIWQRxeGwzKp9jyo7veeCzWVUBaQxnIQ/HY9X0wdWLffhOgPYu7O32PpIt6oH6AqZ8M9kjhPmtkarelwlMluSgM3kMttpQKKQHtsrt++bjvqMDnPapxe3Mw1EXttXEB46NphYlwRCeRTXXX6HxvryU7JMTvj5x7pgsezykK89SsXtLUplEeVlYq2fSOZjW5+zew539u+01uH6jwQoCSjgKO7l3nPIdvMPzjuFPpzctVKoqJjpMr+/fPDjY/+za4Sf77zcT52tDWOBwOELz4dAhbnDcRr8mTtGgVGVQf+Vknzt0bpU8aWeO2Z4LDDdeGfvV6VowdAqVTIOzWqws5f1eq6Tk/TQuvurWFypGYvdokuLSzhNzSDy5ciHdaAao77cElKCRmOdf5SZ+wW6A1x7dbaLhZKVcRd5z4KiN1IMbv0KGyqjsGT1aOhLZOQYDTzagK76ndc2TwBUS4DyhLXCFb5KUIeBg26RcfKyEW3R/3d/A/R8cC/3nESzk0ZJB/oLZUizlJn1YCs+1eagEM8ApR3I7Y6yKCmhVGUNwtBaBHsa28xCsbamI8GrfqhnFQtLapkT2LyeTqWkhc3J96k75G7UWvko+HKkOEsYER31fb8Ia9gie6dqV0xYDcZZWTJ3OK46UwhImpKr2WqLDcrfEh9JvAs07E1a4offfv+VFhpNMuLoqTJMZ7dMdux7uxvSniYoFSe1eHQUZ7dTzJ/7oCIZKSV4tFWAtOtgaiZJx/gemYa/YEQxFLKW70UNZQbkO8mokI+YTqFaLLncMYxBADspDZgegR/8CpQ9DtBcXrXoOZcyAjySAssfiwsudQx9HjKmKbqyW9R4UaDCkIZwkXoqetFHbPPcQFxFeD1mLgHD0E19iF3hP/S+4mEkxAI3Ktijzku9s1Yg2DZL0myy1cUKIFfod7qQMEX/XT1rDnmM9bL21kMqWiYygA9nklil4LdFWOWvihLtU9dq4ev2NlqowR5VC9UTo0mf2N+NMvPDJyeHbb7/91q/8tevLi5defPA7f/tvNvy/58ymFpYYkbr89KPP7F6QEXJf5zNdmyQ1+avadyTh+dXZ+VOw+jPc+4MXHlhen7ZYsdrL9K8s4E5TSYm7ZzArIFvcKvu5R2yu63uFLSXfJdu8blN84ReC566lgi3BHdtMHxoi+uzTz4wyYRXX+QWdKtbqg5SGzS+MQBtUm2/GdGDSUeSId31uEkuFmF1lo/kJ8jaEXH7KEVrK6qihMg7pYmVJ1H3eVyAWn70Vt3hexjD0JtcoLvTYs37KB3SZgci0CZLfaDKpUibnNTfbWsMW1OuEMtZ1cP/k5P7xyJcEkzRaIRn6/d7xMxw8Y6rXgZvw0s7Dd98WS4O2jK6A4U0T0chG2Z5lZIeV9dgQ8gxvz8/eCGbSgArtZZ5kQ23ycKgsY6oQSUcN52dnD+6fNKYcUg2dSsrjz57qoX7419555Ye/XxkoV5ZLoQFY8v/4uz3yqaNc3PRJZ7vy4iNguS0TfUGsEtuSYIVRfg/7HiDYiFEZXmXZU16d8I1qt6KhOqLiWlWUsQAce/OkdCYPEcLpfYxn4AtPuqhhM0h/UEwdtsgmTlrLZ2Z3pQic9pXQ1g6NykqWm+UwGxk2tgxcmObSNPoHWWMSSSd9fqmMKs00oNOzkKkW+vCrBa/8jaCyGUl4yKVmKW1JR5wkih9kU84wqBIJyFRynE/a0UChqWH9plUoRCfMCluypb7CcnSpPxSY6LaEHcpABn3Ma8Z6zTCad+ZWK8jkrNamA+HE6aBKDb7oZrUo8KJFOY0K9lgViPGTGyH7D6UNaqgSxWvr1jUFuYyDA8dF6h7GvIYtJWpmThXFLfqlZx46bRsrSQexzI3j82gmD/BjOF8LdwTMGHhxBUIezoAaZ6S1ceGAed38qterPtHVcSEZWNDDHVEYDEWGwZHFmnvywdhZ0Rq7spr9jZFgIK9uAqF5XZy4onX5NJvN9mhSt03L+WpY9Imxoz3HYsLN5+vwtFcvi6LPujRVlckGz3TtPJa7GUGn83ihFVS1cNQfHtteZ1iynkFKGmyKjMNXxIakOYSUlV0okvDlEUmP4X0noeqKNiA2uqKqBmpkx1TZznaYfM4S6q9SSyvq/OqfwzV7BQ1bydK9Gx9HyLDQMuAy1lW7DvNtzmYewAIcDKPBMhk/y+AyFikTLn301P/4+tz13SGfi/aySerpDlbQ5lpPIiYu4ncxnrxvI7Zshc51B7YB1/zaPD372WALzzZwEDZawwbuCfZQ5LMRoDvIxfdK90ViW2x/3d+VcItz801KqSieCIj3d7s/409tkmQHedkd3wsEdPDuADZPr7MuByuIwTAnpmM/uyJZ22gyeZVSkfJp1BiJ0Pfq2UrEhqBbDMjA5l+5D6DKN59zs3Px1fL66B0lXcvAeCGibCyzgebiTTZ2u/tBxr9/rpIJP4PhnJdXBCQByLbPXtzuf0dnnXhjsp3ikcyMNA6VLK6hsjjMDYvrnPXLr02G4WbiyHj09oyWV2L8a3Q+hUBwvwGZ1KHPwRvRh9WEfv9/rP1ZzO9bmtj1vfOwhzOPdarKXdWD3W3abhs3GLCNMR3w0BhjizCGC0gIiZIACVJEwgVR7nIRKcNFpNwQokhRpAihBATICYMHjGm35+7qoXqqqjOfs8+e3/nN5/us/7vPPtXVbTvJb7/79//91vCsZ1rPetb4G6fBiBqG7b+HiuutM02GCPxEQJYbomHdnyxYAB0h0ngbL7N6WjUyX1B9ZrYMAwyFOuVjGPAqpke7WiQT8yTFxsRMGYkxBm/MQMkxe7gu3CooHwn51rUPknSSMXjoCmr8ZFy8j5VRe0Ps2uH1RQMpcUMDhjzYqNI2jQCN64vXBoVPFRyzKt+/nmNPrANduGcZninHShSekVi2ydvD5B2cNCXBZHggyOY3ApHuDVVSSFp8NieSIyN5pxJEqUATl6WGSqsO8lN8WIXTetZH1plLisKoVT5kIbCLl9hqGY8WYuv2pU/Vg9JCJELaOk7WcdGfLyde/+LP/+LDhw99d+Xex5/9vr//97/z5Xfs+h2rXXknl7+4c/jZ5eUbuQRww0cdjBT76vHDhzYNB5NoNCcXZ08dxLF/j1XdufoqjpC2cd/j27eHHcNXENdL2Hq2G8Rp4sZLrG5cURO/bsPQ597n8XsG/rpEU9hNemXFlq4pP72jpgbb7h7ePXFg/ONmorF8+F9afDdYOI0ln8fyEhy2eFTTXy04PdX4kmd9OIfc1su14v6gyav+1irPVVjlEeOUPj8BLypkXBWVonXNT/HXM76+EhYxop2mRjW00PVDrdjWxWtTf0lcFfaNM4Lps4B8vqzS5QnVODo+Pr5za9b/7N598TavQ3lykVjNe/j4X7GjhKRgfk/laI1pGMLl80taY/kKaP/Ac5b/WYpFxdBXCvqblfCd8qvdc9o43hElp75KRY3J9+GLsqVfxBcVQL9WDz14+MAh37fv6K2ODakyIhMTqkplwrv9D4KpYpgUtNxI50dEqykcen62f6iP+uRbP//NN77/y5fXryp2PpesbjzID5vqDIr6wiCOZ8bogRtroNjj5at8qJ3tD3UR6iTY0ORbiTv2VVxYnpR1VBuglaelYoeVNKHmPuO6PW9W+i33ugrsH6s7tmsgVNrO9fkbsl3P2vfOGpXTN/78jMJGeSPIUwVjIOpZ8QySNKHclVnd2bVfwhCIGQnGz2yhtHmJ3CFljOUbU5DsZW0uaKg+gdbW1QtXl0avn4CVGTXAEFnKkC8Zui64qhzQccEhB4msc3LVrYDVefimmFG64WMmorgSuENU9fFUGzwSEwTA0CEcPuE2GYqZZFXLFVr0oFLmWCmtn6gYDIJAoJVSzAR7zgEw6ZiLub+7bf0CAey9VypD75rVOUWnklPcKclzELN9A8jWgA/GnNM5OCWFodRjghlkiCJlEjPDPZ7xqoHpDQ+qeQITjtoc8tOkaJiM/l2c50wXMN/aVfgYn2BAk7NemfSQ+0nP4pdnvY4dc7a0vgQ1rKAb/c+br66kpZFRe+8AQh8hhkDlEi+uZ8BHEBS1L4K1QQsQCfQonGpohSShM3WXV8f6SM5/M2FCNwDVjbCZ6ujdrdMHXCpiyjkZ10fsnJR/bQtQqO4ZbDoywRGGw53Qb3vvETehxTkwYJo0lduHU+KO76HRwMMjSzSv9/nr0PSFBacVpYko1HafHN1qNZRhfHt8fC4HJzrmWnnnnTYYBgzQBWw7uXffWUbWPM3hpMStwl7f8q0xdg9ScOGukMvhMVY3mHO5e/CBQbSt8686bpQAVhWC4/aeL1Chb8zEjhF9VmnM6cxijJPDKvT9ihyHifI4V87GeloatXn+DX9I5/lrafLnIYFVPCGnnl0FJP7eNqmtoPG6dpqtVKVWbazIuM7eSRs5myt4N9cXn6ppA7fgKlyZPCtwqu6EPiv2uYcbcH/bv8+QeT5HpVaUYlOdRmZyc7rcYVDYDfKhlVVilDOSVWDxKfpIbfKsN3UjiCXIZvWwrikPmOybOrLo6ZAQ6jG+mhC93yrBFK7KQmMZj3yCmOMecJm5myn4hEqudozx6zdjRZtlv7QaUmsnOQKnxApjRixfk7Uam2Wi34MpUjbYMli1gl3ZLiXn4Wd/QanwtVhGaeiPHcGBHMWXmqUIjSuHlOEPJC3y0aoyL8YXxtkbgIvL8oWwWmb0IdJQJsOWnkroMVc8XK6TmRDfy2BSSgUYOAYPDBOMTUJOA3KixY7oBiMZk0roZV6jJ7KjSDEuwKNv6PYacnGz5PrtIFZa9DOQnAarkBTDLOFXYwE9VyHtA9q5sEABsLqOI5XuSSolmxD3AKFRwBBXxIR4m0JuIgrtmsDQDVS9HcAMH4zpQA/SMsWt3SwxhQjb0YspA0VFpLAjTV/rZLQpcdDxOIYkwnQaC7QYipk9DovopN8QCrIMEZm3MSBDgcEUjng8bA0SEKM/h4fHH3/w4WeffQrPg6ODf+Af+L1/4A/+PnE19NJubz159Nh6mCYTMCEpMhdQDxGrup2dDw3K0xdizs+Pb+0eUIn9Pkl/fZ5hUU30K5QeOIxEcsxcrJow9HpNYK4SzsPf+rYy/CapR5Q38RvAvSpqChRP01S6OFbJw9BySeWWfqeKpz6C3Odzzvd8aqdzs/R7NTkdi3d+mvgk0vTeuX0bjAV8FbBqJjiA3WAbHjc4fU7jSjnkDxY3MRvGDN+E4Xu1LStlHGvApPdZAkTw9PX3yGVW3esl7joKM9HAtqFBJ4ijEs8b/ho8FyILtUFZGestNG+Q2PxO0HcHfp5m5QhsdbFiFi8M4av+ENA/8o1EUeFfvm6bh+F4GOB78eUFIY0OVQxu2LPk0V+SgbNJWY5sQn6S9cq6xMDK5dStIzP81zu3bh0d+ipek/yjvAFnAiTKDGZb6k61as0YsOpWlODYPaVViSW2isgHS3hCrMflsRUYUaquSMP7lyb8Y3LQ5A3wSAdq6zkokTPwKqKaXFjsWoVF4HNXwV7FLyQqg4Qn9RQsmp1vFFmqOe+r/LAoTQO9YVaFnaFRnqKvVksYzrKIY1Bi5sDN6HjBzSbEgqiwAVeG5e5Xjwd8rmJtTNxDrWQeUkwkFDCsC32vG3WIjpF+HIhfvckpXsmVJ2AonYR1q3qQIKaVuGf/pdwU6V3GZxVsAD9L5UHu+QvOZFlJG2seMUwTHMzChcxf5XiYCwOWdgV1kA5ML0VjYPh53gCY8W/kaHMG8+AA5j8bHLE1jtEcpVRssSb7HIJqdbsL9AEubq31PxurmY1aGCbLDAAn5LwpC193f/jYZ4N9N5eq5ymkg1UZ2gwzITMLlD+gEq5WYJBtlH3xdOPKwyy3146hlqomzrize+hMZB8PTroXFs8fHToBeayelqVWXRLHiO47tNeE6ehAwlGuFsjMaqUrt/H7630dm30qUtNGUfQnNL7g5oJcbR1Yr2+mjaey5zivVqbIZlauvmb+9eyOYNc6NtCEneQ7lgZpcWwV2FMNDg73OFE2/3g2eKnHwA/R2eOmHFpNYa2PYQ8booyKHePPPg63uNPZJDu7RyhVj4jnvI8vgx+jdZeQYkCBU9EJSzRyX89fIzh6KzwfgziyU4mXCfG7P9N0HcOYpPN60pGlDyuod+lHN6hCilXK73mJHn1ZkZvHlVq5QZnsPc+1+dmATdMmwSZ6k6zyVplhvKCt7CvxzfOmuBuYzsweatE1ZQuv3s51A6S4Z+lvIv9Of6tWA3BBbQ+A6rJOQfaUjrtbKksr9GMmFeeboO51J42uCcl6+FdNC2uxrfxu+XIgb7zPkdTKtfg9jFpkqk6pfNV1AiJvuXbeedbenDOw8W88T9YZcs28ZtGM6M9jKbmeXUGqzcF9FStnXVVQOYw1Ns2giFnXAYDS2RlL05wI0IijppDB4PhKA0oKcPGVCkXi2KNMiCyJhpmAt5eq2Oie5Phm7E1ea9/dJ6Ynj4/9bllIXKIGC3P4kD7kt8KAhagy1PiNeRGzMaE52PHPnRGpfoyGgHobXZ1Dj040zOqbRFKC4SgJ8hXLjcxJgL6hf+YWPMWvEBOaLBGE74Zev7xttaLEgiqsVfUqtqlOFF9tOxfCsGxDGEquOGvWlQKIcrSb9QuYA1zS2hl1+1TpacfAqtApeKia0kNDClAjJYwLDt5gVpyS3GHj3lU6z8xxI2cN/xh+s3jSONOMLsOH9eIuI2FDY6UMIlN6M5s1GLW556kJVOc8Znjy6ZIqLJAAGQn9nUOwhp/n5615z6vzpy1pZ6o8Q90XKDnl09A2PfLpowd83JdevMuQ/3P/9D//0kvvOPpzZ9+xQZnvTz755PzkjVRwztmoTnXI7ZVT9M9OTmhDfl36Zp58f+fo091bF9dn78DC0DPly3Ob01dCEOeQFspJOfp6sdTmyxEcN4elPQ9Zfr/rahcQIMeCl0i21tzg2iP0XYl7DfwEB/TmwrBTz9eNi6Ds6tbtW75zXAc1v6CWUiyhmJjWjmgJrbfRjO1ZXaLVSilhX71AgSIE3rl1K7+wwdkkHvAbBCnL+FuFbXD2+Pk1CTfkbuIFpXWh3OMCFec8jXbUQ8uLyP+43DpVSa3v2T+0YcNQW7Bcu0cfOhZ99zLethWg3RyjLgP3hsOr4Erqv8sJQpuneY2+eVi34dtz75vH55NEZSLOA7jo6NhmAnUOndSJebmbUeUK9M3DvMo1+wG2r28Vj7z+rvW/DEzcumPRhZE6DJ7JNN9R9txI+YKzgaafpn+r1tA8A5M/+Y//5F/8i3/xww8/vbr6+OLk4e4tw5WGKc2HgaNq8DwM3zSIUOe4zVuVm3kZ1NwiZe8z77vnRik7oYFt4Vi1QVnRxhAps6zp8+RNSj1s/mp68viH0spqAEKs6MJA6mdCyuH8GbdCCjsNEVdoDERLHKijf+Ml99B7A8tV7Xr3XgVdbTurqkDuk9awpxhftONiOXNsOA74zyILbypLfrUbejvOgRF4OSNA4lT4tpQ0UEOvjLHS55Q9YUI2besHT1BjzCHMpRTQQyRHYw3HpAOal4eLDTCgzbOshl6rO+JkkHSa7JVX9qivGsRIQPzHgtgVqwbq3J6lAylrI47yeaiNjosyVoMhPj3/677aLhSw2FPp0IlVKcK0tHU8wBDvYYqVatuXgAUz4xHmKV4rsBItoKd4Rs1OfZdK9zeHnpjztlGh4JK1pEV31AyPQavppK12Wpet6URjDZe+nXP69DF1boSOpdGOj9Nijgai7QbZP+RpqlYM8a3t23uHTi6wJPbk8Oh4thBj6AViagzTk+hxPPc5o23D7nS3aAFkSLNZYGfOHyXxszOTm/kl7FpySKbDYv0NJrKWH7jGQBHDoACJFpWug7aaN+is/VrVdiOkmCkKtU27dJ9bdlG/sTQRkmQV0DzFHEPU5CX2G3GxA+1QWuYjRYKlX3pi27TVjyYBWBdrk8RoIo32Wztxfq5+OMDhaM83bQyYcmR8HoLfbwHr1Rk9Nuh3dKz+X1zQcIsjta0ZAWU766KKRMvrOwCb1zXIva1uGJwVp6WDhYUF1CidhHXGX5l1v+WFOrpjT5PEo2mTcliIl2mJ8LmhpSumlDcufI9rRW+S/fo0QgbegCl6zaI3f0s6RYUnNo/nnORkKHyVu4GuJUs1v/c1WeRaCUAlEtm7LZPX08J/U+T3hvN3GjpQy/Ts4YZHi/EpNKSyE+xpxhdbwzKpjcldWQsh1TzLIkq84UsUzLWIiYYNh1aw15JMMkDTy64ipSP6uNtreunN1LAMtMcbifsBYdRh9AWP5a6PXSbIViGWSVQfIJfSMNCX9qq7Zvym4hrCnQzLC6zfLK65K5KUIbDK1Z+pxIDT35CF1shmettTaLwI4SFmMJyXxRvYM2MAj68/b6XFsbz9akYFsRtA1Z9XFuOSLoM6jd9gGcWjeaJW5rzA+sdshZRlCRr6E4TUjWUu5MOsNLU0zPa8hniSHWI2Im7kSU5GipFZTHYfkutcMQdGJqYI4xm8ngObmEkEWrVgAyzCK9yyiYqcNQMVHclFbR6HwxspTUxA1jWs9jjkTLabmOJvnuOFAozBdEY74+JkNW2CGVhno2CiBZw2b+VD54kObuGwyJ2C0oUaYItGT2z8JenmFxFfYz+dNPbQxGyLrWvrRDI0Rn8OD2iBPwIMPRRBntdDw6YjR1dp67vvfefb3/41tvHFl+/+s//MP//V7/uqD6PQOEbb8NLjx08eP3qELVopMIZXFFwjcfL4YeHVp8ByPPd5/NsHjxZH4PPw8UOB+/sZ8RBA3KILT2T6PGSeiloP8xtbf90VY75X+PdM+HlghS0UhKVNn189Q8fHqm7dOjabgW62ogptAEpHy+4Y0jrvOzsnp+c7Zwao4iSZ+K6zml/tINoKiGfZGU9DXRo0BN8Q9ny534XG5wgNGxLV4gdG4Z03chwyyIAsarXiOmG7OfLy/NJ6dx/5anGwiBwqRijctFgVlqCS3o0ogP8cH5BXKQvVTelD1A1mm5ib1y/8bhBD7A1Ivwo7OT358L33HbWk++T7Y+P6VP2HLWEyfHoG6gYJAZsq4HdUxYIS3xI/P+dtIaIaODmHu2WfnDdw0lVd+yyKcl995Y1bh0fnF09PH22dPjm59fKL7ApeTLVcTGYpVBBFBXz4kpGqpV/NRbyMMBJWEJsxhpKDiNlKIYGxXngek+KBjAnHi6gNtdJMyCTaJM1EVdTKNSzuef1bPKimYJU7EcJkVHMYBC7Jj+7V72cPhHB6cuWHwhjCFObHqMxrbVLtjMGZZphZUGDTED6ouQ08aCVtFl4aOMQTfl7dlTGm8NPQjP7nHIVld6wezkhfzsE/Slf7EwMW+8T32Mt4/n7zygV6hWmNnPFr78WAwE3NwoOfo1io8OrXaMUwSYhrEHumfNBaPCUG9pDaqC/CsCeagA7JLUsco7EhXUHnIxtLKitfg7XogBiHV3E0qlKnTQ2GEEPd1KFuEeD4poJWSUX2qfsOrunwqz5Nq47OshLRGEg80cwwN0DfcjLWW+sdETNpI2a6DDWvgZpGtm6+osqWEPrHZbVsBaI5plw4xGw/ffLk7MIXMS546tLHGw6pzcb1NCq1Wnly2rENsvG5HQ4dtzz3Le2d7WPjoQx+PG+TR80TibGA7KDnUJLOgDmSoyAWQOGOwSNTxENsZ2pixVlDJ+cnZ1LBwllBVShttm1VJo0NPXL/jaTv7BlHcmKxjhJHunlCHe1zalon//AWsq5Pnxrg0Hw3Lkp2OgBIxbeatj0dGMEX+0eHPZycwHTvDFZoPW85lI6w8q0GgtP+sW7b+akhpIakUKoDRsRGx+xIsHpViEK1pf3G5ql52GiQEcNUF88cM2WnRBjQUKifpcfxg2kwVOSuU5HqgxcUyFd9y0VwKeJzF7BfeH8uaj2OanwhdJN+6t1obmCl2ITPz+Y5tQqvUU0YhFDXs2gJGiAt3W94FbXyPZftJsvmfO5G1AaqIkre6/9friFwM86XZRgrqOLubd+6pRdIUXC8+YFYXXQ2wnKGBHj+VgEHRong1qVJ7PHibWo9I2TiC1/xC3yJowQJhZfT/zG/5DnhvLB3YuX6PnECFL4ZAfc0O8opUbUa8Fg3uPmFWg4GU02BWllJE2WQjm00/kRR9DWTWCDHIrB6xTNVdanTMp1pFKpPoC7B8sk3jl8IS21Q+8t94vfwg2xFGGCHe+SvKysZb8dsKbZHQedZ/1nu5qVcbqUbDabsGdMAtfwO9xsMLVthsDFmwC7Jc/D+APuSNBxXk3JB8FhOXiywTGFdAoROrT8NwuVReOiCa6IjQpLpywZLVbZGfAoLiBK711CH0ZzawUKm7CLM1imsVFNZHXzwAcDW8k4mWyrytis7wyrXdMCAJCyZKrr/2Vm4KucmoMgpQGCpiypp6Xsu6+a+kJxSdHAMPIJmuNG57WycZfEZ0Mlab6qh2WCUdyiLkydvV8a+9YWDF07Duq5KBI/EcocyW+zSbAhO48b6hDg7qUzLfwahPIHAWcICJ1KcE7S2t//63/izT548eePtL/3A137gj/2xP3r8wvH5+SOls6Qsw/3P7rUtrGt77+gDo01X5189ubzw/SytQlMKdfL013Z8bQpLd6+/ct2qQgMhUaVEXxLQCXC4xIZHRQauBjl2pQtB72n9ePoNrth9/N1xv+HYfwmXXL47i/dOO4nXU2g8vPviXT79mdbEWjvHQxwfHls0cnn5+OHpp48eGoSrlQXQ0LJV1Ft752eXJ3Y/+EraRnw6ePm4OnRJRbOfM0Ng6pl+WuVMgQujeSvk5hpUiCe1LGyD2iZ6BQoLVFX48uxLOXxzSMDW9pEzQ0QqRcFVKbIWffq2ijSvKaghyRHBpogbRd7gBeYXePXdCHp/Fv/88wbB9XMToRwo2EN+SWGadtjZ4gjUAZ4LFcj8Qs4NcBpBLjcsAqZkce9q6yEt3T7lyuzdun2Xh7Wz31dFh7Fzk7BFFzpmW48ePdahPrYcbXfny19981/9n/yP/+1/+3/+yWePTh589MqX3zmxdSOVvjrY73vtKoIpcM1zI43nL5DW1t4DGLfaIQSwVU/iZbze2jE2z1Y1n9W+cKO8LSswFDM2QSujcbl4S66EhwNjeubZmxCQ1kBD4pirZB4k3TBEKeXtVsT1Yb+t0+1HlREE4MAcTdkoRlWpFZxqLMOQk2I86Eg11wYRAw31ycFpKzuxf8dRMNe7F1uPL68NFev0mux76nvY+3un29vq19Ora19fxqI7V6bWK0zvwilVoEHKBLU4G9BNyEClNqv+wYgq/GpjJJxRGFwO8RHk2J3t8zdZpSs79OpwICRlrqG8eF2DvLX7mcQa10XikKk16Cgx6rRz8WbD0eUFNdtZYTCqxkj77GlicIYlzDtka1v6UZJRPJBcgQ23xwEZgUjOyAkToPbCynTPLEhXm3E7XZxbP2kb8A23kO1INyhwIHW1PoxCqUKVI4U00iZCl8mD7iaghRs3GFSHc81cqddjHYFTrzFc+9EA1jQYaMrimtnlxwLC5Nf9I+JZDjrzQFQ6yxMiDRHUz0QvZKh1PR8t7LQZoZKAQ5SF8Jma/BIdL4xKt3fPT85feOEF7HDOKOtYB0wtOYdBsTUiZbxykib3x7qls1NfGMlZN953cZ6jr4AafntRjg+3Dj++PvOh+VO1yLarsxMf7jvSrD050f3g/ccpvRq6YZIKZddaDWI3i+gMhkwfXtHsbFsM8dYxgMb5D672zhIyyCz45YXTKKz3EXfeAT7Tt4SCMQAc1cXYMTaRE7K1/ciknqkWXr81b2DGYuxWVDvdqRBdzow3ICubIsUZWGvckducNylHIhhlkgQ301YhmCPx6AMmpFcrURjLVtizq1zPvz+LKGFRU0KhaXmZ55kQA1LAANPJ+c6KmvtKJneFbRI8K2W1mztPRTUvORkGB1iuUhak8m1K97jS3UCv9t4knpjnoifq/4db5S5MBvNVTGxFinJtxbP0S/WoJmP0sKkWLlZM5S9khwE1TWzhZyQtecluai+eNgWVrCqgTM9hP89jyhc4UAdeb5RAgYyFn4S9QijJ9PmWK8n5khueFSsZUwGz/skFABW2CbVyixokRFjdAYt1zIgFGGUNZhdMZ1W9VL3t8Vnq54I9IKo7wy/KAh6y3GTmxEnDzHamUKHUFRaDXW+Cgqf+TcednaiKAcFEzsRWJakQ/Ozp62/77BD3A+e5E3UGKheMFF35QRsMDEoKruqumZF45CmLYZwAYmRTu9JIg2EGc5VNotVyqDfNBBqS0bUDvzWF5cWY9iVFzpAUC6/PTV7G3LHYYxf75Afj2XIXDWaGOyqlGGkpgrusKGIDNczr/daKT4KKiZC5eplmxpvEUZIRKEV5pVv/4jyyhYdb3F/PamctTaFjKCuB8dITIEtdGy12nbiEL4OUARqcyqGQ4mJnCTS/PVf6XELLgjA7HQvXhKx526kddYuaDQBY1iZRcVbZ8aPCUdBw13vvf/jk5KERlzff+vr/+n/3v5bDSGs7uoyp7O1ZCPT48WNMJCD+Ls+WcTx5bKD86XzAOHT5WJA7aPHJzN0OE9A9jI///dEhaChU2riTtoRy0o6+RdLm9+ZtE/i3+JF6w5HnE34PGDdBMW4YvTgZSqMnDjx99fXXrCC/uDizBy66aMW1LRAt/Q/nKk3+VQZne/vFl188Oj4ioqRQo9guYRSKTe55ijU8na/VECDi5jbYfg+MYT/cAPmGkLQiNiVBP+WMi7X/gGsjrUpyom6T747RIv1BUruYmEfrJk+6pznO9VwkT9RNIfO78Fl5vhDxvV+eYTjRCXSD9Q3uwRMMJd8cMPbfIEeT7WEeG8S6k/zmZWRYyAocnfgcp+HAuDDm/I1lZnpT4vymwbnyqyqDCHbRz0Ouw+kTfQA7gH7P3/vjP/Lbfviv/rVvfPsXvnX75a/cfe2lRgdqK8ilriq7CzvVctjLkGNkMw5tNayNoLz1u6dR90j6ZWbA3DOMFb25ekxqY7SLjtahVsiQtFJM8lEJuE+W+QmDXm/AbXg0VHoO3oJYIaWrSrd4ghaza3b3Ni966aywRnerhlw3+5U98fgbbmYV93wKwmZHQ2i2Zvs2krb0tMXYXKpIxIizpgiqn+nRtRNmslQZrZaMxhCk+1P6TC8ZPhlOilJD1qQEm0s6EYugwf+mkSDO7Dym8rcwKkDSVXiloWzEAJX+ZbsLTt31PGJBhrBUi7PK6H1Kim1jVYaLLI+IIDQiT2k8956PV8zEjQtVrzqRTa+CRBU5Ll4SHmQmaV7GhutAVCEH8QbpBqwfv2HmCkT6KQjvJF5avADFFCNlXcxHBAZYHFuRQKvIxFkK5w4PMYH2x6QAN2EpvweWx9EkIk0DnlFMBqe9rQsNfRyyajpCGzFkiwCwVr6SSrY4lsve8iMWXgp+/P7+kRlg4E/OH588PTVk1IfC2liUQ2zEfhbiX+3uW013cXx0hMf2LUSs1juWx8VxqautedUM1HjVdcrqr5bq9ORM44I5ZuJRXLJhlUjTayJYDMYu/5vTv+co0viZZrB7MUJVE2mCIp7itkCMMWKvnhrLJNYMdzHJTBqjEjA0cxDdV/oVjnNrRKDGVg1JHS33SXtFy4dFq5wGaxN/Wl0HKEFEVwmBkrCUo7Mr16A5bbioxeilqSni5wobVhFUol93jVrPLfguP5NyCprXFb7u3wXE68q2HtyfTxCoVa75o2KWKkyaTWmbEjdQni9pPcePL36r7Nen+dsImdG4rZsz/icDTi0e3RB8Q4pYpRaZfuQz6aOnTpGyIS8lKp0Jmo9T65SthBHY6pLt60NjOelWwhuh4USKU77J2/O8OeFV0M67kl5enWTZR5eMyypNCmWpJhslUD2oHLYyV0FcIGiMUe/XwdnenrmIOG2YMCsUWj3RIPla2WI6kpMsaqiZMuDYXFsrtWrLlz6oIQYqo7JKsEk/DGD00/jD9y+un465yDBrgisijk36jIhLuo5EaNJNyRzc8g5l2cH2A80H4+uv8PivTt80heeE8nODBCoz77NxdoKofKjALZUA/PQ1FVdbNGsMmRHgzh1bA3zdADbcMEGNSJsq7Xqocl3aVJBrZY5w6p/yr3bOXo8lwYcqZ2pQHuHG+noU1UTGRk9wFqmSXEf8VIW16kym7Mg6g09ohvVgmeChWv6CgSytfJcvz+OnI4vIUY6EK33C9TQ0DqMKCJDzWNC99+m8pATpl7RsSPwIi72jW5blN1YfPMRVsuDYNo2fhEUgeJWw9+0pCKjEUvBa2tn0qHISSmLN3AMGSASWOZmQ5cKcOXzVzvLrne/gUd95tMOJfgK4/+Ff/8afpmrG8l956WUjMs6LjDLrhunk1ZWPf2k5DGx3lMr+wfmTN04fPnr84DNoG/5UHB/X7fj4yAoZ0hISL8ONutZBi9PNoJrUkpD3gRW1td3jJFzHbV0ciOrvda1wLN1cnp4lffYg7vnwkj4fN1jF3+cvCPQaGrXWqLBrVs3BgYA55sd09dPHrD3V0qQ5bsmJNHBusSkCExXtT84zzjQixUA1aqdV1NfGTTG9dTgGwL8ji7N9psjnsfBsNOC9pN93i3GtWKiOLnkS0D8PSkobidEeZKOTNqU1ubLvqJ9btzi78beE0ZRSlWd424M/akRJVuBNukm+wSf+PHe6vyRdi2ublxXUfQWAu7j4ecTkEA5VfuXTxycwtBJscbvqOtfk+pzKRfCUVSBsb8B69RwShag+hvBVG+cwSl2qEEGnZ78oNE1ANXkwjZqaLHn66Pf++I+//+1vf+uTj979hZ/7ytXXTh6ffOW3fLmu2dg7EHcvW829vfUp87RzvmfptiEJ7maGvD0gn3KG+vAGLOgyH5hytCPQ9vecrerhxZv15jPQmeVIyKiH92AIiMgwLHKuwbiQDQs9ulbmlWtWHoMSZcOTCsLXsggbiMpkP5tO5p7n0WxdP24hEEACt7Yc23SgAl6f+Yzd1u7Tncvjq20ry1lzA59P93as97t9vvvoeuuFre2H11e3L7dOZim3o73uOmLF6vDTXR/KeGl7u5mBq+2Tg51b520HYmEtHKd1Bn11MVLxObnOAZEkj52qdka3Cxuq/1dbh/dEmKFlFloWGf8RYOXpR2jQW6PzLIP8BNkKE++JVh6t+Yf1Y+eq4iXruiMrwWJPOjZWRapqccyCmISYGFRwZoWpHk8dyBZABYp3nF3yOFJTkdlSYbcwnIGEzeJ49ySUeeR4pgosGxXRwsFgtcURruTo7CGMwiubG7JCBPXlZvMt0QXhTAk4irQfQJK41hntjb4Z8la8LJE0EBYlmfEWGM2xVNY67diilGaaZEYJzhCH/sOMvre3sDlwBnvTMFVqIqzxhMPF22Zgdm99luFrj5lOwJu6iAe3Pj46unP/3qNMWqtdppllELlf44HBMP6yfyZVrk+iLTM02M6tj71jzeFHuxoXpVzcop+5M7qKULAW6NCaWCN52uBBLmmQjL5GvVhWN8YmGujiHZ5gQrt0ZR9O0iVH+xzmLhDW2DsgqhJc+bZxUCxUUbPY3DxYY4CqSwcDzQoAsOHcKn/ZkzSOJHR9kHiG55l5tB98qJDt7a8AZ+gLHn5qzmSAdjKDapIeWcI6YuA/kaMKZfE389iW9M7b5Px1tzmN7frg3dKH2OQEv4T8ADugWh0w2SZsntbtBuwKL+H8bVJMLGJO1zuukkTPc9sk+p4/z5dTFmx57hpxw/b5VM9F/509YtpvmCEhNQcUL1K3ZRSEkn3szkeezMUXOFxLWTy4Jq4k2Oq5KlhKD5PguXLHGAxIVVpB9doDEMysx4Val15pAwBIqUfckrT8QsLqQhqRAlVOdtlPuq1bMtNw1Cy0g6laZbAonPqrLoXP3McchOSyDFNaUaOt85uCRMEkyGqolWUFD/A60CyCeitdDKh7nisQKTEzI5aXyTFnFoXDFu4wK3g4oHcAVEZRs248ienIa9fGoLbAgKX+/qsQGFWHQp++78SfR3I9GAmDADXWeaqk0gwuzDgafppecEcZaxlEhca2auQwSfsspPh4lf0yLLEmN1Vc+HEyIcAhtswxk8bAD09aqgmFxWlBXcM5yEY0C8BklvgLV6j6n/HpoauM9TcXGZ+n3ySdxITjXxj6z2JAjUZoj2qSesVb3BPJ6RymdKNRC9wqZQO6kihE66V8o+XqaI4lHh5v1phkZ0iW7DRLMoUBmzxKA9E88zGFxmwICrPOj/duPb7/6Od+/ptP7Qze23nh7vE//o/90cNbvumT+bP/iruPrffv3+e7CzHdA6px8fuffirFjI5PdSgD2BFah5CQUp4EhvD4BrPI7UBG3TeusHerJ0JycSIpD9tHPAX++ms48OuCPw8FqxIXzF+X7iZgJLdJNsnDsKwkFfd7c41eBbAm49EDrlLLP+F8eWppkK/zHLbBtEW0VydPnyC14WQ9IuvvZ4EHcImjthBGsWJYlP6CXlgR65rX595X6MKnzN4T6GT0C8KqBoIdxnfrFutCw229sB6FOWmALnpwvEyjD3g+7gXVisM1aFAakZXoN7hGos/iouHZy+cPg9G8fv7Ua7aRclcTFdrwo5XpFksdHh/Fa/8H2tASaVPYlAHlfuMUMAvVTXnQroI60NOsvhknA4Y5EEI3hdfW5iWAkA7nkB1YDG1fxMHB8U/+E3/CvOP//v/4f9g6vfjmX/vr73/rw62/78e/9sO/zZ7JlgrSXIfeGosYj64BHYbLqeqWZnNXKbg6jBpjFeMG5T/wszraZKEwJo+Fl7DR7aEiSubaYAi/Qob9NzFDbS/R+uzCvIgoOE7JFcTY1TsN7S/KFzw1vfItWDIkYAZA8lY5BFQr6WSUq8vbjlfBlRKygz6JaqyzsR5q2jzpxVaHNDYtmDOY4fTN1H1Jsovn1X4z7Y30mMJxeoaJBhunzJrYZE18mhVmDF2cwsx9G4HRU/MnliRCv0ehcMYHWlqDo4/GYo3UaDnNHOM1ueJT9I8ib+hMAUROFIgDcBjkqRZ/w0Eal8C6uKRGqhq3busU4hERV7JUMxAYFOmE654Iq9lZJUA0U1CbKAzHJ7gyyVeaZCDnRLQoXKroEwi8AjLNUgeun3z0hVNyHIPA1NfwT/FuU2CJg1m5PQZussfgDRODqF5JQED1WMKjIpBkpLynafUMpQW16g9SqI4ei0/GY+VmYbuMekQUSFOKWRZVFwIkgWosLp+ensQrS/d9pKwaBp7mFUDgIYggCQdzAcon4BmZXWySXhsEZYqQv50JGsTcVjI7c2ZJrurV1IAuGVHUWeSjhJt0tBvyuQ8RrxhU0brhUsDhMtprlWMgBpnRqLpiMtQAcvz7Aqknront7dSZwczbqR9/nqwJJLei4Toqvapz9A2DK3fk7T78z1ZItrhV5FyjQ0Al7vCdKxz6t65NzM1rzH72vEkyPwXKteFt+CUUP8HtDXNGVJ9n2oCa0MFhYVDwJqpcpV8lFuhpOLsCoToS7mRu8M+/XGLXplgP1gyh2mGR4lOj2BY4WHUP/MWXSrPpnfS4+Y7v52f5V3CJ132d7PF5yAQ//7pJWZD/yZS+DuCqYkqSFrjW86Rb7BdaxHBvc19vY4meFTSwgjhQbrIoqC+9KbFO+Ihik7Aaz7VKl7MpjbZav64U6+LCxBh0LcakDhrtdSqztXJvQnZ7531DiibrsI4GTf8hcOkS1ZpTn7cvXzdwun3wcbQqY5ZpDc4VtYPDO86f/mi0F0iuLiyBUhNCJUJqpaIAQqNG8zID3hVkAZJ+Qu1apmkxEHyJlgFQxYzoDHWZQJRVZXx5FHBLOiJpt14FDCoiTvYPLqvLzPgmAewgKxUrlAy+M1mM8WQfuuTPW2o1TI9jzbAkswvt/sJoMoRGUSs7Iwhi7QsXI1eD+YDAznlfgdjZ/0im2rqsAQxXzVYESBmDUYXkM2VIEprMTil27wW4okJTEaVDWlkL7VlU6eeapFu7H0/E9JxEw3Ks5PXFKyXsZCoIM4Aog3IE8obx34KRfZ9PgXMXShe4hUGCq+RhB4iGn3d9z9U4CmL3PxYseTkuX/HJoy1Uh2NBLmtabt29ddVSv8f7ty/PTt7kudoC1XfjLy7vffDZL/3Cz+91MszOj/zQj/z47/l7FM9LkzFRp4wXPh11pgeFlWHcli17ZS9PnSCkmcBek8A7B0da8cVQhEYrCHNaF7kb5+jNRQGK62TxrfNTZ+9sWLgi+zIizC/emdIT0tAdaWVybXg92Z57n7hAVStuUgXT/yyYvX72jSx4vd1cE1K6ZwBD1DVLn1e1nDMtnGsxK5ItPmk424qWp4avLIm+On3s5CTbAJ6A39k7e9aqDdZUSe0yYsyp2jGqlED681XgShwJTY0k2lVoMl7fDfAu855dH80G4Dy9KEsZsUIF6ZHcj2/dpgym7G/dum1ifLNqV+MZZRtGqBkwgECVKfr4BAMKZFiNfR7kyjGAgYf6e89ewCpoMrUK3LXGjZ7NEiyEBsoiZ6Qcx/0TuZNMeY33nNpxeDySKDzCgwaNTd7eugreFFvqGqOpml4yETlYFjHb3PTCS1ZmadEr6hpvFXzwfoo4+mp0weZCPXqW8+B47+Do7k/8I//wX/rrP/3n//xf5JBcXjx979u//LUf+Dq3hBNL2RO2bYsMFiX3WW2W3ZgAlznDBaTBDOJVVDZfKXa1GGHF7xnvD8ORfg5ORG3sWE9DJ2m+Ufj+RwJKE5Vr2Ah8A5pvdLe6faPIwzypgF1VIL3AqcW2YcuoWRohxt/OA5zZvjyW3qjmKAoHCratB3pBPfay9akRFTOABv5ZI9rqDBxnn+3s3R8n/p752uvrhxg6vhWYTzIDOw9x5XLraVvtdj6ZvQTcUdWZfsHz3Dnz17ufqr0X1uiPF5fVvmq9YLIZjiAu3jWuPnagoS4INI1W44Uz9LT1bOYFGBsmXTLBDGLPkc7I5L3FX2DBq+GoNYjJkiUADOpc/3R7bKNPanJtn2Je2tOo3Kz8bkLaUUijZ3mnIBQfv5NJmNrLUbXZ+2zaGXSuQf0SiU7LpCbBZhCoWGN54XD+TsjsfcuAgRkqZ/lPlY0RJVdkuTEOddoaB1SYRw1c5lFVFT3a65h+DfPu4fbtO0f2raYEYVfKgdCbRtNJEpbPZGIc1H9knbMeGfY0vOgR0VOQY5g/1saYIJffeBNoGDy+eGNPGQi83b1nkGYOILqzBt13Dz/Uj7lyTvYBTmisDrYuX6/vffu+7AwONxhb/WKAcKSwgmoMUi0pmNZ/qIUyfHNstEnvYakhPJzgPPCfaxNZ2KdvGT+yLqMjQLf6eCVMIS9Lc8s+PTVuBjjt3fAtdgppr+3123Frt1ZvDJ1N/29fnZ/6qkMFArWGrvqUu34urvB5sHlUkoI5+8Em0vYymkPgzNjVbQeI9c9StGTqesdXgXG6Xq4rLWmnCjuDlXoOlBEQwxCQSMFqv3DTNyKkWdUeAWlKnN+0hk7iT32aKkHOpOrhe1yzmn8kPmkDJVWZqwET25NgpW3SiRvqVnj3EYEEaaa6vtlROSUDV3ZA2/iywaXaBP2Fz+anlw0LJsQtqvxH2Eo5SJVxES7FTcQmfv2swOfAfleym5jn0kXZBPdbuP/9KR3lIbAKW4iXYHPBpacbznhc0ONXiHaXXGANy2Ry3wBYEdIszqr/ZcjmErG0qkAFD/syXUHMFstHd4E2DTruwIZFZaQmrlSq/oRFu6GECpUoZAJGpXjyR7MEKIymlDJVZgnCKxSVlgEP7wmb/NJRcu8hUKLpDEAvNBeIDO2yQxAbMKAjxgWHxc1JzkgBBEXZp8whAIZS+1Nh6qBDoBZ5+huyD5Up+6AQvahrVFLmDGgVWkA6Cm+Bme9xx0eKUUunKlotD55kMJvWtAq8BCYBKOUFBMVtRcqmDd+HSRUl6ypjbDd/IHrZkeQ4qjNUFTIJG+EOakUMepPac7/D5o3OQGe0IjAJJnFgUfes1NR1QEAdWMIi0mjNxfXpk6cXjiJLYjNr1fwtq49DdCYTVsy6kqun/scA5tJPRrevupxd2lFJMFngkUeJJFamsqJnRlCsy68Y7oCeJG/lqPMcTJYeHRxfnp5+fO+Tuy+++OTJyauvvfg/+B/9K8d3b3FufSIeMuedcLf1+NET+OgfgG0WoOkvwDU4jXpagOE4tVb+LBalKovDCTDSh2lQ2VyY41oULdLidckGwCI28nF1shS9iX8GYh5kca0M8+h2E7aR3Abaksvn4GLvTcpyQqi6EA7+h96giNP2+z584DCkYUWtn21Eh0d3fEVr//t/8Ou/8GvfJrCHTx9pS6QcDSABHeMBP4VY/e6j8tSDWP3wBxThaSKrn9BK3TbXMGGDxKghUcaAcFrvg5pHwcJNRVgEZAObsQeLVdZYuPBh5xBV3t79NQ/m3kqkVKlyi5rCF5vLNjEr/Tx/HrRev3ifkgK1Ca4YbFw/subl4FuTEqdPn2wfPrFlghHIbtCnVCXybsgOyg0mC2AYDq/W66YkaaZEes2B2ZAw1Y4EV1VsOEpGjFqjsDnB1vJvbb32xlv/3X/lv/fxh5/+wjd/YX9n30ChA0Mba9zaNQtQ17tZUXfjkBYOqGcUGT2jzVNRE8lUxlqeNhdOzV5USyUw1R+rJdfiRfeYErUFwmx4FFnPHm6eBGxi1xNoaQF5jfUOPdyLUSt3mgeMKicbz4nNzCbwrhvvz/riiV6QlTV7EdgwspGn2xybq+0HET3rudVya6pEtsHlev8sDxL1PDymlWO0Y3yCZ9b8Iues3Vp8JUUrk7vXFupxcTjBmJBZgpTSI7pE0TLWmpWGEkUclMGSdlzLG1OfHZeAclDwsdTerSNVsAm3CQ/gwK0AuenShqU1LEVO88J3zCJWc1u75VB5be4M8otWm+mGZU5qETVLkQZPXfY+O4VybD8zvcaZe2JQuUo3gkgUs8csHHL61ELIOvSTGYSNYxUMeWwf7b6o/y+JXe9syYho0M7ApzPpCer74q/9pKtOrgaLlsRF9hV07j0be+Xg/EkzLI2xJAymi00G6dBwyhhkeqDTceQshj595VqJcFSm2FEIJdLNcQ4+5Wo5gzhPpCTBJStXz8W37QyT2z1iJxRCaqESGzXSe3TKkCTjAnCsL5095rRTE2W6IxdPnyLDkKKS4Mgixj19Gzwyw7a3bbipug9rqCz3ROd3eiPpeT2pxhzhZgZAItOtUDw8cMKPeWlmeefKt72yZoBo2NOUptbpfdJOfwAnZxCaCJlhwcwyIqmlW2Jqcz/xmRyycZgyEYHCAIgJcBurhQiHBIVs3Tx5gfErhcZdEWAT+iADdOO+FKfxgKVPfqtElC2HqztUiWGEsspKOvM0YvrNb9jvIqwIBgaqsk7Q/Dy7TcJSTXEFx+jNJTzbsUEDkHXp4sS8rqrnXLMa1dNNotRpU6TQgV7saNOskZoxGBPh08OodwKSZAseqTzdhKSNU86aSdis/hcrXuXpZ/IobJP3iwSUopD55/brEpfg2TWwKg/Ywd+9HvBwkEY0eh0rN0XdUFt+iRaTJ69e4IRlNOlQtqge5ID1I8wn6F5Nl7ZPk32sGWPHQ0tVVf1q//beJ0Nfg040ZUZoVEVGQeWViXkVQ+cbEg74IrA4MMuTvfPkBAwd82mizHTLfu08r8qEJhr9WsP2xtblqW/Rhaf3gIis3Enh+75gKQhjBmjjHoDX/yWk5J22C2LkB5k0HoDaSUq9gKqY+/SHiQ6yeKVIvRFzwH0KJKPHqjo4IuqndNVM8uYWZZG5ehNqmT/5M9NVzNaxhF7cF4VA0UOmEZeiKoy9ltlZFt3RC8mMSBL0xyIp/frgg0o+N2YwpkBer5EDOXAacNIklUZM/4ap8wuEK4Bj3TzEKLkqH5dExrJY56V1REAmAdbD2H/UdYhnFseKA1ZmhjYsITCCqPlsMXcguiqvK7RDIbYGrCdBRuUtXD7b/jBt6nizECj91keVaJC6Z20ORM52zp1yEu/1MxxluRKyl0A+uP/om7/0Sy/cuY2mH/rB3/Y7fsfv0sA3ljkqdNiO3r2jFz659/A7l6drHDo2aXoatcn33Du8/bHDVbedMT8XLoQ9/NMyWM33Yju/iCUxBj/8KkGNFUwWosVO6uu13tFbzFuXRPOw6JvninDFmJVmnj0+e/382WBfqyRvYhaUyczypKSdNzXi4y0ZQTeurGk7Pz391EdzuUFPn55owLjYbPe0cBaTHL/08qs//nv/nv/8L/zXDx4/uPfpfVPuu/ryC2e0TyELb01EyOUjKUcL2rJ1Lbp7ikTkUg85i6h5LRxPti/fkmx7l1VU9ToSYEpACnuVddCqKkoHz5bl1ccbwnKItp1LJtHMwQ4+XmqB6i3EuLRoa+9TsLxUVr+B9zPXjeXfzN9OqkXZZv52Qjaxk2NyDoQbGAWr0bb7n23tfufQ0fsWK1883if9ZVckVCWl0jQuNiSJ/oYlU8TA3twm1HO8jSrLiq6ePH5454UXtrd9mqFRt+KyISAEOPjIa3sM0z3l7W+//dab3/dbvvreu+9e+b7wvY+e3r//yisvZ+VmzLwlmVTCOyFo+RXkdvlmfNr9sDHy89d5D9d7H2Sn2gNjzBM/JQqrrshLsoPB8HSMb0wuDEIhN4QyW6+EZ6P+KuWHZdnEFkwwSzr9FpM1m6wRM2ah19ZZZt14afSN+bIj09OpUejMOTN42cehOkqh2Qwuk1p+3/cPuTVW+lxf3/VJku2Llx3pc+n7D3ymrfP97b2LnROgti7vgLOzey8fVlUIDQb6eGvvfo2aT7cM3RogQ+X1DXxPV7LLl3UdsJAGR4LS0zpYK1+DAuFlZ5JVXlTs8Bz1IzNhEEYax5FEk2r+p5dpmyZtTInrsjKubOM0EUl8hwdigg4vsljWRB0S04Gl8A64FLLnCEu01L5cHyMmgVdKOKhKHtQU3t3V0Weh58ORllC2t6ENpdO++3AMtVWvIynMjY34fFXTaxr0D/IYXXBqRZlpadlDcOgbfAlvnRRJ7A0L1AWQRBx4ChLv4/bh6sMrJw9NPaZQ6XNKMJyagrmhdWlUIXT7vsUtXn0tn4y89isn6Oxbs8OjMFWQx28kLvO9zW448zNQs30lkAxUNsK3Qo60TwkF5juH7J/ecKMXxwdO1nIeZ+dNY/3tPhsal3wWzOTD8bHpPVjD5+rqVdhfbr8/vKR/6mrNkQQ2FOBFDVC1KzesglKJneujD9UiSjhGASp9cNfPWCs0YY9tV3Gh2tpP/PRtJYBqXaVIF/KvrnaeWLPp3CsSoaV4LQXzrv6a+Bmtyf+R3dfAVHlo7GwdOskf2Tx4QJhq3oCInJEt2ALO3SdEeojVVm/Q1OkXViT2JfOeDr5THtAXlnAkkHIgE7i83FHkDQHrm+s36/hF3lyrxQRt0pdnXVHdldZtrs1jxC/Yxd5E3vxCQSklDdSkTdl6XBh9PgNQaNcNjJsUK/Tzu3BQc/1xB40L8OTE0WdvJbvJ9Ow5mL/JtUHzN0qx0Ad2CqlohHnrPrXjuSI3MERVpgz9DkI9yLUhVL4N2KFqExodiXeuVHGpXkVWqIABFa/CYJM15VENdIizYly9gZCCTmrqqo5W2zNsadm4oFN87m3MZBVEVr3Z22xnglsFuI+xymYJXjBDcFwK+acQhfmXuSojDc+xcMkV0qUZm0TZ20Q4hcZAUEbzh+Y1PLMePQ8zKgnoGsf85eEnNlUAVPwTVpWEGLMD/1zzjIuGhV2rumcToj+2TTK8C9dew7F65z/QsbynYGOa34qsto2omdZpW+ZI4+HFiDFAEInrC2RGdTWGg7jQoFR2d0CBVMMjqawjrgGyGFJ4EJeNngzVaAgWKm5wnpfwmzGsEU6NQLER0SyiGYCL0+0TX6wjBOF9INHhLTOeQWFiYMFB7GGBxmyc14j0CnO2NZ6KjsYZsywtYhhTdxZW+9do9NbVYUtRZS0IyVRAEYzxycMnP/tz35DfaT6HRwe///f9vSa+O4Z5Rj5ydLad3Xn6wQcfBi2GpIwoxPemnCHBQtsDpqujnJtLMjgurhc2nF2R0RSSaYWIdKwIQs1bglu0rWuSFTdkBSWBrMybJPM2zwH7PFsvIz0/K/QG6LM0wduAniRKV/TjJ08e3H9go/MsPHjSkvWdY8Ra08AHwTVpfSbgpVdePjjae/nl1/6Zf+qfe/fDX/tDf+AfPH1kjuA8ZcCiITKAVHZQqdQRY78VOwfwFRoKlRy61Zth3UJ2OCQkaAmxkeiEkN6DPFVgT3Pe4fp9v57cxS4WVvZNiYvVU9iURQ+kXyNrhLmKWWyXfTEjxALwDL0p91nQhnGD/iAbAZNzU8xKvl4CvWMHxaOHD46PfA/u4t6nn5ye3rp95461CtXclpYNxFBZElPSIDAwFxoLWAHVjPjkkd30n15bBgBMLkED24zQJJw0bilvK4KrPTq0zKmTXv/gH/gD77///i//8q+9//FHTx893HrprvkTW5QvfCg0heQCW3uR8ZUnd8n4hmKNhQbN50SwcEb/6D8fwusg6nfk3i8M48ygjsSQKjRvIgK7DadKMbW+mj85hiNJdHLfAFm/0qCvlIvMASG/civE+gO4cZxU8SplVmM4tnuyx1tDJP+vBoy63LJ7xfyU1Qv27FqTY5WQEYq+UZIbGI99iErTs3V5CDxZAYz5qyZ6yPUNnfRc5vGFsyxg+D6gPgnPq/h6d8tAUFtBzFFrq8aWAIgY4fnu04euDHjnag3XxJYAHeM+x6z5mwewWdoYVZdMivzckquHzoqoV6NIn37iouKxgV5aMKdEzFoQFpUHHOsUyVWlG4q2F2LXsV7AQqWGCkd18+Sf+ZVhDHSV5ssCKKUdcbSV9KFpnMW9Jv/ywvK8zDxvmsD8D3roV1OxKke5opEhfw10zVsO+lyFjeF3OMc4tyRXO5CqD6DgcP5NIDi4wK4YPX5nohuXcYpDYnKS4Opb1ObW+gKMSJ05cSY++koZRlWoNspcj6/hqj5mAA4Mwu8fHbnPNIGxHmQpfc/iz72jF+Xec24nyz+Tw0b2F3lqn9nRI5ypW8Vtvo0Q9U44NQuFZpeU1bJIdFM19LT+qQ6JLWGRKapmKMHIbenRrOBTrwTpZhzkprbuzrFWkvcXJ9lF5/lakSfPzsHuQZNSp6NkQvZPL2zTQsoR1W7hFeds3K6aMjM+R0ZRnUp+RoT0GBFG8g2ous0Gi4xuwgj27EomFrkOfQgYL839Vlkzy6CIqos7RnqEXpWvfYsYsclfmvT+JrmI3/SiHMOKuY9ujCp9Mc+ET7JVUrHVhU3OZ78TJqboFYiyBWp15SdbBSyF3f92kfVFhoCbtNszihMN2alRylVzrbhN8QYkCOthlVTYPGFm0Obe2P8NOZux/wqc2Gd3DzdpihqwcwNeJWZOSj8WZaAG2X/3hcGQMmnkzWJXr4pNLIuuDdwFvSIWesBPAmsZizp/ic5t772byAc4WNnFZURauGbVjx4btoyyKNMVDOk1IU1jMirjD2e3pvQcqcJDqGLXnQ6G2d7HhuchLbGK0WprOGfTS7faiLlDo31ZQxUKFbEhohWxaoJKPmyv6icfaGQTLGQbIepszECOKm6oftb1MTECFQK5BFr+wdErzzLOWykLTHAvLztotVk+nNnTSa+6eV4yGaJ2dy7ebo3y1q8GLM3QKnTCcmSOvOTZID28DTHsXZ3p0qOhdsHQxkhH7O72hd0Uinkfu8gUP3eMW+FIKjCQAcG8ysAWA+LO1E/2IVBpiMjUaEbqjw2EVYElED+YyutZKiVBY10rdhApvsDiVnSR8z4hYzqnsBmlaVgqgY+2BBQaxkSZTfuronyYsG4DZxOEHtEhQZFAT8oVF9JbFy9Qiuvdz5pbEIdkGtEYxYmTF4QUSN7Z2wR5fXr90Xvf+Zm/+fO3jo5Ozh69cfe1H/ux372A5+7GktpKB4BePH5Dvuga3BSVKuJzHtL25dM3d1oUnic3mE05sVsGxQzOxqHDs4AlE72P+NmZ4kgq0TChDIqJ5v5vXmPQDQcKXdck8Biim5S99bgCepnXFbB2AswMwwBXrLH/SVtjSvQsu+Elmx1ySbeujjWdDvlR300F2LWjYrzyymsvvvHYaelnF18+vn349/7eH/urf+X6+ODw5OqRaYPj20dXT9/KCh0afRzkB8ko9IrtrmHsSDD0lppIrFWICZ7g6QfHwr5qNO4Xlnvyr+ajiqDFPHh3+/CoE1pYlk7CGQhQX/9mdX6fjIsHbCwtj8kdBAjBI0fxaAaN71o5PLWJNYJOCI3hkHQ3S14XMiqWABpkdU68d9916FaZyWeeNw+lF1J5Ez6qREGcu8cq+STQRw8fPX3h5J2vzk6PpB9zpog4FPowXQEDa8BUlqgSV+4QSYPo6u61b9Q5ytLBTZyPG0bVMRiOwURN2PMJbEMqVsOxDdYg/MGf+Id/+4/96L/xr/8b9+5/9mvf/CXnH7/zta9ZvdDIta1NuX05CCMzhTlYx3i/csdHPfzIp4hNlbngu8JXg4LgBB0JiWy4EP2LoNhhNix6tA44Kw0TaNYiyjwOVUVLAwjIwRjWBKTHZyk9gboGGmIXgWkCry/f5tPu9F0nm4FsiOIa0V5Nj08E3tm6frR9dXtr+5Prq5evt59cX9y9vP7s8vq2Q3kur50rcO+inUIvXG8fX+w+1EO41Dps3brcl+ZYDb9UZRqFt1fJd0DqHJh9HKXZ02L0ubV8vauLpy9xxhHovrvNEz3Ti6LTN4Qx27BljYc6Q8y6DzWBlAnbGa2iyNYPDxETVkesljcFlerN0u29H6fNuHf0Y+sba35iCpz8uZi/kzCBi7x45FizFm3zR+UT6vCOx1cdhErRtbIZ5GS9e+i0tO39E24FNy9p1mcIX3kqwWnVVz5p7yNX2098zer89Vr1vc8OrbBHDM1z9l0t0XuaK2zI6qpIeQHTTYXc1OMhm1uuU2ayMX+gkZs5McwKAnUN0gZ6Tk8fKKoltKMVsS0rjhsa4ihz3vDW5UljjPUooh15jSpNF9ZYD6JSOCRE+Yy6m4c3GVgvBYDRLWRN7HjnxFOuIwdCjKRyLDpWy4YEND6AAReeEHQi6KXjFNNO2MTpGqC9Wx+nDfUZOqfLk2U4I0eM0Vtpr8ILL76Eq2ZIhAB+eHxoqaVO1bF9bCl24h2KzUm0/OZWPrtuYSdJ6E6ARh9csM//53ccWeyagvQhls6ruIV03RnfdbnaO2w5VU0hkLo1jVxVf01dcPW5KqrmgQ/eW1uUrHftE/DdDDNFDSxKj6mHddBGXCoXOe3aDtHK2MYUrre0aHiLAyGQMa2gfsMw+kD146oeAHfz4nj67xSyuVbwvKzwSb4iA/pc/E2W+X0ufBXw3Uk3cEIv1KCwydJPQXljC9QK6Xll2iT8PHKeJnYSUIRSSrbSD+QVsFJu4Hp5HtRN8l8XvAG/+QnsBjq8xyYP/umo8yXVLoG4W594qNvgMmXdIBQAkc8Q8F6WhU9gn5XZU8Kbn3IV4H+wVxSzYHOQyjnBA7n4kq1sA3lgwEs5SX+qLDrSh36qvcGs7E3pEkoaqELohU5pLkOtTglLP01GDUfhFZcW6zGrMOXkLENjamLv1D9Ls2JE9xDEtDLtrPAgAhJ5o6PZHc112ixefd4guFHgXhXj6jeYw8jqNjiTmJuhU0D3TTZLVJFIQfl0PiwcNPJgDbuZ0doLKQb1KouHeW1UuZWVy9GvLwVfo+RGb8JI5VmzCCE4lX+3RVOIgDuTvZoNdA5ITBtMY1i4jCnLPW6Wc12Baey/FjS5eo0whX7xipokAxlQ298cwCTTNXlK4ioM7Fi5YodvGYhoHC0oq9YqwU1fCF7hUTu3+BocSUq8QAa3RzlmZGtUUhE40j1ry25qTmsAs4hyWhpux5vOJ/5IL47X5DPpV1t/4ad+6snT+1zBl19+8Y/88T/6fT/4NUdd8uNF1x+K0C3H/wcllt1Q1HgeBmssC4QfTQgBy7SifUNnkSG/Us3bBMxTNCy2TIbFuO7RP/cFZgS2cgR2xfY+UCfCDUsWT28CvhjtbZj2LPd6LyzOl3vze3z7tmM0USLm7PSJvqrhHXMg1y+j2NcoDX4dXx85RBUbmUqr5nb+2k/9ta9+9bccvXDscAw9h7rF1SqwwYh4t4roN6Tn2duK9Fr1EkzihLO5yjb/hhUhV+aB6kZBMXpn11k6zv+x4mBqXtFlcg28dGqwWDAHjR6T7+WVU7cVDd9qiOUd5nNSH7U1ra7s+QtYyAxCU0LmYtg9gQG8KSQ+zr8CQ3daOPXR2LslvMbtROsyWoWmXqYuDguv+RwIZegfBCSjTvJHTLQE0ENMnPcBrojVGynozCHiB9pv/jv08zY4BJNezrTXomzhUKK3PGL20c6JA+vXju6S2meffmbr7ytvtj1396BR0sx2JCjS+G62bUQQIsLmlo+Q+sAmWvNIixm+rKChKTlIkMgC6uopUsaIr2ivS3ilVfKUsYpfQBUw7Cl240IWvf4G0TDE7LEA5Eqv/KVUuXH521snj3zd6/wBmV9cPzk3NG567+TiwdlTWu6Ml62d22fc+vawPuQrXtvsG81O/NS4WFbKc9bl04s7R0aD+/YgSTeDs9OBznzZRJELZKFjmLRc9jI/G5duUB3lGnKEe0F3WUbYM2hRcmXOTX75IG9pExBrAwb7DXaNp0vqGMYjNJYfbrEyTnCl5as7wseVLPea+Dn7OjIlwTCGS/+Xx9lnZGAA1VZNciQvzM8ypboEksxQ3gilZzw5MFvegXOqkkYEKnxM0wez94HRmPYTNjDXN7HwiCvJz/aKccEZyfQY8l712PqMqWsaMKJzteJoknq+5Kk79pYnmk7l9iTb6k680Y2Zxl/CTeMIx2xykPnn6kQo4a5mdVasQECSCsTI9dktb/Sy1sFkmg/S+2LLlq8KyqVbh+VMXgsXhdaG2WF7qv+rCunXACWXbWOehgltDIMLHAyLCAlCSt96GTgIgY4i+iyTnJzuK9ntN9C5OLzsBHCBMwzf+DqnvDLUwXH2uAA7vngAaxyPyQA2Kg8dZ7CSK2WcEUDdO55hcoXJVpiEaQe4jeFIPzCw0R4W6Vpv2eBEwyPT1cE6nyVeXdZMtH6BkkwObG1Z46RUVu3aitBGFHYPuSnUidolgc2Fv1VGIavCT8xNNJw8LgncZFjvK+bzsGdPX8j/LPSLD1+AuaA/V8YG9MLh+aQrJFAIcT2Xx/Oz839u4ib5VFhJUyN/1cMbmkSp1vg5hqnYeV5QN2VJIngFzfPk/963VKmU87sRaAZ3VIrCiva/H6owYIe44tfDFLSAZApElHIc3EocLDZleDl/K5D7nSMxVCyyxI8vu2clvYhyBWUApV9xwCtElxYMUSAL0egFg/MKCNvDb2iWFHT5BoyslHmsdCYifCcrS9QRa9YQyeofrEuoA59W1fQIyISEh65/HOC6VRo4JZCEvQNb8qFVTFyqYzA6C+/62owJs8iuzWJH83P8y3gcqsHPxVR2hauIASt7zxNVMcYXVAGIJQMEqirTG8+gwqwVldfbH247VM5mPF3nnYs9c5Ds6WJbG6BXpxxNIOSp9HswQ3qtdokpUJn+nphkMDON9wjaWvPWuWi9VFpYMAFGboTjmgYgZqUg2JjNDK4Qkf0OJFOab2LF1uGDEWWdHw3CxJZiBDIpCy+ilmZwD4/C/A2LY7NroxObvNDtqwIGQ+4FcwA0JiRTTRRimR1f5YzKCZwSi91cdDJhSq3JqTlrOy+LSHbkUpN4/WAWTKKKIJgqjder0+Zpwzp5nXi1QtlvHYKz0w8//LgTEuPN1iuvvvqP/jf+sHnjXECD+kZVa13yJxwAumrYcAkTl/bL5B+qRg4pyAZvD5N+g/pirpfFB5k3XJox6UXbikV2GZ0CBFTn3hQ5FMcvD0oSBU4/k9MTPFds8NPqKWDum7wDR/Lrs04/KGcgAOwJgR60A92jEH+BoTlbh7sGSvt3dPdW2TGDDqlk7EOonmtIfE3+D/4j/9DJqaaEsvCNdveON6O5U0iohVJ4VqhrYTVF9Q5+4UUX21NfANik613R6tRQ50WFK7C9yEd3j35o/J9SbwgfvnRb/8vc2H/UwWEDLkqePnmsetfMww75qA7N+MJcSL+YOXXQnLv+elc6DZPNudFgDt+irvoyhIA2003mB4amIOtNnXk1OK3LUZ2iwxyIX/3lX7n7wouvvPGKUUR5qZtSVhM+mTZyD/KGOwu/NfPgICHeVwiJhLKFTQ/ufWak8O5LL9JkRM2wHByrSiyDTauwzOxnd3g21y+88sK/+W/9m/+L/+W//Uu/8GvK/843z37L11+6vvNZ/MhkJ5y8QqA8to4R7Rg1qpKfkT3JXTApy8LAp9VHw/w4HmrDA1UsArlQC9vAuuJ3MpkL0Bt6B4KXYAzFSEigjMM4cgO18aS1KoyxnS5/OiKlTU75HduWrvGkmFxAmqq7uHj99GLn4YmBExt7Xij86haEnuzdfSpy1y4gM8i3zx3UdPXS+aUNbNZ3w++OFshZU4qgS9NuOEyIywah5o4uGuLRctX8qYo8IzbF1DUzjVU5grl8HD00ZHtHH6qndpZmelpNnVbHj8WSGaa4Pn8NwdfbH8diAs7pF62+xkunsE8nDuTglrVEc2ftjQF5VVhhGgWuuvhcxRQJF+vumjjCHEtEeKiJGUaQi1i+5Lkz6ZGl81JwctIMQrMS1Iy6zXSu2eszRZxvH3yS6953/xoUwBlfM2iQsOEq3adx/ss8WjHlAAxPtPsS8CgqbBf/mO9T7IKpeOWhgz4acboyz4D4/Xf5ntCIcaNHDez4Q1FO6ODXHJCipWKo3uIBXG19G2FbW19q9druh82EoAP7ojzaFSVg4L6NyVcHn+gN5Sfo5pgo0PeYSmAGwJdyD/eO9s1Yg0Wzorfa5n+QopU73p7aTuUWB5yuwt6+I/4dL2GZHajq1Nnp0zZm73ZsLc4j6uLk9HD77SjZ+ZaDiNrBPjWAV45ih4JaF2TqQAlH+4fn509tpYvyXZ0Q6liTxy4Ob/bPzp/O/jznIpDoY+3h0RFbV5PWCbn1iCwWS6Y6BgzS1eXTyJ/VcdtXvomhlbVyNsPIyHVgoQa8Dej4dOpuaGgG98hIW9kk5K4xTtimc+rhoWzYQHzDgQkVnoAkcYlZDz09f02o23cFb5KUTaT1OJ6+MG8wCSZTaeSfnwkYkKu8TFfyGvA3pVT3kpw8qwOwiViAnkfu2fPUOG9yURwPqwrKGOh+RqEGkcIqL8RLurm8/e1cm7ybEga8bGUO45QvoRAnUfE0aXJWASlT16pyK7F6RIPTNAo2mW5K73XSiANp8zhpJK8KFhR7KrE6kgpagdb4dDrfTDDFqhEY3oKiFBXQQJQ5ZdNmY5BAp2qwgCa7VQWc1tD0kiq2mtfwT5ehTQPZ6qvLIzVkBhOUrp3Tbe7QNHo/GLIdVqFluaIZspTZI3QVJ7jxq3oX42BuWLIoTEHHccxQmWKDp105jYIDoAJMKtRpXVAtDIdzA6Y+w3+2kS02Z8gz0OzACDg0QgFzItfuGcYKtb7Kw7iST+MlIbqPH8v0w5XRbjleJ0u6pv1WZXI6NALTigsOO+Yj0SeRrDBCiZ+x1eo52+ZQvYVA0NID2HvDh1oS+IVUQAbR0C/VugaTjGlSFl4hrkhZpW3IomVxMr27id4AGVAr10RWVLnXrzxC4R4mY9hHo5pSx17BrHbjQK0nDvBzdzqXWFiZ8UIQ1DAnI954FdXzs/FlNxkl1rzFR0ebOE9WVuSlR+3O2/vk43u/8DM/e/bkyZ3j469+6ct3jm997fu/imfoxkwrSiXrC6hcBs2dpmVVi0EdZ+I/Zszf0BI9Xrs/Q334M68TtGJKthgrbVc/G0Z7WiCSQMCfi52gSTAC25TludcBGB4bmIIGnRWyAidhKSlJz89CJRWw8hbeVTuhcCnTvHlYuFDzSVkfiSwO9m6/9eZXPvrw3T/9p//zN1576e/64R9tirzJPs3QYBGfNmgNQZU2AYsJk6gUK13lD2ZLtxaeGZZJAaWFJ4/cZTw7SmAZc9ZVBYn4Z1d5yjwMndCVeJJNRZq806mejDO9HvIzvi6Hh7POyJkefFp30emxArjdLnZDHRwSB+bnqEzJFVn40t4cL6qrI8qfaJHto0cPX3j5BYbSOYmNnM7H5mCMvRnQEccGzpAYcYuWylFVwSMQvzoVuTOcjIf3H9y6c3fWQBfOj+vHhO3lztMTo9ds9fbOkaEMk2gHP/zbf/Qn/9if+N/+b/73PnH6zV/4eWh89bcek2A5CBsqWd28v6EucgZm73hgwfThvpqlegpH3aRaIhhcC1n6KT4muIpY+hfHhy4BK7xyV9xEVUw5/J+EywwGsIT+dRsfeFQ2n6vR1Ww/3zMOiuaZsni+aqadYXQ5WuYPU+ridWhLyoVRqUd9MKasnfdV7sGG7ciiFjOhqgGKGybwk84OIqK1IqHLkcAfo6OWi1hIhzmZjBALHneMGjl4qGz1miIxRGuwtFYAbFoSkOLs5IsVtUrMIwFJjdcOfqEE/Czka0y0yucnXM+pwE0FD2+Ura0LOg+9MqXLDjTiBp+8hkEfYoxDg2C1vEJbS0kHGrfW9Q81BYHVCjEiUX00lLtWAFombkeBzV3ARUtaMI+6pXK0gSiHIG4y1NxM5aE40pBjAwaHApYGbuq9GMGKF9mQjYC968fUxDU/EzEe9DyFQaBVfNGntuADoaAJoRfRqkpdnflAILWvkKlQhIkX4DelMF7+4JoU4s3G662XrrXmiO8dHBpzmvE1PaLO07msl4eoIaN5nmGoLbcoMlrPq7Zw1KYFlZymOZ/UDgZL5qJeC71/eXa+5xyE5m00SJlU6HFtmvS4sBSK24RWJZmrFK+8K9ML5xcmrOr8N78Xj3kS2LFjGRaeaApxA5d4XER7eXEyJ2Gc0skWC4gcQeOJA38wPCY7DbSBzksf1WkCh7CTYFquWqRNEEZOshKcvtXVriOklsUuFkytyP2KAcY104rYL07qHIqkUTy5ot4DwkgQzO9xpYdLgb5H5ASVrxQpyPe4JlBB67r5vXl9FlFukc9AbIoVMrX3BvCzeAHPJ7+BW3zkPbuGWtqwCQdWHwUH1rrblfa7gD7L+10Pkn2hyMF99kT7+uznmOd1VhddvrDLXbw++DD3jBSEoNJva2E3pTpNP7Aj2ymgVGUeKjxlxA/evwksosC4NbQlyB6lEnR46+jSXpk61ivhSpm4ZZOqQf4cdOW1nL9eoh32BsiWWmR+jqkyDc0IyjDcrNvbc/9TFcM4DSTQNhbD4EUaFhHZplKBXGMZpu4yNEmpyJJAwIJWNoe3QvGW5uUzMAH5mehFEUvGadGW+wpm7VrjxIGoIMiVDuL1I1STKGPLOny3gZ9SjGWb8pQYUrJT9PIWn1ksl6NiVJ7LM7TuOzFt20Ig497MmXHf9xmYnasvm/GreimxzkZc1gfqZA9GYdbuR0LEo2+ZyFhd7VL/GvaABf6NvUdYNhbdQvN8Y0vYTo4l2RuuFbT/7TaM7Vg1iOevKGJr59OhZmhym6KUrrYzBP6urDXC27p3ZMFYvFJS5zsNiqOy2YLaHKXvfzYQImqAj5XBD71C5gMXgLWQydgavoV8hhrbB+1EJVuW48rowuX+fpPyhTSuysRJ7tTkxigUMIsX2aMHa9iC5Ik1Ditboq3zzx7e03B8+SvvfPbxpy+8dPuf+BN/Cr9nSIasyE9CUymXDx/ej7dlB7T/iQduFeIarAqHo9eoJIBG8b1evDO5VlzBLiHPnqIxEJuQosRt9hp5gkdx3XoUPe9JIXW43jmBzJVzx11nzrOfNL30AHjyrsSNdFIRIPJrAxC8BXxwuEGiqGSW/U+rghrba8JpEYXyKsKAlrbxYH/v/Xe/9dN/+Wf/8l/56b/nd/3j+9u/9Wrr54FQ6pRW5l7nqvQeAljwGr85/3JYlmH9LE4OfpNr3hdI1YcE88V02DhXJDkdckU9KyQgz1/P3p89bEofUcrImcLMAj0v0wJYf8aNI7aXtPDa3mgrv2U5vXoqkL65v/jSyw6C2uQomYiT0aEpMKiQ40ecORmd9u7s3wNzd9eJ7LGYf/TBex9YdnXnhTuoc3ZhQvLB2jY1nqjrW9YWh8HmCpg5jXQllhVaOTW/dCISTE+cPt0/PGizbntbWUcjf7qzb0i2f+tTpsFCoSxYlmfr8emD3/PjP/rlr7z9/kcf7+2dfnT/Z09/7rXf+sO/1cnfzf/LzhyGKjuZhIjDgwjP1TkF1mbQjdO4Z9ugYrJRnkOPurlvptZ7Fr7uYCz8NyknGTYDPSGxbsLO3+px91MFV3jWQYsjHceLLqvXvBX2rWz8Eg7guO5zLLlQ57f70kvH3h8TDe41VCMJA06X8iAvMXTfWPal9fwzlo8zFwTNFx4blatFPRMGe+JQSm/S5aK1XZIFYoIsVbW8g0MJR0u7aKo5WLWEilZ9slUZzgh041EjhQK1PUkMjIvzC2j1c/vw0zRfN3AaKoPk/phSuFvB0WOMLz8jAFKnbWIG/1Fra98OFHZ4AtYuvYLUmDPDsXt7qL7a23/iu0bbeycOg9vf9qFu3zB+2IdpbXswKLXzeOf8ld29R9tbL17vPL66ur2992hn+4WdvSfb16/ZOMGi+Azawe4rlu0cOgq+ySWLUy6vnZ+keclBRDOq1hANgY1Bz+7k+XtLcWxemWZ9z+ZaoXU56gITtZypGKl77TEL3DzG3ocFJgkn176uPe7MqPhmcR0h5KMD7Y4Vjtx1iLOw6+1vOQpHCFiXe796uHsIEiMYs05Pa91TnGmigaLq205wMl/q5NHDi5PHRHt6cjIyud72NRifzn56srvT2h0SmF730tkqPfW5Y3O//gYw6g9RXBk8oEU+t1zDozOIQu2+5pNB0etmwUaUzTog4fziMXHatYKii/MnTrCrnPRsS722PH+UsJ5JE1DWAvm4qFGJzDKWsdLnO7wyteDk9etTw/TvS2cZ246zsMwT1L9gfEyR1VPAgLoAPm12unOQ/lng1BCt2jorfIHRJxl3pL1SaoslRlhEiPjR6iBI1iLMp7Vr+jaeAEyW4CTGWZUSXvbQajb4lgLJv7qU/sa1mwvcZAHhiClm3Vd8yRN2GfOrk8DzuTdQJqy084Uuu7y+UIQM40XPt3Fuij77cnmnPdIBKO8X84RFGrmuQfEm2Sasn+JXoqpbf65NETclFfTcFeDJ+BvE32SXZpG6KRuIGywSPMUfMJMmUMPb3j5Pr6jqYcoVlol5NbkbRgbyJufUvcFrQ1AxQEHCH4ukDierJCCYLUuegsFSyWsaVYywCoO251u8Pp+2lZEWyCU8rSAljldKxEwWGJ9VzTgYfAg301Rx9dQVFejWtKBDtjBBVuNzow6QxpCFQ/BCCcLNUoNYoUM3+AhxATkNea1KQIJJx+URyZDF3UwHPPqTADayBCB6IyFA/TLcoeOtgmHPvPPI18vwK/xX65cFZUZRNeMiSgRdS7aRCTRCIRpnGm2a2DAJbUUNkZKERf+X9cKZip1aNHiFIesfDkkrtENWIXEhfnjoN5RBXWxkmQIYNdXSioiccoDmN1+A288GDIqi4VVs5QUnLNc1hUbyKkExSyssVt6xAbUvyzZ606rEVhSYFbUJuOMNWpsR0rlgC4FQjD+UA2MbvXICgbMVocKW2eS0dWS7ko8LpB62w11cnzXwt3XlpO+RIevXwIki7t3/5JOPP7k4Pz0+tA3rhb/3x3/vP/QTf+Ds/KTOGDQMzemu7uw85P5/dn9QgMOUj9bhRMbu5uq5ZkSamLOCw9mj0Hj8fIT4IlZqCaS8gVSUN9KXII2nljX1cyV4hafnqkyNZQ5ovK3qmJgqM/NMLDJ2ATIt4mhFhQYOk1OtDaYVXWEDFrLalUGgYbZUvSGzUc4oAWIQm0aAh2O26ux09//xH/7Hf+bP/4XTk/OXXvqbv+0Hv/6l76ttjSX+hcLCvnuPwz6/say3Z6GDnnc0TLVfaQuIri4jqa1a322ZLHoJa6EN4R6kGwTXrxevN6XNy6SoSPyZa5NxjEMsj+e4uyJDLFSm8OKG+2O7QnpdHh4+tPv5/NadO0Oe9MVU1KiKTGHeqDCes4eqzhiuEgwuxm3OTn0a4/79zw6Pj+0TePW11ymAfRd6WBaQ2Bu5uJL5mUvx4amk4aG3Zcgjp+Ctww4NsUSbgqR69F4adVuJPuJ2cba340tJl4A7wlzl2/stX/v6j/zo3/Xpn/tzF2eXn3z08Ysvv0yzZMrPyxTT3uHOlB6DktJQGDGeM8cqZhYtrOYmfmGjtq78oZ1di2zXoqCHYURBN1d5nyUoXVeagLX+CxnDMxqkYGQ5krEWBz6MnWld5rUVO8bzWs421Zob0kE2u1snnNR9g0KcUURebR3YJswrmNMHPNW3gKcB71by0OR9cmOmWblpglQ81Y1u4FHthRFS7QTDaPc0hvG7WZ3L3aOLXR+OOtTwhXuaeIN63GjMOysGCa8NfKyGo7Eipkep+exyzoznvu806UqgmoM5TMCBsS9Z9uGIoRiOf92Dlsuictcyj2NH/F86uwnDQrVNo/qVvli4t/d06+w2M8d4XlosdkF7oVJIzh91vXz5etfmYJs+Ke3tHZpi2CXGHuWo7xz4WPTO4V000GalQrtGQSfIgp4WhI3WYBgCMn5koTMgkIsfwSpWg+utbE/+NQqzJq0d7U0YGASqlq7xHNrVoT7HluHYeFQLipmXu8f5/QfH0+qS/ohnCqYF6aT1Mec6JIKsaMLmNd/CJ9bxgG/cjMtKj0EEOKotKluqxKynZs7O8bSmLeR6TXiFUkRBud6iypU2pIotZ0XspW9qODVhviOZuZgS6pPU+ptcITLKZ9pwz3fo/QjHueBBkyfO3hLifBRBM5j5qK7pq1g/FHOWUZp5hrqlFYv1WEVbqCxAlLZBjSq+r4FGHGWxsnlnT/fBaaUQ5Iw1VdZZJ9e7hxd6tJJS3/pxNrajK6sCEqCrGRpCgKmkGhicQ/nkE8q4JZVQSJHhEy9CXDKouJ+fwVxnmwMnMqzWVaZn183Ls9gVk457KvS5mJvEN2kC+4Xru98nUiAYEbLs2gCc2yT/wgzABto66fnZKD4A29ZL4Yx1gVNoKt6F6PVA7hXjtvoWBS8iNjlWsu5T9KD0edgXnm7KCMD0UTbcyAgqsvyjJ97HE8+fTgYRmXG0/bReVwhHsyhCKpew7iVcEkteQ4HESS/jsgrYJIhrU5nH5FGAWLiUXMIgzyUVxcmjDW47Bccua45qUNWAepELmVRHePZz4VeRdI2KpXdhJ0/FhM14mt4bA6nW6shP9d+46rUKIVCdL1MQoAyL1ioKa1negHEP7+piBVf5s/kRy7kqgJZXeOOD/lo8F0Xh7QbraqwUVZBYNqyYqNS92iASpclIXinUTOP+qjnsEaWOlpc1jYKargVYxctZCPEoqUZKdfFWCao4WBgFypatTEIX2aMEBhnKNzjBvN+ho5YDK0ZGMJrgABdYRR7ZwQTq2oruVXjAJe7d6w3Y9eudyZimSmpJ61mtU9Wn8Ip1QXllrFCnfRPh7mdKZAGNUG7tWVm4ddiIpsM3+wIPx53tAnFAMruePMocAvY59LNvPGbkhqEZugra135sG33sFGo2jZdvy5PVUBb1nF/4iMuc2L/jwIqH7377137uF3+hs5S3rn7H7/ydf+pP/RNf/dJXdq/fsux1e1dNqSxtgNNvGMqd669enFwaGxg0RmI4HGOliyaoVu+GUQlGgMucm1+IV4lqqvuNlrLNz8Y4jngExShBi2lZ8OSfYWetnQtB4ccXp3dy8ycbjAZS93hn+w3n0mESEtNSMgambrV6d2C1t8Mi8GBmgdol3hLSqlDjU2kT/eM3RMqmJRs3Ltg0PP2tTxT+iwq1JN6PFVAx7j/6+C/9pb908uQh1XlyX+Oxq1vFyyvX4CrlIioYSTC9TZEhevpO8G/iY021MH2+4VVP8dSld8t92e/QT7G8f+v1YnG1ELS5DZNv4G2qkMzFBrL/c4u5C5sNy9MxjDNWBL+0cXMtwL4n4LrZlRH5O08V5cs/sdF2vIszI+6uRYuRfuHXzpIf6cK70WYV3xdL8BFMnAkXiaKMzPQ5JQZKxVj45h1p7nMP2wso2ZgRmeNH2GZkXPMwvTWsGMKyQE8eP9g7Pzi+9QKrsLf1dv7H4fu6xdvnX3F6/+XtR2vcIRSM3m1df9/3ff9/8B/+x1YfPH7y6OhXz77/+17eOf4w9VBAhlGZw5WQC2uECFL1WoWQgqgCzPvGDJQ21kntJ18ixBJR1mzJIZAAa0kK8kYRj4YrPPGg9y/qWJX3MkYKykwKEGOFHurNASKWZeWCWoWi+BOmG8nTAjA16kpc4cXyt/d45ExCmY132iwbz3lw+1cHBsKlOGnI9FbTpRwgtejKpkxLB9G7zKpNkMrmEKJEN4FDrMy9iw58w6XLo52L24fblmOc7lycOcXRaCnGgJNx9Z8liIyqknpdPQoDobAFN2ykr8M9ullNSDeKGAi9Bw6MQuYhQ4EJi4XD7dCdEKtAXuIEb5uZyaRzKynX6dG275UbwL7YOvxVrvDOzq2Lc8rc5uirXWf+WH/i1E5Dy/eu0e5ciR3qoQ96niXhQpOmZSkdi2Q0nYOsc9RRO5WKLbtZm1kSF1pLrBHcHFS1oIaY9UzAY0cufakLbicsng5MJggQmo+ja2K45m/m/fYskDO+U3M8SoHjWlKfp31Jo9FMDpGlktc292MoncBOrqbkSWBK9zxDQNrfGSeCg0RTaabJT+MgrWssz8H+EUA2eWtOLNwdHTNtszffQad1I5KpG/VeKgZZOozAKV9jBEGER2pJRSLQkiPfEjg+9IWFZb30dFqKV73wUFKf4E1/28ULgo9ztw1Fy1QvY3fb+i6xGjvl50rkn8QPlJhUmBVYWIH5xPTx1b75DVDbth6Zu7P+GI8TRPWOQUXJ9YUDT+HcqamB0ovlkGjVGB7VCfOayWnjLzp8nGGUmf4yvxTnq7phZjWjkSbHbVkwfyYeUu80uOq89x39txY9Y02BsWR0OUUunWvd+wmRErlGLHBbGZ9FFlXCZ7kKKGSuftfXBpKxVM8l3ft00iX6OAh+Hv6muKgaKBuUFriFyQ3wFda9Cv3cNfpzk2p+QRG4oTBcb2JXri++PQdpMNykWSSW9FlpBYGKhQRpK06uNlVN7ZZ3MpyNxYXPPWW/eY/CZ0V7uKG4sBFW2ReIwWFsjbrJ0CSzIbM2uFZtsoC2AjM0A7ramKvglUGwIi2DTaNp00KqVDwM39lYE4Fjs4GRIxSqqyDQJooOUGYc+sV60A0vSWXkLtLXYgdXCMofb0Yny0KhNYCUfsDl6GRY4QklgQ0DycMhN29p3Mzjgh6KrI/0/iAeb6ZBkXugAlKShZqn4A8WG4bWPvW+WIIUzSXQhagiPQzfVjTwVUqNRIFA+5dBiMkJT+AMu0szeJeoij6JR0IrWNoKyaQFOI9tSvKGSzUcQgHpb4Pb1HyvKjxw3G4BNbeYp9jSyeNvXmK6AbM217EaUBxCRhkHo/BZlwfiB3Nusb/wpUGAjsUMmjn6xiLE9zalTWHKm2swDTUFDvpKpiRi/W6wnXyTguerraBzGiZKhdEGz2xEwUlDLBeX77333unjx0avHz/67Cf/8B/+oR/4rS2FZSHxjQFzafFOzxyF9ujho0tjYyHV/6k+iB0tyrstZNiI8f4QdkM6biymZcUBBLYogf2ULjUtzbooVtQErGuUNmZv73z8wfv3PvuM8T0zltfGsqaMpsPYvtK9PlDphJlbVnwYHRdDiSiXZXwO1tvbvW0UuZUO1lU1pdyWCbyAbO3umI6DgyNNHv6Hb/2qC18BU3W4s4WM6gwDEBDuExAFXtTce/c+efj4wfbWbVpgtcDp5f1rnbS8/xvSRmvKGe1R6Vqggr8JXPHAEitOxk0vsk76DML+riFAx5JqvIsyuDB5AESzx0k5qQX5lXkY2k85ClqPBa+8QkKprBMw4pmUq+RodN1kW0+TPGqHBezPXCYBUmfdK5NHEsrjPy5bpJTSbp03RM1uqVOhI3YUCIODkGmt45a/Z72BIouXf/QiK8JJWOyL1sE38JCXB8j56S5EeFAN518cXBpcEeqAGEOGGmCdRPL1tYcXXrhrHLCzBe0I3dt76423bCDWYTjcP7738QeffPL+G1Zmpa3Jqno0L8OKOATRkTBBiJVCiYRej31zjfg2iD7D2EO5k9DwMRIWtzJ9cylv/kpWqorfgAydrt61L3Awhs8f51V1ald+WBVEy0SfD3R0aTijlgdjUD7ThxWG+G1cw2u49fnojCW1NxJjCMH6q7ynrYZEAeK2erEEi7+okyDooDLaB2LJUcCBP7VqtN6ALyrvWCp+sH3Mk83lbT+s8QdrbmLfsHKIDH2eFf9/LI6oguePWkWgC3sKaTe+zmG2Ig2JGYGqgCZ54Oh5hKSRmsxSgocZLDR33OkulGtmK0zZXZ857N2MPDlxSMusW9rw/piU3UNlWNgbgi3sqembBhaGGDaTI43iKem20/LPt4w7cD/SDX5fjJRP6ykEfpRQZqHzEsYthMp+1PUZ0cjdCvOUYKoddtf6IDBTDQtk6FXAJFHz9H3uo7FthTa3qVOuAyIqLMNK/auZ4DIkUbassf4rB2PinD6AohE6igOnkJ0GxY9MZZOfBPS800GVhrJEm5y+lq3uaIvrR4aVcMWVE7djgxKp/yYDUmt/I1KlqPMgIS7rGOyYhJHKGlUnF2O1lWak0zX7KPbOzk4cQZQWJlzoYNboItiWPwNmkMyGFuUZR9P84VlINvi/eIuyWN8kEtWPaMANZs3eAuucLWzcPq+vkJjCcKV1HkY2R1n5IbEky5F0JsnU95SMKrSfIMqkVgHSy+gT5N+wmtDjrysVlXVFBXTSjcQnU7rsYSnARAfquUt0mSWbNPME3IL+LN2k6u3Zw7Moab8r8SbdpL6JmlSV3KjSd0M5f2fh9Az4ttP6b3IOGY0PBfbzb0YOKhH2OfqLiCr/yryAlu03vxa1VX35MOPaWQRAtBdbgBJIQ/ut6/4RQNcXbwvf7quKEzulkGG/0NkI5oaZkyiYpd2kSrWqlItCP2WlT6Md1FIt4JTPEJUFA2PH0iPJxl5WTgKXDwyPLa28OH97bNiH/EaOyOhMCdlIlVbHhZ7IX45ALxMRIO4vD0b1a5Y09CsFEgpo+Ln/rUtulG081yzItpnImBwFmYlMD8deIaPKrENVIsZVKsyrMeq9UDNjM29ISOq5gZDV8LIgHa2j6mRo5kuxAVETczAtQMyditqYReMrB7DIiYtxQYzxEUXOIgvdfOmMaA1akpx/SVnTjoLD+c5Qhe/MWoCQLe6rMqpW87wTi+lNq/IOs7OsjEQospawxQYaQYxiLrM7CgJE5hB0hgmEVG+sMfqenZJSBE4CpJNm6PcTyEw911hiUU1EP8saRRSqmmL0G5gCXANogoIHy1g8l6edeywBHDIPpL6GhGC1284DQZBAZKn7HX4mnYGzomAeQ5Ef7OLiUeId1ekkafGYYF9iotSn8+A4aUfWbL/z8N6nf/Wv/JRTfZR1fOv4X/tX/4c/+jt+jARJ5OLK0ZbGubYfPLh/+tSA7t7JKQeqsf9KVMZc6bl04ZCTVfETHfm7Tq4gAv50KM0lzUi+/HLSFbohUwQQCtFJG1uHIyQLZEEVWB1Bgk/Rmy4+PzltzB8+JDBd5poqnLUe/fL0yUMbzsgXL0QyuZSHr29cByjOpVM+jPQAGFsbWdbUtHp+5+Ts/PbxLfi89NJLt1+4q9N05wXfp3rh8GjnzGAoLbJ4eqdNGQYIwedrQbdGOc7v7BkZg3x14EQ9M+788MmHe/tfsyltGdLhQ7xZD91JbWpcofNa9kQ5muPLxFhwfdQoVkyqYktJV27dvu2znTF/OLhz6GuOzgJgdRdAsCUsk0q3gZywKq+Y1oyqZZ9b8oXUlDKYSJXsNlel3Fzr28w3b1OOlEm/sMpwysbjh9bs3L59t63Ja8ZgoeNrBuryzreZFQE4XNdLSNojYyU6Mr1ed66Mz536JNfuy68dz9bU6margMZkpEmRVoGYtvCbSjAkp3TRWhTFUHmvth4+vHd0dHR89C3uaN+lujg/2foV+XeeHt25c9eCEIlwkd7++N/zu//kP/nH/8P/4E/rIezvmT979/rqLeXSTNApj0ScWkXjGG31oBQimD/FcgNSx9C7uW6eBEpdpjBP3ecCY6VPYENOMzDreRFHXnavkd37lYm6DXC16jTjky9Elzv/8vzypDJiQonigej8TZzlX7VGPBuoOzCOHU43Yegrv+c2Yj6dkenP9owbQKbuq9lAn8g94QMKafR1C/xA+rBWTuLOfElVZWWTy3x9eLl3tP30cNv3AQ7VrYuDcysPzbaN3ayhirCN1LArxqnfzX7PWwNYsSYGuseq/vtLALla07kqrphklsmcLButSFSAMZurfVOtOijSRxdj7lBRu6LluX7a2i6bIuoYGGn2xxZbHhKxLA9fUrdDw13zpOI7wqiKjoAMFMQvth/abXy5+zLmWvqkramtQt2Os0MH3WwYQcAwRZ+r9g05RFJw0IA8MW6NfzDWa/BhYcMWbY9v7FbL38GUNlfU+jURkWxSwpHRbmV5Cu0+DRSPgKk3eOADXY2iZ1VzG5xBQvotemFt9aisHjy3mrA6krmNaZAFOhhhm4EDmj6kj6ZC2pibyLgqpotMp5YIohluSZFWa2sonPLAUxCUTLDkvBisBAwTnZl2eeEgUa5/rZ/OmfwGphp3mWHGqsZ13ydRZu1+uB8cHjH94QgsXatprkc0LYfSq8LDaCWTkWEvQEdVEVJrUtFYEWXRsvXkyQlDapVgdaSxT+iBI6l5BVuPmf01ZZ0AUrI2jfCGfPdp6/L0lcDZdwYQiAr2TQ/NjI0E7miNoXI9k29lKggGyYb65Fv6P3lDMCXod2WZ8IntffGt3yqDS+GTdl4+v60M674SrOSTouBen4/Oc24nVeW3qTreTiqJZgZglS5sLqEL4LqnE6H9XPDn2W/y9CvUX7oiubLKVr4bVBaAZ2Cez/pdz2WX08+iIww8ykofRn0LL7prHudlaoj3xb/C/d/AeJY6SJswKUOzP9BWKd4qaLJ5qqqwoQWpT6n31JYo7D8TqVB1pbdp2Y00kHjDUVR07zSXiKdHI+angzF9tqrhFDoK4PjHoFBEVoj2qaw5LAZxVImM3sHBYd81NMc1Di4T09xaXXATmqBzHSSvulK5aMjsstiQh2qtVPoOp2iYm5KHoZWlqlN8h8Ll1ncefC4/ZWfRYk1Jq17pMwsgW34VsKUZJ70BierWcFFU9i52AqDFRVUDDEbQO2iybaaqayNnWcrGFeaYkCWHMZ2TGyMV613VHri91Rz50GMs6S23zmzl4IdZzfz1HZxF45LRtI9JxkUGiKl1i0UDBGMYVye/OUiM9LMjftOEdG/0AQLV+96qxaXCaYgl+8XNeZhcYSrvEDNApC2LZm+oCEDY4FgMjIwsxQbAaHbox170lnCBTTt6DZMeYkCxY5YrrVZMSGVJUDeMe8IUf+Nv/Oz73/mO7Zi8sS+/8QO/5+/+3cxltp0B2zcBah32w/v3H3Ri46PllU4pgU9nBlplZk+9V3BiZcAJP28pvpYs6zzEQZ6iCsbvYaFnvKY9Mxc0I8TJlcbieZRmlCFkCiJ6zXobH9rZvX337snTTxSqFjWEr1nWHzg/P3mqpYxSyNc8NSOjcIPQ9Zw1FKGhhUeyIju/vA7hDNHZUmZ++/rJ08dinjx9uvPhDBk4n2r/+IUXjg/2j2/fsUHi9TsvOl5WIXQLVLPJJtw7l7bqdnr54P4j/pexB138revHZ2cP8yKmcUgrYsLwbRhCZRJvNSKZhjhAWKgmAN6VZKk0DkwkYV47R+X4+FjjpEjZrOaSfhNdlmApY91ln4cpt8hVeul+sytEbi75f/31XYG9BnpKncyE3jfjnpqjSBAzEgkVqM7lGJLDR2NzklF2SXZ/JRhtrshhB7mc+PKE7446LfD0qa7ded86iKxJk9bnRcmIeQUNMj30iJ3g8NTGANned3Jq46DPA2URlTSVxIYZHw67deuYXpoSUsSrr7/+9//9v+8//89+6uz8yfn5kw8/eO/Nt1+2VhywyhqHsfyQVFy1VOk19/2HSis7NlZ0EPn8liRLHJqrCniolgTn82TPPw1lxfk/SSTdXJMpFADNk1913n2UrRJCMEWdiqDu90BthVbLWPNGWuHEC+OvFeYM/MZMQnPJwov6Pvo+hhHhHPnKUG46OL+DGVDqg6Gdet3iahecp9Lsw/TQ63hE9tgF+csdVfGPAWv4BmYTMiwd9ga+q99so4dpX4YvI+HIXOgELnsnkeQUkmrJwugoKr9SmzbxVsvA4umM8pTMugdSnJ7omWELeIZObrAGVF4w7Tv1JdjcwZZF1bAy9UwNtt3evtIbt+SS4AO/JuZhMG3rIF5TW2sEw97huwxclhSQjeZHtSrfnERqFqc1asFUmiqfsktvN0UjcB2HY4ahGhZTqkWNinsWjqTk3jrSCzsgppJFiYGTlkemBLOoDn86iyT+rKVdIYglGzSVBljYmwT2pxTU+SAAnIezibbiLDSa1hc9LRijCqlIvc5W2/fhYujVjtTpsLgKKB+eOD83wH9gI7IN6VYPTrHJn6bwdvIKbFhWlDVRDfNrVgwVKc5wi4U/PsiYFtAfcx9Oz6gZMssU4zNGbMvwtgfx6QpNwFJa5h2Ht40IkAbAdifLNe0Vx0Epx5LBlniX1CAfVlGtBlECFFtymy6mbtWY6n9VTS3QMsmaMuNcDC16EqYhGgnalfLgEQu5YlYaL/BPR7r8TjRAz97nYRN38/yb/t4AA+MGypRS+Ar4ruyVusqeGQCxK2SSfXeODfrPghH7bOz/Objn78SFmRPAmmSRUmHorRJtP9kkfQbmuaw9LuaE8bNrcCp9vZa56P9KMfcFanbKP4f/MxA3VXAZxxsQn/9CMhs2SEp79lZ6sGf0JVRqBoZHiVuS9Fx3scmyololnzsMBVpLXSCgFeSFqLV09Hrnvbx7c5LDhupF7bjElCgrW1n+KCBtpIfjVlrkR+suTl5WAbb3P1aUdtGqaAjAM++ZztUcns4sgppPoQMBUvYXQTeVcDoWkFKQWqzeRKjMbIu6wIexP6wqLQgWoYwU0WC/KZPS3UND/MCFtoKy7+Fdpu0LHEv3u/adJIBj4BcA8yUce0IubQ/a/w7qr3fnuM8Mh/JU82aca3kQVN9GZ7TVe+pWbAGl6uPPRiTYT5HEoOIhafxG1Ti+heRYDV+odR180IRAJs+xGGwLAo7y+3HWAE4X1KrNSNDK7ds0qw5XyzGqKY96Vz2zKVpaWZ5xwRd1oJnNB0S5A2lBLKTI+adBrpikbvBAv4cCVWxikNcnTZSw1YgOriR9+wIw+oaB2DcKBVaXnKMoBKAEuhaL/RslGrNU+xLja1UsjnTU0uX5/Ytf+vjhz9h8bKX1n/xTf+of+8N/7PU33oxXzcZenZ8/MjPw5MlTm7e0LmPsKEYKNpgO/CasW61kuEeC1NkJDPh57rvxdMd6VtJRbipSzUzosS6azs1fq7aNsV1ufZvMLy9ep3snJ+eS8EtM9eACeQJo8RLYbCYjz+5v7Tz86L2PTfwe3zbxeELtT56cHhzvHxwf+srO0a1bjrTfvvJxyn0LfSyfnYaBXbCrQjGkWRWhXykPFmtW4WzYzFHxMZKOnVg+JK9mkoS4+A8vHj99eo+wXnv94Q/+8A9rbZ2DJ+XW7omdYvaRJiho2/Bm5zT2kYj9cZcHZz4J6hgSlQ9bV0XDuYQfIwuLnQLIakm3n2GxENG3dIazCLhH1yxHODpai/4ncyZlPWxfvDMAAyzjguk56M9flTfFr5MfvphiFDREns/x+fNvEDzp07ioGNxTS7UFH047KWiPs+/vsB0CvkGezu/svPXO248+u3f21MgFaWfw5NrugFpSblCTXISoeOT72SdPOhV598QwAe/fcizpsYPipYhSlXsUXmhcnTo4bIAJ0d/UykYzBDuKphqUarJhrMXRkydPdKv2WyaXKXbqyPf/4Fe//wff/rlv/IwPEpHdxx9++uobb9CO2TRSMZyGjsntNCEGxUl0TjRiXpyJqp6BHr9GKJ+zNCTjv6gS+J/PkYcxrJvgiSzvJCudf8gt79575Z6wONZV8xQsVEy6Hj6Hk5UTrA3SUqjc8Sh3yRBRnocxVycCMUFYSH+NkbdAOmujDO5cQ9nysHt2SzSeKrCTrlplriHz3xlLti6RmsFPfYfdrfk+wAVHCU4HFwaz9j6LWRkJK8i5XxCy2GYZhkgP/2a+s6tZWdiFKmo1WWwFjDO22Xhh0w6tGlHOeFSKeYwNgvwDterir/KEd4ckZzrdiGd9SMtqb9+n3dp6ULHbhhjq6dAHeyecVAl/thjtxNvyqDoDJ40r12oAOWOl8gjZfXK1c3K1/QoPYGvrlvZ4df+gVes4bmOcDk/WJprnFpgxB92FuxOeVFWInPraBiy6ur5FOLViZiBrZF0S0FJDD+jIYm4YCUDNyMQPYw+PjjHfvNnRbYc4ZbZ2r74s7/Xue2OR2327u49A/y5tKaPVWcipU7U8NZCOyOUM2KSLrK9YKkXbm5ygRgeHPqfd+hlzO0jPDcoQphKWauE1C2WFmPP6Ln0+wi4gVUv7Xc2ddi07bD7WQQa5G6eG2ozCLPpYvDbIWvoEwzhiDkH/XQfA9m6HSY2EfTysZjZghM2tgpwJ3uwt66z8QfMtZez6jN3Fw+udj7AcsDTClFQzkM39ohSiaTEwldVXspMSPhiubTArMajYLEat2Pkr9Qwb+dULI2L51BXM4kjYK+/sZxkIFIByIqlnAS7ra0dANZrJvJZ9yiKw4uPAJFwvTrQr/TrdbvPFlRUzqZcln92wm/S/yQ+wMnVP3pu7IIGdDjRR/QzkuesA9Ps8PiX44iW2JlsrHx0owt2VbWVd4EZnJ6B3hWZrE0RpN0kWct9V3k3cF5BYMCpuMg+3K72KUcKbTPMwFH4eVh5S2RA2yA5BMQX6IstArt2T24ot0hukVf9MDLmqMNwes3SG/M47lVaeDEkmLsXQzgBCf6Kw+pSLL7XO9oAQGf4qnnFZjX0FhpCUA99vW1VmglJG3owRW74QtbKSQ22+ZMwdiCtx3kDOqZpH4dsqB7TXFvFYcRtXFNZdo3d+quucsg+ZFJdPyeEWorLFmpkohC1HCHW4xRSG167v4QWEuVSNPck0k/h+rbsg1Ck3clWbmpnytZokoXipQLkyDe2QNBWiPmjlTUM6tLtxAo19cFDU/h9GhfnPz2ZcqoudZVYlDKlkWK/Kc/8V1vvcmXcS6EwdjVU7qfQLzOxSdJg3cT1rGJezEWUxF54hmLDSgVmVwgCl2Rg1TUe8UAiS5j15RRcAcMLEoucCKahzeVgJy9p/jChLL5i9YPRSP2jWsuqxlBBCJkkRar+XO8s01r1sLrwKys0V2t6xfOnvJlyCTariwLzc+uSTT375l37l/sf37Kn68pff+Yf+4B/6LV/7PvzgZVu9/eTJ43uffHLK2+qb51WnVDEzNRxPeGE+UzvT/00FnGrQ+W6rTNy2941EmGMMGUvHRPSLq6zx0ycnH31oL+kVx2v/1sdcOp/GOL519/adu7dfuJ0p1wCPrwZgBt0ZEbBxdiQF1EE8tQfg3JFEgnwmwlk401vYun1wZHz3aOfA0XROkFDw7n4Lc8O/uzZqozL5S4141RhASZWsbTayVYO0c3pmF2DzeaqvKvDZ/Zo5TPzk03vvfvCtd97+8te+/gaPFj15DKNgSAPu6VPzcmpFC3XOrp7YSHny+MkLd1/ARoQkqv5vflKAFRFn+z9vmx/vozNFwdzKFaf9HLW/eWrRYstInFbALem75tbD5irFhK6Cvyv6+cCSpUA3OTf5nr16kPvz6GfxwQzzAACR+ep1EjNRJNWWAF8/MYY/sTmpRob3D/Tc9G9CfPJ6yrNc2pXKMQBOS8uzoJnEITsNBV/LjSeBZSsUmxCnEga/ugWbHOHoIUN6n+jHCSPWy5MLa6s6G2RXB5jpsYzh5OzOrdt9OLi1jpenpxc/8IM/9Pv/4B/65jd/BcjP7t1/9Y1XKSC0xV7Zn9+aBXrj47dPUi3HyKTnHB92vHPeFB5V0ZZoh/AJKiyCMzArOiP2jAUhvSiJrg1fZETFgBpwExM019TOJbawQx08KWPpGYiMbc+tEcry50qFlwjFsK4GqrJAVc3MN5er04O5iYOFyqfXfXVoFFfbcsg5n4FuCDAjnANOWXvFck6PjSefOVOnlUVbe2c68Dikvrb1SMeIoG2yJAaJl7yqdxKEu66Ex1xZMsbCUf3a0HQd7qWKF5MmqsdNL08vk2bDjnkTlsE2xtugNtXxDVfdC2P/WKEE2VKq7d3HWRqBVM5wUEyAPDqM5evfewVV5ZpcZchSTHVn7pkKTHQWkU1Ed9iBdgvANFGN2g3gWCDfQn8ISBbZ/BCt2J5KsxH7ZAdHAYIgwD9PmnQsj1Y3wmiIlskxlX6CA2t5g7FhQZZ6Ssnzl9ccqWh3ZwdJ7UDPtLGviSrHIFhumDyVAaPKCtQ0FvPJ3qTEmwBy2/AKTl7t3UqYo0eHd25rn+2dAVuN5KwTe1+Q1JHc3tHv37eA8vrwNrg7d4TUgVFQm9y69hsZ4M0LtnJh79Ytxh9ckuM+NFKwe8vnHHacc1ZHwkkVTMJ+Xdls/vHFEVXnFrShBxEzbohSa5zqumHH3uGtW/u7LwJvpF/zdOUA0HTcUKwZCLPHqOgrJkyLLOFG9Wwirb+alHQ3mqhIYQVNK4FRVVhcl8aWzeuDeiNUFq7kNbodF0sEpwSTdMgkoZSz0Ry4jbSKqZaM01HIJF1xN28ryNv3vgbO9476XqGr2LnD6HPYQrzM+9S/TUwdgCHhuWJW0qHgJr8gagLv4uQPktuGkJ7WqaLFdOFJRJdg9yTeA7SJKnZxZIJuShDcKiWR01Mp0SQsqJwDQojngVUVGo7fJBA8Jaxiii6gTh3R6N/DX+/T8/TUW3OW31g1GJBXu+9FV97lKrukGiUhZ2eGNjqy6uzEcjjO9duZgDn1orXsqPGdQm6FmsGoMCI+v5IrqwilsrQtfvPgH5yqHnVrlx2hQ2amjFlTKTXHF/i8vs/qjh+eWWsaLz/9Ql8gTGtCfVOD3qoEb4zSv5sTP2QsnkDSggknB9cu2R1BI9MExxpAsRE5DayaykCo52xo6pyyuCnww0pRYeQdAvAhTS9J6j71IxGY5ciwC5VhtUg9ZmYzZw0nm0n4tjmFvC94wxiNcnjXoqjCatO4aMLB85jEAuYBHJvP5BwzffZmxFsdyyouQQPuWioQdSKM/dfTCUQUZ+kk9oroEospfRj78RZ4p2d6SB+o+DQbzEg9fhSo7mDJVWEKzhbFC2EVMmrcz6gatIRJOekniYC6DRE1Rl4TLHqu/T0205szZMI1rvgH0wEfxFXPJtGAyGDN/yXNIWNAR0+e99Ko7Z//xje+8XPf0Cg6E8gY/52jw6986a2Mkuby8krfwHGf0TYjtWG8mgQcj7FDAgl5auxE4M7JyQlpmXQ6u2zWYvfoO01wPv5ydaExmGVNkZqCI8LnH6kvc2/pxd0XX356duvhfedfvPrLP/vRD/2Oqzfe/Oq18zcou2U2NhQCbW7dFl6dQOdQ+2TM9VccM3Nw+NmtO1baPCGjuy9q0jrHcDqxfcbl7sn5x5989Mn7eydn+iIf8n5UOhV05/x1zcPhrXsqod2lMZgu431eZvoOZ2O4LUvNddnXpEmA/fzOk6dOH9rauX/5zcc/v7d7/pWvfPX4pdty0QTcMK+NVFMbxg5rW7daOWWv5ON7L79w/CXnbY9UKdbSsMrNh0x1XKME1nynPlb8T80LmbE/W9svvvgi33+W/aQ/2wczn3b5lZ6XkqU16fCUsm4DeI0MWXlfvoT3xev59GM9VqqVbmVY9xXyxfypQ+ldPdAIyKyKvqkFVWzdrAsNLULHh0gLz88uj2/fPrx1/ODBQw37TdUDoypZnVD3VIyqUvUq9aXZJjStG3Zq7aef3r51bA+0rFxL52mEwXl7vSrffSRytf9eGnv2FmEoIxHDh+d46QjBplKJzkCdNOwJC6oEvogRU/1NSRxk9Ht+z4/9u/8OB3L34aMHv/LL792588bBLcME6IRc6x1UOKektySgpdhKgDcslu3MVsQZCO1/EFYXb4pr91RNi9PuWaMWQ+hyGCypIWiOyLOQJclgqWYxdtQmbnZhT/cJXyo0nq46mz8Ev5kjlZm2je8YU9MOKsfgKSL9bkwxt/hFDD/YOgTTSCy9vXjytiq6t/0BH1P4ITfHF1cdsL79aH/HLo07m03DHcfSinO6jyEXZ6+fblnydd8aE6dNptoGFPq8y15bU5tFVfxoYT+9dKM/+B4RHl6tsd29n4d0CSvhn5VyDTj4brqqvvdxHM7dhmomqH2GAs6/jE0bZYw5ZaY5cvRXK48d2FsBBTUcQZR3dq6Od7bfG35yjtOXtpLu3Felt+ebPFc7n6WBV8eV2uZpuCb67U7ESbEYlsvrR/WrzCFoNs+nVu7b3Se6UTMNFe6HJHp9+0LpcI4KdSVEY8O0OO6DA2Tl4jI4w+2MK4whDCpXCfbZhCBGFgdaXmYYdF+qiQF7H4I1bHXjlYybwWAc+BTuaVsY0opv54uk/9hu5wMiOhWBmFEalXDDpjnrT68B3tJNR/1q9/ieFsg5QAIBMb9nVIKC8DQM5O3e+iSWNHmf5dwTJcaE8PG9PZtBfEUBd1U08phB9xTS4vsL3zO24fz9A6cBWaEnTWN6Tp44Ub3ZCV30HHVpVA+zfxdvk9De7mcsgjYENtLuX/g64cn+oTlhx/pqC9K3ujeGhvY/q/pcXhxePDyfzo+xQZCdvO0ez9FCX/kCmhi9Dt4ZPlxh/qW+PF9Mnxhvra3Caywmgu1t34XObZCfCKba5+I1fBCDYIpnKmr8RpG0aaAfAC5ZqnTCfXvr0zFxpZdA4i9eAlkPI2WT/QtxE1Xsu18Ifvbytz0z8AXQz72sAqYDQCdgGxJz3aD53C9qY4QkhBpl63WenqF0k1ncpA9mWZ4D/sVSUsR1PRdeQOHl2/yfMjdIJpGJL10plrVUZsEro2ow4WGpKvmpgaAwEhVWudWvgibAjcBW3CQIEAsiZd1YR4rUrlQh3Y1W0QsD9yCJDoHLi7XDcawx7VUN1OBKApW60BxGkBX3xjqGT6hnv8tS8Aa5+hCSwaYoEbSN20Ena4yikb4a1tBCNSEAJgXLa1SCyN4aRZtBoubiXJI2LoRY0axCyTRm7Eq41bSESq1wNlf4GHLFLT5lKZUTL6LGX+YU6ZUVz9iX+d2QG+LZUMLoV/rSpDtKaH4kBmCc3I3AF1ypksWFIKN55cXBnhJrUpYvB2IxxX0KzOQJZhH6MTyB2BDTsQm9pkxDzzVKMbkACZhk07gpBarKcM9ixCmeQ6P1w41AAq/hmFxhUwpvYR01AlYJ81S5hUM9FsaqQoI2qTwm/4xxdAEUaiswkDfZS7x5K1GtQ8AS+0TAVs8xqOiv2WPCHj949Df/xl//4MMPb9269eILt//AH/j9P/lH/+iLr7yMLrh8dv/eg/v3aUdlDivicGgkhWhabOlRQYwdhQlFBtT4bo5ExrGxdk4InmUSN2KNiFF6N6NnYrYN4nz28OG7739weHB768n2r/zCr123Dsdmja3TJ3nSTx87q+Hp7t7RScdIWzlw/uH7n+xevfXh+x8f3X3ghLur00cKf+E1naW9u3ePrSW1n+vW8bGJ47yxre27L969PDjlCVhsAjHT1RC8ePLYEC8S0NTxPtJpXvpm77bTaU7Oz446TruPzNsLQSc1l9Ic2x+sHpjL2tn+1rd/lVP45ttvv/Lam/vHJta3zMvx5vp0kuF/SyF8BGjLeMBTzoxj/KZ64aNalGjiSVUqtRo0Rq+IsL5xPK4iaEh39yxzMnY1c2LlKxASEuF6aUNsJBXcG93YhK0QwUH00pUU1++8Pn8rdwlvkn7+UAHPp/S8Eq8H94FZ6LPwlZ5Ox3bB+kOzwGZ0paUzMbx1/VlI/Kh+oTsIg6HGWWAB2OKhLjoba+vwzqOHD+0usGLn7t27HRyOp9ruKnloDIRVegDULfovTQxT2aULI405vswsYja7Nc2OL1Vci5XNTvTp6+03Xn3rS298+YMP7738yuHHH3/w6acfffXFd2rgWS8w4r4SuRvNn9KrJBoK2aXF5oWH+6RcZGYPl9HCrBQgID3iSaalPBEB+fSyvAirs7GglbTgjIZUmwR+saHxTM4V8z3cADKbmdKwfA0BOwR7IdM4qO8W5+0cXm4fc2/USiToE/mUMR915w615v358LzDMQ0XaSS2rk7tgczfDCWQPera7bP+e9OFsKkSGif4qtOwu3++s28hnX6b83/YhcavuxDaPW1DzNgPghl1xhj8WFSP6Gq3UoKxQIh8lkrC0g1TyhIz5uonsP6vAqTMjiuhEB24koOqZI47smprhqcAJjgtw8howMB2MrjJ3B/NJH0iT6XoCXbrSGhQTAWk6tIPc5SQrBUM7qr4aaQrTLKGtebiAfWe7i/cPRCP4IRIOXVc0lFGIbNhZtvBSzVzbVuKBdoi0rOKSqRpz1hR84TBxsVLeG227cnDx7YKCgvtOKDTS9hVRaMpQi5PTh15pqZ1hHRQqHQ95GqHb/sdOJTWWgMj6DISuKVjfWoZWmf2+1sy0yT7aRUL8W1QVFlBM2lwePLkqd1ZiKOIkulaMK15GJeXB8fH1+ePrevjs/sK2NOnT/M4pr767BcWWO1nYYWhFeM2crQt9+SRXseVJuLJydX1U0M5FhLs+RTDxWMf9ZAFhuY12tpiJu5Qm2AFhJ3Q+ydPzEU+UXg80/UJO4SmK5woYqujStktRqqDcRseDrhfJgi/2IWas3KMgGhU3I+ZmCBLkx814sQ5upHKpkqTqZeJyzzIBgUCd6NyARxVAdC/0YdCet1c62EFPh9+E///1e8z6Eqs1M+Lm8cprcV8cz2LnuBN4CZqg/XkR+UG0FC1SYhil5A5Hajz+1dAxQawt/5PVZiQdRM013cV+t2vFfWsCI8zBb8CKhR+U9yCP9hWm100rTrNKAx2g8QaxpWBdaNEEyHR5gpSYf25TYTvqHR81QhaDWu9+8bSzZfeeEdTy9V3qKhRdegB5hq8Rsd2Dj7NnmjeeDFqrumIDezQao2Z7PRnSsbd7cvX88+NxINjyGGan2pk9tAd2vQPAvAJ7alNGaMwR7c/JgtA30iGg1zyTU6Ku5KVZDkr/VowatSKdtuy0FkBINXHqDy5p8LXcKXX7hOlTD7RW9kap1bL0TXG0FhCbXYvvEAtKXugzss1hYZj9dGvIlQRkLFEbqCLM3UnmHNHaK/U9dn7oGosswLaZVGVq1wMVvDZG0raOsArCYJXZAc4Y3TNKkQGt8odAkZdqqzB9B8gFfRZoqgIkltrrqrWg1vcmCbcW9H+B2BpXo/+S9Ot5+HPoL0svSggh8Tiwj/zO474NLbAjmgq5RmcpX2BLFArMRnxLswtUn2rpm3/AyLxyglA4M/8zDcePn50985dqV97+dU/8cf/+I/+zh81KsP4fvjBhw8fPDAOhEMgDGUL2yknMxenB//hwMBk9se2wcKiDrO021cnb6bP4wNNlhAGkdzcOUlWsFl2YfHXL/zcr77/6Sfnu2ff/tXvPLn/1Ofif/pnrg7/w/90RlghvHt+enqeKtQL7bPUpKvzd/kGMBdbnzY7dN0nbXzfAL/GgTN+s2uhfMNShvrsxr11aCS/Q4F2dzj3+3s7jx89tBLYSJIPSdbfNK99dETKlhWhXJtqM8ChfoSTRFu5buxs3wepjg5vG5m/e/eFs5OHWreTx2f3H3763kf333778etvvvzyi28c39l54YUX2n9veAkzquKdMehbs9s+H+QLNBanblp0eJGsQzFqn+eM7D31cb4ktnN0ZBzWF1MPNbp7h7PGN631P5bWgnpqtLsKmqakWVU8BmJ6p+luYlqiahyoBKlAgZJN1Hr1vLnmaUXdBG209QtpVjYpekiao3zRS+U3kZOBwLsGP0K7tDjqhGod736dz3F1/SsS6arxndXRNNNY5eg39zXTkJtWbfU8y2685EVJ2WQmMwXi5ZWPjCrm8umbswiltneDV7OvBmS/tNHhRQKbEW/U5oxE6OOYKSwOgWE/gK4unj55cvclpz+J4OucvfzKnf/+v/Yv/7v/p//bL/3CL1Leo9v2ghsX3L/an82QUS0XRNSwhh0ZBJJuoKShdIo5pWDDxRthFjZqSaaLVa9aR2UQMJIuI5uMSYjq+ogU90UDJG44iR4MMupOZTNB6QQ2jQiU2WEJBpooHJfeQfVWIdOZSlUc7eMi2o+tJYJi7PW3d/WGLvXe1hnv7/Dq3N6afaOolyf22Nhv6dutFo445MVhuldbT/CjHji+6d0yh3MKFgaGyPXTUDr4JURU6ToaiwPGIZXw9GLryF4B6yjtR9OckaIbHEYtCWHQyTvXZn4GXRgmnN0HkwQH+odfO3v38E9zMrhnz4LATq6TkdiVagJsXFgYl/yvcWyVpwKAflgpBinSpkq5vrp9fXlsc1B5zA+kwlWqVvwPY8P3yo6IhFRp+FgFmtoY87mKnHIzmw+0PdvbrxDS1t4HxEMPcH+K6OzMkaAKm2+QuJMzWfknVZkqNCQqvXK6rLfyKkyRhs+pL4OmaSyjIphT1aG6AAaV3vkQPAmYB4ouCTCQtkXQETcW12q/50uQIiCQMefOgqYIKLTPygLcE246+9V6XabGLPHiA0z2XvB6YXWoIrNa/VEOk/AO0nm8s/MgVGVDi+92MbmZM6PnKvZtkwAnT5+oHnEehjXv1UN82nn0aP/w/pXPPz/1+MhksjrZZIJuxjmDuXX+1LeHI2lsha0sBPfR2fnB7Rdevrh89OTRKU+Hab2+ehQdDkdqasNpRTN+S+lP9m7fZSW2H3eStXXXJpdQ3egPQvDBaNc4JOQ4LSzsfWmkQ3BVhDYYlnLYKj3mdo9MfIJVmgBcSlFu8lr1tfets+YkxwOM34XIKSb/cDhFE3xOLmVrpmgkX6IipfY3qaQR2lmFva8rYH+L629jV4AiK6wa1PlFzwAOxYLgOtMuNxHfu9SFrTRlk8nDcDadXjS4D0MGzgRNnqJX5md03ZT0HKmfB33xaeXZFDAlrudctecKXkhVjOgFVt0ZZJOhCHnpYph0JVdhUz97K2fBww2v4nsnzuzxsqyGEFiaJgPSarElV/88lq48Y7MD1T9V16B/cHsQK1c2vZQquBrNbBVBrYNQwg1izaSLGQigsoI9b4JYK6XJrtqniOEuQT3q1Loqmwn1xKZDlynHrYxJ+YaHmUAWotJAVzZEapp6H3ozV4PPBqFBbRi20IzkRYzA0F61ZZABZQQOQeFwmCXmSYM1rOXAtAxPTJdtOAIagzHZwzEIWgqVvrrIJOrjayQad3aPFrgGpLqoDKaoIuuOMZYeow1Ts60Apwo1FdHvURYJI2nzE1NGlHDsiqMxJp55ivUFAuE+Q1yxt3KkGQUok4CVdQOiSLhXStk19OpZIIINUYiVS8sVP6QptIdh3zwNPE9LLYvxT9lCoJT0lVE2MT33c7XlzJ+f+Zvf4Gke3j78h/7QP/qv/Mv/7ZdefunRo4fWxnz88cdtFOnjh5tsz0oNf2H+omOAxbOK5P1TNa55Hja/w1QYHKngAhJ3oiqaFK/G4FKnibLoBw/uPfwzf+Y/vff40eOnZ9anGg22oL8Br9M2FvvXcVe+C2NR8eWWFfAtmWtR58HelgU+Z9Pg8yx0w0JPT0eIBb9muk/OT7d9P75mZvvio8bSN4zlA+zk96c4iksPm+i+/+ChKWYz2jPMrANzum1ddwRXVRFt2/Tbb75957ZzYgzIt6Eu7/1q9969T9/79od2PL9499W7Lx1/6Z2vf+Nv/gKd4NyPHtoH/NT6wKePnh7f3U9XbazRM+kDrPqfNttcG3sLGQ4/zmss4n8r3+MRc1Ins/GyTU2haaNxuI2pYhIJa2HoiYdnwUAUpW+jgR4jIQmkAEsrxU7YTdzmZUS7FDW5SiPryn2TYv2K3QAK7LpGCUNFwE3g4jiIA240s2PLn54Zub/FO+rAD37noZUBDl2JG3z6asUgr4i8GEsuZjl7uhP4im5ZM99iSH7y+DEu6e3BI8dIafkm1ZqhIB2J9PW+MJ+FDmSQbIGLG+YimpHidqgLL7z4YiecKGhn687tOyePL77587/4wQcfGFx0JNbFm69QVRWeUGhAeDaE2rcOhskVRhlhUv1VQIyPMRu2Txh7k5EcAzTmKkcfGnCRZfyzgTeZx3Al1oz84m586MosR2kyQVCn7VD6Bo3s5S2JYuNAHRpmlfe/zOPILbWpEjO73KU5Dt86O72hGQGleDrLZky5JnWzrQbafLp+Sh5h4HXNyxiyBKQewi/7A4aB2r4ZXF9gP8ybLYQmjKMyh85LHmpZgiM4iWdUuXpxYigW5MWf6tFABlswNT/FUl6GJkoTeReQ60GoUkNrIVV6IeveQ8Zkyx6ArG0Leyabe8ngNw+9hK0/xZQIqsJkgmtMHg4wandbrLh7WNZALSqXnKQHLW0ofB4iU9YSJ1O4BdBzLJIKcKC128kyjyBBGTvP1WdwAcJM2mcYZVNaS64UEG4ANEpiIcKaur9w9IFpCjWmLkBFSgbvGBdMtgdfZXbTQ6xrjW9410CoxEGj7YNpIdNlACBjA4Iq12l+jT1N4kxQYNthZwU9nesK4iokGxah1D8NVFywcp2MnOg6I1cpfANOUI7xeANS+ExwOg1N/ECsNc82F2UPMQGTklRjL3MgiMYojdCJZ0PPnp47hQDrGBNsw0yWEy8rNO7qDmQ14ETvqC6IuBET3EsfXTFofsgtHqcIqbrcamwCyhK3EHRDZr8rB1bKA5uk49fbgjhVQLfTWIBYt/ktdhNf/lXs5kn45++F/f96TUEbRG9gp0Y3OGhwK2KD+U1pq2/RWP5CiLzaArV17dwP9B0PLau/ErCuVZCfg3cn5bOQ5x5uwIMwWTZr/Z8FP1v9X4g1lK7ZD/Bc7YV4hVd/ilZetWIomndlF7EiPyeSlQxN55BUt/PWr3c+EKSdKPMsR6GrU0eyAPOwbXRZLdraepc9z8Q1xqEZO28PQK38x3gxIxbS0LAaipv6npebCdi7R88aA1bIxetZ8b3PJjV3GJLNHAi0sjPrk+IZKldjP+l4YAMBqnUqq/10h8DAyctRRYy+WKr3acS2jLl/8Sb0qb76crl9buTMHPBHaW+a62pNN+apt4YEVBQVQFlqlSrcKBeCM1XSVwuqS9BDDQ7Ax1q5BkJiWW7Z3icqrufoqhZklVaD5B0qLWy41pYzm9YCdK6hQVJrKBrYqIzayOFZVRFS2VElaeU6yc0XluyFyM3LUB58gKLIEh6jM+LSX+9/pKws2yLf44UxUW2+dZ+DDzwZsmiKJFjGBhmlmZ9QTQgTVKAnNGc4wtBrXG3OdT2tsqWJ04UVH7h1eV6Q3VcpgURu1jQJDQlTxqFchjELLyXEhrheV9YRpqjztwK/5wRipEwrEcr6D87sT2mhGuOut/6rP/uLH753/uqbB1/7vh/6p//kv/b6S196ev4u8Tx5/MQ0Lv9BEUYCaMj22ZdHcjfUVXp1wQUiboCZHY1tUMsZ1RppOiQSWDq8ZCG5+ty4OY5qWpZgnJ6aJ3j8zV/9tQ8/+azjWFQSM8J8eQfezTkkFODs9ImWhXdOwbkh47XTjP2LawdxfKs95ec7ZxdOu7Jq0wiQjek5lJbgU3p+BWTTYufvTFvCOaaQVIw/CW3ePydj7/L1Wz6je/CJ4XZf1jh9wohpjWwyJwP0Nr0Etebvtvbuf/bQqtHHjz+22w0EnQCxB3wuSn+18/Di0Ycffvqrv/jBe599sOdIO/t61Jh6hIeaHYlee/1F/DluL5tvih0aEstVo7tdHWsB81ag1Bwa9cKAGjBMlNI5mCgTrDZJm+JMFdOQHNiv0ER8zis0q3SL+UGZdPObWHtYkUlntDIoE7q5eSlO6iXpFbwJLWL+d795HjAbIJ6TvOgbsPRxEqv41K+Pkp6c7/zi9V7fL3v86En1YgZfGvWvD1DW4UfVMO6MxrjnjDNEaB9N00hLKYEv0z3uG3b7L770Yot2cG3stzEtyvA5Ivg1+wGEo1nNGC3O+IQBLOc/693xChysc+f5ZA9PTh799h/9oRdfvPvee5+Q0Xe+/e5rr7725htf2tt9iitwTYid+QRqQFI5NjEryQb5W239DLKy93ufqoTX56/zU9ShGWOqJrHvvLUdg6Dpv4XJHAIK1JCkuYkOP4MSnH2P1ue36ioYms/a5qk0TS1vDiSekRvfpvHgaHSQgK4mD6NtZtLM7JH55xoXTl8mJzuh2qvElE+AdXfosHq/BdK7eWgSKsXKqyfXpxxcrpXOwsg6NVBgaKJe9z+n34iLCQOFXtmzY2bg2B4zor2+eicjmzFYLMe9oFRnZc2GSJPLqd7mWxXbH+FQ6nowCipUWbLJY1wfcwRx5cWOdRqz56VStIesVG0rhqgj2Pxa1nXrkdnf2BjLbs8njLjFWIJGDBQYa2AWTmCxqaG8QRE+IGWm+bfN0IfPtrkFpe28Vrs4NNatCOdIzPQOOYNncMsiCBExW9Ja+9oLZQkbzdF+x4cUBEtyeh2WAwncrTrRs13GxYS8TNp7lqH+EyOXRpYCdLbRqE745axiRmVPLYUBTHGTUqQYSXDr/E3OMnjZzJ2ZQysRSEbZKBLVMNj+Vg3rwQdUkjpJDKZDlYsNy07FiYp2DshbAvgwXApK4QVWPeAmO9LjwojKtFU2U0u+VDOp01/n6ThC1NaykcTUs/qS8hrsj6/BtMDMomuCa4KL9QS0VrSP3yh6UmEMmmxIyJPKdIR46/UnYS3aYIpDEQzMOD/TrVntXbogcv4PjWXBzW7e/VRSPKrdTBtp6JzZtcQ9As8bKlk6g/d5R6RYIxAaYFcfQmHylGiu9UX2mzcpvzvB51F/R0+JCqhZj4OKEcUAiDA4zFdZpgMwod/7FtYbfAb7Td6U+/lr1H6SrtDKW1llj+YvJn8+69/yWdYAVH/8VrP6jZkRQeOCUEjXlDO3UFTBUnHhMb9KPsjQLhVv5JglyEQVsYHRQwLLWBCjBt8BVZemXCXV993f2rOvSKXu1Pl88+B3qEhqlua6sde118DqJWveQMyBTwQhbOglqwd6tc2ZdVFXhVIFc5WsNp/RPk55zogPudvnH8AppRFZjRlFqyg1UL8hnRvD1qhDXd2z3bOtA7vy7aq5a7xS6yR1HQBl6u73xY1jnGtsrBbqXF2RTw1jW2CjVuj3K0aZVX2mqdpUZZNjzCJ6UYN/U6vCPdimBIezkKsa72q3c86vbrW332FzvC+wqxSYIz7TuNqHXrVUHfseQ6piEVeFyropmaHPykzF5m5JQkzll6rRrzRNWo+SNOYnp0g1vlGVm5elkIliSZ2pGus/KUvd/wGltiNSMh2jev/ghdKIbeWWckoocF1xJRWVLvDds9D9umX/PWb3Jxb+qXOMW/gMNK8lL0iysT7xbHIEZh4qBItWKIZuffThRyc+C7+7e+/T93/P7/6nv/79XwK9r8nu79n1S1OSVL3GDdMC318l9bMBH7tjPSZq823JnU/d8+cM/1dpJJti6TF55JNI3GEUjbmYhj19enrvk8/+33/2v/iFX/wVSBOnJs3k7xuvvv67f+x3fPnNt770zlv72wdHt31+6XrvCGu3Dg92njyyfPXss3vnn97/VGPoI7+nT32boo0HzhHCrc8++ejBgyePDbafXn7y4cdPT+6nGc1iN1KkRds7OuzEc9+b5MpZkXyqfbh+dO/+5c6nKrETItTClEQcNa6533HujhF6i8L7vtL52ScffeDECtsDnMKPjdKe2f28vS0ZBcMkvVhLROoLpUwkfObkw2zFxfnTew9lsYNZ9Xm8/QTTNJbnzg81jT7f8wLNKiwtDpzBaXDKoYyWyMPKidfpQ1pLKOmOOMp9cfHg4ZOaM+3Ztp3QL95+4daIiQySUdo+SpAcRzE34hnFcxMt2c1bwu66Cej3Ruoeg1VkwHssenTEvVDvkOrfJCt25c7QiW6QpD663qY4fUJ3xLJfZYysSJondojNiqisW2drRHHJAo1F48DJozbXiWKLAkJstFdZoQcpirwQTFXn3wa1uDj8kX7Uu8TY2BKgh48evfrqa4m8WcX91155+0d++EfmLKB9U1I+Jfb6668xWTpwlgkwGxRBKfXllAdl9o0Jyu4tVy0BxJtqajUr0WUfZ6I3l0ri6eBkp5kP5pHBzNWTLypijv98aiLE3gBilVjVzfOYhn69bMSuzkzbpBFioxQyq596LouAhVKmUhCew0xt4sH5OC79P8+2XxxpEnZ3HtuRv3P5Ys1og7+ho0TUKq8FRJ4HB7OHCUCFhmIeliNdxWoEp0iq20TEDT3DjpRSiPjqC3iRFX4TlHQ9LWwrK3fbDRR6BBp6i13uVGCGOdLk//pBd4piBOt6twPBeKIUbpo4kcloa/tRrjwtyG1LS+tOxGBoBCOYGxS/gFtqEyyMM9dnz88Lxr5aziFV/2ViRBK36wZYgh9JhviE9xOVkCSBCF4iLRc1KpES5DK5l+WI1esP43SbdazIo1qkMPpmGqK60Qe7JNbNTmbODjDGVinxNh3qgoPIAgJoDGNsnzIptqYAnCps6eAEiXpnCmziy6JMYNrXrUQdD8H6qHWc5YquprNpoLOAxBBCNpwRTXsiidTg3V0ywA/ZzFmSoKxRAfAjFfz4YL764MDMriqVka7boZL5jkCqqBGXwPmmmns9gCDWe2ngcrrOYeeTY9Sw7k9mpe5i8snE55lMdeSVgAqb2BvNG26NQDIjYRvq/pe7q/eVcvgoAWImqrq74kd/pJp8kskTeNAoWznIJxRGJiOfQAZ3pVtPN0ELzs194v7ObhusBsJC5ib/CKaXIeAmtIK/uwMQSZszpKUdcxDinc+zWORQkHmKjBixgYjazXMMAOSmkMk1LxPRk+9fzs+gs9gxAc/fbs4CGp5uCglUNWSENS+x+PlLwb1uUEF1qUYbC963ii6Kkn4ySfKTgN4VKMnm/1TUrTsfUYxGQjuhRF/TikpDpzqjH7FOILBU9B8cTkKOqVz67UbsbLJSRzV3zpCywiHzZ5btnjK0/h3MO7o/wx7Z49r+4MC3E5Q7y6sK0iAiBLWQ0La1Zmq3OgGIeqITIZvWiY26sIMmBG4cNHgZjby8tt4ObrcC76vttbPWHJsG7iRQx2EAdXbq0BWTZ4Z1cueGC1gGNhyrojiDKxmJfnNfMhPyGxhQKdm11APfhh9lVcka61cxuZ5jexsRsEvJgWq4cWUFBr/SksWyBXV80yTXi9EJ7W4AqzfT+nM1s/MzrsMiqVrQUOM1pYDU7UHPNIlIudy59dlQMWddTz0n/0Lc5mcRqXCvteM99DZk9DTKIRDXehmVGiIHqVAMbyUuNavGyD4oSxGEgYarLynievdectG6LQKzYlQCfFO31cuVeXKVZNDo1jXR18b+hxEr/cagTDQWJaxU5+q//gv/1eOTT9780q2XX/rtP/EP/8ThnYeWZJDXKbfmwQMQGPfEdPalKSV5Rd3CdYpadGlmCu6wj7OHD+/vbX3NjoIdTq2povP2YBE5D4b8CR8XGjS88uEtUHcePXn65//sf/mX/8pfuffwwa1bd04fX2xdfvr9P/Db/sgf+SO/+3f/2CuvvWjxKG4TvbaDD1bNmHUNQ5op73aJGSNSiLXOPl65f3Brv6cjs71Wzaz26+TR488+tVP0k5MnV4+efvbgs5NP7znCy/Khnae6QHs7Dz57/OjBJy+99M7tF3fOnpq1e3z36OXDW1pRSF5++un9Dz96/9HD0wePPnlw34k1+qQcDgP0e5ay2khwdnl6dG7hie8jqwW7ejVPL090ZS/WKok8vwZxd/Ugjl544cW7x3fvOMvD3oSL01NjogaBnxqJsqPhgnU9sRMB8IP920lgx+Ii+5cN8Vqvu/Po9IERvKqT9pkgoUFNchPHKBw45eb67OGrLUS+OjZka/ezsV58xh+MGwmOwsiUYEamKVE6LHajmBNCwrSdqiyVWxpWXXBlDLvNYwGlDBGB69r8PgtIcV3lQe47EjurpwZSDWxhQ7WHHuHRuUQM7eaEt6fp6lQfOwSOHDvJPIZqxlJCfSb1CxwLdyUTrmpzX3QnjBTiAnvU8PfgClJIhoG+2FuDUgga6Y7GKKqeziMTBB9U6e7ZiuIj1vOpI7M3e3t/6Cf+0T//X/5Xj55cONbp/V978LWv3L3aezBoZJmHrWPlG/9Qkxl2UPmF7PMqGx7AG36cGebKN5fhs66SnDr62NddjBBdXxtwebpjJEQDenXr2uoUK9R9mtd3cnZPcst2uTxH9n/oM3LPOxLe/ojrVvxDBpdraTqgFHHmfCmMelq3ZBlhuEwrlg3U4016+enM5ExV2WNj4Oj63G623as7NvB21I8KwZxuvbRlD4BC+/pvLK+N2fs47l28zMh2PiNgxmGz7Cwv/3zv1FDY9tHFni7dS9gqS0Icdo0tgWVMGSVh5gDWeL7Y6+4DwVfnd4u1E0AEIuJpZjLXtNXwNUoZN3/+R/FXuu9/JwRrHGXwywb34XBKoI549H7lbC7+I3Wql3Wxc3m8fWleBXc+7qR59UbeS4c9qUCPUKRuBrl12IWJVCSlUYRWywgDm7PjpCDc3zYD4N8tpxdwCEynYPAoOFTM7fgOhqoNAiO55nDUYrJj8Zpjz2Aml5otdLZyEc7tWCAmcI3rs3vOM3D3rAryWonboh3naEMRWh47FLCeXV5HKPvLXdZNwhGsNKQ2SRFVQHpVo+3fhdnywyczHoW7sb9eCbkFxOi6bbW+6/DxLguj5U+9DKY08asv67iEFvB0fCFdeMd8/tX2+424X9oJsHvmFNZmdxTNYL2W17HzUdUet/xnqWgG7cQJhpO6XPbNpd2DD9o2hSw9GZ9W5OfXkCvodaZ1e+9ePQuu1875jknFq8d7V69sXT6wNdns2d7FVy53nlzvkGl7MKre7ZdkNKYDcPlG+uObAMomIUNXFT/iVd44LcOBWIg7o2eJlvDR4UftGms5SgESy5ZuxJgSs9BIGguzROC1q26sBDTZeG9DDDvbfXIuGxIfIlb2Ujy7vvDyLPT/i4epGOWbh5Al1hXofnOFcygM5dbg1Je8uSZxPPj8itphG6QBk3ti1/3zZJ7KF0+mgGGCgEm/KHz+Pskn929O/cROWeEQ3/oLeDH+V+QG3Qme8KKKL0Uc3ySZLOl1kUtStRNSEWppIv8mo1RlLDqjQkFrkLaPNEKdwAlsvd3GFaz3zeBiEz1U4Tm+DBJdP1R4i+QqIebxbIGkSTnWmKparSEEbxWTB6Bd0W6CZbJVw6EIeeKo9BtuwjwkQQyxlDbtYuajM82mmn25wNxgqKtR9SCqdeELcF2Xej6KhB7r2+G76i/ng9ZG85LyNA3q7bCrckCY2HRb7nrwaxQP9mQjLvebdWpub1AEK9TOHbeCXL0Z27FYTGAqPSSQF/UJZSqJgDYFzpq9KOtfvI46dYg5A7CaDAJ4A6kBED04UAROPwq8DGIuyFRdFodZXOjHxgRScuHzHFnz4NVzWjBIRS/CBUahQDHYWzk3VzkGxwGxQnvcvE5CCdZf4VDEFXfAE+AmZQl7qfjJ7kVqGE6oZ8QLEO8Gp+RcaF2ys5OzP/fn/sJ3vvUuhfu7/+7f9T//n/1Pv/b179PHOj1xzIJ1DgaeqeUId4NXORW4fjZ3bwADnlSwuybIec/XZ9d115wYcmM30WCwzcfESAJSJ09O8iSut3/253/uL/30T//cN34xZbJwYufyq7/lt3ztK+/8s//Cf+urP/DlE765Hbh2cTU/q02tF6w4L5AyNsNG8yZ8o7c5pO3Lw86dvtg7ODu+c8uWs9u3WdL6zjK89PorL7781v7+1206beFEH7XjNlmPvMvdBvjq/Nb+4fn+3t3L68fXF8dOK5mDwk9TN6suNN/XJ7ZRfvjx+7/0zXd/9Zd/8Zd++ZvvvfvLOgP37n2iOljQxGd4cnL29OqM32lRuwPvVCmdk+LoGgiax63T99771fPzT/Z5SKqbLgAts26Ii5TfdtIpdvvn+wd3FNepc44McuZK3tTeSy/d/fJXv2/fJmAsN1huTE29jv2IVktmTlzL7lCLy1eNye3byMkHtI5LI5oRqd2S1pVTWsaULImmOYk5zekahV6gC+i1hKUvjVwUYd6KHf2bqIIWqAUnWOnMBKfGpZqiAuG5FnPAY/OYPv6CsQY2hMmLui5RKfJcKisqxozoCtrJPeO+M1Kbuk4B9BC1Dx89tGe7Q8pnkkQ5gYIhwis6vPzLyBHxsEOCoUBsVbhUDPTO7icffcz86tS99tYb+7u3dfG+76tf/cpXvv43v/GNJw+fPrz/8Y/82I/sndracbF/dGAdGQNJ1hx+2T34lhjvjNomsCiL4gTR0H6mgdVJlzkixs+vnH7r+GbDLvwSFtOyAP4KJ0g7Ef5ABm2fj8PuQTyaQztCGAiPmpjuK4Zd81i+CkKHFkdkDMa7mIHQ9CMQ1SxsNLZsk0l9gdrDkgctVyXj61hPJx5e3tV9znONVcLV7Ozt9HYWSBl8kFujRLjYUL/Mgr1I3D4AihaOtuASeTbskzTiulfIgDsUKHJGDYpuzADHcnsRij0GsoNSQzE41orEhVg88gveXDV+KfGgWmpDQZY1HWhmr/dOzx1WA4h1WLtP+ISpHVa2FQKoBpZjXciBC0KkBmohWKHpkTW+dZGoJXt11Sz6tq1Budq13aRnWj1BsAOAs106G0auogaxsR8M/n74JrPprg8BQ7UJBTOUDa8Bb+KwRVVl061UQIPudRQ67TvuDLnaNDbS8UA42Ges8NlQovO+MU1N0gxeWQQ5Y5ODQAXDX0sYB9QiQPf3zs58BrFaudiXazOaAXb9kEEXB4zfNSIiemvv9Po0ZWLd0qxYaCTI91dKY60jgqsHaabSOEVUjL7Vj4fMTt5I5ybzgHAPLp35YSamE9XY6kykw6cc8WkYv9USxjrVt/MDneNTFjvV5bbgz/W1rzqIVID+3Yl5BWznczTO5XQKof6HTLJEnaf6gSNLN+8+DgCpmI76JZn4QA97Ke9kFYbp9fh4aKNok8CrVItFfqMkv4typekYJH6UPtlXxYZb1V85h7HC5vfZT6UGam6x/u/8WgBBDrnnrxuYaClupfs8wSaYh7g4IUEPN8ni14YfK/cNuIEw9DwrcOpBFEbI5Au418zNhsLeF4iJ6nXzPo/f+1bSeLcBF6xMUhVUBfRvbe4JLpkJnzss6gTr2S96FmZBWviEFDwHtWqwVBvRDgQ3KQbais2cZTNot83jjd51UEcDLck8f52ka/Mka6DWYATdx1d1MYeAMjDUoTgVu5hGTfPEF94cl1DrX0tVcrzSKK8eak5g2IRmv1GtPP/F0S1owGI4wHsSe90QkQKoJsS5GgZP5sBEiVVh5/vSRx6augOwg1NO1Z8as2qBkSqIMJGqtk8fVFV0/tNqVMGtL2tASryOzXZ7dPRwNoyfGgUZvNv7oDTOJm/iQhIAbc93CgtjyrcykteixvJlm6ZvjnshmKy6luS8+BsBTQwhkCzYEpaRDDGRGTV/gbeBqGJDOkhSsZcjQ2wZwN0CXVz8NSuC86eDtKhNYX0T2nNnKA0rQ6hs/lLAnkpZGrhpwi5fKoGR/tJX0oaMvc9gwwRCOsNXif78ozR1IqPMJbC4/rvkHWQDs4pKGzcKgcS8YwTiwoiepu09evTZz/7Nnzs8OD6/fPoTf+gnfuAHvt9KHE2H1SxPnz4xis9GBnNYU4EeKypiNqXNG6VpoliPoq+pWCZ84nzLs+1v2zS764O75r7kNEh1emGjpIKpkc+1GMP6lV/+tZ/+q3/1p/7ir1iB70vOtn6+9OqLX/nSO//iv/gvfO1rX9dYPbh/T0FAgzCIpPyUQVlqSVYf/Wr1rvniozPDaQb/a5cojM9vnBo21wccKVv1XwuxvfVYv/L0vLXa6TUtzLOxa7klz7t7jpu4PtXZUKO2Hm+dVVcwfGbeds/OH8u1t3/x8ut3f/yN3/kP/IO/26p99eUv/9RP/1f/5Z//T/9ff+6T+59dPVHjVPg+GXR+8lCf4vJ0x3mgnEGyozSaaE7kL//qt375V06O+tB9jSeeaRW12frfW1evVjsOPlUW85CJ0Oo5QX3rLR8c+NKXt37f7vFLL9+x21ntsypo2+aHPmR3fvb0+uTssfC+33m+f/vW+wcHd1/oAyGc15Ojw+OjO/dMI+5sW3VNfvpF61oivd4++E5m46xYoLNSaQz28Bya1i/d+Zcw/Gr/W7XhpbtRuR6LLcSq+nRzZV7jo2vX1qQP9lziN2e+TfKgVfvz+yquqR7AOr5DaOYl3yq3H3DODn8wNyEF39s3Lu04kxMV93pOxgg3qatVQbVUgDkZvW1MMcdrabLYQbz0gocaK/yzqldWtAsqdWl1os7OHj55ROvAdfLGxeXO137g+/6l/84/82/9W/+rvJnL1x7et/DsxKb5r//g1yXZvXrHN/B29j5hgK2nNICug8obaVdmZjb2xt9Y3Cp7DI3Pxnt9V+v6bP9y7/D6YaZ2536+7PlLu1tH24fv8SHNm5Hf2fapQWY4shx9GkUlswEm0Dl2s2Rl2hlQL45ZmevdT2JH/NFYMN1No5Vi7wFr42PWwwPAYdMXfU8s049RdOIQfn1som4jD/6MZd++eEWV3917wkrRWo5Xe4Yx7vz1RLUog57JnMPvxMPzd+wWbszVvgNzAgRl6DpHqaGmGD2ZhNdkyq5mIygfCWvuF0QJoHv1qbpVk8UN1Bg26i8HZzGQtU2Gwub4hwCpO+1c8i9GjSg9bYApwkfCaVxdCXhu3XXikYaNfbm6un15cXy1e59JKKuP+1pVHzGfwWIAApIzH9BGlqSafzltlstrFe04slHiQRV4+zG8Zo7ixGcNHY6U13f9YO/iywBO/f906/LV651Pri9fN5R+ffnq1u4n1xevbpt8uHrtavtD59ptE9/ZD+p34f317qc7Zz+wu/1pS812Pr48e+l677Pzi7dPfFz58k2LDR4/OkvNzAepJ75xPmMihI9PRKNF3jozEbF3mzPOwpgoNUk5i+WQk5s7CsoSqeWtOiAyUjar6pyFC85xO+245sQe2fF7xxFlOQfMI8f8QMaS+UCv84ovrgyaYPK5WjhDn5qb7QMrTDH7Kc/B6lNHPF9aZ9Fojn+tNsqr8PEN0BxEkYJTY9B33rOsOR5zynUFLBHykTX2IINwvn34cWdd7b9snsEciHqx0ylVcp1q7Ey8sGm7B59ggxaEcliGccazx88mpYN/vfN+1RFXSZX2p3Ht/sGTr9dgggABAABJREFUsQSqT2YFRL2eDEOqLkMzRTR1TnGwqJvaDWsChOsUjuXC9p4hX5XqYak3dhecCtlHoXr0XWTxqhEqSzn6JvHS4bL6X/B6mPMznz+rZ2JvbmtH7vMn//z6kE1aYKsp4TOPq8BnpSovegstGdVfGDxLsMk5uQdkOQbtlXAAgLB+V4qp9QvCwN2EDugV8Dn4KbAEz4Im9XffVuyzQpLqZFohxQ7HV7YCJ2LlGpKT0wrbFPQcxhspbKBI9zm1U8iCOo9KGegDjoaqH7nGhComPyw8Mh7+WfBjxIhXq9oQu7nFLqZGqlzAdLQG2TPloj9hmE5pMsaeQSjFApLB1IAaguByRKok5c9M5oyXufJT35khNw5KySBRDWP5wDYMq/Bp6jYEgkWJgYdI/hwQNBy04ETGpPOUe+kdEQ5Vb6ixecZcz3oLgOx1SIraN3iWWFq4I1XIGPjmMLj9LcuODDQUq78s3RSlTsiWb4Qkt3yRkRt0/HUN3KS4BOB1XPUKC4qR1KqfJZGjzVMbsyqV5FJ+GXpuXqBS+zfc7bWEgZ5g7/49dxWwUue4zTNLskk75mDl/kKWglYJN/BLqVnNCOFx8RluLBpaK3NKjcGfZ67A4T8MPKyrrMOIVE4Qplmdcnrxy9/6tZ/9az9jfYxBkH/pX/4X/5l//r+ZE8G72z949Pjht37tVz+991ln0BhNci3Cg9+Lm4eKHi2YBNb999EYbvf19hNfZbJXRDNw5gMufVaCHa1faFJVDrXBsSrf/s57/96//+9/8NHHV+evHd2547zAo/2DP/kn/8RP/uQfNU/w5PSxWd2scy10Oqy8wQI9PcUNikTJQKRUqWN7D0ajWGCLNh45ZPr+p2Gpa2EpWW0Ofjpf16L8QxNcuTuNA+3u3r5bDzUQyjHYnyOuadS0BbzqoWnUL1d4quF064vHDx5TFl+I+m0//Dt/1+/6XX/8j/2T/96//x/9l3/+z7z33vt3Xr19dMvApzV5Fgc9TJ/Hc8UKIPknjr9Te0+1YemGmnh2pZmrhjt6xOw/0s6QNjountsKDTMnW+9+9O5/9B//R0d6FA5ZMpN+pivF5zHPwAM7MOPhkzd3Xzh68c4rVm+9/sb2W7e/osflOFTnldrXgTnGzsi0Vc+7u7pYU0giQVT93hgUh5XVa8TXqLMM2RtrCvgEnQFALmrPUoGlH+Uanci4BSNVWZdwD1PRJsUKvWlLyoaxtcAZOp3JBhAmbKkZESuwwvrPG2A/6wQ2VhgGcnFRVZe6DBV9U3I1QKo2BBvjnBXJKQxMprqFVEnBreyFVa/TZhcJ2qDkeCVic/7gi6+8oFDbuwxPHB3f+cGv/8gPfP0H/tJf/ktOA987ODIs8uDRPTUICJM5unMpVF6vyjtDtOMEIFWR6zGEo5tZiz8OO+ApXmyfWJ1p1LLl80KZcv6uRLm8YzZphiUfY3BbZD7bLjOHubfTXY4JANZGUGHNBzgJJUKRpa0BKe8oA1wlGiEAP5Jlcs73eEUSnDUB0ZyS7WUXhy2PKfXe1hOfaOL70dT50i3/GNhF7/guNW3ERlSExMtVeCqVM2QTYY3dARQBg9EUDq0qu9oQFjE+IjWYefqw1VzhZ334qe0XpxxFw75hvNVRO1IyOC2/KatyGiwoFgsTwwgT4BD1CoMGdctt6s2QFN4f4LGetjUhvlJAu+iY42Mip0nroAEV41LDZAhhzyAHX4KJUDZv2JSCLv3d0UxsNLFz5mwysGyY1fWgr7unQGOvCmaYhJtJRzTn50YjnLvEYupWbatyWr/6N47FOtuy3It42xNn/5Lxdad8tNLHOt/BdF8/5UwZl7YyuRyHH3JNIWI9jszysw7H7HNXt+6+8MKuqURnjfkabna+UXmus26Pdbj+Nx6J5w5Nbg9TrjaT7COGs4r36tCncueUNpOUvppiGR5xazIULPO+QUPMNs9zxbTqLfmQou6W4qrMtiM6wG1n51BnbjkIKjQ3wXQMftC22ZEF4V1nMaPABqEmN4yMWJKEZ+wYfOz1MkVgoR/1zhCYcD1i4h3RT1TNwtFg4fQHxSZX12tutR2uIDEKzWmYVnajFqwcCVPSqkNCpTqBUjdJtwJYvmpgxcXYtAGLU9TWYtHyyTfpaUgjUymummZhXnqVRR11SQ+V5SeIruUTStkgnTBNRuybypF9uKmf8sXF+ZPNw9/yqqi/g2uw2qRfRW1eNhGF1feNISFwg8JKW2hm+CZPTzdvmFOOMvTfquJerM/zfvZ2kQdGC2oEcXYDf5N2qPbcVfL1tLl/8UvAK7AyKwl+i8OEJMAyO6FJLd7O9Tmsy1cK2PtQuu2LN4v2NdwpbCVdtHbfeKFTwqJ40ilU3EgromuXMgua+eZUVR+B81OZY1gBpkDqNLnLQP/GzlCLspjpkiWbqfpIerFtrbAmjSNCvfJRAut5wLb1xxpirYvVCkrOwomZaJa5nFAbpTVaEyLC5tcyCDo9bQ2NzylpBpEUMK1xHRWnEXMLUq39MuioG5AUIBCt0tUhCOYwq2ZHoItFrsAEip647vMcErWSMcWXuTyLUVaZvwT+jDegaLoWVlTwoozTS5IVlimb1j3sqiLgCR86q4DVnC5mS0x1rSpWRZ6qljgmXMPDtfYyprF2NuiD40CV0MCSap06BiehSwuRmfFA/oRPkTHZ5XvDn9PkEbjSE8eGq9E+Bfl1Odlpk7Pgm+dhCdjxfOiCaPrgp7KLXoLrN7SETkhisARmIFk6LAf8ZQuIGPJsaHln9+zRS3/mv/jPfvabf9HSk+0zh/6/8cf/2E+Ce+H7VBcX73/8wbvf/o7DzvP+c4Ez2MAEdoofVleLBveCAfcB3AsfaNz+1cNbDuoxeHN4euJUzaZvqHFctiLWzC+O7O6//9H7/8l//J/8wi998+HDR0fHtx4+ud57+vgf/Ed+3+/7+/++3/rbfsgR//QYqxVaC5RdVpyc1DcO5jOQTjTTrtFnbrNWICHhZPINWcOOxvMivPZ9xwBxeQPi5r82XhAYnnnHYvsujJ3FM79suKsveUOCvR+2ayNRJLnKgSsHVhZpZepqPz6/Pnj1rZf+qX/yD//dv/33/xd/9k//0O985+s/+H3feffX3n/3vYf3H3/jG3/j537+V2z+P/StR7p7+cTinUbaVLqL1xPLzodN8MVvkwGfIu/y6RuNMNo1VIm53VdXn+4fkNGXHz/aefDkA0uMtNrk5RsGrBXZG6H2rapbL1x8evbw6lsf6IO99tq73/rg24eHL3JIts53X33ZaN7x1dYvv/zym6+/8cKt4xfsIrbQyCJeK8+3zl4z5X59fXJ46wVnkJoKajI/jwb1qQFWbB3T8HQhD/JmDIzfRURVjb0seQynkSSWaqz6UqbCi9w8TMpuVchRpuxPSp6hTIgDYPJINuACmOClrHqXlkVSt2yFNLp8jOSt7Yf2Rs/RC/VDxD559JQ2ArB3ZIG1xFP/B6PUZbB89lNwJ8PAKyzE9sPijJfx2PeJfbb0pZeUv3O4Z6/122/d+SN/+Cd+6qf/PMfjg49+9tbB9vGeA2SUbID1vf0WS2KeYZ0obyl5M0EGILI39ErocCskRPMBeFeVfU1MVRnhrEBo732MI4zwOO2CmgPNOOPWqheQJJiGLCI741y+YVcZG+3Qk5w1RTgbZL575fu2bqul5MHRoEppovWpRfA7l0+37+5d2EmzdXB1cPvq1u3ru7d23z2+OOTFzrFrFI99fkBc11dHU0sNljdDMKInbax6czjJU4+iopxc3gQn+N7mvJqiuH+vxO29exjgDRWjapAbSRpBs2bcDBcWWtx2YbkOhPskeAzDZfNuO3rdYGJCHvXAT5IVXQG5Fb2E1rShtb0yr57kbVZM35y7agmW5nN7+160WF6v7bu6U4PaFwloP6OkTdfnMcysG6afYAEP6qfwaBQLGS3xfa311tZLWa/rszS2c4iNpj1We/Z2f1aPTh+go5i2v53Etn6tnsLeT9VobD+pKb7+1hxG+p2a4P2fgXv04eXeX0srdVnyz9+14+Bg5zumjp5u9Q0TRaQF1Q0s5GP3jS2VPD9cc2am2gqX/c+MKVz5EJaTGKSjjQjAMlqavUYFy6bUiqyf0aqzvHSk4KM51xaJwcQWPU49Ju47up5GGZdvkEO/RAehDpwJrZqQfGROvPOaCahvAe/ttr1v9+VGhVgT3+qyr/ewPXgzUdEHFtvmO2eaHRtOOuizLX1W7OyYhVSr2KSDnSMIGV7VH97f+WonBe19cueFlxRHS1Lpk5O9a4czIE2JPtpljIPm39EB6piRJqSuTw9MU9cWXF6dNIhVp8XxcbtW/mQN0p20kbbqMRDM7CCseZ2Zb/VPs4YBWgdyl0o1svLPlPIYNhxXQ5taoWZV2xyjhDfd2lEa2EID5kknk1utrhZX52vyXFWN0d7NWz+Tec7pvz63Q48s3p3Y3/S20uiER9eam5V+pB/8z8vYPG4CAj8lrocmv9IvV4hu8mfnViB+r5h+yjcKmQ26SV/SySdlwd3jtXgZsgDFfn59/lqi73XdhMs6Ffsm/7ASw0EMLObmzbieAz/FfXeRvc8VXivxhJBEbysPpKv8VZNhoojYoBAVejxV9a4BRVKfZuymVMveCFfFq1EqrmYl1BuWWJ4KpRyNSv0GZsUjZ41hx9XRpPhLqzBOASoyOzNaXqdymqCaWJrEVuQ8jzBiRq0vDOUIMWUwrWnnWmyHmqptVDHcQR3IcJ1i007T1UrNMsaBzeVhYIMpd+ZZ6WqLcImn3nhHbZoO5hQBuBSlD6GWIXFIBebrJU2GRkGc4jH35rMb4OF6RFdA2KDxUGYXQfVHWAUCUT7x3Eb5Y3f8XnwCORSkADZClJ8hYKpkKJWQfvz5j/Min12lfvYSGet1acOYAUHKAyBmTWx5gBrknuWQTKYbcP3OC24JTaygFB/HxhxMkk15k0ABQ0W+R+E1mWWkT2AVu3ALwO69zx7+jb/+s0aNE+rl+f/oX/8ffOXr7zw5cW7MtpPvv/2rv4LSW8e3ZGJufYGl3SBEGGOSo7siKmX9Hzk7td/w5/W+Ta26gg7SYfxmX0eo5EHTPedo+sjXz/zcz/4H/8//4OOPPjp21Ob29WtvvvS7fsff9/Xv+8of+1N/n6FMrG9RrJESnVKr6p+eaCe8kgdyUvIRYJgMXcjFTYGD0eA0DBCWCm2Utci4iaQUlkCGJ7IlXCy93rp/X2YdJBMFmoVDC2aODxHlqE1tli3vrjfefENuTcDxrdvn51bbN5MA4v7hgWOUTh9d337x7t/1Yz/yg3/XD9165QGDb0OF5kohDx8/+L/+X/7v/+7/+d+hjzxuB3g+eiTctiBDcnfTht2nkainlMLVWlw5d0+N3X8C61a7ml5xMMDR/sXTQ+3Iyfkn1PHoyMa2XUzCij1OWsI/ffpZY9VGvJyt/9G9T/7mz/9V+8ksMr59dNdQGl9ZC2fG4M4xMo8PbVLYu/PCHeuUj899WPPR1Ruv3X719S+//qVX7n/4+Pt/6zsvvvSq3dRGIUiz6mGoWeXkT+iL4FpX/E+jsXKjElNruqGl21IXaSbL3ItyVbNVhywLUU3lAhBQgTQuWzTJMiAFV3dKmgNNAYgrt9JxHtDj0dmMy9kxCri+5TkK0Ek6ULaAB9989TOtqSc/GhBq/kJmKmU/ojbYTdnrWdGjJUq8ePLokUWML778EvnvHe//8A/+NmuobTP4zne+9fabL/nWnNHSp0+eOpwxcMl09JdUmbJVVuWNqIcpQ5RkjW6qcwqyqmaymcjKkUZ7feh0FeqtkqDcJtSa8qg5k2MgqiOL18/gx7GyVxgprtqicPCwmxcX+RVV9AzGy5pZUFotPLuvT3X1dPeMh/vk6uLJ5e6LW09zuy+f7rWFhodoFbXTrgxn8UUrTIUHlORGJZqmAHwjb26DCE4bl7L5sTgUL9KDmCXPkJuUEatO9AAnwjeodXqiDxAZraYi+vgp0dRgg7JreDUNnZ50JmKKACGJgxRmaeuGQaIT+NhJ3WCuvLXuxpn3nA5kcmMH7TUhOcMAQJ0/HPPBSRILykCuqaqRic7GeqHFA2wPgLY6smT2yXEa0PoZ80VwMS7NSi6hZIk2pEawMosI2ubVu8e4tAhpNU8NCxlacm9Fmg+rPd3ZN+hC40nDSQz1sspDDlOjFtnVLGqDSTgWKZnZ87P8cV4rMrqBrIZJlAKFPx3ZtPLUxKdLcG4qrFTGIDeIVpZcsqq55lst3dVKW0LDdtAKIUpRbkJvEbKpDjvCNNnaDGyqcQcu80Ki1RpLnCBJVzt8XHNlbk0X+uzCmn7dvUMaOj3gtI+RNGKFJ+1X2Ls04fvwyWPTFvHLIkgDNjNjSEhnjDxfvbVKNS2mVCwPrYegT6Q83v32/4ez/4C2LTvrO9Gd9z75nptD3collaQqJVQSKCAhkSVAyEST2sbD2Ab8TKfR9nihnz266X7uppvu16M9ut0exm38jEEiCQRCBOWSEKpSKOUKN8eT0877/X7/ufe9VxII6HXvWXutueb85pfmN7+Z267mcpgL0pCl0ojNiQiQE1zRTFMSZQ+NWMUL7gSmwwaMYy4hQtGTHCriwlDYCPKRUJnKfyVKugCfqiwfyZRYgJRbABE6D95MTa755fYVF+ElugC/6poCuDNcBPgLooE++2gOUxwCi/doaZCnlV/wCGYlXUlgohTg8sW3BM0efClXaYvITSaY0XtkKZK7U+pugzP6bXLK0x1fb7djAteaqlzlIawsLZbhCT+wwz2XyuovV/llDnoQN4BnAoGTT7NfAtgjn3tGBmY4+VXB3YqaN6CEpZhwuluorHQFDORPwaJ1uEoK11IGjunsz6oXdNW1Y1ECNYjvbC1IsuiYv+FSAEVRiuxgH6CgHkuswYsdgUjzMAf1OA1KijfdoZZSEwJfJEBFNUDv5Qzb7AIHQjItxEKItup7YdQcq4OopANJtF0DE6L8AA7UeoKNRw8cvqdIkyNrCSAmOxIUsYiaXbyAd54l5twTaukqO566jUa5BFlm2NOGyMPTdihTXPOPygCUJNH+gElz7hptmElGk+SEFGmeTChiMEFbFE2j8eB/gpkqCWPYjRucXYFAvaoE5QrpY9ShJ1WxcNQJv4KyFYLclQY++cu7Vb1GNygaao6JQFqhCkSG5RIFFSgv+RSIfI/lIx8rUv4QaWp8D9+BT3ROkCaUBSPgGJUxFsIRgYF8t62IOsTAZCrLZPDcxU8wzIX+sbfSkZXKg/ctMpeS1VTUyv1Bd3F5Cb3ATYQCXe9SRYldMJWWKTFoI0FUPU63H2yILjK1Vqr0u05HZg9aJrawPQ62Fj5fuVz5tV/9jYs3n+j3OLK+hYd9z91nH3nBI9/8ra8/c9dpZsYjF0HSkUJ1Btrdk7Q8KtUr4ajE2MsIdTU3z1UnicusdDjdvAymsdTy0TjEILygmrApP2SaHOKV1NzgLf9y0YnFXBfSMSy9t7e/BxyqK5TbsEpla5NxFUMqdODVqTKdJUA1wKABzU/aPNvbsHBbYe1ThTj4gIfKatFDh1Z/4Aff9plPffwjf/YEJxg/eO8LX/XKVzAAiryaTUbCXelGfUQnmqjoWCBtCo3HWsFcGmBOqbO+QSuo0kbdvZedPH10aXml3Wlcu7bOuZcb6zev+29zc/NGv1sb9HcHB4eZXNua34QzgN3Y7k62KPF7/d5obq692GkN+luApE4d7i9YKbc3WW994vjR/b2PHT1+bHAwWPnQfG+3/+ALHvzGN77x5JlVkGLelK5VZ67HNiMOVqMMSAyExUw2wtkw1xf0VcvMO9HUZwJUDu7ln48mCPNLeuNAaUyVkAswk5nLFBTSsEWCAnAuLWeG7u1urW+vrh5amFvc2OxdePYGXxYWFuEsDgeJegddNJBV2uPOfMsDlR3JcfzUyxymoMUtvWgUunKObPlkqIiC6d7O3sXh+ZXV1YWFOceTa9VHX/LQK1/2wKefvjzYH+xsHCyfOWSrj2KHw4JZQ7TubcDCUPMJr6aGz9eQ591OVWyMOo0HxyQP/Etm88MLTAzoNEYuk/TYaJnYtlKp99liblxZIhj+yDR+tIzF9hey0FV6b7EJoREuylk+8UNZQ+qkbKNzURJtPF9x2viMNpLXeMxeQ06OoY+bI8/wkavDxWalM48fxZSz6o7WhZ3yqTiAg4xoEYB+ihUroMl20rwsbaO70WmbGGBQd3qbc1o0UiqnVhq6PCEHLfNmXRe2cxNHWBAD79oETDG1Em0kLL96JSzEA3wMFm8UHC1m66LTWgZ3kZ4MBDa9isTJArjaMEQlIqz6QA6jDtt61dwkgAbNEb7V3YiJHvRtnRNqMMej7T9nMAaflmRBQHSdxGuTiiBmwTvji7MF+DCpHJXvNHhYbFDb6jNK5KnReJrUpMpDwYdmJcPf8LjVtC8yAoglFh/yrIs6HNAz7bY2pGRUl+4w/P4Rh9RWjlL/0YGmukGoOIgS0Eybpk6tc4OeHUbysV98xcKx0TCeMHvs4HOPa1eiaU4Tws/Wj7frH57TK8Gg0UkWzg4rV+0pp2sdWthvh8lG+wfciWK5rE4W5hf7DAHv7TnISu6WiDFrgt3cuUGnPsZ+j93eaIXs72y6Gx89IczsYU5XFziAofucfAdznXlUY39vh65GGoCgoZQZMa0Rscf4ZddpTvogk4Nevd3FFHe3Jl0mDLE31miwQycsMF3MwNZYiED9g2SHtWvd9tK81o9BJdcz6uxUqz16E9h9Gv0xLx0t19boUfnVXvxOh0YsXUWsokE6cJgakg3okAHKgcqDCjiaD9qVesNSJe/9Nx952/fPP2IRVymrkjxSEuE942PA06shZxJxJS8feAwmypVefwOalwXGSdIlau7mVl71sXm+AwAZkYoTukooX6ZXeZrlN0tmhkYIBBGaXrS+Ejh9vRV+O5SgabZ+5A/MoccSN03kDyTLsqSHkPzeKq53RpwBuzPXO+DcevyyNMkBLQ9YIVCGxYTHKSk8lhSGTfEosAoWYFYiEEv0+ZY/X6d53k7l94SapQplZV4uIqkN+ZAQ+qpsZwcPXVwSopfGtzyrHPRyqwmBGO3ko98BazZJSnETstppqyAaJeKgqvudj2ZnOsu1RszE0CqQPJLa7z6nFY7+kqsfzTu6RE8QxSdTemyto94SRxT+iBAOhQgiYbywLwAwOTHNyvYxIRR1XrVuXFh+E/MMqYUD8k6WcFggVnaAV6RJdSYOiIiQILw0MlRg7oYu9pAGToy0OImdRhreEhFEz7JoWko+0wSIYZYizy8+qsUMRg0oxRxFKwOYNAJOYJsjS6jH7WgI0uLsRSTkYo0V7koPV7kpieQQOogA5kSFRqkPAWLjJdb5DfOnAZIlDDIMvTLbcVaMNNO1JwN2kWMcEjNNLmG18aClAINYnnzNXQ7EjyQS3SqmsMekur2+AUC2c11ot//23/rRh1/4IIzBuLEWrNVkUiZd71klH8qCM/Pp2damA1fSjBRtWWI+FU5xcoa0dUkxaJhpelyayIFFq8zHAInNra1PfupTf/juz91cu9lYqFD1HDt6jC1UvvM73vyKV7xsb3dn/2DPYzN0VUVTCTMQu7CAYc48SkkpjC6cQagRsEyiMtCIGoG03hS+PJQ5XKAN2HLJg3yXSbqRXoVlEAPqfA8TDSchTLFa4pdFb25Rb2x1ir7P4aTncHt1v3cAsTQGqKXAmzY8gOntWlhcoCRTzDdu3mQ4+5/9/M//q//jl9c21n/gh7734ec95Ipk0AQUV7ClGFigFJkogJUuDiPvPfSTjO234yvVKbxaXO4sLqw4Qi8lIt7r7fX2Kteun795vfeFpz77haeu3NjYuHrzqWtr6wys02NNLMYxJktEr+4e7LWsie3/c0hbhW91Go0urlqjfuH6DfqwG+sU89qF9Ytb3Z0f/qG3cqzPeNhfPbxar3dqzPCdb9FzGCxVMy/5jaQscIoBpoS3PIpk9L/oamJzm4pFVfI58ppqczQg6ks4eE5lKV+MqAhSTnk52O9dv37txvXrzumqVg722ZWSkZw2B0fMLyzqXMFEdJPZ5KNhcwLVmEZzpHUbeGYuwlO0plkR5FOQ48evEROrEjn6d3DyBCMKlO16bfmf/+K/+Jf/6v985+/81hB/5mD3S198+uyZuymw6AazIHBdyE1J4tX36dqf6qe5TTlUFNTlvUxSQFlZS6vwwbuYDX1KfTfmFYEG6flfUstVUtt5JLQpJYUasufBLKblYxbAK7qNstEBjcnUz5vGgB4LBVY1TODm9AZcTKFwkiVjc/06Ws/cJnblAgWjssWD/rg2G2tto0Q8+BBSeaC0MEyFroxpCKHFHAwKPfTyqBQUeRVFDkOC2YIm34FRyOABNYeZfIA1frBPGRsoIy2kogmjVDhLAtkZFKYKKwyTAGDPrgK8hAjFYkhLm+kfBzCDszeodthPwGdKHfPzQMBHcoFpcQqlkkvFABM1lEeSImbEwRoAPMPxEpxLtPa4tisqtMbQCeTb7zd1LlOCTC5sEqvXPEGllWxgRkfJn5YYjGCmnd44nWjmCmOwCVQJsGyhPmRcDtIRAoaeaIGlX+E8K5VJgkGH7m8GOVt0T8A92qs6u0gPA0dHQ7NHvlSl9tYDaw6tdJdlJzsRq8vUQA5y2DM+ubB3QKPJaEM/TrSj8pZLJke6a9D+3q5aD0bgaFU8YCyz3nD7Alp/LB+gbsOPZ2oxhpaWiFrBQifG8mn7cj7AeOhobGY5W5UgJurnHhv/o4a6Juw1UUQQzZjUPSsUt2G4d8BhkXTsW1thpckej8RSb3Gy3YadwKNfaFfmqPbH1b2DLr1YsKIy6brREQnUbdgD66EZ+XInK5eauErOI4eo5WxzUcTRcFHT2TMDcVODnfRhV2KYrlzgiwqfBx5T5IISWk1rExOlvNAhhcSzxcMkgOW33Kfa5E8eS6gy/YqLVHeGTiNMf2bfyitZCt7oZjR7zuPtG7wnQqgxIo22JBPhabISN4DQSxQB/QxQKeeyCIIvZJnyVjZqR0rvLJAvswjllw/shWwKGrjl+opMZ8H+ftUncjRQWJNyBluMgvHkUq7gJHolnuYGnKaJCtF8kwdAyIdSTvOceII3SiSC9qlqdPOPxwzi063olDLa7djFYiZcEByyvcsT1c+0aJxFCMXhUF9allOO+0Hzwj20lP4eKQMOxZCSYFTKkLY4qkQp5jueI5ECHLNICdMFJ1xanRs9rHSZo4mRuILeMiKnOUFZsyZR04qTzY0kEqdWM9WOAQr6SNMrEC5BmsBkBoUFauw2xmTKghTsoGwNTCeJITA+ZpvSqAWMM225IB619Gn3msiG7pQyZj6AlPwZM8vNaXlUR/aPVeEtoyIAcuQcw0kP1Xj/MKxkr3RLlzKF95f4HfVOEQBzeKaxQSKmRTKGPmatFa0a8IaxldVIgPY3BdIJRWzkyDg+mfIuMFnGBX2ySODRcKsdLBYAxD+hkaQx4Zjx8onYUqiwK+NVQ9nSgUijQ0ZxfwnDjEtgeabjF7rokUJMsUbUQuPGQcaXVeJwTPBqDi+GcMEB+W9GsXp6P76DC548lSe78VBzdBfaS694ycvac01muJBsMOy155ybKdPDKoym8IRmlTrFzh9bp3yl6x/gOF4jpl9oukKf8cnc/kx8xhvr13/tP/zGuUvnyXthtc3BlfPt9rd/y7e9/o2vn59f2O/ucfyuS8RJjapSCBEo3eE4063LKLaOchxUmV09CNOlT+JArXYR1ZC2QqM5l3IcxHMzosESkv/U9c6YrNJrYlIhAVHLTJ8KbGSsCcINpVVpKmMQYt8MjKFOQ5HtICtKHCYhpTQeBj2X7aG+e6NtT1GoeJxNzgRo1Vs/+ZM/Rrc0+ry3j1kgBQXKOhi/HFhou8RLjgDCC9AhS7wnERV5uMp4eHOwfWW7PbezuLTMcQfgThFgqW9tqX/f0n0PP9J5yYvv2d1lcH34sQ999OlzT3/kg0+ub+/QG95sD7tsjFHbXzq8srd7vb9PxyE1X5+5VrUBi+pGG9tbIDLH8gDmzTbr/QP2JK198PGPbW6uveZV33jy1Co7u1YnN46sHh/2P++5a7X72LiaIRjcLV3UIKkJKNiX2gsaYuuKEJTal1/E9hManW+WM2p9KwbVQaqntM/lF9ZpLklA6QBwjkWrcQoDbS2iZ/qHJmFna6fdmWeg3/49dyCox3ug6Zv10HTPheHIUhGbkeA9FXian69BDTTIB5D4O1ewDdX6vZsbW4w5cNxErb5z5MTCT//MT373W9/0Mz/9c7u7e1fO36iPl06cWeYMB1ZjOoxGSnBlmYrWGLr0FcxQ/iBv2yiywK0POO6BDfxbLMSsTg6YXOQy3Aqd632P+61209GOEmI52R8WaqMUWiJ0A/7za5nNB8DrbqPQdhnR3y+XqYkIAyx5MjsD3wOUANRSjUEF5VNemjy1HzVPMnleW+wy3WSysDdqLo0W+iyXBbhzKg5wvfpsRUXPjbvjYxvwt7DPKc/jU2zE5YgIJ1lgidmkpt7ltAt9QPWEuiINPHA329wKNeIJLuUF+dDlzFcAafmtT+Ub2kgEKjjAWK8QnUIkFM5Bt2wRJJvhdqRpFuF8MlIWpUqmxsr0sCHzweFXp8E0RpoEDjHF9yUiRbPmKhl2UgJvmzsEIhF1GzxhoA6oU30IrjGFkgnnmy6ZBVvOZ5jMU5IrkwVWI41Hy54+WNlnZ6dxhRW66hb/iplGJuhKYFrV+Kdt4mrDRnx0jDdHiQ89UJkxDrbQZj53r1a9PmR71fEiZ6H3OrioNACEmrF36IddCFjlxbwWbpVGqezRJ2aNwXU5g21ktKV1DbVVJUmGTjB4Q6FkfKCzboVMfatN9ujN8JUIGeQfhSyPNYBBwM1/G0UgLiQlyoxKz1CBRuEzgOoCc3UWjSO+RZvU2HPUiQ0/qahgNQyxsDIxjQaEDSCUjY4ZNEe+0BNB6bazhXE36jGFJVGQADD2/nFUy5lRWnPchTJ7Cv4w0KAksaqiArWcp6FWW5URH9OAyrJHELRIIJ1BlYbDMNT+FmTVT1dN2hpVtn1gOMUdh2iGIDPVUYbKRMcvLEjhFxqnJsgc4hiBi/xtTvCcQgXdgcBn/geMEQXnlQfqx+nnEnjrHpjTN5/Ldfspuu9rAcedXM2oRLkdkadbOQaINMkcnJegcAuhaR6BkCS3gQiYSz0uej79bug01ykYQJdkU6UK0ETJ0xSQiQJiGvgVPyW+EIDFD4UnQHlUKGGZ5PIv7AaxEjMpfE4S480ungPVXBOBX8DdAptXIPNd+6k0jYcrriHkKRoG+YETVsjEALFQYj1MYCkwLWUe3UwVSCMeHearzhHweY3OEMlsSFBMe7wnmheUDUa+hGMRoUgw8wwjL/qxPiInExLCE9gFijkQb0gXXw7FJnf4g+7DIvWQqtZFLWg4fTkMHHu8Et38fNUOKFnsaGEJRlf45JC2M8aYsjMVvSa0ODogxvZkJHaGrqlLEtnGO1aWcmnJ1M2k9xo7wY8uQWESRpdE5iyfZb0GgwItdbb2BRfWwyP/Wf/iboGVjqIYeqNcyxniiiGtCjTEI9UIsPNVz815WmZEHqQjsgWACBGlDDR6kI/sUlITlCy0QvDOu6lJlAjA58lsjSBWAvGrDCcwSPmcN0TvZ/ugwlugaY9NJCD+85m4cFfEXB6ZFPlqo81L6Ixv7u5sX1+7xkKqVm3+tW943aNf9wgdqDhNeqLMocQVZTMHXSIBiZDIwPbynNxknZpjXOb3oAcMSLPqC+8ltoHRYbSDWZrY+Q999EMfeN/7r167PrdAJ/g8qwq+881vefXXv/Ls2bMom9JQMECPuHAH7JTF41Un2P2fx2gIFBcKCttCT2Qt2bIM4qMMciMo5yHx+JirMCs8LR/lqIRxSQ7pVANAGT4Fy9cCzkglbRJPEyb3OHV8Nz3YxnLTh0sAKWqMg3MOF0ePDWq95cZqr9+1TW65rjOBB0HgxlgTU0UFBDd0jzstPthcNDT9tZQ7mAOzyDUTcRmepyee44HRIY5UMz7SHgx37YXd2dzY3t+69/7n3X3fA89/4MX3PnAfxz4cO7PU3at/7MMfft0bv+n6jUvb2/3tvbX9vcrJu47evLG+v7/Flkh/8O53n3vuHBVpv79Po4LqbNAbfPZLn3v62XP3nDn5pjd826EV1s81e1s3Fg8tdRr7DCRRCdqghj+qpf6XeEcucD9lZOqhyUbYBAUSC3dVcAN94NfLcCA5PdfCRgAw+ZFwACsH8yAMzUFX8Uvok4OlmAyKk6k9qZAd+XGdK4cZsrBKjobXGwfMMWAqBrMHXOw4zTr4lOzNyCsZTn+TvUUBFBAAnRCj4YVz5/k5eqrRrM7rQjYGHFV93/3P++hH//TIkUPnzj+zvdt55CUvZncUkAEzuhzo0zDDkAFR0R1yAKSmsviqo9oAT4PmPt3REIgcp74L+oC/hMtV/CQ0Af8sBjQ0YGX5ygAUHReYK9NCAXkQjJsU/pkXyeEh7OO7dk1mlj2dZCjWFMZjgC0O8eMBAL58s5846AwY8RozCrDXZ48it5zhHCg8PtY/DvHK1UDqWwqjaDmwAHXkxxt2jtFVLDfzw3GXkRtqAyZmZYTCebVDtkOKyEEtnj5cwASh39goAuC3PURWT0Se0mY6QEA7WUIk6mAdIcXhAh8TQej8hfLyBLkKts4qEWbGMHxE02S/NWGNqC0y50lpojGjtDfsPSIVOFtbUtoQa6MNWqDJV11PHrTD4EsTk4XObRbMgIzb9dLbNVrkoJF6dY8jHNjDC+TtEeNKNaUBnxolu86VFOkAKTwz45WFr6zAtnwhl4yoIyy+jMYcWKiT6t5imUIMwUBnHwW8Z+o1OC1n7F6hQMBA6aDscEEU4WGbpk8OIxH9fB6tdBCkw8K0iaKOhFjxOnWKSrTYTL0FagFEQsOy33UmKmbcnjSFaGc8UkaJmByl1IFkYQWM4V6pOwAPr/gCdszUo1ZiRr9efeSMlIinwKHNPcH1t7B9tCKRDdu80RGigXSOkNszABveQR/IkiePqiXpZaS/MRdFIwKU5qLMwIWgnQUaEOc4ABoklGiXTgj81D0LBeLjVFA66mwKamYG9BlCRLQAMpOjFIIrIoPPzriLTTDrKJT81vMJx4EmP+TPlNhEEhQwSgqQLIATwI3oUlRizgK/7LekTdQvC7c43LryLHNmIdOP/hA2rYh5yUiJFBEMKmRNx+tJIzXWTEtvGTd5LG5+drCPixssCCnyxpSIxy9es3zL7+1g+v5vvdx6mEUuSe+8Z3ZU1T2AubzBTNU4imWWXvEF1QxfxcGWmaTwzguXRJX0QsiLfnIgCoEw1IBw7JWq7A7x0oY2snzyJHFHtQtoRJ8ao6e7g34IlmTCIZqCbozv4rfWuUoxxyh6Fgz2a8BoPEXWVVgw2LasX6OzImARhQB2oKaaQFdp1PYPjnG6x6hxBYxowzt1mOQgpXMPUZQXPet0eJEDWPDIqPNlcA4p9rXHshBqkYvp1L0mMhaCViw/jM1R3xJRChjTwEfWNGsnQc6KVr6BIsSRnS11d6wzP4KZQOm7LOasJlrRtuZlCNkZaDKoxHTif/SZgIGJAifaUpYda5ZSL2AcbXljJ8gG2dLWocThlBqE4RIUNQ2zDenPAy8uiNIzkDlE1reyecaP35SE1aeNAhJjOkCh8AWrITiBiCc/w5O+1a/DgGCtEH3IiZ4Tzo2WGv8L2kw1lGRpdvKEnw0R5BP01rcEY65KISZJjgASQ6FfhQWyM8dY1nl0OqinKCv6EsFKYSo7zaYMCI0CAQQii2bKKppS7//gB9bXNhY6zNHk0NpDrHOF3x4vRP7j0fraOg59oEzRj5bNgdvYpVnQkdUjaPf+gbNHaMgNhlQo9K2iokgI96jV6XD01fVrV/79v/+1586fh21UOayM/LqXv+KxVzz2whe/aG6h4zxpkGNRCCPRqIgnuYK5KCsKruQPzqgTAREReEm40kC6M/sKbl5wgrtf+MxrW5uas8MTHd7xSw7WWdW6ff9mFa6aBup5x2IEBCFJYJ2ZmEQolXC+BA1xC1De/CafvSjvqALPyXd8/cr6n/zxH991z9mlxfkXv+TRk6dP00SXQEq/w2iKi5yZqQ5NpOEfHf4mt8yhhZREipEZwKGgBwc0HcNub1+FnqchwCRQ4lE6mHo0ZIOUenV+kX0uVjvzHeYLvfQlL+ksLaAG2dZ78tKvewG9+88b3osjTwvEqXQ6kziXNOUmb/v+b3nnr//B17/xVf/fX/gXT3z8o73uiFlwvQPaY+MvnL967pd/5cEHzrzgwRe88EUPtFvHap1d9gIZVzY5do05RPhEhWPSAdpBF6xUT/opIVWJIFuZLbO43L+C7teL0BuR8DU6QDIUyuJJbL0EdvQpnwQrx4SUWLpKcQejAupV2DepbKytb6xvnDp96ugx5mGjwBqh0figyxG6E8Zm2PGFPUkALeflsKhIgZcqWEJ5IdRSx/gA3B9WB7tbWxcHE6ZhrR5l5ISl4TX2Qv/H//f//P/2D//h+lXW0vQunh8/8oJTzfmN6BbAVDFLackM4fJcdBn7AIukO26fioSXxN6Q9EZTIYAGo8F4jUw2wMMkLiH2YiIz6AeGJQRwQuPfLZwlxiBVWOihyVz9T/RiKOvrmBR2oA+HAZcyomcVqrUzZAj/dbhgHp3AgcaKcgwHVRUFj0UC7Mo5PyCABQMAkzZXX1gyHL70ETcJBweflx58jJrrycG8dLiKnPSIFFGzD4VkYAEnHJ6nVtmaw7jwCDLWIJCGCeAtNUjrJhVCdXI3+Kegql5yShzgAREFx59gZ/dJTr2oONLIJ447oKtpkTEK5rwwnaZVGzVpqzAEBhZmCXmsPiIqA8fWFnLAvSmboxZJWGrfm7C+mWD7ebGNNIxZp0Fq1orY7cyIc62+ievtCm5obLLNPycQH5IOUCKM2odKxQlgNj4gBYZDZvwWeqaZP0b1gdVgKR2HQ9O2ZNk76sdhz62hSDE7f5/2KZt8InAKAdRSeabOFC7geLaYCRqCYBk8tnDBRqtEeOscB5xobI96Zj2PoNxJOeMvvASwHfOczMNMsAqb3pocp7ledwIVRo3JQczodzJk7zS13IQVnrYALIJxgciL3XswYjR/yrgrOoPfAl5OUi3ZDrt9Gk/dg9LQYs9Z0KRLCNTtd3caGiAgEXcZGtRbclBVMIIwTY4SkexVAyiw40Vd5h33HQX1dEgHLuB8dbJi6aut0WhRb0zkbCLoAmWi4W/QpUUtyCAEm5iaDRlgeKwTedGM20SETHL2axSNB5JHS5kbqgcGz3Uz0Moi1qS1AxPb7M4KY1eZoq6sQS36DeqAgm5zLGAFeucFNKm9FWj8O7/nuaAUhDSTgVoi8WgBSJL88koQqy7Ri0kf7xS7d8a4jJlPAXsOQLCYZTRND11Bd4pL0J6iAxRkxD8e/JwHX772dev7n0vVV6e9FT+5yNnEkeRgE+HALXKeIjmDoaT4o9kXFS/BIJxkuti5Cg3wcZqRRgulnDE0MBk3Gg0P9shlXO2xN/mgz/ZS2ilCSKbtEg0pQtmog3mhw4siztkU1sXaGnQa54rFdhbazIVDa4voRFOnW1CovF6EnfdkZPe/bYL4JvqcfEd7p5YQksxTzMHZt9SIPIeKfA3ZlHrlSEqZhK4ShVcsuGUBzY1hwAZqGUsjA99D4Fwz1oAfvcMqO6ksQDntyFE1/H6wYhUXNYvMw5gwcO8zI8dME9X8UZrF0DYC9YyrQi2g+tCwCuZQ/FMjk4veEEBAkhZKUTLbFWLCn014iQA7DQWGV03AsQQF7YQFGOCwlF9qVAOEBTdUETCXLCPkspyRnnDSC5SIMkWyzS8WvAjFNgt1IWwa9xjBlFG4bsmJLwISqIUMRKZ36QYoXeD6fp6QTLVHRKsI7uJm7vyRXNTKj/YO7HlHokEmYAz0onO/MeiOPv/0ly5cuVQoPnb0yOm7jzcX5na29+cWnDJxsHdAv6locQWKfAhVEuju0IyH0EdD1z6b0livMKuB6Og3EoQWlJzPm1s7n37qU7//e3/EoUjo7crq4j333P/Ch1/wpje98dTpEyyulVsYXTrzJszYZgK9ctCws3Irk5HAIHhDJ9VQoTGygmHkZ0AhngcZaTMBoIYLp6RVOrMrJJUXCfJDRMfTLK9whQ+qI6RIOL6K4ucyjzvAJYyoMskkJYaZoBWRQNiWXii09hOf+cRTX/gMGg7U1cOHun2ZrCZqDcjLhELnl3zEW2LNkmcYLgem2RNodt7Ntba9jed58tSpublsdUcCer8wAcMBe1+22h2c+4WFBbavYz5Sa4EhB7YQl0B+yAvbxFo9utgGAwzU2I7ySuvwoSNve9t33vfgfQv/yf/z7e/45QtXLn7i45/qtfu7u/uDYZcZ9k99Yeu5c+dHlVe//KWvYAny8uKhhfmOql3pthcWW3PUjvb8hQWiynCQJd0YMTMWJUnmG3G8hxZJDSv9wAE/IM8a7y7Ok95W4sNaWS5nULjiuNCdT/uyxkQLu5y45ItZeFFnA37t5hpJWIqt/wHrgYo9ofHJAApmByMjmvI04r6FnhAIVxzlK1FAAEe12WTyFQeOYqFJRNc3WJHXA/c+9H1v/YF/+2/fxbSR+kJl8dC8W0niD9IdiSKJmQC9JIIXgqBHklRd/riRm/2LdJ24XJHOUzKUDBmBUZAHSD52DD9N/IUHycLnUQiBbmaF2Xo0MtcPhiQTiqAx1FcbgHr6/qnBgW9njd9jW4XMbBPdm644TpgY46BVRMoKS/sQ2I0eDaftm0l7uqohlsEB++MBgN9L3ywnNtGDysR1CMS8q99xhoI/Oo9XSJ5aaC4OU6MvLDNOXTTPZ6pFvDSO0nCCoWipVjBOfhYmYIpixcMJwiAYOtDAsDopeCzySCq7elySqz/J8Y4QfkCnCwtVmRbjtA8BMqRJO4Dlu7aEZB2xIaBBm4yOf9sCqJSK6T8eQIh9hTgGi60umXaL68f+P3APJ5K5U1168REyiFfZtVYaTKaZ137zDCQMLHjjIBsLY1E2yWDGvFbJDkE6y+2u4gUEeyNmE1ES2m3OcdMGYnjAAi6auX8Ak0z7q2EwHgoSZHYWDFfgMkJpEtN6lgpUGpgQyiQjayMKNd9EUZjAFjBJ6H3IyXR61aRSBRiIcD4Oc3sO8GPIWwLTBIOsEEJCWChKilOlgn4igeBUC8QRT4w1S5gs+xXG7LlGgVaToFrzDK7u0hr5Um7IgGYYZhW5qBfwQo7yRGIIt1SlFIo1+dAG1bknPv+JZUSTQSl5AM5SAvlgRR8HIFA7og51MjzUT55CGYUBAfCI6ETFvEEebkAUKPIGtBCMGaYZ7xdaskiA1k/RQ+t8/R9BkqNlRWEEK+Vrct7Dfn59+bILXPgaYhNOwr/wMlrg346k6oF65FmyJnUy5xfIiVlyvZ3IBgCXYuPHXhwmgjo/PlEEGXz9PE2qFvgozRDlhWgKPSVKwv78262MiVmev2YSWpzESkQy5Zl2lTjVrxGWyogXy1Eh20AIQM0plKYsVJmFyXHEcDhdlaJimUbQ3vLPaJEwsqY+kE7u48ZVPuMSOUUCK64amqNaA3NSCIHmQFPdkQr7PxwpRkPQBuEPD9iZeziuX1G5kwflKqihmYKzlIMe2ZAA1DzBQA/Zck8wUVRO4xKhMFs4URY+R/cDEEW0EYEu4yxbSDFXxJcqkSUJBVk+wCCAWsgAiIa7FQJ5OZorQ9Bj86XOP242zZuSor0AOTtN6CYADqikp5CopDVDJgJSADy9RNYCh7EIO5fq/ZNOda1yOgQcc2TAZnYhgLtg/QJKNnSsTOgjQYJ42mDpPyRMDLKQS8oFCJKuqECGxQQyCRCWVZANOGUjWFgJrtIlivBSZeBLY00tER5362elxy1WwcYNefhOoCOCrGVSrB7RkLlMANfG8gM0CzuwKyM4hl3dIETxJyaQ6x7zA+H0GZfuUIlwngytItIrSuAkLwtVwUnkha3UgIpTqq6srd/8wAc+2Ov2O405fMM3fOMbXEXFBtKdNsgQgcldcAnh6q4Bw0syKmyhn6od9WAie3aNQ88ZT+iDGf1R4uDhUDRlh+fOPfNbv/075y9e6B8MTp+9izMHHn7w+T/4Y284dZotJhrbu7sO4ssxVsGxjpAHtYA7lY0ZSo6M8zFyKoXOBAYSDUFNI0YcSE+cASLTeRAYUbtJncDAIpSYflEXjCR84SaiGZK58uafkI0zzZXIcIGggphpRYI/q4moma+AF6IJS0Ue8th3GxeY+oMpNQeeICuaIVCwwCAvtcBcgx4PUUBzTyAPiSg+XGYdvCWc9u2ARhQNAOdogMF4vLG21uMQZnub2LTiud5+rbl77+rxw836HGPz4GbbNTzHu6DmJJCH+aV56zkn5tWXFuZuXrtWG8x9/Uvf+JM/9fxf+G/+qz/5k48wj6nfna+3oKaxsXPwW7/7/ic+8fTZu06/8OEXnjx+ePe5NWt9tw2pdZbmlw4das6xMKDOvjsgIsr0hpItnCkGKXSoCDkHZkoZBE/FQ8Sx0/c5EndIZypoT4WHkku/cob5kIw64cezpSwNS40R8QIkCcgR3R6O126szTPwNNeBY40GG/iwaqUyYOK0E79VPe0D9UNsJaABwZ8Z8YwU1MkEiSizEVllNFk4tLWx85mllSU2AcWBxszj8bzwefdurz/DMheswM7uhZPHV9hbiQlhnC3BpIoYGQBNYQGYp2pzU6GMDsfYYGew93QWstaSmxHQNrCWcWw7o/tGX1SYiN0WRcGlzNpngkijXXzgin4qbJQLIvkS7qDLUgQT2a99BV4DPDUHQRq6WFZsNS4vwCnlni6FmiYZM81hSCeeKY0ucOgjV8aFmbc6Hi47OtXcsBWAsxvscE/Hk2U90tZuypVTgSbVDuCo9YI+XMZEslcY6FHPsL7+CAumhxMOJCELfS8qYIcXqaeI4bRuNsG/DFK10Sk2JGVWBrU3wreHQvlJMYUBwxQ+gDFmSoaEOaX8onv0caqR5Ft3+06uJc4aqI8PUQfWqs95sPB4RUKqN+E4C+Rhx3gwT78+W4bBK06p360suMP/6HC9eWWxebbR3hgMF5n8Uq2s9Jvb4/oyo2r0gY9GCxOYUFsjZnW80WIZGE2h/ioO/bB/pFq7WRucrHQ+57Zm9d3J4Fi1tVEbnybfSX9lWKd3/FittlkdHB/Xb0yGq9QUtfHhamNrPFzxeODK8pCVXJM5+t1ZKT4cOc9QpYBPsBp9iYYgc/jCsIGWoc64H4f6stcwQ1oaJdhHKLYBs1XF74cCWK2msSCaU+Cog2AjHEXDYDdOjQtV4Cffa8MzqkfjMlWvY4m1lrPV8CQa9AEVHoNI6pVi87XxVKto4KjWZNsu0aTiRklRdjBAfzgAgJGI+fl5JLRHm51N/JEPMOlrRGUpcZyWmC2qXV1D9pkvRA0QkaPiZAFd9ith5BiHAib1LDuLjD1fBdHSMHc2FU5IpbbhOBjCTVcjKgEj0XaJg2MWQDu8cH86c5y3yHF98sYGCRxVax0eU9scnVDp4CsIwUgqLJoZcSx0N9L5j4rS+lIdSamZMefoLPFqlywjDPeRAV/I328Q7t/0rqJ+5cXn2SXk2ZVUptcUzO7iKHUCDwYJ4DtsJBff+M/4mFfi1dcIEEvJ5Xs59SmvREmGd+Ya8ObHJ1MkobBNTcn0wSvU3ZmwBH/1vcS5ne6rY/y5IeRFFUA/17iv+jpFZEaxdMNokhEpFb+Uiik9G7SttXLYRakNERgem8XESTyJCv98U2LKWZUGABlRz6RS51eIRLYCIR8zDATrAi6fwyN+g49NVUqHti5AhIi22dbnuwpSAAANq4NVDRGYUTww4xAprAA9jXmgBsGSS+jVUxSbotlihzqokWYFMf54maPxIAf6oCBqr7ZKjxQpzcRMcr+APqUZhpqaT/q4KYsEhGPiKC7k6ZMX8GGvF4C99CllEGzln0gkR8uhdbzVfnxBceDPOg9HlHl7gCmAxI18zdQn8SoSECPQBoqISKdfMStK2kfMhyCDGV+JSbBJ+MudnEsbIyxQwLKaux4YV5GCUGBa8qCLxAUMHmQDQNZwka/k2YQiRHvhpF+a0DqKVtUOyGL9nEGFYtF6wMfRPHvYTcQRXEXJ9OAvIUDkUf4YygtKrGPN/93t/cc//KdO2pH3Iw5VWT127Nvf+mZIsFfCQOdSMwIguJDEA0D8Qw4qmTUEPfQ7m9vIdNgftNrZWtEqx7n7o8ngfR98/++96937/QN6nSHhxMkjb3ztjz366CPLxw7YLIi+FOSDs+HQqiWklJ/QIGfTtJOZZh9uk7W1swTGK4H68pUg+5hgse1mtUKxE40UJg/1geNjQgTDc3KbPeY35EbMPAFFlS6gSgJYEwCBX9AKTgXvxLeaCWzCSj5JYTT6AYHnA/Vioqnp8jQRiccV/quohIOE/6d0SJHklxyNoa7mIpLRKW60u7QVuWhrsMaO6g7DR5OzMuZYTDrH19Y31xmD5rwqWMpuYysrS0xV73J4A1uAMyO+5baGVI24UVhLvFUi3X3PyaWllf2N7e96y1vvv+/B85ee+dQnvrDX316/uc20L4bjnzt/js3vn3rqsw8/74H56vyLHn3e9es3z5w9sVBfglr32gM7ipKogCvqywiejAqDddTkbZwSKZMwfiVDltPQZo4Os2DSGWlMmeOfUSMTIqWM45/YiLUvkY9EKWIgcowpKeD81StXVlaWOcYL9aO1C9Hs6TmaG86hq0pAoft/yt7w2GcDzHJ28Y7ikQnDJjdu9u8522T+W6PJWaqckNp5yctf+ZIXv+BPn/z4Pffe8/kvPNWs3b+6ephhk9b8gt5OASKSedbmhhsULh9Ud4q/OqNp4CPlWmXAt+AVzvAuGF0nrQjxZBfSF7I3nsInOet7KJMuWtuhz0AezI26g2ycY5l58M6ZxPKiyxpeHEmWHTADNTadsT9ja9MYk6EUM5WLoR7gA4HJMzZu+I9nrGnGbUYcBV9mjcIxCjejg6XbotYGAI4fJZdSHLSoM3Dr/aO916WXYq9B7++osumMatA1vTUJTwV/fuhIhQHWTXEeoRqeYHzx6swaiwbCsmjWKoDwCM4fGeOnBEkYKIqy++XYJpYJzNTBBtPt6ywaOqcQA2ZNBRRRtoyZVHbqla1xo1/brE0WmN62M9hq1fYcz64wbZLJspAp37s7tE5vchZYpbmFHR9XNtrV1mi429+DAQcTNgRqrlcG89X6dqXPAersqzY3t8CRZEyYGnASS3ewPaGDv3aT6VOT+jq+N3cQqzU2x4NetbHL4mpYOceKA44w4Jj3DIDj71ITu7Wgfe1I2opE1Nkaw559t6/hmfNYOMlEftHoUd+s/mCNdSQ/mQlj3c8YD/Jl6hahbkCL58xkGE8psZt8eRG41foiRodiC4xhb7y0uMRCJ7hGnxiJnN+A223TYsLCfQogHVxLpHCAJQxFerQnuds0ZKeKDhtUdJodNHnY4QQV1x/q3KuQYMhJ2663VgUwRzQfOb+Qhg1mrskq7cyiYMk6wicbJu2gu6iMx5Qx8mF8PTaUuEZPRZuVWODPXs4YLgyOamblTbPHSgaEWWbgA6rNOCmjWNn4zjJoSeWW8ghm/kev5V3BgCdDKThEU7lQOphLYbK+81nLYxLULFloswij9POnivrAm6B9yTX9KS9/nfsUCBADS0MGYO9oPD+xJ2Y4zTvxzVoyJCCagizJtKTz9ytPICupxMvCkosHM0ka8jH/QKQHyO9ljlGJeuse3PJWgPD+V7xMGRr5wTVkxyba+o4ZJhAXHzrltuhJVbFCcECtIDxiJS11V7STmOhEQBZZFjgkVlyxHxR7tVdxBlto1GYQYOWvxNVWE6gFJAJeKj9LnfGwrXw3H00E8mhe5WiSYvV0IGgUUrD1gYxGRJvB5iWaWBpZA9yganRgkiw1JDjlzRDJBTdBeBFPLIuCBfLMZwnqRVLCJWVCwLnoPAAwbyGBdIFCBB6pK27yY8FIMgHWqB3AFhiYwVP0HjPDrEjB/khGkGBo46J1kig51UTOM6bU6jDDVDpzfiGpQBx+ysWCkRUO2VriLCZyBFxgkkyRN8SzJUcKuOoHOKnk5RTA4BNReLKhnhcFhiLkm/LwgUovxiasY3IXQdZm1sz8AJRnx5f8lwBNHv2p1EI09+kEdZIkDVGAObSbKt4OPJXAJgG7LwOFfgEbAGStLUZlWvSotuhX6BDD3hHUEytOFmSiCuZJHTRsKmX4BsyQbT8QXBlWvvjFL9y4cc2Ok3qjXW8dWlx87BUvX1pZHFf3sZe9gyrTIZgwbTePZ7VYTCWD/2GOzWjexuPePueCYf5orlR6e/uepsiQ5XD8+ON/+qEPP36RrX7Q0FrjzOmzD97/4Ld9x7fdfe897KnPOVlAwhFF4nRXyzzbPvyEBugoBIUqaDHz/EmSdQ+EY9hxuegisoSSO16vEWWKRSaJZKGwcgdxUkd8KZPRhMAiGjwiB9t6wiAgxgC9SWqFUnBSHzTGwuQhDAn8fC7RSp5m6rvR9Md4Vo7ib7NnuMIgoP3RTIRzDYDfC5FETRbTd1cvWGew45BoJVLwmyJQMOSjtbcJ8Vz09an0NVBomUqSAWU1gv3sadPSneQndubGpSCUHXI2rly+VO9cQx/qlbOLi4tz80v7+/u43EwKWl6cp7lSa5xbOlpbqjZOnn3B173qRZTS3b29933gfb/8S++4dOnZ3R1dfPLa2t37xKc/PzwYXLx66Z57H7j/heyh3trf36lWl4bD/WG3sbC4QqXJGXB4hxbczB4Fd9klhUpAMgtHeA/hhYNNetIZge+VaimoIyNjKluNgD8HrTmVQelZWnORAUExJkiD7uODQXdrc3t5a/eus6eZEkc5G7ByejhiSyBKo2g0ryj40WkwALeSnIBgV34ESMaWUJg4Osuqx7UbN1vt9vyimxHVmANdHf1HP/l3v/hP/pP1Kw1OfNu8+pFXvOxl88udioMPe6gxOxlqAxW6dzkwOC7Ns2zIODUBZVW1Tl5kpm/OJz0b6cOWCWNqpZi3gJ3JaqLJeAXtBj8iAT1MKSnIzopNtmMuceaYZQ74xq4+3fgEdhhuARmuptQIgikrimc0YIoVDQVGs5rO/AF1+sJbLFALRiBFzTRnp0Vzx04OMnDkFm8ce+5oZpUtaygXiT2Y7I8xbJmMZkvAqTJsR0d7apcpr32m/Aw58GuNAWHbfg47Aw2QOvipjsELYDjYp6EEBMl3MjylzuN5yha4BAsKDwjRrJu8T3x9lalkgeJHYGKF4QYswV3mUDM4tALY8ehBjpBqcEgfAxyjo1Thlfo++bLhprJj09BqZb+y0KWpMoR7dAufHdQ7Xc6VnXB2nm0kzmWnt5iGT595O+z25sY3y6ncjjBzftx7qDfu1ofLSHo0OCO7Dp5nX/V4kQ5ldr1jwlG9cWLY2BoOT4LgaHi3Uwwqp1hHS++KGjg+YUdIdc5eK1muL+5ssQHzi5CSfIIqfih30YYpKzSgFh+8g7C0WCobdgSjVVAZIdMCdF4RGal25GoBJgrLDKiu6Y+xW0olai3d5GU8YpYOM39cAYUVQ+7sUUajBPFYZlEF5k8xWMYxwm2WtLjBRqfGHongxlf4bsMXwJEL82VYQs9BxZQstqdehhamg3EuCpHpSqBsdKjHNSP2/mDy+A/63ButRWUYoTMskGICncRCU1hHhB1a0ES6wSELCob1+UaH9Qwgqe/EadA0DyBSSTMSIt78c8Uz/RejTptDxlhwtQ+ZNmn0x9QuOYoLBkJJB3WWMMuCqkfZCzoCAjTxihLGM6FU+BUpgaFyFHeWddG1cwYQrEwDpoDuuAJ4qsAET18nrMwBjuOlswT+Top37Zx+c+E2xYJvXmRZUCiJxEAA4zk/ZvSVsS6jmBGI+1CmACXerbyMUUCYMM8lxATlE0xJZryJRsL/klvifQXYvyTJl33WaqrS5Fi0glxxWVQRdCfDNNEhEqEZNF8bZfTKaIZpG4g5JS3Svm1JTcl/cqD5qyDjpoUw05gFl75jHig+hGoGgRx8fEEb0HtC/OPGP4qthdN6JqgnmqbQGOqm+hNQKL1K4v+IVwHna/klGqj5zepDe0AIZcWsrJEdu6bYBVcBzUyA1jBUgXcyxSQkfVwxy19AWROCR8k5uNnigGBTB08SUxQYRIwNUgQkERvmk2prk2myFW0i00InAcEkokgnNt+DBxFAQnDTVwDQmgZZDaSDi9FuookGcSM1fiIlGQC7XDygtYeI4JZUckYzGSPCbHeTm35KhALjv1jk4ompoOSIb4cJhccYmhIlP+n3MTmsMCF37FzfbgaX/JkT9DmUoBAdvg62YA9cEqRhgQ3oYCg1xVb4isR0MsBUZDTFcPqUVytZ4qiUU87ULpx77hNPPFmUhD7Vhx9+wT/6uZ9hMS78x913sXVtnm6mNIIZV3WNBhmJRTgHWBiHIaenc29nRxYpN1ZrNJhqQsjl61ff/o537O5z+kpjaXnx+c9/8PWve+MrX/kYPTicpAu2uKjcD/ap+FEGm8KSHSRnTIWNEhS1kW2hkUyIG3otr1QeYAEveYkBDSCHdgVVIATpAsUs1DS+iy+/yZS48NE80FJ+/J/PUiko3/0pHI4AiQnPVcmgmDjEE2yew6eSSF1Tvf2MenFXWPYkmSlVI5MZaALakxVhkpmEk5nZB33wBLlSHHIv2Vh2jHkbhbxCTEYsZ0bGolLiTKNLuBQRzXJkZyroZR/rKoccsWsI+9rvNBo36Rpnd3DiDg4Ojp1gn3u3C0QUVHUoCaZrrrP8LW/81tc+9q3Pnvvsv/zf/t1HHn+8Pd9idWa3h8NRfebihXOXr2zsXnrxoy8/dfowudp9Omzsb3epyqmiV46s4jSwZ18hP1jCphm7C2lqurRLOGPpLB+vkAU6SXQZBeZTgvgeO0ChRT2JOaS3WHHLUqIKn3rb0knJkSUs++V4omvXrtG1eOjIIRQe07G7s7Ny+BDCybReuyYUlLKIwUxKgYlA2BjYvFj8J5Unn3ji+IkTz3vBiziotsPxaoPRY6987J//j7/wX/yj/54Ds9gP68LVS88/dI/Ll7QVQIf50cYgGNkbIHRgqgRoEAVFU8Y9brO1hle4MH3ko25mLC1FA0CBRR7qVVKKr90eGARSqsOlIBDMd9JDKnaFB/0OEcvdvg1hAZq5hvSJM7g8j6cN5Eplvj5eGFXa+J3M76BRAMgxe0KIIT25nCaV/g2rMzEz9yAhPrwRG+AoP44utl2mODsDZ3+fgUNWFuHiIbK+/e7MT0kNSMu2CFqkFQNvwKJHN6WyWFLJF+fciGcM6UkCjfktHgtAKOhETLNVhyGwEh3gxqJWFtMCnyUeZJHBBxspEDlcsEiLFg0yptCQxRKJWQMNf0MZ9OEeswxXprOixrPCafK652kWr0qBa4HlC7VBRq5JARNzUgKg2XmU1hHVhLOO2Q+WOFXbS9gRhiRgIMjDSAonJPIcY8g7ykAS6zRJ1+QqI+QCTGejTMsA8YquyCm70uzwRi0YqIBYAlGJmGtCYA09AhwUVnQStGM9oIGGho4/eXnEnu4UWVuVk566j5MHUHZ2KKPagw2yzrzQIyUhq53xZY8bzwz1hP/2efE9FIWdTAqmyYQq2eq1V0US+GwVmRKBlwCuQOdU9XpbqbsOITN7Mxov1eZolQGuGgprfMRmhvZexKrDB1lmeXeMgkTAJI0MIlcTEp3vWAgkTybWQypfeiaBCR9IgA0kftwdfm2WqrHI3XIj8iaXG+TOb/kMISgj30Oyv0QkgLQxQSKhyvubnG7dCLl13Xq+9WDOfuYGXaQNzQTMPvglMUqIeeYSabIL7olwK9I0caHKyXAGTMGWSLlP2n6osp1WNIR4iTmVXUgpichHXfhz+/4F4XUL7gy9EvyX3mfRpQU0ECjmC20IuylRQA6ZfFaB9B0Rkt0sSJzdNLHXfCJEzQACd2tyXlUIdBDM1GGENDysBFvXUX8C8StVUetvtYZSJQP8L5CI2miFcbVh+iTaN3gtSoZOAYO/lHOpYON3NMJVYHisqi5QtO+CcuwTfEGV9rStUSoxlVLsiO7xIFgSsCAZkBmpEwQB5kIMJus5aJv6glSU46YTweGPqlw0MTLi9BwT4TpjEexlcBJhYChBSozazXtRGzElmQ0GKTdrixq0KFH7YIrZAZcIBe5doxMTCH6Xy/AKvElgqeCC2lrzGg/kA2yLIyWI70nBd/seCKpzXL3FCyj85Qcn21pHPIanwLHRvkYrz24BWc43+UGJlrcYCEwVzKSAe3YgIDD3JiVH0Jn9qSsjd2nQz/cbzIqlMCbYqwA8AgDYZCQI/sskTIBxMC505duEcGiVSjiMsHbRCpMPaQHsLEV66GUy45gaDQmGD6HPjKNWxCxX8pQ5KpArcqs1Zux8/OMfPzjoasqH9PR3vud7vvtlX/fy/sj5u4x1o/vU8KwA5kREp1FJfiCXjHDZwRaUGIzvwd5hu8VgNId89Rg0YHurX/nVt5+7dLE/6i8uLxxeefHz7rvnx//OWzhOGD+P/5YEPF5KWA4XgwNTl0wEwTZoh7mSYLb8iL9fEdu0BaiKWuNaZeOVApHizLQSnqkAkFyp4ORx5CW6EYylD54l38A3Q4u8srWRiYBSbr1HekZQZMaLQeBZfhoKD0odacWQOJYrpaNP491JhkqP74Ilc5cr0uXfvElF63gM/WGCA2Di+ASEkC07yJou1Blnph/8mrNQKEvsQ8KzASIoFCMpNQBxhgZ93eNtP4KuYEtsWWw8KbPUgYOvjLyBjI9EsAKz+qxUtnf3W/M78/NDprWw+wdZUA0nCzogxwsr9Ze/4qX/jxOn3/72X/v1d7ybLUeGdqUzuqUz8cQnv/j5z1984Qvue8GDLzp71+F2a7nFlHv6BYf7W2w/dWgeV52crS85n4gnVUJFLUSDcW14t+xtXOATmFI22bmfPWEj8UK75Bhf3ls25uZst0wZIpEhtndSGWVlGid8U9aqrau4m9ub27v1/YUlzsGb41QTtHNve2dufqFSoz+VE5Iuq3ucBjDjF3ALnt6VaZgraHhXXV5ioKN/7tkvPvyiF+j2yMbhvWdPf90rz37x2c/PNe6h3E1G8436Ep2XTOVn6bVmIdjCBgUhQGlFYzTFZBzdwqoTjo5qqGLVjGZcjBLmBiAkMoFh3IeH/G7R0UrkK8wB2DyFB/OXEKATZVG+M1kFGhkxAEgJlt/6fSMW62q28WkZNaQ3kmnxtTY78dPtP6yw2Tuuv9OBKl30nIVrDH7rzUKCc2jYwohcGWW1hZVxDKjGr0dF4U9Z0QZJtADIg73eMRR9R2OY8YL9gTOUnSBuJWgxcmC9SMHyBo0GkphuGilVMxOfIHgnfQYKfZpQXYGMzDUIC/kY8WoACsvgqq0h6hGZsuTXhj4cDWRrQrKfsKZlS8zGHS0r/dqMz9Ml77ZbNC0RCedUYJeoUcAGB5hIkRLMiJRAgQuLLjUes0WjmhJnjc2wsLs8kZ34gz31PbPUqIMGHNnLQgi0NIuRxcMhYFhEBsHdChOfIGpiBjzJG8jiPxmbLSAhCwpNbwb88D+cHA3pxBGEbIXVSBJ2oXuJ36FHn2rBxY10fWsHOCuLQ4F7PVYPWJO6JQ6GkVYbm8GaJWCBjd2jaoE2l0CYVZOTBBkbZDUESylcxuLCGxc5kqaYDlZLZwek5oi2F8rEjob1SnfYYwIPbGGQ03w5cMbywIINV59Bh74bNgMQEmgNQYMy+iF3InjnF5EGmfENCYiOCxWo6htDlgKxiB9UbaPTcmNN82F0elK5bHzao/DFESqYY2cCwxE4UjRVSS4jLSSAQ3K8MsGIlSGoJWiUsT5HwGjFUI/h9ziXzD4H0rF+mbn+gDwDhuARYUAOEckGkP7DU4KXeaJX5rRSc/zKy6y/+rp9UpapcyXiNFXCGDeDJNbPEGWqCkZWl7iMrhJZqbH2z6B8vH0vIXQH5CNvJJk9TtEqr9G68hjgU0oiFFOptiXpn0+Mef9fvwI8iKEVYlsCRLZoafp4aSWzECZ1CARrexAu5otaAfkii/jCfgBfRak+lYtfS2CRPkE8YH4cJ+M5VipGWiVTqPQAwFPrOTAohKPUDDChOLlUCZrVuoWoYoqvk8WZO+LJr60WllgtwnigP+ISJ0YPlSy848KCt/WFzgc02EcwbumgqGCuCYQNwGIRDGBtNGA5sesWeKp4ipCn4bLXFSZOOwRBsiuycs9sqcLn4nAs/GPKG53TBGgujWpM9UarAapW4TiO7GMDXewfTM50UZBKkyT+pia+dQRFhbJnUUE27mkI6jQznE3ICKDuAm33ZJFM8iqXrE/kNg9uL5xiX2/TgSMycgi8giFomUeDPRmYOCnaICOXCUz7B64AB6tMJ6nUGWgUgESwQuRdUkt2GB8aSswlNgDuYXX8CP7lQf4JEPKojd0jX+tqweZVkfDfjaSnQqTyQSjWGgJEwjCe/842TGQYJb1SmgiqkHGgEwKndPqFP6Xvd2xJ48bla09+8pM33I2HCZfjYydO/vAP/vBbf/Ct3QFj96xQH8Be8aflZ1cVGzmz5x41gJmTIb/QgzVkm072Jic7IvDIyOygf/D+D/3hRx//6NNfeubQ0SPtVuu+++77j3/u59s0RDs3e4MuQ2mYbM8EsDktpvwhL8CKI6SYiZgWQiTDUC+++8n4KiflhCqo1ZjHPYU3MsVmlKKB43TFAAWhQX3wtSUJP4FuweYnOQlGikJbhOiHYGEoD+QrBF8Sl2cVKAm50chkRB49CUZoeFSfQJLof1j1eCUDmRdxUAICBgzRH+o92o1CN17BR6SnuVgzFPymqAbfcG4ansyNJJJJmGdAojklJ/gjn40ZHIhZ4vigAxXNDGm8kqNx1Vv4WDhlcbx5/SY5gMbS4uLSEscOz1MLYjukd1zZ7+8fOXzX3//Zf3iwX/ndd/0e7UBAxBeloV7d6+1//JNPfO5zTz9476mXPfrY8VOH2m1WdB4sHVrp7lQ7c3PMQgMnjuamvKTowTu6V+Q+WWpmRFn6DGU4nJPPOKxM7oRDsx85HCaw3xGazLl+OiKp7MN8wCElm2qgjdZof1CUaD6fyGhnZ+tQ48ig12t3mMSP8ss3YoJGsgpGsrooR8kONLSx4E52FByGR7LVW6+Gk4x7MakdPXHiv/xn//S//m/+q3NPP3f9+vUbN6+220uvfvWLsFqCBV4hTzqlAaIRoIod3x1BEMIn4kVZSGKrNW/mjhi1LdoUZWRihD0DLfOMxbsyVeVSAOlWlwzLhb3eNK9NjeNkXhE+mAjcTAuaTt3EkDjVB0BM/GDPX7u4IF3c6ALTnZ2LeWWatZUM5sthAaLrzzGDgvm3eNnMn8GSa5XguzniQcvqOsc4UZYoV9qXoC4CEKV5tjUCVOicfgQ7Pqkj/JNxEZT0F7XRgkqBZZ9JOzOxkWEokEUqRdLxovoQhzrJMp/ODiLidtp357kFVEg2j5zvQ4aj5REEKiRCUGKUrTOpMfzFhB66jfc53wqs6GezcRu/Nm4F9XJx8Qq2KCNxtBt2pNnBBx8hUZdE7GkaoShoI4azYbuE+e0w3Cj2TVuBUhtR5CMrmIEE1QWfkKelWXlLp+T5JPlhCwQTgReypwlTINKHCAgRCkOSFvWGq+7wRvuW+DjarC1oUj8OESvn7rnOucHSm9aY9V17O9sktXODo7KoRNt9tm7a2dhptGGWbjfzahzrYTfbFuWxyZq4BVuho+2NnSi2Qx6soWeeFh0KTFoFSzjda3cXFxa6jDzv7uL6z7Xneaat2Gzs42NQCcNtnRXFV5tjy+MRFRObIuyrVzZRoUjLGzaQD3rJVGQXIcwvslCbAZrsaUELFFjwhRiwga4xh8ZpmB5Q+YUlKUfYFvqr+yzopzLVaIddfochioP2MjptNggVfqcqZedcMKFr1m4+4CIiJWhitVOZITBCEDR3DIvKqbYJ3h+epcOAW9edz7cC/5KHpCnlA/ioB1CFzU/gc5eTJT+1RSz8WlCZQecDYSjB7Q8lWblzAoDp1DK0MIwzYwbUTprClftkkgwLBgHvJws04QV+AhJ466ky6STAGU5fdmWH6elcpfJhzFwo7JvTxWz9aUYwTIIvdBXWKkQ7bJhlRvuSnojjyqa1EZJlEA4PwqHmE6+UzqTnmXfkRGb0VF33XZcbmqldVErh9I+TkhN2iYc6komXfNcHkgm81G/wqEbCMqZbxvln/R0QsGdgLNrwTiPBUk2i4FLzRYulbRUNlS5VPubpBBXdqH5d+2RnJEaQB5KpRaooE9PGZzAvtdZVfUu+8gcMTR6DlHTSWELoKRcyKxAkLFlw0ku5fIVAUAgNgo3JAeHwl2AcHbiADZQfwsawBwXNkJnRyyaBgUT2MiDxdf/i71p2mPY+xyaGYq5HjmUhpWBISCN6+kYzweLP1Ry2KO/OQSQFkqY0sv2IFQP9khRJAI+rV2AbAsfW1SdnBFe/FlefR2UUH8aMnF4oVriSMhh4gUlGoEiQSbXaZbFuQRoVK5jICgRSHCpxAlu6rBWf3Ibv8IU7YIAmttaZoKj1sZont4BS3NgDoyJx9U0DAVp+FRfitUWPsyRTUAlXEcMCFGh3t/fUU1/i0kQy67bV+Nt/58e/93u/m8wbDZZJDVn8hGmW+63K9evXXJuL+RE7grRoQEUNJ43z2H0Uhh79heqZzU1OQd3+l//yX129eRXAnstcb37v9771G1/3jQsrG3SpsuctNQoLnjlVjhpSFoqksoBzWFExJKxoHgi7lTV00DMqbxUgKFCL9I7LsvrVhYXFtZvr73jHr154Zu/oiVPNuRvHjpxhu7uVlWOt+rFWc745d7PRmGc2KVrDdJh6ndVw5EJXDR2Zzja2II8Oe7c/OF4LdyorSK2ckUpOjMY3CfvjiqiiTgqhXwfG15mETpzMjIAWqIYuxMEQFCJjlgS0uKM8NB6oGbZrIYIbdb0VG+hlIITs1DipdAYzOLL2Q4FGrwRduFKY4D2AZInnEJtP+RROGZ0gMCVLaKm0L9IPB7SEyfTg4M04ak6kay4QiEBUrTwEARVMTcudRPgadY62BfNllia02hwPTAuQJjr73O/trn3xyc81eid//Ed+6oknP3DuwrM3bqzTVemiRPZOHNbZNfRTXzj39Lkb99599t67H7j71COT/uH63KVGjR4ElqHXjp08herbNke3yd/CHSTrF+ML8Q4ysNRas9VpcZISrJQFMktecGlY5V6FbU+dbyY9UTW+caKzlBqVlWaYLbQ6qaCzdun8JRYxHD16lC1t8WBojBw+hoYw0Q25yHYu80rqGev8DUh4az5GGw3pt+Fo7c21zZNn5hkJOejtzi8usCLxpS9/5HOf/fzewS7N/929GwvzLdYDoF0zkVosAodMIglzs8aMjcV6a3diL/iQS0qsYkjJuF2xp7gz0hhNMSiIpfxKDV840g3dJpocBig51HbprAwljqqROYDVZqhT+sif5ggFBKiwF1cQ48rukgssQa3WL1TYHx+1ZkN0llGQL/mDFC4vbmytyQQvu/HjZikuHzCtMSzWWaGP/g4Eq9ljyjXQa1VWE1l+OCCM7mb9MTiLflLQYJemIxRy4xIvvoEhxc9iyB1VcFiCmpb6Hhdc8RHLb4V72p8CI2IFAJDmCK2wf79QoQPqKb1M9bE7pM6prvQ4cLotNnG8bM61HWvI8aoUj/v1KlvoMmkE43BkPMZ5xWZi3eiNpnPNla2MT9ITxqigc+FgWaTNHYbilUAV/xkDCP5SJKvFxI0gaVMTqcFCizHz9JjnCBkgg0PCEJ9sAGdlmQJrrghKyyrrrW2QJxZD1VCJjMZ/PARE0MYGuoKCqTeN9lWXFFtiiitAZFUAyYg+KGAFRpMWq2NhpPl2NRs08+s19tLFnaavlL4rusix2EzgQmAH44P52qITHUFkyFgS50M4d2jcPw53a+50R7Vjj5i8ZGlQ74QNSEWIxb1q1sqCLaFpMgxbdQYW6iwMJxGLlOAMHYOVIRsEyfDh4Ajyq7cZ2aMTi6PKGKOgfW/RsYVONeCMAAcJ5AsIkZ7WrBLgXAkOGmLGNyN0NaoqGeZWhBC5BuWYGpCg3wBqUVm8MllILxCLrOw7VScBhr4BWIxHR/kZV9cosW77ZKmxT20yOo4W1Js3bBzbh+KeG/B/1D8FR1F87hE9GNq2RMy88091VXyImRuNJvrsv/Lyw1eGfa13abHvn4tcyYqA8qY+EaSyGJjHW18T5datJCkNgIKADMqTyIi7rCYAEoKg94APbdOMwJxAqRQVc53mMPu9laFMEPJf6xJ6QEZa4SvpCxgyFIlg6gOKQhZhtnVz4UGiKBo+GeIlqiJDEj7IJB2IkJFQHQAsogkwGdT8eB6u4kUL05REt/Sroo4l30S2Txg4+HuaRFKbYXiHSplLVFFrRyLzxcYJg6hpttrAgUxQDUklqUNNfI8HRkVOT4yp+eMfRbvApQhKUMyz5sPMBFsepONWiKGEW31pKIMgX/2VCH5Nr3cDfnZBaHYoRLCBftPUADq/QEyGlEV4yJiYZZWSR1pML+iQGCDF6lNkeNNYQpmYeAsZZpNcRcAsGWSwWYATJkJyXx6mMotDAy3JSbvmYCK1F36wa4zclrIgDUASg7v7G5ADHVNmpkoojdyF706CeMR4OS46m0UgP77lnxlrJ8MecKjSQ4ikIB0DhFgIt5EkuaiLzQgyxfqRiZ1qdJWBM0YnQ0LkGJTETvH4G2MdXYj49NtJyjf8obL8gH0PP/GJz54/dy45Mo+o/g2vfNX3/8APsvIJ4LCVrkpAYe7W19dvXL/OFAteU2JRUUilEkcW4/2DfY7qkqARezJi8SfPPnPhl375361vreG9sa3Mt3z7d7zu1a999NEXLS7N7e0dQAK0UQ/SDYPYYWP4FsBSp1WWTzLKwqOYJMncEk4wkXGrqNuQBcBqT3zsyT987588/qEPD7sLDPVUGlcRNGujce4blcON+lxr/kajueAJEgxL4Vw25vDJGo1OozVu8txkZGOuPj5KSK19jeE0+vGZ3JIZcejNSYZ9aVSwdwStF+6Z5Namzmu35lh9tji/3J7n+E2WQTKripE8FLWoH6i7jg0F1NGnoUvZttfORruilyI1J+fyQC0B+DUZAaAgWI1rRuSYolTDZYHcMDhc4ZVfohjmP2P5qrBNWp4s6IhU9aJSykcBFdgBXYp1oAWg0EEocRUR341PDjR0ooq+QBQtnwOWd+zssenT0vLK0tISFT4DMvTy3Xv/g/f8rVd1ljvf/0Nv2dpZe8+7/+jDH/3gU5946qDfhf0gQvNr82D/qS9+7ovPPPvQ2ZuvffXrmr1NJt7gHg0q7CK1CAqHjnMkkGTCGvTDgqEPFhrhbeEkHSkMPeFfYhfklZzQwlhMVCo4124z9TSUYC6iWGGExVnOhLuQxEeLGg40HZu9/pX+ZU6rWFzh+IIOvYzz84sUPwRJ9Q/8aC24yQrlIINkvNnz5pNBsGNzna1XdSwWD620OnO4Fax0eNvb/sbFC2tv/w+/Sjmbp3uyw/wBdkdhjNGKAkjgJn2peehAABzvBEKkApnCN4r5kak6U8LVFfAsMrPIWO/oXwGXJ9wr4eGGygt2eRRR/8NZKCv2KV0RGikX+gK70IZdwlLCWQ009VcmRrMNqDPBYB98t2TSpxH3iJoH/zDiot+KvpXM/yGl5o1EGHzNGiRYmMXdoU6eMKKEkzHjo7TyGTehIGHH7PPC9KbiYFy65KodN6oM94+3yMOgmEcMGs/WHPSnI+7oviwmx1w+hwfcTVuCC1QIo9gSQyvKJA26h7oMBjG1JYtMpZbpUtA9Hi8zp9YepRFb96ygIAxLsoUODh8kwROIJB+kh57CLYmnIYCkbBQRJBuoVUCEDkfcW7xJBRbJmAIa+AuM2t4BU2yYxrnfZVckxl7AhQ5NBiWE46Uewzr+OZPUM7vZjoiOx/5gf8dpM1kMqkbAYrmFvR4esKdEddLLZACdBuwVtloRSYEKMuWv3MibMnOSFuY2A9LGZKYM4uWJ+tkJjtDiBTew/DRRtQ9seBFCsUwgYKWE4WN0hMQJx3dnz1LVkxqRnMDEEXXOY3ZZMNyyj8B9e+2G4JTf5s7WLoYdt4bGmWuq8M3BPwY5ZiAs8QtqgGrxD7CkJpz6XYVS+yTHQUemSlq+2Sit1danJ4b+B0Mukodaob02QoEBW2iUZjcq9c2mEHCicGoXHgUay4+KyZUPcJJwfBy0ySKNglgGkZSd0US3QwkgAA/Di0rKGLDTjqeM+Apr/PjnX39ReGIDbfr91pPkK1WgWganpcAfY4qzEUw9vRmHT3kzeHY5qWYGvWRS7io/+HrXtKGsPEsBMGzBQBnbY8FEGrUClQVKj/5mesJo9p5JZrAokKbZFdjE/qq+/xKhrFO+MzJb3XqZbwBOcS2ZeqAGSkFxMkaESWFCcZsbilW0U7mAtz6ZP8FVUJQnYaFX4m9q4ROFEhFjI8WeCEvld2mERUCU6BHypLmcMaCCD+diaqPZT1btR9tiJoacpYduaidQHr6nXFjkKRV2yIRXmlbFRISks07jE8RRwMg+Zgak9J8gh9+EhNJJ/QoaTGtBMv1vZaD7QjplRpLKuHkV/KXOeihyiiB9BKCUCjWEEyERi5qDhhfwEwV48gWFjqo70GnvOzaREmNTW75yF4cCzdqJ6GZksZKz1mptuM3KjISboRRM80gHOf0xJCMdpABMifGWpHAXk+sn7N5xXqpzNx3rZ9s0skATGc/LXsJygzRBHhgabbAlM6mBHoEDR4KESUzESThpeEeU4hReaPisRaSBIARKUoghYtp41P8aPURAEDGpVYVgv1XhrVLzouEkSJzxnLFZSg3Akk04P97nK5fWMInsV5lUN9e3nvjYE1euXnKTR+vQymOvfPnP/PQ/YHqUWzKg/0NPR9rcWJ9fXtjf32MOAyUzKhCEGPfEK6CP56BHvy9YcRxss3psY/3GRz7yO+/+g/esbe3QdDp55uxLX/qyH/ihH2JPyZvXbkI+mHBCcJ+TgtJ6iR0TW9nCTXKVqHLVAMlH3uipkg+2YKli4TAy1Ig3Wut7u/vvf8+H3/H2X1vb3oJjY6phzeM8ZLoRBZ1Mleuybhdu7Fbop57s2btpBpLDb7CyEkCIMcVmqDzNkf+a4lSQ4sObK19RJjZfwoetNebn26srh48eP/I9b/6uM/eeYP8jwICkdYyTe6ic2M/KRjHlGKyop9UTx23YNIVpU8xN79LNiV6xJqLXJQSqFXq1dU2cokxBRnT9JGLROHGUXWgpHyQE0YaRfoiCG6EwkRJtvr6XQs1TaC8gE6nFKEf2W5Pd8oQf42Me8uSb/1iO6MzUcYtZsPgGGhl26GIj7tHmGXq45+ZpF3UabQ6UqM4dPuj1Nir9s0zr+e7v/ua3fNcbPvnkpx5//PF3v+v9/TFnKtUrHnNU6w0Hn376o9c2n37ovrMP3PPgkSNzrdb83s4GPe8bm2tspb+0epjzKGz9KhoFI95qiH2fSIY3JgTGXaFnMWjLG8OhBMeP1e1p/dpC008lmaWpFCUgSCPxEyhoOpkBQzOAUCg+tLiys7e3t9s9fHS1Pce5ZuxyiBIqLPEJX4tU7mCozBdXoPUndE+ee+a5lz72dVgC4uNK0rfI1gesoTx0+OilS5fHzK+sMth1oJMUkGgSzR2BzywJ1NB8sYxOxWd5JnJ0gIixSKRVyUgIcnStBwdg2L4krgjCMI23uLEutOPeMlhe2eVxwkzmQSZsSw/i48qcXVU4vXSEkGlJJGT/mLqNLZhU5yke2hgTd2hrDgYn3QioeYEVvfZj6OIQn/zLgATDCwqA/OkNL6pGBC/11hFvtAoUhxN2rOcLRFBodETVVP6KCy0Q3qEUwaGMsKmA4R5wETFi4gpwcuQB02p5VE/YXYdspr2eJU3SJjVz2UwVXImVetRRDFSfRlO1u1hntjqn9FC6bcrUx/UtBhnHo8VGZane2sJ29MZ76BGbkznfyQrLtpQA0x8AIJUM++kyIAfF8f+lm/Zzg2MQwBbsIA6DiZuMi29Nje9AmcPDZb48MfEYRzQWbP1CE/WlnWPUjjGWKA6skggW77ErE3Wrs9GGB/Srw0brHyl1uRcP1dpF2m1MsG93mtX5S84LpcteBmRCgDYZ5otVdXSXQmhdEj9YI1Zc2L6OWbPoGWU7ODnkSI35TXminjMNl8YltLN7phLjiHBuLAgGbVopDB/BY9mIEayx5ynOOi2cwaR2gZJLN/wIt81+S7hg5WnDlGG8WiOnzrMNKIWJuRgsormLEsvpAVCOR8E/EcQnaLLTgMf70OmJAoAy9gQ/iq8+hQQJ8Y0w/ApMPfPyYzXRQJ7Y64l01ZuRig1g01r4qGigXb7jiKGT1sI6UWqm/ENubMxqbJAJo2LB+MIpH2DH5ECVwolcbu9jm0gC6QUEWFEDMBMmzEFugIICgKnxcv7/wlVEZsLyVIiZATJMboRGNUoyQF51zD9fEzn55zNiFO8J0wcY15sihsoETOIKMTbEPgjS+yxElchoEk1AaqrkbF7BZAYuYAzJB7lZsJiF/6W/IWAWS3KCp2iA/O2PwUSsQrfxycesYIGRFS130pRIfkVNE8FSSitSlTEJ8jUO1inEWTjzSdQjXfOe5UQUpYvzHsAaSa+ghgYm6wI1iqmZ1IYIwIdYwEII2IEIOuOgMDBR2kKjcQKHG0mifqJCzFCtGREdFE5ESKY5pqCoeo5TSVdhlRFNF1xJza/uWYRCUito05PjbF6L6mCOpk88kAMfdZ3+ZBUsjLWopMxJH9aC+KBgOq6CaPxoX5MHICQbjK0yRb9gKG6FKsuPDrY6R1wQC+KBoMR4S9ZhPEW4cAQLgdxSXSjBIneaBDrtoYGUEaySJE/gB2JcjGhHEAnv8yGvZmeQsQNGbLAt6V21IYDZEhmxtO4zpQiW2KSUG5Lpk8088gVvPE6iKTNoFaS2AzCh1ByNe/Pq9T/7sycvXriQ7eEhqrK0sPSjP/ojD7/kBaAAoK2Nrf2dnUuXL8D6tfU1GmSqK2qE7WW3C7py6HdiA/led2F+zs3kmUhTq27u9f7PX37HU089hSTZNfLkieM/8bf/7vMffn6j3djd3aFGITvm+9MZ5MFnTtkKA1V00FMloTK6ILU+hLwwamqtoYjZI6YcjemJv3bl+jve/o4/ee/7GLGpsckDoMIpoZkifntgk4M2RqNETWchlSfWjXyO0M27vMLwPJrAekJrLEYyjwyypxDUM59bAmqbw2vXr7cvtF7xisdO3XuUSBR8eqfsOdNek46az0kgtBmsF0ImGShVMkRCtTaIYTqo8z2inmaOWqRcSr4hJ7wRbyH6y0NRBtCehpTwfMw3nvxEertyg70OIG8oGF2Ps5hgKXjgTC/TSLCBsiGXuiw8/Sae1FUY6KfCW6MzD399c7O2ucXe9hyFS8TuHl5+pbvL/qEyhrkwr3n1N73u9W945IWv+Pe/8svPnbNbR9nThzdXv3bz+vr6tc9+7vMvffGDDz3w8MGwQ7lrDmuX1rfm17YPHz+6emiVOUayHfcC9gdxUwcPZ/nT1xxCgzrB6i3/YTYnB5MWlRblECYUHi1uIaQ8RCWQEt6P/a/sRTgcbW1uffYzTzEguHrk8N7eFuv7KQqRUUbJFCMg+fNHkN7AS8SUMkYNR4M5CHNNmnntpjD50u8Nf/hv/sj2/s6HP/zRhx99wUF/9wtPf/6+s8dJKWoCAxA/WE9MDxkSGluuqUTDrSS48086NdvaX9DhDVX0NW8wJVpusAD5Qb006s60gXqebNTLUtNKAGpjd2yYTAzMP5HEB4hk5RMZ6qOpUDQYSIJi6dkzBER7AS+VpopTR6pM2gYRe/Thq5oPkmaTAgARkpJKx1CzL5SDDz2r2H/zgXr+y0t1GWYbM4WXtABQGQgnN+WaSyUF36CtCHwtXSayByp4B06IIh6XGYskv16iaKCZ2T6q2ycPVsPqft+ukg62ULlSK9I5yLDxcLXnJve7oyE7unW2a5WDSpvDavGXmdICj+FNpFTAOTFmTAMKJJEf/Ipy0gHOkmmMBlgAWWJIhhGCW8TjB+OBAdSdRg+xF6WP3rmUwTQKJ6sglgahFYtDAA41CIobn+QV/JMRodpPAoip134JILGJZM1PABEEkEziv/ECeg7JaSVtDBU5EDOWTjZaaZBC3JVBnlyrhabSmYKwRMGIYBRc8IEbdleRK0PEzMBx4pBNEGpEmCW38LLRAKSHfvR7TqhCO+VGtUP5ojVrjpKD/2F1qKKJtRyg1e1pNgiT7jNapww46KVQ36orRiKB/b20be3lkvGolx1y2HUI4BlUaTqw8hh+2O2ouytb9dvznzaAiihxlB2jpVjKnTQ+qEfTLCFT+GJSdCP/nJFBQkuI5cJ+XkhJYZIgMxM1dEnQJAyhohDxQcJf+SosEmhJwtP0oUgZtZ0GSABZhKUEwUuN3e1rBuMOHFztrr7Id6+AVAuA1BKCffDQUYDmXp7pxYdyKZTTpIzhoaic4lk6p5CEeSsxL3+Fa4amUcVKdEUxeaUOkEZxtQ9Jluo6o5XyWv2geaogkQrm7ZgwGjdCBdHVEOvUUmiHJ8G11rgKwsKEbG1U2IBFbV2nW8aea4J0FLGbLncToPmm7GSlBKjJMaHrtaj6oq0piF7zon7aHEYjKWvsY0B+o5MMmNpnY+bi5B9crV8TFXIxB270pkfr7bBUqNoafi3rqi3dOUIzCbWdF4gUagJGUKIHZnROKw4H8RzDSrWrDQnLxUEaUAnqABeaYSrNACboXSmBcfMSej0Z3wVIbY8FGn+RCaD0nOBC2UVKZP654AlcwwQKg50YzmWEny0LnPvRAlq2RlYmk2eaTh1lBBpXHcKCOVlTKekhIZcrGkroBjH2/NbiIBX/Ja5RUlx5xULRR2gtrPkzJ8VpTDustCClUma3EBMzZjLNTSnzj4igaRIoJUuaiwQThs0i1GaHXTKGecSgWfuRuCThThKFAySiY2t60QdiCz945K441T0qKu3reLK9s/2hD3/g/IVrTEKwUpmM2o17XvDQSx955KUsJGefn1azxSGva2vXtnf2lpeXOI2FHns7b1x0zWJBGIDz7ZRMzkoCDYx4vX7vxz78kXf+/i+dO3+N8NW51Te+6Ru/4zvfzFFibP/S6+6DM1gyUQQI5FtvMdhF1ipaeAZt6lU4RCiY+yLB0bdCEmGIQ9Foq1tPPPHJX/rXv3T58lU6tOynUV+YEABiRe2UKrSj5AKPLfMYHT+H+TBGbxjNhI/GLNw0E/PjzQyDhX2W9pCJj/WOPE1xRDkoOv0++03sXb1+7fqNE816Z3mFaUhUhfjzS5XqdmWwzJjDYNDpVXaatWX6FF30YUctZpAxhAWguoKaHyyIMx1wVMABzthoL3e+8myzkPBgA46AUPQiq/rxK7uiFaaOBpYwdJQAKGeil+VP7K0VjU+CkpKfjK9GYwTKd56VhSOoPM4lNAlbzJ4XJ9EIBpM+e1Bo5ExVrW6xeHZ7e3mFAwMW6OFbWFlHT0hBs2h78/q5C88dWV38hf/hv/3v/ttf/PCHPuYcj8rBuHs3O+5UqhsH/cnHnvzS5Rt7j77kkdWl1aV5WovN4cHexpXh3o0bLBdoza2wfsT6Tx8WFOM5hJssQaQnFYyCmahLnIjhM9SYtsWOHigWCRQtFEEE1kONk2WcJSI52RMDwmjxRgT0sA43NzZbtXsPLR3v7W+0WNLpDKUMVttSpyDJf0CkbAJVhnEJF4XBOFUvErHXba6v3bxn+X66b8GCSUYrq3Pf9m2vf88fvO/6tTX6STuNw/ffTSuFHRRuaMKGR9VePQRY5B3nGqfdoFJkzME8zE9RIFd7qJMzOZiGQqBQdI43QK82XA1S1Al8YJSbGU1IwJWmfGV4mgmAlUpHxcBO61vjkaKR9tNHV+Ac+3uSB+liUN3PBye3Oao6DYZmAy5VvXGDOWDggTszxH7DmeZ6PK3jVCZ2gfklApQ/PAAM8JROHnnQqipXF1/q1os/Ipab/KFjpolzJaflwvAkofXGVRLCCwQe+ObBd36mcKGCN99lmKcFTwHIPSJhSSxWYXpsCZjTz82WPKdJYNFmISq7+8OSud1mh02BFljl0WL7NOrhxt6ACmBvmdVAB82tfTS0vghRVdYc0o1FBnANo6d2IpT4gFFjJie6tymfNOugSC7M2HFje9GCGJRDQpg1DjH0kmM72viwzLWv9JgEz/ofKYVXUCcdDjUQVoo5tRQh+LNM+xGW32WQwHgLmVJvUNhCFnE55KRsEmW1m8tsCK7iS3AyIHuIpHUhu8DQ7DS6UAYceFvvVAdsDEuAoKi/adlAHBM0ewyWYpzTjUJkeeIsD6GjGh61VptDTbBoVF8AZ+hC0x3VKHOmoXGx1WEe1Nz8fK+Lr1WQhHNXRUZHmTUM6wAuDV2zIPeoFm5ERl9wsjPIBisswlAomfQRYSYxJjCUdcCeokKBhVOcsoxqWZ4oAEy4wseiKcIMLww6q7wZzmVABtOEowg3ravkHY9yxjEQpISN98oz5cOSRbdS/wQcmjTX7RgAI7CQYfD2hBJg3SZ6ADx/+GL7gdowzFOpIpmA/YtuZS/N6T5XJVJJVNSeEBVIJSgBUQdyJtBvucHgxIiQw6vpFyPfcbkazQbALdCzVMQBQqGt5CVg/ohZsqZUa+iSIfzQwcpLbkmZfAquwe12Jndg8Oc/kkUI8ev0YfoDZQJHubyIJ5/JXV1x1J+cUEP6PvnKCxUxxckkGH9iip0ar+FAD/JuFgJU5ALNj+zUF6IA+0A7nkQZ04kM5QEsx0ASLquITi7io4/uG4jyX6zsMokagSep0TgSRUXIk8TYMPtghC8ILasFVA8qMEntymZ6GtQoXHhRCvNx4B2JxLriD1uKgKTtBQRPlGBwkF4h8M/s5BiqiwGLiy5E269mKvYmCEH473Tn5N3BN0JRZsftjeU/vWr2/U02BNusByvMpjgSgWdKjiWQsmY1zqstDpmkvIAmfMyfPBC+lW9qkPAL30dZEwdS+YUZpCK5lY3s8kLCJTt+KbT0XdLlIof9VL6ZL1moGdJnQp7yACY+YnRDnyyako9u83H6J7b6qkIAH++8gA9AScyzlZwsEVs+J5rx+JQXvsBxsi4fjUGcqb6RSAKnuEEbqPYGwy89e25tc4d+FSqChcU5dmx65cve8NM/+/dWji+hCbCSPRIGo/7BAdNAJ93uQcMtHVAtILnFDTM36ZRBQGgL1md3favVXnrP+979u7/17u1et91ZOH3qzBtf96Zv+/ZvajHzlWmeIljt9Xs8U4LY7h1OYoVBFDyhI/zgZ8oAkQ6FCZH68oWKDYbjVrDr5M7m7u/9/u/9zu/+3u7urmGs0VKl+QhAJEAKgGB90RlzSV6UFwCkDvV9+seDIitOcNwOeSpOBY08WZJ4Bec85CMhMIRc4LEZTka/9Tu/vrF1bXX1xIMPnZ1vL+1v36jVl+Y4f2q8RPU8Gi825g9qI7x/eoyohvv2L9VGrebe+sYW3QtInSmvB719txaBaOl24imgC5vwFsg5lFodEp6yGj1RFdVY8aQIhuRMfg1lFAwZHpcodDEcwdZ7WiHAAVVaCqXSLX25SlDu3mY8g0HBQ9apljEGyTNlBkiWGmvB6jaNgM0tlkkwwZ0RG2YAgweFe6G9cPjQ3Mri4isffekLHnpw0Gw/8fGPXHi6u72z5dAQhq5RvXj50sb22qkTp1/+4ufPtRc4YhrdG7U65567sHxof3F5Gd/LBiw0e0kBgoAP+Df6WEEv1BkB7Wm2OqtHjzLK4nl2agIxklQ6JM8fBT0NRq4EQgvmiak6/aETdJgX99CpRc76WVtnnGz75Klj8D2c0fcqvFMKsiWwRA1IdGQzbMBKrwMaEkeP7cC49tz8sN/ttFdf9MKXveJVr/jYRz8y4CC17hbrp+dYCkBq3VugS5NmLPaK7PD9mCFpRQm+M8tCLB4JEAd+YgWtMUqtgAcWKhW6KiNWUQ6tECU72MahD+Kg7PQP6w7AurY9NR8KEwVMtqGPJrfNaIo5AzK6S/agsDwHJfYYFB1VWw6l7x+VIF8ZlrQUyRQe8VGp/K9mi1zowPrZE0yFgyEkFN2mqQEjyAR7QDTqSukgTGuk0IWBCqhDSo9/ioGL5FxqB90H1OAzNGLVAWL2XnKcn3L33QvQgImGWevgtXEaNrPlafO0LVr7pOrSiVeZrNJTPRpscr72gLN+mcTCMmJuutys/XWbLECBXIBmSlPIR0PMFGqn+IJAKFVz8Sgo/HyKRhIDaQZtFJ4BEo2fyiJXTeajUKxHZBV1NxFJknXV2Jlsq58iEBcytZQKg0Jls0vpJfMwBXDihgKSpaKx4HiZF1QVXuEx04BUCARHQKYnFthBFP3oiF3B2IwxEb1GrBuw1hc+X2yTE8yfMwx0Onhydw4GFQGpvEBIs2cKtBFJ4jezn9hCY3Fji0G5ZA9y9gHZIKegiB2YUoBlnUQwcZOpffy3P4JM1RYjwQ3i4OCTgSRQ11l/y98oN6qIPGglZykKPg4sZjo2wIu+2oUESxjnGdadUJd+wKBKRHtmqT9Kj1S4JimKGrqBxM3yzBM05DUyRWaIg54OGZNyKo0qTkoJHNKVUwCh09+//gWOs0vChQejYQa5WrhKoB+UCJc3/pJu9mv49CrwIMQGqISVVPwCYLZT6RVgGWUKhjzNFgaaORQqLGJ4gxNELWXcBF58LTkbebr79V80+7+kuBV/+no7VCLV2GQMGuTlPwIIRLa05BjcIQSTS7ml/c02Z0yUxqbdNHebAciDC67pj06nGVQ2A5O5UMLybozcw14MJfP5IUW9157HApChemHW0XdJRVNsZqAloKFdIwoT8tANlFpfPLKg5FGAGaE8kVJkr6dCFEXLt61hsxKXBPIKNL0xnQf8W/FgPG2gqc1URMBRX9H1BWQLgg4++k1xcEAWooFOntxpiZpDsWloPnOeW+7AxaXw8MPotZJXHDI6cv8FGrSMxQercI8SQnPavjcZi8Vyeq28koIQwgfLY+N8OH1fihMx+Ae/LIQOqev7Z6Eq9iJ9pdwpk6Aa8wnhmJYBLABvcA/23MnFOkxoytC5gMhLN1fmioOoqI5EECF+TE64gdZAyCQEEiycwpiQxvES10CdKOZbLuNEuwBhcL7KTiIKE33QMth8kmy7Q0q2shuslaDRTRrM1GGjUFgkKjrHZxAwGEuVecyckHjj6tqXPvd5qj/1FDm3qn/vH/zdN37Tm07fRTcVdcVkYXnhM09+cmd7ixk7/e6Yvn1UgE/MTVELItDx2LWMloLWeH/34L//7/75xavXaAqPusde/IpX/OiPffddZ05SazN3k5XNDDIgT7wfkgQ1rHnhZWiRjbnCiFAhZioc1Z6tL+f8oLlqvvxpfuZTn3vHO37j05/5DKMReNLWKFANatUemkAXlwY9jFAxIw4yEPztDOEnPOSCP+hhahvC5J09rBGsSu5aIBio8aWtfAhg1fpOWCqLI3SBaCEqnZs3dj791Be+9/tfvr7d3aBRzTSn+rB3vb+9/YWrFy8P6/vbm93RoLuz1WUSKiSmUnIsgP3wyuRpvEzm8g4Yb2H/lGZ216aQWzeEoqAMdTHO4qxe4BvAVypo7xbDKBBtA5Y444DBR4QNBGFYZTqbgujRMWcdk8xmEtGKVCBUQYdjFoOiZuM5aDcQbGSdv+EAKYVFxMQUBoaEliSyABn9x8qkW+n1dobNBgt/qZprcwudU3edxAtht6hXvuaxI2cOMzHou9/8+ic//pnffOc7PvHEjXGDw6SdSby713/2/EVOJ374oRcdXmENI3v87da24dBwb2v36KljrYU22cAJmpY2eBAF7nGz3tXVZukwhBwQAep1ItkDab65VFna3NrM2YZgbr9pSgkihnvsfs3+J0U31DawhyS7AxmKrNb2e18cN+e/9PmjO7t7d919bG5xHvsTY6UOEt2GFiyYXqImY2Apn3snsYijSm/txo1OZ+7sPfd0D3bmFxbZuYRp0P/4n/yn/8V/+p9/6Yvnb97c/ehHP/3aV3x9Y8J0MvJMt7ELbYGm2zFpXKM0VsYnzaSYOUycmpxpNskymknOml4yb7gfJdtPdvBw2OvLkyLYHKzaZyiecuwqFEZ4Jiw5o/OScHYM69CXP5wssOByUl1gk5YBfflS08Z7ZKNGqgD0izVXDkvQr1lt0QVdAwFZDXLMCGQaDKWiRe80XlOf3aOZsz5cZKJ6tlyjRCEbIFKw0RG5hJrCJAub/FJb5Snbh7XQBObOOQmETnj3ducBeoztgLP9OzjdpGndUAYkAkDRUtVTCRIIgrLQguDl9wQoHy5NTxGdWk8RME75giXqnbZIECW+KFkNJx0XSrAatdE8YLS4Uu1MDjki2t4dVFqD6jx0aFrMx7F9+3TRUWwmvfroCPTTQKCBxFZL2ijygj4LLGQx1yW9bFYS2AFO/VK1VGbiwtiUYBWtPj8/TxcZvSpsqBx0yS/aa3wpdoszZiMxmY2DUeqN+QUXAqPMDK3LDKfB2K8nP2Qb/ANpsm1j3lmOQp1Lhx1tZiCEbcQCF3ihvLAqSJAXIhCDsl34b7Y0k2y1WdHTIKQINar3MNI5qV6hiCIfT5dRwtgxxKAk7NWzKNJWVq8xaag1nYFsK0Fjmb0LJ5MDMqUEWOj4QitTLUTjWGZFAxXlmvTgA0397O+J5wE4xIZB4keYtBjkIzWL5hKdSu3m+L/M6B9lqfKkuWYuNfZlcl8BVk4DBwtgAybHz6Hf+gtgQcmPKRVtfSVU0/ysjb3AJBzlLSuzGTbLUgH2HlTt4SdYQLmL1Xiu30xlBXMotJRlBAQgGhnrmGjV1cmnhXy2rQPFRCAwemsJIrevcX1Z3//teKQp6ApG7IVnTacs+Ue+BKttPBnTfOS8hczPt5JPYfLZFKguLPKz2mVM74Lnm4wp1+yXN6IT2ZTGncZP5GmIsJK9URI9wHj6K113ZDWNX5AROgy1hxRQ9r2SPdqWoTc+otkynvYiS3yIi/6m81NGQBtCkkwuEurygiRfphRKkF9nzFPXrQ0YTEBynHtBZtEDTz0hR/2kKGj4UMBmuKFI3jzweAJRLqMGTsinj9zWq2O3yg3jYtuVCCnZYAhW5KNnS8SgY3MezLURWmIKgHhigJw1aOaKPErF3STY4vDHHhjzly7iyTdiEp9X8iAnx/OZsuNQe/gDFIYlTUDBy9idQ3rgHBwFZYaWBH4ZWNO3cWoj8+kspaIJhnlLTIwke3dZ3CnPLlaDo5RkaktEhITghGSR1lpfCUo+UEBKmxDcxdhs+QsjJJByqZ0GlxiKfA2PAWVbQq1MPCWeAoD8bNsb04z4zYO0TmPyYzYmIyhPEmFsQ8DB4BLDqKYE1cTPT+jnS/4XOESDrqBN/PzzJvjZO4+S5z8wRbFgyM7O7qc++dQumy/ap0LV0njRCx9md052bqFzFQu+dvPmzjNrdNmy6SEpg15MJzi5zJeNPtgfqc+kDk9eb7Y//NE/+3f//tdvrF1jF4p7Hjz7N3/kZx554fPPnm2zBzw1P9NaWCJMdZ2Rq+AGMlBr1YTIbNgW7lAACgvyCsGST6VCQ9AWSNZiMmABtA9+4H3v+K3fvH5zDaHSDCZmoRKvw1mg9guqJzGUCEh2JUvZkEe5Xh4UAP8t9VFo8+a5BKu4SSATIq3yVnRGOUmIgrNWtoFuoRw//aVn/9f/8X+m2mi3F7oHOHZshs3e571+f3dS7+rDKG7mDXNaAigB2eqIQoHWctIRbOAU+VRPgKfSROWQsg19sodd0oJ6+sYXniy6hlqfIWTaJ6AFM+lcYHcBLQlgYCDstv+PWtTh50ml17cKcbIAWGe1fcgFgkC0EoX8QqO0litsNFCmGDrlq2UATMMOYhrDEo/hAJoFj2dqSPox5tosbeQcxRED6wtLreEq4ZzqU1lcOfTN3/Idr3z1K//ojz747t9714Xzz1GiYQiOy/mrly5fvb6y1L7nrvvarfrq8rFK/TDrGHFRjjSPMiQE2XCihULXm2hvynXBl8zVBpiMAlvZV2sHHGiNAMAK7CWWKJJXKLlNdshIBKdfEw2wLfYD6Q9YD3BodZWCsLuNmaosHzqEKOAAPJe90k2e/lMFcYqYkjwaogSgga/WPXCgA4eqd8DSWQRGUaqvrCwcXz39ye6ntzb27r/3UHu+1t3v4/syCdLF5o5tgaKl3sKi2cfz0diiQn5RGcCQTMEUtoNMJiFoxwmGcjuKcUpIrCfhOCjhNC9xT13167R2LR9B8MmGg5KrV3Vq6ORHFZ2MYe4OtwIV1pUeTbd7AgUh6xjr4zBRkMQU/QEqCHY4gCwU6HtH6QBU1pWmqgryKkxRG8WAyIp2WQeht5CPC2XTg+PH2EgfeUKLfa5kLCgLADBNl4QgDpdkBBCgikcok0+lEClWaiJmj0IOhPKBf9xlH/FgDdJWbbzxQg2rCsAa3h0BoIZiRAsXj1Oyu24+Ue/WN6uNxWbtELXfsM2kR9qYtIj4x77DtHBBEScCJrFulfkesGGe7sU6C6TYrYzJL24nHk1jaTjFGA5CAt1Hbbc9BYOUdzAUTy42KqMEMQTB0lnpkwHWCMSQUkia2gLRlk9AZFnxXEdXBz7oQQqfz4kh/7kAJM2oF6WJrnTeGTCZ67Q820vomoxpAvIRErkCyyzp18Bc8x5/QWc6ydmfR4iTVWJXm0wVixRwcnuDheVVMZez0dyMGGA5EDt7rNFigdeNNpMkiYO4KTA2OxW9MmL0ieOA2Hus2ZmvLBw6dLC7q9vQo63rJC7BxhmXgTRG4HWHLeC4aq0GLQpHFbiwlUSW6sEqMKvMIyYluOJNebwSVoW8RsxFZjYQXVkxwzKZfi1qUksF5QT04LPnPfMsx1m6QB8HRcC2KZ1KSoVyZcs5LRyKLXUGZCMO2IRDiCzA18XWFPgUMdKkaiFnBaWnFjmRJ6IwPlhO74r8r3sVXSKhgKbpJTy6LkcEiDjVFAINJr/k6bu5FxB3ZnwrDI3xMj6XCekud77dFGyymWZiDK9Cn0YNiREx7hfhFmTTm6cFpWRtCMD+gp1/+Hjrmp49zFzPGQw6QoTFTlSyVoOhxljCDUenIVqZOasg2aIaFinEUCgycyFYCspzypjWN1hN4YA3FzGUWSIqxNgjflHsOrPeyb99pUnXjLUUBUQzAxLqRdQtEWuTwQn0u0IPEHIgHI3BLFMKqnTtmCkJdBY0eeo8QeFalF8qme9Ix7y9JnDWUT001mmuMBE3ms5yig2rj06pbcxAtbDTIOGsQUDiXdM/JLvxsisDVjgwBsL5BoHCB4CjvVADaVpmyglYq6P8YPnJC4z438Qc2hNvmYTPoBILAHoWQ+CAgovIgE/i2GcKgwzj4+i0tAM/DPU7wBUTw8yas+iWZp3KUYKNyEWOyCX2KFrsnu58YcwBAqZUEVc/zIDS9jOAfMWQC9CFHmMkmjIYHKO50WhuZ6CT/lS5P1NpUNMnI65kioyghRJS+CXE/3h8bpNngxCBmwC1GJ0kc3Zk8pXTW/EOp7v8CiL1gTKWS2gCcrJPQZlIcvmntZjSzaFew17vmaefuXL98rC36vri1vqxo8f/zt/5qbm5RXwzWMhcsLWbN25cvRZDI/Ekx4ZjBIHPqim8n0rjYnNc7e7U3vueP7x289onnvwEff8nTp+pDRvf8aZv/87veRSvqNvfA68D9OyAAR9qBMsUiIAVd8u0YhG1UE9teUKOslpGVhTlZUUdqySzvs0mGfp2/HOf+/wfv//t7//AhzMcAr6oh/6cEGUoio9aCJSM9Aq4O+6OBFHsXH5EOoqCO5/ks11QODDyWoBoMReoMoMxwHxJ+klt00+5ZKuhwOFe54AQPbJaBwXf7x7YHq9t2+ensilAyeIsJH9oXZMvHCoVn4gqvegmU2qZf3Xx/NX2QqvWXKAyZScc8qq7MwwzsjpMnyEO58gycFFjbih9hW1mzdIlwdb+HayBY3qDVbrAKvMXcCrcxwwJjE4vzZ2qN65Q9KmBqItY5oEPor/mWIT2AizRJdCziPoG8UCbESyxIDILk3uEcOUhXPBNbS9pYDHvmDMzAQfYJcfYMJRZaLTa2TGVo7/6+kjM4GIfqVSmm525xje98XX9g73f+o2NmxtX6XanAdpszXGM8JXLzYvnz7c6Ow8/9PDqiePsLcJkqvUb1xYWO2w4xJ5pO/vMQTMbXBaXOtQOKCa3sEI0PjNSMzfXWZjb397FvhdVkBbRDYKhK08hmSIV7ZVOJEf9z4TAOhPk1s+ceYgRgL19/nGwA2Dnce7JgVgkoZc98SEM54E9TwpITjZjt9/J+to6C0bO3nM3HbGttt29vYPeA/cf/+13Lt1/z/P2ttef/MQXn//Q3WyEgnIxYxoQdmuovijUYaYaVzgsyeW2KI5m1yKgmjHRQrTJE6yZPe4OKuqe/hCBUytaA0+cD5sQFVTLKflMU2FyDVlQCrBF3Fncj0PaHpI7zX6mj08WKUocjMbYH34cE3tqODnD2gIGkIaPKgE/52lUTCb09ONfzVmHukUQ4yec9WXFg89Fg8KGYBaEUDox1WA4tTngI/rke0xpFbGwekrtdHiH7KGzWr8+sPv8sEZAjPkMcdhPhynAFg9TlQQ4/7AeZDsr6biddMSjG2i3bCO7yH766IsXoUjR/nikScs1Iym8YOeBS7f6wB0C60yV7A+o0JgjDlVHu0OEyRLUuYGHzjtawdIeBl1YdYrWDGn7sLkcOHH2JgsHKh6URYY2jOlVllkQAoFujMq+mrKFtpkjnEM2+4cp1rGjE9ZEbWeEg4+joA6ZOzkZDbFFl0YNWKIogqTpJ3t9n6vX2XmZmZm8c4Vu2S0IIqU48BCbSfD0v1Rbj6nAsoV4drDRRBEBKwc0QVMHySCg/aT0wTHrYJ0r2ycybU6/xaFOktCwHI7YZplmJ26GyuqMfHAQMfMiFzqAECT7SM1x0EFcXrbwFkkss4Zdmzk56UbTc1s2E4E4sF8DyhA5Ek9Fk3IBuCCIzGkusgqYNoOdRTDY/k6PdpYD1T3AVirz+A92muCu0sDI+UoMODQ6wHMDN4wKMoM9mCw2HZNN4gyN4A0jMvWl0ZjDJiB3qwF7k5EFxZzmRbwTyIBFYCn/wQJWUS7InSeUfMIGTWl+wGOgY5QjLYw+2cos5IopUGh+AEDkxilYwPuyHS+B+TUuoJXL3TUVsD6G+BCqtJHD8LR5tC6Z3eCUatS6KN52PvhFEBKB0Hj0KRB9oFr6sosMEiWQvRE9PyYqiafveQUPokifwBK7BKkoIGAQ8fPj49e4SpxZzFt5KjBR4kI8ZhMbxr2EkkVq6SAa3BE08UWPH5Sa5wKNqAIjUK9ZrHglVlg5JSSKHdh+4JMtvZRYEqJH+vr854OZqLhiIl9NqUbbCsdVEbofMZ06fMYyrXzhSgKMjLplcqWFTvlBhRe8zCNcDcS22ectzlLDg7aOGsMqBwj66KFZs5PizbuBEsV/wPhcSPRdhmDzOe0Vy6W+MH2RQD5p7UiDglMx4W9ZzLCoBhJKToA1PhfH+9JraI1F1SpiEKPGKyaww0smAVExPyCBReEvhcNokRmfiYbzE/hBnXJUev7IqLBKAkKEFlBafMs/KxUIM9AmmRmSsTxMzjwHLhykMKbu4YsMFKKSgXmyJW/eAGeS2wGzECOXIRe/JleLlhlZ2vklmc9yJ/8hLIHhPN+wzhk2B8+wMJiVm5RakzF2v7W5+ez5c9Mu8tqEPVa+6Rtf/7JXvGw06tMxhB+cMV75bE0Nf6CFJWi9AZ1udq8jRjb97A6Wlpc++cTT//pf/1u8LlyBuYX5l7z4kZ/1wNcu8/yzcTUimPTw/hG//nnIEfXSblHbQoncURKw10fD8qvK0Fctr+xHaV27ev3xD3783e969/rO5+G39hBgxKFe14lJDoSYACnhB5B/yQTGy8lIQbl6eVeJzHH2Xr4Y7CUov00TTtPl060b2PIMpVQD5EWVqHxQTZxEdBGLL52WSgHxDJlCpNIhtuON9B9BMIn4FueGM2BG43f85jvf+dt/7Oyq1gK7WbOmAvVvt+bZ454d6CnxjC6kC49O0ZPWMnOXmo15Jvt44gFuQnvJ0wzq89XWhWZnzoI8qC7O3Xvf/fc/9MKFQ8uHnco1Gmb2ubvhcXYmG7wO6/giFapP8IsFUb8lJwofCpAeHCs8JBavUhN+Kc3wSLuRYuIXoiqY8m463RvT0IOqd3gw6O/TXz43alOxato4JWpSvXFl7Z2/9+4vffGz3/PW7yH6777z929u3ARMjcZnc/FgH4dq67nLF9qfq77gvoearZXWuG3f3B5QF/q9fQ4DnV+cm19Y0K1U78hRBRCTmFZe6NJbWlzu7h6oAZpVCjhRiXn74i188A6tGS0ttBNSca/Wfu/zn/scy1F69DeORsdPHL/r7NnG0NYFtAm31OdoMSVqQpuHdbRc8FX1xhXY3WNdODOXWIyhq4Hz+q3f9t3PPTd66WOv/JV/9/NX1y6Pxzt3n71/cYW5BQ7wYpfTqR3EwNx54Skj4IcO6UbDbYmVZJ4szzDAIkWWuIEpXRBEf78mTYZoVwHlQZHoKEYZSUxtsibH6TqDRpWWIiwAqk4apgZVYdzVMQnOtxtzAlOTL5y9aj8/hsMmCY6e/dyURoiHAxKOBtDbKgPEEZjEot0OHs4z1BsTdTjBZ1VLvYoEY5yFoRsEofoe5ENrhxhWZ+YIGLk+oJuKw6ugnXoGT1HuW7fwGc/M3ggeIR445CQmlk35L6O4AEJanEN7a+nfZcSBe9xovuoK0xRnPhWF1e0n9tnYCd+TIZJBgzl/tX02rDEzwNDXVulBoSNvYEUbYYTFtApToKzuRfAYMMRBdtoCNAcZwiRD2epKyRJCN3EUFFRB1FoxdRKv1HsoMPsfMJOAV3kcLeXBjmiUK44yZVvq7c1h8wbHwVkDABRUFIiqABxSeXhF6uTIM3MRQZXsMf4MbXX394wL092uDJ6hcWYARUADlgyMBhY5AgQ06V9g402alOZIdpgj3At6DmkhkGY06fZ6kKoglL9GAibwQETYpaaxbIJ4UIYYoy3GDZ1q0ag7R68IRzDscyLvhKY4XgUFARYjYciSNpu+USFUHw9KTUHUtI1VRRgKPcI3gZ46aEtZ5lfaemNgrN3MdBZ0SR45mIZVoMnlZg5aRbgdWx8WAICiRx5aejgETRBj9Y36wS9OyuEr/IMJ5mrWJKQ8aZBsTZEW0ZLemk4pEEGbgszSDgJpZIGICn3kExjEEo4/f9XLrFE4/kgnP2cXFHEBjTAhzj6Zlc8RxzQ8UZRIiVU++zobAfhy2HDF3LymkG4981A++CXGK+Vfvohh+Gwci1fBeIpiIHyNmxmV7CRzcMZcpmv/xYZP6DSZQLMRkX8QmSazOJg7wRN6vsFs2k5StEZXHKYqaRMyRRLIobdALiSYHX9Ex2dFu9FmQyJ+VDvOgU5bQgAetSA2GDSuACJ5ohhYf/ngK8aQsoAhCeaGCRPDVujRqqBAxI9xtzCodtrzYgfoKiFMlBR705Y6uq414sHpswISZLlsl7PiHuvEO3nb7+XAL1VDwYi+CJLCVdLgCUlCDITFQj4DFtNA0UDNzVH0CEyJJUAbJLv5qHNcam7o8cn5yhQrCA0Pg7GVgekp+WGaHDUKmSd32WKJs+IQLW0PO5aAHdZUQxV5qFXj3kmpbl6zvEGRRZf5rJRnrQVYWjCxgyTWDLFF4EWMGcjySn+BNU3/FF/dhQAJ8mD0SNiMsfGnQHRcZ55xMUMy3FoQfjAWDxemVLFY6RrsydovNjcCH31EiYwiQgxogrmKA4DYgHBSOfmPeLYriAJBWNfu5evn8DkIbc5tsh363/qJn3v0JY/K+km1e6DdvLl28+DgAK+0yU4pLNi113/Ajj1EoVd/fnEeVn3xU3sf/dh7v/ilLzTmO8zvxdL+8N/80de/8Q1bO/su6hj2YKgrNaF9Qnc4hhufEhoLK4K+2CmZSM5Czg4bipsNfOxYspsEYcEqOrcP9roffeKJ3/7t3z5/7TJuKhWJQiy9qYNVBDlu7AIPaOE0+0QhsDT5Sg7w3i/lHtaNlo1d2+GOBPgjBf8QjCqa0z84K8CP7hckFB5VGm63wxOKHKOaVrJA4A2TzU7WKIl7VghjGk9Ny4zbKpuiIO8lP9S2kQUPEjtmanVMvG4BLRiPyqxW6EIG6AZVFcqrHIlPOhVfHc4bWfsqiZgOahs9O8sHRTZuEOlYkMM227WzZ499xzd/+w/+8N+gr3rp0AIz9BDocnPlYJ/jcQ/2D3q1fv2ALUyiRjatdXrIJdmRI8WDjKKihokL383fWKLAO3+5+9Wo0ts/jVg5czcxxTtOEe4mFoatZCcMCTQODhiUwDtZOjT/trd9Z7X25sWFeXr0Xv0Nr/nIRz7462//3b3B5vxytTE33Nlp09B8+kuXOaqo3z+6unLq8GHOuuZkrf35DiP8zI7FDaMV5tG2aD9GUBIsLdbB8qZeX1xe4ESvLj33oC69iUC0mcTZHQjMWdaZe7jrK2AYa0XAXZ7hGcylQ/PYsRNHjp1ZW99GiU+ePoMTSgLQSBtAd43OWfxgQFGmZAwSrE42Njf3D3aZLcZEDoKrtZ0Tp1f+8T/5uetbW//7/165fmnj0rPXjh9/aL7q4mn0AsuHFugTIGTdCqadU2lh8bS2qcCYJ0MurnEiF/67UEzPiuZoWsXaP/jhlGwW7NDzY6UhUAwIjql7ODJZXzq1vjgfxodFDNJopSZ7xVEilW2IIRMtmJrN1j8MRrGzUMaeCeQoU3wqpphTv2DTAGSbgbOlMk+flgKxwwUKED45biHZqLJqTvQJFrHnCXFUOO6pyMCBHnCsBHsSjA6lTeQIIeKDCbSRoDOelzY6vh1bxjBl0SNKNPz6eeDBSAYkk691nxYh5Y5f9Tb5y0JtrHKGD3h5eHq4oRYkREhqQhkR0X7DNzfWZxcZ1lLU68vOfwIIMmFbfXr/x80+zQc4B9XoA7umdZlPDyEaCNUON7u3j6/ZqLcpbKxbgdz4yGk0ETLdHAzRs5zoiI0HxoQhoKv7ybgBH9ANvHN2a/BVjjBthoVwnKMEWEqYwkYndaibNL84XqPe29/HpMNyqi0dVMVkhQIwiocyH56gzDKMqXZ1jw7t3Fl3JFZLzjQuRogcGDYKM/TpRuBgF2etwFTGnSjjiEyNpzpgKVOHwVzy73dJADNgBBIhPsN6+wdd1Bss1QgwicjlDKMqXdoGtgw5esNFIDSMUpsraCWlmjaabJkw19qf7/cOugcMHO7gSAOJyNCFuIp5BCCJwHZuwTLYZzQKhkBpyKbaID5iHTOfC3otO8RFA9CILqM3sGU8aFdG25zJBGW0CBA/U9JUEfYdZlRPMyAngav6MP7DbE9VBoZThsxa14uNL7t9phSh69gEVgUxQGYtCR6WuPJfs+gzsnFk3sqb+JQliRaqTk7eiGEjQJVTecG9e/slIb5yqbPU4md8/uqVAFLsmehQDCZGVwpceW5cQW8toHxuMh+BS17N8iQqFY6cIllJ4rOfs+lvHgQ0SwFtfptFTYZJcMdtGhc8uCyjAk8XTvInULAFv9uQ7wDwlY8AFCZ/5RKBokFgwwd1lRiIAaaXKIk7e0l2hhMa/JNqigOREjnpeBKUAQLjLgxhljglBwMVXPhmoYGpytTsQSZtdxNJNQwu4jbaLUDqKAkAULIXiBDFzkKtzEQovxEswRZx08hAUdSrCBJyQyQwsgSInXgg8hRidFC1Dj6BGfJCFU9Ih7Sqh/iQjsdQzrMPtuPBFkTIUwREhB6aUBNc7PhkzF5jbtEuiItRXhOilgFPctEHq+DYDHPGFgFe5IAv4uiLhadkGDr9nG/BAIzIVlA8JJ384C8Z+iMt3DUi8ojkmCFysb1CDxi1Av6h2Vg39Wndu/I0TMmdBNQMQJQbgJNweao0yk9oNICHZMfNDHURwNWEZGUqqCacL/43C6HKzwJ22lAEDSKQUDLMxv/UJETHKWUj9ms31q5cvua88Frt0KGV17/m1a969dcTmVPAmO7PxFCy2t50wxbIoi6JOGu4JthceyRarbl2+7lLF/7NL//bvf0dxl5XD68uLB/6G2/7vhe/5JG5xQVWiu/ts+VdrdfrgST462eATwSq+ZvJS5IVWHQPyiQOv4J+Ji0oyPOVvgNmf37xc8986PEP//EfvZdJNTVq2Awk2T9ETRPfVGNMZKQkM7hCdLiklkcg8g1V8EtAew93ZFhJx+/sha95y0+4PXs3ZAqw8N6oPPkXyAJBMIQiQkMTIHVCLEgV6QcBA8FJtCwlqDPC4r8PVK1grC4wvQ/FNxP+AVF6iVzyIVTI1hP+AkzlwXfKGLL8J71fpBd/4fzFC7/0//s3N3eufd/bvv+Fhx5uttt0caK480yiX5ibZx5+72Drxtbu9o5g6F+QhqKxYghkf0QjSMf+iBpvIhhsggoRjJFgEePNKxpQfjA6vFL1sdcXG+zRFzCoMpdiro3GccRWB5l22dmwUj189OR3vfVtr37Nm/6HX/wFzpegfuXUOXhTbw6fPffM9etfWuocvvfuo/ecfeDQsWWcf5rMbD/DTqzyCwTwVZ2KYGEq3eV6BZRWV002+zXWB9POSfdHOisKMeLPJfX5Z/1mqlKglS8hKHS1ur3DfJjmwcGFK5cv7/e6z3vovvW16wvznl3ACGh0EF7Sv0szGO9V1gUOjpEMun7txqGVldaRjq6bk5vH7UZlf4N5JNXd7u7RlWX6PiGHJTD6Kopan0ajo5cIKFDgB2bi22IXcUtQEdADX1TF73hziQA5qg3YqCTAodwgTKPit+Gaa18plU2WooErFt8OdlKxw2GqCFsQsanRQvCgomhW8O0mc8Pu/HDSHg2abI8x8sg7GgdMc4YefNOx0zbs+bdAghyGn2FvWeq0JB1qx7NE2txkeC6+lIfoidweOaLocAIips1g7z+7lzp8bV0A+YyIKBo7ra2wdJls/5jKzlTlrC1XKunFUUPiS8kG4vnP3IuqAwim0han5LAuP5soyHv5jsNMLORBgHyFlyhZn+U+aZIRyw+473Rg0+YAHfFAjKQUb9tFtLcwx9gxWor1pjlYx4giiZh9T1SqJzZRUErmwnRTK5pKk6lHBhCdXgt6Q4ACjuCdtiZrCwwFDBU4TbwxC2cLH6jDmVRJORiwtoqMlDGR/RoXE7TxHCQGHxdvCyuEQ4B0aNYUAYFtLmG7zSVE0Tnofn2gLqczjwWi0nqUUL7WWNrIShBHVPCH6f2mSkEpKYMVOpiGPZIrEq24dSaqrMZCPIufAUGeDDCwJDd6RwyFqA9Atwgy7w3n5hqZlzehh4gxFWbPpwsJrwAhgTl/Sl2h8MPgEEMrnL/B6ItTE6UhWpF4ka5p0JCsQoRLuPQHrREntcg0jnNDDmSBBOEelScdGCobWIEWy2MoFhDCeWQTVqwx8mcpU5iM49HApias9liiAPqVFqfDYX+w31gLSgNteJVmwiZ7bHXngiY7AAGNGOS4Ugg5MUCSI2VIWW5CBzJIXaCWRUMsTCVR3g2Lguf77GbspJjFBahBXN7zVUAIJeFGJm8v7YHlOC+znxKtwCwjAKCZMlPSJOHskXDBfdWdjJOfSCht4kwtg5n5BwrBIt8C7mvewPKgRJC85sXpsyohFyWXIBEpuZmJT0YwMJ/AhJ6mzEdM3IJJiUa8wpXCpMAPl3ITStSWOCW+hc9IbBWC9oCPXaXA1yOFq3YqolFcRgr7iC4PTE7B1M5bg5LAML6RziFfpz2KrbExrDRA4WQKOeYIHdG4W4xJojFjUaBWTG6SyOkTadaaYzIhHGgxetgXRvo0PAkshQrGkrvaSROYFH5SqkKzi59fjK9VlxHlgeSxE4+9vJodZ8JR8wDAj+arpkub/2M2RJXCSkVOGbG0UA/yX69R68yArzPzCKafA9NjkcamQidjlcADG7ArFaV5gxkZYfmlRU6ZT2LBmUn9Au4CtZXUONRHW2W/OmLlEN1WdDSd0jSwAzqc1c4iG8f1qJbQWCpxwTWuwCCJspKXeWBEPv4j58a1qaaYq+zIBT70fFPeM84QrIkNB6aytTjwP4JSMDxhW3XRVBWMjaSQAu6qCWRKVO0plI0qGzfXPv3kpzY4KJcDdfuDB15230/9/b/f6bR1o5m0u7CYQScaAz15Dq80xxCFlYOfJKrcuHblyY9fedfv/wEeD0se93f33vLd3/u617/u0KFDa2u7axdunDh5aOnQyvr1G1hJoCkyziXgHlylg+f+ST805QBvyD6/IsxfZE1mk1Zzbn9n90OPv/9d7/q9y9euUSIYDx+Nl+jjq7X2RIf/cK6+C4c1TBLuX1SdBx9lhWBzn2Xjh/oWEWSTSQqC+h+okDyNACuNHQF89eWYQC7SmdbLtHnUHeINEFOlAlrJnQjkGWOoFtIRumWZjm8vIcSysUSInVZOakIEKirK4OpAACKFO0oYn8g2twI7FCnxRIMpln0xAyzw1U89i1H94GDy27/5zkNLR87efXRhfmVpeW5vf8AMAiqcyai3OLfQn8flOGAeBd6JikByrY1alR+zFWNkYCCv0EZJZusYojpkMWO5GBKZcMdLCTV2rnAF5efFgsgvviZT9cDPcUH61AZ41eo1ede3dw8ONnfW3vQtr3rz2771f/r//POLl26g7/Pte+js3x5scL7Ywd6l5760dfjk0l1n7n/0lc/b5zi6g+35lcWg7hAaDLRQMwuDLM3OGQgMFuxsh7FkH50n3GJTmMlZvGJvChNRlqSEVyYbRX8QNN3mTv9DcJXB3vH5dnt3e3+us3JQ63VaDJdh/mg7Z6JXyZV7rA6lC8O1sb6+tLw8Wl6mptdYOTeYiSS7D72g+WM//uP/9P/1XzYXjlzb3DtyarXNdu+MOWj0gODkFvBm6nPsJe67VQlmOyJSwcRcq1smQtBRSdcpLRA5nGH5TCUnDhqohuCFkD/QsHAs1WLZYhtu6bbYvchWMEOGb7KrZ1avYqXo3nS0U98Ob4s13ewf1MFjIz39orokLBjG3ZHXjPUyYk4W/NfW47AX9aZu0qaBQzh860c1scDMgrV7KpVL0TAuHaQIyU4vYoiM/vxRFxuN208vBX4V9MMkd4LC1piseIEiYpGyCpE5eLm8UqymAg6iyZniRl7mgHkEDysCy6aaIUHBjCBfSxeZoESRYkruJWMi8oyHZ7tStk9FYmFSC5iMGoj5QPd4mF8Z948IpXVTFMIDFXPaewLaGf/HZvMPrqi3eqWCNndejE2+5i2eOqZwXTLppeJ5cHLcY/nBTbxjkvsPeaRRhm4JAUjhVL19le4fzloBS86jqE72a4ymFItAiLpY1JCWzwXfB4cplfJXPbSRo7KS/eiMnfdjpg+BJ8t/rVhhE2VHWbgGAlxAz3cf5AsIW1/bxuU7mcIKtgCSu5BDIdVxF5RlAf1hTIdOeIcrocpK3Kg8ajlJoeUMv/B2aKDS1TQY0/KAV/5TMnzV2Ar9Fl8wTOgbqWmtVYYLROuz2ZOio63G9lkc+1BxVb9d/vAZtdYXmnL9AC43xt0uGIgNg/fUvC7SqC3SuGcDaKXnOZJpENogImtZQ9mySPXZLlllc+MrrQ2XaijCvNpWkkLlzwXZMa9WngkgKFH9GH3zgWu6hrC8cC+RiRG6hEMQsBSkT3kzGv/cDY9PDJbwougLaJAxz7Cx/JS7cnIauL8+JUIYfCv36QNfVWTI8vItf0Cdhgg/lwU2zyVCAZrY0whf42cGawqUmAmZokeewExIeeARlEDBMCJNv/pbLgURwkpSAoPv9Hs+ka6kDlyZVr6WjzZzKQSMi2UgnvRokglQJSeQxR/SmoVo1Vkc+M4Q36xqNBKuKqGaMupkygIlk450JWqxocmPcqNPDiDqLdsJEt8UZFL1Are0WVV0AjFf9Elk3wrenaJo9QluKCDkU5sFCvCn9PkQNuESq6VwS4bhirBdjFijNCh1qe7RcEsJA4i2oS12xLWz3G44ESvctdx6eRdl+UJxTONIS+nkSh1UyISHlDD3PGGCLCDtp6LQUJDgA9iDgW5u0VmiQixMofnPNjiABIY3qNP8gQ3FWdHo3yhRSG5YNVK4GRuBfgY6m5x5GSLoSqEWGjk7mTmhJIXP0E8/nAyRdkAy8AoaKbOEAVNDqCJZqKE6bCcQwyRucNxI4kN0+WD7QdYYwzm6Qg3rYBjOGhMn0AigSJgU8J9EUCPlGD6OGt3c3KZ7XpeuWr/3vrt/9h/99KHDhzCx9LLDEtAYZWFi6iEx02IyyD1whH1hocPw78f+7OO/9653M5OkM9c6fHz1u777za967LHl5WWXMLbmllcam1vrqCLLpSQ9xBcagcabJJR70JJy3g2hzrPdY4U4oMunzawMNip9+9vf/tGPP0GDVeZxDKSzC1Bv7SWE0YVUWBg+F0jJx5zJzhx95BIJLpVu1jzw8+zycRaVdGo4n/NjlNufbie6I2wKxZCSzsQKT7Cz+zTSFJgS8l+JabQkJs/E58304Qx1Gy8mUBnF3vdcBhmnvAlEgCVbWIn4gOE7P6oQ7WI6omwwU8ewf/mv/vqvfOqpj33dyx77hm94+fNf9OLV5SPs11QmpC6sLLc7jf3NXXaqoSqlV16VKgVTgGoeymU5l10yLLTnVpCQCKgoH/gh4gzRgj2ohxIwLMmITg8r+sNwFCoEJlwsVWRZAB2FlIm1m5v3nL3/zNn7/8Hf/9mP/elnzp1/+tK5A+wZ5YXTJZidUK/sr+1fW9vYriwyFNU7vLw0t3dw5NgRphdjc2jKaGSsZMWXwgVbDh89RqE42N4DVWnkU+pUFYw3cfZdMoKnuPMBfhoWCjThoUBzO9nb3j1yqrG5uVHZGhw5cpz5SMiMCXXMIMfskUiQ6DE97i6ErDG7A8O4t7czGR9nvEAlD3w2dnnta9+4MP+La+vrh1ePsR2QxkD3CIZhSWAaTWysPGihGZZx0IU4UieL+ILg5SXv9W1iXjIhwUYizVGceD7jhOHKU86AThcEvpcTkaHKyoEfTBIzeTBKNBPkts5QDc+HBgA2j51NsCJUDnt4re5ayGQzVc+KROwUr5s0gpe4kybNYHwosGKpqyZOJBLf2y1VCfbeJEiqSUwBMJ0dr+SqAOgSIi3UcNNnVMbWI2Bu7sQOnALBOxgAgbi6OLAS4F5mzB1Zyi7/iAJH45CxngeE492qIallk4hSJtMxXqSg1vDNchG1SRhwkRJMwyHmQvQUHip3q9IUTNVJpMAYEAbqhkZgcMNe85h9DRLQjeCTqMpSdpRydx0v6p6i4Mlf4KBDLLiB1ABicmcWgEGUBtbH8jMYg9dA8Yg/Ih/UIu/SBgQoAgn4rXiKLIkl3igQGYktvHZY3FJm/sTke3TRvJLQeAwpAIpvPssu/qNBVr5JFZUDZepaNBvMlAdZMQahnANRsRuerCERNxzHww1O8SiiCcWlVqoASjw1ghyLRElMQaOKBmFLpW0V+CSpQRzMxZ3YkoHOUTAZt2BsB1Y70sEeLBRImGoLVEaQMNj4AKd0NnC34Plw0M/kBIhzvl2bWV7jLhUeU8BwFihHSo7IXOTGBboqugKhTZlCX1o9iWN2gR0ZmSfBKBSh4gotfPaaxUYY0F/C/tw7KfgMmEK9cYRV4iav28kQJyHl2zR6eTH/XNOf5D99pitLeGbCv1sIylliIBUzm371uxQl/xI1X4AtloEQYCUO0ktSk08xiMYFlb/oVtCaJiz4mKUwZsjl0fQyz5/p1+RzK2ZSTb8ZK5eQuGbgeZwBg2GFfF0rYlBUtCi84JF6abJK4VfzclaFRR/zGzUUkNAjUSWOm26BJI5lGzUomhpus/Y2uLt/eQwuIBgjc34hBYWE4ELvFClNRwjljieccveVw1WgV8cOGxXKH7OmuOtauwsQWE2ThGdSK3FibcXKM/+wO9nm3zShmLjaBr9SOgiU3zwS2XrINwGVKFopOk+sgwBJvz7blhCHTeTwF+PcaA4pKaEXUmhpTgZHtOvN6wRKDC+pF6ews9vPpHGRKJRLpmUOevru5GsJzp+pUEqTmzH8wWCRr23earfOtirWtxct8PtkHzqdx0e3Bl3UZEbcJmYLOydZcB24QOJuV1cpnxpj4qkD+eHGd+8ksLEDAsgEqFreyFEuVbpHcPartasaDi4HvREoFpguU8aYh3hNThSQS6IudKWMFZngHl2/eZOmAossjxw58j1vfssjL3pxb9hL+RMRBlHw9pgDjmRdJEf+ut0umGNGxrPPPE1P/LPPPUsoQ5KLzef91I/9Zw8+srizjauztbi8wtgaHa7woNlgCwIHf1UCEeE3eEhenhuXRJ5vvIMfprjPbAd2F6EJxgrQTndn+N73Pv6Hf/KHHKnrBhkMEssu6lz8ii1YFF4B00JC+ikcHq1FuXjwNrtEI5plNSTL891nL+5TWcziT7/cAlDiBcqtsFlq0nxZWIl7G9L0KYmNCcbl0kwlVCFNLYOIISrwUW8RMSURITKKteiX+pYxb+cnURYSIREcZgavkkl9ckjFy3kFs4ROm+GZstvvd1h9+PhHPv3kE+d+89d//3Wvf9Orv+nrHn3k644e7TCrvtUYs80m04gXFunf6rIwYL+7R4lB3cxfs+MfJRXlLjW3aHi+x4wcfmdXFIAXEZ2FKbooNrLNnjnZiZ+vVMuYjbHLkWmZ4g+z3LnebrO/TPtVr345TQIaCS9/1cte+Q2Pdbv7n//8F375l/7Nc18cMheIKbf94aC7WekP1uqf+OLJ1ROT/rC6tsdeP/RMdhY6qgfeLQiTOQ5N+tooacwC2h1xTgsBQ/Ky9M/QDGvhMJ+mBkuDK4mSoh7xTHQ5YeNqXLvSaI8vP3PXkaOHjp8ddrsWNxYcauuIVuSMhPnXuqhOj86gxb2DA7r/mTVEwWx35piPZ+kfDW5cuTga7bDVC+55d38y14EheDAxe2E3eeMfQAq8pBjxwa4V3SqsEc69FsfuOo7rrTB0gAvFEknGClgw06mOD9gxyY3/R3OT2n5ltFRt7E9GC+PaLuNsQw6uRusYXmOlSo1T9pYq9d3KeHnU2K+N51nzWpmwwz3HCMxxr006zfqgzaIh5/wgQzzFOSezK01GU5mfzSZ7jBD02L8HRVU/xVNHHg1XJ9nISMdZTys8VY24fC51HzHDcHpeJvQa2QFE7+0cbjmbtyhVdkzHm6R3IPWGFZkbwkWSyG4KTa4J02Yg+VFFJoKZqBJ8NBMufvLEKFFKJ1RRD7geN5qg5N0BD1juWmbOpMZZZfIPTQELY1z8KIfD0dZElBh1nvn6VHdHYcO4tp6syBZw3K04SVlrbOAQp8/e5Rt0dSVbtCBwCkPUHrFIEnEW5Sk1/IoDlWZ008Z6tF7uiwz7B+J3Ym7pS6Km4k/lhB0kcogAXCHXn4JYgEOLX4pHECabIdnqo2Kq7h1wcPfQtbzMhgdT3HIpBSLCqV1No3KOT7Z7SaNmkl4EhYwmAwc/ZHDYL/V1lBh99WMQyjgPb9gfuzAAoNdudUo1xSMbBFE/1AfsdUC7AbBUtQ76Fd4KB6DhEjlSGC2TmAKHkGzB2ZKBDUgyOVph2+AGkM6S/a20nZEhRjljFOGvlbDmhBftxti2gbAkp4H2YawQQSFWpOQGa1EYImZlHcxmko+RSQ7JEipHHGw3WwShKwIlYY+evYpllvmclgEBUkggqwp9ZHUorB+4wrD09PPq852XSnPnuzmH0RoOyef74LTpGlfuiJkPs52FTBPIYJgMwERZwIvZGV+XxST50HQuDwWX8lxosbxN/wSIuvlViHywGhShmRIGGN+nGYYMEhBSAsUgcf6qt8Q2I3NLYrMS4CzLGTyCuEo2U+iFUyWCqaZ4+eA1/Skvt++BH7qSI3w3omQrVl7kmpJE3dACi8eXQRJLuOIP4X4kFUDDKHXBgpyv/sbKGdVWuuWJ3l9zkeZyL4bBbNVaggvD9UKsVUzmrQiBBgNAeQtaSSTwgAuJPIqbYIQY7CxLBUwCysdkFQLEvDCfH+PmP4hb66ZXwLGwzKKherCcipH2h5j8WUB5UPGENOVMcCPalDNqthkFK7mKTbX/GADKwgBnDUmJxZyCR0Fk4CLEUcyli2/FnpSiSJWOWQMEJZidPXDDW32mbGLdGPfnWCrLZ5JjPmhE0KLCwhkiUsISqMzwIutpi8D84YJclGbMEF1FMKOkoKe9zyba7tsI5WE1bj8NBuaoUimyxJOkyK1IjdRGAzxLjp555rm19Q1M0rFjR376H/zD133jq3vDLnlh5pKbmG2s3cSFcniHxgd2CIVJLy8d/7/x9l9fW7+xsLTI5OwHH3zoR37oPz516sT6xgUcFyLfvH6NjAOKFDY8Qp5ZKwJflbJEamKUIEEIwc4XfKFOC0Hgj7LVz8Vzl977gQ+850/+sMsW9Q1GEqjD5L2RC1R/Ag24sEjES4jsKrn5Wb6WK2Hly50hJJrG4uFrXXeAuiPanaGKlE/88X8KzbA745i05Mhda57XW1nnU0nCo6rsFV0nNO/TuLeSCNBoZGO2iWaAf2athlCQc5kon2SjGk65YbIEe5Zy0vPF7vo7fv3t7/nAOx950UseuOvYq1/5uqXDS6vHTuNxDoYTjtqttQadRXbM3Ov19ixugNA8eKGdvM4oFZPbvDdD8uXPJ4WOKEUECNoQP5o4EfgFNyMJWMtHq7aHW82WuIxbNpcXG2xFNWCmCtt4t/HX2fav/ZJHX7X/loMPf+AjT3z6U2oIbcUO880H5889fePy1YVO+8SJk+ADCYdWl1YOr1pwyIeuwrK5in5I7fCxowc713d2d5ltS3kWjVLkEhWUoHVqcCRdaqa455EbPNAv4XDzzBtkyGR/b5vJ8KB0/vz5e+++j/FCnAHMDhEVlITrAJluUtnc2FhaWaJxDld73Z4lz/7m6v0PPP95z3/0T//sc/T1u4Gyc4VBAN+hMF3p8ow6TQs6u5Fgj0qnd5jMmyzVtJMrTQJS0B/HQBuhWBVRsWNFAwRfnJZNVUGnkYhSjp087giq/Zz2aMgcQJhWABZMrATpGc7osP8UU4g0Kc6JwVdzGhu21I0+GTcwOVTLO5dKcSedfDD3qYaUB3kkaLADQ3kk3YUMXnjUZ2OEyEqCAOsAu2UwQCTUZRZlfTXJA/mMQYd1oo5TVlxLaphkTCrBl8vs8o+oZgvvW3TpAMuxUy8Z5QenPzGFm+l5UW84C+FhOJFgSyl92GQXCWvU8Vz5p84pfXuDCLQm0khbuUlIdInP2D1WALPxjhWCyBFLnvgICcHCEVry9tn6o8QypszSX6WYi639+rTFUE69VzKyJ5BP1Bwy0FLB4A/YoCCRqbWPgGmG4jYkh4IBwmVNC5BlbXAxPlGpBaicaJSBBhphrRS1IxYpVcIQAUp2IJJGr5rZATrRjAIxjA0+CFWk9aEtiPLEPsAyYKS7L1LAwhHnQStqCHFw9913LmxmnRg9CIpgpj3ESRIGrGwR8ay60EM6QjNZSiEsRSAh5AzCpIDbYgFKvsK31FyipL/gEkAU2A4RLohQiyUcBiIux0rAjmhmxBqSNDjA3aLH3VTwMIJSzWJyzBIgfhEjUDVjBRtxpzszRcUUpvG7HxMdDKCZd/n95ZfQvuYlrqItDZY8n2SH/8vlA3/CJtfykaeINeFgySe/k5YoJaKBNg6numJo0lB2LpnT4LQCrLN/P5yfK2Bzj8dWwEmd+496HzD3GhBwZnax+woQh4cTMpdQY/wl1+2cAhwmSrakBfNASCtq0qRFxXUrwZcBlvyi4LMYlWHaXrScSDFth7HTy5QjJE4ukA4R7QBmdZRduKhQikIErBpQ0OjAwGRwWM5xnCtW/QPTshjlgtc0IYkGAcRx7iaR3GXfV3Qic+p4w+xS9o9TROgXd50XVSo6WkZ+zS24qeshVB2CCWqd3SMmJgl0UiHRfXZUnN2TPnRzixom5ZQFGjOm9oAryNEJw8wNSxLwUG/4DHJAw+EjPgt6uMhYnePBwmZejOdR66Qi5LRErCL2ygx70k88+WMpc5k91pTpSrHIwmiwawTDFBxAi1W5brkMZLLwoXXFOthybac4JSikOsZKvo7AQCOgQTi94OJkhuUiMnha7IjLpEmFBhT3VaCfy/nVbB6kLa3jozsmC1vSxSQY9BvwpAQ98w8+yZ9Hvt7KiIqL4XXIg2Ugzz6ah61669chYVi5xK7tzM4FMvQITtFj97BEzLC1KrG2JeeU4eRWY17HxvrGs08/G5tcPXn0xGOPvXxhaY7uH0ywVYJMGrMFDJdeCKsQULxsbfb0UwcfeN/7P/vMH7KHBftO1mrtt3zPN732Na+9+95DO/vXBgfsgsiRi2gu8/NtNZkQlQg/xVHKxZMglUnhFlrdJwFhpk3Hdoqcrko3f/tDH/rI7/zu7zx3niGaIyQdTrYwtzBMfYaYNAjVPYEI2xyEm2ffYoYJV0YJzpeCCbkZlfD85DshJfks8h2/twAUGNN0M1h3RJTIBKtlt+BNcbwVb5pPgRo9vhOupTDJ/c5Xftw9eZIdh9gZpuCZO9HQIPU0BYF8iFg4S729IgKNHdWjvgeAfCh55y58wkjsQLxTP/RDTvd74+tXtt977fEPVit/9Acfv+vsye/7iR+/59Tz6dNcXu20K+05Z8uzXHjV3OqV3d1d9r1H/AoD93DM7FgkxQorM5xSpgEBu1kBR0XzSQjE88ZFSWSPHRNHrCWKnsmsYsNgsKZ8uNHfnps7WFxcwRIxPQjfhrUq+/21Bx65954HH3jsmc89+eQXnnziYzevby4st6uVBdyBre393Z1zWIoXHz3z3DPn7683l1fmWKODnnJyD25ghkA5c619/NTK8Mpuv0untAyxhpGt4Kh63aIjSKKRU6sX/hMH7UYeoq+K0pdZv7G1fbH3ufmV1ZVjJ0+akccs6BlhfySdqP0TRVspaGy+tLuz0x30V1cOL62wkwlHPdDZTCtltLDISaz7zXmqCDaAZ1fTfewCBooiC+8wBPFy6Ptkjw7mRx9y10InW+LWYAh68M5DjifUjMxabA0nvWqTHU54Zh42o3+c29udDFcrlc6kscZ29s78rGNsGYRhIy9ee67hwfBwXAQnMWA862x81GVF6WSyWmGvIFSRSscZETYvsHvZdonJkPv0+E4q256Nq0lgi1fAso0QhLh1kPaKWog6QusHrzNKQpi2iNKO5h+XUTlhRpVSzSkXtFpJzCjRMdzjGjjrGx3E4GUApHj3mcWklEiIqwjbS2NjeFLWNW+QL6UMdPluHaqsuZS1mZJ7n3o8u50ktVymZ5tRSvpZSdO0d7NSWSN+jdknFEVH6fU4McRib2HmopxyIXFLhS9QmibCqHaFeUu4NQREb2AL2LjxGvNM+M87+2HomFHUxR80ZU3yNU1Yp3R5xu9kF6lUgiiui2LJkOj6ClRUUKm7yjibph43HRm3MnRCHVhm0hMfzNBe/AzKFyjJGeVCeOkkggi9ai25n6zhUVE+NzDdstJdd6xN3NwT5rpYrkjXEkXNBCYtyp3cAJNEFjK+gjJEskqNIeANlArzpLT5S6cypsALNgw4FwK3egNkrUrhufHIlFMs6vOLC8Mtxg0ZQGO9yhy7EjVzRAbRSFWf6L3U6hvYPeplPAybNlyhh9pVQQgRXliJmr8aAS5FgrAZRncYMYOdlXqkb/OA+locONCvzZz9WlOHgIJUZVosy/ptqQJHH4Y4bY7zo92AbadbE6YFfYWVzGvuPoR6QaptZhDBsaFoISVwg2adRDnhygFVo4NAqpwlQUCDFVZFPbKz5VSlQ+Dtm+SgMMIgtTD55VKtzBlK5bn++e1wYk1fboUV5eAVdWM/TJQgO0bGh3VfzSnkaUo1qiT1J7rLb2wAv9JTUNF1EDniSIpw8+ejgd7VzIQTlktKZvR8xadpjD/np6CjEgIMPeKhsOTOuHdCmyXwuxmWq3ASnG9HLRH5HAJm8UoivvE/AggQuS6nDC3/eaUYC40KUEVQcUtZSFz4CKYoPRoSNCiI7tNXFs+Fs7IzwiSGkYpmERbG3hZz/Fez5fIblmIKMVFJWYjiN5mCCoSibQVfrRlXEBdCMgCcZPOfMhPj5MCXmMZ2UdoJNEkwBTAX76T2v9lY+rAJviaYlJoIBgGcalgy4SO5myNRuRFR2kxBqGbVh/I/RaJ8I5TL+NQ5GC50DJskCra8+NHt1o4TyWh+EagPNl38saUgkPCBwqmnQBGNlOhPSZF2SQDjwMx9gmggySP+4lLYHCt5hVoeZQVfxVlnFLSxTdbvPlvTGx3z6f7RvJIdP1oB0InZmAIGY9cWQf4tyMCBPBWpcf3G+t4Bo//j1dVDP/ETP37k+CoLmDRbM8uys73Nsabm5EiIWXLC73OXr7znjz76zJeerrHjfJ2tDvpvfst3vPm7voepU1euXmq2qb3opAUNEEFuck5sCZFDM0IJASV5Klgkxg8TvSFTA0xu7vHfvHrpxh/80R/98XvfW3YootrF3aAbrHgJkB1CYBUCQqgA5CJD+SM3wsEZ7fmQKEEpcWe3adLpq0xO8tnnv+C3wPlqaIlOcMEnAizE/gVwphH5aqICL2lnAExncEgJYL7AIkNkoReiLxHyXMJ4pCwQJ2mMxRWg6IksLyGEEcnkFoMCF54ysmevc8l6dP7KpUtrz+5OBveeetn99z7/jd/x/MOHD1Nj4om023ZJsFMXW+yTion3ezsHu3t7XdbKKneVQQ9hRhu5Ur/Ll5KZWNyBIYiIvt8KggaUmBZkv1HUyxobqlmOW2Iy0vwCuwS1D/b3cJSOnzp7+NSpYbd970P3vea133zu4nP/6//8L86ff24OV02/FJQnFy89R9v2gYfuHnIGXre6sLiADkEtf6W8Y9M41OLo4Pi1y3TWWNpChQwSHdlvrThle/AHADH9SKiSgUTcI6tPlJZBNCbrsJaG4bJ2p0VZ6zRrzDdkPkfSRSJSbTIE4eYt8G84ODjY73Tm9aZoK9CaG9Z2d3CM6FVn84MD3DfsATgFMVilH6Lup7IgOuXZDkYLmWIWK+HHnbK0Y4rBFp+EbXvAhP4XJirQuUDnkSvr4TY1eehqOXmmOgfPdQgJGvGVoRg6aFiDSw1Ely0uOwwuy4dgBE0Hpl/YCiETMsoeqDQwURt4GrDgoh2FCk5KoOh7WCSshQmqTpSU3pyQFNxlUAiGYum2gyZ6y7tTfEr3NzHMkhdsDhMW2YSB6dWaZjJRJNpJ45DWvkhJ9qajwz/gkqM3eQUggsqr7NOwwXclouUBuPE8RZsfcKdqApr1gVwpPTGIg+jFm/GLXKc+sHIjhl/Y2hg3kTXupgOcPf9UMdZ0fuaGcjYZdsBPdB45iaLM5iKp5h4ceZ6+BnmqHReCAZLmhJ04CILc0UoRpqMILqH3eqlNGz9Z6aeDCQncTQ1gVI8NXY0IPjXGlcHMyMHQrLnEQvJ5pBBRaXGmAAGUVqe/uteNI3V0LeD3ynpbiqawiUAlK5NxXaQPsEJCK2sNupKQWygkiBgOcKFQqDSMS01ro87LZEKUGXKHTYRYCcSf20QBlp5HPwZPYuRfevqARBpYSnG1VomZodWiRmRnoqgkGFr3qm1pnuCPG5U06DXbZpivU4pS2dmhap8lhCIr+1SUuXLQJ1AKEuKENGpuT0sYs602KgJPVDAoAlg4wksIQhgZnCfx1OeXFunWApAPmERZURQSqOWoRuGE1sCoBBeyhchbLuUoWeXH3xIsN5OqfDQPRREI0/ASNdkKL/HNhz/hFMiCKyDzUx7dQTw4+etDgk3rEzqi6SnpYEqew4eyWnlw2uhl79Ly7c47c5WSfcKIKMA7v3+t56AtpVFn75Lh5b1pZZC3acCtV3AsPC3Yzl4T11TlwpaW5yIONXGKW8myzq41BY6lSDNBwZE/yoLqiTY9xgWtGneux3qlfua0VJSPeYfUJJQZLJ2JUOTD/tZvqElcQKOhmZ2G0dkqcwqBi2ai4+q51Soly2xtCKOs9vgWfJyjlh5oYxaeWNCj/e11kuijqrkATkECZfIM4mgheqhNlATLDv914zA1FIspdbCN3poULeJgLTiiNFWgUIjdAhOAW5NYUKWFfXEyjqTaq9/Wdqw0pRDFzAFRb5I7zCN+dU08fcCAKC2jST/tcgjBRsZ31/DJDNCP1QQTESZpGC7qdEVWhqctYfRFCSvsteibp68xUKzeSycW8YBg5tSZ4uPWQJo+oRJgAYYschPTgmTCkJk0W7r5BE7W2gZVmzeKiVIU9n6F3VYSUGcQcbJnCn0RbRUJmy/+wMCqWf2BwJ4TuK35f/In/6PXvOE1xge4rRlSe1aXPxUHAdj8Ecy2t7YuXrz4h+/5w6tXrs8fYjekxoMPP/zYy1/zqm94Va+H38UgEv090OEyheqQcwFRisuFBh6TaYpS0Qq5gcEFY/CHHYi4Ne7tsS8IswZYZfrUZ596x6+9/dJ1+jDoBbIOn0w27SKhRQN3NLcQBrYwUFj+lotMkIUB/HFNw8vLNEr5yd3PBcAdgREEKSyGd15CvfP99nMJvjPHEiISwXAatcS4nW72pHxuAZeEfLgV+9YDwRwkDMGJwA3OKlpEjOBuY+eXJKLUoflEwVHjhykEefabQplyLnrFfG4BA5/asrmrErIiybP5KDJsU13/s8c//mT9U4dXVtvtH/mW7/yW1aOHaxw0bu1Jbxal28G9JpNxOosLyyvbG3u7W1voCdIVw2TIjRytNYOcLwkS9eBSIqDF+ZDbdFy0R2RLA1fGVDn5RPFbJY36mzvV2i5+6eHDR+bnaoxL7A0Orly9RoP7gYdO/dP/93/29v/wK+/5g8dx1QYcTsXUu4M63f9YsDOn79tzCyz6PzUmzTbbdEo3W9bSojh+8hjzgq5dvcJ+g0EbzGGi9Svo3r4bjC6nli2K6Sv9ndo00AYmA63oOpU33X+Xn3v23vsewPQA0+jaIs1JBDSFS48hM+8W5ue2t3aXllc8/RCtl9V9pjPMd47tbdKIaFYWFkeV3TYOrnxBhfTvqGYwRrXxUXyNes1DzWp1dpSH613ndYg8xYwZOE7iocSCl9OEJNw5RdqJ5jNQo3UsbThb8ODJmQU0RebHzRvao9oueE8mO5TzCLQ1ZgkUrQX7LKlCMCX4+gTS2YdnySxneMiuLPhi1Cbu6OT+IbYuMoc7jSysPJ2c+kyhR0zhDsN+2fOKU35BotCZVGTL1A5Y3UcLxvWrVCIOt8Bme95Jx8ktk0l70w4MTbCbL5FP3LfapH+CTKrNm5hhbSc6YCTECuYIlPi3Ruw92abaYvTY/C2cpNAzp/+6NarfDJbuhQI8awhkiKJCH6zE0dfqu0ZOO8fVvEwOnFOr6aNCIircoRPYWhaGWOImHA/tHst4/ICtthpzUISKNCanyZq9gLC3lDXuZgrqyVpu5QkU2DWBPXPVN8YBOrTr+AQaMAI04A86ybiX/cQgDcY4Fmx/i5wYB6NtzIEttC+lMumITyzwwQFQucjABowsYmEQ5wdAEUGSHj3HHWHfLpfE4vGjgC1O/KLWRu6syaOvm51gkQmrdKyCgQNdOsK1y3RrUXmSij6zMXsN4FujasgD+faP0cIbT65LA7tKISpUWRZaJssS28noGBpbqW+ExrRV4G2rsb21wyDfcESfBC1AtjCCIPgmHwxxpz7O7Vmk9UUDlEMIqiMoYh8fNkvFO2jj3ITBnDF9AlPQaGyrfvLMKW0MUzTrrcF4X6cLPwIdyRxcNy83I0oSVjcDmBz83KgwBoAI6SpBIJCv4GFpaw6qLSiorsbDJ59j8tAQ7SPStVNvWmmiP0gFFpCDnJ+0qVFLNZBiYtGZaUaelb55RhG4Cw+Ivk9f8tGbUcFCOCgen8HAEHETEyFz+QQ64shX8QlwPF6/J7c8icYslcBS7PkpUIg6eyhJCug7cDagXElN7ALl1n1GQonEdwEmmvjOvhr4l17EvuNKErOR0sKefJ3GKlnwWaPpRTTuU/Yk5M5bkYCxiRlWBsukMxOhEIfLITycHrO0qR5n26Y/SsJmDKkrzMheIcYvIZIxNpKRBgtEWkfixi2YPiFcOeFf+lnpxQ0vzhMliizZai4zFRVmZo+AH/8ozI48KFyRoWhg9AsXQIpKDcFb+erG081kXQFiGABSxnpKOs9Bi+4vLxCIjWRMjq0gtWqgKCUywm+8E8AlwgAOH/DnBMOsWSI5ec6CQ+Vi4zpJPSfL6Fzgah2uvcxpXQqOL1THyQhWYapsaidT73nSZFN5CIGiR/2D7WME3Z51aSE9v0klJjwJJMiasRHE3azARBp5gkvac3NHTBCLKJllSBZgFy1AwLKAiNgNWS5EzJ1+TgAmIOYqhMoiJaKp5VE22VFkCnMniEd5JIMwR1BlsYxzAWSFC/2jyY0bG1cvXe/MN/+n/+0XX/rCR03EB0u6s54ACpIEXr5Ae5XzaNhQqPOxj338I49/ZGNtnXqCDp4XPfriH/6RHzly5DQLfpmwQHIabEwWCnfUCy79cECJgHhLEJcqCAkgrIik1SLqvj4oOGs7Lz179ff/+I8+8OEP2jfLDoiJT9epPJ2aRdEN14vohMoTeQCufEhW+erHL7tE5Y7L1zuCTCMr+fXxji95vyNhyW8WMAXz1VneEUKcYH0brCHJUDBK9NZVnvl4R6CxSykx0a0PCYryEDoFckeuglQaJUn5kTwvmat6IzVZahDE65T4iWcrLpxFviod2I++Xb957X0f+cB9Dz94NytDl5at5j2Uhz5rouE20EdMSW+vHqa/srqxft0PoTt5F7glp9s0FHyChp/KpcL4gT+k6pO6IFJevPOsIok46kMFP+G4CsrbYn+8sUGVX12c5ySDxsrhYz/4wz861zzx/sffe+XSVQze8so8Xf/rm5c/8vj77rv31P7uwcmzd6F8TOlmZx4mXaBqRUVXDx/mKIzrV29sbW1CKdmj2zBZAyvrwljonrI48hFD/9nU17tjtsOQJizmESu6vb19+PCqfZ7aUxU2fC40SSIpsWAk6w96K/UVGMui4eBD9w1Fr3754kb3YHSwT9/o3qiC/0XayFE+YV7ABpeTEHx9nfu4/pqCvIppQTDMZeaDJVRz4hSj8FuEcEvotKbVYTpYTC++KLLhAV+1kGkTWCRhCZYSOqkCGgx04t+Rkh4mTKf1RHReIvUPMG4wjbCU/XApGmhgbEaxhtpFrHmkbIh1DfkraX7VzqlvhNZprLghLtngP00lMVUQsZM6L10lLbu4EicsDbiYId5pRfAVVSNLecC/Ip/gMZVQeCcvdP3SMYFzS36i5UOyIp0hUoQLy0RQ3E5BFnBEIxM5nJqayqE2N8d53m32oBCwTJVqcuET7CUp9Ir0kLNtaafSTOVMLYuVOmRuCMQUPBQMrGtxNmntqAfmW6IZR581hcaiDgpqDCDYdMFU7E9jpoiDfWmIjLSsFLXXTTa8yQARmaaiNDmVm717fEf5wIGxKccaKgx30/HPROSunVBUOiBd6rXJiJmpuOlOTLI2EfMFqK01F/Ah7IQkZrXJavR2i3liSFbkR60FOUWcCbMPOxltrg85SKzHSWuoSJvOrMpwXntV57AaDj5vNzk7Q8fA/azZPX/AxDfGWOwlpKWJdjGItswmthyPRvGY45zwTqPDGIwDGKg0B7XhTiGjNpPznLxEK77WYQIbmxEDIbMOJ/OcndaY1BcW9/fGNNRoMLkEjrZ7d7/hnCp6UkALDw4A2AMbDVy1RtsjJGifp4uF8XNFTrNHocN7UI7QVRrrR35leTxsZ+2qC2rXVJ/yQ9TI2SJAmdVWRxm0VtE+VZKnyFrAJZisDPS/D+XG3ULGN7ItmSRCeS5qVlKl4jBOAS6EkoMQAzBBhvpgvECk3V++Jhi6eZ/23BPDnMuHWcJp7NLrX1LeeU/kWQpn4+G3HDZDVxGAr6bkr3KRMFAKbFIkQBZCjMyYZcSvce6Mx0vhjIKRI7ev6Ys/AsirD4XSJLPAV/r2m1aa9GRUqXVclNY/bhx2iOcHLxvVoW6grGp01BXUeDLesduVteQU0QyhoUk0s4f28RONya9FBzAhHjcNU8jEeVo0M1prKAo1H/UZ+uOAlEaLzCjSwGbInJJNnoynHQfKpLkeO2fupXlb6zG3npn01z3fsc7kcs5koYky4wUZiZVdGRzkg71U/Ciy3cSUkzJrLZwNPVo7MrOZQDqBWGi0Nr4V2rGcjCYyz3LofFaOzKBzhbVfOKw05SkDOPe+8UOjX0cGbspx954GDnZb4DyJCtVbuOGe/U2mXw4ybZXoWDFplBnUYtmeD5uQy76tlr0+lRq7YgsRRIGJMbRlK98YT8cgGsI3EE/tw5nhfbtP2G3DOgZf2zoTJKiBQcL8LO2JW/QfUCWKAPhE7OCDPmMXkylEGJq6S0FYj8pcY0Cl7hFqw8zRVJphRt/TUr+4u7vDlJ7Lz1x76cM0AOjPsGpQuMacMPHgyT/7s+2NDfpB/+zDHzl/6fInPvGpxaU5fLrDh5bf8j3f97LHXgpZm9vX3TY1vVXUwdAFKhJSdz0P1JSQoCimiEZc+6cIoQeXxlysXRLSc9jvfvyTf/rrv/auS9evM7rqWBax3SDiMNhV6zs8s64C0SFbsDUD8YYB4QWZjw755N44f41LZIzuTaiC5hnWqSrTC1QSLxTxNS+wueDAm0ERUR6SKqHT9Pk+e07i2yHJ3W9fkaCgNUuETVsSB2b/30rgN3ngveAH6iBfIkxZU7TMIHwHkPRB7eBBlJNOPZ1UN9FmWK5Q+FF8xJb31HZkT3wKTqvR+PjHPrVx83/5ez/zU8dPnNxZX3/40ReyK5QTbHJ+DeXaCV0kmHQFURqA0hZ9MMspygRNrxnlyTFhZh3D5Zm7Yffsp9rkxBWvghxlR6GAWWVysNfb37na6WzgUS0uLi60WW3X2O/tHPT23voD3/L1b3jhz/+zX2TfKvz8pfl2rTm/dmMDk3fyVG2//wy98tkatM6IPFN1KW+D3gG9MHMLc8974fPOPffc+s1Npi+UDRYx03IxTiWcoi7XbMFLkNRQilPoBSmMmJFp9uvNTCadTodNVD3RaarBEUlhThKRlpLIMv1h9UKrsziu3EvDmIKNcA66HBK8ydLTbnd3NJyfDFYa83tkRobwIQ0HLCCWCNuFxaPs0J/MHy1zLDbVBCUd+4BRp5jbNY0/TAS9Zv12JoDE9WTNAFUAffZM1MHtYZIPW/kwvbh+jToATy2zQGhw4UmRa4OKA4YQA9+ECR90pLCWiGW3WlwbATCTnHT1bCeoYyzYMA2Jo1f07Oojy1BCQAg+RCUY1w0z2XNWF1SW8iHaCzT0TX8eyyMscUl5jEYTiXoT3UXnwcu+bNVPRCQWfG/16GteBRsW8hw43hlXJzpP4qJMIAB3FpLovjU4V2IaGmcziVVIKwLGVGC1FEAaiaFhPDxj7SKtKWJszzQaMmEux3vTrU5SO5uwK+ge7ifsIneyhoB6/ZI79nUre/u76cxxPol4mrP/g6nZLSzQn81cLHxLjqRiX3kLIf6DXS1EhvfUalZPCU+tS9kfNjTn/W6PlrA4KgntQ+aQ1TmtBWbW6tdhQ4xwOIKrobphkCn/4k2PO1lXmzQkGqPmoFVzkFA+yEmqZvoVoRzIgGJKA74+NdRm2M8+VBDP93F9wcYR8+WQL5yVxAWWqQBigVYKrhGt9FZ7wBgGcpcIRi8VHGtHAb1MaHuOpYbjTscmC5Puej37SdnmGzbZxrB+5m9P0VTmwQQLRnBrif2sVyh5nO/FSnGi4L7rclia6ATppyyvgBOVO6N57iVMx8H8zXq7z5F3MFmFh7IOjRlsIBQwmgHHiQ3znfBLKYNEyyh8cBc1vHWm/NlqUsZ6MjCDHMN84ckbuBn54nYBDpwJUz4x37O6lzhRS8gXgLIlEiT6bhoSxQZbIHg2kK8+3b7UcGIx4sqHRMh39NK4AgtCU+1g+OSkpaB5Fa3gkzmgtepwzjSY5i7I6V8eqFl9n12FxulbwE+/S4GXsk3QFNc7UeaTuXorcW7/zAK/7FOi/fm3aW63cJPD/IWHU8NQcptmeetF9Pzzghvl4Y67sgz/iMVD4WBsUeKTdIZqyY05tWx5jWHtGB81TwkXtGIoXAFZyjH6Y1pKHjBwsAghIczQwvNPnaBcyiG+BrX4iBm3TTl2Zg5G3kE8C2NIURNVvcg/Ow+yVS05sb+BVhBoFDO5M6rawKBK0MCmdZsBxqBILLMFvtpPqXWMkeE+zEWPU+Lp6CID8Mc8aDkK36gY+M5F1UVeFDOGR0mNLww5fqROYvDONoUbC0gy3WIoNFaTcVdMCiUNeBxzTweWy4igHDS8gTatci2fBowwE5E1HQISzhYzcNpB6FQrKHK4RjyaLhjT8JNtRRrWxfY6ZPBOuDJNpQ/FBPDZZw0sZFkszcupkEoAiuFJM2ukCFbD0h6BF5hdcjEy8ayWhcwLMUBTHUITjEFQfhI9zwrYNJb71PG+mvb/T9t/QOuanfd92NfLabe3mTsFA8yA6IVoNCUWiTIpURQpiaIoRzRlioxtMYkcR1pyEq/YXlnJSpadZHnZ5kqUtWRZJFVICiRsAQJBgkQhQKIRZTAzAAbT57Zzy7mnfb3k9/vv9zv3zACklGjlvfe83/vu8uyn7Wc/u74A5QdEzAS7lvVbt24DCJqeefbp/sZf2N/fox8IT/gKG+f9gO3uzk6PoxJP1m/duPuFLz2e0376cIdRje///u9933e/e8jpQ9MpgGU46pPxTEoXMVG2wxJ0uItGIQnkjCqyQMSsK6XfmJXcd+/ufvSjn/jd3/3YmGPcyVOOZLEHhHxVEs2oCnAEzVJCMA+5gF24tQr41/xdZSrAIACuO0KxCg8Yi1Xhq8CStpB6rJhSsY8FhFaTVcIoUYUPR8leQcVR6OrBzIWyb4GeJIFcgV9huUpZobkChQ5BHjeSS4jU8JhU1A+FhBUQVuiMAYiRUWdJ62grclhyvOtTX3/q//5/+6/66xu3b27/5//F/+nBh+87ceIUkbgkjCjY/OgVz7rt9pgvazIC5q59wKazV4qyIJUBHGSTgZVExS1X9RB+yX7xr4SQMN7EV9U22gqDxcAs4CEdHh4MNzE5XdbzXL9x4777Ll+6/8G/+x/9vU9+8tOf//Jnd2/dHo8HW1ub2zeus3BpMOtTac5fOnvixEmWCOHSM3Wg/2znHHqnFy/dx8KmWzdvcTIV3QA9OBCGIVgNukRgkwWTzOzDKdcqOCoN4SFSzMBP24p3dXfnztrmer/HkI2xiTQhKZJMysmczfSN4fCQ3fbdrqM3ALxzZ9Jub7IFu17r19qjdm8EmzX4mjqrOI6Y5g/E3TCDvKY0CQzs+B9XSReUf5obrsjBpxhMIomFXFDBhqT7DRgScd6Q6yXAEe8fh8ppHlYi0tTgWDLYr11C4uYCMGqTwZK8ok9GhdI0VaVUi05JOimgbZmUBRt9oJL7D6LihYqqGfITdFEVcMTgC4M4ceRBT1+WRsnBJMDUsISRnSDeNPkFTEoRrPDlnygIyXiRCp8AKGYppyRNDiHRDqIhWj/yJFf5TSOZslCHCqbpCxW2YpRkfkDTFGSMBsNrZsMZ56CLyJKZBl9bU6zYZ6RTJtNQA1ZdahUFoG1MaTyXsgiizW2xQ5/yDvYPRkylir6tJyPpkJXWBrPtxl/KpP23CLz7dovewmQ4wt10CBAFdgMBLNHscpx00tGZJKBr3YB2xn84pUqYKE8ysfyHxfZsW+90PQfD73YLCbRxa/ILohiHBUe9NXt9G9Yp8xnEzxggF1OB8R8FwpzINUuUWv9Hd6XcDpEuDf6M52NKAht88T/oFKWyQSAiJEBfaDDTMbD7Q0HQlvSlPyS7nXxp9bpQA11U59rYHS14UaQnqcg0cIEYLpjRHxANEEQkTRYLgQoVwdlqpstxFfjkMmzTc0k9BFVKYP5d6SIDRl/5ig3KyW75Ca6FOxnc1MS6OPf20PqBQv6ZE34YgE7ahfKCO7HMqilweBaYfCMTj/KmaHwijrTdyOqCoKQna7JUeU0fIBECaa05JUHAViUQhBLlhfwgZ67iYJgn+BNdfFYDUmp+KDf42b4mtNzK8yqEX86O4O74veUUclIfU5TIpCYVJMprhTp6mh0CARw1KGADppT2r76bpXBbKsW42CnKMwoaZFzBIvfCxxJV5TxWijQnecJiqYRTSCv5LafGt4QBqiV18IC/epfT64nCOyvgFEhhAfbKIBTL+VIqHi+WksocXlCONABGYOEkxpkQmjVqNXu0CyQKsF3HqwYjdYtXhKfpRfNJo3VrNO4Qo1uubyxDCsmcWyx/WFeJzqPRZHCwgRrmgBANgZUnttUJQaDTa+b0Ctu+2pyv5gErVVeFsisc9jo4RLWNwuP+8QYU6r0Eke0i5qTRvgFl6adgQJi1Iy4GFEoCBMfUDV/gMGWtJ7nJyUnHtwinNvNGWfCLQkShvqbb1xh4Olxy8UNe5YzxGtPHpT9yRfqBZUdKcYmTFckevEmJmzNFC79YC6ssjHZOBhsUES44HQJJYUa5gw9AERLsC2nVuvlrQHS4S3y1gBxzKG8bDEpQiNhRDLCjfiYSKyyv2gQ8/kc+wLWNcT6AIPKDEb0O0ly9chVzy+HimJvv/74/xSmfUiccQWG/9u/uDg8mG+u9T3/i4ze2r+/s3GKugDNJvuMtr/lrf/XfObV1em9/pE1l3aXmWTkz0uT2EkEASWDiA5k+lQYKglkLwTMG9ArdMHjCNi10YjxefObzX/idj33ypasvzjjOdHFaFVrsyCJpQan2cgCaTKe5hLFcEu7vK69/nbF/TsXh+vYpkYlx1gWhO16TckIXGuKwaIqFUk7jgUZWQkcXVuiY3xB/uYoYeUEjIj2f1JzEBtQKYinbROWpwDFdgvht7CdXQuZbgm7sFsxKEkogawk5wqFCJDmr8rTCvJuWxIBZmSQhiqmR5BMeItASmIHGRuVGs7JscPn0159HTfko1y/94j+578GLzK7/xb/0Iye3Tm9sLLud9UZ92GpsjRZ8K5SF4HTz/M4l+o/eCNj64VPwEIfqyYjyYmleRvAnDj76krSgVt6JmGDzcURZ3gNJYK2iEX9nZ7BcDvh+2frGCcYoDgYHJy5u/Ad/92ce/8J7/8Wv/+rjX3l872C/3dq4eu3O5fbFs689+9IzLy8eanb6HYZNu+uLbo+P2DKpOWdzOwBPnNpcX+/s7R7euXMLp5z1zPV6317O8By0cKIaJWPenKayp0R/2nGuxfgcijOtXXXFeN3Vwb1+f2P9BDWTVR9YA1RcdShtFTTJeNt14NRnl3FLDvf2+/1+i8/62XsfHBzcXta26iwCmZyoL84satc0S3gqzIuRDfGERVR3mxIWggofU4vqDliDkNPTLYM/d4LhPDJiSiasGgPbgALdxRpzAUu+4QtazLI6QMTHy7rQQeDS44N6c75aumB1BN8I77FUmqFxv25bZ90pwzmsR+UXZw7oVhnKiDlSr6RWLPMDbs6c6MEqdYWGhIEGGrYCKhw6manCaCD6CUFEFCsXfdCbgmdqE+H8CUTdMA14UGrx0S3DNBQa1eF9el7Wt5jZIAbQSAIIyR+EAkiccoEf3xgmg5fQyoNOHXmij6XopCBEgWCueXJ0TedbBDRqlldO3eTrleBOMyIbfEIQtIpwT4vNaDeF6DeKorYUIEDD5AJepImFqzw5dS5bHYOzQGYA8Iw5i5ZAOhAYXBCm3ZOH6IPFUYBjfZyL6pIidCTDXIUGElTNUETBiNqLjPcoGkfggMYg9mIyHI9unyCo0aHlktXgQNWgQAb8QHg8HNPoO1hEeSokS/VQLRGejHs0B+A65lMzjCcx/+4Q5ZzxfYoes8qt1cMh1vdmQkkfQ/TpLvXWerNOm0/Xs++fwXvIVCgg4QQ4FopS6AqbYevESc7MOjy4e3h3D7wA5vofh97oljhFZu3Ll7ywDydPnKLVO7y1A1zYMnG5EHCtWPQUOFIILUI2ukeKSbaundxsd7cWc2bm7rLHxNaN1oMTSqbsumnzQQ3n8KGR3QFu7262mZLodjEvrJd1QxtgpArJXPPs3eX9qoj+BfMp0qPDgLjodWNXdJ70NBCXYlfdsEHoQCr99AJ6wpwVtyV7FDlX192niY/GRO2VDoHRalXYLPzlIY+Arcb+o1El3mR+44J0bfbDqGqoYH6YSXPFPwipFoLgx7F/pWAGRV3KSKCQuLSMRJYX7t/u5Qg5UwVWgcMbVJXc8uDoSvFHbz6kPpeQb418Rcpv8xKcoMbCtKr8g2QrX4qXUq9yP8qfuKO36iFptBCFUK1fQBa6hEwxACezFcPCyFJKsjsboIQQYx0DjoQLtbiepIgLakTxSlXQgBB0wcLCI7sATtEae+qKZdtikcL6oPsFGFIgVXLbZhNu7z9YksvcolsGsalWNnd4mZXUs63ACkmnljYEEMKzTZQmUtnToD7aQQdP7AwaRBkFefGBVCYIQJzqzQolOheFHpGCN+n1kpfazIgbyWllCp2kSyFacVfeOy0hSwq2LsHjzWEPMwiBP5CpZjAZ0sIYWxYxIZ5fbA7FwmFP67J01Z1/Tq4bLixIE6BUmYEkAW0KyaEREij/aWGKEO2zYSsEZTjBzINr951podpLPFH4Uh2X/aXSA6uwEDddg50i3dQWnMEN+ZGSyw2IWZOAULT4gAI6O+I6vd2dPb7txbzzd3/Xdz3ymgfJK0yEwsrHJqOZzadfvoZv9OTXHn/++eeu37iFDRqNxucvXfye7/meyw9c3j/Ys2Qwcowz2kV5dP4sWuWhKGWg9vDfcikfHLD7bBMlJciPDjlJcM7Wgm889Y0vfOXxj/3exw8OpyyXxESqufID4wy+PKqC8s5nWVU4w+//Hy7AO2qLbCMWi5QIxWinL5hIJQ9gaCy0pUrKCJIFSbWHK2/lMSlL7iogoJOsEFUigVfCzJAgeJvHCmIJFIEqWFQo6ehtFVEVHyhSUNIFvaKUQpWdKH8yqx1E23xSZhEsEuDZvFZ8CSZNQFk5+CIcEawW+OQnfo8Vt+jtCy89Mx1O+/32O972zs3N1mTQeO1jF0+duthfZ2YNnWaRPePQ0VDrphWt4BCyCkuKoMXu2BUMVywiXUGZH1HWa8JgkZy3AMmTcY6Cs92IBqnOebZbJ0/iVGzfufWaR1/7s/+Ln3//r/z6Jz7+id29u5xfdPvWzU9+8lPnz5158fkXTpzZunjpEo4/k1xrG2vsgWGEH+LhCWsbANLutQ/2+VLwHmt9sUTUUAYhqBDUI7QXDOSeSg8CVD+tBwaswm2xYDvB5oktXIVFzmgu/CS2sFqFp4Fss+F9Rj0FtzHrKjEE7u9lFQ8fZWOlQbe9sdFo79bbG02X1lgMRVotFZQmhO0YlsiRnfLNlQ9wQ2ZZDiVolx2pMYIhfMdQjbJ0ciBZBm/aZAP1Obs27Y+wcViZpLLjFuFsQaPbJqkuDDRYz8HTPp6F8VfaKkCFeN+KeChFjRI9FUpurSqPeSI4SOARGAUt7B+Fm2EFtaSTGDsaLtxWg22pxNHSHVEyN6+SLe7hEnEqsskMEw8Al38JFnmjRI6HgrRJfTRCAP4T7dQIi+AfERXcQp3vIgSxBKgQ8kxe+cRaF5xIh4aXToRyUSno/LAiHM+8tba25iZgjStopyy9UdMxh02vwqILKtKLJjKaRd83gxcwgsrmDLn2k8YCbx2kyS0+NtgubAFbZrMoi8rJMDSrWOiXahDct4MPX1XWYiJScpEVHYAMI9rTUCayHbf+yG+wKaHTzEZzvQe+vuceAl3m+PPO5fLKhvAp/4lnnsDvvpPfasTCLs6Adj2u37+zCrWYZwAvyWux1piWmPU8rJliN//EbUd2sVQCT6Cy4Zh4jjrdZRYO9CYeMM5aNtYgUZBosmON9HAJ5U+1rA/BCycDgB2+i8ix14M5K91Q9PmIHKxqxvhzjC4tbeq2/nn+MU/dGrK8YUaOfT6HByfQMLs0DgTYDwNX+B8VoBNNZ0UrKDnzsZWJKXcqnupL90Dfw7M4ghNhiB2xAhSxgTzJJ0BApZmxpEtAPrgbrVMNsCamcd+RicFbJfMy2KckJWEC4UXCiF6FlPBk8NF0sszsufgxC+n5idqDgdWc19wNrvIJMwOyMuredfRGB6CCSmRJUWW1BBjTP8okMVFcE4iDfzymbJOW4GQrmQu8ABDVVQFVicdik4Sljf7WR96PPwPbLEnvyaZY5WqEyQgpRkWqeJFa9ZBMefxiDIbXBscwy02rI18oJAiNkrYVPtYsQwF8TCR6VCWFtHOl0iaj7/wRG7amkiYvgYFS4PhGRTftscJSta22KIo8FA365dDh4hnzEMCl+DXJDkhpDO2hBz39H/KimuTVuPjsfxlDRvvZViFRTOm0g04SQE1SAMRfiiwcmF+UTk5ygA4aujLQS1sGBhScJkVAYNth7D+9EQpz9L2+mFwkVb2cxKxewG3xoQAKnNdvQQQPIq5jagmAKpf2kaaGM7Abzt1LOKUoWJ4FZNIOfVwQrVxA4QtQRCXQsnNBcH0EfOOpxQERcoUKo63SsR2kSGWkCFpPiRPf9jXu4EhziqEEiPQBuzFj5dScrUrU7RDnmhueKQ3e67FZ4S2Ok7Aptn4bgTVYyUcFtPOooIKj1O3cuvPSSy8y57i1efrv/J3/eOvUFms+SeDFfb7Y3dt/6qvf/If/4Jc3TzZv376DDeVTwJfOP/I3f/Y/uPjgaZweEcYZ8GgYWQXGYbZMsAA8oAQU7AmpWn+2a7QbDPPYTC/G7X57Mpp/5CMf/u3f/r2r29sNlpZBER0iZbEvYbQvciPisBQLMuTf/Pr2Y/+o/wlLae6pJhhcC5S/dsbkYdnHZw/QZIbvBpcwQfYTFm1fbMkIRusJdDQF7jKOxCWbvSXziiIquHtXSCNI9JAkeU4CbmbJ3fgEApxA8AxUgwXqreBmcHIl3mgRKspEUMnmT3rISh7yVBxWtKJ9iDYOq9lUwQIWyW6qlOgbH5Ft7CJfa5k1EfvGiX+um/nUx/6gTAR96lOfr882KHTz7Gy9v/mWt77psdc+9tijDz/08CPzBZ+KYIzqnESxmh9UV2hLRIVd0CykmeCIukKNmbiCnVGp+yEtzC0ZgEpbmdxIsL53wFetbzOif/bsuVl9wBECf+Gv/tj6uZMf+eBvbV97aWtzE9C7N3t36/NrN585ceL85gmqW41uAJv+7Os6ej+g4vHNk95mvbN2EU3ZvztihmA+eRkP2IqLG0HiHLsOV/nCqVx2rpIltZxzMmt0bmIqd3cOGvXrFy9esLedL8nqpmu4aInkuqIJefRAwH84GHA0S73JF3YXfASg22eAkg48Y4Jna7MTOccmwiCPw/wAwvPAx+wx4OlZ75DB0ggqliMCqKheG26GVnJ2NpJHA2ERCLCkGiLYJYlN6XDQzKzmhsdZu8d45JyjSxp4iF3P+anxKWLO3mG8n5FU5gE8FIUkjEDSVYh59ghipgZVJZARuvqizLA+tbZriiI69MlALR4/WEQ6RpLAPDGDzBwyITeUcVFREilSuU0Ydy/81RgWvKlEUlq01xdMlVPP0XcBOWSG762OaDxbt/SVePSS9z7LSWVguV6JL4++Wkh+DEqSVK5w0IhkWPjNH2r3y9RqPFSe6JjRT2TYiy8W8w4rYQG1Bn5BS212Qaybd3hjpgUfL4jEDCowlQjMaHYw/zTcNk22zOCo5LS8zDVBH/s0dCLLoBWWgkT4i4Gajj1yp9/m7DlrY1Lt4QBTwgs0vTulPLiD6x8VQpltFcHILJQYToItOIh1WJSxfykJkwmmfBtt+EoRTTSEwX5bcsBYFLTgC7CKDiCyVuL9kRhv3Gmu6QMQCi4gjSLQXeGsTJ4p20NSyc9ZQozbZSMZ3r/evPMEgHdTAOv32NoLUjAfIuEXQxWkoaOo68zH6yNl0IIq/jgkiIxue7Q3wblSTL+Bpl1Ihzn47CASq3a7sRSK7o3dGT5ztqU6z1ho11xwjrajeDYY9DcclxesvotlUMWoCrRs8gci0G34Bz280ss4w75nHUNEYaBCMp31lP7EVZkzvZ9+kh81o/F3iz/8doaCtNBVb9+ATpgnV5vXbbNoiCmPjIJIQvfZog74MzZtNtTRX2KTxpRqt1LgKcFFqAS3mWk0RCnCQZNCYMLMxD+E61N1gfnRcwlydwHJhtxfPQOwynT8l8LUOIKAU+EiBl4J5YUYC5FToSSRx2+rrIYFxvHIb/Nc0idC8GRRDvy3nltUwnwhNNexR97hBySCTziyKvMorYlzReykJ4D/ZvQmE/3NZcgqo48V7QWVkF6FoK9HGZKuvIt/BS38IapKqVFQgEgPO4s4SWgv1YpCka8slCiuGBTxkzgyALz8x3qhsTyTnzDu1jUVETgYPiuYK+2wfSwNtD0GgK2N7QJGRPKp5aGdm1iJAhGh2SAeTZdCxTlIJI0zpdQzs5NEIObnz9wSQ+HWCkEIh+lHKjTjBOIEC2RCIcR6yKvWlQBQgubYrJKC7AlO6eECIRRJrASUK7QEwRQf7QWeNsz85NVsBxXBUT9CFR1+gYMR+Bbq5I/4YslKZ8BREIZtAAVnRKlKh3eN/ygN0CYMZUg5tvGMTMjKpCVICbL6//bO4eGETyReuv/cqTOnh6MB5erleN4cM7DdF1546YMf+lCn1x4cHvZ6DG5uvPXNb3/fu993/4PnDsf7lVwK0VGLsMH2JjjIfKUJmiqVfAFlsGQ4k6EmxjU59gGH5tmvP/eVJx//zQ9+mKNIafRsEWgrIEGE1ZhSkJTmXxhs1PErsccD/s2fo95BAQaCEiRmoCgYaguUC4yKN0JxUliqDILmObEAsbkUliZWoZiwMEiuKPfybmum8+Qb4YEcMKaRhbx4gUd4Em4YKGKk9slE5La25c00uZKmJPLdclPHuXOJsEpoaqKsKIgBsDbtNJrEQg3Dk5npkcoktH5IUsoQEx54Ye07o5JsGU8h8Q9qLgDY3d1lFfLtj29//OMfP3tm86/95P/sTW98bGPrJIfTALhCrtBS4IsofNBAyYEUU0pJeMoLyuGPqcVHHvhMdHk2HxVLSgQHbGoT3yjDFN29fWdzc2N7+8bGxsU//X1/5sLpS5/8xO9cfe55luwOR+Net7eYDZ9/7ukHHrrIoaIM/4/4pkCXFdV9euBqMiMkAF/U13obrRNdTvUZ+6lsvBMNqYwVHUnCBQ668NiodNrhDBxkBHDa7vDrYKG5RB+mhpX+AoWl4SpPhvxwGbEhoXG5xvFuLJaeTTqL+p0Wx6QQbt0P+Tnzh8YVEfIVPZ1pP55IVn0iXZZZBvENsV4aSBtAjMP5dMDpMhhKlcRj80NfrPdvdCatzgDvhxUUqovw5KdKQEqCKJwwYCFQhUCsypSWk9DyXxrBVPi4VZFIZfhCtXYCG0UQ2VlLjQXhcGFGhllfbmVSQVFN1ZNfaLNOkQeScLU8d4XBU7OCIx1bFqC4goWaByBZAwSoVUZBFd0DXjgOXgU38avI41EKk0ByjJBI8n7rpZqJjD+mJJVP/mkMixJLV0apSUoQmhHl4JlfG9+8Mx6E1ih9AjUhguECJAogDWE8UTBXbIywiPDbG2n50bMPIjwW5EWGS3lJLaxh4awPkZMPmSdwDJryMoAOTi6IF0SujO2QXiEUtApsCrVYYBiqpMraewIIVDcBIP3ibp9Y/ohh6fuYwngJsTg0EU3VPpAFAC5egmyyUQ6Op7MELKKndpuigpbSmXKgSIAJQW2hwmp8KRkd5OJRjx76SE8ICNlW0W+Hqra7E1nGRk9f7VA9zOyJQPLDybCAEpKOE22WLrzyghBucB2Ajt+HU8Jn4kUE1TrK5Y4NsRn2qxd04RV7JUWqqBP9dBMCo4yygY44WzvhOFsPw0U7COwysKqECikjk7SE/CJMMhQVC+UUU1iTxOFmYZkSM7s1ViCFeTIRxErW3Aumlgj6VXk8QVNeFHFegeeTelBy83b8MposZQYgeY/FVjmiVpFWSQxeBZkST91nWpNAZgkK+oAA1BG6xVaSuPwvXCIl6UnFSH8pd3XPmqcq0NhSCklloUVw4/uCPnqLxHhUcLkKSVhcR7Ni0yigirPs6Wlelw1jw2wS0VMkgoyFfcEkOVbZLKuCb2SBl2SAEoqqVlLIihRXxCd+eQU/kSnZCUSJNCIpIZrKMyzDgjIgobpbpigFMeMsCGDoHsqBUdWmJF55VI9WWxxc8lkB7NKWnEChSkR9bbxQf5LZ4NEOstAPvbElAnNBUZ1Yv2vZRywBm1K9pRLvMHC9A19CGTgJ2aggEFzMFxVWB2wvACvuWhuKqhikSaV6AY2aYbQkU2LhCdaZygwUXHYwFnn+Cw8ERC1mxVzCEyOeeZQj5fK3/Dl4kQpFKuIRlo2s9bhktHCZbXRMCa+x4sWmxSKCDI29cFhlK7Q0E5bGICbjDY5dWa5GQyqguHlDBGzlQL3YOIZIKASiMIUsxJw98bWvjyaTtfW1h+5/kK1n4hG7wZIhpPLFz139pV/84Kx+uL7VunFlsLm18T3f+yfe/a53txYPDg4YOdiHaIsoaqXEJSs36NT+UDnDEim0YIpHsyxmxsQlDcrLL11/afvlf/5P3n9z7+6UHqBemkY4IgZA8sj1kOIrV0opKWRoFZunxP9/dWNUUgjY/FdeZWYAI2/RRTSUDlFsZcOzQWBMjsvVTpPPO5IMwpwL4cGRPNK4KwA2H0RFFDDzMCvZEGMAQgxjmPYHEoKCQgaTiOUZ9XNIyyZWukvjqw4rXX5UAgtFHUSdWiSveaC9gos26Irf5IVZKzYCDkH45o2SaYbo8okCpwTi2tFQUb+p5NzJDy4mognl21UzvmKHhBhITQzzM5YYcqyYDnhjIRiPw7eDBIHSSLN+dg9A7eYaAcvxBpp9/crOL/y3//3b3vrYz/zcv3/m7M6Cb/Q4Csi+N6a21RLZDs+ED3v5FQ2xlkiARZV9rOiOUIgwZYQm84KY2cxVzb6ycp2YNFa1Fl4+i2rand6JM21oe8MbHmo3v/sjg/HgcK/Vu9Ve7126/Jq7d/ZuXNmejZcnTm6xtOHOwe7WyRpLm/SIamc4I2g0Ge3vHbAMamt949ptVgYxwf8yIyEaGBFGRqFHY0SFrDV6t/ihHcfcckBVFsUAAQAASURBVH4J4yGDwWjrVE4tRKzWZZjGKStwS+5DCR4QWTw7geMFgRmi1zema+vsbdiZ74+nB63luFdrjfAWKDDDAw0+GlubH+LoMwfFN/motEt3DzAqyLHx5xsLptpeWLLEvzlcLtf5gm9jucZO0cV8bc7OJdb0uxaov6ixoL8z5VyuWmtcb/G59WFjg4iZRz6gSwwMoywZz/M0JHgSYWFa1VHUBJOnbaHhJJ1LiFyczboHPKkZi5OREeGOUWhJeLD+8wTTpAPu4NbzMXBWgFhRGCzqcFZjfcGmyllr0deJshaTFP/MvVE6T+ifuCEEOJiNoLQ5aLF+U6lLwYsw+hKcDsXpJUTwvVL1qehGqr2hhnnzqfyFGp8TbpxX9Q6lyRS1Kwn4itp1CMsyb8QTYUKc7q1+rsKyd639AF8V1xbNdgeoWZLqyljC9PTCn6r9hU1ymTdG08jGB+YYdY7OOPvk4TrWAVeaMAruiju5rF/JSDygEGNcUX1pEbKlAz22+Lpwxc8+029Mc+OJdeTMf/mj2EI+1AoRzMBefKnFeMnlAVsBDe4drnevgf9sfAaCck4/iGnaSA7iiJn1MBk5wv5g5az51HsmGAEBhdSUZo3N79RiP/Jd57sNkFffxg4ycYZKlxLBixVsaVthrCsCooRYbEYYl2gMw2AQSrAb11FMVljhf4bPNdbNqwzblEgJHLdLTSY7X8V2s29jTYZpsZ34gy5rB2MA+ANkV6ou1RJpxunIRjlEqMo6HdBJGKhZ+SCYE9Ic+EbOJJ7SI8fAeviPhOoYmCd5w0jy0dcBMhn5hN45FY+ztRAeZ1u1mYXj+8fZ96OvYcFV+TySFJ3RCQJIUVhiuVhodIWQ8lJ+o7HyBYYQzg/AdJxW9THJUKIGvDIjXi74CK26KRMSG0JYfksZBpdQI3xyOaI/vMqIKjRPr7wVAK8M8w0ogVB+hUkh0YPkkIoqE7+rR0OITsbquYQc3Q39dleBoObLYWFUIUhTSgvUqhzhh3n3SvY1qayWXrzJ3nLztQDxvcQCQbaRhNiUUaAJoOKnABJPjGJaZeQxkAlJMclYPZEGXFDgKn3w4QZIzKdjV5qIKpRUwE1aKo22h+1uanAyy3Biy7VC37zqMyvc9HTT+qm3+II0CRo9dDWukv2Igr4jWxzek52tzk1bYeSNBKUk6xUXZXBZN9TSEBkxmI4wEKPooCyyoOcdu2Yu8C+VivpLVDAiwEICi5T8F5C8ABD2OiEA5kpKalJoN5cMJjlw8mQZVaEpLmUHsolsdASttYOhQEMApVJakgURKgiApfKJqzDIorlJZmUBGdhoApWHwAANzbb6JiplW6Tti9ASQhNIO5o3bDUjGXO2/25fv3ENJ+897/vO/+Q//Xv9jT5nTTDywZdOGLzbvn79V3/l17/8xS82O9cY/j+xsfGWt7753e9+b3+tO2EvpTwKeimIW3BIIAYjnTy5EuVh3FKeugqVY5dcC4FlZkzuuRdf+qV/+EvPX706HrOkCf6Ia9CWCxVDgv0xNhIcovyt6DXl/29XAX4vL+9HwIyTw5YXoRec1HhQhbOYcjgM48VVe00lheNksf3ixrMMiVIdCQKogAQCwuDBSNhta+EuNDjgeYks++Hdj+MIT+epcNJ6VcgWiKhFryzN8HA8YLX4KV0aTOnLKqtEJRVh+hk0cSoGzTb+vWpkc4sy0ZO2iUFdLInELBLglIEmuxRJTatC3qizhHjBC91B31I+D7zIGjC0IeXJizaOUevuguNlv/iVL/zCL/zX737Pu77v+/6UGxyxETaoMpIspdKFRyqVXMs/SRXlwOdXTfQywJtXhVN5NlS8Sg4ZxTvoF6ygj0o1X3Z7bZTz9MmzP/aXfuzXfu1X+TjA7du7ZKNP1O01b1y7Dtps2uNLw4cHB+OxThWHA3IA4eBgxEG6GTmpz6Zn+dZRDsrUnlKo+ynFhhrgqmXKoi6KDpxwmI+tk5Pd3Z31jTU2BlN1bP9DRIgkvfWYlJzfogGWN36qC6IbjbV244RL+zixpb1XZxe4lsUy5R3OzWLKjB7lseooI6pjpa2ITKVi4/syaonXqEwVIPKiMuP5ZemH6sdXr/hIIKuOOBV9Um9P2QyAtXa0E6JIIDd1/TTRvii+QkCYD5ORKCEYBkw0LQiynOJRqWyOpnbofmq1C49Ey0d0DWikwK3HcLCobMpxN6zYnjTrPRjv6UauTWILMv4fiEAR65D8YNVszNo5+5P6/9YRJjOREpuKtHvipzT8EyftJFqu1lkTNMu5itDITng0vJJJshrmg1C8wDlX3qs4mUMa8xeGSJcyRQfoplCLYLVss1NIIjTcxEWC/PKWD2I66GYtIq8yl88pjSyWSxDTu56SjPCwFXJCXGQg0oMuk5FJvYBrebMum5am1rTc+K/JIKnVlFQO0NH5Ai2TITfQSQrAQJUwSetYnqnJksZcfKKl8rak8VQIMlC8IweYy+BYSoU1dnrUPY414k1gQGCxkBzh0aVjLZdBeq5ojI6ASCscVuoEAhiCC6MuBAGDV1AkMx0seEYl1C8EtrWcuSs5Iw0JC1elnFQIKtRwowaxhZfvV5AergFFCzZzTb8rdYFgeum288mDDAKAYQVauh/Aobn1FgGRRm6RSCtoLWV9ECW5OEoB2USSnbK8oSYqMDUQVOVmHiQJpMWAgmIvNDcmUDNIFfJAUTwkjHdZmffEGSoMf4J9cocjRilccwEssOBTcsO3ArIA8TmYKMF7MQUFkpjdq+hYHr/9Dbsf+CLEw6vu5ClwSnR5JhBsUE3w5PAEXs0luqaSvxFntPDVhZq67G5OjBlXSaC098pYS1jFpjSLYO9/eEJZaBvFGhhLISXq0IpTyVISBLOybxoJogjhnZTzHBwKzBRIaHURpUegOFKOweGsEHgiTgxL40qKuAKil/wpZgUJ/brgM2ceW6ApUjT7cgyvN1hbRiiVFM3kH3c5KYEAphKbiGMEqA28M0CAvkfxCgOtSaSkruls+gcbKMBsGjOajIiIcQq6zQAGAHDEHH+CEQqXO8cjYaxQsmpjTFvYQT7rB94HWaxyNiaEpACKxBCJoO7LsrEdIsApTrK2gHTUfLkI2jSENqqQErJAruIGkZNLvnLCj2Ek0WBAwpGEKJJ8GaiRL+E9aVFFsLFpoShxxXcKY+SjoVIhNpVakBXKyRQLABqdazgHzfn9AJRTli67ART6WeFHqFqXKCJ4xzRQBgM12xwIELMJT+xyAY9S+eGOvSUwVhdonBLAKmM4BwKL69t4/83JaPSNJ5/evrK9tblOZwCxKZHl7Dc//KGvPPEv5vUD9nGyOvnSfff/4A/9uQ6L9VnayPlUqLj9CdCRXgrTcaS84CcD8lg4k9pgYhYRMXzBWep7d3Yf/8qTH/rdj379xWeRmd9ocM09oy53Awn8QkC4HTJhA4qN3IADG4BOSHWZVkZUpRccEvbtbwU2UuEBj8R7lXD1yyvn6nBv7CYNToVjQgyzZdQfYuHpvF1n3QZPDE1po62KeCJ0bnrdAR9Pnu0HUXWDEipdkwIUUvS18KX6cB4U2pExIUf9GVfi5AScbz60JCutiGl5xYh3kA7u5k4QwKlEYso/z340WVKqCCax9hlrGrVR7fSxEIyfyoos5qdVlQAlKY01is7ptHhhHGGhvko2xNKWobED56wnaAHMobaKSkphBIEacsqCWwdghTKFA/T52PXBtAl+816nw3nnjuByUN6XvvjU177+/Oc+99V3vP3N/9Z3/Ylz508MDod0RsAOUNZ3YTmMJs4UI1EGeavuPCSR717SKQMY6LRG+60Af/gqbYmPTpHGemQlxhLdvn2bmjEZHbLR9vS5Uz/17/7kJz726U998vc4jeTkqRPDIYcS1r72pf3XvJavCzt6OPPjS5LDmX07t29zMg8+y2TCp3m3Ya7LEZWZ/z2sHd8AE+fZ4lTGBV0I+IJfy5IhnXO+zXvAVNy8z+g+zOLLGNozLpRHcuE8M2aYFlbBjMeM1tPvYLU9BzUumr39eWOAUWY438FFzttGigiY/hI6xJE9mhqYeCJmEt1iZTGL9Tml4aDWHFDvwHbBt05JhR5a2mlqMt/bTvWGh6o02ybHcz5cUuP8IO50TBkRpRj1UKXKf0N8UNdKiDKw8x9bbRC9O89SYXosQxicHUTp2KJk0/0CJGDFwlklxqPw/uUfR7ajKwuGKGajdnNK17jG3VPdqRwcfsquSZwm3ET7VLP5JI1PXErhuxic/gsc8Axt7Z8sksEUGQvLumpxKGgnwjfxSU3xucohel6xavym4om1uCemAAZ9VKsKI7uzf06oQbx5dJ1Jz5mXjkcnpcxPXutM/UbkqDlktNgtrOqTtbgUaMkksw5bKjNneQBSGSjGCt1BfViKwLA7HQTohGwYbSceG9Tkg1m2bkJ0QkC4pEFd3Lgypa/k96YXbAR2hIOCKUZxFgxFJGQwgwU+9DK0Z6TwBpFAknxZTXHuhWET8H2el8sRsplUN62pSC9UjgPIYDrZWFd3ocFmj8aVYqjo3vklHf1svhREBmlcdq6i7NgHXh0l8ZvaU6cCiKeeEArYEIXHzym8GCP4jRZ02mvLxQh8ZhOMDAxkppQcsaSdGyBkd50fjJ4fsaN18EsXVHVYiL2OoabvhrIBn2RyLiQUk05OIgiPII3hmV4WfRuwCic5a9V6DaZIlA+DdcdLiGUXA2eOLtl4Ye9lfrCgMlKf4RelQapcUrLKGvgUTkEagkv1SbfWuyL7eNZMSrdG3jlkMgYHRSfrrFkyJn/lxovvEV55LgGCSTrzmgJdDOiYpva1AotEiYxQeMrphYYQEatbPVeQDE9GQOcx6JUZgISAecnhW0mU8Oom+gLApOQhvBcH//GrPnsFqaPsRw+JCw9KqmBVAquoYy/38FgFAseyLZTL+HBbgvISLpZEpkPgqdgmzmsefKr0QzRRBdhqNRcGT+YL5TwEFpLhfyLIZ6pS1ckb82SGRAeJUlD4UqGbUgMkoFfgA8UQ/qixXHZU43dSv6xaRKSGSQVoqdlg7FgPhsueQHyy0CKGJo+aU248CXxESIukxAfTzJ3hingQBWbEZlyQDNOogVR1yRU5k4mclU17R3PLFLJ+McH+EzJ4+GzyYO0P4ckYCDIVPG2NqEQVLyv4SchzKdx8/CMrxit5Yx1A22IIELR8Lw82m1o6uxTxsg32uXAPOAV9+ULhpC2sFmVGfG2KqFXEkkGDL+clm4IcKQGa92AqMpZPQHKTjQx5MyrMIiO9M8oXkpYCwDS1OniaXSP5BUyD77s/880XOfv8zNkz3/nOtzzw4H2YGztts9nh3uFHP/pbH/mt3z7c34fPHJ32p37g+9/w6OtoEBghBhc5A4u4YAQUyK6CJOHgEV+NRy+5h01izwIDeBDNEW+7d7c/9rFPf/z3Pr1zsAcUZsdNKDTnrOnyaeq9KroDs4gnQGV/eUiqsCtPITv5yusfdTdzAZB7UD6eFlQiBQkrbLXIHms1aGGcjbHCosbtnG8Y3rMylDFEiWH1MZ+amXL6PO4zUEkKXjKJ/2IYchAeRPISvrmEhjcXaDk1DGgWRpAvOoYgYaDPwcUwMhb2p0bkPZEWxVt0tQD2Xf1M6aFWIx4syhvKoJ7oe5GMS6FmSzmF4H+hj5zsyVdxdF2cpGAXCtptNxPHDFCWA3eECRW4w7iwluezBHIzDZ/pIITv4KB+DP+i8d1W249M0OtAQxqLp5564otf+uynP/v7f+b7/+T7vvu7PQq9lj2IVCs8EtXZBlPgVCFhhyGUUJiTX4kpfxFgeREHA0ExP0FK3HwTTyAytMynQtmRstY7TcJOb/2Bh7f+7R86/aY3vfnq1ZtXXmREYMQxoKc2LzEMPRiRuMtCc0BQcVmTc+78hdFwKCecvrDSUZGong77ZZgfNloZ2TPb6x3s7uG++yVEvzSWPaCsuGuz3QD/W1Tlnz9xVNOSm93uhluMu7VOvk3WZwx5rXfqL/3YT//9//cv7x28fPpMl7PHsY5I0LpP537B9mrUMbtKqFl21exz4klowh2XxzXhWXcmqiPXQF+6CmNlGyGsUnA4FA+aU4gxJZ7GAjlgWnioDBByJCMEglUNnvJHGdofnikLVweFQYUy2YWykcYzobWpAtR2YrCId1AYzx1eThl20PvHNHQ1ZLY9HQgsmkfRLqXWLjmFBZc5TYV8mjPHSTDOnTbdLURAzw3BqW8VxSEQVKEDivnPH6jwIKrp5CSJ2qZYiMmP9PnPjKsrj7CB8NVlDt9t36nFahvz57rdjjuABeqvXsKhSN2sKUHhl7yWkGiTCEY+Fqj5QdDMyeNB2z4qEFmBXkUIFkQjzAXUAjzFASINHAwMNKmjt6AZkHBaCXxpYIh6XEpkDRuFkPQOE+gBOJtcEAWXaE6tmQWRutQ2BMzRYOg8UIATt6cHA1qZYj3FB5vD8LcoqCsIlpSaQBcvYUVlLi64K2ps1bj40GfmAcnLegFS4gkIUAOmWhcJaVQUAxetPRwnWnZKLL+OWYBcnHBwtFNE0YWXkOmKenQU5WHmwP+AbzuHp/hQMJhrn8OiKFEhKSFjIx84gxTgpwfzROTE05cgPANwfntAFlIoa34gE12HmaU20fcBcWexSBI4oOwKtww0pXaQUkKUNYrAhYq7UR7OBUzm+YAvYdKk7IkUR15CpU+mEGuDyqPv966VkhuSrJEXAqquZDRKUksaWFCBrd5L0lJkYBRIBpM9aYnkP2uhpvcb3GYEmpCSJYlUacO8hHH0ElTKW+4IJ2CT/h72JUUpzPy5jgJLyCvDqz0Aq7T+luwlpLALCDys2CHl0SluRZSqmtovS5R2yRUIkQSeMXKuTS4SUW9v0xMNtdIOaMEFvgWLbAowd0Rq2Qbmf+GD54rQJqf+lry5m9NUAAGwJedc2FBkeKkyagjn7QAC3XR/LmMSVBRW5QOcrNzVXu01quw8H96cg1FsrYoORo0wT6QmIb9xJnyQLyqdNTOo8IshZiEmSq03is7qT/jDNiSbJzbmajVG5rBSy46iLk6nOz6xWI49M4Rvx0atpVDVjwzMFSY50awpwcDih9HwkYSaLBqmDNt0TQsrUwDP2XsACgAEgIbC3JoygVJJrS6BYEbwYyIbcPA90+HaQjlCNYZXeSqYSWdRBDwkyeJ10RyANHtRKNzvXosJccAvtV26ZdCRRsdISUfkgYCMsZo7MECrBgRYqr+vnoi+5DKxEBZCNIIFJ8IYsLmxfXU+n/Q6Gz/1Uz/9Z3/oBzjfkJES2pK9Wzu/+k//6S/9o1/a3Npk5pbPlL75jW9+1zvfi7ciJ4IOSkDRWFVZL45glCv6opzB0O6Q6bvdDgXX5y1a7oO700/93uc//5UvP/3C04eMIPvdGXgnRfUWX/Zlx1U5x6D0ACgEXgOdBJSoiJFc9EXGpcgUJtPy9m1v5np1hDpwFHj0UEGUrzXWrJuN4qypkLrR667xmTM4gGDotLh01GYWHJERCdK8sEq7OeIr8ygwDKBtwq1nJW303STI1vYKITjyhOjiY1CnEJlq5BlBtDou+/HzkFEBrIMlUKJWLv9km2jmvdzDiegMHM3Yj9CoZ4pIepOTEHMpJKjTvKaW0uQhBsqB1QQhSPlOSzqnRwPe+WgOygge1CWgkZ6GHnNBDQkQeAdOAQv05qHCCnzG7vAlXJqMdqutdpUYgHR8bUh/Ez2djTkKAqbMW09/7fmnn/jGrVvDP/sj39dtrzHiLOs0IjAIrRAx/hfsJSHFWFUKPRbKBe78zwNndlHf0B+kCNcidlJLnYmta8gJV9zqzsgxlNY4YWdx/ebttc21x9782Jvf+ebR6HAwGv3Wh35zPHhpc6s/m67pStphBSx1juN024ODfQ4YBaRlwUvEiZuZi2dFzVpqVhOPF7PRfH93Dx+11+LjG3wfqcY2hK3NLcwpthflAAKYFX8IfHmH37zqkiAMxrNT1wlpdA9/+mf/0ne+982f/+Lv79/crs2HuBqwC9+NoXPmJ5puI8m6iTgrjHfyIdNYZmXBQmhikZpoF07IM98oJoqh7hTsSVEd/K/3TPcsCVa8Jg8pw/SKyVAtk/kHCfKf+HilOdUK9vAOQOoGn2+P7tkVgDLVB0FTC6RzoM813WHZWat20Fqw32bQaWw12aKzPDmv7y2XtKEDvsqwXB7WZ3xjmDkNDoWk9tGIaLq5zycX+MzUsruLrhPmBicOfhArsBbFXNCZulB0Q3UJ4nm10vPGPgFSM/Ypw6QV5Sm6FwghdwVOoZdE3nFf6T2ZXkDwGpdNx45KkFVfzL4hX+qC6ySpUCT2qjAjZwwEmdGjVfUUJ8OBRzMX1lcFghVXVTzKgJb5AkCOzA863GA50DTRPKQge2HYHBBghRX48KmKzlpvzpQvu2np3qNNKTGJvZF+6ZYQ1NNBHC2by4P1ZvhKNQCQAqab+g40SulvrcN8bUDzqqzwex0kYunvrMW2DmewWBnarTdvNros+AFVMENLGZmaNDo0lHBSC+DYWdQPqlF1FsG3e2C8aM2ZnQJJulgsUuNSxGpRGYPqsPulwwRUmw98ii6WiQgwgA+Rlj0y9IbPbIN0t97qzhvs8FpvLA/a7Z5goYKGljYfwx5nAlwAgIpZfxQEwXzyq9HpdZmTk2YWM/AVSwgET8oBCFqA6GA2H//kA8kehdFDH6CTNJoflrnZgFPl+aCq2woEI6egiEd6PuimO30QrORjMmasHZDW6Cn6wzNcBjktJxeJjhTChyWfYeEXL8voSneMKM/RZBKETSUjUUaatPwIgCsVRc2usrauqSSKqYJagUni6ubxYoBBWP6QkBmApE5aSwoCJRD8kq7cSgSlVdDvRa2SKUu4JJAi1HtJfDLncYDHY/+o8HtlkVvIXioNTyUOiVlt7VsSosoiF7xV60DKDPPMKXZAybCQnUz1yLzxphRUkqCWXCQtJUQqEpaQij3qhHiYhmd0gv8+muroCo5k5SKlWVfyDhaFSUTG3DkliK5GwW0leGeUy3oM3dosCHKqDhLnrKn0ixlMjUmqvLbrwM4uiGGrM1AYLaZQkqCKegkor3ae/1bP1rQ9dzuaNp+CMMxlaxQeLMM/OhlKHhySH6zDSYesmChj5QF20MOSw1hKETAlFjTM6VATk2LIQGXIWJBqyQuVhmgGcxk/kCnykZLMQ2Egz9Y09pEhHQbqpn43kSSUh1FgnIEUIkUWIIO2T5Gys5BYHKoa/RvApRSJkLfqDeMV5JNSv+uO7XTY2IqfNHGPVAPlovgoiELTMvoOWCmhhks5a2I5FSMpXTnCcKyugXkoVxQjNvkv50wHDKTJgAvDuUC9tb2DtXn3e9/5oz/65++7fH4wGJiovnzyyac//JHfms2Gk0nr9KmTP/4Tf/nsuUvr62uHh4csQiiIaDM1d6UChH/oPIQqBchV4PAa/uEwT4cjrCYG88knnvzS409+7NMfu7s/rWH4PL6jWCwQhmHY4hjHoBEGAxPCERaNCv8gg5olH5WXUZFDfo9ozNsrb6YPRwlePfIe4AVKgFFuia5gyzWipcuZ2XqXgTaHwJlSLyqAWniqXEENHCEblUNVOq3u+tqywwZFzrtTyAxHKj80JNJTyFKMMDXf1DnYg+pKPvQCveCmVitHELKKKciYc6VLOqAEZcQhwaIdq29RxME32StN0UVKJIAc/K1ol3wQtv4kDLlS96xqlmCvmdIn0+moOWGVjxNv/LNky6NC02Ijtei3iBJqAxz0VqUIF46x09YhRbcRT1nPbXvJgipW9DnvZPcV5ra7OG24FJP3/8avfvP5r/7wD//wg/df7nb7kEeRbryzFiqUUCJDJMTiVhhLHiXCLcJIlh/zwDPjCDPWKl2yEkgiIu3bA5+RZgY4iLYDjODxlhmObDV73a23vP3tL73wIl8UVmgyX75hTLAtVI1TZ87cunF7PBoWBaUc3QKpr/CgC6TCz5snTp6s7c+Xh5kxsHCI4xO/B4PhQbdv3WT3oZiCsPZKmeEL4yf54BeSsH7aWIdFGZbv1N7xnd/xxrc++P5//Bt3b+74AVLVBi8MY4T15kRC0ChMEynXMgtaRucBbStZ5ARFmt273TyexVlHD1zaQMTXdCdr+Goxcr5iqPz1vzepVgikcBB2ldKetJ4LVaXOkT5xPaUUpw1r4GBoWgiXrSzGA9BvTYe1w8XGdLYxY/lgr1nzMFP3LuMxc6g7w/p0LZodthJP6x3Olx8tODoXLWpndAQqxARSrbHKXqY5NUKnQ/l7BVViTRwKxNtHKPPXJ/4Ra2Dijp6seACiXUiMHPMpF+Dl+ipACHmrAqOxZKUCwWHtKayFAezZEBo1gqLRLq0prUqLkRFJILDwLYoBdwVHxdISKQixlDLS5gd1Aq7ra6mZHOvW6/p9FV5ikgQHDMqTQ446kFIzy5el+66FZjzQ6RXG0G3YVIXUxdgZyMaGG4p6WJ7ea7edDb5wzOWLdOlDoqYemBkuU5OY31MzcP0d8Ub/s0CHGuLHwkQ5HQeptUxe5830zR00URpI1GEVPCzQafU219kWjiNCR1LFhmuypAUzqQX6F6QnMZ/ilRN8brjL3C11ioQaYi7yAYp9tVQW0EIsDDX2OzWM/hoDHeu2/a0mvfc2q6OanBYwQSIZy6cASIEIa7dOEbQ1u7VNtrlMoIvKRdltz0BDrBkWxE5KF2Lyz1XNNb6WzIgqWFKz2GXESxvLSO/QtEifETuoxgRKuXLGHIKhYaBNmjwR48VPnoyKxiSUFGLiRbhy58nyS0AJrJ754TIFuXzwyezR8wCoUqh9VZr8FIQEn0KSytIEwwWkUqLPwdpSNLiuKPLRmyHEkxJd4FwzXkcphkezGSe0UoR3MyauBPtCWJlV6FwxsEIgj0J4VUgJ525pvnhGKY9smfIn4YLkAoEwxFfraGlXraXEpRImL8Xjydp+QgwA5J8uAm+p0oHBeDx9NAOTwnL0daLlzDaxLh+re11GTM8DxTHvaJtlAY9c4oJXBISYdNukqKPgLbpYOpGcX9RH49sFxqB5qfaFJjCQLMnBKjvrTwODqxicaXRIreQRP0PVM8Y9mYvDY0Fp9TKoSDY2k/N0qGk+aQ5rzRvQKJl4t4ClvfKQMcolSA6kDWBNJC47gw0SQQwfw+AQeupqHAYJk9kwkB9tgvruCAmLDOhl4k3F5YWmxJNkwfpQ0pNGroOrzRbLH8koHyw6LiVRVjpqJNhbl2JldJZSqAXLsKANTbKK3DBg3noZl2DBGd6FijARZjj6DhbFikzuw7yRzDlU1sqrHpBMcTBUILCFpgbPgUV+MaYyBM7bVQffiFXG8Q5NIgVsuYjF0lNwPatfDTSNLBIgKe1ROCkgr+tzZkhwm/kWKQokLYWFDnnQfM9dEnpre3syGP7Bxz/z8nNXzpzdZB0zx2x85Stf+Se//A+dGeixULL+3ne99+EHHqHRmEyogJ42XfgqMqIEVEWj+s0Yy2GFxzUFBZaJgwNE48BNR8MPf+RffvozX3jm+ZcazbNQ0myN4am0SkIEkdkPHtE3AyIfq43Gu7I7tflpSqy17lLyqy/C5ydAb9m4S54w5iiJ2NAH9E79Kpf67rsUlat6UJ0SJ9dSo1EQRh+7tB5tvnjP92vx6UklmewoVEF1mmkM9XQYcaWsWq/ZUyY1FnU4/h+Piv4aTqy6QwXj2XlpLT6L5gHItkU61vh2NJwMjXSwHoQji+HIFeTqqPoBFaAsFbxKr5ImQvXh2TE60DKM1drUmaz9DT0aBrBeyCW/WuA7qBFyEvj19oGpOApGOLs+W+MccCaW73syzEajirahkno8NqDEagHCbZRapNBHoKgM/lAEHEYJ7YGjmghdjweeqL1UYf7jqpEPxaUk27/a4uJoMP/cH3z18S8/++hrH/rxv/wTb3zjozEUmoEchAsz1D93LvHkvDHqohAos5QsItKgGiWoIGdJytQ38OSZG0nVMkJlTGMDRoPd4QFLhKG4zVeZer31SX3yhre8udNvXnn5pfGhwx9Z/1+bjDgzl8Xxk7VeX8fdr1ln7F2XRmGDZmWOLAoSEa4uFevJKEZGahwoMHyCJz7DYSLtLZIXQM4MokXUnIlHJB0e7m+c2aWb12rdT83lK6IsmnjkocufuXql3d50qkQbaL8bVsdIQyj0EsIvU1KM6DJIYWOBPiEItBguyQFlh723GoOEdk1bhhSBwLADdlDHy0/8clevYVmMVPVF7T0QhVBjOQWLp+aez5QjJximhSZ7MkzgKoicsydkBIsTxyCoCrlsDIaNu4fd2W5vOoHRG/UxXyH2k1jdZ/gOQW32MOcz1peskmdJEm3VZFwbTJqcZ7zVWPBZ8i3m1jmhiAFVcePzC607OL/5CrINAeNLfqYyldgaFH0If8IIWcAhyJDAlmv/mcQLONfQfthmfckFOSv9p0HMKCzaaO0rbAhzVTBohdhyEYlBU/2sH4s29YLBcOXr/3CUu0phPtBBkn5gzVF+ahzsIRmuLyXzgKgQuG4rSU1Page2ixYDB2xLVW3ZNOhw+iELUUDGrDmxh0YOzXbHVXm0DpBv9VQcDJYDShUpzquUoYFgFPQoBThASk/GXxxTdnSr2mLkyT6MawvfQYklPrHrvV25rhUpDMe/BwrKqhaCLa6tx9Z6/g9sFzaH5GpwLJLsLCGzN23PRBvXJiHfouYzwXyigu9FOJLi6fLUMWwpfLRCNBYXqY9NJviWm/XGN1ptPPWxrNU7MI30uviRuQVG8vDXydNmhVOt04U/GmosTa8xGdFJwNMnmi4CjAAzOgKw6Ly9cbrj07Zr31kARFfI0SJmBdlyg2EnOaMdfkAAxqSbRAvZdv+eMw5qlD2BMed2MRaCpFvskMGzaLNxiIxkVWXgg5IFc/CFNZTBxSvPaRdkWOqfWBOoEtH98FA4LU9CkT4NOhds53+S5LZaiXMlwSVKaDwludVhdfmUqiF3AqdAsm6QbJUnyfMqniX/0dh/QHBzKMKEBTpUqdkVDMo3anUFhgwoAffigoRFU/IrCl/lPMrwx8S+sqxVzqqsMCVKiAbza3PGT3UFI1KixFQVaHG5GsKiQvAa4kUORSMfl9yzCstEnqxJSif1jvB7HCGP/4kOo4VBXsklRItBdnDIEDtRxTEs3BCq+kIGDZCicVyHymZulcl0uvtcluKEPKP4ZEiDLE16FtChhEWTBYWoqWjqavsmFYCO61lKCXVClk7NZTSetJ6OVeFDXobbqMmp/OJmC6xHEOECT5iquQwCW1tFQFFcY+IoXZUs5BMbDOKn225qpKKHyQkFQLO/ThXR+mpxKIcZA/vWWBHwJEnhK5RwZWafCiQSoEEFh+QgA/3ggbBgmDJQ4SwfRCk/baX6i7HWQ0LC9jQq3UlyhRQJy9EiV8nW4mPxQEKJapUB6Btg9QMwNsoOVLTgbgH0MtxxkDxTignBK9oSUJQOxRLBGHMam0Z3f394cLjPsT8/8H3fe/mhC5DG0vwvfOaz/+gf//LTX//aybOnNja2/spP/JW3vel1wzFzKGpmhmwgUnylmD9ulkCg2i0TLEU3hbvWNjJ66itf+/0vfPZTn/z0hH1edo2Y1sSWa4BITb9FZpMZmMoNAmwW5Kyv+MRRPdISkqL8JbL8lHtexCf5StJj8UKvEor4vRiyVFEE+my08ZLECxiolDQ5eDy2o7aEONVwGGNPBhIoFds7kxYYUK+aKphUcAbB5JgH0EGObW8ibMngE7mVstizTpYOA99R4sST8LDd5Zyc6fjApaKooqmCV1VvQZWwsN8IChMNZoNMZZcbCqRGUvJTsSEUmp7uQeqVgCMtzANUFkFEl5zsAxpcYckKFCtc1JGPeND4EY7lwLUjP/UNRhUeWpil5iYOXOKCVpMZNTRCzGKrKrZBDASAFRnDvgWr6h9//Mvw9aHPXn7w/ofe8o7vOLF12ilyhCSSUoDzxJtdMIpJPQe2bCEs1Ip/cXZECNDGG5l03PKo0Cnc2oO3y2CEHzLTa6CMKTP4IjrtrXXf8pa3j0fja6MbbPbNcrAFa+SYKJyMp4wsbp3Yurtzd6Pf5/gmx7IFCd2UZ2HeLB5Qi06343QlT1jBqZsXeRocHG5snmPulBYCRCJPTIf1jzpAKwKT2bKPl4Lg6P2E9fQqYdQ+nyd74xve9uUvPY6nAFQuzs3ne4FcDfxm/UbkM/OYpexH1EiKGlJQbOg20Kl84Y+4arY1YpSqVUb1Gc1CijjuOIqSQl5ranJEmgmU6FxaNq/CcoqVvwFqpwOEGGAyO5qHGWCORbeWus9+XjRhNqgN9k4up/3ZuM9CU7oO2DFHmGlNoc3PqFIl4V0rX0BiUKrbao1mrNXuo5vsDmYK1/ZU4277h8LYFNH30OFFKSjHphejCge4JEdx+UIQdIZ48ORf1AlyKFmZpSUgDXmoBIxgUUvU22QuLDFW+imBzPIhrzzCAi6Eq10pSlFlLMlMSCxWPkXJFIKm49mwNWx3GBh2NF53maNVXa7jVAfaltpHuPbSpkPIiisyRctsbsGGZHBAmBQfHRBLtCuNC3O2MIQri5EWDGWbKGKyUQFtLZrAoQ9ApJRqlAtyKFn1cRIjH/uqimNwo4lVMZnGfM53ee2FwkMhgb655Cmozl2wpsVdTkeZ3paICS4+222cJEzd12zEdJIHDaV7innEAjghTmHAgmZNFSgxmiD7cXAycbRs9znQlu/PNGZjzpKSyzghsAuNBJ9UVsmDX5hGVI2CJnN6k3xXwoaJccMZX6JA3rguDMJQhxQizHdHPwXTNLCUCdXhi4CL8YilSPMlvgqs59BVmIQ0ma+HWoJYBQF72QrV4Msh4wFzxcxXdOZzctGN4RuZEwYfaOun1Ag7T0GRMovAfKgerbiquhIiMvUuiYhPruT0yVjoC+f99TLXUUgylOASpkqrLOVNxUnyJCmZ83iUT2XwKiWt3hJoRqnIX5IElySnafRSZP7GX0uhfLikBFSYV4ANM2R62fRtTzMtGOanqBbeDiNDJV/wJm8BL2SuUmZJscI3hSayjP37eO+CxWaVB6opaKrJmkr1u1Rs20sWIALIHi7+Dk8YLvU7Vb94/zwqyVRFU2oFZQKeAeC1/qDHVwADRgTaNwKgFG5W9Jw0sSKOhacGhS4QsXWUPhQZpUMHRbJ+lRh8A7CmtguC4hkWJ5ltFZfeTOqL3AilwUzsSERqiIF2Jr8gSugEFnHKAE9QpgoynGlzIa3iRKUI2TRXss3la3SXsSLu8qLfm/yoL3GsBGWZIdWbUsAGkDzDEjKApXlIRC2Z0JH1uRQt+BAj/pZJDKxxmSwDD+EUueCPTJAwmhC5SyuAUOABtbbCQqhBnNKgxzk5SowsCBbU7DLgl2VmiTN0gyK5KDfssgljlIhZRixLNM+mBDxJKCTrD0y2RKwJDZoCI87Ulh2WInxwxeTfZzvZeFlSmXgkgeOJZIYZxMsASIdhPCi/UpI/EZhcxwoKM+Ijn3wklGGRu7s7dPN+7Cd+8m/93F9f63WxQlevP//f/Nf/3dWb2/Qtzp48/ba3vPPhBx+YMteC6tJUyiXNZfCFCMDyKDm6m4ivyXcb6MW402s510Ri8Xb3D59+4Zu/8WsfeHH7Oi4xWz8UYp3ROPgENCCIkV6+0LhAHd2VITIcIJbBVQojYNc3rlJ+HitceObEnnDRPBXApCgvmT1YtoRQJTPSKsxrKSYBBIFBohSYSsLYJIcsYttt/pQBA03uAltm13I4iz6znpJhKJajrs/nQ4bB9KYczcL/N5MuglCp4YVxyIUWhtw0LETT9KmljDvSrNopIAyns82RQs2DIZsKzkgHOxMAtzghha39qF5GBPUz8PPO2tjV9sAQ/wDQOkC2OlYrl5jaaYXbGohwGITQ9ANaJkaRO1DVOaBt8wQYzQvtNtmBLBC8LhaQs2zOQzHlF7ajrPCVh0JLKMoZ/snBFKHe+KCX4BoqUmEeolI2W6gwBPEXLkWvmZ1gWRBbgaiFtc5Xv/TUFz/3lZMnT37XM+/+mZ/9mzTtNrSNMWam1rwK9PC2lAUc85SqVvABtmXCOi7rA7fob/BMkAC8WJmqNAaBSc2CuxywjVWajkYjdHd4OJq1xg888PDBwej6FTbdnh0fHlCclYTVMQqyfv7C2b27+3APirU/KR34Vl3+ImBoRys2Ntb39vbJjvWGD9PD0XPPPEeCXn9tfZP5N3xdAOLNYQ5wUNANvhChojiajhXhpCAIYXCQk0Xxqibj4Wzx+FNPXL7vwY3+Oov9UC38FOwgk7ro4nx5l6yzyRaCc+mmbS2ikAv6YxX/gQyPqAHaRQXFWA8GXVXwfyYNsFpOIOA9IoawzvS15j7w5WI4LMf9+jWFGMvCeR4pBBagTgrdA+rFAPxrzptQIP0KDvdZtmmsGDDFruiYrdVafJGgX5ufUkC0I5Nmo/cirtYCO4xuczwpL7Ux40tLvuiMMeKcmcye0dbINYnDwlOYlYpTd6J8DrGqxypfKohsBhMxZkxX0ymqIIpGQYFNnzqeWiqToMFQ2ycrLJS3XNcOOB65zJtnCxANX5U/UATjjeIYe8krIdEQ4wkXABeQ0SSKwwU92HNgET1E32zhHFssCFN5HQ+CFsATTkZQJq9QxJRvP3T4T8d2dHBIJFGU5l3HFBXzvF8oJX2GbdR5Vwrhmx6yAtZ5RZCnQNpEKq0yc1zfiXRqNDywYYcTuMvj6fCAL1EgRnrmCJpqzNYykmNBUXz6Ksyg6v6Sle0A4awY2gXF+2mzbodNB6y8HdP6Ij84y3gRw5KhDxAZuvY4Lzvq4FxvjPyISW8+GowO+DwNSFMhli4yxlnA3qKnmp/Gc4qwf6JR3zo8HNHD2T0YqJEqBzwYMc0AeuCBsBgWZMBrbeyJ5+zPGR6MAYDs6F2TAI1SuM5igpTdDv7XGy/RmVl015rNk5gmxvFHA+ZSFCLDAXQA4ImKxqBPpK9FRR7wu0MRi+EoEqQi4LIB30gWwjXYtgBOlKFsKVYrSqEqHs0tfGUtEzMWKiSUOPuB5GGOabgMo1WenbUh6LJ+hCAlL8VcfgmYivhy9UpI8ZmjNiWJCUhrdQAauJvPeL0g5o3jY1N8lQih91OKsw1BhqyJlWXiU2U3MM+mWs0A+FigS6GNFZmqjEbxuEpSpTR1yVNhYApCgnRg5UbGey/Jcfx9BeB4klc9B6gZkaeeFKVl8Mk6o5sAfATGT+Rt5qDNm8H2uUlpmrjqtNHw0vSlaCqtH4GQv8ClWjqJpzeuXOPdEa5bjy1TeMCsKrnxKYMqYonUChlAaJANw1FmY1Fh1VQ9oU+Zqa+gK8om59JecqVdF7WYtUIwlQfLUhQTIujSWDJunc2kPCCZgKTWZ68EkUz2EEKwBBIQ+2/tEQYjYZJs1mSXYbamEb0TZdKa3EQU/CQLZglfGNEwcND8kSbaCLUmgP0qe/JbWCorKId/BMtlBMltpdsFKkjYrwN6EZFsF3lIKTQoc94MipC8IbbIAy45CrMCKURTeyVzoAQFa0T+g0QiA0uQvucq1GHniBJZpSKNKd+EQohogh4JLYTY/FpkAOtItLBlLMjhe0bPfvPF5XTvu9/+pq2trfFwwKqG97//Ay9ffaHd5ZzP7r/zk39tY/MEdjgMc37IUtKuEKIme1GKTgLtAabNlKCBpaYpctay/fyzL37g1z/4tee/tr8/YNN3MsKimGxxVnnkENkqRvEsmEQSrNz4IT73V97MX8WVRCVaQXMdD/J9ldpnryqZCauk/MCvxHlXjOBoNEiSbtZx3B8JuAOGd+RleoWGRa6zQmYwHEBce5PVoth6SIJWZeFYlF1s3tF/HuEf4YK1eYNK1vd5pCOhJKdpdICSEvAqGfdkVVzadHdgi6SVBzdMVwDdDm7AZeWbq6bNqHjwgWgdAWiFFgn9DMUjAImn0bM0IHngBFPQ9TlnqkzG9D1KW0/1KZRbp5SIjdKSgypZfiFaHhEiDyQ01lBGFYst4/yXS4JFWNwTxouGjvL11KnOJjQrQuFHhShZJUFcYUSz266PJsPPfO7TNBQP3H/pO9/1nq0tVuYyVaLNLOposZah5eBejHIBmBKgp6BFCRGuqXOZiGwp2fKrUOhVUfAJPPQvMx6gVMNx33zkkUc5s599wewW4thQXKFmiz2Crjno99eGA46smUiPwCAq5YodOECkquCLEpCrlGyzsFywD+eJJ55kh+J9D1x86OGHiVZLpEQPijxyIy7IaDBm6LflOSO0FwRzJuniiWef/ejvfuzSmYt//s/+uX6XL4UTTtWVRaqKBPLHq6sxAepfYUlB0gK0WiQzfHU3JV10FUfdSAeSZJFOUgmXy+fVX4FC4oRJB6arAhr3D3+RNTzxoUNiRr9ggatJBcbp/nxwb4Szr5taY/ZNmVFTOOrRFUm2GFFitqTh7OOFNVnxNlt2aNrm7L4xUpUPwiIhVPhh+4Grq5+K/0kIZYa1ajLJ4AkNbUbZrRzRUkqS8USSXgkGlEB5dxDPpXvkVraFZOJymYHUYkFBBin7SHz1Q1gIDoYF4QRVimhhwMjdUTwIaLaohQJJ6WCoItFPiDEGvrX83uULypXahGONYrLUMJS6PS4diDCJzfbadSTNXBI7yDluleNv6W8x04XCKCl5WnZPZORqjuvJVlIWCVkBs9/c3hXN+YzVWektuhQCNqo7rApiXYED6cByYE2djwpWlQ/B0EbpqEgbvh9AoQxq5Bl1i1AAFQ5zR6FChw0lQoR8SIc7qJq9FGeScJu5ND5yC1/FhYgsEx5PXUMLJo7MLzhaND1cuYwqqDW0Yp7sDFiG9d3U6AQ9+LiIgDBlTSEGCRmZU0Nj4jFo9I0dYLF1s6FWpVUNe9ROFyAq6qB5gBT0RL0kLiEgqsaQFCbkoDUlIycBQ9HCKSJXJJwSigGnTmdeCGNPoTTH4hVeAUb2axNJrrIZDC1c5SeMBukEmcuSxKCEJKZQEABJ9kfdxDyZTbAqxnKKOA0t0aAkLbn4YcCpPFcJjBYFq5MxSRncfK1C/LHvUsXzKiSVokpzFJWH4zezJllJTEm88cdV7nnkljOk7RWtguWvcuNPMSBqvoiWIBt5z9gRj5AWLECatNAfy+Azik4aQaRS6dLJDMaVL4hWZ1vLCgjDqYGBV7ggUkpF2ZY/7lwgwTwWnUz6eahKa5swShFCeEgKCzWh+PJLVIbeeKZg72RILMoKRigQg/O0E3ol4JzhATI5409H0jbHasYPnWxgUZMBGt4HNYtQ/gBj7OIcYbUGZ3GQYqUIelEGi2dERummpghMO7k4NVnS8+ePmgBEyeeVBW08MPWXd6IkyAsYUJojFNkUFDptMsMAgVPk7Jwo0yliQLSzU2Rl65rxKM9lAqfm1VRD/RLm4EpDRYHiwBhJ7zp1Vm5AFnf4oN1AH/gP0cWFIiG9fUfp3MURxCiBk3qF3L5u+0X2SF+cJSS1VC6gApxEiC7R/wEkhhfzTHhGWyzI1IVj3AHiFe7ZLpKgiQ6E2QDiAfFmvGGA6Vs2DybDw4PdX/iFf3DqxBkazb2dnf/d3/1fXbuzw2GP505f+MHv/55+lzUMTBQ4QWGrM++qVzQRFFSxSVHY1kCYyx0YznF4GTm0Wr27Oztf/dyXf/t3Pvr1p56u+UF1xynE1jwwpfxFIfUKeOeZQKkqN0kxpMiU0G93hcEBKG/M+0deifTYkFWKV2cIZgF4DBKpFTj6QwOoI4KdYuwUZ4MC8680Bg7/cjphrcfM7WTUXAyZ8512eu0WJ+iwI3FOfRkuZt1FjR5Cv9Zi1dka3zSiK8FkGuM9TTsMnen8oDbvN1oci7PGnPNyxpGOjMMtRzPcSVpkqjcjrGqImpNvMFtJmRtirMpZGmtWvbYzW7D4tcuy1RlTbky60G1pgjxLJKzizF8v2ju1BqUzmAomnRNnGIleHxzcbNR6NDKcb3NzF8Xr27qhyegSbZvjqSqZO/xZTOqsAP9ZmMtHAuZD96SqysjOKlFxMAKUgcBBmwDnWrK23RrbbnLoqhlpDkghqzUowiSHloEAhtmsW55ytr83/pcf/O319d6Xvvjk/Rcu/Ol/+8/cf/kCRTNWp/VjUZZNpvWqYMFrdE6+BDjl8BkKUGXMVZySrKAr2swqqKXBSMGTKytlIRYIejb7B+trfXbunDq1fuLEa+/u33jmazvzOezHleILVLgNjsmtr/fvDA/xExiXZJ6NdRq28BRWIZF5FFGiX9wcT8Z4VeKDZSYIWufzm9dvXzh3afP0Bq4HqzvsaennoWXsR2BAX245Qqo7xswT/kzj2otX/8v/6/95b3C41hvW+MCC1DFtkHF76i1FT7egSG7b+bJAgPBq05SKETkoMFnIxUP5hTGUbGK9Op7Jap0lQ1KEsCJ2swE6PKU6F4LhLerijCu0ZVyPZZ/zzrTWZ4aJdRuMczqlhpZiZ0aNxRrrf9hmM5qN98d8NIRvE9Y5dKm2ZG09G3D46in7nO/jBF7cVKZOxm6qYJnIfFSnmi0P5tMhYtMdxg5rQbTfYE0l5t2hCjSLAXU8MgdlVUzto6yHqtJm4kkmGAtHvVcvSQ1hx68kiMnSZpGdVISVa6XXhRHlXr5H0cKXACl5H66T0pl/xW/2oodS6+yL4d740+3LuzVdaZ7zrc0uLwDFOZaACCVtK4kUoBAREmW6FRwMCY4HmSYh+2YJ4eKedpcKZ0VG21A8ahDA8XoxAdYB3PxJo82ae1nluNmST2Ewcs5ogqs6cUYvLfhIpIYObMkbCUiD9ouWACvB0hhgwgFxi8FIM2LrixtLU4cfpb2gUiDDaCHIkBAfB2FAg+SLDD9B3dS63MpBUZCcHwfFQTx4sPCU8dUJLSUgtTqsRWYOAvOKxXD43LkLgAHU6uDCSC5st2e9wTa/bALySoPCHfoAP9ODmDgYxQ/1kqZdJULZmkxWTGQl3WYZT0qSKq5omTEp0j0v4kP3hwBQsEcDIrCKiwoOhvaKM50ozZZLH5gkVmFVCUUXJ8XMsjqK1wxaEsnlFqy/wRK74GkZgvBioI7xe5WEizuhkXKhM0gkxvCwfZUgnGqztzZZc0uUmsbXilbQko+XIprIxtJW5Slwn+FK8WxK0oJHASq5JVFJJq4E5SqPgeB7EMiDJVRElXBDv+VKAYaWkr4lvgooyeSkCQslIp6eorhFSBSX+ilupk3tA6WoVbG2ZNYoycdU4MC3KooquoCb5clfnubrnA5ddjSjUCsXuCIDgBfwwpPo6BQVktk1Kgx4aWT1of1HaioSus6V7GQRGhUxmHBLugpfy2GSKwgQbkWRHKuUSNoGSZIKXdQX3BViWpvgGCytfrTu4Ff00CIBpS5yDzXggfEv2AC2kKf6cJG5YMUjD6WbVOWDuky84DeJOshQuMUlLejZFeZPZh0hBhOoTXrx5KkIJ4xc3kIeKVK2+AcFcaFhlp0STSL/wN8hA2q5k6/mNYxA7jQazp5GI2BUpB4rJ6YFuLGaRdAW5RQl6sZCBT/+GZeUTH3C6hQh48Jy4qXXwnmkXC27pZtFZPIgxUlY3sS42WBMh1nRwYA9ScvhcLi3t/u2t7/5cO/gw//yg48/+dTWyZMbW1s/93N/89zpLRtHvQzmeYBqNwC4AZ9Sc6N4EYAruP50FVgijXfIF5HubH/4wx/67Be+fDic8e0iV7dUWMFLx06CZSiV+QWWyFqIIfwFtuVJ/R93rRKsfl+ZNiDvBZVER0nlUErNg0/lolzJrV7C99hmyKB9bczt52TTCN6bPV+m122sOHVx2W335zM2N5Npcv70iYfuf5iz8Fr1tVpzNJ/394e3d3fGs9rYjSd0FXCA1prrvU1Gfpv19QkHHdY2OA5u/6B2e/cmu9k7HImz7Ayn3cNx43B8iKNQenFomK2SvZHmSUbCOQDPoSIEtWi3OGVvMLGl44zO3mh8wBIavETGVRstJr2ZGedzsB0GvWYTmhxcpua/9a63t5trk/FOc9mrtyeDQfczX/7ctZu7ZYoPDmmzkLEVABuiH+RZUvBnwoGn+OXqug4hKbzBvbAysi1MtK7DNL7SivOKZ2cbz4Y4coOTM/syvKg+nCsagYWKjVUS0GuoCs5KrMlk+MUvf/Er9fnueBcT9ejrHn3TG19//sIlvvMKjhm3szYX4ysq1Beyi1vBsOBnlTXSm5FqW6k1eQk+FmkqYFkfMIOLwehwEw+IBQfz+sOPPDo6HF99aXv/7sE6/axWazzyEyWuHuDGqB3HJKAjml9Xv1VFBiAMwbdfX98EvSmHhwLaMVR6g3EUtDYkp75IuKiGLfyCyXA4bra6k+mERRXwZDwZHuztPvHkF29cv7usr+0c3B5P99Zxo2WaMwAUT5mk5J8DBEjLZod/+hyUoJUj3gS2a6RIMH4zihSu6G/AnRydCY/jcsBVgoqcZVT4FkYXUxbOy+CIg4Eg2Qtkfnhk7f6sO5rrltLBXfZ6TU4rQnrEzj2Hkp4TK6/n7GNoHGqKWRuCHSY748jgPaMDgJNH/WP2lqaG3q79kkWH74oxtg/jNHpWFRsnlqrYSgGcF0dzbTiIxQlEUJJMsTAFbacEcUaahss438kYTSEyAb7ILu4hNnwgQE0rcUosF1HVU14Tb3VJ9iQ3F5lKdu4CkK1JFHC2QsYLyyxgHoxtzCzU6epw3tQmMVZqkSCJ7WEiYJHFN4XleBq2Q1o0KqK9IJMBJp68Dx5rIdqwhgcd3PJCiaqTnUBH+XUSaAkxPSiaa/NQajuoNukiJBrSw0/aFAMqZtKsQIlwAplm1kfUm3sYxquGB+GHxRgegUEabrEpEl1usooKpfPCiCQAZZccSfFUJchgXgPyNdrUxPAFIQdVdVKWc4k1qVEr+OMhgSgAdXIlVCALmBrlE32lyq0yq45BQZgaTZ0HGNgKl794EMkrcpmqJYdtdyhSOBkjE6ovGlQA6kkB2GqKqMIruSLYIh7YI0fjcQVnEeRC3VeBJKDfnlyqM6Kh/gLAdCFcPMsTgQnhPZGmMWV+5GViE+RTCTEJKUrSxB3lLQ/GBx44WGz4QUDgCdPsGdpcATEuJafokl8FJSywhFBQCWCBcxkt8EAsQX/cvaCRTCmOtGZ+VZZqRVRFQqKRu/61BRX9YrQVRaACtBgnU42RfuGVCiXSyujoWVddLbcolADCeMBOLRrXRWHhYJ4C4069JTIJpI2LH8Rf8SImTazF20gwEZgWgTJMqZfgRZl674FiuCnQsdQlUWN3/oW0yo46x1iAia12vBnCcDTJ7ViuRtM1StQn7nyZj556NjnQX8C4WkSU07FrmMGO9hsSYST6ZyPNC0MwS6Z47SVwnBBmh8zUi2ACCEYcYZo2HOIhEDhGAsQRLau4npf/JRcHxDRgCySbrMwiuGtVPkK3MLBMoRiq70gJlY9iHX1BOtAm4hbGaVSMVIg7DTZkpzJprKg24lNEAhUUU2xM5KNFRqiRZi8sd0lfrXPTsjWgQIcKznGiz+0MhN0e+AhBVmFjpJgsPMVGwCzfbIH5l7kO+ZhQCPeZCx7IbYcKZAfGAmBEmdtmhjC4o0a5DGx9Y/P61SvsX3r55ed2b+3t3h79Z//Z33niiadObG5xJMnP/PTPMMDJoBqIImnMKVDQE2bXgZkiQdExMwpVHpkvNsr21g4fJ/18/sufe+naSyxqFDl8T9aYShDLT0kk9tYGBUmgJMiZo0tGqfzcFYsP/wZXAVxKKJAIKa/VeF76V5YgTsdKSqLZFiH19o7E4hjJbdIjdpnKqDtcRTisxBjj9833OWJ7Nr+7mLGOecQBE6c3Tl443VVuywPH1monm/X+/s4Oy8nX1taYMxncvfu6y2/cXMNr5IjRzsHBZrM97q/3p+P9Vn3MITO4jnyOhrNlTp/uXNk+uL07cSEGUxAqpr1I+laclL+Yse6ZQzLcDIiDyjHXk+kea1F6fZalx5jQ+PHxLjSYYTgHBKi/rVofM9VlWzafIO50DruYmuU1Tcbm+W6f5Zs8qlapMna20QhLxUWl4OlZrEujte8RFWha6pJ6Sw2HNZFsOM0NyrnLNxw9U9MXkSkeRAhAXdOkj04oATWCP7NpoLCHlE04aaneSsoP2cL22sd+5/cp8TOf+QrbJN797vf9+R/9wQceeM18dpg1HhgiKg7IAN3qgX4qYhaWgA5BAg2O3o8u40oo9FYaoZqn7moDobHB0DtfJD137jx144EHH13M6MZcGY8YdJ7zmTMky9kjJ05t3rp+p7/WH4/YqkuNcjxVuqiJi4twdcGeLstiOqXF0ne8XcP54kL7FqiNh0wMoFmQHLOme0CwhoqsLPcfjQaD3Uc6tY3u1g69nm5742tPPosejuaTze7pteaJBpvso7iUIVXwAWDKiP/UbRSIcCopEgM0f4dWuPmGImKpPeIqhWLfaT40mAiKL8OAkeOmcgVIshTu8cRjrGiEFVYbbsncwYSSdETC9HoXLUWXW5yyvhi1Jq1ubX+DeZHmLqsxGL5nFxFnLi1aTG1wkIqHj7IZtdvgjH/WyvE1EfSQ9V8cbOLynxaWmAKYDjbvtMuiFRS2xll1PfjuVmBeWBkiyrgZbTZPRCl5LaJGocGQlOJZm5/V9K/dRt0wmGAPLAkxbWjj2XTQDGUljjtPPofe8CGUJsRAM3AyDElQ+LQdVemEsDQGnzLNhQqm1aY0ctiUIYysKklZoowkjUNPhIoISW0txVpXpilplEhQgnjOD2Sx2B44mkNUGFmgXrBTgmlwhsHRSb7yQnaIpitB8yQKVFXmNl2FYB3n28BnbWJSjRrt2zQQ9jrsMTHcpnHQyDW3F8091rEXfugb2EUglScg2HaY355pNIJUVlKpiKb77lwnwLKIUVTDC/iL008FNL1JAeAzZsq2yh4ORsiR+sRq34q6wx2Z4zSiUzlg4sqwcEDzYruJFvkITOZDFqfpgrDTDAx0Iig3Wp6UZEcZkz4OA9koVG8N3XZllufruUmAUgAcJ5EEtGkWKGYOTyBOBih9ZgkaVRfMYaXqQxXDzzBG6hjuYXaM2RhsJUmQnWKw+QGYkgVouJ+apMCijDKMizT5UVv0O8yVZ1kHAkHJFDyZN0/VTWQ5yZD7aoyfRIFYJS0ZoJHcAWRAVWKBUVAsmZJI7ERcXpg6IKDIx+BdOgBVSKAanHfxKZqQ9FVBhSTyc62KI37FnRJhhgrppDnCMuUfvRUAFVZVzm/9EYfgCsYKyx5b2AqHXUTmzJlWXmWCyeAMx/mfsngqikJXIReIITlKIVpNFHjBkQqjYqkUUe6ksSAlnn8VxSVElSFjLmBh2yNs3T5Nu8YI3bMZAR/ti0Sk8ggGp7/kpO0GG2KsZaqIp9AAK5pHDeKRmsJIHksKDLNukBQqMORULr5Ur0kAOlUc/LmwC4xpuV+YC7qpgPDA4ojkzqSXA9NUXau9dT7AIdNRCkvGBIXlBgU32Czb4AYcd6QBnOxzIWXppbAWlqzuwCTpZT6sEV1egUkSECApxcc00DJQvkMDpNaUihocZSELhoNgaAExCg3zJVp7IZGgJFjNrhy2FCBrnOA5rCszdiSVywUTyMSAsCFIV1jeRXAFRR7FITIRWsBGUzzkwtJlGTcHFCnMkHJF3JoXy/K/6YQueHHkzn9M5bLJtqSDu6Pzly7+9E/9je3tK//7//TvPfnEHyKpE1tn3vW2Nz/2+kf3D3dBXppp+zSpygCjWRw/CVeU2QvF+eJMUjE5uhh1OuvXrt780pOP/+bHfvv2nV0F4iyqHBGrvPMMdV4FxfIsxUeXJBZkE+RbgXCU4hUPx7O+IuJbXgI3BZciROEot2iVd+6rCzR4TAAEokOonaZThsQQE8V/GMXhoPMJp0AiEnbHcvIOa2ibnOO83kOv2MzGYC3LoFBIPrzSoWU6eeJEr9vf2907caKP+7LW6c3GddzEzXXWBeGUcx48cwmMj2MAWKDPhAPNQpfvGmkmKkVFqiCNzCf7BzubPc/Ac8kuKtzQyeYfg+ucQlOQNK1KWl1IA9DYBupQx+mZCZUUnSSa1mg5Xeu0t5pNN70lA4WqaVQHMqEQ+ggGpMqIj1K2+yd2tpEWZ+2y8CoEJVKwKC8ZKYtYJjwVNSkE/uqLvARG+CkslTglClbgGAFmXSCcseK7g8NPfOrjX/36H/74X/mJd7/jbe1Wv+2OUwp0WB0AJAXTWJ/CCAkBSFVwUooCBVYaR4wIWPflVVJoS3kG5GwwmO7cvbO1tUnEfZcf2Lmzj58zHXmoMWuctItIut0eHLIXXIeDeV0MFePa8sBVwq6vZMaMGgR6CIsviMEr1EkfQp+A1Vbj6YRjMflMmA6WxAdBisc8s9iIngZTAZ3+yFV3W5w6woZk4FMsp5ceag8wH/CZ1GCJwKQWVJAfEuVNs6bsDJWycBbDK/LqOCaESM0A6YOATQQs4W5/WHSI9s5POMoDL15G8RMIFs8z9YfEEd7IDgYuJQMtjNdj+ZdTlpU0mQ/oOJDR5AB11gvRo3blSI2ZqTU4AB0Ycfz9+dI1b+6qlDXUO/bzdur94YITqPvraP6iS3eAVYnkpYWhF8wmArx5x8EoM2bWtgMWQBj/RI9X2icrCoH8xxE7Ypk6UOiUNGmpxFFRaSChBsLbkoKfoysRFBDOOngOJwrfC0N4Y/rImuOYgmgQrfkNIjyIK2BRnjxTLBqSugZTgJfBLLQ9PoYwkXwkotvtluuQWiqt6EEZgrAjyGym+mRzIzH8iVh1qQSVMy0EzIaNOP4JzLESO6jER7PAjYSYEkIQOFfQA668EndZnmheyalps7RgYv1SOSAH9OUSUUjbbRzaE1AQYUVALsII9FfUcBsEJD+505JLrNSBkSJLejxygJin4p54+oYqq4+8klLFDpLetFc2gsSBekhNZDARVvLIRUvgVTumcwMgfh0Hgf0hHaKsPKQTpPgzVoix9YVAwFIQ25yQl0FQZ6UoXAOymOMoUbsc3AQwmSyPFCIhZPVKNEJFKDOSYAKIMc67AVVonnw2UxCVBUIyRTIHYMlu3rwaG2zNEiaYQRiFRdEi0yRhYkggqiIQNP1JUYasQgWV9XnmLVei3KGMjt3hxphIgiyrgl6gWhYxR3fThj/Ww9r0oq+O4kOc+6NzOiwRwcgUFQWlggUUYV1j7n0POAWSWQy8fI/oLZVQxUrbSSuH0bfJYTBfKWJQKEht5I+0WHe13LF2e5nXjZN7agHX8TfKQIeoJ9bQ0JcKD9pqswHoFdSh2c1trTVgirkobDYjPgeFVg0zhIo2tkJk1M0QwSAKhDkhWG/fIIz+AGCkMZPpplZL/KNAFz+Y02qKwuIjs/iV1R9JQziKy2g+DqP/HYu3R8TaM2opQzeuq3RBK+2fHgitN2aEQQhPtbMnj+10+rtl1xeNEoewR04U5qcVsnrBY6wLnrGC0Poo0Izn63tTGjWGvFBV/ZN06plWXyRJIsNIIDeyUtYlPXIxfCHWJMZb9QCo3GIPVr65IwEEFP7ISy5st0A5W4KMZuYCvpaJF8oWS+ayWS6pgY6ZpCjRStEUIiRSQYR2jOwuN+EOx0WAXhbvWBBY5xwIl2XOL3D2cKNzS0ZRY0RCSyEED2N2BJctJhxhw+GGu3dv/62f//eef+bp//z/8H+5cP7Sic2NOzu7/8nf+5sPPPDA9Rs3NtbXpJkOnbwCAoiphrz5Q7OBxsk4+MAxIHNPPd699Lsf/8Tvf+EjX3vqOZSONrq+OCkJzX2AsLqdOzkhDHD8Kzz2eXUlDtLVLiGbgnLzxs3zxcHirgHlKieON3ZX76/8JZbMR7GBbgpxSKmWYd/7j71wNvbgMMMgKgyshGinvyQBoSq9Ra3Xabz+0deu93cbjQuH+6y8R+3ZPjHtNruMv6OmHQ7WsWmkWdqfLvbG03G90R2O/HZmq9FjQS2jbLUFft6YvWnD8aC/cQLX1q/S8rkZGwt4zda93fX15sGUMylw1BUjo864vh2OR2RvQWfN6sDJ1e0Ox8mhG512FzdwyqcbFD0+EufctdmrRL/A08j4pE6TBe0s4IGUeZfj6PnQvSpyzkrUGjeaQyqpH6F0Eg+mqeq0UHRJGJTyWPXlTsaqWN8lQ9GNxnJLNnPqi7YIYGxpYBoB9ZRzLFiGEJcwEc0J0HpcWGMUGNxQ2Qx+zs4Iq3kgd6u6ghjVOHUp9Ux5WZy2DmikxBbgNtcb/clwfvXlO/+v/+f/8LGHv/M//Fs/f+4ijKJf45q35CW/fpICFQdVMXVFaZaqGp023FJUoPwkJUIgpBBDPLyjFh8eDLBXa33O0Oq+9R1vxiZ+7vf+IMuQapxeuubGivWd27f3dwcUradiTwrNc0dQ0HA3BBaDPxhIOYvmDepZfXJBA9ne3t3ZPXUKZYD5QQeSC7tpmUYDil02Xl621ocjl3a1WzjJPTbtdCbNze7Z2QRxOc6dOlwRAxvVYO+snh+AikeDRwBwYTlfhyGs0rIaMm2blkLRay2hvXTXTFg4j1x8xGspnIJx800fPQtIqIYzn0A4IVBd5zRSHHH2wxDUdUKWw35YaF7rMxnEhAiTAezNgB+t5Tl2Tiybz7OtYrboLVpi2ebjvmiO2NDEWBg+P3sAODSXI07Qz+lipE1sssBxOmbxFSQ01hmP5XMBjnE1UH5myNj3gsLlHwPfFAskVm46WuFUXVoN5uFRfI5N0kxIYoip09oipA6z2dU/3vw3v1Sb0uu/RSw0y9VQWJQKUKtLjQKa5TuaUi4S25LCXlAkgk4K23Q0+dTE+SV6g+ydw/A7dmyjqpONeZHtYTDYgQN/the0qqUM6pXDBzZIcIZZaOhgUoNSaUJkGKA4ui0ogjUP9DetY054UJ9cQkwkw2noZVRBXtQ7zFkx5YJZoBzAAN91hygtld62z/AVBtCqxso/6/78IufFNNyxwLs6I+VmkB71mvozuaQw6jtUB+miBH4B6xn2QJ46pU/bg7WZn1cfOze1BPoMtrBckIlu1KfnNRp8K4ZMKGnaVpwRB1LSw2CJM40Tw1xEiwiSFnMaWVrOu6mMOukEWlOIDX3kpgbBmDTWZk2JduaxsUK2f7mYjU8010/PG9tp4UEeSlSLaJfzIXZMIDgk2qZzQhdnPY/ZNgbPHe+EX/axYKluA+QKmUIoiKg8Ay8OsyoRNhMF7T5yB7RgLJqn6uI1XFYk8M70JCIyOk6AOiKWCV7y7Sz1WX0wqkoXyBVUoowQRKScvAYmLVRq7fJSUmE3L4pU63pKTBQ3SplQs6SngujvCkx5uIdEQSXlBilRkL8pp2QKGN6r+EQdvSaQdKuigG8u65L8vXcRUIElHl5FhInmkX8VjBKVcIYmqJS0xI78NtmqVcRWZTVXVbgFhoI8EIyBle0UiGbkmZYRPa7KLdlEgz8UAJ2lRsleZu2xGuq9WiKeKrFmyAK4C9TSjPCi2tulFhAP2gIJ0ZBbLpXM+qUl4eJdmOSs2B+NMlkCPSKXsUl3/7iCp3SyzUctpZJw7q9TryCZXisGzPFGKo1QIdNRe84j4JAtTtP18y+oJzWZXgeZ1VCREHOqAGZAhGPidDYUeCo9VAdVytAapXYkLfypaoqhafXjxtIzwyOSL8IGdBgE+dAuJyyE8AgEgEqlKAghiY1OkNQWkQBLLzElWnSDKr+EFMYRQpiGKHl4IJdGgNASRJEK38tMFcdFDygyvJRVicVkWA2NY8qnyRSg4AyRcKFIZkwzyqGEWWSCs37j2vVHH3vTwXj2D37xn5w8faLHAaCN+r//P//Zi+fO7e/v93tMsiMahEuLKJ9wYYEYTokOgFhbwgERtBV8tp0V3bdv3vrmMzf+6a98cDB5es5+VE+FEA1zl5GPgiV0GAw9RIWepJExBvAX65PAEE4I/4+uiIeEZD0K5qFAOkrFw/F8RylL+FGyqE1BZRVW5Jy3FCFsHIIogWB8t+KEDIWHEBjB7XQXJ0501jobNNcnumdqeJx8/9K5dfR+7Ec1kBWOB80GPYBdtgIvdg7vWoG56ovbd2/xoWScds5642hNxipw5tY5p6nb4fBpPjbJMnkw4zzEzhlOOZ81usuDffogY86jZMJtje9ZZlqBg7U9Rl38+FxZm88iscpoY+s8niKtHcK0pcDP5Ks0fHFpyiSFhFAZmEbr+B0d3qigrMlor/XOL6Zr89mO9YaRDNBE7o3a+bNnOd5+f589I7vsT0in2bqdqmZzyEMUGFZZ59A2lrYrWf0qNAieORqt+4gNk4WOC0SExCZAacpzfsyCKcJJw2qUapcBcnKkIMqL9pMB3YZ2TIdjFLMnnnrq1/75P/vBH3rbI488RuKiwDa4sa7kMYPi5Mq9PAYOt6Ow4JLkVWIx5lHs8Io8wn85HAw6HU+HauYLxo899titWzc42ZNUVEo2YfOLAeIzyt0yVE1fsDhV7AyG6Myk+T0wKlW7def2jhXbdZJ+gOjWzVunz2ydOnsGeSfUvoCuBstjmOxx6f+kN+seeibycmNzi5kC+gG18bDfo9vDmeJxJqyF2go6oAgJDcDuAh4gGiI/RCg/UG3nCmwUMM3AXkmmUKBQOISK9A5GoEm27vyvLjgi3/JTBcljA3Kt+A0D9aW8sTkSnaKTyYJ+V26jluz0dVUElgu192D3LpMcKIpoMYSvzoC9DYCuV42ONKT1ZTVhAqXdoefZ1XFaMrfGByVtJ+gButzUQVUV2e+8MtdNI63+awNi8RyRVUP8Sz7AolQEkojMxWMPjZU1tGGRIPmgYkRfYqVWxr0QLxPCTcvnDznozSIDcoUbBtoB0CrYUDoUBXvVoYgutYP3oFiigruF4bHmywDqv+nlu6Wpd9FUmlWJxJNlUMHeprvw4YqNgutViLHZ1c01MzWefRU69VZAOMAogHrj3gDA8DlbgZGJwuUJE05kB1g6ZeCgIjiQB+AgI9v54xlaeFAXEWRaLxIZLttJTQ6aZ54BrGjhhowJcDWWbBgEhMFL/gEOVcZx9NV8ppByLVZOXxc2gUbwD94WBB2ApxeFcZFLUmHFAG9Tp6A84c5HXxSuQhcKiJeCeDMDJYMSLODVorR1FbnWl5JLYqGUDDblpKEs5Uj6FErpzhmEJ8IkEdFYEFK45EEBBraR5uWizNBqGi5zBZ/q3bA8JjwpvJkOAixeiPnPrbypQjz5P2UK0yy5Vz/CJNZgc4NkESih8N1hTctVcuVBvvNemJaMwCcsEIQiLSCOHM1BWtMnmhfP3inECyTBSZAMSW+OZCtvyk0ueynXWpuTZ1aXI/qWm1tkYqYQIwqJCjiexLKAZqxCpjMBX+U0skTnbrLZRQpetrdJAUccKqndx5EUywanruKjV6tYhIOiUuf5KqFDa9YxyYMv8YLEzA6sJXGLXxct8XvAcEj4jucTaRr7q76RDpViASSV2h48Sh0OMC5C9IxeF+fJ3KQMSKUodZ4MXsg7tUylV3O5LUYXsY/sDbf+I1uzyDCrTxADXxLyjzEGnlFSgdgfFzGAK228fw2ZEOGAg//mAoaYm9+araFlcIYDjSmHAQtYoyebIlUsSCQbSTNLrp4RR0PACdbaXOoMkZJRuAJUE0u/xsyH2CFCZS/NhZCxbwaQR2L9p7LS4QI4FJOMGNsE0lm4eZQZnEgegigD2FRNIfkOS43kvy6QjMIoBaIAFAapZXSMBdkBJs8iJ6Ioh5oTEMrB1Fl3uRxfouIs02MuZ2LDKdCsLXv6irSRkOrxAHggN/HpFIRUUxQrjs+C8aJ+PYQrGFxPqDg4vPvCS89+/qufPbhzuNk/cfPG9Z/6az/xXe/9kzs7N7u9DgPLUoFk9EIUJeNxkiiOnEiD1+IGMsTEaYe3bu7c2H3xA7/ywSt3rh/MhvXmVhosfbtlfX/FG/gQ2yqQgPEnIGUYF+RwT3FKzzT+lCdfaeV21S5RANhJwhzdLzAIUUzHLtPf8d2FCuUiQSnLlKs/Hl6ZMWlNmoiCRUkPSUgFJUIrHAZC29EYBokYoMT94/gfzDduTHPAt1vmnOKPAFQynCw1fsT6nild3dbGWr/NyZVIkVK4LepdljbT+OIap5/V5XsM8+Xm2oYCZNXIvAfDUfTpiPawudVfZyJhsok9QfWp7HzUyQn+RaP97NXnZ7PeBh2RjXUwY5EYUwDnTvJFpJ4qouLJKZSZA/7RBuhC48iLihzcuYk+8rFUOittdKB+h8HjXqfNeYtLtIgaw7j+cnFya/38qRPDtdb+5vzu7uJgdGc+PT/jIzmLQzvsjT10rDbbCiMOFLlb4tt2fuApY44yhNqNPrJAGKeEvgEGRNod4ZPBe4oJQRFCDUfHyF6nl+WC4lgiMycFwCAhJkFQctQKxSc20d/G3d/52P/4hS984j/+3/xHb3zT6xQFJ/lYNnjERkA8xSn9aIXhq4vwI01JEm7gFoySR2IMQUu4sQJnMd/d3Fzv9nrQcu7SfePx5OLlB5/66hPg3F/vLBebGI/xZCBbgIMRs0HA0DEmaggdieHgEEvFKiAsKsNGjTbjtaKGEIeD8UnMiUYWHBz9zdGfbbYAsJyo3XpwOVufTL5Bo8A0zne95931rT4fjvjg//Arg8P26ZPO4oklqHjXu7JczlOad1BhWbxcQy2YzGBkBKeZdOAEP4yTERphcvtIfjxrUtOcWaNR7Dgs6lK4AUObBz5bsWCTSZnP4UaIz+wCkgUa23zqjhFovrpA9ccwEdhdNPrsrHAf8ILzslAYJgFi8Fgjz8o2eMT5aYyRd65qs2evbc169c5LpRhaLCa1yOXBLZDtBjNw57N6sDRD3XR7pAubyAOLMOm/kQ6W2MV1ugA6tZ8gTjKoo4uA6ZZSdYvWhXPbdKblBtyRlPwyqg060iJDhCIHTHd0VUoD8j5RBjDHF2DFsoWHQCZQhSnU61TN+AsKvc2XVcZKynhWt1Mm35BSmEVKPLeW93Uavc7aLSgDPflvAr72c5nfWuc6TRyYeiYNvWQWyHLW0rK3HLfwbmt8qwTrwINAJcn2g1khJyXQhAaHC8yohS3GdFKsAkfv6RIwZUdzgySZV+TfJYrm/DFTUatZpOURS4URxRfBl7vrqlpZR2dOSiqybZr0DAzhuzq2wQxCQYFEREfp10B1gwEROEYCTB5zZTCzNb+I8tUbroDQlAgctgkf2+YoNwz16714ICdp0ZrduxJAHnozQOEsDLUXDWTGiDuNN27LSTFpYANJwuALh6eBAIdT0eGkWWeexHEULp0HAMzOkHPpbLNCgsfOVJOJQRZSl6TRBcUNT1CBmI6wVAWyqlm76fdh/JVh5uVQSLpzzsvS+eQbxvU5C5u34YpEQcXstLyub1stDQMA78bwV6Xxx8Srq8qrXht+FAXB6iswTOmLP/wlewHIc/VgZHnmOwDIi29f5FUYXKQKZqQJtiWtDQJf4zZlAPMmIwoO+MMs/DBjIi04LyWARGaponzMq/fgKyiQNlwa8mN6ripxklWvBvueWmSY9TgJYsiMLuB9OrpIk/DkPMZncYsh0CaSAn2j0+y350BEtCUXnoQ3BRu44j9yWa3tshesSwG8EmydSMMVfqbwChVgWLy5JJVU6AmmmFDrMDrA/1CXlObyPVgwYI+KKxSCyI5vES4IUGA4x+XcdwUTNSBRQU7U88RNY0dL4HlcONgBZlkoYJJAFrFM5CWPmaSEHDLIgX/UnAcQARM9FZrADmOWVEppknEpK4RAEcgJl3LhGDVEM4DFjukONUApI+AWxaUuRB3IA5+ClEyRdiCADDzgXWttVVQAPFFVLcjCc5cp/LO+R0R2ZkCFUPJhk2W6MAyC/RbKrwWGd7TfqIRFCJd01GT7B6QyhYVYXtiiTKSz4EpioRz9QbMeIw2VGWm/zW5quSEHwopUMLBSc2AaQKCXd1MbhMFudflG6Y3tmzs7t0GYsbbR+PDEiRMbG/3dwzvdXts5+exMkmpLMCeQCutoLjy5xmFF+y5Xrl35wD//n77y5BeHh4yF0iSwcKvGqR2sZFXKlFc4AZCAMiDP+S2PhHHBHx7yvEpREppFlhy/UvdWyRPxyvjjaf9VzwJHQl5HQKI9ohhdTApLw8ja9UYy6jYMQSRkorVZ1A6XjaGD/pCNlFkawhNpkJZrpTmLnXXhDvCM2dCIaYfxHH2DtvmlOItDZWme7SsAHCBApjgcxkhTnfK780wCAJ5VzeiQRXdwGDmCUyOKvWE/LxiYl/pB68YnAQ75JM640+uwREIRusTf1ojcaqvo4j1QkWo1vtpDDx2jxYHfhwOmFmr7A3YVMw4ptxksXCzYnzrl4EbWELQ79DKapzZ6B5OTOztbd+6yE3HIkhh4JDtxMF3sBLmonprohlGebZ2BxewbjSiEAJkHayv3ohk8RtpoLQBgCx0s1xyicNZAWWVa8kQsZOQiMaWY1pF+cSCRFXrvYO+f/eov/5X6jz76uu/gM2ok1SlRM60XyRNQSS8mBZx5YSkv/hrJL//Kr/egYautGXENT612/er1TXYDbG0S+9DrXgv+Dz/y8EsvsA9+1O50tk6eQnT7u3ugyXowa6s2AURs6gHZ6/X9rjlapX1WH9g4gqvJxAA4oBKwxb0ZYGMk6uT80s6dnfn6HbYBLOrj3traaDL77u/93nd9/3t3d+9+5Jd+pdmdaum0dVoJZCEJUXcdTYQCczXLMpcn5IVmwGOTKAaNuVXTXy2AI1maFGeZtMouUkFBQoCykX2oKpnIoKTykJ9jj0FAZtc5pgrM7XWCCdjkQGfWLPmJCQ/zpC1a0gXlnE5qDZjhxDMWXWZvUTCcOjKOXZYIh1IdUXwEPK/1c4AEs0zEQKS2njYDYvV0wVeZqidAjV2VrcIRYZonMmHxwYtzmTrghfrKFvaswyJy2pTIISSPCHnjLwygQPkm5PDAdElafogtmqkkyE9iUCjPeZOMoKq/F6TQkHqTBfZMG1K01QbA3KSJy3JRDL872GxTzQ0kBfgrCpxX3pjz5eQwvXNIYCwHtrLcvMviWQbfcB1CjY4nWMuwoE7Tbq137AdPllkIFjU4DJE2DNQomAoVDVEroINqKjaw2pkkfMI2p9BmVDCssNKQTKjIC43UcxB7e0JWW4XEDVjoOf0HjV8h2NhsinXPDMsKoAVYTH6awih5Dv/USQYK7f4RomujcLA+ORmBZ14g0lKR6JTPFCB18vCOZ2I1FkOtu508cBBNFiYzbgbPwRNewlxgKwF+4YEwrREMXLp4QfNLNFxHABRoUygKIJGFjpGapIlf8SZkDIxm1lfdESg/wre+c1lFSYLVMgqK1Q2ZRbmuKrQ0/pEoLCZrBJp3w+5dFdLwi5SWlWKO4gmQlkQkZgUi+QzmoYSRKghYru2UUQT4I56mA/OSWoglSuh5g+VmN7O5EkpqHYiqgBVSiTbpIosKch5z4sxWEuUnN0tZXcqWd4N4WoWW33t5gyuxRzmPnilznJfk9YNzQYWU/BNigIT1ADWUc2OSwXuE1uhuZxLWyq7czIe6KkOVjmO5tU7sFbROEAL5eqBMXwJONUcPLYbMVpnmTYEAIiErDnIUJWNF88aU+QeWkV0zzdwlOQAkRHuN6avdFeaS76io7wUC8FFRFD6MAi7+N6rjAYeL9h0sHenlj5hXl0+i3yeU07IphErvPkWebAlsWS2IehzXV00gO6uBqSZWRxIQh8YgeiMUjoWKm99+wfrZmBIr5aHdR4HIPauuFQ6IM8YOzc2zpXA3uV6C1td3gRuYW56pNs6HIEl9k9Ck6qVOio15gK53xkHbgSEUqjQV1uT6DfjHBGoobRkLGZYHjsFSbKwD2l9ICyIUpsBhAHKlPMiHCzBFZTC9n2Hi0RaaH6w8lk1oXMtm1uHBMjMq0lgvsrNyg7YQHcGURjk9SwBbbFlymELarFXFsGu4KQy4NAJXXnx+5/YdLReWtrFc663/jb/+U/dfPAskvjbFAmIW0uoYMC4oCFYlghTnu+kBaLLmU4aDGCXZ3r759//BLz773DMsQmD/If249IlmrFtgLQRfGVM8+QOMVPpcaOJRMr0nXD55JZbicvFConCBZMnLWx7rzAaskq1y5f0IvMCwjBUoIVUXretWIncJNHT1dy9JtC3Jg1zoj0T0D3BtZTb6oOwcwM2Gva12+2SnPVRGSlFND8nU8GgaDS00xiyErnii5CehUwRUcPVazSQ/OVQvslAgGscvguMfEwRNl8zlkAk+5kNbzufiG43blNWsnz97Zv36neFsethcro+X+7hIU32sXTfgLE9QaVBBLckMl5WhFpwqPKp+NIpjEKmW+kocr843h1nMsjvZx60Ek2Znh1rF4rHGrM3JVmvN7rx3dzyf9VrjXo+OzKDWODg4aA09WsfF1ovFLq5Cp7PGdgb8bQZxXUfMmY4oJbq6OKXIYJAqWpgDkakyyleSIxrZASf5T6Zus814rad7BF3NCmPDKAMj2flJbfRjYalFCE4zQAX56le/fmfnv//bf/tvv/71D48HYyjHUkE9ooCzrtXUNMUYpWTtgP/CeRUlihCZVRWSooOldRzm8DOv7ezevr1zu7cGmqcplBF6DNXlR9v3P/LQk394h+/rndw8NdkejafuwKHo9JC1lTj9LB+aTJxb5nMBFMaRQXzjnMN/KI6UB7vDZ59+vttZP3PhtPaGXhznCzEA6hKRGgf+zNZeHs06axvrJ0+fpDN/+typrTobwuly3L9odjhAkz4iXyZAgswoRgnlDG2F/VAaDmRSP8DVlo2OxGhQ+Ca0tni+CXPYhQKdzKtEG2lKnCNFZ7H9Lr5wbwmI8H91Q2xWU14TaIRXYWR5JgIc7P7ZBeGgdFw2p4H9cNRso9XkBKfOvLmrN8/m9Hp7zO5guoH2LNfqnR3ap3QI2e1wwOybwCm0xjcr+CIAA8XtaesAcAtPu5I8MIE8qqz6R+3EeEERlJFRJitJB6cIB5BNIraMqoGz55F4jPlaQ5HzzJpjI+OY7AKHO+oJtQ5sFacRPgPN7oL/5APFq4yFHeECKYBhOOsFxDAomgJHgADVK04VFRJcMNM0p2x1GNdlAjEYCW23YK3SjU7vZqvTx4bk5FkNChAsvMu+RxDCmwU7crDRiIwOfPv14xbfq3AwW1NlbYS91EpedJIhFPALCkUftHaAg2ywlHt8ii3Mo/5ieUCcfWBXWdm2ZDwYzexc6/b7fBuPuSqQ0qrZdAYtPooimVDfdho5XQvuMXEcT4xQiOIW1qF/ca3Z3FEa5ZZnf9GtBQ/saUTZuuPohwaSQsjGUU9oFrO0OwBBr4GAlwUHOWIN/W7Ue+45zOAlVYgvSsBBGmDqJBQBFwuxXOxnmzgfe5kw9SGyyhVbAZNgDhTr7qgJwAeLxq4QkNNiTm8/tQMBiKQpERoMhOl6MtQXrA7ml7OVOHpN80+r3esxD6ySMJsLTBhvy07BSAOe0IJbDW8DJHPFTrAAvdG5C3xbuvQWrJjTS+qfX5kgrLqESyreppcMrlbERBdNkod7ifIkXNMiX3+8SvpyJ1pBGd26klh1ALVMLhQij8TDJF5MGaNJJjwK2UnCI4AB5L4jB4QKiMBMkVWyEnAvtmSuQl/1Y1xBG15SPq8p4hXJCmUiopCqK3StXvw9VgyJrKuhyYhQmRQkqiAA1CSKugkx9ompr8K3Ua9ykZEWAmec2Hj8JNcmCNtUbq9hzp8Aqmx0Wj0RrJBz4xG+HPEVs4EaohB8FaULUB4SC591RLROQVjDIZTACogCBWnCKNXTO1+extsD7dKZW5WTTDo/fPdPAwRmlmjZZuURSQu92CfRTQ+GHNZ3jJCLOVfFk8eXQjjEgSnY8VMUxWafOFME59wACAMgmyJ1ZTgXDiONXaI+Z4giTLBDIgOpS/hGMWMiJ4qEa2nwg3UB0gwoMLW11GQcI4FbsqcxVNIBu4wbqSyQq/UGCcI8qYvtUCIn8uhHBKUwYbuM9oHiiMeGsWiahpNpf0TPuIrD5PzTkGmBlaa5IBAeAM5OSggORwWWiKihRlk7SlF4A5QLtCxEtmgCGRlw1zVGEa+ryWQtbYmkc0rGaMiwlnzkxsLwy/ddunz5IqabBoVzBIGIcYIWLiTCETZSR/vv53Yw+uJCS3Hr+u33v//Xn3n2m1PsbYvxtuTQGyBFbTrGWvloMQJTB6IbhiVkdS8lWclLVOKNJHlC5EeFT7iEHBN+L8fqdZX13m8BbsrydC8mjPf1laUeJUjpEk68eSnaxPoBBnmJFdLFUUBoo2aD8XJDqW3qj/1YC7ZsTt/EN2myTZMT+mmDaULIKWG562hQRTURqLuVyHAqJBVEqVmKN+SF9eeL8Sy4YRZ/zjGU+Ns2kcSQoHuqd3LYoyD26PJ1TkaeOAMx/s5s0qZR9Bh0zFFaelWY8hVuSrY7GOcYJxBfgzasQ5+R1hifDBzUMg6IZGCuzT5g1lWziCDNN19uWnRObZxicftk3puOmTfYYyVQt9s4c+rsy1dedLjRmk2xUM3AhB8qjnCxb7AIaxPVAQlJLHKqhBP5WwczZB6OsXSD5hBXTCrMQ8WSkRGjdVgLbc8Yeoij6QX169tX/tv/7v/xzre+7d3vfM/rvuMR/CRYPeeEGVin+4SnqykQMflfEFHrvCIOf/2nyOWbNy0zJGCCcK+ZT5uOZ4f7g9Nn8CRwpMyKke93u6999NFTp888+41nL91/f72+PT4cTN3qJxT2hsBzWGMWCgI4RsV+/Xw8ZnjFM0PxJw4O9/f39s6cP8kEjmaDZX6CV00Gh4dU/FPdM2zI4dvd2H/6WrPJgHr9nd/9lgmHQWEAcH1gmoKWKH05eOQAOuLV3wrTMfYoC4hnxhJ91YhYjK2HPyIHRzFnUK0xR+tQLmyXIIKO6bwiEQPDqxK2Yp5vZpBejwbGmjCKz0g/vVOWnTMPgMuNj0hTMWKjPBwaLqdsqWH9B5+cwOu2H8tMATWRmTX6nHilyw6fXWCYFhuHS2s7M6dTwYIeDKDouNKHYMgBV5/EC48OhckgM1oocdIHd7TkJFVLScdWeRIx35I60MTN88uIuNLpRGJEk8kaSHKy4aCTK7AKyUgJsJVeadcDPgriI6ygpPAjFiAEYj8UFw6nMmjz1W0UTd/T8WsVHhFCIJjqwlKeJ+pgwB3LNyA/0CJ0S1I8UVdOD6atIRFehhuBmNNghYrIwxDKlHYSls55pCRFqqbS9A4oeepd7E3jLzGk413L5y8Am92uB11SuWipRBMXuNgqMPS7fa72lYGoXFwIOYVA0mjbaYEq3SDysnKM1skzCXDlF25Wgh/mQR1thJ0UoKp3calBB9n0YQ54RPfpHjBvxAyHAxCOtHiuqRUfbcaN5msenGLkKAvslhBxpwgNL+l7Lughd7PTaa2vrcsjuSDW1Nq4NASgHdhMyHYehsnedq+LL9by84wtTggwPZQhTafwGyx2kB9WJ97ZlwHwboe0VIEW5oi0zO8hakYLtTOQaj/Go+Hpgjo3IrJgJTUgwz/kmwvcIxilEoEgi3IpleoC0WNv5XkVoCpUz8qXq/wcxa8Cym8i5Uf+mVrNLVe0pQJiiTyaMgpjGutFlXT145AAiLuenrSujUs6blZ1f47dgSfIhHA79syjr4BI/ZQ/R6l6PgmNjBZVIJT4e7DuZSgZQ1+JrqotmcNjwZSIMK5UEgN1UqkN9GBDNtkKSsTVETaGCAahlIopbi4CLPiQclWPAlmYxJhdIPwGfhLDr7y0rqGSFQQgo+Xw2aKTqxAJHtFBSZL5R/gI0QB++FXj0HzA8xfZmiGGwLJRPCoSEHIOQHTR/MWQodeCperRptJ0YNzkA60a2ahtmFKGADJooGmi+pLYv7YTnAxZq9iUb/1PLS/USlg1DKOhoXLzaUhwgL3aLP9FGhhBRzeoSMw/NpeXHRZg9XwYKIogQEr2oZOXL+zmnVAS4FJAr9WJAqxUGEGquH6GIfowMi2003XxkGJNCmsSya0JlxRsFkjj61BgVqA60wgP5EPstiDIh+lp9Fvs5eSgd9djcpJm9mNaltU+5zwUBQFhGGrxSpMjdyyGB7jKTA2s1PBpDliiCCyMVbF8enPaG/7zUBZjAhxF4xuiHn/ACfOd1umzZ37+5//D6WSwubUBbVhYYCsCWTYq7CFkNik7pVjrDs717e2dj33qk3/45cdtT2h5SKt2tIDs0Kacgm1Cgl41V8bJ8vJUnqNIFHmC8Opsn+NJkl4QBvKifmaoQ2VJgOH3riSznOMXgSWk3E0D6/ZK6Ar28Qx5NnEBx716QIIuWOdMcQeXrLkAcbRJUfCpRzYd9nA/cKmbrYlrgjg1yCSWh7KCPgwq9sA2DvWgARGEWPBgP7Z0A5W1MeqIygAyBBjPnVFwfJ3BeNhpdRgAp2XjCCI57JDSuNdsXj57kkZhOBqxsHs2HdGStGqnpnxQuI2OdW1BPdx9hOdgc8gzC3savfqcMVaKW+BuHs4OGVZurtEkcUgMGgZ5+NM43mRnFwJnBW01mneWY7ZFjVmUXV8O0DnOIeIYnFlnvr6+NRrPGKja6CwfvnT2kI0PS76Q4BKO8YRh3oE2T8VEyyJTCYuPyS+cX2zKfU+MSQqdAbvQcA8Vh1oqKu4cGrqI/ckDjNiU0809uGkfO5DIhzeYuty7+vLOS89/+Itf/Pp73veO177m9Y+9/qG13ub6BpsTsB/MJWLKsCd6K5QeofALRMDxP/AwndFlhedFRbR5Z1riYG9vxjGvzdr+3TuL2WX8fnPoFFzcO9S8szTobe9621e/9PjrXv+ar/LtMgZikaVNwIyNIdUoD3CtR4r+5KlT48k2JDPlwalQEOaADGsU2nwWnV4AG73YhOPcBQ+D4aBz2OPkqeHdg5NnNhrurG1Std/3J/7Uv/j1D2297iJ+kSfnYD+wRrpi2lVnjBhOjp8RPqHI0g5iKGN9sV7nE1tQwb9qxNdIurv2q/hHF8xt3DzRkSAmLZcxElAupUmCo4DlhpYCzZFMhpCI6DKuufTL066woC87W56aMsOEzHEPtWvtyfxgnw0SjoB6DmqzxfyAtYyvKjSWPZSOkRpC5nQs6y0ODVq02HPNiiK4RXWiK4UtRm4onHUSHxQR64uJFlUQxVMXASYhodcoa6QdAbgEtgFiQ4Aelm4T3XhHQbCUGVVBDGozuUitN66NIk5V8maM3QLZw6vl8US5vGEY5LO+XqpD0CKNFjVNMIP0HWum51bQExIFLAXSt01yHob8rABCE9KLBI1SqkVZMH+wgiIDFGTQAB9dryIJdmCBCaXorScXZoQbHzbFMyPl4gunPKx8pA8ZwARlCpQS+Ax1CMWV+c1bYMCRA5xjRaEqj+10cLIrSXG4tO6UkHwMx3wG7ggCMPF56AIOGKdotneni0lr8RBpmDqEbLLAddpWrKBtTVAKZbJRJtLYe4yZXUQc/Myp29OguoGH/gfmziWCfNc3exeRbqe2dXKTT6yjJnABGOAHrgiNU5OsJ2wnZyGTn7HnlNlObx2mRVSluUfdaO9Iz5AEKxU5AkKam9TGXvsikcvabfYF8UFGOYTJRyfUCEcM7XVZ0Zgv8dMBlIBaWL+czog9pD8r3e5XRxSI2vVaqKnTFyoaKgcqlKfkHW8CIOc7sN8VXslwQl59VWP/0JdUakgSr14Nn93nvcOafqB4RcjAY3MOL8N7mX1Xv1LvfSwBuRMOHlF/3lUTosWKJ6JWKUt4CVKOeG8ldUkityoMj9Axq1LKZerVQxXkq7nkiAmPBRvilaAqnJ9gl4gkt6QUWyAn4nimYwCppeRepfAh1f4YRGEFE3JVQpGfvmkxuKEIRFAg8jeFNViiglV5rArgZUW3XFRJcxUEhCkc3ihBIyNqFGFwScjd96Ir98J5IoH2SmYLBx/CpMGhoO8j+qn1IbHoWtFM4o+4SojxBYItgn2fAKXKM2yDvtNjxvKQji9baCUxAzbz9NhxHKm0VZdJzvgXjlmWnLGSW6J1x9676wuxYuBS2kLTgzTFahDtBjBu4lUqncRUjBCa6UjPT3HFTCjJAI6FJamPFA494ikupuG/3CSxEXDZI01dFkQ+zZO+nAancCcdQMys+TVwMhHLbRNkB4OhYcpBjqIuWBsBEU2IOOIh6wkZy2v5AYZ8s/MvQzAiCM8RjVWA+EGJBkJ1wrppm1gI4qxAk1XjFDLliJhu89T6xuHBrgeZ693QvrZx4gNIk1v9w+clZwt3ZH64O761e/d/+sAHP/uFz+CKeog39JRWCY8ACy2a4FXxCEzEmUA1xJfQ4EMuqU3YKiAZfUHORxHm5s32A1KPkiaVuvit1ytLuRcPlQAKJsr7j7tMx8WP/1NruGF8FbEDlpDt0lXAwKr9eW3AqDxDjnomylGZ6fIrfJ1oKhW2mpUJtDahjRsaJmmlulFYoOH4oBJWJItW9sqCd3ob9M92B6NdFtyMxyz+YTH5vIn/RPo0MY1GnzF+Z4QsnK+qEs68jT0Hepn2HRjIZJamWlZkDdC1R5nUTgpE2Wi3adbwq9rNXr/VQ1FopBgwZ8el+lBjE8PhgE+eoRSd7mQ4xMEnmAzMcKH6MKFDg2kr1+hvbHJMJTsL2P08mTNE3rx15+a4rCLWPpAHkqlvICS16G+pcYSqASoNHFCVxRQVR9fhGVNpGbOPD8YNPUzdJHEySL002Su1xlHt0NR268qVK//jB17udn7nwYfPnzl57sL5U294w1vuf+DC2bOXWH7DB0UoQkzUN2S0qu+AK+oodHVQT4h2nuGB2ZK+1mQ2AjV6Wf3uGnt50z+h4HqPfRKMx8OWTnv39p3Lly8zUdftfHM0OeS8/27DpZ6O59mpqcx+vitnlSKcNPqqOBYtPtj38oX7zqxvbmIhVTHZAt1Sx3QBFfzuznavvrhwgSNcWZ43pqvw8OXLz37z5Uce3GCuCCfSpVgIW1JY54HxwOemfDgHs6Aa5dQVzlmxhKeaWE+KIHA5ZYH6rsmNdbXDyihyJanUzeivWru6eBISabwMT7qwEfbiHTKkzofGoYm8rnRxtqJMonm41Hy0bB7Oa0PXpaIHrG3laxlEsz+A40Qn6DOH/SsIjnqds9LMIRDGlpkBUEa2EYylwl2kKZ5aaGQrSnBOi8mjljgIagIjXGofKmAtpbfJN6qN5ZUGmrMq5p7IBaxopcMsahkcM03RW96UEEXJM4nOlQcT8p8K7YMYxHdl+Mk6aCjuMd8NwRuF21Q657EZ8sXXZ6qVQWCqmnj50OTcKLvCGOBui445EEBFwDHA/HoJU+ppIowVc91hXMfoejxQrBNqYb8L3pMAI+FSVzLgQMcY4cBKnYyjZIIy2ljIoAmjRSIXESSRML15G0fyYLpgCFgGGx1ozIwc1n5G7Ut3TMxIm+GqCeMKTHahAZSmFLS0tjVOT2FBpUNe0BMGZQxImWSnZ8BGBeLo2CpBcF0ZUlJDI51nZ1XAhia70+vaI2a9UrfJmjs68PAJhtMpgVfoYXFOVHiICedcIyXhvkqqc05WCxVA5tuhwfngSb8O4jOKgxaGD8LxKTyETaobThKegh0BmSrKcKMwO5KDnYRxwQGkiJ1RpMpI3YL8yNYkYgBsWR4Zh92WpTiOLgMSr2aaw8ufVApTKx9+hUPRhiSBwUldspgw2UycmGQrjwkqYG21SUfqKhCollbgCuJelJBVbn9zZr/ll3zcq3ILmEJniTuK4CHp+HoZqLdeVs5TTgzADrASrsTyO15hIiNK6aKk9lXFSVuVwYdXXxZSsvIU01GRJP/9x1VsCS/hq0GSWjFckQrf91JllXCpIQFFYEmRosGhYCGC5itXQJjs3kVU8UjQZUAXCSnIJMldYOQBg5TOk/FcBcpRWXmvIlJGlQYbAXal1OCVAQUbFQCx/o+rdRVtthKWO6TNL1CXas0r3Exu/aHxw3rwLVJC6KIz0+fIgPG2T1Qxh8k14nICZIJmCq5P7pdbnBWA18GJEHQp2je0kNYPrTJXkGWP5HWdMQwdCGdmG4yE5myJIeSKptOWpz7MzrHYbtm8DoJhWik37KKmLXo+TU6BPWsccdqsgV1OlqaV15xJqKVgqy+ATb11g0J8xW5pDbATsp1DGSQIC5NPsQJTaZdxNCOyE4gQ+aRdpsoLHbuGBSBYo6t5xb0Xyzjg0AXjZIL0WZS+ouzkPzyUATS3MOZg73BnZ4c+F3b0wplzf/p7/+QLzzz3rve8WxvKZZ+EIQ1MkKDw5VyuANW0zA7SNa/dfP4X//FvfOPpryMAWUQcq4ZducccQzHu0TpFf+8Sq8WW746+gyt/IJ+ruVt+EybqVbi0GWbA7JQ/LVLykgQlihdyBFxySaTx5EuqI1DVg9CLhgfyvWhT1+cnzVp2FySgVp1oDs5JL1hMrufn4bLQ5jKH3uls4mGs9U51OQgI/bOzt8IBj5/mEwvPmS79tU6/xzjxZMCo53w03ts/YNgYqUfISAkeUyijbFxFLb0bKh/S8tFSUMhmv7ecjg+H8+H8gIWEh+07jJXid6N9Fs0XARgfxRnC22fcipk1138zeIyDTguE1o346JJnAjnHVpxn3Bq9fBdN0D1wFKo9G+70O61LJ0/S1SFwPOabAGw/GHFkyM5NPjQ1G/OPhWXU4ZzuVXBk70iqsUPUcGkxYbW6TTQ3mcenCdgj7qEYiIGyqFQgsWKuKeD/vnxY1RzVEtePOgAebHuFxUzKtzu4hnwhF1ax81gb0txXYtHIVGVffC16MjuND+EZHTJ7MRgfPvHVZ+vLZ8Fq7Td/79Tpkw899PA73/aWd77zXWfOb42GjOVTU61xYOHUpY6RcqnP7hex9jVqHnQx9r+3N6Brs2xe7XQZGj/Pyh2W7+uKgVSdTwQModF+Oh2z9fXe6S6dvwdf+9A3vrib70dzNldKYc3V8j6+3jCYPD+d6NM0Oh0W9LNTX/vHSG1tMRrzea/R2voJOA80LCOGQq9HhV5wJuva2vqiwaaLyWLE6gUq9/zc6Tfs7h4++9KtNz34OkxVxwWTYz/Yh44xEMNZ8g6u6t2oFVDIlzo0fDgx/Hg6kyYNkURARCCKGG11lSudB/jLaALPiJIryTn6hCx+4SE5i3iJaxwkAUdckZksQGFcnzd0ALn4Za7ZYgMPblrrM7bgZ7w4AYmR5DbtxBlHTN0F3J84TMqRA1rjxoKvB2BOMcRUArqdXVbL4ChPmyN0AhbhEkIu0HHUWR2kJKig0zPOZLa36buy1giLJ2EK2laME10Qi+OsdNm7t/G7iiYQQ0eD0WAUbDE5w5evFu1dhqLt4yORXDxBrs6qqRnopTdzSq1s3SQCWvWVc6eWYSzQZJx63eclExcaFAoFcVYZscWlNmNAgfmc27PR3en+uVnjkNN45lSQ+Qa7TvjewrwxWNZO0SvBU8bnRZAUDtNUfKFqD9NmcosLDf2UB6p4rh6QqkyhVDnBI60bGTHmjpPXmnzgggkWdv2gB9Q1iOJWqJBaoHtDxSmW3Rr45dQbAHtkGXDpznnoAJcttecXoVEu3SJc+bvyDhgUxfSFGPFVO9dNU9y8N5v0SOOpP+IF34DGslKsE3qSZz8LweQiBJXVDpBiBxAhYSjQT3I5qQJclx3SAQ7GNvp2hzc2163CtpH0cGS9EoNqzZ3s40lvAh0AfxkJc+GO2AAbPjoGQXYphHyaaJY5TMxKsTg6ndvU/Ax+OKICR81mE2kXS1wAGh+JYhkdafWpC6wR5St2iMEuAAXC1cWM2Vr0WwfK/TgEufXZxhrCYAxY0dbTBOsP0KwrCyuEgpFi78cuAspVaralqJCQJmERb6c6MzP1Ok18crDM1RTVBT8C3VsJLKVVFUFg2W+wbF01pYxNMqmWfn4M95KbiTUMoZZLbQM705erPASfY0UmrgJmilWUQffyViCOfijy6NmHCsAqz1Hk0UNS8GYR9/JKlUlWEeUhaUx3L3ngoxoJ8kV2FCRAsuB8xCISVUCrkpLEPD4YdXQdK6pCgnjhy+yCVREgOUvGFJxEBZuSbgUwWUxYZdeSIK2ok4AAc5ythpdSyFFoEmqebMWNp2BRKmigtPZzaP+lHx2PUpiKUqgA/lAGA1b2xEMtRrnwMWBClLmBWUwRNZGsqbAhEVMRtIIsEEADhaMozEpKDTbWU+IoQotXcJFsnAxmDHW0A4wQlTXWQFsJHaalhrsd0ddAsSnW76MMNltiefXPNV9SaUkyJVnlBO8UqqmlpnOzgDBC7gZkldmYBDlKR0RiAwlYvMh7wZHZMqTFUP9XWTUlshkb4XYrllG27uxcnXpK5Xxrfe1H/+JfPHf29PrWOk4Mk5CmrBBNW0iTyG5TV667Mxiw3/jacx/8zQ8889xztokugaUgCKnmOngOS1aornAIMqGkeqpQD/pVkJRIa+G6YP1f6ChRMkrtqJIYWK5kPfbMe8WABBqdJIWBihK4/iM4QiGBcYYTeyzvUfHqAM0B/MEbWSyGJ9dPnT+zzgD5bH7IuhqO8N/c4DO8qDUVhlajaGOUOYXn5Ltlr9/jc8Fr/RO2V40zL1954faNu7Z8lK6eBCstPAqPQomozUDGpCjeFsDOHpt2O52NU/0WK3UGOPr4O2OWr+BvgyTDVpkwl2JWadjq2ZTjY+k9O2jm8lIqtTrDs8uZaHDwVGyedcoZ5odKOhEUxVik/jZrZPuzFv4cbsQGc1YMYIMyDTPn0IM8ukTpKCLKT7G07Xg2LFxBDG54oDSImM8ZYsdjZ0QMqlAaqEW7UNAwXAHAL575Zw+etll3TTpYfg1pLDxSRssl0+sjBttZwkaDy+E53TaboWEO9cC7HeUkJKcPBlaNOryOHwRwvhNuIk5AHI0nN69fuX7t81/4zJs/8wc/8sM/8Oa3vI15AE+NFKQOU1wnn4Wo8JyLgCgWDszcmReLMHOvBIMR8BzOYMGSFu+dja2LXm8Nr4WPNCONKy9e4yNuSIFxfTgA5ToM7mKyJZaLMA1Pxw3BdulBn6FVdn7f3L5+9hw79VEK7IaOOwXDMfjLFwGGtYPDw+H+3mFnrdbvd6njZ06e+nf/xv/yX370v9nqdy+cXu+119GDGV8Wdr6J0W9PSlFLLAOnUHVl3T00hDUEsNpdmwyTKZKtifoKmf9isQ2oYqMdcVElrU1yO5cCLY/hWAmsokA2lS2vJHIPAB0Jtkdp0TRXLK3kcBa6EFQBl/0Pls1Jo2OLAVPpWBUVx4mDD4FGxwmF4z+TnPrzVii6NxxVT7+B4YxFm4EPiECQyMaaALm9NqrNzhJPzbHgOH0ixQq75Yx15E5MqEts81UnqRF0QNAbLS0zRWDnJgp4hwhofsipgvBbHkFOL1DdT35EBKcLn3RBbQV5l+8oOkc9weqi/UJRqMTQQ2Dn/KJH56XG5/yc7KPDP12yG579OV1OOmKH/iyHiOA4kTjeNmXStlBjQBnfFOoAp2fv4lgIpWZTp2GUtZx5QSsH6UkHWtnaKzHUXo6EZaUOGQm3W2NVAiAOPiBDKxJA+OQiO6PmcBj1cG2S0y50ZUfDQ4AjUAYU3C+Om82AiFDtGKRTIZlOTAGe8zyZ3XGojG3r3WazM6b9mcxZjogxcE0R+8D11fNRP5VmDFedz9ROCoMtB+5g4xjmwXA4GCIAUKLhg5nYhYiY7rNsDzFzFucM6aK3awf7DArTLUj/x4lWSGCXOUbZwTiYwyl56MIAYzEYqCNO+CtiCtOMoY1ssuogFCwhGFJr+DLMAYuLKIrtO9PxgE4K6XVWqPnadiqvJhbRWIUY2eHMhPWNyfhwPkFH3QpDx0yB0GVXc7DsTC1g9NjrkiVbKLT52ETE8kV+2fjAJyD9IIzqVSpaUUcYlAdCj1+oSXSjRBoTofJrfsvk7m/R27yr4avLQkzBRRqUIBGlkKhwMhdoJZlxVbxpy2OeVNEUH3FatiP3jrWU8k3kRZYYiqOSDUvBAWY0ATln1AdTi5tPkXpyFwgVtKQ6YgTVOQtqG0OiE5XfchOc5os2iAD3Mgv26CLKrbFM8puIy+jgVs4v8vuFEilYa3nq+VEZYZ+1yZyvgJvXwKmEYYoKchXMa6ExEQZatshwD85+v5DQFqve+ZfwxJb1XvlGsjFgJohVQZqvkp07MXnLk2mSUESMyVudE4sJ50t+lsV5RCYhjmfU3zbPIiqnhAEAPQ+NiGedU3OFlD4utkCvCNNt75Y1yrbchRzTNK/iyaDmGW3AkmKY0kCANlB8xYb4zYR656qWTgMBOBwfxn44MxFLNzShYmBgETQ1fSK6uA6WeCgupWcqmd4AB2648kCvBTB4O7UWh3lbJ3kGBWwZyx6ZwGDe2XZCa0qd5tk7z/FqyApy9A34oVhkkh9xJzU3h4odkJOXtmvhnOiBGSplOY7/R3TSSh7CE8CjsSYGMKrso61y0hQR2nbFMNSXTzz1LPPj/e7i4rkLD9x/EcuM2ep48jwluQQCFPAAzV2MFEfGNGYHt0dffvyrX3jyC1956hkorbf4rC8JaC/WtWJ+9bNgRfFc8GbLX76he3StnkNawHNLtlWSQBBOuFMlkbaM/Ze0JU15loeW5Z2rAPZJJYEXqROyZ/UYHpEw8eZIXm9pKRv7El0us0FX8J+d9LlxF7eAZZ2siO20OQAH/+xQj5mRSgYmWfafj+NEBU6YubWnLFzu6QiNolq476jZ3sMDwbliEyoiAQekK7qK0/Jlf7wxfUxxBzeURCyJQvEZA0OTmp0GO94OJvURI9Dx4hhzNz2LhVEh1lbgUDosRF7cSpYylJFoZ58oBmnjVUhWrUf/mGXiLGSj2dP7FhNaZRTD7/HR/jFCxREkslMqWJpCmxqdRKetGQw7gRwaTB3BoRHRVpcNA+Bv8Qqmpd9FuOBqW7jHyIRYtZpHqrlI8VC1wXkhIwnwNV2PDAkgTPPKEVUcccMEB50TPpzJpgha0PryJNyr13dTkxGi9sKbVZSKhX7y7Mh29urRslsWJAZdbL5Lur70h4/fun7lB3/wz7/nu9519sx5l5+459aj53Ho7ed2rwOH+o6biHszmrJLlWKWnuZuX4jFUg2G6vmKgm4hzuzkkn2d9o0Jrn+cCb7i9uCD97242L576xYtN/aCfHST7hw8d+HkhdkQ51/xpdPCPrH2aJ+jx3Hu9saj4dWXtl/7yKyziQbCZbQCkqCcC8wQVJft1432I532mvrMJ9jWa+98x2O/9GvjT1z9/He//d0PXT67rB80lt3mki6fvRv36XvFw6f+c6A+3QMXLtP50ZuTbBUTpwmGueubyaV44aolzbP8RehhpYYLiwHo+Wl1rIz38wSeiw1/COEHnEWc70DzwzcBAI5bjX/DngO8cyTutDA1i/2+6EWzPWpNh5ScRoAVk1p37BMzWeJd79Y6a+ybZdeDVpcgziAjvxzQHcVZYj7GeRyKcbAeOiWdT2w3FlvFlaOk5eI8WC0at8GPxgOLj/7gxdbq6ygs3TMOx6U+JJYZXOrVDh9A7DTWESBNDL2mzGPgLzIXrKFGGezrAqzBd3vUQVUCZxHe2hDoYEN1YzFmaSbbNmh3XPOypCvr97gd6maKeEbvZ0oHoDPcmE5eaiyYw6AkSBnx2eOB7Sk7ePD/mmyso81kajKYQ24WyVAqZp/6272hKzw9R4B4WBXoZk2mI1xzp11cLIv4IhoKEF2YBFeZ9nXbEZkquSlj+gAK2qoGEaT1S21oDB1aVpkyx2dL1t0dDPbvci6CgKm8yB9GUgPxk1GpMR9B58PkaRPFjYrImjRSesQcIwfs+6cdb4yGI6wNpccqoYwgrkLGXgKarh2IohPIrt4auQKov96fDEZ8mw8fOh0AqiD13PYKWwu+foGEL0rYb9MIo4Aceyw50/NgO2/coDIxA4Y1w0hQHvA3N/hQRns8OBzsH2iCRITeibbMZ1XHWQXsOc4N/WtkJJ9nvcb8Yn3KaqqDMAqVotbAXtTD8RH4Ek5bhewB9oDFFmeOkgNjNEWbqcSsYPRkAcmHLqJcKLoTttZ/8EPTbXdMRs0xQ/gDg7OanxOBEkaw394mku0ZyDNJuQOxygMMpUodNK3X9H6f2pzzswpJsGs9COA7wblUAskpb941CZ2r3lPSKsLX2hSsWJ3BCg6uqnBahhShi2hoMpAbQEJeXUcl3AtaRQmT6OpGPh0T372AEqCJBdESYSAhBVYSltTmyFVej6CswkoG3oJbBYG0JoxIS27uCalwML0ASVIBKK9HiU1+DPQrnk0ksHuBQlq9HeUqgYVhRR5HhQkhMAqc8vqKe1W6elSlNFrYq5LDj7yUkn0sapwsBKpKVQaeKsUqQLjTyXYQgXpDzaIqwAh5gQZiksoMrPUNmLQHKIT12sV45KEAbRlAhes/KiDRjMTzM6Mltj0Bno49qWdMVwHAkzT4ISLORBngwYqOqJ4ktOZIAjqve5Taht1n/KkDIAZNXb9LdcWGOKIDGP7oq2gGLUcX2XEXgAmFkoKhNBnLzXd/dMBNXyKkmgwWzo9J8deseqET6EdUks9nLnsy2r8Ml1AYOMfQlEjBONpCx4VUhBXPrVhz0lIdGD26dfvWnbs3yMjq8B/9y3+u3WcEjMUhLFNGKtiY1L54aZzlz94sjT0DLs3+E1//w9/49Q/cOdxhBazIKTkJ07/UAPIuNSFl9RvEuB2981Be8+utkJ5XOZL/BJbg1K7jSV6Zo/AleBgRHPgtASsIxnAV4CXQpDAryHDTVcIBXiVbZaTJUBEthJvM9R0hDJfNPi0EX+HF9qKAjvowUT0b0qgzBgVEM6F2tGrynf/AcEEMnAo1DNm1PaMQNdR4Eyz3oj4RHUXbxBaUiCC/+mIvhgibZzABlP7ReqfPsREDhsCTAtr0oKHIoVnSpUjwsmErdQM1ypnqaiIJxRSwZGPcOa08sA1BidgQkhD6v4x98gEAxqSYC2KgjqqAPi/7fkCasWS5AAn2yh3OtFzIo4FlyE7mgZvqxxNJaXklmTRQU+IoDQNgSBhNOWkPcHIdVoQ05YSHpeqFM46RwaF6r1NjHRIYzGttPG8WGoC6pQmcKqEx4UliYIXDbxYASmnjSQnsLBGHIBr2Ru369vY/+9V/+pUn//DHfvTHX/PQ/Z4+pBAd8gcFYOBEslBhNGR8ESthfZQR8ahYdj8ZM8Dp0T1WTh0ohp6d2J+y74GlFewHmDUfff0bL1x4zWf/4A/2d2/Gx9Y32txc80BPphHooHQ7jDxwKsDW1onDXTcYjSdjKtp0Oub7y2c3T8kmtEHFyJNawWDFgqNYd3ZurW8wPoW20WurPfza7zh77sLXv/T4/uD2aHqqx/GYrOpjrm/OF5r5ZgTMhBfYFIauXDuK6mHuEA++KSqUEuAKagAbZCERbDFxPEEm+6xeRkCF6QTfe6gilEB1qcLVn5EM/LNKhx3kfIuYfg6dVz6nh+zByG4lY94Y/w4fuCh9FUpEk8mnVYyFE3llyoGKdJxYvWkftvKwYRmfE3DNW8SgGcf/souANN0ziw1HfnRBsOKLDRFj4RB3ikEzmJ6CTusZhS6WLLkbD/X3cMHYtEAlBtB8wewDykcy4JoV7Q6J5Ip2ycvEaJzVB2PFOnM+DB8pPMw2nq+1gzS8Tvjs19yPiuBPut6JkQIUgDVBbIVG3WiNmASgq8EHCvj4ClJC6RgzBgXNgCIAlegt2ocbxMEbRNEXioTVGeogJsPNpsWX5h08xY0C6M6ILMt1GLJmjpEx9L0xH1uAQDfUipWE2ICTCP7rphLRbW2498dGW0sBQtCCmKwgKkXqI6czAYj5LpEwJ6E0ubizhEcJycVUNQwCOypRWEtSskc4ERBv4Bk7BeSoA6qJcrQaHKCrAXEo3lz0+SjDVUZqLLAZdoRYPoTMZAVctAqDfKDKObLBc9gAv0urj0phfVi9SW66kCCBZgUm7HTmBeo9NU0nQM2BfBQnPTGEzNwsmAYH5SLsSEe0ZYwXilZa9TBUMyVzRd6OrNWchAoVE4w6M3WYxkDyIgm1imgS8QSjI3+hK1HCZX31CBgyw1l+EpXURSXsUMCK6DHVWmz/uOtV8a94LcVJmsG8+cNfeS9QEypZXqKYTAw/BEf7HGCORXo1JlWOZKtu0pJgM1PGMJIQTlb/U2xJUO6UVZFfsktwdSEKTECuezmOFVgCk6airVBl8bShTiRFAuVekCJgUsEsAXCW8XiStBlPqq4VBkdlWZIv0REeSslJfTxNyV7iy7MsRp8Av7rCUcsSq0BaEcxbeocFL6OS615eOehbVWR5QlIFDPdKx1Y/BXr2oZdEKyzIw7rJi0vGUZpXqHPUKG2pX0sNetQeJEcnnPE9+wB0+ZGhzSHnH3PnEHDJskSxFB8yYiMaV7E1Fo9dkT6AmKDJmcQk0UYRRwB36yWe29SvKmKYRE3PPgpPAuEvh+g/a5SdViu5tFaU6eahVGJaIiwgAw8YExcjzpmxc/qa4tssYlxyoEoHn+g6tFmdKFlUS2kUonoaEuhx8YIGmFgnJU4DEbVPKhIT7KUo+Edz4+CB9lmqQF6bXxym5Mf8EFVdAsP8YIdMVh999ck/HA+HzJSeWL/v3KkHMNE4JQUpTJ8libJGgHXXs5H9tVltcPXald/62G/f3L3rgQ5IBNFQhFYfm7sna71Wv4W+1Xi/EYmuyMizxSRY4RzRV0VVP5AYXNDlP+q6l5kUFV+PFyZ0rvLjs6w1IMNjjDXw5qF7UMO6YgqK0EWM//KwQK3zTUey4uvg7dX4NgIuSp/TL/UzcKv5QA8NI96gzhBNA0p2UFok3GaAw0ykBM/0Q9ROhKbvjp23fKSJRsUkWdf9I1hZqJIJJwRUzEmUdZtVPkwpABs/2OnFJqclOjrYmi3wUVwSnXS0HcQ7Mke7oX9r243+sMEO8dqhxbtOO0RrSxgMd0UQo1B0oDkpgxPYW831nLULAfqEtKZ8KJqFZKyQ4STGEOb5sAyI6/m7bhu8+LRmf8JeYtYrW6+ZRsDHw3u2ynOOEOuD1F8ZDlWb0tY69ASexaTX7vJJuv2D3fTrWTEEZ8izBU/nrR2Pw1j24TA+O5TBTTjY7Pahf7LAxR6w7Mh6BF8EDROo5gg3/yxGVzuUEGkLC+dwjDBB8IMSVep693A4+9znvvrCs9vve+e7f+hHfvj8xVMyr7lHZZ/NRoMJuyFAXm8FGCCDRFzQ4CCw54qyGABXrru2obT5MowGxKQ43qAwmh7im2+c7LzvT7zjxRdefOmFFyY7kEkChMpXXJg6qDEuy7qutTVWXrWave05GyI5oog+3rhx++adM+dOqrHuT5CHqJXzD6rHjW6zd3P7VrfbO3v+tIh19889uPy5//W/93/8u//bw9FyMK33N9ZYH89wCacTQgLSpIpRj9n5z4VRRlPoe7AIn+E7hwnhDclxH1Ee7Z6WFt2gWwPLmbVEEk58qaZIU2gy3pm0XFXVxgYdJKQKJiVaqkEyvaMYnG3IJw0atXXuHJ2KVWnM2Np+iPu0aF1hbLs5PWkHweFOzarCVTEQAg4lPhZrhMDtEs7RnK+h65WSokwG4JlaCvyiulBFqXnURz8ODBzbIEgj+S7IULURBRpClBKGap3DepexXFa2zA7ay7vsUph0tmuz+5fL683pxUb3znJ6uVa/OSOkuV2fXJix9Wt2flq/WWMvQYuUlzxujlMNGVqen12wGWB2ftm41Zhtddu7a+woW+w3lxssFVksNpYN1sysNZaHrVrPT4lOGE1ncw5TSVO2qEMVroO2hAEs2rjWIX3LZXfDzzlkIFhvGQbFbECzDA6HKV3zA2k2d0wY0i1lHsuqIoVhalFCtFmlYLoFhZzzJWbm3UiMasR3lqf04K01cEuO2pXJr2fpoqVYQVnKTgkwRPAaNJTV0imBl3PpR9+qltEQlJ4HZQZt5aMXb+8H2xTQoKtjG0EpPuc5rbnQJuWGAwSJgYdAMqS1HI8tXrDO5vCjZUK1RcvVXciXWss8PyeUQbMTovXbyV6mOoHGVKu9Bfp5KEgcFeZqCAaYWqSrgUotLzHzuqhvp12mDQBVEIFDGDnO5Lm58Nwz4IsfApEVQIhcwMAVCpigDBA5zWWDJGpKgT4RT+zVkXghuNKNvS70DoAmLMmhckRaQJZ7cCU8ifjbV02Y3DRwFqrvGgqCJyDAivckKhB4BQBpkReCvFpYmlRCqq7456uXf83fIEfaat4gVlp8CRJlJYjseCrU5SExPB27RN/g/HI37+paPYtuVM9kUlmlTuJC7CrLCtC99/K0AmXO4xfwgmkVVrAIkACXXYWFKfIIShUZxMBGVT0O2HTmXLGCF6AIaqXUKxxCuzEkPQbhWEGJiWitilwinF8qrL+rbPfyp6ykLHBKigrmPdBHeYmPXhxhbN57gHk69ibH0HIJsdqoxngDhY1RSsLJwTgAi31xSTBI8XJKxY51thJCRGy3VcP0yle4uC1QZHMYnIwlPzaLuAKYzoZW0yrsMInpnNKmcvGsnoiVFzm4y3rm+JmA083C+uEciZ/GDJ5TIAaJHZaMwWCa8d/0AknjBy0xI6AvftYsUeOSuwqeO5bk6IWS7VZoMIovlLQmEgexERVzJUS0YlmaTRb4Yhq0S8E+8VhxyIhTJGVA9s9MNm+y4ubNO3d3DtfWcWFr9913Zm2DE1dhLNlY2YIzZ9IgDNGOwdFZ2rl158be9vt/7TeeefY6k8ExOKIkIiWpOHOJ4bdehfxvDa/Sk+nbpwgeqtC3jy7hFbIV9NRw0kenCzaI6pVFV9IlMCUnFi8WGx4jK69KHvPLM90qYCqewLJFGbOCosnXFHCjYbkDvKRmTN2ParmNL3Ijl7qqq0G7l0G1qKhzy26+ZGC75aiweCAy48RdvZQE8UBqKpoFR2v8KXghXvAjLXfaDwanHIWnraE72mgOp6il43YuOgVh1QgC8NgdJkSHlRyVg2qmekCDY2XUCzxJ0yeWE685nY+tIrYwngnEl6RoNVGJ5plTp/r91uCA3uGI7jyuP54ITTb6QkKa5AkbnZkicB2E9Fgp4BHOO+ti2+stj5F17pwSSRBKLLNUlrX1/hu+4zuee+bZndu7e6MxBwqRgAaf6mg3Fp1neN39bro6FEH3lQksjiRiEwvsgMA45pJYuCWjqj/4mqbdWiXnSkstc+UnHIEN9KBwi+mv1LdvbX/wQx9i+f73/8B7L128vN6uTxkAbnXYdsEAAa45RCFdqgmThIwLsh0Cf5N1GEymuSvEas0VCyXLnQrA5GBS2HjaYpPvev/Nb3v7A695+KMf+ijrfkYDqyuuj4spmo1ep8teZKYCqKAWxBYctEar5LSD/9EiGminNNQu+Uf0fP7SSy9C+7kL5ygNVwE/7T1v/a4L5x48GO+9fO3lRY0h2j49Eda1pHcUo+FwPtDdv43CoUVia7n8eVxbn8MP9JV0+ohDmJw4M/Rjk+0xKEtnIVaC710V30EsMrA+hfGxuigHYmAXCTo+42AfdZUtFa1Ofdh2ybtDP6wTaXZ6M2oKXSTKtC46xl9EymQPUiCt++I535b6ls0AfOoc0GIFopCgcwQOChmTaJccQ2e3L+oJOQ4SyQ6wg3By+osuZTkNbi/NBscrnWgMe0OW47sxdzamv0jJdn+Wh7CAMD7kSCeQD2ew2cVNApP6lC8j2slHYgwJsZrO/ass81FH0cS0JmiC9Qa2x6ezxjMiYK3kd8jSF6TKEUkzdoAwEYbR8DhXvW8xbtY2Ob9+4r5PFBYmMMKAXyv2kqzWWQ1Iz08C1RvflW4YoaDJUFol6wXpUETbXJsQ4miqM9KBHihJeUcWOQufSG9BhMi4lKZRcedP2EkCS+OZ0ogWMR9Alv4X4jCQUJseoSBbHisZkc2ywDCtY7BTVUMDGS0ZzKnwdtWQsytxRQn0rEPWDYtHxLIxGPrdaMLsJxnl1CWF2GiSxl4fsPQ+grMuM+OPICkRnlPILiY+kck7UJSf8cwGURCnutvWogtRIFSVLU8k4Di0Ro4rpykAM7GGcyIJVUKS7FwK1Cn9gCUtmGm6MdMkSDb1koKdxIJPmSIgCDZYMWATD2pOKqPkERAOUIb/cll0dHyVgNCwOXgj16AETjwQTqRQePYV/MW8QrgA/Fffk8dMKbIUtkIHcAldweTFDkDS2gb6V10FjLwvscfuJf0q4dGvSY+KLdltyCtECmBXRMGxb7fiv8Ap+fK8yglHjspQJKsX+RPyEkBGrxKbF3CnsDwuGRKQB/xf8VPKBLDKpbRNn/dvczuKPVbCEYBjcIvwjgAEnmwowhTKiksFEHfCkuwo0/GHezH3Ci55ynuVVs2seJ1fIz05h3PTp7blxEYPdRQEGcVD02wF7Vprxqi5aCsn5fOE3x6L5TSfas0/bGYskRIgxJtP1BcX7et6QR0hOjhqdvIY5Dwa5Vl7hU+98RUAViJDqVA4KeDAWDFHUVCRNSKMA75kkzs/i7+F/8eQU409FRqRTa1Gm8WgjDE6PB8bFEucCipuBQPRFlVw1izllZE3R6yqYRVMp+/kUPut8GKEn0dfozg3oZCmxTSp7YCBCpwDfvVHsR52b2gwHIJlaJZnZjDnz3zzGx4+2F8/ffb0n/sLP9Li0/EaTJjIx4ZwgovU3d7LtAbFdVpbV156+hNf+vgzL+A6nCN6sdwTtYgOBKFDPGXdt7/k/lHMsV0Brwh/xYuptVbWfPl/lPuVD+Yh0QrlgBAXH/gTq/K3ynYPEALQjTEacQnCPkCPNo+01jqyRlhAKl9jEAZky0UeWOHRa83bDI7jBWHxYRcCY3TdoRrPtEH7AOEAtRiqhEjXNUZ4FMBkCod2nKMjW23GWXF0WO3GVD4bhDieH5Vi/J6FM4ymjzlj0UlFOhvNUYMzmJuD2nyNHW61+bqfMVmseWw6Syf0MtxXx+BRt79WY44Cx2yxNlrszMdr/Q4bTxlS5bMAnJrC1MTW+smOJyk6+dbHx2rUsIHMG6zPavu15VqD5Scz1/4cHix29+8cDrrMmNH45UTKWq/T2lhjt/Fsc40q2eAARhg4GtL7QYvZcumIO7uF+SraYG93wPFRnH7T77G/rb1W57hMxsjpJstm1wBg6nFS2VTHu0sgYGO/0z5zer3TfM31q9uD4QE9id393el00O2zaOMEfGTpvZKDZj5Qh2ZT8dgOyXlMLGigXit3m3orj/XDv2hJapPOkfEKlHClqXxiRnhgYwNsyQgU4fw2mh/96O88/Y1v/MRf/cnXP3ZpfFhf29yjme71OVbTQUSS58zc5mB0IKnNOof6nz7fYZ0QQ6bkN4Ul2ZK7DUCPwM3zlEkPfjY67K313/S2tz777NODQZ2pBQZ9WZqNx4d+kQaK6K6POHnJc5yozs3D/UP0lCe0kfKt4yhu86rEOF7Kjsc5OyA5uYshReRDrhP99pve8OhnPv2l5XwXShnxhLGPXnxs/QyKgZmcYJHBBYOGMi6WDBCyAxrOsPMKzeSETTodLNfGYiO7WMvlkEUqMzSCBTb6UuygyMAndFr7vIfDPPGcK7/E51czCxH8z4g7rvRGjR2tfnWetQ0bhM7rnABD4g1MGotzmK2CFJ7kJ7Rz14dkDJuJKjrdNCdUHPoG2zwXs4FTDXjoslBByTK73/xTAeJXpa4jHxBGTiQzPCqiYdHQxfjaWcWSnug3nm4rwxf4RnGz/QV8+AVr8ZkGrn3DjantZ5HEYv5NKsFyecgId6f5TXSq2XjaSbXlrlW8vseEX712l+Lmy32d8NqhPKsfgGytdhCjh9lBsHyKHnXlUCPmfzqD5aGaxPZCV8fEatGdwBRwr2+CJ4KGG8V7JZ3msxAAjUoD8yXttl8khjnOJBT66WPbp6YzJs2M/ZA5HKOHoclDJ+kawg0QdNwdUTCDZyMTkIXhsiifjLThhbngQh0hDfLyfAKcZGqnPvqOgvHiTR8YoFyiBiNSLsoMMRn+J7trcZaTi4qpfQtiAA794GEq86WaCcKhjAz3g51RXHABmD4tTuE3Lxq3YCqpxIvvoC0b05lfOqdE8LaNdoxAQ7SYnhafJud06fh3uj10ifEID+5Lt1tu2CIwCriN1Og+ZHk/9VGk0lRIINvO7dSApqSp8mqZjIat8IEWgWRWbQyD42t2I0EIFM0RF8g7KeE4PUBSIgmdnPkFFaR9BwhRXYgkSsbITBljoeVKoTIjYXDEvTTRjITYHdRUskMA0Cz7EqZo3rtgTfLeC/lXP5UzIY/mCqQnmbwfgRdsrhLqvPwqqIhXNFYhq7T+HkE4HnjsOQgXQo7yfzs4YvVHFFFKOQbzeID4rq6iaqu3e7/qkFJEwyj6CGOkIyaBUBFpnggtKBJYSTWwSlGJCUADV+mSIFpenoihLAukBmrgK9pKmapfka0wy1+xEBU6KyAViqvXV/4K8hjeR+w1VVVcRW3UOGEUDF4Wj0mwYabDbD3kVrVo5kSjdbVJU5Ajv5v8aO5paAJd24ju2rwTIj26wlZdqCYF3Nbk5EGI4qm5wmpigLAl2E321mD+iEoOTBNRDqNi2oSMm8GALs4XghMnZiZsfqgyTkVquoWCIWfGk46JU6qQwBAJVddlj84b6g9hkY+4FL6LrfinQJSCYUQKtHD/yEAx3ov4qO9pD+RXWljAUk+lf5VAkyWKtm8ROcN+GL/C5lI4LyRa1K9fvXH9yjYxs/kQ43zy5BZAnHhkUpkvQVIIo9kuEhW9TOu3PvP7n/7o7/7u0y+/xEZoSC7cjNmyKQAwIccvExx7f1XssZiw/Sj66OFeirChCMfAVwGu0imEIxxkLcw+ShmgviWEcBObooDmF8Nrdttd+I+7hm1WuvykX1SNFpMJrw07j/V1QK8xnDRG81Z33kKHWKJCV9PDRXDYScWSDVJq5l3ZrLLRWjkWhcdqv5L9fdh51xB3u+sX77u0yfZFv+poB4BlPLrQbqjlY2p9vmjTaW42moT3m61RfbFWaw2by81646C+IJwtLmv1Jp7F2rIxwgdu1Icsz7HDQMo2J2R2Gx32t63VFhwrIdrtxsZ4evfuzmRjq9uq91kn6eGTNZSBrwyNl4vubDlgDXatRR+SQzbHnBK1P7p75fr+jdvbfMaLCkcloqZtrHUXNBDtDjXG0fhaE1wn8yH7X1k6xyGWDPP3et07u/uuJIC/nNhjdWZJQ2syYdhYD8ZhNVQRX5dWz1FmTgtlgc2Aqrl/5+Bgd+9Er7e51nnuhRuc/96nAe50Su8Ce2ZLqTydl3D2wwqPK8b5gYyUAhJPhKpHz8QKjNpaixW7JsW6gBxIQZUoI402w5qOzPApfQb53E3qmiVqVv2bL3z9H/6jv/+WRx/+Mz/4o7iQvZ4fvQYKGy5xcbA9dKrju7PCZ3bh4iXBUh7gQRNnCHzol+NUgLL6yRVHLUOtLO+5dPm+yw/e//uf+IOXX3ypv7Y+YwUzky8oElbC3iR5rfjYDer+/v4+n+9gvbsdTgeV1VKZoYZxU0lv37x17crVBx95GExAodfc+vEf/+tf/uI3sGk3b98eDW7uHLzcbywvnT4jnnw/zqqNzmZkUT5RF3D5mKgBIA6vEza4sewcZnkTPQR2vzCWg5jrDebB2LNIqas2RDwKjZILV191EVBsWkmHhkQkLDFK/VQslC0MseKKtFQ7pOnQOYgQRmrSkAU2y0z7ITpPZrbSUYhyVkzx0UxuEEB4Ui1U5gJBqaghK7x5dD8I8SLi0ZNMSjd3XW9Pf1u/16VyKcICaBVcTGNnQ0viHAmlYknZKM8+A5aSBokIJxyRBWDtF2jJL+NIoJ6CEzpHpyszGHZr2DjOQLktOKDn7I/QXDF7BpnAI3xN4VO6uswrCdUFxBENFz4YyUzSVZFhjZy06y5HTKSogVjeMIK2g2ZxnsKUThCpjQUaoKhLIE0/UctpfVIi6D+mrjBSrtpmkxZI9g9ZqCLQIt4gE/UgmWABDkQG2ewqeGQCawG6NrQGirtlIDDeRTR0WxLZjOOCKaBNKZT4/6HtP591y+77TuzJ6cR7bu6+3Y1GJkCAhEhKokSKpAVJFClpJA3HEzgaWeVXrnK5/A/4hcvl1543dtXYLyTb5ZGtUrDEMCYhMQCQSIIJIBHYADqHG889+cnBn8937ee553Y3QFBj73vPfvZe4bd+af3Wb8XNWW2OKxIVLcLRF3mHZOw2C5VL5jKUIZroluQ6sAeDHdAxZbq75EM0JE5dS3lFVvDQWSBtuwWLO6z02wmwh4aVLNBLEUwHhTnojmQHVbnOg6pGOlWNnAiY9ByVZgFGQ54KjymAeEZIxMUgRK8KwQg5E6D5MVBRVsATbfIQyxus8c4tyfPrU8UpEIa7VXxyJT0p/P0eLpJRWrmSpQRIiBGSA1klzQYmYk9MEWmWACVvwKhGPuS27PtY1jAp3WQsgHMPu6qieLZ6C7mURw3Ke1V8gQg4V+0LtroKzLxcelzHlt/LESVvVErwxTABnH8EUqj1WvPKVRSgKnlNY/kVTME8P3P6uwxF3TVXYUDO8Kn2DERznkKifNe2dWh6xxTNg+CLcUGdsA5QmeCUF4EncW4Fh/W7dJTsCfGNXdukKbsFTAxRPSPxG/zxKvhsXi3OQNUPbOiz8xhhEKB+G6o9UyppmZUTuhckpZ4/1EWLXsDbmhurcmvrfafp4Z91iB/haioAYljKV+EIVq3pJ2DIzG7tsj7x45/UxK0gB6bcOTgqMNW4AonlTWFkmN9SonDTroIj9qvaAXOKU9x+Ru5op1n/6MJoxjc9j85BKRELBSqkpWErVtPr4s+aZs0irTspQAxzip3MuA/DhzKCRSU3iV217sNCd98CQU8COAEcVlJtSaMZZgZ9cpsthI32I5JJh3/Ew8Pmo0eHjdU+ntRo+s4HXnhhsN3Da4EDGjundzE0HSepHU9hAcmQvF/60pf/+Bsv1TkgSHady16Lhck0HsCMkAigCGVU3fP4rluk4a6AJLxUBwt3SvYneRYHgm6iz/wWe/UkMk8pHKh+RRixnVyKNmtV0GLfx/Ld3yhWxTflQD54pok2iW2TVlxGWk/lWzGkDiIynuVgKcuAR8tFn+n+o/MV572zY6XXpYGmuaqzbvvVN96+crZ99eBgd28n+ybHrNd03EaVhcERMs3Gcp8imt0j4nZ2UT6ZKdsZ86LryhhZB0HY4rZWV1n60WTci+N6UEM0br7bqO8tGemk/9wYquqLC3yUZRMPnsU4Oxyr5dKaWef44hW+JttqjgilZHSA8+Fn4+njwzdbtWe3tjlBBI3h7AtGuvEzUHemGhhnnnJ8yGzJqHy91R2OT++PxyjIhOEyFwawdYZFyTrrVJQj6mar7ngtXGWFPktRx1M2yaH/4LbgGzvTWZ0PFUERKfhuN7m6vcXWqjebczZId3trV5b4JSf2BTX3dnYY/iU9Gz9vHlw5Hw9PR+P9m/ujNziKhxFwvNIFS+Ntra2w7gwmI4yCbuB0aCebKGqdHk2qMJP9jlOKHQpLZUKoc/iDv4Qe8gbvxDyapH+AQ66MMosPvsgV1x0a4c07d+/fff3Bsr7zn/+Dvz8arbb3XFB1fnZOx6TevMtHF9rtfWS3v3+71d5i5LI4NRRpNcdtzKnkjvzHCKBn1DHrpzoHKXzztvXjP/VjX/i1Xzt8dI4bMej3PTkRpVM0EgDaaCzIWjcns347a3IwM5ztK1hkxD9nRPB/6I48enj0wgc/RBgILFbDT3/6I7euf//dew9WndNZ/bxWP5jN+vgbrvVo8HkH7JA+PueZrVZ0SY/Zj8E3DBoc++P6fNY28NE3rOfAvTPNM1mqNYC7FysWzdf6VhZsA9jFQICK6Ho3xqv6tdrJA7kfE12W5LDIxIFnOSex9pwViO5cRnT1rKiriE7vnzglahqqKhsThMpBPgGsDNMKkz3l25uZXxUAWFBy8xFmleJlGFliIMWWxLkXMuAzCeg3Q3DEeZUpnHZtF5yY/YAaVv+32KIuK0CCdBju+Jett7Hl9cWzVoR6D1nX7S8xo8d8HQaHFkHkKWxZZzKHp7SkGH+dVN5xQUEZbJhPZk7vXDe0/pbb6WvX1efmCBr4hDyfO2DLMpOOzLHRdaNN1HDF0VUfJIx/sEgdhnTZYxhFFIUBLFslaco88YkeNMwGvBopQ0mJQjn+noNuo7oCZ5BLAdnVgmsKnO4KY2Gak3p94Ag1884sAQIEfAEeJSoLhEJpYGhFRSY+yAd8A0adGDm7BlsarYcxvXrVGGa6UYqbjgYWzx4WptKutDP8nK4DlMY9Zyc87Mz1i7SRUgxIrfaIj0IwkMH6OWTQ7Bxz0rEqnbk7l2ipJ3xcuuOSPpljqmiJqseRWhicBsMxVBK7HppmCKFkCpBuskgRbb8HsbovWocAbqhbwAqlLFAkwGMMI3LBp6GHhZTlVINaSHsaLwOIEEFjEf4TzhcqkK8SkS1ITEOtAwLNbi+R53YQaCQo1OUzjDYwFlU0TIXmCZA2cvJaQZQmT2kEqKpmODH8uAkeQHkGNS+fv/er5CG92dpvcRNcYGyiSiQY8BBGwsvYEPfQZgbWmAIDeZrOq/ohgqfqpcRUkdJUMiobISikQgb3hJVSyVASJ/86ky+X4JbHy5FJvUkTDTADDxVOIk2IvMyfumIC7ul3Vnkvw0yWAC5PkUPSmbWk5L65hJX3KrkRJb4qy1fieOOHagpAqpCA0iM3vZYzoFOAIVymKPeEmq1EeK9e5KJpUsuqHLwXfKpSLNiwSnIpK0m0LCmDmqK1oh6jm4TQCgEi9qRSVIsTR36oYvbpLUyTbPEgASAikagvVUrxEjGBUvsC1FT5rwksSmFdMshqQXGWYvUnZXGZA4QoAgscUcGykEEjSgSz9y68nmA7KY7+FcO2TAXoRrnLktqMtKmsgWm5RfMEZ8lpr8QbSNg2+g36HHigQLdZBL0wX80lWtJZOmrLRxaCqOKJL5wwBLiygngSsIiZIX0Z4TgKu3/d0IwLe356zgl/TsY2Znu7DN1h8YQIbYxTMZyJM8w09mLBCN+q19s/PT65mA/dX4RFKQPkKbdYbbH60y4QTiJ+19fTmS5FrBNUv+us4PfUJY2BCvbKE76F9svpkqXwo0oKiEobBQYM0VA8/U4Pe4pw4QAONEaZDd0oJ6NAWg60lOc2x9rhxXLSOvdat8fe2MX5xfFoxFD9eGe5v7fTZ1wfv308Hb719un9e/efe+7W8x/4AH3AbKu1tUAy6gRNSIqmFUGEuG58GlfzzrCRw66Ul34n3iVNHsacfbQMvrEGQPnS8LJYg3aLwShaFLSV1pEVxSwZoqFkUJ1+KKKbn5+zQmPxzv23Ee/BlX1gUabKtqhfzGaHF6ed/k6rt0NaVEG4bmGz8QNJdprSerMIRQ+p2R2OWAU0ZjCNUXu4NGcDa6bCcQNcF8yQHljBP6oyq5eWfBOPdojNncvZmEWxvW4X7eWigrNehKkMFhB1tnqN7cEVvmDc7vRz6A3+gOeHjMfjXRbS0gDYjjL+jr/fmE/cWOG2Wtf5MIfQBEN9CbYadPhKlGVLmpsvpL7DknHqFOvd/DoYnIJyOc6DymKthK5KGWQqMf7oCCMQXjVcWgJ1vdKudPQ5a+V3/uBLJ5MHf+tv/J16c59a3O/1YTc8BON5p8/hg/3tjs0XEJC1mxVYV2NVRYgoCA9RBFEQKyurF8/uH1h2fvgv/OVvvfTy66+/4pfFOLGrw6qDZZeDlrr9iyGLzfiGcGMy5fyhIYf4UlVRHIqC22gsZegbOQnZhjPtnk4etTamq9vp7n7yEx99+dWXWj3W7TNBdHwxfsjidhKTH0SQLSlZCRg3G3/OgV8HncETb0MnETb5H7sIhWg22C9qAxa8k0JfVK5KJ/4Fv8X6hV7Sw/5CNVl5KmUqHPpBcU1B1N54xlUoxd64SUlMrczokcaRTvBaQsSKCEUlSOguHdDoE86PkQREO9ESX9IE283Qg9K51+QbISbrS3GtWxrQQJ7qUItuD0fiUN1wClmzLznuBwV7osEbWLxRODojtYKzimI3JBGGpSh4hA2RiWGQ/LS8oqI8e2ARMGgGBAdpEbFJEAXuaLw9s7AgUKh+2IH2E8fZEuWbLizMEIXol2+XguSpbCIWfulRUlJ0PvJVOMlv+0zZ4sF+XBKgYwyERLJEEQrvzK48EXMhQSOxYBYU/MAJA6GN0HnOgiwycUVPJJhENj0AVnIaWzlJ8RRrJWa1mtUo3gJ2JroEdsAjh/vOORRL71buoCVMuUOSJkkBKxHQA2+AY+DA02EJERVb0XWlJl0K6o6noAJVSOGG63BgrjVCJoIVwkvvFERVfkrigxS479QPCkNHSOHIHJhIu7uhIITLnCG2Ii3coqTYLcxOehXmca0a5bCRBHJEFCVgF4EAaCIclqKHQfeCQ1ZhC1/KIxOMRdNlaSwVxdGQSYESihZz5xXw4sDlU4Rvs2k6VYU42c4V1iRVOEQB65gkSprvdgsUblVpG4gqVa6qgPICAhZA4qjrOtD5L54LjCeQCGDZawl2AVh00IywQBigXSCU7Otnftcw/PUv3NhkWceaIRCezDMY9PQlbWaYPeNTm3NMefNxjYPQlbEDPPpTCEKbTFPP2WGotbJNKaXYZAVAgkpReRSG8gn7IwTP70+6FOhTNNSyiOeEnyofQyG3kC2nT5CGMG0NhiFGggIUOxegjCpKYLpCBiGlekjRJjFPZew/EMlJgX5NmWyl9ALTwtB6AZAZ8gMkxQEhxa21Er9D40v+VAXQwKl1HpXMwdC7sTJSLF3eSCZNdhGA6HEBXRNscyVsEzpNG52ifF9Fk1TqCJZYO2yLgRXBoprbS2NVfIlCCgYGsOSxXurjaKdwrcAupWScwKPxLFEktDW8YWugnSJoLklPaiqbPCpgxd0MmIwHJSP08B5b4Y1HkwIJ+ook/CaxHCU6i6dLkQQUAVUYEGlB4NK8j0siTYGKQLR5LJyezDtdNjjenS4Zxm4PHc1nvUqmpy0NdOQVC5dZd87RyMv5kHHE84sJ/lYHv0M3OVBNWYDzI+iaY/BY09MSXe4i92TFf0Ff4k0fIRJvGl/9DSDfq6v5mAiAJk0J2zxWD5EESY7LO/dkIXECSmjjNIGWIsOKdkqrZHQ63WdvXN/tMpjKuTScR049dR8igt9hMmTGUS/4kVTYMd/8pc53ak0+HeSXkRjwoUlhhc2S4x1oR5gcpgeBGUatlMHFEB1k+t+WGUuLlF3vzppl0oFy45Dmida1P+hz8CMjUnzcBf8FKXA4EE05fTaO4uFgk27/FG6hANYP58RZEnwfBfZVxwyiUDD6nixEQ/qAfIPB/4vJ8fn45OR4uHvAJ7Nw6dxFwNQUCwpGo+PVonvGh3WG42ZtixU0rMxh1UG3ts03DVAMd743cc7dSqLO4Gn2LqYjTtdhuRrfPN7d3oKIDtPa9cUW1claRRMqgdBpIwgjwPvgYPD2yRt8/dg5dho1nOEp53We1GeuaW732sPpiNFmOgmcpn9xxjTFCi+13hvP6fLo5zQdlGvU9m4cIKb7LF1j+J6tCWz4ZKMnksRBYDmG7hHl++fKC5ZCZMIFRjpOaBcLfleKgdAdvVY/4h+qBjbO/ovrX/RDbdPwFN+QdpdXrAFSWJ4cn33pt758MLjx9/7Tv8FQ39b27pAu8vE1ahLLgvauXrVqYGgwZFQ/P6oAGxEVzCkMil0iTjMA5oFNFTWYfGM+aPt9n/7InRdvfvUrXzk+Ol6sJnzMqNUduOFYZBdTegGz5fnJcGf/KvVXnabjk/quB6MVAhA414cX5/QGur0u1s613a3Wz/2Dz37x936BiZQxVXsyGI06q3m33uLgf20BroieU/NQI8yOFPWYvSXkhYMA9JvOfqFZfda7YFATdjKEzIIxl6LZCHuWf0wZqrinxWpchLZQB24YN01AeATBkYvC1vIkFvnIZ8cbTLkedNAfVmaoAw+IzBdCRCBwCBAYmebX7N4xE252g1KcN9M4owjyNjM+cOMvMksA4zbAc+qVMuhb6xLSq7BXgm7t0B9dsdobeU2vwwA4Q6vK93PkyeLZ5CUUlnlKD1UUVgheLYB3rLhzoL3WegsSV/NnKQS1Sa3Bq6HYvqM8tCDuu6A4MGJACeTig2cqSh5z2NVyB+I8lAcZ1YfKq9F3EpqdPxJascSy9Vx5t9WTgxRsa8qD8mPzj7TTP5H5oE+JtGsy1WqBrBzegjY+SsD0kM1bWEVirQ6p7foiFUesMH2kRRPZo0wh/kvFAoZGEDpixgjLkIrC4zMTrKTKBattpVI6dpLhBgOwn84zuozZ4/dcJEYp/MfA1vg0XOtxqw03wAConv6L0+2CVobMGXpu8a0W1jKyQk9G6zu4mA2LTn5J1vlnwsv1lwyfQxtyh1tml+sEq+WkVSWY/5Rp1AIgyAXGJNg/gEduX1YW0DtHyqSx9WD6AV2nCdiS3aKMSWdcSX7Cl8JfMFDc2AnQQ/UgP0yWZvEoY1AUAC9pHJgfQyuo6sYgSiZKwYOyRUdTBy8RCs2SAuTiTiTZBaHQyyWu1m5FVgK5kw6R+FClqqJ4W6cyUfUGgCrZe34C4klmxvXFrcFE0xPYycR7qjAM8Rc2ZWDLwGoPAHxKyktlJVMCN4gmVoKDvrmNepIHbkidN4vZXKXUVIZNGA8lCfcCgfvlTJsETwooxXGvyieDhQnTeqUH4ehVq83qXNQS15PYkjZIST4pq2Ke4B01L1CCQUg0uqKkEkHKWj8X4ktys+ZSCfxzsIeCA8Bbkvlqbl7RkYJ2oBkmasI3tw9Ga4JMXAItAMgmtgJLN7lMSVgeSm6aKk0lmkdCmmoqgrUUwOZNXziWQHRSQOCSGmVPCPWByiL8oBQOWnDkTvuTvreVwEQpkzieAA8EDbChEqLporYJKGIgRANibOpmsAdKqpFUQwYm3Qz6CmbKTQDKM4BAgAw2w8CSRuQOuALRYoO4KKVgsgIj95Rr+4rFCOQqbeIFRSBmCdRIb+7w18CSPXejkoEExUqnpTRzKdyvx8AGDkophwxOp6fXbuyydmIxnuB6kkmwlEFXR0u5xG8Yny89TBk7ge2TgAJ8g3mFQBi+JmaDxyXk1pQCgMe021VsKAqFJaCiIS8Vd56C864XEZA9XGHAhgsJ4pY4tZoHn+VeklZcVCP5nNYcR7LX7jw4Oz1lbYds4Ou259uN7tXOoN/iyMke9pLxWFpjjgGHKey9arZ7Sw7o8Ps70/2dXR0AhuoXtW6/T+uNxuztbTmDj2StCZpu+IcqojGov8F+tkfnDKXhpA+qDy4vPUzHfxgvUI+cyWHEEeRZw0OLF/WCBBSYlojFYCiN8qXHgJur74vvLpjO9b1b29uNr37l5W6/dTDY4zs+fEqHarCadmfDSW16ePH4bDw+Y39ppzfpD67sX+nQWDVmY0BPWa+v5+rsUbs9uDrYb93YWfAp2+b2snZB/wSvlENWlnyGSK1BWag5cFK+eQYRiDtyP5lPt/j6LX1I1kAxapVu5DY52MfH9yVOL4YnnCI0GTO4PWcplftl+A9JY9xXGIYXN2MbrDUJw8l+UJpzPkTWPOUrPDgkbcatqWOMEKKuZIA3WFqHW7lDRX055XtbqMRszg7NYkVIEkVIdSoq6+AfUCgkVaukUGPEU4Nh5VeEkKcHpTPUnH/xd74wXVz0+zuT0fHtm3dWs8n3feoH7hzcnk3HrEHCC1LXwIWdIS4LWGsnYH2MWgI6OmlkhiRSovWVsYPt3e0PfeQjX/nKl5cTfG4lw1YHqJg5RqjbN5ux5WOmTWT3OXN6nAyvMwEMhWEtbrVGoxEfYu318O/FHE2689zzd+4899LX31QHW6P58nTV2NXHAy/MsV6F+gSpyEFXCR1AGOwJkR4GHElAJ1Y5ocoLP+CFa9Wn06gHqFeCtdXShn7pBhK3kCxeqghJjGF0RG8Le+CYPhMXfm7NEsHBZF6WY9EGBUz1pmxSmShUG64FR19tWahBdsJLfhlsYQzdgL8a4qAwFBJIfbG/CiiIxMpFvgqHPID3H5AZ+HFOja8lSMS5nwBHK9FvQClhOq32E4ijdCu6riZxMg7oJHNRmUM66pxYy1+wkhJAiE34UMXxRgItiBtrIBuY9geoDBoPNlxzTi5iJ1X6lZS36KER+JE2PpYESEkQvpfssQqFpSAAfuEPsiAWncJfJ4T6bpuodkEJlgaEUAYkSr/PKg7P1Dam5ggjgQwiBdgwdG4JgmafLGBhqiVDL5+z4Oq6IBk54+4Dlh9qJ7/s2DAVvi9vsAIL2PRzhMw6ogiodJvzrxyfanap8Hw5jCIklVkvRgF66D/jFHO2MNE9EzPmKMBjyewX3x8ESVBp+QUPbamjAlhTVilCKUuAmK6SJUtGH8hLOB1sVi0B3wOf7NaBMdDgQkYLmWyk4WQtZt05TW0gp/02OSrBURI9H1WblCoM2uEKLmZBOUK113N+g6k6KnCbKgy9kAaiEg5LYKAjw2zmcYSxwbydI0kOKMGVWnfQp9rSgaKNWi74nJFno5YzsKyoEhz5oiLJThYClAZsjoBSElxWCyjT1KpalISUykkdyQNSI5FgS3AVlx/CiwqZ5FL0n/64Br0u7HIOC1oXxi9olwBn8njnPwFVguqnvGo2iEKwJkiUt1AYIku2Te5NinXp64BNCh7KlYeGp1I8uSSZHJs0edrsazYipRsvl6wsqLDD/0gRpXIU0frPZw5ZrmfL7ZgQ6YSriEhbYKx5D5Cy+j9lJs6nzQOZCgSR9ClyCTjLb99PldSca47IhuST0BqbSzYJ0MsHEiW7FYcAZ1qoWYLmJ1HFRCok/pHCCq6NA6B3tY5/0FPiNVXwgRVdnELDnjaMPJP0WoLijmtUVCvuaDXVfGqIJtqaxyPM41UOaahEykCBE5gS+aUqk9YhEikwUXDLg5TJf2KpzZV6OVgDE0iP4SK5wEox8fIJB2liDESC/AegydxGEa5bE4AJvToWmN3sA2Yu1PJlAiRZmf0lGX/euQJ2DdoAIZf3JDUznCiJky0ZSxLgrNMKin9VukAxKGiShhigSDROE4bIsnGvGPxozmfD5WwLA1NfXty+/QFNMubMpeXaaIjEWNFe4Y5xihtDj7//B3/44PC+FqjQ4cwKEstcc4rH6olH65SiIhTKEoFcjL6e5qEEFIsUTiSJzPJKw5yncispSngVXNbxexL/d7jAPbMQq+bJpRTrsiy/es4PllcDDRawiFH15eKi3ti+GA0Pz0757GbGqJYnTJn0pp+++WKvcXoxn4/mtcPF6cU5TQ7fj2PcjoVC+PfM/J5+sre/56g9XoYz5Nh6huNbbbaysagDY09xLjDCFsQTyRAAH7boLrc6DbeZr7qjqRt/OwNaqa0li9qx0HrA9C5Yds1I1KzR4tidTLczs0QovIQSl8uTBocEChEMLSvLuFgMBLSTyZh2c9KlZeuyeGbGds1Wl+ULo6sIevb8dHlSW+w0e+NO++aqyQGMndHkMUhxxh0tMw0Yq8C6jAIzC7GaXBkw7t/lc7u43bMJDukEJ3eyOu+0duodzrdjSmS0nNPonrDCvlkb95rX583j8Xz2fZ/svvTt9sHOZDHpDifHjHHO6+OdrSuTxei1t7EOk17b1S2McJ9dHHPGEcPlnFCJUKAP28WWX/wRv8IHZ8e7rL/aOVheHfTwa/k4KJVPa6Lr4Ce4kTGjAHSfHFekTWaDMqG4TrhLtpb0BOxkwCmYS5W1kedoRjsA9r5KGq0YSWKZPI5JzcFD4q6GEUtHb7Hsng8Xv/pvv0jlR9A7W7tbbHVYDT7xmU8Oh2PXAujPsh/C7cjqmP+E4Q3aNFCxOgRptAhTeGZLjQAZ5Hf15vWf+uxnf+s3v4gfjxXCeDLWQMXMfA4zOrdr02fr3QfAIzvRuh0qLiPxODTsEV9cXPCJ5OXurqORwLSsZW1r0Dk6uY+jXFv2J1OOEmbyBx/lAgqtvzDepRfassqmO7nC8VD65tQVzahjLXqgHHaqg0pbifviuVX0DDXnwCF21TiSWsd0MdtxKOUqYLUZsMImTAOgz4qHw50QCGEcVQsNQ+RIsHA0XQwIEIdwEYHp5wcj7B0Fyl4CWSnunnIxxR2DKVhiZscYLbaRQmHITvlUVuCJqWZX/qMGjoUTGjgkIhQ/XEvawiw0V7sssZtPXmA6kL03dmFs41v50ioEIgC2rgCqvZrc8nB6ZrGYK6Qv7WcKQIZeGm0c3Ry+2MDOChajM+OHJ+p+YlXeUQF3/+Mm8O4wqEPIIAqtnCOJxOHNSGbC4kUTsbEzpskZAJDfPmODaq32DChLkmRAFYYahOhq0WmkFFhHXphNBkwGZcFwDC0A6E5T1eBX4Q/cttOBVbO/x8I+bVej203nD9/c9plLR62UBY90WRmHwEfmiNmoJcxGIvqyJMq5eaSWnPrjIhl4msoorqBcbz0mKV/2k/OcptBkUw+4UqMgU25y0mqUi8Vvev0MXblvJSqEwMHRT/dgAaGe+Vz6DKoBAiQEIXcVNYMJVCe3YWCrmUsELDRQQTh+DQnENVA7JYsEKkmqD4aCGs0Ub6/WxwpydgI0YqqBqcdCGnsAoF0pj+oIPnwPnO8UAq251eG8WuckpRSostglIWaE1VolyqCiQtN8QeeHNIQwTiT+XaYt9jGPHNfG0bB+HY9qKOqqrlRaa33zz5EiDALZPTtRpVIc+Dc0TpxYSH3IKQXaotQGcLGTRFZvYvfeK6FAU7uevkRiHVLyPgWhOapAprB1wvIb4VQFIqbgA/+cdFOHLYrXp1FKcaYsV8oyibakSl4ykEZO+0c5JfX6nrCSnmQU7XU5zSZBYt59K7Hm2mQGe3HlPZgTZRWJMUMrOS2bgx3gPxfnXyipghdEgrjP6Bk5yW5+kUpwVc+M31xyyiwmNUuSmskQgcA4gJoVvaQNLSjFZ6A4Ry9QMzSVrAHsLWwAAowULJUUOK4KFXz+uSQuKa27YmcyzBbGBTtqNmJTumBNSv3xNEOGSWiDMGUMhuGkWD8t3VqJxdG6qVVYD20gecnqKAE66yu/WPNCJkyTMDbcaAY4+oNMchJSKUpsAEK1SE4tSxpti7FlFVfL3VwVIyWRQv1LHQIbkXe5pQ0XyRnXBDjRqXHBifbWVgeCgzEDI8hakoADE0o+CvMFYKHKxIToeWiuBCZ0Y8MvSxdXQ0oM4eY01aU/Q70SUZIWEVepqjzSi1S0v/CHsSrWD/e2F/MLxou7/TrnuONIyTSncTGo6gprDmksMaNw8ZXXX/t3v/EbZxcjLG2USaZINUVbXsGiQgWdCk7lVpAqUaYOYmpDwfBSyjUpSVTCS7aSZ53y6bd1KL8lgvvTVwm+DCnPqA/o0+6KP3+oBXyZcaDKhPH4Oscdthm2lTZqC/adg3fak63+To/jUBdbzUX/3nx0woZJLT6NOz4ZG0/pLPmd5NpsgTsOF/mujAO0aDzOugoqdpjhjNubdbDVuXLl1mR2wcJ+98K2O1udHZbo6CwxwGwri9zIa/tNXgaf9FOREA6oTa4eehguaJ6pB6USIUJrg8pYOzo7Gy5mV7a6vcGAU/nZYok9mo+7W/1G58budN7nS1Dt/qDb3Vu1Jsv27nDap6IxG8QHtVkx0q7jiGcNLscOLnuMta1q9BXHjWW/0Waxwe68fuDpMfUhpwnVW+NWbbfVYYJkp9k4n0/anJHUGbx4bbz30Rtb2zvjh+/QNzqdT3vN7XG3/VyrffGF//Dtb76x2rq6s3dlf3/nytSu6aq3215M9HGpSEyx1xq96WL61t1H3/iTlziXp8sClOPj3b0rqCjnaXr4OwMqtKkoljyGJdRvlmn7neSML6bGc1x7FkjJNEfdEDyprc6IJpXRmstwnQCoMqaxIsNadIB/sR6+ppWEv/Tm6Fb57TUOguIj5MPV9D/83hfOpo/+9t/+u9euX8HqgAZ9APACGhUwxTkKjfIBqFyx1cGdOohaxCxowRyutPMAoj/453741z73b0dswbCPhxlV3jjJZ6eH9cbzAMQt0ekENxWabsKUtWk4HpDHZpHJFGXdE3Mt0mprsPWxj37/b/z6H4b+C+eXVueqZqoF01Igl4qBeeIwSxTNAy8baD6tCVvDMRL6jnqRQOBAAixHazlw/yFx6DeZ9dy1lfgjpAnT3NqiTaUg2wyqAOHE6sMRzEoJmM+RS0Aklmd7WvwiESRjl4BcMzoBUB4OYtmJlWItLRedFPmS5sFgpCe7NLPyBq8UdE0tSrY84TYJgKfPJjjbizhRPBpmk4G7JqK4V4BrNi8Wzem4NfOzu6Jno4PXT3YIhIU8g78sCDoggncPVRbjV7XQspRv60wOjC1splV1LkIq3MXijx4qLm9aE1xYOqJ8GZM+EVZagES74AaFoEfRnq56zBKxRBwPUN2BVTBPRREL520oBfoIIBc4KW4Rh1pa5SkLHKWDNCQI5yTOfTtwhc039ALIihgQLqttxmzqZ2TP/eAQboOlH0pBDnjS0aBGsJNnxHA3YDFcMw4U4FAwUGGLi4tqGddzGkPx1/hOFwcZh1uKAUaqYSDJiQbOMHV7HqDv97A9YUOFAVkHoygZgfvHkbtMmjIBSg8B6uULp7L1ypyVI1lwEvtolWQ8RQXEbUC9MgwPH1lYZ7eFw3zoY3mIZ7DgBhIoOpua1AUqDzrEjCIy6dCxV2sZKME+QTY8lwHqXHgLI3xSfMiczRDKF6+nybwEJ54hT1yaBqOiEINfkRNC4a96A41ov+o/mzArjJIgJOyAHUVkxaeg+QQ1GYMRKWEnabL81GZeXQEAeWyxAZdmO0qvXoklAHlgxMQfAyNoTYdkhIoSWOLMoVaTtoABwCaeJO96I7UpjdhcluDfkyslJWsJs4qax5yWxaMzABVGQKTva9jdQN7AqhDhI5gWgOoKVzU3MffQ5xvh82cNa7/jvVx8zYM4ThMqyap069inMC4lbsoljc8UkKBSHO8pEU7Nn1Ez2RsQjun+WjUxbqgmDSYuAirBMKuqRlWVeqSGLpYXga9hWpnVI8nzmQMuiARjxnNviQYnw2zSJnHkREqp0hhpB7SrdCG1H3U9lVQ99KQweEMypZoJVLhTH8BKm+wufLDEJbhNo1pr3k2NpUaRjK4t9QM95uKhZJcVKrkbpDQh2hNQYQQLeFrUdYMIXYYDG/NKsvyDL1YP645Qw+WYGLEjUn4xhaepIoAWggri1kdtmnVRiFQ/fmQCnpFWQkDKJ7YQ2PAdXMJTqDAFyalIGBcKJ28ALaisSIvM0S3CU9mBmt6KiBKrKYMGgGHdoBhYtvQy2xxwHutB4SQof9wlXOq45jeIrXHSMCYYaKLKBUo+FtQNSHJey2VIoUjNSBNI68OzJPnreEnMB2jAAg06p7fURhfDx+0eZNEn3WaBAKaGo1U6nGxD/4DvPTGsPRszyjsZsTZj8uWvfOXeAwYMXG8t98S52jCwxlPMjEUQVD1X7sGuQkMwfpKO1whUSioiZXiuTRARPG9ehV5SZ1y/PHPn2oDIW25Pjf1fwqGcEZRYmWxmOqPwDTON/YXoFhoOm/T8UUVcMYhdOA92MVx9+/54u3c6m26NVq8Pp52zybmnAGbl6mrpOeWsxz0979y6wvI+BD7GISOQnar99pUV529i56NfTXoHGYNzsU6tfev2lVb7OsXNxldnC450JLSnEiE6ZMfnl5WNukObZi3Da0I9NQY46Q+s3vObCGXZvK+ucGKYGkx7gwraELCzFun+AF+n4pAavgIAgZ13WLi/vLgyHY9PD8/H421msfGMx2M6MNssmN2ubXdavdHw9Hh89swz17FasyVn+LsMFy3W/ajTRroggNXkOSGe8TdUnZNkaNTpPHBspQfXOALavHe13et1Zljc0/kpX5zd5ux8DDnbHVar89Nvwe5u43ynw5fKZvJydtoYuWB3q9XF7rDtDaWlfvKNMUYQtrq16wedx4cXy/o5TD48fEArzEACCjeZLvkAFK08BzFhJWw6YZhuMWPzDjdoemSTQliudh2pq51ZGUEyVZumX86SykDCMD52htEwOswqIMHqW+yAdY0KhpHQkMUvhOvMRrTffuvxw4e/2axt/9Rn/+Jzz7zgqS9M/jgrpNprEVPpU4liicjthfBiOE3DMwi7mIczSVbTmzCh3b/71//uz3zz21/7o9/+/Wb9+nRyn6NQkeyi8XC6eLPNjDLMQj2shpoVJI/ugnR0YHXv7v2DgyuoEZ382ZQvOrc/8yOfbP8Tv9XQmA+YdGIgs87eD06m1+hlC4rnfXqoZcxUByr8oBydXcTPqaeuMuffMOVxsg0e/LlTuHxHQpaoHvJYTUVJbNZo6qzp+qBoJpE7VKBa8zHKTrQNIRUHfqexYogSt0u3FXngBpCIjTSkwYEDjpWJOmF5OHaUImMpFolZy3CGgO0Ku1xyBWwoFOMHa4hVlspasaYpBKjQYb0sLEKK+U0zYvG4XqRmQLXRHExHy6NRvzvnYxpMfmxzov9yvrtqnPCZAhYIwRw6pSvW5DTPWUTJ6YJot+0JS6Qa8I9vgo0YSeBrUUy/1Di/a8GHLUCJvbxjNmvo2C/7y8aQXd9QxAi4Q/wQRqu07G6tJuxKYvB2teRbEowOgDXrkTjhyy74ZHiNk25qrtNDDtQEbFFRqNJ40+7LV4UKG+A23MLpndNDZFLCVoJ2nDUt7tQFYzjtriKel4xmIDOQoKKxjJBt+nrSpFZAsA1YmgSYB9sxKa1Jg3Ns5T+tAr3YGSsK2cuE6/AgQsC8UTnd0EJOovAJdN21Id5pr9nzz4oW+DgdzejMQqfOhpaWP8FyqZXY2MVgMhqDqgcr28AQpzQ55o4VQdhQBEDDxlQqHjUIWgVhCx4QnHBt4Gr/6i6qw0dLJnxHcAJXbc0xLyt243BHyywRZFCq5ZUrN5hEHZ1NLy6OccqnC85fplhWGHZcj6fXyh0ltxIHkxoTANvbu812fTxExOgAvAJbKh2mtXIMmE0QA9d71tpd5gTUf3pN4M4YkIOwyqFM86ZrQW1BUeGUvSk/49PqwMMlc8lUcCu7fShbOjhHOpQXmVrB4NDito4PJYRXEVMMU5QFsHIwofyG096qSDLxnH8mEb5BmzwJi1IERF7fczNDAiuv/l7SagysmOSe3+a5WF7CStpkuPSY9wKp3AmIUmtavAxN5a2oSEAVvE6QVxI+VUgiv9stWIBn4SApCwJWAK6Kei2PGGDCtIZxNfLlF6TCaIeDeUTaOJULw6WRgePINoYwsAAOQOSG5ExI5ce2uyKQUEeEUic2+JtChnGnUBKxdMDzZdIqYipQPg7v49N01jShBlscZzi1ocjMwrcEqi/dFxoO5s4ZKh1KUXukrHSrUyN5YVozpVrzsL9xQiSdGF0ZqHQslL9QzKAZ1sD6r6dl1Sab1dsMXEbgYNAbxyTIVeQIMibG5OOwhJ8UwpYR79QLV03b3jNCoYGwyoop9YOixRQQOFDcGY2jCvY5WGPFyEEYYA+EkUR44+KBDN3ZN1Jos3aXCs3B3kaRl5ncqCiVGz3TKIAZ/9OGIVnHeeSNN8hwQxwOmURR8UjIY3ktYQQlDvRktzcrbVKFx+EySWBCgSMJa9JKVunU4sAjilXttPIyGJvjGeHOvOhSuHC51RwsZ10cMBJiG7/50lc+/ekPUtdAlVT6jhTAoLYHkA8wKUfsQaSRVVuETIkUIj5V2eVHyemkVteaNkPLtUku7vm/jnn6d5OBh02eTSBpN8+bh01gCdnkWgPeJCxFK6KAgU70R13JpKoWEf+fsSeaWxQWRqADODeL+vTN86PVxclqset3rerbjrW5CFWfi5qCBs5Wowcn929fv3Ktv00LjFvCRPlozNw/p2HaE0NT0FMeaHoxwzS6NARo5mw2bbXqva1ev8HcNEKg9aVxYj3SkqF2TYSn7FCMFddRA6o/UkDYLQYvaCMQJWNsruDCqwAgOk5DTM1Hz5pt5hEcsSc9rTKnijL+hJbQHIHOcH50PhxyshHtaHPQ27+2d4OF7Hzqq9HBvR6PX2b9yWCwx1mHelkeNwfJPKP4nOPJXDkjTJ3JjC8GsCYV1VN3i9ahMNivxoBuUG82vN0fN48u3mEcb6t+5eL0nLH4xcTN6OespJh3V81tVg+djc5ajW2whCXbKB51xFFz+wFsQMf2oLdb3f3VznQ0H58Nj5muUYEVE2xzi4RHBjnJ6MQ+osFlihvtLDnpVGBqlmOiVQUkm5U02oz1QZawDPyLETdWo6FIVCDtjzlTBXhUOyKdVGaRZcrHw9vntcmv/rtfvnv/5f/sf/pfPHPzOtughWICBCXMIj1wg2NEFPgFDwpV6TEBMXTc1Rq+A5DmoMeM0cGt4/scnIr7f4b/Ph5zfCRDgfapMGrBCp8G9EpZMoKlaCxb7mTc0dVP6N+yvbd7g/6npxY2JhfjC6ChFCgN0TBCzgkiB2pSIxxWADj1hQQM4WBSIQMB02qkvhA/w0ridrAfXhMtVrZZVCRsERj5qS5eIQ+LiW8JeGeCHf/WE9PMCy9NYLF/FJAaKOspVmHrr0EbA7RoiXZSfx/EZBjVUEFRX6l+noRjd8KoMByUZXsp2PTlArAggB7AlgRimAXdXjWJrrnKz9o5y2cABQkuT5vnnJ9wxho73Hf3LLAOzk/18SlkurFMgjElMqLAJYHoITveXcVHZwl/fCSTlxeU2SxLqviql8wdKfkFBwmANMuKoAUpgyhf6AMdPzTebIy7eqyTAbTCJxXXbh59b9ag86E0Ri3oKEwp1hYPGsVAfstJh5mZC8JNJKmOvAlgIKPy7PZh2AfK/eJg2IglFARBhMMD3F7eZI5qDIZaTrOrwKJivbBAAFqRVGs0g+FuFLjUuAz4mRwg/ld8MlP1j64qEuHxJijLSAgPCk79o+RUIjSIOApSaGAlimVnLWxD85Sp/2ACIIHOZSGMBZBWWdOVIp+BYsTo7GzKBOuMr+Hh6iBxOcM+bEijwwAUMqGhTIHaRXJzFOvhJnT4cfohz10xdFSwv/ynLGZoGI6UGc7rgACtK9u3bFzptNPbQRZ0CzmtiIlWCEBjST7DqGLfrXtaCT7HSZ0QaqwcSFKlIALOgrK3MFw2+cwbgGSTtcq+sbXMEPpOMtKEYiJpqYfylyxKdXMRFWD+CuapSHJZboo2B2Bk/jpzgEdyVVSwWse++3cdGVFWL2tQvgrNrv8TPGgH7wolEQG3eTIjX8Dhplb5losT63npJBcwoUkIFY1BF64gDAkxg/ACylK/l6uU5F1NNL/s4791p303fI+SZcrOnQBUmcV1CqnPaNTbrMSChWi2tQ4XVi8tooXTIGV+0OUHyGJEdQr/seLkoipzu2sGxeC/gghJo+8qDgow44isKbN2tjfLJYYJ+9joayWZC6tyEpiKIXOi8ZbrE3UOlKk6Lnt0zGm1eh0Ks1Gb3+BuJUnp4Vqy0PfEaPCHBBneAQtq4Wo+uYoS1xm5lDDsOFYgnAuZcADyIbFQQnZXzjLnzfHScpUeOfUCzlKvHOVLvVCp7QnBJWj2/H0/kynQqtrTogMpVYHPt2h2qCAKH5tHYigTGUQzvUVTBZKass4Dzr4hmcOoDEN44iJ7fRgYc0AdE2GiKS1o0RdGRB+KlWNShOko8eLglx8SkIfaTBJzQZ6PPksmiM5vgGmt8yj+HZHqYtJo95poC4W0HhJOzqQhL8VDk/DWwApM7Pkt4LL3g1yYEhLy4HBUM8MYtkDN2eJ0NDnBS6IYBy3mTOViLyBNGw+KcAeSUwDfkBphLCMRP/9Es0WypBEvCRBh7qXeQSdv6Iwk5r9PXsqoPBecS+j73Em0SbF5eJ90FJzQy2lK3k1ISZCEtD+nSW6YplG0IYQO7VVHFFenNIWQ7+42TKiejf6QnBbxHWiv1w5oBep8cxFZ2N0NDMWYMc7VzvHFbMwhOs39fJ/LXbBY78eHJ4Otg/FyND4ftzs9NuP2t+qD/jY1slHjuA/G21BQOmYwFzVkNTa+rkNICfFgCtpJ/CKcMaQlzrCScS7K5bsQIMG788vP8ARZ9PsghyQafHAmEKsivTT65OLckpvkX7beag1cR9TuaUXon0/GwwVrPJosBkOIE9z9Zued7vZg0N/ne7uoBn4kWm1/1qYRvQJhwNGGsT6YUT28t2t2dKgmtPzUNI/NfoFSO/uNzrz12u8++ouf+pHF6aPxaDg/u7mYPGRjXq874YtnS46b372Ob3rGB1GPDm/evA5zD/a2V2OYwaolbAgT34xyz/f6TDH0T9n4Wt+jvXT0AzZQ8e0LmGjCygTRQohqAbxZ1BjDsyfkQCYPUMuJNLhu6K4shyJwJDEQ9IscQ6Q+OhkQg1wAhaHRdu0hyStdVgwUb30kXNvDzPt8h7x//Mfffvnb/+1f+pE//w//5//IVoaBY4XJfxVqObkllNY7AqPGiY2RClQRi5kUAK9114G8ZbM36L7w/O03v/3tVeu1ZveCIzzZ48EBQW+98c4LLz6Pj9ocWKPx6TWhaVUgTQXXZlmdUQ4gapVqo+devPUTP/Njn/vVzy0nz+LuTuY9djHU6ie4M+CD+7FkP0CdjSAoA143HELJUec2usnasnnrjLoC6kCk4Yrtu2jjvUxZMAfjXPjODJG+IBtkGDJhiNu9XXiYdIhbnKA5rx3bSZy6DI/9HTrsEI6qkQKgjHxHf5UiSFMSTYMWFsFYTYRFN5kxXZsiq4MmF7HHStqJMxOmzFZMVsJJYFGvta+8AEaG80LTq/xJZI8uEfp8zM6n/aFDPBknDzWJkV0oo+PNN2N3XLle26t1WB5zkCmXXZRxVd/lON5FbYsFH7XaDrSD6aIFXdvInuVXUaBdOkQZ8obbe0wk1pZCW9V2sC+N2rbueW0bJDnPxwGkOhMC0LHtkjg5wH5u9x44nbCkouIPICWG/qGIz/+lPqjMwkV2evmsMkeU5cDW6TV883rnUM2nbPmjpaDZAwMWwSN/uaNSwnKQkJdwlPT8FynBwoNrtkF8SwG2yVEU5CqNzmL1ICMY7JcWIXQERtAXkHcFpISxbEk1hxyGo6kb9iuTADlRPnyxElAAHFWfxQZEhMBXohGzlgpLF4xAjwZuctVwzkiUV8TwhoSwAZr01Uy7XWsfcqd22Mi50aI0BBSOkYEYWcQXG0wimVzwBBJ0RGlCwHY1u86nJFbtC0ceUT8Zwh4plIgmlAIcQ0TFSQiAtKHyRvuMMjSPVKs6G+0gngkf+KiW4gpiMtkkwoQcTgmvyAX1wFlC69EfFBX1VpLMyaGwabFQV7itnEBNnYYiBmVsBkDdWkWM1ZYydECQpgSh24aEOplTAhMDxhl3r3vSozC94BepyrNf82WfyVu+kZeo6bPEcQbmOvU6myIueQzxkb+SaB1eRXfe9sEWqqQBNYmqs0vh0gxA0lSANmDeBclXZWwywW2iwfCJQBOcZARLg/cKteTfUBtwT6CUYkXE69JbVW6Vr4rIG3WrsFq3Fj8Mj1/KFKOH/WnCFCbI4VXhDmfMAdBkS7/ZpyAY9AWJRsVhyABhkXAp/gmeBT1AxvrTB+AbT5wtTbCcFaJz984eo7AJSAXzyTjLS6EixTs3qrTjDN5VZvSMYan801AKw6YLpO3SO5ROSOiGtlKmTDFnaCWJVQ0glWaR3IwUBUWqKrlSQ3kxCR0IQMMqclG9sl6l1IhAEGNhovEaMzNpMUqlIaOPFGyMhYCzWC5ZikF2WW0KiAKKJIim/RwzhDhiPXtMjMAthoXCgGF6awf56RLYgAMQ6FoyA2l9ZYAEaVwCTRDhL/XOrF7ReKtAYYsNpkwtldT6mQykRmcUIX+wo+hbwJIvYEoW0iAccxmZdLhkUIDnJpqLKWs22Gc5RVLtQf0v/5UfwkJCrn6kQD1J3hUFHGI3YX4U6wPltEiKQngpUgSrEB7ybHx5rn5IUN4Tv3kuXH0S896ny0mJDbinciVBCXkq/D2gkrAyfFUk0BQ2BDHDjjhUFeSD8KiAznfZTBOicbUBCr9hntQKySk3Zt/o1MILm0z4wcXhE7hCx6NHz97cm404RJ3g+sHB1cdnj7uPukeHRyePTzzWrdm7cr3zse/7eM+vVbGeQc1WOcBCLUXNbJvSKqjxqWdgLpl06RAK5ZLYPzSwSFe5mIIKigxK9wASrK6oVTQBx05apJyKAZ1OEPW6W7iG1IPxheu4cS9o/fjKllMQ4CDtnIPkt8OimQCj160C86Thyl3ThkIxSc+ahyxzFj2SZhag1+/0uzv9xsWgNt3aWu3d+PDxbmva3R8NGw/Oh7PZ+Wj06PyEqZAjOD5q9Yaz81vtg4LqcMzptFRlPmfXdxXvotlnj8R83Km32NJwMebLBPQaphDi0jUXpjhgJpUSZZvNIy2rjAknIVuSZJEtv6J3gEyeQQ2h2gy625zlj0+FoeUoIcjQOpBQLeE/yQsHopdy3uy++OgIIXqgzZxfDM+/8Nuff/7Dz/3ET/wo5p8SHbXQmwee/xCuv+VFpgVW/AjNo5zV1zW0sZpOcUObJ3yQg9lYBi94XdQmk+ajw4d3nn+m03EXROlGqheaAshD2NTyxenJseuT/JIcXoVzpZ1Of7t/ZcrHIBbHzdnqnO3ne3gkKA0OB9tJO+p3EEUAuqZwIExwS4bULYqOqLQ6JhyY5Qg/S7VROCmxt4DdhuHRFpfxwFFXvzHOPNOliYetSy5scUW3sTXp1dGRRIIePgrjZRSUMN2kY0w6qKO2qJ5wSAWX7QSXvQTQyDM1TSwirMgGFK0Kqi8RXJFZYMkrWC2BgpNyFISzaOEVLpn77xn7x3MjJ7Wc9S1MCtLZwww4cSoiEikj2LnT4Mg0ksF4sXPES7Oq6KUxCRGuld4mgzgwo1yAoA8gSOIEgQNYQjqU2rg5dGX9ZnzapdtwDNeZFNmHiqh29CBiPSgliixTVfGYOx4xbXa0REN1Br7JAEG5BGFuUE5sSPpgPNvqmxhhARCcg7TIJb38CDkwjb3FSSorvMTL83lwmqtcKYP0os4ViQsz5o5yBBZUYEyeKDnQwsnwgnCjtA6KjwKpETRb9CRRSOLMATI+UTJKQaeX1G2ca2oTpk8AlSMcLvBOErdWOX2nxSpUqGk0ipKcmyXzdXHozqy6VlndFB0EqOamZ1qIo3OClmsew2tFm1QqLSVk+BDyNSx6+yowP1QNllM5wiQ2jEMpC14RvexXRUBFiNHDcJGSTYzHAKJIUbfAi/DwDoJVHhp2CFOChJJbNUNwPsLFIn2x5QoHk52UVV0JuBLmY4FvRl8sJ0++cVWJCw55tySTKfIkeZKM9yggZUlPAAWAzwLWiG/y1MpqIUfxCXxSkdcJAJGiVIyUVNb6+5g/y+CB/8K8XByYrYvZPCRgHWoml+iRbeQ9F5HCLTd/fCt/PFOUKh/zBJ+5GFSjdaDuoy51vnInI/mP3UEl5ICrzlIlmdEqhjVA1UlSps3CinApm+XMVeP1zkPSFECJKoB85A8wwOWTT+gaoK0ZJMUYuSiIlWIgB4qmCUxBq2aFB9CAzqRnpivAuJIA5DtaV4oEJ+mxQtIDxqiDJu4CAzo3sMX19qHtjbO6UfIUA3QxE5giDu4p16IjHoNkmAnglC01KxdVCLxyuvKiZY7gShJ79ixQfwTH4Bp7OY2p1AYw2BsNAtnTsNG8Gc2hv7gETuzKI8elSGqpLcczlJp2JFVcKUoMPg6mH3IYF9KGtO5TLwEWHQE/TMYNedd8gHkWcwCBKDHz6+LfeSz6YF/yaEIoCFQemksRqi6526JGIuBzH1CYIwCtFjdobRvth2BWIClLo7BBIEu/A6QPhekqXsIcwRI9YQMjgsXxX1wsnCi2J7WzdevK3rPQhJEAH+wMd9KCB6vGgOAnXzAcgPcE9LWqABNU17DzHOQTYiSXHgAxxX9ZP8uUgpOR73uZ5H0ipGNzJU0JeSp8k2D9UGLVF91zs3muAOygVWXZjhrbOFEQOiaIGaeE4XPLV7WVnzUWpkA5MiRnPV8abiy38I0BpSiEy5IemoD2/Qd8GnhYm9z90K1PXt0db7f3aaMZ9rt5tXVle3uwc3WywOulXcUdrE/HOLCeta+G4904aoQmoPAoEMplabxbw3w0EHx8tOIU7iMZN2g6MG+INXzJ/hyfb6kzwoJqAIN+0SogsNDU2NrqTRbnccwEX3dwxoudgJMRbgTbkXudzs3rn67N9h1jBdmoKFVMKx7bVjwVVj9Q0pJ5KtshSqFkGjOcBx0bpN9p7rFdorO8+tEXPzo6btTHb3Ya+42r9zvbe51rvRf6HxmOv/y7X/udyeFAbrdpqtrzV17bf3DeZFxz2tzjZB2WVOG1sla2vhjSrHba3cYOzTJHZD46OnZaEX6q3Hi6qGmk5XQWeLkHQOlIvlhrx1D7BaeewyCZE5UwFMbqmUidVDAixwMOgQ5j+k6O4snnsDn8BYRJ842LZfMU/BQQ5S73YvQuMLOc1/9P/vE/vfvm3f/6H/5DzkDDJ0TrYBTfcMA6FDOlqFVBIXvnlwhkTmEAjLDBHL8fc/q3/v7PfPHX/8O///xv8Hk11mGjxWfffuPqzVsvfvCDaA8Dj4xVYA+wgtEZLR87OnCq1SYVAXogHcLmf+4vffIX/k2HL4Czem2+vD5f7tfrj2HWgplSGqpGn6SqI9xhRFMmelLVarkFnY6OI2L9SRZh850GihshMVxFEEalo8YO8ZOWAlnvLiktF5NgqdjSrY3UEoAYZSJPlpHhhHkcChgSrGeTBJpR0Rew4Y6D6OFSoyNPimPwFbBQDGdJQmJkRhJAJacQNVAyOvDVCd4M88nSHHdRJLLfEDIQXN/qfqDFJpTFW3M/d8NpUdC9vNLii8eslKP5gDw2y+PzTZaO7rMiqztlimm5tVqdUPFXtdFy5d4qdtjIPWYDUIIVvX/2dKKlHAkPxiwpoavLNBFbXxiqY/CFOTBaHB1S1/+4EZ/vOdJVn7rLQmZwg4Wygr1LiGtRO8NCrxSiaqwK2bdiSesBFC05+4iuLjaQFxU1LJd6JgHQfEf2yEgwHAyvtSSy0Q8+87VD/RECGCaA00ZRRvtBWmfeDJNttHGWLQAVkEDI03LJdKufFgqmB0O6ixmcB2kQsq0lC5mUY0BQKSxV4EKx7bcrgrVMAZZrcXRQG4y+TGkZScsZpEDBjYZ3yUYWFj5xRO0j0uJ5aU2LlloqFcUeu4f/xHClwjsGJA4FYcCpeBCAMWF388MuMxAwSiKpR1ZdHxEGKusICGqJBw/yiXD4kiGSo2YbObqVgWK5CuI4NfBC4yx90BoOYWlkH8QjRQiEKTbuQQOo2IJrFMg2KLAys42CTVHFtjAvAiaSzWeQWY5aJwWQIxdRJs86B/JRboy1lLaDhNGUUJB0PCH+jNZbpjnBdXXpDEyZItRyDzjIlLyQCMSUsU5QUhJmLwvikrcAkEN+gSR+jEEJlkG5glmeJN+rFB36CZCVJaRwAnAExARWic1Scq5x3gAi46VrnehSUPVY0hXyCJJhxlgueHsFD15lE+TEtHCClEcvl1Edk9KgIU/FbiWkFmYsWUbxv0IKXwRlkynWUjqQ+gkOhFMivV8oKRSrKGQp5aPOqATzcQxh0bZbPkgE6+BGrVubu1Ak9lE1geXFm4iZh2pIdl+5G5BACiYo3ihkVASb3bTAsYk1Df+t2w5fAMgACidfAZN84OIbyU0gPUmwhuUwSi7ioVBcKcOqR0pzmN8Qa0l5oL+VaBOb0mJMLMK6WNTTGe4LT1YJgQaUbC4pCbQpIj/NiytDSJcvrZIAiRSDKJ5k9AZrghilUIKFaqExSfTliS9QLUO4oiqxXKELGAT6L0R5C0NIH2BCswyZJk78UzaBYbEGpwxTBQ1qvXlEhlTRHbZXsiB7yNJzlhrKksVya7vR2ypwoQ69xEC5rQsBUQb71Wzv8olQC5BC6RAHiywElOeCQ2KU/uWozXNiS+48lhvR74VIVAnnvklwOfASgKowgBQ4pOfKc6Qqs59cCYJGlBMpcUkR9Y5pVbwGO5FkdcQGvqEo1qlABmpmf5Cm5zYQaFvJVdCjo80y3ZPx6fG3h7u7wzsf+CAH7nz1jZevXR/sd+b9wX572kWYW308g9FkeNLje0A5u9NzbmiIcJPUPKw+WiNK2OmYRe7pPtGoSKjE+RNtV7C8eQuRoIzgwFqKaYrUoVzJQD02mXrCPyyAdYYenicgsXhmXKvvK3MUBt8BBczeIdoElTLKbGkWxiVHSUnSANRHJorMVCzaRRbWsf2AFF996c1ld3Lz+vN3x8c3r1wdTobTU5auPwY5RjJnZw+/9frhxYSZc3xKjALn3LTOLg5fm+FbLDpsVl5wdKkDWGw54CBTgPc5/ROjxgxGq82iHsZOsJyRJv46SyIo02ZYSv2vEMMf8UVWYMzSxyxlLIQQyaUFSAXXCYzdI7EZucgHo2CXdK8vyiFA2gEK4mGIIEgvg6IyJqGLN/mVz/0KR4f8tb/+E3v7VzKcDOKOPKTCiVUKrUALsxJXgWo0QYzfQz60/diP/+Trr77y1S9/jS5Bu8lnFhZvv/XGs3duM1pID4G/CEiMkUnQX4xH55AMBAJFGDem0f72H7189Oiov7vLh8zPxw/rLdamsghZFsmMQj9dOZ9iLlyRy3AOPUW0JEOrri4UW5JzVguyd0Els9Okkl2sZkErtHZUHZWFAU+WfkA29hw/CfzMzrMuIGwGLVwvwviP/dbaFVTAwYkII3Lpw2FXEZHblDX1LDoitY6aHp5NjzSImszzj1c56T0SLnKi+jrGBDwbJ4SXTMEAcK7yaXKIe6+1hypyzgxFDWq1qyfjvdpOG59+OVh4aNj2kn29td0l+4P5vF2b1VlbbL5aLYhFXfv0/VjxN9c5xHpM3GzmLAjTW2MwZ6G/hw3QwVg4DIzbwwmPnFbJDKFLPuqcQ8AYtd4yXgw5QRZ+gTG2mkA+jOGSkNqOLkEIF3tTSU/Itj7En4Q3UAs3YHOpHSSIC0FKdddOluyCmbEivMs0lcA+lamAqKsL8vKcC5DeGG5PsRZMo4mv02EcCoilUpqUP9655DfDTEbbwBDB5Imomd7K628osEUCnG46kiI5k7RBTwLMb2zqtedPOfuG/02M4/3MKFGiY4JOYmNmLS0ZdLu185YGecSUjqqUkUWY6gW5rHEAgnr+aMvJBONJRg71zl4GyXTLU/Md+4B+gWbsJxhqQCDWUsA6VYFhX/lgEwOFUKy0koUxUyuB5Mk60pMOxUZM4mMU2ejfEkwSL35lL7/lJ5RZHHSQkleR1NUB4dBtihBJEuXAv4J+grlZiAWD03uuJK9CzV+Sl3v1XuCXQipAImumgBW1qly6VQYT+56yGBN4koHxDXsnppS/rMPjkRX85apA+wI4z8bBZN4NZPUEDuQZ0SR3yjfp+lu/hq6JDSwBJO3mTg2vroAqz4V3ZhYCuw6IK18FDkRCQ1X6eUpz2eg+JKG0GyMtyttH9A1NcEyFHyICUrAKRxVTp0jFk5Gte+pqRSnjSaRRSZMN7XSWH4oYFsuPKFuVLBAVxoCKs0UoeJEJPcKwSP8IAZp1KarvMhKXgJfE4Ix19/y3mHoqqJpMFqYVqAyPYpYxW8ChjRB/xd97THVMc2IZIgMUIWg9sjzO7iB0EWj1IyoZQZG1xMQwNOLSUu2d8ES941zKchqJt+4mDQCt+Ug3CZOU0pbPOEfKanvunNzFKcU6F1nzwK3+wC9ZLpl2xvOhHWLv1m2NY+sQZ9CWSgPHiWRs58ElJlFI1zqFNH5ap7R8OBhird8hEyXRVZLrGsg7YdgDc8FM2E1tR14xgowOFiESD4qpEmoNsdR3KI0F0J6JkX6PwyKgCkRtBKAwUeCPgwsDGa/iV2QolESsbdjZ2VaTPKYAHZx3OtdqnFzRvig6phWkLNJjbGz8WMzL4m+NL1ckBkCR576+Lj+XsISUsf+Ssnpe59j85mSe+nvO9Rdp8MudtBa5vsrzJorgknId72+JFd+oSHnFf/BBveGelomEqgjNCfxnzaUHKCBPx1BJqsiIhyH8413lJxCojrQy0yVRpXEqBTF4SeO0x/jd8Xnr83/wGkfzPXo8/fHPvHh9f3/ZP+cAfnwIltd3mgPqMF6sClXr8f3dzAFmms4qraqwOFoN4LwvSqb1kipHUpmAELNNLVWdGLuSqPxxRyOyvhwJSqkxaEuWK/BOxTE/sqeOXL1+A2WhMWNU8trtuV/9xUd0hciit9V/ZvBMoIIIw8/OUopc7AN4rGeUsAMUVDijzjdaR8BuLg8a3fkffO3R/+Z/979fra5tbV2/ODtcsaB5edH1Q6rsJ+LQyMmi0TudnPkpBFtr2mo+koo0Ovg8KLEDvNCrg2+jz0YmOHxxdoLRIJavMkdEYMVovdUppCED4hhY1RfEG4AFPK9m26kLFxgjWnStCiqeZRlK1OrDRVYP6zROJsXHhXjTqf4kzP/Ud1DRAODvnvJg+Rafv8aRTzq67Mi7qqmqnf3iL/0qdPz8z/98bYW3p1dRvitARuO9zAsPDKheeeGQklvwptZgvlHzDh7t/vKzP/0/ee3NV89OTvkmw6C3dfjg6I3X3vnwx57Hy2cdFBsiY0PpVdIjqi9Gz54v2hcXQz61IG8Aqm2pDdrd8ZiP2XksSb1+0GwwUXlIWVo/90FgJqwNEMHGkuBJv1cvUDeWSaJOxyZGZ4jTHFXZ2YRPFPXF06ohv8JmDCcCMhhWsqc7kzIQBgqkklpuaRDhPEvnnFjT1yFJGBMrB87gpHrBIG2sIiMJwepeXLVi/azNWu84SJphgESioAN7ZXcBC2sKo+UIf0Ea6YNMYkrxdfZToaoUyRkrVk86AFvbSw7LepveEhtr6T8HE7o4J7Q3bY5uwievnbSw5bVTDURrxCzBcNbncwvaFljK7k+O1K1zejwtDoyeMeFELaTezDh8lxkDhxjoy2XdkR8KABT7iTlWiyzYYxFZ8fkFZmagCPGwGp0TeLtYEzob9FLIoSXnYwI191owb8D6hSmbbth92KgdO9KTagDR8BVFNjEVXUo5e0t5YitgJR864QwC6ludzTq2O/H+WfCu+joyRtbwzxbJXoptFTBdEK8zrZBttJS24seMXZfr7SORRHysNbWm+IErAJEK5hsBRihNkZDKYu9GdQNG6VZY3/W+VRN+7B5m0B/PGPWx4RcjZmU5iZRduuyYJ68qqTZAK7nsSKBpJAcyqNozpRjh6dPbSosFP3O7pnTH3Iqd03ZiSVnsDChHLnTYxEU9J78790h6bH8ZUWjn5RMMstT5AS/N9mM1uRBIHQNlF7yAMhqiAvInEJHBlyOp5sb0lNV+VDhrD1iQVPLrKEStdSinUhI3MLFUjDPAvYjCQeAFJCwFwoKAXBEwSVjTz0M1rl9lMyuJ15dCyHMBfzmuFLNOaMwmTRXI+xqSjPI5rS2VL/UO4ATLcuwAVacqidcKAD/rjJdCAnUD+1Ja00inyuE9L0+AVSlLCrB5NwHl/d2hTwouT+K8pkupbcp/AtBglfdJMnNIJ0yIaNENZIM4aQs5RpfeJrFySOcqAAEAAElEQVTYhpCL5ng8DYADW1hrLqTATYmw0wjgGo5tUaxVHoFbXkqtMC8ZuScDsWtVLQSZhUhMkY4l1ld1p95hYK17WTMMbvZZg1CBSryayiJOmWFtovJYQ3CwMs3BXDa9hCrOakbttd7plRoKKzBQ+smyIKTw5Dwv5kcK6NewOJO0XMAhfQsDhxHYIpug/COqUMOrZDT4gAshnQkNI2eMMMBio+X2M8wo9Z4NNNgYGgBQ82xBTiNnlqDh4e58CVWLh2lt8fUPP9tBCVZIC1L6ldDNm3KJEDPPt0BqTv2Jnv5ieB2axU5pIXBSYsJpKKGOrEBLzVdUYA4bZDzPQgOWIciYSa0qnAqdWLYCyhPkBW9kl5ea4NCgXJOdwyFeQndywT7n+nj8eFXH+xc7JeJPTsBEhA7j8cko8kcvAwoYguMK0T5IEZd0e61/y9tT95LwUlBgFPY9la/A2EDaPJD1MozLzyXNBhUfrAWyMlGUQliVI4E8F9UyHaJn7G254itXi/OLMQGKVS2Ws+QLFF+ZjeUdVavCLKTwGWguI1EtO8tznLAV376tv3bvqz/y8efYcoIAuvWO37ZXSCxSV9acWMX3cihYyDZmVCqLS5ePRig4M/tvUlDwV/7JM5Co5AuqvCeNyIKrKUMcEAW2rp5mMYEXd/Yk80tazjzqMKJC3ZFjjO3RctF0EaPWoOSk1yfA4yOxJNrYBSlZQTjeLQ25LRV+CfvXVh0WAH/1j/miGgt4Ls6GoMNR9KjUcOUKKEbjOLDoYlUbZnYDmrlCO2Si3ZTAJL4GTzKIjSch2ozIyn+9FlImJOyQILkjeVFlv1ZW7IC+J5eisbqGfrpglckCBPCI55YaCr0uIOAkGaK0CHa7McfQpjwAEH7LCR6iGIInP8wKIYLkHQJICvQwZv65f/tLu/vdv/iZH97bP+ArD+BmNU7h5kLZQmnBQ4AST12G2dCKguJB46bYW3vuhef/0k989hf/5b/h2IPz2Wm3PfvD3/29nZ32sy88Dw326DKmQm4xBBlGSGZs7K6zyAtTBs5Q/6lPfz8zEvSFJ4v5+eidRvt5Vzkjx1DCCC6KaodIsbCEACixjTgJrlxWWcENK+H0DH0tlqkAVNfRpBYpTSqMlMktV7SgWHYZYZu8IlA/PfNfJtaZRheSLpxWA8PLwhVqWuAJUsYGVcrQyEK4iUMt6iOzxMJw79WV+ICW88YIqEyxGedfDDvpwzmFLq0B47pRFuye8l0Klvk4dKn3jXbQR4R2x7HosVE2/GJ43AhH8dn152ANFQd/WzUkJbvn68wAWoo+tZyn9tAIMHsAPuAgibqneJLWOZiNRMp0HGtaWNrBOX6UjWfD2nQK3OetS+9QA852HquYWNQHdCuyLZtGlmUV2CWdWKyWNiKyyfpPMUn3h9YD8dBng7HUbQ8wBQGRLrafpiQ9obTFhbUKE2zhAPxLHUT4aoK8jwiKX20sKY2xhvMQyUSmqrmZudF/gBuuedMRD+zoFDEyTLaCvS6EMKA9qpSS1MECFncBAjheAeqWSyYZlaD/ESUGgYTULbTEr8PRAe5xUJbHCYix8iyIqw/6z1QoYjjPjc6Qw57wAlmn8ym54sFdAykW+CaWhK9kO65LV5QKFREMqKtoIEI47QhOkU/qvcQVnkAY8pEfsjiJgZiCjJF9EIhGmSTVQpXxPzHlgfTrK5ZJXksfF3ikGAsQ43AmMZdvkGZUIt/1YChBBZovTz+XkHIvOS+HWKagE+PvkyTrxxC6Xth6qaCk9P3J2D+QS37veWKxYjlVtBQawxBzIJM3KJfy/QKA4Db4PXnaBH3XB04BN74+Eoa7oQUA7A3zglT0inpTIahsi9qYl8YIVakzXkuF5D+1HZWJ3SE9H2BXK6jzgAzrwNfRKY61RSGPSNKo9SJYiq7Iw3LzgprO+XCKTQczt7doPpg3IEl9cRufts43Gq3r2KboDAZrIxVCSIByLQ7EsHufOkkfnWFLCCOcKqH2OePsAA8tuw4DZoXqAnKp5CCgD4rdYgiZCkMDwKAIiMob8MzSNdJDc7DHUCqJVN9iIEhEfRaBIBZzYRoIKt5B2Kkg6/0zsiyXTM+a2JYInlrXrCpSY7knGdztUJshhrljt2R7PAKm1z1M1karO1N4TU4Y4cSAzFkzaaGd4N8cdw2TCr464tR3qbCS65rz7FNwVRdSx6z6CohUMVjhcDSCJkpnnQBsN2Mt1mJG73S2NU9gElJ4i9/PS4FkMf4jAnoFoTD4SyNEMKzREiUifFMqZFeCHjHB+WK10ejC9QA06Rwd0ugvlufaXEdNKBqzqUHCDC8WzHql06BhIwFKBScLvKDnTZL/I6/1mf3fDUS+7Mvux1LEk5SLPZ+rc/1DYVI8+RIwAq+YWHBEKOAON8RYFZzvamZa5+rrssU+eRSQPY6uDwHegs4kVe5MZnNmOTLnVG9y6foHC5nKhXRjv9kV6OJUHDuae5pemvEBB2yeHc7/5E9O9z51o9e81ejdXa32J7OjZv0aB1fXZzTMVKE+bjGd4zRp8JzhOuqmddX2GXlq462LVDm1WGWuKPNVURlecSbKIVompm/7jsROb4T4tNslXM6kcSUpQDIojneWjGlc5ZD1gYptYWowSBAAPFQbR/+x+0EXu/iyGBsCjEMh5zdpiRbN1+qM7p98e7J6UJvcwQPm27XUykZzO/WRxptNSDgrlE0dlQCtAAVRhxq01oDi6yK8AxXN3pO6BvyneCojyJOBsNLes6oeAAwek8iLbOirh9yLd1rc1hnhcw5MtzRIo+rADdkEDhxqppSz2InkqD41kVOPzI55bDHmvWKpzZj90OSQYcIAiAjKJx6wANwrFMRWZkLvOeH2ZEB31PgX/+xXv/LFP/pf/q/+13s3XNfByCIZHCWUomIxTAkneNVNgiXseYMYJrv59lSXUVi+iMTnkWp7u9tMmc7H+5wquNVd7uw03n7znYMrNzqDFV98Y1AZvSmLETx1jQXm82eRMgWpGMhtPv/Epz7x7O0b33zlHsurFrM9zjevrR6AB44NlChiOZ19nLaeEgjZ4Bd3EHsoJHxGY2AE52LZKGOBgSGTWPhshxACl05ExM1mmb+KJD+iSZItx6lTqpvbDOhzAJs1YZ5+6+oUY0qqAtUXoDEhoKELnwAngynLX0WeRKJrCU8u3kuIKQNUSUIIl04fl0/cLMQEkEkgCYAsRYrrCtxhv4Tl+ektEjAaxWZhOotkASda53Pbifm2fGvyNUA8fs5+IYNL/3EJO5zDtxp2ObuG1T5CZsgfmniGGR43yXme3P3iHi0Op8XLIs5RgqHoLQeUXZCFnUhIiqq0pMpwIKlb1ikdhxivBggjc3EUKdWTEGDWOCYUulHnUg1CIBbIZp1uOSTSfLPSHkGomTRwjBKlkaFk2QMbsG5qAw+8c5NfYQ+ctDpTedBLhOmmDrs29nNpfYhAzwl5LLNhOa82SRLMZW3C5TFQF4JQHQb6lfapwjMkYJUiq7oZ6YAn6ejPcHQyH3K8okSaDwnSWgOp3WcZ0nJKBmYLr8MaGjNKWTVYMeFBVcCCEB17YLRbHU9pW0w5ApASKUPnBOtHKSisE53WKDBnQXCLD7bTjrIvX/MEFZIJh9MFqrfYb8DIGYSAH9TALw5ewuPgoP/OfPY4BMpMtAkMOANOdRYdoFGn4AgmyI4NmbCaLjpVr+hsq7iw24qsr4LxUufqzSP4CRHABCp4KEoKn98mda3DqYDWXi4SJ/xZhO0JYyIYs18i/G5Vwc5U/OUiCXNHBLBM1AqTqOrHBJ4OpPfrvcDJQ1XYJsgcRotFAQ4DWHMhZAZ/iVqn8BEZOvBJ+hIaaJtHk7/rIk7AuVSPclnpBFyq8yZwHb1OlN8gVhX3dIKn34JKFVTxa13eOuoJAlIQkkHCOuWrhJpDYalbWiCaOsOsRaWmAEJepz7owUNDQPiQGsXXIrJrqojE5PwzDc6aP/IQkbPpkLGG1ZSvZ+Pu6KA0PAJHmxuCUziKk8RkRtXUFBRKBHxClcnDCDXPAezot+l0oVFbluPSGybExhSgdkgFTd00e4JcGEcFIBcFi5vYiEFKRF9RQzGn2hPBjSgqg2d4yBaj+OGyRJKtA4SSQgLMYQrSYNOAwnPJEgO+BqN1Jo9nAyzZCg1AcQBluM6DZ8EY6B+kSQ9HNnEnSBmRmmQ6Zfw6VCLeSU0G6ppkKiBMga0C1pBYwVgAl2UDGycbQNgOsoiq5oaLBQ88QJ4ImDKgjRIBb6YKMmEVACleRhXyyQWCFp8FDBQWH8vShahY6ks+xdjkY4R6a3RcW52pB5DZ/CFcQkoy8WdDG822c6jhkfrrBfoBmJc//VbShur145NMwPqPuN63+IKWzCmXv2mmtJL8QxCwJugX1kKVKqvCKPYax9z65eP0fxyzC6dJUoQgpvlTPcKmBBivMnIJPOzndM3sknR77rR5+oWv/d6bj2d/9TM//ZEPbznPO2eQj2/oYn8Z+2EDJaOs+Dq0hSzeIHRBZcL80+1MdxAY1gxNh/qlHNE8pUmJKdJipYV/1TsY+0Ta3LkVtqCQ5s9FAl5p3uEBD6ThQujquq8U4bAm6fNia2TXmD50vBBGOqmJTTo8LFB2zyJqbE/I0fMZC/R7LJleDq/Xplda/f6EIAydNsf5E7CiHaUYsOTVJwoNCja3tvCACzWUCkwdFrwJTBS1hqIo2ZJ48k8q+Q0H5BJVgmYe5DMcTY+Xgh0K1bUN22goczAlezDxmMwRpkApCw3pGbNTCzSRM9hgSlItyJPaBEcMt/B4h5GFCkAwciIN0bwV1GSaddDKPuc8yUnt7Xv3Pvfrv/bTP/uTg60tZ/CpYPYvREAuJKcvPnDDQ1iy1Adirlzd4ztuOAF8XZWzmz7+8U/9F//Vf/Uv/m//DtpGs0ezo2nvrfpzz33gRv86x4PiQ8ArxpUBsVzimret4CgZBxxxsBfTmnw1qdn/cz/8F771yr+Sc43DVf1xzt4MHspDETAog25Ij5ZNzZC3Mc5KrCSTCtLwTSvoVIq8SEkqH0SoPxknh70Kjmwkc1BcPgo9agAn6G6JtnwIR8AFOPKBtHIjdxgsbwDCf0LlnsPawktqoZoorwlMXpEKHKD6zzf+qpfAsmkpuaQ+BfMKWcVlxgkEdOsxwnQywHF3Sqflc7TJGgojWq5m8dhNhCUHoDGj+xTGS/ZFNFiTopuHvkzVAVLhskml2mA6SiwIqAiqHMSlp0Gw2+GdCmC4QlZRYfkwAJ+L6k5XfABsSn3Wr45au/eYFatu5BdB7YiFkIlfFZpSWdDFWPuUc64tgirg1CT5HUgSF+lX/NYoQOHUOrXFd70Uu3+ok4uh0HJMAIfoU9dlDb0UQoGhuNkFzlwC6sQ7MDAVUoPjC3Rl1emWmWd4IUwItILDr0oX8mOjCRXWMzklZKlgGLTV5lhDTmCiXO4kxnzLT4bqCWGSxk/aY7x0o6QETkS4tuB0zIDR6fIH4zgwsdnvxtZIDnjo5FiJEAJHpeHA86py0rUYbA/8QBLfNqa/gQmXBxIM3nabDKDzAFNZtmU0+SBQfEUCSvGq5ABVylYAB8QPHrumDv4BJ30/9MTeg8lhB3jbZ/ACbXmHChIBL+wAEGoyKKSs8EeRp+oo7KCgDsiDcCLRJFbPylU9Jek6TIGso8P7J8nX4d/5VwTeG2uZhKLY0mQaeA2RT9ISQM0pl9gEjpB4yHMVV37IWaIKWTybJ+BI7Ks/5csA2Rtg3awuBVoufoUTWFXQn/bDh4FS1LtyViAkwoIsANGgQ5JcwbSFKeSQjJGdtPS4mIKKnhNPFr6zaDq034dcEqas4V3SJEXyhUxDLRGi6axS31jCW2/TM1bswmrep6JjadPB5X3NizAZQaCPWAAhtO6b3hS6s+k1kFEti6PMuUa2pnoqtDhoIEWqZwpVpNDjWBkhQJP9fCe6JMi2ACzs7gNZP0wuoOaSANN4Q5998E1atCsmQe+BARrBI+gFw5QZnoCDQMwjq9wsJcMwilRO7ZJ2r9FhVAPnC7Wj3dKUi7OmF1pAwmEYxz1kPEXqnbsQU9e+lInpFDGzaR5ipIiBEgspVIoEBMAQeC+XxEeKGNuSpfG9oNQofuR50oMuiUgtHFlnFQ9MUvhrctFwXMd4Vz0iN/GX45pbSginY79BUCQFyoDPks837TBc3e/uL1h4XTsPq4sIgC/3dIwZ0mOcSZzgPXPKBAORu45FrvVv9Wp0dV2OSWCJ2cSXZLxeTrjOfOl3Pfa/CaqyNE8ugypAvDePL4WrRTKBCGVKDJL0XdY4OhtgaDwqoTrxC8loHV9GOE3rDntNGSzthKN4Ehk5Fumo0/LcEWv7YrT9NCpULrcA0vhQmRrfeP3s7ftf+uTHr/3gR3+IU3n3O/ud+hvXr98+PhqNhod+/3HVOz4+fnB4CMNv3brx4kdfcNy4zEvR7aQilCZR8RWWFSqRceqpWBquKpgij/xy6r96A70SbzwEOFcmHPhAjbIJ4aI1IimJnPJh+oKWj8/qGcE3AKigVL1sRiSYbXWsyX0GNaMCeCoig7V0ZvAL6o3dK89cHK/Oh/29/Q/3b7zKxsf5jNlRx/XYI6UOUgc5PiXjAGm7qtpUMdORDk7Z0DKwQA9dLZJSmaUMBJFOkAIfVRTtJr11I5uzHYdYzXcgpcwYQEs5GQw7FeUng6NNgtN0pXpDoJyBIBb9Od9HOO4OyuAA5ArvmZadzpkYkJEH0vJMZLFdmU9Q9kIRtsDyq8fDixlrPT6r9Ojx2Te++e2f/Tv/aDFuNXpvkRSoOkaxdZGPyREJyCAdmHp4+Gjqx4MW3cF2r88ckaftdHuNF+7cGgwmhyfvXOseQPNkPPvG17+6s/OjnGAJARKHHDUjzRnzFxz3o2XWDKLniIPTlH7wz33iF3/xf2DOi9NjGsurTUZPFXjUebErIc0H+iLlq70QJJszQI/4HPKhyoCyqpPv0Y5qjR0NEWlCv8CsTYiTvOxwFTzKoDIDn1yNU/jDgVgplYFtgvB/MIZYeL1ULlknKoWvOI7RA6uuXQiBG69aa+h4BbhqolE2c2AIn905SoHuUORjjE9UON8790WNP2UgVUQmr0AMli88YQivwdlG5xsyA15iPSY3bdbcp0vFYLUoHV1bOVMjSY93FEu5gjeK1UclxNEmeNV404QiBozrQMdFrLN231PqPfnHY+Mths/NsiMIi3LGvbm6Ahg0BFO8bPJdbTKfQvx8vmPfN/ShEsTjOpYxIOkSY+opDIQYvyIABPFn9JwVe7RBLHlF44qORH1dn0I6WxUO5Ee0TPuhgGwzwW+GLDLjuvKsyawvbsil9iNqIj4u+0TiPJuk44QabKQTQARoYIctOtrIPmuwjK2BUCBwQYI8Q0Cyi2FMIMM/7qvZVaXGmT9KBAJZB9Hq+RXFoQjVtxSWKThkgVJbHU677tDSg791jdj59DqjFPRKGNoDrfl01t9iMqbNl3h3utuMADjt4YiYlUcMVwcazNaRAzOqNmOhtX6fZ9DGYvhFgthQoQfHNMaRN9UE1pTZBcTIYU+L2SRehomTC9jsPvSMViDqPDDF44m99DJZBNWN8bGRwdbhwEgaj5BKQjmIA2PDhKL56nCSvI2s6Uy8HTFJA0mBQBwAG+37vGMP5CBjQIIkS4W+3Jd/vJYIYphCMcwUQYCIJ6nXY//SfukyM9fT8wMlDODorEW4ex6wserruDU+mQEwsGKsOvHkzcfq2uB6GavEVTgUShIi2tBexT6h2YANSYnN+wZAFfTen6RITm5yjtv6lXIsIUkSGkwFrDIS4bu+nl5jtIH0hkEqgkzrHuugItKAmbPUkdQNVMeWoiLCCqPcYhcCB+WYO8HMi1LX6ReVDFliHrGRNHZgEhTJrJbwzA0VTQmCjO6oR0aJnQ6Eznd5TmuVPCqnaSoEAF2yJBsA+R/Nsk4TZe8cgGFPgSYpBgjNlrWUV+4Gx9GOagNKRSxKZJnGysXYZMBqkEyvcts8u3WoRMdjAkdsAicCAqg0FYqDZkcKmOcjP7kFI3p6wVo/ayyCokWUPxYYkVCW6kxeeJV2B5OX+gg1CIhhh0DnEeooIFYNiIVcybAyIAnHRXihHBkld2Sh/yyNH24gF01JMwcWxHmGDJcUGksgugKSKU7czMc/m0TMH0CxMMz70xQM+Yo8LQUOA62IhCAXRa9zs+Q4e7c9YbWBKQQAFmApL0Ua+l0vc703QWCJ1p/52mQpD+FJ4UwFStBSK/nRN4hCAtQm+ZHLH9LITGJ41pd0GZteQg1jRzgPwoYVMsZs6CRNe2ReQgI9HDFN0lNZ8p/OsB1WVAlHc9UatIa18Zde+v2vv/pmq3X+2T//k5/40AHzLg/uvcN233fu3eMQ0RYf5Wqurt3eOz0/Y5R35ln0YGxrKf4VMhYsFeWn4BXk5GVRF1Et8eiUaKsvqmsoNYpn8VWhw4GwiRCYYP9RY8SkLCuU0OLVrGNvskMLjIfCp7n4gy6aFOwJLTz6UjSHM1wWrf7/41/9wtGD8dHj1/euf+JXP//HNKmQQXEgQf8gSgklsWFgC68SG/KgSksouvSPmf8HUz1CLRXGQ2FKT2mu5AhISl3SIW0u3UN+EJI0pnIkG18zwCG2VKpo6jCOAQTj+WI0FBPp8z9ZqVquCiBorTCqQdr7hYIldUoFICeXgt2UJTeW6CVWIqM48qO5KwaTVxyVV197+f/y3/0f/8HP/8+u9MspyYRiX6xi6g6JrP50wCSdngdj/JxEc3JyfKO/TRIYRh+STUzbe/s//4/+6y9/40t/9Ft/CFfGHC51ev7aqy9//Ac+hRsAAqwFBwIrKZAUi0FpC7BtToNQElRzZuiUTVAz3I5FjRmAQ9UFecAkuegQBWYMnQchsQonpS2VhtjQR1J+oXDgN8cAoBAMgXvAU5cYkObSX8SJcwcrHUj0DDKZkpB2sgA2FlB9Vykk1BJSRhAAJaKgPg/eKYzotE8KlpDcCcSQBomCOOEAJ0QAUuVV7gW8pZAnA0sF85RbQJCwPJTsWIiHrpB3Ds/mRZHZZcR1k3j63ES4jdrBZnDTd0YB+A+GDgzgvjMJC0i+LWBLjHS0FaRsLBhYkfeFdzLPeRJCMOeCE2s+fMYP388WLbiLgnB4KMB3cN8JI0hrFmKROzngJiYcbjr+ZDZFLMU8AhJrr6A0bISaAsMvmxWgCYo0lDrJmJKnf0axxIk4n5Wz+eFZpdXkmZ6/csgBts+ZZOlkwQ+MoEMLJmg76q0C0BXQDTBnmCSzLFn4fFwFowxSROl3VyL2VQCEc7MD0PIAVHAFewIpnSSkJ5wHN6wzD0K/hgjXR7Efiw1ITBEQUOtiwjQMqh3+AH0GnPUZLaJESY4AZRg+j5150Ke3UgUiGxLpm7GNxdVXsEuNCmSe4WrYDFtJKp9d0QCWppTdjonCAaZWKYI+tYuBssKo5YGz5KKuyjDqL96K1lCMALUWHrnxbGzxxYWblFuoDbgisfMUYa5xAjmyc9nY5UGMeJIbuQzMS+G3seVa/1av//E/ABZFVAX++ZSSpMu3NSa8XJoBoLREFu4GcW6gRGi5ym8hDiAIui9IRzE3JJEDSnkteQW6ZkJFdAXsz/BTlSsqFazIAgiJWSPEW3HTGF0KAlU+slm1qjx5wiYqNPOrVIEgRUXzSynonHUI5SS+oo8YskCgDCWQmmkdxbxwfoaAEssva4Jde3yYlJKaCN0hkqB4FU/5QQN5i0aRqAx3kVyYxloT/NVtoETAkJ3RwhggVTHArV2aKjEzABShqxgpAhOC4QLjVErS2DxImtiQiRD+m4cylCwDjwxz2BDRa4aB1M2YAKuV/yJ4QrVFMAUwNq9ynjUXGhd0DwcP0wOj3bvJlO5A+uqs16QY7aafe4qS0njjKVChCJNiQLhoUg5Yp+UKBaaNF5Uy20BRRFkgQBB9w0lAhZJLzgBI39CRaew7WGsLHBpBT+zXFf6QQ6dTdsjDiMNYWCPaDsYzKgM4/XX5bJsN/9QncskwpxoEy0UcyxDh7rTROa8zlDt7tlEb8AErPvIMRDeuFRabGLxnnW6j20UdKcjR0jor9iCMdfkQ7rd1ZUnuZnj3tYkpVPP65PJlE/xdoVR5nsr9BE71VCCUl4CVw3JJ3VFwteWu5TF+tr5kGn/wUkpbLJSbsiFMwshGd5G1sMQBByAM0dNmMzjHQCzLooSpjExLXsFbiAqJVnDOBlzP5LsrT7ocADhbdD2tfPXMeNEYn/V++w/e/PjH7jQaV48ePFiOBtPFYOio0HGntc8YzfzqzskpQNrtHhK3JuMcKFDUlh/+pciiSz6Dji9FKyISqRYrYv3No4lMGp1AXVM3CjiTAFxnW8Uim0vI69vN9mAxP2nUr6xqj2v1LRarLBY7ve1TPt47Pn88veg02m93W8/MOl/n23H93U9/7dVv/h/+T/+vvZ2rtN1Hp29PVxctTviZOl6g46Ib39MddhLPSohGBaMKMVALqrRzrkBIi+3ORs5aMYs4WoutA7pNEgcUWG1LJ+rGWNvrZ5WpBDBylG1smswvEQzfaUIKYwBCPQIs+SiWL4o6SEk1trEVVOo1qx0pARo4DclfS5XFsssR3XaDw1+yVztYyve1vpHeKhVhxBq1zs+GX/q9z92+vfX3/t5fx9tg3QTsIcqeV7EWwgf4qtPqnhw+4nvli/loa2fA+gocBAdWGU1llUGtdueDt1aDH3rz9VcP795/fM4W39XR8UvPPv+x3WscacAZLlR8+2eM2V6cDLN2AEwc+QAfvq3QRKtn+/avqP5zBpUfADcmBR0Y8sfsCttUVD24F6y0ReqGn/2y3WLUW5wwh4zksUh9R+7QuBS5ahnRXeSCdqa++AwgfC5wQCv6spNvvau+TifpeLEIQo/IGiWf1VHZB5D4w7igd60Q86tGJEEMpi8C18zS1OoD0mQqZisBGHC+EEUHWACW9I79kybFUViSm9VsoGZK30QjU3LL+Q2WjtXn+8ZrD6WL1JzcBcvRfF1ex+9ofXBgGD8nCtNBa02Xv+cqOI/9BRyeNJaVUX+x9FzTBieNUpLdUlb811kMiOFdsIAHz565AloKAFMYJbJOnRrS8+gC9uCRoHFBMr7SIInoHhWE1f8AQpHxASulh6sgQxK5CreIRuJwnIc65+7qi7OCJ8KTaKlurLpJqCfOjIXMpR2Qs+CJakcwPIBi6xhaeKCEDBspMN4IxA9FNqlmANdr4Ebx1qDwgoLA20Ab1sAQQR5I5FLEogUEMCsl401LodZPPlfJmL3Ggde0cSmW+ZAJvQPKhlOginIhCGVEI83L/Cr8n9WO3Cjp1j7mRChq5vmciGF8ID5+u5eOGYVpJKiGcI7jW/lug/OZjq4CFApY4qizSn4Zyzn9SL31SFZLM76K8x+ryTU23zQb72RJjwYMOmjHMdzYl1ptKyv++bKhVBHd4LvyKscFVMcDIH0RHCVRAchikTFDahlP/IA8TLST5sAMJGeLITlL/Zfj8lTWRzKaNkXNnwgR6Ip/rgZ7SBLhiwnWd5+S0geu8lxSlJDLd74TfPk1z4ELx/mFEAHADADwFzAioqKvOwC8xYaWMogsRa7hrsGZOdBIbVzyCDcvuT+V0RhLMqZE8Hg5RXlNfEm4eQyw3Ciq6GYJKuUDpmJeyVHibMOq4jZZZYGwLZY/27lc8sO81qgk8DmpCqs0OojQ/TpcAUsyoaGiBgmXLOiX7jqNnMYVrNZwo0neSmpzlDdC0BCeYw6Qg8EWEIBiQQIzCQkl4kYaTZjhxqBe4po8xjrsRD1UpAwg0gmGKBKsAa6Bkz5aEMxBVnWOlppWaP5K0WLmjDYpAMt0ZEZfiNUqkIIaA2cYPwU9UQccBktDTGXA3omYVZqv1nOfkD1dZXvw9rSlTAIgRBtTXp1IgYOzqdtzWN3oEgntOEltaLVCWhjYAAQL1t1wvs0+yHLOgC5X4Z8MAktQ4u6CL2j2H426S/GlMIwjteZYKZPCkkCoSgta5rYMicavtW8DZFCiyfBFvO30WNVNBVx+oZuGaNDrbk9YBezJaBeNBt9+YikXJaSxLExWnAiAk9ehmLNiiIaHWCYBKUpv3oH8/te7Yt71mjyB8P653xX6frkvJ4Fck6gjkmvdKFhW6FY/hFasMYA3eK3awmd1g4kixt1xLmWFLWMYApNaY/wVz+5zMgSTjoRw0Ol6UYh55UcuVwIgQxllboqgPrMKFW+FXYAoA8Oqva35/ZO3f+Hz/+569/bN7dmVnQ8cPNsbH02GZ+et0Xx7sDdmLHd+sbe9TQNTVt1Bjh3FMgdeStrcQzOlqSeqYxgRtSVJqiZYWJ2LYeBBbQvCBUUTmSDtbhjEgPNbr73zL//1/7DTv3blen27deVgtzEedx4c33vhA5++9fzg4rzVbV5MT+miPDy4MuCUzd7WoNnabta2B+2d8aR5fPZoe+vqfNLl4wgwNm068DOgFlmk/KizWqrsqDlBONXWaPxORqZZmQBFNr/xtOwwywxz0PSi6dTYEXeXYJkMYm0FlQIlawn4Szdb50y3i/Fn8MAnVjJxXAgLNE7Hoo5ZkKVhZ5asiECAsds6rdZ0vGfxtK7p05Gu/I/TGnOYd3EUSS5+IKd49xgnIS/rk1/79V/Z3an/+I//lCcLE2irLCxiUcnyiJXDQsxnQ5Yy4GOMh+NWuzOdjuilYPTAGi/zA8/e+dm/85/9k//u/4yfc3x21qwff+NPvvLDP/qZDgfClG2hDrwivtFspj9EAWKmvXIlS4+NxTgLjbfntUOGKAqBMCgmDRIzbRJ0VDTYpOmRZJjE6FJ4bXirvjMYcOBMBwcHLou/tY3EsMkOQLrW1tMivXQRJFuwhsLl5XyMVUcADkbAMMuxAQj/SEjySEzX0xxKF+kgPAqTb8DiF9nFmhmUq2BubAJEvojEB+uCaPFoqaZJwgTAJqBQrmHc4t61HtGzYr0JXM00TVEiSKUbyPIfl5o4vASOko7hdGcXS4P44gYnTwvQ8SQMTEbOPVLTRtzPr6QMlXSJ5muIYLbFAhBM6JWHHXQfmIawW2V6+MnWZFjRY1cAS4ayespMMId/NiLWb8fLQqwx4RehccHV/YRVr/xYnowROJedbbs59CocEwFb+7q6lqqz3EMTSSdoGYZFjfiFQPoAg1fYV9OE1UDGVrL3YEKvDFMLJAFQodixANN4QfqjEeNxlC4QYlOEOlEQIwFPTGVTEZgTU2BGqpYa2viUna7nJhErVnTWU3nzAMfZvFRv909d3Vfve9qqhqF2cY7zQOPIACHTfRfoU2PBl/LoYp2CNO1/j3bAAYrpfEJrMRueT+xgiDvtRQYIFh0W9DQ7j8GGTiPId3oMHTDftz0ZjRieiCLLPbiBfWO5l+MIdhCpSNRL2hmWBbFHEbnRdbSDZhUSWpQkXEx2nuRVGrCw0XfFoExkVGShW2OeIp6wslgbmcxr4WQS+MxDrpQoFNm6Dvz/8a94BjWIC8JiKZEp0KXGPqtjXGvRJyxTdtAKZ9ax6qyWW2GTJquLAim5AdB5awN7TdKasPWv5VSlpmzf1w8FDGWWQNFIaWIYa5WE8nfNsUspyWNlRkCCoXjjLElMwnUrnk0YQwC3MCqcQEw4kDHG0AQ9hQ8aZ6to/lvFzQ1MUlg050ZTQpP93aqzjSRVqtNaeAoH2pBTlpucbcyedA7DBKa8Mru4iVogoYw33b0UTja69wGc3i2FkhIGc+4QJoilivpPqKdhTJzBBijU6ikU1Lo+u8PvonmfuWZSQhefVSSH/6WESC6chBRcoaK/aWLotvPyhNGSS0FUOA4aoPGGOW6ewTiiRiBoZ1wCcNg900uglCDhNlGOm4m/pC44chnjshhzGPmUzgGFoTpRD8pgNEtBxWChaFhsaGKcjMS0iLPxZDIf8SVmYJGHQ4UOGYa3IMZ83IGl02PJeA/ckAaeHG12F7uAoQBX0ODBIy90L8QnbQnjlCJCW2mHTcYyRYCsI+T4kq64oL4bA0EYZHnEdivv6D5NI4NB9elwzkkqHC8tw+2WMFCURY0FqfF8OXRU26WZ11aLHfY+gWThp9UqMsUSMF2iiDiO2g/feya9QkclPbkfSqQ/DJZb73+RZH1JpfwyKM9VRHm+HFJFXPohtkAqD5vXkgSYYhPQFRwVK1f1i39xIs/NSUuQLpI0Rx6QBNum8+HCoyqJdbjK9QAO/GKVeeJi4wR2uLHqp3nCNCECN8c3OLFEMWhqaXswaPQreXB+xpmXKT6X63qVPANV7MLco4H/o6+fNRYM9kx2BufN/ul+99YPfuTmfn1rtnzUnI1O7m/v93ZYaG8jT5OuDrqpDgJChRU+VFfkQldswJoR0mWpuWEGqE7KLveEl3gTMMziGRFlJXTA2Mk9OTt6682jra3Va2/XtjuTnc7k8MHwm3cf1buveVj5hMOjTlaTwc5B4/kXHn3g1my31Z7Ufunwgg9NXH90MtreeZapOT6KPJ8yMs6QmmpLGVLQGDU9lfyMjygta2d1Pp9UO1lMdzq98XI6wJtnrfOyPuSLpxxsspxtz+qHrcb2yk/tXsfhJHbFQClcsO6gjfQw+GYt/TE4gETSFGa9HwxJvaBIGlH2KKDR0I4LwLid/6hiMaoGAk9ZI6/K9liJWehrKxte8TPNuKKDDtRAilMlNeaYHTUG3nOeeYYzgVhvniopk/mfIvxDJWZXeEWhjh4P/+//13/5zttn/80/+s9Z/sV2cQpkDB+wYKIAV0wATdut7UZjez47Yz3DfD6+4LPKve3ZmI38L5JyPH+d/Zjo4la/d3zOSO3s4Ori7PgoXABL9BKW26gPLzjtc9nFBLkQiDI8GGJ3b9BoHbrWZ3alNtut8QWDCmmNjG0D/+Qa1OmNkk2F8T9HVOEh0Zpo64PziN5xrdmnbmHEXOPCmCjZkAKUkwcryiPB3ihSXQtvye2vuGLuNGtadHvgYJC4lGg2T6RE6PNnSJAKCEQHYmyqEH5AZ6Qc+GJeCQoEChoWSSJuXiLGZZjBCQ9yIp+EyBdsUAWgkVKIRFzLYOoDJRogIB4e0/ehZj/wVLwVA8lgdT1GIavnWInAAZ3sllEsGOQlS3lQWJbw8wpcOqaYBw7ixwChJ3SviMYcUa4f61uyaoVy2Gh01WWKTeZnSMnVXnCOKwLiU8SldyGDz0JaiNAu0Ue4K33yLc2uNKfpl/OQBAcxZjn+GOaTT57YpEofii9DnPjRTyWe1CTXiNqLTlfUAgklSEkDwnbEQhIsokEpD9gAy1Ny9kwk0ZIsl1JAWJRAOpzgx5oeROQyFJi+aLWF8YE1uOkgvanEIcNvuM641My94v/gLZgrCYRHWyjwB9TDFdtPYAxDe9ja9Cvpk5iC73XQKaOu2F17S9wQHAizhomVQvoGlMoxbvyfLGd+VB4/HfpJt6y9gSyWkzAQjOUY3Q0aizdZqcdH4eCKDAquEOIbGowFxYxMm3xLgq9s0PFBnuy14BuNcEnauEhLSe5FYGjIhQOQRZDM1SDGAgIWXOdtPZ7WFvEOacFCak9AEK3pCzciSxKINyDMaTWL/2OIlwr1fuv4Syz3knnz+q6H94m1qHUqWQb1ah2BqoAXdzF2BiDxBsEo0xR4qKTpilBVzxjVSMm0PKjaJqmuko2XKpCcKepymiTdJHySNpksu4KVn+T2KVg9HUTRppWZQabC2maY9KXoSgAmk+sV9ALsCSMSmdeqcGUbIGqwjEtrQUgACyX6kA550QwqaLfRQ2dBShZa4RzdBwGqFs7BGssKXRPJPNJVlUrV4koVgtdEAQTzpoy4HNuq0mITDHD7kQ4sdQI/CGjUt8nFmFHnQGZUmY07jqWLDEAE6BP1jhc4C3aMdWF6qQlVE2OMlxTachfGyh8eDeeW/7YN+Z/es/jIkqp22GKnQ6FDnJaDmipFXkDCV7YAPDg73inNCu23xhnJZ+KQVrremkxcJagozIMXjhUhHwwKSx1kDGtYH4xR0AtklMYPP+IpyC/S6RWCqU2caoHCQjMLR+lmgAAsdLm5cCjCSXcsAGF0Lvx6QfoV8hXZUXMqNCKTuR7oFF56SCNTjTKh+H+KT+nxSdDxBeaKkar6aHrMGaBaTJt26WctEDxCEmTiiC65IILFZAGgsFqeJ31+/5QbiRVPuTYP64Dv9XeTsTxsXslfsIELT2DxDK4lwhQ+h02FTN4SBweDHZWBzDS3pSdqS2AzDt0OefnZzla9273S9oCI5tnZCVyS79pUAJBNXUFWTHynZMorJlvtt1tqS4nUAIdbg7a4SZPeHSsJjscXq9nRSW36zJ3lnec/SBM7PD07fPDW7lZ7f28bNFnyQUsmEaGP7hxlEQxXtRxFbcVfXSSJfCgpQS0PZg1z1q0g1CeN8ahE1MJ8BEpFfTXodq402FnX29m/2t7fvlofL07nw+O37j66e7/eHvNJjRWbsxc7q9G9r7zxZrvxqDU+sBvZPuALwKxJQP1PHx+h7INur88QXa12ZftKn2+A7Vzd3qJ32+/02UjYny1Ou52rg93F6KJ77/6rvd5eqz3b3b7abk3H50yInddXO8Ph3dGovWievfHa+dHZIezs9lirQM1aMJE1W07m+Fd6TY3h+Rlyw6yEAZCM5kMaEol2yyDIVUeg3zqoVqsnagd/yjGNPPDoirv5sVTncBFeIV9I0mXRxsQttFfBNIAlOIKHy6N3hCIJtcjDAoVQROaLdhG/z4Av/tYXb9zZ/hs//bPkRotKLpRPkIBqNu/efZP1DduDLWFgqexUNtDDyQV9crxlSbt67fbf/Nn/5Jf/9Zce3b03npw/vH/3m1//xic+/WkaULQ0eFBqtJRXNVCnhtHLbn8bM8sw7LJ2uKwfhkEWi05o3mWOGltw5oX/soEuNOjJZohQeSRu2ccw2YkKW2PeeAzWGjq5L7wAJbhQKC+UAdHEIxOspekQLgjCDlgtdKHygACBRJD2mTpXsAELA9VkQTHUA4xUC36DgyBK4WJkogTnhSfzFi6tg00BMiUcPqey86Z8682HOuscLkWppNIXpFGhKaZThD2w4mPoSWl2ZdZWMRzdNQbQrNjBs0EGWATlrI01AsmgN3rzEgae8MtuEIridIulSwe6zjgCnCKOjC6rw/zwPUGNTDhEIv6HBRFm1NUOXaCKGZFwmwCe5REP/vpTXRX28oAY4tBGlIcxJX9JRGZw84d/kZAKKa5mhSj+YBYpyeuBngFEI69UAZtwb7DI7OIiAGEHeooNLG5ChiCL4KrqklmSS60QTSG4Yt5n3pzAQlFAgxCae6CoifYaECFDM6RZOGYnVdpy1oCyTYOaDVj+eMq32gAuSHBYuTfIZ20E9HNOKmqCZ+CgUib/tSl2gS1LjF327xgm03wUh6RDIrUHXSFW/SeG4tLE+mYBoCyepuG/mNOkK3noc80h4wzW/Ki9hkjuFFFJXNCjf26YPONBtion/4hWBiYUNDHSZmhYy43wYOYjl+Hf5SrRlxMB7V1X4FdhxpbCeAg64lbhILZimVLtAJRLvMOT2uy2Ic3HyeqO/ipF9RQlkNQCgcjL6JXnEnU5wQZIgD39tob/5BfkzUzF495gWTDMimL5xLOlrBacnIqQ2JmeUBEqcDUEYpd7ocko6TNQCJ0Hak9qF0qSNGozAP1frvltLGCj+6DACnR4yZwWo/VC57kEqk+AAmXxZiFK4HhD60lDLs144Ki9VWJwSMFa6kDDASaNMKxsuI/cq1E0FDYX6kbl0M3giXaSBqzRfA3rZLWaDVmdUpxt2zqabasx5aL8ImUmUSRS3WaOk5UzuMAwGqMCpsQZi+aSz//YFBEml4zBXY6hg25DwDVgi69APNmMsT7BWtwvfQgrJN18wAqg8BaKZQZppZfxX+iNsYMkaieeARHL1tsWErkL0CBzEAiiPPKKR8AvZeDnMcvIBLFfeCMBGSQ1dKcwAEVKYEUCSJMeIJAHZ8JjBgAqfowKXIEbjNWBs30ZCmBgVcTtLy0nVyh+vrpgqJkDkGccDw3GzPunMME2WOUy9EMxLGHh+IZpjRMU5tNzrAHfqfUgCEwiGMMfOx9jLThCphAKLyZGboNPiJXg91yLfZjBdzHlz2KXaJ3FYPCepN9DQIGWM3/er0gptzh+rSkIilRyLyUm0hCTEKKsfQ5DSBSDSDjOkTM8JbPSRx2GqMpi1u+1my++cOP48avsKTq4Mzl7Z7/ZPRkttpn8ZSEYwDhGfavHxyVqz9zqLSartx59a7m6Ol0cNesHdHvrjT30mUZzOkXjd0ChyTetnQ9nMI9x64M5R+Isrs0nk/MTBjyu1ZZvN5q9o4dnk5PXP/bJ567eenG5YA0olZIeqysOKJFLDPPrrSCszob8wiYZItGqTk5w8mgo5c/CDySTmheV5eT+tMpmKN/VXrHPoTXqd5r7V1gico2FKN32VmdvzFfM+ArSarYFm9uNfY7Kb9SfY2PAfPV8bcAc044lF7Wfz7ruFmEWe9brdD/zmc/sDurdVmN/r9dmDqXT6/XY8NZjDqy/tc2d0bpvf3PywQ9/YjDo8YnZ5WJEN9tOrA3lpxnFm9Unb7518uWv/t7F6eK5D9y5enCTNP2tK4vaxXK21elz2PnOq69+4/Of//LR2TEHMVkN0X0qrm0umksTCyfSkFO9YJWn3DB+esyd47BSv0jJl11nfA/Zc2lo162s1Hd6aoxjOJWKRbFJVYtgLvzkslY63OhhJH6uUS/MzjPmMXqotSQNolFkq8ZxcrGMnPmQzvTs4p/+9/96Ou3+rb/9WXZlrZgAAQd7AkiNkdf5R7//E1/5vT+cNKYeEcKHvJiGOFm2J3w87qS/1c9OqCVni3/o4y/8ZG3yy//8lVaTbRurb730redf+NDWld2c1OxZbZPxdDScbG9viwNqrybQn4EWKGJQc7e2PFitHos7IbHBqNO8ybeTMTI7sVnOv2CLGdVx7F+tQzr8Jwse1NjeMm6xrozHFkIA6e0kwCvFQQ4L94dil1typ3mYSsseG19kps42xbemfiKDLzYyIYBaYUrkoGaLd6TpyL8brxED3hCRNgggo81E6iLCGFJcZOVNdJCxbBNj78Vc0fCu85dw8qcsYaEM/MWDMgcRntZOhsWNBhM9yyPyAQ2VotPLmNa8yaDJdm3xAafH+bLKDLPL0kHGxLAr4o7VZmx5WdtCpVgxtaifzxfb7dpRllyf0kgsW90FZ+i7T5Yz/qkFlMDh3XSqaEdAhbabrUWcSeWWMpaho2J4tXOmnRTZ2EXfK3wSeCKFEiR+GYqbsC6gVAGCVHY5aTIk4Q9lSHqujAmSG4ax4Tceb0bikDP8YpMs+8apCxSR7Agw4o2AeZFatZclBghUxQlvLc2iELHuAnJKMjg6v8nTsu7K/vqceXVOHHgElryWHAWr8kZ2WQg/LY4k/FjJg4SUERjaU6zWSFrjM8gVns1KV9WarHx98YEpBJbOM+gDcE47TQVwg4tWxJE5+BGrzQ9MsKXQiqKyNBK07VLEm8uaggGyBoOQ7+i7SCF/fpQCZp/WnhkHIIMAebEZ1hPRgekKRZ6RSTGIKg9uc+QZaIidDzanvSINQQjQFJLPI/+Yf6YUv6sdor3JTl+nzwB4hfcizT0sQ842FFUTUJ6JeM2bzwlsv1Pe/0z3CkbyfKfnyp9v+32qkpCUICMptK1BiIc1HklScDRQZj251kiXQLKsEz5Jcjlkg9ITIEY/VdSTnE89PclBsJoadIvEfBZI4EAJz4b4rpUx8RpW5L95MU4FodlSMwoLMLEh03sBqZyTB3NMb5Gh/mhiUpVSw76ifCoayclSuQ4Ga/LQcxFM0su4RpNKxJoAowVhDosOOFWyaB5hTL/ZUoqVKqrNJDY6TDlkwXeBIAyVq+UoFHzwS70XeBShmQSmRMItZrgWDI/iiLoMyUmKjIRgpBzm5r+Ep0tv9QxLC1vMDRR+IM3K6UiSHMDDS7ogh0PE/ixxpvozri4eoC8JUk1yK1QBZONW1gUwKJw6aj7MH1QD2AaL5Jht7nDbfLrOjPmAAnGlj0W4wzS4mYSSBNIL+PxatEhqxzUXyoX4GFyKiKPpalzMtr0jE4qpeNpe8gNE1UBy7DKxM2LCsAQouEeaDgJ2B1FQuv2JZrczcEJmMmPacbE6n0ynnvXvKhdFoNOvA2PHBz5jR4DpaWYWa1EWWh6qu6SsQ4z3NVQmnNfkKuHe/0wXeStYT2czMJBlRi61c32V2PJWnmEtJMiuNVaSWsYd1TH6Z1hD9lCwRI3j63BkldLsR3/kE3/3r/zk4b2X+jufmO4ePr7b226Nf+M3f++ll19mOSfZaYc/++M/+n0f/eR8/Kg+7bxx9PIffeshX+FZrrZff+VV14TYcuAfdunVurhTxXVPisf8caPBa48Q1vnsjePps3TPuj024c7nzf7JbLzPYKH1RV2LpldUq7rvIhe9iK2J6sg0EhSGlIrFGhJci02mKtaE/OdCpjwJpbbiq659JqNbi85yMuIgz+mycXE+wXVv84k8fBpGL5mUAiVbQ2dO/DSpC4TdlM98PBqCxpOE1eptfJUGHan+Tr+zmEzc9YoYGMNsrzodPQlqyJIFbG02Q097fCyZhWfF7VZg1lA8LJZU3Lhx++Yzz741eXhl/+q1g6vL5ajZGHCAd6u+z3wDn8O6vv/s9uDlk/MLt8fCCjCQIWlE1Fywjf6WPmAMQalO1BCqlu6Kg/i0xA4l8Exdos7JT4ikPqeCU7tRZ5LaYy9RdAVY/G1KeMysfWnyU7gpw1hLVyKp6UrTMQ17/Xht03/zC/+q3Z5+9q/+NFLFwRQwzXscwIvR+Mr1g+nwPAZca86SKhqJbn9AJx+QfKaj9E22W3129YxX4znzeo8f//HNr/2Fv/LnkRHCQnM4vuno+PH1m9diJ2Jv4cOiwRJqVkjUW8fMAGBLKZq15yEQHHGdinm1vstQgnAtHM0uy/+lnxQUseKbIZLnS2npVKdok+3EuiIW2Ikhr9aRskwAY7SoGCCOHrNGo1ogo9iAoibAMu0/HENSMOF8POQzDuof/6mHwZeEdszwW/uLXmcvPrwwyBVQloasxRHA3tEVC+LZjjrPWnDIsEypg3/qEWO6GAeFWK89YlU4pjLoYPnppsw5L5aFbh5sT5PjCUGM7qPVDv5wjBPHLqJhfHv9fD5Eo1dsjqfprp+1J3yM8Gy/uWR5Jcylt+wppawInyEFtvA6eg1Dgl5qFOhg4V2ExtQuzHDnQK3Vp8PbaOz0OKEeDsIPVRmyaPTUeRaMIDrMG5Kyc2ErJH1cgJAHYOmhoPS1ZIuaaZEObHsoDmoBQKopTbZrElct2o8aXZ04FbYqpDUcjnKRk/8tD9OH2zxbyfgP6ERCCHy0AHo5/MhdTIqGGRkoFBEraQOOV7Oav8hQwJGNP9E3i06+KAw8M7uR5qhSEO+LgKg31kM1HdwBwUgAGKqJxqSp07KRnfTg73wdqTiPizAk4K/Dh1ShqIvFiRTB1A2wyYXOSBpxqbzgQ/3gTSYLm9/EA1Li0hhYnUqciQQbFIAXzCmOgJCVvorUyBSTlktiuBjfQ+IpAmvGK/nlqilJkkQFYrAQCLksusTxUlIaUl7y+73d1pC/Y2phV5GX4FehwTGx2G7RLimrn0t9kTWUElNxAe6sUX9v8etCK0W4TG6FUcZg1tgt+ym9ggi4Kn+EvSpj/8UsEqWGFEzEWDiEVLQEU1QdACyr4MdlAIEHxNlNs7XuBYJqx0UAFSX1QBaYNhdP1Wvrgcqh2qhTFJ3shXbkLQ4xA4SobSRWeVRHn12zKpZxxP1Vq0oJSU1cVD5lGAMQrIXDWvwPnWYR8XI5zkAS6SWhlPrm/Bov1MhyrpYlAwVkl9Prpmc6lZRRbhHUHgle/zyuP3DUXg1WYo2m6lJdS/MAQOwVR3xgv5gfv0U5tSZfP2XcBbXnoj7ZnIvM/BnZ4u4IQlmD4WIZV9rEGAHFNJbNzWEvIrSPzvTR3LGJglPbyAldcIAnUbJJEHmqPmRhUfKtPum1NbMxjMsOH1bz6yyZWHYex4+DdXHVjb4qsM5jkmOZHGZyzFLOygvLsDg7O5ghZNM6JVSCSEMkphtKaA1srKHrRHXQ9yJaSYliEQ1y4ER3Fl/s8M3zSaN+tbEasS1wMsZrcX+IY8P2ZDB2PFiuINKeBSUKBCf5bztDUtCo7gVfC/Nyh0DBnsKPzZW/9d3I97kc6V/nvRz9nu8AJBKgjprILtmXS17Bjz3vnlBUXXLKNKAddlaPxNIAIG3G4/EppqiQy35qtf5Wa6tfm492+PbqcDj8gRd/6IO3lnf6t9lFwMx966B/djocf+pDH/ng7u9/9dVFa9ZetZ691bu9352e9dvbjf3dF1987rnBlXand+cXf+mf/f6X3p7Oz1pNRl4vpuOLRhfB9JQVemV7wfHe9K+Yvm+Ph6x3f+HB+Uuz0/ri8Xlj3pl0z+985Pnm4g3OqWi22YVGVzb0VufWg77OjDKRC7oWvFtRqBzNLG6lEumUdVwF6zIChjjx6dAxdMOUVNpAAQDheMI38WzaPSa2J/PFeDFjSGyC8s8XZ0xmNnvz+mTG4SRqlKoPCai9Yxbg0O/jz6/2d3Y5WY8dJvXVpNPsc7Rpv7u9v4Ovz8ZJvkk4ZgMA7g0LeRr941prZ+EXfz1kaXfPz3aOJxdLj+8Gf05vA7k+fnCrM+q15/MRmg0fqAvTyfyUJPX6ecvP9z5mvGDafPz4nLmXcaMza0xvOJ7XYG0bIqdhtzOu/FPFeJJvzinxwBeIVAh0AELgLysTHTIgyjwIiDhEZc3Uk8eqOOoqt+PE2LrzanVnetBPnnMyASG5yCYJpVzz5LI4/EyeY0+B2hkNp//sv/83d984+i//wc/1twfsjVSSMW2j4YyTgpzp5tPkHWYSMWbkw8cjO8gUr27S62994EPP/ac//3Of/9yvHT+8324P7t5/++zRYLCzs2zfZR0W4n3z1Tf2dvf3r9J3slPK7Gqvz/E7dN4wz3t8CRgWMBDqSfMIl5qlB9uh16oLJOoej6IGht6iA7iXMhk+NdxHBC0QhmKRxF4BcdRH7n5FO1JIuMCQjrzzvBHAwiqPzkRX9XqBxk8YVThIfNXaYFrtlMxqbMxkf4njLnpVdjoBRMlk1SlvrW7Vdq4t+CqIkNKWUpqcv2Z6weHRHoo8GeV2DPP0Gkfq1Jv3dFFBgEeHIUXQV4gF1vL6YjVZLPmuDkP+rRmHKHBOfJtRli1qDavj5vWL1WLQxL9V5jQhy4vZ9HhaPxrPLlyvzkwgXXxQ7nYmdBQ6W53tTv3UJTN1srsflDaM2TYwRJ28q2t0o9UITFv8TE0wqrZo1Sft2oyKxzgB3HfiHBagsXDMR00eMcpGZYZeq0PmJYjAsbdt5utXzhO7dyGKrkTJ0uz6aS3hYDeAQF4ZwXpYOrxd6qEKLnw5b2xe0y76lP8Rr1WVgkCRMJQWhDAatGZ8uIwzNQ6BAF+4mszI0Sx71gIah7nKlI4S8g8CKKKxoMWkq/0w+qMvr5y4FtcRZAOZgiRyloiEc0t2aJd+IXnDMVAhSgA0ApPhDfa7ZdnVWs8B5aZcW9VSToYk7a+YxRkjoCeOm2XKYTx/ZC9i6LMYmlVzn8YZXpHbODqb1hK0FvAwCKskj/lPFnOBuFQW+CbNe8GlKlg/hynPxyaaXdOy2EYgWuxe9Q2fCK/Aw8C9Y0ZZQakTPBuEYT1FxwSxuSw+L+W+CX+fh9XsWVPntJ+SrT57Vrzfff6PYeTfQPTBbw8HnyeASQOpOv9UvU3iJ/F5KgU9gRXIxpjhaVKSvtwuQyuJLoXAXdF7zxWIwOe3aNLlFBFYFVCJK0CkimsN0GRW6YStA9esMJho4tQTc5FcHjxJmCCTCdJbUnMLYFMTRiUrMebzD00xJKlCnfibiVYPeVeKxDvVXSVYX0bxboiYUDtVWPGJSlo5ueLnE0IokTgWIS8J845m85UNfVMg4HNg33HaiAp6/Go2LFe+VTl4MQxIqXNBYM0bslkWW+741hLrpzEf1CktliXwx2iig0hyT+r8rwmgqus5hzm+ACc3gqga2KPyajYrpVwJhvxgssBHy8nHP1oLTgrAHjh3x/ifjoMFcwe6hkAjCDCNKPbMOOkSaaxT7C5owXnSaXucpwtLrdnmJCHoCwlkvQiz7+CwjaXNMNIZdSmAxZesMMHlhwHF8H6klK0EzJ+gcQDhggYkgFVg4pzvxLOmgtEmz5U4vfvgFRZdMGxFKuYxFJc40/Q4xguhx8fnGKYEyk5UR/RCOOn8zS0JqlCDqiSbuE3U/8iHAjCFigSva1y+A2B4WGLEScUgh3LhwVc4pxKx5hvbyTkwbJ0abLfpI3Unk/Gkfr/Rf8xihPH8cXN6lWUbo9nF8dlwZ3DwaPh4a29376DTb9duXtl9/plnhqet0/vT/vZ8e8p5Jmezs9lg2N/vDNoHWy+++IOr5cnDByfn48d3751YKtO4HCfl5ACNGXMOtQenr/zO11h3c3ZygvP7cKd9Y9J87UOf+MjHb3NaBZ4BIojOQYyqYa3JY/QPGlUF6oJ3HkM0gorLokJGo+SATR0fo6FSAAA2cIYdLZwqiXLqxuI/DWqrfdSHhXpMei3njEo6vjsb4y9wcgDZWIKsw0LNQTMJGWz1XrjzPAt8drtb3R7VjQ7AjLVr7a6f3GkwqdJ2526G0OC4e4OoUbjWOLF8hohT+fksd41pD75RThXksvJaHfUz6GNQAfnS55JP2Lp5X9ItHpO64nAbxylr29uDa63WAzZUUECUVEFLoXzikSoiD/NGANB9VKUDjSRoPP0eLACwtZAxB7DF0X5CrDFur9Eb8wIN0iA+kfTVOs3oNFm1qFZZS/BvfacQnsGJ0uGHcQiLCs5Gv1/7zV9ftYZ/++/8vatXD5AfPKA6Hly78tbJCWmRJFUSLw1aU9l5X7b4whG7mRDNZMxcyw9+/w+Mx9P/zz//f9OTeXx09IUvfOEnfvKntm+06f61u4PhcHR8fHRw/cAzf1lkwnhwMNEgtU4Wtcer5V6YpBqpT2iPngyS50FcpSg36gxiDw1WKP6QOD8KhIRyTjddKGYRXJhqEv+tL7IB3Wj+ELPQdXljT3WwKBMo8Jb+hgaspJU7LoLHVoUE8Ionxg8AGB3HtaQvyFZc5nY84RHIRQ8ABQgriEVr/GUjSACATgczQE5JUWwxgyIWLiBlNzWrNO32yWB3tVvb5Tj/Brv2G5N5fX/IMUvsuDI7ytifd/i2E/zRzLNllKZqNZ6ygnaexXiEQht1CD2au3RqiFKJIH/8Y60HlcqWwpEg8YQ5cAA09St9ou7Nm7Sm7I2hB9LnhF0qWEBYO3NJaHlEjoJNEwI8BSkh3kkEeSitU4P0CdmoSrISyIyAA91KH1BhhKJQUIiWqo9ZKolhl/oMRHAGc8jGuqg+JR/xcBXzSjZ+KdsKbCbOpOa4pJBtPuyDQ2+2VrxU+ItnIUrlSaXiQXxSPW3cZZRoixb84tlqLbYgCBFiLYoolPnVOV0Yn6NBCESZE8DkphM9QUYMk4tUIiREElm2VQEZJkxuEMpfkCAxEGSZjELPjDABuUi/FkoyJE2pE6WCkDClkF4hkHidHp7IzFQtARaIFWgYKZEaKgAgCnFEYWFlFnxWHCC1BXCXCaVcC1K8azSJsXDjDcqDL9/tEmKylUTvei2BuZcYifJ6Ap93kFYBonuJhdacoOSL+FUZEkeyEiyMyyhWBZREuRN7OdD0VYb1b4SyBqJmcULFpSsl+15JIgC9FbCcqX9bnnbKGimsFVdFoI+mq15pdo2l/wqs1r0EJzk79E1XqpB5uDbg80CylLuWWRW/Jj5QSBIqyh6JwGR9lTlbd0FwnaaCziuQQ0elYyprCTCJoKzAwCyqJR0Sot57D194SaEVcMK1CGQ2oQCtiEJy+ywVnRcrHnOa9k8thgrtg6PlbtfTDXW1PKbZ//E7NUIk5S5Aah2+7HzVwpxqSLQ0PJkFKbCO0M2vmHDicMLxBGLrRIZV6VYUxi9su7ALzlHylRBxBTG/Es2eivspCOoQB7iZD5p8448xEkL44DqraifO26za7taQNJ41zeDOL7kYyNHKibtM4lSvRytGiezikxILj52QiY3mkctzyB/WkiMGS66Q1bRE8mKT4cpETJWBxIUpFMAGA4VBOGlrTIYgIExYOOBgAOg7RuuYmoaY2XMG/s87Pb4DjErefPVb93f3WAjQZdWJC7SEXeksaI8mk8fHR/DNGQtxyrJCEUr5FQ5i71WF5gmciFVlpEPUvvtV5g2+U5oC+Ql8INIcB6qB71vC5dS06Huk52yWIA4/iXWcSa1jcJwOGkeXLJu91s52d9hp7Gxf6c7rndOLO8vRDSZJpotuq/WVTpevuX6fgpstbw1u1q/dbNa7p4ev1BY3pvPH80l7WnurudhtD06xu6v6/R/4oVvPfvD69v7q4ODm2clkd/Cxx5PX//E//uJowSEejFJzOB04cKg4U/osarj9zVfvt/H6nHzambZrr3/9+A8/99JHf+5j7Va/wcke814cgPaKb23Wx6vpc8wq1GucgXPRWA2yQB2e4KEyrDtmsS4rie3eQLbqA7NwUubdNl+j7HMmFetn2ATOrFS9y14RjoQ6rC+3642z2bxTH0z48Ndo3vB4kZbf0aGuMIDfWNEDYJVCTjqnmrFYZQVKThnR0sz4LkDvRq+xaC+7s8Z42eDDtR129N69/+rkuMsiiPl4cOV6t1G/vayfTedXZ+fH09n1evOiUbvS6p49eljf2sOb3euxS7i21+myhm172T5Z1Xdnq4ccbd5on09GjSkfIht3ByyAWbi9br7Yope+nEH++d7WlTt3rh0e3hsyJ4CHqiJb9xC7DqWVJBaYcSWiFszJUB0v0AOOzbJ/vvK4WztEaq0OIA6cK7isSXibnOJKzWLEmjTCFBxWLVVBw2Wj7yIo6iFrKeBOlF8djXaW+lDpd4weWcWRZRU8UWeB/yu/8oWH94d//+d+5vnnP9Tdbi0ms7OT8353MDk/ZW0VgwFURE8kxFHlo618K5RTg3DfkL3jLxhVzve6Mh7tdTrH548ePz78/Me+//rHb38Un5QZGOAfHZ6MnqVXhkRLbW6yIouzmurLK8vF3qp7CqqQRhxmjKEO/EIrF7KGk/xp0+AexhnDi+Tp5pGA5BjiiVRw0oEunGpHbnI69KJFKsk0LKvaruxrnJtehSZtzp7nmwOpoi6OY9tK/qfJ0Y1xGCYidNzU4RQ4ptdWVnLLVtEgLDAgo/Vg2qZmcS6+yFIMYuCx7mlgQOLiVbOO1wR2ig5z3jmmY4FJhUilUrwpf8mkuoFYc7nfnjd6LWYJKPCQ7bisAu82qHGDVn1Mo0LHV03hGHUP6OTbUqPp6rzd2G61pmzlAGWmrVhpNHMXEFTucQA8WqAh93QsPz/C3iP92kIwPQExh8dgOuITHBBB3xDnGcWks+ASUYD6gTWgkMum1Ky8ynlSq6tFDYko79zDL2N4ZqGetdhHTA2/dF/IymoFQuj4wiEnwFOEsICjWpto/WpSEMs6ogirJJGLtLqskUtDhjjAzIy23A6BMOxCNiCGRsEqJpRI7vNgbvwKiSCEHn/9uKo4oEGEja9RjdYjf0mD5qbJDiT5QUDmB3DwSSMxKSXIEx8y1EW577nDcNFhDRwVUSA1uIaJKq7DuFWmDJ9LK5GUa/WA4bTpZJdx1mrtUCYMgKQ6kZok1g+JkzkkojDWrTGFCP5FYUljLHzQoKSZIK+bc2SrhRQhSAjv82tRaOohSXWqgjbQZURYUoiWZckuYwuv/I1aRJLclG3u4nDpuYQn4F23yyP91XlB+MOmT2EB/yQL+EYEQpe5oleqdh7kJonpKkvL5jKsYMCT7K5w2yTwoSTgQYhPxVQvorK+hJhkiKl6yjuvJSCh774l6kk8T3lB4rL0KbxKKmhVbQStB1ZdJizXOoiAFFwicgdkSWNcHp+kcATjCbg1MH5Jt6FSPhd4VVkBRDS4Cq+6F2YZnNzvhWtamjq9e5RSeqI0sd3EiYrBXigcCcU8gSlGJacOA0L1JVxY5oumYn8LAqnIlcklDVXQA5RJXq6iSzLCOkDtwVDyKJxSGawwGXewxhCo9gcPaiY4w/3Qy2NEEqgSQiXD9tk3sCJSHasqIYJC8vvffGuQJhbPH4QCuczBi7hSxSzxiAkOEw0VsdhguEOwHgHE6y+AuLHad/Axn5hgJ0Q2EsjdGB40QUkjpoYUxq6VifRwA2aSKMk40p8AzmlmA4AeC+OT8oeC7DyQHGI7/T4HErNPYLG91716c5cG3lUXTXy4TB1gADv4a3QGGAXqtfscKB4CKcseGhyP9ES7IF89EJErv+K/DqjC/+N/qjoJPP7LhnK9C/5Tces0l9EAJ+tNARDewj3PTWJwt91lBnjaG7A/utfb6g66+61l6/zwt3e3+E7QfqM7bbSZ4qe3tQUnxxfz88ejP/qD352McEYenN87Oz5+ZtA8OB+9c+3aM3tdzoka47Nev3b1YG+rN5j2m/sf2K7PRgfN2my7e2148tAvydDOsFTGdbx4DDTvNOpg7aoMVgCz4uds9vB3v/obP/rj7RvXP7jda/IBSxaAe7qrjiltAR07tAuB4JGjV2wFpPHCkcFdw4FFDRzKCr+of43XXn3z21977dazu1s7V/u7zHgMmp1hY7GzmI6X8z4dGVYpc4BgvbXbb1w7fOS2hNly2mKg3nNOO5ysy1IidoqjQjRXDNSr1Fbt+vZ2v9ttc6rwcDrZ2eIL01Myj2bz7mD82v3Do7O3WRdxcffBYrzdHpwMLwZ0hluNgyXbKFd7jfbFar7d5FSb89XO1+rTSefajfZysrWzg1N10GxfdNs3Wp2zVttv63zz9bcePHqLw+ZXvedG50tOKW3Ut3scnTrEv+3cvXfcHQz2D65evHMfL93KprKm2vBokyl/c2GprEtFgdZGpqRELioIVFYpNHnhYioREVg5DVqYTNViAJK3rKCT83EWynYaAaz11aICmaBN3SjV3bKQFjWTfaNf+eof3r332l//a3/zx3/qx3DPCeEQ5y4LqBhJpvsexLSl9FdYQuIpq+y3RkCMCgvjmZvPbm3tzhenmEs+cfrqa6989JMf0ksmkv7ixdnp6enV664Con7rezjLybqRo5W7UWM5nWLVicd8ug0bIeuF8Ccr0TpNIN1v/UsC+Ic7Drc96ymmOKamWBpIxnYUO6AJ1Pcjk2YPWy00ea01UVkhizitZvAwTgbJLYNDO9jwmsseqHIVL+IBCWKKI0xnEal+NmjqSxIOA8IDswdVQuRYCjcFV+y2DYfeG2ARMoJVbZi7jnChunGvyWI3dmiTnc/8ebI2633sMvF5ZgOXLAtssxHaGQhmCWr7zSnnLXRasx4LzmAXuskvHT5OfeO4SXtXvAsND88f/sfMiwNvok1XgeVqcw4E42sArO1WY9AXimVnDuvAWm5kz96VWAQAQBBus1RJr//gMTf+y2DiZWwipFjiaQKkhUC1O1eSCavIgjD5It94yE1h8lSu/AbrdX5KsRMuIgyckFQhiYR/Dk3xn5fq3V/kly43DW+bo2xolukkIxHbuBINpcheaHTM3ZmQGQaLVQEhTN0UvNInH+27+aXbBr5apu+MEwZERzzL5C0XXbWfhdvOG5dUIw1rg2lhuklgMaGABIWivEK3YG0CeaKyhUrxp+tOn5l6YlBQ4M3fcMpcqgDohTViz7vekWUTXeoF5MBJWehIQDoLoTjFIhRZZVVIltQC6ZMWoRuc5PKwPKoNJSzo+1LF5NHUm+vy8ybwuz2QIeALlFAa4JewSFRVNPSGtIJAqjOP6w5AgVQVF1SqkA1aG7Cbck1RQtdoliiz+FdQqrDcZCeiUsd1ru/0Kwwv9ySQXZNlD9Brw07LUDCEIGzeSGl6HlIKZ/Ybci+5ciMEYMwPGMHT+14JZ+MQV7WXoEpmUYz3mzdXmQfgJUiUsPe95zM6oMWJRgX5qEusojD9Y60C2h47UWgSkOWszYFZYhikVsL9z6iGJzwUfbaxjHFT/VsP5RmVKtzwjuWxHcQGkUuk05u1mbAkbBJtRlQcS8DQm8HkNmcqq8XWHCfD0XUmkpkEapBoWOmt5xhxklONDcFSUDdMoM1gBvsu1gFrRNLV9BZQl813qHiks6aSjYE9D7dgsAqTvGC2QfQpC5BNBnVAz0q8mF6XPc1HJKLpATajKYTIA3UEDkAZPf1wjjvjTYTKdSMKsfwQVNKAjwimILNjCjXTpKhAFM5EJmwKu8rhNKvVKayhTDK5/xoiXeyNALGXq939/s4eR4k/XswuOq2dVnNrPju3QWI8hhUFwKe1mZLS0Rw3CXJgOIL1Q0sEuuss/ayUDhHrSwokgYZy13sDHKoAH/7HXYFbuCNrBJYRfdf6+yYy1f2pPQPvClcXlDWsQTxwk/4iq5/t4p30mltbbb5v1dre2tke9JvTCefVfGTvxe3pdnvKBpA9lk+u6jfmdUYud0ajR4wGLoads4tJb+vO1186rLW2n7t19fW7p3/59o/MWN/cutnfOm+vnmnUTxqrO83WUW/6ffPWy9eufeza7S/eZcHFgq+6wjNOXkJq6P10zsp+huTxxVusKt6fdpr3L649+Pbo7f/2Fz767F969kMMDz7//DOTT774UzduvV0b/0hr+83a9OP13suN8ffV+6+sFjeY61tesFfhNXwC1hPbjCNWV+m4mO0rX331zddef/ler7HaanRw52lc290Vn3mjU9FnzB5vhtNL2KIwnV6wwXK7158Pp2eT4cmq3+1zQv2iv9V8PGIfvw0qq0bwL2AjniGHo7YdQtxlr/Arb52x4PnR2dH5eMwotceltqi2kzr0Lu/XT3qLxinfK2222CjZHY9O9ScXR7guqPHdh06RvfEGPfsOew+a9TfBv157lWlWdsnwPZ96szdbTN5465u/84dfZfgZt8wd6nUG7fpsouVTvGgsvRbkSf2gLqYWoR/UOZwPNESrkQfMjPqZekkRbMKMDlEczS8v9KYwUnaffDOT+y6oABPNgV8R97JGJakbErQjfgeAj/6RjbN4dQVYGLO+UkMLKKGKoAhYp0Vxto9L4Vutdv/+8f/zn/6Luw8e/rWf/unVdHRy7/AKO0zGU3ZZcCSs1YAu/pQPAqA6+k9oJ2rtQPaqduOZxU//Jz/wq790H0x2d3YfHT66+869D3/446o+R1FNpvfeemtvb9eCQHHCxwH4gtJ0NdtZzXdWtXPMBdzS761NxMZ2CjYy+wHtVhxNtCedsEAQRjFQja8GKHjODAA9h442MwRJn+pxZLNRJmOpbxrUY7hcyC4ycseXDHRZGcsiyYh7o4fjdwvVYvxiTa1THC5RxCzZdRY5IOurEmuPL14bhcLJxXSXj0jUeh6gtpzva/RbxxResZxfL00jAg5h/kCGhWvsiSXGBD44KYcXyOwQyW7jjTepZcwI0HtvzsGkOR3zmRj6xfqPBHbu8Ymc+uR6g4nq+sNObb7VWg1nJ5x91GhNyMahSRlVmXb5/q4Y5ODsxjlff+aEFz15dMyeFZigVmwb6NPTaK22neJ2jwpnAdFKYo3JjfUGAGlBlrMHEQ8IQQyqivj4z3JZEJfFcN62RkaFfFsE2Ge9QJFwblFENV/Rw9Uc1WcvonJeqOzukJEpQKiYmGeSl4uUQikllSBSokvJFMDaYOUPQhavt55OglXNf1xmB++2Xgfo8CwSyoqtxwTCATquoK3rv1pcZ3NRrfmQ1w1WUGVV1eEWQpOThfQggprihbd0HdBPADk9EQUjfMmAB6rEPJZ6bImC5BcExEK0xRFmlTUdWgw5SzUwlQKq9YjC3yA1KW2HM97H8jC/AKGvAGbAkvsCBJgC4JcuPvB8s1SRZ9kB9oRJfkcMmXOkKGsHpUNC4YqJ+fwn5LnVuyAqzlIHydJsEoEieUn1TXn4n/BcpgtlJaDEbOJ5+N6uzAaU1JSaPNU9P9z8hVO51qWI3fpZnuOCuMKCnm7e1pEl01N3Ia0LqiJK6YaXp3X6UgZvoV48jF+n4fXPeiXLGkyAGrIuXrPCa0jjQY6HdsPWJYXh65cNKk9SVMCrFILz7/2vKqZUnXUSARhRSuTJh/KyTpLfZK5QTTS5ql/I0MA8uUKpoEhQ9CsWRE3jbxPoYHGWCFuAg5Us3HF4mmSpzBhqn9FF7iEs9oli0WKbcuqVNVg0ck91Jo1VhbrEiWnWYg02FcpEKItFWhVRnfaqx8w4loURFmpLUSRSiLS2jvExXF6anUKo9hHuprg08IwJk5uqC0SDKcWytDrgpmGyhtHYAJkfZrypkFh9RgiorRCKcdbk2CoA2BX/4phLinmV7sCWqFJ6CSKUJAYZSqQJNAuEGYo9pW3kiQdDwnnSpbnANYMvNCEACW+JhRInNWFI7fTojINKOq3t9m7/uRduSqWLWsS0IEM2yPTLxHhvSIn2JMzD8mDmtCBcIpSHzc3wgjNRIJp0VbKSNCGb9H/2B6DmKnD+TNBKTnlX2Jxf/AcC8A+WfHOi0+RLnkx3z3c6DcbZ+nu79d6o13ln3jpddPeWte5kNZlP571Wf7Ssd/cP9q8sV1/unRydD2vT6XT59Vf+5KVX3hg23j5qzluNo27rZqd31Fre6DjCfWXRfKu9eq7WPqq3X3vnAccDdNEH9AqpMMT76U9+5sbtHT7uNBk/HJ227j5+++7Dkwlfge3S81h945U3/+Qbp7XPv9Fa3tnaffP2wS9//JOLazs/fOXGYWv2scHem635h7b27o1HN/t7D3/kY395i0o3x/u3JkTPaMC75xeTE8bnG52z4dmgU+c4Es6A9yxeTqJs4KnPGzgYtFSLyfDinAN7zodDatnFZL7qMMR8wR7S4Zjl5dQzdjDbQqpPaANrmOnMsmOx3Xjw6HAynJwePaKRcjTa1b7sjQULPrRX293bmZ+e6a/TprGLUFVcdrrd2ZSjZm050e8cvseoH+pIxelRf9AilNNK7EoLV97HIkSrI0j8GhxSzrxjKFyZ8jlP6pW5IvFUInUxofEirENFjaTi0pOqIEwqbqqbWkxKwEEID6YVVUFZ6fjTZwJLJFkCsQxUcyoawTgAopGac6kcy16XH6p500oYnJlC0jLQMJ1Pv/DFXz++ONof7O12tj71ief5OpC4cWFxcA8dYFYCBbWMjABi2e72b928AwrE8c3go9cff+nf/4cPvvjhVs9ZAnpuZ6dnR0dH2ztb9LLYOeCqdbf5Hi/5jyNuCVR4jJ2dKA81hSciFgta5K4zqYuqeIiEDOzggiXhOK5EOIGg6yT9sk2uIsCAIU3xoFAJw2WFPJImRiuQXuwGXhTNh/6v/RpMndMPwBAid4rX44f9TMxaAlg7EqvnBLA2x6ZNa9i1Dme9U8VLQd75x4XMcuVFEngTVRNQlu1TXkFMIRPquhbX5nugaqN9z8M5ccmCKkZEs8iX2ZZ8sg3UxvRIF6ueYzwyFzIOprOL3rS/V5v2WXHKyJQfuy3jQ7XBatZwKaDsdHCHbWbLnidQyH9wjzayk87Pym+hioagbjr+HAVLVccl7xlPG2djxAo9bAYkgBNYZ4tI1FbGpJVUOaGG8pp80hYpkc2FZC13isuIyBqWqL5WCoUDd2SQNRFoeK0lzKrle+oUIJOcF0UPSl5mtXeazhoQFSJAnZXhQpBWAFBShgRYDInkMy1ns+2ucuyL3xI0gaeN0etnzZsGhE6udQ1KPIbL73iLaeiTQMglwqYem1I8X6WLMtk9gkV0FbE5ftgXEgjjzkEbiIwG3RQEqBpMsYoqePuP5twJMSPI5xgS7KC4wl6MI5OrxNODzQoiPXUEziHBHbq0HG1INnal0ESTCADqLTgjBZTdLgArgQi3I2CHmGcosA9GrYI0PuSHeCFbhEAQXHmKyqqO5kpgHmWu/IR5po1ADVmLM3gbJcvDfR7ffQHgz3wJ8tIlbAVbLh9SpsgbTCSXL1wF1TzqaIWABBtk4ipq8wM5fSOqr5eV8MupeLbIdYT05zn3KrKEJGrV50W2cTEq9v5XQVY+Vhi58onB7rdKciMqEAlQQkohl3E8WLJj/9VrFdW+l1QBTNC7fysQJmbsvxSTu0ktgFKkInyr7gXGOiepCUCf1qCDiOOFm+ISE4FlCJ2UQkJa9uMJ1xDrDVtBdDRjL0lElVERuXRMcbvtAKO+ZEFjcXQ4IxA0aCCLKrqXKWMOQBCw+KvXso4OgAMjHqnBR3mIyH9uWhCiSZ4xL8Ott6TVOuKNUFr8br6eiA3VQ+bORQ5R8Ym9dJZjrSdUcNof4uSeWHjCAOTgc/BiAGYEJ6nXbc8xGDnwI+yGFDZ4YVBoq/SYeW9yoJ6c6TDp7i5PsaFOchAchZNWnhRsKFBLJ0YWChrlSRslneXPs8Y4wQUh6FgoAJ7zR55CWNLzhn2ot07Y4Am+zqe4XBs0oQ57ohQgE4PIfk0aVfbIdfv9QX93NlUZwIDEppGZCkDcGL+Cy2mxxQZQrjZxECKJ1WqRLhdkBXE2FCZAMkvQ+mSeEn4pi0Jbp8kTEk+AvuN3vABAvqdG+r9j2kSUUngs+IG2XTVNLh7OarW/v/03fvJnGHJmJLvbn+/u32FQ9Ox8NDoaPnpz8s+/+PLiN04ai+3x8mS12l5MT5as9a8Pxxz2MRqiwWcjGNK8eIS+MTvUvnv3G2hho/a4YQ2950kXDnDinj5w5c7iZb/62mbhPq4Vw3Xjbm/wqR947rnnn8UZX02///z0/u9+eXLvId8aGzLI22hw9s0Ha3wkcvFRvhhwcvriyenJn7zBiSu/2WC5au1PVhy20/6jbo/1Ov3BYPq//V/8xI/96MCBog4zgTMaXjRsVb/z6qtvvfPwwXjWGg6bF5wQtDhbzNlLelGfD9gIPl90FnW+Ht3iy1wOIrbvXZyhCXRs+ALYuL7sLFb3RiOWHaGzqYxOK9PlxYfX5WWTMEPB9+4/YMe/dZkG1spAGkbjT5vLbZLSBHIElVWBla5tt79z3iPd5Cnn0KJPtFqMddXZMswHU1nQ3+QIJiuozjdLm3qc/ANN2h62X2Y9CzxPTXEhC4vzMgSM7pZqZMOZ6q/QrR9A4kYYL6rDWiXUiFIjjcJFLhYp0ep7VIYhvVRbXZoOFSRLOwjRAllzqFxgweGMbK3G0bEE6KNTDWmcKkJdcvYgRZW7CFVIaADkSb6uTTGOawIAS8YMypf+/e/vb22/8Oyzzxx8/Jmbd+bz13s99lN5DCh0OPrNlNySg2Kp77AGkwuJ42s3d37ib/7Yb37u1/n6aK/PJv7h0eOzW4Pr8YR0zh8+vL+19SH2D4yGeI54n+S6spjvrepnqd0IDvxi563h4BPDFY9IuesKY0U9EBZEiYMR88W5p9E73UhFwEEmF8YYEeGvCEWjQW3DtDjeSvuhncdqcrcFCROAjAI5HK6HySM8pDiy4gBSlhLSkLncnSVovEHwVDCNLm6SDnSkg9I0OndXPXxxnGZ09gQEYr8Ud0ShuUO1NPDoqwLhCUikhplZHeWzobYuSDMAeKhNbnLsTn35uLbo+1WHxTY9F8bm5/XTJYfnsjRlzoRSxntAh/rROO82Zr0GczZ8AxtyAMTZX8DlvM9GrzbgCdaBR2O508CGUClUoBHMay45L4i5hQGnaYBqozNWFdnHNr/uKv3efRSGo4dgKN+JZnTN74U7BEV2IWIUeGUiTgXzipIDwuYP3nLAFwqLqJYs6cNFVUhuMK4Ih/88kSmfvrE5o3KDf2nF4tRYC6i8/AuvFJxbKIoHK0Ot6ADEAogDjOVFpsvZ+uKGUWzc5zWdN2UShos91bq0z9yr6ks8bRiKYTp8B/WdBfcNPhbOrm9ME8gKwTJQG02fz7rQDoqlMVO5sf+8WKbcFDjLL2Wb/jPpfMAcwTHdeqgwiYoAfQTj2dOEap7Q8QaHGaBHpqTGo/BIgSMWJMlM9OTogchdZtTZJU7ObGeXatJfhXGNZdtqD0MxYOIkZpDmSYVMGmAo7QCKM10eJjqp+MDU1skl6IQRsFf8Mb1kpnsAEtglaBCkogqvAFpq1Oy2ioj/iRTkphFiq4L4I9uqEF/Xl8EmL5nWoe/9jczXiXLSV+VhJukasAphaQqpwOQlz4TwfXpuJADDoJSk64Tr5MEzgQXnNSrr+BCyDiy/BVieCzliUZ4I3DxUxT15fxrKpfwlYkMyr5cJQieJEp9CLNHC3CBo7oISwYqn4HIpnnATbPhgjupS4bngVIFa7pFpSVGVaXyVzN9N6aXgRF6i3PfEqAtAyJ0fRkp1/tQREKX/HRUnAaqkOlljSWUWGo3SiKCTGHUqjKfu2lpGoILnv0tadSKFp46aG70tPCAxZVCHrArkk4eWwdiAZZjNCmAM5FEAVRPead0svsKjECB8k5GempnmM2wWioylXlOKHPIuVMOJkCuGJIHmhGAMhtZTyOBKDoqy+lKTrabUY+xhGRaksbPb0fKT4gyN6R85hgRyIEgthXD9M/55laJ9ASiV3HdqtjvxZKq76jjaPyZLuMZuLu0WSOsLAR7XSF7DPLGVEoDHpsApCrbfscJfWV1cPF4tn2E5MBYKC6ijRosuA2SxI4YUpyQFRUhBVcILW55odZhbcLI4kCNVQW+Dpjxfh0rlUxSUtN/LvcC/TP2fkquURSJKhBhoAQucGJpemMUWt9m1a/t3PnC91+mNh0evvnb8W7/9B6+98cocfwX/u7m9WJ6tZgM+3FNbba9qFy13FrIohTPyojuoAzA9QRQt0vllQtYj//WjUEk4qceDVHA4EIdfdYhs5/Wp2zgXo+Oz0/b9/mR5Nj2vn58+/va33piNZ7iCDGrBRcfpyYSSAanJsTzYd+I4TxR9UjfwsGj9KGE4/sa/f+lf//m//NnGEl9+jqNFW4FLhafwjS+/8c2vv7q9f/vB2d133sK3POSon3qTAeABQyfLRRfqOMqdIY8mPhPbyhe9dpeazVA0m3TZM1oDC5wEl39QFGR4bGCDndEHe/un5ycn5yelOYJmajtdGZepzRkV7seLqE1HE8e96DBQH/gCAjum+RBYE6eJdUNwjCE6xjiN1LC4yE2/xFaMuoC22k7ifcSNAAHkJhOtp/IFZlX2AyYT5nk9G92s9JFwNRFBcPel/KbiG0B9gSL9yxJhCE9IkVoKDJ41TeQ0i2/8o3Wm7UUCmj6kz9J6h//8p/+gi6llJHlRflXQnBYC9KpGiGFsFPC1alAki3GPG9PZ4o233n7l1jdv3rrOCUl4/3TCBaHtwLMBMozS4mUAwqWRdOxvXb/D+q7xguOolm+/8/a3v/Wt288dUBxHf/Hp3wm91ynrpTRAHhHLVwo7R7XGYwfavXS9+SF98PEhbJAODZZoi6iuubVJ6uj6utAZvO2YKRO0QL9QbpGYlDhVwMeW6SDyQyJ5C+2yE6uDKnO8J90tek5+4bl4W3QHMKvyDS+JZWqNBjvKXarIqIrQEbxociMJgPS5RZlFMjmYSBaFBEFIWFL5ZFr/ChIKYM18goEmQKsd0J0NJf3CTaude3zyeuJ3LfG5OYDHLpmH8kQRPWGZ5HDIOs6IANt2WvhtzRoH48swRmWAXOxpinbkNw0Fe3nhCuzKd+ftRE1wDeGj1leBYJuZmKFawF3bOjoErJnyxC2eC9VwIwIRsiYJ5qmB60u5SaYK4yCIyom4wYvxD1b34dpSvlVHrpGKELWRfx46iiGqc2Scw2F8fExlES3AQGYmQuwqQ00ZJIj0Qy1tCrXaSR1nt8gD7JJZTCITtZ4HShZgZgmKqCSEQLmp1tDARmQp16jkkhBCyA60XMBNIQFONnEMvVZe/sNpoKYGVXlscMWMQCDARX7Fx/pLyQEYqQKMUAiy9mgwqKZ0Pi0E4OilcEmD5WBkIH1J0zHwQSKbAN1yusHqBilISJCU6LJT560x2EhpYQyOG6MDTgaAEP00lmgxAkmsmFKCltCGO6QjKs0kPoaIOeYKwEKfdyFyT2tucYaF//6UZAVMWPjkVvJViRMsmIAz+3uvClZKBHRVxpN0JZep5LDy8HoCizDDVaQkCgCFw6untdBevOUzvOHOdvsNATMMH6bvbe/Jm4fynOxmSUnT9Zh9LNoGGsdrpMinMq+BvOtXtIQF/o63lZfoTcFboGpTVWIB6bsZ8xetXMdXVKi36wRPIMiOQEo5PKtlG6kBLrGFRbxcipGclBbSk931hfBtkhItSwn4Wy6fAKGGqD4pmXdLxLF5i7iluxfIxQpLVM6zny3Z/+LBqRqp4xg0lkkynEF4vAKNfNIRLThsK60C2k+tBmOVPWCBrIXCttqzsAie1mwyEalJybEMkGEFZRhBxcdxsSmk9toTTjqMpeOvNhYIpTRBFsrlK5DWzxViBIMbFiiYJAHgcUrE3AFJ7RqONr+x+FBhlBIHa0caeHX1JLaApouWsz7BH2QTGIuWMTJiTjzREszy5n25xnnVYiNVKRjLvc8TH+gJsF2RaZ+ZVctSlUZgucwie4gnDtvhClrPrEiQjBBbxxdAsdVmRpJ0OxPOeZ+C06BWZ+0p2Z20ocwU4dwxw4ugFuOE7dbSKAXRBAlLjBR44EpcebQ40xmYp5y5vkmxRlZwGDJS6bStLzy/9eN3/P3TU7wn6zoLxrXCFfedwWYnmga93vags9vd29oZrjgRaXv3yy/93vx1ubhcbU0Z1art0mms1a6orrUdu3iRAYYGbBv1ETv5/HKWugiD7bstGxOO5saDla/4AcuullqnhCY1m3aX26Ql4cVo+cu/8pudet+BUbZc9Fgd3K93htQYvu6ZCWo6G8iEL33CsJaHwDiVwPk/+h60PtPp2XLJB3SntcmHx5M748YuQ2udzuu16fOr5hscfH46fHT/IWtk2vcOz88n3UmdTbp7NlvZuMnhP+kv+r2uVrNPa0M94uNFnNBPQ0X/h9qJ/tJDdDeIrQ+T0OBiXxS1OOMbxkwO6NSpXc3llnMejRGbFlvNc1VkdrXR7CzGzDR5UD4CmLmVmcHQsf4oiyAYNEY+cKNmGo4wsv2iF8VENxuxs+6fngHHf+pdcHoMxcAJF6Fz4Wf69dNI1S5W2t+er6pq5E40mpbGkQYYvDASa/1E4fU9DKGFpsvFXmZdPkcZkgVzQlWi3mYvE8KEALAmHgOV3j6azvie+wQRLSTi+du0O0TOSUWM8sU4Cq5gJWYqaH5Lvck7AaAXZ2IX1Jf1U3ymJXMhdND4Slf3hEE/ZAHF2CEeUbfChAJZXtiHxwaunrtz68Mfff73v/Q1ATea33r5T37ir/4YJlHJzidM9XDWbH++9eDtB4vRXoutqyjq8mBROwYus34Zd2HxDIo8bdoR7ENUzJ49TkzaAiljY/mSHd+/8vQePN2xDIF8z2djVTzTX0x1ce/SW4YMzu53GysfF67xRTzwwqdChUjJGUQOomLpOdFVg08H1IN02Ag/BQUqYYOxClwg+tR8AkaHt9l1dQiMAKxYYu/gLwzltXSvwc2l84yIFw6bmEcKLuz3jhemHHxSRdAAhEgiMEABDIefDokDVQNKObjv0/nzw1VzvDhfDXuL+j1mAJZ8eX3BAldMdLvW4hBcKtFJbc4aNrSLNW/Thd++4EgtPPLSf2PPBkuEOKqBEGZgcsa/RwBNVnQx6Ezg7Xn2Dp1nKjvbKpBJ394lE85Ow/GBvgdUDqqHHzxgrtvvHpMG9j/SYZ1fVX8YcrNrCqXoM+QzZXgDrWanEPRJkmnQIto7zBKictcHzr16pC4ajlNr20276Qeq6ZKRiXCZNmcbNLrI+TMkoV5a+qGVgDjyYRsUj4DgI3ZTucJkvodD4q7f/+GkJoVmCwdUYZqY/7ObyooxYLCzsU4icjsSoCNBmpLByoUQLSEZtc/OWnCRAEzJyn/psQ+j/eACiBDQK4bMgQRMFItpHE9ZoAzmYgHgkt166z7QMlOhrQYCcIEiOZp2RwLbXU4mG3OyE2yzDwAoueAODNFgSIONIQwzoQkuLaYZ4JV1kVcsGQhobDhAJjNIf4wRdoYpJsVJ++IkBo/IlMRUJ1x8qTZvdNe1BvottPsoHZIgLe05XQBKsD7CzzqfljON3g27Q9EjeaMwFXYRKyf6wz395zAx+HirzvYpfnUJjaw2Cb7LA+3su69LwONJMhcBGrlkMTiJF5Y6eK9TlyQiHCaV9CLPvwSR0GxPRVepqvgCwhQB+j40JPxJpu/+RGI4lzSCkokbyIQGvIpeEDRdFV/wIOZSnOJQINB9if2bZyI3hJotJZfYCLGUR0DCAGRxXGSqUOSlgKgwXqdIIpOS+FKYrwYI3drDYWd+8V6PPDYSKPZEaSVDBMrplRd9RXI7PkPh0IUFo9ZThUAlUbRK+DuBrfWoKi1R8DBsJE9Bm2rHp2qSzZigSDr+o+OOWVFPqTpp92OwbL8plHYgiIqBqQVYkZQ3YXF5B1vv/JHFJ21V+A0kEid7qg6lFB5q8XT0SGetIr8WkH/4TCSy709dlxIYaOtGEwmWTuMZQrlhltAswELzYITRvoKGwL1EiXCRArBQxVPwuZPcskWb7gemiWEHhw/xNoECg7WBpMXtgdOYIb4qj4UGm8aEL0zx1eC0EDDO4hAH7XQGPXRfpI8mAENV8BQ9W1OQfM9VxFOCQUaySko5JJ8Fwb3gHXjvgfH/rwAQKKXDKocq0R0NfX1yfnFc641ZcD+9wF9p3H/j7I1v3/eAReZqkKEignEyX0XV8YUQHiQnCoMlLQwRnHzL2Bsei02AK6JRe5hPZWGgWjmQV94AmzqBB48rTHM+Q2wc40hnDJfLVthmVLZRCDCBksYvoqZwGYmQcT05vRt5U016D37jC5+7+/gXurUXG73XtjofajePtgbPnZ5dPHhnVO/tsUaAT3M1Loa2MBIvBLRAFYtIcARCrq05tR2FAgEmRrYGbJDmm7NtPr7Ex9GG4xGZ0J/JbHQxHOPJ4eLLUodlVfsaDhLat+hngYiyZ5U0riTF4NT6dWopasxmQ1tLVgfh16hgGA4r1hRW8DEnTjyxD804he02/CBP4YW5i1yEzX/U3W6SFsd3//lLAHTAZASkIKkI/DMu90ihUkee0XPwwG3SY4AKVswbysoHfFv7KLLN6i26ytTTNZE1zX6AaBDwwUEbfypyDj7FPpokqIIGUERnHZDfUi8gxFS6w64m5vMGIrV6+OidxZJxLtxZbZyTKPCaKSog4RoErtZQ9oEsixW3PvKh7/vGH7868xsODXtsDEksG3w3eUmPdrm8uBixkGQ0PGcGCiRXDP/XH2sTnGTRfrLWABx0aKCF+o8cFI2LrmdLnHgGtaEIi87QNyyyPzZjHRAlZeKMT6bgmmCKcVlYoAUcuwcrfEbE6hSDH4KmGtJRckIAl0xXdQVuYKqLh9mBbxSazqahCIYQ8JMHDPVwUhnZKEHpw8zwt3AYBvOBP8br2W3CI/xB/GYOp7lX7PfJBPygKTATegBl1dA5propbeZvre22Xgyp+Mm5E1XiuNXaTbszo/rRQZk3l3xrG3e/NmWVCplmS/YDwJzaajqbDlnEZjtAWfy3zKKoQGXWg4EjzAZJKVfyYArGIR/hpWIQgV7RYrJ+hE9n2eiyzd3eCJi12IVDRwcQ4kxhqpVAsC+kS73GD5diwHKFWtJW7DDGICDISuRIDDar6DlCF4TQ4ETcUPaFMGtniLrKQBHIlaLpPKI9lg8Smae3QpCdLR2WgFzpwLrthGOrTAWQimqx4tWargCQBgViOhWK1tdxdJOYynJViJIDPB2SYCUrS4Wpmctp/OhwQcRR5gZ73wUemuEjymuVYeeSXT50UdsDXPScM5ljaEUXPmjvycjiBVjrDIzqJuPIAmjcIbWr3uv2FnweEXUEJtpANmUIyi7iAS7IEjBjaEM5+VbYolSk2mYdwNIUvhBQ8pASDGAdC8usQ3r/rAKi0iFqYkCTaHEJz9wZQZ8VfoM9RoJ9bXITKKSUJPLwB/W+CtyyJTSg/LVAL35Mfekhb5dSlPfv+V7gFpiXM21CSABi8E0kgl72XohgRv2rcX1PtimwqqShAFqkIWfsJDtQJLC6W6VDj7DLU/VFYQKoGYwY8cs5GJcx+56e+Z5flRfIBS/efRCWHOc5VRtcDDRkI4mCS8mGqictYBgpMS89J0lIbVCMZi6/pgGIqUhhfh/5KQWkeuY9YWpASg1D/r+s/dezZ8uV54f9vD22fNU1uAAubGNgiO4ZYLxhcyL4oAiJipAeJFExIVEKSv+JXqV3PlCGUkgxE6JiZtg9TbJ7Bt1owzZoAA1zcW3Zc+r48/NGn8839+/Uqbr3dqMZ3Kdq//bOnblyrZUrV65c6Yg63zdm9gsKeLMwihcPaGgYJg5440TBB6TTJr82ua2sUScSlRqL/zgZ6MAUirGtX5QlUorOS6NoUWjxaBpTgSN5VB79ohRNuVjLAROY3xxCeSEtGgU9zIo3D+ST+AodLBWqK+BcIYDqoo6akREccIQtRRXFMSdNqNEoMWqlGjWFkGoPteUPnEsW6D8jQwiMoSbaIEoZqxFsfvIFNEC+DK9Sme3yyxD6/UBjwoSsMgg3qymwG/fr7lZ+BuWAAwHJBo3Wcz6zOLIoOCgCP740nLdKxMIrQaaLAabln2mDdx58keuZQ0zlx3uhYDi3InZTmgZoIE8AUnbTdXNMv97VEIyoI2kaNBqnJqvaWLDCqAIdmgQ0Js0Pvj37dqDAFap8uHalWKv3RPKZB/Q/l8Z0iCJErthKGH4N0rVHv/wPeRUckFJ4XE4zkKtrz5Zq/PCHH3AY6uT82YcfHvzkg1+cnJ6zpCPEoOhFImY9hMO8bSDUG5cKkDIGSxmCd9jHdjNs17KR2RzeC1fpM1PcI6PjFrVywQTZaOdqgYVHo8twhBNggNNqDNxLZtKlJa7VR1aXNecEgypFihBQuCR0TRsC5nNjIobrbUzO2uzu0eXkd35n0mq9x/z+bvtdTsjd2WsO2X6zjTexuRhf4kv9zO3PTG7OPvjwIfO20Zj0aoAOtmDIRA7sNhy3IOOEC7JYrfC29piuj5RMp9ZPqyXOWvyXlKKyWmNevg8TJCjjsZDHEkw2DIVJ+onxVHYa3WEPVcnA0kW3ub1cscih3+ktp6vOdHXcqO3GzdmN6dEHsssEaiP2Vp8vjjqtvVbjjLMOFmxUuhjoxXfCLmLs1FmyporK/Fi/sBcFR1WmrSzVhsrPkAmDE0UOJTacs7DUJ7zYQ7YQ8cV6SHanz4xd5z/hhaUSaVqgB5m7hbWs4UAObsTacZqKDj4tVmb5omOs9iJWAS7TXRQ5y726zDFBvJdAQ5Y7PrNFkqEnFDf72GistC8YmGEKCTv9MIhI+66RVWMN9060TTKipPiX/9gQ9ECWtekXvvq5N//8rfd/8cFycl6fsd9rnbPAUGCUHv+ns8ut9Q7WSL1zENNjZ7nYWqzPQRy+R+21NTmQcIwcrHlycB0L3mh4wtM5yyEynIK3mnZKLUfvb7E+RVaXa/qHKM1J7FEOmaJ20J2gAlLfWRerl3XF6Bm1Q51AjhwyYVePA7PUtdBAKFfYRBcCXvuoG4Ky09ih62AsdSWmMDKA0Iq4YxckFgoqiwEEV3jaUqhvAVhKQX5b8Pnxly8QaGV20QZ6nhn3lHqMfphBpuorovMyX9w6aSwv259hgj3im515zlkdVGtdUmtWyz3WC1GbV5ymh8/VbX/O5sv+vDmeLhh7xXIbLNcAGDYbF631dq151OC4Zc7Xq+3X2h+uFiyDob7vsQFufXVj1TherXfa/Y8aViiGC7bXjIA5ZHcxXwxWrUtGBmhqOCSaEQWkNz5++PRIL/XsjijbtYB5qacdxgfkUvWPmhA3NcUD+5BimEKvlmrlyWUUi8uISUn58rmoaTaZY5sgewVIkRypPSKmiWEi/hNHw6jymv+ZiBLukpSqAXPJgXCdiPQVGNwLJkYBKy+KCjCNJjvsUXUwsBmWYCdiZBbxo/eUAXbB0D/q4bgiLqHIj7qU0rOMKSvLk/9ILz4Tx8IdQdJ6Rmiozgi0pW0v3cE9StcDMsHL4UGadL4VaWOQ5hZCAVNIDCet90iH/CQOqptQ9stmZr8qgMTWQvlETeFPgwTSaIRBYDUft1ucmgImmkmr5jPA1pf3rGwpPLmv/UCSIC/D8cxROH5Br1iNIBZWhRAzK/+l1Nh0N3ig7dGsYoCUxQPZc6G+uCE3GljOVxfv4VFFi0gL4vqO/oZxQRLhj0LXVfIEXr19wsNVWqyM+34vO1J+PCanNySLcMw2zVoYbHh01qhfc4FfoIbJouOHzceXHxO/im0aoSR+kf58fuV2DdArXz79lTTBiBhJLg3V5YM8ToQSCgYRkIJ4Fa9EyAuxxNO7+ghglkgJ4F5VwZI62Uog0sot39LaWZ6El8hXnCIOAAwXum8yMwj5xnvSJDPeKiDUkoJKdC0HjaAV8ftQv1DH1H8AkLPaOHa8kK18AhAHW1TaxYogKyZYSS/xQh1fEpkPqo9CtRXAxwBLkVMr7Ekgzhqp5EuOeKIyp9Aao26QAIQ+kz/1YZgBMMlIVEu+VAs3CbU/gUY3MOywaic+GKsQQVEfk7yQlnRibHWATwWkUczHIC4lwBJhsSr0eI8mKL4C81EL0IrQfPESPggeNORNCs8fsUi2AiAgd8vCCm29j2YACpyFEWIQAEnom+jQ+JIXqgpVwIzNBOIjlGJzsp3GN0aFZkkCrolOl3Z3HPpBzKIhQuDoe2baJ8DRoDGPQALuFXSBm7yN+rGrIiKfKjzJIegZP/CTnGc58DEAfpT+T7tKok9O+mlpDCdFDAnLWPCyGzcJAvPbv/Nb3//eH7I33+iCySwd2tpisCn5/iHKmgE8UrQwspR5ICIU8Ee3T0jjl/qhfYrW10GETU85mEhe8JFLKASaPW9UKSIQxVYTuxlnIoO3BFJehQ0pYgb6EXdsaNshc+M/ap6dNpFUxqA7HvFlqwQKbBHCCBuCAKnrZbczxJfc729vD7fZMlIX7aQx7AyOL46gvdcZumaXFhqwuI+4u8MmpY+jt9ntkmNtPJlC++UFi0bpHdLcQQCVQoLyR82h1bfBJVqo42QzkIcz7q2E5XJj2Hv7cw8YcNrSP95btQE1mM6Ol7Xtg8mjn/wcMwhXMo0l59yyS+hyuzlgc9GdrXu9AfMBhqPp4Xg9fP/08TmrI3QqaPZDG2ho+fFqnUMZUTPsVfolvSwsOtbSFUZrIcm61DX5FNwllSaHkpbjpKM08JQPO20s1ZCHaY9pi9WLP50QdA9zH9kRqcdxB9BMvWbTGi5MVeObHTD5H5HI3eIql+FeL0Kq502AiQBj6aNVKBZ4/uTg0WQ27ndZNUGp0nFHN5lh0ZYFnIDRUppXlGpje7j7uc985qc/+nG3VT87PX34/nuf++qX6dbiOF+znyR1maJpMydNv+KydsrunMgL0DeGlAyBLZhEKVTqPkYSaoh0shO8oDHFLdG44pGHaE7gIQqRXO094ajCI1hUAGQ2RpcKzUAtGujEr5xXIkuPHTKKSFsg3AifRVXZ4zs5qEyNR4RKCAjLN+exrLCq8WGJoLGEqoRyia53/lujSoDpjCJqDEYgBIqRVbb4oQWhLQbjOQ2aUmmOGZi27+l5CvRf8M5T+hrHyxV7cDF+COFwxa+MrDAtzsNZMOk4dFyXMgtwZ+vFZNm8RJyYONVadxutEUdR0szRsWi1Zy3gcHYkSXnO7pxLziuhu7VgYejUFpFVvAu6e06EonmWDxE9dZcNpQGFncoUBHL5FKrlHWVruchmdZVzjDLyRqtK4co80tvCkow3mG8hu7ZYxsAk3vLkJ5hJoCx1RpJWNVa/mQgmhUSn1qbZ3NAtDFA74mebTjoAm5xhWcucfLTFNceXcd4jMs5oAiwGOr4BF1UgEk4DpEZQasbkB96JkhRaiLDWTVkdmErhWn5GKa06Vj+xKUNC5SbfFM9QECgSzSfAKVjURxkIlu5zQFefmP6DRxQyMYCG6Iu8Ee1o0CGlw8GMm8y6xWoxMSCgO9aAOBd8CUeKTaIIK6JiHGmnIIllFoA3e1KADb/kl3x98ovAZKMlLNMFGOyTh0mFbYkLhP9egZgv5f2le4l0/W6KT4t9LekG+iYqGb98CURhAM0gxddNnAo+4bSCAfTCW280413Bh9aK+gIf6suDNAdmiVpCkciwsEhbFREcJj5uElbBr/yUUYKX9gVKAmc48XCF0BUgcy/Ila/hujE3+Wx+k1EpcCoZkBiz8iFWnpEC2yJVCEtGKTWB+ZqST/0UFatrZDjiwevigTm0HivixAdOy/5c2sEiOIFhBpHw5MfmA5FjIMVAQfsvmWAKbDCs1IpgNTY83iSPQCUT9CRYoVr4yDPnHWJYU88s6SiJEls0RcNhNbJAVqcqiqAYDRYwiHh9APaOOURwQzC1u/xb4+egzVu3D8CWeilCVi/JCx22I4wggAsI4IABfT5SbxUPNHRsfiteMkaVUMvUqVDh1AFaNCGYRpWKqMAP2KCdISvi6o1QGYuokA5m0KrDm2fpJg07MT6vtTG1cTkkJ+/8J1urKFfKN3kRXEWxYAFSb53xmaaFVol30pB1sBJY4ORmdP228SjwwExrL+OAFDkRHW6wBbsTVoco+zmTzN0FCNPGeZBmwRUIjr2vptYWtT7c1T70AqB5+5R/5TkBL90oU76DMHcMryp1oBu0iQusF9+qwI8FlHDSJLOS9grCBtJf8VtwMJW8hAhElQvvCOTPTxlYxSGqzcxWfZR/xJhysSGpZIkGghI4slDtCyEeTnfO5GbInDpUshzgo1WsELrlwH5CnU0/kYqUhQotlFsjRsEEipi/i6cH3+oUh6VFzJG0mAr2XdksCAkrifCJgy5zgjWUwZkWMcDsYtv0Mct+acPbWG0tmdbd2eVwruWMaR7N5v0tkBpzqlen3mY4gOXP6+3hTuvRo1388fNLLJTLVqO1bODcZ9apLl5oaXaYscPUDzzObIA6cUsgpBqKUABUmNKzTw3h4AI7mUgyTbNlBwdmTI6NAmJsi+k/0/vbw1//4rfPH/4YI4l6xMiHyyqZj9TdPV4vPvjZo1mDyeldNjDd7tZ//atfe2vAgoNpu95tsgtKfYvewai+/1u/ePdPfr7cu925sb373tN3zy/7jLIwHx0X+col3YgofQ1wKJNDdrXA1iPaSNgYfZdaY+c4LK3EzLqtHaE0iDzm9WTOOCQlSDWhHWdBRGM8HZHs1vbeveFefTGeMdOgt/PO2dOj89nczZ0YSnN+CO5Pl45ocKh/+NPEUWtYk7y4mw9Ckder29WuVqATPVxrnqsxUR319cnp+PD5yZ07n01dHMMaegGUtfYGIMnEW+muIwo4K+Txd777Nx8+fP+dv/j55WRydHLx5VZ3vpx3WFfBiVKLMdaTozz2l/BK7vCvXr+wUjgKk3s2UrPQxRU8GIbV/KKXKPYgZ8aIohYKphOiC64OkfLMHbZW7VWaEASEiNqkCpDOXC6j+aopxQ95ERDGAVg1TXzUkh2hF/WX7AlmnxwmwYMXyYyo1GHHBXlwYfn0elyrbYu5nJGtNgrJReRIYe4i4YMwQR4sLR5Qp1ryIYtWpF/zEh98FDotw7y17xZZiy1nY692TTF7XfWLuMCZpGMqdhqjXWjDsqUlm69vMBS1rt9ad5GmLcKXiy+hbajJ9AGatS9D9Ayrlh75mm45rLplaSy+oCmHXOFrdi0KpbDLRKxOc4+mip4FW2LTXaVI6PohE7XlXYslpQaF1Ii8SjBPFY/lhJQrQvAFjaUL221kqLyZkSTFcsXWHBAmsEeqgtIfZdEr337lVwamEPHbwwH3FCI+DjN6RnHkwmIFglPMYSZ9IFscC95XVAwKFwlDYMA8K2h0trFYaMUMQEjELeJouQXI6jj045ypPgCkl0E7CxiSYUmQA0wVFgLJbsNAo0dsvxbmoJapM0QyZ/U6rXwDmOrtuwq+TTveDWLSX2OiLD2zY+SVNQD4G1UbSIdZoRlsGNIjdopaagEjhyzfPiRVA583qMENq5NE4yHgSGg2bmVQRe8lu0atbkEuWaNwIFg5kRf8l5sJ4VWxSt+Kau4H+MlP8AAtGU/mpdqkfIiUxOYJJCSA6G5NZyIuYfAN5+ADWFLvYAfyJsP86Fff82v0F9dL1m/5fnV/Eeva0xUMKlLJnRCuK/Cp/iLPvBs/FQKN4luiZSl0AeR7YiQCb9UVGoldpUnoi6+8BpDBJVT+XI+bBJvbhveb91/+N7kIt1x5DVUl30LDBodNrJd+iW2hCYNCp86WIhFZoCkK+RDTgneuElGVSSS/Ci83BakIgnGsu34od8s6VYU4yatkJFeUDOSMrM0TVFKtAE9qqwt5YwWacSIbHsSEgyCiErSMNCPRzkZHCaJfcH+4mJJ6oXIVlqUuvcHInrA6RYnVP63lLYE4AlJDSyrCq86vWNnQh0PApN7wUcbJv4ptQTps4ImqmuCSzjZKjEsj5xPpiCBW1G/JQ3cQzKw7BjDEwZsI6IXwGZ7LYcCoTfhM7HKzrPIMKPUsuEYDkICkBIKi/JFaESvp+AVawgkwieHk6EU4vlW1CdiZnthkz1+eQEgwiWuA/SX/iSHv5GQa4SQ6N9573c72KXOyaboasxW7UOuggy3SUoYRMfwklYkOMxYKE+6cIsGQAbDyIBWfeF0P9jnvJRA8fSikmfjFk29/xVUB+2uleQUkIEyeZgFaYbtkY8jrqMaBqw+IGCk/GjIfpZsSgtG69zD9LX6hpLIgE2E2cfRfa48hFBQYUmQqOq4UACaIM5id8UCmdB6U9JAD4ykFXpFvZBLIycpSJSYvkUmD7VfHbrJkFEsvns2SSmQFQUK0Na1DrBZj+I07IwFnp8/3bu5hYuizZW4fFCwavcHgc2/fHQzpFPQuRwejs/FiPmal8GLBjNnlaOy+/zqZ4YLSxk7/7G9tgLmSPxiEMxjIkglywUrkrKoKDAYhzzR9cqT1vLV8eJdZKMgasyD0nu4wtjSft2eTzu3hzeezC2RtPZl+5fW9b7+x32OOOjOU5iyupZ8Fx9qj5f7fvvX1N+rzne1Gr3XzUX/vL56Mz5uXx6P1dD0ZY9CqOkBFzFRCHloENo7daGNoIRaPEkwwYiWZkGEtViYIQT+Q/nLOkQbYHJhi2DFYJ5DEetXmXQbPsK3x3jbbjw+O2dhxNZ1i7ACcLVTa+BeAhZoEGtwoXEpuFlce4JR/r1x8ugpTuHgBkhwVL2SotrycXc45HI1NfgYD7fsVW/6zPWD8E8RHDBAOTFiEVlDMQl92u/37D17/8Bfvo8l+8Gd/8mvf/ZsNdhF1eyimIiAnrLWARj2YzfYZ/Q15VmEHRFUWtQH7DbHlkT6S+aAt+QCHC0HhmXgSNUIgoUSACuWZTKTD/wSHsPISY4zSQXYRYJCX0CTjBojcqRmItotBwIAQBS511jysjGAJ3HzgI3jCLGHy6MJHSkuuYzFLTvipKhb/axffCmDLzG+KMkip3NUG5phcFus5ZjqkQisOc015yFcD6BxBZ7AfK1OmplS6inBY4h/tIl4cneus2YHxoiDPAMtnGhpcU6SQg3RBYBC1DDyp1SBmbYKXZEuK0pMlU4SuiQMHmUdi8YvPmYyGpQvd4pfkwKPGVoJIuOyHY+iG6HsRBg+4oj+L/oXL3zF0eZWX6b2IPHmBq82I0JkDgJVMFDMikp/iWIpm4Bka6JWBA64KoNMXpRckHWEtrSh1SrXA0EmsCTlnpx3sNG/trdCBZpTBkZjpfD1lHyzGOR0XWeFoQFoyu5Z2ipzcDlO7BFSwMuwAA5N8bTXtP6EBpUDuUfepNnBVvwku+RVT03C60KVjGQDSBRJoBxmiHIpnOrPKA9njuLO4QBuaAW81YNa/ZZlU5qrYKI9ecAOKndFGz7XVkVTnsfEGVjHiQdu48pcchCvWsFQdwo8FU+wR4CrGcFrXo9RgK0CLaJo8IFIUoGBa7gTCAd6uIpiNCSADHgo/rBGs/41axbUu/nIX8D7tuoJRkHwR8/qHF4lLrOr9xUspPogp6U0bblwllDX5CBEMVUMGs2xfuUxV5epaAtxDjwOQsAL2Kn4V6+r92gNsY5TgBWbXPvGY8OBSIVOY6csVN6vs4PonZSMmSDg1s9QugVIyXi+QhUhLtgrgx3JUJIjEE58RfSMkLzmlMU0PzBQC45cIXBGeBPnmJewqvlJs3hIUHGgpyMe2gFdGEpDT+R1TBwUQINg8EWB2QwJOvtJBxuNObacqrqf3UTb15kO7u8YVC3u+YpV3GxSbmngobF78knjO5qQmGFEsiU0dhdJoNPTAY5QqURMitze8LwDMAvUTDcQ3kBWWiPOWZrDwmQrjZ9jJB2FZg2PyJ0MRA7j1BHWkSaHTBD2oUuQZA4kYwZF6TABQUCaCInNzJC9+rXvW66o8VO8hzUobfluC+S4hZEASY0hBqr0Z8mBOpCglLYSqDvMImrbpZggOaEKtw8QQGz402U/lotFmivZ6dLk6Ob7oDZgJYKvA7BB+SIL+0nJi6iInwHKavaap1lTyBYiebHLiScAi87ELhlSfQlpFZoICxa+LXQhY4/uUS58CZ7kn6Mo/WlCoMiy5+/WV65M/lFTetbnNETwowQsWkGTXTrt8TndaYaQSy5OwFAFaayx7UtmhhWeWSUwivERsjE2X2OVfSpF0YQHopHe3z/olLd1yQtvJhv2UBQAHzKNpMt8dVx3zVqWZ1hGWD0AII8CtOGpdfPCUMVhZ1kIGWcQSdS67SWNWoSN5IkF5jwag2JrNCwVo2WWiSrvd6nTabCo6nTS29/bv3L7T7zAVv3Pv9Tu46A4evrOazjH0nbzNFGVG9lnet5j3MAWGHGZZu7xkog4DAhDE0bxkoz1GM5jSKpyMTsDwUjQaXaaUMU2BJpu1DAThsFxMep3Fvf3G23uvd2fTQWvKYFO9dp5tsqhkTLI53t5v/o9+7cvff/Kjo2n/4uDR129/fjBtdhYdz6htnZBdvTlmOkev8Wi7dXF/yGQJzmT76EFrcffNncm6+fySw2afv3ewOl2cTOd7TK7giAOONUCY3QxjzSiKLa91NDWs/FyJjIWQkqO9l7fwXxEhmInGFAHNNDKBAcCEqHa/udvr7I7XZ8Ptvcvjn45xnXuaEu0UXGJKh/qbniRFYodD8zD2rwCToRKSOpPfF7cSXr1bxiKlnKmJEUNa/qdPnze++TXmINXWo35zB0XihApEpBIIxNJ+JLVeYPQHMToW429948s/+N7D84vzD9794Pnh8wdv3Q8fmIDBIVmLO5950Nvunl9ezhdDFld02M9KmwXHJNnSdri5k14CLVVeAYxlSo48QxrsMi86hSBDCJUFHSHjYp1En6kMNVLVYkRj2Ii6pGbF4MUPuXZreaakudsJiKnwNOOExoUOVsLRPFYnPkOu6pOLeR00RfSZRYJzubDglED+YxghqkzCR5exEJnVMobKJX5LVZKv8pg3Lj6Ykn8KemlXdFvRj2NiHJLNoJJqWtUNNXTll4ykMKGHOUv6rGUOCiPmersNek12ywlcajQAzQN9IPEsLcA3wIWxWjICazzdliLzUx2GMifECf50aDmpmCKbi0oNEdQ3ixxz0cJmJAiFhC5RoYG+HRGJsP1BFlFoFIZYGyDN8iLsSJMgD0QVTcckQEScSb4th3jkutwgQW4y2SwIgAta8PIj4JAP1NP8JtnXOW2XKOQHmyTMBOYRVOBcYYaU850Sch0RAgZKdpEQKYItL9QHE/14pCPgDCDLQi/C4hYrT2puM+UiLtQ4RQ9fYZlWBnUUXNj9yZaK/L2AabnNOYTkQ+eycr6s8VnULo50lmvr3fWCpdUMFrU4dxhHEOeiNBtDNnh1HflqG/uJvhsHnbAggW04Hduc1zstug+Mi9ovYQ8gp3W5Rhe32Z4SyDgtXh7mLKC6OE8TadIfhNZnMiGSw8w7MKcctDfAUe2EtmHEguNSkPT0oEAeKujGa/XDCjaThU5MJCpJpEBGE4VdlfyFEDqFT22zKHCLgKypyCnBUgxGsQS9dR5aOLI8YUSL/MD08j3hVVoTvDTzhXBSXb8bpbqq/YIYW7i6zKJcZuN1FVKApGZWMSj2Qg72PIxALsr/kkyUqjRVfH+CdSXZJfj6XQhGMtvqIZ+vkLge+ePPJbkJC5xrMQLy2nuihEa4WVIkx1BQ4GyCk8q6kYgVKkhtRNePmwcjlKToBtpUi7dUrJKRSSlvU3oRF/WavA0o/80ntasKyeeCnxkmlmYNgAIFCF7oBvLM18DnhtpwShvdVFWA1kA617Faic1aJhtLTCLqK6QSD4WufqFuos4USzQXP1ZMSYMIAJGCrGNXqFYSAHjbHBYK+Q21qrDarIoQQVQgvhtXAAHDi/QUISaWl8xA/4iLFyFmkyfZrcWPjkxEgKHfykAhDyBK3qBocpqseGTUzzZMzP9EbzFTAn7TxFkwCi7kgY+jFuQEtNRAWzA0AZUer6dKMFjJPy7p9TI+iJXCKNpZapQXba5NRQ63iF2RYDJzTFqDnZGMBS8TArVQKlayFVr1hXQbqz4r5LCQtrb7w52BGoMk7D6DcmHHPmxDFZzDofgLW5wVjB0g+wELnKvLR7P+S6/EJ90mUnkQlCEWXcjJ578EFJ+uQJSESfGJt5ciXsUglDzlVfkORDhro4ujF3vJJY+03xaudgjqW0GKuRsey0CviITNFPEpDpoX7DAKiH7VDHC054xuYwt12uzbXr936+Zn793qzZiRfzFp9ObN2UePzw6On7PXN5nj8kZmZHQ6F6JY6T8rGSWAfDIdgEZF2ysVJKWcmqi8gTh38LTjIm7UO5YT7m7tbO+zeA50XGjc7bLPENuHXByenM4OMRwf/eIHW1t7Uj5lBJZGB2fiYornf1Hr9fo4sy9Pxmfn51Q3Gx8Lr2gVWAITSlmkSCM3fIatdPat3VRZzlXGjg7+g63t//F3vnm/Pttvs+/pDEGG/Y52y2M2DKI97Pbqjd3GYHJa390evvngM7d2VovJUZtDgoiGUFJmCijnVgzbNaYDsRCZSXpdPPNtpimtm/3W9h6b2u4PRo39szHb8c0ni9bR5OjgdDVaTKjQJE+xeeO/2PsLYQaEbfG7shQblDDHcFgkrsLOPxp0Kj97wQ6GTP29GJ1NcSIu5u1+dzkb6QxezpnmBCRMFGcGa3+gJzRzqmySXV6qWyo2wC3uEuSLl0rgCkXFiyLmy3r2ox/+6d/61S/t7tymDNishB3iOVmqiZXoCCGWomk3+UhfDm1o7u3d/ua3v/n93/s+Vv3P3/3Z6597DZhFXzL/D3up2xlQ3K314+3OxRanLyv5lA98YKaC5qcCplcSI0y7kDmT7FtpM6A6MUOGCECYOzUHJ7h7n2JzEVUlTxlqvSGfZV8SdCHQYHDpNtdqPaylRaMzg8XQnYpkYVslrVTFdKYesPOMtqJqCJiUKSs7iKIh5XwZF3s6e1x/M4kRyzZbjrZVzDIGjYzgyVxxD39940v4zxOvJVYUZyKmBEHdZgi5B7pdH4xHbMg66+L1gizY9Z/+mWtoLG8aBXqEfNEWJymJyJ8lQUz5YGEJi6n1/komafmquNBWYv6uW2y6a3eC/hSlySF5kSnLg4ha6WoqVQUPwUbUeebNWSsGgbV1hkczLsoNDuDbt94Cg6gUKp+lyLiO6BEMF+m60AVwHEIG8d9ujVH5UzbJQiSyekyRI4r8sF4QiF0unA5bgbkIGHg0dNxJReqqEMxfYMLESbjilBAbUcgXXTgBeKbbKT12JOGOaaVMOaSX5GoKbGZkEabQKiNpLIXwvAhEgOE9OldAotcjouQFhbCGQ7ZQAPgkLBztdCEDEe8E7OekDc52Bh58cZl7m/XorfTtaPUpPIpGFFQTodneFsmmU9QxFR/+oToZSGNvHtoTmWLlIbJlKgYwChaBP1s3hBtUl3DSrhxsrdhhHOICh7Q4YkCfki2J0w7oKrJDmLSQZ2KI5Ap8Y/KJdkJlyf8oPXiK4YQuCiQjyxojGg32Gt2kpdDLU0G5PH/avUok1p9wXX3120svVQCpCE5afwsQnkpcuBWhsgNQghQayU0SP790WU5wkt1SqZAoOFqGRxXjjXktdrW/acnvJRif/nIt+auRKjgiJsZMTNusd9582WQughVRzMgHxZwBnFgUSUcsmfePGOsfoBCJUiyAlFFYRImu2TOVtM0nAHuBVvWE78bc6y9OFwa8bDDj/JlILElgznngt1yGl+adrwhfxMnHCA2OBIahF6tOp9HcNmUFFLQj58EwsvQ2zRFh1BMrDevzW5wuVO93L3CUMXtPDCBBnKnKYmdSH/j1TeVCmKN6RHP6HpVezwgfHUuw0zxnUwovU5gHagi6aBLmt9U3nWcGSjtd/1vkvm4+w25XHYgU6bDIQyO4k3p5z1bPcRIUFhniIXAosja/53ho80Ny6XTdE51WyHqlvsS/5HxFp9BY261FWmmQPrtNnV57jp01UbTVcsLFqQu6xg0HvFkfxZQItqdUapkflqhCfAH9FIY8D8w88MXkRveemwyzCQoZ3JI7BAMZrSpYyafNmKxXEw3edf3LX/vy3/iVr1+cnVDgMBc4FB9xZCz4pHT+5M//1C3sagPZTEjKDcwDT+x9eOWSzX7gX4EVXK5FKh/KmcFGDtXXvr94bJ4ETMklVU3SKbWdYJCIV/OnXyT7+FPBSArASXDMH7Oxkr0o+umUqdVbDsfj5UF8CbJk8ceAH94IKTap4TzhJ9PvS4CWyXra77R3t9f99vDW/tbOEEf76uh0+cOf/vE3vvArX/viF5rHT5fjwbTbPVrPx9P1s6MPMnqNLwh/8yW77KxqbO7RbeMiZDEA0yJrPdZp4OhKM0cjTgtIj8HGz8zBWKHBMtFvBn4GlAaBLl5z/eDBg7u3dvGK0kaRltpBZwRTz2Ta263+oHvv3mfv3G7v79+r9aYXJ9PD50++973vPXx4zIgAfv/xhGnuuq7wR9KaAxtp4ERn9VLjlCxhX3oHRco0CGimZvMpVYRnRzOwgSazz7zxua/sbe1zDML6oLfor5anOAlqjYv1knMP8FEPmy1W0m5t7y/399psfzI9Zjbzdn3eaXYOOOnY7arY+1LbslPvTDvrfsvN3aVMw2vR7qx2GrUTXHT1renZbMlBuVjrM7Yc6g5m84vpxWSJUWuvV+7Ulugu3s4U8I1EWgeNANIYc5S4ZpY1Bl55TgK6jHptmbd0uOIMdPfPi4sLiFUiljt8rNcuKAX/AWgxVFiaZ+aAlAr+DGiRnty9pXpUb360KE3Av4JakW4VG4xtNnrHx+f/7b/5o3/y6/90MBj2+zdYvKGW6j2ku7We31c6I8iixP+ggtmDQvry127+8Z+dTKarP/6jP/3Od/82/XnOnsNnSdFyEvhscjG6OOm1h43L/WHnrI+mnd3NTi9PkJ453EPuEHKHOEANA5aGilGRG6LMtCxmNiCJLjnQGb9cdzmvWi+Hbli0joMUcFNRarL5PR+YAVJvc4AVZwiwlHq1RQWjjztlw5VFy24A+8nSgrBLgYUyJj/XwxR1TtHQ10DTkzPEztlXEzMZjQUtdgkK97D3QGndbS17+H2RT0owR2WlpMMeSnbHyOoN2wA7D8Uq4nwMJKVxQkuA0FHwdL4p37i7sM5uInS1znMs/DYH8XUXtXkXk03NQDhFR7swxwNNbwQkKFIvwiUIMlkowsQVQqAJMvjTtMNdsCB+i4UdqhaqEinxFtF/hyirt+2fckEBIPn+8MY/v+hsAqQTE2GSfLLZQI1Ahn/gYgqzilntgnwDWDsHZ5pdzhL2otmAjwB3mQdNDklNJPcKVGkwjLIGNVCwF+ZHdJTxshNgnXOLsfuJamSmS1FUFA38swg10/CXlF4BsaAFjwNecVluocIzPPrIJWTQFeHoDzQKm59iecgUSordGqEpugjSwke7Bcw4wFnXOtT2t+9ALAobkLyiKMAQwXnTHoZU8cd+CdrG7Fm7qmU6IqYBolTvU+xzRl/c0aurR0gZLr1OG2gm/nFHD1BsZKGe006DpagCG1zYbreB/aPAjl9y47IM8QDKW57pbxiP5Sv2qSALQPIagihDsFNm5C+rLgm1IMVb+xZWYg0QE/4qEjCREVCF3zxUicSlJ8UD0IEhgoEG6aWgzcrLHGSm93IZlFO2kL6H+VR92Py8En8T/MpvtY9QoOVTSZbHkl2VYxXDNzmgaIVSy0cS6VDRFfPrBsekMNImrIIkGcSR4E1I8PctkEMucRKa35dvsrlC58WHgAqEF2HVU4kLkrxXzy8y3rD01aQb3KrfKkGSe/PdJNac8INfJKTkYEWkILNFF3o1KplXM6/gmNRjJviKHizMJG1AlrSbuLLv5cvsVT0woRJAgVVTDlK7U+Vombs9tpZFAEFMzKhDGpay10KKziElQbrRCXT2H2dZM+jvGCXxVEL+oqZCT268FYkURcSXWFE9hhMCR0yZB3jedjYCrlYUJaE6V8IzELFzQHzSwEYhKypWQllJGJwXdS0XQv3AW7SeqaxFckoeCMPPqmfOn2m3Pe6bGmnLh+KDQhU2ifXPQCN/WBc4MQhnYw2qqaNvLKCUUWhMqigOMII0METFjEBSDgbfBFmzwZAIPME/koB78XaEZ6o0HiBDOiRPEnhUw/CsQsGlrOKRPWhNUhgf8DCEcJ/Z96XJ6bbrC0YkpmzpPjrH/4tLK/E8pInk+CHojKLcsQDj/rdXFmaCgRH5J//9F65K1ebafHvpffOy+YUFPEJgCOYnYF8BUyInMEDNK0n8QDCBn3SVuJ/wJUJRUgFpvXrzjbe+/WvffvzR++/+4sPnR4czTHkYV2VB4aHEu74WDLgjhRQYtgGKG5cSQ6md+qDd+fz9N966+8b+brNb38JqsbPUmR/22U7vcnx6ePB45xbzUFrNybh5enl2eHDCZID5lPVti63BgJYHE2C712GrxtUE/8/CrapiUNEU00Wx+WeNK2KnwCBiEuZdMkGO9tO2CYIQLiunBe/8dQoIyfBAYX/ry8mUyotS5ROLQp8dHi9rRxOc151Zv73Ntp6PD589P+M4UNxaGisWDOmsqIppLtvcSAK5wxX+xIYaQO6E4BojLxu6GrOl24PtVm3KIWTvtnduDvps2sfYOYYdA0rT+rq/aI2YWsjA2NlodFrbaa62nx7SSeis2juTxZo9jWh418s2W2jQ5ukg1rJYdltdK6X5aR7hFGHm0ZzJ2Y0e0TnkDvFnaTsnW9N/YOEdY4/BPHhuZEbSCC384wenNpx0oRvUOX9DIwUSoYUi90C9xHcOt/5U5+Hg8Rtjr2J3sNU83bNwA0uyqNCUUXKwsOQSuVk0ucIsXksZEpToRZwJ9Y20gOLiWfXiPJnV7/3h958eP//G1798+9bdrX7zrTffAj3ckNpMGyBJjCjoQYFlFOWdO3dv377z9OnDx48fvff+L7781a8s2Io92gC5GrQHZ+vxYsGUgGe9+oCJ6qge6FVg9O2DJjaKk6cBhwhaUbWJVSwYGhgsxHJ2A8aDO/ngcOWIcfamT7eo2Hy2FayBARjsYkIVnnlYgGjSb9BCx+RCyu0wkCEFTbHmD+WJ30QTV3w0mmxiLAEbJGCr7eK2sNsGGsR3XyZRxfNLBsq9rIFDWmxSJRWWvOGJ6d2yIcRCIgKQ/MajeBJgAkNyER3ZMzrR6BymNTF9iYErmvrCa2mHSynbhqnUNYYBpmVJHDQ20KEsWEqyK9+cK24A0mfehApceVDlky+NaHngQ+Jg6Ka60ihaIF6UEqYvzx6EILcw8SnR4pcDAnwFknSp7QRP4dg42e8K0WmbeArVqhgp5hbYpPGDyQsMmBXsrDYghXkL70Ve6kI0pefKldLTKDmRHiZMp0wEstVykN+p9gBA/ZGD+zLghgB/N/k2I/VPnDMyg1xEA14pMBIUZNM0Eh4ydBkipbw5LBQxTs1SshmqxFgCOV/c4pANslR5DVBivh+aVSObP7oi+gAAYibEhdjIo0MGQYzAlFS4AgEghsVPHKWUuFoLEiYmFqU7ClKIcjv8zEeYYomBD7RGesxMxWQSfkiu7AUnY1alAPGAJk3FbxwOfg0DkilgZYa486edE94Qo8Qysi/8ysG8vXxL2NUH8w2QgAyUl6O/9HaVLKEvv1WZFngCymfRKo+6YUrwtXTls19eXEU4iNp6JBR2zhY0+/PwUlG0Sbb5fZEYaoxX+FGCN5Gust0EBMPNi7/plZIapx217bH50pCQztyJUMBewTFOyYK7oVVMkMwfBUyi+X3g4EXO15KLxbNuQ11hvQnN6/qVvZKMYGBJlWil8EXV0k1Fup7MZ4q0XMRRkvLiPdlSR5A8Zs1xVh4GCpWbgUwMU4wl1HUAI4KCR9bRYjy6rKboXCCjCZZs0sHGH1orrDPS86qy0ui8ooj+Ny+r2sjGj6zhBzXH6ise6HxdYeob7AEaEjCKpYtBo9mBsU3L8JSvrmojb7UOQB6TDh8N9VzWWpmit4jsYIGWbr32kbDZgkjlA3tJSpZsU/DB3DM3bBFxZvCZ3cRYEUklxufE/FqoLUfDUFnN0bmcqJiHqAmbV//LHWpbeu44BaCaurjMuRYrduAG2zDYfAWhMgt93iHRxP5LfZYVSrOiQo4JVgPmn/wixKVOagm+p/WwXSYxDFPj28RQFu1Fp499j18EzxzamTaYadPY/aSDTEuOiYrujOzBPU6tJEMZL5b4lkqRi7i5EpgHKch7+WVbfUuweQrYJM3XEGn6KnbiLnd9a50WMAJM3Dr+Zh700vFr7aAB8AaNCfeZSwb4E1yIsmugpygU5HwLluV7hTZfYeddTKNbu6vFTWykH/z5n/7sJx/SX2WEyaTkgsOOrcRlduYiInfIO/ulYGM0Lvf2el99643Xtm5ssRM44+dYt+PZdH6B6V1fH7e6dKBacHHcWr/z0dGT4ersor1uP13Xu3u3Orfv3aINZqLVrZ3e9vC1vRvD29s3MW0b6/7h+OHDp88un09Y/HZwvtjd3zu6uPjgfc6Bov+ojBd6wlIKl18CIUYHmQaExkGLnkxpEzDkEVbPbrIuYfrTAE2xmY6O6h8+fAcznUmsC9YBTNmZZ0pjSZmDFYyl2D25AkOheea8Fi/6MOdWosAOGgoF5Vs596iHafSRPswvdyRqbzOgsLP3xfPz+cFi9uTy2eVienrWnTfOlowO1E9by53m+vj8rHa8unw6mvV6zX6j/X/9/V/cHz64c2PWndxvdR/XGq91+6fd1d1e/5R905n+363jh2DsBWcE06667EHEsMNFY34wXx+cHN/YvjdvnY8WHMLEvkyczKQOUQa5Guf6Iq0dUJS6xkeZ2LGu4cbjjWOYCbLJJCVdKZUE4z0MFEHPnN4EvRBn3MC3KD9gOi6vNlktt5XJxrmqBxnif+PMuxJexgEM90sRxs09AeUmAHPOmw8ijJpigSZtR+vdDz5674MPBr3Bg7s3/pN/9s+Gvc8gd+hh8MQG9EdigUD504OluLUGPvO5195/ZzKdj/7wez/44ttfw9kMligziq5Vv8NCn1n91mJ5r1U/1lfR+gi86nP3CuXEW4454sxsmzmPoCIDiau3jxiulgtMYcnkNBzNMrlxIO+ckkRTwFyhegetSYWosYoDZZXzJWoXHTqBnnvHkshTxHO93KJmwViAex6GLkyGC1C8AFWNyjLKCKJYWppsCNd3akcZAcQuJK1rsuCYPZYUhrXVpcByFLPOLlH4aplSLgVsUspnWYepd2YkNRoBspz8AarOl7HPCcFUZBhIlQrithdw3qhGoDaifSXJbOMGo5WgVogD9QYwopPIKNmiS+3DeNlsAYgmyjaUiwpbBZGLvA76xLNyW6+dfurYRfQzk6bAkx4WGCi+gLDdsSEwgY5hKROIDVL7ADzNxeaSwUYYT1vgAEQu64MowROiWwjWiBDLs+Qmgm2g9MgnCUTKNQLSK+PdsjeqMBwGgnj5i3EMODQVHGHIhP6zAZQbCEEd8WhZAWiR4dogWXosocluV0UDGNjPgfrH2Oh8BUORDBfBJSjCTc5XhtXAgf3whwbkoXxZPSAC04fglicJ4EsIYcgsobXlAwheYVFAbAaX6ovXaAvXdWa3I/l2lKmZjGxEtZKST8kb+Fom8IFSTIOr5yIlCBciXBrzfMpzuBeh0NLBtSEPLG5Kx6UOxEKPpVIoGIxJEc9RMuojxSFrYWqKprG8D+BG55lfBWDxBX4pTeUa+CBhzqqsIhq+p2CY6lDm7vP6l1xiKyn5yf0vvb04RbgkIXKVnTLlc7ITuZIvRFGo3N0uo5RiilxKwbyK/1KeiqfGEN9kSWIaIRlVIAg0jxcfCwSBem1+y1sVUhDipTwE2xcR8pRcS4wKxFWiV2K+9CoexJccgEu7zCDMB2MqqJt881tYVXi0QScRK9xfxBZC2Ek0dCRqOSFENgfTFFZXUIJHRWF+yMNskCorSGEfbAUUPWTcN8ihWKJhUo9igIuvpkBJpRGE99K6kW668ZVo3XG4BvU/qQwIEyEVIfqbOsWF6AJbLRaGBN+kNrYSTUtBWpwZTKhk/h2n61nBiO+sdZ7sWfDV6mm2qgTA6rbHomPPBBQIyKjRyLzM6qFa8VUtEa2kIxOliG6ikXRFV61bY8P8xWg8nrvihwpKQ8lCH/Kib8AhLCzq1Ggmc7CTZC0ndBrzQWUyw7zihQXF12huyaJ5KiQSQ2ZY9rDbBkchFnVQtYUKE7xDirEUdUkzFol5yK+mDXSFQYAxrQBIGNOw5IE1Ab8YkalNpsvJ+AzrH9cLiUjhiGRRgzCIwWMmctOUWFLJjtzNFYiEBMvyVNAzo+qqYhinwmDzRdZfuxJRYC+ugC70vIgrpYmWoKsEvKVwTV0o3TAiASXYe64qmfhzISRMofDgUgxenLkctLThmA25S89lINPziG+ZKJqwQVFBOjEFmX8yrc0uWK43ZowLvnkQap1DGtX2q8b55WRZ7374/OD50ZNWa97sbPcG68+9/dm//avf7XQuH37wdI5TdDVuNrvTxeW7718w3tBsDFb91cnl6ORsfHkxOZ9Mnx0fXYwpG5oTWvqgAELKQIjwXgjH6LYyaoHrzMKSpwCxUBEDxJouU1VuCAcJJlP2DGXutzOEiNDp2HrRG4ApSxwX9S4tnOaNF+ebKm/pKpP0SmSTtRGCiygxQ0anKyiwhT+WAQ1pd7t72Z33GGmarX92ePbjo/dOx4Naj47EzXZ30a6PWs3RvN5lBshs0G30kPX22eLy4fhw8uTn64tb89qH6/X9/a2z3dbdG4PlN9/44vawuZishxpBlEO92+5e1Ld+9ujRj04OZo3e2eVh/eyk3anjwpuxp5NMg0BMDS2qDe5wTQ1mwfKRJw4bprFc9lLuEbQYHcgI43a8+6dDEFONARNKjHkCVI4uIyk24+ACV1SzVnwil9JR9q+ukh1xrbKWJBnnXp6vv4pa+ZqnYGlFslnnhy4qZXd48vzx84PP7z9ASbkyklIO4EQsRVIloL5/+Utf/YPfeYgw/Ownf3Zy9E93bw8pHeo7kxnGHFG7bs/qj7QbmPiE0DC5ptmasyKRrTTtQC05mJotWdjGUpOuwflqqLAVm0LF3QB/sB3Zb3Y14ZRhDLGIJwyGMzBAq1xfCwoTTk016X2DaiQWfrMnLaKHpGhF0+wbAb0JnVFIdgd4tKD0V5hQhiGbmocOaOWL9TWx+DFXY4ht0Vi8pAQJ9oPcKVGI6h+lHI0qA6tPAMNf7cG+ZK9uBDXgWSzcOM0JhmPRalNqmwo0rViVg1iZVwrCzMnFIkI6LH3pMYJNErhxmTPhhvqjVQlUsuNN683YfhEOUH3Kr2mFRVtCiUIYYoAeCM+Ux2BsZFtiPlC/tdH5J39VDhJs18Di8n9yMbfkYqYk9a1gljtvBopUEONHzI1CzvJWKDrfnS2UAvU4RNAkdwoRX4ZxzNpiIyx42KlzYioNeKqSQB1XJ4b/Ntkp6akLGvTF52D1s40Tf3Q1kSFNTAgnHbUdq51grZIgSiSabiMUNis+Ya4c9DGKURbBwgwesCgO5c4iaVxgQIKH0bXIqn1vqOG/oxNlsaIFj0DrxCuzBhzpImrSiprUhyIZL+e8DJCi4AQZvACVwgEa8Zi6pKyReTGr7DQFhmEkp1jByR4/H0jEM79iS0CJYkxDje5lHvktopqwFzdTv3hLvJdfP+kt8F76sMnEwJdBvvhyPRW4JD2urFDAS7CXqkKvn1/BjICQRTDpOYlDVnsVWFVsfl4CUiJUHxO93GDXJiUPVaprIcaqQhuTazkUSBkNMApXCSnP1++KgFf1A2EpGF9ZvPQ03yj5/Fp4hRMFGqFVcUY0BFJRm5LnPaziR31QUnI3zYtyNgqXATxl/cCa8ZNNfD74lfpELSgIMPWNHjC6uWh39QhCjkqicRVYlZEJrTm0H/bx6QozrXNxn7HZRkPfEl8JNDboqC9sMgx3S0orren9MeYLfPKi3rCiyr3EhD7sGNojKgMNnEZQFACxjFqUMlB81bopcFV02mi6yNAxPptrssBc0FVhCn0WqCx8oS73xzRmG238flBWxUeJAJezWHBosV/Zwj4PXQjqverRT9kzEvDEXLKNYosNxSC8wUgO8Gh1pIZbaAURIIc0qWPMH3UFquiQHXBrNM7QcDCL9kpUCwdNmf+GkEpDxwBeaHxFQsVBeYQiOEfui8nkjKLD1etMjClzsd1eEBaAZVijwZR1wHhA2doFL5qwhUryZGNWlp+CmYwTxUj8N28999DC50RI+iDlNy9jloCyEsBXA0oJ+dw8CSAfCz3i99Ll91B3LfRT1wMUXIlPHvrJ3LCdSTqL8XAwPL94slxeKEGIqaoW7IoWVjhSRiYUjfoZrGSyw3JSm52j+jml9RKLmelhyzkDBbizODl3MbrA/Vjb29n68dHBtDtt1G6s6G5Npt///b/4vd/748aCKSpIFMYTVlSHWuU4DKduIyNuFtRhk5wm29F4WBuLAcw1XMU4UrfEoCcQ9oKV5ZZuG1LGZGIqLI0Na/LKNFDnb4CuUehgWz+62P1YslNWrq13Oqxt4SgivLGMS7EpBxAVzBFVVGOLmdtIMwdj2ZFtMLBAz2dGi2b1sSzkkwjBMyWe08fq82m7Md2u7dzorh7cef1zf+Nz7/35zz8/2L633fq1+8N7W197Mn44nu8t60+Xs3uLzslitTfrP59MdqbLJ73lvU7vg+3W3fats9rkm70bH44n356sDpqLt4b9xaB1Y0Q/qz0YM2OqOZ6PGt3eBdP0J60aB6g+PGMvdCbp3YCtuKodjFCUYRzlyA9cgodwG62FSQF5VIjEIJwdPiGItTHS0oeYSDMhNvMYTFZVKhKaDqDeGSzQcpLZtu/kA9eISLXSuxc43K0ccgeZ5GsevVeXhWdUIpUEPiXFJga/QVJsjbrcA+l57Rzz6Pxs8jv/ze994e3/ec/NQEcUDDKUCWMk0TMBphY0WDcvb97ZefPt5nu/OByfrz/84Od7t/49DAsy7/V7u3fPDxaPh/W3G/X7HUbhkAFS4tVntxuWADS26W8sF/uIHznbs8SbgZWOCaelMWvQa1LSGaDAed+ttej0eghDo8bGPuzgjijqVw0nWEXQi+anPhGCLmbWNV0/IqPY8NdsayFqp3JQAeKE7xetScHp69ePRIMCEzAWIRHFj1TTXbCbyoCGulP5Z1m4Cz2JgawgwdpccNUyUhTC71IWMoD/fLLjwQsFB5MhhnBS6umHAfoIyJTCSo72JDEFKRk9QcGGsoH3aE6WN7BVC5vKgyE5UWrBlXbEEmE+m4PJZE70oGCqpOUr/i8TmBKJkj98MkuoyHIgXEtwEgUt6bBHNPUMo4LYi4oE9M/I3TGrSCN3/PrWU+hOZCiVJ3IPlszvQCar47xTzyUHJsgGwMss2eNLxTM9aPmYgGQBO3MlkrmUh0DRD2cPRyggodvNo1AoR6uSVkXyyKMMX85uFcPXFK1nfIRMegOInPh6JWOLzNS2gkGdr7KXFxEntqUi6sGbZ/wbSS2vM3GACZIPqMuMDgIsImECqxgzzlJMAmk9CTmgTkaUA1bZIRY9SWwa7NjqMENYKRCiMDVAxG1BeDAOGpGHdMLwv1CuYg0OkiVj7FqinGW2joagDCI88IG7uU4RjASFsqgWI4MDNSYaOFyROcRcNw+MB6+FJvTa7L6MKPv9AziBJpEKMPLM9ezwY3zCE+qXciWmj3m4eishxDXVJ91L6s29OsWL1wK+pPKNctPyBNNW5s4UwClIJ7RnUqAZSElJ60OFRxWwyWUDvbzL1Cpk81tFfJG6eqp+XsBJVgV6+bZB+FoUH0uUj6HxibFeCczrq2DznlLbxA4VJRrklAeLlisv3qSz4FJ98bUqMTgokwumilspSMIqgTNt+U9WSVegC3UDN9xH/PmiRxBdhY6h4iRjtUKk1U6rZWNl5I77lDdrgK0F7qPVvIeZY7MTq1dAkdpkWojwayndgkrB3OIOUhVKTgO1BkQDkpuyHjVKLFQgujWYUw/BBOjCNDN+SchlfZIVAGBoH30tMTRiRWHzXSpQzU6F9phVNlFh1m/qt/NwHV0wDxcsuQmdkdk8EUWF/zddBicCZa6PI5KODziVmU0H+GGfsNL3sUygAjUKKTKD/7IPevwFHyiRhaWFozSMTCoygyMiQJwk4uZVXmgSmblioYtX+RLoEB1UjchJipitizX7iDNFhVOPoA6y3ckCdYUWhEoWxY6ZR+LGahh/BJbS8cGSI7rF4/XSXbr8I5uXsHsR0adcV9gJwci5rh42AWRAmGTLgVevktRvgSKLPu1KpOQEa5B/4C7YAx83FRN3uu2tXm+7tjqmsKRPIAGGnPkCQwpdNEsIjCXDMVvtHWZ1rUYKe4clSxjLGEHMoWf54GyK97lxcnx6e3iDYz2XzGr3OMrpirlB7NyS/hXsVUbXbMjoYk1L1jmpFIEOUAcfGPw159AmR4MF+CHnhS0WQmGZd5oF4lrnNGn4VHyTkst/MiUCXdEFR1fR/LVbM/rkTPrCGKBny6Z2Gj8coEo9od+qFAIMy25/b8tZLxzLNRycT85O2a8f7ytiqFSQnVUx5dNk2txXP/v5X/vW6/OD2vTk2f7NO63Ly7ffurm3aOwNb9xY735+Z2ew+3ZzdnPZOMKsnDSfT5Z7084Js7Bq8w+X49u9/aP15a1W9+h2483p8v2T6f548pTRikV71u5tn2J43hy2OQBqfco6oNH4GeclHU8WHxyfM8mJds+hxeLjs+BgAHhRHVKGtJmWHc/QZiXimYuvKyer8IGzY2MP2FsgQB7wK/sskugPdhiFi1hW2Eu4AmWqESrp4Ic8A7MU1SaH5JM8ErK5gSFXbhUEQ0qBVnE2LyCjySHmlqz9jqPz48l8NNzabq06DIbaBSs1oVQHS8YCghC2Hbxx6/bD99+fLObf/94ffPkbv2JNX7pmrD/Y7w3Puu3ny8YxGwdp2VMlGHJadoZrVEOb6SEUPv7/VdPRMHp46IdWY97ESreRxhLRDGKE1LO67GTq3HEzJSVElwsR1LpMqONMNzoplX4jE/jI4hjmUrCFC95VBlvjcscqsIJidCFpyq5lCjTsW+AIPT4ahtsg2oqjq1VGwnz0udqZmwD4YvH5UT4X5noPlODJG7+Q4AGzJAQDJQIdyCS8kXSbFv0PAPLDZWDnHF0pWjYFoY1f2gMqLwjwByS9DEyYpKIID1MdTjLciBXMK1wh1EyUF0xCOkOMs2WXGroXyK7tKLpWO5cEGO5MjIG3hArAZldhhT1wmlXX2YKJmCxTUQaJSfsA9fTLpEfeWBts7HSp82xJwTr7O+EGoBNN61aOyK88kSEXcc3XqlCEykpCQkILd1UX4KUy0PgFqP/lOX+oFBCn5wxPrIMkLe2XMEXMUqbRJS0eB8uBdtYA2CCPgkKimZR3GVGB5yPMYA5PiQQ+lj4wVGT4+CxdUhisMhdhRQYQNtBFEMgIaBQc1AEuqYxkViZOdGwEs7QTamFbOOQsREkDvNHBhIfkZz6wIvGy+Bs0iUds8k0cWJ1HGeKTvBVFIVQ8lJPB3VyIozwD0R6EHwgSO/ESJvXPLibkEAT9hcmJY7xCrOmMe/169f36Nwm6fonIp11/KZwKV+NYCBUSQpNqf/nvQ3jkuyPX/Lx8XQ/Z5BfmJFoVoroWbCAWuNWd5o65X/gmHlb5EcdiTE7VzwaSq875wDxIfxJ67bbJ3C9Xz9e+57F8+FhaUuRLPvBE//iuAe7hU+VUye0VQGNtyq48yzavKv9CrKfQwTn24/cDrLyedxVz8Zpf3PfGyiMIViYQVYa9qC4VitGjRXcgew7UFtFT6Jwm6lUQsdz4j9ShWAgS8np2B/OfHYKtbzNxIY61k7iks46oSSoAFVuSFPhVMJmaisRCVkdEn6BcZWKghAprj1CNoxFr9rzGyE5uBEUfunyT0IgIkVKj8hN8xEWNBJZCx+1EA4SbnOmnaHxa3rt8Xq2fwy/NRajBAbxmXzC+ky85wSE2rNAZEHFGJ+RMIqCrt8FO7qhCpEOjLRyI7hB76CCqetamAf64Ew6xaKHSboTFpBacH3KFM/X5XUcOVpe04FW4aoUc1RuoBAvHmZkT0KNR4/iYjge+2t+h6LQhaH74NMdEpe2DgMXO7g6GAeUuCHbuF/WTTb7BvOTP3Yw+4bIcS8QX0ROtvL6ciDCuEpa7NyFs7n4u4PI58Uuicvf7J14WRmGYnGWLenjBJiLM1l+1OrM4dyhqiseGwYpgppaWtcKE+cfN2aRtdsg/Gi1nDdz+YMaZyVgvTOsHam06Pzs+Ptnt77PLZYd+FhunzLpzDpbCqbjqcfIyu4hMOIeV0hS61gZ7VLODCvtr1Fi/ZLOBhYHNgSRxPHDfzEt5sqNFULLliZzLKXGkGlF4adQZDcPzmmInDsiZBBNKixWBQzjp8Z33B7j0z9tNzv+icCcYc3YJGOGibsbaxcYlf1bA39jaXY4uaRzbrCltrC70YGGl3FKWmucQYd70KJq1G+3ev/+rr7/9YGd9o71/4+7Wzp15fXo5Zr5/8+jg2aD+xrODv1ie7jaaf7TfvdOpz5rLG+364ei8czn/+XI0nNZ/fGvnm7WtJ/PzwfP29xeLm2fT91scS1AfnZ5TtUbPmGgiadsMRmp90itp9G693tr6yfbpxanEYsbhaEjttpHUTGMmEI/oIBkPRRqW8nwbttWb+M5hHmc/ExcmUBpDFYMqiprDVA/+sHSpNdg+ml3MAXJpoiLNUXqxWI1jRQeQ8WU4L8C9fgm7XEb8+KULnEtp+qQLesHrlHLHBrUm1lqHh6eXl8vdnS12Lld6sSoVWm2RKD+xIo12UK32t/7Bd370oz9vTGaHTx4/f/b8/uv3cP8fPn/eYu+lfr01e7Ca32g1mA+k3QW1rHJBQfTY0aiN4x+pnk3ZvSTHHaDMmvN7lkDzEmVCXXDP3OWgVh9xeMSqdllnLQSnSiPJTAKlEwDPOQNXGaU8NIudX2k2iA28xWg9dQ3KoodGQh+iYXF6M4gPy2OZ0ZXGTk33OqzWNkKOWUZPIOM+nOA3n1LuzMvyyG3IBqEeRQ9wy14+yBpRsFYLhFKyrvMUZqEunUVO74GKpdGF5p0t1qMxnSQgYC6DMCxu6scWP252AYHlTCTrol3pZn1KZxoyljfgYb3JfnSkdxgNpcpZ2lMGCLksF7NN9TRPqpZ1COkEKGdgKX7Qj4eKWoZ5f+QoNPqFE2qjl2QkHMGDAFoMmsA3pjJqXgMSmqGX9Eot3I/m0C6lb0Np0ZEARo0TeelR2FfA7Y0qotChjIKnlIIgiIdV4CHPwLLIEiCIl69ysepvQ5DNqayXQHvILvIGOaMiAIH/ohL4JC1cUWV4/QmBUaW5ckQihJCX4Bb35BVz/QFnCKkIDYZm4KP8BAvbS2s+QTraUxnzDAIUGgFSlwg2iCoEtIjxbf1gKgaiePFrPSBDImsqGETr7QdqGOUoqVETPApXJFQd9NceGL3zREyMxT8+inuuYBmyTSHXZUEyC37GNEM8jxYIFzEikzIYIogV60F4haVgrFGk6JYBMFL4lVWp6VaZTYUkv+bqZ08/EO3NBZruvl+taC2hQuG6FqsEBEaZObJZ11pFfTl+uFKSmGUpJAgIQDLPutaUKSEGGkkGsO7oU7VhhUJ+AjRJr/IP7NwqvK+eS5SriNfhXHsu0SvA18JfefwrI1TxPzm7KpS8UlIhPM+GkLIgcS3LJDA0EXzjv4XqZfmXXx6ukpYH2Xn1tYqXyH6+FltwikMJzg/FheBRtTaCiAWM+GMhmRT9zJcCfVOkfEAOrfFESCpqgQEoMJfcawCDDUKcKH4r2CmX5i2mfufHy7qRhyobMaRZwIJXZdPjFSGBkYTDW8CXPBj/pmILixdzt+5DnE2O/RfNIHVNUEsuREoGQIqRZCr/gRFxdZMAxSA0tDSQvXDoAgFUJWJmiUw8VD6b48lzoyfAm1nQNUcbcPmRKIb6ymV8ajugIFGK/ED9NzMeK7UOEJp4IgS+6aU8AEhhp0PvBHdakeTIXpVuhcZZkaJEazIdY+txACzW/6K31RoM27NZpV1gE7SSPwfLR6O6T0IfUxHsAyw/yUyCbSz+iitMIE4QNfVL8Qn49EvCrn3Nc9jlEzy+9u2XeaxylueWJPoePx7LN9qN5SUuNHbt77MbNqUvbKUO+QRrsrGgScKzbGdWq98WF9PxTx++16+xnSU73gzpU7H5ZJu9DpmHwYyIeWPvznBnu/vOO5OdTncxWPb2787rxzc+8/rw3t7PfvKTi8uLbq03O3lOj9L5Zez8jf+U414w/JknxsIEmpsgIAvFg4qjlFsQCgmPUuED8fwO0jROCD+Y02/MNyqv/kNMLtp/bQu3F6zXb+5usxUPB+1iSHDALJlqYLGmn1UNAKY3wvZ8gHQFOJIz3en1GBaYzev9Vp+JNtY6/4iqSxCxWk6xPyb/+Lvf+c6XvrTHWV21/mT6/PLkmH7O7/3wZ//2Jx/WBkf722/eu9v/6q98ERC12e6MCeHL7YnW0k6XLYKnNy6YJLW/1d+7u9t8MBphLG0xSLE870zZ3rOxz96X773z6GR6PGSHx9kpgzazxWjFZvYPOy69oCmBBfbAN275Ui3iJaYxtUixntU61Ci4k5m7eKTRcE3WAMAmNiGAFmVd5slgHzEQZDoshklYwthwrP/oUUCujcCcwh6lK50orp+GJzwHAC952Lz4kf9/+UUKi/yVK4ATHp3CeMfq9Oz4Z7/40Rtv3INiJpCIp+WYtJomXJhn6Ggn77NiemdvfzIaXc5HE6b9NRvji/H4fHR+PGOh+rL2dNnYWzUGEoS9q7oCAFs50C/FgsBex7juqHdY/OR4EEsE2LLTLZPIRdliBRS9Vx0aWqasZ1EvchUpha18xLMfq6oycBHOBduhcPVYh0zVUvVmmibPjkaBh+XJyAJEQSQeEDiKhtME47w5tiyb1DkymqqC+ezoFsJEd4GsF+j33aGTgCQEeJRsqcaWpMVvyfBsg8Rb2f4SZKRd41OaMNihgNK1DTBnFjE7BafFoCgNibUQxUoNTrVCnFmojJNk4TERssXdTcFcpYH57pjyvOymatGY1qJWKtXRPGrmMxoLExMocLajIU/aNfhAh4P1W0gyINFfONmY/IPHxu1Q49KHMHqkjEiCCrUgXmR1ApjyD9IcwlYYLZgIipyQAto0fCFia+OBxoscGdfyk3uSwWfaBTWNLCxNEDGCefgM420UiGwnig/oFwvMALK1k2ptwkpGULnQHFbLlAXxyQp5Ips8JQefwbkMW2QcSJxMS3AMeDswdjIVAvt7fieFPSRIQWmqv4kOJgqYNIIRlxw3v+CbIDCzeCkqW0ERgm0AY/9f82MvIqCy85RCTI0jUK5aGF5QbJjwTSzfRMY3Ow+Kd3iVyNxEDrnjIo68MC0MsX/L5Y9J5C5RRJBmPO8yTaCFEfyKguWSIamkICTZVZwmfYCYFUxQ25ub4K6ugu3V6+YhFJnZ1ZWXSMNLwVffq4cq/7yZrzl78RDMy5ukFVQrsMTYoHrVAXj1dDFI6AuI88mEUtBIHmbgewGet/JS4iRn5yTlwXx7Zk9FfeUqICr4r3y79no9p+vPBX4VMXlVWfJT+lhsHOslWoUvZXegMEcZKp9kzlU0mqh7vujdt/iqOAbxkjQ8ZcZVcElS6xOLuADHJIWSJ61BZlxtUiQ9MlEyS2kIr+Ijv7yUlMhoAxx0lzxFHj1phRtiT9qIj+YqcckeBFOy9daRI54Ip/AQXKCphPK9ZGMJlAySp8INSlYLd+Tghbm5vhk7NTc1wfw1V4sAUSdpu9iDn6t56Pim1FnFA8ougnIP5subtUU7XCKQCkalZlPRop5Un+RNMhicqgk5mPj4yDETnM8vEY0DCOCJGBrcPM1vrZlRXXtElUZ7OiDLClOIXtxet7fq3VOnhjBvlKYV1ScJVnRUE2DASnLyzLdw0Y5VevjM4wY6mIdRRrbqSxF/MrPUalldeLtsHeHe5dMMLy2bmbG7iz0kmBRdhp+Ila+WBsc+DWeTKdv89Dpbq+UJvIxOxo9LBipoFBw2EnO/29nGVHzJsXEiLmSAxVQMHRsYcfGemw95BMXrQUW8siMKMnzqx0+6SHUFhocAqUJkTigvoVfRPgnMx8JWu8H/GG6Dud0k9/nBFGVTq26jMbLQ9FfxVa+VCyIVPu0TZTauskgT/IRXCNNisujq3Ft1EBEmVLCjz2u3WDDBBpG1+rDzxo0b/WGv/6Vpd3fwp7/3+D/+T/4Xf+/Xv/bzD35ea/Uno8v3P7y4bBz88//sXz47fHfObvXrx/XZbrt1urN1t90fjc4b09rhYnmfVXHkDJIUnXIgO0BOceXHYrV0QRHhoPJNED/2VMFQYdWKxg8sQ+Y4bxWp5Cwm9D7ziqbT0SXGNosSphx22+9uYVcwtZ/a0GcIYzLBo9ptMkDRWmCkr/ts5OIeWFjYWJEcbta5cTo6fn52wXE17u1omWAbNu/0B58b3Nvd+hkmwLr+oLOzqvW362yEiklSW3Zabz65WN/+4je/9Q/+Z31O9kWoMs+Dxfq6JHEXSgr77XJe2mKynDS73x4v8SJbHpBPfWrOu3/y/P+5PLm10E5lv9rBuskZAtuTy4ftxg6LgdfrcWO5Cx/WjTOrFgYpTs9MetZFbfXvaCA6OonX4MyZLuouvrDFDRHHaip2iC9MtuDp7MlplBccpzdEhxFUwQnVgTqONYCpl+8UhnBJFZm9ViMsH4siV/kx3suXC7U314vYmxAhkzK6g71JEFaM3eXs0fuU12u15jtO5WKKCeonugzbM3ggH0Awy36/981vff03D07Go+m//hf/8rP/h3/GKRiDQafbnjTr48VkZ7G4PV9P6nVO5mKXUzpKQzY/a3RPlrX9GuMk6y1WiTcWXQp9terO20/ZnhUFBxbwQ+sqHSNGuGhuPDQAhaynPzoCVHggFmstPMeVISesWPQhOxwd2idwtht7QdJO0Z6o+ZRrGKxBg8Cqu8nEiOGHAk/1Y/gS9ba8h1pet5nLjtJE6/FnG7Ru3W4tttcd/IiCo4ICxxIi0DpxIazlELjuDSWf5NJquaU8t5ElbU6kyHk3TMDREkRn2C4YCl6wiG+Lfc3yBnPToJVI9owlFz0J6dBAOvIBJ009y4T0EsFPkRANV8WGxNqXQUOsFF36b6fZlUuvVlKQBxILY+RJmSctJoRRZi7CYSF+eKBZygMtFN0hOk7ofTO2vba8wmGxQHbpNdmNqXMUGbVyxcoNDVBxitlK+y7CzN8BlA0kJWS7KTlCsp2UHXIZz5stFjABoTFgWmqHuHqXUvKn+0beJhCEWJAZ2ImafRE7ESahtiYezoenJIUpkmRhyQMZPr+PvK8az6IlAEfu8AL0HO0sqiOtNsKBFkWahFJwMfc0eipWCwNxZYmjZQPGBVsJh14qmyWnLrKjofuRgVmxQC0bh1isNBCxzBbRlgMGOKqoTQrvEQapdAjBol7ck0MdLDHCSMoEJHuVUhMCRTslYSoZx2tyECKAK4uBwPI5wTyLU/hjIgO5JQ7pI5ywHaz8xn+yIpMS34hlN8vAqm58f/WKAC9eM/janpaJJQweLNQXt2sQ8sGYRKwuC8WAKimPJb4ANjqxip2f6jmprz9fA/lScJUNYRu48kPRC0vNT9ZeIVASX90LxiVpBer6T8BeRQ6z8/kqwdWDwUYspULmyp9Swf1aJB55t0SuOH/ta2BvIF1/SZzckkfoq74HUrKpWFDIrxieKik3RCxpww3z56+EW/OTFmkxjGgITqITmaT8zz9C9TZpQGsX08RQd6ix1jrjK8UE+6kqhPIspslOXSESmysvCikPwKw+qQLQQflIGOBUj9xpjMSNqq6WJkXJsRCsWmIaq/WQSQ7RShlCiFVu1TYtKlhIMCQT98kIUGSg051ZBPAB1xSqBSB4/tge0G46zDF3brZSXFCVwhUNDBw0C9/pq/DRiksMKQgj5YoMC0/4nMSCkNXqTzBTa4AQ3wgpXXfecwVXkCFGeGszQwuNv2k+n07cwQjs1SNEMXcAMRLDFvbwEC/gcnHB+UdyKSIg/LQt3NnJTdWHZoTX7nFmC+5XmgB8YjZvolLhLU3VFUxKcIXk5ksCr8XchP9lvxK4+X79eRP2S/9WidXLyAaygM3BAWew2d0q2LemyUlnTsqPqFogckwKU6jp/5AZ3JQMpYvyRiLgLRfbw4z391tffPOz88tLJ/HWplsd9lkatxr7o0l90b/48Yd/9rWTt5ez1tHh2f5Og/yYfXVjb3c87n3jS1/52ueHnYvdZuuw1bx9427zJ+/O/9+/+f/VCeQ0FyVE291awIsBZEnRKrVyJ01LPtP9XS3H8/nFatkHRYwprBS9kbRA6NNOa8HiBA482x7cecBhUq2Hjz44v5ixpeMMBwG7XTVb3Z3hTn+L+S1Llkb09nvdXh9/p4uUmf/dH3Raw/4WoyUX4wO2j1Q4ERXyny++83fe+uJXt1dkwHwo5jss8dD2552toxE2Vq/f2qWB29ljQ11PW7A0Os1Mq4tJDWHAwqZsrTh6ano5p6uKYQJjPZiixuwO1kdzBGenwXjVnAPU5qOjs+X8lAgMm5wdfUi2UCdYvXTMoLI2wqeUNkY/p5E4NiJHZB0T1rsyk0c4w+QfBHw+pBGGm/JbhpPWMo5fD+aG1lZjyigKJxkwndE9cwDIeEjmOVBTkAaSakxZKhYTPzxcu5eXEp5gbryZLA8l7PrzJpa/xrQOKsCYZ42f/fyH48l5Z0CAp9pxJw4yuwEm0lDA1PN6Y/Dm658b9r+/nI4+fPdnZyene3dub21vs9sn4wHd3tm8dThlS0+cwfT94WqDKY+dFVtcuPYUq8zlKCy5XjTG9DLpLLMTEivUMd+dMkEvq75iZYkSqZ4GDysMdQl9hPkro9VinH1BA0HfGwy17TlWFRQXHKeFFqU8GMwlkbTpBQUMqcibESrgEkqpGAllSnCMQ74rThQBQBEZPpc6EQ84yFmAZC8w/qO1yFuEYJQZBi6YqoRhqh+p7xjMGuQUMyt3jMV3VSE4+OS7kHzAYY8eJZA+B/8NB2OhkFxFAAJAIkeOrI0S5mOCU5q8iDCAQ6CuiQ1iPJBKj5L8h1piRMiYkBkmwQxyIbhAYLhWLSGH4QWABYW0UOVgCz1tXwBAIBz2v+IhZwUCv3WBsD20xYZusUtJMKjKdGJbIo5PVia4clhyF4iX8NGlXDaLEgmlFpmlyVe2xwArmZi4ZuwVFnCPlgOGLDZLibNA/E56BYgwGMwHSSA8EGQ6qoO3cF/mC8JXfkgE3j5vsiILioaessY+saNI1eLhGPFhAzwMJmCAYJG1XTD9FG63QKVHzaLlre+0I+GzKHOVuzgDz7/IrAiXgE0kCCjYJwV5EdO7l7gAG5wrcAKNVEt/+AGBpghRASmbpDH/DQeEXCdeEpdUBARFY9mg28YLMoEVnFd/JMWwze/HXssHgVwDA1iSJGFFRL6XWHks0Y1noLETPwl58VcXTrmS7npiZy9trs1M/evfN9+u//K9IGTgujqR17nviZSvQUNUwl0RuvbR8IJodU+AgSW8xE0Cb1ewqq/JhWDaP79W8UKvN4W4pLLQfCxFLQoVhLqe+wpuFcEfrwItQI2CDKOIyicOXEwis0RUc/nLZ6NaeZWHXEGkyIyhhIFJoJb8sHWNW5JHtxOurxRQKnRrmun8ZxD+cT1wKPpUM2MUjFM5k4HxuHymXqpc8mr6deaoiQSfIrNoQJQB2s/pudYVNDVnPqCB8G5yf8xSVlpot+1H/9AR0PhB6zhEi88XS6bZvtQFWHMlJmf9NmkyWk+tKSUbmj7HVOlJLNjShLsTOppT8Wd2KS0vjquF+yfUm4dWfSZFO6WCypyarpmgpcYiYN/beIamVGf5QAxaQgLVo7DBx8q0TyMmifxHU0OYpjXSpxMIZSQtMlDnRgonlp9NgrmUVKoT2UQjhApjyz6aZJWx/mM/hDw+qNDxhrKZzICWYc4M9lVvvbpotstOguQKG0GFdg3ITG5hFaiYWbqxdQWlPiU/50HiBJB1Plm6PJgdX/OcL+VmMp82v9c+vfSYSCVqFV5CStKXon7iy3LPjD62FxBIcYmauDFr2cbVzZ1YSegwyZjTSe3zYEnU2BU+bIa9loNsBWQaI2DE9mKtLEKI29KNV7pUAI4A6y76zUt2qceIxrocTEfT3s3d+XT60clx/9be4eXp+8/ebbb6jX7t+PRkvTr/wX/3E+yq3e7d14cX37n/9e766XLRn8wmSGPjjfVg+Ox0dNcTY/RPM3Zv408BSsd6oJ3QvLAKFD4jYhC23KMFbrFIdlmfTFjw6QSGeq8zr9/usWdp5wRjend39x/8k7/fGzY41JtBqt/7d//uv/0tjEKmHkXYlvN+r39jv8uoF+YkE1306Zl3G9dim14Bq2CHs8vFZbfbwP3OZi8Y0+slZxM273TebC9uLhbv0/2EggYbyLC4tlm//dqNh+ODzk7v/s5wr7ffYNoIfuBsOh4hTdWAv7boHAxGq0yEMRvLpN2etXTSz8V2+rQ9PGtNt4g2O28upo9qk15j+NOLo96NW7uj5fN1c7RessElyxUgnLPt2KBmvTXs1pZsckVfd9Sq7Xe2GegYtJpsDd5/ePjRarUbexINQSVmPBmj50rcqHisg4fHfbVpbFD0gptiMV9LU4c12+DMnHW0IgJl8VhBi4hfgdmI/KcLfqKW8yvcRwhFsSuMV2X4CqLSqCd2VTs8ee/Z8c8/s3sTMXZ/IKVBEVdaEfbizkAp4dmtTXZ3u//et77x7/7db+M4/W9+89/+o3/6Dz2pbnS6tcsA0RvjxWCKx41152x+47KBrQkneq0f4JJ0OpqMuKy37Mti08GHORLeOmT1L7rYepL55Sw/Zxct33TBetII2iyv6DgCiYlaTpWiwbPNy14LsI6WBftQ/y/9cXRjUW0QgNSDDatvEXVsfXoIpKeYdI2oV9snahzsP1QditP58LQ59O9OXVLPvkMyJCjwC1frZ3KGAOpR65hPDF8hkHxT0TUueNIwBjsia7DGV4AA2JQV7QsQsN1V9zaP6SDVXA/DUOkJHnRm+VB/Udr2vMnFfNJFXt3ijGXaGgP4R+ar2xZh6wRkqC2M6oiFvDRnL2xPlq1Q4xd37ZM0nzBH0bJX1GjooMIdmjSOAzGNGFtWkA8z5uHPE5o7esKdHuNf1B+LBC2xnt+SpazKs90qCEIP43su/SdHaOOzHTfncdF3ICfqsWyEoCbnFIK2V4p9cUeEW8/5CuEwkUpBG+OTaJGJCBK2WtzWim8+g0sklpB8JSKtTW3JyjqGiDidQOp59CJjaAfrxhPiG2ajmd3x3YkJbJ5ZbqwzZOfizhkBekWE7RNxwchoYOFFcdKogUTyILwgoGzzz3KigNFd2BapzwIhLSUPEbDOSMwdVjwQRcU0LjIjkKnhMpTHbmRNiTcp0FJIciQsV8NrIaRCSCWfYSYYSDso6p9LuJToYfQONP8iHYazPa9JyqRNMSiX+ROHUTUXjLn1km8WEmUf7IhndCPmJynyuoHxym+BXaLxKa95C2wgCzFpClizMz/FKpeRDTCaefJbPYhasEu48eWY0HxGliuICTLhf9/rJfwEEjQqaGFPnkt2waoiKcESEBSqexILMg9XMctXgiXPhOWzT5vLMjCaEAtLeEMWhB62VUmMcwUm0KqbMDfECCrxX0ALIOEj7H7yi3/ETGmU5tZ0CU4J8pW8jBjA4mfKCCGylz+qoiXHD2KsbohxCU4A9CKW9QpJJysrRIARnXCCqDX8JRebLh+EFiaYV7Is+QacuSV/ah3q1i+C9GattOph03OqtkoaMPyDPCoW21bmMHn767ojqNLqJbBtNbutHloONwnRbLH1YYMZqzQlzf+oP27Exl2CU5dBdvZsYQ1n2vs2h7w7Iyhbg0u/1FGP6x3VB77a4pljgFAhBpoZqDVsmjxNy4FgV9YS24bOKg0l8kK1YP4ktYAyDRSfgx9MV4g3AkT6Smxyp2wIK9QnOwoAxaRWUjlrUdHfoJ/CR66SEdq2127j4tVz2Wgvmm1W/RI70qjVDylywdig71RwPitN5QokcgGHWEuVXJT8U6gpKD4DoQo1TXksmPj+171C9i+T6NOyKADEGzban1mvJ+MRHus5Z/DWutqLlA89KD7AZtjGQ5VhqRlW2gilxCHk+pr5MRiLlo7nBetgYRn/ajM88I3mor3XGB589JNbd2+fHp1eTsf7w8EWpwTP+6eLs/Onx3d2dxgz7tZPatNn+BrZ7kZRwMge3Xtz8NmfXM4neg01aRBH8hIzFQiopfB5iNwXvtP4EqfFJCQ83Mz78ThqyOp3m10WzDLED7G9fuOzX3htuLN1eszZx+fAhaRWm0rDTPpls7fiNMzFdEYby+EATI3ChNBxDi3s/YIoLGuzVXd3+1b92TMFX8Fmb9sFFWu9eNhY7LPRUY0DkbnBk/ZOrcUGoOs3b81XzQF9hm1MzQWrSWmcyFbpVUoQE2ok2cQ+od5ipOtU8LIIiAK1i9rWajWA6VTl2dnx7vbkydPpdgtzfnH/858fdO+889EvmKfLkXZYp/CH2RBb3c53vvLNk7OnvQaP48m0xbILOr30dlbrnZOzy3PGKqwql1i5jRquBCtulFYegoPibC226LE+maVU9vtyzYSd8NRESVE48ltJTSHg4/fQde2mIrr2KpxX3l98BT70wxBRajfOzo9/4zd+4z/+X/9HbjuGVmGQ0k92oxTxgMFlC3s9sbiz/s7f/Vs/+NGfPz98/PjgfRZlISbtdv9yMW41j+jH1ms7GGIUHWpuueyxbJoBGEY5Wy0mYSKGQ52/bruMrjsPW5jt4/inFCC3sktTjqmhKAyyJ2JUt2Wcf05Q4tH/CCTak0EptPRqgFOmw0Q1TKkO082AQdPvgu4l64jhcVHLEOV6L4ZeGa9pdvrl0N0MQJE/ILOzIxkxwLne3mK+GknNN1KECAWJ8Jfist6WT6Wl4bUUonIIUs1Bjy5ye+YGvVGW9BFJBBDn4a/maAycNR3aIcbyWK/JQl5QabN8ihEBmM6wkxeZcy4W9LG+CPbheJIvgoLDqPgWG43Q6aEgMKw5MRajzUnt1G8UOJ8Ip9Plgc+qJrjmWRR6r4kCl5y0o9uCZoms1eN077CGaWVouqietHos6CIlNiYyAfUNJtZiRcPt/Em02/MQ00lNlLef4T+gtIOhWUosBIrDFsKGVVEHFmwkmAvoRGEwxGlASWFOVlyZbOZc1G8iw2bfCCWYrwBCrCEYcDwLX2ixsYXLZ+hV4SlliJQo0VSLG9DNRCUWKAooIGlz1ZAaDiS3PuWvIAPmKpxIDLmBjaj462Ng8qromo1fDaPMvCvYyjboBzC58CfuNB5yQrb5xQf4oD5h3jEMg3xyRXrwToKQCwoK6wiTB2GiiSu6wtXCFrEqQEtcOZ8s8ltuBYj5eiUGMHlKgDdfDUiEEqkEGyJvrz68+pBU4FxdScUb4KrAkjRBVZxEvmKnyF/PmeeEVGFQV5LxIN8qvJmrLlv49GIn0RLv5fvL85aC7MsRfCs5lI/AZLrpQ2XiZY6EprACJGTIJkJ5ViCKvCRccVGMIzaJEUJKjEJhsijIiMALPlT0S2pj8UAjIvPGiBKYwr9CLwKlOAnBW0VMiVMVail405UYJXXghKUloXUyABKJuKUAwTsyDFZ8KEhzR2B5BwYujTmqQbu10fyIuqfqVpko+O7wYO3FU2GXVwuSqA4c4zpEl2Gj40l/fT1j64yH6ki8RI7rWhusVKSxxwxp44rfCUuN5jsQs5mDk0TFDP2Ghm4sOKgScwn41CT76WBk1XHv6DbaV5XGmKM10AkA+FDJGcQ1xEOj3ojOY7QKiQhRNZUiR007EE1hq9u152odznSlVdvqzLrYQuvjTCHApmJopY291WwcNZl+vdSJXuvgT8INw0bsLuzqNmdsjw3/GFVYY5JU2suic64+qiMKTtcVL+lYlZJCw0A8Q9CgowD4nQcSqMVIpKIoAkW52FqkEJa3mNhSW1/o/VB5QZ92gPRAncqSmKA9a7bY8YOJjL3FDPTYRQ54ZKFeNU6wshHLCQsWTuRKTHjITMmMJACVuSEG8gmBSBGBoA/CEWR5zC/v7ome0E+7JaEfrx4S8+W3lxKX3KqgV/2mm5g5VUBMBQwJYje6HDH3vd3cmixOWRQLRRYC28jIN/tkRNtUHOBsKIRayFWGe9gtihkc0X5qd2AeExw4ohGZRO7Gk11OGViM/+GXf23WOv2L3/0j5hMsaxcXh4PJ7Flv1Xvt3ud/8OgXx8uL7vJz68Wf0Caz8nDBgtrle3/v63dvHTR/9uRH83FvXjs7u2hOVuMGa58cFzrGoGBX9XQkEZ0Vxgj7bTU5YZehjNqN6eTictTZZ/smpu23abLP9btmP5BeG/QWsxlbaS5b3drF6KQ/6C87TOeZ0yNtueEgGxI2Bs1Ot2m7WsPwQASt8gpBrcvgyZI1CiwjoS+Q/RCpJM1BZ1Cf7KxGOyBZ7/YxUbrtXqM3H82P5uOLrW38VExuxRnpNHDQRijtf8JeMQuvbfOpp7SLHjiOGEagzTNS11x3Duaro1X9zrrZ+ewX9/6nv/6/O3r2b376Jz999O4Jpk37JoS1Hz1k3eZpvcG4xBizYIvymT0fNNa3dihcNALHNrR22cCSmTzMRG+dNec7VPz1qk/tqYwVJZ8LK4NLw8JfClxVBTuYb00Nas0nVDGXZ7CHktaAdcz/glFoEpfHPAnhL7lSbzb+/iTxnNpXEhTxr7hhRosdBBhV8+HDx5hrOCxadM7MT2vS2FRn0EaaU3bMvLJP2Oh969tf+xf/vPXOT/p/8P3v/Y1vfAtVdnlxfuvmLWzubrcHARQGYoCFMppf1Go32PKrz4jTGpTGi/bYUabWcX19q906qTUGiw5zhHaZKcQcMTcVWQ1XjdNak9MDYHgvs89Iy+yyrlN22FzAnqgGHmgyporeZmSWf2ztZO9PRQaPsUZ5dyoSLQUcRe3FqkTxUzC2IciSJxBYeNEyoRRTi2SAxzu+rO8vF5yhMUoBqi6JIntKgRb+4iWVSTItf7xMiZb53HRjm83tQXfGTqBKK9a2SGOKIpou+x6TcLHoIcfNeg6j5CR72hHtcTotWPsRIbsLmsu1+jk97NVyQOmQFzHr67FeKlYhQoMmb8Id3PBrEJM0s6udOZuIxoe80iUv5LIBEpl4Bhs8S0y3babZ6hxZuRYodka8+SDPY43r3ag1j4RvA1N4h8qnF0Fbycg5gmXMtUUGI22jaePocblIAzXgqwViN0CLhNNKDpHfRvz0je5zMQ6PeTC9L96sGOzun2pl5iWSyrbwn6rG+bVSbRNEClq5JK1xeros9SJduhA2nCSVFrdygN8H7JgDngU7osUIIXaFDk9ETWqBijtpkSk7WpzhQ5VmeF9pIiKK1cJDeGjNOa8aWZu9wUDMev0knTdW4IAzOcADLpBDm5GUomRNtvBZjMSdEqColU9Q01OAgaTXsnQ96m3GNJBiJBZSQQTJp9kAst0DhVAuyUSJ9ZIWLqOTQO67qWIIM4Qr5IdPRlXjMlZMDMY2Jf+lq4AFOQYJ3pCT123s+QOzc59MrpJroFeZhZeuXqjy2iBbMqgQV5BkS0nPp6AgWdVjiS0JVZzyTXxDtcFyjp9NjJLkL7sXsgrQvyzex75ZbhUCG5QLrJdigshL2BfElCYu2CBDTCajCrNSB5CSKmFREH40qQJYxneuaLQokrgIY8FlU7DlYxEJIRBRKCWAtzxUdCjF+Qw+EZ1kaUjJoTzwyUa44GPQFQ9SVZFeMRcyiNLM6UtCXdCSVjw2cSTahMaVCTbi9IfFzKbdXebRdCDMiLBx9CRibJGEqGauk0d1YcEDJ5wPh2BcKnHMW5IKnU4FdZQ1tzQo9AQ2jI6dTHIRQ0uSk1ULV2JqLblSGe05UNmpy6VrI4+IFC9o4ISryjNFQ2K2f0ax4gBFE6JQcZQSglhKCu0BVdUjwCS1zxQL9Cl8cSicGd40pRzvZIuEoYRTaEoXajqZ0w1p0v+BQUR0UwNQsBbmaJm40/QXMQLAcjoi4U6t9WhZ9TG48M/WWaUiKyE17BLnwjGUDn/8QznQ5BEoi8NP78obih4zjMNrG/VJp9m5vHzOnl+6pkrBFYFM7wGYzYYH99jk6WfSvPAK8WbIYAg3C54f/lsNCiZ55U0M87kEGPGvuMSzQEvE8prHq2Cz3lxXz1cPJbvN9+u/BYB1wcgSXJ/NmS9/4VrTFZ1VXDMdTOPwFR2vuOXftVtJK1QUucvzUPFslEkxthrMpHdZazddY/zd0wktpruZ7Gzt3b1/k3MGfvt3v/fznx3O2oeNxp1aZ305aX54+OR8NOt03l82HrVYwoe5g/8Ozk23b3QWX7l544294el552B88KP3TqbjWq/bHfbag8HO8dkRCW2rmeXQbLx55x7zbVrNrYvxaafDpP3aYIgEMhaBY56K5h6vCIsKtT6/uDzd6u3MplOWLzO3h2ar06TPQ2ePwqSUmcudVYNUDvbfd6DK+RvKGu5fN/PqX7rpKVqgi+Oz3e3NxifDLZq2o3r9oLnsrvGSs2AGT//s/mJ8OR0x+7452Olesq8PRh3Li+2QA49LeUZOMFCoh8mF6QrUWERL0orFkGNFmGvy2npxczS5bHIY760P9odHtx98dfzO0Ucnj+r95k57/0v3P3+zvRhuN37x4cH9O8PRfDkZXYwnY7Y8Qogn4wkKCW9ob90cstagfpv1vrThkQYoBBVlFSrNN8jxhnKgcqKtqK7wD17MV84wRNIxI0jNbrns+6g5RSpCTc5F+vKQt7/GbZOK36rqFGjcDUoVq4CTH4OUHz1873e//2///t/9hyhGikOKUmmxRGWxWkA/iMXHfJFZ/9e++Y//7E+fv/vz93/wx+df+MJXLdwpbuYJkxXxqKMbmdWDumms2H0104Fq3T57WwFkfhOHyxJeN0b4U5jpgbeDGYRIBk5j/MqMHHjCXXvgeZEclc0WnwoSRjYLhFF74EMvhbLGW01hO7ltzdQUd9UlDGWBf8SOWNoRJEK9SqmoVERLlQ0IzWo4zwwXGwwrKbDUdzKMb+E78SxOigxohPrLpU40OXE3V8QwCdX35KTetZnJM4nBgDZG+edSMJIaQAInSO1om4gAcCWZmlN8zM+yoAchcMQGVAVjQtUMkUAodiTgSimRyAtdzd1yM0cqEB3gNns120sHunmCJXnQBFFlrDy61kDDxgKUUeWcPwjT3EYISUlTa14AhBBZJQZ2DVB8tBliJasVY8gWspnjDAOD/A9F0khqI3ABjyQC8cHsvAqfInjBnhYWWvmMnDBZjWwLf4hv25IBClL753S10GzG5IUYwwzuOtiTaXLkk+VPVsGbYRHZgla2xMwT4wBhWtL7lVOUqi42x/HUOCkEsrGYOHVRetCNNOeZ0Sl3KXIOyQKIOrHBvE0VkuelQ0CXkRaZ7H6bznFzPuPMVhc4FolYQiE/QJHBhqnyGNuiXeFZfskqfrgjwxQWNygWM5ITy79chARsXoRfrvL16tW8qw/5whtkE1rw2aS6+i2R7S5KfoK5V1lexXrpwVJPhBRy5KhYj5t0JXW5UwobeASUDIBWHq5CyLtET0aA9/tVwkwBuvb9JWz+ypdN9i9FNDBcEQVYnEjwgN4euDExOt/zs0H2CkcxET+isCsRT/aZrFH2WHngKVyXnXo7Isb2J4mrHIdWPDf3LNr2E9Gwvce6fKgAQLw9UVDC7rynHLeeEDGpIww8paTwT0gDEwpTTcnbWmjZlWr74pc57nypd56INKDN0qvQHmrUd+aBBvEKHBgjCeYCWUZmEw3aDutii02fMeaVU7YOUW0z6qyMg2JgYTfj54AW7WruxGHe8Kz5HuDgQSIxiMyGyuwRjdpKpp60ACLiZ57kJwbggAXDz5m1RQbxQT4yHIpKBSwddFWqiXB0iBOq2oyt8xYIUHmnrYoic4Qc6zrxhStzWO4mV8wVBKiB6giLUmsEwJkLj3yIHxsi4lwiX+bvqEWw+lYzFLKqGCgMTagnFozLrmYjjEMgtRpttggkPomwzmEj8sIXUjHCDl2hszBPGRENfbyQeFtDaI9jT5mrs02Tsqyf2wWABpsGElJy0fTOwrcYc39WdKCkyxDtK7ijtoRIhY1wpo3SKdPfMLqgNHur5QVZyXOBRjtKL89T7LXQBnnCZ/BGsJiVcgzdR2mg2UIE341CuFSYaS4ern3ehPJbYl4LqB5fib159fcK6MdSfRqwq4jSlr/UJWgFaXcT7PbvjOan1H0mjlOS7IDislIkOJ65JK8wkGQu9jiHiU0mwXe2tob9LhPE2R0FN9BsOvFMNfhG3WT+9BSRpNc3O1v2Rt//2e9//RtfvXX/7cbe1un47xw++fHxIcdwnV9eNi7nz58sd6erm7XGGX1JGw0qWOekwbz81UdNNjjH9lqe7A1Xp/Pzbqt7k6ncO92Lse0mXGauAe13uz7ruzT1YtBcXl6e1we9bgc3N20eizmd0oA2spPNzu1nq8lla7AL1sxGWDiuxr7jzCaRNhjEjAxkO8cUa4IweHbMrIP2+gZWGxEg9PnZ4bPnzybsgEIVmzsSgQHIKcKD3oPldHc2f7aYny1a2/1Ordt9srycdjqXsES/GnOLlpiJu5xwSd0GH80CRQirAMKhHDxp7Jl5QghFADs0+JigZSe9OR3urA5OsCDn08uvT8avd5s/bvRmLBMebA2XzVOctfde63EQ297bd5jI9Ozs/IOT04Pns/2tm402q1koVFjF4EZjiyG9+qjZO2PnJdideodcw4NIq2IWMbc9BkPf+UXucexiw1B/bazhrapfRa8GUWmVlEVOfRbOf5+rpCoQSvrNc3Igu3rrXLzZ5mYy/4Pf/5O//7f/AwqHWRzL+AVJgxGj2QpPMZ2clOKqlVXzkp1//lf/y//o//x/+T89P3n+9Cl90Va33x2Pu88ulsvPsB6ov6hxtjKlckbS2vqggcXf/Kgzby/qB2VSUByth+01p18ft+v9SZ2FRHDkTO9Q85Txg1b3p6r9ec+tgWwJGdJx3pQMou6oamjpmFEGGXxmMbHOUdz9IRVOwnNRp/TRrY6Big+xsR2j66L3irYUIgMgYYtVJ3wyAWentFHbLF0hV/jph0orVT8lMHcLMDrLMQFDgIO+t4bZLMlJdEKKXkmIKuC7AJVsLXxzVqWYdwQZ/Yixi0qPBNHQmExaEERWpiHpCrymOWliuZOHlYFvNj9mhMjapFh3CBMTeSgt5M4dGAzOlwTSSaMIHSYGFtXaWalUO9o/9BLsJTk5pC1DL1AZYr/IWHErlwUmbmQBH+Syyy3IyhKgUQVDI5MpsECFP3B55KCNScEovjM7QSaArcGKxoe3eJEEQ9JcwoOSsFIOyr0Atephh3OGHRH05vFJ3oKkUXLzlzoIBrBSE0pYpQNn3vT3QRpSNPVp9dAhMjxOdgWR2Y3NBf4v4vCnN4duhHqu3mTwCksAQQR9cjiw57rs6Ldg59qOLb5fGVAEJUdn2ix8khVZmVAKRiqUdQrNcRiWFNLDSAcgWh5s0+YqRumiKzy2/rIiTKGcGB0CX47E8C9M91cu5I+YxrUA5Id58amwRqVEgbMRrRHkDDBkm3HKPYGYTuxZVNKUrxkNqOKST3kqaZK2yoDI5WvgvXqjQMgkpUyXq7o28Pkt1xUuAZawxAHX+X2gVyMAm+i/5G/JpsC+nkRKNjlWRPD5CpkqavXuTyJ/EpySgwkQENnAxS9ijawrjX5BZ3AXDv8tIeSeIGcHEtlZAn5FyuNLUYytcdZIZsuYoJybZfL8CUGcyMa0HqJuei028/NNcSBMrLIV/RxXDVMDLiMmBhINHEVZ4rj7a6U2i7yawH/seax8aqTSY+UoXLbZmLdYU9X3mHYtXSQv7hgqA3F0kgFJVUFjUzARpCd60GyiHHCMwwBiUfMwn2NgA9u6xJzOmKYOnFLxFHLdPyoMUuayAVaOsY1Xc3e3RNmQL1TYJwCeaJNDmg+2uJeOaAeCOWXGDryCmCY8SqGQCzONCehwsWQWsMwBVC2iO8TGjoAMdnInNd6c7SoIFfUpVDHHiASJxXyGtui2nS7EXneLdgM7esy+hdOZOhLNiK4kqZlRm8kCxHzR7AQX50AjPPM6jtzpbOl2e+TLPusOihsRdQgTLQU7KDFEAk7lztwrnK/xInvQJl+BR7wULtnis0QX4TXCzl2wD+Rpg0lK8LbM1kVpatqAihc9cNiptKFEfRXJsMsSt8xhqTLlVcmTr/7nM2j74Ze5CnYlJrjm9dV0vzQwIgLg+v0KlIG2Wxn9ReU32P7ygkPcYNicrhaDNdAbh671mquCwo/UBw7SABPhGV7R+RynASWMPdakiZ1cnB8xFRfJeP+dxyy/bc7PWPO7T8SPjr/37n+9WN46WHz05PD9xuKMpcazGjMHWgPaHRZTMqEC3GAymbCUEkNHaUDuUIUsUul3Vs1eY4w5dHFx9uRodjme0r6RBOXBKBOubuZ4MI7BvvlId7vbYUucmC8Apd5jfPBLbxkjiwEfTrBiYgamB2tr2QiSPi0dci6axnVaQEuZf2gjaiGywXQNGBLrF3KJz6LfWEViOO+0lsdnh88n706Y/LPoX84u1pPnt/bvNupb7x4ejea1QXcw4VwpZL3Nslomy8laG06xogMjpsicDFZLqBLkQ+QHURc1RG2102nu1JdHzW530frFrPVDTF7WNKzw7+M7pl3uMvUCR16j22genByyqel2fYsTAvCc9mAeEyUotU5ra9ju49FY3Gssb2pepkI6QSW5UK/z4C21G9QoF7SN1W0xX0BiahhlBZcgyWhaS+oHX4N1gVUeCVOOPv3io9R+7Pp4IKhYKoFLtaSqLii/Dz746F//69/4x//kb3qUb+nKx6gxvSKMFRklAAHLLuNWr7+5/7/93/zv/+//j//8hz/8IUnOTy+ZJHb/5v0lWxyJBOQAGf8xEyPYHqq7YvZZfbSe7dFjdjRGGiksWNdn5tGixUG+6F/ob2EW4QDyI3oxTnrEE38Jxau2dHIR0OUZs+Fj0DOb3tgVG6EvSiaUV2wJtfS7GEwwOIKJtPKWAiBD4IYpCnn5ToY8UBqiauAn8f96mIWcTEUvKaTRLIrnZs6qcfQCNQD+Mq4GOtQpWiHIRSnriGG/BMhUtmnbsncQ6AQzUjgrCY06HY20MtPCmZ+LKigbSlL1CqppZWilKAfVdtzhwtDvQxPExs1paKk0EkdKeEAni/MKsECxJLRTaYycsurkPfdqtROF/OKLQENxgaS0agwzO4W2hhpHn4S2i62igMi3eAvIAMm2bbDjoxTJdE4Nd1MxIootlUIRk8fQRTnYLMkHAm3LtYLMDzRpbcicWmYTQx3nOwRSZejqU/ssDDMEGJ/0wKMZqG5cMhRgxuGTfELUuOcCiHFdQq3ytLMbKCk7aXFOMLh6AgK/UgDOYE0ZwDEPjhA9mz2gaEckT9tZckHHGR8NCxoaD5BnZwTMNU1s62n0xTMEK7uyFbrQYyQjOw0LCoVny9ReiSyWSj/CDkkO1wEq3b4juvK3XH4uEQEACKKUkPI5nxJgQj9tkhn9SvWU0CoAGMIvXJTt5dE4JYwfP/viUx7ybIjRcoHLi5dNYPklFclT1wsaGxDV2yZWgVMyCOwCHFJ8Q1389S4TVShtcPMMAfo0pZcjxtcxCGngSjMejpTCMO8rIk3gxV4cXCUm56sRRxZqf/NHOoQYXaHcUaUwgWf3+LxuPrKwC8CUz2r9HuLsHEvHQ5UGJhcivpoeMU9ni/l6eU4SNl5D9F8kDSDxTO0DFSubksYcy/uqrQ55EexlXJF6XwiOuUlY6lvXakn3AxkFjRIzCQg1jUGhjNF+mn4rF+YnOjynCNGLdnmsfu40A/TJzUlmcaO+eLws7msceoiV3CY1aalml3iZ7JzbOmg+2VXHvZwSwO7A0iFro6e+iohZm7tqqElttd7LXOJSl6jrALYE+A4TQoSGHYgSoiLCM+QMZriM8oBe9u3CKIelVj6oL3SaFTDNGh1tcZKrAwf0QdE6jYfAAjmGLUg1c9fnooX0X7opGPoOdoOX6IGMAIAw4SBJPG5oBu1kzGi2MqQPdYeWolHjjMCY5VCfEk7RoOE9ZlJvDcq3+aTZ5lzZDgg5s4KlbxNmYHgkDGjbhpC2qfc9hNAw0Ymix4JDaKabHlZLJkWQnpIo0oima4HRwwh+B0uXYfo2W8WglhEHMgZxdTF0cVl8mGsCduJUcmZcCNKE7neVI2LrM3tiUJTN4yILCbf0vRSOT7sKBI3PF7Gkz2uTPHEWN0LvaRWYCC+S5LXcSiD3ErPcq1e/5f9qP86kU/ZEZ+Urc6Jm85PZHMN0isDjdqSllMrrEBXDpPU0VqAz1kzHgX1lrSSyfU1RMzjM2rrOVnf1d//pr3f654vzg0HjsrU1nR5+4Xj0i87+ydPFyUcf3js7Pphf3luwDOnys63hxc2db+z2zpYTeq0Xy9n2qnW5nj9YLY8btedUVVqqFp2A1mWdbX9qNzn9lfFknPLIJnKCV0oPJI/WaIz7WbO7u7W1ixt2NacigJ1tNIXJyCHD5Ot55+z0svG4fX4xmpz2Lk+7DdarzKY6vtKx5wY0PLhaKbT9q9ssnHGGLSzxXIhar09byeLpLWYHEWSjv671OvsX493L6f2t1sFqMWx1KfTn8wABAABJREFUO6POjQ8vz9+bzp5eztaT1s6gtpg05xNw3Gm3j+IwVfsxPcQBRCpPKXZg+aS4Uqmt+F5khJf5kk5OizXrnN+8fKtx8SvL2o+b9TuDrV6v15qMqUguGwVpkg/2OOiuc3u2x0QpKiULkZj5z4EG23s724N6h1GG+Wmr96x2eYOsLFrKlM0/LPPS6PDIS25UdMcUAc2uKqjRGN54rdvU6FmxcFCnYMvAGtBwqaUWqJvscIl9oUJKPunaSNor3whW4q4uxS4hYOUDOC9ne5B7dnT0z/8//+Ltt9764le+VG8w/5hvROAOA3EhQ64rebFZceFj2kwX55/5/P3/9P/4n37/+9/7zX/1WywI6VzuHbIl8IihJFaIOrsdEmw61kOKZz39Gu7vdfujTClm2BMW8a+nucSQEfOkjc66DYSEcGrCW4gTnWs9PxzAHDsocsh4FLqe6kJLMeK3ttxn+UajjkhDEFyCaVrI9sdAQmgxDcVGPzZaWcWui4lmhKxUOjAotZUEBqmR9EXH0l0NYSIVR87lc7hJnOtX9VqYHc7xGP6SHYhgfLNjMC0btiqowcduxx2DkUom/SE1cIAuAdoSlOd4n+Y0O6LsiQcUAMu1dbnMOe3MdeiQjxRZRHabUNQuHe7ZqpMcS5N+OoYEytyF+O0G53AQm6zZX9fDOmjB1vTuqfToHFu7KQvMsBVg9Lxta0C9p7tChwGFDn9opIQHThzpDKlKsrWLJ04BkdvYzNguGL4ghS8ACaf5K9Jmn9l5fpAHHG11GnelD62Siia/ad8cGsbLluk7+MgdFadQbNvIyvYkbSJZ2nznE8TK5VL7vKvnDUOT2WWllSUE/AFAiOWXpk4KCNOAkZp8tvm15fOFGpeStvET4qLWear6m9xj4oJNtL1bs9CtgcsHhjESynJ4lBwbVzXxvs6YsoD8gr29XCclYWxgbTA8BOvoAKUDACE09XiNOANyGj+p9gPiSvZhsqIrn8CEjgSjBayloAZSESwUBYsLQtKAOkca8x92Yy5IVoDMCo1SSZiU84FE/FR/CeZGxBIl0UQhsZMgyfgqX6qkSp8sFVCBanyFFuiFr3zlKZDM0Kh+FbCXkTiN777Pr54GQBBZQT1xiMmGyzxjY1+/qozqrjcAArNpTJME5OEcGUKo/6GT97/GVbB9NUEh99VQsypoVl+ucoJ6P26uYOY7D/KOS3YpoMg3bYzSjiAul1O8tggF3neu1piqLNvCVfJCZmK78Q0iOVKwTRCKMGiQHM+vk0VAKhfiarEIipvZk52sFSatczQIBjFFY9UqcfTmqngS3Zx58NkIYrkBKU7ERBxfZBGqSmZIKqotWaNYSIc6oU1G8bAuqqgRqgIJNBypwPzRBhSMBBisSQ437Pxil2NYoCd1v6lNqWNaG6oipF8ugCSAcpP9PqosrS4FZ73taEych6T34BsUo3SWxE5VsG6DJWRBV0pH54SEuzSLnknLiZiwEGZouAEZIN6t73zCVwJqulHYRd/ZTM60ZioPDgxgjqZ0BLCz6aVAKzoayugRkZJMZ2CFV5LRxFRlHcRs7dBhXB7FoAME0BAIshSJfQuptSzxOrhmOriAaIUYRcofqxrNUVRLz4PPpHNmJ42B1EovWhu9pIKjF0kvDInULiU7q7A85JNKXWXMNu7bLEV1V9TOij0rMwM+LFRkAGivxOKmC6G0wT56aDLJf8CyneapmDWSRFAyyYMvuUpwSbEJ+4RfAf6y18sZmGqT/asQiHkFOA/WQTCVG6h1mLmenhw+ff7kWafD9he0kY2t3d2Tk2P6A0hVZA4QJPV/ITGZhas0ix1bRfb88Kwu9rasTc+p/I1thLnTn3zx7e3Pvv2r9fZoMTmc1Q6Xp1+f1T+3WJ2OFh/1vvt3+t1ntYu3V+1358d3ZvOfXpytx7PDi8YUrz7CxEb9OLLxlrP6vLliH0PqMvPK6LGdY0lwTDD7FlH/UDm2Fg2klKNJh+zePzmnjWmfL6btXod5Haxrc4uVNL7ILqKNLDAy8JOf/nTxk8WMednLO5eTSaeni9AGcebGiT2MDg56JR2B0ErCNF+KA2xAtuvDXmfn7NKXIvmt1pJlJdPl86eHH4w5AYDxy07r4OmT2s17MzYC2h4tFv3z9WjR6FyOTp4evrfVXu7s31Ji2TtpunCEi5z4r68RfnNDsjWdybzKg2ln9WG/vtNesyUXRxH8tF77Qeui0xmvtyg+rJY2hxJi9jmNC6b1Bv3phIU3rWn9OdsZsSUqu6kMu/X7d7a6WDyzxfj09np2x0V+hSyIVIKktyhOkUqpR3fYTIMSq0RsFskJJRgdRGr+UjcjU4ERxZUnYZYLaC/kaBP4V/7KciP5GwR9UWmUcDt3ommX9dnpw6+038ZERvPjHHFg2SF0OEgsqipo6n/R5ERfN9ZvvvXWs2fPV+vf7ve2V/XzizFG6znSh/8V2wTjUiNyvdVEofU+aCyG9Tmz3WAyRihstlVSe5sf/gYe1ULwpmOroZomK0L5jjISIJ0QJIyMdfeUOoVlqiVGHwVjzLbIZiBNqWrKAEZ844RV+nzXDFNjC8CGlASkkiHCTHusHOGhUkuiHBNZppGAlzzlgfh5KzcFsHyDn4DOuy2IxhrJLHw9KVYIl/nbhhAfI9HGd8lyH7R33wzRmbABN5lJoUUu2UCGFoYLQENWAdrVYjSnnIiHu5i15Cz/Ja02pSvNKDgbJFz0RVkBk2/YCbQGJNUc97uCCDK8YcS6bN9IeOfcLwne+QzZgHCzYzMHQ6iQFPDnAUTQCxyuQc/DfpNvcFWaZSsdNqJBSnx1cD8FAAxIk9NCMAdDoAqNlPKR2yAFED6WVL6Y5UvcLyVCqA98TjNnvtapADYFWHEptTwFgtklfgJ4g9Ii+eZhAhluWhjjB9rfyCF0w0n9CroC7dzRScNyYXzJEqUs2RuaDZQDJfQpknrxaCLY8BVe8keXEBwdYmE4Fb5qgcgQxJZaQ2cJtkRjgATIUZqIfeJIU0QqlBNoGRSxooKIV6AocFYyWUKQFIlR9V5RXn0Lu4wgoIpbxjUHE/gpV3kpzyVAXorgFUCCyb9KUZLJXINz46sF4DvMMax6Kb9+KFfSBoW885qQTTTKRQgBQwQfrBEGp+rzJF+UvUSqoP4SP8nGtFXc9fW1zC/SvwSVl4oQMHnh6QfKq1cVsmJOKimmlJIy4gu+H6aEOlSHJNJLXtU+8osuoZCm4ImUoqqKlDBsQkeusOQcw7LWqTmlnZpaccXkaiDSAoFPUUeRtQgmn1hndaDqKX9WSfSD6gkQVY5UTMOJYVcVjSvK/BdkJDKxxQnM8odRaH1TFRZLz2qjX0CS9Vy4xTdVGzdD+rJRw4qHdUJVE2x5JwoVSu+NEyK1KagOChV1CMNWnYSnhP/gYdNFBTIHci/0BM2N9EmOSJIlsEKqTYrQSCP3kgrw5EaWYSYT963ajQUbl4w67DgEcDkJJPIkgV3yYETpqaEpQJTycv1+5oQ4SIjZA2QWQOJHgQlocOyShd02OLlszNyruNY8ZKtllSDEsC+bygqXAl8gSBVsA8l+BXhtUChiJu0Khesv8UrowCDA2JKBZLBznwUF03HdIyB8Iz+bD9EpRUg2+OTsVKkeKR7lR+UbDwPxwQA+JCfEzIkhtd29wcPFPuH94Raj1Riurmu0G4EXBwtKyzJGgEXlBA1yi1iQZTIQC/ihZiUGBDZODAhKIl+uPICOV8H36hMhhNuPKg+J8/LNUQWjnCbiqR8LkFeivfz6iW9AsIbCHxpUXhrnFH27cbfBxvIXi92tvRv32ns3vswuk//Vv/ovT04ujc98huQXfvKKqECufU+kVOll9xI22nM/EF4QmZ6mTb2Hfdlq7Z+cMtXmgLjLzni+7Dduub+18c73z5Y/HWtI/e7ieNYY/xzZZ2Uq3tJGds9kC3xM0Xr9g2Zzgku6gZXc5CjSebPLYMwMu5y4Z6xnpXxwTGE34OMkzWLe6e6wG1W33dnu7t68M9ze2mruLpjRQ5XCCJjMJ5Mpmsna5fJf1Q2N3+NG65TdPpEz6iJmNQ0ioq0EYEVzQjYLOjH4akwY42gMnI1j6jHDFLXaKUfGqguYpUqtWnWY4Tadf7a7+8bJ0QcnZ9PHJz9d7e7d3Lkxo9fd3Vt269PRcLvfePjz2W+f/O7t3Xt/49s3+gNWSveX7MEKjnakKRdqsRWc2otVSV9bn2Wjz16LrcaNdue4UduZz5902dhw+q3xwZdrtd86O3vOrCedaqztoSV3UkNtq8dYx+BivP7xwc/OZs0Hwy7Hm15cXNwf7A7rg+Xygsit7cNZ88Na7QHlih1KGarMLXGkhPKvih2kIBi50TNNLZ7hQejT2aMPhqOXFcDt1Q4OQ2bkp7VmLhi1agfJqXO+LJdN2NUVsJs3ZcyryPTVvQSqj8pTIvCY6CUWSXwQZSRZI7JeY7zxv/o3v/Or3/ru9l5Pxej5Jyg2qqZgSIymgrGkYJl6m30F8MCPR689uAvz2QWozygVE1xWnPO2s6wdoTmVLK3Ys25z2l/dazYu1Kedk/Via7Im09v1JnOEBnVObEBUcJggac6nICPUAvUaHEATgwlzCF2tFsEVrjemcYmXhHMeNF8bj9BcjfWwqCvVFGk1zHwCACo9xQE8X4shhhTzVVPEbGS8cqM+17AmjCdkyV/39efiyZ/CvzwaaNCLy1fSkWUaPmSSsqMyMNZHI4fnCmknT5qeVFBUIDFBFf6zE5oYqC1Zv9dgXKj2BFDssaaettsD46HI5MgbiDvhJBoahZL8NGDR8lq1NKUAoh3hA7FQxbRL6PDZ3SYLY5oPIbm0dI48IATR9qsVm4oyE65qT4Mc0dTNsTfBVXAUArB5Bl6YZ268a/6nElBCRoUPqDzaHXqD7jbKCJrdFW1SRyDQ+8LB5IccejjQnUARhyF2OUGMKDjO5ZB5ewWFtNVEhGelDYdTFpD/g2IsHgWW8Q5ZTrcv6MAaIEuI4CwAfhQ0yMRIwX0ALs7ClzSAkYoYyoIKDQ9HrA10RTxpFQlm7mdEC7LEn42OCVRcyVo9ED8Y9j/5mGWETw548rQK1RWSYZe4EI4coF5BAtD0x5QQ+09IThC3LRExkvCj80JZyXwQnBdgk1wIIz9bq0Tjx8vA8lQ9Gy1XYUruBoFIYvBogqtEiVtuZEp0S1peSxm5eZfPJi/lETqIKohwvILbM2Hl+w8Sjgbg1HZl7CaXIls3zb/aZahChJ8QiHnx3GyUFS6/yvHNpfa8ilqBrSBsorz4NWLeoKJ6zk+F9IuIAXntlcdNWn5zbX4D8sVL9TU/5mWBCz4xEGg1gOHKjRUiEawABlggxpeVVTlpSBIR7ehZfUAxYpAhJgYZBCVBwS+lU/KCSex2ya4CxNbYhmf5WrFOoEIofPAb0KkjVEufRZi/QteG33nzVhAIIaQMElFK3lTHRXqVDlRs8gWy3n9TihA5wAtAmRn5Sj62ky+bPovhyYj0wADZyBvmM8lQttZA8tkga1L+wAY28VPUUBXm4Huh2/4FXMeshKhUelJ5UQPRDExpZSYfXjxX4+sj4oNaJLoQ2U/HhfoMR5k6hIJEIwbLVEgHLWKhkB3lnBar6EG0LguyV7U2k7DBhDRAQg85WMHiCd4df3cWEB9XoY30pUZJOlehLpn5ARbS4LhfEH0P/QnmRygRMI7wEjjlg8wNAOAKWxXeSLjah0+oa7lHGmi0QMxPVvOGz6nXYXewQ1zYb779Jg7gySXLB+UEygscAVAio7aQsnbMXAobUEAgWxrBOLr0bREb4BZuefLBkFcvv798lVifFPd6vJKuSv1xIJuon/4l6Cg/PlgCsgdZwGm6PD8fHZ0cfPnLbz9443Xb6XXj+be//Zu/8dsMfBNJdslE5V5WC4G7jRvZEeASM+u1C1roEXfr60F9weaBre7obPJkWmNzSRyb616P/fLZZYjhAmahsDjSTRs5WYvDd1cYKOP1fIpMpZ3I5B46oZ0lKwQcy3bLXMq41qH70qsNv3jjtY+OPnJaixXBKj1vTmeMQS9WvWFt2PtMd3843L+3nJxj8O/f3G3Xe7PJGMLYAx+c+322wKEfi3jTyNXZcZRJ4xQwNDARPy3okoW6y/UEOWj2GCujs8w0MxpgZwFhlDNkuVcf3tpi0Bsv5ZSZDWkDWdW4/umTd56Pz25trVvL1sQ9yTmPoM8+NfX1kF4nS3hZKnxy/IS1AbDz8PHh7fsMWzD60nXnJWorDILb+YPJ+OF++uMP3338+PS8Oes+b7b2B73m8cGIQ4XPLuePen/y54+7u52j8YwT3Bg3YG8+1GGt38P4J8fOdDk9O7ngOKjtQfvw+RGdnsXl7AtfuMERAozIaQ2MH9Rnr3vaKZxncHDtEnBLgStCAiaWvoLFTZXjIytzmKFn/We4UR1Cgdp5bs2mZKGmocCVEmSFr/xTkF7cy6Ofq+t6gM9mm+jlu/K2iRpA3goqxPay88Ncjlbjww/f/cM//eO///d+jbqpA4h4oE0vkSTIsGoAK4OWHk/mkllTmLUMG929ff/J08P14ojDIhgB4IBqzodeYIVz3AEbhTXYYoryW2iVrwczlpHUew694hd2ayndrgydFT8+/lDCsY8tbbkHnogoq6/lSAqXySFoSJST0woJpRug+RjFFfWj7rHeyTOe0S8QwsUbhABN7mixyVd7o77BBCs4gZaU+arA8CUVIHAhybyRqrr8tmE0z8kxX8291HfoMcMA08TkSo42FHRpbKx0K2O02QCFWoaNiY40gxGNiyItSd4hSTQLSbwqJQDPZpE0OQAlYoms9skYvpoeb1TsYLs91JGGU6GU2JAsHJSHSoImoZo9IlybII0LnvkL5FBc8iVCumJSxD8n+tAloehsx9IWi650lETgGvkxblggUF5sZUQBTiBpiqpCJmZyKqUexppJCE50EyV5WE24rMiV3HgCZICAdwoPvNBRCBufzMxL0mKnElvDSzhEg2qDSSgPeQYBq7g4BQXaTkUOOFreJKCUJNo2lT6v8TJWKi6hD6BY/dBfWCAvuegXAZZPQjCESOAgY8wZbmrXKb1AkVEAJ6mrDlQSoYu0eoxLbTWXIqmBT8pAtvqHioAOBWbEn/ETVXQSh5Bc/pJhSDaAaFcsrt4LuteSE14IC/6+mdD/hSC5WhIRxsVnMSpZvoBTPpbUQY8YEEvMwOIDKQqk5OALMZT4APTdJAWOHQAjR4gSo4R/4r1CwvyqqMkzrxU8gXFVMfPM7QVGhngeZOH1BguiG4WdavJgHHYL3rDU2k05SiVFRhRELgVG9dMo5qryI4kmKuJiVAN1LZsCWVJElG/8atRmNlcWCNEsyJCfHBJCVti3y/vus9b8EN8XAMDJe3ISOGrGF51DZG9vNTQYMeF+NgglVaGXpHwlM7uD+JDIPw0ixBMVB5Fd8uIsk5/QFqhyggcxDVUAlR9SCRHgxF0mhGJjpP8d0mSVdUhwIhRFovIiGoYqH4nAY1CCt8KI1wMHEpRRl5gvKalWIegncogyl01ZAY1A1IIY0/5ZJMnO/EArmYtFCSZ3e/XqNLKlGju+TVrQEb+wU/YAUlaV8m0e4KSAa2iJkjV3WUeCFduql1gMF0AHzZ5lkJwrNPJKCBEkkIz90V+QfRwMtNwAD+L2GWPe27aAYlCSUZJOLMwBNXlKPRrTEqiIRBGR73LOhIhxvXVI3B/+0Y+/+/XvYIWFeMdqaPgtVX1Owlu61hzI6C4qI3ezdNAKFtjc2BIyfMp8FYuSiGEKtxfX9ecXFMOLF1Fein8VfH1H/4wGuFf69VRXMT/l4Xpc/JRBzrLDDrJq4BbHozu/1d/CElowK3wyW7NjvUZhCiFQZQYMF11It5ZGIOpszsMhVHQBGFLAOrIH6EQLOLHs15eD1XSLLbJZZQt/GoutVX3C5pj11pApPnoK7Z+2W9vNMT0BRGR1We/067ORuKXw15yotWC1/QHbR+mDX57TFWx0RvP58U53ut2cNnuj0eV2rYsdPuwPmzdv3Njdu79YnAy77ebsrM/cwt3jN+/uLWeD09P5eMr8Ag4IG04XLkzBX+UQGD3S1qLb6iwHW8x00/53QNzidghT8UUEQBProNusM3TGuWBs2EI9WAx6d25sjc/HBy2OBV6smQ50uaTPMDidz8cnzv1mC8LdNlPNWqN5vd9h9ueqsa2Tvn+7cWurff9GY293dPPWVxieWuNIVrytn1YBLgLXrNxlv6DRZNobr89n87tYVLM5NrZMptd0efCl5xw9sL9VZ7buYt3lHAK46drnc/YIss/cWr11f3D35pvjWeP04uD54WL3Vnd7a1eZrvVYujFdvzNfv1dffwZymc8l8bXujGnE1hFL2z+LHmGw72Q3b8GxVWwayAlLMocPGtrNM+xZrFwPkGY9DZxrnSk5VgdJ2sjm1cMmgN+SQ3Uvub4SDbWW8GuJrICmzRSpxQ2zaOGeZ+ep2n/5L/7Vt77xrf3dG6vaeYmFvrBSgo2MJUPwpLuqEmQv53anvtXv4+xorruMZ9CHba44ZuFdtCsmpj3D2oUx2WGWTf0bj2oMCrFDlSp45BBogzsYMlCgXtGUj9UtOySf3oLrgtVj636GeTtNBY1dyVEgrEPTKZuEjlNR7to/Zs3/YIyyVGFCISxWuRVmhJDYVGrgUAZxhiadVZzYjIFQqgOVEn/W3einlzgZRlYhYZPFBpBk79RR2hUwiC4vPzYEoIEckiWqnPpMV8AXZpQzXLBofURzDnH0CoKt/jmwIZqzneZ3wbL4TaNYQM7hcgxwuZeYVD1Ist0MYvEbqSPq7KNPo+BMIZd+gRuBxIk/SoOArTRwbMEtZMECBhpa2+3mQJYiT4sGl8o1v0vhrNpPYb1NklnDYXkYCCpBDWF+WG6goBtODACIrA8wAEwpShqdDPVIMVBpCRE7oqS8BGl1MYkNEZ8s5hQYMfhWVCsJkrNYo3V98RMKluiL+742HhZifRaWSItnMuMnLaclRmpDk199cYe8gr5iRCqgJpktQvqqFedt9GNLUcWDViAXRE1HiYAKXJDsoAAAfs2LmSPJkhVHRYMXOQF+MqlCecFd9xg8PP0pZEi9IiotFoOPpvFGLhGGPOebCOcSajALeJKYrLpCtiGR5YRbGuZkXoUgf+f3DC5efF69jJMCM2oCRKd84wMPfucDdnJ1lXyZ/Jd1tlBvYQOeJ+WTtamb5L5FH4ECMEO2a5YAmiKTqeWyjOAF7TRBm+R8MmoV5WM/1YdNbH/NsIq3+fX1WrCv5VPil0p3FbfQfvVq5HJdx0qBoEBpAtjuMbArufdFYZDmUsUkp6JH1sBFmn/a1JR+4S6PfrmOogUWHAAEtnxS0DHH4C9dY91Rynys/ET1YzFhZLGfA7sABYiWimGqJkAHP95Lnimz5GcdsO4ihGxxgteSHrMUFixUFEQTdxKirwoo80Wvi1WKEL2DkYPuw6q2kx1wGh9wjUF7VEuJGKJCAoCsmdJZyPXuZ0Sm5AjlsJS2VydHQKIejU40/STBUI5DlB0EZY1PcAnNFHoFWOL7m5yMTDGBvhVT9LgcwIMavCMASL/AaGjnorfUGEUbAkNlJITg6TwvtI1dO3W3CjithKklJuTIeeOoMvwAbBCI7rTmJ6RShca0KETVD1hlOCyDDM5X9Voi8AuNDm/g1aC4aMKELnD3fCOSOry1vbfH9u20PKeXR+M5G1MwA80dkx1qDQsEQ5ORgUvdQ9BCQ+Sy61IU0JR1eg5TRArlBGSmMM1OzD71ykcZKjXGNcUveZUkv2TkEq1AL2yvErLBBP712mLGjpiL/nCIUTm/HA86O13OSLa4KASvSsRFkz8FMI4oYsS6QLyYeks054VeLBiJ8QgY3WhrTGIP3GKOL5NvOWiADUJn2JpLVpTAYebvMMEAMHjzWErA+tRVc8ZkfrtdFLzTWVjbslyzbGy53RsyS2d/q7VY3d3v3KwP7ty/154uDi8nw4v6+U/eebLdH27v1HHuz0YdPPwdlhbRu8Dexp5nh/f2YLpcDLs7jVaPA3HpriEFDrXxx1qcOV2gOe5rVrAwWIXQuOuJS1pdL47wgQg+bgjF0c1iATa1XU+ae2yw2OsMOYlv1ZuyhrMP9ulTaIE4Ho6FyGLhWmen16YrycpdN89mAX2jy8AxRw/0lhPm6J/ucCxyBDbtOsJn7YSztuHNW93uvUbzKWexcqQY8svO8osZayq6rL9crJ9NFx1OsmP/Vpaq97osTm7M2SOFWVMWDtgysYqhl9b2qntrb+v1W/aj2l00s+S2OfZ4fH81uoWzmglMlAInsLJDENZ7GmOKmVqcekO5YwJRFss5PUOGGcbjSWfYhULGE1mkGbGyg+wOIlp5TcZbkGmTKdqvymsRxkoM+Wo12Lxde9qk2yR/KVl54U4uqgU6bKmk9Y8++vDPf/hH/+gf/MPs1EIEZVjoWstWbbUti6HYEdQmCQ5192/c5LnWnLCK+nL1bMmaDXcsQZ+iWdElTN5k05uRiHLgBNAYAaAAncZYIAscneRkB0Lc25OpzDiPwA47FbcI4k1bQbFjso4YK/HYKlcpMQRHHEYAaB2YN0e5ucWnyruoM9oIVbmWcBSLHyWXr3RCzSCdZ3lgmorMhKfs6JelmRNPUbNIw+kNTwsBQr12GdkikbP6bqgGsIz5GfZiNNVp6ekButuSFSS0OzuEGj+nTtDn7cxmU9FJAyI6MIguJt1ft+bRLox2obmwza7aCymjGKiT0EuzBgY+OTkdrUwyNIbamV7oVP0eEI5CIHT43jlKjRoLV6z1eM7ooVIFGexmfbH/dOzQN5Ao6SUv/RUgwqxzNgEzO0e07BkSw9EAotC00wRo7mPcOJSEQZZWnwAVozSSIbLEJ9s7wJC9bOVGMclvIcnNwlbhkTTGIYVTUAkaIgU3+Ojxz3Y5EGkH2eQwMBhBZfpmy814csHdAjWZaQww4M4gYBxxycSbYiyfgw3MNcuCD2Sq3U0N2soG3htXVaMi/BZGyXggcOdXCdNDsckW6ikqv4l7EoCjAiK1XiGPXyKRXk5W2REjqCQbYwYbH4gIRDJLVAGU0AC7/ij5UlL+jBeMN1ECMagWNl0DlCii4yXyuV7kU1KZdfWf70YLt4wbEfKhJBaJKo0JqmBFyhQVDuVLARkQGgwE8k8LUmiAlfPiS0DSeWLUFWKb/Iz78SsgjMzDiySbJ+D6YXNdBb8UuvlafgtOm4SbFFUORHmRDyJqD9J602yxL3YMOApAG4J40ikvIE6O1uZ3JZPz7Zw6Rq1BLyim+qCEwp6vOFSCQzKVA9YlgQhHq4Hoy2b3gBqCGayS0I6w8nCnr4y4r9uPU29sUVUnguK/bSOZByHeUa7yPgUNcOsaFdlsiEceqWSgiLVC3WdOCzsrr5gwzOA+JgrnxeAOUsvT5LVxLLJ6ksY4c1K4l5zJXVsCawfdxQx6MhVV2hbwoD5jLKhEQCJdgpS8egxvBimyLta14KLmXhOS5tQIUXTwOSwFEOj6Vc7Kd/WMVUwVlzjFdNU5wedSMCIioMqCJzv4J48JA2x4QS4Y2uZOjaX7b7UMd2SUSJiNbM+dMLuCKAXLiEQoIDlMMpTj/A6+9zW7UwMeVWkEi4x886AC9cX8QaPcmTvk9IzldD9dkWd8RisaH7DOTEVNKne2HMGcLyhOnNR8q0pd5MNWf+A8Ga06bNLeWo4uT5497k9Gqxs3s4xShQYyGWOA+dBICAajm8R36yt8ilgEmBqLwXC716vt7dx/7/13JpwRpHiIitlQlMEkP1CZ7qkxDCiXwsVTkbLcN18+/ff6aMD1WMs9AX3a1+sxYansLZeVFELbneHR6ZN3/uKd4Ve/Op0MObwLY7c/7I3HbFQP8kSnmUJoHf3g3Ch1ePuUsmk3WruD7lYbXzVbflA5RjXXe08WM1bh0p3AVm1t7XGaB2b3SX2xtVg8X8yHtdoFdvFicbpcsux4vJi0+5iNjUFjOB2dYE48Wi2H6/ppg1N1e2Psi85sqzvtCJ8JvtRHihVbfVnf7Z+dXyw62+PabP6ZB/tYVv32Nnt7DjHRF8zo1yXdXn1xNR7O5xKiqDL0nHZQ8aaxo3ShztqEAxOJ5bzqIVWszTRidp6io+KGVxMaM0S4zlymWq3b2u01J30OPJucUZHa9eM+p3BzODEziZq1KcecIpmK/MAVEdhON2984bv/4enJ46Pzd3Z3OzeGHF52cXl02u28veiC1pfOp6eDJv7m97RfTEJJ8h8rEAO9PV8e9Hfmtc75qnbRae8ydYfCmvU6ywXbtdJYc87CoN9rzfEvLDmM4VatNmJylcLrSo0ZK1cbTbbN4uRiTsRs7m5tHx49Y6FjvzfgDFfqwPninVXzrFYbqGSw3WxrwhtrHpgg/fxQI9CvTH9y1laPJQuDwZqBI5zvZEFngvPIOQkcrFkHCKDoClwQmS4IGNLu8LHWPAMWV7n7dDWi5Usus0sME1yPmteXbomBX17JPwENbHT9HhhJy9n3/uv/7ru/+o+yE6OqkHTE5gfp9yWKCbWIptIwb67v3n/A+YboYyYGnV/srNd36a9KOzPZO9RtJkct27W95nq46ry3WtygOFRei70KX/Skest2jkeGZOkqsVbAnY6bI1SDbgOHvKgpLIixm8Uxw+oZGOjUDXbOoQGgHwXU+HrrnlxN5QS+OgUSQm7UWNQLOg5hJg5vfqWEUrNDK9wgPNziroLla2HA5jXcuM5PvpPFautFGAseSAck2IIGYJU6XvB1J9atJrZTIzF7eWC33uhwyfegd9tz7HNtTfVhGhtAxejXx9I79K4hDXyY4Hg/kZu112sslGk91cUM6RINQ9gOAJiQCY81iOVHc6CtAAzpAkWs5DXNBGcaOo5V2k1G7WiSEt1JX+RFh4XG74oh5N05BizuB8CCcGfVYZsnev9M1gYrXV8UD40AJLJ8nu0i9AKUDgEcVX0WEkCBvOr1oU3F8q7hzQM5yWfFjOZXZxa4UIk0kOWRsfgK7+iBgHZMICo+oboOSk/GUqMlVQkT7xleAQ4ICcG2N9FfvOXi3CR42Xka3qnnYYvE8SMeuXiFJdCs4otcLJj2ybCqeycS7C2XS++UWFfReJkGXPkL+bH5g7wh1RfwQJ5RYalmYiXVcAQCoZRM0bR2kAiqL+6x67Jmgri5Z5fbC9mNY46BmIt3Lh7AjaBXL0O5LKLNxXOJikTBDcYjn0ppiWG0DUzT8ZwP+OxfQBCSbxDhI3FKkipGQcpkVUD1k1cpK1eVOi8pO58CKDGg0AvZ5ioYa3XkNUFElgncDMzcZn5F+BV8rpKUhxLjlcCrlCYOErkVZMvjqymuRzOeWLxyFVnIh5IrXLaiUPZu9aT+ajOlx+N1MGodqAOoVnjKiD4mdLtFg1RZ6jgX2AZUW5G5q5xQQ3OYbI2uChFRHiIWqVFUfpS+e/5iVqMMaQmIZDxyXM+z6RKTOpA/veFkXYywpE0dEG6kQCHkQZVjEM9WTukVOwgBP+46YprsGF5r39qrDZBd7R43cmYYGs8XzTGuSoekdWpiHKAg0XEem6VvYImHAWyW57P0U4ROtaRfgP63IqFuQjD1xBEC6aTCqHeCDexKXVYnSgtssifhGwoFWD5ax1S6YZe8gB5Ah4xQpsSZFfH5CJUqUNukaKMwD9tFrmb7NYanyVdJJBSlDqspQfJ23YWY81FUSY2mFF3zRJf6a6kLzH9AsWnTmdRmJgcxKGi+GjupCijxsaQ01dQb6Q712JeMUQ71iizzJlpspRe9WXz2QLGtkFYQg58IlqDMwzvkgoi9gfwy3KQ6whLqbM86tBksZrxAAYFUuBNwlHBMXnumzGKvcdBSfzK/ZLvjr375S2999sFrd9+6cWv74nL5n//f/rPJ87Ea3CXIWvlkKl1gLH0i/gkXcYzgdyP/da8rqFVOSV8AvgwqRfRSEFw3ItxGqlkZWqs/f3ryu//29+8/uMW+NO8/fvbRo8duS6LfDQsc8S4VhV8ZiajSjaXWbDWbQyaYy1WGERZ4ljstdqhhLs3FeFbbXXeefPTBv/wvflFf70+mT1azPsck1dl7tH7JxKFmh53COCPpnCnytSYeg/5ydVZb9VdrdmHcgos44pmlz0RA3KR45lnfyf4cKdEWfWl29WAbQjzpy3Vvd9g/uTybseiQSe6jy/6gh6WCRdBm68B+82TOtJzWlNG46BxrEXKX9ldp075A4FkSwBrfKakoDKe7wBRFCHuHOsUDO1RNmgzUsiWRzmYWjCtQ+Mxho046jsZk633ViHuOu4cZa+2nrCa9fePt/RsX67dqnCRVOzm5+OjR6cn4tH3yvHv8vN6evk1jf2e6M3Bk0WkQAKBS4tXEcl8tDg7H42V7/8a9YYuhAPoJrDpY9bq96YQlpL3G8oP7t/e3do9HR7NaF9franRhdwVlWEYZkS01al45oo0y3er1Wdvg+QqcY1DrXZ7vNmt33PiQbO1Cq0R4sQ6WSgNFMonajS28uvf6zfv3buwM9s8vjjgEbeIpLOTnnpYIFL7hJFfYVDOIiNqIvysJL5IuxF/qCtQXqa+nsY7xeQO9Uia0Aq41enb0cDq73Bm49SeVWoFXUUmF6eAviKfmIdIYZju7W8RjxTXezSlTGYccFEdFRnDaTNj3kC52n2w/Y494CGSrmmZjx62qgICWQO5RSQgCysONCLAxe8wFRCnCU9zmyOKyMZw3Zix5wf9NG+GOT1pxKEJXFyzZZpRaVu+rJRtUCiSrZTPi4ANloUjgzEhROKYM5nAWRaiy0V/rKjguOe4vVhfR0MqwnRg2skXZ+lERBYJKJz8JM5h0ECRNpuPKjXqOf4t9j9sgRCI6+HNlPsBLDPMka2WW/DDWrWCa06QhX+ARjoULz5EVRuOGO1jh1GUdyaCHVqeRY/iwseKsWSLoD3CNl44eklI9aXDYMEBO6JZntpeDrqX6EhclYOsDMMYRMbEx9CGYaBQL4zC2XOwlJtLxGyHhMoFyBwEAQS7oKyFtVtYTD++7RjJZ0xLDDdtaLBS2DhN/0CJmTz0P/vyFCmnkKZWHxU40y9BIPsolKALctOWNeCVhmAy2tFlpXckrHQz9hokvY4kkK6BEi4F+H60ze5PYt4oQg17isKEDtY28uESNUGtxilF2Eyx6RqFaQoQixHcbSV7AErEylWZ6Mo4Hz5JNn4d46BZXrosToTYfPAikMIWHGHgpNCGGRfxUlwKAaPNGgtRKcoTOCIyF5Qgk3A8XhUwmBceAEqvwTQCC9sd/Ly7Rl6wSmpx42QT67lWgJo7wCiNKmgIzcfxOSjA0J69N+gSXoCqsIOF30dqgpEz5XMIFVyXKT3kJw/3EaykrUNoASJAykV1C152yS2jBdAPjCqyJYEvf7Dn57Op6aVVyIDvniS5tWaecECIn/6tEPGw+lMerz0Hbb2BbnqWRf1BCmduPpxJigzGgiUk0viMHO09zJoiksbKUn8XyFD7VOThdLy11i/PlOFwdQYuQojfdFagUp+CRbHPjv1WoCLBVkxpNYgSOFV2QwJ9gSdA5QT4ZlbcBxGINNTTbnEsAj4hENuvWI1mNAR5tWuiEKpIokpiYwEPWUTC+otbpiS1a2P3dbqN7H1FfNU/4HN8/ycoM8g5YrhY3SVqrn6gJWT4IVmQNpYv9bvtGs/Y+FYmhScLRclAmxlQObGwo5sTCOCmA0HRJHxop6onYqrUyJkASCNNMcrdLCFjcorteaxxCKf4sa2brORTJNGDDQqo/39AIq9ucFtRg3irdreUt62rzQL4lb6LpuKPlYRh7dU9Dp/4EbClWIHGwqhsELdZMtEW7EELHC6AgTZvAK80WWcBua6Eg+VNNobpoHCCn3j1gxoKqBLWrX7lclBQMSUPBJzElCgDRjb6YF81k51jgWXRHbNLTx+qhOPWpOEQdaklEiai1WJYHWGan0lCzfwvi6VgTZhb54JVZcBoQ8Jk6NGVPD3ZpYSYIYABL7Mic+fpGM4DdeuPm/dfu3Lyz01t3/4N//zu7e31cQqwVVXe3WcIG+np3rAxshqkyVXzkg7IHl0rtLvTmHjn148f9oNdi/RWPogv405eiAfPqIkLipEASah2SuYQgk/RdsRc5S+rps4P/13/x/9ve2dsZtt/7xfu11R48qtVP0T/szmN56LGjGOe0vHV202cLxds3v/LG5+bnLE5tsYK319/iENYu9DCnGqU1Y1xgevB8tFycM1PAPqVWEfuu0hhdWgbKMDYvS1opFaoDi3ExwZu9oS0NKCpd/qIL8LVjyE3Z/XKlLYaviD03O07EYEIK2/ccOjS2e+PO/dc/yzRw5HHWoc/NUk76MTSYE+RDjys1eb60UtV3kY1O84KFnnMQoK4vT+ncY/pzWisqgbq+ZINQWmJYpICjSbBpdpr1rVVtRNmuBxPM8daU87U4ReEIhdVd7/Vt+sGZYQr6ifQqTyejR/PF4c4uB3Bh12C0NMftP33v4MFqum4vbu9sD6fz0el2/eatjzggj8UYcLXV3Gq3dtrd6bOjxdHkp4va3vmKrScHOwysrnqT5fklUy1mb/Y8fZnW+HaNWeg1jhhvcTIwrGCADWVIbVNrORwRDuJh9aS3MTT0+ttYPU65as4vpk9qrcP18j7LNtmMjTXEsR2pAdZnytzEuMUXq25j3Ws3d4atQbO3vjwYsiVKtz0csK0QIkxkGOAv0o46QjVyi3QBgGp8prSF/9yNVCTxSm6vgorcLnaV2pwKF/E17UaiN8+po4aDpypdjW0ujAOsVmdnE/ahbnSPEbH1mBnnFCH1UYEzsrYsv6reOcsnGN3rdA1b9BYcPb2+3e6/tWz+nK5BhhrtZa5wXCw+s2oxJMWWQexLxYHDgMNMB9iEzlGjvt0irMEuWMCfuT1VJvOsOSqY1amejSCTNOKwi9GXracoutXyFk1ikyEF7p1z11BgfDqcrX0Eqeg/2jjEWPWhxsWAg7HqU25Vu2hZRZeGJ2pAy03/LdAwtbJFKfT2SM6PnAw7iVNdCZMndMijGczJSEBgkQyFi18cVxOnYfDzBOmi/ZKlvEIoQxc2BIzN0SjB1UCy26nxZPMmOAgCdbo2vEKijl6+wI5yCbP2zAZXzWkHXvWt2tFxzniKZcwTG4CRQFRVIJEGRNwqyn7T+ibkoTxocIo8yVkzQPYASpuvVycs4FPG3GQx8PRa2d+wz4rHDYiAIhlgTWDNBRu5ygUQy0CE4q7il9gyK/0GOpBAhTlEAnbKgmc/09db0DrjQntGWvNVLC3bsJo7WsryE7RslIHkLEt4JSEJ0Ndtar69hOBGNHlbazKfwtaXlNjSAJQo5MhohGhbwX+csghEigOSkfBnfDETjSgJjs5A6FhBYcspdJIDf/HA0mo9kS6C0weTXcAzwGCigzA/8Ks2Z39hZOOx+fMV0dCXabchpVYKjwzpruE0gSxsJUZqiER0L2AHLoflwVAa/hKYL7Iu/zlpiisz+MU1UWQmIb4QKSUVFhmQPftdf6L85c8kifvyQ41ZJFzZiT9Q8tlb8HiR4ipEKJuYZFUKh69Bqkq1+akibqJfh8ZICHSgMTaB1Jhrl0hfQbkWbliJWIC+lCjxCh7Xk1wLufZ4BaVEtfh9egHQuFdhFhHyhzBxEYnX/FOk3K4Pzhf58rOyHbXFA2SRlpSkNY1AVAsISISYT7E7rQxGqSpkwJjGOk2DuoEa8UOcUheEpzhoWQITO4MsaN6wABHi1BzMUscQAE2YFUMJtr4hh8pm4Gh4UrMc+IujHp0K4WljaBxLLuBJWFRQSUQtQhvyDE8ksKSRKY3mDrOY57suDkt9IQiAZIG5QZdJut17hEREQQhQNRIEOuZBNOUYXahT2pccwNFqz9cTTFh2AR9gw9ZwxZKYw5lsktVEmvF6Z0jEFIpuk41vWhyDigLESiIinZZATgT2QykxaRXR4ew34katzHbgUCUW/7FLeoeJCEz5YNiOWl1YaDtLDqAIfjRXGu5hL7nLA41jVShN5tKhTjd9sMCUCLBSfSMt6AiUpAzDhUtfxwEiGosV53bCeGaWAIk9RtyFEHOkh8tWu4MIum0IwnBbMPQM89EmTtlhkxmqUaPLlvZz+ok4sgCLnYVz2ZO/mq0be/fOz5hvNr2cnNxKx0mbCpkhJ5pnEKTjZhuE/3Tcbfa+8uWvvnX/9t4eWeCiclyITuZkgs04IXsQR7givGELSaUQpvDf4nv5yqeXg/7abzLwkxJZEpvw63HyDN9KotBok9Hi4N7V/Ojk8OTs7P6dO93+cHK2Zhf96fJQ+3fZxYGHMBUxhB3oUcp3Nrs8PXm226gNm/WdDtNCmPvc6bHFLNaJ56vNsDEZDHTR+Xzs5AzsTkf5XGPKrHsaTSpWFpjQn6CWdWiTh3tD9mdEvsmD+UDWEqxPWsxWt0v/c40VzCJYgikhEiMhQ0q+UTvj/DL8R+PJaOjRBERnZjAD/gwdzBozFl06UOYOLY7aIS8uw2Sihp2+5USho18Q6aLWOa8Ewwk1AbIItLVDF10b+7DFTqPONeaQAPboYedL9u6hnjKPJGYlgDBccLBfIorDVuvw/Z+PT49u3GGvVcG1pw8WkzfdahB7r3cxnY2OL3662xvt0tXoMAaxO4Y8tp3h4HJEasUUnQYT/N0SldmGELhksv7ywiW/jsCsVx+s6hf9Ad0Sljc0z05GW1vwAH+wdSrdJ2oe3hgVJZ4X+MG0Lao1X2sLhgJWo3OWaN+gjuAMjTiz4KFo40iISh05sk/OO4ekDhhTgbvMcmSr9Xlrf+vmo4en1AIKEnmAc0ij0oWmU38pnFQCgBCct/zKUoMU0XLfiOq1X1NvrqtIPFx/Lt+JWQCBufiiAajgZxdnd1E+jmc6bgkS5O1/NRIi738rua57nLv0/VD2/FucXPxs2foi3dUocBU7c6NwllDBAU5qbszU11KjkUaQRAlBsSVieMC6pedeRYxuY8iINNhZhABJqtzXloxkE40Sv6s1gwjYc0wiA7amG+LGFyScWgDikVgRp6DCAd1APEQ6w2cIC+3C54PSiFyq3dM30PdqjA37SuxETWhSVbeAIIIZJz6o0n3EUAacGs9SNn8JlWQh2OAwFy4s4oGeAFXUJsAQKSV/Y/mUNiHASyY0B5QDqazUoC2mxKdALCbI1jCHGOxW8oIrQCz0YJc74YCPZo9DjswqlPlFFZNLQc9XoPNCdwLUfAUfxgsIDTyCkHIyTF9NJECDgrA9wp6F7/lK5qZ0qM45S6kYgSY7RJAOiIuULRqyAbPQHcSChBwhZz6DjFnwpwVdngQBqcSUuegocYUHBgU5hSB+fTlZgvhOKRMB8bEeAxjOCVCbnywMqUZgbFK1qiwGpNDMQUW+m95aLP/FUARSCvDePyLrp5FIIEpXhbTfYINu1JIs+EodlxmEFIueJ9+sehLlB5iFf0EHDO4lDA9KJDti+S1wCtCAEnpAeudzkOf36uJ7UEiWJvfdeFxyy6t8K/cEVLeKnOtB5sFV0l37AMzrub4UxQ9mm8z5fSXiNSjlEVgVi4IvnL+Kklx8RSNUJ4RFJl8B+iKHJK17Dl8powr1srpZsJuo6dNUeBqei48v8uYZbwFgJt6zspv9f5J9yaWCdS0R6EKtBMhKn5Ez1u+xE7AOjciVxYOs4BigAaRxV6ioLQitTS7x0H26OogWXKMvyilrztOK6lX0tOatYcJj+CATBLE5UDopc9L6myInWkrDd/4a3edqdGsAIKjssdS12zRfxUv2WgMSQWKpQyaUPL8gqdTBRgeDBgixqmv6/k2zKXd2v1bcdIaUpMkLAM0T7Og2Ew0xazE0UzFR9eBNs4xNQAVr1HqYJ1Rys6MSUSMdJ5Ac+QKjJBrjye48PhmMc/YaXHfxceIDHcrY2Q6k1JrbKhbxpdKSt9Wcv0ZtovVfeyNbFB7xtVFjbwoxJUOMBEKWLQ8MWq8uHJZdD7HoocbjXZ0HSe/IaZa90ZsUW/wHFgYR0OHSiXKkK2KIfwiBOpFBXrsPWsyzuf0Nu0jumYq+Ymdl70ai+N2BTB2n6xK1u2hymFG7z2Z8IMACRFYR4FjGJ4VVj7t9iVWIlsTY4jmNE+4Z4KQ03OeQgmZvRPqaEJgiXK9OmDrOcT9Yq+32zRv9999lqsUe4wsIALLClWF6VC8MQUDgOjP+dZN/6StffP3+PSZ7s8ZNd8ZqyjaC6/PTRot5F3QttDIoFVQZ+Cs/4bsy5BXul8d8KYHenYT9P9BFpuXa5KpIEnL1uomQ0sEuilGoaYd3nwF7Ztc0LnGdYnk0OJcUPz2mCRNSaWNZY7lNAs+L9AAQZrjUnh6d7XW333jjZocNVGqjJkWhOY59vmywgefyjovRcJqyS2d7D6/7dMTxWGy+VO9vYT4zIRd2M6seq51zg1lS2ezudLtDTbHUOSSH0TM6xtjOCGWTKSwMBGD0O+5ixw7kB8wMmrEqp1PvsjvNos2Kjt3B69P58ckhy1mZfTFkynuvs2IFLb7vdhfDmlabynU2rU/GUw58vWCvHeYdKb/s27neWq6PF4ut5eqotrjDpOLl+myxvGQy/XR1OaZ7gycfaw5GzAaQhTS5KGE+YJ4mHaIGR5nNMeWbDJNzR0/MjjtPP/jF525/kY7PhD7s+oPx9I8nowdb/aN2/Ua7/7Nh6+279wdf/szu67du0EmgIzGes4L2sjbb/fDkndM/+EJ3cNrjHLTW89b8zUbrmGby3t5Jd2+11T3YWtz+6t3l27fPvvB3t3/2o8kP3/+j+eRLve1Rs7W3rI8XHEXcQ8jp8CPanekUzntYm1tc4Zxuj1lGcHD6izmnJiPfiHPUmQpTwS8yo32DqNB90kytdR4fnp8c/6yxvKTTzUDFJQThg+l0OBCAAVItP4StwzLlqaNpCh8lyY/6IZe1IKBfCKLhfK5yTCxGBjbf887t+nt5LiC9U8+4qWzMh7fmyfHZH/7eH33pi/8THCvkTouEMiEb9EwS2DGAHr0juEZajUHrtW79tVH9iPHN46PhYvZg1fwzewTMs3I/OnRCp9Y4YzNbdi8B4Gp5B+s/fSzEabSuDZB/hpRc8iuxqGJmwqDKWOn9njvTL14P4QoyDo2Vvp7bqLQa5/OoZboQgB6OA6wQpOsljVBFHqYScNHh9iWSB/HUTig2QpmpJ2G5oDYMhSP15Taz6tdNnTXhTcU6Uhi1vBGvXPnlRunDnPqKFoTsjtFr8JSOcqP+xIy07Z015owv9SXtqc0LEkIQ1MAdOV3Md7DjQQPV+PSieSWtr0S22SUh9YgMoQJOgxPZqrDJNE0eAGF1RNKeAiIZO5cQsENVeFYlMLnwLbFHK8JKlmiHx2LGGJ/xbarRS2CbkUAB20uTHPiv9wb54UKKRWDTl8WRJIg0pJgHah8a9sIu8MifKPsECvC4tLO8WlxIG00xEWVC2pcaIxIxuQ2QEX40O38EZHrhS55YkptlLEApT6H5CXLQxjSECGklzUAkLXEsw4CrpN2sCLBvLxq8pCJgPzBO8sBJXsUmJNSPYgBLrM3L18WkzZgPtf+ZuM3u89joPLfscL+JqU027ssWB2o6PAuTuWgCnlNYuFNtl5nVRRuKhqB5ppsBHqIhHqAbbU++1EonTVMjSccPsAlkhgXkQFK5woM8ygM99JH26mt4JyRcp+ECSSMa1Qtz2J6EP4EHACjytknOr0BzZQ5F3jefS3iFwbXAksQA/vvC/zwpEtZxrvlr3hPOfZNJfqsXUmg2sIK0Sh2BgJW6BDYwA+NjYBJBfm0gE//jVwFyFX4tzgadV79di5JPeVcUK4Su4gMgTKQl4dHDMlTGxrN3GrlS8IjPAHGqUyqj8KwoyBIsUdYDhmR+UQ9YMYhjnsnDCqZWMogsEBU+R7iJbq/CYkd+BMTFR8P5NXey4AOWu3mhbkwLkkRXkPluFK9S04RUdJKVwo8OOFCDnKgnQkSogJsIBEtq+UPdiWgZnrxFhbaEFiDibvJcVALQEyFrAH8yQYIEaXUBSbLmEj9g5s0AKRI/3SPqVGxm+ylWTCuqFix00YjRdMgNQZE6MJkjzQvdHjMUaHLJV1hBVNdjmAHsSglimWADOLCXRbz0A9j6A1TZHT+YSTpUB5pFLE20mvxqypOMwSDsDkoOi5L8LBxNbNpLspZFGusS67RdsQUCrtR2V+8LNHmKfAv3J9MEmVWLCqHhdR6Da87U2pSL87GBRUKZR86UNHSGxMC3+GhK3OFFzOhstNzTg8V/bHrLpvJkLA5wAxBsXkNSFSxcpqGYLXe5mAEkr/Efu0RUFi63WHBSY8taS0RazN4XHmFoQcbiSonyYCHwzafquv68Cfvlf0n9CrxPSkuUly/xUTYcjkfR8ywUhqhH03nbTtzcnTNajdGUTiAnZClkdA/mtUvFkBGAemM0G03Zxb+7nI6n260ua6qb9YG5rCZMd+np7l82e1szWmWa1eW0PhgwcYKj41p2gR34pZz5ZSYbqwe6PSYHs18h1gNs5B/8dQSs2e6w6XezPayz3gJxpH9Wm2K8gvdourgY0eCzdeNqWG8/2L3ZGrKH6XC7zfLiwe7+PvNanh+fnxw9vXj+fDJtdvot1q42G7Nue7/Zw/GE+/5iNsL1xdr+Lpv02+WgOZxPOblCjy1rADiElBWutSarore7zbu3d7eGHA2wmo0vlqMRmo6VQAtPK1h0u32On2KJ7vPZ+YQZ+bXmcJsOQf/R02ecWrYcc/zGeGv1lbf3vrr/+de/9iV6Jzda3YcDjubt12/t29Oqr5B2ODGkuzsYvjWeXLw2POsNOsz8YbpafX5vyWDdsMXZYcPG6/2dg93W+c3VUXdOF2v5udu/evv23cmoO5keTeaD8fxiMLjFbJ11ncUWjNfV6H+Px5dzusqYU1bdwcXl5OiMCsGey5R7ESMKj0oE3dZBZZlyUunRCXbnkV8cPmqw+w2bQVMFj4jGmCoqlzMYYCbmFSKEPWZfgYIzdeT8ejUQvNGu6oXy4mXka1d5fSG1vF+9vBLVpH6LRo0pqpVzORkh3dALBWZqHP7QPuKFPnGqeDyQzK/psoNStzM7u2B7maPLHy8aH8kktZB2N5ssxYYlByx7rFQkA988kOnlMlqlyCKntCM6VdMugA2XOeKWliW6XogFHDsMCL0mlVoa9cKUNvJgspCaHz1JokSg0ol1UhawhVLvsjdf8xyGFxYm2/KoAkc902EIeyhzsjGwvIphUl9ju5yqyl0S5Bq3tMvoRzQkp1WQmbXXqGhH8GBRPqPEsEDjjyCqDBIxYwAkeNq2kgQ5wih3bQyDjfLKXXeZaSeX+CRyLCLq0jXCLYFEsz0v7bspQZq+ArkTTeRFkJlIzIMBniioDOgGeEwfmn3BYhWTYIeo5Nmgq9VrMnmVUuIbYcAEa5ZkUKdInXbEnQzAxcHy9ClAQVGBPJhlCstOkhkLsJ0pRrxxbcaUvqAlEyTbecWRNRglgIifv9Zy34AFeKJ755nsbF1NGnD5HvYiIUADKjgnfiwWIjkxId0ZxzFooO3/2N0FVIqFx5hDkADkyFbKQXoURmYDJDK+LRZmkAZErBeMmImwU3xY7wEotokAB8weOUjFp8NmZx8ZdjBFx70tJjfa+jb7BBAhjYlEwQ9G8vlOLhQ36YQEz1XtcoYXx5cQVPxm4EBpMi4mtmAIy4kua/0VqIyPQCa0FA4ApSecNGJShasCNASoUhfOEmCmJqgun6sXfswkVwkSQAm9/m0T56Xfq5SElkIUk+s5baILNLFDQAWfj4hciX8FSjhww/dC0Qt4mzjCio7YQH/ldxNvE3z1TsINF67Cqkh1VPzmWl97NsxkoLVhmSiTPMWJTNHpVd2JsnJJcdlSc6nysO3oKbqzDrVJ/7g6qb5inxAG79gVhFpnMUYmZA3fnanPxVsytPfghYpHtVHZ72P+Mc5gFHSvJa1Jk4fULZ6MzGcrmnB0B1BvIzLRTFJk5fKz9r1yJh4+QYXvEmSlEhRZMPF+y3pZPydOgSF8ogV5KizpacUBguwLCSqJubiHf2K9+hAa5AZKDVzsVwAL7TPlxTrjR9gYMssz9T9YMhlSZCERRUdyiGFcTtuMWsO7IwPsagwuMUYtlcDx9v9n7s+6LUuS/LDvzOfcc8eYIyOzKmvqAT2hBRAEmpBAECDIBVGL0lp80wfQm/ih9KwHLkoL0JLEJRAE0BgajUZPVV1dYw4RGeONO5150O9v+9wbN7OyhiYAiTtu7LO3b3dzc3Mzc3PzSR6hkjw9Dl+xnysMsAqPDQAR0PwleUjOHtLAp9FK+VP8gGQoL7f9F1ETBT00D7V8rlpLcgHKEkQa8lnmQUv5rA9kQvJ1O0mHBMQ1YcsTFHQKK+Br5p/zVkWRRhWUpRJdZZqHXLS7Ioe6+gmUEUKFguDpNgCcfiY84kiGZXavT6+g0IsPcOQosPZsuRxNZ5Y1iBA+SN6pMg0n13haArNZ16uZudWb5cxkgRAMC4WAZnLM2h2bwISbQQy3xBsmAjIKox39C2smLEUL1ZrzfXdz9/9d1gAUwB3c5vln35u8OmfBJheGx6oUO9Q07TGJLDC1oaawQX/1wZOvztZvf/wj7uRzY1RacPb+wk6/a7258bC/Op9s30z6/eVxq3+13Xww3HvVnt9ztkBr+bXV/stu++uLzcefnbY/Pv/h6mrvN3/tXr/3cNs6c46S7dUtqbd4tr+3f9fm/2eXXNVmVQ33bBBkas60tTnMthzr4brzWX/4wDmcb09nZ9Or+az/+uLN2UXrfPKytdlftC83eh3t6X/2t//T/83f+PUXTz/hR9fc/NN//L3vf/rdyaxzMT1fbSfmFX3jayd//2/+ncePPhyPndt62OpftlsH7e6kveH1PzN/fr548frF4GK6WcwciLCXugtL2NnaVvGj0Z79M7tHh5YqOe6htbjqWCc6ZF8M+9OJ5aFm2DtjbDg47LcnvcHo6Hxx6eDe8b3O5fP+5rKzN15fXVin/Ht/72983W6kxxaUO+F38XA+nehbXp5dvrl82x8btGJjxqHpFOTXb88fPtD2a8UvyPeq8+dhyjB6vzX4ZLsc2U51vTjqDL/fm/f2h38wZKzu3x+d3L2adk8vUXRhbhzDDPPblQ3gNLtqO0JM1pdX85eXV5ZkAGNNxSp2AAlhTFlGEIvLvJ4xHY7VWTOkSceIIxzjZMoK3zNhiq6IwjLAZ5wIm4f7DRFFwqISRC1Og0NIGfsn2bsIRQlEIxL1WOG3bgJzJW39felz0kfEcnkmwHGQM+NePH09NxaV4Vkr4hjmVCitRvVQETmHKM1QlJ4d3Yb7Jxcm5eu1mup4dT6eT58YyGqvR8vshHMEcWON2oRt67BszNGyPbOnQ6m8o465WpikN7UiyTKV9XpMIWzXYwtdNutRa/u15WZgACkb7Fgps3bcL2wPnS7c3h4bul1vnTM9XG1H6x65MG6QFqgpUOnw0iXKKJFWPpoklCwjUomaUoe0Ca7XED66LZ6KbedVO8sScmQDPhes+wGWOKHG5hDQbc4JzmuT3HPzsG1flP2GZKBjDcEOgV8uZ9lmKuDth+u8OaRcLDZzypFqbbV1VQ3FGQibzenEAivXathwnx0CFwvT/9K+xE6ICi2GNNGh5t5iTVOJhM6WtUNqQPAX2KoVHrbrNYhl1Hu7fGJ8rzX8jAVedrvJn07Ss9CrZWMA/iBVa+eANPR8r0QnOsGOtUt6fuPEeqHdi9QnPEzibNl1IAstrmZTzSIljnyQRSap6kfXw+SUAVOW5Ojyp3WJ9RtxkknkMnRXC6xgqcvmQVU1Uy0Xu4VhG6rbVwda2m0iJAsVGSziTpfWS1OnqZ1UKG7wGQr5kVcWgyhfxuFloQQIiEJld2V4NoMfwcRJzII7r1ObHWuiREsVS6y+DcwW1Jg07Z4VgJHSSDFSl/0hLexcm64VFIAHGxECZfQmaKKXmdXV3UsJkKO9mc8JGvUkVmSN+w6wtL2iZ/2TCqYf9A5SOABESsHUvH9RTehh86VQtYq8K3ViFJRUVz1XQUKSsCTMkkOhWK94Vcsc0leN5O5z0oa6+e8x7Xx9l0Q4MM3PrQc7GiVJEe1aayVma/FB7gN+/XrNS/PYvILU5FOoySe+/1sxK3qTIpj0P0nAbnwg3E5om3wrYhLqANy63uWSwKKJIH8xNJO+CW5+r993b7d+QrKfF+c6Aigh3M2r7HYvYfjIkZDwS2idOi4WoGdxo7f0hqXwtWQF92ldgIN7TLVURUGgCDy7UnfXOVTG3nAYgkbaQrVgUBXoA4OWM7byDtSourISw7E7uMVnVYp08gN/ByH4i0XngBxZLj7P11wQrqAd7PwE4fhU3DFSerZ5v27TKnvhwaIiNh+LLCmyUWOmahRGLHg/YioOQUp5GbXlbAMvJEozkDr1nJLX/5Q6hXQHNM1B4AksPZLg8F7UUp7Sm0m2oV4+5En8IC0oyrEWrSYJMkQrVLrklfTwDS+W3pIW8eGt45GiVYNawJvqqBRNXqnoSh8KVAnTPU2acEIBliaVkCLXLVVZCLqXbkpuwTYNVmooEemS6h+wh5DF8GVS1fShphJJQAFB2yjBKkQoz7oNv4Hhf9qEjALnqCJqamMZerZtXc3mRvCjMwvlpgDJPwiiIlf2enFw0D7Y5+GIPSFaMtNpm5iGxRSwE6P3huDp35bXPAqzSrjLPkkKr7z//+pqctzl+y77pozBKNVveJ+DH21gxSHZbf3N/+Q/OR73njz+xrp79Xt/8ON//fv/culEI21WimDto5ZoZQ7s86uzf/SdZ93VUWfw4nD0leHwzXrycL39qL19vzt62m19uB2dPX9h0vrrk+6Dbw7vdObnXLN2EjGCove0XutaECcL39uHd/YHy5lt2O3F2R/OePT0lpeLwdn8aXt//uO3r//V739nsXi7Xh+s2lcbGzJuJt32vn34D48NA62G/ZZTb81SO7nz/tXk/NXpn7w8OzfdyJCB6S6OErMP/jef3PvqB19ta/vtUdS92KwH2046AyurAYbHk2X/7bNXm6mmKN1GG5kzbTRjxpy0Wdzos9bMRO3xwaiEGwHWl6dv51cOJnO4gSmIpjCaITUc9Y43/YP2YjC90sFsrV794E9/93/8pV99cjm94pA8GO+dzj/7ofXRpg7hpfQSyZW+JdOfaYMJdZUdDGwgLU1ZlkEQ2XBXKkuzu5r3HVW2HeyN937c6R1k1ZAxeVvBmuSjN9uZDHpfPRy33p4xTMt2U5hKzpIrvmVfMRweXl2+mpsxql8DsCLiA1rJJsVRLSQoWrM4ltyZNySxt2j1fA6siIBa9A9fAB1WT3kkK8PFayCInvCYtp4i+IFKMJK+uXz/3JX4EZ1KX1/qOU+3o9481wNwiaUqYmw4TwLOpWSo62Qsv4AMPvEUZyCQsVcbms1Tajy9IMKT7ScX26eDLHx36ITZkixbJy0i0FUvdp4JJ3S3/p56mffMqGRhOlFbZ0wHeQCOHCxSykLhYISoqGTRcDZIBJ8RCRhfqy+WZkGJFjcJDWyuhWbmAxDsUnUehFlvfoqGQb7+sAIQpQbzqai5U50psa80FCSz621WIqBJGotQL7Xhveib0d4KVOzkANOd7k5O2rp0dxis9kdw9llWWFlfjtsTic0bVzjXMxbHpGmHAjS9qlR0OKjaHYFlBCYN/4K8UxY/ItddhJQg9ms2D4SbysGKupuoDZJ+R88urPF+WbtFtUogQpoDkOVWvVYaPQ3Ucr3q5xQ+1c9cztZf+AHmGlHb52fWUuVlHZ+nEFn7Grs6Y8NcQSa6Z41ShK1K6Z7KsI2QjpR2lTZJ+pAqcdJFChG8leWdtlXvU9NZCRtCJXKCnaEAB8PYhjJQtxp3PqOybtOCB2RILnvSByYCplaqzQpFQx2yJm6aQJ9TllAuRlEax1Ro6nBjdZJfA5ui1O4LihEWMLClrsI7kRLlZnaHjL6moPCND8trBnS0tEoSYqQwsfRYD7H3cuBDowGCUKEtjkmAsZcEZJSANR+oVGlSCkd9ijW9o0aFVDq3ylZBAlNjzUSiRy1ZioOhyS5ZiBAcU14vSKQMKVy+5HLPxyDqB/apEkhn5WemM1Sk5BVIDZS85L2+7SJcvyZmgUT1Jlrdm9DrgPBIoDVX87uLsQv040+Yv9vX7rOgd095CdIVcjt+ZsbneheWp3dv756FZQVxxXbrmEv0+avOPCt/uagNhJvYn49ZeDQxck/j0ETIT3iiuULucE1NoVbpDtnUbRoZcdZVb1g4zSm1kI37GmfSNDoFB+Njzi2tQvczBY8XqrGhiH1Yp6kkOTVZ4MdrFNQ/NgtLcg3/mNJko7q4B6JuyUsk1pXeesQKdqrKtx3ThEvwiPylCt/7y1pyA5CfBef1I3lu7OMrwxLwpGwQwXl41BTPzrmYsbSD3Q7Vwp+UgXAYt0bnIlsnmCvasB9G654qNuTBg5js8Xwa2qwwS7+6RvRo2miKmFpVTsqCCFFcAEciZccUp4nAQUAYrexjo6SlC4AGPOquYrohQlNjiS9TbYJhaxMnGL6IoITgldIRtWQsAobAUbHsWrmLEMpGo2Z/UOWJDZEcBLuvHsqhM3hJlcq9EKx7lBPtSKkxoQ0lDK1WRjQrLyVULPcV1BGmvANpV2FYyKeO02BkMgr6IKMQmpDvIV0j9UfNWKkSlFPv0bEKBxshsUJgFt2WvWv41XqfplBK4jiqOHe1JYnJ3QMejZ+N5dOgpjZBig7Ht3mtEnW4N6wgNT0px8ok/6jRzJNhQba6U/tZ6el3tnejtXpnXOlxPIUVSngRsCDvwIOa/U98retmL5Td+7/nnyYb9+R+ndd13mgQCra7xBaJh3iPI+7qcvHh+3ceHz+czd9y3vzGL9/96HvLe/e++tHrH714nYmn283e3AqB9Z4J70uH2GoT5kdvLiej4X6nbT30A0eAza7ubeKAtJn9dq/zgX39u+274z2byXBfmTK+n5kk9hoyXGCRhSnWo6OPT1+9mu7125foyoFq80WT1y8mq6tPf/TD52/OrrpLe7HzX7GPM5X9gHXcWR32Wvv3D08mZ/PT05fj4bGd3N989unTV995PXljns7eyLrkvfbe8EPn9tq51BDc+l5n9BKH0BBxVmwuTJRv9a4mr6YHB4vZcnvhaGILGnoK2I+h1u7Nplf9ngO1VjGX8b5x6vlqPumcT3QSDqaOx3KAQJcJMVzDEXks6Bn2R63pamqf1fnLH373RAdlvFnYpJ8HdRkbaeng5PRgRWZVqQjmIJl3lG58a6ZMEbzVyvgS9UWVEUasWvLf2k45lyF6edxun2zG5wfrw0HnWbYpzJwXLG9EdG2t8mw53WyPcTMLnvhEBDJCr3W1j+HV2dWnm9YU1E6mCoUdS2TmbGJuYxsQO1SY6Ufmoyq3ozgqoIn7gwZBj1TC1SPAhCnKHPSMqBC/80ZOw/o5O4IFfYEDqwlvGpB30vATHN+w50+559QLnPw292LqKPQ8R4lBw3+regzjYJ7gC8+YaGlcxZcr9ODPHzzcs149ToS9/cFoz/R0aK+fv7zzJz9aPX7/eLYc2XDJvH82bn99ON4z0XBk5olznVcr3X7NmUkYI/q918n+lU6KoJtslla9KSSdZv69dTXOr8j4pHMkxB8zUNcd88/MfoQeIOx+xylQ431OdZ3qKI04ljLFhRgEaR6FkN4jxBUwyhhjlG0Y+kaKmytqMl9CE99nVjvNLMEBcr29jEVHnqVP9Ulo9cIOaBmZ0XWhZD6XTxqY5ao3X/Z0TDXUmeiFU+ETdYuZsrgvGckq5jVYujDG8WIjVtOO7Jk+FnM7WVLanG2UuMukcvG7plH5SYMnjA0pK+suiAXSp3VWlHjaYswSGt1fh4zoLD3PVqCxKMDWjokf+hhbVp38ARqdtFT0vCYyDWmRK79GNp+HDDAPIqGdbJQAbpLH66X4IXEKIwJbJA0qKmeX572d2idmvmb1KqxhauwUIFllBg4SKm/RGbSSPOAyJSA9T9VCvukAO0qF/v3XaUj0N3ekj48FrORf/4SjgZCYA0JXDxW2039Z/RHv8WpB0tBKSXqSbblglEkTVKB0i1KlaiStquwjKRUtdyjq3ihIuhY6TIbHyEjt92dKtwhFioz+BCntOAhghMPyRXGiwjJyKGHqUQjyrqwWUAGDl16FQcXkIp1sEYxgpFUP6PylsKllVYK7FH9Zw4twSyp55l+DbhrWihthjxFShAoWvrtSrGL/TPdVF+snJpUdHF+k8GX9tvvPE8+V2sjam5w65aqs8tBcgdcEFdzkDxuasPH9X0dqfgMlWd8kSHSfqkYryi6giV4fm7jl+7/5GCtGKsQKNfyZYykgdfA5/JK2Eony7ktyzNUE3XprgivDJrR5rHvh2US4DasBk/CCFrZripTfXE0mHnCCRhTRw15bbqczB4sSo9V64qNxoqGTN+PYpoXxeTrAODbCTvaiD8KL2sNZjseq2kzRia9vha2sG1apbFNibBoJEA6MaWXRWQv+uek01Rycgl7kMmJIDtyjUMVPJYYvolYqt/Ar5ueD9Hk1n+Obdnw59hCMJ9CM8+zmluiErLbXwKXZpbm8SjJouBGuBTgZJ/d0njEg/SFvOWOdUIqQ2r1rsZBLOruBS6lVIt6a2BpBK8iTh1C1KK2Ngrd8S0iisNgK3kIwFul6OptG9IBBzOiyEEiSyGWIVreIWcEj48ZhO72xLViz+CGTKNMZC8XUSUZC7S3EDlcD/ofc0Y0asWFWKqcp2vkbIhC0FiRTCFPro+EM5xmnFS7zLPTO97WVizrhHnk/KJw6clUpaimz9zjsWE9rvcd4asIoMDf3BtvYATHnw61yVmn0VhYwZvJPiByyoEaotLslPHSuwAqPqZ+voWw1AnlHJ5XYgKOiNlsH1mqxmmhNMsROK5GEga2jcqEX1mXop8rDuLaTMQbOcW4ne+yK7rJNLjlQyXNEd3dVDXgGqB6b3+vQ61j/wX+/NEOtRMRBY1xkw+Sdqe1pfvjZDx/fGd89vrfYTBed8d/+6397091/+wdvX72ZIJ9WftDVj8LOsHb+BeNTsJn6vcfvHV68wAKXw8F+b2BG72Ayn1imfngwONjvHDEY54c2S7FhaMcCj40uHEd+xoUv5/sY8/DgYGALzOVFtsXabi/M2e+PBu3B1fnTWouHAcxDQmBSOWcXmJu0Nzr55V/+4KtfeXB098Ri4MOD0f/z2392MVn2+nvD4XbQbZ8cdL754YPh4exq+epu6xsabt2/si7SiuNSOVnGbYNye8LmNIB+e26WQjleU6FxbuJGMsV3MSXD+P3qanJ2MX82OWXbzDeLUcexciYT2/vIUWK65SY6ZuPP/f3+eyMrxFcf/fl3Roe9+1/5wB5Gi+Usvl76L3LCYok+i3Jczpk26oFlY2pfpBeL20lBccsODPfgLMzWYb6aGPSsvZ4eH51nk0QrUH0Lt+oxWF1hhKyv/04NkSaTK2M9qapchJYSO3h76kM2EEhY+ujt/YPxgqBGxWTIHnGYxyLT15G1gk8kFI3ahKeWKpIfyNSCooQHJC9O3t3FhxjJiGz4l9cGUb9NnIR8+VWRb30SP4W4dfdRDk3ZqDE6Rl4uWvHS/KzMa4qO2gFSBOpLYaBt68/GdkP9rlNt+0O7AuiDbbsvf/Tio96DDwTnAIr50uqJ8WDo0C4DBgoxZTKwg9ORCCPaaV6fGU/pQPjDoGV5qcHwDcpSp+qWRcTFvKdnaRsBC2x4eVK7UbRlHpX3AyegHjVsf1I9xGCu/0BjRaunIqKQQ/KEiEl5Njo8lZDXEIABQUGFDnH4Rl3rM8d3kp3R4g1TUQgSkoSS6kTa/Ljwei6fEIpcpJ2J6jS5NN3AyjOthShJS4nKTpzwsbJ4DFmiFVKOsAjAhbxw3xokFSS8IBabM9WVHPnxlF6P06r0NMmO+yUTkYI0AyzSKqJBcuMQaaxiQ8BMRmlCoqFDlsAKDcGVPb6QNph6gBxbV9bNGEKwQfQ4wjVMIVTqMpHhXBwvDZyThTEaq+cNKswvzWLPBggL2z0FXkpoKBS1xFRkT0WEIiKy0DDBCYWbZik09hoRS1XBXX1AyfgKm1vSuCRyoWywDo/Eek4FVeUEmfACkE0eoqJ6QY8MBnCqssk3SFW1VHbVAcj3VHiVrJq4pJFTai88KS19XA0ntRDqJns5hHRKRP8VTzR8EnygS8WkroqbVE0afowdvNKR29Uy7s3Up6g2zaZ0JLGpn1BZ5CAWtV/MApGiQcqQMoWQ+bRDPSh7dZMtvP0LlEYugkeie68aN0SJ28KLqYpAyrdrMuX1J64m1q1gAZVFgCbtrU/JLlV1nenuU4Kb2JXjuwS30wpt4niI+NSV+DeR0sHMlcBrQIsnCXF+W36aqx6r05eC5sp9h0CTcLcjECCFangkZKnItzLcvefnc8W8HX6dLLRPJDMotITG37CBnev0v1VyzARijPipaDpoufAKTMQ73FqZpmWVIE1guB1/REk1KIqLD6o2ETj1FzqH54oH130KMWNN+C8zC+NfN5G5q7eXGL1TWmI3EAxMikMwYvWm/H7KUOagaLd/hArAl9v2o1i5Bui1nhw7xmxzzs+6MxwRAf1g82bSYIrfwEz3WoglXEE11Oy8DTPQLokjELxQOppH2eBa3ZsS2yiQQiOO/zIFIkTy58ZQnJAZ3n51JUBIRs1NaBoP3vTpClXRQEyWAWtKBPFCI7hEAQAQUNYMJYK6oVNnU2aZaTRpKpK0cgIgu1anAqqAMC9kANM3GOyZQ2lSBOx4gpCnCpUa+SQREFUDlS1AdMfK+VDIt1cP4Nbtz+xWRFTZUMvZXXVtB6EsgYPe0o7t9pXvVrr403wNwBqllZdy8pds1w9199rdU12y9saiW0JvB27Mk7KlpClx2KreUJUbVWKthLblfngKqxpDXr+Nzo35hRptftqO+dzh2/wvFRzFRFdpejRFQhWsu9pnT4SuKRRONq/0LNjLza72lsmGwOdhTc+p9ig+Zga8Cp/Uoavuu5Am/Kfef5G1AfHC8gndzf3au5/nL7tk/ZMZO78iKjFGLuMmJ1hv13bX33z88flvvn/UO3nL2T/u2+1nY0/79ZXxARTlwr/QB7ZOjz8Mf/PcOSdNw99tjU5G7y+23z+2xf2YSWWR34gHZjpZfuXx3ZENKNeXttEc8gnYRxEn9T6SsjW/b375yeHojunas8P54jKeKHOrZ+VWdMPZJmSvZyb4ZgaWvSaWYgzw7v7e6usffvjek/f3jvdNilG7/5f/6z/4F7//x0++9vXuqzMWv1W2x6PxN5985Xh4PBrcGRycEtHUabiGKrAHzjgL5rezod5DdvnkYjzW31tM2/M5J257r7+dXE2Xe62TYwsS+uwyor1Y9xbGKI4e7x/ur6YnMySjuUYH2VckjmEkoWjuHQwPH+7P77T6F+dnb149W82n/Yej8dEvzWevs9wzNkrE0w/etI8GK3HQNjbSN6iXtsqko0jVvKQ+/kjqLiyUGRF2Ynp/2RnNJoP99Z3OyceblQlHryPx8Wl1zMKmw8znkgPNYl3xenMG8gobZ/rc27Orj3WiSg9WZ3XbHg7smJvt2y1YNoTruAFZZSQs/QC847esk/itYRKVJDO4mSJH7azWtTTWXvK5rtmNzHTOvYf3qIqg56HRnY3h3lg8SbO7Gq6OL/ALV4p+zef1nFxcTcNZlIzo0TaTTedsPX1PJ3Pb+5GwyGmaDpwUmwZSsRQM1JB/1jkc46vhhjWh/XihLocPl5oz08P059d3V+09KzbSjMVVwFrkpTZvzrl1LP90YI1GGjQxshJNaW49Eumj+sp1nU6cWjNRUD9h1DP6aq1kmhpiA3O9BnfZo0yECUs4EMI0CghRv7QQ4ofeISEnFNfDXWU2e7vqJInFSXHy30sqBYuk7+YQlOhwTBT9lL/YweIkaX5VRD2EOLs4CUibkBhSiU9PA2EICmH0BYi/5Ijmn34OQX3Ae9PuPU3kqGPMmakt+DMdhN4naUSQSOmhVXgGZWQEMNNPREojiJSO9MBLWSUsatUaRPRus+YoC4jTPoMZ5PS1Lb0oAoUJq+yFerqlEAS2DG+4R5KgX4GqpLq1Ia1m2D0uAHaCp3QmlE0ewQ8tg5V+Rtgm7YldjJyDwjQmVhmjxFU+8pkLDeljWmA+1magoI6UoTtgDVBgcIriOnRcSz14UR9T4zFpRE381GdSN43L+oG2qp09/hv8nab5PAxPEgu8fNWQBCY6IVTTJOPN4oFUbmjVxAyABpWUMJklZVIoBFb0AihODfGtdOKVS0MpjStdYxUFbjRWCEIvSVzPDfY4wbfKIhkOXjQJo2irQJV/iii/Qo/APQ6GTUyVBmoGWMUPCokXKkhSP/DKuT2ApX7FrsImJpWVKJJALIQEPwRu955ZVsZ7GUL0n7mncLkntdOBkskXrgaQwMTItwoAUbJqbfPefHNvrnqQZ1VbUi7fT4zavbNiNPGvo+8yvUle2eRjUbbJ0D3BGD67AP3EVUluANRnhfLboFBf3EQL8So89+vn4Bqa7ArZxEyEz10FZZfm+kMD4QaQ4MRSIzGak7tbNVRphHBDZEG9iRABw/+QUK1JEL5usIv8e2/82JFVIhGwyax4N3wdhLOFqBIF+3yUyhXXMzuYVo6kUjGMyzJfU2Fp6c3pU+shqDyCrXhVfLFlQ3XIOliRgdzhTTMkgxiiNhrMQlgtx3bJXxY5cHKp/MUomle5pHIlcd11EnCh8jdKnJ1e7OEQpahl8eAdWalfxUeIQHSj/ZAwHY3sYE3jFKEapAs2QCz0UNpT0gMjt5AWmfzCvylmRKeAlnYsXCN9TZ7uiZZTlkh9Ko8SKs0JYuiqRpJf5eKDbgHrSjgNhxZag+SLVE3FFGAlQjEYiBTEciUSKnKD1b7rKkv9RIVn654gr0o1H6ZF2CHUYa6pNJnjgXwzOcusG8xjqi4uMnsBKQ3PxDZSlZyUQQMSMG2Ir25hHjwr++xb15Q5EfFPCJLuTbBT3cN+1xjDGcdTRmf0Hnsm/uY8+dC0KGl3M4c0Dfc3h0d3bHNGTcpUI8SfxhelEXI+FJNLtWnfkkhXLg8UaWjtr8Gk0Pn/663QaXAqxAqvKDXchx6qDHuyvHl5Ws9e/uBqc7G3WJouNtyMHdK5V/NgDTjFzYVnMBeRiFSbyRBWlLY3mLSWZw8P9u4/2M/K0KwG3Bsftl/MPnt40nv/gwfblZkUQ8MMJDM1aCzKwajr9/ivr87uXH73Ba9j7ewU0cN0Jwfjt1e2Zr8YHg6c2MA0VZl23aFUbN3j5JqHj/ZP7sW7Q1OeTVf/6p//69/9vT9g1L+c2T2/8+je3cNx/97J4MjcjdaMsWfuverjbAsP41JmQZpSHT1+9v54dHy4MrvHTIzRxexMU37xdmYZ8fd//J2Dozu/87d+KyvDcmS9ejRHZn+0lzEtvo6308XxEVcBpTcybW5hX0hnC3fXB+aYbS7x0WC9uT8aLc8dg3y12rw4yCG1ER0uBtyYRokg6EBF9cQiZGzRS8U8hKWmJWgcVZLHYiwS4MwyMvF2/ekenHqrQWdmJ9KysvbnWJOgYFSjKlOdVWtbJ9PpJWGLe7U9WE76r1+ogiHfQSMsaZRjekmJMiYFwCRyirHd1XMEOn8oFpHLSHXeI1B+yWzD3PleCtZrPl9fsBbLW4hXfFP8d/35S39FD4OJ2Ny/NJLARvypv4JP/PFITiukRqJrSh8UniW74IFYetYvjZ+eT683yuJnhW0tzy/OnLjMTcKKNfOk3Z6y2UxzKCwGmV9uNn8+RF2hpnpkDtMf9JLCU2FgRufDnpY16TGaDMkWTEgtlWRSUGgxGMOHeRcYB1GWAaTRkyCdgYQ2TV6jR0KzkJG4VQAAabKKVWQSOQ6kFETLQT595X+rCTUxMxFTNzMtILzdYAjHqKgyHqMGdu1BtGY+R9HT3wnGCHGGBNfwq080QKGubClgGAFMV/BP3SG+wISni1vyJkyXSeqyE2DI520bi5i0UfoeygqN5Z0w/8s4hSA7laGdDNqOBeG/Sl9BvvIhFra2q3EzrUORpPpU2tvMPS6o4eZkFSapix5TpKY4sQIUJeEhgi+5klVIqig0PsWYSqMyGQGhTwiicNo8AwmRzvB1U+XxxAW0tCpH5NhBCC5VwIX8DV2SQLRIUb6VuNWruETVDstKWA3fDXoZ8KjEcJYqSVKhwQhZG3kMLgEY2DDwjHrRLhGWYJHKT43lCgYwT6BUTUgquJ5SqKawEKc5lS+lqqSVQTKtYlb8YFn0V4iUKgiksHmpfFNGeIcETZ+qMAxVkqXwZJY4gFblJKkQoBrMknfFQXa/VcKgcx2tQS6CJ8NklQJKGtiUrmg3SSpqQ6jAfnclw+SqEEkbeyM/dfcr13dxm6dGiOpZtCZ96rae6/Vdiibw+j3lqgjhkOvAd79h35uribqjf5PoGhWV6WtJHzApVKR9h/bnADfYV+qi4+c+3mS1Qyrv4DZXg951em9omv5r2tGM2SXbGECp9jStEUzzJ7GdNIvH9hDYdj5pwEULyN0/QoSDXEEGgFhqu0qiAooPmwI3khgcAr80jT2VQzW9coFV5fla58+lVPkLsFxUUHGUH4SpXoAAdkAoJfPMvqTrOe8oArlm4DWT5+KiCP+WHWt+oQcu/4dMWnumR5yqnNEClZ8CpywAW9iX0JLWqpuQCUFSUCotUtNamgVoEsobJrIsmUXp4YATJSdm0AwyIUMVh75JWRLYSDI/SqN4i2IURrCl8qxSi8iX8LJjqszEJZnEyoubwomoEFKeyLQ0NCsMqPSS/Iib8qcoySt2oiO0gnSWXJGjmNmb+X14bcxHjHGiYROZfc9O4/W3psI+LRsei8JtP9SusdLt8GXSgli0cgxPJk/w6NQu0bLgPlIn0O+13u+17aph60nqIi1aTKGk8mfHYIQJixRjCCtMU89lV6UXqJFRrQ6N/TS1ungwW82N9kYfxrVJld8ddB51u6emndy7dzy9vLC9qeGL9GJgEcKYrGuf7kFrCI09eRfmCzOdNst4yu2A41wF6j8jRiVNaSlFI32pMth9/vpF/PpNit6b/KZb8dOv5uvP8/3v0l9LwjW41GthqFBRMvANg7h1Wq9Pt9/+wY/+2q9/cz4zY/9VbzTeTK/27fL/Gq+EUdHP2I27XeM4s60qGZjwM2+/f/D4b/7V3sDBVH2mzexicjBZni8Wb375a1/9pV+9u5gfYLSyTvE50TpRsxTBYGQXzrP+/uXWfp6doRWWU/v39XhSrQN+ab/FGB6GiBbpE8M0tT67+61vfPCN9wYPD77y+sXLN2+sIP7xP/vn/xoXrpbd6euX+9v2+HD/zmjw4aPH947sDrpviyHbDPmcs52Su8rENhO9etO89W32D9e2l7LX0GTz0nZPm/XV5enF9OJic9X+waff5yf/j/7qXx4dDxbO753qHvQfHR+fvT3rXF30pvNF+xis4cGMLb6ZGkmZHCwP7x3P7u7tdWwYOqwx0t7kwtldLz7t6weN7xh7mC/sD2MuCgcBUmYwMvPyMzE6QgPB4qV6ySw1Nno/k3SRnKQth8aplvOvvl20986HD/rvHY5+uNmeLLpvL6d9fQDjEG66TVdvLy7Pzqjfy8nV3j5BHViWfTl/63wG3e2Gb6MsjNbqV4Q0FnZQRfzZNBasCItRA7ny89fQVrYfjjrhnxpkYywzuCZoCf8wUmSxLr8J2F3hr91r5Oun8vbneL5JcAvKNbRbv2oSZMhSYSel98yQ1gq8pghi90SJI3AQC2qJZ3onRch7NEfqIb4Y9+aLqVEkhvnbN6/5+6HYWp3QZnwVVndEoypNpsPHrlZ4fFu2PuYHg6tbO2erRIKfucWaIZnZ4ce2TuscpYesWR6QuY3x2BvpdM+zBwDoYtYlv32UPxkLBPBBihJWvtAy+l+LSjOUYRO1GBZO7kngQawmgTfR7xqJ7PXOqXWNG2W5XR8S2nbX7k8IYxiP+GUudcYwi3BVg3DxZqYLdGHH5W+CjfYIbhrJexoRu8J7Zp6ytlfORogvAD0pQhRPj0MZNuZ/p2QIbTwE85hGZT6S8YE43GAZD86GU4DYPDeNiuHgD8AlDQOjrAMohwAXg1JE8DdWS/AgYUbHJhjRRpFsPhyljDDJlr+mrIZkYhDdznshzvCCVtnoL+SMSqHUXRi/s3ykr98fnmUBq95zWjEMEprz58R6DKvogEQudZtSNp9ajiSBWA5900iZXlcLNrAYkzo3SlVl7yoDtGrJIe9Da/OeYeh293XMl2QVTkGI6u2kAv0JTX/CiHkcE5dIi3/kkWFn4GFQOhBmSAiMf5EmnYTUL8oGXvik4MHRM3KnlkUIzepZvBIb+JbZUME+gZjv16gE6SKAajXwGijslidw2PY/TaR0nBIpqaKXwBUKKT95BQkt0NaboIzAxTkvNnQSKR1q6FeLnGY9TFyrYpIyQMEuqvgxF0N9Gn5xxaBwqkaarIof3RkkoAMcbtlljS2SMeSgh6PDeBXRb57rf4Lqqo9NiaqkVodm9OD6W+Anh8qoibZ79iVpK332CHKBrJwNxApoUjWPN8+pnAK4wx+gygXO1i0Us+5CdgmFNWh4r4QJD7JN7h5CsoTcRMv7zbVjgbw3yW+A3ES5fvDl9hXKFlCAPTcv4UM0Dh/485tix4uY7yqucYQAI1Gl89PwWL6GQg2escskL7UqdvKq+k8xIlYNn6fW65tkSSjPeCRxTSA1inAHFN9Jltj1CbhUho/YA9LIfV2CaFMoY1uaCuCUoYQjkMhM0sRjwTDULmQ+Z7oD3EtpFcv0L/rTPGFe//JHfQTFQk04htR9Tp7aiIAMBgpIBkoZQTK9juSV9GBFKRC+uBYSUAWpVOgX9U2fhbOdhMZlGBZnx+Ul8w+IHDM9C1YBgQfM8r94IsPL9r/nPp/TUyGvu628KntwUn8Vqsy7dgYeKQ3ZCypglagHw4a43iEkU9+yk3BNLGbR0AKsRaia5q8g2cOfDGZiMkJoToK+D1DwMxqO4MyvC2yYAg6ml0ubw4lhj9hhEV/SeKaJDH2gHdJBNdyUt5QjHSWGpu4O1ePsprIp2tazadCbQcbUTDvbGhofzJx1TZeVgJDZH+8rGFBT+8wvFxM7/gVpKzWnFkGkjZCxqdss/5Rpr7Ued0JJ+jG2UYRBJBrwf+FXCAlF/6+r1VPoqFVn5iz/1b/9l8P2+b29B2Nu1E17b+/46ODudnOaaULMFOybWUMYTAeeBl+b8r5YfDLsfuPJ3a8dHJsx1Xn29pP1bPLg7vHJSWvvuH1wcnBxfimdWWhZTZLaD2X50nUCD1b3+wefzVjjVrj19hzytdxbv3p9liUGcrRFYntvbTQPN6fG9ep633Qw2/358eHB0dHJP/r//PN/9Uf/tNMz4BvuGW07tu23aefJ0Z7tjAYWagztFWTjdovl7FUwH+SQclfJYuZHG1BQdguc+49Oju4cj6fT7Eb6S+/d/Yf/t//7ZDY5n7/99OWP/+P2b2NCnPmVD76urX3zZn5+vjjcb42Gy5OH97/y/lfZiS/PPp2th870tb3OQWft1DgTdogFPWg82hSH49Wg/XY5u3zTvnc4PDm2wSyGiUkSPsu4AO1oKRJWRp60gMVUZTi2e2MLT5hNVF7Vlujrq7fT2fnqB7Y4/GBEt1jCZIaJbmsaV1tvsDCPT/YP9/ami+lodnR+9dnR0Z1PP7Np0KFqTf2rErdoL2LY4zO3ZyHSRESjp4ICDAfOEI7rIKsva1yX8uC4jT/BtpdRl80VJUsK6uUmzEOUg6vuuV1/q9Avu5UaEj//IPBT4hfkwBMNzhhF5M52b8+iDho3Vlo0LfWVxiCiST2IWuwnWQae+4PxsOscrkxT4d6dO/zCSdVZre4kDNvTnhc15qmnnOplcCQmSCPjYKEXrsPQPMOFLOhSVAcg6l4LES2YhZpxYfjA2i3WC2dzikR5qneVX/6mJBeSXnZDpcK12tmGJhUOgvYoJZe0WAQzl0gpJViAGAsHqNkRXwWD0GxxE65HL5UJ48pLXQcQj1XIXK0NlSc+hFYbsiIB9rUG2rl8QqOCacxagGdXiSJn9F50su45zZj4YS/TJU2ijZQPcsaLNjBaObZrLOpudqTIDCl4GvvrZDlq9kLdmt9HkDMia7lQwptGUtNmRF4OOI8uUAfmZJmmZc6Qmq5cJTPzUH3EfK9yZqUg8JC1h5COTQpbehy3ZIQIej4jVMgIZFoQmj18RCgQM/ZM2IfmKlddMWNCBOscViOovEWFpK8GI4wR8Yo8hBhNtzbkFVa0iusjxBYiUZBy4UI3BHJp5ko6adku1YR3jOpVBZW0hWMqh0pdEoii1eFoOljqFvLhJbjIAAs0mYAdwILIhcCSWXFzJap3H/01uBf6SlfNokCIlh7OI4BNVykwM3CedNVRAnuHWOIljYJptqPNKYxUvughGhRwc9jZczLLleiBSSh2r01wlTgpESdYVsz61ESsjPKezHOLIqMxzd3YoVOJqlKQoxLtfhoouYuyw+Pd03VQQ5xbkSqjJj5qXEcTsAORkIaelfN1Lk2mSeFfokbx56NCv7twWBP6LshTc7qYh9RdJY6VFwIXIGHXeNyGFRCV6w61SormDYB8/UWuyiF8BFhoW4RONnip1ET1m9dP6rtZbuheispOLGQ2ErjDqeqjKRy0U0t5CaVSa8ExuTTVHN7D7w3XVlcuqLY72bNCpKQswysiK8nqcQA4dU/RVu+lhN2nJcFlN+YdsweNphThv9AsMh+RAK0IK2Jp7ii1GHZ0pimfGU99Qz+UclEIKqzqHQFCzFL1ghu9ELABF2TTWBJZN+CR0Sk9r9z9+syYFJQWN0l4N7ggMK1AmAqkMmLd8jnlzIy4gjJbngrnESx1TPFlf27yVYOStbYvNCHhMOMdUEqaUXNAH65s9ahti5bMWLc9Fli0xJIVbB5CkIu6j0DXix0urGccsgtX+hiZXpA57hqu11Ej7aEMlCEtW6io+b0IAZhhuYIAswEgXZ1syhU9urMqqsVDXh8zCUOjx/hT2lokYpLDWX9ko0YD9Mz404wtQCn8pabMzue6LdqmLhW8uk+aJ9pPJYZYykzt99ur9+sjvPUKtPjhU+3Qtvfj/uGzzWfts7f2gJ7Bynxp2r83THeIAfDg3sMXLy/OJuftNffx3VbrFHHSSiqK8604GUfd8Xh2rluoAdJ0RV0pDuoVF9VTaHlz/aS3PoMruAC1P3/9ZMjnv797+8VHFSpN+D5kq0puMFSchCKXFpFHS3s6en02/+HHF3sfPj45GWyXS6tzD/a77GaHbW6XdzYW8vYv8WY3C3lNaZV0sl0eMI/OZ5aBtx7f673/6HB8NB8ML/7u7/y1r3ztHgNyYJeg7CGKyGlaoYFwPduJ22N7YR+U88Hgve16tpi/vZy/2ht8rdN29u1wMX856CxHg3mndzRbnsZIWc0ePp6Oui/vHX5lfvV6MPpgOns7n3fGQzPdl3Z9evJg//Gdk/cfHN8/3r+zt3e0D0kLGFpjlh7bePAmDoX41Lvt1RPI4xMjALYBSHPTuerPZrrSy/bEJPJv/PLB7//p85fnp3uH+//s9/9ofNz7zV/+9Tv9o4urK/sWtvvT+WT5ZnHx/E13czD47ccnv3X3w+nk7brzaDs3ffyqtbJqnTUzzPwE7tDO5tCoEc9zp/Vq9vL87Z4xiWy+2bWOh+mjlTXVxIU40YqpmKatiydlOxzOR+P+dv54uZrYbGrueDN6wi5s22+M98a2KFobLSGMvQvnEyMFJ+tQee2RluVSJLP96Phb4+ODZ5c/3GZg7YRqViUUE22TnX8IRbYAiFKNZpB3tkLCG/Ex0CUWu4yNHbKaKCC80u4vtvOZyXvEgaBFhSZR7mGy5hbJj4TeiAPeS5T6njhfeimu8MSppx3Mz0cNcXyvn2Lp3gXjiQTbfqK1GWfb9ZxnD6+dsRVahsjpEnjaGx7C/vvf+/PnTz9TT0rpbHHjAkwt6nLReWrBSXtp7S5+Kf2cA9drPkz8PuxrkGEAIJ8QfCP1VXlsyoSmAqm6zZjOMoeEKjSDEeUytJjlSZKAAH+8aRSoTEpVj+BNM0I/BmBTxJQzF+pFgfkTEo0eiidAyiKy38BVSfSzEuuAZpqZvUrbdqkiP3ghLTFly3ymtdNmbFrWNNOzGYLQ2MVAh4Q5Sylp0z7qH27be2+5VtLKZDa9ieLR7VoXSJTVWo6r5WNh6+7zmCMsVwgv3+taSWsedqvveMDUV6xXpDlDxu12n7omhRFKJ2znCIDIfXultTAOa3DVvhX7VuZk06TtZbd/1wEsNmiyeZemqZPJ3NvunoHZw621OVXewcZOrs4Yf6GCOp0T21vED0TLWM/l3MbOnrl7vdZrCq3TGhe9kCxGiOcUxtw41IgDqwbxkdRTmluU1OhlwkA1x1SlsmioMQNJwwBxVIlWdRYuUCdqXwMLuvNzjO7E4kXkfKu/1HCitVYPYhcPT6nEypXKCDIabochWObPd2EVLjaKNZIEvlVKj9lNn4RXvsUM+SrH4BF6+03bFS2A/YpRw6HhbN/lkihqJnIe+cxryggx0BPmLwaJ7IcsKziETkDne+LTXjY/2GWIzXRt81FMpcUvVAyCyiAEBNl8EFYZZuf9SDbqX12nKKmJFFCO1FOyCFx8qG5IH55OZ6GILGHsr6SpghYqUuNYuVP7HDC4yIKcGlZNTukIiba7ijJFmOsQv1X2vN+exy/SF69dSFFglyoVuUsemqUooWBwD86+psaah6wTSNzlkypAk2wHMyE54epzU4Buvt0gkrLXlU+pBClCi6aGm5yaCNcRg0qi5D3I5l4/TbTP3X29SVYfGgSaKhfQpK4oucX8jtaLCo3l6TF9PdESMZzcZBtQxZUYA4eFOr6o6QYfn1ypp3yt4PhXQr2ygYuO4QnpdiUQKX1fiYDzwT/I5B5dF/7LROFwc6mqIpFIkNYwxGT1EajiJL9ew9wFPKjXY5mwdBGIcYwEC9ImKsjpQsQCzZs8kmVKixErtZ9wL+uZAy/+7NIIck62kTlqQ6sa/IFwMJ8JJ7Qz84NzpfCJIFXJjIbyOlBPaU9onsEqh4jCjdMunpdsNBSZUYbMxaKV03Yz/eWPDHGF4Em/cTpWtLhBsJkQtDHTH7gqedWBVLC1ZXq/M9rbm1ly2Bs4aREBlCilTr8oBEfbysHbTmuA4mItMLgb3BnwlADWFD/SG1TSxWpyJOYl9Qmuaqx64JFDT0mMsWc7oFIh8CuHjdxpUUXNvaqTeT9fzFhUQAytNoWMRWle+J5YRrgDdeAPpSQYDGzZ3tlM5pfhXU9ZALnEwDVK3Xt9ejqdtM5fT68uX987snGS9Kx/laofN4T7sHf8H/2Vv/3dj5//4R/9oTQFM8UGu1ijqf3/Jd1D3C/DLdyvRqhdfOGwZfzafnn1arp638rVu0e2OBxbRJuBIwo13O4MIEy3fvj45PH9I+snqftB++xgOJ87XHc1O/rak/uHe0/6D+wDZEfFozsHyKLtseA71iO1gJbllaHnNHrbxd6bTxfDIQjbvcGd3mY+7u139+58+uJivOrfbQ/1Au8+eLJsnzx/+nK7HNw9yRpj+7dOJ7PF+uVHn7waj8dmqfGcWk17/3BwMu4eD4b7vV7258kho2l9sEHYNOvhS+7IPknDQXh5YycgAwgbrl8i5fTQ09Pl809fjnrmDx2SoVFn+M/+xe+uB8tXz17/zv/qt/bHh7ZHt//P6urqYjZx3tAnL5aD+Ysne3f6C6fzro73jjlMNXx6tRkMS68Uy2Eexk1n3O2/p7luH7x49SNbpdk2NCuLuEJ3lgMGVk1ho+vGngFKNvF9xvUM863t0chqXK8HhKp9ZU/LbFSfbXEZJ/4ygSeuuFgc8eUrGREeDA+nF6sffPvUYQhGXqIPUAfdZAfByEfIZapc2DhaED8TltLejuLmIjBnJhpHgdKXjvagDeOVACK3ULiu+r1+qeCS0cTaxbj1I96ON5tiN58C7vb7rQS7CMEvj9dCFzG0J49TlRVraeeufEvjEq0bdawIKoP+Gw7Hf/Cvf/+//+/++x89fXr25tQ2QPPpNGt5l5ur88vemAVqzxkRHdHIjG02CjOZhwWNOMGMQRj3RkoVJRzxT05N6UpPRAUjZArBIqEXYq1gflIkavno29kjKE7w9GzBolOjB/k20pLV5VuqptghWjEkSbNRfqD0GjBN5SSWSGIgQbmmWaRDnfSFVsMBckWp1GXayrQP0zBP2J8aTnVDNZO7fCb/g+jIlX18HSTWD+cx9s1Ak7PvdkyKFowmkF8a3wY/8qRtiAN/a8ejyFXNS4lvXzqaQ04pGa1fWwh4bVhLp8uJj6aAOHc8nJ35RbYVc84CV4yddmy0xcZnz3VNYms7O63d3dMb49rVZNljWv9en4N42ynChnUE3oGDOj9kPSd56OljCl3CrIlwUrh9z7KSjU5Iq0hrbHtZKFS4iISCyosMSkhX6BBbmpN9h5sWZ0Wo1BrKSxJRDeWua0g1Fp+rIUUNP2CO8EraxvQM8yt+2vRERaJyhzMjIntFfqHBLjzRzGYxJGXHQ06vKDA0V70IXg1gkMUowFFlOLy+g5vPYZLKr7JSJ6o7akFwag4uSkxGIsA4PVaI3n1xT9oDJQgTFB/GqqMhHfUWR1mAJziFhAW/WrRHtkyEfzjDXhHBxMdkxzKRQK7IbSZW+n41XgOCGaGQ0LI0IhV6FdM3RPIIvKTu1TUDrwiXcslIEZRAUVJYDXyYMzyoqxqRZCGFOFiqIceOVsKCXV0RliRPjFvX5152UW99bh6vE4Xkxf8hVj5BMXURIN6hhpcKg4Q0oJNWWRLahBSAJG4ugAqU9vjmSpp6acBUtruP6TBZ1FURzFZEghAqH3eJmoTePdhJ4L18qjN085CcKre8vLtu8hP0+c+FekITBURmb2rGb8PdvRfOPYkbJrWRTwqroaBmUu/hOsnUUPqFasswHpVRIVwtgRqpUME5XMeodM6HKARC17SImlWVjdfsSAEO/RZ4aEBUaT49p2IX7Dh8Bb1IWRCIEHqjeEUN79Z5nzmixUt3j12MNFUa8Zr2Ql5Ewkx5lnWqleou2iJuU+WGtMKeIUD+ECrNjEwVNJkpfuXGW+YvfqV4AySgY0OHdEmqT0FRN77ndYvbm6KKCAWvlB0aiRV4BDPOFtTMZnMZVuGg7g4sY5WTLW+IRKqj8SHJOr3qjNLGCqjKj4J1iG0ODqRerRbQmitdazm9l6K2PpNpjPaIbxwzEe0sFqzjQrMljxn787ICS/w0P6Ajbok0VZBhXtQm5WqO4nR8Oj+khbzsa4uqFxZDg69gKBEa8bUrj41cM+2+BDhzc8nSYrZ3sD+2zhbh05UvsiUzLILhLWFEvXkaVmTkhM92ylm23bChpcU4JGkCy9hx1Ge4JMULzeN2jfdq9Ob1hQk/g/4oegoDp6VuNI7Kn/UGjmziGDxZb235bwtwFdNfLC+c9tUfT/7W3/2tO99+/aff+SNn0csutVrMWLwgq3pN0E+5fnFP/08CKN//tnum+H/BK3yQJMgfvmoulUJ8uNNs3pVm4PT86tXZ2Yf3vzE+eG/dfvPokXH8tRM3t52zCJ294bubr3z48L591FvcbxYLPzrsdq+uNvsnrN+j7mA470zEtNk/Q2q1uZDfenWEtKZSqAPkknFam/V8s31x7+70b/723zjck3fvajbaHz/av/Ph06fnb86erjd3/uDP/sWb8+HVbHncv398OLTxp3odHY9evTz7f/2Tf3Qxv+h3DxXA2lzrlX/9W99aTy+ODvp7e2wIjQE+o05GbD4zvjrrb+AWpmtCw0q+m21gfjJWwqXKMsh2wPPLJ09Ozn/wqS7E0fH4G9/4xrN//Om4d/d73/9M3P/8d/7uYvFsMbn6yqPxB929ed/eRuuj7fjIMMN+1zm/1k07jHfZu+rYkz+uAsJGW5kAYXqU0TJDJ7YUe97fy9T7afftsnWHcsHQFlSUDx56ECT40ZjbntN9ODVPeisdWnP0acWj2eLcSqR+e8jYH6732uszywk623EmpDuOKkqPgWTZTpShwYfMxl7PRqPe06ffmy3etrr39R0wKgvSzLiZs9UItIafl5boRtF59S8aPJRiOwkqG6vMVW1tFrMujBokIkV4w+3XDLZjrfyEzcJtN3FufauvNx92D0nQcKeARpQasO/uag7/hJcj1zYQ2wxHWKv//pOvbrZTzoeiO7rG6gwQlWQr/l7fVjsK+tGPP7Fh6OM7vzpcnr7e/Blrjm9FCc/fnt8ZPTTCE5W2tcOVlS7oyfDP+EhOc1USVEGXTEsLhWI1d/in5cg1EJUTJRrCMxsv4whbHcO21b1SKkRTuWmzYa5mYmtmHQiuREOVojX0ocE58PNcDZICEBqqlaIRV8cUJrGhAYIOdV+OKnq0/BE2dbLvMiM4TW80G7A4CppiwkI1VnOWVhPxwp79HMqNEWUaFqI3ddnTk91VV7Vujo5mXSkgPZ86gAH+CIXTHbTuK+FpSEURnJ1eStY9lovZb6oGxo0k6t3eHWw+0BG2y+bgdWfwwFZj3e297uAyo2fdt6t5d91/te0/RMz2wukeV4b6lsOz7vY9hwNsNuOzzfnzy4Ornl1ERzmiGDWzeCPZpldtlUOOvFOPXpQlJI0UZgkCHNa2Mhhn7wcfQiL/KbeKRnsoBftUH9c6fW+sDY24mIbxpJu1nHSSYqY+2tsD1KBIc/ZvpCJzhdFVx8k35s7OdI+hrBoiD3GKwECevbdVu1D3AYbyvW9+Zad3hrjys+cslx+/SwiNOcI9nuotDaBiFsyYI4oeOInYsAaY6A0HNRAWjESkuKmGVKLI2kpEUTTFDw5JQLhScy6KNO0mcwQLhnmFVwev5nlf+0d9yWk54lc+US+RTKpH5yLNazoA1WdK7nJQDICDlVsEQc7C8at/1FAMvTT9yBdLAzyck2Jh6RSt4ucOdCAwfMLIYHe2E13WzKcgsLERUtiKWA95wuM7S7gJSsiXXLfiN6f27ubg3E7kuXCXnHXtzXks0YcqqqGoD6F4Ubry8NJA85CPkaxI+u7aAb/pAHiveHUPa+ZN5SeT62RNmgpIgaXw7AFBpKjwhAap5kO9vQuv18/dfsq3BDefwn5V1+y/eLqi2+LTDYNREjwM2CUL/7zHXscKasnVZJOCqHy+qGBV3IkC4eOY/mmkY4Bn7jieKKzLo1BZgkzi3HVeh6Z8ls5JZzqTUcKg2MvHZBFsmagRzUhGEC4m4x2IKOYQu5K9iFHljj7+0gImdrGTR7yHeeGeD3GcFxVUaigsvEpVtKkshOYSWlAxptpXz+HiqAtOiLjgYiy75UI4/6Mu9MijpwQLC1rAlkgFVuQ3TUXkqjdg2Ppq0qtNTji6Mz8n4MTIeBmFzyqO1udsSddAXGdxqJXaeZ/FIMN0zvhzufRkEid3xC+8pYshjQOSJu3VmDAaBDRFg5uXrYAGSqxPkxq1FxqvoXp3ftjKOUW29Intkk3zojrXw9Ge5Py17ilAJJ8ZYyxVhcb/NbmcKpTA5BuJRZ+oK1Pzc/B7ORqkKyJDrtRS6YgiXfBH2LIF1IyWO6rLLEqBVEbITOE2UYXncN801YPBAYJcXV0hneGAIlJVAjzwsUkO29FwYM7K97bdcy1ciB5WjmsoE6Jad7W566XDZepKYxhE5VSXDEPE5uU/6F0exRc/L5NdvGuUKg0swzBtO8+oiAw6xXC0Met88eL07Kp1dr7oHdnwcu/YpCe1hd8MRdPnmpzl5eliPiXY2T1peIVqh1b03jkyfyZWSloLfv60j3RA8XO8pqFJTBTVjUH7m+y8s//3/tZ/9uju4/X81GoLtq4Ngiy5eXDwyAbD55eHncXhvdHdh4d33r/b+fSz52pvb//o0Vc/+H//43/y+o18OR313/uHh9s7g+0HHzx++aNlxvfDo1mXohUyAx8PqOIowxBAQWPKUTJWFCi06jbDbeEg0aVuIZf6/nrafXj0+P/4f/hv1r35P/2Xf9Ze72eAqNP+w+/8wfJi9rf/k7/CSSnt+ND8pIPldtE3j6K77A82BqFmg5H9AmmvqBQeforI2l/2ZTwGthYjl53ZZmWUr7UcDUMPRxxIgG/DujEF4Ro/HOWgQeU9CFGy5pRtYqaDI8x651F6zhxwvLHtiDYmGzF6lJDqUCcKKBPWJHMvxbb4wYlrF2cX6/V4szqIdeL8YSjhc2qzOChpoijQizUMKV5Duhm9SFO2B0JCc9mNP8TpYO1ke81Dnnip12L8tDVf5MMien339Re5xAqvVrpK0dRYg+MOBA5JNabpgDWlyH1zcHjnv/0//7ePHz1wVgJcI3zBLilCjfzgQ0kyJvz3/+v/Cif/+HtXy+ni/Kpjkn7Z/93F/Ori/PXo4D7fSXeEsDwNRhDR1cICO0BF/9Je8mNGBmR7pHsEkzL2BNCgDfLoqtdHAMhNbJaq18I3ZdOWhG5lnuS3JnhqtmIyYh3+kOgP6YuuTY4ZUEUFtY5xY+qEBimcByXMDNXgJWElNffBFmvpVCROCIEGSUIyIaSyS2PRWpWUjZsKT9MNSpryAitRkxBC0YwySmuGKwMzOVX+KdMNMrEOgwVeQsG0nv4JKmTjJ65WD0nSAKyXJ63uo/aitz5ZbXVlgxxWt2mqCW5aHRMEdcO0LvbEzViX9mez7+wYRqsM7NbrwI/LdQ5Tk2HjnIJ/iQ1jINSArotE0UnucBGorAnwSBll3AFyVFVKqYiI65P38JcPWfsLAoTWvXUOVwucxGxsZ+IUB7/mQZOrpIHiQVAyC4VRisYweh75wjppnkLCgNFWpUoghZVkik5eqo484Vf9S8NT5gDZXiQkDy2bigTAM1tiVytxrcTzLUeAUzchukAkCP0T2GAV+0oJ86K/E6tDPiorSoX+TjKFS5o8qXBPARYiprLzL0VMUN2SS2KKmoY8rW4yQ90QK70vj6nypl+R8pYcSQQOipQ8JZPs91ekxedVdcE7OUla9Vg5pXRBrQomWuoHzKqUPOdPhAgLmpCxNDg3FElK/xs6FnxvCUoxf+Kebz/tkqC56iH10oRExPIoU1fwK8ChVV0i+quvUE3QTdJ6049oItaHXVDFCtgQo4hfhfTIqyGTELO1epSPdkJN7Gtk6iW3/rNKm8eWs1FTh+ZK/vSLu8qV+ZQusYFO1q3V+wnI/P7QnBnPPsJUmShZtZ86yHuZ5brF9GuuJG3bJziGxqfhlvAWcceEkSGCJ2Gsf40ih+s2MdtdOw0Hnp5BSKa/kQVpGbfqxEIURGyYs42mg1akhEETQZBB4MfBI5wNE+wibkmUs0UzqQZetWtY2b8poY4s/pEusHB1xinwcLnSg2HIHtIWp0PMUwm53yhGP/6hi1Z8vRnEDCZcZn9W+fysjXcaq24SRhQD36WljeQG6QIfuPRCyawAyZUxxNHgpeFRbpXg/APz2Pm/SwRpP5SnCgTJAH0bksKIAkrtmw0ZhcFkSNYZXOx+ogfAixr87DYtv97zCI39XGbLnhHXAKLsiDArJV4tjp8aP5ElhNuOAFCDOeo0pCH7qVXIRTyj8dFYuyJ3nHMvkrF9hUTcVOkmVnMkJnZJVYSocUuxlqKdauuZIofhWlXiK191ICZeiRkYihNm1zM0IGB8J1iGoxCCPkm5xMda0PPrSNo+69C5tdP5vH18eLTevFWiFBOCmeKsv6NBXQy6DzqtQ0f/JHl6TqwA84eYUJPuaO/i4hyaWNy3tnNP1W/3PCBkV2ygdv6DXLdWFIRPkl9R6KdldrNaIOQNKXb3Oqu11TqXnEsknJbGBX0GL169+eTj98Yf6Me/5MPZ2+9MFma7pKXAv3hv3BuN7EK5njrgcdAz8RoEc27utHsOxzUldGZ2/d5oFd/o5i7lkIWp6ZGGOIWtdm0Z53v3wjyD0/OnGWffXMIhI39Ev/uGQ/Jk//K9e73Tt+ur6bQ/PqYVHjx2UPHyH/x3//h733tq7roZAVhN/S8uWkcPH1kNMzKvyGqXuBsMlGXX8bCS4mWby3i6jE41ZpqCRvAi+yKYcLDPe7fpLu4/uTe7WIwOj1keb96+Gmym283z1eKRbfrn09G3P3pqnOCbH3zr7gmGGW+7s8wz2O5te/vOKeDGJI98eqFicLNziKnNV9wjne08BIgvRAJt9nCY+Qp7A9vXry7XvatVe9Zt7a+7k83W1CNIZlSTyJqWZYGqRemZfGeQ0HSVzqV9bNu9qVnmi9WRsaDNdmwV8OV0+ep0dn41X6yds2azIF5qVXM5NN259/Zqutofm8xz1dqScRpCXUTKY6DUTHdVg/SxCKGeQUa/kUuuFNVC3NA0x2zYDwFtHctQ5wlY2h0t4Fxb5MzRctdXNjUSkk1ZohCUpTrv15/zu4t8w5/Nt/CI/2rmJHeRcGz3LTBRvgmxMbPnaELWABwhbU34N77+jcGoF1YgkvRKoyPcY510B2MtQrSijqve1fT85eTyeadrCpDNkWat3mKxnFI5tpydT856B+P28lEam42dhQzOODM8ure0RA55L2S0Do1GoStSVVATjhtqE2q9BhGp2gm+iICIEns4gkCxxfqXWspqY6KxNgO+dzamLm0ApfGJsix7Dig8o/jyosMib7G38hMdXzLta0gR8kWVhul8DVJaIFGEpNazx138JGlrUsls7dQztHT/sxkPAEDR2YDrL8WvhOxF+QKjlUpAGW7JMzgICQ5NzNAnCfiyUsLAS6QkjgnoI9BROMzwgQGo+XGfPRBb97Jvzkv3mQO0V52XcXANf9+QuLOxexrSzmc655vOs6wFZhWY7r/6ZL+9Pba4zXjHxnZtoS/oQU7pM+00rVE4vbJVX9g3HWOaoBwUotqSKzalONDMn546MBmVxvlh7awAjPrP2T8tyw9I/LM0l2xaEtT/NL601QcRelmmpKm10DYg7cmRroey8QEgByR9CwMDHHeSqtG/gLQRwRqDCRav5Ke6YytkvhEEbXTksTxdbHR1uXgQ+F2jLlgdeAnS/oYjQ+yG4HXPWQ2N19mr3FNLMu90DUUqwEjb7PwG4XVEg+a1OqLhZDkDSkMql+6Cvm5aXlC8uhXNQmNEg4rXNCGRuzCtOMYEivhBmJpNjyo9z2hcspYHsxCAFZxSl8gWGzXoAxgq5SX3MGlxdoUJUbO5qrwUWUIA0uynUQ5KosvfQ5KTljIQknlZwoKTxKe6V6zd003g9aeb9bfvItw8NejVygHwnDScAMURQdaupgw3eeWhJCWIV3UE0woM3yTFdQegAb0L2tEhsCUoylzHriRFh4YY3oNBkzzRr9NWxOZWYG695/F2fpXs9vfgmAjXCdVx8LfR157RN11UM8lNx7WEp9rfTKFJrfiFbORNhcXgs4WTSeJ2YgkR4n2uQjeFZGE09ZlKWkZlG4Iq6Uy1RX1Z7GOqX6RQEeMJb8jhA/hBL3rEPyybF3n44/vGwBgursFoqz7PJWtgGAsFG2UYQUTsjZXLg4Cb0nSkc28HkSWPhLfS2OGqgPZfhkUTdn/okCAMmMBkHF4HNtP0oysg7xsutH0B06cgFJcEUAlA7H6yB0z9KzVCrkOuyj25FksFZ1EKVyqhyhgrq2lSKIIyoBVW/lH9sW3BTfuXH0vAIpZgJSt0lkcyKd0QEqBBNpCLK7Dm9aQaJDNtNWSKd1KqqLlMaQ3Ojeq5bnxAS2jorZcBhQh5MkSVRl7T96BKuC1L/UGliowMvieHVBMFFDJ6QPGQUtUy4PR0uYTCezFeKNXUqWGMRuXERW1VbtI1cShydBG5uVIp9pKx+0enO7GPytXrhw9PECz1HQ5IyfxrU4scrxa8dq8UrmDCGGhz0HHkfczz6sWblEm1YqUQpEpxnZHfJuhWwH/Ax18sL7HqCoPCr3g4DRVhiS5NhTLEuz1LXZ+d//ib/UcOgGzvjwYHx1fP3hLr9ML78wxPZ29u9FIhmUjGbTdZvOkMnCbcHu2TTUZh7DPVG/KnMVSVKiSz4DJ9lv2xzNLYUc+BueEqC4KzeYtBoTQ5xWat7UH//VHn9XRxxn67uFyMx2b7HP/we3/yb7/9b1glDmZFeps54rDR4fzOQzC6tv0cDfewrvKoaoMW08mVCUgcwzoM/IHh9ao2/B7GSAvhHi41C3yxWE8vpwtz+2OuDo/Gx//pX/8vWNT/5s8/TV+0O3UA35/86PvPXpz+N/+7/7VTfnudvfl8xpYH92o9cX6YoThT6+3DSclUe8NcLp+6O3SjwkxMNoEND/OMoKR9QTlQJDSbTK6sGdUA84gzTaavGkdWTgc70utWcWmNlxcDZw70Jxyjp9OZFcT2p3r18vLl23NUodU4UEyGWWfjo8uWntosqri/PemtTw3eYdvscB5NhXOjWg0qBrcIHhWEDehl35GRs98RTTYQHpa5EJcla9j+vdEl0TE7IS1+R8pSX0XjuoVLKP5k9T/vKk6VNHJZsNIDqVoLN0fuXBujeWfnL47ah7woLuPSOjM+SE3rKw1LhC6lMDCYXbzu3Xv4w+89H432hqPB+RX8TBDPUuCjw7350vjOIW6gZxwJ0GgYCedcHEgSEwrjJZdkkOHuTNJOxQZDTEVXQcKLkpdSkXWpFQFoHW5z7ZRdtJ26ljYGCk4IudLQpIcTWpZyjmaSZcqbjFOs5NTYNk3GAREEhIWp6iH8E9h1QcyvOBBQHx6CizzSTIOWdcG75itlRKyiYNP6Qslb1ERgvwNZDVOggkCoU+7gGvAJTemUrMkXwpkGmHYtI3AZUhK380aTKGw5d8zCzNoWhunQIFm8ifKmHDpzo8zxfsUXz55Oj6SvLiiXfeMsHceW6H4Oltw2RSHNDVaFB+4NleOdpC58S0AQDLEltxpauUKCGNYwhSGE4V4PtEVGB7ASBW81SKRM6x3ZUaQYsoBJXl26MEIIhG4pdZ7SIIcV0nOjiuSNPFISpmjB4JGOAbqmoDgI0iEVwqU+UgR3f/7XYF4iqz6e0HyTEQDKprLSDlcCOfsSMnj3ueII9OBDgt3zvvvNO0Dx/WfHvbTHRiVADasiN7tNB1h0fZuyRaIhCkvQFS/6OsKY7BquEwCErECOKkf0LDRMwYMvcoQgkZ+g2QRkHBImbjgkAktT+hR6hk1FDlWb/mSDfRUhZQjQJAWtCBB554TBLEqUVDsuh6KX0HwXrXlOWC4Q6ktAVsQm+C92DybXicsyqtcCDVC+yDsoJ8hr0MuLR39Naa5zZyAmQRD+kguYwHCTZ4q4A6chNQ8+SZLNyipjfZ0K2T1nZKCBaDvIPDpXT+SfGAfY5brz/TcY7FDJp/6n4FfjERzUXqaW8HU70i/jaTr+nAmKUJWgmKoi+1eGq7o9eyxEXcYuxF1Ro6GTao5rTIElilQsM5sqskYCIVpRCq0gLAmgYcRUfBrKaGM8GonBCaFOxL2xk6vQoiUTAoxFNiYpxfaM7gtjY7ykiBxGDH1JTWW7yszp682jMTvmMcum88YXkRu08yxBVUDDgcTRW4i1PBGybb0Ed7M1lybRPLF/2ul3pIVNpcNAkdFRymDNQKdJKe44ZMiQMnL8QKyafxKnjMimEHz8EbCUtsQudnXIWQIZKUsRK4eUrkkWYzUWia4NQyKtTnQZfBEe0v3XAsOYpfBLAtEnk1NRM/Fi6viuroJ40TRjJjknILoAXqWFFRWM2Ifcs3dM7teARnO1T6mTzDKFQ9UWaWW8IDevXbUNyZwqLzVBaUYQwg/RNSqqSF/E9xzCc8uF2AkXgIngplD1ktpHoBQMkQw58OUnSUYA2KxG/N++mLa+xpSyypn280l4GGvdm2wHc8uyUzZByGVhs2kf7XEaC03SajuZXFpvkC6odO2zGHg40HP+/gNeIew1+Ob55vU6+HO/16sFrmMFxbBb0Q+yKAbz0sYJUoMZPfnRs/mvfLi++42j1mgfPcaj2Xr2YLqa9i3ysy/FLHugZtcK9W1xBJrYv3PZPTtd9IemiHxq2MDkm3Z3vG5PLOVZ9T6L83h+v1aMNa25brC2ofxe3QxXWb3HvF0azrT152zUmj/e9K/2H7x3/sM33b3hjI7adv/hP/wH3//oo+zJUn1uLv+uSUebyX7/yZ2TB93O8PDwXrczo3wYNG1zjOZb+7u/99X3rCYMT8USiIBgFCXVrhYPYi5+BiNdM5temVo8n2Rg7OziI3vFXE1mHz4cHR58+NHTj//t96eG7gbd8Yvzy9/9zg/+5l/7yv6ehTXds/nV2caJY1cH/cPBZsQ9b9QU6FV3wqsnm162ildGi6MW8o9lEKX1Sa83zEIYUrOxvT83tOnn3MBn6dB2DtZDngfTey6snaj24IVdtawwDocj16r95vWRUanVcNXuDxxDcLmQw5Xq7HUfUnTqqt/jZ3l0cRXrfXR8NG//YWlEnuwYmpk1meYWw2dv+Mz9yWKdSG44mMhEw2a6tAE+a667tv+3TsSpwlRPTmfLQAdNgpVoyhQpfJd72JLvv17rhSJyxaXcwH734+nWiFZFLv6W+HZ4WF5QAOcvijWNRdQ/NVNLoZZzQTr2uMNEgngBoaUwNgKgOSaTCdQUZTS8tz/czC7PuqZ0W7447JsKphdqo0ijWaOhQZVXpo1lMqOT/tZURZTzwD5L3OHWWmuPgkHZaLUqw/gPVMqlKbv6UhnjMdoyKGf/UIjSyA5ViZLS9Kly9pzp1TWcwutMecyzaX12vMngecqocrBm1Zk8RSGnKVN0EMLlPZQUsR4Sp1HmqYWI+O4nGpvYpx1NaaLRcJ03LRD/K6iphtR3PotLjwHAAexSCo1K/ROaCFqENAJpUaJYEwZY8NNOhDJgpEmO0R7s8rVUcjrk1bKksZFjNPXyyHSrxfa1oYeuPkim9xAcuGXKy2b9SHqrWfSIDT2SYKtZLOFyugIT3rxUE2/mmwviarEGD70GUEtph7wg1XmBOzfL+8Rt3X9OyNurR7XujEW/cT5gxEhrpKzxbQOdRhYhFKH4DNoZmLSkGIszR/RbQse8PqiqS61u1hl841EUO+cqIFdayhQ6FMF5yYM8K3hG503K8jX+xHBQ3A42B/CYeKmutFdVdcbgaiMNscHJambRkyQ1D7YdDqG6eIyb2r3PUEkpQ2TpxQCj/gWk+RpqOuikdJ6li9+MA467L5rQ0gV8GQuN92Jl5nCg4RNx2Gke9anCPGEb5Yx1lHt4XT2ry7QZ6eW4Vy6R92iPoJ67cjZ44wsTEGvWnMF2FqMysYjSpws7BbMgFB+Q/wkAp7JOt0CuMMp/GVUhw60ZN5HMFbspLCqGfJu49ValrlqpUF/zPcDDm36L5gnz0tzrK2D1OS8/42pSmNsijh2EQvpyQGOlAl0g8zEP+Z9CVF4Rm4TXh3rY3Sj8XMG+eXp3bxIUbZrA0KRBPGWvK3jfTviTxWhCxLkdrXnewXiXY/O0yzcpdjEoXAYquufPo2pg8kU34BBXJCn5hFGy/CgsA1dhareBk+JXHHWOd4p7UoiK6FNiF2dE8aW6wlMx2UGr58qm4uVrsEgOyShRfHDPfwzip3ST4LC/YJwVtrqJteOAiLnMSIfRfNMKWt2ZbmUyKVgNyp5d4db63dGkyFr4N3iaGaOj1eVKQJkwbVicNjAzhe5IF8hbJgjBDs/ErKZ4s1EH9BpVLU9ldzX1jETNyGqKGqvbAoyMZ1QpkVNBm6HqBk1pi9ShXCokUumKoKFAdJOk6VUIjyG4u+pVtICNf5z3MESLZ4XZ5Cm1EsLVzBwmvcov+mhcsEAJZPIlvWmJczUcV2jyjSot6rsitJlYEsbBJlRkpvBgLQENG6mItFCprCJFgUqdAqmPw5yDigLEr1ShzadUAGMreAnwOQik0OZOt03V6JqKfXb+PEsGTWcO+PCOjESE0tCy0hE9mUHaMEuQASfAVnOj0pvJxLGjqaM4hvIUpvQv1C08gkYur/8erh3Qa0gN8OssrkN/ym+lreIHs5SiMMxDodzgHA4osqrC7mTx+u3k9XxmukXr7vD+8mhyZlmgXlLnwmCfzeEnl7PRgOLXeJrqjqLT9fatjsFsPnIMYNEx8oayaGUbfrrBsgn1wTzD+NvNLKN7sTxtRMltwGjrfvdHn/yrb//RYf/4sPfAjh6vXz7bf3TSGW4vrs7/9Ls/tBL52ctLnYSqUK2sfuSyNbFFBbyujk1pNJ3AuVp4au18H8YEVt844xdfSRTOhdDuiozHdOSesg1mxsRYfaNeZ7zZ31y+fmEsc88GJBTJevCrv/Srr87af/KdH9gyEy9oIonev/mj33v52ZsPv/bk8d33Tfk4uffo4NAwo1EEjZkhkvAEs45o9/AzsnpG7ygewxOaLES2bjXDAhE7RcJ2OfraWlzLSc2fbjsnb2BTXdN4dK24BSSMilSoNODD/v6k9VofFFKb6dTMN1ogKrY6FFY1vLo6/dEP/nzueILhHh/GxWRuiGDr+OXM/6CNmyYG0xJQphBWj2XbiAhSRvjDyWpwfTm/sg9YyUN2Z+Q8CONgpDBM2v7IwY6wYap6bFhJ90HAtQbYxcnPTbxbYfXYpPbo4RroDcwmRvAi22EymiYfbePlHGVrfBQkZoswEejMEBaGbee8HewfHBzf4VzYs2abBuhl1IUDIuY5Nsxw5+z84uVy0RnOkMS4Fs5pzBCKNi7nmOtIHMgsSejpX2HDWFORrspMftVGqVSRC8UgS1OnNEUymKd4ReCYzDAMXFysfvUJoAt4IjSkbAgR+NHd7kX9os51lKILsPDwtRpgnxKwg1HfAjE5ucpog2gDMTWNjlEAFQNqIhQAX0JPgPFWoiNnZtHo4Abv+E18bvAo+qShz5fKpkGiihGAum0OpGGJ6/cjL/tvOLw02VIPi6QRN7szZJISGlR3MS2gFiFWBr9Zze7kx4nNzgOgysJ7ra15QCstmUrQFeZrlw8I+DxGtVwRM74nOTOppUjnsQCnwODY3SItbxpBN2UNoi6aRJgWJM2SEbIUSRQsAXuIJhOtoT59z5RjhYx8hoIyq7ZZBwKVEJMMLSmbom6Mn1CTllo6eYJhoMFPk0crXOceEjJsNZPggaqQamS3zICYN8QNhdMZoxjAEyxGMstwgUIodhUj7Vdp+Ogk371CPoZPOgBBLgu1yIWVQUs7M2TvFd/kneGFDCVSjtw3qdK0yu4hTtSRZj81HKHTfnqqu0+FlX3Q+vq4ho6DV4bJwIJT2D3WSwqpWBCgMxuGMcugtDapThESJXFCdm+wltxzXoJDAwGzhOyJuYumdouHgk+ToGHuoC2mBK4S5kL6OqyCqxz53hCrefpZ92t4O7DBTKUVOoVR0GwQzUODa35T+mBR991bnuvbrgPQvO/uzTykZgVxZ5pA8/jrxy38596QK6C5LPnpk02yzM6mTZbXGVdKs3XrN7ekqftNyOcfCtGQqnAOxZMg7BBtEgOQhwMG5IWRmn5eeLd0VngOWcJYmDoAYiOmWcAQGCCiClSqLf1NLSgXjhf4hC+ipsL0AoiWgfy0XnFUYyKsY/rxZ9EXq/tkvd1/JoOOMwHyVY7FWGAOP8vUv/VDWUcSw89hRtuDoBJFRNyj9WQpZRzvkFIkLG7nWpONNRVvUDeVm3LjwoYDgQ6ZBaYM8stXJbeDwKm8u5P3NSXb7Xnw0fJCWxSNPo+gnRYiZaFR0setk35Sppprjbn7mBPAShmUgG/Yt+pALt1PiNk2YzsUKBisBE5uMdG1EPQYnealwTpTaFIE/0JXWYddWuv7uHXbe0VBhtKZ+IQOUbLEMPRIeSCMJqktnyjvFFeq4K4M4vdtgRjZzGzd6K50bxRfWW3vsJmaFs5ka6pYZC5JmoHDYWYFA/6JK4wu05ywjhLAdaNSqk3MJ+xVNCiEssrZUL82CNO4MZvi2g+3NYO/qYSUOcVJMX1FkyxE8SGzT9LGANJ6/eIUfl1nRqUa/U9VJCltut7sD44UNmd8KmNAUbJh4NgZnDobm9hYlQZddJQUvCQOsTzs3vz8+7yaDG6y+Rmgxbmdd5NE/HrIFyMD169hlHAmE1AxV4eRmfXm29/+/t3x4OjwfndzfjgePXl0d7W3+bNvnzn6gJsI0Rw3u15sF3xyw/1x5+hqdnKosW5/sFo922z3bKuZThPhWS56na+vbc/cnqnpbNOOWyL3g6wm7Ywc9mvJDx/9k6998/J3/+3Rnb2z2Rt7Lr04/+iXvnZ3tLn/+ur5Rx8/X87bw4OBlsp2+O1l79Hx8H/7d37ngV0/O4vx3t1HD+zC0+oe2dadLOPL9N0pkYOxPoyZuHqRNcgUKy68FN7erga2Eeh1zO7X+sZxt+lMp1dW+F5dOiyWiJo6YmaOTsfm6LDTnzgxrDOdr81cWq32v/fxc9vCfuMrvzKZXjx7+nS9evTo0XuOLnaaVE72TUcnPJXjojPmwJVM90XLwKAqh1rhvdJG+WqrcobAS6JP+oS0WrY9MSBwFV92qcpO3+FhimKnFPxmltLlqj3iLW2tzZ5iHFl7DNQx60Z1Iq+py8+efTbnFzcO0IsLP13zTFO+B367+5I6DBcY1pKObPM7xxUAQcF+/TQtbvygs83mcrU2fdNxY7McApCh3obvo6LKRGnYSd4ou90c+mlZ4+Hafc2X5iomvH75wm8TS4x30W9iVDoDKsEtioyCoaOVanpx+ekPX7/34Os1I4MtFS93zG8/FNli/u0//tMPPvjqN0++1R8d/vCj75++fT3aHzn4YTya29tmvTTLvDM93Vi0bbmmEzDa7SdpJAb8eUAwN/v9bS3WppvSo4vLRmcwtRbzBiXi+ki5g2Nc0FIFb79IGp2MF5AM0dS/tLFxcqE5HGnQjF0YmoyVFjGRMjUdEKmMqDNvstCnKjoUFQq6FPW92tOE1Fs1GTv9H0xyRUEHxaCHCaLwkzj3MuXpPTh6z0KcNBap3GASmw6qsWGJSV4lSTFiWCdDbe6jIN19EcHa6VJiLoJ+lJKrNWNTikBrfjWj2Z1n5pp0WMa9Ubt/wfrfbnliVn37Zw2Zi9aTTAiucZjsHkYYOkdm++t62RqLTs42dxkftvsQQxVz2+Pf6BmZI1IhVHf9KO1IaqGzWT6iCrylMNFuEY+wt8Jnja8hO2VTaxHR9ClpLv09RQaJPIbVe1x2jrgPUwGFjv4rC3oqfhy+WCGtZ2DmL9qkvfwgMtX5LADM0tN4NK0nSNlUwbBH+kvalf5wTAU19Sh1AoN5OAVcbRVkMoKJtBFRV7igrB3Zx4xgrzQ2TRo7aEArlpIWLPf0Y+AToQlx0okADuUSFFAQWjoZXcywpyiAqc9Ew9rFq/CrrH2FQ4ofgyJ5iSW+Vr9Jke5FLvtuuSeifNwz1IDyYRevPskt/J+AFD3gAQ9/FZ75EWpvQDAMn1aRA8dlp8fnoUBF2c4fwTRZCMFHyaSSLrLbzzb2YdFMlISHit7DCSlqouS1+dkBSmjAJbi58gxOQOzCgzF4u+/N6QHZ3V/79rSiVPJk5WpS1WPdCiXA8jW1uoPpV2dy5555l/m7dD/n6RqbBvGU9uck+MLnnx793ZeQJP9dUSYRGMxV/KXJTGlqZF2Umy84pWq7qQh1rA6UXbkjGklbHBqLIaCjYEStSCWliZv2ralAz2LJJnkKCxw6BquWZtIDKXpWDvg4OhmooNB3IJE9gIh3DV+kFKDiQvA9F70CBVpNBpwUturmZW90QRg3SOQ3V/AJiOYx7Oy90lZMCkxWmeWc+fNJS/FEs7CtI1Mq3YPiB4cCKWOd5sVqwRdifaUcYF6zGxs5So8k3SEtQbY7I7XVjjMSomYVi6RBR2lSHlkS8uRVeHoOZRqnfuiSzbno62CPESN6caTkQ8EKkJQ23oWICwn3hpChTU1LLL2Ts2acq25ik4QxkOUhcjr/cY+1TK61SztKciOgPZ2jb5Pl15yucSXZYVKDHQsszTmj0oJSjpHGkpFVhmphDrlqbwO2kDYhXdEo0lADkpy+IXGVNQ9YKERL0bL8QdlZn5wfVqmkoUfo88lbO6Iqi6JFo1Xp8TA0rs4uV/PZauzEGSg1/i5IxiviWCTNRFgtDWL4J3RqGKgqUaZF1Hc/Cfl3uFJD19dNDtcBX/6baGGwdyTx3nBF2CPBuysskUtk5Q5HcjZbG/nJy0/++OPOb/zaQXd4+Hh8fHr6ZjAaHR+OVgtTSvqHJ04Ia1txax1fp72/PX77uv3m7fOXd99/wH5abKd7mwPTo9j30xkL0tpWnS7MaQEPL7ne7xXnfHu+tO2OaWJqcHq5fHN6tpquNvdb44PhbLLu7R/2Dw4vz+d//L2n3QMNv8EbVv2g4/ypzeJbT07+1l/9Vn81mk9e90Y28dfB0//IDDvcqa1VylhzvFrsOXwnPKaBMhZtGr2gdXDsBpSYv5v5aHg07F/qH2q2+cJKJrqGApbD3odf+ZUfvPye1nEdpl71BvzHC6Y/+/7s9QV19fzFcwsKD08Gh4cnJpX1hpz3mYekTURTdpv8M8iH0nXP6Bt2zFa7rAoESI8WsyEHS2m9te6XL8BOpXRP+pnszgYflPRJ0czPXy4NTpKatND4N14U3sbaeWlkBCPb99udCx00t3Gwqg+nBoctYtWgUy7VnnvDBYVeJCFMgs0JH3AWMnOTpjdsBwJmr+5R3ONxnCYBWcu9OCxlAS7M5jcCWF8rWl5+gasR4Z8bkcgDHbOJ66A7PuSYmHkJJ7urcMWgOrDg3vjew/svXz0//72zR++9f/7qdDDYN3PMjCe6Hc+YiEG21xbsrkY52CjzPqfMK4MlxTH0jepCojRDWVpCoRQzxcdcliQS+ISGaXTSDsQMCRXUCLNIjUcY6TwPDW3zGVuETUOq2GJlJCdN4S9+GCWFyXcPHqupUG8JaTg5OjsvafVSh0KbqgyYpPO+e6JhvYY+Qc6tmtE8YoxSqYWxRoTubpRt1aScJcx4WGDCOr9NYAJSOMWo4qTaq1h+hAS2CMiWvIifLoG5PZbJwJbrhw6+xGB819gRHE1LNeM12SbU9Ie9MxXX/jsRyYyPKW3p9nCf7Y6GxMHBBzyOGSVLToheDSr/WPBKcQMJMkpZ9EEtPEOQZZxF1xHR9NfpvsQOGHDCPSFeWohQNTUnIKYIdCn/EDBth7JFwVTDmHKKh4KpMYBMcmUF4ARS3DCnD6LGMAjtyLJsCnAIK23qKFVUeafBT+bCQI49UUASMRnkHg5AOfggRepOSDilIqbVizQ0oJPMc+qb3t5ZLNX1QSs9jIoXIxpMNViYsJzilkuqQjC4RX2kEDd4WfVe5ag4kEmLX5OIkouswhaBCSQSe09deKxCCo5spJaCasyPsBPREqcYu+ov35IIAuImcsh2DaWSew0MPFrcmpckEVT51mMQqFjXH1OqipN4SXB9fe5F4Off8xay3IodKAmo39RAE5CyXV83T0268GVdzevu5ctGABrffxN55/u/hvnF38p5R9kGhwbu7fsN2kl8jfIXAeU9ewERiZuxgiJ4PhQEDJPztjItJF62mrStaxjDOQNrtg4Z2D8ek6fxxb9Ry1E2jNpuV6+XF2CitrkJQwhfSQpRT9y8hwWZXfFKl+M5g+akiMGYssSzgB3sfUQI82xSwEMWatRqWjv5hBXCXesnJCK8xSaI+Bp/13nQInPvMUrwg+di+mhWBaFjMkNZKTMoWVP4G8aLpkoDkMihDPhBIiwJSHkQPOoI4fvVllfPDoPNYVgFH9okOkMchpmzWI95WRNvfQAmaykYo1mnu+IOQR8zALIS36fwtPghBQrNHqX1gaGNV4ZfGQxMOXguR3EY4XoGkIATLEkvm9YOUcOhowVfZVwvC1tTtpr0x0EO231EQKEQZfVQ224vIDsr21IlNcuU4G4kx6VAlVqubK1u9giBzRjIbvcyjSMzpdFF6fOppIgdW55rXq1QsNDBBbYxhZwrW5NyzypUCk8VK41FnBpjSldUhY4SVafUux5Exnyc50JThU9QLy5QBpEn1ZesNAlIm51e8R+XkZLgT3qdZ4/zrLte3G0vD/ZH37/qXJ2+mi+m5oebvBHTMd0SK337fZOhs5Vt0EnDSo/B2xPU4bxc2xTHzC6Y4YWoJ4T0ufGiNUzha3jj38d1A6V5aO6gf/H6wm4qPqc+g0UiQzY4pY5vXb5VjNRT/mIG2csoxrHhl+6nn017g48Otp3DwcHR0aQ3Hjy8/94nzz7+7scv59OnZvCTI44xW9W1u1fr5ejBndnv/Ob/af/w08krFLzstN9/+fLjN6/boyF7686293prw5xsN3XICNgu9p0fMJ3udzuXnc7+un0m01/79d8a79+5upjcvXP49PXl//i7f/L9H3/86vVZaE/QZgu2cd/Sgs1qPBh3l/vTq49s3cKCw1kmdSgi3sD1cFIKkvT65cv3F0+yJmH4VKzJ7E64adMa7WF4xxssdjTqrE1I2rYv9EQWdh0ZdeaXuGIzMAGn1To66pzc6e3tj87PT038QMfFzLBGd2FizfnsYGgMYX7xek7Mn7/cfPWrraM7+/x9jG/cwTOPY1HZPAcH8WLwclrE6OhyWzq4tONY4IWJDXpdrfXQgVSbjm6nU/pyUPHC5uM9W/rcaXXO2q2jTfvNej1SP+Pu4Zurq/nMvIaMgpn8YK8ZUmHhw3Q26XVHKDtj4PLepf+qglLBphi2u+daVhSgrSJ1/koth2qsUCZppNZ/OjCfqW6qlcM2k2B0UcJAaZkxf5k4DQhJAmj3Pzmdp2WL2AqWmZ88F6Ml7KdeAdFg9SVRwsS7KxAj8cHWNOje0dH9rhlcm7cQ0byXMosxsl08pm62qz978fLl3tXJ2dvvGzEcjMa9vvHzuTK11vN0rdhVZvyrC7qFodk7ZdHUbBMbN8UaziSekCf7OMXAiiaIP8D0NzKEGgLdASplJSThcIzSiIKFEwrUPeZHuKAaHTHUYAidVgj2cE7KABWx+ZKClEkX45TiVvoQQI1JWAyV1i5hUiTjajILQnJMLBTJ/+isqhJykNYhnypZKqkQFCIa4AoCUBUiyG3mxtiNUrwUpIVJqoDN9/JRP6UOgr2eTEgBSvYnrHLQJ8LEtukzqOaso6WFK3hz2Ort4dH45JIKTz21R1Z7u9+l53sfI/h2e6QPmilD28Nt+5SuzqkX8dgv5jbX6mJy81bucBQBE9yDXBwBwBlHhnqKmYlacJFHvO56CumXIUw2qqh5hfJPYRJfWdPSWVCSrpElaukkhtZWLSmxAgNYU9fJaXojaJnTVGQblqBFtQhhk87z9JvSRIQHMteBdgqOMIFOmmbgMpRRFEeVgu1HMerZPXhhIgS4zzJqdZs9HqvqUqGilWynLrS5GNqshffiVMmcEeBhV6CCakoXpkoGyR/Dokb2S8v4iGLUno1wE6H+FzGifY1myLIztDIz+QS/rXOKIdeMGn0Qs6T/WSw8GeFGzX+8eBnVTwtuErU2HdSFnSpZhuDkXxFzd0tZymkYtFMXKV27NUo09AsrVUmCfSte/6SrsIAKKomEh9V/89b/LNXVZJK0nsKFYudfw8IBwStlxA/F0LZo1VTD5+7JrOI2d9F2cK/DK2QHIbrOJUYKFXSG9c6KLkxv3xMQzP3CCoHE/LIOQAD8wleDregNYPd31823d0Gf+/4u+OYpONZLkKwXN3yFE9p6fvHgpobJhOJmzY5miawsVlNRzGo1zQLbiw0IQGSNC23Qt2lgdpNI473ODEhsU3d+YflkmCoKOlWarrOMOW/Zi8SMdCGWPKV1Zd/l4EWetHG4U4dESJn6iSnzcDfODHdEfTedlrBiEronDoEktUBiY0EZLQU5Rx2UnihVW/mU5kzVFlnCU3SlBErGWKc1iGvtJRm/W+aY1KGKiSwj2sHEZwRK01FdC4F1RZ0MWKBS2/2XFNrRUCKM63N0ABtZVpRADnjMngiELwedr0dxcWdBKnmLGcAnKi8C7yXk4QLs76mmnsNRjUuIEZ9n9XO0jmC7kg+9BztEJgy2KDSHL734fIllAK8y1RuXlp5Z9vnJPFp1FVImAsWXyd2hqAZPhyjOkGBC/qvI8WbyAId0qQ80CbnDST6wHDIa0Mk5jtUPk7lYaXk5TOyzqK3urOd8o2KKV67QURodzbHN2mm0qrGwWwCj89oO7bDQVUo99darvcHB+OTw5OrMeVWry+n5cZEq6KanlHgpKYWdYZs0FqVAg2K4SC/ECICmZc4iCrGaSm3uqcWUPHnXdfv5Ouwv/ttA+YvDSsVBJrgVsyrLNW6FIeLWu8qvdwViXESFZwpWt/X29Gx59YPf/NX358vNnZMjw/Kbo6OPP3t1Yc6MZRQmz7A6M7pCdK9wxrPLj//Jn/wPX3vSe/qZmTJ26nz86Udvnn+2und/uLX7ZO/Nerm/6Z9uNget1mmvdSenREwMdJ13Oyca9G5n9PT1CycKffr0x/3+we//4b9asFzZZKmCjJ3hQYPKnBGdzuLOPU3Mme6pcYmmiVNGpQm/QD3NELnfPvrw/fHxiQh2D7N1zXB8kFmmmKjZL2ZpQ7KBCtejqEo3GWAPJ81N76I3+BP4z23Us3/PQmjbwIzGe5enV4O9HB4MG1OP356+oEr2DvbMWji/shXnZHw6PDJxiVxEVqPrdGy5QmjHbEYTcyGLdnQycW92GWBer6bnF6vOyAmso05vttpOt/PLzsoUILMiaAmL1J3He25Po5wDkAGozkVv83r6drpdXF3qxZhIp8OvK8R2XU9n09FwffrqzWK1HA4POD8aZRhVCumq6aJOtTeRQuSNPjEnPtUfh4sOM9zDFSmBNEVWkShTL7GmovJ8zqcCGeZKgvotHvc54zGkpl4TK2/18gvdCtpNTGl3AHZQdmwLPyRerSfmmGXDrnAjjULPV7wM29mqLud62AM0eoQeaLV0Si87E719LM/vS+dfTc/vbI6qY4B7NEHcV+hhiCbQqGITFgNSVGuiaKRYq2mDqC0/TEcUodxL9QVVVw5LhQflITTE81stVxq15tnXtG5p+Wgb7CE8TVUJp4R1RX82hZdtPQXsNTEVKFaGd3mU+gpJSgU2YCqFGekiVlVHPFKPgSVZgAcuStKBzaPwyqneUpZk4aLhpYyFnBQpcZMRIKUOIRFEEhVA9JMwTON/POXVd0QDxZ2Ipb8d0es6aw1uJr3R3xljJbl0rU1BTZOb08faNccLKuOaQjBiJjlzIovSrevm1zHJj6RujQ6Ko0JS6Wnw455iFJfhm9zQRMMRXU5zqIJoE6khqbRpp0L5NLWhTvXLtHF5bqhbHyP3MNasVnfAJ4RLdeYvnjUtdxZ+K3qY0C95z8StBqpIxZJJnwrJ0Sd4jNMK/6S6pQhliuLo5jlBAOUvHFcErbfQuImch3oDvUAEIQ+ptqQMlilnQkFJ9RQnhFu4unzVC0AJSCCT1rXJUO4lR1RH0MhH+dc3KiBKIP0brpa02zHMPIuaMuYhCKAC4kojoHgmEUKvgAK0ojWvidz8zzePAdUUv0DuShtgzWPYLDGo7CADs/BgpDChuV1nUw/h8MpUqSr7IIBFK14VapcmSH3uEp6g5FZoAXP93YPQJmETrQnxHfQqR1I20Xc/lbqBIM51YGLtnq87ADegrnP7RX4Dw/+btO/gv0NCKb4Y/OWgI6L5ktpvYjSlIqB2vxPsnFTyVnZh1IrJ/09EtJo/spT9fQlZioj00Tq+RcCiEjmV0vHstAeD3mwS7gOuapSLi1TYtyGVWoKKXbHle4ze9uC1Pgc1nhJEvvwss6A8gDl30oTRIjkRMFMO8g+rxygv5oprOdqY/hqWPmCbykLi8CdtnRzZy7Cx2M0SwbYDQU0G5Y2gXLBy4O/AwjVEDA7UfzAJZ6aUisUtDQpT1kG/vbENy3xNHJSQr0wqMUXkghCczXWLTEU72RtQGCsMVULAjJRQfLHaCWvBUhpyZyFByLt9vtnO2WKZUZBSBR2OrKAkOZ1tc5P2J/1sexqTHZ7M6awWgj2VHLlsVDUtpCwvUp2I6pAh/kU6gs5FcHtlIHn0POxi+nVa2f+bOZ+OBieHz1QHxE0boJNHigIN72zpeD+q/BZAyzWSCG+6xyZvoTmnQE4vpl3rU5aTOCvK2ItZmuZzVx9d7fSviLrdFsKRkS4UR+6CFajwSO/T/ElNhKZlMZs7Q6W0aOi9wXKdjxz4upjM9ga918/PP/nok5M737Dok/sYUrRY6jDoZUqRgkMIRdMAY2ikwJRdB1ROYzVk2omWRsZsgNS7p9yhtLtSfbsrnaTEzP0nvfUJvb5uf63nZr5+Qb6Oc/Ob7Oqld7YL89oEIk6u1DKfQt2vIyekrmBf+OYBX0chqzY1E+raQHJ+NZ8Phocnra61vw7DOet2JyoEOQaD8XI7iYvOURDzE3U9n3zlH/+zZ7O//Gg6szP8Haz14nQ9wQwXh6vW60z3ap3FrO7Oeu3DnK/6Zjnq9vdHJ465IWGHB8NPX046o85Hr1ZPf/TnDsDsjwbVlYv2cfUGZr2Hw3rt0ZO7f33Y/lb/zv+QnuHsPRxfjXdURtzUzACdxVb76PB41B+ZlNRePuah4ELQ7AZc5IvXf5TzBDAr/oxUmrK27A2og6wbsYZtNhNruzp/cXjAPluOR63DB3fm8/Nt135Bs+ly+4ff/uGDh/vD2YheefD48eOj915kYcmzO/eODsYHne7hcsPEGWL0hbnmo8nk3FHXtus37XzaXo63rdnZOVVxtdr0D+/u3zt83M8GJzHVmINES+t8edF6/fqTTm8x7OyPHKLnmLoxB8psHkmKvzo+P26FdJJJ73a8d6guTA/aP7Rvj0lQalOB08jz/VMprmXsV0ilzx35CXsz0BinkaUMTuSa4wkuX4kb3RU44RcBdkQ88jFvXo0aNey1Y7KEFqsRl4os2Q5mpWi+/wSf73b+aaLc3L8Is3nP55RWBptD+/YO+gdtJzNsz/gFVG6wKpbujp6GJUgxac02FRm/8N3akYHJ58vhaNSfLK/4lMi5PWAdenffDq9Ok6b9480GX0cPiFAGGdc20OMiSaOmjwAUFxYXsqlsdCBniqhkJ6qOKOGhdfwV92Ia9c/SI5IGTOgHR6i5SRmlGrOIZV01lcQNdcFK1g2x/eTafYn6q0YTY0d7pduW5KlMLhFNnpiVE3FWhgg1O5nSZY43tqmxYnIqxWnaEytMTFdpPSstAEiwSKl1d7z1nwddCWUlRUqQAO1V+FXkYJY9dlItlUwYnilNDcOgRQOLk14Ka90Y+2q6zDmDl7qu5vdrd5bLB+vNgWn94cvuXbEr2XSzGDtzot1bzLuXreVByJ9VGZTVJCtcWnsIt+r2HVcHJ/MKtKNZrBycLBCHRhqg5F19NCRNDwYraLAhG/nRtAXrKgXodh4CKQ0QC77bGoXAyl5lNXxZ9aUlzWbW2dy8PAiZBNNx/jHS3w/HGKCw3MHkhqgXQwPpTKJl1Xh+8hYyKksROQvnrvMP1WLO7KrQm30RlSkE5XOpkikB5HOlptVWqkmJnMoMazUjtW/p6uS702pTUf2nVa+J61tYvLSDGqmBDh3FgEqDHjeohLHcOoNnASlFWjq44zWL5c2fBF7/mO8/JpbyF8aR9ijUIjiiRSzCCDycz1KCjVUcYtQZO3C9uZK1bBJZnprwFC3/K1KK3gSY+YcUkZcmpMGtUqe7mRJX0C3QAQxWQK0eI45TFMT3FkLUDP7kVFeF5ykhOxp4LGCUucDdjBiP/m7SJbb/N1deoOE76+4a9TwU3HxIYBOjgaOYSZTtVm5DvYH4izxIGBgFoXn4yVQ/LfwnYgZYIu8EI9VeKAoLgk0RmLHm4pnQwk4yuyUTgcRS/ekaNMlT1NR/VUFSJtibx5h4USJlsBYAB/8huwFE8/8aAYmotlaXKLPXnxFL/ke23WIxjb6L1ckAyEJCth/GjQrlJKcGgmWkBC5V1XGUe2TnGZBLLgQJlvBMcMSJ1Yjz8CsM2v3sDmixIylPnww7UjwZNKsSpLucuPEEVD6RTgWIXZupJNSPyTrOR0ja5MVkjtqRD6UWRSCY7tSMU3ZikzjUgAS17BCjgiwhTx6zOO5+uPJHVOYA2EWAL2o2ubw8Rwdf47xxNSUpHQ3B6P1UR7e3t1lZSDifzew5zrDIFFhZpslJqXKVpGsmUy3Uc40/UELZSXwxnVxwQPqgKSVeyopEChbSUujRVHlBiFBaAUcUEZ2C96cT+8AYTYidARPTsLJ3iUlicbHriYTWGkijsiY1yR35eIOzR2LUa2+QYURdSiSyq6hKWG/Nz456DL3LHSR/n9UCcuass55+jqqWuiokZ8BFVcQhx4ZPW5CxXJC++2ff++2/8o18i1ZiNgYwguj6VX1hJ+GKrYZSzAws2ZjGYa59dmK12UX01In/Iufn3/MVwD8XZMVwS/bNc5OmEhdOUIsUBBJy7BBNZeUx/yRQAFo1fFgDNjawurpcvRkePBjvt8/fXg46R/v9e1ett47H0PXPdPNyt+ghIZqJQG8unn3yYm3tqdZ3teqZI6MqN4uJjfq0n2ExR2ukh4328sBFfHdYCm2z5c3ZZLKarj97/bJjkN+oYIYXIk2pEfYYtNhR/ZnjA4Yj/ZKJFbcWHEA8TU86mIpWc+XhotXP5AraZRmhq70Wq4QiYTxNdlp3s9dWtpCESzYqGi+tVs+ilX1Tm5bTuQ72cM9cEWuJT/7S177+8vzNcO/g7Kx7Zb7PcO/i8u3ldjo7nVx9emX2SLs/vry4+MM//mNS8PjhE4sLBqM7c1PSNsPuyC5Jw3X3tGPTEnPWplTCorM9MA3pamoDSn3U4eAYjE5vZBt/ZaGJdOQ5R442nYvzSQZkep3hYG8z6I9Gw5iMlESsmlh2yBfjz76fncGgBhmWX3nygRN8ry4ywc9JfaUg42u0Y6E9bbhao4LwcljCTc3n9AMGmphhHFWlGBFyjOFKi1pcslMTCct3P/n/JVeiq2PfpXX9lGg/mbLyS/Qd/F2MCmiCKkbeYxwmHht8ftbt2bhTg8OGtYiC5HPahD5qFCvwxaT/p+/KrM8opVUSIymcBX6p2wc/PpTu2mhPf7BnBiFNoLNYHMcQkWSQweXWyDCOKVXgmt0aUy8z4RRVii4y0yq4DrvtDP20IVS2kzHipcTFJYM4NlqzkE+vrVGcWDY0SzsUcgmteqkCBiKeuO4JRH4TIViHTKkZ9ySEcZCINRaaxyDzl+dGQkhCGhg/vlYjIRVhEcUZSgBkqoqOggn1cYTVkEaxSQzWtNGFVaw7KdKZKfUoXdAoAsSeTrbFM4VelScKlBsCfiA4evjKnCtVhs4WEnX4FrIZq6m5C31ypFd/RnD1ZhiWUFelOfi7dWhUQEtnIi/lIPO9xf5Kb7d/eGXpsGO/1Zv2IgZ9CMmmL1KhZmgOM30IZmXxvNIhREoVZKtzuCNSxmECXNpQpIjaNNfVbOMlLRUZinESy0jMNPpGoh1EQyYRILRKMdMw0TMap1ROxBZT+Vy9pLQ4MhAnMQKsKliGcmfYSENDNuDZA6k5EHwN7UP4Qq6KJlbFdEPi4FT/4BVWU46UQmb5kKsmuCbDtLVyFt1LEseKUH3ho0YzqEx5F4OgYD2lCgPXL4LWBJDUq+RIr3okAChsk+D0rMALCqFC4dAweUL8CyCXDAtEsojARHSV0kNSJWIeqmh+U0kB7r+UaeyLLPUqqrTwLhnzJLTQDRCw9R9ATrrKOJmLISA/9duEJ+R2DK9BIHEqsiLVbxLeXDsI3pO0Sb6LVdJQEQWkuE36BvF6axJfu+vM4hLp9uz/Srzzyn/ZSoAmo5tMbx6adNf3Jpa35vt18Jf8itmglNq7xjmkqpTqA7toTGx3Ob+6ylYv7Y5eb/z6kYmIlXopQxkP4q0wZLSD55GF+9ETG8d+zGcOGFpv5g9jt9Vc9qZim/qJogGm9ePU4cU3cdd27/V8vry6mlppjoZYDWhLD7XkBNEYfS3OSu7BOpyR+scjcUPSDqVf5vOMU5AEqEbyeFDC1oWh9hb36GaS49V7w+2407vyWGyWcpGaFMsjXVmO8LjBraRPn1VJw8My0yNZT7hDbQ8e/70WRQcDceJRcU6wA9H4ACeXqBn2xZahMd7NMtmmhxDs6wrXtlt74/3+iFtaUUTg7+dEsRn4xFyYja0VY7ayp6NUxEjasNmsStnLkmTobm2aZ8/kzGZJPSpwqjCRk1U8HBC0Rc/Mdj1xX5Vuin7StUvqR2Hc7nMVVxnFrxuirR+pO5s3ErsoOiDXS1s6IIIaMgRAn9UFNXln2vZqwYVjZXDTimAlLBCEV4uVKRSZ1hUtoBXIqINqArdbPWnezohwaQ0pZK4YobvfKkZDxNLeypOeVH1jJKmYHCA7HPdfvsIsmweP76bdnTP40y3IqEhGkDsz80sd90jJxZdRbJhmCO6ynWpE+r2H3c2p3dhRIRVzTb+mBvP6hStwrq/P7XF+Hbj7Be7sXdDt5xRYEX/iKq55FypGUWEXvL4rzdac7CJXPjUXOnjIop3EDuQCbVqU+kX+tAfI1htdzafjw5PD4bo/HczsB/PeycO7d1t9B8iZEsS7NVi0+OfQarJePRna8snWnGTbMl8N/jDHOWdPfI2htjlNo04sQorPiNb31te1X1wWg1xNJ+zvy9mb6fl6/8BGUUZ60pbAJqp8YyNSk/LNDRsejEd37h+bsr1ZPjYA5VAhGqVKppDsAxUYCw6T2LBHUNa9RxAa+yST3zSmKX9m4JzronY2d6UwIceRW+RFZ3vQHW0W0/3x2DJx5yUfHXX/q7/32y9PX25bg/nqG3/87Y+2o86/+RNHp86ZAubcX1xNvvPnf054rqaLw2FvPrWfidVTED/ac2TY8EGso9YDBDC1oeXc4c1Xjfp3+2dLq6qx1Ozy5ODu/j6jfZQxlZq1j+H2j/cMRFycnU4uPzx6cDI+vMDpmarmfFnjkhDlzHdMmK4rAvR46Ryy/IgSRfi7B2OrFOxbijhRBmHUzF4huM5bUhFGYIl+3DYmO2X8MCSKIIVWVGL8UHWFg/LATk4VmvtLts4rJLcvv1IfFA7qh6PKII7+eBf5Nm/ffhal6vJdzDwJatLmG7AVxZ0KvOD5teHTch69m4iqUtaxswy8ZNaIjpyDv/t7WYyhESDHTMjRaNTrXfRGTp5eW4RhD5psI8bxBDx1HDTUJ+JF18TeWLFAp+vVwGpj/li+FFpDDolerZ7+Gs6iEPzbru+nDei9in4avNE+wSows1sdGThlZGkkU5IUxxfqJ9OD/MR8UklhYlETIQKKa5cPMpRhZnOoWW1RxLYhqljN2QtplVKE4O+/KxqMnBawssoiCHaRv6+UvcFLGdQQM8F8G6tS9xBWoWQ/o0Jl8gUPdR5bMbgGpSAX+IV8/brVlQY6H4NBxWpQUifpeFcCRDkSt07t0Hea4kNDsF2NbMshjHH/FwWiuNns6Ztnv16Tsi44AQkJnZ3RDCOH/dOBvYTsnRLU9FkITZ20iX7wxXsxsnVtoORfFgsGuL394uFvDbOSzXHkM0sO2p1LsxM7bTjstdpX1iFYtNPbHlkLoDr7XQsYRtkwYDvqhaVTHIg5cptgOSkiXsDtrLt4YGCc31/MjJTaxcjoQbpWqAKObJdmFNggHG9ZnFbNZWgFKbRKtS0fh9q9p6FfqBWOjViipZIwdFJQidMlqFY+0RPmJ70p9v+uXjCQx+onpC5awzfxkrUsmw7bhGDhrgKbBkBNaw4UrPgSwEoOK6aZvnSTfzJCV7mEvgrtQAbzE1wE/X2M2h48y0u6AApXvMdSiimeRGzDlDTr/tJ0J//kLEdmZHogzA/3TNpoEngsGvitYgXrfAmtqkOV9E15jcbHaCpoEaMgFaJkwhZCVMVXamMpyTfikZRFvS/8Jnx3NY/uQbW9vps0fZsE+Bxd+S59vTQg3wWmcE3Sillgrm+VGJFjSjWRCh+t7g5UJXn3/As8BStXUSeULuLVb/OhuTeZQeNnXIXk7vsO6k05EqxcyaDJgYa12zepknMzvTvcrMr8NVxdxArTVGXxZ/dZ4USZGJiAMbWrOjLM+P61TjUdKJNvxc9VbAGOqkyGKBb2ycyT+HmA9BYvXzERHcD7yLtTjn26Q3sfTIIPgctclBiE2sh0BvjX51ZmMA0hGKD4FF7CQx12sPtqMp9OO+dvws90BlCaT1IWXktrbKWsvC26y1ZaAvWqZZa424WRAOgu2BIcpsUuDdGUSh4s8M3Gor0QVlmpCIlSzuAso0xJjyCIxrg22yd+BQWCeZCBqzk//N3VUkkCWpMQcs13TJ/iR/dF8hBRCZODUqTj5slVdQShdDwoKiOl2shIUDGB6NGiYiFjYidV4SdOdbUDVgLEKVwLZG7wRNPdfOsqYtQAPxvrP50SjswQkXoNSo2PtqCjFGrk5r8OSbSJWJWfyFX0ZFDYBz/GWwM/+CQpeiXQSzRmdfDyAyfeOBMAbALIalw//eTj0zff3BuNpU7rETWNmVuHR8eTi8vUFaqUCg090TCojDtbc4jmzKqMgeIDBkA8OSHO7krC/L9+/wV/JfnidSuoqF/fb8NuItzklE8IcxO6+9DI3S3gO7g+ewLZQ4itqt1Dxdz1kTov37x4+uzp4N4+4dETfv/+Ho5z9o2Rrb4V/gvju9x4+8bl+t19ju0Y0DbBGfWmy8URmiIYozfmStGyk30xNV4q0xo7O11x8LH++9v+ZDq5f3THZI71bH1wNH57dgon2/PbxJ20HezZ60eH2mFZm/HAOQ2L/mjigA1d0vTTUopY+SZ3uKul4V6fkzfjNAoUoqj+NI1+GE81YyaT3KRnC6t3bKjb41DYru6EvQgdK3Z0FF7NcH9/uXL62+DByb1XLycmOJL/s4vp+48ffvbqOcvbIuP+uHdwcLBEim3b7DJnfA2Ge4/ef7zpHmSkJH0YJJYTB7Q89YqPWZsUielJZNlZX2l70z1KTSCVro9/xlggOBqzRfZGBwfr1mvTDPhoVSTXMqzNbrfqKr1o9kY1s4qIELh+PNrTDSKAqVAtKshRndGr6lu1EA9Ne5haubMLCPLFsggt6yV8UcjktbkScs3pwrxdf9lFuP0TXnIxAlwFq55+zu02wHfPwaS5rp+Sfem20tzbScc2hkrHBNez5L2Oio0v06V5WBjOMb1KrzbDg5vl/JLbaji07Q8HZpz+B8e8PK2ZgWUDWP1sFcx1z7TZLiML6/nEIKTelVaitBJJWfGopK3GO3Ei01E+4UD/XaW6dBQ4FFggMIUMlG3fBKF4M8SJOgzrRolUj6CUWJM8bBwCi5AS56G5Kj543nb0b6gEVCD5THJLy3vPJdRD9H9agfRnyBzMyEH0eqAGN3GCQ5M+9FM60QqCjylZKI5/xA/YFCmxC5NqeYJQ/jfpdvGTbTSkyql8omRFmoPfM50yoy+oRb3yHmRWlfCiHp5MDRYerWHPhvtQ39cpKfpqmkUzV2i46tBEQ0vmh6zrpm7EUNIcU+A9ZS07RA3FPmZt+eYyWZ9PYmxXs820q8r1kZwSk+WItLra7+MD6+EESqebkP2L0yaKpvyW7GsRBgY75TYws0qY1gbvqVUMQ5q7g0m63rJPwQxdVAdK3cTYVUZqAjIhZdp9T1XelHn3r4irmOEt+kmfQ2uYiLF5Ilz0a1hDyqrGyK5IIW9onnR1AaeqJapBmiiAglIVV3kFdZ+LXsAlmWxS12nwsqdzOLtw9TXY7ngzfYZ88V8pGizCQmEDqjc9HkQpJFOOaijLJAOjWgQ5wQ56bIAklAAWIUH+EwsmRCqRjkqRYoIkXeq3CB4bLsnckyZFYnDEHAiVJMwlBqAhRSjaXBK4CpTAAtJ8+Kn3All0CRm9Af8lVz7U3/W3wG6yuA7xOTUg18q3hPB2kl0HYLuo08Xepbp++jLf//W3z/0C72run/uQl2tK/MSHCmi+VjUH/QZKiFgoS21vnxLQtBjCNDphoJQsVCZ54mpOMsVD+17b1VOmDyUym1AabZvobPilSbAqWar+S8kxQ7RN8WB4Mnwe9ZguhBauY/ttKoz1iwewB4TipSlSisniL/GMlVm8kfyCvSQGGSn3su+36/mDFUWfBoNz4TPr55rKiHYMG3Xs3ZNOCudh66n2u7Ug/PoUYU97/1V7zq7JAYbJz+xJKwfXT5U70hOCNV0BhWRn1nZkVS6ts88yoIlqYDC9hWQtYUO9CBN8RSkwqTzgYj4Amc2VKC104fiMGRDJ1u1XCiSCB+d9ugPZPAHpiKriGYiELwXFdODDC36qpio1wAOlMgzlQ3ZLNiEvk0yoIuBVv4UFHHovY4kXvomC8HGL05Cv4lQN1gGZQcA4wwhgRJgareH41BR0NdTtFm+B/UPjs2QSpazQFztKxBANIuQd9gKUpzt8wTmtAooo9EDsirKEUnT4hGYx9qJx8FB7+VDdtRd7rfllq/MsWDGBkLzl0PjW4f7+0dG+AfxPPv500D9eTtrdAy0+QOmzmDKxmDlQNmqLMYFQhVyUK25ct6cmjWy6p92RmTBJ0t7ew8a184nXqsfU1v+MKxSovy9PDpPdB/OnPdW8/y+PWpmrxLY4Xx6jMcvEu/4cfsIz/Ihq9VjHN6Zydz692n709LO//OFfNUI3c0xu7DkbcVoWcuVMsI0Vq7aj355p7jLJxYZRwyGHvlN4h1rtTFyxBJa2U/ONgmD6l6k60I9FLpMnDBgYTNiYeMEHfnF59tVHj41EvX17h3fcbLHlzMrXva9/9Ulrcn58pz0cnHzta/c+uPeV6knAPoyM17BgaK+N0JUbtI/uHNMBKtGGWak+OaVmTMPFgOkb6jmk77a+s5xd9fZfqd316qGOCB+wlSkW/6fbu+kMrANy3Ouoz4hkBAzbo9PLqw8eH69eXo7Nsu/fWcxah3v74+GBreWvZvPlwvw0bLs6PDqBlsWpOdgvs4PhFsVFGxip22yeaRf1xu0+wz99acQpA13m+kXjkV2KR+yYDgYQDU10f7zunM2nC2OJxeDZml796kCJ312wcc2Xe8hL4JwEnn3+govzq4W9Vhl7MfrDV2AjhTqSpDg1jtH6bllMhuMQMuT0DxOEZP6aqx6yjWMeIm/NBerPuJr2Ny6hVJH/7xL+jFS3P8nnJ7NoAoNeo+vEgbR5YWlljG+Sc41ABYIVui/mCbdUZbXZ2xsOj/YPOq07P/74+7b0nc3OGPVpdVr9iQYhBqKehHebFcQoCUdxa+WcXl1XLk/SEdlByIwla+gUE4npHtKWjluGrTYdg0U+pMjBIPos+rrdice9GiV14d1XVyilfqrpUK5wQEMxNUyvK180TOeV1c5mbfuW0idJRLxe8izQj6wyySXfQ+/8k23xH74MLpVpu/cq6h2dCrlgGvYQEkDR5fi4rMmgmUS+l3oOvJhi4RSIIQ8aJB8qP7ikHRESFFNE7yKW7zmFjb5Ov9sBHRwpvPVDjvZg156a4qmLlVbEFkD8AzZws0EWtwNBXepog+qoYBAdAq4TB4v5YEDcTD3YV0VRMTBIpkDYOZ63D5rp6MYbSFGja2fBYF91V31zurbLwbZ70DofOI2gd8FV1d2eGf7Ytl6D0u2cWn/cMzbFuHeGiWY/7ir1MA9/aWu2tvAaX3UmdkococZqYSzRcE8/TpCew7n1FPqWAZg21prOWmM9CnObbFyXFgq2oKaJMokMlYtMUDW04Qzj0DBcE9p5qdpTkBQjfoJoBUMeBkVTEyJUTYcHm75T4PqQuk5HJfWn1QtZyiPHjAijCI1MBkRuyk2cUv0VBEXIeQ6KceOkK5P3wgYjpRtTz2ol+StUz7yAStAkS3hQCDLxXVb8tNq4JThI6FOCcwV1/AVsLJoUK/knTphKITEOQGHLpvNTUpAyNxQIXUpm8BdyKhqkAgVnpScQS6W5YBes6ntKlA8p2M+7CtG+NQxShs0ip7m+kLZgNzkU6ERZPMl98Gnu4geEb03MCohGSFCD2q4DULH/XW8NdoGcS3l3mTTvP+OehIm7A9DQ6138pgz0VMqiptFXTODjoFVfiS9O7sobK2pH9gBNWDV06jvvqrEJCxWkCesKEhaYBSfvoOfCNFEJqdhSlBVR9uRXK22bh0WMOTs5+hAYPgFjxox1CtQGRYB9KwNwChU6x2Nw0QKbwI996BvyLh+B4acldy8dUm1kMKQIfHY3ITEut/JnQyxKHFGCKqGSf6Q9xatiCEAtykP+pLjyx88l+U3Zq5RBNxiFBoEQolDqBJS4NKtmq81hnuf07pSR3EZAGsIlPziSupAqnbGIDdyoBhCCnJ/Iba6GrBG/zLlntDSVJU6Q8Z/EVtsESIkRTKUWPwWUK8gFKRDFV1655z9CB3GxUsNNOZBX9UaVmu3F4WI75EgqAokrbWomOSc6zOgJYGWSppV7NuOR0ePVyGgdJY0f18R/g6qqJUBkq6Q+VSzlDfzyZ6lKu3yu+GfNMFGbLz998d3v/vGv/aXfkG/2o8C6pg5buueQRiun10Okgw4UYqzCO4u6VETvV37tV3/ll775L/7FHz5/9bzGo0OABmHZy+7LrqqeL/vw+bBg+yXXF4J/Wia3Uxbn3Q7YPX8xLSKLqmfZqE3ljTyb/cJqiZ3a20xMCdss7C5V/uuFlmewr2FmjfbMwl+woQ3MG2qPfKWdZQalPa5BrphK6VfVOE/UvC4W2SEyaZw4yGdX07QxVU+c9o7yFeqQLpx1MOJWX0+vrgbb6f27J3dO+OtO5m/fdr/2MAsQCt+Mi+v6Mq2xTzq6LfN39u+M2OIxSXBHaiQljMaOJYL9srpdlc9nxuvB6dljCoeRafEzhyBMywCClR3+4rMn/phir3dwubm6s7c3v7c9X/f2Dg6nExm0xsMhk8G6FzwyHu7NZlfYzLO80/2RpcUMvcxFsfYAr4avjXXgTRQQSX9Dv2k4zPZBvRhBgnGe2XqqBjXBmDl/S49IX0IBY2aG0AOrgzedH330gznj1goZ7giLhtgXUV7qgCDwq6Ysqh4V6BqgtbIgMvJUruGHDIVASB4Nf4RSrtsMd/Pl88FN/J96DzOEBgHlL/BvA/3ydIlYfz7vss0TQE38hClDXjFawkwh6zlorqMPk14+i4p6U/BG4eBqOiUjvszJ1freg4Nf//W/ZLe1zrD9w+8Q3jGbzPT9p88/652e/vKv/pI92vQAdVvt+4AnzT2P7tkYqLF2JEoNX2hrKNds0xwbTvWyxyRIw4GK0RXBEPqNFEjk1ScoJ3YVjMIoitAvDemFC5IIPzfqJG+xuWmv6CF/8UikWQorg1SXn6hhsVz5pC6z0jk9joIXZqP+lF+vUuuWYO9qBz5kQZcpzvI0DWWohRfETpYstSjTQEgGVY4oi5j4qZ2QosgiYhl2KXHhGeBNARMfKohB4yZTg3b2DcP3vZ4TwU2nIclGYhATV2YT8TiyQN4OMbiOGEcA4UveNhCDVXpKy4GtMrrjMwMJ9MoeMcXIqIWxpY9vocgVlOWo96Y9T3PYsEzg4/qZnbPoKL19Qqpt8VclTAoSpDHo6ymkv6IziF410d/QCYrlPCHSjNPU1sbYklO8tcGkKv0vs4o6Q866kV+7WYiUmQd0lNYFR4GXwYqsl85gjBpDtOQdU6CuazRQgfJJhSC0iKmSat5CMWHFA2Eb9RPKqEAZUTxiBSKUU2KVArBaz5X5N3kJtPwl62IgYDwnl6QMgCYrGHqI4gnvpsY5VgyOpSWOL68ylbCSJXEwS96+gBj7KfWK5oDHjsrxa8U+IunUxORXPckmRQnCKVBw8AtKiVGEWrTwbYEuUgXzwlnmhXqQKNQrXMZJDk5+xfDuKaBDgfppbon1C11SAqDgHlKwzyeqr18MvI7SxA0NFe5WpBA8JS38guxfvANgr56AtV5td8lAyOeyyReR8uXnXUm3I5P12sHMOHiTsilEnlExxlo+p05iDaYKLI4h2p6JT5qVhEX1FcCe3q3v0lAB0SwhBVOaux0x41yMYsv3okYDpOiy0zgNpbbrx1v7i7TMMy4Qsfa0elCuB4eMrvsaT4ol3J6S5D8ZhnOg+bNj63bOu4cfSHpFcCtbPzKcEJgwbOHAEkwaH8lsuDQbUHKFFpvTqMNW/2yxvWobPTRhQNqUIAze3jwpxnMyXMkwyfQUXMSg7MoKCUVLtpMp2pWN3ZAsjItcwSrIMAjQDJUIXlSW3kqs583iYQD2nY0HXbEiqJVLfDKRKyaEHk0cKrHUEyFgG3Vn+msVTrgpzaFBYUeoCTpAiBEyKDj7ykfohYXTKqQgwQVJVV8ZP6FX5CI17GzIfXsha0v0myiy2GnSZeYsVf6ybwZ5WEsblEl6sil4gQmL6LbodohCGP5VO1Bw5kBqWlzrEwDk9vOipul3yi0w0rvpPY/O65+3+ldprYoiob6egj2os5EQH/P50cHBZ08vfu2XDjadU/lZRYlOWikTr+VekFPauCVSgSkpPqfKfvVbH9pj5Tt/9mfPX1qg+RZhwsmpwUYmJFWM4JzSBMHjhDRznW8/J/T62oWfJ36TajfKE8I1V0B6uj1n+vrTzW/ll/Qiu4VWrrol9EuuqOYY6/hQPDG7byhqBGy3Haw7762HDx4++Z/+9E8nm1e8yg6dODw0WVZhu7buSdtmA/rtxWh8YO37xGSJK8tRzIDnOD+w3S+IKgR7MV6288da0nb/dZoqQTFR8fLAxkzIbV4RhipzATKEbrm3r63VBWh/8P69B+OBWdt7liE//roDvPDfXCw+sc3UuPy26+51ZDeC9cqMgAyxpzOffoGq0dLCmJYgaxmRU6mOtLV2l0wsJ0cshIwWRL5ZG7oJugLmgPD8ZdqvkmYuOw7uThxicXTSnpgucra6nF85l2By+WY1M5Ugu32wbqYr80imw83BYkrn2ABbGYcKZR0+7p1P59nqVz/bpJ2cW8II/2zcGe7393kla7582WPIoLOfrkDqwyEe+kuHo+GgN95aNhU5jjEnte1rXl3OdKRrCEE4Tk3N4VbiGp4tUQXFl2LgyKw34ySsNl8nl1f8CIkbTZNP9YclQtG6bh6KoQTdCthF+ZKf4is8HO6SAi4qzNM7fv6SRA2Lgh/2bbJpkhc7l4xkTUs0h/BIdu7xdMYskURQmpaUGuPFyEq/Kw9t8/5Jcq8/Xq4vVELLpPPujHmYA90uTQWa2ck1M8E6j+KjHLyihlINWChDtq4wHJw9ZwKrDqKeW7KkMriFMUkoH6UVVZ82ICozOso9sArbkMBjVFxT/pQkjyLUAyb0MTKTvwxnZGItqEYmjWVE9/oYcCFqEHQFJEwfRIL6b7PYrOSutb6XaJ1TDIMCxrYLNbKmb9+uHimFV628Jq1jlwiLVlNgM+sNljZQrxGrOiT3YkQdRl1E57qW96L2e2/klS9ylJmf5V0gnAHSlDRlUPvqotU2od5SlVZntGnxvoNnMn3aHBv/b1vnhnTseY8fN5tjEwiocu7zldFXHfTVGNdu2mc65Gpkz+HAy5WOsbP5jELSV+kMZIpQOMAcuAFXvEUapsOlqwLiMuM2UUe6CukAp3u/OYxV3j5HdoJvvYVl/u3sNkFEtFMmjup1mHE40B+J9bpNs9KjDUwRS68D5lP31da0SaOeio/TlEorLxvDHdxqAQKcfihPtzVC2b02CjasnDsGKPXe0C80TEBuIaW1AaHkZ7BUvPAzRmsYJrFSCULC+SlcMVKqiBsi1Z9qSQov+dpamYvBf/iiwCcTJwWldvsvKs9UUFR0IKp8TrFMWYCkyzzJSBdHYUFO4oY/CgywYX04AFAZ5geg8KsyasmhH88dqxK0xNFdVwckMwu4Yn0VCxWEKlRERxmqLxT2zouv+L6yDIzmyUMRoXnzMUjLtMHEe0jafAzlcjUQBvliheHPv6STfyR9J3jNGt3mBICcBIyGz67BNDmW779y/mJ4894gssMnQX/xDoBE13k1MHMvZkL1uq5/m7db959M18TP/TrtregemxThlrSIqk3Vxrau8Tb1LwIhSoZxMNmHEVOmmuGzAxjIoKCkD56xJL4Ap3QGvUKhpksuKIouikb0InieQKraD0eDGdYuwMGEXgYsTxkHpSgBCMNAJRXnIZwUfCtrYSV7mA74eHjiLqqYkEsRwmty4bBmB+vNp5cecedXK0XMQxH8NcUpIwSA39GrDFsNSOaZBjwpAJzGxO0i83/LD8JhSQWVVSxpnYumEZFn8E0p8iG1EVURpYzwKG8bhdHGmlSOkyqP2IkBoUhq9HuahlAxtUT0zEUiauDHJA+eLIB0kjwkqyq3xBwy9EtcHskcMIuZeCKrcopg6AhgcNIr4iizcizzB/g0+QXKt5RKMS2Z7cN4ye4kNEjMq0hxGgyTIrqjznI5r3BJQ+MQ3rit3g27rd6M3qZIaXW1vlpb7VZeQ4LMaKpJQOmaNGiVSkBhjTHsQYgqUggEjEaqywxgXhit90AbabfEP/rD3/sbf+Ov7dteQluQ5RyxBO343n4TFBoAYZy6+Bo1xRakPX746M///AcWDwJugxEzskIoCb54XfPCF8N/9rtUQfkm0runzwXffH/30MRs0kfK3qV8F+cnnrAJDcyyCa8ptE17IhCZMWWZ4PrjZx//i+/9+ffPfvzy7Bk/tIG2u6MjBixCj/YsxY1XHVvtHx187ZsfDgcWmTGAl89ePJ8tZuZjKovKIwSBvvwsjN577ljo7PGDfr0s+B4P+VnjUjVqb98cc3pxqjnWD+/cPXWY073+Nz78yt52duf44Oj4kD8NxxV+mf2GmTCIDXQimeRivd4/GY+OxyvOeUdtTe3sacOWai3i9KddaiUuDjF4xtW31MG3vJjXgP897JaVQiq+zOSwFF2CK0wGVsFtOPb3u4cf7I0ml28vppfDftfZc5PZxdByUlNEALV7lc3/TEc5Q4hGco3UyQVtt/Ye6BsuSN10TDk3gNcevmSHvWhvPtn74dxOXaWARMZQsraMYe7cC0NzOb7QKimzC2b2VMoBLMRivbXJlp0ARibqcn8U26MwXqQVUZqkl+YNrCbYb0ZJUtGwMgNzbkFLpDnBNwy846BrViFBN5/Cl7uXd2HFrV6v+a0e3aRDyuaD+8+8oJAoN9FuHppUXgP91o/HaKI4d3XP4oQOx8tSvFhI2Br7xVqvf7Tcavvg4Z0cB7Lk7MDpuqkmqqlj8ktx9U7Pz5cr7n9bIOAM/Vh8TTUZvzIXJXZKyQdLjxa1Tz2IPJpixWEQLFN3ZClqE24m8ESZ+2vqANBolKAZZZpLSP2UQosaxpEYI9qqgOzAVttRDJHUJC7VG7ABoMAgutyj6N2z93HeKiTtTna30xpGSyedBHhFc6Cj68lp2XKrtiGTSxt0w0vQCPBqHsFSFiyVdiEP+RMnWcstZddIwihB/pX2TI9a/IwqE876YDY/hXBpzXR7c4GZFVQOumOm5mzaFthQ0MYIyLiZ9yoVwhYNZjuK7WYc1J0JwLFt+W53cNlaXHCE9YaLPq1V4/8hPzy1CmSRlkjNLvTxUFwJIa3M8ch7sYqDOl8y/3X3XRmBSDuvw4Zv0qqUZR9XCN5AiSQPMeEfe7Zch2msoirpt4wGpNi6kjwN1g95tkpP1xMZdArQT13oXoRWqV8OhVRiZV73PFXt+K3QipdA/6/vIW6eUy/X4Smyt8AHIFhUbL/Nu7dYS41O871qMDELrIB6uElTLNzAiE7F4Yqe2i+wySNULgZIBkXx3T0/iZdgdxeGK5xgFxqmqZfa10xvS74ZglTFsXsROtvCBf/6JhbpLI5LZMVMGZkcGWaDNTCJuvtJppVvPngI9EaUwA3QKneDWqFYhUq2zf9g/HOuwDTIkwQlxFVWzxWQQDCa5wKWW4U0D76kCFUtoiWiDzffkl5gWCVhv/j1ZasCQsNrXOo3IO3Tn9Da9zQPNxG2drpVIiti34UVbtUrKlDXQBrAhXQ4STC+pgHi/tJ5aWpAiHry0Y7LYcwSS8UqtZzaCVPhDZtN2FDNKHs0nirLIa5Uhun3fGaZsJEqE+ITeHHqidbrv+6vp9llJ4aF4LQCaaaToVWnnI5LK2zo7bQK+CvtOUZmg5pLyBoVLzv2RCFkz015qMyMJdL68auxBZIhtlSkeCeMB5N3JjT1V+VKn5WyIL99hUCzXmzk2mY5ghgdaHHB8GUQMgEvZZVrgEBXq6H03YFVevZA19FhFfNbGhvM3udps6Eb25zEGlb2j69CzrM6Otfk3+gYjRl9Y1Jhr/1W+blMwvG0LQIxZWG3uB9G6r+gbTJk7axUKHCkZOINuz/y4WBRWqhqkZBxl3AYpOPFiSR2n1mmGPFo9HrL0oN4IrJkygZ7Ll6BHKZjaCI9CoOjcW3iayq73T2zCErOtm2ImpNrmMAfzG2j2c9yTeZRVYxgVAm2hB1VaeKiPFpVlfpiCwUtFb+Oykl9uQd4mh5Zl8GWigi7wCRSn7gehIkTjRDEDYL3LeNUJbLL4PLzz96enp7dvfeediE8rO5aJpXOMy5sNKB4A+nhXmyW9l6jeXgwNtnz4uKCLtPUwBOjVFlCf2WCQzK9uW777G8/30Tw8JPh5Su9gVIFu53gS56byGI2SETHCErK6/uXJEIsX3dJSRRRQUV1mNrYDK5W83/w//ifHNll/Tl3pmkn7x3dX8+msDs+PFY1tvQhaHeOHv4Xv/NXlpPWxeTl0pqZ9YsffxoX/nY1nq+u5sshoUtTaOsa21Ctl2byjvbGNl9nzxitM73Z9jlEAJ/bB3w8HB3uD/7Gb/7297//nffeG3/9G0ebiV15aJMszt5YbYu8sce596yl4/GzU6zat1nmwMHiT3/8khXOnFZrw9GBHUP4BuTOF0yynImhL2l/ze7gLIf7bhe2/lwsZhdvJ+w8Pbo07mljyDF21UunE2I9aYSI0WJ5bqP49x/YMNSK8L3p4ejifLTYnOYAYPMb1q1RFpSSzgVbY7m6XC4dMTu3ealdDqcXy5cvn2cJos6VMzeyQCiZqP5t5xWmZreoikZSMHtUX3F1hs65GGMYYUeV5QcF7Kprz1zTsdinjLNstxqXsRqUQdRmdFjp1PCBtTHREt3P2DAIsVrP3l44540zE/PnX2i6JZnFEXV3y5dbV15+kqPWh4mSfVqI3mG+Ox8g8RSt4S5gynOWAiVsdzWgEpJetGRJlQI28ZrP15G7Z77lBX+uj0Of9iml5nDxeGf4WYNs/KNR6KRy9YTaVguCF1fH3ZMHx8cPlwy/jiPg9jQUk/nlQrdPG9S1EVD2lstO/zab16zQXNQ8HUlppkKwA0NWXXnFgsGjqKw4fMMUj0PKYRai+00cIx7ic0NHcBqNm3Kyf+onaYq2opc6lh1+TVe5mrPkoEpSzclWfaddkTSp62N+fUu9VcjGWqx8jhJOPLLcf5Mk8VTszM50xDlZNG/4A1jx8om/SDTSfC991sEbTXeApHlN4kIjSEod0ILqOWzmrf8yOj9F9JKc/XfLWF9TADiFFbVpw1TTZs+BFvYMMzjW6VzFks1Em+yu4wjNzWYMlU72oaJ6kz5H/UTJWnNLW+g/+2FY6wkP1p3JfHNqv932+iEfjmEz7qrO3Jl6xgEJ1ards8aLGx5aTiAx6Yh6uL/pZ4Z/tqo2d1T1DC+Uocx0nUXbaqWZqh3sTqwaq9llwl/p1avG9CpTQAZ4eDucwu5Z3wGq3XmdiQmzO6qx331rh0BclPGgNFDaNbzKTjlWumpSpHaGAE71kAhFtZKXInOAp8ZDbecApGblitDzhyF/96mAfExlqNXmqvYu1eBTzKPmQv0drCgH+BqZL25NzCqF03l9SB+HHhHbKvdH4YReVtBRS4wXTJLKNR1LfSXbQrUwcEur7K9ePWs96iUB0nsDvbV6T76ZrVDR8yl5oHDZ9OEgKGeGRdhJEjfYuskWasWAwKYyA70pfuAHlNvqcWt91Oq9iEEnQpO2ypIIVnsmHS3tu75f0S531VovCSpQeXh35ePuQ9Eq/AoDDYL2UC24Ksrt54SlxLnvrt1DkL0OTMmcLRDK2U8MEPCzGdPnU1y/+m1QuRXwuccmB3GSRaLuHhOpkGmC6i1hP/O6lVUDBox3D1WI0imeRiMtXAxHZcPqjYnWKDVB4X6Ex+HYKxZq0OJyY0ulpcqmG4bbwnYkPSYqbktPAspF56iz0EWnwWFAoAltDVZRCQUqUp+YAFPNjAGji0mNlaJA4p0FzTN0V6w6MfcGe8tsLIATgjKkrEjKYLX+A6igGKPvZc9hM2ywCiRT24Y7WToBFH4N9bat/YHDfnvsQR2J2cSWPilvKlQ+Cq786leWRQdkSOJohJTGaGGGKnRfysRgdGqX0FN6N+H6R8m29GqrtRcae4u8sGWYKRyEQ84p4GVgH03ZKk/RnAvjCHrb/rQqhaGQRmoTWwGZS9eUlV01Egqn14B6Mi995Bjd4Z5jdlMSKzsHffvfx+RIwYu90jFB4hzHS5XCJfa5sPhx4ySJN0SJ0hjHqk7JgYp9U+VhKGVyc0QdzfIjX0QLcSLrQlOQZKAW+aWCXOb48tynJkGj9FIZqeqwVNgFLsFe/tGclRYBxY/6C0v0V+u5XT9O7t776OMX8Vy353uH8RDzBNuQktWvb+LcA3CTgpIL+QoXt/QlG8iD09eT8/ML7VUsrPwrJSevJBL13/0qCtwGEyb6hYDvogWNYr38BtrPutCoaFgZpDZFLrZiXqnm8o2nmJmtZ0ceHQMjKSOdO7sB9ca23n189/5ovTwYnOx1V5Orzm9989ce31vce3zwZ3/66acvP9ZL4G/OgkwbwGYjIcdBtOz84xzcXn9059HjztVcl90kB8JwfLKP/F/78L1Hj7/6G7/xjeN7m/M3r9Y2F7XENitodbRVi2UFK2NPs8Xk6N5DZwZjOwPTo709TfrZyzMrE3Igbxrpc5ZzI5cUy3rNv2uyFwbU2wWHImGZXIQ/KB6MwuSPEssxvAiRri4vo355Imz0XUmGTszjo5NHd443q3G783C5GE+Wb87PCMik2x4dnfQnF93F6mIy65xPXjt2cL64BG/vYLj80XOzOAwZIm8mYNB40UEKHUmRA9l3ykR6/FnXEnMfs2fXedpAVJWCG4NKLOVUGQU3s3NVUsM85iPtEJdkaitaKDXrN9Cj+9hZrCIdrWXXWc7JAhTcGyUa+A1U1f+zOMY3UZt7JXG7/VbPbrurGLKB/RNwbye7jv/533dwrsE1eUfvKePAGKPpTNmwtSSeH1n5m9YohcoiYGRczJfz6Wb/QA/OZJeBCh0OjgyimjqikTBURUVqBpbc53zR8QZTkrLGQJQ1johdXPJku0/KJ50NFmepJWouSituyTRopZOSvsiN7jGusVL0iCuhIYOQvDWUQ3rKN6+YAayQJfn7xVVx11dO0uxSB0C1pzvy3MCqqgctmjV5Jy++rthk5nIYOtYUySRmXjW5pStVP/2f/qcnXRyKlXiEkeQnRlSP3Cqv3KWvC881TBNOg3G4MFpbltcFELtYTFsmkCRixc6F5qrVmVhvlXZHWxE17wIDII27VCMZpkOU1ngaxb4+YatnhJKibx3SH/utvclsap6hBQNkU3vQsajDJE+dwMwFNALAc2TtPn0VUhJlefSdH0IdEVWTqlqLYX84My+Is80UHotzMxtOX8QcfgRQyzrdymXnLjqQIGXMv4x15RwRzq0hQHnHHuDYwC88YjtUIMrxAHs9bDkqMhKTY22/kmk4EEaJFTBNTBocQWn8IZnoogr1vanzVCRqpA5CZQ1ohQSp+M98wXD+JPIhYFMHEYR0OETIp9RNdEVFCeAAFCO6IYoocSpxAKTDFsTClakbl1tlqxZ37xKnturym1AQm45hRblO04AWtEMw4R7xmwc8L//cvXpPV+QmYpBT/cklDyHINaIJEd8/H9QsDo+702vQaPq3Qc9rpRaa+CFDUgXk7YyuIyb85rpJvvuaagZjJ84VrYmfTJS9ClohTa43gHZIePeUiDu0dqkKlfQmr68vJL8O/qm/N/GvARcSqV251cf+0wbTL4JoZyTu+vK0i8VgzFMzO6roFeFoOKIKEU4uj1NGpEnx/L1ov94nODRKRlAs3XBlGFTKmnFCrWh1CxKtYCeweFp0r2PfhrhgkuSMhGCIiGryjCLTOcAK8o86DrsIdKSOWFX/UTRCM1VeGYSWG0+LiMME4XwzPXQS4p1jK2aPIiwiLZfQypGEim0faMgVOEtFOQgWprxVYhoigzMkL/xjkjRwUjLaTShJq6u9NowVzqzcFTsSFd0Q3pRpUE+1N8gqKXOzR1HVTF/Y1qB+GBuR0EqhY7jkEpTk/ldRhQSJktuUOJcwFLH4wYWiqL89jXmRwkIuSXaAUoW0T0Y2KhMU5tni2M4J5rHwMqeCFkRsFQg6c4sCyY7hUe/pBdALHJZMwawxiteRSoqhT5HHrEkRYFF9gMo2M6YwQFJQ8AoSXYwM2rqUDYH1zWAanRicfAx5lQoYf5k7WDWejFJ3/bUdTgSaRxgcUhPqLVqzKCFaRodc4bkKSv/CpXT2Zlk6ePXk3sH0auaUR14/JGBFKGMovljUvlUpbsgsWen8tMLQieagiqbPXvy4rH/kALrEgM6KWvFd3bhClp933Y5Z3LFLsAsP9oFTn1TXz4O5i9GkDqiiR/P609YeNMCbONmVT6J06FqboxQg3lB1hDgE01pLXUhmED/7xliA6Wsn+8fD0docngNHAsyX/b3XzNeD0fq9xx/YZ4dp9vUHR9/98fDpi8vL2YWzN2bry4uz4Xb1dq+zt+pfHToDa2/x9Q8O1pezcfeAK+He3cfHR3t37tz95je/cveuGfM8gtvj+3fn8/nb56+2PXuFtVeXOm3ts7eXP/zsxWdvpn//P/9lx16xL3qjF/cePvj4o9b0cq7znH5nmjCckI40LouQbfewaDbi3q5Ho7ENcBqrSDG5/9M2hxHjS8CGyhwudE8jFWLGS6vlH5kNLEhTs1tXsNqO7h4Q0LENS+3OOZ+tJ3YXbLdPL9YX56u354vV5vDg3tHHz16Y53BxyaDBNdh+OcrCXkCYXBfb5b590KMrbYqyGZsgEQ9/N1uucUfk8OK2jsSY43LY25c1x0HUCHdKjncdmW/Q7+7Z7ub8fBb7LyM50X1h5YgT9fcqesO86HR65vzfEfMwmbE+kYoJclPklNfTl103Xyt+E6N7US91VsDuuQSuvkbg06KXvaP+kNDzLot8rEsFVpiX4OSngV93pPcb3dXEzr0o2D06OBkN7OTbfJBRiX3MVh7oTzJDjO2wWfL4P3pyd9vZx9MkWKdAV+7wcPzi9E3pItNgDCfd7bWP6Bc1zT1sTorpJ5Qff26Wq+bgCKxhOkqaHnolC0RxF5vRvU5NLn4JwtEV4T8pIAY7Ra4CpOzFUomVRrLS8iuodsUcsQ8AAQAASURBVKyeXil3RGmSEEE5Y27kn/yk8ScvKNHPpRt34aBxiz8Urd17U6TOLeteKmOfMWshEXeYQ3mrWcPC0cBoJm7UWPcVaSnlTq0RHlPWH4nf6podnuybOlKo0uKFENTWj9MsDOzVBsHCPQ2Qcan7kbr+i5RyfQLT1vZ1BrTbh4YCdNerObOlcjGExbUMuGHshvKLZYlwa0nHmHY4ygiIMdLgYMhOh1n3frHfcXLgZKBKrIVvH/dHs8VquGpdtFYPHFzSXw1aLRreBDnYjdf915vlnW2PC+K1RfXz9f5EoY0nWICvMUzLzSZQrVOUyERRraA9DDkHnJBg2NwSHR9MdEXI9mVv61wImweZNNA+tH3w8EXHcMTGIhJ9mis9fP1I5cAZORMgWxDZyyhHhhthjg8ta55NDzIKYfiT9KWSUIOaRSSSmN5n2rNGTEL3uvLQbn+S54pR9RHmwDnCqnFVMy6CXnznBe3zNZMQsJMyV6pUVSRe4tx2Vx6kE3P7SRr0tIJUXZKkzvMZohhEgG6xPAMwbT2rQBS5VkRhYU8VtrvKPOg+jQNeVTa5Js8o4hQu+ca8KEtRspKdjIYF5RIhEcBrMIgMvMPas+Lh5f5bnTsCEmjJAlxaxY4LLxPQlHJ1LwzqzOZA9rS7t5fvJcrnZvAnQT7nQ0A6UT6vfaMlEjbqsj6H71PWxLmOnN93Vz59/gp6ouskVmrpKmk6ANDOc8H7fKKEVsg1KT73OZlURmUUNp8qj2vQn4t9/QJgJbp+//xvZVd0DyQ4hV8SqJ7Vgv00wt3YuOo0U+FQPYQXSy1i80xUURRd6TA0K5AZGEaNhSZ5FBMGK1akeiif8GqTjSw9NEai+i3+K5jA4pxqNZucGqSTbXoF4ZKwlUwLD1SWV4gdn3TQj2EX8zpGMN+bj3EZEPlo9kKYOW6CThy+4jiHMBUeazAcXqah7PlT4KQkoUsKHMhBJQ+7e1FLLnkPUunhUjNB0r4eob1vbpGoSEKeUqbS1V6byvGuRwTNUqxAJS5yKiflxqUSaztpMoO5esARTKUvWgZqECiqwCHds2RVUhSfIYB6IwCli+HVzOp6SpFSvnSc4tBiFhVZhSV+DmCOp18Y1CKoGs86H4RYZ4gjaJPHNBbpGRaxxBe4nlfnpIZRUzf5BEL2W6DbTM7xIt9QMoon81ohLSe1AKwGUMklEhsRQ4PcdcvgkRKgg0+qKhoksZQpWkX9atOGrNfM2JZ28t0//7OvfPgfUz1dwzg5zoK25AJMbxRjlBqTQ6oh3RLxTD7rH5+/zYK80nVK2FAlJBCr7rcfmvDr4M/9fuFTk7YJzP36c/2i0vX752DcevEdiCbWzUO+fzFh87HJ7lb6eiyOlcRvkSy1iwfSJcNsq5UzcWK/OlMOux0d3b/74A4nXH+jRg2DmY2LH+Mxh4pJFZ11/5tPvvnND4a9PQd4O0fpaj7bn0+dGNyfrt/Yrn84XP+X//v/enb58s7xPadv60o4pwl0Ln4IhAHChTldO+dqYIkstjUzY228bT6zSf+L1ebSQUFMrM7IGlzzBBx7DekoqCoQiY9i4OuFV6ap8ezZKdOMSExS/C2CTTZ9jSywg6So3uwysz6wdMqefQVRpWFVhsBoVLu60xejbmfPiQHDkbZ8PRwNrM7vDQf7PVucHtx9dLKYjs8u33zvBx+9efV20B+Px0fmK2Np7Kj79Bu/9K1ud2m5xHpzvlpyR/p0/PLVx1eOqO1v7t17oAPANBoOqNn9Xn/6wx+8cf7EgzsPrTVwMZV6LSN1trJxhJLTwUdTuyZNXtnrPmVX79FgZD5SkZpUPEYOee+YfqBcKVNKFULcsMnneKdoeHMrTgrj7NgkHxru+iI3NaEVszJIzLpklt8vZNJEdw+cwsdP87yLnR9fCtHIuajWn4/H9k8i1KzzhEArpn+VyWuEX+7tzoP7H3z969/ctiZZBDzrTqfzxWpxfHKy+O4Pe/ac6h1iF6o/g40xZKJLg6ZJKVEtOoy1QjsNRmoOREZePCyxgWhmHYPi1bBr0A7Fg2k4j9IBwpV2oh6aW9EhLNogGTQrTQoSMJU+vzRgLCVKiWu+GpuoP4UUq3JVyYnW4CZTosDUDC9XOaKZBUZpp9lLu8FgBj+H6rqimM32MK2mNmyWubmO4Yg0K0Qdp0oYTCt3TBMDEaRobXAoVQhkQCQRoB2ilFGYbnIN0wKmEx7DEcUsNh50N6NxbbLDye6f04BTHuaAQcW0bKiaKih43Y7T68HOKS7yyqK31kCX2sTU/e1ed94fOhHAWYEZUztc6Lkxuq2K1/vfbIar9aGNtRzKtenOsw+w8bvRlC6w3bP+W4TIVk8QdioYC1+RmeMwotuQt2isEEUxh+9l3QQjx0RFmW9ziOC+LQItIzBBV26WDjupJL05ZiihTENPD5qFNkQcJc2FdGkorbRSaQzUdL4yOyqqBi5BKBws83Te/NWVH/+BEKF+gRFQ4SqIjNcjZH0l8yXNwKSCcLW2Xemiw+PKaa5wo7pKBQSSTNVPKiPoGdDgp7XUAtclMW6q+KlnXTi9AHPb5OupzI+kxA9pZqM7g4w0FlhoTvU/4mutEqFM7KdiH90GOYFCcZqfaWBVkcPaKU7iNE6BICxW8ExkJY0zrim6LwUi5k7Klj2G4BRkAqHUteQFLdRIpXrPLb9NlRSQekuM3efmU0UPvHrNDahI9Q5OgWnSJN3tC6AGhsDmoUBXFO9gVHB+msI0iWM2RYXsgH4xJYEPvCa4SbG7F0rwz1VBgbFL/gVwn0t3jV0TeI1KQGyzKgDYAtJQ4poewpleRl7JmdZnO1/wVW3bH0Vb8AnnwkYlPyJBGvOpdqplJ0L7oKstR7Skc6xC41fGZObyyk5sTKw9Rg3VKjmFottsRCJrdkgvW4MuQcXoJTtyZcduCs4AHPYhz2HKzBj0lzj+anav6a7Sx9kHq6SIuQIt6qbPwZ/uo63KE7DleFCafjRphoAJOQy5guzfASxNzDlJEWR6UAPMS7EP/JWhOnKhQ4lIlareIkkKQy2Wyye8T0VAyugzYtMeMVFyxesR5AQSpPQUoSU+zZ5atjE7ZlyaUl2VlOrK/La44A1NRvZSNMVfa+EcjgbllRWF9lqJS0BwyAK4xY/FHtUwREEzCwysc4+aL0TZ9ThfJ1eTML5/US7AV6tR+RbzkvkIc6iWtnAzyHGwhmJS3+Z19DNJFzqUOwUX6cmcZgWhBaN0FQcNwwCaqJQt/UmEiSEmWcYjJLWwKmloF37NzJwrx4Z7TjRKk2eudpCARQiZf+mfWKrBrgOIejOdy7IN03s7Snd6/mYz67589Ubzs5hbTl2lM4qii1a0kzrQqpEPkVVLuFobtXj4/v3Nv4kqRGMBaUBzNfnXY+iSuD5+LryCdrdq8OJK2V1N8iZ+c78F8Nbjdfwv+b2JVYqi0RaFwufWGDSxbuLewMnw4w5ve61UdUP/WqlE6/RaVgOQspkBMnjPJqvz04k+pwG11urs6HCs/qJ3XOFB8pQmrdWeObBT7SHfcHveac96+8O9LD6cH+6PT4az7sFBl6WbaWQXtSdN5lJARsMVMGClSlXmVzBxqzU1z2e41xsftjvnGBsnE0922tcW09Fi9kYnIZXYC6fyPGQtjeaHd7HNMDZ7iVAa8NryEJrjZw2w6l5mCy8VZkEntmQXONnDoN58NLrjuF6dBbXpwC8aSynGh+MPf/mr8+ml6TpUgW6CKShWjQ5HKGFuHobNYIMBDdPnCPTbi+OPPnu+uni5t9876Q4Hi+FkejHqje4cjL/59Xsnpi3NL6w+XS37TjRfbEwBGl4MHSW0fvRY32pIJ+RY0zjRhxfPDXR0RiYxs3Lik2bOO5CCy9Cm40gw1+9OxzaqQnVF+zVMEK0SKYkWVg0lqVkHgK46R/QKnItRs+vKl1y70SFV72piNPFD4uurSVvjANfnBlTkMMPWpERX1ga4irnyANS79LsAIRUm0jUbR8oaCUwaPLo9NVZ7dHD3m1/7VtRYRjuapiKfA5TEZ5/HzDGhUH7n73z1l//yw6dPX4hqO4Hp5NLX8dic0prE2EuXEclKwabzz+jM6IkVQbWoFt3SWcKSaZe1L4AzjFg9GgjaSi3EbA6bleXhXmgaoXmstWgPXgdyAlMy/BfEgmNKUtSsHmwKKVTGIZhnH5MmcagednmjgNJHISsBEZ1fzg5Gffc1icmqAzpl85iObvVeSypxRooiRqzM6GedS9ZYlDby9EYUqalR9phWDOrWrFZHzodRJOu9BiZLE9O0q8dgFUMRDdKThBul8FoDpmqL4+gQyPqEKufG0E3CyYQfewSlL7Bv2LazOui3GQAMhWG3P9GSmqhli/3W4siGuO3Oq8BMjy5bgKXDQpFnik6RWTOh79VzDDC//KLbuujC10zb9nS06q23LzpLm/0vrM1jdXc29ufqHCwG696PnBk2dVqn/nLLiMRiuj1edibr7T7MTIVLS8PAx2HO8U3ZkBxBp9nNV5LUE32AABazsWQOq1k2SmAXoGM2ALdC+edmmUkMO1iTyLTlkxyzHfYIb3QtOi9GMdeAeGrsUFTRQjCxY0On4cnOfqm7zNRHzDScDZ2L+uGMCvG1mqTiFOy3fIRO7b5UTc8hNVZCbyEiDlk6cVApwoY7SQ/UpjsQ494HYMMkxVjpmtioRw5ihxeSFmUACH/yxqig0nUZjPJZyx0dXF7C9KvgCWJZ9lHHJmug5KZlTnIDCnOlSwTH2ClN9umo5J+AYiypvMkFndh4ie65tJpnqUIXmq0IRfaMzqU3LpwZGsT1+5IiMpfSuvpWNQAb8QQtdzf3+PUrRPykbL76lM916XU+Q6bW9W4/4oj0068m09v3W3GblEGsgd88JDRtcFVpE/t2FonaRL/97Tok2DTy2UTzWiHX35s0P/Ne8ZPqJp9KXAG7hCk1DaL2kDWD5mk8cxRwvLI+pZURVnXD+sIPNmKLBRDpx4Y4Ww3rPmo7Ga+TySReYDxBU1TbFTHxzpGoD5rhWp+Cl6kp/aGDtYOak3dny0tCF599mdrsyajyXlhM9YqDR7mFtM7aZ1oOrkxav1GWrZZTezCneLIh0qzIaLeY5e7F4Pm1RnjBL1KMrpG0wEjacDnI4scfyjW96joIWbFtcE67BtegHDs+ZMgsXlSUjjxyI8qfoyW+/2wtsmw7Xik+i6QK3lbfQhoG6cCYq4C2putmWk4mVHB2kSjLD51hPL0iSzAw7o/yqsMYHHN9t3Q1chQyatniwEZvGZjfsrT3ObRIZDSpelRhVVnRcan6zGzJHNAIdEJ6NnqvAzIDD4y69EJK8ESOrz3p6M40VSk8+tgIjTLiNjXp3gFJVg6FslReplL1hwpkA5ZsxyG+BhmJUDtSyxOwQHU6yIge3ul5RoEBj6var5lmAEUTJa8qoltqOaZM2nawlCoCXg1uPHpF2mCHM9WR6uncuXPv2fOXZnm9On06XUzMbEFMS1McTT0cDfFaSuE/yiY3dRP2TqbYe41791QEVZ+A6JDEkXNiBKtE88lP3X/BW5OkidwkFPIXgnA7o5+b8MuApyw34Q0+hDMP6FDk1ola8sazHeyds1pfTabc9g7qZXi0B+NRxm/sv6H66OXIYjUPYeca+qPc05vLxC0TibRay+kloczQXMmtTELHVB82JcTJWklC5HBUONbEGJB7ncOxk4A2BsTNsNXRSNuaU5/mmDuo+pc1PaDVkFeM3WwXm0tnWudEClKVeuNpgFV2B9Ekl6nVaV2e5yxvc+Yvzi5a2+nx8Z1Is/lId47vv3fv3pPHk7O3TvmK+WUL4PgOLE/kvw8MxlmayWL6zWqfedrvj49O7rcMG6z35rPu5dWbzdqShuXZ25f7neOBTVE4/HVSOgMjKfujg+1iPhxnWgm+rPls2JEHdHA0PqAgQ1nFCGsrJT2DPikzAUAvWiAKgSFZdFN1eBIyItHdbkI4bSK4evvYteo832+zz5c/34qS/CpSE9Y8N6kSUqHQ8JBP7xJW0E2ad+FN0uvIlSalKLagDgrtAqTq27/2W7/95Mn7v/KtD//Sr3xL1dFmOK60WQwCpQQHHYpr9coMTA4vLueP3nvg8PXf+yf/9vLSQBbIuml8EVZMiau5MoZD1ejZcmxFl9PwjdyHkqG4D6gmH9XLpuMsKuHQTGU8JeHKE+Yt7RFTI3qJj6uhO5WbT6Ug0voAFYGIMksDlADx87ojWZRi86xXym+hV+t/pqzY6CIzNGQZRsicNRNWeJ1MiBfC+sQt2N0GstDyP552Ihq9rosIbYUlDeQIS2o24nrpjui9ZsuckDsCh6hoC0SkUj5pBRBD6WGYe7S2EkW7Zi6UZHGEEcd8TTsST1uqLU0YQxgV2zoGSWqqTOz7dWfaNhiQzXy1sAHECu3pNqgMh3/h08zohCpUCFcaUL51sPvtve52amc39LDZnPqDrg1E1ysbi3DMx9jvby7MjutuhpYalAvJdLd9xek5q1DlaOtUgCIFdGyBqhWFCE2zJ0ZqpqkyTOUKz0iuhOb3y2PRWgyoI4vI9AN0u1JSc/3LykEVEw6VOOyJmHb/1LIbZenbiSAOTMZRVF1amPCLLCWs/LI/WJkPqVzBwSgcKF4JspqPXZHgCgyKaYeRgmej9EH0hpEZsBMQXk7ZJKnvACkJ7km9FldGYvyJXmqFARGfbFP2so4KCZ+zf3oqHVunNpkggVLFQNfYR6ZrZdyAf0L7H99+6Ks3p86YgYUDciTD/AsQ5kjSQR+xIBtM8lh5ehXgWeOORin1/5e1P+uxbNsS+77YsaOPyMjunDztbaolqxXFXrJMijAEA4YEQYABCwasb2DAr/4CfvWLv4kNweqpzqQsikWqKPJWc6tuc/rsMzL6HRH+/efaERmZ59yqoqyVGWuvNddsxhzdHHPMzscJJVVjQN7PdPkyHkNrhmVFTNkVF1jDUIknp6ssR+qCRkq3KaQIN3lV5+m6jrR8ffvnJvFUwpTmOuUyfZ+u/0b8KevxSIZHyin523m/8/ZulNK7loUtCwgZy8d3kr95vdzqeZW3o2vcl5mMgOk28jn/yNdZM6UU1Cm+5DVnfEwGte6+R7BBqHoC7ADcQWrxJ10gpq60Z8NISOGB2ChyNrMTUWnjjMUH6ZC1xzHh4NiYRqNFEXg455Ojaw5TFZOyJU/kO11iVg3zIJ1ABG0Ekgpvm+axUYMWL/93sDm0U44BTeAUg/tAloHRCeBKlRv9enbCL3/B1c/hXh11KGMv8YHpFCHbXJ6sj62IjeKfnJ4MrPnm67nJvXE1FA0dPSStsljk7AZMuH5pOvLZqRVIzUXKqW4j4Q4jpN1Np2b7clPqmZBDCwe1/x7J1YBAfGcKadnkD4eNn0Q3Yg4JPTdCNyDNPvEw8UDDq1E5NgHBGMQdMPcoF1218YFmaq4EU4subksg+Ki5AQGd4F4bNSkvhpczR8vxWuxEgymtzqAO5adu/oXkGIQcxzW1iucGH4ygUFnxTUApHVkcxyu1PU6Hsi3EdW6LpLYJ1X6oDaGmH4bHcfG+Fm+1/Y4G011TE2kj7/mHaDtbc4a0l1gvVK/Pfvuv/KWffPajk5O1P/2TL/6//+Cf/d2/83dmq0d4bjjCOo8pfVopKuMHs4TO2kS6be3y5OSAYbeyblPqlzEG3OEgmKUvBkL99Nbld8Lx9HrrDqffedGSrsUDN/spud9KP+WGKfbLef7C1194/cJ5/6UYGLydVCEqKmRZgfGQ8rzWfFHHQDwzFe3iV6iY73CWn56dGX85vbgwW4WRcmZF9aa4TfMt/pUpQ1t20M88HrO3kNXmUicnr3gftzd3yOj5SQZN8qfjnEVbNZWXzAWSvzEylkmBrUi3XZi+0KT+yic/2Nl4ON88m53fYVgcPT07PXxtGYLCqJfsHoKsvSaFGNgwv4V/esUtK1+184+yRDp3JNiRbjaGJ+r47cRA2uX5wddfPj05Wzs4OFpdnPydv/Nv3nm49uzZ8/v7W/fv7Z0dvWJIUSgBN1ZJWQEM5grFDmoSz8KXic1nK+unu/d2Zzt7x4+/5C+wrb/Tqw5fXdzfuqNCjqO6uHq90n65bUAJkZt7zXkaLMU2096qvmWOvKe2N/tKj9hYAU3UNlosidVTGxAZmOCeNMpyeprFhecxbjQqTjDSRbPF+zXBvNEU7+URfTzhmJJWFmaK4mF7uiL84IHxmgF3+4oMI+cpyXWyEt2KqT6u5BInv7pJP/HZMvNWm5D0lzdfl6Kj2ikVpJanZ7xHxngczj/++OP/03/wf7x3d2/bAtC6W+Y9plpkK16mhNLaaWlMBVyZ7ezf/fD7n8iKc+G/+y//u7//n/6n+/t3tre3yHTdUtpzcYKVTR8zEHh8yH60QAC/NaJc9wAuW16Vz7ZNgWrSdlBlQxFAAiRLcfGJbFbmTyiKgUmKVERIegz3gA98PvPUyKho9QpZyB+9BuYVUdPRF8o14kgzLkXX71Uz7OULYuf/SqOOBkyhWWF1RwfKYeMgzl7JjB75IIo0eqrFs8empBoKynR93f5UMKe9tOUNiYlp/I2lEQPCdLYyJ8iFpJAHwJHRPz1+dp4G14IVtRvTOAUnCMau+OdDUMxWd5rhOl99YE38uQX0a7tXqwc1trPXvlrEcLWyRwmTdY1ApK9WfLow5LxwfWEeeJiq9TPNfrZxTmQcssukBq3LJ62o/YKAK06dJUeUWxnMJU0VOEJ35XS+/qRJCS271ynaVR/didZCLJdVDFe8ytZpixoDcrkhoPpAY9qEljA6MZYgbjY9LGpk49QNvdppw6LsEQaHSvC4mZ5wOp9tm+cT6mQWwv0NNUeO0HuwASJgDvv9Q9zAObyXoEAF97LkcyG2rJW9hwQEfLOfe+HDxEyJpiG3kb9PntNMKimvwbDFkJN0UTJseVdOL5WtsoMV5Zw6AbCi9JA48mg9OemD2TuM/0WCtDZUy4IJFp8Pn6DxGtIxIFSkEhQ2aIpKQykFV8DWUwNFzlgXIKZ/wROqGh0CbmxbXftYjRUrUyEDLYXIrHjjYeDFF2/TVcwSjjRCR8o3Ib5MISN2z7dfxQdfGRe+PNN3xPyO21Tk7futrKb4w4q+HDs7TZkO0KckjQBIsHy5nf93BBXtTe63qvud6abIt7N5k/ZbBU7RbkW4jjFIEoRmZhyfOG6TXhy8ytwCTIX06kEkVGpWl2Z/8DPyiIFLML5Jvs26rddXWbio4QNat7kfuFgBE+HpXAVwL3JlDwnKCqyQdFgJE6Vc/em+suE84AOkEZpDgrNxJMbPGhSQP1KsYMsi7VGbD3WCkZnOrw5Zi4MzJVSPtgaPRhJgUon9U572tVkN/uoGJzzjCzESC17yRFZ2wIJVEfXBOekao6uHvJRQ2QoHDLnjFef+kJVdK0anmSJO4YQ4+WjFdbzs3de4hE0GiVqmDNBGy6EBgGNznxi6lVWNJpFIOUHSaAzqVPgXvwyAB+QwlBcoMYt8uTkmLEVEIcu6RL8QkPoistZJRTzv5TRADAvSqtRUL/gPbbV0rQZm9Hpu+nVDKFLUXQEnHYpLjBB4iHCAooAZ4hEM/uvqmMDkKzvRv4FYt3ENcg4sh3GfFVSuAVKN2Ae91ibVn5F6e/vuD3/p1z/7/KvD18d/8tM/+Le2/t7CLg7Gc3Kg5ko0TVSTm0ahowIwwCJwPar59tb+iFalRUPr6HytRQYuKn0ETiD+z7lXg3HdPFxnqCzXdB+P/5K3KcNxnygn/a1C3uS2ZIOpcvFL7atxm7kBv4WBnXWz6ptT03L4TWMC69vbtrw4Ze7vbO+v291z9e7K+r7DuYzGNscLAVhUMLyyzTzS1W23zlBqHH14lsK5YmB6Ql+UHs1C7xgpu9aEhNnKj37ys/Wde49ffvb7P/l8Z/t06+r+r/zyA0eEHr94dfeeaOfzrS1t0HAqsXf11fUSO/7q4vx0sqnPj0aPZHa+bcLb3trx0QmfASrr85shdrK1+9nP/yDDy/Zjlvztrtx97733v/cxJBiKy7gigcSiNs4VfwRn0jj1UMGtwnozd189fWHJLZv+7mYeweOTxd7W/ZVXX+7vcMdad3JCNs1Dd6rgjCVqNAJPjSkFVIVuC5D0Ro1SW8Z7funI2pevD5/b/vB0xo0N+Q4/MiOOQNEpwIlLh+HiLbZMcoeop2CcNKzbIiwLQPZLJPtShd66eh8pp9B3mM3Xm5DpeUo/eP/2x1JfC8SUUxGntCOJR3Dcvqbggb1bIGR3jmuhA/bg3p1mTdJDfEms9QzQkauZFLRD5p300c5wsVro2VsbcXx89pM/+ZPzcSBbpMIV/N/ws7Cp5MXW7ol1HfZnpqLY6vp2tr7VhzBSbc54lqgj75zoxN7USq21LEqnMRIh+gRaHT4cm55wQ/7B8CnPqhhTa+SW1eu9ulPdxRsthLesMK/0VlkO1BVBHfibCJ7wolY1DY2sfaQoSQbOpItGY6KMutMhevQlaKl4QNRJhzHY+sZjzRI2olRfHnuk7xqQDXKhNYLYwj0wlI/rp5egSz+XY4q9Pd2aopmFhx5FkoTAZoWCXNFaQ2ma4rA6O9jlRVhr1uXlKszqOGzML2zf9+rKIQzatmzJgaVc5vXBRtl6LxDJxoYAN3TY0TguViltZQgY2IU5nqG0RIBbc+9E4Qs79nDuNykQX1AGJGNnxVqQkElDcGhUo9rMZCZpcBG9msFoImTUoixVrJo14ys7pcHtSq/AtjHXjJVVIy9mHwKg2QkG+0cUuwghEGkm45BNDZYXsgUSNgzNqAkqPzVksvXUXbmVUTHgUQ+tZGwBrhGJBlAwqunlFHvKObBHgzh1MidQB1F9GfGm38AdVZ9KB3bohIoa5IinqgFMc1BQ6Q6w2Y2RKVOvr0Y8CDXv0B+TBWo1g9oGQZBM8IjkQyKn8BgUH5OYGnsyMqFa4pFcqlGPQQOpEqhR+VEL7+Nr4A0EDVkZpBh1j18r5foKU5VZfAyjnn2fChifRJzijBTjwzJt0HS9k+MU+Gfdb5e/jCdfpY4PU2llfg1FZdTFvM7z+mGcN3bVDD9INC9/uiQc+RSfw+vT3jY+u/769m/zlrgDvng7dMqfXN/k6ft1oUUdOd9Ow/cP4CiRdXfM1WfaTVZwYRE8/CLmdOXLq67nH3HFB64Y7Sybtlp6lNIBacAUw1B+tMrVPK8JdpQbgRtmcn4eo5OkacXXtYNVO3cF6eCJGEbpAFM885FV+QElMpt/WfNMQWFL43X03SDlUE/ExooCAA0/WkSZ9B2eLV+86j47+0B2dpatzlVmCJvw6k8+UmBDr0lODDT87SQzAeLE4uCbf0225VehiRAjuFJzeAQxP58vFIUsA46y0JhwAjDuc7/DjDYeME3IS1/AMdTj4KpMc5BTemLk7AMsJw0yWOY4Sc0wCsauZhUNFnsJg9auUOKBAMhmEMoEdRL5lLVCDJoWu37L0AZn4oSHULM6PO517YYwR3QAJcmBU60cVeaYRkMo74HmavZViKUdOWIM/DaXktKVjDkICNijwd7PxbKkJG5H/eoxKl3DNUwr5VRRjXzGKEJ0wvQEYS1nZRWBhI+U619hHVXDZEGhAua1ztdPz158/3uPfvzjn8jkH/2Df/aXf+Uf/N2/9zf0p3jZak5CYKgE8sBzSqNapaQEO2Hq9dXqa83V6IoMfpdzqBTnbolu5joL/IteU2WVHN7HbOnrkJHxyKa8q+Zbc/p/QQG/II4qTFcAB/HNfXyZylyG90ko0tbmefCEIY3+sS8ut5zCydnPo31yeLi7fX9rc31rvre/c4pS+3tmvO5t7P9svrF5efKR44Gb+9ao/fpYW7ZxdDo/PLBxJxwfwym2wcpJU1QfkESsUAnlkJvQEVKnC16uPH75+Gixe/767NnrO20e+s3Zyeufak/+lV/9wEafr796wXDbuXO1oZdhXZ6T6Cz0NPF4vnF4fmCHvyvHd9k93oK9xsQuH+zuHB/wZujyYShSx57aOHjytY7B8xcnH3/08Ozq6JuvXv3w197bvWuOkwEETP/TnHZnj+ipmIMS23wMVnI0tjYIZ0xGU5mPDi+++tmTu3fWd/auPnn44OyIFrnz8vTxr//yX7//YG1x8HBjnZv0hWUSj7865J83EpUrU0OrxmlDzKD11XP9xiFiul0rnPcLc3iOLlZ2MnyUEprGbIaJa0nnwGa2DbzSfzEtF+hTKuRU9Wd2zWwnpCHXQM2QAXDkHU8D+xMfuP+ia8SK61U7luzqZySZXm8nfSunW59vRgZuhckk1Vd+7v3PyLi6j1cuV7/Z3txzrMPctDMq2fBurmwQ0CY38Sl9A7D1SnVNMceTb15Y18RRc3R0IGmzKw0Lr2f9k3abyrPJGIUUwHz2vWagjFNXESBD68qqUVSjgRVwPlZDWMJpJ6gcy9qy/AvrP0Wq9neIeb2ziIdvqYZhUtGTQSUf+i6C0RSxzkD4UFf5kOoUq3yti+f4YIoAxfm+MVXpAsRUk2UTWMzRErTsTePHBIYnzabGKGVcZGnLCfq8lkU3et5DuNMnbN5Kej8cJgI16aNEiQZXiJf0Z7kSxKmZqNfhOdSLLyF0NdPDm+QZ8pWZeCDRMHzDkklxFipc7Olox7yL+bnZ2xcO3t7LgGygQFssNS+R9TDbDAiO/NnqQUMc0legYbCoZpUOftZnqXqchKtf20Np7epho31mAEHW5SaKrG4+J5Va2Yb1L7et+bcQecURBGkz3zmYanfUszWk8UOLiNWaFx/kY/vR0XRAZk0+G5tnzWh76KjNcoI4yDsKCC70HKksQ3Sk0G5Leh6eTRR42cTJ6o5LHEdgowsAazGvRWgQBTCDuoJrE6NL7400BpCfxYdDQX7uJTaJP2TpY9wymexZSXVOWfX2VAXAwrzb9Y7Ao+HyFzi6eNYpQO57zlZbCb2Ha+fGtF9xWKysvli7umfIbna5N199peYXBmoWH1/OD1cv7m5asnV1Zz5/fXX54GLtyJKoi1VnLNxxUPpsxTDs8dr87pWYlklfHs4W3ztuDrHxYXMo7CMXNoN8MCWGiVUspM6FimNxzmCdgec4eWBdIAYas/Wgc2Lg2HdwKA6P4aEnTm/qf9LnDVb6i4fHJauSeC7bwgVMX0a05UshI3kPt8JGcJ+mB1+mjKcH9+k8rtXjIry5buK9CVpZj3b1QbpGLYKE8ZjFONr+8eXNLcpfx67YEfvW5x4naG4+vRVrSitoGelN0refRqLYLUx965oCB6ihG8s1uZ9fGfGITEQdvBq06YjyEd5/CiZfSkbn6MGjXDqhzngkR6m0izSRP+LE0ehUGPoK8yFJRVx4Gx80cr77IHoTvT3gp5Ko5tCi0XiKQRZTCeb/bCpVSrHKW5rBiaWpVMopHKW2ciFXV+pAQRM+BPQktWxHkZ59Fa38ZDFilIVrsF9VCSRdJEpBbrG/dzNs4AXeQFpEJVZxWdVVoPti6fItrxK0fREJaVe78kng+5nqW59igii9GTS1a1qBYsBcof4QLTyG8l5Tj0AY/XWvmbu1H0Jq9kaUtEqJlLZEtZcaD3ibygG1xyHVkUyPfiotFA5YQBIsuauqO1kVDd+IrZi6O31XkfSZ8OES0Eo2l0l+/kVOKSlYhacy1EsWwAgsd2l7GKgeVY8bZRtWa5yQFcT9jfug0tXazu7d3b39w9evjy4P/rP//D/6a3/9V+/c3QcWte2q91XlRy271wMZRSvKioQ78DAIDz/VupiRJm6ooOUVVOPRvfR/5nUT8ybWm1TXT1Pe72Q1JXwn8CaTtx6mfKYEf+FkidzY2iIuSLMPFnFw0uzw6sWL4wd37t97aOkgABhQzC5IR1D4IZqXTWbheke8Gk5NEOVgCtDm3Y39h/e39X4ZcLZggrn6kv0bpEpI4RKMQrEN/KYtTs8XBwfMN+MNNnE3W6N1JBxs97a37m3rYFgBcPH66Gjnjil4V5YmHNsB3mEZLy9mL5S8cXh4yIF76pzgTIgTnYOODugUsJOf/fizO3f1CNYdQ+bn+TOj9hs7m2dHBy9nW6e7JuDML03zs9MOaBKQAeuEXCwz1ECAYsggxnYxhOH/nd/6zd+9Wn3VGUMrO7b7XF/94PnBz/ecF7Cxsjh8tHJ1aLvV18cvnnzzT7gvGh9hqMRNmLdDkIYnREfGuMXa1sbezraRsNUjs67Mw4K0wftpvtEVx7oqNnEJqNizIbVP2cqHZ0cdvubcK3gq9cQzg5GrSQFTUDi/5t23GGhEE+c6qlgJ2rgK7uH6dwpd3q8jjdfviiFsEH9ESLFdg+UDrMo7TaPGm9tOQHGUuNNzwhKcV/0U9fRS60F/IrQl1LT+88cnz5588eiTD7/+/EurzuTPp88Y6xCLzfU6fvM93mvjMBcNKph/rXCV8kMdjWlC7ftKcdFEDHulDTMjePuK+EMJDIWUIkN9IiN6kId70KVageqjwDpfkqQQq0ExBA9q1AkoMCIODVMhIyu3ko9Xvh/60KuS88ClO40hueK+7ED0Af+4KkWAtTYy0BK5Bipru1TUfHqrgnVqWydAxRIzAA3WaqPKEgcaIFK+7nIWb3CZ8OpuVlrhLvFkAU/SjLhDi3IACsj+zskyO+QCWjgJWJ/0jCFusqyhOYAcL0zDkrFyGIr22F84sYvtwHaMEPUVJGm1Bdtj9uLFqb6/nogdfTI5tGhkVCmg0Ky0jRBpsk7XoPnwNhkoM4Ns0eKJlYU5dXFPFaWsdJ/1maJa6HULtTW6kaM6Fq1RDjWn/ASNgRsJxiYcIQedRQSbrrVOIxhq8ZO9VmSoO85BHfmaNOVT+46GFuiNUMLHN5hD6KnpCRDfw3cljC81fMGzvPqg4IF0wKEW5cW62LZSsCMQzCJuaGDNpLWNC/OeeSXqu/J7XNwxvXd1Tf8KI+5FuZX95vUstqUylFralR2euhRvk5roHSO5/BVQagzUjq2GVkwANgvRKy0/VpiQKhttrG7jcRMXTe0+mi9eQB8Z0X9TRbVQ39AwzK0l1yRzKBKDGT+hXZEydvOblECDDkAHBo8MQsqEAIJerPBhbJ/KXYaXsCr1Nz5fh4dTf4MWPve1MsdP5L8Oun4o/U3aEXcETBEHUUZSt1HS9cv177uB432Us4wxRVhGU9B1ByAMDb++eLdnHV3uVNI7p/YW57PrIm/9yq+cOZrN2nddV2S8fPs2fb4VSeJlFiMyPiTtOB2DcakumkjHbUByImj6EVePJXaImyQCVA6ra8PTTGp8HFPZhaEoGmjW0iQTZIld/2s4bdFBEbcqxwxvLtHHg2FkKUMSGHISjYuHZTP/Jn5ITGDsg9TMhrXwMgGvu9VRphp9Cu751vMEpvxJUd3hXCr4n3ZO0WH2xJQqitP07Ne+klKcuechn0EqiTX1Mqnq+Az4ns+af3feTsx2Te6rWekyHa3yQI75Do/STfZDqKmCQdjjBkjtxrhD2KmPlBgzuvmEZZ8hrcwmXvsvvZBgkIPq0drSQiw0Qg2cQO0oEyMBjCEBi031bOvNjBbFEYBwHEHSm03NWDEzeFS8zKdhKMgJ23XZc94od+0LKKL+5JuaylDWYlCLUBT0VWKQJUbwUHFSPVW1EFKJk3rbbg+NnhFG7lilGlzOn4neFg/gOnsQjdZf+gQIrBKWgkcxbu0M4Mcf+DRAviLjvBGVajXqHLcAAuRFDZko1y2uMPSwtvLw4d7L59/c2b1D5Tx9crC1eU+jYypGC0eMUWkVRq0UO9Ru1KgRWL3Y26Nb5WUdiMzGCEN6yjJQdXpVYT6WVqGum3uh37qmrzfBN6mE3DxPCavCMl7z+0HzYrxeBy6/3fyMVnf0PKegW+kLkOytsqd9WlZf9a2oy+9XF3u4AuONhsaAipN0jrUvfGyn2uurtVeHZ5ByeGBD7PnlmfWWlPUdJFtbvW+3/fPXuxs7hxaw6oGzQeMYy3Q2Om6ZnrdOZ2umLdnEguz6psJWrHyVT9cpVAJU5CaaHx3snZ3uL85/f2t1xfbvL54843jbsPbxYmdvc+P1wcU//dGXGxtOcps9Ofl6+9V9grQ40/ZaaLN+NT+Zr93Z2LRdwQ41MVvdpcSuDva+fv4n69+8d3j0+BiMc0vAd8/PV18f6IK/2JjvnDlPIMZ1cqH2cmd9DevW/M8uPtJ4YzScNC6jCo96sJuEr3Zkj+syDta2fry2pTZNYFhZed2Q3co39+6uz9Zs87+2uvfHVgTZa8Ci+O2djYvDV/gpxZgc+myVyzYcrPB20zaWaW6t3tl3iPjFNy9e8aGa9q8TzQRN4MBVp4AMabH5RDIyKA1jHaZ3C2WcmHVpH1ZxWMhLeYyyYkbviSNSNpXefVRt+jQ9F3A1zv29st//m7CoVaJSXafracry1sMy19sp3zAhYZo+UCMDAu/8AiS/zDkp1dEI0roF5FZ7yqptG+ihhJCsMqsnRy59IIfNtY8++9OfPnny9Uc/fPTo40+fPn7y9Olzmt5ZdMZ2Mtpbn7j46Hsf/sr3/tI/+Af/YHvl67PFZxcrd5XJJsQ77TAxs+GMoYYN488D9ujDOwDn+W/RaiBcHfqa/Yx0Q+dED5FH/3SM8SJHHubR0vQclYHJTy81aPyTAzZJRsaLHGsx4qW6010R2RVp8V+VEEnHJQWobrnYmmBae7TUsQORqeYssqELkQNWKYd2SFtZtCqsrbcEjzmQ5vPkPG9uLOELhmFjwkh1hOZowlpj5QaBXTYbG0m0fa65AaanSECLNhYBI1Rl02XJPsN8x8y889NNsrXGBs2mV+czLvUgIpVVVr0c97K5smaB2Zbt821wM9DV1EsWtgU8YysOGSH/KjPUTCKnUFvnY1rs6opVQbLdXJ09W6u4zfPZrnerNE5X7Mwjk5NV/nDe66jkZMA1/TtQ2J+H9XB1dWhyXaNBGpr5EY2nSo5AvLROsokD+iFjFBQ96zpsXsw4wkn0s0ugXlhwvHPBBiCAdgjtKGjY2rpcOGlux55DF4uts/wUlmdoiw1LqmpOa70wqg7rJNK1XAOdLaMaLBCPJLeddIsAhos8j85AFBIfqi/a6Wd/e92o6tr81dbq/ur6y7XV/av5ix1dkNnT1fn2pTtz//JA47Xm6O7F/uraa0bIYvHk4vJ1xxS089URlbG2emrF4LoBSVh1SuPK1wtUuDymx40gWtB8eXF0NT99ffHq3HKLq5NVPv6rYxMoG6NlllzumSt7fvnVxvx07WL3dMU0k524KSapRVeJiTW9Je1EqRYXHrTQcXh/xY+v8KBVo/nkJl3nUyqy3vXIJ/MAz8BdqIjLh7otg0oZV5jtNVal8VxTnICaUHwTdeB+4vcRawn0SOR28zrlPN3fmkczxZxyuM7nOnXGbVBM825G4hGlHZy0EzfReggFAw3XoSmD6w/XYd/1+6bQEX0ZRVa3X4VOmU+BSfEUMt6XgW/nDu6wBQOhOdMU54XA1HAei3SeKAPwScMpI0JH8UR3vEirpHF56JP0BURWeidxk0dO4QYTfKd+IrUYsh7aSsKYo3ijo5Gx60ksmZc90aaP9CPJlWxYvbFWKVLgJEjkoeOa+q8SgZYboNFbDXuFBULSZeI+TTHUHSO22g1bFvth15ipelczT+5SZIYPkBVaY4L5ZDdsxXzvlEItSG4EFpUPeXSC2uTfkJrjQQJ9+oZlyxgsw/QwKDiaHk3XyFY59F21I3OhsdYiLlEwAala/Px2KSiHAUJNzggf+xxEX1HUKmAUrljGQUjsqfym+lbpgZXQOkRMfnJMEbm0iBWKCkNgwwOqoXcx5FTTZwx3Akg9fciWUrLw+lTlORGu2giNLyC2L0Loh5Q1iuAvnyJ0mZhWGd5CdtSSWfcyiLijnzGyLatljcDRNKSo6lCqlfXdlZPzk3/0j//hD3/w6eHpWTuyjIaVNs1ImHikKkaGUZf5vTsPP/3ko0ePHnzzzasXL56fnBxNYEXl2K6Y1eCta6DprZBvx7n5PBAwajIFqYMa3XweD++8ivFOyNvRx9ttmG4/X38cOSyzWX6PqiFUKJtjodc6VvD3SqCs3dWLe/7q+e/9099bXz+ZX+7ce3Cwu/3ogfGV3Udbd07v7r73wfZdLJjRBLOJM5av6yfAbmAGEY0bcL8ida4z2MvtpMxktX2kI3WsYvOrk4Oz8/M1vqwtG+qff9OKDYt6V09enV6cPHlyfjbfRtLT+dHFZ5t21+nkYM326etXOpMH84192xve3Xn0xcsvFgtbilnsu39x9fP51b2zs5d39j7YtzTx+Uuj53YqfHCficZguTQ+8OEn+3/t3/htO4+BMPYDHHTEmRE6WRjE9jJ9WbJtUXyJjQf+8F3x5DEYTM1IZTXupJGLK32PdqdvLSpJHhKYyDPKIOfUVktQsO6AbjMSznkxvyo78fAxvyiZHiBh8WZwhD3/ORJ0+fkbmwh5fHlhp4IxY5NbNT1hQkvaZtgfI0Hprvl2eh4BSz68HTKYWxHVfQqvvAr15n6TzZTBt19vwm8/DIwOpI08y2/KK5knizSEUR4HsS3ap9UZkiWmaFtTxoSijc0RQ73TlVcvnn/+08+fPvvm53/ys/vvPfzJH//hk6fPLUPc3CLUVwaC7HNAtq3//tf/+r++tX33v/6v/usQbQ+mzEeMihd5QqAocyRU65vmgNGexKHKhcCh1blAanq8V/ehNvsZ9HAXZ1SmCINTDESP1iH8Z+e6EKUfAd0zYnAN0quUQuRWI0LWOG4pMQljw0TIzInRpCUHo6HxRRQquLLywQB45AyMkTuIqPGGicrdra2bvXJF1Z9S1mgCKl9lbRZ1Q0wPMYuaSRzsZLPZV9mi8iLMYMJvNSPei1z4qAeu1J+lS62zWpuZH7Jihc7a1akOAIxnKPPdrGJruTvIUmO0z/o0f0tjLyfNI5TULVE7GaqUhKC1M65xD6tAdgiFcQaLNRozgxNrXWaO/b40TUgbunnKS2AP34Xeha17107P107quJgPgzo2D2Ti0z+23tCfgGDW+rSXD+nsvBf1ztU5dJdawq/pD6dNAT4/swAqy4IrAv4A57HFNpBb/9LIaTsiNEzZ3R4J5F40+B0jLbVcw1tq0i+aUIOw1OrI6ysOUs9BLDh3CdB1DemD9fOiRm7HHGgRL9cWhzvzna3OB7FXqglwasZdb8ui443ZtsGUQdiGGTlGYKwljhSdYw2c5NKZyLiBRrjYCIFNoEJlyzH1q6r4xblJskwWPQR6RX9zzdana7pyNofGsHRTe5MY07UTK/41l5LyMqPKFMb2zIKD2BkLwah6DQaB3bi1dzUaPypflQfD+elBfdGBZ66Iadj+MFp5JiykSFC9X+/FSQogvLQji6kZ63GISIFDYsu9svqdfpKYW9eIuIwhGPTdSvXnXFOEt6JV7RJX5+V9BKnJBMxNB2Aku+37rzCVMltRPf8C18h3CeVYRbBcA7AMn3K4nROYKnTAd/P1LejjRTw/T1lwb6W+4uvhgaUDz+3eox/bjiuIItxccyGrm89wUaRS58qQaiu9nZrA7VHfPz3KYciXtklvovu29iXzleHoOdU30G+vy4jNrWB3l8QBpYfti0OddkmJyJNYpC/amM82Nldr39hKx0gn7Z1CCHIiLRMaQdwmNnJWY43LzoS7mm09Uxwn5eCgYWhiq0xNq/Msfudptg4XsaKFOVCDge269lgVxKtG7QieP65CAlIr/5zSprl0vm1NwVQmdowMNhSP3eiqgH2Mb5ryp6tvf7FaofgkWxybj41ENzgs6IfFxwSs0ZW6JsMLGBBLerHGhwiUcvXiY6cIXa22AiQdhAibTyI2f1mNvxKrxxAVWpyf8NHq5faqU2B9tXYydKGIUprkMQoR9lE5zJ6Ea72VPLvlom/iIKQe8yvagYdz6BW4+W+qaYMAnCZQn/03lLucCW25wK1yHLIEb7P1ZzhHft1DwSg4LCbtzNBRvREuDBqrLSRV/XZNbUeLkCS7SVXEIr4GM89SXjcPv/27f+nJky9MYtlcn33x2dODg7Pt/b0a1BYzQCZtMyyxkbuAKEDFXb345NP9/8O//+/9xl/+tS++ePwP/+F/+5//Z//QOsHR81FCtZei2wT5eLp+nsKXQSOa6Iq6W1DzoUdq94t9Ua/3TnknlZgvb7KYHtTs25HeifPu65RglF+xxhMq8vr9JrvlTkRQ6T+ecawNsmoPmFApdTJvYsxJm2xt2jfl688NHC++mj+Zrx/PN073tl/92//e39pc57c22TQSYSeOOsm5knC1WQGOi8iun87xQJhIR3jN1siksIkHOXj11Dz9V8+ePwOotpqZvL5jHoj5D2dr63ush5OzdsY4tE/pfOt89r3V3buL+cWrl8eHR44bkd/uyXN7fF3uOVTYvkQ8wXjr/NXC0Pb56dbGncZ0jq+2LWpeOd6br22v7p+e6o2vmRayc+e99fX9k8VBTFFzUnMzCDVwnoBD2iCAtTQTlieZLxI9B6lDkNN6cal7LVfdYK5lgwwaWW2+ZZGgb33Q6wPbDp8etWv2YccAX668/949B5LyGJ4enrw8PnKGnb1oWrxZa1frWGN4/r6f1e3n6BGiJUu2IMyk6cXh+bEJVIQKNMyaQG7/t4Arcld3wdeU99jbaBE8TBdbgPuQZtovqGfXdYrbj8JuJRrRrm/Tp1snA1R+kXHxKPJNjkRuypRtw+84/7f+3n/wv/3f/L2rC/6zUREpMYe7Mddw0YYk1Mvjr3/2+PnTk8Xp02dPjs/O/8k/+mcP3rdg4/Xnn39xfkL8k/Lt7Z3f/Eu/+Tf+xl/9F3/0ExjAhw6sduyJAx0c7RRO2nsCM0InToMxTAtQBUA2xGWY0iu1JeEQRNRTrqZBdHxcdP2SGpnRJGq2qiKrq3zloAWQkOrDCXig7EYetUqxmr6damYUxXKGjL3Jt6rX5elTRp/9IGIr1yClZQoBM8DIAd9T7R54a5isQxW7mvjfxHRCpplIKs1lN7xfvTRVQhLFyk4eY5Vs82wwJmp4MJvlLI4V4ivPVD/gykFdkTBW/fEv5ow4Nbzra19sru6tdCifKeNc+7tX669gol3bQ4XSVZiu0KazXkFxTDrG9Dkm4KZ219Y6mgHa2KbZK6tO2LUR1labGa3evZgfm43NMz2/3Hdk78rlh5dXXlVIg8BODMNWhlsZfLR4fnZhEzNwXRGsxh4N/Wfkm6Sk4guzomr3NIjAFmf0plRVRsNwNi1G24VCYNGm63feTTfmceQf/wAxqbVaXMavpq1mCoo3dHi4PrDABY2Z8zAOgzaQNO4crXqZpBJPeHVF2njM5l9GGlm5X7sRjcGHxvca78NDrOwHF9sfrL3cnp2u57B/bf0TBK6svLTbuE6APRBmDhfv3GtzcwyZP8cBs9mT6Dl7MTjlRDNvf1X7PMxDoL4ZKrjOmqtJ7dTFZvB7Ni/ILv0bDtBMcVW+o5eNurxcOFvhwn4G/r3gwaB1MEd9vEuYrlkfQj2kJi6pQmof4ywvNC4wuegh5E1IGN9HNFkMhIT+8cz2NLU6niNvlQH3EDRx+igjjMlQSRU1zDlECY3X15sng9IF5qefAq8/tZ727Vk5vf/Zl7Q3VYMneRZQuQnzQEBv7L2WfF1fkiwL7ek6j1sZXUf87t9lxGUWb+L84gzSSW+ud+Ity8cIuBQ08/UNU38vreA5N8QjjCQZyidJGhUXStBfDpNCFcYfV1ypkESLbU8GDdfG2sbW5jZaZJWT+prFQa9s6MHY0CNhPgC9fHsat3umbLbMQ8ugLO8s3XIF1UByj7ENPdUs0E0SPAChK1YvLXsBISNmfrXhGJ0a3iQIH9WK0ie1mSQ21upukq1tgdLjzNMmxlBa4lCBZLQxMCBQLfngTN01dQSDB2L/gghzqUKqhbbV1Qmw0SZ0U0gaU28ZL2JaBeQAYdwMQ7lqpA1TpMOvTkKwiC3qSgA+jVFOoHRzRdBWoQt+yq56eRg9DA9ApU3VBOujlWiQkqwAduAcEkUXix4Rpc6Y6HmGwr1pFukk+gqY9Z8hyT7ToY2C4sRFT3aSSohfC+OoXctpHZboGFWkTj3RzlQJmLNZ/Af8edPDZa9IUUAnginj3FyJffmrGcxy5JfGZAZdsvbwqdcohnRRSpW1l+0R2/6qdP2ooArAZ/yU7FVcsMcsJeUzOj8zIWK2vbX3eu10d3/3m8dfHB4dbO/fF9dJrmZJKx0MsBcqutAROsKHmj96cJ+76dH9j//mX/3b//i//4NvnjyO1QbbV0Ao/otfvzDyAP4XZbYUyamY0PEvdQ1UpIZGSiCHGu8B3+/NNWoTAw9Zs+vFaJVp0ubXYrx4IfGXgDErGIbhLboxP0+OFy+PFwfmrpThlHm5SxK7FoLtLOzV2rfWDXMiVGynTfURu2Id7ZPZ60evmQWzszNbh5y8PjjadhjY+trJ2fzMiLrBpTObBGw8e/3s4PjZ8fmhFbzYUw9Wf+/UIkMb8Zzjo8XjwxN7g+xu3tu2Ls4C4dn24vjseHGEH4nR2eXZ0enB8er50U+/eX/v/oM7Jirgp6PTxYsA5vHEf29qEfJoh1GzUZ1wF/aq2ngsRg/+8FH8g897US8KKEPJlYhwleD6WNtkP+sQqbC2WDQ53akfZ598pGtRN+LwNec3bbatmQ5FqSNII1Ncn2t5HQef41356qElt47APT09ODH5QYqkjMTF1tkZ0e26Rj1+67qGfvmhV5WYfq7DvI183gqdIt66L2NPCLl5mR4mNN1G1pSn+oXwwZctvvnX/vW/8dGn7y0uf16zTzkQbJVSEYaJGhsWtVOSyRbWgK88PTw83dm7f3j4+r/9b/4Lqok39vjo+IP3P7p75y54Hcv8b/87//vf/t2/+nv/7F+kRcxtO716dfDM7sBDQeFCvGd45YwCZoNGakClFWh7SiA9lHbT6FR2ugIZkBaX5ucVvw2cRlMYiSfPeFpEsxGH08kqNsg3KhghavwqI4++u/CaovDroZ+B+mg8VPHwnmCdYdnASFlcM9yk72p6AlFpOgA1w8AHQ8o/QLi9+ER4yoa2LKsoot0bTUTMUwdzlAu6pv6Wf61ArF+kqVkxVCdYKBDCwODtaBMLZl3LivON1nhuvogl7PXbmr5v1k0LVh3VZbIuxdFAcc4pLQnLlSLp3BFQTPgnGHXSzeKfrefAby69aaM6de2M7d1uWdnq5pwYSKgJZPduVae8DUBwVIBWYs8pb5mV7d+Zk3y0PrA7WvCQnQ4bNXOPdnW+pvbeL2XhrHI/cYhBmDxfmCTI11jGcQ5c1HHHIQE+mjOshEVqJbMKtHgyqlo1STCJsuNVdEN30lbQMkSsgYGixzQSyWAge3wQMlr81QMnH3+4sbO9blqOXQ5MWGLP23N58KGW0gqg9i/WlIOd8jbwqu76O5AGF3WA0ikIwZTpeBdmzWTfIRNoyAMUgYtyNVcqh9AGnk1vi4trcBEPpe64vpn+iwFYT3PnDyULsTpQsUfURQ6GnapUzZAbl6iem1jxSwIykFSVCwdpEZZo8xOCBpLGb3kO6yJIiplZ0ecwyfSZUqo5+PtYSeV6fRX71utU3CjxOsby93Yk2f851+3YE/xBe12PqWJVywUdty5BARlUb+dxK847jyVRxvV9qt27+/+8k+bd16nI27mMZ9GCAj7TdDZC3ty0zMOaQAajJJdXryIj33YXLSbOoadL6xYGjuoDDO1i7yAPQyc1p7Z2bzBLTawy/EivPUvhYRYdhCTQqBofoXGqGccVBi0mqzcLAbOkiXNw8NB7R/6cx7ScPiF+3bA9iS3DOtUTH57vxh4aWKtwHd/thAEHc5jPzYSV4FlshxAGsWa2h2u6P+Ne1eMhZKqTBmSAmx5q6PByk+uJkti2K5aKpHWAFVRpY+JHTOWoaW+oToXUwiRCPgXmiGWIvqom9gSJXysPcjfo+Gi9ydTFh3YicCqCRinzN8ljLMz27h4oYzbbh6vyNxFoyAHswRso0zJytlfF/GBnh3LeWdjOkNaFXlq+FisJS2OHuPie6Vvdr87Net3YMAgQPHZx2drh5BGuWoO5AkLvXxl3mf7OF0vqRtdOmWphQ0PTvK8uTYxZ2dy5D6m0SworC4YiYLY1HLxp+DYuCAb4pHzU2d7wyW3yqXa1pgBzOo9a2517agypJoWjiE8DacOmyQgYbXC2kG3m1gyTwk29LhjCjerDIuywG01Pp98wAb/3g49eHRy9eP7SPoxrG7xIuK6O6dWrV8CqFOkVB4oUdpauIam9O3v0Zq3m2us7+3FBE0+Nhk1SvERT0MXByu5p5DVep9B4octH7PZyGatXpGHdvVymHtW8/jolme5i/ktcy9KkuD4fAEBvLp+n96Eu34SD3CdIqMWHDxNRdsyhwINmH4RUjSfK1VVDNU5903j1hGF4C7EuFnsOulu52lu52rla/xepssUnyul/ZcQSnuKCUUicEtt681CEIXJJVNsTxkQapvPt7dU7e+vHr16ZoGP8jLAu5kblrKU9ePL68LiOx/zk1Lzglf29DYMEerCrYLDi4ILpYct/4xWnF8ebgvX68YXzgDuYzmSkTQvcbDJj1cyWBnH/ve+d6BbufWghxNrmj7EHLzto8VVMCkxVuY3GnkeAB58nDlpGG/IYIfXZJWY64HEcLqIrYxG3O2DEpiKOCYMRTG+XdoIy357t7+2+OnjlTD4bjEjQEX8nzlg8042ASy2q+2zj8dh4GYroqJQRsjQzYm3FMVivOVKHtAUYBzIFlaEESK8he+DaA2GZkk/DsJAxVamqVZX4cjkOsHwu8O1rjF9N5/6O2OPrNcqmqBZGTzl1nyBIxm7yGWjtRg/EBU3sPjr7/Gf/6Fd/Zdd5gRwCI26cRNNjDLUxW8FeSWfnR6dnzP4Dh3pZ96x/9/r1xevD144g3NjYPD4z9NCSkt317d/4zV+99/5DM6s4ds3/lnBx/N5sYRfbr1OTGSlDZ7UBsVIaT6aRfcjTMIyLGq9sJcpHVIYh8lnQEja5yTUhgzqs6kZNM5rX+G7j+6zE8LgkVPWEn7Dvd0OD6N+wWJqzVGe7USSfcU6pFIELaPCJ/UYcyGMHw5YIsvJj5veQpJofIVR9JSs+h2uwqXaCRiNWTOn67koHddS02kmTCqUAQJR3RtUGv8mS/OMhLIZIFVptPJRaHpJqgTTAFsAJydrzbfFrzuedXTyb2Tglp5B58YdNKrG8/nJ3Nns1s0qnVUBrVuBkSF6caBA7mw3KbTFsj+bzJgN2fjdytJ2O+wEaUMEUe17npvV3rJgRttUVSzjAwR5lQAjar4prL+ebnJfbqXNLBYCmcqyMCKxvTIFA7SbNkN+KfaPR1nrMttoeCB7813zrbtrcDIoYJmFJQ0cT2jNYCbUFzj/h2zAUAC6HeBqbpq+GrNJCBJlLE6bJV4qg9k79WC1taj54A5w+gXBcgyysj3z/UC1YiFJituIDXfu9u73ycGP1S2eirs2fW0hocZKIJk24QY7pG62tMkKyutEGWlzykERyhOsapNlCxOig6BliAL0jzr4OwsjKitk7oXMc3EYR2ekZAPo828M7oqqHiC2DqysrDbhddRsMnRnVP1mx4xD2jUFAnFzZeldDbRhJY22yxqiP8JrsqsbJK+7Fw9Cw9lVUHiwWkacsEC0MwB8C6xJ+ZOqWsVtN0Mr8q8JlFiMWK0RZ+xxZV+23k5HIKhZ8/mF5LC1kBVxf+f4lHRlch/VrD5+b6+bjlMxr1wBqevzOe7CK1KTo8DCuwqz/ZC+O9MJGZuM2PU7x/vz7TZJgKtc/P8l1jCnq2+BPNbuOsYQqbMaE40qC0koCYknEi5VrU7LNe6CWzAMb46BYQwWxKw6KmnmMy6Us4o3kYACNVQSmMioLT3D/c+4GorgpIbSUR11rfJAMQR1+pfcY4ZA76EAoLRfz0iT+NJ6Bg6YGpfhqJR0uRtpxn1VlbYWw7Dygw7p+DU7etLS8zrLqDOGQLe4LJuDGeA4CZDqst6egNlm28qATCfG0KipsUHIKJ4Xn6Sw+bBrhamuLNW8CQM4K/2tPIACI1UVc7JFIzBb7mT8bjOziuUtNSzgZ1w7VAxKLtkzGoPrrD4kQavGXbkNKIX8841be54yBizMDgUPjgF0RlTW9DtzCjPJ1vgxO0KjVk7S3FYOySY6spUIQFwh9GQMXeeiRhzY3uMnjOD4jOEpB9cQWkvpHuzU9crR2kbIo0SMaqReOQfSACs9ILLgCE8Q4rCz8D009RQv/RnqhVQmxACASNMgIRLA3EDICYLlhHfHspIg3tjZ3jw4P1dTY6tfffPXehw9oCCeUSSGLkYtSwkk/YNRpayNJ5Ntq0ondRFa3NjZ3Q3VpFFe0oThibFev1/fxOCozPQ0mXT72U52Wr0qfnpe5VtH/Za+phGV5/Uw1uP4Z0MBA9UbCcbLchQ0kHW1DSYdkVMBnUsYk5Ta6yZBVUMiDOO2NntJLHeuJgAJr3BDHv5F5CdV0kHlAMAiI26aQevIKZApv2XtOBzEeu1js720dMbasOLMzD983D9PV2v17O+tfH7w+Oduw7+ca6+ccKLEmHwJNwHQwkH9i/vec48sp34FvzW8OAiJiv8h2HdnZ2d7b2trWGJ6fP336M7/HZ99crBwEtAoFC5RMrBiuJhqqRYjyf9SnQM+jpoUPc2+KOugpJoapfwsPQlIPOs3rtgncNoXp0vLHfBuyoUnsCAxHq1ajard5JDS3s6tcJ80apiW4m/E4xqbIBpOkMPlHLV9YODTk8pAVbN4Li4UqGbMrB0SBGvxTklG3puGN9yKMKiR66rrk2R6q1J91LeOMXEceI3KvE3DXaZdv48NNmSPV9U3ZYXFZIjV/fnr29dc/nTs8gbYDfp/xE3eGJPhMO9RkZ4PKXJ7cMccnNiJ2ureeTOOTuk+4aFffUQ9fj3V95/1H72/uGIpGhHMTO3N/czDR3GMmD7TjUV39ygI9LaEc5ix1Dnq6iTVr30mDKmiJz4CIDYdYiDzM04n4OVVjGdDK0UM075JzXQkNhN7CKKKSsjCha0SRgUJJSviipkRzeR1yJssYMlA8jJh9dqVFU6XBqJSa4grwN6KF8b75NDIfwiwBWGLHSlWPIsgrdvIkcl/dKij5LXnQjwX9Mq+2ZRw90vHwlFGbEFZ0H70c6H6cLg6swzUw194Jml0QrvHZt+5KMyBXrQgZpWegqsUyilJ1e4Pa7VQDa0UBMjRdR4tDmE47z0syQIYHMVgFhhaaMm2D0SCWmjiZxB4sfIBsU7Oh8t0Eb+QdFasSM0PEw2FUNWBXQE2GFq+aSQ5gSkdJY3R6kNDUPcipJ5BxkxEiCT7Flr2Cotn2ygRdJ49zx0/lRrmBVvgOSi+DMUJmhPMbyoWPP7cIVIjHiJVJkH9Rv2frmzVrksdBbxz1xczPEAp5OaxgbrVMAdE5cwrAZdbu17EUOi85gl6yaZAsGWzwErEbvFChgA5fCBZCYKIesAzsi7opgTEWkfUswHh10USa2cL4r55mJVWF4B4HVuh4htmCsh7qVyZZfiQifFmD4UIVhYykIas3aC6d76BRo8hUd23gr2y8+RxGu3JfhY6qLI66yMbLL7qmsny9efiumEuIZH/76/Lldsrr78I8Tl+AM8nLIKFw1awJnTKbApdRb2c1SvpWQKHXhSz7KGefyH+ZwZtvtwEFyTTPyfLtMNq34b1omvsy4g243m+ewzpcW1o6YqEqW5yDbmqpbfcJy3iav6Deb3SlRj3HEWRWW9e4nh6gw6xi8ihBIHQTGPrhRbai4YALa2biTUtZLozXU9oceCfHJrc1PJrF34ih0qUCM5oPn1b8EINjio6b1SnnOaND9GTZKqkPx0BqIgxeMRFYB4ZrC+dxy5mRCjqn0Qe7IhI2IybFGcSrm55e0tM0x2jVHIHGLyzM4a0zzMAcapCs/nbaaLJHW6CUpGhh9aMNHdAZchESiQie1VGqKQLTu11oIAfE8DD7POeqqCmoZFZ/g9VZm09UgoOLYrSHYmcLlJ+/rCbo1sEYZx0IYzYFTnP0oXmicCpA5Kleo77gKdUAu848qnCNRiTKclDTYwonsEMiZOvBKyVE1ae73Nzaa5WSXO237DBVK4JoB6oEF9RzsqYInO3hrOcgVjomQ0gzmp1dKWIFFjGlREzkyE1SrKqjlkN05ELrmOjdvELnTK2w+pAdptwvTt6/OOWh/6KEGjD+IYcSLC42zWCHRgMm6H15ur0z393bMh3IxLR/+nv/7C//5m/CH44DehhIHdGIwat0EMSWtQRzfmV5Gmnc2prf2SdHHFGGRAEPkH5l4ZKTp/K79ruP4GoZ9MuPU5SyHyFhzlWq3pdZjbf/JW436wemAt5kGf3C7BQSUBNgAjTZG8O/aN+ZyC+mH/SpwSMJDYZs6VEPNabxjZdZ3DxMdWXPScbG1en3Bi0iavzcsA2yynw01XCs7FBf8yFGYGReZCH7NpaiNcVCQ2ql5sbmYmvLCr8WmyGeMe/tfX5cKoWhoEtwxwAPFjw+P7m3u4OhTl6fbqyerc+3LB6YX66dsQXXeaTMa2UrXuzvWLdg9ff6ns7cFo/XYmuNd0rDOHt45872/OHamt2BrHuZYKOnv4ks9hybiIPggeuK+ONHxQqdvg9ieqyKV+vfZI5dPsJoQytmPXJqYiez6dR9e77x8Sc79knhfzC/WXfcdIOV83vzzb2N9+xn//Hh65Wvnv346mQL4xMQZLLpKV5MLVEYtdANDhxdHD1+8dqshMWFJY8E8D6QLq9e0iNphqEfgDpAxNvgNneGsViGFAk9RmAH/E0fH0QJ/iJ2p3Ixqrv6XtcyDHhl8L26CfdtBE1F3Y4ppIyUNyVz77q8U/i0G1Vf4xpl1hCYiqP/M7OepNnVIzgTIZ6ktn1XsTpsL3Mbr64+fvrzg4Nj2Z+bBMarY0KYseCtvDpGA977aF9ngLrd2dzL9War+Mtjh8zM6QjorMyMiPZfzcfNccRYx9sAMPCJ8Soy3qTLaZOby772A+aBZbzNkPaV7/BrlYW3qpGzRNUajcQR2EqIKgpzQftQNvCPStqdUqd++5bQQU9oGWjKGmpfEe9pYAgIm5SpssyqV7bmzHOCNJLIym51Clr/WiLyq/irhQlmfKJfeZFzGURg8lzJokHGlZOkZebcFYGDS/rkI89rxu6XJSPmZa3zlRodEWuGzRvUmmruapJX9tdnEK4tINWIontmKwejczaghEci0C5W7f55YeawZhE6TtZnm0IdJ6IN06cF9ULnq0VxJtoYFPwQWixO7aCMFZsLQ6ZsnefNa6/mxzOLB+ISTfNn+JoDbWXleG6hLHVNh1EhizSVBl1dtaiIWoNXNet0hWm100iFYaaq8vl+uNWiXvynjp0QoQayYd+rfl2G+WzTsn7tV8j0eWTbPF+qL9yVMkYYhI+l60HUDl7Z4TBL6ZuRauBZJLSdyCttqagR5RpywIHou75qp8GVR6tbPwfHGPTQ3q53vFot4GFMEdJPpHaAGi12tTA5ijl05EM7HmjFOi/ZeKlzlM2zeFZplzs4bmgqYGlhMSt8op8i+U9sc6RBHKbg+k+qwsqn0HO52KsDaahh5ZQDcnZ1JARmJyZHYtyYPNXJUGe0SwqKEJ/QeMMKo8+uHoOBhZXurWUeHBnetfTKihRRRcjal22AamWYPueSh6EoQUkPFwtWqCx6bkiiD74vd8iEZh++fUWab4cuQ6aP7rcvkJx/Enk2Ph9EevNZRr3043dSntV5EH/ShHFJ5S3jjN/bmf/LP78p/jvTQm7A9Hf7qvz+bocNwAQMDgyj/V84FMnOEgzEUmCUPicRiDOtYR3LhgrDMrgwJm4amk3/9OsXvIn6yqkprdd5Ru2ofNwwyq/LMASS6W/BAQFZGmgp/Iw0nJw+ZBfGkwGM+ZQZJxEzfjXzjYBjW7TUC+agrRb26rXv2GxjDCPSSUOP0yC5YWKeVNcomSmegKUkUHMYptVTNByrkcX7c3uS0UNEJGxVU3qi9OlzCo4bIN6O9Yi0WsUWaxSN4WI7EYzTzURukgw90c7LJUsCtA2xb5snM/Tb19q21nWEDo8OT491aXQ6ziktdSa+NKsMxJwopyhyCdvGB7Z3t0wj1gqGTh/EIF/JDSg8Jh7+g11u0IRIu3vEtXGXw9eHY6+JkEhiilZ8v5nI1WmRBwVmRxcP+RNgWN/Y2mBmHZ8c2e1N7w4wdK2ayPbO/j7P3NGhhYwMxUZX+WvrIHa1oW9NRpiqW9AkRWnZ76d6Dpn33f1Cq9b1kjdXT8tciNX17U1ts/6EHos9CuwLcdmZLzAfKww+sWrtlHenZij0Xm1ucPhuP9elXF1/9vLFyenx9va2qSEH0LiiKQIE2sQQHqYLHlQhC6Eei0kkJpjs6Ij6CiuALs311Xt/1+9+R5yRs9A32V7HeBO4/FZA3Hgd4S/0+06Z76Z5U8i7ECS+EhOma6AnJoQCaNfrV+vYk3Fs3EljXOdVdpcsog8//HB7Zxtma9xsqd541+LsiKf+1eXVjiyRu6oQJH4fV54bFpLMAkiCAlIek/z1oQTDfjEhVS3wClkXxghwIGw9v7UNm3yeEPD5LmfenYfvPz3ueCCms+69XbF/+NHHFvctbBtoAS01gBct/9lYv5vxp9Bt00Ls4deasKvLOzubd3e3zTDZVdLKynt3Nw01PHwo52O8VtMCyqC6pil4x+OSWCGtb+IIH3UdMQK5TyMa+fFUH/6VQw0snd7YdVZBjR2hTFXAAO8ai6UNysJXRAk/a2ub29t3jo88O8FHOEhMxdxgosi67nTSXwdMbq9PDvVt0CdIdJxQTbm0BUiIQ0+9dAXacHAQuHIVM5L0UvET2NWna3obuZZwGTo+TTcRvhUu+kBKIAzkFDCiTwy3fLwWlunTlLdndoPaQdGlLlKd7VoabpFQk56Ph6YcLnWlbIPOznn54ujotWPijqNszuJGfR/cv6sPAFHUznsP7zvAgjRvb1M++JWPAFb4R7TCifNkdMTdI3cSPyqf52lgplYD9JPqFKkH7dTwi2VPp1kDMFWDsCo+8oGemL9wj6LlkfE2MKOIES5kPMikpMu0ChhVL9bA5Mi9BEUI0CU2C/JKWVfUpAMlmihe7Kg2SiBrmquSZXkF2ch8ymfkWTLx86/FC332Cypx+lRelTUQFgzTGx05omrh2906TwHY3VYPmlKygcVbDajr2sQ8E3E2Fpv64Asj5KbxbGuap+Gc+WzLJh6kwiCdFS71h0dpiw6zq8mTfqxRa/sJjZ6PGhpF85KFEG4+zWLDA1xF9sB3fJ5pitub/He4wJ5AVs5o0E0WDkTb+JM7oKtfnSe1EEzyqv6oYaNo/rE8OBhEGTuFwEGol0g7h31U1Vyx2keJ8oWE84ld6n/o3wAzPHWDk3glVFJ1/k+069sg0YgnTpWaPo2EpQrGypYwZKxufs0egfdkoyZMdB2SY+82HmVqaIaZ/c01QQfHpa/qAIQ0+dSWiVfzTjvY0wJ2IBOksFJLh1GMHzLWBypY8K0QwDvNuLSwtdqxAfjVIpChVP2pWgnAXOyxBg0uDvJn7cFnccbKjQBhY/HsDvGrRDANkyaVBfBR6yTOl7AEPujKOspmAXG4Ewx3Mh1EGq0JBMVzJfI77DpJ5BNCSzJdZTnep/sI9Hhz3Qq+CZsepjxGdlOGAX7reue1MgUN3QHKajqBMbhhymzwzpsspuymT4UuYZlqMRU2fbxdrj1/Rkkjm1ufW7/MvPryTfYDQddJxUSUSvCHIZbJp9/rNEnxyJ0PlYmdZcp7WjNDntGbOLVK3MR4ys8EAHYhmsi2Nj3siyEc8TYyCunZTIgYECuZ+prTJbnDwwoWip7xCx26uvg0+332mX3LZDlsBZZ7pjLtENgDOIkY5SNJpgIRxMYtxRktqGZwtvj0cnG6mH0BKMuUcXOT7CuChNK2qa1ax4gTp62cPmLtLdZeqNZAOWtfHL42dTu7XOeHPBvOt/qydM+Q4qGngz5mRXN+cUhiqgLJP3XbXNk6OrbEQG3UXQaLVMloKYpaIjge7JzZofOztn9/uMBpQfsCHh3zK8jWHAHlEK2hbKJE4EPQGLOAbRstmi9UX8u4hgVtWfDi1LIoerIKUG1UTY3VMrELqwgp2MaP9RYGJSBxyR5RRXXCrk/EUQ7CSLdRl7PjdZtrmiSe8NF9sFG6xNa/iNFaZ5Iftms2m7sQkmUI7pAXBCvn78PD5fwrjTcSMetzQstJbPw0xN6EPoFViNYqNq/v+xy7K/N/YYsyb0pWbmVrZ8A/6yTXVTO84knTwOc//P4vv3r+T60r/ZM//IM//aOf/85f+d3WTWhmEozoEK78dpMItGmocAPEmfNEdV9iafujl2R2EJKo4/ixVEPK8fWr61zE8kGOwOlnilXU4r51QYZMpthvfbj9cnEvlMxfjnzGh4t7QJ3NX5bbVMB1MTfl3c5g+RwHKQtvV+ASbBBc3EUmm0kz7BHIpvVmlNL+o/PZwneypylldDuBy+6Ke7trO85qulNbRqiPNllX5JFCOF3ocGmOOdaN1+G08w9lv7L51cDo4ElqEf0XH0HwysYXSY8INTKakxw+ow3RXnD6rW5x1a4f145wc/F/Xpjx4Yiv54u1p1cnDxcrh+v29LbQZG2xsbu2squ/vuaEbS6iU2MAs7WH+/c3NludxvXfxF+t0Xn73lnwYjXI3Tub57YNsg3E5cnD9x7Gc9ACmEGQ2eKDIB/4EniD+UGrYg39E7PccMFE2hItPhj5EPA1tqglNGMXl7GxCS6qSQsFbA+yXQ6aOJph9SXjKCtWG20Pfpvic4TDVvJletZZ7bKGGIZaQ6loEycE6JyjkbKIwahB7Y9cSxmTuEYtQmH1qbRB/fTwGJEefYtlbYtRnK4h7ze1imVCzYg4YQQDpMavLu+JPWb8j+9hsmIGm/kii2UyL73PD8ZXEAfp0AVqwQWzTQ05wA8OGGnMrFREBRQpBeWp44HnR8fPnj19cnL02MMYFxlHH5moua5zv0+28TMf/u7uvrOSTA0zuQyXmzHU7uwMHaPTsJmFIWbVGk0CzWXI1+QroS12p2OmStcqhWD2Kn42FdQOrUFeG8UjixjrXwrxP9pWRTdAu7cPbBionSgQu9OfjJ5yGz7jIRrBEP0uPmwIdO3rFPfEWZOYsp/lTD7kETrHX4IM1argo+SVELWVvP6kFjOp1NwCn2P3icokdP2IV1sHqAnY0oi4+Zi+w2JFTAWGNARYXZM2ayzFPem9oPeVW9CThp60ec4NVN4Xd2crO2vrL7T9jb231sUJUxoufkGT+rJCZ1cOl2WrQiGLqDPauL/iXEPBTaLJ+N5pDs6ogSP/1jfMi7tYHJ/W+7K3BPUuYU1/+4vOKZ3mEDBB2/1r9cpmujtjvYbJ++pgpECDQR/Za8g9UE2YBQoM5VszumuU25SY7Qunv7c24EwfxY53NtQzmWW0XXDF7aU2gT0aHDCYUGDLHaThNwFP/Qmla1ob4xB3EqIYYhBouBqdIlIbaZwQR5+9n2MRdUaDXkSIdz9/FA3mj2GqqQVUhcnI2sJTzo4HV5s/Jw/FTDe/sqGR9ZkXV1ujy2QiHadmZ6JdOfr68jC2avSeFWTnK960FlivXW01hZmNA8GAqXthP1VFbpYnJFzyYJ5acQ1yjasDv/Bkw/wadKjGdUOzXDUvw56gR4vTlxdX91rGhc60nEVbWO1yG3L5NAXhHYQAciY87kxESSp+yxZSzeZBeKg7acqGloVCiEDxb95ZH5SukcDnTNC0A9hkF6+G3cRg5OYlizQ0Xl/T63WgT643X69j/Rm/U+QSlslYUeAhKQFaV/dJ11bJEVHdjFaVwNhdX4uGS3q+dS+1a+Q0RXMfAdPveFwmGh+Wt+XXKavbH24/L78u9ZIvlVCEQpaA3o4/1NSoUvSG6JboNv8l1DbRX6XYaqMVI/btZDCa8FQSHkVY1cxW4s4dY0idU69MieAhRqZevKeIQk86dAqIuuTILrOZt4O2QTnQ4la243VISgEjmxHTvHe5yQBg2DoIPYtRkrRcVR2v9B5Nhp/66nttnKxwfDbIaPGohI7pBW7/KoXOrqEmHsNlB13NxqO+RoTEXek6yWSJFkyYKNEaEYYoAz/FqWmRE+vKQKE2nhodiYheaUEDt2wsFjBuByR9MoRSrjoc82U/oSYnqCsq3AwyhgG5jfEWSAZEZvIgE8gbEIRrTzBQXSTXrhGpUbnySqg0O+EsZKQOBq4E8RBwtY/iEsNRcgBQF0A5s86pplb0mjnRilEHYVIDBekQwbeqw8EoKEDCAGIPxMtLodhOXF5NZNIGXdet7NQFi6gZtMQwMlBJwMVSU8DAg0wCXFnhNq0VunQgV7Y3tk3+prdfHdpD8tSmKwjF/zQmyKmN/26wAwwAFKBEhciBJ6OpxDt3R6sTl0fOkWBKt3yE5pvL48S+gfcm1s33Nw9997dMW7o33956GmS/HXK7vFvhU2ZTLtd5TWFvIhU+/V3H6B2sqJIAnVDYi9Nt8zztCU0oUSpPGBtk8fTxN8++/uajj+5/+OgDPSiH8FoKboaV9hVJVOTURvcXp5tr7DB9V/66GA9JEB19Rk0HUkaVo1d4R6aYXcPT2WFnDSVlF8xtaEEorAG+sArfmvqT06vN7fnf+vW/9fS9750drm610W6N/O52i1jMFMAcaxalW62jF2iGj+G21fmdzU72Mfdm+AgWq6dH1uX84KOPfud3f3dnd/bi8fM7D7Y//eEnei8DDZh2AHWNrwH3G0SJM+Gu7xPdqlZC6CpkoHJoG0J1sX/vwf5dcM1Pz/hlXo805CxbXpwkIsGs6SJCRIw9n/a63N1Y3UcNAylJhXW+4mWQGiLQJA8Z1YtdXW+r4bg12e4qtwHFG2CmD75RRSPmFKFYEaD6+nF79ypomdn0tXv5Z45k+nuvEgMjvYSCESdEhJYpxyHOfR6vI3xZXs8qhenyNZLNNEn7T0/atOyr6rX1nxJgbYi0uNzb3r23/95Pv3hMRw1FEM23t9b37+w6UaExnzWv3J9V2YHBKRzdhFVr3Bf6jA2lcOvwLg9bJksE19mMsgkqDErNiIsJonx8ma+0its+3rWWV1ldGUGX69YVsC31KKbKTgih67QjcVJqaFwxjhxwNj2mIpTkwGFtJrr7gm2dgEFlFT/kJXqZGLWIRcjdNMrpc/oTBX2Pd1j0kCmfwMhqcim/MeLW1pUyvZ5FLjw1K5nnqD9wFGqlFb408StK0dJK2rirpiTBFC8GLvO0v3oEVS16LXD5rq0e8Ek5oznPf1+Ys8x3e3MN7RrjwIAsYFHHBobsAqRXlgdKcPUn2VVYYvjKOIU9HmSTQEOI4sQGC4in3mx50FU2BVjTDYStVYsN2vAUATXdTPjo3FHbIRsz2PzXQHRbB1i8lOW7skWWTN3VtDt7QLUuL2gw5qatBwDK8NeEGSWARD1pmVhSKKoZzMQygQi5OedqNqi+wE9o/cb5Q0YGEQtR6S6kCukM8WtCxENLAanVjlahVUENrpdu/sVizSp3E67MjHAMggqZSSXLgFENWoRAZdAkVrwwSkEaAGpDNdUjW2XMjvBbCXFEPSL1NftNrCMzXQ3B6UNICSNmMFDu841jphvPSRwXDhh/J/XgnDzgXJYzkmVWsBKqlHRjMWasjvtSULgkQmfbxCJxBRuriMKSlH7hx3SjXKQDZxjO0E6dr6QvERA+RECE+FBIVw8hFbuEgIHBcDHhfIS8c5vSvRP4Z71e5xzibscbtHort/ECGrEGeMsY1TisjE5/zwMHU16BWi18z1bzPN2nsFHc9H08vrmVwltZK7D7+ufLsJKOxxn/2XRN0eSNwINRhhz5dpNkxPPGehsnW9ipF5WFyqKH2E9SvGXMqUXfORRDfWkiJjLjnI+ZArPNb7T7GcGqRFJZfEiX2yNddnn2MWtj5gRZYAM0CHT4rD7/yt2cwJg0ZRJ0fZyoOZE8VilCJnC/uCa1UtE4J0h0yz+vWaRKrccdmCkWzvW5dOoh3PwSMlObsjp/TArIwCBKlao65T985DiV+qOGUnpKIub5Hlzeqvm4J0pFie2CFLMGqlnjFJBgiCMuySVXd2cI1Aj0NCCGulxTKQwl12+QhVIGhsptXCDsl0QJAp838ZUvN/gyLM7rgCTyHMP9I0byVl18gdJ0gVtqXVCf/KegmyHa/gNQkKSFgBB9/uFoFb8QGbygjKKRLJOFYkLY1bMPAXM1s4rfL+wV038AyrmZkUNHj/CRdGA51S9o9XEQhWwqihGg7T8bDaBvgwLhbqjRKjw0kg/r34CYmhhIGO0JkGS3+MhspbXZy2lMV57FuFw8+mD/N37rV//wj/7UvghHx7pWtRP6Glmo6bDBBMvStCpp05Aw4E9z4kw+1tnp6obFbfFRGLvcD8CxY7r4gaty/b9+XgaOL9e36dv1G+oDG/yut79cx1j+zl/I963LLP+RYhn+dmrMARtxzbvqapR1ndeggyj47lWAxx5Ya3Zstd3W9oXjbeu0arlN5FMZPloHy/AqzZ49ffXh+59sbtlMPalz/OQ3Xx8fH32zMjf9SqHH6/PN3/jd72+s71xtfDmYKblMHLqPSudBCfHJBRtpAIqbEnqdcyTIqBMln+HV2Vkzd1cu9zZMCr66c//q4dqWfcE7wcIRNOev7ffSRmW0wcaWFqOxt+wiDMa+syS9JfI2DDYocbmxunt//sF7j37jt7//6MNd25B88OEPHU7A6Bnwjc58iI7CgQoyP8Ab0lDg9G35XkyPyzgTYhObruytbDs4v2J6rNuwWBMFEwb0qu9ARPogzg3/Q+KM71OXHJCWCw/FmZcRo0oRWc0/4ahs2vSqLf91thRALgdQqvsKJPkiAhseArY6TFfRuiou5LtTgNVk3McHcQsZEUaMKfp1FsuEzRbIdpBhFGzsa5nHZLAWPfZDHg9mFXdNkAwMFphyJE1jhFf7zgRpUsP21p3Vq43D16ZzGREVLfBqQ+olVJQRApYT+/7Bw/tnR+99fmfx+sXvDwRQvou7d+5bux+1FezUVqeCrc6PT88uTvRUWzDKu26n+TUbusHiqrEj+qxhyWx408VMYwg02LXJjDd2DuWg99iMR4Z+fvQawaa3pTXoufkTrhcokDCNFLarGj5msuq/sYlaBVs9mkGe2RfBadDBASG51mQ4fYx6PGbnaciVMjIbvNFnVOaOMf8efNo7Fn5ZMPuS4shNesO5efxeV+aPgwNxJi+3LoEZZzCUH8oXeQPVM7zGWBRrbWmx/QsnTNkIJvcYjCKdLEjKcECrLdNCTRxFf+RLrpMEUGifrzxcu7x7sfhsc7Zztfra7PyL1dfoC/lXV7aeO1SXdmkiCcl5fa2EoN39oYOvtJxZD3DZEFkedzlbyo8hDM1DoP1bsjf8m60/ndFURg+K1qiak0AM226sNUNUfCEGLxOL2YmN/9ZmR4kRDVN705YB+OHUKr/56w1TENUaeuQPySbSOPI2BadEBgJZs8DAg7EltLfmpjeL4xrjMFgAjRGlIVMdjehSR2+QIedKPUGYzNW28SwfGJvb+/o3+atwkmvwXrSE+rn2VE7VfDTGkbm+1eWnq1eP5vOf5dzQGvt+ZZzQ9lYc83ZKo+WY6zvo4Tj7fHONyYAfpiifZk5IEHetUOxmyjG2CJbN3Lld2Aw+2QJIbMcKqfrQXTRwvplt1kA80mEORuHaOVejMIhgedgLCmlj7T6ZySKJMMqUGzwrsVe5uGLRUcxovPF5DDkkLm5TU8mzzWDh/FHKfOvJaJUwei31SAyTHM+hoxTpoLKcnuG+IOwN+xmoo9RK/tY17fe/3B3oW1/fDVjmE7R9Gvd4BUjCJsiq5biufwXrnnUVggcFJD83103Em5C3Hm6AF296vp1AiMrexBkpvx1rALcsvyg3OYyoN2+3yp0qFIKHXoiSUvWv/9lGIpd6QrXfRDUJyxfcG4rrJBCdevO+UFUN0jltGuONSXx4DKXlRwbSRfLz2rPcRRqoAkKy6lOl5YCoTOwyqD+g8TJILWb9w9EjkdhQGQYecWUbsENnEoF2MKRKooT4fui8tENVqvgKE5y0WPhIXzoUbYzXVpX8UqLqjcZ1VVz0wM8IH4wIxuSGYIa0cCaawDScKyU8OhpVtQz6J7AKaRrkX97l6l10MBaNgkhlexrObVmoVRkrNLUY8J7TyZXDmsmYC75yLnDkUu4KFLnMR+pq62GkFq/f4HPBUfqpclIIscISk0JAmQWvDl0heqrflBm6gtNnGU+RAJLmIZ2yZ5iFm5KARNmjmm52YhMHOarL9FGphVBnQZHuGrBWCyG2BGvstTftG6exA0Sxn2zr0AV2KOA55fPb2dza1hb/5//Ff+w84Du7sz0rg9vtJ7VI5VXRWCX94SeyDAjr9VjP4fB1vawYVlkTdP3QjIEkZqHX10Cil76M+/WHW7/Tt+tkpfj/73pT1sir283DNSSVMAF0C6xqNGpVTfL+XT559fxksbazfb44Odzhy9+YfOlQfWXCNVMo7BKOTv+xmZZmfHF0cvj0ubWVZq7Z0VUea7969fGGWWCjUoOe4g7GCphB4SV6xns9iRokXI53CX3CWDQ82ZI7Tbl4mXXIfNmULE8btQlbjta11X9bBg4iMPexDrentoMHoLkcWv0OArU9zPrdD+5sOed4be3u3e0H77/36uAp5hqmVXw4XYP1wlPkVarbwE8PvSZOPblGJDefuk8P1x+LKK9cXyLIK50AtiFYqZEhnkmAf1O2Eow9kbGhQb+xJrvBMh4DfSLsKSN28OXB8Wst5MnZ2ZnuWLZxyQc4gdZTr0ls13gfsHqaqjR9mL7dgOs1JCy/3TyM4OvA6VfOQxKrs78qIPqtxFO065zHW3HFGeCNvOm7MDkmkTK8bFBOus7XNnb/8m/9GmIadqsYY6EdEaX+8Y+cSBzHpjVThwcnhwcbp0crH3zw/tdPnxoE3t258+HHHxgxqmfCcmzlUgNI5pfv7uyU1gy3pqicGw/Y2dwBy3BoNAXEYQwhCkClGZWqktSCsjJtVbKdpuqTpR5CeRqDjmQbxUMTsTFwIUXMuMlk78pWG5MlQhIqqowYylIdOWeX5101mOCYh5YpDMwmZopN+45q02hAVjQAasqAkW21dOZUjjpc7OCylflhCAch+WmL/UaYK4h8jlZX4joSVTEy1RqNDknqWiYKiX/AWIR6PoKzBoUNItTY9hhHxtUBNr7aeYsf/sloaJjRLgb94PZkIN0+KEnNyj+CjrRa7qg94DEKhN9hjycInhrk8zdGeaRlpobqEjNYtd6c+3IB3OgLhRvGdwoEi+awrw0wxcZohNntdtmuTIi1acEZf5v6qSHyGKvwSG2A1kPawywwe/MpGmZQEPD0Wc2KxiZHSRzbOL/NTesQmiOvlWL76g+wWjzVEJcW4mTdZIk0U1NxLHDPQTAQEPTjGoQVFIRdUIVkhY4GVq9GVa7mXzqoAfA4U4bDqYrQnvWf1VUpjKA2clhZ0xOQAJURcPQYxzuAItZcJwozbCVVkrjX9FXsstH2pJIRXY1BwR+hT7WXg4YRO2wN6LuwpJjVv3p/nUdCByPapKNVDrjBWzeFAMXE+EnFVWgICLZZz7V2ZW+oYd/kKxl8qKWo/5cNFUAVH1h+e5N9QI/QAW+RxjXIE4OF3eKMVFWrhMsoU9R/ifuUUIIlevxeBynIdf22zHOETc8D7pFwoF7g0q27jCpp0K1M5/iuPSu43m0/416Nyn8qYoR5nL6NT729CRlp3Ea2UxovMAVjqDhyu45znUvfl/nffBp7wEd0HcnFhu1ThvKq/ZIpgibzaZckH6K9kAsqrlU2W183Nca8aQWkSxE1uxZfju7q4PqNL8CEuDg4F0wsGYhDJSUtDNSRJ+EM5vEJOD1JVEggi2XzKbxS09/YQmpxmKVNQ9PZoDqtJJQg+9ypFlkX8YURMv1dg8BMQ714LJVfM54bogasiomHcWEA686HZyqAdmDmLB6kJda/FMKFAIQSmn+8eEiVX6y2fwikpnrKUAQIw7WD2BwLtHASoBop3mCXf5IiVGND101KbWQTkik5Uxj1XD4AzNW8fQNWL81GHc8yh8sApMNskSfjwK4O/g/2kHuwVDF2OLj6KF4o9clt/fF48TTQHcuI3B4FGkBvQZiqFL2cR+6Y45EeyXzt51VgTM2jskQ2+FLtRErUJQ+8kig+1Xke9mQV66UlAkU/j2uhgwYHlkpa/aJsbWrqo7C+UkF5dwFKcVN5o8QEbHXrm46QlCLFFcTadYvQkPGXfvmjn/78s1cnB1998ewP//mP/9pf+8vbW/c3t05OTyxQMUuRKqysygQcnT+6f1SXPpfwrW1Ng3CxRhdME7H2OvxEZEUHWKgbl5dyun7peXqfvk+fe8aAU6Q/6z4lehNjSn7zfp1D0QYl+xJ6vCZKb5J7EnqT/ObDCIzEOJl77WrDaVJHL0/mr8mGNvL04Z2dD+88tBBPVS1mhSBLzb/++uUnm5uLsRaPyQLn7C3tSBtZnq1ubxlDd46Vdsj2FFh8sMUQiBA8EL1EUoBmA3H4mNuSSW+960LHrOV+tumhOPa2diuIRLeVuGPCFvb0tI0+/729fzfXV08ogKvVvY2dzY3VrTWzTk8bRZzbuoBDl58P2LPdzZ2tbfvlOlOMYJ+sb2ydnL1oAshYyhZ7p1X84J0lua6R12uIC9QJnzdIHB+q0UCsr0lPLX9VTK3hWu1hsl/eeaT8V6j/LWuZWrjilrYE/MQpJuerzI+0jsyQvIlR1OCHSf/zg9cHB+enOdZqoF1DsQ/YGBz+DwNI1rK8uabn6xC/I/4o1vN1uOijAiN8GWO5t5VTLK4DBs+Ll1CPfz5gjVHnqZ4UwFIl2p9k4DVAeqqAUFRecIA6F+f3cZ1dXOg9n45fH/3of/rjX/+lXzMhiBbP4zGpMlmW7KqTjo2S2O+L53jry9Wtz/e2Hnzz5Dl/6Pbu9qYVP7Q+JWefgMum+iiF/367fZ+UR5nRD7YA2De/TPGM42GvZ6EoPdtiWfmoQcrHTmDDpjdBeXg6rs19sYOnVJJAwKCEV8X0PysFAacOA9NnosuoxaAbJZXaHHFLSsvRhQxatmNAwGBaaNjd8s+vbCefill/7CZvYjW0H0v4vVC7/iRK2ltJBmaxDyuMyWmii3IWR40MXBoZMMlWD4WBRC3mj9K4033VTluF1UYbAfjyH+AZS3qUCb/2JIMz4EaVA0JybW51IDQmbzjADvyzq48XF+tnZyezi10D2/PZnaur5ysLtuMr50YF3cWOw3qvnCFl7133PPSm3YOcm5mBuXl2cbBiS/7Zga1tCSRchg37E6eN8z4N8EAg8kNbkK1u8v0HGRW2uLjDV2/FFC8gwzLODNN6fo30ARi8ZgzK9NLUF9xllsS8hXNJZe1WXyJ1vGpmS7JWI15KoeLUoLNPmhrdGLJPsft6KxPowA1jAgyg2sNlmxifTH+sg5Ad28SlEtbxiY4uuBVAjsZ9gO1TVYhghMSIKwH42FT7xdoXdZAzuKxbaCZ2Y5jVEfzHo77MSIMt1C+P87Sisa2KLNZuQVuRbZanwrpndbeQxABN1hwDxzQcmbbKAi4WZIAat6CGU3e2RikFZvyMWddmZlaeX56vLV7PV48uZo+SZRXM3tNhaFIDAkBldY7h04ShsBzcxybO7fvgtd5+iFUDuUDe2vMYCz+JWWxfoajecoSqaS6z8gq77uEwLGLoVKusPPa5/52JDjGTdd3j9ckA4/nPuclkXBVx6zr/qBdrblNzKb1BSpGHYlb0pKGLNOVQevQo+k1WHq6zD9Kb5ynVMkSop3c+y+bta3p/J9Z1FMEjB/e305V3f1PE5RO0wjHOW/ak6A7pVNBfrJoZGO79T9HV4ULEDCd8TU6G3NEa5GRU15f8gWPPrzKRrszKcXQNky1KU9rAiND99CfOeIugfalINShf30e7UDGLxrBqKeM4w/1dCW2MYBXYGGmSFd6UvvF+AKdXKkTV8KB6DN6ZQJAMQcmB+SIGLs3CzVRVvWAaHYrYUs+f7ypXqCrLdADZVqTNnvd94MZv18AAtA29rtKGnbkLQqCP4cKlHaIStIWLhj59VBwlBcRiDHwkDhwyA0VAHUDnmvCRbKjCwNZgfJIYsuBKsAxGaQOllSVBqaYYExmLXOc7KD1WcGI58DKilws697WCauIsVxhbNccPkSNjIKpUnB8gTSVYFVXtmkMCWXSWPMKYr4rpP4z7qU5yrugyR/AihiRZBRR9Zr5Hfo7gmgoNkRXkGCDbv7JHB1st6y8vunrlBz/4pR/90Y9Ozg7+k//kP3zy+E/+5t/+N/b3dyhJNob9/k0wjTfEG50TmHf8cepQ+zVj0d7BRb5XL0WO6g3cDUtMezOADCvXV1XxXD1uB98KmT5NX2+eR/Sb23cE3wR5mAp9U2bpprAph5u4A7Ej7E3QdZRCBialjBzRDS10dHIqmUZq58R5k3C4/1uXOXcw4OLLr77cvbt+Z28/Bm74355yq6f1p043N2e2Ym9nrGw8PILexmdyqw4uvUHJKBQfKhKnxO/zze0tfbb5fCfkG4SfXZwcLXQMOglgfXtxaj+Cwc2Xq9v7+xs71NPmyfHLTctr101E1R6ubNtsqgXEzgS3p7A1cEfk1xDFysKiQxtf7e59/N7e3e2d3W39viGjg181oYPlAAfOULK8Qu6E0p6mK8JXlZuQGGO8xQa+pjdG1GrHNsBWOESuoyxfBt9PSPa8vNJDhAoucDe+3GXdkAAuDXhsBLVme/XylBsD9ycS1wJduvGfPqrcyvLwLtx9euua6nlTDQkmJFSNP/sa9bxBVaWNvFIqHnoeYaoOjF7VsXuhk4IIT/7ouuLUZGQdtG/vHrvBVj+0I5HPESNRMhdyhjPHYt6x+5F1PWar0RJnp2d2+n/48MGWrV/gvIaG0nfsQn1gXQIHpVTQpeWqZi/oarJOIkqslxkHsctXoIAk8KMReKnixH7KNjCWjFLEsB5wA+GjQlV3yoKezIqsV6OmrmpPsrSONY8VUo3Tt80xlwiPlHRkV+S0kVQBGecUdXTpl63kZLgnf6mm6pnTtLIguEuClJdJUDhHKWmzUUAuk2KOhtWz7uWoVOmWHFtCuBYAyEL9ja8BNh5lLqBS+iSCZq/BVtEXq88OzjefnD/ddvYyk9Gm1rOztQum6vHCDJMLHl/q2hJBDRlnkIP5TDvsAK726JvzW7OpjegcnvkhApgCKmCtV0f9dc5M/M+ID/PBw0NUdQb41vuwRQrJJPFdC2LQcsRCFDWaeLHMGGOD75p6Li91HU0f1GfMyTbmC6cS1cAIQ5L6ItiAsSKgm3kCEYlrj80B0lDjr38DPwN5IQoVtDbIMWJMEUJtpAqrVUboeArKqBQn5LrkauRsX996vr1LP+rR5nZRdb0D3hOVtyXayvmORHa3c9rgJp1so085Bso2D6LULB3cQs5W1k4tu3BKelrFAMlF55cpwgyqVVsj2z41o8l6GBsgrpuqZVvzUXX7qhvnaG90/jbCRwNbbbN19d7W3BoPHQyFDdRbhQy6wbc14aFqYBcWIpNPalmMIUV95HebLCC4HLu2eI084RyGwsUSUZNgTJkOa0GWoVdEVcXn16XpngmppD6Ph1tvI+jPv02p3QfIwd41Mpwep/cRnqJYlnW7TFDFIN2amrlM9ib1d89DkmqU1nHZru1xX96k7XOXx6r9JrdR8nidbtPHKfJIMQJux78B+Xa9cEYZNxuVZDXIlUbLAs6s02EjCtEmI0kG+U11yKnjOKWlR4agGKbKESUDoHF5/GFSpNmWaZbMa9kk2SnjSYWlcMojnchy+LwS7c8d4KpQNRPqlJdUJ/EbzZNEJr1sDcsFh7+8xVTZxemx2dXZI+Cvbj0DjtaVDJi7x0WkQx5Y1gvJODkDB6fb5OtVXlaQDYRrcdMpjYQagzTvMMxQCkxS6eBG/9nXzW+KUz2aTEn1ii0ZpDSrXw1CjFpxIYzmASarU4Oa6Slooaxr+GoX45dUcA1kyPF/44kKQQxazDafDtUWOagVU1RX2h0PSvOA1Vbq3ZQqbBnaLHIopBS0HFymg1AoNajoy6Tn5T7kJ47yv3mGOV+bDNVYujB5+ulJP+tZ3G4bALZ6+y3K3cKp6lajUXHdq0UBKTIevxFY8wKkSs+5BMEAgO34qjy7gmX8DjSpxWjhpBtqBSb9JvEVFLRju1LciNJpEKyLbHGAOojxvU/f/xf/4vdOjs4fL578p//ZP9i/+/Hf/Xt/q6MDLow1X50c6wGcz1oFYQLCJyEB6nMMSn+1uaU4GnMLR6iL+QX9DrauXpWOse4qZezMM1U9qKrK5d3uN3vzC3YNoKfHt56vv0ghynRfRhs/b4VMmUzxriMVNhkEU/IpjsCbh+uY41d+4sEYnNU6qgq0Yhb8wINeq7NmRuncWtv19Rpny3xtYH88u/jnv/9HHzx8dPfunY293Z3dK4i0+6pT6Ljv+WhaJ9+aMwRtdhZmaVxI/oMblBZ3KQMj1NhSMPbt27Fa29FWRy+wsIm2aw/u7p/L8fz06y+fnJy8fv/+X93YWD1Z/Ih//8Rer+0ZwwHloDe8cLpiiu/iaHtr5/DwlKN4Z2/XEEYz6Fsqe8c8pp1723v7+/v391Y2n+Rfv+K/wbJmSxs3fBRfEddByYGUcDHgBds3EbLxtzir5zGvXXWKEc/op087/2CE2CH5MEJIm1z9UkIdF4o8NOqEhSGYIse4I5vVK+OH9MtjAbP54cqK/8xWwpNlODWezBDcfLW4lyYZM/6HIKYPsHvrFEUYQAdbT9d0r5RxNZHAN83QKFacNyFTAh9KXQTXxLfXb1PYuMcxMf4UO7aRJlwu4wwKC9M0GNawu0iOIWmawBCyM0lTdc8zTJl5FKW6Xq7+9//wn3z66Pt7m7+8e/fu5p0nDWmySGrTpRIJFs9fvXhpxOnF4eOszvP9q8v9nW2L0e+GHZo3mDChnSibn+DJRkwh0NkCCjx7dHX24YrRg6gDDjHSTj5JvUTfdR36quj6b9V0aKSeVGRUDWELH1cP8YYrREoGHz6HlesUE5ImvKXYa3OKUH5VMbWT+YkD0uEDGg/liXns6+9TtPeTTitjydulZwDiY2p4evGsgeIsiWMvjRuDxYCKmtiPLtDaOUNqdGkerOK8x0CRx+hApASG+/qziHP2QFmztecVOqGjUv0J8J9iVxnl4cI72sjjq0dmu2/SHxbSzu9LOaxrA7ID8gWtorHcXmhfbfjfFsDHButWz3Zajj/bWbky1xwMJrWzfzb4jWTOoDu1JLWZ7lRwPTtD/Sb96e1xIAximuT7efrPioIx9WAQV7VHszqhdriLBkeZGEYJwQa2UtOqE/Y8wiT8ONhT3WLpWqmB7MxlD6JOyIdi3QsdCHua8a+fn/HQQ5b9xwevjjRlNi7oAQImj5qSlKe/rJAwPK5BkvFFotih3lIGSMaENZb35lvvz3d/Xn/jfNfHZgTIc2xGZFzFrvyqLFPuf+pMRrJesQI7l6Ommo0+UMUpphZmqLOjEgK6Kn7wL95g03Tw+kGdnbXn9Ojs6m7dLouwyKoN1kGy/gJ91lY+3Vy93Lgy+nS8cvmoXVdztiL1SVsYDP5mBuGoNkiRKhbrrtD4BoPVtYJyl74T7VS74LttTdgoNcDgjw/FbPj96vJ9ymR1wzwI7IGXRInn68YDKIYHNHdJ/V7RGZ0Vu+rAuOm6/l2+/jk/xR4zdGZLT79aVIGStd+mh5DR/mCFfBWlq5fwfpf1nJhlhDQCMKVf/pT6neu7vghzLbMtiymTfsfb9H28DuBGeNT3PzCmJG9/H28lnLK9/iguHkZF/127mtJ2f4V6OqoMfS6uEJVFkyzOsil2J6lUrP7x6opBq9hcIJSwEXj2GKtYP/sW2cuHZVC/oieEp781/Tvb0U72a+1iu7K2rZys7Vi5zoM3htsEN0bCG54Z2Qal5C9yS2RifIE+q39uHoADxHJAhnxltTtgvZFaJoVYqRciCimrkLZq3jBDRFwDyaqvb9A89Yr0VeQwlWNbT9mEckrynJloH//2H1jvrEEDaEv3kqjyAZLMGNS9Ks4kmDY+SgWZ2KABWrVvHePBM3DhNvdH5qjOioYozmKDdHJW3Q9A+AdhEhrplqfpE15gyhTtmjOtrF7OuLyUAJRlM/40gRAXTbvSUe56aENoaqE1ntEIfYZ+LE7/pQgOEtkY+RCBwRq15fBev2+qIEwBotiC8MpUfjxDdBWXTagHaOySWQ28aCwoQAJqJBS5Sy6ynr7FCf4G9EVEWHmpOJIDeSqx7tpAr1VbcnZsUvZTilCCi6PTYylNCeAhXrVPDCbEIJuOdve5je2C2Z076nyxv/vgww+/vzLfdN4cdL46eIUswRJDymaoAG/VcYDYvWuKND2P78vH7/wZab/jyxRe3Svr1uWD91+QbPpY7Jv0b4JuZSKLJdQhMlbLQQVzg7GNi4xJKRpY2td2fcdnpmm1Rd7Z8fHz58/Ozl9//84v272epa5TbYPYZt/x053aKDZXkw5nbGJE66b0ysEW2XyAQyxaIg7uOImNjTu27txsaQeCmqGhH7258eEPdk4U9NFvaIE+++Ln9+8/nC3ut9H4fP/i4vBqxYyC87UrR4PpA2/9/A/+4OTp4b17O5t39jbub25uOlLX3AFoWBjS115YNqA1pYH6N2EnKDwiar/XKIvVg/BNgNgj6JoQU/rYteApbam8jbQqXQs2cq/SIo140g0RzBZZcvvIYEoFrP356v7VpUXXdWhBwJ+hMXawymgTJ1ymKAJVDj2qjfzLblShB28D0uL9xS4xpzq9Hf2dsCm/ocGWNa/0rJXxRexgipta02GKvxAKwk9e0hEIZxyQZqjbiWV1/87eD3/lhy+eP//wgw9++YcfPXv+9PVs53sm3m1y7WOGVNDgTPnYFOrsxcuX+gSPn77a2dnjSjb2e29/886u48NCRBqH4nP0Q3vL4FVFQzNHOzcm95DNQA+gKm0zsDYhHQOG6pqGAkZF/CTgQjL9hY4KDjaREjBTNPeJga4TymUohkooo5GfoIwrrYigJAwi+s1c6184moro40gYxiaUKvkat8sMfauYwQpgU4rHClSPZXnl1uP0Sp2FHWCMcL36CgSEgisvM3MqdcAxtVagKrcwGoCSRovxb9R65D1wgffkQfdK2M6YF1qPOhztfAdUBu/qysmWwGGexxJYelTZPBs5GGvXFJR/lqbGlMoJHpphOCREB+z6Il/kkF2Tc+SaFz+9TnkHKTOT99rVxDmdinT9hBlWyMAcLgXoME4RJAh88J8322TRphOrb8ODs7EtkCjZ68XUISkvpWRLxBMVyMJpfwQGKvUHp/ZxCqxillNJe8Zw4uhnmPfezqQ1d2wkvOCpatfNGIRBEb+1aP01BC97kQhLezB/Jbpd17LRM5oGv6a3IAGiLXJoVhJU0adKj7Aw2hoGFo09WBE5PhnHAKfj80XKJPbOwrYOBygyU1nRMqDAoaowNsFX+6BfTXvnStADAcX8/J69OzP2GgPgHZMdw0BN1kqmOBtcnZ8ydULKQEcYyVhQSm4LtWsnAJC01lPTY86bpKaNAN8njKSfpa8IOBVkjDFMNC6+RewgQSBDUO25XF9DDhtkHe77myRLrATF61/8GpFHAdIAvpRvMhivU1ilFCFhuI7gt49DiD2M4OF6ETzN+7/l+3+TV2WMt+n36i3ffx+XWSlLz+PT3tc/7768CrbcvkxaUeD1RmJhwr6k8L2cC3VdzMhxvEwhow7RvRFWOeT91SHLxCpCrVFSjX7Ts/Rq3TCrkNHg05q234B4OInMpMUSHDk0tJTHd3ili6xVKI6QNJR/+thGp1I0V5ffH6+jYqNggclM3XCr/QWpC6D0PVgTRqzi2g1+BabdzAZWNrPd5t+zRIfXdnV2Z9ixCUB7glEjdttVNq8GIMZyhDgPa5lxy9jvUMr2EBluuGaL+sDBXt21ZwQawAO3ZGTtYt1xs7oi05YRKmrnQduAG2bwFZsOTh6iLbJIBEd+Tiy0V11r3XAzeaBHklmkDRxpdBUAp8BC+btEa0JL84dqmaovmBXnACHyMXgCmP3zXKEhcrQMgxCCw5h6MbSi18r21vYZB2rcCZ+jGM9DsBrWoD6ANKy00D1wruTiyqrqs/NoqozC9oEuG+WVRXgCRJpZaFpK+83T35sv/SI3iKCiHkujk+FUwmpXXUpeNgEwFSlMTuNThaTOvEnk7h9+qQdYwz/KU9eQoOC1q7/21//qP/offs9O0udnayaxmE3emcu8S5qZtXkzSa1qoPksBTNLtKzMmG0vy7v76x88vHt89P7TV4/Xtx5vrNMzMebABs1eRRx/U/3evgLwHd//2xFunx9c5OuvU063776MYq5j3Py+k+w6iyntMscpzjLoJuX0UIKRaNBshBETXi2+Q9AfniycFGe9lmPYjk5fHCwu7KS9N980P0e7guzU7fnxqUPc8ujZsnPTLCxkNRWnEWKMAoFEzZXpMVR9jQKK2IcBd206r8OF9w0y7WuyZ/Nj3J04rG9u7/18e3v35ZOd1ZOd+d7PXr84urP7yEZ+l7PXaxe7GxuL+c79k/mPZdvmTjTN5fn23sbs9Gh7986dh9ubD+6fnBx2vGWnkejYG8lbN1OcCom1VHvx3vSTOJOnuGzJcEvUIaqdVcQUzFPBhO0plCWoUi0eDb7FzWnEeCC5sE7vfRYoi2C8pQjjQkyTFSGLGnft58ispxXnMLA1aCmRVl/ZvYYGcBDnSgce1w6OFjc0WX8yxDsZvVrsx4edqjskYUj7yE4h33VNvn9fAnFEEOL5zTjAFHrzeYrzXVkpWKESlyLtVKQC3ScQ2BaMKq5BgWZga/tUB5xMPsp+8Vu/8zv/3r/7v7P/4r17D+6+d+f0ePHFV198/pPPqDVqYuwtu2nhidM88MeQehnZfqWNxdc2dw5evvjV7//yN0dfb28e3t35aG3Vul57Ug1/UGrscsv2sTHWOhXnlxnhJGBbAi00BzmzMPmklbDPsIZZm+qTFhpjKTkpoDhdm50X6RmlYNEwqrSFQ7houHKL6WuqDBG1bwypmkeNFWMRGTNMgVA3tBWbXcwfkSGwhHgvEmf9pHDG2KVAHeCJayTBAOWL7woaKB4053f+MO26buwImGNXiyw5PCJa51cqw5SqJDHD0wJzJJCxUyOjm0itAZBrDbWaxMk4PaJprEFfk01+vi6m4WrRo0dViDEpz6LV9Gh/4MtKHE7/s5VdpMajLbQZkrN+9pd0EC7nP4GJSk6Ny+esc8RnZ57Eu2D2B8zqeWPF0zkYW3SMOS7RBejOxmFXZs62YWt2czRLX9SjlO2gneqMikDXsLuhfgl3LLFiA2u0Cz51yGANNR2fJXk125iZFVMLALEZQXVsODJ4HXNgqjAMRgnJ8aJFUObbXG3ah5YLpE3TLk2AUcm8iEO4wlwiEmKh2Vvp0UeIb664cXmFeI+Dfr5rXeJWcLUM7eT9+bYt+35qywzrPVjWFI1iLi/uWYAxW30KCYP0uybx24a/ra6hb/WFIlJtg9msX2hxtglC9kTCMDEBe4tfn/Fjt7KNlTWLyAFEYInN1sUZfWuFuj3WXrdgIO9sWlEf5uzSKjqbsD1ZLF5fClkcQyjko0fVHG6Wei4mTnCRQjuLRfWqtad0oFcBqcUmNdWBzAdLHenAOcttmGPN8TCwpKsVAT631mx0QghfaiS+GcgleHoZWMKpkHZ+MBHUieDwGIordInriSa9/0WvMkjfD7An4K+T9qlrzWjAt6+pctN9CUIdgCnRAKm36zyuA76dz7dCRpIp/nXqmzi3g3t+K9vx0u3dZNfvvgWQnySrpVgYMYEtdLAtCiUZMbhchpaJ22NZIk0UKTof4F2YbGSVcLM1xU68JvGnCyUbEfP/iUPQyrr/U/+zYiSV+cS8yg/0lFSZyacA/0go1RVMzduW0ejRcxU0XQNYYxoCI1la3dIqRxKwi9LDBEBSH40wVV0ROgXG1H4GUOLXnCQF0s9qqMKjaPBONRM0meNJbHiaKogNgd+rMkYhVX96ZunXnfBa7m1IKTysJcmiUdbBI18Xe5QOLj6sBH8ghK6hfSnfcKD+Vg8PEGVkm4IGFtIETUMCRpWVveZxgKdnohMyFPfl5s52K2UDUT5hfxCIlFfZ1e06J9RAaKqAUbuGHSgCqKWXh3LKjdFYxAAyovgPbgkjTRittzHaC+BnIVaJStPgaBMRqf9VJVyoXdipYVZiuKjWiCOXkfmIeI3tyvNvErTYtRx68xfACE8Xre7t7u5s7x89f+IQ2a+/+vK//i///t/+G//a2WknLudyXl3d2dw9cd5Vo8sxC6hsu+5Rs2fPRc24iZVX5kPOLWVrSDFEDTDHYzAG29vXTYCIXSUbd883366/jN83tynu9H77+U0MT8t8R9jt57ci/QVeRlVCP9JE02TL4P3h4uir1083PnhvNIDnR+fceJvaaBSrn3x18fzFNw/n9/f3OgnYElsN0vnpUbP97KNRi4yQ/Ru1HRWOBZkEUG6rR4xV2668ur9EICQWvfZDD2O9fVSM6zlB6Mg5zq9ON7Yuz06Oaw64hyzqtfOoia/6nudMRm7H2enJ1eujV2b7HB45z+b5+lYtHDg5/9ESBIg7TKwqjPBVc4whDkDBmdgOkOOg8UzZiMmEqG9ZAswL4swrFBcty0wF5deDfwWPbiRemuqVbZQyqZL4Jj9GqnJELfGod1hyrc725nPeCvuVASrV1kCKcT96KK2VDkhfDFB7htEgGX8hOoDHJUh42S8DvvPHx2rzL3ktIX6T+FYxylVRW0UjtF1ZvTmKyDaCZnnEXfwaeof/2r/2N3/rt3/n7PQ1IWuRVas1HGuY+lq34ztU0YyMhoakkmLyqCUgocwY8zxPjo+3dhyAuLK7fefevvOeU01hZahmvJdBPaT48NCy7/UV+0CY0nry9Phob3u2sbHj1KfajnTjkp4Ys+FZ0yRihvRwxyk574JpwaWYHjWhhomZ81IU5BndAL8RatKOwJBdKBVWL5pg6AnXxORP8RzhvGe9peJiG3CrE55oBHL0DcankWOx6XMFIKa00k+j7vU7vJ1Z+cAEeTGYwIRdHBqiiqyda7kosDs/QXpMqS1hPGYZJWS1wU3ByBjDnxJn+re2lJiEBqcorNswDQByi2kjqqSZpYOtyDGeZueThKBfmDZLMnKFZwX2gyi0BYcat3ptzSgV2sVmTLfJBti5CfQSmx5w5dywOg28LPKFxJxQEbNeFtx79Dv+oncII12hIopQVD6OE0GZL4jI0VevizNTQm01L4G1RGs80pIaSNTS6zAZYKttKcMKqYJOCKty2GCAQ86dMoCRKJownDTmadQQ6yU4jcsv735T8Zrxq+Ee+UVcsKqgTEdjphScN8pRVBVIyFNFXqmGIeOht4gxUYaNXMPlN4DmLqshtCg6krgk5pU3FyrKgK0GW/5jKACcrC9sXDUqSYcARXCknNJNE2A1yZ7kzd3usd6qPlgLclS1ZMDBMIpqYUybICnFkgygXyz2KrcDS+xhFV1aQ0zPwnInZ5MwBhXffP2CCnUrvgq7woBuW+LQsvsx8GNkAadCb2e8hwhQ+lGo/s2gPNQErcIwlvSDCLytl1oE+pxAVlZx3Iu7xPN48NyXv+i1jDvlcCvpTa4yqk5gfCvLZYIp+fheSzVd9qp/Ky64tgowleovdg284V87akPCrWt66UCHUdfr0qfgq+WKglvx334s2kiSIMAhdiJxcZnOWUZ8qiISQHXcitYUR7IvroSD77R5KQPKl5qB+dpOHJWqXYI9lGOqKlbTrDYyTBVTY2bdp9eGKGAS4irfZDe9llk8wadUI25iKaol9z0pQx+ZF4HH6GLl1GogjpiTxcXJ/GorS1IDpC8wXx8jjOJfztcfO7eoOWyAK6e4BCy4Ub1sNlc30lPHmvHoVPSQkqHtVcu/ktS0+ycHFRcJExMvLgNMmd6ULLHoyoFAfM/Ox/B0BEqOVMxKh/NTx5rWGlVVCx9PTWSiMKhNSypxP+vF7M32yFMZmGDd24VsJG8ZQ+MqQz59kQloElZ7DtGyKVDYmZJU194GTXLOGlUQEeQpNaVUz5IbbW9cIuiyRKhhBA4Lmo2h3WoD+OpCh2DYb5AuSc7Gssex5SPqHJZCsP032uYfMmThf0CQXkRXugyMWWl7GpsCycD05JfqVXSMFBqBcPHx1blDDf8Y7kFX8mgXZQYd48JhcPhVgIpWU7E2tjZ+7dd+cPA/vrw6WTz++uuf/cnXf/Ov26+m4WBaZ8O5s2vbR8fQVYhapFoMfFm4FocaMPjT7b3VM76pM6eowLVceaGg+84o4lVlADZMuKncuDL1fNAYTLWeAq+fb40PiB9Wbl3LHEbI7ecpysj2Vux3HomAayrXw7fTvxN/xBZvyDJos1BrdS42nhk0efxib3OXJlhb2SGOPImNz3byV2tPHjx4sG0WdotqtlFkf/8u9OCG6q3ghfmRxLUZk9gKt2ggm3G39bisonXGSd5F+/zEhIbHZEUlrKycfsr4Onzy7MnnXzz7mSlYWV44eu/O1tbOpf2I9h7sz06+p5ansz8yf+7q5JO9uzsX5iuvrx+fn8yZnZaoMQow81Awzti6OrKsjYVxsr6+v75KV+yYFtLoeXs241iOKEIxFFrMSQ/Sdbh2LKRJiLzAZru2m7t+df6pxQdVE67yacXKUi8uXh4fO/p8j9XOgHz2+NlIlQ4jNVV3GI2JRQJhhPW++8XV0yg1P15dOwXy2tqFkRXhYsfKySFUpUUhuAznuG5QLsGIfaZXz4M9CnlzLaOMgOnL8rv8hwtg5HDr85uk3/G0ZHdfbnK5fuyUjFHdfkw8wAecjkllUxfM2dre+u1f+1/9zq/+GzrS2XYUbpg8Xd+YbazpMFxtbD9d26IF72gTQmlYp0izzo9O+O+1S2umf9vN6eJiZ2vDrI+dhc3f208m1kW2pkmub1EINv3Z3jWMAPM6VLOL13eff36xfvfV7of8mrqY+IuacNa7ZsQEtoYx66rhxtzLxiE61TL5t3o16mf9mxdnTsIlJ3omV0uqVIE2GmYHbqaMs8HUnsUZnioDS7CoWF45y31ETIHAomaKXFOZCo0hohSsxX59qUpMqHITrr2hp+md3CTh5k9TRXmNmKVWe9bnJP2AkTlDHLa0RMWkrOQVLymKgGM8lQ1A7COz8Nzk6d7dR0envkeyOLGsPOIwECQgKWpwCszDXka+EaIrs3/bi1tX7tyZsPooCDTffmHs7sIc/vw4KGO4mJ1HnBiy2rJGbwiSzOdm+lg0zBbI7M8QYXRm97MI1/WERienpn6QAqShSEoFsVec66UxcM4A57z6Q3J5QpdsRh8e2ua2GFi5OvKK8xUK8VELIdjwucPhWL5559RKttEikwYlq6dP55oJ4fjM9F3K4dKUJF8au7KCP1plPQ881j5h4zAkCgLWmsnLO9gGzkA31WG88Vt67zFyycNnhy3PZsfH753MHpyuH3FyylvtGCvzizuXl08ws9WKp3YHPr1D9W8sCAWIDzU9rPWTs5UzZI8BKJWWLdpXwGgK+OVDYERIDxkHsHPyzK4PeV6UfW6zpM5qOJcmNKzyj61fGhZYZxGZUrl5fnW4uHpxfnF4ebk/MZ1UOE9pmVLxIFUXrBgmCqTWq1mbscZwDh1r6A3jo5pvxVBlnQzKTi+hTqWlx4NHGSsIZYSm7RFkopDBHmBdvGdo/2r2hUettgmAA2+k86PsJXNkJgEYZVf8+cfV59YcnOsv7/5evRsHjFF+EMddNmOFmN+1rwfFRyWwT5/ileW98hoG/e5rZPPm05R6uk9FQF15vROvav2Z15vPlT/l8G4ewq+Dxm/FwKNaojqI8Rma6hBngSlxoHJkhhioW3QqLFM8JZL6HALXSgCiKz5i5TwxXNPik1QAK1E2IZKuHGR0UorS609nA+P2IbmVXgaTJImprzBBizdSfEq26dvAQ8oL4NiFtkwyrYy/IgcXp9Lom2pcHJSNS5wnzubLNCYiIvN0DliqSXUhARY7Orhg03bcW7l5ctMnsmbnh61kOYePZyUbLsheqUUPNuNU5raSrZPj06OjowRHBUEJ+FHx3EKlw/fN0WfHSwh920RBIGk7Pz8+YpTAIjw0qJfVQVdZt5B4VHBIG10ySw6c/dHqzEYtOa3XJB/kGBpg5F9ppTMTRm4BLzkgiaVDREghZLPf8ocNck4aa9KdwY8K1PN4gi+gwjw0mbRRa4bwaBWrM/kNnnbyEn+IH3gpFeD7TsfzmNiJLB6AUlAx/rgNyi72wS3RL71MGaGlGkTZICiD8VMqqBEfQeBFZiFFapmAI8N3Yh41BpgS66/4tjr/4Q9/+Ud/9MeLxTGmefz06//oP/p//9v/7t87Pz4xhd2Q4+LogGZHYkXWoWK75ccwBMDGA0pK2ilCs5VDs4QM9QJWphFT3UHqijAVP95GyAiYAF++j5Cb51Jdx5me/4L3iS6V+Ode4gzkvRXx3cARo9z8pVzhgKTqzLG6Xhy/PjlfbK2v3N27s6aJvbT7fl6WJvsfvzw8PJDEOaz1k/NL7VDCcD5ZNoO3UWmCIHGNU1yYLUQ3co/akwTmi4NVpDRWH5tYibx6fnB+8vhond2O20yEX1l9/uL5KTneXf3er/3y/Y/vbNzZ035w1b76+ikXMZONHyHZ1r8/zyGkOT56dfT64MXG/M7Z1euNrf3F4uXFxcbD97fWN+/ONx32tL3UzQRB3dnomq54r7d4mE4bjZCnuvvgJ9GUUX5NQhPQBEz4JCaE4+LM8ZlXzw9enpydn5yc1V1XcZ9xUviJvRONXK5Mj7LU51fQfGY4RYdKZ3gIRG2d6CzO3kULHD+g8+dWTiO3gdeKGA+Qm9QUY2IAb1H1W1d5TjEqsSK+I9K3Ui3TTCC9+ToAHK/DQ8mkBoXxfU5Z3JT971iu1X/n3/133vvg4dXKV4iTRYoBmuY7syhgmKK1382dAcikVsdoiPTHPCOb84OD1zhQvqcni907dzd2mfsMuRRoXiArv60+TeXJWn4hl36hbVIwzIkdp4Idr23tURtoEb1rANA+hI+xX6nDA3CpAYvbZTN9K2y0h7JUQp79kDxaNbhmV6NqpNKBoTImDsIgRR51SUHJpOKGM200gvH84LpIlj6MAgjpAXtFQ+Vk0wjUMscS4cXXaDV4r3wUqL0cJFf59sSTQPVVOlbIVSaf0FFGWWcD9upccX3xT3YDa/JSBlgVkh+jGpckpiviyKm+zUAvCo7f1WNgWQTKH3u+YqMO+4adsldnF4fUaNvQtGyX1blquS8hdzoXoZ/PtzTQG+KCfnXTgrwNs1eSNYv5UbSpREx7m87oeaNTtiRk0/oOHDH7NAgBpx7WjHMr6AxobgQgaZ028hV+tDpCmO8Lh3yhh48gI4Gy80qkw3M1UwfmK8+bPL0zXtNGmjjGscKlK4qbUIkHNWEG98KMNMqupSxiaZO70DNQFkKHNgmj/fMhDgnCwROaGzQVHKaH4qlLB86Nx86zbr+KC2smbF+xrbQ8KmbK0XGqfN1lYspTJCrlaJSoRsMCmpY1UJrOMaKl7WI54AFkqfMifqN29daCZui5muHBGhpC6DAQscEJmREOfj23S/0Ah6zvAZc5FcONxGQKI0JNSi5ero/R1hk+h4TEELpdbjFUWKvyeA2Y1TshYiIkXYKl8xCmdIhTuBk7g6UBHgrFCFVexitl23mAcEg+K2RkPn6mW1CMjG+FfftxinU7PFBG0m8Fjuyq7rvXiD9ICba3OgBT3CUc177/6fWtbAS5pvt4hNHwugybfq/fRoQ3t5uP0k9p3srpTcSb7AYqgwImcSQyrg9/QviPId3jpRiq1tH/iZypUc0eWpusFwWLyvXzhWiXi4/PzPE8uZhv20MqC0BLPkmHB9oJ+25og2eXJ9xm5CyFtSxodv6JHHBrjDh6YyAJjlb6NKyvQ9iIn5AN3pFcSQ0o5LXALHXU1zQkzVo4XVtsXRCM+PtE+vOrg8TT3IDOGF8a5UBjtqq+OWuSOG/onMiMC9fTgy4YCDnKarNhmMWP1ICr2eQl5P3Y2jbZ/PTU/ruisUQz4T3rp07DAkyrOkVMns7pYBYz3BdMZ6WQFJ7mZKSr7GJt1ZnzfFf8WKBbwZ63NgHvwMujPLDM/eG5D7zYXy3a865EVBE1lnfeQNvlLo9Za7JXX708WJgUb8EcDeo7fKSU9XOsbLaqkkqs4Kn4wQBFssJBX4JuaHC57bQLhAE0U674/RsjcWBIlbrSluuGCUWId2KCdKdvOzt31uzdmmhv1s+IkYJ5NJ/cftEjINjdKrX1eG3FYtxABbAQmdR3OPnQ9oFX8+dJRlac8cep3aLr9MfqqiDIvTt7j588xS7/01dPPvn+Dw5en+6s727tcZw0CRKauDhqRmlcoOlP4KvVq/cffXh48ALnHB2f2J7k5NkJm4AOAiutq/0ImLAcuvzEvLGJO+q/uabgQuLuN9dNHA9TnJv7m0jvPI19h1ZWXxY8Pd8aT3jj+59STQXcLvT2c6UuQRhinjHUZNDqhB3QeW7DCO3P7GrLSaq5v9ezW7nxiTuz9fzMEq6XOtJra3cGL9SSKhkmZ+tfp7VjwIoYit02Pucbm5a6E3knjuuZN6y+svGnqH959gHE097W7p6dH5nueXn4ukVkdpoOFqKAInrwl8fHx0+3nty5t0OXrKx8uj7f/+IP/j9A2tq4OsLSe+htBsHZ1WLHrIKT11d/8qPHL5//RPP5wSffe3jvIXPjaO3ul1/8/POvPrv/3ke/+huPdrbf33vPjGRnxIKKrtaIUmn22QDNw1YQ5H3PFLEVydX5+/OL7bW1wytzbVdfjyaT9gtjqqobbA7uhb1L7ZSdBRrsQ1uGFS+hXGS/2vUU5zMEaXw+a+hUP6pBeI3x2HVk2AeZa6VY2TD1OKGunMFHcBK3pTKTmYCWGZ6M5zNKeu00tfHcr6cROD3f3AW+fdH8rtzq37quMzDEU7JKGZeX1ZcxV3slAUQ3gMP+PZVdXX2ZO+/i8off+6Xv/9CU6a+yq4Cb8QtjxjbtQ6h2VBZHRqZAzTe3QajJy0Di+AvuPfjgD37032zvODPibL5+cP/R7twOXdnDTh4A6qnpXqpvaKB2SB9ygyqzl/kHCx6d2TMSeTG/w+9iHnzd0JQRmzryAC7+QpGB2QmNQPM27KBqJefJcg4BVBVNI6RLRikuzB4zx/pIIgFlM5qNBs7SyT65pzFUL96oflHKj9CyFRS5xQZJngjtrAUUkvoS5bM8sUNg0auZn6PkAIXuuER9RhMwPg04AqdLEykLxlnShoP8B3c1GzCxa+kxTKvrU33sOgUlmio5bzyXifqKqySZrFw4YQDZngK7CmQT72qnzxcvh0fHKQQibZ0ZD57tLVZMc3jsBIDZ7NAA/Oji26v31IjB6vzA8G+i1OpSzi/zigLsypm4OGTxCAZZxf5nfSq5U8Zp549zKDRQX7cITuZX9wE7M1s9zglTutWp6ThZ9WAAPfPiTV38xBaIFQZbL6vCxf7ABfzzsyuqbojllGMoWGBtRPkNfCkWmSKY4rIO2it5TIg6mYZDVxYfoPbq5tOoQpD8YUn4RtuwiKlR0HqMiq9e9hOLJT6H1MEb6qeNVAqQOTIeXS4eXm1RDirgIIWT2eLOVVMeUFMzaDWCvgG/ngSAMhvI2Nep+9XsQCchv6rNcC35u9xtBXBr/6CIsKgjathBaI9yMxdrwCImbZIDjKnVwJM5eqblr1CsR4tVe6Oh1PevZlvWv9nXdT7fNXhKBHBV8x/gpIOBvcRLwtkKxo37SLMNbDSulodQ2cyewvh4xMglNFxAMU+rT/VztCqMlDjaNr5oyugQKw6MEZ1e/5jnc2EAf5A86yMHjb7kV4wiyPDPNW49sCTfPI+Ad28+I4erh5uP2RWGIEY4zeYa3+z/E2GnqN2Tg/F53NQDnoH6dgfgJsbNg9hSf+c18p4+Fv1b0W7ncSuDKe70cWTx7ZTFvpU6gvQaZkkDNhyCqnZZeEP6MtVKk2CImV7GyLioiYNoHYe78nIRyrrc4qIXY/aEQw4RJZN2dMx91eqZcXNZA6Ad0AD4N1QhJHrLv8+AU9DU2MA0AIFJf5qlR702PQYDNUM8dtDG4JwBR7JaCF4ua62gPFWQiU4vU4HMNxyiQaX0pRiw41TGvZ0hjWYSqzoXnEAAObcNmdxVnLxpq3BkuZESybuXs2wY9Q0LNMYwLsQHjrrU1IcycI41u1ARmOVgBX9PjNhWWqUckhoNkvhoEj/xxUI2dzaABluLZkDUek0g1RRUzYqoONgYdJzC3UWRWWgTrZKmMhq70AXIzFUcTPo6EUhoUVJgKS7BEmFielQHwIQlYXo45bnsoQHDrttzK5vlxa2unKmZIbZQrWs0tPRY9aFeBnsNaqwZOIBvLgZD4TV7oSi0xiV+sJ8HTNAbrZZ94GRXW0CO2YWKpL7ViaYCLIpIGyXKCTBWSdVE6GPVj5j/5m/81lePD46OD22cZLn502ff7Hz0qaVb1EvkjzSqGy7UlbXBvDXb+PzsxEiLBaSbG3d/+Mu/8g//h3++eHnKF41m4TPqmA8ADuZ+UAN2ZNWjS9D02t3fiDK+vHubvty+vxvjf/b7lOl3grXM8xqs0O+KIRPaIVkquXBS23oz+7NYw7jFb9CkJ3TuuK78PXUXCVZ0T4HIZkLHxPyyrFNe//P3/vE/efhg/+MPv/fg4VadyA7/MlR9dXF8vjg9XV81dX/+/Omr81evzl+cPv/quVWMqNefRQbm3RIojxvnL79+8odHT1dWdk/Pn81n+8evn92983Djztx4xcHj5zYvnW3Y990O8WtXq9uHJ+eHp+e21P/pT3/6+U81sThfvrOjsyeff/bVH/zo5MMPfvA3/9e/cfoae5tnMrPU2Qr71c1vdMgvzk7W1rZbQri+ZbB9ZXb3au2486XYemMSyKRkAmy0A0SV4X8OUgsKL09SGQQplPYDO1NjAePyHvzhMV2QZbBiC3Xbgakj25qcQh+GhPWwZ9jttPXZ5UBClr/JSsnhOMKE+kKWv1Hzncunb183gSPht7+/E1JpCeuUrLflFfmH6U/btBcnWUpE2Saba2fni4fv39u5s4dtVJaGI26JXkOhbZ2g0vz59LRWZNSRTLcY0Gc7Bb0+cArA4ssvvrx77+HLg+PNrb3t9b2z80MpF4vT9o9VZ+aj3dAHjtNNOam12TLRKB3PrnYX5hBebGtp0vppd1XIxqAfBsfHuqo1Om80wVCINJnaVI9oCL3IQs8OEkwoV4x8lGLFeRaYZsyHqCc3AtOgWUkHorQRLG1YcsUPnnwZ9S0KlMptwBFPgJuiIWzJXV7SWEmjUX7yqTEd0gqAkacsljgHkZA8sn0p34AZhqfshY4uZ1s4aOMq0JwhslUBIio627h2xz9Jw9EAeXSVBkzavqmJz2Ug0apj7DYr3+QRzrji18aQM94yNqyJhVCp7W1gHeRrHMkQtcOmM0mACm3RHmwPtw4kaG4wBndLjfWAeKB5Im8uIV0TKK6V4AdabICelNpSrLYqcLNwQ3+sIJ6ip8qFOIgCHbNFXLwQIYviUnEdixpWIlxGfO6j0mQwwyFcJdQTqrXKIIA9PSWnj6sWFhx1j21AMS7ZjLBiYvdsK/wUcTNdYpX20UjI49UwL3tEx/qqjlNt+WpnAatiGfdYWhZRCTyYlZhtAT6Q4CIcGbYeZIP1Fu96Bnpoav2Aw6pz1y5hdKgXjp7m2tTJwfsJXx10Ayid2EsF6XKYp4FqUl1YwWW/h/yAs4uthWPfQg5QOhooVNTyAyXjG4sN8y8/r1IalpB1Vl+9UHfQI67WQ30oPVOauRP2jFHMdyxWbkEJbFdZWEmuGEvRtfpwXMJb5o2M5Uh9Cs3L2ch/6jkAQtOSBNPPd9zlt4zzrY8+ufqKcO9c0zeB04OSpmySzEoOxUNqRgT1KvidPL7z9buAGWntIOR34/OyHykj7TLb70oEgJEucfhFJU/hZ3zt+tZfjPzoOW+xrwOoK2nx0D1FJBtnCkLp4r2R81Bza5/plV1dfZSIxWToNWzW8w8Kwe55F2rNBgyIdFwcy8KgJ2WVxywqB4mEQxcRVZ/X9NWAUjUIRJCMFoWg9NU/iTFSgUv69Cw+McDlxWPJ4ddN9iAj3qd4ZNi1A1/ph7LxUlPADM2kZuXSAU09HXgeM/s9aXpJDlA/dCzRyvZzs5ktDzNP0v8MIMXGl8P4blCbCskwUkOJh4qEA5NBxZExhMgNvvyPlf0XmbIbn+kD9QrcoZNrQ/VJ9HgCuzGNoeIoI9oHns/OVzcYQ3DUPzkQDNYZI4YmGxUUqgbvj6oeRYjLD1abJIW+JQjxqlyrNprR80d1CTafhRixJ+U/ChiNms6eJvKhbCgmqWQbLRwJ0nSFi9NT44nKqxyNxOz8A0hKvcl944lPyG5NVRbNxsaFyZ16/zQrfQJXwC1HUp341MQ1dEELyi1fh3/eUTZk0Aru1tVkSEQCGPVJpMiRQwFgwc9g3dvZ/NVf+d7/+M9+3zEov/+P/+mv/uBXvvfRnaurp8wOCIgAsJJRUEEw4r+xq9eHRw/u7xuWsXmSMZyH93bOF3bFMQi7YXEAAKPjSBPk/o2K9xPqvnVNH74VLOAmyZTQfXj3Ke0X70a/vUf7bd//u/Gu32/DcQOWh0YPpvyvC499oDR0SIw3rha7af2LQ0pV8wEv+l6b69xLl2sbDClrXTD5HROQN6yqcC5XjIaFCI/EA6fRUxgCCVk/Ojw2a3RxsPm9T/6m/vvWrhm0egK7TvG12ffh4fxkcbK6+uDw5MUR7//qmb1pm5Wnm6CJV1aZdgYFj8LloSbk+NXhmQNE9/f2Xp8fvfrGiNbG8fmxWdoLC5OvXmknWBkvrf7Wfz6fX547gShTDrPr23XIwez8+MXV1fGzV798ZhnxznZ7aFzMXhknq503r2Dl4Ojo4Muvvlrd2f38m2evDi52Hlx++uEvf/y9zV//wW9sbuAEejJv9yTYJ45FOzWYSXLPacLR7sLJYA7YhXDt68Qo2SfwjFnxPbVj6Op0NjfjnPEkQ5ZrYoDrqdCkKWOv/yN1TV1uGi2vGtUIxrddudOGO8Bj+V976K/ZYfzKuYyWz28+xXdd3+n7nz6NTLvd+P6n8EqTY+HBUusMK69NyykmflnbsYJDf5zSa9xU5FBMYqm0VmoDqDkdQ4DJfTZn9bgwTetPf/xj28L+s9//J5999tPf+rXf/OLLn2zqKq6ebqzfsdlrvgJ4svXH0HNmOZc5Y//09eXK0cau7qCF6iZEH21e7W1evp5d7djs/GyxOd86m19tzxuMuuMEhtnl3uXK69nljiOZL1dfzjdeX559crryytzuK2OwThVdNcMFo59ZesuN6uQQWjVXTA4mhtsQkkw53uLl3iaMMwRpN0Y95Da8QPWdISCD+jiiHgH6MtrgTiujZWQeRrWrtS9YxuuXj5x0PhpxCkdVxEHyE6sHbXNnc3QrrKyzuirEkJSN73jf9Xb0V00Ex+onl4vd2frpFe/v7Phy9XnwX/4g26syEMLuTIDXuTVfy/xs8LPglPWMrc6qZqNibtDRq2iGtNql2fqL0VakKE0sUf1cy2qQr5Okq2hMjQUuZx1HxfXKA8BHzb+mjjEFf39DDbofa+bxYRm93sXq4aVuMLfb+Xv2Bx6dX5Wgb8SXleknH2drVjG8rhRExySrl+tfG5+eI/VwFmhO+1rbC55OyMoTpPQxe14Fdd+hBt9loV7us0fNOcSxq+uv6bkOIrAjofSxlkqJu0nAjcmHNIUS17WDrF0TR9f19R/AwOrK64qf79jUaEWLHA1Z0IoadxY/KtpXR8gkZ07JGFICYRebr2Dt8tJJhXBuMoIpDJMKzbV0tXh4eW6znc8uVnZX7Aa2gkwOViMtA+3LZUjQbaNMdMQG5kPGEoZsw20HbtRmJaOs+bnJBfCjOJjHKljOZTYRHG/VE0SNLGlEH9VtrhEWOWruxezTy/oDWyeLFbstnOMQG0Hz7GeTkAWb6eUptQW3VTRmRWwZjmxrEv3z9lhHbXlyIVoJwGNkWN8MT9JhJpH9lNZni+2L3Z0Nit5CzNPzlTtmG49mha8IUcY8j3hM8mA1/qFB4uzbxjNXl84D5QdQMeitjzEiDW0ZzW6uCfc3r2XkWlLk1nMiNz4OrI04+Pyd601iBbnSq/R7Cf0bmn7xkfd4YeT2bukj/M23Kb+bwGRpehk/QdT1Tqx3Xkdl3oQNbTyle+fLdeD4vQYsy0k9GhIl7/g8ymrlfO9/3ATXAUE2BhkwrDhIBVjaDJCp7kZiyA5LlFnb+qS0R0bZBA9hSLCIlh//4CqzMl9XdmRdWfpS0aMsJF0+yERIrS3hFzrSTgjJ+lcwqRzdzkxColoDPU4PqA5KnMqFHnuGpruatCeXwNM0K5CnOSMGt9Gsw5ERdLGVnCMHMutOMK75rpQMK3Ub8leDClz4LsUn2sSlJcWR9WGvzX8KVCy4HRuqKE668OMvxEvoq5eQ5T6gy1FGT8s5UwOmfA8pI/fwA4GNMC6DI4EQmQ3tOUTCi/QtP/ApoqWnI4tS+F3yfxddkCuAgS4baIoWuSG9jKBqpISJFeUwcpGWDV+Rvo08ilXm6Qf9F4pojA6hAjUdpHinodUqw000oksYEUcGYsCaTlUYiXxVd6kzK71Yw6Dqd2DbXXkqMj4WJ3iKNJt9/5Mf/NEf/vj4DDir/9M//x9+6QcfN4tKVLBMRYeNkrbU9erq/qMHf+ff/Ls6USdHTcF69fqQ9xF3Pn3+Ym/v7o9+9OMf/dEf8C8BKZ4E9YCogq+vAcX1i18RBH0r2hTj3ciFvhvW+yjoF2czZfb2fSpRmilZuUx5xw/X8IxI45MnFIcFmBLRiPPi4qjFbUXPf76+QSPDSWN2dlknNqa9XS5M7BlCFp1Cer2JTFN8Y7U6qq9vr989evXqy9df/yf/8f/r7PByvmHjzofbO5albfz8Jz999vL8Yu3F7uq9q9OXlwfr9/dWd9d3dA+JU7hNDIa2SIbzKtrQNXYzgGCkphlcx4dnhtUvT04utlIhuTa1kpYG1GJiKuk7HGrIff0SnVDDR4vjo9f/1d//+zsbuxvzw52t9/buzDc27yrZIQMnJ0ffvDjEPOevzj77+Revzi7WD1/97CefP/ijy0///Q92to2GYcjhbsqleOG02prwtqwOh6ERSt274mrsMthgUkQT9lUvHmdcNgLALGpqmWixMTCBnkrpJUS4UjGC1SAKpW3qauQqKxnTIRdsZYe1ABi/y3uQDKh6eOcS9X/uNSUFHHGKdQIQCsJDi5suHt6781f+9r9apdIkvB7ULEcJquURzunaTjDxm7r7kYtkDH3z9/7kj//43oP7P//5Ty3Ff3Vw8vro+M4H92QM03ihcf+qrv/QES4OAOOVWdve/J3f/ht/6Xf++p/+6U91P+/tbN9dX3tvvvUg3pnZsCZngd2reFdzFFD4be4ijOKD1iaUWx+8MNfZsTZjA4kaQ0AOqyup5+jGSVmQKS471dTwoQWOdNceuKjD4uiiDEUzrOPc3zgQxbOzwEHPaj7pZGThKjK8rD5Z0HPr0Lgz7xr94jPhBhltrs4Ac4eTRRfRgAajmuOczceXb5syGTJVm1Sjj6grUaZre1wvVwuzcAFyXFnkwaTwNmml5vmt6eYtJ8ouZptnesnBH3PFacQsXkx/qv7gRlXvBZJwqmY/rsSXZq9JJGlsh+swbnZmvVmBo2HT1RElD0+9pgMzTq/OH7QGsK/MTj6FQZk66YWMoXpPqW/ZyVqJ0K1Y9YX44agHLOFw7oR+i64mj0xj6WLZ5HlhFQqLQlSJI5prHVR1mmNF6OUe0sdp3kiZJ1JGiFMfpUjlIaXctFMuQwbMXFixngDJUm5qNOfRaox6w5xkk4AdgMxZPXoYuEKcrIsBZR3f9AJHIc7tGhqNkLj0DLqMIzEw1pqr0CSFk5C+/pQ/bzHX1wWKnsE4QbmOBABpktyO8h/qQXF+p1Lwas9eKml0lMmLinuVlAT5nxlXfH9KFh++pYmKLjwaIZhJMljH8xsGdBbrixeLy1e2ft3c2YcsYkzHlsDCDKbRjskKWQ9zWzs7EtpUKN1UzheYJOLbSId7VYUzbqtpPrq1NtnbWD17vXlmY26D91vHGYIdChHV0I1ABDAg4r6BzOpgvzhvVF8m1Jh0nTbG4obd4HpUQfIQMq4RMD0OeAULmj4uo1x/fes3jF3H8/BWNuPTuIXJW9fyTejSWfLWZy+3S3zzrX1R1DNPeb8jw2K267/fKd079xHp3dsURyLUnbK5VeKU05RkOk8gVE8xPdA/ShrciUlwWO9Y6/1anM2vCuOZoDkWH+bz10bnPC19rIQYFYtiZ9zQk90qNfG96gS/RNULBucEtqdDzFgnQb9/2jQKY0/txOD2uDvgBjJGRUZRuC6tJ26QBiu1QdLo8lHnBhYF44uiU0JJM7DFpVwadRqSEP+QiiK4Og5LDXpOQmkYpQ7m53gMgNWvSqkBI/3ySQlSAZkkQAxJhOry1MxHmiBLlGsn/WdCm8zyjmQuhU2CKjLU6RP5trp6/tAQwNXKj4Wv5FEwFPEUCwM/XAV6mfuv0CBY+XB+yZX1mU7Wyvl7IlytfkPZQ4Q0a+tELkGnvOl4mLlafxKiVq2b03I8WVk/yN9UhqABbVSGZ9IuzdCs/Co1xb4ytGBPRH9GhML8+ldVV8NGY+iGc8Tz9fG98UwM7A1gS7G6+YTVldUuQcJLR6KLOuc4Yij5NwyodFWEdBv6Ull8ESqLP/JJ1GMwm+iknpxKChg4TD11DVMgVS0DzEjlO07OW8ZFFKZjdtbff//uT37+9cHzk69+urdmC5GzQ6PMdikB3tD4lZKByC29uNjY2vngk0/Mkzo5NDnV0VTbY7PQi3v79ze3t54+ffwHf6wxGGgGkKdAqvyb+7tz9KdvI8Kff/su7/6o0VtJB77eCvmOl9vl3n5+E/VWaKti0ITri235PP5j9NgTKR6SgDT70dyuo6oll2vrh22V6AB5mF41RqtjbISQbngyGBBLz86O7/LnzVeOVi9PbetJ6f+T//5r54YdHb8+PP8Xq5srjmp++vzk2MHAOzvv71sYeMG9++DoeOtk7b175/vbd+0JpB3U7ZAvetZWr7xiaPMUHZ8dXa3cYR+trWzb/ev08qVWQ9+AiJhAaEk/dXR66Lxn8jjTUdjcsvLg3CR91tX5Ys4DrCf/6sX5MWNvfqD14QddXD5bXJ1uru3qIvJQbt01qsBHuH05P9ze/RWLT+/dx9oPT6/+kKxcXn6A7zAZzND0LSZJXGNSZi5jN5WQ5AxTkb7pcwonoUvVtgteYbO2ADIS0lKldofDUakZuRC8+eW91cy+A7mqS25ZV/ZZPFtGymySEmWRCa1bFD9Gsuv7eLy+DQivX777d7nC5NXtr9VjupozTWe8rKY3l88a9gIAT4vScqBZZ7jv3d19+OADH9olrPjpFuvKOctX7XQSnpgSPH55kkYhTSpbne380R/80cHr4wePPvrsp18/uP/o8bNvdnd29u/trzssLB4dtnUnKFIMem67axt79QuOz37rdz79v/8//m//l//z//XoZ19/srvyS/d3P1g7tJoHBzmFduX8wCm1c25ytsrskM69vHqZSm/iEIXmKNvtxeyFFWyWGWU2mexnwyp6gRNswZvO2j4Cp9S6fpCOnpnOQEINH3KXsoDx4SAEls43n23FN+azSJSg7gaEon3dIV0YImQKBCxF4EeY0DYwKTXzzWqUlAVj7P6mw3GaV3uzojszgd1DTWmw6H8lHtsHIfWZNj0yLYe11eysywc8/RiymTi6qdiE6UxkKWE7ZczmR4uT0wUWNBc/3azJpgiGZtOVCW5nfqBLE3BoAZtK9zV+5s0lYBp73QskFGZN4EYzPFl2dYBIraUzDhe/urgH1LWV921jcbnKRNSHMK7Cej6enW1ZAyRio2rzzTHfwb645AuzyJLwUEeQoNT1OmpCUwlQmQ/ZnjUG7fxApwlFLQBbbHJH1yNOn+XvwpYiT/PK11Y2a38zHtc01PW8AtNclSEd9toKfXtgjz7hkoXRrBlqx4SXPO4XO+7aJ7ruauW1SgMsjVLspB4V66uAPRXA2q5/qToNrIzAlGrNFgtIfJCym7OsrVpMnwz3/MXig4OVhy/MAjp/sLb+dHb+3sr857PFJytrT2cXjy7Wvj49f3R6+c3q7L3L+fOVy/uR4+KetVVnp3dPL59ZyLQye2aRw+rK843V/fn6q6vF3dn8+cXZvtla89n9ldUXqyv3NIHSXq7/eMXWZKsvbao2W3++crVvD8nFYvdsdnh1tX949fLZCaRa0mcl4cU23ah5MM0W2i50vNXqcnP91ELv+ZrNTRw7gC8pp6NGlrITTQNCS/IJD+c2YWH/MfV1/2FGU7O+9pJ94uSBrCfoHQcBsBprnf1FhNr79As5AnABto0ea1fOP6R4ZvPP3BIVSC5icW9pqClkCn77WaSzTwpqls3QYdd3MjVywmcuj/6Lvcz9OnCZpE99H2Lhee0pYMi2kCnZiP926inXoP9W+Ij9C4KXOX3r5zZgfZT8W9dN2E3kkBaQFBOSYNkkO6BVxUMcPHiaNZWvOawmeDT2VDucPJBOShKGKf7KmvEeWkC8IocauUXIKRqlwg1AAE0MXZD7Hfs9g4NI6v0Oo67WbJQ0AEV16jFC9IcsGR1mjuGF7PALM7Z1WpF+JEll9iWN2gAcxUD7ErRs4pbDTzBRD4lavERxJMyjx6kAfiAaFe8GbuDrVspvbikk01+06l4jwMPdICIFpAlgoXCm0CVtiym3gaWBsPwtzdFvJUBYobvEgw1dbIDSQDLM48EfP6HIx1GDgbgBRN2NAZoa0S1NpDfJFmAdTUgiBmaKgQRKrhlWr0GtCkIZAhlSQ8B4EJxXruSpP3Nz8tBXORqz8gGjisscY4qRe3T0J4Wq4hP+YN4LzFNQZfc3Qau09B9oXCWKreTIVmoEIAoPLCxjxG/FFAOU1SI7yCw0AXFWWcdK+c0ajh0KVNWGQiinMpBrAOqj6lvanjqL6Jd+6VefPju1ic3B0Yt/+k//ya/9+kd7d+6oNl9jp0WXMDQYXc2wshD8uNNkWaUnR2aVcH1oZWvuT70yP9VhABP4o1oB/Wdfo15/dpTpa7X+M+P9uRH+zNS3Psro1hWZxjUe6lFbCcdkalj8coFDkbrN78wDHSfsnlycWTHPkwMvJ05Ks4LcJhXotHo04WTM4t07Z0gvTtfWd/f22btnP/j04/MjVvr50QKOTw/XFHH+89evnl4cvHj+5dHrxytnO+/tH39/+5O99x+urZisY3+6EI8bMOKR7evWTrjjNuYPOUzOLlgsaw6ncRQRQhJMs+Wba04WmjuK2xC//i6wTYk4cagA51ozldf0HjZWLFI/1GnQxdNfjo8v187sXrJ6ateY9fWdHd5Gu14wnC5mTx5/cWyhsY0O58/1OUCD+0MYzuCZNJld3CTG0QSLU2OI/MBDjYoBs7h06g1IGZtWndKNX8fxQDKUK6kL6ikwMoXzvaiMGjW0qibDGZt8DpkR2ccehzDLFjNfE3bQIUYdV6UuH0VfStrbQct4t2PeTnH9/PbvdaZSdU1w9av6+GFnb/PT7394ftFR3GoB3tydfPgUVAaWWCtrlu5E3oHPACb3a//ov/s907V+9KMf2eGnTFdXPv3e93I5BTrtFPoc0ceXsr22fca+X7FrOz/6mt7gLz34+O/+q3/9v/j5/3N/Y2Vv5XwLcwzfP2PPPIvma2CW8oFzos0AbEwCbKDROVEVfg0W5tA3zOSReKpglaJVmc2AH8RK/dS41NjkD+baROz0b/jAFVElp1HIVlysXKD8cljkDYoPciJreOwRoY5RHxiyYkLrJTLJbY+jBF0SM3bq7+WtgbO6FrI1wyqjO4eGvkecwzDm45CNyIAWkv9NAv9SytLiYZ2AVlDoJmxoRzjSITpdXjzZ1n6XYLRGtRUCW/RaTUd4ipgdXO+tJk9u4qKM5nKcA0U0uRHa47MGVUUuNl7bgnJlvmVPftWya1cjGFbatA6n48Ehm3E6Gi4dGu4FsRMl5OHzjjWkEKiQ8JoE2Q/EfjVV0idx4iw9mSirSA20aqExk0PNUvSB2X+ted0uFKkFrUYxFvFOzqZp9IMnfEG/fNNSi4HCJD0l4xo4VAQLI/jYEMaI6g5GI3/1AxFz4GugVFmiTyBcZw8urAhLVUtvJ+zNTmcH3zjH7uhrqnN2/tROuFdrj/VzVjdeWLt7sfoEg5xcvFCCKaM2QYMUfoiVjWc2IzifPYdy5r4drWez53p1a+svTeVfmesYcLg+M2DicDFGHdRmt2zoVCDUC8MQV+LEwR2Sczp/ZVrj2WxhGplNCphAjkAjL6EtFtVSqF5z1BzhlreFQq+doCeznkOBE3XijGwMtR4ohqAmilkI6didWBP32BZ2ZYvQqf5g6VALSXFNiA7XpcVw6DbCoxcuzmLtkwhqE4/23GvXiNpbSb51/aLwZUSZSZ+oLlP39OatWD4ImH568FQdpwR63yWIX/v0Hdeb8Ot9gW5FknfyVF4bn1Ww0zS7RpmIHSjfvnz9rqsV9xidM2lcki4jDtSNWuk9Gz2/spN3SqwNHNFvuCoIlQGfj1NMFCBtQn+qU6qkC/sKTY9ebGTH5mC4XN2oNxeDJV0TzNhlUAf32BSkUQItKl6nj9fbaEVdFZrAX+vjUf3ENhRivVRTgA8bdcCQi4LMGghWskpJTgtPSkjEIbHmA2pjNliTl+ePiNfK+hNgp8wwDecCJjLLU1e1Zc2JetveNLuRG/xRPKBqgLR3BziktNiNYqs7sNGy1qF9d7Z32PcgSzesMoYIvRxCl4ZpqpStUKSRa3rGcoK6sC9MZdjKb22enokK9KDtril0RtcN7w33eQvsrtbXzVI9NNjbzMm1p7b24s8Y5jDZs1KZS3TiwEl46KoPEGFr85AHdOBQcyYf9QDEIEoMSnddzDYO1x2r0VjBUO8aq2Yl8tGpK3K9Sj0ttpAGQmpX+MSGjgkf6KNdDKVJo8bZLdwjvZfLD7DMyvyb0cFRbHoaoQjKiBUspaX7hktUICylPyTufPlUP4LGbqldvIHagV+pEleX7jJptCnorCytfHNG1jft6nPv0aO7X3zx2dMvXvzssz/9zd/+y5Bg6mheB3nXcjdF6urqKEZrf9NGdZGuU5zX19rHiUG5MBYEpsR7dnkv2NYOlDuq0u+AVzAWeDl+rm8g+/Ou0vobMadnOZb1uE/h5fHt/X++M+fbJb4Ba0R9B7ab5MvhSkUi5wi14bVTwHgajWybSYoAvDmbm0evj+7Md+br72sWoIjn8snj59ou0hErZYTgbUSC0ueqoIu1tjXbubd5bI49NyPpaKT8/Plrm9/anmvt6csXXy3O7B84t+/QxemLZ/OTO+ebh6Y0n+5u27PVUNDBfLGzYa//Cy2EEz+2Z+vfrMydWnfiIPDX58+vNvbOro7XOCmNRHFtrto2yrqUo/W1HSJuuYAzLBfnZsey8u0QdWJKrkGEVhRgLS3qmfke7J7X2u1Nq0m1tKvrO/bpvVg/OJD6SHP26vXJ45OXd+9+b3Xl/cVRwjmJD6qj1ObaDx3Osb75nAvj6ZPnehyUyCAd7lrSVbT0E9PIh4u72r2ry6fxDR/z6oldwZp7PQlRzeQwt5pk+MrQRZMAM3fSpJJHH+8ToYhOixaAkZ0qeAjDRPUkpOvNfXoq/fhwc7t5VczLEXoTc4ozvSLnq+uvN0muMwkVhFLjcT/Y5q8B/HD/0YWF2Q7uAl0VYCKLT+qarUTwHNI+uDzDzFgw9QInr024+uzHd+998PT5072te/O5U54f3LnzQMvAROK8xZaaAnfzOGxG9d77j0zPs3Y8NXtxvr2x/m/+r//Wf/Mf/oeNirRgk9HMvLBlisIYMm4mqKjRpIHGjM+mKePe/czL+VNkYc4MTJeGPQQqaink4qJQrPqaxRzRTdDPGPLfOJW72mWUtfNc/QRDnuzMYfxoR0A4+gBIFbXghDdau6panV0g5hnXcYtJ4JMyTyWNelG5QWgeiOL1ML2KyHGOZc20dnahvkTH3wwQuepbe1b/IUU5QLYbT3C8ps5XVi2BYCYfYqOL+YmZfIR99Ioqu0GYepw+YlrdY3hMNaMO7HlW50ih7hr6rAEh4Bxj77BQp0aLxil+TizmFjM0wOGUANMFH1lOitUv1gwbGiwwHGCuocGN/dWNM44h1b26+GFFNTtI/wfOYXKgX/1rBcI0EPMQr2zXcjjSgdVdZwke40LmLi1O0WgKmiAOtxFUAoKbDRmfsDIEaKBEa3KR+lbAysrD7gYSxBoiJscQOJhlZpS+nHwNDn/ED3c4b5gBcXlxJH/9eUx8BoaAqRNSM+gCb6mS0aoZT/kmCgSqUvyoxtBuapak52fvPbuYPWexGOG/fC+mu/iBanJJNKd6/h5Mnpzf1y1YvbjvXctoTct8cR8BT8/vJYnaCyVc3Nfj3eDyB/nlewq0Mj+GmN3zB6iZ/sPFAwx6eXZnAGHGB2C3sNrpxV2Zxpw8jswsVp7p/YirkxBA0Ci5U4y2B7qZByeG5XASjmq0o4XDCyfJ263LTOBTBxnDShvKacEXW1mMWg77ezgHEUWzmYZ9BD2opMuVKows3boDbJQ7boUYYPuyMHBjx8XHRRDip2v5Yw+l3sa5Qz24RkY9SDp8/z2/e0US7Hedy7ufe6/kNz9vSmw/NGQbgAF2RPqzb+J8u6CJW0bCd/N4932ZOx6a8vmO73K7hvhWUclarEEV0ZAogqEZTshMT9ILWhftGVnxW1X4s1HCKX/khnnLn5PBzrlez4D24MrIiy+OhgvJ5JbGxkWIq6zGQidPSc1aBjKlJZxkVgdlEIFsfuwFYvkMaVGx6amPaaaaDMtGJg6JYZPsARuDPO5XXpKm0e1PdmRrZK5io8ohoZzAqKTUzDBbaDQWN9CAFzuWTE2Nd+XoL824PMg8b2DOG0pvY3d7Z/IklStFoOkQ15fhzx5tBIdEKk9DYUVsNcbjHakLwKzMKqMbbck/5VFbOLUVWpppqaW4BmDVH8o1nFwDNjapdH0gICsorR2/AVEOUFXPO/T72i4nctR0TtUAJqH2Bk5dEWvylngvB6B1mILeQqm3NjbZXqNJhBE+8XpKts1BUeAKUt2oFdnpW4XWV1MFJRlwFJYy18/SviAx2ogjQgSRqqY1kBWMY/yFui5oDxIEiyJj4fVALY4Uv8lV+MQ1xQ7v8VKxQwLMM981wLNPPvn+1199c/fB1uHRyZff/Px7n/5QnrULVRxUwR22UziDXnV8BYANb+S6oLpMaTg51tIILH6ldQ+SgdCKjKduXQFRtFsfCvru6520RQojy8g3X28evjuXKZX77UJ/YdR3P1SvGJsomCJ1tr666yQZlFVP4qHbdHJ0tDp7tb3vzCXTIbhyqe+W67K08ECR9L+GucenLh13uFHis+Pzzc1tcYis/XbOn5sgdvX04Ght52FHK8CvnOJDzdnF16cvD//06d7K/XtWGmf0v7q6smKAcb/JPb+/fm9HB+LkzMywu5vrXx+9ktfZjNmkWcppdd6kiI2U2ekpWOgnQ/emHa2bl9AqSRsRHke0nFDMu3icqCI1a4QDzWK0b15+9fqrn1vaSwLuWp5mP72rU/sUffSDs9nm89ARq4bgrB2qq129dJNi2kEdvE/64osR4snvuOKa8RabJqEXTYy2+hAOCMpS3xDMwfAZhySAhYBLxSbeKa+kRdEkZfCWD/FkpQiJVsur/JcvfiZYSnkT4TriW7/LqLfDbsC/DhRwk8n1c5onqFJartqCi7sP99a3VjoYIS1eE4E9ah4oBqbruq2XLPTN55fXg0HQniGzL7542e6NqsNpb3T0cvbBRx8hkdT0PPD7r/oXjoc7/exnPzEZjWVL7xwfH2m2UPTi8Hx7c313f7a5wQd6tmlDq4gNLFbNpGMRjohHSznmywByjliozIdQC0L+qaPR2hR3YFA8bK2i0XjUUs7RWVywMRVDepWPSoGquavdaBQ6gsQVUaXmTY2yJTWqlA4LliMmERicMRSQwqlOIajui2TYwNB0rrBp3Lk6JH1ES/Kpd8JnoqjWR4/+VHpXQ+VrirjaBj7wNERBy/ta5WMhwE62LfiT+il+jUo0rV7BMt6is1pR5lLrl9HwHqXJFV3RYSXdyyJjhl+unrbIATJSrCheC9KIzsqupI0KU7TTvg8VpclTvs+A98tECE3VdUAymMx7Glzq1dUt5qJ8xVBe1YK10BXXbZhyPD5EECnb9xL5yL8IGRLgCn5ZlwZixBrNU4SK7FjEIh8tYfEjgSvlNtBG6mshzGyrza99BW3NIeDHMuuRSKTyCR3+YzBpxzWQFiQslmhatWtR+VucQEeejYxEJMDRQuwyc1ZoCn0/Bjm+pRpqq6OOzp4hTy0uV6R5OOExsXCQnuwn0Yl3VzVksQ04aGTlewlluCTsVjhIOhhb57UzFZ3bgJgyCjdCLMFv2iHedBRQncILd10MDDBwqruvB0Cd4km7JPlu1E21WS4D24hj3wULBZRv8BM6GFzsIl6miJkAYkaFLYVsQtS4owh4q9kSq4MIPQvvz6fp6/XPiPqtGzSI5v7d15RFXHP9fcRe5nwTeP3xO/MaM7NH1G/HHwmn3HwcD9PbsoTx/foLIJqlNL3+grxuIPEAEd++plOBZX+7BHnme8Y1GnWDVmvnhsF1XWzqYiypnShM6LJ98thrFtZxCPZoDx/tOH7t4MDD1/wKScvAv1lfjWAZnPUJoVJeyZKOhDnoeExp2GJuJ5jNrQ1zME6d9RhLST8J25DclLRCLCXGBMGcULDVGmmQKSZoEv1Sx9jA8syBHeuyx5IEh0mCcygX7kutgrUqw4mbxllc/nzDbpTYksnRrvnNFanu1rMYj9hiDtelsceOhmp4mT4PZ9YNgeX1fGfLNhQpN1PEUzz43XEnbT/JBoImJ92pacoeALw1STqpijtZ+6F+6F1ruLR1YE0hM6OJCFO17dWJcjNqaNUgoSZGN1qgKaENVcThDJpz3uhhRqe8K0OE0baqSqqJKTLFnc2/apB3LI+EVIRRE7hLHchPHpT+cJZwCFlUqTufkgbvqAFc+G4Ew0zXyNfJxFFY28KFGXvUP9ZWq3Mji9U67oMWrCJJyLOLlEQCoMBQj/GXItSgwR9tExm12rW5DoT3Gr6qaS2E08caGULW8SUuU8ESpLYGb0SfSgoNiCOqvoowOPRBiFgP7nEhO2Th4ic//sP37z/89MNfgfGK0JoOlOFJvIW3mSZqVjOGzqCb2hUFmLy4ufrxpw9+/5/b3/Qg0VF+JXdV6eVV1Ovn6u8tMAfA3pYJbse6/Tzt0rP6opg11H4yK5fXLf/9MlFZw+3dItz62qvwf4lrmV8pLvaN0HKn5G3EJ6bKMKO1A6brHp87UOLlyxebB+sP9t+7/8CqCVtYGhRG2+bfpJ4jURocI1Xp+bltHnd3t49fHxMLzjbz/Tb3t6wEPn7y1eXrV5iQVVCD33QdTfX64mzdmrKTRl3Mw9netBd0RxPMtXsrY3/xu5vb793dP3nxisOT98+4nmzJ8rqzgyiNyzt2mPJqsj9ZN9ngtM1bTueLOyctN9zkoNJYOiJAJfd3N9977+EWB77cz8/t7XHnwZ0//G+/OLKC1e48p8fUHwH56OOHR2ev33v461cXuzaTqT2OJyGZUDC+PvPGq9mZgGNmPx6NX4vhKpIXf4PrNfXPKTyzlQSenx9qUFs02b4uev6iafvq4RJ10u1Jr5/+uTzZhV4zd0NwmYs4nAyjDLFJX5LSNZV7/VP0iVFiihumndK9cxf1Ov2IOzh3xCn8Flf1dYRMgYAaklRRr7JiUtFO8bq7OIuL4gjophxxNV7iG247RhXQ4/uBnK7mP5Fqcf6axv7qm5+tb62+PjpEkYtTx4YgY7OkKERR8o+urB4eHHz2+Rdn5wfy/cvrv2vyMR3Or0CmKfaHjx5erG09P7z6YO3+1drT5vUwN6C/rRCowfdlNFuzu109ppqlqXKrj2m5sW0PfIE4JRpCLHVNGWzDHb4CbSaeD6Umn+nKdF/Yif2ZvMPAzhzUPUydmAZTAv4UBlob3ZR/Ypa/h+3f4dXQUzuBR4JODmFFfL5kXA0yuqidNaRw4D1rSj9WgVokVqFBcOpUR0sp2ZCA03MyfxxrXTk+Nh+rmPHY5epBJ7nCZEXWWdBWIkbDM0oeFmDUlMVgWM9CXfm7sn6HHQiNmvL5YSPDpoxPM49qEDW6m8Zbss6v7rLqLqzbT8Tv8LgwWzdWdlZXX6Tf4VH33iZFFoURcdvY18pYtWybyW0LIYjqld3rO1Te3vnOcj6d20KHnrGW1BiCPX7mRznvh6pvku9AdOU6WhjmAjmDMwd22/XodaASYoxWKspGiKxYPNkgAMTpjes7iUPAh/BBiLEVIdSx9RUYODcoI0nb0LdBeva3OVq98MgZymDUekYttC0iborzjEtIN6EyU7mykEoTxWPGO8GZlzlctslLp+dSiQwYjKWP694y7qtz4arRqIqd/uOJwXsZnOWPaVPDo9Ahoqo1WiqhKJpGydzHhyqlUQeqqgCtimu449ZUUOIYX5V5fWetcX1UUDnRZWz/Yp9Q5DCJe2VtZ3XzRJMqMzIiujnPWzlWDGm1HlhHxTxRtVDTZlrnHzQzzxNjjYtOrSU1YDuQnwryrkx3AFfzleHdt0vkkNRxq7Z96S+kmlT0xXgteHkJL7PrmS/XwSPw+qUI189vknmqu1NftOtWjPIMw4k/joqgb76+eRojAN+R98juzS34XbfTLYOECb1+eTfSSPXW7TrylOJ2hm9F8zJ9G1gb7cj4nomCI1Ge08xZ6IlKTjI6QN8dHDFxBFb7BtRrUqyPdB61mNKKDmX0EyVyzvem0W6ItO1XZIKAVHNFDwHAfrivDsDRMeM1e9M3nGPokw3ajDYjDy0zTQexHbMmeIsGd+Pe2eq2YS2WwcXCEbzs1Kw+pgT9zJiv20AmzZRHnVy2LdHT6WyqUvnZeBc7Ax236tlzXabqa4so2vzaetBaBVMHamCru1R5rRY2I2SZq+dZZguQBZtuop4U6PmZmQfxw7BESd2k4qGtUNySccDFle09RoX1kXR0aBZSQEEkjfYVNnsBeykayiku6gMhRr41VBc2YGkVXaoCpSGZOZOeS2v4Qa/AUlp4B0pWsMFZJOQNYBLx3rPTao7o7BLBvA4DBF2etHlCE4JAK6ma0z0pDCs9jdjap0vkuiXEmT419wh0yqRt5S1cdSgxe+4XjCFEj18y7+BQiC0YUxF9ivOUUDGAGHVVv6och8RRpZR31lMdnOonJBYMOhHKQ11HglhXrACczCeCOwzoMm+K08cff/+zn3zz4MHDtc2rx8+++PCTB+2LFsLSQxkBWbEdUyBTi9ZIAVUFm3gM7QexUUqYLSzjgekKIcAaLwNmYC+v6enm62Ck8UnQm1jXsd/8TpmN+k+BYeLN57eeflG4SH9GqhvI3uRV7EEECEY9Fy5rSimWQz+70Ztcb5LGi5NXrLHZ4eL4+HTv7idrmxx4kQJRNUXgJNhQmdr2weoXE4Ac5np4srlhgNiMhXxZBOT4cv3sgstHD6MjxZKJDpZmx5xprk070+s4OmO4W2NGTHjxuNnXFmcn8w3by+GI882NHS7g3Z0tPUsz7+9sCm4SsTEppSbObTh9sX/vweHF5dPTx2a5Kcpa3zsbLZ45soxhbePew/sbXNCMbEdlz9e3N7cfPXzvzp3tl18dNCF3Ze349GRzbeOT9z+5Oj568D5GfGpZf00szuDaILg82YZDVT9hoEjCYsw9LiEY2EtuBaljFjLWkQT2SaRQobVdtq82LheGJqKBCBOXkydZynRhO/0OSFnoaav5oF5828dAKc4QBU9JbZd8gmJ6m4K6l6yfKaTHcSWLrnGbQpb3Ee92sIDpdeSWCI4o8q3OQ9rL3IfLjz5+9K/8lV9nPRvtzCd5TrdDg6GimWnKchktqGXhp63OHH5OQ518Tz/+k59abXn0+pXdYAXv3ud42bJXBJ7q0ADb+5+cHxy8wk6YigFxdHR4enrksDB2UxrbPqBnR69OXv/syauPN+/s7CGVzl6KsMNhYH/UYRg6A4i0TJRjrg0RrhZQNLQRNsqAq55DNXWr2Uhx0GUh3zvXQzZZH9Pi6a+unofayoxoDo8YI8mE66FwlEVrymrqVNRdqHjMxxzLfgRZpL4yBis3ilcZlqKZk5NFW2xEZ9nTXzrdkGoub+zgM8W1Iz0Np4GCcfYbn5I+AKZh3mLv2j1rampZAGAYWaUb1KX+gkBZ3WU5EBPmPIWlgTJIadrPqObozmU4I13dMFBaFcoHZry7yTxjktWlPW0q0fFO7Mhj5S5WtzSzqEKnMqIBKWsw0wuBHfpDsTReY6BWpgkZZ+kQJU4+jWrbjE7InzA7XgSokzJq3rXtA5UxKlHKe647aqlEHiK6amwmE1OG1OgEkFF9GWrmwieaZ+ajaH0AQIXruQGGWrOBhaH/tDVdGbqYQtPBLKG7SG4cU8LydYWhJDyc+hCqTRCAQtXVlMkXafKtyRYWaueN9Dh2lNRrbrF6++wO9cxKSSOVJQIgZGxR0sFJLXUQAJ5KZoZHcO7N0XLHhDIc1Q5I89AYd1YLONCNNaIkOMzl6wEGjFTZ0gX3R7H8k+YNnJj+ZD6DoQpbfypSRy/WNaNcLzTPLCyxkayEtP2nyrUXrZJYeRyC8GQbCGt/697E62o5EBpGBl6qSvjpmn5HOHROYQWOii1f3/qZvo2gW483+fVhyvOtVFPOt1xvt7/2cejWfiW+yfcdILRGZ5+W8BfOMerj7Ws2zr616+2twBvo3s59gnDy6+eZgIIp6Fa0W48yHBlNjVP3iRnbXpsRiAmzJ4km7GcukS8/eHVAUptdBlrUK54qahL1Rl8Ns7YDF1sc4dA00cpbTFOl+gCV4F6dm5uFxF8nUjni42/tZYYAkacriKrsaYOzTwF32VkEaVRqd8BlP+9PCcvl1eOgOPtIrpcXr8ufPLI7UhCiYvt24wsTl6zT1Evld1GXBpdlCWLrwCTMxyZidzUd3oN89rKTKUBBmbyO1KFn5OTj5OUklFKpa/5pMxNaqsbTIv5oG8CRiQzCqs98JKENYZBiDYG1awQq1Vpfx/5BXO/p9PjpYnFEffsyVZ21KzX7IT8RL4GzMw2WndjXH4gwzM1p4j7d0fwB5GqKdT2c8lV1fXIwqIjCfaH0AcToshW6ws55efUQVD4Fzw4bPALjAau+XaHIIiHSXliTptlY9EJkq6kwhCLKsIjrKRgdspeZ8cAtpbN5tPfrVKQeT3wm/tTESoIaSkqThmNuKkXFAyFsFFsbGm1As/igcmdfhfMCBamroCoWIuENG7SHgs0gAD64Rg/QmqSFwxEz1T744MGXn3355Rc/+ebrx5ZFfPq9j8wfsFIOh7UDd6U2YgNR2lk9IhbnqR6RqgZetpv2VNeYmwoCcFcUeHMB5M11+1loVfT/xk//7c83SScv/si4Bl7MKfFNhHcepq+3ff9T5pV3HfXbOdx8uo6yjB0fQMBhr2aWw8z69snhy7W5Efb56eJEy+5AX62J+Tx6yi+eHdy/a6dqu2jBYy6lGLX2NKpEnFqlUxPrF5vrJ8evWkJm4nGjOsd39m0W8vLs7P7D/fXNs+3XJ08OD9+/XD89PdviQHz48P2PPnpomadpPXYaMjIXO12+XpzdmW2cciqaHGtt8cbKwaPgMd69f75ysLm+vVjYBnv3fO1oY2bXGBL38OTi5fbF/NNHLFAjAC9mKw+3to43N9cPF4eLk/vba8emTxvh0p6bDsed8fT1U54Ejlnn3eSL0OiezXb4VjHA2b3L/x9tf/5s25Lch317Hs50zx3eHd7Y3ehuNBrdIECQAknYIk1RZIiUaJkyJUth/SLL4fCP/sH+E+Q/QhEOKfyTpXDIshiS6LAligMGYiDQ6EYPr4fXb7rzcMY97+3PN9c+555732uQUNjr3rP32mtVZWVlZWZlZWVVTa4v20/ZQLQLPiOA52dTp01nozMBO93e+WQSSSTztFI0WGmQtKK/gDNJmDMDNt3ZYsItdnZ+Yp6BcUxOETxcXfxGM0ZBOLWOh0y3zL2NPzkq6cGIQBrYjRwhczQAh51SGunISkvSWc37WmNfcIP9fLzpHeWz8iXxy7QpoCkmIhplU8AuvlJ63jeo0AmHedA9Tq7oz2T9K3/1r/zSL/8Khwq6BL/Id9ecCrd+qd8sYw2rdB85ysnDqAuTz9PJ97/33TffefvDH33Yt0t4+/nB4S7db88QvGAgMdqxhn/gcAACcnh449HDhyMhCuE9FkXZhe3V/t4NI9Yf/OR8dPLgr/7Ztxin3MIwRF+E7vUfhWjBPwoaCYvkKhh7NRVNuxEFFkByZWcSqankPK1Yc75O9V1ZBA/SRL8TcBkyMHBYSnQIfWSXGw+ytjvBFNFYBT3BkEqJAvU+/gxOaBEUjPs8jxlnFg4wxYv12fQeUlKZIKJgjZPiy+cFiiIu1yxw4n0+8YaepJVIrd553XuYt+taw8Y0gzcIknatdBIgl9HIyhLPKMdh/G52nkEiOMqqsbQLTApf1Sbj6SM1l36ETkSgHMwhx434ygbCfXVxOpsstOW5jxu+NUxooIB4Q4KYd+4dufMGT3+2HXIe8GbYlYazhZfOKmT9UmdHTdrtHaxrFj5hxfyAUYOZGIzorI29PSEYkBBq7CCR2O86YgF00d6lM1GuliSGslgt0qqTywhQK8T4VD9gF+ly/cWTrgfXtmmS6qrT/afJFZo6lwfIS9BsN6IwLS6iwVw93JSAYFoO08CHvUu8NYHQBgAhR3dVv4UXgqK+EDu8qaXb/ft5NL0Xe6rLt80mQWT46LtN+8nqhh7me5EaNAWqPiQ1zrKbFVgsLGZ53qphhn/0VNjJcIE9pLLhSRhwspSxQTFngFc6Qx+GxJFMQpixW6bmYNyLV96pE8vNmdMNwoU8NfHZsgNUXIIM1w1sWBBpnp2OkwQUH+mYVX9srJFFmcXwh4iw6TyLI0kEQco32x6fq8lZq1bISbt71BbG18oMW7sdmQrRtzIJNxfv/v18NvcXd/WzflSi/HTTpNq++x/31UAJN0Q+Xct7Adt7mvvIciQ3DJLf2yu1dxuRLtwjJ2rySpqLtFe+m6IarMMZ21cX35//s6BerefV+wuIn1dyCbQXSR9lA9toQrVsLCo8iPNRv+gfSyjWpabIlcrVKVd0RGQtvI2bDcB1zppWgkQMVO1jneVY34Z8KSoFydIQJMBCQArHq+jFeABoI8VH04gHBTVbAhDr6JS4duFUaAdbytg7uOaZPLj0As9gmRfAcKtnwAE8QSkbjvCWkJWmI5b56UGsi0DD1wgBaFJHSkCX27AoHCmFZB6EgIQxatJzVYApQaJusmehDo/CqgUJqXStl5AFJFW080zCm3TkIWs8z7zyVQd2sypm0i0DLo0Adlw5RhhBJcOHeEYZGqhj4FT9kx0rBM8QS9BDKEAZqvH25HdoQHcz7akF3rfy82eyNq2NKNS0LoXzo1nAldqqqY6nKpjWoWt1HdFZMU5UOQKfXlHUh+rEFULMdQ/20DEDzXwbj73JSfaZtNERZbl0SXRIiIiZSmDSoyXOCml9QjW8mCKCNLoqJPSBZPSnL+mpDPcZzEloLjsGkkIQ0ju+VP+8przQz7o/alRoFvyZIDmnuD24c+e92eIDrn3oTmfnQrdUN4M2BaXhzUeKw7KXmXIyD0PPKcRPwx0jy7gfLYMdjBURxlEqqOnkLy44FUOGjnXllScvU9TTqnOTIJ+v/Xz5ou6atz79v7hewrt8e/HqarLtsysZL1OFzp/JWyKG17zAf+btDW8NcDc2thmOmOK26jCaWsT0NR1uT+jTx5vum05wTJZqLG2Mbn6mT8kQWqfphCagRMcMO8M9G27y+WTleu/u/U8fD0Y3b9y9Zs/9Tx+Kub/RtSP5mtN3emPUuTlmInBwba4NentDNsVufyACbefmvXHb+rHumc34rGicTAeH1web2e7Z7NlodGuzEVEzXPfOeq3d+eTF3vje7s3N/MSWk8/ns4Pe8PlG8MPmmJnT751Nz28/PXtwdDyfzyYTWwRZMt7b+cmPf3r07FiXpr8LLczqA2DtR7tzsvj4fPMYTxBv1aWrVPDZ86P7j5/p1FgTWeMWbnLwtCG4ybYMs6kMZPAYJzna9vmzFyb7zk7PTV3awv7kubPJeMf8JxNxNJABrAW+e+yH1yMWhCfNErGIMlCytvQ+8ueKpmoYLc9zNTzS/JKqeVgQ3ALfvKnPgvVqnoY9mmyV+wJsAyc8X8V5DLFGfN3TVkyU6A8zad/8xi/YslWD8g2GAnGHEsap2cScMddIRVRrFIvXfJKMQbJKqE9OTqy/H492Dg/2rx9cowJM7czOnQFsu8HJ0bPnlkIdjPdmkzOb837tF35+/9re5OyERRN4hrBCNFub88XZT55/NGvdFDhCqzXS2bh8q8vRizWU8x0Vy3BsWFbDBkxVqPCMmIfY0ckUUoQ+ec09VedTKk1CJdALKScvQ73mfxRpaYqspZUzyjyuMuPMdFwxp3Vo0XOukLZMJM4SriVva17ZICRISkAiQaB/KNA8wB26yyhpW8SkL4gzJOsnwjLMNXpTh6O89FjkMbMoCgsUqt5IlYZTI/TRXSqGHz5zxEoodLwLIXLYNS3LuNQDZI8QSjHtXSggjEbXSacWcdunvggGVcn1crqLCvTA5pqaM0tfFRTlH8SfBBL8kCfw0gXp3wKuoazSy5QOk0c00rMnRhPvZdBWjRdTJFDkTu0iJyFl/aXDiMuy+ZF6YTh2Z4gQGBkPKRdSyVHE9Qk+h2BRGhoVoWi4Ak28aHpZ06O8BeAlgmCqcdgnfa5BAbamIOjBdBDqGbJhHYjg0hSSxwr3LM6+iqmBDWiMBB2YFyBWDRUpTCbA8bdaBMdKiBxVUUmLNxTtic+MSEKsNLM6+ZGerMYWLCAJUukqIfMA8oQMoXyeZfAGd/4QbvusH0C77I6FiYKz9ssut3AWuA9bdAu3FHnNh6Qr5i7RujmNAZHCUBl+hrYpiv1SQOTS+Rr7qfVOBlHtrDSoMpQY7Kum9SFjLp8qfOUKZStd87hJlff1G7ZXr6tZ3b/68krCy3RNivoMz1xeuYepPx+pUv4XFZO2nlUm6x8+vcz0J9w0uQKjOfc3SQvi53xeIYJsdXpAkuc+34UHGlf5zQOPGmB5WfUIhlvy5nduiVSkPLayimBsTUYJWb8fTtIc2CIvpFbpsGzcADGgs8dwIDzABInC9c705HISwDFS4dKM3gCh7Io6UXCGghGOdLERETq1JhPNEsR6yKouSKYemVUQB/hpZgDiBvDxIMP2je4fTC9LpcBkebMwuR9M84IoZvwSbSirSkZfg+VKRVKjUCpll3qhkPUBXuVxvY5cVZq0dG5K9ys2KEtq+iMbXCBGiAO60TvDKJN2ygvNgghjXX3dMU7jbfBKHVNvM34JPo6nJP8UAJ+GaPCTmR4HidynTjoPNEPeHMMUnNNgXgjN6VKjSzYxTxUXuF5D1ASRr4lv3tJY+pQb/62zMdGOfHsmJ/InZgKSUV6qlOA8YOt3qmkwklbw1q0HeUnXKCI6LVyiFV0ISAUMRrZPAppeiGxr8KxWy+IoGkBj0AJaEOrxucqhVQBMFSEDNv0Y4zyk2thvwX33cYrh+49nLd0EmlcfW7TKSE/51TRxMgWk1DW7VADNLPDHMNiXWTJ1/cbO975/NBwcPnzw8OGD5/fuvmPdYFgkLaJdMqM5EEbe7TIJISNYqBzbwHJbw1Zs+d3N4mbLacrZhYNdAbu0qNaBhI/6ym1z+SlvyCtF91k9jHn0ytX8bD5X15K+2YllfS3J3L8G9JXMKfTzrwD6zBswPbycMWgSpGgcG0ZLv5ALu5LxHXvUny/1+eK9RLlMjYhyuDaOy6k0Nqd7YzkVhCq2xwlETg1jGZxo5YG2JvwAikKwnR14cqPV6kQDknxBVOezxzvd8/Fod3+wO+xylvasJBvs7l3f32ckts6Xb9+5u2vQsZpd393dHzoj3imY8539a2+8dzvEjPUdbjk7JxaOjVr1d9/oWFSKFwUL25p0upicDN/60huD4Xh6cjZbjAX5rxbifLDjHbIxslN5r3t0vvfk6eLk6HnG4cP2KYB/8MOdvki/SWe+P1nbg+8ah+WTF4+cL3z8VJTRflt0coYDhJFQMQey2QHYtXdk87xrxSDHZ/wF6o7IEHW7Wb44fvb4qQ28LUTqnR2fHr94aoJYIO0sm83zCdCBTCQjkajWCCQGDKeHA30x34i+RyWieeQuHyFI6RwTLLJYToelU/A2QcOY+LQRluTqHRdfFnpSNZzgRZMn+4fQZg3vNSXWi8tk6UE8wS2xSjfto2C1Xn/zm7/wV//qv/LRhz+9tnfwpS9+kTSmMuvs8rya3eMqQHJxgOkZYl+FhrmL8uT0tcq8dzY5/7V/6dd/5/d/ezjauXvvzf09HsH28dERpyIJjaG5Xo1Gg3t339rd3VnMrv1P/upf/saffWtybr8mi8QHglLH451FazpfTiwVae/szWxQu7RT9GnHiFHs2nrEmnGUtV3zbSNjd9lN4mSANVH0cGm38+7zNXbLyuzYzXEDZz8f9jdHLN82nTxwKrDw641ddDI5wMClCpyZyouJGykircAG0/hGuyiqZSNc9sExNkSJ2HVRtX0l0s2tza2Egsbxo5aGh3qHU3LU6ZrxZvNV72tb3hBcFArW33JFNTI50JPQszwtzCgxISxwQT5vxWil95WEFSnkNe+7hZlHCYSLQRyvfJowXiiETd9oloVFlmOtMzABx6DVt/YSqZa0inAYoFbjDM5PYNQSksETdpJTqEol5bW03ZIDfGFonAPIiN2pbWSy5b+d+ZzNbF//jmlWGjs9MMNV7qIzA3psUGzwo44IUJPXUFEdLIfSj/UGnfWbBCMdl54l7IHkjp3WO03UF1bRZVDmNIvlAE7EEYywbKc/h5aOSCAxrlIuWGCgiX/Nd4z9iEZ67lV/tjw7n6OWtUnoWsMcZAwJ9LakOzY/81cQY2YO+9ldyrvq/AIjcczkfgehOOGtzZMjPe2qd7/6B5KAnpmZid2NDAicls+uteYLJU5zoa56oDpKaHkn86jw6noaITUEJLVptR+nQ1seJrnS+Nc1CX2Xk4w1FLZPjZkEdsgJVNyr14Zk2vBUt9p2OmEIqgzpVC0TBLF/wE2fexIf7IbgJO6i2OEAEaq70AGL5OSHG2sA1UBLuQFBgkh9rWdoW4cDVv8JfOKaTLuYckUQQqQUv9N6Vy64vXolTVrz5ac7qeo0lYr7/0yWSttUM9RMMfAJ4QKoPq6AS/Z6GupKIwCvSdSkTpvmDpAGCcCSJb8i9tsZ2AL4L/axhZbMl1dBvPx19c3lw+1NisxtEe/qy4JXGBVq9aoA5SO6pPDHSOQ943cGiEanjrVNgQQxwIsGGXcHVpEMU0YPeJJwMAxkxI+LszUbP2sARg4VECMr+kJWIFES8QsMcdJtRFL1f56DFJGJRZkAHsXXaDUecwxd+IAJIkCpbTDO/F9MjohM4OZx0FKL1MANSKllVMTlf+m5kpWZ/RNUg9DSuR4wVaMwGZLQukgfMmF8mCEPTi4wCspMlwqRLjuk6Ovs9B+a0kh0ObXoB1PXACBDBJMD3FqQ8pkugMJQd0sVhiYWo62rk0OPCDtMmBToQE5MLJBe0elZB9HvDR27kQRQYc3Yt8TcLuPeImR9FRNfzSlVuyNDYCfOBPuUC3Tuj3hcaBMkj1VOKWamksoJwa2hooro6KKjmsbBmfYIQUxF1ADGrwRp6oLB4QSIGgqBEUoIUnbD09kneMxKpXQxNJH2Axl+KQ+NdX6NlxScEDGtqJQY9zGTAiHTF8kVfR1fik/AMRQ9q6HyEyIIW6xFLtPiCF2Nr3KhfwIw0gECv1zMzANkO0ubu9+78w7M7j/45J/8o//u3/jbf2fHgXTJFnajdhS9s7cDoZ3dndlsenJ0qmHrAE5VxR8Im02bMjGbYVr4MFmDStRVyv7cq3jyc98oPBR0bWtx+X0lebho+/PK7UWCq4+u3l9kuUhX383Dq8k89tATV31WEhzMzp2eTruT2eT6/nA4Mss/0MIMlIPxzuHegFXNtZeB1OTTpeHA+uTPfO2Xrt8czaesvSjL8s0Rl8xijQeDCTtZa6ZrC7V2h/uH4+uPn74YmNUa7tku8NQy4fn56njWWy9v7O1c3xu9deNwdv7s2p6pGsEBA4f3CjUUhdXLcoLY3fr9/oiyEWwwybyQ6Qqyhv8xnn+jcfYiWJ1FSHVfpEGgjrUNYTcpZ935Tsyy2amefXc4ztkR0+5f/oU/98s/99eWrReL6eH373/7eDI9P330zrtf/PFP3t9pn/ZYZlxbixlW5o1mBmSPhNQRf9EyyJaxj7JqHZGBAhbkLuT+FNCEdXuDwS4hO3lx9sFPHh2fLPYP9mF9cn6OoTB8LP/oyZj+9SAjdcymcYJ+VFgkpYQnQhANg/FIRKQoSqHpN+uxt96nPYNFw0TVupcN7akHTeIAumC07RPwm6e+KmPznc+0b6IoY+oVDLXe3x/9e//ev/+Nb/7i2dkRYclIZmrShj9Iek5MgQXzzuCsW7sexB/BdEgv4H/qYVmrLWN/8qOf/tPf/t2z89Pd/T27+mi6wSBCShFIOD+fTlsT83SI9eGPTwb9t3/7n/zGl778r3a772b/J7OtrD3an06cLcfj6Xh08GJ+utPdP7WNOc+JIBRLxnkTHDyaXa95fvM/QiwCnnVL7+QHgqI8xVe3akoPlGs7jRKby9LG7EfqRdamx05Kn6Oj0wKhR5oKeWJVphk6rVnthqUdLKTRmGYwxqK8y8MfuUAAY5B0hZmXoE/j74pOStXRJ26bzIK8bLAaRVRZSiitnfnjdFT0bYosVU2l04I87liV8k0flgZHd1mxaQzahP6rlTo7wSKqtzzf+M2Fq5M+Eq2LTXHmAKP6YquhinlXz/xbJYhGdbMhPrRNkm7VofLp8lRE7lBYPjgAkfQySOe1X9DOszBdSKzT8ap4Iz103pVFKWHWTqsYQzMTG7pG+49H7DNCLFaSJD9BwZ6ASxeBqsZI06RF0uvplfzQanmjaFc+QsVUueiSQU+Ui8/ZypkkjARevsQPuUd5fJ4OK0OYKqQGAqnVFlvFNAgYGzCbQzYNzQJQqcgI+WcfxIyWBRrwcOtHKh2cw1L5RnOEK1ZUKbwQRgkJUy/PG86UtWoqd4FJbYt+wcdNSZvqex3yFpU0iMdASFugiupuiUCg511TCiYskYlKwm+RyVgBFlOoV4loQCpFstr7q+pQY2B4Or4AA+JwucoL3LTN0nbqvALD0lIZRVVbBKPc/YlXNVmlqFwN2V7PEfRff7ZN2YBv3m6LCvZVbkj+Mht6vopMkWpLnHrTNP8FxLhgX7k+F4ttUVcSauS4z9s1lg3j5LrEI2+aRy8/mwcXSV8+f+XuAq08BATvaIJq5hKNtJ3G1D3jJ7KkddxlHK1dJayGThGYmZuBkZdp/ZZNgvtHdrEQzmXiypwRde8p7ElNmEd3yFeaguSlNegO9h+rN12l+c+xIagN2aXPLDHdw9D1OeDBGPIsUhKkCzwGdAVsxKq0hpcxyShgjtEljoSjKsjD4EU2H7AoV1m0XbpikgW4cwp1IeLYVAgSeUZbWagu4tRJMtFy64TN8/WkDwJYZLzDxYpMCWBQJyp/teyNsmkDNxCpQyuChXFZ8Jg6awIY8AmPiyIv5gj20TLJ5DuuJHCQIsY/3Z9n3lQINcdPhEaFTNSZp31Cv6hH+oblm4k9oSwou6xrVoruiMYwqqZanISIaDwEMuQvjv8Q0SbrqpSYePRDJZtFZPmXowZ4ZQBLfe8rorN508jHAR6il01UyIsgoLF8Y8RHqStPxYgoFA1CaFDWHVlWsLQJbWZ1Lefns1mOXLU/gU41WlEiObWRIF+ZxC/aaglVOZwoDKhuS0ivQ+whE+n3BsLdJxltuMV/4fnqNOBTydKQuJJpFYLWjwqnilMxKKOlK6sqJegJHc6OTDYlab35zs3vfPun8H/4yZFFhhYOxk2ddc9hd8UBb4iVGvccZxeFrf4WbPoiIKPxi1/8xo3T8x1a+9HjoxcnloqW6txKZRWYQl9ekZltGu0W2XvlauSyqqHl45tvUsCD719Vqr5NlubNRY4LMFchXr2/eP/K95U1Bi+fByLTIV/+goam3YzOTmfz8/lYED4CLjbjER4RwN5+796X7t0dHT8/fnD/6be/+72n9gFLEPZxb/nGX/iLX8LyCIb66TDCP7gx42QOfqaX0BjMYgsP3tq9vd6TF2KKlrsDZ4rtCNAZDO3YbAZGjL+5JDbjCdejDs/ocmKJ+nJiLuKwe1i9B5Q/IRHL6RvMPrFbMSHiKlQDXLHYHQ8d/HV+Ajf8aBdITSxOjzMskxGzc3sRLfo9imbnyYNPZsfHs/FgNh8Md7S+ZcUPj8/Ouq3nX7u7327ttTvXbbn9pb2vdUZ91V84mMw1egjOevHWcj2JHelQKqdHqXLmkZi8iUTDmASWFAgfW60mxCd2EW6aGYu2T52J1l5//ORoMhM3SJR74zHy9G2NkCA1+osOxTlhctHGAvks+XN4mbG9hsKt0YXhjjQYbokBYSeilBLbastqbiIoEd3wOHg647RytbVUueppwEoT4BjgqPmuHxG6q+nrVxIRwpi90AB+vfmlb/7SO/dun548TTh/LAwA05dwfIQa3Y8SRpFjs0i5WC8+CG1c5ZSdxqw3Qjg/PzINc+1gbzG7Meje6w/4JqNRwTdB555G1NuggwUbZ9MfPD/e7O7+O8hjkOpV4ik2m+ePnyh4PR+8OJp+fNI/PNjzZpOZJxu2cnmaTRqZ7dusxwHuqKI80dPtmtbrU49LPG8LRMffIm+Wk/E5U8LWqesaMoxc3LYprhlysRU1vwEI17uJa6u5yp7mvKZRNFsoR6kGfcqQlMV5kpaluTm9bukfolgTJxMUtSy1BjcaSLfIqVr6UyOyolEPzYHUgaQ78EqHJmNr9g5i4jT9rs7Sg9AY2cIcmW5JAHd34nymhIHwvqfnNHp+mnjx5XVk1TkoO6OAqGAcBONwizcxBSI+pYy0M+NXMuyjkC0hAAEAAElEQVQpfbNba0Qda1Pxwscrtj7GpXuzHKJVFabAMExrdTd9F3QwYXqrJNOeF9xZfQK8y3AI8UqvKhgiMXbDUOWyWb8FnGmKdF9eppcNGUSh6h8tJEhGFMJckRFUK1++3FANizd/aAWw4rzIG+WlyHQ6/qu+i40bXybtj/q2t0EVDQS1WBjBp5xNygyW6dB96VrdpkGDQcQFGX3IE3wCOCoySHhYCKWCQSttF36DL/o0BYQpRCTCKL2NMoItZ58Mq7vpOjNXnmrXu0RLOzcgVkYQRI/UIuUi9fIQdhnxxsiQ0v152IktlvkuuoVrcVfZjs2m31QO4GBYBEt1wlJOSr8OAYG0CdbYTDIZ3j1leqU2mROzPsQCGDrAkcyPhPdoSqpXu7MEoMMr5FAzCypYCarazVoUCwCEkkaOQkKIu4pAdfcv/CFjTrtq8l/kas767X9y8RuB0iiw3SZMkduXFy+8rdtwBOfEZd78CuXrqpsClOxNg+ZFg/hrA4CLEirnlcK3mFwgc5msgF88rTIvXtWbBkxopcGTrJI2ryS8kqZSbkma+7zakjZ5IlnAaO6wr7Z3Eai4w5M6sMhnWhanhZtwfv7jJOKtT/IykSlCT+wP6U4iq0Azy234wFPM9kpkmLbP2DFcKZ5MrAjDa0D1Jlwl86qKs6bEbl/Rujx9gRtkS6JJDtC0GMExVwXjbC0cSLYkwUgsARyfvbKaQQsVShzjxYn9l3loIsX7YhJUs7CMtWs0NPixTFOKula1YlzqmbPzJsnwygoEXnJ15fQpkYpg+yc7uHw2iMYfYJ4hVqb/oWFIHP1cn6kIEaAvjQ8avYBKfIbGImRDaqQuo0kO+FARiN3cJ/SfazOEiEeh3CvbHj7qKqYV4ioNfdJCEkJNayVOq+QZ6dLnSFxwIa/fAjHqyMPo42wsnPESbkrUdw0kFAgc5QLJGIRZMJxoHp+ZHIKeNovayQQFLc/05qUf9fo5CHWYISI7gMGFq9KTRFGZbEFCU9D9hDzEF5W6ewMID260Dc2WiKo4eELH6DVJQsCGqd2kofxzhdCNlBZvJnlVPlAlr1w+AkU7WqjSuXZwY3f3yaNHD49fPPzt3/6Nv/m3/5pGihaXCOkTSKtBMhMBeRS3ny3QHvhwA8o7996iPZ01NR48mv7o/fOcZgmN0Dalf94FlVxA/4wEeVmJ1KYS5jPXNudrt/Xq8gPMK8kuH/8pbrbZt184KXLR5SrHWboKDMH6GYvQsRhgMn9xdPJwb/e2tdQSDYZ7QvWzN0+vfTZ/Otz56uyU/i23UlUGrXBtrJlOfzyyhJ1dRridLtw3CTDqPLULjAiL64ci+gSAGFWK0slsy+zs+NxJbTacYj7jvtoJBw9y6pt/x4LG0xpJ0zlb2DnPu5kdkFJrbMx4aYvpdCr+lJqxSZ0GEvGjg4GZxOphQaDJivVe5407t7/3QCT/0fUbd7TwYjrFzZOjM1sB2w6Im3+ubKsyD3Y3gkc2U0oijY0ptFkFA9vWIjFKK1vbmF6K8UFpmKujoBDT9jWWF2Cw9HY5bqk3MjWxWg6G106Pju1Vmgr2jVydqezcHFIUEwue7CeDgVAuxkRYh4BH8UZXO60cR1J2xd7hgTAwxMKESUzgIicRjPC24mFVTQKKJ3m2vV5p/5KnFHblukzpWYHO++KNaluwGcLd9q/++V/tj+rkDa1TQY9kWzhWDi7P2qbOxFBItbCXsRhMKZhoRU5Ulz1b+8dHLz766ccLm8dYK0LHq3hqSaGBF3WhiaGglTGnGvCH2Czo8HAPPqGScuPp6Hz04ScGCIvl0EyT0wuP15PSK5jFGJZ5Bj5OizfK4CpuYx1L3OTN0qF46NOh+AwRacrc601KuciLi2Afg1C7GFtqM9RQFSlja6YLo7bLRA+z6NAkrpbQApTI2sFIFF5iL9NRJWU0LTL1s8cLcprNaFqUFUV7l+5AqPTF6W/kyXskuFAc2yYrdZbWiU9GMtaYOqteb8aKx4PV2Qd/jGXUkbop0rBd5RK2FApDsHRdsUzKCscoKdWCTdZa4VAZUnHIoHjmMpJCPcvJTRuSjdKZwEEu+IGBLA2mYARoQ9/0dV56k67Ai9Qqj1KTICBTXicNDMI5dFPM5byvB2l+d419nFHBthxoRiekh8yz5pPUBHyjtlkmmSdRZf/yX3GpixQaBdD8kbQE/chXFUiaApVUaZBcWDWAPS8TH8e6acyraISmtKaqTR0kLiwLbOqz/Y2yaZrUPJ1yehZVaBCuApDc1ko1b5RcCJEE+AaA9P3UDsgZtyZrGo6uBpDyiDmRKUWVNxRNc2qx3Espc8ibvI05EF2d5vAiiFQdjOowB14Ksl5paMcCMTeiptMvZ/Boc1mOyIh4xhiZFMp9KasaTGqt0DgsariQleJOTxulAVOd/MsbJbxyJc8rD4J04de0wOVLN0Hv9eSv5G1KaD5Tt21iGL8E8yqQ4PUSgdxX+RcPt4XmK6jTRK+UdxWjJnb/s6f/wiPQuNMa2gYVFG0u9xfV2j6pr8qSNylz++Li+0q6K48KUFGO3Jt2wS9GcqTVQl4NzbiiwmYIYXSuvtWoQSsSGHMsDA8rsXrOXndiZs08wrNRi1T9xhx9u2fVtsVCt6MQ+p9kSLG8i7cwaQ0v0nCULEYP5glDF0ag6/4woJfXYxxmFwW8FjVKmUaNcl6FvbZ2trtMUNIELRNzPbvlpZcxQRk1NtN9yMXLQa3jNO7H9P56UGXFTwzhHHvAIWVTk2xyCBVzpDQyoRW7nIAWNKHQCE2ty4nSy7Qv+HKCT5bZFJFLez3wCceEjq9Z74JCxtQ6mGx+x3UUcsWuqhtUIJLRNMHEiNXKYAKQfY3GIq2F8DqB2JSHU0h5Gk1TsOPtyeWwAcw+shZzcd7nBLPtEPnM0mG0d0Ag5ZctLlShkXs4GNNnVkSDMFIWb88mjkR9wbOUHU07w9Z01HUaT/d81RpMbN06y7yH+VRuV0M8lIewf1z/NiplwGVrgKg7seCjHLCldYj6TK0W5kFmZ2emABhXcffPBws7OTs9l3sr4yUKycxNgp2cIpswjIhtdHi60FoqqElonfg40CofrJw8KCptlUHxejRJPBMBq3sLV6iw2CcMWvqfrmYmabqafFCRKL6kEu+jI//yV9959vzTdXf3wf2HTx+d3rxxp9OdhB3VLVLBGlCw4UnHuV+0JXOs4b0MCRg2FJt9nIS1GOvoyycHGXq1n5XwKcX/YH/1yiPPgsLPvuptVfzz03xO7jyiWi8g1yjv9czSXC26Qe0S1mcwLQTCN/EGYVibD1pSOVutD8Y5SdU+9+vxycnieMxFPjvYG+/t9+aT6/3ObNy5N+xeX54f9jcH6+6nJdRRpQwbrZb9MeIfL7UfmSJJq8Pbw9ZPOyenZ9cPDve649n5C1JQhkR7ZChv/6CZkLkhW71np8IgMxDoPTntHxxm3ms9f0O3w8JksTCeHTqJqbnKhz0yHh7eGQ0GIzEfcZ0yfGzglGCwbGdBANXi1NKBbv/QNj5Pnh3deOPesjM+ecFGZaXO1FHIxmB4MBy2x8P9/h5Hw6C/u5tTolGUapze1mdmZiLneNjZa7lyijejprPot4YPQTw629kdHBzeZPfLvN6cO46KpiqFvjy4ftDJwQYnnc4eexTPxVzgJMbXsXmZ/qadyMT16CtbHlGry2uxyuyYEbpi8hiDaVxthrKkiYOamZKpt9JJqOxeopgEkZTqTGTYdhnhgoY9XmWaS+7YPga+yrlMlb45hfpHGEFOccPu4Nb+YfCpTUuCRYQneBrhULCaPWhTixwBYQyZ43JRWYo5RxmuV7/1m7/xySf3R8MxuIc31/3xGSjRepW6+KcR+HRUbIvpJNuLD+xqY98Bv+0o6H27s3/zUBAQ0XWewIpzkQaLg5P9umvHTAo2kyqrURzQiUSHgrMFlGJyABbmoJS3Q0FlHjrGcD67tq9hd+bUE/xDicllkBInh5Q5xogwbpc8ZraZtyeUTDQ9JWrqFbPqPAiXOajqCkpvU1kqqx9CqXyCnklyrZlP9WScaW+Snt6rRg9UFUGCeloBlRGIkGWUUHQNZ9TjrekAE0tD9EuDTB7VNHeGSSzC+Q3MkYDNoGW8mhG9XpG2DlArEtl0Q+udAi7ED2Om4cNQ8pjQKXtdtrwXSpRBji5eBmMJcyPyqRG2x9TBOXM3ruSSSFcVDYHmYKYqKpKSPKo/WMWSzrOCL1VGDBJJoKFJGzBSgOwxOEkQpkofHPyS038deo2hwnToWWWsaydz8zzEI2VX6cFjnFStc78V7i80Q/rMRqu+pQt4h1WjfR6Hn3NX2ZPKr7qCbzips3orTI4HIDF4lIRJAmYur9J0y9ssj9bwiYTV4jXGIT+xpGAQ15XnWiicUtWX13OqLF0/hs8dzPNYU1S/DZuMABlzOq14Z/0UlSfyAcCMprMnpy7R2hVPmBWYueP4LrsbdeKvsLc608SAOGiYky3ipjzLfHtjXSufKLvCFCeHrEhjHrwK7jejS4hgwu4iEbvd7ummvb9p25thZ5OTK5wCMem2DjLX7XiK1slms7fun61aOzR0MXCaK/+0VBq7ah+qqWJD5y2Nr3yhUpPAs8ubet/8sg/n61nxjzyAN1mu5PLErwbORa48yHXx+/I+AEL3NFSQuEhYN68NAK5mLmif/Qj3NoXkzv9LeNsSr/x226QpMFdefBbs60+SuMkQIHWhdk9YovvViu9+K0tO+QnzRUcnoQI5gMWx9oeJe4lmrPgW4EofXBA0aoKDPz1vFRNhVyA64UoQ3Ub/RI/Fxmz0mV6bHvQan9fuNyk3MhWvWol2SVFEElg9ZvFGHNO8+3SrZiAi3hAAnWDUabpUYghCpITRGINBIvjRr3kbKHpwrJ6AliSSUvDaYj1Zzgccn1F64Old4nRO5xqPKPVctkfCOeN0sg8dRCZ8h4lY0Jnr41R2bcd0pJAt7iOlr9kKWeqQY71UzkIkWxgulmezM9Y8Y6LUFOdgNgaHV6+nDzMUMQAQYKBMGjf9xNn0BKViVBnwKDjTGxF1Ai7o2HPDHg2KkFCI5mC7xMKwBR+j58iSok3rRExUKKEyJugsJMhwSCH276EgeLNUGLWChzWWeu+++AwbF6aFrHg02jHZbY46OzKKcdb1MotVKdOKhmhW3XJpahR9RuDgA11DJhvs6ghFUQ/wUgiy4CN2T7RhLB5TA9kpUm2TNSyHklGuYVqsk2byPMqWgnfnNZr7ig1Uz5UVwYxyjB6UM964ANAlr23jg6pON5tNZ//4H/33/9rf+p8P2QPaHuIKoOKq0Y1WxBOLAzIszKxIiqSiYnAjitOpzGOGWYtpguKVC1a5IFV3QVIJkAlazZvtTf169SNJmwzblK++vvKrSXblwcvbV9ApgC/fvQL/4nFTaghZDiHYRsjSmbTax1Mh60e6jms3bvTHNldhM/f5emP66Ng17KY92llef2O0WpxlS5Ggj/sCA0UbmWIQAM35FKfnYLicdnYObh4cPn748LGwfiF/rIfWfGbxmcyifZbT8+7hjsmq/n5FDTGIM/4UsX86vrFnFAYQXgGffylhhnGhZ3/Wgd1AnTN2utjbHSszE1o0yar94Y/fPz2ZOyJqd/+a5raX5A9+8NMff/jJ5HzdHo0eTY6Wp8fhLROJPWcRJVDufDPbG+2M7MVioK9Py7GWNEdOlMOcUULOJ7JHsX2CLEHF1hjdtqS93SfPf/TgU+uGnUT76e3bO3du3YtSjXJF0oR+nz4/FaDSbe1OExZlfU6k10Ei1qdqHqqiOD2NEXFoOv4oYE2OpqXUvNPxI1tsAQcljEDwPuMXXEq/1K64jRTKWaBir4RXA6dayVNXmqi5+5mfQeVlGiBchWUEFz6bm7fv3LpzaBvWGr8wcfFSqAm0aSM6rTbdipHpTRQLxjJ7mRVLFk85RM1sz/q73/muUtTAug5SRx+WzlYCWfImIhTUo+Qt7O1O5ytRfGS2qgMNUryZz2aPP324u3tAgK1eGeuqIv3xh0ZzRLEFWgHMN8Eu0FEa+IkvKVTFWEkTkqJYqpGHSR7PSL6pN+UWEWgMIACOMzzvQqzcyRTV1BQXnaVDSutuXRIYqN75rbky+MPgtYnLLLszi5gKkwGieEIW7POEYg/2cXUBGOxK0cakDNpewqHUn/MlIoRMMfyqy/aS1qXhQwddSsDExFQPAxUzEIb9yd3glWR15UnZY+q1fZiOphBjB6ZLjrJHV16x9JRlMEMa+FjO0SmhFDSAVA1fRChz08oPmY3vk8xtgZUmjaQsb+vKY2nruQfVhIheClhK5nAUgueheuGtWyv6XLRIIZ76qkIEtUDHzRSrGUSwG8qlnKARTCMaahiPYRR/CvYm9UoWfy4NkI8Uur3zA1t7YMTe4FJclsSSZmBS0NNW8E2fU8kaeBnIypTWkaAsCUn4oZSR9iqeg0tqmnaBXioMFFmMBHgRYuatPFJh//jE+iZEgWRHRXvZc10B1BEiZkouiNg1JKNkCoU5goMTmQ2F8Az1JwgiEFqiozOmU65cAuQ0MacLGLFBQrcyPMJlWEunHxcxea+3cWGwafiSIi/lDoDnMJFgGf0GZzSECjBVh1SsCJ6K53W+L66GuEXhvMyri7eVevvr4tlFtnyHXK5XXm2BpxFfeeNBw1J5/srlcTjKsy0gX1t04q02hnYlfujyYaW74vu/fJGUTSmvPKofIPhevOnjagG1j4Hirem+8rhKSPp6FnqmSZpZhVlKyZV34SX7/DQeJ7v3c+bOz5nbqJ/QrLD1sbyB7x5LyUSJyi3sJ5PvGzHftk3UvO6LkznXtDsATmo8yL3xJ7tqeaOYN2/DvaIelVx7h9v0LdYfJsLvfPGr25jCFMAsDoPE7PLkmYsPq2dvGfyNLbIWdqgbBWtyh9m9GnwaIY+WzFpU/JiCfNLlDYzkidVt7G7I0hkZu1sEWMppTndyoKcXUEvV0oNGE0/vOIqwNXiAgzNGt6lf5xNI1ihJFxsxA4RrPGMgrvdVjqoxex/Fm7+4hmbrqXmMxDoZ6SDZ0n7LcX+KFhWOJ01rvcessfjQ2CA7bnVZ1RqUfFC3+kETcAJpVDnxSMRWkWuxBlnraNCCJjGmESnf6f1gZIK2F2+YZQ0wFAePDPxSrcVQVH3/xWZWg66VxRfemudQV2/1SlR32hRRVE1Dr2ZvpIbDRz4oH9axyC3np/IMca2tOg/KtjD8p74Id/ZOn+dQPx5QVbR3x3o9vYn7OoNn1VlwEUjWRbsQgOYqbRlVpNQ0f1ROEFGf0nrRbPGVCfu47SyCVud+WijKQVOx+HyGJYuZkcIvb6tnbeQoOldblHmQvi1n2wK4sz/86s9/4Yfvf/zjH/3wgx+e/MJXj77+i78oEqO78wB3AhlOD9UsBxH9hTmxRy+x17FYshokvNVZ7+45hqjXPj9uOjelbeytDsLlHjv5EfzqIzeXV6F9+SsJXnvymd8vE2/vmjyN1/9z8lcqQL3y39Xc1+3245XnKLdFI72GX5kCUWNKeTM5O/x4unrvrf7R2Tk+cUjf2WS+02eiTbHd/mgwY33yAo1ujnYsk2PnvpGeIDuRa9QqXNQp99PmNs5Ztp5gpu7QWLZ149a109MXL15MPlo/GdkcdLjTbb0wao0MbVrnzoVtnZw/wFm8otxkhKI9e/rJ8wfHu/tCfkxsWc1CftZnL07Pnh1bdTY5P7v37jsY2TZAonc28/QzA/HelqOetKfHsx8+/7GhQ38wunH7xtlZ69nTk3SIBnlmAzW5AjBSuzPSsu2xsUS3vcP121vuxUrv8JYNuPpFFXJfhl9Jn8XEPQ5e+I4wZQIFu8vdncP9g6lVC/TE9LTVvqmHczz6GlZ2/aS8nj18uFic0ul6RXDMSDisMEdxsBpSd/yezWtXm+dwYtpI1uudRNS2tiZRQttIggy1bslSh2y9IfKSfsT6WeFv5/QFcxZuccinwfMXObu4z0//cnnU3NSvz/kI41/L8+6Lgsa4ZBgkn9qPh6Pd8V5kN7agK/ZcCBTxYchS7pQsOyAmgCFOljPRQJWUc4JynE4nreUdUTvT+f3rN/YPDpQV2KSvqhoSx4LRfOQx4e5dG0QptPw5KQyVaJBnT5//xj/6h/YIyqkwMUEaUwqZUYZVlb4GVHonGiJAm5rHVR8zhW5JuTE/1AJ5k0bfEboBplp6KGKhi6Rz6UjNrtkKOQE1pU6purgyoq9QAw7kIBoq1nY2THRrEGMQwdoDmNsWHe2wKY/wSOfc9kyZZZW5CZb+B+n2FrcKTck0pZzhC58EqqChqojrB+HJ9Z2IMpRjDKZ7MwBIjIdA7SqzUCl1iQhRdNrQG8rf/JmuKrIavho8oNly6/JbF57mCr71CxphRt1sPQdQCvYBYEFPdy4nFk0PjNYGyoETaEmSymSIA4Ggmsf1ys+6VUR0RxXvUfBMOfBMskqy/ZSuxjqQVQIRqblr1ZU+3QXx9gW5yDdAacMUXufupVmDTQqKdaEUJyOFoRqUkjPFhnK+ucaC/OB+Gq1YItnDItggDVwooGGM/7zqfepJtl0qQCk3wFIg2qVEd71HJIRD9LJqjfswmkhyPQ5eSw9saCUPTop+VqavhjWrfrCLARDnXnhBy4bPM0cvDwZLlakFWOJ8OZk8YigVK7wR3unXzCCGfnyUWFCqPJzCDwNhcWUWXQZsjbZdkmFfEz3rzk6NU43DoZuQIaHdaVPLA1Lr6wnFiFAkV2jWesNood2+ZQyw2RyWGDIZAs+FWqwwtVONoOQRu1fhzSm/9YANVEnFmjZX5cxtETg3ydd85Ob1K43qWbWE2+Cd07c8c9pAWjkvG6CfBeRJ8ypQRbX40X2ee+uItpe6JF88Xv/cqwq4AvFlhisIXBTYJJakqJmnl09e5nPnjRf1WQncJXH+tm+a2+ahNlfbmKcinhMMEwY1NaYVDAqIIc7EeRklUliE2xp8RMJvjc8be2WSPboxaswiWsqdzyd8kmFrZKMKlyfzVniS2tDJ6yqcMMrmowVZesG5QkBEZNbmIbH7FRjrMiil5GoXynXrQIpc5g0GqRS5TQumafWA1ZIkRyWaCseypKWi76KSkxJzRrbTacUmly0uC15/+/mUz4hijOPXGdiUH96MduMDZ6DHM0mESCfzHjkEjcTOBy+DKGQU9JI3UYNMT4Di/SEVZhJEHqXUujdDXhVXT2mKkERbHsY/vDPCDgrpZDI8Z/B4HNzTOHzyGWwE21DBNAct1+if6icUmvYL1UsVp9q0jxZDNW/gl7FKzG4N2c1yyVBPsujDRFmFP3IV6h6n7ZMPDXV+jimJxMDTre4r8/HlBlIMIhTvRE8liyj/be8VeGmVtIEBjWFUBC51CoOWbuQdFBoR2U+1oivTzGGBYFdEjp0YlVXIBVt4lN1aWYKTGkX3hfCxohBJRPj4C1/68v37p8YUGO+HH/zgK1/7cm8oAgGvagHRKfg3O+Vh12KFdDCM0MwDQMAC9G5O5cwcjg5PUTEpgmdVMr/rCtYpWsWDZepVd9vXlw8u0r/yfPvjyteruQva5dsGRAPx8uGf6iaohtBBtS5dmiphL1UjbJPF9OHR8Wi4e/1glNi2nNBrRaQ9cFeTuYNZV73+5P0f/tFbb35td7CD78LH4ITDNA7q4Ns0IcllyWspsysicN669wWBe48e3X968oy/xNaKw9HmYLh/7+Y142aFJ0pQNiyyNAgOP5wdn9g/89pkf+wcIa6EkZUDHBJic4DtOuk6+0nMHcMndzb8gcTidLE6nR/s7gpS6wvVEK3a6z189Gw6FaUzcqSx+Rz9IL6jJiJ4YWx2Z8yn7spxsxniu0DOIcTl4ohs4fcE71hcEEOfhROLZjV4+vTJydGRlscWWNNK4cX55MXRkSG72YYXx+dnZ4+mE6oCUPNLZILbIlBNdbqSg4zTKWlW4qnSiahQkWK2kDUdZTgLK2JRWJckz2EQVkWtMK8UUZlaUfLIRQlNulUAcwX+v+BVvBWIlUf7h63jdsU2kS3bZ45NfUTZuRrW3/JS1KAgKSTdZoKZKrEE4InwRXHWbueD7354fu5U4P7BeH93b8cJzcE5Ih0pCtbMWBKd/iTrRcxDP39uqYYoy6VwKpjoeewQ+uz5s4ePH9XijWy4Y+SBFcKIYehtpUPTaJWqV7gejai0Rtf5idxKad6nOepXRMRdtYLv0DP0CF6BEFSrGGUW0igR+F76h6ncy5H0yRU6JV8+2d1xyHiZ+eJ0NvMiizlVb+ODiKpJl5ucYauCokLbigQLr1JsArQLEOMu0aTRjswvoRoGw8EsSRWZVki1qesIeqoFMyu+IBVqFI6xx4DVzOUYkgKZ6O10GF7VsF7a2HXRFIWrLi9mKo6O6EI5Rl9RDQUKcjCVKXT15QKskgR8kPfpXZo9z/153iTwCZRnygK0+iAdXMMn4CepmjL7gxHbLPurRobqBcS2fBh4MMhkSgiSjA1BgklKC7Omus2blKrMUmeYpJ5vM4bwQdEldXMnqV/p/OojtVY0cyG8G1jJW/+qNskXepbBok0RNvuHJWlKCoKqaBKg6T2TPNzqBQpnjBuYSQ6+dsUC6Z5SuJYOLgTJjDUi6OC8hH9gilBgm/ezX1MzAODdwz8Jgg4TlpkUr3yzuQvDzgDR0MAgl48DStuKa+q0a8wMZAvSKJnCi2iFD8KpVDr8eqs22iYjs/xvaBZ2gG769mQsCydAwr6pGtS3xK1fLz+8TYbmQb4kDFTXRcM0v+pBPa93lSUYJF2DSAA1v7efBalAV6rkk2NbVkHJkyuIhTddDQ+bMOb7f+26mjqvmgyvJQoaKUdJ9d65cdtytgVs01fkouIqneao6xLiFTwbFF95UI8abNRe7xX245pfNrNddLmnYh+jU1g6rP40T4ms8up/mqsEI+VXOxU7Jy7FCMFK+ZKu9IMRxbCnvilnSels485P3gDFD77xjNplgxraKu6FDD3j2s45hVW2LBABlrQUD+sNnq175xmqekfowzykutRkZCaSbzlxlZMKVUvDQ9fL3lAZp4AOMry2O0TUSQa7sVIV13uucvbXB9Nu9IigQwbeCaFQS88X7ws5WWeHxDghzoW4dTu7MVVsORcd0TShXXdghrgwmXOYh6BG4QTG4461CgleJ2Y6UuN1qiwy3MrGNdAUAEB0GCwZPsRrZZGAXa6P0JSQRODNm8TH9kBvuZia32A3x0BT25gyKhKa8b4YvsTgDSGRaJktnALD+6JThiCqx97K5FyUe7v/IqxUlkRwlqOlW3KA4yObpptLMTnT7b2gcrJtCz2SuoCKk0Rj35A3J1sHBCRpjetCpTrDI+d9xAxMmA8NE4+YigOfdDCNf0JD+KnpwhJI3R0+xQv2kQGt4cU0v6yQisspyl6HrGLhpCjEQIMJFCoihT7NtlA4xwBXyMhwrz/c7y6eH+90O9/9w9/4+pdvfvHnvxKl2bfJg3OLkN1BUVZ8y2SthcAnvKCaUUZwK39qy2HHIw7rpynR6EeZm+7JtmQFN3e5CS6u5jsVq3ufl9f2vvkKj37O9frDBtDl6cKXOZrnzc+rea7eXyZ20zwPV7uPTyYPwiSF+PIgtk//RK90dL6ZW8QuoMyOPSPHcraPTo5nHOBElJBOOn988ujenS/86je/0u5/GEkUKRtRfghQWkeL9R+TXC2YsW93yp7eubF/fNp/dtR3LlvG1suzwWpg5e1g2Fqyy01JE8WQPvNwlprF5KylsY+fvLj9xrV+f6gRcMq6dTSZ4PyFWLSz6Vlt1SEChjKxy3vOKBiO9h4/ez5ZLEaDa4ab09lJrdGJI3nTOSb4/c2+J3o+leEam3Mf9DoHu+OdvZF5hlbnhIPdJpWUROZ1aZXOR+hk+MM3q/3jNcgwnk/kCSGytZlFqDpsci3C6McffHJ464aVNp9+/MGzo9PxoP/s5HxmUXr0R5Ysi7qV9sw5WHHeCQcJgxN8VeNPMQAJ58WhXFyO2xOUmF3HcJP2wmzZF5ENkeCUGEP0Bu6nTspmiTKIGMbAjVLK/2rlyl33+YhxiImb35I0rBFGwP7Nz+5xmEOK4u9YwdZ2rCZ/8S/9hZ//0s95VjoSrpUkbNTki+xEvoGpWrRX72zm5+3M3LJemnKyc/SN27YSs9Q8GdPmSMGEj1zLW/9CgWQZiEhstfb3b+wdXld7Jj7VWsV1vvvd7754fnywI3RsuHdtH65yF0NHwaQmsPdE22DM/AiS3jDDEaR5WKrESxQs3m1wVHASeqI69Q1cWsBfVLFf+hR566lCNQI7JxUosBo0s0RScUYUkWTUXcqXHsErfBQ8bJzbN9e0Eoa6md0NgoMHPjqb2kUn2kZx02jDlm2LG1S6UlJPTsFLcDY1m96EIcm+o5mlEQgUQP5S9TLSg6eezQMVzVbQUWZluSNJ/S/g6Z1TR7xh9xcze3x05hkUkNTpIoNiiFJVBtMbF2qlTZLMsNa4JunyNO1ROAHvSYA3SVNc8lTKellPkqq5+vdTyuJe8hPDNA6dlL7O+wZwEoRf8lAyFNDwEYRig4BqWrvwCsPngeyGzZUk+ryQK+Tdga9ptaU5Or0VGmjW6Ir4Eku4UniaNQwDpVTBm+rXYhjnbRxMZVUH4YZg20oFyXR2uYqOftJF2papE1rCjlVykVojRNuU+c6CIFnV0/FAp1SLo4JeQi9UnwyhA3fLZucxr0drdS/sqCNLb8iNBVciW91pKGljFXSTj+pBXCQzRjCjEM9IzDf7VmVBg/NwiqtjBamwF9BO4yYVOqRLx2L1PA0DUporM7ipoW1b1Mj6upA2pAj/azEewrBJpZUswMMbOQO4SOgr3/gpgRLbKzeXP+rZ5ZMqIC9ffb9NBK16niJczQyDZ/mVcbfvKqw+yxK+2F+oeVxg3MrenA2chNsczdfVGYAqY/taniZBQDQvcldPm896GGpeXleSNY89yLMm5cXNBbiXOS/vLnO5Cc0byCofmScEMW7wTQFU9xCgWCE84rF7bQslBNKw+uGM8bVjAynyFYh4MzNTojhxlfceytf0SaUfavScPo6pGC0Zu9b7FIjj+ciK0xpSMC2zwbhCEodQaVJc0oalNFPKLObDXIrOWpviIRIgjN4PLiHuPvoNlEhdUMk4nBdSDbJAMLCinNP5KV2Vih8vwxPj4qsKq7hgp6UNjqBcBiJTFegMVZUiW6zMbC2XbfcRpMGVEAAqPaqrdpGFyDFDmfjELcMA8CGXDh7OBtcVCp+nqQBhQpNY5UFPzZo+E95FOT57fX0pYRtxYLm0YlKpqRRIREq1AUOZXWz2PcuAsgRTh5N8pgAdjWPXFJ589GewCeyPfKaDjCVd22VDLF4BzRCzOza6pWz0n52jo54i9mqJtom4qAYKAv6lpdP8cAjFWTK9IRLGrMkYLF7TUFf0c5gpk+PR096rSw5TMm0v4lCviQ9tmqFq6s3XlOW3iQpJ22nZElkgpffbq2LksKedqdKyOoFSp7ZVkWQ1HPz5v/g/PXp+bJ3pdH72D/6H//fbX3zXJqHaIAyTgZ2oqWIISrCGram5+qfrtMW7QUfNc/Wzhr7KK50WDssFgYb3c1O/g1Khdfl98cuD7RU4WwAXjz77fZlGygbEZwFdzXWZ7OpD91cLCoQt3AZYeK2pQV7g/EgaO3dxdjafvejvLw4Or9ktkc1lQ09zAZaq2IBPY26G5xsngmnMRHfjI7xQgoeVA5EhGw2QJSY88Wzp+fpg/8bO+PnJ6UnPSZCd1vn6/Gx5zpG7tJH7PKZ9+C2EjQ7AaIK6hR1OJounz55dv97ZtW+jNaPtXfN9s/nZero8OT0Vwtrtzcej69DA4sPdm8dPjsJO3dbJbCGQadObdsW8sdOtAAoxoIU15hwDYm90j0LGlotpf97eo5eMdWKm2Wzc+VJn4hNDv57tgoRrCzqam0NISF7tgkeVEubReOf4ZMIJbamd/emdpTDen55Mzh89fnF2Mp3vjc5k2QyNEmz7ghpi50gfWqU3tqQHuQh9LLgSG0JSyiFPsBt33qDH8R1WdH6ZmCPmZDREYgNTldLUapfUYJT2zKQAvNOe+cqlAbZ8cPmoeZHnLx8VNzQv6jO/kyJskfWFhjF7169985d/cb6c2bM/05Ox/6L/Gx4tBRTBTedR+oLHxXvTF2X1ZCpTnp/++CO+/Nl0YW35ji1RsxFz2zyASemIdhlopaAd7cEYi806HA73dvZE+8gPumTGhB9+/MmLF8+YIYBkb9Da41kPAGmYRCkQ5MiyMmN2oWje0eaonGR1laZJffMu1fU8vy6+q2pJGfm4EPykuSBc8m0zJlcqjx7Ry3HI5EHK9Uy7RLGmCETJkJDgCFChjoWc0YHGDJJKhT/CGfQv95Cuh2oKmo3G9xVAfkcfBlgUY2asBKeFPjHaUs2AkszjdCjUPKYJ33iVQWBugm8IU/8bzIBMiSHYlgRN5ZSROqdlvQHPV+rhI1XdUiEPG9KEYgGR3PlLUVtSNL8vQHmteJCTOLcFUeWqRnmAcGQh5YTflBTh0MZyeBSEqvTcpIOFP/LlJqU3eISAAKd7yOMCU7WRKoXWfVLkNVNeMcE2MPyX25uqqzZIbdJIpuD4kuJTT0H60Bj+uUzImFOuGgVwQW3KqV8qUZ1oevxGzJUaXSprVU6vGUvGr9hZkSrAZNGVhg7NMNj+ByJ4tlWUID1wkrE9YJA+OOOB1D/dOJ8Lnz7o+tPUK4i495dtF0wdFYfw8EVOTITaBCLLO4vIRcOUhHcaMVIj5EFmLeFJXYVKEapqkTJcPorgeavk1DEcCGR+p/HqxzZpwOZx5cuNl/UsXz/7qlSvvE6ZBacBsoXUPFFqk7ay1asm7RUwTYrmQaW4yJOcFzjmrpL0WvYflWw7D9BklrDJ2RT2yo9LwPXOL/+Ta9OcKFzzAPWwAZI3lbI+rtxefZx3YLQrPikVSrpqlC3d/aYMCQgOsn2LyC0tGhWUdBkDYviAWDjHESaf4DQMIrExafQ3C7ZkacsHzDfvIwb4icQICCFdfign5l0VnQ2SEpqaoWv6C9/ppopRkxb/BwcTVIpkLjgo0+oTwQDZHEQ+897ZXTLWhF7TdD+8sZ08iXLJNhRrOwjpF/2nUb2J3yXRk73HjABr71i54k7pVhauEk1Q+6wDFCPAJeC8LBbGjxMMv+CGFwzAEm0Jy7TQdb14G9BN7z7VQkzY+2qWo8DW9iMSzZ9um+hR03aQ4Dq01kKnFTpCGrkaVeUnh/2cF9U4BIeH5Pr/ZG1bL88jEdOHbGfGLJ54jrRZd3O+VdiS6zijlthJb/qWTi8fhaMRNGnNn0QzRDUWPUrkleRndXVsjVW/Oy75dBQCk/xtpXZQKSOidD5SIg+gOusKD6PL6lnvU82TxQzIgHPsvGDkghwMK7Eb/UdaUeMECZY+xHpPhzlFYY/awSNSQsJf2JG+aNadL9+yicq684SKKXqkKfLHjZHFFSEyeGn3rICIwjJ6csc3G/8KesahmKtEkN2W/gCEjEzhXXY7DmTM3XljeO/e9fe//6Ejen70/un9+w/efu8eE8Iaj9l0WkUZI73Z3TiE2LkcKKDHVWK6tLC9rSr5d6LlUiBebXQiDinuSZ8cJKpN5atUweGz1xZhQOTxIxR5eeXhy1+vvvXOeoPL/I0Ht6mqLK/CuQoj901BL0GnJskDa5wdjEvuM6fh0sLVqTkFdzl6fLoYHU12bFi4nJ2eh3vx5mDEyNh86/e+97W3vrF3YN6MffuMXztWokZDKkuBrBzR9vHjK4JhT4NM7a1/fW/nxTPB60zfpVXEi+naVj8Wls/tHRGdYM8J4XB1rDW7J2Fywt2HomieLk9OTs52924OHQHM27nq0Rki0tiW83nXtlYs7Kznv2+XnoXVwZOzk5mlP0PrRKN45obzesDVvpk3HIjhie7K0l2DYHvXzLqLYW//+l1Dn/XyVNsoeXI27/R+4iZTWJ3u2dkpMi1XO9OJDc1OR8MDowQj6YODg7Pzc9t7gs5ZPzk9/9YfWIGcsQav9NHZiYUJ9vUy1MBQVg5FdblT2bA3gudee0aMIyTYL6/oSQN+zwykmdADaxF2dylYVEVk9bUFl1pEPxowW9NHcWKpsCEF0zRutOxlN1iNXu2ej7gP6kk+/V3wSNg3mbeXmyhJT7s57dWi5t7jTz/22eWroxRW9yphBK9hokBLfgK0RaIzfNBvZxxFbOGP3KcnRzP7QL04rkF9dAbmIdfpg5I7ohHbpQY1/dFgQkGadjrbPdz9Yg1CFoL9pLSg/MXTp/vja+OB4LD+ztiuI3SCEKNEcZU5FRxk1uSxdbIBKDIrIfveWNfUzimt6dWUiXfz3BV1lU6iqkCtmSTM83Q3ee1Sm4zfQja/GpJv75HCcywW5wZHStz9TTNruWTE4IbEirSGqvS3aIsYVcP12gI8q48G68WtKOMgEpFiVUQwbE2EJcxYBT9qKW9bmwNIxk0dyzCStu69iF2/fqMqk1Tyhs88yyxy9fJlIVOoUQThNGlz52p4ETtCCZdulveCc5KkT03K8EKe5T9UijBhuoJVYApYwQsF61cIF34oannirrGUsnKySVLpAhzg5plY7bfrafPT8zQKUBmjR7k0hn6ygL3NlhRhYP8zaqxWVfmInP+87RDB0RmuJNUFft5HjKyUi28uQibOFrGysITu96aMpmrxZLuggOcwqmMR1C12SeHftGv9LJM8yBWlUrAfIBSPhSCZlCAXQMaDH7mRNCHNwaLIkQYMP8R1q4WriHEokRHGlsSIqICagcD5b6Zz5DiL/y4tHDTD5Plp70F5avP+NKBsMbRgQLMH2XT/KVG+IhLEKl0ShhVyNRQO9nUktlyNnz4tXG+lCTVrXYHbPE8z+yhwCVfLT0sz/asre3DVkyJg3fu4fJ3kF9c2x8VPueq2edysxbUXUEO7vLmavrkvZCpTEdjDK/BztsBrVyqQeQNXLHOm4YOLFCGBt3qUiyf5boppbl6+aMpRJ48uU1S2Jk2eXX2FVvV2m7Z+pN1fzVtJLj+ad02+PLy4843PcBFDuZpRLCxLLuKgh6u3TQOH6Rb7aar+tdi70fVd3W0UHuM4xYehCkYmaC125c8rzsROMQuLdYqX6dxe3HiI1JjO6arsexNvekkHUuSIMIqQeMKjxyK27pCRy9yL3on6FBBfKloET1YUMyk8Dx0ovjg6CLW0UWQ5Hbd0d2xyg4xtOTrnsKpo9XSusQ+LsxMYrxeJbovskTon63LOcQwHNtptxkx869fiNWGVqrYs+QtVYwt5BUa5jbf3yknOEEhZoWv6Cd10XAJeBj8bmWQZYv3wAEnSN0Yl+KPlU51IWv5rohg5imRJRbXDM7EuWXfFEMr0X5Rhugk0DIyU6U8rGMWzzYgzf4GJPKfTVxBUdAD3rCEABSfmgQLLwCkTNJlqTPuZPBZnncYNqDjBAXZ6MA0U67BmBrKKQqLEOcEwmy8qKFlZfrglqzljZzUYQdE9OFlrq6TUI+QIR+YzLFVlRZryLoDwUuyhDHVSPdVqpgGiKtkHmXksjYI60rtvaO2HsuTBPX0H/cwdRfWFd3/uow8eMhlM2PzGb/7jf+udv8NaG1kNwBRNMxrJ9gY7tr/kq7Y+BDZsBRXBRmZvxAh19/YO+r1HzcpvRKk+pdCMOFSz+MpVpQfdn3m9fOWuapbPPzHLFlYlewm3+fnZh5dgm6SXyV4WfPki77RE8xuJL0gYggpaO1+tPnh4dGPvljD96WJmYyt0tuLdTjarxZOPPv3eV/ffMIVjuQeO1YJakUlNIrLSx4ggIbpDDYWre72dXnu2P9yzg6ThrsmEvgPhe+sn5093hyNcBrYMw1GmcWyTP3Tqh9W0k8VkcpoYua6dDafdpy9mwuyZ/AmZowCiNIy57c2VEYhluK3laOiAp950arzS5o83fUFxGD5bqiQa3zEHiibQQ5skxj2wM5+YMBDF03cu1c4oe0RmL7CMD7LNl6Ym6ZjWDv82zzVk7g52HNANVbrElBoyhaXtbdHtmx6ZTkw1zWfzld3CxE0NhsbKlj9lQG+GUfyPtVZRN+HnWDSIhmpEJ4fjRjmTGKpMV03nEN4gY0VKd9jbHY+iAoILL53tezNjGdEEiJKpPj7D1xJ/8NOoJZzFZPWj4bM8rZ8lKd42zd88LU7AFc2zvCpx9LnOsuXe6s03b8zmJ5UsJRfICEIjgJVNjqaM4KAipCzxeJSBIeum/enHDyx6vn7z5tHzF3t7e6NhVsTGfs1oL5FpgKt16KBiRpeGc/P0ygeHB9YDzBb2baIOuyfH559+9Mn1G4eCaW44XWJvTIVBJCuJUTCnwHCFR1/VXGaUlzu6o9g8kdJZ4ZZOIZ1eM/ekSpF6T1IHTaBldR9ARGFXrZpK4XHvI/uuVDhqPh1NU3WHJMa1gT2jA1WD2yudCA1YpckDUW/Mj2MJc1sW4TlOlXG74IBCAordNJZJaMWkcSldpbii9JI7xWr2dJEQyVrLFI3CvkUzRqwbs08adMnLZMw3VW2mXRR4mK1mHgK43oEAU+ZuDOHS3ikuD9PfJm/KlSpoBYliQnSNNk7pAZN8uWnSuasrBKzGrZQF4OJN0uZKrvpEmfyr9qzPWKmhSSqVxKlsat/kDI01bpgQLdxnnyXtkeKcjZDeVW0yKR4NFaMn1m4QzBVoKpDBUfojNVGtEC1Uayqh3JcoFY4eFA9gKp1RZDYmO9hyKtctIAEVkOnCfAVa1WuLdu7rSVE1mId2dRVZ1SHIMauqzQIoiFVDlg2l+fyWJJ16mpNHr4Jl08IxjtL9pr6wK8OtbppSPSk0UstAjvkhDVUUAhbUhggNhiG0VJUpGd2Euj5xfiFVaBTFKkcS5L3rMltTZENWL5v39TbiI2HlzM1lOfX8lY8rgJPyAszVNNuC66upzBbe1a+8rfK2D68C+Lx7yQqWPJVtmyZguM1eXwMgdd5cfObucx41SSplyC/11vffpG8onHtX6F/p64BD4OJW+fxrC5Ypn92ExKMClDbOFfY0m2x/9k3np/inu7rrQTM6xAXh+tZPMxyO+OvVjIoXtOgwQSM8EJJ8ZKy4Wb4FGzE3Q+co9j4O69p1J6NGPgzCEI6ALV0iDEW78gjqBKjkXNbEQYP3RSXm99KDpTzei494h3vrtwRn8Dh5UrxVR+NmQovNmtANfB6JBlT56UFLVkgAyFSnoaSKgtnIsVQ0RaLZhAHoGIJ7EToamSEszjG9tafpGwxl+sIc7Nbn1DNIg9IdimwmWTl2nuuLZZz6OV3Sfhfw5gpXzwhiQtcdG0B+LI5NkxYpBQZYLcCZ1+lOlTtixkCxD1o1xUr67KvNyRRrE22iPHVRkDN2Mnoa91lJ1Jm+SuIgX41mAXcJfMZUUT/JCyY71rYnGdxZrhDB97jq68RLppnjlqIMbRiqc3majU9MabB2M88eVUE0rYodsZtjBm/GOY7UanGvmogDRtuQX2iQLUcn1ub1rRAypNKYGElDpjeKFqWkkTaay3K04BlOKHoo36jLJkNPYjdF5+I55lOUQsoPVXxFUQlc0njhR7VjNoHSTIhXd6yYypCMoXVIE07yIz91jNH2WofPd/H2u/f+wq//S3/0h9+anEw//ODTx4+Pbr9xWxACYiWIjTW18+jNL3b/6J/ZV3BikxPjqyz6TJk1x4pTgImmglUmS1JqGM9bta7/ReYwHhR8Fh4+vHv9aqL56/TfvJL0s/H9r+e58hvEGsbmUe6vvGrur34Waq+keZm8QS0dqvbZigVDnBCVV2BjdQqTetV+eHRqlpj1d7jPtTmeLU77veHJUe+Tn86+/OW0eMQHrWGj5XPPEMAOpJPBmsaIJHVOmSVEw3476ym261zbu8aYe/DkjFCsWqeD7DLFO0BSUsHZGSecG+itxyP2fXfWtv+sQBp+vN3NZt5t237KHrO2WjezxmTkXO8bdE6nm7PlSXuzI6xiNTfynZ2d2uJVB+kMkLljaFJth9n5tx69OD+3lxXLGginEAyNFbStmQtUcNggvWT6sNeaOOKqOz4/OR4d7Dx77uTg8WpmNH1sV9Gz2WNA+UnmMyK5Pjs7afd2B7tdy3RFs9kOyLCI7az4uUmKmCR0pUrNwktxWcR2ksSElOG3oXQshzLq5rNrFcvxTNMQJuZi5tt6Gcmctc6zOatA38x4LizniaCUkdHoeQHCxRuXnv7LVgdd2vq8fLa90W6hTTF5UvkRkYpmSVgz9T/o7rxx/V6mjme3cjRsMVbau0mdn4FcglhPvfODoMRiNwUqimnw/vfe/+ijjzvru9lunxRXofSHoU0QiQQZ+VB6LLYMApj1YCzaD0f75zQhUme5VHvz4x/+4Hf/6e/stt6eTM7G7+zV6aQmXrBdlF7UTqwi+OgJardloGM05km7/zBMLrWLngie+pwsyYBrMPIgaHfWszt4q9V5Fta2iCu103ANDeWHoPtCO/uhSeRc9uDsEAHdG2zxJZeWiSyKg0NNTbMJj50hzPpmU7nbHbNYa71DdnC2/KXTTmS/jkqHZTLUblSJol5nnbT5Lo7xrsUAMLELuwUsItiyb2S0Ln8dTczCTcXDRhCJDEUm0/ellnGaJcRPJSBWmJNfVh9SpytArNLGoV7UN8ZzU5RTU/QIZXOj5ptxjjG2iDlPFJgrxQWTNFkok6KTOyRtKCWxZ2aAC1C9bNDILVAXeVNQfgRImkkuBIVeUkmanqRy5EfTzJUwHYe0byB7u/skj8JjKTOcFaWtEg01Ut8tFjr/8EBmwhVRPtE7WeDXf1rD9Yzzt8wTOcskQjImjjSnomZUqQhJQ/d4FPF7YR4cwXVVvQBJstSp6NIyx+JRc5JSMSHShupV8dAsNWMuFdGKpnmU4mMmxMZJvVypY7EsDslgIIlqCA1ROYJ1gBjMDvM7xVf/KHdH3B1TKvwQAgkOkJ1GxR4NtkFx+xeC5VYh5bN3HjNlFYXmkVf5lxpX/Xw2V+oeGM1bJWcWorBoUqpHrKOLvFW/5KwsDYjmMw+q/CSt6+J7+/OlHX7lRUA3Vz1cvOmrbQ6zisyjlwm26VLOldv6SWjMAzyspnn5LrVIC71+XWTP85fQtlS4TNw0RJMA1UpqgtxF8Zc3nqWcXMXJze0//3NLrWQ3rVXbTCacOjzsMELjDTtu2OID80drxg0MZjBIn8Mwcwg7pg4raSMYZKIoYhjOoyA4amisYTwlxZU4MorHS5+B4AUPSnbV4EHEhmHEQAkcicIE1KO+JeAjLLEn0utKFR4nC2xnvuqItVEt1Zr08VvoISKSAZoi+QTDhfHu+e2Plzu1iWFt5rRhuDJWUkF9MBJw0vAAC62P3hXpbrcfz/UuFDBhTpy9mja6OIsMhqMyhHQU9risxQ+wIieS+uTmT9Eq6CN0dG0GQxFKump+Tf6tbGMSf3teS28TEzjqXRA4Iiunuqtyfqttr7fXP8yM8Xqm9+/0dkxRpl9I9ThN0xFGlatCnA2pfsjl2Kp0O5S/HX4j0yGRbbkyTkh9WL2ex+FaraWaDirSUorEgolm7ovmaml42i2LsuPf5elXbsAaWADUWbGaEphA8+mycjRaaKEAMAAEy4f941N2vDGIXjSBT9oVTC/cAlhOLigB4F9qmJQ1eJEto9OwCL2MSJk/SDLGOesUoNJs1W9oOHyVvYDwhfgOaGp7rMJf2BvcunlbTLYKiBb+r/7L//Lv/i//nRu39xCwhgFhMEOnm3feOHrxlBI3spmcneFK5AK0Oxh3u6MIBZ1rIXd0AHLBP5VOa4QF4ZXP5iOfdeX99vbi99Wff9r7V2CltP+xV+FdqBGKIB3ui1wAyDjwifIVwRCKh/hG4PPWXqyQlQCU9c7iZPpwurg16o0xIQ5Py2oXsSkEJI3kf7QB30Av0Xd2vuwdXh/8+BN74S1bs5mNdgzpO+ujA0fGdcc3bh2cnU7K30ru2uN9UTqLwdCmmU6amDm2bm+ww9Cfrmfcq1rGunTMPspEQXfKMkxnTMLshWJAzTpxUK2dczqO2Gs27MVxox3RTMZ3PWN+C76JwmQ62VW4xt8bWOXBRiWpccmyEUaOGKMJyJcKseGH958c/8b/53cns2V3FHft3njz9a/8ojN1yDBZWc4Wa+ONVv98uhrfPLRcwEljYuWNqI1bgCHahDIqLVzrpmSD+GRhcp7FQ1wRbxkFoXO4DyWsGbbQeNrb2+E4iFJzXsLetckUvLnTGXMyWe1ylXaLsIQXNWVYwx0pe8kleVNPt+9ef1VobVMAQ6lBmHhnFNRfrc5u3niDPrON53K5Q0FGELfFNaVsywImuKgjRigrnBxKO+gLAHv+/PjI26MXR++8+97BYWyS9B+kNAVmZY6MqXrUA8ayEDF2tRH5weF+BlHzhACNBsPvffu7ZycnjiWE3niXNazZYmsnVyOQpUdAg46PVD5/IYxPTwrDpHXlRx6mq/HaX6ShnrqFW97LW/Xawgic0sZaMo+UK1lsTM6aClaNM19m65jJlMGFNCUb3CJQTY5MhvGpOFROGKdBaSRG09PnNo615DBj2/QPhRvkkEfXUFnljpyhlIFFPs0yJYBWWlIcuqYzyhBCUcmBrUGIVkPu9I6ZnHE6TWqrjKpFpm5Dt+CqVI7kRh1zZEkf0gZQ+Nh3USSUCtpVghbP67xtqLZNll/J4E2Qr7eVsm6DaWWv501b5IVy8rxuU0/ZddQceqldysknMBnvbAtKwcrXtW2bpHI1+AbRAhbRK3yTGkE1c/qt5iuUTEfKa2C0UbVWXMAHSuGZgCD9V+ocxRb9mfL9h0yQ0rHnl4dh6ZhQqWxKKJ4EK4UEaqiBFSTO1eTJpxdV+QDWiMEt3Y8XFE5l1celANmDU/gwb7CfH0rNs7ygjIO3sWVcV1LJE0MqKDTFNEAkDkFZ/6mW+6iglBQ4TUGhGQjJmXJdEqQJrj4vyFWO9/mRHGrTZCyeys+qUbImTVEvyeoKHpXxIks9rSIL1jbZZ7+q6Crz1XdNIXkmxeWl2RsVXLhdfZMkhUHQqyIDWQsGQH7XzSUgVfnsAKDBRdJxQZvIWpDq45J+W4zqYRPx1v+4qWjaJrQLXvW6Wr2pwJWzBS6QaIq7+llvmrilLZAwQfXsERhd0rD9ZsQ8rk2MFVXBkFRk/oUlE8+TJZw5CCn2unBsyTdtewI4f5PpDy5L2Bz3HZDjFY2/wfAAs0dCcSLHdrU1MRFfwofNIyhB+oTEKUqYRb8Qw5CmCe6GSiCVPa0CsRHxWHqDXAYwMSaZlfyUnf7K1vukIUyPCbmiY6TqrWHGhItu5MGN1cg04cDmrSUAsORnItxwyVtrEy1vhZXd/8mFTdm4yPmmE3ubFQBowYxO7dna3DWsC3v9LWdWbiVZiYDRM6ud6VN+dGVYc8AMKuPQluD2uFtvpsXUTv2cZq4AHdKx8+tEdcI/2xiGaGqLEgk61QUMxuNp7CT9I9oyVc3ASIO+fU4p1VZuOCjB0rqJe7L2Rs+Mn9qrN8Q+r1dHaLJ2CIimdt6h6Iy2YFkHqtqIXNAtj1TaOkIe6VRKbGvB0rw6uod6ieCqHmMaVtmPxAy1cQ7FmEULJ8v2tQwiMgsyb7aVC6vYyslDasdISgRz+vKoLRFHad90QFXRtIWaKhP+yIPCVl3eyqDG7JAwkQysu4gtBVgQcZYaSkQ/5ElO6wzfgtafmpvBRBZixBgq5Y8z4swowG5298bf/DNf+/YffvfB/fuzs/3/7uCf/Z1/91/OWyymW2F7dTrvffHtvb2v/f5v/VOnKBszyG18a8M0kSjHx8+wVVyP7B6dQi1TRi34xwkXYrlU6Fq+xeuHormtj9xsL7+vnh7QPP3sE8+lLKAXOeu7wIZHXnt1We5l6qvZr943YCJ07vKXYpKg0W31I10s8msgRumBd7zpeJ6N270x3HEEwOnmvNXf3b97cuqE3ZyehQyDwU5c2q3jNF16QPZuxtKZ5mFFtLqT1dnjk5nI/xUDd7w/a61GXcGs7aMzY4Fl62zPljrn5+P58sFiMThLpM9+b+dJr3fIauTDFWBvX/gzXv3eTqfHD64s52m1+xm5M7Lp2N4cH9rAR+ps6sW7z2BS0f7AEbGDgRgeCwwy9m33dkZWGNs4aLHTbd866O5ues+enc/HjqTtXrt5Q5jT8WnczDkHYMXe5RtYDQ86L06P+6PDkxNvOmeTs3fOel9595ZYlNn5jJ45nh4tHY7QGVvBdPbE1KK9sAQWZvI0TWa6jLFRx2da1ErUrapB9EjEYrZJQFo1Ade63bUFrHdfpMeWE4MmAsTEokVQnfHIgHY0Hlq2tOd4rDO6yOQDjJp1RAYagVpdUrJWCzcfEfM/8UriLXPRe8Ui4nM0/4D8vfvul/7Nv/1vDoaLicgwsy31+iXE4sySdbyZf97HPiAv1XXEpdLa/PCHPzg5Pbb011Ly7vh5t38z9XegiU4oar/BmLelVEhqTllz5vR3D3a++HNfpJfKpw7w+uTkucnObvfR7tgRYV9az661ho9hkbLp5QylcF46iOJGfVpuY3lfpPGtYfJXwoBT3fhZ1mTVQqvZI58SQIWk8bsImM/ABT/EJi8gO1pLV8J4TCfWJIyHQNXsgcCPACmJGrstKDbm+2a0tKhjOW4LGoszRJXO8fmqvbQgSVBiq7Xbap11WuOW3edMwGa+ayd7ymW9r73b7fnmRF8+Hdp5oIfwpY9M+dXZp2qpVXoWKKjJamqtC9/2Q2Tprt7D3/awT+3CHtGHFTuKofzLwI9K195BmEpP/2TKQKuaU5/r1wP/6lXKOmTqfxpuXt7My5xNFNLneVDx6Q+ZQ+0UWs9LSNIaQcb/9G6l6FJCyveZKdnwtu5AtB5sgG1e+CpMklX3/ZxSqCcx5jOSTTel2NtyZOVbGizvVSwjc7/qCaMgRg6eHb9IxN3cHkQY4mlAp9eGfDHN8g0P2l3PG0HLsKTmnAMV8zaVUiCxrcoUAZ2aEnf+c12TDjtVFE2uTsUtHiJHJoFiVRSZnL0Vomehmu5JAuQIUVQxAwrYA5Lhs9f1NlNP0GK7V92LcCmZJwMgAcNshcBIWUX84JBJx6TMH4cc2QLf82qa7JrvLlHvDYUjIxKafa065mkuz0Ip2NWdQvLCX31vkwQCYPmqf2n5Kidpt5AC/DKTPaCk3DhjoR7nVTAzOLZ65GIlSe7qKigFprm7eN58p6giXv9+gKXofDbslgz+Lkop5sj7XFVghDdv07SvJ9syQd5cXq9g0NDXu2pory5IcJHqZdHaPeBTVCW+AJiU3jVYN2heZL5IUt/Nq+azeVH0Bq2UawDTAhbK8eJNywsQfWdGDNd5U8PauBzCf7RbQlfYcEJgdZ05+J3ZuhAgCJmqVPzivL9sRGYd/sUcGRWAVsqGKzra1GnSq/XpdEL5FOem/wgnJC3qpokDLVo9Di5Pw56Fquc8dOJ4BWpMZybiWWBO0rJwSsQ+w10yMhstnHCU5XrKuk0XSCzJOyc7gKUo6DrdZ45+nGf2vJszgNP1kIkVH5Jhx1LIeETF3KjC7DNuH1ChwJFJxq41eZ6zjTl3NqcnZwlDV280iQRywQgYABDdEjtuKrn6s0SdEzwEtEkFn+BEyAENYsIh288zeFJ35in4UTws6/SFkVauHH7H8+MzZWh3MFG44Q5GSRnT9YQybnpZ4Q2JrZqMrc0TBzGZzEUK5MwAswexLGIdc+B3WmfTqcWIs7GoXHYZP6qtFNP6xXVMsxZ3Iw6dnk+jZVCENz1tKgAp6iE+cBUyUOL1Nahagh/NJa1OjrXD+x8X1iJbL1mZKRvOYBOWIjLPn84kHJPhpCplW/YydGzpnpWc0cfZt9U/usgIDTKRGDKD1GF6dw3v5xMnUe2zzZAfxqJex2pqQOVXddoWqNC/prJj4b/xxt3B4CeJ4293vve97714/vWbt25hHC5mXC4fNPV3Ozu7p8dndl/Bjqu5GLDh2YvJ6ZFxlPqYoecBFVHAPqbMGwZ21yCUZxGxK1chnIfbx367a5K/mvJlpssELx/V3UX6i++Lh1cKf5njtYev5KlUDSa5xR1JXTkidp5oZr+j+kJ3XyiT8INnNrlf7+6yqHcd7Pdk09kxdsYKzg2bnD7e6ezsXjfHxe4PC/NXJoIdGZ0O2xsZ0D569PDoZDJpPWegn83tAhnLhXXbHj3fPT+bTB4dH/eOz++v1/vz1tnGGsfeUWu9Oxo471rQ/urZ0fR4fiogsW2JfHvczlH2/bE3lgwYmFMAG0A1/tR0nRGlobJR4b2bd+0S2rb/6FliZZ6cnpL6/fHYIL3fn43bo5s33h4eZDZCVNBgwIVPds5zQCbpINnYMPJz4523fn61/H0CEb/sqrs7tIb5uNu/y15gvVpvwJIygHDY9vHZ+cQGlyICaRIEjAswVzQERawPdh7YcHBtZ0+kOsUqFMpwk42frbNESQl2mZwdnTzPbGAxWmtj4z9jDKqB1jRL0RqNB7SSCY393dWz8/tpM8JBEKOZm2ZD2CutfuW2WviCCV/+aLRL03N7GnaAM/QG/ZHten75V77+Z//cL3zvj/9wzXMhbSTygocAD5NEFouVAtTbKIZALZzWm7Oz6U8++Ojk+PiJbZ0Ob9rUiUa0mxBViU/AS5b4UpAikEmZvsOCKdfe3u69N+82HZP08+nsj779HUyKLd986529g53qwlQYHuHYoJKC/eVq7guVYO2mSksX9PLyI9jXIx8NmPRHnjWA8zZ5kz3PUjv/Ylg0GQF0Q9eZ9TGG1vvZVHac6hgNq2P1cnJmTKHGySdsiRsMJ+sBJgniSdhhDlSbmZll4kdfLfQRMRoDmg88G70kcz4zyolTJVj6pgVpafquwQQ6FS9Yv3ST6TrDhFWJcEuwTeXcJ0uIZnkEcGbHrfqwQZO+gYtLwdojBqYBfQYGsTL172lxc6QpR3YAYBPCyVCUCMpuqzmiVNKTxERoPOtRMtsr+MsaGKFokgaCFLCLp6x6lVjziUwSlUzqklI+MIKf+1wKCLrpMVPPwE3tgFJ/E/WgVlkBm9vgHEBx5zVXyJH/IMWPh6QF1O8ArH46aEsgew0y0wU3zJOnsGnKLTpI2uCY2slfyFbZ9bvwC/VSg6oytJocYbH0kbFJLkyiFOPt1uhPUawc1g5iJFP+wzYO1aIEklSd0p0yGpgIhpthQlYT8WSP6YmlwUySpn1TKWO+BuvAC1INzmkW6Zs65Lbe5SvPUrO6q+f1u0lQz+tdZamMhV9lSdmypiGSJrhcgM6v6kkya1alSgDtLVZJnivlN3c+X95dPqqb5nmgvXJp+Es+rfIv317+atBBly3wK8XVbT5qFCjr6+MSqF76/gO5gNZHU87Fbb6b6CW1u6zQxdtKWz8249Sj2efnMlleX1Y79amf28wwaB61uRC82MxIxnB/v23vYT69sylDrCI4SiuQq2oB8kbmGDw9S3izRq51Mpnaqy8h3XEx8Fyx2cwNmzDssJ90EmQrAwk5Q6mUqinHrHcagtm4bk3mbOUGuhan5z4m01YppGFJVYQhfBTlkJPhySmtmRhrEt9nglJpBi4ELR2yHegUKnk0CAc7QU4wnuKhgq+bIUpkPkMaIhQt5cDc0EmXWyRpt0zamzhYTG7TbKLSCaBC6DRVs0QC8/nQhasuN3QGBzOrZgOIjWHeXW2kj/bIHD09SeeE3nEM65mUbqiixgPh8j3hwBR4gqEZpDorQ4uY3VG7JdPEgJGS3HyUeSxaebRDXzO7BROrhjfIk5+2NIwWUnjIXrJDiD9IdWejjs30up9ONtlqPJMYiTAyQpnpFlZtCyOdujr1e8iZmI2VYG8+IJiUltw4wICBATcdBfRVRiG0o9EUDAwZeOVFXleMfGuPhrRDZIf/dSZshobRrgYBllBQMhUjTL2k14BGrZhshH1ThzKnv7KYM7EjxhhaOorgYfxWRjphBp2d2kW1KU/LwVHaMFijAf0wMNPlrJ0OtGIDqk4masL7oRdfqvrXrj5mQls7e4Ov//LXvv2tb7Vb4tFXR8+fC6UY7Nh/Q38p9sM6F2A2B9cPTs+OdVF6VcEd1ofeuXfj3/nF/8WTF89/9P0f2Lj+hz96//xk+uzZc1s71uSZtsBZ1TH0jreyuJW/l9IIcRXJ71QkPL+9rt43jy5fXSTZfl8+b4BcTfy5cwiXCZoiruTa3paWvkDl5TP18TClwXlbdp5pLiw3W9qQ37h/d3E0evbgZDG/djT/9Ps/+OTDD344Xo3+3b/7d0YG2KNnabKMzNPFDLJs1kCuY+jQf0ZEh1jZepLpevH47MknTvZdd969NXrrzhcWk+Mn8+dO3+t07SKlYfazisZxsKvVXm9/d6d9lmk5jLLLv9da7WGE0eCAN1r7jhjs69356bFBNB+gOTNnq+4Md+7demtnuLKV56yfGHpH2E3n5wLzZsuzfmf38NbNf/Wv/eWHHz0cQajfPdg9WG4WT5/Pf+8P//hw//rh/q3Da6vx7vXxAT1ozRPza7k32pucT9qrnf3R7Qf3Hx2fnDsfbTI3HFmdrpbPTrLxJ72wtp4oXkiykLUQCY1rqBlvReeA31oEz8DZwsSK+yB6CtPGj9ieD7JPd36vFjei3IZnvc4ugzDDgQyou0TC++Fo0RuS3hrwRn8oTruVFtVgTTPW420zXn5d8lKe+CGpdJE69gNFaJ8QLwjAz335i7/+l/7Wvds3f/Eb77753t0nz+4/ffAkCpyVEY3UANpy0iX4glptn6RRVDTAd7/9nU8++sQq7b2dnRuH1/av7dIJeb+8ERS6zwiwRpVUL1DKLeuD6SWOmDffeivhKIS/HNukfne3+8Uvvfvko8cWLa2c3yKUSpcUdSxzeg9lshv9R8kYNdtqxlJ07wp5GgMuVocGCAF8RL9EE8e9lGex2z0vcy8VS748D57cNZrWjxjBvqCH4fV6joyDiunCWheXpS10ekJKoKffFJyGeAwbQ2jOGfSOTPX1G2atdBuzTD4y0HbLvt/DA+mUE265x02RMbNuKfPtZheam3RAaoEVVErbqxD+4fNJC2mpgDCJlPlVg8l0jWo0sFdePGUqkzrqJCrEN/OffCLVu8QFCBHyiv4qYU1YxmaxMuN9g0A6J0UqWKvZMIR5oKuz05qSlap+3jrbIz4xTu/q6bLjaWidRGXGSlpUVoWiZwidqkS1xtRuBnhNb6TiyJ56KQn8CFdawZ9BdKBiI1VJQ2a6NgojiKjcMzX1s+GOpslr+4IQjwoP94TK4QFitxweQYFx1hBHz88cSn16z4usKO+NsZnM4Abz4Ku+wSTfASpHUajVz0nAGkCesFDQ377LXfgCamF+A7xYDumgPdVqgR94qVvRFfFD9rgmU17eNTA8hXk0ja8kDxHoEXjooaKWgiC8kgVZwUHmqg3FYjY7TJB3aBb5MTsE123d6q4oEjQalAKpeVQwg0fSF6ZNOSksIGEcmVKjmIh5mj/PmzyAoIlU9TNgrF+9v80ceJInfa5Yy1eSNQ8bLPL8Itn2ua9qkqvPl2Y2wMncwuelfpkzd1LEAARmXj/rXmxFfmC6ZhooP167JNhi+VlkX0+aVirUqy1evi0+ufj5GqoN1JelXBT3SmlXf5Qmxh4hpD41QpP+Jo1CE8eChTDRyjKhTPQRodiC5bZNe8uHFUOP4qLwTzQHCQMi0NJMFxWouI2E5uh0o50aJr5oxTBB+EO93cS6rNbFHBmRR5arC9Df8nnkNDFXxvQlIZEsfKvUMDBUIzg6E+jy+sX8j8yBW/MAJDoO9mIuQ2Dy5SfrLhqWaRubIGZiJsoUHPMb56cgz4kXEpBmnmPRDhlD69YNAQgofk3gCiJRBH5S2alMblM+isZAdxcY/sMuzyWoN6EiXcMH6glLQWbyHCUUe6EnmiHrDCIrhUz02TZN8UQEsGHeEL46AyQCgC8pFaF6UCTmbxkWhVx0l47SX9Rj4juBDqnSbtWu8emzuxPvlYW/KRA9YsJQTGhdSkQForQ3tkVJdy0LQ8WhPorVyoDau8kKh9QdnNRTORlMqGdImoFCXiIsfRgShyKVptHnwUueWOBpqbBe6QVYBpqHgMEGJK9pDPVRYWFSeZiqoAwzJrokvY5s9gUZDN5++53f/6e/axDLyfpP/+nv3H3z7b7QNDvJi8FwIICdyBdzczXRUdQ/7bdpm0pZZfOTu/fe+sLXv/Y1E/Bf+tJXv/Pt7/zxt//o+YnILo1ipFAtUFRsdGkQDk2DS0PbInAEqLman7m/eLJ98f/brwb4ZRFuquDLB1XaS1wuCy88m+c+kxzJ1Qil54uzF9Ozo531we2vf/rok/d/71unZ+cmRQ4PRm9dv2lH9pDeWLAaXoWN1NNbGSU6XMaxbAeH8+fnR8entbim01r0b4yvLdaLp8dHJ+fHZc1kTsbMEvqbhjnYH0OGDTKwEsMk0fK4xDQqjIIxV79jmxi7BwjbY920ey/OzgSp44bw7YqjfX1jf7CZU9xZ8oON37zz9sPHD7NPaWdKoK9dGz19+jw+dQtUswKZF7735pv37Pt5886bt2+9PRy+kHg27z5/fPLFt75MwTx5/Hx0IIbnxfnE+bTzk9PJ+dISp8HpbPHiXKSecUg4O/o1+pSmSNfeNH0MVPOC/e7+ztCwBmKWCcWeiiIjlI0cZEwr8s6V+bCw1MSkR0QgTZGhf4wxnL0cLLJMp9Snl9EJ2ymDi6Z8rXGrNbdN2iS5TNBoYOV5EvEmTe+8895/+B/873/tz/+N7mCybj+xFStJtQ1SYdXIYBR3SB1lFOy2sHMXKcUyIPpxdnL24w9+cu4khdmMiB0cXLNsWhuaEaQ9+ZLBlBoYECjZqBcpDRdGo+Pz06/+/Ff3Dw7MGFiHblLm4w9++kd/9P39/d07b/bvvflW4gWjeZI5igAWQcpcsHlO0pxXQQKyUUPNv6Cat1rGg20tPKmaSJlK5b6oGp0TLgZVrmyUbF2vX4knE2YmkJaVpqoASsow90nfdy1VWVpSFW0bYy9IqF3xLpMWZaLBlDC1swLjTDeRyq/agrtipSZPEDF3rY0pUR2VZ5nOjQr3iI2YAWB0YXxw8ItBGwSwSwgCjeZB6dlUyWQTD9oibORNOq0Vaz9dTYYxzvUI+SBDWpUa7i2nCjTDi6kBN1BoWCFsGX3KRVfjGtQoRBpuV89MgKfM0DWIKdEjNyoV1ELOkF8xqY3fMI5KT8XzCXr68zLrM/ZLBxRtH4HxA86RrmCTNIUev4EsJS2qB2RJYc77k1pFU2oVpcWqZIOE4FPDCiG/+iBJvHTVXC80CHPNTQkITRVTIATBUr/qe8EGq+rpeYwn+KU2qaB34TuiFVQk8qZYIcW71CXfIY8fCKKMKM0QWKOrVsBJE5YOKxUlsQ9QF7wtAe1VFSrUixTJHt6uQrahmQU+oJArSJo1StvALCSVOAKbVitNkGehV4NY8hT60uUpMFVCfSsq2YNnXZIEWiVtBCd4hHpNMV6FhsGk0m+B1CMPkzUgq8QrPxvgRcB63/wOHoVLsnz2ahqmSdCUVqCLDxTxWoaU+tojD9SkQbF5Vag1CWP/5Xq5Brn5/fIzSDWn+fLffwa2l56Bn28fg4+Ts5lPuKhW5RJ31VyBd+V67efnFpC8GjmMFI2DrrWiDGvGijXXlVXlGisCkr403JpfkQSqjiaog5Z4hjIgHWuWjtD2mM7pqGLDB/XIkieFm9sMJvVpXvgsWZE72sn++qgZ/vMOrHLc6gNKhH3G/SABBMqnYhbijkjZ9uCh5wUwScUDsRioAzUp2RPa3hKeD35ndTv83XpeVaCS9bZLUR1VYng0qTKGoBIeNixqYrHhRXjCS/2jBaNbw6HUtGzZvsGSeQSIdaxyJdHhvbis4oSKcupsZncounbvUxrQz/RsfN00ZOJtJESeECaESqt7DaYXSdGYytw85fzOiQSlQCARYiJ4+pqiDPlB+ySAT0ltAALBoWN+IkVYX5aY/WTdiqIel8iHNkqTSyMoV8YosMi2f6D4FToXej41c3BmEPN+ZFBBCSGO1yJ9Ur7NqrUX1DBANstIpxfIW9u42iTKC1WpUrSUOSil88AbAKVFNsvbMR57j/wGPPUFPAjlu1JtK2LDWD+DZbR1XziBcGDaWnlht2odcYrBOgs6ovsVupjP/uKv/9qPf/TT4Wj3048/ffHiqHZfgWuXuSO/9ctDO/gZE9axtzb/EQY0PT1i4LUGM/A36/PW5uTG4e3d8bWjMxHwRmmZ7ElB4eNUNJjmd+Ge57maF819JW5ut8kvflz5fiX3ledu/4RXryZ8+etKkckdHBuMLmCtDpK4y8IDPs2sLmmAznFTF3TWxWrBeA9brSfHwx98eM6L8OyJpu8eHN7UGL3x4bJ9xOjiIcFGLBnUjx8hysT4uT3c6d1988btm3e+9YM/evC0IzhCMB+pn4nmwwrrdzIsbz8s/guT2/KSO38osiYrZ6z0sAgn0YDFqFEn2vVgZ2TlowA/Bv7CRKCBp8gvJxnHaLJplXvrfsXgkUjRfhRG9/ykRp3rzn5/5+bB4aDf2903+rMrVK9v71/RhGf9py/Obt678cc/+KHhxXA4UO/T2fm1aweOGbaf6M7uwWK5+8GPHu7v96dOM2gNqMKnU4OPrEBqZaIwcc/r9tOQcGPnDVe43jP07SzvtufXB/1HeDbzAkRFD79VAeFei5nDWni7e4J6tiRGfIMpUFQ7WjINitMn08ULk5SUTWnXkiQFrA69TgDV67xSiFy0uXI3y/20FayCxBE9xUCNMK7Xt27e/N/+7/6DP/urP7/cfGAbT1qCybuzu+9YvYUlyBZPpGu+uIJPU1qYH7kKH7fuSUfv00cP2PGxp9ZiigbZD0G01fnUzWb9vIvC5tOCRKpgE7b4pyLeK0MGg7Fsy5ZBvJ2gCOT6//af/z9OTo8Uf+v6LVHWsW3TIYSGWfWRLimKpEwzlAmzY63oJP8UUKwdRi9EvZU0Bedq6CHiJXOApdbkqQ7DuwgGbuz0zQXpLpZZMWWUlqCZrNqlqBipFKFk8lh/JnLFL8xsnUaYQ/MDS7/GaWJFs+ltooEjLM5aZclKqGflET8Vzk1TjrPPul2AWucJRuFwL9WaDjfuqXRTZLOkTB0TiR5/byJjSZ/p/VpPIkntawZUzEYRZQv60t4PNNxkvQJc+ZQ3NU9kjL13hYKaBYBzIFgQ0nIGnzgl404H4AhstQ2Xk3Js3rJrtGICvdOZZMWjPnltPyv+fdaCRTtDcXrt9b68G5sXWbqwFhCFUJbYTdcrCxjkyoIQRg84NqtwmHG7M9q04GBU7mBjPYkgMKxhysSeE7ZIMtd77gTltsNDNvut7llrJQDM/e6qdd5t7bd7FrzttHpPW9bC9Z6tnUzfe95Z3Wh1n/RaN7qdo85qr9M7FVvY6pxu1rvtniUWo+X6pA1C57TXGa0HgWkLDBsurTdU4u6qNzXYzkS6SMS+cFBr6cIN2W027Jaen2jGYAqHhQMoNq2urSIP+ZfHnITEspEZAKrPDICt6EjmXl/VDPTwvyuWVZRIeDQdcyAFfm6AKH4N5wKPhTNkCZAIZy43Df/nhi8WMDmS2oPMsW8GD4iq854jLqkAY0CPpgUpq4IgecpiruB4TzP84C4LH5pxx4ABKXMuRUfulJ+E0SquBo8gCow3lbKy1QNPSv8UohcJYJ4rGVwxwypv87MBlLd5mDrm8wKHbZpXvgpOJN9TWLHVhU36sX30StoqNe+uPsWoKSUFbe0KPxsAmYb7U10N7MsS6gbUKg85twV7fOVSmAfNs1cQeyXNlR+v3CZfQ6Y8junmqjh1pOdmjhmfFtNkRK2IEvaUJ4UiGCWm16W5MiZOW4jZiE5FFC8KZbnlUUqM0aAIZLwWDRfFXxWN5CpTzHPv8UoKTd0xVaWNNR8ey7NUOiApzoLNGqOhIAWEB7ULozVBSZPctF+62EzgpfuJrUyBxw8iT1WCIi4nSwIQipvlhIbXjay5QZxi3BQTbJsxd6pdSQIoXbj/vvIwIhhShc9TCpwvPyFAsWb/9HJpSRGoKc9t1TRopAkEVjVCkARAEtrmSvKiIiqlVKKqJwvxUp7Ctq0VskKocG4qnFaAYVFRtnSOBgIIEoWiLRvFktcpK42boYM7rRI6aB1VjskHg0JdIr1ytE+4ROdgqXKqRFlAWPtahCYjELHyoz/is/GVGqW6aZH62SgJ1cn/aumibpriouKpdUpxBaD7ApUGtcA8ag0i9vzOgua2kGjqrfa0CJNVPTI8Urx08lNKboaDnbu3x9/7zvv2vhBy/pu/+Rv/yt/465vlZLjDipUmvjlhGwYCFoRbsj2wAXtveD49FQ6VgTKdvt59962vjPsvjoQynxydnp0Ns5wUVkG8GCCIFrJBuLlSybpLBauJXk9xkfJP8V3l/YumbzDYopX2aAgaEud/g9NLYPldidPwGehRcZH40D7hBL3nk6c/efDhrf3W6fn53n7nS198d758+pOPfvDLL24fMo5nMwa4oAFTickco4yTfnl9//poPmgNrr996+z56U9ZlXEZxClo2Yrlswx4fBzqx9RBer1wFtcYdfNF6nQFpsEMT2tMMA0F2DoGCtaAGJfqOwX9D4wapLGgX1DFnFnWXVzfOWAtzWaLs5YAuJHok+OT2eHe4WiwGu3IlZ12BEion9U//Pe2Nnt6evLP/uhby+W5Jcf2L1rPzRV1fvrBJ48ePXbIWKd/vLMrZGg8fX5mRO3v2cmZ4bvxDC6isVhsxboRz2pz1IRz8CZYZSwuRb9HuCKaEXdvNYxNF6wl0CB0QHQEFdO2dZXQRDvER7Ty0MuoNtdBuyNK5Nhz2jSyGE32aoM2bVutWQ18+RZeTTOXmPHLRFcAotzNfDH/i7/+67/2l/6ivSaZFIvlHB4ZITsDkSslK44WdnGqjhnauVKXFJ3qhk9C0igtEy+nJ7M/+MPvfPTxJwbX16/feOfddxRjXjlh5N3E6akOVVpupqoDrcsUddiwUKTRaP9g/8//2p9nLqPVaDR69OjB3/9v/lvNdnjz2jtfeC+zsimUEUplCR6L89KjPM5WFFFYqhUSsdDSg7gQUO01u8+4LTRLWEsd+Pb5OAogCPU2uqlpx3QNkhoJdZzkZXCpK22s/1QZAypE1hARLFrQJEBrhGKlH/IOnJjVQNtvwQo0M0aSJYvpp2zzgHLQiv6ca9F52GC7/ajZ9Ex5EiUzQ/GjCVEnBYl8EptH16WL4hZLLwhP2GVgIA2ty3RTCPdUlq3pctzYesKuqunaNwsHSzDxs8mboCEtbawVJw5s/EcNjZm+hONH/2kMJ3LNaRvi1ECKH8l817Imc5nJdnsK94bo6VIAJNjpdEIqeFHZcW+F4AqEufoozUZGhoKGIBn3KDXsg5SKS6Po3XL8X0YWq6yrNRBJAAwEVE2/j3eJfTb+6gmra4lObVvjONysRHgKZrO0bWi/Q00tF0pUJ4UMlItYLUd0y+LefgJ926PMDEY7NppCQBsb4CYbQ+vIhzYPWw+ELxoZUhTAEN0y/dlEaXjUz4falz8yaiq/wjv5wl9IC1MVylPPVb4yND8rbRKlHXNVp5L+9gJwbv2okoDKT1Dz20eAFAuG9eppyimt4ibaAaNFxgOkQKZB8r8wSoMpEgR39Q07MuKvgPmOtEiiFsQ6hWZdaGDVVV8+lKWwMGssCrAaZFJIpCdk86ikDeBkkB3m3je4+Wwgbj89z4MkqbQXL5tKVE2q7OBy8e7i+zMPqi7bp8B9Xp7kvYJBk6R5cFHX/Mp987RocVFifTfPL26ruBxTc3ldRatJ6/MC4Kbx/W/BF/1fqdjVzA3EK8W9PFNtW1jANMxR5FHIenZ3Mz9vtT7EEVQUvTjfTHp8ZuL2jARGFReVJszMaloKo+qFuRPiUSOa3NXn1TXZS3RoFl/8R0pIN6Z3Mnp/i+owjxHZoY/03KSWeZ73GSlXc3rQtLp2pe88jq3JfYztZEnW4CBNWHTZu2/7QeqkOEYhZQPSE4pLGlKlvoSyMW3w54PgwiyANtWnP5IQj2UozbwIcEhSmjpsGBXzFTRlZoAUTz/6yJMuOMzbaMOACCdaXeoOcQjrmncKCoukgAB0cz6uTMCXSe55SlDLqrMRYwoX6mmRwS0jivbgUYQTwACP0ew85s7iWrt1Eq0eVQgDujdAldTUufRD8Aoa9iUAvNIHQlLEgDAbrFu1U2JVnzSihdigZa9bqy+kA7/9UIFFI6nAdxVRY5/BsxRHNniJ8Q8iYmcYlUCe7F/OAl/Pb/K8bbr3a4BGW1sgfFH34C6PP9UPWrBKASmB9tSZRSWk+iFY9mdA3CSoyQFMCKOiXrRTmsKVVZe6Ip19yyJQNkRjl8hknkqSWg7gPiUzGtP56VhrZChC6lf/pT/3D//RP3z+9OSf/f633/3CV95794s90SlxxXKTceylgsUaxMPxzWwdPdNgs5zZZbI/Wiyn07feffP7P/zjt96994Pv/nC93M1JaJ3zVGh5GDbsHqWiqtOgnqrWX/yymPvIr1xJ+qe8Prvbz58MIH2pgoqjmuKKfpGa/AyOWyzK9184VYoLsNVgMTWSXkeLjKZZNE539OHjj4/Pbm1mm71ru+vNeG/31tH5J5Np98bOwWrzTGhKr31Aptu9ZxqRHsDeA310r/X0xU/vP/3BYGdX4YkPrBghkzi7w5PesGOrodmMn9J6pOn5GffoYDA6SEjQurW/t9t5/lxUYDjA7qKZixPUY+YtUwGwYguIpljbSyonCs5tuWK5vlUqnM1dDAz53kCQ9bB/sL9L/WjK1dgxYqmVXUNTRbOaMU2yKHPW7k5Ojp91luNsBrBs7x/cYBuOxwfDUeI2xKZYM/L81Mri1tlsMWNCmd8rivqw6VHMgNYO5YbMIBYlI33pEjtP56uJAKWtxsHrEuF7YXmlJdXKhl3MjpjIjhbpDOMmzhYoZDARqGtbRNKG7dP15pTey5NIFfDRpDWTs23YYr6rDRtUvIsypLa6x1FtCZLk77RUI/vYyDLesXyrdXL09MYb1ymenH2erqJjGdZivjk7ur4/vtXbe4ZwBSxlpfDS2pHCqJFIawjX6T159OSTTz5R0GK2ODww9cHhSs9HyARMSZg1s1HItBUtFpvOACMrTW3zaZXJoXPDbgXbdvvFs2f/l//4Pz09nRjqDfv7hm6xsmPZxWGRbR8QM9YHWiXaJnT1Lk46LZx7Kgy2VErMSIiuHC/jH09NxiF5s+ZTgEjiODJEkKbEOZQp9ZR1HfzWuXfms0JV2BAC77nTFsAGJwSJQx2rogeDKSsAwiAaV6n0rgil0oyKxK8oIPTeoiazHwKAFJyt1cw8sV+z8G/5Vs4n6T3KaTNKzswn3souFHCtLaakoxkFLi4owa5VxEYIxl8ZD4Ng8GyMbSCLUDzl/awEMKeUdcZGclMSZBjesj7L/EC6v2WW+sQLriLH6+X+qnM8b+8t2y961uW3JtZndLun7fW1TesUNy7azr92CI+FNzMxlKKKuj27+s5sopVq8uVjozqOL/MM2cHWuG+6tLVRa79HZtfGsWeb9Y45gfbKfBfp0ONMHNbRbZ1vVrb2Ojufj1rrp+3V3k7fan5hfpOWuTc4r098qlROp+lOr/VMO3y42Zy1eserNkPlJAcpbM7nnbP16jSUdMQnmG66KX3VOVllhu3UHMVyczRvH446Jxae2KXbREevP8kmXZ3zxWo0WT+bz28tHT9iSKBPMHrRmjUpE3sCoapLS1+XX/lfnEPL5jf+wBxl1ISRQlfckFQYzzdhD/cnj6ZohCif7iUK7zJLcouHpc8gzlfav7Ff0pFKXE99QyYiLkWUAwMssBojS3q3hQBr8E5pn6SXUHJwMv6EjKFaTKwSiuhwTwgJFgUgnAt6YFYCX0or/A38IjAlkm4klMpUUvAOF1SwFvjx4hYUdfBiY8chdWXpbesb2CkjF5/JvRTX7Gw5fzP1GtwvDKrcqmal/Od9NHVvJD1pCfFbqPiZ+B3lVuUuMPgs3MIvjz87ALhAOvA/m/HVJ9uC6uEWuaboV5P9zF+XaDQpXvtZlQCvYYYADs9JhNSNk8Ynn1UxUTFxwzPVmD6wbda+xG8BBN5GKkpfy1FR4jd5G3S9sXCpy4vGwohKYPKx/gUL6Z7jdAjPxLwLTYwshduCk9KROJwbu6vC75IyxrR/JSF6CMxPpSWh7CSJkhXmUmKl3yBwiswSnXqp7EIgTBJ2ZicUOqlBxKwqggMiQRGgho3cFMuWTo6aTm4ZU6niz/QFRUY4b42qEgSlV91jyacNUkHAm64xwmOA1HHmVEqHK4C0Nr0qAdFJvx252ZaTsoJ/app6ZnxilFFR+7CpHi0/0x9DuPAL9WrLywAxnaCUIJ3HfHkZ72wE6ngRQ0FfqMcS9Jng04injxABWeSpXNW61cD1QLNUOWViZCZH7xWco89ifzHuskUoVWiJZBpDtVIf+STOd2ZA0phV2ViQoc+2wpRfYGU0lqFWcMYREBIHZnwUlIOeIQUUwzh+h2lMdjPIXfq2TDggKbrx25SeMVfrAjDzc8xHhEzz6hc7XUtRd3f2WrfsJLX8+//t3/8P/jf/4Wi0d3pyutezMwx7xdSzUCKbcLSd/xpLtL0Y7Ax0Y3Zx7dv9JX368C/9+l9+evTfXD98IiQkrR8eTJ1Us5AsTvDglasIfPnEy1cfXL7JzWfffi7IV/K8/gP41zBIkSn08nFu/DVPK39ThdzmOYPGVzxkaREPsEuJDc5tPTs/3u0Pn599+r3vr9555zZH+U8/+dHtw0N2CWJInR3Qu2PsEd+TZpKnxYa+OZt0T85eXLvxxv5ofxC7HfTN4cG10ah3bJugXl/TZNjAL9q1oQ87kW99sz/eORztL+zNxPjJ0dQJhxMTMcYDsOLB6+3uCOcZjg2I23rxzXpPVIJmXPdtEmQtE7Owy+1npx6m0Ho5yn5a7CQrVbhac7wAQ4yqmc2Xtui5dfMuThuM97iqYXV0Oj+fTM9Op3u7zq9Nizv0FxVsq2X/deEeFYiCeq5oji39cocvkKM8IKuZFcD7wpYoAEpECAZVaMpBEFrUR07l61rYO1PDnlgH0yCjTn9vl3s4ocmugh8NIL+VwaP+fnv9PN10CIDkKJMWc6WdU7SyX3mUp2FSslGIwYyflXVqkCZpzixb/vKf/9X/1b//d8e79oowJCC+fNilW0m2+DiRR/PFqHRHAyPFpZwwD0HTchDVZMTZFnI//N778/OZKSCDOdXXoaTWZM1BuKulICt0tkMrLaY9pmv7Hu7JqjkY5URYpcdjYSEQ7Xz3u9//e//V35vPZ9dv33zzrXuma9Qk6jRKghqJajCOSgOofwiR26HVJKERjIXli73JtEGZOOpuHx6J9HFURNpQh+Ezfw2Q0ARYXF86RIgZfmFsAUD/ceeT/DR7ptJjzEXrOvuC3nH8Ok0NkMrawCL7+6CJjR0y1NAthUj+eaZfTOt7ilEzbM6gvZmASENG0xcPNVStptVPwS/KUAHwKJPMqZ2pJdvZBnxc9oYxsQuN7rKzQwKUhvHBxVsTf46z86RpDXFTootColHgEda1IC86l88/wDjLV+vhRAi8Ef1mPRac52E2pA5VItzQ15GbR4sgcboZQZjgMIdjubMKI6eCzKAqJa77xG1RnCGcKXLsqOWCUloLxeIrc5tVelEbGQ/ZagMHSr8aLpoZyQx6w2JyYWaZIhHzQRYjmJEwtAydUnaG4rhIGvZKgCR16C+zirpJawsuWmxGg9ZwZisMcU6ZQTCgtM+hggRs2aBr7zjehgEHpdkoa+08Z9pEqVXLgkuWi1syrZQRZUiSd/DB8JIapWrOyFqaL0iHHYIp+YdXNADbQQfnvUN56hkuqSMyKFYL5/Xxion/i1G25Y0qK15L0xYahpARbzTUPikoZArkVFsf6E1xt+ku7Yf/9L2hlZgmjofildAmDB8KVotpCSA1c6ZhkEO2EDo7QQFQFY2F37KZH6FOJFK6xSSlvGI9+pmV8ckUqoNvMJHSMSIvAYYPkKKl2/SnzX01nFepSCQ6pIrY5MuVsi9/1rvm+dXP5vFFjoIAmrzEqoH0MuNFqrzO28uC6i7pLlJUCfnx2QFAk7nJf5GvedZ8Nsi9LFSE2708G3yaz4yoAreuV4FcPL3yfQmlslydZ7iSqKmLptT0ne59G/cl7s40pPBoQbId0XXt3vB53tKeVAChibrDSlSJtmE9as5ZZhcTqxc/KXGyQzM3GvWobUhoWsjVE8WLlcuJEm7L5KDUcm5pSq2YiYtYsdpyJVxYPVi6i3ss297oMRVIZol+mAQvhLeiaVnCUlrHmfFo9tsJYyV7n12mn4o2xOVBnR9aAKHis96JCa6HA4RnOhHFTgBIXZimerSk8qmaNbFhjRclkg2ObF5yx8vO8BEjBq7RprLBPSinMLztVzQw+ajuGQJlZGdIBY1UD03Np2rVuCnhX1LNN4aOw+eFrf0f8qqURcDZq7g7mrcmhCsSE1pop+iqO/qmVucRyuu0AEvfh479B+iTY4VtvQpA0wMmgtNkqxfUtn1RoikVR7msOg9yxnKxmT4DcEWQpRjMjpWhr3TH3H7ppLNPENLF6Y49NAbzKn51WzOK3diLa637NPiFApBF3EXXwsz4vNLGsPcS9Wm15kbrp8kaEcQZaJdOTjK0RLTygzLw6FpndyVSlT6JtoWMz0Cis/m6DGWiUR1o02eRcArmtE4fahleS1QueIlESyvohtMb67K/+Us//w//+986Ojtut88//eTTWzd/fmzPpQW93zmbHu/sDZ+L+lnynknPBLrVXr/V6vyUduR+ExU0m5zaA9XYQ3RyWBHepdTi+w/+iISaW2avu7TgS99/8+jik6mTJo+UXVw8/R45Lfi1y+xB6vXaU9x3LY9qbiEFXSa5CvMik7cXKQKo9F9awhXk6wbVmkK0SVgGp3mD1UJJbIbjEruuH5q2z/dWu+Ki73/6ZDUd/OZvvd/fHH7x3VvXr906OFhl+YSNYqPhcb8OzrIdFvDinbf2N/cHy9nz0cZGjg6O2LeFv/bZzJcHw/Zujl3DwXyWIruYhnNvdD3XRoM3dobGFpvWKGol5oCY4jgDSHtMtt7s3u2Dg3lrpzvqTO4JE89RdbPOrHPGw93qTbBkf3Frd7gZdYUI0GLXDvb3xJgQLQZ81oNr4oj/9PaNg6Pn91eT42enkxdnxx98eGJ9AOFPrRfT7qp3PhfWXA1dY4Yor/AAPPzhUb4ItFJxKsNdzKidkYHD4Ob+/t7Y0hlckwiYmLnRytGQMgsqXokGXzowhA6CZzYMdtR8+mBUKBHLrJkAD0p6MNsxNiBkoQEejzgoVNFKrO7N02pRH9smbTCUO2hFB8a3YwDf8EAkJq2/Xt+8ebfTn9twsyC37Pzr8YtnnMECsz9hOPZ7NwSwhGMKciQt/KHuVJmH0lM9g4f3P/3+d54uJte4k99+9yt7+8MgFzFWviVKHaeNGxVksEOMuGF7+/zvJFqsIwazsfOt3Ws2id3ZHX/68Yf/5X/1X8hnfuD2G286/yDbJETcFW1p7J2waP9ZCSAUGG5ahOZIIF+2tljZBorNGitKlmiDaIrqX0K9aL/gDGv4uQNo9Va0TffTapytmJgQorzi6lBsCKzHlB4AvUDTAcFDC1lGMBA+ZQwL5iLxa0YO1C3qaCOKTdNnaO15onGiXwfuQ7nodNa7wQkFHq214fuEkdTKWeTsnVb/gd/V6egh5ElTqwS7n30/6MyIUKd9FJE1joaxUhSZKutOp0hjcz7tb0ciqLYWuxvKvPc42LEixMW3jgcEcPBH6YE3d+vozXOs2W29GKwOOjv/bNMZxi+rH05oFbsVtmnCvkmqwfshX2+/iEpuWPHmAfT6+qIyJILPsxxg1nnez8kGR+VxKyYDJ7URiI85T4xANlansKg7T43PW70zbnvx+u3ltfiDg24Wy2za50zybvu4nbfi5bDpSawUNRX8k5PX1fhFmmzwIz25Xg3fb1rPAOgOP86+d9l0Ax09j4PBqYDd/ot0jovrm80ODWdwZvbNIGISdRj2yWbqgotYAjCOsGtnxntGpZ3VTR3TpvdEgxnWOupHMiSZ1vT0an49nSXxS85HJQ34IhwAg6xeMCYfPeZrGDr4A6MxvwyXnF/o0JFJ9joOg7CwsvBQXa6DEn6wcYJNlWk9k0cRRlMc6jKOGcW4gF7CPSL2rmIXt9LhicQyiERwLl1n+U6GXOFtBIn2qsS4BjnjmCj9Rh1BwLZuLAaL/hRfnGm724S1mdezv/ptiHcHD+yIa4gpXpfIZJld72EgrpxDVa4hXBFzUj/+CfwwGyRL/lIwJBsmtyOQIkoMy06OsgzySeDOn/v1ODfZe/NnXElaeZI3efK3PS/rc7NUMbJE8tynyepe4uZJoH12ANBku4B4AeTi90VeEFwv0xbEAIxaef367JPPT9EAff1dfhcxfWEEZSBuWCd7AnB5bnuqcIiKRREyavQzmFTSMl6jG+VO22BpCWJQtywgErSK+1NCciEQbkp/pkCaNHZeiCYthmxSeYGD8XkNPWNORC+VjR89WrZwmfZhMqwF18hAXgG27QsjVwqEcbpSOMd/x9YlhjXkoOSqI0qRuhdKGyRPskUAQ7pUN2Z0wACeLPixv6NP5YeLX6CjTAYGBhOehRjsY/YmgcrQyYtCKGmibesJc4lyYZwyPKmksmaze1qoCXhW34JUgoRe6iOFfd9MmuatXk+yprIKqr4owo/YIUz83LqEDJxQqOjd0K66uvShYNB4gjsZDSx5DRH3ObfX2Bip3ZlMhAMJOGXqZJe9UL4YAllJuDLYInC38NE4ofSAfsyggm4NaOgbf7iNlg+dqxPLiqCKXU3r8K+qXk41ze53IWXDQyEsdojy5VbxmhGfllORkJn1pdAYM3wbfkd5h/o53lXdkRZZoinzPISPMFZ7ua2m8jANpg7F3uFKzVIMqXJpo4zfDCf6t27defu9d89/8H5v2P/dP/gd87/f+MY355OpCBFesV4Pqcw9WG/Ys/ltdo7CNeZ7kX2T9aC93i7G+dVf+eXf//3fnltop/wwebFDcWvhAIvQNGLQYBys8+TKrzx57WceuZLz1at58tnnV1J9Nokn4DeflbBKSzp/+Bl9pMjv5sqvKjvp8rxwz3BdwpjhCRiQII8zcEy/1p6fnp3Yb+f24RuHh7c+fXh/MJo+e/psvT7+uS9+JYwa4yxWG7WgK+4PD3/xy9/4whf2J8tnH/742ZPnD402qRHcGaeoMnBcBgBY0wBg1R33WB2TcxH968Px7jMb0mDonPDHtRhfvlO/SROM2MG7w11N6LCsYWe02xHBcNxbne9193EkT3N24Vs4BKx3atf+aQYf2e9Q7DUrOicGVhiIVm/3bh3evH1joICnx63vf/CT5fxk0O2dn76QhtzPbPypuxzHQ1q0q758S7hMWl00uefhBdYG7hv2Woc7TsGKTU8KIvZ1U71v1GPFW2cYsTvenE+nzhZmpZ7Pzha7Nst3ekmJUkQmzUbiBCnMT0sglFGlY/9ozLSO/34Fl+0VuWgarmlkVca5GofmUifGRzwsirf151d/7t7k/IUTdqPryGptaOqcDtpysZqyLU+Pjw8O9glU8FZA/qLnU18f7qLiDGY6v//733748FG0JgPUJiv0XLRTENab0C3BEfKsphIjmRMGE72SCCLnBvyNv/nX96/ZBGjfCSbf/ePvUwFvvf2uqKDoA44I9VCTqNZt9UDYUoACxKXxnLDC0S8Glkprd8xIrhVdHVPh7523cd1Gy5F1eEU1hcDYN8RMpxW9E9WSzsCdGkSbU5BSa9Ag45MJaIw04EKRk9aDBtPQiCdmJjtIN2rQM7TNdMoM0eCF89Ua8IzdUqArxJQg9A1aXiotdYVBGEFp+UipksWsNuXFd+yJn8E9oNMwoUnea+8AxH4kDDEVGPMwN3HbpvC8h4K+I6auctPbuzOToB8zLDFcFwQDGoMvzmzupQrtgZ71ssFcxfnVaysL8ZN2xsrOFEbhhIvBYPhhW4wwfvnmEv7UYABNeIfiabs46NAslMngJZH4WXgqeC99e0atITiipGFUQDUmIq0goYF0vsjNbyY76ofRQ1d1Y51I78Yb+aOe0n4G6WhjgS+HV4+AS+Y9CQ8wEw+Zvlhx1UEFi2gHOxPoyDKhxA0UOqUptHIw5yfQyAiVHssTw4WwtLIwIVrsQD5GRpjBoeHYETlk88CIRjSUmcrZsjZiqkaRKUedmADg6qrJfHZ/xkMpc6XF1SwzeHyMsAmnpMvT5LhAO+Znes8CH6LlV+gXRippJBEEBbBEbMWZyA8S7lDuJV7qXIA8zkNEsbMCV0SaxoNATWxCLIf09epkqCyAKhMSdHuJetfMe6wYaVJQ/hkasSDSTTR4B3iAwSX/6r8fdaUUBTf/kiBoqJbUQbMeVMLL+y2sfG2vYu/UHTv8zOtK+sD1f3sVzfLWX903bXDx+iJpvfWw8EjuutmmaoA3n82j7Vi2KSZC61LzC2hNoiufOV3PyyvrCupl6JI8Kcxd6lhszl2bmyzDj/gnjfO1rLLaFhKd017batoKSEHPuqtkTHtDpWtHMGtl4gZOFxQdEVetPpicaXr6nK0XCMDmIgMUYCkORflvQs26ocy1SkSIo8QAZg2k+STUh8cst4HII+gpGXyvcDcmdsMeiLcsS6BEtOSkIV25Zk9AWogVhrNvhk5aZxaZsjihqhC5oChVLgZc5E+8OIhsU2oZ53ZWd8O2gyfWkG4pE+dikiTKsSVOl6SzQW3Mb0OQBODCusjsE6bh/EYh62GickOH9CJxUZeTDyauBA2mKpRu5LJKSPmwS2pzxhY8loYiOZ6whndFRuaCiyqQrDhQ1+uzNldN9mpVRjqBSgFNdpElqc7EsvWcs3L0MZBjw3jDncMqD1FHg8F0MRuMHC2Z1sq8JIyjLPzOp30JIZzhgX4/n9HTlEMVFDeNm/5gj1YyTlIf4A3JwRgwE5E43YJGINEKvOjTNYIehW8qaic8QxeEL2L0NMMb2XgX0EjuQAys4tPQPw/zv+GwcEbdKgIWddpYqbq0zSjqV2isJjHSC5WTMVnCk4rPEJHH8atf+9IP3//2cnLrW7/38eL0/O71t3f2Mnfaap/nTImBcGfbRI7Pz0+WS+dvKJkEaReejUW7xy26fuvt21/44lvf+c4PgunyTojYPcJs2yYLMp9zBZfXrtUNGLev+vsv1wm8lrL5yRzJdWXG4ML337z/53+G/fw1ejYNy9ZKrpoxCNW3V4NsUocH/WfikLV0o2Ly2elO2utMl9n5/5tf/Mpw0xsMJrv7O2fn09/88R+u+6df+sovyuwsZX1MukfxyGHW09299qi1eno0vXu3a/OT+ayHIdaztTl39GWr6x8QnHBmFlCkgZ3ye5nRt+OPXVGoCyHM/RzWJ36AaYfTjNByJLEOx+hNVznYHR4c7sxmO29cu3vnkBvP9I5BhW1KNrt7MY/s2Nlq7WA7a7hj3jDX5Hf4F1btnO/tZbU9DSmI46N/8v3J7Hy+mAhpcBBEFh2wnrKV+2rKRI9Hs3r5cHS6tLqweejmni1g4GHNAKtQ529DdLonkkIU8Ftqip7SYy4kzuhnMNqla+ZLh68sOyKfRmOyg/2z6tSSRWEkCBXh3zjIjurI4icfsXMyFQBm4RA1FlnZXo3QwApehCqC3bI7inFW7ySKfHWNhWW/0f/D//H/9MX37ONOZGIhehXMErs1tAvQj378U4fvDmbr8+lyNN5B0VQxo44AJvQyuGTXkk9OHvzx93531ZrY7/i9d79849Ybzihk6qSe1AeTKmNyOSFUZcRKBoBWCcONhjv7m/W1gwOmxNnZ+XjPHjJGRzvf/DO/BGvJpInqcpsbv/yFiozXYtr4SICzWsNxcXlfSFZ5uStaqaFWmFVvQzfrFVhRWiSuyHbvfkgrLZCUU67KlEqifqy6+CoCK+Y/vPOeoIR8e0YTyZwFHIxgRzYbLVPaaYiYvnkVguneFJfY6IyCUqwqlAWsg+UGByzKFE31FUHGWelJgkiEV/6Ya771aoQyrabnjAMliQELZaNZNXXDJ+Rcnw2rtHGQpW6tQ4tCTiWq+SLkMnc3drSLgRsRFpLHalsOhQ617WQFZ9sBMQyMCsDP/JhniqaU34R2YwE7IDmzz4kgyOIZrTHsEkb1ofL16ObGzCFz+oRmSnF0PXtZV2ppgR3AyzJIrtiHm4m1CY48bnefGXBoudTQbGRyoQAT9kZ7tbvOZkF6yPl6kv2FeuO8BAJF0jh2CEzlsnyCvIZlFm/ALPtraFZkSlQX91Y/Jiw0e09Da3Zr3qoFCU3r24Qgyh6axhnmZMDqP2/sgeLeMDgBj8dUc8ubp0Eg1kIxu/MEkr3EK5NOuC9RUdTwE00XDpcxRUHRTKhJJMOJGOliEzC9a+MMDZezjcMB5kTRIY1JtLJXX6KfAUwPXgirW1BIK0XqorfSYVHoyW5Ipa15RArZWA4yFoOqfaQAi8JfxrAt2ygmPNuA9kEf0ALQqmuwREi114NHENUpon6A43IJwVm8EY2iuRhDdASrKU5AnUPIEkyLTOFCdakLwQI+f1VQag4Ti008EpDSJPNt5ZVk9TjpL64GuwKRR8pLmkqW38nTXBd3LzNXvS5eN0mLAEkZdHzGTL16XWau91d/NXmupG0gNAgFbHg8r+v5BTIN117J9TNug8sFLQLr4t5zBMil7eKwSL+D6jEgooPxW/SAzoPpLOwhx2HSO01DxyQUWTIakcY0DXUXuBE8uht1eiadeIngnVaRhFnqNFBMxjUniefs6MFIY4mqS6q0tvZ2ozfD4ZnPCgkwFA7zOLwZGpAzQNiiQxqBJuCiW3OF4VFisFhnvw5yEaQNLgf0SJAWwx2hLMmOeciUCLNXbSJdEMONWUKaMbn6LLParmMP8CROwcxfKCGadHLGRWV62krCWMa56IVCEDpgo1gozMVVpkPK0g59s3DxahuW0ABqF/3Eyc1CyWutQCqiMxQUadDf60jY3LFiCGRC4qRXFxgXMoSaB4LxETWpWg3XBViSMILIZKYdspwVffUzQR89KwFEQFbp8Gu2TFEvzURJGbIjI9HzL2YGtCLc6dtyD3a4JpouBr7qKdyNVirmSXLNoeegG1VuZA0WOrMNKZJSRFpSuyNCjHSVgBYVVgwQ5kC74nDfzW36oNQYYUK3cIILivn0FAISpB0LLXUPltqEDvUGbtLGlCklmwz5TzfJUD7WKPHNtf3rLJKPPzGOGj58cP83f/M3/+W/8ue0aFTaerO7uz/jJZ7bn3CXeZu52TiionkNFBWu5ce7O//qv/bXvvfdj+LmgBWVdqXE4F+IB+2qTXPzOZ9ppM95/PmPLlNeAS7lq79eyfrKq+0PRUqDpCHMBXavJHz11SVAaZJzi0Uwb59Pzxjcv/2t37l3/Y0bh5137ryJPpZJ/LVf/7OxXdJf+o+3UVd4DdFK8Bkv7N7o4OTFyfnRfDju7bB353ORPRkRakUChet0LYao9AmGFBttRXC7vyu8TISPbX7wseaWUnQujg6DUV2r/vhwOp/Z13+UDVZOxqPV7ng/YWQGdtF90Xy7uzc7R2eLtbMQDQCcXWDzHaXFT2HqWhpjvyweWvefPn7+5P7ELgSseOMBQxxBiTx2s9n5THBSZoeIVHXSuUMYvAt/ykOr+h8ZQi975tBvqkDKQ7+wM+IncamdLUXJFMUUhWD9hCmDnajoqJQo7+rI00uia3c2nU+OZqcv2NY20sF+pbFLV2wHh0CWJlUExJqWi66oNBRbuI71kZIjEVJQZ++888bxs2eLezd2dsZaLOzho0YCELWdP6Uuw9nJ6enx8/HOMK9zpbDUpKxkv4VUPHzw8Pe+851nz87Gw/Hh4TUSNJtM0vOgUSkiSoPFC42cfih7apC6x8XJH9t3IoSzCN79C7/+FybTyR/+wbdOZxNnd1y71izUpqSRGNbKVZdY4fndYJM7+jz9qQZwRXEpo7nSP0R9wYIZ53G0UWnLpNIdhsSpJrFPU6JtFIt4LOgHHL0UB3MLt2S6kr6NUsxYjjO8DCh+DSf4qo5IyWCm6HJS8EQJGYgSTPhHNUd6rSAnuyFeut50C/Sp8sMfqUQuYGBaWgbRlEdRVo0aPovWs2DDq6LjurYlDaPpRYGP6wmssJ6U7jW8TijfQa7pJnILsVAAcD5s2TNeyY5H6TXDEUyGSGaG5YW+0QChrSLAsxkcc58JCKYDV5SWibrYCxqWF4/7Pnun6sUJOJWtP4/5UeFY2e3UvdoH1cRfYoOyO9HWjfpDmvjKaUBCCxeCfuXyHsVm3FPVchk6AVLKPoRujJPUHkFCyaTKhWDwU3MzAMoWwZSWqpIzi40FlMI1YHWEXitbHOFWGl8fW/gwGLBu5D2sHEFIy6WvUSq0GqSJbNRA+LWIHGZVaFDxmYFR+q/kjSEcezutlClzfjgtSP0IQM1eaqmCLM1oIbkDNRXRVE3umDkVQRvOgRRAYUHl5Su8W0KRsTHDLT8DBa6SaKRiTmVHCIJKkUsJxfkx6GPR0ackJ0KH7qlpNGs0i1yKhSSqAVerHcAPiyRtahYaxf0AEKVAgiTLuNWvLcWS1H2QzxUMq/l9wj8vXQXo4kfzSBkSVG4vfOc22F1myu/tA++ii37G1eSvlzK8vHJfODSglfA5IUCXySUKoHy9AiUJmrKrbu4bcEG+6lDfTVmVLhAuobr5jO+/4MmeCMt4+ptCU26Karctww9X+5deKPadd4n2xjPr9bSYZIL8xo3J0hRdGcrKJfPULGEmyrgvpZkXDrOCQSbxnOfyR07zV2AjEvRktiMgrIn0YhrElGLfRtHGtUwpoGf0avrHtEmcEzHwROFzOdQqT5wUhYit6R3yUpEk/Mli2y1R6NRedUSdnyEDBLXLsh5WvlnCRhIjo+pbK4/4/9LvhOPwnjOAdWkgRX6gFJFAxxIw+45bjVBy0nJc1HzYGeqrGHylofSXmZ1spAtHW6io6kVywEnI2rlRptGJd4YCWV1nywK51I8hbvKCBklrJ9h1adcLEt5ZzbhLpVmNhoOpDVKyUQa4cmSa0GCLIgnPoBm5DktEsyScrrx+qVjR37wkqioHyXkDtA33kyZSUnbPhG5q4UHTH5P3DOTpMTulUEVpB8xA43mjryG+9LLZ/0QLUEmohETRBjKFaFJrURGu2kzrJHrCBg6ehRPyVVo96qX6M6PE2Ohp8OIm+ZOmuZjblg6aW0x3GxSjepIz1Q6f+Z2GzfCLIg9jUJH+8wyJalWAaUmfUfHwisoPQ0bDViAAIjDf+3/hL/3K7/3B+x999OPpi4PvfOfRn/nVxZt3by6nR455tpf1zrWBHnwgDHrzvNc70tfEH4RpwrOY1nqy+e0bt95888ZHH30qvj+9Rlgagi6Vqe+mQkED2hc/Xvv+k/39ryUOVGzz6nVlDcCrL1751SBUmDWooB5M63EM6cLaky3i8EXRg6TpHr/EPRX0L1NhSI2HBa85Ec1+4ra+2fR3d48Zyie/+o1fNmrvrndWyxdOc1rND6ILNvcZAJ3NAZ/4uue55nA+gL7c+o2s2DEKX9kLPDEGmGc+tDqgPZiRAGbTbGRmfsRjYJKK4AwosQR12OcQl/A7mmHktYMWpl+uTk/nLWEKu6O98c6uAweyw4pk6br4eBd9bsA3upM51IyHxYiLgzQUFt0t9mbd31n0x3vzSevjTz/6jd/8lrW2OyNrBmIsny0mWePmxDiRriy2dP54gh2Fj/fCnd0E5RQRVRj7mu+zVRodmB4ws55IHYVcFPWB8UNp7JEvLGqKEo9lrO4dQeXXraUCVCARTCyQc9wX0+MnT0+nluNOKoyIbDZgFaWYaOCUmdYNaiqeRvMs5bIw/Is4iZNmCEWaoN49okj/xt/4t81rVdGleKKLakzM2i3Bw+Tm3ByxPHPiMRuo6e6jdF0pq1DufPThh//Zf/5/PzeoG+7uDN98685XusNH1GCiiWghitlXfD7Rt5omUhzU8SGdbl8gk4WtyXT67MmTxWx59923/tnv/cF/9B/9n4fD8Vd//mvNeDIFhsIhXLRH7wU11dGSZUqklwroTHJSAFkZa545VYnxFjcYFMqYyeYRAs1jsqMRNCxBCenlAjyKK1ZNXXxdzF92esfOrDlPdyYGi1+GpogfoqlE4lOAp/87Ff0SAyfmsvAnupKqVMc0uvkwGGjp1D9uFK0f4mgsZaftwzBSxl8TPKrC6Un1ZCEeD0sUdIiQ7pkCN35ADO2rSTnRTWvtu6u1SakDXdhsLZp6AelVqKQD1gpp82h5RPCYxYZXHdTetYZH2vhZq49Ox6kK5tQgDEU8mRYnh9KHYtWZmtoxXm2FRbjXYGaGLicetM08z9AgNbbaW6y4isTEpBj0HKl31GzqqvKaK1xhnUh0e3oyZVlJPE78EF+ZZEFH+iROk83fa80O2sMfJlPWgxUV5WSPauwIU+qJPqwQefxSYmVPFfLQI0sNRJMTbVyhFRNJbyZuvDQL0d6NaaDN1FLO8JMmhcB95Em/GYDAuh6lNuHz9BnppLUV1imSWcWnHCbAdhmuNP4HWdwm+PRWbrrPc6ZgdKzC8Eki8cQbbTUDpCXvZt6mvbjtvj18GpGuvjFkSSMagrqQAhXdeJ3qFycwnR7k6eJ2KJBxeDQBafdc1TfrN2IqSJv4t/BLCajsqqYeHkJMAKbM0TxVhkS8J6jnoT8+SpnQPB1W7LFa+lz3aJ+mLHSCadoP7qGb964QKlfR5eJhktejfLU6VmE1T+rn1Y8mQ+pasBtQTjX2xF5DDZQ8bF7U76vZk6J5VU+DSpEwz+G5fRVc4U1+Xsn72o+AkqYBdIHvFeDeFcQmTW6btEnqPlxfqfOmAeTnRZJXyyo4ly9fTYM/oNtM/VQ6v/FxtMaW1KVjagxHojNyM/ZMM8bexHjGqGagzEEHG3wexRODMhN1xffFenLJA2+qVlyamftsQoZbFuf2dohEhI103Xiw9JqSMHzGIUqZYx0h1fQRA5sqi0DtHCB9vAdTwev2hnOkl5dszlbHbhUs9tpm33NDkawBiD+MCslcdlzpCrQJD2sQv9LCVqcMzMXj86z5EcjRXcyj2hijwntYpbJy+fsMriTeIIf4hZvjMvepGZyI6SuSEXd+w7XQjwyoS6gchajvSTt5buQzFDCwmDv4ho0BcNqVaIeYG64+PxfzeVv1QYem6Y6BVa39yeQcQZWt41QLRv7SiuYSpMiff5gDWTP4lqklzCCatd9W0GLCMoB3DbQzLspsBGyNNByl0+eFye57XFbcOvRXPApcbjAKJY069FVLK77wCKxKb0V9yU3Rq7dnG0M/qa1tC9ewf1OzhDsx1AZ8uQKS+rt4oTLjrjBYuhdVD5eE6tJ7rdJpKJTKXz6iBbOvIpIi/iUnh4fDfvUAgcOatKg2AkgPDHF/obu/hCaG572IrklXHxVcJSjVPrXj0e7bb7794U9+ZHZH9U/PX7Tat0x2MTsYd3I7FGZ2trx199p8ejbYrWFM2ji7nIZo7fa1g+tfeO/nfvrBR6geLd9gCqlLlBsJhfTVJ6/9bNL8//kzdHt5vfyVZvA86L2O1stEr2Cv3knqqgFYpEONEeDF9Hj25MmtG4dPH35y/XDnwx8/ErZz88bOLMN/Q/fiQIbBXNsYTQ3G7d71cffW7i2Myd+M5FiZhSuyx0Z7llsIwPGMIcL/v15N8JtdO8UfDM0ysRENjrN7v6OAsf/I8N8Y93xileryYLy7pHvWs35nJmpv2B8s1lOCRtlk6izuioPxnf7JKVu/tbPjFAEzcu35ZHl2ejTeuYaXnSH84nT1n/0X/9gBxjvjfWLG5T0VV0crQLIsE82c/+l0/UPIcK6PcB0CEfyYISQzk4Q4N/04nRJviIwhob9Ki/vzwz9wwIYMRssrALefyUJmMdnDJ4+z8eicIjRuinZOFnQKKtHLEqZFt4XkQT1pbtySgkY4fJYmtVHCwrZXveuH177w7rvDMcr3xer0R0OQIwlQJyFRZbZGWBowMRAWwqJm56PdrIqpIoJrNaG9H5ff+e4PXhw7JcKJToP+rpMSzuzIkKkTHUYsSXIfcpR2jULJrxLWiKg+NUWkEr/26792cP3aj374o//kP/1PHzx69O4772WlUC51hFUyMnm3Yt+QM9ULPcOXaFJqo3T1lt6VEzLxaqlTtR5tnCaSrarTFE65sl00ACDMHCvJZZKEEqTsdHC8xalx2hYSkYT4dD3UN/J165w6bduMliJOy6Rn2DZOuLDmAJCFLRVMs0ipaW7FpfnKtNKVQKlpMwySVOkC9JjRbGrvvcKifXKmb5oK/8b5ki6vWBFZcpVSizYP/4VV5KjyoATlMI2/oJ+rcSPq4gI4p3Ck5unZO4nao/6LRgDpDGyiDxKzUYtaloFVxNdBY0eXpRZyzvTJcFrZHwm4cKzZHwMAeZ2FJjFsYo5U8fmd+oOgu4GbTCAbptAiah5ffeQE3qqCdMEsGCidny2J1SgLISAjlZSZnNmmQrxCPU+SLbQISSxQSjurFwlJntQliU1xaB2L4sTdBjEZQdDHO8iNJyAGRpXeACIxygx7+0pJkga3EqA0foNzbuiS5IxkyUQWqrLSp+HSlWrpwlKqaje/Y9LLEEPKs6oVyG6Ili7KFQaI9RQ+CWfUX7BRjKd+JmzPi8RPB7dgEjSTMPpK7YyvNJdnTQmhEX7zHLqlo5YiP+AYnqg5PXACJsUEp62Ip0TVrZ4xJC55x6FpNcW6gWqGB2hKqQbhApMn2z9f26vwTKUL289LkWdSNUkuAOUJNL3x5PKzYCLXFnaT5+LHK99JUkCbtMUvl9kqZW97au/gk1R+C2qb2i+FbHF5NVugFuQgVkmayiNU8ytkqmZp0Exb5HoNSj27fGEE9rK0qykDtdiGcgilbXAXxdQ2vi/w4diwNe4CjF7NMFeAXgWsMumweQy8cIEAocm2puuFsBh2ZOZSMzSIfMSkLI52eqPZMrZne2WBpYNUKSksOucsyEx/3NIUvY0ZROsxuW3UR3kqAZrRA3g/gjWYjnv7JWhL++6Jv2DcS8IxG35d3OUk7w0e4vhM3+dA13ho9YnFY9mOyrhCrSgy21BgO2v3BQxAkegaoc9s5YxiUpC4ClHGpWqid1XbDAAwaBQ85cQcFjbjGa0Ut0PoK6kVxnFeCFbOMB2YmDFsxKVdIwcz3rIExJc0lZQoGmRKXzLEcuAIabO3sM49LZ7YO3MF9l2jbmyHqNuxS6G2SQ7oWHEh+FhT0E1awbiArZ0zkvQIrcVwHL8oL9v5xAQuzRtoGeA748ROEPJoq2AQBZPoeXUrIU/Lc6r0+zmdUvijXaPjvllzODCOWrM3ilseaacoDTQWo61/siAD8RAi9K5alYYSG53tBvANkYeQU1q1WmGcPpJPCPnSpyofSiriyi490bs1IoxjxRaCmSNqLPtmNQJwRmVwSA8bBkgjaB0eMbuVm3XBujRSZlGDUpggdcWZpV2ja6M5/XEQdzfvvffG+z84ePHsxe7+7v7eoRhLLjksafwkuHw5P22vztvrOzaKWSfWMPFgGAVUf0pg2DFGI+LaE4n5wMIT+WuI6itXcGwef+Znk6Aev/6R3lDG6Md/zvUvMIdwFQXoA1gfVwHn4asXO/S4QbDQLxipd1Lmr+wLTYwrJjOO6tZ81n7/p092u6u9/a8+fDH//o/Ovzbiyx87eqvduslM57DuDU46vQNc2WuN7Md/cLAzm29GnWurwckoR+Aa6Dt09BSbiXkjod2leB4HhOQssdvXW8eTI2G+rf55r3O46RpR32Bb6Ok58OwyuYhT/OzaaM9ybpLeXRmJjojfzni4m71mqAGGCAl+PtrrOGhgenraWd3aOTCOHdmsZdh78/S0/fDR/WfL59/61u+cTdY//+6XDTCenk0fnz1fsHvMceG6IgB+xldhpfR7+s4TRA0zhEXYNb2D3R1qjrjya2SVJAkJM8ZZi4j+xRQLKN7rR2kQ65GQNxoYvaOFFJQO3QWwX53O8enpo6ePh+P9rEYg3bEVFE+/RXlWs/iGYSOWwG1lxKu8QNWYlX4QBWis37hz6+u/8Asff/QTB3V9/Rtf/bkvfeH4+dOdu3f7DlRKZfJB4KVWIzuqLsxqZhGtvXRIYklZymskghTrTvqPnjz8rd/5rZyg1u196QvvvXHzul1Zg6BUpT6oMsjzVaTSs0Njj03nMfFnpiGKWkcdtDp7e/vf/KU/M5vOnLn3/g9+YCB3+41bxNzbwAIhLJi4GfNzdgwj0SEWE9AxWy0O4JjDglKwEbziEYrnqoK/qSdayQqUDAipKi5tO+LvrVrHndU1W3hmQ8uuOBaOEttC7q7WLzpLHGTvaTShlqzCmG6sCeksh53dbne6WI5XvSer1TX7yreWB+3uaa9tv3zn3tG0zqY1Hcufwld41F1fC6ts9vu9F/P1ntnF1fLAk8762qr9otO60Wofb5Z7mzZ2Olh3Trvr/ZZFGsu9bvek09rdDOyUv9frWDdjAUzmyjY282kbP1vGYPU7Hotlpk0SuNJ5ToGUki/E00q0SrPSQJUlxhFawdjYBvlyhc00eLLoByx+Y1KHFUO0dFjaJdtLZNIgnJHZBkcL2AKoWAWzxUx03/C5HXv0vsxwJTZo6FexcQz5nLmh8+pPTZGZd45sJBEJjWs/zZ+eK8VuOi8C1knkxlSWBtHR1LjnwVYSr4pffHSfbPrTqBaRRvEisQ4MUEONIKha6QuKsbOIMBVQ25JfH1nZFWg6ocQrq65uBWLccJLiB2eMqw080xXbpse0uuCl8FYjJyUHKUwlyWQqkf+K1i3lVo/a/MSQXgSO7xCLELMsxAKoS6f/WEc86A/39/ZsgBsc85Tm2pyfnYNm3o/FoX5yBv2sAQBGkdV5pv2QLlPSqAlVtSBuoVm1LVJHK2zuMFmakWTEIhZg/VrfiPKoIZM+uSoRpldZ+VkpzvE2Qge4HIGCE2SFYJinuUINbNcV+oA+aW6Dw+g9vh+3VfckTmcfSa7RfsbQIUYqm2avGxGGMI6T4jJXCBeS5XsLKZV3XUlUgPK0edMknL9VYCtfZdAq9Q3z164Gj2QPKV57mZ95Vi/z42IGQFVeXi9zbWvlpWdNkrrP7ctUflyUlodJWsQpSlSyJuvLEi7uLmH8rASVMDQEsLocLV0ikaVSOqc8D2+GazQPAS66pGQSlK2atvKj1dd6Z/WM5mjKJd/hEVmjHvRvIEuBHzKlmkP1wElDqxKeiTpUz8iZPL7jOQ2bxaDL27CwFyA29SMTMTcTNZ50wuH0PemPCF2cazo+7pN4lHXsHmXoAkEHFBVHlstJ6alRVVLyuBU8CtrBudFduC4UkKwIkRtpAFJTdQpV3AWZVCYCEqFIIsKUSa489ZwoqD5kK4UYSEkq8Ma3ApO9km65p90yqimlXHTIO5aCuQomMtpnfVV0AzD0OUg6urST6kTPVnkZzKmaAMHUWLQgE57cx5wOVWjVkhM9rnnZmNwQRpayZQsfXEH4AhToEL4oDmasJcId6KiF7vHuVGOm4Dgjq06Ro6by1dIhC2ACsOd0TjRvBk3hjXJoGb05WDRaw57ozk7SneSKoKWHMX2TGQm/1nHEJ5I1DEkhegIhw0k0LGdJZ2hXccO/+FcZQJlpTxsb9ySqrNgdY6TngC7YSBRChsVFjsT/ZzTZ+upXf+Hb3/nOuz/3c//4H/+Dv/7X/rqw5mgr06oL6O0vV73J5MgcNDBopFmr1cOdOiSNcuvWjd3dnRwG3OiBhmW8dkGmua7eVM6LF6BdSfby6c+++xnpXyvwZ+VvECm+lSScukXtc/KnpEvEC2D9QsomcaOuwvP4E6RMUHXakw8f3r95a/7+sx+9/8PvtFbj7z2ed9s37r7Z++rbXx93lmfn3f3rm2s7XfvvODDYDvonTtwS7L1ejPcGewbDp96OFvYZHFiwvmP/99msP1vPXvRPhGTduX6nN7ptGeKqfbJcvbF3vffitPfi2SMLhZfr8/a8P9i99qJ9Ojk/FgmwmE8OhrNh997NmzcdsZSJP7GOYoW6xsbXekLzzk+my97+wd3dw8HxufX1mx/+6MMPPnj6T37vvz+dj28c3P7iF7/sNIDucvrRk+difliMkf5qsTB5Wi+CX41YlAyFikrGyYykTDw19MKg8R1bAoOJikewH7JFkUZc3GJPqin0xKF5VKQNvPTs6Zxlz4oozlMKUV9NB7LCSzyVGwRK0n3Sb/WxRTZv02hAJVFprsKLPvh3/9f/3je/8YvPnz3+H/7BP/z613/RbjuUBq1KRgiOTBmClx6kjmbTc3JPQhkBTjKeTk73r1n2V9q16Vw23T/69nd+8P4PpzMhGgPBPCYTrJUwTQNUaEi5VV2N1sk1r0/E28VpAcHSpbEsIGBDw/He3Xv3dvb3vvyVr3z1a1/78fs/unbtmnk+4/1sV1HEM22Zvc+EkndN7pJc3mHbL5rejIuaMgthY1oOhmOuGdjXwNpW/eZltQcr2rDTZg+9s/X6YCoAc+FgcYYt+JxJu5vu2aazb8k4lTe2TVjajRoZZRpb8JhtbS3UcH5Wb7zo7Kzb+/SPlVA5ZdeRI0LPkoZoCGxrj+yY2JmOO7vcVba+TTB5/yD2Y+/AtPdmeZjIpNWehchKjOd9c6C37XX2BBkszGMJrF/aMdPi1DKZbPWQLWtFxQ2WZnQT+o4kBkLYKCxJJhOkUc4iKtWsWyhP5Gmu4oao67SFAWE6RMSPC1Yz+IWrsjksmEEkKybCO+n7arCt0VC1GUkaVUc3h+XCuhwrjf8F+9iSIf11ZnJF+8UINhijRe0MoxyGaYmTj6ABvt+RJ/wUPo16ClB9SZDiSjRCRLq+jMXkJRtJEqRzZbhSq3uZpCIRQUQiOb1K/dKFSmrW6EK40rWSrsw0CjcmVQ4gU/kA5tgWaB1SGHLgGuFAniZcmBcTjXkOLZ3udGcR17rKygjywQ67pEZpiLKttUzCA+phcJHAR/0M8f3I+LWMjf29g5tv3BiPdzBamgxylZOcWSvoEJvjk2OOy/Ozs5AvcudfxEgzqIDwJD2/gAGoIjknXjWilE0bwjd9cTxWkVz3QdENEOobsivUR2DCTQlpBX/ol7V9utfMfRlomrzxPmSNFgqHFI/IjWsyocWWYDYEHlQVmeShaXL5Re6VE17zWDe+RSWlBScpmmdwwkkpoSFovfZzewXm9kWT8+WPaoILeE3ygG7gN1rxIktl8rLeXySFWiVPC+RN/WpeXqQkndlJdJsydNpeDaB8bmvmzbp27zHaBsmmF95wPFxkTXwSQLUv6QWUBohfrxd+UcpLlCppFVfvNEaTrX5taVtgEVarULgcxARR4zU9UMlHNU4BRTvJiRy94pTAO/qgVvuRxk0ja1UCopde3PF43RFfFSjBf9tu8vEPvxPvjNNtHNfXfhxFDGQEEi9KaxFVs7yoeDbWqiVT/lE9eOcuWI4hNH7lQgPcVGBTbp5HGpX/FHel/wnbJih8s7qtQk63BUYppUxSpH9kI5v9JZZV59nMWYAfxxysMFhsbDokQxy/8Zx2kzhyZDycHiHrJVI9OtvzxFMG0VKaieaUXb2I+kiHU2XW+V8BlA1G4j4MRtVQ1Trt9ZvZNgFMo6yBM5hTG12h9YqpVCIj8X08XgTAEznr0K2qEflMYwQgQkARVrGDN3faS36CKecaZgryMeJp4rfjG+o+DorokIFf4lhUIaRMw+nIbq7bo874uS4rI9u8jBW/sdN/BgiRw6RL22XsFe8R2i1v5bc0FWmDylnuzCUblZdtv7AaVUkVhSMErtpZ2e757Sd5G7s6uRE9zVRFplKruyvLQlcfmZfQaq0pBuA/SOEy0IzSsDj3969hROpZ45TqxU7gBRa8Mr6s/bVqlwaPU/MQOQUii8I2X3jv3rOnzx88+OTo6en3v/fJr/y5r6yXM+5Py0Znp8/X60mbT67Vn87OK/ZAtZAjkpLw83bnK1/50t/+N/+1v/f3/r5wh16bN07twwflJEt75eLzc3WO/Kyi82v7bpuinrz28bm+/5+R/hJyKl/t81rC7c+mL6yply3JL3MqvUFum7T5aj63TQTpUHd74Y2E+UU0KHtUiT7fwWmPH/X/6//Xb+8Pja9mP3l4Mhyv/vBH098aPhu0Tqer8y6zvrfLsucDPNw9OLbN5apv7u1v/s9+9W/9nX/9x3/weyP7sA5+bnR9uH9jcbi/Y+Pa0+npbLocD9vD8ZOd3T3GtJZbzO5axTtd7H7yk+89/PRZ3zmkrcfvvLX38OMvPjv9qN93euz4+Mn57sHw5o3xan5ilwA24rL9XEdkaKcSN9+gfwzeaOOO4wgO9m/84//kR89mz+fL2yKLdgd7BuBPjh588vDhw9NnOavVpBclEUMgPJC2Xu2FbNnBCV3QIWaDF3rJwz2b1gxDF4Y6ZklwBiHAf4TQKpn8lIMw5qIHirbRPdnPmzlI3+JpJM/4nPRnJY4ZLsP4zHBFEu00YB83p50qI42nZaKBtX+jKtJYut1tc+UroKIKgr8AgM6f/ZVfeffNe7feODRP83f/7X/LkojzsyOzoqYCbatgvE01kJMguF47K8N4GzrsO8LGWJxNFqUPC0s2x2r1/PGz/+Q//r/G7O3c48Y4OFjYwycLPUVX0jYQCINCDxWyCYG6tPvPYyVEiWWU7i1lLyDTzMCgc1dspJOhNcS7735xcT6/ef2mkK3gP2Atp6L9GPAJ/cu4X2wZdEHqWLKVKEJKUbfB4LbFGhQSN7/S6Geq4IhZr3u8zwOTh3ZXc01mItUXi5E50Ox4lR0tl10Dw9PebNpZDQ8SfGZG1KqB68v2pNM9Xs9OR+YMLULr3qd9l4vBujeB76w9sbTcAKA7+H67e77ufHVhamtg86TTg76DnReOm+Mf6/Uf8uoKqmobfsy+uGifcl21Ohbj2RPreOmA6a5Te3mFjZI72Uy9fTzvTaaGH+0p6nYZDwJTTVjy/6/xwT6RtOOUVs8oKAZf+BSbxomaQyYw3TQzA9Gw9CNO0Hvbx52ZrE2zvi66U47oyHhn0s9Gp+mIwnuRfirW9nRQTaeTOTEdgFGPPAEZL8940/k4wcGtWyhPHwaBAoFR6H/Nw3Y0hLT4Arm9otSzd+fww/DmwgF8xCBaFCowbK8cSkaSTHHM24ZA6cfVK++jxFNuMgRPSApt6B2XHIXVwlgSkrKkjMTp10ooGO56ds/iIwujZ1UDuygMqONstbGZHQOxlJAnPieTRbpmHRcXo9YgBaTE4MBermaEIs16NiWBlcgeBRZLV6FVcFCI5tBhpbfjIddZ41x8nLSDvV3n+pnYs0Wf83wIRmQlFnKwBxhMs3AmWoX63uAymc32rfQT9YBE9gvTWQKjMRJTodM0VR4z3F15qFPTQFE4kLlyDBx5Ix8UY2Q6gdPEiWDHryFOI3onnBMKQr568zjDrIaP8UHCQMpAItiRMk0C3zBVuCsjBAZI2fVhkowuU5e+c6IQ+3bYz284hN+s+bpjhn3TYwVVWwXVhHloL6ny7Wq+StU1D5pPKKZuaUWTVW/lff/jiwR5Vfl8J1VddVPJtw8Wb+Umtrfckgdk5ar7Zb3t0cwB1Xwmfa2FQ99K6Xle1n3zILAqdZ5v3+Ru+zYAqoZXbwK2QdNn0aJJ3TzL27oK4sWP5vu1FJdAquzAxHdImyYlQvW0YYlwapqZ1ETWq7xwW5WBP/Tw3pbAYfKkxJt5Hvw1YnhanWSul2AkRRxg5J8iUqIHCkxHlRlJFJNSw8e/TQ5RQb+I2xtyhKvCoDLlI4IdhnJb/VzwS4cUHRXxBrokORhE36C0v8DPBKVE1SdgJyKngDKIAzUIJE8Aq0b6teZquDdgMrQJoUKNpKo7gtGwborytPL7VpNMLwRZWMmecXgWn0GvKSowKo98UoCmgFArWrKAEx+6xDBDqZGiIFwDi8JMucHBpa+Un4QHeFBAz6AYWNW47htRjFRmZ//UwBOvJSqqR1tX1m0tmCQhj2rSTj3dJGe9S2oaDw8ENzinvTwF14/ogWrbKjrQAtLrwjR8wqfFZtEJmKhBB8wnNzaIpuDKVLb/iknJIVqgBtXg5jsYF6INwxT8RJAzgxIYimtYOFDNTu5hpiyUDKA0bIEAER+Gn6ROgwdDs0W1hz3Vp4Svfe0b3/7edxn9P/zgj9/5ws3ReByPIiCdUba/MO/ftZ9F2AOThDrqXYvNDbfu3L13cPPwH/2D3z09nSk+DR9hkDsAUliDzPa2HjdPm0/PC6Wrz/5H3F+Cb/L+KUA2OX92hmqNl3V5iW6yhFtKUtOrI4tWRNji3PbZkmvDhrKtCV9Ud/6Vr7xxrfeFn3788WKz4JIfj/uT2cls0jkRZ9GzFZdR75PBzuLOe7fH/d5e/wu9/U5//5nmH1iPvRPnnAbs9GdZQJg1RMITrq2nJ+yEO+++9fz5uWUy79x7t9ubv3nrzp1b3em0v7e30zNp31/tH/C52ocxhoihRtfGgF0hLvFNPvj0/uY8+54N+m9+9OnjR58+eNFen5yd3bq5y1394umj89XRmWA4vn9GC7YiB6loQzUPkAABon/CZ4xyp+OwphOmnEWRej/RgNXpi1QU4IBVuUhjwRNvDI6VonyAjGBHm+kcC35KcUXWmiJAT7xf/2D/kP+Prq1xhRWr5xqiEPIBD8JVq5VyMFM1ESBbvgcxsMrDPnvrzt1//W//G1/40ntwcTrZdMKYS+VMqkUIU6MAhK3sMM46JXZz1mQw33KUB3XOApEgpbPJncR8bTnc3Ts7n/h34/r1e2/eXBnHTxcW7wIdswa09BsJ5It9EMRSpKbx1PrmNHSGB+3JfPnzX/vateuH8vy9//r/+Zu/+RvvvXlvZCXBejUcWp/KZmGwrUX+hMimkbjcjSpySAuEs7lM9keP8W+XcSPUiiRMqEksJtUj+axKddECsWKtSVmP+KoQa8dWeIndN5HbE7vIhGJUMkN2ey0LVzJhux4J52FM27F1hLfSmnvr9nzV3TElk0Mt1rOd1nqvtey3d+i4tfOw2wzz/rzV32fmwJ5oGI7x1sbSU2tWuNEpZ7MVDkgLm+Fs05vjPFXLumhTtqY9RufYgeLE/9lpDUfZnUY3MwZzRk2Tv3j10uToyRKNAYdVcEgMXKtnEccPPm9qsORapozm0obklyqO8qOQazNl2GHPyHqK9RbtjKtQL0VE35mXYHZmrAqCLTmOmXSZ6IIDWzxGR3Rp5r/4yDZTg1aiCpk8NVioAKR0AzEKVCvsEK1cRUYeUiQ3ljbC1bzKqhIrAufENoZE1Lx01f+Z+d84mVQL8c70daW1llCCSGJTQV2WFk/6kECXmq6nzGxebdiS1ngHIW4fJ4UpC6yEADGIrWtTlhKNjazUEz7G0HE4QILXCHczutZ5in6OgyzddGGHQdDNnD6EtbdK6r/Y8sRBgrA7GdxzxHjC5oo9tUUsHEiXjEAmICQNfbCuUYC9GXWEaan0gG4MBoiU3nF6fuIVacB1un8lwJoAbomUtkm5nqs8gBbyITm829lzharLoAQJ0qyZVMi63rSxpiS+wUrsMW9rOmeMlXFldJznVAc0/Sgb5f9L3H8G65aliZ3X8e66zHsz86YrX+qu7q5udcsigzSa0TDAjEYwAwOCCBABgftABAEf+QARBBAEfAEiCMwYjUYhBgQIjYTcCKlbaqmdWq025bpcVlVWunsz87rjDb//s8+5mWXaCCTY95733e/aaz3r8etZdruVhEU01QN8TOJYyiRi/yAmaioojF5JKUAfaVswwnDB1U/plbn8rvxyLenu59F35YLN5HyaqTJLWci7vcpfYulL7lKvng5a8zFlJ9OCZXlo7tVV4oBbYD5NXn767PQexd0RzGF61f3Vp10ErsEXez7AO1bIuLCs26tSy80kfP+PpWIw4wI9bz4m3huAuENK52vfqhFKLJhcNaNdS0XEr7u+y2ytaG2IniDa3C8TPeao+ZlkZmgnwK2W43AAMKNKC1o1aDSLMzy9eHKxqXWBolWJli1OJ5QT6WQriLEeUI36U+EXQmT9HTp0fqGnSOl2h1jdCKqpSavCUJ2lKRoU4TJ3lnGyonEYGQyDNsKUbIGDP4sfS0nxKZv04rkC2kJb6j6cHKaPfSoFz7xYOjzXWCYrQCl4RmUS1DwBp/JVZy1xcovbhpBqVxa5xNZEPt/V1qAXYjbfgCeTamXqoojK5ef4GYc84CO28YGZWu3b2XONs63dm7ww4e2f65Sh7Xu1cePImrpMqcwA+h4xtSXL83eirz0ApxtGWZLHm/CExnj57tY3HmzsaEfqXzW+z7me3WlSceO9sjUMUyWwijcQO34m3dl4Nw0zD4APG/fdRotALV/GJ2pniucpHgXKu64/ApfQcsJBvPrwC2SyG4dI0GRRI9Ohb4lBRnIOkI0RoHldaGEEvhRFCWuaSadPqkgyxYwrnXKQ54uDyBE90i0KF3Fwc1C0UY/z27e2H772oiMf/+7f+4U/+of/qMMerRA4W31yfPpkde2j9oQaUzGiqRIahDbwjFGB5x2jJ0+eCHAd890eAFe+tErGsibnb3JOv5z/RNcw7DcrcemrvieLgl3I/35XcxTs4P2n6JSdZJwN727mLvo9iSnXWLcd7DSTRAiXSad301zjAB1bPb/F0D1ksbf3rv3BT/7eO9fuf2nncGvnxq2bW9d3N9581xKva988PHjt/sr60ZNNJwWdbexef+bmTS+9+hbpnpwZU+3slIw+ndZS3fXBKGvEGwRd295zaMv13ZvrO+u3b924++C99zd3H5nDcjzpe+++5ZgAzQ9pMndvCy+2WXuxY3ZWzvaPTvb3Tx8b11vbOz7YevDw69987Wt3n9t48vBN77fWsN7bf/fhySODq94q1sgF+peudS0g9SoEWVl7KH38Z3xiuM/e3Luxa8M47RB7GBEUgvCcTFngya614NNFigxQ0dSQizvMzaL8P34+RqfsflD+/uKB8OncJqhre9e2HFQla5p+ToGDUMkERBYazY5PupjRqTEaD8bxGEtly9Zcb63t7d1+8fnnn7l+nY0Wl9jq6Cgk5wudthGIXwGRCfuM8VUGDyHunTWnI209IPTtXYPn07GvcYfe2ptvf/tbb7z5O37Hq5//tc+vbx1ev76/s/Xc9tbmxfaOp08e7KF849oDltmb1wZ+XGj7V1M6i7EXS62K/o9feOXa6vY7B0/sN1v/y3/pP9h/vM/xba1fd+CUZscm4Rqf4ujs0dwOoZicWd1wbpsFOM/nePg4dGutem+63gt1xfEG7BruabjUoXknnG0Ecjs0ysH2LhPRzcxbJ9kY5NnZgWZvlhoaNDVvsLa693k6OG/6MkJwtuUlKIXUhkYfdWybaNe9KmyDsKv9/MbZ6gNO4VRsamHsmrFn+x8MiOCbMRwviNjd0FnY/qYAf/aX6R88wnrvmzYs5CAyq2c21+9F7dqxjqwAWvLqxvvOGF3beoeT1ZydrXtvRMhenO7Qvpam13pQDoHoxOMtZSnEzWYblqIt4PDNkJfbvi8Ziy85TkUpkiOSV1a/VY/77I6GJDvU57nYY/4pRktpwdEwteQ1v2yQXjfnhGLIQItMEFFsiOQLc77ru6io5ovdlR2rBo7Pj28YtFldNV9iQduLXHPLjVqe0Iy9mRuaiCp/Og+165a01yhbU0DiwOtHhEvTwILU009cHF9f2XsNZy52vqr/dX5629Y2pwjM8oHsUeVxwRk4vdXxVumamOb/pytRTi3fdk2WCbamuA/0ea3Lqq/YFj1TFoINtIsFBC2WjGKfmYfULRbVfCM5M2pAgIZPC0gZ2tEcrgq+aHnc6ub9FK9qgX9p7fz6xeq7pKNfkFJHV4+XJi+0BThkR9hNxMWVcuE6U0ci6vVyaLD9WI417u1gNINYzHhEM5zyK1191yLXLwq+Z9VS2ETM1Gzj/NQaufpoVZOiyl/zSbshp39lQRfFAGRgnWcdcrM/HSGsCDF4eT4b5+AwnQdLiOzkQldiTDeS6LyqWdv91qoe1dDTZxWmnYWLfkE6MnoyTJPSr/kt3Q+fTzNImPsle9mWPN11zSqbZe/uGALM73+ocLcf+qPLZgYkZWkL+yLQpfc7Xdf58bSIX5fVlesSz7Jcpl5S4udSyYiw54Ev6SltQ/KHYF1CWFI+BHgKf9dHgK7yD5FZOY8IOjkL1XTz9M6YWYFmJpq2jH26s2/H0kXEyTj503IglxiLx0y0o39FeLyMYZTwHx3l+UZvGqBlcS2AsV1GGNcZbTlmNdH/ZeMqzasDkE82fgCV6B/VGQLUP4rkq6ixooZ++JJRCK4HdsqmHwiZllaVfAhzTWEnChw5aHd4MXAuLQD2hfHo4FWaO+sCZkEBJYDmx2MJ0tlWuCmBfRlMJiULR+GRhzmsCG+sUARbjDrehmeCjXG1MgMxFckfzKxv1vkEP389LrksY5BVEVJhzAiXyQDWrRY4F05UqBcLedqsKpm2RGEEiV+yYSrivMfNMFKYVyIFhEf9k2kP/JZc09v+KIJMfCzaUaKttZ2OTF0mEQ3vNy6JyGUji2x58AhmgRm9QkccyQ2QvqXTjckUNsmLbldkxTmyU+FlQtQMfyS6hlPxX10YQhghd5kfZ6wEOTk83N/c2ENQvAviFOPFEO8HV9WRdcl09MiYYE1LrRFSNLZ0gBacbH/0Y5/62tc+B/wv/9qvfOITH/3MD3789Ahj9zbW9o4OHxnQOTL1azEliHCEf7DxGVHOTbU9UqNoSYMnNQHREY/9W8id9H8qH/HqN7zCzIWm6v4nvSA83H9aDpwhdkm+lNJlHWWKvESd7iawBYDoAptK4Bg0q+K5iwdHb33utZ/71Asv7964sbmz9uJz1+/euPvsdXMtL39m5d1vP9n82Edu/cjHXtnas/5C81oQsG5NT0zMblTN9ps9giC51yqk+C0skXx6+vzdFzp9zga1PcKoQ7t745nrt2/ev//g4PBhLyQxZ61EjX1aS1gH+/uf/9Wv7ly7dv2Za+/fu/fFX/ny/UcPN9efefLovmGMB4+eHJ29z86N06msNj16C6QoeLeYkkJP31I6xEwvzPLYfGujWaoxzucJemIkjswyGDEBhQVAigfdUBo58Gu0S9IlK+WajCVHdz87MiHPlunax7+wXa6suqGQhJEZB2UpHfwA+qX779yzH/m9v+df/RN/4u7dZ59/zjBQtt+xpsdnT84OZDk+Pnn2zm1EAATI0F+o5fgwIKw62N3zsjXvRTFWGkxiIGqTKP/oF37mP/grf217Q/dp9Znnrr300ov7h/sGs4VC1m5sbt6U3TQCnRkRgMmdGMnPN4ZGrsM05PqrH/3oweH+K6+8emPv+r/zb/9b3rfw61/5miXR77339qNH969fd/AESONKVT2CyM9ANF2EEmZBSS10wpdHxkqwLJXENm0HfzAyaIWQd8MbXeZn2K8W66wNP51MU1cJ3xQueEWo8N0ofCESvedxG+lOA+xysWxfHyPwcFAst7d+YIurNoC4G5CmKQl7msncJln4qIn1KNQVGhwrnSyFkVVbmSJhlMi0yw1dXDxaHO/ZugBUn0Q+K6wMGAnia4cNXMO9cZBcZwdrAdigVb40vYlphbl4AJpa5NeG4NvouUWaE7qGkoLxRQnomwVBq0WhY0gJDH1qqp2qYunDpRLp4gmkAdDFFCo0TNCkdZQdgsidqm+2/C7GhQNtsa9bIsqECdLqpunsFh2YaKnhH+QLQmMkrPojn+ZsQ2TO7SkkaaBOjzn6orDmYa4QXVoh6q2Vix94ZCRNG1UAge0JZDqK0Md6jIG4l112YOl0hHabaWnXhdKF180Hy4dDYYQOX8pAGvB0jjHBopeQEkhMJPR6iGld8lPd2tGR0YiDacSdgVbxseHwz6j9HKNWgRpHlSSkUzIs1eEm67YJ0PSCI0alksNinpfWvLRNl6CWYiE7li57luNeJCC18a0hyAN1dDuoYDxGoTkLJAhk9DQf5XNw5akBrXFl0T47PFB/F6H4N6LDZ1RPjZlMVTVtGSEjppjYzVAa7WPvy9OF6sm2ZL4sshQMRowZFrm9zPIdeZacZetKNeZOniVlki9/+YqyCBqxXmUeEifpQzMAU7CPqlsAdDfXUoXpWtfsBLjshbxcwtNcV/dPWRFPh6ayXVEz908/FqQvsfsQBUuGEhZoOd6pqJB7682JhnOV0eZjugDMDxPYKGFtOBVD4YZPDi623uD5uAwAJuL3Xbnz9dcZmi4y/R63LtEBfXXHZTQFENxU7MS8cROziuTK6E0OFGfFxg6xqf3iKnbfyeRGnVgqtNKt8lAQh4U3VDOO1LhLil8PhlfgXyItDqxv3fOEUeliNmc6O18NHjT8s+oYU7vX5Jq6AbLKBU4zrAsVTl37t376EtpW178tsnCMD8fFyJm6gbO0XgPR43QCeu4a1Y4TvaMAyI7FXNmRb/XcyEEahb5pvA1EoEjAIqwwjgBjDbmWhw9lJMM/tTdk6uwCFnjIIecfNDOOrAEGuO23zRU4C5yYHOHTSNLWfSmWzmmnmBFEV9beXd95sm7A2kgYx1hN3q1ayKud5dq3mvi+p8mwpNCYIg8BPWM5zrPRtdgwo+kVPCe9bhln1zbePT1/smKQyyEJvRLaylqisrTCbChvcU/tOtRqP/ceRJvhOrnF6AiirbglSty1HTDvhxY44PD52bPOg7tYeW8aImJLcxDrGdVKE12bb1lkuXaEY+K5rRkjFH/XiHAc+hTkHdp+igE1pEDbUIKctIUc6FQnfAiIONo6tGEivoQ9vAgGA+10ONI6WvtrePjVV6+9894Xd7d2vvSFL3/2hz6tw3Jidbgpq01cUjOfTAQxlN7l2amBkS7Dbjw8gvXknMqhU3H+bB5q7eFoiJKypTGpwlwpzXL3z+zTyH328eG3C//mdV2dI5TjnOtSub3f4MMFsTXsfU5IYbQsq3OeWFxvOl2jI06tTdV9ekjbzxxnxQbP7rz15tmd3bfWtq49un/v+Z0XjrcOTh87s+xb1jB/4vbtP/A7f6hG9GhWPJ8dnVnw3KkYQPEhWD1NvOght5L/IN6JCmhy+9Feefk58RRF2Lu+W0DC6CzYWL12dHH84DUu5XDdzks0ZuM3AYRn01k1uidvfvHr99+5bzvSyu7Kw4v7FzuaYeu1D9rohok5scSVhY41txcFQnFiwY1vuC7Dxua+Jf5b69tMw8RT5pNvM7zaHMbiL+h5ekDvfQV3fG5tJxvHyxxEDjAGDuPjdhUJY3pJB9UtUKOPHNd0iZqonExyAdiWejcluag8GpFAEPN7baeN1Te//utf++aXv/w7PvUvUNrjI1trxHQsfU0noPj+2jUvZZhuVlP/OeyMh6A3nTdytvHG4clzFj4bT1ZEnbphHLF8H/vYDxwd/Ad7z/A81iF4IdPG3vXegiJktdFife0NDyyaIKeKCQsszmmUkQUTdGNChPLSK6/+vj/4u+7ceeGzP/rZe+++9z//X/4vyIzbuPXcTSh97atvvfLKs3efv+FlEY5J4YhqOKIW39ikd688W2QtIC9uzWVyAJy8eL7odvYRlVY0TYvIDuM1cPYAYB0a20PUyY8Ncts3IPgkmglPsPX82vnZQyUtAVJp4eF0FWyKXlm3YRQfHBCqFTgSJmdB5zsOEQBP1ZxVVF/sGRe/ON+7WDuI5HasqRZ/edDbiiimshxdQ9K8IrQNtYpTTUpYX0YirGCndexG9O0r7vCi3XMzkMRtI0F9tGvRUf0ZDh7D1GQGMemmrTjBr53BHKsNrHZgc+L8rt3KNItvw406J1DDnLW1a4SOe979gE9na/u2v6ajMKm99j/jLmZQUW/G9b2n7VxbeSnV3j7i1AO4dN0ZAppqlL3ReY9iaCxrXgWQLQqysfabqevJc1ITTs0HPEz+P+/1ICtrX0mgMZEEOowrdqbWrHpTpyHZbb1rrd+FbdlanJOP1yQahsN++tD+XTyBjPbCSvZX663FJJGON5oDY4ZB3qQFT1qjW1Vj0WyAp0aATPOCsb6y/WYuxtx7rxpI14s3+JSMGogJWfA8xJjngmLSuLyYh9Fupx0jLhRQo2/1Jqa3Tha3W+xACk50xMX+ggHslO/76p4/oZzkVMvqQECepq5JyLAaZEzmITPKcjhg+ASim1LchcVlJjotqrB8ADItjlB1tQdnctPLmj8yTANCaVQ2S7p0bvSoFpZAL0tRZk5C3MDRqKm+IY2EHQG7hY0aZv5gEFGqaqsXCukBf+lmGCVniF+SsZDT7w9dq09X/4fchx58+HZZ8T8plxDblwvsUmCp4/K+Hycv9TQZTZnqdxf5ru/XASh9eeor/pYg6RLm8uvpZ7C+A9nLopVwi0sFHB8klj6FLws+/fEU4tVNGRbRQqHm2R4mJ/C2Io/gmIXDWtgNLfdcXTLjuH5a/euQNRZnQmimkSaLRA9ZhLwNXJAV13BVtqdVnQGJamWYiPZibTsgFLJtWM2K0pecQj6GixBl5UI4EUlUv1101ut3mA6fh7+wMuyzmBh/lbest55HVxGsuRFFkdWwIGcPFALqYOibbKyIeS82TebXqCNNfN2YkxV9NWwGxcx+650rG+3eN4rUDec8zNLVJbyXu6iPk9pavXY9b4sF9vW2Wq6hyjPhvimM6dQLFtmTl4k2Hs/dOpLQq4F3zHur/dgLFp2jzOit2rzwlvRI3zRMNktJmznVusN2x/mgN/gmQXydmVjVOIUOyTSgugmYqr3RTQNlzVytV6bu7FzrkBATzIemdM8OL7gs4s6LGd3HLfHYxvHZoaUTDje0SrBXG4Ka7/Y6VQxy5rppXYsBts1GX7923cHNBKHvgMcsGAec7QFvS3/3nOyxtnVKQUxK144bf+KsyRGcrdnHhMk1ezXweTmLAGOb9rlAZtiUO6EyqRQI6eroa+pJtyzNLgokDVrTtqSqEYen1pwG8eZc+BJUmq84PT5ixrwNzavTIV6kCQ0GjQvX+akjYTQykJq9emMUSdfUUOTHP/6JN9955403vvGNb7/29376Z3/8x3/84okMyYl9mFMHMuvg5zMciDTGaN2nE0Q//QOfee2b3zo9qq8FwbHH6mAjWerYRHYx13f+ukr9p/F9WVWG+j3X90Nj8PyenJXONq8+3Yx9X6ZMU1GeTH9ERmL4we9LY7xkaKwRpwwiEISWwEDb/v2Ddw7O7j67t37y6MGjo/fOV165fnPXbMDx+dHx4YGlPo6f1z1rsThPxQbMBYz3gEYxUYZqmjG/kz+sidAqFGukWLYaiHBoiM2hZw40HAdlYcF1B7OsN8xM/wdlyiwUc8CMDgZ7efuteweO4TIicuIoleMnBzRh+9R2OqLVguKCaigBWtVI7BE+HjK3QxtdExTQeEGRQEuUINSqgIzaYQZIRftNoVOggXSlEx54FEmyR1rwg9kfC2Eu6l14PXAiOgSiYhZbCu+OAK5XDI68Qbq6QhqsgRC8k73d3X/uj/7RH/vsD330oy/vWsOj5IxGW/xjMMRbtPa2C22bqcixp+H8ZWyQVqWgaD10s6cRQBNz7vzOFUcvff0b3+TmWNlLL9199aVXIE+GXr/Ancx6CFhx/cDGXJC4auwYhNOdOuoXZz/wmU/t7V57+623vn597//6F/7v27s7r7766q9/4WuPHu1f291++63XH7z/rdNPn7z6sedCSb9lOA0dRgnIdBF91nx1RjENJZXorHYPhrVyStOQDCKaC4FprVhbJntpJl42XwofZ53W1RQRrW878mGfV8GFkM/vgcMxWmgmYVnwhYLENl5XlwCd/HPNURKu6dpo49ZM1Ey43XBbKpDkapT9YktF5JoUjRHXDfQMWhQ/X2zVNm920s10OQxeGJ8iLo1jTklNFJNqBhWJyZdb1nywQ4XoIAxhnfhSpXzxQlOcpPLxcFAwvt121/CDJL1L+wdBvtZuWD4xnMlzmKrG4S8sxw6Sp4EhR2sfoYV4FmvCTVw4YGEqjyVhxtC13Ebz5sAaCMaiNsJhlAbRK3TMxpgvsBl8q9eIN9QzZpVVZVwFvdMKrJx6AaAcHTwacdOooKCfOtBA4kC4QDpn3uUrMAXf9ENzSYekVorlQsut0STwGpenM9q7DhrnjdrCMT022ef/cG8Ii5PIu/xcjBKm1R7di5FWcbXJRz8CboTO1gkuBHtLBXABN98Y0jdFiYxQHOqnLJyPjntrojaoBncKR0td3zGSS3B9+c1XVfsgg5nBXJCqhsuqB7UCPMjQNMVydv0oBc9BKC6a8bgwhs5oU1Ry/b0pFYE1A1Myu0zrJoZMQdIMTzPRlNaj4RnwV1csqsYhF+rd/9O5Ft6ClWu4uiYxzobIJC5PVQqTRR6D5eXTsvxGHYAFZlAWLgfCYuJAT+kP9UImbfIvlS7yknr6aqnWJ8VxJ5E/vZ7ePr0J5gc/LjOWtpCTnJgr19IupfQd73X7672mRbG/4qcvZ1obxl+9VtNBzdG/Z7YrhaYPxDfugcssMs9tbk2ITp9UAULjL/xjK1JEvukHGE72EOU3TKadxkdaWZjYGFtCNQxumR7lHRpoz5hpvVuhaLNlAsYZgBeDdQaIbINZ1hh3YaFGQ/DOJK4vIIc347Fb2BpIbKmiMHTdG3+8dSsHaPSBJ6pX4jc/L6pMY6nqysbuPVRwY61+KRaHTEz0njGVK5iG42XjyJozeZ1BjgLHvXWkvRpnSKDhCJzRCGJ1Z/IYTzAS2UhUPlyT0jn6q4d1Wqw5bXJW4IJ0Aa8kS+S9M8VUgCP/OgKifa6FVyycV46y1ZanI2uWRF7wjec7ju7QwJwf6e8I1zVjDsMOd+1Dbg5vWiZoI5oDMNXVZEgHccIQreIhfQDBlJFsjfrGyna9i5WNowbtev/P6k7Hb3AV2ntHgqx7cxqRIjNxZrtFgSMMLghq6KidogyKTdOzsNgxFe+dHx+bIRjJ0koM7TwEupBnAonXmBAkdeBtLnolwTwY25GKKA7JMN2RyO1Ep0QzZkTfIIhHiFE8xlZ3XaTUXZLVbsA2yqKhrJqaeV9QcBjHwfsvv/jMa1//Oq3+hV/4lY99/Af3vU/W3hQljOo1iWJkxQEyWgiqTs8bARVH2rl197nbzrwhCVtczi7ea+hCK6kG/KKfZ8+OZ3zfb9fo+HI7n7+99/h+qMBveFuFLl/LiH4dHfVpEOf67oovk7/nK/4Omk+fLCnDsDgqvfbQkAg+zGuh9JRaFRqxDGDm/UwZ0dWsy3DpqQOANq/ffOGXPveWd/F99PkX9HPPjk4Mqzmt78zc9wmWiqgMemYDprKdi0UlxFgJio8gv95bt8zAVLt05sqNzUNf/SPoYjN6jehR5QMnOzrnhSWtXR/83PEdF0/2H7377v0jb+AwamZwzwDVxdm7++96xRa6qK9IbpiQdxyeEj7YB73eNfeGt9k93V7ffCBaMrRhKZhtrM0tGI+zDuN0s6jK6KYPilKUw0CGnpQewtrmMAWwNpFjaPm+8QJMEG1M/FHrmMOJNUN1upSpKMlhNjSrp1F4JolHD1l3/QU4LLmz1nzronz845/8fb/v9/7Yj/3I0dGB8IhXWRp0PGw5jlkxQxCsZv8ILTx14zIqirU8w0DGGbUH2FhOXpPX+eY3vv4X/+9/6fHDB7du3pLP+uYOJzGk4YWG/Jg6ZqwTHfXAXVwusJkS3zjXrGC8fuP69tbeRz72CWVV+v/8y3/5+Ozijdff8E63rbXrx09unB8dPD5491d/+QvP3P49N2+0CbIOTIsBTfdpaNRUsDuHjfEQUe4k3/Fgx3p8qRPnTyo5Wdh33LJd2oyZ2zOGShM0Fu28LawnnRFLE4unm6fXT9Z21xzVTz3Sfz51BmDO7R42z3NABrMwiOdt6spROSeN5ph8pjAWZDsbdAzy/Ia6Ol3elJP9AI6W0jr0afpUfqPimyfr3oyzdWpZW7vKCJOOcNqdq+aQoAcXGw96i8neztqd0/P7G+vPmZk5PPNeiErlS81+rT5ZXbm+svLIdg+RoZUxlp1488ZGi/h7X6QDu1ZWH5snWzl/uLZ6y1FFXl/gPRNehrC29tjmHP3ha+cvrqy/d3x00xtnN85ePLz4hg38m5vvnJ9+dEbBHSv3rY3jF89Wv312+sLBxbc2Tl892Xzz4vAVPeu1k+fsozk8uPXkzK6M28fnD89OnzELd35yA8PXTl88WH/j5OD26fqb6xevrm2/vXp617tDL45ur2y+t77y4vHa2w70O9+4d35y63ztfQa07xylkxv755YSvHC29f7pse2C76yfP7ex9f7G6a21DXtFbjqP6+TwubWtB6fHd85W7l+cPHN+cc9ryNc23988fW5t873Vi9srGw9sTzJPvnp6Z3X9XRO2K6vvn55cO9Mwnt0+vnh4dHLDXMfG6XXtztnKjdO1xxdn187x0xFn7XbYODt+9vjYW3p71UB9ubqYNS05JB9jc+k00xn1kaLtoIoTZmeWE1XV8WE+CpavvodpyUzt7Hx/a92uMzqk1DwM6jhepi+51P5dVlFT6CftnsE8Wkzr/dVPqmnjf/iugQE/v4rJB8pSrP7u0uSqhJuRmW3o3ioivzT5VEe/q3ToqX7Z9C85Cmss5RtTVp0NCcw8L75iK0KdcOMzzMrAwamRxLY7ipUwrdgmL5uvDQfw81sgNWIIZExECdWdprya4TQ49Ow3vBafEqq/ybVkGh5+v5yxv5rm2bJaR95+L7ljzEBffO5vUtEI7DuxVvKq+kugV9Au86llJDRPk9jU9R3FPlTjU1gLRsuTQfAqQQ5NirUj/IazrwWKxnst8VaPKJC7jVbeU0tkBMgwtzPHGsLnqqLXbl3jCNNChQM58Z/ytxosr+viT/0uFuS7qTE3Zpm/NoSzsTbGWWnpevMPxdtqSr58d3T6raCxfgqbKqRpTMPK9Ub3NDPSa2yE942/AjlRfPam80A75ozJGvIWhwzAgj2VQLSGa/QakoZNnDgubtPyDtLpN5UdrkcVYieUABkAGkwv4VvrKmxoutwGpcw+mMApq7MuYxOJEzFYkRzDWhd3dnDA75861wup2ZCwRqvrONDmUAVRbJSHLydfgjBmW0vZc4kqb8NuXI2p4abKrFKSfsjsCtRHau3+DBggzdSGQo57cMh6jZQGjVMAuaKzqMIgqXjX4n4YN7oO2YZcYmxo12BatHvoVWS9LblAqoaUHmx5byMSy683hyFK61LV9GLiSAWI3Jgr8WJ8E7UUZRTH2iCa0FQfbSAZ3Qo1pkAxB4KjCR40gFRiTGiYPi0coJMhBGJOUq4f5xwSHT8uEJXgQYWaDcD4hpmGe+mO8bxEnu+LkXJOFZLy0XgNzsqzz9z+yEc+8u79d4+OnvzcL/zMqy+9+HD/ye6794+PD6y6smIof43GQjHLodJ2CiBo+l0/8bu++vWvGPv8+mu/fu+ejjop4tCICru74tv/j67vWxWKvzP9O399GLXfIGvmgXafWLBI5Hxna+PW3h7FfOKt1V4TJdbBTosc0qZmhNomhRVrp4/PnvzdX/3V9+8f37x58M6T1y42P7F+zZmMtmAmFKes3lwxWk9g+syMq8UnTL8a/cNlEWUv0j7eu7bnAIwj0qIFHsXdLCaRgkSa0wwbRKSB69vXhLhQ8nqwDhJivTPmQPne+uZ7h/vMTrDWQLW3DL+/f3xwoulqFQ3BmsOj42lZqBSl5yCiS0Av8BUFpmF8gLUu+bTTUxNWXMtY7Uj/0oEYS3BOX/7T3KsoHP6mG1v4bmc5JHXXHSzO0sXS0LvYsBTniZeQwSKoLp4iZcquHIVI4zfsTmX4cluabPe5h+PsLkWUJSRuX1PKD6Z757k7/83/xn/1+eduP3nyyPbUOMtDzHiKG1bT6SVGrMss/EWnVLnYD8v12wA21wdunO/MkDi/5kVdGPf1r34NQtd2b9x+5pmPfuyjFhNBe3EXbvSHGKEWoRENQ0QAgVD1oynqYEnnZyYlbt95Ria7Qx4+eKCUyzuKr+3eefbWnfPTmwePuIOD++++511jN29e5x69Ix2UMX1Ahfp5ZzSBT2nMVlgDqRHwepQNg0x5bPqR5+E91M/f5SEaJUh5uEzHyAwLlhUtytCQTYvW11cfbudHNWQpgyUmZLKvw7BpdoAuGtACXvejF0odI33rpG7h0uOr4tOjBmOJ16CM3zNo3ygYFhAvH24VVoup1GEUwfp9Q8yjh6ZpkxX1g4X1ac6pvSeIOnmv/TVb7zYotrGP2UakZ5uSYSZ2d6AHafz9/FhP48Dhp17abjjH/Ib2a+Xi8cjmoXDMq+3rw25aC8pgn/itd4zLF0fvWzN7vvH20f7+poW1zj49v1eLsPrOxtHe6rmevLWZb9v3q3tgve3p+ntrx7bv3z+3VvfsLeeStkDUkMzmE43n8eoTyr5pCgW3z94yKbC6cc9k+PnFe6unzv16cGbgfvVdw/cX5/fW2OD2A2dVrFpwhcZVnQca+fjs1JT9o5X9axfn9vAb7HrUwlsdGHlO3jdat7HyaEfztfP4jHBWdTYw9306sH7+vvXHa8fvkfTK5kMqc77+nhmR9c338cyQzbmx840HBntMZbE3/fyMevNQ87S5eUAPHfNAaAjAYrjzG3wGxdbfrDX2yk5nnbMNbXkDjAXueaUJYmugZWSBeZWi76aFfDZCzlXKP/qI86zOuOBxjkCrV/zflZAAG9+b5rmv4WGdte+MLC9xeHhwZI4+V9kSi9KnA6BeaMis6lQ8SEpc+rKA10BDVWIzD1Opp2G/wI4cxRvR56H5UEHBzJNYPDIW7bMCLapcLmuW0as4y4+/l1QLo/SyjMxpELwg8diQGbeo/4Rzln7lDLLlAiq2CVkmxfM46nfbwaPhH6Nq+Yecq9qGhnm0RAVRNGRdPvgg3/e9m+yLBK6eq0gNET2icTfg8akcnnpUS+Cnz+VNwOZjv3WZu0zLo/KDNelL/gp8KFs/yjTXku+ybPkMO7+epMa5R/+S47LA0x8L5Aro3Fess4Yuwa4uq5c23+C66Qll2LaaQhhaeMip8FBMTjDUcHu4Ooc1Og1Ik4SEIkiRpWk4XHcRv3KpckojZNRcdRKcGjv6I2WqbQi4Izgsv5FVzEvFgARu/RtqWz15viAJeN6DvGkku9EG9gyVrKMU9FRTjUW+XI6WjiQFiPDsTSEA4ygBtYATMgrUphhxo3+zAq8ehYpEsXqTXprIFU9zoza2ox/f8E/znbghYd523wPVRSD+VLtRaENZ62zq8PhwAu7hRsYxej/EyA8UlHHj4BAofPCS1POdHesI17zZigvuNSg5B6MJ8NG6bQq0+WoGV++7t+UBebyze82LSpFuYJTjOTH2P+tdOXXreog6drb6FhrS0oEdo0yNWp0devHy0TR3lc89JSryhW2hzOrZyVGdIE2uOvUQ2KPnnWRz5G06hyfeXywyqhXlTjDz3NmFzYlLITWC6VOetZZPzKgVKy6U590mZt9wJua647lhqhLGRCy9estq2wIHytOAOejhDbn6GSoa54h7I+GEPPKXJX1e7kvLB8i7emFATtur5VgqusoXHgrUI7URosHUAjWXTwosm0Ex55Tjt1OY0lAhnU4NnfndP/6jf+/v/9SNG688fHL42uvf4vv3zeRrmS18Slk0a/AN81rkQQsqN6+v//E/9vsf6SD+9Xffu/cafWkBsQcQgUnj8VN/CE6hq98hdbX+vnuX55ErzrzV53c9lTLDiKjr6W9yBee3yvP9iy/Vf/DsEiOy8i/r9Mj0RxKgryJQQ0AWuglJROitQvXCbCps0z/TNPzfUMPmo5Ojr76hQT7b3nnu9ODWu+8d7G1aRHZ+wGIvLh4/ePLc3We9+hdQrx68WPMeD3TWGq2dvcxcja8fHRw8ev+hF3vvXbOlLIdDZjkHKM05VCvOyCLZhhVgQakpXDOIm5s3uDuHcuRdFDtde/fBvQfvvVn7RC35tzyLE3/uHR09brsInOWLz4ikjbRdg6RGqXYcMEj/jGVc3NjZ2duxKsFw2cmGVXP1qjNjWplvsUWHagr0YSiZ0reScf3atd2b14zRsqojTT016jga5rj6Luexev78wf7xu/ecAMOi2sqnF50LzCwy9RziWEF7O+3zgeGwAOm1W1Hoytjl6hd8avN1VJhNHCsgqF1OlZPmeF1oBLfznerEnR4+pvRGXDCh0aLYJFgB1n+jOK1s3NraunXrJijPv/rZlZPnz1fe9IbXvY2Pnu4/61BXHg2qLJRZiBOOj61MbD1l4UJTJ8WznKuuNPO1fE9jcf3ajTt3nt+7ZiPHyu27d37wh3/4H/+jX8psz246cOzGM4e7Dt06ur69s/3oweHXvvbtF+/eMV+DOGCJiZbEAeMOvYVQi0FG/N0uhaRIjSQWbQvdYnMLqLQf/ME0HYI0yueMgI3VbS/oXV97XONx3hJEQb1I5PTMoPie3R0JNpcSk7jyg9NrGxc75+uPkw8FbkZ1w0tuL852vdvFTELNjyleJ/h4912rJy3jxJu92Hhxg4CwIcVkrVZ71rzyj9sGNIoPUziufud0bd96WOplxscisyOD+gc3xfcbx7c75OZsj2vWi2nHbCHkgbOAvGRShD0KrMXX3xBHqXPv4MQ+0c05ds9bDY7WLyxVdUTEdaZy6uQuPtLbLTDz+Ka3XZ1f3NZpPXtyexq1O/BZP36R91w9MgB/vvLkOYq9smonAzV6Ofd98mLt18Fz+rSG21edw3NE1THsBnFvOPPnQh/7OSq9sfactnX15JW08Mx6er3p5wFYP3kBC9ZXno8bJ7dMva6sPNMs/mmxjXeHnJ8enJkLElKcPdNgwcl1zFtffYZCr5/eMM2xeuhYCMp8o6Zn5VYLdfZvUnmvli6KtP1ANas3mGjbJ2pPdiaq39bxbQmuGSIDXs6DMsSj3wNJOqbmjjMmZOuaSMk4acf/c3HqyonEIHDFE8jFdobZxeYyGt6k7YFauhrslijpZtSOT2SfZXevthOvVl1ZcdQXvma6Vd2nDNLdsSkgBS1ymo7gYA4e7dq4f7r6rt/AqskbqlXKZpUJL6AgEk8MxYMVfiqDbd/qAZ2hn97lx1e3vt2+OH2bCgDiGSLIivkHgrdjE4KtyDSat3rNmUteRsHU1OYfkOubOwYQvSCBcFXjjdh1UBsxaPjT0gDvfuEQbHeMml66s9WoZdODxlxItpUXzhXUVp9vvSvE44s0BRGBE6evhNrm64N5XCq1/wuToueDK6598Os77xbulvaduYJ2VSiw6V3AE2hyqMLh4sldXzPrOtVP1qeglpLSFlCXP5+mTuarj8HkEovLqifjJRZD4NBe0/MBck+BX+ZTxt3lj0vYSRjatNQfpybet1Ta4cz1HrWWxt159txQOSudnKma5mp999qu3t6+ZbrWbEQ7HuTPyqNdbIgvmfPfygxbytO5NgRXJ7Y+h1ix0ebMQLkTwZposThUv9gDEfia6c+GZdiENh+J2qegRUwT0GodC5sRcq40q2l0uUgrJfe7cFYIomWpgeoEaF+UX5vVRAdonTJEY+XUnp9o0Xny2kFP4S+rQZKsqx6ArioKuNTmtRbTgbg+PuCLmpaaV6gWdMbjuhbMxn1NCv038uBRPjjXOGt76tpaWMpXnFm2ojYOQaPeEkMdp+RU8wyaiho+h74icaB4E0a69vLDF3PYeyFKIgOPVVlIbVpcc7XUiDuW/PRvUYlkNOMNAlo0QlmYkpdUo6p4ioiZEXOGyKU0VQ+FkTxuhXbWKRuxGvPSqgrQkJiXqXhy52hj8YwfNBnE9xlYCVXBAOHWsSTTsNJ0ZVPTgMciZZPZgi5GoVtd/et+0Z8pEUaRnYwwIherSS7XqHAsoZ/JoibV01IKz2Dd8FhjHfgpSRHIQJMWIvmFF164c+ul9x4/2Nraefv+vUePH9994QWzSmeCW9vB1jfPjseFhUuXZR8Y4gWNzz37/JPXXv/kx3/w7TcP33jnzXgSNq4MZOF/aPyW15D5W+b6zTME4ymcp3U+vfnNC3/v0+QBnP9pWmBy/X7SnpRVZ9KrjM42vU7VAY7WGxjXR/+WcEVuqorxJMYOWffByVt3P7rx3qN3Hhmr2zje2tvb3Fl/4q2WJ6ePHz6x4E9OR4BaH2aFmfCN9iRfQ5mHx/oG+/siY42QuNnbnay7558Iuc4x1VTvIEaV0sE2uK6uv/Gt12Fpm4Fe3tGBscOT/cdrDx8KpRqjysaMuZ50GKhwqCYalTn6GBEg6pI5upjDaHTP25X53K2b1t0VureRdFwVc8qtwkbN5i2DluZzayw3d+KwIMDrdEjO6PJIbPzM+KLBlNFj3kVrmu2MD8I+4FGWkeRbGppbNYSmoayawTXfFfUq7jc+5k4UGYH5efPm3vWbLfFnNvw+QwMtP5lIsxU+CsFAPH70ZP/Jw+2da+ZjcIhMdNHN7FvSE+dF/9vbXMfW1rYo5Od/5ud/4effuH7t1tHpAy8Lu/XMDbGBCEf3QBSOhUus0IpBfsPbuToeWGCd6iRgfTlMbbpZJ+GALB34c//+vX//L/xfvvzlr9jdcVwP/EgH0wRFMzlwILjj469+9avC6zu3xZoGuDGE4+a78LO1eBFZ40A5D+OSI9FFH/k0szG2Yfll7wT6xePxmpXyUJb8na45ZlSjaAib4plhMPXHWxpAeszx0Q/YKFXzVzu2drZxpPHCwgQ57LMzlE90mlAroN0kFa6yARw7inOBYjQSrtrxqOSV4Oq60iR/BINLMo0YnTIEx+Jh57voT9RBzbnl/+gIYuMo0Y0mI5DNjBLAsJZo4s5aqlFNHyP4Whq1gzHq0pJJyqY97FurYyxQn9bI8jREqCUw6Uiu/xJm4QrtJnSMwI+/jYvaZ8g2xlh8Sst0cHRmqaFYsDn8/tVkpIGxE6QW/2eMHeWTuuIHEthU59p0/hJWz4Cd7koNNJLaBy2bJhzzczFaFe24+FftwchvgDZhQvZFNu3RYocjpxoOrnu4HQW1Hi62SJ98Q04y9HomBYYeEmwkW/bii0vzCz+F2mwto6zxonxwireiEUhg5mKkQxnMumKdD/n89aAfNUk1SrUdkzlrJGf3ZY1VtC+noa5jx/0ceU/eyVEzmdjZe+s8olWokl8mhfq3VADI/AMjYCpReY4tTepDo0/AYQ7rWsh4gMwEJGO+ZrCKpQrTOhXgNVZO316hBU6fAEe7ErWtKZsIpby66UrVZZLdagV5C3waxMO2ogvIA6lWukSLQqqfWF8FsI9LYXJF12h7qcoPj7q7vCbf5c/lfnkQoPl/lXNJ+M5ifoXaQhXEAu+qiL/LksubgMtayrBoAJfTNfJdao6TcX8pufl6t8evyvM9hUqrggSVovlcCl3WOb+WHBH89Jqd7P1ecPG1tZxgujt8OdAP2z+1VPB039ttWA1/Rl1SdZo7UKASuezqzCHDJjGRbOBuxvCrNVQzFrf0nYEIr4SS6Ur+PN1N1umf//PenuOj3lfeC2HBPX1ep3WzULxJzlRhbEWwXJxukF6xVt4nbzC3jj+yuu7Fut+GTyu8ebO8A/CaFqjEcZpF3WpZNSOO6QUAaUy/lliOFK1IMIXMJc8ptr2UPvUcYDiQdl2yMVahDWTEYhBVj9LiEpWlBY1Y45NLjljUbconU0j151FbVyf6Wz3/hIH/8wvtWSWi2MQR76CBlNGwXC8WwBSwpltV44KPdprBQ09hJsXKqnI4nNshfLxvyO3CqUcDbsQnG+C8s7nTSIOPDlreJJ6hZS4dGK/nddQPBcAknIPP2tkr/MXKxdumUXe2ds6MsuSc4ekDhtSETRaIhG/80cp42utCRQb8YPOhGNiYXjarQREq8PgmCrhuEBRy2ERxN6bEomnDFBnOlVJi/4lDnjgas4JaemgmEbfLo+bJ6crZ9sw3gTacb5hgIXbpJxoPS2yKWOs7Tr0JK+tE5YrLafqwaHTo8PjBH/qP/q7/8G/99LsP3n3y5JiRaH/efPu9T/7AyycPHs0gnSJWHRUpwi9kaNna2bXre6++etfI3Re/+LVvvfnNZSNotOUhw8f9ELIQ8/T2e24ieXJ+79j/kve3Ma6/OrMHF5cQuFTXb3s24OyZUL2qfbi/YF6rPwKaGxpFbVIwRn2+W3d2c8+gtCFOE04ZgzakGbB2irTIzUJRrPCKrt2f/tlv3d54/4c/9uPPv3Lv7funjw/uP3hve+ua9wO8sHXN0h1vW3r/1FbMsxtCTfLfsC3u5InF+ScnTxq2MBbaenv8J8hWzqycPWN2qT4gQbd6mFzvOGv8+MiE/sq79x/VgNBIHmHtraOz4/1HNxtIxcl614/OLnYOLw7e239so2RKPGKmrox/lE7zxbGQNaXPL2jaDHVf39ttKQ9rMs1kSEuGUKIMNb2KCnypnSQBdC1pR1IFcGIy47HTuuUm2WrvFD8/McC8J0zNKRq2KG8+8Mo1jxG0fL32WUhuKtJknfMRwsjD4XpmMr8KnmhSGupRPaMnj4++/rVvf+Yzn2C4+UasapAeApDVB/JuTsPgb8l8dnH02LuEDBg6AospGzzvhJ5rWmqDRzu7L+7ubPe+vPW1n/+5X/hzf/7/xBzo7M3rz7768kc2d56sbR5bPVKrnwPu2GJwYg3EtfXDymxwbcVbfnfWPqaijd37nLfXPHPmDx8++IWf+9n/7f/qf3Xt2o2tzV1Nx8bOgZUbR8drN246luDk8YOHZPrgyeP33z/8w3/0eUcbba44qsuug0Yn0KpSSPsHK+tGNouWNHs8ojqRLLbWShgN1T1tJGrzfMeXw0+OHfd+cctOH2+MJkKjWCaGvd/JoAodd4LayvmhWYWVU9pFmO9R6OOLa4ZYNoyai5023uYTzOwSnsy0ff30WQPfuJofrgolBP6keLOoaf0BZnR2Qg6a6DzUcPmlQyOMg5SI+1qDJRd7aOHteK1TK4+8pbiFQQrxtyRNRzgaoblEJcEx/2YM5lX3Fxuvs0lMsfieK/bS2KivYzbtWegsGpImpg6pjDQlj9ZOXnYunrDdfeYekaymdkEvSFatdEEE06hhTPdF2G5tXrD1r/C4/WSyzeibNg5ZNI8hVrsNba/WQm68U+yrVI218WNMfDmdWn/HgKVIpHErNtjpc0UZKmqjXQc3qZd5Dc8cvbXaIWD65o2x101Js8BCa63PRa+RWzt91ft8L9bfzi6SkUbEIUIMEBxDc6bIjGC83HzQxkPM1IzTW6gkPZ86cZWiSakVRicWnMvocMCJVy9mTztvlFAys6yLLh15nf8DiVoyBhGf+5isZc8WG2F0Tbc5U5lroTpwRA0Ys3Vs6JPHLf06ObufjyBR+l2zSpwCj1rRNNz/QdDz8PfTLpWpiy/Tig0OPj2kvaRqkwt5jaX4LRLSVUYJ6QwyKan+2HTsE+XSNaIXXRN1MPJpqiNRQwndU29nc+mZ08qUj5nW22w/nuBNPjjylhR5QTd0rNNMq1h1nlAhdUn3rrzXq+mScZO0cDHEFhQ9v7p6fnVN+X5cctXd5eMraMuzJXHJ5FPlDhzDmvg2l0T0Wk7GrtsErEBc/uCahOXnh0AvOT7AMWl/GJkpsHD5ErN+VGpJvAI1pS6r6951+evpfb+fktvtZCCLOnnWOpByrbGoiVkJgFyL6shawxQrx7tZHMkS6jYHoQ9YJ1PJGeMYnF+1MUV2OcZMlIKw/lbipv9Mx4y3CmsPaTAxp6w+/DD1Odv2W7TDwQ1nAaHSrLMt94lXmwckz0ObiuzKheee9X9+V7VuQX6v5Qf9G8dQALbYhkkpfofXUbcUdS+MW6BR5ipShzGLIZYOVsN4NSQooCosoKecd9Y57E83klAIIwwK8SbOcLpFiss7AQTEoLcQgH3igmYltxeIAFm4F0m1kZoGbsbSCiHToAnZcPPZEBWHKJgawqVohtmuq37CYvR8n3WYs05aSaiooqYlAcV6hErPOFm3pz3I8uDjM0NVimvnpqNl4ZIveaILgeIBbIUbWhr/GNTljUVyNOQZ5hwZYAuBKhS9FYkAXlWSe0R2NVkL6+o60rtaie7gEW5u+zEjpgGLFylPw0oFW4HKe05ivJfSoKLP5TWOqKmZlJNuxisrFuXmPPNz1l7aY73hzVNWIky7bNnpgwdPDo1YrL/2zS/99b/1l//la/+JO8/eoU5yaJHidkbChx03cSSpXsHenWdeuvvCS5/74peoVhRddhIi8ze/Qn3YgaoP7n/zMv+snn4HtgsykZqwaHhy7Rp8CYcitKRDFzrJ6hDkrWXO/DmYwojKcvMNtq+sPbp4+8tvX1w3MLG788md1d1db+Za+9IXPr96cf+jH/n49pY4Y+9jP2yhvHntMx2KrS19sAaitm9ee3Jqd6ThiFn5JxZpHG5G8S2lI4a1G5TKkDGzherMbaq9prJ5cSvW5PZy58LfXmLV4s3T88cnZ09OT7797pOvf+vdBhiQxJwpSGiPgnZLJ2kKrabwRfBe2WkkGl11aFHFuJC6WF86NsFAYRP+ePeNJdjmQxn2KbqYda4nOaervt03OVaTmN1JblJB7T1107+qSfOzYS5Kt/rEblPBqT7X8iStT06ZfJkHOKGMW+Kyrt/SxboRdYumpT/ZcsW63KiOd3WgQUe7Xg5PSEVPbsGUi2WGazdv3aL/1grqnn3lq1/DaB1lzscK/r29HSd+yuzwH68rhgae6FYIqeyVb11YXj8MGSMv4nWm7f9HPemtrn3y05949vaz1/auW/24bCXnsK/ffO7mM5ZqnOzs3rJ96Pre9dvP3Xn0y583GfHiC3d/7Ve/8GM/+rHt3WvsmgeoB5A0IoVu4oxV7zmkJKj9rjEZ/4bR+JBnVAhHaYW2EGLnq/sN92tE4knSndZAeTF3TiMXOiLDMCvTWlVvZ0k6gOP4nuLI0foZO4cmb+ohvhGUJ8hFPlTUQ1xPafwfUcB/RDwCkpdo85o8ZOaDmVtHzT6AjnvTheoliezOqCoS6rIqgHrEKM3feqrJiowuDjzmqK2baRek5TnLHW/mv+fyOsJVYGDBlNdOi63ls4ILY8MwUuNSM3QVSXPQpalHPhpDwYgvjdcp8RTAnHgNlVuyBgM0dLsJXrjhQ8yYbYdBy0hwu0eO8NCMihSBqBGupVMREQ4ZvmchcYDmbzig5Gg3jqBX7jjOlrFDXyYzG4EJZ/uVWRAT7viUPRI8n/TyBWuEXEk4waOpHMn+6vPAPWa2cchGpmqLTImXSCDQ7/5FPT5JlyMAZZo6YhW706SebdbKhGE0ySxn3FepvKL/Q+t8j+z/wabBBEOSQ1mN5/lWMKynILZOSsJZcFueT4YAS5YxclNGoAw0IG4kgF/DigiNjX1iU7KaKsoVOa7QG3yzc7kuAcxIgCoitimKcA2hss8Vz5V2LTgMoAWmJ40yBTaA1dIVwvMNRt9RfvVwUJinH/7wdHnwoZxTcjINkEuYfQ27fIbtJdwY/7TiaClXzYiPp9eIYIoH5LJkT6fuSy71yHvIPlSsHN9R4EPPLm+DNQXL6/rgvie/8QXHTuSY4j4YgAhYNzshpxyLDKb9yQbl0NLNYFUCSmTZmbOHu2wVov4TrmWfxMlPUp/dUc9ZNmlMlstKYKgci81swNBSEak6LGsUZ5k2f4MKeQdelpOPk8bDkrFuA6+RWWxsfvtik/fXezCNx+PUXcFjNcf7aU4S/SUqNMQoEGfzkuodWZ1lpMvlg28L2Xni5olnsCgmqqTqU8hC09gEYCMaCYvvzV/yrIMVh5gnGjcR8/xdEppFuCrjKlZQKISrbmPzjYbcGtTDSXG/G1C4nVanCtfhZphFI+gBHPAY3sUXufZReqFQZiZkbxDElO/K3j1+AkWVwa1UyqcSufsQc6v++Tdo1ThOtuolRTlFEhCq6EYzRbnCGNXMJic9/aRENE6h0GT40y+ZDAk2vhIpQUib1JgoAuoOOnCATAmFZGSPx3F5vINUIPvpJhxIwdfM/ISMtL56TtUunVAZ0VS3lApHpqEa5Fs/vtWhceDhiLIdOlpOYYdTtFsMO8sePPIMPzRpMjdSAqMmMYzWNUl1pPfz8osv29R7cXS9gebV06999fU/82/9uf/mf/2/fe2mg61msQcQLpZEpY1pxErjgPsvvnhHAUTy3R7bFZlM1h+GUBz5za5of/o8HJ/++Ce/uRq/r2SjPlP508/faHfBUs+Hy05KNjHmHU798z/1SUOZklYwIZsW3/Z2XXvF2Y53foydWlBefNpagGmqFT09e+bRkWNmnjv++nsPT5/7zEfv3Hvj/sbRje21G1/5lW9e215xlO3D92+9+omXbt21LNyZ9Lb86hbYa7nhkPEnDyzTOLw4vbG+8vj4sbnBhxZqezMuvLZ2H9x65s61jU9bKXFo+vj05pOjd89Orl9sHdosSh9WLq6vnX9k42xnY/vgeOXO/YNvvXNv9SvffvLW/Xfeevju/sHYF5UZf3fhbRUitrUnYc4uLs56Ldy2FSg7et/bG9vep0v25jVyPqYEEx9NzapF5g7cfPXlF82FMR4TqdRLCEsVrBjKIoFcfb8g2Eiw4WAtNye49j5Wraw8L24Db0aL6/M2G5klJQM16FIfnp4dnhzvWx2RL4z2Ocxh2p7URgElcoR+KHXmjc6n25/4+O9/+cUfPz57jaaW2rPx+KOcq5vv5MzbysiuLSa3RpE5NG4sY5bCg2+t37Tqac8qdnitWkb6S7/0S2zTCPWrL7988/rN/YPHijPG44N9C+oc+mZMZ3vtVd5tZetRHNI3EyQx5hogS8U2NnffxRRdBlZz7caNg4N9+wr2D5688LzNyvs7e7ynOHRrb+fW4f6h44VNGxjCfuHu7fe/dO/Rg3sWdJ0efsybcg2agz9eYnx7kw+og2ejd3kQvjZO4xLyuR1NSqqcba4TDZSw+sSbHFoUjqiRZxJFv6drRuJbkF/62uOFgdFjLZjzTNbvDVxEKZh8PSke9mbihjZVFEIBymdq2O6Pt5aN/phi4cHgwnT4Enj5zKa651mBFF/y2qunh2aSzfmwMlXAPKAANuavYZp6y36J3tabUoqVa5AjjzigMI/ph2EyxfPw7hv4HV7kr6u3V8KvbN7vVpZOCzGN0NCVH9U8japewSpLkXWzMXVP448CpMwTDFVBi+1koWyPB34rpC5WzTgFa57LFy1FfMZW613AL11bObUT4HFtB0hDM54PoErjlSH/OJaNNy0wT4lC46nvb0LBrJqymjuGaNQWh0YH5pS85mxIigWWH+ZOtnvLluixkEqRS5i0gJ4k8QEGxk1xkmSPhzokIG0aPvuRoLOgOZQVBAHRaDFcuxIGcRzfjY8b5gr8AtOvLnMF58e3VnYfQkhztlxxyF1/dJmAVOgz72oWNL8xj6Ym9cmFG8S6SGo4XuV8xYJD0qAbqTeuJ1OO5G6fTmQKY5UDifAxKQD99yt2k0H6SrYuZjW8uowt0n3cjXCcUXs2pahqLg0ggwpwOJ7diU9r74Vwjem4OJWkT+ZV71b95j1eooryGpHzoWv5JSlgH1x+LWmXT54+XW6e/lxKLD8XuMsneKN5fCht7NbbuwdpJWJBSGeTvUw6lf2guitULut4Cm+yVF8p8/CDHMtdTHuaq5xPL8/DoesK3vLr6veHUy8zXmbwpATFn6a3apZqwF+7LZXwyZppJAR/lInSE4CWQK6aNzZB4IQWQ6YAw0U5qAv5QS8SUoqMiL2f6jUADIypd6EafqVYtTk6II3RBcCnzvMoYKAr3Df1K46oh63q/uAnW2NfU67B3FEqepI2Taya81FI5FpWCsdEkNLaRaUbgUMAcEHo0/fwKaQDG4EwWNjZ56RHMMSMcdXXWUQxzJgMaYNSAwce6f5YB1QGECtBdVDDpbzL8qFwhWDpzRHzdtpNOFsNqf1cUIwBBc7RFw6+tcQB1DcnGsOKal5cBIKAhgZG8fOIQW9sSWZii6m+44y4XeiYAVkIhNKQHgHJvK/q6aZH0Tc/ht0eVRrcDDr8hsdxYMmY9HAy/sflPpf7MM9lhyd18mthfkxPF2WL/ggPBHAVnN/RmFtR61QUX6c+XcgC9yBZWmRr4Ob2DnoxUg7eP0Cz2tfGPgplKtHK/kDOv2rpLzpsn6AYHc+yUQZHj9+4fuPRe3oEp4dHT25uPfOJT33ayYmrTxwDVetm/BXx6kCLoxcspzJvayXywcHprVu3ycWBfCHJwhbuqfFDV3z90M8P317m+47sH37+T3YfH5R4Cu03qvUK6vL8afar5PkO1gIv/g2PHX4hGGtBFG2wk3PHLnRL4ve2LR14YrVOOiMvJjjK1soB+ol5p95aJKp759F7j7769le++e3nn1l9Ye+ukz9eePn2xunZ2xaAHz164Yd+4OLWtfONa4dbji/ZWb2xcmPzmV1vjnrr4fHx/ePHFkCI+qx/2e2lHrYIUw89wL2dRxenT/bN3VhytHl0bij58c1nN50aRLs2Nd4bF09OV37my5//6uv7X/z6l95/oPG0nc4SRbICLr3JuOHNiIrJ/KyTbefpnb1rlvwb9rZ0NUPhJAU4M+uYDnNsvF6Tqk1cXtvZun3z5uHBY5HF7q6FGUDqLFh8Yp5JsDKuMgdM0bVvWJQFqFMwaOlK+/u9Qc8mBzsbW1PFg6RQFpvYon/ocE0YG6e3da4peFfVTvDka4ywNP8iSTEicmQTz6Ez05SdRwAG1AfMawpym+Mg0+wGj2vNwU12gOVdVl6sV9MAP0p/+ud+0dYAkbQ+28c/9bGjJ5ZjNX5pYNJxqFvbvb/PC0eQFnXIm4sS0YsY19r68929YRn+Xaw8e/uZVz/yyj/8hV/83/yv/tfgmMRzyu7O5vUb1/Yo2u6upYlnh4cmB2DkCClpJu62Hj2698wz9tS6QrxIgneZzgzidOkLB9vcjMno5oUum/MIbPhkRhLiA8+x7cRaGxtlymPazibsrmdBk53ig/QYNE411olphIATTc5mR0Qkx1pUY+dkXKaWzYhMLd/h2sSmQKc7WoUavzyoaZLCSdW0tqJwdmnvENN/q2CEq3nN0908Gnh+TTeqwYca61JCRzlUKXSpD3Pfo8EqPnh8eY3jXe5hgqllXhAu1bq76K0mPlIGt1NPBITltOYVWApF+qWI5cxV0KqJ+QcyiJ4uFQAzrAmXikAuaEqluguH5pGHoFzudB/jHMoCPTQPgMQzTJ32I3BTaIQVuR4OB3xOw8AkRAIy4ZWaPSNPDwfj+ULRwg2fMoxLgBhk6VW2krkqLq3ikuabq0jNVVd9VTs33/GZymVrPRtYCkztUiJrSvQJ0sxwVm00QSIMK+bLyQZGrMjB/TTGZQNg/gOIwTkuT7tSlaxXXUNlbKjcg/lcXgABAABJREFUwJpqJ+9ldunEywXVdQwVtZc/BCqhMOLBSskHGykDcaklZOXInbqal6t0VxrXsx6nzqBFW76gLzl6Ulqahs1uinfmcQgM6KmrzFOnZ7E6iB++lp/g/9bX+LWrbAoEsSs0qUjgJfgfsJ7H2VixZJveyRRYPia1s3f07e6X1Aqqy9J+TQWT3McCNNZeXVcqsJQYzs/Dq8qv8l3Bme8PwEPXVearStPD5QdGzwIs4wtN76DBMxzmmtLmkxdj14bzN0pEOhktdlHOnCZ5zPHXKog5sYZA9RhW7T2IH7kpeRjYyCQ3IRhyHO+MZbypPs6WuelXFYxbaVfDM21heOceR8RD9sIrCR6NCDjJKgnnkUpxMjGA0AojCOXN+WtKudkKPFkDBLMAZ3Vj84rIG63BjYxgDkjf0iX232VdLIBWdvL6UO3QPedY+a7++TclF1ghNtgzA//7aBC/C3jsxI1E0CFEoW3728nZUWdUblujafXhR2vXCnWRYfjIeFVHXMAoIN5PzJLW3wAKPXCKqsj3EUxfU0lfC7f8dEZLiJ/eBsLufgkqKK91RMb5QOdliMCdtIxzaEcGLHrDq9bF2FiqUD1JAgnDo+GZZhVRjnadQXAc7qlr9fyFXmy59QA1eVmo5iuMhjqbAqRyxvfB1e8BDj6fZkGRX1LgPWhoG0BxGz9LcskGW0cxCD2dnOh4C12Irc09gJuXNjtRC05Xq3lqiVdwULyqq3yhYr4MwTrm2xQN1WnX2fHejWs//hOfffz4Z700bXvr5sH+w/1H+9/8xrd++LOfgqMN9Dnd+LxybsWn5dNrdHvr7GL/+Mnxk32H1ll1YMhKjgfDkJiSakRZV3ycz+Xn05Sr5z1dEuf7Oz9+8/H7D+UdUVzWtUAbbTFu9eBDub7j9ikCH06NV/1++hDrxZ+E0krlfccDrG1c23JwtTDzwDYA79Iz6Hq6bn36kfNmE4m3lloX3cyeYNq6at5nj5M4OMbMY52uZ4yr71w7fbLy7r1vXbv56v7m+eHZKxs37x48bK36zs1rm1vPe/X07toLN54RiB2+/603X/vHX3z85NHh2aO1Y+f7nGzuvbB9d+0zr/7oydaj9RsOGj/ZWd/72pe/+eU3Lt5fOdvf3zs4cvjg1rfe/uaXXnvrS2++5mQah5ZSrqVjQt9b8AbBjqFofmll42H6x0wNcqxePH/z9rOG/AWXViQtGo0vjKnxQWRFZ2Nc9IJ+mqKaBX+GQJoRosvELXodX5n6VfJaSpGFpw42EXiRsWn901OnkhfJZYKaWYHsMF7WuVp3UmRgLJc/ZF6tBZcjOAEuW/jw8nmS0kn8PUvkd294s/X71vhqXE1ISmZCqohM5HejmGoZUHSsbn7bqwUvzl6Vx9kku3t78ijMreztXPsbf+mX/sbf/ttG6M1EbK1t3Xvr3evXdhNvq4O2g3Sxev363sHBgbeJ687wPXX6pWbOHVy4vb3d6hYu4uLi1q1b/8K/+MevXb/24MHDv/ZX/5o9yDe8xU3Iv8MJ2YeKqfhn4aV1V3ovTjHY0NPe3z8UJew/ZO/XL86fJEstzWCoCC83PnAv/7WiH0KsJmEbPEFRabm2+jaifAjPWJ8F69drtwTisbPJLT8LQjjMXi2m5YqzCicdAynnWy1z5gv0gBFdqp8chJczjvNBoP1oehmKhJ3ay6/F5cbhw4h0JfVPK3V2u8DKO7zl4qxSA4rqBi282yFzWOlwIXsXsKJWFM9hlNfLr46ArpQqCUNuhoTAoZNML+7PixsBd5uS+AOrsyVQRomXkKDXzxejYimuUO6ITMPItraeip3c8WPinCUFW6iiLDhI0FEcgpI6tCM9nci0Rifcqj5oFFShGnCY+EsLdVYBIWr84Evbzo/DRbaBxU4Ey7qEtHgCN+s525TT67dbO0xVuXSVDOYdWUEDw45p1EQU9kQpieTO1an/nUTt6hkhFzTDWi3pzJiE2qtFswguS+xVV1cn20ZHnMGkaTKDCCscBEeTH/eqfnjoc8WcCRylT8Pgab/AEL1sesnPNcnx7uoiL7fDTpxMMHrBThKTrX+ndyNuC0xAUoegEkV8pj/VW7sJldO7meHmO24DmPqPgm+bA5RCqS4lM19qHPwT3VL70AmEq862aVJg/EG3ZgEXlxuPISZllCG0lBxsC03crm68h8C18xdMo/WOiJYcC0sYOBz4n3cUpbStN06PK7NQNJAW1syt1GB/3+v7Pepcfxx7ZQrFhJWTV/vcdAZmFybrl1UZTC8BEN88igLXeEvRIAwn/enHb4TH0wzffVOBK9jdXdYXFh9knft+yznJV8/GfC6Lz31lrh7OjR8D9OkX6yv468p+Ug6qxW1RlDRWxlRNueYuyaDyEEiehN2S/SUljZbdf01e3W/qk8ZNUsUyZkYLsB8EKGtB1mSo1pypXGM0FVzwpAE5u4WOgC7eRG2wAGqa0wyeEQAWYmmfYmEtIcrG3kAHdszc7eSR0sz78FMVl+jKU+VokDAgfITBkloT3uKkRsVqr2CBUwovMMdCYtRTAeSl8j2xFGezr2lKQowbQvMSDPE0Ls2ZFjFo0K7+qkuxGsP236XRN0wkNaHJFv4qVEvjfxKLN6J85KiGhbSqKy/OzNkYmMfzwYsjGOzjztO8I4f5ia3VM+wYSHgO+PhJv9ly3azWcoJCc4YXISYL41WuZQyBmno8z7Hns4clU+dQEpQCJ6RhScjE2Zggshc1CG6qbnBFyHKhII3j1rwCoJ3PPHEIh4WE4EyNiSj1G21OTfAh0bvy9ypSVaVqZ+KZFey1dCg6v/vc89e29myZb4vc2vrXv/7Fw4P9T33ypZ29XctAnH0Oq6ockc8n3C3TOnv0eL9HGJ5CgC/PyGwheliCpsvv+fIxD0tdbq6S+7lkfZry/8HN94L9PkCeVrzk/t5aY6mrfJGUFWR9Dx7vH1mWfGP7+uaukyEtq7+xsb1x/eba+tHr99/CViKmgCn9TJYORS3cZwhiKpHog+N3X7t3/Nq97d/zmd+9f/LweGXrC1/+wtYr9669uHH4/uHuszc2tzdE820o2aS9zvVc2b629cYbbzzZP3IQ6OGjjfcPv7F97cHHrr98tna0cfvm+vre2ZMn73zrvb/7j37hH/3yFy+++N7JyS2v17FJgNd/571D2wFEEIbC+ZJ2JgzJCXG0AX0JqH8EmIVs22QqgEn/xzVR5DaGLk5G05cqy8yao4sjTYdEg8Z807j2IGb2o/5ZaJ2EwI+/UpiCPnz02NC+sIUWsq1g8IF4Vy+2i7n36U0mJxeH+1bfmLPqNd6p2VM1cesafUtM888N94PXN29dN1dyZP5lZFjOufOlzc4Wau2KX8dpCXrcglFzLBQ3w2VY/9SElxMtj07+7t/9B84efOGZ29eu3/gdn/rY4cEBjRfMEqhzPzPHzG06J4uhDR3oLjTDC5irZsbNDfTfvvPsJz7x8Vc/+urnfu1zP/8Pf2GzgwjPnehu0MACoV6CRdt00w18GjfxVgGqtr1z/97769c3js4e2cexox3mN7PHCbm644kgPwuZluVMtURj9WrO0dSKD3aCSnJylK0ewaE9yxxJzI//MYb8et9Cn/4XCvadt1ZMoAwIMCSr9mAo6MxLAU4ZC3dnRAxH9Ocas/cvv5L9EBZM6+eJm6ZpiwTCTj/mM6mXp0h2D1MbAilO6rjt2QQv96xLwdgmMdAoe1pBfjHA8i1dW02NRZvOORU2poEA5AITdw4rLaAk7TFDiRvNFzUdh0grtD411kGWqMmOvwUDIRu2KXH8kRiTVTGtUHkaBjYoV6tRgwjmUrp4NCeC54lhfHJHU6iHyHGOts/gEs7wFCPXBswgGfnF87EPCsUwella0mmSUINwwNliwqgWYNNr+SMa7GqsJzeRRiaAjSibZ6nOIAA67sFuuFTzUkPRQJ0q8Fd9+vVqU5fS1Sa9jyqoP4FNo0kxJ2kQel3hEIifvvyrTAxdMghQLmGCmzRwz93U0Wc/6JfA2Cs6p2tUjdELyEQUaWNVIL/GEXVq7V5iWZKYM3xoZ3DVHwqq8RBpsiYgqWnaUpaupOPVMxd4AMkJ1cAtkJb9eLjAeub827RllAQC1sWqTWnFFBjZxcaOHQxCeMWMBLQkpQkj0GgOq/Acd5bpLdwKYrff5/q+iR/KF4DqH9wvKZjHEQ+VRYpSwmN5oED3EEwofoDxXR2AHteH++1cC+ZX0K9KTB3Le4KdFDSXyq6eDrbnpgJh33Yr37HAJc+yUn/Nq4gur4qNOEcL8z9yk9rF0d20deMd3mG8j51fb0cdtxRh4iAX9aUOJU8tuC4d7EZMqnhYkNkAScAjU8Yb76zfWneax1vWV6/hho4iAQezqAEEWXqberirICcCH1oxg/Xi3KrOe+ZOuFEDb4iUN4Uc2Vu/CJ/dMM6L8RFUOnVzYHU65nFIgWdN53HNqXwgaLzrtReiGRW7OHkprNbfHB+igDGGRmJ4yAx2480C6971eDwDT3ETE3NikQ/vaJ5h9Zza2qoT4aIvU+HVEo9LzQoYPYoYIU8sDev1la23rApeOX2xDX3MQ1WtO8jwOljwwtAXqPkefdO6A5gkg94wdsI1SjvjWX6DN9vWXzjN3lt8DMomdvV1GvH52uvBxMCGf7a8fm9wgpHjE6ELF1hLwy0SqXnutxfadDobIsglcZfP39z3kUPlY2CrkqXCGaGRe/Od1Q0z4x0hUp6GnEgGzZq01s0rkiLFYrzIs+QTzl/aMOGw9fbAKkCIyeMCFncTGlMKwBhDtbDfWsPqB9GVdmGebJJIqGHN5OFRGM+Hz6SqDUaahzHKFQ6wudja2XbUyY1nbv6RP/YHvAHjZ3/2Hz5+cvjk8fnqK9ZcbBudtdlg9j8UpF3Yo6IGhdmMZRGba1sOoiApI1GNZ6iG8j4TJY279z14Dk4adEk5oMtreXb1q28Fuj486v8bj98veb/vZ3C+F/p3Zl04hjuYMHz+0OPKPi1PCyy09TN9EEIfnO2vPLrYfWZvawdjCF2ofrql3ZwX2zRvlvsCVkxpoLwlgWnCHA+LcY+f7Hib0F/86a/92rduHT954+L4/S984ZtfePcv/hef+ZOfeOmFT37qh3e3b61vPb64uHZy/v7Jfi+mvnPjlU9/+uOHj1e+/Kv/+JuvvfHt97/xkU+u/Z7bP37y8M2DhzsHZ4e3n//EnZc+9t7DlfefHJ0+ctLoyubGrdX1Fq9vWS1yYMWQU8hoCr13bLygtnABu8fY0gpuJxpHPZnfqeOxOBLdBlJL4vqctJKccSZla5PPNO1Yvb79rtmRtZVXNNGjhkLhGtteKcuyOsFE6IF37DHf4NBMHskD5tzzHGv5gbbsQxamPppAnw1AWiZkPBjCHSwJheEtUWQUFeLj+s4u/Zt2v245RyAL46i/PUaSgGVI/8vPBkCe1TVEyE+8vLKxt975PQKyQijbfLc21m5ee/b1b33jbOPttc2De2/v/8gPfobfddJPb/uyk/7IEa7rzmxV1/7JvkP9uSnQvR+43jhnWX//wvsZVG2uQO3PPf/8D/zAZ/78v//n//Sf/tN/+6d++vOf+6JXKjBAq4gO9g9vXr8j1CGYdZvBCisLcfBwZ9ur6s8ePnp3+82Xjj/+wmZtmY0EnTzLjfrYaLqaG+n9XfxvR6Jx/RSOA+r0KtMxDBfds/sqYz7uRTJEkNn2aEIDB+B1+mmHU5kUzcP3dKQe84QvWMovt/FtHOcw1QGY/F2BLz2fwL4gfJqVNI3DpmnKqyclmzJp1fp7+bqJSucxr5S7F2Y08dEbD082d67taAxOXvYqhrX1N4cyJz6Y7q2toLkzbq2W1CkN0s2yoQPN9cbPLKe/WHcWjRmI5+qjtaxI0O/doNaoUUxDT1gsgoPtaU1vTHMeaGfpgGmBPAdI/TrRm9l3FhDgWG2yBk3qCQN4khHtZUc0lsBjezrdKle6pdPSIWFmSusR6R0oraCjTjVAvbMgo0Ibxnu5iFOAjw+dGSmYpF3yO7KJQEmP/MCU1Qwzlz6efXQfbED1vmSYRjt+KOD40XpWtUHQbSCLCxML18n0tGOHoc9wAZCnLdfhIXcHhasd3g1OZc402etBTUNlR6mc/QatXdYoEqIc8I8ucBc0iF7BcQsSuuSJb4AtE9dyAzFP5qnC4S1TfqCRPN8WnXptg56wI7ZaY4PrdpXQRtzWN9YRogmxtGa1uUl5dCuaoCOL83f7VUg/WF+p4VAQUvHUj7RpMnXqkepbiKjMtKl5reRT4NFuug4kVkz2fI/s7I5vxKuzFSeJnb5kunJl652sjwjT96d1q8xiPwsNuAI6M9iAkWXJTfvTxkHLo7gexzw+fjkMxEXzMwFc3XnqyZjRQVlFxctDny75T16eu6WE32ZjXi/d/wriv/vAL/WlCWG2XMmsvC5J3zMDsNTg8yr/AvWycF8KX17BqZLvvIbASyq/+9mHchIHfnyong89C25/Jcm2fBJnv7C+b+SxoELnEqWsOQPhcrip7rCUDt5KdVM78C5RGruSnFLVbPYov3NFbz8WsFo9p/538IK8wNFlZlSXrom2khNpHF8mBiiypqTfw9qid9qmYDpHi1NaSSE8bi7WKcuzAsPtqI+NVNU8aW60TjiT7qP4s4ZKiLLR7Llc3BzFy0Vk61y5XVbZV0wabWuQEqqpIKSdPOgw5Dlepq6LtIBAIIrjsXh3XIslxSl4mtTgBiRzNGGVQYYcaP6jLEwgXOahtWfVXRMw8HkDvwabIihGtWSI9NyYv6xR4YwzjnguGafghTPRJZTP4C5TMMSmPH6UKdasTLZYOqTg6EQzEgbhyoW7f2HmPqfZs4IU7G5oX2qXBJwpXknissPEyTAmZuND2UOYDMecEOAanH3UEvbDjQ8Q8nc15DglcVhU9fCIceXpbQ9raxwT0sOqdmsgchqRE5TYx0HJgvqamDivkfOZZyzNpWpJumg0zgIMR9etrT9/1wmDO1/6wmtOW1T63fv3XvvGa5/42Ce1hQqGnrJh1EzI3Nghunnjxg31GhcBcLR0wIf/06syFZuE+VxSnmb4/8dN2LoWVruJzx9Gep6WYZDv4Ri6hLTwRDCq42x8V6S8tuHQd5t2BUwRyTLTLDITjribAy5lTfwVd2KgAa+vv/X6V775/ubK0dbGDS/yfO+L/+jL/9Nfu/vsnedfvHNj6/kbN45v3HhBDLmyun22+v7p/tqb3/zqjb2XX/vSr25u3XRu7Z/6r/xrH/nsj1lf/+67R69/+cu/+Mt/7Zd/6Qs/94u/5IwioWYCMijhPU+8XMepxP40eJxJxup3OiB1kWWaKDVytRfe/ndhd3j7dEI8dUd0ZS5LpbpcRXAaA+9ISnVYx+7tgezLSqEGVmntuK/somCqPlCH1Vv3c+DQHAPmdQMGNaGK7n0iuDRq3I4GOt4GxHPj4l4jNp3YkiMlbsrD9OK6pFyOxHyi0xQ2b999VkjHGU5qn0gjxSQkd92zOvANoAh0BBEW1d24fnh0OHNxtjJ7HaGe39r9d9/5t/7Mn3VGE5dz7dqOWPrx48fX9/ZUCIpgHb025NgDsL3lmGCmoGOwbsFPOxcmgkcKFNUhy5ODxx/5yKu/88d//PD04N/5P/4f/rf/+3/z5vVnvPlToEUt9q7d8F+XMbs9O3HiZ0MJjdCs7l2/sd5Og9XDk0evv/n1H3ruGp6TQNLJ6CGTqOxRjQ+IQhxfN8tdYzOfkQaQmt4F+Ji0HOYT25duecKtthRhyztsdRmHy8riHL9Hpwy+nzhVsj6Jf8AyB57IDVFxMgJrkKtMUWLfLrJ01/m2WK+mlhV5IVxzoPM72aUzwOMeOWz3hubatpPT672gyilN42mp1gysjBnRp/HDfFItRy4uZU6mHtQRXTqrWkDEMUyVt1RmdcMSKa1eTnXmMMdv1+oYKiIBx7miyBlp3gyTTrHsVmToHmtYnMeFe+kPHtfiqQruCnD49SF7tiXMGJR0MWDWnm4etJZVaADPrErP3FNIcPhI7qXUsSbNTU8wUPOmI2XLh6mShBYToQEyvElIxV7JokKQDdP7xoDoEuXAjo9O2DKEOUz1AGtjgJ034lhgpkizHuDST7zV0a96V6lpAm+ABS3AoyL968OTjibL2iHPo6ii1LFdVlzwMRJCTrgiB1iv1LB8lfiCqCFp+ICC1tGNnbhA4G5brOHqY/EAbtKNcUPGIrxLZUYeqlTthEOf9WUyNPHblFJdaUvPlmBq92ffSVJOhaYCdWJnJZZSC2k+zcMP7AimxwtPCvRDb5zeQBkE4Ck95YIAj0Lcw3gxiGB9iyepc6JYAxLxktuhmA1kEOhMEV/WmxzzTjXtKoZTv4gwiUuYpED05Huukdtwbnk0/KucAn1915UU5uor4H1nSEst35N/ybUgsyAtpTF7PQmri+YaBzRuCECwfC6VLzgHe8FkuVNmufHZtYz9f+c8wPLEZwgNUgtml0W+M3HJLMM8jXdLCskU/azfz/2NplsMR3ubVRy2DZOS6xK+Qd3yy0vb4FHwasnW6BfV8ZtBElCpgRx7Wd26b2n2+ulHRAMnq1/T0q2evMrQV9ZecwyCrt5iTtR4WBMgbilhpqZDHa2iGtwDRE5edoLn+poZD8gzXRQIbeXoPXyjGAWyM65zKTL+RBw32BxMYNx2utnHOwjXArH2zZWNNzkhOl17nNoCt3Bq9Pz0hSJapzhDM8SwqHUqsR2d44DkG8eCS7hJaS/jQrBgXnip1fFEeru36qVUAiB1nb2iLzQDc9Kqt46J7K0laKpgsFG00SlyiMd8lmEaPWZtMY7xivkPrcNATIZZTqLtMB+mPq1l0bC7LUCpolWMHc8CumIwHNoTNMOszg4hyTDzqzmkSewgOkngalG1FmPJ3K6ssS3mlS++EZoUykAvYv60Lpmugg2OQ0URTBiGy+q7IaPXjev0rkstR8gjo47olMMegHwaMZLU6J2vau6n/5Qr4YDFsV76MTwhWL0dVBememrkwNkCpHq/UrxZuNcieChA8RZaewCuWe+8d3Nl5XB//8ntOzdff+sbdiS+9db9v/QXf+FP/Wc+/axl//GmT3/aA8iTrAaFXv7oD//Qz//cz377zfdy0ZYNBP1Bxg/HTOtDVwHxcn1H8lXih77/Pxr1/1D5y9uhP8HA4wPHuSB2id8HmHxwp/QUWcpJL3TpKxgEZWRSaPjk6OzFawIUI4b6tAZ1To2nHp8ZbyQ2qhsOIqTFy2vg/Ki49NPktXp6l2KIgfdn2YfJvfffP33vvXd/5QuH6219echgzLerVWYlhSErq1/d3dhWy9bmxX/3f/C/Pd547AjRk6MnT+4fHhzZPaCpXXP4pF72ygGrg2MBt9X2bUcZq7TyrBaI3MgnfYWNWa85SKQQka5agLK6vXnT4wlFFpQzOeRQ9/FjUZg+eDhs2Vp5df30Fial/1o6lU03PT1kWulB+WRPjVjI2YVXbwlEnGgv/naekkXe/BP9FO6wmMySsSgBxOnR7s7u2dbq0fE+n4IpAZsrgCEF1yiq+kwPUgTQAEot9YgijxTGfdXud8JiRqU4L9kbviyNWllz0LhQHiG1BoOvof1f+Plfvnf/3a31vaPDJ2sXt3e2rp+eWIisj7HlKXDmAfh+RfS0ChYFwli+vOZJhIcdvB4NOD1rD8jByTPPPPvsnZt/4l/5l/9nv/J5JmiTiCHgm+L7hls39g/3rfZBReOv25u6AXZF7+5eu7a+rYv++NGDtYv9177xK7dv/9Crr37y4uLhLKw/zH3pg3YKmA1CpzuOKrkcsKFx2IPUk1hTWG8jc1sNDKfyHXxXzY6ZBCItQjVjRUqbtMaAJk5RQhBEN7iiEr2lze2YY+KrIBZPT7etO1KEdouRZ8yDamw4K0jEubluGU9zsE6kF7MqgD1KYYj7kRe06kUYKdbBIF7H92cuLf56zEs5dyUKVu8ZJqefCdXwFlSyJU3QYYJf3DKppBNLACuWmnkPSOTYIQs+/ScyMhK2e/8DP5YSX8qoZsD8Ks1rGVW2UmXabtH5zOmzFC1AJiMKfglX1qxBx4o4Sw9q0/iB9LdYMcADXherDGML+uTpOYriqvaqjUWTjQJjzqixF3XnweujTky/gi09AEMmRqVh2WiSAf7DjRR+hIIpgVsYnNE1E+9RJeQBjSBqcOAaLLVwUdk3g1BsDETiaSfSnG++JdWz8JNLg8MeGy2dlo1e5BamlpjWaIP6Gm8QsfcshJVU1OFUwGd/JTIJZIcAY0GFQaiTg0P39Z2GHQhQS6YzhqNStu8wwBYmAEBSjcThcRxb935lFr7xOgrhOXGVb/n8ZX1q8j9M/AqBJFsAUZUAoBK/I2ueemWK4nEWm1xpyzAmGSgya/RStVE38lQYUAwz8IFdF2vvVL260ryX6nJs3hsUlFD5MKYziIwfyKlkaNMRvqivudKPq3ojZNbxT95hOJWLwKvLrZ8b7/Z9bLy/R2ifrBR2UpYY+zRerW69ga5hpWoCMkzwHdBzOzDdbr6RyCSFUqz2RHrdrN/2dZUXfy5xiTNRu+B4WXu/0sbf4KpoIuuxjyugoXaZtDy4+nWZnM3oGqZHWrWOWWg0ImJEhGquA5relkgfwOURfMVa14JQ+ehKDUWtIL+fkBbm4WG2hbi06EpRCq/USxPSuNHVRTGzMrhnaRlVfe4JC6ZseMUkIFXJI3PNzN/POtQoklRuCWCm1jU8WoxR08Yb185y4r1mhY8qmG7YgvKlb4wCeDCFbWemNeHLkXvLd6prKKbtgHAzb60F29wu+Fhf8+4bLZkaMVClFcKvxjsgYD0mB3+gGLPBHNk0WAgzmKVBBB9Hapx7uSQgDjTx8hpIuMTLvMjYaXaVODaNmI1HMG6agnCwxxqVtv8jyqDJEiEbckVMDJpHxhXIXIywen3taH8/ufHzs3pz+uONdeEj9z2T7xa97nq/akzMH2oRVg3eashhAI55UEPZIajifFOi8I9jNzS1ueU0OsRWtuf50EVk8oRQow65v9HCRRWB7WecW7R3fvmNOThHKLREU5bkXWNgbmmNf5RzWoHU3c/FhAI2+kiNNCN+wkUt6exYb8eqaDkiooVtSiKfsj1Fq2yp/AyQNBSjB7Jlc0/HyAD2yU/8wOc+/6UnR/tk+tprX/vHv/aP/oVXfgT56W0UN7oLdhPI3PHq6u1nn/vn/9i/9PU33vz8r/zKvXvv1D1QAZVRc/8HrblZfkL5ey/5/hleQ3rmPNVc1bX8wCXYVnk3g8Ty6fYy+TKj8ilJssnWLfs2FcPuWJocuKm3ae44pYn2TLa/GpqkMz+YZLXlGIpzy9u7KQo4CkXouYOb7A/z3Hp33O39HotWJGeLIL1l8OhofeP0/peeOAro3HtdW3WwMw2jmQWHOJm9yWqVuhRCyAxhGQ6MMkpP80O9WigkJTDbZ2/e2N4SrlkCIqIzjL08S7mgko9M0RpYBi8y2j5or7KzZU8dk2PMQkWaPxeArLLK8g/Bz4/olBTtrDrL5533LGR3eOjptRu7WzYcMPbQMJRX9m5FK0Ctmb2MW4aWh7dqwLW8RjjgbvKIvVnlpPmEIcvbu26jdmvBU9ulKY/4/CFclJA66c4A1XnjNEvUITFzYl0c/V9f23373tu/8PO/IPx4fHS0vemtCscPHr17fff6wYETC2CKp/HarItAfdvmicYLJrwK0PmOweu0JndIbfz9p//1P7mzs/2ed3o9Ofx7f//v8zw7u9d+4kd/7Mn+/qNHB7eeuXX3hbveL3BC0CIeIc/FypP9R3UNVrevO3j0yT44jx89/rt/76f+0B9eefWjz/BJlCq+cORxRAgbAjPwi3bqQSaeD38spG+Pd7+jvhDouPGRAqlZXKGhiSpnDIBXpNtbdxuX9PYoS4IsVZlFTYX+sZkDSZ+KpL3BV5jKMacfwIsPp8UQQHuqvcAcwpe9U+1lmrZJZ7g2KJ55oB4XWrwtXt3n1y/Ore+thtjHJEDHknGyaePg4Fnox+aULf0DHHJ4V3sQVzwc7fCtfHkTyKCzcCJjCT9jTEpTH965toCTg2doT6E0KM88SJUvKFWYRQUzNnLu9XtLrNLpO1R6ismsldG7C2Ak1d5NSxkdcAXEui5tfeveaLXaJSeyaqpFwdD03ZhRqp12KTp3QOVcqlm2+Tc3VS5LX54oB1LApInXAQ9+hlS5bis9d9RblvDj6qbVzNBqC6DD/Q0R7qfaeYRBIHqKECB8duXecAUtuFfNkVqYIiNSz47zgKM+g0MffM3UMripfTLnHD2B38I22s1TdMTtEs15MhYJH0wLYfIT9/CwcQWRqk5UKks3uktxclzdy+RRGX0vqCfl6UPwfTFOelyJiMLGhUL1qyzvN2VjwChnrgh3luRgJwVww35hcpQ+/atGkF2SwsE1AJefl7e+FmKe/i5/jBzsLvMOkKvSH+QEc6EvKEvy1BSIJSkUu1uAJcn5tSD/dAag95Ndlp/sEEh/hsDlHiP3J2V57mT9wSaeLSlXn4N5P672AFw9uPpea23TgsdlUpDA78CESYf9AF+4eq67iU4n+RhOWDdxe7rpNGVurFNZaIDRGXZ96amSfEK0Lm9rZ0u7tbu6u+W0CyABDeqMM/fL7yayRkjJpujNJzNofE60fY+4N053x1weZ/rnNxbjjeQR0gJ0a8igRdDk8UZUWbOIdsNq4q03jJxvnO/RShkhV5xRd3DIHdEoMo1WWi7op9VGCctoraOWRwQvut245qEqGmY7b8bQuj5DgpiQIaKjYvnJJozVs/O2bWcX53s6xL7ZGi5tbs/s7SgDXU50snbIn8h4B/ZViUvm4HDGoiNxJENed4I1QzIjqlOMb+ZSt8xLY4/YgF+TkQ4b7onFdWaKPmMm1DOdLYfq4ZXOBHIvN3LJ6KA6ZljbPBF3s6WWB+g/GP9svDOShtUzGY28mIfx9ZUYogBLdySe5H58tCE5n+ot8F57KWfsymtEZGSGUprg3H0zyDnBS0HGBvzJmaQVOirV5gevwhd0p99VjpNnG6p37riEvEaNBjzXzl7YuDg+WXGiDkzSBdVV1RiIYYV8hIYg/ZQlRZxPmYbIpvCRrA7ReagtVU+jjCayyA/bEVFtKAMX9Px9M6qNDgsCLbBIajvGNE2uIn93d+NHf+wHf/7nftlKhu2dldff/uLq6u8MAcNVBgMhVYtYUCXz1vrG7rXtP/Yv/uHVzd2/8x/+zT/7Z/4v0Q8XFZ7dLEvvBIgVcz29uUr4jb6jCCChyG91fXi3wG+Vd3n+FIlu/MXX7tA44rtKWdJTew99+D/2OvaMhV4A5VhQx2NsblJUnT+rya0A3BnUs6uLFftEsU03zE9CBAMEcKpr/Dz76E1sI/4K0P2z8/s1hNXSIStLoEBraqoKPm4lwfMHGYtOO2BndxL8+kOGU6U6vme3QDcPk/4ka3IflZpWPFVIjfSNFRZjVK00Z6zcbMP3yoGjeR6f7Vn/Z5FTtMsCRPRnFy7R29ratRs7YpjdXW8LsMB9SxCfzrWsA7JGuxfOQpWCPoTy+sXt4SIwBsy8qOXs8cna44uT7ZOTa1tHz928ka+Y+caBkGO15vr44uTR2UHv/2mysJF59jGy8DkoRQ1n4rPubvmyjhUvAXvh9p0MCnWYcfZSxZz55mLQRMlmbSrMdVkkrTZRxLHt148fP7l+7dqTJ4/twbAr97XXX3/3gbFn22E2X77rGDczZmcHa4dH+0frK3dUtLm7z4O0UzuPWnMPcn7DKSX83epDePJhhk14nT/6z/2R3/V7fveTw/2Dh/v/97/0f/7iF75gwkFpr7k1PLWxsfcjn/3s8y/cldnG4p3t7du3n/34x15+8803fv1Lv64b8OD9x8/evnXv206WfUSX/tEvfu7O3T9wfVc/50mjMisHUGiJTWHIjON4gwTHnk+EVN51Vg2RnnEUojxxepSV/+SmL5pcG/W2Dj7nQBydR945PGL0lrF59Yi1npb4xGOHgZLpyu5pUuLSO7nG7rc0Sk29g9bqUGMBVnnFYhWqPIse12jv1XhGqiLWBY1gKQoRNYdgjsKMROtmNsxsaK1qT3UhNL0mzrqFGzevIUCX87UKiHPDiT+6Cr5latjrwnY46vhSJtD6aa/kuTvmNQt3xo9OKTiOjcQiaAOsPhqlity1h32uF2+M9Worl32P6XNFfcR9lR8EP2UuZ1qXSpYt+uID3Muc3gY9h7yy6jjm3K98rYXL3FTduHeGX6OJwDiLqHhb13062BINAfAw4uBLNBQOA78IbTDjYXTHBpe8BuD6FzRDy+yRHojdNQrgYtkr6RT/KHZNdknTOPkd3qd3y7n67eGTD1nBAdWoNndg5NiVr1s9e6kh4+17VLKeWy4g0RhqrNmSQfN9+kpdi9U34EMVgQOvmYbYlyoHTbWNvRZkRyVap6MaOjzszlu8XxjBUsXKg5y7wjn9tYIK4QImBSz5sQBAE0gdwhBaqFBMnkEh7g2xUV6GJebIjpT0M5Sm3zBh/2AKcMpcd8PTZgNFHm/U5Gd91ef/pQvbfBsYWAQmkjx2mJzCxpUmZ3X2sO+uJe+0QYP8pAwql09NX716lXPJP798PF2n0/1l3K6WuZavEFjufGYpXfCicFkWjKY6+rlMjE3eBbWl2FJgMi1ZJ+HDHyPHDxIqVl1BXgB98Ow77gb+hyqZhxi1FBsQ35U/KQ/filSogf8Nz5rxc2OkRwvRGLg9AHkQjyg5YfNzLm5YsyCRCo6AiNOiOs16IMcKQ4Y+0SphpZQ6thvmssWgFp4FivWnSaJ2t4kzdAvk3E0tfsNxaFgeqsWvFCV85AME/+nWAOH7FF40FbtkqpKxJCSkoDCc5pl/KD6TlKsQpKuXzpXC0Uy8CHz7AcUW2b/is1BVnVauThBfL8hiU1Ugx+gv8BM1hh7esjUMdCEXztyGOnNr8kdDqpQ99E85vRGpBsj0n0+tfmzuT61N9rs7gW7Yr67posFqZkXil9XVAyfaju1Fi6LFrUa+dklnadNr7w0MmHY9ObWoGH1y+x9nF8SSQqhYro4bqBNjOM1jegvxxcJfCLT+6ISzrSiRKUH1Y2x8vBTa2AHjNXyjeH3C6qk3kp1TNXpSrVN3ZWSdJspIIB08EzY06TKMw47eGQwUiRz7AwiBXL9SmOCethU8hcaiy3kcQH2oYxBIKMfHwnQxhFpDEP0ntpXp55neGSUKSMN4SSdY8FwAN4Ynh5Pld3lIgk3bvb9oc/vlu6/sbH7p4fGRs0m++Y1v/Nqv/cpnf/RHMQKfjUPiZ+bCk+gfUKBNe/FWz45XP/MDP/bSi3/39Te+PS3oJSNwQ04IxJmrm/n1/4cPfETiB9eC1tPfT3+6mWyLhfZ8GoXsr/Saa4HL6ZlV8ic2JhqixnrrwI3E4/zYb+SnrSQ2Ra5ADLAEmZ6MGZBC1RUjhV+NhRKJ2p/goOYs0Wc1Hqi854TQeJhM4oaABjAsK5ma+BiDmR+XUgiTrmkfNVFEGSxihYsabOhbEdY6lmjtwivAgIsA2RXxMRVoyMC25+H555+jp4qDwhIpO5zotN164wKma1Hrnf3RvYURSGpoZdVK+msr28fNf50c2cX/zPU9rseCtDR/OIPZhyeHj45OHh+YbFm3aSB2pabLNUhFbVacXKHF9XAB9uburf3A7/i4ZW06sVWNEz285A9M0RJNdNiyzcNj3iyz0ATwEBCrb7B6cHj0tTe/8Q9+4efqHPXe373nn3vOCNHx/qFQ9ODsYNs6G1HH+fmutyVUnGQK+0JTGyI8Gxdd52dWBnMPBjqZ3ad+x6cfP3nyUz/1DxzgCMlnbt958uTw/v13yZlWHRwcco1Hh8c6Gc+9+Ny1W7d+4M6tH/jMZ+wK/ds3/v4v/PzP7Wzu/foXvyjqfnjw8Fc+90s/8WM/vjXRV3wZTcTERrLr1dAR4Z2QgsbiLEkb4RZgmx7Alzr/uv3+mwtqtqRUURZEzHY+Mee9sbGdb7NtJR/CMxpXopInGyvX2ggD0Pm25Tgg2f7oeNr1jWtq4GPzybVcTQZXUS8PLsLFFJ1Z33QOw6Y1xEICBFwcj/Nu6byhJRRcn7VJzSePj2qv6qJLZDfUgZp0s5pF/1PEMaEa90QsW3lIpoBey91KnRF+PnZRbtlIsmIpLKVPilRJ+dqU1Hya58wh5UmDpGYVmedM1YaJfDVuVVqgFpkicw+mwKDlA5kuQBUBH36G+/TINKTDoYHcOFkU6l9PfdU72Jo5FHzEoqFJVX3nCMI+VMM67i5Ehkz1RBC0KjfkTPbpsNFiyfFtSgSsmvoIZMhGDGy0jIkQoP7X0C8Zqqv/MW+qWgpUMPuXOylN45xIhnFhCJjH00pSmArBULxRM9gjCeOdqjRM5n+SgKL/BS8NOfgWgi1b1SRLoQ2LHmSCLQBu8y4cptugdL5UIkbGqn7iMuj+1JRXDPEYkV754V/VVnMfqe6wcnDx0/NBeDL5PSnzqXwQPO5vtMWvSzZ5cMmvICx/AXJdlltYOvAr5krrZFbhZf4l+epzQAbMY1dQv+MK0R5Cys2g5vmHsi16fVlmEMaLnKZMsrW7Yal7qT9oVwAWKB/6dGrN0+tDVVylTdGn6Qugq2ff+f2hSubBFd5+KL88/SCPsX8cnAYWsq2csf7S1saOn0w4o++tV54YmrYxP5Pu6ys7e9fP+F4vyQTUoFV7ZnUhj/CJujRkSu3ZX+tqluo4gFmEXZA7D+fUNgMdTItSOVGamnlA9wYh5t8P1dHsbCO962LTPou/c7Ncj6CWOwAHreun52GrMJEVLjtwnAso9Mw3WkOnfhqrB3LhmfcVCVL55M189Mnx4eQx7rZ2dHQ8rsPWw00rcK0ZyAI5uTNDL+tecmQoTx/Uy2060du8wurmkyeP8CwzZVqtWpCzhmosNuGNuVQ7zmpPBJShebH66MFDSzbPzw7b7N6RBUg90zTm5zhkbKmHFTNXTl92esbj47dMa6IdzNyFMbHFRHOA2J4fByj8sep8ZWd35+atWyfHB7bW7e87gFug0FYBnYp8ginF2iLhNSlrIU6819Px6/LbrdX2BvR4W9DenpWltgqeHJqETIbx6ug52HpHxPRVJEW+LsTs3FcOP2vDFr2DI/7YPugoDzk9nsEIkBJr19p9dNX6ESxuO45lAn9nU2joG9KK/TUeOgXD5dqzgik7KWfkgLuJJzE7h3QJFZ7aVH+5FTjAQmPhFAKtpF5uegbPTL3GlqpQrXHb9KDNFC/gwdnaPdWsbW6Z5d9Ym1WYq2fP3bn1+//g7/zFX/ylJ/tnxyf7P/tz//CHfujHNndaE0Bocz5Gy73SWGZh55/btaPnX7r5iU9/9NtvfVN9CXD9QXr+1MWE5RAQEd9xfZ/UxqV+e9dvvlvge2YS1JXdXtpuVVz6r8zq6rq8zc/m+nqUTuYKuneEj+Fzw642aG5jZU28Fzh1eMrpkXk2ZZxnlb333sq+JVQlIA5yGeX02tHOTRfw4B5BCZopH+3Bo4IAX/PDN52gV8JJUuQv3g87zwk23vI0D9zlUZSyzbHqHsX2sUtJZY8If1f3HuNwieqiFYzNB0psOnUyjJP+RPit1A9a/scHvUOZWv20smWXtxSuFIgk7PsZ9/mzOp5iSV38sFU2lJV5ZugPAfqNefFn1Tte785yizetO2KwRUKwrhObozk6O3v34cMnOrPeJjaLgcYIAMFGanzJ22rppa3D4POzuy/e/ujHP/bcs8//sT/2h+3JHRZNjLb5thxd033lguKIXy3J3hSsC7hvXLvO7mbhOAQsbdr+yb/zs1/5yjd3nQKzut6yn/2DGzdvkPrWRu952Njat/Dp1s27evUsGmTWEFQnqGHr7rt215x2ogiH0JDBH/gDv/+P/0t//M//2T/38PH+57/0+S/9+pd22J1ThI6PHu2/e3DQ7pFHj57cvPUMtrZkcRiuyy124SOv3dz7o//8HzTM/zP/4Jde+fiNb7/xmNi+8c33Vi+++vGPvvjic6+crdzf1LNaOeSf2aleDdpQals4tpJb2qK12tjGbMaL0XHczLf+SWpb61gH1lvl8mI7TkO1yYSI1zcfivrXtebelwxyniRXlQdwemmhu47jdpOpzps1e9Bww4VxBWAaR9K9kqVJbWg04dKJYUsknKWrrXWDAj+9N6RzJykefq4Z9znqjXfKlZOgzRhgcnqids4vS/A45YpKj3KEqLZmDBYjZU9gdm40uucyWqtu1HzpOitgv5n0tKjg3DRyjf4oe3YE3PxTz9TSh/rQ3qP+0BIEfwUI9LsWB2LhUm7ZmUk7frIIjbuXtRdLwASL7LLT6AkG8GTyy82CqGYpRRHYGbIakChuAdUE/fBc5okb0zE3XlsBQvpeW4nTC5+MDLPUPEzWGifimVFqB9o4lciSWUjWQPetumoDIf3QrAgsGuIBiu3yGOXYehOXgCGxyIyO4cTW21KG+IKFlMmcW828E2+ac2pSUWJRxEGYVuyss/zjUKvCxrRzZsBGznDPrzSN3SdsWVPcmBvboyiGsFvN60yD1EtJENUnBmhXBh8KNuUp4hIQ8ORxrLDkwsoUAw9U04FXTAcfeGbp7KLVlfrPpv9n6qk8Tn/ShKcVibZJjYKd0YTBTt83xYi0pJm7TM59LFdPJQ5pZRgmDJ20Xf5yyeA7MPM0zUoFl6Qe9iAQ6ab7+TmPP7j/cJ3BvLoWUKR5WVeF49WCqPvADsYB92RS4DEAcLYlGU+BDZr9WopcpX/o+2neD6X9E91eQV4Q+N6iVxUsvBiGyrSwxxeJH+wfnRwdGio29EshPBQB0s+OsLEcJT1PmhazGhJxqvPh/hGpaszy5VQoQWIE82MPGUE6728EQBH4KdO4qeROXXnl41zTdwoWdisb2xdmxknp2rA+F2F6BKheijnoi2tkIy5fPXjy2OKXuhBZZh3jKVq9YwztQjP3DJIUSl/zWl/n4vTopFhTU8sjrxojrxNSBkv+T4+4bG4OOIAMujuWhw2JAgshL9b1EPLW2reTM4fgafWdeK3mUA7xqBCzD/oMr1UHxb0jBJ/2ITTHwgc6L4wnbWzB5wQK4VnoCw6m8CQsZxYyVr2xOtaIIfk+aperzKuqtaCj6mcse/yLyEPKmY6OswzWvNdWa1QfbxycxldpnqDNjwXqND3HbE4Z2/SNPCXFpJNVQ8+NHsG4jKEjuxqBY9kAUxsEAA1DbOSgGxwish67b0KA0plHgP7iyCAckhVUbr5KssMu5qgg5Qh8GjqqFa8aJBlym3BsPjShRgU9AWvAQKCi8lVF96Hejf+q415rYcQAHFYYzChgLRY8RlhhFd0eUwLithM5f1doRrFZw6svvvrVm19//71vw/JLX/r8f/i3/uaf+Ff/EwGiUA4jVePgrsOpy5eqXTj2ZOvuCy8KdJoxiuCu/OygALfQ///7NQyJeb/JFfIeL7k+QBtXY8+iUnXWjAtoJ/SFrJ3y4lQLpMzh6oTjQBqUDlWLhst3k2XpQtNLtkIKtlKggujAxs3yyrn8kNg/OWLc02cDxAfZaR7VLnahBNRya6Ihuh6FcX7KV7Iyge1uylcPTCaglhCACtil0zo9CYN+r53OHAl3UGhE2x5N6uI9Sf5EAMDwTYGjpTnTLJ0fLLnqga57wbNVe9PlUe2JEeRTQ8IhZJDF8qGJGBcWDO509VwfwCoHZF1mZKGghHkF+5vL7+hTt9Xz/6U//V/+2Mdesf6H8eiphkzh06UXgE/3cpPDLKTgrMlLj9lwA5eX9Tp9f9uyxfU333z7zbe+/eJLd99/490f/4kfefzoye7O9vW9a3HyYu2FF+8yMOIbLgmPFxtcRjfI1L91Z2oxcwNG5hlu3LrxiU9+wgLPP/1f/W//z/8n/6Of+5l/aPpyx44L3cStnaMjNa/bEn3k8EdDlcOk3Z0tIz3H3nyUf0xTNjd3/6X/5L/sLWDvPnj/7/zk33r7nfuGhn79a7/+1tuvffYzP/bxj9zSV8pCe/M0unG3o1DaU5vl+hDHmLJLQmycRIzwe6s3idbtGWcwcWezlOvrD/mDjbXr+OWsYPkpa80lGA1CaxpSM4GVoRMc1MtotW3zyo3soIBL1rJ6kUFCmP7lnD/jERxBKwjL89kGm6LzKvJBjogYVMdlXpzt2TvGtyRiPeeGWuKNfDl1CKCnv0UTyjQK7oN1sDval/xbWIe8sJA7G+m27y6qBtDl//lCQtyhIXz7jO94npPzV3RcJvAWtfNlEDCuD9UDKJR4xfCo9U+HJzP0bRZBLZ7zurDM/bu8cg0E8IMsUcXOWtIoJzGBiLyF8GqGda3OYKP7hWBBQPammlqPwFyyBUuV8Eu1ivtUu5V1WikJlL630SznmDlcEz41Mx4kYPpCJA0bxSoYBdofBtQiG1T1xNhPWFW5hxnXLCsAqDLAg4cDxQegpIV179I/BcAqXzyoQYG+lGpMdmPq8lQ78IkOlUyUOGazgOyVoM7qpcAqjEmxOTaQeHFeMVgjsRo2EsW7Wnmfvmr1afSCfCkjsZgXb8N9ukmAUWMoyQCWkcQehk8UqiyBDQPSuer3gVutiUAJzK6uye+j55F6mR4RV1k89H9ABipPtRSYLMkgistdzWVefvVzgfEU1BXI3/g73gc3QFd1Tu5LUPOwRyWGSZWonxOZtKdVX2aYst/nYx5/n/QPkuSI7LToe67l2fJYnvC4wqi8y+Pl5pIz1Te6SCkW4yLIgkIEiEiLbpSLGsdcszwdZyOpjVHTR1owamxT2t24u/6GrHMmALApxZo91OBuOUtnoNDdpsUwJV+WHns6dNQi5Fn8VAnVX2w2y0qS5ZPBia1+WrupFgXq5qqVszZG4hyhPGnn9oCYYgYNFYXP09JgRu834CGc2wN5mitjswdVTW0b/O74mpDNy4D5EmrPLl7nFmfIIa0ebmjSF18HN9MLeCNCNKhQPzzcJEcLQOk5NoJXbTULPEfqPuYVr42H9vTs5fi5+q2ME3MCIFj0FZ6yFzzoIrDCzbfON3cztGFLMqaeRQ18Y63IuNFaIrh2XPUIlOiwQnkuIfEKZA9frpbe+dep3jlKbx/E8Pr6ngwEQFxnLxgLWzUGvyriiavD3PwN2le9ryB9GCvPrl2Y4He9Fp6h7IttYoT7s+dXLXlfeSDNUISyJQI6sk8sMAHP4trwGIgA1I0rVdqwEXr+hwItqVQyrWlRcTmT6+AZf/g3bQt3aSDHOks7EOAM/+pIT8oZzZGmW8r1B8ZAXIKLMKcUh0DeWZ8lPAxG1yJQnfPr13d/+DOffvPbbx46yn3/xS/82nv/0f/oE6eXYIPOMzQE/vQHIksb2Sku5xd/6A///vcfvv35z//6G687ZCADxIlkDR+VYgy0PrRqP6qk/OZXDbl8S5z5m2f9nqdLqe+F8BtV/CHcBtaSD/ajP0mJWKy+5Qn0pVf0phnr2fmhDmgobtgDQBB4fN1ij4yx1qzQqlW2MYQgRE7NDywyIkSrxQ0yFTV3iih5eSaxMAEAXMPCcdbqXpQDPE+NqPFgPvHYBIL3EwchPzONSw05pgfCR04vYH0uV6tUW7lNLufPyrO6crC9sbuxuq+pvLZtEZDg8B7KT0/uWo3y8OEBlTNEwmY62W69Jf+4sVjIyvmt4Bhgu3BU5/L2a7UgOFswBJAI6TN0KFvL3o7W14/W1t9y6M25vbXr3r+busNUzgx55eLA0hyHgzTehGpWDhd6h5AJUCKikdSMaTwFffvsZ3/sR37kBxp/KCpI29GY5/J/eNk3jEySbWyeHrdaaXXlBdnfeOun/RR4OmPnznPPG7l/9s6t/+P/8X9z8Pjosz/x2a8cfd5SmReeuyNgZzKo6SXBp7o6K3oE+vQGIITtVYE69dZ1z+XlCtAstt5Y/fHf83ufvfPMm2+9dffui99683UD/7efvXV9+1OYtLm5j/rn7m7DPLe3+Pf1Na832dnaHSazyzr03jK/vb3xX/6v/am/+lf+0v/r7yD95N7b0k+ePDx5/91fvPUv/YHnn9Xz2Z+oiHdoFQm3SFXo0ET/arOkxHrSfTyxaI27sBqfTHsLe/qQbl+stwr5/MLY/421zXfXO34NMz23Nzy9BUIHw1jH2umrRl/WN7669DQuHLKwgQ/6HK8J+y5OnkuRN4ywWvn5dvK4eCFZbH2jiFjZBJRqpCcElXVZmwTB+AeD89ODc5sBzl5gSmdr7+t8Dhoy0j0jSUotFxE3YpeY519tyshaFaMJ6AK82/xuFY9ovBcm4zD3osZE54eTtHyP922Ws4LFig3VpUoF2cWEfqWS4EWSy5hSLrScRYm96QLwklJrsaPVXx5WQw2gbpJaGwzvCByNdE2Ht6y4jl7MYoo223Ey1bY2DmcKFpyJZDZmmCUNJy7WnIMEUWNe0+wjw5vQgneSvLiXFndpKaApDPYye533R2fHeqcw7pjgXidsKgDDQynqYxDi8cSNoHyhdOHt7N/ocI02cyMCIZlnnNO+1BCMhUqv+kj0zIGYPIeOaTzGA7RlI+Bn2/F/Kic4LNTyD9XDWRGO6r2ztkgM5yhMcoRtrVkMiM8jMB/5D1EagJgnMNhYPa1KR5EgBk/b9eQo2Pfa1nL6/Jy+oIUlmkdtvb54scGUGkouF5p1JQSHMVdBR1114Ko3pCRHwszDJOPqHOQqeqmDUeA/MZSvPGE5biEGyOXiwcYfySCH58vFZgfopChbu9A8VddVzlLSrMk5T/pYQAzsp2nf72YADoAp4SfIoRm2C5jLryndUzdmS2RA/uXvq2ffr4Yl7cMZvzeXp13L1+WPpdpqu7q+8z6Du0Rxvpb85b2CdgkuVzxWnqiSkxFibdbEYgnJOGUy6ruAziVVl5YKKUm7pqKcimzdRz8wo8DDp7iWQAXpRiZy3gVEdCVoV1jIMpJfAEmfetk225qYy/P6HTSZyxu1zpP581vLRsX9hOugoIg6xL/MpBIhGuppvhw1/VImMitRCiscrAGzXSFsaS2TociBjDYIUlPFqpWuT7r8nUPSP9ypEl9uc5NVx5S6YmH/hpd9KOfRklhMEMAp35NwCRb99oVo03CwQVFI9IEFaX/IBDmDqjMdblMy7HoZsG9/xa0wUaJBlFgDwiJXN6E7uRCLNKJRKvwhKH/j63XnGz2dvESf3xyyAuS/FMWSXQeU9NB9RITMGO/QOpXl+4MjEllwVVFVpSMF3W5JHR0Rs+RYfkFKdy7UFqg1lJdXElvIAHvqxRaCV7v8EgbNmDEAcQtSKglJD3OCOODPv5FUmBe5RZvRiVEW6On94YhS9eTSYGkv3X35Bz/zQ//4135le2f9rbe+/e/+2X/3P/0n//VPfqpuVWuiZ9gQ+1UstxgCyk4E+i/+F/5Lv/q5X//3/sy//fbb78MlfUmTo6LPKv7g8nu5vvvBVfo/22+4PMXgaU3fgeBkSLsH78sGnJqirF64d2qZWWJOdKNBPSt8MA7MheNRJW9z3xqUxN/yIYNSIqrEmbmqToPVhAAM6sBNVenKVJkqlaOHc4vLCtbflsegvOxt0LQMxm0A5VPdFRLxfSHzktgr8iY50DlHlmEhjHbuxMpAa/FpQZZFG3QpthxJeXFw9L4TwsxuWGJyYRJt9UbrMZL+EDAIhXPhQ8ozCMMmb8E/snMpsqZk8q2KpW9tnzro5mJ3Z+ParkmlVJ3e1fDCSSfpgGHia5uscgzIAoOGuw3Uws/qkR/hxstffO65vWvbDj5dCmTvIRMPfCaK6a7HJ/JaW333/v0nD/a/8dprGztvf/3rr71w9/mDQ4t8LNG7+Ft//afuvfPQaOWvf+7LH3nRIMvZ7s41TILm9o4zNO1+3j09OTg+PLAy8Oj4iF8O7ciDb04Mgw1eGMjd3omXn/zEx557/oW/+Vf/2t//2Z/7xV/4pZvXb3qDkbjm2Wdun1y845T8rW0jIIUvxtGtewLBYWwOhNDfsiG44840ZJtrOhv7B6v/3B//j7/88c+8//Dev/dn/8K3vvG1d99510TuF7/2hWeeNWB/RoJpRWiM0WMsgDMYmWJw6bFQHzLWyNb/+Borh6H8ITyerKx4pxgeymB5jOzmfNhAklpx4BU+mratPethvmTiaWMywPDGqmEVpyvHBhWqx2ceJwymJsVgKJwAUarEwlr6EXjdUEHvyTUrWImOBCGcesktO1YHq4prIUpUNEMtpURlgqiu7hYHBTZqCoIH4aAGD11ypqlLudQP+KDKWWSeQksqwU05JaWqFa8BG6oio9ngBI/xSynZqjYcbHEIyJRhEq2k9Qg4JdSGG8WvGNeZNjFJ7grMLFxt19iG8bvcc1SNMQnn2dzk9XVpkSHsL08fC6JBteTIS7M5s1yGyGHOl1sdZLFpvZU475/42DhpI3xxQKSAunRg2CgSSSH0fzyFvBzxLaJ0E0wncXagRT5mEjk4+OPP54JNeMTAiibEhchJSlF7cImIHMgI2Kxng8vwBdlJjj5Xi7oXjg4gJZnJvNBJV5IOmWcU1FXLJTv1SVK2GGzRA5HgfTTWaWksMcya/4Flkodhm0XzjyFLWLZ/RolS6JiGVu4I6i8XgdLZdBf1Y3+AuXJAw7yF9iSTkJe/Jcuw85Iflyg/ZUUoXV5lm5IE+l1XUL8r6fv+jKeDwKhJlrBkW8ovD0uZ3wvEPmFMzlC+zFfSUvI7ai1XpT8of/lz0iJpAfy02g/yXqL/HeCeQrvKdpWpXJc5rwrMt4/RmnmMxXaIMhoX9RrFloGPeRYZc2ia7OMBqQaREvvQ58OSNYZSW5sKRLSeaND1gnJVtfu5BH6OPc2Ej59TVVaX280Ksr3yhRa96Tu1Bu78dgSsOT5PxlnJyhPMepJW+m2+6TQ+m+p5qKLayA8LEGeZba30ihHuFI+Bs2vKHRq8fx5BRZRY756aNuEYWasb9xFBUVt2aX8wHJVwFX5CBYQZ5ZKqxTG1OCPMSbzq5YFBpqzAQoiGyihCrqzVmR5P2+ddn8xj4/1IDP5i+piQDeHrmBbDDHw4poH+PtCs+BVQ0ZWeivLWDNwJg/V76c9C4DLDq8ZGGnrzl0cN1jbulbPlTVWc63IHdzWMW8frjbUHoHMBDsvIZqN9kIfIMn5T9eHagwV9v09fSIrrb+sXrbiX2SgpdDbvbW63XaQoeGhZHFlLn2KUmjSWzxHD+coTlFVX3b5ywT7mnb6gKV1bewP4YcSwYpgea4b5FequRwmBpi1q5Z2IvY2oR+rqvztQQ75sfcAWl5xGHPQYtURlubgWGDwvft3aeqwGumbzx8nJ8cbu5o989ke/+rWv3nvvTRr+la+u/fl////yn/83/uQP/uAP9oajFJR0Wt7rEy3qNnXPxn7oM5/6ff+R3/1X/vLf9CDpXyIfNlF3tWq/5Ij5rS4u9//L63sgDP2/FdAwC9/y6SX2JUzXTjhbjJwF3BoGFmKb08Gxgbr19b3NlUPnAgl6jH2eG5J/iNd0gJ412VWT6WgsAmBGA31aZYY/VSwG4JaeLTJMd5b606pJlSmJNfC/pJAlyOn7aN7ytDGN8qQDNRIDpfzzeG5mJScz1j5vOKkp+7C62474w+rMn7GZ5yiOJYSChtYL4ALAmj8nweSs6E7RDmQBGY8gZBcw4lKRxUgb3CpNOWqYeQMua23DsaUdcG+A39sw7MzZPT0+ELwcCUZQuLZycHL06MgKINTyxxSdgQNY+EIYCrN31uRe/GOhioG5l++8+NFXPxK78UK1WcrlheM54Qi7ujPEerry4MGTR0++sXVt//333r/93DPCeTugrIH8xmvf+Ds/9TduXr++/+jwlefu3Ln9fAVP7zgWeX3zgSU6PJZXnx3ZiMWfnPXW5E6DQiMiIUraGL9w3vk+W9u/4wc+9eTw8MbNZ/Z2bv6Nv/Ef4vod0wHXbt+4ZY71Pedn4mXHnRUx8MzWUTpjpxCHcKVEkbc8bGw45dULAdY3Hm3v7fyu3/NDR0f7D95/8JN/56//w3+wY9fWN19/uLn+9Vfv3nr57q2buyaFbl6sPqlPURAmeOoOdvQ2cdNels+KE51DezpwNpkWZlFd1r1rsK8T4TR2Gw/inYCqU+Ud5+/E2xtn51sXG1pDW+NI3LkRIG21pNOi6v3fR0POVr98fr637qgsPV4nino7b2Mj62cnLxqSnqmwzZX1x5oPclSLwHOONLtlXdXF5qOTi42TtSdO2j9ff8cUOx3wGoX1zagweJu7U2iUnvZ3xy46AX3ldP0NKtsyHhrCt0Kx15CNAmR3NYvE1pqv5jC5Fxzwn3LHnfQLvOymlV3JMnMaBfRMm0KLTQCBm+urGaGgBM5k/PXanyJo66DAhAGPuMAhkaU5mgoUmtkPNcb5Ympj0C/BXOOipLZBqL4ZVnA31DVLF5JcG2IiInnVSnI5uon0LVew9W3atXJ+1ysXMg6eyknzuHR6pyBFsUhkzJb+Lz4NSoYvRQIGodQ4kvBKIyCRHPMgtsyfcAjK4v2ZWaqgxwIAZ04ExkD3/k3Wp03XNgUAXQ026pXO0lGaOK4i0ITuMZjxECCQUjF0q0HFUElR7cTzSP81xjhhcRSaknILwaoI2kf6ORe8zAYLwym306hYWAMl0Coo4jfi2vEzVT8zsRfr7zRbdX69OTzzYD5Wj4mUsPQHkO9mdiWTbeO8FHGmB9KPIQMO+Etl2hVZB4KBDfNaFUf88y9GhWU8rLtbySi+uj50W5J5GrP6+t1z0pQj04Kq0GW2tHDhV5m+6/rA733Xg+/7E7WTHoJhOL/AnvTLSsJ2qfnsju/mkuZn6Fw9WXhxWcV3ofA9P5eEp8luVFjZS75c/rqEdvV1meMSlSlUwaXkBzcDBCWTj42QWcPd6+enx+2RpRrUA9V5ELpme60KRuA1WwX0yio2LDZ+4Qqfy5Sx4LjUMErlZWu+iRXJk92OnJkADmbveLjYSeZa7mGum/lZPzICxidlUW6zK4nhmBnwAwKOvNc0fmpOhZJUyq+kf/2GfJqf5AaHEJ/nAeku2+IjJlDIaIE1hgcROETWUJW/QUkYBJZ/FNwzj6UD0jBS5EyVKmseIOwbBB3CirQDWXRpDKo3uPjnUW1YMFGNSaM1jVGJjQiISYnI248TbYCn4OE6BZr+4Mzr9vtHXjkytdrsqmxU5gyzdz+G0lgUXwggB5N5TgEfC2OThFuImO8ThKB44U/zmtCpw1eWEhODRM4oIWTgWA1yftaNt9MHM8eftDFf6dk9FFrwGtEiwRWPQsyfAISzXYQRDd2lqsknzdFnqUEdtxrUhc6QUpspkbBL1IPJyG/IrXYsrEM05HnMl3Y/9fbZ7bBtWEHjR4j6DyYB7JK3yKPWtJ9Ogtra+T2/9/f/yuc+//bbb1n0+/bb3/q3/81/61//1/6zv/v3/wQSuF+V8ZGAkq+J7MaN1tauX9u9+/wrmx0cPvoR/3EQ9Y20LdelQFKVrqfpy9MPfXoSzv90ru8C9n0BL4kffuR+8CvNTWqJ7vrkRydPzrYxYVUoyN3fvHZrd09kfHK8/9yT48eHTms896qo7DUYiYs0aFEcTi8CFmsSGVlXi4wjJD+S6HiJS7T7Codgzcflr35nQh5NT3fggAq+ioHtuiy7gOp3oCl3h2PxkOenGxt2Cunb9JagWmSR9BSlQnMeIgOTvzOGN3Y84kDq9sMRUguaC1pcxWgQnIZImBV9U6lCBtp1dOwkgJ2Ntd3jkwfCDGs83n10vzHJ3krXGPLq5tb+oUMIgF3sNwip53TshQdQqtMRUaFQpHS28tkf+aEf+Z0/nFuLnx6h8MqsFjPqd3yLXm8wefLk+MRKJLC1C5u3bu48fvjw2Wfu7B8cPnr0eHfn+uNH+x/56Ef+yB/8w5/7lc85kfPs0MTjruVPlr9nq6PVzh7Ye+66IcJxGeK/3KMgWFc76fJR2+vOD/3BH/wdP/WTP2lf7z/85V/a2tpj2g7v0p3YaEJl7dpejsGGLl0Lh0oJHratxyjWWNnetcoRa7w6riFa5s5AO7YLH9fWr12//p//U/+53/X7f+x/+N//3/3jX/7li439b77xrfOLB5zwswerz9w4dkYrLhStYghCsYwGFtLFoMTWws+UmUbjTkqjSzDeb93aGycoWDwpfrKhK4YeafVMCtCNlbPdvEwH610cCswn9tFCnZ9ZzMaLcW9Wg51utuKCgIiO4x87qEGTQhI6NZrOXv3LpYn5VAYlD+lyZ60K/y+cu+l9wJZbNVxLU23hakWrosXuGeJINVnz49arQRPaVdm6F4M7wlCtTARLky2joI8o4IRz/ZRjLDFwHkMisH4QZQRNFai4bMxLbmoHxT2njUFz28foHkXXKWJEGWb+2AVK4FPpDJPA4/+gPWWNxfmdififbDBMqEuvQw8NyodgIJQLy6EkjIcPsCTZvLFPtuRG5CtvMbKHY6o1R/kJsEIO2TXcOMGTB9OzYIej5AxYPyEXMtUY2ID/lEc7BOSdv+xRLWbrmshUHQNZxCOD5HRPwaqLC/KOQVaVmpZ/iLpkimd1E+hHYgFvhGaSPFEUiSwFaOkcmCJrGUKLrBuZo0KK+VYUq7EF6GlYl3S/Q2D4LA/Vkr1MfmQoLE/ZIQ3bgyOATIwREEK4qVYJMWpQlJmBetPRdACQItVwWM00uVKOEUMMraZL1qW6lwlTmSdzDcirH1ff4RaaHvr/z+xCGI1FzVQ2bEndrq55wiMsZC+py+MrfbjKefn9tOyivFIHZk89urzva2FM6V1L9cv95ecA6NHl78uyVz8nfUmbT1gn8uaJLMv1WnP2aAghcyRDfoeU3+B9+N8F9dQs30Reicyq9D7VCtwi+6kqMxUQF99SAaAyCTmyAYYztjJaUdHlMQCQmX/5wkWfs2hlt95QLHplWnO2DAZ3XJpWiQPlnKeo/uvA4ChDJ8gTfXYf8lJSOXoZVnr2Y2vpcqbRuPSGfT/ZeUgUsElrYZ8yGRqUcl0AdYln+mQei+RZnUh0Is5yX2pGzpRpM6wGOjRjcufjVDAEIWopDtYCuxTdK18zZpAfG+yHM8NbyMZdqdW/xLh5qCXnunM8iiCNRkR4iPABuYO4Bn1UX2y+M5Amy5bRbhjhpTrDgcNuJiFCnVORM4nbJly0dfQjPiKhjU2go03DS382zfjTIqs07Le+eBT8i72QWtlHw5pTqMdizM4nDu1pTIEM5TqzAc6Ebu6VM+s9ADC/HqPU4bYC0zbZg7j1TsxpLiV3hOHD8+FnpHUpPRzmaPNfOAOs9RpbTmHfdqATrvnPRS7tnQwJXCsHn5WL9zli7zx1JwOSr27WjV5frLxP4SYuKCZQTiSvBvsyPv7Jl0/OT27c2HrjzQcWILz3/nt/7a//dYcS3njmhu5T7XrrpMR8AqMGaAVIRnVv3Nw0SOm9wjEVQ06v84/olnu18eaYOJ+/5Qce5cGn6/VbZv6tMlzVefX9NH949eNqdqJ7CeWbvA2aSpBE55wLkc0g/dx7RdrleGKXJ7uzDdLiCSceHq3e39l1rtKN/aP9N+8/sCb1tHFBEhwTThzBq8pFqlkscNnIVJyluabubpZrlOpWyWsP59ECqKwe+eFRujfzk7kIaaXOgzItYEpxq3kyMFuEiA5bWY3zGbV1YICDMNrgC9+8GpeoXTd00pGaK/MukRPew4tW1JsSVQPEA04hIWCAvDOsaorDuHgpY267TnGQ9WOW5e4fPbJSxxSq4O7gSExYpHh8fn7YgnpTA8rX0LTJIasJzXFrRgk2syb1wcB26+l2ipvRe2I2YVsNZY3UuVuolrtSxua4MqFtftw4+/7OLlquH+0/OT0+dgIP//Dwyf7/4y/+pRdffvnw8ODw8eFXvvzV3V0TFivruwfeONpZCVGNRD2ZI7r95MG1tdXd9bW3miuGFkU/esG7jc/WXseMk5Pzz/7oj73ysY/9ax//+P/zP/gr/6d///98/drN69e8MWy3RQWK5EmmnTIOv7kFsSePD7gI9nRx+uL62cuOD0b/iFeXAE+0Zc4thcbyqsTjT33iY//j/9l/++d/4e//5E/+4q/+yi994StvfuuNR889e+uzP/zsc6tbZ84sZXkO+toW7K6ediyqZcw3BfpORTg6tV5In4NTNRlsVJcfZG+Ae9f1xskFsz0wpM2+de69I2T9bN2LFNdPd1fW3z+zheBk2wvrHRW2dr53umZt9M2Ni8eOSVntHRTbJ+c37GJYObcn4aYV/2sXuzoMoOlPOKlVzH+xssMVqZmWnZw4fGjdYPb5lncj2xa85SCLJ6crTsvqnArTBIL5cy+nOLFBGN9oFf+WD6cl03QXZ61bKZ4/9rm05DSzrpMSCQ2rRzEq0ehR4/vUlNDQf/p8Tf/6O/3g7/GhilLcfGK9psweIJdiiW2UjFKPsQR5KkrvxxGX210FepIQ6wmFB1FUvmikOziY6JZ9ejVagKLfcvB9+hcSWHL2FgHEEdmGpkNfIQKuRjaiu/hy/YU2wHcUnC7k2untGaWxlaJWDNtON75BjOenXvC+tIJ5/IbYgY8I2bwDCE5cdpNdfkqdVkSrgWfi4/CaFr/6oUaU4ZgV0+ianKQTxUAWhtSiZZeuIXnh4cLEARF/XOME+/ar6CKE4nP0t1B1yVaCLkE8kQ37cQIe8TltL2KKq1JzSDL1xH3QA20eIPelHmMBt3wD2//pCCWHmO8TXKQlnhGbKmb5ZooQhboXZfIvNPK3KuwjisJnKIqEfpRxeWBXjDzecBeS0VKOPvwNNCMHb5b2HdclMybz5YMq/o483/vjN8ryoXRYhlopsByPFAvmWr4mM3K2Wv9SW/j0ukT36e8PoyPvUtzTufHxwfOnj6ZsEn/68HszP4X/naWukgN89eSycBQBiu+sp0YqoQnkUom6uBITVVmm3nJ4Toq8TSmLSrnjVxbUhkPJUOHlfkJqP69iRvqRSuXSIhk3lR/KRgOLOPvlygymGKz6OWlTwA8xOENiYtwYKBSraWFgs6VUTy0ztMCaNeNR3MNq97wWM0MFs8rlLvQXqs7AlaBt8qeQ8UFDpr2voyxFiAidVNJYn2EYnoPZ2uao6x/q8kzHl1dQjDuvHV0YMuCy+mLHxStHaxwIGV82si1URxlxDMdxoUfT6TbtKLFhY6Xqdagr11qOguqGWrmeWJ/1pqnq4hMGt35doVIOefKTla89ABeDBL+qzhEgTRPLITQMlIMDLjS1sOnKhAsQ0AG4tmOrYi44B5YvKwOAEYFJI8e6KwqD4PURgGNUEWIiafAHggXm5QkjtS4Yxn15W4dUZBJlqje8pCbdNrWFV9pR/pR1PqVnqF34Q2qk4eiyraB3DB/kVJOGLSqIbuWDFnH9IzxJENGcOEQVitZjkK81x1GJObI37QKxi49/7JOQ+fbrP+NYqu2tHfPmRxeHN1avha5+QogMNqrDETp5sfXxj//Aqx/56Fe//GXIOXor7NOv9HZIDInoiqDf5PotHv8mJX+jR/Hh+zz7fmkh7frQI1TGUWyrm5e+WKGnw36kH+mAXQfvIt/rJFaNl3o1QyOZa9s3d2/ee/z+RCEgojvRDB/8ADBNSUyJ6Gl1KklY5a/CRe2Wp3FwmlRfKapPOVyDap/uh7cDcZJ9TNUeDgXJ3dh3MZXwED1JvfNJL2crGMaQ6oMS8THrhqv3n3CZ1jYUtJ9dODznWmo8DSrgvsfwqQQzVAs06AJm6BQ3fb/oMuKfPDm6/+Txu+8fcCx81daGIWQzD4JMbOO9BEG2VsAq/Vo+aE/qXBe+5EWTh5cm+BsuZAIf/6GP7t7cWAaG85Np8XAn2l0Jb+xXOh+V7V+/ee30ZP/0+OjGtZsPTx9sbexS3s9/7ksCqXfvP/jUJz599/nnty2+Fyjh1oV3E+YdEOe4INF/Q8hOIjt4mKXuOKvNEha+SxbYhjvneXRycvuZm17NcfPmrW+/8Vbd5Di48crdl3XbwzNG53N5ad0LHNu7tpOfjQDrnEzLhDdXItD0VId/78ZNh9qNhPDdAaaHH/nYJz/2qY//7t/9z//UT//kX/y//YX37j80nv7Lv/Yrr7xy+4Xbr+xuA7JpZ3Pn93vDpRHaBL6pA2CiRadvzWnX3hXQ4grD/5ZBJIX11X0LT4puc+ArOiVOnGjxVqtSW+2ZQVussb722FsjuT2fK8ebDaeSqtmD9aPzQ9OAJg82Lw4yBlGXmNqMT08du+R0I8S1KZyK+DMDoDeoeTZvRk/4meML79jbMABRm+a0KNktvWqJS4vNajcuG6BUnXApZIYUYml6KkMSQNOE9AEO0SK1RiCzyxoLFGtrig75T0pWyyHF8FJlW1VGakvAMLAVQWRF3ZHy+HO9rPFx4CqFa32nB+FTP7rm1hA9hDryZwL+rFcmzWtr39IEDUnFl4Y2RJVP/PMdFdMQmXnRicVjTW1NO2rlgG1eQ2VNR58dmU6zklfhKm7AQm4r3I7Vh3n+D1z9hhyz4jEMAIzvUIPMGboe1ZBgg5ZXazvkNF5GUoNeBaNykFA3JfXZb6nhfYldPxUeSrrtZvkoLQhTbFKnWKQmpyszRiYMLV1OjklTMIBP6hs5T33qrdmVsXhIhwQdLNc9ImPsIDUgE980yjIPM4oH0hf+xU3ETblYpbRE/Jq5/cUiNJFVKZHr8hlyI/HS/C/FNWQCt0CcND8WeYXhZQb1LnmX/FP06qMn83QKhvxlpkHgKtd8L0A+/Pnd8JZnC0RFejy09t2/BfagdcX4gZwwlssSIJePQCWJbq4S3MyvUr73Wgpdlf1wVqRdXt1ccuVp2lXVV3mefneGq6p5w6dXeSc/xMjY4h8rGuc+nUEfwXE1RfvqScWWogljNDd9nwfS4zhF78TMldMX5ew0g1FLPqHHUBx5eAGOaJGNT/ycl1FgYc7cB0tatS0IBmXCYEp0lWOpcNBJ2eu6zAA2JBpuqbSZ2EVc2aXya6cvZQmb73SQ0XjqJcYc2bEdMTdPk8G0Jrhok02rr/hdfqs+auHrZ+CGeqgt/nDCOIcRM0zComwMkH0wl6NZlcwPV3KpkIBTNym9GGiehF8mLEsRqieuSmAO31UxcCbcZ11cy3BIekjIaVrdpwBCGdYHk5lh9zS5pXZVpy5VhBgqFehuHAUaFv6rq8OMEnc0+CTNwSEvLXrI5fbAJHPj4nxBHtXoyYnTCr1prFci10DIjUhMCqG+R/AwqD4OF2l+1AZpyTFar4IfhSo3FG4gxKYhy+iMVfsKCf63BEIFMeqdvoKX8FiSG7yo6rqiMAWaxL7655IvXGJL21LRmt5E1/Czz5S5P2iPELpZuOQYpWJZeaAX9+BP7MpCECG9tqx9MMcvvHjnB37oU9/42tcODwzOnn3xV7/8yr/4keNjIeGgkZOue21dLVoMFt+8uf3JT3703ltvHBXUGAt/EjblDtXBLOR/q2vQrQP8/a7vPrHn++VJq9Q2EH47+b8PjMFh4XWsRC/9bzifXj3eP3hwvmuZs0CHllgIXju7trFlhYtXBQsIchJebyegmRmAxQkkm+4CjStE86F6l8RFqEuyp2OQ8W117f1yT4kk3/1TtZC9aHUg+5p2e3Ru4FxmzWAYWRN3TdhnC8yIorYUu7X19GemcXiYwFtXIWTd2XYozcnmxdb1G1t79ttuL0PyNEqMSJnoT0MIYt7aS1bd0G5ap8tgWN8TayZ4gqOz0/ePHr/+7rsHZwYXHTwiSOmUJGPQJ3ybU5ib1WsVUXMANNEJGFCASG00rsvbQDt9dwzrxupOZu1tVKfnTx4e8yfLKuFhsEwLJxIZ9UytrWZJ+0PMJQcDt/DXAnozdWKjayurj5882t7efvbWnR/8gR85OzkoI2ad2QScoSJMfCTYbYwlNFY2rr2PffkCnXbrATUtG/dbyCRlff3Hfux3fvZ3/ti163t/7t/7P/2dv/2Te9s37t69+9yzd+3rncGmQGRCOXqDDVZkbR8cMBqrd2wzfnC28vbZ6W3MFAEThcUwx0f3NTHXr9/EWpYm+hnyHh/tnzz/3O6P/9in/sy/+ZgvefjoaHdv5e37Vg+//9KdW04aRbYSnOiZ0H/cQx2t3rXciw30B6CPqQRqT2g9hotbZw6zWnliqYVhDac7W05NMqsntxpEatORlmWzXuPK9Q7AXr1GY07Q0YH6W4R3dv5sHv5UPweV+AV+oTF3kKq0iVy7UFdBN8ID0b/o284z0qYROEiFNaq1q/UZbppboJxKNn2dZ611SDHyi6P3fY7O1pz5kVA8puQgZrbzWLL6U/ka7Cprr5IVARoZDnq0J+MBKsmOiGoi3VHvaYZSH8WmsjlUUw2pyhiDG350BocW96yiMRKqjRH6krQEsHyt+vw3r5XHVRMCmVY9nNQimbeZ2kKsQpaoiayW4XPZwDA8ZNRcgBYhjc/CdNPQ3QkMTp2lWzu4GLihm5NinxcsEpoGXg4Qdf+cYuiVyRusGbfUZROKJreWnXWd3Y1LG3YXqDq+YOC4/PCDFlWct55rrk0idZWrr7nJ/Mg1PkvFpCXDyEKGS5gxJHB9X1xsR92sO5v0aA4q3UjuITDNObIrptBkAxKzCiF856f5lkYVtb+xrRkQNQyKjXHNzAqg4alDO484MlOVfssmK3xMZZr0wOXcJkCsUUM9+DjtcPBvGXmc9DWgwmmuuYkP47USaVrk0CGf6c4gPzn9+J7rKZjJKEeZnhYJ5/n14XILmA9/9lSZSep7eSbx6U0ZCAXfinJipPvk9cFVwiBf3mUG4CmsKzomi+eX5QbGBxB60JOF7km/rGkSJ2E+UuXlUsMHdwu4q0dXDz78/T3PFq0gxHyBeSyO+czLv2gf51bfcIwwjBZaFpETb2Mbcg3AhF4kHN4Jsn99g4aYtJ/xZIg5uE6XoyAeTPbpIzQG1qPKAOPBIK3Y3Iz3WlrqlKMLeIAJYziWaKpjqoVyzmz6Hqn0AkXxIuxUXnAmeOtJctAaCjusSfAeRzbIjxYjKq9ZLsiFUTvcJzwSKg19DQ4zCdeQuux5h86CeOsvIVdLPQcjRiuQ6Y5EXkYzUg29Y9iVQSMjCSzElBNkJYoVJlFNDNNinPX256BCk16LO4MkUy5A+XEBRDTGS7zyzYf18o9BPIcQIv1YvLC4wW/1iCryBzGp4UmzzNlrF1PHK9gujh6vkBny8xJiPAPLIw35dAMusVFQtgUBj9UCHlbajaQ+nQ2kwbRIPGfB+5u1t6YibMDxjYXiZFP+zfSX3GHhMWm0jAT6B2O/h9rSFVMwlPq34I/hC/FNAeTi1I4z044pHCNllYkU+iGDwvPfrx72GEd8NtQHvLBNLVUo9gff0uTtGLD26U9++s3Xv23k0VEP12/tPnkiprdkeQt5S5FlXSy0Me/6tWc+9pGP/fw/+Pmt9e0n5wcoahIJjrS2akZWI8HB4zf6gNdvnek3KvzbTMeO6P0Nq/Lg8sI7F+3FxulOr9578N760eonX7zD8A1icjLOa7GXjJ3io17B9t7u7fOt9w8OUoQYv7Qio7JP66z2pZblzmf1DEbL/Qh9En2M4oUL1QKxMldsipaBNIKtwDxcbi5ZSXmnela/lCb0RYu0+UKBPJIMKTTVZF0erl/c2LnOcm7uXb/x7N7Bwb7D6a3kMQBO6L1L0KZ/7iX1M1fU+3ETtQi+kQLjDuteN3J0vG8v5v0nB1/65je9Lm11s5OCtbEdEipY7Ah+WpEhml+Acare/7Gb4o2oHM6L1s6vXdv75/6F/6S3ET98770bt55jb7/39/24MBG4+FP2vONC8xC82BMgUZ3hWK/ZPKbcmcUzz9752Z/5f2198/V79x54VeDJ7uGDB+/eun694wsZV0qOT1qGejdCZD/1BBwP6qna8vwT3smQt9jqRfJeG3z79jN/82/+9R/49A/95E/91L177+7t3Xjt66/dunHbpEp0Z+gNfwfE6L73yW/o/m/uXe+4vZ297Ws3dhPheIThCcTPHj16eOPGjYQUKSiSmD/Z2L3xiY9++k/+q//KT//sP3j43sPP/NBn7r/97uP9/dcvHj1/x6qkcU3cgKpmGUkjvcXYdWZ0XOmmhwRuBgBmtkgeWZGIO21nNWzfaIFJ4TNj+lv2iyik+sbSThwg4JVJRU75DEqOx2mVHLlxCsLVU60ZYsU3x0jVYZQtbcPXTIPzbo2KXnQRGZbARMeAbqQEWhlbf/VObd7FWPAqF0vmf0zyt3yBR7E0DjXFiXtyjuTnPq2ObVNiNEr9+U9Pi/rSGiqMqUbg7Aq7rGZpaJT0dMJTaILU6NI460AiWqNbo9Dq4p4DiypiYkipYDWzDi9dqXq/qxXtqSsyszr/m0axn4FG2WLQEF6kDUuGWwyT4lJG0ICzXqoiZRzKcOu0Rq2gNperamqjTETVhsJosB2DYsOba071Ld5XP4h6rqmlXN4KkoYWIaTqGlNY6g0vTKIuY2Z1QiIiKqDvBQZxMPJDb5B/KiZdDtCqZCEKD+Qd+mJOdEZi38HoZ2KZqKpf/b584jlofkVg7cpIxcMozpGgoKHJwPgP8ckbfZVRtmxhmJx8BTmVSReTh4RFUYIFi7EPewHFDQl9ygR38ImhNQ0DoMSpdMF24UOQv+ea2kOvKwSWuw/dSAiXIaMMH840rCnDVanv/71UsjyTdfl5VabvcUOXbCfHK5Ytefucu+VnXcyBsGRTGqM2Xw/66e0+vS+wRwueV59BmOvklcBtvh53F7xPXg6c1UWX8Gn0jOuvGX1ZyvT8stIl4ennd4z9P03lKF5WdtUealrvH0Oi5tY/nr6aq137Zk/DkA3naMJkkbe75soUGIFSpdHt6Fm3/mkZfmKUeaCxYfl0JajRY8HoybxcycCfEAAE2UfDZHnV7fl6XEqPYnF15mR81Q5mL3Bcb4arhz2ujOaGYcOTBx7dKpZVJcfIkKx6fxOwpp5V6XldX66gdjWvo2HmVte3cxIyj1UL8jqsF+X0nFHXHIyZqPfsJTbuZCGocWTjKaZz0b4CPkkCXL0nj/+Z9+xwORmJn9GEmswQNxoSHNSh1bnFUDEK6JwRZaswX2NgCfX5I7ReeOtx87wihuM7HND52re4QBY3cwc1+UmiQFY3hj3k1nKAcdKHeQW1RlNVwYX3bewIFvVX/awucbmTv3sLpmZ8JJwPyM9BuNfl1E9aEaOfnb1YV2rjTajyaArmCZroI75aSTAhpioiAgFTBlOIONCQ+IWCnC0VmWEUvSiedBQJo4Ao5u7SQQO54R/UDV2eooT/JVzkk2F1yepjUQA5pcNH1aGgCV/QykfIUjRfOcUUwQYCxO1pBwh8EqXlvNWY0jSLagm0w3+kcZNUUOtifFCvE5ft6uudUM8++8yrL7305YNvvHf/3k//7Z8+eHj4h/7Qf+rMuS3rr4dnfEijRpOMfa/82Gd/5Euf/8df+OJrmIeHFi4PvuqNnAWRQVKbfitkW3+/gOnXXJfPr35+5/eH1+t/55MPfk3TdfnzKv9ToJCIid99SQq75eMqx6T0BLuKixGI2Cenq0+2VhwAZC1NrcL5tiEGE0fOT5ytjWIVL9d+4iCutc5PAOQhDQIisOc3g7fx8Kr+pV42eKuU5WSeD2Oy5BsosnrSP9dVucv7vi7TPFdPvD67qQDZxHg1TqJbxjctuE9Zt9dX9y4s/JjlMeQojBfQTa/Z4GB6cOfOrY98/BPvvPcFS1CckX9w+GR1ba/1LlZtmz0Q6lmY0P7MWhTDbr2pr4GFYvq6AyvemHB0kCOm9+AZkbX+Q6AmnrSe0KjMTQPsF2vvpiLpMBRRMP8WeimaCk5PPvXpj/wb/9l/3Y6UvT1L2LaZiSk14+MVq1ycyYktLIpbuQ9pA7TDNNXgbE2OU5fFMTynJ8fPPX/35375H26cv/Cxj/zIj/+EE+4tiLowVK/Y3u7e1uamo7H8l4g1TF6klnXmh+CEzipr+MCArk3A56cf//gn/5N/4l9549tv/IW/8H/9R7/ozV+i9ovbN1/qvQcNDEGqxRhOxxd5nV+8f2JNvp7SwaFj2XUF7EI+2j/aMbeU+54hAtTxDI3Ex7oincWTjEu6uHh47ebWf+e/99/6z7/5r37+177yuS/86uf/8ee9S8H7xR4/On3++ef3nOi6a9LE2x6Yfcs5MMgaoETgPYBGIyZgbfS6ftu1s42d4/MDCNLYZGHbwAbltnifJln1w4k0+duUAp+RyHBZi+Di1uDqaLbC2c12Enu0tJgtp6w1wgDS6AGAfH+NGlaaP8MUaE9zpW1dPT3KMem+tAt9ANZNiPScMpYvS0Eg2AYPcuY/A8yBjSpA6/S5TG7znsTz09uawVVn42QSo1vpRWpWe6F+bMDbYHeNJnmgzyLFmzf8K9ZUZoEATO90B+z0mULuaIkHPl25xvW3rBxZOX5+AnIDXZ4GjCzjUy1TA4gYtT572DZWnHyvv1MhRLWC97IbDPHYHLKYSWX02uqBiMkk18ZfVtyrjtFeO9FpS+Tq7RyxREtPgUMSWhnXpMZA7U5UkdlLFr46O8ikkFio5mrDzorYiWRN5bg65Pkn0R8+EEusLNpKmYAq2PZ7EOp0oyYnV7+tMOQLntWs7PFLcb6zpOSGS1yL5aIFRZNJOoNBuJgscMR7eY/vZtgbb02YMaWASiLzxxoHGCnawl4sYbIRuOkswDS0eqmGumTxCWz9oWrD58G4/EMAE5HgP5i6um54tebXZYZWb89ACumB76QpsKh1QMIC/HCZQ3Ub9XflhOA+vJuEEqeGvpanw7ZBbDi45GWoeIiL8ery6swr8YqTgkLnUuGuHn7Ht3jYtWkOpysI1s74WlvWzqhC5SMA0vcjmB4TyGXuKbfUcLmNcnkw6QPww78vE5aHTz+T+OWPS0hPH6kS+9XXZ6ztSYrguiozCJXw27sCtxStU6ohs4speRvLFI3NHhnVJTkBijDIU6PaWpFNrCh25XHTKuoOqSWeH4BZqj9wGrPCtn4gLfPY3GjCeufmVmvPJriytBu+Z0d7sq1s3lhYAK+0eUjLDFA8cLQiUNje8d5swmgABQa8i4waVTjYN5aljaOiLFZsp9CaIzm0sicWYNja1ildytdyb17LfXjTyamXm8wQytG+Mvb1aTa3zFg7++PMnE5jeWKWtdPrhqYuNh5jiNbRP8gb1CuWxc6xRiNBGQyHWLcnfnZuMZbMfDTmFDK0x/Zs5caNGhX5RUfnjZA5+tpAVQGApN7ABU4b6bDbMdibO1YgrJ0fPZNlbhzw73jmni3V1g7TroRfNyNe7e7KwxRR682aw9W4SZ/EUBqnnmlJjBCiuXeRrO949xB22zuY/V9YiUuW9Qo8sRzWVHivRdnVAK1uX9vwLk8LfwcPEKcbgREDftlBvmjHpbI53YMQjlMMzI+6ufioJpD12UzG1AWSbjb/5MRYG2HMwWQKJErhj5zpIU+8aEtA8iP5lCUF8zJW7Ku75TuXWlKNgGYZupqW9BOfR21KT1ELqjIyOWUq+M+NrXSQeacynmJOw3kN2NetNdChI+RWgcP9k5df+djb9x4eHh6/de/eP/qVX/rsZ//ozu4eq0qfBweg62xwVment565/S/+x/6Vr3/936ZpprFDOA9ebyX6p8zCnYVJ33P/oeR/urdXVYfG0+uDe4/nuky5+hnK3cOfTuKea2N7/fHZoydn165du3n45GBL9LDiTPsciXXyGI65znS5cIgLBk3JICS7xBxIH/MduA/dXf0YJPr4AI0yyjkKIHV5MJj14LvylfSha6oiH8UpjH/jaYs/uMU2YSbMXFNeRbnUrmm9zYKts4vHjx84I+fmzet7e8+/+dbZva99XWy1xoTaTdBS6OOzk8OjutEpt65QKw2y7pZ5D60Me29j7+GJA5KcmylNJMdOU7CJoalz2gnPBdUPeJL2SKM/eg9rn/jYJznda3tGys+OD71TLFsAzjU6FhULM65+ZjScjxieSzw6OJCZDdLeTWv/L657H+4zz9x6/96jm9dv7+3Z2W9xnrB17fjAWhpqbifwzv6TJzoA1kRNUFKwgFPqw65Maxxz6Bfl1EN4/PgR9A4Pnvy9v/czWphNB+turn/0Y68wNe2MIugGIxflMYuveVpXnVcueLp7jWsCbCJ1HXLwxXis0gsZOvUYjtG4mDuPRtc0EvoUz9996cW7n/xDf+SP3L39kb/61//G0dH7h0dHb9x/+8U7NhudUMhm+6zl54WyfuuAtDLISanyCdxGcPXa6IM6pKHIhtDzoxaKtTzFcFrtxloS91q3tW3Ba+s1x8YpeIGTvf/IW5+Ic0Ih3QwNk0mEc4f8+JywUUrNLeH2RyeA1ngU8tKcZpIxGJrCr3YnN9VQ1hnpaChHNv8Nk6U2Uz2BtmaKT58OYExCYGLqSoEkNelaSoKrIcA4OOb5yuYvKwiJZizynQHgV9WAtJ6O/8zbNeYSRP/IYogCoVoDo5XsCE91BIyonXg3aIScXJrjAGgphwC1LCagqHtMKrn/1QrjeBF7m+v1S8MFZR2BBqVlS6ByyoCougES4qbcNRV4vAQSWaXi/SvCSb4ZXihnqJPUal2gMD16gKzF1wkzSpnE0riyKpbudGGD0qE6RfzsQdymZpOhR/EEqpLnr2Iwg5q0IcDX8gOs4SSwS4wOGjwv/4GDqTobdTuqvRrCwceQ2zJsP+ESF8oz/xFR3arzPYimRvhQexgBU34epL/AVWKK5wUrR1iyYXG55g9zBliQXRVaUM+cYBGzSiwKnevy9+C0IB2wEBgMEod8l6C6nZxLqQ/KzoOpSdqSa7I+/Sh5sn/Pw8sE1XUXkhVyr+Yc/xC2lIbRJTp+U9/JOjkrQkiN689VsUkpS3CvRDhUAbLMFVw+9KVfMrMH8UhU+XK1eutbZaf4IFK2y59z+1t+BCFC/BM7cqk7O97urltfP37l4pbhmZEjqxHOUo+EJN5tGIl7Pt5dUqonWcKtPjoUMvw2o7vJYqcGL1f3vrlXdSo2tp1ZKzC1EtdVk4asOLvz/ojVfK7nbKArmzTe11FoEUsBBaLTKsiglKEQKjmsl5Wqd/yZ0h38wvAhY6qZojtoQgJt1JZZnnF4cQC4gY5eNGNWNjboKjjEwzSx5Rm9wCVXNwyuVu22z6GSA1sQUWaxBz5lcEGoHIXkuZmZRowdmbM1IXgIRP8WGqJu3fE5sUy5RLqymwUFTY/CMXbrZ0fP1x50xvO5l5lzraLxCjiYJOZNY6A4jKAIYlYcW+Z2BsQK5RttyIu3EY9UlowjM/lUaFYafe454I48ATsX3bhkP4o8yhju2jZtQhPiTvve0GNa3UWOxQmWc2N4Y09yJ3Iep14N77BwcRYuK9dIFWbjZqOCV7ImMwPqarN5bkM0NYxE+6kWrcawRr0zGsBCDZ7y6e6td3SvajAVmT/s9mMQkdJVZL9oz3xWVzmrJJrT3GWoEmH4oIuFfGAnt5EuK69TnugWtD05qs1vfUKro2o35KytJpHzi2t76y88f+db3/rGyTu37r357b/67J/7N/7Uv0GdCch0zWBSIx60uHvw0Y8//1/9r/8X/51/6998/VsW94rR9uN2jLkUlGyJaEa7w/ef+tVAFM7pnF9dxtfRvvag324W1l7dT0rce/r0ku0LnDn/IKHQIbFTlO7uH579+rffPjxev7HuaJdrZ6cP21g7rws+PNo/95Zby3GtQTt9MMr1DIDOSMEdXwDFqOogxKVeEcHD5X6QCJG5Rp4LYokuupZI4vL5d+a+THxK4dqj8i9aoeKmr+hegiK8mt60dndtZdesBpaIQw3eiwtFzH41+gDDtZVHB8cH+0d3nnn29MmJLs7N64xkTwjT8G+Sd6CMQxtPznSDzegBNO+gTkEb84v03e2dj9194bGR7uMj3VwceHR4ev/he6udLUoz3lu0MRJjCBgxB5ZDemEKD+CMnZ/48d9lkHzH4fHGLQ30mVGgxtm2kovyLxxBGhiR7vfa6d3VNr5+i9fVHHA5KNvY2uazP/+5L/7y57/iXdc7m9de+/LX7tw8ufXsM/qujt102iY+1IJf2Op95LUFdt7GPNahSt9JcfQ+LA0DtTT/mVvPOJrzC5/7sjd/ff21r1zb2bpxrdcP6wtSEL7M+JJZNkVX1x+PHBoY5ymePNnfOIXU9s7FthGf+FZgGRVsDeSHjw9um27a3tS/MjqbK2uVdl1vO25W7KnuzU6W523+a//Zf/l3/vin/sHP/OoXvvy5b37rrSMdscei8vOda6vGf85WDwkVDDE5GLnC4ZLYiU5YMdSWKDmQqN78h2lNtuRMuV4UYAyZzBunX7VPV+NA/piwOOgZLTZon3s29kwGh0ijeG7BsApI3yoJnXXC0oS55iII2tlH1ERTZaIAN29SivWN90l1feV2nUyxLmRncESvD8oA5llzVBVMQcoBq0lIMdOfoS13vbJ+X/ayyFEnQJniZ1h4fHH6cnNDzgCUMIN60Bbymv+vcTz1GsSsFkw8qf4CB1RYhJaeSefXk+rYmrYq7p08by6sGZtBTu5wLboOT4CI3Uu06nmgBMI1Hhi0TFLD2AX2RKLoVIkZlcbITS+LNBCgo6VIIQE3Owzx4UE2GIFKEBDEh/lqqHGVHB4LD+dLGeA23tDW8QdTawjhTtxlzLIHcBhdudCaK464qaXG7Mu07vyPuo03zbCHQEkqD12IiQbhFlpddTBAcVdzs4CRKP+ldZFUKy1X1t9EW5iABynYDX0LOiCA4v8UomYeEs40rAkFbEMI9+rcnT7rfm3zXguhT++oJvpHYnF52dLfuWdhM1gBacqLBtKC4qjz3uBeexp7WSdJjkrFpv7ZCuSrPtolPcrAi07ELVeU+Td8iXRJWZWPIE7m4cMCbslQHs89NKI/kEC9mBF974QOWJAFDi/L49yeEhr7H2g+l1h9ecPAsHEBvmrlzgc5k9JVNYOBnOFWVU3nhbTsIb/AvfoqX/hfXQPl6kffuF8ZRSNhck9yANQo4TIttC7rKcNv87qCGQaq6ItyEgxp5XM1feZ/BVVVj0jGXwQ16njSlhfsbz63Ns84SSpfTgrWQpyy5e2rxShXqibEn3jPyLpWM5sdmGcG42cBpeKyFWO7K2gcGrPzgRwnXLXBNFUFcjK/4rj+6a2jgvtXbDEO4IaFkWc4qmY8bBheU+PqmMJIqrFcMmuSDThlAw5YG9+lbj+HiGiDifB49C5c+19kygsHHTOqs1xYloF4iNjMNNzqLaJmZrGzYENBmQYYxsrmYObmBLi5BqR5cKRM2FrYMSMTOXKS6a+VJ4v6cG6DmnRVkJqfzTkPFrCPBM5KTB+DOzNnTnktHc7zXGaNVEMrGnutmfYDALsO8bP5ZG1XI58JNJSwOnH3O9ffT2FrS60azCX6ppKiC70OshMWe5sNstm3NoOukD/jwIDoAg5a6k5sOFWhEUgV5Ma7wiGp8/YRuwhMGqEvEvRYO+iZzIm9O/eyjsYmjxGWyqNcoXmWPP2srC8d0UQ1z2I+za58MnU5R9HjYjisPDk+pH+WymGBBh8egfFCxfoq8e/ZW5YCPfvuvdPN7a2vf+ur9+698+ydm9kXourDFC/qZ0aYKi5W7t59+U/+p/4zP/vz3/qZn/57R8ePa8FT9JHxQlZ4udQDxeVzSfmn/zk8GLDfVU9ETuUf+hqef5Dak6srTRxdoeDrm+uHZ4fffufNV+9cv76zfX6a5L0spzfpbO4aYFg5Fl61ultDiEtgFLGNio4UlmYyUSSby+spQh+gPE+Wn0+zXWX/rlxXycPSpxBHlpyh4GmCCVDG3dAHQ9piFiqsPevIUoOwrlH6dI5raO6Mnzs/Oj15cnqw9mT/0dmp4Yd5LVOjHDqZo3l2gdtWu7ZylAslYIUzMrS7dHlZ6u723pY1OzNLKebzZls9C9EF9YXSosI4kXaEIq64ajOXRECu7964tufNU87HzP+oIK+iuvgavQuDqt7FOYI8IcqBoz0PnhxfmOGcHpRNCetrT44cR3P93fcO3nv/XXL6+Mc/9of/0H/k/ftfyevadrrjHQC2Ggv2wVUH7qijNmVAIz2DggGzxSL/tyyY29z8oR/54Z/4Pb/7H/z9n/x//OW/sr3d2f8vv/KRmzevGVCuA7bZKnC2F3njDZa2g+6YT9HFQYNzV4+PvPmrUCzX2FZDV2MGR8cHO7vFcJc2FKvbf58Tmrf4gaqZW73Y++Tv+MFPfvp3/v2f/dl/99/7M2+++cbp4aPn7r708it3Lflrg66FPlt748B1cPC/0JUZa42Efdxfffski8Hw1YDy7Q7k751lw9xk1HSlgZJ8VtwHx2e5jUJxKQJ7YLkpoPVnGnszGNUchKueITWkZIpoMdOyxnLsECfEIjN4jRujmJFruJe8ezQ9nvRj2JfME/Z4NUmcjxya7ETiR3FjCkSNcrh8dB5qGpu0pUYtOAs/8645SFnwJNVFjASGsDjF2v3pMOkjDbQlBhx7QpVWgjXRidiVeUQ7roTjUi4PAiQu9mgQ7NfYKNVK94IPnSE67asw/CHpBgtCpRbDJfYX9w+wAC9F4bD0iiZLaHBNE7OkwAFTL6Na8EJtNhgPqhHaASrTsAViA5eBwmu49BRImCnleS4OK+dxFlm67JkfLiWVGrwyT+XAzzVxzsigts+jyT8Vj0MYDCvNaSiw1Fc2MM/nuNNu5y947v2ljCgmd9+XaXEa8CKCIqvaNyLVWHGAOFGZsQI1pb2p1rB8aUDLmc0tM1s9SbxR0keP6s5FQhSWFsqw4SqaqgpUn405L6LNreX0XAuYkf/VLzB6NnD6dC15526p9DIJ76NNpiWfHG4S4NXl9urRktrzq4eX35e/Rzglxeqq8a9H3XTlj7od8DjVz6Vozxc8LkFdPehn2SsVlpO/35f3fQ+1eiqSz3fLWW+m51NsvqfYcvebfw7ak2XEqpFxMMscvECb+YJifkNACx6DBFmu7u5x0xsC1X0TxCRD1Wu/hKcZz5LihkNiKLUIS0l+oqp+XTvhTSmG/82So9I4gIhcFktoIF50vnQoontozznFDjUO/Y3fOHVGFUZwwH/y+HEqmZkbUjqsI433jJ2WLgq6tra9ayENTdYstT2K+zT3no5eHG8Yj9va4oe0BOYL5+wFraeAFW2nF9u98dU4XLPzvA0UWmH3mnotwOT3TeyaRdBWHezvR98oK6nQXZ4U9blFZeJDUv1/s/ZfwZ5t+WHfd3LqeLtvvncGM8iDSCSSIGiLgkhKNl10kGWbtC3TdjmXq/zgN7/5wVV2OVX5weWSy0GWKBKkLJeYg2gRJBEIgAAmYQaYfHPs3Cef48/3t8/p23cGIPXgfbr3f++11/qtX1q/9VsZLQpVM2qmuMSH/aYbyWxUKG5aHFfR1LRgv1cfIcQGKnnU2uHO4DzQJwS5b1SWDTZXLKsICxtFWDTQhxkMOdvaaQ8QOStN/JWjgzYbSShxzc+U7SmQXtQbDJFSzboSS01C/1NKU4OanuS9CjQyXYaBsNH0BQUX7RLodMGqbc2Bc7Mq2yvvyoplKq2IONCloINjY3PvwCRoQEEdvN09+xpYVeHCrQEfLpCdiKLwHyYZBjBMEdHuGsMOkeBTlSBf/FyJTN97xtR5GEDUKksnE+ncxckuToR5Q7w5+3iQrXJBxEfC7pdV1EcFXdoHtSwWEdN8zJW3VpBJdJvXru09/9zN9z/4Koy+/rtnn//cl3/+T/5xY1DYUqtJxhFmsxGwNIsMPa3+oZ/64c/8+Gc2Nt/8B3/XehXCV3pAhZfrgpJ5vggK34WeCf0Dbx+tHPiOKPENGP8VXtopgowwTMC9eZ1MTm6UcuPeZXrxJ1yMeZzweboY2xEwCKtug0pLFAajJVsPj88+uHt0y/bo/CHNRGda1ZF3qniZc7LRCUrit5f6qbmI9tSi82cP9EFVb1Rr+qoKH0Pi8ansB4dvu8EBXa6olPRJAg8X1/IUkhcfc0RQoV5byWJUEGQJIfKlMInZSiHTWB8iq2JeRZw/6Sl9OrNJCJHqXz58dH704NG9ra1r13fXj50CK+oppWFlc+5MCdxs3GA/9qdFik3rhL2mcY1oMS4AyoYltjjYmIPGQoq7cB8JC5dHP0FZqBxwGLe2duu52y+83J5sNBdI8MI/WvHY7ubWrLwdA9Li1LgSwZ8+Ov7gzucJxbODMyb66pEe/bXNtz9440u/9znutlJ2ePjO/XuvLXwzWfT69eurZ8/k7a/fqwHX5v1Ey6ltrKOipnqYY6H431x/kymPjvYdmWcrn5/8qZ/89X/2+bffvqMN0RQr04eOjRGZNMUEHRnIPT+9yZavrt1fKH/4aLbVIqKm2Fs1tLG7dx22KFD6JhfqppStHR0c21sfXSv2fQ8r/NM9H5sdSyEvkxF55StOAq5tdvaf+uM/9sLz//N/8P/9m//R3/onv/M7X3nzzfe/7/u+/+btm3u7V0yqbt8eNgCUxoU6FCWTHddaz3qiFbt6opuD9tCVGbJE/rJTWdFkkXWVDTZXo2Eei+WZdyy+MJ6o0zPQW9d/XT3KSROWaPBUPPnjDTSpTERqAk8HOmiifOiDQXnR1s4frFthpauHSqI2rch5qtQQtO65jKFMQz2DqUAhJ/bp7/mQ3E1BhWlqVOOqlhydm/YNPOCcBT7feBc0JKA0QgoPqdOj26NtClEf0rHcVDXYWMjNt9PEzqovnC6Dxvxp95CBs2aNhJ2f3q7Xf/rTcTVOZQTcqo1nrpO5mLclGvWHtoOfO6yj1tegUhHJK+6+ZjUCzg85xmR8Z6vlOm5JbEjtJYVhN0sYXhRwtvI6mpn1RakiBWwVJVAdidMuHB7lUFuvpGYXhScOgpSSCcT3qoYFulgeRw5kgJ/Tc1RbAuCEwVHILSZDgBArt6gGBSVzTS+nN7HmkkPrQo1zvDN5yTc6RpBQx6ywhExwIjNK3dI5pgQbSqGLgZ+HSw2/4pgYYVVzlIfTqhvRsrpHZiIoVtRC+R6QJQaS6HBMuzu9gkFMo5OOK2wWnMPmsK0Oray4T8oHE4kD6JRH8uU21PKUMtoBwW9XM0QWaBEQ6v0DaOgYHhT94lqiWCU7M2UuQxPDR5GAM+8jFi1XH42ufBTFo3+TYplxU7xCJmjyXRuLLTTZXcgiVhcllcdz39ynAVDSuRZNm8fJf4AuoC9ifMePeKW6iLlksbwUdfkSKR+FfUTIdwD7toAnLFjC4axcHO8789HJF4aL835PdAIn2shJJUlLJwGHa/3QnA++tHmschzv6lJQ05BkehZMGMHEPKyp9tP97FjQ84PdK3tZYYcgHuidSqCIUCZkJzJMlsKi3lW11rOeOcxipbGVJMXzVJ+TZ7WpJNM7m8mkiDA2ZTMhiF3ebEqLAogE9k2zDcBs6M6Ui0K/s7F9P9HnwopNLV1u2s2kDL5+p5mdkjsgl3xuNNqPgkHV6ohC3ozGUua8pc/ZDk/0XJMmGJFGsS/kBtHcybBsYenRdCc2XJDCZukUyphQQZNSecA6adb3ds8fPXwgCvMfCsgLmaXXxutcAZlyi2JFXROmAlidePjo8OGDB2EiAJZgitvjsEpqSDncvjLoOB/T9ONj5sKGH7u72IBqp6LOMuWK+coh6s5sn2RVgDPq+QxZC5ljUkDrSF86wirquJJu8exmduSADoUEBZfY4aUSmp8T6akAWzu2HZZZSYwEhv+fMdfIHA7FXherzLplQxdbAoOFtMlKPbFE6yv8Rk1j8/S4Z6xjtp9JM3BjiLRoGnxkF3LDsVwMlXo04hkgvqGBNQf6fO2Vl1994833Hz58uLm78+6H737wwXvXr9+EMYKy4RTDAWojlVwWrVln/Jzu/PSP/ZF/9qtfvP/onnyXC7AR9MXr/x9/LkX+cZAXHPp44NNvksVtP0gnsuXbEuJ5SY95C/gaisQVR01bOLfV5T4/ipDJTheworu+tq29eNWekjuHawf1/NrixeRnY2QoV2u0UCj9CKabtMmia7nP4wUeT4cs4R+L9x2fJ8BNBt3B9dM9y5cc+UA2lafCGq/ZstPTRxZ6iAmN1DVtZS+mP9sRuJvbN67u6Ay5dfPqtat7z95+5rBxgEeHjl1tAx8WwhqSNuHRkLCMnvwzWQrYlHa4VgiUx9FwTp5gwPVKHNQVjXGD3ehc3JBgKuEhNcyjgTZmKE+3t813DlJ4DssW6hA7whnNDh5AOL1IqmdbfPbt7Gxnt9ntJhGdHK8/eHj/V//pP3vv/bvX9m7sbtlg5vTe3Tv2OLq6d2WZzGOFA9okk3UWmx10Dtes14qjqlpjIWOZj/b3+fovf+IT3/9D38/d/IVf+Ktf+tLv4ORjCwm2dl/75rc2v2d9d9v5CSTtzKaMHQKbNBKu69euXlNg9/f3tywi31i7fuWamasnJ02ckzszJzdUUJS7dz/cu7p1Zfeq3EHL1dHBtOqgrC1HT+tyMpQhieqjJKfGig+/57u/58bN/8qv/OPfevSVR7u7e/uWBbzz5suf+JQ5Tjz8ZvjMEkvgzf2SUF9Slp412tDyM9Wq8cSjDcfdrSvq2Zhx6WbapqGgtptT9hMJbInbA5Rys5gB9NatkDXpPpXO+OioX0RNssPCJiKOquTJcZg5XOpNlMNEEwMPmsiZiZRw2g0ZkYBorKa6PY9pTY3pjRGt8dHT8BZeCardOxUAHBdMcTW+ZiKlwO0c/akGrDw4NE+4z/RozHLCqNyXGScvW56xHLIGQMIcncVLROkZk5z2JD3IiQNWrMqFFK71NXowqWwEoqY2cqJESSLBcGaUX3aDcJWPB3lmmtN68NWM5dR6grhR3HKNGzILZ44K67MgErHkFWzsziYwSGEtHYJATCOmwhuty61O2fFL1TnRhgfh04caQEHT/xFFg5Y8x0vKL5/qp4wyAXKI7ygbDN0m6zgiZVmMLshpODaSjNo4LSjcS1kigox+MQe7Ms6y+NwTFyV7FktzKMIvnSTJqfZEQUw1HL9pegaADOVhaKKRHTYNUmUsX8cDVqsiuCqvenewMpPQ8R2KBImkQSo+v+KHXhdc509JIXZ1bEwcolKKwJRP18Ts07xd3pZIvV1gs0Qscvz+KHZAlqQfB/AkcOL3Tbpk4RGlF9mPwi14CIf3JZ7lDIRPSwNggHu7mFE0PfdLuok30Z/cLj/ESRnhqicQhC+ld6F5wiRqbbKQp68FwsfDnv7+1HNRT+vgsTct2STBbuyY9UuN1aqBSYUpqRjbjTg00g2V1sSXXmIIhBveeslXq5JLfacLQn9DZdanOEatY1XXCGM0bYQ+qmjyOf2T3Rxiwm2XDSVMX2oRjp6lJ5OPHjXmptKoS7UOg1X9zaunR/XbKQFFq42eLg8X02QQ6sKZHYRRxPpb7TCRIc5eavW2EFaR5lLXJ2F3MZN+F+QRDj0e6MDHFqWDDBrYXfzHoQqgZpDHh0OjzLjIm5lzQ31WnhNquCkT3ISTl2LlySODvetrb2TRZhcQKNnn7uDgcY5HTewpbAMAMooVpjI+U3iUuyldDOZ4n7JXFYwzKm58rqJJSgTBgcDV7MeCx3QyK33Z8/gwl/VxuoXQx6/BfOGYbhB+pQYXedafJww1q2cHenFV0Ry4LRSvHGkDnLZYkbPDkTvgGzmSRrCVcIZUzlZNJVBt6gzuFPqAYCdb0wIqFkeehA0XNVpoh61/GYcxVWNDoZ5CiElWJDJ2mZ6CgyEwbpdtylyhTcejaVieGMcE+EWxLFKvDK1MkFN9J9vKWDotuKInsyTGS6NTZjS6hIzhCoujV9Kv7bey09Miq0LQv7i5ev3G3o/86Gf+2T/7df26v/wPf/Hqyif+zJ/9M2ebry9aIIuRasLygOcZ+5XDH/5D3/vf/O//ub/6l//y22/ercyEY4KPkpNrYXaxS8+TMh6SIsxdpO+4Lnf1efpDViOIy7WAevo+8C4/P9X3P0FFXBIvSQa7C2hPwj0s8ZJj7JpKAged9Xt4bL5zu6mTjbbdletrazubN9e2n3tWSVl/fHDn5GT74PjB4dnOyQoHbO1o5ejeg+MD067GqE46YC9zvyD/yesTvP+5Dx8lL9q8kXmozv4k6QX5OzmXhmUoKJXxG723Z9sNTWy+3mDh0a0p4CbzZbZ2dndu3L62s7ttdt+2xs3GsUU7N29e/8rX7r7+5jvNha7MplcJVTfBeHC0O3Wt14Ce2xjp7aZ+nLxcF3OHy9al8fDo8aEik5KlhU7lTJONQkR0RjWJwCFlTxw9No5qnFY0FIlSvi7PIttRZLHhC9dKlp9aJNZAj0T58gIzFuYxnj96/PDv/t2//aUvfW1nZw9lL7/yys/8xI+++9bbGgDWklqzywwen79rhAM6B3YEslD6iBkHuBLUPM/UuG2RMcqeuTvrG7dv3njpk99jBea/9f/8t/jNFmYpxdev3fjuT32qHpb0XoHMe9jc1SDh0dIaJUVJXNvY3ti9sruzZyc93LRMmVHSe1JGcolK5oVyHZ+/9s03b9169upVbZYmKZkNeqSj6+h8Z3uLmWzCjL0m15kjo3CeVXn3bt7a/mM/+3NH54/eevP+b33u8y8+9/zVGy/u2Y14b+dsC6ONd8pEZs3QGkazWXriDXGxZbZfWXmsBt3ECjaPheI9NcHG7VAGUZWexRnC8ONz7QbroI2mMl/5TNURapwcPBIWQ3Jp/EsHTGXBwywRW01xOP35aqc2rLAawzgKLkunhaPKhWlavfmW1Cv2k8GfLFstjjSB5NPALLtcesuIt/8EnFR/Z0dGcau4ZDbVl0SpYHVHZQTu4SGDdrVl/YxupUhWGKsFQjvDDh+m7OhWw6rIgxVFBiE3mKL6Wh+zg2EicCyeGSAyjFfUIhex1c2yqpMdLJAtsejwcMnxCu6hQdOD0PiAV3kXVGNipm5GQNnLeBiKWFE4EbEkH/ds9S35JpaF82EfAhLWLXf6CXiubODk4EhKyx94aIjVi0Qra3CITIwRSglclUTAwKoySZG6l0c0Y+ekH2OiGVmhrfc+ZFSpHiIGFNFI19PZ6rfSj1HH1CNME23Vm+9Hzxe4/q5QQOTRb4KfERblXI2dciVZlk12FfvSAAVtkbHbV7HmirscD8LoIbyjDoiaTir8NNcn9ShhWchnRmTLi0cGEtAM/SlthRzz5TS0eE4BST+fZuu9yRdQkWKXp8FpyW7ejl4OwSf7/MSniyg+D/YT2Q2GXQMlfs5zbxfYz8Py6l7ok5BkMVcs9aH3JWTubqn2pBDtIu5liLk5lw2AUL2AMz+XUQu9TLV86H4Jr8eLLAqeiAVcXvN4idBF4KR9CsBl3D/ot6i4lRqxt41qKo5Z3VZD1t+sDNFCGpTTxtUWmV77I0XdWek7q5U+lkrE9IlGVCAr3y7qm+4zatOdQKEmj4udK0dAspetEk4PG1Md1WVHpgjxdBsZ1bUgu5FDYBsZgDi1gYEMprTHsTxCpS4X8olsQj5v7oKftLPCrSQ1aMUcZ6zcatiOnlTwl13ASiRbZW+pVC7pl1PTlljPdkjIeLYdPl8fbuk6Z1b2JtNnUuE0U0lITE4jyehdSI9lkI2YwDj5PTybqDM73kzfRhKSgCkIqii228OomlXsbfzC+fTBQ3GKFsQehGMVgOwIMK0/jYg0Yspy6ZLSYFMCQPwXEACYIDyTPMZAersQVngxJdIq5iL6nXmwxp2DBYg8wdEQ3GCc43QwJfORNDV5TuecEhY8S1UStA9KHgbEYr8Hk3KvLdL26bLLyIk/CpChqWEw9g5zy3scjeLM5VtMjyrwJ0LsCe0ZueSNprrFjzPTZJy4lM57qBW5uy7PVCOuRIk8G1UZpKb6gUyNJQmVDz8q363nnn2O8/H++xy1s/fvvH7n3nvXb9fiiYLYAsgUqbLpSq9XVn7uj/zcm9/61l/5S399o2WUE7tMkR6n4mbXQs3y8OTeh3/OdZl2Ul/EW+A8gfbPSf30J4z4CNiFSvX9SbiH5VXYcK0c2BBMOjTvQqM1c2GvEgdMmfF8snb1yq4lqudn2w+rgM23vnp8snl48vjg2BxHvuiHts3BnhElVg34i9vHXp7+8NGzKB/hOy8LI4O0fLsAMkxO+5W4K46b0hAnZB5ELVPtv3V+o/mDiaqS1aBdrp0ipgasbcwHpV2jIRW8M53/j45O90/PeJxNQCDxNDbrxbLAoiHJCv2FdCWhF3l08cpBpqpSK4APDESwlGnAhdegWNDZ0rniLrhV4qlQRWbjfPeKoylyyqRL34paxGHLqFIAe1hgLCWRDebR379/D8C7dxrvdk7z3Yd333jjbT0IBv8eP7y/tbH+7rvvm8/3zDO3JnmAzE48eHD0eP+RphqPHEPY2tq3QZdFXR5Mt6jGPow1f+UbX73/6PB3fu/rdz88MDhgIoftU69cvcLabVvrTAQzcxyr9LouBR0uYtbHzzCdnNz98EPTnBj0o8P9K1d3a8VfElf1gce6x0/P3nn77fd5sps7Bpw6brvuzLVPf88nd3euZD3iDZkaqq2qYxiOjw/+W//d/+6/9Kf+xP/yf/W/+exvfcHw3fbr11755HN7YZ+8csp64oaCZIUjkR1yTw8OohnaPNVmzoLNLXKnQoLSKuxgxNQ8lCqB+TX2V2+JHVePrI4QjzzyDymLFMs0oAzkILrQx5KrAzJSppHl5KttzKpqPfJ2O3RQQGPXVTjDEdCW6gPeggAikSpEuLGvTcElqOrTjFNo08ypYSAsAc2eMWY4hFx1VV5b2uYpRcW7hn/jjxAqNK5Bw+1V5altTQHKPxnMMHy+AezAcwOsnqmp/6cinpYB2GMA8UnS2QE7Nlb4ICtX+GAFVlGIGhMz15CqDZqLVqd5C8KKUjOMQrlqBJkVxr4v9UMFR6GEUx1s8cZNbjEKpgN/ZghMhRgjpMQ5ETkCrJZC29QJuM7keXktahuG9GSEPew1QILeUsYu0pmc6eC027IeMxYBBaytZeu7/9ANp3RjkpQseEPLEh6jQWeaBo9wiv9TT0kEt5JU9wWrEFdy9Br4uDFQo66Qap3ydueA1ayqPCb68Qp8QsKMaYQWbi2ZgBSgwYxoyliHxCgTmIzmCAvMGEvwI4NSQCbrRex8zkQt/zQsfHwvk8Fn6J48oid2JI55KLT8+ym2hyC7TcSLT4U8uSZ9bz24LiH0O2mX4OXrAE4pnvqyfJ8ML3K7bABcRlpWE1/Gk/giz1gEs+2+dD6ATqfXoxPJBc3Xi5wWUEPT8ukjDMLpo+vifIBl79KPgn+fp7XD3P0mZeD1pfarxLQd4bDxhiHkk6NnleuVtXfDraVFtdntzZZI6ibW406OHU4/rs+IgcbP2IKpIehjEBchTuFf9IX+5HMT8PDRCYov4sP5wqWTVxLa9tvzFWoLJ+hKcOxQIcna5p0xN8w7/dYrYKEY/FhbasZt0ig2Ve85XvfKtn1wMy0++B0diPnWMhRudB15FQFAkeYHK9SbL9LZ1bV31GuZPfTalyZjkIIqngHrDKj6/zl7o+GgqLeorTn6mfDRnmyYbGWZCU+ZBQOSyFa336s2MXemqXLi42qxewKhdggO+7ClA7Kyku1l+xJWxqEMyO7SQdc/CsGT5zJ/G+9NQWLIROXHqw1Q17ieHFXkYdG/pffAbMIXgm9/5S7NoiZFNY/w9Ln4v/mBGT70A7FVfkMcBBg6dQbL3d7uKoBO9XWava2vdfzD4Y0xe7eHGvaOy7xpg6WNDq4/4MfUh2o6tYGCJlWz75xBzRtU6GjT28dmIKUdPE7MCz98Th1A1PWY6ajLtiok+dOoTsDZnLZWVHKoYlwUeRR7lCyTwLYCi3FSWpi5dr6/o+44WzfV6QQR65YsZKRU9OwzcMmo4QHipic4zrkzzaH1fAYfcPJ81fxLPCCu5BZjsm/Zd6Vje3ftM5/5nl/55d9yrvyXvvBrL7589T/7Z/+0AbIcmzHFzcqqpNNaoyJ8E5nzbPbVycw+1o4jCOy4ETKMqgiT1fLUw+xev7J+9zLkD/yVZknp3tXPEPkRtAn/592WpE/dF6AXEJ4KL6TXDBklr+hse6h+ol44YKzI0uD1je1dO96ygCfbZ5vHq/vbbap7tHZqy5RKscnkvCcDwg3QtaqEbVSheqWwOEe3ZbBwY8n9CZVPkbF8WQJ8X9ZFrN2fgBQGdgPyGnZ4oiEbWw+vbDpjCsL23m2aHyOoNOreL87RM+LkNNaIZQnIkVZsAUIRV1dubK3trqw94BfsHzz+4O47ohweP6bbdgKr9NMcbi2jtWqfYF5Fm/Na0IMzZiFzatY2bB+cObv36L5lPvafRSYtk7B21Ob9yWcKFp3EpYULWWWBAbcF0I/+yI+0jabcRhARq6BMlKzPcvVQoLvSxIgmoUiQG80/evzw9PV3X//sFz57pNV29szV7edf+NSGTa6a9nN8bP2SvV3pv7RWxtePk2Pa7jQgVvpirVbTHuNMyXlMdhEW/YVXXvri57/5K7/0177+9uv29D87vW0Lutu3b730/HPvv/eBB1wJwdQzidhBLgci+zhu/fnKlStXZ7dkzeTtnV04jOOQ3x13YwiLY/SGqs3xKccnB9kJlvTQhKzz3/vS6w4b3txu+bI4ag29ybYyax+jDOWHL33yuf/+/+R/+Lf+xn/wG//ka+++dbi7+3ht42YnsSmXW9lVaNFFfTbHs/0rEMC3Kai+z+mJgrl5DMyD6qSJQbwcHiju5CHGnDFwOG4S0OnZwWHTIqMZ4vFKNcP2ml0Ou9KSPEqybGwTAPhs7EINkJVjTB2QPBvrmuruZfqTxZciXK2jeWWek3SZ4wV2wsqu7X7Kqy5Af9qlCVHVkLE9bs4LPzfu0kcGmF6EBULH0C1eophKYt6hb2Cxxq0H08idmfeWkesRpwPuCMmNzwuNYxWjhe6x6ikiw5xq4xzyElrOshGGHIB4qQThvXjMrE8FtpKhajoehSoaAXD5ClD7aI27qZLag9pctCApjIqRkcoRHop4FBYd+JAZAPEcCu/OmW9pOx5UlaAgEW8fnSDqWE1oi7zhp9pWYTIlrJ2ji370fBXP+rtpBSRNsyCECi+50qH6v1fW31e5n5+85NPaNt8jAmrnYCeuxX03FE847IkVqFEaH8QthiCwva5rsV+oQX6DVENt8aJGHGD9Mk7Txkijo3xhDjwxtiwuzGOigkmqJYu+iSF9qoiLAhIFiMOyUKU6kzbbueRJsPm2FtndLv+t9yAmUyXBSgbM9Nl/IiD7TqmSl7OwwqFGFP3K+7jwpdOMEi9XPLkIWIKefOkhlJ4EXKQo9OKKNcOeBUShSImifiMUNeW3MKffixAIFBzwfgLjZ84NUB4KeCqbp5+XTwN44j0VrU/AXcbocy9PXRcUXQR7c30b8Kdi/0GPC2OWjBCRguS29eOPdqS5wCrOtX6H5r5xepmnmrDpgwA3nFKQFAxy4g1P4a3Ag+qZ0QSPhUxfSzB6wEdKYWUjW0gSpztjwHKotzKo6VvqEMcBnwjlIhpty5hOqkb4Yv0kFl8eXMtMGIDghUaHb6dnEAUrTOqxAGnMq9/lqzy4YhkyUxQ0Uegu45LBGUi1yKEclyr6DY1MD2HTHxd1hDOvLbQy34iNsqyrIiJTYYCN2xehYV0RCLyrsgxOqaIovPFHDVInmN4hjQUklWtfh2hJQTGvJlseVpDzIWtefSm9cCY2/noKI6XdO/yIN3tdMSqv+u0TSbkTKQVuTqcvIpvZ1ccBUQ2p1tFnhBvmK9jAJZHm/da/ltHnxuIzAkVpu7c6D5ReyqF9YE+YEpJBXMl0qG7kCb144P+qk6Jq5jgWgYW306LRGrul83pEo2IpQngiNCwiqvdJPrfyynjheRihnX8wtWLEqHjbv49Si0WL+FtxiMuu+8zEC5Vvk74btGF67O1jMYyWHn7MtF9tGKfXru9M5xP7fKpAxLQqntx48lM1qpgdcXv71gu3nnn29Tde2z8/+Mbr3/rgznvXr12f2ksKf9HgwqZaRPXZUbGNn/vjf+LNdx/++q//0yPtjkue+IaS0Jr/hX90RfW/8FpSf1tU8L4t5A+A852xJmk68Z3XU4HF6hVho1i2GDaUxA00jHbIvzk51fe/8ejx/bP1vdO2QycVvoAW4akVomvbV6i0SUKqizy6it6UxrBeUCqDweDph+9EaQnBRA/+h5LfC9SWUDrU5RsFN4v7xAqfbdsMi5RL58SPyt4QkmrDRbAOXX6YHkCL1rI26YM6MfNI87fWd29dfcbQAXKdjjUjnYrnma0Ujs5MRH/8cP/oob3RbGi5tXZt74pCQVPH9Tl/fHDw8PFBrfbV9d0dix3NzN5sM6rGB2hzT0NBJTi844zr7Oj45Kd++if+1L/28wIuyO7jRc29sG/oHFov2BFDKJg2CjV2otfRowOprdT48pe/7iixilSYnNveVPvX5bASk2r2ruxBgsd/YHXwTPvZf+RM61Q72yNXtqJuP2xjkLUa9JOffXjnzq1nr//Tz987OnLCwM7OhoPKbG/w6PH+lWdu3Rz+V+AUpAjMrjH7ckeC6e8Ml2JnF65zU413HRtgf+lOTelCsOy6wjffOtHlLObXdhQxCCfHDx48sIpgY0v3hdlE61evWkqwt7d79WC/BVnmGJm3+IM/8KPf/30/+Is//uv/7r/977791rfsKfTcSzf3ZociwCHWkgcTOauMDApzo/I0fVGqGY4IqI2gwbr0x6dH04shysiNOiQ4hYC3LXBUSiKsah5Y0cDQR6cKwgxZBlKrJucdNxJ3nC4c6f03pFmNlM0rRXq93EcYyaO0RRg3Og/aJd7CNMa19h+Jlq+Kojqw7pH6ZZZoU1un3YpAcMZNCOKSYZCl7ZZPgE4qgAP5BP4CGs3KsgR9L5bEDaNE8UCRpjiL+g4p1c/W4+hEolulkQEOqUA4HOnHpMWSwTKwXQvHB4waRwdERSAMZ0aDqnBikaIoOcGqSyIKqyonUUNt8u8hNOPeVJ+9VxHV8EQ97iei4UPwo7OhlbHvHGQh8X7CWxXHg1GbyU4eEz+OzKCZe7IMuBwgU6JhtbCuwEAEloUuYIdvC74TqwrPRZAqu+hZcqKKnmzsC2Y4JgOchV6p/F9yTUY+PLn6dJF3TZaJ1cfYdplz1AnCjGFIcEszeps+NGA1uQBGZ7EtQormRm5FDOeBMgpSPkPu4D4olGlwXQOrt7gRtkXtvb8Fq4skfVvgFjB5TsxizxdJ57nXJ08TcpFVgWUCt0letOGwoCXlxe/ys4QtDYDlMwACL+IuQcvrU9mZ1fRWn0YkaUrxFzHEOM/+R90loAtw57vzQReRayJenFs2AX/wbXDvRkjxX+1C8wCniVvvcI8ss8nrXqsHHbVs6dQBvleRE6BayNYuHa2Rg2ho/KjuiKaBgqe/aAwgVhVtOOMW0sx4xyMa8nQ2aEVR6d96V/GeWmN1dfvdfNzwkjJWZxoINaUZh9xr5V2JpTUKpHn8KK+5mVUE7vTZ6tGNu57W2/8BWz6s8IcINVTw/KX3sBnL5ZN/Po8W0UPFOROr5rX1vo1PWZ2T2uiZiVo2FXux+a9n9rJj+U+rhWapE+rrybM/PXpqOMXSoMfDbDcG0HWsr5Fjn+f2lxZ11BhS4TFUZHMV11cTysZb5RiZOr/JGij9McLiXu52n6JpdfOD+DZ4+okSoeym/WfEF1PIyc2Q2Hi3zv6MSbCHG2URGILkzDOBGx/ErJPns5Vrd/FLLmKDG0UcESP37ixamOhfmToBbUg8uYULCAUT9/DgbO1oa23HZi8ZntODrPPqfovB23KxbKYuadnfeiMAgy+WHd7iQZg6YoKIHhonHFI2+FIwngQJig9gA00jvlmsiWQsgibJuUKHqNUYFvPxyrgD5gefrb1lo5PVlWeIxwiJqnCbR7PYKWxamkrhQb3r5YCQqa7nK8brSiEHjYV6yxZNKaG/SZB05Xe2vbXz/T/0qffvvW5bxS9+4fN/5S8e/oW/8BdWd2rfIhbyoCcBD/Ain3ypkxdfefa/9uf+yzYy+tVf+mc4dd7YINfsIbVAqVRR8+Tn95vlv3wu1enNnv/gOAPuMvo/5/cCzt2nojxJmopPeBTVHL24REgv9brS9frhsExxPVo/WrWx+Y7Z5tp19+/f33IYxoajObS6T+2Rb28TItpwzqvojpurRrRGwnGSktCoBWglMU0lnhT7P/EF09nvfxKEXroRKcuTDg47E+hMpGPbW5tcN0hkLLRdiRwZVWrkrASatkFvOP6kbW6KnfLrUFCmHlj04qhwaru5ufJjP/7DNQcyOxwWrQUz0Q/u3Hn87n1bIj348PD+4X5mbPvQ9rIrHH3rXynVg8ePP7x7z0waLQNzZpywq3DVU3xk3vML920wun6/YpYTM9zN0lJQA1DOiD2+8/Z9rayzU2NafWYqR0JpWgK5kBciLt+mkjk/fFYLZ33tNRNsKlVnq++9/8YHHzI+68+/8NyD99ZvXr959eoVOxmZJ2SbDrjF/cZORT+988EHGKSIWUcqxwre4oLZrOEou7hlte7q+a0Xb371y7/72utvv3/vQ+yziODmzSPHUt2+9QpbamWt8xcRo7TntxOLxkM1QKLGQ1nsXbES+Hpi2jjW/V9FwRpNOVJGGOoRUmJBQ35VLYdaKRrtip1dFwxgmENuw2fbvz3eP7tz9zHcHG125co1qzf29gxDaVR86Ezj3Z3td9/6SqtQ9jccP/zqq59gg69cu3W28YguKpxYhTaqv80wMkTqqJYu0CgY56EaEdFRks1XZUJFWLSwJ0pzvVRNZMlw1o2SNKl1HVgJQM89+s932tvkwsAFQu9801cxZSQ4xmRGjBcXWXZJOLak5rjWT5qeaQYHr2JRHGP46wmKuWQmX7WRyuX4Jc9r23e0WEZlpuKI/6gq6cCviq9Nm+UDYMkiWaAp3ASgPUrUhhnEYpmJU3cSC5ozHZfKWawGH2AgfIBfABwgYoKpoI2FCWy4G8ZfWX/MMurRYZmx/aJxpJO9tTOyFAs+UtUDNXxv27qST6nPfuAbgHUu4Ty5hw2M8yxwqITu6GHf+Q7DvF69E90Mg7PPgjc/CLKMRT+9Ve258m7jKIqGXOybhL3ZAFOqnm2ge+MOJ0uCcNn8MKlMFqfr7z6ZLRwP+zwohVn/KAfSU5g4u1BTnPKWBR/j9GVSPl9/u5ZcFMJzfosF6SynCs0j9YO5wCExTFLJ6KeDaYuKb3qlEtNgwoLBcjyUmCafNEyCYJYy36Byd6EkgvkLyKb6UFba25HFKeajcnpZAzBMLMPK6aQwnGq8pU+Tb79lg5YhUiARFDR592WeQwYSQERLQZNuYl28+jrQvBZ5gbzECvoERswocKUDrGbltI63XMLvInqfyn95LUpvlz9PNwCeBC4PTyd4EjLAlzf3C8Q+evdUsgv4F28Xnxe0elkgfxTpIsLHf/qMC5flbvglqZquvp8Yx5i7w4hIJ1ePgmwU5MfuBhkmmsIyJOaUDLWEPBkrMLiag6v3oNrnIiMlIU1MMs0p1H6gxNqFwfDPL33llubkLAaiajiSyn1Au8GWbpW9jNt5Hngp5JEO50ONePwCOgxZythCc1rT0GqRgWRIyxwGoA1D5Obf4jt64CQCKXKMEG+JNmQnCpmp59vGAeA6TjJT/sIi4+MvrgiEhGJ3cS0kRTerWGTw/S9Y2vkdSsUQJ8OUSOCXN407pSybAMfViTAhMPSvmDoLU9VoEUVrjjXPVxh/HCnlEjcvUPIK1tBN6pEQY7N9cBsBwjBMiAzOhgBiBbICUCMkiqM/nsSYwSv0gAl0xAKaJKslY830+UTM8NO9/Bu2iVOTZ4cQTd0aEzz2LbfGXoHM0BBbB5YMaI0UAiE3yJtcM8LSllw6jcIiZGMbdLUzq1ROO1StgY74k/c0/LnkTk0+1KRBcufbBbp2SQTp78WGgPqvTzQ3hQ7gWrxTK+JPxL/44is729fu33v/4Hj/69/8hm5dEylK5Vt0xivxXJiiozQHenX11s2bn/6uT//aL/9WY/AhENoX4iru6G/k/AHXAPsDvk1wkgX2nxflX/Qt2i9g/f6gPoI+uFeE+C1055jt8GyzlJqZGn77W5u763ataUBO10DbhSVsc2/mHKo1u6g0WyzvP25gGetCUWtsLLnE0Au5PYX3guATPJ48DD/FoxXUZ8E+49RzlWNTINbX7UxqLaMBSSM/VF3geFqZn8rPFAQP+kxXbDRschAp9cr91629a7O0EVVUO2EQ3uv6nrnxDpOmwLYWvvdApzmbh1yTLU7vPb7/8PH5tSsthtQZbuhJHibb7LTpfW1eUZ0scX76zMHR0cFozVICw6eeZq2Ute//ge//9Kc+8WM//MOQ0YS6RDJVvOAVJEedsIvKDck+8o8qAmb17F3dufvBY+6IBs/nv/BF2Ip158696zsvXd3bmbwyRMZtFK6M0hQfKLz8iVfu3XnfuN3hvpUexFo/0eRLc1NgNYi8N/SvH5195SvfNIxQJH6B3YSuXud518ektddJLFUDagneIE4LrWVVAei/knZyfGCZzWw9dHC4//jqtb1Zu4wpmYCpalQVUhJZnnW5JwJhGUgcn098UkMEZca5p1oHj44fPnhoZfMzt639fYbj9t2f+Mx/6mf/1c//7m/cv/fwjdffevz40Se+64W9q7u2RkUL/sOzZhc0oVUG5vhXLU5tZMhWznVtsCEim0WblZxSj2NQ05+hFyHjxh1jDqlhbmNKPNYcKcWbd+qAusUu4/tIFGsqVaI0jFCtK9liMvBhGJaJXdLHvoJSef/QPY8F9CFaxtIamAu6bpKZODpR3VAoTUkqADLLQ8DRYM0VMp7RkEnDlvJAdZbTIyWu0F6Y+PGox8L6iOJKd4mLKjJYPgrX/seSXMoJRatiT7Mxuy3CXCppiPQw+UzVm5mm4DhbqYT3THQp0gImWOkVkYw5GYdtCJpuMnhTXrEHGb/RNISowIYiX4grekAEc+yDiGxYlZamob8+lmpG6LGKNIeO0ZtQSUbusV00r7D1n8KMC1GLYVyLIqY53kuG6aXBtEERzILDtWqoXEGgXSOd+AoMUvufzEZuCa63/KnclWQZQv2VhYDKkudeSGHEEzcnSGI2KWRHJcIoIF4lXLgSLjAsPaDxU4+qo1dJupoyYqdozxHwCbu8fYgXkiVBKRO/6+JnnnsNx8Gzz/N/4oW9VB/FuIzpV4TQ863Hy/u89/bUhyVsGNqH0PJZ2svIZXKBQTy7fB4sJ86TBsBliuIsufb0scu+ckPpBBbn6TST/WX0JwBCZF5snv0kcEn3L1oDILrEQ8lCTxxROqpBdFmNOcl/0iOXQVO4lCJJTEY0wkkjqbfRV2mOZqjT3gZ2Y3DSRDsFYRU1G4lXSskxhzU1qgAm9ZVjWzgoHY4zOTrfl8TXrEju/rS/x1pP1WKioZ6Mi85dKcUyOmHotbm4aoY64Oth4Csw4k2/CCvx34Mtr7Bet/X3B3NTcjmvvtLjqF8eqgVWbOO/W+umUlEdi7i1rQ8o4OwCCrBuHvnM93guxfMi1YOugzl3rb6l/fN9rkLhtXfx07oIrBwdjuPwodKlrkrGViw+NydeGdn3XWCbbA6RJhSJLIDarW6+baY0Tzj+ND4/dONpBR9AOUINgHgeGN6zyqZZSA2XxjF1KrMzPeSQizN2Bkhp/HMb3d4y+3+ER6Jt2ZHhJCNYqhpX194fCe6SU0vOJjvsnZJtso5GkEEAvETLgtaw2DoN+Z7eDDJvKpBYEiPkHtdgPHMhbQ9RFbx6dwzUtbrXxW3uAAC5GGnQ+oe6h8/ObtdumL6d4GQwLNPE7loVMV+aJBhp9UJgfLbG0a3ItJ3FsL85CVF1fPjS2sZegyXBB6v1ePo1s9rZewa0SyqjE018gzKY0/A1LjRp4roPY8iwhL+ospdNIaoo9729jVdeee7xY1MLVhyhytNNy6qyWytS8knNXFe5pyXUuxrtT/3pf+nKtd3Pfu63fvu3fuew0xvMgUGW8SJUKSnJr+fvvIo2kPxO3/+TaD3kKEqpbp70Rf5PcP0+YwhPoMprgTAwy/rjmLU4hLLiGJlbAGoMa83xGape+2pbQdQCkNXNnc09612VCDRqFyjMin8Vz/rB5vbp+razAtrPtqKUdCavmblLBxLsFIBLSj6iap769hFSqQctmnsT/JQQXw0yPIQ3RaJS22uO6tg2Rb+eCgfk1WVXDyOfF3l0jJA1zZRmpW9vZ5fDrwOFKk5hTPwUSllVUtsIeJ47aG9Tm6f9rTd3DkxgMRyij9cpGTrCZwSM9E8cwdWSR3oxSwt3HZ1sDUQ98jScWbCZzOsbW3dbwKWk4OmCRQ2ik+/9oe//C3/hz7//1pt/6Cd/RDsDN0IIpSkyHoz8q8YWhtHsPJKJpeamFO+sb+07QIsqqql/6Zd++Z3339nau6rNcmVv74c/8/LhvuERO834rjt/xwQbxwvb8Gf/cJ/HA9DDu8aEqX1FJ7jlCG4NO/8YsYPHR7/0D371S1/7MiOFh9i7s71z7ZrVv3uEgkR7dIYpC1rnisLFy3jG3exqDvLa9j1jM7FE6Tq2enjj4P7ju++9e3JwTeMKSu1KtGFBRSCiSx6caz1X3lo/ZivOd5gUM4bCrrIghihGcmuknZ3au8ykxuO33nzj+qOH21YIbB78t/8H/6UHH/659++/9n/43/3v33r7PTN/Vlaub19V6di5zrHlNRc32aUV59Rq4REltTFOyIDTFSPb+ieODBJvOLTEWaQrFiHQgaNVNXV1KJtK3/EmSS16yQRlJdVWW29VYU1rhZ5DdPwiaiCCQWmGAn+mCwavzDXKAo6oox7rx8RUZCwNGKZkosuHGtcBx56pd1hSlicX1gW45sibmbX67f0Il2RJDhRVY+5Z1iq1PsVBqFWVVzbSqmHvWNGlFhStHHxQNKpVZBj24vXfi73Baksb6CtnDgDZJ7XTV3y1i9EM9Vc3qG+VWSxnCjSJZWzBIu01WjY2uVEpbA9HDMLdFK1aMIJCI24GOU++ej9nAdgKtYQCQUim0qF/tMO9Asl0Z6G7IroiA8ja++PzBFluAJ6uvm280zCMOtR7Dbvit8OxVOv6/nEGHEEnz4qwtvkhnmGUkAVyiKS6C28HqWKXxcIwbJxiHT/HmMWXBO/71jtxoFIIZ70q+CsW6mEvDpIQq0L2RSnMhDTazY2SzFXkMWTJJZiLlOKcuGNv+gAVuflflvNtWFISmCwBzFo4hEBw6U1SqOk6Qs/ZbHwgzOHfv+D2EMilFAx8ucbDJa8Fx1CYoOXBp4T70RXD5+0yeHl/EmX5ONgWdQmPnCfXhPp29CqcJut+B8wUhpIsErlMcgFEGVdWP3ZdovIxFJ+KcZn/xyi6/D6JxVjAC33ysPD+Mt5T4U+Cvu0hUBc0Lj8JN+o0OJcRSNXVubVvdc2kQf2nqUxYppKNqMj4xmhgTaaN2uip8pzPXOsgm6F3fxk6zPVUFFIj7uNaR0MrSMZNR9Zxk1bSQGaBoiXadd5rFUxxABrtq/iObKRKTRZ11vVSqwXglFYimCrw012OF+m1bJUjjQ3GLlceUVkFesyBqATSLPFC2yUkDy9VQomnPmR2wXZSRjSkuXn4ZehfOdrcEsTJDtyZey9mfeT534NbOcFmtEdo0TC2U12myVHm6pIxHrBt5quCgk+WhErqbDMhwsp8uIv5pqw0v0WYfNhTXSKgDEsyNHIZPYksjojniRXeE/GCaQtY4JJvNi/cSmlhtRVt2TpIY2FNFUMu48NVrZJqhYbI7PspN5WPiuSCq/FQR2g9JiqLmIbzsS7HfiSZVFAkszjuplkSf/Pu04SozZiSg+Q11GAlAr/ZN8ZrKQ4pjk9ARUGgQxVbREUv7BelpST1LGfwuFLe1HD0zEBJUqL5aXsSVHE0eyEGxOip7FIw+uEAIx9F7OAF856UBB7qEMHzN7oJQzF1vzQVF1gq5/f0aPX2zZe+uvaGTU4Aff2t1z69/Sr7S6YL06EatVGhDmsEfKHXfKSf/xP/8h/7uT/2d/7OP/obf+0/vH/30SCEl9grwVIAI/FjV4Lsa9K5vDxN0OW73yXooyhPffr2x5AbAN8WO4Zf5jVRLhIuWS2RP3qmnRNbI+tAe9AzxxGzNJqo76PD++vbz9ogKsmeb3DPcM7kn/XVbb3eu5sn25uPcd2sm0onhnUeOXVRNqEhlyUjUL8NSR9GuYu96MxlzH5FTns7PI7VqTJMRyjQjt38cyAuRJQWjj50HwHBeYqwhpsd9x1j0IgQ4zOuw7qd6SWlaeioGKf7YzuiLgO1sbJn20YTf1J/iZKogcSaEPQq92jkt2tTUWV5jowIRAgr3JYQ4k3NkQW/PKH19b1rV37qp37iuz75yZdffF6rIwhl6ndRME8XVzzxwT/p52NGqY+nuvV51aYuffDe/d/53a8rtk5rsfbhytW62K9eQalzpnjtdcG0tT9Q6+sHBwdcDVvxXL2xe+/ePeQklWAu8BMBlOwUdP32zle/9a17Dx6aPiTGzZs3nr19+9hil50zcwNMd6pNQT2GY3EYUqEah8aOqUxOjx8dbF2/dogtyurZ8Vvfet1ahBY8W6C2vrqzs6vTBOeVbTsamdjDSNiklbZlFTOn5h0ZsdFcb42mI9hIk+85fa3xxPjejZvXbz33HOzvfXDENLEKX/3y1zetBzk+v/vhuw8ePH/11s3TowNu9ZaBkpr++X0QYmW0asyIbIy7qgcj/CdSAQYbcz+bDyQbXf8NP/q2LhVShl0JIntdKqpW/Vd1EV5dBI3O/tU31wjVjGH6ocmABCgDOFLHtWkqC85kJOUseFIHYjQPf7OWIdSfLzIwoQZRsNCnFS4ip6HT9b6knkJQfMzMXEIzICE4OQPHmBEcfOmq6j463ARa3hMREQesAjAZTPe9Vv+Q60vkp5Kl9CxbHPEoI+95JtissEaTGsG35tbjEzbG34iSR3TWsCgTyclSXRoQAIK+FAJ4xoiC6V5uMc6JINZgkOJQJ7sueZ/CM2jBEPNGKmMsEm4gqvdC4+ISJptFBombBmZHaphAO7bLq/IyZCbFMI2Ckrkqo6FbaRN5sOqeLRq0E8ESUzSo8UKCHHlaqRWjkgMKIrVEHecKvNmSKoWQe3ZQAoIuO9fgVaZlUUaiFXO+hODwulgLhDIuFA8UAUwQNwwvkoztFAwxOlOFW2dKOQYwAXiUfv5V44dsFLC+Zb4Q330ARlERJsH8LqiWvusi6OJxCXySZGJc3J5EBPjpVMvnJbA4iwguQkPiIr0fj09j0IdvawBM5OOXitoZY0+l/QhKgC7B6D/wduB1+PtRpCXCR+ljH3kOBoUq/fb/mXSxZ8JTmkWmF+n6HBdrqcy5NqyilXktvWSVzEvPdOp1Io+8mhLr2qzEtfbLyjbV5YkdxxzaqDFfH0adquQppwyFB2WTftN2qiATfXnUThZ8ZYVc5w4NmC4hsEIFimf2gqU06x9gLQeS0k0ZLneXstmgFl2GZ3Y/ESBk2iINCRdZVHo11NtLoU+p38RRBlRVoDCZ9TC2dhPBQdB5JZmKVWrDr5gUn5SZzGxgaX/Al/J6tmK3WvTqjqLqVVUGl5l0zjHVjg+jR1HkadoGw0bZJ8bAT/ODfavHRdHCIkhrYziCRVZpfllFBo4HTusMQ0YHvQYfQ+JkBkf9Ebrli6VkGFGqI1+n6dXuK0UuCx949bLTP4A6MeTvHkdDsFIYW31SiZqPG+QRxcnhC2CuGYFBV1bVOhEHJgO7qZNWp5Ypvh0ArBmpw81w0NmzZs/VPFgxecPMB8ManqcTZdDUGeyAI8fy0BS7HmQBbHwe2pE3WKC9CtTUzLPTaw03YUOqUlNVzLgWraHML0evJ+YCyr6MEJNOff9YEH8oReFAEBkVqplaTkCPfE9eiu1bM/sQlY0JGKIPhmiGXzSJ8FC+1nRaJmj6b+BZsnWduwqHlZoGxJJfZnfNktZk9OonX37/zve+9967D+/t/zv/t3/vj/3RP/Jn/gt/tu3C68YetMhxatSQgYGGTq0fV9r4n/vP/kmbDf77v/DXjvWUd5jDkOYehZH/sauAUbTf72NhS9//RPlYwj/wZYn6neCWrCcc1h9diW/e3Jev89pqvXB/fHhiJuj0KmrpKYvVEycnW48PnCBdEaaQ4zt52D453zcDenf7+FwLYWvnZO1o9eSZ1GPlYb5NJ+bKIgsDyJLrBSIXL4NDt+V94lx8WthEAuYW272d6hNZHmQStjmXcPp2xh+mLVXT3DVbXNXMzQTlXCg5V/au2sNH9mwL2RWuQDT444KpHP1ltdqohbTXHlFIJ+GurDgRe3/GL42gnp8qXyniBzzgNFLjZ3rHpZ3ad4pEoDKBG6YbmcwcUQ1DbG9d+a/9V/8regT+8M/8lLkxdEbypc4eBUmnwm0S489IJb0NnG8q48FVTg6CNBH/4cnxb3z2N/aPrE428nLyiVdfevX5FzU3dFIo+jv2NN1y+EedAoAdHj5CHSDmZCNAu0CxGv9psI1RSgHKldaVb3zt9ddefx3TdVvv7l65ce06+3/j2rUdLSjMtgB3TG68HNzyAzbuMZDwVyJYBKZam0TFog7RwlJuGiGJn2YGHlgLfHLoZBsRsZpM1997+y1z8K7dvLqy8j5+OfcdCbt7djGlkRYbQEw9CNWc5g8/uHfvwT08uf/w/uHhNTsFvfDqfqO1r6x89w/96R/76c/8rb/31//J//fXf/d3v3J+/skf+v7v3Tq7u6095vzvDnXeZqhsKeYI4612GJ5zMFePrXY3t4gAnCm/enrlbP3R6cr184bB6DPDufv47OHB8Y4NSO2UdW5MIKPR2qrklNtZPy31ZMOjKMvdYgbT6mfQvfojy17vjPYYSjh8QI14GbYsqgKSAaynpu3smMoNu9bQapVhKnr0UhZz8035ybpCosZJJ/zxU5lKL0KxqC7tPteZgnVZ29QgXfQhFBvXJaWjW0JWNt6mv8rNYuuqTpTtcb8TcSnoYfGzhOetloZpNdWY+srNqlOHG+N3AGX1W93YUl5UVOjOGOjEaRqJ/I6dgQZUTZWqPAQrIJx+36pLayRUOqBpNYoILKo4eJqGjQXADjHUojWhGWa4qba8q4YUDfqlcKk8i8/ER3paCb4Qf1SdhNosDjVByBXk7Si3sC8PXUkOwy5QFo9ooAmpkWTQqzHO4kMv5iCoBp6aUbPppdaCr7+TUstXNQsFAJO9qMOSyX+EU80o4trxi9Ocsytg0hNExyL1/IBR4ys4h7SxuyhW0YGTf5SIcy0iRlT8TmRhuAhN9FCTm0BPS+8IilJF7N60QQCsqt2S/oxd620Dz4rJ2TNNjmBJnawZQzSC5F/mDUDqFxsHQnSU2fwXhQIgccGrFDD46FoC3Oe6eJvXiTe3i1O5+OFdF3HjYDlcAnzyEG+Lc0l0D0evFLL55oSHtLclsXg2NvSaFJ+6JuPenzw89fHy8elvQ26xiaJsnlyxzov/obxcS5wFU0kug0Wcx5iVMD/6Ipk0vU8xXlll0Dl0asJWxBCC/RpVdJtMqjInavs80pNmcNlReW97c//YqtfTTiPZmk2Hk77lLWSWIeWhKcANzVdTdqd1VFJ/yQ4Qhmj1ASjRbXfH8aUHFMYwLlmvbc3pfuxj2EOsc+Nz5alKDZSKKwj6itBfs4QZrF0+Za09HxoflDfFyrinWVw3o/m84fS6vZbbT1qUiqpYG+sOROtbXpceWJtgcs05ozb0cObl4IclLAxDPj37VVLUm7VDxNRYq1u7uzWHlF9Zw3suLzkU1Y5qqwxfJhNmegDaQbThOeSAADsYyhoEg+CWCW6pbElBAvrPmNTfr8dt02B5x0DWOa/hkTba2sLdkspyBlTji+3DlfUtwHUkW6wH7oUdv3ZNViNTKNbQiA3Zd49J2ok5mRjZOqQ1Ic5UIludOWqNhNV2jVGM/VM+x8ZmPdt8TqWCnfwl3VponX5K7GhMnNbOHo4I33JiaKPmLHkayAyYFY5MskcFPBZjHEumdsqU5YRX7nVnLBYi9Z1VwdmYNGyUZeZITd0vKQ9dCjIaPZfWb3h0r0y7JizR9w4K7mUlobHkUqW5fK4MqnRpcHrOF1QTkmq8k9p/UI15+B6yFPM4h089s0m8It68ceP9d99n/e7fuXdwdN8YmJaFeQzpSkiViycIgCYseH3i3Ng2afPHfvAn/8kLv/aNb32zmH0aVIeOoaGgb78m3rcHLu8B/v2vsFlw+vbvofcE5AAoYELm7aP4CWOiJpOuiRWTxw/ePzxwnpIqojKb3jIWenX37z/88Lol4nggiS1CN9cen6w6D6xufwf8nW8edhxuWhA87T14VoX3UyYf/V9y9Q78BQ4Je6IO9IvQQbRqdFyWEWtg2wjqvQcP760+pqr0WW8+hDQ2iPLa3voz168b+qEi8jThxOz/nCUmjx1jE5Qtk9ln28ow0OrlDSsWvNsUtfyx4vR48+xY0xddNVxRwFYAWYUv9qjnzpYmZ4NjFddqwSrM2FjcxWeKUi779Vu73/cD33371g0jBov+jCJF8JiPOI9mL09Yc8GXYqijhfcFXFPb6e79uw8/99kvMh37+0ew4O9zFG7cumWRvJatf2wOJnh6+PDB/YcPZaq8P3jgoRHZ+BvELFzd+VrIVkVsbb7x5huf/8LnHum/39qFzJXdXUMKhi4tvpWLpDUqGMmK+0hZ0AxKMP+AsSnGQxiZhwePvvX6t+wPwFhevbZrStLq1nbFETfsXXpyat30IEEomVNN9ft3tSLi62Sxtr1jlDtvk/pRgC5Gc339+s2bD2x9OsN4BnAU+ceHtjfVGaJuXP3xH/9p9cA/+ge/dPj44a//4t/fO9//sR942VJr68U3bdDEkT48avKY3iVWk8xqoNrfU+2Tedc/4oEqDTntOkClIG3MQyHgqEKmOrMxzJjG6WRncJK5rVLTs2ODV4wR1B6gkOYSttYuM8dgqhsz2VPepGNUxLywjouJJ+VRwWEvlVSjp31GKv3EH2qmcY6R5ZxK1CEO+aqGkUGutJySBWNVDavGlBP4pZVEjeS+sr0Xbzf3ICJl0ZEAtSKGhj8fynPdcFkpdOMpPvqUGnU3P9AwKz8imNPqaIrt7MPFHZcdrNp81uDRyc7WlepSBRCfKKDC6CnFhi09hS4s6pHB56kxoK/czR4dix+K3DwEfCCWpkVdNgBmJF8jIS9Hoze28pKisiv+1gCQBjlRnx+SYNrTWisOxSBffJ9U50pT09uMip9AD7SRMWxcSlTuEH7HtQQYxktNZ2KSUTITQeO+CKpxgGvqVHdLlIHxe4lJ6K2v2MygNofbUjDH0vRSR0tG3Z2XV2XrIpWlTQhKVefgTlzKVs59/jzE3AQsiiQ5JYgRsPIsGjpyb0aII4LGCSMGslYADyrlPcBjF2TCqAD/GkjzjCHlL2GuQHyPtKF9SViaaIqIRRoT8rHnXiZ2t49fy5eL78snL/5FzUdRPxbBh4UnS4yFPR/Fnkwucvq2BgCAyoUW9lOgP8rEEzpHdEXwnPu7XBfcGTKExKXjVxNy0KJ9ofDi0xJhCevbBTZgK7RUZBAYnkWIicUiVIz5+qbCOx63LlInvFr+Nhqwebq4g+yBsqkr1xH2uxvbLJKst872Xj+H6Yk92s0JfS9hnDyfIc6qoqKug84Q0KNx+FJbExi0XumIOIXc9DCkbVjIT68qtCur1z7gsPrN9bUnYAu0OIqpG3dfgWQuYpLv6/XiVM4M8W5vHB+2te7wr+QLzUNaSjMAUs1McmwIRPOL6DoX377jeuEQIOUa033Cb2yCBk31vXZ7hwZjXM5g+4C0tMEHCFRl0Hp6z4Q6SPtCx+vNlVMRyg0GIqjFGfYqeYUXAaXyzc/+yxXyjbehZl206HIY4AyjnEBVYei3Yd1AdMosA6GZlKWsvmPepoysrbYZNtKYCYIfPlSI2l8wJ7iuue09FfI2qfSZolfMPIXV6Btnpb5nWAncsbuRwZLj2gFy3Fh/L7NlvUdMrDrRIdI67HMmRk9SrMIUEm9dRBnY1t3BZc6kNz3GNo6QjRfbx7xj8u8chvM1e1hhyhBM9KbiNDy+YQ+YrJxsDL6v6iejT3VYyFSVlU2liNIzsxDPXmOO30Ni293bxRNou49Fi75ydy0mq4TRCJmK2nBsqSrON1/P4uRWikprMwbU4vzYqg8dQO/mn8uoT9WK7ZWho2jNnMsEm+YdvVxjtfUh1Kt+Gg6aZvOV61eODh7df7B/dHD4S7/4G1euPP+nfv7fiPBOEVYsh5/lFVHYXu03bTYiP189fP6lq5/5zI9867XX2H2AXVU0kPMQGRJWacO8++93FWv+Y1OJIL9E8yNTSRne7h9BmNcL8EvkAHx0FTasHRDBS/+eZLNELNKAz6b3gJEpf+pTvWnLJ1Vep1sQq0rlpM0/DSGpkLUnzcZG6cn9Rw81gOkm5q9tPMpeqF1En9b0ktFk/QSTwcOJufJbvz/5R/fK2bVB4P5i9CQ0DJVSJmd6QBWTPyfi8HTLBvz1glLKziBVMPXJrR+eHD1/bWXXggDdrTt3SXZ15aoqr1KLDCVhbX13+5p5KFQsxFrJg26OoP42FaHZ6HTI2U1nx6cPNZktAAU7zqx9IOb4SZKetbn9TgMLVeLRVl83iOpg6wTqPx7wOnRvXLv5b/6bf/5Gu1i2D80Fw/sq9Ug76IIX6YTUxeW8DZEctTy1PqEc2Sz/fP29d9/6D//m37TBftXC2ub3fvL7b15RDu3Xf9iUmt1ddoBhyFvR9ZC/IoPs2WXeyhTAygc6lJdTe384H8x8emPH9x/cXzl9UcF88cWXrl25srF+uLNluJuph2yl2IWR/ShSdcf0KAsagsf6n7BBB8rB8aEd/c2RPDw52bnyzPnxY2pjWEDhNL/Ayp7GJht7OCSR5WRLpgq5gNpUCYYZgLwWnCqDFIAZ37KyeOvQadU+bt4xlwsGDHJjGqen++fvfu+nb3/ipU9+5Wtfurl77bVv3PuBl27tbd9aW91Xqa2cPW66/OnBRmvDTP23YYaOn9ONU2uQdtfW7tVFsvqhJfDrK/oImfTHG6sW97y/dnqwcvzs7H1N/exEbI00zURvuOen4rbxVYTXQMrThSvd1HmLbeent5WN0xM1qe3T7ilOWVZ2NZ75zFVsl7bG1VKkypDKzOgl75kg/J6vfDPNORqbZ8ceveaVtTG47K4Ksf5yHMnUxil3UGOnGphjrQwrzEGHMo5qOK1ufKBey0SP0cw4rraTFTUUBXmLusRew7/Zg1OqZSAMlQBQ15x9j/Bd2Tw+VhyVNvF08IHoDHrLCKFaW02f1fQmNQcP9ZvV47or89rV2tubShCo1d85Qdx3re5GkakticBJ4Fjw0Eofjlp9VKVoNU5mo0UkYg3Fda5NilEZt6YR0lTKRGqDMbYr1Uf7BvqMEmdbhlgMqpPR6My56aSxpZabwHKSXs4mNsbIBsJrPGBjzUso6lr9hohnFoixEogsGhhk2fdBOzDyKjScwceq1+MtI5T8JIEDCVaF0gD6YcDQb/gdvVjgxptqHyilf0OMhzJ0edh8K9kZiyAMdBRLv57YlaKwhcG6wQ2VeMOn8tdnaPir1gIg4Q650BVCCegvbpebf2g9uQ15oxyUbu30hfoOnA9Q9EiUkQdqMrnguXTD9nma1TXKs5LVh8srinsf4gv0sFXf/0XgEtKH6u7uzi+KJN8ZzATt7yIH2C+QNt/4eB6l+7brYw0AyZYcJ9m8BWt5GFQuvj8FZIlaFE8XMZ9KtIRjzYBJvhPvI7ye0C2m5D589K2gwihF0aTWdXF4oNq1Nk/HJIXXLb11cuxsmtnOMrdATAbn+HjneHN7/Xj/4PDB483tw5axnR9MmdVzRqH0l2BcGqFOV/TqtLNzkLHdESL7bXc9GbBJXG3lIc9RweD10xEHRWetaZLauEGklLmBBQWf15X6iC+FZWDo4SmRuSo1QxE9tS8DN9SjK8MikX4RxakSV8+4cB1ONXcrFdlVJYCQqZihAfM8lIFyn7k0AERXLFNZW7ipxOFaeTPHueNSBQFLdTyUsXpHCpYtuqRXDFWZdHoWBdY4Zuzr/ecxGIBonMSk1FLOWgtIbzrlHplQx6ApAZVRpQratWRyQEXIvOKw1oiOlEQ6f7nICoZoliyyzCrqLKlCV/8Im8b0FbGGRGyBd8SLYohh1VHy2Nd7ecS6uIEtef8X3MUzFTH5eqi1d6ajOvtQH0wamQRqx+lZIuYLQyKMS9c4aqIm05o7xKykqExUTtZMwQsW+vWmrqIJWje7mwbqaYTCmMcHr9oYEUAoGUCEqbQYXd0dLQ/Ub1p/IxKO7bFCGyGUgCvMg5mA0RCk04/hRcwJZwE67HEaVZNHvknsgbgfYDAL9nJeqIxqwBDiafkpJJOZBU1j1x89ePzg7gOVzc7OHirvPXz/N3/7V/d2Xvi5P/6f0gGX+oSWJFz/oFSFCok3zYlXXVy5svmTP/3j/+RXfvHevfuLoGVXjME5DP6TXGLTz+icqzxTGsHBubzP47fdBj+pL+M8gSHePF8EBG95RFMwBEwefpb3jlU42DRvxlJSiqqVFj2OrV2/feuaXtb9o7WDQzM5bGb/WC1tmYBDVh8dNPtm1AOUi+I84DM1cpGnbObZbQphd0H9LZenhCQzju3EH+FPuqXcDZQkMCKZZjMYxD9AGpTnv/NsFIeOisvbGJdzepY1+zM3Nuzc2jGiWK6MANPn99xQaRnXkAWuTgAe4cpem9ebFyTuyHKyEdko3Ob1K1fSgtG9hYMwWS6DaetrO+orKqrednzWc889a/L9aDL1WciN+oXnge1P5DLqKtbEpMX+BiGEKn1m8//u17719W++4aStx4/2r+xtPHf7mg6P5597NiPd/BlaShp6edcMVJp7yS8ziZ+NUw6JHYkjj7LzwDicHh7aRP+LX3jzd7/+VY4sO3D16t6N69eVVWMsgw2BBDaHFu9QnpAZGXPqnLTLKBl33pl+E3xcul1032bbjHx+8N7bAUKF88gziYds324dHwySo0Q4YXZfZRURSmprZ7odwnHkrfqAZlpBDn6NOW9xSyCfZedurG9nQhg6tFmLfuXK/+x/8T//5v/sLYMQ77z/+u/83v2f/YEfazmHbK0OyrtikrhUPDe1Rrufrqxcif8c1zWryfGPqUcv73DVRkJHzY00mr2mL3s2TLRHSspCerA1KVR1ZYSDr6ReUv+Czz7KBOV1Aqutq6dk1/7IBoc5lroDoqfTc6XW8lSb68BGk//JRA61uCXknjYhlpnCHW4lmAShhQlmVNBeWsFVTFEAuNQfVU72GDV0OftF6tVXVSkpWMLkYmKhqVaaQiy1KD4DEmcm1rTSsssEw0vltI/LQYRxrW4lV1NxAh5BjS3r1yFo5lXDxbiUOVTJ1ayTfrTZzcKc/OmJX/fT4kBcZUpFE9AY8uqQ/iVZ9cs0DyXoq+VJh62hz5NJjngPIf1Y2odeIJOOIghvii6ZkHmeyUaI074yfoRnIsQnn6uCa2ozA00bMFOwVosaDQpLtadipx3DqdpORIWE6VAbUkK3fMVPaeP+8i5iuRMuhKdWBHe8GhHkP9z0MOU/zvpfY1JzIwE28aFpQMm3D3Fb5LQQ1CE1/JfkqU0fkkjRKymCtIqqE8cboXGdFKWanso/GhGK02LOHFr4LnlRBOAtCzNGlzWbDRJM+QPWKqlcga2HUIyL4iGjnj9bohl3DQdZXnA4PJb/g9PFawz76Jrny8+Xwd7RuITOc7wZWO7yWOI9+R3WFeYDpC5jLrE+dr9sADjPzDWz6/wOE5/EGwgXIGPmwBtc5hZiF6FPHofnVhGUtEirazbSEU99UPKPX08CpPKsfPZ3mUsw/ZmLoAxT9/0HD9N3gtPKDPZDZb/VABIoLGkpXygHaG3l6sGDh8eH+2eHN23bvrryuNZcfcNaq49zys1QLYmaUVndI7Szs7sZNCphDJOyKaRbe8dH9x6b9YhVoxvEnV60NGqlFV2CZ8EQf0tNQAWyhiCqfsxAVSBPRLKDyOPDQ0wYlayhrKxQPIVBdshuNHC7gzYrjZVzwjQ0S+nGBuFKW+swNmyxCpnBlNJhjtizeqReUdXpx453Chid1t8hcj3f/XFfx8XP3E3SksXuzOJlJ0nmntnO3YS+/wq5aBDJFm+8z5Yqjd7VppMMDklGBDVcAJVPJUdKX7KXcBSc4HVyrJ280j7IzbYsC1FVnYt6sFZT38R70dmyspGf9wLCgZavnb+Us7/1dlVJGoJ7gGTLq9iasr1EZnmSilwgpfnComoqok8/UJY6oaDIHHrjPc+Lm3mZxoms8cQMIAE6YCSIjA45hlVFW9uLD9C4Ya52tgITrUSxmT7Pa+mBES+6GdZsUM3DhBBBHES/hmqCv7W7rc53SJAhiGqamFYpQYu4Ge3k4M4uocunxZCqCbKeWppxJxXCZly3BeV7bHHpalbVr+gLnE83PpzOKjnEb//PN/Toi5PE6ZFJnoaSTFnWMLl168Y3v/7m44OHRlF+54vf+srX/s+Pj+79a3/mjxa/UY0nxhGkBb3ghcGGXsy1Z2/cePnF2wf7+1Q3KiKpTFOFLmr/z7uWSBeWTsQwLnVXrPBzAeEicL4sNyGrp8/0vH7nScjyMPcF0pIuxlwCFhIhesF7SKkIgkAJiUcwDG01nORne1d2r2xdOzr72o3ru8d3tt9/+10uJY2p25cu16GmC/bZWtYr96cTq1Jov22Vy8qqmSeg5AZFSZodPSvr91OP8fZr5Pq29pClScdKQPgDgVdv/x+VYIPpjVLG3aNbjVuu3809gLCiv7It3LztA10kdEl+xze3TG00oU9vpVIyDoeDsZgM9Rk86GI9ZOkqFYaWCjcrNKbg8HzDDJb6RbQaiH/MJizgdtocYbuQHh8pZzCFQYRJmYGF9mFThPM+bFG6fePm89ev270ekDr6Em3EjaglTgDLJQyEKQm+F8aqYcdwLNNoLu765377S//kH//G9vbe4aOjZ67f+N5PfeL+nQ8NLhwe2whoa++Kc3MrZUqzFB+83SohKzVYDHDDwVkGALI37kjLlVNcNq4/c/PLX/nygwf3JL92bf/lV25tbR5sb55ubu1m207ym/QwoLXE0auumRGy7U1TwPaumi5kqyVDjnV28BtwaHvjVYMS+ul5yPViVnZ1IGWZP3j/Lufy2vWrO7t7eWyss7EeQwPp04qgw8cHIthTdTEheJEpzmqbMrT++PiZyiRhbBUBz8i2dkdO98onv+eZz/zkJ37jl50r9sFrb5z/zCdevP3sm3DS55k4G0SjIP70e9UwOl95z7jA+fre6obOX6fl7DvtlVpCKct2+szhyaMTJxN23qEJM7q6dbodrpxe62idk0+erT46Xr3f9KGOpeeab01/MHyY7CrEs7X3TTPzgUnaMDol4+xcc9wrQHa5Wz2uztHucNX5zaYTfPvMmYzJo8ZtWC6dOSq/vH8CmR6MnMe6zdSW6VTWNM2i2JYQpOF7uzsmchFyXJp6Dw8psyHYXECyt2Sw4p/iL/I1pc80sHy+1IhAyV+7V8UAW4RLVTMYw6UJnREP6EazMU0uAFV6a0gM0GhQZRzWehE9s0lsTTrnzTR1YGq5eFLhAANgKRavFYyEnMYNg5ZCp1xEUR+YNFrFs2DW/R82V0uGiBREnmPTW5WFBPwJMKvoYhfFGoRiIKMUDMGhUYVe1Soj4sxCNYsLpEq5AtGCECVLh/rUy4NdzpWS2z2S+S3dgZB2sXLjwEtuIg04nKk0bbAFVVqfiKPuDPRQeQwP8623p8IDrezlj1IKRHg1uMsUyi+H2LSMV1Y6Uxlb0hAZowZpiJXA1FY1mueKlSse9jDix9NYK4GdnTlsaOtIDt+U4XcJ3tCC+Csbb8brRp+kpdHiA40SOrO2cvS9UF7ZfF3EMgFdkekqypLrEpwAPrrELoFLGmJbEFyQzEuP7V0XIIBaIs7PAmiCijM59eDy6SLl8l4D5l94PYXYJcq/T5onKE0GJLdc83bB1/L+CNgFmsOUi+DE6cLI5ePoQYxKI3KqOG8kouAlnNmhjArLi4oN95eRpzSDbhu/cjjWZpueZU5dLD1ryRqkgTmJteEzMQYva3PLyVe5q7BIVLeKRAYc2TcqcNoIZd5pFVi2gyYf+gru7C3jST1Tx5k6BwXkZiGuY9xnSkCNR7M+6yKunI21KimAGRFWkTmpLe6qgEOFbjN8NiGhW3Rg04Qiznd7703tJR6DWbV/umm9ogaA1gIJwaaSqj9lkJD92rqqcSCvcDeZI85j6CmNCh+g1Bjd2Rq48XPzX5oVu6n+1jWib8nG249ArJGjN7gtaAA/29ncBuUAPhvNzwsZVZBBmW3InHEoK/AINlH/6Oj88GE833gwXLY+TK3Q5FYYk6n+yKvXrgGK74f79g8/SBxQSwlwNi6vntjDVL/HI/ba2gN+gSs/XHVqvYE1bYYGoBUmUmF0RR0DzlRwtcpUKLhW5W31REXarX0wdNOIWDnLGJE/3sGr3r5wwB88DZp79FTwqkuYEk+LbU9sFVQAKKsqfFpuI4uIIsLSSa4R0hQBsyTx2qgFPs+oURwllsyci1RgWdtsKjNk+AyOW588JtBw8brY2VEOWVTO3EHVAkzWmFG7OEaGXskiIICU1UQ1srDl+8HB0dVrN15+9RNvvnHXmntswXZzXX7l1/7jn/jpT7zyyqvWA1R2woKnIJNBodq77TKIgnK+8uqr/8qf+lfv/JX/4OGjh7pmy6iSO1mGc0kurshYvkzgEEX/+jqfCnjqKuz3u56G+Pt9H2AffUgIUd7Vc2IZXvY6+GASXWq5SGfn1RdWISGKmteH6/b6tAB1e2t35+oxN2Am3fPA7EOveNfBOqyl6pWwKcb5rzGrch1tUUJrFoLksAT6WZ68LiKWIl0dyflYTZXGpaeDt5SwrxjLIKe9upwaa2xbDEWnVUiNLx1tG6NeNwhO1nYtO7JcQKd2w2zEOblKIm+NCj0EAzXXZtAwBW6vSZXMnZyXYiULC5yUJgrWFHVeJcs1ACqtSyESWweiA+zCTgv8P/Of+/kbt6+JWd8HVPEnejEhXZQaP8oAabFHcJJxVfg8sZJdMt18770Hv/6rv2mZihMYtvd2XnzheScW71zfdBhWAxu7Ju53EZyS9ujRQ7O1TCBZPT/Y2t5h/WIZQ19OcPVjPIHL6+jfc4cTf3Dnfj2o6xsO8bq6uwdbhZXB4bxVohQg/8fjGMdIJaCgGHqUu+lQ2gmcXC3JuADtlhGBsGuyD7AtwI+LWai5Uq6z+/fM/L9Lqts7KpwW8ctSFMPdp2df29278uonX7l6/XoijzlVUCq41jc3x8YuCJxaqoel5dg/unp6urv1/B/+mZ/7xb/16ytHp/fOX3t49JWX9FweHXeudRaBSPWr6wghodN2kLU2t2Xf2pmP109BfnR6dKdmyfmVw5XHB0cbh2f7jOWxBcGaGZa5nzugmB5r/h3aaEgfl5MVpgOF3rFIFoMhlfAIlrTxyOZE2H2c8dvuhGatKY0LFY7vFFQ1EIF1yS0Fs859He6NPubmByjdiA2EWw0OuZxOxYT65wlk3uFU5QzmojvKr+oNU2UoPdmRICbiIjTt60Z+0NM0VsglyopPFrhk4pkSjrFlvFgD05wgznK3cSpIw0uyWfZwBRnZIIzSZllUsixgdlj+Fbj1rdox/qqnQqQi4o1Ozpuki3pUAsAXadoYnr2EiCwl86G5QpjVoywrMw28oyjixM1sFV7J8jGqCi7u8tI85voEL8oy4qvBMzEOCbGGUcOyci6yAk6rpFT2MaAZE6BwpCpM3mpTLlgNFoPRWP5RgYZW+rz8SOlh6KmW9ABp9+TnAUQc5mXJzQPsNXGDnkFVYPylvoqe3xrkTVGQsjoulwam0gwLIA5M8zdHp4bsSebwdGrcEYkxPQ6WUelKEDITHBDIIFN4DgCNQ+8gW3MqRGJ2jF6SwEI0UYla2LA5edH84I4U+p1sLu9LeDkWC+/CYRFsiaTy6hqk+n6RcElQ5GF6YPrmGgDzs7xP4MW35Xm5XzYApu//SdQwucD0As8F1PDnKShLzkcvFTs0Od1v9HgRZT6XD7yczHIJ6kk2ApYoeCr1cjLAak5DcihaYvaJPnYfxsR/dghDG7BWt4hTY2tKoEhhAZilpbZJrgXJVJSeYlXumJm8fzk3ieJIkTSyVL0pVeXQ8nzdZPsba3u2Q94i+7WH66uiSQbD5vMFR36ztdmInfL3OvY3xOt8b86PDpZMBSPC4usxE46CS+pHXeLZ7Ms4C0qoTHikqvDtNHjJ1Z0oBFJeKRnY2t/FUl/XPg4g07KQVFI8GFta3xvK6jHILitkFW3Y5u36Fz/Z94oMlc4qYiyHRxCWWhoqy1SdnR0IOinaBwX7uIXIMf4hssVs2gPjgGQLZG/uEIk1aKuNzMmOmOCufSv7MeM2hvXExP+wr8SqCV9d2b7Z3lOhcXRyZJuapUQtJDEjJjm/DpivyrMDWBHXiEYhXRkLA816YvN9ZLUUQfrhwEg9LPUNKbL4oHtJW/B8/7YXY9z5skvx5cUiecvMOQh/sn44MxTT0mq6NsOGv8Ok0yop2vA7MWCW9od5ZzIxFySVTf5YUyJqFVP8hyhpGnTkA3FE3H3uoCKrGImdFkmocyybmLT7zEAJheXCqLXTlybO22AVQ7w+MILTC3XyApzXtt/PRIqBrakG2dBGMNWxqjoCrb9FEhnZvlHP5evf+iapm1Twe1/+HU3E/cf3dNodH+6ptM4O97725Tv/p//j//W/+J//13/qp3/A9iPXb12Z9e0mtlqG8zyOOQVCjVtdmvSPfuSHvvez3/+9eze2v/SFr3zrm98aslAfEXPFlB7CDgFD3jz2enF97P1JyuXj8u3bAoErZP3Ot4cvDLqE228KvMRaONtLMCtt8Ex8uQlUCG0piiJjy/mWQlO9pvWtPn9+oHV0ZIdGdZOmPe9Q8/1KszBsl3+f3pj/AJb1c8Cdnt8/PDnQe5paDQaUZnkqqyqWBYVqjhGqlTrhbSeCm1d29prXVllYO789CzQ51nAjzMRIuCsrz0PNxA8t93Rn5XRnY/36jk794DjA+Pr160DIWmcmKzDL++B/vVzX70sDH2jmZokS7fBidRQmr/uMn3/WGStKPsHEFJvW/hrwXGrENBXiERLeY+jWTp87O8aRb1nd/9wzL3/ipU/TsSlp3YbuCy4sNZuetrJlLYc1AAUr89QmmCTifC7808j62ltfffODtzadhr16em1n7/oV85QaIK1ZZpcIg6FNOMF4NGiZnKxvPUCSLXkCeXq7tszKu7qyAQ9XM9I3dvj8X/7y73z116grS7P+ysuvXr1yxQAdeJBtBEHO9bhzZB/qOB7rwgIaKTI+sHbVJp6cDJ5JSI+VrsKoBXK88jrk9RYoCJlJPeT6KXIH25bUiV0SGjQw50yymXc4tiDX++zh/Yf7zjw72H/hxRct48ZwcjRvEI3mmu1de6BP/ez4JjOVh0xd82fIXC6bR/ur3/zSh6qL9W1r+V/Z3P2eK7smsx2fb79VTXBytHG2e7Ju1tqmEUKhbN/myU32ZuX0xtr6w7PzayfbppLuGAo4O9u9v33/yAhGpxJrG3Dw92zxeqh/zQaXpxsr19+rrujcD3YYdcTbpNz6MGb/0elL0ZMlYWtvVaJmYWaUKHYDHoKbLFo1m9jreKpXmHL742OpXXc4eu+DuHL6HNfrfPM9ZJ4dP8/WUeocMe8ZXkpkAlUGVHZBjtPwyKAyf0m8PKgqBFk4mVTuABYCyqJ+gGKEcEB8KjyvGGNZiRq/ApR2La9JqGRnPYAe2w3gZAFeZWKKkzLU8Nt4AfDMFIyShhBWtBwDL9QyIoZJvgcVWFBNplMsxE6vQAzRuBSXQ2yqUaESavGEfO55NVu0ec5GL8nzJMSLYPWIKinrzSAIIsViB9sCAL1UFj4FNGlt2C5PsvS4CBFGyREyVSuawmkYAHqYpY4YnhaYQqwU+IoiEh28w5kBqaBMNPBgBrAATA4RaFRMa5fUZYfhcBkdgVG9uQt7qvRxSq/l+5F18lxMkj7aR5dkGDjOOUJiVpjE9wt6hkuhFaPCTnSP+CEii2Qjbjp33JTKbCAWYFZ4mt3BOIMaKbGDVpQ87PSiNFMfiJGRCJB7em+fyUU+I8lRsrIt9fwWvLxi+6Kxw/U4Gqz+ltjzeqEW8zzp3Yrw5Hrqy/LojstLHM8Dtp/RjR660p6LLxNnAj92i09wGfb1sHwcCVzEw+cFjm8TeaG5qAvMCsyCyZDseZgwoJYbxRkHuBstmARUvMoLm4iFKRkMLrKoXTaufRuVjXVR0hlxE3MGmdS3Ky2Kc3SMflQmK4i8bvjXrWUfjDUncOXPiy2O4qXi5e2JIfVYhYrVgBu1wgr2yqeMTWVjyjp3MHnKfGGoTPsuh5JeUr+wKXyqm6QQPQbQscUOUX9aXJmQiN5N8REHqvRMsEDPabafUdUZs65U5dFWgmFfG2ZsGfSarx91vIc6pCpUAYMe+1wnaJruQzJuwC4qFnJhoirMs+CRcz0gXbFqaJRTrJgsgCQUVstlqQLrxszyi15p1p7JMsdOliKJZhkypeS6aDXYSvJwT8MD/KY3wRgjQJ0Jz2WFsuwFl4g9hiMFoSjCJUcctLEkuLHId1HdAjtmr1aCcm2VGXI4b/qfjCkFItPYfglEIje0RaMFEzFH60D/uTELSDY/IaONE7Z10Kvqc7IdDqcwi0zNrPY05j+bxGOBSVVK+OTTTaZFl3xZRlLWmee9ZL2hjxNG82/MZboWiIY717b2B8GqPElwuKbJlJN4LD9aATVD1XZI1fd5vvKNr38TElw6vfYWKdpb/N79e49seoZ/Jgisrr/xxmt/6S/9v9ZX//POe33x7PnrDh81KSbFaPCsQhRkAyblc/PWrT/7Z/+M8art9WtvvfEOgAsa7l0hFequebx8Wd4ELd8mwnITcBFzPj55firKRwC/I/W3xZI6ACOWwD2Jv3wggApQa9qq0lURRgKUgxRDb6ut/1cPcI8jtWWfyQ2LJWp86z60mIZt2WuSNx4D2wkYnHItZDOsH+yv7FeCsjOJGQayXijxQjGFe+1LbB+0jq2v/eRzz++p3ULHVAHmmk+macFGaXwI4U2RJSnUs07jA2lyRgsPNYe39na3bj5zxe7yNBLJCozWpj1tRjWmjYpI2WVRlIk2Hauc904vLfTU89YIgDVQwectbm2Y55J+Zi2qynlRlacLqtKEyAQMzpYjHx6++MJL/+P/6X//+u29kzNjdwLT1Wr6C3sYM5bnkYxbFrp7LJ9y7UELBH2rW9/42jf/zt/9200Jp1gnx3/4x35aB721Snn/FgZtm4ZvvqcCqoXLmJw77hfhZq6Tk9Kp66Gs40Y9HPJ2boAdeJ69/cKjw+N7D+5b9+F861oSWzt4krjwlJtkgn9rsta3ty3oDWcZkTQQ5tx44JzjArrxVsIRpoKn38es+34SzOxewEJYk8Zs7D/e1wZoiEEDvt4E/4pTOXUmwM7OzWeeUaz2ru/duHGduI0tPD54LJZVN3Tm8MBo8OGVK9esXbhyZSdk4iAv5diMltP9lTe//uajR/sWDK9vfGPlynuHx89wM2UgC5N6zEQx+9/Yx8jxeNNUVVNprZRjMNg6mKQFftc0Xo+07BUMm87V0E/Y9Lxqt4HcBrEXxWZ0PGUR8pOY2tnGpoGlGkFNoJanF2j4VEWRAqWaQJVbxSzNSPpTUiIocOmVKn58LYA1lcDvIAB6qCKN6QDkphUz9aGvjVDhv0SNAfip1w/s9M3fcnkqoPf47ivqQkApKOslIpqkZwpQT7j+qeCsfZJfhWlpG8M12U0Go8IDMLrk3L8n+Y5aTzp5jZOLlbDFv0X7B79BbRgKwKA1jKG7hjjKtDCf3FIdBDSY4WdsUAW78IW0Uk7Z7EYBXCVMHdz9Fi9ow4tm75m6p91a9T5x4T/aIGb6E9wix2wv+eeAAInQ4a7ALk6H2YcBD5eUA/rqZ5+wxfvg4g06MzYV+waJoMw/mJS85wtpeBpqhtnxD6jQicMJQdwRQyMbCl/1FKqjt/xDRkOOMeLALIQPGkHr03AtWmfyxsKSIUDKvKOiVfWXSw7MDN2MJ+M9AIHJUfI7aIfUEDVpLqgr0DVx4tjF4wTOLSgX15PHhbVL1AlcUhYtnV/gX6b6A39Fm2zrb/w4NpPkSW4fAQi977wWOBtvfvRl4k3wkxRPQwvBC+lOoes1ChQnzG921NOxFwYu8ac4K3fJKzF0dlHlXlclfaSbY3Kp2PjHMSPvjLmqAIxemMFOouaCKMObZ/aESWyKsVKuEtWlwDBpqGZJxnrbt5p9ZJvNPFlfNetRvBy1MBWtHiH5pvtrJ68yf+dOrq1hDxojE5Kg1+UgSWqLsohLSkJS0Vpf+snqxd58Z5igqq+UlHiuIGR00t50fuobOafQRUCsdg001GXDp3IQlRVhnq2Cl+37IWEsvlrae5+jOzPrl7cpiYm5ep57qvxWgGTRJTaOTgm2ZFB246ey4JoetmhmBE2pVx9WqKYkQcWJtm2ec7/kXePZZjSQqEH1kl6stS1z0Ce7cT1izuZbq5u6mhIlUDxp/RgZ4Lo62YWaf8f4kl8PUJNDpWIyc/Wh7hdfczWravhDOttjg33xWumU92/EllpEr/BqgmSRfIYnU9cjd3Xl8GVZqmFrRuBtQZOZlQBTxghvjCWHJO+JdKjkNPeazZkA7X8FpbU3mKuBSP/C1gUV3cXr+3pVB3k75x8d8kviUzZD9VlZcB6nCsuYBzylqAc4t5RBej2DEtj8xVGpMeDcTbxYeUv2VtmJjGkyHKa7gRm353/xM3ztpL7zzp03HjzKNT05ONq6enX79s40SNsi+Wzlbnva2Crw3DYmex++f/A7X/zGf+O/8W8ad9LlNr10isub8okbo7F+8ROZn/zUS3yfH/7RH/m9r3z5y5+n25C5SwBUOCRGL+Z2+TLkdxOw3BfdmbfLx7hUN9J3XMOJJeV3fItZMp0oS8YX+WPkJeCLEGmxDZvtYWhLp53Y5wwsrKU5Lds7Pzxc23+oR9V+6ur+/bXzw00NtLbbclRqlXd9XPTXnaUxG9R2kKTQXl5mCKRKo97hMZQPAmTWX8XEz5RR5Ty+amM4gmvdpAzLNDMbjWF2xm7x2mB/GqWSCGedprRMQdNEaQU/9das227t5jC/4SDT2bMZtH/9bquE4VqRahMsbduKaMAxgQ9htYr+yEemMZq7DT2GxDQWJlGsqlzvfDLWTiLYsa4ap3KixZb9rnzjaOXBH/vjP/ef/uM/94nv+oSZ4rSOjvuUcg6xSSumDDfW7YwxytTHSiVIPuAk6IqnYHOy/+7f+/tvv/GmUr67tf6jP/mT+/sPb167lrKjwaUBNmNZAHt79MgRAUi+cnDwgawNXJyt3EEvdoEGPtPL0z8+PPuVX/nld95+1/J31umZm7d3d0z+0bdnN3qo2CBIBsYePrToct2huszJuW1bWk+sRqqJzho2HpISRmbGVgYdOLK0sPCI6cIw5c6HVgPXW5BLbBXwkTUJKLXR5k5A2v9ndeXW7Vvf/wM/oPvfqvyrV68c2K6lXa1NtlEPyGKFcqzooT85efNbX2+mksbZ1ta1mw4tuH74+MH9u9/6ru/bXf2HjNP++dHLX/z8/Vf+kLrEJElmS9WGAVstqNUPcKKps93WGmdagBQb1bRpWyPlbGVX8dfJo/Mj88tANcVf8Sdk6atgTWNkoTUtzbWtay6dIhCxRaE3DDmKq9RwraETvTf00RC32Sc+tfUPdJBUlZTqVGYFw03NpzmicZvS2JNJfK4/i7ty/oKvg49KYeLnTKqi2UDGyVfFIzDhow1Q46EUQkd5ExXRSumBsMYNSO38XwzDvMQmF5YHT3Xp3IAm5VvOl7UudoWhQpPEhwGlUVBTgMjxinC9XmiERqY7dviYlYZcmEA9+lmLBWzVb9CnwAuURZX/0HR+/Fw5WMNGCxYq50F4STY+LMshAnBMSJqu43a1Ot98e/CIpjgNULIKOTEnQC5+sRaZuQNLDsUvVxTVATqOB8RLHEFVkdXRalv2AGPEDed+jRtwnJhGbykR01MCfwEUF/mTUQFxYxL71kNRwmYIKoygvBGHEB2EpQmgHgpPJy8WpTQXiaczlmhSsAtw8h/PbySfqBfKHRwCkBGYbnMBsVS1GjE6kwl6mi5iJWqCChJQEGz4VfkWAMGD0l8AVkRDP1Bd/JynvOUJWr7GsACF9yA2v5e3yaLRgzK7hDCcCteJvyRc7kuycLwE0NMgtwRcRBbjwmY9HfVJmqfjPgm8JCWABV6+93SZ3RMZ+ngZdgHgqdc+Xr6S4SLlAVjo5X8PY0yyji27UWQUNdMXGQWzDE0XSR8U/WXtkPSsSoxsvY3ObZ5YAKgtT5DcOFbqRspn4FGuCTHfsQImq1S2SrZe2DlGh61yqA77GPuAcfHvlhK14KVMS65cp/06IAJSzHhT8Zcyg+0N2CUX1sCDT0XL4ZNgbshRROMpHDygy0+s6QLS0yAhWkCBrIiDy+vokMeyjtqMHg9sci1uGYdRoMNhiVZ0yae6zhDJrcKOJUyTcN8kxvHJP6YrwEJZuRw9w58sola7Xm81S8iHHg90C7MbQOG0mCucCSkfCcci8NYzgnkqVQRS5dxkO0kuiUSrW3iHAYsyJnZ6jdac+eBUrIwQiEbAjcHp2zmx9zod4C6rZcotX0TdkWnDv8YM8lMyG2zHMH5hpm4cseEA9TJGBT0rNntXMN6pO8QptMo9cWa7knTctNGF8w8yFbG7uInGx9b85ihkDQLta6kQY7zgSIckcDokrVLTKFjkkwTlGMfsNMFr5Ppzt7dsqFKXAwyAT0OGoYPJqC7AxivaiiSlIBYqDsWQ4mRodXiUvfDBDFP0Sp7e+/C93/vSV7d29p5/4fm7d+48frh/8+ZN3DSd6drV6weHKx/ceX8sWXt54MjnvvD53/zs5z/zw59yCAOGDD3p0GhgD0kzufpYRfdDP/CZ3/neH/zm793n3+RaNtDsU3zzP2z6DbOuAC1Py+vk8FTA8pgkPgpcHhPDR2GTwdPvfXoqjbfl64S59db/Kjj/SYDvyzVpKDDXg5dNtiYCWn169HD34c7z120xKYohk6vHBzqY9TZv8lKpS7VMyrqoik4KrE4DK/LVH2l0DIj4+R/3ZA6NUUrppU5NmTXS1HKot7lOj+KRP1xjGyVwTxPSBc+jGIEcNQyJFH7DPKD6NYrpTyvxuN1Hthgtvm9mKXbxbZUp2aTB47cVLIKl7QYBbHZ0zA0/eqwsX91hDEf90EpP5aGOnelkOBY8NsIOkh0VtPqzf/SP/vyf+i9+7w++alrZ4vfIJLsFFdelxMOAYk+YZwATCIrEY4fXTbPBB67z6W9/4Xd+67Nf0G7R4f/K889e2du7/uxzps3kfq+vb+81NIEFs25q7fH+44cPH4/VOr1y7erBY5PqD3a36zPusKao4zyfPHx08PY773z9ta9vb/u49alPfXpvW9uPwIlVrRJanFAupHKqdGkCHR9ZYCbbTSx2JoQig/G1wHMIpMtGTnOqmilJX1CsdOqFMM0jO2Bn0Kb9xA+fEU1n2t0t5PMWldzT9+/dJWSrqR49fkxGypcNZSBkEpFUEGz4Ysshwlfl3oYuxydf/72vvPHGm5/+9Hd9/nNfvPvhfcdBPHr80MFtD47vPDhxoIPeGTbPJjzueknY1mOOeP04NAaxLGg+FmvvM41VcNcoB5vScOyizGncCC0pzf4N9adkzSVI/1Sg1DmVAiLCFu3WcGCJqGPwObvJOdkrI2WOUnoISOYq7UrBJa2rLr2Ue0UgrCbhYrHFEEIVx8hRmKDOvTLhv8qp7dry4LrIQ6CXqd1S3wIlATabKUCZ6jZfFkgVXo3kSQkvyFdojIdQI0W1AluiKEYQMxg0D9UYfsb5lY0yOTxeHH94V9RVeeQdnOqcGQCWWaCCiEER5C3Q4vQS4Akp1CU0BBYCJz4kvYlDS9AY4oEs3ZJwoU5IrOhTv65gT+YegylhIRXt5XskdPUGdlYvAQGi9hZUHmUyNm5e1QXlXsXgN9elHCDgPgycSRqBTAJ9u4DuRxx/WRnltfCUqSB4AkFc3i7yLNsL4i7wKF7xF6JBSaewZJLKbLIqlyWk3AZaCBdcePj0079uAgensiiOAuIh4n0rzpKQJBsSj3GlnvCJGDaBj39+/ZXi8lMQ5ktfl0vywUTsMpp/pZkk3xZX6AJB+BK5NMu1PDyVoDgaAE8iDOTLuEvqy7T9ni9z9Of8MHSX7knSoMapQrrHyB7+OdcgtqQoVhxZKB/WHL/s+3n7mE57j9DAq6jUeFRo6gVY/UCq9dNblaHGhxkKME42tx8xnlurnzAc//D8QbMUT2rAra8/rqA6EUzVVYN08su6PIzFK3ZsCg9RFMtGe893uWb2Sj8+u7O2/qnxbCwCH5SbyV6Nvsw0Odt6HbZ1NGQmDAQn/NhRV4lXriP7CXhdWUp9Hekpby7d+sZ7Y3jLfNG/WMtYVWhFt4pON3BWw3eWwqoo39LjDDKuyDEb46uytJR26VuJsPlODEVCP9N7veh+qMhEuS1ePg+Dz0SVRRD6GC642VNVRUGWRRvUN5hHZe0RIU9Y6Hux+rYmOVzVGeG1aWU08SSmKoK8Vp+rELQa1rbfy0ePEQisBMK+nMjA+0giMYRk+ZeHqnecx/ziVCvON5beRzMdsMBS7+lmVaGdvFiTbOMt9XDd5mvbVuWp66ytU403T2PoCjoEA9gjvBXViAXac+0HZKvSZKGZMZHyBuQfw1dOXrKRxdn6Gwhspoeu1fYXmjEGKTbe4TGYZBzbzrZqOayauTFZxuuoW23LbQTjVa85AcmcD4GX0Jz9hFQI0hZyYT3DNL4FKsZ1LTUiBYPl8iF4USIhNUzdU47RKDHSzM73Ojn54IN33n3vTQtb7KWoEXVTV+reDU6J3uXNnStQefT4nukOXMWT4/ZUsfjy7/39f/jsc88+/3yL22URq0fMi8Sw0FXuCl2D7it//I/9xG/82q+9/tYHCVrjKEcTkjV+BnP3oSLEuQY3Cl67e2FGenn6WlIVkqT8nF7vxQ76c6VRPfj41BW7n3qdhCNood8Wc8rAyS14YKYFmB/eP9iyMY65zqms4S6b4B5c2Ti+vbetAWqdijXSmI63iSJ5RHyCUDhT8KaByV0BF0jEVVbDn9Wza/I+XwtzOiJKeI16pYC9KmmOs9rNzpRGPgQ3HBhyvCbgJ4mTvXQRxZ1KzOZnm/Chuj7entUfdi4nGFqq+BgiS7X4WvKtfT391GdtbMGqUHG12rae4MPj+wdHd51voKe4UmExxLEJM23cC0vqmoKzFPX66XLRYoKAXYTO9g+PP/PDP/jn/pv/nf2jfYdw2T4YbqbJZAmTRti0cOoAAQAASURBVJYnIvsfB4b6eSnAFZwpC/AE73T/0ePP/fZv/MVf+A8dcXC6f3Rz+9onX/ykdsG9O3fNftnZvX716jXA6aSO8HovZNZU82ij0tUQ5n6enN2//+ja3lWHJmjEPrr74Y1bNz75/d//G/+Pf1sfhk3Unrlx8+reVWQaPTg/fSYObdzBeK0LxquV8uen+46fqUFs+s3JwYE5RRsn5/f0vxtpkbXCLuvyhX0VBBaTSuRy1o8eX29G+s6d2YyBdQHqJR1ZnchhuODk5MHDx/ix59Swra37j+4dvXn2zK1bdqA/tylC+SubpTrsFUaGEvd3dg87RGVt2wShvatr1gc8c+OGJQLPP3f7b/z1f3//4L6jCNY2br179/GjtR9Y37l1uvr+qSE9a+3MnGoimTEB86McgXJwumpkwDCpuYFOamPurGiiRfonTAhRkZBJ893SowsJwsWAADOK7PS4GiFPe8PmWGjXJNBKmbgUMjZkvNJk+qDVlDWozsKikxeqZ9bfGpUAUhWdcgIKmlpvMfvSMxBY29cxximL9kR1lPhazS8Y+/WlosE+pV01ZhxZ0SmR7ZdfzZrOUbfqgtKXkD06el6O6o5sZUpZ4r4GDv4soqlghwZbWAgoq5er8VV207QWXsMgImtJqyMqlMb2o9u4ijetLByB51zl4HmyiAVlMtW51vlzwVmrt75/F8UlENKsbb4r3fLs1cd5Njbz7vAX1cO9JUZBWRQrtdSAwQKwrIWLpmJ/vup0kx8ST/zR28U5mMJNjGXq69rZLZmvrrwbRae30+nV98qfVlSnhyral+g4WEu3bB7nZzpFeICEMDr9eO1fdmH12Pnilha9m3D63ls4Tm01fAaVBCU+HJ7poS1hEcNAG4ONjbKuJCY0zEZ/Jpc+YX5x0LVk3kvhxTYDZUTgFowBMumLsLyX1DUuTd+lUoIyy22UBeYkbWKYP7p/gYDEC8elmWv5CW4EzX1l2YfT+QbFWLKcR7wYLSzICsknXy9WzNor5TK634vnEgb2+NXLVL0tYZBCQgwqxxoAxe79IvFFQPle4LHEKNZHVwy+vAbAZQZLmhh1+bnfp18u4PaToFObjwj+COySJIENgPpK67LKeLBAegnaAE15au6KjhkqZQSSe6cPturWmjdbFm/ZlI+ipCxcSIPy5EIR9UEEl3gzUM2pHSud5leP152dCWDKdfxc2zIokNUtnKz5eUmWk+l//bJSSRZWEsOIMrpGP2Wo9uptqZV1KbERPsVumHKgFMJSg4K6do+pO80sEVVO9UgAValLDPaiPIKflYVjtlP29ptTBfHiWWvlgrNSN3cRc87RqcIftER3RUv0gx/SKO0Z9D72pW8peN9VaReRi8GvF18NSO/HCspO66oGBMNUBCBw001egbrMKYoTNxIWZVlwj/AFj+FBYhchjMBwi0rWXxYlV/YqfhGF0YKCVSd3k34QGvM11Xzlsw1/anSZ51qYqBgRnLH3DLEEmARsfTMLyoNm4wAUxj/Zpwktm5NOdrgRHo7S3FX3J3HfNbBMtMCpYEg3yQ3oNzfAhkj6kdOwWNKFiuFMuPdaeBow8D3mKPuU7k9QdxSP1JJTXydt9qwqGZcgSLfLCExENQIgGgLhojxgPI+BUtWm0mw7+/rXvunbp7/7u7/4ud8z5eClF19wdh5yjTlsnHRYsqPKbt269e77d2mlXknTr0/Pjj7/xd/6t/6td/7H/+P/0YuvPG+bPEqfkAfP0eSEAiciqtJd2bhy7RZuwBzOQ70cojiyS5Z29HL5P7qWKy352FW6y4DLh+V3Sdz9P9l1kedT8AZyWGVSFBp/9OfDh/fy+3h+te4fb67tXHOe+HmbG62vXW0D0DzexA7UomG9D2XYEsmzaoyVSO2ScpwCfBFr2MePizLnmzLEJjtnpArS6JYjDcOlGEuSITAc5eMKZZIdTg6kXssfv7lJmZPZLREwkVdWDg73r/LFQ8KrxKneIED9hcIMLZLpnXUQnlYPrbY4fNds86OVQ+ouDedywEnhdeAqoh2JYFJZLQ8wDw6P7rz//ocfvHXt5k2t9xbsVwajZsnwaeY/kVqEhBWVZVuiO8q0RXZ37nx492/+9b91590HVl5sb208+8Ltdz94z9aOzz//nOXqWcCz0+3dPWRqwyijTILp7xIzFxWFqKeGXHQubmv2bQxgWOC1b739T3/zc632WV0D7dnbtySEhrk/J8Z9zODSkm+JYZvz6J5PiJpU9kFe27IJu4JsjuFJ58CtHh0/rMmbaX3YLKnGLpRCR4p3ugLnvtXMh00i3di9r00yH6FW372GcenOLQt+bPXBd336e1548Xm7aLFQ9PC1b7wj8NqNTqYXC0oGo9KW7ZwzyNsc23QgYjIeVdDq+TtvvvVjP/VTP/qbP/XFL/y/qaGDyF771hu/+80rP/zdP6bfiSvVMHncHo2vc7tqRsTc8R5ROqMftFHHT6Y0q5VpqfYjmuQoZjqWIowWSTjWXUWp2GCpGApH1az6uNmWWmhlnCfqYrPSBuHVka6666ViQAD3pRzVuVTCtwUB1SdFyhr2sWxLVt1cG0DSCepLBCV+2DXVu5Y0MFIpOsPtyI+KCKlBXIld3roHbSw2KGlPZpQarx0KhiedSkW9LBgEKVJhkwHpZ0pTefpSuBgVW8ZwgT6Io6tMu2puxpbS4so8LswWVJQ+BakIoVfdNYGFTC2Wua/ZSQxF6RbygYpvEzAfPIXrBIhVFLcQCTlgICnihPfkAzEViwZg6iCHeAKdL5mjTEf5FT2JTHI3mqD2vGBNGZTV8htuF+9LHjIYhC9xG20JmAyF+YrA8GMjMINkY0oPSW8hgArN61CU+KMT1GKm4y7cWvJNqYT7cpF6YpeiHEpUgHu5XchtCRpu+EZVySqblWJBbWFzzZ+MQGwAQvKALndPIk7QEjhfivOxa74taM6nJ98nfVEveHKR6oLSwi+Qvvjw1M8CcwIGnMpguT5KfIFowaKU14BD5cETDIbR2rgvF2XzrQFxidWSxbwNw3q//DYRB27QAfapTBaz4XFSCJ3dYCZ2cUa0SYFcrzJ1BxYq2TNCg16pN8WH/bQ/j4+1v1fOnlE/b1vG5dz1K23fsABYX7nKjz9de6S1286gJoycW8nHOlNoVYM5tRx/rnOunhVe505YNDm+jQ6uySEcSNuU6BVDsTrU80rDDV6pIbMFz/IKB1695khd1hUEBcDRY/wAX+ps87GavV4xu1rWByfNmMtYEjdmwkmZKjxlDCnbE/FF1MuaHj6oklZOnlVVO4WOA+c9d/XkWRmuOqMOGg3ZaoBULNfOdxLieXtrLkUpk1fFyGdHFQ/Ze/ZJgVP0JYeazxm1k1fm8ZsRV4PFZExNqWVGGny+VVM/uVWWKonWR/CMs4Z11U8JYC+YTsMmY0TEPHkxSu1Gn53xJP0U4CkuZa5cSeKncYcAww0Jog4T9GfYj7/Wlzo2Hsnq4PlaVDtmRnJ/TeNuswaj+FLoH1OvR7J+6ZhSsQ1Wsgl0LrQ/4dHoF76wrwqcKiTbJr5wAwNo3ti6u7p9mMvb1Re37PFYAyZYdFQme/Ebe7iSfdxoGbHYUDZ9gKuNdU3QmQXNZQuYFAiiyi3d1Q/HpXbsQyG5F6CE6aBTguqSafXAa9GVsMn7L3z5ukzTqv2HdWXBpzg7+epXvmRryFdffeW7XvkJn569tVObB+rV2Ck0L+vmtT0HMNpI8eT4WvXH6hWfX3vz7W9+651nnr0mVbVUzZUastCi8Jfskw0tMBfk+F/5M//Vv/4f/LX3PvxyWNFYIl2/H3eq7Kduj4ZUbnXtbuz32NuTp+X9Y3cf4+T63QkdwXQTpmT5yegGAqyJOq8Xt/j3FOwlSvexHvbU91FNDKXmdVVsoGrq8jWl5Mrezub5tgbv4cmhlZGn51xMyhXkdAiPajL2UkWcw7l1aEWmDsAt/rRuIs4eltGEO4OdXORAoQhNRjiA+8dmstoga3PjvgNuyz+J5E2MXjIpcO3ZjxzK+wmVVUWJvnLKh1093tvdvXV7p9Jw5oAqnQu2fSpLFnMoS93qtqz8VKjDLfHD056P+5p9h6cPbQSkAEPOLscRDYP4DA/KGN2Q0SEggkLWxMCN9Z//M3/mU69+at0xwVevmJpmBx7KZmFq3BkOQTI6PsIeJ6xVkLkZSj5VIl04Cvw777z/d//hP3n37ukW9LfWnr/1ghXmH3547969b929e+fWM7deePET27u7TawzL2d9i73gJCtAcaJCWr2giwBzFDULglH5eP/wuZefffOdz7725psK1c0bz7z4/Iudp8J2qdnaTetBu8M3sX7j6rUrJuA7qQlzddAI4dwrLS2StFLHHHnHeh2ajaPjnoUxPyweVU6xptlAOatszdnae8hy3lcCFKp9tvomnNObHNbza888893f++pzLzyzsb12bVOhO79z586zL946Ozrbv//YCECDUPsHW50DuXL44K4FDlb+71y5cu+Dh0d7lkUbe9l/4803Xn755f/PX/mFX/vlf3pytF+rRAf/xtFvffGdK9f2b992VMHV3Gq1mCGslGmzs4U7tY1FasWI/at7XmF/KkyKfuaL3nikWlQ4nye40UgL9JTlYHv1kSKhfSkJBqJtO7VpNPTs7FndMqsr7zTGFHx8Vqy8aMxYg/Z+3WyB7ao2GBaytRmKTLECNXMqmFWcvGjCyFD0RhKsXsh0s0UUMQ3HXX2BEpOaKqmFVg0aoyg6/CKuOquHHnXyvZnyL++UJpqL6b9gdxDM6asqZmv7VlcjiqXIlAVZNLIP9RXr3CJDvDyAcPOpeoL7LImiGx1l71sWYHqOQ0bB/qByNZOk4LOUNlHELnoIAYprsi+3ggXqy5cT28J8zZ4ZffRhSTIMjTk8+Bob3A4fjY1/OJVKQAAPctxrAOfybwo/IOv3YIq8aoj1O2honLtRhWyOooD45C8SsMOx4Qi9oSLLFRLJB7DiFTM61tXamOMT0MB0myTzg+4gY3+5V+md3M4qbhjxSBer8YY3WDXZXCQtUbgPAwY50hgDOVjIzcf5GiL5SBI2Jj8sL3XsSDZxXTg6+8GeQbw+0KVQ2P1S+PGLAZ+6g7LQ16Q0OA1PAiZd2EymQeoqaPXi1KwJWD4Xt0/LrTg9xqF+1w4W1vTcmsMn4wM9zmW+O33G3d3uy8ydnqQIxmprRSqEf9BVNqF7geW3RZvQWHtx4dEgOyiWqv+TTxi6hm/zsKT4KGnILHGWLxNp+ewenBJzvWnu+UmDnTvbOj3MwaRrxys7LLvJeJyb9luQL5UwI+P6FXXOyokDz+lYqs4KNDTHzFGaug9yqaTk6tSGUKZZAEMiklP/vb1zB8dUJ91a3znasuF3ODbKzdZLyHVmbccCwlBqaVlH2rwgrHxX1OYf1/zU9hRQ4HrVGM5VUtXz2oufl09AvAX7aipPQejAFeV+Q96sAFzzcnGiTKhVWS/QVefILKM2mDcKGDbZ0Qs7iBP16aqp/JmpfNz+m4CVqUhmA8ddHfqYkyGnuPLIRKn9jHRz7RTVGWBTEHLzjL3I3LR7OTSgoX5RCvjcIYea0CgP6TVUTMBUsCvbOt+EsTW1II52SHVt07hzOXnWyaeHjdoQzLpdS6AmF3BCr9a0n9GDgrC7gX7TUlqMDYbpVHax4ZnVU4eMpJkbvdRZsQ3CLKwvAzF2c/hGvaR5YiPmYwhHQMbRlWsTb5g7molX/reVFFRhPp8KgeF8zqRk38f7H+kuwTAAE7I+C9bvp7npak/ANC65CRsLlXaq45tjqhJTufI5aslImAbDJFtE1YHqjwR8Qq8uySoFEq8RRKYRZOh6CLmI2pEOdz68J5W4r33rzZtXvv/Fl15as0+5FcmHnX+RGxC7Nmyp/szKM071AstcEsUL9qYK/KNf+Xs/9lPfM9O80wiKjl+gUYGLzqG4pNitPP/sCxsrb9798P2R37BuMRrk3kBEKeUU9SBfMDFGSt71dNDTz/Mt4par39RlCodnUZ+6nrzFq8tvHz19FDM0hpWJdXlpooVZZBTGyRbnt5+9/hOf+a6vfflr9pbZXL9WE1FRVPdMt08k6AvXoTvkK1MB4cLoeF7dPDizeBe0Rikb0xv4aepoDPw5+xvmTnA8oLm6vru5Zp3rzAavcguxSv8lAaOIFwwocFCnGqmXfDTpzdM7ee75G6988pUZHsvfkoPqgiSZEO6M7WurypTSHjQ5pRUoRE6rdox3aKtzDDUWEFQx0GVyZD/dXDA5umVlJGp4lkdmbYvZJvy9tZ/5Qz/x/Isv2D0o4LLPXNP/2HrB7rKKFkEDrLcwHzVQFKKoKE5j2P3qV7/wD//Bf7S5ubdxuHNle+8n/9BPmHyjXF7dvWJr/StXr8rXCEADboCwMivnnGVb3gcECJnmI2zoBbhydefw+EgcZ969+eZ7M+VGoTt/7tYzQEXXoOF8qFmAQYX56EdHH5wYeBAhAZQHnyVBt+jIVqGGFTR72B7zDDXdWUhkyJckFVsLBA2qOdRxjiBsNlFXpkOprtCfWBkJpjGJk+tr5z/zR/7w++9+AAE9A6bgbKF65eyNN996/oUbxwcHhh9Uevt37925f2//+OjWjWfe/cY7X/69r3xwf/+r3/jao5NH5vYd7B89++yz77z11pHGJ33TwZDfuvrGu2/+4q/84z/ysz/8yvPf9Xj/0Y3r2/Xfmu3UcS6aAuwbFavLXwXHWFXWoZUn7A5RN3CWrs20IT0Si00aj5bHkTZUqbGhNTozU0gUVm3iAJlst4LalKJYGbvZlHLJuvYlgYkfizIIeiVcGp6yjnVwGuYngKS7xA+EmCVJLSGa6WvIQQTPMJxrAU4ywgGYxB7gOZhMtbd8E70IJc+w9KdG7rLmBxiilR31HnJAzKTXGhyo8cUD8mlamNbJh8qqU8HxSN0EADUPdiadUx7liSBk/Jc+FCY0EPIoshzFXCIM6JAbA1Q6l6/QqwK74OewBTRXhAcmk8ICSzny7WPyFg4txT8aK0mJuIS9g1utI/8qZ5AGoqcubsNF2fYCo8ImhswSQZkDM0lGM+LmRZzaA32J+qj0WOIlOgwjt/zmHvfmk8iJpnBslzJaSrPgBfuBHy74I9oFhFraIJVnmC6JLnJcIs+nybOI5Rs5PYad1FgrZc/pXVHyygaDyTO0WNpxR0u1YBaAiyuQpS77y7CnfpewvrqejrCECJyHJ28Tb24D+PL7R8Hf8XQJ9LIBsLx/DOAExWrX0/cl0iBXP/1QMdGiKMQuhLk8ersIjXEXiA/MJ7clj0lV1AGzfBymByDFSNyZJR34bTpgoudzuXUbduVL9fR4nW58QCPWV28v0/KorwJpIDchVTJ5MPWHw7BCkNJoUzgnzDZ9DrwYk5eC77QJZPMjn1OZVSQMCzg/uOKi48k0UMcD1A1chTaKFXrj7ZdT5cccbs5N/tCaynBqzzhoLlERfFdbyD0fKFOr/SFfzywRoxWCtY+BAnXrZNuU1KWqwJ2qU9YwNpytXT2omJ3fkA+u3b9vMui7NHE9DiFOL7LKPu/DkdSpfWSebKpBKhrlUm9wWlgProogJc6ZgWLmjqeu13Jt8732t+DGdHz7dF5oTtrleVOrfWNVJbhxvnX+alB23oYGirjm58efWDNnZNWsNRgOQFmmLfDAn3dRqVJOUrVMklU4KUO4psarg3JQrCcDBM6UyBOB5ZjWHqtfT8ZcrWlce2sRImbMpzxQcJfSN/KpwDcWj8tjn6N98klrx/ZVLRBS8vBYpRLKIeLFaAkEqibLuEYBgDFLlD51dQcTOH9F78WS8yqwMTcC5kMfrTVZv7K9RXxVc0k29XSPE/ggpkhnuzwbL8IvQj7KK8MUDV2aBkSHgXYkqG1MDOSrXifcxGY9t37Kg/3f/fKXbT549cq1xw8e2Fx8e++uQ60wEi1UnLMgLwp8vnJ/Z5vy7z28esVh2ECtr251oNLZtS9+9rVf+Pf+yr/+X/g3tnf5wTvtDJ43z1+8qHhgDQ+bB2LU6vr7n/q+K699697x8eH52j3kRXqIYxEn9JmIXb/b/YKQS14OVX/AbVg8kiHAfmtK+MubjBVdvT91lSQRYL8kviUHyjSmLKEuxjBTXlU39Yfu27O1x/Ca8yCPt063rpxd/8Szt4/W9jfXrn+wen9r89aD04evv3Nfxnp2JYKJko9+XdCUL3wqtG3zwm7RQ+MJ7XkfGmINMucctbXnrl+7ZRmr486dOLuxcmXzZe5ts3FEGtyjNMUM/VBCtbe5y4RuDOECsWJDf3e9HesGbTQ8KLOyQMQcfQreySTpg6WkWKDXwEDhmZU2GEL3dBOcb67vavGcmpGyfeLUJvOjlUEI21HSPcRlk/mrwB7U2IBZwVo2P/9H/2u3bv7I+do70NWqkAcP8/jkoYxGr0Yu3aA6V4R5aX+bJJlETIZuugjj8iv/+J/+2//Ov7v/4Pr55s7u9v3vevmlazvbX3/jde7yMzdvMqA3T05u3bptFPTk6Frc2DTcsLp/4Ewr3nv0KEkzGlCji4rC+M69++9/8M57d+49enyoz/65F/D+BqHhCi7VltDcMfjbuWIGXDeODh9aR5bB7lwFHjBLrstJg0H7vUJB783mPz1WEu5giLa9Mr+6rqUhNydFsMTTisQfCIx6LszRl6ngr+3cwQCLmBl6IxvVUodObMQTR9iu/fqvff4v/7t/8YUXb9997/7dO+9f3d44ObCs4RACezvbeojuPrr/4PD07sN7DKukZPHgwf36X5S+2YZqxpnJYevd99775V/+wpXdr//kT/749Weur63jktEFFYx+nrY6mvJzqWQZ6+qpcW/q+vdcn1d7B03cKqtEd5kwrbQ7EcubINlm83Fxw5Z7jY9+YDOrtcc3QbVIJJWuyZEVyPTqPaWy6i9IyzG4Y4DJTC5SU810VuCSY9pTfmlM+9N7lcviy4vNLIuHyQHnOhR5qfYq2iAOlCk+lXhXCjxdojm9aO5NPPh4TNFnCvHRC3yGs5WvicDijQ6PynJOUCIf9Wa1pMS4wu0Px5XOTROe/fZWrvAN88F/SCn+YCBln0IYhAUrCWmDCJMMqErKwoDCfOCT26UqEHQYYEmD4b+4RVk1ttMbQxSiAR9rySgNnnEY19j9qPdW+l5AH6ypVbIBJLXC1tAfRHqt+igXLAgdckgIE4IEgTU2WjFYeZzEQ6xIMllKxJBcfkOo4HJG5/AhbgzJidKsh1CLOVEckr1fwBkWL5yN+3Ls02A+n8I7cBPW73LNGb2LDGWF5CX3iF9yEBMPAtyc80CmUMVdcRbWcKyoS3Ts8c88e5pgpsNkdpHR8iPaQtHkD8cFH2CHFqFR+PvdJ+uh9wLgrJUFLqQmgdtAneRP9/0vCeYbE+NtqfOW4Mv75HsR5zLM7wL9gjzvA/wy9Kl4fbi85rFb1F4GXgDqdR4T84C7uD0BkGyGMYkxQTYmr/gpiuxv5shF83T0G9mluYo4rjv91MolynpkJ/NUr3i1z8liKQyDDwGpYHL2jVzWi6fX2HTKdhvTkc6NrgNBWstwdyvQo8QjsxniTI3LfsjiPbe6NK0ZzRnTXQ9vvRBKGFvOQypKJahk8AYT6aHREIEJpuzlUv1cQI4ahPAP1TSTIjMAMYMJWKCW2qzyKIKOKBCaI1TpjVI+nL74upBtA12Hri8qR8fUqwyXQoUzFXR13rSEdJzlYjbNVEHn0q3blE6GVXQ4J7t6k3JEeehKAFfABhLrWwd1HsWgpFNXj1reYlxtpwxVZqHOGMnQXNeBKIu1zQzgR2Iug2Qcx3VGNUyueqhs1a3ScUSeJzV2zZrgPFSkTMYdlubkqpNpwmSXFnNEB/S3gAkFfAAaAtUimj119kzOyWJ83ywnRy1dKdr2jiQNmAyXRmrQYzfHkWJAqd10LKWGi0iLKnkXmuCbNsxLt9g6n+WX8H0ZoTZSgfQuGiNGc0rEBZRukO5ogxCVn0uyZIbKya6WiEe9Xng2zxp/kQRaiueOOiFOvLRf5eqHDx9/6Xd+F4BbZk489yyH4/atmUjG7nB8rOiGjdYn12a16UlbaxvPP/usHVQe7D/QkwjU2dr+yunGP/5H//C5W7f/5J/6eWthxVTKYBiy8p6Lp0VVNUSuX7tyZe/K93/vD5mc8M2vfX2W14T60GwUIocsGiP4IvHFA0ie/Pv4NQHdZBmgi1R5Z/kWIXIZdpFwAfQESkTMxhPfHi7GRRDdrfQZDlZCqxOnAraS+/7a6d1b164/POFb3zrf3d/eu3FtY++9d/cPMx3cu+wN0qgpOZg8TUWtHHRwsEkW5tTvH7ThSoVxSCbIdCThHjm66/mr189PH1lasXO12SVZrWFJXC1W1I5SQTPyEdqH8K7gL7yCO6sjc83+o5OHBpNicBVR01ek0yuN7fDS+YxrnC+aCVU2g+wzMDbeOWKQdm2tf2Xr9o1rdrkS9+jw4NjMyoxMnk+2w30cW7MCY/z21d0f/oEf+rn/9M9t7zUmK9JFw76d8OFF+KGCn0NF+nqh3sOFQqewMhEA6r0+ODz+3Je+fOf+g62155zJ9eyNZ1iQz3/uczZgunb1ypyMtbmz1xg3amDAnbVRDphLuUkKda5SxbwH5LlT4+0rV7/0y796unqys71z6yYCr6lNDMBaYcyBA0ccdgx/Z+dQXUf1XrMbTbYMy7YVwAcFhOmqwvBcV5N5eNq0jCJ3sHKXRanRFcNZRuW35cXjx6YfkGFh6pDA0bNXPvHKZ37ohx49epQJtXhga/25Z7/rf/9/+N/9R//gP3589+4br31L88IChkcP89V1Cdzaum3GlbGA5vSdr16/cf3ew/1KfwYWgBob2ImNxDpow+/M2gmHHFvzjEqCcGo7Molpafnn3ckl3cq7yRZQiVaF+8uEL58IMTOkcKSE6Xo/oiNVbC+ABCBAIwRVjLW8HOLUGrlpaNDyFAERd+EHyFOGpCzGxAkG1pUV/MqP4o+lFkeyJFbcEJ9qDlAhtUJASeV0x6ZsoVzaASuKuiDOSUutyqSWnTRzZQmLX8HxJDVsDXPNkLxoTHADXHAvAd0ebtBw/6pA8x8y10BAViSAImB4WHUpv0lZlMG/mBdUe8wgwzHEw7085nuxuwZr6EVx+BUAfsY7rIpRIk/Vw7n8XoeiUgqpVVyIsCFBzOFYAdE+lacYk3W/6RBCF/53H3oAgZ66MPYvWV4kgRZE6A+ZD5hkKvNpovTjJUaFa3hKtuQ1ksd/mU062CS6ovjtK54AnczmmvSL9pVFmA3MwHpJG4f2UYi+LyEjDTgS0yQpZiKDGdbnYRZXQDClXbyZFGLR71J1RWeIjhOE1emEsPk6kptYT24BLP5Hn+QfQUIXgAPNc9Eur+X5Iu1l4JPfJ+mWkG97fRJtHiabBdzSAFiALnya56fzlSTyLkgd1Ad6YUshDGhzmFzLOWc9fcf17TCL8JGcfL3YZag5oH1blMGD8HT3sXmCWHpUqTGiSg+bDa/z6fh8K4/xdGf19BmTds4M0jG3h2db69sP9k/31W7ZIt0StvPfOXXQiWm7bF+FJr9Y7bx6qqvf9mhi7rSUtbkJzplUkvXjvLnjxBZ76OJCo7smL+oMYzTRjicXhZ4oy6YQmtO47xAHerUIUiohwhgRMThlVQ9cn3jgmxqXjgWj/nd93hLw3bK8aurSU8b6s81htQIBfTKwO1xlT/Nga6ddpUd7uba5uvXBi6MCUvfVq8Xam91hekxd/moETJSQAUz1y9l/CVix7BnvA24N1I7qR1ZI5IDil7SVYW4gml1wt34/MvUhZVrqdt99xxE7SqiylFGWTYYq6pvpMCVpTGdMIS6YOoMXlrbTOD17oKNAynr9eSdVyVXv0Sa6meVG25Uwfr+UYQO3ZtLHzSWb4PEFauHGLhtktlBv6RRXu2NKUeNz8W3DAb/JQ04Z71NH9QZ7hr3jTRIkYHEg4iFJCR2pJYw+9x7QeTAp/+XY277LxRNIGxJKDShzrrQ9m9gTA0Mkl6Uq4vIqULCrlP1mAlUqEPC8se4gnwNTdk7tXVCRUH/rslV5UqVYd/K8Pv6VjbdTvFJZOPP4vXfetjLyB3/oB77w25/ff/z4+VvPO2BI+0qcgwNrUWRQTlX0aXcDLRqaO1tbN67tHp480qnaQZWn7V9kk9K/93d/dXfrxs/8zM/ZrQZSKln9nKaZjbbhzgW3fvTHfvh7vvdTjx/vf/l3vvR3HjoV62j/8X1seOwwBFyxUxcmLnx7Qiqi5R8/P7oWZly+X7DG60V4SuZKbylugfKfoLlNLPm4uhO4RrokE3IRrWfIxOkG/Xg8bXOed2b3YB0FnC4nz57dXl375sHxvf2Hj/dqI73B11M6daTWWUC/ST0RyYCbmBOg9G2ct18tBbCB6umjwyO9cZPziJ422ub1dJONOntsXsW6c4bP9NwnEWoBGGuwYDrygWU6cfnc0yjghGQcGjGkZY8enLz71r1nb1+vUDgAS4Mws5MHTAsVJjPWycNsZas16PPpqZ0pKfZjxbpd5+16enJw744tR0yF1yW/7X9G8LiRDcUg5Ez+cThCk53sznP603/0D/+3/vx/++H+vdUtZT+Fh2tGYxaxLK8JZVQbJkNCLB9JzUOdBewvNVb0N3/913/t13/1VzUjz04/eOaZq9c5/eb+bZ1vbXR0rn17TG7nKLsszD07f99+uQ1c8Kt1kTdM2rL4LHM/jFZGznTBt977hq1lHOJmZuYLt5/d1nFuF10d+Bt66+M3hO/e/3B754WsZttIbtWHor9/a6sz4DY7baDeGo0cXRdpCMv1IavExkqOmePX5Jizji5KVWtBuUyUua329FGK17Y/GM3dfPWVV3/gBz9z7Ybtdx3FfbS3e+XOB/f+N//r/+lv//bnjD1e2d59Zm/7kUHew8ODo5NNBe+ZZ28+s/2lr71778g48Oq+BQlNGFMxpas2HjDJqzJIYrjJ8x5JyPdo/+j8yvnq1c2vfeNrt2/dvnHr9tb2rNnF5WoE1U2CQkAFeV5I0TJuh8UotuDIZsqW/X9wc7SOkVdS8u25uka30g4ZIh/Nlad0dibLbd7NRT13voW0WFX9kFY5MzU2ZeLp1eiDz7DQtZUzFSaj5wly0RepgFgsdkW3N8IbqouBjlD2nv1TTEO1TEo/htxv5UW2as9D0gx/8Ivkf/qJE+WQkMTTnHr/zPrAdmTljYRZyI8KDLaSw1nyBcmKyMAJ7KCEt6DmcQ/v1KcYAcVJmI2fummJpOZLcNMfc3ob2ivrzaXMtUyhl1xgVV4QRvAgXYPKV5RBzH0o0pFX30tAmn/kO3di6qMJjLVRmuwHFk48c366u7JxN8xlKPT0Rpiv3YXxUCkqroRLtFdnzFXsuQadDGF8VHckanDFXlghUqL1+eR50wLOt4wZDmULmPDukowcjUASxELpUC7XXBUlj3u07CgV2aC1G5JgZ0EA0ZjnstaxVGBJtKAsZvF7m5yKGKp9719ESZp6TLaDSiip09FoBWzxJm2NmESar6PyBXiYv7Lx+kgbzCWLMArwci3e8tbM1B8MgOvb+czaX7Vq9MlVtpcJe/Z/oEx0jxdhE+tjtycJl4eAQDm8u1+Oek+SRWyXyE3Q5W0SX3wpYSy5CJu3C+wvoz/9+zS8b4u7IC+t8D4tn5cEAofvwuazUFbkyMmHj/ZNIW+Cw+qxuS461TQGTlY0BFQztqI40MmlZXu6dba9fWZv82bBrDxueFHDIO2jEDbZ4Cyy1FztqptpNtMt1YwpDTo9V45twqfuOD3f3V6/e7T/4cO7Cl8r58yCcAQP763CVuM2UXPZx0ttcLAFsjrPs28d2c6+mXh0yjmwZdvhmFAFhWOpYFfYGjBkJfqXoRlFodCVRL01ytmRvaI5EFl2jmPbt3P1mulRfVZEjQd7mKqG1RsV3jjm7Hq7PLfkVQTTdOyGWSVlJfLjfVV+JYopawBBXc7ocHXNG8EVm0Kf6MPaMecEFtOqkAeDrzIQWVWnNENryxQpfHUhSeUJRCW5PhdgsvDnq4cm5mqvWCInu8x6NGIYGYJQyZFYIVP7clnMzLmCGc1aOjiC5qGszLEGULc05YhVY6uBzt7aNkPtW+mkH5s1ZPqML71njKSc/QnR1TrbiQhYlqQyMGrMhiTFpY9wIIHe4ICSD2dR+wqeNBmG/mWAfUC1w4AdzkmnBIq53Jf8Bc1DqBDulJZA1TTiLlE6Ymtiz9iKIiwWIhwWULKVUQjUevM7OAeiGsOQFy+SL1CjdDI316dJxrNOJTN0tM+bocgStgEHM3x8+ntf+r0H9+7Z7P/Z55576cXnXrj9giYIZwEVMjHgMX1C5Vv/sGYSHisEZ+fOJCKht968h/XJWFFcO7r/4MO/8pf+ilOEfuZnv2/v2hW7LtYkc8EnbsM0nbtyZXd3d3tve+XqTz1z9crtew8ePbj/oQll/+gXf+WNN16f/qthD9Keuj728lS4R58WXo8KxfdElFb6gFexEEOfui5SXIRwg+uRgtu3ZTKQhAYunuPJ4sqn2qRMydfvrK9/yDM/Xdt++/79l67edIiskre3vWuJ0qFRlmn75yHZYNGBFe1Ly1/c1cG/aQRmffXu/tmHDx6WcxgSenUx5J0zb9syc8I0Gwye1bQuP8UpuhbexFqP4ZcGLiCKFqRusE1gtRno+cmGA6ZOHpsKr6Q0X7v0BEue/k6PDjWtNw+1W05tJ/9gZ9MZuKyEdTjMQmX7vffuf/ihhkBS1Bpip+y/z6eSD/eSkshZt7hQ6ytBvX7t+q0rVx8f3d/cYQbbV2CsImTzw8TPv5whrEgI/0E7csZodav8VuqSzsr9+wd/92//x48fHdhi88qeJkgLtpS7rZ2a59TQpLJXP/FK45frG7sm6liDzFne2rEyuC079YnUjcAySdrCGFxiJ9567Vu/+ztfMSZz/bkb23pPtjZtyQ87xWo2xYe1hbb7V/ac9lBCepwTivxtlhxXW1STYIwgEO7OlpY3B0CjnsQtZFL6QKM6dDtmjZlexKbU+wYl/3APsTo1PD7/4rM/9GM/cv3mNTrCquytbXz2tz////x//D++9tWv7e1d4TsZRvjg5L6iSAR7V6+c72ojntw5OLLJkra4xcePjs8fPHh08PiRTZ5UFowBevXHWEog09QDgdFoNdr6gzv3/va//3ecRvyp737xx3/ip24/c+PqtauEodxCKRT9LKrW+Eb+JJEwwWMPSFKDN/ExZqlwxpYae2gcl9RJ3it5i6QMZS56qqZT94lKOVWStZCXDdYwNz5gdVoS6DGJKUkvrnHlCcHrlG2EyFDkUM00itj/qVLKXpoiEoDlrHm/2YTRyfmWhkWaK6oXuzHlsQzBlSgN6nv6WUsS/pp19VTpFyBGECA8GSkV9ayl8iiWojG4cLhEJFzQhIHlHFkRM/TFKB+VWQlkgSmjPwv1g87ErLQMSG8RLBr6eorhI4mFB8IqnJP/fM6IjEn0PVH2nQ3MhhSSQKA+/Irvcw0VPibAseaBK/tJX+4K0+Q/DCRYAa4gVRlXg6YxBItH7G1pmZ1SwlViH4ZXnLU6Didjnzx8JD6vnAnwAIrayaS34SGDGU9RTxzD4SWXoPS0YLSkijUC+iJt+gtdMpBQkBevMbaEU5eQlMtrajXR8E5J4rhNEsQjNfEHBwIlHBb0OA8L6IE/0T5++3j4JHgS4eNvS7CwhcZeB9/L6B+HdBn69O/TMZbnoa2GfXy5uJqxhLilL//cngDephVywcgJ6BabhjcSpzjh81Hff4gWa7lMGHAtK5EvgpafhUvfEXP5CLovAxgOaXGNPB4pn50WVDxVSRsqoJa9kuNuO+61jk6cQz6WzlACZM3UdG17Vgt0u4qgwnBsNn9msbNdmCITtLPy7JQOSZ1+jijcYclxZ9VK39PDo9XD4wMwqQ6LmuCZrzOngUJoMXyVhLPDF6ZW1FBYP91+w0BwE2V0E6yZicS70lSxcaL1XqSY+kuNBToJ08ijl/RF2U+p9sNI2X1oMeW6OUoNd+SC13TIm3YjqSoTmFNAFIDjLbBTOPCO8RoWugNbKWq7bwzySPN12clFT5EXUZyRnCFRU8oZd4ECbFwZNsvO02fcRFBnXg0PURc8F9bUVtEPT+0hXbHSy7C+ZadVG0p2MBVvo36vsUdwKy/RK1mYF+FSnJiR7OnM4IyBlZaOVZnWo0ey7I+dZGJYzsaxPf4x/J0sgsKALad4a7Dc10jCEoHD14u1lMIYmopT/4c785odlA8Ont0W59z6ASgYClC3LcV2NHBKSZxMF4WkAGoA6bjNwE5f+YDPfKO/BEQhCO9eS4T0Je2VdgCzISoBBzOv7JhSb5+WYuKJOPK5+D8aAuUle18uUw+B0/at+tjfMPdVT2beGsFq35I8SwQsvbqztWtWWJp/dLD//gcf6DtskeLZqQnD+qyfv/2c2cw8w8jRb0orWouICAhrnTQhuM5vBYbXYinA9rXt7btaj2trO04INrNMa8o2MZ/7nd/+E3/6J5WpGByZdHXEU/lTVBuaoIlXr9pK5dqzf/yPnqwcHh6ffvD+e++9++E777xZRZ41T6DJKEYEJWALO+Z5XqbBmR1YMpooZH52XYJVO1S4UiptolvBWL8XR4Mz7O2xMaLLXo8en74WAaRogcdPCSsgo6da/nqM9THfWt98+dHBF452dz88uXd1ZfPW2pWdtfUbVz/Y2djen2lvWmLKZTDqXmFxOmN7a2OXVCyysS7CitCckjLCahEZIrQactxtzGnq1dwwcWPG4LMwaOudED5+MYomAztn+z01LxnfoD7WyDf4Q0HT0EZSq84qZszaWpTeQon5uinG6pV7zM+9x9tf++ZXHx88uLp79okrz7Q44fwxLeJMo/jk7PGJbXnWrvLYWljSmihtdLe2p9TLsLFtS9CXHz58uHXl/n/5z/+bL7/yLGedLal/IwPEKozbhJAyDu30qpfuCCm0uMITo9dYsKp9cvL3f/EfvPbmt9ZXn1k/2Xz+pV3N5ZMjaKwenDyioBYE6GF5//2389Q3r9BtimarISprATDOax5U1sbcGD48fHSTKp5sfPibn/3C2tptCy2uvrBj4/8MlMFV3eDtM7HFvTs6Orh6/TpHXzk1nMD8HD6+blM5J0PgoW1QkbdJ4e58oOQ9v/vcgb78ZYad4qSR2OzEBMdcy51Mh1RWgd1W1KO3Jtnquc6dm8/euPXs7Reef+nR/qMrh3tOm7MDwj/6x7/4f/zf/m8ZGJsozXLuO0793TUAcu3qzSs3bUFkotLhytHzN597cPfO1oeHt1+4sXPVOWbrDx+evvHGa4/uXblvrt/+WwoDISjaFbGKNRR04LSAgcjUbq+/9v7p8Wdv31Y0n7Gx7zO3nt/capVbA+1hWLU4RZJY0i9GIsUyDTLxCXLPX02SIzr5EWbyHc9IVcXh5V8Lyo+bSrlqwIRSgJT7OiyYjmousVqFVmFYVCKVXjl86fzg0emW/dFTj1GNhjSX3AaCLzgbqyV2Scyi4jSh0/iV0+dXHQt0dOOc1d1+P0dC/Z3KiUY/K+L+hlfz2ynCyqpaxiv0DfjXbkMRZc4HVKiVWQmMsvNCCsRRn4f0jjMYgZ+8EMb27PdTdq7qu0DmSJJM7AvR+QxTrxCudFHbyrCi6sWbCvM96X3P++kztBsoi9VAValFNlc7vlaLLc5yBGbHSrw0ZjyNNKKKrcYiXGWy5AHSgqhfTP7AAku5SabDKp5aY1B9OuSxsUF+L5Rn2hwNGxHoadUkNx9Enq/CbMAjY2p9SpCjUjZRkVcWI6wTyy9LaWSN9MjzAfBRPErrl04qqWzIIOxl+kksNzcTxFECiTCN5NM8J3aJK/tLbpD2D1eTel9qvbqXX1H6HANKlh3FMrupP0e7V1bfIBLhPpN+hBy/JC6O5U8Ew00n7FT00rIBBcWG8pFuiVUuT1+Xu/RM9h/7cNn3Pxx48iUMe+Glw6QS4VoSLxGX53JfPszTt38KyBJRpCZjXLxdJPP6MTB9ffLJw5OkUJh8IvEi9An7lg8fuz8N46MPT0I/Cvro6SIrku8v6sk+GdBJa9a0GslFbZFT36Wk19WdcqgCRESJCn/WIep5VQtTMBUstVOGKww165b43iOcBimPOYZ8/zPdPdysQ3M27b02h7ZDwyQcBWlsAY1NocYqQJHbSltyfD1P9oyEnjwUwUi5VyzrWl3cI8jrM8hsqf7rFF7oVCqEQx0QsGSREy8CAkCuCsmghqyoSBgdK4sYN2mwwud5L6iRPhRpGsWVNLi+/T6nnMMI8LskTyC++RDeo/ZjcWKNDpHmByxL25skxY4e84nqJ26zthJWOgGGwLRHAFVMmvnqt7I/eLmVMyliRXEVFGkwdfKvePuXyCE6pLpngMoBmFgVh4yrhCMJVkqTpR/XEDC0uEVHhRDhETFseRLTA2TEH6rDDpmxAa5CB0bfAhMgxpXnEXeaMVwVRm4WzWbUklP5aOUdmjrBDYwFUE7T5sE97gCia35r00ZTTvDMDAlc7pMTAlOYGHAZjHvgl6uo8XbqAN5YK0Cs4ER4gy7TdOtritz+NHk2Q+Pqu+/wuN/R/uT6X79+/Xs//d0mUch4ai/1qQnH9fqbRaDq5N1HNKzcxqhj03U+wo1n33vvfVqbDGTIs9lY/d2vfvFv/e3/8E/8yz/Pfx36ksh0kyQ7QFCI+5wQ7Ssv6NLyef6FV3/6D//0P/vNX7t35/HkMzj3MbIjsluXh2HQ8nYZVFiR55rn0vqnmMzDU9FLPjIeQPPhCfS+XVwX4OZngS5RIqBv6SS69fvfXdm9f/5gb//4+N3H779/596PfuKVZ/Zu8qV0tTYNjZ1ZVkpQYsakwuGHKw9Wayo2OnDeGp7h0jIrkEPk8+rB2qp1BFac8lzTxLQGCOViKahpodcALeSkFS5q4QrTBXVfmbtymGFx42/6p6u3Uv85iM36Dq09tTSVPV45Ojy3v/Pq3fv7nyR8K3HT54Yh1td3HQTGbZr672Jsp8ozR/D04Pjo3ft3rz1zff34unbmzWf2nrm598ytmz6G6VxZMVjgRCzsWhi/SAM2YTwly/ch2PcCLVj8zd/67N/4a39DIbOH6vN2X9pbscm9IqfQKV70r3bv6unh4cn+wd0VG5X2ap6KSZJKx7mzwdoUqFE8o1s6+puCoIj85m/9lk08jw5Ob968cf3KFSEEvLHNvJi4v6VH/4P33zdgZZa8mrZmj8lFxy2vwmky0ZY9PGyR/f7x4b0HD/Z29oxztvPo9ubhkcmra2bvgIw//B5kK/wWYpmrhPzG2TLvBi6c8WzzIidt7P7sH/1j3/cD3/f40MEJ+pzW7nxw92/+vb/xV3/hrzp4Y7ZTqudFx/+nP/HqD/+hP3Tl6pXnX3x5b9eOvet7Nw0rbb379lu6/6/tObrYBqA2CF27//Du44e7H374wWtvfv7u3XsHRw/fevOdg8PD4YZKSBcT7FJV+2g8fHz3d750d9vcrrPVn/kjP/VTP30NvzT+WfRqpDHZi7NasUJejqfg/kZQ3RKx95HlaB3CKT3aC5oYWJetIQ6KlSqysppJS3t3YhAfINWsXkeT03wAgp9JzySOU8vMy7x4UCkDX+eqOJRfhneUCJPH+JKEKpAdavEYFarGCaEpSvSu5gNQ9H6KSfYtityHBxSkUZHLfo0CKV4Uc/uCXWHjWiwpFOypEAHIzRCY2iM8TBecpxQIpabwzDMWDn7dDTFZtCL7mh2OnJzK/i6ApIv+1FE+jttNrzwFocYsZAkqWEWbewADnRzkK16mWHsEj8MqDsZPz1OVRX3e1UJLteEAFBrjBpVFQYYDqKjamGBZ9q/aOEcFZFC7D1mDTmSXF4RlAXefhuZi+h/GfsMpYYTfAmJJtkRiXCry1YzkGbXBfnLhzcLbrFkfF8DhL+4CuipVal9l4HuW1ktWC7UILadUvt6YWtHkmPrwRtJ5fBaxqpCBTT3mylULmq95F0sgSB/D7gma83CB2scDvT0VPly8CIgbl/DC/amIT6W4gLaEuC/5z/2pWBoAgVvA2De0h+OX3c9nD9FhyyUmi0aNREqFi+tm8Ypqen3X3L0/uQbwMp/pSZiHJUqxPS1Jn/48zxfBySOhRD6BcvQSYAXWprn0uHq17TUYlBhN0vRpevrXLX215lF1MWucoDuHuuggsgqPYCqlOrf45SaUKsGHdiFuHr7NEJSsLaZ/9WjX5JlWTp49koOaR2u/0n2+w44oY5jDy6MEF+q8oceXihikFZLDq69cq6BpxGCryaaXXIzROJSkS6MiiHyTYxhXa9SEQeHDHfBVIvIxHV7mGjm1Zs71fGeURpsjB4jhToUl5lX+6K4c+lejiDqu2xQmPwbmKBqWiljMClG/klYKLEJr5hRgmCxIxp58iMXQsxdMu8vXL6JZoaDjJYrbHQKPfJGpP45PzJHHUuTKIKuHyMyIwSbChEt2yNvoVPLWd3L8aMU5iIvgK1rBWdvUTzAqEXRh4prwnpJmK4+fDwd7E1WEK/wpRn6/BhXw+hpg66O6nOyYVHyz64E+jHpVu7e3gMvXCIvwMikHEllb3ea4pwBy4f9Xo/RB1KxAz5OWKa+jDQoj6OHt8rE4U6dakHB09OHh0YO19VvbO3adkiQU5QgEeELk67kE8hiLJHlGfvDRirB+MVQTtDbASmdbHHUSwtrW+yDlxRuDOT5+7Ztfv3Pn7je/8U0+xnd94hPHj49v37y9t7MLemiOcOMmZmT5PC1B8GhJQQttkvGqEarbt28/erz/4NGjUDrb5UXQK/uP/MVf+GuHxzv/2r/6L+1s7eVS6h+MfViwtLXjt1oSbu04gpNrDrndsjaY43R6dh9XK8ioP7mBke02Df5yDYd7jOx+5+btMoIgPVVFqPjQz6qazgZ+KkLp5iqOS/Tf7+t8W25gpKlcZ+agCmQcTrme3dI7fHb27jtvvblxdlUTa3Xlijn0W5sWSLQJ/bHFs8ZlkC4LAmslDkiUMMOiXt7dPLfD8MGjhRiMinI0bK7srhk5s8TCOIxmAySxYkgKDozp1+GLkZgJTFvK4eRFSlbJk+PYiCI03cdyGmq/rXfbuJqu1drLs95UkbHfufTG5izYOD15vLu9ae23aeJHj06vXt07PmfumNjDo7MD877qVXHMILCjme7jUrOqut7W7ljUfPLVKxs7/5U/+d+5fvPZ5j5ClYWJwbgIN771Bbdzg7p8jL+LFDwjdcKXYMVs52vf+MZf/iv/nuFSowlXdh9/+rtumNtp61+aJOXGyjPEvbXjzBaDrGZXHZt6pjLopBRAW8fJrNRZ0o/twjdMhTre2Fn7lV//Jx/ev2uD3eeeO/3hH3zx/t37FtzXrcTsa+Csnt9/9OHdh+9/4tUfM7RocBHjeSjoWLMvO8iaFnLSrt7YODQV9XDfEbxmtGlsaA6xe/fef/+VV17WsU/ViTwSNaUY/80tM/uPWzzgtOBNz0cnxw/fffRTP/2TpoXt7z++euPG2uOjt9555y/+e//+X/8b/8H21o7miJk8t5+5crS38wOf+fQPfOYH16Xd2bjy0tXtTWtybm3t7j18ePDj3/0zN541BrXh2HuifvstA2tvH+w78PjqDz/6sQ/ee3tt5/Ddt975pX/8j+58+B6roxY7O9vVQ6Hh5GCDre2aJCfhe37nfTOIzl5/83e/69OfdriyvVJbSIJ2os9o+5dA6wwmsqlZUsLUd34SK2M+f7nyiVQqv6MA9IbLyfxlQJld2lq1LUXAXanMoimePRKk/6dbb5+cPD43DkDFN9/Vuq6qy7RWAeRsuWqjMNrSANuZAJVdNgdVvm5+sLqze751NHtda6AbcJaX1p1CcUCh7L9q1NROIlNvG44g62NFVf1F7f2qp0Ac+8Ln31zVULQVYPPhThR2WTW8vqFVjyRFHo/cIVHfv4RKpmRTXG0EMj2BlYGFW+EuRjzsfwg3epdfjsr6D6bGERQp/kdanoMyw45aaj9VrWrIU8eGaL/hCh80hpTp3ME+OXpRjPPtd+seqH6B97O0Yfva2xWVmqy5AclNIu7GhhEMXtb9lrmc3YDPytqHC++hJFzE9i7m4Ghjt5htqsvxSFZMhAM/O1VVG17i1vwAilSjFlgUhgd8VQGT3gcx44L0oxhlm89kmJ+81KtjQ6oHqQDnrGHW+lCDA/dxLbAzOiTLsqR0mM0oRhkdlKtoemoaGhvbkzTkGd3AeIANK7L+TiM9dVu1o17bytejC4tmBHJ+sFHFgGwJ8Qt8dA0m9VP4PMCi5Z93ne9I3jwX9+bgGDVaVgU8nQjYECymr/0sV7lVfi6y8EFMGh2cOQfgo6hD30e4LB/y2AZSNCxALt5B+Sifwi7CRZq3svSwIFbS5fsA++i2gPzovUxGlSfoO79exgxYMYefqYLJ6ZGf4nJVkiktqfZMPbwvlkbVN9N5aqOZkpmmE6RC3+SOjTqwN6ziVUW0EuDMGU3kPx3OKZsH3SJLY0IchwTUDDjTuWITdM0Gedr8EsUHW6Wqfq4wXnCByWsxYLUOA6ezsA9qFzP4NwUKStdG+9vfQ3awo6HxQNmjSeiFQko+BgDtWjNNORRO6xX6+DHMV05zReO/v7R6HrziheiBYlu7TLHpo8FVA7fcZZ5Ck/IH98pQRgFWPZY6qnC69AGNwIEDL2CL5ML+SnewsnrKBW2Hm3z6JhD3zXxw2iWL3KIIEP2NiQQyyIN7iRarVzmclPHDExwyYX3OfcfpzAUYogNVyQYIHzQGNTiEQrOmd//mEg16gMC6R+8RF2WTWbDSWmknUfgnDrH9D+RCkCB5i9g3sHIJoC/rBDKRA0O0eERiUg37wAiQGJN48uh9spjw4xU1sQYAFJiU4MJ1as6x4GW84AsmMQ1wUZZJBW3b2uyFqAjDlC9xsVWpGQvE/98/2n/9tTcfPnqo//7uyen23s5P/5GfOW/aVhOWYmaWy9IZjmw7GnL6QjbUU0XIhJRW1WYnSJABf2Woi/OZOMXAplSbG//wH/9HN25u/dzP/ks697Z2OFN6TLAJW1KnZo7r566sNoai+WzYf8dU7m3Hcg/3+5nHkkAAt6L9979ELAI0S3xx5WlIqpoeCJfBH/8V/eNfB05hT19DfXkETTmmbNUeWnyP9t/61tu/a2vhnVWHANwzgf7Ikt5jADgPNt3adjoYnIghFQnHlJi30TyHNtPl1Oxsb1w7P38glP7MFkMKt2Joj9QD/YQmSMl2DEjfn7AhdOJQJCzw5ZCC+6lnYmXnyh6XhS8hKziT3tGZjV61AfcVFLKq0tQ8U2DbZLca6sBpBisbL5hJsvpYAT58fNeIKTIfPtq/f+/kzoNHpg/ZMqEsYUu32IeG6tMQ62Gv7ezd0wA4W3v1xVe++/s+df3mFWuIgPVdXCpbocCEHpaLGoyYosKHEeE8X5iXsUr7Dx/9rb/5D95955796bVS1nc2Dg4e8jodaIKEaLfvftZWolg3Gx5kblHtml6HqZONgJxYEma0sm0iv/naG/cfP9zZ3Tw+PH72udt3H9zlZ5ulGBtj0PkH772j+/9Tn/qEVQT2ZW1v3LV1JwbLoqFNBltfUBMntpWFu3fvvvDCC5gAvrJ52Jlp9UKRNImcHjury2qKpuDDaH1z6/D48Itf+NJ3fepVI8z7jx7t7O21w9LVq3Yg1R64/8bBG6+99X/5t/7PX/zd37XGGZN3drc+8eqnPnz3W9/96e/+8Z/8iaNHzqk82d7c2dRvr29ra/vR44MNS2uu75K5IQgeie2D4LN35crBwYOXP/HKww+v3Xjm1uPjd559/sXt3Y3HjrXe3H77rTd/41d/00BH61F4bdoDp8dKN0X82te+8sY7b16/tuecBBsJvPfO+5/+9KuvfvKTxilIgRHI+mL4qDVbgyPK+Oinm780cYRKtBXN3jMfPeO/FCNz6cRKUcVIahMQ2BidNizBZdeo94wqk+ei/RRdereBOVCkm/avFgZFG+85HcggjAN4Uv3E6KndpZoJUNxxltPorQlSOuhENnuPO2E+G8iMoYkxOgwbJjG3SytyKdOKhlFnTWmjF6ZPOjq9Hdvsn9tghoSyG8/bJEw5CFBAc+/5mSyJcmNxTyvblGRle/hRA7WyipNm1EkShpyBYSAew6f6D2ExCP5xnOSyHidO6TgzGQ0ruTSyEk0JcULPRCy+9KWLa7qMOK2n247YcdZ46mwTrMaQO1A1HOTtBn6GXRNiXW+OudI6WKFnKqmCzncKGVcP3U3maipSzehTq3QACdbK5l45nl4lZKlUTbo4fKtWrz6JPiW2/FIU/UTNLaxado2pIV4xvcURyOmpsDkxcqsfxwJNBG0C0s3TX3iT1Ak72+Ca7CCVGEbfWszDohOw5VaIW5iL12UzPzX3cLiMF1KI3vJ6DRQt/8hjf5QblTH6F+2PXSUPrcRaUjYlMx1FviHzQtoBfuq6yHhCluenPv4+jyEmnqtcLp4rDpdhy8OT+5O4QpbnJ58ukjefYQlbfrrPOMDHoy8fJ+ziA6oE6oPs03x2+3iij1AVPlHK6enn3n//q+gXMSsKsfQiE8Y4HSKHfDqzHpT4Cpn4+h4pA5efFm/oI9e00o2ToOrzXzneNbPcUJVx8Jbe5quVai4RWl5AMRL42sHJ2lU7926t7W2uH7YZIIHrFl87SPGbaaGMtYsEvR7KaGEOuT5RZpWCjlqHt7ZtCuS/zkLFtOZi87D5aZRZSMVNWMoPmepoDyCBIro2SkSuUldk2JWdDnIjKuEKFZr85VJlMkikUowuRrDiGXUeFJD6BMATr1ZHjARAmfGeMYqkjrrXFcQLlUUdt3pSglf5TOlBhlzTmgH2Lvvjl9ByuvqtbE4GBWvwHzi208T0enx1D6ipowtQf0VMVmgWIazDMRWoQ31k3jrD7XdX9Y5PE2sEBIdBpDZQiiARvoXVGAdpa8xvvYOb8a/v1Q9Nx51NMetTpR3o0aBi6xsazlOp7Ujerk3jAJyT7GV2TR5Dcia1Ky5Qm7ofDp8368nZCLHdHIN4VMk/O3wR58823vaeF5Kdmgt42S6WGLPF7hRMAJs07/TQgwNLwzd0z3PXJxdqmVIsl/h4Zd7RbqP8Fm3WswS48JSy2SZxCEsZyPOz15iqNnKBqAnL77332tePr+18950Pf52GWOf36P6j6997zWJxc4EgF01Z4Fz5mfNvTxizQUBGT+ox7Eyj0GoIi3Jsqz8WO7jxKG6cXk+jztYe3jn5d/7vf/Wzv/F7/8rP/4lPf8/37FwDPk2SdkonmBiGCwrv+snx41UDGFvru3vNzcCuFEHGa/dkPdKTPCFCz/3iyh2fqy99v/j2JFzgUuGd3izCsiqgJ+E8RUkuIfTyB12DQfkm2GF2Ko/Gyu7x9ccPDB3eXT5rENnzRBE9WXm0bv5IQ2KkkKMfX+NwSNbBLCTpC31sCnfUYkZ79et5fKaYTvE8euVs6zUMall3/UnmMS7qJ9VAG2AXeIOcCqS2sDNx/NOffiW/Ko9p3wjA0ZFZ5Se71j3B0nkC0SJPYOl9nSDM4vb6tiU2RiRuX7t5dmp7gJUDyzpM0Xag7NFj8neMcSakylrDr5Z8fe18FSWaeTrffOG5m6snL/wb/6X/xrPP/Ojh/sH67jv0My8xUisCZZOh60rCSMhQDCV+RIhBhaBHh+/q2d7f/Bt/65/80i/ab4cW3rh69ZOvvMplV/bWr+Tl2Az0+PRdDtb5yg3JMEghmE7caRg3mdK+QJY92IbfeqRdSJh7c+fu3S/+zueFPbYL1g98hvPNDduy08G6rw2N3nv06K137lgjc3Xn9tHxAycOs5YHxwfT3DfUYStVWmp3VLstmIJ0qLRtbGzrkMZNO1zl5h/e2Nm+7egEVi+qHcIA1cfNVLQtkil49x89+vJXvobYW89e/fTL3wP+L/zCL/zuV7/8Pd/7fb/x65977fVvfPl3v8LtUmxwRx/9F77wW3u7WxYINHTDiG/afUsPTicq8v6NflzdubK5Zqdm9Bnf2Lp1+7pNMm7evvryywdks/7dOweHj+/fv/6tb3zNTlw3rl35xHd/16MPH/6lm3/585//7Dtvv390amMw2wWZGXrsPBBLJix9dvulX/zHRwfXCeP111770//q9Zde2dZ6HxeWGoy3zFQTMBFPH1aGKK3SIHghiW6+t5SeZsQudm+014kH56emM21rTa9u3c8bTsOJf/lc0W93IG/qO89jC0Zx7C/7dho39kOR8SWlWqp9ekUXSzzKxBSWNJPYhhaN8Dw8OLhvXzfVMJfWAnX9d+trD8/Obxyff7h1cvV01ZLxm2tr940sOQh8/eD5jZUH56c7DMj58fWjtQcra7dSgwbDNpwASDw60bZ2aTLLdcLxNRNt3ayBtf21093zNVtxXFtb2z87ubay/vj8zAjhI3dz/FZXrqpEVk+vtMmYkzo8dzal/Tr4sYdZypolKmWMs5VTVkDzjGtgUSFi65rMJqOWgtWUPj3aV2U3MkWHz53bZ8DuoLMlbXOoTOToVtFX9MRmdsjtaHt1S05bTjdaNzbiRKOsUUMxlcJKOl/eKsjj1c27eQ3tvWPSwR3GkMAXNoNWHVm9Q/gc6jXTXpXDKoz8BkWuWfh26tBNhUAteZNLJ0WVJZlDDC75INHBzvGhG24ZCwEBZoqfJhM9sGp9xQsraKrQ5j6kOVUaDNXCLvdG+M833gR57fS5uqZSBPgxhvhqqKus2JTmdTuZhIMIoUziUmfMd9HZlXTSA8Y3KwxRmtxmyPIpqwohQg5TKU7LkEEM7+GM21ADnRwQ5PnQX0rd7TsvH0wddA2A36fv/+lEH4MyH5Ycy20BHWvl8zE4T0Molvciza6bxAO7C7kuIJ5EH4yWsG+7T66FPZ3wSbonkQeVifYkaB6WmH8w+IvYRZio3RRZbWdk8kXS1/z4qR0XS+QeVS0IGNVUKFTN5DB+9eI084uyrc2XoOW0wX4J8miuSzYkr12Gy4FTDf2u2a3moMFA51yZYwr4SLmSgHuVBqVFjhQ055VJoq96ESAw3+Gk16EinYvMSgKhjGW5AFjmHXpv0UyWNfNVAVJtqcZTIX4rdzVKK/hjICqhsk/hDA1wLNJJX8Im7eW8KvMSI1yu6EEXl7ozjzMitUGarxaLGdJGJlh3BSN/1qBYsJol2di6TC8knDGBX8UlLsMX9+QWJQ1ws2V54yIRk5jQS/c9L44w6sCMbZWKybwWRKgO0z0lQL7h1CgBysjqtgy9PPK5JCw6GDHQHyqTQU/hlazDEeuKBAvtOj017Z2KcDGwiOBqiFxAhNcUz4AgaOB79iYecD314xPWQMysGoLm5+mSkGBizcCkLQl9ODvMEY+QlptIGsvI4oLCwW/ALdWYOMuCAdsWZmdlg+qFStC9DVt4K9Y4WnUAK4o5X/oWZ4aUYUImNId7rb2JPvzw7te/+vXXv364s7Njg3DuzO3bz/74j/3I3Q/uogkb8TaJRSCxaRJ11JtNDvf3bR9kPlFO26JqwgcNOa7o+6QeOZnYpQKuFxAfDlsfurH1W5/9/MHJ/f/ef++/u36sejRRwm6JaMLkEBxO2DGGbjvFr2Hf/UeH6NHkWwSSCi0cC6viP319R8CTjxOvWhOGF6ry5Nu/+CHMJq8lg4tsoMVIMPnopOYioFl34UNbiq2f751aYKpbigDWTKQhBi7l5pHRvpq7uEv3lr9UlFhSgil+2lC7W9eb7h9j1HOJuMLugB4jCyOL5lZV7afPU9A8jHZecuVSMRZNIcv0SLY8Tm0cotjavHq+cgWfd7a9NdsnRR+TIke5wJgFhGpnibQeoH4EZvJ0xaQs+nC2s3vDvAcovf/hA95BijX7ENQIRtrGur40luRf/zf+yz/y/f+yOZQWN1OHioPRpBF5LGMSszPZAZn5nCZMIbjQ854r6SlyyFz5/G9+7u/8vb83TTXauHHlyhVeCO26en3Pdkb5PAZINrd29b3q6NPybzQDXygi825jTYYH2Twg9MoL7JXtvat33369PVpX11999UV+P9NnDQyfqKCNlfsPHnz9m7/H9L7y6vOrG2Zh5Y48evy4kdvOLqvmwOKzo8705cyYK/Pii5zd81opQbCppdlt2hKYkLUR13zB99+38v7onfffAeqh87ftwHa6v72z9yd+/k/+sZ/92QcPH9y8feuN11//B3/v7//yr/5mi4CvXmVK6k+kQefnVOoTr7y8uRUbW2bg2jZmtqfjQZfB+qapg85meNTY2trZtasvWJmwty18Y+3Gbc7lgfO728ni9Pu+7/vUmY9t2vXO+7s7V/6rf/6//uc2/pxTku/ceffv//3/+Lc++5tf+8rXdK+yL8mYXmatacjG/uMP333/jRdfepbw0pBqm4RFXKYz5cKxNil4iiRVilUZTNhUXuWVcqdsS0mmRAJ85MBVGRYMYrBBEHHewUop/n+s/Wew7dl12ImdnO+58d37Yr/u1wGdgQbQiAzAMIoDhfHMiKRmZLvGNS6XyipXeao8ZdmuGpc/+Js/2FPjL/4wI3EosTikqBEJkGIQKICAQOTQufvl927OJ0f/fmufc9/tBkRLU/6/d8/5nx3WXnvttdZee+1Eo4Z2Far9GwkCfFLXwWhmpnS0LYNmeiDUrBmRSWDRmdmK0MiT6Lq53gBKspinlh81JlyujLpmuS6eo3BeUw8Gn5lSf1wuDUZVjsYalEZ4W6bFQbHW8xxpkZNHyWWfzioA1pTVKCqu3bSXR0rgOkTfvgYtDo6xfpAAf/Ef/DQi8PbHtHyoO1CVFgiVml3lj+LRiYlZQrtyUgdhVgjkgUj3T16GHYgCDjsXJsCXWYYf3u6HYmbs5xw/HBhkTWKHBQAAtAonnNTZ8aKDDmn1qsYB5/06iMa9bt1IBwe6vKnaXPR0YoWak4mjyWRMKCsp4BPkmrZGt4xap5zch2iCfFRDVghV7DkhBZxGde4Q4f4EWcO2tpWglUY+rWw9y+ySwjdHElCle9WUQss4UuJMY1xvXGrdbQF1NGJfsoMK0eQc33GOs5OZxnSVB/Qvt2yIYZ0SUAngIaZUScc/eDvi0NergBUxDWIakXzgE8ynbiQLn1DdEP47TGHkod/XY6vkbNpPzYaeRFT8TIxnI8m8UkGQUWT8iEoHNKF/8JEIYvrBJ1B5X6ACZQFy4vyD78g8T50gCdM/k/2EZ55YC/gDaaRFUC4aKhUUEM6lg4xiPOMF6HpWhKHpR5ABEsx/+21hj9KeIXGW+/0vkYEgzyNCyPtKuAf46DfgXAsOnhYL+EeQWl+2PVpCk46htRdVOTHPCNsmA4aiOcSmN5Cd464WUpQ8OB0pZLkQMsMUHWLL+kucc1XWCCrvWThPuocU0y1Sb048hMH0hgEcyUXR0M+jC/AcKbes5EVqCcCSBqmY9gsu1YajMCxE5E0pEDAiizgx7KYezlOy4A0pD1ohZcglSo1jJ0CA/salFE5yKZP8i56OUgtcXYWLiOENDU/NXMcfPMxN9RwwwpJSLvQETXqIOnp7PO5YI86sExvNN070LhSq8DpcDahMnuE7nRulaCVUmAeGUGTR+k8uvWMwGg7KOsIhLmrM/hQlc50Lk8e5Pa33SS+swLAmxRvwMI+IS7hMRT3FoSh2EnjE6F6dzQNx9qGFCKXqhXjyMeR8Bqi7jYqXciG59FvUgH4guhkhk5FyVCvQ07EipibdAdpGfYPpafoUC0zbnjYBK9oBWkNs+RpUg/7U15iQCRXwNL+V1LH9R+TSMoD9CluhC6E8wIMDzUY5ZBWe/8WHH1wmD4ZSxxcSaW1DBBODhElSQjNYNPmzoytaRQU9rAnQDEfbn9YMBiftONNqn2w/fMgAgNNUC5XDdrfb6uZffuXDLz7/LPsFQVXYgADsaJ2PSW5LfQg47DOXV8AsuUGbw8WjZLCzM3VpKWlqNVYz9zvdNs2nDZfr5F13yq4YukD7B04RWV3aGHN7Lk0nWKtpYrUhCaKZqTy7RkaD+gKzw9LX+tpFQmxLCXoFNVKcsX/FE5EU52M7/oQ9AP82vn97IuiiUa4msbsmhNp51hJaRwbL4sOrTHNsUBkwXOKYfI5jyOdYgH2Cf5FBNrXRgJb1rE7Iuq1nG9qz082xkxUTGeBwECGMAk74QAdk8rgJ4STZk3hzyHzR4JIlPeBjuwjAGBPK1Lj03NZbzeeO8UDTJ2MqIjD93rTUYLgFayOksaBCuDSdaoaWQQ9Zt0wH1BQQ1wmqGpEEKjHsHeUnLf2X+CnCuCY11jodMqvFrl5//Nlnnq82TqIuB3pmUYvR2qnxMFUxUVMFaEPElrJC+giDMSSv+lAFZ11bp0df4tzPfsjFeFJv1JabiyDlIh+UM0qKykrcaBBUP2xHZwApoAhgoBITNYx/WKWNU6NQavdh1Ozug3vvvfEuNm6TA3AX11l9w1AOBcq2Ia/wzefubz6Y9teWFpfWlpqALuH/xwsTN65g9dKWmBBgCmEx8Q8eZhsLFxj0wg+Mh9GQQGaxyCTLRezFbtuzlVnHxaVirdbJW2+9y7AdM+Gk3WLNHkcPPXX98Z//xV9sNpZKx7uXLj82GI+++hd/wRWU1bjWDPGkRSulxvrGwip7KsajxWYTrY3tD2M0GwvVWn2A33O8WmY2Lt9DTYIVDUc3oQpX59LKzlnXGtlitdHp7Q6d1ZnWlhbYb8TBSTS9R37hAL9Q+/XLv/Z3sr/21b/42u/97j+7e+s25mzw06RUwnXNe+EbX//2rffee+Vjn2zWnqywgrBxGJvqXO0qXRTMmbDaiHlOqYLHbWZaBEUG5wMSpjZRYXdS4JLmrlHseAm6kjAY2N6AVmQ4rfSTAzbzRbUB72JnwuT0a6anwRUc+TYELSlMHczB5ACEEUGePWOuUOR03TAZOcWOxdYdFuAt5A84Pnw6vT/uYtefso1wxKmqPTz87/UZ1Q96bK+eTnfgrDb7ZDgjcHwhhBc1DTyWCSEq3AXAsVSenFeY9ig746I+Cj22+y9swo3aKehNJg48CY4iOA8bPxSQKlre6AvZGHODc3iL2WHHBQgYvuhg91+zfgyDngNqW1bd6iIhoVAkZhwaAp8xeyWlIAWjPSiC1HIwBtjrJpR8aHezYd2DkYMktqkz30MmTAosEA3zXlt1gEsH0XVxe3TA+UK9VmHNGDTWbI5GNpPF2apwGQmxnLSNuR8GeydKRNVRZ+yt6JURvsmw7+6LSe8C6OVymw6AAIi9g0zJ7ugaxpZFzA4XT9NLeIwWpMD5QhvGfT8YHGOOgFd/eZwCegMaAJvJdApCBLC0QJFhYPuC9Q2jH8EIroIBQBhlw/KFPLYgAwecbZgBAEBoURYyMtoHgtFoPPAPOaw5dETIs0NmQttHaD1qQ6hTEdAL+WfxXLXG3eC8In+SJljXnPAq/IgJBkUmsdUm5iLUVlHI+Y/g6fPBMzyUptlzFnv2EhVW+c/SRMTsZ0p0lnkO5NE3CVhxyu80AyCsOWBz/aT8QZ1ZonnaqKipg9fIJ9sLKr7nxUV8BJ8hO4/6N38/KkkFIuSojv0P7avXRwNXQdVmVsHAm/SchHEUB6YqjpHBAOeI7a8qcnjLqLmY97g3ftLCGNeYo3R6WDgUAevEQBGYmPQMwT1LP59dYDUMRy6itRxzyrJDbXrBOoK123OuKIRdu5yf2n/IAJLssJQ1D/AzHUXZO1rE2G6KAQQJ7eFFTgaCi3zgLcmi/rV5mKMlhmlf2VWTEfcPwxbOJoPwuiXZgYiR7any5Zrk4Q/Rgotx42iTM4LGKcSENcMVDpZgzRTHquL5kJntSq2CMMaTDkAgqV4ucqCvxAnlBqaA4oBtEpPcyoGqyLByyNvrHQBQKkN3EuenC3TV03xdrxmYukzFutjnqI+cxVYfiX0YW86HeoC6g6gYvFHZclXrWmVkVmBL1Gk+tpuXPESlCKqQGkxAEWUxotvG4jEpfyG6DEU8KooSAU0N0II6T4ijcWcPnJHsTihJhWwTMqOBaC/WdmoBBkyqreOHaKoaGAGApGIYTwTOindoEPULmbFxA4jp5DXrT9XQeqgoA6hH8qhbfdJY8VRtyvKhjlSDsswcOJgs/UuUJDkHuHS6nXZra3Pn5nvvkaFcZo9i9fK1S83G4nPPPb+8utTrsRxcoQETgFoGrc8LqpzlDXnO7G+wzK3FAgOTRKNSjN2suxRgNhqzXIJVWNNM/whCCBo8CQ0jRzbzzntvfumPf/+X/tov6HTBK8otUV7ShMcEg4o1B71ag0Nj8pxuvry89pnPfm5p9e3vf/fbPffHp06d0qyxtTv3JPgpiHce3tNLQpOmmGFwLte/w+sZuNmLbgW6IpBR4ySiw+E5jhjusxco+NRtW2zbZeqDc39lNHcWxrAnZFMcFRQaM5pHVqG5y5ViI587JZA4MAwVABz21etCo+1pIXiUfFGKIdaRtHzbGpLIqgEiPrHXzcEY0o5X0qEP7BLdrcpCDFoHtQVcYtKHUgwYHpoFjaHxjxJk0lM3ID0ZzuBYlTcqZgZM+RBpSsSGlWptlCZ9WrH66ic+trLcYN0IB+SrlgEprGD4QBr8ETzEAT+gq28phx7eCkgT4jRtmE/LYx8NitOlb//lt3745g9hSMwjbqYrrWoPmCifZcCBVCa00WfoKMUK/RKUoDcGp7QrvVTgmFrYOtPtsSNj2ul0bt66ReWWlpefevIGZwaRC/8CNj77C0qV/OuvvwVrLzbqF9fXSpx7yJB1mu10e4BjQR1qXQtOJ5LNcXB4MJmsNOo11lnhfKWcULhUiZU5RW7Za9TVvCR9uLl5794dVgdh2asjwAhWyI5vXHvirbffKpVYn9PdP9z5vd/7p8enLRyj6MrBsFNkQ3kpc+nShTKzzuPRtcvrrEpiKoAlXpXG8vL6Opuf7ZVcfqi1P8Y1CiHzec4VIJDpREeDTIdwLzHe3lKRLopVhtV6jaELNznXF5q2CLqM3QkMsZqwYmGh0fzc5z7/9qU32QZwsHvofJEeojFFsbfh9u327s4fTQbLGxcufeLTV688dp11SoyabAuJHw3AN498Kr8bYwto6IGNSg7lpTD5EkyuR5ac/FBgNOESrNA1ZKGLFAZb2GCBkBFTy4h0vPZIYU6ivIhFsJwmioXZgJO14ELIjSOdN7a8TJjfoMeDcdu0Dh26E550dCJk6djdsumkTv/HBXy+M0+pGDQwOt1FL9oobA6k1V7NZjuM2ayA+CNagSFlUmtUAIxBpc1CjA+9Ik3lXjXaAy5WZVIHzQf6aqXGwxHABtUM3ix1cG0Cipq7EjSosVHUsVF5hVxjJyrOi7ild0oMHpM8uibFDsz4IFgkoIhhxEZ22ye6PyCicAhjmQvGNjXQqtFZo+kiSiG2ebQLaIIkdYa4UpJBNISBhEDlAzFkUzBF4TGALe169efxyeSfXQ0WsU0EGgymQIDeGdgsO+DNbCpMWpMS4Q00WpgUYIQlpIFtxaiBnntrghnucILRRkQJNXGUlab5tF7oxSECnAQnyLSgRZvj4WAFBQ5b8LL1raYMRv1oB9OTAXXonIT7KEGVrg6gWAmwB2BoQEwQxMQ1I/ahwDMnWW0PcFE3xf9oOcHHb17OHsvxiUxR6vwn3wKJx9g5JwELwlBO4Gv0HMbZi8WcBaYEZ6AC3rkPfbrnfp69UoUwtuJEUssnJopMqYOtzGlVIbkvwVuRMOjNdrKrgis+CEyBRsNiRhvm4+lAZHIU8pMe0qWi+GZWS/7ELmdszOrO3LDI7ir6S2jMKEx6cCWErIy21Ctvsw/tuIqm6YzHXF/PAeatSaZbGF2Wr0hGR57tlvP96WQDLs7kjnD6DLk9Tsag95zA6zBBrnSXyYdJe5l+FI3KooBingPm9KPDfXRMnOjoWJ84lQ5Diotgw3p0CsAMzhVZIgzvsnyJuQZ69osSrLAZNr71DuKhaK4w5M0UHsLqTmyjo4EeFEBkSKZCwC2uhkEomLhxO0tuDDTkdRtVRB70hKeCoNsnnObkLAeyBTwUEvEh4fQyTKQATj88nY72vYoK4xciIvwyDtKHpYPUW66dDH0tHS5L3+kNueoVC15jWdc7mYL6ciQthuZDKApbHMdNbkZKrpsN1QqsUELqFfWUogi1nC0WhyiU6gKWBNafZOIewwzQUD6Bja8a1eDAPdgODSL6fKKbQ0Syk/4av6Fwzqse3JLBmeakokK0KVY3Ks/SNR5ASaiAECiVhCbIMyFEANb/tJAaIT5mBEmNRqQMPHtAkIesYVynQJOLXiBIHUyuFEQwRUShgJeYCpcFskbUNuUGXzMAEVRDNVMjxkjE0xJ6GwUiMFrBi9Jo5eH41ns39/cPINXi4iKHgfQH3eWVlY+/+smNixtDziikSbV7cN3Jpyqz0r7dJbrcFoEONCbN6kwVyyAgN4gQHItbBp12GzQh80KdRQjZaavNQgdHp9bIQQVkg4VaJ70//uOv3XjqiScee+r0aG9vZ//gmN2HDj0Z1fGPbUNwEyZIoZj7hV/82Y996uNLS9U//OKfUdNH5Ex0BaJBUYJf73sgmEGmjNRJkGZJIuR9yf9tfsiHoeWAm3oYpIRWsfcKPqGvqTghyd0mYUGErkCPsRijg5V2WsA/BEFcKwotAy+lH85Qzou7+twmmK90SXQpsDpWHvE6nApMZcdSQ1o7eCk+wAeGkldTHaPKxW1C4BMJYjjdMcd6sv2UqymAzvAYvUPLscKf8ytd9wDJETTgwnJkkfm1N+jr2dfBF5947jFzOoh1LAlkHTGb90qlGmJDWyEUWI1kcu6vw2aVaf7ixeWXP/xKu91hByncF7WVgcRNZH2j/yzl67s7+41FZpY4KRX6RA/KfCUUoLdXDUzhokqx8tZbr/+T3/kn+AcwXlnw0qiUVhebSEe/D/WTwcNiYtStbQFOCrTSI6EpyJUw2htM9i2PWOhcPGV1A2e0cLDPyfEp65IWKtyWOGHjuTcLjnH4UsH8D370OmPUaqlarw42NtBszkkCUFuGP4w27gCmpBpU4OZ1zbRS7ZQTNCnQsmhphk2xOV6jPF+D2izMuH37Pjdej7Mr9cVCt/8AQ4QhB/sOfuWv/81Vbt+jlOn0t//xP33jrTc6nRP4hMsTkEHydlqnqwsvTbq1bq91/ZnLC7UqM9m4jmiJRrPOdnv91IDLHnK7nFaze1pB0EELlxMk9g2Nwl1mPXb/u6uhXkXg4SRWDYEGbcWwkIx2ZXnWKe0d7R9/4W/8jaPDT3/rL7/5nb/83s72w63tnRE3jXsCrLoYUOPhw82tnZtvjW489tTmgy1uLmD/s9o7hCaJohZAcLvampZWdrCf9RNp5MH9Go2uL2FyBq1Ctwv99IIoYnJO9AXBoPR0huPoYQkJ1A5NRBVhQRIiI4BFZ40uQ4MpZ6IH9WI22C6UBqEZteKhUKEyxGfHJRtQsrDILCYT+1HUiXAKD9Spw/X8BLFsZVnZh6VHpumqRkH5aFJgwvYaFdOhLLvaOeoWZIEA/iG6R5jderOdBO3YZ90gva2b5YjV2EeL4rwLDz0uRYXbC0lBAPzQAwzRgMg2AsWUP80P/ISebYgRAw9SUzLZg+vs1li1/poFfcJMhrwpcaRFuLCo8WoXGdzagdPWDqdVR5pF2LBwk40Py1AZVIWyJbwQ8KgK0fzU7AAhoNNqNA0/aSQ4DMPezUB03gB1kRVUL2Mj4dqAt+gp2RHAqhysKbplpo2pFCLO/A+8wGiHNMxUAoNiw6xzYb/lRoX5yk4WIH8mf0iRLKmQlZR0iRmDIT+z43VmKzL5A5EXE+qiuSae0srXoAmZCed3BPPhqyhJNl/JSF2hk5SMcJNSP6KwUGJgzpJpklAS7LhttvFKlBEwHLtCYVMHtehVN0UEO1MCAYNk/UBGgtqU5x7i4yErz/xXCksRgW+K8O5hnljfH01DV3NPZLmXwDoGBXixKrOHl3O/5qHnvh1o8rwPqRQ9K3P+w6rwQJl4Sb8iI3Wao05ognT2MktBzpRDdNOrv39CsRbiY9RZNOKdAmhmrAe09aTP3n4XGdN1aitrNNK3OCbDS8nQuu6BCczPN3DjoxkLFWZi4clKJtNwuS1raRxmog7Lw2md+2wUuPx4kMfzjOLOsPKURZygWi4sDrPtRrXZRx9w+hvmtX5/scctw3HuqH0MIZC1e6R6bHJCKPCWewMUYWIncNiGUbH9VciNtmeqE2KA1NiHzUQdEUqTAGH54UFX2kmNqW//yzpsezs+Wd5IX8aonHM6+ixHwL877lIe+3oAzew4VgYqoVJhB1uZ/WHFQpXboITt2Bm1oB0NiugtqEmnjBsKbAwPYyzRn0+SRcrQExrHcrGGMjWMKGlvFWVvNKIHb2jdBy9GOFE4rLQMqCzyqrKiDM9Zg2YIBlHo8xl7qHOcOiDGZhUBBZ1aW6STP8SbmmyGqCZRpwHdN4URrUWBiCdrn1i4H+oL6ql2LYshmQ5NMwdIChFRAAsNZQNDWUfNHyvJZI6EE0+bWWFX3sWNX6nyEW1QPCa1qVOyGdfP4sxjk4IGIQEzvkRvlkTYURq/MY7lkpAdoQZo9RY4Y0Zmspubm3s7ewf7B+3WabvTXllZefqZDz3cfHD1yuWVlWVysAJMbqKxbFo+HNIIZ1YDK8sDKLw2HFbYZ8Bsa4s/KeFhimMAGEsRkEG2FC90epxsyDppYWgMharNFwd7ew//6//n/+tvfuE/eOmFp5eXl1Y3NlhyAAuXq3VnizDKtK5kdpiwXq09/vhThfy/gusSAmARNAiKidYMS7FPBBdTn0SrhHkK+Z/ySf4Z4JQ7wYt5QXfvo7/pe2AV+k8cEFxG0+MoQl1ydmAwXh/mYCZMbxdnE4fB5Ch2pndtUF/hEeDQju4RIlHJqfLEHnQfji/pZQbQWbNASkrVqLn4wMzgOKOI7Bax5AA//rAhMrndnc3TyjEby5ntqzc5s3WNFSk4hinTtTNAUFTDWxW7gJjHRrxwDM/2/LlZFt2JNc5EjYjgCe6xxtgVt87W03AkxsSuFIrHrd7FK1ebS5wZyhoIOmDsDuiBPU4pUXsMU4wRxTT3xg9/tLReffmVVxgAGOhYXR0UKhsRJUf+5LjzxS/+yeHRKSvQuMYLM31jY52r05uNerkifCiEWkWDwmshAhAhrVhAAhA/iCgCzGeUqoz8cZW4bIY192+/816pUnz2iWenfe40hhr0BGU2yTB7f2fzPjzMcdEsjVnfWIWBcfezbYItvsETzB502bHuvGihtLuzw4KjVrv9xPUnQ5WpptH+qVIYQVCGZmN3wptv3mOTAIuW8Tmzub/AsSv01KpNVo1UV1cWmZ/5jd/4zR+9+QP22zD2oI08kkcfT+mpF58cdRpHx6cf+cil5WWEg6EBk51sHGisr1+ym6Gt7WCwQvkPYAx5MjL24GY0DoWBOIgqFGFvdwOV1RtwTzDhego0r1W6yB3dEJ0IO4vKjfrCZ37q083mAl3Zz/38z/30T3/+5rtv/4//7A++9e1v07vQ/EwPwyqcg0JXwdzF7v5ep99+4eWXXnzpRZpJtyozHg5bpZlcoDTxR2PxiQIHSQ7UizDwAD25gvYhB+lQgCpcFDbp8RXL2zAFPUvoKs5CxdmmW1pdBPeYi+qRU/CjmpLAolbdZWQEiKvsDQQVBJXlL0wE9bgSboDlOC1w0IK9KWPTkDASkY93lDyyyfiIGTO8Y7AyqnmcG65ki5yHCjAlEMiuDeOLk8ERfNU3xI6OQbQYDYZxYFrwUdECHlmiduHmiX5CD7J9Ch0aC9wJQv7VDcHWdMmUpu9QAAAP+iHyQrOLE1uVPlEWSQEwgvWlRGVK/02FBWPOHYgC6ZSQ6Od1YjKA9kAeChFhSmC9BN9BDqHAOXylNjANrQX6SBcP1DfKRozDV2w4gLjXEoRhKpDDGJEvk2EJt4Ec3MpCBLABFON20lhVmgbcXJfDksVosGAYzY8Y+4WZIsNYZYhDWRBHFP0LvpEqxKYAMPGHlA/uEF/1ZKSWmvAQpgO0otGkFTT3JfZ5BRgBCS3+g2f8owywo/8LyIKjWdTHLomkBtbBnku2TkiRnURBG4pJYGwoAMQvIRDq5//v5yyREEQtMlsdCiUMsAkIX1Ao/UjwDT/LnjISMkueMkGPs1RnSQNROAPfPGXMgEJ5qXqWfVZuCrH+ED1gnsFn6PsgwvkgagZeovpAq26KOMsQ4Y8+yEDULGd0eJjFsBZHzDIuZIM/w1Gud6eV8S1x4ButAFMzAGCtB9zZqOaqjLVLbfw8PbbYZ6fVkee6ee0vXjqZDK7nFMKiV11anSZSOKmytY0evVoqdHMjfEXdaQvP5ZDD43B2hE5gQD/iUAjWAuLmxtUdvVyQhrlCwBQPGGSz/gJPAo5URuzK93iAxxO/02jyQIbxSFMJJlES12dvIejILCyrc1AZCV5GqqLWLM+3ORRUoKXOjzTvwQkFLoUvctL1oNdmWf97gFSEYA57AsUNGCz7JCVHE3CIAetVNeYQLaTfv7B0oaw6x6U42GgcWkfXBYLMawMNh40nXSDhpiYdPvUwkPXu0/l44F24nTjwDo8DtyLhEsDRxuT5ZNjjZkkXEIMJ6syBO/JN9RARzV9IzwRFtlSFYlzcM0LD0i92maknDpJQfdwxriRWuSub0jRbrruVKQ3RqQmqt93qYLWzPQsVxlEB4SgccWkOHAG3sYOQaXx8T2ovnrDgABdYARnKihKQMXcJZkwFhSAcNI8HFiTWhCF0IeL2NyJlhMJJUjkBsJGMYFU4wXMYLqJyY1MAMuu4iJvJHSMBgmbPFPH9R8ORCF8UM0fuzXCTNm0BNUASr5iDO1twymnke1u7t944KbMvkpVb+GOzmZ3d7Vc/8+ovf+FX9nZb2Txc7xpQenGVKPVyJg21Zx8MP1GyOiyEWPFispyjwiusKV8hptV70Gt3oQlmCgxAg1I0DEWNsH4wnjjgUkOB3my4ACz2bwH5ZH/wZ3/8tWtXrl68eLmyUPRoS5YokwF+xEPKEJG2R/FTqWx2eXWh3qwfHR4jAhI3iKMy9R1gM80i6vFI5XiJeKzfRX+dP/MnYv9tP2ZtQ1HnNTPWAuVr92cwAtT+x+V8hXPYoWKF04CZ0uNAcJ1iHDRVHudZW4Wtw9FSLIZFq4A9PU2ozMBfw3d8hYDRhCuZ6PRwYvUzGS7Mpj3Japep61G/eCBuJeEcWwW0UpgJ1R4bBBpP88l9qCUHxIMe+oULy+Fa7NRetbaMXxtjGtyZC3J8BcPROGoHrD92n9uex0fd49O29YyjSGANnFeoLs7dwaIcIK0wDCyKw9vLTIo90hXLyyv1SrmBvQG3eAdIsgxsq2T9R81x+lLQqP+h567/3j//g+ef/ygKKVBVyRFDIm200YDzMP/0T/78W9/+LqaknstJtloqN2pNDkZE+cJwErmMYsE6xPqCcYJhUYMMWtAx2BVM52prYi4y83fi2II532H/nXfusH6XW72wszlvF/sehuPwUzq+o4PDu7e3yMJptEsLzWa1ylqZEtYRlXBHIbt/i70Bxp/ragadDgpWX0zMuXHnF1MrqgwOiMDZzOCQE0I5xqvb2z8+vP/gfpZhDHMXw1M5eFxGYV28eukL//6v/Oi720dH2/d2v/Tmm6/RGQAEkqqLuHu+Um4u1pq14t29W2urS+vLzRr30DCoYIyRzbL8h34rdj6iUagnfAn1woxTjcMO7MWBMNLUCHor6sGiZ+6eS7Z/iJ+c4tx79rS1x95YFq1Vq4XVpSeYG+RI3m4nc3x0unFp9Zd/+RcurC3tH+y/9qMfsSDQ5tJqdT0VQyb48c3X33zu+Se2Ng+q1UajsQwx0O26+2VNsAAhWk2HEj2v0qPfFxcTkhTqUW+CFpOcbXI5mURol5nCpKFDyBEQLXrXYZDGpvfOFpIWws9aOiCVCxG13605D2ngcX5po7kDAz3l9XYx6MgzluF0K1By3Qs8gzTF/AJOesmW6bA/wW0UxXshYtUMPX+GeT8Pe8nlK2ilAgzq+ggcGSCt/FHDybTKKh/0qF005i9zDli9TpUDFj2PvoWCjBZBCfsEMqRle/j47Sn1IVIenQNNTjWKW9FRrLNO1y7WqtG69Lxh0Muh+PK32J+Q5dZbIgvb0nB0EXzcMw9mQYEc9xDTPXlbSJAYvUQFKGa0ATkphXDhW1XQjhd1DuU4tRttYQ3NJHb6DEgLJcnAXzIeyIi8OTtBU9IhiCQ8CyA9kB5zpF+JnhQSxgjVU55o7uhzcKnYbjoLMc4sJN+RBnE6PkCCObR2gU467B9bPLcnAAiTuEgRQMgM41Fd+zYbvFhhFRN8EEs1qA0YooDMwpSGQEiggcG7PBBP6h39gaS7ZkQSjNdIjVwBDU+GfOmeMV6gnlSRVslPD972YZIrTvfH0jyzh6NBoxA/hldM9b5zeyLOcBB0NQc155W7uaxXyi3z0l2smMZYyjHOUElkjXyNqPQWP2cfZyExADBpZAwCRmGRgDLOEtoOszQ/9iLjiM9Z4lnBqTBC3xcRobOQH4+YIThrSn4l4Jotmk5o2QFLUugnmVy2p6K7YhUkjBKdC5vaCRmWqBa79BnA03kMkXg8+SyIrOvCY6yKdndXLhyF2h6XmUNAGcBcAMkW+vTOuWphRH+IrNLVL8YRaHQH9Osx98XaBVQqCyTJI6uR01EyHyBpXbW/Qde+ljiAYjuBsOugwz9hnfjjXzQP7w4ZHKFaWdIjc5ieKhN1Bz23Kgomoyz/FB3ik6Cqb/yBqomQgGsqOdIvgnHrISh5lAwgtd6EBfcDIVAgHXg6vuBRL6JoXQlqo9ro+isADzFRrc7HoQcwDXjjtmR0EHMU4CjWnGzG2R3UGpHRUByz9gTrEIWMFgBvJAJFMCNcoh6hqGl686onx+gkhFyctMeKXi1hWBklCEBzabwgbpjlnMunF9UhBkN0V/Az/uIflpCaZoK/By3MjbxUzN6yDw3AkTNE0J7QAgsYiJoU/NMsgm6qNGlLW/ItofkjKeqPUQcZ1PB2LzYt2kXikpCG19gTP3pcsHbSlbakRem0AxR0t4H55UMxwTPUjMaAoq7HscGkNfFA8gUsHY7BbvymDBtPpIyhU8eOvnfn7p2bd4ZKxMU7N+/lajvEr1+6cmFlmXPXAHthY5UuG1hWzNYFurWnAg6WQEjVbom2jR2a7UhZlFzMVoZDB61sNWNSoF6rdrp9FmRo2o7cl8kc23DIcAuKQWq3WpNd2qghpzu7D/7ll//sr/+N/1m5ueLGOQQUuDGVGjwmHRAJ9P2FC5fr9YXjw2NJAAi1OQjDnD4hK+n1xz+jXj8e/O8U8uMwxENTj1UxgY+Eg+dxNFy8tJrv4E1kG8qEI0xNgTWAHkI+8a6yDBAPl3wB+tFYtr4cRW3hXgGzcUxClzCOtN9scySYBNQXGVFCaH8+E5fYOLZKQACsrSW3mSlGnogqXAREF4UzCYFSo2XZlFAtLa4uYT1TAMmRD4BgPYsbHQeiOWF+YHB08u5Ju0dXzf2JnBHIpkeKYzPlaDpoHQ+KFV3QiCyeZBQsGgzvAHfJPfXM9V//T3+VeX8SI7GIJ/8lJNjKaTYgImBD5vAxr3Al7W/8xn/7n/2v/zNGJiRBk7A4gFgYAOfC9vbRV7/yDaoIgWBLojjOiFTlMhO8ijbIswtKoCraswcACCIrVQq4MWf0Vkw8/xEqc8/X/bsPcAFcvrjeOT0p1D0SFTMeKCedzr2tTfJDmqXFRjVcQwztoMpgyB4HKoPzflgse/cfTuFJt/ehZ5976603V9fW2KFEqWArHgx7mQfAR65SLezvH753+11GUxga4MnqFbBhGMOV3z/12U+zXKrRLH//e9+8s/V9CnKShfkaTiRHS/YHTNYxGjg+OrmwsvryS8+X69rtQIWt2EEDVVi0H/MITqVCBusu24RGRsPFBXLiZZ8o00At8BNV/mF4hfxDSnZlqrtiToDpHMjF5oDgdy4fYOt4Y5GrjBfWr994rH3a/dLvf/EvvvG101NHMmhCGguFD7ccHuz949/4HfwNg97gYx//9EdffcGRJyhBURxKFA53Q27UC+wa2gt8bDs5hFbVXPOxCfgt5xgRH/YRyou8FKsdgSFI01lGfMoN5AkgxEV6BSv0t8lCf6DWpSBdepieOEw468g9hGSxLxYkLwqc6OPtslBIPEMRJwgWheccUJrLVhx1Ygoyqe/JsGXUAiQ1ktlsMio72hLROODgLC21UsXrhyOl/nrVpCUHkuh/OSa0g4nBg1Ykjj84FIFFuZAACqVAKSARqJrDK/PwRAB0UhClSvBGACEFpDQMzoE5JFbQDTY3t7wCgwCC0DCEUExaAeJBV5DMGjOJwry8KIBxgiTRfMLHJ8VpV7sUpdEXU1thXOjRRYazj7JChdlTO7SjcIeHWt6SznqRLdo0tWJAobLSS8B+iB+cbQ2N5gcUefSSamiIbSFUKO9ARhFBlMJ55d5FeAZLxsqJrWxIescICawg6QswI8IZhOWYUBIsiNKszhbSykEbIQBnBshxBVD4JXoJOV8fvfkrnp8QNI8Sd94Dn0gWJc9jCUnV9yulnBeQGsvY89BThrNsDrkia3CUUJnRuWcjxPiDsiI7aaAdDUzGMwiMTmJMM7wySzaDmr5maM0QzTL1Nns993UG6nziGZSUbB4B79lpIQts7YLIqE82I8IpyBXs5o1wLhhhbt4DZHDMYxeWWUCou5WznMs0Yi577GwOh+I7S15hvTxerXKBM6RqwwmLRFkdxFKdIWs9itluHQNo0uP8qUnhsF3olicLbRcslhk1j7kk11H7kiO+wi4UsisDJ3o8RUC7ChMW0xgqEsDaXBzwcppGtfRTFuJDYR1dIs80s0UMP20MmRxNwYBfDidfUB0GQxegx9VxMeikldT3pAgdH+0YzUmYBijxZlE8tW8TZOIcodMLYgXa0emSB1FThxhAcXmWGBCmYtFsAZsg/AvByMoq1Ufu7W0QX3EwH4qDX8qzuPFOdhfPoMg0rEO/YPJSJz4tEDCUZingQ3lxDDZ6XKioHtEXoxCxoJvjJOxihnRYI2EPEIIoavoATzXBp7unvFEA7ep0ADkFZG/IYCuKg2HWaRTpwsOtw5RCbKSipgGKCqIJqIuniPKKwTYerNEw+ZL3APBP/kOdRSRDH1DVTd+9OoJbcw8n3iUnChIS8uDtsEbAhpKoShbZsiZhhk9CgGQkDuKTBj8Ko6MyJhDuOu4iwYWpx5Pzz4ajdqf17ltvcfoofv/B5G5/cm9ymmO330c+/OEXXnqh1WqRkg660mCDoB0quAFXwwvqYaBIE+oEO6WhoAjGX7SZCm/3tHdMr6Wx2LUKiRuoAiUCjJ4P/0elkOmjUe0FT9GHk14DKOPpMTvLv/ud15ZWrvzCL/0ce4tZORNsZU8jeSE2/BBemXqtiN0BT2MZi9SoLra5A+iuWT1/EukSimLqW3znj8+iUvC/82fKHxSSE31cJhBdLx32oa5V9Ea2xKRWjdk/zyKD0SAkm0RxIqBycOAxl85KJ6xHz6qR2PagIdTwOF0l51fqMucqIUxGFhp09f3A6YVWyDXuf0TAgQd5lSVziQqAgmb8UPYRGXg2qQVI5Dguh7MeHwL+ikypUEUeuLQNK2XUh7vAQeHWpkHU0Qs8sCSUL7EiJc/qF+ZMs5NGTCuxLNvunLEce3xp1DhwBul2bmYwnGDvc6Lihz/6sY3VC6w1IATIYiJIGgMMo+aYl+APFdTOp7VmeWlt/ff/6I9zlcov/Hu/sHFxpce1VjmH/SwyYkj+la98ZWd/lyElHMXxY3TIqysXkFZwZAiKTwcOBCU8+tR2gsudJc7oEJWQTlkJopihx2INRynX63Aaen57d6u5WFlZvABclsewErLXHWBncPDOOzdvQhTW99cq5ZXFxWqZ1U14R9izPmH3A4soOm2GDMdra2vwPhY/1Xm4vc2aukajSZURBbU6/gAEjHWjHtUwPDg6uL/1EG8RFOEjzivhoqnxY5ev/tJf+xVUFE2wf/z6ve0fMZmAvDBzRNLseHVpoXH5eonpg9GgW6/Vrly83GjUGe8w9GYxBxmXVxbz+OeZ+caqVgup7FCOSX5ZmCd79S9m2flQOFAmJL6dAqiq02gJSaXIYe5wSjAfDBehNsWXEWBZjA+aQ63eqDcZL772xndQsC98+MXDk8O93d2jLa6oY9JoFz5hywK1G3FLwqR/clh57QcPNi5euHjpEsdgUQ6jT1gCPYNupPoKgHJNr6bPBTGnLIarwcazXe8iJ9Lx7Ud0CuprUsNYfMHzidNY1rtDdQFKQKoaeon+jdykSYHEOHQwkf0o6LDojg1pUDCbrXKkB1TJeXQmSej0oekD+oPclLk120nWYy8WUlY+nNLdT6+GJDO6Z+yzwdwd3bYuRovkkyUDyFDCFhSYrDi1w5X8PBw6gtR5k4/Tt9jLqAGbjlppB9hEjh6tjH0ieNGfhC8/1EYQhnQE2jjEI120Y2EyvIyDS/NU22hDUAoiqPOPkk2aYZdgonigAoBEImcPgvsgAKSQ4NbIB2ThsRicAkKAwU5qJBEm6WjVHiJ/FLDE0c6RQVK0lKWroxLX6YujBdWNLLUxpd4LlQwPHEDSmCUwr+BYSkB2KxBUBUUNVChDRv6rtojnXSJgVEBJYaBl6cXohaP6hESqwI9MVjk1hbTwoec2l0R1f3fwZ4oJnrNRoswUxmmk1NvtHPyjRjP4M5yoOysXcIlh+VA3S45HTgdK9F9z736q2ww7U0Xi4oN5nsh49pGs63kyILPW31YucU8w31EX2M+HmsxqGO/gSY9lYMREknNvsl4qkvUjRia8TJwIZFYeCRQw4nsWllJHMcbOH1t8HkjK9D4PmX/PE//49/kUqaBHaWRBcaPJw9HLpivnW7M9bCEbEb8NB6GxyayGaa/XecSp5Pq4ptMOqx9K0ILUHpNNTw0wOu0yC0Tpf5Bv7JLClLVCuaEDUYakShmdqN40JEFrc6HM7F7W46gxYscsD4V+ibgwEaVEL4dBRk+lGaSFiYoe0pcyWagIuXjI4T/OA5WjDImEIDXSO2iteU5SqJAYSKUNA2nEIzx8agqThpyqFb2EuGEYbxCBDg8mh0ihAEQvmfsSjtTYi0CQH0jg58wid5wRhA1HXbSZyXgJXkrF2QzWNv5FywjVxuaf0mKFxc1AP4IPjImapSBkhhfoDz4Kq2NxUCIt/1ST/EwFCIHMDiGMFZzo0JyUE2mMFzSZoK08arKA5S9+clYBQx4uVUXd2jzMt5LGGMrUdgJhRyMQOJm0Ko4ghGCA5ZJIlRnq2BeFgjKUcZyBFZYkax85W2GwzaYDhDbFBGMwwNRwJlOb4CljgQdWiauqXU/PqzxsRSyFdPAJeVniCqNgf4g8T/qI8QEld7UVXHmFs02/KY7A0fDw4Oj4gDtYe512H+cc/stXP/6Jpz90o1ppPvbEY82lRe7yrC9wL2xQjUMs3BOGXEAM9xDTHXrqixR1JGaxs5JFQWqjItn0DT/j3GWtG/Z+Ps+FZaSC9jQfQoLXmYSVEsfGIzlMeGMQybMu/pSz6H5ZIV1847XXPv6Jl+tNNt6RF+h4/fH+MpLBpKM75h+25sK1xx67dfMmIoLtgBiaEJIGxwSjWG7CMjCVTumZhc5//k/5ThAToDNwyh108HeIA3zDkYvcHsM1CCgFOAYZH4Atg30WcXANDp4yllHkc/T3kUNUyM67lQEeHjKsLm7HJl2BEz+nmLMKgiwGr5IUmy1+K88KeaxwE41Y3qC0O2Wg9S7LZjkRcnV1FSdHiXPxa9pkLEp0tRj8CBdyPJdAyUEp2v2iZeuJGACczkJ39lgsx+5SpjdxanQ89yrkgYahdkAYD1jyodrB5mZD49b23s9eXv/lX/yldpcbzbCykFVbxvaK2go5CXku1zo92d/b53jNH37/u1T79//HL62tXPj8z30GU54D/uEuzKM3Xn/tT//4z3ArM+kHAHzh1XS/HmNoIDn/1IdhIAP+H/Bh1sJFoNBNvymU9B4seBvrdGER4qPfS/V6kTt9OXhf+ngPWo6jlyAAJ5Ifc+T/vfscZcuyekR6ZeUCN4sFNzJvSV6O1OTgxuFpr1PgprpSscfiH8byHBV6/wF62HX2GgETClXelQJWs0zv3HmwdbCHxEAM0EJeoAOCMOmNnrxxHR/Ezvbu0tqFm3ducdWWthd4snZo7K0a0KdW5hQzd50xCcDdZ3AYu9aoO5MbuXxt/eJFhpi2u9alDajSoSAJb4EIF0wCI6tejLUtaGk0mG8+ibOCBeABZk85IEhZxaxBCbhK0jFJWMicgso20qOjzubmQ6iKl+Jv//qvVSYb//g3/8lBa8RBY8MRFjBNQPNPFxpcPNz+ypf/7Ff+1heYt3Fi3Ptk6OtwCWP1YWAkLECYouwFgiVVhoSofEDOOLW6VUof1EntSzjKRt41goSoMBPYixqmMldWZ6EEGAnlwwblXW3iCnKdOPbMbPJFIsMAdT06fWNMkSFh2FLM+IW8K0DQHjqN1pil8hQg+whK0gSxjDgnl18YzoncZKAkINtz6FOhe4LlyGQeMERSGF9BcXWnHTxYQhDISCTNZlr+K51+U3/1gsqDMOsPKLtaI/0IbWvDS5IIIyVJRSK644iS4CSP3H4Kj4ComxAFqL52tChUq2YaEvgmnUVVJA238FlZ9qKEhPtfu0kNkzAxgRWEAnIXAMDKBU+iZ2XJyR91JaFLaygHvtYOpyCRlx5GCVAMxcifKYjPQIJ6xqDF1rK0lJhPSxeUCQUkR5AfKFKXcFF3FbSYQAsDwCcVQgLLAk+FQtwZInpEKxSApGjgM5KijRzVSISgILWaoc0XBKCx/Z3AAzQiCZg9FpMeIh79mAeeRc0ymjvwBLfZI8zAmrh5tDVJ0Wcg+X32HlH+slH5jAHAo+hgP33/KUmKOMt8vuAAlFYpzYqL2PnJPxE2x83iUqIPfM4wnYVOWJsIj3TPJYpszDDgtc0/ZB5JscZ9OVjHrMqXj4L0jnUmg8u4bgaFI9w3g86oTo9Y4JB5bJeH9ImyhzOt4fnOdulKEG/W5HJ1n3LLrR/yN0w3YhbcccaogtkzBR/O48/ucw7sZLrAQp7MaCmGgOF/ye9BfJZ5skKUKW0YQJcQZShcMDWqFB5jCtsI3LeeoBNKgd27NCM1V7DgqextEw51U5jTDFDLwaRNFOKAIlcLBp9hdoSAMEoHCFoS5lPhE8hHtKu/AEHeZMwpcSTV1AM2UbrW7cX8h+YjbWJcyqdqYkWMYKVbwBaiQfNvOv0QHn5DLhWBEADGd2RhtLpKzTPZbYf4ACLcCRJXH0qH4p6+IbxE9lJxmDHZfNCXQAheAgLY4NOi6NEaVc0UDwMJW1LVpHIRscgHJvaNuclKqJx9IkCdns6pSRV+2NQqdYI1cjLlfaVAAJhb4BeuFDsoyCAN+MRqNhq2cxwleUqlY8wwnqCROOAijnFFgJJaqPkHWAVeAAE6DEgmuNboBeENukZ0llQClvBc4wMD6zALpWdtKM+1YiT1vD8WWNnilIEJhV//wYMH3fYpHiBucGHDBYeac9PQ3bvv/trf+U+whjCRsPMZcggoLbjRZERFuvkS/oTFwNmVTFQ+xF0axCPuSIE2DDzLapCBu0j7Tq+QGM8frA4nV8sbw257PN5nNQhEYqVCtppjyDHwmCAWsSChOMhZ3U5L5vYPjl577a3LV64zoxY0Yx058yQ4y0EABYzxwbbLzJWrV1mizIIjJSFzBPJ0CdQaIluRYEKyzxBN6M4/bc5ZgnnQo5/W6cdiz5LNXwQRYM6+9bH62PAwB7RiBgBPAQeo5Ev9QQs6Qze4fDptMMZEOt1jiTeObT9ZFgZQKK0MnYEwa9Pwb2F1cWsP5h2dSsuDymkT3AKMlpykITkcxQ5+3fVQFzMSWYFBcEfAO9CEbxhBSkxzC83q6uqCTnaGkfg3S12M/2K+ImNlFmHzabZtBSgDgRkvSL38qcygzCsq8G2x9jDH4VqTp7hRC1Zk6wvLFYnWHqQaKiNGCiPXynL8TKn42I0n3nrjnf/ob/1NrpfAzqMoxSMaDPB8IzFkB2UKXmgu3r21+YMffoNtBrAjtfiDf/4neEJ/5qd/BjFBdRbKtbfe/uHJ6TEH0rBTBWvXfVmTYuvktMqwFbMXPzku+8mIW7ngnMGwN+iPOBOHzht3NNsdK5XcaYt125yKX2Y406hx5wknIvQPDw/ZFztoTQrV8KPHikRGCps7u0cnp7DfoNdZbiyyb6bfZbkg7va4zM4THabY+rTKlUsX2+02zmFE9Ec/2PKCZG/XGpaLNB9sn+swjOgPuZT34GiPs67Qlxy7i7KHZREi9tc+98LTn3n1E69/7wfMHjAJ9gdf/H3OxEIpUiePadU7OL2wke0Obt+62b9+9TpN9viTT1Q4XieGQDYdJx9XOWOKXcuO17i8jCBUARKK7pCz2TrCIhWUO/eg5xv8tu1CbGw9OZif6jSlifdIQZR6AINIDZDyeHQsqzfdXARH5keXr6xde+Ia1L51+72rj1+7snHp8hP/y9t37/zmP/xHd+/eZ7KLY4jgh+HkpE/Hd5L7nd/63YuXLjz15LMbl9ZqtWaoRXD1DHgmnCmdqS56XcxaBMpjHZEPBCR4XgyStIONXJRQF7f45e9IY9VSnD+NlvUiEZ9UBstcX3imuEkGiqBROPEJAfbkJfqp7MJoxBCOI/YRYJavMK5iCStiiMJFL6Fpo7NFQgr3EeppoaGNl71kGYJn9mNXLeoSYvQiy4kwGOjq6Zw4kh4DhWkEHCJoBv5h89PEmo1wJqsdCUOodB+AuqLOCETdEjVS0YE+uCOsuEbs4IBLKpuRHBoovFkjE5ia9HRr0iHoRzSU1bi2V6UOPmY1Bf/sf6PsWXpSkFbSEkBtrCSVIDXQ+aHy0RTmp1As0pyFfVLkxuvG5OmdKVQfOVo9kqKm7HrIQHUDTfpQijEkyhK+FQmvh5AtK3poxmBgAeZ6RpxOl0fsD02T8iREAw9goxU1lJgY88hB10LLUcKOFMDmB1j56YiSBjU9FogUFnVAGxv4zLJFfxcVgGLSE91HiqCG5zjxONhwWRP5Jk3mHbndhaLQ3SBKywXfkYWSg9SRZ/ZBSTbyv8MD5CAjTp2HFCiXiLLmRLz4fa4Kmo9gFwXwxnt8mpbM6d3Q+HP3jC8BdBbK1/vfrNa5J8o1P6HpM0VS93Op0utZyPmE70uVQP9Y9DyAmgmDhtAzFesgkQoGAvaCjO4xL7EkSMOdNxzo2dZJW2ZGgBPxWnjrOErGZbxjZpVd3Iphwzo/G5htrFZajqUxeRRexnl4JzH9p5yfx43Z6HGOQ1xkdmw8rNBj590nhAxzRHSM4ukzR1zuyDYd/foIP6wKJNhfu5zhL0rbkahmukwOv1kYQwGYMETGCnisGxJtLUk5M27pU1EOtKVB+GPJGpxNdgwj3f9wMxxPzRFUvuwVFELLJwsPXGh8eDjIZfGAEB/ygWNCMtpeNYSE2CkQHRSfsUv6CgLPQMtzks6kDkvET3kITMxKiPDp3tCtMzniJ4IncFBAECEIti8mrpYvI23VElHkBRi1kFUTTII1WWw4xRUeoKIASLSKDFG0JQKfNA7cUej2ri4Lc8KcXNr3wBdZvpn9p1xP8FBHBdYYWyBpGYDxz5aWaNFw2ly0AEm0t6CTiYg0Nigb79GhkikaPWWMSC05LF4yaS4He8T2VysZRdB85KJ0iQdIES6MsCf4HWZWttPG3OixyPh73//B0lKjUV3A3YaB8tSzN37+Fz8fO3zpxwDPnW3FaYcJMJd70DJkl1wMRNyFq4uO3hBPI55UKMF/VW9QQD6KOoFBhwUJGLeQj3UajAW48IiGG7PQnL0XNEHOPQbkVQdKX5YuII2nrSMoZydHhzqe9ibtUnmp2+seHh2srDYpn4kIR67BNoxheKV7xnhtYrjVi9y7oxgxMNe4Sf9CtwWRwFJaBa7xPQ99Xxg/Uio+U8uez5HypTTEzh9f08+UN/2Un2jdYBko0Z9me17CwcHXMA+rLbBBOwNOwNMcKGH/28iMEIINST9jkGBl6O/sDWHVYoUVU6v1C1v7hxCPtsAJS5p6tdBkX/u0zBCZa/g4AMajU+3MtbFD+oMznel2GIBMqAFjiIgdytocDGjtZ2Lc54gMOstDx2p2K2TTygZMbfIoXm7e6ban7BOeDDjNCeGywkRibbrSIyQRXeWKR9Bk40Jt4fqTj3/4pRcwxGXYEDU5NoieGszRB/i6cmx4ctj+5re++dWv/wV7JeATdk4fHu38+Zf/7KUXnl9ZrcMM3UHrR6/dLFcap70utaXpa5XCxvoqJhvLmPrTDgNMWA45hXrMkqFhYXA2KMOXd+7fW2hwfH9pa3Pr8WtXgcb5PnAUZwexwbfT6jHJsLK0cvPmO1Vv/uLGruLu8dGD7c1YJModwxw0tFIuMWBgY7ESL/NNMy1yjnrLzSXkhm02cOIBzvBuB4FaWauvrS0NegyEOTeuUq7m7z+89XBrk9rHkiR6HQdjHKfD0aIf/fAr15+8dnRy8pFXX3nn7Xe+8a+/ySFdaC32/UJnZj+YV1tdxlYut1nGx2io31lbucjJRYzecUoRi4rgvt5mruxmG1ctz5UE5SFFtA6jE6jNsig6msTBiCw8RePGQ3GJD2XMeOdniiIRCflFM4b6VfHzm/0M4La0dKG5sMKtHXiyXn7pI4899jiIVVqnl69c/T//V/8Vmyv++e/93te//nVUEuMcJ0QrRbZW37177913br/wwrOf+ORn0e5Ms3NFMjfB4T3QesafEuLtwQaM/EPbypOoVlknFHMgN68AqBJll6pq4vEjKujn+x7rZdWQsKhyRLrcnjDy6u9BLXEAZ3vApsGJ9/jCprgRx9M+yjMOH0JlMVuMvU85CKyOq9Fk2T0AqMzQlOg74IWFiwCxXgqyoh/gHZYXeQyJa4ztIlC8Ng9iRnI+9aoQQU67MI0Fhg3WmcQKpY9zFciIzWBbaXGCiLpBythe/pcGUU9+8FMxJz/hZiEius6gEhRGs6RMkiMIg79BaFFAAOLDXMRaqp8BhDSAt9rwaljVRAXzUJZ86E8g2hsCMjb1WpZ2yNxTKbQALSkglJWxZCGIagwTWKZqTWbUIJBSaHETxX/TW8VoAQjro10k3cLhYpedcBfdVJeomSCCahEqcaQufZb4URV3IKiRNeQ1rngiA9ks39wBjbkjR3CkwgalodELCSx2vyMQA8lL+sTSihO5BWeDzqEIVphC58Of558UNU9wPkbI6UnZoigCZtidezGhLRAVSdVPNTC7bxJhVrIv/iV2NwFEjFTxKXnNwc5MY1hAM8tnWLxbCBHp9yyQX65bOh84i/HrHPgITR8pNKLP+/7PYND6nKtKJ0Y3BS/qQMWa3VEeaT6QxDulccMps/Q6GCTYTiUO/s9nm4UMN36f4mXAhySu2WNNGOWKFuQmQq69P0Jm88MLIcQFZqRRE6gpBZ9NZdkL08xRoXg6LbS4RHAybU/HddYAAY89doBFqu1JcXs7aIcvw5RS0TDGoDhH/8Fz1B2WkcnoFWE4mkgFw+7ykBdAiV7o95AE4Gi+auuTSbc6ljQw1TwBCxPYFUtswuMTLRSkwHUabSgs1QbnA3h0YX6LMTv6z+kqICSPPz00Ow4N1JMhOuIT7BqhiAdCm0xzHHIsoOQ0A3lC3MVC3wQvOFEoXTiwPXKJcNEnuctxwom53gNAFjpr5Z4+C9JwGrqaL0aeGJdhmqNVSaPjMipAFooYZ4t48S0RMcrmDt0KnOOMcwkIAPCAYLQAhGVUj23baXneRTbPrgzdWCBPMvyKYONOHbMNnNhhxEUB3gYISpAetmGkCPZDNrlFHckH0emmwrRR4Qsspm7YI8g8MV0ekq9LQSJAS1U4Jdg6/Ff+eVBb+HVD2wGIh7Q0hONRKhyOWysXUZHRV/NZfSbQ6SzMzjIbwg57x2+++fbayovPPv25w/Ybt+/ff+6ZJ69ee+xTn/rs6ipdtbumMWaYamBHJOjJmsmu0Z/CwhvchNEJqV7piAEs09rE6CnqYF0hKwtJsMGHrhBgVc+gzzoTjzPp05DWBHqOJnsFPLAc10FPJl29VqlaqyGb41G10+ecGMIQ2Rxm0NrKKr3QD773/U998tOVBjtzErFC4WrrQ2SolP3IKy+urv/9na1tVh1891s/2tzaChaWXKKqOpIufoDr/PnAz3PB8ZpOByoc+CMG2PME8S2VP/AwRKR5ED3LivKCs/lBi3piWCVbwEAvF2vbnPrSrCwzyV+qL+DRLZe5FmpQGHPVAQM3PUwSR5ZAj+BWZPidXVjo1r0DdKU6LZabLJ+6+sbtbU7rmziH0OeQGpbH1Iv4Mxz/yPOe7usMiUxePBXWeIGawPXIMWJXZo8pUjFwAOZ8WpYNnWU6/ViG0aLZqQN4JMbM5ts0ClgRxgukV5bJP2ri/CYN4gTavDixw6IXeEZepXQ9FNh5raPTT3/ulUKl9srHXhkxRoCf7enMQu1sc0JQJSzRpO4cjzO5Pups/eU3v9ntDWSybJaXcrF0672HX/znf/p3/u7fwkD54pd+/+7mHU5dpsLcr8J6m0KNhVbMZOU4XQZ4nFk29LgkBIIxBMQcnZ6eYHcyRDltH/c533HYWL6wxui4xJC5PygPOOstx/aYWp3E406ndfXa5S6H9uRzd27t750cjsbLVQ59Hu41FhdrlQozxhyBTGw2u059hpnNO/fusof4yetPwmrVGkcJjR+++y7XBoBCc+HxbnfAbbpYDFiOd+7e29xihpONYixSiuEdQtdn/f7CRz52iWmK3c1dpjGOTw5v3bl17+FtRuQM3lQKkxzL9sourRsPe322CF+8wDKfjQtrqxIfYkl5tEyxhzSNnVjrj/rFXA3KDoZLqMFRbmfImAjGUijH3H3GXgkm4SpVZ9FtaCHYLhz/xAt4cYqres9Bo5u2Q3YoihBTEq6aQAOjnuwlxzduXMfHf3xyykmvLNs7GXBt2cGtWzdZVbW+tv53/u5/+sJzL7/xxuvf+s632h2uHyQJEwHAytx+9+7m/U3ukHjq6Weee/EFhIMTBWNdJdqFLoKVRionuh57TosOdEMlZdwRh8sVKyKkLr7kNF58SMyfn9qEUsqfAYLNduuKLrYB2swqEUzjWIb1dLE+BS0wJdGGqhz4nUG9MQZoMAB0vp7hCnu0oltj6RJ3A0PgSekALeohB4ilXacqFNh2LE5yYnunmUykjJ6FroTbwV3HCIeyYpB4brijsoEiChjo2h32DPYCKmg1mnVAdqyHaWw9elIqqH1JMHhbZf70taVX0qgkrCtYEek/AQQYYfoIUnCSwp/8dqlb6PxIkegUCBAfKfkEJuDofeB0EvM/QEBzXxxKOTMfdLEIjy9zdkfDKqk98gsT3z+FUmHoC+mIRsdCDXysaRaaOmDeQAoXYjGBRx5uqKXMGSGiXJpQqPwPcKImOmCFKSEdeKFzt1nElGONd4DqaVGkMqGFmRkokqFkr1VgqtJjB131xb9gE14UPqsXLUXNbA61t0wiv+EmJYSJXCri6SZBT+pFCmtgO9JIWqrspCIQLSQoEJ8h45fViM/IEz/S7/nrLEVkMau1EnqksoTAUpDG+mfO9GFCtQK/WKHD62wHQkrFZwDn29sDkmPYzEKVEAmM3/HD74jxV4SmYmY/CEmxJIOE//9+JCd/0jfkIlpJiUP1QQ1Nf5WVwqM6cJgplVCa7AFtewd4zqtAkCFnqR3woYPKBsCt8oSMqxuFanDdGHuYRjX5LMulPPBrq5Dv97vruO28PVsXMvqCA1BAAF7HnuZ7iJPBobaO9kAqKBNznfoBwNzHhtamx6pjMTbqA4PeWJAmVktUEaGnp90YYACZ/0FbMqKWeaeecJtSFrEyKW9JiSCKgJKTBUZC8gfhEHvHM46cwToAkshWC4OOtwhFgDAXNJhVUPYDMFiUakprxOpYDhFCkv1JQXJkyFUApWzLpDXIJYIgRl+ni93OBpuSYkTOvKIpR+sGxuQI4aGSBDFjqqueFhELFYZTPZKICogPBQBKZQ0kquyoAWgOIzLZeqUGEHw09Jz4azXfcS/oh2F85AgBtxrlUBcmeXRwWmkMZcjDAIlOCTs7CgNImLfYIWh+/KmSl91erDbgWE4sH1iBekV16C2lTtIU0CDaRjY0zCf6XwnCE4HSjRzgBRWsmp2KKQm2DaWlKYBFPG+OaieZ1kkXRO7cunlhfeNjH/vY4kLzpRdf+OgrHymWi7jnqdDu3l6FM1s0IHD7AwXKxARUYMhvQuj7BRa+JopyaQkVT3MA9hAUi02vwqphoVTYPdwrletsqRxycB6poSlYIene6grTcvA9kwoiyXWwjBkqoxInBSFQTq1A1nxu48rqyx95kVmL+/fvPvP8s2QBA7kgCqPdsDtYa4Q79kMfeubJJ57C9v34K/f/m//3f8Ox61ZBPoM8koUcZnv/k6j84+HvT8Uvs58LjDbzt4z4KOosiS9RXEiIyoNJ3gI3hLi1n5UYePCqjQU4rVxzuAtVoGS5XL+0cYW7uWVextssHRxh4MMxEBpR3YGxmMfF6K5kS5dXL95+0DoddFE7OvILIzZCa/1hy9N7yCFYHDOWEkv5xye+wIiTabrIgkssJA+Xg4/YDIDj2C6HVRcsNUQw4MDI6IecJR2tNDEMVTDkmTlntp0I/iFwlEsbpCN3kEQ2CGCksskbi0bXd+bDr36o2+sARR7WOEFKGYGjZQOuv4JHGMUUij96641Yn8NkCfFIJ9VhwDO8++AWC43YZfuNr353PGSriO4GtN/S0tLayhI6Fk80+bWU+eakZnYzc9ySHp5Mp9PPuA4IjTBhJLC2tgwpTlvdpeZCH07tl3Z2NvudXrPRZEEL0wiQni2vLMLZPeAuyBwzu4NRf6FR3ri4hJHKRbrUH1MAxgfq/e3b7W73yadu4CukUGZV9g6P2GyGqoCyiOPJ6VEuvzIYDu89fLizu6u+dqRFXdEUDsdW15aeefLZtTUqNK3WF06Ojt59722W/oMuNGcVE84JdNH6+oXr1x975423qgv4qvKXr2ysrqw0m001GNyAjY7i7nZpDMb/o944X62xYEU1RH+DTgJlFuJzSMC4WyuMFovZVpfplL4rk2jbZMqjtRjFqRDJQKN4bR8aE0aCP3hUufHwW21B28huqCzmSMqM/DmZl3lCxh40qudDFQovv/wRnAscadHvdp77yPMf/fTHn3/pxd/97d89bh+BJ0dfkBI/QOt02OntdgeDdQ4kW10pe2+a6kKzitLtLO2w7BETCsGd/ghGnGEVMipCMc5MgX6amAdu8ofymwLih6EypQxt/eV1+wtYm5kzTzxia3vZmXjmVIYV6ONVF6hGkpfdOU8WqEoZLGTkLKzFNI+t4DjEA7aH2nP2FP4R/SG6hwgEDbp1m2bIZhbHzWra6BbQ4FaCZoXOdnrx0Og2CgHUDhDRrfJJ+9AF2swOXagb7Q1YS+aHqayvtQsfnAAsf4YE8WZKWSI86J1CpQK5/UymupQUnFlkElomYAPT7kmolGSRom7d/W0mKWALQgQpAF1lMadHolDSUmW4NapGFUxLAGqAN8uzTlaImtoH4QgSBxEzLxUluUG8i4GcYQLqiuYlFYH+wyTDg0l6sYxPk6U4PsVVAlpkkCbUFLYJeIG18CQybBIpA/tgnOC6EDW7YNqanhQAsAWWEVkohE9MOK3LKDpKD4pACCHq0CSQV6oi5PkDfiJp1Dm857F+n1XGRJF0HpsAkf0MooB44nfks+0JiNaKqPh4lB6ypDwpCDPo0TMDlqAZDLefrcgnMgqYxaa05z8DYNoVMN/1/Ah0euMeTR+8KWLo8xPW/Uf42YdQoXUIsozpNDGb1+xvx1cwfSa5+5KdfY3YO+NLyORoustNjdMMt7XTynsOQhlJw8GTZS1B+0fknLYsu/hc+zCxUQUGzZTus514Ot2YjmvMqrP0f1K6rw+D4womdAgx8JCVKJJmHMcoE3h78qBtBS6yJ8ZPMAc6loQM+mW6xN+sLmQtKcyNS564yCQXwvIwZIgN8HnHzoW3+WScQ2aKFgIp5LjxKmw1LW7KCSgkj1V2XE5MIIKJxzh4j64gVDvUCiZ3lQ8C5zJ0CIq4Qy5xcEIWbnU4wW/Xp9pXkdiVmoBgSSrnipBcVQnGomJZrHoFGoYyKSk5ug9MbWbHWauKbuXmSjs8vHhEKmP2LtQc+VJycLEp6pDG3WI6/uirQZzrL1lEjkcJF7RWJn5mW54SWBZB8fgHp5iboZClGLv1sHtYAEDng4d+6CaHOpYsXkUO/3BJZo7DNDziImkVUKcs3JrRtaCntCywelSAtoKxLkhwHgBXx2wxOshDbKwKwsnhoF6VpQa3xQUicQhUPxnrn2RRe/pIHzsBH9UTtJj1gWSL/thUNqDqFfJzB2e/e7h/5L7eQQcXXv9o56TXWb3wCy+9/BJHpGtis25b1Msb6xxdq3cRGxUYonKGR6DqNLQMYIz7L6M9CLJnEhdRBitHekChLvlptVruUS504ho8pvLFm4ov00dOMvsQG+vfZSpamvAbV+BlDg9OPL913IQi4/HBQmMFl+HFC8v37z24du16rQEbc5A8K60xpPkHP2B9gRWDDe7KYPFxaWPjmauXX9ja3Ob8Uy2+RBJZTvQiE2Ggb/bZM/sdofOw2bdOUlsh/c0CP/gVkGJWahZDAOSIXLYFywGnpeyEW8jL3J8KN0rKDKYrTcUYhnmThsiXxlXuwGDUCxd5ZqayxkJAm9ylwRuY/lCWOrN2+kKz+szVle/ffH0wcXYxO1zGhIhjaR30YnGylN1hsJ0ypEQdWbvERfAdQBGmAasXxkOZGUcW+UhJctkYEiHjwV6cui2x1L25SZ3mnmRP4S0X6TA2Z8uBxxtyXIJTTog+/SvFUBQLl/VUKNlVNnlfufHk1//11z//s58q5Sv9QRuSJ6WHboF3JBWFqIkd43Vb7a9+8zd/+3d+G96wQJd0ceJng0UXhUKt15v2psN/9Fu/d9g6lHpaBnDLmNvl1i+sHe7tj1jEj8bJrhSK7LY/pOsFUVUS46lcpjvoIFEsyYEKg0HptIfHZ7q8ushwptXqsRxrpb5+eghk72Q8afWG0wHX2DKuopjchNP1p8u1Jpc4smwUDeNOjEKxPbizf3DILSmsv+LKkJODk4WFBVzF97d3uXid7a3M+128drnf7t/n0r2Do5N22yGWWj0z7i5yDmmhcMo0DrvxYfHNe3sXr2wcHR7evX/3nXdv4UJXU9hkvHCPBIeJdR4+uHXx4iqn6F+7do0FdYy4aTpozZCe875apy0UYod9/qwIQiNz7la+zEwKx1lgkUyzDdRWjiluOCHbH09YPEZz6XeCb8KdqtgAUJXOqMA5QGSJ8y85rspmkkNQEnH2QIiS4CJM5yVCCTvI3OVppVRhV5HKMj/t9jv5QbbbGrZPZYBW+96Va5f+N3/vP0fD/w+/9d+/+fZtRiZ0WeyrxhnRa/X/4stfrVVqy836Ezee2Xjs8rSX80oelLj8YokURaH8YMCFCsnld+xdGFrCxIRKEb4NMlRi82l3CTvBNWgzORXFSgxn4ctlKKgEPTPhjH+8+Nn7KBgm0RBHen23GXkcOJ3DIeOVQa5KP0zbFBQQhjqcLc3MG0PSAbsMB/l2OLFxGsbISrGnCTDyr429NHqf8/1ED0RxKWMOT5horXIPB5TL5PcDt1XYLhzpmihU3H6anfNKGfjqThft+AMNeihEG3VKJaO/UDVHxTVVpJOaOhIWttAnmcG6ZMrjLkEh4dO1EFSBWYJyvLiNNQgoO4iqTjKJCu0tGgB+yH1qDlZbrDjaEYEIMpCE8UdCNkZTheKxv4frOAfYAmIIXgyCfPSyYRtM8g94z0wvIv0WgyoAnv0tFhetHdVxiy0P68SsadDSDjW6ZpraG3LAU7LbziLi33A5LIn9WLwFXXC0uwo/W9qWN0Yb+rgkhVSk4KhdKCq7OV7gETtuCg5NPgfrN6nREitQb5w/ABGXLwZPMYuWyd8jH+cHBtm0arj/mGayicwK/ipv9LgsJSrWiUcjhyJ50qcUDZL6SXjKHqG+z0JM7xPNYyUSr5k3qoU58tD3weWEOK82u+mimPy+sbNyzr9EkFa6vWOkj4Qf+KC0GcAZ7lFwQvIDSR8BSWk+GD3/PY+df8/Dz32DzvyBNIFDGn9CWl0beO3DZqFI2Ah9h0nIk8gTfJVlsRBW4qm+bHShbSX15Tw4iTeJo+WjY1kQcA8ZPN/HdTLa3MTTtC3gTscrlDTsccIfHX/MbpMlcaLtodzJnMgKUM0J8YGjjMEO0XbBcpSkAY0+wS3N+ISUpFbpKhOYcNQPe0H1wHBFKiSqBzNpLRFgenWEJcltFgxvGmLJkUKDgUcRCoSModLIJtGkRSDNTHLKDnax8saS0mjeZeeYVjNUQwLbgnXjbDBFsIgTARhdlDkDi96FliGDXha9h3hItbp4pSfBY1RAM4hj4OmQAz2chs5h1iuPYEL/TqDWRLlYph/Bs8xJTeLusn4VFnPfGDpgiT7F80y/xhCBctHmeufABdXCtc9h+DhVg1VEdbEwiGLsAhV5oWUVRztFkFRKqVwiT3jHiERjQwWYjSjT2EuRN5lTgLR2tA4QQokC1JIhgDwQUVHVMGwgvYt0IanuBoNIEbQAGVuANiBMBiI+5RYlkrGwZ+vh9ptvvQ1YTgFaXVtefGrj6Q898eILL2IZ20mAofMYZGQXoF0HvknLt2sEW7okAdJi6qhQzGhrGj9xbfoKdqJ+wUShE6074x+SMgDFsV0q93KMqsKXypTLSInj0K3xmBXAsXTL9fCMFdlEuFAuHQ56DNhoJVpm8NzzNzhu5YkbT3/5K1+5efvtF158FjLIfqpIC0sDAMhic+DwZXdCprBQW5CUM/GSqNYhvnkzf3xF7eLDEGvwKITMs8fEZo0/3xOcFPvoVyRLqSzLJrFBEDHhMq3PyScsdVXpsyLOA2AYRHEEkm2K9UcLYJKSBaM/mpkzowCRjHKW3ctoAZGGIRwDpz+8vnJleaG2uddmzc3V5QXPtqGRbDtKBgcEwHqHlrLWQQSA4ANwTqHKQLnknAGDQLiHETHsIAAgMEctiexJ5Tw5NWzw4MuQCgByhinjERra7irGfJaABiKrhXG5mHtkvEQPu3tppf6f/C9+PY4G7ckeM6EIAYl5JaSFgbgcPi11e60vfelLXIyFzx1woAcKRJAky6be6fCf/vY/+8bX/rJadutIWDakmuzvbzcqbGfG48BaHuccMCg5hBOdiKU+ZAkRpz9XKsdtthRDBrUGW+HZGtBoVjGFxh1OeV+ABL3+6cICJzmzSaZfLJfu3LoNvVkzhaBCofX1FfZPs7oGbYLfgRX3TBS0OlyIdopWgfdHo351sdntD+7f2x72e5VajSX69YWFzc0tROrg8IR9AtJH9cCRN+w/xs0xWFxuPvn4jQIXEBcLV65fHPQH9+7fu333NoRlsQ8U8LCJ6XixubC81KiW2bu/t7q4tsIZn80mUzeQ1P85Dhj11H/c1TTu5DDfWFoq1RqcZMw8KnWQjdQ9NhDryVT7LFzSirK5eYKPRc1fhtLQoffIA1MRDf8oWz5KOH+hAuDJCNRDhoet1qiF5Yrjn20J+Ozya6ur3Za7/U9zrYsbF2mvfre3s7nLQqyPf/xTrAv6l//qz+/fu/PeO7e63Y5cmOfk0MHJ0enuzmRn9+Dl3ocvstGZYciE+zHV53YmCoWucvsZKqMmpQpRSxVSRCBGIG+1o5ZqMLNZGXo/PyECfGhH5pOsLjIDQEeDU8GeeEWI25Ex9p2VY1AmPZVvAIMWi3WYKUZtajOgV/ER92OdD79AAJIypsfm4m62DCuBgUM6fOHRFvY8lOfoiQqCEBkAgnDRTAy2lSrUg4txXcOnpSj9RTz6ppB3MbHDonH5isoCI7VpfFptg6UUtVS4eSFUc9NAe22wSNpLOkm60LiQgl6UDsvaUuno0qiDhCUN+ALHBy4TgzAr7LYoSAMmmsCOJDWOgRKUOhHD7TpaV0ZSoEoPOqSSSKS+gqWwybCsVT6UiOcW2QEA9hsIsZ4i9GyUFSxJTS2alguHHxHyhpiCcOAKFZzdcu4FXKSHHxKG6KAKCVOtEq4QmwgAIQ+AjVi+CJQYZDXGNynCd1pnzfpMipZgCp+zb0oM/2kyPvnmj6xUQ6YPSBxR4wIgulF+WhFD41XgszJ8BUGRNTpQjiCD+Xf+iQTzgKhehMyqZ+KzFNLg3M95pg9+z7IUZiuEzp/nM0sqmECE6gOdakTILPasvNnv+MJOeWDKR3U9i430P34bwKMZhrOUviQQNEdAstlU9ronXaSssUeS3AH6X14XN9oGE/0A9wldBvPsE+/xrU+mh3QZmVyH05yzXAhgY4ethxsv9DeGB6wKj01zZVwrufElfQG024gFfIt04r3sflvuXmVaL9a8qR/Fj64ATi/u0uozNAEOGhoykMrOQZal52XFGSGgDx1VczauTI9BquQok8Rrx4lc9NNS3P8sPJDbwvwN9U1nRVrOjGOlo6oGiLIPoq3rx9f0KUQrSywDpjBlxRKBCZnRBE8oYdbwEmv4EFsGz26/d3ROf806JcBQA0xzvGTpABuqS0nA595ZZ9jZAY19LhB6Q0nHh41lENUvctaHcJGe0ECqe0+ZUEkiHaTXnUpeEmn0ko9yGYdolTDRb4tbWjjbvAiOFdegg5OG7PQiTM9BS8xThgMq6LjsTxQ1hxzY2Tpa8nQAupMhMpioipFVcFQ9ae5bNL0FZEHXmcOcBPpmE6sJQQwbmzGalncYchBY8bcBaXFTJpcWcEIt0J62Mon5pGjMR6y8mNJRBWEW2ISUbEPaSWjMkabX7W1t79IHPdzcZW095MH7yXKN64+vfvYzH2PJxNi7CJ2aICeWAazoCSTe9wyFwBNoHvuD2893sAEE5dgwVhSa8B9NT/rAX7VNJUDapjJa5cVCZ9cUlNkxyTWq3NA84ejRfOGQDSQUzACgXl9G0WE6sO0CghQrpcXlenvnJIvEjUbNxhIJWVy3vFp7+aVnT0/3WifHjeYS8DEp2bFAKdJdRmGkAdVR/cNSubVyQWpKHAb5toSrKSMtHzaK9Z4/4jqLC7zjPWTneJ5EXg86p7iUQyipcD/9Hz9nwAxB7m04+QAXGg4/hpZVppo4bADzzM4exgodrzjDwA54XbwB7igUi6Sl9P85JYCRHEwBZESdUcOULQELNey7eomjykDA1RrIkLYRY184R3akdEChatQM9H8Qhva19ywWK+x5IQ1tzQkuXFyLRsixjjZ0jG1JeqqRxUel9FFCNtdlWAJKIw68pxyEEY1dOsmMn7DMIAKdNaMZtY8Q7PA4+4mQXL+yUF4pQgb5lHjqoSGhaFAjBjGYQEzb0WH2+7/ze7+1e3SM9a8Z4MoKWwwqyeaZ0kJz9bU3brJkTGVmXADBn5nNPdh6eHF1jcVU7Ex4uH9zoblQ6HFtAqPIBtMC7OI5PfEIJjv73DHc3Gl7eVWhwKQEptZ00B1gUGD0A5XZQMZoJzir3ZbCWibUOxsnio1anascqRh+Q6x89vOedI73DpkpYG5KkSkVy3QKiF7P3RGc3Ap5y7X6EhU/PGRNU5c54dGQsQ0qx6FcJntw/bErTz15o1Iq1rxxuNLp9t5+9+brr79uc8HZdDD0WMVprVy/eGEDtY8D4srlqxsb61jVHE6KqMIhzIyBM1cCI5KZbG1pdXU43F5bWvUkYbQCyMUkZ/Ap9KSZmayGbeGNKgdWKuKlhwaYIroVCpYbwdINAN7gHmxOrkgTjCb/IKS0QllouZgvoh/iVuTiCTcjYLVVGpxE5PIyNowcHOxz5xgs3WdUmMlShQ+tfahYmb746rOf/blPI79/+odf+fKX/8VXvvztTv+0zJQYGj5bPjg4+fIf/+Da9aOnPrSxUF1hEhoOG7EWwL5BBwYejbTMInAKrmedNhRGVdPFyD8wmwo8asAHSgf+jiGQbAU7IiDBTqHGlePcAyrmWhyP6UPmkNASffqItRt0Z1xt0cd9Aj8zlcoQrjzNt/E+kSPPhFiGq0/KXS56s1Aow4P5gEh0s/R601Ouq+YWO/pJezSqACuP2YQC/8Tl0FRmuMpMAmMzPCeypnNr3lnqRABDXqUNJYH2toewpwI/RRdGsYqgaP2iNX2nJORN8aG9EDhU42UGHQ5uqL3zADR1WKhkIZ2yLVAgIHGIIXiaRtIC2aYGJxSWSWh9xFj4vNLf73CQ7XS6RpcT9glDpXQkMemp7ENYykNVAOXeS7e+O1qixwF9uxXUOGqGbdQbCRP1F24Tq2Y/Q8cM/0epYCIbZaZdEYVDMUBYi+v+I0QCVONmEpGFSHwG1tQlt08VIAmAnNiJnHL4cN0+GmprdcH4wKGXRKVJapoP/yAZmbfBOwjd8pOBVHDOB/Iw7YU0w4v0ZXtqCPQxc2EjWswasbKWu5bhKoDRMGTzY8xsAMbXFtBRv9RHwwFK5li8UKhygHyyB62dwhe3As899/JoiGhUzF/ve1J9ZQbZ2rrz3xx+Qmj+DS/He0QowiaItPLQub27xtn4hPlhVpDnRV/mv+FJKU1qaVIoPbPwf0Mugk3/Y7Ep5BEUE6SEPwneozDyRa2wjzlHF7qCuCeZQH3JQquAGqyO1Rm9IlzGLVeYS6UulxRmsr2wcly5yz8zUyw55FFYFK4io5YQG7mwVVQ1buIhBUtXukzzjfML7LQd4l9VgO1tgcOnhZMqODqgRm0sJHCHd93aonecEHDTMDMSvP1EUmzCIIKAtI/1ihsUJaRqW3XKQpyVbWQmMpE1oRHkND4qluqmOuctRYlMUproTeSPUY2mm7klQrCqigBUFFW/qJFS7JoiDVqdFppfdIqshEURk5rhAMdB0h3hzHTMq1UiZoBk8SN0dVTPEl5H+bZTaCzBQ3YS2g7M5yPgIEJ+CkQ5qMeEQkjM6tgnJHuVDJGF2KCXoupNoiz4UfBVpcoeR05wIlPQJujE5EPQXR2NRyu28tst2lqWDKz+IGbxAhHqBbIgP+rZ52TohkUZcjFwoMOmcczo8hj7kWLUM8NqAUK0gDUWNa4YTurtoDGZBbJvo8qQDR3EQoA+dTob6KEbIHZ0/dJopqwZ4o1GW9s73/nWD6rNYnNhcWVtpVKpfu5nf/bSxgVsCxChDKlGpYKVyAtqah+66mqFq5cpTErhv4GCaFH+QUEtadz0qiRcsFGiXGe02pokZuLdTD6ImyUwpOOmXpAtl8fHHNhYqvT6bSBjtpbx16LtMJscUdvr1CoNuj0qwwKJJ7CJnn4MCBhkzz739Ftvvb69vbeydrXdOWL9FWSVzxilYO16tZCOUoiJGcSW4iQ4NEeQBWQBD3fMhEZM3/+IvAnkFesQP86SSCJ+RKyBKV6IPGabv6QYQuxTPOTBzpb+AIL02Rc4wWTRZMDNL3syNmMwOuZQGEAgCHQ+dG6wD8XJ+fBTDBxRKZAdDyKWiKNQmiv4to+EYHFwCM/Ia55IgUDRA9L/BTuk3io6ft1r5AEsWQEDxlyXXanWwmnNXmq4LwaECmOQimQkspMnxCkIDHQsSWCoStjkrflId4g1xII9dVQiB9kjHFHJuXqP0zZRg5xaU+B8W9SpU2eKrd4Kl9cBHxMP41g7Ljttn7S+/b03vvOdN5RyetNICkSqDOkUMD2po72dfUpE1m0vaEW1NG7G7e601ecWi2yxWilW2a/ZQssMTlvN0eT0uIXbHv2uNe38A/NFLI7J1es1QCJbDUZUnNnCMhPu+uI2Fy5oyGY3N3fxCyAE7Mrl7taVJdztGu7oHMYHeBNQa4dHHXbRV2pV1g/W61WoigV/dHzMWsDoz6ecKo2I7B8eY/2rfjiY1PEDlVNal5aXn3zixvLS8qDfOTk+Odg9vHn/ztbulg4KiGB7cEhOa6Feu3L1Uq/T5YSneq20tn6Z7ftVbASqQ0/Gnl5mLx3ou4wKYd3d3Okxm8bkS8HzjZj9gMyaiDKyVGO1n1oJJwgqWldptDitGAx2xtnQfMb9s7fEGTOWJ7lKQA6OEFkTCHR//UoVJ5pzraDE8ipqi76EsgWW+/e65Xqd5Sy5MUsEYVbUXfboqMUc5M/+e5//xV/+uW98/bX/8r/4P7BwkelgThBCp8J1nJh00rlzefPi49cuPH7jBr2EnK87GFWPr4u9wuxih/HgEmBi/ONiYqOKNjyMpvMELgn7F6kEYZB3yaK8RTA/4ScUHf00lQqTFrFycp/L2jB/8xxtNtSpxzB1yC2NI9hn2nPQyrlpLo4NLkXex30k3on/SZEDpxQn4mDRGJRzGtV41Gu3kXuYiHYDJYyTXjFb6g5bDHcH3BTGoBWbU7Wq1sHAUA3HDD+XJ9J29hj+55VahVlsy1KKaoBgm1jZYHjgL+rFb5ie3pGaMSzBsRCqHa5IkaazKWkmlKk01Plna8qy6BXe0BumJqUbKAHOwktsethZ/kk6hmQqrn6HS2gYAIc+4NNmwTgCDF0YWKtS0H4cx8sZYhwNATAwN7N4UDq4i7Dc5lJtaoY2wJhC1WBUaHhhDuAixDervwPXCelpYK0s2lJPFp0PyxTheqYD6Vp1kQA3SGMaB0DUjIqhkmhzSoauYaSpNNXejGEkJKEko6Ig4wkZVhbOqlZrLo/yoCo6ZtZ9saibTVvc1FFgFAgPghFySUoXizkOgOtkdod70QtQPXT6KC3XtJ3D5rCbZ5ZcUaV0yuRLsovJ+5957PtD+UXWyGwm+4uzzLwTkkDNo+aALex8GQFEQGcv/oifs2Rc53jFkPO5/M0zyzMrmS9PQiCYwfHZI/pRRSCYPn6fxUaAyAN9BmYW9xOK+2ASU0YyuIp6BqFQ5HRJPZhEYwaeQu1RsL+xBeEeGBkZKjLoPm01qqNirlstcXevjMAaRjKUWAHIonE2CtsPiy/jO51tdBg0sv7h0MKsCh1xwl+mlikyQkWJcBcsK2VJGXShZFjIqiEYYAAOgCNIhYwug99YJ2AHgNwkWUaDmER/ucJh3Qiw/7ODQGn5icByYCnbjgHMCi1pSk2JcMG60oE/ljoif+hNBqZWwu7QTxORhcR0DdJ8dMGchUPmQ4DuCCrG6KR0ZQfQAE4KZBRcMD34wmwHyBTvOOYs6YGGkich3Rw+rz5rjQHFke8oiM4p1gGzz+AO2dRF1Ii0rM3BpxVeOhCesHVw1FuVTPlDCzJltCuV10iiTOpIR8uplzXknV+tdhs9hyWhqGEfSnZsrFQKdXTKgN6ahbH0Gij2wojRSClXK3Z7k06/5QII1mcPc93xgK1sXuFUrJwcH3OHu50CN6ByYguYxxAFnBmpYxCrmPTFoOfQErQaFS3GcYdQBmMbtNURaE7UvXBUBAg/RtKQrYRMD4mqSUPgrSY/QB69Bs7697EXDZBK8Bcnq8C5YwdC6kIMRz39ALl3595xq12tlw/3WAA8efrpD33qk5+6cm2dozY73Xa/P/IETlSTTBRsA3zVIWRVSrBpomui/ejiQhuqMa0XLcXqLMcAMBosT+ORcbQanLudWoWEmcEFdF42vyOi9ossYzIvCDcXaxTDLg9V7pQTAF3sRaVwtQIbs7KBieaBDCao15uVci1T0KfY7XavX3v8jdfvfe0rXwfxyxdXLl69kvMmPhaFY4ySHCPSQ6UYEWxcWuZgQVaecAyHlpayZnXPHn5Bx7Ow2XtwYPAhCVPYLCZS8q4qTk8wfXpNQQRAEGBSIcWPdxcZ+kU7IS+2PxjhCMAa4x5VeopR/3j7PvdSMTXAyTBMT5HL6R0nB+zzeVd1UE2WiOAxBW6kgej0XvYcMj7OSO4N5L5nOxoQoKNzAzHHX4JApVjHakbz0LS42twXgdlKE7BA3KvgGqgXTCwQYhRcKtTqjXBbObGZKXJnHZLuNmQMfzpPBc2jrlg538UCdnZxMlzmKjPmw6J/pHQVnP8w+cBmypaGQbZQRSDq9bV6Y204PMXrimeWKtBeWACjzhpr1dq9m7RSZ9z+wy/+0fd/9Dq5MpM1dLRSDxt5BovffMItb739jupGzSFvMK/iKiCmHhHsHHb2YafTpSYcse8lXuw4xUxpHTvSR//hrIn5XKx49hot1JvwTfug1Gwu4H33Tvc+J94wZ1Du9Hqs1mcTy3SyAPHqlTJrVhaqdUBQMJqF/Q90F+3uSafXwsYAN1YUVlcWOsP+7u4B3QHKNpiDDqZ8dHp6hALLNvKlFkpTgR2zqyH72PXHXn7ppcPd/dPjTKVmI7575+3N3T3WyujuzeaYocCMvXLl6tLCUrt90mw0Lq2v1NxBnm8uNhlNwfPY/5DHNX0aFmy9YEv3kKZabi7nYAy2g0A7xgbqQBtH7uH/BP8oHM2UVClT2gyVpWZIvK3MyLUkQLqQSt4J8Zsog42N+NTm7s0j1jEbSvH4+FR5RFOgEBwA4H6DbwYM+LjsC48LMbDRSmP54mXuABZBGhLp741PWyfDJ5+78n/7v/+DH73+1r/4F3/AGarssyiVUUYdHO3cDdJrnXROxqVq5tLG47gVWByVKzqjMs7GjLejs0AVRFgKxgXOXjpNT8E6fjZ0XARFtBPI4oNAGaGloSKWAbWy9thxjnLVyIVqGU8/DKNloGJikmec8UwzDjdyMnbUQ8OQkUM+0GAs8oY6AEVZImTIPaYffuEy7EKz0O4QCJc9wDidCrlCybpwFTJ62S/HGJMAi9IdA8hOgR5KCuP5x1SVZ5ARvAgEUQy8RQi5aW+wJSWfGA92voTQQixmiyV3BGLI0vk6h+WCUlJwNhu9FZUMXoA4Ghe2NUcZjT3+RJ1H302RBFN5cSOF8172UXgiQGDUZys5xjaUc61SCGWMIpgJ6vewvVH+iWH4wsXEOBDaMrjBPgh5QWbY0ghYfKx6oIQFJtSU2rB1yqoCEBqzAA/RdTRHf1LKsSMf0YYEkEaDAHcK1wJSTWadGXLK6hSPbmT/JZM2KCwP3bGbldwMBGAatFyOC6kBDN2C0jSs9IYsFBvam/QEIK0ixt4zsB16qwkGw7g/ONJepIWFKAmDTIhrzgM/YDKK5HBl1TlTpmALiwPNyw9tQtshz3yIFiBUkiIEU47VhqJw2RV+xiob6QCAuMeXtI8eSjX9PEBA/gRoCrKg2ZNOx9LrDyaEUWU/eYQeP+gOIoof5J8D8yWi4+sMNAm0aP/Kx2hBfjDZ/Hf69pO/qKTgZoWlrPOfCac5ViY796Qc6VNIERWffIAASGPgMhUMjzlt5RiMblI6R7EIDCEcWgEBuCAmPyq2Op5mwAGGJEZXM+Lkbia8BzAgPRipHU0CIfp2TGlMHuRAS5mVzVxJP2ISh3TTGqNgT3wasdrExTSIjf2U7iu5DcNaOC5XsCV4dIzDb2DnOjB9BLYPZrvntlkiI3flyjqR0W2X6D5FjQczSBMEYCBLElwLyhp1jzbQHnd5GURhWxNaD7XCKg1H4mhNuBOYNgbvenv9F0a9UxGigWNfA4eCEHjSw6OhMxURdB8OWYCxkBdCQBcMFBfrWDKublzL+AVsHCuLOkDoFa8Z5xMUzYbvAVMQNYyoo57oM1gFREy2yIZycqOGbDbTRgM4s4JqLzvwpwfFyddtd3E0YC5DfUivQ51DS2lufqliMD74gA4M6gZoDk5eY1sdYjseIN2s2MNf2S2ylIsbG+iu8lMcGe4O1vZwKwc1xvNUKDs+Y0SpVpyCoTo7eg1rQu3UzFZWDQvSCDQa0C6a7Gg4PjXnHT/gMoKmKLeQfhkqzFbzoHOjV8Cc0KsmI7pknF3VGH80m7WGS3zyhZvv3jw5abH0mbXLtUblsz/9Ch3JZz776fWLa9iRNEq5WoUsYXzTVDbYjJpQJBoeRAmksVHvDDUpAX+V+gl+Ay1NQNDzC6LKK2ov+ohoOeuvsgQmMQTGE01lk1kAvCosvVAwoC4faECj8BBL6cwTcBcVB6egapfXWIfN3dmuiqlWagwFdzf3v/K1P+f6gpXlxf/df/G/XVm94DSA9fDyVPyqtm+usHHxysrK6ubWJuwLYSGZKayZT9Rkjt0sJL6I8Unp0vujkHluEhBow8RbADPXuYeYaHpYgkqTmLoUXH5Gd9yGgA6IMDJyeEJLV68+VvaAQUTSiSPtSOf7Q8QdJ9LlwFrMmPXv33/Itc22M20Rwo65vrjSZNU4xgO9BClhT/p4DBHI4PgWrh5l2hyqwmJ8TJJQEuySwGhgjQYdjiMGxhEcBYovHIXDkgQ3ySC1nLsy7nWGuD/EAico/SzL+fF3o/mcpcBpaftzlxarGpJIygsKu2Kby1WjWQuctX/Q6l6+eu3q9XWvQKFKHhFL76axou4dZ77zre/c3/wm5+Ic9Y/u3X/IehvGUTAGjOIgH0S1OuQWMEMbMEYlIuwQ5YgWo2RsO9AGPqzT4qwfGBdrrw81HJFzEbXJQkmBJ+9YNJwfxOIpVhyxOq6Kx5WTWHHvMbxnOqCXZ1MvW2g43ZFi0WpUbWN9w2U75iYNpgNkz21v7eO+hME5U4g5Dc5WYpXP4fExh9uTBh5Am6GTOsxNZGpxbzfY0tCcGpy5sHYBuuAXeOLpJ1Fc92/fPjhu7ezvtdudcrVsZUe6Ki6srrGEctQbXFhb6pz2mOni+H+O82K7ALxGARQPesgc5A9i2BWhbioco9BcpFY2v3pL1CleGVTz6n9hpTo/lWLjlHUTkCS+CJHXFWu1LaxgwIzZCTZWHSLgkKn4iXD3nT8HMMTXbUz5lKQgRq/CuI8+i/Ns++PT4xPOhmXljBvYwqrknKXJsDu5/tQTH3n11V/9n/+Hf+9/9b9/7+BtbkVGxmnAwVHvMNvbPjgYdI8//OGPv/Lic/gkwIMOIyZEtd5QywgJxq6TVl71DBOBqTMBtLUdWQm7MDtgQgjuUt7sMKI2WlzR0dEFw3SQJchGArSe1i504D+lqMrRLlKErGIgJCpCGmoLS9A5YuohbugABD+SkN/slGWxpEN1SU80OpzLGhIBYG7af0ErYcrSVko4ahbpCmHp2CAoH2F40Fz8R3HomXG4ovioRvU6UydogLWKNPDLrpEq05rQRGQUI/LzM6KpNt4pG5XaYQhTY8rkywTiYkZq7dw1weTVEADTGACRllSmxS4P3qA+EJHKyR2ypgxhDqc/yEXXaq+orMfWpyAs6EgoOBNQ/o90UQr1gw62l4H8sADSwInQH6xtQxGH50hGo+GAE1XLDd1jWyAzgSS54glyiHU0UeJqKkcamR9EwzGPHsQ2CosfRxmJQZCy0wBAeyGoz9pyOEuUUOkUZm5JIZFVZWFYSVILp2Gtqej5wWtU1/kXwME+5vKZf6dfZ5+RIcWnFCkggUyfH8jJz7NM1DgQC2LPg8/gnMtoKnNBwVQR3sPK5PtRskegU8nixUMWF8bNTxVNa4/8zZNQOf85B/f+75Qi5Xn0eb6Ys8LPXgQf5aLmOJSOgVmxxsBdPqRZFe0oQ8mhkUIvIr9hM7ZZzcmFPdaaA75oJk7bQGLLwfx4UzBSk6sSkWStKrqAlmRyLdvHJVktjrKLBa8AYRHYdKk4ruHMY6adoTgcoBTSOYe0y6MwQmoF8LgIEuP8Fh2NQ0ZMH04GYS5B41quJa0cL9YhRHCH/IdexR6lPjRRV34aLykGvKDMTGMGkmFBCoHawJnKpABZdlqqsMhV2y5EipQQiPX9THwv4zWMflhNyFLhQd8BRtiRxGv9Ba9jdYAxBukGfotxYRP6kpHKUQ1EkE8GGuPuumLA+QMx3nAFkP5O/iF0M0bIDjZy5XqmtOeEHdlQgeVdMQb7xKvBMOKpYDJ7f5GYfK2Xz5UbjXon0+ZY8MP9A0wiIeI7dHUolgE0gAuxei7QBGPuqCmV8XsZxtDNxdaoPKpVQFXjGwu9zw2aVABbBPEuozYZVoGHfQ2ahrkfFaV9MIuoQS9ozNa2VdAel7tQQ21HzVD9qa3QD3bRlMIt0fQN5NQWpGMzJR4hbCcYZHQBmFN8VBQjcGtKc/NtDoZs2EPsUfYQTWIwAHIutCgWTk9OHzy8x+aKxcUF1qK9/NJjT954ir21LN6FP8AbCCTn37yzU09GjYQc5ytTDom1c0CPa5CJx5RisDQaXyDNeHqiQoVvQA0aIBG5bejAYA3MiKbFsnnOpw+4LlElXEljLt4m1uJnSGZpWKHqvmgTjCTjOLypBm09aYT/Iw79YC8Ni+s46xEudx1x5rS9D8139vd/+IPDV195srZ0CK9KcMYJ8BrMNmHr56DdbTFznGoNh/vAKsLlkedBP5tO+s8fR2CER1ISRcqULbLYofPY+mY/e+xP0kM1lAt+WgzdBhnCDGDyEPpwBgt2Ld1TjkNcivv5LMNH9qTnF2r2/nAOdGI4ijwwoJdLp4sOofMtfI7KQLZyuFvonjJxR5MIGpJXG4UnbzzOmUD6NbM9msO+Proim3raZWU/wO/dPmn3WSYO12gCLi0tNxbqynq0nyNSKY/mye3uH9w72MLwrtTAGRyGnNjjODFffLiz1e5oL8IkcB/OMGeI8mUGnFpysIRDfiqMLJMDkwwAOexvvF0vffTFn/+lX7ywwmwDd3Fg0ygFyAUI8JcrP9zc+yZu9N3drcMeFKho0NjaJyHeFdQIAxVrpPXF3Be6FxHS/8LkJDD4Cc1ZMKme4RuJgofC90qK4D6dBDyaO3b81DnLptvmYgNPbglcSz3OpGEEAa05jZW6saOXS7hwrMdqmhOsxmKmyXQVZEdpIZy4HFjrc9w67va41K2emRwpuNMJ13WBKCMLOgssClWsLkr22HAoJOSAp5UWth088dh1DgztttsHO3ut9gl7hbk1m6PxGTlE+zo12FhoMtt4srtbKTY4pH95aeWFZ9kDMClzY7GrSiCnag1XiqrXwTC9zEZ58cLyc5lOe3Dh4uVhroDbnIN1xtlDp4u8CwL0jyBTdtJUreL+9ygSj77Q3KHZIaOCb2cQiotwGR8C8mb24Hq1iY+yEm9JFqg18ZI6Nr2goTCdaaHQjpEXHNkgYIc1KfTao33OsDo+ZR7P7gfHDNRjhFca93rjnb1tRjt//+//vTfeefOtN1+/e+fO3dv3WVyUn66hyBhI3t08nQzfxOr68Is/XSxVh6P3WNjIbDBzuyz/Qc+CHFgzWENucAaDU9Y16AyW6ZrpIrAjC8wgkIdaUUFKp6LakaLKmIQZUZgHT62DUnQR7n5T6XVhVIWa0/KDrihm5AT2D9VBu6CICIdL1YQwLMIMh0hk+BCliJyYDQYRRUjuoFctEHajGgTgyDOfbl0zIaxsdyqZULcmTAwPHE1whygzJ56FSEnbZ1oFLDgzGiEdtYR0VFLpsSYOjCjbalMJZFujVMhgDRPwk2xha5tGqhCtikuCBzdz8BFIgR3FyPOwJF2U+SlLNUCxioaEsJrQhKZHzYQSoKaaKJQK9VQhIM1KGjtNBuO2iaXSzYMuIIQSyjKwsa3BOjt1ajXIRWLnIrjxgvLDQqNUWgq8LFdEhMf4ECgMsdKcPK1ieJAiyCCeFAW5DLevdphDcwDZK9vABfprOgDMnofS7RSBQ1oy26tbW7QnUKU6eTEwHJeKMDl8l+0Sz1BRBcmfQAkI7smJ4aFxKTI1EmX+xAfFQHjWtTbi5Z9VkBA+rNZJLwb4No8QNv/OP7YwQjELjThzBJLmhjza1eji2TN/OfedCjN+HjhPPMPtfVlJTbJ5nvRtQPoDv8D5XJIZ1JQy5U4ASTN7HoVKWAqgWoaZRwXkE3WnrtKYlqYUrDrYpY3pOOEkPbxqCIJk1LiRwR3W64nVFWejkTwaTL+O8oM+5T/ZyEJOeKBEf083aVeujaeosHKW1g8GgK/V4iH4khTeoZMLg0aU7NCixWAD+1fKSuaFckBG8CbEriAeTDGrSCWVqlQv4ykXaFEiiKmUzQiSQXPFMwgDF5tNanmcZRI/xh70WlEIvjAPMAlC4Z0gc7Jup/RXDHwQKufacmNmsKNHYWOeva/6BD2KZgUORLJ0662SEm1plVACC4rHe8P9jypEsrBLKBofhFGAoQTIAp5RYUdGhXojX+OQSCzIar3f0wlKpxjEoU/EvKa+Kk8yMPOBqCoXCK6UAwlrCjiMJH6AofW2IfW2sH3H3iEwVq+DBFhIV/Gn83BUF/GQULJQbZqcwuihWUVDc6hJeKgZBDAj1dU+oG4wAs0U1dcBJOH5U3nKVlQyuM60NrzdM7T1UxtI1y3XC3DUNsfeH50cVRv1q1evHe7tdlsnv/7rv37jxlOcBEKTk1qVBRvpe1H7R4l++sgBQLcO/OfDH6BJL8dKTRfb0w70ynqNcJGCFbRhuOiOc3ZN0EfG0Y0kk+VjRajVkDy0FeU5ruLdUgiWfUN7R2FRMkvoWA3CCn52l1I5cHY801xhdr+DwJDx+OAI/y6bAVDZIyYFxtnf+O/+PwxNPv9LzzJbADX03VoxSmHA6sWjiBGlQUspHwzEz0gAdtbz3AOiBkkP8CPaJiLEnOeSSSgDUozf6c28prckQ+3GFFVMK3nf5sqxYJ8UbH5o8INw5AUFNOz1vEfKe/rgPLudyC40LSgYNfohaoZNhBs46S7lwr006A16EbonPhxBOUY1KhiSZmIahxNxOOEWxsWk06hnhqXA4mxbFD+gK/IQQTyF4n1weszaNvzdoxYXY6HfGRTrs2f2rdcbdftQmm6VlfGseWCZHxtm9MRDMFULvCznC45Qhnv0kxhcLLz//FNPPPP01S4+eKwQh2qs1EJkUSn6IHe29o4OT/JjhuscF9MGAmTiHwoTFIXKciWM+1AFQWZ5mbaGPhQNnyBq/NK4COpLHPKrWFRNYEabGWUD+YswsIaZ2iddbMOFWn2hXmXFQrncED1VzuSIHQOdjgoB9i5kWNnPehvGIWDCAAFkmIxj6uDOnQdcxGa1YTSRUPotzVpQBbsYwzWoFG5mANwYmZmsLi02ufIrV7h2/VqvP37v3Zv3fvS949M2h5BSMTiCbqNcL9eXaqw5ZbVGqZrbWF9ZXGyyXpCjP0GMFSRUQRWFL4DGpZ8qsAI+e9IbLi8tLj22WGQzRD7H4ro4xRhiOHEDdhYvk0EWDCDoQbsQDISIkagwv4gH80MyCJbCDJWEfEcSqZoeQ3mLLz/oK1AOEIFiTMWfRPEreR+cEyak2mAGiV0BVMDuBd6grE6P5eNeJsikHwxx+dqV515+dnXpP//eD77zxS/+KZ6mf/Un3z46bJXqk+397fHAW8ROT6ef+NRnsmUYnpEQ4zWmmnVjgCrrv5EsGoASRB3JFBdqp1mn3UyANp0V8I9PAsTan9CPtsZipf0YM5HTUNnNSkWPoIrhJz2w3GWHZl6O1fIoWgSCpuFQS2jh/h+KTCCkr/2MjIzLA1MA7mN1geqMBpX5gaIjRnwtM2gYOgFSzflMXEDNhvUl4Ih5YGiOaC0qZAtTT8Fq0wvWOLOS34ZRPHnhoRoysD0Rv3BD85qKJx3kwllvLakwage6aPqCkmVAKOJIH1SVvyCNLjMAQkMA2sZYNXICS1gpXJrQDfIC7aJeMifYJJ4M0ouTCIsh9GDSS8x4N6X2GWoPTMXDfp9v4tVNQQByAB1kyGGQtaMMPHrkQzRALRFEbKg4LSEEQdtAMkN88ElSElHZYAXqnxQg2dzHIPYWYl3gtyiKd/JRjpEiELUAvj/A1w/yRLHEJsqLNro9yoXY8Yj5X/1EAstPAC2BYj6Qy2oFJpEwAEYIP2cpxSbl/UBxIB0PuIIf6Wn+c490OnsegYuaJ3LS48W+Y/H7wJNCZiDiR4IGJUgZGM6/CTAumjYlmiGWYDwCHDlZv5jCxdqJY9jM+kUFFGtJFMxFK9llqg1YrFmkQ5uw7KTE4otctprJtkjLjni4I4b+MRhwdF4mNUIA6jQ5aXSG4ubEwhcehYGqI046fUahmFGIOoXDLraxI+FgazQm7un8VqqrrCNPqK7suiW4JSj5qJCgEz9dMRyVYYdCdIQMf+kTggsB4dAfABq1gg0TEJQSQejPZQ6KYHsbcsk6AZEEHrwNmixyrIy57YdDvFkEQzje7Q5WAOY4FkbwNyVpSwNZ69qTrYsPXVDMKh4UWnrceYCFgw8XGXfSOltk1x02HyMEKAHFGEq5HIsXqJTPnxQrnBDP8kkDXIbi3CCIcgYFiezfKcs2i80JufI+B03WqsulKmt3Rp0Wy9xdLEQ5EAIFHTOlVAgSCiBb3GbUzxVMWEZ0ssw269/BHsCyxVub57bVAS4oNqxBNQwMV9eiqmIewzGWvp9EJNoUnY4GyE16azZCcdd5JM5UpmK5KpWjSBU1Z0hryqgp4AiX6k7W7V8L25AAJGWYpFcADJ3zeyRkLweVzRX2ARy6jw7GzViachA71iqcHve7WP7t/YP9w6Ojo5WVFZY+f+E//I8ev3ZpbelCsRJuGXhMTSSd7a5COcqWco8k0SigeH6OV0MwuJ3UQUtq01KOvSj5PkbKeI96N4oLTBa1OoyM4S27Ri2zbOb0tGVeFmtHZx6vGifwEgkCOjWjVqx9oO7MAu3xHgrTdqcBsGzou9nFwZHpjBhYLdbrohxrLPwBDH15v9/Z291i2e2Q9Z9uwTx9973v/fTghqwGRVlUC6exbjbLfAXLuK0PJhFlMwECY7uBxwpb5Rljvs/3n8KiEqoWnpRMWbHRZwEAEEySThvU6PhnilkexiPxTgeDW4v+jvAq7TAclHAl5zkICOs9f4KVI1uEQwGoDK8SdsCcZg+xAkDd/RZuCicoRt0wIjKC7Y+fHlexuY/tK8WENnOvCZ4qsXLbEmTBllwo5LoyH65XMGEUyShOrNAkJGczLOM6jtuCl9FBNLf8BU/QzRFLNKYY65VYUex8Gg8+Y1nKgT3jWOBBUehM24Kl5gDVNStnzo9PB9wGhSXI6T+nnM6JRAAO819jGhMpm2uuLLRarWGHmjIGYrsRKFJfBzPAYoji4TbMxIEru6jxv4IDLWA1lWde+MEH54GAtoeQJf1uU+iNho2VNbmcgCZZs/mWTcsFjVVGtyVGMQSiZrjJy1Eol5/v7RycHCEFyBv1gDJry6sOeNmNXcWkHvf6k1afdehtEJxyHzxWwtAdOdlJHTyy+Y7oUKJKEToyzlmmOtymzHpGVi4/ee3GjcevMXxlovLgaJ+rA067Jzv7x5JADw3VYBDFXVolpu6YENp47EqzXrx+4zJQqws1K+LROk1YHsOU2Zgi7un8AmcY0OnU13IrF8vdDu7NInalWyNJDh3w/euvDmadLsNTNDNYTpwh51ZadKbDFVPLJUHgGFlBP2BQdHqMNJFPJASGK+Cdg+LDtoEEEAD6rct12f0ElAge5oHD1B2Xs1fsRoq7nqmidaSjBw7MTa6UKpNxddcL/mrL7m7IZDq909PbXLW7/jf/g186OTz87tdv3rl3a5wtLK8twA/dTvf21uv7f/KAE1qff/KFRp019JXgPorEirIPjT4dIQNDhq+YrgxC8fBfLoyZG7kPTqjuqBgSGR0MxeJCcHmOB0CgAWQ4/LGIBl0GKgvMMBo1HOGR0JaG8CSzniy0vj1YBMIKJKNkAiQv/6CqCpDNgbrEZBweT9qgU8fqYAKFa3Acn2Aj8CEDUx+8htLRJg3yEyhm1AsXDRhSJAWbgmpHW9hPhbATxWXk4MNq5CjOEgVlRQhhXlqkVTEwoSFRAkAoQdAyjLWg2sbhw9bZTmnE6EgjzJSksnKpdr7TCfADFAMqVFI7W7BSSUoxpOJOoclJ0lb8LZ7ieEXbofFI5E9BEyh5o1Ddhe6dsmQJYeXJS7S2l9nAgfkFz+Xhjd9wILLN9jTUF30OM2iA1jxz1sUMyA0hEJ5JA77IRZlij6alGlG5AEv7yrvEJDSpvhQhNVg4sQY+xICb06QxZAo4wBpdCaQeRsYEnqIJv2T9cpugyS816YwzLVAUxOT8Y2kC4UMZ5Ikks8S+G0tkfKbvWY6IidTzXLMIwgJkfEWZs5+kS0mnHHKLPMTPFDIrd4YmxT2CkFL5e46OBcgQH3xSwelzDtBk5I3U8B31pYHil1U/wzTe54XO4RoYGeBWNA1+adfCaZSQT8tEWCZWauQNiok2Lbbz+MK6bTYOsLWI3qXAhe10sAikuAQa7JdxoTyinYeDcPHBQK6QzU46xy2m35lAljMpCVayd+Q4POfH4ENYFanmoZFhOuChR0hiJ4/XFvBOieW4SJHuEzRDmE1JPLGBg+g6MnAyg2XhShGY0bOiO+jFrSMWpOIpBqExUA5RZXdhMSigNBeEYEBTTqeNezLMZDkVjMb9LvfasCGuqmzQeQARTsaxwhp0JAizSyMF+aBcyBcdhY5vvRes3Qc7TpVRu2HN4YYRbVtP0xGiMGdfrailEDIMmmgnykXn8mCM4MWlRIvj6hXwoWiyigP0IiF/+k5ZssLsMT7mPhfOQmJunuzFIQyRRGFEtm0vuhhqJwLSjXNCQ5s4bNfHPeTKGtdb02D01CUK9hQbuIYGon5pYpvbrOxrXSxkpdM/7XcpMEMKEktZ+IlQnd/4zgFho1kBclN/jBu1mUyojjA39IBzeCNQctK01DRcnWTkBiPMaV5oWAw5tQs+y3fefZcdc1SfkHq13mjUWBycGeDUrDFqjQPaJQC1hn5UxupTgm2llqRs2cdYG4QEFi3dhC/CMoJTZRwSSgzc0m+3aReWNw9ZOY2ZYmPBDKmy1MhRHkXwSTXJgtVrpSQXxfjBQ7CvqYhUX1on3KVaqdH0PVzjBVqi5+SM9hlTHWzJXpAobFRjn74LTPDRugpK2sMnfqAu8xc3Ln/0Y5/4o60vOuxSsEMExEYC8v1vfoIUIOhDsSnx+Sy++2ct4j2kzuRnj0WwqEDJlun4ablOYXMxYq7I4LYB2bn6FIMNwuALg8yEWA9J45+J3QtIBPrKBej8VAu4j4QWtRn1uDkHHb2M6UXK7DzSm4JhFs+ygreIQqpIBakAi2OYhiI+OAAM8CmzS7tEqxmsOQZS4kGbsiab1ewwLGUC24W7yH/oEuCpZ3gCZ0diXPSKFvJ+KTfkTdmZl2c7VZsCID4VooFpFQxBXAmI7aDHXszK6cEpRn4yFEiGmNvLWgUQcCAUDWetLImyJBwtG1XWdjMcjBA+qejf/GuW3PhAGe4kVeb45BRwS80lNHSr1+aQH2CWy5z7eXh4dADRIavEcwzikhWXITFEY5PmcHx4cnLMzgqMBKBivEkc+FDwlqxYhbaCjLIBSsDVn4r2ZHzx0qVLGxvQcfnC2iRXfvudt27evnNwcgia5Ne1z4ES3NDA9YSFbKNcZVKMkd6lS6vcIViuNhyeWQAOlAGLhRgVY1tx3tzC2gLnfXF1IWuTUIhd1gPhQwGZkH81APUGNUqxFW0JnN9EsgEXGSciiAkKQXDZxJpI9sjjNzl9/E4EDn6yLVLE/JNgnuAWrShKs3wLF6wHgnLV13RQtoHLVVxskhrtLEvi+FikeSY5dp2AWIYum76N3bqTTL3Mht8px7A2/4//4B9853v/evfk/p/+0R/uHe7ApKVydnt39+HmLc62evmFJ5abS3E4D7W3L8EpEEjQgcJV8rB9EI98lRg3qiTWJIhg9QpIwWVMz8HxTqsxHIjJYRaUBtdLCNfBB68wUmXwLCkoj6z2AWz+jKX8lpgoMCMnrAs/kBN6BzFlHVW+TK0hwCwZjWJvZxtFfqWAFUESnQCwm7cIIGzAaCxiUmqzhNogVWo5iw6djAJNjQ1AQ6yvAHkRS6UpasRQFgKQPwrU2iaV5CKLpTNSQPYJofRERSTXuKirlCU0pI48ABYR+wh+hNkgkQCUYlj2EymId3vRHDVBwKMWKWamDViiZBdDQGQjFZEJOTLbjBFuqOovplOsNbAjnrSaWICBSiLBeIAYIUrIKNaKCcduJWlZ8UL7ip/w/W81QTC8srSe1SEPKfjUrJGEhpheRk+R6beFkS7Us5hEFSKILIKKgCiOn2b9SQ/JZmXOYvk5KxKCp3wEmQgIkXoOxt8pc8TPs80ABpxIOk/jj/QekB4NAIRqBYj3TgCmhvZN64gkpeSTrFbJYKEE15zFphjZZQbG9GePN/5CJ7wU8QQwQAgrPSmE93nULNwUUSJQiQwGgSSBidxraLCVHB9dDi3G7NRkVOPwxumYNbh0lR5HjeMbDeBA0c5PpsiyKwD/PdcGcPlL5oj9pOPMIkIxyg07HHaW77Mf2KZ1otuhp/9kRIy/6OFsGteXVOwa2ANkV49/DF++lIITNebH7J4lozyqslFtKcaJSqABSRmT4F+fd5RxcgsArRAaRazpndwYb0vLgg5wGMYAiaE5gfQlJBaiM7DUiyj+43TVAMFGz4Mc5VgEtzl22NtGbnU2o+qwLxIdgYTdzjoFJn8xA5hfZpcV64HcTso6crr7SeaeFE8LDlLrkUkljU0ApbFxmY0ocrpWkb22zAuwDqS4kFmk34SIHMhjz231NYJoWQhF0QtMClMNZhH6HQ4P6Ze5XazcZcUIF0MWc5fG+fuj3sVceYsb70b5B4XJtSxL/zPXytXtYW95WtqbDC8WikfTaXOa3yvkObFvK8sq/NwBG7inBe5349CKWCSa6TCmn+Aqm3KsNTigPSAxop/ucwAzzAPsM5d5yX5oFJS4ZhrIhmYnB+mhY3GHtqC9bVn7AFsXO54QstIQtNu0sGvyaDO0C30PIztCgMTKnE63s7PDZbdxogKEG3nt7qc/9ZlPfPLjWMwcLNbjVtJhny6TjgSTz11uqhQx5ls2sMEJgHB+UGqmuA0mxiS2iMS80wykaJQXYA8FlHg1rJWlVWU/rVLbgvEs80Xl2DgTsib2jGuCVmSjDOq5FzKp9SouIkF9XVqLeLiB3uUViA+3uRXbJyw0kZE4iAZPMAzrOqnQwFiSe9t7nGRTry25ppPfsZsO3sb9z5HqDOc46j7OFGL0Am6UHn80TtgA/gaHc49kSEHqFkCmBLNgonwLrINkys4sPaE8kSC+cHFBKlJTmIs6YmTPnFNjPOBC22G3g0XCSbRIPrG0qmZr0DDgaOBrBWilUATp+NI0x9hTUhIhsddhr4lHyAW/zVGXqECzfFgrXHQKNZympSySNAgv5HVikOaHdT1CCKMcE9TtGBTlenewYKOJe/qZSIP4JLQrFJSVE5r4iTq4yjYzRcKs62jv+ISJmFBgpdy0mZnsQQXqGJ8qQPBh6MpRMJ0Ox2Oetrqod7mVJtYI0D2hZuD0gF6np5bIoW9DT1mkbEoC+macMjAPvnzwYd8j9cMpLpYiN2sVaCZl86dkRR6A0+0xlGWZTIu1gmxEXb+w0Wg2ukM2I5wy92dGBk8IMHqhuVTixBk4sOykymA82D08gIU4zRdCZJwBtij+c3+FDIFIaTEaJ9+5d/AUzYXR8/SNG08/9dTJ3sFBu93tDavNeq3Z3HnzNTQFTRJjX26iyXJcL6sqBkf17PIC+92feOLpSpkbzYrsE+W4J6+XGYyay81MeWFx9Uq/U6leKlZXL+c5zX/kWbGWaycGxRyWzBpYkkWt+FTd8zjjlBlz4lY1W7BvDRlUxO0DaPukZUkj+cg7e6KKEWQ/QbVxkIG+CQjly58EFznJFBDwDQHxJ4lgIKcGs4WHgUjEgLEC6iA5m73NB3DoQviBLOOd4ZyGaeZudMyo3cml68X/+IXPbz7YZQ/8n/zhn5+2D7rtHpdoNxtX94/7X//m65dWN65du1CtLOTybLau5jnVzUNcHZDRKoB3yxpzEYWTcp3DW52t5UZsPtG7JBFn+cTFnzAVI1kbx5NfYAg4wkWuMWjHfoXOygn86QJFhuoIbfRdWA/DnuqexXqIEUxHfWNZIKzbo3oSSdpIMEqTaJTJOwaAdoNRzsm54ERHEOmkqsmDwHwoyRRt2tjrSEb8sgKNnr9GkzODxZ+w/aAjC6et7abM+mmTkY6q0LXRHDOceKc0MKYAFISNDmNrCydVzzu5I6vJQiOQRwjBFIHorNzAmHdyACdYRaWo0yZwj4qBm/WTF1QAciDg5BeB8o4KghmsRqqM33IcbSQ/p598gQE5JJdvFJloR2Vl/IgCiHBoKE9EVL/Si1GI1ZX2qGVrxHuEGQfiUccghJVwqIacYeTTYMqvIIFp7UVrmuMuCOpLKYENGYxSS5m4sCn1Ar8I55V0SM2mNMD2wO8jPwhfsOmZMnsMHZOnfxY0i+Irra/hjl7gx2P5qabxaQHve87/nhcxSyAuEtdgeS8o5pfvkpLAmKnht++BvfE+5+GmkPSZwmekOh8R7wI5Q/0sNoXGZxQ8T5poIprny0u/zzL7Yi1E0c7C5eeyEtwHl+n/okQA8GHjz+iltduR120iRNXVptoMQDKHfRFJtUZlfFbhUH94CLioDFbHeq23jAiDYLSTMwpXL9OXkkVloJQjBGKvnrWhgjeUryQliFsSMusUlQSbOeX5bQlUJ1JTDWup9okG1+dk78kkl8wLaqhi3221YErJIePFN5hADbLTYURqQGme0mNjeEEG0SQvixYEEg5svvEMqgtVhtoFvHHMEusEBBxgJCFoBCnBVR8P3sbAFaoQjE0ZNbAuwe7Wi65O4waVWsRLyry2K7zVaZjamtQ0Q6RPtNBTAtJIsvsTWfZyaXnxYr1W7izheyxMr3J+06RylUVJo+4l7rzPTy7jRhlzyGkh3y2utXC2TCqVAlewNLL6ZBfsqHOrrUl+WKlyN8t0gFOtgnE05Eq4fNXFz/SXbBpGMiGtdaH64fmmV7ADQUmNGnHyPeYaGybIwJIPbZew9agvD01js2LacvoPHOZEAUfRUUdMaiwzh0tQgO5Kk2jogYkcrEE6DiTFst/n1tOtLWbMWRZMJ4Ed/MT1ay88/yGMYBmSleb1GvsgT45POXOtvrDISaYUT9PzSTPBB5ATNKRc0JJ6BI8rLP6BId2WZqj8OR1wKGccgDjNbj/c6p/iycbFxVmTWFpZjqjMTFqgrlMoehSlBBFTkelWoTChAsrSpJlsJtUUL4qgaPAigI3QZBmOWbaXPT7cGo6OWHyCBei6n2nmYP9I28wTsugMBg8f3Lt969ZLL78MZ/JfCbUczh0fXr10cf3ChdXVyzdvvcfUkJVTWORK0oFQ4tAZMuJ19iQ0/ZlwfPQ7kJ9XgPjEf8Kcp43v+B0fgqfaQWBPm8McmeR6rQ4ckut0W5gUMjNz7oGcFqOCBMWS9W+PRQqG4mLtNkStOgK1Sx0xUogrHKIUwuEXPA3OLJLGRQuSRbozQCQCAUey+ITmqTUol9rJlZSRzTQbC4zNTcAmGhDDzezBBZVOvwM07CF1l/0zbaYwy1GgnyZ9BGW5qDsQOuU21xHnnDNg5gIQTslsgSuRoZ2QF+rorgYmy1bXNuqN5p2bu07DU2qoQ2oHFPkG4VGDuOHeCjKxKe+qmngcDlBFPqlBapj4kr9stkdNR14rKg6Bp5MYHEE+5Px+aIwubg+7g5Px8eERXlmKYwyq6tL+8G5eS+dI+0p+lM+3upw3D7TZgnWbn3bjC9DC9gcZ5TOyo+9oQrrm4ejy5SvVSp3NBWtrKyjX03b7e9/97v4x+y76kDcQB+a0WmFcwW6BwqVrVxgMXL5UZSqUfdtKEkvJMdO4WK1Zz11au9/PL16uD3uVUc1ryxn2c0i8ZpMtISVpKr6CFMGKliGh/COW8RwgmZWScaQ2MQgHYQGBSMPQP6aNWF9mJBSKESncwijJXyHs1Nh4aBvxvqm9iY0WDSiklGFSvkCIeH5GEOzBRrjAJRgMcDgX2BdNu+TQhBCt0Vj627/6a3/7P/67d+/e+kf/3W9+/S++Mpp0T9qjTCP/3r2b24f3q8WFx66tbVy6VMtjTnkEX5hplMKEF0t52RrNZDZKiIu68FI5UKe5RCjqSP8Dzuyi4a4OHHSetWQUVBJZpvchH6IrEdX6cET05CFgqfURWqYKiAmgJrF6PqpJ5WRGJgEja1G0vB0vUpAXNzxRoApOABDNzGG7k4KAaFAVoLAFCATqyhAUDlZmQsMSHuIeMy3Q0NZILSsWqUCwNpEAAgmCLZowZSwZI+SBSKgCgqg93K4XX66LflgEZD2xsn6BbVRaT5P2ifDIjK8QGx858CGEYCXRvlQYBs4fWkFAUTc9BERpG/GQ2/TUO6gmbINTaOBgGuP8NFzTLuhjfTg7FGRhUQCEKo4iZA9Xp9EFIkEEacEBWZmSELwnQgfS87K0CEMpGWAWYQWCUQ2RgI6iIIWjjgaBTFSDz9B89GvaYBFFQl4SlxBrZj7N+mMPYVG/D0QYBt6S6HzM+dS+n0EkleAfJZ7FvC8sIKUksdQ1Xs9gsKrv4fmyhCYU6iQNozCLiTTnPhOAGZhHCJiTVNnuLGYOOoF4X7p51Ax9ckV0kJKWmfV5oqNUYGPZvPqPCBpjNGDRoZzQ+Ohi2KuhquKAAqWNJkEIWXtKGSgiMgSzwzryisKQHddz44HTqpgmrk1n8WgDE4quTnNZGsASfESb2igsnLCPZRMoxeB84BVhkr/VIFDK7fQcTDnl9jh4gvGi1Qnes+t1SCJY0koLpibw0YE97glPa3HtOCCwBqywbj0rZbcNt8PG6jlJK0/D6HyCBh2tQjsZrMkFOdayg4v/LZc/EAuLgnyUKWRA8xWKhoDAR26LmFAD/gAyGam5Y9mkKYVPesBaC9QxpA8oSuXF/GQpl9+nmcA/BFOtYfmS3Rf+/CA/APzit5LqBW7T/OK0uz5YqGVvV6bsJb3J6dGsysX5Maq2pxwcPu5gsk5KAxZbdjN0+qe4rdl6l2HtfhGjyvsKxtnTNseHZ6pe1cKySW9/yPQY13FoAKcKZcssBRi7WtpiaRx4x1q4TtE2hBC8p6akwyKOPRBgaR2lGCSHrOhTBi3U0ZbH4KcWvMQvu0lqGFW0coZzft1guLe3d+vmTcplHQ4Oy9PjY9aW/MznP//cs8+xTgBXGRuDBauNyARKoU7PNb6Uz9aLlQO5FFgUHHCngw0oNy1sSksj4jN02KxlIhCxwSYf6CtWNKgxiQEfFbA5seGY0qc0rUzbxGkq5Uuc2cfpeAauc+jreIA3RElGgu1AODBl1ANEmDa/yF2xtVx3VOY21etPPcP8ebeP19YuXw8olqiDN6jDKXBFDLj33n7w/HMfzxW5eyVsRFmChpi89OKzTz/9X4Lzm2+/+Sf/4qvvvv0me0wdjceAJPCU8eWm9MjLvqUQaTVZ9Ef+JEiDb5I4nWdwLU/osvgmZcrJynXD4SRjfVc4+KKfxZ3ObFm5289NqhV2a5QW6gMvoKALZCUMbcLIm8UFAIeFagwD8/kjVszA0Qqs3SQS6upC4ZB6JkXMzDAwxjKhGLiEojABXb+jaFE6Iq14xM5I4RBuVkgPIejVbRZT8ksfJ/ybL3J7KVN+DaSeZLQJCLIAo1rf6w72R8PLooGcODAMl0d0LbIr/wCPauLYmcHwuN1DQPiFpV2rrE8mDQQoLAjZB/OE/HKiB/jmPfWfvR/5HGvrCYdxlA6EQy7C5OaIUlpVFSH1pa8wSKNfAPorYSgKOmd4b6bZghyhpUkrdcwZ7RLDBt5DS9k8VCGXYw4im+lQuuaN4wk8x35xMy8kYMEbF4NxJ/Bh+/jw4MAiAws/QcgGkKWjvQnDkgu9bAO4RotbKZ575vmV5VUaAU7e3tll3T8HKx0en7K8Cj8v813oYCaZG40ydOBqsHqhViv1HrtyiSPaaIvhGNJw61t5XKsO6pfqFx/brFRZANflPtfpeK3eruYbh91djkEox3gSDJgYSRtIWEVu1wDVoELMNUl4BRJ0oAunxJTxVkoh2zWi5B5yWD9CE8mDhoaZkEp6xbhjMz7hK+kBpUxq/zXggAK5jTa3FLLZ19i8gvOFciCNbcpLAmCqYEmK0OlDKCUECiZxzkzOzXCaH66Q4fhke9eNYY1m6Qtf+OU7771569ZOuTYdjOvdfpfzu8fD7e39vVey9aWVaiFb4zBY3CyTMVuLYHUHEmIcbS1WoE6N003G6HYZG0VGaSw7QgCRNTunGI2zNsm+CZN9UthFrWf7GxiLkDn4J5FBfe48AUfee0uUzMykF3ylG54GsDzIwz8oigP6IhCZM4EgYEUIiFE2XzYAT7SFMONfoBvBxCsW9Ox9wUIuM9sbjj0PMNz/oWyluz0t14bYXVlygopGiLYwH8jQZA5wo1g+0iiBBKNLWu2VfWKdsDU1f5DnkgjmtwJbAnHirFPzaWmXSisHPFQNtAfrigh1tO6kZA7GJG6yoK/grEVlXi0CEGeY7Sdy06HnIhIqAXIPgYOXw/GNhMOisC7RjlE07+PLllo4CAZmVTAo0iy2LmDBiw8QYthC1aynVEtDLDDRwJgMr6MSc8xfiaVNqiaAVZEOPswNbJCl0wN/OAregKc4Ddnc4iEgiBgUEhtxD5MtKKzK0e4KwwoOS4IWSYADv4kIc54Isb5UoRpkAixhvn78IZ6HHZi+iLePNAc4n3FbV7b4IGIFE098WXikSTlSTPokf1CdFCaZ5Tqf9dESoAQjJUmf4jvLBBRwmqMlQj/hMRCtFGg/ShqBISM/luU8Pmae/Y4KUeKjaGlg2xgTja8TS55IIO0TNW74aYrof/BCdpTeGQHgE5IkX76dSjSIfJAg2JyWR4PiEAWMDOET9h5NiA7gn2m03XmhgupH+2KLCYmMDoc0PPRlJnZtPMeJRkZpCFRPgAly2INaI1EADl1S5PEFjcmIIKZ3YTq0A8aVS6X1naIZgEIRYocGhzdJb/WBJEJIHnzNq8KB3No58kksJCXOHZq0ERIGCE/8oT50AVqzhog9nwSQJaQF6rr4N9DkgxffHUlHI0VFg2jOFAQGAFHLU4bwUg2BIN6ExId5RTjBC+i4ZDBkJnU2NBSOs+N+iWX9DvHZaCh+JOeWMFcy0fouevD+VD2dDBnwAIIN8k2tsrj5uReTU8G5YtMtX7AKNfEoWHwFXiVDVs8l8RxOKCR9oK8dUqhsxRpnv/qewWX4qzSFRdw6zHRW/ORD1rOSqfkABQVI40fQ0ViWKOCDpK6H+0dbm5uVSvnu3TtLy4ucDv7ipz5JIzx146nmwgLVgidYyIE/nnJG+qfscnCbcSS7RJeU0C1eYIwgoOrP8qOJAxl+2naz1LNYGCEWFbMr0oN/Ip6uKqYumKpggh7TlQXlrusYcbdjQIIgjoAtIvSlRSdFDDY0ARYN7KfN675qdKuHq08KFfacDA6gc+twNzN9Es9svVErNZoseeJkQGwa+JjUEJ3Cbt9/ZzDqcH0HEPEPQhyUdZ8TXSrkqHfb2Z/7/ON72+133ngzcan1SrVLbGhtU+OIXGA4oxJVkGYGv+8lAh59WJNzTzRn+s2rWFGvkGBOW+dK0ePRpMqChmp5cdTfZh0KSeUyCOQ5eVyTBEWqLOzCiUBzyeV2dfBXrrGweHxwoi0n/sCGWyA7I1N+8YG5ECUG9wTiEAURR5/ReTvLhE6Ax5nQY4EeUMUtLfQ3L2EY62QhGOccthfgNCMgOIb88sIaF/Tt7VQ5I98bkxL7yDlksFz7R+cfMhyec9hxzzhi4uAEJTNl+N0mnY/yoVVFQc51MDZiHO3FBY6QNbDgB1d94FykglmO9gI07nPYGE1FIVTVTpHDucL6pxcGKlyvbg3lGHXnPcqLUiUM+QJR8Ux04qd1JBhcTCxSmhpQAqvCvh6Tk1TiVypxiR47dntcEUDDKDVRDp8gIznUx1HmDFr8tIufjAbVUnN1ZZWxcKVeXV5ZeXj//u07dx7ubLuYEvpyqV+hMOj2GotNmrZeqg9O283F0srSMkBqDU4lhU4lRlbDfC1/+fp0sX40KfSHPQzwcnbYKBRPh+2905NW/+CZpUtlPd1WWDpBLCU+OgHqaagVRj7DrGboSV04sFhahCowVvrEBzkEMCPfLDRqz5wkc7dsMNcKMrVkkIh8mB7bDmbzuAgpMFM6JiIBvxOhSCgn2yzCtqxIimxL0jkW5FYLBSiPWqFZwD+tdHW5I5e29Pvra0/8n/4v/9eH97dee/eHf/6nX+UwK7aYs+r0uHvwnde+ywFK168+UceVQ28F92CjcgYX6w3dvWHvlDT0jBusRaIIjKo5jgCG3sLIg6jweKqDvZU1N71Vt5M3MY1FPTlZC7NSd0WyksAbKbam1AzVZ3evbFMCSzqZgIjlwUQDVQJS7RlBSORoxXxBXiWInJIvFR9uO62G4PpAwp3EypmL7OncSCxi4sUyS7dag6g0lI9j/W1AshOE2nZ8wLQFrKA9OyTiLEN0qFYtep09ykyVkTaKZdThWgNrDu5qDwwQhTr4ysYTPEM6/VxIE2sNiZMCeAyQN+CKL3oOdoQPgpyhH1DyJDFcG8oOI14wqimJ2lhkai9JHt1ntHCqKp/EmgOYDH2ttBZXcJPUZT7UOkMgBSAqYC+PGkQx0SKAFnHPiw21g1Jw9ELaYCN+IQHY3YL0XLdYZ4vbgs7SAQAoSy4UCm+yUOAqKkCFmraDshmF2NzQBX6IAQOQZftokqgo76JjhaTmT3reHzHDPmWwiATG/LOEBvqk7xQ4D1MGAzHi3w83sszCdImdf85gqCYeRcwFhaIk6vxJSdI5/aMVQ1n/5GPEWbpANxoy4uYJUpJ5IaRmdZRV5KgKIUStAob7ByiXS51oL5fz8An7yq886BKxi35UIbE0eITjqFngkuOKbwFh8jD4pbFoBO0q24Ki5EalmnBYWSbLe0fYlBVa9F4oF47MowjYO7QrDE5p2TFnI8A4nHMvIIRJI5NsUbZ6QQbQIkz+b8bcWPFqbB9iaRgOz8qPhxfsJov71AUcwAKkBM/6cl/DNyaWCWegwk8wm6nAAcLlS/vKCXhYF8UH+BSaL+5FBcmCLHtkDohKPGoLvTQiohmpDzudYWAbgT8IQCUAYqGQJqAS5R6AaBRDbBoIFemoKz47qWcecFO+qw3Od1PawInCJCRFRIuCepQUmWUl+cTsKgFLsBLsDB7XC+NKIbepWZjzjAXuoKABJ7lTEnjVIRZnfjvpdKvvwaAclchNPcVR8W0VKQD15+Lp4Rx0TvZVg9gH67zBNwHFPOUII0XqigVEsGxsJ0YCUUfy0DlStNFRacLBlfryiDGMRo38A3MDlA150y8fPiGdm6D7A65z6nVOd7Y2l1ZWnnvh+d2tLbb/PvbYxY999FXKwYcBILJRoqxgCTQEaHHc0WG2gtWiziWEGDHmKW2lhiAfqUVHRFKSqJYtGHwOqxA/XuOiJLu/0fJ0uoX/L5KbhGrBkw6BbH0GltaYVgEi3vookAoiYoRLHHk16j/tXyHnpLhtxwKhoPW432H2JdNHOQ77KOhGiYkNuqoOW8bWAAEAAElEQVQBCzDYlMJuVJbPehQpQ2jm5d/90enttzvPfXiJ8koM5awJK8+53G3EkUGV2sJgOFq/sJrnUEuRYkDHwBtCO1gFE8ICkdmnYUEFY/Mn8TOCXKFhRNQ1XvxtKv8CCLQHCsH8WUS8BuvGAJ4BM9fi9gq9Fje+dff37w+G8FNma2ufJeYsQaNuJY6Th06Ftn0hA0yox+GYNI87csesWceowMONBqMAFAVqIDwOiFDICG3gUmlQEk07PLltUquzLo+7ETgaH1ubf9xtxZE1UJV8stlkVGHiqFBkVybm+gJZ2ZXr7A1eZ1e8cZYPi5DWGqXVo8IOIzQGHmorEmuuoxjlDkQUluPGhqPTUo8J1ewp1M1muiWuauYm3QlV62o0gFzQKeFmc43WxsPVTO42BiX37YJwvtjn9ivH2NyXUa0cHhz2ut16HUM3f3J8AjlCU7iHWDZGE7qHiSrjleSnQuSHX/PHsNQqEWkjUW+ZJTVr8ptORw2bLdeKOO79wC7wEFLsy5P2CYzU6qHYyZTGWr5GaSHgM24IjMBP1oIkbE7N33jiOW4ceHj/3osvvbS5uXd00to9PL5z70GO1f5iRfOulgv1J54u7uweSDTHAI1LG9dWVquFssuTPPyLmyZRpPVGp5DpsUyRdYXcXqD5vcUUyU6XY5dHG6XmgJWM5UmRy0nYIQ+hdRPZRlof+SPrO1qk8iLOBwmgB+d5czhMngkQqBL8Sw6iR1fCwtujFtA2oqSedeNbHaLuokMNg4lfESdEIkkPE1MKtJDy0ipy8678pXdSRLepilB9+Ts+I6sA6QJIjdIIShHrdKtaBQjysPzOwrZyodJfrC49+aHrP/Xzr7787Ie/9o1/+Y2v/QBlUq6sMq1093Z/6957F1Zya4ur1x5f5cw376RzUpP9YigMZ+Loa+gbWHtlCM4Uhq/OWFAOXO4cr+dH+47McGeCHSW1yw0virnUtLfB0wZa9qSmI4Qhli43RER6WUHO9vEKW37BfNqIzryxF/DQynhujEYkAxvVNXRhcsaVrR3safCBjBBDG4EfcjC1t2PWYtUBJ/XoL/jFazJOUAns4LNAkKR/4GhU+UBsfChM6tvw0UGYjqYSZcwWbWeKUoPlKjtRnDsDobyYm12+olIuYrBhQxMUDymJaipewSfRysDax1vOMmHGF5IoOkiPt0BLkUzL3E95CpYjL8eToeTKh841EqIVxBJc1lboWE0EBT3oholC987ZHaTPcn4aMKAENGAmJwgBp8AmVgyuBMfBJSawsvkHbLSHt7krLnQ0SBBHQ+9IAQbX0kaHi2Tij4UDEptV+OHZsxLuEoF+pMTGKHJLtG1ABbQYOLgi4M16m7ArgR+JRSsAB8lmbzYecPgl4bC9eBW6rUr56UNMftKTwiPdLDrKSJniDmCCgy58k0yg0+FlMZ/HmsC8EcXn2Y4CAx89RvMfveEE9AyU0SniLGH85INnhtbsK0Ii9lxApJFPI0PKkzKngPPv8zTz7xnA9DMAz4AYwl+AlRzqdO2rOR1kWbki+J+kIQmILnnwizAhjrz7bnvYiWgq67Anm+rdHOamwbCKw9KhgclQhoscHBpj2pTb9EBCVOELh7ZKVzQxsE1qArbFOfR0REAHzwwyfYAlJy0jjYGGMYeQcwg0S1zwiiH7rFMMsWf+yivy6LrgQK1LuJRMsKqIigpf2JgucaMj04xwYQO46uXCS6H6kxyih5zinaInRrsJg73OpmBWUXzIyxNkADl1AORIJViifgUjrb0oMlVmRagpQWLH+TBWSpRMljQNRgSahDQkgiQmVyVIt1logpgyxTspAMM8q2qDVVj4v/e5PCw76U7cpSfFGcLN/PgulAJTvRc0LX2oO7epFoFxKrBrAqn9uDJk/y8dAAeaxuFOIhMeBGjtTJDNY0WsjbUKo1aqUw1pjTIFK96COxIRUmWDRlaaPytv8/jfvwjmA9izGfC4oB44+aMDTglvsznivXffeez69Vc/+fGlhYWXXnypwNVsHLNI40cPJERB8Q+MMbXEJyhpOAWK9uyxoFmUr6ntEhIpLaEyA59UBVCwBDSesSJNz8oNHkRB9RrQogZBEQoyMDoVmVymi4rBM3hKGIbDs9GVkBB7wdO4GecMBqMiinRYwcTZ231wcrKd56IDHcD2cH2sGgbVianphFyVcfyj17//7Ed+ajRgDYl1YGCCRy1TLqysraHbYGGu87NQp62D2OJFyvQoerzNiTL7OYucfQVpAE2ilI0XySIxU7Vn4Y++TAHdKIeqk3Y87XNv1Gh4Ms1Wu6yOYfnSgHunKr1Bt73dYXUTxhqXO60srXLpoIqDs3TthF2FzDelsGKeQYlLsQQNzRBABIhxarIDYEsduvxkhEDvLQb0QxCkz/YDrRC97dxK22rhRtW4AS9m8KwC5/+w/2S8t31IhnaPZXKspCkx6tTMnLD+ZdwdTDjlLNYy4q6wSuowVZacBqvTMHwet7teOuYpYTKtpmE5v7TGyKwdZCAZfaRH4sCW7PAcDyatVofz+Hu9QalSHg8xB5SaWr2KlcNB+30ien3PmsrnuO8C6wZ2s3SJbwtwMJd62R+6SIKhbah49dNU/uSJtrJB0rsYBWuqYlQ/QT5SxRsZWbqDJvdOsYPDY0NDc6dkgYDZBRqc4RsQUJPuaFcgUaxc37W2ulQu1SrFS7vbhxzU9b3vfWvv8ChdZow1RhakgXVBO/vtYqG8ztFAo/HViyv1eqFaLxXYv4p1B8/nytzDtrx8uV2u6TDNYkZpI8ViLNy8Q45NqBZyp6M2TcmmLVpKdYsgwO3oJYqJ/3xJKbEXbQNzPaQjRWr8pNpbMSNVbygNtYOPlJNo8S5pIeGMhqSJ6ERVBQ2GsINQ7c1zk1olKbyUOqSDUIudkzRwPJclNQuf4beT3AFQg5GKoNjpiNgbDU4dtmfkJp//hZ/72Z//7B/8sz/7h//wv71/7w5rqGCa7mD4cPdgd39nmLty/cr1UoVzESgI7y9qIbBC0OBJ6hvh+MfZ/YEdKr7YnF5NRQmMSekGwF3Ll/almlQQ9OkIGVz7O8BRH1gWE7CIbk72rqzhVJujLoUb+mhGxxSES+W83JEgvErwIlVDC9jbIsiCD9RQgRyRRu9vGbaBtIieV3FLLAxvSHAQdOoPxqby2sxwEcY3usXBDvClW9j4ktdmlAi8BNbkQXMEO0gS+hEYQHGXvak+saAPcLsG48gNmMQ8gRXYUBQhKprAx8Gb+CAbjmD4j+8zWJCaxq1HUVPAmBfcMBoCpr/tSeAbyANYM6sjEzRecYFALoZN2g7SCurEEMICGalRV0duYEr1qBdeQmjC1Jvn57HsV4vLEaC86mVNbk3WQrBYJYIXFS/GEhUd1whkJoMWsocFaiS0JBk0hqTwDKNJ6RYkgTrJQJoROjUW0FBlJAlZ4Mu0lkwFSA50iguiSobU3gkc1fpJz7lUKXoeQPsIPf7Sp60VEGdgA4U5TJKmEuf55xFnUHkJzBgAnMNrlizGE1nPAuKx2Edf6YefqWKRGd88UEoPTErALIdv8Wqa4Ay+CTA81ebsJxHxpMwp/wyK4ZxuDneezS3QviEt0+El4bkGOtaZ0YquwKNQeS0/bsAJeU9HhtF1NNjQmtZE8gZEqkCYg3sFzSYjkcpDZyfrL3NLiXERLAvi/0zjij5/YUMi3g5d+TBIJo3hPTBAOk9PTZidkDCpi8wBKD7g5D1WYyCcaCy4X8Ekit/jDbrjCWfJowMYg1oBBy7mslQ6S3zZR8qUE9wIU9gZE8wRdiw5BE+4EoziEinFLbyJyARKgAIFxh8UwAqhWBkd/Yx6cT6DXyg9p1a5rDFUCV2pp9oJTZ4WjzTDCHJYDix/VrmgLqkeG395N6WN4UOWYABekWzGX8ZSPE/QXcKoys1Bh0djreBVzuR3lWYOgJvgyMfZCq0cpk1Ha/AEh4CTGxuDM+45u4nO0nPisW49fZ/VX7jPjieTq2M2jaOlVZ0DJ1pZ/Y8WstbuZRYeUKCCykU6iYnf6JVwE9LixKEMUjdJdamKDymlYrwbMg+P4JAO11lK5cnBwX671dna3uSo1ouXL9YXFij0lVc+9sTj17m6Aeuf7LjESAm8yBJQhc04B38SQirVpT2PmIQi490QedHHeohtZnjRH8hL4EUGzEeaiVsO4APUpFNSYVlixuH1D50c1bFddMpmhhv274Ud3tGq8B8yh6oDvqQYXGDQNc1uAnfqrRfKB5+IGHLEuIdqjLn+dDw6bpG9Phk47On22xy8yJmR9At0wWYQIAx79N3vfvmTn35m4+LGNKc44J8THmwpBUbw8PraepkTtZlQgKSu7gVPclM9+ShQt9WkkjXnzw+rL0XiZ6SNQLJA/oibR0VqI889KSwgjpuAgIeW62tXL5VX2M5Z73Q44XS8tFjhZ30Ql7BOWdJx3D6aZJZXCG7QfWOuszIbIWPNFQyEk54Pd13L4jAfK6K5k6rCQrbkB2UjEy3NtcmYQ8giZEezYL1y8xSnxsP342G31cNFzKDiQAsflzkzYfiwctuOF0a1Fodb9qeHPYYAXPYAFfApxporBgexvgz50r2gn0t2w5qA76kkJeHy7Yz7p9zdUMR1Ajz2r05dhjHuLizgJeXmWs4F5lFmKFJeAjhKtnHYm96Gj2jxTP6Yw1oKRVZJsUVHIaIcbuDqD3rukoFtKJvQ0APwlNYRPIZNJUcHVjK42KUW8i29pyaL5o0wlDVakbTQk2+iMVBOjNcRABAsrTKEa7d73FDh+jqE0dWPXO6mAR1+x1lhCJTqm8LY6sCILHeKvGAdPvXMjSsbF/a3d+qXS1wwfH9r786Pvn/KZgMXLzmQdn6VonOnbPPtdsbL6wvNRunylSu4fRaWahxT7xwyh+HoZxkWV1j975XFxemlXKZbyO8Puayd08KYmJyOShnmAMqtfmchW51UpJLMC96JreNTL7YMbxsQGQMBiq8x7coJe6FUCY4oG+8BjI62C0HSVJPWtqDnkLhcLXRaUJhXbaegNARU2UCOsG/IbU6TxRfgU0pT80Rj+GETILiB6CyQyJDPSGltRAZ9BDi+7SHjTVmDPnYfrPIs5HrDQz4/+9OvXLhQfu/de3cevPfVP/9ur88GjyILxW7d3Tk+Gd64cT1O5umiw9zv4U48Ste4pFBKdQV2jp1FIF9kj4p3yXu/BcvT4DmukadjoM+B+TTA0QmgYj+o6omRtUSAW0jMpiw9a4iKhDdbdPcWlDJqBUZNE5nsGaPHiJ/6s2hfBIaelHNhlBxyipjUAlGkTXwTCKATL/kZXSOqLBvDvQ2A6PehU5iXYQnMIZCUDAGH1o6mA8lEZJBmwKDHnSds6NRG4m6FbWLeVNyCge0DmJhFJLxEgLpITI0jRFRtuPQZpCM2rJToJiJGlsJu0RqSf8xjq8fAyI4iEJBCUg8KEGEt5UnZhgSRBrg2UZBS+55aiEFhC5GlfcijY092IpWmi5gknofEVoIPrAiWRXDIGCM0+ixSsyyClTqMvsluKv6hnVL97MmAhmIFFYYe8aCzHdHN6h2lmEvDiZokMgXyDNWsg83Nf+su3wiZT5/0Ga+PPoQSj/VGOc1/JiqQSdIQmNJZpwQmf6jYpR9RAB/EzD7PzQycAUz5hBNrdlBks5D4iryGzBCafZ3l/uAL8bPssxgzRPZHMIxJcCJshvks/bwgv+Wbn/DQnAAgkhFbqcSSFdNA4OmAWWkca6g/KtMwsEiIpOK9POlz5lxlxBVOGOHYv3AXU1p4DTBnkBK6RuVeH5ucg9nNbU9EO+83ztbZEkkkCcImpATTUEIUHubg/If4BOlNg8JwOj1lgydtGtwIcoZYpSRwBNqKbp70oAFM2RBHPfnAKs8GVTouAakrlKNgaN5JSBQMZmdmsTPuJAZjn6G/DQ+Xmos0AZcSHNWIJWxKxjS1p8wTCh2NUsTUFZxHI+PC6jJGYOw42aL4szsHnVlfkUgDHEAwBicBuVDc/KYc20AADjmAnXSkYfz5KW2JcP9jkhJsEIWyl3WVzn4hg58Ee0L2jo6CSO40ayLrYaSiGq0Pnn4Kw32gVyfbZYFLblxHa05GzXDwjDJ9DCVQghZUjqpV6I1jGGQ+/hBs0KH9eU1ixafWgGQRWzKDLT/mNUpvVsEEPjKQacBBdWoWRk98olN63cFbb77TarVPjg4XFxcuX730iU98+oUXn6VwDsTQvRJaDVAQGogwgIgEeLCKZgJPlQh1sETxCmQtNN4NEQG/wMHsMxCCkoDUjm4gYuQ01F9IVYTIFjaiDl/0vyxn3QO2fGvRCXgAhmDKo0eaYiKazgBIi7bHkOWfk1q0wxADmBbsARb/P4tmuXiAE2lYHA9Fk5KkV4PrH2w++Pb3/vJXfvnfh1XwB+MGkp2Yfe9iqGKucW1BuV6vYV7TI8J9toislWr/6IvfCW/pwhv/3//YTJHJFwhD7cgtGz7KOgMR/aITpOmBhsVOPtuuV6ujXmuhvjIatRE05I2VLgtlFnkXht0+u2FPuqeDzWGj3lu/tIL3m0aGWNaJdfQcG+nFT3Id5jKV2N3exKinH8OFTJ90dNQ6bh0ifY42aIjMuJwvrS4tXby4xqAIPBuVxZ3NB53jweLKBXiDUQLL4bjkhNvWWHhwcjTucR3IaLraLA84EtGxHOY+4yacbm7wttbBn5COVsYYj3KhqReZng4Hx1z2gQbkfBWpEpLGOJr7myuk7dDBk4uaBukgEG2Y7w1H//rr32StJUe+QHHkX0uFhe+1OsfeD/qc3lhsjVuDTK/orIL3akN29wSzgxqGmbjdBKdBapFoiPe12aM2jIaLuPOtm5oZdFOg8XK2jKmyAzinMOPNsZGRAsq2N6F+AS6+VA5yAhnsDoDFsp/1ldVnP/TU1t2HrJS/eu3K3s4hjXfz1p02JwuQQZ0Q9JHpM41atV6pMjBcqHCXIaLAHhA9jtyHZb+CoBTKvXGjXWwcuj180mQfCYqMHgZGxzqBIJOMF19nJhvlykaF3ocbp0HJI+9EFAx5swH55wosZFKxpIn54OhSEkQNIxEZRc+oVMGUkx8+M4om/E3kMwu3FQwICiXVF7pAOBGayM2nSQLcuY+zAF4iiZDViqn/igwJqQQGFKLdBOGcIO7faqXGeQSeHDwaFYu1T3zqUz/zuV/cP9i9euWPvvznf3rv1q3GUpPbLLd2d7Z3txbqzVdffZ4NBJyMVWRzl/u1OAuENgeg9HJzNqt1ECbs9mkPVwqTBWgnh+LoLHULkogmo3PgYUqBuRkaV7OPzhRAHF3GsvBKTfaCBogBUsBIXPiRzqKChmr72EnFwjZqxbYoKkkqjU5wkQbIYwhg6F5UWXQ6AjDak7lDzxNL86L30diUxuofgBAZNbLQsGBRIJ6jEH4ZMxIsGNnYtqJjdPqASkkNYkNnyxNApkmCRJIq6YNUOwlGlApqxiVGWy75zEmUomUl7DkNwJ1k5pn4QBRw4EFALFjKiI8v9Gv+YHqT5V9wr2DAX9a2FKoqYgRjeCNVQRQQ13AiBg8GuWX8AGQXwA4WvFqOANwLQYx1AS4gOTAQD5VYkZBSoL3DeuqCTDnbKEiQYHgVkmQnh8gYZhyIQQZ6LOnm56xWMRiI+viheqFI60hGSccT7+KJt4MDNBh2wtikAQer5Ft6iV/v/wgiQ4So6DzKAsgiBL5TcfGSglJ4inzfp7kkWAT+FR+xSukRSpE+7gEQwF+RbxY5S3KuGCgnm1m0XJHASEB/WrcU8pNAn52N+oGCS1sCDKhYmOAFoc1fwUMJ5R30cSernySyEaRkbtjAH17InLqQjSMg6ePkNx3vOOJsNN2rSimag72XhWxJhuJ6Jhxd+U7PY2PIGsvOgEsOqxzlFnfFQQHjsUb69/yTbW1uyueR3ZwEQ43AIESLX6QnjPkvUsGrsiGziiANK1oIBtKWBhIzklEfmJHsnqMBaFK7jFiJiSKiJOVVUPhKwR+WTSUFfFQABTG+BjfpogPEJYaMVIxAYiid3MaG8FCItcUkBNcJFMAGR3jIymocVCg+WvMZgGwpqVRQQFHswCkLB1d0UuCiUGHkEwm9IT/cDXIIG/KrdDg4wG5gdIaY2B/m83XWzJZzK9M+SxjaLDfMZk7YHMKtWGCcybMTkVFIDTR4mbCWKd9y9tHrfUChTF9bKN5D+AZOTuLthFoM/7i6aUKIJGfdOTXP16igU3z0wpLd/hMIYMiLlQsHTkQYbnD8Ke+8kk1iQjp/Sz1eUNP0DXAVyyC4Vw4FMOLC0V6nzcJjjhcYseuXtRCXL1967rkPAYSGocxYXRhWB+gHhwD9ERqkC+ISCQ2x0GELUZEV3/+IN4mNirmy+B0/A/cZE8WA01spbISk74wODUUJ0ZFYYmGH9rKmxNob2sDSiYc07DChFLbkyO2phxF3eJlBK7dB4uHPTVeYtxn0pr02qhnPPUCnXA7R77MohVZJswDRd2D/jkd/8qUvN8pLv/TXfgZA9NlcBuSlVixpU3Fz7g47QMAPBvdKZhvA9qJ8azj7mtEkKGP7BLbxAZmDZ+PD5NYUszyYMUz8CPPDx5zRznCvq9IzuRYsmhnXWWnNoUeVbK2a73VYPjVwvMpdT9wVhKmGwbDQWOKqs1Z3dG9zi/udr197utrAwuN8mI6jW1WAFwjXyqz1gL4jGHrc7XL9EMZxrtg4zrU4lJfjc1k2BjPJTViuC8sVzg+lm8R7j/O/wFzc9OqVdRzuU/ZVZKo6vZhsGk8W6tn1SQOud6kRO+OzXKiX64/aI3YalEabu+2b995ud6oMCTxhWN6TC6gpItAdjo65H4QwtzrYTVI0LdrvZpu1OscsxmIHBVneD7VFi2D0f+svv/27//h/wMjRBmVKgftU8sXl1ZVqrcKgD3cNtMcKoyldTlEtdHssVVcoqTEy3/fyX5U4lJnxW2rPaOBojvMfZ40aL2p+XhCX9KSGA320lr05w0629dmbY5FbBguQGFF7PtJ0egI3qLEtNdgl+KlYatfKlWZ95ZkbT1RK+Weevv7e27fHF5ZO+92bN2+3B+wQgzjsbRhw1SsWJzM4MGdzoU71mtUaB4BeuXKZnS0uHgCxUZF2qTVqnP47qI6mG832dLSSK1SnbzVs23I3eqFykWvq8wsl7pdmHcy4yJQP3bJeYWfeqKMVg3k4Ws1vd2iyRCjQRslRjcq0UMlwRhNVsQVpCV/MZ+5QJ8FPYR8RFyfyGR50RzQ16cgQEhCkjahoEWnjAQbhL4Q7tm2q+JeSW5QQJCOv/AzEwJ1brlHCrA4gQo0javz3jaJpofljNEMhx5DVKsclcK81pGW0xu0SnaOTIw4G+NVf/cLGeu2//n/81sl+d8QELzzcX9jZPi6W37l66WqtVmzWqi7eKOQr1SITrUEyl6DTh4/YLaCKxSRk8aG7n+2S3E6M1HiKNRyqUolhmH4lBYJxMwYAdidLhvpdOqLoNBmZo8P1EDtPhBBxooL9gP0FAgtkMdPQZ44rlvyh3KI74E4iJ+mG7ARwAszWkVCh7CEFKIkAv3FX2T+qJHFH4rykGwGwjAqdaW1wQM3yDhKksaaERwVQwLQzKZn6sm9LFjWYh4JHAWlZE6EmQk17si0nToRZizTHsNk2oi2jQS1Ty8EaUgxvkjhMGpSEBr1uR3LSz2EOUYjMCLjo9Z3X4AYSWp0S7ezEHTyZ9I7EIJP6Wequx00Kw/P4wfAfBWmidtTSuVMHANDoTEfYAjoD8TiElU6UKOpFxOTCrMduVxKIZGTNgEWjD1AQnVXQ0n2axTVQqzsblghCAwrf4hxOuHxC36fkAC040uz+wuxBXMBUnqf2AQ1iSfKQO4J9yN/EpOFUC+tnlXy0rjEtH520GcEiRrhFmXKeevZuVPy3AMNMRWL+OpHRD3+e/UivskwqETPXEhMKs1QRQv9nreYZBZ7SCSsKOYs7l2b+6rfxs2y+mQ/aJHwMJx44KZ0Jzt4i4Y9/pAR8zp8ZAoqH4KJOAk2QU2xKToiki4Ya59oM72lBjWI0QzqwBK2MeQPTjGEyGI4luQO6YbiLhOxAmbBxZMQtoDV3/zC3nop81MlQKMIQ9CIKXELGLDPwUBGIIz+kHej4Zodqc0XrMsHgDwxkhAGpQ6JIJKfKe7Os6n1YC45EfhTWBFTimsQ+U9DkSgWThjht4zjZTYlFPhEHo5EDI6WLcKioAwB1UNBSp52+BKFRKlU4S0oKi4gK84IGjfIDDlBDxFJesvM48rDnswzD4QLbwmqwImTAYl/rDRTVbVKgA9c9D1EVelFzdN29Inc2545snZw7e7g+S/pRMrYmK/5BhrEcUd5jhR1VYZEE65QpJJs78jRYWY+x9wqtmuVwGU0dRFlHJjTKcqi5hgoeF2lpIwTmFiCl/O83X1ZDxRevfvCHSiJa8Z+HB2YmjhTSJ3o36bazf/DaD1/jAMG93b1yufBTn/uZz/30z0Bt7D1npQAczaLeARGoLnkTHBHlDe4iJBoEXa9zi9J5KJSIKFomS40bOSPSt6hCxFkK2oz7sF2hYSPTOiq42JFqZms0gwwT8E7IDJA4igOPXwlPOjuUqJ541T1vmJH0DPpzqb1aFDmi+2OExVF+HLvSp2sf9DnphQ4ItchREtIPl468x/q3Qv746HRrZw9OkA74UFnwQyLgjVk87bgCKyp7egzrI3CUIoazavsW+M5pM0fZwIikBtaZvyBI1JfSVdxW7gxAghJgYHYFgnW3JLIw8rYzrE1gSik7KA4WWVXMMAURloP41Bqga6TDYwMnglg5bh3d37p/5coid0+xVJV+T/EK4Fxx0axWNQ+LFfbICiDDdl2nTUpVtvliH9t8uPBxP9S0XTE3IbJ9NJ51jBmcg2Ktb4NeEH9xKRgZZcF8F24Ad/+Wyqwyr1ADnHTsmcwtL+7v7vc7fclDZivL2ZQufB5wzu5g1KMqjmQpCOvf1qYDIw032rIHeTxmEGswnogguERhwUy7Q+8PTCRlhPuWu25Zds+Vz71ev33axlrSwU3nyZCu189jmNCPC575IrAMZRYqPcAJEuCJ03iL9jr7FZEJ8dnrjAXmeU0ZmXixp3SaxWZH1SvtWjORnQLANwojViVFTTAGaYYnn3n6yuUN740K5zp6+vEPPfH2O2/ffO8BIwl8+1AFteM0jtsHs1R2eXFxkbtta9zZxPZQlBhL4CbMWdEWuBsgRbXc4Hbz+oVn27lSczxeG44rWDuw9nBSZ7nUNMuIpEzvMxjjrHT0i42qm8clCHQEanJ4IWw/q0dNkB3Qo3XkYaxPjo9kbBb6ICoTr9A22tma26wzKeHb9pfzifHhNwF+GJQC5VXy01iQh3rQElBZUEpdgEx5zWFUEDxIykfo1PhxBtFkSi2A6aQiLyULOHISy2by0ajb7cIYzIog+v3B+OT0FG1ECIxerS7+9b/+hVbr9HuvfW1vZ2fMOLpSOjzhTueTpaWFp288/f/l7M9jPduy+z7sN493qlt161a91+/1PLGbg1oiaZIgIVI0qYmmKJEKHMPMIMGAZCCOIskKEgjQHwkQxEYSOkoCy0EQI4Iix4FgJHQki5REUS2TFCeRbLKb3f2631TjvVV3/s1DPp/vPr9b91U32bLOrTq/c/bZe+2111p77bXXnuDKoMteTyPwsb6j66hKmuPY/biBkHXdblRViqADHf4xUIufXZMV4U9vC9XFC+imMpRSo4vioYu+oxYgLBxvjBURxWkxMq5lBaVykg/NH3SjH2ibRVZa8io8KzqmKRmAhhSPf5p00t5/evQXDsPz0XmWVjkrimPF2p3USTCLDixSQT8EIkpKLVFiF+1t0cuOWxyS5cIDMCFHG1KZbXcF0HTRK896SmyeGxbaCWHHbaxph80qfoG96ZDvjGaQKw++zJmkpLDFQWYpFRniyXXRs7jkHzTpWUFjLRveKaKRRIx8Sq1S9YKPxCbjFCwUAL0QroB0WAcBBbBoFMwFEJnCAaVnr0zitdCpjBA4pXb0tcGW3JheU/qKVOkmg0LSrmAIuGTufALHokMrcpBoKZJoWcKgXjJPviCotuEzH20PpA+ZiqNXPvhgQBVIGHgRvQoocRJk/E1SU5XLiCXS9f1rI1VxQ+NNQn9LkpshaPObycuz2XttkCpvm3uJQxQebkak+H4iEb8imTXI7FPu84odfviGl6JKsoH2Nb8VChvY5ZVYVTpdTRsKKETBMb8FUuIn7k720L3Ui6/2JKa1BQ824okRiUg22KvV+oiDqNRtJYoJuI32BQPU9dqh/uk0rUSzcmjXgoi31fyOMlF/jOTQtKBNqIHKnFEBQmwekA7aHnIwKgHUeGKTHFpRB5gfQAVitr0Q3diEOaM3CUJtNSaNDfU6zicJoQlU6osVy//kjo6zFpRnKyDxQAa7BGqRqWUHFk2xuh1WEAwq3imW+DtSQTochu7/ZUVn32UnzTPAz3mfc9yTEg9lVGxEAnFOOOyh5sQFVWhAy+UOEqXpyvgKc1sxNdB/5KLyhRRqI3Bwxj8/TCWJV4MizpnfzKSFbXzVq9kEC559AGxRMHTw96P9IFi9R0disWbfayb9Y2LyL634sgsf1otbWKer5uWiuZrUu8y+1htgBFQhi6+1rVixCssoIf0DsJFYkgF99KrYNR8VuhZqhkzwXf4VsoH8cnYPVtbaj1XKYTOkRc9S32l6xleX5+cXOP4vr9w18ju/57t+7Rc/d2fv/tbWNnBwOmmA86BmkR5csCY/5JB/5gRvmf7CGOJWZrvSnIizoUa5VoYbCKQXe8H4xLPsTKDDzXCegSQXF6LVIhbkUBLQNrIoQs9i4iNvCJ4qmh8+8WOmqr/kkDJnRkdIZwuhbY3jRlGCYR1czscsCD4/u48t1BtgwDMHhf1k9PPRhNEckgXKMcBtI8mCI8FOT8Z39l9dOeZja5euKcc81brt1tbWgCaNmLXFtni3LuBbRYdgza2g94IGIJsSUcpKZ0hkv/MhdjODSJBIShbyb0AQDTuPwggaGgCgWeO87z7+JJqP+eJZlAkjUUxFw6tHRcOExiNPT5ZT1dase51Ph2x+M5ut7t0d3rvXV/41ZeC83r3lbNLpMXuIHfopE3kxZWQ17NWmTInibCP6Pmya1OiynS1zSzSYwBQU8GYyL6jHegDm7PCKbGOGWMsxELIVBrX1iih4hZcTVsedsjwOhzJo9drTJkFggRaiswEZqG4thjtro+X8knkykGl1C6D1+gXUkSiYUA7INHtdplYqsREMrSnEmNUHj9/96ltvffXg/t0n7z4aDne3trams/HZxcWjZ8cKKpYcfvHu/mBrezodYd6NphzLwWxMGl3g0yKE6lFDyr9KMvy5Zmi+gylXuW++FMZWH0gkE1NDAwD2RmgVRmwW1o3smlXzImU+IyP0k3pfC4SlU0wgwW5vv37//uHe7cP9Qw4+4+Q6pj4dP3/25PjZG195V3vO0UT2JI5uNJtJf9DptbtscUoj2mOp9M7t3Vt7qMThAP8R7QF8c1LI6cXz+vbWzq3to/nV9mSxvxw0O0wnQ+YH0/pVu7G933HHYrBhfhHnnyt2aUQwe7Dc0hUxgHFkpRIt5j9FN8On1FN2AerSO5VInCpACnZA51J0KWoskKrZ9U1y8Zsn3tBePqswqlaKp81XssAQRGcgB47DB2ChtvC5zCcQ82JCQnLndOE0Z4ErbkmPy8uGEVeOydJmyQ+0ogrxcnLJTsCxp2vsJ8BstJEnO1+1Ohf9rdb/6C/86NbOzhtf/qP/7J/+w//y7/z0s5PH7eXe5fTq8mo0upozCMDCqgVT9pn5toAabI01a3VoLPyjwcf1F6cUHKTh1ZJ2HpZbaCxX0wM21FivzlIcm2261nYFCgXV8KVXgRfGOT7QP18UMFundDLdYIOMIEn+0fG2L12m7yBAxqFv7oR0MUodyxBUeAMgUEEm56/SGrKvS+FJWKEF6XAgL6hFta2nBoGH+gnFDNDwwcjpAJArqKNdiUwMNDO6PbUBOTIFn0kCJyiKowL68ngCKcflUQxwJLW/NCHylgSk4j3f1Qb8BRkio8yjPwJAPstcitkBJqO2QAMANyUb3Z4GIwG8C5ZP8IIE6TnFRjKJNdQf8xVn4sogcTENwH3xF9Q1DigLwpQhFnRlItM9Fg4Iyxkwpch49uzi44MJPWuNbkZZTGz7pFpAMHDQuJ8xGUqwlIAk4QEUi+UQHCU6vgzyJx8LE2yW9+3ehftgakGgOUTPXv6iXS4/KA78JCBf5A5X9ZxHvhqtRErMm7fE3JCr+mCeXI428PRSwutXPAfBq0r08k+yfSnwZhiQK+CRqKBszdBQ3uQZ0r0E41/l9WuxJhX8hwoSNFSrylGict/QgDiNK5eNhl1qJD+KkR1lflI14BSdAKeLIRFKBuJNV5+asY1EZw6emp8QRXdTnvBZkAYgUfw5KRBgCgF6n6YvTJXdPgDQHIMClc9CpOLxBSsHG1nhjAqMjCpswFaWqS8CQaUjSSLGi/VAOQYyhRAYodQoAqnxfDCHAJJOWBzkYAWJ8ONGYPY2vVKv2P3UOrQSQ5l44hl2NJTYiP94NAbUwKrjJGU2p8fVZ1YmTVmYvmuxrGbL1twhPwz4GTRv0biBMjfG82i1qE3WHKkTroGKCQGlScGb+VnHCWHRJKPGZ6LTwyihOUS7MeEnXapVG6Cix5QhaAvXXC9BDvTTyJMeAprMKYT12pBheiiE6Umnz4nLrCpmyTU0ZEsJPCz6NgCq9Roqaflo1RDDNjh03RTUEvvBYH7MXte1/EB+QmzA6EVghHN0NeLlK2989dnzZ/Sdnh09aXzi4//z/8V/uLOzjcJJKtcGpOAyLvlKVIDbeJoDgYDlm4oGxZ0v8QCFdIklihTQlHCddCJXUCxAfCliT3vCSJfzHZuN+YTJzDP9VDjH6IIsV/hmScvQO1M6KJoM5R0kvHAkiyTWG2wVorAVPwubwtBWEg0OY6DrqUGkXRmJfmQhNvPez5jVi72FAIzYiUaRoeg6qS0lBKQugH6z9tU3v/orv/aLP/j9P6xJi9bCm4qLmrnsrBvo1XEs9/o9NpWZjR1EIMdNYasy+wpEL0loEZQyC6LRDdqUyH4OT/bVQ90S12SFeKYWhmlN7QNISgicBY3aCN8AosoYMyhPqMTsW+QZT3CTwhCLk84464wJe4OL5dXl6fjiYnx1dsGGv7dv3xYoTWGT+SCYlwgsRh/7w05d4yfdO3d6u/uddCrAcDVn+y5I0GdWQ7cFscEDqWO3IXDBpUl1weNHyajR9A8oIKspeFxYZZDtLjaCu6DQjDPjmRrK/CWGy5goIttIb/MPU0eL+cnVaG53QkZLJFgFrrZnGgH8W80nnR1Os2qzO3uqu7qy3ek9ffTlf/7z/7zN4EzdszjOry4uL86ZNCHlVE/NrSHbgXoiOAjhZJlfjor24jMSBd7WV/IM0QvZTfo11wvubD6VkIh3cqsSF3n3RXWrUQJlUCuKGgY5iPBNqUPsoBofWfOwXH3qmz817Nxao9+ak6OjB2xKiRa4Gi++/Mbbx6dPkVo8DqQQpLqFWQf1XrcDUwddTrho9todRnKGwx1cqvS02GzJoUc2/60vj1j4jmbqDh5cXR7Nzt/HADPzoexsz/H+l30PiclWYGhvPN84oFhL3WNSGF4XRNcODCrQCQ2UZcrm9wZLMDFijQAVgSl2BvqnvPKLNCEG/qpSo0ukyYZI5dmIMYz8IuONaqRwJHEVgvzlzVyNQ6qISsnOIMJN6G+umy+KvSDBn2D+yQSVeomZ2oWkYldDMhqbnEoOoMZkxGHUM50VXRbCrvv9/ltvvb23v/OBD3zo9Vd/sl+/81/9f/8e8kb/lgr16Mmj553G+z/+QafJMYzvanvLQZ5UG/wP8s/y0kZHHkQpU9oI1dxHykHOBhSqBWeaBqoIj5GVRKMhoxS0xdaSlCg0oPFNwkIHVTRAlDd9+DQP1iiAVTo/OjDqS8rIIP4pXUahTpOFBEM2ZYokjQSrkMySezKzODwHbaBooEhT4eDqoR/ESBRQJDTDH4CRuLRWAjQvgGiYQ5I88xbF6MrnkArBE0lShnGmghZV4UwtIBRrTGjB2BSm+yF0M3Cog2i0CaaExryKdDAovyVIaTK57AEEjACuaXhVPySFhePymcfyj/Yf+ZdtfjBB8AU5YxqLLMFMIASIPc90vq1W5CNjiIHRYnsmu83ezJMQPWEyOULJ7RT5VsG1gCkQ2RDfi9/EsbkhriMANG6bTosIlVil1OUt0MxN5K8hlW83Y1QhIFKBqcCVrDc4BYZRpQYo8G7QJkkFhB9CSyCNOjEL2OvAF/FuPMGiqancld9ehZ+cz1RkL/lsbhYH8J3EIRrP1/P7b0D8xo8FI4tQCsJPRXOfKpb70Rwq9BUDy8aOs0zvr10po7TR2sFUcqaFs42GbSQzD2J+yCz8QfTXqSOL5hlNs3uzUf1r7OCrgz6cJxh2al/DAUlWP1pimDpriAmeUhAdzMQhho34zKy1NBk2O5EtcoFQRHFvLFamOcuW2oKwIYSkUcEjypTJepfqpfGK2Z96SBCNPfBBVqUSD4R4pKxOeisWlW5eEit+mM0HYDxdXTChwpN0dT8yoWYxuRqzKg0KUePpINCiIMsqIgafawuHC7UhnMsINpwaZJ7BKPJdiB1aB1s788HDIEYUp574I1pW6RruX+iQOgXie1Q+FRX4N57Lo1woX02EoGztnOOP28antVq/Aws0tDyRFMuD2SAjt1SSUFB6m6FHJ41g07CvBqCEobYG3WbL7baXK3r2I6aQtBtThmzqDBpQljoTKvr6C9igw0SUX2XLp1rjEQolDZQUFFFlz/ptTAccSA4+DNg/JRSeEE4VJzwmBdN0Xhktzh4f/erZ2dlsNv3Epz8FIT/20Y8e3tsdTUYOR4sdsb0HKCUpOQCOwvLsKZV+tJQAhwuOU+HOjegTVqor/rX7MCgjbIFmdKHKr2Dvc7LDc4yxyQLP0ZmT0SHPBCuNf7ZisjYtFHGFYAtpzTKb0q/ME1KuL0TCZ3YsfARE5H+9nN1lbGK+fqqY8h8vaPZ2nGNQNQZwhEEPRjKen14BwJLZTmQqnAo35Fvunx6PfuHnfvsH//CP1hozcJILFI55RHKGFzZJYSHpet7HiKSYGhEiRmly8yH/JcJy18DNOQDyNI6tMh2Qag6BEPsc9CNwG7oKpkB8zm8CBUTbsFr3l+sB23+yHQzGs5WDkYB1mxWek6sRFYbVuIs11l5zPB3xEV89Y1mrRffibPylLz88Oa9fnIzZ9Rd3P2PgMybO0H0YOwVBfUF56Jt4V0lZYmbNLQd0phed08XRcbPHzv6dyfx4conjmTEWVhxOWIbN3uLOoWt0WF788MHRZMYiAlQGAj975db9W9s9Gt/Zmn2GaucMIHXqk+V4gfJpbuEcYZjsYnR5MkN76WuQ6c1LeS53lH/sEY653du/vX9vn63IYQK77hEz3KnNluOj58dno9PG4hxRGD/bpwqQEumyzaOv2Vj1uv3BYMB+qRoBdqIktl1xqhFFDKGltRIt3SU+Y5X+qqC4DPYy8nvviWWYDL+Ox5NvCDGJkDx1Ni+XGj+BSekUHjFk8uBye2v4sY99DK10e6eznNaYzz9dzC7OJ+dXpw+Pnj49frZa7WoQNM7tYblV8arbrO/u7W9hkDadyrU1HGwNu0xeZyyIvSlbXSaeM8DIgRdZ/Eu9bdw+X3cWjEPXOjPmmXaHzeZle83Z5Zdo3Faffa5oUtHbrPledximofO7nLCnGTxm6IvpWyyVp5+OiunTQai15yv6kDgg5us5FQJ1xD5ImvuSqaO3L+SQqjxb/oq8Pvmx0J1BA0jRxE8fK8pgmV8RPFQlvqoZWqKv9C55JZ8SW65VINmRj0d25DN9/pMqeogo5Z2HIIkkON3GbAs6Wmgk1hNXbFX6R6iFxeQOGM7mjx2/bK23GES5tY0wdgcsCtr5iZ/8kf2D9i/8wq//05//uUZj2N7Zpuv0m7/xhe7q1vbW1v1XGDrtz8bT2nQy3BtSGtgBT2gp4D7tpXoH+XZlINWfjYcfOAe9NoCSiIXS4b55FCEumzX7snYyoKHuUjPnrza/a0XpHKMNIlG07BgMVF/+0zDc1y/Yeoz8UakkAytzuHsUCyRhBhF/IQLEVSZJ1FhzFqzUodHUj2ob7RftbFsNSBbRhnj1OfofugVa+xHPmpvpvSD/WipEmr3isj9WLWqeWJ7wL/pUX374uDyUZ60nYSeChHoL21WNvFFkSqD1s5of+F4/Uh7Q+Wis7uNIVxEPqRDdRU5WdabAQWtrqMkAwqwkeIkOyFReNvmAaoRzcY4yBOk6ypRLPC0FyZSS3DEAqo8IZPaw4lVqSJRIXSgKNMOxf+6JjaflgAQ8sx7jtEm7kVZeWpEDd6wIO3WQJ5xDBjzWBUIIEbJZKvFILqBcZtzZepYrVE3nyhAtGvbHg4/r9Q5qNCN1SSqA8LDwwdfNf1F57+UMGmxYdrmEkDxT9R9ArGhXgkhJCisXP4KprgpMfsrzjY8vRdro2RKvSlnifA3c63xuRnsBOjwwKQhKrWC2ye5f91dQm7Sb5/Ib+NffKmKU3CUQCDQmK1QKGlsjEfVJPUJrUgosaqx/tpElmkveyAOTEFggjTEeA30Lcxkbgc1NqEW09nSpqY+0arCJGuzyMoOQYHjtuXFu/Y0gARrY7ErAI/aRmzyyjR8ZqeKsys7ioCriTeQBmVOuLAuG7bqrXxlJxKeBDe1FrxQZAsM5R/9QV2JM18ibKOoZVWPTZVMY9NgcmEjjcSp3to9YjNvovMlVZ4UfhX6JWgjPur9qrEwDiMnmmlopQwYYAugaJ0IRjQCRFkcrquTNnxLnM8oCSoMDsQQqDIIEwz9ToQ8xsA2HwvSI1SJQnY+VLpKoDocQCPlQVizWZfUhfh1wxzU8q7XmIA3ROMhQNUh+0AQrwf1KdRrwz7JVXmEopI1VW+0w671GHcaicoqXZ4exb0ptzXQaTDU2d27FegcTcQZVS2HbgA1GmHy1UClQClvKxp0vDomEBJTV8rBsCC8C1+hs/cYX3xgvH12NLs9Pn9+5s/dHvv8HtraGV85MDZhSbkut7qLI0qTK0jAJKOjNDzioOos/hsjQykbdSEWuJLRALEgJ5ofUvKvgkxHWGARcLi+vxtu93uH9u4vR5cXZOT625LNicCcQghCtpMUWCCXNr9BAw25a2iGAYpX4qnQ49oPmRCARdd5zCA7DDcyEObscHbd6u6DKiDzDCUgU4wPM75W6payKlDRvd7vz2uWC3g7Fi4seqeYgLaQapjY7TETASLIdSqEUf4porhtSCckXLx9kK4T2RSImwDgGkWO2dQNC+ZKv3q4vk5KJMCjpsnaBFwOjjv0s26vujJE0CrVesSyAWWX0lulf00gzFkjfHxj421gT2GZjoPnqbHIxefqowzZkhLpLqqd/9Ld6rgeUd6VJohV0lhp50qalWLbnuPKBzC4zWeM/9YyFIb1hbCjG1rFm1q0+/cbu1ezynaePmYbEVlkMxmAXdpqd2aQ1Hc+JyTbiF3O64t39g8PxfEQPBGJC18n8nG4htc5+B8yXIxVxqFtc8/mEedT0RSSiTC5xIA3nPMw//4UvwUWXHUk0FSuuA5z9QEEmcSSwnc5kxKnCc0ZvOI1L8SSu/JAlycvXEmBg9SS4chnJKxUmslgkMzmWL9U9qQ02D3IBfhL7HLAykmeIa5POrJzh3tZuvzPY3d5ld1p0DHJ7eXWJvr4aT7/4xlevGGzC6FJSrapWJvQ/aoW+GCdXNdtbrPrlpK9Bc7gzvDg/73ZrXXpisL+Fk3mOfcfU8W5/e73cv0TIVkt2Hhg2pt3GDPPT+oNc2Q1lp2KmmIMRVYPFmzicGD+gb+fiwY6DPZSdPZERCbbPQgOi39jQkDFPBbPJLniM9aCErQ9SVTqAszROeRWo0LqQMqSQBFyFQoZbtnJdx7LgbgmlRWgtC0V5vo5qVmaWdN4rwodZyRPESRnCVfEsC2IkLGOo9sVC8NRIroBEkigZ9ZNDJBhUVpEhWyPOU68f3OWYhdq7bz04fjL+zu/+wz/8J/7sX/sr/+E/+sc/i17c2WYghpM/a++88/Dps9OPf/KTW8M+c69waVHBIBd11KIgpSmNE2loTchT0kHZcNp6IMfRbKAZSdFBhJiLp5fqAAaKq6JlWaIJEa5CEpKllAqtMeCADzRWwvPVCOGJUPIYIZM6oiZMosi4iJ354ZULbfhKUu7OYaPdUW6MrW1h/lxEEHPqH11ISKueEmQaER6AYDbmhIKnwTezaB0gCY2LCPYpjZMy8Gu0on3jQMXQIRP9pmaGtPhjWu9ipBCSXsOLQBtWLtDhv3BByBejirFX8rKAvFpVA8mHfAkiBaFgVW7CymWqpKgChMOfycufhdS1aUkdZ/GbmtZf0iY/ICQ73FMitgEQ06aAstC5kl84K+ZCMiTFMQ+5pxa3XSx4GZQncygPJqkuAwJoE1B+X0TYhEOLZF1Ka+h7XvkqKBGTiptUL/+WNIRmBIDfIBR8CnbCEVL+5zPo4xHfQNT3X5IVUN7zrSBQyLmJnKj/OrebAMqzKL0oemFSCBqCiy60JYAq08eBtVwPaXYbjSuWSbG9Zoft2Zhni43oPvEcU8fhjOwV7VRB+v2MF9Q9lxd1cYWkr5Yd5srS0rIGCIMkkkSjj7/gnvZ/HW8xusC2v7G4r3qoP4xVzpI5tPUcUaMDoN8XVUJ1dPYBKl3kGFVgiC4wKYv1k/pjK6w5UF9NbmPIc9KwPFGwqMrkwtRGxv5ZTeh0neXsAP+tO+W7f5GqheZEPy7yiS9xsQ/YevO5IoUQ6k5AU+Dkq9MlQQ/SelAH6DfQPbIKUEdRMbgKwA5Fg4OEvj5O3Aa9T/QgDT9Ikzy0B0fULZgtbhN7VX8sT8CTF81QYMh9SmTd5FnkRIRLArROKXN9cUutxLPcJIZyxgYX9JgXLmy/h6MdfWX7sdrj07J+vmiN8Pq74s2OBDtGn+BRo8vAzAJPD4j2K30SWdc6pVvPSVe4K1H0jI9ktwKYeYTK44QH3bUrm1gQBAfythSQQSn20XuKci23nCKsold9rS8vLuitsTIVMtNKAYbh6l/+b38Jr8rV1SWuwu/6vu/d6va++Zu/Zcg+8XpAV6z9hSrOtkpWioEXeZFvmg58/1XW+QJNQEHmstC5hznNo4lgrSyjO/PUpkh1Rp9S1GmIrlE3l7wgATKluWSawc5Of6u709m7RZ/1wdsPWqx14dAEJrGwFsz9KmWeRffipwDjR4zTkQtGaghwK3oc6cUIhaog5cFzyCCTQOAYyDK5hS0fmDbNINhyMb44PaKfhMhAdkRIrASthKxqJxx6PxlvczQZnlWcQYyhcWX7y0W7O3z1/YePL+9hdb395QcTZtmjuESgQtbKJ+b5BffmmSUIA0Nny5LC4HsmKr1HWK2X0Uje6M5ZNwOG95LUBy8dljQILABgVyL8r7gDTnEUzBeMMc7HE44BwOI+xwRbr7bJBlLQVhdKjPHdQpk15i/7GqGCEDTMOyoa863sADAxhi2M7QLUL2Gp5QXC0l3/qc8Qp7/LsQIdp285kWQLAnJ4N+tymV2PcSYhqcmcmrZi331U2WzVBBqYdOqdHbrAA3pb9ekCnYBWmK7mY9e/rK+mTE/gTLEV+9Dr6pQIssOLCiF9uKAP849YlIiWQPJ1hmDGMltIs2Ha3W7VOIwJZcIHknESrWIBLJQFjhKmR+lFAz9OgKa5dTTDyRAQ06zIEHBmzL1kXfKPnz6YlJtcESvvL0KuXzaBlSREbklhEn+ArWCYTX21a37NExh669bdj37oI1v9FutVUH3deuvZ46dbt/Y6W8Onj55+4QtfGM1mLeYKIpjrS4S3Nt9FR3f708Ggv8NBHv3+rZ2t/b09ugLD7Z2zq+MWGwChjdBkDWZGNseY9Cxt6tLthm4Pt7e6d/qv4dA47HbvbPe7uDgACvVbTAQa4hflPFrqeav3jGaK3clFfMkJJ3CNBdaSzY2Ooa1jiAzSarRlQNcz2pnmRb8RDlnkSp2pH0Ki2Cs8OQEMGVNTQTGpw3h+vAlE5NqQsbBm8ybZ1PpJhLKh1dRZDTmFYCwp69WkpTCWysZahI71azRb+WAS/lPxYnISjRbSGognG8icOpIaSKQAprev0rYZU8i1sTlG+upf/urntrY7h4f3P/Lx+x18/LPJT/7kj/+ZH/9TP/1f/72f+8efPT89p+s7W57Nr5qf+9yX+oPWZ/7gHxzs9ZdjfHbIfcs5Wu4RyUwq+7XARW2Jg4XE4et2W04EpVmDnukT0EewL6RIo2QJtuVI4eHwUx4aCzzNLN8+Zi5JyhxQAGof8xHApUSWyu6Gfi7oohb3SpMT9zzgrQjWItCRfGpGIEM1e1Fkin7X6FBhorKaT4wowgYJljQ8UNXdQcjFh/XOka0GszZs1umpS+OwE9i0rwwL0ss8iypVQDgtHtckez2lv0F6YotlucTb1EydoOP5hIwho14KBDhAxVhEVRcEkLXERenxwKtEzo1GnAgpLeWlSEQgK/6DA6JjGRCsZB7PEiABjW5MgSUjaNnwoZnBW/UGNML856W0tR5volFx4CkZsm0adzowcNMOOOnJETxVosQABXLib36gL6N2kmCJgeEHcuEl/p59oTWhAPikGTKZ6byWt+RX+0jWYWDi5qXZkXL8GeNGdSsJRNzw6jcv3G7sFFSNA5iff0S1pKTmuboIKc/XIfnqWwG/iZjf60iovwLsPcF+vo6yeYqsVVBK7tVLMthkUpJR0hvRN9828f/1foUZEpWCmlHIIKrkUKhntmZHzNmiuZiyvhRrHFcW5ogeOprD+rzFJpOcNsRa8TnTSvCQsUNJGyeD0qstsKxxhIBHsTDV1Y21tBTgmtn4gOmN2kgzifdLq4uZOgB2RiZ1gSmJygvham48g6nyalLkLci5cxURYWWYw6N1jyR0NAxSKDF+LYf/EVVW7qoBbUB1Y4RpEMC6Q1b0QczHvoGVjWJQK6BSerlMOF8zGRW15UA/LifJp4LRhEHZWeZCWauAMLXq82Q85JvajfQWbAuVrSfUMe/++dWoIb0FECKokUaTlzdQSkei5JCYpYFIztIWfN2oYT1qMV1nedZi48EVU5U6y9rYqsPwuNs5UU+pydR/GlP6U7R8XVhtBaUqiwS9LWe6M3fI+pvp/HARZwVR2ISmVmNyEdDwqOHaomlJdbLQavgUAeTsDVgw87PxAcnq3Xi+XVxcsOSRDh49Qc7DPT87Pz46P7u4ZJI6OLCZ9f07d7/t276VwZlYw0xJwhPsZCo0nWWNpQ6oZAHAknOYbVAuSoPIxA/DB+1vNZs6KvoLGKyucioPQyS4y1heG/UlNPG10QLztLKKGvuR4Y/2lZnETK9lhhJ+aGaj0zNRQVNUcowyqPDYIBeMQIp/UAWYoo1bp2j+uIDylbS2OVh+EhBxXrG95Hw0GnVZLbluDCEAsyUWj1mhaFWMpUieoTDMWtemi8vZ4orVsEHFZoNOKV5ISvmnf+zP/MR//9/FnfwPfvpn/ov/4v8pgcKagqrxE5S73wru5VXkbHAgiHkROXclhlojRel5Wywkv5QxvwXIBkS9NmpwflBjgNVuQ2BjpQlDRQUaNd1AK5jw1SRN9ptih37pCmysaUQFQ978SaNtwaP0DkmtkPbrrOeFugqnT8y6wfo3lNEDDm4D5wXMhjQpppR0i956l1ESvjm9wU7vvN9vdJlFovHepWitdQ/zB2uG6MwzsBe2bnFWg13osNACpWOftorMC02Xo/EFotSi90pUpUwtx35cRw+eP3j3gZvhaDAZpilVNahQQ5LDVOWW6WEzBgyYdORgQWGBDCpXyad6+dqfEm0T2e83n1/EJ1Qa+VmiStZNUKkLTALBprxzcOfu3cMh23JRXfRNrqjI7Ok63/NI4zc///nTiwtmAaXH5RCwepxFXrMZJyFuDQZY/zvDYbfdxvqn4m9v9U5Ony9as93Brmc96Gehl7jifOjmAA62egz6sOXpuv3azu7J44cs6mDFb5/9LgfsOceMIPiCwQ9bmOpOTmgl+eK0dVbOODPB/SmgMEaHfhlpBZewYBgghdH0CmKXWNkVtFI/I8WJaewIpLSQQBKn8MCeu0FKPv+tHYkj0QohuVf/KpIiuNbbKmHiR0rK55JI8J49x/CdwSrOwAdswDtvBGFOpgiHQ2dWACqEXmLwVzdaXaiYUD7tlQlt5Kh5HKN7eP+QnZdazc54PEH7fuSTn2CDoFc/+BprBX7lV3/x2ePzZqu/vdO7vLqi+/W7X/6d04s7d++9gj+BbjOumYwHKIWwj16BjaKFwOqEpDZT/MfjR5aSzmpJc6y3IgVPQwCtILupJKA1nFL6Ag2viVPIYQwuihsFYVZSW4KTLLRJitSXZAgG5TcQZQbkstEnpUmSExJNNDUOsOW9nOc7ddvHVD53jbMOJktJbBtJLNOIQNZDUXzegkl0Gg2EBEAflnz4atbGIkQ+WRakznukjhyp48g8X4CjOVwBNB/xTEVMmSJlpQhAMz6IiECuFIE3s7AEBBpBETXjENCISRJsIAHSWJEzOJokjWuSS2ZLTmixYKhjwgqOkpUP1T/jm4v1yeKVjUMMgAJ8pCAuDeYDFafC2WZA/CKxgWmTSAiEV0IUY6iH+Cw8URopKs1GEAoWBUsz/kZXQe86FgmT4XXAjYcqqkB59HopccIsLA8okSpSQvM8f8Wf0v94wZ58r25QpaSXwIVwN0TfNFW6Taz3ZHIT0u/3XMAU+JLLEuUiaIP25msJSZQgRyXosQv5zMPemDzAYB8tmOqVVoyNL2xL0fELdvbAVqadxs5goBsVfpu5JczstZ56dq+708NHy2GQ5W50HruHN62mSCgO68YRWplBQjSYtZLZhqwOJJGyjsK7x4yRFd56KwiCpL2BsU7CKF2NeMLs+Oo2Wa+7R/XFJRkDvarktK3sMaftwflKYMUui0/p1QJQhWwNgw7+E0eCmo/EhC4uBiC62CmPTuGktRYhz0dE+hVNF86qNVQ6xAUyZiUL2FbAX01cJBgVElQkMTgix9zJJXtN1Jozdnoh9ZmfQcEUAM6fAapHbS874Sfhop/XjE4oI4RTZGwQ8UEBNNddZv3ga6MvI/0bLD2kEBMMGglbP9FLuhqCM1tM0pWv1W/VmxTBvRLTWMJo57uzTbQzv+j0ARBIFK20W/UR8dydGiw5PlMPDShGjBUeX8GuKoml8WOK5JKulI+2aDG+HG0Nh+Pp5PnTY+bCPDs+fefBG5CYDWG2d279yI/8MMsKUaOM88MNiqnykvXgQukymFtlIo+Fb6blnzw0S2knidhJ05Xcsk9BNAh6w/Qm2/9hawOOfUzo+9E/ZPY8Ct8iIhfYH3hdGQFbs7GtTQN+L9iAjWJWzGJgg+uUFlGFlocUttE6KrJOFBUhdWl5SDPJji8Sg2TixgXCtoK2FDCONiPBMEcaUqDVbRzYi9Xj0+eXhwf7lxdsIXXKrmt37x4cHT85f3gE4qhTS5POAIjR1i+ZqoLxEKlhDi+5sZ+lmrTZ2h50Gc6jfnzXd3/HP/iH//XJySUJ0KzSSYKRSGGVcPyBpSXa5eu6cQYEJVwZBDPKBFlCRzMi45TLQlmj7V4STcnMmyHmwGFbHLkKC/CqYXAzxrRan0+vpqstG4t6bT+5pzombXaJhK6KNULAXqDUV6bb4GRcOpjAwhWWlDCNirGsS3nHZ6ZIrSe48ymLy/ew+bD98dOLMG0POgIPJifktVlZATGJw7CJ43nMiKUYloT+sFRhnlWvd6vWmjBRnCGZov08jHzJIhD6E/g+0QgcowHnpAjViQoNL6QbRfcgGzzQWgMAJGN4aU3l3b2/nIzBDL2vfPlLaLc4GmA8cgmheK0IKtmwpZbTnLvUoresVYcMa/KFxnJBhpX/krtcBH7dq4p5/Zn36+ckIG/VBc+wmhrHhYDCA8Y0OD/hCpvvw+//xO3be4PeYDzmnGqmmTSPj48d413VvvSVLz87PcMKdCgW7Uh3Bblhqhgjhgedna0tul2DNiqpeXBrl0PU2LOVfWhGk96d14ZMNlmxxIjtObURFswvYu325eW4d6tFTVsOmd51tJ4/29r6wKA56LemTCJCK9EdpAFybUH9GdTFBmVckXYJlLH49ZFro1AaZBvSo+goG5GJi4SAYiG6EgpBFVsrVIKN6SM1Qwqj8SCIL3wwar4BwbrDNFVDAIzoEs2myJZFsLk2dSqJvRWg5lA+GSvMJAhlC9mTseW4BsEnW0sugxJMcn7ZJ5Ai4c0h1Loc/vHA2T6cAY/YE748tF2rHzNw8saX3l6v3mJx2mCLQVaPC9m/Pep1V//DP//v/tAf/97/7f/6P3n77S+NHvW7w/Zk1B6dn50eXT19MKK/96EP3W3vMkmIbiwr75VniA1t7YNQ+8CBqgn7KBIDBmQnoVgkpwuXPj6ioHKTLCFB7AyD2o9lhcUnfmFKYiwOjN98ona1vHzlIaVLmQhRQVxf8IRSEwESEllWCBMx0KXgB57hjRoKXq0X92mT8MRH1RNVoESimZGURMMoF1cyjxVT6mdQk9AE507lFjJco1W1XUbkKKuABMdV1CoWToe1BBRQv4cIgL64cvNfynRdHEJXzlxHmJuPFShP4CaficrGklKWIhw+YEvotkO7aFrQ0lGNNSuCIDBL3FCRF/JavKLvy7Ou85Gml1BxTf1H/IA/Zx8eEGVdAfKI1cQ33LmQgo400SEv9EEXwWk6S9DcXPjHBU+hOtUdFQiN+WB4vhLfdXfShmApbHz5CuKRXuQWWVrcc7DM2Zq8kK+o8C8ICE+aS7jqKjQ2h2S2Cb7+LRFLfNNtEhJbONfxSA8+m9fQNl+vY5QcjMK0AlwL1x82afgV6I3Xm48vRb9+vY7vQ0iZslDq6u0mkH+1Z3CMWjO2PAy1Qu5CJHIq2csDczOBfA2rbNWYSEAMO3qwi58mGwTEJa14yxi3y3IgADpJRb7GhFm6jQALB+RXMhYP8yIF1iWChwcNdxY73hTWY/9EWyCyjs0hw0VvJ31G8kEsBqB1W1xFvTCKPGM+GcgFYtRHJMfC8J4WjRY48WlBqRvkQTDKlNxIjdFpjVeCI/9CMbb/AeZKMj6r1fk/n2AZ8wEHZGhCGklqVuSpfVmUmbWPXHznSn20WuaND/4CTWInO+CrgSxlGBVxJj8LISekpF/IoNTQlC+ICoxIjtNgVDTGnTr7e56H9PhdoPBFYMuhNYfLABNEVYgAB592Xq1jeJCZrqV5Z6VmrnXHiEFIPlgG+NLDoF4vaH3JjXgWA4JIhqrmWGYCAG7JxI18LSaUgQ8UfDLBeqsdPz1iJthkNPnC7/xuvd1httfp6dnWdvff/sk/+7EPf5QNrWlcgCIKEEIKCFUimJPlk4aAJSTZS2/+qqtQ2OQwShYlXBJiYtgfROE6+wJ60OlxB1cFj0wCQ6RZbIokLVCpHMhKavYYMVPgRdlzBgz4I88sACAHBVZ0AKBhLgNBS4HggRKAsoRinEmCWzICZDr4S0tppm2HjsX7Z9cLEHTbGHdm/8WLU+Y3H9w97G3vv/HmVxuNZ5IF1LnkDPqa5GSGIcuo9JYjWhz0yCQSCMs8YBZBTWePHpw4WLFmR3B22LwMrhlilt++iSj/c4XO3KCGDDXMrMqLAdCMj0WEcQ0nEeQKa/iJVIVDAgFEs82UfibUtznPlz0/2z1McLRF4+LqAmOBBshuLCqG/V1cvAKLPJ10SushTc2dgTiWpY8ZIKpNui3s4hlT0IipRFvbIGtpdBFsuaRxSKEyMIW4gzARkHM2kSGYJPxx0algE17sbDDQc2ydW3X6TWb4T5jxw5Lg9ZR+QqO9g7FASbFr6MIzjQlesZqNNp9+FZOJnOhSGEJbRXfJ4Xv2/mI1kp57BbYat1EaRqPpP/35zzIHUbpqoICDBOYfzy4IpzzURiYsIaIoobjf+UT83BOvSFlI/57bNRffE2rSBEjNl7/IOUEbnu8hICwGD7ZWteF/3+Gr73vffY4j44A0piWxodPo6hTzsTfcevLo+O0Hb51cXbjFv51amIJQW0UR+ruHBz38/43Gdm9ri0UDrPjl1BIbdbRo7ZV79zvbV7AXKtJbb657k+lq2B3sDvof2r3bGKwGt197Mj5dnU/7LWZisKXQGIXMcAE9cbp64qskIahkCAeV2JQu6oNn2S5xrX5+sdIY3ZfQQcG+eb2XzKbwf0nsC7S30llfyNhvYI+xIhZF0AiwY5dPhZ5VHtGoJgxI+YeOKJgEquFKAR/UDYGQLHxKKhlvDIWFEHEVBVNRekMiFZACembLaqIAKxdPZA5P0WZd7P7bCCqTFzmogj2pWu3B3cPb//nf+bu/9Cs//x/9jf/DbDbu9TqLyWo2nbz75jutrh631fru3u6dRou9RvsIhsNhSLW11Xm1bI/m2LkT3sBPEYDmdM61J+0RyWJxTzcGWKAr9hCLze5oHTAomTWgWWlS9DFlQIzQDbCWhARb3ly++uJ/sVCBhix84Nf4MomctePRU+RX6GmHALVPA8hEzjTT1j3yhDY8wUGgBQTok9DumPkSwZxtzXXb8GBvwp3byJrCiCG/pI4YgizR6GtU6AaovDKaPFBFyEahJnMEqLwZkPyc1uw3EkkWH9QjSFkwVJrUjuUWHIFrOSL1EK9AIsQhmCprf0QeKCbxMXnICoKAnYSpJMEjSY2Y7O2+lBT6cO1y2FnlxzkAImqoWAJO4MzV1IngjCpsP2q4nURFWIQCCgQ2mZkfJRI+9JSNQgCMMmb8QiDuMJwczTB3E2y+Eu0bXYCUzSVa9VNBSzBA+VdB/n2B4YMoSG/wILa+/yR/KaU9BlwPt71fz08yopTKz3WyhJZ1AvYpocnk+puvX/e6Lkj56msgh8OhOJWw0J1PtuBSwQ95S3SZQSo8iVRlJQ6XGGB6pf2iVaZWshi/jTdl3cEfl349zRgr5bskYf9tuMtclABXS8IX2w+BhOZIGH47fcpCV2/KY2ZoUvVcP8vUbCTQyKRExyNUjA84+sMyBCQ5OkAElQCEQ/wRejWF3zRFXIdsZgAgqKICMZ3ZwlcD0gkgpU1OslNfcvoMTRvgVOymJzkw/MOWimpnc2tPQtQ8CYJWSZmNeOKMtESpCeoI+hX6nciQcMyOLkeou1cdcxxA2GqKTqK8nNOsfuzppiiGlPXLVMSySvpYqjqYJD9I44PRuKw8IJqJ/I3Vtm3oegwTMV1w7LOeWjVHabIEhfpo4QXk5pL0EPhOVsy/ZDqQA+XuD4BdSyJox44cnHToMPqaNfUAYU099wZLLEjDUm/hio3qHGiSIn+gVwbcnb5PEJ/4zEgOpBhdXk6mI0xn+gBnp8+pyEyz7nc/9InveP3o6efu7B4wpV7xDCfgoA2G5bXAqhSp5LtBPoQOCvHmMkzu0STh7YWWzPPBg6IXFv6l9Kwgge8cfODcfYZFGqyQphFi9hSMxehs6ThusNsPVrn3TnsQXc9Xi8A5u2zzupwh7agmepU4tY/hPpwgQAnKRREW6yeO+pAdOBEOYsTTUqXpwIFqf4FOF3BwMDtCZbFZpngCSRsT5ojX2c97Opl3dlit2jk9fQZ3gGImxOQPyEg7Zige6UmdNQDkheEP2WQLrGw4Z5ell40u3Fq9/eabz49P6+tbNNjspkJKpJtGO3SUaIW2QK6zCxBEJRvgCEriAzO5xm6h1JaY/DkRi09OWnDBiqyJECsZSgUcq9fYBYjjvWY0yLTG4/kFZUBs9R9SyMiklZhpNhguboQEle2buXbZrdTZz4S2Z7W4WF3Mz9nrvH40xwvcb2xzuijLUVZr1h2x5+m81eqrujjbjuWP6/bpnPXGTGRkqQ+LfSdX57hy2RJge72+YioQrjAWRGCXnp2NHjw+pXMgQeHxqn75229Zj6hNsM8aXJvS58DuZ5tJVgJxzqomH8DRKjRqdiosuCoDLQQ9Vgd3D5ge85lv+5aQQQiZMQFtsGxqn/3sP5Na6qKhHeM62y4XrQKpaU5RkNoZKEE3dO906dMZ3RTyoiKwP75E3Iq+Ybjj+pJ/teVO3hOnrO6ovpOwpAwQaxyXsE1F1qlHvW77lVfu3dnbn5ye1xZjz2pbrR8/fPPk9KzbGY5m063DW195+63TsxO3+UHTe34TClOpZgrf3u4Wu3YuJ4vezhZT+dkDiioCHXZ3GVuuDXc4bfB4ydZkOZmBaoVH+kOv3zs8OHzlzu3pxWlve/t0On7w7NnJaatHp2P3PvURWYNB6SRzZwxAyw2FCuYSjB+CKYd9MMQyZUxZ8oSQhyzeLWJFg5y6Y7sMAEkQukoOZV7BVu1s6MWvYk+DZDXcVO5QmNhaYHxIAqAxxGTF0YCucgskDKaCXvLiC6E0DvxoQQXxEk+EqxQphc8iKYbBspSQQBNDiqALJYxhLUJNt58xeI1coawyYrJidfvxs2NGFFkPsL3XR2dMp0c0vrfv9v/4H/+h0wdn/7v/+D/udLoszVrNdxzdXzafPH7ORKCPfWTr7PLJB9//sR6DAejKBRO+lm0mB9GvRoDpvbOmR93JKy0a/rLKrkXhqwzs70iHEFbBF+MoNASrVB+pD67dE9pxVDhwYHh0T2GXKqX4XpnlRRklWpoIs5T4OnbkGt9UlK7jSUyaUepnoROjg6y8Qru8ov5pHxE9NiWaEDFGOWv8Q+eSGWlAHvDpw0h+/tSnMqowRzZJfORb4z7tvGJCDN068pT23mIIrI4Pnizaj7CFmOgOOKlCuEVPmciOXaF4DQosXOfRdsQCSqjiMKSARTCDZyDQqMh7sQpmvoViXQKYCyCRGVdBq6VUKWPqjTVGAtkxIbMu+/+YXRFyygFArAXdeFTwmCRQiJ1BnG7Aqn3nZzKXm3h8c3SIWSJclt3IBjqRHLNNFStymagm06oyE1bIjNrtHNErXK230geQ9hbDAskF/puKVwpUSukzYPPFr1//SrahCt8LsCriJjBQC5QqqNjt7F548yIj9zPM9M2XIOX1ZlyeC8Dk/tKXl19LpmlMqk8lhLtAwkjIlNJLlBdXhW4CKlKUn0RCtDb0EYZiVGIWqlZgfFEIQ0sHtbTpMVkQPfiEOGOmsioPE9vNOPyghw2LGKGgijozKCxpsjs6h8C1Mw8BRsPgcFZGZwEiGXDoJyLocBI5oFmQBv4xyhyfPJDZyI0j3u1iEZkapSSKmbWrW2p84BXXArPEEF3aYjYajBWecgidOaRMdgd7Jd70rBtk61Cdi8gi8XsIOVdvMND5Gnnirt2i+wJbnirXcJCbPuxwy5129JOr0Byx1v6jubM2q0JAjiIo+s6QztHlGIXEgXTMD0IloXCcJiFxbehZbJGdsq2lXoXJVnX7MzQzCr+1nyRKO2+yGrLkISnY0AAbl0I1L5ctlv8y8ks9v1ILw53sgIljtWgr66dKKv/U1/RoaERRm/F0cu4Iiz8a9djCZg2TIQQAeaxzRhI0nmNLYqpyBhDTOaRsEFM9WQVDQQgL8nQwCtrp98NE3KrjRw8ezefkVecsJ3acYL8Opk19+pP3/p1/59/uDp9jEOJJYq4q/nWKCZUBmfJScqmgHPrEb6EA9zxXtxBHMgUVei5anEoR+LDo4GKGW72s8GLWKrFcZbACH3afd+cMFkvormD60RUrErBcpmM2w912RxHyQZK05pGkyXS8yPJlZIAWA4+axIIlsMJaRPno664WtD7sdcP++yxMp4J4aKImMkqRzNGfDBkDkfk+8koViZQjFbaaxGE3pNEY03DR6Q5AE+sTlyuyZc852YUYlh8ZZsQAZ7PjVZRV85q2n+oY7tKGXzhT4fjpCXWt5J+WhSha/xUcHwppy9OG3uZFTHVI9ZkQgqybhlB2uu+UNIQXWoFYIkOxORM82DORs3o56RbLHb5g0dO5dGWv1Yj6Yb2VaLESKAEDLMzbyCoQhgOcS6xLDQc0moNlGz124WkumY83rtUx+icNdsdjixj2GdJTz1HK2FMd9ixwj7HWjImJTjJfMOZwjMufpshKTNZMOLxka9/ppMFKN+SX+LRydgyNQ4g1qLGeMXVnzXp0Z7vo4wB32lzkH+UY3aoaqySTmnD7YO/P/bk//9GPfcS5WkumTLCSjV4lnUyaz+boYjW5VCVSouhcBTsUty2k2wiLaT6Rivm6xV6g53QB2bEE4XFAXUZA9PAjfCs8S3oeX1xGKdf1NxNuAsOkilOE51OESpRYP93tcEYsXNlihS57aO4Np1fn3dadINC9tX/32enJo6dPL998C/qw2xJg7UjTUWH7QlYRdTrbwy1XWw+3ObwZRscEBCcqCBtJNFgBjOaBClR2mM9gIGqIcn7k7mF/2DkZXbC1BJWi3dl6/ysfuF/f5rhg/P5k4wFVTs1kI04MTW00/oGwAi/1LGDUok7C60vu5M+Qigb8VAWP2jIUCEWF5UH2B6YPJhd4GBDJoOBWVU1YjBo+xd7jARDUx1LTq1yTUakzRUysNaF5ECKFbiHra9EPBXcjiNZ7riIk5peCKjm2faImhiRQawvOlrvgDxwQ4RMBaA+bnnp959bO/v4eJjtLDu4cHDJOePzs2cXJ2Z3bh3/9b/yNh4+O//b//T9nziwqmkaSdE+fPzr/lxfz1Xmj0/rwB99P3ez1epxQFyJQAvx0LL6gBSHTkJLRAOoRU4RpEOkH4omgHcIkDCnByBbKETADXA4D5pn9S0shBfnAHAt1YUqlkqNMXjrvqJm2K5SLNcS2uNRJUvBL0UIE/fesE0FmaPsocCofUUCAepdajCTSdXEamSHBlqVznCNBw2YjTOygGXwEHSKCL+BUnKUkoT94UF7HFySyQaCWXk1hVeFXWAaCcjbtps/BVlDEpCCkpv10kwKVuRFKRjwHgyqwgEJoiCG06rp+g2oWG0TSb6H4xoCEJIjagid6GdBoyo4SJHU3YHlQqEt8nomJURdFhSK3R4lBQyOa84HaIVabppParSPXRjE2D4WDwMhbET+Iglq33nASeJdUoAdWZVNpGAqq2kvN5mDQK50xELN8/BOCajcv/FggQsWTq3r28fe5oCSlIlnSlIiWPk/loXotQV8L6kZCZwl7FYgbKCXs5h1EeeXAIOYO42NI9GvwG3j5vcaDmqC3VTQrhINxanGkQSA55xWWMspPwgAw/oYUUAj1tEwrxRiCploQMS7e3legvvUHwplXQgmPfAAGi9iKkwpMcC7aTM62UhTMvMStMT5QwALCDxiubtENz12rh4qPsBnF4iBvRLcSBlWAIHQLxhSYSsmYpTYANotIMFOWY4Wp44iFWVSimVqDXCdPcWEiFjVFS9HReClEt2FTd1EoZoadAZCUkYSpn6BDANRD6ep2oU7T+YhDl3JANyDTzGiBQyeKg+kGGr0hpp6rEGAL5i8eVgsVpQaKFIDCkVIPEf9xwKACrFZuagQNKQ1AVC5WOxBKZ8EGTLJI9tAoWoA3qRmvqogCttDQcqCuRF2Okhvp4Ma6xig5enBUr+1Y3sV+vfUA3cc5MGJlbiLApEy+8UPHjWydOmJfCECcrsraADJhR5R0KmA438im9UTjjq6OButlMN9mIwjACdTxAbyurE/FeAIfyuKCxUzl4nQD9fJkPOm0Os+OjjndDDI8fvvhAsOYfRLXi2//g9/5Iz/yHRwhjNnA5BVLqv2qXlBeQEetA4kYQ+OB3X7U1oRzsqxfq1MywNuw3KUUDBURFBKTeTBAW00OPZ7RI2DmBrtezyfM0aCPRhwERFo6YDtfsR8LkrAYukiivkNvl7HtBl0itovFOb3Yw3XZ6h6xKJjeUzqATA0HXv7IjAzLXcqyqgFE2TgjWstPygjFCbWJrP/ftoeWh6+6ZZAVPCl8IlL7q195m+1RXn/1fSwEfvb8OWLTY0fLIhzLXcSy3jyVFzwzk8Y9ExAnrEzyUdphHXI7n02ReCbN4FM5Ojq2A9A+UwWHqjJOstlm26z5XMqgvPAM/Ur1SATwJI6PfgyDSudIq057jn4KwYg6KWkKjedwBItJOO+11d7fvdWlXrMieAQfVzvDnfHo4nLE0V5sMEIfzHpKjwpLt09D3OrVWlvsPXFyeT7lmBGECksTUuMzdhPhQYt12etdZRUcaS7qfbjk2QII/wqrFTh0v+f1RU+/RZNVxBRvi//Il4UAXdCG3IwxADVTiuzTMniG2nDTMxok98/lZbFgQQVCSW1DPJkwxgJU1kMxYWneXO3Dw2bnkm7HdHpF5f6jP/RH7x0eXp2f7N3eS3MGsbno/Csq89rFd3znp/9/P/1zdRa51i+tggo0qpFDwVAl2FrKBUYyHXsI7sbFKEdo4/ApnjwuBQ2c1SUxaBxzM/DGBfW5Nuc55CUcJTN+q7g8U2fzstqmljXbF9Ct3+VA2fnONvteMQF/9vTxMWNpd27fuaCrxIqsVv35s7Onz57hy1fVWDcvAOFOAbgOWzjut3d2dzHomc1PTwDrDF5enl2h17c5AmBrd+vWcDyiZ4uXqc1ku8Vs3ScW+610GA1YDAd71FmSwOou9W04YAirt92+QgogP1LB5GiKrmhp4Kj0KAa/3qLAiFc1ARFVeE3s0Dh04FaVv3poPTA8FFMu0jRaz+CXkiDsF0lePAKE7FSdblZiBiydCvByVwHppeYNNJEAaow3s+KTQcmWAOK4qNzEpXb5naRBnYiccYuUZ36BuRKvXAW6IeaS3IUGzRmVVt4AYqgpbFaJQ8Okdl2/9ZWvMgzLEQHO3mGbmKn7C19cXN59de/Dn/wMMP6N7/3kP/nZX/rpn/5/v/NVlsWzT2hrNL6khn7uc2/iSri9s/fB1z+zGG/vHLpNc7fbZkBPs9naBesanLtHbUKgVQT2+uBTs8NurQgyWHGz6WZF0MLjdpk3gEJky3HGkjLFy5rINrr0eTn/wX64/qDSzVPwmWpeF5T5AcxBQ8uFxsMMADy0dGaWw6ioJmq38DH10+tgKJz9Y/EynoYFLMqBepBQQVLsMBgkaEY1+WJpNBGKhpRtGLl4/Iig5qnobq9EClOJbPdhHY1xmjNbe8nOVoHxJ9ZYDwA72GgsLQFtU7juxAiVEyqGSRKV7SHnNCRAjmLxH7wIClfByGzE3g4w8FNuWSyuRSacfaByUD7YE68ImVD1S1JeyScMP/CIDSZVyc6yFJHJVz7yFVJyYQTxVd8Iu0NCHVpG5DX9MvJOnQE4UgZ8UsESzSe2TqOSI8ZSNPshgLcWEZSR/LBKlUJj22V/sCHtMx0J8RaIBU6ZjGn5s9N/vf1EAhDAR0/IJgreeovq3RM2bsy48SUX82v43kmtN3KuAtZHn6rrJd//Jtjf9E9LQMnvRrJ8Lt+smGD/4rqR3+Zx87FEQwhShBK6SZq4sCp/fqo+SBouhYK7seQkv5AIZe3mFQih/tRNElnkyI2c97/+XS4g8CwAmFxjWqAGX9gqD6sqQlmoGsDP5L4N6cGhBEJ+2Ev9IUuiRgSEKnKynQe5GB6mQKUFo8TuMRjUHdIlDn8ImklBqyqW8qgopEdLbEWSVELUjArUyKxOOkttSRVmI5WiGUfgiDKggk5iWQ3AlvknfFe9CAHIwlBX0eZonVA1kHq38jXTFBP4ZG25EO5UPXLC7C6tavDVWUF2oBDahVdBAA3VxkHZ4IBTWhFxpEDcuYgORM1Tq5MYWBZ0gxDzNdFoLykMjQ+DNY3aFae2LRpX9E4WzXMHZjz+g/JTBAqDHZyRGioaugoXo8zyH5q4xjFhAMb00bepq1KycwuDQjWIrYGOc5A8sahANt8hFRTA5rdvUyEVfisU/kcRo+SXZ5dnX33jDVTYF373t7vtXnfQ/finPnF+fPan/9SP3dq/zURntjqR8Bi04KDuSN6SRYYoCH6Gej74nOzLzTcuEE0Ea4MdQovKjBK6krZNrA1F/RBFzwrkSBo0Mr8oPFty+6xI0hQTj52w8B7ruWxjdtrpw9eBi4IZLOMrBpqsNFBUzsBrjKLY1CJRCp0fhSnh+uxhnVklV+hCQoUZXvLPdxjlZrJ0kVpO4m82OD36zp1bzKljO3hG5Ls4s10XJpktZQQbfBV/BuXW09mcPo71mo/Iig0GE42cj0bZqWDti6tLGsnkCwzrCDEpudUov4Ku4Fd4JqdCHhE3grcKfbMKzWWVrJPwlMmYwA6SCB8LZ5mfA5qsAN/q7ySFgklfYN3tTZlKo6nNSB3orwad7v4hG5bP3HlTX3x3Oprzyu4xcI41vJ1GD2HR5KZyomRYOSDnPJyQ9h1/4GQ+anac7kaZHZYGFxxSDATMpihEew2FGam3THVzp6SFvTTWg2NpgAz+aVtHtgnOOdl0iV2ywkiGpZPgYOEYAs06ORXXAwJCpOX8fa/e+47v+INsbbW3ywwldnWJMwxt7AoiFwQjRwd372MVQySFQHoWstKV8cSlnZ0tTAKGO8ATHc4sC+o3FAalSEwqgMQlIdy8vsLEvIGiV8Uw+VW9GyKnrz9HAJUhel6gh7gPdfn3IOflxQkQZ+MZk3kG2+3Tq3O2v3r4+Ijj0tSCWDeBi4BpMFnTJOvu7s6gP4DqQ04y5hjqeh1nnlPmmNvW7O4d7G4NOxxbASI0QUwi4mgwyF9vt9lWlPSTy6sLtgza3qJG4PohpNvrM/5xdXrOUggy7g67DL0g5GiISFlFAbmSghqsWEYHSIhCYIttAkueeHnMq0FeIRIp0D98pFJzB06+VCQzEvwuUHggRu5Jyi2ssVYnIPiRPAkihwEXzAo26F7+cgVV5Dj5EcX4BYroBGJcBOJUEmhlpjC2C4KRmXxCHxOOPkEvEJCkaXrVdSh+aqQloLE7OzvnvG00G5N4iHtwZ//gIx/mXAcm/2wN7n7mD337t37z933nd3/H/+Vv/pePHr57dfWIznKrs5xMLh48uDp5/vzRg+kHPvTh/fudywsGnFn0yYinXGAkn3xbOPaoPvgkuljwdlc5fc1mTERtZVI+ps8RhGYgHOm2FvKdScXwn7EE1CBC5RYGTG3UgIwjDOZadJUmxwoRISWnZmp1FqedUwnS5W4xoJuOEC2px4Or/cGGKYZUQC4gIcihtlhxhLj6IQpZqttq2tDb5pvOFBSSpkTMnCQIaUs1pj+A2PiBL4AUvcTXP0M7xCQ3ag0tAqhLBr5hqSD88VtGYPluY61FnIl0oktUYgBOA8DcKW+angAjRxECI+0EKUDLLp4hs0kQA2QAhJQOYEGtNEfQCbDkJwVCQKUzf6Bvw6X8Umi9wKbjnQdyQ+UyTEKnI04TEGZbZOLSuvofUBDcFBQJ6z/ccUCA1WgOi1m1rDT2MYAZCqVY7tBAuA453ZasQoFXIQfsJnNxs6ibK/WMuiEsS+v9xudNtOrLi1dz/JrLfN+b+utGe0+6qr8l8qUc5etLCUWPK/fyjEeWFJ4NXJJdI11SRshMcRMnUiZa8QCx20uFLIEOhwnKywfTwTd+4Ss9GGko7cJC4KBPnH9GTMnJn/8KM5BY4tKs4fql/3QPIKsW+/UGbCKSShlAngwTQJDmlfcIst9jemBy2a5jU5Zjj6wlkcyqgMmZ5HERBm0gApbcyEHnP2aYvWhwkvU0xuIplMhrxMskok/xAp76R1NkRsFTgcUzqnYhkvTARHAcX53KPBWMDgKNzkQF/E60OXisBclHdn7hGY2SwXhnVruPEM09ztaydAnaApn89NrxwmrNbo/2YzpmQ5IVDadINTjflL17jYrLGcVLbyJn6+onwMAxL9szLYuUTZoIOaVAD6Zs1FOpAGqWRQwtN2qWW4Y48SIwPsMm5bs6YtmMtcEMfufLLjrndDTqyyFWoBN+mNzPdBEWNXYe6rFZxH/P5iqAwvTF/Y2D3Inpmh0UDsQtpIpioJh0rqjT5AUCCgtX84HC5VNukSnaKgOIUK9dnJ11uv3JbDKbrb7y1huZ8DV9fnryH/yV/5nj/HpqkedIOGW0IQdOUfEAgCywB43t7it1VoH6kS3YvSeL+EQ9A9jcctngkoJ/RdcgOPhOkQt9vYwzQJ/1HZhRr4/sbDC2KTGbcxTPkh14yIbVEUz9BwpGB9XcSfZIc71xTmuwd/vgK7/zhlKm8xURsaTJUSiWXqzDJuQUYLTDzt8wmjtycLG7gjpWrUxklCU1BTbj+UaboyvXM+ZSMxEJccXi7UIMBiDmp+c7bKLe7yyuGKk4JRGZmV771yM18OTRrDrjhow09EWChkeI3WmzVzu9OMXU1e9MoqXdPJHN/wCSblI3LU1FTmAjMkUSSq0ns7A4gkFsy4zO4NfUkg9ySocy8p7WDGmmNnSY3W8LTn1E4nl22EImiQNkwftfr3M6LHsVUhdpGp1vTzvdmT49OeX8vu3BLo7IOV7oHHBEDswax9fO6QD28+RHbTZbvPtscmt3//69AwTLDcuzrxga5fnlydlJb2vQt3pF3pA58n/y7EiDn/K4/GX+yr3D1z/wynzCnqpsfbPFqkdk5vTi+Iu/+yx7/3cZQ1p1hst3zh8cjcHcjiYZc3L2EplhtQl6oo4TfDCUcdFaVBSFUY8bvpV2861332ICMgvpqsZLgZdZcM0OJ7OF2q3pdMbv1dVoMhlJtEJeyR3Rkth2ZpNSJlp/rCpykjhENN6LK88lABiaE3KuRCG405/grW+3hlACHdVQSlrsQMUmpKfziyfPIDAkZiSJaoD7AILDNRZrn5ALyzDQfL1u89buHj3hDud8DQb4+2bjUa8/GJ116drfvT+4dfvW9hD6MJ1qzrZs/cZWc3wxH2kXMqlrhHDMJ/3LAZhzEm2338YjgNgjOnSHqI5oY3TchAOA0bO6tMAapwNL31+zuB1G1ylQiMCDBLGdZYRwU2howSPk86EEviBP+RjKMQmkuXwNCV013wHAddRCVKNIfLLS9BIBVUOcaIKltSURcfmH5/6uEJpP1DOMjSPMBtO23vW3nCBbUFkYUm8+RTaJbKvkRnJAJIB+7Ns5dTq8B6zlJNjZ5ObZYxY7cQXMNxjIXqmc5FKqJQPphAPQVm9+4J3TbTextf4R++ke8/Mms8vJk2OoeuvOfnvLTvayfvKd3/0tH/rA+x68/dbP/9Nf+Hv/1f/r+DE7ONW6O10Ggy4ufnfeePb0bNBp9j75qY8uJ7PBEOL1aVpBD82lWY0ik1wiqCdbdahhnKkuqHoNCcrIvG8wQXaoRMSlSuG9JDERUdDO5gEGo4pU0xiUWb9nsx07le4rtd92A3PTcQVjE1GzxAEJv2m2YF4DuehdXJikLn4L6rA1h5psB8xeBMkc67O+qhfAOOkBBWh4Qzo7DZoXwMNMAWU+gp4b8hAJC1aFz39wZkzDaDbpAAOLkIBkNLpUNA2IaK84BDB66YUQ2dYDEP7PKTEgqPtHMSm9JIVAaqF8AYtpkYvcpTrYgIFeA6FDcYmSD/4ik/iGXIhi0Rg/TARl1a+W1VzyT1GPvEFDOWcJ6GWhH5Akn6A65hrUo8FifR1BmSwEbuIPKEtOMpDvME0Ia1C2+MGi8QkBkdypUzKLcLKClgWAd5ACJRBKkSHIuv0ARgBVGicbJhIax6hyVe+Kp/8CNWktMw/8RzTx/ZeYfquuG48JKe+m+ZqrSruheMmjxHwZyktpk/1LYQWnG4GBUcocLpRPCZUCwT0firbfUKeCIDaQO4rLOgC/rjmZ53yV8yUarOcFeIoT3AjRJRRwDTIThaK6x0igYsHUhBFBTsqJ0IGYi9JE4/RT61gLadbAOrJo71CjNo0wo32ARTqxS5iDiDMc9wseJQAinTSBBTUH+KgPGccwN0PJ0IQRFs4/6umFWi3x8THbBEyIYo4Uh6nGuNnTj2YNLyWtBj9S0C4JQXDJIr/JnC1TwIwTmDTFMEltZ4ThgTRsRe+G3KxkZWZ/THZKT4moBhSSppgS1ZkLjphTwPF0rGTSe4L2dIEQSccywR2MJFvxyksdSeza3HCWb/yqToTOjYcy/bkQW3ZQfmEQD+TA1KrMwSzygOW5jJJP2OWwVn9ea7Dycgfjb8UAg80SedgzEDIODNZWcm4wBVVhUkYWU1LhqIooXKf0udBDowJiEFlXHN43vrqSGCTEEDQiRqGz+IsbBE5Z6DrANYz08RSdDHNRcW++9VUynzOBvtn8iT/7p+iIbG0PKj5aqsCIcgyYFBb6UjKAw8+ShS/lUjKrx2Tsd6OVS4C8Kf46axljpkXSxY4BA2j5DsaqUq1WqAPmqCXGJsGbLFVSXkjZTGLz1U5E7eTibDqnUPISDSSqKn0vmSZzoIttn+iQE+95NQKvxgJyMEd0TBL9LxjElM2maHnFBgPo+ZlbHPZ6W0dPnoM/J0mZbZUIs4iGNtlS6ZZsOoMGBLKtK9C543qiHuGjZUo2/rQJW/uibUXpRUUXE/+EFJpYZpWvpQc3/ElKBkyWWiGpsVPwFJYyQgZTlQLyKwQLCqZiiHQ1m/Sp3FVWSEiWNVfi6OW1RMSC7nQBOP97ioNpzRYkNsH1+ZQTADoHt+/gCqfP4JpqKud0ysEMsqQ2ZgkHPkcCU2ZLj2Qvp6PlfOxelPa3V4wlNGr91RhBZpgkuFID3ZSTfQ06RNnqDuiDgRUlwUg9uL09G7G2GAd2l51kOQED1Ha2GEqiWW9R3Ra1Qb/BsqHOZDVBJKgetOOwhXGYB0/e/ps/9b//y3/5rw4GQ6pARSKzsyNIDosZs6q3mdjjYnMETnQsii0kpyzBVYmh/EgniUUT7pyuYCdtLSRJYtn4zn/54t+Ly8DyKXe++Rr55BFiGaDyQuaYzN1mLSedcZ0SxGLO3pjdL1GY/EMG2AUe0WdrLNQqEqF4xmIQCP/qq61Bj+08mceF15ddf0AHHgGfYxlbjW3Wm+7dXXc5WW3JjHP6gv12v79a9Xb7w9XW5N23H0IH+kurendre4cNwW7ducMZwdP1hOU1UA01S342E6wuay2wmEIL5EaZROqsaRLav3KTIqKWONJFKm/uPl0H+VLeCMozbKJiW4dU5ip2KRLYSeUTAYFWpSkpk6FRTAwZCfV/5JQUVnb+TCwbqluJRGAKkO/uHcxX6yDpEVHRIFAJgT1ha4GB/mbpNAQSSpQMucMahlwUR2SEFo21Lw5nWekYZiUEMQRBpTHFgJnWBTpgy9X+rf2dvaHGrIvllhzv8OTxo0H74OOf/taPfuzbLs4ufuNzX2CQ6q03v9rvDbd3t84uTjkYdDhYfumNN9q19r17t4f9NQu+mdMb2PYWFSqKQ1tCfdAFoDMJo9NWPEoFzGCoEagmdKZVBZj8tDs6BaADVGEQVgKp+tRO1gCpS5CNEM+8SbwwKtq6lI1ACcYFjfJPovBIi0iF9xPJ8qnEIrfAATlHToFoQ5bxf2wHayN6VX4sXSZmLZC/cAH9bGtsm8C4OmoKvKxLEJro1hfqF3OJCaxy0rmpp4Nh+4gqbY362RFJIuvIh2qgA39ZE+d+6BrrvIMUOGKOo3ugcBLzSbrwFXVhxvlTW9Kaq0bEUzpbJZQt+gXSXGKEaiIFVQqxQrPQTtoClGefeCapVcM/yc3FTT2H4BGIiWXWyD8pKEBgy0cEkcIjiMnUGixg8AA522ZLBnEA6tBnvgkgbBVLgsgoIiCO4r25Kpw3r/waIu2qeHmtPn9t5IC9kfgbPArUKDEdfCiYlPvXQjfG9ZVILFzjkoW8JkHZ88d+yUsXESio8l4iuvpY2ZeXnk2IhPocsBu8gBnzl1gQwPa/ZCbbYbBtDk8yMeRH6qiWUXPmgazDbGDSpj0WskT0IrqvCmSBtwnmE0EyPZGwQ69GiLDVtLQTCh98TsoIRdATMKZJtvTWAqeSuO4Ou9ORSn0I7IDBDHIAI+fXmfLAPyU/1AOsc2iw4zpuyjWfztyg3V3qIRx+QqjnBinxIESxIG+Im0B01TRWh93mDqexunsBC2K5UnXogDD9w+qGWYYi0HqWWUgtis1amjIByipu2a2WFNEWUgS1CN0iV58HHGKDEQoEOsBx5NHxc8SeNAwYmqq1rM3sVUsmOCIljU8uggOanLbI4kglocSIQcpnRcbv21qs+rNFh97HcnlnNmXK+6u13sPZ8s5ivbdc3Vo1Tlar3VXjbM0W742z1WJnvurNpuzmxKz3oZgsmSqNRPVxkLMqlc7Nkt3W2U2FBZcc/7DurdrnM84/avTcM4eJEwqTqh3uKwCgZZUGJ6lE6zIeTTCsZ9MVmz92t1r//LOfXS3ujkZXH/rY3R/6wR/61j/w6ThLrP8FSIoMVaIfM8Ov1noIZMpdhEtm0smRMuSTi4/WCL5XxAgixpMjepIQJrU3iolhgA4mBb4ZzE7UeoMBH/pvaKYOc8XZAknlirVHiagAwJBr3GGcXT4A0hyoq2Rdg+kQdCzJ1wq4dlcl1vmQiPLIsGI6iKdo5DWdtAZLHXSmSjwUH6ec4B1i7k+oCODM/GTWrLYpHv2T55f39g954N/21h7Hc25vbV1cXtA7IDKGr+RunZEDb6MrTS4LbXMvJiGs3vu6m4Sury7PCWzUMG1TMomVh0LBkPoFdU1lbwHPHTzRISVUKmyBSkrGZCC0e1QryL4gk+RDaSiPiwE961Yt1GFiPShiHToLwFYARKEUMiMIcbWF4Bnhw/ifMfRiA8gCjHoDZzIPjDpTB1g5YhZiErHBjQVKagvaDnGnxWMwHPatpqwsYDIXjba1iJV9azbymcFqnbWQCZKi+eggMxaU5ho2yU6s8NjbUxVE/Qrs6/UL+tVNTgag7WNFiHgs9ncwV3onV5NLetx0MBfbdExYZjLodb74pa/8k3/y83/mx/+tzGmWuPyH4+RCzsvl1dX4tBSBQkgInOAy5jkdDA5MULxUjAhkczRhNQqsBhUHpAoohzqAKa4yqWTAe8rlLZwq70mRL0Yzr01VIWLck/j9WTyh0Qsd3AirNmX6ldvgQlWZoLZlAbTcyRwGqYvWheyIvmc097v3bt+6w4nOqFB8MWrOGSasVQLO3L673N4Z12YshG5yEPXt24fUG7Qy7pXIyr2dQXu4NR4Oh6z0/cgnPv4bv3LUqb9/Pn/GaCouc9ovJNqppZwqgCxxEjyLqku/AGcqWbTw8zmpsaIAP0Wwa2N/Qx1Jx3VjTnC+GJYrb9UtZMZ3SMmLyBMewvtd8vkXIvNj91iFoQUEMsoKZEJoaSjQ3rWGGqwYYWZUuMaDvv/gJK8EnNNhw2de0X5k3a12FAQPvgPUaFwFGTMCzkOnsqCWiW+DUjw19FRxuNAcsnqNTqbtOSSEJWy7RE3LUJmSIw5Ap/3oPNvZ2dm/fRf2M5+HzOYL5gFNJlcXe9vbzEkcTy6pQ3/xL/2Fwdb2aHT+1/7qX//cb//61fFtvGTz9Tl9tidPj3FBfFfv27f796eTKyizmE/seKhVtfLgBeIB0tCKbJEyCN1wTU40Gf1hy2bPRJLayWR8Gp664kZ9zNCSc2x4QagAhm7hCetc25oU0BmCwApquIIl8SEJUsudr2bKM1EtN0BBKu1skqlM5Id1Hlo7NA58/iAoCpQhLMCDftpmNZX6mRFtyuGf6letW7QgkM3Hy+bFkyjSDUN+8UDpd6d01i7isDiQvp1jasg2SHugKfUKCQIFdDtqwypJGNmRAY9kpyj4KLLaJo4ZYAbBZApgMPYduEMYNqq2bAQRPwkYYaSxZ+Kkrkw0tl/LLUDjzDIuF2nSTlG+2rIv4dhnXG6CAziqB8JNX/xoae0vYVKClIS1fhAfZHhlbBTbSU8SpwHQTamu1X0bSLJgqSRdP5B31bBGHhEKW0uxGWUNW131WrAw/4oS/IqVZXzpbij/r8MR5HeNUqxun/47XMmighaJJa2vFD/cIJdE+X1ByrlNqkT8PVOVnArqxExxb+QAIUpGxkgsKGWFD8EkU4K550kM+cSlyuKPShG+xUNAEwWr9FERIXmpXgvYYFuwDM2rbG9CJwoQuSnACIE94bQpqRwoRJJXlTAf+Ix00PdVwGnkuKy3tpLKqpLFhHOSKW1aS2p7w1OK4MdnXtP6Oy1VPetOpVZEMrM0yp3VJU6H0MNa4XfHnSwekUDZ6hrqSkTT0uJYjiw3Q6wJVY5RjE5NIpEVlB9pLUrphfMkQJVM0FMtWDut6hLDYvEZXSJJeAY9Kq1veDcFh2JzbZGGgkVn+0b2rvEJZU7WZoWeYA6Fvk2VCFngKEE5cMQamxOOYG/nYtTqnDbP2Saxh/Jv4fzEWJxz9K21EaueOU7svKod3BwvMD1mTH2GFSkh5GMNfmPhsCWVGW8kFgmltZTZzp1BYTpX0U8Sg1KILYVTf8FJcIWS2FoodGazd1onx8e/9Vu/fT5io/DRoHcXOD/+Y3/qm775mznvk7iRgRTNCi1FBCJ1ePXZO0SVqhGuCHJ5S6Bk23wv3wgIp1IRIJmdW4ck64MGPk6G6jkgmS1xWggXdHHOTXLFrFvoSsmBFplVFW4iOJQO3xvFLHqM+gWzbD8QGkVXGZCPYAq24uldiigwUmXlOZpscYtOR6c5W0UiUx4gQCg7KEguFGuzF+1s0O+P8bsqZ8vnz4/mi9dOn1xubw9o6ZoNduxm+yII33JiaVpX+KBg1PBIjWGxbRgiTxgZ2M+nD8SBALRYtCD6ApFFKaYfgQfZm3qbQMoYWKCtRuMb6LpcjK9UK6+UKQUkeSIbKgWoiXrvyJr5+vQ62P5GzFAEmCOrESasrQP7MukM159nvTBtwVXMeUKcLkeXaJBeu08LOGateGwp4LDfcFxjUEDrASSyTSd2PFY1yzPS5tGA0nlAyucTRJGqT8vID717VhvaqMIeqhT0YopH5iRYSa2glBXOggbd4FEkvsgW2XDKGJ1eWCa1ICmjYbVpc7u9PW2tpmyHyDdK4fQ5mMtUt/Fn//nP/vhP/EmIiHSEzOIrodU/nclEfUDJJb//eVbOoYxueK56G/cHwwvUJOlDpY/uJFXAyQTJzgUVZEOAbfDNh83HEod01UMSggkFgVN9juTqUXxcLaUPwLjrlC1ukbHsYUREjMhuDwqwKzxrjJxOCUISP1OwhoP+3tZOjx4LdroWe4tRFvhMXWOuDkN8+7fvYEiyHGByNeluNVhOoH6wODhZ6p3h7oc++vGtWxfUAjoT9Ho//k0f39oejqanBFA9wBrDUfWENQXxmIDpEddqfkgLkhUlJSSkkiAWNfdCow2lCL1+NDIFMCiSVO6mQwsjT6kjwBB4iG15jayUmI5wxCtSJC6FLUYxCbDJgBot+4htXpWYmwH/YTqZFZD8GKfgxhPgNDtLPonio1eFrb+lfGSFfrN+mhqoSAo7yxFkbL5CTyZkoFJ4pqfHAcDw1g8FRyqQVUAWk+bBg3fJbnt3ACg6cnfvHe7tfoxKeXF6cTW5evr4tN5edIfb23u3/tP/2//17//9/89f/ys/hS+Dvtjl1Yit41i1v723y4gZqoYxJQYe+Ipc0KSTHS5zuvHAh2OwDrJCS5fp8J3Ka6Mv6ZE7TV+dbhQBhktbSoUkUETUsQZiEb8iAjY48qSQK51OrQUZrIyVvxCb9EaVUjaeNlwSlUuSFx7S0iUtS1ZsLKmtGMSENNrsaQ1uJBdJGQAFUWJma/UUqFjwoWRhiKD5j18fwQRQFB0YGRjMlGGLY8OgyIkbn4ARzSjCwpVbpgVjdQFPShEx81VQFQImlrAFknQmFkQMUItse4afAh8eNUcTyBYWNVuaQctcahB0EhkaKIkD7ihkgLD1BTmVgtPFyzfxk0eWztYQRoNkWcJkWv2bLnCnbQA5zkPn13ZTPpJFUAvKFM8FG5g3pDF7bpZSsEaTEpAigZvyCsBI5aqilBibwBTkxcuN6DcDv/FzAW55RIzregRg9qqv1e7+RCsoGvZ7XJUQbgpzvR75a6ObqRroxSV86J6Aci9fC06SCWmhEkVyfKHAYhzVCPZBj4RVKSwPcWAIEkaYZg2RknCTscFCkSvJzFcuYS0OrbftJwlIP7C0sPMDe8Stp0RFbNRL9Cw0pEkKIPNEHIQsx2UuSNc4AQ6nZvOxyBOWcExR2wtqHcOApK1KKEKhBD9US6uiwAMWadXAwG5F0qzcthNoD2cREOTE/0gmH9rPapw4NLmNd3C1Rv2JKcik5oikg5GBQ1uFVZsaYmNshUl+Qg+y1lBtd2kL+azFkrFsAQPyBKnUaE/96p64ulcBuFzgHyUyKzjJH0PUKUPgaVHROrTH7H1IGrQ86EmVZGjsMAU6o9y7QO9qFM4POISvVnulW9vZ7d1p1HeWq21WMTZXrgGor/jE5r2YUAzBN0+vZiMOWm32WB7cWHK2EqMQnVu38e2xzzOedfac4eBVJjdjz7HZIm0HlR4aslwPUwb3/iGCw0gRm9UzBgpaYoaBzDbz2XIFe+bx44fvPvwKu6xubw+/9wc++Zlv+wzcOjs/62TdEHBsgZIKSBDf4lF+RsMoviWViN7MUtLmyfAEXt8TcOPGvhlu+tB8yHCG+x+jXDjLDlsQBGWGG7wzNQr3C0IwrU2vdDph17fxXWCaRHqccMNCUPQdAsNVX+9gFrXq7JESZaeYscE8H5y0Q82BRWlUwJRGIrLkumG2TWuxAVFKVNUB5JkqYeeP8jeaVyM2Wcf6YcfQsTuSMocFu3JVPzo6evL02c7uULFZjzmIiSH6x0d8hungSxbqU4jCJnt47JzNaRExbm1YwNmp9J6rtV5MGdA/V4Bi3fC5oiQBEoQvyLW1nFJYWotse4qi5que9Kh46GcHQ+lETiy9DCJOWnlFElzZcmi56rdbs7nOfMYBWOrGB6YhzVbsBtNxjYkdi7iMxNVmAzAQATBX45F2XYuDqRfjJSeIzZxHZ0eiMbzVaYxwNVrLEDR8hKyr4bwEK6ptNv/10LOBpFh4/it+UB16DBEynyikklxoPLxuci3jL2l9KQkOS75gLQ3XtWObRWWPH5bS2B/DNo9tRiCjW5i557XVxOVABNfP+NhYdlhK1OoM93buMQ2DTU8AalWmtJAGMnG+xOT00cOvsGERn6S8FOMP5YDMMH/GtY7TyZgETMAAVVLTNCIoPogPd81ivBPeSgBwzIf36qvcEXiu1a7hnu3gBTTuyB1r2fkpW69ATBz/FNKpIMSGkM6FNB2bRb7vlddZbfnWW29xdhthaDnAgOqtvZ1buzutOjOXzkAebJioAPB2l438+uy1sre3s5hfsRWQqpMlTxM6G8Nl7RKrFOt0MavdOhjfeZ2ib7HvJ1mzTLM7PJ/NjnD/W8ciikESgQWGlQIrSGqCHfYZnfBcjCZb+CiLUmgLH/zLq3fWCXhVX0Kfa5JKm3z1JtV5ZcWRTxmxl0l5885Skyl85iOORMildwj9QWvWYcMrUlr3afAogEgVPgsAFppj7n5KXtzMWuTFAf8oa4QMKd/DV2MaoEDwZ91PCqJjoVo1bL9z8UPW2sWpy3CWjZa0yZxH5D5FpX7zADAu+myY+4PhkAFh9rqFKXy4oh87WR89PqIqsZMYjpHbhzsuaOEUbWbNNabf8m2f+h//+R99463P/9Zvfp6WCQOeCbK/9C9+5X3377JJqHXQmTAKA+OXrqOlmmNpUmhQV0kgAD7xjh5E5kBbdrcfoRtXy/tWZ1e44TLpq4HxAsQ5DT9o8URcFSSfeFRlEUTDpGpy4xPARRYSg36GlgBrxiw0BGBlHM8kgEaFpqulWz2zP1kguJkCQhkCyT11gBlJerKH4EpzmQ4k7ykGUC2biIkKIsp8xfvWteYj9TzKTJ9PtO6qR8YZuway+Icuch+wMfGby9kBqNX7RzoXQdqLopGFOXHGvA8t9sBB76kceEP6gkXaU3CiRmjAWytDKOTkDhis6g+gH8s2em3ad3yPKnblxZUGOBIfwsva4tWUFhgOrZm5a/AgIsaTXFEPRsRqzA6g5DnLqN5gIylaJuULmJZLUkgxPW2loH7FY3lX2qr0zIe8012DevIlWwXmSzCX/IkmxYJWIOcG+Hyrctp8SFablxe/Bsuh+atIYKVOQeOlyywCV+RLfjfhlWfvmxGAKv01oOuHlwDffJWlAv96V7IteX+9z6Fp+XCd0wYSvybkB3HIRBEfk5HNDCwsCSupU7KMGoVSktHyIrTEs44msjDBdUPnCuvyzbtx/c6tZIU42IMXA2QOLis/5i5y6kL6pFg9fMI5CXSrrxGoHcHRIENJnkeknp6hSgMAhEWziTatNdBSORF06y/tK9OKrCESWIAC1gwic+QbllmVEc/crP/2S/SpOwARYY9dhaYLsiJCDjpz7TLj4eOVLgQZkxD4eNUlAmiQgU0nSJmS4mqyYM3zhVpHw2Ui0EKj2T3jkZ1AaCKc14yuESlwdaMD8JWgpAZPP0pAnkkVamuimok9H7DmiUFERngZpo+7Gmhu7jlXE3B8ppUqM1/EkX3WoAm2CwMs8zO8jMyixsZtTdgsjApMMRcM9jKFqE2vnd05mA7BDPhxfTXzbKVac05r2Jo12JIFio0vzJGDqyCExbEpggGjq6udnV2msB8/ffb2O29C9suLi9Ze/Zs//em9vV1aAgxSiSJ3KJKEkR+Rz6AHnhKgyJUF9cVfS/DiKgE379U3IKO8IRtoM42ss+iRMBv1yD2Zqe5B+pjRxBhIF+sTIw4k8HyarZgoKCKJsGok6mrEwFNCWbGmnYOfAgayVyzOeN1DlF3kTS3fkBFFEA4BPeMhqFo0taWlq4ubhFmjOJqc0T7jk71LJkF3OSu1Pxsx5oAw1Jks8vT4+ODeLicP7Gzv0QHrD2EHfjN8+fhBwQFJQuQx8JkmRAtH24nPj7Lig4nn3pWTYN16dvx4MoOntkKQ01J6lXv1Wz4kDELY3lgA9t+0gbGNCUWkCg9ELokFFoklbqSXyXsI0mqPrYQdl6Mjhh2waHVb8xF/zCzHRcg/p79aMxmfYhzcqTs0kbqLbt3eQ06ok+R/gJHvrrKZRMcen93Gycno5OREuYGVTUSdUysq8zqNDmt+8dZDFnqq1in+yRTaaT13VBfxNVeEBFcYNYPP/JfpjhE020gBY2lRR5YSInToP0INKyDksP/P4ahtzipwWb8Kztpt/XcXf8gz/97v/Z7ekCOW4DwZmyXVxVm8rDHYuvvqKx94+41f5iRdKUhKdACIMDeLMT/E00kN+FGZ/qi2yR9AQ3YJn4sHuWD63BNIKcTDsIo3vpiy+rVKQVU/U2grQAfppSO2xviXCekJSQxKEzctaW/vH9y9d8D53BdMMqOPihTRRjfqbBrDAV8ezQsRGT0BbYq7mOH93d3dY/OfDopSqakzW/r8cj50DTsrXC4x/lne3eFE4U6XZdMI68JtLawxkJB1BD3OilZqQxoYSHPCWnjWJsE/NiEknX5kP4sqQlNKHVrwLLur65o4IUsi8MXClziFEgkpVDJ5Phe6CqjA4CkPVAwe7SaxBQxhtmOkUE2AWx4LeCUPcaO1SiW1h2JbURCRUQWJ1CX5ITCC/G4OvnNd3/OQJGGuT6aCOEwC6tHuyVLpgB1oX4iHpFYv0RdFsbjHnZfB8sXaKuMgJTxE/8A9PnD2iAYecz56HNm2w+QbHBP9IT235dn5Jbr99sHtwWCH0wH+4n/w77N109/8qf/0H/7M33/08AkbfrAA/NnZae9J6/DOPQ5V0XQlI5QAqjiZmj0kRuAov3YCHunQj6qDzmQSCEJoy6fVmYJGBdG6Q2xKSHyqkpS1gIUIlKXQhU+mic/eKBUpjStbNQpCIUknWHKUOYVOIYf6yG6byBLOR6HYyHMDvLnKULIUIZAWMq8qB3+MIOVJTSEiGlRoEvHHShbb/gLZROBQlBMRRLxg58hkFQB0RYgGM7lYO5KqEBPKmlWVDtqoEJVAsQBxSOW/FFlTm0Bwoi1b6f7nCSRt0ah/KSpKx9ySCFgA4DHQgcp2ZCIZAqNvURpIvk1iUkSyoZb8ZCAUaoRtZGHhxYWiYKtQDEokYPBB+SZfIxCYMiouktSSk1aA+VqKaRH4n6s8WNTquvG4CTIjr02iUMaAEHsTaoARN+/8Vm8ldbknlreIRN42HQD2E92krWKtmCZBieI5qIJewE9ASfBSsuuoPHzdvG9G4LkIjQgVnMtnqElrGrmm7aHegp02AjsCaeVCXGNzwRsrgUaqcWYwz5DUx0008KiQNIpXGFhy4qX4/mUk3Kxwlp2dp6gkY2Ovz+4hbu58YlUwc+SU2sInGnARkd9UPfa6PuI8TjfI490GEyONJPXl5A54NNg9l1wIcTlUugHpR7bYA8EBaDzs6GTajRQKyXXLeTN0jYDD2VSfdBMAYXTaf2Zf0JQ1V53j1WLk5MEEW0kgg/LJTFeaadBv4Mu0NoV4rg52krc54cqSYoJ3/iJjqXaoHbyGBUiz/6hlfK6zXzj98daJmgTTrYnds3C3DZ6qdS80LLe1EZrPoAm4aHCkjoRqPsoFDZkEMB9HLyyRqHKQlV1HRqtlD/Oyvt7GybGcDz0DlynstEMuNMJeVGg1pxjlnsdhsNyBYnVGCahxDBcsl2OGc/F7gxUenEzqsK9LAnaQd5tQ2YsqihJ+V0+HvmxETnKhvqmzLChkKfaDBw9/9r/5mZ3dbYiMO/CbPvGp27f28QUwOAA1igpCPsBHybK4ohb0qoe88cyVqlvkqwR4L+/cI5mgVR7hLB853QI73VPROGwU04QTK7H2AYSRBxeZ608k9nxC3U86bFJZ7zIe0MO5RY8AyrNRUp3JQowLoc9mjK646WPtzIkgGH0YnvOxu5307owZ145djwWgT7qoMBlUKoXT4UajUQRGC/S6qKACKcdnWzCw0X1KYr4yegJt6QXiRHeiab3x8MnR66+91uv0p7NLeI+dhrAvRzbV6t+oe1pu/p2fnWs16aCxDmNPR4jxW7vpFKuxeWARK2wCiZCskFzqQ5Pachto6+ZFRUUxLbEgESCplVRCelVki8hRV0r9UlSRYaUCAZMH+pMYbKHhx/HLtptM9GC7TI7ppQuJVc7uVNMZ8wFWPXaDnC84LJa4nByYvru7xJAtk6ZW7ElFv6qDxxG06JBjBnLCYHPAcXz0fThamwUF69rpFVvvl9mlqDgb8JmvHuGGS1IqcfKXE9om1AASZYURqolGln4F6EL2SBcl0qdDXeivdf26MS7JWXqMQc8gj+aR2xQ5d47KsGrMxyxKtfMRekIhPWQNTKTPfM+/8X1/+I+ORs/Kfoh8ISPVWY7SXaxGR0/dvlouLLdCvkveIH2n1adsdgBYOzOz+YisQv/wC/VRvE6pxfJQym/uiZ1b9ncqHOadq3lhNLhcWAuikJTMGS/Ub8suq3pdicFKBglWP410iSJuBcrO8nEibG1xVAg7oXFuevv23v6wP2CnF2xhxsI7Xmz93nVUgW1ptOtZ3IJKZGM0mNke7Modlnezvyt7N5EHKGB+DoeEz1ER6HsIiXKQJym4msY5D6pqG4iEw4IGxwPgiuHVGlaKX1KklBb4+qIqFyE2RLi5pEPeSC4bchGYZ5MQAH1wfJQ0vPOpRA2f8+pBED4gMuII3dDFqkGqH3qUquzsPiEAmRopIvwrJppokUHJM6WwMMGKCMEPApWMcydOymIyM/XiyUdIZN/ZTog6hDYIZNAIZToZ1Wp7axvythfti/NIQsAnU3LgEJ7Fxfk5Ggeth06JT2l1enbZvTtgn1AGoJ8/O799sGaHn63h3v7+bcScTSD7g8ECf/my/Rf+/X/vB37w+/6Xf+2vP3j07vnlBf1sRkfOTqcffN+93e3doEgfQ08zmdHcogT5o7SyFTJILz+Bv7xc3uORvX4ZNqQy882BOxzyeOekgBMpqSCFAt7tnKMmMyezzlChzkchQ3EgE0MjnRqk7e2bJSQMemhXE2KmPLjZFwLpHH1x5oOIUaEV1fryPtE4rEYphNwym70AWEZ9X760j5DPxvJARjePLJqmOO6cY9SDQ5n0bVSQhMvEOXQDCUtCAUSH2MSBKBE9BIkRy0dAznQABh/FWlLho4TRaJLukdOA5/eJ32g/xr5BzrRyhCDqwqVxQOGZEVULajBicMwbi/BRtZhM6XkVjU0cjBQg0+69KlamKsiELwVPEHKqQoiD/qO20tTQ3JQuGXRGS9OygymEl6MlKo7Xtr1MDDxH8BBRyIBShRbUijQycsz4DrE6Dk9dAWVYBgScd/yV9jo0Ehn/e+U3WfkcGAkv62ldSUi4AMqM/+wdlAgVgA2cAohoJaCCSKpAqGb3JGEyWXsGUaWFS+hL92u4m8wsXa7rPK5DNl+uf3/vL0QBcgHBvYp4I354Y4llfkZpEFLW1Tr3hcabFIXgmhZ6pbXdUNSEyzT5pd3tS/7LU7LxuzXCxEJ4+ZLdREsUotqg65R0cqGWd70jxpxnHciCsWNnHpjXiouLP6g/cL/e6zKnwlxpj3CDxz6rlsI4ppg6E6NZ+WZJjd1IqgR1Q3uHyUgYO+JhheKXv/ikyQMVgPMos4AKvtRJayYx+Aq2FFtkFEgFGPjo1U6P/YXw/jEqNWBWLq5KC6/sEpvKRY1TG5GMIpWOAS4xtQ/HNrFfmn0BHIfs1YCWYxcUUplsyYAjezN2S6PoECjdCT2Xc4x4jkvBDJJExGmvOvpH6asUHZDdhCgauEpJssE5ydBdEXPCKmmADK6hUOdJfddIqEWXmFNY9jzZ4jIrxcJDVmozkRuMoUJA2hFkw00YwFWaYwSkzFnGQxpsQHC2MpPK8X12R80xt6yLZZ3lJevIxqPPfva/JTGzTvdu7f6RP/KDn/nMH2CjEXIiX8gl8hIud99ePFBw3hJmcHnITynM5suLX9lYYHKH5+FIJFV/B+WwJIoD8dSIsE3TmQc7h7X2kJlPdJXRZSz8ZXo9i6q5szjYiI5fOvRps8PhtHQT5jtsR9k4GE9HlxfnrAUbcoAR9LfDpuBYKJsXM2AuBxSgyFwk56aOQxaZ455RJuLgCmenWTsRNht8538TCwqnLCL6/OT08fGjj3/oIx5cxjpmVmx2WLTN0i5bMRln1rZTzPDRv0O3UMeeokyWVgkmlC+xuFlnT24UXMKBzIbKEoR4JJEm+QwGIBxG2ASHTUqKmeoO4yiufCRhJXESmXyNrMyRNSZjg9Wlva0O8/EjrUZG8VPvbY+ZIciMLBfluuSEb0AvyLElGJNFoLfH5zF7iGan3qGJQ4upWtYtTpEYMwVj4QwfjjgDb2hBrVIIMorcZAyLjoBEj+TbaWmBEE2L1cJWGdTjmaRzxAYAUMMrs6fdTYuZAPILZ7+uFOYsrbrsMMa8FPrVY8ZaFmxx1hljOjlJikyhWyhHPigPOgbzs9H4gvOwwIwv1OnQlSJ3f/cLv/Xu24+YMie1Q3pzRjBpwxEyOxouT5boabalsRJMdwsl5kuoblJebr5tKgHhgoYsfn1xEZpy80lIdRQaa04oAO/G5WNKE+1p+ggXm7cyI7w7mSw5xxljvlVrHRwe7G5vkwuGPlrAhEykazW3ttIu0ktTKtGBKgfN0G6XeYaMdVFGjpQiG9oIVrPcf+XencMDeIf1QmTVo9gW7P0JYUAM8TGLEFLkfbSI/s8VDBJdVhJkQfkuUNISrVCiPFy/FvhhkNGNaaYVAiV9cimpjWMseV1AE27xeVXWUJsMZqArDAJP0RZFfoI+4uUH0xdQfApkbmGNeZFAw6jkAg3lTxWdxNQv370HedL7i0ijtS2k8/7tzNEhEzkG2ztM7GGTN4R5ATNELcmFDMoOXayW40WHk/o8BwOpYMKPawBoKxmsIwIrQNx+mEPb20wDnTLg4NHUOOqYVkf1Wc4PD+/9J3/z//hbv/ubf+v/9J+dPDsh+cn56fubh2M2eU0rSb8uDaoMVnNYat1j1Aq5Bf4qWltcL8iGBw16Ioiqa4UV7UiZQ+YkDwvgdYxjIii6FCskD2noMABWbvIa9VOeFQYC1VT2KjU8IQik0+YsyGAd86Stj/BgPuFtVDmDFW2B8EJ8XkhAhuTKc0xXGhREXDSVO4pkVwyykwhzUb+ShY/ZI2ooTdYYwF2g6+CgGtoLVmbQZsC0CEyWcrcJtlNwJioNMoFJorUCTXiXkhAQHZjWnQCLBqhiFlkscsVgQulaT/X5p0BS37zJr0hFKZzlk3YmlCfcAIiwqNzU0gUDtp7TVpe89s9o/mQjpZFAKUbEFLTlloECzQs3CQmFyEl4cSylrppdKXckoaQjqFyb3+qVn+Di3XTXl2jlW3W7/mAwV0m1CSWhwaBpSElbvr03XsJKHFLoTPXFNQDoP/chLgByGlmehfrSZeFeXFVPBQjXl0y9GeX6Qx7Kl5vfbz4XFFJ2aibb38zuax83nkpo2BRmAWc9vSsjmEPmupAy3l06vqXCwEt61VYhI1d0kWXyslBPubC41/wyIhctFcOFjEuSnOhUiT5eARINqNIANF9frXoY7UJR/VvfkR5knRAlm6RO0SB4Xetdikl9GPSDU+CsV5fk0GhscUwSkEzB8BanR773CjxLQb4cPOiUH9G2wjNqiaKko8zPbLRL7Vo3H/NRxSiGTOmkt0wfNAv49VU6eZmP1CGqtObBkk0z9WANNTLBHzLqooLNoKRSc60htY85gCc2ivGbeshglAdJur1eNv+jbeBcJHauwEZkx30mrHet7DhDcJ9M91EL9eZzphGAHv0jfBLaB+0TFHuLM5GyoGfOZu+zu3Z1mifM83GTU9xwOPs1Xtk8ni8H1M4GcNYM6dV7bLBi/ccpgyqG424LMB8dKBWdI01f9SNI51gAdAjTXchPox8iQ0K8Rx5xAB/pq7BWgfadM2t/7mf/8eFr77v/yt23v/LVb/+OP8TEhm/9lm9ljinNCQMqgFVvywRgKA9A8DGOBEq8EbcX9VB+FWEjXtL5fn1VVcpYpCkXWegToTPGTPD4ErSw7O+QJYQzP25kzgoBdHOjMUOLMf2EkZo1nhJtPzphNsC0k8TkGTA4T9gz3mn6nAVW6zhNY0L3zD5UNHgpCqNZr0jsxrtOLUM56v/hAuQrxJzX3gX/+vIeO0msGm8wgK+xbSOoNqYJwXPcY5otJydMb+OVffudp/fvvH8yPhkOtrC/2BSHKp1dcqBWagqv6/r52VXOs9KvLmHBWlJesCHsujF+fvEc2xLIkElMVNNgK1r+Qo3WJXgQiJD3B31sWGZ7sGPEejXEcgZfoTkaTqbsglopB2EJMf0qYggclUMtoJOz3t7ua+shwSv278GYIEOoKQhYhVeQSSMAsiuuWNI4wYL1dETR6TPDMeaFoxDgD8MsUB1p7TiflBEGxuU6UJUd47vUMduKtKQojMmEwZnbg/YOh/VaVzGEKJ4DOWOG3KizDBWSO2xlz33MpmZXr5gYsQmT3ent9bK/nHZrrItpP5rpwFqwhP358dWqhdcfZ3jtajKh/jCmgDzFS43hvg0lWFaD0H31iw+fH1/s3erjYEe3QA7bThRUZgC89e6bU44qazLWBEEvtRTi3cyRqXBgOZlO3NxIcZROEDRVJGrrRZ0w9YtL8QntvSnY/uci0KcStTyZHz5HwnmHMKUipvjYF89N4bgxv/AU/TyezliSgenImV1X1F72FejlhSg6O2hWYmp4uiq7NiGa6kYFnkpFf48VMHMrwYjug8Nx9KpxeKxX+zu7h/dfBRkiRjGq7YKqeYdnBUG1cQRUC4bsrCueVEMsHiO9PJZih14puOEpI7GFy2WsXNev5YF7+QQu0QqMyNIi4xV+t0SHE8C6Ts6jZHP/KyCjkE1vbgoD6t+C88H2TgaKIxck4Kw+1JFRNygFgZJ/FcgPNRPptoMqYRAaf+SI1dMaGlWDwpHTfGAFEa1YfMMihLsdvpR8hUbvmX4a57Gc40JwX2DSRQMrWXCGOOvl3el8Pakfa3AvD0i7ah65n14KRVU+OXk8P8qQQr1zeO/uzu5gztK52pgGjvmL1KNbd279wL0f+OJvffkf/eN/wG5bV6OrX/313xwOhh/98AeGPTaOo46uOSOADNXDgWuDl9F+kNb5JDslYNim86vTajKW51GVYIw5wqIefdyhh5g7mU1HuwnKyDaRwMg43EMySc9/QigUgHzVkMWabjn7nfL7MTeadTYsY5kqWNBkoumMiqYFPWqrTkypmnkH9fYDgKw7zwMyHYDGudRydywzxTnDAw0IY95xM9Fsaqej/TYGv1oTRcmAon6RSAmtDKjBXy1qMuBANIFKGoqO6z8NMq20Cnbdehb+M6PHCa7ad5bdGmmZ1LM0PbZtFkX1GKEIyXAMI4gYEhKcNBWNrAAkrQhijZQviohSWUrGnee0aFVEkrhGChaTnt9gzIMJ+SM23RE+MbaLekCu8dIwtQzqUkxkTVvaFletxJQKPDS0hJSCS80fIKLk/+DCU7lAzODNxXMVYu58s1wGvbgSYpG9iOUugvzmfKFSeGgFUNYJ8OHr7cwJOu63jmV7nXnJ92VUiMIVRHx4DxoGfM31jWN8TZLrgJKNpIKICYXhqE58bvZgFXPUES2qheOCDQ7dQiG+pZlHECCuFZUomsIb2BKrpCqcreDLHL8Yr/yXfqa2FsSy190JSoXaMBrl5WXVpTb6zz9CEA7kURVGXNWrhfBQPk40tx6r9ZRY8lFYFQIetZiQRO1rZ5ZEVClFcglafDUDc3Z8AV2Km53yBoI1zknctNhIJdnSc7Dkzm4ngJy0aykAXRqyUKETgDqyISdj0wLBc78pMv8gLwS1BAo2T2hiftLrSUcm9SxSj7NG0hhB6xxfZ4YBKZKzRJhrwBMe9lQBiAEl6GZgsUsEELbOUpXICc1j5wIjKc0NMLHY7HKgaMgBZxsb/Tv5FPiUS12ALtFVgJjjVOAUdixCbDVsVqiqBpbE8pFEqYngQrgMQHyas8nEIoOBxNKDTjxMfM8tYny2Xvvyl7/EWPDhq/fYB/1P/MiPfO/3fT8riHvDQboHUpSiRRDIgUdzK783JMlPypKfuRKjKJPrt3yobuV7Fc0YoOEFqbCaoHVCLJmCEy4ofxCKNoiSGp0OFBHgO2rTbI2pcjaMy20NgIKWw9jn3Sak1+nOG4upJlwiynXgmYWtB4Y+LaFear5KUhCijHiPYRe+QHW49VNZkR32ixAupa65pEmFbDienR3+7NnTz3/ht7/pkx8mHtNbaHqloCa3wlTqLAI8urrkqF14QdkQcm7kifgprogaRraqGLaLYYVRKBMVrbiUmsOcDSb4Mk8DvOzgWc1sVkGVAA8BR/UptyLPc2AR12iqDRUNlWVBE862DhyhO+hTEB3bYM94C2hDeopHjm4cz/we+o9O66ENYGp4cz67Sj+lNmMgLAaQmTP9hvOiZkwuam0P+5fjiVPPWYWtPWF3jwta0AdfNGaYDsBhSW1UB4RAv7CjPzuVUBh1C7yOmuFcZ9ZFMF3DGkKvGPSXy8vV+mJdo9fEiuQ2Qz6j2fIrbz05G41mjSnn4I4nzJcmdQPknNnkdAtITN3THwndOLT56vL09sHhfDmm5io+1k8cBM7VfuurD6ONRBhOSLcoqCBBj8hRHbapQpaAGOEQfV5NcPOS/7znx4fyXIDmkyJXPtxMa2iuqn75+iK5Xw1BcrJ9IWR3ntxiulhM0TXwHJSYFjLPzEgSIlpMS4NLgz4ypgS4SxZtvXRWn5S5XXRmGWqBOE06Z3cPmEc+7A2VR8qulRXdLh5WT0kSLKiKqY2wGPbwiWj+BH9qKiw1fpIllBAyF1pVpBeFS7lehOY1cLxR5PKpAmW5krUPfr+REIzSlPkp2St3pgcR1XMVZp1JjRO+F/E1y0vDegOe31LchHmT7WSf0tsiWy8pJ/WLsikZEs7sFA8T2J5SjRxJY0QRvTP1fFzFnIpH950JkDmdl7jMFpRPqasUQH0ssVKJVEHRAepORw8sqqA528c5h1oRddamX3X7tEHu9sRUT84f4dg7xg/wB/+lv/w/+b5/87v/N/+r/+jk+fl6OaJdO7867/W7nUEfLDgqApgWAqh6x9AkEgs7C7EHjWu+gx2uAI8wlAvky1SFQkzihLdhu20e3yEOYCRRKlPeIJEK0mArNt8LZxKEECPGtIbkQRlLNCkJNfA6wjgUD1qBpHZX2T7CMQGd5/IJyxWthBiSR9AQBbAU01KClEkdCHD3QUJta1HAHUgftMALIFAVzSdBtNalvVWssJM6gRI0E2iFpmTSBgP2gLIcgOKL/FHYeeTBmMQjb4IUDWnCPwopE1NKy+hiM7OnxQn6lihxwT89fhMJz8sERdjIQtAEBS4QkRxllILozyN7srP6SYlE9JlHZZkyQk2o6vxthA3bxnoMDRBdWmGnolAoEri5KvKMF6xr81dJekoCPuTxnosE5SoP5fOLSKXc5AMiJvYGtfJWiLZJ75sw/E+EUkmrjwmrngucAsFOp5e9BCGXNx4385ZyGAfvmy8V+Cpeft6zF2nJyNjXWb5IejPV13m2cCJhbU03S5HiiXEJ65AttZ+KLNC9fmS1km1kZo+Mi2KXgkRaeAzvTJUr0AUVMSiSLgT/e5F1ICqcARwRITQ8JB/lLbQwLPHz6xMVZwMF0tuOBiCyhmCkQJvyASRCQxYqREEh9cqyjKVSo2PFKOKpmlFgqwoTvMTTvGJyYfNQvVUxVIrWsxRHdIIm+YZqzPe1eqsTqcIIMXZ7CsWpW04rh2zKu7jyiQnuTrfnlSyQbMmKRceiXILwRuKPFmXMKHUZQVFPpFdTY80TjwJRRpfqYv7JHXB9rNIKWQgXePupXAND3QioBmu93fnGIwCgeWUtE0XcQ4nFFevlBCj4PvkaLokxHmEqHo5/Z6QwH1hi8bn5gBg2cXZGShMbcuGoYFIEp5YU3QG7nbhClNXzp09x/H/oox/50ue/+ODddz7y0Y8+fXr08Y999I/84L8JtZkx7Nmt0A5ySA8yIV20EM+8pU4WuQIe0RJnE2wQF8h8gyuQjAN/o91QNTgU7KgHZeaVYifKGmEp19QBlG7hocHrzkOyprdGcuhMI8WsRVMj2s6jcgqHvmSs0OYUGpNSVJk2xEix8yML5Rg/eYRIN6eoPfvSQKZ1BCxjAupoPqErG4+YSg6L9Q+JgvlgB7Mu0sGHGeerr2ftc3CeLZuPj58dPr+zf2sHO7k/6LQvEKOsN6VCg7/cbHI0AUOyTLdgVKIishJI08tJYExqoqPJ5ozkTMHJy4FXCaGgeIEwF+9tGl9y73Tv7HWuLq/YDxwDwq3crL9schIjQdmNjNEwFeUiBCa5UVa7H7R1FJ3fPpPo2H8pjb3ircjZ04RFkIRF1HjGreQun2A0gDG8xc4OJx70WTnqPCzscwc0mGzA/hL0bl1Ie+eg37+qT6aX8zENGgdZ9AsPKQosgM4Y9NQL5FP+NPVT4pTQQGdMg/laEEBXGwtWof7q/sGBOpAJxJ5uMR92bi0mGC4P2cv+5HT57PLZ2WhxfPJ8wbIERw87tfaYxbPsloKywUqIzUfOJ/a6mThHvVmsz8/xmvfJUfPYGRlURLrK8y9/6Uvvvv1VOicMM0l8IlB/bAVtySMi2G/MsEAWoBC1jwKloeHhWr7DL1LLdkPLlYfrt9SpDW9vhNoQm0w+KgHiUN6E4lat8Jc5Zlir7ubOahmMvNElG5eCJjHQby4Whv8kgyD8NGsHEGG9xuajnLhIaOMz7ZPatcQb3aU0q/llk1W/3e72LjvLb736yiuTMeMzgLCOmjX45AdkyLyUliCebVj4JJ7UMZWrmlACVS1Wle4GhUhTBVq2b3hVBDGzxK2zro9Hy5t8gCYGBVaaHpFAp/NHVr4YwR+R50eRMxAkobKNGhGpM+vFAcG11lFgWYSS44aXVJzkWxxoRk077gP5YvGV6Cm8qU3PCzsuUJuQYOeR0grAGRw6XCqHLEXH8MdgFJ34tv2k5FkCQx+Cr/IAHq1jDbl0CYjl51I2PsN3pjWOz9mdmD42Dn70CU0eorGc7DFV9ejq4et33/dNH/zUo7fe4WAHJPnNt98+vxh9ejh0VQ/eE5Z823DonsLZC3C6vJIsQ+p84qJMRKCkkJVY6fgZxf+qZT+gZy16IoNgahAlIgA1FkbIk0IreJFSJKVA+CMOGoLWU9mCCMYkmqo5hEi/SAubN1VF+8isiEbGjcfwkwUAtNLgITSk3pQMvKMPILtZSDT2SBTbI0UBUpOtrYIDIDT2+D6IwwRIY7M/FTFn9wClrDutDoiUNyVK7cKfIYcoK42ojnNQpdwkI9D+mFuf2RzAEYiWxUtgLM9ks0j5T/7ThIEnfxJGVHUzARkNXgSCyOUfX0nAG/n4Q3pCpIlWvYHQg3BSEw1wTOWO1YQRT8zQxzLExrRZ4CwFCex8btvAgoJdAkqgh9PSY7XhekHYi/0GymYr8uXhped8LJ9NnNf473krAeLdeRdkS6GMYaESE99/IvGtBPJFkrAbEg83Lr/zGhqsszZg0wEwUvlaQFaQk/YFDMEm6Pe+yY3rSEIUy2+UqMrBmFykkbOWDkGgWQVkFUPCJwcAo5etJ0zEpbVXR1gw421KQKOF8EkR2ZcH7sgcOBXSRRcJj3ClUKi8EZ18bYDLpexLuQAJ/c0qbwipTgUpT1jUVqKSgXmAX/BNhSaB/CNqaoY3Imk6gD1tO5H5ZDolqGRH/OBKSq2eTfGIShlERaEVpEBLVrxICoN8iPItA/QRTEtHJbaaBRFe1ekURBeVdhiaKwTLYskAAE5qV/r2kgh/J+4EaW448IIZdQN5Essgb0YZHoNR0W7A4koCcVatG9caBi4AtB7iZGDKAQrCvrTbGMNE+EQOoI+JA7FNZbkCjfF4/A8yHiiilMIHrtQ2Q0gjSkZBsHSK4CKldhfDFlI4GfSdt9/98htf+eIbb+xu7Zw9v2DXwR/44e//5Mc+wX7eTCNBxeMHxQHMjBfap2SWrApcc0nGFiQXvymoKPgsxl/3Crovf0EESAZWuejUTK6uRnhlYZOsTS78KLMqGChm/jwrGPAH9RlxgsghNM0AZGSWPiINMblj+OmkADUnXkFUtKlPcA9Y5B6KOb0Ta5y54yxm1WIiAe0KpREJJYYMYVqRLD3T9hVY9tXuMAkE0WZ4hiWWavT40R8+frC91T85uXD7xk5nwSFXEWMRCP9ycs/l9lZZNQUohxgAC7eH21tX0zEawczNV6mRrkIo6CIfDPFzZnAve8O02KBlPpv0Oj2kh435q3YNaZRWqSM+QnxW1dIapZuUT+llYdVhcTAAzcwEi8UItdITacFzz7ad1AdQc0kup8BuMY0H+jBjhuDVLmXodxAejuids9LSpdxQjqm07SUnBLdagy5r8jpXV+dXF6vnJ8cjjq2ij8AO8ZSOYktrILvoxyoFtvzoRmNgkvE9OkI63kTGprN2cHe33xkyFtxYMcOFzR2ZBrdYjXHDzy/OR2fnV6dM9p8vRiy8btKb3cYJ0G73J5PMf5UC0iP6iCKylKfJ3ImvfPmL3/6dn2J7J0jEqJ20wFPUHHICAIHOtSv2maiFeQoRbSMvqbYciIiYFaqWamBGssorJQory3sCCeWNT5u7TfTLV/n2nlDrAcn8S3zfvCLWZjIajVlewu5UVF6EEfoyEXw+Z/5/i8EoplxCSU8XolJgdWCCMrspVoE8Y2uqycheAj3TTh/60Ctjpyu7OJYC+JQ5v3CqlNTqGBkj3CKAl+rMmD7Qh3e4p8QR40ThN09Ej2TLk+oyzoYwPLyInvDcShQf4dcGgIEFpYqoaTA2IansSZHK5FP0hhSDetz9500z6MVzsgqQZOZ3o93ASyVS8aKEAk0lwWWpKrRKPmrlkAv5SxpekrGVi28KVNwKqKDS0JggqTSyVYmJ4Q8VEJ1j5aHBtAh+QXGhRaQDf1hlHLzNuZatoYCZJQhYlpHgAmjVegy+TddnpPxLf/V/+qlv+8Tf/Tt/+/GbnHfGFgiTw8M7dw/vNbWQV7QF4gY8uEyLpb9ATEqGhZgImVzM5NXwI7JhF6UgQhlJUbViBJLeifuFPMo9fxWpLBAGa6Fa8iRtITCZo8d1tylvKmjSkAfh8eKhPhwURYNAFrLjuxn7pzKTeuSdd76iymOiE6Y2UC0DSjZFCSfA+LSeRLAsZK4bnhDoAbXNnw/aZmANbYJO2MlnYdpg6VWRh9YHGw3zJzKaVCTtTaF3A0FMKBnUlRiUxC6ffRWpF37raTW9HIDi4FQm1yUYqMEe2pE+tOfHIkgEfkNUOxvWdv6o3IXq3IllCQyH+KIAsihBRhPRv8FT00aSuTYR25/4yI6QGXrksHAHXWTstSrgo/RP5v68dOVTPlo+cy6X5SvJAOAFar5bWEPKPV+s4ClJlcLADZhEeO+tdACuI2we+K3WLN+MLmW+0VWKYETWYoskc7y4uyLt974KXPYdMmb2JVCYobX8UaiFarEottKsbcg7jIdryDFOFWyNJnu665d27TlwaI1DCJLKOpEHJk0nd5LZqCptfKJWqAsUL//LI4bVkiEBipmiYIxI2fzQknAOokHIRHhBZZjdtT1m3rl80TdMf5BJAzE4ASre6S9SkBRDsbZLTSE1pRiSZLYQbQsXA5MabNQpF96yuxF1LABBwO6n8gzqKZEjclvDApSDkkiFm4QySqKgbXmhpSVTKPDN4a9iBxMEF9oR7jQd9SIo4juhFml4MGCOFnJUS2qumUxN3lRuogqhow0ieKYCME0ixxgFCmha1jk71C85BqzD1negASFAg8rFJ/lS+MGvDACqJJHwhRFOuyKG+YoSFg5eU9z2Ko1SEfntBWP7B9hFCooGmVQuQPgxKXdNEH7Db7HjOMRDyFlvnLk+GZcl01FYWHBw60tfWpw8f3Z1erG3u33n4H2f+ebvODjYH09wRaNS1C3wi9UF24MD5lOQq/Mu+ESeyor13ptF9Nki+VwKAgyD/Jayl3deuaoPeTaGYPxtN7czNDRlt4ru9D7zEOqctCqhAl1+IadqI+1rfiLbEplZrczqp0Fxng6CxMwFzVLcLpMpE1RaV5fwjjFrHM9oXblIdzcH28Nz4YIAoRQAdz7bHzEnh+V37KMywfqDYdQjp3zaOJBzRXBnS9MU0Y1gynmd8XpmTNFQcloCZydj2yLrT4+Ot4e32L3ZSfUMFLFmQeVoeZBJmG9VdgQJZznuZ2sl8hxqrF59nTnNSKCUsx5DtsWuVarJKpoSKG0ASNZMAKJpQYZZ5Mc8GpZ90uUYjS7YRRQR1htFKf3PvHnw0sb1PGCZtUP51vjC42FCvePn7rS266sR0QFO0YjMAQyOc2QpHCMD+3d2vvUz37qaX3DmBXY705W7bFDdcrwdl7+TzBd9xKVJdiSuDRDi2cRzeVrDzvageXH5eH41YXejzGhjxMbdcJnsf3JxxWJiPEy6qxDu1jl2Cp0xylyafJWTG94ylMI2RWNrQnOk783dheYnj55wxFGzPr1/t/lqa3+1vHV2shjPL7vt7UfPl5ecA40D2A4DXswQFrpSlSi+Y1xNOp3oM/kTQVYeQLA+e/780fjKnlj6KRIDTVdb7VARWa1BfEUSQsYbZvc8PKugRLaU+Op68SRjy0VYefYuZzcfrn+rEGnJ5T3RqDewMfJZb10Yqh0Cmphr9bPzC86q6HYOp2MYTSDdJwjFQIjyu2qcpj/H+Ak9tJGNOpQjLRMSW9QUlgzRZa1vDQbtzuD2/r3927fU3l7milrKs6/lIYXOYxSPIqOggxwqj6nD0FktXUUW8Y3uKClTKa7BVfGuoZdk77mXKKHFJnYhT4EHrQgmfzhDiPzZ4BwyEmBTS4uTrejtn1BAOC5eLzIyOWfjGACY6oul8h1TrgAXNpPmUcfjF0ktbFAIGiUtkD3cXDiMRftGHNrMPEcqFTo71uDM5QgA/g0VvgSXZOpfmhjzCQL20VFogQkCsNjCWlyB58axEaPlr/3O54k6QLV22T8U45fhwS/RFxhdsK5mdXB45wOv3vnw+99/9PTRnTsHt/b333r7HbYV+sjHPsS8L9yD1BGytbcc/tJWF4KEp8hNYSeqxvF2Gl0GNyBQtrRxwNZ2LJZBoTC4g1nGNyiYFaugTAoxDmMUSMplL8NxbZlI/tkTQCnXqyVx+OzaKsoNclRG5nDyucNKIdsvyMBF1YXIKHPW6iv9mlJCY9uGNicGSku4n+pefyBtonLAWDFm5iObrtC0TDUkgEZfmjrfWrwiBaALUWzxnazMkDO+Fdxn7To+HUYvaW3n7FUEkigxojPsQ4FlEeMRnDbJ4gV9bShZPBTwZT1jpZLDP0wBoD7i/VE0NLtFG0pRTPxxlIsZBJTLKc7GtLHWhCM+1AQfIjt/k80xGqzkZAoArhBrPB/EheJgxGArwFgljiKYVtnnW+SpVHeogVJx8wYQMG7Rb2gQMrEUCic1a3G46u5w8KAldUtD/sT8xWU4/28GvfhYgkt85UuuEnYdeZMw0AuaAsu1iRr0b4C8fqwiZl+gauAyqHwNPhuIwdKXrwFJ4DVOgQ+yJV7eNp8TmJCXby8gEsdo0g5rwBog3UN9CGCNosWhWqcuSGq0ApxSSZCGOS2QnWM7s5JbVixp1TGdia+ghM8lM+oFSQRZ4JOtwqoOIwzmwtf6ZDQGqgO74qMI0BQAZ0Lru+Cge6yzcyod4fA7aCPcl0BudC/ZHENr3SpUY/8UJMaSKFVgHcEVa7UBspQuAdZPfd3XeYagE+j0x9IAuGEcubADCZaOZHHvduWdDAIhlRZzB8FFuKcTjpi24hK5SA+iC4bgrmUmhexdKFFUAIGgiQKKB6QM/2K32euzRTy76zO6jaMLRyPWb5OdYCCEkVAW6mH6KpTC6UouX2412PPPqiETQYyWQE8ZBUWloGuuRrSplKnkZbUSmKjKm26PpQiuXuAFQ59QcNHQYhiekUHP/WU2L09Od2S+j2KiAg4C4EA+BkEyrD7ZBAWgG4aJEf3gb4Va4boGAGVP30dMm3cO73FA5NGbb9KD/NinPv7v/cW/uDUcsvEiCVnQKhec7wGJ4BGrZyCCQC0J2QrbwlWZVD8gcvMyY6/QKL++ifrmbsH8bgA0hPLhJDtXMO0KBYppR75+LnTml2PS3UzNtkGfSSZhN6fL1eVoJHNc+UxJYQaVBX3HojHW1RM4dVaRR0JwoW87ECsyGamSWFZEQ1whiRFEVwM29QnF8WkilZLdA1jV6/fQ2ukQ1lhxTjiHddqWtJYYU6y1HtcnEIkSoTefPH38gQ+8xkpKdkojDLJRJFjBZlqcIDYdT06eH927d4elwFIxzCIzbEpmX0xctsRFWconMIwcUXhKpzpf9wbsmOmwoX02lQbwmRHUGDDVvtc+u7xEUEtLGWJnqhsH+gSuGUZS6NXZrbKVWF9Oz7d7HVYS2LDwn87xssFcehb3dtt9qiW1tdPZ2b89WM1QF5jU6AoEkRbXVh8thGXf0qS2sPZsaaDdKqA9u2IbIBjTnlzNmfvEZqz6j2xX2FmUBceTqyk9f7yezCIGEXpQNMBOh+XmjHXrjuVf1C/niyuwYj02zRH1HAi00uw1Xx/U7957hbW+dMYvzs9YGYuCYT+VQXcwYviFFQpqJOAoumqswLTe9fERMHOeBixfJA0ccdLW9nD/7r37x8dYgdbUjfCqmTH5aEejTGWfcMXSp3IzgDfuJeT6tYRUn298rZIl5OvcqvQWwTqYq/z4qraSmjYdLUwNJgIdXb7r4EmbzakUKhWGM+LQfJglql60eac9SBOE0GNSmJgF3VN9K2xrWz+8vff6B17lMAEEPFmGfpI8lVJEeAxGGxJE+ch4bCJdLFRTpZ6o17QIWaoCQnFVVgge0n2dgpNHMn/506bwYmAUSSA6ZnUNKw+EgZJI+D+RDE/WBWqaHj6mMIAylrhp+hhacOanXCVCGgm/qiqTJXnzbhy0R2hUIcIzIcmUVHynZtlKUn+dC8RBLg7tizshNhWYVbaPVHWFKghYHWxH0pYYWXyBm7kZ5krtN2eeVDbiBTTWhGDA1R4/fcw+sJz0zIAPdQ4h6G21b9/dmo7Prs6umLr33d/zXTPWjXS7v/lr/xL5YQB4b393fWs9rGEDIBjJylFvSCWZhE9RzAz0ZAD5I2LMQWTJPXMDmRZOy0s9IYrNoyRBcbraBN1CcksANFRXOgkgT8EpHTFtsWjh0sCRDqWMXTwdc7gVcsuOApmiiJmPkscfmh4m8s0SLhVZegpASR8DLjqfk6aAykpOoIBckoV4AN9+IDkQGaebzhaoXqYoQE2aYOZ3ogppjDEn4BTGAuKMLSyBVc3On5TSanmEjDpUX3CsCpDsaam44DKuDCwaWjSKFx3B/sZ8cFEfrirUEtYUuIsnkcEHVQkxIk1QRYogYtJb6qCGqb7MZqZbH8+pLQKhYb8mE7EmY1Qe8NVZLaoyBLd6xCNJVKBzcZwHU9FsZ7XvZZFZQIMs4ZCShKYZtog2myCnrSEO/INsir4/GrEgLoCgqEgYzas8JLh6vX7O95duqXaGFbECeIlwnegasHH8Bi/Kx5tfSqJyT4T3bgNKAmN/nRRV0Nd8uc6fZFW2Ck4UxI1zhW/m+97nFxBR1UyG9S8XPzSTcBMB0K34oq8W/FRDKATEF+JaGSJ4nSemLqqV6Y209JM72gHMNYfzCqVKABG38EBY3CX6svHYOsKCRTqsTqKFYdZdNnvGygWwAknNMyMc40jwO2LtaVSppdr3aFJ6G++qHrEoMGh03is+ijeVS+ooiqZRilNQVlAK8a6S6i7+VEXyoCCJTkTKxV4fyrDYMrdBi9Dq6lCXsYIqQIFHDmoQ6QB25mWgAQwIWGqkluR0aebUJHdEcVg/0Wiv8bmqsQCC15JNftKpodpgONl9IL3LDGjZiWYpwCF5SUYaTzRTa4Y5qTEBBv6DNOJHsS1tCZdj5sNXS8TSUsuLhaTzJTYYMZfrGe1k0IcwS+ZRoPY11O2mYV1ggvCsDWRWtgraG5QOwqjWnTYGHc1bXCWCrCc/CKMFh37rc54Dva8e2KJl2D2JmJPxlYMMTO+Z3729+8mt7T61njXBUb9AsRTwcjZ7e7rYQ9lWwEshk5vknr8iBVoPzLdcEtUnUVn3fcia/XyUlHlIcE7e4CAzQ+QpZXTwQQVFgRoPQ1QDFGRdIPAaHnm8kwUkhUWWUxiM7PsEJXHW4f3M9LG4G/WRQB3MR6RCnCAnXGMuOP0+uGHPWB6ZC//ThId0kJc8cbVM6UnKWZQzWHCsHI0D3g/6ENhSzMUCBxfDcmxwfapPPz1Z6gctuUp93T09Hz94dDQcbmFc6R9a78FXtqNsdgY4WgfMnNnaXczZz5T1mqxJwGRCBpVCms7bt9mnigpG4UGOwpzGed9l2JBtQqAAO/HzhW2siLNeYsYhSsyerzP5BTCYegf7fQ4Jev78OayUpQoHJaUskDg9+caFjQqFBluo12CuCOcPLNnatsMMkk5rZzhY1WaDybzHccrNxVbr1nh8wtbxEEFgVgcknjoGSjQ1MIj10qm3AgQyqgbbUyvEuTr11pgOxnbzcrKNEU8zKnUloc0KJHdOv51ap7lRXQHtdhsyiH+UgNjEoQPW06ZQuukaKBz9ne3772eTXPrNE/oTy1mP41GfXx0j5bNZbcwy4cV0tJqyXbl1S9GBVmo5VASG8iuvvPLH/uSfwFwArPIrLj5wiur7P/jqh7/pYw//0Tts+Q/vKBTXunkuITHNMKttI5E36Jl2UWyDMnC4RHxzCZqPuUur8kBIPFOE34xcfd78JL6OgyoSVcCShFyqnyH9UgwdhNtTAuaqXUaHOhfzqxEnBqI2Yo2gOdh5XXucZtv12OwjuWKaHwsA1Lyr6V2cm+3uGQVg0tOz42db29soKZygiD/YSRZVC88YkcgO58chUPcUrtZDOe5fSgj/Zreyi/FzGo302bVRVGLu2IPgsrqJmPmX0iQZVOz59eYoOnrG+A8N9yLi11LKEE+EUCm8dwSeoPA8aUkMh6z55OQO7xQJSaKWaZAFGT8haRU3+ZzUJcekM3/cuXe4r+tH6vjaTGiWTggKbtqM65yFQLifx2SE7WkbixnuhPJ5l3OY168yAU67kqJ1j/DaI1Vwc6PeVeS22DG2hG7LRTYhOHzwqEEZRD7hkRSy1LSzOMXWjb39289PTnBeTK7GO7u2Eavl2WSE1UYDAzbLy/MzJhH+uT/3P/jFX/q1f/ZzPzebLJhGeHLcuX9v8S2fucf2CQg6bg7ukRSxiVrGxCeLxqr90EIv7oEDa43nrPVZDKIQqWextE2GmUGFRUVhmRLIll4HVvT+UywDUaf5RtrAe36PriM7emHOkJwvnD0YguDSWy6nd1bseTB8wtCjUwYchiUX2kjW/uFQ0wbAaJc71E2UqpaJI47STSwhvDijdNSLwA4doRvAsUE8RBxeSF7n2dgQOqdRkxscbA8gbDgqrXmr95HvFXszYgDRi2ixkwERyYbPshlArHoiyaqOyxKS38F+WbeeEiUmnYbfQrVMZLoTZWa9q6m1F0hrK4ZJgzEGW9G0TDk4FO/WQyxuGjUIF8Zz8/IHcYTD6qsxJVkumMuHk8QSQCJFWx1AS8Fp4niI1CNsxwieSKOiA4XIFhrpEXDZCGMvNruY/ip8YouslAvl652jJQcP17ZCj+Rfnt6zK3/18RpXsS6XVBSkOftkzLxZR5JXipRPvkbs/WIKrhuPvn7dyzhlBCCJkiRwvm7sf7VA0m8QEKkK+xtpySUIGlSQLB/lLZXW0vl988yDZiAhjtIr9yUSsWUyUo0aKIWPTUhEksNNTb4YviRxNj8/JS2fMr2Hdxbj2dirKGgMENNKmcB8JAXRFX0LhOBqHGiOgEX+RKN8zINyktoV1FMEbqlFxK/AmFnacGWSAlBFDcktUfNmgKqLYlkwIpLIDhAYGJdaan3gEjAEIEgHv0dTJXfwE7OIJHSwYhMR+4d76fRb/yLyTLewWvKc2W+0UPTn/SRwgKiDqDaqJLKSnlaUEEF0qABY1MIqFywwgX1lGlfQU8+gIIlHHJ0NchOEGVyBLFTslIJqDGA8jlQjwFLh6YK7z0P44SADsCgAtQ3WML5iLPAAFkqRnZ8zIozHk3Ov3K+MiedtdrcEg5BRvKUsSODGwPPKdtG8MnABpXBfKBjQD2WJc8OyrUYXzJjmIGH6NVq0uH3DBaeEY9hxWCRxJHIx6UBFTgSn0Evkbl58CjVL2CZiwjbRZFh1AQso5dWGwaw3sMsjvCl/qR0ypERApDBhMJ4gHGyA73Yanb2tU0Ty4r0O/TmGFA0+m44AiLcajZmNcHgDUsElaKZcSAAUZ5wBT6qTwmpLJkXQKtAt63DGFdJIf9IzWViMToMsX6EYJhTDAwxNeRpZezpll5UFU4Og4eL09BwuoMIRDNRp7NrZlAOL1tPzZ8dv/O5vf/C110hFGbGVS9Et+Lo5vprgFEjVoOh0OJ3r7ivYU26kkVxdKcHeORQb95Lz01TZ8eQCg1owHPTr63129phMsNXovUBiarf5QGoiIzQUU/rZdtan88XJ5dl91vRuUSSM/tr+rVcZX9zqrpqz0XoymPWAiYRx+JrSY03K5HgqHm2jf/TeYYD1PQSm/V3SMWL7XtYqcP7xmk7PVpcF0OggRpyo0Q6aG9VSA1D6Rw548UEWgRnT1zQhqDEz/lFpkU+6qHQiEPTZ89PZ9BK3BkDJkK2+2AyUQwhgoAyfr1i/6u4eHKLkmmaVHOQiVwnWqN+5vXfr1nDKaJGT5q9detL4+dH5k3cfuCWLRJNYyj8vFt9tVZCA1HQDU+Q83LwZP4yVIKX63PxcfUwQ0RLnvd83b6YvnCNv9QwIsQyCww4cl2T2GdPPRjhuEUjqPyXDb0unS3fiYlLvbad5oQo050tFC56kH4S/WWkgZ/UnkkBLSV1iQ8P1+tb+LrPX1NdexEkZpIJvahoTBi8CYVNC/aquRkz5h5gJ29ot/qS1ugnR2Ny5UKX8+pYP/r73KgiUsJvPhASSfgHLIUrekhUfRdkYJQvTi4Vh/KLXSIQWUWWnJLK4JDVKhRipN2CIlNZawAWNUnwh8RQDE0WMnJAof4SW7JK37YN+aepJ1LXjdcyUI7b0EjhYaSO7rT5wtLc5DefFOiyi2vFN40O6ghgSa2socgUts89AouOQy267vbWz+6GPfPzy7OnFii7AWEsTO9URu8vpdDTo97e2ttnx9e233nn1lVd/7Mf+zL/45V8+Pz3DjD8+fn583Hjtfa+xNAQ5SyEsuSaJbZL1nsKAAJSUpLai8AJzlk/ERJHaM+EjMSg60bRCa26QiZZAy5JG2glQa1uOGLDgiE6iFnkhGeQMELKlpzpftznfroNrCizowkn7NKnO5VWXAsMMxUyGKhJY0rSB5EQMcfO7PguoRYZBAdSIx84MZUxPhWafhzJaZHJSS1IYShyQ6hLgaoQD1KE0bGRQ1Yu6YkKjpVLHUbFokgREDnQzREdoksD5yQChdLHhGBEC5aADSsAxJq8iKgQf04nxJ/Bi7fBVDP3vTUaRSlC0Y6CNpeIO4FQ0spVx8IW2Et1Lu5E0Gp6CtOxSwbw87Ih2RkuHeJYxUSUZQeQo2iDpMwRFBvnhL/kb3YIKV4JfP5i4BOSpYGsYUKp45ck0ZJWwzQfjUbQAyHN58jP/uUo21SffqpQvOgBCxav9PuO4e8B7gG0S/v6/yUpymK0vyYT3QpoKZGJVgK6fkwTahDgl84gXUqsNRjcNKPIcHoQ010QvxVYK3IsvNTzEMQcisUuJrRnPKhHYSAOA0Qludg/YhYYcSUsLAe+paO5GK/r2g9VGvoID3iA4CiDaV2ovqQOTqDzhz4tRtWJmOfWNU/R0faE2yV5hbaziF2k+VigVJp0DiA4Wg2A4XRgw+DfxQ1NPwHBxh2kmjc6xfet6N4qTTfbTbDgmmsyXh2LeekwhMXEUYqhM85I5eZaSQs7vyn7XKmCBUTLqHLqTqqjrgkD2lsGSG43pEHPOrim4gwdz79bz2532eLF+7MCIjgPCPfGIwRQLzXmBKKnmUcvNSOQRQx5NiKcWgNSY4HSmsIN0ruNTR61IB1UBlhhZS2K74k5SxzAidU+XW2mhnaBFCdAX0Qb67B3PhTYYmdh8FNsalyqrQQv1ne1OhpYOM4baWV/21ysGlDCziAnHUnnyLBd4R7Wg6wuLOOqL0+EvLhnlp6jgN6tNPYMZOUgroq7BSHRZuEMElEsfu0rTkgg+RcoTuZmjAmdg9eYDmeZL+V5CvAfCJi2vgZmkqiZeV11/6kzD5NfHqBUKg3ghpTYgqFkFFFCgrKHeYCIMrq5W/T4dgGUTGVByERVPbmbWJnUBwW25opHVHWq4bCQF00oO3CmzVVI9jtgjGipBuKH/KJPoMKRoLZAhmEKvg1/rvYxwUlG/0UfU0O3soj9hV/wreIfG3QPJ2ezs6PhUzxDdrvUpRhcMx+ODGHAA55d/Z/X93/uBdfuL5KhQIrSUWbaxotcNdGyn3b2ETdtpuhi8yraeoArk6bhHE4ioqrDP2YVN1Y4vvc5ogIOIHPGGeGwNt3uD/uhyfHF14gJv2iI+Ur9taqMRyNSSuyUkHeKT8Xx7a+v13t1Bb95YMkuOnoMzc1hIuGyNHP8CQ4nIf5Y1aEnCGyY5OYZgiwvCl3RdPW3DEkElNrkCIWfNDbfar3Tv7u7Pu+88Px/RiYUwTZYEX45REaghTuqgRkADymRbpXzQTtvH4Ku0wf3fYE4CbMLtSsUhEt0sWnCchBOKZrpG82JVe+70g0Z9xtAJC4OnTEoAGzzkrIlEF6hDqJDQkYUl7c5wVesxJQahp86ifxRRrzVbtT5/+gh1Mpv2xat5RcltTyHdapdcy/x7hUcyiqLX5hdfjs947i1VCc0DVDGN8iNYr/JrnBJvE5JvZeJW9LaiAvshvYLMrk0KAV3M/b1bK5yvLWbvQJRdKlSrddZoTVbzO6vZgP087NPiDaZhQMt3B5j4kIrOn4RB3VFq9lVTDIdgQHHuvfL6weE9BUosI5zqXdUeNdRHS82wxCM0uyl4F3VEkslRjK0eM09Tc46dSTktAvK4RTvkp821RlviFJW8NkSAKpwh6gfz9Duyz/4eVlApYzDfN9ETxW/JuG6X8jqm8YM3d5EXAZ8iXzzKX9/9J8xESw1ULAy1zIDzn5JGiL1HPlnhms/ME+Ik9/ijIIAXWQkgZUJ4VV1ethHo72AofPBBGhl2xa+zmGJq0R89smrZX0a8Y6nND5CwdesEFKC3iADCykF1o96hLrDj7lp1O4+JkuojVwiwbtLwdZp4eSkCR5IMt14/H02Oj4+7na2t4Xxnb49Rhl5j0Nayrw9Roy0mgC2/57v+EF2C/+xv/a12+/Tuqx+YTfcfPz7a39sZnYx7PRQpa4ysd9R3WyMYSpWdHoKPy2OhjDSiMCgHl0IRrGFMx7PGdEwQ4SQ7yscB1NRDzq5B9kJmo9EcsXMADbN7HNFiIp7Oh4JViDwGDvVwMauTys4rp4owsGX/X5YCXtuei51SEGpUAtwxzE9IHluTOb0QGkHaKAp30MJCkYFWAOqyDCcz6g8McPa+IKjCWDGwHUc4BUYUZDxawGpms8naDyUpgwMAluqBxEw71A95R2BAzkabrRHaz6h1VDZtAI8bK9PkSg0Df8QUiggCTMLhkM1AAIhTrfkkPxBVpzby4CeVAp9BCBx5sCRZgcOAKovBNFTiDqb8khQVGk6RCGGjydxXZFrHYIAhpNZNhUbwnQk63bNNbVGjI8xaYrCEPDSuwCGXtIDa5qyScNQuFBVZwBonrA7ySZGwEm78/M8HLPN3eKvPtdJBJJ+8o2qSiJv58k52Xjzk158SUgX75kkpNzoAJWKBsHn+7/YrzGRTZUvxeHpBi3wMgptcgtPmxmcTwuoSBy0BhKI4YANp4EXB3whwPO947fmE6HmZG4KudQPL+GBlcR40CZ0Ak3AjGZX0CKatnYNK2LcemAUl/QzvURe4GZxXkE0YEQw70CQkvio7SFDt8WUGUSoEo4Gcs+FRW1ZVDt5k+xE8pzUmV2AuM+EkEeF6Nqpz7m5QJnf6lGwaaHlpSBtDp+h0WHSIAJfZyRYDU42eZ6zP1mqheqpzTK+H/oBF9EKd8w4xNbQP+Lpm20EycA8TLp6o5xzcy45RCr1iKnlAnypY0UpvrFiaHLAYMpRdvoE+kxzU6IARvLEyLiFYNVEmBUallVJIXDYNdGwd9SetmWdONDWxlVMizfAvlmqDxV50uKJMEif7QHl0kVWOLLJGh7jOXprT0KKcdBJAHa1ypj/LVZ3cMJTSgiIJMexw9IEw6MpT5RPfJ0ee6R8SEZjE8knpA5WkLVhTak7KQmnS4YAyqig96zGjUAy6bDzNNeJm6ZEy+RqBqAS0+ia1XlwlRt5JBDYlsnx8Eak8VQEAvb6MDhnIyf/Qlfz010TOoVjRL4KSELXGrZ1d9FFteVtRZb6jZiheYDbgx+hhDRwzXKUASwiYwg6n4IeqULCAkMtm7rwdMtT9pBJW4RNTDkFwVTcBHKjUw0j0I3c9+2hVuF6bI2xMpwRor9s/u8D3A6HQsHryONcT/oIuVVNqUB5zdHuZ3/iNz07nP+EO/htlwHd55XF1rNk1nFcNrCQGIGU2f+4ePTbr9wfID5adnhyYLe/CRNiMEJKchnrdHG4Nur3G0bPnSxY2Q8kUHfi8gFpqOBhmqGPVeD46/uI7y/1PvgoElhVP2F9zPcEQZLCBDrhrGBQNWymREl1Km5nelJY1vQ7MY8VIWUpCS2N+lBr9xdFs4s5JtUPWc7D7LV0c6jR0cp4VDSJRpYC9KSDb/qPiaOqTESGcktxsy1aUmexXPEAE2QV9XFmeq8qRY2z8Q3VA6TDeczVCil1Xx9ZASLRUgtmyA/Kwk2nt7PmT09Oj/hZDatBFoUDp4SNFezx79pypdtjKs+wRDRZqDHHMrRQyoRbLpErsy5eU8H8VnhhJdB03KYlQYsp3L3/4byCfzBJlYluvRlcSep0W/t1he+BetEifUoz6Q4Ny4f3VDxEpoopzrCyltquPTWOwUoX3gQqBgAifjhGBbITFoOT+7f3XP/gaqoIPzvWMqWFScFOWxaiUAwTli8hFgeglJURpQbHNa9PZerKlUiYZVCeO1q2JJZiQuAEhJc09X/NEZMFfU1aWXV+kTtIE+CSlAo8nE5rUm9B54Mm6Ewh5EB+qNj4O67mWterEFKV86ByeC54GbZJripFTYCulPFLtQlgzow7yU0bQiYZ6iCyzJg0FIY+i6gFSNG3xrYqYiiFZSyfUnKrYIWAxNsuqvFLfix8SWZ2ht7iKAowgNVxDbTt+ruTrs3I6/nQ05viXL7/xZVqzV+/f7j49YsuDO7cP1otOs9fBL3Rydn7v1dcm89knPvFNP/Fn/3u/8Iv/4smjY+aMsMPY6n33Xrv/GjtEdfv1Dt17RjgpsmXJyB90hJIeAghKjC/FO4WBi2ghqOhIJ7dDTVFEOi1J6JZSWDJUEaVwynp4zIgf1gcxpYMZOT9KL4z/NJyJiMOcxg2FrZqVGqkZERlzknWQNPRzBrKj+qpTI4CVvQepZXPCb8oiMXmwabVyoNthhPSX1EVPUuuAiDOO8pqSkoK8JaBQtuPUMfWhk7f0+ZmfyCV2to5AHlDKZAtO6Vmo6kShsFRjDD+INVnZ0ds1VcYKBIlmQXm1fYH49CDJANK53RDRgKnPn2ZMgw/ykAIlzL7eTjMI1dGTyKtYaLjYWAquKHNELgMClL94hO0O1Xv9fo0tMSwb4MhLPoMZHDBvCoCVBQMtZVhcCOqbpCz4mglfy2vCNuHXL3kAdPmQmLkZAFxTh1MBtUn1EsASTGCg8Ob3PGvHvLj0/QdkInw9IDdgvEhWnjbRwcYaB1pVSIW7YdVlyPWLYZuXEjW4yfxwg4VnicCUqwIiJc9Npc5MQTJq4UcXSBSN0GUlZqHUoa2KLqN5tipqEBBZAVLbYaJrOLZrr7TW3Ub2N1AGMByXbudhBOLLADrvr7bqY/pwgAAs+SIQSLXCTeb1ZzTthChToI6c8UD77smUyKFWiCKEhFizqdqIEc/SCyMiDazZ4LcwKviJPe269MQmTluyIVXnaENlPpZAi8NV+CdR25ydjHBayIqYgAKcFTylp1JIJ2qFAm09sCtCk8gU2SfMDNcQAguwEUlqoW/kUGs/I414bZoGYEJD5B2bA0sCaOCP/c22wvg9ouzNR5kTXKmc+MHuAnFVP7aqhn9691nzC5hwJ94FHRIoUYrBnC2BQbVUM1jJUjx8Ki5PECEbKwtHUZgv28JdXKCmLSgJV7QeshQUZAHo0G1wlZSoQS1aI7wR7d4JYy+whR1WEkUSU2B6GsTT4izvPPvOHygFGrNyQc4AAb58ldn/5bNRqkuq8Hhzji8BppfcqzonKyuxiV1KlG+hhaUgjEtVF0iNEY2bs3Rw7rSZjytifAYAjMZaZZST/gAb+4zOz2FXlDdzPRFOLKmMrpBEwwWFDu0Zy4WbfKd/ZMeMbOALupx3nE5jlkS76N16ZccXHysPbJaOE5pRnmZ9fPwcc9aT4J3SaceD7+BO4eR+uusk15GEId2pn40uLkbHB9seoRJppbNHudDfV2zTLvOkRcZnljuh3IWEiiiCGh2Ai8uL7a2d2mrIgFWzObbo+oAZwaH1IVOrKJPisRdbneGr97ZcHVurXVw+p0U2I8kJ0YjWwVzmGF6mmV5N20/Ho/OLORuCsCygB6lcLoQtfrVudhEbNy9qYBFbIEWV0lhjnBG+ng/rtd165wniTbGpy7CC31RLnsGdZp79Q6lDblKkCLHCmDE/6cR0CNUXvlAEdcYMn3WLXX/YqcTVEIy0s1ZxiqefzZDJmuoTRkIQZ+5i8bewsWrL3rq1uJosp6sFE67H9OTNkuERFAuD+7T9zpttrfadqtS6QMAn+B8WDPcx1ZWRDokOWrAfkh4fP2MnAcnUuIy+hQ58hXJw4cxf/ssjwn304vHFlUYHMbp5Gfe6MbqR0Di+VtHLlwKcZ78hHVBvF36t1mecvHxnC1fuTo+1L6x1mS9x64xnmF+1/pApVjOIxC7zy/VprcU2DzsMxC49jgK3LyeoTRddGMQOThwI5V6o1CwkdHu4jWPlzu39b/q2z9RbXddZN4bzxQUnp69q7HXLaWvscNBl4DDTSfGqdpyRxcYnuHjWXU/cZBCvQQe4OwUjumu19dWkOSTUYUZlDuQpSup8UY8pp4qEj8psInhPxTEBBLHe+79YFoRFXYuzqQgvX5KeEAMiWnngu+8ozcpaQ3KTAN3AofL4O63ugVkUiPCpF0BDAaoclNPSJAsnuaJwCbUqrqb31aqshiINioK2hmU9E86fA5oIRi+p2IpoIfyW30KJhzZlB58u1aVqJf3GR+oKPlTaXN2w1E3yIrp1hsKKYChS7xybS3nnjrKCwSavs6tM3Fz10fgCdwOYHh4evu/VDzENqN8a9IcMFa4vzie//mtf+PinPnlrf3D7zr7LD9aLnb39P/kjf4Ia+Ou//qvPjp7t7N966+1HjElysAn9a9QOhwZoKshKKgLCDPKRSmp8JrEgWiIprggcnQVKKv6QABkmFdhj7KAtKRlj5YRglkIMhNRi0uChZCyV7VekAkpw1oruOvz+TPFjgRFJ2ZEe8vIHPUo3DD0OcCYucodEitGalbvAYPABxRVNQOD8gMG/de+YLLBpyRQ1Jr6O6+LQwG2hj5wQiWleZFt6d46IphmVC65ZcqQBFpGVxra+usinxKAkUoIFSCAJPrGeCWFNJkpp+YxOEh3yqH3lW3qWxVEEzg8Zj64zYoDdxuifsxK4INw9Cd94ojluy27eQETH8p5F3nS4ZAAjxoTXZvi/W6sWu1NoeUkfFB4CD9ao4sCk9SQUtB3xsCkOJWCr58lwyNexx7QzdVmrX0VIyRkJwhExm49Xs1cbC7LQR2KraE0O2arVPg8tlpCv7zwoAF6b3/KWexBx/YBJxKms/8maQyVC/JShDcwkunkrWSXE5CSIvXGtc0vcKucbkW/C+Fd7LjAsLjJSCpMcE1JAlPAqs2uoRuZLVQzjyFmNZaZeS0RIqThzqXeIh1pJNINMSb3RFq9gIGbGySfC4w7kYy6iqj6sVTzYJRA92nGX6JGM+HzxH9IKVPrqiGAUIia/uaYKikqJCKyCBGgSV0XJQ1EHyjjoB0UJYhKrgKF5tDbnUSzIOjWFz8ABy0RLuQpahOaf2CWS+QXXAMtN2GQePIsu0O9VEopAEggAtUE0AtABLo2iRlrJldfUdMms5Ic1+SWRrAECeYocCZzKQUKe7AKgZdTsfiID+hNRH3YIIC9qJPQgMoPg4IRuVcOumJcPHjbnrvnlZcMWiSKXuKsNsY0CmVKowFyXrS4gXLGgMlsV1JBBXNokMWYZAEQTMOBAm2RX0NfUnEBDDkyJvyGBwLMkpuM/5hvnuqcIdjgwgQUZOhANQRNRXsU0dz99nev3/WhCAPCjSJhz3i2GwbLCPMBajCQzjDNkk0jRc8iYdJY7/ONzYsCiIGkbT9mZwMruFGhN+gsUp4iFVYGiEorSZRaRd2YJuaENFiuDvGZpjzEeHXytjCrMp/aD6XLNZ90O1rXOKOZT40NsNcacnLToLga94fzijAoMwWkB0JJIOoXQcIftFg97HM8N3L20baAN0x2o1RtCkyFT15ThigopsEQI3tY1iCOnVldXY5xP24NtXui4kJwWlbJTZMkqUT26jEKy0w5zxXfcs7+/vzt8/OQps5WYjwx+GDh0aO2XUwNpoV0MXLtaPF+3d5ZTNo5B8MatTo+WHsI4ymgjnXl6lCf9UdpOzWuypYm3IaShEEMqBF525IwV0uIOxtgDK2bKgZ9NGhhaL2ARjRX9YZthC4aMbe9uX16szi8X49olhuTKjYNwWDO951LvMqWlJ85cTmYQjWic4HNnPWeDoDYmzFcePae5w94czVv2HxjLpMLi9VPEcJXJW7ZFZ3EzNKFfzBZYne4eXIJmdPaQiBRy9ejRE/mmP0/qQ0zriGyJIAZRnxRfg5VCHstzXhP6npuCWsUmvES9TlBiiiVUCLBNWvLGoQ9+EFan9XI4ZNPaISM7W70By3hYksBXnBoI3uG9ewgy/tcHD96+fPyUQ52gPrusrjjsjL5yjYpgP1dbCpsYnjPKR24YYS089gu6fKcLJgmyPdOkSU+ebrmTekbN+mC5vup3t/s9tmhjkI3RHpDJ5obZ2hK7F3kQP2wuz4OAXrOd7tARURgrea3WVjlrvJdlLGTMm5Txq3EoqWTwzdCSQBCFaAQFTsIFyVUCFKDNq/nBeRu80hRgoMlD/hc5I5w9Yi7PL9jwHnFNWqLzq31ObVLtxKEmqlGDoECguRHFvIQcNGi2TQlMKFDwCSIUA9EmSVAxrgWq8jI+tqZKRiAChCaoOuIgiQGQm2VPGt94UBFY0TfoBj2Ht6ibxmTbnzlDV1hQ7c7z45NOv//40fGbb7357d/5Xbe2+j/zM//N1Xi61em/+c5b7x69e3j3DlWz1xv2WVBeb3zw9Q/+6J/+0z/8x/7Y//mnfuqrD99hWu3pydln/sCndvd2mUQ6nuBXmPd6jB5nuI/aK276nvF/ZIjHGbUoMRSoHT8rjmWxWLoOY2ogk7qTpUVaI3W21V/skZU006BSaCrxncNm40WRsj4KhV3KjBoGxpTUtu+2eM4NjXXjpAdNFCqHfbmAt8mQ1EqjCNqayi+1EnoM3nmMF6+yQvoWzgGY7Hm2rJSDr3KUhoYQcM4fOWtgaMABGurIjbUjtGZNPDsFxBGCVoOGAL0AkiQvQoguDfhH3pGnhNCEq9gtPFTA40IhwTetl5jQDvBmABiF7lYgM+G/xYvDBO0NIuQp9iRQ61u1pI95JoltCJfp2UuAArB1BU4lZnKjLvAg2+p5NjxmAsJFd5NWDuLgjEsaMy00spwvX+L6e14mLB9To6Hoi+jlsbx/Hbi/J8zNh5c6AIKowHztzgObNL/fb0ksxuF9oobk0pGL7/yW5/fAMaExEssv8huCOTsTmZWr3O0jcjVogcoMLtpffeF+8kOygkDWJTvWtOFmyRNiW+Q88lpigyL6hapH69bqPqt1MGsIApiDV8gD69CZbOjkWiUYzw4+CbqPxErp4C+1RMHipjAhUhskLAm7wCLifKBuGyE98mhutCi+RbCKKKuIs1At33BTga+NkNigDVIEoNSZAmFXgTyUOFp3wiKVGclGytcc9gNMbQjFVJ2BGsU8sYGzXULQzYo7uDrfSdLZM1JpW3vx8LlxpxWVLjw4WAeoc3gx0RlY3iBsPMuNB5KeOloHY47o+ZPOi7ugslo/pcCa2Ex+lfSMuB2g1GudUwCjBMi6zjxOMQBX4KQZ4LHhNIZkQn2W1Nr4et55Bh+wYNyAB/Fb146lWfKOEgqqYgzRcyeVOEOPGDqp0+BkiUQSClVEpKSuoQzNkDjQRnqMbs5kJr7g0az3xpcLFn2y4QyEE7t8DE+MJUWVjnAtAUm+AXINjdCEcXvvBQoE8FFZ8qrg81A9rdlNCP3Lbp+aZUpAicb32LqhLRQWPpLgj8ypLh5dzshKOFJbwVjUi+Q7kiJnJAB/UlDbCmywExECzElqy2Q2Xc3vSqv6Q/pptzo7DLAxswafSLZA5qRMgEg98Jc20Jo5Qkxv6Y+aY3iMFGooAxgOoTMdBkc3yyG0JcMvCt6MqTCy2rafrPmUSKP5/Cq8JKnhjCek6HmUT6KOLNHgYdkP+qetBrP6GEmgMFtkgew7WlSAcdJwo9HvDjC96c8sJsudrZ3uq/3j50+fn5zN2GFDmXYQjPIwzafWGC6m9aNn8/WdO43OOdtad5rtfqd7OrlkBel8gubv0Nthbgcla65Z+8yZXCgOPHa4xvBXsa1P6U3MWLvQodK4KyD+IebgI3ez5mLWb+KpbnDwNVvphDOsN6Am2hDP2bWpzr7dIzfb4tTq+fHZpPO+nd1B/9LNRue9OZv2OuGwNVnOR7M2VsvlrH5+Ors4G80Wo8m83t1qTesdyjWZLi9Z/gzvadDxAtqoc0Fu+ganLp52TIzVv9tbw1twDxNV2YHutpXL0+fHnR5LR+a9PruXRqQiKjwFjozkIWE3q0A+R06rmFXsyKaS+tKVzwIq4b5aUf3NJ9PxwD/wQ6ez+fL68O79e4eHnXVjd6s/n07ZQMx9Ui7pt7d7w8E3fdtHUSds59/7XO3Rk0es+dffhxVLE4Ocakkx4CJM1CXQyZl5WL1+d+/2XZylo/XsLAtAdO07NtzTQG1B8/b5eLHXHDBlnQEvtmVG/BmFUQoiC7FxPZYBIloa6oa1myOZmWpFzlmTBi8sFt/RO8p4EeYXIX62EVItpDUiqtC8F3WTtxAowUS1LpJEwFXc/FBnqE7FyOKp+q5OjVlGp0jCVJESzfRkElIjf0QAR81UbUw2mqfiorTdY5rmDpcAi7AbbXZaUwvYWKRaUlR7AJNDEW0/Mj/SoGO5QJuY5Sc5prFEJtOS8F2iiXRBlnBCLJck4TfF9hwPIDJmG1gEYu5yIsoMG7iBG+Ly7PSXP/vu6dnz4fblxz/9iS987vOXV1dHx8dg+8Ybb/zar/7a6+9/5dHDR3Yh+4NzhiGnV1/60u9SN5km+YlPfOrk+Nm7H3zrzTff5DCUH/m3fvT/8Xf/9sXF+dXs8vnJNrXszj3Wj7WpOelp0C1FnvjDkeSYKTMeo3k0S5h3afNFEdCEGPdLD/qgbukvwd5gSwtNZQqo2YD3BSLi5sdjo3bGxGf1kJanpkHW7cMZ/F/007AISMTWNnRdoS2soRdHTqhmOsDQHp6iPJzVLL2jY6S5smezDdlqzWN1s/57gau/iartwgt3LBPKp3IiAl1E8Qy/7N3yRGy+0CUBuAYKqTBIyBFVj7aJ2UFKTBS1CuaBsxlNS2FI3j6mWcWRBBiaEPjNZfa21HaQwHDVfgSuoA/RTKJuVxTXzQfkiDigqbvZn8Buj9JN5hQ+zb8HmWsGcGHfMcrFykO1oK4eMqKpUs5oHwGDDGnaSKg4NNWTlQB2Ogxwu7medk2TA4kASxOB3wfdDfxJu7Wa95+1B3QTtqmslFVc+SETPPcK7vVlbfjG13tj+eY5wf4CTHrkOZJfTtN6765f1xlcR9yEvNQBKPlYNCC/B88qQYmwSf37/FaQEuO94ArYipbX8HgoBSowDSci/xqdDtYwI9FUpGLDiZkKKAiGxyVywRi2o339agQ0DJyEwVVGcOA6WqQrH0SJdH4RCaXTisqTYlopIWXO5MTiSaqLczhL4OYykvmLAPwODASc+Kl1iDJmK58Tg9F5cgFBJIcEKAwqusdqoBvsYSvcQOJGDWbGDBfPfNK36Cfh4LfHmwUQ9ymmTlrmZKHTyf5ycvQcU0pHD8FZ4F6AwLJbzzkNlOMztInd8B5ZBTA9hJkb3rDXdXH/2JUiKASCBjiZ05jpvWcCsXXVXNIV186yMJZMUASDJIjG4uMLPOWVUoEo5IuDA79kF6SLYSiRVS0WRI5IARhBjuge2h7nPhJO4azXcsxhdNQWIP0lwKrGE0qDVsfySn5ZAj4wVL2jB9OM/AZq/tdbgMJRA0J8UAyQxAIWTHHFxfrxw0cfeP8B56mKYQAYQ4zKi7kYkHt5DHqb9/KZtzxwuxHTOKAp4aR1lLrwxN5vfvCn+m+Yz6k6hVy2ymkY1ZPilJ9ESmxlA55g9Le4j0aXdP4QDaf8qgYhOHFLWRQYXjvdXovV3F2q4PJ8nl0sCWconmklCA/Sy26SqybHe4EwaZBUKis9WtJgDDABD7sAv+xJ/Yxwq5QNiq4ScgZZQiwCjQEHrLZ7s8X485//7dff/72wRWZFJ9tZWdIwdBFoKpOFShcO9JQNQGIL8AOPdEx6vsz5xejWLny0ocBKtpDFaDApTQ/FRyadFEUcdDeD+EjuwcHdbm94dPqUWb9kLwVZscPuUi2mb9Quxye3brHvavrzHFxQn3Z0obFj8GxydsFA1mQ0Zd4wgsqe0xMs8xwb7wCBy/DsLjJeMGi0OYSUPYSGDWhLW4GsU6c7NRzzbPwPora/HTri7I1LJxi2mEt9iWXC0l88zM3ONrOhbr+688GDD61nl8+ePsFtTwEm48X59HzV3mNt43h+fnw5vpzQd5iu2FLg5BzvNlbE5SXrgnFyZ1IBfIDjyhuWK6RcxOnN6W2siK1Pxme9rR2FxXpE01Z/+M7T3/r8rzN2rEEz7cCfkNxql8oeES0SKUurqxJWPhaxklnlimiaVACbQH6rCNSupC2frIxFNo0p6/zM0seYDI1hr3d4cGd70O85G9v9c8kNMx0JvByPt9qt4YB9QWmS27dvH7CLjFaRmp7SubJFucX0UAMoUgQoJOKFNuY4ud05m7YyxIA4KEdNPAHobrTLnJON2DShgw5iFhUSgzjDrMiWSgQcY+kKy/y4A4m15VhwqQupZCrIxLBgEiQqk7iUWuqEJoVQkfYUPeSQGCHHNQFJgSVIf6aiXz4nVnVTa/GPGqfn0zIC06qODrfCqyIqhWN1TQUE96S2BAgzK1XYq+fy4uLq6hLsnFbv/okUqra7vXP/lXuFsCQRlC48CJ2ilZJYLktHBMJFiJA06gZqcdIW/P85+69o3bLsvg/7cjr5nJtv5dTVQDfQyAIFEiAIgLRIEYQBDlKEBgVawxSlV8tDkjX87gf7QRrWk4cfPCzR9rBNQiQhggBEgAEEQIQOBXR3VXXlujmce9KXg3+//9rfuaequwnQ+567v73XXmuuuWZac2WrEIRTrBxxTHwLLhxfYq6stxIGCAINBhrs9DvF08vE0nzwjXd/81/95v/8y2/gDDS7j1f/n1q/S28F+k9PDgs9mru7O8Ohez9wvt9kPrt648r9e/f39/ewk1//6lsvvvTyD/7wD375X39po7+BZOxd2UPNGStgbPTdD77BAYOfb+7cvPnsoNnF1jEPxAFTetpQ6RYT7SwkG1LRvwRu+DHUXa5GwKRh1tBB/Bv7xae0nRhgxf2E7PiiOAFIEKVXrFjp42oVe07kHV1RbqKPbCE29DJYSmJy6CFd0QJnjxs+NNheg62rJAjWhJUnBGvv6s0ZM/409jAYuyR7pRd0Z4obdTpusZ4G75zPBcLn8/MAZr0oV21z0M1tTQoi0h+q8wcojTx5YswojcEEgijNIoJJgrOALyPH4wNoYSAB7RvvpJW/Gn8V0WlQjAeQsc/wj3ISKx2d5GcfLnhYeau80JBNmYkA6qpeoiJspALzeccOJyhEbKDhG4Bd1FRHhEoJX2Hhng2ZzWrxKCdbQCt+coHIIMlINRlhNTgMnZOkyTUxIEzXtZpQY97rDpo9jhnFY9GrkWB6VpQrwg4JAQHUKqFP5dHQb3cRW1LmDrxcFZjyAoj1eyJWof+GH7o6kvcnoohlrTFcY1RAVfldiMgE6cxJ6ny8LldiVhGphPPV/Q1yqabloeePOxuQ9fqZRz/zv0i4hYSvvDNVgVU/NWauYns69xU9uG77ON5DPMVCF9MDhT8LwK9+rcRHCCiQrWa5iCxqG6WjtgaOZ7CMZ40dt5I8vZ/0UE5wjw1SV0ABlEwrfuaDmPnIc5oZ5I/EOGWdmOqTHyyF+QYxUhrJbEzDR/4Bz175dNCbRSAa3fSmpIGZNMRBUNV7U0dPjIEZD1CSoLFi6ytv2JIO6SFApieQ0HpGUFhxqOrcKmSeqahYAdwCzLibBEEtEVrUGPIGF5IDTMtkzYZHJSXFUVPgk/ywBSWmDVbNUzbi8a8U2Z57pviyn0NsimxwBoaqxyPkjdKbiBJRZsMLDIJodZCdmg98ktY6D6h17Quhow3niQjMZxANbkGJwloD2ogKXbQozKXmpdbMmcpC0YCFbyYimlaXGHyiISRGLBcrvVOBHdCIE9G6OG5uIAxKRPBr7pTE7AVd3k1y8fKzsf0ticiOtKa/eJXvRi38vfDN5PzlrACoK8F41XeRPhIKrwUUxMihM7lshuJkQggzvooM1FYfEmNvf/fs9LjX67OOjXah40QUMEQTLDtPA759j5hYV2oEDnUeLFnX+0TOLpiuQxa0gqyn4QRH0tCDQksh08pxrHGTLzGVvbE86rToNJmyOpNcyMFmLNyX/hpYc0Eg59Otre3Pfdfnnzw6AiXyp/4kMnmBNrM4ONaALfNTEvFRhlO4IKALjzgJE/2gWmewYnz6eDnd296nGSIAayKFmrQuQnDKmTQ2NhUTYxHKEoOB082tTm/wPNOZ7t67S2uZXf8VBrYG4Ujdqy8zHWCv3R5Oby86o05vtDnt9Bajex/vvf+VryGBeJacV7NszSYL1qnN2JCy1rGWZ7LOxFWm8wF9oKNRqz6AnlMOv6Ria3LE3ry5dWdr9WDaeo5Knm2ZZtNxk4nmy2PGmRs1lBRDDciN1XLYo5FEMY5qvfFqfId1PpMNDqiaTU4fc6LwaNHfXM66H9y5d/vRkJ3+6+0eoxjjM5ZG2HsAhdAWVkpLCrr8lHv+pL6Cs6ztH+z8wOc+wy4BzHRiZIczv0nHXunQDIa+/9Fbv/Wbv390eMSWu9k5TSVXVKxoIadPXoqQwEuYIVW4efl6fiGbBPi1xCVlBSlRCKRzcMfnxrFRxJjY2ug6K0DIonHGSMul3Y0rB1cvb23D/+WCmUudWW2ME6S18pQlq2AOceh1u6hIf4NFHe59ynwQ3Af9BlQfOdAMMzOERoIeGDN8+Nrr7/Q3ODj5aL7ZW7QH8BCtR87A2ckdoNRi3H/DPZlc4AEh0A5UYo9MRRZza18sowtPHGyZbYr/AseB1rL/6L5FwC2IhOAjK8av8ttw9c46BNul1aCbw7pPRG12gnEOlmbIlJjMgeZq3SlwcNro2gy5cg5A5vsWgGaSC677qBa6iIrRX6is80jjs8Gp0o2NzY105uDfxxJCbPuHgY3cutqE8yLw/BFrbPHmzg5YUH/sbm+TBVkr9iGBNRiFtqcXz8pdUPyef4TnSklJ4ZgrMWlLMFlLq6Pe0oZ39Tmqgu+o3eDCUZZdMe2UQrqweZtkpBPZ/ZrhoHXMfMWssI/fe+//+t/9X45mJ63emfjzkaP06H1r1PutmxS8NThjcQvd1Tdu3rh8cPk203ta7d3drUePj3Z2N5957tmz06Orl69fuXz9ow8+vHT1ylf/8Kv7uwfs28GWoOPph43e6s6tg+3BzsGr7fGQBjb1Q4e1OZwpwXA6LqLeCgfcsmpkYwuLNlvN+wPX+GjD2HoOB8QYbCji3ECc1U6TqZSe51tnGl59E61HsBvNM4ixanHU99VV/bS57NLmnK44y2+8XFzDztRXA40KNHYzW/oLR5gXDi+dL3ZXzVPmwbP6fD7Z4bhupjOOFxzn3Z3ag9fXuZjbH8SQBPWqnnZxrxUNRhQYEViypIwi8NYePILaq+l1ja2+vDrMNIpm5yHFgMP0m9em1+ylsyWMcNNUtHCUi3EOpiNqhexQdPISu47rlFh6WUcmQLOOoJ9DhYSbODC6qfQ4Ibbwjs4dBEkR1gqQSlHyxbAVmxjSnkPUdRoVB2oihUcV5644kRf2IPUOUCGsQkcRQcUWF90toIAiYgXiiCDI+CtMdFC8SAlxYAyfaOlBNId2zYreSBGvdx9QauoX/KSpvQxAVGjFk/TCKIipHeVZxWT9GFdOCvLh210qCjAEksfyFjRLQDQ9YL8diApC+SxpAu1p7AtZVIFgvc7MkKoABfmn6cpTWFHF/iY0SsBFWE+Tl1BjFF5KKbOA5ZAPrtXdKFPyQXy0O1MHoKxqVEHMD9LghXmE5STG6qINQCMNd63e+op00O+IqGmcaDwX/4C0ZIxqOhvX2dL6oEWAILtVhkJEFPATYS6xIonVRoRSDEQHecWcwX4CTICEySxlATxFyUDzU/ts6oIkH/2vYOfS/aVOQWtMYF8dNa41rxAtGbYYrSd+4CLZJS+KLqqQKzWmRETaEX0bDMkCIGnWIn8AlEq05yUC6pFJeCEY2mD5ZEQwcpMBRzkYnbRlEH5FW1EnlVmUyJa8LCxP+ogE8idqqDpag8sAWgB0jRN1uNprXRR8JQLWggLa4eaf833EDgBiLCUDj4wIctaQlDNxxiYEzgewBqRCY1ZmZiWDaTWimPNB9NROsrCeAwaIs/yRB2BIbQ2dSZ1LBfZ9phePx+wMQkqDAQH9NCiSPQC9SwIz9nsJ5ykP4ONvyd7P6wh55EMiGoX/1feCbcG3+lARgUiJKmeJzJ8UU1Rskll2ZZWwXHmlkVanPxRGv/DSi3Rff/zRB9IH42uBCm1z5wW5yAU86E6vB0cPi0YBzQAzTUbtt54TtIXl0JMaG6bICzpbmCvDTr612v6lS2fDu3YARSr032VNyNBo7O4e/Mif/jNXLl+mx+r9D9955t2D5557Dt1B6tjOHbDTcf3J45HNeHkdOWYepl4tWPOPfEsZwQ3psD2AG3F8ena5t+8scNlts1Ehso7BP6PvyoaT/gAiwCt+tlMcbABvDjZefPbm8dHp4fGRXfnLcXMxurq37LaON9p7HjrRX/Q32p3ZgKk5VBnUS1Ry8/l40N1Ks5QV0k12mKI/iJ1DydN5Je12b96uzydUfNSxtribs3aPrQZZrLu9vUlL9urp9Hh+CGIux2/O2HoLT8IKBUO3qLHaeLlZ72/OzvZWj9mEYqu7wRhOu9VnoPR0tbw7nh+f3Ts8XZxw2tecAQpOVubILyo2fSGVypJS08PmIiqxdLDT6pcpkNOXnr22v3dld7vT2dodjYbNrt4lxUcUH9+f/sZv/O79B7fT0us4swHENIMRuvxGKgzwuvCFzAww2yoe+ZcnP4SB1YMCGCnkMxkEjHqavwTIRyMniHIx3f/GlWu7W7uDDgdPs8i23em3WTrBwdJwMjkuGJ5iLIpWLLZya3NLZ10jh02DKsi1Y/2KYlx/+4RZCMxMCtpKyIXdinu1wYBOY/NmWgfmCpkPEtyJghRqk5VDAWnZ8N80G9ohWC0TMQlSAPJznB6LNyr7R74pMZFNyz+yBC0h+VpokPLmkxHyVkhVXhLN6AWxpPV7ofiakELW2wEtlIChDTdJC8b5AjXaNJHUESjJDr+4PNRLKou5mNY+KiwBj8PTM4ac0E1j4rEyDN3lrG5m1qmV4K1M2dtq1WJq7smUQN/LVYmBBSvM5keTY0VnpckiJZptGtOSP1DtnQYAtQK/8JArJQ3lyJbUtF1xJuf05I9nv/vV3/31X/u1j+996FRGRt66nf6ANdyM6LRvPv/89UufZ8l4vX2v3+tfu3H9ww9v/exf/ek/fOMPQd4N+1ngz15ADKNRNdR7N68/N+OUgNHk0sHBvbv3vvzGVy5fPrhz9/7O9vaHH3ywu7u/cUBjuTc6PlMM6LEYTpqdFk1oSsREIsYWNgcD8OfwYY5JB1EKRUcD1ahrR60MmUeECywyAgABAABJREFUYVhyhnd7NWPkEQ71au3BxhauMRJHUlbvLOZbVuWrPv35Z2wqZdLekv2llEmIDu5MKGrzBQPUxgzVSMU3pJeB9g1qUvZtGOG+1mpn+NatDa28x+ZoVgFBBCQBMXACaW1Brzb7GNJKwFoDutnhzAQwZ99hzT5jqyyFYZ5Go91HPFQPhoCbdHAg7aqKe8/hZtKxQTdHr0PjjjZHvIk206scolXY6YJBuuKwIAs6KPTZy2Xy4ltRB1UHZWSGE3KpSoGfyoNLBmf5Z/MUnPhBdNRr1BXdIwYXXpLtDook5pLb+s4qP0quxKKiJaF7u2Efok+eq0OZKBxOP6GmNn+46lYxtmnEm1JHW+hERV3IyqMpUTWyU3ZTFp/V57z6JTIfT8FIf4KrQCOilCiXYPJ0/hBNXX/+N/862PxtYhSgfPZBXatiyn2IYGj7rnnbyixFMeI5uFXWKZ+/VqmNeuFyXxQgEYs/Hp4+h7W8I41OlSMbkqnv8knDLGLUkwRIRXP2sTCbaayeHKbHUpxtbZY1INH4heIyq7G4ThRmM2syCE4JBWaUiFycC0QCk27BdIEwgegH1if2325FhS38IHuddGb12qLH3OnT61sojFS9Yojvkje7R1Lc5EbXTQTTMM1CChREgjRtUsrLknPrEFBeNFhLTl8Be1RbRux1RDUVT/AHAP1f+7KJcwkglbWW0TDMWdhJcxwk6emhpjIWNSK60HARC7qBvoKm1UMdFya+E6oD4vX5vqi1H4EieGZEL8SIGha9JQJktzMHfCAA3CNl0RkKkHaEcShpuIFa0ZsuVfhmywDyAh5iam0oX3x3gxKFdEzz4zuU4IEa3tYROTqbNjpMRHgCwTgKCOLLSS6GC/DwsIY68eGEHM0nPlJsqgz3hwY1ejMIcZqQ6QIbvDyTodZlujek5IRgHakl800jU0LykvjlAhWLyFXufljHKmny8eJtveoG5Az2JxLpm0XP5Tc6qkCNvcMtBpaMbxYZglo9xhuRiiqHNbeqQ+oCodF9QHwMLOOX0ylHQGj92DGIipZmGo9ma8bAvxtpQxDgLgzUecI7BqT0DIaL2Z4OdeOOMR1tCGgZhs104kmjc9SeOomFTVmYNc607CEnflEsyEozDNAgrKg0Xnjhpe/6wueOD58w4/Yf/uIv3bx57eqVGxsbXQbZqUApyHR+cnyCwCdzFyZgjJv09/Aun6QINCNr6hGGCxzppk0znp0dnzV3tw+IUk0RcyNqeLvBZ0kXUeOnwai4qzRZ7UfDBYceCN2Dg/7+3mVinz55cNDc+MJLL2w3rjYbH2+uLq+YQjDdWizG7e7lzSu3Tk4ebG+9xkDl5hYzoxat0XI8n00X7M7hiADHktVqW4yo0TnVHXDwxIrTe5vdzf7etrt+Levd+narvbN16dHxeNqmej6EoEdnI/ZoZZ3DZqd3XJtvLhqP2/Xt6XI4fTJtAn2yM97E+boxaTwZHXZund6/dzI5ni44v4PJfEzSmIyojOGTG3Aoy1AIAmk/DnCAFstHqJth1oNyd39389UXnrly2dEJODUZjwa1TfQFJYBN77z3lQ/e+yp94iZAKCBZXDQFUtHm/ekFXc+Dzj/kgRukABEcgqdXFT9iDKeEiGwgiZqBY9KEUdbxycjMl8sjXp69fv3mtWe22n3m5GKMsbIUfDhkCQeHo82RD6y8czxo0us9ABNRpFEKdhqEam4YuZESrxFXpV7v9pnz1oT0mAS6b9u9wfTkSVlNjFcCAJCi/Ot2sJpn0QSPbu5hMHimDMVRsK6Bmct9Cg3WlmzFvrm06xygUGkNkSKgT2RPbiGkwAQwYNyLLFeyMY76RixamsQzlFSBTwELOlY6hrhe2X/rV6LyaGLcdCaqwFv8GB0n5jdZa2ExJDKWk++8V/ACTK7ybheqXcP2rWIHu6zx6VFPrCbXmIa/mH+YahnXcEojFlfS7NC1yRXmmzL7H/xEIejyJPLc+fWmFlM6vE3NL33/ZGGeBlvnkk4koCfv4ml0LgBGmeEhT0g3y3vufHjnX//O7/zzf/lrJ+MzvFDOhpDYjdq1m1def+0ze3vP/uhP/tjzLz7veO/8KpUd9or+5Y3Nze/87s+SB5X4gwcPzk5PHz44OhueLGZMLaPnZ8MRvFbrz/7UT37hh74fOvy//1//w927d3sb0698/VfGi8/duHoFQ8d8Qtqb89F8esIUsVln0MViscXX5tZiZ9v1QlCfVgoDp7jmmDLrq9UE2WWxHSiyUbPGezlmQ8rWfN5vbbXb96FkozZi2KLVoLHPGYDEno0YLVBudcqxM5Cj2XLnUddCcAj46pQRxm6TPRKhJ3M6cKceMOQEP5jziM8+YZx1dWpnPbMDmW+Izjh6gsS6PRYwIRm1MDMEqDaZGwQfWtMDZIvaFgY12APHRWJOOmhMLin5NKGpisldGbZjzkDn7WqZmx5ZSIeC9QjswqmIEC4bvTu2O5fPKtWwEjYwnXnqcH2Y6xRfhMERhqWWD8nAqUH+gGvrSoOuUBShdzCYNyBh2cBFyvCOvNgZQ9GUGgVQyYRGWEQo7lJG2ECh4jxRuRBNPQGoOKlz2i69DRhmasYpaOzyp48aj0g5n/VxRmxhERW7DgRjAwyELM03XX6t5sJ807dPB1QQRCfJcjNSKWf1eh5qjk9fRMLXokEBTQPg09d5/E+mPQ+uMg4cnmGzVAIK8f//ugrkknqdi1TPBdGBjijaJpSvyVF3g3esdtxfvphzoQpmPSlFiMalDTOtislNARwYjFQiDsVfx+IRQdc8Y7uxVkBTdGBq0ioaAQBkQrBEQtGZRo1xnUmDaimJOv2aKoWLCNgpcmWIQfGxiUg4/0gIXP6RTglmcM02AOpf5WJpSoFA1VjW3P6S3mKYFBIBBP/WIAJKwUXY7PhCHcoP4Ols0vs3jEvYOl/mBaZpI6Fo4EecpPShXHQCQSYLwsw3e0uhBHqMioMPJEQD3RsHXJAkt9Sn5GLpSkbgM6PSHJyoqx0HNSlvLqodJ5mi31h1eufUbYrE1BqW5eAzgWS6k6mJbdBLUQZK8QOtyL2ixhlgUzysG6w+yUps82A1xROKbNFhE9lKA7NkY2/nNFgLOm8VbghBwsIDigK2uv7El9oSOKCle7bLZ/xZnefSxEi5YIGlMQqh3KUl4U8v3tevRsqzqT91iYMw19H9fRpNoLm0qTnCAlAA05Vm7ZftImippJkMTETGN0imyOdqMTHnlBFzWCje4MqptCKSsoBZRM3fklBcNXwKngWjW4c2NqLkttrsrA4G2nKpDwpERr74qkkFE3Nh7WWrNWaUgJWuYi4TnX1qVHqBastsLrnY3N568vH7f/Gn/yILXimJAo5UMDTODJhJYzwSujjFRwFbtnykMmZRK93VaXP6zZrJlg+ZWHs9OTqhw53pvOSZmbhlmIKIqjwYEFmtTh0CtwFLESUL3tN0Qs8myF++3r/W3ql1mE1zssn+otQXbk1N3diBHEwL6m/1tzYu0Q9HOtqR7e1mZzqc1nrzOltPMiuBfXUGLJugHqQTrLm5YKU9Rwh1tnvMyfHsm/mAXlT2htze6+1tbJ4dzdnMtDEYf/Tg1nC87LBhUH3pyWAtxv5Xx83aSXt6Z3585/HhZLZxMnt0NhyMaZtOM6EE/WGagf1yhX1FeuNRA8WC4vmxWll5kNMqAp2Ps+94/aXrV/YH2zvM6KIXHQrAbgSEuhi39PAQt8Oj1yRXjA+JFBBE/6m0CknK5r/38h6eJVpil1BVKwpj/EhckilAcoBQL4TAAAfg9Up54ysSjr1kEfb+/gF9t/TvLyYTViUSZ8lGO47k0MLtTSBdZzCePkbRSUqbCb66NKXZx0XTWyl9/+qMdYMFKpdDtfg4dOZ1zyYA3G51dxB4pZYpQFBUxDUXIllKl8Iq8HwoBAkpCjlIsCYFnyfsYGwJ9VZNrWaFkKFcUTuiF9BJ+BRmlQ2h5k4cRdZM1pTmOX/iZq7GQgelZJ68kUUSWhpBUCyW40tVo1sVVMnIl8egkt988TvAPCEHycbu6DVCnclJv99v9hhDXjJ1Pr4d3Uw0pZx/xsLyJApWYasoF+DeQwmx4nJrN9pjQGU+VnCU6yFSJAZBxLQQhnzGyItNASZT2Zds/PZ7X/3Fv//Lf/hHb0BtqimGElnau7u39TM/+zN/6of/9PMvPDeftQe7mwGnJWeAiJ1AOP8OUoAALUEYzIEAl69c3t4+e//9d09PZkMKggPhOpw5c2EuXT6gZfyX/spf+e/+m/+2vuh1W73R+PTDj0ZXrhywENfz3oBixcrGUewcBXXx9/HaaSNNWJxixe1qNCSzyBV1kJwhnO5Ldsqhv01rTi97A+SQXFVBBnCzqeBiDC7cV8hACF0pzicLKZFml6JzAgnzcVI76rVSkWlRGZHcxA3HVcdTxQBHx2hSaCLo5J7ase0gJI44LQUGMZFP2EkzgOipMUhBlrwKkAc6XCGYHNKTiGhLR8hImYyMMZaz9ta5Ehk8QYTqazIZIznMQ2Z+jzU+bgBx+aqjAuf1VoKzXat62pAHw0QsvtlA9ZWyJzytGIlIGUkmrfjlFYSEBZljWfilFARRA2GQM50YwinCdFdaQLC00k96sReGYGUOCVM7kCI4EtUs4yQQzWaJkeCvZ9kAJaCipsqwkHwxTSADluf8N6M/0ZWyfTJmgVLCClyeBfyp6/xbwjGUiVNCCx5BsGC+TispcpExV7E4PhZKc094ouRm9PLdVyEGRGIxS+mTSCQFny6GkkTy0DULkYHlxERgpN1ZoBRxlaem46OMIRE3hQ6R7XQWk0sytH1fs+A3TS3xUSoS1Zv3CaUexCMRtoJlUmZhclLRqn5LdxNNoiZ13JxclEp7buBwoYLznYvfgzQihLjJzFMiDfhgu5BhFZ59P+iQRTnonXKvCXTRNYgzYJEmJhTJ17emnss8CqUTrzfyjdacxePS6KUMKCl77IAQjVR7YkgM8oSi6/HxJPeywZx7BN0OWzuG+aKDRr8/qkSDngONKC9zGezRxpE3Mqhk2BtEOrgnrMnkyHXbL+q1kJZHKjeb+mbuK4H1xVUIyLIq+ivYURu5LqQMT7QnhaoesZnhdcrLJaUxDhwSLPeiTt4x3Rp0zgeQPfRpqejseoAFdNEuUaSRRkAVdDMKB3xpQl2W35zrrJxxcoKmC/hYJrJ3vDE+HmnURfJDzSmA7ywTZFoFfYFl4oeVBztPUoPICi6LLCMkD4FN3Lnr9HgwsRL0WSBSyR5kcC6BRQGAphv4+RbZ9on3yK0BeYVUIlS98ZvZewbkkjDlb3bTgM7tEu49pw2UjxawFEc3Ao5CRbCAEIgMUohxNkUyQnhIJGo0coiMM06L7WR4zPTo4/EpXRlddi2AFKUSIaq0gkykTlKtv71lzNz07Ekyaz2Q2BhhModV6pUNQtiCVtFZxFnR9SE+AD4BG+R1ac7hCiCNSJTiLRvoQGFVa/3P/sSf5QDX8YRrtbO9RX/Z/fuPejevIt/UzWwEzGpL+tBAh2KRM1nSqmR6gCO+7PreanKoGf46xWXJMdpTbw4tOxVYo3l08gRq7O/uO5mntmFyFUkols3KCHyY5a/lpxpgpMx6hHXHdfbRpztqTKr3Tia3/uXhQXP5ws3VVpMdAns7/Ve7W7f22p8fXH5zY/CF5uat6ezmsvVRb/HSsvFe62R/0b4zH1+rt+80Z88tux8sZy8smx/URs/W2+/MZy8fd96brj47Zcug05fmja82pp+Zn7w5nrz8aPL14cnB/SeMwFz++JTeR2YI4Xn0hstHzImYLMa0K5a9F958zHnB8mO2HNgybzDrB0HeY4rxsnZkAayr0JEYDYtLZAu7qD1Z4oMqQBRxW0vTZLfWwXPXn2VDQ8dkaHV36SZvM4YBZI51wLN55xvvSCUEQvFAg5QLtXGxr4A1jgIuN9+FXa7yyAfZwWUDO5cYFOFSKH02jm4ExktGIyCInHKWylmjusVbt49nPqdhtrO5vdm6Sf9ot3/a3dpge0e2MWXqPvEYJ0EV2MuATjvcmF4PEtlabfVcrc6GSbSXGISgQUTh0XnsnnJr33OLnX8cBOCdL5yFNugtJmydOgazgq5GhEt6pnC5GyiNJTS2wAhrKvCCISOW/oxfOpwBQDWD9Qa9lDLAvPk5usH8fh6ZfOUV+pTckmMJLfP+2W8HZiRdbX7NJy1nQElRCiiAksKnSvYxxDiHlAhNcBjNUXOiUfdROXTvk0xGcKU+VV3ygvEkmO0r6ENhOo3csdx0/TNN5KhePybNdDIZDZl/Rdew6xZcMk4V0Z+wqB2mENt/sS7+hmKBDa8ZdhY+8WhFZPTJ3dnd48ZECnNtdln9bdwnUqlTzFpDh0eLdM7g0bvvvPt3/4f/+70HDz3dASPf6V1/Zp9RoJefe+lv/kd/a3t3azgaIRbs4srmdiDM+T/Ybabl0HKwY4gahq5qLr2G+tZ2/5nnbvzRG1+nf9zZoSv2giUCC2S0LRu9zf/0b/9n/+f/5r9dTuuHt9jjZb44Ge4cHLQ3elT47ApKDW+vEavx+m6mgImhUkaW4dOiZouUCktLbV2D0lJdMT8M9wA0TrvsN9UZczI4K4DpU6vPLzNEsPRs2ilJEA/Ocw393b6vsWC9Lz5tqiq9dvqnqXRhLSrPfoaIL4s3ukjdvDlkvw+2JmDv4VbmzzL3SGEEF7DBQcDGOnLoGUnAdz6cqwNwcaihrR+gtKLFL3mgriCtVU7FW6rtqLYTm0nCYAgR4bTg6LbCjCt9+PM8guBqesXD2qkWiOSsW3D2DmPBiLiKB5ShyEoAkoBbSDon2kFwCEEgyGH0kFt8HKXFcWOKBAIZuVCQSeRr4CtE/JmSXdbMwfkRFpCEpvBFs+QXULRCgAl0LCmw8k87GOXlC/zjUcS4IxXsyUxhDSEDicq/yDAvAA5UZ/xTpKyG1SdMTrmvH0u0p0HnTwIA7voqWPIWTNah1e8aiKidXzxnxgG2OKDyzZuxSwre1g/+SqvyXn6TQngElucLEQwvH86TQMyE5vbpqIF8TpcqLUpNGxdmQRo5YCKfFT7VQaZBPgvPZ7khJv6DUYoH71hwfV+tCUyL9TE6Xgg/1veBRvb0UcNCYpMHKcnDsSFHd4SIgGToADEmmzjEZIh5wN9kmSwQraLQLpu/ZMW4Hs4t8LEmcei1kiJbvBdkT2kBPqJG1wAX226gvSla+sIBw2cLp2mrKFAxgcxcqiNF+U4nTNCmOEx/ZV4K2Vt0PvFEFPo/ggochBj4U3ZeOphu3jjhXSMhwCCH5Grz5DU0MUiJplTRK0rOa8ijGmC2sFKVHukJ4IqR0n98RMCgKlYIT0yf2no9hCrzsKMtcjC2A+WRnoVEIUxwSFEK39VHmAhb0h8gfMpCbURKQsgUJltsr5iiBFFyzBP58EkE5DhUcJFQeEAkRYiDqhjFtg2nwWLKKQUhIjJFQUErhQ5o+rogNzvVuBenNIoNzBZ4rKRl4gQ8b3Xp5/ATJUmiUMTY1UMCiSKhzL5EunAXvbg/Jf3FKEau3pNFSWVpYCmmT9nSwCmcFjZYkIgYRIWfEW56hpYThlnH7BI5m7PvHb4u89epDnC0Va7SnoHmYg2bcNzNToFut+g9dR6aWmZW/AEbBoiLhVb7EJkVK8c4e7fr4ioUAtFTvuxzJSrJTA0P2WSIOouZtdtbW0B+/71vvPraaz/07/zo6SkTZWDINIc1dxg54GiqQha5il5Rh884/bozno56PWYjd+pnbO2Pr0x1ZEMyRVU4KMDR0TERdna2kUs2IwIPAIiJVYy6w12Vg9dph5om5RVL+uicONSaNTgR7OjWx7dqk8P2hx/U51+r99496L3Z77/Xrn1j/wabzzw7r7/XnLw1r304OrtMs21ydnnR/ng+fK7e/cZi/Pyi9d5i+Gyt8/Zi+Py88/Zq+tqy/cb89JVl+83l8NUaDYMxjYE7eHIrtuRbXF42T+rL7VrzFHw4x6fF5nu4tTA3moXGpzVk/yDuCHN/LARFKMKmgVMGeIusVOHYlqJrcos2rpI2feHFF5975opaQMcVUs0ZiMzfsDpEqJrHT47uP3xsM0OhQpfJELOkrQhsBUtJiQiY4YVLon7yUhSNTNqShChRBvkRddPekJFtWziJkDG/fHd3ezLssvsKGzMS6dqlg53NXUYElm7U6OZLbKmERfOoV2jgtomA4+AO9B03CttI0wEbiw1k8V6/zhF2zNDq0UvnCevucht7ZUPAff7Yy1KDQO6h5+ZsXk5qF2WwB3psSIoQWSlF8euniZDCAcUax4K7ObvHDpAW/8XwVF6hpMlDVI3ZWu+1JsnWrKtLjvqYbE2RFwPNw/qQuogtpaeTbMZFNYRAC5FviUt2qCgJSlJzt5Jj1lhsn3DypSARgI7Do8t+oNHQpasLB44jvS0WaanFKsj1OvPH2JWONhSWBMOUC1tKiiSXCil5VQCRKrihtpCdZ5JQpWJuSFSVUm0Ff3ITqSI+yjj1o5aavgJawzOGzr7+5tsPHhyCQKdHn8hq72APv/9HfuTfZeiHOfdsXUTTgvldmmCW2DMLXzvFyllE3b4tYafuAwKZMXF0b2+XRcDvvveOCwPtNwdHqyO6JFCWra2d/+Tv/J3f/p1/9eZX3hxs9u7fvX/pyhXWjlNuei6ocdHN+A8KJzpLRhRCA6hVtgTkyJbyuAJ6odbEbEzuKB4UcHko2kBfk7mRgr8ZprC+dDMKdAMJpq0UKrEzA+elQ2+OH+kyoRcxQ5mbs4ClDlbOMO9NthWw55smtgyRqthy5sCITK3Wa9aHzHXihMfVkgmRaryzg7QeUF8riclEWRQoa3mQBwo46g8BAopFewnkE91rABVuGKaQjaduRciOaJy5xZkMZEBbD0uGgIiIAGkjORggxmQrgfyFDGTkuESqXfSOQP4DXTz1TxQyDVTSKTgKFigV3BV4LCbGn7QJBW1SmKlF4LZwEQP58dWyURtgAcwpgmFy1ZYX+riEBoYFDcvHU8GT4wQzr1w2g7b/pZ8PiSGW5V3YRCDHT13rz58KzqsJvjlc0AFT5XQe4xz2N6Wz5vim7G2jB0/5nLTeOMjQu2f0CGadP6Xmol1+3V/29yVxgoy7xlJ4Jqk+lBR+vLALUEmXmMaWVcaPO2ur2TlniAdgiufN+FdiMAQPYCdySFn9OeRJHxhJo48fqSYYnXX2JrLjzrhc4kzyZAE8ZA22wknlod550KxNGElmKuFoNEIWsAsZtiJHAJORgwBAiecdgaUBQCNfoMgDHYfP2roePKIq4vAYTSp4uQYd5zJ9HCKAJgFFgECKzyRGVXs3xBIauSlW0VtjFmUiHjAjeapEJuGRDVaYFjHhUAwI5AIdac26CJP4DplFzs2Xqk57ZJGxFJCF+JAQA4TuMfzKEDnpsXKk5S/1sdIvJKAwtAjBGr17PLfmDmXSeYv5Tk+CgPhKFsDCjFJBU7FiNa2H4KEk176rP3bDc/Ckqx5BejoZrxZnWBDypE+6wz4NbHCAbrKNGntpkzuUwsXD5rHKfkL1A7xb+DDMqyaU7htaHDzQP8O7wsB+Be5b/zEfsASwLLIh/ug2AhGxqR0fnwKDviIqEvrFFV6Ln27IyG44gxDdaXV7bCGCGQELSE5JrA2mV1hx0Go/JE9wVHgDogApd8CVK4Q1ipQwl2++1oHQ+enOwUlB3AI96PFGTQmkcgGO3iZoGpMJcuAZMeC+uAHQ+fIj0rNBPrSHN6MpPWQL1p8ytvPkcOxC0xqHKw8InCKecBvTCMeYrGXbFv1hl4P7PSbks2OkDS3k1lFT6J02npNJFAEEUWRRE5SCwVDcrjlTaUASrGGQlQqemW3O+s7O/pOTx+++8/ZLLz53fDZ+5TPf8dyzz/3Ob//rg/19JqWwu9BiMWlz2u6S6S6PnJ0FQgieQxhOQaAUWxsb9jI2Wzs7O60Rm1RSc3KTzykDo0cYutrhySHxN3p9pcXWqi1Y5TqGG6wsbNiRuk25Z6w/DIII1EwU7vKqg6/4MiI5WbxCEZfjz56OprUHV1bLR7UPWI3+FhypL9+z56l+h6c6B11bR99tMOy+eriqbdfqR7UVY1ZndazE6qxWe5lotdFroNqYv+Jw1+pZTh2v127oB6z2wGg131Tj6j1W3LENFkIuj60MqceRc/oq2P2j31wy4fvUmQPWTSAQUdESUk4IoLDBKGZWyAi4Cx2aR1JzVr+6f2Vne4fp8laMqCqDMrSiNEDI+Pzk5MmjB/S5agdIK0jQcQ46QE7UFTJT8M2Sl3L5lDC+PA1df30aCTklAjH4w5MBT3wUR0lhsD7keDw62Ln2zM3r9CxjjzudS9vbW1evZCRKUeN8M8yMo5hsc0wLCeHDb+eszsnRiR0MNMn7W/KRF/vUZ2yTgkjT+1gfgLAlQkIQiVbt2nKCdhCCiCNRTEbEkMyYwNVmMxI2HYNuCjjUs6zizCUp/GBYPqlzUqPQw0+11kPdi9muqrnsLVd9OmVBqeGB0mgNekfdhhlHl6kBgKhYxoIlgwKr5FHlk1U6hhfiBgFX5ZHODHHvGO9CDSgaNsp4oFshDnUZtyUMwYAUIg0B2dOQNULYBXPQwlMDstXP0JLkv7KDBwzGWGwq7x6z41Rq8NTrEwX/A88qU1NtnYjRoGVG8UonQtAluKC9xlbEAGLFEarpYmOrEVfmDQYqHxKlfddiIDJck6vk1+jep/LV5C+Xb73xtS9/5ct379+mq53KgSrj+77/B/7z//y/3N7bvH7j+q2PPqq3eqvxhGljWCdNZ71BIdAIenYoMtIG5lZ5sICuHM/tQvOc6PvyZ5794IO3OPicKoMFxHDOWFQWbexGfe/y/k//zM/8SucX3/7G+72N1tn0uD1Dm5zlkgoBmDTGPE+RrsFYPqo46n5dVyTUmbIWn7pJo7icOSEzO/hB8v5isTlvnNYX/VrzYxaQaJiWW6yKWrJKBYvurMMc6It6oo7Uq4tBvTlmHhZGjmmPnEeLGWZtIgQFDWxyBiXGy3mXQfsIBvJOpyATdtiymREBZmrSQGV1gsqP/DBswQIKK/c6vg0lwrbSQ4A70Wan43GDHYhcjAfpYi/CU6VKSSSV2qDBxTfBE2GLNMdqrRdCAmyS4OGjQqL820RxdR+pnPELIQQVuaA+s16COroITg/jE5KB8MVCUjakEWOt1044YLm8syJB8ZXLGM0ERMucgAoIQ4rgYSN0PTzsC183gZXkER7Jq+Kar5CtF/gifrzyRKRIF68svPbLGgDfRBgcjF0fp8ZRN0WfH1P6xdu3vSBIMPhUnOy6WdK7PrAAq96FZUig55d3WOxc5yrP828VpVUy0CipLoBZ4xgolO4cLFw5T1GhJqYpSiJ5S4wk/eTLOqXkyqX4wClkiikz+tkYLFQDwEoID34TdqGGPhDVoYQNbUyOKhAfEaFxH2dUmzWrc0TMBEFwpA9Vcz6rDIzBrNAmchgUOpOXuRlDu6B0IWO0JawHyJ1XMLG7ImIpEsoAg1M6u+jihH2i3QmBsmOjCsLGQiHJRrgMP9BMZ9wPba4sLNNuiGqZLLUPVhFWwJ6fh9zx3QoF+pMLd3rpmATLXEM0LUoOYugbCS0LG2lhqgHAFlp0sqJnFJ0x9Bk2BA+4OYnDK0npRaHRT+VEVUt+HHgBjqxVYpcXdv9wdgiFh2YMcNlImHdb9InY4SYpsMKijXiSMRJNfVvcRjVP8qRQ4I/N0ymRCtCKOKAJqbRetu9dqkPNodtgNHkMrQVrqSUG6WQ0eULl8J7PTm1K3haYqqtyUNn/HJp4fgotORHDcIAPkLNBBWYBSrI6GNcHptqGYnmmHrTQlCOT5E6+2EiASAGIBP58JhI9PTgT1Iv0YnQwLyQpV3niTtLyfP7Au89P38/TUEx5Zq6AXgfzGwgkI00kJzcj077FD6a1JWPBTivDLQqSuKTkj5Ky2oJqCKnvb/TczkUDXUcqMKu72zvsjXHvHg2hsgcfOTYzww0kHUchZ3xCFEeHBb9o7jA53WNwgWkdgEJW1QSQwNZDzEywni8muANISU6pw+DodjPAoHe1XNBD12nWN7v9jz/4+Jf/8T9pMxzQre9usrnNaDz5CHHiQo2YtDEds7VLV52G8FAAbrEGjRE29rHruqMR+OEyDvpQbERHOZXYaDyGOBQcXnstFg8fPmxeusIOSPRLISrKg+KlfMlrjXdoD+sNpE5TChBMJEqfFCebwXBSyAXFNZUbPcxIprTHd2ZWoAPTcEDmygIgn/O58JVAsoqshtfxZmxh4PibvzwPXuRjBQhtLbOWCCEXZKyCLVAw4z/fUgqKCmZ8VGwNBZBilCa7gFUo3syAywhEXrLW+dq1vVbXZdJ285MFZbEBwIx5h3HY7vDkeIgnrXoKMa0LthARkrR6CjGAy62EJz7wEiZewUwKUjYoHAk3OLBK+Vc1+vuvXr3KvGz2VmHMstNixyWGp/BX2EPdPbhhFnRXCOE788VzCtWQ9b/z0dbGDqVEMNjPlQ36WUiN5cMgcTYw/ppdHG4S2EEKnVvCVEwWZ2AxGGyaswEL88lq7B+Aq0aTdcGSjWX95GTV2kZObZBVxQ3CYEzpUjLDQ3TLty64z4X10khKwQPGTRg1Zl4HZLYOc8YJPIM58ikpJJlUKqkkDCGKQsgYUHw//5WNiolhEWhBRcQMof/FmZw8IUZmlRunlrbbm1s4KEtOrIAyNJr1flVhJAJ4LhFBZdjrE/IKEAVilYXWhsXVth4AJFbaT/NGUSEpXiDhtDwIMlxBgsUZFTQNl8FVcf3JP8lqODBs87GFDStPqFXx2HJpD+nLyzPwpI3A3XgU5jN7hw0jaaP+o3/0D+7cu8vOZqz6/f4f+sHXX3/9z/3Ej37uu1+nOUfa6zdvfu2P/oj5gi+/9BI5kxleOXUNe006Pck5KFInNFAJMCq8Um7yY/LMztb+8Ow+PMCLTiTmQrpWAfeE0aTRcPrSS6/+/u99udvqHz48/b5/91UO7hhzDt9k9NUvf0XCMqiGK2LZbbYy8IwBdLGcxLBKcoWArQv8T6ab4t0yAY+9PMcdtutItxXkIba1p3NUWMK7YksKRjwpvJpvzyeeOJv8IlsyiClGaDwvFtbBBCjWY3Ut1RQTiWgPsH0PRkyxQi4lqKMCrLkaNLe0l4gEs/PdQhs1oAOYQUHo5FKzFa4BONTaY619b4Ki2oauRDDSGL4aUzNqLW52zp8ip8ybyDittpF62dpDR8ASRHrjvKX+S3EVND7ABeoeN90lQGZpqJUEXkAYe84LZpFqi+jy0gouQwPEJgohUARuKkqRIA1xOFI0w+5SIfPf7jBiOfiibQ/1RJOySDKEOsYKcRBQkUxSCZs2RptWjZmJuXnlF5TMTNUo8f211inWw9zKF4KNWlI+vZ9/9+HTlyAFzZW7mVV5K2EVjgHKa7liwUsacrENQcsn6/Rjt4IA4IxOK9Ov/ALJvVL5ZxsicZAE+x5Kxj54rTMpb2vciPSU4EIgGqDAXGTzUn5BWubQ+YdnEzYAghAjIShObTET+YoFF8nAiDAgBmgDFQZ+gB06aoB0xv33fB9a/LAQy2XHERLvUhXGehQj4ERONYG+8itkvHMlVWleXALOqvHQmhTBJlNyizxYYNuPqPYdPMrGqueRKcgrFad+pc0GxLQ2vUph2f3DzJjVR7u/8RAHAs3HdaA7jkLT6UcRwRFxyqkreE4aDcLNg2zTxwpO9ktxZpBIxml2NKB8BHuQwxwDkpWaqKeEoM6z25teGRruijj+CrP9LAMFR5r5RAEhi6VnDNRJG+RoTPdLV7jVB4BgdYmp20dqctK302oTSKbCxGA5iKYjpaBjKbMBYnFgIBWFAvHEVALQVSiD6Quz+KzmwSMgwbXG4hJWst4+hFDoWem8p1jWOlZuGC+S0P4BnulSfHr1mRELoUUJpJQMphva8eauCEQDX0pKDI08udR2G7UDiUweETZSAgFKJw71nGtJdfXopaDopGXa0OZjZdIVIAI1vuEAKCfzuScAH4xaPRR5TeIqPB/XN2AYjBD65FWi5qd6NEL+MKA4K1Scfm3dApPl5EYxdFVSEGndhT966NIKhQIBKi/mLN0mdGv7MnV2v9c5G3an7GAzZefpLaax0bHPRnLACwZICPkhEizqZZyE6aRqIgThIRyGxQKlgeEIAN1LDZdu26sNQ+zIof8LYWF7HBZRDJCrgz1mtc5nI8Yj6m/+IZtpbI0md1649sq//zN//vTs6PDxIzvscUzYEWP8aLE6ZsGtXFTCZw6AL5c9JsHWR6zwc+2ak9vcTbrbae/u7RwfHXOi54R99R2MQv/oE53ff3DvYHlpg11QGQ0v89GtReCj+2/AZcCj1wC1CWYTZ+LvakDgoj6mBPCeWoIZQXa/eSCPPe6qqVLHobEUkIEpppmhMhCbSkfZko+QnCzUU/RILeOFr1bntQ6aHBIB1tyJyje7suzzgqzEATt8dLKm3GLgaJ+0T5deg6WW6BnVlVUhwmhZFHr1kCKo2RoU/vGqEHAjE9jXhZecYEDv33LS7FLJ08pr0u2dATHI3GAutechKATRWr1WSkQRgE4LkCu3UIocldnFjqixf7+fohElTkhBHGE5TV/a8cU5AIva7t7+1mALl+HatSuXLx1grt3G0DKsxqdDJvkgW0Mf2MFsTsOPmZMsAcf7Bw52gmwZ3QIyXbxnoyH7gTLt+0u/f4qjw9oShnOYjczkbbcSIN+2ndlOPgBfNwFbdgdPOLhusPE8MsQMDLok2EwV3aq3EbaRNl60JV/Qlx4pG7/QEnYT7hcFaX1ZUtg5vyRNoJp9Qb3xovlosnCzsdUO+9PUGo+azIKgy5cNERAexNJWJ9AijRo/MhByoVv5EV7imCMklM1w3EuBC81Z2WKfEWZTBRRh9TA0Z3SF+er4dPZLLRmnpQGA6KV8Vq+BCGEI5YXVBer2B9gP6x53abHnmQU6kWSh8z8WniMpIZrRCi40GALEvEULLNbzBUhVKFbmAqwyM0owdMz3exQ7Vb9GxphVmchHuaWky8btNlYEa7ao//6//t3f/4Pfv333Dj1cyPT25u7P/Oxf+Ut/+d+fMl9zNKHmgZmI+mdef50igB7VB6f1HT58vLW3gyV//xsfvfjSS46AqbYotu0fHUpqYCLjZLeW3/9DX/it3/7dh/ceznHNiUBnD935qCdf2T+1U3vltdc5Duz2Rx+On0x/5zfe+twXPt/eOD05Pjw9HUIy1PJgdon+R5jaYIffFjUv48joNZUO1TgcYG6PfoLePmeYs48nk6AanLNOkehc50hjzmyfcdC43U9SgDUAcHFKS1hjy705asyuugF97ZSxXCrbbCEF7XAtWKbLkgxG6e0RazdG7Ofl0eGLzQVnC3DqeWvYmD3HMX9aHw4pn/dHtWNW2vdWZ51ZZ6uxGMw7zQWjxN1le1Kb7XYZB2gcc7zYtN6e4+u2GKSlLAgF/stjpG+13A2zi81QHprNx+22501YZP2EqBK6h+YoCLA0PCYqNAIA0qtNHMF9aIVgWBHxgzSSD2tdsLUKEAnJGQ2EcMqXUBaMoOqnIf+2/ylTmIm4KktMkdK0Ui+rq4pugYN+oudMscKqMuOST1oVrTfSLzI+qpWN1qH4T5noZYh4NZioSTLWmLXoVPWrp1ODS6wBv+LpVSFc0Cb9ueaWU7OmN8m3XOXh6Z2n7K6ZM7jWkSy84YD1QYrwK6LmWeViZF+N8fRyBIDL6BKOpOXZ+9OYqY3WiVTDAqokPA9fPzzN8CmEp1BNDGy5RKCUSCzZU0IJSgH8IEoaFilIe9HylD96PE2uuJEctLkXEAGI5JgUBsM/0iN89sTTv84eXnxC+DSCkVYFglUuTv1EQ4qt0UBwEifWh+ofQMBPzqIuiQBuxpokjCGU1gpYvSIXXEicQfiihAVjcbXkTO1j02+LDU2tMJDuPIOMTyKgH4B6k0QBBkRzxWJZ3Hdkkhi02YwJQHsmyI0sAaGPoF0ED+H4j09giK8PQNYhYdPBWonmEfB0gtKnRTUQHEGFJHNHO6U2tSMVg2Vl4iEd+O3WAL/AvQkoCNKuVuBt4CDqDkImTKRARUHy+K+wVuh55Sb+soMHrggB+YZDZmo6AUsXCYlieLerjzEB84QiRIet7v0y4ZhxMCXMlIL2z1d+zcxseZHwEizcoeyaeAhtEnW95EUs2oX4BdiLuMWkhm6SNsm9UY+x45FFRhbdQ0HXJJ+pJj3F0QrbfAxLQYKFSc+vIOqbHORHsfhkrJIcxMqHwC9R1o+Kj6RJ8SSaRUhJyZlQCWXDxu4cDFMFkEhIJPUNfUf0ZlLOiA7R5AiMxUvq9Tc2to8OHzFv1a5m3AJWzUpQ+l0Qb71OqWQ9D8/JmPEouk5xWeQc1pjIxojo4EJSrXGiDW63vgW21SVl4Ar3tIxQ++DSweh02Fid0hvf7fV1LKanN545YKVmr38wPDthWYUDvDbdW8s5I+OgwEUvVZeDeJye0dqgnY+/ilirLM0GW3ETi3ncO9u7HGbEcaWHTG9yfpoGgeY1a4LR8MFGj+4yLk09upD1ctBMMtElrIio0YqYs/vo+wQqb9LTJo1zeWlXOGdGZvFPDbC2wXvgocgOlCMZlArxkC4hQEA66SrGKNMQFl12jx0JRHSydngW2TfEqECJ3gJbEVaA+aA7bueIFyEINvtLoit4A/zYhyeTaCnRzML1VfLDKZAjBmCX9oJf4czkZq23sXF6eoaIMw7DoaKWKkqOr3f79j34j6SQWjmiEciNnkdJUcRSDAT59EfFz0XUlIA7UgBlipIAgmUieLxMuBxN6cPY3dt94flXOTdiYzCgYJhot5mnWAyPTse9AQIyQD62tu22xN0XGdZudrp25HKgkqP5ZkEHMMOb9Kiy5fhzewfXblzZ2trqb9Il0xmPOLZh2umy/ctD1uoADSWm4fP8Ky8+efIExmFnGQ6j/mcFpc84fizW5N7cQDJszMEIy+WDXE+OpaClwAStX6unEj+0Q40QEZRwceYRkywbQyA4he2saUbTfqO/xXQj0wGjADe1NM9bjH8oDvECN3ENkbTrqyQpzith1BQKapwXRYlLVUXr3fyAWgD1oRdcHaIKoICyRtlwag30hxDpElL23MLRzipzh/lcCLACTn2kviBsRE4efiQnkVGkuSW4IEnUJE9RYXY+FXEmPgqFqqCwKTtptVIRWlJjfIEHdo7tY45n83fefvdXfuUff/DhR+PhiGl+B1cO/ov/6r/4/Be+j3YhPQ6gTdZrAJacMliFN5sHVw9oQ5LR6fBsOBputbZAV+i5FFXmBbm2gdZOvYth4Tjt+aLTHXBCqBxJjUSZEVYmR+G4f/Y7Xv/w3Y+ZGTUenYzOjvt73Z3dPRqHbNHV7SuTIgJckEDh6S2IC0u5rVTIwz2m6VpYsBZnp9Viv7Eee9ZhYjioS3UhuvaG8tAHBje69AiIg16B3aAILa6CfjJdovaIO7NfdbO5oqFY0erFlPXnjdaotj1vDOe1jawgBix9MwPqvFVzwz7BRv+UJse80Z21djkXkLED26gwl6MNsTsuzVmuerB7uOrSvoFo8DBujIzWcEXOKGtpcKqcNIRhiUKl9MBP3YZIDnJFexiCmk4LbN+qk8ZgNmpHhsLTbVPMkEBDIEny8pPC5T91NGIECsB2+ANIGno+YmBJwbOmLaJFkiJ6Zs2fzj3gmT1uUQMueKOn0F6IXGIYwZZaQkDFBOvaQWCbBwswcNuQI4hvRgVBn3OVB+78kfoTV1AL+GRz4VtooNYQdg4hZA74EixyeTq/XYCwfuRb0iHZXjxb2PZt0zgOwPOdfMmtFMJYFFYa+QAVpjd5qNv3H9YbXsXwN7wRoFdyy9M6pIQJrvqaKKKh9plEispSTJKcTrgfoDBMRQIS1wD6J4RdzYAEN/U2efKLOwS/2fmR1r0uPTI0n162akwZrVaxfAgyFXBEyqwB6r6celG+6vnE6sl7JbmISGPGrgvMT3hMWv0icTRnhIjeYGTXtr3yTSCloZnukaSL9hMzYo9YlJ+9/J2WR1747qSn7w6mlCJosbWFahCtfNQFOsR5BSWjFJqQhdoC9fH+1api6MUiJbH8ECDyLHL6DxSLGpSp3LYitPD2DlBJUGKmXDI4wP7HKCeVK3TGJDAcqRFkrESyCjgtB9SeosANtIUGCv2RVCdUtLQ3KlxAB09Ra6dN1ysJV0XdGLqhUplROx0O2IryY0X4oJ6p9jIgTJi3HpJWNcR6MxkRmjO6Aklc00MGpIBd/GhT4+nAEIBExuAL5XTTUn5wAj02khArZNlG9DkTsMAUu8Z6QbpEIVOkUayN4kVZVXdPUbUTV74aTDYsMsHKKC3aZ5N4kZBp2ea8DiGwPK9DjFyup0/SRQD+CoMnmS0gL57gaTJCavninHow692XufNniBdJJpCROtK7CiVQlDCewiC6POnjGa0WBzCBxrL9T+w6X59v7nKcLZvusMcM3j+scY9o4SBcTgZSmMCC/a3hsyNoY87ToIv0oR1ZdqnSC8/qN0SLszA18fCQU3EIoQSKJ6UBIlJWb25tb+Feb2wOTofsFrTFlON6rc+G9kggtnt7q8GUfuYwd1adyezhsnaGlyg76fLKtP7JeHx85AJ6xvm4UwurCE7uagLWXmy2gWSCEHKOftrtx7TWyfHolJU51xs3MAlwnhKgG3bea+H7FJVxBQrIcZv8Z8yMDgLZYNBmxJoOMxJQj2Ly7INv1AZ8XtXPkFtFVHWmlMSyxskF4TWPlWViKn/CI+c0OxMTMAzfm4Cz6AlRyHhIRK0YVLMyc4Wf2XvX2jB+sAV0ZJgadEm3n+rB3GVIESWwOAvOPSWetkv9orgECphPr3zHa3/rf/0LR/fuQ6/W5kaDbcF0+JwQiKXEHkymIyZXWCCQLnKJslkWWhr8y1TDCk1CCRebWvPEyADS9PFLuJUz0lqgaImWtauXDnqDRr/NAt7B1uZguz+gTJgPJRbRKWaedkKXpYkgztZl/SghWqYfBVvRdooCu63KV3XPjcJwd+hC7hw96ty7NcNQ/LW//nOXr27e+sgjX17/7r2j0+E7778NOcyh1hpsbB/c2G/06hs7++DUdXdIuuUZrWozU6zB7lBsxcoAOKWwQBTF0vNHQXxNGaVDQhMYCljkhIVosEtzYWooANZdRxxtWLJ3G+NRpMMU0g4imu01EksEgiM6dF8BD87JHFipzAjdH2OVx2BDDqlyCKJP3UFuaQUgL6ITWfvMndfAoWsDz8yz0mKsORcWmqIRWnt8O9yw1l1MTXvyAnNpWp07et12JQSBAjT5R/mwqchpunhFy+JUeYlmkjQfJXoQyBPbyEu3qkCldcG76cGRi7xEHHQmV6moGj128KP/RTk5O9r6F//0zbt37sIJbE9vo9trvPz8sz965doANaeFCYLIOVV8ICl2AnOqC59oQdg26LQ74+P9nX6v1jpBSGJR6UXxkzQFMcf4ls++cP3+49vzmZsOY1rgDFUewKENoopr9OJzL+JHTKenj+8+6f3gRo1jd2ej7b29h/ffwsWg24KRWqCRPzOXdBFom1mnMaBJhz/dEDSIF915Z7/VuMoCOGbB68OjhsgDUkHtBTF5Aoa8ZO6W3YW8uac2uCKQj/TCIY70sU5NhyRjBQigckXnBceRMx4yXR3N2LFJNaNZwmnfjAYf0+dDFth0hixOlyNmttI836hNaYR0a55LUKs9IeNG7YOMjjixngl6WE5rP3VbKtQWB6BCXbD+p7lA0BqLPUR3Vf/IV1ow1uVKTzwWK2arpnh3WlYANDg5HrWKPLBxlhlgIXE+6Pu3sDwqG+XRZ3LHxEmOWvsBX4CuuQMvfSmRg3wkZT4LsREowUg0L3RQmko+JmWgNFRGJGIvfyJy00vSgGrQKOMlCIm7nLQ4QoySbUdCRYlqNJiQ7hx88vj0jaxByou0NXf8M/n6Ks9iUYLNizigkFwJ5FuVQLwupOPVt/XHxAfr8yh+xJiso5jWXArcdbzyZlSufFuHQNkSCsTo7fpdIH5Z//pw8brw6uP5Kw8FYikHPKM8Mha14RPypX1U3zT9cs3EF5M/zSVEARqpClqqMfzDZWNzB9R1MdnkvmxsOPqJgNhw04emgoEfPDBxCMeARoItAFDRQQANphw42kdO9JDzAdcdjdWWOPQcI+uNqlrUCqqADhbgg+cITERJN5Xq2Q+wsOBoxwbOJxqGiMYuSw8j8D+R2RguboAxgO5XEguftG44oMcQmpRESqPw1RthqCe5VIkCNRlQMFLh0FNqyO0ESqshLmIj4rk0UnZJ6oZY8XOXMnbEGZGoYGJVA3tSzTsxlxiWBSjYXPXQ4z5Ip/PBs4hbB4NcIADUXhnMOokkPLApl3GBTpPFUlMiMqX+8vQA7QX9aWymBqT0SMMFYBmMzoM0Fa1QyYkRYHAombV7HXqybILQqiFHzPCZJoLs2QOEAFpciJyZij4XEMBCQ2YRdDniYAVPKRAU5UgVWYpI10/fE1CFn0coged3gK1zLeotcK2OMSgdpVXMQN4JHJIZY0Ma610kOncXaVAgRYemCumoHioXxF4653iw1z4b8yBx9KMzFV+qL9wQiSYqM2MhnM4u7UO7lywfWcMBJB3sVBZlhOkveoEyC9OEz+2EAahA7ci0Nw+mWblimD6fGkNwwMHhsggivMJX297aHh6fbW3tnZ5NxNWMFm1mJqMoU6YPGRMvH16z7q1Z3wCgeTE3vecYLlSgQ9dVCdZ+4OBIAyCIo/gppNRvtcuXLlHZ39WLBW/yaDIo8fGtj/e29g4O9sBNSVUnQQ4svEVu4TnP0hukwwSLDkxIbAgGIaTBKhBPp86YJs2Djz5J/oQLzuJ7Gcj/CnaCiFtlWwCYunwIIOtOC0AiGA5fCFXfeJDlNCoQT/YekNH2YLXSbgHD4ZAFx/bsA2yNDiwzf47629za7PfbtYMtiDbY6AR1F3qYp65A/fR0cufWPVwilDg4E24TvLi85yiKqcWWduvfIr58EFaEtPpsXoMeg4o78H5/i17/Xqev18U+NOqXsgUsWwDOXbSLxlBcCLt8cT3tctVBn9HIlN9AxziDkzI7X7BrEKMC9A0fPjp8fHL78PGD/UuDvf091n8xRXt3a7/d8nDgLnugOd+aKW2Dnd06TYEucsWR8+RIM45G5rw9wUmv9dr1PrYwepkCQvhSppAkEp0ifvJGFL5LqvKAadPWqWmWR/YBNCIGG52oxlcGl5SqwFeBMYKIBZ6WZCUafbXE8AqhIzKhMJ9LuGaTEI0z+Xpj9Zdb8gMB7KFn6hgzUVXSTiXQR5sGoJcyElcktCtMT7e3henjCAEQwEC7rTLSF4YuUzCeYQ4pYAQ5AkeNBASZVZfohRQ8nAf6LRkV3HiplKIE8jXCto5k9WMeKDbD6ffv3Pnlf/iVP/iDL89x1xr17/7e7/25v/q/vHrwPWenxyzoUBfi7oOb0MxTHYuImgtyDmGxFgccKIHM2Itn7VZRCa3i8lV5Q2CeffbFr3zlDfof2OedYlpszBxzJTULkuH6M6xOv3H3wd3VYnx0+LDWp4KDze2tnV1w6A96xsLp50RdZIyaih5U8ot9pnuQB/oeevXZoIZ30mJsS1bjXeLSizYIaXmsYxUFmpI4NdmoAJ6EboqonhNA6Uy0AxybK3rS3W/Km/4pwxL0U1ALOm2S8jlDjvYUUw3Z0JTmLuLDjCRQhc4698oG6a2GbXcppexE5KwJTwhAd7F/xIFewcBsQD28SxAvIgj1pZk5yQZfVefAtgzSlBdgiC4PxpALRY5941NIZl48ST0jm8SXfCvxTAUEooFtvA4eog9miPgmAWEioHoVGAEGYUgN6lZCokJ5jO9T+SF6VbIQVcwqJvBI3cdEQ1IGdEhhsm+61viXEgG7YEFCsjLbCkBy9VlcvErC8ly9+nX9IY9/zM1R5nIlZVWyzq2Emf8aOQJAzLyq/JQ/etyJKW0q0st+U5yz269VivKQbJZ907K51dMr4UbmIiPgCD80oNVNgDaeLwV6EY/mIi2hlisWWLeQtEniO0gIpD6/gQ6s2DdAU1Wi6LjUuvdx+fjkVndmENunlERcyIChYJK75wbVDzywaMDg/7J5qIg62rOqbzwWadQNIqDL8J0YEIqaA/VWu1lJxixMy+YfF7afNWDpupBSGDJDCQdESu2Lug1gbZc9DADGOAjB3EwQcAWeu0ozD4GWqGkKkHwONGWb2JSZFoL9XQCnlMDF+KC7WQDBqxWsDjMWJWO4eAyGYAUICe0Za9S5rErhoCeKyvokuoLIgXJrl/lKj6l9gxNo4c4cnHjgzCE7ju0ZqsopHVIQp4OQCE0BAyDQtTXosze/RlmGwzbHMPW8G/VrOanzAdSBilaj9rTaWqNUOkCWSmZB1rJLXWFoTABbG0AlGURZydxhb7Y2qLEFhDMoCLZw2uNTxm+1myFziC4JzYE/7Xx8I+c/YEVNmf9hSVbRVGvwQV647vV7YY9/ol245NgnQyTvGmQiBu7aDBC5QJUPGl3LjH7o7DaXU+b9e3EngKKqZcGZIBAvsoGlZz/qK9euTcfbdPQ/vHerV28dHz+g35zpsnxlSJz16bQBWOnrGkUymF8FZqN1F8OtlMGU1PRZr0In1R16mGnc4kpeu36ZhbbwbDJ1GS57SdOHip0ZTYZM1WZQRTebvZrSKNne3mW8fnt721kZ7cZ09oTWXHPZ/vpXvjb9i38Oh3U8PkP+EZHB5k4dQXN3bppwDBaLFSWlmHiEk9mkM4O9iA3N82amAIk1tEJ5+GFJwKWDffLizM5mh4lD7I7IBpOrk9HJ8nDOpHNEyIl2dvqWfT+GIbswoHNhWET/JCFr4DFTmIRaAw+bWCBb4ppI613xi5cChe/G8/Ir0fLKc4m/tPe6ytFPJY6KAgN5M6Jx07L1F38LyT1Jeh3lBnuf2PcvbNSNycMw1ME6GgxIt6Mu5KnTxg8GotPqHj05Hp2NB4MdThJAlHDzmKBl0xq9c54kJ6k9fPTgnriqX2oiVlE0Ka7lWeOZ8nBbl3D9LnKYIdIGr5SLOHvbO5f3LwNu0KDXX80jEMnCTyIyYLEAdhqwMQk2euZMxR6ztpiWM5syMul0JgqAMLB6geIgf0zIxolZ1TY3B3QODDb7tcY7bHHAdPDxmIXvVMnTje3+1tbm6597kW1+NDK2HthNKh0eLQ6QxiiyuoCOHm09Oz1lXT/ODgcCTzweQkaIJ0UKjcOuTxYZzPl4kQj5bvQkSdHs/aASgbwDqoA6s5z1LpiHFatSaCsY6csfhJb6sZCQBcbw8RyshJ5dN2pVD5rez4wyt7d4YLscnqGiuFWWrcHh3xyfl34ZDYOqxIJatM4dfpjfIhC8fn01W7w4fGjvx/AJMBSPDM7OTtl2AtQ0P5VQUYxsKiBOQUP8LUkwShiFYiNUBejpVX962knCU2QTAdhYZELjAuNN0MfUFHa9NZpf+eIX/8e///fuPXy8bC3ZhZlDu/7C/+LP//hP/ZSVGt0YDHxNpoPNQVqGCqvJqUqxQV7Wj8CkjmD+2JVrV9kJjY16OvUuskTdhhhSExrPiYWaBeSQbvovfO93//7vfgnc+GSnIrscRw0RXkbMGFfdO9i6c//DZufBH331V75n60/12YHK0cL5FCF0G37aLfTrc+A3K3Dn7dqUYVT4p4V2YNDDY+n96KzYTHroXuJMDFQubQlEZWEi4qniU23CCDsfWJvkUVxUxHRRIynckS4XNVEApi8W6xEqMvqNkw00HX0Ox+PwIBRToUSpa2fQuLUa21nWHLdBGw7gq+AnaIPoQWCcAVEio668YRpRg4HTDUpQX22Ql6wqnOYxMirF5T8ZwMl8LPKsbSYBf/DYqHxTyo2utEJ/P/MPSHxtcG49RQcQf3zkDbRJaBKVSTLFZ1hcFhHOqInokFzYiqG5lASRXwP8ryTwq5MX3M0WXas1ehIPusNa/nv5TERkQmRM62fSggKqVDISZ+ZDEI11ISQ116S+8FTeL9yBQDSYy1WeeSR7r4oIKU95ruiYr+VW5cDL06cLn7/NI77XU+zWccy4PAfUN0eoPqaGM2aomUApfPG6mPaPxcvISQBHQlw1VF9N8SW1ZPav5GdO8gce+GgEL+mTTymEEXiTzb7LJj8qcSi3KpUBMlLj7KJJIXFx/pjGV2OKIbvYwnzzIZ0jAIoaCs9/VlZpTbTkmgxMidOIBWVVi+bSHZmOEhIh0Bgsi0Ll7VrMyoMBMKIMOlZ1pEWkI/cYXL6Il6KeflM79pR4C5lSSCbcPoZiiYKFCjKYa/XZ0oZ0KTVIx30QHP6TfhIWkrFIhj81at7MUatSZz0T0xroImUP4x7TJ0hgG52eeOLgwtH7J3zMKyIep989yDGR1KPMNACZ6IwaymJ87KsbBLjIwtV8mjn5QDksiogzkyf7e9qMItzy0ugoQEgAXZxwSKkFy+AcNtfhfjnOLU04FtwQhXeJo2UAs/T9mE+oZTVGTvyLMEjl0Mhei3SOUkw6FMENr4l+0MJZ8xQYgTIG1jlkxBCABWFdeAHBi6j4n8tbCc+9ei2Bfl9ffEgKYn3yKsy11HkSCuw2L66kKvHNnr0YGNFCFvFlMMrG46OkD+JEp5yigLVFTshSm2XOHHXU73vK1eZWZzZZTN89XbBZCovTJtNWq3/9yo1bkwenZ3CefaKmbHIkXE6fsZEkP9fohGlAZNb5goqkP8SXRzCcHtAYj5f0wT56/JilBcgZbjqeZbqikTsAzRlrgRus5FQ+2i3372QebYtT+IbsD03ZmNVD9z+tlEcPD9/40pvkTHz4BUXIh73aVTpqv9EYHbx0ifk+ztVx4I6ljVTbjAxQ+02pzKmpm5f2D5gNcnx2xvm5aLfTGGaz42MPQ7hy5VKrzaJDt7IN9ewapAhQtlBMXUP8irUJlUPVitPSxvcS5m/59zSEj15S0VhwvrCqvKyDtDIyaA2HuEYO7U2ZZ5lr21uU5DLxQVK5VT7RN1tMdnyy/xKN2zTp8SxRT9wZ1wJZV5KYTGk8d1rD0fFswco//B5oB1hJyMf0UYjxR+/fQa2TEXlFEZAptCLqJq48FCkzekE+RRGWD7FrtNzIVjXa3d25eeMm7TbnHA36bfb4wVqCOOXhx/FMxletZUlOMbjQXAR2c2PAws15y92rzBN5xXYxIY/OKBiK4K1WHCZ95dolEsHdza0tOmpGwyee/CE0qLRiB5JBb6fdHAQx1joQynIB7R0GgIltoCPa+CduJ7qLDDBNiL1xdUyEgZORpBYVZP1fQqTE+hPP51chg6WXelw4lEbVkNBySed0bD0vjHdy19HhRgLtj7UL2FgpZsNqgKwz5UnoXhGT8oR9MiMKS6jhsQIlogwA4Gp5fHTEwhjQsC4SjmVhv6BLlw6EUtCVaoA3B8UmeRSLAqcgDDsnkYyZ7dhtYhK9oJ1chaKIKqSpXqNBoVCFPzHMlf/+cAmDyEhnwqsygQKvaeCxhasdTBBoeHb8R1998+NbNE3tv/rO7/nOv/ZX/9pP/oWf4jxfvESaACy+ZYahcaEh5RN9Xnw1va5kLj9pHjls0IyIkVoVReFZ15+H8MhBgFbnypWryCcDajSfwFcQGgqG36lidMxfeOnlr735NWh2+mT4ztvvPPviCw4ns3hgRbOKTa7pFTMHRIr5+Ky1ci9qFvsqV5ScHhCe6IECP6cXcpIh3kRoDmVgFeIB5uSjPvFsXWltiSfjP7WaOBguZIA/dCTcAxK/Ki7f1X4i8op+aD5MYmZ29mUaD74B555gX5l7nK5SZAPLaMUKVbhZ3y4XLJ9AT9mEzcEL9QPcFF6LUqhrnjhIqcAJ5rsmPBMuVAIiepfpvpgcbCgSjgoFLNwSJsZNMSZEF6FEQpKJIgPyq2Dz1bwNKKkDosSCFMSwlMRIjiVZNEIakmlp5JOTeSivAgMcVlO0wBQ0MbKWNZ4hIDSlBfNoWsDj+rsLkMhIlwpR4Xmt38tb7kbkQ0H66T0lSQppm4xE6ULCf/vHC7nb+fpJAFJ/jWCJCNFsIYmbomZZCy688M93rtkNP6974g35dlh+ou/fiNUllaR2bmG5+SshsKYQ3fcgYaxWzhwQpTWE/Fb4iFfWJzgnocQxHvginQaUUJ9KCsQKbvlJ95avdIKhps6bqOAreXAb/dQyUC844il+CgfdyenJ1gYiHyZWUJucYMwAGQR0l88IOq4Fkg8I+1JMrtSwsZrnqvC0nF0DjUbTNd3KGYnRLj0ZNgDG/2UwVvkDp3h3aKI+kxKrnUAzrVLEeH6FSKyCV5vITmkFUzqtwY0o9Dsw87ODL1EozGzmTGdifWUXTJkgyWd2OdD91g5mdhAdA4lOy4YhAKqu1Ls639Tl9sNRk/Oize/jfJAppdVfK0SU0gVzKUEo0euLK+6QUL+TQX7VMpWd6g6WuC867Ww/QNlXT0hjMbFJRqIBhlcBC8iRSzc4xDdDFThMJgV8wE1QIMRE5ib3YECLxhbO6tGjI/C3K4vVUxRdcNnRiBQSSBrCnFbtCl1EreZJo8YWT1QAQJO+FpCfsopf6nOZVfr+81BeDeKSCFUEIZTXBIUZYrnGXmztKSROJanGA6HZTbFqfgwcNm8lXaRLNFLIWKUyUkcMeiwAQA9Slsna/6u0pXFFM7ffuHTjmZO33mH7OZxotoKBsayPhAZ4zvpB7jAAEMQVuW2wAQilARQjCbCDZi8coYlHabd2Nh4/OWTqBay49dHdOrVx8yrz84eTjx0L4pAB6hAGVWlZOAjtHFz6HNn8czoe4oIhobYvkMxm16xYjkKz0VH52Z3bH7MdbXSHBiAt2DrTRhhXYLEN3OLw0dOz052tbWhDalheY9eKCZucDIsAUlr4zIyjze0NBOrh40PwpsHAxvKcI3b3/j1OQ9vf33OKII0pDA5qRk2J5GhhFEsfwkQp95RjJUyerK+Qf/3CrwJkgvUvT0Yp0QTFi19LjLysU5nOlHNmG1OJsgQCDjpNAc6rELCEtTuYKZppOArgCWlnS3c6xpthPYAt9AGd486jQaFS8cNBTAA4QGdWXZ88GZ0ez/Z3N9k+lT6ABrtJcV4S62jZMWc+ZxulN974KsaONYIhATIATFzk4Oi9QjJPF8ruI2XDOFpTsgiEida8MpOwl4PBN/Y3QYsmmf3eWlZLBcEl/JyzmaB4LBB7dtEERRaIi1fg5AQOAJlgMKEZMLERGDukESSxWBsbA6AwLZDtjBgHwLnpDzaZFeSyng47qRttb28w2GjXxge12RbGZzae0F2KVHD+V7vfJQ+Is2QeJMa/yU5WvA4ZoGKMSPmXj+FKCuyNvkbu88vnARa8umLiYZ2Ms5rwHZeMbiWwhkQNlr5gajBRcI8g/szdOlf/g8cIm45dMlaFS/WbiOtcyvq3UDzpSQS/saXlfHFLFKHRpLI7Po0jRy/ZXBU9ZSY51Yb6ERFXEqPdCllKy51Hs1+zOhRKHlWWImp8RQxTU2pSoCZTvlBaS4gpiyESGB+9V1dONz9H0uz4aqGFwObVcIa0JIBdiMVbX/3ab/yzf97sLNmwFWm6duP6X/jzf+nf+8s/TacVesE1Go63d7atoAVlQtETO9tRvoS4wockMY5sLSUJ+E9ESJe1quETeLuDNpGZIca5AZyAzB5lzOjJuiZUUYjsIaub32m+9NoLtV9mEIINyrpj0dh99913IXKzs9lA9nETIAJVfo3dNid95l7ORoxgTN1df8pgPhVrt9Vjzn9qQBgzy3QbKkQIQqiURktCGhx9ulQ40IaBhbJei4K6s6jySxtggY4Q0TZDRW9kzDVdoEwIBcVKKIjsk81iCl159+mkq4slfz18EVSeWCjvckkD+xhLUms/sh3KvqVq9iVWzs0aO+Ba42CylAzxtg6HWCJMtpETf/JQZDoUJpWVZ3kmoirBCzcugFvXBG8AE1KiKv2JBQNRG2WM0nKZW7HT7QcwMTyWr8bmx+8BLUjy7ZOuXqO7J1EIUj2d7yGawlVeyZZfBYKAFNLACLlj0a79cKzF9piMcSZC8fTYlIlHRhcNIHlQNmMeRLg85c6sAV7xHLivRwBMVZLFo6iz2lb6AbGk5A4+hPQFUXQ8wP4tbpmtgDA+vcz06cWbqJoNBeQHupy/JCQYBNWkUqXKVWFZvf3JflK2UjpyhPGUzswNh0mFwWuUCgUTe51nySVB3BIKQqTMla+G+7/gqTwmegqIxSuxqUdkXOLIuLUIJS3JEUM6yRGiFFJhQFYVNy5zQzmRF+Y4gDpONgcuszwoPegKpdHItJK6IBT3DpOWEQnm23Ggj7CaGzhemAlga6N1izjNHuxGaj+mxoLgBLA8K/4S1UidLlUGwZ37LoSII20gNInOfloYZG7e6WNjnBfHiOENpsGQA6XXStMNizllCizdFEsmZdBWoDRAZLiSSqvU5XhwwMeE2S8BOKQ/JcUmUWStFrkkI7QDJRFTMKeuD8mNxhX1oqagMFJblZPLWN0ZKz4RgDLK2cK9s3/FmoMyK/VQM3M4sMhM4QKp7OxCevto8RzLlB4MPYsZwJD4WBb9JJJnDN1NYkRULOnWAi61xL37D4BOZxhrto6OD+kvpT+aaIqh7TdLTCG4wwrGahd00sDiYvz5GlUxmo8XL4rPVWi/fvAtsc6jSqTE4w7QUlrtqfkpVtEEYpyD45mvBOhAcZEwuPq7hlZC/GaQZYFciLfx7UaWYnSVUVnhWNMfz6jQ+HTaafWmkzku0vIUKhZ2Ix74cMS3Y5S0yYXO1JmT83MGArDprRcdt1pfPXr4IOPhLcYoGAdwio1iST8RG3d4ROhocmZ3ppyobww2dvb2VodnZ+MzBt7oWotDyMo4OoNZnmiGx8eciOkYEmCoftiRPHl5PhNMB/jpySnjCGwgg4BolKnZ1Cn7wilhLIEUoPo+2Ns/Pj2ZjMbMdELgcCyZEoTY0KgcdDf3djkPgSFyqRTKZ55A5JUQGVDRzxfp+umLRN/6Q4koAMTGWkVLU9iWsHApQAVRxSYH9KJgYmb4NNxpQMlcIfDGXX3BdZ6csam7/bHYgzLDBX+eHRXhts4/TII0yi2cNwMH92iHs46vh4K7XTwfwGzQd6yg29148uSQ3VQRHuu4yKHJzNKbKPhYyGCJSpAfvcgIXwH600ZHa5jo39zb3hv02OSJpqOT/LA+6B8bNzIIZKcy2kyr1rmDtAoYQFe/FVpVbnZ2xjYqMySKwSUyp7y8M3wAv+A11m9ja7MzoONt2en12P0Ro3rnzt0f/8k/s7e/r5GjhG6GA3w2j+xDKUK0ObB+sepv4v00WKnSzDJiRrTwpGbD5XKj7ZBSvY+9w6+hkGRd6J6ip6AhR56kCJcB0WNZrJhIc8JIiclzAgbxXK2ernGZApexUWRiYWV6YJBC44zNFY585t2g6mtyEicZUTLNo3kmKKJmkAgZSGqcFOfsAUJfhpygvONm2OuqXSLYQKvQPgcvmACrMks0A/hfYQhIUxUA8EWYvinGKKJ4BYIPKROvycsYBuZtDVEJoHqUQ+5IZoVyMnryP/1P//itN9/c3NzE4f+pf+8nfuE//oXNjc3xjF16zZpcGMpQ5zV6SifP5UG8xLZc65rYkNRq6AgRRUJbV2IKBteQ6lI54fCt1mde/46vfOVLdIy4Bh3R0NQ4objZ6FpIZp3t7eIMctzV+OG9fqvxzDPP3r3z8cyBTc6ZC5k51RuHkR4NcPMfAw24/jRTgYbbPmMUw3n21Kg0HlW/ikSiZBHMU6TFUqNsqJWqX7Bq7kOPlCknSSiFIQXFk7y04NVyPyKA/M0wHyCS/m/quWoza5wYetRsrJorZpcEzGKihSKn+I8DyghdbeF2avCcxna8n+gw8NZa4qN1DYS0Y4WfcJkw8Q/HJBvFCbJyMK/8FiGKnNho0t3nT4eblEKUv/LLDldLT0KTS5m8E5RQA01bsCoZkPRpjkVEjKaC6GIpM4ALwMAVjUAjb5JGQoigKTdJysL3IL2kA4uOyDhDxC0JxSQQ1sXyrYSYjWnz2ZvvQbkKEQ2RoWAlpMCovv5Jf0ib/Nb5PG0AVOCSrdBWZScKvJzqEp0kFof8KbqGiBF9hMQrYKGHcf/tLsQRxxdysmsKKZVN3AVDZldciG0PARlcBEu+wajk+jS7vJeP4Z8ue1gkQfnop5AzwCo5kUWlfHlAq2SyVFEmiE9iRQONTHKVlpgqHkABx1eUKEKOhHupbxgDxguorRlYQ+viu4t2IIMykdBwLEexjFjLVv0RCemI5jTOiBTypeICSku07JkXWZG51AGmvexkxz6KvFKbqbMYp9Yh2kGvEoYTv1ic0HWny5cy8eZfzIA78eUzaoRdAiK6hcUFDQmFeQImFgfLorAbiiumosSihGJQA+xwtuAaJaRqZaRCcoikqM4uS5Mmpx/kgryG00J5SNMFsyBkjKiOAqmwRYwp4bY8st6uu++ygKgkGdxnRoqDEqXP37oTOCqkvSRplIOhIyVWpZzRK8WUKBoyjBqFmzb3gZG/Rv3+3Ycf377LFJRLl5/lwNHv+q7v2N3ZGg/PQNRY4OENW83c9YecDcTJVHSfccKi382b/4lUXrh/+srXEmiKoMz9PJgwdp4pyf06KoWtAiCNhlJeJLEAVqVvwKKZgPASx9ew2GCvpIAOpRljnlAsCQRHIrSsvrG5zdn145PHdJfOF7fp4+9099rT2nTsWLMRqcXhZmRPsXFQgnebD3Yo2WEG8+ePHzxeTpmPO2YLRrx8JHG+YHUB3hQnzrFbqLLjmBPyRnOT0QY6qrMF587WJrN6OCDSzU6YU3863tpkbcAxLVXin50MWaVAleqputR2zAJbMllpjIe3nG0wCNDuuL3v8ckRo0C0AaAUJ9SCANqATIMfNaxqgQTPloONzddf/czh4ycPH90nJo4zVIE+Z2fDKafdLSYbTDbvOX0TSbOHmkpZhZMDgJKEaxNX2B8W5AYSfDZ7YxaDws7QvjUQJwpvX/7KZ7u/hJN3VMeQKDpE9lvQRYMU/wa7MyEDBNpL7ZfpajQ647i0VjdVYH0+HdHbz6QahuxwuSknA1UbDOPpoCQL8YKAVtO99BJyiBLTi/d73d0r125wdgJgwQecSEFuKCPnPXHMwpKpCygiQ4sEM4EBaKpDKa+gE3DhVmnkDiZy1ThywFHDuez1Wzv9jRtXrnJAkqJj2TQQlBRO4YcAKMGaBnLB9POJIhdNp9efYbcJW+i32N5zxhkF4I/pc6xgUd/a2WRdOG+MDtH9Qp/xcHTCeM4TVjDcu3d8dHrtBg1Pmp6cK2C1MtjsDk8fuSPnok8TgrzY1IpZgGS29PRc5nbvUbJF6wgJ2tjuMS2QmdOghdNSWa4IgWim7z+MhDLWCFb8KcBaHCIS8A8GY1TJQy+KGdiytFhh+Y9y6NURjYjO6AOBospQRqXlnf3rHPp6lFyc1BeZPOeFUfhPuBffpF8CjSq0eLFurMcy/Qn+KPvKyyCbAUbUzIIAL0U65U5gBi+eI+BVDoBLqoJE4NOmvGkfAfW19SPRZWtKzlo49F+PIumKkoiWZaxyzMe8CA1Hz00O3NKKAR9OdcD7/Lv//X//B1/6InMC4cJ4ONnc3L5y+dqlS5fZXyeoquRYlV6rX4oORCuh7OvFwACvXHwSKzG0gAVRswUVWMLDckCgm+FAEB5AgmlbVtYUqPHyay+88+5bR4dn9DhMR7sMSrQ6Tzw+g4pstWTkYXtn5+TwuNPts8sCh5F8/PEHw+HJpcuXafVyBgpnH9IUZcCp5XZLGFbGuMjmoZ55rBXVDEbL/Q/BnN3uefa8IPCSUFTAjpQ2HysUos5ax32f45ChavCz1ryDyW943gIVn/UHjDGxqVDlA5IxqxcaUqD0qIydpGxUnIEh+a2kgJJOKhnkMgZmxrJKAdeW/N3tftEYCq0+xKbUWCVfYxYlLaKgxwfTIt/ijU0iCkY2b2bOf+ncumWJV68EDtEFhLUFEySSZ2IW22hypc1OVX5YBkbNAwBbJzISg2eWcIev1lTKLRA8Rpq0qaP4BDUEzlystKzMTmyMQrpAMMipUJomnjTG/hRkIk0iTiKwsHyQDY4QgZXVttX5QPvrY6bT1WsvEFWlBhOgRX2SjdhVVzzn9UsJtSTZk7PstFk+iqCwuQlTtCmF9/NEvly4yrqaT8xKKF8DpKPHHncwxQlufi6FS/HOcSzJpEEJUmoSI/HLDQqnUJVJKIHBsqT+N92DkBFCJX7pMNK2wDC4wINC7EcDq0sMChWMvw71l5fQJ/IXkOcB5ylEPzCNvk4dWwD3ZLzQYViyln+8msZ/MFsR5F6yghs8mIL/1V+iMrCGxxw4+UwafouICLL8Iz9SBxbdezaU4yIJUflLtnajEduwUl9AGf+V/KxN2Y8l+7LZXBA3o4mt4s6zFow36lyS2dzAwhDYYN2b+hCskWITWRqtHhEBJluxTuZATYwK0oVIbzq9EzBFS5O0Rgr4IuuW3qlGuBTARoHIUP9B3EzDAyWTiBYbx1314MK3S33uLFtTUMNz0qcJmC0rNP9EwKYFO0/qwdjHKFjiA6pUZBY5TR6+QplSGKki2BgMCMpLtJmundt3HnBcFB2Sf+c/+9s/93M/h63E5J8Ox2enJxAdxMhYG0J3OCu94BEzC1gXSGtIQlfiIbjALL9Q4ML1ybenHwTgW/me5NIBvCtB8qdEeZqoPBnpPExJBUjSluglAIyIREgVtTzAcUuU9NyhGh2yl6/sf3hy317VGS4UQ0kMOnWnLAiDiTYLyQBsk0UeU1ox1gFjwiN799SWR0dHM3pWJ27PihDNRtPNza2rewePHx9zSuv0eMiCcEXJwVP2gJd0k8mIY5hZHoCMAY0+zsPjY2eMNHFTVEEMKBvAc0BBVqHBONuKNCyGZyO6kmlds9CTY3Q4wokm38nJCR77JrtTmBQ5UQ5A2iaxyCJ29OI5r2x3dxdEbt29SwSbIjnRgvUGFIGJ5vv7Ox0OGWrTbMgIADY96QEWSiBT59eaDcIvmZRPov+USSZchyiqphLHsMI6KaIADLKgIEWGkXdZlkydp0xbxUWW09GQ2U9nkH5WY/OTDUrlUlmhutao3xswwqfkG6gI5AarEf/kWSirOrmZOtOqaaTphXOVlpKT6dT64WTGYAmNAaQyMlOKxh2MQ1Ch82buRbr8gmaTNSWqL/YPmFV+mX7P3e1dh2QMtKxYIXXK8QeAC5CbT3JcvY2wuTIVjEWM3hOqxQ798ZCHhSLsQosZ47TH6XA83DvY7fXZPQoi0a8/Z2tYzjPt9zvPP/f8H/zB7yEV/5vP/O9wyIIXFgV56zMwZW+D0xcjVLAYcyLZYI8GhWxXjU67t/XiC8+wh4D2SjxKucMXCSDqXH4sT+XuJ0L5wVjyxY/QNMRi6xX2XkexFQBCIa2k0P8jEwqsIQ5EqQFdLTGRhUiFgps5c0d2hQOwMX9+4hIL/2tLi4gCobiJVQTWuQISzrrFs/s1yziRpLxYY/QEzS8EkA0prxaJ8iZ/YoNBFWJQQktMhUB3ya98CHaA5IFqLWEVDAUlMEG/EJK4BazF5VuQQh5Yv878eIzFfH77zr033/z6F7/4B8PRqNvxwHpS/9xf/9n/4G/+fBYGaNvNGgTTpAeFUjYepL7/Q07vYlleUyMYzjt/UECXTrKFgEE1SRVUmk8UAV5g5cbDoZ1k097D+4fbu8fsMSVIV682NjZ3Dh8f7gwGJyenLJXe2dme0l9BJ0hKF9VimI5Orim9C+zkADZMyYXtcQMgFmdsaUGhinYifW5hgTmo5dxcZgo8B/aJgfykhnKSsBab7RekYSmCLLN4KXZ5EoxKTWkdxYDSOMR4+ZlpxHIgT1YFB3cTEw1gIZy2G5kFFEeAWol/TjFasfw3u5W6NxhQHSgQKUulH+9ARvEV0GGmGUMfRvgc4fAfMcO2iJc4Wig6LREk3AAqC90HwQJPUSmVPYnNw9QKUnlibAF4TDQlwA+WN1fQ4lW6AUnBLCmFWFL7JcDyIGZklJrXSknDFKihp2QMNiTQKCSzChOSSBf6rDElMNS0fApsn88v4xO+fi+vgVSCLJVIVh8KlHWCBJa059/XkP7YX0tIpCR39IossgYf43qnEFMQaStXWazpGBKUwkAIck7iAsoBtIuB5VMBIDhhPr2qhOuAkIe+AYL1OLnkRswGNHzEYHAFQcqKrz9GIlaBXCFTsZUIsXrCA4xGwfjhOo8FiCAsvuGJZ0xfBZsH48cDTtICJAYmsZDMWFbm7jFDi4njdyp4KKKVqJnHGrr8FKCRnQLJ9ORQkCcmIsszMm0oKqnwRYpMZJDVkQYam7AWKbG2BPyo/ERI98O6SDhWV0hSa90VopUMOohYg4gl1GtStdxbgOWvuP5ECyxcW2sb+1nLnfwzwsjCQib8YbY6nkzC7EBKya7/VhkUR5Sdq8HRmexli20hX2hCnuozlqTWwNNKUdXDUqwUYXE9yDwASVSHTkfiz+fM7X7gEgycIQ9PYRdzgcqbNPVjShqz8a5EbD0JH6UGptuIlFj6KQcrTg/gwVIAQ8Ja1UIHu1eMA5Xu38al2vjC9332z/zpH+sNOhPOFGrZp4jP6p7/EQz6OTiEVLI4G4Gujg1OlJL2RVrIzizIvNxyFwPfi9Dw6FcFmKvELmFJcz5bV6oEkDDyZBqyWkc2+afeKngpdJV1pJeEihZkIIn3APGBgLJup6PcYtb3d66ebD948vBkNd1m87dBf7U16LMqlinydP7H9BexpL/Q7C07lQNc8+gH/HB26WFTditm1lniVK2muzTiXnr52f1L+yfHp5eub9+6de8rX7xLP67pZ5fms21kiLocD5Bd2/tbg9rJE0QAH5a1wXQp4ZbDSrpY4ermJptiMzzIbtDIG5KMTLBlh13cpVyuRI8ryXwe+odxDmmWAMlCN3B6bOagiS50wY0C7HK5t7NLZx2zv3ApzjiPjMlUDEWxbHQ6vHPfzpUb1671erjXkCs2YbFJuTnxkRfhSgF5lH8S2JByGR8586Xeemw4w5i80Gd2LjKoszGAqF5Eco2/nA9olC6WRxbSKT84CDvcx9NH0zmd37aL0N0+6785Hm3M6vxDGs7YGOzO5sYWhyKzIhulB0MwwGQgv76AEjuG6Y9ZeF/hYetkY/cq578FDUQd5FQ1xg3UaGB22P7GxZH2DljCqJolLVdVZMJNKz28i2HrDO+CXYYOdg8u7+85p2fdO26rTDOGMdM55hzWApewaBGOMDNk6ODbA89a4xClY5ULU8vqyx1GZqarB5w912GSkiWZ9Te6O/tb/Q2GffQAMnSPozZlYcliduXowW3WiTx8ePLk8ZO9/V2OlWf2S311rdO+Xmu8jwuUXQQYJlV9yQ7FZzMDGNLtnTHTcFnrczyvx4PZ+aEBS+FCjxiYigwkLhc2KlfoEvZSKLFSZ+i1laWLXVwoBUlFsujYLe5M56QPZ9V2YSUL7lU2R5jxhdxpBsdfu9k6nAZHO+/YtUmnLdMvotdAIj54KU9c4GsXif8II0Om/qMGUlmXmkXP+LSeAUwWGYQmTwXbCggZAVdllaKY1h/+mYcZBHPfzy+/gQY9i3SRREEcz0Y9kXNe6aUm1fk+RQZJSy+pGgzzlmezEZqVBdhwykf7l37xH9x7dI8Kp9fujufjq9evffa1L/zID/8YK7ZoBHabWB56zqEh25UeTMdMsT9UBx0Po8hlZkF4wbS3FCMoWN5ka37Vkz8jhJRfHDxpAAS70tRoRquxM595/dVf/9V/yb5nWKq9zc7wdDbfZPTZwyLA4ZXXX3rrzbc6tF4n84/ff7+7scEoQYQZnaDQ5MRkIbo8WNDCkrb7WCUO5cGykRo8IJOx0mdfn+9JAPtYmIhrH/MaTbjQqS/YQYuhY6pIGqjIPwJ9oiVY7FidmpVW0DkzRTLnu6n/+AKZXbhMFGfbymLEyXzr7Q8bje5qukexHfdGFojHKmW0kh0/W4cMES5W+2wYgRHx8BFGijkne7ltCyHz27AUkrKIDgBt2+g6MP7h/m+Sk2EnRo451/gaquCSomKWILwyTDmMZQRZAK7YCWDrmtDV2Zg/ayXeuU0+RAd/awHoq/gC1szduY6ytR+SPZsCBmyqckGRiG5BRUsIeechBk5kERt7JyKeRLUcJLHrssQXyXoDXV7UpztE4PyEYAEFTAvOtdUOo4fsIWZWGjnDvukCrGFiW554pKxeTLZ6Jg95LlGMQ9zqVn1N4ur5Uz/fou9fiTCHgCE6g6Hn14Xg87DqofpUpfKN/4qXJOIx8EoZqjI9heDnb7o+HSiBU3KqKgufXo3UP9BetkpBE/ErFjxGbeV0riRWU/lWnp8qdpWgxCvR1SGjCk/sg3UVVDIJpBK55G4cs0MaTAOKtpuFbW2crzwLz0jB0NeSkYgpBfxRmvPwUgYLFxnJK4kVuBIJOth4xpBri6G3/4Cd76F/QUkSUXA1oNySC305yGgSas/tSHJaDonBhe4ul4IFUysiOjVoqufCwV2OhkP0DT8K7Og0Qq/Qf+baAh5rgfZi3Jk4zZQDRx4abI/gAQLmuMAI4g5OMMTdZW/B8cETdndhszA77CgW1aq0szPQ6QT0qdgphemkayAaRg1NQWhXtVi3gMqTMfWi9UAhbVEn4dEdSJ5pFfFqGdBbPCZst8SOiGr4JJs2zgepDaXImTww1q3pbP7k6BjL+52f++zzL9ygNoS+7U7v4MrlRw8e0cUjVXWnsICUQMyZl770zCZAQkx+z8VJvokll8Hrh/Vj3sutRPpkQJJEDAsM38FWo3wh4rd+LIicZy0WefGnMDkEKRGMDGQuuxFh+nI5phueQ2roXGwP2H4a34O6imN0mFbBOS94SER261QkByWFHIBNhVj0QWNKFYmf5lkC+N5T0rLFKquK6YtubG1udPvP3L91xIJuxs2JW06ggVFMQ4khou6iP5KS1ukru3Png/1dOpb01LH5vY3+9/7ID//Ob/827FAdQlzkh7wxy/Rg47DSBw5Kk4kLPxgZ6AxYimDiFBUKuD4E+UQyCOKuqYaVjcaNmzeZ//Hue+9wbBCrd8C58k/r9cdHj3eWDXqSpVIYIYbFtHCXL9+KM9IqIkGUKrai8lRXfTJO+SeDEEddA+MTOsdJzZnTaJTtmfExGC6dCIRrztpNFkQyfN/sD9hGcms8HjHtn0ESur1NDoPgECsa0saFYEAv+SnK/sXAKFxU4EyuoNNbMuUCl+iOxQKT5tGj4/GInV6AKb6GAs3/5b2yRVUGCU0cZmU1rxxcYc317vaO6qMlExFrVovp2gzgC8qaOHBQcBARuHkLh/VWSAu9ekxpbDe2N3axKqMTVp7QRGLxp931jCNhKMgBZxa+ss0PBKADAdLtbe8yTfxkXD9+/ASvkPkYOLs0ephgyZQSmE92XJhEmoXIjDYIxOOzajfcIoVFJpnzcF7mwkfxDYqiGYTLwyfuEFPCYz4sjs8kIj29IXJBVttI02yF/qCC5kEB7CTeTxoIktnlTXajmqMmHXeP8jLLG7ppzhW2imIAIxcxQ/AkpoiKhzEsLgHqjIKEQXN0S+bAFcUGeUDDlug5oK15C/65kywFBtCaPeYhGXyPnGOFSY6CEtWsCNRKBD1QIqp0yJ8/XtVPVMkEBVWipteMWVubg83btz78rX/xW8PJiJOqnxwe7ezv7l7a/V/9x3/rp3/650fzER4hRh/DTD3SZMY97KN0VAdA0/tP+a3ihA1G6j5PosLlM1hI7eBQ+IymUDRrQ0KlAsHIr8Nr0wk142D/4MrpMWukFpvdq3Shz5Zjhp6YSgbJ4N2Vg2sbfbtCyGAxXQwub5xNGC7AAQ1v1QJWmACNilUTJBZublZwAsNZHGnRBC2rL5GkCi748o6DnIJZhFI/kJi84bhjROlPIJrJLauAiS+wAsQipWDEwf2OqONxs9UmJ+8wrIoZ1CqUngN1iuVbnI5N7wxNAggobek33MCmsu+uzSymtcF0ElgrAJ6MFE4mmYAFhCJv3pA1Pmj1K49Ix0a0RF/cNM+8s8hYGFURlLwUxaR+Bpph/i/G3Fz5JM8JKLbGmGKKkvhoWmKJGWH+5GtS8OqVaKKSOHyxELzz2cIIQ5KqSGAGMPPEQyEKjJcPJqH8S1p37FUd5Q7kAh4A5SrZrd8KfPI0BzPJPRJbRTFhZIA4n057jvtTcN/2SdzPQfLkFCCvC20FSRMUDD9HxmylXXKnjCVTSaV1U30Uu3U6HvgrF9DOnxPy6XMAqq/MMDOm03xJUkqJAUvdEIFLmLitc1EvTSzRpUvFG+nEP6Gxr63Pa0r6nOgVjCTymStYyPfEMSCXQP3MrVDOhxI5cYy26pR57VVBlK4AQdw0ByBJSFJXHySxcAsgJAopSj7mllrSLANDI6rlUTToJcIlu2427XtF3GKUtAb0k2O76STUYbXPCOgfktQNyBB8enrowMcjyOpG61lOAWm2GZbEZDNiLgJFxGnj0wHmmSCKeNYhgzsf6XtwBgwGjK5+qicmHFsqopVdiZR1Gt800O8xCGhfBlYOi0nFTK8JEKxo6Lyi10nddmQfNfbYYc5McZtqceMAqTY1rmvzo7MqG1pmPoUBYYaSaD1D+/4RmyeBl6RMe+xcwy012PDTnHKTmOCQdFg7MYdCNHE45+jkbDq/1eiM9nb32QvSfZGX7iFNA0XiZM0r+LjDuKO7EJTiU0NTc8oluR1WBX7hsEGG5ddnr/LpYtgnPvNBlMCMpAG6/qxVKNf5wzrgwu/FbyXrcwQyJoOOSwUgV1+X9Y77aGl2tWPsMbW6dPn5J0fz4fiEVZmr+vs00LZ3t1r9jUZrg+nyWfYAp9hKBQEiFaaaOgy2nyJ97TrNB0wse2UwE505FmxC/oS53hhjNllkp20EhTkasFdBo43QPVk1Hi9XOzQop/Mxc5DofEVMlacF83BGixmtuyFD/y71PJne/+i2DUa9d2IUQvFATXnaqI2Wky22Ler2yFo/hgYnZ4Di4rD6XbFb4vPRrPXUBHvQqR55l6eabWd/txrf8frrbH1z5/at07MhW2G4DS6T32fsk9jifOJ+Z0BRWk3m7gMeKQNmWM/bms4gx0V2coVgHjAOdjfil0P1iIuJCIe+0N0tXKGjPnH8lUg5MYYxeI0nh4enZyMAtdtDDgC2LlvQ6cfsh57T9Bu165eu4h6xFzsTDPBs0f3jU5wSKUg24Fs4DkLOJxZTkMpSPXnOV3YOOuh1rkeDnQAA2ooef+TqdMT24cMHU0YZdKxt+Nc8yxMbcJxCWiLy8Xm5baLGKWrOL+06Dll7/uYz6WEHV5Y+wlnigZXaWi4tAN/wLVK5GhwiEofgZvvE0UVGG+cT3FXc4EbncafTmCy7w7NTmnNsyAIx4fR0OLdJwI5rzBxYtTjjFHPHiuNu/3C6+AgryDdGeOzDrbE0BRfxYb3zkB6QOWUb2+sJAbsrpBVBwZosOhxMzC7yq2EaB+B8Q4qIHywqFslnkFWDlEkL7b31wPv5jkCWrlCJgiK4B+E7IkFD2jOYAAlbZYz/IFFrBO907hmsYbEC0TGlbMqMoEAjpncAkL2bZhxUyUJml3y4WbuYACCELTpOmOQGvjQERTz7eR/ZJ18x8Ss3XvG04/p79A05M+sdtphElAqGAAGqBRNfMU7BE2CwxeCut8yzwx2YTiwDwJOXX2stdxKrl5NSWsw/Bn4SSlf/eUGsoAQfIRa0poi/+S//xa/8k18ZnY1oqCJFN28+2xv0/9xP/vif/YmfmNVOPd2hXmeAEYXs9jisjazrrY0zhIIiuryBMTBQmW6LZPvYguc/OcY4gW+dMU9wX3F2dYUFNeqGODnH3V/VhtpG2+IJM9SGnEz9vf/Od7/99Tfni/db/dGlwefbrFlv3FJvWO52dW9jc/f40cPNLbYCqrOAiSa9c65YbA0cfH2mgNVZpeDkutp8HzI1Gh/TasfPlh6OyYMukmNPOAVCG4qggIGd+nyaX1fwdIihmd4vH2DAco6MkdpArbGj8PT0K0rkAnr8MNYUC06ZMQue5ZUhAublOPOHEDgMGeUHloqURDBZj5EYmiEwt4Ym9jqNeXfaYOrgEZvpLpdbtgDEhBQO7oEdIGyNMTLAxCHPGGaa6AQNwyzqtdBr3/pIMa+9COERQ3IMuSkh3oV1EyhrDIoo8swRjozJU3NpM8MivpGpkWWUYivPGEi+xwMvpKbW9sni8AdaqfgVP6UfmglILYROtyl/Y3mTlkzBpMSiXEhWMCSNfKnPDphuyTGVVouLbUbuaBvCPuWNdk7r1qqJdXpWVGIZIEUu8ci1Dli/nn8QfS9SYkmwPMjtHaAUbeGN4E8lNs4fd30Sft5snlVXgRkSVhGjuT6bc8jn04WcwaGYtiQo4nXhcwATp4D7RMp1pvxeLEh5RnANh2vkm1IrgRC9mIY1WH6VjjWIkkvgrR8VWwP85xVY1VPinOcNnORZPpY02kTe84mH84xQLfERXlU0U/HZIK+ClA/qQbQooHhUt4osG61AKRGrUOMURKtc0pwOeO0h8IgugVDjuL0YdwlFjU89wdgk81/FyysIaLcRdvwMenpiI6QKXVCY6AyviWRgJrrdTjrXYicefBIOz6Shb4zt130NBUhoR2lKhI5RHF0BFBu1VCFBDP8wicFCHU2tDh54EqnhbaaQXA2VNFgPgHNneqtYiwDVf+kjpG+vUNgPMUe8atmZOs4YgrKiIksacQmpCTKymRMa2vmFeObkKAHfVw32w6Z23d7Zu3Jlhwoq9GGzObZUcq/8BW0qHEdcA0ya5BFXRljJDAiSqECvyGQR+F9dktaAELG8VF++xU++A8z4koVsfJAXUreS9vOEiXj+FkZdeDvn28WwKlDQICl8iQxsxUSvsTMYvPL6Z9//4GuH80PiyM5aY3tr74xNVyg7pti14XaxW1MLjn5WTPmKeSft5hZTsXUlQyM2zFZhAQy7FFe7cvd2r+7vXntycuIuhHxcLPtM6R6e6ebNVhyUA0h8NaYdvfvO17/vuz+Hs86KBHwHRPvmzRtbWztPnozoxwWNgjrSxCi7Z3HWmSiM/zR15spiwdJP+g739vZw7ikl8XW1rQksuN4XfVAzfEFcT4MoC68kvHb58nHv9PjskKkSQ440cLv0E2aCtRsn12+wP28hXfH+w6cib2ITKJKz0BMieaGYUtpQfgAAS+0NJ4CvdGAj2JQBarJygpn9loSDbHtUKjbqt9jnZIm3wXFRtMmx142tjY3d3W1mXeG9gvrw9JitMBk8mTMlCkXAU5cjIhqxIROcIitRGVYqMTvkLDJsBA06znv9NkcmpRAEIPwMBaKI0Kbz+OEh+HgoCgj5MVcpiq2WcgUcAoNfwdpGlLLdvLS3R1kBjniwygBOSY5chK9ByUeysrGtVBEHmBpJtlrkF2edtSWzeZsjAPYP9jg6GvFTImo1lnqzMak9+jQnM5cFaQUwTUsmZ7t9MROTbRawoS36y3ZhjgykHwMr02A7R6Kz/oG8STgZT7Zrjeeee7HVo9HYYRMk9gU9GZ88PO3en57hJjHEBFGlGlSkFOXZnxDFb+vrKZVgggmIokZXZcf0YMDsG4ZPfCE6UQiia3/iqa7I7KLbXGy3ByQzVJ/CA9GlNxPrFu7wwlgWblqXNjE6Cu0AVwCVzPJGAKwHAklBxPFf9BNXUM0kHbgpbDwgHnOZbu+5rcdw1uZZjCWULPBKY2adQ1VeiiXlExoUGE5BDhIQepEWBHJVvyGKAeIh3tWFuoVcth6sLxqNd9955+/9vV+cDoebmxsI4enx6Pt/6PP/wd/4+de+43WW0tLEJT0miMMftOYkqtWOjo7v3Lr9iOMI4XKfs5y8mO4InsvWxyUz8EU+TIAoAGb+jOO63bt0GRBAzFZzw4VJnRkT6rZ2tjBpmBWKaWGdjdVwadOlqx/2Pmgsu9YkOLjIlrKIP02X2vK7v/P13/zN32TPseHx8JmXrrHvcOotaEGDDkAs4IFoOOiQXUI0Vx13/oRykov9QENzbuWzGgexdGmoeNXwmGDUWhojRkCHsXrf4BmIKD7JwZWy8mOcpEbBXdOPBcdN10+PQeI7/+wRofPUyZwIJ9377N8Qu8+6sLbHTtJJZ0uRJgS7fNvxiBM826GRaiNFFGPzAW2ZwnjwijwlzNqcLYqsD2JhFHuoQVwQKSiQsYWjCJZI4bHgcMa2EAWA46AE0zTdSqaspB5n7FpBjcjyLYCBKSYlFY8+k8ZoQY90kpTXUIcbKfmHrbUas2pQXZUgKiwDYLBhflBttKg2IQKOFBLb0tC1GV6E8H6EFqSxOKVM5bG6C/GbL5FMTqQqyas4weqb4/8xISWVFCxY5H7eAFjD9Dv5hpc8iHrE1WDoRzQ+MSWbfmjWmdCO54Xy8xIqyLOS3C/Jqjys4fP2iXMABGYKw3EupVN5Sz584yuT22xaJhKULNglXmhqllUy6VwuGpryAdmy60RPhmQFiRInZamyNhnfQuQCjXzhdknhl4ANNXhaRw4KJUMBKcnrPHwDEVotKpRX8iYQX6eUhBiQ0s/YAfUQ6WI/PDseTeurXSkYYUjBfzwD4jq3njJliR6KDjLoBTWdag8MLFoCvcko5qDRI0c4i6larFq1ocCmCvoBaftaCxBNxeE37q2G18ZGcf/WeGtC1ODgAG1UPkvl1IsYPh6ppFJKMBZ/M2Ann/nmsvY+FQssTBJmaqQrMQhidcVPGZLDWjG9IzLSX6AzL/kDT7YET3pJDhx0az2Qu/AVb0BzCElgsaaCi2D+QJHKLKYEuhdRpwMbMqvbAShlH9x/RN8Su9A89+xL9BtOqO8lB6ui9BIm7bGVrdMdz+ocYBl6abzYGcmheMGQo1JRXTyEDOt3vwivuqDh+vHb/p7HAdnq2V0soCC7A5nXObRvAeIcl/NIGd8TC9GQibIxIkLyYIPry7AOX+lkbX3mO7/r3a+/9cHbh86U6D3GndvZuXx62hyesSUO1YXThCSRibkjtZyXx7ye1aDTOZtYQ1h7e1oDEyoUQ6jc7zdZ7Lt70N7eb89qGw8f3mk2e/SK0Us7brWOTx8z1QW/jV58lgNMRtOjI07xZN+VIf4kw15I/Ge+49X9S3t44xY/fFbw4DlNhAazO+rtfs/jnJZuv41RpmN4NB6zKzzqYolBld+4CCCeQKRkpG/VYNZ1m/ltTlFrsGh1i0nr48nsvfffYzIS6kKrh/Ienxzu7R2gO057m7JGOT2+kBHhpdqFdqniastNacvZwHr2EilUCt9Uf70wlJoNAZE0NmRH+w2jAYKf6hFRtG8cpsBzHnQHHIVG+5auT3o9mU/P7pm0cFAWFscj2jSPkOPpkvOb8eNdDssnvRoOBU1PfJiEDMkuWaWGiCnaQZYEzJeHbKCUCb4cV0KvmxJilUYU2hyL0cnJId1QCjy74FOI5knECsYKSfgCpUfsWL2ji8+TpPa3B4PtTSZBgG1VxYiVeBBfkoR6eSsirpxAZ4Ohz9b2xvMvPA+tYIdrNtRYV0tm+382KfE0wKZng+Chrlr01stgUNenGB1vTc4ata2zjUEHgtCwgddMO3TiYa3jwhANLsvc8SicFUY6znUicHNr48bNy2wFxgF0Tg9q1Heam/3h/NGtR5xfQWE9plfczQuMVCSpkC+QQAQYaLkstsYj3MjESTyFMGF42AyBsoNK/IdYWj75edl0kyZnUtPPCejmFj5uvTVdTiwnwLCCiKhjB+whQ6sEJom5gGfXzMmedS9RBJnkTiWiR0ovBmLncZGJQc0SJDXsunF6c2kLkTuTl7eph1JtGpkIxtX2p3oRROG6D1JAelg6s2WEn5rLHdJMSVs7Dxbdx/gMxk7k8q2CDxCqJ3UEgW+Ojrb+/v/379159MXv/v7v+Ve/+uucD9/ntOrdvUs73/PKSz9Sc12NilMKSjMPho3Pzr7+tbfu3b3jeiTlmz/rgiDwfjKUIoUxKVahAd/f4hUh5wm+E0lJsr7B0d/8/h/4ARoYoCYh3Xu+ycmDMObatassP6DTAdLNlh8xlQ4gWTJm1t//g9/30YfvjU7OaJ4zEY4xeDIDMKjZ8z3n9NwBckUdzVk9UsaNquF6RsOWfQLqzIYg02CGDiqAcpVaQEujy4Dl8TOELZUmPKVwjDcWfafgGTdwvrvkF6Q58WdrVh8pnjjxMWFgIKQyNhWpsGrmKBbi45th+RnOt/rEPUCXB7VGn1Mm8M2arVP7x2s7xhQBBg6fkNtqvktO9EyCFmrNE4dDwo7ORq+f/giUurZ8GTq3On33MAQ2B9rYO2GBFBIukqoc0o4XTLEno/mWwQrDeVbsSF1IBfF9CmkCgWTheqhlXMloOUMNfQGfSICo0OPOowJflppBKELj3DI7FG7Q0AEnVkEwP9CmEG4ZTWqXT9h7mHUajGuwgI0lZ06uIjNgQRfVhBIIOoQSRa/zMTHDc7Gog6vs8FPtEVS+lQQl0jfdzz+ew/l0FIottQyG4VCVHpYLcc4BFNqdf0kJSFZ+xb1cT+PznoLy68dPfChxDVunq0JKRAI/EV5eEETIJRzvmr3YI5uA0rGQkpQVSuBmdScshaDCQE77wusa9fJa0YCXT2Sd9KRZo0/6pC3SUbJNkKJiWl7CTZAtgCJmySPv6JN5BI6uvKmQttKFQD4WpeBGpxZeBdqFQgKWTRiBSPVEzUU1DwSMDlLH2ko8IZEyE1KbA7Yb80ccqnxJE5jkA34lob2LyCZDwCbChtkDwXrdsq1F2GpJ+C/1xFwcgCPi+RNQNBuRET6B6JvZq2mEqUMEc5mHZQRzAhzEFUJyJiVYoT9iLQji+acvjS451k9gwVvZRG3OOegj+SSoZJRPUwgXTHgDhviTlUOMdKSYq0kqzHgppQmepTjuCN54/PiQuoWFZVcv7djQxx55mADOvZO/H88ekpA94yEjeMbGUwCITacHWZAB5IyFMicuMc19/VxQyLfcpMY6QhW1BCXc1PLRGBbHLJIRT/xpnQr5qtjf6ic5Gv/CBawKZhVYIgXZUgR7kxQPzu/d2t3eurzlou+ZfTZIFg4XZg5ia5sd37WZJx1o5q1W+FniZb1EuwjJoIqzJiVHloCsnPffBVS7NcC/x1uZjukV9ryqI7aZZ8+fRY0psoCmGaFLvKgfn96fzQmfML+f8tPFuxp7WCZSDHcwX0RmTILLHO1xk0oQDB7h+uM36kMPR4ONAZ4AjWdwlaq8RBpjARsMJ+tP6w3TtnF/J1ukNH8XrF5tvfrKS7dv3+FcMwYTkE12B2q1B4Nel6PD6NjGPaW80CuqlhZAETZ2K1cWzRBGQQGaFvgNo7HzoOiNZqay1kDvLamoQzwkYeGOQ9YUeGBz1uPh2gw6GxssbmXTzOgXbg0u+YzWF816SIageoytdSk94JQf8WQui4DJPPZdnlStEB5884vyA3csFKWPS0nVZWtWaZakRZ351DgbnRA5BvlcnspDiVsJE2khRbfbYln1xkCkOaeZk7jSnRFBJt9cWgdFQ9ngQwoQ+UvnNMjCsmvXrm1sDeicZvIPCPLZHVSoe5lAxtgRR6pOp32Wm/NF3GQBUkG971hKhNAGIedMM6feYmMN6EViMoMH30IDvnrGIfMspAZsnzL61G52ET+T20xj3loNkZ9NW+zUQsuIE+1UGDVdCy7u5/SoykIYbC9XvlnI6CpR1wLhZyf6u/utzr61AX65fh6OlVkzO6TVntXnZ3iW0kfGYH0cWgN+oZoVBTyhyxl7pbGssjVHHn0VoOnZIMueIh4NLJgrnGKEqqYJZFxEgdEV8HDApJdPOFt6vCi1BSigzci0ZmMq8/GT0P0fsKRSggggqIQ+TV1F8ofE/IvmqpYgI7+oCuHJl7/4xu/9zu8Ndg/vfnyHFtkzz95sdzd+4Rf+o+/87I/jaynK5Jkfx/EsbGtrZwfPejIdwVzVGvjQBvlJYQsiyVWUrLVlikTlnq9rVE0IaICuOAjvydHRzt4uhLGCwYNfLjhEHQiDzc1L164ePjpEvBanZ1SHKpWU5WAKzlPv/OiP/9g//Se/+vjJ0fsffmwWYGPliytMy5ZBVeJyp0lKZiR0Kg7tCuwgs2WqeBYATXdYQlsSrjtqAc5YCJEWTbwAi2HriTAjhTqUkbIb1cTGFYBvKA1w42zkE5afDIOjNwrkeIeibhMFGRUwXn4Yb58a7gkWyJUXvfZq0md2FPPvyFU0ZQsSYBL0JBYH6KRg7lOT/r/+xmZ7c2dG/oy+UKGQEYaGbc8pggH2/bU5EFntiEEEAzFRyPCo6YegjI4aCl70KQeU1xAoTZLAuJWMQhRfLRY/XYplPuCK30EptdUC4ZtY8yuZVS9X2BDV8pg9tT9uPTtQO2jMxKqA1MHHtgiQ2VPWJNxJxnJGIgQj8tUiFRkD/CeviwHB8JOfP/UmlqV05x/Ke/Vavp9/u/jwFDiRoFt1XWwAnONyngdCU9rx3aRJj5cJYcLdNQR/k1I1q3U+hlwr5xyfI/btkHqaSyIHbIBJTEyhTIHWfORCZ5Qq+jngTL3kDp9g8/ya7GvfT3prch5kOX/8VxYVCUK482IOBV/FiXIhYop4fX7dLNquK3fmCsKf9GZHOvbTJaRjqQMvkIWkACQid8GbLQ/Tawpv67bJjZtAYqL9eBMzj6+K7Qb/65iqVv8+lW3EMXWvcJ3bDtlZhot7g6aQGDVB0KWEeZCZrg+yzAfEeI4zw2pI6SZG4Enp0QvapyQlCgeZM47AMZoE0qGHQjqp2gKAon1+WplEXbJn/4Kui4eKCjkKiWg4CVe0Ypx8CdlKqVzJZHOS9Lg14EZLBJC0V3httu822mcucCtah4knFdxt2MejS+IiA4x1Rvcskbg4/ihmlFUjLUe9hTOofethKBPTgK1AU0WaKDxTTi5oJYVIDcHAKeykAwzsLKbCIXSXhOLMnZ4O+xt95n5cunSFwtHUJLELIeocUDWAUvdv339w/8ELL76ISeDSh8TXYgdVljuHeGQHwHClEhuzL1pAT5VxxorRJy6jeMlOW/x11irI8b6AbP1LDbJT3iQLu1gIouQiSBPzTlriRU+rkPLzqXtJZ1y55GXGPuVX0xvg8Y9bW9sHn/ns90Ocd77OzBS6S+e7uzvL5RNmSjAvBUvIeXNIEZAcpZHAyJe9SJpKRMv9KyAjTKSvGpCc2zVFhjk5gUn+pycPEUNqbaa8PHr4mKqGxQN41JuD/oMH92v1Azqb73x0PJ2wYwSzPBxbZxEBPvWlK1e+8c4H2gFss3YbikAGpW48G9bPlv12H00gR3w6nICz0Vnt0arf5xwsetRcf6IdTusBGQP3VqOLoCK/HhoBWCkNgDaOOvaf0fxnbz5388Z1JtZ/9NGHnKbHnvJPDpf97gaHhSE/kKycDgsMcYlor5ojEFPQcNhn88dPHuOtArd0yds0NQ+UqnCTV6tlpvRwZ84BbU73u2m2B3gZg56yzXzYhX4wEKznUAG1aIfX6eIIdsI4RtXA3nqLnkXdulM0MqPbSGYsBjyBTFZogKRqJTotLavgJ4+PhqdTFtRif8RJEqkx/Ht4ePLue7eL3PmFT9wriYzocCNBLjBkZ1Xmz3gYGfNfuyyuYPwENWE6gXWkRJIB6jLZKyjqJthbGZcuUkh485lndy9tjydnjHa4AoQp7lDMtRy4XrEYHIretf9PQ60ia4qABHoOirTuthoLZmBLZEc+mZtL7yAUIgEAOWNORFg6TO6eFSjz4DncppuJc2Qd0wdR7KY8bYzqXc6TNq4OjBQgt6rlZrahawgAXfgYXCRTwvJb9MxPqgYXNImn6MQP6iBAOPbiPG++N9rsUsvca3oj5xMXklIlcOY2TIEMnAaN4CzmfatbItMITh1Za905z9GHIAI6spJY8cdingtCRBBXWro8wQdSaJVVJ0SDCRBDl6Az8GCvNIaVJkqKtOrFb6a/UzhErkqsUJRs+WFWdC4UTExS5EIWo+XVuFzky4NpgxALw5DAxnh4+mu/8k/efPsbjf690+Mpg2CnwyHhP/Ozf/l7f/B72t0Re87wStGwOKgriTXa9Me22xubg4IXHAQ8GSDuIupdfOVpoY5hPFeinjdjkLygY0hswnB4agogAdJdBOgTcTUd96vXLn3jG9/Y29tmKbrOByzCWtkl14Wq/dbg7PiEVUn379+hA/+Sg6OccUk0boyT0O0N39liYWxx2IITlqsQDDjiDRNCA4955K4ToFlIHCeCMQC7gsJOceO0BUxXc7mxYm3Ssr9wkzoGFiYcPNJontQXW0vW6jA9nbUNix1WOCzZGqjxpL7YWTaezGebs8YjJk/VWqcLNjczzibnk9RXm7X66aq2MeXc39UA+ZgvweGUYVuWWjTq28v68WK1xXkOHDHeaE1mq/6qfVTn1IUalLcaBn/O2oaOtMYjFCo7LXH8pxWLeWiq0N3nemLUkhtCrwZib1mq6DRbySuzIAaHosqLeGjIssGou8zAbPKmGtrAg4saE+wBeusDUCKa2AbeVZEi42DCAw0o1RxgsUmRP1wW9l0ACnMvEUKtDcIIUxAxgPNHJ1G8rBk520JSfPlKOWEKb1Olh827yJHoIqvCYXRwQkSZryBabj4op75ePAcgMaq+f+N86iqfcy/jBvqrF67z7xdDcwIG9uQ8Hnrp85KDjM5HAMT2PML5A0ElVPqdh4q6FyEXk+klGlpFLHFKNMPX8S8+JPiTUIAKAFXNBOojhsmJfjp4ME+vEA6SjTUKkWQ8l9afrEsgz5q8gABGFdF3r3BLQVHXgBiEDeSBv8RXsHgJwBIifBOX/+ui5jd4JHfBewFdBEKSRAkMRRHEsOuaXdyhfEJYkRS6gexgMHuk29k+eOpURUwEwBfu0p3JFxyW4CuWIoI/XTVk3REfNIhONP3ICns0guKjYlZpfNXXQNtgfAcHt8Hu6oTYxaPuakxxCOgZa9U1o5gM2ggQ3SYEXv1qwd7ayZU6VckntiHojXVqcHIwnSLgSqyY3kDXJvrA4D2zFt3fU86asEOHHfpPTy7ark6qKxbOOqPuhu4SJYUquDuICWDpA+PDLCOosKirqpw/4CAJFt8waaJ1YFGf/fqSLN4fVUcuFqp2Ht5/eDYcX7128NKLzwwGbAaPSss7iuZINEuMmfpzdobjy8xcAPIKSDB1YSL2PnmTSxEXiiZ9QgE5EKwM4uItXxOcZ78X4UyJfBEAyY3Lcylp0ipj5FFEzXRP4eXtW90Cq8Qsn2URQIJBHqIz4gLc0uwVJ6mIcC5n3b57InLiFgMg9PE3WbTqrCdoQxydRRgPETR4TMWiRxNWwlitiiwoZMgEHlb5OkmI7n9OAxsPmdLjZvasWady3d7c0ht0UkYXhwbF6HSp0k7ntWMaELMlpxVhc3XlWKVNi4BMybsoAETSpmth7b9nNw4EABnGhcNbZGPQx+PHu3u7NOfo0bdcSA+fZkwsQQDhY5dpSFIbwiN71kxgvsTXR4ggCiDpgKcgGxsb4IG4kvVkPuV03G7b+ehIlxNvVNM4pLQpGS4QClrlfAD3OEI7EG4cdcvp/jwINbJHGxiwTCZmvjuTf+1aopiRJTCkGoWKeDbVMjpH8FBBK1DdkgXdw0710Y7R2HIHXloICCccMYp/sKCSRZ4tvF4yCkEZYnsoIPQAB/o/JAEcVRSQf/f4gopf/cPffXD/PothdG3OpZFIiomCYqmTBSXusvNSp8Mpv+gtWEBzxiXACLZDEGJrhzU/CraiEhFPkc0Z3JAQd4vimCRbazTkwsowDlqAFSYJqLUazkc00ZoWhEkelPCZtAqcFVB2+BHFrDZhUIjNlNjGlzZ76WCma4BlCXbGYIQQZkYSSSiBotSBiAWgodvBDCBTNPjtYVVWQkizDLkMkRjf4oIy60/lgZKDt06SQEynnsSFJTmQUvHJaBWL1kzRI6LCaxYoklBOkndpwuEUIkoStySP2yGjgSyNC8/RU/f6TLQEkp44iIqcMGaVPgzBdq/GZyNkCW7pWMupKlLKWkqeHC1gSuKvIQWBPJO79Ws+iGCQDIAk9VYIR0IRVpxhCj3Ed+4//L0/+NJw6NJzBg1vPHvjuWdu/PW//jdefPW1NtsIJCFgUfP43HqZlJQadDwcsW6e7xIpdELYJV6VU/VDgAUyGEKvf6piyWFT++o3kj988GD+KgtIcFH5oPxgaojDqOaNZ26+/OpLx48fj2ZjmpS0ClwDYGlA3Yl86M7x8JQj+1hng4FTiBzUh6wcaMcBeyNMHGDTGmfrH/rlcEyxqKhQa4z02exUWtyHR21HNsDK4jKIxP7984bNLZYCaUHrkyX9CE06m+iBpkuovWxOl42pM8tyXznFbFxzsfKY7g3OCeNwRhsMxqcpQt3HyCOOLIWdOHVnMR8yVMXWbnju7MnQpOdyzMLiui0QTmVmzqRjasfT/qTbWbQzIkEz0kpeC4i05oZnggVAfWmrOGHRFTXaBPvykUHKhthUMqsKhP4IHcR2MMDyUmAsbCwUZhHvANcI820jUGZRX7nHCVphYqmPJdcKxwMHdHokhYRYq1PqOUTH2AZ84bMuFgplfnwkYsQIbvEPg4btBIki8U5vwPhEiqQ/yqlsJBArRG3EEIC9sSSjbuITBUzBzC8P4m3SvK5vvBnt213ls9IOHrkbswAq9yplASLsTwSX9ypOKHthBMDC5yrAq2f6I0Uy7CHoIoJ8KPmUqGGY7ZI1mBJcJbmYsPoQcCVyuQdabJzkEjx056ELPZVI6O1+O/Cvp3DUnZe5ajLrEYz1wNKjj+gxGwEyCwIRoJ7XdkZvwnlfnJsOANeJmylB2Z9YJpHKrLmMUV7oL6Lvn2+GhE7Bj6ewkyCS+ZjkAmzdAaaOKPmmcOVOEOHUQ0rfjFEClPEhYLQWkRuzReIEofkDUyBQCqADIdVbwc4AYJOMqyiG7oZo8KbXjiWxJCqiPqv2C1NpQOWFoA0YMqof4OA24zDj9AERR2S5vE1HXsboAATF6dyg+Qv9H4BgELHICLfD2ALUelsoysyjcg9UW/0Ulc430mg0SRnyUTyJBwiZiqWYu2ML2YcUCptNG5vzZIJBgZClaGAv6c06RZldMWrzPi8YGAtPWWSL2eBMybHpZb3UJrzmQjEtrw0bKbFkA/jR8Ozn/sbf/umf/Mss9gKwu5qSCpKtmNDMBKH7X/7yl06enLzy2qs0e9g5FeB0FOqWOJNY+nAVhDAaIAAm1q0dxn/C/URYR/KXi1TKBdh7d49qWhfQwHmfFibYyc0Ut5AtgmRiT/iz56BKa1CglZ9vyq5kkliATSTJDjhf9HikqNwLurCbOcpUENtMiXjts1/gyJvDu+9PzlDA5Ue3TjitQznJumh8EtmkNmroUkXh0BhCTtwpBzNfdmlv0nnaaO1s7NCtjYxYTVoNzobD2WafLefOQIdzM/sbnTHbkHB886gxOVu1NuvsQUmTGXbg4+5scrStBwMrsKUcCpHEtBwMqE9YG9qfTdnKiU7LI/oOcGRPT+nQqm1tbbrPaRtjonXG03fBHeMXHfa0HkNwZz6HJYCnJNEgoHLWxKzb7r/28quPjxjK/xAJms3G48kQuYPRNEsQNce8FF2n7YGKvrqz+WlFMBMAZVQnaepyKsf+3p5zelqsL6d3P+F+YgdD+54tC762vpfFQ++AT5i8UWGs1ZQNLnqCk6nVE59BnTRUe41TJq7YFpNA8jXRTBFds72UB6zFHgCWq8PrN2/u7B1AJU+FgsdKAckp9/Dtt99m7MW2P9w1uyI1RYnJcR2SRjuUxxhMh6Nu49r2BlPST6INomY3glWoyW3EhFa80YKR0loMwGt7GF3Z2tydLs6wTYwAOM/dWdVEg1b2yWMU2H6EMzmgNqZKLQV26AW3kEzy6Q/Yu5adQ+3SJjnNdtoSoyFtVyYKYVIwFLQyWzSyxEw+spcxKzDFEmdZ+QzOzgKgm6w9z4A/1jOM4ZPEVmlSIhCAk3ms0CgRuBcT50dTUET2DocD9o/abFbG4JXtWcoB9xkNgD+4gIjUltQ1tgwEUqJjyeji5QNxmqx0sQFAPGOq0UkRWprKK30WaSWRhhaUaIOGKpAcw9RITzHZ5AKe45N9TXjrDhDAmyR4psGCppfpQSjBRDd+nrkZ6H8/i4v//VhKz1OC82t4LuGCPT1ejdbp0fGv/eqvvvvee6yPGZ2eXH/mBqfqPnPtxg/90J/63Pd9Lw4p+0mz5yuHX+BKcwGaNhwHwNGenwynjABwmLf5JmMxkWda0ZJVVVrDg7akS4ETVdR9L2jnhWgrjtzmaEN6Q3o03SG4s9qok+zCGmGux6OhFtQag52ZJjqnlhfvn/649tlofjacULXh59IRRpPS2VFYxWn7lN6EZXvEEoHGsL7ssx5gxvG6zdP6aqvZPGrOe8d1VigNKMFiOai17jNECjYLzp9p3a8v6bMfzZa9mfNP6JDZcUygPkRYl43NBSaAvdrYy78zQdpWy+uZWz/A8nFYL2g5Q13hYfS4RfMAdJuLy+zaRi++vYyrAZacxgNdGZPVgRsqcrBeg02n6EUZkBlHATG8wXof+uhntc6wNRq55sK+P4hnK7l5TzMyu0x1iZghq5gtqDZu37bT52yHdp0+OZfE0LG2n9O+nfR7Qi1qB6ai1VgDBjg5aA+HjOSobx5xoig3Rh5Ti4O3mo3IGlV3qjN2kFperyk6EfdnwV7BRIODepWyWylxGbldNyUT9Ar+OFrLR30jyKXcayY0QtoKcNBYoT4aSsXIgvpPhYlQ6aAiDXwjvRj4l39F6Cy1gdVV6cj6tfpSIJ0H+rCOGOQ/uW+nn4UYUvny9KL0zCYg9dMcC6iAcfi+ZGWh/VcART8So1Idzc8ncPrUC9Hi3iUrM3uaXYl5fi8fquTJkbRit47hY0WwiAhOkWOyUh6o+oiIkpq9zoPAMIWESBO0JwISk++xZ2ERH6z3kQkZrsbCp3W0wkoBkYx4SKviJjVKkBn6ZLZVKl5Rakv9lGx8M//yE2jC8MGEPinDCh1prAKQX3wU1NXvSlZqOGUncAJb5LTXFZhADzjbr2bOCxHIA52I/cHQ+8nSoRYlY10H4/LGf6rJDlEWMyeWkAqDFpRQITaY8/BF+ryRYfwZENWjVSfpMbNFTnyyIQt6fTsDVmrGcXHUDPNEq5oceLQImWhhUfCqydsRBokWJ8dSMU8DBHE3wUqW2OdATwI6DOr852vsKfyk5wwUJVHKkELBQgqFCpoWsLQU8BKgFQIDX/DAxHPRpo9WqpnQ8ddMIkRWmsdPzu7cvsdA5a333rt8ZZfThUjJAIigGFrA0i/re/sHwGE+sz27dkgEB4yaYy3aLSsY4FqEIOe8SAP0P6QFz1x+9rqAvthIG2JCTA+jpeBQjWfqFns4jJ0ERi3py30N7UJYCQoaF0LzWH2qnotyAQ7EQzR+gn6iKQVckI8nGMWRspPhGfNY7HaZ4i0P2KLESerEkzf6W0UBISxThqktmPnDRq5pW2otuwPqFRnFJpsPHz3kLDAoSEIbEXMq16FeeLvDTpZOA2ElDMLbbI4m927ffv+Vl59lKZkdsSs2bFztbB9oopUE+5IKBogjOaNZ8p/u+cl00NlFtt1HkdZaw+kxjOEQeYOFtNTi2TdGXiLMEBkOUCFaD0FwVMZuRSWaXPiYcqpajc7e9t7w4OzR4WNkRDYREwFITWBVpl4rHQCyTUCFZSNKN9Sayakmq2tXrj73zLN8pKqZjaeEY8mQMqWNeiZjKXhsAlPfZL0I+F0lzHsEQh6pdFZxRMCHVdKounGUmUhmL7NA5LEPYaaSFo75UfVMDUYkysDe+rSw0DI+kRwBZon27VsPvvL7X66UMBABmIsSEE+wBOtJ4ne023s7O6xRxkejmcc8/hqbmaK/VqV25IuuF3wgCeEWDxR4RsycBUi/yHz25MnDS8P9lmdhacY1M2SmHeCHEKQIn2aFzwdtMUcAFLg+lzgMFyMiE6KV4pKnYg272YORThfgosgkKpM0iIhJYtepjeVAD4/6gW4SdRuK2+qA6gxbpbMRqkjAUgxgCj5UMHJ5sIDl4qMlTSRoXX0niD8I5vQjmE7CWJDQ0fiECD8EXv+IBYEQsCyToqwIdYfWrK0neK1/b+TyP5TiUWAGRYJFikzEA+1C9BEV3pxfhYiZc4QM5os0hQRJaREKzHGAB40NuCk4cQYaaYAfbKtceCVtla92mUsp02YWXMyLQGEA3Ix8Aywq02zREfMHX/zyr//6P0MCGf9hUtbnvutzP/8f/s3PfvZV/P7ReOhsrlqTfVs1O1RfSmmTo7hQLiAz0PTO299A0+EpEaI2oYsYBzMz4788KA++pDTBo3xLhSlBDCu2jYGFu7fvvPjySziRhKNewVrLv7W9NZ9MPvrgw4MrlyKsNA8Yu8NwEK0xnS52dzfG87OT4bjX7TANElbCPI1PczKaUedpBRotHH1NGprvMpU60k/PAvtKxkKki9yzUB3jD7toe1j/tBSI+JhRjsIYxtWjDagMDFc3/VWE5D8AkBaeaYaAJHe9XK5MnQYJShauMouSwzRYUq8xJFzrhL+N4DXx8+1J5D/ecQf7xr4PtF3o4tOFwTFWxnAWWAboHgepnanRnfPD+iUOiXRKJNZe+yn9YYfd+xz3YY85oxxghBFmoRgzbJVDo1gaGKtvwe5nsLTFIB+dI352OMYWC4fAjNlFRefB7kQvpJHtvFFxvRi8LvwbQVBEjIryrak2Fu9omLhoUSlxIhFDSVBglBgiQEdKCnbEiMCYkChEUJuJiWhzk+RESJAfk0FS8JaEBnp94oX3T39PpIs3mf3N14VkoBGw3HN9i+gEpVBuA+pz9Zboq3ImgL2M1aXcPL3K83kW558sM/QxIgT9NJLJpeT1iU8l+XkCo6WAIk97DZ5Rw2L6Yn38CLs8Py9XSGx+SUUSxqd4Tp+/IBuz0WVqs1b3vghhFhRzhXzZ/Jgk6FxKpjkK3yIyMo/g0MTaL/wkC7kLV/0q+5HxkLDQMeiE50EgEMwSdH2OHGiVAIthCLRa9z4hLVadk1vjQcmGCMRNIi0jaMWWCcZPhTQUIBKmcRUtmhC0/hFPqjbUlZjunQmaVISIu6VGl9kpaMGqf2wlcs8eKSO2uKHqNR77cnHcutMJmNLTwx9jZy9gQSA8FSp4/zn1gF8qDDK33sSnAzwOt66cVMc4stEG4SAOz3CvsBBpp/ORQGBo/9BpTZDlkfpw2PhQKTPpaA7wlhoviOtVEdE+ObIvjJIrFB0LU287IiFc5YQOwVa/N+Cun08+ziCvzzhnESeL/l35RuGxXKznw+NozpeTe7dGG92b8wkeFOuDUkaRjQslXrMP33vv+o2bt2/dOj4+3dreBk3tpw0jiqZF4NVyYVkgRXwvuzWRM/oaIXw0AojwTET5v76qQMXD0vEJ9JQF0tB40LOW31DK4kkubz5fnDW4hlZ+iykCsnmVHKsH6B7RCiZ8AjDExwcQDeXUnIId+Vlv0JQDJmdqbW5fuf7Mi3c+uDOZ3usO2lv7u4dPHp2txtjW1YwJYLBC2jO7IjBG4Qx5UQkgFA0myMwm2NkhIxzvvvf23Xv36Lqjn4bJYlRW8IxMY2hhPPP12UfoCULMpPfhiJPguhM2uGefHyqZRnNnp3twcPXOvbtY9BBfsTE59OO/Y1kwAPqc8Nzr9I8P2d7dw+zpKKKlgcfPNBUXFtAZr+sP5k41QTYCJ7N7rdigCIJCO0dXku0RM81szo5+rzz/wqXdXXb0oyVjrUKlx+aJMJrCMtJFXznD+GxJhNrNLzGTrdcfs9HkxuYGUbtddkptTugSZOgeTcLpcUKddZXCnEYwLcDwXWZqgCwPMNXRIgMw338WGL2oOCy7UJBWczRiQJ5/MpSgLF3mVUBAsCrmHwaBsmETXCfAWOj22TFLXWktu0U3OapneAXUpzTwrcaBQDsKkqTZI2J4ANtKZPOYN20QK5bAYTZG63Z2trY3if9QDWAaD/Uu38VJMRZt7AAmmjRokQaGShw+svMpi3oVbk4dzIJCtZ5ZXHgDaUSIf2RURyBbqiMwKiBeIC2Hgml/0GfPVkd1MGiE26pkjTXlpTVCxo4j0dioNyeDDYpULkkOhkzKEhPo7YmE4OcK2SnbAM/HGnIVSD0F79LvEEoUFkgS6FrAgRKfUuRSboJJBfLQbQ/ysdaAGeL4VDPX9+LUMtcZSYDTZaUQ5UWlmI2NIdiWwkkKEBqRAiE32qzU3TqARRGqnJNLEJW6sJEA/osOfxGYqKt+H4yz9YC9QXIhQUHaOxzt3AIwvFGU9ExpVSY9jCJ7OOZl3OpOsLwpwRQWXG+Ss2vqxNj/T69EW+Ol5WHq15PHh/+Pv/t3wQaXejI6Y7efu7fvvvbaazefuTZkyx0mk7U9cbLJ0qHlM/ig9dYjOM7kwNmYobYVzYP79x+8//574bLGXaqtsy14PUVAxV1/SxHyYixLl6tEQFPgGxm9/977TNbb5UBrVo6reZSXSpPhxNru3uXu4B7jnDQY6cDQqy2tG3octgaXLl++c/9ef9BudjAUJtS79YDmzhDqN/s41PTfI6tN5vez58dym/63Wm0TEzJZ9oFmlclQwHyga6rq07dCHc38GQ4adjLSstZdNJn8g8zqPrP00MItreM4KwCZte7GX+WLJr1L/QsWoMl+TZqXxVWSYsFM5YwDTBkjA/jZV2dM2MloIqci8KlTZ0M/djHascJHURAMRZIOeZridhFiWT2MG7O5ugr96arHhGLSJEmDRSz1GmsjGWBnC1Q1iQyTKWpc3qAN5QUBDYZfdQrkCHYQ5NBM39xeDoml8xD5pzA2ErBFcAqHxxWPrt8iL8oFkNahd8++QGVwveBBDlQJfFSEvFWsgAjT8T2SI8lEoLxIG60XK05hSOs2ZdQuCsQvPqhuYRBZe/k1KlFefcu1fiUaUIycmOvP/kaRErqObGiJeTHE0PUlLJ/LXaDnMQnnr+gsMXgOHT1H/OkIwDmckpGJC7xASoJEiZqfg16nMjOEgrhCz9/5p/IQYFXYxWeCCvCCuJ+EIykTYlVkR1GkP3KhHGnaIkAlmgpHIIkLFYyfN7Uh1r3AJZItWdx33b/KvoGzX/kBSDzLYpsIJhwlpR6jyS488sUtIqHVNbcyxTxfxDhAYuhBnihkxQN6QbOXqog8iUMdSTx8kZQxI1VMr6mz04QdTtg4swEUUplj28ECo0a7WgmLbCI4ZoXqlyqHGAzEYXmoBCfOCMTHdasxazEGwgAoJdmQA9/IM30RYGjKQi83W6BGxOdAJZj7h2515nV8Yatt0OO/9i/1DJ6Q2VtFq5gotBYlU3QKwyGQCipfpKjpy69IpsgWC2hMY0yZjAdENFs1wwUCYd4kW5JLgwqI0qDJkNsGEhvLxa9kKiroFzijHcXOyjQLLQy3D3QCCS6B7SMXOCQqBwPdv/ew18VnGPzIj/3QnD03IA0lthSUDw5yulD3+s1nbt99/MZX/nDQG3zhe79X75YFpk73ZMSZTPATMVIc9XJGLuBGDzR5d7uDzV3mjsf9L+hb9uAq9Aj3+l0fa1V7/PgxZ5Fa6FhH3E27KtcFlGTqRSlUVTS+ej19k+YA57a+THB+5cWAPFBMKB2sAiOcO7diIEk0mENnW/3KM1dwZGdn+8Ozk9MztqBkdUeHnVN0mIinvU03kdnT5qKKtBGp7tSbZ6dH3U6vT/p298H9x4ot4gwG9jchDOjGDA1JW5QQvA0xnK2GDx7cnc5eGTFwMGMRfGMymkPVP/WnfvgPfv9Lx6Ph8eEjaku9Z3JRDi2TJjjOHOeAYZA2NrdYvkAhPAKWaUZnZwjO/t7+oMWpZyE6i7aY40pJ1S/2fWOuUZFhDQTiQjSxRI5AlMGxeufy3sFGb3OnvzkFcRSNri8cOnv9UI1G1r1wlB5bU95gkk+3N6KXOuhJdC7kFhF1BbySRh2JFyPmccAot7lzKeYSkwDDClt5C8dglOVVilR229Q8T8aIJO1zZIaENqFNjwSqZOoz5oLcKBIVs+VS3Zx+wtLqZocZMiMVxcUM1J9agze+9EesfJEbosMfwMzTrHlNmAG11fbWBlv/MD9gZ2PrYG8fl9GKHXvlmpkqSQooADCGnjyJA7349PLA3RCEcfYrVy6zew9vjr7RS03LPRNXCEJxydjjGla1Hkc+0aYcjljbwWIDjv0lU4rIrq8MPlBOSJQqA0JhBV0cBXVoSEixENGxJsxwdmuJxcO1ZOMOVFtnRD+BFcOeQUYgiyB1a1LqENVnyOu9UCYPeS7MqqJKO0MTaHzcjSVrJxt7LIias5qTD7QK6d1lb9x5lsbY1AtkSQUPSx6BDyg+AZJbeu5pxyq7+Ui88lCyTsTEBQIv+Wag8kAICZEE98uSP/AUdbDgaLLFN77aSwpm7+mnQQAlmKQ+iJw5Gll05KfA/e9fvCiic8XAG2Y04xpVw0NNik9mJhzu+9Y33vn6197c2tnkUHZ6vl9//TP/p//j/2F7Z9eMW67gxrVmfQhshZsUutnrIe2UheYZK/Pff+89JnOyOyc5gBPhpcTmy1OwLCUjX/FYe16WNZj761XwFEs/JR713OHh4RtvfGV3Z6/Tbb/08sucSkFLkrKhys8+/9wH77/veRT4h8xQwiRav4SkywU7Xrqvp8sGONECaYxHywx6YtYbHPLHfHw4gQlh3Bl7gI+OrooR7gWOgepnLx9AqbdXjSnrsumvo5OODnps5WI1Urs5HM8BAk4MZPigT9ywSxXDysAWlRbDa+G0l/ziD8ZxptqWJ/mxP1T6eNd68wD3gGZ62jsuY4ru4ibRpah4sEcyTMcjp0RuS0sg9kPD6caD+jqUSo5IWxoT9vJFahUj4IscmBgFqdFs8F1jFbvDV6IYRiyRIKpdnNgXG/9ZNK9mWlyWG2lR17oDchZayy6AHOsJEBSQQgqTyGZJTg4ep6bls8kL54HFP99oNZmz4ESUMK6CPXdfw7AUwQQlglgHlHESK795TkkCg1KdB5cAISdSAfM0kIgX415I9q0fC4Z8WycsqQVvKSxSOhIIrrIUDo/l3FBfjJbb0wiSJJ8+eSeCpjYF5kuJX2ImYnU7DzfqhQ95Zu9b83MMF65BRkWTB2y7Mk67khQwLr2syUO7rPxo07krvsQnHrHsReT6wJ6xGYJljYIIpQccW88Ym/6rDozUAGq6bOdsWkKuaQlYK7ErnGferqbsD0Nf1l3yY1SLkgYL3EwCgE1XOji4EwtvijIWWr/QyWjIHKNe6cK0m5A/MLXXkCQ63+/4yixTT7Rn0BA3NN2ba0OmCtN6tfcAHQMVSqrOgQ8+CVUXQolDLyLUXnoGfI7JtnWr0kAcCkIXBKtwAEP3GvUula5mqsWmgSQxFGcMN2SxZLvGko62Cq1mOlscrUOl4Q16TSqNp2VD94npHIY0vBEp85IptuR1meqLLtv+LpdO6yY4veYUIOzmTbUWaxNOL8kH1k5Q+aeWsmg2W6NcUpY4B9RbqzrrQCQzBAil5Tyf2WmSMxpdbclrEBQhOeKfdosip3rFek4my3feeQf36+jsvY3N3ovPv2x5cDbACY7RSzBjevrp7Hg5GAyee/4lOnMfPHxMDvXpdbJbLe8BezzCgK9GwzEbtkxGE3nNN/tUbrJ8oLYcaUPt4AaDUKRgKjq5AKPwSXsk9ez0zMdGY8iuRL3+1obdQuJjfgFSbEV5XsPILsJ0m94SYmLxm9KbTuUopChSTpB2zwLwRSPvXaYBlb/KWMf6KtcG4SeBHztwb9568sZqudlovn3lcuts2D48ZKK2u5e4OtHx3LIVJ31CyENKhdyxz057h6805KfUz0zSt92NAEIQ/UOC8PDgHb4wKoOjFrsNgu0nT5iXPkJ1yIWBXeZhMVrw+c+//vJrz52Op//8n/7GG2981brMnblRW+fmwgG6vUfT8Wa/DwehOp7ixAMG5BRTBZgMhjIygeTqtauaBJaxyTXJjmyjFogOASgXJVe6rLloCTBUARGoPRhitp/q8qV9xAndJKXeNNaGmBgHpvoombRYKDz76+uhYAWIRixwgKoQmY5L2cM8b67mWeQmWKjN0F0ehg485DJR/smvsA+uyDQ6p/EEmNSmfVL42eJDXX1ibsY1FZoIj7MJqT3lwM4nxzeWqyeNDgexuWOmBjHUoOw0Er78xT/Ep4oMZQdM5MSsvbGXiOEWaMHOS/j9lw92OaWLSVaUFXJYN5MLKGG36AimOUgy4mPNwIy2x5xDuGgTMg7EOnumR6M99f2Dg0tXd3HSkUy2/ISo6goldLjG/hQLpKjdHJ8ypf99WvRn2BUbaw3GBLI+GGtmOuaMuVhzORlOGOgQhKkxNdkJFGp0eqwTkN1IHb4Ly1DIisYEEhXuMzaFXaZLduioDt2SAAZCyo8syKbCmuAkTaoA+y/1SQypQsnGzNUoS4JB7GC56eG1IUy+EpZ6V9/xHA6TvMlEHkdjy0vRKhlLLy/ecwSQ8ZmIAuBFqaAlqUCRgislRpSY2nnIQwDKQqmRX4hnD6i1ioUjARDKQ1VWm/LsZ2VDF49dwDPsGwb3TimgpQSsVDZzHsSifVvkxMA36cVFRBXWSwI5s7Q1Ptn+f/7f/v6Do7dHo/n23uq/+i//t//gf/wHr7z8ytb2HsODyGGD9bBuNeFQD4mXrUe2kRi0YMCweeVLX3778Oyt0XCIDloHAlfVKDpEjuKW7LwX3Mwe6gQR0ebf7IYRO7csgCEmNDIz3WGA+xrVn2iPTiDZYGPjpVdfIXukm8tFPulls2MI2XSZACYtU01qyxdefuHNd99mIdPpeER/joPtnB1L9d9A7Fl1N6PPHq7oZcAHZu2zRpjBObigsogl0SIG4Ida9bRL6VOn458vU9aNaFFdPWK6dHTDRFReaiskgHHMwQrYfmuhQZ4ic/jufKKBUuwTFkBpgzUOguMUp/6VmCiOFh4UFRo0GMcgBpJ801iAXh2yjDG1rRFl0WGgHNI9NIXd+DqpjQlSqUGFuNwl9vSaOHLqLe8YWR2opAXtjIMQLlj5S64KgOJtbDCyNe0T8CIfrEOgc4m+VUUGpwLTasyCi+KhZ0ap4m+QuwgQhXpAwtMuI3Zcf/gvdopJvZ2VhDwIyQiMCQiXMfkSidCgXHPrJKZ2MySbwsvJ5LGEU6R0DksJ4IEYF67z4CosIEtgQK2jn8dL8qpgnwYmjBgQciupJYEo8wGklI8qn+rnHCzJiLnW1wuRiPGpNCkL2i7ERDwHciFZ9fitUlefwEsRla1whaqTyWLsPUKdlGGhYjuKg06OaJ1iImEj2xo4+Mo/69PUMrZKWXoOBEJtTVAgPrC5hLubIBUMvOLFCt/mrYy3Y52vQMbcOJ9Fvq0W4xGL4VatY8LVdvSEtjfko9eIRrcTE1mRzPp6iQsKoIqzTmcSFSDQ5jgxHESDWgSc8oOtQnFVDp0w/CRryAX+BSv7FetCSjlFDKrjbEFF6nTe6WOBlu1WfC8KjCHQtVIsyUt/Q7T13ExiQxx0Nfb8ESTB0ojm9A2bSzo2hHGACNWuRGWkDH8LKKQwFaYHlLTnVFkAzbwR9dBKA3gkBH2ppvcU5qBdALIfnihqLKFiE3BRYaITpDGkBQJU6M3/dPXZQIE2fCI+2GiALFxS8FYBJKfQB+9P95+R+7W4GrNcxJEw8AH0mQ6AADDj/EtffOMPv/rlz33+O7//B7/n9PDJxqBHTUxfPiO8IGjV1Wo/uv+YbeDZ1eS9d95fTGr3bn2Mm07nN+JENlSJ9Ctj6emqt+lW5QzfcUs4kWbU3Jixp2NKHFws/RoniCY5kOEQR6rU2e2OQ2eRVw695+v29nZnsOlnk5m4pMmzNC1FJHRdVGOGRBcSlHTEEIpwUA5lw3D7PShpnsMk86jyKw/ER85hkSPDy+XVZ688vnty9nDZ6TdHZ52G0/3VGr4hHBpMLiczUDnjZeh5RNBw/SdsZ8cc682trdotmQCmssWeJKuICJxb3HFVyLXqw/GpHbdU7ERHdajH2pwhsw9rrj2zd+uDj/7wja9T46EtpAJV5RSo1CNYjQZTgDhwwFf64fF9gaJKt5sTtm+ark5OzuhRpk7DCcUppj8P+hcgQIPD3CvDb+1Cu4Io1DFIZkbqaKvQ+6VuOnBEcSgHmUhgrIZjQlN7ndAZyqit0M6AYYwQlKrUEOqlTssIAMW0IOtL8lkg6AOfCkoyW3ykLLKn9WAEXqDGhZSIKEAgImFyl7YIAyg6cOy8BL4wBJKREX86DK16C4cGV6TNpPoOrinkhDPNt99+63R4wkT5CR3nucIY+VWQAhIDO/u7rhS/tHewv7cDRGbRmLPlQCRQZVlMhs4YxNjJdZYjos9aQo4MIxrLASewxL1HapvbmxhFh9QoGS4QxXFDIQQVO0wBhQVsnI/h2ZCWIfQkArP08bbgC30Z1heYEWz8nG1nUWQ3XhkxjQf/kFECl9t6wSPshUcyzDhoojuecOZc6glwpdef/uY6BwJ61i5bAA26m+lwpNxQTkRSkADyZiB3b3yUxGCoOaCQXOBIICGJZuuGnmLsvXWDrIJRkIbVG7aJdce0nCFh1FmembGqbWQZTQqGa5GCfEzWCoqfC2oiobULI4ilwIAPNQGTPx0npraKOdSbMjfFyn/ahuBJdEXTlHQwMTbCN405P8T5NAWIXOVMOq81jEIc5dGgIClO8JRImPvh6ck/+5+/9Ed/9PXOxlCFrU1ffumV//p//1/v7my5bpWLPT3G/sto3hRtLRggaRjau/fOjo6POK0EUQ8BkBn7cmFjydDI4hPa5FnSBL38KE4GgJtx8uNbdSmnVVqpYyW6WHByPPDTvW0xOZ4c0mj/8UfaIaBTDGCSZ/MxTIiE0uhjXhO2gpntyCG1G9UyEgkVGPlhci59dhnPl/1k6CIreItxtl+BbcpQStwMvuktGMcfNB195aN0IhnZUNVTg+DFA0jjk2KpbClyzEQ4WrxuikdMSAxlSFkaAepoCoth0htyxTz54pYR2yydVU/ewIFmOA74U3jNDOOy4xCi7dQgOU0JVWPp6n8RJS1QNFApJn2uoK1jXhQcVMjJpOWfGSqdKUXpuNcfBWULRBHISE5HHLFl9mFwPKDzxWI10SM7/NPOhEPuJGAbWAmxbBZLlCCxrpGE1D6LskIONhLZF7PjMrCIlvwmmhEML3UP4CRkAgxOKUJNkwuoQPSbV5W6vPzJ7gL/5kvIhHr7lhHikhnhQtKCeXoRypcqIFEEJHctTbB0xTd0cc7QBRjrR1pLXJzPytX52Ps3X6xEBlKB881fE8JqZTFENuCsXSMoCCPqnv/CBWsUaE68x5HWJ1FMglXsl7YUeSKAZICBE4wVtpl4gwyxzt7KLzYP8ZEPdKULFZSwk1aupHErOKoGHtzjhY83nU7XvB0ZYU7kmMH65GpJIsbUoKxDYUEZoMdUtKYGK/SWXYbM7iFLVSAi3QSYB2QOKQtZnZGHyKGtlogq3F3AU064pC2jcUxhQZvpq0bjv5U1JZ5dFn7rASXVxDufgjiU1Un54I9sLqfXKJn9GeAgNGNqvxkB58epyQOIQM8DSKKlKjf50hrWxtOfSnlYkW+jHyyFSHuHvgsn119SktuPAnBKQLv2HLMyG837QMYVBkE1isH71qLjbBAmw2A27OsL7VA0kAZCqQOEDcOhZ3PziKyoebnjOAAHWgEFNshny4ByP9GRZ+Yl9ZFQ6fqSiE48pJ7X2yAREVVtilDEN2QCigaLVgBVBZNKb929PR7Pv/A9P/jz/+FfBTb7S+IkmQvx8ONwmVaI2YhMRienr7164/GDz3ztj9586+tvv/zqC0oSWwbjLeFtTWkLUUUxsRu3AVY5cahWv9Pu4Y7sQgv7XJRQCM4zvYlEFzPeuCwZIWALj1n9teo8efiASUqz8aXF5HK9Tv9u+JyoxrNc/OdGEDxlFQR9DxaNxIIFbokiS0lBTGZe3uAzowS8IA65YK5dwdaW7NxFGs6sIHbQC3jSI4T+o1A0wIDTal+BX532dfb03Dt4XG9NDu/rWzOmhKdmlwydhQ4Nh5DaWBBrzKdntG4Qn5PTERNy4j8L1UobR4aFciRm8o27zYgyfnYEqH74+Emk11ogsgpkdr04ufbMPj7JSy8/u72zRUMLSSE/GnXWQWQagR+xizzdlVS0S7ei39nZJaOjJ0ecn8sMExppd+6yg3JjE7diY9Ou6K7qA37Il3UM3XAZ30cYs60e3VZ2Jc2Z0t9kt0qIwIR1ugIoRKrC8BQJpMCYhqiNoohCghBiSbkAyCxWKQqgIqAt9rggiRwt9/LRADi73JYRzLOHT3DKxYVwGqO4JeDGqfJAuwqVxeuhVkOTwZqFdrFNkU0PwqWwkpvczRhZtCpFUtAYovf67WvXr7GzCuCRtSgQM6Y67MRy98GHtYZz0iq5wK5qJjUp7GB65fKljX5/e2Nje2uL45wRKiWfAlgbqsPpd8Bq6eXaq2lV7pag0Ad00Fy8b2hNuwlvGM1U/fU4QDYl0z1Q5wELhBAO6kqLRv12ZzBhXrTZLK/R4G70HjICQAcxmZKc2Cz/URyZWQMJiUfDrZGxTShE5ztYijCMsHceRjIyBOt5x/ayAIV5Z6v5AcBms3dhu0Y8aiZyKq+XulL0zkIn6OmDGKt0shCYMt2yQmAor5+IQ+J0TcJhDHUrumwuak0gazQsd3S6ChPOsgcCDvrUutg9gbMZebIXH5+q/mx3CdO1U0wFhXuUWW3DMZ4zTEQGabCZPQ8pVEG4AAtWwYxU8ddSGgtCz2bZfRyLo1BVmfLrHoDMabIHV9IgTAFWihECWYuDFTxl6tZ8PPnH//CXPrj1wWDrMfMAf+CHv/fg0sEv/dI/+k/+07+duq/UiKBW50gMu+vYG4AdmWn4Ieur5t07dx4+PBzNzoAcPZJk2Z2GH4xpMoxE+oTvARXZB1MiJYAYyiHvrEK4RZqSgs8FbSKx007irmMCAMGGjdbOkB7asgIBq0sL25Z2Y/6Kben+Y7SVMlJHUKeeOTpBDcVyO0bo2PHCZeiejmgVDCPQW06t079XRbAz7FLBuBRjBY4msF8Jr4wTsPkmtWE4bgnwd/mq9MoYVYe0qhm9FGkbiDhksVD8l4UwS+0gAD9BwcSwW/ejeQZyQWoyMDpFckjX6gJ+YYDNo8ZBQsgveokowwLCuAMyNoe9H+j6EWFMCehFA4QERDIXac0awb6AZKhIMyEijhyvWrdwqGzUiDkpg7XoKIi1BbYIiWLnJRTFvIEg+1oPlPMlI7ryQm5o6/gDa5w6nR5aXDTG+ESR6VQyAloIfDf3AZI4mo/YAtyn8FfSUmLRdZyGMP8TO0+hLjsQGlkrZ2WxvtiMwcISjys058ensstfMktIIqxTfeJ3vdO/uJ1rljFIYtj55SlVXJ3bwew8mIdEm10zqHU3HxJisSwqd+p1LkILHtVnvlUBF8OrXM8jJ6m3C2mrOCXkPAIPARjwF0MvPq/ThBlUfyAhhvxJR4jLHSLrjlCHsPaOd9mDNBlkPHVBb8GJPjZnydUslRXjWDOxGp3GLnUNkRroGBfw7eFw+14u6hSkpvQ1OWxAxQhGQGXAlBoDiIoXQMGG7zOXmCF+DPQDqQxqUWNM5+xVR0xEwhSWDUFSdhSJQl3QA5JVgehFKYozDCK2EKzVmepJPlGemB1Q4AUqoGNCsz6xFWHnA6jaAxDe6QJTFjnt4leIB2XEAYSw+cxuZ+TSxg6tCpRG54bhOQxKlhMD1oEN9BlcScMN556OOecRAR+zhW1S3KPOsgE0IIAmGzfH8oBlmaLjuAcDEMyGYLIvyDC9gKVvNuhYQ0pdiAnBexYSvjTx2rYnx2P3m0NpnfiLxQSungNNAvoyqQDACpRxG2xqQCvwLEUjWwkcFaWkYsabyEX4lq3hydFv/f9I+69vT7f1sPNasVaouKt23vsESSfpKLgtObUk43Zo2kCDoW1G04N4wRhcwA0DuGVwxwU3/AXABQyim9C03ZZkS5ZlBSsfZZ28864dKq9aefH5Pu9v1d5Hks0Y8Naq3+/9zXfOZz55PjO+/+prH1vPs33+Q1/9wp07d46P7B1PAIOn7RDnB08ev/PeO9/4k28dHz29/8HHm9vPff33v/Pmm2/94R///he+9HkBhz6HMVkw8Z8PUX3IWMeSx06Yanz8+IGwUncraYfBXMkTgqMDoTZPpE10QMTclPPmd4xndrBxzA5cVHRh0nL5Xgr3aBIBlr9kKGiZgO5HH+7mRyX80oApQ7lSliaLp578LtaVZ2pVJplmVX7XlPPsRzdfvnn7pe9/8tHDQ+9H2ttz9N7ZY1WhsUPgtGtkFB4TkrIeP83jmSDR46YcDcTbU7Cz5VgPdRWKJXPdKEFzNVpwxUG7O107fvT4nqkD/QE4NT7FYzvBySHWbQnY/b7Pfun2rVte0jnDk7XEC7m1ZjOUJfDFTOQoxRyM+NpfaCiRa0lniu1OHz1+3AlR6xv7V/du3rot1oE4SqkdImDLUgSRqVQiyhJMF+itsMvtJdwnmdpiTCs2jV8xDT9wDf8SNygr8UUixYcRNaHBMggL8Hkx5EVWMiUIYKT7CgycJpyabwwmi/gGI8VxW2U+lOACxFKWWh0eOsq9OASCYyxYtFiFXOFZ0521be3sGDNTUjBspwTj0ihsXL3z3ONHF02ijNscHqbIcPV359atz776mjU0xtD5EUMnFuLT2eCOOtKtbnOjfFX24ClxF2cLzPG/GCJF0wfoM1tILTFOQU/DcVjIIcO8a6ZBctHInpA+3RDBjEX1OFo5t5TPVN6YPmcHlhOQUW2B2bm+65DvRdSGJ+BFXKKvzpH0UzecYBgtPuxu7T09saPd3KOGYgwj8IpEF7FE4Px0U2rcWVjrFwnG7SUbomiJBLMB0vVTZC73CggCrK05mYk2xzrmjWgETIwYZ6R572C2u7OwBwKkZSI7pcPGWpbat8W3jHQHsrsgwa2PruOjU+frVzk4cdq2loZv2xkF5WQRQ0J7cZiJie6Vd2hJQnEh+H3Pfb+DOV/z2YMADhqjpUvxYCQ/J0I+Pf7ab3/tt3/na/kfGnXnuR/80pf+5t/5m0pqaZsGV3Vz3y1z5fNbBXR+cePGTZh8++vftH3r8RPzpRPAqWahse+GgWPBguAKzQU1dK1uZHS3KM6StqBa4nI3WSu9CLH8ORk01VqVnH+GkoMnnn/+pQ/v3s+5LQfaSaVzxDyzWbaleNEe16F91WZunPcCSusb+NRCUz7KM/LzFpPe6UdfYdDIuhCcZC0LoE0JnWlUvxvI8DiUquGzS7WLs3FMq12slKKwCRQpraZguU8zVZJiLMqhGYs0T9jj3A+lJXRNU4Lo+gyqjz3cxjwNH4ohU3FUo/eTTLqLlsSzcE02bgbzKii1ByWnDT6CimVQlVpWAKMhLZC0uPeyFVTIizcQ8j6hoBd1wDkQCuUnQ7yhhOBpNyaCWbJVmWpbiwQGxY6I4bMvBXo86ENDObFZO6szwESQ5rqtS7DkreLQ7Tti+i7lGWULjZPak9JdUfns+uThs6RAyfupTM8eufmzyUuFC+diiUyTtICeT8nLtfpefTWwVzoSVqUSzGUSRWkEyOC3p9E5lV9CqlyXkw1c+v1dU3TuVh9yD4cWtCbHgss8+FROe8/L6AUWqZ1SAvGX16y92Hp/NKF2JHeEeYkwsRkUrxVu52gSaVGDL09ZQl5r4+zwebtrNvYeMYz0VjQ/JuGYHANCpLt0ASvUtBmzTIPyphR78z3QJqQHuqG+aq2CeJUrqIZhzCBLk8J/HJD3Faxf2dXSGbZocICyKS6z0esmyA714Ifj2i+IcRaamZHbwnsbHwpE1FYXP/WKIZRcPH9XRuvtJM2pHVAwVRqayJZG5eVkH+wgTCcdsqJWoCIQMnUYeCJbY22BFJHvsODOoNh0PJfx0CsO6zWqrawQquPAtIdNGp8fHRluaUBvcPa5vnHtu9zZlVY0Xog5qjLDqVFRynMbW03aHB3qEGONkMUEi1e2PM/znW2+VzHppkmbD3Us6cnOzk5Hj49nl2zEmYUas2rHgcHb9SsWck/7WQDh7Ss8pMHfCT4AXwxwYViqiCkJTEIDWbXx333z23c/eIdT+IHv/8oXv+8HDP3lr8jeqcPyOPjsycHX//iPyYXj/s43v3Fr99rv/PZvfvftb+py/s7v/PFP/NWfunpjz0BOQ4TKbmwcPz0ygoyt80qp0Z600bnUJzdvGeZzcLU2/amkUa3Fz4yoQi92cZ59au4R5NBo/Nv+YGPro94rngQTu5uoipgy59mkNQLkuzB6MvQzMfe3aNISS7ztp8lmz2rDJpPvuWMK743heDowB6fyLOPVVRUO6j0/3yVR3ZO33z988PGDl59/dXv37fPHR15Ye2DJk1OiZe5w7vOjxo56KdjWjoNDd4T8OgLOZmFlFsi0OLKVac34UUA5HYFq6ZpB+it7IskrZ0eH9g6YapZotP3k1G5j0YDpJMvxxbU7ho/3r2390A//8BtvvbW9cYdCXaw9wJWhqTZLR/bkbH/j6MrOrgXcDbmhfG/HQq+Lh48fFfN4Y+wVMwM3vDnI5EWraq/AaePa3jU9VdEJUjYvbMPQKHW2GNWphfTiTJK6YAXFT+NAoI9DEpZWSlZeBT7JK0klmC7sHgkqWNd5kmJrxUfK7vvtc+H2xQNydz9NrBxQxH4t2uNcHq2o83k1kr007dxphBYaCv2dWjOTKyJjbaK6ARmwKzzmV5Zib8/m2p3bd+yDPzywDWP36PBAOII1b377zZ//6X9qaduc7ATBNAYknkPkfvu5W6+99PLZ06Ptmzv71683MkNDfYz5FbH5Ue94Vj0ljCIcSo0F7ZsXdZ6cLPG3uBNwwToH03vEtr1proa/sfmULi76jJV4vSyCCBeCoEV1itY6B8xeTH4gHIoIe6Xg9DE2Nyx1yb2cvOg1I+dtkK4vgYX0AUyRZXUkwCyQqykQ17XTN8Cy7XcN4x2d3t++asID/gcO7/FS0jOvU107HN/XQVjeqbR+ejuXfuEYJY59d+5vXXiRS0Ohh+vn3jb91DtNNaNrJ3c2Lw69E6NYkOcXg5AB/99rlRqOKno5v6VV2N4+bLvnieF9PRaLiZMepJwyEOXrO49x93Tj6toVI9vTc9CPbRiyTJtvo2iEMmyflgsARvn46ElDog5F8JqFTkwRXSrWINAcnpljT2/TboAKqnBfqiuhgj+YSE0xyy1b3wWi82YS2JXtk0eVyCFhc0Bq/2T+1V/55Z/+Jz/DsRvUt07tf/I/+x9//vPff/Dk6Ae++EVLs2SjJDp4BkJA0w8zJG6Th8bk7t27b7355pH97hi4dE5qtau/Cjaaph+E4tjqKp2All/Z5Oq2hH5eXpc5Si7Nx/I9ZM5TnK1Dy5/UM9EZ2Nnd3L+6c3J8YD+6NeIm1lKx6VbZm7d7de/6rRtO+n/w9scNIGJ3lYNX9KCT15Upc+K7jbGYHOcgvKV1/dD7gLFVzBB1BS6JKXTTgHoHYD0LDkJObgqEC9xD/JC3xUV5rMk6UlJ16ZFXxJ2fdkeuHnAlPrsK8rXWls211HFTC4/VYycbVh8ofvxCZbI+wdHzOFLnMe3oIZDuMS8dr9YBW2J5RhG4s3oMQE4WM9IKyZYXGU+Z/jbJAaZtoE13m73hBXhXiifg0WUdBTi9AybzkXVqgAcs8CwERvXoXt9pc1UO/6I9ZPrdXfCV0TZNXrWulH9jw2SvNrmVkPaUhaddKdBartCrtupq3X8aGJiQjCOLuUhWT9QtxlS+5Rq6n/08fjVEi6UvP+NoKHZ5tMBYfc4v6UKFIAelnPOjm/l1+XlZxwpeGMuTdU0VwZ5H8E5/PVxIm+T5WCAQzqquapirB0PHfJe0ZO3u07fzewD/2dTl2QIa38bEWJrBmF79yZ7oF13NCAyWFExn8rBOKV3pjG5AmAOSq8oCdOGG0LK03ISKj4JJpgbChiBrsKvd8l7TT8GCYg2M/rgWojEIwCl/bfUlmr7Vyb+PGrkf+tXdDSiJX2bpuYk6Cp3dO5pXev8T2KCriOdhHTZZ2dw1GCALjGDY4xp8yjf2gg7jHLqwHpXaYqRmBWYxunlz8byR0VoTQ1o6SR35Y7xILN/mKSmKwcLZ6q3ZM2avGp/eoTMO1y9rF4t+xgCFF5pxzEwAsN1s3CXPoe4o7XIT4/pHDq25chkUlyyOH6J6CKJ73zG/cDDnFI3DOxH4AgPjAEez4rAOaj/1w2aGE1oMLfSmB1Z/pqYullY+hg5SCcDN8NNKdKHR+Vvv3BVoyvwf/IO/9wNf/n6bUFdw0g/NIICbJnDuvvcBhXr+uZee3L/38gsvffHzX/72m9/RR3ly8PDGrWuGjakPxHVmxsTVABnYRMfg0R12oVZEBbDcNfC5qAWhtANNUUqwmvytKwo4ktwOYKLzFyn0NM+6okYVQ9GKKskLgXLqcakau/onuwfz5dFwa8mJ21qPgMT0EMnru/H/Wf5VuSlYTg/ky746y3ljZ33vurj++eeeu/X0+OCVV1/96MNH86pgo0QR2PhWYZyw+9zpeNt7ekd+Ou+FPW7v7F5dfOMirBTAhUkXTmqfIU400lQLMfSoej32YsJ4Nf0cwXMscVT22k/91E/+i1/8pccPNVK9zjVnqwoRJzzY7WkHd4osKYrl5piMZvMAt27eOnj6ZLY9rt27/1C0bKmdvtwH7z7ReD/YfHhNe76917ndR+fC6a3tw7aXFLOlVUxbm9i6lOa/JUEsZateXiKZ4VahmBpHHZUZ8eWQVrJY5Aify98EV4e/5s0zPJxh3YFWoXooaUFGh7ixymYw2lct7j+/51bAlOhHHRNdBUIwz74If6kdGcxKdE5nzs7uPP/crVvXz06Fm+3E9Wx7c/+Nb73xxjffsqf+9OgANjSdWD1js9bXWvbjRKz9Xaf+SKZAeeH0I50qhM0O5O9QRO36MmlZPnJmaxiuIgaoMEtsjg/vNjb3ep1TUhyJxEnEACSlGEkN+MvppT35ME9daFoqH9ZlUJYzNdmPEXE/vHLg/nUS+angfpgjaNsHqhBz84p5pu2rno4m6rt7RfrODlXa31x/7eZrV/ZhvZ9YNnZZsU+k4myX0xtgKkRIaRvN2FgXIqB9H5YUN0akq0y/hd6OWePW99aeICNPWC+AiJCKIt39mjvrLIRUXGO9GBBqZmRxpQ7Q8GnIS7fgife0njOo+D+eNQkkr/Qq1sSgEB4vCoCpXsMWRXxS4YorZt7aXJ+PqlEoroxtPqqy+vwL1vKzZ37F2surpCWblFG2npRrrsonDRad7Kbg+m//1u/8Z//4p53Miz+06b4T0D766Cd+8ifb8d/Zs9BZtCVjz3MG7/zKzt6DB/fffuttK7TwDcuHsbxNtuOqpgKszPRTGC4PLz/j31wrOla0TdIlLbJMpoHSXfK9pIhLYQjDQU9SRZ+sT0caQ3VFoS+NBOMMMzSnQcG2jaUqluIEKU7Bn8hliUmZ7kQsbnpVOBiWSyLH6skWygMFkneNGdGoF50URxkgNxIZLldufFSmCbd+DOay16AMXaiTGfL4pqjbmgxf3dW54apVKjhMrScPq4PfMF256s6/DV/6idzxiFFBj4ItS58wjTr5/QyfSG7YdpU6NhL+g4VfQJQd3WlzoU3ude7C0wNVJ2UV6Gt51Omf+eYixMCsICvlAmu5YvjqB/yU94vBh/2gF6umaDBBS0IIntqrcTLJrcJhaajGCD8nz6QXBKA0YmVcrk/qXVV/+SAMnuVaEifHpD3L69cwRIZPIH0CYu4G91XaCqLykdO1fC6F+3ymzH7MpG2JI/yFkIUflUS3IY2F+GcIDeQButytTiVf3huw/daquop/cnWy7ILAKs2P772SW3Ut6GoOGf7G7jK601oaD4oTCI7atRYuJaYL/cuqBr2YTxfSulyntE6VIcb9ZJUUe58Gv5GWK5nLayyERfXYQMhECW5qkmJU/d7BahzrSEKqGnJJ/aVWMTo3oCVjshW2/hQAh0iCwLE2+11D40wddSmqCQFX3ZY3aFgVcYqF1cWvd9D+5ruNuyOWZl/J5jQLflTQqKRXg8819FmS0xG82rz6whBrlFv2D8Re652dqKVia/CdkF3cUmvSwkPgsq+NE67FMBoc8lXR4QhtjU91dNOZoRqhhVxpra0cdmUGfLrRu0b6Y0GlPZs2CCPZ+XJmcs12YcHZKzoiGztmMM588t2oaWhWOZWftG/hYqOxq4X1w+fF6yGp0ERtSCknTLfvhi7sOdW8Q44uns6/EZmsSUouF7fzjW98+43vfNvQkXjO2hKHORpusfA71uWbmg+xpOvg4IF4z8p1UvAa2IvTw899/pXf/o1fPDu8uHvvw1/5xV/5+//1f9CePWuFc/W1VLolnKagkGpVdTrh3UrPf/jO5qOjP/6+7/+CZRCYMH5bhporEiD0hW+pcQUcK2SpaCvUnx7MjhKD4NhTv1UU0LgdVBf3GGk4nQom3q5EMEwYr5I6T0o5w0iubpJRSlupyorNw9mTWqYB24/uz+6AcLH5AU3zLauTldPG7bXnnr9y772zP/zD71698cHBkdEvgfuxN7hacW7IFHi0utcrpX9HBkTWNq9etXKnKBZXaT2BTe/avrjnzo9ube4ee7MPXHRHb966oaehC8EH3PvwgffUPnp83LmaXsi6dra3fyNr2ra8Z+v5Oy985vXnf/8Pv1XgiKljevGFSrHczYdHZ093dDDaOOQdY1wCCWzs2LW6ufHo4SMnc5GA90MZZ6iRXPdGG1MOHZe7tXlge8CV7eOtPZ6hrd7iJuxt0NWFkbEoP1GLRO7nN+Cwtv5w4S0Ozhzz5Cnn0lyNJyUCxVdCg1EqOvnSVCcY+VpCyVYVJS8CouIcHiWrGT4+abD/GKZ0ZEZJG6xjcKTKzOYETGNm8Go0MbH3kVDBGltQfd/M9/zi+edecDqhILUuqO767M21Ov/47ODKpsNSjclxfecG7J+7ed17vuzUfPGFOw44DV7ObbiijpPb0Fjf+oCCje3X88eZUaYCNTkNamHzLL2hF1A0wmKKdMOCpZ3dK/ZpoGiJTACVs35CnhZpkY8SOpE3ivFLXyjwHrOmlgOl2gsfAhAnW1Z4sbX7Edqtc4qfMWEUHlvFwtsOPL11cXr98NG1i1MHh5sPhELRuXosT/zcHa9ibegcs3gbjD0/+9j7Q8xGcao5EGvxt52V1JyX4ZaNtYNGTi8+akWHfmBTBK3m4C3m7777RtxXcVXWqBg9skqJM3IY9Ob2PTEfjTPEDWvR45zxMgihyiK4CMBYBR34iM/6orTUoEYtNeZMM5WHwQN8xDG9O9anhSCjUQW65d7nLAA5tQG6NUCpYtdwb25idWzs3+WDdHZRqRJXnI7fs1LZesB3yqnUwu0kRW5LxAXRK17X9Qv/4p/boKHtIIL/2j/4e3/r3/mbzj+wA2fP4V186uJtcpJ1msDiY48ODt/48Nsf3fuoyWTogBluYVC7PuipcBDyuVyTevljRdzk6MGYHY7FI3UMTVNyVWr5Wj5XENVLGzo9iUzjNAdCGNdvXG2mokypD5iaG56c0zafaXDkyYGFkmPFrVVILoN061e1ZOZBk1KwjSmgn8uqvbbdjX+iCDUrVc3/Nx2k3eFHCZMiqCnkYdmXqmlW/qbIVkuvj15nOE8CPY9lox5upiMilkiyEzqgKFcDvfK2a78sGVs9RRnrk1Ji7QJPrd5CMWP/PUoeVVCluUSWClqApcpM+T1NXtJ99h5vJwSG4iDU4+EbSafzIUz/M97BsMa5ZQ5gpePQz8fMI4zTYUaq9RrqeCllmRZt+OlOlUs9S8JUWIGkNWz3mUQ6+SdzjJiFT0kZoo5YhZXORukHSi0uLupiXtfyaTVA3Jr6SKYHsEFvQFcwJ3WVP+r8Pn6tZ1kNB/l2pb7nGtjfs7e2lKkZI+bp+tMFgQX4ULaAmOSxx4Xey09P7RR6Wf5Fa+f34DqFFQN6oJU41UVDQJc6x2xW6aV2zfMFoQWFwCxPInjg+T1QSr58ttxMfcDGKV/4bqbfBtKpiTo0JGZwqDaG0QWu/vACTX9Sy5EKjeMGIFzGaFK0KtKWKMpr0LsqFwOXLF+LerXdMibmoGa+4NfaNoc79zlPw+vCvigI5Gi879o2EX4huKLsv4Uohci2Rs67XT0GVrhTqfbGtaAUmeDyYbNuNnz7C6E+aJ7vMaQZvmKtxne3OpPUNf3dQbL8GlEF8kf+xDfg8yMFMql+A+3ocjxGB09rKwTrxjuzHgxohs9TuwEzjuoL1IQ1kv2CEm4mDU1YhI6HguQ0QnXWDYGDQ+xxZlBPfHG6lHwI0IEqfjEN4h6Ymt4SuRSnTEY0CTYwwF0lPcjkXlZMUDj80gHRcCUN2rLHOLsMjrTlIzmNrN2ESmi41NJPEvjg/Q/ev3t3/9p1scILL7700ovP2YN6mW0wVu3Z6aMHj548erK/a/jzCL272zvvv/XxF77vB7/17X/+/J2b9x8YbdUCHHuvk/pzUePVksfgkHQadDwVJDkp/8XnX+D6DVE5ojQWYxlFHIxQ5AaNGKzBP7Fd04BoCmF5vXWH6Tr0mvTIbRIkpkz2ODvqOiSmOFEZwTENQ1f6tXzFTo/jCcVTMu6mrYuEF0WWY67LnEuhCpYxYwpCuApVdvedhL//ue3XLNu4f+/j55678+jRIy2ewJ7mFxTaF2ZPr1CoRdo6jcVJqUpr9nbW9HGsBGs7ZnNuxNmaGJKfYxF3rljZ2eAMdvzyr/zyX/pL//bF5tPbt2/vbF9LvsUE4NPftd2d/b/7X/j333zrf/f44HHIhZ3mDlkRCI80LXOzxLm5o1pFCLZ0cMP7qh4+TBJDnUZdu8sz6Ic7/sVlF0pLaV54wfk2dwTaKKuCWnHsy6tgtx8TvYFKLYOdYJwCSN6xtUuG0pLQgmJTR1EQQwmx1P7PcFTSqUVfSKgEVyAaF5GL9g32w22oy6zRF0FFGiOXpoCgycR4rcJvlcSrLhnUlzHMNdScO6Pws3//P/x7CLcNwMi/+TEZPr5395d/6ZfJUZXKsTFac+vG9ddffX23mRAhqpcBnZhLARDNuDIKNvxXX8v7aUs0D3VsPHb5Iaf7cQq8Fu9oaPzc2VDP7QC85TXNlzoGx/oGrJswlUWLpBxIAXhaBpixfDxx46/hHtfW8v7CizlLLZ+eH82R1OduPSHMj0COKZaaKdEYKybZ1G1BaGys12EMOtlQT3RAIInoWqFzaHQEQ94HkImey1ld8kS4ZY6tZvQj5Kec+mttRC/IwIW40bV85Q/DIbfLETDsGcZshYPBm1qcEBjo6le2CikVeBvHSNH5NTO60iPPVlDBrwxCUliB29aOw3AVoyXJdPReNMuxG33ZqwMJ6wp9+gIthJckX0P2J3mWupbPy2KTqx9qSeZDb6xm7ZzwOx/8x//Xf/j+R+8R7+OHjz7/uc/95E/9hEOkXn39tSN+1YDKdBWQMUVXzGJTT54+fvfdd+gk4006MoAeKil5t12Lno+k5vfyscK/5zGwrJMUd+aKSd14hNglMarhsGS4hO4XT1JflMIlAuw7X7t67Qb6ChiELRrHcTtsZeTfGOve3lWHgBoTEZCbiBbaB6A1AaOgjR2sUAefG6EMLSUa9YVxqBAZffOB2wuWyTFBqmURCybM88Zr3MhJyM1G1CwA3F/f03Ys3JvkNIKvm/zlqobMqp4lV6cM0ygn1QxRt67wSgCUW68jVgyz5uGAhS6jmXBLJkYyyOJankk9GfXIQrnGjKrJg6gdjcJNSIRL43zT0tYMwVb+LFS8HNyBM1iFzSARmQv9srpgF9meD+JxYpgah5aMoVPy/BxzjAO6PvkNndVazCAGY3FH5ZR/BYA4VR3eEso2MdKCjKQlfQosuFUs+yz3gAjas1z9mGv16FmOy/S+Y8Cfdy1Q5plb1/K5ZO6+u8snZnn88yuul3kernL0tQggJiJp6B/BJUaPXEkxGuxBrvACuAffc7tKDuLltdwvlc79pTRAzrhaMVGNANXk2A/lwRKjE17UL9UlmEggglxBJRWpFawFbHRfWuIbK2vBCzDZwEXDZxa6eI+dE2Ws/2kiz74/xTQl3K4QrLAVQLvcp5pRo5NX4HSxYZ1Wjl7TrPnRLJ0fvcRqTy/eosoAcnhGHcOsxeJGRtv9xhOL6XRtaTvLNG8v8lBJ/MXJ7TePnTzTCyjzHcsyA9g6tB7he3udsW1lPWTovOET2DSjXeCid2AoiPs0hsnL7FgP1IBhoy98vIysiwEOP/EpGfjhGzvUsFhkY9IZowx5YSxSb6EEABVGDEuveYIdl4BhReDCHWsEko5J7ORltVxSK/9Iww3xbO7c9ZNsq1CNBX0pVbzkKvY+khhlvJ4HaYDyftduShqe1NKv73yAOAFjbVYdHiNk1T51Jtx4GdgFeGD8AtoOP0fO7GHG8Z0f/PJf/74vfKkdELXc5VGjLSV4duXaR2ubb22s39jbuXr89BCJ21dOvvLV7/vFX/q1g9Oj+/cefeebb772mZdrmuMQORoVbilz3rJdpMNMtW29//Towf1vw+7DL/7gZ4S/efxI6n++O0H45x67nIG4c+/+XdIVWl3Z2W8IOQGkuI0eGVmJqlHi05caUdu6O4zN3RibB+F8q7cTDDUKxUBYKJRMqiiFGdaUvFgubo/JJO7y9JnQfa5vfQjRSpTui5+/p6kNzvrFnZc+6wCaBx+/cf/ES+0f7u+1UJINPTJRMhFMaz3YFiM+eu3EOv7tg0b1N20kt8Fj02y+VSvUb+PK4/UrDwTkIkJv9URoR/Jc2X7a8XkX3/jGN3/ip/5znU+5bYytViqDLfQ09p1p/dCPfvHWnf0HT97e2ngunCEfpZSW4RMQfU5Nxc0GF2mMh4wOV80C3b515+j00PuD9ItJYHvnBozFlMopTn3Mv3384N7B4aOr+17me92RKbrbS8PfSUXNZVOCrOb84l7VnW9N87+8EbkANkNJs1Lo85N9fN/YfExexJSejIzWzq/Jtr71tHVD5xaZGDcUwR4L9rGogyrZf+6H1l+bldv2TlAfpIzoRr2J1QRT+uGuzlWRelIefcCI2DKyHAtNrAznL/7FH7P+RwW6GDVgac3mu+9//J23vmuShSfkP6C+t3ft+rUbMDa/aDW8R0CR1/SAUg96sr79Ye8ErwOmtsbJ54Y+0Qpewz9BTYMjDEGnyB6NjmQ9Orlz4/mrV6/XmRlFBWFZFIY2XhSjRhwNzTRlhECxk4oFi7MMJBV1DNeRPsx5r9TqbSfFCuob0xax4DoPQrAJxxNcBjlNp80AX3n/bP3x2pa3oT1YX9sPz7BuWIXJGZ1Vw4Y3LY6ZgWAwMpNsVJ0EMh+93QTcSD8W6DXF7wwXjBhfaDVg6Z+hChXXsCkyEiEn4tBNxX6vkcLb8jtHGitNoToey6iL7OenOsCe5F3hiIwNJ8HLL/qHyMkroGxceQ/GQ34scBMb253UOzA4t4JUtaYZoxIWZ8dhe3I0H3hRaQVDTbbVfz+dM/1KiVtOGunR8nByjWh7BpfldKAlQ59xMjyQYyRj6+Do+A//4Bt3P7rn2NcrV6/8O3/7bzx3/cbJ094z7RAdeUcuw7qpRjpUmfzJ0YHXsGj6vM4mxuLREtgOxuxlaoBZijbYjwzmh9/SUm44Tv7Kdy3or26GAKWeXZe3FYHS4qXjFka5qOMELM7HePv2q4fXb13jStZwidMzO10MUGusQO24Hd7Jed0CSCpcC9Fir3R6a/cK5giASbhWMV8R4Im6zcs5s4QCUsVX2eb5ZiPEDf/jgu3iMuaQUV8TUUcUfiDk+6M1fRn8E/jQqwLIlyMNckNABmzoMLdTY5u0EpqeTD+yN5GYtxMz3x7AWXJmME0RE61TkEKbFcc/MJI2CkGVDrNnKRjJaarUmXhMrNrDYpBRHFBT65O/Zd5SmmRTRK0dMaRuKrIVWgmKpURUlKnr5AUy0mdJZxLYkmcyxKt6yZFTgnxVL1fFV+XdVpGvBSdfI5LCSBaG+YouxMoz1UbkchFCFElXM54pmYtensNn6pinz0rMDTxYzaz476lr+Vzyf5Ig9VNJk/7JR0WWYkvap3K6/XTRT+dqjxNaZwkQ4Knc90BZVRg56VEcXQHOEubHZcIKldXjfn3qdgV0SfleBD6pMMWacgmmW1Wuhsz9zD/qA2yZxeSXC4lChjcvBhTf106scMi10YL61wCFZnSBWOrIaBL4FFBB0gdgmZ2BkMLZeMRD0mABgBd7X9lxL0H6WFhgPAE1+xpEoQuyHy4ffgz6M18B1ZlVj7djVfLUuMNE06J97CAiOh1A6lLMrcER2mp1C3AZs5usS3UoFBFUNNdQYFfxChnCgWEL7+pR+IUdZwdFp515D2Usah8eN1ThWrDgWxY9DAhlLi3k8YdJZlvRUhoDDp9pcivlVzB6wq4xexmcntLyezb8iGPwa3QE3gPOz+FPmxSiotqSGeTq6F+QQrXHGU1vA64QAyRHE7nldVdnjrD8dBMze8JrTs2tWfQvvMo9jPIxbK/E88+//Nbb73QS5eaND9593wLq2u8VHvmwcT1rDqK5+dxzH7778J233/r+1z5349rVj//wO9/88P7NGzcfODty4+J3fvt3XnnthYZzCKx4EZ5TC8LIYMgTqho1uXHtxruP7z7/yiuIMcbZETmLBNOWheUJRxr/cvP2nffu3t08sHmD4FqRXC8r8bhythRicWHlHzkNE1eWCwriQV140Jeyq2vEMgxRLub0N8HdkmH1aHkSAFWuWLh48yqUQupIZXfYf3xw8CTl2t64fvMGRbDnJA05vG9bhT6MF9P2JiYL0dK9rFWYWQDdZtsjweqVnSvOhCF1plwHCsk1XhuOpblulsaxWrnQna9/8xs//mNfdSa4aq3L1+uzXt+Z/dbAoOratWt//7/x3/pf/6/+l5d0QDN2kUIrhYr40yJ6Rf91rBAhTERF0xQCnw3HRm89fnJoBuPgyQN7DCOyhs5KcbpeYNGbiI/u6/jt7mxf3VOhU/MrHCfRk2Sw2lG8dMmmcNrAqdYgKg9DtRgyjJ2UudwjIOVrHkZKPk3FFfEL+ZtcsiRG0KOPEWsiLPVIIqLEAuxEEJVhkPKluC02QLAV4e25d9ILkqu9WuA5fzCtZNar4mt7Oz/6oz+sfwHbnXlVgrZWoT/4/T9yFJBxA9VX9+nZlWtGyLdOHJblNEaDYfHT4HQ7arXQDNu4JiTArC7FiuKtDBTYFQrgH0YZ77918yYOONSdE8BHm4xRfO3mdSzHDWO/jlyF4ATnvvMg02eOfGirtQp8REXBE9NHpt/0oXDf6W3eyUFX5oypobougbFY7nFclpV4eV09dltuppmG7HaHkFnraHQhXuVlclCqy9WP83E/jijnicQUapAelk6ZBRMFgl8Ph8GOY4LzuC7Awn/AJnmVLbUB2KFYeJWnTzxDfL/NXQ0CnccQ1SEXnKTYvU6wHzoe/axYl1r6gy+7Ix1MfHr02IoxjjIoWAfJ3EXZUictybxUeMqPGEczPwWueoMKv9XNZJt7yCxPlrql+Zv7kqcbqcLmM/7ga3/wn/3jfySSOnE47/ref+2/+vc//9nXN639Q1JrQWVPkRA1Am5Npi2A9ii889bbdz/48Mb1a3oxrFgjR6BTReo20GNKJUsdSN2G34KM5NWz7lZkxI1VtklcBDm3K2rni4kN1wPnhq258tIlxEYHXfB1NL39FGy8oLkWPLXb2n351Vf+4Df/QItAYXd2bAy2cX9iXYrWeq7cESE1yQ7iKCVLDjO0XZjmiiWzYEaP0Is16z7kdaCVy5+GFc7INbpRA83Z+gEQwDAHaZl8quuS+uU6eFOqHAFGLVtZIyLyb2kGKw56jKjq7Hw0qfNwa2QxfPrmdLhMGu0l4wCo1sQdOlW2EFvrHlTyajEjHo09Z1TVURig3wtnn0s+NWIIGjO4gGoOc6Dos1tJdjzLL6Ijkoaq2CJb9cSXymRT89xvnJ4VIAwgzKopBnUFQ8bhjI/54eeiZItFlyu2hJ4syk5KN8gZZkoBIg+QqV3WEHxXdHXNg6V04OdakHA7D1eJk3+Ve5V0+RWuwe/z33BFyRAmj5xLkeV+atRurR53zij1qn/ZFVcCHaGX17PbWLACVaQVGp9c82BV+pPU1V0gP51/BWVSu19VF4u7UqPi9NQyJY2Dftsm9JLpzw1rmwxglJ6nLRiswfCO31cbTYgWYYrRoEhRkq5o0EfneTuhvjEw7evGxclLDrc433l/9LW6Zc8kaDsD3XgaZI6UkfZAe/GOGwqg1kRcMAAHzeB72eWJlWRMKj3w7xmvummIJQXuacQGhjuJ0vVePUNxloauh7loVtna8ZCvHWD5CnVgCd0XepqKnrYKLnrLxTpKsZHQZQbY1bFidWzqIglL4mT+S9sJWvgtwqsqWJBmnsgd94DzqsbSqOCyC2IWIw52bY4K65lgIujW12Kt0alKD78XPsYwP+NcvmBa05g1KhKZscGP/iQPRtU4+ExZ8s+hQHzxtrExaAHMkKFTZgldQVB41r1dnL7mQY/JZfP01dfvvPnm8+++99765sf/zt/54eeevxM9A0W01dT/2fmjhw8efry/u/n9L7zwvjWPqCb9F16+s3n/45/4qb/yxn/8fzl4cvNrX3vzJ3/i8NaLe/gbBvpguAkS7zR8xEHRGITnKCfPjj7+8P7+1Ru2s5cx/GochmLINXRCSr1pro5fZ6Sa7xovKktEjRcVUFISwuf/jPRTbBCCFGc230s4KQj4qE0aPqkTJCOyZwTUL581mfFL66O4XCMBahxMUFGQMsla8zow5Rg+KkZmFMuSHJH6/ttvfnDvg3e8IHdz06L6I8v2Dg+fhHJLUQ4i7srD7R3L4W5cPLk4PHi8tvb4xtU71p07yA9SFk+jhckwsg4qIlzS66B9J67UwX3v3fdv3vip527fpuE09v2773mx9E1x6OaWU6ccVXnn+f2r1288fngwoq/hHOTZlABxzB15hhjbb9OreXRU3Ahv8eTEaxw2N+w6sB5FwG2xzcnJEbEpobHRWyWvRFaUdPLo4Nh0gc7CjWs3zQlwQUmj+SkLmmpOrWkaZrc+O27FBXmSdVg53yx/BnZ9aW9iNR8Fq8OjDw1DeFOgwX69FI9HjUdLEtKEROMlnHREa2wXqhltOLdzTs0BtqfBdKM91DatNEMoAshn1VEZhYQHzYCT/xLAoB7f98Xv+/IXvnpir4tOzoVlWs0JvP3227/w0799fnLjYu0e9Mco1vZtgzXxtr1ji4dIns4DaHOH2kVjfBevSwmlN90qp34U/dpzqk/nw9qoDLEbt/Sgb3A+RuJt03XBx+t4h1jhn1GYfAhXnBWsjwGMe4iR2JA+QpvUsJb7AUknByL9M2DD4+cqx2/Abnkw8afMzIo326nbUp+t0X0p6Zo+VW+esC+ZEcJfLVVSnVWoYm1LJqNJ8F/qolLj7sqi+vg5OiexoZi6fi4C8G4BvqwOoeEYWUYaSoWlH0lFfXLyP86M76er2jO+cHYalfMGrg2ZkR5eoTb4Wa+0ptXwq/G8ATqP5rEcxGFlSpqiCh2rZD/Q1e0+7aoeH/rLJFVS75T11Tr7uUAfhTT2X/7+ZArDvufq96d+LolJItLArwGxm/Doo1/8pX927+O7DvV/6eVX/92//Xfu3L4pCwdriUVjqxWJcdFAxZ++ALCm5enBUzpNNOSWizKSdXqxs7tDw0+PXipt6x0lk5Yu8ulrpH2+/maxYtDCJnBWeMORDfY7JizXVLa670uJU7EQh/Rxn8v7ixZKBxjHQD1Snc51aObnQux0/Gh76xs679vb75jwCor+oe5sJxrzhHoxw4tzONjpftKBIEEJE3RdrNlEjvsG+GSvHdm88G4WTTmvrovQcKWTXsKiE/8IKieS61FYvh4UnYz6nJ48fTn12357UhKBdAkXJy/kyPY+wKmL45dCbGaMYzw7mHkJmWllVQRVJFMtU9e0C6oxyNhrzoFdtHkqb/wh/5oUxiI2Lq7GBJB8+hgM3QyZ9fDJxqWyaatQUv2bp5+t967t1qieeIkT59mbcChQuUdpI62dEJjEokRBY3J6XTZM9DaC3v4+PFFn3HGqH/UziEFYljSmJKJCbX0aIGua0D/yHC7G11Recc7EmE4Go0agoZA3nxJDahC4BZ9GOkOzKrn7Ma4QxnMn9IsY300E0zb03aMq8NX9fIZpN30uqfNo9fEs62Vi5ctf1kWFl7KXz1ffPQ7fBeiU6cmUXgrwepePe9DTruHCcjuV+K00Ugc7yEbGQAjo3Ky+V4gtZft8BnNJ+gSJIXZJDEAQB1gFVIoN1TMG0o9JrOHsvXrE1VSR5xUqH9/dwh2FEuBItj5l5SYT+MyGBhRnGG0K4jycqid6WlIa2ckeNOYAh4X/VADTsqR6EQNxNCjsBvPaHmpQIBdHpSkiu68YWMqCJ6+cLs2zaOK//KsqScJ3pQffSFQlKOGak091yaDVCgj0s1ZH+6I8X8MAazhDM57JG4VANMlruGLT3kcNgCFXix8a/WKCtdF7JszXbSLJOFvULnJllI503N83L0/iRnZr2HldCF01zZ/3Kyo0vurG2KGy7gVkI6wkV35dprnsgjJAYsQEmhKEFJxFywKa0Fcwq4FRYonLDUaioAGeSAQpGrg6tQoa4DppcUPxVFKG3vW9sLEqZUFa1Ps3QPHI+oX9/VsYZDzSRsa/8e/8lDFAkEcLZv6EYp2dP3702Dk8jqcQrzx59OjBxx/s9C63rau719959/0nT89u3bht+Mqb3a+dXXNQjxXPWnm23/klLTuJHlQAZdzRYezinbe/+4Y9ji+98qKJGKGZYA+94ckz0cmQTAMs+vQHefGIqQmDHAYvm6FIyeCPIvIndLGdFHu1iQzTpuWexp5eCKCGfL+b9BzISqakde3KX65UrYGiAZ3Has8ZAjybIijiadUi0QduJjtanBAr5AaVsLr44le/fO/j23ffeOvgoY0T+6fHF07+efLxI/pMz1FoZIxtaMUN4P0H/43/8Bd/8Zd+8Ktftdrnp//xT1t1no+dGQVu2RH9RAyCM0DtnYPfzt7Vjz/48D/9z/7RSy++8MGHH/zgl7/6o3/xR4yTxzVb1+0Rulj/9h9/1zL56bhiDgJoRjjTMKqSjtSVrfvkrYC0TrBVSJIObziBxFp/i1KMT+/vbzx6RDpeDVvcDxQdjv3o1Qog2D/nuep2HDgr9/61/Wu3bt0kylbrtimFROpsqxlrmGB9R9W0O4nXKQpTtshfM2W3edfMRI7aL9ytYYwAX2RX3cysICph9KGs/hjMvfbKXMp0ABA6MUc01Rmf2ac6VOlNgEYR5jtlGl8kJtnTx7rqHJ5ciF5DjzZ2Hj96evfuPZXSl0YX1hzSsuv9CYX6vTUKDvlHf4XyXk++vkWs+9evWd6dMrepyW0dXZ8UGjLLiZ/NGR0eW/ajI0e3sAMVWJS7yHXQtKEYeSe2fxzu7hlVXQ5HRq+BnuhPPdNIhtAoRiorcc79hFSBftOhmQljQs9wLL3GaIF+6wuOxuazj61OxMma+ODMykrPOaAWGhmkugCPhY3vyZA8QiFM4RsjcRaLlvyjdW5lYS0XTw8OTON4tzE2ljPjCv0lO5wHQin4YP8DrcY6nA9OYDCZX9+NonpVkhSNCRE6BmndQ25PCBJyy6VyN+Hpwx0fcnx+cmV3//DxI9pMCRUIh5AZrKKH3hbfAEvx41sQF6ADavmxJKweDEIDaJV3SViwkAcTZqChii427n300T/6x/+YCdMiPd0f+/G/8B/9d/7DB48eoLXXp8g/DFlKo5ZiGCoHxITtk0ePYbq/r6nytkTbgV7kIf/pz/7Tz3/us9//fa/Xae4MWRPaXNP6yWGnhbLwFSPC6hLvy5thjPTV97PHC4MvKZjvjCcIPpIXhagfxXh1OLEtXnri/J8b129++OHHVTq8i8fTz6ej5uPMKDLYUxtQsHqMmz4kRxYdbOpY5SlJ5kWRJzWlW54HTgayKl+KPdWkK3n1UbA8Or1YQU40g9wobWa29O/ourZzgaBSJltxXqoG+xLqQntRELdXE8Pbp3VNKKkvNgx/iZh4B7iEusI9QoOPOdErAiCZgg068zmNCV0s9hl80VXoE/FQKuSOezFqQalqq1c6RRkurBAY9wh1aOjnRsEUGY+n1lbnzmqCM1s0Yd9RVx0ZHMu4VdwDsyKDHMjKryBUMxn5lWWofrCxnk6KP+AK+sMyA2y9YtUXr/hdf9qbRoxuJIPBO21bgFfb1DI3PmSp0mfXn/69PJT6510lB3cK/Tl5Vknz+LJ8P1IwhbK9yGgF/+W1aOQCNrjw78yHTgQqaw9iXBTRkMlQtoHkFCDXcSOv/9rrT9MzBSf3yCLQXfF+OIabrW+hSFk4FLg1EZKoTxfb9Gn5W8CD7bMqLs9D2UNWg8CgaNqIm3QMnFpzU0NpfBa4vu0f14Jytqq/1KFxXuw7zaJ6QcutE7pBtudFcutbraAa9RmU8OT05bFeMw/atvoigsGFNkBYnXaJxokIW1faEPuu6tY3O31Wq2VNOTqNSGWweiHKZkao8JXf3nCWUVbQwXxSxli6y5xVVcTRk7Q8jmBdrQNSs+DFwcO6GYIAjsrqWmiQ0bH0FpTvcfZ6+Nzmxf7a2gcd5MMbw78zRYW4bcWwXxBFYCNJ7WoxxIlTekDLxSqe0R4mcmQh4ZeRNaZmrNedR3AVaeVKwUwqnRwiy4p4qA7zi+HkVUtfyKmHZIwFUqiDhPwjCODkOXk9uINNUFmpEx0PH4nvjQPs7115+hTL9DqKC+JaMUTtjXX/ljrsJIx1y6MNDuoNGLMRjbz80u5/5b/813/jd7957969n/+Ff/kP/ut/f3HO+mRWdJ2fFEUhU/sguuI5LHoluh0HZl6xwXG/bteOHc+RzdtuGtpxGzGRMGhAQISXAxSjWuve+c/pAQFOs7BiUeIi/dqMiKVUtDVy08aUJk6CSzbxbtQ2KsuNdT10N+o1JeBZu5+YYlnfscVcxIChDmPpQJQHPoZ6ctZVtrZlKG7risW9WzYuW91x687tjZ3zR0+eCuLOD9tSeXD8dKtewPr+zrUf+NJL3/jOrWu3rh4eXHjdrNf6Cv60hFtX9k+IhLCLP/T0ROrWhxw4o8UbQ7/7ze9851tvPjm4/+Hdj37wh37E9utImZ6otR+PHnpf2NONLSOCGYWKIiKOlstd7Mn03diic67756kgExsEgPqnJ2cHRpyOnlp9tPXcjVvS79+7n7qu2rBeoOB1PzoP9ZSKcs+eHlqMcPT44OE1J4BYmXBkQXr1x6zem8HGbYC2j6FeBDXLC51ZhSHEbMybIQmEjaXFT/si6OEcIgn5sZXAkE0y458EEbpGwvPdnYJCgfV2MavA5+L4ei3nxX0KnAVwMmYStzdNyERxEAQEYzUK6BGNCK01cvbnf/5v/V2nE2YCuiwmQMzLt3ngbHvvfqN5xecciEkGiiYo5yrQJ65OSNNXbTrKsP2eU1OxVEBfb75qWvJUTZm1PoBt33oLtKrIw7k7rcgppE1G6MnxjqRaNbN2dPz44YP7IOgdAWI9XiYAbgpKMrnHEavBjBfipFFS1+mLF8d7G/sfJQD4UaNTm0mMqdPkMQIBApmwa1FK/rHXOZs+gdz6xe1WDjNa29NTnKWGxRhg3U1V+l7eqbn5bjVCWcYlZdvK+yULoVFCjy8sUeMY6MCcBZd7zAS9KyAH2pslknGAgzWh1qCtRTh7SZ6Lzfc5gvU1r6a2Z9QLB/iSa2G3GPCWU+3lpMntARgG0qWQAnA++hHOLpM13tuHMQWfIAFTtzsUOuXJ2QwpVdmBd975UBcZkiSGXz+qfAW9hNImqUqWispJt/ktxcK5ZV2859HRP/nP/slv/NpvUJIXXnz5v/hf+LsHj57885//hR//K39JxeHTgHplqxpa+mSWkJ1/m3Ie2Qaz/pD+xFfeYGPn4MHTX/6VX/mnP/PTn/vc5//Bf/i8c6lEgfX7hLLO+Lp67+DxEycI0xxcXIEMW1spQOgarOG8IL2k/ZnPTp1/dn2SkwaSUy8CzNpiGIdPsSlbaw7pKiQihcSZyazC9V456xs37VvKz04bGIOGwzJKaT9TtNfRxVVxWVodgxOKEShfdv+7BpPVR/qxkBh9wNRxYHLK0pZI97+rO/H2u7TdEB+LPL/ygSciFNLitCZvHfiyA46u2hxDF5qTBhfag4CbS6Psp4RR8wAPjqtqNAgIUnlrAZZGGWy4uFcoNOqjF5lUT+jXwRnr8BDMGDoZN47PrBRd+DIkeBPw8GQWN3bqVg0vXqfF40hzQY1dhj0UkaMKe/qUFhRNZwYmgpswMg8oJR7JBIX6QaEIhUZEBBiDhgBnCsyQLTjRGTGpUqWm2xyWQamThLKoEkcZx7xYnz05y+OhWK54HHOGH92mCJfJvecbjjNPNQWW3OUq6xS6Mut0nLr57NmgcpljBTcmlr1MYTQYIu6Tegca6ZYp4j+5llKKfTrR42AsH3mNbvuYCnMF83gq/ATUn7l7hvSCYM+nluXn3Ma/EsHD2hSE7rE66WZ4RLNMrv7jFfGrq44/aaV2OJkGFtWnBP11kVJRMKiSGAmFqalTB4UIVNV2gw1j03EktoQGgUSo344yUVF63Y8yhDtJegq4ysOYKikXGn0FRJ7GHYURauGDdUCs15ktL2M9kSYMgiRdq7tNrelgza8oIktMrRhNtWQswzS38BVDCINxqXkReWw71nhHLGTKItPoM4TH1lXOjdYGo6tjoaUL8ZVtgYkz8by3dU6grwFeOzIOiC9LgN7ZgGJdfeomYTs+3b0RW+QXh/easKOMwJAXcoQSVmo6YdrbbMCylT7/lpdZljp0Cgc2YKngwBfexCosXK6FkckVTCEiYnJQkAE62c4QoILoG253G5SBtUAZBkR//HMWpKrbsGu55t61bWSeczLxBROaJnz3zbceP3qiSaqGDqHau3nz7KMPPty3pGH9/Oa1O+/ffWBFisM0RF2PHz28vrnr5S8NWajAMSoyOUFyK3YhGj0I73icrQ5Uee+dd6yVV3kjwqaGm/BHHIRzfygCk6C1lxOmaRIMyjaiEkvmIwFPEZK7pBOQEXOUlrrQDR+g4mdpc5Wv/0uW6B1Q0mpb/RtcZJ0cPpbcYPRgpJJakYGfagtwskgfiPHGzavG0RvXPrs4sN2XkiUls9f2evG+Z8baNR8nT7auX71poc2ObcBNrRhZyJP0nh9v5KXcRYqjVq1tsQnHrPqV7TnO0tTQ93//54vJi8kq4vUAAQAASURBVA/s9VQ1zlNCy2SNF7pPjrVMMMwIa4KhD1y6VS3FzEfHVqQ05OwioF0v8mleyv5y62ccF7phBuP6jRvpr/7uYSeTo9YoI64CQ5uwkc1KNlZ96J3S9+/lVigk23YHkUb8iWB4THozhOEhO6YbDHsUGY4ecUPenKXl4CsahSj3MFlbpM+4p+toAX4IJ2v/ij90EKOuf0mH4Rd5DHw9FJR3cn+Di7AEdmhNUZSnmj/41a/823/1r/7Ij3318OgJZOywxh0aTEx//MffyNG2tR1WTdTZPK1q4TJ5ih2AcjO9d8nxoT0VGSRGozz00KAi0pEb5gdPnhjHvXHjFgSWgC+MCX5yxoEwRHnUwRYyYLrdpSN1OOYBEwY6MfYzg5iGXqWxvsmmYaavqR2eQeIkNhy9fGbfuHN+6GP440mjM2CPQL3Ygg3zx52yNs4EhKkjxiEsfcrtjylMmhR5wnVBLpw9mNTIsbpreIKV8MSfsobggr+cJUSES0nbNhpGaPJVcphTiB53TKlxhIJRSJe1eio/XBaHglRLFjDFJsMCQhEpIDU3TYlZlqGJ1tehE7+jUDvo6t0E2V2lmVNqWbJrEH32Y+Avv5a65n5IclfSKmvIpCkBcKTSr/3ab/ze7/0+P8NIP/f5137qr//E/rV9Cr+z5zUd03sZNid++tmqrFb0YrnTM71rXOtBS6/fuHb//Q+PDs/eePvr//znfr5+5RwFsLO/S+/aGNZykN4BR9/wUwdgSEgVwyvqloTV95/zNVmWfFCZS7ESIm7+Ss9AG2VrmAT0JLxu6eP4blqa6mtNpm1vStPpHfxMA89cfG1tWlHsiDnwDcQKydQD2dlNtcXAoKQUCX0ll/BRNmWKsGCVEJnjEJqokLAqJcPqnhcEcVRP9pzi/PCdG4mM0SoFpoYKThVDMuWBSE8aANFYUSz0IFelkAFuXBEwA3XQq2qXz1CPnPD2fH73ZH6MO83w+r0qouYArTK6dV9DOXIsG3REg6Il2sIzGDpLzHl8YUy1y1/CEK2YLHDnJ2diVIyo0xAJZQ6tBXgosiy1qZ5fASKGqXhuwiImD28nVxgGINdXUb9yvC3/XdU+0Hx4LHMAVvdze/lzeTwoT14g/9T1p1L+1M9PZR5QUTBZfCwsX9UwGSWW7l740tdkXfBa5ftUiiyd/r56cPIK9V+/sqw4HB29fBLTl7F/WZfyz9Ba1t6dN3T3yRUOk2+Y9yz9kkELDFo5r27RA5a3V2QwmfeI3OLhlLbhMepXY0gsylw0HpMVcvLiEMZFHKnBJUM6Ry45yRxECjTiHu0+eVGK1fw19GFXppRAztpatilkfJ+2FPmHfI6O8GnfprfisYejl5P/5t2BL1KZPn3cCyJwfDYvoOk5d3aEl3GqP8YVB9T+N0VxZTRu1cyqhkYKEUyn1wROTxZwYaUGWwDaEs/zdduQUnFsaWbrGVfnJr64oFAOK26qMC4jonEFTXfNlTOz46NDjXZbUXr8uCk9yDao7bEXWm4feNcvVGKIDy0T7rtEGmqO9szDW5DJyYhiDW1rSyYCS5oQRjtUurf+wc5R3QA89cDK4LZVVZUBVF6fcGs79YkSnTbADqvGlvQfQl+6Pkhz3EZZdDnwbpnHGMHIEb3DWk2+sHTt7NHjx8fOmdEkebsm6zd3aTl9x0qkxnB97427lkBdvXVXELt2/qKo1BMxIwL4Gg3OzRs7ei03Xnj+6ODot3791/763/gpI6g6DErrXaDIGGGjQLt3rzihbJzL7dvPzZKMqPFq4Qa8Ny6eHh+FW6wZyUCFMFKt2JWCGP3vdblJLTJ6eojR60YI6qIOdSsQHq6uZeRg/YKVyXBZeJVZnlJW10gtFmUK9iBaCEJRbWN7TcrZ1tuTN5cJeBpX0RzjyCL2Dxw/LdJYv3Hjxfs7j5+eHV7bf+7w8DHh713dtVZedk/TXl55e2v/6k1vOzaMTWmPjNLhrDUk6f+6EWsxa12f3hKg31igeKUeN947NLRg9Mmjg1vXb9+4ee3gqWNwPJmrvscN/UzowWbwwqUbtIhQ5KDzk4hMDRhj7USg5g6bVDRIvEPZqO7S8aJjDYQjwMjq9tbVK3uP6IW3LbXjYoNS1rMdcPLry1WLFr3O900oHZ/f06JksEhxWAUoY3KLdp3nwAzPt//U+hTLwzItHYWLK3BcP7uq5NbWoZFouJn3qAYLOK4Yll47fmrDidmWJ1VODYCFtOVVuwdjjk72zdUwKSQajNTNwLRpofGA50F+q+qtrL313HP/w//R/+CFF24LkiALQ+ACqM06vfiTP/5D/MFzFUGb3KxfNvzPv+GENyjIVo/v/Hk4r21/aJu7Hlp0php8QrrbJj+gkw/T3vC2QR1vy+oePjq9cfOmtT0TK8wAatqei+E2zr1xWShswFe9iOdbqOKcHYwD+fCcUT4ZgzZphHOHlOL7gNj8YHPnyKxRvTa/eJLmJ40H0mH6W/iro6gjs7b+FKZT6Vgf5lx536jo9vaXNtZt7zb+XXMQ+f2RqnpjBR7xinHTLwT7lJqvm1ufycZH/uTk0LpArzg42bIaBfPSCRlpoF5uLJexanzTNhhjQj/pARzvSvKDYDbWEXV8en61RsCj3NTEGnYFdEv/TCp6S6PVQM+H0epEkUqHc1VSXfO8+mkNTKwZQnf8QzM0TeUMU6lSHWVkIHX9YifufM/496jCeXrYi41XdPZrbr83QYW9z2cure/J2R/+/h/93M//LCRv3rj26ssvXDx8+cP3r3zx+V1WQF3hXMvjirHgzTqeIvvTJ08eP3XMADdxdPDwo8fy37/74Of/2c+9+8EHB48OrQj6K3/5r1ucZoKFJbaDAm1ir1M6duvRo/uIAC6dxAzgk19sqarVf1+fvmAeQeuzo2B5kB5MWuqdodTu07marh6s4Gt+br1464WHz9//6CFZc+oUbjEu7XXYNQ/sHGQ+3MhOkvSRXghb6bQIB2yLVRZMPUhjFmRlnLmIEUJzUNSl+MRvZaIo0vx011CnM+5eCbi3Qfvhqq4hjUNdjJKeqBNz8j8T+m/SkpDyv1KreKAbydLFVr7p9ViuptBQpZ9gczxApML+RqmXCkNoMbCQDLBzVlTY3pLBRmbfYOQ0AO9zu7UY4etR+ZZAZnW/at1CTxZiLc5Ra0q7tInxA98ytoUTgAxzQml4NDY9JZeEiKo4AmWcv4G3VNkAXOW0CHDJfWJcYgOWotaHzk5DZMmQafrNVKlxO7WMnwIVoeHsFgIDO4z6Ga2rhnVuL8f+l+eV/bPXv259TfAW+AvwpWRVIGzq/VPpoaXhfIbHs6oG0rNff+pmiBlykBq5n0BYyJGygOzRv/Fa8q+4MDn/dJER39ToCU9RcDDSkJs6tvuq6A06syglg6dIfcnc4LXZrnQ6fCm/ZxNKZh+URDqXMXVkPqETSRBK83K52KOsTOBPXC09fP1V1aib9iYU6myUe3gdBM0aHWmmKRsDY4I9xzpAdcaERiZTJTyK8NlVexJD3lgBfEDoZ6t4AtxHxI2+ImY6PzX5A9pgg6ZaEJn/GWKgLhcdTX0VrW1OjWsyAccU1AzhNQidMTLNEWhainIKSTX2Nbi9eYZhBW5GH9Xi1Qf8YI3HdBHCTVACYG3tYtWhrERMn6hOdB855HjcOeKQ8LSeODM+1/QL6C+8vZXsBFtDOgkCmVhksQRDraMJwQQdfGPteRGv54TxBA1DVOhEfyqaLFTx+MlB671Pz3fOLcXu3EONCrDYY/QXRU57eXTv452riDKHbKELCFvf94UvHDx+ZO3y+sX1X/+N3/row7tXr169tr/71htvmFnfuXHNWE/Si0szYWjcQPCla0H3tAOC3JPj7Yute3c/eOPb3/rqj/zI7vXrBSatMEm9Qm88alNbSQY+ELdasfgxCj+50NPv0bGYIl8AiC0qy7dkvyw4anNZPG7hfa5uLvUsd/C1udO2kIZyITMskwUUwgJzBXtV22VN04ZA4mL94Omj07WjF1996cP33r9ytt++K2P2LHVTJ50WwVogeGxpiuUi+m/ew5am5EDZgspbW9i26TQoj+5joY3eGQsmMtkpzXPP3XT40qHFOrP/hJbahjGHSArsxKyhP1jSB767mGlldqgSEgJdbGr6eDV9pKasjglFCDvVMdjc39tzio5BXCmeOQFU5Wa3PEpdZfRlUrnt2usWFG3vX3l8H+i42UOpHU028oCWFm2KLf4HgZbCj+o1CxEbmJIX+m0KZba2di3V0LXH80Tl8nYI2ehXikpnwrUsvdFwqYudmmYhu2wcAhtHTw9onb+Cn1iQSEfkttYev/LqSzeuXTvRBTU4Um+hpVO5ss3tw+PDux/e57NAmYvhZK1Hhwd7uzdn2U7wEMic41pbq4nPApMjzZ4OS4ajG8FU2emclKLnbPhTx+rB/Qc5nc0to7/hOS4aiJzLrPCMP+2csfSrEQH1mnWBiKHcTbNH9VWGDHoHg1HUqIWi9+7uX7VHITPc1l089krG+i04U+eipUoiUdLrxb2LmABvAMIrFJ1W1EJsPbvTM+8ngk+DedkGka74NzWX1IN4PB8JevmRCcfhLCbKqJ9JGIO+aq59GX0eWLJUmhgvSy5TvEGs6HxN7Yrlr3fZJIlzbQN+aK+6mgeHFGTEZpZG0xcYCqvBh4pijg6DnsvGpnktBJGtZcyzLSEXXaZR6EFd3mzdNdQMRQGFWdcCWJ4Fy/RguU9b3S1lVzeYqBP8td/62v/5//h/9lzD9N/77//3bt28fvvaV+mcTL2GL02rZMjGuzjngxIJ/f3pnFulpt157vbzThD6+h99/a133n1w756W7vu+/yuvf+ZVj5vQ9c4Wr/3e3TGOMPyfVoYFgR3eI6+FCL+HjFCf/0OZxIXE1a/lxxSrwPz0Swm4dDNr/Ogg6WIWRT29fvPW7Reef3DvkbVnDHW6oFkwenT5hf+Bzg9kbLZ6DPMkMNssnRUoBqM0u8mZrikxKA2v0RGXRhyhFcf86BnDCa8pVhY/Fq4GcUDl4VhQBXo0/0DwvXxWG1BwiKTJqArKATBtnp5CFuGxvTINvSlblf4DM+OSI8wZDJ9aqWikATK1VLPyY1SDbSUHzcEwWACM0CreP6Ze2Z4MO/pYbGnSV+SEQLfy6e2HzDCK8lfwsng22a8FUDVPG+Fr9HY+B4JMC8KklZerUWdqwZkOwYI2RvAvltBNQxM6w8ukwflXq+owfMhaKKj6oQy+ZbisrZvl0Xz///gx0FQesODPlYhKGKIvE3syiPVUoytDeT51DYw/kypDxTp7p+9sdVVTlQ70y+/J+imAWGpU8l93VbT/1sSD+j1jDyrQCLVal59sAHxBNe6SCKNq2cVodtNx6KS/KYAfIvJU1KgPPLUMVdJoUHkoQ01Do83skQoANw3S2vb7GUF2riqek0ZCiVZ2Q1MkVmNOdZhWaj4raVMTd1feL3z2SzUKqWpEXWGPbfrN6gDntllRetUgViPqGg3Q+er0pq01EQRRQFtOW/+5mqhc4+6aKrOlNXJ2mm9fO1vf5pUuLt4ygpg6joSYb1zRMBrXOd87O7fWuRPQpx1QB5AG2WRlaUC2ilQcgLrOZolfghehVfGXyoFaO30NT0/X34b2zq7h0gXH2pK4tP3uWF2h4fCkt82tHd++uPh2BC26WejOLZII2lMkXQxxMo5N90CCv3gEhnuZVupVQQ9qsNxOauVLHC8mvQKlzNOpDp4XZ/RKSoPME/RcGDTadWw4vlcGD6pDe2ONthX/pwevFjxuPNEn2TSvYu3ozpWPPnh/7fzj51+68b/4n/9Pf/pnfvY733ofLx49cP79TUQK4ewujgtXPki48apIyDpgg8neCKbXJNrwllzT1JaCm5DYv76XkOAVboO36GTTRkBDv0TMXpyzT2GxfqjMOuYqryvMo25++iFpxv6HI6UvaQE3FE1B1TUT6wXkojaGMikCoaI247gisfP2AuVAY+/8W6nQoLiqOZTHXmoeooDT3dndYxrXbzx/cdUaTUeaHH5435qwMRfhrLHZrV1kWLBrZN0xly3Aurihg0Cvz0+v88VejjEhV10+NYubO+i9o2w5XyNkdFrM22wPRzBSJk/qvLF/5bWdrZdOzj9OQUb11zYeTY5F7jWpHTxKzE4C0RUhknbrnpi1p4TRwNEvMWiksazN3d0rmyfs/FxMLgmPru9dFdiSDCbYBky4YxHnlszpKjTvJqiHZ+PNAr5pAjgNmqBy5Fj2k6vBRwyzYmF9b3ffAL+1R35OJCQcx3fWpwZ49FF1uMbGNx8kDdYghJ5Qf4K+FqtlDZ5M203xLLaxZMhO9zxHD8AbR8hVXlxc3dt69dXPPXf7+r37H6NxgmBkWbJixfbFr/7yb37YNs26BHq89OHqNccE7Fyb0z/T06wRH6EpCPN8y6FZT548AUEqYgiLRMvQ4p+mxoLSvMd2a5+2t/dh0D2SYmaubGgd0dkk3T9jvohN8RplzEfFn6qNN3mPwnRZeiKCqgvBw+VU7Q272NoxdSaf5wpYSmKq8EWr/WbYpWmfELcbiiY6kcU7vy+etsbsbHdrY//CCGW6NerNISOkiCOTmWQJXX4REpwhIkcCmiYi/HL4ECsA9sgCbolTuh+VIo2ijYpP/sqrSQJd8TdBVjqDok6WvDiUdavh4Z0LLyX1hodNO4Sc4nBkKamxcq+rwBMn9IfVAvISSzAl4qG3w2TBK3bWKOBMNaoPrQy+Bs8tCIy2n4Ozm7kDt3H90qWUuvo/QlFLXLjM3IyfRvs1qx9/6Rf/pTcQ0Irr+1fffuOtV/7Kj6/tvOf4NRbm/GDtCkYoBkMiAdPILZXxzhwbthTEey8LfvDR/Sub12wV/vV/9WtWDtrIsbO1/5Uvf8VrOq7s2pnj5RteLDJnQ2/juz3ApkmfRHv2stKDeUuxMebOC3KFdyKdH318cvcsaW4yIUgicFCVjaWlE7WIcVxbVvu1v+88/8214xeNiV9sfBj3UCPj+sbnvvj5xwePvvH1bzrot87wlYabevFCGhswmNhDBmHZYW0qO7XPT3g2zF14K4Odh6ocTzdVDBE9hWKU5hI3nVWt9jDwBJJDGwp6P8n6RivpXVXBfMbXVzVVELdEEdWwC0Vn0SoGMYkTF3l4ZwrRmLyfEjocRmbculOFitMZ0APX6KNi0X/sjUl2L92VSdPmUVmKn4hpMO8DX2v9FZ3YIz2Enpw4k3XJsZDic4Q50oi0UJXx7NXq2novUupvQ6w1Y5EQZlNpWTOsimXX2WeObwVTDeLGiMl2XUrl6sdoDG0ksOZnuJkoCr8IVInEgSyRyHiWOGCFwZzsZF/g54O5ZeZQdtfU57PTgUSvtbYj5H79/3vZFeDSgoe3D6gmFafUpgFawKiZ5PmcPHUAvueSc7lWCF/+7DuZoXfYg5vxS64haVXsWelPF/vX34fWSBHCg2MAu4FgdS019QMxpFmoqtLlt88sp7Y2Fra0bggMS3nybGClA3mZTEaBcgbB8363EpRo/ctifFfB3OXQ0xPW3Vo/7indbtgFfhUp3XN3DZHLOiYU6+mN8CKnmoOgbu5ZW4xbkQRTYXqTxRSliLzTdhY9hZ7lmnKqUeOuPdXG0Om2GM3xhWbyGYZmTEyhYnAKZmrSNgUjVZR7QGgo1e9pdYDYYhAb+WtftxpksEy/lb74wWaHdCPQMUVx4CUb3gM3HjtHyIk0Btt7abzugSo8rR0vVpjpF8UCMoaRmBaSIRtpC7PjA3KGk8VuWv8RFs/T0GEsLZokzGr3Lwc0Yomr6VtQA5h+J5xL2E25zmwqxie2hAgEPiaWJcgja6N9tTmdMulVaelEXZGwTfbrb373uy++/CI9K5RZ3xbXpeybG9eM7jx9qhf2wksvPHfrtd99/g/ef++enQD/6X/yn/77/5X/4Nbz12HSa4by9i39pKgoctSS1Z+kz+8XDeCYt9g7x/qkmCbko2GYsfDHmbz2BrfdErQDazaMz3JSUHDJMjJSZGFntLtiWd/l8zkwSxjOSVAwhyVF2NpGlDSlYFTn8fiQn3JAe8et6KxQsODF9gAO0FXZ5NcTaW7UCZ0QU1yVV6/vXb/+mbbI2nt6dn7vw3sWkFvCs93Z7q1IU3Bvr8U2+/vXnnvu+Q8++LD5o+1dWmoJWM0e/JtmBr24lTbQ7M6L0qR4K9bJkTFLIh5CzuE7/BQ06HdtOJtf78JLxzIUBAGSeoZyyjLE5N8TZuYvhRYRkGpy4Wl7rXB8Yc2k1yNrX7TQolbHV5n9aQOJgHVvd7feFL+xv7F3df/B/fsX50/NYNiT0JiCKmLN1CGimn5FvzpPE3jrTK54Yxo+i5B8qjmL0NLI2qLnhamYAEZijuOxmbrEmr4RB+10IUPwJRPOKM3twByTGX8E9TwIYbV4uYtzc1lW1TiMFalprKayg9W3967e0EN96y3bBHUvqhmGsGE7e3u7S2egPuzpmXF2jWfbZ115tgxZfB9e01ktmbcBgWtq3o/jIkoN7objwPavXg1s07iQh76//mMPJD1yYtjBwUEca1U3BMsT+jP9ghxwJrwengSmCwnhkN3LmjQ7/qH3Jal4C6Fkt93hH4x03Gs11nzjnAPpGYLJDEGr2rA69zpD9/QAL6u9a4Uq5iTlZjx60M/VE1lGUHzZ2XHaxNeMPgwRgzv8EvdiO6MtUyYFaP9Jw0PYh/BAipEvtm5t281Ku6j6FSk2UfcmsvV2viLzSosNeO/0ehoc6AyuoyvsAF+xI0knlRApcTBW8+h9GqI+tI699HRoHHIG2gJzbj/9EY6oijOjrcTnImtUnB2e/Mw/+pm33nyDvnzlh3/87/ydv/72d75jrEeQZyuUCqMRGmDAp1Zmifxawf/o4X1KBV0NjibHbNe3v/ntX/3V36B2UAX+c59/9fYLN2na7PM2MNBKesjTf/socq3JJNCrfwu9g+snBAyP/1TaJ0+f3ZUtk4/MgesTWhIhwORUN4q68dLLr3zw1tb9e/foFg0gLG3H8DtjnwC75Vj9Y5yI75aLpEhV0Bhgo+2DdoVDuog12cbg0Bj3mKggEUrhtMDxm9QS5ZJtcvejn8EHh5Wt6MCdZVJRuqhWDKXiaetDrHmLwl4g1chGAMgWfEirLYZTOpWeBCelGlXPPNMm8dfkDf16d4Vbk5qNZxMhtlyRvMQztLGIxbORYAX8HwuKGdJjg7QandiucvDrcMgZm2A9uE1OuWNh1E+V8qQUShAYM+yp2mBRdihNXQWJiFCqL5GZRQK6FGIwRBCnv6gb0QxkKdBAV+9FUc4HhAx36J8HM0grfIK5+lFqt8v3/Piej6VEyP1/vZ6BmJsp4uNToKVfpv4ZYFxkHJ7+sdFePRIoXRb4U7lX2Cyw5Fmyxa+lAl+uVa4/VfZP/VyVSDIuTJuvw2wibII40Eqnb4IVNmNkkdaRXm306Mos9cL/aTvF6Qu3KWqK0WXNMdiWYyijfw7XCQlGd4TQQDe36iAFnfKGncYFYomMuRSKSxd5HAmMQuawg5QgP1VPRahv/dkJNCE5hhtLwCpHdKi61UhRUsxR1lSIxoKWjtlN+NLalX07BzoosrKK0j55a1mBSF8D0PA7kFpHz+qFw3Dn/fOtR95btrHbYQMGIKq9eWEWYvVuy2HPTf4zSQktfbICvmXWDVHVdbHGgJeGTgZVHXGvyQjEx7SSIakrv7Z59UNjFbPfNUbAH7b95eeW8QMhI3vJJqtp+/21TuCNInZbiUW0cBzu4XOnJ50cnp+/DyEDwTAgOCSMbrhRUTxME05fqpO9/iZmOgMEdlYNAgQTYYjRV0UKjyRFgrpGWpuH8+XIl1OrLGhJQ38dpt7jxJAsL3b2d/Zv7NMlW53FNy1MatNa/wz3vvDCi9z0xx89+Po3f88g2eGRKOXgYufG2++9s3Xls95k2pKQuqKox/DDJLV2ZsTH6FtUW26+s/PR3Y/e+Pa393duWsB649b3nZx5lZUB5nRTNban2ocZo9IcK24FiJEwnAtR/1c8iSvuixV8upZMyAarjIDSI2xbwrKkY+fLdxsuPX+tLrN3VpTzFkGLGeUWQiWxhB2n+wjOcGh+4+4quXeGWH7+TgJsno38kV+DfnbSkoVXX3v1ycHXGzJkVrqOxl8vNr1TeWtj90++/id/9Ie/9+Tp6Re//8tGtc/W7nVS9pZV9rdxALKZOtRrlVLANptbCEJfBzWDghbL1NxmiuYZxHxne9eebu9+9OShvl3dOdzzHJAhcOEb5bVybOES2MypVUCHdZiJWD0p/Fh3DhztyIZKoevWjqVpbs5P9nQ2Ls4PrTAR0Hp88PjA+h9MsFcVE1msnp6iBUDjFwTP9tc6Blf8KwLIVaRNWHJOgWx71oOWFAMRW+RdyxefOR/3uQ8EeUgc7BSKSVbfQXjhAXrxx5Iqj2pc1bvhrVsOXG+yKw05vzFCtHMAmpYlbOuGfeZznx/0jExn2FtMIRd2/vjxw29+6+vU+Pz0JnCbewf2IdjBAitTHEKtshFksZZy/hb16JtENs71nDut3CMRA5QT5tqaFf8W+4Vgq7yac2i8o7Vb4yXwOsGkbOTcsiv5RtOKwk9eBMHkXFwa8QE78pOsWOXiWSzqpq/yx62mBpIoXE6Nm/oSh+iRLZLBEOUGbTupDkf5neK6Ni8Hm3hC2SrRtJBREe1gVWfWNZSFyQgrHOd/WqTfk/qmv7JR5s7qj6jw9a4Hi3asjbMqZFJGq8FziuXsGtKQVCobZN3ks3FkL8lum4D5PGxrmmhYu2xPbFwKJeMywjCMhgGjKwNG58cSFG8hFB2HxDwedkVJWRKggitbn6jLgxJCw78l23x3XxV9r75GFQirzha9BfrMFN/Xfuv/+eu/948w5OaN577ype9T4Ae++GVKfu36VRtC9qbHGIiQDxC9g9nh4+eePto9OfnYJhlTUNtXrr333nc/vvvRP/nHP/vW+3d3tl6h83deuP7lH/qh7V0zIVAkacXhT7KGkLQRr62fPry4+BA+A9ln0nm2cqFKV9cziv41vxfScX4CvuUsxPOj23Uik3FxSarW2lQR/2mnYe1/vH7gRfXONtWQN3MOu2vXnPGqQ7hrNSizrZuO7mH3xYVRHvGJmhLTYLphgriTJPIkBc5hzzlpRN1YlZtWT2LihnlaQiUk4+Jo1ahuYskMJpMfAtjkKTURGbVzG+vGeqm8LTK9ZnnUb+te7tDeJBVtfMTbWDDbugAesI00hK2xIHHUp0+CBYqsddbrt09GWGKTUKLVyuQb4KeiqnYjfvEkJ6Kq2KAZB2UeMjQuLCOLIv7Gc5nDG9aFUJorSVIG//ohYozWI4iUmJ/MgG7YI6GkvRCIaFeP6nYLfnoeDxdH4W5cSPj4BxDA9lv1efpKKHXeVxFWzoKyGQhmgFkc/juk+56MFFy961sPIbx2ei0er9vFRNJ6TdYivhP21bpcQa2+Im2EhHIJ5ehrrsnw7Ndl6r/++xnMt1dwRt8XABBlVXLMFb0xs09YtfyndbeX+IWM69lv9ysok97PCPbp8gU4DXJNQY8uqZh6Fpr+PDqCsqprcOljcPAg7AZmkGVi8FpP/r9m9drm0aYtXApzkvjrCL9mMJrkZW9UciIA6qidreAyamjMoffR2KTb+IFJfUZIy5hZrpZ62SJlwcEoSn4MmaOQV2Z/avJnCPRu+sFQDFs6Gs4RLEag2OBrPIpdvLx02j9PLTTBLFkZKeek1sF9Kq29X7f7T4sIzPr2VUciOPWDiRShGuoYZoLMC2gLM4boNXaoPaI3ERGNW8a3zrWs+JMiLiJx06b4K4J11qvh76j9K8iYjdRr6+KAUWznMgihekMtgxRYNOxae9VRfYNAFssadra3W9W+ZnOnhRDQEY8Z1Fzf2bOMYZYCdLJEJxsmPtZSZ6kDT/gVCNt2VtvQCzubJMN8peYwChsLjKJYFcJT6oNhI2501ejSslKSCK2T0c2ikfWjhpUljIqRBtn6Y62YEEvLmrQIvVx0lTOwgTi4ywGmedj8BZw2N957Tw9k7Zvf+MbNf+svPHoouCxQQ78wjUezmOfd9993nt0v/fNf/MKXv3D96puirOPT01/5lV995eUXrm9cbffGlV5xMCup1GXYYGO3/ZHQdnx1RzPh6sHTJ/c/OvjiV7+Ih0QY9pf+KD3rwFqkrp+cGa0/cAi7+6juSiCu6FIoI04BXPZLeCSj8TBcsi62uCNlmAJxzm0hJgm6ia7hatNDstUQeMg6MKOflYtzS3V9+6vgAm8+R60nQ8+W/3losQZQezs3LHLxtq+n3vXqiNAtb3za/oGv/MC9R4c3rt3SIupcFfTgGP6KzwuVctDWI40WUdsW+uD/kI2W/A789N0ePz3a97KIGNJgqkNWd65cu7LtnNen1KIOXST1SKA1NNFulwLw9D9u1As+7RDclEw3gtV55M3QqafHEjVrhFFHygCDdtfJHmdPvVZmff/aNaAoFi12CH7d+/objcCjPfuM5dCoyoU7IxAJaaO6jXN3ZFYuZeTCca1aQajVhk1Bn6HvasQiSFI8aUSA08NaPSISlNTDJugKomWARj3AyEROhpP3cTbJ8eHD+x+ErbZ8y6JBWhs3zDU9uP/k3r37tZXzNgawdq9eyx3ojNr6HgjLrdsuiz9++I+W8IT54BDqXRiGcbyEoVmrwm6MXzKpZZQ9pusUjF8fv0iNytzBqTLAvz0Jebf+pZi5gmQ3gV58IS+/eOzh5jyNP/lJ5IYI75RR62tx+/iiRAtBd6zx2axTJw/snEZ/fHpmIvD46KyZnas8Id8mUPa6AFOFWPXUfqSdnTpaigxxoNckdY+bOmDmSPOtvGVqNb3ueqwmSBi4ri1HHK8JWjF9ziMnwZvUPV87qo8U62HeBAke0rKcPwqHi+myQR7MyXNFGn8xetVSjCVTmpBOROXKVfY7bPpXqu0XLCxJldWlzp671NdPSj7JfXZJrOjyPbklToGpbfJ8+iPMIiRtp2Z4+Lu/+Ws/9/M/b3vIydOjv/Ff/s998Utf0De+duM6MnmDOy/uElgv0cpIlDVciie8X+9hnOD61Gk/Z8cHp4d4uf7PfvZfvnv3oyYrzQSurTtwbG+PeOv20QVaHrasZiITAPN2y5VQsIXtRMYlZT0bcqLw33Qt2K1yKD9AxvE5sqz4dfjMV6iQpahq15Kk5iBSDSbKXuSqyWs3vZ4RrfD6TlNbObuQgnPtJ9Ror8YoP6JaCSBo9gXbS6dQAqSxY/RqcSwL3RjoSgj+0zHRUmurZioP7iE9yklRhwXKXtIdCgO3+tmLrPBo1WVl8DY0Fsfb6Z0iBNTJE+873gPAMMm1ZDwar6iAQK2w2yjSkXGPIHnd1fbTNw9zc3lDF5YYIa2PMrvyggqNYWSsjILEWoSjP4xLiU+khLYIGE1AQn4XvOaOYsfQrtoya1TrO6VsU2YYM0/kKkt0xBYA+/MxGd2npLPnAX8MgWqEIptwp+44pmB1DAbANPRggMkgkbXWjKsIIFzmc8l4+RNpk9zXcrcCtNJQaZcFlnx/5vNfl2OBFooB6GtJ6QeLKGEgF0D3uNMDVrfLzTxNZgNA6f65SkBUXyQ3rkPWZ8CnWPpYhc9SF5CXn1OzZ0veKVxSgKeGJR8I/Sy1nqgxWedsba3v21PZ9K44gefVAZjmw4QbH5LOqtlxlikAycF0h/O35Lsx/DFBB+eMGu1ubxonY8P8c15aExioXH2EVWODg40OIqSmOtHLvCBeq6SDETMbgPINKt0EqD5BqtpkZSaHiSLcbMKYU2bDwE41YOdHr5HE5t67KevGR5qB7e1dexwzI5qMucXlhVOQuYwtoiZ3grvT7hZIOzFegZoQI/n1ECw+L5onJAtG2SxdBlP7bdylZrdWBrLqaP29pxqjhq64bzhHIDeicdvYmg5R/gAVSOHcLYXABLVlF2STsQ/jhlAloxw3CnDHMHUclr8ghCKRZfiogwUGnW+8ZYAYz7TIg6dihbbxQAm8VRNHqhkd7meSBNSZS557psZUutZX567cozduEubosApnliCQlccTVlo51EO4AN2ARWO1jkpwrhz67EIeKmRau7ByQxF8+Mt/9S89d/u5R0+f/vRP/8yDB0/ygamGvShB4La0/+qK7+dbhydP6wdhxQiIy/vOt777la989f5HH33/lz5b5ywmUGWjF1D0JkjD2GYMDCBZt5deiQo8SZWZWlJIteETl+s8mmHgnRQpXA0HrqnmpV/pMWZQcb4bxSevwqU2R5KzvAr0HCQ/+XVRTKG0KXl6CKnX6hoe9UutAXO3vC98WN/PeRJayF5ff/jo0Qcffmg/pff1Tjx8tr3/eGdv9+XPfOG552/feXX78PT+7//+2y+89NzVG9fO36KLYj+xANiE7h2ZjZDNkF46AvqMp285CUWL8PH9R0zMW+qcD15MwyLPLWG6Qjh23+nfWqRTergqrOnIw/Z7tKLbdLegjZfQ4nkL2HY7aOdw+lEJp7eVl75pM5r+9q8zSo9OHig8AeQmIdkbwHZd8vSnFRj9oSSREi3DyalxrCKuy0ixahAMoz1NKPwNUTkLyzcg+QcijJFlVyHL7L4eUnQkNTpHgO0wOTFIUa+k981BvD+jBEkvqBzRY/nXzm8CdbFJIms3nrv57/29/4oJmzGnFvqnWtBZP3/zre84wQkl55sfb2zv9C5msbL+le0Q2Xg415CzF8wNDR2jO2ra2Lg3RH0EY94A/9Eh99LJh4aUAoeZCGmoYqBxH4DErpi9Y+zQrhvkYFNMXWi98l7dySvPiThwDtWxtvz5hs2zl/PW2+/ngpKwmPKlQu0tp7TBBQ5iKEfFxffCBG+KmKliVfPqpiAa+M87cuVwdt7RrnFW8hZ54Kd+teo2t3RWcShGRv5gBge/O2mpE5NYUBu1hxZbryXY5rqr5hQbaqevdpjs2rehxERiG6tbrpja4LeLGgPh8fnxy9Gy+Y5a6/j5GKGz7AqNGk3QoSiGJId4DvKzq0pSki486gyGxo/PjYMavMXrvB5cEqK8qUcqJ9GvZ4Cy5wEpz6eAh3LX8jVIQqCRl+RwuvbBh+/+9td+89133/nsZ147eHhw+OTAOAi7hi1ea+bwtk4yUoCtzV18XH3X0/OPPNHFxKlNjuPeg1/5tV//xhvfpUznx515pff2ymtfunbrZmcrmIs7PjS0UGxKPU5fQvaFc5muePFWlMeacF/wH1ov6ajuCx1RZNjbEC2XTyJtdUW+ZJ++KNGcw+akGovoHj93drJj0Huakx5zEhzX7v62rT1Pn3bExdmRE3/E87zH2rWrN45P3+QhnprqXnuqx8igocjN2BmjBUCzl9dgCYWMI7Z5jDzIP9bmBJI18U2E0iCcWovZi6MHTXRSPWRbfJSiyo7G4UEUgETkVGyIGw8g0XOtTc0wwJfDDIsH9CgPPKrCRZUrhch60kJl3aZclVXj5pUPAr0EL03+FoYVeJeYXqk5PwKFpCWjZLYihYBCMBvSCxgM1aSGciy4late9KguTc6sw6KCbjKIWMQQdI+bjewCw4GVg3F0+MHfSC6a0BuLnXgLiIxQqVNXDo3SxkfnWvsAh0dcs/wEig6eiegx8vCeqAuAUxGm/sEj6CcQrLNB0muM164CENVdg+3y1dYggE2Sh3/3c7d2/Hq3nfQfSt3/f7me5ZHf9ewzuJcQJs/wvxxkMde8faJZgO+5nsFb8vRZyRWrL7Pidfq3YPi9RVY4xFcPFnz+dI4VmB5OhsuMS+55Os8S2aCbLYhpWJMVrp1fkZ4bLmQdrQuUhw/trJDsIVXOu6V+nRFey1lsoQ3yiDkh5og7KebxbHS3Tqs8ci71hbExc03gqKvm2ogbuLmqlCKppphUQmtBy7OhonQdfAqW2YrurA6AufvDAwO6OX0KpJ1QgBv05iPo8FbqZVbmyqHz1BGHKggdwYdge84T4CJrCKyqNtBeq1bTWfN8auBBdTUea2sHTw7Y1IygGFKxuMFIQ5ZRE8KyNqwWOAJpViBnhAePDw0gmoy3kyxsNabBX+eunVH45PHjvavGc68INSa9g1AgjDPs7MjJ673m04x2LwPCxsZsrZ4JPj/kUYwFE4bq5a2HfMjoQ2BUpo8Up7BjOsb3q8XEl+Nt8Xmq6uk4ruE6gIvrTARZYuHG2G1WuojPXfJLVLFytIW/yD+II9ISqmCrdKWnJxYyNdu//7Xff/3V19584zuf/74vUjGjVt41q5tp1IpbchD19tONm9evffjhR7tb1+7fe3Lz5u0vfvEL77//wcMnh69/9iWDmK0VoSP6iiEGbaPG7RbFDUG6gOP+e1bOXLzz3ltffvKlVrBAyCzcaJVOlzEDbk73ownfORJUc8ihj49iUhGc/kWZsKOzVlE39ObviH5hiyyZJ+0kzr7pr6kVOOEDHwcQOc6wt26q7XXBAXRpKhWYMstXfO6a1AXs/FiqyPa663/DYA4bOd+9unv45Kopb2uVdcoI2yL+1z7zqmkgnau9zavbdmDuXHUaDObQcFuldGWEBciDo1ZN2xIPnfXITg4NRh+IwtWqKbz/6N4VB7zki+u0ZybH2z/5k3/zrfsf/cx/8v+mAqiDElApBJsZPRmGwDA1QAnvEM+twBE2mMgRFzYSH5l4hBDKADMvIZ16R5rRqFK9rouPP76np7ln4/PeHhfRNvYUjaSEnzXDMSgPWXQzCAz3Yh4fwY2oo74AIRRkhwpsq3yQj4QK1C8XDcytzRJGsUegAtNM7cz+HNN8a6ahDGUPrTU7Vd0HGCOSqvevSmLx6dlb3/n6l37w8xzbzG9NI0wH1zY/+vCjo6NT+3m0aQpo57z+wuvDc5e0KOo6FndzV8iMV40rGNmYzhvYMRDG5Bfu0xPQO7p+8zpumD/0bLQvjUX9ZJVxsFXQ5pHWSGSe9AKTDFaYdtjbu+ohQThFcYEfnEYctzqrFNdxx8jBnAOTBTdmyF7hPgRrIY7bGqJbrDdCdAO5AAs03HPB2WpA483nHdHYXh1e36cuKzJZjb9YmDgATXtoCGuujcm0804ueFmxgidcipPpqax8mgPOWpacloJxaS6yAX3FsTxhOjOeqkqQmGxwko+aTMNTOPSvq7LD8/m5fIRb1+TpPg2oOJ7X6LAXej81T64soVwIKONcS/mlyu67VigsP1afpS21+UQWnY/9WoUPPnj/n/7cP3vn7Xdu3rjxmdc/8xN/9d/Wg7b3Y9PLeg3DkZ3BMWVqlFnZtN1Tn5SnT56a+n765IAH+PaffOfjj9598833fvXXv+ZdGI6Z4kKvbzsv+OTGzRZqevechmnz6Gj/2lX2MKREEFoyvSLh3H38GH59D/5Lao9WZJRnlVjGoW0h3O2KU588Z3QnBmsE2guAqSJlQt323rVrp2eP8Zxi2sZ8cmEdiPy9/d3G5ibo6iNrHDFGRZtnVowYeelEsWkNqIOaGz6oV0prOoAvLQ2pHHiubwR5iXtkQE6p/q2YUHOeU6nVyCJHjnyO9AQAzvhJZYMWKwIQP/pb6Iry0ZK0tTQ5fM01vytWMpRkFBGRavn6YB8B9CtVn5sB4kFWV66F+yl8HpffWjLMs3Apy+L+ltrCLULwZEiaWjKfwaPGy0huSK4EU/EI6IoOd6oe588WhjOKwt2YbAyJDSNSeOhHUCMfi7vAo5Zrgq14DISG+irhE/DlMwTn3BQP7VbfbdlUbJunw/Bwubwqu2BXyid3Qe2nPzf/5uvTpSbnSkifpAclMP3XsE6mEFa3Rx2qeJn3U7cVqkz6tmAzMErynr++nB8vR5nK0fclwkPuAF8eXEKYLMuH7AGZ/0v28p/Pm5Nb77iwzPdoXotzPGUSVpM7VY4IiJnLOTdQReScraWrmlaNhTkii9rzLBrIgnQjOsY82qHpLLgipNkQhqxUAdR40pA2e16CjPSwJrCuovSicHMLlgswk07LFa6JVKZ7yBJ5PQpdH6DeRI2xHkYrYYqNvR8TAVqCeXOW3kl0Oe3ECXGCwfO173q1uTMeXIpzoOJ4DmLj7DNKbey8y4KMMDlFD6OmSaiVODrSUMV4L7dBzoml4/qhLtEJ4zaeOstMdVX4HU2+zMPmesgWh9DVHI8eyzhHzp9LtSkdkoxKI2F8iOfyRk4DpXbBIgNbtIg1r21+mmZkjKVOBqLtC2zl7MzHnb2mK3G2/u4MftbwrK/tWRLl9F/BsWkQdmUISJeol5XVN2jAQ1To7I+zpy8BuLV1L7OHcYoa4suvlA0lxvY0EThk1N0eANCc2jRqMsqITYX1FRoNSsHHp5QYsGmGw1njHQs2Lywoh2z8/P3f+z17IX77d/4AV1996XPbVnZsXEE+vTAbAGhzvJsOCzowuH/79vV/6y/84MPHJ9/91hu//atvf/4Hvv+z3/d6Ls9rRmx9VTFx0Kzmb9rr2eylbQtHxw/vPf7217/5tT/8gy9/5cuf/8IXDOK2PHyGWi8urGCZ8/BpDX8PEP/fuxaGKDQIC8YgiiWgLNgY+1TX6Oqo4gQNETQyCo9cq3/xomz97Ns/cUvNlnOFz7RSjtw21faEKOPgXHGmzGDFS7fzc6lwxehVOnA5x155v7O7f7F+z3vv5c5ITRoLHen8Gn4+eu7O/l/6yz+ydc3yir3WjBZVF1FBR0Q3sXjDMrBAuMbJCvvjnVPr2q9s7//8P/v5N9/4xn/7v/nf7ASbYyreoUmHpw9+/C//8K133vrZ/0Ss1qqP+Rt+1UkYTYotCxPUU576iPhRM1DLZUFXjeO0uB7o6zY7U3de68yc+QusIxgzYyoQcmw8eWp8/ezWzWvWexhfZg2K53nUH/rP4ZVjcsgqSIgcNsbFLr1QFdfnWAbVx8qIK8mqLa7aD1THOHnQUvcinuaXBhp49Y7YTP6hKqZYI4uVJda8zaInD9jcxel1mNHBq3s3KGWZudOcldefHd9/9OQ3fuNrNcMs/fzm2aG91aIxOx/O100GxENDcWnqUlYCBNY2Pxz/N8o1QfAyrBcbQPIyiysNarQyLHWDEFtQ7xCV2Hny4pqzsycHT+5TiNxM2qISXQybhreV9vLxlBjMii5aZ37BMWR301T84cqKP3SfW8VHBLLl4DUGnIui1odKZcDiLdtzs64C9zAJM/Ol5jucyuWkBbzjNltEtDzFd7jwFxGQl8/nqY5mmgDgzSRdzIre7fXvS8q1KIYLki6ECehs49veq6zASDK+89i1JvLJmXWXDZJjn7y5d+y0Yrm1pWvelAeTeQtsWmGo69VQ3n4PtHCNA/O53M7+HG8DABuGleD29XC1XxmUBsplG7oWK05OjQNjsfo0N6gB66YKPQnRxYH0JIRKKAkWuVrsNBT20Xt3/4//p//T8fmRUy8PDh/Bn53eefF5c/Ym4akwl6urz5Z3r+1S2bywNlufWLN4fPLEact2xJ2e3b9/T+Y/+ZO3f/eP/thhQEb2TAS9ePN5hvijP/bjL7zwkhV0eJYxYqR5xmJvzvu9cW4knhSh5yEpDCFwHrRDvYR+/KnzBufR8jFZnzGCozVDxbiNELvihhfFOJZeRaqIeq1DHnvjs9/32o1bV72o5J2333x4/8DKubOnEc4O9dI1/B3HZJortDliDoW6kEWuY6IA7KCfTU6OVjfmrWqatJLWICBzrBsqFil0mwTHzRTXYMgivcLdhPSMaD5giBkx+oD8UFomVuRZbqz0lGNpTpYo+hJIJTybUbZFXeQqzOmk8PwOWjhWAxyNmk8FQY7oHhZmDICFgK23UqOz1wPpsf8YExb9n2skCczGU/WIqpecwF10uo6BuleqcDGn/AnPsgyEDXK9bQlrZ5QtnQ97zcLURGtYluoK4BY2z95t3S18WySbdme7wsTmAPypImd7cXZTF433Ini+WvGL0/1ZFSK8EBM+cfDRxvotgKK5nM8oUnrCvpBxfSp9ecvvn02ffH/ex1J2gbN6Hqef3c7NPO4jbfG9iHleNJSPubw+ubtEKcwHdRjPU9xNJVQQw5ZrhcLIb0kZ3VFkIc3zTyD/qR8QWgFJMv4tqD9LXG5GodXMnA2xUXKTajRN+3hiJUDRa8N1hzWEeedafco37m8kzppqahoR15x0rnA6RevmxBV9AkOzlL5RHfFt5tZCZHE/zMGu2fAq9frUkjRQ+DfIat+tK9WXn3n7PD5PlDH7gCtkapYk9mgoHfWnfdwFJwXeYhV40Di6BE1sjagLg7Xxy7BkxCQAddWqJGHfcZWr4D4nuZF7jOi8Koi1BqWj9wKlmdkqcjZYX3tmuWV7sKrMERixVBdLnQ1JXvQI2sksejT4yqmLz2PdljLpC1F6UKcdzfLyv/oGkKT3+Q7rHRvdFJzMo8FTm7PlXB0jd8eG7GqVi/wsXRBgtSEBxxa+RTbuhV9CW/Dvc9HAlC+tgVJYyZZ1jlX2YFGV8nh6qXhuKG1U0YE6HK1jrOWgDkkGJicbpoic6+JMw1de/exHDx89R0Q80QJcC3xk7jakgdrfc+Tbrb/2V37q//J/+b8/Oni0ufXK7du3sZqjmOPG0ZJGIX+OTaqbZIyhM1eMkR09ev9dB8W2wIyMDo9MlZZfZbP1Y48/0yLUa3CkThE5QqoVOfwmUEjGbz81jLElfsUQDxGdbc9PzJxCfQ27hoExxeP+94muY8sTLPzwwlcCqCVengRqdcVrqZVcUhYQA1Zm7FPIU62bUAuyglEDuJvbO8Z1vQOHHniKndoDvcH9/ev3Pnz00cN7jms0KnZy5tVXjZMU8vG700iGhmvUgAYyjaeHQDnI6OC3fuu3//bf+js/8KXvG4tOB7U1ArOD+7ZMsCkKmegVJt64MYxYCB7S4LvwRt65z0T1k1ckwkTIkSeIYamfUKNn+io1LTy7AaAcSo10snOJF+vJVCkNLHcyVZbQRmIxCUOFPAsLAa8CCKWXGfdwUoHBsVWkMdyfoQ0jHDrQsg2S8gxSG+tPaU8D5HXjspVPA8//5KiH1p6Myqxfvbb94ku3QmQwmKo7odUpt45mAuP0+Mj+d4JhwronXAqB9hc2uZ/qxtqGMetpTGqergxZGbgSoyqtzVlbq8FylmHHczOl0rnSIU6kDncbl3NKIBh9VxpfE436TUi2iiYEghX04OP7UOYzrvpM1pG4sLR5EN5kSCzLogvBILaFfeGZoFJ6m4RtQqotYHFD4zC/2pLQEHPJ/MTBAUZhz3Fi6rcj0LKhiIUr4iCIFrCQycQodTycqhOqK/q7AQQguOoplTwcLsNyRa5r9TW3cx9ul9enbuVcgV0VuXj86PG4XPt/lFmqHI1NNtJCIwQ8GVQCOrkgGPGSq36BOujOU7lW4OJqZD59/PSNN5yJ8P7F2pFjAP79//J/YXd7Z/fqPsfIGUadimq60+TqSOAFkZKNIj01Sc5j9sK4px+88/F33/jun3zjGw8ePE4ZehfEHrXbv7Jzbd85Wm2tn+A7ZAXXdduSNszCWgewcDyHabIo9l4S8D2cUnYkERCX+z/9WCrGzNNuuxlYBh5ODPT1LjrlBL41LBz42bn3Uej06mvuXdv71h+9ee/+Awbaywqo7EzrUhEN7rSTo39J3ynnif2ypjhOcbLp6YgiBIswORyT1eAqNzZelpE24khkCxXyYUF5fQ4LYLCiIBVdcpWwuuQZWfczWMuH4jKzdEBSdWhk20uZah/kGpB9xsxMhUKMOxoobv2QEUlumumdpKkkmmL9mOzg6dkCPrG5r7swt9l/3tXjcTjh2YPQiYXdpw7o1ihk9kNRrmZYlrbTPZlqSm1jzG/1NtkJ38e7xLCJ2fLnAYe2xsVdHr8KG9DIFfkIGbkaG6gDnAPK25dW/OOFeraAxqDw+uSK2tWvqvtzryVdTte/Ls9S8FPQvifnUnbJs0DJVY4WXQIcTrYjKhT/nGuFRF+Lg4iLzGvWqCC2K26uru23w6W3lA204brHQ/4igzI+q+mTgpcA5k1vq+cL06oujtZ4jiph+4xdkUqL/jvg4HyrttG4s7FTISzp1HokaYVUgr6guG1oSVTVKXk98KkE2MxX6F3021jdojclizz08DdOXmGMa+ffVaY3eNBiKhblNEe2tC3jj4pW2FP9Ws7zbUMiRZplL1W2IEzrBne/xfa1evUdZ2kRlGAMic23JlpKPqZPxUVWHwYAyhmzv7QPDsYmhW6nhy+eH+9bMnl+9PRi/e0qzSXJrRduwU3OCZ4Acyjuz892DLV7s6xhV1ZdAAo3HQEeTcU0XXta0NYyWbGXFk91ajYcLht3Tc0bU8yWO0NQQcgVPG6/N3W1Ja5GhpDWDw0htuRHUFi7jB8cIZsxmoIhYwEx6mJr70PpHjcKyG2jANDlii0Q8BWbu8H+zcZ7Ln96IsvytLTKjYylWRmsyPnF2yOjjFrV0wEDCl9rei0ofu2zL//xH/7h8y++cv/+hz/3cz/zn//3/satG7fOejOfVwsR8+7RuSbKpNPuzEcfnJ4+/bt/99/9F7/0S4ofnr35a7/25Ed/9C/k4tBo84COVrtyDVcck66IyWHqTw9Ovvvdd08e6fccPfj4ked2+s4yll5v7Ohrxa/evIn+FPzMa7P2KLGR0SePHx4+Pca1SOe7kr8xJSP3Vlw5T6BfqcvJ6xaGrW+/taJ00nDDw4ziin0+5p9eiUHSSJxgyGjrLXZwsX6LXxwm99z/PuLh6n5glry6Jnnt+NWyeC94p9lafa5pxF1D7Al5llmZiGvDbm2kt5Y2h6Z/eHq99TPXsryzO2dH3gnaWL4T9WkC8quYNpohImcq2CZL3fOWb/l87+69r/zwVzYO2/9qVMahOFf3r4PMGpImLco7IXBxd8OaBuajzme6XEsUW1LCLqvgFHTTy+D4ECO7GcQ0EYhKZ6zQNaFb+3GMIhXRIQY45zVJr9loPgEIaOjQbj7GGOgGfqoa0yhUpXSYIxn+ErmXqErvuRGtSaYjw/nJzXqQ549FEEUbRm0zfQDbmC5Y4qyYailkMQaSoEcugzPg9T+gqWu6tftEMH11/zU6SVh1zre83+KK9wbg93feeMsCQsA4pSs7j+GxtXl9d8c2bt2BWeoAcq0qX5vPinzcpKZQ7wqF8XIUN2frmiCMkxWf8WClNJ9VP7BApBZ40gjEwVvtP5mZTFzt4vUMiGT3pLlriK79LXPhT7rLbQFVnJ9PcV94k8vvYeTXaIQY50qgxK9vinCslwpsQhl3XHGoGDs/fuXcW1yk9qgeKTavn75CYW3eEQcgsE59/jDXX11l1I1+ucGUxvG9mt1ocfMqzNZUU56vbdlhCvDkhlL4wWPhwOhhwqI7cw8Bzwf71iUv2SS5YTHvuVk451NOwHo298/28nlEQLB9enBI2OX0F9WWRZ14ea7aI1Sl0FhxakBUd1c4VshHqM/Pqok5LqVOsn3nmTQusr7+td/6rd/49V+nP1739wOf/f6r1+8/f+c2BWPXdMQ/S2rxIXlOjRgMOq4S3cf373sBi1lSW6S+9fVvHB+e//wv/Mubt++8/vrVN7776Nat2xsb96/uXf3ql7/w3O3bC0DMNhxF/bxh+tr1GxDBQPiYanbkAMIInXVKUctwcNAO9RX7VnROyvJRTnczi3LJySnVCforKRAQZVNvrUbWKgPlDhgtHFnkCK62qfylK+u79w6/QeEJblqcpzVEw012qUzFsDZlojPI4TPtRcShfELDyapDTEcFVi5SMjqmQabNS4M8gkwTkg2EytV9CrbcVwvjeyFgW/f9urzKLq/8o3Or5H5VYBI9L3xAv8kuDXrGCyMuBVplVEkg+MPsu0akIE3lPnWq2XsRsowoyssitcPN2Ttt3MBtTxsKrUZjOYYZ06eOI/N8iFrQ0hLCajxe7Z96tWXhOcMIqRLw/TNI+77785M7jcaoAujRd2lYMvVIGebx/IlvScdSNQcHhgYteKhGOiSqL0ogykc7LfjYbmBprFFzoP9gGr2jopt5sIBQEyiu5p6HvXLFsZUkcCBKl2seRf2zlNWDywwJ8t98LRmWz1UVg1glkRoKU3VscfXb53A+3yIqrq5SY8z3XJ/8DHvSmSuqXYl5vruvsgXypA2wRRHLNDXMAx/z7PLHfIfln6Fz0JQ62K9+aPYYnUGCGeN36Kq2pk2TqVRupeU6VMzinPqjA5OiRlsjeIuWXVj7X7QKjXJoELI8q4PIlXb41X/UpYZA0sFaS8I8baFQ5cYSfWcSQ4AyGR5g1TX/Y2Z/w7TYXfXzr3ax8c6Kh3iZGFKFu8+iGi0zRyDuPCehIIdK6cJ5J1NuHDmy/UpDxFXfltrq5P60TYKhBdQKdB4gra9k7VNON3utrd32WiotejRhH4NghZqrGcyT5t4USzuW3XClKZA8oayNxhXb+sbhBKArfARk2ulio6lGqDqpcQcqccxT10gD06N5WIM4x5okGsQMKzFEL7ys5Z/LTezqGums9Hvgrbhb9CR6mErSgvDNgwV4GFjMTCxVG9isPdYdX3xw96OPPv7wu9/+9uMn9x89fvKXfvwH7Vk9emKl9cXjp0/EoCjBSKQJTK9du20g4+GjA9Prj72y/ujwV/7lv3zJawJeuIVn9k0K6Hd3rcHqRVGIdmz0/aNHAnsrRq7u7Vtgdf/BR3wHyIazhqlrJ08Jem9t06FdWKJv5uzRF/DT2enyvPHtN+hhVOZAZ+JiFGMZn8AYhUaBIwu5YA7xPRnq46B7DlRSRVMF2+gdz48Vmp94VtUxuTtgVgnzPTBBGOMpbxnnD+BcNVSronqwyR5043JhROppFzVswks/W8O9e7j03qcNaP7/+HivQ7da1ZbzD9VK6a6S3Y6jf9Y2rZdTpXjqrbe+e37x10JTE2DagS6vO2a0osLIWtMIpaKZb7oaTtlXtLkiL8TVQrlBqUzNKtuht3WSpXiqjHkrdZKpaa0aBZ123CvncF9yVwo2CLMjv6poAA4TUzVPq061dCBuJcaVXQ8+9aUpdVsbW3XWqYJnx3HOq6mC5nXIJeWJkCUhPc9+akNr56oxbHwPdf2oOnR5Ga8Znl7otf+Zz71WV8h7pHY6tsu1c+XGw4cPfuO3f3NKasp0GtqZ0PuPLy4crIRe74mgCzSG8kRJ83XFLNU+H4vyIHCoTy7QM4cgmyryBoIZgAyocCzOFOQDZVbcqPvJ6ZODA4s63IODqOXq6QQxdGipKUpzE3XkQFZF6QvevvtVM5AOp6TxXSVUUdCrL+P13R7SLdggYcfC9CI2XO8lDyyuM6NBGE+Ikdwc3NZPD/e3rjJ50HKOoxiLBg0DBssGR/J78yMslVa5UvXPJl8Ap8UYvx2fITl+qZzoQk1pQQlQ+f3qfqnn8lPaqmK5lmxTQmKAcDUYiuOlNQu6K1BeAMW9OXJAvtFD2RfslhIBfHZNxSGNV0viwtRPqvRk0eTzNWf3/8LP/RKHRtlu3HruP/93/90nJ9/Sx7eKkgJASasXlmZCtzcY+7XkUmvy9GEv/DKzZ8fHt7/+J+KnF1969Z/9k3/RMPHZ+vsffGha7/DpQ2+wePnOLfBu3biGS0YKdhzo7IC7K1q93MJIhrnQNZwUIbBRvc36kHHLf9jOtXx/ioWrdF9/XqLski+fpC4qsxL5yGYgC1yHt3i+UmesJ2Wq2cz5Rm+ArLWv73q+u2sa00vWHHlk+MwSZT0fcDkBWj8Aio9Tg2JEXU5pGJb7FMBI7eoAgQQ8361JGBlEQVo0CoXeRWr5tNL9Gt/ufhQwXBe4g3S5hjwfgKyugYLanhUKpwJxzu/QFb3Yte8L+Ixeh7zX3zp1zdJrWQh93JSKEgXUikJ4rV7Ukt+LolHLxW57XqTA5orZFfajYhXKdU7tiO97ZfYjmUgsb5q9ZOXcIFc6mB66up8b6RO2DbhIlMHX0K08Bi4+bNIxjVUKKsGPyFOzl+YJRYY0sO2nLYawJKS40KipgdGyp33d68rZkK7a0Kpy1YD/DJXBR+Iguvz4cz4V+nOvFGPA+fyEuGe5l1qm5upOYyLiWc7wiFqX3SevluXyFKDS5uq9g27sULlkEc8V6YHqwfylpl2Sjl9LlZbck7Y8Wds46Pl5r39fril++aOinyRM6ZBdMW3qIAZgRzdzkqe56TTPsYv0jrYMSkoU0SB1BEn4d5Luxt2sYqIPYknPxslenDwf/7buVjkMJkPRyYlesuU4H8BAIjXe2HDSvFOdcp09ivEr5PMFiw8HI9ga2tO1o+dtyl1bf5eqiRYnR4YOda0h9yR2OD49diZGRY102zna+FSq4JPjUJAxeDHrLGmwdTgMs4HOKnHCwFNDrZRTmgaJKznZeWd956oRp83Tx2aeJ+LMYlJLDfcYkZ/DBP3UHW9FDVba752Fm71lKbkKozYglm/t0KR4qeKlyWPzxhuzzqPnjQiuX3lPY52pU/f6XgO+fhK2CciWzpTU/CDQ6tbeDKOZh6HH5vBVgX6XESADBS41it0nPXfRWCE6lEsjoidWzDWodTeqgpQFuEykUGzhwWUeg5nv1EWfMDeRtPi6hj917Qp5jZG3T1698n1nR4+Onz74gc//4O7OtccPLPTccFCMBaxaKdXXil2sG9u7d+9dAdU7b92/dnVzZ/u5K4ZK1189PXreEiCBRZ7H8qaDY0dQHT89xU9rWE0K33m+MRgn5Gy27lrbsHXw9PjOjZDnVo5P752vPT4/saKRaO5yMBZcFdJYPV+YO+Qv8UTa74Cod4pEc6SeRbtRKwdbRtoQ9qmPqmisxRaajMulmPhM0Ckm6wgmgiELPIl7VVURd1nalJhSIwgew8NmHhxkO2dYDbMVyvy2dradeO3UnOODNufZKb52bD0a/efW4wztPjs5PHhodmiWYJojAsmmYcG7lVggm0CZdtFYS4fYGgp2UqzdgSa4SHLn7bffq4m0t4DUHj/RY1X+8aP7FptMpzH86cTF6bWLs/21jSduIyeuRFDUe5yqLCmRm8A2GmiveYozatA38OJR+8CvoYbrx2w5KaVJCbYsvnEeqChaqO7tBCDW62Ex1e9z6tRMxsZEAhqGd6sTZBUJUMSguTi5xqhPzh6xtTa3wC5Z6GrUQT87virL2uZDewyqfMF+KKmOzIfuiLONzYMGevFxtXAjp2c3rl77qb/+Ez/wpS/cuXPLhMzLr76Czbxaz0XGfZ7Za/m7v/VbJ2snZhs/88orL73w4tnJkRPJLBrEoJbrqTiYnKA7xtrwRMwbdag6pJy80M3mB+jVVeAJCHRpbkmwoDsHag2YhT1aFv8cs7Ew4XzPpESsHW8wlXKCEzKWTchUP5KbrykGXj+yVZ9VxzzyLzSA3lRzkEe8ABZhruvA53UNRXcOco8TazDabS98tB3L+QSc28c2QvNXMXiA5Ch0VzbePbEQf9ZhGYCqDzCTKlNJHPATh0Q8cGwbQ8WLAnqGphU0/ixfCRNL/7St0y1pLh1bxpmnOTrFKU0MXzjjJ5S7Sp/7lQpM4vIhA/YvFSWJpQT1XTt98sQ0VHsYWp6XsoQR4A7lOTu3vBDLHFQSR5daAFRcjoB4kKUb5XznGfDLavln7uldcc7G6asGQb72h798dHb86P4Hr7/+mc+8+spHH93bu/qKo1Hs2Et7uN9BrFaADZwcv/fme9du7J8dv3z/o8PdG0cOTPvovbctrDzZWv+lX/3dN997S2//7sdv55h1/NdOvvKFH/jM669RyJ39Lce2bu3au3U+g5e+66ZeY4lNMjhbw4jG4daVKwyCRo1u0Aq6kblF4CUNy/2QVuJy08N5G9JlrrInhr76BgVvrGPidki5n1M0UU6u4fY0fDvvHj2+q0tDQaxPNoPx/t17w4ZiYRVyMmmjqGpgTJRDEnEstYYQoA3dqaShd2FzDExCh9KTkYHt4DRKMpRJQbF9IxSBM0zAUwWF5zHfo2rm0+AbZxJxs5znp8+bXl3f/lAhVhSceIHIF6Jo6yNB15kTlvJCH1ZNyw6d5scHQLmuQGvoQ4N/wxSlej8PmEoDxZsx0PP27Gmz3s1ghqNFC/bn51midLw4jlpAT1+IrMWNbKo4PKzAiXn+cnThXlpUgMZdaAyqzFyJeOL5IKZ5kyPCcCsAgxIYyA/51CP2I8K1yAU8v8LSJ7uePQQjAz4IbTxbbhBsIwthoZrRb6IS/0Pe4CyP7P3iNrXuLHjKBj3oXlJTfcOdPnq4onK5n0cl/tnLaMZrlZgVNwr1j52CvtLb5PoJQDBmnsQ+JTivwEXNCnhDMpfJ31NZz2Ov78kalUsxHEA99ky5efjJbflX1budHyvwS8bvqeOTH5+gQETPci7MimuScp5WA7T0WVtIp2iGERytbhqWiBdwg2ayTBsIue9RhuQ9lhWGI8HsIbGMHmc6C8q+a5rSNEqa90qTplDfCVvVUGkBTr97OE9GD/2KcWHjM5WbwaoMfZRZx3Bnx0pilSindcxlWF2T8nqbr9BDoKnRW9QRGtAPsE6lQwTK7JpXjTCkaqouehwq9HXxHE2JO37nyPBhsWJjpFvYp0vaAAz3uGZctRE9fpy+sjT8w64wHAjKNWXQckuvLAV63eis8DHHkWU3gRH+yQivUgdYVtvcLaqSfzFsiU2dqjIlMpzhVngn7IEtg95RvQVQGi4y8ipWkCHoaduM65OtEE+TjlhVUsjFP+jWBTaQw/wQy9xGpiOHeI0yjmtGUbGlSMuFbkCP7Sg923jxpZd3rvyRZfoff/De/+Z/+7/7yX/7J//KX/oRp63f2LmqFRWVGYSdMWYnIBVRfPbz3//f/oHPP3xy+lu//mt/8vjet7799eOTzc9+9rP27Fm2QnkgRbxHx/ZT7p49fvrRg/stUxdWOvGPqxc6nnDlwzIae+YoOOelmBs2moLHhtMMCJ943T3lH54hqGku7A/vul61xEPHaNqorAwYueIDrsQXmYfxfozO+woAjsBQ5hqZGDiiSWVxz8eUnR/ZYDf+TWof5JK8V1VQs9729fZ3v/vWt76jI2m6yW6/7d09epKoxJ22rG9qnKjd9tEBeo1Dbzp5ZQ6PapyS+oWsfqP5FoTN2F4GoKPq2tx0OBU4Tw4emjKwMt7hMPaznE57ZBfvUIN0JbRGEQwWpN2OZmfr6eeKhCHnkho5kcNoalyaamDV3jDgtM+WL6eY9mTb3g1g0bmXRtko/PRDBxFuzCijxkyLMcZBLLF11JiYMifT/7i8ZcwS2uCzX//D0RiS48taiLVp5IwJZsh6Za3vKeDFpMb9BfOj+4lFLlzKKkTnOY8asNSgPRieZCOIJ3PH1fzIj/7Qf+M/+o+2vTuZ7p/PG81sttaBYdvwdejq+cV3v/uNye9l3+uf/cyr+7vXrMnBOAjipQr4W0hchgfNuMdItc4NnqQHmeLwVq0GX3PImOKKLSgNaZ6td7dJy+dK92l7A4Pfv+qEyvP9q/ut28AAcbIOHtoMcHSEmCgwGIhM3wUntg3Ua4WHkVShYCJSf3hGf1F+X40O50huPnfb2DN7Q46sgNidsl3Hw94eew92uMZZSYonzuwymBcb9RnsSoGuGWAjIwsVgS0xEZAyyokqfgin4ir8Mslam54DI46QR9VFDO0W6LS6VAyQeDd5sqexwsjoQS45jzqGVpK7KbDKHojVNXJwv+BTrpDSZ7V4MVcxPJnCFASOdi+TzmgpTlRafqgmU0BWNS5SnWrHHhL5CN3nsKfG6/zg4rf+1W/9zM/9k2v7+7svPf+3/tZP3b51e+/qjtNbNXN101L/5nIzYWSouGGILSfjHR88vbp/9eDgnQ/ufoDBXPI//8Vf+Y1f/5rjAU6PqPNRruns+KVXX7VmaXd346s/8iP37n2k3717bc+i39393Y4HjekFACkaTbBmVU+eWhc0W4mRNqDo0r0Nx0qY1MvPZz/n8XxMnuXnwvyoHhZJpACzMnbc7AKbRq9y146jmmva2Nw1OyImtbGO0tlRI9mrtYcRNC1e03R7CSjziE8ljcRNr5tnro8zzSrVI580gz+wU2IQV5qOdFL41MxZMJL6cuMrejr3tcoBTxkXJHOMI+i8UJ7Gw4Ufqww1P3Jk2hrmWDvEr0pzCgTII24PRwatPEjx8oUxxixumxdw+Al/FhLV0q7nlLopgvEVqYIUdQ96+Vjycs+KZ7FH/sfzBf9IVBOvpeEEhp1O4RVRAo2QbbAA4kGZU3MrAyZi2UMDOB4kKTLKBbHWFfaS6pgEQuaQKGfGPLsEpqmNUZBuKQqu8GqZxbTXnblelZiQEEhrc/0qF6ZJA6Rp48AtPI+Qy6syc798LsnDkJHQZbZPvpdnK0iBdI14l5sFWmVTlXm21Hz5WbZY4mOKWUq5jP0P4Hm6fGCC6aqBRwDDwdXTJWfcc5enWzJNDZSxFcnexudzSMCw3QGTDFYIV+bPuz51Lu9Ai51DRR9Eq6m9su9UyiP7fqs+BCgsGdZ7nLF1fTPqMdLofBiIWyLjuylsuWzuJVA6NQoCaqTJVT3l0SzcG84ZjIQhldxpOivvCAyzbeFRGkv53GWzmkPwJYE04wHGwAoS8/+SCims32UP8gcaEp1Q5FHVT1Okci5D8wCcWmqgSqfJ8rAB9VZ9TqEov559OxFVXT+ItcFBbMrArHtz1vuJXQRUQOhQhUmKJbMMOFqN7bVcOi8d3BkOmCeDemrvmqf3z6+w4H2rTj0juFi8drb5AXduCAlubACReXXETrSkRv1QlUIvi2+W04Zjb3hBq5XfhUoo8TRCgcZIqZr8Jj3y5MOHDS0HJvR8CIgP9U66lKs9AUFSHm40cMDFHoGeC9zVV9XF9/xa9G6c33EQCgQF2YFf8ADq/OzGjf1/8Y2fffjku0/uexXDk8fOVueK9646EeWh9akWPLVno0jMdt6dXfzXkTvTGP3D//t//Cff+OPNtasfPvj65vpXP/eZLxTVHB0lN6cpHVo/uu5Y/42dtRdffdlpyVtelnu+/ujhY66C48A6q2NnjNkkw/nGzgN09CLBk7pVSM0LDRFYhIQoGqrTkHgN9/oMuDRPilaxJeJwQhqmDytTqIUtMcSRUAIaXClCjcEJOakmy9H+ybzcpd+uHvvX2EP/kooH4xQ9Qa2m/fjR08P7T7zVxysG3vnw3o3n165v7dzYNe/Ua6euNBwLca8q8yrc/e2NF5+ef4sGemVy1ADJCS+oXCKB58ZV7dK3mvgpVjinSszs6Cp9SkdqOGXIYe6Oc9ph6fHDFRy2vP7gbO2pJ8lhRd4Q0YecyMSACogVorDelyuPortdH88bBzDzROwbfcpoZuBpAYCKNDUWL+g8Bv70Ri3c9hPMl/fksFlKN0RZ+5oJ5qpSN5W1U3/kE7r+CpFJAT/JwLFbwwWpc3KuMcKW+d0acT+sgGs+fbAv90DmpBufmgqyELc5w8+8+qoXYJmjIFWmMh9CwMQc1RixtvWbv/kH58dXRbXXbqB3t9ctlVsW0W/ej8lxPshVl2tqZ55wbpzbOkxkmjVNTY+f7+nWx/W4tq7Ub9u6kpoOztQdA50Jw7qnajGadvuctZw8OXMisAmXhtWmY5MeCvQxKy+6VEuKudWYVwX+gzvOZBVMrzjjwGSaOLZx7H3GduG++OKLt28/7wgvLn/2qHjJSeHi6ePTrT0QzDVxVhxU0ln4j47A5SfN/zcuo2p6MnYUQrm1jYMMxlIQmVtFdK63sk/SSRKOIBfLDA+DtXn6OkfonO9EvSynWoBS3fFm6YiiVe3CJLPcnpizXa6ATF2r38++lgwhSBtlSmFb5rR25Ng8xzdXWX1JTcaF2Fy5+gaT3efiRRWqbBV2ifPewWS5BqUlkV6DFGY1Kht2kn33F371/3Tv7odPrmzdufWiNRHXbz6XqxcHypqEAjXKr0RSrX2wOtJbvecdOL/1r37jxZdeePTo4b/4hX/57e++ffXatV4eePL0ysVLOHz7xsVXv/xDVPj5Oy88fPBB3GjO/3zv6h4E0coEhNVOYL16dd8AAch71zdvnN588PHH4znjRRisvi+pmJRnPybLs19/+uaSS9ID4z8uLrEjOZY09kQwI5saKbl29tb3rm9v3tt69Pgx9TmywNWoz9npDS/WqO9a6DnjdGNKoGSSyJGGS1pJ7eSqsz15Zcd3gWzRJSWstWXkRqaGQr0FG1Zy/BeOKJ32MYBZz5BeBMxbsMDAhGvRm/tzbXpSSncMgxFaicpt3Z1sjqO2APpuxANIVzz1A9uNI8xQfTbJ/WA33J2Fj5tO3Zngyio0Kzyzh+33RTn578oXtcS2/o9d+XZTT1Vej2K0D1iANSrUT+5GcyX252omdZFbBfASQY0zLf2qnMQ89RG9oDoLTDFjLHv5+Jy/RpyjK0e4DKPgUVHXaP5g58esfhQ1pPhcgEgvav3GCpg0TowkJXP2HRFp2kobuGEfcFdAY9ICufqW6/J78qzSfA3iSWS564GcA2JK9DxDv3y8jP1fFGlfrB2W3QXPS8b1o58LErDwYHVvBqAnl5CWos8+wyC0FwLms8yu2td54n6FTkAWjCeh+1Xm0K/UlKx0GVbXJ1Rcpizfk/dT+cgAIgWro3OeYD5l0NqkT8GeP3VaNVvr5gyuYfsCL9nEh3EaNbgkOM8HaM1Cj/1VS2YzxZJsQpdOqNXgQThcOLLTaJaWsUY4V5dyY5YIIIcEjTD0Pw/lfZIiGKDNcHGa1gQqnmUOVoXLzM2Yt+Bo6lcny+bBEQPI1MApFPhqTeDAgyrCv4sdIaCmXiNm7MPSXq2stXj4on3j5m1g7fxNSybs5xNI2awGj4aow25m0pt8noXChf12/hqQ84rfftTERlsn2a/v79thkL6fnztxRZ15FnsJ4IA9cYBnkrhEGTNZiVieLkAhb9yUl8h4UDojYTFnuNtiaze16RwhR7OY8YhJVdMViaNYwvPF3DyIpQjTqeg2bvsGJHldavSieD0mtPFf2sCRqH6gtlyXoxp3OxvxyvMvPn/3neeOXnjw4Qcff+FLP/D1b3zjhRdvfPGLX9SCgmzcJQcwQnSCDd4dPDk0LvjS86++/97H2jZLPK8I7pdjHyYumcEVDEwpZf7gg7veKPzo0cnezv7B04fGeaefU0iBewm2ZlMF+dVeY6qYO9pG+VKvhY7REUjjQHnTUH5VguxpeL+VXZiSEcomLe64zXkXHJDLpHiu3Dwd/ribjFPXfKwAxdT+94+N1PKVsMJGEtnXbIkUj48O1r/zxvsPD3r/xd27H/3Ql37EWpr40LkZazs7153rc/25s2u39x7e95N6WHduy6TRFqvS5cn151v9iwlGa53LLtBsWa8Q8unjxzdu30S6Ztg4LobtX70u21gxGQ2iIdcNLAdfd1RjlKMsWd+iK0NGXCk729B+bvf629hb12Dh3tIa1a+O59klK2ykQC787A181vU1qB97GbCcADagr94UZyonN1bck/lJ+0IxO1PzrKKDANzCRYJuyTzKWS2CyYHQ/FqjBECOWUezFotEUhVVCjV2d/e//NUf2rxycfK0SfuIC1tGt6iBeeoqN1QnbtvZvvLCc5qQFEk7qs8AsszTReVeipJHM8M4dSqflthKjG2kNPINnx7k1BRVG0zzhuPW5JfY+S2olY4nVYBBa1evX+ch9q7t8+WWV0m7zCJbAyj53uFITIwzs/J73HTuJisIZjqDS8XqlmEyJdCMR1jKf5ggFczbzE0HDlmivftkQ59tO72jto0ZN/BxuYlMRaoFjG+fScfRt6k/PiK05/S0oIoNpVELZyClXu6uYQ28L2tB1RjoUpAxlJhKVqxRaxgeeV9yKFAmuIuiqmDylevffCWSVS7cqKUwksKdPw235KJK75khbtUu6C/fVTDSWdyvXynEKO5UvoAdK2jRyagiPxzhG48fPdF7v/Xcc3/xx37kr/7Vv3bj+nX2qzbDRsmipgMnQJCf3+bY+9kEjgbuYs0e5Zdefxliv/Irv/G7v/9HmfuBTVA01BH/Rzd2915+Ye/a1a3PvPaiCRyWA4rlPf7AH5i4iLEOwzU3a20eVWyJ5s6uUa4ceyaiTCzH5NCImGdfc/9v5utwP96D5RoTcKcVSssG0hhm9lU92CJdcGyx4s6ODV+Pnj56fHDg/0NvirrSkXfrJ0fHXhoRvGmDQjE9qF3LjhhD7cAY8vAuoL3roPpoUdW0nCzPEoy0TkLGtNAZzol7vnLUS7LvEcqSceSXguZoXVjPOvi3DHma10zZRS/VWe3VljdUxI/Cr9prZoOMyUukk6nnjEW4oD00UJnSKFknIRAkosAg1Q8PpiqEjZPNb9Q8TS0hsxDmrqxTcG4/Se+njsTEbfmCikgL4z66lKRmMWDg1bVqGmHqLje3AXrWOBgGcRitwNK2Vk6aUhWE94Qu4RzvVMNVylz1MaFhG1KE7YqAuRnYSxV9Tm1LlXJ971VdrqV0TPLD/2f5+p3mlGl1LY9LWR5ePlvSV5mUWSCPejQp2YOlmlUWX0vRFYDylMFnfK1OxJY04nxWSsLJa5eVlXsBPNC6//Ou2HdZzWXfZZXvElJvLfV2tPdI5/Tpc+vHO5sb788z6mLKr+nmvL6v0zugrW99IPAyITC8KbIflOnji8bJ18+tLBQO6/VSBVmGIjn80VoVZYrZTm1fr5att1oKm6cKNRS+p+srSjNfDADHKe45vt2w99r73KIepvxUpdCGPlJ9dpWJFc9pGjhGg4n849Qq0fR9WXnHxFMo1piNKX4IcaIskuoXijdAUNvvblq1OtA8zRjv2s71jzgXk/yslnJve+GcbqghduO2xpK3vT2H0DYcLzMdifVtL/pBskFNapsxNE25MGwiYx6rsztz2qKFtid6StvzCCjWwkGDD8E3DZ39i/Jhqs+ezdqJq1eue0ECN9NTU4NR5Kn1rvwGDszsWcs9GtbNp1n+BJYwKjXgKpJsK4gsHOn0UnGVzIU72FTVmbsIQYPZ9Hpo96TCk2dRryXFcOcH5LS2dkPPJV6P/4rlZ1avPL79wgve/ba/d+Pw6TvvvPWe900+d/OFx4+O1q/QpbLOCJqarpxcvIGiq9def/jw0d/+Oz/12c+/+Eu//LsOUvz2t9+0ePpLX/y8hnz/mrNlRwfbqX3uPWJf+cEv/9av/caF0xsNGGzuHh606KWO0zh1AIfzBUdYlSPJK7l44AZS8k4LU9JTaqJYjB9Ck4kTPZupMNFs2LXxYwBiYIXiicNecXUc3YX3M0xUN4DSfhnmUk8KSKsW6yhxoaLEP32VV8Ewg5+l/8dPjpyH8PTkgeW4dOLo6cH56ctrawYFdw+NgXXWviUoUDq0cfDxo3tMyfurSZcOHx+aE9Gpzjlzou0UhW18OP3M66/euvXojbfNWmy99vrLz7/4nCHbYotavtTG/BkVhSH1GBIoYcM2iV8ukVd0DFndUcIILjQqBzm5PSzp9DnE2KTRbhmLi9o3z/SERDoYpo0/wlU9nBadcQnBHEZtPvRj4sDRx0hvpk772hAdhMJi4Ay70mtJI1JvTybZaewMZPbqCfrP/I2DD24z8rDxKBpc6SwyxOI1SzXfEbKYSTTmbHgso//rFxZG33nhBcYSDsye62B7i50LpOov8Vj+LjZ3Pram7fVXf7zuMIhzIFhVyS1Qs7awjCmrx1FYQx35uJ8MIipENrY+zGCZyESxY7srBZSKBPbV2fY8QJ1e3YyHCDDNIuix2d2oRDJKbyf3SnmrcZRY7RmEyso01EQRl5LoFVLzWA22n78+b3/5FkxkdyLNocXj9Woq7Y3ttEtAybldvfI5tv3k3o22se3ZM1b0ZgIBJNVcaNEC/O0Zxu926A6BjM9oInTcuPXg3Asljp0K4CzIJimFeq3rT9bYh6qjzTf4He2GzACqN7ZSAyouwsOq84vdjR3OkAdlyKux/zi9MJmmBm5qnFqrea4SJ2VufEyeKdkcmt41SdPmqaSuDkWhQuTdoLHP1LsbSVol8avj3cwh10KBliX2cBmvLdpMETc2vvPWtx2C/P477966edtkLxQw2BgSpVIgEy5lMMsiw5+702pY+KcROzk+eu72S9/+k+9+7Wu/N6zqQK64dXZ249bx6y/fuXP9qy8+95WtzfvqP3zizYy9fQ+dcMlmzOl2zmyNReY1GKoiqmi12nsgMyyGykueTXJALhMG4ic/Fp72mcSXbAPDbY5OS9CqXb8WvVZBPFL1ZEg9Gqp4eKyTafBva23rxv6NBw/ey4xYrryuTqJkm40lFSyCkFIDgUWxbDhetxA43CYGhV0Uf5xjMoGOKikRADiunD+JA8FjnKD/VvS1ZkFPnAjKHfOwz5HH/GWjnOluT4r+R8ujrbTp25cnpcu47C2p0b2S+9UMyxbbiHXwjB3xMjqcE2JTnE59wqiC5DAeVfWVHKbLPBYS+MvUvuNDf0NOMIOPnpjV4/6prXijzIMFCgKqSJkvKamysCoyyGEdxGXzvTr6ApDJq1SAAhpshSNkTDfYJcs3+KKtYIwJ4Q6QXFlyE4YGtSE83ZwsW/7BmQjGbCvPIzj16Nl6/cvaqvR7r3lSUoUuPxfsrrTKZtKePasp4l3KHD2pxbCi+KO3JSz0L4Xcl60fPhqymjL9/t6rUktK+Zfb5ROdlHf4W4Yy9mA+/FoK+nx2fXK/AHj2wM2fSVllBmcUcZ7TnlH7EqswUS3HNI1kB0rsTliabTkKgiUHTFpfsWVloXKuhBNly22F/e8RLWVvUwnZxkNLfxRfqYAuOg9nZYuBKM+qxMlDWSuFyaBEaxl5G3kz2rOTRkLPBUYieQOE44m1e4Zt+bzGlhwSfzKjPhtPnhzQo7H2PLI1FZEr6jFAzmB3bXhqzy6DNO6uKpMAhvrEy/gjgFa399ciVajC1TM/UblgRNvv9LSDp0+Na2KDna0oNWGqLxNRduEOcxJGztkbyw3dOk+NB7Ui4NiSH2h6kaFFtHF54wCPjO1Z0LzsVtARcpQHgmAe/6YDgFLBg8DOyx3HH+Hv+pkNaFvBB0dNOzu9zsFgjwZjNie0MtdNbzVu0JHgEniOaS6/bfmy7SzZ4k8dAJnyLV5qYClxknXN5yL3fsVERcHJ+52f2wMwITWESl/zhrTNjb0HDx7efvF5C0sMwTHwL335C/+v/9d//Pf+q/+BAOXhg8fP37yFv2B6J8DmlZrn00NvqOHer22u71OBhw8e7u1v37179wc+/zr501ESYSkWhCCFDjx4/ODI9koLS/acJfoYDnt7erO57EOn2NCf/uIh32QFb6FCw0K0CO4pYk47lqSTBAf5EqOPkC++9jtfs1P2tdde+tJXv4osoPJQK9rlSbXL6s56Dnq4cGkaBzACPE/HXNwvv5avYdQk+IiVCz4DXErKKYDgjjecIr9+cn9tf2d/7ezQtpOd/WtCPepYG6HHXlyr/7l7uvb+xfpjMbo1IdZmPHj4EGfEHbVwS6+yWMG5eApuXL9+7Qd/+IfvfOeFr3/j6+++f/e99+4+//wLYyitp8KJo6f1ClUNo4qLdVrzYIKAnkTQMHPBfeGCT+l99DsaIl5mDBWX5N4ZQwOPpWeMuNZMnQ7bhEoDLA3qv5g7zKub8kMJk3wsIqv2eipwkKFa/VHEGhiKDWqSIPcZLh7DLz4uuwfi0WL3Bb1FNgCqLgGG5biRqQ0d4BUHJNurV/d2BKhUsyZLyYXS6g0fyrG+ie2PHjzQ7efTQhe4RJ2oYKpwDsRV/nFxtGXhyKQqED0yZhnlH1qHzghQSfmVbSilOfi0Wy2TlYzYnfD0ive5mhQ1VBEr5xpmLwhl3nGoqGb+u6PaMVXWnuAUd0Fb1ImvuDwssL3COcVbn/vcZ//ij/1FPSscw2UwBG8GY3/4R3/4w7vv1JI77KPuwpH1kw6RBNyfyd1Ag4+ExvL60aVSFUfCCH5+l1xslHOhiDs789a2s7PHT55oEVIqzZVDb7xBtiWBQyS4Ay+2T3loezIcaixjaoq8BHeZd1AKp+R0CWcp3qdrSayGiQgXVZjlSYqlbZOpj3EjcZWzaVwqOS7wQT56esifO3Bi5vRS70qMBOScv81f+oV/+Uu/8ksC8P/c3/ipL3/5S81Iz5lmurAz8VPXS42JowEjvNcm9UjLVUB6vvYHv/1HX3/rO++8/b4i2jidX/3tgtbt9duO/3zuxisvvoAMAztGn46OT67evGGOSIPHuwY25tfc4K3hf0ynBvilitgQ37uQk5tcODMpq4Kr+8uvS3n4vbq95HMqVojrdxrK0mcnAw0BdJJHdgNITvE52o3F7O5sejGa5uyhc8rxwjjT3vW29c8L6fSGAaSUfH4RPLDsWfFAYk86BhP/FmsYc8qljCBRtFi0x/l/O3dOHVkRDstSgjoDGIMVopGGDTnoxUEGNW9lgcBJy/DYTC5N1ABStbh8Tn2wmqiGxRFEx3c260eCjSXCtAJ5oYJhWYbTU5q/UzcO4VhUcVeyDPPyk5GWaoeLPFSrFiRtqfauWBp/R3AxRZr/k9zj/nrsgyaA0p007EkG/V6ShpbVD8lpw6jOArKc5ZsMg1Lpg9mAX0GbyuVDALobZ4StnBNtVjrKwQa5PDGia5BZONov/8N4dS1ZLn89+15Qefbzk5vJ76MMC+sWNMsRiyNkeSxhfn3y/BMon8KgeYpP4fOpPJ/GdZXjWcaYhH4lkblkHBaqc6A9I3fgPSvWr8vsn9QEwxVFq9xL6WHf3DpzBnQ1tgjVCNzmk5nuFt7wyszMSUwUa/Tmyoew4Qrik3U21aZjXa3ArTvbhw7Wb5/n3BHNpfpo6XHeTevEtKOua4xSJ5HKnb6SzW3dlQQRaw5RmkurjiqID9vWzLE4ISneZKRq4wBFZrU92XbuV3jtScbrPH7jTFtLU2GsUQmZjWpkcqrXkvhUEVj2U65fOHjGwK13lIahnG7WjDg5RZubboNR537UDTg9bQ3m9hWNd68QwqYWFDnP3gh9XqaWBu7wJEEV4lh3qlt36IJ1RV6shAa4OL4ARYZlDOaenjzd2tpTofUaoYdTDjQ688IbTaZKIo5VNLCU95Ji/boVOxrmegXGBPn306cvifrX174Vc3BhRBzhJspjnoxQARx6Y3l4O0o9TlNPaCYWE7N0XJ8zNHtrgJRalOyOSBAIn+Vy8r0R/PV3gSExAYDRLoglpWSXHnd8U8dNOAR95+To9Ie+8qMf3rv7e1/7Q69We/LweHvn6vW961pJ/OIwCzVOXnQC/7ye6cK4jlcd/+W//KNmrR/c17Na/+ju1tW96wfbj3ud0tYOhWkX5fnF9WvXfFq29ujR4w8+eHByfHZwYBG5gdjTxw8fmSdpeAYS646+sbB9SzNRO9ZuJrTqUkRTJkY9IXP6mT433yQ5TDJmef/+45Ojs3sfP+ltkjvlHxaBEFPXnP/Qqa8yIx0zSgIxcAN4AT5Z+z2JPjB0GDWFVsmej1Aqzgt0IkfWdHR8uH/r+tFbJ1tegt4UuD1gGqQPtnfu5RDVvKGFVsNTkwTWi5uyOz//YG1r5+zo1tGTqxv7T7x5Qs8nO0LUTHnNCo2TJ0+8hOHg/r33ze6/9/6bb7/97p07Xh09e2kajLjYv2Zd87AoPEWWuk433PWenZCs/7zmBOfs1uo75ldDIpuLpc/o526at/GEadAlqjo00n6ZseEu9E+PvK9Av5U+K5uO5i4WkUw8PQ5EftKbZrEBV/B98Dy3KNDGFX2eAKp81vgC5Qd0ioyNrW03X6QXiIyWz4zMgdPPSf26iqRVmtQAEv0XnMnfQJ7HVN3NFTN2KoI97ISk5Q+RZAkZNNhkubHdmnuaJAT/7Oc/r2jpdV7RC3hoB9E/JYHNcfCuHEizBz3ybHEp06LLFRlzQTSiRj3U7CSoPGLdWrZwOiucnWh8fvX6NUbfmUO7nZihmury2dFB6gOhQ8kcGFWiMelByNsb5aJ488s3Ewtb2YVepHO+9Z7zRglLVPojX/3hvf3rzWSKqr122Km+lsFfufb3/96/by/Pz/2Tf4ZRDx/ePL/40KGkvesQ/9JW9dn19VZLHLU8hU+CII/AjzXDkwWdGCGlsC9JN5YhCVa0SD7X5M/bLtTFUuxZni0wKpgXjXmTX3Exm5wuxYc5C2sG4uRZ8s5vdspikpHKQMiXVq0grAZxYVVPal9AjV8VSP3kIB281ZBsPbz30FDRH/7hH2P+5z73uc9/4fNsiSqphRMmXWvwzBI8ePTxv/q137h/d++zn/3ij//Yj9Mvh/AslOLDVISYovPogoH/5xtWziKUqzA09fTJ+gsvv/Cf/OzPvfPBO6ZxDJFcaYkgHbz4yg//EHt+7bOfefFlXL3P6Vo8uedMq+dujFpYH5kAKAS2oIH/3L747M6eXd2dJnF29iAaU/lFlrLx+0pc8nyK+xXvlyumX95/8p0+lhybyjtf0H/l9OnLUdTDZyUXXspLyprf1OG5Ozf/4l/9sbfe+oYOz7t3Hz16dHg+b7uHz5ZxN1OeljCkXo0cRBJJ6EVd4TzXnF2LjTWzoQ6qW0MEDUSwrLEm5OlVG1xpxzDLbbUbdDJ3sugsfAxxwpW0VCVwbUWAduEIoeoMa3uruLQ+5Clsr8oI5otkU7WURiU8GS2T0/35TQ82tgxmVe1AYCO4bQO0xnYGY703ZQaA5Nf2+ZdVN1/THsVUDxubaBJLv+KhtR6YgX9V307UEHcLAenhDdmkqhhKPPF70IopkRgmIxvAe+J/kiraq91nIBnVMGSBvTxd3Ek91kg3YiIHYgmmXJiTB4Cf3NhRJagYKIKrtG2G/5UNwwu7MU/vrF15J2wGVO2FirffDruuQXO5ffYZmkPQs5RPbuZBbJ5Mg3O4fHIhfYAm52fQlx8RMFmn0uW2lTU2JP0brwX8qs5+PKshV7jQMLDn2QL83whwQETBp2/cLymTPJVAbfWjG3+piqFQJ/2tVAcmzIZU6ESR6xC1KIAlK/ymgcbYk/hTCr/Iq37wQMOQiKmBstBGU+xBI+sUpF01CRawvGQmEfdUVZuczm0aFmzNAcUyvRVmMlCBsM7lMZqGTCoTDoJ+zapRZyqIb6M3ApPeq8Wl5lgXsAL0iJZjvkLe/7S2trjlRppO5mqBZv3phhlivlbR1gIHsukTTDsInHqERzxCdgJCVC8vAx70IMY2gTvOIDR5IZ5PwQNVhaSHrSXZanaC18lQjYw2bc22vdqmgQtwEYjSGgYOyNkNGUT8iLcLFbVATTXai6CWtt8UB0QVmFlSA5/yND/iU8H5Q7wb17Cj6AqpI4aSYkxP/E2uqlPWVeVVv8oASqQtT2ufkEmLMAowtbNudBnCtzJh7/r+h+++53QkL5X76MMPnn/pJcPM77z77s7VV7mF69ebXsCGw6Mja79xBeanR0c7u9deeOHlGzde/s633/jogz+5f+/er9/9tb/2Ez9py4XZT0P7UHDcTTxc27i6v3/44Mnx+amFxyYBjo68AOeALjnVJs2BXoONXOr63tVdLQHJqtOoJBWq3V2YutAd6Upgk7+2UmPg8dr54dGTew8+vP3iTVTHnGQb/Rrxua8BTa2Hn7J4iBOxtK/FUgI7vBoYk2lqWzE1na7efLA7nPdtyPDdN947ePzhAy88ozKo4fC96ffI+55lL0wvrKMPa1cvTnc3tzRL3rM2CzGPLQA73tsTbLdFRMkFm9TPq6O3Nk6ODo6fdoQOaz08Ovnu22/+hX/rL+opQJLiWa5w6h1iAzzEoeZj5E7EgCxkDkWDeUpS8+SpjHWgUq/hVY1rpC2cKAtjpkQNQ5q7am6B4hsJg6XmWPZZWVO100jFm4AZ8c2ZDKOHqTURLbsiTMcAhFHimZl/ReQDQa+hYH1NnGTZHs2UPoMsqkF6ZSDZl56+lQ/hNh5C8eANGI9h7f+jg/uPH9+/8/y1nk7rrjFzBwjrbvXd5tbXv/NNb78+PXqyc8Xwt85EngsO0IFAvipwykzrKdYo3AdvSINaTCDB5nfi+GRVMJmgXaW1oO1B4g3czAKvmHLUccZbdObq1asvvf7600Nr8YtTp7bA1LMiJvDVV3JRyvwltMZLwOQAVewdd/aAWwN4xZISVmIz/cXO9q5oSFaLf374h39oe8dx8ky1vUYEQHD6A/D4qb/5U9/4w+++9cabjx99eLH2xEI186Kdb3LFQZPRw7nBJS9hg6WEFX7LDbIu8UUrF13gwpm6hvgwL2fedsmZik2Ry3Ll/eQhgDLicEMm2OgCVo64OyD60Y2M893HwHLjFsdUMKUSWIm1em4GwRTWVRPnYYKrhevwZ5ZFWF7RcLHx9htvf/ftN+4/eMQfm+Dc2d/hta7fuqbxGoaT+NrTw0f/h//d//7+/XtX9z/3V/7yX93ebau9vrpKtaXQna5QuKR3dAAm0z07MaR0eIQvDz5+ePp095/+s1+4d/+jo6fHu072tEjx7JQlP//Cjf2d7RvX9h0VurO/9+ThI3gS853n74iNEz0Tq19RPegSq9EWL1LU2aPDBiOG9qhfsTkWDYPi0Se3sazrMunye0ldGLyC4VG/s71RQy1annlseoHQZ7kur92d/e3tp2cnT2+/cOvRk8fotR+D1m0fNXpIq5xthjP6igspBBXCjkTl9xvOQ+IYUNIb80OqUTpxA/eKC14UYomxDkOHlW1Zdchs6X+D0yoQqcpO3tWVuJ0eIlpp8FDTy37N+3uqoyhbWlOKr4rSHF8ypr+62i1niX2Uxe2E3X4XlVQitFLxHOr8TZhe608b7bM3RFu0X9xv7h2Q+gaiI8uJA4Bn4ybjnnSzEF0rkB6HiKve9UicaoETNpgyLiIGjZ8q65K9MnFzMBrwEBwS+tQCVmndENljVFQI5HLl+vD52iKoJcbxTICQsCd8GZoxWbhFHLl5YABsmWIGMpiFcbXDcal2EpbU+RzEPkm8vFvQvvx1+T2pcaH/n76i6F97qX46PkuGdDUAnyrSrSVAnwJ78kqZl3OBlv3LemALJ30BkBoZC++0n5EcOYx6Vmxh8Nx98oFls7K/tZKfXCB9Co9JX5LCcah89lO+OIiVNDlfEg25fkwX4mO3waSemRQ01C6D0alRj9RcBs6BjImXuOm6si4N2XTaGktDgWaEynkyPjOBVoktaalwUNavfJB6dxqjGri4T73kufCrRnF0TtZUYblUNNIHFjLp22pGorWhYmaWn17J7I2q58d7G1ZrrQ6vwgVD3WkYdZcDIGtPUvNx7g1lBX3HIJHOhZbVLzhbcZFzEClOkwwlVavFo4kOG10ZFiEk7z9TjyhUgeJCSJRbnuEzc8vC8btWDYEnpot4g4YDOJE4thSL/BiGgbX0UDXNqH4LuouTPBxp6XC8AMrazgeGOFS8zLCDX0uPh87MGtlI6Q89Zy/Gbf+Jc8uBylWzkt/Ca1Q5yyLiyu+xgoNxKWVJWPo977mZkEst3CXkDX9WotzVxMCPjk4fcazWorz++o8dHjwyb3H37gcffvTwnX/xiz/41f+utewQ7pWeqMYlOwU3vJPhaOvK3unZoWboW9/6o8cP7l67evXDe/dvP7dnPdGVK9djnvVOjw8YjNBvBGrARkBrKdjG44PDux/ce+XF1zeccmPL6WP4w2aZhmqmiKy4XBzd298xe/Dw0cM4Q5WKLL2a4o0kWx+MY7SC4Whr4zWLmY8OD0ynUwmJST+JDJV5qGEUYV1aLWhpQr9jRLyoOZjr5DX6trxpeHhr6eurPXDmQDkAycUodnH0quIXG2+8/gOfX1976Ys/9EMU6Y+/9if/j3/4D/HKgmcrozIt0m+4C/ufrm082tLpcnCBOZ3zrSv7T/au2qzYiZMFdWBOpILZqknr48TR7Tu37n+bW37ha7/zR/+lf+/vYRFtJFvq2Wq12qnAZ/JsfPthdV50iO1QRNUst5XBtRBLmD0TXeAkdgcwfUp9Y9W0K3pu6mekOBOVemVprEZIpK4G5oDN5IWHtqrUhwcBNiwOCMn+kdHmtgMBASZXw+dVM5FMyMTejK2eacWH5qy2jaQ1zIMTbneFlsGyqXZ+LsJE/U1YrW3cg6ZG7C/++I//xF//ay+//JKwIG8Q2JHymAsme/ndxw/v/+I/+xemDM+OL95/88Prn329vv/0/2VHQiXybKlQoX9NmqUaUREOVlxMcLkADhllMtGEISuChJnt/2bBClkKHTeODx/fP3h6srnjDMe1jz/+6OadW7aAK60ebEgbhSPoV21OaNog4AZ+msaz++hFhZxzx2vaPUKP2K89Bh3Masr04MmDe/etS7Sv4I/+5E+++kM/dO3m1Rk5ia3j2DaePD74uZ/+WRCu39i/+dxzfJN6hVEw6H0aDaKL+utsKFIns3NXqMzIIeYgS1W1L27SkIVrkCY2Jc8+s352cL711krrMEWGCiUIMLudK5n0CF5rF4cvdb//IdBxoiqqa5Xbe0Ik1Ub7rkK/pvTcC7QsYXx8JxZtv6ftcAMZUZt8NkFwFSeHBoYhq43QeOLw2u7ujd39rQ/ee//tN9545603Pv7o4d0P7r740os7u9tvfectO4vu3L79mc87a9xAhi6wF5M//r/9w3/44btb1/Y/9zf/7g/eftnLhr3p5Epz0S3igmtcKfron/VVV1WzXYzaahIDG44Au3v3u7/6L//wV37zN7f2LTA1ltcYh3bZYr/9Kzefu/Hi93/5s96lCMr+jRtPDx6/8tqrjl5wxh9xZ9bFXqzKyJTP+Hl0/I2T0+cEz0WiWQ1Eqh53apxqRWQdLpXuuTkGqD7beXj5tD1LGv+83EhMZrtWyGCW445v6cz1LWL6Mv2ubzIiKsuISSl2sb3+2vbG3uaVt999cNdM5cGR15hYjzhdf+wIu/SKxGbVZ1684scv62edb95nGtx86j9YIDBkWLnr1Ergw4vjF3QVTjffN0TS7hL8DSorfbHBlisfRc/mPXFs8MeV5do5fMOmI6Flz+SFpZguVpcmFXkPI0Y/kWZ4zuDdyNFTD9dPb/WSx12NGhk8HBUlBHkqt95BzxqUANnqWPPUq4dMsAdq+C5Q8MCIaxVNXWETbZvvOQes0S8W2qtEOjGl9gsHRm7uF12WGrJNfQjh5PctmvK2H7Jz6Mo7Y174WVBO+nWB4FKYpkbQ6vfakGIVhkzrm47J4msL/QcUWYiAYKVTqmLjbnx5ToyA4M3zu93evlo0VRH18LERkdcaJ7K+YWa7TWUpx/BItmj85H4o6EMiizYz4JU8r69ySVmyLzf9eHY9ezAyqthACPQ8CqGonDLLo7BMj6J2cvvafk/aMjb2Z0E/S1ndXCIebAAWIIPjp3JO7fN7qv7Ukz97u+QYpnyK1MF2RY0yz+6qsUYoOCklsQsNeF6TpM6i4j+IuScrkdNmTypQSt3NabuCkkrhVJYisZE8ys/xOFenWDmvxU31tNE1UTJ500WaQGdUrLDHMAF+ReY4o+TucX2JEUlFgsOMC5pT4eH+OKLCetBnLSMUC9+FEb7DYVDupp43ZFq/wnyUByoVTpRdHur71xNl5B2iZaFtA1b45uGMDo77gHvKyWm6U6o/Os1o40FeI2WJRGDsLtjiGYOvk14vSM0wEMAa4289D75YYpJBxz0/RUjiAgMiOJRlkQs4Aa6bU6XBc+MaruYIqjZsfALVALm/uljhN89zUyt1lVZZ8QOWE/xERXJGR5+yYmDyyvMsNK6Y5nkJozRUSNx25gT3w6OnilCNAKZduw4CEvw4pFnOJwcGVzaeHng378Xrn/vcOx++t7e+fu2at6l6evHEQMuRKAGZJl5NlRju3Lxx9bmf+Mm/8f/4f/5juBjzfu/u+zt7hjgF9ntn22eOxREBOvzH+Xb2axhgbNu2cUp7CPZ2nCUED02r4auCgPDCsiK/GGTd08bWK6++eufk+Y8//BhLnzx+Etq0HzFJH6kWTFzZ3HPunHMmBIBUOJnKhHFN8eA34hvAHmmguKdl6Lp0qH4vIlmeDOfKGAfj03JNWeBLTC1TLQ3p8aGz8vf3b40czh2AIVZuc/f5xf7+XpNV1ciT1nPcXrtuYwXfKnFmY4SXtQm+xHBUp2Wx7bDPAHt9hZvz7Rdvv/x7v/tN2wruP3rw0f17d25fp32GwNLvRrymEx+iMFRZlMF81LLFLekVDZsJK/buIUzoixps6mkOMAz7P8WDgsEOKF8SptuF3mwSe/MD9QSsaDOBYwICPGUpWE9b4tJ62zwR77LgBBcoeQ6RhXkLhkCSABL049zDuA6qnkL3ixin7VRDJCjUk7Ci/pJSf9d8gXtxfuf2nf/af/XvffGrn/eSVT5OHlzP4tQOulMJt0wyXH/46Okf//EfWp8W3y8c0dO2orGU+Da2kayxpRpX3F03zloQZoKrPqrF2bFDuKIKhikrvnT66Vi4oE3/wqj80emxF+J1cIFmcXpQFbdue90Jid4XUfyn4NSl9gijllWs154hpOeJcj7zPLmKYcHkUXsi2PCyiCcdwtuzhkIs2vvWt7750ssv3X7xNoDMp7m7Fkue3v3w7s/+zE/feu5V8aLza8+On4hu7TG1No83snhvNLtleINVpLmJ79lodY8weu4HvNzEfUysr02gKoqBKcsopTxT0EdlAtX/1QcpLXCofmR29TTYk9/d0DVpS6Hl4ZLQZ3M7ecKgew15P9SVhHiFmQrzugd+Wbz48//0X1zZ3/id3/y9l157/tHDp15ofnxI/S52d/b29688fHh/88n6Sy+b2+xgn8MD+74cM7B9evrot37rN957573Njee/+sNf+fKXfxDRTkOGozUvwwrCStXiQHgTX4O+NnmZkxFzORzsxouvOwb5D/74j7QqUIPh0yeHumrP37nz+isvs+fnX7rJJsPcotGDp7du3TQjWhufSRLEpSiEabR/gnI0Wv5qFoJZR3XaMN4077Rie/L6hFfdrR7M3erJpVQW3kdBD3xQThSVDOLTQz0HVfR8EdPkGxSXEr0Jeufo/MxKyCsdbqDbI39muIDIEaEl5wUIhR9o6ImiVuezuUxAy9F4H6B6d7ZMNStsLrQpQO3FliOqU5vNM5sSa7FZYlQFlcmMT2KRgV1UdLGp6uTzTLksHFlsbQjF3IqHmP9ZXNzO/gGARWzlVJL1ZI2Jg93Q1e0QwqOIu4Q5O47F5APRh2Arbc/MMHIc2n2jaGwkNa+qwMhS/23gNSYTQgPQ02ES0EZZYKsSzjl+zsFKcMuZ1x3zhjJB3QJvkY1cHsXgODMiwzTdp855l9XRFCFAPMALwioNLeO+BGDhaCyrdLKI/mnGLKmVEcRQ0tfJgTcM5OK+B92FtaEuEYZDzWViPybFR9S7Yufy3ZMlu9qGmMm0JF3mmW8fCsH18tdlwdXvCs+zQXwA9DOe9/W9MwCNK1zWMWP/z4Au4PuUh8nGS4BHJfqa67Lo8ms+WeD3jP2vHiksc5+Vgdry5b6bhNH3kmP5ovzx+vyF9TNTtO+rfsabMTaBJGFCyJxqBQdcYwDdY33NEm20oq6fk8gy6AQD5N8bZiBjfipma+dVzytNT9RtpWqfy1/5EfKCm+Qs+Oylqt1sr4ImDPwafl3MJuP8G20tcQiLZyIa3tKRREX8Yrj1rbc3d6/l2RZ6yllTHTkrbqRZovbRuVSf2p15C0sZIJSvDGuPL3VB9klbGoMAQj83ILW+cFmbCpwq086NZiQWrp4fvagxX9t834gs4o1+2b2ap2bP7cts5X3mVwX+8yYTVx2+0BIBb2DA80G0sC6rU7DxDo30zAnksUbAVe6Rtl9LBY6QIGaFh+D6feyIbTLPe0Y31h+4XQkoQocokLynUNYr9wBQbQgNYuMI3Y2uIll/aqITDfwiSTAGA0CPDh/ef3QX5hePjr5z5dr567c/+85775hS+uY3viV8//f+9r/L8VpfIHjSxGo+OV/vrxXpXZzfnyj1VOTxuc+8/N5H7x88uvXgo83Ht57euUOm1qk4qrJxKU2aWez333yPg+L+NLdOIlwUSe9nGIHgFcv0bBEe6mmzWRMrHMwp2yHt/Thb1g51rKuh26PgU7EHH3x87+BbN7ya+Mr+U8E4/Oy3y0uunRpt1QAZhLPwSIfBiE4CSnWD3qjSDFdDsS5n0oyLRi6TnZ/Wfr1WXvN+sEsEHoeWH31tvUtke9vXAi7FiEy7VpzNQUf0Al/ymtgGXLzgns6Icte8C/nQwOva2V5bTE1YrJ/dfuHOzetXtWresNamcOPSzmbC65ypBVfH771913F6h0fvrW0d3Xtw/I9++p/+t/+j/7p6vQmUmWgrhLg5gfrtoRXXUpa60Nbs4ZKpwgn1o8E/mZtwM3vWhGBjOf4iajTQXYFsh6nbsiKDwg0KCQ0dU26clbKZy1cFFM9PrlfX+v0FMiDFcrWW2RkJVN+0H1pzqSpZTK+cdQ9CGfA2PLC7/A2bgFJas3roK4NuTCuAiQhoZUlgQqPNR+oAwxTgj/34X/7M6z9wePCYqowvy2dXrWuMEVrnGwdvvPX1J4/svcb+l04fX7V+QH7gUpskTEmiu5W8ai4q124OoqMnDSE3cNFa3trdKSIp3rbQxjiCe2GZjS60/dDe23rwBAqLjc2rt25vX9nbu3rV+T+bV3ZLSwNDszrDs05QFip1um08HcT5EHphuIwuKZTrPn1ubcO+k/fslSrYnZFvGmRpkL7ZydM7Dz8W1jcvqlMOVwrPPNxsbO2Ip3TUN7dv+W74xUFlem5JlkniWztKiWnkMlzv4VCWgOcW6p70x1vmUmsE/G2/e34+Aw0RPP/mxo+Re0QugIITuX46ken9mLx4pvxVJgVYAnezGvtfIeBrahp44y5oDjsV+9Vfo8ApeXD75IwOj9/41jd/57d/69GTg9/49d+w2fb48On2H1y1vez52+YN2qdkIF8fwHERRideevFVPqrDo497m41Zo1/+lV/9nd/9zb3dnceHb/9bP/5fAlVGlMQoeOf4a8YohpT8vx+bh+bWjizx74CgrUcfPfnlX/pPfv03f0f3RC1nT2/07vStj29cv7V/Zef63o1XXr7tpSuHTx4ezhASob3w8iteG+aAiPiw0BxJXEkTDZJoAeTtSNvxGzQ6ECLx1BzjZTMKFQCGHeBYLxmsBZ5Hw2A/4/DyJAFNCee2KaYK5DX0CKhVUzPKkqhS28xLrv4lzQYG3jl77IXuV+4/fEolOuXs4FjrAeXkC/ZSTSJO+iGp47jxXo/Pb1AEe9gbl5RRq6PDbcaNsSELFtLW39ebdfYpE+RazzYc2rHr4Il1XkgHUhW26lHowoMxKx5SyEu5W/cVG8437qtpvSUUozrCle5CzXckR7yG0zm5jfE17sbfetuJwwO1XI0a3ARnfeMBS63T5Uf0F0jlwjhlBm+fzWmCK0Ra39s+Pjdh1zGuXCjK47onU5QnZAOLJNKkxkBTozCRZbAhH4MGUSS59PNjo/4mp6wRuFjfe1yui/2g+h2wLj8THBL6VM5CgJb56aL5vbZ+LWjUJVZzHuydm3X+yQsle/9x3CiGiYL5USnnxWHA5oeNfZx1lC3/E2IjHZCk1O9IaVShgGuR+uWvvv2lM6sWVhb3z64ePvu9glKa/997QTBQUeyB53JkhtUO4U+uebxU+v/h7D+bNcuy/D7s8fb6m95UlunuqmqLNjMYjGkAIowgiMQwgnIhBfUB8EZfRhF8QYUYAQEkQSgAATMDYDAYgmO7p6dtdXd5l5U+b15/H2/0+/33czOzunsGJE/ePM85+2yz3F577bVdgqkbq3yfxflFT6bLFQygfmkSCDrPnd+nkVZx/7KfZ6VK0MQsQatMzrPNF0nPmBBKWHpQt5hEi81ixQNL6YytrQ8vTaL8g+iIcyorBj6tGqIYvQ7nUYTwSV0V1vGMMNAwZBQB3whmikJMmZirajAqPpxWcqJNlSgfZL8SaOUl/wBOE27W9igTS1vCNjrcyY2YVNjYGI5nGSt8IwSpK0Qka/Cm8dNktQhyiyRZptFCHSUVvDWd7U1LAkqgkXZAygKsX0ShBKes6MPHVY0RQ86SCyBwI1glhIBL4vqDOmkwW7EgLLk1NKC5X4CErIiFbYTb3tWENA9Ym2RoQTbHgkz5QYInYQNT6EkYQ9DMygISPOF2kMgxQLqPFvigX6iBXGzkwjcS25yYg/HIFxMuGyIBjDTRp8JT6hlVHIUoGKTkKlF8ERPqdJSUDSrMjKvVT8l2Nl4Oz5xhf3p6trG2QShefBqk/kb/3Y/ebfdbW7sbH733zsULl9guPcMgtHYNWlnOhMJAxBWDAF2/frPVWPv//ot/PhgMppO7k9HtX//mN3EkCKKjCgMkiZyBhRs2LgThqGawA27JH5Km3oI4r3YJFJnVH4YTw984XGestcUAAngAZjEjJu98zrQHjCic7k286yygKguUi9uUloP2ysEKR7FBn3RIEeKrnPNqB1ISAhfgWR9DNUEiW+gKnopaQMHAgg1SVFTIrVxOm6ESEdl+uNaA+Qgk2TtWS+YkJDfIQbeHPwxHzTcNd7asbTfdnZY5wLMpwxidFjNtph0WpU9HdCvODlncvP/gyT7oUy6b6/3oh98/+Lt/Y3NjnZac4prNtgRz5ZjQUbKqHgALoAqmW9BirAiU+NtIGUM5Kv3SCAqplVSyYFKJLm1kDyLDNGsTJGNFqKNdEEt1xJQDDzWjj0GdynAi8RFCik1FMR+pFXKtshY86C05pbAw2jIhJ2ohmloVi5Y1yRQeCR2QlR5ri7MG8mi2+TOCmcSCXlQHJ4eL5RkNu1IEcQuriI2gETMEYkNF/ngHL6Zlr3XWwYvhFwhFiVAEjBOTFBRaKAnRVCjYIUJbp+Kz6bBymCKkMpAACrqroMZwIkfnFWSzbkZ3DPqI7La3d3vrm6yIUAVpwpEJlApfnPoPO5UW85MIyAnKgTE3Z9/ylbgFGcmlVGkZQWEG1zBhmQgH7mcnJ2wjnwnTYGRBEIB6BH21xFyC2fJcVSrGZMAOC3QEsiqSRoB+grgovHZRGZHR+ilCL4YFrCDOy4qqAqEaA58EpiLlm/EFN7/lJ9iuHv3IV4hqzmDBa0JKSRYAf01vbiWfcl+VVH5KeVCH7FDt8KWMBjDiyH4QhKMi2En3T771LfaKU549BVkLf2d7C9ngMF828mcg6MrVy6zoxcCjm4VIcIwNlFzrr//Lf/E7t+/epoXs97b/7/+P/+vm7jYEgGgQU9JHbkVABSAfCYOR3EbjAYJ1sLdXr7Q//uiT/+n3//AYujP0tGBmhQ0xy14319bW++0rV1h4tUkYfbLB4Aw3xUuvvMIKYHKHeSCmLEEletBWBh4KCUEY9qerRiyBoRojUbDCerTiRyhYUihSSfyMmqF9IbHMMu/EVSx5lyMynNBqTSfLaIgiMm+DCo9KEmN2O32mRTGAOBkN0MZ0kHEf4ZipbdGSKvClfOAEC2Ao+lhGgwqOnTFH8+A54vgUsi8poCR1jwkPU10RqBt74Gnm4RUbejONFg1gdXCTyxQCPNCNVshJvdoL7NlB1abuSCyaWsfEyYUiYFihlPpphY/1GjgRIzCkQ8IXGp5mr1Pv95h0rTtDbaltELWVrEgs2YKf/ROOMiEmxVAmy0fYQK/bpDD8jcRyBJtUgMRXF/7zYy3SUWDlp0JKYGIKVW5ALt/5r6Vnz59ETbYKQOBj0AozpRtfGTEqthbAS1rxplNIS+kRknokxB0oANQaqBBLErRfNIbFEIjQpV0wfsBjDo3ZZ6dEbCmoyi7OUFBbpe4GgJJwRQrB8OUXX5/+FEEyoiU9/VTyMtisirz5xkWcfE0R5SnhPkqkfC0ZQdvEl7zJSPeS8c6vp+WdBzz7XRWzdJYV5GZvUTiWSvgszv/iJzOFVYIFxRlG5J0Zn6WsVYmJAmeQ7fmi87hacz9NGGbFlrfeIHkTmXcBoWwDP7/IUqY9MBNBXYAvTOO4UvxS0SPUF7RgjEq4q3Ws62hVNdPCUWdil1r1+KRzjlywjxEI4CROStyLFFGBDKVoxIGfVJ6iB01uxXNwlirKKigkTrzN1lqDnkR/iXJtdp2YixqnRarqLKXCLpNEH/GMfWvbRypIkgaJrMlHMKiHioxjGhJAUIQbsNmRhTfmo5ANbRt4Ep9huEoLo4FZ6VYoPhmHFUUYMJ299PDXcHVnOoLHCGDpwPkSLV0C0xIByOhA1Rl9Wz+I9qFiYJBJXOhO+8FIPFZIs3lIw92od6Py4EcqDQnYYYlDi1qPQi/6FdWyIrZe5fhc8FDt15p7NvqYZIicVEqtDoLEqLUeIzLSUqaXZkBkUCb+gzgSkdUC9HaQAHQjHUg1V+iGTq8y6Wn30lbXNWRsQdpzYk7nyQs3r7/19jvLaXV0Ovl3v/c//r2/9b9B47sglVFYh23oPk7ZlGbA8gAbJ4ixODk9gB7t7jGtw9ra57Dv2eQe4rB10sbWFsBdvHLp8cPH0H84mp6e4a3EsmTS5FCdIvnFhr88a0QaxB1mVllKy8pPPMRKFCwSAmhCqcRiJjSHPnRw8GC14ntljYqdPlKSqKAJPRAoBVbZoCqQse0FWbUaXQ7nQQ7JzYUyCAQYlT6S9/gdESRaY3U15Sstamzlne+5qzMJUtCVR0rhuVGfLe5W2w+Wy6+Yb8xo3MEATC2oMg5AJLoHVFU2XqRUu+11PF2IMfblbDnDDqlMOeCT45yADqfROtsOViqsbz15750Pv/71r1doUli8CEQV1mg4jRsYwDIiwg+SALCIDZlzIa6+lgEWmk3ozSdJTgbQRKEISsJPdQMmgAJCmysniIMmy3fYv4vFsrRe8wnVaW2TPGkj2YSEB6lnNC7LNT9ZCExmLLeER6rJOi8o6ytkA3huG3KufkSC5XyDLHkmHxKBFDeafuYIkCxIlixM7UfUVb26uXnVqbEomZDCiGaujIErQgMfMOL39/byodbsn63t4Py9jCWHhiGCcAqq3v1UIciXuo/OgxpKHnDSi6eDEf01u2TWzSd8IAec9MRzBk5txKmv0KaFRQo4yC3bYW2uM561trWFUwahoxOlUC089TYnWVKV0Sa2zZZui8OyaGYq426gorGY3uDqlJNiF9U2dZ/Dn540ul23z0du6KBDqtmix8yzdg9Ymt2Ho9kH8xnncJc+ALMc3W6e3JTg6Q44L1ITKYJqzfggGgmDlfwX4ysKEj51WVWoqIgU0pdKy12msuOHyutqkSDkgNwlHameu4yZoPJQvpibuBubBy6RUijRDwR5EjBBiZxfeZ0v/IRP/CgntSr7RJdRQc5cI1uqDOpuPBjQH2B605s/fvP//V//vzxsuuJyE47OIQP8F0R44eatF27d4jxdOoaDsyHyweQf9rFkCKXPEZDT5R/8wR893LtHJbj14gu/8evfREboOiBFlIIusPzUvMrcWsCsdNDnABhGulGqnprZqXRvXHvzjTf//R//h8fDEwcumW7qicz7s+HJhQsvsFv25euvXNy+3OtWGOdcME67nPf7rA/pzasj9HXEX95bo6PKxLrosigj1sCyvzCqDUvhnPLnlArtJO6q6km3/D+nu1lJdnngI8SPS7tUWz8gd9AMqaAC1g/2n7zxgx9/8UtfXt/oKDTJLYJprpKDliMSy8Iw8kDUOf1wba3ZX+ecB7QHVNIkRfDphUI8dZD1l4pAe40xjA7UaAEeyhZdDFfqVvOMSc/z6tl83Km3J836dq02YBi4FvHHq83yEbQ+FpEMUf/wz+YJwBkAEDc0uXm6E26USaxfonkBeL6ZTOmWiURV7blIEM7KZuoLj+RTRh011EmYOPkhrtn5DATYPJhDcgjtgkGBugYsJkFbhkTW6EJKIQA1CNZyR/KzZnOEMiUX/ocx0KvgAlyra1l/mIIoMTGNT7bEV8oBWMgFRwJnUEFgC3BoMsPBEYMolyiTEQ0BGLJ7kgTEESukREtOenZM09wTPUSfL43HPAsmCaQEmsaVDGRZ0uTrs1shVoWdggjzHF+YjoUGJQZGWuGzipVkefaG4r+RkNxcORDs/FL0B5EIeXrnyX/gxE1qlMx9oa10DYAfn+X4i57E5GmuGqzqfrAm31LUc4n+47mVyKXI3M3nuev5l/IcFCiPDWg6nHTrRhwYyEiNyQMHHNGssz+DWs+BtQCsWNnoM9ijwsBGzVkYEkN0uFtF5FpYShBL8COLZIPoU2HUoZAN81fxSQdAQOh6Z5qmchTAVAGIgX4v58WyS5C8Jw3i6GC40yNjOMVFiWyxzMyd+JB+uYKQ6pukTmEeL7pC1UJNoCBoUjD5y9wJG0hXWbnkimkJyi0dUPa+6HT6zGxFcaszHDRky2FE2lsceTNmddL0dtjjkuNXaFoZDFHPOB8DXQqsVMriOac8WlDIEx8eD+CPTcHsf6dD8MgkDdqAIAPs4sSFQQzwxMQkQoqhZBESELDnTRBdcA4lhl8eHEAJiR96Ym4oYPRD+MSzLjTApmqiCyBMTCIrmbjCF+o1jZOyR5AKKrykCF1DlCDl5a7/1AhKD6Gx+1Uf2Gw4tOdMzjQTPkBt1O8MpbRgYLNPtrpBs4sbkzy+8pXX33n/nel8gjtqwEYTnu3AlB84IoDT6QgzAhljiBz6vHjrs1/68uEbb7xF0IP7967duLa9s+XJTjgbGSVo1hgcYMZzZXm2udEFEBw82bNeO15IA3wwYp0ARklBRUyCrrqP7hvxVOhRLlAI6BF/ThdwaQE8ZkMO9JfkKWMyokjTFYOdYD9BNjMHA1iL11lhgNRWB8d1XZP3dCpIyIzrppwnRQeSeiZPyAXhCdCRc27JEgbFENDVyxkUbmZLFUzdCaTI3LKJecoiC+SFvkLqCm1epdvvTgdDRBLdiTcaPrPEBUjYGRNH8+Z2m5nLT44PKRVXO/X/O9/90298/Ut6duoV9inpdNbsXsuXVH0Io0iKGsCX7j29HVYZ2OpEM4OGUVZ3fySPlwnNII8KmT4kDEdPA3DAUH6xtaVNFxcUBzefkF9y12FGtibLXR3CQ8nVaJZZLn9XcGo2qTF0N/u9JDAPH0lsXEWE6kFLz1qWkkVC/ULtyk9tPDqYzYesLTcLMS3p/QiLeccLALz7Tw4ciFPDcIAIldjut2UhMTzbGRPwkjUIathjMHNIQsChs0jtbtbdegUKkDN/JCAQx6e9MgTPg8jVHrAFyHEugOTO5Uvb2zugStuaDfREm5gWZs7SQ4hjbClO0WIEIvb4TzLsoLh6EbTk8Cw2KNOWDewqJ+AfDsaoRLDtdteYB0RvBCax9oHukxpOYF35jcyELxjEEMNNAqhHhZvoDzDkLiFW0hGTjZShU2gj4fkH5so/MMsiIFESQEvl7gdFy/iEBjcfDTh/yVf0txQ0IfVJayIJSZE8KYcrt/yGm5ZjmPRU/mEsLYBnnuFGpgvEImw2LhucjW/fufsHf/SHh0f7jUab/DH1mQzZabdeeeUzFy9dWO+t7exsQRV8IDvbO0xrW1vvQV2Osz05Ovnu977LWV00Cpub69/8jW9evHiJqVtU5ZUtWaBM6aoq1Q2VQkbAPqZQdvu9Rw+fjI7Hf/6dH9y5/2jEzFL6qW7f1Nhsr1370msL9lNot26+eJklTGyfzwLz4XTW7PSu3LyCbgZDGwYqun4LaR8CEyAEIg9/bD4UPYgadSpxgQHi5Eo0qSb5zIvHwpMQkPCwI7GNm3T+BLfCJT8W7tmEfHLn7q1bL21sMIxmglQysiUqSZATRkSbw8nZhUs76/3eyfHJhd2LN1+41VnbUDFaExlG0wunzQIeSNlKfaDRZCE5AX98Fh5Z1Xav1i65Vrud2rzTqqzXmmeTcbva6MyWG+Pa5GjUmOAEZVdl5Y5sbS8KPslIHIJHEI7a1YgCeGoe30zjG3wBm6AqOgQCLNjBMAYxyIKaCmURNFFWv4RK3P1LgVYQ6RnmFMeBHKd7jkagi43fxYwtmrpq5BSoM9SCSyY+rGIRwaLKx/M7QQU7o/E5P0JvKupBALe+WlKJYGvjZ7lldSlPPLPahLJTANwUJ9/Uh9CQ7IyaD4SKJu2WFbuk4AdSkLNizz2SVGqACUknKH/ZFTyMUKKtqPg0TT4/fSsZJc/QmESWUFI/zanEKqEmTfP0NPA8STqYP5Nz2QuosS9yNX0PgCMOhcT0V3im92clLJkGFLP+BYU/LfFTDyXiKnqSCwMe7qfXc1mlb8TSSmq4BKJMZ3Cq0K3nGD80D9kKU2WNZM5v0BrNKvc1ZXAnYv+3nUKHHU6zNKWzHP44HoCdgXmiidGyc4zXIm2qACECmbeXtYI4r3hFl7vNE7LBqGlmmxeaED1Wk1UJz5FNEnMXETlCuTDNnYOBS8oqZm0RGObAMGNR77utA5+YiEpdR4Et63eQRXaNQTcwfZZs2BoAmSIVkOIaoZTF+DL0X9TvZgYIlLBJ5odIloZTDQwadxk/m842qLmT2ZCBEBKwdEnF26UppJEGLicryVx5rKCz/ouawZfsn+4XzPV6C0cyG7iNavOrlDBnDYb9d8eUYTrmCChROhck1T0JuOBmzbHbgL7jNDGYIg0r2MFtuwDO5UVPgdM99fYY+kBJNn3oYknqI3HwT7DIDbEANQ1TSe3AgvUMrYnu8JsiiSQYWlhHOcqnn7KHAyxiJwZYDhExdDD37YHgjLSHRIb15Xh8xt529Iwa9VNcToOT4c7u7rXTqx+8/+Hp8dlnP7v94Se3X7h+S78OO1E6wQBry1FYm1oP97HXz2ZvnPtFu3j45Mml3YtPnuxtbzO32C0CwAgn4e7FC632h+h0COc8ERLxD2Wq5rApoE0EhWRmf48YICKybJjjHDW2Npe8BTt0jsRHXDiblu2wGAtBjnEg2RoSB+QdrQIAzVUbS2OTn3TTECcOwzXMimlwjjXB1eodZBZVHboRkczcMYRfSGwrTCQylQ12G0oRwsjT0rny2F1yChYaZAxqIUA6OUXuSygdSi7WEID5dBs5x5MEOcPNaqvDrAy76wgoEAgLRYIOR4y16s32CQu4nUxer+8fnozHiw57O7YqnR5FjCtsqFSGwRRqSqKWI6NOk8PzDLuAgUYokEtXoclNaHiGslDa6ig+CBiVE/nVdTXbibF/ZLbhkPofWqGCyIf0Qill/FpolHcLIMg/Y8BE4wEYqfLkWz7z4EUWUOO8RanUjvxschUWj4o8VZq9v8wr3/xYwCZoA9J+8u4dJJyD8QIWccITYhHfap55g7XZ0ckJXUZQxjWCTqM7yvJQVaI0oQ+AdlVAKY+6lz45AniVniY7SBAS1FVgDhpU9tylmaIcdbReMNvEsZrlQNpo52sR0YlvVdsXL11nY1zYYRUmvsBDV9oaY/EmsUSbrWPq8+5jnuULpoOzAoAVkWEqM112QN3U98GBBrbUxOKyHdi9sLm9tXa2vn7v4f354Iz5Y3S811yWIDVwIVh9UVHogNpjx9M4ORhtQM6iC2gBAxK32cnbogkspkW46JtE57YiPuOLNxQYM1do+JR6bYHkUJhNkqTxN1cQNUj2QSDSIlf0UvlKQextQso8R+x4KimSqWMmkK0+FQrlVoU5HHD0GO2LOhxNPxmO//xbf7Z/eMxklX/2P/xzeN+odlihDlvpVDPNf31j/YtffB3j+/TobHNrg/zRVCwVEA3GP0bT/kb7/sOP3//wAybpdTqdzfXt7Y1tBleciumondvPhwhIJgoKoIdpdnVa0eueDYdMGKcsOmh/9q3vfOf735s4TqPyp2cIxdBenG/T3+xtXdza3F3H1zYcnwAFLe3Fq9u4rjjPQRro3AohfZEVCptKv5AOFUorL0NgP/6lEA166AgvRA89CSn8NCuSEo0QhVYVoxYOCnwzBF2BjCp+akCIRziXpG5C4cnlg0eNGzfVYwTlCxF4SjbgCIacGTmr9Ht93DOPmcE48VBIolN9yARDxqqsV4KsFV9OGmGOp31ox9bQ16o/TuapL2fdSnutOWB1RK16Wm0wC+gYR3yF46JreJ8GB/Pjs2V/YmMAvoi1aCLfFAPglIVAu5IJ3wSKF8VGHB4EVWhRf9CMEk2mBGs4ixEkoJ5ECqWWOtwCCDNtkLaIXODgv2BPEIVKObIKj2x5ICoWB8YRX9QgUFzQtNQ0y0J/iyHxoLhRjGbd8ArlZTtwkwWakKwJzJ/Kh3pj7MxSWdYeGAshFhOLISofQTFwg745GlLeiZxoQQBqAWhxdhc8SS4eBRAALrgCHWVg20gWJsKl3RXk8VXQWjJTRujMUjB/5npuzW21yglCQri6nkZOGG/5mtBnJwkQNyEl3QqiT6UsxYIjMROr3HzF2iXXsgZglVGKOYfgPPP8nmcqFQsyVqrzqJLiF10W84vCf1FYAPtFHwwTee09uILT1VwxDoZDT5MtfIXFEh0vAUKh7chED+d75Dup8D0rRKgkImn6GRvj28HuDFHZFFEQDmyi2BVW2zA9AvhRc8xhcVMSxYjd3KmUrIONuWZVpuJiqSjpWNXkwMAfGoEqQy561dVGqZMUy1PqINmLFIUrwTypezzAjMiExcgzmLkQzt7XLlQZ6Gh3xBYwxzhHl2xDz3Rwx9zdxcQNV7DT9WKhPpyHBtMxKBFkdCNu76UbfDM4SNvAQff0dlzUWugqYVSUlVbODKKbkXB2KUZTs2shVUvs9JzpPkxdFQHBLzUTIYBBwCrc3PhmhlgRVncwdVIQdQ7CFvNSoeTKnaoPEd2ACMekDv4wTuODtORnepWSD7JMRaGmBz8NRAb2dEioksiuwHOeNxAqscDiqKisgIds7CKyZqcWIAt6wrjCO/01REj3YKfX6fe625sb74wnnIbzyccff/zu2//wH/7DR3t7a711mIFIcKIU04HAMDvvKDwce/tXvvq1T+7sTbamDHrfv3f/6tWrNGn09xiedmga0jO7s8nWBQ0gnnII8oTt4SQ2+KjZbEwA2V1KhFr9Au9DWyhP6wF4qtQV3fiiWsW+nSw77MUnRXBzUgPsXiB3iqupbAHMy9pDYqy4Ds0zvnTkH7eZGzRIu8KREBtuOYlI4vHjHf5mARkJEzOAAHRRLtZRQUXPcycJ3FMm3VleezcFo1LBlHEw1kFTK6dyWAa6RMHBDaAlsRaldUrfGFUD+af2KR44vjtulhSOP967e/fuxy++eJNNnfBTsmbj4GhAyaSnitCYMn1PjR3J1DWobAAthuqqDxkiJvicLhSZZsWFzBJDAuQ/KQGIvFKjEUKpgoohcMWyPAVLIiVQPVKKIFszXhkTSUS2fARYoTJziQzDQybDCDIUQMyDOHxdvSZTk2s12homAsqcYpDxZX9nDWct6iC5msg/5EEEgMqsmKV6794DxANeIpyqNrv9i1bfKQ3CCmcZhqIIR8EFB94sOcPCyHYL4R254esPuzjawu4+3WM0p4iQ35QF69Q2ji3vo0WpcoxzNpqMcgow0AfHABe0I8wCKmEUcna2ajAWWkwYJInVh4hKtc3ALAfKsrCeuRN8tM+cVCajd+IYBcC2aCxQO5ww1kPTIeXojlQ0yiZ7EQrrfKYLPZuxSnVNj0DKUwCU4wKNAAOtbOWBQJ41LTQeZISfiWk14xvqurwb8VkMY3EljF9S8V1i+eQD71Qm46jskDEqmgWGUEUUA0DKMj1cKPmxWScJQVGVAR9diY+/drKxvv3hBx+//e77BUjyZMo+rQzzhGg1Ws3uS0z7WVtj36TrN66yAydH0XsMVZzHw9Ph8dHJm2+/9dOf/tR1+fPFb/6D//TKtcvMaaH7TxUAeppGVA3QAhIlwheeeQIKCI4+Pz0dcsTEk8NTHCU/fus9thoCLehGxWaWP9F7W+2LVy9S+9c3NmnRKJmNV8eD007/Qr+3hY4EfzIFbISLZMhwaKBWWNFQLqlH4DFHmEEQB3NVgEQUGigHPFBLysrPMCxM8yWgq/5kn3xIzjYQ5iCZCU1TV/iUeDS70JmulF9JpD+F0sKNsJJ6g4+P2oUnj3Nc6APcufuAuaDhr1zighFY/+aQRjFIuL+Qo+UaunYzJGSjuYY7CBdmlZlDnLrolGdMHPRrZInUG3SH7aTbp6Ito/4KvI4aYHPaI+jwpyVAUwm4vih6Tv1EY9ssS1sLJWXhIL+IIxmYl/AQIIFkvPH0mjt0AXEkK/ZWictnc/araY1BWWDiwKJoI26sd6YPw2gn8kAqaAjk/hRuUSz6w7IiZqV0iAxA5seIMoxJ9LyXJgjAoqdwRjod8Iwula5YoZU5qZ9QxFoNoQhxUjHk0QlIWyml+c93arGLzbQP2e6P5OTLuqBM+neQ3GFLSUW+2mZIm3SzBxoVTSDTVBRxo/ziS5ie+xIxe+795x6l0c8EPs39ubyIk+BVUHkWc1mndHt5X0VEfMvHkiz3rIIvUVaxStG8JLZiTt0reRnmh2qTOetUweurrEMgozjQj4R0vf+FV7I2x1Jgua9i4xmChUqAPEfGrd4oGgmCYCMGMhgIYIKS6YzwUrqipDImnlG0TJBz6oJVnkqALYVA2ZRDGKUJyTBOdXYRQJjjRQ/O+mfsq5bUfGSOqRRClDTCbDHkIXyV+RUqWrX+mLwIotFTNQR+9aMGZyDlHqiQEYSOmFHl1iT7GY7est82+pOjVWxMWRBJw9rB1Ski9Eru0+qaQZQgFo8SGgVAxdLUobJNrgoQNqplprlmRQ6WLjAo+oBPTtYk6hiZElkF5J18UWcQk7ZcygEAtdYQ58JKZuktablLa8hiENAH3UIODW7QSlOE5ci0BSZMIzlkUJAlESmo0ankhlGuSahhmpgW5SVI1NGUgylIahlpUZRtqKQGBadvmQQOeuebedjTBUpzJsDaS27hi5iVP2o0RyYxWI1LjHOE2G4CXA+Pjnr99Vdeeuno5Bh31d/+3/3Ndz748NaNKx7dgsmDh0uyggIZ2rdEpyBjA4734sjkZmU0HOEno1xyo6XDtTMfgahwQjmGr2hSG+t9cpB6YaUIsYBbotVnI1a+OWrBZ7xBUIdQ1OfxCe5h4fYSg4LsbHOzx5k9jKRQQdiuW2+iCMN7lr5qqi4rV2hvKsxWRMYcF+PWHSMsk11RaT42koYxHbzstmGB/IGexZQ7xWlVF9oCrswXFkrieLhSI2CeKBFTNjJnBhXMRGRZQbWl1jkPn7VstEsoztoBGMbQt5/EikKEnfJIijbR0ITzPNbMgaPuXZI44Z3uKFLZuv3Jg5ducTrB4tr1S69/4TPf/d5PKZY5DOre+a6CWzsGYnQIFRH1HmqpBqUrF7+lRREN57szvAcrdFLJEjklEagmbFoqMxwTKDITpMMCouYiW/7KZd4WU8oAIwhCbkR1Wg6fuJV2VEBkqHS0ZhahgpQhLEkgI3iY7XM3EpmPRXvnWs76/NaapwuGVfTZYVhQDCUnJ0WBmOkqQ5V6bXAyfvDgobN3mKBF5YA+HKIUJ7SdgqgCa6JP5uRFMa3HpVymiDiBQYLaTiP7UMpoHBRQ41Cx+XzIYi1MlTZDj8Mx3n3tBlwTFy5t06x2Wl1VUMk1CkYcUkpYIyGoVDAHnaWqAnJtCMoikK4+eYx5B2NIAIko2roFQbJAGcOUOWQW1GljFB7s7XMQ2MaGp+khZxIb4SN3maA8U33x7QA19lXhJ8hGqwR34hfgSKH4eFFJjRBIrYQrhtmMsH4pkAzlDv+hTMlARp+Tc9H1uTqKajKaJZDj+LIrzRv3pGXiG0x55JByBch8obZLY/cePeb0ktnwAqOsrN3CoETVZibMkkHbs8rJer/PHv+MyWB9DUeY427AQE+a4eVv/sbfuXLlEouAN9bZOgyNddZf7zMAQB+AFSEff3T7j//oDzhb8PHjvX6PDY2df7K5uaGuY0ZcGkYK41U9If1teFS0eWa7WLol3T6jC93Jo8P/9h/9h4/vjhsdRjlYda1BT31gv9pbN250s/9srTE9OalssNdZff/6lVaj32v1wUkXhgsI8MHb6NOru4L8VuroK5QErhylTmcFQxKONkv/RvVWs0MNuIv2JZUUTlWURXyWnBjPZdUKy5PwtDGijveLffz8p1CRb6mX1r/QmxNFSM2B8fCcPXBbrZdefunFFzaRMQW3edd6Mrsho8ItZl7RiE0c+kDVT9usdnfPU9xh+Lri56O2w26kVsWgauE/VMV6RXDVxTj7MhzEzDVEGx2N2nPspIlrj0k0LBKm/jFrnLp3UGtOKqw5pt1i8Q99ALbed5axs+0ZggUhMdNuTeOtSaCsSRakDMVoI8xtC9jVyQK0kjISFGuhxkkj9CwoS18q0ckldlTySn0ly3Xbijo5hM7q15TshqD2CSajSYWV0OMZjlW7Pk7twjnp+pxae08YdYQBmEUAAZQye+EkjPJkZR7lU6qqjRTUQyaZFpLm9BOWW09H8aAJI/EgCBc00T2GuDJj1rnMOIn4CIxofBoqXBvKMLQAETqwnLeIeqRbxX+OGXEghEoUGkodGFpkRD2XT3Y85FB9ffMeh/uAQjSrsOcC8mCzqtmEPQ3Jl1W01Y/y9iykxPS9ZEFSYU8MSewjxCyfjbwKxE/JW+bymPhZlsZR2X06NG/PBZWcDEixK5DsQFpeIppDcimvq3gGQdi/+EqS5z//XIAfCTTbVUmQHxJTPeKiQlaEQTnI95itpOAtVV3hBr9iuxhTKbI6m13IQ3PhFNiSXBVMjTrPE+PEdSqwPr0NGuaVHgEkhDlLQwRPCJ6BTmtEmU/bLBtvGiJmMVIT3RSLWgM/BIQ0hAoeKaJxqMoaT0GbMrXXxUSgKYIK5xynYpFYajCwFiCx2fJRzEyCRjZDayiZFByRaXDBbnW/HYGhFuBvMbFl2L7ynDrlFyelEMhsUWu6mQqlsIiJkbUMqb5kCzn5EEAIpf5LEWAyom6SqB86/wBnbQJISxX6QjZSSxKNVLO02lNDQ6fEBEJASdEwgyaHipkPZrOKwU/gKJJAvgHB77litro/DmWRPRrYNWqpt9gqxQjAm2g3pca5RQJUZbybDbAvXrr8yZ07tHzf/+EPJsPptUt/D0WgKQ6V2TIK05n95GZ4OuMUr9XW17d+9Vd/7d333rp9+w5N31s//vHnv/xF5o2po5bVfrdHtw6Ws3iAeUQb630GRlDiISKQQs8gAp9cXR0TMaRBPbm/D/uVDpkpFxkTF/KNV2zObpV9x3ddP6Z6UxD8c+oFWz/011B7/dlorF9UOaBnYqMCixBQ+720yV5Qv7BOJoVlChGiEdnnSfchk1FJS+VGJqBnYaMPCoIElrTACkNt7IBWXMCORJZLM5UlKtj3RAMD0ykvKl3KVdQBCUlh7ivZy3Mmu9U4o253h/2UWKE4AJLpbHj/we317b955+NPjg73JqeVTquDrWk1Qo6QUvgUkCiRao9HmrwBUuhsuXiO+y0YpGaBu+NmHAEDs6CJjxlIBIiIreIOOMAc2pOdGHNFFouwSQezPP9XCCSmfpFEEir0gXnJAhrzTjKj+JCoEISCSkNIoDSkeAACLz2tiW18MySfVUHV5YVLu521Mt3FrKR9SpbUyAQzdBqNjx7cPT05s4LSy8LEcFJVLGPtLPUMwMA8dUF6nuZAZnTHNCXxa+o8A0K+MlbGlDp2eoEpsJi+QacJr6bYQBTthld1djnub+9exOd886VbEAIU0K/OcwjglFHoEN4ILa/UKFQHs4jQGRhOqpEyxK56yLFHegVEH2rJKagjTKJclm/N56cU3W53OfPr7OyUQuwZlewdrYVkgcHVjfDdM87UWiEnAKr66CfAMsmLGOtjsh6XcD3fxhVWkxTeWf18EZQE5alETOQkePoUcITauBoi/PBqJCljPPPOndfyqaQmBRAy8RIKYKSw1VfGn4nDIgfsSIYn+RmykBeWMcABvhtr64xBYj1eunz1y1/+wue/+PnD/QN232Kqlf0iTo8+OqEWMnHlYHT4wQe333zzncvXGcNkptDmb/zGr7708k0FwM65fcgAyYN0gD4CLbLOluGHus/49KOHD3e2L91l4v/eXtG3zmEh6Zz5XZWb169fvrjdbFa3Ny/Srrca9B4njenws1ev9y5+YcQhN7Ue+aqbMH4plhmScxZ/AwTEojHA4Es3zPIz1RDDAO03vQAbnBwly0wsdUNXWRlFVJleMARjmrSTXT+3fOY39Sl6yWz5Ax0y0JCSzJaAnFS6a13GKxxUV+HKQDI3bdhEJWO7GzqfePMYcWEij6uBwUIDUnjgB2PpCj7vQILqVbFrbdJBEBCMB7webITQ7LCHucuCmTBltYiwY5ZQGmhixc377AlO8ymwmvmpTchqkRfohamrMoXw7nOv/Mo9ywZ2Hj3MgxfGjgClQa1E5q1xUkMxpCTAxDmD+M8ZMcS/TXpjoScokmoBUPbWycV3fgCQOs5niSKKVHjSom+YJYHkOseJ8qUY3/mbQ0kreYlOglRACYp+INCswkgpJrkFknSMxji/QTWh0kc3orhAUdNLcIRBHBzhEBKokVLJ0Pz4ZzQ++gcq5EINYv4FA2oE0N7ZHls8McjYBkzcs7mJWbBs0G80X9imRjI/SgXuCANlgwRX+eEuUs/uq68JM075uoqRjwY+H0vsjSXkTyMY4n8jP5f4adySf2oAyfKGxi8qpXz7uXvm9eppMOMS87y885IpTwpO8cNxSVDFjny9EUlfSD4VyPKY2zmYRMv4QDVjBZ8ijfHYNDCIMfG30BjFrTSRXFlBWniiWGopsW35sagoPVUIbq+8zHTxLmP4VeuPqHqV6SVgYyddksBPlpBVaizlscuYIXRypdlnvZruTmsVO7xS00RItOlS8yheEoWJeJRVjBgcfMxYNZwICoZw4tNXYxazjQCsa16IhqBgcCpSyKMSY73A2CFnXLTmkvaVXi9zkJ1XyzE3S8bfMT8Rd2bmoBhFXnSJbU9eg9SLnOJxtGHjVY2sfrdXa1kSViDgLN98VWilZsRf7w5fdaEFUrHVTWApRLYScWeCAY/5Js58s2aRFTXdCLIFU8l6CWroSHvM1vmUFZCJA1nplFCJqftexCOxoxnqe4z1ZO282PryemXGcP/HEtXM2Y35os/1hyQgVfACSGBIlKAJ5JQOZZxtnEzBA2cXka3blAd9G2yRIWzmM91l2sBoeQ+TczAYMmPn8qVLp2fDwycnL754ix1G2H8cbw6pmc3jsKD+MBUfSiesWBydHvI3m+yeHDCuPYAyeCPgOZBCI8Y/2Za+iZeU84eZwMUYo0ocPoiUMWQpbnLNNIU04bToqCYIB0e4Eyj9BDcqOL9AoYNEyUcmyZC18tcUjtY+k/ybzWM2H6pRm9Bt0hddfKHmioW99BVlZeEaT7LCPOWmH0gAmeDrai04JC0iLcjCwp2Zl5TVfCjXgG+FVKTfumNvNhgi7Wjp0krJ8Oh8wOQX2aevRCZOhnb+A80WklOfcyYo20WxWSDrWza22oPHLF6hpnbffefut/7wj/cfHB0f7S+mZzsbOw8ePpwwTRAypmKH5qEu77EjaLli/FMNKCmrgRU4iY6khAuwA9mG0xEk4IbIatrUFN+iaoANhF1w8fw/5VA8rQtkvwXxsodP4qSOF4LBxNpy2zyrBzAWIaD4UAj+UPuo4OgG9UykmMz8hSUQ1lrmBD9SJyygs3LABt29Wbq/9Fd/xRXzFfyjJsFWC4q2eiSy6cU7euc2e2WSBawETybqAIEcYNYO8xitDAoXnR3FW98kKgiLZNpdW8O65KhdigUQNjzorXHU82zBzi5KpZGQb4qasMMm8wr0abC0o/uFr3zh/v1HIM6MOKQZ6hWkySZUC4kAGJ0gcRA45cjUiAYtlVMCTEbfA0sd7yiZOB4o1fBqYDvyL0LLiFzab6owcyVYGe+sPzBV20bG0fmMN7nVsLOkJBJ9eR2ljrgCDphCOujPnz1efnEru5qFKUwlDgJRGTNZ3kVZUiIXeRGTCXzb1pjm0A5edGhhRMpKeZSp0Cl1hYl5Bnhml99nvzZxli4dxc7ZuqbKzcJ85Ee6YY3EKba8vWBbLVo2N/XRkEWH40SADt/+9rfoC8BYD3BkE7NpdW19/aUXX/rs5z7b7bZruxvgSs+Bgph0weDhaIgftPrdH37vJ2/9lOHD5WSbBvXXf/WvfuHzn0cZ0yIaE4dTiGJzISSFgTxBYM0jxIYBpWZn/uKL17/1hz/4V7/1r2Z4rJuA0XIpOVvVdHsv3rx59fLV7hqiwcY1p+jo+nKTCf8vX710vX9xUDnkJNbhFMOLuX9rtIDzalt+1/elLUSgJgIM5I5/N77iomaQtkO+F9e6NBa60FYBpQKkb8w5M1wKDzTPc5k7TmtiEmucldQGy/qm3oWqWBAMsLikaHF8era9vc3Bxta62Q0KULNAg/yjqQUkRj/Ajto8HMKE2dngDJFgvhn5I1ORMkCS15oQUlKrwB8KdrM+Lva9pxIAAqe4QHyHXFy7Prmgum/RvnCE6Ki2GIE2nqVlpY3KNAfAUoErX8kx3rOgpZ1NYhDiz6pmTZvSQ6jtK/0EAiXqa6quNsp0gze+mietCt8Vej5wgwv8C2WZp1A5ECp0CTKk/aSUkyHWMn1UfP2BCXyEwCaGHKkK9YdunDK/rvA0H1F6aoWeDnOnJdMVAo1CIgsnIl/5jUYQIB+UBf5BS+7zy8bD3jMPbly0QTBUwaU14T/T0LgJE1Dgk1IJMMIDwC4y1ZuvjnLTCyBQ06RrgdIne/EG8niiVSPCqZgtZldw42IdoGU98YnSa/jsfuYCRGDMtfr5dATyXkVZPZXPFnmeMOmg3yqitDj/xmNEywDPuk4kKZmKcx7RgBxKnxyezzrpcnsWqjyVt/LBirO6Es63AlERhSIhhDxL8zT+ebLz9H/Rr1kKtBd0XODPsPFSTylG+qUoE6ZHGnlUnLgic7DRqstr+IusJRdUWJmaouQUcbFJLaKoiGjyK2dYevSDtd3Jk4jKVh6Qb3ivxClWyVUskQqA8kJTEK7sAEoCaOCtD8ikxhmNE20Y6g4Dgjyp3TbMhEtgELRtQipFXa2d5sezt2RpcCR3Ki9SSZV06r+G+ApZgdRDY6MInAExsDP/nrwlI3moTYjH9wBJYCgnUlY5IyHqwKFLmRCyF0L+TM6za5fVihRg7U41VuFqDRlmuSJDdpaRdEQjNXDT8lr/YsLxYE1OGagkPxBZzWC+4a1FCbllcyU/v/hixpLKr5DHQEqV/qjOEsE40hlVqD4CSKcsD04xX4gpShQLzWhFoLajfY06LSjOS2YLbGxuEuno4HC5PGPTDKZk/ZN/9I//y//bf8kAgjOrLEzjjVyBA74zQ30wPPvc517bf8Ku9UfIFZm8+/bbt156ASA5Mhatj3u13WL7PNxstd4a85s1xwEfcIBS4gdeFTAfZImGCOjR0AMr1MOHF8SlBQIAj+wdxMmNZipcjfxAD/4FNhrXJrtH9PDzATFecjQcJFbyaLQkhGgIAxepJI630KfAgKo01zRgEtToXoCrLJEmcklxfIPZqmO/GRweWR8x0LhjidOS4V9h1iT0IxYZ0FOVpCAjv5POcHJeVIfDMTuWYI70e+utWrtWOSNVq1M9Pj24ffdBr96pNdjzkU3lbbPu3b9Haoe1xUZkYGw6x1iQQTQQIjlKhSgKvIAhhxyHZ511uqfwypkgLiJkR0UmW2PnR/nLh5QkncgtypfcyDcGBHFis9KHyXfeoSSYzfrOwFow64nKQcLIfJ6kb1hPfhbHf0EkJdmSyDkEAc7vIlDiQKrZbPPihRs32bwStRAgSl7nEaE3tiypP7l9GzIjoukCIzbZ/B4qWCcB1T4Y9YE48MoKCi4N8K+0u2y53MxCDDx85O6S08HZxKOO8M14korr1BuMpKkAaSOVQKhCv2ZjawMB5hg7es6USOEFC0gfDEKzUp3IWI8GiRRvBCgxBAl+Ft8cYgSssBCo0RmAgSEGS0kQzpKEcqne9kIYAQAaACkKB7nCo0Q0azCguGfRHH0fw0K2YmJkJ029idjNbK0LLFS36BbgJCL9YYBRwkTw/Bcu87mEqG/gXd7DR7koplwhqV9Jzy2/5gEy3CIRvBGu0OQio/L8tEA9NdUyOQHVumDGDOWyhzFM3djcAq8ffO8nDx48AQz6LWxGgDvjhRdeeP31Vz/z2qvsF+DGcfMxHIGk7PHAkCeIDk9HnAv85k/fOTg8bbN8YjLqd/q3XrxB3wBSR1b1+lOQvBPyQA9oQS7oQR0cHZP7d+70GxzZ8eOjkwHtF5ImfhKncuXy1UsXdtG5HAFXbdCv7zLRp9mcjB/u65RfHE3O1tm9jh4HexvTaFCYHVFypzE1KxgOj6Q6BEdIJTikVOcBGYKp0BJdgkpSwwsxDV9VuIACbQO0EfgfmTQ3ZQqLkDLkCG+hvpKq9cxKJlxqTBFBmdOWEZRqaB4+qMOgeXUyZOCRXTqO9o9G7rzq7tjEETD0igYHd8EQYNMqDsTTM8VeJpwFhpDha0N0l+5Ox2EafDJByEmrRlGTGXsgmKSB9W/9IBOIpuzBG8+lBmFg1n+N3OMZolZQKRB+dLFT6ZBGKtZ01Vs1FVBx2jZfbNNpo7jsKFAHIAMDcgIcYAm3nLA1FIYZ5VP4Qj9A6KlN8oLU1pmoQr0b6fZkWj3ZqumBLJnAIykRwL3Z9pkt8BMeW8jHkIzCQ1JNKUjKpi5RLFRYeUBkaAP7nPtg395IrCaDALQL8tmhAR2v6g09nxCOcPV/xAR+8SqOgsPATSZ9hXuAQlLtKl55EUL7TPwgEt7AwYSBUxqurlVt8TPlcRXWB2fobIipym8JLTESkpJ84qJAyWQchbRcQJ9scyslEOC/EiXk8pEpQKsk5Se5PRfyqb4LUfmuP54NvJ+LRHg+rX6U/iBcMjsvc1W4rwWsZzmsfP/PAp4+GZMeDGmdbIL4YZbhAoffZs7lJ80vtS4Ot1DNQfyohqjYCAcQs3MFWbCQljjV5qNgAs+kC3KJ5gdmJJ2neusJ6RETnPCYYcRhb3zzzJYCuZOkSCojc6TzpmWJ49b4fAQy63VBVjD1XUg4MEHS3cmXvHEl6BkNBACiQeIGh+x1QVNrwSgLCo6gU31htJhWcCdfZzp9o/0EUUWYTU9qErp0spAllo2l6VlHzsWa7YGp0/gGm45nadwLGQklo9YAMZkjxAAwxyoxJQCl4MgXE4FoWzGLnexINCuICAI3UzlxibUwP50NA/jJy9qQSgDV2WwYhcOBL8yHoUSMA+Iwxgmy1ETMbXJCzbXZ+g0INTX8nI6DFUgaAp3qNaf9ATmY2k5TOorjgUopo/RkySQeKSymUETWcgNaIiI6ONJQvpQ1rU+Zl08m4EA4MfX4spU+JYNz45jNL7TZ3OtTlfHZz37m7d/+7StXrrz95ptAcv/B3c31LTyL9J+Rlco8a1QkO3qEPY7ULTgHO/1jW8FJ9fHe4/76+vaF7Xj7KxxGxUGyKmihoocgBwRTYGN82tKRGVoMasuhCAhWrBPh5SPxTZCXQnM7q+TGhFeQRsPC0Ux3aTAL1vyhV6MydXI2CR2KYRgWsB9hShmSDgylWE3IiCJ8EapIIQceXJUPzQfZPkQuC69l+WP+cId1KRE2KiGvPGOCExPPrQ2BF6xi8SgK2uFst6WizTpvzJBu9C/cQRCVMcEkMeJBDovN/tbxfACfWdqyvb3+yf3HgMi5VcQ8PZlsXLzQWatWnsz6vY0uG7mE5bXGKbIErRQolsLT0tH6Yf7a35bnSDH/fIqw+EuvgSPVgD+apDjpgGqFqHhakZBYJTwjbG5ZapXXPRwUMVKIBe2gJHWe/jPBfeUq5ssqK5nK8Pip84onnGubndmFCbxX0PgoiSFEIucBUxhoWEpYjhSlaNmkrsDutaYsZ+v91lXOVcskCb4GKo0nB+XMQ/7OHj/Yf+edd+WO9GnC58J6tsvEi2g4lLXRJVfgcTKMY5IaCXalWGUBaji6kh7dWGHxDHs0n5xyeCuOL0qps/UkVKq3sJAos80Z2mzbcHh4tLm9yQR0AebfvB0cR1CnUAYcEGv+USJUdhQMeKAA8dFz9jhopc+osIwEYICzaRq6mXZbOWOIQGMf6JEkNn7N8IxrFWD6YnB2ErcGBEkRhLo+Cq8SthCJr0yHFxFavslbed1gkxae6cmQJ7Aok6oXdbJdDEBxuRUxTSOUpbYAKl58A6CPX0BWRgSLsMB3dsuxAhuq0iNIsFJRIDmJjM7OeMZJpNx58psX7QjtB+KJbuVwVSabo67YeQb13jo+PHz37fcfPt77zre/zb4yZL7Qrz/vrq1/45e++plXP8vKgcvXLnE6GFdBih7O5sbm0f6TyXD4x3/wrYPjAwBj5+Kd3drrr12/sPEl5zE274dNAiCXuASO19KI4JJTneJARQ3i6em017///e+//eF70BjiM5l/PtpoNVqXLuHPmEwH087VLlRiIWing/LEx1e/uLl942Jzcni3u9OcNU/ro9fqy/3q7EatcTCeXFrU9mqVq7jCl8MXaVaqjUfQN8RF4dAqRVqFaDX2VagN+oAZSkZnLlB9ENrYhEIbn8XkY+7LDIqbh+jJO+LJ5krZp0Vdxws/g5P6/ekn169do2kjBI2ElFhKWEnbZvPtLGvWDdQHk8mTg9NXmGuFGa8ZjqqxZYL4XApVKZDMqW8RM5awI4iOoLGdgZWvg9lAKzjn+JQq+6EfsEB+OdvAhlg2zqbTs2WtHVN0vc4aktpIi1qZdUybCl6t7gMjY3dgu1zsqMVqh/piGFnHGnH7DVIHMUmFzt9Gcdcbx9KkdlRUBDwCauWcyBLb/mfMSHpKyEfIQOpUBePJG5NOJ9usXajM7wO9NU+NpZRb1RQl9CSCcN8MuKxLcbPzpJ835xec81RClbT8ktRzhGD9Q9Q8aya5a8TVW8v6E2nJMTvwEPGTaypriYvhgRmCUiZ3ukvul0DzyWlFjoKo+qQAFCMpqSAimx9cAtZF5RPyIY2f0leAPz6SBlMhD8vanfgkLlqi3nfzCF6KzWo1rCtjeS3oPn04D1DojJvraRxi+0EiJ0X5LXJqpPPwIuymLVFNIQgleULNP4F0ALxKaasMnxVtnqtcn0G0QibpVjdSUEA0gtGTwfO5PCuCJ2L8z72eQYwFQQFKHYQGwWKCcMfqpCSCRILGqShS31ITMeKw5x0wJiYZwAvA1FJXIFTNya5YpUgDgoFlyvokGOoiSeumpj/VVmlGAvSIO3qsFMpaCAhFNL8oHVkiAOhwRNF+KF2YCS7mbS6YywpIJtF6Iut4UYDfVSbUPBpF4EHIUA6sj6LbLEntpyN/Li+nWIDhmBZwWEz7yHSzM6QQkEd3U5F0XSPElEMZyKVHtFSZBwpxqi1TdbrsJ+ZJ4HigyQMsaDKtPKCgINtL1tyiOWdzQDmlvS69QL2K/5h1ezQiPGdiRoivmcycATBjfwnTa7tCfwcvqToasrUmJ0lyXDwQZQKJCBJAH4NmG2LDIKc2QlrMYt0YTHlcW4PjirtEMCcykruU1WIyPCyR8WZgLKLpvywVGniJG7YAtM9EB0AG7iUwXhn4C9kli3qWqAbj2aD1atVwbXJAfQeqwBQss16vPzwbsIfDa59/7eOPPuyu93/wgzf+3t/9u4fHR8wvYGoBRUtvTT3dpdj8i2GTMy53tncPnuyz1hZb7ejk4NK1C4AZPuqzpwFALoAS/BdDTV8tHmCBG5oNaLToluJCUBEJKbIkQdWgIg3gsA9+YAyxpMBJGnahEC9KknrMw3ZcSmLg7dPOkD/E5odKkCoAzc0b2cZ8hxaS1T8uyao4nF8pFtMHieWj1JU9IXgiwTuzsmzUY1ILOKU6M4PMMOgp2VTlmIqCNRJOqVYi3bFkSnVjCSesVSZFRAW+sbFJ7R/htt1itvJtBFvHYbV+5+6dSzsXkdlur8/Rthxvq7xSqrlleE08sMUYVkNIHUZQdriEEoyNzSdRFTDPg2AxshZCnWOK6KUYLrJ8BD6OjKIWOTtL0YSk5ABStnLEskdB5SMvpNRSSiwgyJv5FIYIQ/J1yMmxfscD7ZwIEjCRm3CTgJi2pzwryfjR2e9DOLC5iBK4ZIGxU2c21jf6ffrt1iYLNSGNqK278Zj23Ow/fPDug0cPyc2SON+Ate+IMp1RhupnbP0OPPYM4AhgSCghQZyoR7BJKQVN9NFkMOoyO2sxg+x0S5jYNuFUO8doOfrUVVLUZpaNXrr0Ettd4U3Y2t1G7ClSmgcYMybr8ipGwkQgKhp7sIOabLambE5ECt3YaF6nQoMda+zmzqOGKNJcvRV+UiSHjNK9hP2PK5yaVD0bTdE3j9l+fjhlC1HUBAAwo4TJ80qj8oXnk84Ak3lInRCgQt3EKgNfycA3nowbYliYVm+oJGXFwtmM6ntqgKxRx+s9NZHpworCkBLiPR+5Wa1SAmoI9WG7U749jSS9IgYmkWKwx+ko6Igl/nvYQRLczcMBW2Y3fu/3fu+Dj95vNXvgwTwlZIxO2he+8NrOhR3GAW6+gEmNfpuvsQXQZNLtsmB3Qreh19t66+G7H3/8EfUHLLZ3tv/63/zmV7/2ZVrDSDvSqAjZTgCeukfjVcWKUISJCBQtxd6j+9Px4sKlGz9+95+fjGinrEdSes4Cle3XP3edsrc21jGS6cTRTcRR0ms1qsO7Fxvz+lGrUj+qTV9djk7rc+bMnFXnR4v6E/YLndVGi+bJxCP/Hk8YCG08sJMl16SzdqUVv1QxtSUSC4eAUCJGymSCrIsOACCfAcsn7s+eV+EG5BPvoExOoGoO2L6NRw85G+YLr7/6xa98iaYpGZ+rAXU1/cYGfEHJHR2fIMEsCWD3GxKTD0zBOoBWZG5dxq0Y5anK0wnoHDzaQ8pBMll6D6NpwVypbrNAHplkk34vcrOs9Klxi2mXXOYVdkMmQ/PEdwECSHs6PBSlvkLH0AmgCarUOEcMyacoVrtCKeu8PFrJuRSJBw4w4Dsoy3x6vvb7pVWhl0WQcyGTD0pGkXnrNhwnOlUuMMAOGUVwrA1JUKIDrjmWSwKfUz7ZW73846WUXGKXFMBPW2HN1cBQMkEIdtHQCEywocECT6uMH/MPNQ0XzHL1l/oG0WJkhk+kJ4IqEpESaRGTtiIWWKCHRdNakyAZ6dglWngqGUKDQLKC3Gy8CjoFBV4F1bvZ5sFbSbyK7c95vPOIkcXzDyQOofK+YiI/xPUugCU9d0H0B6k1SSk8BT+NwsPT5xVvTPIp339JSOYUAF2SQuh9X8FuYPlg+KdwyvtfekseUDGEQHQ8OpR1PzTRTs+yiaLhhP6wiGeVKJSHDCZw8I7GNW8CBxBIniLt3DbqFo2cC8xm81Fr0aZVoH3iBHnaPzrsnAZTaaiY6GmDDNVa/qPf3feCLHFmUEsZlaByEk6zbadeNbS4Tta1xgNmgenjJKjG9GtdlbSY1IPoKKBFOrExOHSGoToEki4BPmlgxk2rKY/ND2OYo24FUaTtgKiTcefon7zLsb4cblNb4D7UhYMFwnnjwsbcs+m8jIGBsoFQSZczjV319OQUTKcdwNZhxiV8Tg/ism50e3jiK1iT1BHDOH7Y/k+TGXE0mNU5uyHhDHygeRrKuqm/D3xmT1Jz448KCb1CkenGGs8zJtPjpgJl5AINN9H5hQKCMhje2NzjxegSYDTXnuBUk75MD4ku4lm9pAEDGJ3ASGdJd0WBEDFQgnmh3il0ETMfCZZzSD5mdhZ02oXANhmPJndu3wFirnQGUIYTekYAgI1DHwPC86DOZWd9hs4nk5dfefknb7xBS4kpPx4N9x894uTRFvDAENf9e2Y7AOPUchbQ2ckv/fKXJ9P5v/2df8N4IUo1pywxJdq5vNDU1ZbVBZsFLU/7LDWBwefNkRoYXLA+MvZCZKghRpCUF2DTVuMYWhVPnG02ZXOmlp6enVbZ4TsOaWQZ4tEiIKByBy1GuVgYmP30fAij5XbWNEJKYbou6LKSv2qBBAIJ8fiPEPrO7k82fq6bxC5nIxuihcRS21RCyKMGAT8hny0GsC1Z/1ar0uH0E+0OZS9YRcEuQFQyzS/yojgAc0Fcq814un0zbSf7hDQYNjwWoI9pBtqdVu3CxfV7ew9Y0jFdjB7vtcfu9rhgLSPuz82tPpWUggM3wAgDN7Y30WNNiQVUcYS9tuSE5HliSfqDmG/A/DdS1TVqZZZyBHgwgQqVnqYngoFrGnzrJx4A4kgbDprghO0aaoqyAB1u8t++DQVxiZGEstASUujHs6WUf5IFMtj6JNtEJF3IxwdERnKzZY2Fkhux0B/Vef1kbYslEz2qtnWHUoSNH0cCSQADAP2jj25DXNq6+mKXlrHRY4by7NHjJ7gSdrbXyMtchcfGGy1ES0HXyH5OVF+rlUVJYAVaoEcNaNzB8ljMLkNuxwrQj/XG1sXLV29cobO0trlJHcOuZeSNIVwoKVAmVb2AdEANRbiJEDLDUtU6Nnnl5Ih1i1gRDP6gGvEcW0XQkjNq7NixDuiA0tCBh8aNx+JsNBvVpi364pzDPcvZq9O7d+4CA+MJCJUFwkuHg+PjcHehx5XG/nK5rWBb8YVBMiMMvFhfAnNgJbmkcEqeBoT/ohCRA/4BXjqtplftk4QciMOPqBnCBe9LoKkJ5bz3xisIW731EBVNXHKTNEZL/Egb4UVogAfr8+joiClKiAUpICyWWcO9Rzze6+XPfObtd9+BTrQ1GJxoAzb6fP31L3ES+cULFzgQh0nfbtQzmzBliDIYEmQYdjwbvfP+u5CInht7TK+vX/785z/XX+tMZ/fS2qpmI5OBXaUkbKoD4IVMdI/X9pAlbP6Hdx/+9//db92/+5DtXeiq1ZcXaK2uvdjc6FfW+u2N9QtsCQu6tF/coVN1PrlS7bzEUYb4UCsMJf1hm727Fo9dXrK4M62cNqtPqtWz4fT1ZZPVxWPHzpnGqEcbQRIKQYnxyxIvm34moVF7nlLcr9aGMKFElr6lGoauBMr4FYkThWdroAU4/lo4WliAzKFuT09PWT/T6WIolDzzkULZuH/Kgdx7W1tb/X6Xr3VanukRkqMeoTxIhkWBDSZUtpzUNuah0FWjF6e2iEezVtlhxoLnc8xbjO+MZoxnoWoY6GQ36e6ixgYSrfFyOlhwwg/STw9ju15nWNlayRiEShxfOLDFANQQciHvHkXzkXrG6Fk0hSDZUAC5ZKDGH6q6rAnRizQ3NhbIPDexUY9l/oJ0JUUR8uWWqTm5nJKj6KQcjXnjGEhoblACKJ5oJOb7qBgt0UhqNHJEjrhST9SPQLNYYi6kDoZqpUlErklkjPp9osQYcG5YeGe61UOwobemrQ/BU4vJjSqW9l0eENv2hj/TAYwuK4C0DRELhitRM49J7q4QpVTgW8kJcYXXXEJjG0m451iirbmQm2dQtCBXuppCKj93n9zwrXXX8GQV3Eos+eBXL3AuDwHgPFeCCF5FosgSxZDyWKR8FQw4T8MVvhRY0j+F6VkW59mWT0pNsn1WXNTUeYGrX4lTHs/j8VoeV+E/k+Avei3JJL0iUQhJ3Kcg+wyxuePEhZlai1ZEWIeUYyjDWYTcRpdorssgH2cZ8IVoWMzyGe8XasRFtfhvmfFJx7rNedulTefHOhDJwFC2TdCsokOg6FCYBitE0MqZo/iGLMWqNVltWfVILdapjscnxxhn1ElEDEVJPbcWkSfGLsxCxoAeCNCtnOKO958rGwCz5QtQgghWiO0NUstB71CDRlyPsYdSgZ9Hc5Orewxjb7HwjiPYsfZCATACYrAjJoP0mAUYZsg+ylebnSkXfgK7kGxZYVYolEGDU1VU71xzJzuiT8fsIWObBx7qEmmSeVmkDjrmY3xutPXxMci3cMBGlwYaV0arBcmAgmYbG0u1FqMKrtA8szk5U4VgE2jKMiGzMSV/isSoIBVj1mxUB1gGwkZ+4BAoMcGFtsPhfNktTsqLKs16COnDO2NreZRFlhIpEKJznSnOcAY0hFZwAYuFVxDNkt8lezhsX79+eHJw9+zs7r0HX//GN/b3H2NwQHKSYUADV9m6h2LZeOTx/QdwBmcxjBoNT3784x997tXPaYOquOZsj82GGzcvX+WMYdz/cBZ7PHWN7dFIhr6jcQM2/0QRRqs4dWvxQp6EYsyh+JC/qcc1tBzGFWWiWSVgFazmgctSQSw9PTnnXHz8lO7EDBUJQQRJyxNibVIvAiKaENTKYiYQFhvRBpdHhFvWQEtYZBwunvhq1UDQ6UrZ29GiKhk5EY786dbyB5xioKkH9+makX+6O04iV39qpNHMkJQhBJycuEXjiKzV2TPkzoNH84YjSOMJW7yc7GyvQ0MYwZHAdErZfwSiWa8gHESrN9jTicQuzwo9IZGfHbVDPAIyHVFmSVMp6YvQdaeHxAR95rq0aQyy/hU06ZCQL4gLk/JUkNbqE9AijtQK8qYXQUghP0Si2MT1prjSQghgwuWzwfxFHlOBKIXLimQ0lRfJqEe6+qj6MNbEJX8ZZeL0K3TMT0aQGXUDAWSuXv8mFSxNUoW93n/w/R/y7LkR0wYtMkLFLKSHj+9zcOzmRt8FGtIOyqk+SQ6JNPkdP9NTyYaD+DQAjuludswcFnDCc33J7lKeiocfHEi3tzauXLkKzOhNiA/Ydu/NT9RS7yhI5EkRAkBXKICJZO9PxTA6nhyeYnuBGssenXFtDqpMTE17wVrOChEMZXICadzabIQfpztsTKfbW9NKk64PxBvghZ1N21UG96jXajfpQULHKwCNkwoBeU5l55OeYwVIogoe+Ic1gC34CY/OcaUYkZB7sqDaMGGbhV7KlZWUrrX4hYblp7wm2HTkVrIzDzqWrjpwHMDK5RcYzY+0SiGGWVIi1IYwEocO7OZcF3Z8ZAtgmgmVqM3T3uMnNCMgK6ruRt+4dHF3g+5xq3J8csh0f446cTFGrTYaDHFX9/sbew8fv/nuu/cesI7fMerLly/88te/tr27xWibQASMyFiRf2QYQRc27nmm+9HARfXRBx9utb/26MG777zzjiszUG5T9Az+i1q/291a3xgPBsu1HoVAepB2zVVt0Z3PrnUPLqx1JuMTJxpPd1zW7Aj2hFmozN0ERgYSqtjBYTcqHHmy24sZjkyo3xXZMX10l59zCoG1G+EVRJtpf2x75Zd3/xsK+IT7lYwMS7UxdBWBX2pjXpLUREkGZTlRgQ/l1YRES0LCaNHQxhCZBUxoMkarGlXO78HnaBtAC4bNQlq8jXCUA2Fw7+AwIi/dSeRlY0El5WwaxsHIi0FPDgBojqh4NDqLGZtLkw8HpR0dj4/P2AenMZqeNZr4Q2grdRNiigIhVQuwMhClQqJIyOZMHiBCi6BssYgCCUUqyqpp7kEFLSV1fQWZyCMv4qsRUGgkYXz2Mlmo6LPJiIps2DtEp2Ma09BqhkW929aYlcnNIYywRvs9UfzEF0vjxiVZbMysILAr1FYMhUZTh4d8N2PyMKfgT3Ky9c1QnlYPvvIXP76Q+1X8aGzJ3wBKNAVh/uVBWSGDqHdCjE9EaWZbCroKGZf1UCdXXnLLI7cVNs/CDEl4CsszH5+PVjIBpEBRgCthz+cCKMKRhEUahc38ktKoqxISrDFhWDn9l5mLhWqrLPgWrI1ivkpCPont+WUQ763sED+lH2PM8tG8A8n5aQDsaSAkZJr7eRZ/8W9hPtEhbUAxO3gtmiUX6CGGKCACvRFZATIMbYgnQ28xthGcJog6KRqoeDaOcuknRGKzMWcGoyvFkSDW2tMpZtUaWmPOXFKkF3GhyiBKDCIf1GmQxtdYUlVd9GhCMTA4+W22GJJiPDscYMGxZayTHKrNBn5zWmz3rwjAhPEws6cyucrTvHof3eJe7NW17tqpkgiE2PPalHT47ZvE0mLrjBioVHobJ5s86i7oIGHsN4azLAMCeOinnBCMukGEw4YQA2Roqmj5HP5GOiWZjTH9BGuTtOPYTajoGcSEVNlTjAmIlshgORyTwjzUWV6JRS7dlHSgZT8E23eqBP64S1BqzmkJYIRSoeKzNd2E3e9VPkSnaqPrIQF4xYARFuf4NhjTvQvtozHszdN2UorNOQXBFhiA2mIRQq1ld42Ok0IXEGLZA1WaOk5ccdaRAoV+44L3s2uwfFl7MhpAObhZn+LmGnHSGZGUKx6gXrsH4oCWGcFwGlgbnIo2bne7kOfmC9f//DsPmNY8P9vebL2GQXv/7p2NrU3Md6wVmDmeuuM4nie8MGC6t7c3Z7rrRnc0xjE3ajS6k9H8wf37DAGzWSK2KEsSB6ensRSVVDGELXghxhfg/XJB420+AVKZh+BgBpnhV7V9X1tlxN7VqHUob6XU6J9s+rX5BO9NjP+SUDLFwVGYZiAbtNBrIJr1JdpMZoHnnHlZ6EhHAwSLSz5hJPkRM4n8Z3RlhSRzs6GfsBV9FyzSwBI5AqJcLKrslURCAgilMKQLPlIj4CtQb8v+ygHdW8iI+eXwGzWKdRR8t/uKPGbMxN43MoGzv7q5zt6G1eGMESEQrz/aO9jcXOOcHKaANlvu33o2GEApKaN4KHzCGc0QVKjvZfAhG32CK+a8TSMo0O8kS14Qct7BHSMDRhif+UfptCMb+MJFHpuYVFQfkfc/5OpC6BVZ+U5wmiezMpxERDe+lc4k0jk/Bijps3W+LZZHQE5nmEcu3uEQElxhp20yqZ4kG/FaZWIoNpVCQ81uMxHFJhtVJ3ixRYjAkFfzo/dH9+/hWkfIMQ8OkFsOFfL0ALro2daQZaS6I2Wi9MeqBSuypiS8hYNTDwMDZMaY+LpsPB7XzmZnOxCHfgTrgOmHr9ON6K/tXNglofIFXWyYbQsdO81V4PWbtOBnhUtkinKJxHTp/qJ+zNS2ZYUNixQi+wbVgbqY3UjUyAOtvOWGigSOoDeYP1PtzBoDThGjyjBPmpnuEFKKqvMtUN7BZdCju4eFLAj0hxkOxOSSe9wjDCvWrAAsMOKnXvXAifMh6rewNSlksYgEB4rHte3u4ZYIGcwy2aJnVlnySnlEEAbODWWNE1GMH9nwYyFLiQVR+Eio4bPBheqkW6HVFjkqFCON2H6LtbXN45Pjt95gFPrCbPaYTgVrYLa3d37lV36NZo5ZPapD+sTNxoBTutb6SNfp8Um92r1z5/7v/97v06mjzULH/oP/7O9/9Wt/hZEBKgt4EUTJoml1cUTLF2sgMAFPLOz58mi/v9n/7P079//w299iS2W2UYP1mK1rm5Wru+vrvc3d3Qtbm91m2yF6UqK4cbr1OJbwdLrdaVU4g7J1yh6b1epjqnKNQ0xmQ6ZnoXic1c3G+rPHzJGtVLeH4xGTRRFZmrE4pyU6wDP0Va15bFmhtSQrEEo44hArDUToDDWNluqrQORBBhQWFkYkowiMUYmzYktqJtrGmqn6SDBfEUTKaJ01enutSefRvQf42WydmV/sXBu7hVIPDbiogAWjGHUO+KKjw2peFkZMUI9kiNaY4W6ZV4fqThbqVBtjuhAa9D09O+wwo45r0cIOBkfTyXDR2lPWWCuF7sLFw+FBnmaFv4AMycOKiAKHaQ6wW20EA61ctoZGv8oQ1F/whRhFzOCwRouaDeqpiuS4gWTAjdiSxAj2Gw/hKzFpQghKvXdSQsY38IygBE2WPzRbvD++6E7xKgE+pBRZhrSdU9cYUhf+MXdMHRuQdOCAoTD4a6zCJFnipa6L5Io+8Xz2nmexTFohSKncfAhi4i76QYbQEoeUoEacoF1QInGgpeVQhxQKnX8vyY1irkK4uizFS98/T+fxipyu4pRUjHdds4CGW1xIXfBy701U150S0fTmLv0TEnXx1LaXxISv7tWFbb26GEoQXvA151UMczDQrEp2fljl4MdPXflUmJjIZpn452kTO+D5VGJ+Koe/4GWVWwo2y9VlHkgzcMMLlZBSR5i2ozmh4C1D5z/fqBXIisJCIkSc2nfez0R4UJ0QDBmIURphxFvFkJ7Gctx5qjlW0FL7cLqzqoxpdrR9rtIkW72WkezkSrtCTVWg0MmE0Fm3aKKEksVUcootl0A704CyaXlwciJqQCwoWNU0H3hrLAOXjkrUsUOAxOFB/SWHWCH0F/Dks5M3tjrg1T3FHdHUeoGzUoh6hoMHvRFXycQFCdR5NEqj6fxEvWbUKIwBtLx1gnjAipVN2TxiA6CjeaQhoU8hUYWThpwheECVoARaJ0VaVSBXxBfjiRaN6U8oPQfoQdB6yBQgMAJBXpjoa0vso2Nwzp9TtYAkKJo3BqQWDDQMlEYNFYgNpbERJas6S/7H0uK10DBAKQvAQ/dgxDb+WnCsbKtv7+5AQblrcv7bCYQ+LFfQccuUIE7WZV4AeeF1bNR7fWYxbGxsrN1+b/JLX/vqv/n3/803vvGNr/3yV2cjnfeu42WGBNY9kxxw37Q77Pp2/YUXWez7kx+/ifYbzQb1ZvuTj+/g7up0HaNod9v41Q6PDq9xbCkD2sxnVc2DOn/oYFcuKsX8SQclSCFSUDRSEA8oQQeMFHKzijdUdSh53WSTUBkAXFz8oK/IOTUhvHKpigMuKFENcTOXnrCTUiCLwuOEKGnEf5hDMjLkObGIHJ14DhXRycisFTjiV+j4SGuiIZQYyXwjTqQbdzDGFqY09mim6hEKMK71V+xd1mId1mNErmpTOOBezIgRhxbBmvW1rU6rl0aelPMHD+6//uqtjIC1mOqi/0ysEQ+zjxySGU4endDiofoGs9RcKQQFwAjs2R6HMyp5tBVT4Ixs5QQGUDCAlGAVJ5bIBlRrrUzyK4Dz39LLcyFRgnhcxSEL2blKA2wBrFDecQbSwgeoAc34VhgBXclG/pDU9BQj/1a5wB1yWVR66z1OX7L+kj+wwFOVEm+IVnt4Nvn3v/fvGdkgppW0Rn+JhfXVEZs2tqhIThSDBUQOqJEhBKDgogNlyn7/bRfwWP+IBmugA3Mn8UMgm60uq016xydnN27cpLMhYgVSeRn5IR1kW9HKfFNQsLFUYFFqGPrBAewMBXQTWrREQ1Agj7HQ4vQYUVkhgHMxyFW/gLNNGG2YofFazACieBYgMTdiwGlZGMopTYVJR52MUk3AYMnwwoJTMsgtrAmZhS1djjCLZ6KtCgRlgYATouMjP4gDr+CLrFj9kldICc8EVFVJ3MKR0LQQglDZaFbczSTsMolo+Z8yLGUV34IqbLMzGY6a2I2MCnG+kmLp6BkK6Nvf/s7RySmMQJMSitx2unSE0EOT3Qs7iBDpGW1G/Q4HZ/Ku1nxw7+73fvgGZanzG7UvfvHzX/krX9Zec62XfmlhExSAhas+2mqUzWFXBLKW7V699j/97u+z+9CTg32wAk706ubOFkNFG/2NfocjxoCLuUZj12Y3gGrWZiuF4f3tyni3e9Zpzti3dUB/rNqHdNHljOt2OEmRE64XVU6c6HIwLvtf6ktHUkFQwkf1q2FyZjDjWvSKgBHJDwGhn7CEhFKR/+pLJZgX/onb+VcffPcKvsYJ9gQnomw3GYoBYuDV6lb7vPqPy+SylLlwUoTVNTk7EoeeXjVoh1AqM0gMloBO/6knyeCMUAGSno2PyJ60OhGTHzWQmQk0oRwRrNoBH12Y9HVRo6ynRoTxrkIQ1oB3aERpSXXv2b7r3KROB3k8kvQwTQ2okJecaJKX7TojX3QJGCvTWCHYImzQeUE5Ws0yxUnpxjXVaTHnNQZWkcsIt5VBdeuW+FBJG0czgsJhlIqJPMdjGh6nDRLBIJIABXCAZCRfwEJia4l9Ed4UfmtVCYes4kJsE1ICj9HTACvQRVILAolgFiYFY9/FLWWab4kgOf2fwnwo4lyqHNkGOL+GbjZ8RA96ycEPvIY25AwU4sO10tc8kVhUcp0jWH6TreHl4WmsEtd7Eb18kESiIQR+4ef5BD6HBibjEqkV1UrA+d1ccmXgx0glWgk128LRp4lFDtLJpvyVxOdAB/QJ+4QUHMpHGfnsOj8JmMDnIj37/nNPAV08zUbikp9KJwAU+It8PF9OKJOWXQlB2+rHUhSoLSJJZXRMALWHF1NMkP2SVyoCzkIHAaibiij+cOf5OvovUfEetVA3WGajvqvv8Vm65WDHIedKhzNP8FjPOMZ1idpiwQ9NhVVFx3sFL0WmrCAaBnnpVm88BCkqiu/NvWX9bO7gpmxzcJP+Ras1Hpxhg2NBARTqBEUeS4E6gNufQ7psubFeVvPFsRPqD+q9GUOmVB8VnDSIeUcnhzUGxHX0ACuN5lU7urR/KkJpzJbwkMrJ/JCKr2guGhfyYdgfe8IKCxSkD83QPwAueKSyHzPPHvAa6JLWfoc8kMSWpd2KY5LIPDBizQRpiuPdGKIdhQW0lGX3AKdFKBN5kXtIAlagXS3BXVXzVGisSVSJ2ekdxHyDqUSTjgDL7jSUTvuOnY376Fd++Vf++jd/9Zu//ut0QkRFxUQSZgVQALQCEtwVkNSRDXScE2z1Ji3bvQ4zbrcv1773xm+3260Pb39848b1y1cvAs/p6VnpVsGSKa4emrRWl2OqmGJx8eLO48eP9PLQk0Q+dJ06FAOrjo5OOo/2kTR4YQMr1NUF50877wgaqn4d0QSjdGBAi6YUXi8m15c4NdXVkMK4LmlkbjQdVPS5Uu0/aw8qiILd7Rc6o8KpxBoEdCyXA8wdJ62paRE6BRYg7D0CISgrC6gzJb8wfKWDFQiIVlzNVA2i8Q9xm15VipoPrEKOPrs4h26zXUVHMwjmj+YG25pT2BjHSb7VY76zGIS9mZTJsrwe2xf8XBigQYPyoW8ryyXGgoWnDPT0+o2jMya6gGfz4Ojs3t29yxcvMbLBymxnEQMywGBDUjQPXEEnsPIO/HAd8DAZETP+cPJTNTw2GcFFvkQKBUH1hXquT+BjpVlv4Ve2XkgxxJ8mykciwYmgCY1p+mQn4fLAKwFCb2w4wie/q9HyIGqF2vJ6WTtJpoAgDCFjcsIAQkFxxL0JzXVVsnEQFisI403IFlOIMQTYrYeyIDzFUwLl41/+8IN33/jRv1/URhjIQE+ndr2/Nhn0ziZ7s+opSsVOvv4D++eiBRGihe2cW13pz7MM1xUFSg4cGm1X2zh2W6zSbs5euHDl0nDxIRbPxevXScfMIrtwIqIfASgDuQHwRNKFQpC8/IbshCK0FNdCHQRJyqJq49dg1Qf2bB89UWMOI+pouSFUKEicFFKYQuo4VB2nYqNRqzb1g8rdmk0PMYeIAklSPDJCFZ9SZwObwzs6BCgcyUDTUxoVk/oRWEkiM3hp3w/tgwjbyYiEniLxOY+S0SMzMtXshryofRyRgHOUEssAjptWPhasa/Mb1ZlnABepAVBQEyBJ5p3MYCS1BDgAfV69N5rvM4kLncM0E6xqNldA/Xzru3/2P/7RH7R67OXAeBWuATt0L75wk633mx22ZBJ9GI0CZLkLCwnIbe/B43/32797POOcYHRb63Ofefkf/OZ/irJRPetuAHZErhC6cA0hAQ8b08iIRi27DP/0jZ/eebB3ejz83vd+3Op14Dm4s5K+XWmutzvbm+sXtje6/TZqcElVUjks6NJD5c589vJLLy2bP1lW13GjLKpH1eUGU2KmiyOcSE72oe1oeY5BbTaA3svFFuJbm99ESy6qj9NWIA42DMWIDY+EGy7IN8nsPVd5kLKK4XNBJeaK4oQvlA3GE4iTaKl3Bpkd3KFabW/tqpNhlvyRLNZVRRWqLydDOmYoaDJRTYMZjjhPa/ASNlpDTHQVEb0uMynaQ1OE1grgWjRuiD7zHdncxq3hKFRJsyymHODmV0QxPJAJ5hbBiKt+bhykXQAY+ET7RdnRARTKhndUHVirhFaqq+16Uc68WOXNON9sYMAUcYMhJLOhsFkwmiooUPBjxtInejP+VOq6JKIegJol0nlBmBgJYgGYNTJJlMRYyWk/wB3tRzIzi/Kh0bRaWWy0UEoAbt2IaIfkEZADLyDnLBrq+qPwXUgLqIEZ0FeKyJh8sIxsduI5V8q5OPIHYVQRVlW0UIgNZRQUq6wk4xHyAxWk4dnskqG/tssESEReBaSkNQpXov7MU6JJwNX3EscCSG5qM+feZJQgpZG3sVmdScgqUR64Pc2Gh3NxNcqzglcx57vkyfq2AlI+r+L4YzkFx6AoQuqrFHseze/inyJ9Xn1IAc8/l/y4ExjhSoy/9Gaeq5xNJvr8KUvUcDQ3VQUSwxDMCtuVGCXyxu8k1KCJ/GD2pnJifbojiqkEmfqCelWCqU4yy4ppQdyYf2p5RmNskWi0/6LHvDwsNZ4RCiqqR5MwO5V6zVpSRda5iZEJms94Z8lXMVJQSe/lKwKNUUKg4g2TFLzA47QZKaTDk/3XKJE4FkwklCJtIB4A29y4YDjyw8jIsTY7T0JsLS9aj5RSiQKwGRkxMBWLE/GbNMUGXYF/gt1uJAloRlgw0vlE5XJpchpDkrOLj0pHXVewUMcFFemsMcQ7HSX+8QdiMAWq8kg0Fu5NnMKkyWtJuq4dwzQ9BrF7ArBwk1ZmsRgSnZaXCHJAXyP9HeEiS0hCWpIAA5f3UjFWZJUSQJq7ZFjVdB4tRysFsuCnYf/+/9P/5b/43//9vz8aDnC8owKgNCiQmGNaoIywURpMsbMBTQMtm8+Mhi+9+OL7731wsLfHJhsBYPn511/76PZtzoO0jSQmGphiGGHArYX5W1levHiJjfDu3nmoGcSkEcVBiulQTlfT1XX48cYjDJGCG8RlplOzC4NGqVDSSvlXDiAwqYmpnCEcCg5yB5p4e3Xz0cngE5YQ1FZIieNF2tQaxQi2UMSMXhZ4IjgTjEYpi3BpxUtuSlJZ08nwUHpaHSZSMEvH4qAYjZA9Igdz4LTTdcgwlBdKJw/QnGNejMYUpwQjXTATQUO6rUOWhfGCSIARpEPqSMd5yju7OzIek4l17GURCFOE3YhW2+/0ZPD47gPmlGG1ANe1qzfvPngLTrt8eV598Pj+rVtXR/SXOdKv21OBR0gtH1qRKRmDgMhBaVnMBwgE1SQwal9Y+OSwD4yCAp6HlGslcQEdywmHVuiqeNHQi2PIajZyxsY+Ymw6SxYGuVVgEZpSWwUmcWyM41UlQLAT1y4/M3LoC2PtppJZqrmtqkESJ3/5F6SW3U5ne2cDq8zNQ2AinIf15i8oi2njd3/n9zkVF98863oI7LH1O32sbv+ofhh1ARWo8ilGIlqnxCAl88u787AJ0jrQ+cjoE5sUvvrlL29vbE+OtqkOs/rkow8/ODw62N7ZxXsh8cXfWgkaJSveCy7nASlDHIivMkVgnATmMhU4wgN5kJ6uV/QLsdj0FhHUwWEB5qxbxaMCqcupb/QaXegCu1huOh3PPf7PYtUlsN8f9Yz9CPbOQUrT30v+ikDhPgkKAVeA+5MLiLGVqR1IMsxTeMIDxjwJpK4q2vbmmd3CWESXioGGV1XGHORHMso5qWMtCxqSQBkQK364UyVRXsShCOoX3FQTUM2w99z6WZ+Opv9keu+TO7/9r3/r4WNWO5inHQiuev3v/N2/9dprn3WIg5kTaB+2K5hMmbvCZEi4zyLd7QuLB3v3Ny/uUm1h6F/7tV9h22I3G7CtEz4w8Vcx4l8glh8EOloFoAx7np4wbtl65613Pv7kk2bXwWtbhkrl+rXLWJDXrl3a2OyzV6yOC9QTu/vbbmIjs3jh7P7Hv7dX/crWzTN2JaqNNvFR0MC2x835hA4Mq8KqU4y0eucUZzcH4/Z7lM2BZfXaGA5w0BLuJPd1R1AQ2giRkCqtktCbr3nMr8+5Pv12HvrsN5Lr66cihhKIEHWL8mgC5ShRUq8pjj/iI1/101M686xbG8JDza04GdHCguYqI9KwnE+S6p+xxtlAMPpMDiCkD99tKdDxpEi2CkcRHFqKuXM9J2zfj8ygrYqjh7aFkQHyRMPb7NIWKzMlGVwrjbzcKRxlJJiGWMUlQt4jlTpEbFuoiYXliI2QOvRmx1Sy8uotLz5FcmVAQrmHIqgT0Oc/ezgADQONxKS2IM9FYVosxcnBJCYrk1C/1cOhFnUZghGfmkJxVhUXPkr1hFpkMAxcBYSEKQ9c5WvuYhcVl2LIKfxKyRaSPwvD5pIqlgmlzMF8Cu9FPJKWnAVH3pVCJLVZcy8hvj3FKx9KSO4lP0KJG4Dy48vqLV9KqvN7yE6UZL8KTNh5BH/L9wIIr+Xh+UALQCITk10+ZEm0Dj+WzoucTUJfEqZOLHmX9zwnTlm/7FrmkiNfuMrz8yEl/H/JfXJNqKufUIwGmbZmRukjd6pebWOlOZXHSsQrnEMYeXQ/QfqhFoh1ASQFUWrMUxgUa9IGNXsFil0yVFNmFAATUk/U4ox54mxKkEGuE/fWwYdBQ4QBAxzVwazC5jmb2BbONtDjnkns7rISq4Ii026iMpwatOBocQq1+qcr02yw8njKrIyrFT89RJcxci0atNCawLQRTHGHAlQVrQPQo3JiwnJcC2jR8GAd4odn7IC6QctHJKhFShpEDCm2K0aXmJEOVSXSsXLoQLOKjnAsn9aAvT5RORjHYKX2INRGJAnjCbCho/kknHpLX4GRCrpIKCsJbqWV2DjlNTZBkkk1Dv250xxF8UyD1BpfprGutR5AauwNtAPTq/BSADYwUKFtnufwnehWLee5KqdmLTjwxZqYlkR59FJsYZ2sNNVT/i7YwVdM7uHxWk6u1WY3mDTJSaYsiYatri+UL8uzs2MmTUSruKgXgigRTjthdLS5e+HC8dERpd68cePevbvNMQvMGv/P/+q/+sbXvv6Z1z5boWWl74B7cuoG2KMBjkFW3VXZTnS5Xtnd3dp7fIhPHJrbmcpqSE4Q2NnZ7XebHKmKvPAJYqnO5IfHpbN+hMYVQqqFhRPUoS4NAlBGtqOsET/agbZ7qdLtPEy3Bc5RYWmYXXdOxoiPfQPy54hccrGJGdVqCAWdBvpvsBpWMmzloLGWqI4lOga6VXn3rCrNDgSH2TVuUAt96UfyiZoV1Rjg8VxCPgqm/bBLyScErMVuR80G8mmXB88svd+MHVEcIXjxNjOX45g5UFgkrC3FSKJPxpa1IC6bw0se4MXhQX10Mjk5OWN+EYceMXWF/sB8vgOcD+/vfXL78caaqzvdXcTeCZTUrCYttUBRxqYEKYgoEahC/PBNweIj9I3gQUJotkE2lcojkjsYT0RYwEMgIoEiptjAG0GMn4gnpY4eEAUpj7AL+iVzJQzycrd7hrIiM+TLrMmXUoysurKoZGP2fk5bRcHUroX7dieIbPj1Mgt1nZrEO97W3S22rMa4N2OQ0gHPC8/V+sP9e8fDQ5Zx09ftNVu9bpc+Kr2ts7ODZeMIFO2o0cKjciS9MKQKijY5BG1bf98N4Jfp2BBnyGYsrHRqbD5xX4Ja9ZXPfrbZYTsa8m4Ru1JjUNErMK9uAbg8P8XH8sBNbYdl7zYmTHRRbj34tz7CX1yrnlU49mg5YNnOvH62mG8vaqeVCnNdOEq2t1yeNOpryxqKmkOjn9Rrm3W2SJ90qHnsysUkPdSLGFpt4DfTRTBDJT4OIMyucAD0wHGlx1Q5sE2dx0+gnV7z2S2DMKaZuUHXnviOGYIvOaOgwEI3AumQxN7+mIP3kD3NZXKTQHyDSsZQpYEvio+FGPewi63xliM7UwOocLPDw0PN8QueAAEAAElEQVTIyIV+YI4P7GS5Qq9+q9IcTGcfdnpdKH18fPLWm+9+9NGdVofT1uj5ZB+w2WR9Y/P46Hjv0RP234Sw+IzJBzVF/56KgUtoOBp9+zvf2d7dZRNd6PDFL3zl1gsvoiMAAhWBurDVEBmQi1gCm5iit1EgNEdoDtwE83feepPxsQ/eP9lnVI/tj1lwVauur/UO945ee/W1nZ3Nbo/tqvGhMT2rezYethudxWTWXIxvrncvvPxrW80pgwN4uhfNe/oY3OtnCKIMAszrG/UOe+08ZFnWem990hjWFpeYh9LuPC7yCf+gLHTFYxfYIJ6Qh7yp75L0/AoWvHxKHHl3RjWj8ffOw6laOYPI0NXFJ1JH+pEQFe2IyVc2FnzhDxpFunix9AUkHQ/H3e4a7J1OBrPJsWKDOMFyu2ckzZJ0jQ7EQ31hQ68NyUUYWt2qbOZKBH/IiGFsgYpunp1ewFfCGGXcnhOC6419FhvQttMzZNROnRLuwXrl1ivyaTdUqAEFeQBwtRDil7wFz6EGsSUhmsSU0ToGgFhg4bOtsPko+UUJJYMi1kDMx0iy+skGMJUtbfoqPiiTv8pP48h0/LcQSocWiBBdB2gTTcuD2aeZJ2cpTjb8+cvVfKC9YkHiWSAWl3zmPKf0NxBskhZ4mAVgVOVE4gtE7gRgPHUkUJpgXAlgzHEA0QQEai3baaGslBMmSeF8E3JR9xuX5Uuw1TN0TCq/859wXs2OZ7A5bwpKfNL4KX8+kU9gtvxyPVeKASWLfCIKthNyUnIo0c/TNbSpdOAlV7+FvyshCdFKSEnmvRRMxGRcCJt0JRPzMlbu5fbzIc99/I89nmcUElEoV2mGgSCDWlYgqwRVXvPJGqRNjCxiWGD4OrNCHwMRTBwMzUwSACwkpOLAOZPZAdeApPF2MoDbgLi3miYlNgDb0aHy0DLUXXK2H4JVxSC7rTm1gUEDpp422DHEmRtUZo0gWGGOyIhSS0EGcdei56BZfQfKBR8p33N0MJY7vVplnZ49ZqIttzuTgAia2FqMbqOdiE8UzYvnCYMGyw/rjUbNukH+qFdsDZLgBhA1zTkrEDoaGrkgecF8UE1oOgurnUOp3rRP5IIXlGY7uyFhBUA2GhIaSEgFVXQ44ap3Fw4Vq5QgCtmaM0SOb0mPUeiplEIMYgVrEuCuGU+ZjhsayHupQg66KY3L1G1yJQyQnfgRk5UCZJScV+dYoB1AWONlLlLQSkMVRm9SThHAc1k1hjwAeTo5zA2eD0HUbYhquJJsJqUbZ80O8JhCVXOH8vKM+SzM+nK2OoiyYfb6S6+88tE775ydDSn58OCw3WvTwJMAnqCo2e2BCsUuUG1wpDWBi7PJ6cmQRW+j4Ww8n3Q6VZo9bA4MEYgHqosx83cxhYFIHa8BgVPd3h4SWJQL4YQRt6jvBccSc6ASmTibyObBsjn1E8JIWLUYDNI4Q3XS0ENFem/UE0WQUpIRc6xYLkvXjbUHfOu2W8OzIQNa0jQGMB0yy2X3KC1BXigoA9BaN8aSZ0hb/iCV+Et3LW2eWeHQ21xDZljVxjyobk8r0ChQXWsJWXMXIFc+LBEwvF8cyoqFVgaLIEPqIuxFeJAm9ofV7dxgH/fpyNMqPZuu3t7evPDoYA/GMs1gODr46PZ7r3/2FeSJxpDeLjtvKAwgThPChVOUrod0gBhqDjEEIh0GyipyRCx+xAv6YSjZqhHXS6OQD+VSlRhevpoN/CGbRMNyPTk51tdr5WMrEqxteNqEgWEQt/LPLEgJ68lPyadUaWjegiOnpDb5xDJQdRDM3XysEzzDUJ4En6xUjwv2H6Piq1nMPFlRQ7HUKe5f/ot/9ejBYwGqVpkQcvXy5c2tbRajnxyeIYKwGspDKauldoY0CosFjEuU61YirCQyZ08ydE+7vrG+tt1fWweKOtM50BXaNG4yRnz1WMnlHDXhFzg+ikDJlgeRMlxtR+cihFi0+s3upbUqZ+3hPKwP6+Nme8rGTx2nKy82B5XWrMqZBXRi0WhUw7VMo9ApXK/sDNqTe8u1J0zAZlnlbIp6oSIIEpTGGcup0cBGMZTLaNeMBTtssBY8xVQpN7J4G18I+cwFEVbPq2BJ5D8ig72PyAMCoxGLDGTWB0JMKkpUsonKu0KezLV+zDolohVL9rmTNa/ZIIiBJ/IlT+o+Z2mdHp/SK4fR7U7LDcimS9b+7l7erTXo7aQ7wZ5yHIDQbv+1X/l6j3GhC5t63+nxT8fsX4zOZtZQq9n96J0PfvTWGx999DGln5ycfP61L/6d/+3fbnIsl7s4gIUSCLrWBfAGuJAr2lH+iUdluba59fEHH7HT1m//1r8eDIfuLjo/RQ+wOQV16cLupWvXLvd6mYwHlvU6LKkztYV6vZisLw+/euFi+6hZaXK2wzHTtyrNnZYNaI9NfiuVdY4ymMw2WvVpa3Kh05icVXZ1fbu4DGGjUkFDAEy7Yy+Lo+DAMha0nhBA5HPYF4rKurz58LPXecyfDX8uBZwLR6ydmoboFgd7Y374SxYKMZ+RNvekwCWBjl6urfdHNDGC3eCskZBOrRJ5MR8IBXElb4IAQbOFOoR2xe1C1oZQTvSXGUB4WjL8ONRcxlvwGrIDchgixyKB+A2Yp8wVDNSlaDwHi2MqRdrJiHyE37pr67lSJyFshhYi0paNGomWYoJPTFgyXkkEyTA0FP/CjtAoUm3jaoU2vXMPyIHNA8CNKmyzEppb54VGuAOq76EJ77CTQP77Gegowpz9DhkoE5oQzoX6U2CpvtFYlGmuSi+wkY3xQkUpsWoTI+SESkYVgmoPvU1uFgfwtnX8qe+0pZxoFqQDg/AWWLV8ZJ4l8t9wSXt+rZ7DX5MkXaIkYpKUuJZb+JX3RC5fTBR8EuM8Dwstz0nFcwqxdJ+fy2QV0xCCQxxH9rlkhwaZscmFQlYQKOyGmKKQ06/MhL9KCDOQkn1YVnrPJTPvSffsIRF9hRtd79kP1Ye/9KLgWuY5VQfXcCMvax8Li7zmR8+1LbU9N01YzF7twtllZGSBhyZhS1reInfQGAU62zVh7aEYKibKUxA3Q5Wd0maHEwe4ao9/KiPFKtMdeCERjnkmCGDD5cww5JjKWz9FG9QXXabR4liBAsCWXjS2gKpauK0mpVIjVgxaYuRpgpAj9QGdi9eksrxjYUgkvl7G91iixWwNejJMe17vnJ4ezRzJRafgRNYEZ719r9/HjACyyek2/oBF7QFbe0EYqzkb8QgEjKx1ej0XSrJVeQ2zjEDaAASdOmP52VlnxlCy0o1AkLUUIsK82+1CBj0NdR5ohFixSvNexnBpYojP0DRzapjbL5FBdTG+IF45HRZJg19svEOrQwSq2XT5CVSFfdmWkbonIxmGgD/yyI1+OOaJnqs0o1bDJS4y8cdGKUXYE7Oy0Y5ArrgMlU3YF0H2R8GmB4z16gxfulWHZ8Pby+UX4R1/Ou0AqVqFqvtPnlQmV5eztVr9Hna4Uwtor4MLOeJjOzw4oPfy5EHrtc98c16//6Mf/ojtJn/wwx+x1yGHhXKCGFPwkTjMd0apyd2emNZ8/cWXXuLjgwcPzgajVrs+2MdsYg5M5eLOLsYBA9l2BVb1BYYqJciVLmk1WzQZMgoJ8ILOluxvg0OxNWPHcFctoPcVWZdMSymrhbwjiBeExE4smfBfozBfIQ6mPdENsQjnQ4yHw9HgrK3cKJCENbt7k9lwOeZ8BuKgFzGwWmwdWGtiYagvEI+UZy15SnMYwuQT1nq989a7YzburMw3eq8fHW/Ve4eMiCCN9jqmZ7WaK5+BaVHbx1gnA04DBX6AgZ8ICQ90dHmWUYggnuAp1oA9pePjY1pERG59rX145poAqbNoHhycPDk8ZH6Ae91CDJBQZLiQEBbSz1hVqJhY8/muInfDz2i4Es2Poc6idmybDBx8EEn/vC02ybTiHH3YYUeCl0i3NLUn6jYlU3poSWDqqV2+Ol1u1uFrEttXNy7/o7nY/s96kZIBj4/magQL5E3sIYLVKvpO3Wxq75ILEGQicc3jq1/92quvvqoeGc9aHGHrEJ+wA+2H77/39ps/xb63c1ipbq71GcbizAonyHdZrUvnHN0FzR0sXLgQiGRMGacQ+kXRZlIMgmHJuXKRk1DabFNSO+tv7PQ2WKAJDGlp4xZAsdotrCYf4S0AC7SSWjhhivNw1lOJNFzmkkxIMBJX7W/NR/g/7rKPcHe5tz7Fb3zcYTuU5eHJfDxfbLbdmOGIQYbFoscRL7U5y3c40PgtTLPe/OsbHHHABl34VZAr9kdn3hvTaZxLyTgq00tabL0IDNPhhcloR+8hTJatoS8/YK4UQMAEgUcLzxkwQxhhhxy86AIJ0wgXJXvy0tyUbsOCiWafoDK7bg1v3Yf1tjPlkrPm40VIESUEbPVZoac0qyGMxms0mXKw1MnRIeJA9Uft0m5Q11rV+d6jAymH6PthnS2Nr1/bvPnCy5cu7lAI1QKdAWio4haL6Hs9GrIf/fSN773xY47u6ve6s/Hg9Vc/s7bBMhh0l8IcGERIoEQYKKzsYs83sEZR1GqffPjJ9/78+8cnw/fee495pfTkabMYX6JtWFvr33rxFhMdm+2eYszernNmW2H5McrtWOLrL21voDg7x7U1GpszNlFAnWFtMScQnqUfzkzNgdjX99gXb1ndR0I580S9FYeY0EXuJD7c0LmCaiNM6vPnldn8jkQRAOSr0PLt/B5L4/zL+e/5x9VvYdHsmrRAJnHCs+ummkxTHbLAZios1FvUP57VmZJYm8zZ2hv+0+qN8ShFGCQg/WQUhuokCkrrBfjnV1GfFU5wh0TWeZBJTdD2tC+BAPCPaza6ZC1kPxLzRme6UoL5A6gS5hnpsec2u+AEpeojOUhJJJWr1j65qfqwBIwdhZMYQGW00EhMI5EZKyCt4wnqPQJxeJLar2pTYUqWuXtLBTco0ew72hmze1al4w3ecBj+yThkAugkA+w051ylbFNbYCqXElC+wVt6RCkTgogH9QL45SzAlPYIQS1100pqNC7G+LjEAlx4KpUOwCSx745pE5clRGDI/GU4U2NJNm62Bm4RKiHAsMME+61THEnkt1gIQ/Qvk7XmDnMl3CwDc4lQoE9cwkmxGnHSE8/b6rP0lAXPX+Xr07uxn11GPU/uczjCL3gIYT5af58lN20pAkM2z8aGCE8zLsWbiuBESc68I41E461knIxCO6OVZOdfnkYxg/81l1nKmwgapQofjSE6wRaRr+yuxXSJCAbsRBz1lvENuWGZL9ylauD7YcKrqooEWHvodzP1xh9p+CnESGERMmsBNYUtnR23RZ7QpCppZq3gEkXvyqLiPuJ0PoQJ4ZhXZ+vYdZwYgSvK2WPWYKcxUEmQB/JJf9UJo04JjacWGRNHNBtjrNi52Iy6E5w4ihYHBwBlV2N3YUYam+wXw5aaREHXkI7Oh04UgEctY2iqm4mGnnAGBOIpX8TbJ9WJWTIqwkq4QixEncSa04wyuwLOCgEmkli3JLvlROFzSw1UZ9njR6mRq9S2CeIjDZAmV4hJluIEgLHc0jRqYRJtZbivYigsEp+Iah/yMQY6LcMLmeAkzYhgX4HMVVCAykUgOo+UajtkN9HMzL9S183dzPnPP3o8zr8AaGwFem4mJy8mvGLrMBr+xvff33u4t7u2Q18Nrw1J0MyAB0zJh2mWmJsb48bw67/89dsf3z0e7yFUmMxb21s/efu9L7z+OkY57MNoHbHmAeJThpsvNbCYGRPod/ustmw0PXbn8ZMnyC07tx6fHu3sXgQBSaWNTrkIDVxyc2v3P1Fbiw5BEA0eojNg7mRcY2IbJ8GFFH4yIcgXlUS8kAksSSsW+YEY5sGzsWkiZtiGAEohtsb12sHZgP1T+OhuiM4Hs7YzscOJpFk3RmVrtrsrmkYzFAAo2mzJWLexSYHcRVosuqlUnjzZ+2f/3T9dNu/juGQ2EeennZ2wh4RHbituZgcXZ2dnJ1gJbNdiZtROzBW6rlYbhRnpYASCuUjtRmu9v05ngUWevS7NHcVGJOqTwXh0+5MHL7/0MlavzUpBVfFA/pRDpZB6SoYxbigkGWtdITiShiiEKokoCqokugTTTbcxgStqR7qTt0+KXHgj+vynYudkDQCH3EKth4KD8M7gHpU+dZqYptJDbMlQN2QIAGYp6ESw1FR2QQIUPoAK9LIYf1YJQBaBYaLxpYtXXrx1kzOJOAykoEas0IFzAFq/9S9/i5Uv7M3E6ksOisLWd71npwd47e4EJ8JoPHJSu5xzIx1IBmcthPrFPyoNedXnnR6it8FK/enRfdYaLEd9Tg+zgXcmm6QGSGnubBM9IKIT2RNwrxXkoJDcfc8lOkQN4tYHd0XHwmEjRHKbMamE3UrawMKWCqwFbgy32tURRg9SVVt0pggMUGJaoKXlXJcjplrVtdpgxmQg9mGgRz8eopZ1EiEdrCRZX1/Hthgz61KRQDBC2jg1z6GQBXRDgKxAHbLzIkbhJbIiL6gtMAc2SS7jBsfE5rsU4L/qixot88wijMndeBLcy/QGmoUVljtF2FfUPkSEUB7z8dBp3yhtOjMUTXYcg83Wn/fuPcTtTgZoZOZ69ta6L71yE43OHPQe++4DhaNhU+Zt0qdgXhDnwd2+e1e9XK+zG+xv/ud//7Of+Uys/9iYMIgegztP6OQm24I+mfCi1DlnpDEf69h+++33PnifBVH90YhxPGZN6tbodLrXr9/sr3VZl7+glSTZHBcD8/vddJau41qzutM54qXWAioYSw1h+BTVY8cV4i/drBB5QrRYI7vJmHSltq7jIk0kWhp2OZJeCJcfEtp8IXdQxhNwnn3kKa/+/kVXGAik578+APezC7BQtQTS1PBse0wtt90J3/gSdULNYFl2rXoK+0D75PAQXUpzQ6OAg8AZws5GYyfHKQOEGMSIZTr4NqnIKPIAAuRFMK9k7RuU1/YJQBTEKwzosu2PO386ysXQSa2D96q+aMAVWA2EdnchB2JPDWVgGEgp16wVS8wN5pMhwTzgIrJKkrO6n19jCYHaDzHzFcqKfUnLcygFfDIrz+VuFLtEpiHEX+gGvDa8aalSMcyeGsF/Pmu9aJOQjXXRCiLe3kPtKFsnNeXdVsLLaSxWgacXHR8br6KagQFQVezFF0ZuBT87Fmafr5YrjYkLdIga4saqa0ikOkP10CKCnv0141tjJFVysiTa6zQQxCGC+Qag4K3J9Dx4T+E8f1hFLXGEL/n+TBJey6dQh9vTq3zhY9R1CJ6YT6Pwxp+vhYN5zlcwPY8V1knYp1cIKJIklx3Mv8zjCMI6W5G7X21Gk4YY55n5/vT56UNicft5379jAohp8f2cRysIy2pFxz4xx8yzOgYBtDFMUy1CSiRqjQ865smo9gjuwAmGq8VKQZJFlfk2PYZl4xFxxDM5K9Tn7CGasUnH0ghcDVW2h8AVPKSPgTkW29Ea79mT1DcBQWYmRF2opEjE1vKLumdbsgSn7b5Z6IAYKEhNsKBKu6MO0kj5bI7AvPcIcYAp4kf2fCaCWIOF+gtjSN3LzHDm2tJQOTkEoZerVJyIpMaEuTQfM+sC/Yj+UJqhPdU+FFVkYZi9EYa6IKEFILco90wKJbeASWlEtELgXWkAx2Kh18SKZgF4jlX8PAYSHA/Ku42Q9R9sKJGGihO/HmFjlsbP/GKVkgnE4uzDtMG+UZX4SIZQCnKxlAtFprYCN8tUpoWZOOnQk79f1IH8EA4g/DmOAbSBhVRwm+98IIpwQ888QCTbmjbzr3C7Yh/02G0a/i3v3buDep1VOIvglLOYpZzqlsSZI8jhRpNxr+XIVbX1+Gj0Jtsgbm5ujiZj+hW3b9++sHOBgwJOx8eMAjhbykHo5Xx0mUHFk9P3hsOzkxPOqho12w0OhscHAvmQxIPDs/X1HZQfDRgkFEwZTvunWVWvsHZCxwh4IJFVvFM8DC/AGmgfsksZ2agkhD0yRa6SynSqncISSWFGRJOS1CC7uKSmt0dWedZNHrrjk+bMJZh0YT4YQij1aeeRNl31arGTFFoAljclY2DwCTDoJMOuRmux1uu5FwubeuzO/7Pf/OXD46NTxy6mZ8dnH5395OjodDHvMTMBc1kxZ5zONQ9IuT0T4K9X1mAvAwWyXhVK36O2xiFBZwwfqHGon0gHXsbx8SkRqN3EHo5nx2cjxo/oX43P2OUQqoKxNKNfwggZ0/air0Bd33boBrcpQq2Sdte1ERIPTHQ0rJzz1jTKa5zwIcInNRNLChhb9HngcR1oCluWy2MZg5BDGJgMg2Yuh6jUjokNwFEQIRuaQGYTm/+uIWEDFaMgnqYjEDejvqvkDEGs1ovZZj4drq31/vZv/ie/9PWvsai32cECmA5PBzgF2ZlnNBqwJf+9h3c/YmlmE+Yy8621tbnZ72EpzrGqIiw6kpkQwkAeukd/hXoGnDn6g9LlPQUj1hzEgV+Dwy7w086XfbxhjTbnm+5pmQg5uSVDWUSVTJAaVcSk0upRNKVGgvMMt9H/ZpBuLAqXSYDQH+wRC05caWONTmBfozttdIfV7Wb7w/HiyrJ61B5drbcfLWc3ZrWD6vRyu/6oPt7h/LYpM4LazLrmTCgOT9lstj5m6JLdgKEox6iyi/7sZKNVuzlYvsvox7J+//Dk/WrtClUe9kh/rsiOkCvw3MGgfPAL36ELVUnh0RS2Jsodxa3gG7lKG+BHglv3aTyUdiKYpZGNunqQPPyzUlschLcUXonFOKff0gM4OzrEJ4FB6egQM7FG7DI8v337ww/ef1fbejGna7ec7V+98fKXv/yVw4MneJSAkC51i4PQ6CC6iqByuLf/e7/7707GA9jNyVkcdPj5175SqTFEDKxgoByAmVQAktlNAK4279jTi34WJOzxWvXBkyf1fndvfw8B9qSUmeu++NTr9HZ3tjfWGFrA/mc6NZ4F/NFuvQDNkA3Op/zcjUu71av1+Ul946eOAFe3bFqjvh32YOS0PhDHZV+9WsfbPVouOW8HkPDTID9odJ5XjQgAs4Gz+Q8ZXMUrx5+XbCm+//L+P/cenv/CyOy8Hl5BE1acMw1HQbW+0LeU0VJsfp0hssrsjeHpqVMBGlXWNZ2eHUM3PWsa3o7gs5oK0x4k7MUgp+1DFhMiKPTQsTphGTnhkWEAkbIok+yByEYYxUgjxcYVJNf+YQoPo/KorziJ1F2okbEnp8B7wPPmgRpaSzY6DOVfBKxK48iqa09BMbMGynCeS232xXe64osd5IKTQyTJYttGqnGgpov8K8k2Lqg50BdQyUFa5ISimWCQGBRAZwcDXfQp1SkGsdNscPUwQjcIMqsjaRgVsTVSQ2hNzJ9Oivh3qSVEo7NqHKeVljJjr+v2ZdGabIdM3KinDJiz3E/nFGwSEuuVpopR8gw0Or7oBEFSiNTAnET/Q+R0x0xGwRWWMNPEmTXIkRnPUgp6qSVhaJkkVOunDD6wf/9VYWadrem5+BLRSogBn7pK5ufjAyQh4LmYJduSIrlAcy1z9Wc4lkJIs7rSXuU1bA2wgLAChZEUU4VT3JNhCXi+nPPo55FDM26Gc/FQrvNcz9/z+wsDPxXjPNrPBj7NlyIQYi9EzUdUDw8op9wAQAe9Rh8XkQIWn2kymQDkslc+UWVgEhLs8/mYu0me+uXUt7Q+hLElIbNb6R6xuwCSBp4WzR3L1ZbcZ0xswKDCI9l6OziYgxKWeKmc0YyBld6i1QhNJjURemQd6AGCtj1CgBBFrvwucDgUiIR+RJYIk8ZCqCKmptn+C0w+iSaRzBSmghHCS/FJRbL8kQP1RTuC3j+Uk3wkd5/Kdpt2QlJKFsPJx+JidvFDbExkSlKvmWlBQjjNm+ZBMxfyBHAbDKOSC99JDpfIzYj8kIOXDnUHb+kMMKGEyU7mnmy5O8CJUSHO1Dc7MNA6JBMUcaR/Ar6lHEHiDWrwByJWPVSUvXwHF1eXbApaAWbCetHl+MnhY+Yw0IxBSN4xibAQ9vaeMK0WXuDWBDZbFLUD3mhwpCiWFCIODLM0+usbN268MBwMHu/vM/v27OyMeUH1TuPe/bsXLuyy0wg8QdmhOIhD6Sz2WA4qm5vrIxaL0fnQK+Nd2BeT/f39qy/cwMbCWa4kCC8z+yELzUmZZxm5C/VW/JFJEg7AfOQq95UBSbgRvUReafFfUq3Ygd0nI6CZlKLyIA/4zOQ4ogqbGOZs43fVyai4qOOkbljrIJsMTaEBgCjmAzzGAC/kd7bsswc5hVSqWxv91z//uScHx0wBe/D4vfEp6vXz77//ASx+9OgR/BPiTJyxtUtLxqAecy3RxmRrcV5wGobon4YpLALGukWeLuxeODwix9rIzTJqw9HZJ3c+3tnddZOb9IQgQ5LDcHssyozbbQstH8hUsMEchuFBZqK56x0tqazkJR5xEDDkqqjOgrLpuXgpdOCHfzwjmCgcSoIM/OcCQQc71BYr75DlklZqmYEPpHguo8K43EEkbif1TFZwyAtAIhmEkHQWMHvt9c/9H/6P/2fOomDuHW5h6ib1iQHD0dh9IZvjye/8y3/N7lUcnIRvot9jp6C1ZqOz1l+LjZVuPKvCOYOJulGayFIF7AkjrHZoABArpFJhNRR1pMWkAzZFQG6bjYvL2QbqKfQQYeIjM0CZykNwIZIPuUK6Z2FB/PwbqFE+tYBKQLWg0WYklrNO6f+A1IiFlNXuvMExz0xHbGDLT2uzdgeHTbU+8TgzTkklJmN7p+wY02oMW5uHJ2ziuD+aHjC4d3xyShf09OQUm4llKvuPDzGdqWCYQaPZ8IOPP/hPWn+T6Y1SFP6GvipvYSv8DmNTDQyS/0oSoIoNd3A3ZcFNFcgbNodEMc/4ZaSMfg1YmExW2RM7WeS1kATZw1JT/eYLdc5pyvwsGG905Bv9zAHZYzda5VDg733vB3jfW2t605ABpvPtXthlqtDa+nq7y2R8qFRH+bAVPOMG7db6ydlwMB7YlWMbnfH0xvVLnO7AJEMRIF/tb7CjSTpHP2amVV/JFvxOq/vg7qM3f/zu3UcPmH3E5B/xtRnCEVbDJ/Lyyy8PT9kNmaVxtMYTNvNBcliSgQXcWk6+9OL665fqtZN9xxiRLBs4fNU80F2R/jZM7BljNdVpsliuKfYctIfuprmg8UVZyQEiMNIEubHW6JMuT48HNslwJjYkCKx4kidv4FiI/DTkFzwQaXU9jS5YXt5LBqhOd9WkMAMhHuVb0WE5knvz1ktEu3rj2p2P73TaXXeeQLnQ6uid1IbwRG1iiwCDHvAFx0e2i3Bpn1nE/S/NNWFlBqRBz9jepf1Pi+d4OCtU2VuccFIwMYs9xKk7Yz0IspTmUhXEvTRwqiBC6YmQVT4bDzsB4MVBHQ9GvIIgf8qhM3XhsFv1ISgkgqsqoCgH6EEOYpIJ9A6B8kghKCo5i9SD32Q6GNIPp/XFCYmllFTu/kFMx45ZpVO259adqsQzgY6CM+lQ7aTphH6ldxjBBCrnUWFv0YcXZuqa5j4wIS6gWLD0ZWa4LS/SSbfRyMSiCNCwxQ0NoI5AADCbFSFVVEBYShg5gw6kw37RaBBNU5ZLChR5EFezM5NPXXwvUUjKldunIhhI6vIF7VAuf8szxRu6ymT1OQLhsymf5vo0cx/M0YrB9/wZjytxcCSTra/nfZTVq0HELxkRQfqgJXxQBAkv1FWKchGyyvg85Onvp8Kf5vj0sw9PxwRK3uffjExx53nzi3ipbSkdPgcHGJpH5YsvRRhpKlIfqRXY04SizNjl5sDdKpBY+8CxpdOHg5PkiA5FsJhNSv1EcpmJiLPMllyPJrpFQccuQl6KsGikc+mLABAaIEBjBrw+bFpS1vzofteoohOCzFEE6WjY6BiYFZfBkNvuBGhewSvVbJ8oSNZALjIENKwV8CQGryKnKHNZ0/BV7TIKXO8cgKMCGkoT3fhSyaQCQSkYfBFrHnFAoJ+Na+ngrE0kya3Qsjeqi1AH/mhlhCVxnbeKFKh2jc0OgGRAv0N47AWZJUijrgO77CEsBXHzlwvIoUouFQ2w0UOhzPJJiSsiZi1yAAaDgxA/o+YLMDh/XHYgRYAQNtCwkYcdAoKMmqukARZh4s44BsLQGGbZAyGspcO8Rye4Dedk3mj37UqAFny2AoMpVkgbI5jZm8RjATVJOHSRMzVRihtra8enZ3Qeev2NP/qDP33h+vVr124t5qfs+YDHCxtssfYEWcK27q63wZCpL7MzJ2bU623G77GXRoP57pZ8IxpzlKCFvA8t2AHdObLFkgIbPkyvSa45k8ujziUtsdXtIJpk3nwkNlpf8eQN9qnjyKKwQhcLLUw2gYWeqHbqEiamM81QkQz5eOFZQa+yX7UQIHLspARROHianDO8WqhM0ar4qBfzJxR5QKA51Hp75yLNPKsWKuOrzerNdvc9hgWuVG5den3npVsfn54+Go4WB0+Wp8zQw3KvtXAjIwyNOs4M9Qybq+jWsSJTgEvPqTjsKcN2jUzlpL4J9Hy7U5/22/dpJVodpnof1ysdJkMzFyKVREGmyoEmkgGq1coaFpRA2y0GIaVxMHQP1pBO4jGIrpZ3uQUTQKEEWOEEcqxeUkhdkvEHjCuSKp8JIL2cWB4tq8c0GhLE5qNEMyVfq7UzCC6fRMzMZDtRzPw8uHiIFxuId6V+ws3GPpHDVFL6z+f6MRyi7dvc3Mb3h56yXDImX8Y42m2wYB+Vx4fH3//hT+D5Yj5gBnmvc7Hb2aB71W42z0ZDerCsAOGcLM5narc6CAIA6hujVV6hi9FYh0Ftagyjltj+jIZNR7VFg1Xwy/rx+mWmdTBlCKVRaARotsLis9JmPJQ/pTeXvyECHwwo34Uc3nKyistUkAKWGbA4FMFbJ0M89LXGUWX2QqXxZMlar8bhonZl1D6qzV9odAbt4au13tFs8uKsNj5cjNq9fn0way7fHx5v96vTDsM3x49Ojk5YHY7umrN6tj/b3D4dPdhtdJqdtfFbb77//tsfvPLK5xhokzlAUgyYFeUN4/Ie0PkNUvRer6p5WnvqGrkiMl7JBCFE47nfACoLG4xPYpwY57QgI2WIf6p1qYLERt+SBcKPZiLK0F2KWUw1GKB/sE1IoVbHam61DgZH773/Dnu6UpB7VzO86Z5a9YP9/e3PvOJcWXyXnLNLVR6PMDt/9IPvfue73+u1mZzY29nZ4cTf1z73KjYYQKcnwviPYo2GgQ7ANa9/wgNQEWIvmhGPRv3w4PHde3c++PDtP/qT761trIGmGNN4zpcXL13qtfo4Ma5euowoltyoyKMJI+Q2RRvd3pdubldPBrMlrR5mOyu30XgPVevOCCEnd8kjhY0sLZS0OsFqq1bOoHO1wogQzbr7YhMhUwAAVzeNMRv3UGzV5a0oSyuENA1hw5hz7hQ2PQv6jz+FcWGxmdpKMjjMMnqGULAdGeMlJMpHaqF5+uvdr3z1K7/+N37jf/hv/ynVeDxiPHiIex87ltpNTIpUQ3BrYDxwZLMqUwpDf5Sx1rxZEcOaY/HGtt1krpDyFD7xHXSdz0H3grqHuxx3xoRVYs7yRHoYVqVzQHOQNYFw1dXHTIitN5gmlPI53932T5CgLherJWX2vicNOGIMUx5gSNJSNZhS19hHHVcGu+4vUXui0FAUQJKen+kOeVVqTwgwIaiyiRe/Y7Zt8yQPsgcWhYlP3tErjlzZUDcexPIGPNpenBs6WK0YHA4NfDQDWO+tOzZNs4vgDMRSCPSFgLzIkPyRWbLloyMSsRD4TBuA5YOdBqVI4Vxu6hQCBy4kZa6bHnG6OrPrQFRpsa+dOaGF+AEqrR1cS+YPD7yJsMyLdPHmayqy4voLL6JzPfc1KwGYU0Nqv2gr8pXdexwxSDww89ec/cl3n/LMnZmQstDY5de4zy7tAQRpFafEI8LS2bxZA/A06FmaPK2ygzIQqiBU8i2s/rnYPxPwc68kDmar+899/9kApR128D+qB3Ai7MiIG+BACMgNH5CwwMcvckB02e8nZAZiWkvhN+yzOtGwAT3ePnWIzbvtr/QiC0SWVw39MQZmnS2fKJ9wsnLiijmXHAmnJ4p4YhcoxFojEHiNc4iY94hlYh/CfBAuHMvo73AAoFBYRKdcilJsrG9QFnTo2CKGdENSOwRJpAQX+Oy4Q4PQrygywXJiqKQxKkXarw0NchddGmGKAdGAaZvssgHqcghJb7dFiwAOMppqE0IDEx0dF4MSn66BEwYcKKy6YRwx7DtRNijX2C+I7T+xijECmK6r3xFQkjcz6DIdC9XuqQJNlhHjwJC6zHFxXim9aF7jkFg1dfLZcUEMkxrrnftMgSCABJQG+tw116E7KxRVN274RmGKhLgWnKCVrCcNqHvxxs2NUBmrhUITZt5LNHK2E6U2kX+awWZKgyolFBNSgozUNwe019SRExq2N954A4ZdvnR57+CtC7s7B0fHQLuxvfbx7Q93t7ZxzikoRLWVnqCPsa09RDn58wmri8M3c0DCwMEGpRIxUM6j5yiV1k7JpGgKL/il44c4YBaoeGh9Bazw3mgQyjuRQzBZDx1Se5JNPso35YEtj4a4dTB2cbqjeieZQ0XSQhnLVCjIFIisrUoIeTkm6mMqn3LFF/K0RONIM459D1XHdH2RI/evYLNON2ZXG/fWK8cn+4PTerezPV2ewspWk0/M2MH9zPR0FsnR8LTgk0pciSRHh93gINPV1zfXPLFtOPRovcWMQQaI/NLLtz748AOUXPw6dGVT96CennPBj2i4IRgc0JNNDKVGilAAm53DGt65gob4EJPoyJq1VLuT71YlqWAkJeocazOCAOVLcrBAsiAocRUzM09yDRTTpxYnszTdgWYV3c/5X1jKI/JMboljjhI8LyUIYCAhvSZ8Z8gbioLya50+e2Ky3wYLELt/+u0fgA4zFeAqRwADHX0ePGYcbIdqgvDsT7K2tmEV1u6nF+RmIkBMLaZ1hVy4kNc21plehAI5XY7d4hhHQm3UZYS1crNVuUzbGAgjKNTM6Ft+gFNwhTqc4CHPBvMQNBKJWyhkaHE+I22T6uHRcn+fLe4502xeHSymm5XKYYOV+rV99AP71rQcOztir/9K9QTX4bB2clo9RcNh7damZ/Mn19rNDYRFS6La3Nq8CKWYtM0UPipmd631zW/+jT/5gw8/une3Ux8c7ldvf/Lha69/hvEGQeG/pOQB1MR3dZ0/qGUiXlYz2wFBL5cVTdNMxwTLKpQlJZk3eZxMn8a0PpLWonKhl0pEyiQb3BMuIKHNcu5+m60IjvePVbksg7ZLhFVTx/3/3nsf66jE/nRzgDlbGrEW/NVXP8scCXsQrvti6iFbf7IRantwPPj2n/3p3v6+JuFg+Y1f+sYXvviFVhsxGhc/EYAIEkKe+g5IoBOk0tjoCWL2Xf+f/eN/ykKDH/7oTTftRUrgHNvz0PNsNG/durW1uUXXngNt8CJpLGrQgZBzyFiufKF/sdU4ms1PK4sBi+I4bIumiJmjSLZmieoLMvCCRx9gcp/36OByQrDdYRQ1QsYXyUcnGDICsmQM1xx3kWUQzozCM9/N9Nn1cwHl06cjEZbkz5KtsuNHQi0WH7z/IWO5RLtwaefFl16kSQybTQDmUKbX7jkut6g9erinwrTtti20y6QaDfeDOc9k6NwutCw+ctCi8235Epj4mTOJe4a0DtBC8ogpHURIxsIcLryY9N3rMzZMU2rQ8HV85Bg9GB/AK0E0WOAtKhresmpAbcsYNCRj7AbyEovVeFB/3kA/03AKD/wlKUjzyfaKMNPxLh8ASNGNbFRYg6RNQouK5FMcq3TI3vXrVFoZDSS8+iAR0dlkZBSyo9JYkBGgQGnHcUgl1DlD2rNE4yuSTTMDGdyvjv4QOtpM0iqSK8TRpqIsOjBF6VMMxordaHQ+0zsYdEFjOm6AMeVsVHlBVKmNOcNIlMkJhvjFlorDVp4lmLtyGByhLVG0IootZbIIjkQTGP7KldDzF35/9l0YnsV+GtE8QjhDkpkS/TTm6tm0zy4zSp39uTyjip52ANzFX6JzN0ky8KFkpnyW+CVn3hL1uchJROynqUtMKEfLBL9w7PHN7H4uht9Xl9+fK371FrzhrfIlWzLIi0TBG4RVUYYQ3kV1UZteFtz6Y1UIPUS6eCiNSCgTBDPqhPhjTJIcmVU2nA7BHGT6drBvNmVIuV9lvxs0LHNGkUhrFPPKnJ/tRrAUS71lEgJVgq4Fvts16gBbKS4bVBo6yOwcac1l4IipmepAnRlazjhcFdMMVOEVwp4jVooYNDrMeeijDpA5wqWV+C7YyA3hBD0QJ3qn1SGCws97TY9IpcpmCwYy+MrlZLvY7k7vBkloTz6RWJoNlQgHDuMKUqbBSr2MGY/MKvI06vhpUbeMfyjy6A83gYaQULHLbtOAn1rCjdX85Msej0zMoJ+NoVf4a8UQResYQoO3g6pF1pDX5FHVcApLgvENJIyLCYFGh3eO65qQCgkW4KiaIxdMGfaGb7dVFmQRaw74ShlWP+LaedDLYDr4YfsM9oJDvBlHsbC0sdp+/GAPGyBfGbmFS8SZdRs398f32v0jSV7HUoK52etmMYQjQuJkKO3tR/cfggjjz4Bw9fKlJ08ed1ptzhB45633Xnn5M9cuXWOokQjqLUxV7K3pcG19YzIaXbh46fjDD7Wa4JhosR5gxrAAppt8pwjkF/3LUM3qfG7lTPjFjfZNZJl7vbHFbCItFC70vCJMLPssqEWRF4WQSDlJZVKoMpdAeUi7wTY9mafEANKUPftIwycwtDD/nFTAi6zxB43rp7hgFSiyrcy7GghMyvCFiP4an8Fn3cdsJoX7me0smovGo1rrseMC4rA2nJ91u9jwZ3TJWGUzmx873S4lIINOZ1yerfCwe0jB0MYeWYMlQCy5aS9w7DIstBhRXx7xqT5Z9lut0fgMA3gx3abm0YcEMltB8cXnb38KBLiAETEjgP8FXrYcYeaMosYliJDRuGSirNswMRJFhZaqoYQMMae8k6dsStYJQvBC9irLdYDcusP17MYOEupSFELImLzkvMQ7z4bYJHV7+8QxI7vWiynbttConYRRYmHVIYDDPDm+A/EGF/pdjDF1GGVicsgIBj+8d/z7v/un1CkUJ7P8e53+xtYFqiMrRDEYkVEmp3FC06N9iEnPcOAWsS0OA3HAHb0B/FYrToBg7jinLDMwypwm9tZiF7MK4ltvbh5WWk+q1WuIDZG1BmjDlYfQWMxFLETwHlrwsCJ4fgzNt5DDpVGo3FZ1Uq8+nC1vf9ykqcYKUV980kBtLj+kL+ms7mW/Xv24OkWbvRnD4JMzjF/2CmK6fP2Uo/6q3f3OLuLW2ugxX2/U60yYWs2C99loOB+zi3zrlZeuP7h/797+o2atv7He3ljbYnjAQU5Bdl0ScKoYhVvYCqARdhHwE1SqP5YXwSwxEjtY84pEMZqFJMHAlZiUqOZmrSM2ZfCVi65yiUhUEvKVvjrTlqyAs9lojBrjSIEYQ1RkWi92x5qz9rONjwvF73Sv2qzbaWzsXrh4YZeRzbXNPuUgzNTowckpGz0x1PPtP//Wo8dPsPaYvN5ZNi/ubHt2tnIM1gKCKhUvrWr82UREDFIb/SwN6I0fnhy+/uUv/Tf/9T8aTtwuWQcHWlU/UfPy5YvMEZ8OWWvSwEFOc0YSajetn9VqOr9+89IXX/9ss/LY2XyMxTY5kgXF2GdlMhvoURmisykWLxKUES6hY6aAGmFox4rVYpIOgTfvkNFkhuEnaTMKQXsdVSg3WMF3XfY9N5faYC7zLk//kft5xOBfCiIFOmKxGJxxFvwpqJ2enVy6dHVzizWBRgNxnVRQL94WV0vX5iyTYG8r+mRUbldXsyV4l+WCVBeVcKBnvhPvRaZ0NoYINIkO488wrnGjY25PL1lGw/0MgYNGlnaRsxJQrW49jM6gEmGfolTnI4Yw0cAywoZVuqDXaKgiSkzOQhevJkvD7pAUSj4yY2oAP7NtJJX9l4DGRpuPSATx6k+0RChmpcwkB3DXq9QIp+vLdcYcQI3NUcgNox9PaXRmBJ8sUppdOOsJvAO4CL50kwiAk+32JY1iSF1hsgXj4apR2yDzKxApAOCF58ei+JZfngAPasAPewkhJ1GdXuF5c8A3UXSL/NIaMSmOFQiaJOYirmYnhjxEEENCCs9FqGjYhiUF75oKfiOYxMsideSWjAgsWZkrIWU9rS+Wtorjg9FylYfyLeUHqvPYhIinVE3+q0TPfiAZn2EdlwotCZGpIYA+HQHI16QXifKw+qU0EQE9kTFiIqeAZ0++fvotEc5v5sjnUni5n3/6ud+UbmjJDzrCP9oi5l95bJMSwH+0KmDBNkUEtUF3jYaUaRuIOf/xUWXSGtaYXQBGqFnbYVeV1IxiK0yYCNRAMnfCOa56DsihbziubCzH68sRy0woheEjDf+Gc05YeEgaRFL3c63JaarLuQvw0dMQf8mpmjS61c54yebfHGeCuYmXW2vV2QogYyQtEWolGGADU4uxpNC1EIb84Ydl+ipiobb8JjLmLzsFKGdkci5o6Fxcy1RYrBygQ4Cx19EscIlqbpMC5bjDOMZGMR9r9dXG/2PM8SabY7t6SR2AgU4hkEhTA7sYLxllAgyUzHQRjrhyywmInRGKEXWJzUjtDTc9fITpI3wGU7AAY9LhZgNyOwaM99aq7HuQHUgxCPXjY5oQU8Dod7nc3tYMCOEerQFUOT46AdoQFowVOm7wERx1WI44cE3x4DX0TIzqko3tmPZgiNTOFwlJzjR1xIHlfkgqyFhjVgPj5FhOv/Qrv3z2H/7DfHo4Gg87TcwsaDJiaEMfC/xwSwDap8bZ6XG3vzZ9/JD5QaCwvbFz7959BjeIQbbXb11/6+2fuo2Gu/JNOG0JosEAhn2Z/krZgyM6bFWOCUPYKuyFPaOFbDNHo91mREg+p3I5Z4w/dLWSBrz8AjeccRVdc2t7+8mTfTkN40hEGyOCjG/IIXKgJQBkIgRNsFUfAwas1KFLsB65Oe003QqYQR5qyogdZUB1hInI9hSiFENOOQUMdNUAA/oinIqswPlnrZRF/MT5DT4q7GffFHiyYyaPXik2UJo31tkTCSHBsHHPGUbG79+/c+P6NbLAsrEKOwHE3KgttG88mIedIPqUdLvZ4AN7ggHd2dbGznDM9PBjS6RZzfie8Nga+UPdR0vyYJ0nDTpjJR+hMPkSD2ApjnCaR/QiVgVWrnqTbChdk8jMgqqxuUwmERKY7yUTw7jIXC3EZ5Oq0RM534jNCyDlExkA+4qK0pLLNx8ghUyiSpc6nTJXSj8IzmYYRmoAQEfVJS69T0blOrVO/c++/ScHT45aHTcbrXcbfbaD6fcYz6T8thvDVzET2ZPEr3SbGs219a7T0rDCgR/xEke3MlKQ2XSntjaesnwbSYGXJ7gBlotb9colEIBFdLwsXTRJJvC885L/wSiP5ZMI+61cwcqvBOUD422Vs3qHPdxqzSEeRPZxRVF7IrlrH7En3P0TwjAxjf2sTDRbdLCnxotJGwHQqVefjvq9s9bJ+OBSc/kRm4HO2jhJqSRMfIe1C+YBzZY9MO6vo4d661u3Xrml5zUSA0ChfwHxHFKYArwlzO46Ba/YtEJFXps0sQzjPxkiQzzASR6CJG+IG2RMVKK70S2mkpIPEbiozsgq45aEUJ3ZiWR4dML8H9hEQkcYqTjMWKs2Hz3a/953fmT7xBQgWroFS/C729tbVHVEhjFJnDjtWgfZoFBM/x/86E0lEjq26r/21//al77+RWPaGrJqB+snwAd2dTLxlFUgUkcLd6V6+OToT779x598dOfo8LSR5WSsWYUVmFNbOxdu3Ly5u3HBDb3q7JHJpgr47xWI7Gc/aS4nty5tXWiNKifHrhpw3i2OOSxDoHBj1sqMlo4L4kEu5Rl2o5NwtLk3V4XTyrBnCI+KtGKDi5QGTptaG3kSWfGUR78U9vlixJ+5fnHoz0RavZLvuWSXvGQsgehqBI4DXlzIxJfwkRBA4lJKgLu7Pjs9OTg44KhCiYimdyoDY9NUXDcUJ5OAaxHpAqHiSQphM1mliWuKlt3pYPAhtQyE5aPkQJ3b2mAgIVU4B5nNibJlSQfdOHSXPkAHh/gK5YCL3kfUPvY8n1AfJNaWCi2RSzAgVXomUYlKr24Qi3ZJAPFWtMyIgQnI0tLAQmZqEsE//oVGpaoYSUVovgBPoYVC8kVZC+sERJbBRqpTJNB4tiiFn37lMzTV+o9iJ0iai5/Wj11uE9qKyR35pvDCEo0bfiEFg2fYSQBBkyFFzAviaCIGDulmYtKZg1eK4EdjyfJJYgQBs44omVz5YHQjkNIAwMj9/GcVwqdE/5lvq7jnpSYx8VZAlMjck7FUei6TwHP+yRRitHp/mvD84WkH4NMRSlHJ/TymWIGiOZGdIrpC6zwCAVyfSmNAWaGc8HMi/nwkI+Z8AKQ3Iwa8SlR+ZDlCsJIpmiS82PrD2FFLpxwcR2Mrwz5hKDsWDK+ZaqE8NqsdZyLjn2ZjzYlrN2g0rDr8BwfaCzQGYo/ig7WSkZrTxaPBjLjqsXvsY3Gw46DbetLAYZo60cVl9Eo2LnYsA2x97cPZApuVfDglip7lJSVzPsAO0hSbMS1EoUI5MVY1xfsEz+b2UdCpzGWBmrVJq7e+zjlHVBQMNfDH/iUlzmPMR6w9plO0W+3T0wHgAqqChfBSmHOnOdfW9TRs5s6QX2XM0ipa8EfQDiitCTHwyHY0whHOQAU6F3f+Am+QGoYM0ZxQhDoWos/wg0F6iqEVrev755Sc0YDzF6+iKtjdXx8ZszBw6pAbW4EHIIz+tE2yDWyZObiYXFx0tmrtx2Zr0yoxyipdKIgwgaP10mqpieeyTwjjViRwWpsHLsGUUqciDNq7SiIXDiV/hdhXCaJrSOaTpoiqiZEeIlnrpxg78MKehYYE7SI0Rk4uXat//ZdufvdbdwGwjC/BFyxTjM1kthwPSGXfh93oL12+9uTBPfZXQcm8+rmXf/qTt+ssc2t1//gP/+jKxUts4DCa4tQHTiDBL+CMcrQQBjeb40C8FqcYMdu+3gPO4fC4PWTd14aNlRAGU3udNniwIxwBY3QSBFGa8OUZSxVuosImJJ1dXOgCKODLjhUCC1kqhZ8h0WJ8FUup1ryvPgpsmD92z9yNG3ExiBbbwhAISC8BSR6929gDlEoF69zWgmaKmZQmMkZgpsrJMRS7hcsMoCMfRCsAG83RNcFmm4vxbLDV3aTDzb547O1FrYaXwyHeaL5n1SCZ63Io9rFVm0kHtWq/7qz3BVsWDs/oW3LiJd5vDhylE1VrDOHdqSPIyy0TWL4/pRZQlVYvyiqwcpYF/QqP/ysIgBoGCE5CBJBKTZ2hdvMNAbSJEGmytH0IVcw7SflOTVEQicu1nOGBZrBC1tC7IdzAvBjgaZRwpQRYOQEGaQy0klYgk5dgUSqcdWk5D4xi08MhgWSGTJYLDhbe1enf7dEzhlt2pqlmNMa06+P5D9/4t9XGMVsEYj1YPVUd+FJwCeOdIC0er9rwuHl2WOtvopaoHHTJ21N2yzF6IJ13ai2mXItfHDAYdJSOjLDrIEvlHlcqbDf+V6xmNUaSoZaXePjPvbOYper9/Ark4CcFjXN+8Uq+1BwmUuJOmLL3S20II9AEsJczYllYM1u2x4oGw0Coc4ZeAZIt4Z/Ml61JfTjg/NPqNjMeGmhvJpLURxw1NToetNuXZ7W7g9PxDthBQzqPrrmkjiCvE+deq4zpoLJ1KSthIJKWAcIMFl5BJg9C+5SbcNbA565VSBCTP/4X3XOUS3LvJuU3lFJ6pBjGmREVOXiHMPCMkHJir2fOT3Du2hfTBjQH6g59gLPR5PYntx/ce+TeW7P12bLeX19cuXyTUyBY/stJtFil6Cf0A06QJ/sP/93v/h5OaEQIS+jipasvXLuFBGovgqxiKEyUGwiFq1bpoRQZ6yMYrwSKutfdOHpy8r3v/ARPBPWPZRqNOj15XPKs7uVs6a1+v1PvHq1v9Ef0yzV/JxyYOJ2gJmtslPFCf/sz/S2mXOk6Yw3s+CL7ZxCLyYNTvPvV/pwxQJin5Yf+R/aZukLLS/G0p5xs6NiaawBsttwZSSuQuBINUeGR1g2NYkcpVJVW7lsYxHj+X3eZSzgvaeRqsqW86TXrmlY3Xep9gvnnHwxVlmlJGFKjf9To9TvHpwf4L+J1tNYz2EtUB53kB6wlTzCxWadqIhDUKSSVTXulBsZKfcEZbXQYEM853ncNVDzrqhDm71VqbHg7qleucwBZpf7Y5YjsYd+EZax/w6GiwFCrMFZs2iizjvajVGK5GoAxQ1EQyeBA2dZ/ymfi1RPC801yAxc/3qQBkGYiksms/IKOggJ9/2QVxHHCPXWNLglYIU1MKpZnwABe/MMO4wHlA8Ov29Fs7BONfM3BPDTooacmfgABCB7IAoohCe60QwHNBwYRSZhUlX62Y0AmCAOtKt0slacDJqpQja8AriJAHWMO4r1kaySkR5Hjys0fMjND87TXYNl8y2dLlQ98D8B8MjY/uUySdOVWAgkJ+Pl4HvRculjCqx1+ZA3X6p7IpVwL5NViZY+FBohEKRBxnrFfHasPDvkkSb2e6wDwlrCSTymqBCUlHws9z8FI+uduT7F9LuzZYynO95Lbsy/PngoCeV89mgpIeHPoEFHGV43N5k5nDodxoRm0Saj24SN+L1WWG/krK7TkbHdjPOoaB8UgR8gBGIpeyGPvVVHWGMLUZxIk263VT2WjWdJCOLTDHyZ4pI+EEF0rkdVpUZAYNMgu0/XWp2wLyTFd6ITZkEEFzwBtMPvc6qEKV2TwXVJ7iwIHdmbpaTOhDHDhcjRjcZxTtIJuf4HBQwQYCHXeoO4pGLgIoYlHrRQpVMWzK7xtuzwmLaAj+FIv9KPuaPSCh2t4HI0gGKLoDXAeqD5huAsZrTp1lL0XlQCHBvMpjA9FvEtIiKhWcOo8fDEvXhg3UNURCj2BRPuXy+qnr0ZVQnxsbqlNGhp4fFoByhkFhPrfJkgyqwnEhBDlxWyL4FiaVhGbo2idGUkhITCV3EcxThgZ5tXcbd1ohRq146NDDGXlhFLlew37ajJabm1svfrZz3zy0SdOXBFX+xfID45oFAP/TocjROfR3t71qze3dnaPj4+IcbR/fHH3wt0HzAtiHgLg1z65d3tzrYcZ0e13nVWIbKBi0YjIJdMtcJ/SRNcbg8HhfL33xk/euX42/uUrL03qzIgBcKgHrqw2pmUs9gd4o+adgxkuYNNIFNVssOfGm3SDbKFmaqms4jIispIHiZsY0A0EJRv62PriI18pH7ZG3PlkcshLKADpNE+9QoJKdGNY0co/c8iTN4kVFjDNS+NWFawwKOjUVpzV7CJTwVihPFBT3vgIPicnezRJWKSUCqzA41Q98U56AwlmeTR8bPe6ayfTAXVprbM+21iuX7g2/ukPj45HnAoM4DpyxMpixYhqA9P16BQxzlegVLIkkIUgpNwpW+vWjor741oLBNxKb6OSS/QkmdFXj37iLVQgufQgQHFWwRCeTwkt70lpeAE0rOczccnxPGdRAO0QkMBn+RAhMekQIkxsWMdsM1NiyTFhnkP05DX24p/+2beOT4falW6Zyrar7W63h3Qx8AX34ccA9wJOhzm7Q64tK4fskMswl3s1WkdBn3331UUKAFZ4u4uRscZGo5gW6J7GhEm9y8lL9eUlG1TgU9yBbHUVKhfUC/7cy7WiVej1LMwn+8F0NBTA9mTenbYuMH+aw65amHVo0eWU6UmYE/0qgxZ4gxbM9e9w/G3NQ+fWRnYkZ3V2gh31mTdz1uiedmsfLN6ZPea4r+rpyRlVGg5bHYWWmY05iNpOI+cTYaHCY8uXq1JgxcfzB+ELw599MChXROscP9USmfhacoEfduHKa6rLKvfwTS6XuAklIVBqsim6qdywuYrfhk4vipFqpF8GjYvSYCXXRx/edh6mqpPZTfPK2qy/xsRL9jBg3ATmLtiZgIPM5+36d//8+/cfPmSYVMtrufiVv/qN17/8OXw1OnTUkFY6kA0FgJayFH3rH9FBCv9Fs3X39v1/8k/++4ODI6obU0x0pDL9bso2srXLl3fX6IhOxp32NiOferJsujz6V/XP+Gr35LPXtuvTJ5TVYAYZjTqMhZyMyzf7MASLh/k6DM6wIVcKpAD+NN3m874Vm6EMq2Lm+JvynCOrSoN6tH0qF/U7mnL1tgr9+Z9St34+/FnIil2RBJ6to9ygj4/hNU801+oKv0lJoCsXkwvQ24wEu4GW/ET+NBoIpA2EySF+8tRyDs2IxQTmZp1ZmqowKiG5QibasEXVkX96rYQQDe5Qa9jX2IXZtWmbs5PZLRdXiiQHCs0MmiDOUiATB9IhcvQ6CoD6gBuF/hb9bIaOgYRGi0jhu7HUPkBntVZ80XPSHApElINjeSPApgnESEuTYQS0qCCq6LUCNHPQ+uZNJBQLuDvuQ9m2KqVlIWvglNxWQNQ3GSKAICD+5lYI70MJkTL5JwERYhJCFQoIdJqLQuGrkPJ3fisSbQB1BKhEV5E33/ARuT4vRKbx7LufSjhReQroJVPLMTVlUR7PwankaPj5lW/nL+e/T78/feDLL4yZYG4WLyT8z5WyeTIsmfigS+xnLuOHtU4BKiU8i34O5/OZdnyhDyEvEtMinL2k5E+u25UR309fOVevMr2e0JIbyYlnTP6fF3Ce6qnvv3zmjvcIRV2jAaOrr47gH8ncZQCkJ1fUeN2Hapk05LAe2y59OxfjoxNpyCnqXINyIC+NHji4JsBV92wLDTiYsHZJaRaajN8xzZiHbOfzk6iSbTuObjdH42BNqbQfkpjxdTqL7P8wt2vVZz7CcnmIxb6c7qhxMOxpxNhTdkq1ZC6QAqHJVPWsXGdkZBPM1LSQA3xopDHKcXQpi3YWqJ6yERIrnFxMbI1Mh+dkQ8x0CVY8UVNQCM1i/SEEUd6DPKkpOFUipDa5vtjyNfJOneGiLaELdAX/xHJxjHccV4HmuxpG+xtVtVzeT8tplaKSgkujcpP5uPX6/XS9DNF5bO1Lc9J6VG3R8aK7wpJTWh37LXYhptcwSZaVB3QaSAK0MDuJoBP1izzIymeCgVPNBSHSPlXnV2sLtNtj3okBbu5hhdXWfgSmBnhFvlY31p9gcyMbLIDDQzhnBhEr2MgMqGAEBvfg7Ox0eHr95vVet/XOOx+ydwoYgrsZWJOV236v3+1yqteMjSw4eh0C99fWr928QeDewR44oqyPD3vDk/mFr3RonUkFHgzrYy6RFfufdfpr49nB+gaT+IeXLly5cvU639mTEftm5Z/WwebavhdffvnCxR2KhiM09mKKGoYizHvGWcMzcCkcYivxIELoFmoNraYRqxKrxHOfgQarAHEVMQrF6m0OlmOaU2vR+IRdPyvVdakG58yKp2W1/ZBdVqrs3EPo/LKExUto08qTMWRMADBVGE65BEbSjG4fFZgxLnBmUvH05ZpsNDweDI7G99ZblZ3J0FM7qott8jraGy+n7E5pgQqwhE8ai4GEBawZ/SiWUDd71c3aJpbulC2c6h0s1o31Piek0m2j5lMqgBT4qCOoCFpapIp7Zck+JJCTWfigUWhXxCV9V0kHrLSRgioMiBYoqeKAw0d+fV6sWUT1OKVYQcjQFrR+5lHBagGSJq6tAEWWdN555NOz91U0SuRJGnrXSiBHI2JXWDxZ+rHADHy01lt8YGESHmyUoeK8yOw443H49N7/71/9jotHMQtmY7arYktWlgucHJzVt6hRSleny/DdcvvS+CJzqsZrLome1VqN3nh+hqmFTU1lRUoruDuQkiZzl1ln3GYmGSf01pvrPQ4G6Z3UWw8arcsUDsyWLIWEVUwZaYlM+enZRaZMsQQ79ngJunziCWJDcXSIpucMT1yv0Vu/fMxQ2Wx+mQGQ5nRnY7Hfpxfd/OnR/NXh2gdTlgW33p6ffb1V/6gzZLb//mzycmf+ZD5dn3ToNoDI5OyTS+wLdIJ3FBWq8w8TP6LMFGC9gHSq6XPioBlrh3FeNRISDsSIW8EtbCLEesOr4tG6FwaefxV+PsO31YhHvhrRMLntRpyec3z+IbEj6eZ5jdpSrd2hB040eZPqQ6/BYQpngCzozqFPEAnSIMbagcwSGo/vP9h/9733WSvMKGSjecbskmvXXlpf39h7fNiotZs9x4SxxAbHh5/cOfjhj36IVkel07Xe2t587dXXOZ8bgrCMZMlSaclOu6AnGjCsL9bfgSaExWIcTlv1Glse339wh+VxHALH6JPYud6s2u9tvfji5xAOjgAuGpsMYSX1CflkzBDv60ateXWLM6jZzh/vCB0A5kNu091jpi0TfyazTczTWgOmMYZGvvYBXPiLrABQfRzkGbtDEdmB4bABaGXlpHKgXLSD6f225tMLJpGY5GJ98ZebHPyLLzIgAvutESUjBpWcTp3xq3P+A1Qql7+J7gktaSO4MyZGDilKRwbfiZV2qnJ2NmqzRHA5G4+Wa5s9ZuM6Myc9UUxcyY3jQ8cfPIBOjLGBkJ1qV+SDoFJrr8HS01yrEEylegK40hpytl+zfSbuq+XUwuNaYmhArXJcpMKaRMYBoA0ORWZnEcq0sTZtA+0jfUVmOyBkgMCsLCQAdeBaWY1IwJWAskJ/JJAEhOAIBQBDJxZqS78JkkRUqaQmRydr9KM/mf6EONrYOxWD6mg0cHW8y7WAnGDGSU3mjCplmE44tUxo66OBMZ5IkGTqC6CSymwRxDgkJWO0AAeFI3J6t1eUMUMgJCm9YjxE0BkYtSuIwjgwNhYcAVz7ZAnkY/Llh1AKCjpYsyBPSyqJLXZ1mm/jLp/BA+A0HEpkQsJ+frmE9ellbK4StnopQc/uRfaexiKyJIVbjLJKSp+nN3hE1ftqWXBOvJ5eRGLqscATK5TjE3BLlpSujBq7ZO1D3rwJnBFNbCl554EXPz8fNakSs3z5y+5CwVXuf1nEEmlVFi9ICSMzNhAgbNOI2sbxxQwfDVMk0sqU2XWoWjzQjuHqTTQfG3Oau9l8hImv84CvziHGREGCzAzHBvOHZosz6LdYHjKy5qoRyKYX0G5h+YPpmIxYE7UFK1/tTyDztE/QhC2/mFuzqNBZ0uWN3yJ9XMRcm9ielnvRBBGEE4MGWpI14TE0ffIFVliI+LEDOOBBfgwSgtCEq6/GK/9VCzG/6PkIrRFoJLS0SAf+PBdOM+CryW0JaBN8CFLWQML0QSgC5OaqZmN5ClLWPQOcos7l3LkMOtJAExmS8IOSgiKQoeSfLg1xIbkZU4Z5mr32NBelF7e/8IEe1hx0WXkHiEdhorySNjMIZNYqFL4dNVLBttV7IggvXBMD/yWBIeRmEQICQZhRjnqp7T/ZHw7O2KlTYNiU8XREq0b3wLOBKnX2QsFAx2rn7C6zIC9PWW5sbTFfhS0mx6++9sUH9+/Ue0ybmR8dPblx/fqT/aOdnQunw8nhwVF9h200Go8O9jZ6PWlTr3W0rTmds8UQ+M6FCwf7B2wZNDgddtar3W6z1926uLuLc7rRarCGAujpHTEzm/NcMc0ZuhX+4CWVgCYCQCzQ5RUEvKumJc/qK1gXRpfIRBAPSYF5x6gFrKLFhtu4f9BYCBfUKRdFmaNdVKmnCk4hcpRgVap1TThl6TOKm0jiGxEW85VYSlN0OiqV0vnmTNXK8uR4hJ15fHa0u7XFLAXabPaw4dNgfDidnzWZr0/bw1QxnWXKHnCKAdXJmoL4sEspXbkW49twipkP3TYzBOdUYRoM+makg1PBheRCA+OBSumDnJF1SKZbO/jyyew1pYOdrVP0ZRR5ESnKFQav0Fx8UwdNan2QAhKlfJddcsS3sAE+mo5iItw8ll8QVBP4xW+kMKewLOmASQ8/8m9VxT7lI4rOYFI5YqNGpPWSW0gRtAIwFvseH578zr/9N+MJcypwGrpSCZnX8FtUeuusdXKIKdSF1Eu2AZ2w0pTzdzgpkdLYvhFd6jg9b44Yko4XVJ9zY1xTOKoOHnOKG72oxWh3frrTWKdYIum3CI7neIppSBUcfRM9Qvjhf0LLTx41hmQK+cw6i6O1yZPW4mxeO2tM2c+Hndcm7TnPfSK0EWCdlQ7DkiPWU22+xtaHi/qIzves1sUxM1m22PD0lRemH7/38f7pCdv+o9QyzAlGWNdYluzkgA+0Mp4wLaJ6Njza3t3APFmxwJ/wqYDNK9eKoT7lPTf5uIpJKAARS3El3OqiPkQKoTC74Cehn8qAW4QtmaivU7QY+UAGdJ6RJca1zg7jPOKEigm2Y2UwGNVYmVatf/jhJ8wYZCEVY7CuoOq2L1273Ow01ra2WFtr4RiAtTWsuR//9A0mQDJXDA3AWBCjf2++/VOOKl9fbzD0TNUs1lOkUMSpN9yRbaRFpuqP0P3/ve++MZmy7otFpHSWtJhk8HK5u7uBsY+2RIOhavAgIaDZL4GzKSHy5PLW2m98cbe72EeophzFBvdoGDmlYXTUrm5WWGHORHbcE6JPiXYe2NqCOyPHkmLBXkMkYZUwYRRqTXZv55jHtN4Mw6Kj6O8w6oF1IKMiHE/5JGPJ+/x6Gm7Ap17OA0pkM7GyK7afzgKsFeVwWALpf8NBo+3om4h4oaaYnsda9GatRyeF5YrUUSIgNLFe7Hcamzn7s4yKFmAsjEaWfzQ3RkCtiG30oPnKFwGHYkXbQFHMdctWuoBLtUO2JIfdtnAqQmo1y44dPKRMVjNSr6E2LqEqO4fSs5RvtAs47Cmf/mJSEZUNd8hSUGjbnN1EHQJ5zAl7YWgnVU0DDjoSoR6wJ0B7gzMRLRb6MYTFbOV4/SlSdSaJhJaMskqNlgAqk4rKyawl+5YIMDFVehae6JgsVg3QIVbmGwAUeQiIeBEpxAdIFaZX5LnE8LkUTXxIyrl4Ukw6JbmFEGclE+BLsSslH45GEOR6uE9c+cIXIfRNzigVXoaTnzk+d5WE5/JRPhgxT3ngG8nMw//++JH/AS5vqv58KOWel2gQ/70AW8RIpgyvrpJBedEuJQ/zMaLZVSbX/Sn7AiWrhCpJRiIvcvIRE/q6uVo1fD+/l5yR+uL7P39d/ZZoPxP43Ovz33M+gLBTrgLOt0zhQSqBhj6fkOkkoXQYR9VAGcVlguRROcLj+PbhLzKOTGP/pCPrBJL55ArVgDNrrWKoGsRu0Uvl6teWndrkBsWq22xlMVxYcwYko+pk24pBiL7YIVIyo99vazkQQny0tcly2WcxLUdmSjGFO2MOgs8MbNzvF4TFDqm0izFHvQy4lDi7rJS29tC/M46lCaWh7Yo7xjcPCT67xFD4vP4AsVULcy4xe1DyML0i4xsPiniER9R5KhRUhI+6wUCTuoGLhVQsrNXCCrKL+gMj4fhnK2F1sbVaGlhnoMEl3xoPQcqpqIBef1BpbEBWwFHvUJgokScNF1UUvCjOYKq0ekpzj/WGrCIgUFmyhXGY0l6OrEw1VNhmKyzEhRwpfn7Vqtj8mK0UFD/iBB7WJFiqnRO4AdOFWWgUGQwePb4aRmwswlZNHI7EzhMVPE4DfMNQAiWCrHBeJXs019vsK3gJn1lnrcbuzsgL8ybAhz7d2uZm170qJxevbB496q1vXupv3et2Oidng1u3bn7/hz/a3OmfDUa9/tqPf/LmN776VU4VYwcP6IBZRnJYA4yoQdZsgIqb9x1zvmkVz9CaxzkAHs05Wm6yvr7Z6zF9iMNMH0qQySWoXzBiOih6aDZ9Ik+VeVaesO3DcHJ2cbFYz4hcMUT8KtEkA4/5R1VBVap71bQSTHJpOYa/EEl2QDve1Y+TTcbBiEzpsEjjJMYdsUi2SiJrLIBEgSgfoTwdZ/rWShmuJneeDcBAReswPTl9cjbmTITh2mbn9KjF+vBl/RAb5uS4f7B/1O9fZB6LZmeBH2uUlT0Zf2IVhQ27y8SRWBxNTNoQMMjVrtQ2nrDVC7tkuBWe8M/XrXs645UwLniBdRx1r8ZU/quMATJNGZ9QLsTWrpHqIFqnSBnNCf0L18jyIEHBnmxYAqt8+aiIFllD8nEHuEENS8NDT6kNtaKLjG1a0+TGC6AC27Ow1adE0OeK3Y/yWndsqHZslbGtpLjQp3GoxpvV+t11QKEb6LRAk1bffuutP/2TP4MyxpxxMkN7a32DiXOcCsxunuxNWWfOGsI1HWIpkQCjcDrdwMvMZprMtIbq9pp0lPCVZpulPky1B1ZGZeftWWNj5PG8NWbpNO+zq+ui8oJ0ULRRBai7YnrllyzOsV6hKQ3KOEwql+MAUjY4c8PdN2vPGzvH8ysHLPzYXVRfHHU+qg53G9W3J9XdA8/Z+DvVzhuVwd+Y9n9UP/4HlfZPZmd/a9R5YzT+q7XujxajG4vaY6o1EyWGy2F/c+vS9UX3nQ8aG/hoMEYkn/oErVOp9LfXmQ5c3OxHB+Pr13Eq42uHywAZuAJ0OB3u6/F9KgXlWxQc8YnOMEMqJjEK1lQX7cLFgLE3OMla5lQypCOpAIaa3/qIWlcqFnGQWjIhnMFJfa3snUiLQB0kK2ei4k1F8lsMaR6fnv74pz8YsgVWrbW1scmOodvbzgBBXDHoWN4xHp7NxmyYO//4k9ssAKDyc9YpYsBSCPj+4x/+5Gj/6Gvf+OUXX/rcePLYMwTmjKWpGWSGClRhRzlDLejJqV7/n3/8j+/ef6JQamguUG5ErS8vb29v3rzxQr/fY+MLrX1c2AiVYxfIwCVQrjf3G7Nu9QxTfmvexWO6XsVXPWFZ9qTVuMg+EZzcgKDORxvzBWdFbS9qg+VibV4dzhf9RevDxbKXxcFMQjvJ7u+UjmmLV4fp76yAQq9MRjXmis0Phmdns/lmb2NZ2QYJaRnGyHbf/eEqxlOezr+XaM37Bq7Yn6ilp5EQo54zNtJAzBLHuzwvVoeByJi2gwyus/F/CzIyHDUborLoAbGGypOw3CeM/o2iqKed2Qc2STa7WBcoZwap7CoIOdxAZbnCAW1X2s245DDllTHTRG2JnzAiYPHcV6C/qQ8jtbRFNAO0gLYHNo+wprCYzoPMxPa/aD+DdV845lE77uKT6pLtTVVmjj8RU/zEWeNDYtA2obAMR/xsM5ViFicaL/0SWmCskMlkyMma2AOFZGBGQbRNMf1jtdGfFxQzwVywOxLLnpLzD+v0AejV2a2fCKAq6dH4aGhXNwGuRp9E43MxzUFW4vCPomQu/0gHjbSbJJ4WXeqg4csu0GAKm/H5f+JaLgEIXsKld+u+WUXYCV/VaamRIiJrhpKJCS3QR9JwJc5KHBMjha2+lojG8z+f+TGH1ZhDyVHI+QqoXLCyXKsESVXCk9YsoIlffU+WdsvyEJRCMULEKJEBQjhwf6OLCJemETOKDYAizHdyXGW5AuEv/rH4v+z69HdzFVyLQSkjaMECGPQBhsdCgn5NJbWK8C7wLANAhHzS9CShQoaI5AwB7Uhmu2gs4Y3HJubdvpBbI6HOqkeVCuuQkrjoMU0f2sIiTNS0sI5PQLTwTI9MHWOKC5W3bX7OZcSLhuHjbhNFk6aisNYMn4XT6qMeRI72HDDkDYYHXBRF4I+BIuJ84k0GgRuftCUgC8/e1G4ads6ucezOyhbukCHISj5yNUM1kSo+K3VtB0UZolLuakQszQNL7Wgh7BhAMEiHSaEHcVZj/vAca56K7YJjhvv0IrgnJnRhGxH69Q4ahESUZmXCzMUfRJ+fVdX0l8iR+Qa44inXwQcil846MY3Myh/WhEWkhdwMzCjXCl+xkMogqUctWyhpdfBukmCrkAZhRSLSSnMI+cAOG+fk5OTwYO/KlQv4D8kZwFmbSpnMC2oxw4GLiStsYFFvbayvcZp69k2qsfyaPVBYyoVB2+l0Ghd2GSI4PJl/9PHH6x3mBvVwe7FpzNngZPTJ8PqtzSHHMM5w8Hewa+kzQGVOXR1Plp12f8S2GJwPrJt7MRgOGOGlTJACahvZ+vzmzav99b7rs8UCIRRZO25EoB5mtAWuYRaDJ9a/DxpqkEiZUH4QikhBUQ958SsNELfQSjKDaghEGSVhIRyl8YnyHB2mU8UrmZGhdYXGy6yhHPlJZ78phfwqCFZAY1MWe5ioXrLJpxyzSwjLpnMWsiMDSCWzql565aX333t3Nh0EPTY6HDCkhxfNEsgNvsFwGweG4vSTIV/kLN+ot0g3Jr2fOVATs5bVt55hTKGp8qX6kw9+NcY64LK5wl8piR3k6FkomwrCJ1AAJ36J+f9n7M+fbMuy+7DvjnlzznzzUFNXd1d3A43BDYAEKYmUHCblkCWHaEsR+ivsHxxh/TUOW2GFQw5JEZJliVZwAkhiIEAADaHRjZ6rq+rNU86Zd77+fNe++aoaIGWfl+/ec8/Ze+017bXXXnuiZQrOa2zSAxlFgaloIRZq6yoOhDe5wpHw1V3yte96Hpfd65aqkoODy5W+MR/csCAcXT9Yw0pEo5IG/vptpSs8Mapn2N9Zqy7qHSE5BHS++Jd/9Mc2AyXwkLgwfR+DHEiHdvBdJbEgGtehWT9c2dzcdiYDuXmkrKwVzqbAWcIoMJjKZzfkhXkgx1uLV7o5NGTReSfn5gRyiExxCZaFEmwJMZ4Vg3LneT0NK5Lm8yu5k5+YKd9iw2G94xfLy+Vy642ozVn/qjO9tOXNy42tVzs2vHIuRJ11NFpkxdKgc2lUY8f5jRe7w/l296w/2eImrgyj95YX4yOdfuEHMx9wqbCI3SNjQjo7cybG0iZUE/ucjgjesFtQhx025abh3DAt5APElVdNEUKJhyHWxYjz9So+SmFDdTwic3ggWkkQWjoW0MrSZyoBRR2IxTOaUY2CKmMPUAN1eg85mU6lp8kmdHHLlLPsHb05triX2VQ7WEEDmO+9//5w0xk1ghuTly/P1VinfYkvfO/7P9BIotcGZcIWOg9gbW3t2MDyD//wn+3d2Ll5uGVGEVMfjWc3iT/kN1LVqIwY/um3/+Ljjx/1LUTdGFg6Iu6EEerJzu7uw4fvbm72VUJhKwiwtVjgrAVgLs8vdva2Z7NXT14+P333YLR9P5N07IJmAYkQQ+fC/hbMPd1FI+ubqeJOmo4x0ejaqCWNPZw4k/YMtUvtNMuF0x7PBKV141T37EOnj+rYhMWpDWBRvdhScXExHI4M3ooR1OYwRVYlkZJm7t/eNEFGqHVXYnWXf0kUeIFa9wU4H3lJcsxy+eGfQ4vcJuOLbu/mxfn88up4tRTTYdOAiAW2tVW1AX6r6VGZGL7yQKsQzXpC7HhgoNpSFuEQxQXXoJKC6y4awylKOD6oFbalyXntYg5lBjGGOE1Joya3cRUygSJeESOdKGpypgVmCwIuAJSa/TmKSXGmEVDoAlnPqqWK4vhLBq/zIV9xUREkUogn3sduNyPZeCyHOikwJT1iQW4lloppdFJI4VGyk8ezdDygnZ0rUoossdpxDNxX6cEiNBePpClOJlXT7WLPNcDGMgWBLLecvgMmlVzpcTK8aLDCn6K/PcjD4FtNagrDQA5WewpGu4LNF6+IKVeAtTuflcbPkPCFp19MlDdJkdSVr91dg/sc1NsEkjWf4G36NVPC75a+IRdinX+2fuRlKUnvMugoJWmR3Upq1JSuexcc8v8vX184B+A6wRr5dcGfZ1gj16CE5wUQT4nZYiYYso8aA/KozSWTswavYjnjCtRU7yCURZM1n40hEdoPHDbCrjVjimeabEVbucMvsyOE967idk+YwfaWnf2MpHVP0l3wMvpLw9xyJ/Vnk8EJLXmYeT5iNLvz1di7rs0uMrfVRj3SUk1/VIGmZ6xNp3tpuwxe3mYOtyw8qZVX9NfxLOYyJGwyX7zhM/ckSsXpzTiIrIRGIGXBVhuFMagwOc9Y2zk/Kn50PMicscWt6excRFmFhNURBhSeCtP7tjGEIpgJIaCqA/F+Q3tiz3WTg70qnJDmJDVW/LYOVxfpUchyS2xM3MK8z+o65LCu9/Xte6On7JM2J/5iXYqr9sz+wlmAbEUsDEiJKCXRUCNW0vxQ4TkXSz2lDDsE446tkaF0CpKBHp9eVbJXwNoNJFU0rlins3kSXnS3PW+XxDEKXuU9waVQYNEOWIIOq/n5udkBI70YHqrZ/6bF4wmQ+gCvX74cbL2R2YAyySjNdH5tS5rG2nAJ44RKF91PR3urdw/euzg75/TvH+z/J//Jf/xf/pf/DyOrtr2bLd798cef/OLXf4ErZodoo+0Cf0qxc6jFl87mFHWeTbdmk9XW3ubF5eRGDBk0ac38zo0HAmnCWRH39B7EikDBzKc4vxi/8/rVK6P/7k36SpbQiMlVZyVtbCmWwT6Kn1pTvJg/TM3qfpafyeU/068VfZgJo/bPSYaID9AyigZGWf/S/QKEf1F+qLZyAoaKJhsc0EA7AUwTaHSKs1UOc2fgULDz9Nb4RTxUJ3mOr8rBsQp8aFr6T39MjekIW9R59vTZ17/+YWpZ5p2XDfBUMbrleqHKSFjXAuLME9BRrXGdtPEybNmSVxCcOzDnG85WvUsKrFOsxGyfrb9QlTmaq49e0QRLIUR1/IiGKYISq7J8Hb6lH1mAEb8DBCpX3ItTImkwYwFCeGbZFudiFjAndcLDxXYQ75wmTf4naT1pQvFbE5yqGfEptV3ugVjs5dfgtABCwfjaiXkQaE/RlRaUFGsbd5MJRjv7Ozfpw4ZFunR8Pv3pTx/90Z/80Ubv4fn52XDjTBc0R7L1h0fPOxu3DleD8YZ9WoQZCWRxZZsEcQv3k6U1XW5uqc/8K+Db0mJrAEgnEbqNgQDxqLe1MXkzmhz2+5+aNjvb/GS1JZB/P+LG2mwsgSoEQs1HuFe4+i6T3tjQ6GUwizE+2kWPSEpwwbG3T/Y/ev3ucrS4N7zcuNr4MN2x7oeT3qbDpZfDN5Pxr3a2nnemv9Hfebya/PLG1k87s49WNrlaWFrDmvCWrDM3FwjTdmaLE0Zv7Ggk3lkWISXiSosZ48ePnh4fnbOfpycnP/vJq6985df6w/NqFSIM/yOhNc7rmzCLWPK0NKHc5cI/JJKpaLTXOl32GyUvqfXNIlnKmNApOA1i1IUmACh9dJe+VXneVy0jhfxdjYW9aadgR0VbDDQ4ymPV+eM/+WORAjOE+ovb50edW7eXO9vbjoWxDHdv/3B5dJJO8Lz3w5/9+NMnj7MlBcpXRsy2RWFn06uz87Px+HJ3e+/jn/7s5q/9qt1mLFaKBbVRGYca6el1xxvb6A9NzH/09JP+SF3KQYcO4svOE6tTdW3vYHHzjshO5uNCs+LLtKHWLc/nI6GP5cmgv/vB19692th8MTs8vni9mN+cdl8uF4er7q2Nzo3l4GixPBg45lmz1Xfe34EzaFerfYdq53O2r1Ks+meL1e6iz15vLDaeZ5Lt/K7xJjrDkgtnqchbNrG9NCYG9+rFVqvdxFR1sKrz25oYmb1VvRKgj9mDyKZZ1KaffpYuV4q8TFgCK91UlSx4gYPZ2FtKnwy0KMpvJYHAlllTm+f9DbOFTS2esJQUYaPDUMzsZzTs64WaLHpiInFv66K3umNQtDe72e0edVc3V/1X3fnNPvJnW52B0OTDqrBiKAqLYYo78LbjkZWKmj3/oJDa1xueFOb0x6+ExKrj0fCN1Qp/JE/No35mXb2q6Tfsb+YCUriEmqqxtlKbMWFIY5EbbfInAORHLBNtKZaXV6U/kthxLEnyxxyYzhMfIKq+thJeQTM2gnFfp5O2Kl77js8QrqYXlHRu5++EvSBUkYTQsSIURrQiW1YEYDOUwSmiQBk2pZ9TZQTNYORRCMlHfvvUd/DdtfGarJDPs3VKX2sEC2KyhbL88JErLMd4D1JY4K0z19s8XIOoDJFN/kjkLycNuBARKK34FJK7KjM3LU995z4/rx+1d2ukPMwVriVVpQmKKdKyvnqdUjzLQ//rV90lTfsZhhb2xBbkcrUMUidRe/Sv+mzJ2ps1pX5Uudcg1j/XQK5f5SfJcEk5taxtmVHbU0LWmlyueTwGVYzRVJeyTzvwIgbmtDGaCFb7RPnTJrEUVvHmF1WhgVTH2/QXCvUsX6ujebjUq/542T8TupaoJBCLXNUcXo0JZtxyNbKNhiaRSidaHb7s8qyHq91hZ6TLIs/AstfR0IREoxHGG7j1Fc/grORAASgKmuk+oEyrZCgQBTUhNf6/7CSRCUvVB0GOCg5oDBjKwo/wR2BOq3Kt1RUlQEuqeHr4kVpVJIOkgGJUykJHyxzzjp2SldnSUKEiLVFCrW4ziwMEtEUpElXFgSyUgAkcgg4XJl0Z+GgwXKq1sbuSS/CT0iGRgZkef7atICF+VTCAC1rW1MmRS9lhphTkWlfDVL1d60i+3FedkaB0xUccQ85bXaGmCmg3OFw0Fe32/p51Xr18Zqbi+EIgKf0cs2BN/rm6HD9/+tJaOoRKj4HBmb/bdmXFAwxlHzOKwmHKZpHGMX/1W7/ynT/5M3nHj56cHl3tHd4QqhPxQsHTZ0/u3r69IwrrBJ9LW/4Pzo9PBw4hwiurcE27XU5MEUqkP7v425jITiyjv/vv/V3dtBxRhnLubfQgjTiLpWfxk5/8xJGTJY1wMPUnzC7ESpPDkDA+oin+SVu/aE6ANAUGGSGEmL/4Mqlfa43KG9yO5sTIl0cSVAJOs0dRo1hhsDS4Hm0JlvQNrHoZlBzXwAei9/q3/BZtFV8xeTI/RFDZjOB0AwQjb4lsSimEubyaPnn0hCQcM0SihWSRJxOzTpCpF+nO2fJFvTCdY1JLX/KKKRNw7NtUFLCEuOhkaE+jVlFujpC1FoZehEszD7sGFkJZ8SzUFctlKo55AaM8rt8+0mZQiFaBUrHC4/aZr3U6AlEfwptwGBmpNYHVBCIdmKVadFydyoQQ03ECAK5hey53pO+LZKRnA+uMhyoE1EqgALXvq1/+6N/5d/7Wlz/6II5/dnwfjja3H/3syeXFbHszp3fTcHuE3r59ywjA4cHm/v6O3QJV3LAxS/I20yRbgWFNQH90cWbtL+U3TTnuBUpaKiOH2e3XniSL8w2rV2bPhv03Tji1+njZfb/Xqb5lZiwU8tE4FzxDULvNZ34H95+7fu5n1CwRmyTtzPY3xgc2w5r3nk9saWTSkB0XdmfzvU9XW8Oz3nx3ObqcOBPJ3g2i0VvWdE2mLOvo1PyExeLwvLucDK1BNv5LBqhZqual3nBK3zR1KqF345nmYNhbZvj65LE9ahn34K3C5Ip+RHXD9kgcXbF2BOdR6KlUeSdFYV5+Bo3m9LMD1QSlhtEfsoycr1kga7JUhILxfPvK+/aPgbeoQViH6urXmj5kN2HrW6pB7Lx6dfzm+IzkTIdjJUzqefjwtrFKmmNQ0pZyDoK7ebBrT52ffvyxYR3nldu485u/+PW/97/7e//Td/7i9373n1NAIfM7tzfuP7z/yac/uX37ngli6ix1pbli/oxqqUH39aujv///+Qd//Kd/ThmFJwSGRW20ENqfO/fufPilD2A43DWvUod7vr29Z/GJA1IgTz82twY3bx9uj3qHh3eOes8Hyy3n/mbNMQhKEcZyFtPA7nSaEhNonTA4sW+QXX/CLa6oBshfbmJ8xJMoB26GmRmVYoNSE3Q/NOu1T5IFzTZCUOOaBYgEw88Is1heYmpi+6ufTZ5rmTeRRvaBsFaDui94DZp2s2p3lIHNSOWvoko93PEVthg8HRRndm6aMzXqWe7cscE3WW1hx1KLoqvKiurrOX1U1wXxKz2tmBzKy7ZpjLB2tTXRU8U7Ji3qB7iiq4FIS5A/T5kUL3L5qmGuQigORFhAoqEohGJe2lKJJMxrj92E30mwrghJX2wRyBQEMLDWWOF540XUD380nLCNjVYF0iOh0okKeOUPfIgKwmhs0sCFUX6lGoZ/5XLAQ9LqMRS/wXDSt64kE4XN1chHEqEy8YACXFLIy5AXB1+CElajNj9aARFq3uajca8+ldh4JX2uSiBlqFtzzE2qN/lKuX5caYvHyZKELl+tBGjUu2sgeSPj26ugfPHB2zd5mNILjzW6b1/mJuyt4tI4/qWrSvm8KHcAhSV55v/bC4zoZ3zoFNeuRpl0lWf9MF9BJrDWb8KaYqW+q4eZwfnz1OX3+hIRz7UuolIWZV/IcF18+25IVIZVVmrak0E7qh1iUaMJCYnYroEqxUBELOqGpsoaILvWOf6CNTFkYZuKDbtC7/cdqLncWfRO58stM8C7s1Ei+aoKM5IFvplOYNeskd0Qeqa6buyMAN5jVOwhzaBUy43uVK7IUoG9Izat3zHH10bTcNvmxwiROHsyQ+h7b7YTprG6IO5525TAqcIpk+rEactamhrWh7vKklpk9D7QRDGyo5EyeU5xqjK+oI+maVOwiDkIwh9qhTxpZthhVi6YSUz15fSpdYopSBqIsxt+cjVEpDijuNjmgeBogtnSO+wbduodp2qwlZ2XZhN7ffilgdQj4q/rcqRLzF1XRNVWepU81gD0RlvqBUqAkiS8gpTNK1JVomRs32ScEWFog5p6sRQ3BUYsJDaz6qeuRfoGQEKcNxOnLgwLd3h4ig1z5KUNjIUKTxvXNUGnLhzNGvEU2ljqNg6Y3aIU0cm5qrkYkuFoh5+vxRKKPnr9ZjK54H/HOQhFiU0gIyiFiSkQis5nsK3i7ta+J+nn1PQhWxIaFvmFX/mFH3zv+z/56U//o//4733y5NG3/+TbW4PN09NjR2Deu3vv8mq8M9re3d2F/NnW5akDIwfOcrwU7qrR1fRFs4E/gIPub/61v2lToGwSG/tJ6NCIZYSA/aaml+dnp99zjz+Y7X/YK9UayzIMXuVnfSZdCKBnSSmmhffMad4DCgLNqSKwnaoEZtEbyJjonlQDQKG5j82OXhdi+BNWA+k3+P7FPOTyxiR9o/kwgF983PWlTZhPz84uctAECWdqmHkLo9HMUb5jc+SgMZ0YHhJRjlJ3LafRm88pePxqflwUPxwJLrpMS0cJK07ZFh1sOMDKcZbp8PMGgi9s5AvyDmB2wJBJITbMzwpYB2Y7kMGAzfD87FyFCBElacKVgTecrfSUFq9DTKG0OjglVbROjmwXUzSHbHcgsEiFjgdMkM8mHXwuLuWlp7JzZ8KwaKqKG3hBsl6T1OAsnCvRswO6RkVIVL4hGZFWboMDv/Yb3/o3/ubfQKxEGUKkwKv5sxdPNoZmFthWlVHp79O/nV39g73D7sEdCryZGbZVPIWPfKsLn/XT/Ak7rAuiZeYut1jPJJ4rU5ARmMwH2LNPTnd6N+uBN94YjunvvO5t3Fp170dLZ++GPYMnYEfpqEfieuGKq5jX+JOfYUU9zV1dxc3kw+7A6Vjc3ZmMR72XR/sOcV+O+ovB/tli8PLHmzs3V70/7ZzvzQZ/Nl/uT5Z/Oj/ZnQy+21/sj629mW3Nbj672N3rDCxUNqkdCunJ40BqDxoZMl5uXK70fUhEjeYLWyDtvKbF4rwE3rhddj/NDGEmYuMuEqRfzHOYuCarqLGTkFVSlmM/Iam8RGaMVbIwLEVle76+TzKQW60qqRYzSrwl4jg+VBosSJv8UyPhhtcuxpOf/Ownb46PMnocCb2xN/HNG4ekQKV393Yp1ua2VTObn3zy05evXzHCZt2Yo//rv/HX9m/c+Gu/8as3Drd//1/8gQHJ6fLqH/3Dv/+rv/xrOd/39cnDdz9YdS8IIAZda7uYceh//3t/9Af/8ve2d+84bFgblMZheMU529nd+cpXPzSkMMraX9pCZ2z6aSqRA+ydvy5abLXC1v7BrSikmaRi9vEgH9Q6kRssXHd5K9sfzA+V11ne8aSzvFf1VnBN7b2tfeuubic22xF50T7ScDHg95I+YQ3MzaZ/lK9qh7dTyhfjFj1qfCY6fgipTaJj5PhW50okX/zortcAlPSSP7BcEX0pbUtccAuMFPSBCFzWPc4fStBKTaZSOKzRMVe5YtgNTtqRuHOlw23tgtUug/7JhiGrKy38beOXvfmN2mOKV/MkhmN1bmej5Xx/sLyxHL6w+ZIpBAjneMSp4McU2YVodDuER0njkcfIr003jIobswc1sP1YetnzNF28hq82J6FL2uiP1QunMkmpbFQRE5OeTEVWmBJmMJABofCwioOvZtlTC1pR6DwmJB2a9kP4P+9rZn98F9WFv6OBZpUFdTOdJ6VX2djvFbtP1IpQh7UGqbP6nQpKUxb7HkQ2ngcVpaXYkLr+hRfVxQlAV1DKnXLrZ3vWfuQ+AFxpO5rcWzKfcTmSoIrzLoDoZ8uQn8iUwHdpRfU+ky0ZzT7ARDMAAy15feWj/bELsScFOC9yVYp60u48KsTyTlucrzB09m6e2o0zbz2tT8/nD/PDTlahtlK33NepUlw9bh2Aely/62MN6hrRKqzKa9ndvgUZsoNIwK/zXif/+e8kiGwKx/bqr6R/C77SBh66qBqddpNmn+QzFRgzPYq+eZiXlC4tvLbLArWOg1UJxuDafDDtcCXkyM7qdhjsbs83Nu3k6ShImsAZsu2VXcPURNMJbCHgvMyDef9wMdiidivdhmivjobNqIJcdImOnhth7i72zZypbd2sQ+TLjAxbzwyWcVNSLbN5hrhdJjRTXF2NqmsUO5NLMqjPqqsTXAanvMTTVQM2tuxv4K7Wb8WoUynndF5KrY6pirF4HQdfclJj9lXRxUX5RE71ThxLY2mALseEEEm6OJFL6qYKoQkXxHNiudxiRdtbW3z7i4vLqEISRauUKdokdns5vkpEMAcaWAFkjsFI2CmBn2i89KnuxXeDz4a2O5Jl3xXSStVVXD84Y4Vj0nWqzIS5vECLgjhm3JTJFQA6A/ZnTCOaWewqjOCBDggryjW/NItJWvSWUruToi7oaWCqzoS2aACxZBSIWdB/SYdTPvSmjNg0/QpjKsyIyf1D83f+8F/8zrv37r1+/TI8GY5E/71OmHq4IVSfkkrUVXKkng5IdhHNQQ3b2zuzGmYKZ3WrYrtWX/rqh4L3msYnj57tbO0cvTpS8ObG6JNPPr5767bAKWfy9PQCMvYMtR2qgja2h1zkHZvZn1/uHex/9IsfObPpy1/5CnwBDjm1TqT6erS8Bl0ztSCxP8KUJOgh0GeY0+oWxOuBdyWgvKl0+YrY0lkMfFEYiGfD1/islSfPYy7ISRtQgWeURwBJ4ZWGlo7pN7vHIum9y1+SVNgrSASBNMlg02A/OACS04f4E/bomDoX2RHAhALOgtfy/gdf1n1KnGu4evXm5Y9+/INv/dpvwJQSmwgcfIyao1zLR//V/IyeZ7Wa+pO2xyfImeS1ky0rFt1RZqQgTh8eAnJHE/T3xK4cgmtVmZlwBt01NDrAChDdDoMteqCpQ7ujzpyoGpdCkeZiZVle2qnS7aI3IFFdjUhUDP2qBkzVOPAaW5TZWsv2O0xqlxfMgHcJ/5O0vktHT1KAsFWRYjC2ZksQQeTMT5NK3gJYAgmwSEo7eLi/n3069Liy9FkDOrq8nL1+c4SiJMr+ZkP7/yPHaVARt3PKBSEzjdjhUnEkqsY6R1k9gQxHakoQ6kuVx7L1YlvwUfF0vXtp59Vu/9F8eNbt74kKLGZ3B4s75lKF4OoYw45Qqm3ODTHnQUO8lMXvliIYhq48yFVMwt1kKmViprsDnfULXWTbL1z2Tidbo9ENZ9vMHMCoawn7TEMSNtXA2ipnsGFsbbGYDAfbjKZeirAGcYNWFkC8g+LErjavgPFgNHzaVEqpF+M348nJ3m5NyY4uFynBKjdYodYkLz8u4YmGc76KyEK7+IQRnlbjlHGnVCMvVYuAcZFmckWfEysJ/RKTsoR+5EH9wWsxY67TKCSrdoUfbwEE97oz+/TRE4NiEthqbHo1MfkHOFsM7+3tAvH61ZuDvb35xvTPf/g9XfBEw5fTd995N9sQX1p6tPlLv/TLX/vGN14dvf6Tf/kHFOk73/neZ59uH+zv6DK+++4dMdrU3rKLpyfnZgmOdWm7l1qYhGn0xasJeuedB9jLocNlA1AWl9MRxNEeC3P1I93cf3DLIEBojY0uboVg9IQv9V8NTe3GBTTqdBRLtEe4llwZ0i+eKbXqojZZzQ1D6UcGB5RKF5JZRdbAX+oilDwYpuJpwBbPw8akzI//ueutpjbGS1qo/Xy+VONCAsObHNuQnbIqfytqeXC4b+w347yJL2m8YsY1b4vFZSIwjntOf9oE4Ag6PjdyOATYXDwKFFz1az6Kr6JbrsHUnyilIKa0CDGGpU9x6eEa6xviQyxkUnur+RYNVLJH7E0Yrkr7ZmAaecJwyowYdAaieNgXlx7wsBhPS4OjxcU94oFzeJsyMuHC+7CsPj1c89hbIOlNIESYuapRiWYWj8PKZFZ4CIsXD7nSDz8DCYz6rT1JskhRekc3AZDcICd5SkhtgrP7mOqk8yJXWOLKZ2RWoRg/UnYyS1YZ8jMmEA+DXWVOqsqZryqnbgKrik5BITJp4pCU25gCi1kNgwYjIP1hQxIXTgpO7nbB5vpXEtRPJBQ3QosHJP5z1+dZihcNl9CbMhqeVWaV9/bZegTgurCC2H5cMyqUV34Y1ZtgU5BgYxZsFCekjR4nszMB/vWX7Nd5W6JCq56GSPtLhPtX9a4VdVWaWBqmoAhHaMGsObrNNJXmRKbu1B8+wdXALBxTAeY24TFtzh7FEzN8O4M34+V8aOboIjP12c8IOdPT+MoaiSu+ur0LxPUz82K62+m8XtngbvhpFj2ubnEURJdrHkGayM7sjjHzTh9uopDaUjVW5NmeZs7Ss6PI7YxppmKJNMrKGukSIAe2anUoVDDZw8SvXmeT8+mAEClK4dX70B6lqBpVTc7SDhKlLoZBzKyg2SY1ARL7LJ0c2c8mglKEWa96C2prGp7SGYVlegR41QqyjFkBaUp1lZLC0BPTFE86GOo+WZ7lQBbjHfEFW8uEBWxWggTqXjBU8+MEpzGAUtmbaD70g1u0VD1Fe5ZrEl68znUwIRtIe8RYh8xMKor5xkIDiCq/XNEqWbxONY0ZihGM4xcbmZqTRLDNtzQZNIBDKMWTYJCay+T1N1/K23OSbxw+/k7v0aNnZ5eXz549t7nnjVtZGUGfdEIiIqJZMzKjsryLFNT+dzuZMjub6BqBz8DKsb+1dXRu3eronffe+/0/+MP33384X9z/87/4vt1XLA94/urVe++8e3F1fmfntmWnL968suulvhJ3VjEaSHFis2FsDPrhB1+7dXPHc2PZaSZLplx9+Biy0eLGGsEsXgI1ykAKyxQqg1vxqX3VfRAOilXbciNrfpVGhWEa6CQk6HqB/W68x9A8yQA7FAK5xEqJn+mEdJwDbZlaZMMlfwc0sYcmm1YEyWAvsS4XU9uPICIi0x2v0V84c2itaqHtfG4qbckgU25iyeWlU3wXzjAaT47/6Peef+Ore4PtVzE0dvSLDwzcREhaCDOakmYts7OgzAgoWnTT/kDWZvPkzfcHqYQIQTCi1ZCHbHqAg5G21VI2TkVwqz2wZddVhx6Es+hmU4Os2kmTUSlMWC65znEKSzDFzbC2xfvjfaR9DFd0qGKsvsD3cNO//JVocnqA9/3TJqIYMZHpEnHuLVAOK5WpMU33Mv00963FjGYSUGvmIwTcMITlEIudHQtYN+xb1d/unZ8dPX361OuQuFhubQxu37xhixTjACVcXllQGvSMr5oA070am4+hAEMfOl1TYX5UZDQjStiC3B3ribvdTbLtrfaGBhAmjAAHMHNyOpsXncFZt3ML2l17YthAObyI+oRGy3CDiuhA8SBPQmGuYoxfEXS9zUOZ3ccGKkuYsG9NlhAExYpDP7ilQ7Yxvm03n4wPOPbL6G7fbh2HV4PpRff2xdCcoAdbw3EmI2YANbMMMmWE0vvi3OQCnhK5j3nIns5h7JQhmF8cTK/2+oczi/9jeKRdY5svJEWlp/dj45yGngdFjyd+bDwjKPHjfAZyaBBuYHJLc5rhqshlnQYgC6YvZveSoP8y1g0fOHmNT/m0kIYm66XmnfzwlAd8fdTnz589fvI0C9rnNxyItr17cfvObZEG8wwPD/ZldMIDqX3nu9/75NNPbHEmmMNM/TXh/91dA7xqikPR79y/98777/zi17+GHY8ffYI/21vO1lBcRobUU2NC45P9f/pb//hf/Olv2WNe/CE2KM2vHWO69+7evXfvnlqcyK16DmEtqPbYSuBMHJ+yxA8e3tva3lXN9VVS5Rif6DCZl6pnoTaSSJUrgsnoASbtZ779DxvKqiQ9MWGRgjRO2lwWIMcJWnVDD4IVmWYUjgtry/1m3JQUtq7nKQSg/+uvwM7VikFTSTQ5kqasx/rtz2loniWp2hMVzkFAEkfK2aM9JvH9a5heQ8tm0Fp59UIVs/q5PzGZTczAmLYVLt0tkSON9jC77pjNdYUVcMRlUkiInHkxOjx8lUPK0z4n7BgVC5fS+OIJdWR2zGvNasNQxc12hW+x2MWxuMzwtINfTQoKdxqTERNyQrE8aGFxsETdZxU7tqL2Y65262q9gRjxNU5VjvgwYVSepSfhxBjNvN0Ole4ZHyOI6LQt78E1pSuBExEbHpA+SiVy43fy2NsQnc45JoTYSmIOmSw4hKElF8BsaFgbEuCaopK/RBmAgZ3kWOM+8vTKvIOM5manBE/yvwoIhCBfKyFpvZlXOYaBvVBy6rKcnckDxXWHNc5QHYN1afMHKWtoVyIlxloTHD2EbfN5ArvHLVwjVWVB034MZRVDpOoAO7hG5QrRkkQbiapTR1KEF4VK9h2CuZV7sr7dscqPRnxgZUwALO/zLP+S1eNkCSoFHw61D4xnrrz+V13r/MmriMLP5xqEp4Gc1q9pz78Kwl961goqlNqblF8PGyLr5NfFKbHMkdJLFtpXdSf21X+IYHo4Hy+ca8JdswmZjSogFQfXIGRmKTrmgms5Hdms/cox4/bcGl/GjFkexdoJz3f6TGTWDS6f2T1g1r1wgLy1wtlEa5FJCBX5DGYxLzkwRS/DYHGiZNGxCJe+bJqA0F2IQAvkq7VchwyZqwiONUktDu/ruWgUBGMqA9HOB/yxctAhFWbwSEJ35uYmsDm5cvJU0iZK6mjvuFMJrvN3ag8ZIUzKSrPlyZ6J/kJcINWVHpKr+Xyyxua21yo57LBWQYmExcGRVfSwAjUFNDWhkkuA5DgmbeJHYPIWOE4u+8clasEMSZvIGaCRVKoQBmkQqpuAVf5Asq6D259xllYzfOFmNdZRM0gUkvms0msaRh43DsUuRC9c0VCF6E8FDw+0PdGeNfUpz+vt7f1/93/9H/zpn3/3e9/57ic/+8k/+Pv/w9/+t//2q2dGxs0JscKNhHnWAVE1MVVRNlwqQMhiP5khjsG5MzW5DeQq8fnZWVZWjzan48mv/PKvUq3/5r/+b/Z2dp4+e7a7vc2v/OGPfvwLX/vIml/u/vbmFt7aTCmbMGaAAoqcPlMWzgfZc5VehRBpwsg45fmdKVuYOuw8f/ZMlBfM4qk3laDoDIkSr2UeepO3kG833hEc86knW1Y09EleoFKxQqxHseEaCG9COmTSqpF6XkmF6ngwrbQU4n+aH/lpdrILMENeUG48FvrUz4nXQjShqJNNsTQoqPCA5/HX/8ZvmPR/8+bhO++8+/zFi+lk3h/axf30/OLk0KmgIrt8f/pM70mbvmTPj5ASRQhW0QI/0mzYkdKoSva3ziPruat2VY+mPLBUU6dYTcbxuKPGyNVZoJjl2cOujgfJ8gAvRBNM3o4XGb5QNBKHP3ZldDEUFx7FgjROUWMkZsQhbA37/V/f5UdYU9wKWX5oZbUzmmKP9d3LewhMr71nV1IrY/rqCq4NJMzrJtWAUgxHH3z4/oZdX3iJk8zxM54xuTIaYKcpkRLehuGO4e6WXsCGaUDyCiejQKW2UNXO7zzMN69PzPDWm9UPNpF6Y+S/vpZB05wZ1SoFi5CekPOzuKpOlF0cD3uXi8Ud9b+3uttb3rEyPyGNIBqFga7bEB1011c4kv/Xv4shfrQk+Yw6JSvKQ36gcXyp0VTphQC3iSuvHzjrLbe5M7R5kb1ct6fCOR27kWqkOVTZoCYeZbx+zE4wWHsRdzmypD3YJzwTkvRF47IaATDDwDZU4wsDRYy2t82ErTGU1BXNS0a1IHQ23INz6kreXxNBprzhclG0MzEd3smbylVTJkKp8sMyjMpoXKNXOc140yuVlQz0V2Olc/5M1+AZPDRYjx69sGCJIA0q2tjnHcuNth3I2LUHv6bh6Ojo8ObtyeX0k08/lsAoLFref+e9+3fvMudqh/FdW/ewMqoEeOLTX/rwQ5hhnfHe6fjCOQGOHmMeb95+/9vf/vHp2SXcVUc6xtmH2+7O5rsPeT8rA5o2j4qeRgM0TitDbXTHlkC2R3OgoaktGoBY65DoP6JpOAeJshQLMjxQrEgEBvUqdOoaiTeOlgWK41lZcJ9oEkqmCy7fMQUx3BxNkHUOudG87VYkxnv9Rb2LjskWAa6v3HtUV91LrrQCsU7y9l3LF+W+htm8/zKSoafyJnkQzXj/7q4TJjeOj08M17BCde6J9g/+F7UDkJlpHIPpBF/txK9lz2G9eKHJZ29wI/4L22cUc2YJ08LUYjyaAa+NLRuR7TdSfTXHmsqEh0qv0iBqWbnLPKOwiqHCoFAagWF6Pr0sicSHCstjqyU2w0snJQmxQisudRFVFYj+x2Ymb+XJJ5al1Mi4vYlUIm9YFMSI3ROalEOZ0kupsn3mTUHIawIFNWUFFbUgdR4iTcrBouwthUMz4SdndCDRoHJhQo37MC7/oigIqlT8sGCUnkkMe13BrcoL+oqONRbqbHoWTpSviQGlceAG8UblNfy02gVC4jAqPldITa1Pev/WGYqs4vm1CUkBTQhySH59NQ5c//LCAynrCjPyoKWptvw6Yb4DJcWHrxFK5V0nCD/qeWhmJPPSlSxJWFfAhs9B7bqMFE2MeZWcoEYA+fRBWdiCzxM3MH/l819DXlOYXtYSRFDJViUXZhQgZeY+yuh1/pAvWBoKM32n6/gtb7Jmne9xHhHHz/HEXH5vWox6Mu+dL+b78UN0DDL9hqzt1u84IaPedt0x0+CAARyOJhnm7tjbru0fSmfEH/UuRDoUseUg0jTbQcCoBaKcC0vZznur8Wq5Me1dzFe3HQPMoc1Y+nQ5Pb8QxXK+sNpXB7ESGGIyyYETElorkMm7t2eiHyE1rQlFjY5a+6ADEKdEvY4EwpAolXpe3Bo4Bz72lYciLUNBKGFlc4hjFRWkqtRTbUl8+nXcPRN1GmMzAgAZkDNhqdJoERMpZBZYK51b7VlGaQRsmBkUMzTArg1BCs0RLfom8RdTu/DJzv0Hq+4LqMgWSlPD0J5qXcaKh+FX2amEiWL1arFHVcrwIFfKjDQRmIAo8xcGKMWbpo5JFKuBlkpcVcD5mrg0qBly3fm77969e//Wq2efPX/25vf/8I++/MHf3tv56mh0YdqHdjAeeWCZ738vgPvPAyosi9JiX8IMVG1uO7/Lra1tI05prIRT7S5y6dD74f6NgxcvXvydv/t3f+/3f+/5q5e/+s1/75/+s98a7b5+9+KhHgI4e7t7bSOgDPjSpJqdPJ1MzWnY2rltAEmJqVoxDJei/tnjxS5Im1tnp6cvX529OTqOXsMiRryIDe2lDW6q2uBtntRzH+EPCvKuaQTbXetSIglyD89oIClSlsAqnjaIVEb1cR+XZV4xzoH2Ic1q5Jt5h+DH4kIoCgdrjzKkurpwAsI4R10u7J6UcSfKkEF8no9JfPZRPTs/GQ02z05n5oM5e+3Buw9eHyfEpaJezZ6/PPr48M67wLLmop9mrFUf1NyV4WwyT6fa6FySPoA7IsSq1EdnLesjTDITZuj8p9UxgZHaadGeekQz0pfiTS4XW6N9/pmJuYc3MCR9OcpMucaTPh8w7lgG6LMUWxbkRJ/1QxYHuovC7ul72+AlLNNap9a4oyFwwYh8ZF5C5BD0whyQkmTVP/crikUUmYJT1i2kRqK2M01tiiDUAiT6DvthQTJyk35uqjAwOE6UyupeVUZNzEjRcvrq+WPTnGbjSfBYdQ9v3Lr34IFe+q1bt6wMZsMWDjNRf6Fh6kF38dnzR89tF7MxNLl43t3o2S90a1//R09gVJM9ZMkEVmGx4aw/v48PC3NPzWYYZUvzzsbJaniyzJmsqjLDgg4o+iw6nN66VkAP6k19oyXs+fxqP0JjaTC/PzUcCOfFLjujWe+KScq2VOkJDnoLG3+dOyLIAgDt7bR/PjMPuXukYRcNXVo70M8JcbSCULXnFDZOUY/o7e7FGaXaqnqk6vxcvRt7nxmzsnmvw5Hjpmth+LsECofCH36kFrTN76/TpwrXEJBzSLIOrURE3Liec1Tsu2Q3zMTvc0RXgIrO3Cmj90SoqSodB/91an2sYhq18CotO/sI4EKwx+YWNQ2MtSxNsEudbQamFgD8heiQ3nan+8ax9Lvbd6mrdTR8/cn4ivGw+8LjR589ffLMrMVEiJa9b/3Kr9gx/+xEhcqettnSUV/dXH4nK8coZz0YezbVlTSvBscsxekNfvdP//vjxc+sL7GzkNmLMRn2mdvaevfhOzcPD7mhao7ep6ypYN3V1q7+gKqxusX3v3mbIFGKIjSiNNnZzVRHz/QqM6qGARV44cSWXdNmRw2a3rgLjzVOYZEyZrFFtSN72BYVSXWTSpMtCwEIWuvwmNPlipTy3a6kpKGmCPqa1LsvvL1OXBlbhgb98zTJsgapaipIwVWx18kZ1cKmCq60Fkav7ty999E3v/GD6cWrF88zn7dn/NN+cd3pfHtjvjnYtJrMDtPbg6xk/9R449JkAjOwAqs8cCXimaHNTPgypQzIVI+UWTxXP2NSwugc7F3mJa9j8KSEJaTmDyTvDZ5SVNkKwahsd/4w6aPDGMjAgB3vKpGwTH4mMDUszUO1EICn8yEfn2U5vxkaB2885EdpQzudlxAgCnjzHRRYUz29fi7AEmuWOCbfGkEZSCfBYLi4C3xv+Fr3vZfZ/KkTwTkVN1ZAGmUmtJcKKe+2lwJE6dFk6LKUKqNnAFtoQkPSQgV+am3ITCmdMV0FrXEgDSldiAbirGSJyMarSTDX2I7AsY22lJNr2XtkLiWipYMGuAGL9qEzkeCqdwWY5s3zxFJ5KoyHRZ24H2GhevowvNowNov4cYBKXRzwuIQFtTzO2dIu3ouryS7Y+9eo8DQVJU+U4NMAtWdgXicO3f7VucU1VulBkniWJP5JOr8FQqIkXhRX811XY3Jwam/rrmDXGx+BkEz1FVa0BwU8b/7/uAqHhgnCKkPAhar8KgYHMpj0kYZTP1bLv6oYSRq7gqAopEFgUuxOzPbP1i4iJPF4AYnu6iBEbWdbg/4NimRYIJJLGaXGUdwE5NJnW5xZrt+bn5MXhz3Qo8c8BFCMHMmhXrLuxomyXWYqMbtnV6+cyLTLjq06mUMpEK+cVChz3Mnfmn81SP6YSRU0Q3RVXUNqJBD91mHIgS8hn94pO6hnorSWI61C1YRiOY2TAW80L2FXBUnt+MELHTlqMjxRdao5QRtIUuKd8EA384RDt8Cn5nRiAm2uOG1JkJfFGLZZG2LDBwsFSrrgqLexMMiO65iG3pe/jFODmHqjqfUkFSkpwmC3BjRyjEDkMzfNOoPFWQEaxJIEZ6Sxj5ekQIRHJdhwJvfepXflv6uQv35TTbgfKSoXuuUIcnLls14FAo4ScFq5wcHBISf+7PTyt3/7H/6n/+n/+ejyh7gdz4kVGhvtidoEYBEQoAGTcR8JRLWc62VYf86LzTRx/QHStf+0xqZ7cnwiyGo93P17D4zR//G3/xg5e3t7j5899ZBcK1ZnnxYnBmS2tXkmNuOmQMYV+AZlxYiBXCPxhr9g0enpmdj/m6M3tmwsXzNmI0IJbrmKvrpbY1vVqT0t1sCNoMg2DExC6sVmVTIE84xSoqdSt78C7CNyCSLVE5aMSkTd0xolaaDTw+hntT41uJSw8/Gb05OXR0PtAaVWFD2O/+Wu9Fld7Q4uLk7Pz04STl2uDvYOqNX5+MoLC1A++/Rn3/jGu2ROYoahsZ3hzVh0tQbRF3U1V4wC3Mo3sgnoJM6GFkCn25hbkIMhGpLRr3NbslofYAF/Jv7J1ec/BfmQGQ0J3EF/di7uFeOCyZ4zDZeWiTitTPtbtdYiXfV0f9+JS0aNtUGYSrUkbXj52USEo5jVrsbSsE0OJsVgDG1MI2I383BRXyZdTGWqSTBmECT2JvkbIaUXa3hy9jq7u5tb20agxO4VneRb2zd+9IOfmRcUwh1jtzna3dsyL9zqhnECxqlbGAoq91QkWOBjPJ6eXQoJb25sCFfOx9MLW+Zube7iiojkbDHe3DgQLjHEcjae7G2ekxxXe4o/nO9I9fZKW8LIpvlHxzW6pR+RWJEOndAeHK+vqlrtR8zP9atq5mK94nnkoa1k0tJjhAoX57F/YQp4z06RQus2RKEnNUco25ZGz6FmruaWiZ2ZIJ5BeQbXKM2mnWkTPHDKR9WBOAM8yY0Re73KGceD6eLKDhOMn+eMfpgFgRjPXJSNUCSGCEGV9uU9GtNK4De9gTXjCyWx3kTtxXnjhBGP7lRMf3EoAUgyXrMmQOLeC5OXaxUPiXc5tUXBiZJilsO67uX5ZYx4f/D82XOzxpS4a3bNfHq4f3j/wX0dWpI9Oz4RYL55+9bp8emff+e7NhWQeXx1cef2PdP0T0+tb+7fvXsni5GGYhDzy4tzcPSe7YYE8czwtJpuw0qS89Hw4Ad/8YN/8P/+h9PZcv/2zYvHTzReUGbnd7d3bt26wVJuboCPE4aSBJ8m+vPOIlZbzAsSjtZh0DqQuCRUuITcGBWSXGnY9HM1Mw4lGG0TVaTvOaDSR1cqXdQgYKq+5GEpRh4F6rr6JSe/Lxty9CxiTtNGGGs4ZQECLTDXV8EMiCqkQK7v60mlrI9W2ufZ2l0r2n3KLXyhdV3lI7EGgMOhM7a/t72xsdsfnM1Xc2fGiyM6sLpvy6khq36xYS4x8Rnf6o6N11RPKBVfPIzDgWUwIKyFMa6lLcTL5hS1SqFzmOmfouM9QKYYFKSjwH6ne1B8DbJFbChIlnzKzR+JEMPKanmwHxIZ6onjxevNBGKmuNwkG3tbxRwV5quCoKeN+mpcMtTPeGUmltCN06Uz2J+yy4qpzuStW6ARyZZPiqyi1aWMS7LznC9TeDExjUXJL9Ulp+FlXpkEqUlRj8wV0HJyS0yeMDICftVVuRNxUm7Wmqc6Bg6aRTD57fHd6YfNGtn1xFcADG8oL/oqpYOPNFxRZBU6bpykjA5+cBPNNgOhOFjSTc2P7MOLYIAJvhLUCZ7huahtRvDy2u/2ka9cQERFCpJnuZfz8wu72suS/zphy6HFjq5VnoCoTNd5w6J21U09bu/WL9qTfOroR2PCcVBaxuibV3nQoFwjhab2pL1y78blqfv21560fP8zn4V8sjR1bLnW5CiucArkiKcK9VGqldLIkSCr7VfBY3uNbHu+MMfLWGdeIMgc/fg2AjFLgXmdxQwinfe6h5ncWFVFguBRyklpEghc3dB96HWPDWNmX2zRjUYE1zVQy6sQt8N+J/lF2/UcFS/IpL94Fb+o+yrjgZ2DIFrmrNxHL5JOjaY+OiipcH6na2KBna7sQ6MX/e03fKxQFE7THiVqCVgB+GogwqyMZmjD4iJ4KnVG/fiUOZsrg86GPjVriR0iDBvU2OSix+yHS0DKniqs48yk+LRz0rD6kuJpwzmVqp8ZUEDAQ52UClNMEdILyD6aab3i9inKbiklwpXIq+N0AJQF4aCmbq6er/oW/KZh80rrkkhlbEfo01xqa3srkQnbDqbXm7zhG/8qN6EBglGBemOUCRt6nyZVVin4virVkSz8TOKqTQVK2w4m2pMdSJ8a49297c8+Fb3u3H9ne7Y8iletqTLb27JU3ygzi5fVCDzSTd+GmQhzYzrCYz4Xjolx8yVDlxDl1hbvkEcoI2fxl3/5m4vZ+OLi45v3hs+fnhzPj+/fuvvuu++a2bJlXtDwZHtnFE/Ywet2YZoa+kWjg4/KVFGJWJPtUvyeY8t+9MMfkNty+jDBiuFj2ITYt3QimXi89ZnIQWlZHuV5Hsb8+VecLK1yV0bfS1yODqxFHw5GTFJDgQzD0TQI7DOt9utB+nA4WpyQP2x1X8Llc08mJ1fj2Q/+4vtmPN24cfv4+NV5SAOHy0XcJJADexazK3uVi47osc6WU03E7u7w9q1bk+lzyjkc7tgWKZv5ZiRJK54Zcay6ooyh627Ap995z25CmYfltZ3B9L9X461Nr+j50p57YaGaWKcaKbVYujJTwqyGwWBP65GpRcJmaRXiehXXouS6iYiuuoZNee4hWRQj6d5Zurl0QbhKX7ZOE+P4lHKkbsaVVOe4jKu9YuZZWAVKpFGXNQCRh+2Muae0q4UGROq0QZGLlyEDiCi+Cnwga3dw6gMUzyHhTW950+t79w5u3byVkQoU5lhoijK5c/fm1cXZpmnfi96Ng5t37phTOzcdPFOLYUjDNXxoShOcgLkHW5x49mx1gQEffvj+zZv78+lY8v5kfjm5dLTWxerUcc2Dzqx/udU9vbBRSRaA6cN0zzobZ6vBUXfptFcXWxbT1AgOV1P/8jtXfrtCUN20uhkOebBO5p7CULlKpNZauJFDGTKPZ9q3+tdJcvO7l1aMb5yhg1KZFxkrmWAWAy6rCbwOo0KYaWAM83g2TrRm0J3MpxeL8YHTkLubr7QCSiRK0/FStS19duDK/HQ6OeLfkgqEiJ8KxKbEQDZCYrfIgRYHx9wLzaauJE3RkC9KkPX6WoriAfJM/DCltPe4KhuoEWIV0nwDtzBXQzgdGgeIlRGPHe/ORPT1f9aLUqavj47+7E//5dnZKVUdX1mT3b1145ahxbDQmAH1YZF6Gz/95GdONrDxg07QvbsPf/M3f1MfT5qd3f1Hjx+ZzHP73r3hQKTZyYajUvIcAkMjjB7NJo5hyH5ZH3/yw5PTF4vV+OXTyWKys7nnfPSzh/fuPbz/gOuvmqmZalx3fiurdDaX5gJx4g7v3nSi397Nw6kuV6tFlFXcnXnJvnmkSnO4S3QFoTa6GDMLPesUopuMj5tiTthb5gtzSh/yS2QXl8RTscl+U9IoIlqF+1Rn4uj35fReZ3aLPpCWrJIzchIkVQSijxd4lavgepYnn18/9+MLr94+r+LW6ZUbgZYrEBohAquQ4YaJdf5t79333v3u//SnTsLkF9s1+mo6t+xpc7gzGAglMcI2EXlt8Xq3szXoOHQw3cYYNjYqThoNu0oYs7tpc4Tojr+a/IOXGFh6hzKOfrG1qAtyIRZljIZ+77PchZONCGyhZMA/8pV+WpCtEQPqzOtn3WSPA+x4xdfUTEGssFU5Zqtaih8V7bxRg1hogLMuLbZYVl/mEKbqiEzEXqUShWEsLXR45lFn0q+Kw2t2oKU3G8ODGp+EHjmLwbuZLjesi7OWPx2SiGxNkT6BcjLnGmiYlDqFrpjmUVorW76hLiEAV3aPiowqMdOdV8y0WqBwafVVg3hYYEsYNMHVjFxPSop+hdhomlq+Zrd3EpSGoTgioItFYz2Nd4IEPo8XwSHeiBsE5GeYHQPjph5WkiRzJfZfaaRoL6XOi3x0a2SgIbOGVeMJDcAaTKVWYsuXZO1JgKTkfFs/kIY5iL/la563oq6/krdlL3tXrwk7rwM8795mCrLXv+vhv+qjAWxvWtYCL2/hWCCv8+V9mJiiqF4cSjwn+tiOvCMojQBvvk3nMYJNTjUoSW6pF8YY+RCmKXLuOrvGdBPnibrE7wG0nJd48S4Wdth/aa8yw5qaXvkT45UqYmawFEmZYCBiR+IGGWPEw4sK7GRhR/TusKezkZtAyB9M2hVg6nMc14qciacEFU+jWdqqJOOTcEqa1vqpRioSodFOxcWL0l7BKZMdNYMZk4ICc8G/TpA7KpnFshQ8VRDLgoksgVL98TR7zDTDFMelBKjypmCwGGo6K2yGghIoT8mmNX7USDQV9y+dMQBNNRYr4kB7Fc4kQ4oLnu40UKShB8Jhg6EBhEQHwqTUfu8IDiDjKfyWkmBWC0eekTikc7UbnyEECXZ5LZbkeQhfK3ClrfSVNLnlDwh0JG2qbuZWutF4G+d59uxn0/m5QyuTMkwN7ghHlBYwUimbjoHBU+8nTVPSeDu+GMcDMGPs8FDTK34GhrBDZrEDtFr9O3/nfzVd/ON/8fu/b/vFO+88/OzxpxC9cbivmYzXiCm2V3Viqz1eZqvx7MIaisaT6EIhHJyF7gC3rg50tEIJ6Pqf+xCX/+0K2ZUuP0Fo1RVlyZJXeYwX+p6UJ9Ij/ZYhIJOkxF25W6bKUwJNtSL1eMjDlif8yRVRRlN6/dPT03/22//ECAq3Q2sRr8IhtcPsywQ65mcTt/nKRlWORBViefDwrpAhnIhU9XQMswEsU5y5EM+fPn1z9DprLTJgFmSimCZ67+ysNsQKy3O1t6wNSXr9yZWwaHc03J0vL1GSHumyZ1NXGAZnLMKNVJu0xDCJGtM6bwVRLbaRojgpcbwQca/1IcEUprArfYYmBZbF9AYJbeyaUaNAj28KNshp6nyVAueBpyUxDwMj/PUvFciMmqCXw+88rkY3MlBvYkqyu01xzCdzEyKi/KEm5o8MbYmjE7W58eUvf4ACw0SptOZxZ1HK+eMnn42y2mQwm5zfvmuPoLR9zpZ2k5Ob2M7YINHpjrUvFxezm3u3pxfzi6lpbN3xpRW+vYPtzSvlziZy2j5ta7lNdudjA5SGPJ7uDE66/XFveNXp3YJVt3u3s3K+Yep8KQWsc4WyIN5+ff7ZnleK8EWqkFa3LW0ByfvceL4yn8Ds6HhwaZfj45w7N7Br2+cUoFgNQ8w9+Ya22BaYbOoxsJF+MDKEav0IzzDMr6iK1HisbFonifrI55klIH48XzhoqbsxGGVZDjmBGuXIBzXgmV1emYbj9LpsQg91ppMfTHySxvuLJEvk6QboAyQn02uejKW321ZieJl89bXmk0LyYH1F3ExOjALtYDQzlCBCzA6T22z16tWJiM0wW+xkD6s7t2+GVcuV2YkXFxf37t7GBqMEFrabsQa3u3fufvkrX764vMzZ5IONm7e+/urNm+cvnj24d5u5s2ygFntgEIZUQEp7sOr+7u/83j/57X96ZQMNXqcdhN57eHpqPfHO/Xv3LZkTIhUwgbJKymRqUYRxt3e3TH/Q27xz/1acVNILYdo2thPwZk24eZbq4Q5anAc8Pj051TCNL8ejnQ02CfGRUrEIH3AogCJrXKpKVErjd/OPME6yfEZBjEhslfem3ScUfQC6kRB48TH1vmlWwP3Vq0rJ4/XLt4m/8CwUrWF8DiK4rTGKxtRfVCLIJ1CtA3pk+GXYOzu5PNzVj7cVr7UsZ2O7qmbm3HwjPVubqLZDFjIuYlgokg/m6EuUQewuw5CsV+kO3afs0UmmKvxKxZa6UAnCKR2uXgbR8D+VLXgWgrnjOQhfqgxp38hlmJhXPF+BPbLgKQlfp5qnRNVpbnfhjUwf0CNPVDItic+kSKclNxyPyKLKTL2MsY0tTdpiESWzBkXNDHb6z/F2aFwcPP14JlhhLGHEKhNc4vJxSmJyG1yeRBTCB9A0Py4BaJ4CkVfyBnaKCMl5mMTyUNpq3+tnPcnbKiUgKGp8JWY99qH8O+qzJjL8kKYok6t0ybNcIMUyZUiB2yMVs6Ngs/6inAFVqeqzfQS7Kj+JA/X6qiKCqhRvn4KS3w10UqZ2tctNA5GfeVqEF3KfP7+uOF63N5FQebRfSJMnBSLP3sIP8a3sQiDF5X1hmO/2MzrjthH/ed71bKc2607qgJW7fbafHiR942ZxpVHgUeNPPEK6TkHqmx7TB6aeridN1FUrEL13MmgUyW/9wxpRt0dnAvX6nMPB8WgkanKTh+8IWfKiMCKr5MiFMblRS7rVuSHc5Fg+woMj2PWtFwE98EvPMrzo35mC7YcdYhjNvFJR7FiRESkNTtURmXTfU3XNwURmlIMbZExNI6SL6QknQEmizlKsxEDSxiiYeqKpmIJ0By7CVqnS2vkCwKbd+ioKTo+cNeG/c25MB1pN7oQrg+d4UfUSm6ouZRjLNGueAI/L1J3MdynfawcpJiqFrlQ1yTBRu4ao5gNRbvxPdcdOZSslwmxuvVJST1UY7m9Z/fj1iSigrD6DeruCd6l1uFdTj5aDx/anSwAyu7VXPWUw6pIlqZNXdRJIeZY4AOpV877d/8gouSKCMhYRWTMKsnuZ2SkFKu5nOFB8MCCr5eQtaAs3bUkJfDMuTOHx8TH7ldw2W4gsagaUn+FaOkx4LK4n18vnz44X73/WfdnffPHg3Wyuxyimn0l8na2rC2Put7760Vc4GD/7+JOr85M7t7JBOFMFeTOFTAHVbegPtzIwlT0ccDUB2eANzxj0kE6g/M4YPkechqLUhcacpERw+29G/vrX589y19LahxgscQJFKYUE44x7Vha+9NyL0FtMwiyK71TFDldvIbILjzs4ZnK1aW1iBkkcLH1FhZJztTi/ONVxtco2kqqpRsPhZm+Tytj604JXmWcDs9XxfWfz9OTsydPnD99731l5TK2uq6OC7Eg4mVzNLg9enMwef/b8a18/VHeypi3WWwUwO31nNZyqy5yMzeWWvoR+7Hy6Q1oG9WySsX9j/83p8WjLWPbo+Misj/TYXZmbFIIxIJF2wU3RWYwdOVEse0SGPzEySYGs6JCUPmVf2BbMCzF47yE0s52wyADLzmfEQJiJxx/INe/gQPgEip3UE5tkq6BenjtQaQbs+8QImKWAbV3nhzAL3OyUquXJfDosTWOrqDbkdJrIQOyBi9Jwyod37t75m//W33zn/p1f//Vf03NKLdF2lqP5/NnTP/rjf2kimhUm2wc39nZu6F9tbeuDUWu4EXHo4xFxuVwGd371V3714d1X3//pD8crvfnu1jCrosXegGS8VovRVm/M2b65N5ovLoZnVnYe9vovxxfcGsHyTZy2h8JqcQO3ujkHQNzvUVVKBcE5ZJul6oN5zEdo8yTzsLMve7ha6cLltS4WD2l71Mi+roOr2bYN3Aaz0XxnNDtbOch4cGrP/ungdLG4ueqcbq72t4Yn0/nhcvtiuLqdKWCdgaXBE9tDD21eZGTSzjmH887GuPNsNNhXoHpaFT0eSjC3SeNkzPk6OTFKbJN7nIlMgp5/tIuo+DcJ0DOzdprfSJRAdIkOqAJqaDl7lEhiLzyXsjgpK66LzjCPrEoZ/2gDsYX09r9pHzn7yaalTH6h3+Q3N0Wwb6aS9UJXk+lPPv4x40V94w2tlnfvMixBkqoK527tbvc3t2wQZEsoXQi7DjPmd2/fkQJS6JotpsvJ4uBwT7jfopbW2pTSqf2pL9ILZBjB+Ef/8B+pp2n8M+F18Ob4E7NMv/H1r2dXY8CCfcaj44r038Sebm3rsTgnbv/wpp3SUJ9EobEaC2Od+SE1+qrfvBxMLibGN7QVswubb9/o75AUl6nanViqeMDRjjBF5varGGbEuDQpGuN1nK80BTlELIP/Yx27budmmoMUmPz+VbWW760NlbUQ9P7tBVrSu1L0+jPp6mmbmZ355WugamYqcepWtUYxqrpS3jIhXrDpZSVWPZ0ure7+8OZkctnfzESY1fzA2RMGbESDtAe0C5ZGgjczCS0BpwANDpocnXBWKHPe2B7I8X7oRkmhIkRuM1cn8SdoN2qvkQ/rGrdicDzNa/8y1hTb7T/DYL+TMfHlV3ZZpQt8EsIwPcZ06MAq1zwVIEvR8Z2UKaweelnBNCpRspg/voOYKTc+fEnDGUwVjVf5xJxiERubBM3WlunzDv4QFBsKy7EnD0Ix8OSV7OoEo27mWsiKd5YFZqlrfBStT6pgBtKTWnIKHAdRy5uR5IByzHw2atfoSuu3FO4gWb0HMbnAM+LCp0KFd3kf2144wR7xyijnozHWo5QSPfACwqlZFr+7QmyeEEDYndxvr7xVaL1JiihM0rdE9S6CyqvAv86bJ/WroF0nbqnCu7pKEskMi3wkS4PjO1e+cCEw6s019PV34eVNBOpfklRjViJeFxJkry98TEkteQpaF3P9Pt8teXvxl157VW+j8bl8KpgQwYzqpKPYBBQb2bQZt8KsiDBb59ojId6+YW7BZmRlVj1vn4tlibB1N7tOIFyaaJgOJ+tAm9hibZxAiVG3TQOZo+UzGyzLy/BENTNhHwJKq6oiH4ozVQ6VUZqUFmlBRMOwDVN7U5RTLSaXJGn94weEkPBS78C0MIoskCRfuctJEEGgOUQHbFWkkE0RuQRZTixfalSlwqPUNMUlaNAx/WYy0HNGXR5DAuDquwTkWq/1TVNFjPuLuDvJRSyXG2UynGqXeZ+Zaw1qAtiDbFevKlFHmsvDcL8pqmNzkMz15NnDs1DtdIWUBLgGmw5/EY5V+2Ky1TxWIkyyU5o516n+7h3UmSUI1oD6GfdLmxZhetufm7mrUTYswYfuZ8P+8DrMCMlVXL5IIsDgFpzjxbZKUvBRytg30xBOtULDdqWH2eA5AGHHdjHCV07jWi4zQ8W7tFUloHLfyax6ap7IWTjgLa8PeUJyuDja2jnYPzx/hcrFy6Mngt82mH/n3fcObh46acHxqyenZ87HsTHf/+X/9p/t7+wuphsvXr3c3RxZDGDjWDNkaE58m4R3tHZ8SjvopbSYihSPLtT0bNhXuo8BMXypCEGofaxZE1GsxREWNSV5+6gYWHqTbCDjGTmTrIqm4kSPPAxvCo6PsFfxnniXBAUyMIKz1/I2GDgSs4iB88Xr56/M/TXxQdU5OTvd29r98P33jt+8MZ5iIpNDOsjUkRDHzp6wD+p8fnT8+vj49c1bN4Ck4dsjQeq9s7PzibX6/a6jrH7hm98AS+nmGZTWFc4Oqc0MziBrTrMKsrm/o1+yvBLO7/F0++enDlrOzAcElBYUAaEhJIe9Ta9DoG6ARR1FZV6gJdF1Pg1mRLeIWzOchZIJUxk8zCIQfqClxhOH/mUiavrFtDGiyQ17lIzhW/Eah12NjRiV3kJeGtpmGDT8ace1YNJGFjzeQtDKZ7mAjdChnteLpT1kf/Pf+M3D/YOPvvrlX/m1b9nTSIdUGvKinzBVd87NwQKJ73Prjo7FR9/4kg1Axdu0ZHNufA4Gbkyhb1ksdPLyxOl0FxdnV2NzDKaikLPppQlsogNpG7IM7nKj927mWOnCJUT4erk4Xg0mkxxrvjd1vNryVn91S4lxHGJ73DZVoilFfBiQipyCf/6SPg8+Vz0/kjBtM8KRjsWj5e5wuTfb4MYfjDu7bLsZAab0rkZjq1QzVUD4QDDexOLh6Xh0ubWcjFh9iPFMMM6UeAsG9AU3V05cjn/EQLHBbF0wGo0A8c30JJIz2LK10mBuo0zmzuaRKmDqQbxIWwVJyQ7s7+5P7CkddYrHjKUEhNaqvBGYO8JMNwtXoglIksru9Rl5KSco6gmaf1W9YJBvJZYFqxy5y9RADpetck1g8/riavYX3/9pVtgnJBJ7u7unA5yQKtN0dHR6sH/w+s1L647a60Nrnm7e+NovfERt9QW4QRmswFe0QDOssGXW5cHNg4WtaNSHDJTAov9Pfvsff/b0qUVlKjVstrezYuTW4W1n2Wpw7TGqXrPnuOeTXmlNbt29vbe3IzjkrWPV1GIZowvxlEJgGZZodtre2P20RGIldNjeyFY47N5O1Qtjmrb4LJOY1K41k9ptAQ3Poi71mTA/eToOtNe5jKOXF8XiZCw++ygwAVFXcjTg69/rn5550z4aARGN1PnfroZmHsRVKEA+YtLXpUpWYMqXeHD/rsGY9Lt7Dkzbmyws9xehsL0VB0W/XC3WlVIg1ggax3+JFfZAeTHS6OExGH7MLC+8VXxUSt5kYZcUG5PuvmFeXAECAPnzTdx+xC4WyapAgbbtgaawa0XW+MpesdCxOMpObdmjmadvlpjOrHEAMU0Gb2KzZifY2wpBv1D8Jm4C5dL5XJo7b3q2CEucijQE7EXUMKjKiaOxVNjYNVTFOqCSZ8Ngws+bXBKnIQY7ZhsDVV82mfTi/OUZnGNX4lQUg0GjtgC0Poe4YLkRNAcfUNg0AB7KtezO0UPCPZ6bouRlpk1WbDk4BkO6qUmwWzS6dLxYG/ubhYXR1+iu2/wknHpYv0ITq89gB7tsU6BV3BmJpcRixIEzU042BRbnSzHAKnDtu32CmatRljIreT1t4syzdoH89v76WX2Hw+0BBMOwpvQeVm0JSO/XmY04vZNSho/y9Bq7L8Br+AaiBT+FT2I2q9nDpBW3lkshSpm+m1xmHaUcD5MjTz6P/edXld1gtl9BNf99tPPSuplH7pIIU4Oyk1yNQW48jQ5FL2IUfKzm96NTwxd8wdJ+hpKPLLZ3ZjzNTATTHUU9eeSdgel21rVNewsjjGqdvXmeEuBydjtqMsh5pGJfUy3a5Abp2UQsU5Cz1U8seFoL8o6F1+OsOQnOwrTl/8Iydp1vbQPBb6wGtv838v4iOCsaXzjl6UHYPUPnPl55dQb6ViHayEKjlLhdqrpIh4qQsBM3M/WeKnkY++wxb7xqrgl1pWGqUd8oJ+i2uajGRM2M0kOOR8CTWNnkFAt3W9UDkDQSRYbKhnYi85698lGTrdMkcsdlSS0k1Q0ztKkrJkub0cEoRjie96bP5HFec1biqYtApjULJ1OFI7soRBKomUaXscKJaOpVCEOW2X62jrYNuUSxniqnUOQ7qle3/zRsMK/Jlqrpn8dahZ1YnMHuDF1gdWGaQmMnYinilCtaRFMylHmajJWvkPE2aVLx6bIu/rL78uWxkF9YHEjNMwsq1elPwFq6/FO08pIGhxWS6iQNdpqByglzgJcTqx999hjhHNANTu6wf/PGgWlNYt6/8a1fe/3q+et5//mrY7OwP3j/XWE5do65NKoOIxymvaLrwTcST20gx1iU3MKA2QmT3PvEsVAEp3othV+eFZ6NU3lWia9/qlPhYthCeeSPIZMtQdClbRPTAskfSoOEEvM1u9dbbFlnmawyKJVbhfSSY1DxL5wPPsOt0a2b3+x3L+a9x86i2z38+p7h/BtPbhzcPj4/NadYKrKbXY3Pj4/0lyK5btdWQQfxifR/Nr70wXs//fgn46vzjr7kYu5Moumka1pQnKDMikZLTP4sQwIYmIlMGj8T2aDmz5Y1xKq3nO63+pWd/uNMlyaQqecGkcPUOMGQ77V5axxBjVTsjPTkwtc3Z8lP7g76qNFifra7f7AxOjg9PtMMptuMF9zNah5oE62vc6aprzeJHxjeUbvsKIrFZt0QGWETeHQvRsxlTM896xFGRMsy2beqeZwl0wujqIpJo047vF8sfuHr3/iP/vf/ieNWEbtyLpYcioxIJFaDDQ/Mfve3f1vxEy20WUoH++dnl6enR3du3xkoES3krWWzn0HpnzhfKrfWfTJRmfQggFOeADAPwDjJVPXtbM27Lyc9S4Vv6QZ0lnvbq73ZeHHF+dvZcWpwb/tq6dD0GWNYI5lxU5qulmKGKRTXLjHRrNJId7hU+2DUozwu5atvfMWPcMHz9G54POPt7uoVP2TQPevPNh363JvcXm597NAv5ry7uGmnCx3D5eLFoHdwtdG5HGyPRVQ7w7kqSzuBoHyj50IUmT+WK/wOcOZOK93vXzmb0FoxByCa+W4MV8U0wsOq6CV6kcpROMk3fyjraPQs9YiNivaxwtLmprt4UMJkDfA5j+UM6anqxsHYLrKM1U7D4930ofe9kfm4xaFobEximjRKM9MjMUfRyi77Jsu0evzis6Pzl3NrfjhZq7ObN+5t72zOpheZDpU4hv7b5Mnj6Ytn8+1tw9pDp27/W//mv60c1SwNUJiaemspGKwy3cLpwhZ6X83PT05N7HaahMn9/8M/+O//2//uv93cOtw93Lt6NDYUZO7i/bv3vvylL5+eHN+5eSsipqaO3TM/m9Zo8Pa2fVoHdPf2XVhE2OgOTdS3nCN32X5Dc6NrVDWT9ZydZpaUJmn0rDvSubvNZwy2+R+2he1NafKrfocCMOt3bE84F2WJ4hEBvRIHpNdqqJxee+c5UaeiNeVsoHwGvwKbJ62I2YOY2MHrvLDPT2piUoR1vrLzeuSW+2SmSS1BUqymdzucCo8LKC9dAhpAdtZN6ADMLmfLxYV16hEHr8LidWLs6J+zwZFhz4nXGnrqwusIpfxxVoKY9Gi0GhbeGGQualrxnkeN5cwsrRXfZvByTUgMR1APjwplJdV3+BAUo7E22R1ngll844mjWPg7hEQlPRRJoNUx8EiTlrsi/jUXk+JKZ5p0FtynDhE4ryMDULGLtJDtLiZgjRwwEDdSZKoi2kRobUiQUJJ+T7XLmYjAsxpQnGYg5fYHuGqYhUtBA3vC7ian2Ov6Qemvn4Umjx2vIPCr5AhJsegnAyFZtVH/dmCL2xEvQg82OfHPMhvkIbD0lECcF6qZllydYyyrLkMoYIobpm6qflabABAI3czRcCeeWChajYog5GWmibaCzjdBBKH1/9yEFvtn5mEbU4qT6QLKI/dBvkSWhOWCViaFBF1XoCWBDLkCsxBqP2WSLGlatvVTTyohvUjgOWwtERc/pakMLRdw0aLAzI3Uqbvrdy1pSGt/AQ9UlVU6lwd5t8buCz/Xia7fS+3J9XvfysC9alJpaaJyOTdDRWIY8zQekpmvYcTUpAzTaTSjyw0iHTgyXhudxW7mHmCvIfb+aGZ3zvmIhsdFhhONMtyeJlmjwjfFNZ02BwSfC/KCrTWFBZyCaMRRfPKZ28g9NSSs9iPWiHujlzdbOZFkx96f1qGAJXVOQqQEu8BkKp2UISd9DJ4NEjnioYFLL7LE9Wi1JUw3KV/FL0sHvYaHuKnWwcO0jIyp7IZx1Q2neIpxxVlRE7NbEf+e9sIVq1LNnDuoT5NA4HI8NrjGG4u7Y+5m8zX1H1RbbDFndG6K68T2INkcU7lGAFROuZyDS6sFbyNbeKT+dWdbiebycgxPk4+mlITyWbudaQ/M5NaDuTi/4BeGYU4+c2huhgLUivj0GJIsM4eisx9zm+fpXsQsJiZaXh/lLP8eP7XfgPiHEAyMWYrqaIbzhFUCMFQXhtEnb2NifKQeGo7ga4YskYXlOIsmVtkxPa/Lh4rWSFlaTiUCIaWRUKSWXlbr4WiQ+flOjc1WkvZmm9pCxZkAP/vpT9//0pfMe6/RyaX5sv/b//Dv/Vf/xX/xePqSC3IxNihv7N5+TUOBWlixafpg51fHq54pUKECHqn48FYorCilihBl07zl8gxr3PgM1sEvH0VyS1I/AyGvWjIgC3SAIQWFYk7FVcyr8gLKHwlFvUq1sT23njB84Wh4jwECmeAUJ7RKFX3hWm7u7GOwWWAbG1smRFmf9fjJ4zcvj7jUgv66A2Ob7fa30BH1mM1tWHXz1q1sOu6Q6en49bEta7bj6MTE9t4cvbAdjc6Ue253urLFmhgFdbp6RBmbhjS5xrX1CDAnPfNltxmCdBuq03tNV7iRJoAATOiKvqe5SEi4wrMBn5Xr/d3dXQmoCmVLW0ZXoxL1nMw6CV+lxdTr2BhFD7GQgFIlm3Tk1tpwhjQwiIkgM5t8RfP5f006NaJYOwJoTElcnpJ7pgNVK4cJRJe8GiG8V/V+8Rtfcx7X1paWSSQiZQUYouKE6TiPTk+Pf/zjn+j82KZW1rsPbo8nF6PNbXpssfXF5dXB7g4dzlgfhdLC6RPazl+9VZ2t8e1ZXmMIZ2qIXOkcY2uozJLrdG5YT2zC3JWGe/jsspdlVMvZmKwXo/3exu2lLXcoUa3VgxV0S+0yUtRQbKg2VYxeRtP8lebmK/+SMhS7yfO8ZgEY6oH5EpP5mCvsrN9z7XFcpWyhSw+bXsc6OPDXJlBno40jM5Y8Lr/J6gEgLDASyzHoxuuN9wFwlNAa7uCVKpxOHRlyhS0UTmwf26UKVmFy2ZngUz9DnDfRIqIqdEMmc/E2V7Qiykb8HlernonOSrA4MucQkReVoFa0JGCzLNUVzZeGhoJ8dWlru0y76G8wqrF3mpA3L8+mJmeps0AvZvt7diJQg7Kg6Pz49cHeTfsKPHv2QkAeLCx6cOfm/uE2Hx266RkHdbgBUEpdfUJ8uLg8O7xx8/jo+PT0hGH+rd/+51blMI4vn79Wv9grZ5h8+KUPKJlFTYbqsoUxZ3NjQ93FuC07+Gxu2hpoZ3dLkxeFKgnGjvir+5RqihEe5V1aMbXe6Six4bFGal6WpXmZTNLVVTpT1ar9Dp/zv16H6xITUYwW8O4SHtJluuSPRoSUMe/jtSTFNVgPY96TPneBWWDreWDncWB6kI91gvWv66dvH68hNHLXaSET1GSPEixs17vR25ppwQyzcaHTegpEXWlR7AKX8TVr0yBs9lpO+qUtVZj8CYSlnynMNw919trWvWEntGoVzlE6XKN9lF1GCHgTpngROOsrfPUsV7L4oGZxjEXsY7DyLlh5oYZpfTlRU5YVjHKs7V/EcYA5/SQttGFuCouOx2iRe9jtWcYL4mNJAyq9SxsjMTPjVXYAb/GOYEnBrThOc2J6nJA5qLF9xTukhnb3+FWiAC+vPEuZeRT0gnNSheLU7gAhbGpWpUqur8mYQ0oPmcE0bzop+YhZyZJGJ1bWZ2AlUJJYYuVNtfawQU4hiS4lb+yKDFpUmdh+CMVjCU/4CsFB6WSkgWnYeelqSOem/bz+9FNBxT+8W5OEIE8aJvVdaFD0gEmG0NB4EDjrZzI0Zsm4ZlF9tRTtVZUeN7R2S80bQF0Nq7ptH/WJElxNbD6+kR8b5sDVG58KkzujAa7CjCLmR0vQIOZdXUlcN+vP5E6xvtqd54ULPMmZDuV0Sd3TlWHZjKiWM8cnmC8/xvKs2dWc2yBcRerfnJJlx3Zr5qaZXe388YPe0hSUC9Po50MRJNjTVjZtNxPbdtgI+z4b5LV/7rbqOF/dMnl0YjOF5WGvf9ydH6z6IgGHZu52Vvud3uvVcq/TPXVvxGy1ct6wuNHuEvzOzpwPu9rkJBrA4x3TLLohEtjN4ehGmiwdppVcfw6NkKTBdmaACpWO2lzFGSusutqUGDMmUFf1c2m4rTUVxWea4XGUjl4IuRhcYAhwAO/Yd3PT6xbc6nLH903EK+JLFH6DT8M7wdkyhpaiCr8QWdaAOYhE9cie4uoHP1se1sGqR2bbErpMe41SwzmWQusT1ycNFvEFVVcqAkzKFqQu+a8ulR8fYLKGsLTcRsXMCOfdeiZLguGPgFyM099QOadTqyTTZPLUlSFN7vWrRra8hVRMZTo21WmRJuDhxTnlCelNRZVK+QuXshdBbWJ2ACdM/HQ5P3lzqpjRdg2JpO3IHJUQZAkgGvpPGpDwrprMGFv4J4CO/oXt+U9Wx9IkdmEo94Ld7jy9esqpDcndnsk+jn959LMfv/fOXdtcOJHn5GLyg599+uUPv8JqTOaMPl4RtyXn3GhT5NMxU5YqlmFD9Cx2FrOavk/aqdKxzihLM5ZfUMsVDH2V1kRAOFME55VksZxhjw9erEUvzLc/u2WQvuAfr3250CW71N5jAyOsW2eqnL3LDFFRV094IZzFVH0RpogwLVDhoN9qly3V0QaKP1JVtQ/DLXP1d7Oz2mowntuTZ9UfaeQCnD5aQZ2MOQH7g0Hn/nxxAi0+qcPRvvSV9z7+7MfTq1ulTFyR0+1t5xaRPtTkKebb5kvmNIgqWVxM2hdnxgD0hrnOd1++eCXBzo39V29epX0Lq+gtIBBODwbwaBFXUJUEmvZvblkb4xYw7RrljJcczXbfM70t9ZF2GUCz5IDrbzZNTX6w047KVLJhl/CYrur246HanMElz3LOLsXORnoCfZlEW91LW+xQkogGN9eVZo0hBT8oCZ5AXQL6vJzt7m7tfPSVrw1FFxbmnUcnq7+Rwb8SLkMz/LPv/JnVFtC09Tvp2iiHJlqXYcVhT0Mns0UU+kbpUmiqwZhNzQiPsk0ZoI6wBQvZ3zaXyixqrBjP+6OVid1nyb6aDGn/8utCKjt3/8Wd3b3FYt9hXEvTajq2NRdsVzQaaEkmNWF8kVf1pSmsBEUR6qI96A/5UeD671HBiJEOdoxziBTScQzAmBqZOnZ72Lvorq56G8+cMcw/6fSPbPkfv0T3ZKVvdNZZ3hZOcHSAmEjmd1X8daJjYwai4OVqMNrcob8snxX2H//4x9/+k2+b/MC0YGUstiksUI7wSTaNTaHsI9gF/+GTVHDM87t6d/Wm6iOdtHKGPGwqmgqXwZ0QK4xi+MvDVBXcHtXkO00WGI+opO3lZLpmSzOncFnu7G2evHmjOOGa47PL7/7Zd53sy9efzZ4LKJg1Z0Kjc6B555dXRxoFWvX8+M1o61S05cGdb73z4P5f/xtf0aBkJVqF3lmDNa+DvKoTKeh12yCIM/78+ZN/+k/+8NGLp0JAzsyezq7M0rw4G9+9e+vBnfsm/+gdOVTu7ORkb29X5svJVQu46IWY90hHqYnGSJ0NOWBLpO7RV9WnJF61NSYpfYndnVdZK2YWljaySRzbw7hwurKHxeFMkHUF3TobVST+mpK8x0c2M6Rl8xYjANy39r7yeZk2XhHpqCdt2rIMF8uRkhRQxQVfOwslcxJ5HjGDUY8gULdJneT1vwoIboWiX/5ilATMAxoE7dOy994HH/z63/jWb/2D3zJjanNrpB91enmm8thN2oKlWP3YGB2B7Vl3mONLV9T6UoBCMfTJ7mi6COpfmob0aksxC8lGUQgApKjOOyXnbVHmR+7S5yisvXGr25w4nePE1Gg+UQilKLFijIAZflbbWaDM7ONagUvVZkTvOBnFQvxAnd4hyG7/uZyAMsPmRAobOImRqucJhHyTTBjoWRbw5T6xG4VE5yWKEfVePzX8LlaGkUUHbJCMO2G6zEEz7k5SJw1goarduw0SwTdal6f1TnvF/ubci9hTHVcbQJQBtdZBKYxhfBN50oMB2lytCgOngEAp7N2hwa1pEArAP56E8tE9u83Ud3p8hrh+rEY62OFMrGK84YhC7qB7fQWVJqK8KlTxpN4WRdnxzPMaKU229r/xQSqFVK2qx9G3rBI0ovhe3Mw0kIEaCEvhSA/AKXh5gYYQ5rb1F8PCAJYgadvV7qRJapfXLjdo/0KyKqPyVX6vwqwG4gufnhSUL+Ssty0p+XgbUtrD+oyO5ikuapbSEeQoJqyeK00MLzczZ6LY+olOKuEPSIM16lPNDdCsZxdaCdJZU6eqAda+87trdDcyEAt0Qsycxzmcblye74pmJXxEPdUAwwc+g7VAmG9sN3SbVS+8bzWDqmUCD4MmEjLpDC0+0sXVQaYBYVVyGBlPMjUiOLA8Gz3NropHOIguPzCwY7RS46WInkE7O+A6gjSNNSjxpMMPiER6OVCXv2ttmafuIh5VSqAalNTnlp7WaXgAi9dAa0vyERAYEiI+EovMUmg0STJhM2HX2C6egs5z+hUqTDn9qcERc0mrcFN7iMrv5Kw3kVJh6ok2L/66n5nsEX8ltV1G4vOPfPjxWMivQlj1ziMBqMiCUhAAr1I1Lom9BtuobysiCVGC06HR5XFoDY11Yb5YhguQwf0H72xufi+/eN5z/rX5JKV4YZ+UcqyZUyBwxU9M8iZEwqcVHdTT06ACFufNrIXIpjQb/UefffbR178huHU6m9hh0EbdH374lU539P0ffN/SzFOb93Eg+SfYRIkSElteXp6l0UIh3KM2uFPlrOlDKjQU9Ra5IivsCXOuf8iG6Fx5dP3YLbh+eY4KZGukzZQ109mWHSY8YKOH5vJu7+zhiQk2DAsnydSCwWibIuhOU0RZzRsWjYzKAhWVasJJ+USKlmKg9bb2s57V5j/aLRv8ibHoNkRd0zrIjx1WJ9rEhL6KDkWfo5kZo+qPLp1KZExrefb69ev7D28nLpi6ThuNkolLaZhKV4NF3ZZGc9kpx8H+flrR5XRrR6jblKe4w1Re5UAjPuQUZsMEgt9RBvXCyoFUVZIN96OWuBiZ00nkhezysKOuyLPpkNWvxpEz2ja/tH1+TpuKAeBVo4YWKkvecmgKTio8ApGQXeecOl1Skik1yH3qO6HXfWSl7BJg4RGU8hsThWE3dRSvJCybEvuAa1O1Jk3eQPX5sz/7iw0TT62N6Pd3bFB148BcoP2DfQMp/GhnICiI5mVYko1Ku1QVNz29zIIS2jP/Y3vX+ICjdntjoHtvuCLTzp2p7UlsDpDpHk8sE+7ubNRQwQ6G6OqadR07QZURG6RqNUWR4UnRHrtTah0zHk6XWnoL+XA+T8OL1DIp4ZX0YeNqejyYnW6PbxCZnoYTiDesVGQvGX0lpUQFZ1CD5zETzbchgugy5sQKBDLlzUnI/Y2jN8e//7v/bPYbf03PzzCO/aOmY3sZxQSZDWgGpu1TFRpEVQr6FvhfxLdhGUTLIoSQQruZ8JInc1okqeZwL9oiVEushk5ai6AM7UaTzOUIp1JlY60oIWg0hzAA8rBiNcudnR1AHAa/t3/4/ocf/OPf/t3tfRIKWXfv3aLCFuZe2bxpvtjf3Hvx/IXRSKp9uL9/eXFy8+Y3VMrMqIRgZn4qAi4x+9GrrH2qtnBuat5y63BPb/Hb3/4XW/v7RkLMhhMnNciwt7tz8/CWNU4mY3D0fZroD1HtS/bBNbyejdOdpGObBGoWqx7p0bAy2U28PlOwxzAOW4UUdMiynx6VE4jBCM088jNc0hJjR9MLnzjiabAHo+C0h7n1LDyv5pnmMF/Cf1dakqSVtdKvM9LQVC6YVftSBbRiAsCbuty+/W74r98V2726TlgqXjKmMfWcxjZHwa8QXS1m2lCjhTcO7xDrcGR8bnfPEp3NEUhop6DUgy3KzFCNJHuABFiqOSmKtKtaxZQJ1NkQQh0LXkEjqpJxrrqPMnrms7gdm1b0+1Uv8lmsaoRgOlcaS7T1AFYACHsqL+gmQvDl4w+Ak+JgR23fVqvUUYajCJWG5ptX4JdutzqVobaUHy6s79hhNt/kbWda+2Yp0yJHIhy1BtnjGPbSz0YInjjywlWY4UqqDAGiOrYxHn8SVgpQ3aTic//YiLAhb7g4YgTASr+RzbtlYgS9MxSdqhdbkgYi4fo0SgKiDFvc6Fad8Sul5H+xJ8WrRAEeFOo13ioFtwBLXklTwSOfZGsYrr/zoMAFbL2pB4EUTleGt9C9CiH5yue6uM+zBYP8f3sVze1XEHJH8G/fA3FtdasDEMANLC6l/MpZt+v7eq3YzQCqnRwa8Pr0JN/XGUM2FchHUZOfua7ft1/Xn0UQ8FV7Mk7bkq0TF1nsusfReC97iweRpVPlyu4TD1mFOjDipJhGRnDbUhpS5LCoSKJDNe2VRFjWIEUg2W4rmBanHCopc1i8mq7unPYtNhv1TVDo7XV7VuntqLK9lXuuEsj2+jS/zYRarsZIv8rSiGXX8t+RmWe2dpw58U3FiX1PvAwa6V2yOzXbStkhFX1US2OMimhdqhaVjC5HSdNrRCUzGpOdHUijjNHo4o/mgvIFY//iuJSieges1p0tnt4LkYNnUT311ZfFe9VDAFArX49SP9t7BoAlT+Ams/j9zfrLB8USEGTIQ80XI92Z3U0odfACTA0A2IPOQ3MGuoOXeXItvVSOqrPlJKc6aE5647v2MDNM05ka6vgYwVw6rpgwgphkb2VlROK01e56oLlSYxEcqvhoATJ/hzM66H/KRq7JTcw1DIwOhmv+bfEMOiu7TbfLdxjnsyrofGd30+YoF+eXY9N+L8dWv5kUEsNh+kcItbvg0zJ5KBckEGuhU9nvXxdIMjcJXFTNdmRq7+o88/xWWcVritR0snj14uWjR49g+2u/9r/YunWb08Y3Otjd/PKX3nvy/JXm8y9++BOSZbGF2J0mAfD0ih3SM4qLqS6UHNNw9NJrt50lqsIGMIuKVLgofHHG26rbIVGCVs/Dt8/flzcl9eRB5DN8Sp1Hg48EvPvD5/KY4rK9s0ulLP0YrL6UAPXwKUYYoYABX913YotZifuAivdGr6ldGEq9lUhUcXrUu+HVhUk+2QJ658bUwMCgt+lQ3c1ROqLUElbqYCo7NaBYo1edQeK4NCwT6xfL7S0hzc3Ts5ecU336jz/+2UcffXh2crG95WzRbdPJ9CQc6AxKZ/QoFKbeh1bwTeznTzx88OCjr37w6OmrmWVt8IqDFUfZxLfwczW6urhSt+32ok+i1vE3Uq+ysUb4EQUq0uoj4FObWDzkLu/g7aJzvrm1dXF1wcxQiKPXrzOYkOi+qpOOxOb29uXFmKo00w8xMMFBb6p0BFTCjDlTXzLFKE1EURIyIlT9lbOM5kdaeKWLuOgN7Vdrg0VugbD2lDOXA6gTrkvdSGGz2X/+f/8vfvTDv9joPTRycuvGdHdnyxiXfl2Ci1SbU8w8ChbYe8hZgYwPWWRf04xMzrrz8+V8b9PsuK6OoUXU0/mZqUDd+e6lsMjm+dhcLJ0XZIzvLHijJw/Pjl6PF99fDG9u9b6kVa0YnfoRq9rcS7TFvjFdccipVd4VBwgFR1AdfUZCFMNHNZbhBCbUuF/8GjROPhj297cHH3fH253+CUORHUIWBnit74otFJO3ZCNhmsWxM9x3x4O5kafuTR4NH5U/OFh6NDYzhQV59Onjr3/t6zcf3L9586ad30RPfuGbv/SdP7vzO//sdxW6NXowuxBjSLwgykMbyKfkawS6UAt2uQmaqWOIDM71rB4lSmLBbSjO4YaxXCEo5GmT8rM7VCOoSNFaQKPFdYUnmSgfwPhlPqORJIaI8kP1xz/5WOMApbyez0ej7cvzi82N/bnRPEHJwerN6+NeNnGa3bl536ZG772v4y0invUqJRlohNH+wAy2IW6hZ/jszZMfffLTb//Rd3YObme252SxvZ0V9RdnF3cePNzdtllyJmcwJelpCwuribynxWprx36gG/sHB7fv3oGVaoATalxrr0u0KERfq6Y+KTampAeBAbv7uzTw4ny5v7c72rVfU+FXXld4kIqHjRJ6XjzGms/nLCRJSAurVTHZOF/Gu7IQNK1ABKTkSKsqnO/8KrBs9kO5OuYyVPaC5FV4n8Iqc1CvYtc/5Z9Zs/E5Du5Tdi5FaOSfLgd3VyYLBOcClNIliVfpiSaiOzyZLS7tqj2y0UbXYI4hODuPRFJMivlLMaXdK2ZpYKWtjcJiMYnvpALkg6hFd6vglytOgGFO7A3bTmO6XS4K/UBqqGikXyMY3IsXvthYHxM6YF5/JFtHpxlPg49IcjYF0udPY6rixKGPawzm4FV/4yIukBag/8Kj0Coy4zWTEs3SiIdqQZJ0a3OPNVH83CcFpTOigZSgjrrS+WiFJrZ0xqOQLQuLEUvVPEAJCbkkqjaSeCCXrMKiApWfZRXi+gS16E5eMg/RTRm28ktMNipoKeaMH5ItVPi3Kt38tiyL/iv3qSEwalBAUnCh1aMDeJLWM0JXD5wHnLwUya8QgI5StVZ6nCUvgoe3UrQPLwMhY1nJ1d56WCl9aP3bc/MUs06gm5W6LZ3EpWBJUJeik4amFSfa8+J8t/ZAw5wythJgoU3hoJih+PUIQGhb86nANWTWsAuNUAVZj6JYofo6DewLzfYwetDeXKN2ne4ttJ+7aam4w4Fcb/LZIHqQxjuFBcEoCLOFhPiD0Tc48BczIBu1iOuksETKY2ZVo/QqMQSr4k0nS9AvHmrig2hApzgr4xKhn5trxFPXKY2fp3h/rZEp5YIMhzAq7f81qzE8SJbbqQ0xKUnwvNiDY6kJWVHAT1VKwEUD19REBVHVMK+moZha5DbEiiEhPLGbZORp8UgKd0iwAMnGdwqH3GqGVVQEB6hLZcutsmUO5TwVM3xZh+qBrDkiY5Om6JNLMcVyn7jm4us0c52C3CdkVkmUJLkazzaZ0JgCw/9klDVWA5M0V1VXU2rQizxIzTYt7rVSYR8XjBdeCFOFRHq7YpCpUWm35ApUjOaveBrXooxAaAyqod69pPU4cEJymJ2P8LzVDZSKWJHL1aV9D+bnF2f9/oM4RaCDE06lHUFG8Iy40BWTG9ypjJocxUh/Znp5ObLt3evXGA9+pounGPnwWV1YakWx07Tas/PTGwc3/s7f+Tv//f/4j+zSeDo9EzIT+q9Qj5Tdy/Gp+QkKgW1dKbcZxhCUq8mnyAmlQVTy+lhnqUd5IXXui5zrFDJ67m0eECajLThP7eNd2gvJzg4W2WRZl/kqmoPJ1lYm/vIEAi2qZc2EaeSXWUTBtmkushdcHfNTwtY/FNc8fnXKlRcO3Ns+6e3v6OPAA8/pVzKol+I9RUxJUE8qo7hwakXEF80OXjFhYmbf/d53T05fv3z+8t//9//db/7SL0lJ+qn40QRZCrMwIVVIuzSfXFBvOm6q9+GN293PHmcOe/omUQDJOKPKRWQil5TWg4rfY0W6tdXeFDeTpVgIV8FXmzAiwMJYXSYn5mZZgrlTVMlrzjSZm+FPKyB0fnlpiD9+vqZ8LaK1VvhlmglWGs8HPWGB1Ei3PnEFH9fWoPIpuSpEkeslVynOlQ1hMjU/JBtJMqgisxnaL4+ef/bo8dSUnYEzRTdu3tzGCrHVUuNqimugQLyLKMOl9OxtMw/5hIFpjGkYS4GO1ezs6iJ7gMzFd4eT+WnH/kzL/biXFYlc9k43dlaz8ZH+a391sJztJTBkkxp+Al6TSsZM2FLx3bG1HRBVW6xGVeXNFOcgVuWoSoPAqprhVF2lCCWryIuo0wft7l71r5zevWEV13J2KeySeX/gFl8DgNZgDI9p1ncW3C27Fml9twbnqex2ubBbw5yczLLkfOLcwY3bGxY0xD/MunARj6997Rs/+/jpT37yYytc7aQv2jHjAutpTacMRRaBZIgnIiqtWPfRIeHJNe6RYUSZJK48hxos1z8QEqRTGbyjhvW+6mSSuDyWOtUpNg9kc8GydGQ5uVoYrnj06On3vvcDFKX+9roP3nlo5dXQBFYjZqve3TsPX798eTk5t9nFjYO9zdHG3/jrfx2/nP6Q2lqqBX5MG86WDODjhw7G82evf/z9n/7Jn37n7HJmYMS0QHNUstN7p/f+B9Y0feXi7Cyx/uw0bRwPBfKFNHXBEi+DiYe3DrPFEOLT2U4hoSBf4YmbNLfqdYrEg9DYpLZ3Y9+iCL0IoSB92mqZAC/Ghh+t5rpJ+uJlfazZhUPt5+es45vXIIAJmWm4w0SqJF05YeC4bzUrMAI4KXy3n+3z7ZPrElNOEGiy/UJSCQKvrkpMrLyRKhnO2oISN+yNDu7s76t16YdTawMn2vK+AUnTvzIJmVNs+imbyUoJs5iwEnc04QkKk4YH/Exs4J0rRP8rPIVVBJrKUj5IEkvZ1M7La8qQ6Yo7VA+jizJwKbPCT5NG1UyVJqMECO2vZV+tpZ1Kh5BgyqweMUAhgpIBnyxB4LWqEhYom9zgLoZ1nt3D+fSwMqwktfHwcMdlRAojOAPwjpeGO3HLOAjkG5aiJegxGsGz6tFaLIikKpUgUmx/a0DyxUImRb0IHPmrCiZPSx2IpT2SKivU8JK4P1FE+hbWBggsUx2g6ze4lNRfIGNP9DBF6f0qPNxLLycAo+xklbxBJsiXRmjaJMuTQK2b9roe5DZXSyBTuwuq64ftPXhf+K1YvxXw8xfcUPD51VAt+iXNLxlDSTLm5nN0RIk9S5I1Bu7Mt3/HRzfnlrWrFYgyByvmyXV+8eCk1CPPY/sCAWMH6GD5BYTS/yBbfdZ/5ZWsawIy5Fq/or+FcNPtUB0ZS9jbql5XYo9SlMTUIhMDEmTEiFC3mt0XmF4MPks8otkieAe58EHVqSoaLBmx6JmH9jfJpDQRtYyWLhykGM99k2rbmz8enbhyINhIznejZTsTpO32k4Zkp/AGXNApfo49kTLIufGCyY2yxN32Mo1+s36xyIU+45y2uPkC0rRKEkasRaJ9SoMPCbJbU5D2P0lyxcSYmoweBWVEF7CNN7wbO/SoILSQlgcHz0slhWZlM3LiLXhxzOJRp7OeOiEnTd54ESsPmghkPDpQVXATQF6Lj6VvVYpE0IOtV/ZLSQ8aDVCO6YuHwZmURoHVa4O/RXqvnFqPC/Z26ZuBl2GSXHwLrYaoWCb/4GYsIeI0zNEHNTOsiOIaWXy8ubPjsONEShbvqsv2jkgljWiKchTZlyBeIHbI1eRbP8IEzLbyo/wd9mgxf/H85Td/+RcnwsOxyLFe0d60fOG1whNEDBwhpTS7XDfj6TEcDiEf9i0nunn3xqtnr53+u7+9h88WFtqtr7zD/ieffGKjetN+vv61Xzq7OHrx4uXDB/fOzt4Y7rbcwmRIrKl2cHV+KoKHqRFmFAPXYFBGHH9KyrRqVE+zJV+YD6kQXV+hP6pfNcJ9BJE3ocCL/AuHctYynuX5ovdI7Ikpw9+Lk9OFieoTHv50Pvg47VCnNx1f4l7bvyzVGYCgdMJ57nZ2asI73ClS6ol/OkCnR89PT57T/unlxSc//Xjv1v7Z6fE+B2FvP0ehmwJklCQYF050w+wFE2Iy7ELrVQ1+6soygGevXtJHkNH54sWr/d0bu3sHVJSC0dLO0HzT0BhxhshcnpgpAkNR8jv3Ds4uzz/97OPV7MAEV3s+lCSzpaOLEx+NKgDhEDCpFOkTNraV8OMxa1bSQ8OL/pYgZWd5NORP24XbbPmQLYl32urM0OhanJqaDXZZi1Qkp48r2dKC8A4wk6Q1nw7YTnqbVFKuEnRG4etKDYr3gHY3YKsGUiQdun1ube9ldwGU0k5Hl/BTrdp1zee/9zu/f3L8Slh2Nn9hQ/EPPvhbzmMeDr9spbpDwXA+ZUEqdRt4/Kb+GLi8OB8TgInA80vLAe6MTy/OTyFyyyQpk46n3QPni80crLu0yQEV3bZoc2fjwdn46HTMAJ5v82qGNifHVpCDfiqqfwJScQSYDH2ranRjAsXYQmypDGkU099KMXg1Q49jmIAwdl5UZn/emx8N7ttbMk7E4MZ89HLQvd/pPVtd3Z11PjPp30nJ3f7tzuB4tTic9V93l3s2gqTlujGzi6vp6snGdgKuMc/2EmJjdH44WUMmjWXStxjs7BrEYH86WzubJdiB4Ov6GD5k2fkgQkGYVu8+VnY2ntWP4FzkRAkj8LC23DnTz6LXxFcUR7JRvDUQ3xHp5zoMcPgRVeFh8DMyVsPgODv8dHxy4+bhx589Oj470WRj8GhgjtveYDSYjSc4bOah1J8++swSsI0N1nn4wbsfgG25bgI28Mn8DsSWTaEvujSm3ZuBs+y8ePbih9//wcnF+d2HDz7+g99zgl/QsJeGUw4P9t575wPTgXQnojUYxyNlM+y8MZ2Zm2R3LHX65q2DptvFnpJvERcS4QqcPJEk/ea3akAgpaea3pmLIYVbKn9YGGYFYWxKJch3vvKPSlRYhG7V79IVhlspRn3lEUuKHfCnNaj8MZRARjIB4pM+FVqgfh55JVPR0/UTr9eXlNlAXM7ESpMdtOvxh6Sv/7G26zulJwl9UW1N6c2PeteS7O7tlkkpJyDHidq+ZJJJzXOTCOy8aYDNriUbXgu/j3LkottYR3CcHyDumc1Ocog4I5BiY4BSUmjzU+maD5WuUEvBuarsQrHuixvhsToKnqHX7hUs7cSUXP1nqXrz+3pROaok4cNhDlYlOiWpLRxG5yhmPUKkrVs/ytCnpiJtvlmRkMrs62l5WdqysI3g/A/8eAe+IpLs1JOOQHgGNCorZV4CnX0/FSBqQGXTZCE3E//o7i3QSAGIsCUi8ClvY0i7yXikpz4rQXiUahlxQIFJT1n5xcTgcUjR6mnyDLuMM2ipM5My5ZeycHYTXYyx7g7DJb+8w8MgX4UFMRmuJRKUYtLlColJLUt7mwxNK/O6Sklu/+vy1tU+QYhm5nfhE4Sq6Pa6kuGeqyELbO6LN7lJ+pQWMJFDiF578n6S4/rN56UnYXGz8rbngV0UrMEFqN8Nh5YebSkAkvlOOl//P6/kTWMvdaVfw/J0zalrq5JUsIiwfONs0hNI+mcS+xH3WhUQNtEW+2NSXMAXLsErOEtQFEfPAsKPVJzIh4nxXjLija2KbuZRlbXGR9e1tUuBXKCpQGNwGm4g1QYTBIJpUPTPW+W48hlcr3VBIcmrkLAyGhVEQHUn3TobfeWccsCzCkEBUWX/wFEvObvrUoJN/jP4vtW24kmF9wI3cXhxa+zyI3UWPBjxRbMdiNprnELZqYeVpHoo2g6l2RAV13ScuepQxoAKwUkZjD1LUDyoS4Lr7tZDNMEzxPlL7vK9jCIGTkrJgHjes0TMXxanZuEFXhThigyHw44iOXGGOBMJhOBGaXLCcuFoGZYCJW0uIku5IKHRd/gSXNjvkTWqmbOqjvdOTk68ThlhBkamrJJQxAe2otALPcpgFD6LLswlxj2CGy4vlpdHRyfmEQFwlmN36iCFdD9Wpl5cji+ePn3y3rsGmucvnr168eb1N3/hm0+fGQN4zqHMdElQw8Hu1fjUmUVqubJLjIVF3cbNzJUnPmJKmx7VZx6HwDzGiACLKl5f4U2UrvIXKySUIPxyxZ5jUzpJVJp3ZsNK3S+kaz6L+oSKYzGiyvnI/IMMBdQDtQL/gxYcNWXbW3z9vfHF7GpxbtqMqc7I49/jGQyzG6bu12zhTAD7lgiQcCD4DfDQ8/MTElpHQDy/GDvKZ2ULy8X24MaNmza2Co7BOci2qp96mGchkZ5ycEic8n/5Sx8C8+zVa5v5ehyFhmP6tUVmBm9KRfNQ1ozpxbGRKMG51B0XNQNavXADyTSAiM8kqETCrY9NqmJ46hEU/IXTeJu7IKs4MPx5LAmkpUrq3Hml9HR0QxivGSotaeWOAyF/OKyQ4KJJtVH61Zn1C1V5tcNtJ8cYaqNMv/c7vzOxeEJkTv9aq94bWe+aQydGFaDTM0jx7SN6gh9ZIMsAZQzYGVjMQ0RQbf7EvsmRu2G4uW21eJT2M9iYDK8spR29s3Nmu4PNG53bG1fTG8Pd2zYRNCkpQ1bAazrDBaYg0gy7DI+n/zCnXdZy1/TGzGzEFenK7slUd4oPNzJBHvnhZuowhVvOtoaz97ZOb/Ut1p5ebY03LObfMZ4yHZu8tTvs7mfrtvlIH3M5cSBER1fmwk0sp0ikoRtndWfCDN5Q3oRcMlypcGyBtFCDusjfiUhtgjm+KocPLaVRQUsOqNCVMqvQvF6XGHnJFXlH0sE4D8LpusKTvOE9RQ9cSZqWJeQmcbVKlb4eFdVZ9FHcWy1Ojt+ML2dvTk7+7Nvf1TGwSRM9hA6VoU62anLSmd3t9PrEXe49uHt6fPrgwR3HgW3tbrK7tUium1EpGQZ4aTGJTmEqo62vv/edPz86PhaN/tH3/2ySBTNRZmZ5c2Oof+iIMWNuJgglAERhrJLHhP5yw/xYe7XpXa+WzhnY2d3e3t1m3kNoeB6LgMD6GZ5yqBgK6e33pW6xupsbo539XZWBjigx/qWcZJ6UayPVeFMCCqMASppwMkxMDUolqTa+ygpnsdOGjIIUPOlqxhvDy67nNlkqlUIjp9znu66Gfv3OLXRSUglX8qRsyNR9XoTaSpGbSkuwNL6CjHkVBGV0K2evc+PGDcZHnSMJ71LhxaHS4lsPiA+xYrr9YNBLMtYrkk+yAkW3qKONMnU+UR3E8l9li1KG4Skmn+1dsHWFd3lxjWx+FY3pcaWE2HhlTKEdTztmh1UwLmAtstZd+vyVxwuiG49QWRYtYMmLHpB+fOiIxfJ6kq72M411Ky6yjQzDRtYgPEqnFLEQyHBGpkOq93GcmAfFSUrldJL8bwZCoqBSAN0UcxtZoSQXhSr805Ku06VA5AWCq3gCfyoXI4Ny772TH0Fu5fM4jKv24ZpQqUJ4GMA3TFGaCxg2dIotKajKDJJBjq8V4CElAioZNH4kfziRR/5/8WG9+bmPwPz5Cxq5CplWVD6DSnk8XwS3Rjhq0GDUyy+k0P1sb5K5Qc0cuzVS9aqAr7MH67CgKBLeepIsJQrzz1K33hLzNsO/NvbfSkuh1+KLiOqnDwKlQtlAJ1tRVSHBNGGA+laJJG5/KbQEnFOzVKFnstoHgFpWWxLBNwbFXsgdb6cVVcBSIYuoQl7SpHZIU/yqOLQ+1S95YVV2nDOth9HMZfEtmuFJ5J0SpBo+EzkPVLkwPwKghWFrPtM/SUA30Y+ubeQ1J/c2eqKhrz0qI5x0KIwLLVaoclPQnOdq1uphvP7R06KJIVBfGBUYBraCw4v8KDLD3VQueMQ9VbLa5kcSpQ4Y1i8eVm3QiialkF9/u78FRn6BQ9XFATJ6z7DGmUs5jf1YOXBsIZ9YGDEkxizw/22FJImyshWJcTPRDCPRwQJujhTLxAnzBmxWJ4LE/AUhe8DV8sRaWM8nS2MQUcUg8JgZheKsItQuLdtnZkETU6usMC3EYoyIKW18OJB/YXeIDCDOlugFavzlZM2aDI17pU3ypCmKrMI235FpWBjMu9wpp6GpYi4vB9owLd/Wuz8+/5GNOGoOjDhNNhVIjHCwPZ/+kMxevDq6/J++8/WPPnrvS+8fnZzcu33z+bPnABrcx9EKSS5MwDERdHvrWoWCswqwbkPdR7b9iVylYkVTw0pZhRwEK1kQXZ+8Ufus52dd4U8SRUWjHkiIeTXtHQ+jImWmJDUo4C3pKDOkRv6l2/mdMwGyzCuw4rZGiZJGPEeHaj7NTOT5FeL0HEia5z83PTndRWljEAMia6Dn6YFVeCcHh8HDEF527Vwd3to39dhxpwtNuBUSk9XzZy9t7PPl978kXMmTUFma8im8EAxl/E3dDWvVHSokln1x8ebGwdabg+PJ8ZGIZhiAWjKO8fCdnmSxLQFxTK8KBlgaH1pUlJJwkI4W6CHXCJuSkllODWZ0JDBX/TM/AImKpE1NZQ3r5qmJ5Q0EjGfqsni06fixCFCBTuCk0ZUygmli1wB7ELsDXXCj7t5bBLy1tesuAfuFQO9QgHpzw8hk/wePfvz66Li3vOXVxsZFLS6cOb5PPvMrCNwSw9i4wjBPY84c8GeGyNgmLDxNErfyp7M6HfQvst7JXsZ2QEdFr3c5ueTfXa0uVoMD5991BzfGl2Z+71mVsb284g2Ch5sYCW1TiXkBLF0s5Px+uN5/Teyig1372WfDk5id8Nmm5phSB4DH0BbxVU1ZlnADhNKcgRl0Zr94ZpfYUf9wsUkL37FDxnL+wWxDON9hL9a07Np6ajnZno1NOjLD1UCJGb856GTec7r0ZX8x7g+eOQJ3Mt6dT/ajrma7wRiCxWBUpMeyXNy8fRO9lxdX8M0IcuSSMbHoOXVxDZ/lYYiOzPNk9iBfg2eS4kIJsqpYsTyvSqKK8MqPEnqyJinCMy7B3iUVP3k5faiaLbuPJHfKiGk+k+709Oj14yc/YyH5SRsbWL/DFnHIxxeTwb7B0/mPfvSZcUiG1oz8+w8egGJnH36cBjR93ux5auPR9Csm43PdhcHGYHx19fzZCxi/evPaebwi51WzSimns/fee/9g7yDVWKyaYZuaoaO7XrP/h13Tw3ixd+490MdUIuRZ+9oMPvINkcFVRTDMy9NLW9Cd3X316qlzyobdm73hCwLmX0rIZLjvL82rHiyHj2Nv8AUnUtmaCfINq3wSRLSCCuXylq5RMqNtkYYUKkeW/i/udP1lc9Ww3rviNLBuIhXSjDlYy4on8ziVL1C8rbSFvdi/PGsXLi9zVaoGpuVxn2cpg5rC1OhXfq9XJ8IgpVqZfXA42hB+kmyKsXGD9VDj8ZtLg2u2saVxOIXngn2WtfOzQ7IWHtTii642cKLWYGJKGMiwyADtJLimb01EQ7dIMm6UBFbLFHLFFwUQgzl1lhZAWyfvtoqZ3ohp0GxCum4kwVooVl2IzVcg+6MTAqXMPrOfocjDVOyPnqhLQTg9hAQi0wx3hy8jBMcjYA71xXMv2JwwFpOe48Jidp+TIKlc5iJkyn9sQjBtNJZZ5VNI/zhE2sMlIZ+kyIweqes8K/pTxLEf9bLJHrTUG2qz5pg0CgiYpKKFXHWgqrcDK/bK/DGzSKKfaXSkyr+ggw8+msSbBQiO1D88TgJU1Hvf17dZbUKXPx87SjL/r68wpJ64CfTr51/8LuBpZaqlWb9Zp2/v5M3bhuXbrKF9XVa9fVtWK6imALXE62LzpYzkCnNKWkErNLdH3rmtjyAbhawycEEaD/K6wfzCZ2X/wu8v3AIY83oN9BqC7+I28HkUWVEDIswk7MInKcDx1V6maGnTAtGA6EVQptiFjg/JG2aKK7B5Rp/yeV18jGCjrj7BLGNTzE3VkzHFtexUqAgJhMAOGf7nZwpunMmDYmjjIhTNjaZj0iuVO5KymWtudIsBR4kqE9wUXp0QVV7NMusos9B0HPjT8WOwIsgEYzmWdrpIwNU0/WYiAweCjSbm0Z0mITjH603IMzm1e0kBaW11uUfSxNymAoTx/LkEnZI6nfNwNzYoiEObRBCScGlqdQqDw9xKPMfOc/XMCodNPG7RyeLdamklZX+HE2BAWYfAR2dqNU7PbCvTQjZNM6zBisSi1E1lCR/CtsZPY+Vronnah0QaNTKmhqMmg8opKVyNMOpfCAtpid3lMVuzdNpNLaq7evL4MeChoxglaab/2hk1YkQgUWmYIwVtlUiwSdUJWWUyOnfUk5HDMM2xWK1OkAY+6vFbRo6XJtKCBeuCN2cjofEf/fQnW9sH3/r1v/785Wuzg6orlbncWvzx5Hx8dXZ4uJm8xcAoECZXtYhGhR58r9c+U077X1Vj/TOP315ISq66CqYHEXerSAtOVL2MxEt11hBZ0mhMKUPuwkOKBYwPnA8z62fK99qb6EONIBAEo1+HwTCmluumJTEmjMUqJMbZwyuz57PxrGJA4PcD4J4E4pFcTrHU9kGLV2+qjaOkJLt48vjT1a9/S4hxMBppm0BKFY9iBjGWGloI0pu80Kgup3t7h1/dPbiYDN8cnys+1kwzZ8QpVLzlZPEzVSfP1KG2ZVDoKVkWzWGfXzTcJzLQkZf0VfmVU+YmigKS6hQ9qM+8yjtpw2StJreS3xZnyKwy7lhRQI3dtFZE4YVAizTnB+zzmQ/tEpVwLkFmn47Px9Or8eNnj6jOf/Xf/r/MOhPIyxTizljw9/joLFhyLfGqvK8SNLyhlhLIQoikHLAV569OTUgHyAEAy9XpbHGi58YmiZrr1/X6+yaMbJjB39Ffv9KbF1dXITIjdrXiZF1cOjx4mjY5WEZEZhguJuLGmYJvRooVFJdnsw3DQvr4MQeQTScxE/Yg1PTMVyjFw2hZfI1yB86nxidU8TGvyk4L2TAemEwrtmqIL52BRIuJEoI0cmJ/gb6pFI7xi53juDq3UCcXyH7fVg1bNqVS9+397FHYQanjfMdOpptnh4dJLVwx7VIXf3PnrHMRjOKfQ87/+DfyIryEkqyFP1SiTJGgF6VEub9+JGfeEHQFYNbW1NtY+LyErNpAU4YbOfwu/sdksr27Obm6ovlPnj4/P7/c2N5k4hR3eOOQpTq/uLh77+7jpy/Ojo4NLN68eUMP8+7t2/YwKe8/1hBov8R5nAgG84sL8z243MvTF28srzcb8eXTNy9evphY0WF3USe6DAc7O1t2qranJ4TbeEim6mWXJYMPsBvY9N+pve+8c2dr0w66ZopnK+omvLRm8U1L8xXe4tpy0jCxrCh/5/Bwb7J8zYR6ra1gGegDhSRkM7NIPxqR/2mXwhHQ0qdoPFfQNcsa44pG6t2IzfaORK4boOzAigRKUiCAWWg2QTbLcP0uUsyV+lHF576EW2JtYl6naZqQ1O2Ss5Qg2FLCDKbFBKRONwyYRq9u37092jT3zK5x6VISckx8jCLdTVOn6tThFjRO/1clihoHUrhbXdWVw4Q3rWQJbjGAeRnlDtplu1ni1PqYqeCWFIVjfJFUFxWmnhVfQp/XHqlftqOQhxTCyUrrYI84+MxfFB5TwHIL78CJQJMhArLzOdioLekRF07ohlUhSAnz8jLZSCTCDPY24POC9Que3G6OeMbk/GjslDpcylhiiTDPjZlUbY5wA0VFyndVwrRQEuB/qRAMAyiwKFjBSdtNr6CtoxVs2kiGG4RU1CuJ0w3LkvoWXGzYNEkGo/xhOMPsmR9NxYJD/iPSR+gKx1N8TEzYkbv8rmT1o33UIw/bq5bsC6/XtwUqUFM8yDAOoL9ytfytjHWZSZPbSANuEUN7Es5lDUBd1+A88zwAQsw6V/2y1UN9T0I/VFqi9V2Duc6TZH/5Koh/+WH77VVEUtYRdR6uP205AXxh4ykLmXdUExEeRuGkXDPXL29xJSZPKmnpJxWoyDHYipDL4yRLrtyEhnzVdU1DSlRYd/5OoAzEBpKkiTCFRof9SlYtVVQ7nwWtur4qFAUjdbincyk+pC0aZG8ZeFUtTItl95dOlrqiSPZHE+axzkJuGCkoaMBbb7sIFfXTcC+7OTMytXW12rShVXlWIPOP1drs7D7PQh60yxpOpU6EHgw0H0CIVtibya6uX84nUjrc+fcSgGa7oBDrLoys3kU4DnY2EIcpDLwOybEAeiQqEdNtcWFOq6mm3QsmIr4YK8/vsUUmTtsL3wuQRJLA4hnio3MoJIhNShVVYgxKo9cmJx6kQUnnggVd5svs6ZHuT5teibRUhrT0bggjeLaH/MIgH1tWstGLSulo7HS+/o2vf/boE9EPDr3hfhAiquxOxtRUmCEKArvwD0J+4a7jzBTg+Ik4DtEuL5yF6eLodO0IWeJgMU2peqp4/pgeGht6cnL2W7/92++//8F8GvfDgZpPHz9KbCduTWKMp28uzo+vug8Kc5wtJsTHcJ8+DXMPeUoVUeaCWX1AoG5Cor96TFbmwl5rdfIksd+JdJRSeaD0VJR085IzwKTDguVOfvdqtGFdlxLd9jqVZ/bQku9u/1W4UgiUooHN82RAb9t9pNv5VHLLX0RgMT8dVPEcAfqoS1Z7WF4pN0qisKla6bxFpawv1CD07eX+wWp+NZk9zbrwjCF1bdnEH3IWBZlEs2PedS6SGMlBDgUWrznHyuqbMcUzn13PM0rIB1UutaDlGtQ0aUSUbWliEKINsnrN5kc3AyvMzI5kcMohvp7G3mEPRINwuJ7KVeqWZIWCSiBFsuNn5aLIwKFLQVVWtAsyBFmZVKXWIGlo0v7Jl9y+lrr3SZNH1EEVwIfJ9NWz54cHO4re3By8/OzF+OL87/93//jF2ZvXJ6c6v6vlK14DSDm3eNi/d/829TPt2CY4cdGqr4XABOEz88Bl3o99y6Lg6q6GdeZJd2V5fJaDm72T3WpW55dXq50X/a29rY1De1YNswGaPTSN6FESHlynf2vn5OT86sz5awY0lZmIL1HXrjlKtVT8IrRo+K8sW1DNE1n0wMRDtqMYXspuvUT5FyEi1KeO0buzM+twM71E50OXgzOqupNxj10lm9Gz9B8lTgdANck8F+cm6KGbxO9MyJjrhDMJ30afk3nv5bzzfLV6QP0HOdQiHSQettktvOfl7OAv/vTRt37l62LmPG9Kiy0E3CRVgvdBnaILhBvRw7Fm6EJKyihkVD2zoBARUUenkqp0zO9QlgBQRrOIHo89ksb71M9F94XZ+eAPN7fZOTOYRrujH/70e7iq1rGDB3v7tuM0bObEusFoePf+3ceffuJ4E4Xu7Qzv37/LPl5dCccySiIyixs3d0w7dD7J0yefPfrsCV6/efXG0gKmz45Pb45OXr56ozhI4wkiFpPpe+++d7h/OBlfmbTndA0rnhaLNzu7u5o2JwYQ3lc++rLKZwTU8R2m/+kYaHhMi1QnNW0iwowWxY1vOzG5c3x+ebFYndhjY7zY3Oxs0i2cQ46xxjiEzkVZfDrojgwnicaLHeith95siWMIS8fMKAFgBqk8tzbWuHFCusQX80hzRY1jjEDSIxybCtfZOF44rieToMJypSgpf2F3icMN6bELyozX7ibVp6qgL4k8kitiLU03bT3PA6HBCLgSZqWtN8x+FqoE97SkkT2kDBizA/uHh/u7B5fHprvqtTIg02i0WWyO94otc6q2GUAkYD2AiS+QQVDambTOEgBrMp1hje42/YsBa/qmhKXTe0ygtTwg1bkhKWOSQbDR3BvH9NVLhPA5NLyeaGEmV9OzU2/lzR6yqqfx8WwsnBqoL954yz5O+4ucEyqcLvYfNlSvRVcebhnBLWcrLMukHVKLoocVqf25wmC/es8FbHpL2yUJld2uugRWKirimzNVVcZP7EhjobAwOjDQEEEnV+DS23SfOv3PZInZCWXRKkXnfaSooWN3cbKmezI6nrOApIa+9VBC+IHycNyjHCcVOpRUMsx9lR9mus8HAIEfLysSSOWJcU0lDcU4T5vilHR79vlp1/q7oDRy1p/gybRO9Ve/1jtW1fiGlEHlLYwG84uf8peK+mq6kCYu7l3JQt4krvymlFxf65T1swH7Kzi9fRzKQ3ZLDJcwpzHiGtzn3wq6zvj5w790R5SFT1jpVd1fJ8FbUlGcBibqGLUPsv7KFb9OJyt+ozNWNOIpOkvMAH5eWd6iEwCt2CqyNbf1rMm6fb5l1jXLgZYe8Ja5qVhgVdboe/4aVkE1P/O2EZVcMPPHpIWYaCe3JPqWIDp1T3LJomRxjm3fIRnurgFoqmTHCe77NDWap0nP2FTmUA/AYBw+xXLF/SV6qo8vmmbAbU2jseOCJ4rG/GbmX1Cg6ubqyGZ6aO2Qk/ADNPEAYgZ5efIW+0YGfqtJBRNehAN5xxtWVaw2j4/uhMjxVaKAFYAUNOLMnV+cS8NE2PlYJ4SjsDUaXs0vWa5wkiGcWhnW3845rCvb20krvQlC+ADzDGNntHlD6FSRHtaVQ8pk57sX3+KDSZS2FmZqOqWXLtyPfKBj38aXL1+aUb21PTg6foNf7BfWMShQikfSJCZ5NCpOpHxRLEJwX6FcUpZ4ypDbCG/bQZvOGLYHudMS7KUax5fLhSkaxfgry+X5+YVpuHdv3BgtNn/xm7/44sWTn3z8md4MFLl3l2N7jxz1eh/S3XCUbUUM5Sa1dOzSFiZlKAw63oXzTR9C1/oqlK9/14+1zpQZUItK1oERK5UOUtQt9/kr6DQr0PMZJNwpKqqkCClbBWwVI+mjHHXhc1W7am/0J43lxgobsOLoFQVRaRDNQ0BI/gm4pqsX0PU7Gm2a+MoigBjbuAVQ1dD0xxMn71rYF0FghpfR+bQlqW0tOyz1KQWzNfkOla6YdtQUkWncg6ZeihqH0oSUEl3jMSlUSLUUjAaE8FScwI1ONj40Fcp9sSEMoQSNS8pPSkmhkW98qJ9SyV6PfbQEkhgUSofHEwlxA4bF4yQvfgZeyk3OUNb4o+SNzf6mbVpNLRqO3rx8jazzi6vXxy/51xJBqQ22sCv7Bzt379+zWftgU3XB5BiREiTQaZYciAc2bX3z+vT16dHZ63N2gFx0jmzXs7Ob+fCBxg0ZOyd7eGmxy+Xx+cHSpKPl5HjLukC7BxqIG1qpOOidnXavljYOhEb2Bql2WauXfk76i2Em98s4jX2HQpD7IBymwyrc4qDTumh4JMsalSAkIOt4ACpATHuojDWTOx2NDX2esDjHU2T6WHYqRGxmksR2Ov43Yz4INjmBs9VbbW04rnE5H1+eh8c8KHmzlepAoII8opCzxdEpBy2b8paNIS852jbBqS1NpFF2sZK4C+lGRlgwzidioucRG7WJmUZSHpYIapChyKjK2Ho/MaH+EIc6tih6LdweVe9NJ5d49pO/+Oz8NF0CFtjopUO3LOy+ury6fefu+fnV1ficEcPT09PTdx/ecdjZZ58+Mlj5yac/u//g4ZujlxYJXJyfh1fUdsaDF7bfMo708uXRdPH6jcljmYtIKvokg3v37jjT9/DWgQP7MsuoWIkcc47izltqMZ3evHEg6e3btxg4E6UcGUYgBLcx6k+yu/K57Z2TMUNWHSMqL56/cra8SZOEbvddVW/T6YAMxPjKvlVWqQgELVaO1NgabVELHMBJqq6jZVVS9oguxwy3J+E6W5gJpqQ3mEzPDm/dOLh1oEXQf6Ory8mwN3M0ncNwDC5hfIlHpSaUxoIAz1/qeQSUJrQk6J41JMhEfgktdZutSCcXioxDq/8xIBhSYCLq5M1VD5MPkLimXvgnRcQfIae5x8KdLdPVdvpdm+7oM4+McJqfgmQpahoMahPhrwa6b/tVL1QDdlSf0Rp1e3Oml6U+xG618r1P87V+BE5RvkYqX4WttHBBJXzySHJEuZGVHwjB4Op/RJdaFsOh0gpUqJQZUMuIu6pv/gJrQwa5qp8DTJnH0hakG3BNJW/sSeHFpvCvKkN0PC1FGB5DEGRSG8O5cBCwFFlA2UzHk7d8gUMi8WuCZkpN3QmcIgphyQ1OsGneeNAuKUjinVpdL5Mba0N/YMrjbeosbNsQB8usFI6Gcddgln+VUn4wIuH6CUi9jUsSa6DiepnEa+BugG2PpPn8eXvvs8EJvP+5K6IrdCOaVvy/LrniJWkoVJqgy3qG3rwKrfX9+QhAoVEkto91trclKDyRRckIrMHHluw4q47nSfGjY+8gSdruQOu8DY2k+6uXtPUC4yOXglyFJGlDyQ2Moc5cEmkqazeROY9F6YqSApIHZBdIb688K5obtKJ6blHmelV1KyGJ8kd2yUoRUtGSJmshkr2l8D19GOYNnRSYN/6XDirD5A3YMU9eKDGvAqpc8+XwGbNZJEjVwOVbgyZTfvvvQlvAVc78zCu/YJXamOd8IE/XtciTVmMLVj6k0IkgZc4i0OGTDzD9y+WWI0t8CY17ty5RUiVJGsOhEa2UmJ3ZyrrXidSm2OSvJrvY1DzjJJ7dSw9g9YlKGXwiBDUi8NQDRkWLlmfJFdLoYYpzX7Ks+u+5uQeptSlFjZeTBZhnx2V71QcjQwbpq9h0jI9oe76yCOFYc4sDMMEec6CdfprHllXFaVZs47OvxmmnFkyuLjhJlqI+e/bs5PhUbIyv3shMJJWpU2BCsnGRo+8UD/enU52NQAn2NX0FecU0r+ynVqrZiA1LdWBM6crU22l4+OTJI7tqEMjZ6YndOfRlICzRRn80Hy9ePj9STPhLBLF9Zf5YongZ70VUIuFY2HuEkxAo5Yhgk+vnr+JzcMkVacC2MT8MjLWiA7EhMb4RVKi5Ttfj2LWaqLkp4OvPpOgMH9llXNtcJqCARQcli01d9J+q/o6LFZzzzDB33J7FhOSyJi/bB3Ew9B8Jx8mxRDM0sdhkbYHjjE5gd3ZmWuzuObvqavzGFBMZbJzZv7yY2Fx/cyf7P0YUpSWNdh0wXkZ1Sq0UspiVtba0w2wHI07mrph1FvqMxOBIDgiHk2EXq+iQTzPyMlLO0BK1CzFphVrsvxihPsXdiA66ylGrzzDNg2IvtgaaylC89CY44m3xqBgcLuVluSnxZalcawURGUEu9+Dc6Z8WWGljL+M+tAABAABJREFUH1wKAQaZ2xtmrpuPY6+amZXAq/H47Mi2WoLF6T/rn6dqcV4WD3Y2PhxtO2nNFHD+rRqd9T9BMVUOr4xiDY3A8cOuxrOzi/GhHSSPXixN0Rl15ufTT3/4eLA86C5fjuwu+ub05sOH3cP569lkfn7Cns0np9tL29NP7DS/u7+Fq9Mr5yQI28atRIoaQZilZ8/iqc0Mgk1VWz6607eqgY81i6bH6/GXrjttjPWK7cqPPE9MMd4/J3i2MLsdIfGTNkc1T5KYBq/j83R27Ti6mD2wT6EJdwNHuBg3Tn3N/h7CfHEwDAwJIGxM+s4HmG4ag8IM8W9zshyly/vMvAtSTl/h5cnxj1+9eHXn7p2j46MAWTwM03uJvUXR65Oa2A9eLyTjurE8KS4yiyCJW2U1BFHKEAXJK9sIudL5SqjQeuX0VSIwYvEikV/kgpTBUQjRjU5v49FnH//khz/5wY++fzU2eJheqw06jTpi16Zo0Wx5dvTmyYsXpbHi8Ttbm3s2Wjs5NW3pEj82N3XtYgzRaO0Te8jcKFS46fj4Nb/q+YuX0cN0qxw5mTmcNOqdBw8YbZMbvULN5uaZCtJfvdtbOPLr6N0P3iXh23duWEjASW06/PjxY2dQHBzeef+9D1RjBgAxtc9stlIdz6ZXjABTydE07jrqz68S47ZS2/Js8VtdCMEv8xLPT2OUuF2MZ2pftsO/jT+r/lE41RaI04xici0x0nCkq0CvWbXIoXdhwQmh9B2nvV7WTB2jckxUTXlwn16ELKRodCi7a9j9r2N1bRibdohdjAYSndn3o17fKIRfpZklz9Z8RmPrqhqubimfDqXGkkjpc7Kl5unSrVa2cnrw7sPnjz7p921Y7IBF0aK5zrb162l5lWHqedpsTaa9aNSmqSm9MEIZM4gxOgYdYy2hlyqmrYn+uM95RKGxGjsllt2ACCJcyoaW/FG4PIgqtmdCEiiOt84Q215MAwdzymcqwCN86C7eS1GyQw3ciMVvgPJZFjT8THvfeJQiUj88yMAcTOa3wUxDU1UbEGPFSVzwVsOXsFou7gIX3yTIoj82OS0TPBvGVWLKDPI+KmlryCpJrGTephcNFRlbvuq5JQsEoqu+iwMAQC7lVYkNsFeycT1MPkh+9iAP8rIQKcbmefFI7mCS0iLiwjUFGYoJgxK18DYpKlUS564uN8m7fpDbxPj1NNmZL6ZLgrzNygec9x8JwbHZjYD411yVUdbkdkVLSvyeF0GtmNoDIolaoevE16VWzkKyXgRkmO87UrpO7Jf8YVveFah1xvZVmPzck5/7Ua8/h1VwPUshrmhYGl3lljdGAetNigkTKncS5imVSQVYo5hnZBytIvY1vDwJsAjxLa5rTSjiQmKjoZ4WrJIk+N4kX+itr+CQojEjugT1+Mq+PA2YVpfyIq9DSippxJCcUvqZVtCjhlWhlN+VR5qU11CvR61URVYWVKQvjOrWX49yVDRdua14yVLrkjyYAqg+5GdqAbixILH+3OgqU2q3qb+puEG3Jv/nZVA1D7S6+ACEhpCL3phe3rLk+S6fVUnqcIpk+TSTgZaiMkfIF8sdLgCvkdD2VA0KnGDIwsSps5+5Ic3YU7EEWAs6xqyEu55COhZTketK5nmiJnLXJQG75hbAIk3piR3KXbho5uabm9m9TszYGoUFH6ZCgBmGByv/ZK7CAgT5cs9s3INS+EgNsiYZLtUxSMRLaE077UkQVZ60E/GyhA9F7SD7+vhY8VdXF7csNPx0+/j0tDhqE86TV6+elfIA3CLEGa4Jk6HApiQeE0rrR1W0a7qK3C9+yONKzqhMeARAaPIIYiGlekr0zorxbOnTBB5O5V8KrKLewnGTonMV/xOD8YRxrOfJkovmaPJNcCXsRE0Xk/MLUxBmzhg7O70YDW1gPxSw7A+MVpOFreZNR545dYjfmCJpWHa/WHIlDw4Ozs7HF+L+OU3ZmUpLy6z5DWScWGPEEjKrB4W6aASFEmQWeRSltlFvTYUzdFaCBDxTQbhe6RhbB2oiCt+SW5xPoxRhdJgkfYAHths/y6zTtNKlelKEa7pLk9W8UJ5qqxJVq5TMVcNlL3gBFnBhboPQ5t1R4JwZGpavGVhMTeKWRfLUVj/UawtX90f0LWsvl93xuZGz2cXJBe7p1hTyOdyA3HY3Rrdu7aOY+jltuRGDXVAkfR6rmFbXlp5ulr3Hz48+ef745Ym5eVw/zfBUF8mZULMfLm/d2NzfXzw/ejm6e7s325qYn2NfEJv28q8t6O0PH7z/cGuQXpZKwdtT90Yb8R4yopJ2U+U2Lsf19GSbxsRZ4GNuGChDdkRXlpnF4NbDs7oNZJsqFRZm6g3HnU70HJweg8XzdXrX1pYDRJiF9O15DqZEzxcXby65onykDHTIH06iWOcZUTon+p5GkhabG4NdGXOQSITb3dzajgVLjCLJDI2mixXn3cr1hGwocSBFxeCnyhdmJaKmgREsSG8F2KSHBnWe1CyoTHA9ALKZc3QguKXX6jWJyF7QY8kyWTXLuyPNbvfo9dGPfvSTR08+ESW/yOHY3YF1GLOFbXVNxbk4u7x545D5slPW5fl5RncXSydFEIzluQLh2LC3Zyz3QuTevsRFQSZ8GhLi2eO8UZ7z8zfBHSLmN47M/Heic+dLH35gI+Mtwf+tTafmGXdlKs0vsnPD3v7u3YcH8L91+wY8t43UcZx7gz/59p/8o3/+z8dX5//m3/w333n3oQFkvUVqiwUbqezIBkT1yCQtXfKs/SVt/Y8sA0Br7cuQVgw6nCeMycqoNPXRCtqCwenlxoOjXLRHkoza0mSjJSUDYnU7cFDxwLnPi97F0u6WjmjszLrZ7SrxqHjRUYvUl4R2m5bGNQIyAkmb2ORJG4wLUUsLc6NEGatsr8LJSH1dR2UMeh7ECPhmMUCTxVeDFch5EerY9MXp+fj8bGwenBEPcxZN+FG3VMoAiTlKgDvu9HBJjokfXWWD49io8GXEdPpyywQBHaXyKghHvYJZpQxJUPFVV1HXfuR9rryLRcqr6EB4EORDG17PNcPCJiIW2JaysFeHL/ThteleFoWrO+XmeydrqAwEgkhFidyrCM+qk5yXAR0stW5QyPtwTE1Jovzy5VHjNSzcBE7+wSwpkqDdBRYi8j+A86b8e7cANuiRbt6gMOYmYaAkDrlkFI0Cfc1FuYuQMkwpKqwsxqWbG51rV7BO2sKoSAWyanfhSTOzqp0LkxQ0L0UGwWSry++399fP8l3U1INix/Wr/FjT03IWams+XCf6uW8JUqbS3z5ud8E6z5Og+JZ5WkVPMMxN0q1392/zjRqEdZbKmDRFE9ozlLy+ZHYlvv6XrirxC6h88XWKy1UEt4Qpo8G65kJwJqu0AemaB9FYtFZxC5uwp661tiSxVAW9vSvYlWqj9s8pSppCrbMqVdKmnunBV+brd+sf+mcFIx/+N87lpq1VqJdRyzQAlaS0HJ/CW4+Lv4rJbapJKzPfEvjtT77gGoWN+rvNq3oXdP26ziRNbJa6LzfO38egpb2x86PwT21o1TI8awRlFnJaMkDjhQOciB3Gqg2tkniX2lueh7020mLlnPZKOLPfhabNScDyl2U3QGCDDtOJY0XkjImNsDzSfhu73LTDACRDTqjMVdiArxh/6mHG36VHnrflbEHKjoEvAssUZtYnRHPOucUcR+aI8X4HiGX3M29DAJb68mh8r28P5S0Y5grV0QNvi01VzDvvv/P81XMzaB8/fvTyxZsPv/TVmqoUh4HBRYp8pkKWywRt/ywrDF+z/NiUVxFEhw5N51pKXurx8TEPYjm7awpxr/9EOik94Y6GYm2elr1mQjhmSMOKbw8evNPtfWdkHDymF3KDiwtua4jNxItwqthRGjLcee2oTBDCk0Iij3OFrnaXgvIjjGj367d1buVq0OYgShMWa9RtrCncqFWnC5p2jVwgU9okCSiQkFvQ2o+odRUS8NGVhG1wPD260uyBucFcwUwH7U6P35x/9PWvfeVrX9bY90ej588f2ZWQCn3nO999/OlPnSSggza97O9uH/Y2MtXBzj9LXTFnMPUzufnO2Y3NnY2f/vQnjiQyZcsshT//zvf/1t/+W9o/5gl6qVe5FK4SxD5z2zSxaZSycmBudoFkoQY60WFNmchnaJJe91KDbOoIbHnVEqCktg5EOH3TZzN0AD6zvhZEUR+QIT8NjAellkFD8CPJBHBSjUxaSOUutWu8DNv98xW+cSsdxmyh6sKONrjXO03i3lnQbZeb8J9QeC3xsQ4OH3700a9Yw0NRM17CH0pcepLFuxqzcEHS9A2298Zbu3bCcRpY5srztZSd0HIwVF9SW/CCVgZ7E3e6hxdW6/YyVpVJL4v+R9/8m7/+rV+fT146oPveV77hROUj69QFSFUrfDMtfTgUNl9tHO7u9HY2jcWpjahOo5pmdd3KhvOw84ly9Vyl9ciKGeOFsI2tSsN/LclCL/RX7Wt23A8wp9tmfM/sHak+mTSYgEKMXmBQABuqZPCw/7PIcgxDk6TD+bA7f/p8xLLZG47v3O8dvt54/vJqkuXEq61N+wbZVy1SUas3tzdEyk3Uubi4sMjV3pezrZnlEPP+I9wOvIjOd+hyk33e6juP6gIpl9dezB/mUDX1TspEm7E8onSB0etZfdHS+umfLMlNCQ1Pjfrv6QOf9S7eHB+ZTG85y4vXryzSDeVDMyS3r8aXd27dsaWmE8cdSq04+jwaDB4+eIeL5kSP+WRbh4OpV7X52QoXm+D9u7HI3tDHm6PXV5PL45MTEz7N5Ygur5b7+zv37txVtey4wGSZYlSaxSb2bt26dTl+fuedXRZiZ28n3k52eXHcth5C9gP9+le+/NFHX715+47OE5Ni6JN+cg6v5qbkLScLm3rF4VZR47ynQJSadnbI3Z11j1jHxFYSEtYcCAP4h4lZbdIZnhtYi/5mUaypOOCbNMMBSNhAr5Pe6Qf0Bi9Ws1ur4U8WnXvz3T+cX/0bnd3v91ff6g8/FVt1PNHKTv82j+fbOCBo+p4DgI0aOYTViT2dwRsLJVaDV8vp3U7/TWd+szt4M5veWmye2pHJwfX24E3fsrsFv7WJLC0oGZK4HafUX+OcGeVKu+YzJirDbjhGrGnptLi6spadMC8DbapOpjEifQwLboapxRxsbubKWXbpLGb6kz2yokAOnzFwE8AL+27ZkrcnnKSFDvy1nqcVSTWDYdp3uZuyJkUpbinYGmEPq94FtkfTBxZmdTpH+WmOUtwD/ouK9yBBnQCIuAMwQFI1I43VpsmMtswAQCcgdk8S6FTm7Oqk7q/rcpkxlkGlDYY5bJVAFRETOrsLchqSmCj5UhprAaznbqtLHCQK+XynCgHtw13QQUV95MbjuqQp78iPyrl2SdpLRZShTq5crfkrphVPtNc5+VqN1X0nIcpojKPk2KAFg1BSBb8tsHgcRgW3MCQl+9lZmCkDNTt9F8MLoYZy+N+u2iOoBNKeVRGthJa+HlSC0EjQgUCfPW97H3kaGUQIBdJrGJRa1J03snvaXrdvDkc9yVfJuKC0JNdJUzL8w26pIhVv3l710K8m/C++eZvkbYmfP/lLd0Ep/9tVRYRxcGpMzHejKx3/QiYlBedgtcYhaWN+EnQJJBKL1SWoyl4lfC6yQIzMkzLU5duHFtJ0Uk/qTT1tKfIyBYWJb1NX7iQOGlWORNH7ahIZvOhJUq+zrEEVFoqvLJFZS1IEpQhPotj1F9Wt/D4lLLVLwjwrnSSY1H9vy9FJimAaQ4CG0pTQ0uSXqhZOVpudFjp1ppBMn0RTYVsGqp7amMK02lmDqqJmvnIQ9ZLrp7SglxBNu/I4RKaaxMV041M8C2XY4bFPcSAuSDrLSRm7wdmq4oJJyIsnFtiISBZ5KkDLCqQLUYFAKHHaND7cFvt6S54iSzSaTzE0QAGIexGm5AofJAANaznmtTxVJPjozZvvf/97v/mbf81L8WAlghyMm0DDVpUt/ASILYqniR3DUUbPnz53jtjp0YkQ9VRQrZZTG8We27rSAlhtoD6S825i3TiYGSMZ9u2zsTh68+oHP/iBMsiH7xvS+otXpy9tpRLg0SPMiQ1W+vbO7u07yycKyKynsC30uCLQz7+S5YuPr+/jIUWd/C6iggynMTOptPEabxO/Q16atRh9H+GWv4IXrUpeVzG4GIlLnmMpl8tn1CyD+1bp2qJkNE2UvTudXX7jl778H/yH/4HjEfiRgUrhusuf/PgzKzq3N/dH29sHd3c3d22+bjFfZ3x1CYXsmxQHYjUaOM/U0DwkV05r1pf66Sef/i+HsMg64CBQCDK0hVZw0Qc114Alp2KjzcPVeVa3C1THAc4lCliNhvaW50Eu2WOU56tJTj8NY+OApMo0Ry15chtNL0anLruSoEoHrXUbqJ+U6QNEPlHR2AKy88OXPIEVjXbBNxmFNVPdUp3QkhRrNldKScJ379zoYvOb+9ODg+yWZQ2P/XgywNYd2h6+XKkklE+kluuwvU3zApnKOIA3qNLqzKloXfZU9kwr82s+WkxGpv5nQ3cd2ByMJTa8cfeDO+9/4/1O99ZsvNrZu/HDjz9+9OOfUmgIRzNSB0SjjS/YJyeegfFy1IVmoNPLRjj8Q64a2ogPNeLrWM0kJ+Su6xsh0qNGevuZz5JFKyjmpTz9vd09dcfKZvxiKFLxi18RfL9jkyAjDWZvIBrfjG54TQ4RZfqLc15i96qz3TNd/OHLFz/ObB8ES5E0IYlI7GpKD0HFYf4HzChGfBTaBmikHkzXli+/6nfEntuIsEiNuAu3/PLcmwIQsjxpqSWoDCkdn5JFQa1flF/spNNFjK6cnl88e/7q1EG8+l38xNFgZ3vn6mpiWj8cP/7kE694KzMrmvY2drZGhHlyfra9865eTn9k7x21qWOrAwuaYQPIm1dHU5u0Tyc2BULL+NLJ1tnt6PzkJC5qFSEIYksD032grpdkaGBjNPjq135ZTdw/2BfgN8dGJ6EsR9fGVh9+6ctf/8VfJHGnYGc1WIvQZBOYRJBDYriQ6qNvmNFBfLa+3FCL49O9MN1io2c5crQy4R77Wel+02F6xUTSJe0xGWkgoAaMldHTYW9DT9q2Ck6cHSzu9Xrntp21x8VgcWu0+bC7sXuw6uxPrEPTHwdLFzLNmHUBKno2raFZM70PW6nyVZltdthSEC42dw2eprXuXGRykcysxIi/HUPZ9C4SXouzhA5BQmRWyRPPKGCwbCoa2xoJR9G1O3ay1eCNzU60VE2Plv7G30jLIk+0wZy5tHsJsTvvIRvnildUeYb45rNNBzXnsA8mtRWBsU3fSpFa4xodysPo2eeoBo/2vzIUUjVcBuuiB5bpeEiWWl3PUpFjoqq4KHJyVc2NGVBC+IDCdBSCSNWE6FEjpkldnnofoUqeV0xD6karfc02ZoaW9LEbeJkKhx3KLoO/LtS7UBWVaN+BBtHie5775z6IVdL2USmkK6akzOCdLJ64fHnm3j80XZuskF3vy5Qlc5S1csuzLr4lKATIv7o0RV+AB3QVVcjUbYq7vgrDlv+LyBY6oaDlbqnXCcqehFtrGgp+A7GG+kVI7hsFYdD6/VvGeFAZ1bHP34UJrvRF3HzhuYdQytsw/ItvPY3U89ynv4ZcJa7Htn4IzGX2gcnN+mrwW4p8+p0VBdI0Jhu/q5tSBSVEz0igWh9WOE6AkEC4HLsl2zpjBLTMzvmdxW2mr7f1siTdyk4hoKwhF41VsDIjWZ+5ipikU+qacQ1Pz/KyQQlEt6Hag+JBHtR9vbvOWvxJnjWwanYq3/wudyHlStq3MYU0BXOdc/2rPc2LKrGgaCLup4ndPGNvIl1/G8/T3ln4lC2EKTFXickro9XwAz9/UunTpmEDmTfOTUoMPi17cSb2Ki19WkEqH+PN3mCvCYtqx8uU2FANy7lNqbcghXWRChnx64uaPNbr1dySfh4FbNJFYME/QQ7Q6nzQwiEwkivYZAZhWYB84RGfRfn8zNU7s5ldSNAbXMVElcvhDnTRoY1nWryK3a7rSaThXT6BjU+3u7uvq8B9B+zZs5e2J/ICfxXOLnUXdqQG4DFeQb5y8de4UTHROMI8O8HdlIHE5Njo1cPx+Hw5eIyB5R/UzIHIpAZJF/anF2xOv3RsYTTvbNnd3d2ZzKZnF1l8Kaw72tj52cePzdy9dYNYryADSaWLsWloN+7cefnixcRuRaE3DCpxhEthvBgAdDfU2Xa1p9e/Nh5JE8ZL2RhhQVt21MErXs+z3uJysdjB7biUsV/XQiroAF+DCy/8q9oWASobveEqNkdmy4uzY8u7sckA/3Bj6+LM9kfHJhITkMSKzDq9FSr0ZC6BiMa0QyazXhSgYGjMW+TFOuDe6pL7en52FR+it7zgqlythGmrDxDfukiqXIuhNLwJzKRkRHJ2+ubRp5/ymjrL3U7vPIR3U2JnuU2FTHZJvzQnfDlQM01da6TTSQj5XMzs/RwtDzOihf6hMNRyA3LbfkVMlT9MqpYjyxUTBwRoYbsevvZZIBSoNE/SeYhfoUqx2gx4uQcwrM1tqnFwCjsA7exTMSHhjf6BeTpw1sPkso8vLvhxejs0VoCSu6DnvlpODw/vBf3M1/ObvIJrenaZ95N4PHzCLht5LA9M/I7b4thuPefQb1exnFHdH2ydnp/KaS+nie08a8NPp4Mt+5PB8t5yphPpqIb50s4zUUbyZZhV/OwmrgC1JIJBVGyM+qLiZJ4NnvMaS9EwNA5Zqbp7UuOBtVxVz0ksTA8nTSxyMNW2JQ0KKRMADDbGO08PgXFA+8z2URsdc8sX3ZyNYG8Aq0cWZtdNl52rmZPE7L/uSOTl9LIzu8hRICoxMcT46p1Tf6EwHTr7q07MnmcVDX5ehnftL5TErwnOGKa+yFP3a+FGK1xJHWW2L1Ce+IvMPUOjHHkUi1cPK3mye1jWuNLY5ez1+PLSlPrzy3M8NiJhqcYej5827+6ZjUPD8Yjlffr8mXXYw86hGY27WzmvWg2z7Lu3cbbRcw7AoVWzWKWebm8ZN3ASgv0xr569eDqeCj8vqxdmtwJjbMN3f/EbmzbizaClOXITG5pRM/OFzATa3z949/13Zosp799bOxrj/HwyZ5Q+/vHP7jy8c3U5uTreO7xtMa41PTmZLD1po2GhWICGYqOaWshO48/SS3dmiHrYe02TDRG/8/5X9m45OKXOk4sPXm1R6iON1ZpkIpkmKxbKvH5SvbowRWYxZbs28WQ4fLwx3Rjd/H9SgI073+nNx8PlU+tZet0fdC2q6d6aD4+6qw973der0Z8v+q863Xvd/gs7QS1ypMMtowSr1UcLowSrD7u9TztWfQw+uVz92snsh1dH/zbJW56we7jb69+OqLCghFoftJ2YHYyoC2HFmv6LVkNNqmlLmZTqLVvjTSo0T94HKTtcWS9UXmqf9jozmWJ7E4xgLavWOhwgi9cNRlodZDU7UzPZWHWPWQ+jH4oKN7LznrqQjgO4AKYaRuWqZDfN+NSTlYg+1Nc75Ufvqv0UXXjSWWQrvCINdslNRQM0SKp+625w9BNu8wcBPHipHdEs6iYnZ4k4KETLvY7hqZBBCK+3sQXeY1l+Zvg4prBVulSJ5vKHoe6TS/40qUkEAnSy0rJbcfQ882/2jjSdwaeRSCgNb3E4CHhtF8ew+FXuBQB8eh7cGoUFtKiu1F5lRav5gSra0uhTNNYZTYVK7HG6rd2Np7J1pvcDRdnBLEwtETNVj4LP/J0wt22zCFbIsVo1V/Dn7bi6FCAYrT/z6Pr6+YdBMEQVopUEuID3gRZrbhsS18CuaWvQYWO6zMNkbjuVBVi4Ewxr4wYdgALQSi2MqqgwybP2eJ0hSduza1zzHUMdgL7DlVSI/Lx+JUPdtu9KG6jRj6TK44ZSIzNpi2UMtCuuKG2o6IjC3WhPorkyMwRFX2BUuVGqVArthtBCxvFj1dOJBDsWFig3GBglK6zykfv673lh5UfRkGZJAAH8L9CUDA3twEv+oqFuUkBApbSUkodVuALVHMW0FiR+ciVblxjeaeqySjIqHye1VZPof0pp2EaT3Kf8AIKbDEBX44GlahSvOY4yUaSxzPt84luMi89MR8l+Ku48UXVxBTA2ONEI0AIdEqlDKU1W78O0xGLS3AZOFZ/X4DR/KAlZ65RXHAiWwAZ6aIiRap2KVgZfAX4agzBCmhg9eGZ8MEgmd8FNEXnjUWEReLnDc6KJhhAv42FtKSej8sEuPlgRK6/y5Eipcbv8hFBa72z+s9G/eXh4cWWHngsD6wLDmcIQqw1u5ahc+JFfsXIULgs3oWc2+mi0dTV+IZhqRgG2JDyT4fZooHLPz8+Hw6kW1AzUSKDmhmRnxf7y1p1bgtWnZ2PrlSNzSPWnf/btP/7P/7P/6//h//h/Gm6axJALQOUYAVC4ofzzszNkYEuwKUqbahU7COutGiq8KCjGNuTDMZnaJ5GnKbXTHMZh/TWRkXLVEd5jsSwfdcnoOwJqL6KkeecJBxTLTCjaGmxpLIAUdcf92fLy/Oo4wwtZyYktVl5PVEf2eGNgqnF8DQFdcGhQIRxJpbWPZDPJe2f74GD/9tHFZ9wT7OLZ2Ln1G9/8pvghvcXm0oqoXS/z+52lcJkZ1FfUbHhyynBTdZgkdlaEx3Uo1gVrhVISBFOdzxmK6WlLM5u8NAfHkrt0MQxUIhWK4kXDwvJir28XsOF8W4TScCv4yZX6XZCSo1rqMD33xdIwocFocHIfVD1FjbgoznSvtndxpicsLAA8H2ejRbqQGQXZya0sISUdDA9ubOdcpoy2WaMZx6K0N9WK1MVSQweIVvstN3lRsUuRbEZpOFw6cPOlY5ingvREx59z/pijtUw3MNpG3AKnQ+4//b04Wu3fagN0qb/gx0yEohQZUopwj9T9lLB0OEZIc6ZHMSX3YU3LmnoZNlHCZC+tKOxlxfHGMfmILVKP/KsU+pyphsYFphY98EwTwY0o5+PJdFM/jMfc2Vk4/8gkl/13Z73vz3raYyvFLb00VkLlTGJROi0CVnVenl0cd7oWwq43py/Jlh6FRsViIVQLzxCSh1DJq6Iod7n1nY9C8/p3HuVtSKxbKeCQGRFRVjvl2Cd+8ejTx3Se1QTYLj+m43PuTUu6//D+i5ev7ty+/eb1m0SR24hKz7yv3Qfv3DNE4klvqJ+3cbi3w63n/g+5jh3jCdM3r4+ckffs2fMsv2V5UYtm9F5dsbu3b95If9JopLPDaJPxho6VvrcePLyftTeCQBkgtf+sk09muiS3bt76nX/6u0+fPNna3f3xD3/03r1f+oVf/ZXZor9n29mhWfhsBNcfkZRWf4l9tsAUKkSncO5y5Ethwkv9TyN/hKjrzz5ix3oiWaseflHcaAp4WJK4ysiudN2N7Z3O4NzMvWX/udHHzf6VoxOcJaZ/ZENZcf0Nk2pkFCCgpkgLTY6kUDfc5uiZqGWWedha08ycobkpBmO709FstdW9eM9JNoup1eed+WTU2TattMQZoso+pCIBoD2I3qZS5ZMk4VjVLQQyJXkfc1HWVf8tk0qy/+wwyyEYTNsgOEIrJjVaixVU0uIodAbLgE37aQANNXFMbZgUfaecGbyr6gK8EiXWCmaqaEFjxqJiTSXbXf3Io6p00MuDmJr2JO1fWFwPlOtXNYlp/ZvSMvYthywIylhchjtYIqmRoOqFEYVzIgLR8/oZHpS+SypBKkD4hYdhJmG4Tf8bnJJ0XuaHq+Fat0lW7U7ljAAiuyRNKr9BSXZflTmQ88irwAqk+EXJLYFPKLUE0rRYECylrk6VTDCVmkxx3sw0DE09TaYUkLTtHuwwqGqxb+9LH/IUX4K7mzzP7eeXJ3VdfweLzxPJHLyVVY+l9B0wUankq488CjrJGI6sfxbc5ma32y8CbplDeWx+u6oot9JV0uvnKSUw63G9auJLrqRNTdIOtTrgSZKWLKljQ0x895ooBK2vVkb9rGSKqIyIy7m/rgD3lZoTovwQMuiv7uqI5fS49HyjaKpH6Sm9Ind9ALNDbseQjZ7MzbmwizHD2hr7aieLnQEb8oubfqSg/HfFTWw8jMecgr2ptG/RctMStyeVLZyvm5ivNLOCwXx6jImiv73CqLReaF2Ndi4UQdk8WHX2NjZt2pfFcNGYLNO0J4OjgjZ4UXAKddroNLFSaP0vOKHD4Q4KsALEQK6FiZZ8QYFjym5EwqU1ChRFxNzF0EC8EB+jDE91kzkxE3FP7YsRyRmuXhrxZHQFc0wkTZCzDhAwSWBCw8OzaAREwkZbUuRzQ7+5Ofp5zi5k0VuxCe8y55pfluNftTqZIJTlmJ6v/wTiZBdNBN45QUZmg6Ey8j4FZUw26dFY1sNTPPIkMk8aRSeBm0RAsvvfumxYFZMjM3kN7XJRTUSG4OGNA+PsDtB5+fTZR7/49SvrKUMcO/skkNaRFLk8dNQXGfCZiS8ngk0uxvZlvzgxCcMqsU81OOYVpwAy4OaLol1pnk2ibVSkXRd2N4KfrU6HXKDNw4N9U3gxhp8xvrLb4OS//q//x//Nv/cffeOXv6I/VJPU0/Cl6czeFG+7JTHqQanVFnSK37Sf0amwrIReGle3kkqsrsSmeo+z8SkzzaA/eTC9PO12ORuzDSs6NTmM1XX+JubKXdACusHKNxxwOx5hde4Szuq8s5zdd0LzbDXd3LrhXCEtmaS8UDciKwrP9F2kaJatVtzKJj0mKSRryImAUUdRjXuYqXznzs0356d2EdL2nZ1e/e7v/suv/8Kv9uyaEaFTchnja8KfCkztUZtlaoAsj45fPXn2eHfvxrJ7Ej2IXUBdpOvKCEVwp58sB30y/i7KFd5Ioz7J0l0e5KeDxcof8SIvkT2/k37OShxI8YFXTMWWqGbqKM6GccCftaBRpQnfPEsOv0tr6zMec71Ks1hsDYsLVd/mykZ9mbrl9MbFmXXAJnuk3UeEenJ6ea63QiFX830x+l7nbPfgYHPHTpfTzaEYIcNCb6OUKTqloyIYL209bivP3uulA+xiTIQadSR0raLlvZ4VGtYoXEHDXpD89sXqKr7i/AZ/WbAwh7P1No1IxXlmnRJVsNdM4gOqx1vqEJArKqX8LLu/HJu2l7ppmCfGqup40kcDGidCfJrt8rFSpcNgiJfly8tcsrgDRx7LJtW3tg8bU2YqE6d2YCW6vs1o3Jtkf3TddSd/LTunzjU2bzlT0jPhwloMQaKMh0igqmnYet07neXB6xdn0w/CKNsDXF3MHE0nysvKhIHERxyhKQgEuUIwUgxiVcmgFRG3J5ZQPUiiQfaOi7QbQ5IxD3yWl4Fx1NHEJNPTZkdHry4vThdWGDlh4YyPqzwnhW/z7+/evePemdufPPmMdVCXhxuXN2/t2C1GrC8bsnUWmaBFAQdmii+sDlDTZ4szqwVen75Rm7a29wQ7TIMyQYiRvnHIFO3q9qkPJhGZVmMzIeh/9cOvcZ93drfCovl852D/7OxML9uYwE9+/N3PNj598vzZ1fTq4tX01u3bs87rH/zoD46Ob73/pQ/2D/dyDFksd+oZ71+LlWZv8AZ/ep0Ap0C0kgI4MIS0hqOtbFKksTGaFBMUBYjsKVi4lF6rQcTcg5Zt87ctXyoRWAmAdV8VMLEf1mCy29n44WpxsBy+mk8FGcamqneHb8h3VWOhnflOZ2ExwHOwu6NE6+0v1F3e6mz+NLNYrOBajpbDH3Jq+5t/MFwddWd/l6Acq+Ac4+wSVSILYlCJKP23k/29DK0NnvERBThKrp77i/WThqonGYIQrGM016c7G0/O7B1dB8e3KIp0Tv8AyCdRYMQgg3Z6LINLNknEpts3LYKWEtGo07fbhI1EwwNBB4MpTGt565kfYUlE7BAoMWs08KGPnEQb/UzVYRryunZEXKE6rz3Q6vnPDYAGbDXH5WI1VY6LH+UvS2Xc0ZXejTpfNKfrHlFUloz5RsOTNpXWUw9Sdt1E5T12n5+t+jfe0oqUJm+JvDJHkZKyngdKWvzkX248y1KUorNUBQ/VZbxIbLTTf1aQQ0LgrInE2zAqKllI+qSOCDMQKlXQ8tsUrJSS+cc8BoaImRssnVNndgC82cFc7lNQ7pARPsPebQEPqPzBqe3iP6yVeGL/f+lqsOphMa1+y1WZAznww9q6E7x815OciOx5zKHyalTBLp35EcIKK6kSpJAssALEVyvBnXuzM7LbLpyTpkrM82QLgGTxPC9d14DqJtzPw8qLykINYxS/dhCxb01MlZXELgldqdX5qr8qp/AtOJ4mDeh5Daf8ilbak6zUIIF/zT+vQLuYsVgFpZfJaKQLlyx8EgPBGSa11Z06F7VoveK4zy6ZGj1N/2hSdewUxfqW1QInoEpHrzlQWMm3xi8U5Pbzy6/YLVxIiVJGNQtSbmCgsgSdqLIb6VRl1jUtp83Lp2mFgpGUaWNI3BZ4/HmuZWigAhFv3H9OqnPq2WW1Ha3ZwlK0D9OEtaroJAaM8YVHZjzXfACjsyZpqDHBErTsjTHPtEoZJ7ONzYyXTK6MyYqi9Hi4IoCubIUBlaVdqE01iDMvupbYg/ZfnLAiQyEkM5trTrJKOLJ1mu0vs4Yp0mHijOPaNLq2IwQLksGvmvkIg5yaFBPTwh6zVYUxyUl+4cXMIgCfTCotr1n/QspwOROLE1aKbPHgLYOBDZ/9S7Im78ArjVrZi3NnbztBSUeeYiFSNXcxjyWgZFHWOiYB4egMKcV22CikFrDNF1s7W/OzdLewU84YchrJXVdkUCt7Gl1YXZrjngZ5w2nwTVP39w6yfaVSZOZAabsvTp+9fPbN/kfZ/iiuqVaID50E+Bx9VH7VOF+fa13ulPj51d7mUWmwbOFkdJJZDlZ0ZmtrlyEB0KI9kT+1iUh29rJJp0zBff2vwOLE55d7eFDS/y9j/9luW5Lch53bu+Ovr1umq7thCNsAGkCDojgERYCSSI2kEfVinkecl/NuvsZ8Eo3mmS8wMzQiRSOSAgEQttG2fNX15tjt99nz+8fa51YBIDla956118qVGRkZGRkZGRmZmTYHbmR78YdtyGXNN0CNMCHPL8/PXr9WscprQk4yA69rsyx0AAOQdECqtng6rRIQJWW+yiJvhwE7/ml/b/9w7+DF2WtDUCz36PHHjx598uDtO2/wgwY2VP2GW7yB+QCpH0vTZjNnOximOV5HDZIDckmjK3p4i4CIfcrQlQAkPzN61CWYwRIrls4MRArDlK2GnSF+aFgj2ExBwFZA8E4chWwYK/eICNFVbOl2qYgmnnDfw4RJUi8VP9SuVLtwEdIKGoaPBrXtzs9Pnx8e3e5NBkY6LFL61Pk8++dY2hkPIa1vs9w/GAwnSqXhx3qd6V25pfKTGzZTWGDtbKhNp11Zm1keyByrtP36z/zLk15DbhqpUywcnp2zxKwTRkc2A21ga47n2l6Tx8QXSqSlpAieCvXk+xcuXJfWoeWG+pa00lgVGQaFW0OPVFAwTlDoFCprc3nXJ6chNYznm9e0Vr8KxVwRBlPHZidG1jKEMdK/2feewxKuogNbG2KLzP3RGMNLBBVQcWqGqQZSHCMZVpnHV9vp4pxP0dnTUzR0GBfDB9nQKKPhPfnlHIkICmUJcv4Hm+CurosOidZUqc/KVXHqHqx9rctzShi6Kas9XT18/PEnZ+dnzv1dWgNwdkHwRDRtu+O94fHh4X/y1//6F48//5/+x/+XqbBY1jPlZtFLzAsMRtkNNsc1m9PQoaztyd8d9Zza+/LlSy1Ey1LihRKmx5HKcQ828me230MMbbH8SbbmG0E4sRXXrX0OSJPJ2CZms9nMwqHpdPYnf/rdf/yP/onDTzbl3ffee+85LGLY67zz7tcm+4Ojg4MYNcjq5nSX9iCT8VnotTYwCevppRuPP/WWrm7LOJK9rfAU/kwdCw8P5Ce/IVGe6l/RLgVXV6G7aR/3/ovr9WTTPdv0aLZKZ+xKXW8YukQzGJxpmooI9V1hG3kyTEQ4MBCkvijkBhi6HnsI/ep2e7pxQFmmvhnpBYY7d2gVjrANnpHQpZ8VigkL8MK9fgrnYIDbmdIyw2nOd76yuEIt6cejvwR2eFhLMoRbczXUtJAsdoqshnBiJnOJc+e7W9OtTlIj1iKi1JpT74yu1GwMA2n7Ya5In/SwAZmSySTdUfPiY+QVdoysoymhQKKrhWrH+Ql89MWWEfJVKRF+6W3xaqqFDCoyGvckC/9DYDTNqCOdZQyvkfQJ9xoMUs5cadnCU2SVLq03qRoCI2jKEJwrvBIGin+hbpMTWEEklRCkSz0KPjLNPCyQgRf7iLIVFmRkMI79SVcTwlY5GvxyD0o3fwDIS/wiW5U5sqYQTjHyXxa5J1V+UoVBp/ma6fHQQ9KKCrBEiVt5JNXNVZ/y0pStIgmLgNuBDj0a/Jr8EvUvXQ34IFCXnzwVZs1vXm8+NlmF3SsS6PlWJE5OTYEKTr4ENIkBVvlg5XUHqKIUFQCqmE2iQFPLN8jsgDSJdgW7iZhq8ry1l05+vnILKcO0FUzj4I7HaY/HQfoQlak+4tcYXk003BzlMiNa+wQ8tN34de81Zk//jiN31BVR/GBSpUyNYdkaV6Sj8C7TMHpl2+T+prCJHR+vHZ436yUarCuFqKUqRr1r6p85nS8S5oNBmCEcQljbQoYqZh99fHXd/cICn/LIyXyFy7lbYtulkaU5yq3CkiohZ+FP97dNwL69kwntCFTNSP+qQ7KqL+jpCGLXUpzS1BnGyOW+cZQBQBxx12wijENre6Xp422JLSmiZAdrn9dZmslWSpMfZaNi/JeRcDwCDT9C5FAtvUhwRflkYq/rsgaXiklJpvHnY8g+CTuwn3I1FsAkROdeO0Z3oEgCgzYMFEG/ET9qBSGgNNN0zv5V1SmgqmTye2ToFAR8h1kufaQJk2wIF7EZ4VdCOfSSqJonjSm4qpTWoPXOuP/ep598eHJ0zPr96IvHP//zv2CSXbx0qfANZ8ghgsWDXWXyABebq5TjlaHajE7P/dmm8lVhaK4DCxVc6/vBuf9M5pKrID0WFmVLyhhB72Quq9NznOcFH+UV35ji803n3/3bf/fbf/tvwLnRMFjFChdjh0hJDJW7v8okGbma5/BFmLr5VlziQ3L3L11L7jtCqLU9JxF0edhPDf+m2ZIfYYgCZc9jwc1P5CcgEie80qNKyONjgHvG24NhjmO7XP742ekfKkoPpywWTz7++Pt/9N3RXm84mtRgNQrHfHphC05w1TeeNdfkbDqgQExRmCVxbaFrRGyrHG5AF7Nz+0tiudHg6KMPP3v73bdpNkwxeDC4InO3fz59fXXJy1NjyDl3s8sL80i9zsl2fdXK7jpyoA0anGXnkCJY2ACR1U8CyAaawNbu7KJmRq5tzUBJ81BP2A2RY9cvlhNDdpg5cgcVCvuiUmL7ukuUxu4Kreoh0BpgKXUDuz7qxRpCV5VhlXRlUm5WI7xiw5/MmVh5Ikd+aDwarlfnV6dp8bHjnqmG7qa3t3eYtrQ04Lw8ODzCeFinsEuR0uW7YJztVnHu+aZ9njEttQzcZBf9XpcdCZCZmSgAWmu7tzJma2/3yF6rhOPEcT3aTPltbIfdEafCKiXeT7GLPVI2V5rDLgSFw8YRghv7hzhOQsMIASLcisoNOXZtbkcnXwtUKWthwJCxfnNPgWgoiBKxwBxxPZsstgdZxtBa9z/vry7a3feuWhfbuVFdf7a6WC1fDfnFX5xfnr6ejKmqbCuaMm8hnoBhs07/2Wzx6qMfffRrv/Jrk4MxMTVov/dy+nLbfdJwO/LVytVrk3g1oApNm1KnPCU3quiKlH8utro85H8RKOE7nUCtZE9M4aSp8tDm7Pg6nxvOxTRhoYfzEEGPh2H/eP/A3v/f/953r+ZqDfdijj1DPy4/h3vHTkuoRaXxylCHlg5t1jO64Hyxni6XZ5fGApnqQWzLv2ncdqExIBh2La4YM8JjFbuiye7e/XsHR4e2/ekNOtOr6XAwnE6dlrBnSIlsr1++/OM/+uOXz5//1E//xPj45Fd+5Zdu3b5j413uY+Gs681wvEegaUPhuvB0VvSGC2KTznv+UTlT5Ezr6tIdNzybpSS7+i0aNnVcVZ1m4V9J7pL2We+NWQkKvUTOzN4s3rVBLrWgzcDfWvY3w2sCIyvC0cjcckQ62Zv66D0NPYvi0a+sR7o2V8a8KxgjKKU9N7moOZDyT3uti+75X4NqPMX0tOFJF6TDqp4o2ylm/1H4HPCg6M6YsrMfJzCfdlc6tm7f7nHFAWu+aVeZdk4j05PY4ch2Q3Y+6ndnpud6zgpo7bd6F1yY2qbjWqZiVgNHp3TOmaeJ0vb2pNM9tfpj2zmbb+7aBcFhIcwh2b1UBaSjyaxQcBg8KgThtqNrkPfc/zwNLGVBYf8VzUt6dokdqJN9WrmwRlmP5MiAUx9r/sT7+r0y5TxSrZnICQWb2kl5q9/CBAUNEumXQ4SgET2jejKHMEjWe5lMYyNnSqLiJOsglMhp7Hlr/rd47u34AK6iIXeZ+qNUSCd2ieMqUNgjAxMZ4BM0zvHKuIV6kBU+4gCa+kouydD/BOb+5jLplM/RcnTA2BUUbTSmNPiFtm/iI2QANSMKrayqHY7hALN/IFdpmgRfTbjLDAVSZBtVfQk0wKPZ3qAnQj4O2P6bvCsTsWqdbb76oLS7EiWvcJr1gYmoDanfKJGJmJ88lJEoCf2FGH6bdLsHP7v4+dBEa0Iqmm/JEewCkahg+GnqO0C+Ci7kEKPA1LdKX0+78PqWgMRxKUuYxUUf5QuQlf9UxVgVxNF1iZdbagWDxjAlj3RyiZHANOxSEIvzPBY5cwuaySIIBVRRqcam1ccHt/B0+KPQzk1YwvOvIVa9JWZCG6wEQSnZNikKfrgt7JTCSGwndPeCkrJhZI1OoqRNcP0Dkshg1k7/7JsiFwQvvBai41hbmkELO6tLFD121a2O39UoKD6k5ecIJ8n0kuwL7dbQgTK94Xwxs2AipeJNDCArguWBayOxdndg7S+LUUb9rhAzrUChUirwK7vg6k+EZOFjClHlTp5FFLDShYWMdUmdizZQtGxoIlJqQr2lrTLMpHMIyCKhriWWI0iWoctbJuHlV7ggIOD6H0ZQ9su1fQozlPAtNR+SBUj+Er/+2r/8S9/+7o9Of/Fbv/Qv/+U/tx9/dNNzop9dEJWkSXzYNrwBiIRsSJmYjdecnNnbjDoYxWxnAev0Jqn9KqpBjLQiV4V6RNeMzbJDxsIx9a2z06uj48MHDx4uv/jCbL6O31d7mPzxH/3hxcU5g1zN5CRzdJMfVQNCDT7BrbkKzeDptcj0Bud62zFtwxawg1EKAXk2kpAka4FxEdxEhSr88y3xfG3+3+RVWVTykMWbGvcA9WBVc1m//O1fZsxzwOyrDz//7Ic/2hsO3rp/d//kME0rVZ2l5FjO9jFSLKfZPx6xWe3rSqPA0AJhNF9v7NFujHi4fyiJPQxpK8ygv/Ov/+2v/vrPj+wZWnPKxXGK3zZRRjGLKue4Md3+au2A1KNjuSpuChsMFCmXO1KkdKySujnoRb0syZhKyxwmPlSuDMtSWPSoitwhGkn/5ZXi14ckbQhcOeWW8Oaj0uVq7gm7eUqD2sVJRgVCQGWa1CRZdHKDmmgH8ytoXS/jAkK3X8wwnF1Pzddhn85o2P7a1x8aGGDL4XhiaAYORIs7RVTeZFXF0yARSyszuLUHQM3JxJrI6YgfNDeSSNmsYMlSNiwxIZ2CVPpP9jXSYHa2ODu9HNw7MiGTGkbUaHgNveAtbugcBlYOg/vw8AqvdSzGBW1ly6Zi64bbFDziI1doW/dQqSCn0rw09wDO9xKJyc8DzENIrkrWP19zfOJp1hryy2MlH7QOl0tHZSHaYK9/1G1/dnl2+r/9r//mCH9QGEeTywtLKhZ21KFkGw3dvn3r5evPnz379J33foLZ9/KMN7ZyRZ5AxsyJ6YvCj5dRhu4uSMSrMO3Cl1xV6JvXCgvSVVRU9L9MJyq2yhT1iFhmSqANzxhorHgfjfed1EtkyJp5ZLTHhrJ1uO/f+Fu/9Sd/8sS6W9u8Ej9Qm+y1R7aOzJUpX0jqKew3YJUNYw7Gf/7y9fnVGS8Reppm4AdPEEl2AjucHIi+t7eHw7SxyXjMLH1ycuSu//DJmNMUgbkIheIa9Pu//9HXv/7+L/ziL/7h7/3ht3/5W/3B8PWrU16gOelrsR6OB0gTmqSr8udlQBZa8XO9qI0W0OqmURaNRMMb688+++Qn/8rX02OlztMOmoeq9gpBsxCw6LprM2k5lv3gTwqQLU/X/TNyiDWABK/9+0nU1MkNrKAkDZonBGiDiOC5CAfZOESIdbcmgroWaG47018fdC+4J5GOVPB4gSaZW7rTpA6Q9DAQINqro1StMqx2F3YFxi0V7oqBCxR7LqfnizyycyuvXy1MZyaPiWmX7uZAdeiL8W1/btPXOCdmUTUpY5KGq8fxOOeHHUlOQMmc0k/2mdMz/rW9KJ+ANPgI3JQnpS9ExQwqhVAxotfi60IuwJIkmlzxSHYgigMw+VAQFCtw06tKGGAkATmgsmtzWmqD3kNduGSKcVA+hEozjVkMGnCBgsCQu+olCFR4wWzwTH7BVfJQrYyGzeeElTAXIy0yAkOasIVEAV3w9C8CKnKGiLsqyhRlpHyu1He6g8opFArAZJWg5gdWaSoABpfQVA5BPaOUkmnJP7QNRgERTvLV/5AIuCDnsfDbgQ3tbnLIU+WYm5ebK4/5dvPXJNjl4VsSJbv6VwmTIiEVmscd6vAJOwZQvufKS/Oah0poQ9q3E8gfzpV4FXeXIJUW0HXbNvv53JSg0ovfyHkxQtPwXGq16jyoBFCwLzR8zntS1m89B43mElYvDb4VCYDsXpcvEfJhHX0NNYWiF94jzJzqSW5Up9zcIlVZTLtPolJ32Wl2Vxp8rtRt4aX+8iyoVLfKfTtgQktVBnd1G04NUrs/YZzVHxcm9VwsksCq3HRXYfZcVUWxcAc5Cmtx6w0g8LVS/LLtDJ4lMpQUI+qXoQDqdHoDnjvMdPZRxrCaGjhQDb6e/EcVnbTc0rdnRFq/coLB8j4QfHxBTt6yqp6YgV5drG3p1+4vV/zGBuWR3ZBDnsOAaDMkwJq6BQ/nlOhN6IX9dWyrlV4c87kqKcTvxeJY/wXACoaIEyLsWM9jYQC/5QME7w6fKo2YMQSkT9XNhNpWNQmL4CjeKOKmmN6gk1LE8zZOR1JEDREKhUzvhJhSWcnFit3ZvN1aj2tPJLkEjXwtTTo4Aylh/8nXfnrw8Ot/++LizJj+448+fvX8vD/eW60uDXySZRLuBECqswpRuycx+cR5QG6WbFy93tvSS+3gVGl0AyZflKfVf5a2F0eKvKIHhdJYAarnF2eHR0d7+/TOFlXj1fm5OZyr6cVmYdzVefbk6cXry/3xkfFCShQahZCRhYW7/cUL/2aPkSJNaH5zVfFuXvKbVE153CEEKSzdkDqUVwuZz4n0Xz7sDPZa3fgpipfoDXggcGRVRVCIyLupWlHTEvF2LIhcpX/l2992BO2LOx/+fz/6YDW7ONjr9kfVKSJaSrPmM2wfTvN2uGFxvp1dOQyHbxjPh/Q/6pnb2PLy9vVCJ/hjh4StV44CtbWILiXHBlkQPLs4GfZOWDVqABlklIjRjLaa8pgxmy8Go357Rtm8tB2K+Spomx1Kp1TcYkildvRYOCmTWpnKtgQwwkGMtKMQLWQID0ibFp1XREnxVQZA4auGTMG7HkVS2KJcWmn0n7zkWyJX6t1TvQoosJvjZNc9bQIrahnJCol27yKsnhkk+XSXU2fLzXHPs1dPrpyW3NuvxpQebaD6bKsVYkyWV5ZR861WOSa1WK1iEQyhQFF28wnZL5WU1mdDmRsRtwR6D4WSTwV+jWcgB3HI9KMDqSAFH6f9lUHQRlYbziXj4+vt3mZ1Ea8Gu3MQDw2nhCKh0JufEoptziQouFhcqk/beobUUaxDBASQq1TFe2IlxKcYRxotqwnKlyRIpZSoMF/D/jyNsdOc/lH2DJowT05srr5c7V0733jLQ3I/8yS9i3cdYHs4utpsP/7ws8ODUzbOARa5PDU60dRGNjWyGwI+sd3U+MRBdZPD/e7keWv6Igs368KE8FT9zM3YgLkBKhAkkihqsEssuKfw4YXmagpV5MhjkSVxCQTPOrISYmntPPW5dDok14hgvrjCsPFkue4eHxzZGuvRF49+/9/+25fnZ1RlTqCDziVTx/Hx1+bL+f7EQuH1eJwtYPf2DtTZxeW5/mg2v7y6PF3wYsoZ3trIzvCiylSsSUirk+SIo53z5Uz0yd7E/eLs3BIpgs4OCccWlozG//Sf/BN97r/5V7/zzjsP/97f++/vHt3mpIQp1EX8J/HFHuodL67WrcEpVZaLl8VWFAGs0V9bi3LRtKyYTyLQLNNltzLCRAANjRbMjsw0YIXN7l+ICHpq3EOihakE8ALwozfBP5ptRrbH7FSb1ddp6r31fLg+6o1+r7Pc27Zft7YTunyZ6klUlWhDoex6V5UEVk07ROmtrq071Q1ZX4OLW/v/fNOebs7+C5RpdS8xv9ULCS+lNVW+QxMq6SPTljMSVpvpd1Cl0YiwSimFKUtUdlyKEHGI1dAytlBfuv0URaVn6+zp0GkZnVNYdluvjGT6bOR819Zvm4lvta1ecIiE3UyNW6zGMRlqcLty5vnCJhQ5TRyxdvQKrW4uCDWoIydM8grLsGsehRjnxBk4nJzvRLrGDBJPPaRhd1CTGY2o2ayc51z9vGa+o5mQL+AwFoZTESAyJoKnLDKyKdGaBp7mzsRj1qvUabvuwP0B2BnKZPgh5xIHQTKixG8IHYtV6tx3d5kFw12AAms3MKvSpA5CaA1HrBQhSYHyKoV6JyioOQFW8JKJ+JH86j1lj26TSk9mJoiwjW9KkXFDmf+LYEEv9j5JvCstvBHKb/Uf0Cm1prIJuiLV1XYehetmT54kzkUnKQ28XppSVpI/fxO7COHWwKyAcF6lE+axKFUsWKQKGW+wSCvKVT9NvIyWb4IqxMc38XffvgI/OTffd6BCxCYL5EjSMJ84BbUShpJNHpVRVUg9vYFQb2/yCvjUfAVEi2qSEw/qXEfP5qpa0RpQzKdFoX9e0prxVzYxiEwwa4fXMDI+1S7TcQfZpr53WQb1XLKQa3SQylUL9pti/TnkK22+iF/sViVIzvUQyME8AHOHuSxjMaMhJYpC1VVfS4eAvEbmMR112Cgspb1ojwGiWdA1sWAKmzIU/kEMB2s10YYzEtB7lU8q0WP/Bi23m45WW9Wwop4hA0Kw6dsr09RwzOQcBxflB01iQVOcDpckuBr5j2wGaAdViaXB/CXeOOVLmjas7FEmUk5vWTVhwFUrAWgAiZ/KSFMIDkYIEnlL0XQVhB837ayjlLYiITogiaI0BIfwpFZqpEjFKkLEScB5TQ2VNaVAqlsfDITkKyMEYcnisMxLQYGTINmmim5qPvKb3VrdcG56/mJxcuvW40dPfud3f+dv/fZvZ3VJZJ8ckyx1JmD3i9Jp3QALBUAX51BOm/MIDaH4V9WEWvBMwRv/4FR8MRcNOcsM5jx759zu+VQQfwKubatnZHV5udCpn529fvL8i3fff2i7FNWraJLL0vx9AzZEh1k+hMa5f/USEHwbjJsPoQ98gzk8d60zPFEcl69BN3H85XNCGhD5qeQVUIBDFN9LkHjGCkkU6OKS6xaNrq86ds3bG095l60ZL31QAsIzC1gxnbkrw0sJHz/66Nb9W+9+I1OfiIPBdR6z+ezJo9cUfQYoXsS3bt1lWrr88cfL+QXPFxktFtyWTuL0nR429VUFyDZWDP8mt5iY9/aOJsvFW28/5C0dnTeGg8h2RU4BasQamRCRzvc37F9MksIgEqD5U7y85u65iuiD33ptAvPBpzdUl7iaegX44ntzNYCS+03IV34roluQCIYKFjRSJV7znyTIM/ZerThmHIwm+nxkHA3GdnxPk2y1Hrxzb+9gzAOaz9XlhQGtYVA6IW2OKIj6hWKVR3TluHwrN2Okw7D0ecoVt2ne48M4ZQ8YPdPsqHM9PiKHS85u8QCMUTCEsbdta3M2O+cgqCYyDExwCBdy7OjR0DDliLgyPbvKaiWXOkhj52hUzhKi4xDJJISHqBEjIVWsD6moeqkGmKrZVZIfpbIt4WZrVBT1UefNBt7j729rRiq6Lqm/Mbgb2jWJf33m8AwY6Iqus6uLvn0nOQvZgqVH+jGCb5gDWLsXy8vDI6SdcICxy+TF6VlyUsvUDFzELBo7eyRn6jPyoNSOKnkKUeUvpigUKyTVl+pNqUqO5c0FTmCXDokkWaO1bS2Wju4aL4hJgzBHgw3o9KP9g/2H77z9xdMnj548Y3pXR4d7+zZH3TsYFYUQppu9WbOW4NSspKbkxdyYD/uTPW0nK30y/JNzx55Cw+HAfsTsa7YPCo912vt7EyZ/5wQcnRzbw5ejIFeily9f2Pbn448++s2/+Z/ZgvRP/+RPXr56hcSkH+SJsqlVKQqiRrdG/D2GImMhHj0aOgOceQZnK9AbcU4ah/zQOeMs7Iw/MxXlLf1MGLS5ipHCDJBPSwC+uCvGnkZECfOf7MkvRyqE6k2vO3vLMQeJK+dBEsexwDg5y17D4b7URXX4clHcyITSBNMZQiMq5fWwsjLmbLUuv93uTImyYGwNQI4mKCYIOpV5+DWVKYA4UswLx5VfXP7kT1k8zV6mLwnTS5NYaaCibseTUfoXXRiONdvGKoLXNRDfrmfaV6s1s5jbeAj+fTNQOa5Q8ug8Kqm1HvKq0sFTx9NstW4hocBYvcJEjspVNEmOuQRCIqzXtKMI72BVn6oE5EPXGE8d4Q+ZJEOoVAHoCvrYKL6auYZJhRhr7SubWkQvqFhpFOkBZVTZG8bRnJG4doOKcl80EFcdl9UymBYC8JJV8PE/LV2coBzkFEPtyiPIVkeuvuUlHmY2hkiZEjXky72ApiITJnUVnWhJ8ipyOEDlAhhFpVgnpHH5kliJAEDzKlZyIGOqwaYTy7I53+1sDumoCqk8z+kBS4IlRWGvkwvg+ktIwNcVTHeP9fvmPXjtvgSNN7ECSF753AR/FVTBfQMicN/kFVj5S8mCkp+vRAwN8pW7hAZzczXZfgXbfGjSVk55LmolNOEBul3abxW3fpGw/mf50Kx6ToYFsYgsSuUvzL5AOHXutcIKv3ppRPwuXNLVA+KiO4yNvNnjjMgIm0Q1FTfMivK+ksgyUQmxlofjMrCJfpwaipHSZGkVuKnuKn1RKijZJxWI3hfIa/Gi6GZ0AVaQhCe0aiZRvVehUicNxoJSPGikegAoWidFCLHIfCBWdRUbVfUEUYlqw+QYAQoWid/PwY3Ahqfo/QxZ3D+mpKm2F2BguFfGiuWZoyKvKJ17vCq0W4G6KPKl/zrNlcwKmeSZ9oEQQZ4wG8SyF5WrvSbutZQsXE3HFkrqBsyGFg6GGPYD4XS1JMhNRlsKFheLFNj64OzG6GJuTCedmQDCbASPNBF5Dq0tIDKi3BseQPu6daoEjpKE53p6R7xO9zmJsrH3YIqTGoRvIFAG/MsZgb3WkL1Hj53TSoUF7XBPbjGQR3YxKhGFMEVXOvwX266eiSgHTEFTaHWDCB6goTMwSEgXnu2xh7p9StUP/uT8r/7a/mBvvpwtAqhkRKVNckgFEBJRXIqkSwcRQKf3bHJ80e+cWDaRlROIyoJkJzlY4NNkVR1ArOzB2alYDvd59eo1MXrvQTSI46MT/c7de7fotfPZ0uk8P/iTz3/91/5TJhb5BYuIeJqtPYWAyikHVeqGGYoFG+7N2R11NVzZPALgbI0w25KwKvYJCwk24qDYhWlVZi4HAj9t9yc+hlETqaEck1ksFuWb2LBxqiYh9SMlVFSolielzqq3HVuU6EDN9ebKGmMVGxtXGArxYp+P03n1MMPx7dHoCPkVrXi7EdrX/cmZg4Gp5hOaz3h4t33rhx9+qH+lU9hGqT141coW75HTVUr2t5Qi+wjGc12fyhmY78fKZuF6JeJJtHClGiikq7hER7akwgUNN8EhDAy5bBiUlhKUGio0+WT0FE4SswxWVT8VT7AMQoq0frkc0KpjSgcvTvY7PBuQYlaivAWEv5wEXC8VsUIz+k2VVVqQbQjCl3pu7ykL63PqRev88olWZc21MT6jiHD2VLs52cqx3zVGcqyS8oXJKzt6XzXL0CGVnA2COqe2Q9z0rCketttX2pqOrdueWGbIls4XPY13PTVB1W7PcwZGb2qrkcH2OJsmDV/YLfSDZ+Nnz64OtxcPD3snd75mnqE1fJy11KXPJN/q3lUM7YV6kEIoUlpQ5IlWcL1iAxbI59CFgqojm8CubNePZ8h5iKgXL0HSFQ+6gCXTPHl2j4tU5rJIPBKnfz2BQXdwvBpYyLHcLofz9nraXjpG4tXpy836naOj/f744v69++++d3+1cKDCmaOyzl7O/uX/+s/nq/nR4fA3f/M/p/eXIQapt3Y0WC1p6PLRsimv8IfTIlSEL3TUVRSlyHKvhVMKGlTzVk+ph0YKaVNZ96VNhSnpniJWS0ST89PTi1ej6YWtnJ49e/VSOeWFEoz6CHd8ePzhZ58TgWZ/V5er9x6cnBwfOdAwZqRM2kLA9qbL3vqWwaKNc7kAXZy9Dk17DvMaOmqQFI0DCvFcPkvMNycHRwTg2+++e//eHZMM6Zmc3TufcQcyFtI8P/300+/94Iff/8GPLAb45vs/8Vt/87cnw4nd4zbL49VSuc/5CF2cXRLE15tPHa6cjdEGrb3hLepcHf5h62SOTMtBn8CJIFSirMPOOSqgLLRq5x5spg9s/sUrPRUaOta9qBsClgBmVwmtl/prdMn0aklIlWBtj9nDewmZfruzGSyt81pNer3Pul07GzxtZxMwGZcYSC8zI9FMItQ97j2t9rklQGpShVDOwdnu/dF162pz/tuRSnwSUT98B5MwoxpJ1gUyibSW+EOuXz4eLC84xenGQ8iqcfWXeHUZYOtAR5Zex7ve1GYUYt9TcdmH1FoV22rZ5r+lVdrAcNrZjlvre5aitOyjypw2zM42empd93Xbnr3q3CZXNJbzTcdawTv6JLlBriyk8HU1XFjIe2vCQtMU12sQy6A7ci1pvUak8xMzPlJXSS4iYeQLUR8tKx07kd44kGdyUVh8iFE5gmbLiNgoLdpJllUEC+03JKExJPO0pYAISYkD4ZFVQaNU7DStIKKrItLln4mwBIRQMtTPBEp0pG2rkQn5pl5i27t+kHrsP6uSl8bSZiAQH+8nVjJKwTO6gIqs0jnYbi15aC5FwSCLX6sjThttBI69Cn1OGYOd4ZsDBtFmO23kK8iFZGPyCDnCP7nLKFTY8shvME0B6trxdphkF5Ki7Zir8N2laNI1iXIPB6Y4N6kEeWxiydlziqCnSwR6ghdrDCBViX2VNsLsy2uHQAPzzZcb7As4mAVUojcRAkDXmZx335KXzyHGDqmkK9TECZFEuIEgJMgWHYpOoZvvTaiYeusAU7tJaUCKY4BVhyl/sgh9RQvbetFZJX0pqBJEM1aTFanJN6mSZYBKmMzzkgfZqmI8Eb9aXAhSeKL53kQq4B6btClpfU20Sp030KNOiOKtERkV3btYCrLJUZ0aAcYu/TjTYJGKJAIlQ8LymbaQqxxv2LliUU6eTX6garaj3nxua845MRAO5dNaO22n8M143WAgtRdVhDULLuKX6Q9Ha8TwhA9yZ6IkLkeiDbMTXKzpPtPCHIKSExUcFh5LviYECKUq9EzSeB6nU3QWk6ZflnhmWGljKtAtcqANnFKds08Rsqe98QNO5z44U5xef8T2IDzwsxQhXliTiQ5ijDZGDwTkqBO/4aKr+VFbKcs0dnQVLi0ZkWYcnYBoYAIkT1UltkHOpBK//ldotHMSa2s9NFDjyf6REyMXF4yGVY0MfOi8uxoeCckLcyWP5IoJOQMbCEPZsZoIYbOmvEXgpcg+hfPCDyo76482rP5cpzMln80QDw5tmc1/IzawIV183bbb9/hgf9VR45GOjA0YQ/EUk2IHWuDnAlBBdpx8g+nNb/IMmzSXyCiQNClCPgUMGyE/sMzkAkWwC3T3is00rIZkTeQAK/Llx1XgpfM/y0K9hzKYLJ1z2p3lszZbjEz0CmwzSE84/SCWoRpDsWy1xiPLh5v9xaVrck/t8ySGDG1fC7en0Pn5pcjCVTUGe/Tos3feeZBBRSMlFMCIC8W4NafBO12gv3d4tLFRum3gx0MGcqFV7uBa1CGTQ0IV3c1qQeqjQyHAFy2UssUAf2ivjkNqMIs3jIpSJAOaNIAQIlSARtWgdlvsF8WwWhQOd+pz+q4ifPIv2F4rcRGzkGlwEuh/0CssRfabJH5MbHz9J9+/fe94fv6C2U1DxuPMu7Tcmn5rGfnsjUe37hzrO4eDyeXV/OCw33aOECjQ2tUnCrsUGwcoOjEwmK0H2frOECLjKSKIATnzj7wRkNQRYPuDY5surjYjnHHtYCx2nlI2VSOnqtOc4Ky9zPZm3ZPOO3hcHoofybfLTPlDsUjDqPFhn3BLzAoq03uneJtyo0roIVpxz85ny+WVQuGEyZgqDGg61KJPqFJwcgeWiFItksuQYhwpOKTtxvXctlRW0TIx4wHCLs7V/flbbx9NDk/avae/+Ms/95M/+Q2864greHC9+eFHP3j0yVMNeLE4n86vKKZYTtU7JNgBE9pv6Fm5V4s2H0KspZWHyWMPpTim1lKQ1HKVtqlj7OYqKmAhIsvM4eXixWQyGY5JP1tDEu52619Yy355RXdvT2dkuRGq3cGuD4/27Tl89fjchnDPn70w5Rplq9c53DcqaNmQJ9XAA9JwarBnYnPY33NOm/kWNJ5M9rNfHtSc8m4cKW8645KzkDF2dTRRP9vjft9moCqO35iFYbfv3LNIw5Dyf/5H//Pv/rvf+em/8jPf+c53fvi9H379/fcPjg4MGMh3d8VXSrWu/a2vyLalA1WuZlNYVMCUkLOHknXaadC9LlIj0vHxASbY2F1/MGLARhtr/WMUSEdZrcAt9V0awQ3Ni544KTWAg0PcyB/alaeou8RAiNy7ssvrunduUNwZmt+Z4mwKHrYX3XRRdMmox/Lj3cKViklCd6bTSa9R6zwzxr6+/Gttnj/ZIUd43MrVLLzSgpKNJ/kmoNAJPsSZtuC73lSnmShN1ERJA/DKzCeaqV8qfBYoJwOz9kogdnrV6+6lbTa4luUkA5Wa8aG/tRZqtJ6OxWja79pOaln1vF1lB4bu9jDHP9jlL8ci8MiKgCsSKVMQqXuw3r36WMWpZlW1WGybSvBJqPT+0snDLbNwmprQtGYEhG7qJ3RKTDmBlrk4xUi3BYDVK9qOLr9K757VWdq+xJBDDNJRspQK6Q1uzIATB8DGyCKrXKp1venj4wTjjjTwiCq4GWOlazMW0uVH8mcRTggeeUZLIdplLjevAJMSUMly4Rg8DQQyC6oYsTCHFMkz/+Co9QKo1JDMmEDBd1VZ3NcQRVBkHKwATrZfkjgEzxAhuCZlQ0RhiZJ0iew1DzevICes+bILrXe3Js7N25vfJsN8VDBlSWvZvcEYNGgp2ZepfXdVNimlN8/osktVgN/E3j3svqaACLlLnLwCPqTOl/Jewv+BlJ1lAW7AN8X9MtvKQhOzX0czpE+X8GU5Kgv0DMmSoRVEj6Nt2TKFsSsVZJKaGgG41iH3eKeEDdzgkRLVECDKRBgoXIEpcG2Ba2gRMjXvQbce7c9a2UWxCqQ01NRrECnQOKJwyy1R6l+DuXNYvWWdtY+VJE/astPyBnUepMpITwyw8BCs6IaVY640ka+plCpJVY7LbnUpisrCBHsLzrLAMcDTsgBGBHCIBOUbDGwOwH+XeIcpM7y5AheBDPq1GQboJqAK02ctyFYMvhvMIk8aH9ppB9qqDkIW/qV8EhgMmJxgt1lkaWxvyKCuj8o6S/ECUNURRsEnBtdswJ0CxZrrjvL09mz0k8uRk3hjO5sSjunoo06tf5hZHA4GfXpSKtk/za0IDHR3YXXy9RNEY1uBiB0ek9C439ao/HCzkR84PZZ3RYBUaFDiI2Ywsig6H2DJ10PwlHMqxmsC/DXVP3bO1Hz+xRd/8t3v/stf+41fmkz2zs/OFbGqUaRc0oYnQi1/DBhA2aDNOEM+PV0ps/N0scClUEeHzGckclJmf+sMCuzrttIZv3j5CkDd0cXZFU+VjF84L3W2d+/zOW6bBfjn/+Rf/5//+79PmiVH0Dbry/NLe8Z5xhUpSDXuVJV/4ryx/Yvhqkybx9w3tyoOG4moARhKYE+Mc309u7J4TnCCostkxRX7U7jAc2O46ORE5DBc4FSZAqNQS7NAJ1dQCk9QgnKe4mbSbR0ISAOVJHpRCBpvCxPfcnYGT5/B+a2LF4OjY+v2bI5Eh0rpWNFoKMyTJj40XlWtD2Gynb98brxMMfzTP/n+r/3qb5iDbgigJ8AW4OcOH3uBbFZ33jr59NEHz7+Y2XMoVYQZfFLymLiCjIywC+luKOurvBVeiHoDhyHWeVtKbTCMEq5YdwCQMHe/CpHRZn4AC2MVJVIE04fTfoaHmpmRhS5Kp4gwiVyXn4LSvDVkzbNwUXyqnwiT9ByyRp+Hb3+t0x9Ojmzd1Hvx4vHocO/1xevYpLBWhtO9/cNjB91WU8WYELI23ZG46QgJGB1f1kulX4wbj03TmW6vLCzuz7h/Ux+EyJv6d729arVGBrMOphBS+/9olUTQvBk5ZAdPCWa3aSC8bvjO2Fn+/LxztfrUslJuWPpyVNKaDRl2hMscrL2egm6qOKY/pSPIuAgIL1eRGEJjj2KjsKJUfbINO+c1i0cyL4GwYn55qbmmFsKTJeRAbm/YgJVPN+Dg34MHbw0uexNzI7z1psZi65k9qfZ4Tg9e2LnSZjWz5aXaN8GG/XJkLitKNkDafPDRR9/+1e8c4uLr7ZT7y9XU6VfEmerAIxk+GXtl1tSg0DjdfgwRRlFC092kJbhXG8FW/qVO64r2s11Z8/Oj56+fknCzy+XhycF+VOqM+qeruXO6HU87Pp6/uJgRAmZy2DTHBye0d+OBTx99Jrfwj/ForAnLnMzVs6Ijs2KD/ng6tQfcte0/KeP0Ktnx/mcx41IHZwdsWAHgwSGGZLDCOBpN833//W+8+7X3Ha+uROv1JTkznZ5BiFH3cn7l2K2nj54eH55862d+vmv/qLhwGo4Y519Ze5DG61xhO+51Ose3jsZ71q1qOGMLCXr9+9Rd4xDy/L33720X9z766Mfz5aN3331weJSBQebfdEClL242L1KVSByS5X81k+ZHWOjYhLTTX5sifStyOAIXtTG3JmbTZJL6qG3Hu+1b7aUtXy7DiXYXjJv4OCI1HoF6JQ6Hi6w6YLVf7aUdtU8zJbDZT5fP3E7j3/sjrNG5+s+aXkkbLxzERPwv7amFsGqNRSq7mZI/cAA4nXBJUJhV3Tc/lGOdqqozjcffluFIePTk4GVbagL/QBUbzSmhYUm7c2WqyFEx0a7iO8vSZnyid84J7jYx7gzO1S/TSwYdm3sZNWSnvpJJAr+Sd/Cuf00YpGQtQIESgnYYV3uDfMUgFEqqIUnGuqVqU0HYbmqgLbb4gZKOI6Y+MrJOX03C+GFYlUFh81FLES/tO43B53jqaS/BoKnxQiw09jlVmT492rgoZjiZz3QgAKaykSEdDyRlz8MCzsE+PUyAKb/BkjI0bZCjoh7AKqdhYHQM+AI2rVOB0inJKFyTZs0MkqLwtoVqMJXQCMF8XTLoPQleq1spXe9J6CWdTPpZwJaHgJCePJamskmn6iFvyVCa+uIWggRt6XK/+VJBTUDuoUN9LwhfhtfTG1ipvRS3IO7ujQhK/Sp2o9daORNKFbyUrt4yCN5dTUoviVRfE7WihxZ5dKuvSS6/5lvS1VNGUwJ3KQK1ec7Tm2QJLThNWD599UoOlbkHhEbU0LTuDCE0DAPrYimx1B5Iyb4SBUWR09knC7K4lP/UQeCIU9UTtJs0bxCt1yKnAqQEaetJshPl+Z7A+nqDbaWulx3wKmIDEyaVYQHGDmlIAeg9HKcagjqQFd2bdg3ZNKB0JKIkfsNHeFOJYJdkCc9TfgrHFEWbiIwq3SaqFtXDYJoMEjVtVD8ACPWIhOEnsYrVQe6abBjD9mbSIy2XJDoAHEnH0gJBLZbmZJNACIWr0gIhnBJplzWHq+OL6NCFySKKeGLnEk1xwvmgJ6VbcqiS5YgxaxTkbZwAAdiKJodynpQ0E0ouHh1+EUEHbdaZBcVOOv7xMo2ROLVEmpj4CWREQ0i6hAkFT8kxJZJjkdpT0a0wkJnfLp0yXGW14NWFdWsZbujLqcW53JO8+L+SKlSJo9cvz+eLGP59JQ4j+bk3oGyaP90mEkhBGwTCOnQhMzWzCAt1rFLOL88n58x1sTQ4IcD8+Ivnzyy5+vTzH55fvjy5HQWaKZQR2hS/Wgw6qdL85dlVnNAULK9f+SLKmwIU9qmiRAkd8oV/sI6ZR35YpUAguHqHOVZRHfCEfGURWHlKHrus6xWspKxKw7ky0BMZ8Uy3rSszNq1rOrSSVpSks0gtNSmRzo8NbHLArdncvYl4UjgCGNm4mfEiYPyM2MTM6xVf5/39w5enNJKyO26zWCK2xxjsc7EZGwo2QsK+oqANB3umGmyMqGGoo+KukgYVqVqFW+xk+DbFz0B3Ye6hLLmqKwXTLKiqxpNVdIIoNInyp99Ie6F5ew1Z0CEsFuqE34TIDP9G8oQ+2PJLyhfKRblUZa7mJzQuYhZTgVbwANteH906/s5f/dVrxXe49Hw1OTi0D426slrH5uZIZpHIZNw7PDhUC3FFGQyj1Ef0RWjy9aCx2hSeZEm3ym97OaV+dFv7/dZhr/O8UJB7xlT8jzmAKB10BiZoto7/1SfyRjBYtx4x+jvaDTpUSH14iyPRpHu9b9XAcmZVS+nGiMC+z7hBIGASEsFuofFwjOIV8hSlZKBTL+WgbOcCe9dzWmeWIqRWYyhXilg6ErcaYqUNURo6g2W8EfpWgiqfsAwwVIEsbbNCVhjI2bN+0DEhlMXAZUolCnPKWyomMkNhaaPxtKYiXl6eGVMZnDNPmH8za2qaQqkzwkfQDPNUhfaOSyS2LNL0afzJsAVUdvW6q9C0ol1t5lFZ7ARwSuZQrGGtgNR1vK19mu+T2jTqsD85P70wDDYABub4+HjvYL/jxFwiBU/DJIpM/M6tVFZBNsuydoAvqAKfn53a2YOQVCjYIrtWSZtMxaeQNpimqprZpXfbaqZ/sBdXfzr9aMgevxruHZhxNL90eXXxj/7xP3UYwDe+/k1nD//Gr//VLz79nMpKdDDBnJ5dGPydX1zallepSA81a57y+lI5rif7owcPuVfFVhPqcBzL2v8xT6RMMaFCrO2N0MZQPKqrHm5IdyOlGrqFnEXApkmkxRWJVVzTNFVgRuhs36lL7j2U1M5L4r/bulQnEUoeG9ZrkqQfhuY4FWLxeqBnBgdds4y+PQV3O/25bXeRFrETWeVFVEK0KrYqGScWQKTFTyb9AFU/kAE37FE9UgnS8Dxo4oTv9Rm2fdCVZICbnjUKe5chCN9fceQdGsJmIFL9Sdk55aN7URJNvOusCwWl/WMY24fa8WRzbIWNoT/M015wcRQh4NNYgvANUza0LbmVtpgvGbxsppeaAwN5jORpe/3smorTVCE7pWd9c0xuGj2zRhZ1ZD5fLjUhYCfWLLRIG9L/o0EkLW0bs6NulbwopaxRTJA0ykXwMwZKX53KDKHzUvGNT8nZNJDrrEe8qXUol9Q1UoV6IKSKjA1id6AipE/PTATRR0GJkoMWyG3g6lt0ntgmVUwA+l+EASLN2v+EhoHBTJTECQPgDHGa+LtkzQ90buIlcooWmpsoSVVGHjXxIniTWcHd1UUF3NyQaBe1ou2iFMSkagL/wr1SNPImDJdYQaeupIBR0RWJIoLqrz4q55uYarG5mqS7e1OWXWQ/Ca5PYKaO8lpZ1EAgsAUVx/Phg0izBqAiN+l2xCsYBfbNrQlqvqffqQsbUhfIrKzCBlytZXnh2lmytX0EtuI7Y1hf3BM+rpoQLcmDY3rQ3AEObk3xEylPddsRrKkYpSnFu7N5N54K1tqHG8mpApeWIk04dvevsBTWHnyxyzE1n0jg5R+7rKOsEuRqcg9nSZ5AAShXKNYbI9dbOb6mfxrBQbeI3owaZSoL4was8oZMnrDY+i2bLLRblwoZjTpZSqJBRn9tr+9r0p3BcyY5pNLk0q5SRBKDz0MCQEnTzdJ3PUnOB7A1KFOD1yhGaSmJAl2pxI8ogtLyjpzaHSPghJb6CEgKCUy1k9AxFbF+AEq790RZhCdKVVMJh6ox3SUroNvqLYqKk5vlTGpo9ylryhXPYJlo17vWabKfkFm/3d5YaRYP007/MSGVBcqZGxAtWSNHcmmasYI3JK8SuzWIRMqRe45HsGKrb0782nE5fHBMjgNAPhepUxaES6VVuhAS6+nuCG65jky140rewDyVavU5QYQ88UEKnShtNWLybHmfLpkSyfzmLKeZLvrFyxdvvfUAJijEzzhyJ84n7dfPz05uHfKYDv+nROQqs3RkWRGxfkOacELwai6P9b3BtSkpPoSwfwLhk3tuJo8ZymNTIeOpqUzEVmlUjoFSF3ySpiig2ElelBAEmk4pPWvaQ02z6MNlg2E4HVxvWAGpJZnw8T29gTRbCuGSfUwuxgWjw8lP/dKt8RicKAcqL2asuJDlbGkDkfWCAfjaTiZ8JCZcOkyBR0HcLGexIJdhO51RmNpsjOo3pUvqb6ajYW/o1Jy4wk5XrVkZ9sPKMgkbqglMlvPv9mFnZskHPOBTzPV4WMMXk725Y+3iwtb6YYAw4IFG0epeYK+mKQAauVu09Tmk2hxEDHayLpy6Fkfesk0aW4XuuytUgU5zL8HlKwpbpZSfNDoZ+sllX6Ojk72v2/FlcODopf7Zqyfc5xazzdnFhVX9xV1tmzfeufOW2RX6fofDuiPAbLLSGazUb7dvKq13vcedxBm+/c7lxrDy+pKOb+KLrdjISZ8co3yLJ/QVLxJWVeeg9uz9b7ZteUnlPzlYjswVtx84Ans0OBgPl0YObJM1TFveGd+/bcVBNjIgs2nCkXMZroQkGN6lx9W01aBipd1p1IoYk3TH1ljVxJiP2MbLKCEB/dUIIoMNy3JT9TtGr5+iTGgV6lcvkGoNTfvPQO+2byOeB+0P3/Al0p7tPsufncF+bpd9bbXvDCYlSsuQXZose3F3M19ez6ebpRUDc4tr1XP/+dPn1QXJNHIsLOSiwi0eSLxqfZFNGqOpONI2gLKhZCRrXEEKxWpOTb1GFFkAYz5zldZlPYPFqtNITpeebjGdzc4v23PLDzr0eONhYeZ8bLT/avXCimVHA+C0lNR0cVR4lWW0QA4OMiUAtyzjNvx6ZdIGn6KhbizCiIIrC7hvt6MBhSozQpE46837X/ualb6Oh8F6JmlHtpIfDM4vXv+//z//8KNPP/7FX/jF+dV0f7x3dXnpyOAofzyLrtf2QLu8dD60uYIrDEVAZQ6D1qUb0v/YxmhhNUroFXKZ8Qs/fdIePNVppzmEcfFHMEPlRnLBLu/BsfmpNhOi7gKaVlM7oYkYxpFCKej3iglkaZwHEdCL+wYcrf7Vdn3c7trt3uI0hoaoK5FdzoqIgo78OFObF4I/Rz7DbMuzXD8z/rDdnbemDwJXJh3uPZHeae4olVN1q40GVQwMh+C8fzxt959sW9+MAgIlMYN02MOFi8kofYXqqNnxCE21ktV6gJpUVn/XE2vT2gYw2wO7D/Hw2nauMneXs6gJvL3+et/GV4xvmFAZuoNP+K/Vciaqe9baUUpSSvIkOFT+hUqRy3t99AORdJRpAFTk9Lxpkhpx2n/M8wrt5lweyoRSZzKF4cE+uBnj4GQlU9exhIyfd2xXuHiwM4BRTywST9EKg2AB9YX4Mc01KJS2kEeyHiycm3nzKDEuMyKBERsvk1xOcENDQkORAQLZKSWZI7c8knag9qmDYQYsoUCAfaImY16AdUADfKnA+eyDyBET8YZIolDIUMG11NfmgSAP36Z+U3f8O7x6Vpu9x9jXl5ADbkjmp0gJt9RkooW4bacv98ft7vMwTxIIDbidbjx4VPGSe135UnHcRa6/m/eb5Inxlav6NDBvMJFn8vgLMRQ+sAt+g0WDilQVHS/eBH8lpccGUINXoiabiMoA20EUgkaJKZNQOiTyL1ESr65QMcm95C8/Pu4evaWJ5KrAithErjhVZQ1EFatziZlZ/igPcT9JXBUT3ArJ/O4gqMp6C+iQO//qSuHznB//C0oTOXzevBaaYr/BtAra5LZL3IAQITnm2kXRytOSKwOhza9oAZ2sSYKqtVRYEgZfCXBlOLW0eNGiN9XV4FC4Jmri74BLh5PT1RVwinsanZaZeNpeUTqrjWO42iENcgOYLSEiyagm7YY1SBeh8dDpm5hNuWKfgEW43MDA4KE+VgiMSpylZJDPuElx6l/Q17iSabCvNJ4EJtM0KpIrExHUlDRGskev4EsVWrXqHsBoxEeeqanBIeP8OPyFiMmhZJYCp0dJqaJB2xadPzcLaGh908TDZqFV0iWp+Fw2bV+9uffgoU0tZq9fffLJh0+fPTYGqD6luMJNvAKTEpe+YHpRgM4AQJJwNNkzAZ5yGaNmGj9cSqAiI7XSjZLN2qY6zMpnaqLXp7opCSDWDZNfqNPr2m17hCg65ens7M+++6fv/+RDrpwQRsV4dIQxgkpuoWldQezPXxWwC83Xqgw3/FbcFxLdJIKq16JS1HlxNa8bFlba8E8DHaR6DpCEYTJNL88NWE+pfGk4RLRtpedssdbeYhMvgkRX3eA7H2ydCoqM3rbHE5ZH/Vz0c9/TpEU0AtyYJ8mmIhyx5DubLwwARoPJoDuaXeds4OVi9sWjL+7e168jeYyIEseJA9lNlreYw2VShqzsmuFjIRYE0hPUS+vy6oqCwhpn3w5nM1tzXBI/NiRjcd1d8U6bisy/C+RgXHWq3pGt4TdPiZZiK2Uq1GMCM8zDeBjMogUkivG1AFbEXfwibYONkFC6qFQIV8VRAg1itNLrX/yFnzOrT9szWfXw/a9NzRCdP3UmK0ali81W8zHjbXbqxyjBRA/OQM1hvGdTSD4YnbXlAPFm19Q4PuSAJHuAUdBHrY3jotKn5oQ6S/UcpDrs7ceRA1/G/KwvHvesxzkYG0NMjtvXF7Yl7F4vnf7V64zxAV4/HvFpXtqnUK8vRYSCbaUH2fTWONNsnYZW/bAWym9Z49Yna4CxHhgnIJtOmUZqHpTo0cQplPSMHFPIQ5zpNkp6aq9qsukNULWI6RZdP/bwUByfpQu3TjeUM0C0Zpw0WC24D7HQMwxn6zMGTC54dlimMBmxxNii6A6Jux6JObw15Fi9jkN26/mLFw7uIBqD6q4KQSYnIRCZk6aN/cqUu10abzDqN80iFRkkw4O5qiniwgy5vRp5ZnBozRru8j+zp0iHIKEj37z4QKY/2O7tj22wi0fOLs8QIonDL+vj4zuRyMN29P+EEKeaM0ztJMGzNDmWGUeeHH3DAO4qJaQk93OoYf+dd96SueIpuJ1geATZNHQzX/+7f/eHfBcNvX/0gx//hJ3/3//a+cXFvqX5TGJZ8dW3FZWZukuLLHhIXV6ZizChaE8hqJ6ev8T+EA5Z4FVCONQjZqJb0ic54kf2a7AhSOIkmsvPDcE8JVaay5uraWpeE1gvSSxKqGI5iWczHMY9na6Fv5Pr1iVbmpip4jSvkClarlsSIguJMGWTgRdy1TBAJcTwtJn/zLY7K8k0vN5M8xF6QRMHghC8Ai7/g4n2II+vf/1rD997h5KMvIm568lwZaxNWCUTxeml0IMmYx2NNRcwD1lwrCHwtXG1vT9jPWGXYVdZRBluO149FhK5iVts4IVwsQpAFzNurQ4JrvjdyJO4ym8QhVojY2ASLL2k6IX9DRV0o4mkcZJ+UWZDnaRP56wYKaXQ4rz0eUVBZWh6ctKDnQuM7MUQ0R6eFV3X35S+8ioeCGjfxA8yhU+iAC+7DIB9FqG5wbZ50NhQN+FZaB3MkKJUb03SapmAiAdY8FL2aBEpNTo1AmEHKGGVZSChfyS0vBtSNNI7JdeoQ6fwiHsSBVNXAzToG4UVpogjElwqgRT5TTxtK2nzl3/JI5kFRkHPT31qQvKaTJur4t+83Py++XoTkN/EzKDIQ31X+sKzsoXFrpIrJrzE8b/Q+EoepUfvoL3Jxfc8pzC7TzfFCGwgfK+qyNeCnO9N5jzzdmkqdeig0prPyHLzsXBJ4solwf50SK6cBywPFjh1m3f/VJTWQ81cL+5fMzeMLIbDE3rrdGoRJYVGQ+OGPZL9zV8ANm/J4M2TOjMr7ZWTCfYphDN892p4cXM15yTkLL2Ab8oC24qdOFWLFdy8NGycLJv6CGMXqzVckSRpconAai1X2bE0PbPOMVvnwENETI+eaYUQlBWDoqHuDXdK3nuanfrb+yIUb5W82RWYX9pT3jEmS2hI2SOoNF85lpKvU4+/ZixlmadCV5Irnt+edShVHH3aPR0c+1fM00mud6k9C4Yvk2PUXc0g1qwAD5xceQ4ihTufM5a3phhABDe3YGTm2SZ1nlVrHFDs8sQ8U+PqNNLYI5sGU1BDRTAjjUCmPnZGL1vrc7BSYwlMBxy0qw3WHGsSStW0cBSEVxEKBvlEFsdriBlvw8eGsrTljh/r29nVoH8oftVLoIf1JI2nnNCcENmswaCagANtC7o63QmL4mr9XK9uWiDUiE4fRxoX5wFMZpYfDpsVpbM/2dubzed6HLa0s7PL+3fv6R1C+F7H5kKXV5s//L0/+Dv/p7+brrEMUjQYcFAhvOBKy05xQs9g9abV5ONXLl9dSZP4fkqqhQTFXcqmmEgko+IQlVhJKkGTcAcgMStHezbLsPs47BtAhQUYnlJF2Wlrs7Yrwmo4Oe2ePQ30jNxkFfRrgFH9HHfdskLaMISgLigVQx9HDel9gzLBbZs29d5772DL42NzArMff/BoOp++frV88eLV2+8+zInXRkZlEKJLJiPdeBaTr2/dOjw8Hk9D49JEmnIVtYKLFo70yzUlC+LqYu9gL+T0opzh99b11OkiYezwW/XNDN5VxpAojQoXIWMYMIVTznRBlIlUTXRQvRKn0proT93d1F6yybV7z6slNqHA5shLu3fe0AsmdFMN83/4+//db3znlyyZwOl7h8cyOr59609+9w+YyPt7o3hbjbMh7WhyoKH0zOGNDuilncnemn5ztH99eGvOvMvhavRycrZsf7pvl0dHfRyOOvMltjehCn8YTzbsnduT3sA2OCcH473edjWdLvmVr5ana/MAlgQ7ZZFZ1xzBaLQ/5mG9dcIsZas9MXbNvDqxlBFZxDJtiCeYQ47m/c6Q81c2M3HikoXJ/By4wBkpMtcq7Jq19UIr3HZftWLavNou9vqm/qynbF30endRxxAhrgWpoYbtU09p/tpm2kLqTSWE6mHEfFQgPi1s0ZTNBImlOreYSrVup9NFa2W+7ogOTPyWNAZtbSbQFOhsevrZR0/Ozq4m+3uvX11Yk07AknUyaHJUVQBuu8/CSQYDUIFe8sAxyl+DjeCSuq3/DQp5D9a4K7qgyOkZAwJuhTgwJNJs6QSwpw7I6w9NJqz6fWNaKsfm9etXa3uZNnaTbWs0Hi8W3J0zwZuhX+qxdKiO9VHReY34GErhHo0pDVE5ss+8/zWd2Do8Orx7976TgK1DXg+yk2vWpPUGFhD/+IMPMfff+Ju/OT2f3j25ZWUUJY/fv7X4NgjqOjDB5IFBXzRXg3l8aJs+m3xtLq6e371/D87lClpFVugqqakSm87ByPCUwCGBazgT+S4eRPNT1VlEMzX4RcizfqeohmwyESUUy88OdpIqrV43u+uEvgsbVV5vHsSl2wZWzPv2CNLJ0jsz+izGsdlOo+qFV2IqSj1SI7IPDGKN9A/Xox94bS9uG2UPeweZH4vKLufUfmEg2Y3ekC7KtNXaqu7bJycEBmjFDKgoCcpT1NIdEB1dx/xmY8Ja+xcH9wDRfpa2BkqbubVu72flU2d/3Tm9Xu/1O+f2Vd5sX3L6V1hcTcsG18CNFs6GtE0Tu0BRxBKeAb2uL8TcUb5IVPRKUet/kS/CEzNuGMUVJeIuBcsIPrOAJTsBSr1EhkMzkVKQKCmpg+bCpPdtz5xw9ZqYGLGy/rKO1B6BkQpI/omiFN7KdKjyMvZKFgnvPqZf9Npm2KSPChGRkooLAppI7GGpC2C4AaRRBq0MpYWlckqPT2AQrmSMNlqvomQ3+ToaRimbIlS85OQv7JCmSC1J0jSZYqyMgmSkhAhT0sZLMbVggzQNN4SXsNo3UOaIPrerXodGV4zrrnjKaz4hCEoeeM0lQOrqxzP4zIcKar5+9Z50N+/NQwrfhGRmTOKsCRQiZqib4mT6K4Wqy9RvYqWcFfgVTbeJ4H6TxZe5JY8UqvnSEKnuBbcAqYeoEY2S8QZUYZccxbkBfANe6A1W+ZTgyqOiQrGAhMXQKhPLjKtsiLyW+1adarDqMpphoDfEvYFSxUvpC2YK/4ZIBdOtyc5v5VIIVv5EJIJ9mUCg//mOZE3iHYtUWIV8CT24Jj4ySOMf9kEXAHM13/KAGcyWeg93GdekRSlJg1U4PaHJoKBoU0CUbI+Ywf3pcwrcLlpFrUyLgEFA0kidQIrgicVB7eTShtjRNbRgy9rpIBj6a+FqUJ/hSuxS1aXBXUKzymRUVupWiaSNoJCAqmV7lvymSReC4YG8moqURWjJZBDVXl2F5b2uFjG0RhRS3Bubr58IguANLUkzbjE6CsYZyPMVsLGcpq/3uN4ys6VDYq5mpYxxPQVMdnUpC3UwgiKzDZmErIETeRYKu0IWPa5v5rr7PG/6+/vH6+0V+/0f/PEf/c3fvMvMfLY8JZ4aRqxEoXZ4LRLCXEfWb5Pk+hve/6QCbP2pJfyv0Ipa1Agx0cwmPjHVmTXvMy5e24Tk0eMvuDuId3r26vhwX+nYHMfD0avXM0Lx8avHNOOQCEFCllRXxFVkcVgrtVx1XriFUxDhq1eqx3sT6nv4odDKT8MeEUahzw7gLmroL48v4SWtUgRAKiOKDs0CQwdMIaIW6DKxROS8zOv+cNqbLLqm0Tdj+6gEYFBRhCF/KDVT5qnW2DZQWXCRwry5YsrttPYPDy7OzswP+GbTWv6bDvm9c+fBixczBvvVevYH/+4Pfu4XfpoZ0mSuqrcmlaN22hG2VLewb9s28Xi5vsQMtjJEvWDrp1BOQagtWIkt02YmXLjm1hUIKousRSe20spMSRob62aOryqShJCpjdCq2CN7qtQwGNOiDC0EJyNFiVfUFTP0S5XVaLUpaJH6TalvarKpAFgpR/6izffefuud73zn1wdcmpJ+O+yPeLAYQFriik9Y7bnpM0L/7C/9jFNaJZgcHc23XKj2OscTHt/XR6PhyRFdWgXZMGDs5KiXm+7G4ssY1w0EBu39Qec1//gY1ShJtpwft6INanxOEz6x3da+aZBR76W1pOuOtZ486bvqVcVMr+e8VdT7ZnExWvb2KWyr6xHhvBHN1oTmPRTcFIXC2AgShTJgM6YtdnKKwT43Fet7O/o8GyBStlSH7nRurYLTDztLe/Bk64E4Rqg5BNvR7A3pYrdryIdFY5O/qRqK6MLyEfut4AT/IwSK9nErWm3vnNwZIVxOUZc+wrT+9/dMdWw6s6vF5dXpP/2H/8tv/Z3/g7mIGuqLp0aSWxhBMdz9Nkgl3xgGGTaCQxPse/F2skidCo04SldQMgGrQAtA7CGJNROSc2+jOr/9zrt/+r3vzx3HzplnxXkmOlr8u6iKEUKRnFR1u1ZNJgNEa7DHdiQPDSei1jQDNTXy2frplLyhTQnGmIGEHOxNDvaNe+OayL9O/+r8aMuiP/z4w48++1SiTz/+zK6g77z1LrKk5HZgXcxVp5KtZraeCzHqfwy6DB+jzvj88nI8oaSW2Z2kTqrkXhJLXB0Lc7cVTT5oXyjvasi6i5gAQVUxDc4hcp5C+eZHgsjYvDZF9wCaIPtgGuzM8NSmf5G5t85FhvDZMBS9g7ChKQkd2qd1C6qWm70lkE4gtdv+PFlHs1n+pHkOgweOnlxE9dgAJmcwkvmuYH6CXyEMD63KAorW9lAWSqHG3b6UnkacmSPSgZhEzMhT/nE6NetFLbV70bZ9sTm3QeglzCNXrQB2lvK5WelBKycb6IPJQ1hYr5PBdo6QG6w6g8VqkO6KfSoTXxYBmw2Qf4raEBNuIVFRMg8Ujh0FyULskl6bnG30EJTJxxBF0ZKm6iBFroorAA3ERmHQLyT3xNW8RYpUBCJ9Sdg7wBK8o0QNoEM0fQcKBcUmGxQWJGL+e6qH1HeEqfiJCEpqOwBLQge2V7BTugZUqictrpAKnFR+VXDS52P9g3I9wKIiQC91DFZuuXYZVhYpfsSkllZQEqgQLedw2/A8m0+TDBE5OoA0AUNtD/m3g3MDVK7ySfH/Pdcu43/PlwT9xSRABsWmSA0N0SVUagKbvL8K7CZfX+p/r5V9bPisf15phDUAMWl2wGi1Z5VHFbbaiKCQJ2UIXE/bxVthttrVOAHCk29ANfddwE3I9jodap0D0MRpiqW5Gv1IkcQBXhnIK1jItFFjh49yViPRWZWb2eTqktVf4iweSLV1ylr1oAHGIzOgstHbLv/kgfwNhWKtab7s6rzqyzMkcA3urD2OAiLpqmB//qHeAAwCiRDakEPhpMjKlCI0CtzcGzBeQHZ0t2274vcB95IWtCgfkjalErkXVVq6pqtLERNaciigIl5oM82PtlR27VJ5xQNXp2ROMUag6N9G0+gVHcVXyhbUeMPCmzQy4Q7BdAODoeng7vA5LZz3XSBKKR9+gelsYjMw41cYkx0N8qa07+txnb4cstHJKMa298n+DyGJ3lHLoQRraF6hFg8/Lyz33B8TRQ8XxvWNi7wegjpOxIUU0MuAoUYInrmXal5QoA8NMm5hzA1i2T80oJpnTh2AUNNTbKe4Yxf7KBepKHzsnbSk1fIMBah/tqV78fI1p/x/9c8++rVfnpzc6U8vLXSrsTjaNzhDjb0hlqYo+mxvjsyEjIUACme8YqEhdxHb/IesqXb95D1zAu2WnZuVRL+shw7608tzImO2nLPDreabq/O58znpSZZpbkzptkYffvC5RcZHx0eKGdKs9Q5cLeys15QiRK2rWK5tpdrN5ekNiwkLqb2Hqo1YTbziRfUYvkqHojN5SwkYB+283xo/kWLHZhVVgpQlz9jlcYXtKKJr8zGKkQ41w63ltUULzFQ5pEojtS8bYHIOz5pnW62v1KQwBdHTJqNgmI8NkvLFy/3x8/bstW0sZWvFoa/2/zRR41xRLDPuvXt+2j8/mx2dcEjQ0KJFAVXmH6LZEg7DDPKAg4dw5dPWwklJXK+dXu10lLx947wS1y2VqP9TCNhI7Fv6Q9tMrBb4ipKdCBaQ6izzDeCy/YNNxSinjpQhhEONwkhjEi+0D3rBICRMWeu9ft0qJAm7uBHKJNuaSfXerXt/7a//tW9962f3LFyN1aNLEccG6HP2+vUPP/g+u62tbEZUQEtKTGdgg/XJ5no8Pji6sjVPZ8xluLV6f7w87Pc+Vz09Uno1s4SeywEFicPPYMRl4iqKc5q2YTlHiOw7vjfcs8C1ndOlLCe4MBvS3lzQgyCpPTuPYXw9GNtHyvm6B4ydmQyhm549ezp8dtnpLcd7Y0VAJ2pVZAK+NRPYHkYLVj9Wsq6Orbzsth/Fc2tNFHAyPiTvynlaHc2zTcv46BU1tXNSfXzGDUXJMHcI6mwKIohDORwDNgqdmNo+MJF8NLnhowjE7q30EWwQaelqdPPo8cf2vO/Mf7Z9aOZNYyWagKRhUM5YGcyCDmdXy+nVhX1N+C9lnC6L8Hragaptb+5nZWn3WfK6qc+wTCo+Rs2bWq3PaTb1L9pYPmnU3K5K00q+5RkSqySftOXi8vLixRdPXi/nl9jN8Ik/T042dkCxlNk1Uh7El4kZi5T78+l8yOU/tFPmrAyOc7QNl6J9xtGmpPfOO0/mUCGjUOnk+GTQ6d+5de/o8NgWyAhlI1HjtMPjW//sn/8L4y4P33y/e3Jw8pPf+Gb4aEW5Icx42oWlQ45O+/JyblW1UQGcIEfnOzo+VD3OOXnva+9XYRvqCEvJ0wAsWt882MxUN0ZWQKFFn0RJDAFFJC9Kz6JZFK8vTXhTA9IkaW5JFoT8Xg81xnbrRFehS1isJquu0c3Ddv+77dX72/5H2/n7rcFH28X714PPtkshn18vv7btf9pavkuybddfu2Y9Xb277T/ZrN5aj07Xm1vdnjOSyUbNP1s5h8xpxjK7QS16pxYEjwx7QmO1nSG8OS7GMUn88xriJw4MKYmExrV9uuypQ1EOj3eyaaVRvcVox9ojP9asj7dQXJcjUdtQGBdQa5Zx+RlgZrtCOZ3iYNm+cIw34a2/RF69NQlFUkdGC9lY2INfbOALANyCbWRcC1N5MvZOrDB3ohea6XcpImzVdcI9z7btYsujXc1kHiMEKMITgXlIo1D74QsgjEFYoC36eKu+FZXcmiSBkIqCoke40CVQCJW0Wb/JORaFBzKyQiejEGEVFccFf4m7L5Pp+nYwLgTymuaZH43shosEhPapnfriDmJ6o2KzKk5TgHxJ2hStoUBRIumblIHiMe/5FTn9iYGLZyLGvswIkOmb7tMYVzfv0hnKIJCxR0qQ6ys/RYMm9Mt7o/3eRCt+aT5W1l/GI4Kz/mS7ehvEVGjGOZF/wtMSm9JVFskb5tlpLVcii1v0CFmSPr4NrnBGfai3ugkJ/fLP94IbAbcrvvcKC0OFw1LK1BcgN/gmXVPsm5AKCLzmU1EmyRsiJbG/FKGCAAoOadJqpkPB0gtStJDWfjVKnLa0q/gQJFClBM1DEEmA8CpDfoPe7gpGX2Ja0RI76Xeg8jXpAyc/X7kaOd6EBcNK2ADPXYsKoeUYFEJWD/WW8AKfcAY6JmEqbEoXfdlzVGTqe2opCV2jaOG8wZVC0qAXbaMyA00SMr6/wX++RzvX/gh9kgEC6ST63YXFiDEYrU1/58ws02bZJkiVZVSdiVCfnZ3LnsoswavO+rjJOBKfWjvgymL5NSFYvWPQzoSp7WPUCDzZM/gfZF+DDUdJK3LKA7t0/Qit4RAZorbpQuJPrAieo/mTQRGlwVuJo6e9oWeiRyaIHckHS4pyOh7pBWpsekv7iyFFhJzVZvbtytUECo9BvtuzBYX+GJ4aKY3TklDk0yyhTVwxtbElM/06ZNc+35natuFpa/vq9dnhsTjZrifWlqpcOKrXPKvb0IueCiG25zQfFaSzPbl9y1E7z58+g715FXVqp8oIikIOAlyfUmMFKOZbMwY8AbpyfDEc3k7998xcXw4n7fPLs/ns/Padw2y3YQFnpIj/QSBU+crVEPDLgHoXJVg3BIVsOEeIb/m/K0EipO0ithuwdMQ0qhA/3+pKgROSZI2MKTBhRP/BlDZs4FXZIrvF706tXctOoG0m3ixOo/GEGsb3WRZIr0494rcCfpNVMbdcxLDQMEPoZK16N4PxwFip1xsdH5w8H72cXm3PT8//4T/+B//tf/P3hgfYs0eHopfLXnWz4ZnusoLv+PjefP48DQbbhCIpRBD26ymcVBIhHK0UMqUmJgJQIhPrYhndDmmuRRRf/TapGHcUF6SMNo10VHMaE4wD04dMjemkojA1rVW6GggFxg6RKnmwKcyDFN3QnMY3v/6N/+a/+2/fun/37r17tvxLqazDC5oZaeCTVXfw+NGp1qmZtxfTu7cnx4eHRMhk7+75rH10ODbjtjTCVgRsfr22wznruiZc+smMKw70UtjtpN/b32ye51yxrqN+qZyz0fH41p0DaMfYP7RObnjr/oP2j77gCs/f32EgnZX20j7o8ALqzXj6bCj1NiC3lW2yNVO4nxY94NZEn0EWnLA0JxBl1Cy8cYGRbsSZfxzcUg8aua6DYmuJuHbLJ8nxsjOoDW2AKmqZwLX3jPSkQscMwsK2xbiiKxnyleBNeweX+msZomX0KqR4UwtFXhV65/bXKEyvrz4/mDI0HERxrY6rOzSSyU7yMLo4vbBMH8VRPQHqMIvD0+ekmgqT1GNdcBGH1FFRGS3USCGY1iU86W9iWtErIlDkKMTC57G/ZESaYagFNFfL89OrLFNEKvn1Nv1B9guy1JbuE9ZxtBkpyCzdtwGxGQCCRWUZPmT2LCs3FhmdRMiHXX3NHIBCIrMSiKrNCCciwXn16iVDhgMKR3uT3/uD333++urnfvVbH/zZD6bTrHyghBoIjYYTq+ENguPAkwGOoR0JqQnrapRu6zADNBAuhlX79ldFhDSPasJV9HQ3ThUAAxIGQEwxMGFuF44R4IPWSbDrp6tyGxoWIavqffeCBXz1vyREHkFIfKeMRPvNPBXrwZnTJS9H5+vlLStbomTm2JNrPmgq8trhxDguJ87Zo9K5d2YMOtZNxP1H8xeny1x0a97d726PcLMtcVUSuV69CZmf4oa6hVtei/dShFQuzNIvhNwNpmHZYOstPS92MQA3GVWlKpgBGJL5yjsIQcxba29MRiil80RQ02jpNh1Gq9fGat1Lh6R07L+NK8xkptWXQ0z2Bsm/Xd5whF3yz5VMIqqVnPINWrGtCuWd5RA94aEr9gz7lUyt+LDGZNIGmkYEDqAwR9NAxcb1EIDg+1woFFkSNxVUqRHHUwYYYCVp4gfTQBEFpfylvWRQJSAPJVE9J0FRN7BCCkOpJFKoEFEepEiBEq8pb5UnSAXxIJX/YObK6D/RyF3R0xC14pvkhZtEQppxThFj9zV41KPviRIgribTr3wREHEQWG+S5OUGixswXwnLxyZuSFYxG4D5cPOpwhEw0iNT2Sk6JBL85nqDRnCrcjY4NpEK58Qlj+IzVJDrffcs+c4eH0ANlT1UaeUIYsDZSCvx+3z1vIYOrWZXnOU7Da4N1aVKYZqsd1iK7pKiwnMInzeWzkCutB4iFHATZhQ4JKE33Dv2qX12rVF4elxVTqrJa/K3ZzmBG3uepJmICcwgXYI72e3Imp1nvLBo7jConxRJG1ZnyXZXxuLUwio4NtRMxATh8IAvYjQF8yYvuQd3D+JQJqLq5UsZgaRprqJZJTPi567TMGTlHOAyrgx3t2DuG34HOmwZPCu7Jq6yypQZIqpVuKLapzj8y7tWxTL2g+prTvwMzmF3zYwSz2KXrLKPt+LrouzFztJHbzb2sLvZOP4tiqC9r+/Js9d/Kiv9VmxrkYzKKrJ+N9UXsHR0OpB9pNONBXF9heENCGYk0pe29b6wMO5Pa/bgEzjt9dtWGF53Phc7dAqoMIDu3DOpFKeL+d3t6vK658zRYh7skQxFFIATpNk4wliwNb5IxccgMolVTIaqI6XmVJbokXSIY6jU3s4vT/du7X360e++/853JqP9S3uE817S4UkWT0TJau2azTuWi+HQ2UAUJ0ZuQjqkVwBl1A8blSFO0Bm8ZDPVd+ASSi0VTTntomEQy9fg/CLjNC57l/PVi9PpWw8f9oancZOw6cPF9OMfPX7n7Z8aj0hB1RG8cxJkRHAIogDNX37y/NXfYscKD6uE4b1ASH+vFGGRNLIUCmmK5jkdMHToDA4aYJWqaBsOC1VDNDmVgM5DQNBfwofVEiPqdaHRnrKedLJpLYyCglx6irRNXdV8eZVdsoHKPA/TVJBIZfgNa0OVN1U2X8xRODn9gw7CjR6IHFltiSEuW25eGun94e9/8Z//1n89ORzTqDBhDV9poaaYgFLGpfPr1rODQdvZwV9kAJiCwCPaJvxBdPaRULqxMLbXrnWWhppEKrI0OIYAIaBqQpuQznuYtspcJi+AUjnQKpqGVRTZ5SFKtBwSVle+1f+mTprXChA9eQXSZjn+9i/+1n/ynV+bLS6tH8jCvrAoNuLLEYcQnm8ff/AxNcsMbdDjqdM/wnyyWmwf9/cNyI8Y9pabn5wrz+hpr78c2hOFgh7uUQRbndTwG29cXzHY89tP3ttjrsncQQ56d8J0dOX4RSja9XAyGu6NZlODuhR8vmyftq7iArLIYURKjmd7w8HU8a/9w03/atBhCD7n/bVxIHR0cY6wzhmxTcgstgJcQWe1VttmiybJMxmIw3COWaODkg3D/jXcV1eGGibQ2ERYdiGokYWOCG4HnCepQ2/GF1Slap7hovU9FZ35B85O1+/RiE0lKpy17XGyHiwPBvzdr3n47A3vdHtXGfaVKSGEMdR0puHiuN3f7++dLnKIFo+h7CzZtGbykvQLzSv3MIf8422Nr9JPbZYPaNXttllQuIRRRImUyQVrTSatL9N6vuUrQZgRr7kdhF4vVi8fPTa9w4SfNRLXPNH1egSoJpCRoSWhKfz1yCu3NMb+i9fzPUtAHKg4IDOt4s1BbiY3tb0hKkYwIZscs2WeLEx7KgzFyhGEbz94YJcgZ0dYKTa72uzdGn382dMPPvhIN2Se8rd+67cO5OEcDAVkrNanoFDcVNBlbYrPfkFAWj9TwjkFzWAA5Xu9g4NDwj7NGuFS9h3by240HlxNX7W6zl/nNWDyOVQKmtW2RJQkKYp0GmySQrxeQ9Sqda+wauRSWlHeS9K16fhyxEX91fVPLbadi/l3aPDXm7c3273W5ptxs95+k3Tazr/JtrZdfiOHlqy+lini9Xvx8udFbVng+j75lAkPksWwgDxJ+QyfdZ8yyktM4cFK9qnWknBBJA7q3N9a1sslgvZfzFMLZFMYO22nG5LUOXup5RjO2OYyeMNEOpzInxQ6GlEGKPGZO3QAN03GIud+606ab/eFTq2d6eezxdJER2YmbZK4tBGqeVLtNAO1bMDqkEw1E8Il37SZUCyYOOUN3XUG0Si0EfHy1Z9LdFxdpN1u3tquuIGoKW1LtYapsH0ARWbnkjI14icOGez3TaymLpU48KrvkBQEX/E+yogQ9UD0NJPgB57YSC1cYEgVYOJW9ePl1uokYcYvYu6EcqLmn0gNdVOGXFV2d9nrWiAcJpaPTyIGP4k8BJeS/EnjL/n6sIuZkMCqkFBhx3upfxmGVp6yLev6QXanidOGzCqZrAOsABaYJjiPu7AAab7c3P9DCZrvjq1rtOsGcgQevsw9CANf+TZxG8AJDtcKawJ2uFVghrMocJP3V34bxOpb8XdDsAKTTzvYSdDE9CPw3wPsBlCi1jhNwC7H0LIgJqRQbCKHn6LTR2/OhcLEWK7Uoj/SMN4LxK3xKOeN2gEPe8U4gYlAoUFKSBu7UQsahOFXV1BtCuGpqcGGo/AgXn4TK1jdvN1g3TBClUIWilCkSYPZwW6GyA09whu7K+pAiuuWZOR4cQ5uh0BXo41nMgZtdObiWjFFK9LsMIdegIRyJUxQKETMc5CpefAiFzjklX4v8V1IqFOHAyqGOGkCimafbIaNNcXLxQrFrkN3R4Lo89TbMlwLER+6IY1cyHqKfF6yfiCm97Af1GSIfNpw6C8rUXRjirwLJKiCt9FOsK6tL6LWD0YDG4ZUGfShXWYrjjq65CJU0Eimck94dqoBXJbAVv+64zmljv3GT67IUbhIp8hV/NRH0jTUSFrg01Bh7OTLTz/57Ory4rt//Cd/9Te+5azVcZc/Dwlu1aOyp1BETgyEm/WVUzozMshZwqFPRmKZAfd8cutY16jgkiRGqildo3UFjRvJwJJgxd2fTOfr16f0JKy8eX364tbJkb3eSvZt7VHz6MlHnd5v8JBwTLIulu/sdsNhI8iHQ8K8u+vm+eY3H/CDnx0Pe6zokAmFI3mLo6tSUn4h6YmJXcpZBnlYqpHZDZiUIk9Jl2qmYBVpo/okuRe8VawBTr83v+5bUrjXseMbymBXdRFu6/F3Aoa7sLHAaETyFN8GzaBY92L9OKwPybQ0d/y5MqYa+e58sLiWhBW6w2Hv2cun9945tr6C0kVx5zbjk4EW/rEX0NHerZPjWfdStvs5rij7YlKZog4xywfp6nGafAmQUTZlD52oWe4u2WSLmkxKbOyyE84K5SMr3ENIr5A2dKdeq+z0j0lKpQPQlFfGxg0gJChWaIqcsIi7XO4hI0atRx6kr56/mC/4SmVMTqZoUqG2+aTsqp59uX/8vc8gptR22un06Dk28DVW4jBwYGXF2uJRTtvWY0jZs4VI5n+JzY2xkyqxmrpmFTTvXou7NqIlIukzv5odHF//xq//4sndE+hpgPzVjLfZGQcW3g+GhkkhvnpUMasrC9fJl6gDhsnL5bw9HU5s/3Rmu/2JuUzOHnYzNDJhs8RVln2SbzS0rHKdcSiyzLLkA9QNcHIESQzgZN3mwrTCtnWb15LSE+QqNzUTWu9kYNN2URHRQ8eibmIgZL6xhMbYH9xKBKauxeNFZyN8W/1Ado9DPZfxphKizqDh4cERL/fBkAFZEUWIHEvWYeDIYJGg4DWXlwYPqBcKipMeqVSjJAt+/kIzH/yv9pNiQzuvolaxCBNLiTQUc71qg23duCPOmZkCNQJUnCiOpcJoUjHUqhecPxyYN1jyR2RbIKVslA02VqRbk9bmXyBoTgLWkhMisf1vrg2k79w6ht7tuyez6fLyanE1v/gH/+M/fXF2eufu7f29g/ViOZ1evPPwIQaIkSfoGh0NzQMojplSnGiGBEAPJyfH5a7pmDWnzbUODo7soaTblYbQLBme+pGdgDRkh3MFmwjMSI765OvuCoVFThQPSFe0RexGdctryJooSaGG8arfCBj9WswcxnzOdp5tbKNvYUmmqAKPR1Ec6cEh6wALU6VgsVzBRLLUSOgXA/u17VO1ilJqg0XwlHfGKpWv2Mm+bsnfQwnHtTMxeYra6LMiBO0qEAhK5rExhKFFbEugGUJm3wjMGQNSNnRiV5JMujCO8YQomcM3qIiEtq+AwnKks5NHYjFPtJhVNnPnB2Nh9YMHRVMMa4r72cs30gXRQrnoKHXpjFxKG7wjNiOp0rrqfworEW4h4rK2hXdABF2KD1TNvMO3iSx5ILuiVwTfhIRaeYioje0NJSmpEehVX1KnfkVJyTOaSmlD4ABTivwFShn3UobKmTrhQ8VGsjTPAKokgkOkIjdIO9hBrGloARssK0ZgN9h79SR+9QmFdMWsWzCqBE3Qm3wkTTLpgEzSUM4lr7TZUsf1fAlOjHxJFhVnF9AkyLfdU338C7cmRRPYRPtqSApTVEMKUGRXpdsBbOInMF8afHf3ALwBh1NXxhNlxb8Jzasrh02ohXnlucO+ngNxd5klkEFduxLy29t9zU8TVQwYVAUVmTO3IEyEuocHuLc2UELEfNBCSvHKL4mYTeLSI22vT6Pybwe2nENUqUDEmc5qkQQ3MDbpuOlMdgOgmeGO/AsuhU8yDCZszEFY+nDqji+CcNg486Vh0Kpg+YddCr+GGRJ7xxpQD96hfkPqwKQixvkjml2jalTaRIvVPPby5ODojatpk3HQ5jDDMXxFcHgmc8uFExq9lg6YMuEJomJmpU4EBiW5NxmzzM0CmBjLMb1RFiAUTccBQK13COLF5lNWfxZ0mjqNYXp1qbFpqPDVgteraUYdG5bS2Apib6JAyZStMchriPqbmBLQP1Vw/VkyyXbAmbbWB8g2x7u2PhWmD0j+3OQzY6DnpvvGEmyZJlgOtBJu3kAOcf6tZ0aRkNNfKtr8xRfOL6U1yJFfUqq4zFeKFukVsnInfmLTucHym2py0/60mltxj9QcKVMVPNAZJ9mQMwjkkyfTdeuLVED4EHWdnUlMqmuOEkhBMQowJZ4uLi5nq7fuP+xfX/SPjz/77PNs2i0Nm8nSjhwVj6kxIik+HoafGSKlIRoWdfYn+wYE06uZim5t7jJ7trrPDvYP9ic0SIfFrPiUxrC0mR8cjMeT3kKXna0IO89fna15P2d/xuV8Pj19NVvMlG4T+ymcS65iLflUUVOIlLPhP7xVl09KH6bKheTp0BSSci8UggrpPQQo0bGdv7WZ2UbSnlG8ZXMJliJfA3pUDSKeUfG6lnP/aZ6bTBpZvbyvUMqYvoEaSbterbsX8/P52Tynra47I/NRKSUVU9EyH6NnMarpjaM+oloAJrv0RpQc/Vi3devOLa7Ji6nD1tY8s9ng0ya765/+K+9+8OGTsyse0qOPPvzsr/zMT5vsofn0NR07Y9G+LPyk5C4Xh4fjt9++vruxrSoXmGtnG2lEMATq8ZPndNmM65J7hj+8yDZj/jBaH3bJXq4WM4fAIiBZLm+0H01mjDoACi43OX2uQbWyO6TJP9MaYWQ60no5iU2xc151ETh5aO4pc1NHTR024cGm058/eGePlrqM/gm1KEn0NhuAIp11n5bDf/7ow+G4P7242htPhpPjd97+Jr1qOBgvthe0wfFkzf+v41QNi/szszpc8xvWZLnhZVBqKNnn1o/cm+3VaK8djxsOOpv5sPXk//Z//b//5t/+Nj3RaRTKpHWbchvauYdnT5Y2oi3LaCkCaZmRA2mRHUqJejjid4Th2r27TLtZhdt+xZf/uvVq05kw7Y/MDUzPtu1Jd7hgszZ3s20dqrTt0h72H18v+1RNKtBodOQcievRq2XYj+JB2pmyRMCoxkWphnTIVU0APmnUFATV81Sdba8PwuocQtKV5J+9+Yv5r189u7q6OC8TqbkIpyhIJGYGxup3OLZZ0ksrKsmt2m8nsrgYW5NIC3QaaPKUGUxKsWraWmoOZv2nJCW6VSOl3kmSQVLEigyMMnKlQebXGwKwqXOaIvFaREFLw9dAzy7O0oo0EwK2bV+n8d6eHWD51SgKyp7w+3Q+18Fkj7RGIfKawTh2sNhQ2sQszzV8CQ144twIJ1lB47qNYxSX/j4k5TVrvqHt6z/44+8+e/US3/L7eXD7XWchmOy0Fam6RgEXkRQfzgCHhtKGMoYEPnVb95CxNzhNebbbq+nliEuQGYmm30yBqwYi4A0MCGZaKqyVHy9ZVAK5EKXB8YaeoVU+NKkLREPk4oA8Yj+1LpJ7RpnkMWUmuthwsZnOFpTKxbBzQtxsVxOlt0d/7tdI7RlrSeJ4O57mk0Ig59qRcilD51l4KbD8Rt2VPyYLTo0hC4CqRfkHQRgErTzmKLRsda/2pWV7Q3SPPmnIiaFSo6FnYZ5ktETjc09EYXZpzWwDcKhuIBNhL2nq2OlpC3scXTv1+XE08vaM+tMbrijV/CuzYs7YBxk42vWWDsdR89QENC6NO/5wAKXdymv+Vh4mcY+sqvTjY1ga/sElw2G/lIOHhoskSet61pqzbdeIrogSQ1sTR+KqBXJd+pAfrJQ4VyoVISkxiNTnnaEvlrvLKCsFFbGI7yfksOxB5LahjkT5GKNL4UfIpNUl086Lgn2PAwgK0zFAFUfZUrxysgAsWOUPTQFprmCEb6NterJNRbim0W/xQCzK1XKTYfEeMKn6PFex4IN09SmA/YvoIUadhOGwzvij2ICLnxu60rm64wlbVKb9E3eHTXDfkSg///FLjCpCYgWC6w205hFkyDUg8/krjxU5VP3K9QZaPmabrNRNA7oAfyXqG5gNyB3gAtCUR0i4pD6ESJ5vrj+X55eBX839JvTmt4hcwJpYAYbuKpXuQCnoUvEpYMu98X7qM1uo59RSMci8Bgtl1akljD5b0jaMFvkY7nfli0iJHzpGshfSAvOQRpMHcpTwouqFa4o4SeJbEzks8aaogRhYuciHAKfZU/x1ncKlEiJhCtWk9xBBnLhimk/F2EkbZVpdEBwl+HUbWQUbpxlFQIBrZq3Ax4LprsKIBAM1G9tSuCNWIkZgHqZV1FBF8ensoaBUuxKJbfxBEqFjBjmyDsz0BLAd9hi1cTPZJIKM4/xQkdLSivsBkxyMmmzRoJI1IKGEfINOEURQE9hQvxldRET4n1pCl1I0QyaaoiFFETZ2Tentmym3DEjSkYgfcomgWPItMOndCUreTQ1pPafXoeWZ+eQ6QoKWj6mNCKku667+pmpfcZjQGEf01pnrsH/Y9f7eiUW8I2fqOLrsyef3799lA6NXGb0ovmTsXirr6nI64StCFePMwMdp26M0WygBQ2IZxdQ2vT7HbCFS19Huaiu+N5m4wBJIo7N0flNne/vkztO9Z84fwA5WrL0+e+G8Wz4vSiDC67Mnlsz2hibZp0ZeEZg3yIejAgg73DBVVQCSNmGp/zxKUD+NAEq1YDtcmloKF6BPYEYlD4PUmmkG12JkMJAay4meyWEjQvxMzZWnalW8AsFLJQc2tQdLg17DL4uYF1dnhOrTK2OAzR/93u/tnZzwEdEMdFSffPJIBRkX2H2RXqmdFC5NKcI9wU1XqNfKPEFWpjMqBTUb2fe2x0e30Pnx2MBZrss//qM/+pVv/5W33n6IFUf2MtwfKxPr5tXVVadrxsDaLEfgpoigjmUWKvUs+nj+zF5LxloJVz7MEB5oZIUWUZ0lnPKxKKy3I3us1jFUDJnCREmavhpRpWwoLnK6oWp4VaaqqfB5AO2u5Ji3Ar57DBwUCg6Y3AHGGVGjQ5pJbXBEhCEEta43/uyLT7/44imQTPLuWYMz7F7N57fu3m3PbeE47G7Httfib63kppfMwMFTC7c7z8D8TNcAnzg1kuAh1z4cHj68fWu01/32z//C7/+bf/ytX/iGvXGwSaYuMDMPN+ODdfv4zr3XZ+dRSlOukCwdeObxsDSNoc9hZdvPCg8LVhcjC1m0sT7VFtvwp7Zsv9O6NPTALTSg7ojeuTazoMu0hAJrmDSwYmndXl61uq/Wl4Yp83XnKoNfXRShhjcaouUx9ebfG+ZHxFRGGn9DZUq1kY4mzhac2SDKVs4bMCqcO13u2gSViYCIZ5XF1NJ0FulkTDdRzpKD3dcX4mbIJ6/Ur/yE1lUkUG7pk6FKSrASa+Be6x0q+I1EiBwgsuIek8o19gUItEiqeG+D6jVjYfuWMq2zZNmkgLBMA0XagYmR2fm5nUFfNgoQH7D+iLwnxS0R5jsaI7eepJmsjcnFtgTFMFheoSOY1KVl0ca3tslYzG699cDA2oqzV6cvKMoffPSJ3XvA69cqu/v3bQxKFDpFe2fQVa3SOh+gWlJsWOmUbW7G8k9+ZgU51NW+eaCc+WAON1u01f5waBWGwS1lUEMQZijdSnwdq7qq+BVDLHVSzRXwVPFNSGo75EfodKa7cGRLlGpypFq6VC3G4E6NZpdZ/QiVLHWK2HTq0Djx8UraaaQS+RPBKlAczSR9UxRunYh+R9Sq+FSXOColnUVgJKvmKnSaCHU3bmRiqF4oAhbYJvIO8/Q7MVGw0BGzRWEy0yWrFEC/oazpJ+jyGXxae63dL7wsLZ2J/LE4lqJsgTAOHxNvlol3hGGYDFBEgGdIg4JFlPyEZjeUC22rpFGRirDQSEh1KxAGQpYpoL8MhLA0Pz3cin/0DqFTAzN9rfgVKQ3SlRkDgiPVFYhRbIQAUvNWhUeJ2wjd8DO+DKE5twVqDHqZs3MvuR3MKdiipakB4zFVoISxtiW31GcwT3mVOzKgEAm05l+6uUIj0BJUqFZ2oXzQS9uUwEMaZgZ5iRai5KpYASqbhjfSMuUaBKJh+rM/dTYG71h+BgDxSpdzSnolT54QlPrPX953Ofz58OYtKaoAbrt4YqcEwS0h7l4CNpjmp6guebJLyM37DYCv5CN6JeCvdLMG4E0+u2g5UhsY/93qXk8AN6EN/CpWE/Bl8A7Clz9Vli9fK/ddwZpsE5I8GqBI7o3Y1kSLXZMLkUmNWmUtGttDxHfc15Ik9YubVaLlsBU/cJb3PW76r3SGJrMSLdeuHSQfKaoiq4KTX96XD9gD2QAioCtCJZJ5UmxX/NuYlzOW5SxYEmmOQ8PGGYk09ZJkhG/MZ/TXlCQlqwKEzbzEDBBWhnQsfMVMab7UctHNc7BcW3ZLvmoZhYlEDRBIJHpkiysY8wq4S0Jv2o9Y+UQSP8Fw6D7KgeJkociAF7eiZN708sgVdCiXOkPabCAaUtuQJhOgOuY0QlbbqNFUKbvlQLSoIClGB5HMB5yEzU8CherzjCTozd15TfLaxy8jkAwGSjoUKgojfeCnzJEQrmADE2WQULEyBRuw1JFonymXgsNvacNpffwn6V/JxgjNIk5iZHSEDlx9F/OpsdyAD0P7h9HAuX8kz4woTK/bqIYiKT8zJz7u7dE1abfrs5fP//SPPv3Zn/pPVvNrHkGk3jZdG/JQFAprtZdFFM5gWnSunZag7GfKbkIAcOueOWYaC/BK23am/bFtBI9UZrYmhby10i37WpIx+vWNGfzRYHQ5vXLCAGWYaGUB3S4d+Dp98uTcLn/mZ0yrEJYoHNI3FMgd8fPPFaKFJTwmNO+70PwWXdIyMCfahcBqPQBL6PP+v6YKKwQ64zoFK14pybptz5Iqco528LghcsDIJA0yDHTd/czkEoInL3qBhO3Rcnlusp+LyfMXr85n52wiOXv2cvb8lakGZtfwwWj/cKdQz+8HyVo7BEhg1z9uzZc5nV4pjDemmEOHaIsYpJ0uXtkqaL2+tCv67GI1OeiOxnuT/QNDGB5Tb71z69HHn5gBgiJQGiGYPaoq75IcGar68AF4zRC9qIX9s24b66bvIVRLXVFEpEIc2zCZxToMtwRoSJS2nooBCc2QFG019vSfpfMxhF9Wa6yKUsDd1SCVu1yKnyokj+qzM94b/JWf/akQKO9pERY/OP8V2rQsNfjq5Wtigx4lW6b6//Sv/62s3R1NzjkH7PHnHq7aM+q4df3D1WqvbaOkC1MnLNoyaM/XW1WKBnKy/Vb/+vhgfO/k6BvfeO9nv357+fl785efL446wxOu5NNOf0zH5ICu4XJMSHfL159rCT+diDcjJWt6KSKOEjvQhfY6U2cwLbf7T1fd2dL6IZouf3obCinosL3es3/QpnekQFaXdYcjpyYTGK2WuQi7BpmuOGoPzlfutjtcmye73PQmvUxNZAKEORuUkCNeeKF6LuIoCm+jcleV5AMyUhEUmX2UiYR7DYdsTU1FjzVSw+wra5lNGNFv2WhjeNV1q9SVKVg0idWCX/6MLduMpWlw+wHQflK5yRL83CO15eRT0CghljZIJpbCU6aHYpJMMGagG2GP8l0HAk6zwCWdRkw7mXClzzvngtnaanefuHxEXzJ0QXlHAZhijX2GCEKmbe9qOLbmgmCLjxDWsxHkZHJyefU6o6A2vykbEsaTk9gZkDZEMW8qi7pGQ23iyNTYJIYP6v5guP+//It//KMPPvja+z/1S7/66x//6Md37hzv7dsPintPPA/NAye5XnHFKWiKWpO9/cPJ3tPZUwyhjZinbfWe62ZxReie8plTsqFBjvf2L50K5TSGdkSLKOtt785X1g/QjhCW8KwGXy2p6BoionDuVc+hbwW4BWLVQG4J9lEY89W7kWpOhUfS1CQlcm2fKxpEN5tXYXgVlQTAZtRZyGgjqkZ1lTCUn9Hos7RtMqcZyQeTyifIVBtPB11s2EiBYKMCYndTdt3kamE+5GEkFbqlyivj8AoQ6doifJynsTXMG5bHf8CBkvUqEomBItkAVEYkjK1lNDznbHOdspCPXePSIuX19pQWxJItA7MY7fVVp30gP21bM9c8wYz+sx2Ym00hUooS0WAOHssB5Aj2IgklKyioQRKJEKSdRJjx9CvlZP2Q+aHL5aJGS1KhuPZgVh/tMVJxPTLIOlaVbeclWO3Vg7BEhuIGWiVrl2/BLuSPJIEq3NElRigPxJu0ZlMzsu0/RYBt660gHimbCKKAZuawtTkBzuw72YCxdCLFKooY7sjUUjBUhU2hqoaK+aoKGoB7Gp6MpSktHXBCHitmACDH6Bxp2XkuCgkNAVPXzfd81Z2EpMldhpu39dTtnJIkmdpDXpvnGuvGUUKUSugnV2C8efJWmQgQmJiu7H9Fz3yUaLuoPu0+hrz5XPgpVYNohdSbeIj6JpNCPF//wiVW5vYzUnHtYDcvu/uXOe9iJGAXseB7hwTSNGSopvImxldAhauFJ2lDx698y2MDswGVN094k14dlSe6IBmECQnA3BQI23mJJThdtVnXGifo1HY9akAUTjsVtVi8IRucm+zkGzqq7KrvtEOf6i2Vqmvx3RN+aqSYdF7ljlPEzJC96XqwcV1FijwDklYUcFEaK50beLuYODiB6jbBfsPEdLC0opIacConYHkkvPJNdBdscSjkQwxkoPWEd4VmWQSXf4ElcLxFEFWeqRrh5g4RNLhHIy9jgTfcUvmRX4xe9hMAjfEoDQlUDRVupgeiBWeQ4yLrfEqmjVHeY2jjPWUOklGye0St8MCB8A2VEkPuQTHNyYuy1P+8lFwowqWwcE9tJ3lKH1EDGtoyOKWvEUZyVBeVugp5qmjEdAjI9Mc6JjzDiZQydEqdgoZ4zRmfSpXic6E2ZHGIbav92ZMPPvjsB/fv7+cIg7Ki7SZnOO/bUz1ktikNd2d7okfdQ9xUCINc5Fd28yAf9T+yS/WzinPKMBGg0lNfLI0dqwgyS9Tqc+zvOxbN2ao2AZ0vHGG8shNji4vn1XR6iswHt06ePzlX3lAr9N3hrzRFkipzMQaqpfx+8lf/8ludUGlvIVEQTSxkyE3V4DdRBOsPWd1TORZMhlropAISAGSxpeeqOBLObDvtpMfI3NlTSDwRuKISfu379/7sB388W01/9hd+/ps/9ZNm5PWNp6eL/+f/439i4qKwUehMtiCvagh+lT8csJbHVHn0mpRFAAMLqyED5Ghs4/LNu+9+85PPn+BKCs3v/O6/+u2/9bcdGmb+walGpO18emVGwiEA3e5rS8cXy4xhwPdXOnTEsXklFZQw5QnLuYKDCBUSEgtBkuKUsAp0Li4vzBAZoQnmMQXJOHTltAoXWuk+S9NoZE14OZUVuH/pCmETKEFTCSE1HvQ3HA/GeyXQGiTSlNRV9BFqlQUp3/3e93hW4XtTX3h7eb2+c+dOd//AbvlT/laHR9ctzmb248ebHAo5WnV4D9GisWHHwL5L8+X+pC0Y8CK0vU2dljpfrhfD4/G8ux7u7dtdhm/59bLU/ev2xcUlbfpk/7BrHy0DKdb6bWtqIzA++5kvMewfj2xu1VnbO8BSVFquOSCyuDfQT2ujFviu25lZFJR/dhzRRDQmK5gjz7b7dhXobw/0qSbNMrAwysNV/ZFJQF4UcajGDNWmEQ3pqmqixInnBeXUWAXnrqQR0vK2UkhbAttEBHGRdY/0bYccqHH7dvPTs8VhzDGAUtk187KXE87t89ezi7PXJ3fvmpRjPEhtNVwSzkhrkVH1NqlDLO89TKuqvFJKCF9tRiWmY1F9YSKxONpxRot2KA+O/2b8uMzP1FR7PkVUqzkJaXqDc0O6pDA8TQ9OZ0vLbQMr27vblaFrrGLPfjgoysL84flrj2a3ouznbGNzLNIiPmOZuZ/UNlFm3qc3YeBp2XLg008/7F5e7h8d8aZ7/fqlcdF777x1eGQJMRFHb4ulX46AZG9KbWw0urg4V87p1ZWFdbYJkjsK434kMEDxwLbtPIo7928pBBZDtKoXu+go8nVttaCVZUBnmzUSs2kDqb2K2tD4DXHTOIT/pSvlkqdGF6KTaruGnBpQ+YCT206sW68me4epp4BXE8GzsiLPuJooY0lDeAZL376anVdXyYHUuH/eKscGToOrCEGCvPJQPSQY6ZcSPQwTbkBK74CkRozEyBnzIxJAUwcdwClPdB7/tYca7+bVv3zVb2SPIsYyJirrcPjTrfo5UG9/urCP51CXk+TROHRf/ieZP+P0Yj/lU1I4hO8TvqN3kIzYIWNrJXpY1EIUMplnnimGDFyNoQ3Cw9gQDaUKFgC4XfeKxUuApzDpTEzXQcKT/5VdEKlxXiQmpki4MIULdRQ2k1eRxqEwHSZmtqJz/JIZzNI8YOjZfEhMiTr8IpdPUGGstDQ6K/whph9izAuo5BEKILhsvDUICyIxFBLyCl2dGgzAJGWiBRASX5EkRa0GFhAhanOvIAl2gBEgWWX8Vb/uIYt/KJA49blJnscwVYLf3Auw25uwJqDhrXoOkDfXl8nDO3kLrPxEJIICj0pQX/I1F0yaojSv7g3QuACFBXavDYQmToLrWwEKzOYhKZJH862SNvlXhD+H6w7QTc430ZrggtbADMgkrMTyBd9uFfo5lZ1qSSlDUpVvf7lMiGMS/CosjBGW05aUnAAFpmp28CSUyKwu35hCPrfKIdmFcqoQFyXnJnd3lk6DSx8SI3gmJ98L9Ro9Y9v0Wk6VF6tsCWGzHeq4qHEhWD20I5u9qCu/ABKnKX4gRy+3WOgejaXXfwkr3Yx5aTqN4ft2cVfM696LMGMMy2mfoQBYGo5p+bhHxDnHtmt4dz24zPY928MqkhYVQ6zY6EVPtdMMttYBkDvD0TjqrgECC79ukEsH46IdN9bOGMoiSKrRji5yzhRGdo2AL3B6x/iihDBN7YcG4mtAKV0IAM00I69EvIRpbKF+AKR16K1Dgok3DppNqgR7Ump5QCuKpjDwpIhTP6GTYb3LNGiM9evMVMdYm86y6F4oKWRKKbZXDMLapEEAWq1CFuDmPwU8xAwJSlQnGrOI7aX2J/yOxqO98+f973/36f7BnlFMxGOUfNla1xGeiznYB0ZFy1i3r/hHXlvG0LI7iimLnLiUcenWoa37+l09+nhvxJBGPvo0u5yR4vrvk8nx6fn5yfHek2fPuP1TiVijdN8nJ0eXl4+Yr168uFhMr+0L6tCz/ohMrxoNIZWhudsd7l6VKRWSfaxDtDefU9yKJ8RWqQ+Rftv91EuoEMke0mSznYwfAXf+Q7b5wwHqMLUUaZ+68SaDAPZXFQNEeDmg0vOJ6190VGUA1eOqO9x3dGhMI0OH7JqG6fZevX5kN73k5fA4Bw4UrCS2q3Gy8x6QhWEyVEPDUSbBigFtPWkHj/Vw1LfIcLK3vZz2Zuer3//dP33n/jd+5Ts/R+zbScM4azgG2ch8ZXNcnVfGftmSDzfnOCXwYR6zZVM2BelxRJHdkIrDeVPNFhr0N8XxP91YU/h1a3G1mDHi8v4adnkVS0zkSIs51Xg8Eq2ZpElXI0levt2UyW9KVhey5tfNst1k0jpP1fmlXV0u7AJ578HttKb0udlk1jAD3+Hv01fDH/zg1HpfuvXscn54cPjBhz86PNnrLW3Vc7DpXPZG1kwPcNrAFvIw6y55nHmSSbVnSy+sI2DpZIOkfRKwjGrr6fnFoP9Od7T3B3/4Z3/wh9//pZ/92W++9w2pz530NRya3+m2Lg8PtnvjA7ZnPm6ocjbrnE7PhqN9AwG7dlJL1+vsL8QtgaCoVqwarHc39ERtyqdTyCigjoejz/A/xwXEmwa6F2MIZ5/WvLM1lESl/baThVGdruBcCeNpK1AzlfkwxvT+E227yFhEDNuon8RPGdMAUB3X2juLimmOgo+v9WKW6y83s9bSRH0mUkxn9vi0q/lKoZbpBDbcrL1uSow59Yw3+WrBGd64QUtPhVe+fvKQd09Vl9Us3gSH6Xqbt6k1q+0nF+fnNH6TghdnWVbBzV7keLjZ3ZM6z1Joeyz+RlYfTee8ubpTGO2t5sa8donBhsacmTOpmSWZUSIzhrm8msslacMY3YXVri1rgNkg7luG0xmcsb/SwmlIeDjWWpuyWjJuBcboaLG4evnqYtMa/NN/8M/ufO3eT/z0T5rkPNzj9rNH05xNLxR2ODhER3YHzXW1yDG6hJhmrw3xvu1v7945PmwPXl3N4kKtpEaT+gsmFfOapk1sdLaw/KnoJMJ2YaWQJWovhg636z/dri462280NZc4kVyp7hA5PvquWahJkoTouaV6E4HgUua30lZ4LoRJxLluD55AE9fZ4Q7J2HYIBCMe3jjdwUGGMFVz1ZPLi4ogRNcFYKRV2LDyalp68qymm6yjICT7qJ7Mz6luMwvJP7JBDEO5zADofHLQxKb1ZLP9ot22w5JyEY4hj8xLiIkWy5EPOlaSjbTRqDVxPVHFxsLxV5MOi0srByG6etNVLY0g3YBeZ9QzbbvC2xe21LXuyHTbGmN02ez212ndtdPX3usmd1nrksKrgVYkjX7ajNBC7BQil4xoH0E1MU2tZ/VvlruhEJqVVoHZWMrK+8ua5Izo0VG59APamVl0Pebd8ufJGBJkLRpmZoPt/Zsl2nUiU4bZad3pDVRErFSAhgvUCDZ6KPw6h45AVAxl9yG7hMAmY7yoEmmz6MH+YNmFDpIeYhZl3f4cD21XD6sUIFsEnWgqHTWqVjMGgFtsAawoQPvA8qAo0SShHJIIzEO8G2RGTvonnqDc26v7qVi7gSWSENb6J8jgQbsTUQadnAofHQOoTEGJs0MgBlY+zoHWwEyOlW1+66HxygloV93ysLvqpAUlext9g6cYWoTLCQz1mrJXcG75+jB3O14GWTH8r++lGpHO+VpB+eYPdQpQc//q1x38xMkFyg6FsEwRo/nwF+7JF8wmtW8Nel9GanK/eYe+ikh71zZQDgcAnysc5YoqGP4h/4pbo83Fw0J8QRhDRElrBY42JkWVqqmsQAAmRcRjhT/IAVsFCCdTAtI80vx2CVPSihUsSvuvBFXBzYdAkhZCiRF4RIKcAsNLg3mewiKpH/kze03k1L+K0YdThO3o92mNJPOheNcda7D02qQwBwRJ/YdGGk3GA3FB4X+ZLT5TcLNGVum1uL7kSmuOkkq80Iv9y3Gn1Ah6WCCDG1XW+leKhb22kTIl1VtU7GHadcJ2WabQwBVZUgNV58qgEvxVDrEDZcrPR5WQhqDvKn0LJWUBwyK4DyXKQ35pQw+XVKkSv6FhItRFa0i0NJ/UrHhKndhF5EpmZ5ie2YlMaShWgsIkcIJa+nHSIvOEqb6CS9LzcvGaTqvyr0JiFscbjSazS1QaMlft7Y3eevgWNcVO259/8enZ6fn1ZqQyuEHPrlhg5+a4D3q2K9/o0QLPbKseQoyOWfKx6XZZ4JRnT6PfDymnpDSzIEML/wPqyOyKe/bJrdvj8dPVlR6XnLTWjzHvAiHDE7PX09mZHf4cZ8tEX5IxpQtYTaM079A0ZYjmUxxVedYt9FVOnJZXL4mjToUjcMITIXwuRsgRUZoLj/iS9+KAUHDHwaKFwFVW3YTCJV4gNiJWszCyjLhz1o815aPRcDid5hylsHRaDZD0nphzYygqvVvaQjQYFMIZKHoQB5JRYRJTQLYBmM0Xo8n46GB8tH93evXa2JVi9/zl083qm/PFdDQ+1L9QROCR9YX2xxxaSWINevJKGQ0FeN8yaGGXjPENjM3KRJxIZh2w3fjC0cqUYW1ps0WljPIZ1dHLAJhBin/MpZ1g+Rlk8ARv1mTWz4ChHeDGlAmgUKYKVkRrbnlvSppvCBpJkEtOcaeeHAwPT3g3OaYCoVSvQS5ihFpK9tEHH81mVyvbdy7Y0Zmr24eHh5CiUMdnT+swFKkW2LP81HaS9AzbtuhFwyjZEDlb2TKB6bXVHxOF5dh0egbFXu/Hn3z22e9/7mjqzd/+u+3zhRUUHBANW48fHBt58yvfGvts7d96tLj2tWNZRRSZbM2EZamyEX75Lf9XpUONaFYOdIshMWuSB6z+xc0Z8L8puHF+drmh+mg9qZfis+AMAFajetprjGM5xkmtJLwhbDNO00dQABr5gVYAA06pIoLcyQG9PLs4fo2L13zhdAYDJjVX54ekBiKp0c0pvGkIQFzTYtkpiNiFFa1VZelaUnNyLg4FvzDZ4RIAxTvB/vr61cuXy/nConnLwTEMmnzx+VMNgKuhNgCnFT2SZTczUql9mzuxrKtBTG331m57vL5+7QuPufnq8uKcOy7u4JsRXaLftxXPnPxy2llDFGZUhMHgxgP0GvCo+1GvIjydCeC4d+tBHKkxvJpdTQ4mXzx6/sOP/7Qz7J69vvqFX3zfJlekaMiI+Y2JmSJKjybOnJSimVlXWsUOcRQUf+aItPWVWFjAIA0J6duRHpS7VDhFMh2lIqBZGmDUI3Vn3pMzHhKpFQyC7UNdCapGEaPI0QiuonCFVzyAGmKHxetK7DRMVY29qP12DohVyKi3z3HOomgLtKjIqZvkknRiVyaRSFWb0MiQoHkJAo2Yk6BBBYaS+KBao9oVHO9aJOsJ0KQmSksGIDLi7RKqoqSRNTgHbBV10NePxIZvNhlFwq6Aa44KpebTc8dRKgUOu4FAErIuoJdN1Nqj/hx1u60rA9zu2lwfFX2StaY2YMDdTtROnppjCl19M1DhV/USIyE8U54Q3NcqYoqr4amXlC+Gj5Ai8l/jo2mk1sLSQjWjIhpBWCdM54vcaBGWTSp8tHMUErP6KI/yIJS0RmWiqJuR8BEcPo09bMmcVloEKopAhIYrNobuNP6E6e4N1inxwTqkSPJQLJXIskOdwU1CEC0fQqtqv+IkgZCKDUscqCpSuZ6jtDT1I0MxvNR7qiO1Jj8AbnSgMIesk7YQqDLsKlbyIOmqHGHqkeZDG4h/imQB6FvShyMkDit4lXGQy8cqUfNS35KoKWm+72JV3EoTdhbofyUPKnWFig0igdJEepNerq6gV1k3CULE3VWfA7A4tTCtHJIoefkepAMmv7kqsCIpm5fmvT59eUt+iZ6PVW1F3C+/e6rSJEo2+8u5ZX50W+UgjouxYXQBuwfSA1iwqFOYKkPl0FEIRmnP38qs6/BJ5EvqS16xFjT1WoQP1EK+8g5WlW8VKrjLqJSUppYK52COYMFqlyg/WlcRCzqgRA1rOSfPvfu5ewKC1hOTr7v6CEJNfg0YbTeZjPb5oIu/lxcV3mnNYlCxDI27p67X1BhJ3ptNSXWrclOj8gWJit+zkq613d/nJ31h+lUDHtk0PpddpU0Xz7UuR7gzVpLU9Aee+gxAtc8n7g8YWn4mY9m1Je6wUmcrOhqSNqkl66bA4mOdJXLddS9rXrPmi2qlD7puzRo1J5ImDB3cNL6IAyVJu48YiNzfPNTxOFqn6j7FLHuhDjuty0tGzNoQA23TVr0Uk6amaF0lyzwrDiVHMfQ3kRrJpmaGCJLs+pKFue0MmSSI8CG30LOEYK0BJ11j7yM2U5uyJQEY2eQZz/AIm+3Bwf6L51bFTQ8PvvG3fvu//MZP9V++eGa9IEv/OJMDtkty5Gqp7wTddqaAq9kJNarde25YFu6WMUVnzEcCkWlXgzkflMtzdqnRKCceWLyQDClOMQyQoZbCRnFkIFxeLbc6ZKezbl7j9tNTZtnpnQfvnjEg6sjsHBThlKKFuUNrVfi5OgrvRJ1rWEyAAgaNRpCrHzFxY/gmVkT660q9p90HBs7w4JehBmoZXyoIYORhfQBPlETyF+CqJ0l3w71YqaP+KRz9Acm5muQrM2G2xanRjKYbOmda3vYvZUzNEQrhARmrsQAO2m71I490hXoWo6Z9OybpPHyhPzLmmf/h/R/MMww+/v73Hn3nO6vjkwcb20ca8zvuOQ6m7JGq/1YWAbbtmZ0y6OWN32ITbdnNCTdkvFp48cIaapNBRWVg+0wK16LnIhOcM2AIk8dKVHURUgHajDE3vDOU1DxbzIEI3VwhW/41ZbsJDl2LaFUxmmLQtcSfhJOz4xEOD44tYtdm01Z6nfnVMjwSmbL9s+//y+X1E2ZgDmN7R7eiRK2vTw5v9QYT2PTbt1frkQadMXcqSq3aD5Hrz6W+vbO5l7XbpdmlbVQdau+zxfX509Pf+cEPfvzUym1rRo9Ojm6TnWcvv7hlb9rjOzmymldhrK/2NtqwPtvDaXMxsz3ZbMY8b6EtF/uoNTwrNHgEKGyhHz7USopDHTaIT62PjLqBLL6JCA1ynIZAk3SQE4u7C1PgUwXR/Gm2ihvftKPPjPbZQsMnbpG7xTIBQubLKIwaSq1NU7Cvs7Fp7QiZXlj1b1ZHNfr7ZNXOEawEn1RmoOhymAsxRwOTfpEQxW+LizOu1b29vT0Vtl3dFbfds8tQZZ9+pdBQkBQ81ewHSkTLZrW8WnyIQXl605Wwuk1vDVaz19bVfWeM9YYvsyVnmC3nY0PZtK5X1CSj7WXUHjxfLiaZo1m02MwzwwR+pJp0ZqrM5OAJvuTmnUhbupSccySbikNA8yV04ByJFT+XFTiZDDPp0x8x6R9O9v/sx79zNTP32799cGvUHVvnYYVJ5gD1soP2eLhnxTTem04v49CY8ukfuIGutrNjpewNL3NAbabddBPIaLX3PUPr4d65tQn7B7c4BEE3qIReBibPafzcAw05Y0HekQ5PqbKQMfHSi7gb6kgR1kmZG3LnJ/Wd1QS+9TOv3rQspU5FZJiYRT4ODj85Pp47oYI5DGP1jVh9rejZi6ZApuVGUQ7aMk1bKD09ISJkZj7Aey8i88JV8AJBzcI2HZx/KrdQCOas5X7sG4LM7fWt7eq+JhgpLXHBDIKSUgedzjkc3Lt375NHH2dKZLXeu3a03qmdlNoOuL2+zQHhOqdJvGyvj3udZ+3WrS1HgM2ddud1Z3u06b0ath52rl+3lqOusc32XFfSWj3fsx+rbUHbq9n1MUJYewPP0KuEVlpjChmaFjoQRucQsggSHIPs7orcKGqnMlK5ktPLxUiS2Evo0pheo2piMiO1Nu+birruflJljs01LQ/rBdAb0JbXQKTmNUPYDDXATXMLoCjNuLkWFuH0YKQIIuhHknNiYiD4xLCYysiez7LIxjvyAYNOcr1+SEtJptW5ILpmEkkdZKuiUSLKYcpSgkEm8lfSCKV0mjUEUoOZbWuYDobFok01urd6r0KbCJDUKwCmq1FJ0/diCJpBMEKlvNVV470UKToPVVVuUgdO0HD3W3chdb6vk7UqMLfmexMp75Ks3vHqf4Dkswb56EsINxCrUqOGifYmeT1UyqQPVfQ6zXUT7eb9q78pf73nrlBV6IBJokp4k/rm98vUoVSuRM5j4v+lq/m4+wS8PoGSzNGF9ElXTtzaXGU4iEKIvuVpBvn0ihFu6oAk0ullcj9U5yejLrQ3iTMkKCR2HFslKLUTLjWQaMqhYBHlqgmjZD2TqxiaZK70Idfu31fKUKhnqwGZRtzUFpz2uJRzhihRl5s63BU6WVAUgIz/ZKgZ5YI6Ck/SV+bbtcL0+RpUDfWcx6L/DV8qLJQoC5Q41qVBHIECJ0W0a1C8MEWwDlWg59FonIL4miUpbEAu29dANbUhZtLyV8n8ZbZuMJI3284J2RprpFFm+UbEp3EpSmx7RXM0SlVica+BleaCdiE4I1As9yGY75n/81GOPsHDyEb5g3ZmQhMnbbO0EXWhaMgW60KN90o7RSHdWSzBItiRMAKICQS+Bg2hoBOHxNYx+EdcoHIM20aJdCgdZwyl9Q3VM75LRHpczKUHB/GvaNvuQjPo9o9PjukNVNNNZzGexLZ6dvoqq+Bifrle2iCc9wRLWAQEwyhRGKISN7ypasgvIFxbvBKSNI1f7rFJKRwM4oAVCsCPZjBfLm09/vL0fOZ0pU53Nnvd3+4Xv7eeP/nig49+9N43HjjTEtYcCfQcqsdAKdqYwVvKWyyF8SLsqsJknvIhREQezigVR0j2XbGmWXC+IMMgNQtdr+5RVnJFIAdwjRF3bb6qsWo5/OgBcxWYtIWIN6QMApihMRljgw1dzQdlxSqlgWWraXaitDdsoV2gi/T+B2g4oZ6rSClK85VBfdU0IrtrUI55OU9GJ/Zzd8qXI764U52dXswWZ7e4jHOEWMzpGZl1NVqs8xNQxkhFqQLOjc7E0hlu5dtq4hxB02RgoJo5DFAHeUtEANiMG1ukcNRQVZaC+59uCMIhYYgcm5fftGL25ioPWNi+cqwCVh01yYt8xaISNAADGUsYStjMCiH5Rscp1oAk/V2GItqt/WjU+eJq9sknHyE+LXAyYgShdjtsazs5dNRupIET9NYETwoGzexRxZjmTGDKH0p1aQjRWvSn8UAOPTClXdkXV588+vyPv//7MZH3FvvDPZRbLM+t3+73RrdO1FlyVyhCy/p7W91ZinB1mep0dsCrs9O+TWMmB6hEQwxp0uxD8HSf2ht0QzqSnCgKUTVd/jhpj1nNZEgWvVXnXkQRX4jqT8VEm10Znm3td8w0ce1kcYfTAg5W5LPmD3JyShXsGIkEtsLS1vgZioYDyQB1GJ5NR63q5dEfdgzOHbixNyqv51gc4xtG2JKBtg1VdoIKm5SjTrWvlGJ35Sk1GA5xSzsoKek1NZupBpozu4xX1gr++tk4347BrX42p0Z6XYBxuaQpqgYYDuJRyeUSIiMaqhFBhrh1DkA223kjbNNIJU4jIl1xXRxfw9ugeY67FUNaDmYwGkhr4AGjPfYtJbfM+Pzi4sOPPrHWazKaHB4dHOyNOEyQuOk1zJrphWrnNDsGWaygJPoMd5Nvd+8/ePL4sd1ddRlk6v7BxB7IGgSBr+tYaC867Cw9VoQMO6pAoQ0KQTV6XrSlmJbEMRKtHkOe+ZDLDzr6TUBo2oRqignbvaVBVjedsHxIBdS907FQ4tXpqd0AUEC24X5ZZkVEVktntBWgeCYSuMlBcv93wINJWn61zeSDZSRpsAt/pfMphBOYzi7wA01oaRtBPWf22SUucNMFNBwCTlK7o/ido1uPHz2yXnhvevru+IQNqLUa86LTY09t2msP8812bBLVLtj03c7Qntia72AzXhnnO2LMALc15+XTW0yuF2urvHvtef9638ZZDtqYZZup0Lbor1XpZz0qCfiaFLTSg2kPoiiq/zQVzpuRYiGl4gbbaCcpppsvVOt8aPq+0ES5gEy70k459rBsMVmS7Soe6IITJYTQCAViw0WmsEX4NVsyFIGbWvUoTSDW10wrBQ95hHyQ9iMGnDMGTvZBND2pT7mndRPEKZpkkcwpnXoVBEiTVQHJY7WdqjR4pYrLIBuCBHrQ1L4E50txQxW+6FlfC4OgEOzyK293DVLpo3Cmg4nfQcnbZAg7nz2E/OK++bspS6AUuPzU85tbCJUSV5SE5voyTpjqJiC/DW2ayFXWShgQN0CSVmFCDmnjEVE5FFXzLcglSm6Vrp7fIJAyA7yDWL+iNsS9SZakX70aiAn58umr32+e61SBXZQqAmGtnUXnCydHl21dvw2VTpcZrAZyYbWweHv4TP2RYGDpT4nLSEzMcXNVXRXsFEXqKga4Ydmq95QiEcKGINQGqTRR/otacmfwuOH48KirqfuKH0DdJw1B3UlBEGRROQZZrJpXAUU8eegY9J+11YPQjMHCNJqSeP4PnqZEMV5pNrwyMmgGEXAMK4KOKrPBzLiZT2a0YXvQ5WS8RN0hskMcrSj6X9sBSVWRuDxlFlt/A4gkcvFfGTUydKBZUn4o0+OJ6W9lM9+ftmFCXCB3oXIWioyzcQdLYtFRf2Ckwu3YdKT+3xrieEIrtH4hMwbDl1UdwZIyUx0dLR5VKvfwDxPlA/vGjQic7HFhFiXfaxCCkL7HAd+USMN5wVYPY0u0qkSzvogbIRBZpuHT6EoUDLP9tn4uBQOOiYscw/IGUDbNNkFsJ7yLu8aV6+1LuZjC5DfKdZe6eDV/8vr0k077xChjOHZG2DFNPf7x4QM1hRFTTanrwUuafBo703ANLYSlYtLkY8xDJejwASBhM/jBxpkwzcpiNc6yd3J81B33fvzhZ7JYz+Fs2kfN6PvX//pf/Otf+tYv3bo3ZIhN1UdHbyk4OjBS1RgLRl6wTuiIR+AUKRaqRfuHRMROvpniN5daiYqm1T7kE1kZZSRqmwLUUGoHIVUDTtigftyKkQSUnA8JfFEm8g9K7J1vG+J0h69YJK0OLpcUhlxjm+hBCo1bg5kxlgFQtjdJvditIvnceD0mV39gQ58iNokU5RHR3dtbb9m5zPNP9w6GnZf6FEanF0baH3z/8/ff/sn19oIyqbNvdCsThcO9i/blS/XKUoSpZO3JkXN7+wcvX59m+j6SGqvnn1QOB+CGJ19VFsKwMWWxYMqWHrM6r7TsFJjM9w+ePvJ8DUVC1+sDX1s132WXm5Sre94UKLXgU8rmEQMBCNgZ5Wl/f2zYsT/JLNPJwYk+XwuK3AAz1MIqVIH16csXisxGu5mdDAZ2+38xukVts5Q2M/PQ7PeunKfbixf1gtjY2EpHk6N5r60UQgECwvbhExist1NjjahJdLurA0dgL9vnjMudrT2plouLdWc8urqafvLDT/f4n98+yoYtOYXdWtXNqLd48dpmmrOcsLhpx0vc8t/u3ECB6oMIGZjrSRujVzT7tQbD9KCFRXW00IIjcK1D1kaQTgGrK6LjpuEgaepfe49qQvWhzNvnxogojcocBCJ6xDlh1vjxWXA/De0z1QAC6jGlKw2qhH5W5kSRZvAjW0YmazaX/PFn9z86++L7P/xg30LRA7kg9j1LcdIE0tvghO7Xf+J9TTEVrqb72Rte1q6oCMK2UfIMqIJO5EE4pWJ4pXdHnBNdYZxeTDw+oeC2+wzWkFRKfKQZSoQ/Y1sRJ6MenDEnSGHObrNt37K9E9mgnfqDAlUdttHhgEjTwoelXdfJUM6dwLfmaRvWgSjGtrzMtrkSff75F48eP75z/+6Dhw9ZN959522zwhJX7vGMyHR62LI1n87Pzl6rEfVBqyeOXj59rsFttq8uLq5OeneMb/CksvB6CUV6L7MtQDZuhlfZXJUHedRAqqaKnCYUy8zx8VHRKjpfChEZUvHQSN5pSWll+aJsnlG7CUyVqqmmC0bDpKw44AcILdRmSjHKRJ+z8JxJYrMldTIoifys9bdiGtukrm6yDjtVcxNHXo9AVnXuhQS4hVaw1RJLtBpcIS3nU7kaska6W/HFL+psMPnF7fV7Ad4UBbeEo9JCDSbXBP3py9XpGfEzOO3dvfXpPp+H6x8t00Gdje2ivLk0VbPX+mxMye9+QiyZa6PbD7ufOQVgtXV2kJatLRs1OnTPKGGIrK3uBeG+bV1GHd7uR4MNRfELNSMSLR52RGlmu8PHGFJBUj0pnM/iekS3aCPpAVIwwim2IVIsewspqIoOTfwzuCKgdZc40kKVZ6ZBIoTAS86JWOJRpxRtI5xNluZrZumzg084v4RchvG+lDCNO7MWEOmbGsywMZ79NYrON4AsW5LQIEcmeNfwniqk+uSLMRREe0r2IXp+UjgxISBZpazaMGBz6p7kUCKDqEypXCaxYFWHKoRC8e1UqvQdgRUKhHJ8DaqcwVt4NDGH1xsEpkABIKIyxAqGjGFaacXNPR8LVNERpvUlX+uhbP+BkJDKNuGpDPcmchUkgfnSpMuDV1+CZN5yVQQ3fWva0u7KUwEOIowQbz5UYL7l4U1o5MFN0gbi7h11m0wDL38V683DmzS7hx30vxj8l94DNUyWC9YoHpDUPplDrW05ibpl01FYn0Lf1BkGT6KSDFTPpFZ1BSKyNkyWtwaLBtUUsp5AaXJBPlmE9bQKeaXZl1t/xG2+3LSZgPdaPwmut6CKe7OOxtUUobIo4BWWfPIhnMt4WC2wMSUXdkpRs2vV8ReMxNZDZvo01Y6tiocC3ieKOKaXYyKU3kNvHnguri3eS/pwTxCrQ1IRBw50fdGi8gVs2oF5CCBIZ58AQ4C08OSgS4zxIL1omEFpi/RIY4xhsBHZ2VA4Iig9aIx0ZeZPJ52ZGB0J9EQLQIZ6fVKGZ6EzBNWnOIGMItccmjNMsCV2yqrBce8zKrHc2Qbm0bS69rVIPRP2+uXBkNqhGPHEhxLeUQw4W2O3XWdhMyTZyyMWESAasP3zKBaWT3Dfp5VGvhEqa5tyOsWpP7Xl++XF97/3p7/+V3/h6OjwajofT/ayrZ190HiAE3wZvWU0EsJSL1KQUBLM4jFUahhDJVNjpFJwnatk6SViKBbfMICzEEVp2L1/sPfhR49RyEJifjN6L26k6PaEA9K4Tlmu1duRtAObsXL2jfiO0Iv0jeSsGkkzaKoimBWpw3Ph012sCKdCTS2jQb74FBYL6XxVCkFJI73weo4UzlPeMUN+/BNfy0j6IkTECKqnopg11QUDJushPPHbMsu1TTWof5xBcNvaMptL6j+SVyA0eBVGNyHBoNPes7cPAkZLXC+v6P8ZAi1maTvZatDGM7S/5ZmdE+eOeDo725sc7h8cX14+57XF2AlucHL0cKqe01c8g9VATP9MbkUPsCMYigL4r3p4uJU9PpT0Jc2BPhYypDUJyj3MGnqFKv7ykcRIgoYBGlpVeb5SxoBQ4HSWclm9/fZ7/8P/5e/TXEZ9hoP4uZmBs/jSCgY+zDqXNARmwN7k0RePHXGQfcSx0vX1u++9a8n4wWSymC66wwk/yHZnbA0mLqUNuaLv0KH1lDZEtLGB8hstL2frZU6W4JnucCcjZOtRHDpi4BQzQ5YwaP2WnC4vprM7BwfT+cVkOVKD1zYQteXQdHW+eb3tjgYOURpqyHFp00UCWAOAUFLrKgFeuixKpOlVX613rhUCGclmzpMgQkBZh/QQLnzFj8BjIEFJY0pyPz7drJ6aWBglfAFqxg6RlxEI1BR2EP42+DEZFtiwVHoGfKj5o2H4j4I9tpfU9fbVCydb6bB51/WubErZ6S3npzlaIe5VvE97t27d1RxiUmHQobdGMQmAIm3wj6irzMIN+asvuYkjLlGV1gEDtF3O7fqVESbfM8YNJYA11SHSR1PWamRs6nOp1OhhC06bBTNK2KRhZjooek3UIPoWVUN0rBhxDQsoRaHJ/wCJMKBgkSMmYyMLo8TRt7gvEpWvz77ICoiUcb4/Gc5nV7gNhjaH0GXy8Dk/P1Nq+yMrgKFa9rnCbx3yom3vIoaMs6vZ8aFDzdvcSy1Dd36xcyiaGQZ8NuKbysjTVM6NtAlCVbk1oZXJipqjhnqkeK4Uww96ahWeQth6yGM1JnIp3beWGC7Q6aUGMFuaJgJGvILBOXY0hvfecLh3cDgcO2su28ikuzVQEa8gYzNAFTAP9RJBjcTVondKJgaDg94qDTso4rFGOdCKVFgkV/gxwwoRKCT6pvnS4Wmzk5PDJAA6pajEokaTji5sc4gWk09v1Gk9Wa++6G3vmKNjhiAz7eahoubGEXrQPo6d9zaHlnks4tcIEEI7+EdZc8KCummvxmlJmqXeezt2ULzpwPT+EbKQDWa059A2ZVG8QrmojUcFk4FNcyPsRukxk021oagxtA3UVjRRAdXOA6w4TnGImwwMTCzohgxsY5jDfQqNR/Xgyc4/Y3Qx1QA91MZbnik+sEnucSiIUuHS5MGWXlyVAQ+EUxcew+vGqCojXUjIns8KiBJVFvUe8G5BUZ0FeP6DUYXR9NNcXTWj13wFDUmikQCWwimC8+zUg15ZMVJxaJmVZn68psGnfOLvGLYphiy1PfpEFidHmcFZ2jZ3Ad7SHIGVUQ+GYW5MBaI3V+DdPH/523x+8+HmNYVyhafqCg08C87vm+jNx4IbVHexpblBuorbpChIpSvvUu1+2rUnd2t9y7s9H9xT+htYIcUN4jtcvpJ/IZK4b+IEiPhQ3YFH7fJWz3nAf+lqogVAQQJH1a7eTnpe9aL3rbYGrmrUq5diltSuNFV1AVqvaaF5DgcnJsyTdodJMonwDJnyJc3dYybf7U6dcI3N5czgRpYVbqFfoCRN/eU5uXkJpLxVOwrAStgUHXNUXpVHTEQy0UhzCQeaYkR0Gu9qk+FL5gV8h/n5+8SSkb4cDEFhR7pC3upoRuoCMZ346RRiIVtwKUHmoY6kY5o7Qk2Pqy12u1eXl0koKFSx88yc0IyFSVeHGvpv04jTKchxuI1uXbtODEdZi1yXaM2mb/jaAXog6dhyyi3/gGzXkwYjznCk37rOEjLsP5lQOs0p6+RSJF2vZLQSu8vF3elR9kVOAzLASztXDFnT+os+qRdlpr2sl/fNb1z3XtPlHe0DHQ0vMjFERHigIwFCedZ5hisSLNUZ5TthGi65QUpQvg/2FoOzuADNsu+ETZCIPNPX5o2Hg4Pzc7tJWhBsHmLFL5oW2yj66hkcpYOfuwqI6DcEWa81eJWCbGqo4si5ep7goAKyGQrhECtB25mO1gjllSdKdiMlajZoOAgD830OY3Y//+yzF88uHjw8tgDDZP3l2aWp8639fMjQweeipDg4aPNWitZ9XLQKL+KnHYuHR/EL+WlHkVkjtjKAQSMopf71ZcpRHFh0JwN3jBw5mvDqSFBIbkkXCoaAyVOOdKQI3eiX2cs/X8JU1xcXr2bLi6vFfDAcb65nmIoCz31eueh3++PD8TAb6YCa3TykyV8qSFDyjUj2LK/oxCQ9hdjZDUw0NXmCyZGQcpbj2F69PH358mw+v7BNz2L2AmYoqEw7VSkA06bCRLQcDSR+Cx2qXxBQgtQirgyPiVllI150uiqtWmksRR7ijph4DOhhN8h+ia3wMF5X4wrQXN2L5rcJqbyqgFU6vVjR9nrs5NvDscYTT4Bq4ZZpUqpo5iiiGebgpGzp2Hp5+roAtgeT83v37/2d/+pvXVydDyeHWZkLW/as7PtJaCxpgkbQVF5UKmawsFQBagRjDxWEu3ZkN98qfjL5v2mfKkrG6ZT67vLk/jt33nr/4Wxx8fSlzTsP+0e37779vQ9/+PEXP3j61Nhr/vW3v3779l5vO8oWNEZ5aikMLlOagl7cwiII4+WQtu8o6LRndAk7YUZtZ0e6yAJh0X1jF0/jCH1TVyF+aBYtn7o03HMuRFR9JCy6gKDG1Adlgz8k7Ro3iwyaFdS22t83SLF6MJsIMlHT/9DSTgkz2pETbI9vrffCrIcWFh3u7zs1vHs0eO/du58/ufP55x8TQ/cf3L734M6rl6/MVRFFaUPpTTRqqOUh6niDbOEMW/LAh6Ac4S007/mzKqHGumloUCmNCiRWiLRixcwwoAyd2pSyb8bbtYNpKWSYnHh0vIOp73QNRDhZBGYarxzW+yEqrgv/2SLUCB6Z3dKow62uUKzTG3Uff/H4cnpuTsUZ0r/yrV8+PDyg6Gf6KHMLOeeQRxmNxXp6nRGRnmKpTYJjdmXkrFKQ/8GDW8iQltVkYIhiNkeFKrbSdOeT/RMoBrc0pGTvMcwQiwfZWG3IwC1jKpUiESzJEEUiQpSslEBIyx3i+QeQOGk2qUQAS+YEsFRRczFMtZxOb2//SG/Jd3bc/0YmxzrP04pFIIMlSPYhiStohTxNLrgG+HQeIjTZ7jTDIIH2sGUyTiKL4yHD11i/mB2xMn267qWrbe2v9x9yzl8BZMQVZ12IhYEBTVtQGF1eWTCywsPqmltq3766Wf/Cj4sLT3fa3+7NWmft7XsU+8HwMa9YG+iY+nToQq+zssCvhLIzNRxJ7nQUNibUhgONRSFm8SK0/WAM92E9JccffqNgp4hVZjObMXZrYsEO7WKooZRlZ6oiuQCUdkaypr26Y4B/3f8UIXyMec/2XpNJMbP6UIGJHctj9PuI0TTLLP3XaLRZfRlaaR328bEg+5ApB1HLHwERPVKdQ1mY43naM2Yx8pZROJ3EQDCdrVZs5jiLwZRWpVtiS+LoMYnlXptHZHhpRPfI2u+cnmDrFNOXNA3Cn8BxKpyelWgsSVRtVdyyTIWjUCorh8xPYhgDLVNh6SxSuXHVqFTFHcWZYjechCgQFjX6WGjrHlJHdPO6xDQWsBHKxdr690RIWf00/FfPf+5WUJoYTczm2X33BfAmpwBJIFDCRPCQexpNLjmF5XZxmggJrhiFtLdyQ0xsVwOleX5zf5OuCZEuDN3kEPgJdks0V/18+byL5sOXTxXvP3pLXJDT9hAXVtiwIKeZJ6Ap4w7k7qeKjc5YRdxKC0y4PNCSXsrgG+z8lfJUeBXIRGtoovbqe3otf6JkFIsxEyFQ8hnAXAW0nvJSgJrQyvJNFrv6kfeuOhIphYn01yjDjpm4hYQwpupohsERlppYrl1MYlV42nNaqNZGUY7er+FKrbVGbY2NyDeYRo1O+yNwN4zeUa1B0I7ZxdOZAM5z2mghqMuN74HhfCMaaLUwEF97HZAMxHxykTRTiSBJGzlOZeUNWsJdc6Lc5+K9uM7uE8FMUr2X3b1nhnwKZPzACquF61m1yRAik7Zkv5gpPagxhIsMrGLCpLpd3rqwN6uuCGQsk5N2mecwumjRbKh3lCYTDiJYCRaP29jgEDi0ivFGwWMALkNXCmIzdUvtRo6UmnpO5Pb2s88+IZWkKh+r7LUKTYgispwh5mlv36E4h/CcX80ury7sO8EEBN8m6q6mo0JiA9mE9gI9KT624iFl2Baib1oHe4cXU24MmaDViaOAhvn0ixfPXjybHOx3OneOb925PL9IJwWcAqWywnxhrFS7PMIVajwv+Vi8k3fU9VdpRA51wim55TWM5KpnFR9TGTwVFVQfk0lFJPy1LYWoXiBQKkJl10BNniLzWe+9vLh8+uLVsD/58fd+cHF5SZBPDg5ePju1Khoz3rt/33lDBDflEMDg3Vxh/rBt07ZuClJEjykIATGfgeXk29/5q7N/8/vUflqLRYc/+MF3R6P+r/7Kz0+nV5YMWOnIZRnnJyV8ozWUup0hbRaPOHzNUCpjOLWCckUSuKsl4+HysNDetKBQLWgQ8WmnaUdKiCkwDXy8hRwNuilCir/715SoAiqkeW8AFChR2dhy4jg9gu4T9jC2GYxHVvBP4vpCtbLrUSbfsB9D1OePntgmOCy+XvIaGk32LJBIlUU+aoq0RRPr9EC9H9waCYCaxHWABPNgoXXpbtM7R6XQKeaY5Y4JgVAilbg9PX++eOfhw/ff5lX5ydNPPn75fHT/nUV7r31yNFz3r87nUx5BV+3jo2z1dNDazz7Drm1W76BHGkAJNySKt0uqLbVKCYtNmzghOIzOzQCktjMjhIzKmNXx4UacRvoJoK9rXvEtpoEXpbX2aszhYFDkFDoCqDbUeHbeSH3Z0zaOjlq2jdYOTm5fvj5rTdc97tTXHW121Bq/943bByf7o+HR7Vv78WG0z0F/cnQ4+cGPf/DZ55+gj5X3mIQBwOQGykQCpHZTg6ljQalu/3fVG3SrOaYA+QiNfC6ni5zbRexM9rMrg81t4Q5IJmPT0ggrO4FxXMFWSgMSH36aDSd+w9TL6ZQdJO2R/zf+Vf04ReHTFqGTW+pVKy/qJVuGFazNbC+72fJKUyDiXr56ZR6ArJ7sD+wEen6+mYz2l4srqeJPCimu/IvZZDJx5MV0OjPDNjYpGrGHQ3MUuvVj4+GIBmtEc3r2ml7MiTHZhxKR1YRfylCECk6hQv2oaVxAvqWmEkL8ooAy4U6v4CeugPq6a1PCUDXlVNvh4YyOdrWgOtI1o4PkkUv6Agvib5/APEMskz6LVbufzUmRmMEtrUM+sgmc0hOSfURc6pYUln3+Co2gmJy8pfvSVhlxjSdpnu2lLoR2V8NepMlsgK6NyIDDcDhJyyIy0lFXo1Pk1GsVMUfIszWZau7M1k8vl0eb6xNNotOKmTVW4+1soFrsgd5/zEi1vh4Yrtv384D/Gr9/db/WTHidxhPOzI0OvyFJ22n3aMBRyPqTUv89yJOBLDYO7Um3oejFolKGcSzKTu1GN8AzEe8Zg1X11XEuSo12NchO7RYtAGjoBagCp2fxkN5tbSF7KsRnZJMBAhCV0tnRgHJtlg5i8QiFSdo7LGKaw/XhmyRNRfgXTStnzFFjSMZ0OmnqcIdd2IDNjejIDD/rURXCAJc2o0Xo7kwXw5uZSbmz8YYp/3gUscSjQoiGFq7QhiRMU61qd+cIJ+toMuGH0Etq2lSZUZIWhd3B2CVKMQOx/opdkkK2YbbQYWPBhnKKLnmInvjJrq6wWnDZvX7lR9BNpK+ENskrICDTOzdXwCRFAnPlp8DKoH534TuYidhUURKlAX+ZWZ44yD2UDnqywUUVBHbzL1jnz+7d0q3eCexd+iYbLx5yZ630sfb5ToygUvna1Tjh/6FLvgFdLabSgeA9lArzFSaRcvn2lat5FevmQ3YL5sWuF8MSGfbdXDv0ik4FdvUgyHUfqXdjwZy6nbIXGmnHsYLIDhw/gGjoNyAC8k3GuwpFsZvPYqbcWzPLuD02qpv4EqWAtFf54OzsC9bIjdLIkiVwyVxEYkoroJYVWRIQ7owia9ldw5SRUtG2Mz7Xn0xP5NXrvPJVvxiaaKNRdqPfp0UJoSGTaMBmdBEjp++2nPbMpC3ftLJCN2yg5WV5buFQjSQUkarpj0EjfgkncIWHevSQyChNO2QJjXQyJEU1ySJp9dFENSEUpUH/V4K4AeGe6g6tq4AyArw3fEyJM1DneKqyLCdTLsI1SKuukFR/KqmTEx9tsqXS3ZAMAqBZGxknWsMG5WUUpH0ySdhHgGfPajXjW2k+YG7nCIrpsycvLs8vj45PMEP5XABJdzIPybpUOn5rfXR8/M57bys26f/hBx+q6RjpCLcGd7mubq9nz1aLM1IQGYx2YsVENs7ShNfaNovOwkytjsf2IzLIUZLQWQWFVuuVXYm+9Uu/cnZ6ylznK+7vjJ6nxOmdmstk8DOFC60QXjj2U72+h3riAAkVbBYiJCxVlL4BxdSwsJ4zCw3ZNiftwcl2bLfgyD9UI7rBijCWrHYecNqAlOnKQ23cXBjvspdD5bp856PvPX55emb65Ozi8vRHHyCrQlY9gdW9dXyXYsX4wu61KwQ4gAX/QA3Q/AY5F2qgbLp0p+EsZ8NB6/h4/+HDe5fT1xjetkxY+uJqbvFfti5pWyjADXi+vzexgxMOiV6IO9KG09QUiOeDvc3TNEMMdarJJMeGMkK0JP1XEFofC2/1zhoBko487RI6vGwx03mImvkJfNVgHQq/uZryvHltHqqc2heWSAu+c+d2mXepFvYs12NlZI4JMDYSrePTM7eh6qvXrx89+UIBNBPbUh0cHZ2dv8YktvbSA4tefVbaMjuh8mRH7BhWw4+uTITpbPXVNmGxYQW93+43rZn9e7B15J4oKYLsOrNV5+TubcTjIvfZj7+7vr7aux537nXW4+MMiDfz25M73SwZXZr1Oh4Nsp/S0JwCT7l1v3tsysJEo6kxqtHA4cRgUkezTyWu3nmMwCNz+hF/Bi3QYs9Lw1EHeDVEpHBRLDarHENmITyGsf5X2zT2QMfYTKwUbHZBSJdAA8i+QXFiLs6NTpia4tnkII3tZjS/ohGyamtVC/rBwRGPv65zooZ7nOo56VNkVu2Bw4O1FM4U+v0c9NG7hAg8YymUrbpDK4wjwx2XCoXtrslHnidaOs0URK3wq1nN7yzMqXY+4WkzmthgNEuDdi1UUWsIxLWN3l4ThFx0Xm5tm7OdyMZ6GbuB8dSKY8K6PTnilqjKwj3pOnpnstPeCxnkU/N4eXt16dwMRlGK/vViyY1h/vzRC9DMot2/d+f+vfvrZetwMozx3oTOPI1FCZyCYkyiqqzPUYcBFrYwZrawFdflUA47kk72JgZvTMiqNPaUTP/FpRvBlcspcsEjrTgtqCSVMiIvGUDAM59nJs17iQsdnejZr8EQI94jUUBTDjm3NncjZ/pPAoQY8ByxY0f622R4M2zMXuxZ9IC5zBJS4ezAnD1tr83bZ3aWRysVOdWTKw0yFaTKdIXJKNI4yn+kcDhHs+aAKUOslIYjjjqNeDCVJCNLKaZts3aecKjZV2dvd4Yqi25O8CxfPn/9zW/8gtrJATuaZaBHEzc2xvu6mNjwLzRM3di9zcJhKaz1xl4kJHliBo8Sejk04zPbR6DW8MMELn4Cot3u4wFzwXaytE3i5naq34xf33nXBiZW5/Snm+28NV1uLFtSGYzWdvNrr6f3FWHTfYL8BqG+RB6GFDYwrdkTn9dvE/HOrCgSS22Ag6CamDNSDMo/V/rwQlQIaj66qgb9hZJpNiFRH2UiGzNSKkmbLkhTtkgoZv1rSxXMnxiBZ7BhdkzJuAKwjGeTDnkkA6/qdBlvofisMyfACgWzT5bRnHqLJb1qxnAOJatBCpEnyRCmSU3qRvF095MsZljdgUJWWIAtD6UWxaMFUd5tSxrFPHIIPvmM//CMdRYKscGokepYNuNJHCgUt6Z5UdRAERBOSbpKnBZdl9oPs6W6+Uc9CUHb9xGg8VPmz4K2jZdNMPrfd4XKiZkM9cXVLr5IeW4+5PvWJI5fHo35zVW4Nb+5V/ICEfyb84YNACqkSZSU+WuC6jG51Pi7SJ2E/lXZlT/xxG+i7xK9gad4DYl2MG++S/MfucQKBnUlJ+DUX+WSrJHRzw7wn4+bJIVRMqok1ftRIW4IvfuNKNldNxASFGODyDrLjPOTy03JwgrRKwuZpKxkBSTME/GR0NyIlip0UJdiFyeYF2rughqGwRJYuZpTqdjJMcxYwh0UwsnMuP6iZwle4Kci3CVJ3+k/EbPTsOtDjNtGvdgLMzZ1I1uv5G6dTiVWxgOBHC2+FO7QV6tMUp9lT/ssQw4RBx/dsEurTgtPMhhkBkB4GrkzppZEkP4sMNNckiRxQolYqgJTfHDlG9u2mWwtInAqM2A9po029pWIZriH3EpaVVkCuCEAWEpO3KZOUVg/n54mERNADqU4hC+C5UkfGeBFdT9CYyNMIn0QmZLu3UDdagHz1ty/mdxW9l159er5oyefWf7r1C+AYzCuVXpV1bALxExfKEi3ZTuRDGyiShLapAMEiYqMnUUlZkORAmK4huy0GZO9qUewQ4rr27fvPHr69GJ6gdjZTcG5DeZ8O4Onzz8/OMy8zfHJkbpuyBjFqLrNlBj8NMbQu/6Sn+qtfBs2qC+JqiZCE39JAZMs1YjVJDWrC8wXhz6mhoNXo+IkvgApmgwCP9XbxMpXpPQaMZLgZGOJ2url65cHk8Nf/PYvf+s7v06Z4oD8u7/ze//m3/xvLIY//OBHP/Pz38wpSeQ71ir0Jc1v6jz/0LfyVYPpsOvTduysqyP+HqvZ7PL9r33tk08+WSznJDinMCsaJ/sGV7f0K69fnx3s7+NnBnUVbf8Tk8xywiqmpPhy7Y33Dg+PnIUEcP1PDgikayrOwPbCDX5yhcDpy4plUD6//tADmumziv0Sq6JDPkD/w5ePuo9Q16VTPTjZG+6NdKc26AKFSpUcMkaVSQbGGpUG8ejRU2caWCuMtsN264vPP/nOr387zK9j8WfgwOgFzSwASLsksZjXoFFoFc/vMqYtOsvANJoKp7VwTIUx7OUashsgfONnvn7rzsFqurw4f/3y+QUGZdgfHDiv+mw86vMLGG4vDtq3xOd2ZKBvgeLsejuN41+bt4IOHJ00hoZPQkqa2ZidO5QzXiEEIhQQPKhmmakmDTu1FUWxZJqel55ASZsc7hnlKYbxkN45yELTD9dChwkGTJbaGXkzGGa1PSWElLN8wghHEcPQmpTBPcoMlDpmDg0sl5bIwh0zpHxDbd4Yw3GEVr+FznQI00VRk0JoKKTOw6NiRyTiShRXmVGCwijZ/JfgleUKQpGYEZm+IVKEQIR1+DDkdhU0ahUiZABDYCCVAyGdFuUEouQnYs9OBpaCZK6ApuakCiZkHyq7G04rngNEfEGyMZIkjS6uLrju0DRzZnAI6HiT/cl4rC+7MKq4urh9+7apMz7zsPdV9XGbOb841QyOT+5wEKLkZlYnXkDz/UxFGhSxp6YguBglB05oozHVyuwMSTLGCzUiYUL9FKIKmtJrelDMNBztv3pHNZAulx95KEqp31kcoCN62+FxrFiD/eJcGCK2MZK6OcxAwva2qNNzZBj/Ep1IcvZ0+fhcww8nQCHDtjAVhIKLuslToeQtJFO1VRGeffaliBgR1ITrolPTKlnnFZORRUgrTrPrzfn5+Xr+yvhouvmQJVnxJ8Pxq9MXX/vG+99569dJ1HRjlYkM1UkAt+wHvXfv3p0f/GjbG87bA8NCfIgrB4xg1inbU7e1MgnLp/wcRgYvGRSWsrztXc0N17f3nUTZ6zp9UjNIe5+32peW4TuqvNW+MtGu95apzHxNT5iJ8uueVqleklmEy64vCydXcVtWAq1aZk3RSmLtIQoPutgDuzp2VNKEMskoK8NjPsm0eclTv+mQs9Qtnr0NFeXtU6rU+qPsVJuJZQSBS2iI0zQ3N5UTC3/kayooNYRFwjdolX9pkhloNIiVlUJ9VmuUhcyjCFmFrG1nSFmDdZkTNT40jAhK4JXi6B5mKDaoLASkfQoMvrAQTQjOcU+HmQCJBBViRa+UmYiFX0B7DrGbt/pUeflQc5s1Ece2mcGEhpPci+/8pLj//y95VLwqxpdJikDJPUFeQo3mClk8BTmBoWKl2n1GnXzMLWzNTLyDn9iVsKAEQgiyK1aR+SZiFdLoITVQwOSVjJo8kSPP9WG3ojkQ29ckqUr6j9r+E7FKkqi5dqWq8wHYYiujQIZ3RannXXZNmsrXDUWcDpgfn29ok491NQ9JUU+xMSRJcxffPwyKrXEGIBHxvoYY9TFSvklwU9TASW4Vi1ShuJvEx4kBeT0/Dgq9KfmYHPGAV20q3XDMA1RvLZVBwYbxZsrSK0egZJyZTiTcHwkpd8SVLvVayDT3iF0zfVi32lN9Te9U/SQMg2vsOmSA0UYlTAtk5kwTdDUcTKNlEDQXqbvFqvkUhOEXAqBDoiW2P02w3lAq6qOghgBaXtAOY1Vh0SCCgAYgDSDKXf/TFUYYabENvOpszTD4StsGk8BJV6JckdAYzOA8z+7pfxyQAzbCCE9uiSBPeWmtCHpt3+4VJWBKPMTNQC4VL9yQApduIDlpFt/oGC94HGqzst5u7s8uN5988uRbP//rs9lpTGC1h0nZQG625Ccijaks1LJN+sIRSxk9kRho7t+OLfCQqo3WArfYT2hykZbUf3gKoITrAW3VMmCsim+H6EhClA7tVKrLWdnb0dExi6Gee29iA4mgf1MJIOUxBarfPL+5QuYKDidEvBUjiIpLgp4KpNnVhC8vcJW07by8HtH2TIAkQuo3bCY54bppDx+nIgRV2TKbz1ga/g6UFLpka+z1vS+2nUc27T063P+VX/4V3urY0pjq4dv3+TCwRzInzufqbI9tBjwwU5WB4LkpiNCqMSEFHfbwMFM0GmYTK91Jqz195+373/vBJ9KtFx3nGT159PLunTsOVN0/5N2NquscRdbvW+ka3S6EuR4LGHTplLYUvpr+cDazGU5pyexoyYqZWStALjyMObDsadEg7UEI5Jr/YeI0CFFCph3uyeLfdzVF8CVRxY29MaWptN3Y4zGvjjlEF4GGxNCoHazmR732eNt1hkP7ow9/zHmD448jDLqt8VsP3meMH/B5pYalrWjNm/X8DpCr7ovo0NE3AtjVWp+kcP3naYDl2tTLIm2jgMF0MXcsc0yom8OwyeB8ZJt5Qkb/PpjPtp3l/np1Ph1sp93Wi83Vvq1rmfyP5q2D9ctNf93qHgyXZ6vV+evDxeOLg9l2M2N+HU20UZoqw0XxS4wX1pFODjjNHW5nq9nlawrD5GivpzgmITOwRUhyBC9RsFIHxIchubk1LlISUOfmm5Xhh+PStSctROPg2E73U2vmD6xI4Pp1sYqP+7A/djogC150gvCocpFsLMf0ArbY7SirD+3JM4wsia+UtsabYslUWVqAOBqE0VZklD9rpdVN5FAqPOMF9MTVqcFQVmiuMEl+CDpg9PU1Ysc2g6eb7qtKvIOiUsKTTQerJXIrMQMZQeq/atPMGRc4OZDbUTwAI07xPfahZhnqhMNpxFF8NcgaHuRb2lEYyTwYw8xykg23tmevzyx2WvzUT/30ZOiIsfa9eyenr0+pfLZmMjLRoMginQ7NFszZdGHAzoeI3Is8RJf1NCudIiu2jp3J2XNZskL3N9RhQGmbMFCFik9jHIwmIXtKm46jaFNM6ITE4Te4MtolTIlI5SiT29hoO71Xqor1QaLQHyNe3wmJOi9CztZbdSe3tB91zxZ/FGL3TsHZXN9TL5Hx2Q3eCblcrh8rzkYLAoG3UkRdsWHootpzBTnZOC9WiJOJ05GkUot2No97kN6v9xT6gpLcLwTVFC8zu8xup48eP33y5Nlq++Ps2otjnWW913/n4buLRevw9t0qNRhQgxzIIYQ/VTwaDybHexhufX20Wu87YU/Ta1nFESWWTLlstcYSGuulj2ofdZzjbVcoPcjya/xGrfdg2+rYJbZq2hh43RpdtJ0O2JuqDzWWGY9QCXlzdR9H4BQe+KUQQxi8q6ssvoXckMS2DITzQ5jXTbcfXl7dN5/jYGM9lMkfw2ijQT4xYOeIplp7h9T2uqHEZ5+AOO77iorJglzari1vS0YIvFxF98NgmAc1UQOBSrdBn+pUsv6vWHlxCw681egNVyapsjszxODOKS5mjtxzFgTJ9oDwM+4zXZdDg8yktB8t2vPr2YOieVWc4oeSCmbiKr7KptEVsJbLoAM3AfiZhIG4ZmaYpzUVddMFGreXzq5MaJgOPVMvOEFZ/KFosVQxTgWlEQSgDEkzWyKehGvJIx2KGiY27NnvEi8QguG/93oTfvOw+81Pf+cRE0LvEhdrd3IeTeowSPnNt6psOxp7Qr3dhyZCh5sZNt9B8A28SpSETdxqOFWj4SUFAy/8JA/F3CXJb5OwUlXGAeWqSF9+rrD/PbcUQkbgFpyAr+yScZ5vMK3SJgQ60Y+/Er+yqdQhQQNnl/UOK9gWmknvSzKsx0qUgET4MmFRoOo7togGB4kACxyJgoNk3nUbGsZiY1OXWAG2C/s6Y+3TCO3IfaODWEVtLa/RaCm1/T/lUDkc6kecaCaxAYITjVZvmS5eDrq9GgYk9+Ba3JwWiyZgkntBQD9fPYRfXxiBPPCUwLvaJ0M/+NA21PDOHucvW7ZUWQDVvdEpJBQXXcqxp/TyeIdHW4KG8FREiEN+BwrqAaMviRwo3V1oPcRpIchCMcI9jacQSIuq0IaAVPGSWBpVWhjQUcGqqtKdAhA9J5TelVxh5YiWSMISQs6mNaZlpjZDBBq089LTb+/CPKTBqaVgEvSDSdUe7rbcH87oo9zI9mc/+JO/+3f+iypcZzLeM5VQtQeU34jKCNA0d2uVuUIYgKWDbKCXAA3uhT9yluLvNe4ZpKcvJHXI2Hiqo+LdOw+uZkwoEWbWaWpr5hUW60tOwKbg+5Y0DsdXs0UBRA29YUoZCtZTPeS9qCOo+SxmOFQg6kECwXyiXqkpsUNZn6NH8AMh6pI6ScPXVUH1G7rVF7mmKqo7SVZi0gHSUAg7Hxpit/cO9sf7+5xRfGH1idNwDiDLqm47RqqQXg70IHkDWLqCIHkuGe6q32NwzCtMq66y6ZNzwWgrJD6K/el3P6KC0Aud0/BHf/oH//V/9X+cv5ru7Y2fPHoOFzuGyp3F1FyNppM6wvaZ+MiiCwS1ZuD/R9l/NUmWZHmCn3HqJDx4ZiSpqiZVTad7enswu41dCCBYmYUMgBc8QADB234FiOAz4AGCbwERvC5GZLELgWAXwwl6p9n0dBdLEplBPCKcu3Ez/P7nmkdmVVdPz9zwMLt2r5Kjh+nRo0dVCwT1F54yfgsbR4w1rwbhVXvYKpCgq+8IY7QFbOCf95JQmX7+IxT59jOlFJajRUWw9jsPHt3LpLwCXVk4mBSCK6BKyWphtFon/pOf/HQ4duwrp/TARiu/8su/5JDpp0+fEF0IC1RBHQk1fKmfsrqYLAiZmRCw2m2kI+rD0yio7BqZ4XOMX8fPXWsdW3B3/97xZOwct2u24t/67b/16z/4j/6r//v/7frcIYXtw+H69upis77o3swG3YNNZzXprE52i9vuh5f9mXU0y1bPqgz7tHatbxkfZlQNqkS7rZdXTpVazKfXbPfF4mIjLmZlZUvXkk12hXmHQqZBQMCDBYEzmsQEv73eLq11Zqcp68aJeuTAcHKSzlrhkeVd63Zla9LlfNm38dR2kyPKRD2MBj3R1OFYfJ4gk8Wt3fgZH5rPZLUMQTBhwRjtkQ5E534wOaID6NLbmSj5G8P7OK6Fu7DscqXHCaemxwnzuitBCDfgGw+Ccw99RbeUUlQ/AWGAZKFzLpQpESvWp2MTPklZsoeUQKeZyo/spMKEpJadlCGiGSweC65YUw2lipMCQAVCwCmSqzjO6qjut6enk6M59GvvR88+MpJhuJv30MKjk3ui/BOPUQtRxP+AUCwkw/x2eTPc9R1cIFqF2CiVTszV7Y5Hx/bwcWy2Bqa9xbekIHaYwJFCB3BQs2kh4GBDKmq6EZao1wI+K1VzZFtmYPBnKVRZMSSOTcnVMlkLEfBdZaUGnVZ1lqrlAo+ERq1mE2e7GxkngzPCA5qmlMKQfE1JeVzYvytPpdgIkAECHyS3JJVetSxFMETmwyehKDWg5rCJPaY0K9u25kz62WxxcDR29qPJAdvG7VsErQVjyiyoqhPXu11QTm3hlzBsFI41tnaaa/SU9SEOWTA0FewKEENjICcqpbXCG6xk1qToGovTDGtH5McI1b5l5bYPjFCtAUF4dYAyBxdpdz5d4ZniUS/gSk58x8D3Mp1p3oeGQr/WWoebPMZgUTU1tIjSSVk+PACdFOnBa/F7FCS6JpY1kQI7cZvR6kGhnnNfeeb73QclpVZTgRqE8QHARFiGE3onSE98XlRv5jmliQmk08l9ejUCXuGkduyM/ZMlbBmq0KVqSJdWDdmPdjQ+BYXQEbVIHCEFaiifnsFN+qw4H9MP0K6FrSCtnJWcUCq3L0vZSGk2/GE1StfzInEpVUJuTofQG60F5YKg1OtWNeGioN9Hmu/W1994FarCpZW3yBfZylUl1O3+ief7IlNB/idZvpsM+b5L8M0AYJ8sCeulvXrU1lmG0sHMe/EJkpriqmAvi5ApXpp9wVIUXE3dsJTx399wfXt3oKotrcUDyXtXblqQllRR9bAa1cDcPN2rjKSQGe9hAur7fa7KWr/3IDbtTfL8C9g4JJ7N/aNGfhVbNl8qDe83Da0Wf1N02IV1mAeOUdR/KMU5TsmRndngMsLWWw8ObWAST1vK1AcSECojfYvmBgQfwMY2YXn3OrbIUlO112XJgS8oijlLtMKA9YQXltfQG24tBdiFQwZCmknJ8H50HGMIlFnfnCylowRMmn7obD/ubK8qtlLmGuqU6VMN2Tda/ykTOYv4Kc6C1pnTQwUIntKPKVkvu/lIqZvW18CrK8KW7iSk5Bp4yreX0XCkXOsZaenqAElPKCGdZcusEaTrbCymfyJXd3RqdJW1xZEkTmuvhTdoFixKn94x+ogBEn2TyZW0N9Ie1EqlryCI6YEyv8CiEknA7tZM3aUQixjG/eEFyf7sJ68uL5ejg0Mv9HkGGoZj/HHFIfnSZ0Od4CAxKEFgWcJRdKYUtAjKe2fbzhtLIfgyuZt08xoCCKyQbkURoUaIxoXy9Nnjd5cXVvyxlugMXZpNAV9/+XZxvVgtthZbHh4fnl28S7shJYaPK3nrQ225z/8gP9W791cvIDR84l+wYagSWqbjivILwEDlTXQyKOLBIfAEiC87up84Xcw7z1sbqxIFYnL7obqhFSclHsgTju/El7EAAQAASURBVPy23R7sVRfP0xJvr2dn9rQR2ir4GLh4VTdtIOBqLx/A+24tjEUogphsUOWBG1ehzXc1IDDv2wXMFJLF8bEVsrRxdnl8b6qWjDAWxxj1+oq9kkGirkHz19mgnuulI/7BqnhFys7Qwn0gQsnxeLA7w79Q4soSutAs4MSqwFf1Q3EBJiWm6NwHWhKtHByWDHmyBzRF/cyVhu0bl+cRSjP9+IPjLOg2BMi0g9FkCJQqYjIqOsB037w9v3pw/zfPLs9fvX4zmowSCx5O7p++Pfv+r3+Pz1sRReoMTjrdNzy5pIQw+MMkJNJNa/xW2xtjyWM9FXednTJYS/rMUa/7nU8+/aL94uLq5vHjJw+O7z/98Ds23he3L2T9/qPp9//WD16/PB0P+5u3bMIzu7kct62jfctwYHr0N63hwY+7tgVtPbhuvxp2Pun0Xg52H0w6b3N2qcXCG4721ZYrsXtr4yB2U7dzyMailawPIJpoyvbQqvTMAzDHfUIkzLV15SLJPNO3JHjWbY0mIrrsabS9bo/i/MfBJg0y1Lu47q2cI+LYMxv6mC5YoLWmZQ/iBPCtZjc2phouZzZh5FNcffX8VeflmeGgeRRbfwRp3e10fPTm5RvjBoD84//PPzk5fPi7v/t75hqh02kqe4EFKCJFFWfY4D4/kY+zL/7m4hSCAWaOD4Muhrjd4df2+Ioyd6EUZS5lPCV0Vp1MN7+1jToxjB7rdI5arYNW5ypCnj4xcwUR3KjtCEtmwBQVbkL+4pwabOBhCMGjUDnMavKL3vDGbrzT6fF0Mnz14uXx4UFvNLYBLN1rggMrmFAT6sMz4V6MmQopXBjhOzFSQx5rf3PwvCXS0+nQxsmY1vyJecs0Qe1S5kC67iS+Kg9oVmClS4pc1H8AF+66g7dWPfXWE7u7xZXc1/tcme7AueRVEsonIx9i3j3DyfDaSEwjX0FCzGFS98a0xGqO5w03yS+hbhZ62uPuwtnzsjqzGWfAGhBiwHxLBksgvTGY5kXOv29LaHL0XqSfTM/WsFj1/3qb7QQxbYWrdaQUA8SPjBRzHSBFhHja3/viy5ff+aVPs4zbbFy63SiWqga3WIPXGRkbJIrTmqXpZnNgBqDbM4QgCM6K3ib2XEB+DkzrW5vOjjQZtuba7p4bGLU7j9NzC/Snfrs2uuFso6KXtVoptnLmspBGP8tL79L0tL7sebwRHFrnV31lGldJwKWpYPRWGijDQbA3eG3DZivPTbQkyCcmuubQK/onjU/2jAFlQjkdoLLzLOLhpurq6k6ylqz2ClGvqUblp3NWTvKHe8syjtb2XNFxc/qXQZYftIIS0tezBxATGKHNJvNCAbjgZvEQp+jtzZO2dX3s7hjeqKiicCNKuYtq0AZOz2jHtFlgRN1Fu6tH5FyGsTmw2k02tA6okuU/QBSG8TVhs3HwSecFWLqbj8NpMV5cIXXbSrkczPpRnIbtdzS6kP/0vBnGGeJYGcvB+JXbyuNZXbXfZiL4vUiKn7sKs1VB+LqwVonuqm3KaNAaeqeQphg7e+UW+e6eVAXRXYr69gAg712eBmvppkJE6C5Cp8ggvxHqJKwCmwz5mSvMlivkKsYLfAVjnv6HXdWMqqQpILq1CksV6slPt2E2jamyg3/V1dP9owZXefLX194UlPfKSsnRX01TUrjiNdsVtk2dVWNqqcRN0dg35jIdaHYTad0yVnBXCsKK4fm6SnvQ5BjMCS8MUEKeDlvHGHmmW2yzHOqkr8j4QEnKckX20ooGNukbL3gtZAF3vZeeHipOiw1NUuCHBywhssxQE+X8CsWnyJ964+6mSS26RzViAGg7eHLSqsgwN1txpQeUsrb6qjZm9XwGDzbVdh5kVjvpZAC/aZ0rU0uldw6GEpiBQVkhR/eVyGxX4pFyXHHiFavx9qvQ3+Q+aenWrEmgNZImvUp2AMNSFGwglNqZoOUug16ONRY8mul/JIkxoRfKBEdn3J+UKgq0oWirCWDleUpMyNAWK+Z7DdLaNl85ANx3vved07M3FxfX947vnZ5+/cXzz/7W7/zGxeUVilSogOVr6BaTOTqoXEG0irdsSxSL/kp/LBWxwkcxe83bZwI9nED5Q7X2ZGql/ADhGRBDHbr0W45iNnoZZE9UDqFe73ZxqatY1yE+R0cn3c4L6el3RC7+KH4q9kvjIC/s6yEAwydAKD+JthatpaSco5EpLNZ6pvCVZsdBsbT6i8k8pr2Sze5SfbSj8OkiEt2qh07gON0K1zUHnA4beg0YTMIKuoIS7NaftE5MdCeUObrDX0CBMchL1JCfHpjKEKAFiwCuZwF3f1WCwl8e7N8GKttJ2La9ZzvQlQgV63s5NT//6kvHA/d7w59+9qM/+ZN//f0f/MrN7e3JyQMu5NmN593aX2Vpdjzoobmzo1R/uV1NJy81Jn2PSoCRChOkZT8q0uMV3gvaAkPRdi810NyUlBf7S8sK73e//+p3I/uN3vBWCbxT7eOD6YMHxyFT5twi27jEf85W4Njv6LPPPjs8XLx680rHeTu7tcrwcDq9mV1+9dXz3/7d7+dM1eyCG0s0Mm/lzF3ESMDJGYJxiOE3AfGMA+WzSR0mYGGxSslv7Mfqg0kwECzxFFXz9t3rT559hMyGCRZ+9kb988XmaNB5dvjg+cV8sP2RKJusVnSqmuiYTn+1OvxOb3DQ/+Xl9MFm8bCTEKAPO6Pb9Xa66cyoN3FZu86JXctXvcHSITvbC6NFBuhkODX5sM2ZEBQBpgU+1YEFfWfobjRj2/rN4eDq1Xl7NmMs6pHsLJjzH2xeKjINL+twOVAhTeBlIorNHqyHI0NDSIGEEL3d5StlkBFEY/WMIe2wxHqMsd1iSUK9YxBW193b87N3eFv8EjmzsCQBFQjFBBslvBCHRIADKpI1NE35rEJoDKuUlN9eOUzESJ74M5sM/TmD5nGg12700telsGKb6mFFrTN5Y8AkaHhM3xkeKDN6IqRMnmhKvOc2RURX+mo6HW+LAzPew036FNMdrBax+ybHTo5Pjg4P7t8/no4OjXs1rTvqGN1lffJs/ubVa2j0cDSewJ6iqEfMYzyQEUdMmTXlpFxDVvWJnGJ9JkprRwxjzkb1CnRysrip0MAcyEpwkCcSFMiBtbA2a7ZbOMGjO79dv3v31jT4zc0Fqx6/5wTfrV2hJ7PbGyr14NjuTFirRlAGsvDNte+YGo+Q3sit79xr0X0gt6ma4YSxiI3mbrarh2aIIkyhVmAJVRokpj+GvwKvEIlHkihfTUrA14N6K6cXMqdniSptrngsTBfXCuNojzQwhFhPJ6OrxfmLVzTSb01GY2UiRaBQa7gOl4dqw/6oDkS+bvduhM8QYRqpVCUpyJTIsGNTfsEqC0raBFq6jXi/zQsTSutYMDabIeH+sch3h+hsX60GwrRbG9JHlZ4KdP7eNxJ93TdX0/RqsNum7wh6ioJJAnwNoBgaqz2J8Gzyh6q5vE69uraK8i2Wjv6GtWilyGC8ZsbouhrJPQ9CA1RqKnbbP/Awhdb7xPGWJ6PyCJfKdFOGHWHPXAElnyqEHP/SE0FyWL/mIoCJNjUASJUQEnLU+Dj6Evqi+QuGpqwqTEF0PyqxIMKyIWzKJ1W+oUNBTc/NyGIcI55OTULT3dZfAIy9lDND0SgDsJg3QBZnF9skiG0upfh59yvfP/8jSK7Li7r3UaRNQoDv3xYaCh2w2jy+e7lP0hQUer0vMndVlqS/aADQ6j+XvL37KByvBRlLNYiXq6GS0tzsay+Imibsa/Mk1Tcas0D9pvJ69e2f9b4+fsEsgTr27VY3aFS6b9g3LQoV8wszpFlJ1rBZpbf+CajV3m9qyt2+gP2rb4orakdyM+zDhfG+p4Bo+CjARolUCypv5CzP1V4Ia8CINYiJ9ez8wemM8lKlxVa+eSOpEbLfXn4ooq3dfin5gK9YL9HPSekaIS+7EPPHOi/ZCj/FbxQLG5/qVMCT6deqWsvDvIxm9NKdRh622dk2Sjl2P+MprShcoalCgCm9tV9RVDU53u68UXEsQFaD4M7MPIA6ZbBN+XFjaihYarGSG1HWX6dt7dcW3glcZ1Ko1Nsu/0H86pFJCaAo0lI3xLA3OPWIeeyzQGrbCSctwzVJ1ZxBA2R6P1Pn3e5ZkdBxxM4W6VFJUaailYJ3raZImZQfE/hO912YlQ0hlCZLaUsx2IRACIo8XDXSU94EdWSfv1X7nF8n/uDxlg/RPPLKAVJIc3W+/NM//vPf+/2/vdtdcSFnL6C+KXJxR5wNVoq37emhQfowD0PYeNEwSsOhQLB7gQYxZYbZP44Kt8SNAqnOzM8o1pUd5QbUunMbAo7YhjkbRhGZLGH4n7+7NPF4eHKE+JyfcToGgXHel0j6UVeYt+HwxHJxwydZZDYmRqAKwVa7+Qfhk/5X0UkAG0YrGq2KFD6wf6ldGm5mncU1099UdLcJieaQ4OPfzQWn7dpMihH8ZBuZNeexOpw1q9MSrcHtlN0gVyYMj5btq6/tpyTCGymjN5tV0AHehOh5cNL+LhsCadP5LZ+lDXVaYUQXaD7TsjCLhleL0qoMMEugIIdf1vTEL/3ypy9Pvxb8vl5fza82X3z56vu/9muCxBHXZnkcmevt6OjeIfssyN9tZ5cLxzoQvWF28o50gC41+gevMYNwEIkvtEXT5G0+CS/S6QopcmMgxh1MBlRwVZK/7oO/X3ZrOtMet5qjU8+M1wcfffJf/pf/h8kQ20MQmkYS4+IiMHbj5YMistvFZ5/94T/65//QKw7muEURT9vSzUwKUcAJigqQlKAygpEuLz1caa30nMaTSWiYZiwRpZ5+LKKwMRhar01XopTzqTXVgR9mDTLL4Rh0S64Z+oeD6ejgen75L5d/+tHs8HfGD3rtr4cm6BTI7Bo6b7t9f/jZhq7pfwGLna6oYoda3Y9/V6wjp3svm8nfChyyYdDGzNuBrbZW64fb3rvO+qjTvyQm246wBwYN+LXc+FDpD9jMxm694VIgAS3AFMFE3cEbm4BsNo/IpNg9cq2f4gBhN8RlwkrEKhqvtPCMdmLWdaf/bre4Jn+TQ+EnNC9swwl1ZviA6HQDA1Z8MDbI/gq7zG4NtosTq6c2a0ogRWbMGndGuBSlqCYypUycHI+AzcZN04jtzMbt6JLAQsaEgYAjqOO1TXyF8iO+gSqWdOKSrcJ0LpuhLHBnq5cOHu62D8KN4Yno+8gEPNienCJWMjr7F/EoqDgYyJpeCH5ASxpRLurVvvUDK29sWWxnH6aRU8YyqkF4JYdzEuXsVsejdrjSBHa2zWok0JuYKRqaNRg7kduSJFtUOqxKE1I7pGErfVPgM5g0iBxQiRm7RpSAZERdZ78EEnp5+XJ2fW2+eDQ2ht/Mbi/JxtxBt/GltA4PjzitGfz8HYYBZkSZVje3F+biMhRl4KW77DpSzREF44Pxoyfiv0NcDK8ETItjeFK23a+cPRHiF4j5fH+VzPpVOM3TQO5HrgaREgel+Z0HfkbMmXDhFRNZlmnFqMMbpqf0LRlRW1gk7Wgy1tEOx8eOzvjJD5/f/9uPmIchUOnf6I9iGb8dEJUjp1sPtmz37UHb8htLftWWfRHEikOvZowDSmeZcMAsgjcP9jg+N+Kffm+g4+YbKhhfdq2HTviess0XpQGpLSzjR6Dn90sD0zLPKWp4S//ud/4rCpRpYcCsnHmCZNEf24+yms5sSRgeh3mkfKO/D5Oj/0Iz8zzLRcJKZTGqi/EDPTid//8jSnXX/lJtlH9sE5AksirVhpViIaSjjrWFMcPL8V3YzteUUVwltKP1DYbZOdVZbyp5SKdh9TAhuIZILKhYA2lVdEHAja+tvLAaaseLmnt3F+QVbhoPt2Jc0J1Wp1RyN5Q3s7WutLxBkZxpoB9GXLvMNTEEABJCM77Amd0FlyxnKDeOZtediOq1J3pc7Z4qPJH3DVVS9t3lVXz/zeV1GvEzVz1ontbrn02zfwuIEDLl12ehyH148NvPG6YP6MUH36pIzv1V7KPB6ZxkLrRWGU3hxV5KqLbUo2QIHGGgBoIq4q68ff3vf/573qTEKraB7P3Ppo79u2/KKgAqUT1LprB1QflNqvfvqug9tHcpUTuP04NqHbFKCbnPR91VJWm5B0X58F1eVjSKR9KmvyWpTNSk2nM97jJ4TyxChtQxXpMUo/If89BZ+JM5AZaOhN4C0wCCk6ZAClqtR1W8VwWQExxH3DOJeqyRQNNhNG4GCcp5Iy27BV/aA04P1L66ugIPNQ10erfM4vRhQBHTwvdPk9/emhSWBnOneQpQkePGnOsVew5cBfhWhyGMY2srA7UlQiNqYG+QpIqEHZTPVeS2FZn2og4kCsi/TP3H3UrDkH26nF3G2o0DPHMR2XY64XbZqzccuEd2Sgeat7RksMsm44jmjsKki+vQrT9Xb+cgPateMPLMEHDwk800mCuseC3nAlwvLVcUFyBu1OmwJmRXvGbzW/0lPAdlq+Wf/NG/3mz+9wk4WbDUmQEQEu1blO3CiXWEgVCcQRYeF7PFQFQl1FrOHcaz7RvjYja76I9GfLEmreksJqruss3vQ0dm44auiYjD46PTd+/ASDtDKGry1IqiYdGsNovR8LDXFQSiv4T1RvzCfVL6LI5uhDFckwe4pUkWXRwOCiEzRMzRWgkFZkVmoro3WKwn89lYOAe7/2Yl3rnHpsr6CQqd76aYOHMZCMx+g02h2gzJDI0z+6u9tpZH+qzDs8Cg15kLvrAejflRhJMiXQOWAxHl7p+uTlAERIENpM11942H8rBplod++QtneXR5cWEMhnnZwLEu2JmZBOr1hrvnZgPmcyt8re6FPE3U3ozClaa4CmaEivhsshO9iLt0mt64ge2MryCJ3GUb/twVKSO8fmV02ij6QALneYgSCBjJb1rwiz+bKpIm7UqVci8ePbj/4OSexTmhDY6BRtjRs0SA2VI98Uq//pu//ed/+hdfP38eprUx5Gj4wQdPvvziKykl8qQyxu0dlii2K7AB5EGAzGejZkrKpCHXBtRBS1dkZLDE/kda42rjfQS0s0i7myWBEKDTNC0wvzYc7rbOju5tnnSPT0/brxN6nIEEzxYEsNgHXUsUGOVb5qzpq5FZNf2hpmy2Q8pw2Tkk3C+tIZ0vtt3Xy8XxYHBq8NfvXX1wIg6q2sKKjOzUvZJ1OaGfDYW2Nq8xx8ZvHwwSOVtlwn5mE1FQg0I+dlNYNuqUuz+bfFNpUaRibERodx18m7MO2MnCte39qeygzQRCxg8qxhQYiR6JFktJGZRl/OYLb4TeYR2dPVrAXzIR0XBDO4E0NzdW7Ng66Rz5aDZWnm4hzRGQMxyzpsAoV5bbri1pZuOoPopv6WhrrBz9Fz0yndzbrr6qTaGQN116VVjQBsrqkmKIeNOwXvw+bESAOAdmfnt7cXlpEfBwPL138ujeCU//5v6D+1qd/THB0G4ZpAjbiWufrW+GIp2dMuIeIpSJ1eN0ZUsrP+boZjoexYNJzak1TQi8KGHPtPHEQoLY94rojinw9FwaBaDlbHH+5p1jJaHFJkIOQdDLGZrPgyfqAh2TTNWTkXM5YBmCndRuD6PWzeVVpmUy5CaAOkcUTw/pAXLoFLJcocAOGcLpjZgWhJELD5vRGhQW1EFXLu/83V1FIK+aJIXpJk0SJENo7zXkwkBTrtZpa7iEV4Ifr7Ece+1b25Mtb3/rd373+GSqW5M1Qlq8lETJEGYwTBCy0ulesGyz7Rpdm25VOhJDY8KSLk+gkSyhALvf21J+9SREr+k8Q6MI+EEizUwZxVhJMQHLfVkasBAW8TRtkSQskzZBdV0Ql9QxE0Lxakq9p0HShCA77vtwfZVMPsqrrWEK8NAf1sE3xrZegcGLWMNq9jvQaFXgqCKimRTpdWxwL0NFwOQ+P7Q6ujaqXkcJ3DTAG7C4qnTFhaQpURFaIn32G1VsoClq5UVTbMoOKlOFTEmhTBBnW/NkUEhYA1zqoFxqJG1gLP++0SCTrHBXggZVjAY6Ico2A4IgnvAGEiOjQBfAnd+uOmzIZVZ9R0pRd9PWavBf+wHKv3oFD0FGwMlH3fpoflW7mvbl7f66e71PVWnvGAI4Pz8AqCLLJwf9EKcVqozbKZU0tUuTHqtKrCfNmCaxTc2zNDMNdQ4AFPIQK+MbVCbVf8iVnFVNPvwId4X4FsQ89ZGKfNrJJ1/SVvK8CLXzXaB/8zzP9le998Z43CTSiafit9wb6ONa5XK52SWXymkNjHTzJLyeCun4ZylYFHtV6i0Rkjdp9hjT+GjbgCilh7H4U67OIOXIL8PgTX6zjSSIOOIn2JY4WjWh8RzIIgPTZi5l24UnGl58npr45z3HdCzWSHC2ssmcAAWuWju+qaE2REtPFA+Q9DW64M0prGQXCJXmOaJy+1PImfHWEPPawCgclpGqcB1XOcbSk2lOcCXgw47qJjfTcXqUxqW19U85pRrySlu8sA6isBg9mCvgRIOqLjo+T3WxlvypOYa1nGxM21MwWrwFK6yNuZb5Qy1tTLHxS8VvqRXd50FGlAaZPiJ40QvRSFEY/K6KTy8cZGTEk5B+D+NFpI4Zd+yithkNHh1Ndfvy1RsWy0jw9XrJ2uckVVRgU6ByY0bCFqte0CoyRaflZfCgLqTPNkeo4eFoKFw7q/24/Sz2QF6TGJKnY2nphnvL2ero8FDVhi9ZEdYVdcBrivTMsin7TFvNejNtFR5qBUXRAP6KN/JAn6vi+hka7FPlDWtdQPVpmTV4Cdw+/JKo051eta6vO60p9dXdLu2DPBRXalSyu6Ti2hYAAJIDNbb+9drGRIwXcezdJe7mr8QmaamX23G3NdkNvlibQsxeMsU8XkYZwJguP1YRCnTMGOSM9MCYGYminoRpVa4Sl2qauZl6MktTNcj6sM7g5uoGGseHDkkbf/Dk/mdfvk685urR5bv2//u//f/+/t/+vQePDlhTWMgfmrKqwlpMj3REBlcZFprSYUqF0QOHNoQrCBbGCv6j07EHzkrNJMFwjjBSNLoN5Qa6UII9chQ8dy8Lzr/ysd8gtTSXl6VS89HqHIzGa2fwVat1OxzQYSnio+paJ77hfF8tP//ypw5nNTJ3YvfhZPL00dP7x/d/7QffBxW0w4kSmgtnp4YIYJoSANPzhQqBFU9qlfmdmMRiaWK8xhK1l0+Xu5HTHOeIErRG9kBcWB3OvR7p+ZfrSWs46DgE6uvfmQ5nh7/bnt4fLL7eXahvJvxGtE7H9J0tNTeci/jULNNNwoxhTyxz58rGsNvu+PTip//DX0yXXOx9sw5vHftls9spa2c+fXRPFIqROQ90dGcyJt7M1w1ngH2juq0bE2S74YK2QYzu7p5EsaalHr4EGoeKCitjkWVrUsLMFdesiC6+APtcUekYb2PgZ2ooTruUDDMeHymo1X1HWfmCJA8r/ihqedN+ZZaPoifJ6CMld77XUU0UZiKvxM89u3r38u3lZ1DvvK2r86vVbE7ibq+vKYD+cJxlQlh255CNUkAMnMR89ixcthLDuRUGIRyGEVpE2YjoKOgUpzUBJt0RHWtgqFIj78AdQQ/1KbQgzZeP3eb0zcvJ5GC2iLgJAbIm4tnTDy34sIOTTsrS54lQn8zrdsYHU+vgsRYDD3rnN9blx4+qMjsV1xInHDLrTydjU8TLpb3QDI4oPXObK+E6OhTdSHgwJg/5SiATftK42LItY3X+LCLOSs7JSJaGhzWtwXCDjGCg/UVPcfcOV2v7IFWDmFGbze01VRmHl1ZFeHOQPZw5qCFzHBqNnTXHywY9QQSSJBOqBlA4i8qIcOb/N1/Nj7wOvv1Vsj2aG3QnZ5MlLNL89wD4fCDA4D9yJC1ERT9sFofcWwKXJqP7H3zw4NHTpwcH92bX67Gp5VQS2oSpJI6Yt6dTlBc9ddIxD7aZdrb3d52z+I8y5uaVuIHKrLZaWzxzma44Wh2g2fKLFstePzHMVR4tDipHb5PmED/7qFbzm3ZX+/SJWLxASVhv0+KABTbJSoH4VbG+TNW0yDgXAnPeFkIOTx1XwlBMn2Y6Jv4D0z6gMIcfIEImO2WZzk0gXrAV9oT+yErq6/RPI3qxYapP4A73bfAtpl+S3UMy0h7YcwnkiqWv4Sf9awgqi2ZmIKQdTZdRUlFThSkfan3S/yEgeGKO444gPh2Wh9jZ/xxTRiGEL6MJzfUrOu32FuKiS2MUmJ/5yuv1+iMFa34VmsIkj0XChnGWg3kxpKj8JEIfELYBsgjDAhq/LzZmeuqYdPU3qEhhKU/tBVfz89/1KVlal9KLsMmM+di9fBpfJWdz1pb586ZQZYeqsuSuYJE5D/5KnSTQmopvDwCqikBW/wt57qJeAkFw4F3hucDKo6DA0yo/dbgpnsw90sBLEqT+oDvl/oddcqRFVVUZf5X9WwXVreLTyAaK+pFkqTt1BoI9en6m8ip7D3uypjtHVJqFzgkdyw3C79kYaqFxxMNLTIZXYu6nceppuIM6chtfCI3V+AcwNZ6KoYXJCpIGzDssShd16y/mse+CQUJwxatMXTC5c05N5YtmVb9PAHuC9+L+SkPzu27xGsNFRg8zKPCK14pZw3yxKbpLxphGGZzkClLUqzkAzaQZacouRt7geADEOE55cdApzW0Nj2VKZgUF2mBFV5R91oOnJPQ/SzT9qkAmTY1BFjUax0k8YFodq54AqS9SqElpBVOkqbEBLoZ2GpvhhCsqh7aLF0HV6VEDpNoBAZhUHj9fzd7Vj4hLw4bSu42xGotUU7BrpD4lBpPpccq/4WzG8eDi4uLs7buPPz1ICGyWOkeFFbYiyiBBVA7bbDEoVCDzqsFkfISImo7ZmCYI0XztxRR2ZKqeoGXOgeoBCyWLMSgOw1kd4Wh4IO4/JSjJfPf6ZrW5dV+uTovzbOgEExnuBViVBMmhVKF7rwzzLJwfhAQibfSm/BtgaJoLTSbWvdZn5KR3yyLSPyXkQeyGX+/FWNkR8ZSVDkAP2x6x2nXFwX8UfSCqr/TKeON4s5qurFsoOgaUuvix1AEKyGeaUKQo5y4vA77/4UDfuU1tuSkGCDI9Kh29e3BywshYb9lNs8n44OkHH33+pS5KrAIK9v7yh//24YOTycEv8aZ2reZUW/F7LURTHhsII8Vmgv84NLWzIARJKveBoJlpj4WS3xqfyjl7UD/mlxKC6ALP+0D5s9f+zTcP78gTqYd+YRiStB88vO+4pZvr60HOFZJa9WFvUkuGCCxWGXaHP/3xT8kC9je58b1PPv7o42f2YXz6wVMgARX01ZbCTxALi3eIq172Dj4J0SoQEEmaTTKDKb28OPDqxdVOPBOnbcO4XcfutoZQEvHq27eFcbq5HUw7D4brydUSq1zMBKTwKOdQne5QJx9frgaoB93zxBgREjGrBd+OQnziTK/F7XI3HSw316v2uNWfOexnO5pft04Hs4vs5WdaIks1gAEBaYX+k0E6am+Hq0Vm1AmpgaNtzaJkoiPEI2anDiGF8qi65gPbrVGCYGL0U3/KZBGYazNIJH0CxqNzo20bqUCJCGDXvECwH9WgHjcchBbFxqJkVSsocgQhZBPt2WJaxVjX5Eg6eezfu3d8cDgVAHRuS6LsrM4altYgqMmNyFGG0ekZYebY9cw+ZnCvAr6VONHnnB1t68IDiSuMX6IXe8gP4mN6CrekF4CpfRr6DmO60FW8DQMlbo28NRfC9d++vjIUWTx+/KFGYgDb+dvYoGZ6bW5gCmi+vLmBJ+sixNjXgdPZcgiqB2bWdpvbm+unjx4JQ7E+YZEFzV3e/Y2doayrZKeqmLHoqjNxY7XbhnO+ch5f4I/BHqMMNNmlyvqmfnYSAJ4QTPNypmMXa4FmPCgxGliB6JvzC6pxVq9lboTHSkKjRA3P1DU+KdaHifwpLOzukU+lyOuv0JNS/p1XU08+8//beSL6+8fpcUMO3zQfgus4uBWwRLaJ1hD0uf/oQW9q71zoOj+eWHYyiXEYkxrRgacA5iaxmXDI2NATk2acybWQSVWRbWayjTCYxZp4U11umIvpD4seZhKVpQsXusxIiBlO+bjD6D8Lq9MBlQZNX1yMCRckBcdmktnblKINnCK+/IxKTV9TvK/bIi4lxpEJsGVklmGvvgb9Bln6LSo4jHqkgpTQCIUpWUtK4lAPHfJCJdXTuqOWQyz9fJBZd3LJubMJkq/tSQDr8h0Er9G92pmhRECkzMy3EIHA7hPGFONXCJHq8VGA0KKUjg/E/WY325gqJTjBWzrNvPYd+Q58+ac3DLOkK+QN1Cyut6QOO6Ul6snrYCwdYHKGYvmLWZaxLgDUnAwpJ9rDH3TpZg2XhSx27lZPN6nA0QAq+b/HlVJdaaL2aELwm/u/elW5SXh35S4NKMiQ4X02DypVceTdGoC8bXLcFdGUJfY3BfLNBCMKCXaCSWgogPJrfT9F7mvY15fKxYdpbZL5yGfVWxCl0L/palInVVEjN+qF7ZSVajLz8L5Z+2f1ssAJ04RmTdoC/tslemmgV2vJe8rBAi8owNb6GY/7tvXjGKRllW7azzMg1WDdRolx5ARb94zA2MjknKgmNiZsDUmRgsKFqlUop7kRD6T3NuCAxR+L8cPOdtHu1c4568fasxueBeKy8qMzgm1S5V96nUAvox1+CD9g8Oz2GVtos/mC/lGFl1IAZ7N4pKZd/ywAo0BeBExy4nEshvwWwwg4I2HlmUOngDTIK5ydjisNyp8ilRw9hLv53aOeqYM0orjZl/vF45Ck85xK8q5Kpsj5ciivpFS+UhXGvFJx+p50GQHLq6CjlBSUKVVyKYkxXESiSHsskcyHyoIsavKmoHKf52mvB83/IDB8Qg1ExZVlCWF5GZpIaZFh9RJENQUQ1Hjr0/FMdI0Dk7n2dX7jJN5XZ9/93i+D2BDAYWFSASBxDlRuVLAWoc0jf7v2q0ZTaFF13jiBYhTsopOMyR7kpvOILyimkf9RLEFLnGFg3qwmk+GL1wtuFuhgGVyeZ1K59ufeWR9CAy8XmbVPzEKoUr1okFqNyjd8Bt0NZElUbzkBNwvnT37mQXRSpDemU+48WjxsLWdbkLLCHHWsX+cpCaqacoPBwpwIcc2GWlPY7D2qOrMtGqaJVeR1aL3lX0Qe++TZRS6zH8BErHR1TQhm0hOonIAQcoK9/hfUgcf7NKK5bX7nM1iDKGEgrkzW2Nuns/3OLz17cfrq9PR0s3M4jjDx8b3HH4pbCqBsDTMAWcVjuI5vsXCqgyIgDRPvoFPKBpQcKeFFPrZ0qBvhEzWkjCxoIFVg59LELOXgetsfSZ/OChhx1Xeu9sB6nKb83NW0Iy9220NtaDs/GAztdVYnL7eO2lF8ysSl8vPBZ2IlzG3Kbr5dnF5eWmOSKGpjhpOn8d2bPIIE2+uM+QujHwAf1k+np+wQP098pkBPAqhvjBfQXVYQYoG2rUa0IzMPWq+fTnMjqaYKhWEIXZNuNeruZgxTkV2HPTtsdvo/aA8380u+2H53NZtyzq1tT+u8ChFFY7vGtcwn9G/CD+liuRPAOuiNvvbX6d3ftG+NasQ3dbqfWOs0Fum+7LVz/AiWj0vY4vwSj8rftVFXZ7q5OtgeOqJq1R1txPFbV7A8AS+1rK9dbxi1Jj5vsnv/4DSWzuohn7MprKABF6LedmEKIxsz2jBxzn6FkohvEOSvew5Xlv7aOiCqKNRxJoDzb+N4pF4zHomoZtyYdmX0CFFJ5y+jKSs1B72Xn79cfbm8ubZ3+cqqX4mzP/l4BL3GXBQYiQZoUSC5uWToymwkv1gdHDi8Il75kwcn18uXJZkIREBDPgUIOmi3DmK+G9mm4ijkImiJeGaucAI/A01ikiqLRCm0hw8e/OZv/LqgIGOO28Uty4gvYzG7nUymZ6dvrSkRW2ioORhPzUJEITJsmmllJzgt5oZLQiKPj6f37k2OT/pnZ5cn90/enF9tby1p6B0e3q+2aATqxbOT/sWtEMzlenHjkD5bA9wz4BiP3ziTw3LkCJJVxYiSwUu6OMazvhQLM/TjcC69Kux9aWw4GNquilkWlo7nXzYfZBkyDQ8IeLRxaiyChN/D5b6DG48NPH2EJ/P181dwm2v/eSe7hc+SmXwUUqoo4Db9vmmk4gUospmtRXGdN0unVnT788X0ZGLR0eTN6dWDo27rqHRWfAmuDPkQKCyrHLMlm4N122jqaCP0oHtKMk3SK7pmSknnMbgTUBnHVAaQRHNGi21HnMzdzTOFbvt2OtJykzzZEhRDGXIYiWVuGXczglVbPJvxEos1Gj/9Zi61Rcs032lfKUNSFdwVwJUuCiFUgQdoAn/64bJzymiWJrpdl1goiiJKwemz2QBRLmFev1Scfji6ltI3cI5Tscuq9P5rGVKC3c8UlbokKThlBE0UXPQXwgaRJX7pS1NXINXRpgONA6uAiXpvqgqDwKfXZSQkT7RktGCTV9K4S8U4K7XHFrK0aPs0ShAXEPN4WHxHF6Vura1IBXiQJE1VXPNq9UHUSfd1cmWsZQJTVp9USHyc1Z/mxd1VOL778e/4rnRBI7QpEdnbAxOJ0eeu3QD2wvW5j53J6n7pNsZQkOsCZvN+jz4P8tAve6btw8tSRCNDKSe5vvnIr/3vfHvhT35VVFH1Om/2D6rSehiyVuoGWD9zUw/vMv3N3wVIkyx0S3mB4X0tub97nnd5m4qk0KIYjk1iDIXW32QM8E1Gz6StknOrWQiOHfUcTV3qLA+NxS5UFwaCujB1YPHTXQONz6oxUKbwcAD502FEMNJ8GbyQvCAED3NDF64DYZzwscUUCO9S5dUOv9Pd+MMBTaZUm2LwohcBLZW55yVJvcB21Sv1VEHS2EHF4eRrhluwUpn0N1VqOJp2iv+tMfMKvgbUtI7KKIwU1N4F+DwEWBR/IAkK+C4ivWyGiLemg5PqSm9k35XIkozJmgZGOEBLPomPvikh1zoCWG2qi+ZKK0OvEMSl3qRNCamCC7jBKmoEZ2ljM8KQIV4Nch3AK2sAi2pTYjSLp9E+FuXQbD3tV2nhRcGRL1sA6XhmM7t/TrIiYSjYfOgQzauLhLtwdSSCgteFyge56qhXfxE5YGgasNNHm0vQKRN+nkKq22o5LlM9dJEnOJTWuBC9g0cG7NJ+mlEx7A1T49n0pj2bL9iLOW8etOPpYQJaaM9CZpmgxVRhgroYh81wInqp0TZaGwby0RAgOIl8ZEo+efQTpilovgqRxz0mI7gtdNFRpBHryAlvRlDkYXpixigj1X04qegD5wWJAtcH2/VBq30Rb2zIncaFHdJzxLiAZMdFMOOUox3fvgrWYpK0KP8L2tDNXaTEgZfXVwwskzHQlgC2duf+vQenr96EnwWLrM///N/+0bP/2X+ik4UKDcB4soZKwLH7kIZl6MlW0VDIbwqPNBGXdLYRx4SEFUHJu4aF18WopBRnJ8Vl60rLlZP8TSt+ti17xOzfKdzrKEA9IFZmGp48OMSDdsc3A0BGoDNF2soGuPGEGSaPX37+ZU47ts3uUuwKi0gsSYQkEt3H5AZg6dRlDJiBKcCEjVNd86CBz6NgMONh1AsYwQOiCI9pXLaxynAaorZs/7Lmjmd3MPO3/dGyP9dbd7c6ufVkdzpcd25WV2+33eOsGZjY9MesPiOOzznefpvD2g5Az0fInF0KdxnQfnd3Ozeq4Eck6tl2SjtyBMq1wDaCwufnpN6wlO+Ia5wInd3MsijRJ5GIYULmxTgC0oSbhkJiHH3sjBIixa12zGnmkYl+lgOVhEcSNpmWEcmgBXIymwcBBBVHeRTtGo0TQY1ei17CXpQnwzE9vb/CZmESgFVOFRVezXoecylCW5aL+ycndrNh0NteeDFf2IxoPJmOxlPOlogOYSOJBQUjmYxbFKv47iSTKbfX9qvVOtLBJSyWIwCVMeGOdgsYmactIzvEDQmVl4SOd7B+6e2bd+IXNZG7AeoX8znzXYU0z2hsU52MY7CJZloJZs8eeUsdtVcLkXWj5dr6ooTagBz3ndw7tmmaI7ePjq09GT68f/LowYl1KDc8Eq9Pu9YQdNtmMFjvdAKKGY6lv6iuTQ9gmik6UKuj1rN8FcHoVeCGJQqH8JpZ4C30BLJwRIam0RYIycAmsqL9S2VH2HRnRSnkiyg1HB1UBBcpOC48mUPuu+tbt/Wo+V1Q5LefoajPyt88UFeACC+z+pWGm1JFvY1rxiVAwAEbNDuRtakdNRpuoaC+/ur1h88e9Ydx+oQ9273qaBVXYFmM1zsQuNayBarNTM2AZEdcTMgONemndLsbyEW3waYnZt/MhIHQj+28pl/S4QciIt/bbMaCUqLn9FXYlXqB8+AgrWLgpa+orpM45lHzOF2vF2m9fw3VzDGaHcUAJE8FSsyYUrweCWJHZ6CbIFEzECaKMBPRK8Eww5+T4FzRh8rPmEdGzY8kw0n6tXSM+RckRjlnCq2gQHDOMEa/dpN6hYS6mQ8qAVZZGpukUcAluHLWI2WTYShmqUc4FGWDpqRXGK5TRDxvKboGFSqOuki/EO2CERtxj/qlCzOfp7xAmEuuIDHNB5NcxXO5qft8FzuqNE2JgKolsGtexrIkI++C5RSUV34XAaqCv+mjyCNRyvA/JUF6w/nu8qgqqBrqdRK5Av+eus1tPf3WR5XmNwZq4EkDQfm+pGpwEJDTxZATS6mqKaxaVfJRkMnXxOm+L79K9+G0YM/EJ+2h8ZWrEHcH+vtMv+BG7tTYXO7ClGmXEqLE2x1+O+WU6BKZwIyeYez8LZ8kZf+l917Jm6x3yd3kR/n+8VLglMxH9+vasFDhxCBWznb5gYZ3xLtLVOm8Q8lCjgpMoAeEPEyKwCGZJSRlpcGgsIoXeaHCKK4Alb7AeK7/dS2y9EJ//iJbMLYnuj+vM8hoeIblFRLJx7fljrLMcp8qy0YurxKVssr8Y6PeuaohwcGTgNCz4s/gJX5ubaR2BQH7xfKLxYZFfdjJNqnIQ3ZliYUQfRxk+MuQurCjfL5JjQoylAk1UMrGIkisEgv7/IJJL2VSvh6hlMiCSyJsVuMBpSmTTFpBC2BARSt5x76Ui5ooVwJ3gWJ9UhNRGWlwxLKaEJFPk9YfpunmbSyzp43EephqTEh+enonRoEPaMG2NvEWmm4uZREIbdqQzW1kyXZ4wbh+MVHjathOR99b3CwHk8uje9PHT58wOSbTwcNHD3TnPVG7tzzy1+o6Ojo4vneIIlfXX/enr1fX2fEzY5/tvGuS1xqKVs9uFZx/1AEY5ha+kaVSXIxVrYUtWzt76FarxLTw7rP7DcnW87FddJa3l8u5FYRM1aizg8NxrQ3NQBEGSiBRp5irmcvqh9MwWXg9ThGIqree964YZirNFTeTxXoR6gyMyuQyi2W78nEic3ADLRnioEiAi9b2k4ZVMKvRM9WITAVDOEAt5m8y3jTr0eNivTAiTMcTqiF5Uls046GzFwJDdhllXYRRop/rUn6gDvypoODGRoK+8zNw6N0zb6OKdBEwQJnD2MHBJHVEwjvT0cPzN7dfffHig8cfiPFRGhiwt6VZCsZSGe7G3w85ahDuIquyhrHyy3JiHglhoLzV6c/T8F64CAZogwo2sWWt9KDNpzYqqkCvu2rN+4+mHYWCzmUwtb4H8MX6hYMLxKM7NQE6qs0mE+yQg0jZYfCLv/zscrb+f/y//ut0bEnAIdobj49MfIx7H/d29+zaUni5jUiFAIWiVLuHRJUBsH4XCXAeXrP8tbOcZYF9t31iAed0+BqJ7OVlOIXA/a7DYoUTUCNZsZOTMg9sZXO/PT62k9bBef/e4uxhLIEuX+TbzuaiNxvPervzGwHkmfByTq2NOu1qwoXZm6UvNLLsDq47f3izPG31PkrHaxNKSqYbjnEgdJ/S25yjBtsPtICMMBtQRMgnUN/bPYCx7UAF5hNsT9QzRRG02g0MboonzORom33AqDfDFuWGrMoUnKR5Qq4rhlmD2N0G8DQDDKgN8juW6OGd7ZEKcQtIYiljCEJZ0gqNwQS2K3TijLBk0Bw7SSGb7leDg833f/37jKR3b84NIw+PjiYT2nE9PTy0LSAuJQBkKvpM5tqEoD3sOMOO1ZXWRuXRWrZTnuYgwPWkPZiFluFS6a2uJ/LRV+FWT2NpeMcoiv4wC5HK2IEE2wEc0Q274+N7Dx/c364W1vvDn3GKJlsJHeXRal9em9fJflaE1rLbN6enNOd0eji/IqHT4fj2177/a4dTa3XEBK2Gk8k7223ZFXo0ub4+N+JgMgkrEpRIy0LigAT1BKkbilAupt446RPvsu2+IWv4lgPldnadAKo4KTadoegAWz08Sey2IkAsvDAaEW+5jCmJHl4RvOWCAf1iZnegg/WYJ3leDO6uaEFwchdOUlgeOcYgnz9zVWp1J7//ElfKpKm8sjYvgvmmYBiGdulM1lF6s4AJGOxgv6zoF1ZpNm+1+evDJ/dO375zRuHl2epwimraFYsWxUtfKMWkED0267SObQaxXh7sNvc73VPeDCyevtGam0wUHApKM3zVoUUQtTokhwSBi+wSvV76ymy70RaLJdoN2BDb3cyXNrGXLAMIbrem6ycatG280Wkj/uSMgsx0rBrjre7JeNF2IzqmNCyMnxMynMd7ey86uv88rJtO0hi8k/mi9N26dQ9bo9HAzldmtKhYTA5m4xgSrkewZMuur+wb7aKHuVeSoSFxNFfMCw+0KeQGGxdENvqz/kGtyM0rL3lUIKhiWAXoolX6nerLrf1T1NreO1WW5gQX6WkLK5K7C4sJpgophRslachba1Ogiz9Rm+MQidaK1E9C+0oF7NQcKD3PX97IvXyWH2LxfXWf01aAxAzZJsujzgwKY9EpNFaZWpJT3r/xuktTMFZVyZusdxyuxiTyP0UGGB+DijHJAOYujwRJmff5f3c15RdaCKmnKoKqfO6TNejJm30B+fYwCK2nVfXdve+faVhK2YNVSdLt1U2KyE267/2T5vn7zwaMfempLAUHtPBpcu6f4Fhv60kBBbqYRdHpmlL62yDdjQhniiH2VdKFgnVV5hSq8OJJmC12YTeF082pBR/Fa3me6tI5YLoAJHsgqJrSpvBTaLOHGCOT8RwRawpSKYnYlgKQxhUByjEsPc4a2/ll9I910rsYrdiChgyVL0VfAaR4KbOrMfMPyopAnHYs/PI9RwCs68p2fIVaaSSMgneB1mg9wZbA0yZxTHzWgSQITR8CEjIOi/ZM98pKMEN5L+35Zklg2pKiyBiAy5K2ImigfEkSoJztm/mR+H+MUWrHm2a4rVHQnUG5apgEdpmAOBvsje1AR5kGUTAERNSIThfNS1Mlc0JfvVPnaKSnt1sFtwoDFcqDwHBOXE2d3tA+aFAX71YpBUyvwFLTaXimCJSkV6xy6VaWSVxLmZQIKxXialgIXba80A4q0W6fYDAnnRW9rfa9+/cm48HCfti99sOHD588ffzRRx++fXUBItR78sETm3vwzVv19/TpU7HTo4Fd6mIcWfZ3eX5+e3VzfO+YKWB7P2uLX718FUZuTP/tbrZyaqq57p3TSQHObxGn9CjxPXo4rAOA5fr6dnYe0oKy1Z0eHCJEpnoaZdMw8/4TVYsLi6UxD0RVW9I5eREM4olIcdMToUKGJRH5DgAyg4Px2B4JihG3BDkpMVwQEsgdwimFAtXvRNlFp/GnmqTfJtg3vKgyJ9tvjurY9mh0oqROpBQHgp1RFwQOHXPqTUl0OgxAIJ9KJAq0ucl93aR5BadXCrCbS2Zd0FZ/gzMgfDo+tKETozrj0XCuPU5mWlTddrbukxq9HBcFHiNYTq7A3XO4mykxPJN/qT51poH88bgXng0bA0hMFARg2UAm5FPoWCvcnQxJ8a0LkIU13wG9aXq9h/9qnWxWg3QPDicIRDDja8iWFJC+Ehwj9GKBJdr9n3z2bz//7LPx4aGlos5gGgwmE6sxOWNlzoC66Oi7wU7QA7mpMPVGlFCsQWaSNMO8wqAV6apaL28zm4EWDE9DG9sLKDH2Skvwut1Ss5/TcHi4szmZPRsXM9tDtVu3s876XMhvbzG032H30KKK657dwUR2G5CwKm7rUOm5I4y6c1ElttY1sOxeLT667d+zO5AdHmnGLBMov3Gvc+HAaIE8MABozzSiVpQ7YsymUhYQ+DTl1VsRdwPSJk5A4gw8dV7MBPowZlZIg7kZ9CiCrcoPEeWFUMa6LKylMU7s+ISeQ0d0rx5a5rgbWPFYkRJAo/A1n6TF7gnHchVG95+ImIrU4bmy2WxQjXls5GXHpCxPWWYJjXPp4NjukKLtA03GHoB0G6ObJlTXEm4SnBbBJGKgp/HAWdY+kUvNqQOtNR3/MeiQSjyYIXogS3kOvri6upmwN0eJYYv7xlxWu/vsww8ePDi5ubz2wF6jGm+qB3Yvb67Vwn+he3Jsrcbw4+tG1lsmC8EcadiBU7/47sl6uzc57C6XNwhj1e98IfjG+XtZcBNvUfDdosc6dixYzR0fU+6fjjkQoLIUnWiiXWLVJgfj1Wa+WDo6JocFtAY388XCwRCGZ/CcYqo5iR7NIAfvhiW1IgiLpgmC3IR1cHUFUxRugqNgKJgikxAVt8XPCWWKyJXE+U6h7utnHjT/g9Hcye2uuYoXkrAeAw4dqIhsAoPmxlUrKyWiTwQHzm6vR6NfOTu7/bM/+cPJZvDg4R/YhwM3ya1B0clKyYBzbCJs27kkeK0+KZsSnFQaBY0TiJuj1sp6yQQUPGTlg/4uPR9HRgHnSRgcH2ynuqO42MKr4calfWgob3YCRiLiGaTGJMgO0/AKmS6g4HcZCr/ehgT6Dq/DfFoWzAcbwWZeyREriklA6OLs85t1wUpx7LY5qw7HmLI1AWYyCC/SE8zYPkFsjZVTouKVSPelDUleFhqwmupVUqxeIILKOEUfFe2pgXQn7R+wclXBsuET7dPPaX5aEqQH4/gmQ0iZtEKlqbp69/BPsB1oyzYv0sB5EnoMPCUEQV6kqwN3c+9Z+LPqbtADjhQbYFSs9uTQtiRTa/7SMVZNAbrKyc1fe1W5+7epOIXkGV6oV4rc39TD98nTiOYKPAF6/+p9irv3+VaE5739OuLEEjX57xJXiwJsbhqbMsgKzip7lQA1fjdZPE4rq9L6Kt9/VZmi60Vz01RUb37uQwW57mCo+z1i6xUUlClo+VEh1Fexpg3NaFuHSUUrVevbnc8ZdDm0MKya+sOAKbl5XUyBUIkliamdd0qvT4ufNFVsBBbojNht4evIfSyPSE9EtQpN66O4U2oKr3eUuxTMqYGt1uVL+eHf1ExBsorZFxw1XNIxNNOklKZDoz/BkFF7lAWMuQ8qjW50eElpMCNyK50Twc42oHaRy3xcQhcCUxGngZC7M+zIBNPy9HNZ9Qg2Nke4nJphTSbUXAdmF3iy4ygupokQUhYA1aOs9I1o7+hroaJatJ7f17Jt66XVSlHanU02mkj4Tv5xgN3hhXhnDGURHd1h5RCDCaK5JRSqTRpY876dWg4bdFJukRVkQWhJJbPP0kawzdfRVpvsOrztfR006zCJ++g0BMtkoiwptlDX4YjwlqkEkfZYNO4BJzpaGwQ5XGUwr3anV4Ll+vpmMbOLfDy+4L+5vjTcYq4cPXg3GE+Ws5uJMRmHcDYmcDjDraw21M4xV6KDeNpiZvVMZjx4dAJevsXqpoHSPjmZ3F6vPvvsp7or4wHdA2xYkHczv8WykoUZiyFyxg7LIzPAel/dX5cF27Uzup04Z73nn2eBCphxwGCQeYybG2DAQPpIrYaQSEtF/qXI/MrLXPnZRIJCQJBVNndUqLl3llPex/ASTTIUfM7cW2cSmJ1+m/DT1eMsTW6fW/LX24z8DgPCeBSwVMaEetw0RehHNC8zLjsivVjuXnFKVecd3saZkV3Lhp1YGZ4iDly4hnAzlWtBCIfRK1GgjuwVKwTmytHIJTa2jfnBcH61zNloiTrBqJm2Mo5dX1yz9VtOpF73HAksrNM5QhGs+h8pchybTygeWCgm3MJIG/cES2qJoIUtg6GMfttLATdIEJaG7TISNQQliFPGnJkkydx+OrvCY6TVEr5cdI4rMqb63OZK81ydbpb3cZPb8915rJ2OpQs6CO515hYeY1V3+9PB7PnlzeV02P2wtb10YNZqNjucGh1yHHh9aWIE4bBNEFQUaQoPN4Ao+igmkwuWms4CtBE6fitrFK1yYHVl83RLTC6pEd0VU884yioYkert9phvlwroOdrZcHBhZyS72w0Wm4NF62YyOuxdXR/sRhvDLdEa1gIMWdYMR8bKJEvI28eQ398cUFwcU6DtbN9sFu/Gw+Nd/3y3m/Z6ot3M29wO3VeoGKYzG5YANATfHvX7s8luerC7mCYkglpEBqdQR3IwgWJrk6kYU9Ae1rL1aLXWK3EnPJX5lctQCXPZGC02DLONFsQMll9rcG3lwv4OB++6Z9QvLYRSYQjjv5TBw23frSj+lL+qWeUu7dck0iGnDjXEkaHx08lmfUtliIOPNwdZ0/3QH+mlEKKYJFyfbWsBDtPpUGQmqbGwuVTa/TPAWJESpq0/omTiIsZe9BxBi3h7Fb0e6Wmdn79br6ft3fF2+y685MCOYd9yecwCYRLPbzPdZGmyY+CuLm/Sllbn6Kg3X6yur+1ybDnKZjw6ZHJ3eucP790/GB0ZyNmHSqiPQgSqZbKls/vq9Vu7i7bb9wNq/yYYMyflCLHxp+nodq9hMh4MUyPr3dyCpWH/8HAyPZheXl9iSun1PlTxbn6SoW/oSUDT9cXgNN4oNEsCbWaqqe60MN1nRkchDXxtPmyteRPo8/dX9Bsi5HeD5MhdJPt9iqwHyFsepXztP1BlbU8V3PeiHvl99zY3Co2BW3/QTOiMVYCdgNX2oHttPEQJGObyA2lETTS/e/ni9Verh8PD7HmQ00r4mwMTKoMGkMOxQ3I08RCaVqvjzfK41TmN3snkKg9FNjbe2k4txNdM7cqcGOHi8WfMYhU/IRPewh5OVknHfVwKBgbwLgOCnnpW5vBL4ENd4dPb2kNGYaOzalQ1MnlST1AdxiJfmsjD90Ee954HJ6Uno6hCJw+KTskd7kW+6MYEAHpukoTmoMYiVnrx7fITdseu+1ILSsFC6gfR8L3TMmiRjgv+SayL7is6KkyCg5dDsPCPecLUMOpF+dAfbgJkDL+Ax3u4ftSC/8i19GlppI3XNTiDeeE9aVe8Q+157IrKrdYy0xVJi9SjdIhal+F6kFafvtw0ePEgPVU4LC/tDBnE1eswZzoRrwqD5kb4MkzpxFMTJVGQakBsnyZLSsiVpvyVq8r3LvkKtmCKU+jL1Lb+6GfSJ009kKSpPt/1qOICRJdUQWGZJqP3aYX0GQC8B0Ceus931ZzUVdAeP1V6U3IqVUaV19T+Hoo8bYCu99WZp6A0B8sqxPPU35RURVSe5u6bzwKjCpc02QN3ZMl386++wo44K/+KKYBORrSO2mUiRP0lc6rPR/K4mhKJY9i0SJIGVaJo83T8nPTpXKX3XmmRt1L4HNLuqkkp2V1c1DEEqAWflCInIsMcTDqXTNMhfcoIWBFhPVe2hDdmSWQC6Q4fx3PORI6FWjArO1CagcXE1G88I+UMZ9eD2zuXlNw5lL7EOiFTs1myHDzHWWJar5oACHLVt5Pg9fU1XtWX8Ar1N+zyrgNj0tmzB8TDg2PXmt/OCVCEOUrfdJ6TNp3MlV3gWVxxodv9PxSxeZwxVk2RAZV64KGAzWzAEhzxVEE/bSUv48JO/AAmAP5nHWsMqdSnJ1YWqS26JHQ+TkAvTUKObCdCrbANBH21MnuaLiEWP0QloYDZWMMpIYUrPRIeL5/IyNJNWhFOkiivQ1xB7zW8qWw+0kfSXoPBDXW+WTs0h5pT/sICORteLxe8zqBje1mSy/vZ749BbuG1wZdTaZBWn8Y1jfL6Nsg326GW8bh/cnL/9avTtddQYB++2YybUDkqhZvlDAsIuckBcG5AdSM7m0WvrckaCnObW55CBhsEYozs6QFfjIDi9YaXQ+y69q3DFcUP0mhuiUBeh2TKhaj8Za43FMawtplj3KfSdPoagdGy9C7CEqesGLFs9sJ8Nv1cLCwpXSeBhOFtE/fUXU0AbbYPF4sDG5xEHAlr1GsogFkS9sPiAb/gvY6FthVpWjKlpKQJCPUByvdXeDwv8DMsEnPbKmlLOkJ7dM25mifDwWF/MJs7xMBWQ0tnMV3iYhQzP5Xy9AdKAGaG3+kd4NihCjE6m2p95nF6vpJgaGN00QxmC9KnaglMZFScMU9iGNK2QNig8w7W0kX7Vuxz3b1KymDUmBgKrTRPcEPmuBYJ1Usw3jxO7ZDJIHzyw7/47N/82fNY7Gun1HHGGnOK6AsJ0gVCdszhMDbAGiiK/9UauAphYQc/Sn9JpRCyGWchpeIdQmhMbIm41txqlji1Uc4B6K1GA86FMqdtS2KvAk5t2mV3MzTpxoDeOZ5Cr2/TPgcC9Gg6TogwrbZJmk42UMG5sk00LmeTi3fvbga3rRtr3Bfdnl0yrTQw0/HGoFA4kxWQ9Nvcit/uYrA6mHQvH5xv/+D+w6F1BvqotoAzsUHir1hV4UE8pJUxM2vgEa3ilxdWH2heM0sGOUgKWztKUqwdA7M7nE6efvzMqhrCa9iwWszoNANC+ocqoyQpDciK9hN+kAEwmkUZRbOH2hpYyq8Im+eaWlOOJRCxXbwRYyHEUIE0YUyhjCsgp5CNhCkGsXvZoxl7RkvKkPXft7czyAwM0XKELoPDcG/0pMUg2bzf76jBojRwAMvXhOvDEnIJ1MkQSZfhapYdZ5EAMC4uzi8uLlUqKunmemvewJQn3RKTMdSyo+XqYDp49uzJu9cvphMs17txIPDSYNqASWCaoaKhROaNuPMHE9OdXCJdsxyinvVR/Pm1v9BoNx1fn1/y+ltt3KDM3XI+v72+0iadXDRPYSOaN5Lhly7ALF0NgK37CM6JIOeLPlOKQnThQbLoirqH+6A7ElF8rg0Rh5jaHoRc0v3cVU/3z/KySVAl+pXv/M/TlBLMlE5QWqOioirSiYdKkBqNhkOM+q5vrn78k69OL85Ws+snv3Qvmz/YQDOm812VGhWzRFzAsN01P0amHMAxzllRKVu5BnpGhuLv6WS5Mo1JPnAMf03aYyFAAmyiVekEynAnAJuz385mZX0WwIkWzkwegiJVumJtSJdwd6lLfcVA1eAkKAWhZGhzH/bC8UEfbOsMyu5K4lwRilhFXnqdBioO50OW3nj/SJmR/+IM3bL+JTyfjjUTS0FycqfDjkYjvdKUDY3rmUxBKguCyoXoYFuCpKdRCk+UTOYWUm+Igf0CS2kBjXVr4IAT1BVbUFWA9lmMVe0DbJHSwDVt4gFUMIWbtgAOulJcg7zUmscpDzt4qAHVkTQYSfo8zSOVpjwFyIVyftbKF5gJuE2GSvHXfKTmKiDwBhpX0JW7qqXy5Ue9ybtKk4+q4u5FpQsUbipF811tCibzUPDG15WuSZAim/ffvkm+At0r9C1mLTorpGqXuXJWSYpVp4+mhqa42s97tz/r99tYaBKltv0YvSnDvjoBvIoKfZKsaXxTJaUQlk4tIZO9wmh+w1Up0YgEmY1mCiO49AEntIyXF0GCyOg8b5wyXZHrCmNSY6zUs0skTEpOd0vEkzg2tZK9jp5Ku2NEY8pKl9QsWqyYmT7p+Vps2R72dVHo7AlPY/6nP1K+0Zzoz9jEgTDy0Ntk9Q8YDHlVTQaUqu9wwyMvlX8Brqlf/CufjID16aHocX1ZY++Clm9PJ2GaX9dj3kCaZIk1zhM/BCeHhYfCOAhN3NipSk+VsQfcaGFZmPoSL5Kr25kIld+1z0MF0eRBkqCddCo8cYYOcdUAO7PwWpIBVWCNZJLe7MhXUx7GxCIyPR1y0rf6LFpIzhol6SFK+tjF6e5C6BCxWyNsfhI/+m8Bjvui6q2jGo16g8hqQAnWUrUyQrONWECeybfcBrBfUho1pFW5Dz2MnahRfMy/InREqpVgx9Fg0utdCM6Cv5zlubVvzs3zL1/+9qNPFqubGlSZUjpYra65G7rdif5bK8Xd5kq4BAe/tbrMRJUxmfmEHt87/P7VxQ2TlPEleuOa1Y+88U3gB0My0FsWzHYSELO9vpwNp1zCxhUYOsrL25/++CsRIFBOlWc4t3zUWg/bQ5gpSsKwNqtQw7S9riA5f9he+VjSl5tGa3vOKPI4FmQEAx93bjvdWW974NGuN14JBui8tUlwu//SRue2BkzsReuWSub0x/uQmMHDnWclTG3/43TC4bft6Grdvly3Vgy68HpUL7nDWaJF+H2n0cN2dN4MbNoDTu2ImGc/YzFlr+pBqORhwM5dYHaVqBFqhM4Iz+CLyAps5mocHXYG14OOwB8nmc2dLvqh+RJu07BSZSeXaWhwK03YXN6QPu7noLKGKwDVFmyrlYkSiYiZK7D1Ho4hY15mQ1iDoQAWbgyYdavEPEykeTGZp4US4yqP65nfbo207fTyn/6P/+A3f+03EdQhq6TMeMvAMvrHMI+QjTsffOeD1b/4J8ODrVGk7SUXo9n9+0dUERurMKNIlxKbrz2SCpp6tLJyieXwEkHAlzFyfqM5voI++kQbOQ7oN1rOmAQeRMEN+HcJG5qvtjPgDAWlTUe9g/VgPLYpzup21V2tpu1xbzV0sIgVYjYuQXdO/iioQtSuNbaJoU01WNdBDWeBcW7rdN3iHh63nHm9u2pv+Lmd8Zm+mcfe5jTukHXWt1PN49l2drM5XHx5eXv9+uh7v7l58NIBJdiWCSpeBrGIbuiKIRGE39AjK6OIAnWObGaf2D8xHfxLwFhD+11rxuthDmUympo5kskK556jbY3EbqmgOClgk4QiGh4Q7WxsbmiTvQG1Mkx8GuRj59hEYCg2wFtsDdqH44Narri+jZUeGt96SQ+bCoAFxhjYpGS2mO7Ly9ADhCUQdJU10SGpQiKg4dF9iqoFBJmsrjj4CponWIq5vDw/O1PE8bZ1jVGFpxHt6dHh7/z27xBWNDVmkMve/w7BlmMfQIjLbflqMX0WfZqnthMR9XLrwK9nH3zvcHp8+ImTyzIgoRXt6CPWk3W7m6+uZ7MIR/etloI7QViRS3tDneGvnCif4Icc+zh++kgSjQVkRiIcILwZtWyWkWugFY5EgjL+wBzLKuyf0sykEoq4iURpeZCW7p0FUN8ZOCmZb+5h5Gr1CAS7Xu0iH4QVTbAGhAfBwbDPXHvff3Nfn81H9hJ0FUX233f3eR4AESO3KR0kiKj7ay/C1twckGxhUEu8m1Sfff6X726vj4bPvvrs+vJsce/esL11ukJMWIROP2EXZWu+h3apPTSKaG0M7h+3uq/TF5BMcfLhAtZuRr30CU5APhVz4QElPQNzIUuUOGTSvS+2V/qQxCwnGUWd9xnhd191+ot0gUEAIIvplMPei+DQNhEL6IkaUYtuzyykEmJHwZ4IvNc+Tcs1aFVXINIZGIdTurFsg+0QMHVoY9S9Kwo15nE4RcPFpmdJQAL4YtroOFa7z5nuJjaSVO1xP3ylDAYCHs5Miczt7MzGqkmVmKEC7ZI+HUrUnj/Y8DYzBvoyEfA09uopXosqiO9EQe5EvvHmxBUPseCNmpU91ZZgB29Aoy31YgEoGiB4UFFVkJzSNveeEZ3oibwvVCJYigpWcxFcb6VvfpGSaKAGVYhW3W9VnrRJVrYxXZqfqw9CjsHXKRokRc4qCeCMgo9UL1veVvUp4O51QRvcv39Y+2TuG9F0ULWlrAycBT5TTPBSV1oO8MoMP1XBtz738KstD5kmMjfSVm0IHA0k70HbV1wv0pq/5kp7coUy1ZSqIj+b8up9gdu0OL+D/fB6wQecILWEJOrV+Fia0CCMELyBM3kkYRHUy9jz6eYp8ZQR4CIPrriHg3ZB2ChaD5M1rF7JpKSqkj59hMwFT5iDARsesIkozufQTWxNWA0IOf0xSAsUeZZBRdgaqxobGkgAEc8FhkBGBEEa0LM+wV+hL6BHGQXgtL3QQZjiRS5JzDP6PUAATukUbjMIBnGYPDsLpC/ORCu4ARJ7KEabSJvQXposYcl4Qy3p5lIZqChvgwoBKGVCLQNsZAqowXJ0UbXOvZxALmRFUca+9+WiKUs0rQoCaGYqmi0vqmJCT8alAli2+6QK0wHQdlqTcQHICntI6Ymtl+3YS2V6KhkoCq2hZEzYmOBYguORC8u8RiPywQhQowKyRDh6LsQL9rWqL9DBUSZZnCjreDi9nF2fXV69uzgVPT6/5XUWNe5Ev97KPihM90H6basalIjSztNZzumuPnvRjArcjUfT3m62ngsj5pRUbLWk05tYZndrpgHjBeO4Kdo8zGpKwehJh50JClHrYbf26vlXn9/cXg/HwkYx9jb7eetFUBPu31/Kljr/U2S9CqfkUdTNnsm9ashZyFRYguMhtLZs13rsYPMX7aCYhWKgZKxm9SSWYTPktUtvYJyLWFF/qYzlSAtj12iqBGOLOb3X3h1mixoNt8JE/lAWN9rB2rYtmEHDLUCcKb8KAVSgLus7ELtC75KsaqL0obJP7UyXEnvdlAOBUsP29M3ZZHw4Gs46nQvkMLAUrrXYXI+34v7D3BLi1jQ/CEphBM86s3F/Ml/Z8xRxgJt+LPAEt2yQ8qga8uTs7fAcDsPdelZcXKUE1AIWVoPZu8tjXTVhiozXC6nSGFUUgVaffOeT/+3/7n8zn9sv8mY0cBp3WtcfiHjGJarevDt/86/+1b/q9afyfPrps48/fPr69PTxk0eIgcnibe9n3wVgaU2ACONXBcFcpLKeNn1lYblJlAYSWqGHTGHEhYeK4kWVbOMVHFtzd3VzNrs9u7mdGyUcTI/n+u5d92aegeHcqRRbUUO9e33LZhxjik14pgc83q2hcDkbZF0Rd2o3WiPqlg80XWm383CzsfG/Sog4MzVbKgEaB4UDLT72dDNx2BoL0MFf686b2918u7o6aX21WtgUXeSEsGhCoT7KJIYRvquR/QCchhKoms6ewcF4qiB404DZFahUk32HswbAOev4rEfAB5Z4QBB1B5MGgltxY9tmFZayAqTgdn8wynjAbxEyZA5qcUoYtIiOdqKfmxnauIoSgiglQVBXP6qe+owKbNgkfXr0EWaiRKBf1+AtF9FsMTfNYzaElyBaTvkNSbxWNwzQVKXDAVzhFZkHwY4LcSh5hEylZp2BLZCLYKzicKHfzN+en18K/hHiBQ6rSCjGHEDBIcSzbyLGAg9RLL3+wWS6ssP/6tberkq0KhTPv7s8f/LoyevTs8zVWiGgolhXmXCmgp1LkMVlGhwnlw1frVaxh9LOEpvQgoxWfyfBsmszVnEdFKZgwnAvZQdwYxazH+PBCDe3tqiAK0dU05xrRHhqehByFy2dZkaUEl8SFAWZcQKHj5RTK0E8qWTNB4i8UFndfOvFv/etjDLHqRMVFx8H9R7XgBMcBNLFC60CCtOuSmHn/r3jxzwPtzdnq9VFp/M4GWucw3AsKOgkc6EcakIWaSuzbce6/Qwk0rZwdFpIOUdC03mSvoyvYxVQ5Rm5hs45FE2NiHvUN6zN/LNf4jizfVz6xkxoOeKNtk74aBwnqs9oH0fAX3pVbFXYUymPRxgUsxd7R2VSRgEkQfzxnfEnBgURgyDTjauQHkaFh8yeRaTxRmQjgOOHcV+QrD2TTLrGOUp3Mg+svYmaNdJOCaEQVvFFdGOpm06x/pgMUoYkK8JDThp5A2kwWkjwJPrOcmnzbZlHFbCFw1UjAfVGq6cHyy5nSFAZC0IFhJ+atpedFlDxsQblOSzc4QdQDevkHRJm8YuGmmgOHRSOB4PEbIJRBaYCrJlqZYVreMhNA33SBPjCdcOY3+LMtAwuPXEHk82reupJgRvuCMPnVdJVwvoVSCtpHqWgfEnc3O4/80IRDRSV7P0AIOzRlOmzKbE+VbbPHII29yAoGANnMgXWGmzta0wL1R3c3WXel/FXv/YlVfPu1uw32VIs6qe7DQxN49JXRnXkQRWfWxpSwbHpJWyv54908KveS+4uMBRFwBG1GzM0t02m0A0/h7/S8gJVl48Hae6gOe1Vt0LML3ntrqk+iQOT1wECf9JQSrfuhYwl9qdSglFVnhfIsX34kVIsSzEdjDVbipEm3RfbDy9jR6yjVAxX7QNwxvf6KIAFcqayltgIQ9M4aaQT5p5JBraBtf/MdJbnA0K0bZ3GzymdehMPQcZk4aIW4SMb0pNKZ76W/08hcQmkQKausUMkIeSCESuIbffGMk/gSrod/uk4B4T7xvQLJCrRD5O3oEuz1Rvk6+BCL2LQqDJwdBdcj9EmMFDeAuDJTSGlbwyZa4zPZxCFmxazn3fLp8Fo7doUiSvWKtzvNUhxSFFy+Lp0SQxobZUplMzAgh0uXyhTTM/YWY2P+lkWOLAeIwEZhw8feY8hnn78+OIvHcK1On0763bGnGVCmXVDAW83n04nEgPLomnKhUfg9MWr2MVRiOms4MJ8eXt9azNtbtLuyJgndumDJ48tS7i8uHTAMA1CRdTwjVI30ZLTHAFrdh6cMqWX7UzOzgWarg+OJjypmPyD73RfvrpYOHZCaqIROApp62dhX6duhyXDVf7ypBAVhMFl85sjKmYUHAQNrKHl9vFis8jpv50Dk0SzsWBkZx9zAV62dwcOYV3ORo4S2ramm93ltnW46l612pPt9qK9Hq+7goNHW9H/rYPsW7I9XAyvbxyDuIO3UB7BQeMjy7Az0zKiyrdryBy3e/a0L54x3Oh9redCGqshmHG6+Djac74TyXMPUAixCmUUMU9n4BGFvR5PLUYVApuNLbAfPxZEP/3k2c3sduwk7LQcR6JLgnlj5OILndxyPuy1Pnz8YHQpIm7bMzkjNvpG9AVbDZ/AbbYjcfwtmVreWomKJPH+0h9hspwdy64xkItaUEs+XIHTP4TS9lg5rc2DPO9dJEWEBODdR48e6UkUpo9VH6DyZ+TnK13m8OXrNz/+4mtdqqgJxtz5+YUV49SSxTntzlSnkuIhFw8kL9KG5rn8rEo6g7PoJLSm4pI2b6LrNvECGMwnB/5JBxGgs0oe7pbd+e3y4jz7QIpQky1MyMy35U/WzFoqcuKU2aOD706u/uV0N90MJBTCNFgddvsPT3iTxtvpMoFsjDnxyoa2WQVslf18dTocXM9ah5kGJGDdd7vdMyG5dTSbfQWP7HIu5HxgtcDmst+yI651NuetwUe77dF6edEZ3q+T4wzm4xlJd55/Zh4IObmwV6FW+BMOQW8t2OwW2R/GqckUjmfy+vbqcnmhDzjWx9vmdrMQbAMVKLq8PXLK7aqi51l1ZC+ssl3Nbk/WJtzsM0ZSs4VY+h4mU0QuLtUMrenO1e1iPLRpj7M0zBvGwJlMRp31dOHsBLTMFg7ULEaB7zJNihh92xgsH+3m883y1Hymob4BDLeyKopV0SXDp+g+dnWYKgDE+hThk9AHwUtLW/vP5sv+OO4ZqlsSjvXJ6OD3f//vcEkY5EQ3ZFZke3h8cHxyxLT/yZc/ejI54KQQzjUY9oUwcmNr0PG9o+9896MnD5841HA9E6yzuDw3QugM+T/WW7sADaf2Cc14GsZAFdUT2xckqOFLRusCzvQybCfIgeSCWmvj0aBxnBx37+je7fzKXGY4MigxX5IR3XQ4MWlg62UqjKlqlfGKf50mjSbkb87UCGyXmdEwurJR1QyNyPLweHpVn/mfejPOzIAwXQGU5vOvu5Qnrz3UXfvZgLuk8mWWmNRWpYSFOFgXRAfUNBq2i5fDmgQdLT26Xjk9ZsGHdru4/+EHg9HUAiXOrghfJskxm4Tt8dRgeTs7n8bjvzrZbh+1+1/RbjkZN50V8DFxOvvWdsI42HZuCWGpCc3jl6x+vDaLzSo/poCybe6VHo/YZnScxDryVGocQItm/op3RmnaRjOz6e+wEhNFGxHOiqTqwCGM2oYWcaA2ROOXumPAspcUeLg7SmcVxRP0Diw/3w1WY122kjKSYbCDjErTR5ZRMQ0G43nhYYiDKeRq0Fpw0PUgLB2Vjsp2WGUg0CIYPlo9o/B0rcnlI7Umh8SeZEjfan2q/N7kK3pvdWteCJa8ZB3Ro1QFwyZ0wEIBMnmDRskE1fkuRShxTKqe/SqUbrBUsFVywKcny+SdU+4ptihwqcIRMYKiZcOfaJbpfJ9CTGPWpfOpjh2cfqXy5Ms3GAJ8q+Ji8iRs1ry5qzipAnZr9ZG7Xf95ftXLJqn7lOBpfeZN88RdHvtPl32Qz2bHy2gYaauWfMQO+LnL46bwyrx/mYdRZAVOqmxgbdImfWWpVHvZTka//72valWKeZ8tDAJ7aVpkPOZpjesQr6zgVEr3N/NAjRoAYZEShDG7EwIQWMMmLnZKDFhUcgX1LurKEyWRglQeQ7xJ7jNcWjmr2TJ5lgcyVIs9rnJiyKooY5V2liLTk/kJ5CZwPzmrHFVHSckvS9AjWxWS72TIgFJeGQq6vMSVhCkV1oIkQq5p4bSgJHhxk1+pIBkZk3qa6v6rKsMNKsD7MHvGrtwUmlZTw4mlwJ40AzFRV5ir0Bsb1KOaUA6Qe0oaqmRQm6W98fZKr9JMhpfxWjCnCI8bLPvKb/Aa9RcMhhA5CVKazIqQgWAqVxCBmloksoiQZZI3AHnVtC2lyhYo86HZIWUG+nlSyQpNsXuSTyL/7waQ6a3zu5IkhSS07CCxkniALemnwZdCh4PxycmDxewvLYv8F//sn/yv/td/H3BfPf9qs766d3BPhzm/no+mY/4O/RPfl1VwQE+TUkPqoQriIdDF9gb3jo8YlzhCa5iwGIBKsolEbCsn8Oot9Tu2g0xQwhLtKFORGCESU7S3ffX65VfPv3z05AEi2lD8l7//A4seXr94YdrH+pEMObQlbW2aVBjai3ehriBKkkqDtuiVtqd3DEVI9bq9YD7ZrBFsKycCjBgjjAPKEAnYwm46FicupKNGZB4PuUoF7HU2I93LwoGXnXlvPd5YYrXczjpH9g1p39hTNFVmmohSFWcwOuTfKWdoxxqKHD+K36NF9TW5C9+E/pqAXWArI6qYG0BnwuEL+yV1tqOh4B9ttzRiOJ+vWSq3NjQcdO1Sfnr6ahWTqPZWIgLpzQJD5BCLG0OYaE9HqKdeLXb2ez3odIdz0Q9C0hKvcuttiQG8sIaz0ESUjF5eC3RceEyfCioFu4/oBebUUJ/770zUQzDVWpU3rzxpYNHS46NpwisWGqi6WHg0BrYInPqyduezz7+y8CfTUS1462d7vtbmdnZzeHSswmyrF1aLheBfA4G7PQfkLp2O/wow7G0SsME8jxxmYEJzxJJG/miEmAe5PLcvze3NO+5a0UC4cW3NpKmhxS6mbBZB9i97F2+Wrw8EHmwW3RXDN4555uHSLpBd+/93Jv2xOQbtz2wDmJZOdVqNu+txazrP9s1hxe7WSVtmlKghboO1eSJ7kAlH0SpAQLlNGA7un6w/bH39aNM/nLIAOC6rWdXOZvybPhkJVIaTY7E0jhoxkBYdD2tQKHbdZKHtk/7n/8v/BRf7j3/4QwuRX796dW2A6HgsUhuxROtlpy+iLG776Hgdh95jayuk2TAbeCocHrUGRf35GXrGhog7ZvPVV1++fPFSifAomJBgL6/OPd8trxdGp6wE6jKDR3nBGip7tJ7dXpy9y8pkRyvXomb79TNGFBstkdGvivaVSl+zyhuu0RTAwdvvXLy6mBu7ZCsIlVhTHn1goRdIawk7Rt9Mm1MIti2bB4jhn06P6bvb80s+1qZMqumAR8NiZwef7zondgeKi1OYqtVO7RvnVGQynLWUQJN0dLWxfXUXBEpvkFVJVMR4PBqYEZUiGgb1I3F3/6zj7tzUGgAoN4uWHk1PInCDguhHVAwzBEmuF07SNeU46axMOtWulLqtuIfTM2JteKE0YkCW9zo9QGAzJgk3B7/IUixfuq4eFM0aMfwFnw1D7V9I74qk5NtH9UulKiMsKK+ptm4CDwECiS7AjLmDi/kc4XN2uzGNst68efn1T87OX3308eP0oU0frVfT2QasSWdnYHideKxujtOI/qNS1BiGDlvz/xgYpcqgEv9FaAJXJCoaKJPZkEpinASMWWvfTx02kW169yhOKOGmC8mwdHWX6eeMNeLNq/Y1zUw/oIJCX1qZavwoPGbEW5dCGgb2q6AKdqREfL+VXpjXkOjqgjqNTT9TlOBfiOMwQQ/h8RRSaE10UIb1bP0Um96CPqSMo1xtu7yKwGwtkEtHD4DAF1bI5UdUqFwGHYQmxo+uLOrUVYOcQhZM8BeUGN81FehRvsGMFmZWRPE1vAqPBTz1eavsoKKpKSC39IyQmQ4rmHKDM4mfLCwi9cAJkHVgtfdXmWSI1MAX6EPVAB/kpbxqRr7y41vv9k/yJmmbPG6bPG5KHvKyruA6V9X/Po2bu4zvnyliT1Nf34QAJeddIU3a5rMB866UPSjgge0qO6nqf7QwhAXWu3cFUfMRZ88vvO5KvvuuMhpgYiO5E1URl1WKb/CD6nVkM6TDZup0SRyMRPqHr3i5I5opMw99h9aSU/jzpxLVrinKTpl4CPtqWdPg0h9FfE0JC/gXhkgzpZKo8RYEGEGLPBCSUXZqijvETZJiIr5hljIZJZH7C3BqCaME1eVF6KyeRmEOXhbmCoy8w1QGPOGqeAr1Pvi0BrXRJjp/u2tmrmAcaNVOC2VetSJE9Q2jNxaVkQ51KCxKuaAVa6vY+OWzYU0kStCo3BFYTMoJIbQv53NnwMAXpkoAlYxFx/uTLCXGta6l9A4XqcK11lOpCS6B0WFQdfO4iAohbWce58T0z9IHFpmU6zaarPQ2FCqAdGiICMHs2V/wFCqpBhT4qlpSlUSfqiwtkzE6Jvv7giejW9Hkyt6Z/6nGK1aipEOtSp0i7ObBuOw8DzaUo4OpFUDMJeCbRWGRa4wO9Z/9w3/xf/k//1/vf/BAjfPZzfHB4W/86v90tTj56Ls2KhlZCWfxhXBOeIHtyJNyA1xYrj045V6YbA/NZJtnYBoYjbCmF4s5u9/uotbXUVg8XsYJ+tvbhWWRbNQEAfNdhi952hJ9Tr1NlsvLTE3ZoNg6u4GOVkvFJ6R9UNC2i5d6SyWFk+EmmEnrcGX6x0BYOKtkLHuTmVLlAHorL+PgZHEeX+y6i8lBq3dvt7rX7b9rbx+v26936wfb9tvN5l53dNVZH7eGZzaGb/XedtaPt/1Tq37Xg6vt9qTdu+msDy/O/vzLN46Fn4/HU3uAqBQ+Q2tH8lacx2Y5v7nYvXxxsbELEOItHiaIc3fB6khEXAQoujf/gkZwRz1T6OGY7RXX0O3V7Wp5O+jbdfEqUmJAZZOYjTNlzZPw/nbOzi4eHD9cLhYDjtngJHpDwZCgyeIOhmOx2r2RHfFXxjHGJ635XPFMXVUnyr5RGCrVl+RQs0CVQjLQDakvYRWA4arNodQ51idfoHaVv7eOSW51L/OgCIGaSuhsHo5th89cy0lMbWeJKif8F1qQeuFkiz/9kz+JPqMVhge93tjmlCfHJ9kSRK+eXY8OlRPk+FJj9SipNzTPPy/MF5V2U0amvUiMtmuNpo5G7esb+LRfpIpx3xMWszbRCaqIRIin2Tk3MPpksboSGr5czu36v7XXT+fizU334/HGMs/Rctzuv97spjN2/2S0HWaub7BZCqTtWt2LbTdTnJ3O0gzbcMavP23NiPh6kzVF7fYlB3Vr1R8NByfj5aPJaDKY7o7xlWCG1ao3PDgYHAwPZ73BDGdeZAdSTGv5dLVQrwvi9PssH9jjqWRciP+rFRqmBuwJkm2VItHlynjy9JmNcb77ne+9efPun/7Tf6pPYbCmjVFkr0RJMAd4wyGVf51TiBWyXL25nX3V3n48aB30jt811M5omN4pLQrVh5PD88XZP/gH/5VY/4f3oyWCfzLXPveJ3WKRxFgugkVWowDjB00RLzr9K/ELZgzYxkiBgHLFdxAxCLu5KTZLh2JYbO5MDZnYsP7a2nDLqGJSxY/gyAGsevyw9eTRAyvwU2EjQpGdKARHkn2dnYhb1zdnpgWgT1a6x8YORtyTg8H94wdsOSJgOETUnEFoHIET5rP1+cUNNQcvmF5Xs3N4ragvm4PFc8Je7w5HZ8bj2p3ZCQgIHtK/YEoNQiCjmaEmmKjrbhc9Y39uFv8PWGV2ZTXfJvIRy3c67yKpOXR7c+/Q4gR+EfalU/Cmi9Vlp81rPrfBUkdQSdzpPBLMLIxq8RVCqk6/n0q/+YTC/AKQL59oATBAuv/W9S3ff6E9cCdFx6REk1c3wQMXcqTD6Jor7UwtVjfxuLrUgka3W37iEEW7fB4/erpwcrooxF2mO+xNXFMZKcGmakLLEJArfLG4t1k+6HReyh/dUp2ZgDSh+kxGfQ5Qo4XYLc2M+ooVrS8ND8ZhpWvsn9LlNrdjKS9X9unKuiYTNAZmTtCyGYOxBM6Kl8q+ZyasdgvdblaLfAsF7BGjVghiKnhMGcUY0PpsTwzPQRgIocTF5KcrGBHciVoWRqbBq98MeoJuPUtcOBIrh49Zhc52zi/FYeIYHM143pDlYSDpv1JZdEWiHZgUCcrLsMc0EH6DHMWVym0gTNHhM7TRPIaOvLGXOpun6eb0szFb0ufJalLJWDN1pm9OW7n28Kj0ErBmMjiPS1RcAg9/dCEqAydAFhekci1UX+SXVgln2MVOHbRbHZIZvBVtGJNC+9at4XMzoM1pRfr+wrZiItX7K8DXr1V2OBT3n9/NHH7V9D6h9OaIPPP+jhtlAExy4K5vyix5S/pvErNRX+xr/OYreZumfTMDIM9dgobjm899uvxQT1Wm7oCSRzU8KnEPJhWwz9SAlBL3ie+K/kXfd/U22dOmZEsF+WSrctjZ6K1GiBmxoD3bN9HS9A0yKjO1gAD1MC4gA2cZRmkV4nkd8Mu8aLDjs/kL9MrwK9wQWPLRNM+35/75HWKjcm5TQtOQppZiRsITpxrVZRsMjNSZ26SEXOmDA1vxChBAq8biMiyptIZzi7Ok065KH+FTb0Q8G2FhWZ4TwwkdX5AfG57KoULwfOoFXrKqXwcTSHIkpL62pDcYw8xpcRFGDfvUhD14IjIkwD/wxUNg2UFaGdursBGURjEHhcgBj6TS2J0uMIlMHTJg6Sl9PiSZc6Ks9MTqYMVkNEyB6AW9KTSmojSC3rC3cTCZTCGBBqiPdmbcZqOhBBAhXq4G5Rnva42C9sKZNiE63ggjaDt9keSUZ3CbS0VBaXBdLczrBiPBGPwH103BOfszYR8WcNMgExu2bbb/+g//6Ld+/7c+/eQTk6yL28X11e3R8eHBwTh6hIHPPK+eS/cT9Kkqhbv3ldYo3y54c1EqEMQc0HnjiNo7kyN7Iga827m6vpaH1tA4n+wxSTMsaW/mt5s//zd/8gd/8HctnPUwczj2DNJvi9VxsA4CpaamOYXV/PK7nqT2ggQ+hCQlzOAOLTQs+IWgtNhlg7nTV8Sgt4bzznbWmgoAWVnEK4J/SbkOBLY6xCHrd/s6lJEVEFZyO5Bqa7LAsVQr28BAwsihz6PN4efz2/PNKyPBRWv1lz/80WT89eTgALf8+MdfsL3xwVBRfS786+zHGb6tmGCdGbbKXCqYg9hqRFguxk1wyksK28UivF7jwfLWgs4Jx9lovDMRIBo2nVeCYHdv37357kefzme3B6Np0SRqu1EACuelFo2gSaPh5Ma5piW2a4ehJrITeSKqGFJpcFvCUWgsBgw73VG5EP0LP2o2g4e+kB3eK6jRRDtI8HSauALySyqZUOw5P5Ab/Sy6/Yu/+OMf//CnDFsjxPFBdnYXn2Zb2+9+99OHjx/gb1vyC7myn9Th8ZEqitRRMnf3Ko5a9kB/ShWoi/bQwUUCt937D+1l2bm4FomxW9kRUuPijQeXYX8sU8Na8frEcblglpk+N6rKxLgtlR92gX42vRSlc8VLbzTqMMKO6NuBxfSZwbBRUZYFmKzMxBGZ5ykINvq9Y1NLPS6MvMzu5HgvkQs7uyH2Ttb9E47k3XB1q7taDMbd7QB3tQQVZGoy0XXKBkhDRCwdisSKg9L01BnBxzIPt2tH9vStarlprTUSG5ZjemeO1cv07C5SfH2tENJUbsJk01ioZqAEH7RSojHnQvW6O0PNjtOO1SMywSLtgV3PDWNWVkHgouF/8//8by4vbzqHMcuwlvdSgiS6l3p1Dxi//Q8b00+UpNgITVeCQVCdvMutLhbBoQnEICJdalnjlAR6v8CW0YOgQQPoDMm6s9HC1mEYxfSUmUP+pu3mBz/4tWcfPL68uEggPmnoJlLIvsV2ijt7e359JTprPT0Yv31zPRntxMiZGzGH+eTxfYaPA/UsklDPweHB/HZ1fXMrHufty/P5an51cxWoNCT7FaeHxS/RQ73ueERNWkvABI+aDUVKJooB604+zAR4A/RRb9wftSaDrnhC216FC4hJJC2amkhkinBlrzN/o7bNhRbt4TjRjzZ2zq7L2btXoBc3BVRkQBjbT4cVlarmdPlhCw8LCljH83sVmCeBrz7clGgnQ11NspTiZ9OQUI06yc/YoplzS7/iHpgZrXBm464Y0+E2DWmPhodWq8xaLx9+cHJ4PK5JeyVSXnErqBTeDLtsALHdXSm7OzjrDvhZ+D4iJoqOzDJJIVnywBJzvOAgLumDdY8QVe2iGo0MdFKcgTDiqdjLgM+eFUTjqUsDUm4s/uqweOLjZoqCVSOQUm96H/+oX6mDRjkYMrJoa0PRVBpOjP87/qkMRMOrKuRTuL21E0l2wNPHyew7YhSesDoBGnRq9LvQy+x8eNcsZjE5HUm0pXBkllHVFuvwvRlDaG0WnYkD0i+XoMNAtRxUgd/kuc4oRhaTS52xY8CbATZmwKelOLigAkkUVOZyI/I0YDwjCq0WhwcJCwgiTcrVbDhXRRAR9S2HP3UnQ/5DZjIHmqDAC3zuB1ash3IFwMJdEoZ/CuLmcaXJbYoFXFKn/P1d8zs/v7lSb8q+qzZvily+A1nzM09TXYMfJdcbeX6myBTjgdr3A4DwaJP1F38WfFVWJZMbKB4mV73DrndpkqxJlbL2eMztL7yalAWLaVsF5+zhpijMBcrCDrUd1g+vIj09gcxIGYYsA1ZCSdNMSaJfbfBXgOW5N6EKJky5vRf6w0BYqdPxKYIEeFSlSFLE8qNu75q1B0qy7IRTujmNKyEp2mA3vQQ7MLthUBWZq+VZZQcT10wd4iqGGEXBwWzTGbCaCbSoLvjiJcN6OUJL7mT3EGwAEztO9HC3A0RoUmCUssge5rUZs95IC9O6pi02a4OtSLhZKPNVxKoQijeFeLA34lrIaBmmArwbH+rTTRPaaplHEAhnoh9kr1473Sv2DgC2WEGCWOYx1pvn6ON9XsYTDzEaXfulqGLd+5Jk6Xv2cpuaQyipKPzqKXmJuA7Z+6QwuZWaipNE2mA7RIKGiFgq4sb3Nim01nOyC/PpSj5LdidTFQdk+KF3KFg9V3qV81zr44jwL51He7f4kJ9l1/uKJ4HR8vzL58vFLSP7+vrSKWk6OEfb6MJokf70XW9k4r1muwMKbWt7U7qHjQWu+gt8wRbTCnTBiS6A48SBA1we3Ne3N+x4W+SJkAwMHJuDvr5/kcMWujrvtQgVZdnfYbN4+fwNDDpsK3YJR9rIxk3UN/z6DHL2OPJdiCrecV+QhPfhihEp70lEZ20HxtgpfHGCN0w6XI0P3x1tbzc8pLY3fWxaYdt5FNfp+rd3ogkGX2GY1u6+TmW3ORA01e3dV8C2/cAYYtc+5Hu1cbvmG+kw9LrjX+m1PuiLDrePknH77sbwwKjp5uZdhYNMDObNoxqQ0O6soHXrLVUcfZ5Ne7AfTxYBrv7D+jPeoLCTtRZpJd+g0y+iwCnbjnFJX2z3du3w1MGqdf7gUf/NWzbB7spWh3G8xhmtTDiAjMg5XMUNH3tXfIbe8+hwej27STy0Wau5V7phiUAT9gmPBo9+KiE9sqtkP1/54YkVEcUYVYvfKknnWg+9LxVcAIRnsYsdVAbgMyMqqEmEUQBWkVh0HHg1X/yjf/JPzt+9mxwdEmk7bS5tuC9qaOr0zdX55dlo7PyynqAyfHt88gDLRNCCm9ia5LGkp5qawXtaQG+GTTGknxZc9rofPnt2NL89ffm6f9Pd9C5sXZ+OHTUdAmATYAc03fZW2wsEp4GG5h8GV0fLV8etaWv9btKdHG7nw81JPK89G5osjOp6m5tB69hJsp2eXSUnq915ZzXa9W7XqyH3ZA7GHp2TEAdJOXk7jrISYzCFw9vT845cxmRXYtF3LaERJ4v5xcH048GUH/6403oTLZupxkiPZgW3ZWLgwJyZRMYYEpgqe8cROV6KrmOZ4jNtPTMV2x+dEQKaWQivSJqHjx5ib3NuFp6Kgy/DJlrm+P7xdy+++6f/5k+NFqCKmW1F68OnBhTX3e5YeqMh3E8tkCmznQq4vZm9ePVKmJbIQCvH+PIl46+CORsNYNRwSTAf9YU4mB/FMR75uzXtZOvXDHHTx3kuSqdD1xxM5DIEDmApIGxjuKSZ17NbCs02V2jttDsKLAOJjcMSxOlf3D85vn9ypCHOioNiZlF8tNaPujOzNJf7hp1EKCdjmE038fjxfecCiLm3AedidkW4Rw6dWJhKDedeXC7HFgcMH4m1S3B/pyVcKZzWv8jYonMkDG807nOEF5cBNao53WgjHml4pJae8fT44RER72xvd0u2PNtx2J2aFFWm5U+mYExAGZM7+IJ4czxA34LCbO2uuCLMW8D4tnOKcBlCbdr94VeRp9UDyo2DNBu/xRnMjib10SZBvH+5CoflvHcPvAarZfeGBet1SW6lbrKorgqIKkj3np8kTS+c1dbpmXOApKi3HB6nhfoeRu5i89n8go5q/4t/9N99/5OT73/3B1SuEiKGrpLHnDZpxY1Feoani3tbTei8LiKXTrGlTdCY9QDJlYqDRB2TUa5V8kAJbTyjzKMSKRCiscz0favOtPYuFcUNTz5i+KYQWKUC/WG5hjABK4wcm9WxPltzPn6UokurK4LPMX5kSnEG8rH8DVn1p45fpKyqkmDUIAjPC4HzNtIXxo1A6TFVbpCragvl8V6M83hy9dcx4YwM7NALd5AEJo8wuvifLNjLHEK6q7BO0B1hSKuVHzyB22OmVbyciJ3g/PBfGgTjSSCtyXy+f9yQGjMr4GlO+XWJTWwSBd4sbG+G3tYcFJx+4qtwASyFd8pEihsa2DUpEUME5rZ8KGpWlhqKt2JTaP5jRhSUp+dJGWlfpZPSw9w2+Vq8+3/zVVmV8TOXVjXY2D/dA6L8oCr/goZctHWtBGhmA5r6K/V+AFBpm6Q/9/mtKpOhimyeVf6mqIhc2BWAexiaFn4r888V+3M/q3kpvLmUFCzh4XJhEx7P8z8x65RZDC9cb0wJcEgI60A7P2bsR7RKBn9FwGA/vijZe5SLLPqfkkbzYZUj+jfMlxxsm3BLqspgnXX4DYqrbQEy8OWSGD+wgvObRVxwYrOQPFtVBlr8QoQyAEid9Dq+6I/Y+vYCDj9V3WmGefGRPQEz0woSJWYkgHDZ4JnWs59MY4QQbFVGLmCBie+4wajEWj0so77BP3m56h1MA1taQgZgjIvKtoMRkjBoWc0cXfz2NBoQfeRsYFOyFofFLGYRF03ihc1r87IGUSSKtwq6omcz0tBer2J/FGY0M6NxhZZMpONLDxcGgYuQyZCmnipNK4KWQkJuUrhUMTmJurvAiTpFzMAdlveOHvRPwpQcCuUKGwAh74Mqt3G7+6Etnriim6uuNDcYDNHl5PgOC+U0UzgdKXrgrCBjstb69NXr68urJ0+fOPJMLM9w1HSWs60jfsWRJJqbClZB2Y0xbfyloWoNHKmnPmETazkj93puveC8lbpQFua4/mx+4Tp7dz45PAwhQsewkyRfPP9JTuK0QajMNHoWJPLloFhRscr2oaLUU9VVvdVkJQSM8J+VWpDCuE4HA9FQzdQO0aeCtsRdbXtjjl5rl+KtS0YpTXULokjNuh8lJYhGvXg9WdNYbizoinUV5W6TO+Hds9Xt/MHTD/+Lv//3vIIizfjyxduf/vQLbns96L17kydP71lymuBOG1UPsjlm9VOQKYI/VaQLtxA3Z2MZRWT0RAJsH2hSGIegmz8+e45CUQIA4/WdTiaisaH9s5/+yN45v/b9T+QRAR4qW5ILM+Vhiq5SYmaBM6Fix0LGkrOMujezDed6ohWUEZ2A7yA8fzKEWG5zBc0+G+I2CfLo7grw0qQERdTTZEkObbMtDgSrkneb8zC7vog8Ye23mfj/+B/+oy+/eg4qMsnyFsuBB20XdDu7wgMO4bA5nnOVHjx6IG9zupxC1VTCoC5tRJTmX2pml6BMwSxJHmgG4RmORx9+8qlNcz7/8sXlhXghulaPz1XX/vyLH81/73fN4rFscOw4Ww4NH52enxhTRe6vxkNswUMARqQbsLOXb2dvLm9ue9Pz9evXb2wvebOZ9ZfbSwMrdqc5wuvr+dn5JT9DIpO6tkAx+2Qpg+INw8a8/qvtcGPOtGUrIWsvhJ9tPn68/r3fe3AwyZonBrWWxLoDfpg7Cpa/gKLjOADHYpclyyTT59JzS1NmFmVuRpOoQZvORudxkw+HV8ub1y9fA9EZHU8//HA85Qaf0icC8ngxTQodHR8RQzxmP5zp4ejo3gEJZX8Q1EHfREdLWP/sxoF5m+Vwc3l18cgZ4Q8fP336hN3snGa77Ef4cU7UcNQLwaAf3YAqs3thCvRmTXVrMwD60WSLUMDYanTMjfmEDAtRqzgx32EeLG85OLOv0Q8NWQmqmVelX9ur5/7J5bu304+e0cnlbaH6ghILmtXmDBKJ0zV0BwfHdvsx9bUgQNPxBKexDM1naDQOWRiXdg+/fvH8ZnbNK3R0z8oBx3mNc2pBjDcGZcbJtFZGGFl5AOsx6NIFgDaMjsG1QBuoF4PtxHlvGfTLzBvRXZnUM5qfi1XCdly07K1IqJNs0mnCjXOm465BaOZcNocxeRPDVZogBzI0BSOrh7gFywneC7uThuim8Hp6qCAx9wVV7twHr4Xc+tVIcpIrp679l3t4Qa0MjhWGirqyQK4uOhrd9K2GRqavEmdi4HsuYO6yN2hvF4sf/8W/bf39v3dXYkhYrKsaYUv8fVe63lbnzbb7gP0QoKLS1BYLR9NS7x4ij/mtAFHWBr1YSFZiJbLwXZBA1trWYyVFIQOd6jCXrNr0m2mFZke3BiXRZmka8PLfMzf4I3oklr0MsdShHu1QQF6lhMbMZdJUt1H50XX6cVOnKb367qQEbvAUHlCC4rxkO3hfHR2eB0CaXNUXmdTOyq+gsjxXWH6n5w+EruAvBQZVQWckIWRMRamK5lOotBniJJfmhC2MVTlek0GisEgNEBRBCQcxWh/LHQ9mPGL4YEsLo4hoTlkKzPSSSQlH0lgzpMnZOzG+VHmCUxyC7VJvqg6jmCkMQlNYUNq0odrR3NeDf6+Pav8dm95RK/XUfZWWmtNeXxmIBGVufXmRZz9Tz90vifYDgHrd5LmLce++y8NaoexFKmv+pVblFThVkLilvLFi6/21epbbb04Cfv/ir95U2VXa/pSABnRx9grtfZU+ONTFDHsKpqXrp/k5usiYKrwaa4le0XxobwgNBa4CkEPhaVRJ56vEnBTa8oroxgAosfF2j70KS7ATgv2nIjMBWOK0OF9hv4KjUJrfhWMg4tiAmuQe4UlE2NSywshBXmJ+pdB43JoimgxdecRlFOEkqkJNHPCZsyNPMa9EbDglqgDjU69J/CgC/Q5xC1/ze9h/Yx1Qs/l07Pv4e1hQijW963lkFV/wSKUhZuPiDChQosGBbFPOeIWrgQwD9ZabmWgQErgNAql4YPDCxsyPp6CVWT0ul0VCC3nEguSMxo1YIL9kn52YpfSpQfmK0UFMJ9kbBMoYhEhLVBlh+oZtR/w60yYRCO31M+gtfMEMMZISipUDIcmavkRdRY7mQ+VukjYyLtGeCGlgLYwDsD4SwKAPqNGzimRDg0tVoPTOaXmZ0/AbpQ6PDsSvQyC7kGXw9u2bH/R+8G4+n0wOWYyLa+HIqZVzcTDkqqENbAXNB1EIC1HVFs6M7ovuDGApWDBDyGoXpt3tbMH9GJag7RooFGT4B4hoMGkRTH+7+uKL1zc3q+NBpkr19mpxRiMF3G6fyVdVFArS7jS/rgYLfhf+opmlvy62KW9IKFudgZDQ7ll3aMD2AQyyDaOx2WdQ7xwABaycq4D4XxXnqLw686qDXu8sPzEXQNLTUYK/0753/OB7v/ydVz85/fTZ/fsn92bzmX4IMk7uDUVUib4wMhxPDg6PHi6WlyFwoJAX8RSEP82JKd3T4qWUSy7S5evw+QhX8+31xVvqlzvWGs0EkfVuwGzwYTqFcUM3O/Luzfl5t/dLpqoHAyZX7I/wexECZqvtxq6d29syvi3j4FWtgb+2QlrwljYWQwS8cFaeNuL+/n1KzEPDlcJ4mDW5clUBufEsFWusUjRhs+7blZGNErHgvNLWlLKyEdEf/uGfOAlKYDFfma1RBMavNhzMZooe9JyKZ57I2lxdz+3i5qL/kx//+D/7z3/A96z8hsciBuotoML+biMUBdVel0kR1aeDw0dPnzz4j//O7//ksx+/PX2Vafacrro5O7216rc3iD5JOFF71Ft8/uS6e2jDSfE9Trc07N3woh3txvYaPzJuXc2Gs+XB/GTx/Lzzj/75H83nM4YHTtHk6Lh0SOwT+9E0SLgAIGdEDhG0ZNaCiiXFJUj6IIyyuifkZtR3MO2r7uo3KAaL4xUT8IvHqqVARc1os6gvWwhtLKzcjIc99rt9bDR5NouSXG+/tL671TlItxCHEQkjXCnt+ZefHU0n93bHQt3gCtNZ6HwsFD2XWQvqq2enIBvvGlgKXLi5EqfHPsmIHUtbv2quxHLjX/re96+uz6GUdhR0kaWhmFGjDXvTdFWFvEjNcvDCgMSjSDH1STTixA2vhEu2y1cvv353bsPEo13vPB3ILgFFISqU1Twt4VRm6I2+bA8/ejdM6t/4ld/4zqefPnr44MyuuIdDfYLC1SpYKPF2juC6ODM5jM+2K1H986Op5SUHugbnFNhHSwicoEIMJiGmXMzPbhfn7y5uR0KFrrjbDzj7lzzy6yX3UNRIFkuM7p08zObF1UTMHQWedqikMUW8iibj5ijGPHD0g9Ulm/l2fnlmX2VxMSyzmYU8/FyblWOJIQMYRnp6azYbbDt23ZjAKexCQsOKlkuZxMadm3vcL5BqXwBe5KyQyYRz+smo1JVYcJrjJUapPrsQjC+yyRjUh9d91xXsFsxYAPjpZEt2IsVukqa0uczR61HrvhGRnhGrlObHN55ASfLJnbbj7U6WdJPmVG+qlqYyMHmh88EjnHomQI9MYmy7OccgbqjAEt1bqX2kh8LniFZDAr5x9We2zlO0zxoTpwAZ/TrTkDQ4DCkxHVGeCkqJ+jw9+uaZcbKTAcJnCvUI20TlppjO9lnA2n3GaE2CjDLqynntThk+gbY2DR+9HPLqSWKLySW1833DY7ABD4KOSDgFjvHMFFXyYK3pebl7mnKjnvxjMgacqlshWpqHUKAlRNociKdtQocQWSglc554nmy3APWDhklG7Q37QS5SFAFTfSVRhrYma7qYUCsLYFJWfaRBteOc3t+wNH2QxEkOz0qQdSsIjZA6RiPatOmuS0sUAF6pkLKsXGlOGCdZ5U12QEVWq9Vp+M9dqarSv//8uQR3PxWgtJRT3/XhXbJt4Uq9JnD21XnOClFbqkulZolYOHdF3d158O0BwDfvk9CvtKJa0vzMUw+qEQ3Y+0RpYUSjMoUIlfAXfryvo9K8/1Vpq0yt8523oau/u1fqQkIPfAYHlDtfY7nrsExc1SjBzsnwDnmqnD2sdQ/CyJcrmSNiWCpc5Vc9bQiYqiEZwShz/O8tte1RqC1P/jUwhaaufHqmqhoAgNnQOcAwv9kpuD4b5uAQSSPh2MzQg/hJqUqvdPeKBJ3ugWaIYGI+9KNjjA7MkGYwrGPJ4akEDR54RLwINqKPNibvfHadrqpviHQaG2SLNztdRNLDtekqjI7mCynTKXuidcPhhAEBSBCoPH7lqVk/Ti5OoEzYwY/4ToktXbWvdiiQQX9CmSjsmC+hCgSQKvD4neE38IEQC3tnyjtDgmwULqozutVb6YV76S0IHxSY4XWAsU8SG1YOXRjtBMtwO1noNZVENdiiMsRNA5TkUXRhsgTR6A5S4HmXOtKrg4nQZ6IwhC0iFsFjZ/PEZpFB6uXurrBItMt0h2M5Fsyc0Eshi9ncTvPL5dcPH4640ddzjxNcEmoZWujzqTJNj30TbtAuX03lxUpIGWBBCVsWp4pQ4XmsdGG/8APva7a4SSx18cZ+0lMQwtuLV+cXb04efMRJZgUVnxvuVWNaVdzStD+f/oWrUmZBUU/S7lDIYBDVEpZq5FX9JBrxtwni763tY8E4CHWASdsFw4qK0zWIZhtjJO9KIuMOgV+leGXcpt1+ygZzy93Fbf+tsNAFdjB8McmT4Tl+c1ylrs0RmIC+2e5u4jpJZyMmTcHBdMFZlA1fAEdTQpxgrkSxQGB+9e3nlQqdpRovGslY8nLq6XTJ2Ruju/v8+eeLxW9gwWBE9XRDwAke9IrFIBuWH5dwxs9cocImOD7TmjS4Kk1rk0UJ9QR667t57XHxaSZAIk1+Knqfs7I1JJC63oECT1gAYCBkCfhc1801y4KgyTI1Nzh4d36tDZqnKN1JdjbN1tpGmRh1JdDC3CCWK7eF+aDuwfHx7WyGS8PDJdARu0CnsUgZEamroVz1Z8Fl/kJr6zGGg2cffnR0/OB/+Jd/+Ob01HgZ2q/evv7hv/qj+e7qk1/+wf1PP9ST9ztXffvCrj7lhN+2zsPGzmBuDwQUUm1bO5PG+2pn/VFvc8mRXrHpiB7fdpAQMIT9GxCYxsTfXuHgOIYt6iA4WorXUC2Ryk6eu5m1Vt1XX77++IOfDo6fxl0Qf0VgbvAcfIYTla/YrP1/9CsfHR0IYu9Nj46ZHzayvDq/ao37HCPmjoxMKQocRh8LiD84PLT1pfPOL66uD+8fUNTRAUGicyW4ZrMHV/Un6NIaT8ybBa16AaQxB2gIK6DZigCzqWL5ZoYaizkvvLZSQsjKyA9z4BZNj/QUzn1QT1FJ9Hy0sQhth4ZkfSJSDAe29eLSWdiRd6Z9UawyBnMNc+VHyIqWzWMPom/0d3AnIO/BfdqDijg44t13dBdW2YIOa11d2ZN+dXBwHEUvKNxURq//8OGDuO6zYbE+dDc9mgrlHw/H+ixbJN3cZO9pc000jqbroWyBQFSBTaJZ4VSWNQD+oixL54BHO0peC2pwAy/WEOMsbRDWMerEppw5cFo3QRWy3Gc5hxjtbwynRIfbpMOp5+Yjcb1pydmyO5zoWBIsk9BB/ZrAweVwmuUkOq3onvitVBRXty9QFPKDv3BLCNFcgaouJAFP8zZoLQyHpyQuSAvDSeJK6wI/tRRxSiFoSNNQOOYwFJMhJZ9eho4YJqI4NI1lMKNLtIY49khKbnoj+QX/sGI3TkvEHLa+steC5Tfp4gteHzE0aelCZqBIdvCpNarZA5fyPASbw/UydadbggHPikciYTXKjGJ2kbmCXfKk0J59MfsW40xCnRamgSk6yMStYVef/KOFM8YGROuUkyGAgjPYV65UwZF6wicZJRXM4XkK1htXhsapKKzsZxoYrEfzY/ikKEUWbw4LJ7TI6L6QHyQoO+hTQeEjT5IH4iJ7IVSaE3+mXIFKNelcgil/NYcSjAWjjaZM4VqdrPWR5qc1pfqlK2z4TJrmeUpVXRCd6qRUUZWYMoKT9AIpLBX5TPmBu65K2tx6X1fz9e3P5vn+s3mhglxVYL5z47t5mTeuuwd74u5J6fFdOyTYl9M8quffHgDcJXzvuX9fpJwheNqTQppmpLD8r6ueV5s9TJT8N6/q/Y5hJ7/97AppDbjfThNGiNVLUwfXDQxFnbAQDqmKUz+rK6lE0GYTNrwkk+1qvYnxJM5dPJpZ5xhSTWVMwB+RB44QDFhqKoTypExeC1iZnjH3Pdm15zI6lTNrEgt1QAj5Uw2sB/iwYYoudiwt32DhfZO9lJ1LA5zg8V9Fsakyq6ZDou7Ukk0nglVtzuLOCIMkudTH063jF/aa2EwblLBp8Djnn9k+epBZbY40qp+PJMMGumdly+vs6Ac9yqDxSVEQVZf38Jrqsymfs3vTkqqLQNb2brrrWp0GRdq6XT0i6Ft+8aRSTBpASAmvGy03llB85E/gjJ0cjPtrl0h9begYEBY6aIXFz8/UaE16Lbu+oJcBEN+xL4pAJavd8oFaxCxFdxJutUNBtoFXkns0bWzWlJx75SWmieGQdPGTJZ1+Px7BOgYoIh2Zla4wsLlljQaxxcA0YwZXhe9gPEy1/iDZ+bkzybA9uneUXTztENrZ6uQcmmM3zk8/+c7B0b1+/55lfqhrwlCZcZ7VMWruU87qsaa3eq/91O9hW/Ep0Ty4JdDWnrPBr/0Ww6LmZAKGLRSYQtzvAYorzkkOrAD/mCbdy4v5F59//d3vfsI5Edcw397g3WZ11bfPg96wVAzW0nb1v7/27YryQeLM1wdANWAq7S/R25Y8bueHfran1nvwa5lGD55KsmK/bQdf45Xd6hm26rivVuJLpGX6dXpfxp6r2X/lOxHq7MX2L/9/p0/uL2erK3Jo76egIaiyAvNG2E76hZ2hoOUFFwBz7dUaUDUfiQObOyTWnabrUIJMTR9PvhlypAEfcPTFCuFrTWDwepgNmrFxxAI6USgBQg4fiPDw0ikXq4QrYnvYtzvzcQb3jMJhG7y2qMfUwahWhjnhLrgoSdkLTFDcYLoBPeithBI1MBtr3ksJnYtitoAP0rqHhJ2jdu+fPE7wkhAHQaIpPxsysn7+9M/+9OqCLmJJv4krb2BrRROSaMZgs/JBSA7+IXqKcVbf2+HkarM4skVrDqPAKhFORNDCoLiBKsjTAKZe+ukA44EqYx3kBWG0H87w+P7jl6/fxabqdi6vLv/ZP/zHk+HiqNU7e3P69fnNr456s+HjafuznAO1GRnlddo3huzt4WE6bkVxMGqEeP7dcCG2xIA2xhkRVzEujtia8JNBe1kGhAHaS2AJZlzl2dDGVIAGbg7QZDOfrNpT8fBS0nbgLNEoTKZr11R/kK90oUir+XJlL8x1x5EUWIGu694sll3mo2VMt9tDc48QIC1zadL/O3/3P4oZ40QP+3BRhn0rQAamgHQBGUHaG4oBU0A5BpqeYcx5RSZoztzEHxRfuLism3eH6/nBZnOedZE4T/Pq0mBjAfg1wiTsxcwhCdMBssJftJhhTxoQHUX/0+06oqVgQCZdBI8BFOVQzUREpIsSMyObduQvbVJy2uXIXgfbZT/Q8sGLqqsRhW0/L87PPv/88+nBwfXlJeE/OJyc3LPV55R4Ec8sFV2uLy7fffDsY25xM+Tj4+lMwN6P/kRDj+7dJxrv3oiBvJwMH6IB01z7Y1t2toeH9zBVmChKJhBRxrmrX6Vg/YA34AHVU4N/0sHxYVLOJHhrMDq1t3B7+ym0RvaMAKPN4UNyUUn97PlkFyxl1+ixN7B/QM/GqkQnLqT0rTiKBCJTtJRKg5yI1NcFSFilAaeBr0IB4dSzCEbBmsEhdPNbx2BMUe7rVeVUTsHvM/M5ykvnBkgdgHBRcxEIbWPrrDgylvQu58aR0fWNXXVFy91Gr2F6BYR1BdkiqaU7NsJS00lr+7Dde4m4ZtCxlXeGnamSsys5DJAyuZEpDiJDk1kZlXeC6NRmU/q5k49qawPnzWfZsSoSTRZ/A5HIvHRn8FaZ+jzAAZACaThH8/Og8waAAgfUiprSBDF05OYhJb/rfwFf4CgeTsSvrh9OnI8RQx8SwwxMKTrpSZih/1rTRZzTJE4iL2JE/ZY7KKSFYsnCN2mRukrDb566dxJ8pddH6RslJVKTSm3KXT4VAWWZNdKlBKqcPOazkwH7QYjlJftpoBKdPNJ0vAKKyhXgA3cIWhTea8tileqrkiLytVsmbn5vzXrQ5IgM5iU851Gxg6iI8J8n4ZBkTh25wzNJlPvmSeVKxvqd778aLxOPvmbNK1kDZB7k2hedWvaXm/j+4f/DPKn9/oNdrfMvj3x4kLvmAmcAqifNACAp7t7+1e8U8q0CvpX4m0zNw/wuvCTLX3d9K/+3kuRpcV4DSZk+NCddWwyigeHAjIHDckXqWH4NRoTO8MBEf2SnywQU8lI0rBxepxYljDkMOKKppOKUataePg0o8QZZEVWlSpPi04mlyy2Jeo+HFK4siKyiivoNrckM1GO3OOkdegWkwOxKxUWRAJDnOmxlKDziU4hLy5g7JKAWokXy9EkbU6fRDCY6eSijTWUNQ+ef1C6pUkVAre7EExLs5767SQ8K2ORo+IHECCVKtZGOhITXcCFWjATAjsSlAwqcQUiexLMV7egDmdwwu/F+5jIjXJEpPUOaQzXYzpc46J6j93RwbA2jNPoxfSklFThAaWEYzNgsjEs9SVNwUJUJ3eACcA1fpEp2wx7CPA5YCmxI56e8zd6lheUgSA4EslGdxdBhEmZJtYWYNnpcgxSS/7kU6kGny/X18NHjN6evGTJ8fj/97IvxP/+XDx8/efPm4jd/+7u/9qu/9vDJoXN44NueIEFgohEUHLYMfoIinKEWXGeY52dAVbx6nR8sQMvjycGkmfzR99cuaRQ2pCNapFJaZWkT0/nL55/3B3+w4S0LfpQwObu48hLewF7QKzkISsYGH3UDqtSZriBGvv4+CZqEEZ+hQWqtoXKAMvzrn72LqYxCTUpUKywXJaKENSPDutSXNmccFGQiKm7IuODs5LGwi/Hh4YOkVm+mN3hlHSSLUxQPYzdmxkulSxGCFOKVExxVxXVbd/lwpRVpMGuY89WZYpouSkkOrqK4FCNJ+hxcLe5/S3z+9Z/+2X/2H/+BoRaoG44FH5LwieJ89RB2q/bEbZOKnnNSzUHliGIs0iCt2lfAFZR79AYSYAbOSA56NfcNlM2LPbx5lFxBaj5Jko1frINtFpISHy88jUDY++T8MieRRb2JZhlPjo6OHMerx9XnPnh4Mj0AZ4wUuOeiuHdy8i/++T8/nE6vr2cff/qhJSvVz1XNAb9EIIOo8HnsjmSKF7zwi07hi9iLOXKjd3jELDP9YEBiJxGLAVdGUz9+/ap/e73rD9dO9zo5Xp7xMq76wgwQ0LiEbsnRQSmXH2LXPkq/3boS2NixFjHUjbYxDAtRY9KxrWLPE1F6vLhF27FcWsR8Dg7M5zBQdu2ZyYLd+u3ZS1En90/sQCW5EQc+atqlNNniW2GUOjcDzYTgbzcW6zthWhkZdqvj3Zs3Vjyb5CmLLYa+t9Y1NORgJ87m78zGiEyjGbDHaHA0GR62Wi+M8D24unpze/3QAnaICvOoNlIZyZOAPlk5/sIxxqJStESkii9KVfPAmRaGQ0aTiYwNTwU0wNFzlsCnXwo/JKTTzhF9SwKMoyb4pHDSyEUUOh6TMXJY1FcGchaX5pEI57/7+/+jk4f3wWN60MQveJoJWz4vK1XtODEcTjdjinAllj/0FsdjPQZ3XAL0t9OjA3r8zbs3ZxfXt5+f39zM7VqznM0ury+GK9udZT5ZEy4vrsIvvNM1aUemQ4ZqUb4DG0prcXhdC/3IiCe/KfdMoTRB/Qa/K9F6sRoTFUZmCYDmwWuY0jQTZBkBSx3FlehyHKOC6ElDEI6H+MuKE4rNwuOpJIxUFIrchVI+3UpZAtvcl0jmjZryONn2VyWLQq28yQf+kCNXEE41Q6IMcUuhVddCcAxs+fd+G9LiT9rRIl8LV663zjtXn3KL/KpUFyoZJwtczCi596Y9uC/OLeIRE1bR1asq3hybsYRRkDanZ+O4if7SiSrGlAMzF3K3y/GgbfZ2nBX8SohzJ65DUgmGoRlXaTJJ5l/gR7Rq1x4jHqOAV0rjgwtaqo9ErNKmlitreBgfXvLQbbr4oDcQqyg4SQtN2WhdZoFjnyhHZWER36m7wl+NS1VWtehFtKQwo8YwCC6RN/1fQuNcOeG06uE2ilCgeUySb1EsiqT8UKqoHGUgxgWQGgN2uAgYCs8VsOs+ApUHngce98meB/sX9bCSeFC5k0j7vNgzqjLyo4qQLTnymXK+Kd1tU643eZl/VWKV2Tz8Gz6r3vdp9vk8vCshTVXp+ydugqqqtpqWvNXE94XUTWVoBgCKKpCbOP5433GNsTUS4+B6+03efb15WkXwDrqvn5BBZpvPwCBT/kv5s+cAvIe1XjYfTcIGPUrWIP91NTYLo0gZK/sn0bHd59gqdUVaU1gsISxCLsLuIZIbb5qPKK3cFiSSeyunApxWmUF1slLcJe289QQ4ZcpUorv/DEL3SPUld2NBBsaUV1WlzViRgMdgj3r1OvvVpFPTHEpOwjArKY2RFdZnEzVapmpkTydG3ueAUZ5NN9N7ETUdD58HT8EHUfm9Vww3z9na8CEQJb8i+wkSiOWusaunTrncdt+m54jHSy3BSOQhnVAi4aRiNK03idvjVCWtabdr+DpsTPU2LUvT4atoEiwYh/Dqv8pwZHnSafFji5Ab2s6Z5Mcy0xtaCCWiXRxh9jQeixDot2cJBe3MMrUQPwTfBn8wC5LZYWMIYFotDUJnwTjcR5ds0zerdmOW2ZFaqCHarloYcsorBzYbSFhrzUciTS0gmdjDZLt1ki1v+liYFHPD5KhwJmYG2yEet+BfmwIkdaZx0SumcMev3UNIyfpOuMVv//Zv/vf/3X/f6B27Z/zpH/9pf/iXYnc+//zf/tmnP/o/ff//yJnY7mfnFiam3k32IGZwGldzEK4s6OPPyo/ivRhBmBh2TdZbcGsHkjjm4YQ3PSsodN+Ijmso0x4DI3O7tevFFz/9ovEncmh6aysYwUsO11pwWzsTWmWdG6QMgaqmgiUfODuk84UU9Fb68dKVAYoPEl+Ky7lq2Zt7a4GInpglZ34k3VwBjQmi4Vq9r5AsEycxeKGRf8Zp1gpbYG6twhzE0vftpf7w0Xz1BYY0qOMvDK0T9yOEwMYsj4P59ciGQvbXT9sjGA3qGzTxiGRfZLMxqdezPI6O8+2Cav6vWFZpNup1tvOjrSUY7TeZNdZWnL0cmGD56Q+//o//tsFU/AJlkZU+CcVDEssayY2CSZYDOTmRYRh3aklTVeqsGpOjMFu4VWnztDCxT5BW3CGerF8GTbkCuo9ITp5EtH7l+785GB7aeAeodA4Z5ypgOr+5fPPi5Rfdfm0YMN/96i/98rMPPjh99WIy/HQxtx14Yh1NBCiRmZ0uqNX9rd/6rdnVcWs9fXP67umTJ3pPigB3BaPFxw1UEvOvD8dDiiZekIwZMymSUujX7dxt2Z36VvMnBkyjH/zdP/ju9z55+eLdB9/5dOxYput3Z6/b096lPfdpM8LEETs8POzY4NUykAwhD9qT9mW3f7MSes9HHcNFJx5FhH+gmOFBzRnu2wMlfXxcfEEHBwV9F8s+/bjkJE6e0N+5sniIp3RnafCBcBADc4tEjVq5QmAu2yK3uYd5vzpHJzZNyuYkZsh4G82Sff3586+/fG61jB2GPvpVNu+EushEaAyMaESa+cGj4/PzN2++Squ7w7fj6WSzfTc0s5ZAMBVNXz1/c/bhO9ITRY61QgWYp3qivLP68/C81bvd0XCQgJ20meeJBIlKEyZkJB9E13g+5oL35pjQIcFw19RfzyKuFSMq9ORI2d3M5pe2R0WhVBAiuseP4di4ljPdFDYMiwIou7S1PvjgkyePP+RWx/leKsigm6U+n9/YVeLVixeWNXOmHh8d3X94Aky7PDhr0Jpn8f0miiHEUXhX546bs7bRPgeWPVgMbXGT1fPpx0YjK7NtPGCbpriiwz399uHhFBCREcKRXqxh8AhloNPUGO34PtrDb91zUJjnyVT+n87m5sQgYGPGxRgYxOnQJMUnTEjoju6yOACbrHtfM6o71v5xJHG6cwOjiV6OAquBQ9AFitge4bSSvgLpDpwCI+U3UCRJBieusg0YoM19cB7469u9sYkXaJDii7K6LXc4U6hSLVjS7SbMXfuwh+IR3T7FQ1sTrxYtO1nFJViICR3NfQwWBp5OBPbMPEp7/bjdzlrHFOA9I7w28YMxgVGlPABKYOlkHgs2Pv5Nq/WiuHTozGuLoXjTReC3p1CYeaNsPIivgOyoBNMRkfYsMpRLcwoxPtLUFJa9X4eJhMgAQDtDNvDQz+Zq10chF2KER8UDhxM6vftERm47nYCamFK63XuWacD/CXwRW+OCdvsB2unWomNNrxXzJ7ZCtTWEA0PmPEJBwgKHT0rW7C2VQ6xVJ5RDxTsnjMe+w2qeKVwtZdTsCV0ivW9XUFjeKBjVZOrdTJtjBotLzTyn2XHLKiX3+UxRrmAjPwstdV9xKLoYj/Dhs7Sr+2XqyR2W8DRvQlYmnIceuxu8SPlEhrysP/K6ciTT/qoq7n4gy1ff3DctKt//3UMZm7KbB/rHj/LEfj5AgLx6mzpqh59UXTCl2jv81P1deZ4WRBHDyOG+9Dv4ki3/63KTRNUELXabZE3OJMhdEPfNVe+/XXfzyuP3hX6T+JuHTdEN/vM+2q/Kzs4DkoUEYRAlR4hIUVxBuBftM1eE5DiEg9k/zG7QUBnoEaxWvToWTt4oisAdfqjOHxcEXAXS+jJpkj6JPRGXaXioEnqOfRvIK4dyqhtJ3tChaJrPmH+RDdVQDHg7kEUxFV2q5hQmpRJCP/DWEMJTwhLJMYxRq2E20IiFZAEwTUtlGV6z5vNIEwCRCL1KoLaQ338A1aW7Z/anflkjP8CJIHvNXMiz/JVkVdtkrNZVSYGt4I1ZoGvREs8DhUx0WuKULKGMxFFTAEpYugIy2KAvYrLTj1Gy3cxd8GBYsUFxT8k2tiMxNXkQNAGBjCo6REnlLFH9YUMDdTLlM1bKjHpW67OxVcRO8Bdzhz/GzCr68z2KZhd9aQ5FYcGFqdmhqWeb37HFY4o0SMqygiw87poswkF8YnlOazbxUa3WAY/rYGQRBS2fkUTX3jUP50t7ca5fXb4zcmF5iDwQfZGOHxtGI6QMrdAgf9ER5auqRdsJgPCSly7WhsYwUiqIyBYcjl1dYtlMnNh7JBGTgtdZBsBtmOeP/+hPbnjjRtlSmcOzYws/Gx2ujZTgX01R6yFMuKLw56NkMxZVQAlXF8qTRqaQ3R/DRd+wHRp9WS6bHiLIDJ+4UlpxndRVWvpYWt3+oFoogEYrECD1eKx0/IBwg4vr+fODQfvli1dnZ2fU/WDYnXcX796YCmeuhSjrHd/YNTwE+n09qdEFh9UBNY/zoB7XB4ixUNdOi+NZ6xrOsY2Rr7XubGLdiigajSVYmhDTanN9dnH68NFxDP6AZxvWrIsPz6xFF9/MZRASvYgxQSRjUISto9cDV67UHsS6mt9527x7D1jQE9zn2r/yIwTJs5Iir6OIALwb5RSHoNhKQXdhHGzZ6f3kJ8/58kGnPUyGX/7epx999Oknzz7cLO45SGF0cGXxI9NA7ZjKRgD6648/+ri9fWJ2a91+UaDG+ldlxngF8x4cwpkmYVXLbgvQIBk72kAAIEQzTKAPNlhLP0bBWM04OXry8Xhwz8agvdn6ZmmYSfCGezckbRhr8dVbxwHdbNazweLtpMt23own/5O/91/07VVqKJu+1whf+ILaEC4riLSUTBSVABrlpkW+6MfIdExfCnPrhFhpsP9803m9vb388uXyzetRFhvMynsq4sa8kjHwxIQQi/Dy4pzdrqpf+8EPMMP5+dmbN2846IWHXb+7fPTJd8y5IAcrBJHdYKWQyxjeZqW32c1gub559erlo8cf2XMp49sofAtory3ypKbAEs6MeOdfMJpPTJOFGhVZCYFRrkyWHPBnaRDFKm26ES2moOJPSkeVK2dfEHOsaIeFrMKiF6JUMSFEOy4tjJTqAmU4rm6a2yJ1fsc4pCJHvcHaicU5kpkIcBB07Ff26tWrd29PpweH6R/Z1sYuxo02RLKP1sZGQ2u7AF9d36BQhFiI/8rKi9vrnI6cWrS1PzRIww6hCh+KwETKUwQq6AXzLRdDzU3vUxBql8SyNXBGgCIAfsqeZtQYOD0XLEgZ/3haCjEQazagqixLMAwaFGUOORjjHqd/I55ZtY8YMI+yWdAcWUznBs0RNEMOWWA6OEvd7688iaYKgK76WR9JVbi+S5pESeY5AKRJMsDlHri0v7VG0d7qCr/BSRCYJwZLdIu3gM4GHhbCUonEBJLxeaiA4x0BacRqW+fdVfbT6MzbvQf4TfkaGd2bBqkqmxPAQJgs9gC0h1J+5xFxSuMh1bBggnsHnclGV8ZpiCGijRWiPC2JZOm+kEFyjdUY2UKX1O6RKtNEt/lO5XnNJ5F2e+BFUiX4x/OsADFcx0tGOUaHMnczp22tvFfSGnxLlsIhnEOMHWzr8SyGDPObnqLfik0yzFOs56m6dLuaodWaQ9CRLBjRF8qVAsMKJVFpAiDT5XmqCldA9hUqeJpmyxa4/ctBAVoXK1EhUFA68q4UrBmUpIFBWdnx+RXjK2wQrlFcbvaoaaqv2lN9+ryQLglCkvr2PADJlYyB6P1XfjbX/vXdz0r0/se3bt5n8Oxn8gSiphJ3BX+TS6K0av8DJAHlW6XUbVAaWEPmlOOHb+eQJVt9xPefgurV/nFQm2fRZZLd5UyeXJFAV6qrSvJjX3huf+Z6n6CeVvnBeW6qaDVBbo5Gssty9shJf0B1JNKF/xPTYAf7qJAuN+G4cBJXV3kB3VsWQxK2t0w3z3GAA2GUHfpFbWaEQO17kek8HBINT1yeud9sz3FAjMXQM8LXAJamNaikeLBToSafSxFsHF8i3sICMuoIALxdOQkc3K88bv4iw+QnJr+UQLW69kTKdo/HPVAV6zV9VKGiGNPDEmcTW9whpxCj0BLM9EBUHu0PTv27QqlO8iuOfLM5HSY4TDkUQlaOAoIKccxl3P5eZBIiLUqEXrZUi7YJMuGhkYTSRg3seDxC74eaYBooq2fm6XUvghFb3XO+GEfGRhgY1zHfFajEReYIzZK3u+PBWvC8RYbt/m23dVCeex6sm3VmmW8G5hpbVzwiXGOt1uG6ZeHa8aYnUMSu2DMHxzhCV6Xbtj0jbA3I6jiwBXtnd2/XuaYlOj0eXBrwarl5bInFyvaR8ZZFdYIZUOlpoprDXBCuDXU2JTV0HezCXCAPlVwqYi39J//p3/2v/8F/K5fjfiDVlvwH08np6zf2NnTmCeVmnQN0Yr0gs/JDdNDX8L/OKn6qUAryKi7UtIaAbmGbwRPEyCS3zsZsAAPApto0GNq1+wdmGxi3YZ9W9/XrV5fnNw8fHzBqu45eyg6MFss5idPL+V57hX5uAz9wwNA0RR2CLuyU6IHWxxuTF2rWT9yqju9lmcB6XQ4Vn7jMMIwUKaBak3LBS7zTLXQQMzst4nBnXSoeUr3WjB61ffjgl5bLg6v5q/Pl+Z/90Z8JOrLRy/nF2Zt3ttu/imuSGbL+PZv3t3ZnkFY8VZAG7uC/PfiqaUTV3rBc4derjByZfcG2BjbE7I1uuFu5pYdQY8GGOCnYbtmXuv3q1aXgmTsClcwVx1sFz9gB+pg9nvny7f2T6doW5bPz2ZwshG7FJgGsUPoewmAYkPtPAAdFBWmTtgE9ryHFv6ijGhKG+WQ7ODhKHrZebdIC06wZHeTz558LW2JYMBQOgNUfWJpsSWp3OrN7kiKyOiFOdRjX0TPEQwmrTbKhSTrsBobUVn1BoI4Ug8Ksy7LveLf4BMIjEuOwMKBSF5qNcn2R/fRSaKnrdLhTbzi03/wWgzhoyJ7Wcf5f0XRUbCSp0/nq8x++PbW1f3c+Gb07WL05fDK/x8/+YCKaqD+uEI6+Mx3E/fnMMue4HNg/iAcRqR6ErKZCZ+DSMHODpWTi1ZDWI8JiYvKHP/3zL/74z6c97kayBAusgqhscnv0cPLg/uOr6zcwqfGffPwrwuvsfANTNoxpt09t3jmffWCrz+pNQtbmHzQx1oUMXd38OP0Ihl7Mry7fTQ8MqXpmGAf9A/vf0xtlVMKrU6sfp+MYvqwSQKwMFlvZ1hGW0JokZyS/SOOYL2IkgCVhWqs9sT6ihfRl/JsCmnOcd0y7oHVzfcWnq2GS5kqdoXNlrvy5zcN4XLZ2a1g/e/rkd//272SUnwrEOKU6Do3Xp69FAY1t9UNme72HJyfRwwpUdT/eECKU/Xy6nds5t8bm9sZ68mvRSnFzeWewsBFTHnQzLx1leO/BA94Qrtm3786z2rhUUzUoXVTYDl4L0mgEPwJnngVN6w8CcEUWpC02kFjotDLpiU3tdWsy1EamxkrR5FHVpCCso2S610lzm91H2fSWy8QCstV83D7utmxBkW7UkLIQBbXxNuHuwJO672TUvAFAeq/yrK5CZT728EVW6r6+zFLmR/dtvTXtHB0VtFdliVKL9tZTs+/Tq6I2Rmxt7sWftzvN9Jppinbn/M21dd2jA23MFY2vCAV1lKAYg2MWwgOh9tvOT8jybncofxGXKw1/SJ+QvFQu9/CzoNkuebxdcfBLWzqgc+0oRePGit+hvfU62GzfEcQVBjs1Qd1oS5ipm7Sp4EkNdQVp1UofshOwOCaBhQ0kgCT/slQPfS3L1u9HNjKN2R8cMGqwciAqXIZv6B9wlMTCpkFPY+sDDjaaBFg1vZDEwNlf4NXwjKtUTWMFqvzLRwwyHlbw9L9KKzYfqsK38YIEGKuMHzcYuJgwrFhTRXCSwaLp6mpQUFkKCN8mY/OhhjQ0A42mwfkZ/Lu2vefQUkSRQYJAAxDty32YxKX0Vm+T9XK6sQxxiUGJfxjz565kah69f/XNo7u0VaofkuS2fn4zY1CUqtqbJAGpga7JUK3bZ/um7IKlSnOnQ20KbmiwxwagPc5nrqo139K7r+bfQVQPsVxSVnoEq/vK9r6qvPX/m7Jy74ni3j8vOKquMq9xBf46PDrEZ2u7fJA4xLdotCPS0fZlThHKznhgVC9OS4lRB5lyqrNaaP9wUpihXog/A3qTPs3AE9pPB3GHYyO8q4ztEep3B7dGkFHtzUCwJC1sWlXkC6+Fw5QHJUXkQk20Xmqg2XqbPugyQbbrMHC1xUC9ABWubyMX+jdudcuIDpRn6l+FRi/BSLq/mK0UnJRCNkGanj+ojWdKr1m4s3MzzalRwmscipDd5Upy8smgJLkGBvAG3KKPsbVtOli21AesRLoUb4sHToP0R57afMskn+LIefCaZ5m1txa5uwjqCkcEc+i8GxV3nE+rj1PQMAEgNuPLmWXRTozE9OKMhRR9O+qy/pcjAxLLeliKUWlkU28jBDZiRFy0OA4egGzpSL4MwwWui1DPkN7WgxE1CjcjC8Kf7klFaA4zUhgP8qrZR44xG+rRIbCWrtEn6zpOCCWlWarKF92dK3Mbtp2githfjXrKy+694/vPPvzk/Pyd/tlkOqhmt3YCHY/iTRQ5fB23At4wqAmQzVWw5RbKM6cU3KdH5wbVQjCbe0lX3FgiiAp91AbeECyNpfXNzNwh/2lBaV7AROLbszc//fyHH370ZLsQQpCSc3gOZoiib9gwPNm0yhM3Lm0EndrRKdYgKANJUAwQ+WxGEa/oTvAoPcAxzThLH1RkrwKaYsKm+ak0E88pOJRjh4Ur/aAWawkZvLev5y82u3eDVg4s5jT88MkjOBJ+sFqfGrmDPKdAtK931sbF7y53U3gKba4GaUWfAOKvEqnIn9b0LW1st+ey6t7i0dcwCVNWZCY6OJbQcLu8PLt40+19JwZZIVNBkI/aCrx8d44GmmD7H1FoFkVO7L8pu135gy5p8hks3WFzD0pBefdsD9176D0PkpIGcoIzH4XqiANPxniEaRh9Eb9Yv7GChhfnFz/98Wc54SEdd/vo6OD+w3txEnPoOi2Bw5DK226t3cywgaCzecRFqIccVVcHNniuekPAoKKq91k/o02LDyNDmqb20JM4AZNwZ7ehsAjlJGIummfQnS1ubE7Ut3Ni+7y9vbUT+4SdEl8vFh23bja929VkOO3vjJ1g7TCyzN7AQ/GpJFQh9OJ34YVMh475tTdg4UM6SFPzJPwLf1peY3U4K+ijfHNKVJjq+N4x3WV8J2nGSFIozIbpEa6dEJXZ3EgTkmx+MLPuNuQrKW/2FpvN7Kz/YJVJq1jAcA7zLhzInDLQtnwW6Z8+ffrg8bOvv/76L3/0InGbnc3Z+dub69vjY7TY0OZ0joo7xB8xA7160gxNE6qpYFhN02zV7OBAO/zwymcDYrItSXF74AqpUNNsVFNE0VzXRrIGlikRyUKTn99cRdk9RYvOdNfq/oOTX/r0OyLEspG/PDQYntpsT09fvz59c3J8ZLWRxUVUutqMbCn2cF2W/65Hh1lcSxY6veFs/sZ2Rkf3pjeOwtgEGyP+fyMGRKSgTIUYsxvE2bIzhdiCc5OjtOn2zFcTkyC1NFEAzn0Q4zu0DB2gLYoScjTeypHB4b0DtefAMdEt+sqMJywWiyJmK5qw8GeUDu3Drgku5KK88FWYmmdksHFa8EHYJmpSF68q/90EgLrH5M2PvKtn4R2vcp+cbt7Li0f5uX+7v0/CegJ43Ip8aUSmebJmQw/Oix+vP4TrOfhkoM6hPfFYZ0FIL14j++mWBYIzlNVAIqYfJjTajGSre+ocAPYrgMLowai7RkvHbV+qXIcnQeJtlRIwAqHuNreOMKFUhdpmwITRImDVEHzme9/SO+KUqoSyPEaLMm+qmUm4B6/EM+ohOirJ8k53FZzl/o6T/YyeMLBXThATp3sqB1x952Eoa88PhgufaA6uTlAzolXDPC4TKCZ9tZWpUNrZGAkAemc+PSLalI+zigrVugZche5RlEYQ7sBciC5aZzIRh8ZRklmUNCEf9c6rPcnTTJgnd/ucSZQ219UkSovSNP8aCvkZBAYnkqWnSJLKAamFy2LAgqeeJ0FTZFPy/kce7at6n6BJVp9S1dv3Se7eVfY0SDWq24NXyXJflA+wTYomV94GYggNqgqeRDvmbUzX5nXz1bQsJaeGPCvjNjdui1r7apSFO1A2g7DEJ0n9fh+hJv3+M+j69oOC9pvWt6x99t6G0GW2qZmwxT3XXSx3twx+WiiurgwPIndo23IQh66G88bwkhzyo9jVePaIU609eFVdQCrB8VgV/xXN0qToE509ykcJJhLXpFEh66fh7212ASoJ0flaCc7b+zKoCPoCYwic28IvO6T3GlSJaNjjXaGJo47XwSN1hIcdyp1JfBkTa+ETEP66p1GVSROejNYstgYw66YkS13mhxVehEv/D3YOeGqo3DXpd+TToljqJCiTdVG2JJKSFrMoRxrhkyjTK36QxGLi7M4WUzqdR8RANf5n1AGirMHmHYxa0afXtGA2gdBsg6xNz6k+8M/javWPuQ6U0gytCSYcH5JC4/2XeTAT+zD5oeGOeMfs4myuIOOvd7GIacmwxjtTEyYBgqLOa8rVToOgpVlRq92+SbSEeQYpBz9SS7t2IGa8qND+HBq8a7/SES+2U35KekuJabj2xEcj+COz141ZFgmJZIYfAgAfR1ElZaCXNsfhuuCiuXd/ejM7QyQLN82z3s5up6OJsNSFbamPgusBX5Ud1KO2FSg3AFNNaTS9I8KohA3nEeSomSrPawoTchgPdGgIAwvWXsY2ETzACki3qkj6VbMXi8Wrl2cmtexlpRqjPsGX6+uZIktAM/Zq+DKf+/+5q1vBtQ8td2n3zgNWilWLTgW8cAJIozJ+5HumPVrLT5Op/7wywkrD9PyysRNlzF5CzpOG3xrSKALfcfFFBdL/PbMDz1bzR6OhCP6E5E8GI3vPOtvdfuLWeIQs8qDRLm3B0AEx/UzDlAVzIPBwlMqbVXQlyUmZV7XULUoMniMfhdZEzjBTGDqybteClSkTbGDRwyh2X3uJAzj70/wikMDU4aYsxfi/W7zLR6vJyfHBfGYTb/AoHPMbFxVnpNqjEK5zERjurjzZv98/8iT6MFeMhipHMxyQuRbBb+h4dHCkwzaATARUBNW1vr65OH1zKmuEt+002AmewrTsIcdQjCfWi+ADJnU6RcqKbZQAHk0tlFSfj7QhQurPw/zMYAQqB6+pxXb7XjRC8WZWrWQ2v20W6WYx3s5ZJOFSiQG1JEN6OXWDk+3FTl1OHdBkYD3a9Ne9d1kuOJiLciC6vbbR4/WAl7h9Tf5XzhVRjVDGqNjj6CnTfXzOWbYROueLpkl/QQeGwPkf0D2JuxIM6fLTNMBbTCTQwF6JyebwZgKBlAzlOEFt4c+t3HHiJvf2FQSJbvdAFUaZYYMM/MyVtWyYZpwFl3imlCwEIbG6eJEyCOAdyJFJSybpjQGqlS2oQGGYHXjx/JXTP+ghcFgZlUAaJh25DaJTRbZjBqiDpG/nupjzsyvXeFIzaRg0mzM2LSw7A1+TAE0jThUsQYEKAxI5lOI6i81OpFzGgYpvuKs+g5Y8KPLl279u5+PvfPzd7/2qgyZZnpxescHWQsy7796+czrkbnM8v54enyys4oiCMDkxGDc4t3hbtMjV1TXVd3ZzngN9j0c311aDaHdrOjk0O7JZCP7i27DLOwHJ0AIMNkS6vr7mBMEuOCSaLfKH3dQefVKGIl0UOXeFZd30s889qrs8oANtEYAXxocH1NBivp7Nbg+O72cqbP6Ixu4PXjfkt2cr4cWBYUKMkp122oPOgR7CqW1pg5mbsLoYRjWkC3epMBXVZ2DrvQyAezzuv0KH1ROlteusALivF/XhyftUcoYOKgmXGrRxMK5WN9jPKM8oKHHz8yNV9cdXtsrG+gzX4r2Vsx5rt+vkL6BCwyDJMNkO5jWEaG+P2xsbxz0HZWky9tgMvkoaKB+sriFxk+1WHxQ6M/9AUKQPyLRF10ymrr9xzxnHB+Ml9o2eS6Ko2dQbokBiUOFnoNpjJbTzMCRubgk/PZ/DpzeLp9K1hy/IjhwW6yhjNVtQpywQ+wUITBU9dnNzHfVClOwB4LNSqzIOi+0UAMRHLwYwahqENENIA1OxiMASacd7gDY2WpsPb0ZajkiCdlpJooT4Ai/Ybe2OomV3Kk1XKUtn+LJPGWw+9DS6K4iORDnVMzuMcBp4ET5Ipe6tca0vtkde5UqmJMGBlcptg8M8bcQvTsQM1P3KW/+C0iKrNGHtFB4S5H1ASIF5c3ft67r7+bPfTWJJqsL9ZyVpnu1Tv3/rd1NePvO0IGnuK1Flc6h2QMVLmthkAJakcWQUGyV7FHZTWNGjWCXJlNNcxSJyNW2/gzHlVPH5yPU+fZOr+UySfdXffvxz91WAD2QIK1RdVOr1zeX8VnQsbwq9qQtP74RZRPySeByWITimiD8bUXNareOHtsvrmPVxyXQTPO34JRLpAn/IEm8rpsxhNIQmlh9TFXHTeQCXvVj2mX5yQcp1g6JnZA6MBWd4pYoKj+B3DBtVyIG4tpyqxq7xCUgeWVB6pjatas0VJ1Ya0Rj1sTeYC0rtjHKql4CAQK5zik86G3oCMN1/ARkjXv/P6lYdQE1rOUf2NjtsErdwM6ebGe3FilYNtZh6NWmghO0ke4Au7XeuZDk3QqXTXxYCY5LKO51MhSIAI3Amb9v2coZe+hiumgyzYFsUgh2O5jd2OrYCqcO+ieUQNyILhmuKlhRQnGUV1nehWRc5+M4vxmYqWzoh5GXBUJUZdUTnoAenv3GOzi9Tjmwf8HBxS1uaIcZQVI8GRrmgQ0RN0mLa6lZM2vOsmGHQLKsNNEoLDSBDnUy2qBMlguv891k9Upbhsnu0l+5GGFVE92gv2oHchAls2o9xNHMuGE7KDvfz25vLwfAZhQYPBUJJuHbsxUMZYbGyE1Je89foGja9n6CHxvA6+GQrDi63axihhnaSpUsTOsFW+9FP/4KfHV0MeONaT+wQx6uWc9/HF0ViqlmFkEZzBS2ZiSkIm4GHiqRFkyAQthkGO3MzNJTRVwZg4aiSVQ3QYUQvSBo/QZGLm8VzCAzvpuCEFxv7+ZFpNJtKti2QOBMNOxgxCPG2/Uz1AXzWo3U2vyVEUt1aC47yIWGAljvF1Qd01U3TjrxtGpb3yYvmph/CCRCXlMF1DaikQ6/iLFwiSIlZVedgSCtnCooZAgbkXc7niUlxeM0cBXfdYY+79OHDpyTpzbt37exSGOqk8nzmQ7LqdQJmQdkUuoevwK4n2DbpUF86C8QlMHUu3MJ+o3QJ4nJoNpELdE4WzV5f3TKtslglQ8bWoyf3e9aPOSo6Xr2ODdqRm/u2UNA0JaQJcMQ+TNuoS6Rq8NkAlvdptLfhhxCqwRbWk0I4WGK6DVTM5tjMqniUXarhdA5rzGkg69aUB2HQfbNJxJfRrnwc6brnscH8rHs16ZovmKqiK56e9MWs8WmESPqZZbXaF8nM3GZpVN6pKHXAgXGAcSSGBGf0n4+0RKimRAHMb/E39I5ZsLSV8qvApTAffeZPDUiqJyAFoKK4bgeWDReVNRHrEnNH99LKRogMR69oftIGsZbAxA7LeoaMRdmU0+N73ory4K0hEqODyYcfCyDZihHKyIGnVcZgL0pL5UQ5VWQ/Bepm+/lnnznHDXd1+8eZRNUm8AXXWuJHmiUpEkcHoYcrPtGFggy2LKrkyq0qCgENgREqOPNPVSFSoaJ9MJpsr65vZ2eT8cQj1pWukI/1L//Nv313dkYKnA9lSkYLjW6QA6biNcuAxHZDtyOsFfQJMhvNZle31zeHk2ODmaNj89UhZMYChW+3JhnsRo0ptMgoWh8AY14CTKvSwCBcSyk6PAYcrUxfl8+sL8mGAJgzuApVzLEbc1qA4jDcBLYNJ0NnEGQotbgPJs4ljmMijPTJZFwyGOJJejkwJ2yh4yg8nZlteHBBu+1QxfiskAYwgcBXAbb/yK+7q3kVwF1+pAX1zM9qTVCdSylui4nySTbXc3GSOFd70S0TEyFOaIgj0/LgpBU7JJ24kyQ3rPmDqiNa3ngp2bMOxfYP1gAkPm7XeW1YW+PtkCkj8egr8KVsUFQsq3aVHHucBFIgUbozm4RKmQPO8HRABoD/8qYFGC/obsQhT7wLzDrx9PoKCOPWwAn75meMiirDMGxgScludYV6u/65qrRPd2iC6PL8Qtro91UGADVCy4I2/8IROJzwokLi/pDa6Whou/+vmpqpwRvkPJBKFzgKex7ARaZ/0jzsWlHgsf8BlnPikg58/ldz9T+6JAyhc0xxFR6Ae4AXbtB04cdZ/uMKW9RN08LggihXLxLEhDlTaqVReOEqn6nOZ5PVd1IG+CrVY/+SvHIqrx4HxkoQhvQmHz93/ZUH33r//l0V05S0fx1d8E2BTd3ACQjvYUxtd/8K/tTfFLWHJKmrQKh7f38HZrKWIZQim2oLoPoIMDCZXPushQs/k9R4OjXskbB/BvNRDfsM9f0LP7JTUDVlX76vsKRTVjdiWFOGJwhOp0cacRKnEMdGOFn9PD0iUnBIdgyYcekEUBnwnmi92gxEcyhEjA5mxk5oH7ExnKeGdETh2lRezU4y/9tf6yS4nykmwNSjO+jT4iDdENNzI1VmKj2l64QMNmUgrAK9jTmYyYY1ueHzU0vJOahTrF9RbJnsMCTV18Q8DccGyCx0pBuiXZM0xoPWRn8mgGEERqpZFXHVc1MxuxfzhEDUgkLwSe7QNJP74oQUHSNebo2PmAR+vq6IQma4Yx56TVw9CC6Zmw76ExCaS754oAHGos5eW2lxelFjjwyoMtoAvf3wapqeXlNZijmMo+3qP7ePeGvyx7QnModi5DzYTuevU4hS694GqfHwWaGYLdaCH69jUSFVBlTtzYMkCW6IGzdUWRBxOt4q0mqK1lZY/CMN3ZcdkqoQcf0Ln0Bq1VLFxKVhc51nNE+7+2XRIuiVQwc2nHBe5pM5Z/UihGsse4khUpzHw5COO8Xuv1Kw8ot0bJzozlQGmxCHa/MlN8eVhoMqPSbkQUEZx/ZDXAt3gyBuu+WtcjKg9ffHf/jDG+dEVf1aHGaD64y4sDb7O76ihnH34AQKz9LqVu9017tUZF5BcmrWQEU4ftWQyVxNyB4Gt/dOOqqkCBKqLT52bUEUGHYUYoQDXEpOUSkzTcNLt8a4nc14txpsuheWh3KA9bsHzP2IQWfR7duopCaJHDjlYJDdVWQgJYTT64IObtnsKpZdgPI0LxwaAL52R28awWIr+dbvExHo0gII0TNlZTKqZ5FAYsx0wVeXrBYzYCRHf4ejUlza4ReDNrhJNKvIHN2TQd6j/omQaIFDeg1WK7AKAkAaxVwElEDTfBQW6qOepePLm2Cd5AQ3esH25pEiOoOLCq3uWFn+9OlHTn/YbGZRDLFnmTi7/jg2UNq4vq93FPB7cT535JyYQDMXo5EJk0wVhVH9KXEPQ1RiAw2E5SEoQlq3wWy9YxU/4NZoHzQNNiUYSqaIrsEJL0PfnuxWutckDz5gtSAlpmBswc3YEpjW6siIf9teOKU8qGhZtDoytKMGWt1Fz2borY0N5Y24uj2eOQhIIIdWux2sx6aYRPStjB4KKKMhPtAwPwLgxuKoAMtkVZd5oRzqwgEwtPNPNgLvZGjECWOjeJaB6USWGGdwd2DGTFO5OezFzuFAi7EquSKy4oBRogI8Alz7Wq55/w0TomoQP/NZ0VddZ3jxY9yy2BJ9oDAekIOD1WLCH9Dtzw7uPTx59ABkGbfSVWHjkC1I4Okkdculg8+izHa7i7N3V5eXljAeHk/4leLEie4Ne2oc4pZYsXsgFlDgMBpBrsTAKEfts/ktCCX0OhSUJgnDUgEtX3msdgE4v/7bv/mbv/LdhQNDypqjmqWYLW6//vqL+/cfdw+tFHdoCfUVp/V2kxUghX7buhreOs29d3b69vpmbgjgiN+DwxPlDCf8L8Yz6aeiVbpZkJAhKxXip738lgc2a2113mjxHslZdkotY0TJYuCu53jWVl2tyTRii8SmgbUU5uqwKi2gYyKoECna1LYHpg6DJFfvLDjuHNjDcrO5Dc9nyBZVLp5KdwQDisvha7qymoChNkUJLNCDlnFmpTQAiQJO19ZgrRBYKNzfBf2t3ruigo98B9uJ/seDr+tJHnicwnBrfmCmzL8laWPuG0uhZfciRafGkCoo6Gz0ChZyGdt71ABCNQagXMTDveaIinm0Xj/qdF641w8sW9wi5phscpVlfRHJDER1bWCg3yCa9ZCWERACSiT0yHFvG1+TpAyzUgEQiii51QagpQW6o3CAO92/6EKTkI05hEplBvtGFUCGYbNvT0YJna9xbMINFERbZrM/Jkfmr6ojYQYgZFNA1FEktwEi1WTETRCRKhZF6E/kgZDuz/sSfxIazVC/AzDUmPhLvL65ks3CvbRYiwRKT5JIShWCE1SFP4rQ64+hPO2ttsBma5EVAu3RBfLRJhHEIEZmVcln3j4ZK0u0BKnLy0qQNHlVKZpMnmPDYLPywLD0KTM/68qLcNzgua9d6ztNWQCSTu736e6Sf1PX/km+moTvP7/15u62/f7cgFRW0DgBwH12H5KoGLGqq1Ig/X5a0Mk8WHPdNSizjjimAWwPXn1VOU0RQVha01zf3O0fhmyARodK0sBdafdc4Cv0+oVtrec/86Ggfd0N6iFbbo6CTCHTMiqJ+e5ewxuZk0St2oeNvMi74hCkD3+kqw+DxNytUbbk3siyN4bTLcmJv4oB0pQoa2AoyScKx+0qvDSDgSJ/cJIriTQ8gGU6u2BVD4jDhRIE0VWar6i/6MIYyiBTRcx8r/OHejG7+eZFjka4oiJSgMGLrUpoGTArskqNBQdghWM/cu5ShnIDUhVF43tPI3qunqCr3rnx7TfwZK4mShn6pR1REmmF/x6Cr9iL9o0GrDa5S0mpB4SVLXDmGbSTz8S6SEsJ8icb51DO0f3s27g7zrO/Z/FQfaTWKi3kyHQnN2KowDSwh6jyQz9p0jXEtx+TIQ0qYxM8hZEyIKJ45MtsYWtzaM/QoAeSM0stAXuicJZ+xFX1FhxpKWykjqJVWpTXWlmuJv5LE0I9nQ1taCeM4WhsNS1qmOQRy5OYWhAnIptFkazVrgAZrm2Ng8TQao81dQTLDZILiTEsKjHMVnsSI29vUcFu5oug3mYdoHYO1JvLF7ezy/HEuiKWupIyFFAh2z1WfiqGMVV7lCaU3PmGJHVywoGQCxYZPAvzyNDdjTiedwsbSetcIAqWIh7Fyd43Qq2JsqTI3EXc9qT3JBztSRhF3gagcyvCYR/Zbbgm7EfXlojw7UDAVFWhdrFAgvhTplbkqwG5QWC9SAnVor1+rzSSCsHuOw8oNUJPqIfKavJHS4zHvNHvFEaSMt6IL3vGIuF6BznLhq1QqDNqjQCy0yBbs5hKM8MDLrmcM5DmeJgxVkGn4b7rMyQGcHBSiLmDvQiQH17hRiWUJa/70o0tV8MDbd89evjA/vqrpfF59Ak3u2zMFj7QRjkpu7ZcXL34+ovHj+47j+LRo4cSGxXGgEhrq4rA8/9n7E97dUuSBc9rz/MZ48QcmXkz805V3UXdgqKABrqFQDTNa8Twor8AQuJT8QLeIARCqAGJSdCgqqLomu7U9+YQGeOJM+x53vz+tvY+EZn3Fs06Zz/PetZyNzc3Mzc3Nzd3Hymr5kO/KXjBKswJRe974EMKTV8nqAmBMbrEQ3Hzd7a/sQf/SIuxvUUaiTIRcPjVMPRMi1rZPGwUZxOnAo+IT0EMVo8eJCz0q/WH3ML2ktq0wWGuElKbj3d7dfOaB387sBZ64sdC02YbQI+ZIvmTnMayXpJVLZgEX/FVJN+pfTYd2z7TPSzNKzbJE5XHmLjl3YlRNbQrxz/cnG+aixi54l4YFjnw6+S7775hj6XTMm6aAki93Nk5tLZDcmCmAVjZgwVG+FS/aVZNUHrOD8s908F4UOdBZqzMcfSCQ6mu3h4eOtPDyFxclEtcjX0zx9oY0quTYuKXNpg2qpYx0aBigK06jAIPnOOIlESrAeGwrYRxLibKADv3HlCNVJt9ZFYF7hNprm99ClLqW46OTqDXbBIPkC0Xrh0KfEFfLOqJEYaeN+erlnlcHJ4ImXv09OmrV99pSAYSoOw9fsIoVUvDwuoKLKnTOrZ4s6PmOIHMbyR1X371pRI9d6iwfWBsz6Ws/p9ffvfKnqrb7929YDmixtZuwQY0T5KFGnGv8JlkoDn8kOfyr2NCd0q8adUYoOtO3Khy1U45wBQpKJNoE1FHyGUz5WhEGNnTVKVeiNhnDWRoB2Qk7Jpn8zwK96BX3ftbHk3aQTWJ9KvG03BNdzqiwNwkQtkJOd1o19a5akuGT6q1cnpprzM+TVEJYbMUXgtuJySVbpb6bv3l6uaL/IFRRajb2PG21qhfcKlkpGKrTAfh9BNmt86w3QCofYWvrOzVza0KMmwMkbGTiXRfi8jVIDgsR2+lb8GdtGhVA641ReVoVBVT5ffFw3zqLEfFhkt9+wxl4ZuS6Z6gNGy0DqiaTnHh7jUtBzgsuLRSPRJAbthZyoEb5P4rfjozhRc/HL+VB0lMhZQfUTGtej9WL4lHoN2/VKREI2nKKlM5ehaw9F4llmvYmRAkTotwlLQE0RRmIRSwahQcT/yPnlNEb0rsR91fN0sVvFjuJvf8WkBV9G9df+PBD94OykORHzz8G7ch+32pQwRpgjs4PmCwYL9geF+1QIV6Q8alrJ68u96hNq3C4ynl3dMyerT8TkSk4GT+qPwTP6fE+SdJhfe+YcAPAPxtpUpVHSImVpQ6ymoZC5hU8XCaKm084C1dSR4WCSBXS3rJS3Z7+UE23OZXUidCNVbeR/iETshUAO0GPeW4yTju6nfNceXqw5RWawmarjT/W63KJ8v8Y/xVOQ+s9alTInL6e2qRLqA/Wef6CwKpAOJSHxCASefr5gXEpjR9Tl6HlF9KN5vKYMBOHNycIkYa5QMLjZAPzpo9/jNnjwbjaoIgErdhcFHmYbh684muk6L2Gmh+plkkwCgvwC7SMk5SyVRX+0vaMZ/SHyNAhnw/pZnS0Hvl4rPa8Ppvhje1qkEAIcCB9/3OQlOUj+WZitDqWN+JnqurhxGARqIuFrJF5wYlEbxtQ2nW494JWG/84in9wv/BPoCLNMO9eM+W4YYHTBaGEX2IKoIL6eKjNre5smM0uFCuFglHJUJ6j2jYgCimeRG6fakXMxV1E5V76cudvWlFdFuPeri6Jwzo0f7Oxo/+/f/gP/jo4/fzOd6werZxOegYHd2DathRi2gPZsDCoxeRr6omjuGcvCmKaCnXyM8Pc1X5FM9OL98eQnnl9rlwqtWtQ1rw5deH33379qd/+GPOGP01Zk6vLzzow7Tixi+VAZ7/cwN2tUO6PtevuG/bYnrakCcujcQgbWK2XjJ6r1cO8OLueo8Q3a0eD6qghXqpb1vIHvbVMJKCOs20x2pcsQKKBGKssXS5P3noNSl7Be7Y9DrP6zpzHEHmvLlb5wDoFzPcK2OugROsZiEUExeUMUU6/EHSYZRhMnvTzmDZ/WKLtDz9bE0j3xKYcLWplAE7mTw/bfaPaAlZYIDSB1OiuSvtmUrK7NDgUCU3QaagqKEzPXjtrPIj6P2dtSjdU5jhdP/m4bv031+T0HYuarNub5ObP/n7/7m//yd/gih/8Ac/ffr8GZsJAOJtTk41RZk9e/pIl24J+8rGd7uPnu7uP/G4safo7NUfrVzZ//6LOjBUmF5niq3ril4Jn6Yy2mm6sEUIF3RCbPNLBsPt2rM2UWyQLJMuFK/N1dhj5W53f31/9zH7gxlGrDBrs/i9i7vLt+vnT+3Bcmtvrpuntzt/eX6zb6rUdq72nnry935feO31xpY9Qze2D863nCUnRCCPZdYC0dLKrB916rnpFNKc/sIab83JVJesDolr8GSK/c345ZYjGCojEqZBK3bf2ZjAChxubGMSm8AIT7/cA2tzN//i6vUTExRra6+MOMSQn1oOvLdDyEQNiY6j4hDg/OT613/9xSc/+ahiZ6ZjOEiSRDHDDBdE/Juh2mRSn5wer6y9ZtGhwTdffnNxevXo8d4oJd5fjY680J95fFjeEvlPrmxNY77Q+uOzb75l7uAJm5T1rGLqXo+QKHlc809f+m06zIY8RZVIxuHqRlpihsIxtWtIs9zci9zNIzsj/fHf/eDjD1rqBp1Cq4mUaOnNzc8//5WNegDZ2TZrdLi7a0sjq/G3rxtzdsYI3mrzxkKmxqymdfjEKLE9MmO/DVuYbty9b3Lsbu0VvW1ERQIhrymxWCtu+1V6mN1/c33o3DIyvLX6xRe/MRj6+JNP3r59bQdS+2rVp1zeXJydHr1+RDo+/mk1qf0S0pp8qqFv2r3ouCZ6jetMF9obd6hU7e1Nr4erT5MIznSZBpKx+enG2tnq2l8HkM/eaWJ3XyEnLMU1TQMHYyFf4oZTFe8z0b+/5plZ03dXiDldZ/l9n9mPh6zy1uNBfAPrQhIsTjdbRROzaVHCTXXWdm8QKFt/w+VBhEKy1LEeBJ3q9p59Ho5kXbuA+tOV6/dX7mg8beZyNlizQZJemDratkVeBnTtyVTbqeHB6t0Bf0LAqkCG8a01A347JCcTS3FTEQ82v/SxdvlRM/CjKhIq/NcutbQwngbJirgx+z0IEtu1z8FBcxP8BSQUbVxvRScY1jAgtEjnrqchM9ITP/KVg6yQAvkgBvsQmoUK4gjSuZnoeR7NweK8jkDDH3e+AY+Zf5g3AueQoYOd+2NjU3AQJJ2gAQ9XaYiDKHnHEwFYDIC0u/p+VkYyZTcXxhLaJC2365/D/fb2PbMAQlNjidzZjd3MOcTwFGeZkAQw0fRkBHV+zmPP5ei5BBU8RY+55/HknadeI2igrz4p8VjWA3SyTcol+wL23/D5wyQLXr+b8K4Vtouc36Mza24fnvTs/j60/dv+MtwzceddKA42KE3k72v/u6W8o8nDi6FaP2SurQw97iFNYsB7WoqSzTXPENSjSdPDJd3y/m/7nNxLaQvJFyIvDWkAJPzM61xTEBj+VMHYNO/HTCb1wxFPuwixxK773/PQR6zKZAAnszsWLjDjekXMa5CkmuyJgvYEwQSl7PUqbmeIuUDvSUl6eq/CahWu8mh4egYoEWnQajfB9AlJnYqhq3G2e6qkk+HZKEsXUfVSLUC7GPRMBz9GQespa1aaIcwMdWqqYSytn6koWsnvxic1xVxWgKjroBzAEt9f/QzyfbkwBhBx9NINWTiUA6tXK6SIu6KORfriRmtgNcHgpXiq8/WtWBYTym/yBtI4KYVJ0EyfNOmHzIUIy20vWAB9AgCBYabE8G+fIQzCjKlY9aE+UMtLdeKGnKHB03VjCUQAKx2Ham5jRmOJ0ItrPVH58PutmxykPc/+8q3ielabeuw4JWh/p2HMyvWela0M0JQjTTgZQnygAhxseg1STGE/s/ZUrSpPDa0bG7xgpfRC1DjYbi9OgBAIcGKpit0J87+GY2Jsi/62ZDl6e/h6deUn2GRy4PHjJy+//SobAoVSkC6FLR9LawsPidVhmQHIIqdSazijB729XT98Jf5clPnT1nOaqinrAg2oaOPfECQq+Y8jCpkfUXgpT/mllLdKvlnbODQyMlnN6OcDIxo4rpZ6xJoTMGuXjQemry9bZYbpFDRA/UyEkqEKi05LErJC3DYfPXnMt2mrmhfEau3lm9evRBqzEEStc+izFoGyOFLPZeaGzLeRcOLEcGGWbeKp4dvUgujYnvpGkEmdmLd25NraKVzE6H06rmq2oB1qi8BElkHMi3cXeLi8QJWHdaiZkYTbf/ff/ff+0X/5v9gEBBuWeBOiMQoTZtK8tv7dy1fxSTvN7Lr9za9/9eknH+3v7hFCm3LlUWzcQcgWYk2JQ3N3g4FCFzr1M16UZOipiKQOT5mt7AMNK5SjbTNXY6azCo0D8h6GgWHc+s35xpWDPR0FJR7NYsc311uPWARCT1gGlJMlHivP9jce66z3DAmub4wFkJgFUfXzl7OUGy2JcRYq1PHqsIeKYn2lvTPuJElXNkU4A4fQ0nfThVlPg7YodREr1hjL7uzQDVvarK9uPcLujZ14ZLmtkLBW7iJ0c0EciHRck34pKjpKONcYrDDqVBnNR7TniKyBWDQZOY5vxjOcr3bA3949v73MzrHL+oFzt01CkAFjknuNIq5Maq30m2++efXd6+3NXScPqNTr714TIbVgqibM6gaPkcYEozJg6amgU9oDvllW9BO4dGs7BmW6xFpiGed8z9AuQMM3lbLx//vP37u8Oj/Y32WUJxk8wDvbFmLyvrPU50zr2y0nTp2d0w8i61NbzHcKVBMXaHp9e3h4ZNeBDQc73N456PBg18g/0Te4Fu4/K6EjoTGowYW8NYEczIRkVOvq6ts3r54+fV6NmFFnZy+/beRjBoC6EdijlVq5d3bqBi8iXPXOtdxUVLSRjSZAEzo5MmGDWujyjMoai/dOohF7CaKnHqhGLmxvEaHUbkCmd8JrWcCRJ2oHPw4sV0W8u4VzLaJrUpXYJb0niei8fvfErx5lD5B88sU/RZQV616d9FnsT54Zk9iFxHju37Z5oKLAZAxwwhmb0UFL3Do5eb3R5KglNO8tJIn+EC5gBvamzrweHH2pE/IBGgYEgjZDNd495NgR8GiTKlJWGHH1rMefbixjQT4yU52gTCVTAVoCw2Ge0I+2uIuyfqcArO3htTQjXCs2LCOikGj+0POx5q2JO3j0hC4zcEPF3YOdpq9yHaofQwBrUvnNOrvX9rQ364PaoKRVTmyU+vd1HRwtUX/rRbNuipdLqBO/iMX8UdYKwxyp01oZNzLH8JgR/VNmXdgNs8pJ0hJRyE+zA6nAZ1TA7RGmSb/kmuYYIyXvX+WRTJ/9nwzdTrIe+VNkKRqaoOtk8Rwq4RAF8cAPJUnUXW8WCAN2Cn746MXD/e9+/+6L30k7oH83d4U+XIvU9WDQrt08vPr+ewrJgvzBNc/uY4x+84BgOqc0707zXYBF0NLzGYfLrKafN4PeFO7tUKfcg+8DYefX7+K07AJ0X8pATjksTEBzgphOD6JNI1HYs1gyfEg3kJ/qWaC50alIPhoBg7WdGk8tJnoMCH5T/YDVAoOZjwWXmCtBOPswe5DgJ2UsSwq6Ikobbn0nWe8uklQmewusCDhd/WKAJBi1QUQqISl54ITHm69zyTXKNRp2auoyFU1fWjyn5F0ZBQksbTkyD5JcvxWz9c3Y3PsRAxX43+va80loBzKqyPrON00qj52DCrR/tVc9SHTBIIUxwlGoA7XSDzGjG0xw7WxRp1KWzz5IpekMX4qgPUm08Gw8PWYpFQpgJBKzmNZJ108rSF3lmjEWF/i4tv5VJUscIhQTNZ8l3WhOljsbVjjcV38jICOYivPcJ09UzIyYda4L8OG4ARKVqgSmNhf059Yprl3/+J7dUrLUEaShhGrYmqEe1tOu4VhJoES8UvHwT93SXmp+0MaLTEzb8128fXP19Omz7e3TlbuXa6sfCsu5tsKVxlb21KiPIJFaPYQavTec/xa0KtrbVT1rVB5mxbe6K9ZK7qu81zaQRs4oPOjac2Z8tYPv+p/92V/85//hP8Chre213V3+MqvVgf6iVcVDfD/7jji+hsJTN5DB5LJUJyRwLXrSyMZ/KKyu83GiHqUvBGKq4GuhC9TD/OGKZkqoIHdqErAeLQwVnv3x3cWHYnkHMqtC0NSxHZTWN6x0bA1AxG4/UFsTXlZr0uGjUoBZeNJND0uJGj5DZcptNYvW6BzTHNXEccPkVSdqWZx9d3lhexM0rPnwHJMLm+w+FtJ9TmAzK5ycYIB9Z/uASyNXqWb9WD3XpRgbkxfOp3i082hv++borC53ZHiMeOgw6Kt5aHx/Vf17cvQqXUHy3ZHtmUnXu61enAm3Zdufz/NpvzO2yHPGa3XxwS/+4lQsuiary/z440/+8Oc/Pj58w9F48Pjp2s5L0ps8JL9DIWUOhRZWLMUn1cOCPiIe0WtkXA6Pas4czCwkmI0Kqr9+u7ZyeXPG2Lqd6RG0MfvubNHdrY3H+4/pUBsovW8osH31I07884uX9iS927ay20G2Yodu2lbHRjG7+1erF5baGVOZM5NNv07Ihc/N7kB5i2fYBh9DdFvQ2wagfSRxvmGAjXoK+sUQa6DHmNOUtQBr/vQsHPaa4dNHn/7oo9XLU3ODphyw7ubWRM2mk1HXN45unA7WZlyCyhBB8HhrlUZ8GpCAmWcUL1c3DO+yNqKMwY+my1hgFpu5oDWpJusPBfhpBYZpotRsYLW2sfP55a1jyT6rrSaqI6UCjM/OMoUd6LpnNQt3DGfwng0CxFOBRsPGjtGcRJeO8MwNsiysbMOEvBw27WnPCfhxZezswQoVn1fM2lEyX5gHBtXSVUO9HM/wB3/8852dRmyU7619g+YAYXrjT//sT2F4sGdLWxiLbmv8SldnjSN9kn97eHR8fn3z8tXrsOKmzGNqiuPx0ydP7q7tJCP2/ms7OQniUhxZMVT2ybTSGhhTxFW1CIxne3tPtjd3mJLc/wStcYJT/7Z2NDcRLkYRe3v7G7vf3qy9vbv7ibG1+mKP3kFn2hKvpLPeHCJoRdrdopE5By0xx9JoPbIQ4aRMtQbhZhXMy82L1iKvbrYaQS2JuCbmwLKgIsm96kDI6qkmy0cluOvhPKrxLq9KNsx990Aq6UgIcOg6NLi+Pbk6vVy9PrMsWoO9M/1iyZaJTYr144vjN5fnX4aq4k0lnu9ZjYKRmf6ZqFnEmvzr118fHr2mA1uzd/t89eb57d1XtQIRWyunAvPUbv3usd39dRr1dwX0Qm+3fQ00vTqXS7gSVN3axu1eI4v1M7hCUtnJtnrefEq+67vNN0zN6na0yoZmuu2UABLbXkx3VkXp8ihuAEAronP0KPooBlBpv5ZBTAGZZVStbx7c3k1PurJHksVfHTzaNQCKZOlVA8cvwbu9+pDiNUWg5Miq/tMEpAHnzmo9jRNxbe8zZy9YNDz4I3XmGioiL3ZOCLMRh5I5jfZDlhwRi3pq7aXGRTZQ2BuS0/qfGQPAfKKSz40wVG/ky2f/Bcr56jZw3bpJXOaK9a77t/24s78lkqz9yrMeLymRaC5V9jbhCtx9tiHgPPPwPqHMv21LL/m//3yX7vtH7n749If3D0I7Jd7XouIfrsRE7XwNVg+PhxT2HJMjWfnBNXn7uAdSYQ+VnKeeLwj0OXdJiuQk5oF673JL0iXZgESFUR+T776AJcWSZgFc2pG+wN3/nwIqAuFDh83IV5e9UsWoRZwZKzuo3tMehKjbEpu0Za/qs2KbR8mC5zqb1HFXQtvjsWfuebtgVifR8FbhC9WUNxX2MQkrIBLPz4S2AsBNFpQRBkbdyqpX8DqNEGI6IU2tqx+5XkvZUiYizCVsNlk3eUa3aKfTVmUJNFuJhquOaj0PknjUKDIyREDzeEkwVkNwa0alnhTuJnetrdHz6KzhI/hKALhmD1hq9V5IBOZwzCwYaHO9CpUUMrtZYnj6Wl6gRiRTnVhuFaCyb9a+W1m3IlBxtA0csiIi3ZgkbfsfySNGrsNqGAF12T2ubtG5p4CXiNUbZYaehVpRn1h9Z8nLjBCGCFUC/b2Q2I9Yv9QhfnnI1PBXZZeLMAwNJ1HJm2HgchQjoKe04/i5E94zQ9ZNcPe64Rax6T82yDZ4p3NpOWhHzanAYNLZQ1Ct0lOZyh22FVB03ak3Bc1nJ/BGTh8Z0l5xwl38v//f//R/9B/+D8X/oLxzCcxCnNnYCmNHlHT3025ishKzkhihqK+CtRV46ocaTQ3JzUIoWmTzhtBN22qzEeudyxpqC5ni1FBiYKL5kKmvHnjX78Qqye5fpuZrUz3qzY5cXbHTjvUzTDaGJRuiVQ3l6iicoYPcw9kopNAq62b5C4Wl8OXLz9p11uXd8/dffP31FzpRluSVs6ywSRQPAW2PXJWiF4xMLyyS++DjD6/OWN631tIghEAIYQabH23t7z9GgaO3x99+9bU+se6ljnFjj9H9/D3nzb1++8rS+nCpLaDMUme/B69wqyr3JFpeP7xSfTyZpqFr3Pv4s/d1XQsQMQI1r7YoaLveHOXX24fHZwSJnjJI+PCDZz/96e8RG1V4/OQRii1NciHNg6T6NWiMFEGyVgS1bsLQ43mD7xHVr9mpiVqqPeKui02obja1119SIdy7SiQDl1dvrm9Od7aerDzePFvZWd97tHH0CwsqrneNF8/zVqD2RRvWtF73auXCpi1XxhEbR+dXp6tHF2eXgk6wiRFhAzFoKJ86+6vf/OriWISJgu26QyHY08ouziYlovKs0tsySMtPf33Jcye43/JCvNxc2/gH/9a/9V/9h//o5tKJbyxyOoVJVLDQ2qapHJ54y5FruP6KUjBkv7vd33/kSF5hLpQ/5rDjUF0L1bLSBD4jVmuW2Aw4nBy28obq3Xny5MWJPepX7CZ39C//1Z/++NMfb28+S8ZGCkqplNnl58e/93uvXn735vWxeTScAqhN9He3q70CRgf2ja5xbOEZTvlheNT+vxSCLkGLdw+7dlbwMy5SrhiX3gtlZQphvbl6tGOMeycykVjaeNT+DcdnAt1unr947mRfvlNBOA5v4N23abD8ewK/iJgpxayvAm0cCaCd5LemVWwWd3LGmaDI4nxYhgZytpxQLjTa2q2KMv3VSHyi+SiZIGzDBNjl83ao9sn5zq4JG04rYW/0VhvopfiElF3f7O5iaQZ9PW7SuHQSEjLfIFg/jEH+UECVp/o6iVwVfqo73MYHVOo6pjWHaaiiEnHOcKv3jOz4aRn0mWHMyD4Oe1STnN+++1FrmMcBXX7Mm95OV9Ov+YsCzEiUNwmLn9aXkC4Kh1zy/uQP1WCoDDNgmb5ywaEaNlJqrwLIQqbAFaKBw1DVAk8PbbRrAFyI4N3GdwLN7J5aX25Ua+Om24Nmj9ZPs8Kn8SQGKW001PaseGnwSpRqtkjUocIEudG9NDXwqX2yVnn5BPOh0QAs8ixvS5MjvtKTM9XrZ1SHpfSNeIbiZKVhmKfGJnWprYY0lyoC7/zCgdxmMs3yEq0oadkGEOmRxIwbjn/Gt+nWJkGwify0VYnVWcUzG4nD18AhBPDa5FeMr8aR9L4HhBMpIotQ7wX+xL1BHtpzV6XjW6xMhpMjsi1NVfQ91ECWufOjK0mLrAulAhQ1XMG4l5He3peQ/PTK36QsySQvv/v5knuSRd0FzhTpdn4HbfLffz78CuS7a0kQ0CXPuxdu3uV/eHiP6ff49mKp528DB24wnvcPuSuk+98ZAMxrq5gfLhm78sqHALTu83WHHUxnQn8efR8qNqgv2R6Q9kiUeRRkrwSl+z7CbMi+wM7aXcg81Awk9ovnlHh8t2k0ynSC8EikVASMqWRerkUo0KB6rDjXufBVwFVQHoRrXWRTn0qQ2xGD5H5jtT1pVSB06O46ECkLaNEQ8yGM7QtBd6T8ww07i9vjqKsmtojawjHl9M8PL+x5rBkng41Pe5LuG6qk6wif/3X/ig20cigVtpnZak2PzGvfKYS8y40drPvnBahlKmKwGfuQHtUuIhg10gbni5BLmc6MoIhBb8y9jj4nvSf9NTGSdCKkn6wQ/yRMIZccBG6YbhZAFIctL+ZHFrbdVab7y3BALkpgNItsRRuLc7j8aMyMjHu1i4cCBtj6N4/u7vZXt14OymOGtpe8iEakogrgAGXWgLqL0ZeLVmNiNN9a7BIk116G0c1+pF5/XS1un1Ru3YfqT/zT+ik1unazM5N0yFOIYXQGhLLTryg+DkLOx/InxdwnIaOEYpzK3R0ev3bg1+3lqZDN/Ud7yPL28K096XDq7OjMwZllRMjYueiHwLajkeI2xN7ZjY9OmlbjyY0YBibNJB8bsWKR3JCiXWkIpxAFFUeNLJlIkWFOh/JAPP/y86tTlqLp0dUrQfA0uzRqHjUqIiSqkcRj47hFG6XaB0D81O3aETGw0CAFKEq6EQLaWsagIRxtrIqmbSwXoaYOkbompAQPkqigz0c3FauWkviInqUHWbD49aPN7WMmii2AWGxmkquyyW6LIkzvlNKyCjdO2bzHWc65HVK5G+glHOI81GsojLiCOve3Hz3lo1b2dUZJpteK/fJ5FiEz3m71ExR+e3F+ubO1x/7WjrLZCFsrAi4fPdbR2vln9+3hm4vTcxogF4HpeYK/ev340d7JqX36aBI4GIpjCqKMxpsR74KjzyH+0KME0a4g3USWacueq3uzP73C66iqiW5ZXEtdmuo3sLv+xRdf/z8Rwk/O1N/78e+r4JYNrPd3DWkkwmZVuqexm7jSv0pZEOgLgLr29gMJcGS+f6sOSUkUBgQv0iTQND/YckIPYGNNhbDc69zy6/sra7sX1yct+1w93F4/uLw6OD65Obo5MEG1uXPkfNv0fq42knpzent+fHfzzfHqq2P7g58J/TY1QG+Bq96i1xxKuLOx/Rf/8T/96jefF+JIX+NW1a0OzX+NNnVLa9vuxxlajj2QArJsSl74v/vph+9/+pGllSaQRn9OS3ckVLu3bTzaZeqqYbMH1mHS3uPytpnyytZBIQ10K5e+UTSCpTtTSqiBp3yqQmVEAeFbU4xXFxdOvT042HLeOkNLfM3Kyo93Nn/f4lZCle5Mg/q+PbdP/lWnYtUDrbbT6Prtp9k2FoQdP91/dtKJNCz6Zi9jWcwiP/4gmFelBbWjterDWNXGA+1LVJTioQyuFEebJuNWUijX/u7Oz3/2xy/eew9pTw1vrmxGcP7P/pN//ez58z//87/ked/cbwhnzIP+RIvz1Qpj1hbQRjZ2DX17fPTq8DDDXci6yt/dPnvx7MMP3qeacIK9Dt/qWOkKmYELMrUFZ9t0aibajri064LtVOFyd8d6jJWLk6eZd2tfb9mkwFhlFkSbVXvxwftPnz1W7aY70KEjZOkcqlUJoz0wzupBArD5OZlU4WLWU9eUIfLoxA1TxzfE4GhPh6FKhAvJCBppOKlwodaXiCjHdsRTC+/9HHZ7H0GXRujp8tCTWsvkTSJj1lz1SkHSwFtcQGCs9AiaECSkhVwbE+kwsk/Nm9+9vFr7DoE0qKbGIH3JsYKdybqGnwQg6vr642f7jxyAcLdnsHJ9+Wzl5uPb1c9bxXa3u3ZzsLouWl0WbCTUZ8ofb3yuHB2gyDhOppBnGdQKTYN+bT5udePpmBZoKydSoEdBd2UqFbokfXX9iSLzVxOQqj61r6gyWjqi9HtwboSobs1PX39C2eZaNx4n4VwrGtstr8CZLRnsNWUdO0pQYDMSW1s5/xAPZmFATjHy206L7ZcVfLgItLs+f2IUgD7eG88bAGkH6ssNQnUbEyQHBlt8dLfn5hRs9ortKxuf51u5+kyNWhrhWgYAVVMFa99JQacheaGWdf2RDCOGBYtgwKFqMvxGkFR6cJN2Bw4rayzed1fZV7a+ANcqbE+HYN3MbZLk33yOkM9TINT0PpEVdK4F5pxs00/vBlD39xcshyvLT3v7uOZMLRhUyA+uSZnAD6+8WopagEbl5eo1BGPykvhdoWXx97cNAH5QTOhUhmspfsFjyvUkQfSqpuhCXi/eFX6fwYt7bEKmNJO4pw93PZhSYtBD8jBu2KnNEAaMLxQjricaMT6pUjED7sK8TFDSxWPCOgRoh94kZKXA4zr+tdW9vb3AJ2gQriAq1cQoTW3vtrBJ8TTjrOi6pWRkdPaMngG8r5FkoRF/gSWtQLmaHkUD+dtvc3EeDrmq1dSMUMjgP4pNNLZay+Mvi7k1b/waxelOvQwCbrg6OHsSbcSe2ECpYTJVaHDvslBVergGPnMBBBWY0YekvBOpMq1UzEi+PoH43rP2Iu5s1Zvej5nxA63UOs9Kj/hWQ2fdsrrZ7QuiLHKdFxTXt3aaya0va3lcOrtZF67yjIpGNWFhzwRK0kYzDIvDziuBy7ChuBStL8IgpbiNS3irhLr6qaBs97ktLGceR38VnSGFJBIvIyqcpCZZMIG+ed6emCkcm8/LkXBWNWpjkVa/56rGy6uGBWnG+SVtFPYnw97ugVOZjs+vbJC3v7fMpd+IQuZZDFobbuRdqc9SicnvKZUF8yb1jQTQASGQbeq9SOykyeGW1EDcMCFjS59thMD42SLhegT93bC9YCSE+e7VN0ZXWyLcGqW2c2U2jdiJQT50wyASTf0ggFRSqheWiWDRPV2m+msU5li0r3i2cr1hQFFbg0FWYc7GuN8VS4YX82totDyvrtL4V4LxYA2x71Zer9oD9Mb6ymYXNlRFY5HgmlyZSElFWuLu/LhOyYwcwMTnge3dfUHLI8+XBz8oLB9V7ab/C0cOySgZ4ORsp1q+pxFtazW5mjwzIcyWQQoBNwLoll6QqQqI+3qydtnXh1mZYOJi24boR4cnbCb+7VoWMEljCHbvX//n92AXhirR2/mKfJ5lrGg19ooRR67nnSHGZA0EV2KNi+Y5fHtuu1IvGJTOB3VmCY3EOIPABM/UW0+BAX0ouruuBS/lzbs+44g/9hxSj/CXO1nFh8EvTMvX2yRRup1tb9snn8jVFu3Ctb5li8zttW27Xp2sHonY+uDubN+S7jvn/9XYL52AtL52srJ5trrNiX1ysXV+RrVybl60mMJyJs1PR2wxKHPJVp6iwaynR8+8gRAgxFpH82sEAulIA2e/pnSwYcS1zO7mGIFo6cRKmSRZCJ8IqSqrdlz4xRVxQEIrza5MArC/f3C97cQ6tjWZr8HY69N2pXUnEaCWBSAL/sUHHxAf4SOeMIz3Hu0/e/bi9j/9JW2JSL/65a/+6Gc/Pzh4rEmmdWFpspK9fnN3dtOWO4THRjsW4q6xVq5ujcxNzSXXzI9O9SancG/8KeVwrMqpkCqhDwRQyzvwC5DTTpFIG6ybWJqGXMhVR7G7t//d11++eO9J43mVvFv99uV3tt159fo7NuXtygmT1NQg/U05GGvZPfXpi+fNhFxemKRYW983k7O6Rg8X1YPuTsNwTJgEeg3pSQO9rVHAWHGaWTqqaQAm/cal9Tz1s0UxepKiTgPluzXJFl3X767OLzszZWfjs5/8+PWbN0+evgcAFUCHJ29JKciJbTI5Yphi7JeXbqezSlHrNQSEwDG/nixpJwT0YNw0ERYds++IynTa2pR3TgU9p174pJP7d5dXDfMgPUIfvBqLOkg0D6WY1H11Nz9Hzmr+odscCP+JUyUcBGlwDpxWPSMK2Da1MdE6OVao2ha2mFkM75hPDFw2aDq/vNHNCyJaW73a3Hm1tvXdzXWzGQJ7TGDdXZn94rdsjV9z74hwUzgWWM1We+XgyEwBVdcrWkW3LdOdqfVilLPnm6hC6aktnKM/hamZg2BKwnkRaTaSCa98oNWiGqel8ZMQq0cYb4j6u2TcG9bnpyPgtsC7BMcCkrem2TBI3u1ta9iEQhkYnsNaNUGb+YECxjSwu9V9QoLKJ4dHZj6TafgjWKO7GOoRN0mWSGaMNrm+tyvOFt/bMI1JYhNbY1hur+Ri4626OJpQxXAvZe6ryjTx4rLkRfuvLmNeoJIBUZIllWrGyeEYLKP5wufIjyYaxcL15WVUKcH88qL/c//w4WUgJk/PRoSmhGpZztIvIO4/FwCTsRy/e91D/JuPewHcAJ+3oX5fekI6cMNleTqtY9KhGU0yKeRYiu/F/d1/1gCgIr9P3e3kvK90gAMdsHdYlGBBd5L72YPFu79Qo/TVJITK6orSedq8qC+cN7Eb1PW1D+0eebv+NS6XKbPrhd0mrNnH5gRcsnhaS3PdXX7QyUjrE7OeRhNf2j6pK9u/oUrSRf0gGNSgSVgW60d4f7f+pUKNnUlhabLeOMaIJVNP00sLu1LmvkaGaofwriHlSgnt7O/UWnoTVm1hJ60w67jgLl5IxijMpOWaJalwSUtMg+XZSqc17B3JTgfT9AbegqvZB3VwAaCcGwUJngsna9fq71Oo05jF+Y32zr7WxJR6c3ciir/VS36FcwVGy2ihrMGKLvXWXzCzoeqai9SRFMZUK7J6Dhn7hvPk5RFCqCYplCDl3fOxKVW8mlbnEHIowJ7x0N3Gh7Ybul37TcNOJnJucgNqaoAyoLIa59DeMXMRi5Ci2yBMSs1K66Ufhe2S4OZJd/qAHAIpPDq2LnTzDX/23e1nUqoWBCTXF3MlxvB2/IioyckisSZGlHH1cceZrf9a0iFACqNDxG7sLCjAYGN3f/fAbiD7e1vHB//xP/4nf/nX/+m/+1//d1aptpsJJUzjlk+dw2VwzICHQHZYZI39wx+dVShUOf0omwZtsBIHE55scyGwgjwlaz8OaYtr3tw4+c0X//r/8r//v/z7/91/nz/blKtxAseJukzPAwMdBu4shVWnKXNEa+PV3fqrWclDbTOH6M0Zt7TrHEP9tVW1K3cfKzClORI5VKN2ydHisx86RpsExOPuulVh1eJvw2feVo/2b672braO7jZ2BOjrB+v5KHz2kvMZVvfkRer2bl89h1zdksb7ADfmLiUE29/DNYVNscNp8bE1O92F0ehTp8ttbDirqA1UUZAY4C+02H7jTFJcc0qrK0rPnxT7bVxpajtDaI+lTbD1uzA1Ry12VZvDC2Z4iLtiI0aobGI1vIRYRHChc1+YPX+jOkhCJ5fzxe5u72pBDCW5wkbANAonshvcqGaT3p5+51QjnAdnd+Pg8PX53s71wbNHLRdWi3dUWIqJUhV3z2g3BKCWxhp7nvCtzenj2mLJFAh/VrU1d5YVqgMN4nn1oKLY1CfH1ujenRxfbG3ur4jrZSJcb786vX5+eXd2uX55ebp6ufn5Nzc3v/p6+/rbn77/s83tU4HyYv5vLUIRi2EYd3p2vP7r1YuTjfXXtzbccL7ipfHlgjek/VemwInsEFbnwpp5nP/PNIQjq1IArP27tf3tg9bmrh/LxtUKDG2GUTp1byliqofrGXlnZq+a94c90TTLlTYSl6EUaYAn6xbMYM72jgirUk77HCJ0iN7q9voncL3d/Rwt+TQOHm+9eP8J48wpkdD+j/+v/+KPfvaf//THeWiHyg5Z4acMcaeDGWsevnpz9OYNYq5vv705eXlj5fT6lqNTDM/5xK2hbXo2XqRMhylQ7WyKDa7fi621ze+yt4Ri07adR3+5dvd+KmP1OKGyYxIdS23e3j198vSTjz9+8fSJqp2cnDAk/+LP/9OOiJdqbe348Ez8/c7Gh3yl65tHhhxqenl+9d1X39pmwNZAGuPhyduvv/oyJ79WPmQ42Nv98MMPRFuZoUreEAJZc5lZZUfstYImRghuI2ldzsXzlOXKt1zD+CEaxHF1u3tte2oks2GX5CuW6urJ2YXB3JMnj8036okb8NHARcHhcV1pi0Syz5m0Wtp3+mCMIcF0ASXksz2xLHCwK9TavvpHD//DLrnyrdJRNbl5d2XUMvwo8lwetQAJpHX14Vb+fjjyJao1wLu/rj6qgI2va1aT2HPZyyr9wMBR1UmnmzhaWzk8Odrf/fRm045Yr1NwNtEzgl6MCzFqq7Y93trdOSCGSDeIh4/R05MnJnK2z5t0NOP04vr6QysGEXj9+mdNz65/zsw3CDf2Wt14pT3fXbBPHLEBDXrKSFJb580xs0iKGB4ahi7WTrRQjkZVIGEbVMJe+2uIXJc2TnCz9CVrIopyqHJQkczci7k5wWK4xDUFnk7TMgudUx7XBpVGG1dr5z+6uTq4W/2yNuexzl7Eg6t1PIQiKqdHOZyuOpJllVaxvGSt6F+shJmGPGypTU3KHofk9NNaBv1SXcyPcsrMPgr6x8RAhsv3wpnlkPYGppmHZIM+tVuydQjk09iMYEzkN7DmSiRU2SyaXJO601yohmEsK7Nb29ucy14lXOaOYK42Q5mw6MdgE1UhAImeQpg6jaawmSTVTQsqvaJG6YWwn6vTky6JeqCT+bRfW2yh37pGupcnncnz8G6yJPt4EnKVtyA2RYd2b+8Rr9B++cyKmJT3EO4B+jWX7wm2vsf//un3Lx8S/W3vK6SS4uS8D5UF8O8kf6hUj0c8qsADzX7wXc3ur8S2X5WwuGbdyKM6PLu5lqeuMrthSqpn07iRvQaQzaHhSKmXI9yUTM9pNp9+6sMNYKcsuRew9IkHobPArma1/1pSU+VaS53O0mb0q+CQITJNzEJ3yO2hxFoKOQjVNhsE0EPoQICj17LFggxgyfui3dWBZaSxDITGEnlzwfVeUlkBbFeHgdyyeUWLY863Mb6rUrZLvIZwI+KTJRkWjaBhaVfggh9YmGIkFLeMVNzI5ULIlEGuWXVosjhMQrW+VBQptcK84t5fZE67Ui0O3YiZrOUN4Nm75BvQ8GpXtl3Pv3bFM9KW1vSvViZhe6G0NacY9923t2t78s8QqWYzzh3FshYojNZvpdaT2xktaU1uMriiYR26m9hTX2EYknwM1oScQ2rkQsf9zGo6wEtbtWlfikq9mougYdHeV/oET0qk2U6rhe2Sa57mSVldpcEfPX6etoXszdWTp0/+6te/+I/+o//o1atvP/vow3/04lMmJzQaH5V+qApO1YFcDhKgE+buRjCbLdGnUucLu0YAbngN9zhKqaqq2uDLWznKC6sQE1Bvq8HtO5vgX5wXXS1WQfhvXkt+Gvvc37ct2FQrH/NNGJQNrARGGrF+KEwxQoFJRAPsNjZQEILMAKBCFwDVJVT8e6C++/vrPpksEjcQI086qMO79WPa1SYkc6C7RZZFv5BWp5wuFWPa3TEcl2FYan2BXZEB92t4UeUfnoVEP9J0vV3u8cUGM7bw15RYJ2nzTEYgtU29l5W14sGmkemRAU76ljpKhhQt/cQ2K0cu2mD+4sZOuI7g2TUkePLsmaApvq532LmJKZAYBBfUokz0CNVuSo3kIdGw+ObcAoD33n+m0WmYiqgCrByo5HCyDHDlL//VLzqweS2fIguOmLGLuN8oHEDjVvAHtmIeyliQGFKQsH5NU/VZCsbW5MmhoTQmyNHh6cZuJrg6o9TrbxwXq2oA3IoC/+I3vyIbLA4Zlfj66Owby0XP7t4enqxuHV1dvt7btnv8y7vv1g2zhOgI+WfYXt682bx+00a075/ePNtaeWwF46AIy0HJD+oljPpPEOlGqJIlD9PbVLMqGsdhqX9ZhhwdxqXMRm115lGL3RkVDGZGSVp8KrnUNAuiasicK73G3pwJcSjiH0QjuVwMKbrJe4/NQt9oq/Ow20m5IMNcWznYf2JiNSnKTXNmr/+VlWfyshXABw8mFJquiYl/eGT3HdE4t47xOr+4PngEgc5IspsX/gqM2TtIc0FHwYhBhAu4ihRcSyFKLKqfyVL4Jp9wUsJ8JSxZSQL+Lk6Pxa1pvvJQs4fHR199/cX+syfQd0ovvb232zRvBc06+EiytsIKR2wbdBIPYREeUT7Ibk8qJWzv7OlkaBDeIU4r9hZkasv6g1C7oDacrdFmyJubztY44wxRg9XxO7T2t1nbOgshuNEbd7Pa9ve2jw6PheRNkwl/tUg/+S0/6g0rp6aeeM2/1Dh1U2y8JQTGDLdX53dbZsANShKl/nzUd6dpq9tCpkX0g+sR2AUfOWHAOLBeAt8rVPJJMIKXyOtxXEKwJrvbNW4OCpv4KuWB9tUUcinQirbfwO7u4auLnc1dbqEnT43InuljnNViWVYyRn645PlvOJWcSL+vDxE6hUQwqfLggmT2mLc8YWwS8OX1xreLe1GWMG2MpBpMl0JtqW4oRg9Z3XCCDRUhxPOGGHbt0tTv1qyMid90nZKmZSSm6OWq8NpIxJifvQfwgYRuo4PP8HNJPYDim3xd0bFvSPsXscAOrFGPjboMd5vqdSxoWHmfRPvsh6mqYYfBjK6tF8X5aAnTlgNS4cPbshJSolQJsPBAA1/Qk63JaY+krlYwms4j2hpbSJlN0xsQpIq/9fFpDT2FhyYn/Q5VyNjNeNlyb33jwL5VMMgYnIKBn4pDbH4vhBt6he598dVzubx3H1qDXALPHMH6cUz0YoE8dX3I9DvfvVsKWwr4wWuvlrfLM/fxa8g7ZVZjT9QzLOZ1jEtSetTDvwFzeZ7t9YNXJbtP6uv/xwVodSqx0zhnNDO7AN1nufq4GyvB51pALajFl0HNz677r7l/GHv1Iyyqg6Hr+dUv6O6aRTyuqqurv+FeMQRutgxHmYt3gtA0qk1BNHzM59enzFMQODCk3Niwxm799NREpxbS9JCfhEDfoKi93b+mpl2DRHqQ6hM9abJsniwl/pUt7QSwUIKoOkaUwWgYOnCFuY4aIBCxjGkD0HxNeJMAE8IRjUqFOuFcL6Atp6BkU1fSonrbdQG2grsSvkaNGDobdTOLdYWF1jeWo7ZJdeLGs3J/VcQIdbyj8gwVKOPaXY24fi5jTzSDfRh4OnsOi0XFowcyaryUyusnAAEAAElEQVQLLFiZBISM8shvNdBDT+9Vu79WYVXseTs/NEjwk+WnALeWeLLptLW87Iseum6HBFVtuCU0/G5jf1aMeF+9tQ85gEz3NRaVK4ql4IGhUzkH0SqZCW7cQ9ghK69HqsBznYf9YHBtTUiC7F+3o+g1CSyqpi0NRBby6aJJ+I0zYExs4EBDMDVbWfvltV65CVswow6Urrg51y7f//jZ6fHl6empTnB7c/P81Pk5N+89f/HVr7+7+oencB0qE1T41HzKDkYKtt1IsnpHdYOcGKOmJFJ4qB9WYiRIDBAejqxGFoaZVqBKDBC7QNtevTMw++KLb0wGCKE5ePx492B/7fVLu5jUp88cGXd+ZK3b07DKm5mlMITMItTYZzxMfFsNDEnDy0u+y6mv8oa0ZYs9bWM6NwAhpGs+lk8Jqkj8KmU+zoTFo5uD25uDle1TIcYz+arEZPX25pTR72TZam7LVvuU2Aw0+MglY3/uAzO/YT1Pls9elSbSLakgu+qUPIbazfqXt2uHOtWBxgLYvL3an3M4jhv9MbfafKbYM4NhmIDiQnYxNrLsH2ydnmQeEoXa7O21We+9ve29jd3j49Modf1E+tvVNylYRt9ACLfBcOHRNMl5Bu51Ptrb21ftKnN906Y6AozG71DZKav82RoU8WDK/b/+n/+YHRmbjMY2dx8/fibSY0zhutCp/9R9JELhMXeIEE16gzkRbc3qIz96hSN1fL5KsSbqg+I0fBcNaN7DElsilLVBzQjqpyR3dh/nZWxlrUP7rl6+/eb98z+UYmXDDj/03B5H7+rl7trZ7vrN0bZNwEHih9TwrpiHJ6eOYN843djaP726wCKd+/BR6Hnbcy14OnmUe3t4kZS64EDyXbJgZxM6a1a50OyXyN3yX3Z5ubeZC1zMcjBwqaFazFR56hjbp9Lzq37eWLeGBqTWjswahIJk8gg9miYaSUIBMrq28yX2U+9aMLVHfT579piZfUV1EJPrjcO3VDXdLvpFsSQiogPLTiV1ug6+G54W/pKPPnwfe7j/82/jC6b4o07li2s4HGkYgaYF7ta/W9s6XIZtXnVRWdZ5OnO6VtCAwZwEfHVJPJR/9Md/oL8SYqRQW9C8fvvWBit0QmI7gqvt3d29USMw1V8wB/fZy29fcf8Tp9Ozi5Ozo1psAZ9V4fmzp+89f26RgPML9DJo0zqE8feb0ODV2VrbK5Q81XlzfHRot9Db1VeqYZMhEKxeIT5mtIz1r+++4Q46cP6wseymWYWPTAuEfpyKLxRtLXbcYPWK9FFtjn2smo596+iJ7dvL3avV3asz4G5X3lIjZ9sU12cgZM1nupUx+qWQouTcVEDMnc9cR3oFvxfVlG79vh21aQxezBPQkIl0BHb9C58Bmr/u54op098p7pJ3gIga9OXpzza4XXupYOwlKNhlnb0hdA00lUxUnZqMfcPhGnvFMTk21/fpnsZxjse+eu/u9qO7lV/BhR7DblObpiAt3l51bOLth5n81Ff6p2l1/QNjQ9XBs2kqWtysWFBsWG8bN9zPigW2KuY/5ij/eKFMkl/VQsfjqAhn94tozvNpISRpESD+LK1j0hGjyEp5VLUV+/hdHeWZTaaF8YMsSz71GrN049RKxErBcuPRpHaydhCI0SAkOD5al9huP2pWcxxYyccQaZhbww1C3tNhR7gD36Xcql0l3FW1oAzClV93fPWjhHr76/AAz1T7pYaQSiRMg15iAxZlzE5Y/IEDOnj+hdaUG4TIFxbhILNc/Vbd3iTdUw3mSANo7VVLwLGhPlqBU66Hq3PuH+4fviuqZH38zWvezPvKnkLHsASWsFPVoSGRhu8q9YCpflef9NZagnnyDvRqawzYYPNgeTV5fjvVu+S/dSMNmEtW7F9ufivFD3+EVzIdAuEueY9c32eM7suF6ksFUHQMjAwjhl1FNkZTM8JvHCnH9bpACEyobVlTxYDWUXhO2lJzpBsX0j2pGTeJeIk1G/gEDJ8yd8kLq31BsA6Dd07E8AwJBuHUPXxqtbE82ziASbrPQmcD7OdUrS75oY5V6/5PHtUEoe5Y+4VfKT2MbdNqNaIx90EM/2SqWjSSoZjLlH6HM+O7pqdhElzZ9fdKKTUU5kaqWu2QM9JJ6mfdbCQKIKS9VYafgwbwqkOT+RwdOpoXUFlNIQ7HNVcFTW0jYXnpqDE0mQrFMtaHTcaqDVY4XYyL/E0ekXQXeB7Pe28DVqcITFoyZDkBeAFTBz2rFt6iFhJIHf61L1njSaTBUsOqNEYbq9mfQTW3IFeynKDD44SoP9n7xPDuq4Zyu5m7NKAmlaw4m5lTTP/ds729R2eH9j8439rYPb/69puXn2+u7V7jZdxHnMzoZIGQDGgW1fDvXtckMKmJhYVDFWRg9zdOcw6R0r1dFWpEEs8v30zthjUT4Sqp0PB/+o//4//wP/wfCYFA0J29XcVyyHI4cRtzLidVrhGzQUmDUYbq4IJ5J5UcVNGvujZm08szq1aumzMpy1BkOJMwRSAfgYB8UvLu1b1sLtqo9yqW6872hSwY8/qp/qxQJaofM4KPbYc4BMqxNctYJU9T3C0NBECfIit2yo9ey9P7okOwBjHEYn2UqsjvDJWLGcYvoJqwEse+YUWKRXXM0Oo849R6KdJgNId01toaMNi15vTEosbm2Wx7CMd2U7m6fPLoyfmpNa0V6FWtNXRccFLf7u6v+0r0S5p5Q3yuTff//T/5t4+P9Jcd8au1NkE2qTRwo/yvvvjNVy+/aeRHVu0dvrPp4IJZt2A/yiJCBtb3ZIkgkz2Szd0wzsdQb3nl03ivZpwkl4A9va1tMlTqmorrEGYs2LbOW6W0EoJSUUpaW7WSdPf8vNXiWTIbW+frX26sHG5dvTFaxDDNcsPurui0cbm2KRziqfk+58sKnkJMYYFqAwUEd5cOYq9oWUCrZMGSbiso71xuTF8SUhrwlPOcyLi3V2t7ZVZfKDd950Re5OdrJOo164UUkSFK+KkiUaUXo+ZqeVLSKJOk4vUck1ACWWqLRbdPrzE2GpvMrp+mgNYtfuA5oo2Prq6P5E9rkgPV0VC4KY1tTJaeO1DL+MqQx3IyKlzhlUI/m0gKISXMICTTCfa1QZ1UfnowQ1RLMK87DlEUGYJEKPl8lrm1K1cH+3vTI2S+OCaEGrIuC+oNNszAirExt1w8XLQFn1EjIlrlTXER1eRIPFtdSpRBBL92tmdDAnlyeBlXXOgaTEugRopUNSCEOCurh6/fZOvrayGdBhcalJ3z4ccff/zppyfHR36qvn0/h/TqlOIKCHoM7VVdMfFSS3Lrff9VP+OI13/3+nb36mrj9GL37mLzxhDgan/1yfG1meVKHM0DGAh+Yd1yJSfuKkKaRFfBFZ1EJAbJoWz3KFS8AuftPYRJ1ZNJ5WGiNCkWjQTUZFIZnMdX+GaysrKxe9rsDEgTD7pOU8vyI/jSrwvho/204mAqOLh6xwb/7frAUba6/ep249u20yVW+Oxx6s1Y0uy98phnwQ003a2bqKfzSy3xgiy5p8CJbkLQnNToV9VedHYCGBe6ls/euB0ayP09e3pfkV5FpCgSnae1kEJpp4pZByTGmx4MAiNTDa2G8GBE9wYu0qQLssa0upkJAS59A0vUm6RTwAO2KpWmdYGisehQKiJWhrHahlJ/cKtvWyoQ6gGtOXvtJxmTxW2ylp8xqXDBhnT7VHZ0BCKjjj9j0bQDr7qNeqm8YEwxcuQSGe2Fm0OS8Ko8kKVkYhmc0QtFaXEINEio/S9ggtoV+q53P37nZvm5pJH0d37+Tka1G4ARIHnomuLKNwX9Tv7lZwj3Gtr5NObhQ4ZAzIP7lctnPfjdS70fMAMpT/8Ps3/v+y/fHQFVSJ5gFESOeYh/8TVEvr8G6sLm+wJUCWPSHVKhpZ/JVO2Q2C8diTsa94olhdo9X4z1ej/qmyUStroB7zL3ycKgPwUvZLjHYMTMO3j2uTyduzIoP5SD31fiCZdQS037lqI35UyzT6oKkWpwT1wzcHsm0VwlnyuBJvQBT3VMYEK3dZJAUNXaNj0xedX+XiblDo3S9AcuOPAPj2log68nZdQMKrZPTybToBwxe428tZ9kezCsmWof4ZA2DP/6QZ8lE1Zrvx2/KSkJt6frWtbhlmyyBGdq0cBgxfLcZioPTVYLCYHFzdqrElwf0DvTWbBQUACRBOqwAhTot2cSMaa3Wkdv7KYbiPMe0w5eKb6xhzFAloPdgaxbtGixV+E8eibjj4Rom8MjeQOtrBKguITV7J4UqNUP9Vy3g+GGZXa2Mzk7Pf/lX39+8rZ1dtdnxza2YqYLEhpc6vYBHb0W3Ag6yjQ0KxIWcxdQsEuPo+mlJHzNOipnvuVQ29k5OjlinOkh1JnTVANLxgQhXF/+6hdfmehaL7bmbn9vT96O6OGete1hO+KzRRaCK0xxPhRNKOCI4GJjdQYGKkvdkcvBSI5rFW/Ks1TWMCsjrBYKq9IEoeXzC92qNR/d+EkAknC1Mkjne3d23adtA7XxjRks/rDIOlaNVb8T9rMfkQ0Ube3VXhnBui8ziO+upajehokdM7Bk/V4XkRUWjx2Z2osvrzkeOWZA56FnbUes29VT7sk7u2nvcLkVqCCyPVDVKYpk6NjMqjO2RdzhsokEervVPqwmPm1jt0eb+1/fvGYBiq+GwcLflZvHYbtxOIgNRPDmQubSRO1Djw62nRb98R/98fuffvpZCyUbqpmiXLM/AZzOzs6ODwVq3/3zf/6fyBUhb1cfHTz+4MOP2gRzc4enHF0hGh9cUH9H9kTWI7/vv+Zm+RmT/MzcjFmotnwqhO7VBgg845CcCMxrZsZEOHi6ZxHktwzs/P0b9rV89OaVXnFrZ3/LjosrHxhd360fXl482l//2kIi7rWmZNtG1jlfry+ffbDz+OnF6sa5c2AF3W69JmOpjxwDSiQEQve3Vzc6oY+cKS9DOGVFLOcokTsHCtAexDCcE3gngmysW5B9enZ4dn6ysfmBreWdAdUkgIqPHlsqPvoKEat4/wscT5dGNDJd3yHUjQW1EG0IWbtDoLJCk4iO3yOq66R2zf7sbhwf8SAYCbBfko9MsDYBSROqGqiGItZ0LqWToXbaJI3kPu8DmRKIskw8EqHRpOhGAxVgMzFNdFyhDtYyt1zEvbkypWfSMdqjFP4kedSC4YSlxduji3ji//Iv/vqa43zTLqtcRY8b1629UXp6jFIAHzT9iH/gXTvwSwAPXdGaK9C83d85ONh7hEQ2QUrDo1ETYhs2fYU7suFGUejNenQJrjMlvhAZshDb2Nl4/t57VlY/2nhEyCKjbgvE9GnyvFAYrVLpGJoiVxAcIL3HQNI9C5vZvr3avbjaPT/evDpfdy4WAKtnlmasWC22sX+38mm8vvwAxzrbxzWdWUDmjzx1o2I3ebuNeNzfrS0eVvjI3Qeo3sLLH5b1475RBWVkYgCWePm93EkdKYft20J3xF4iKkuipR3D1jQcg/XyBc7erf2yAkh4Dc3SfzMAC7x5NJEtnT67eoZ+keXSucvPDXoRdONuN97ZJ1Nd7pxyx2Ujyj9kVF0zCYtyETDJphXpQ6Q3yt6kpeHRsFJb7t3NZ/LxXYCw/B9BDVgUmX+5g6rYQhUQc2z2yn5ELZOw9rfuRBVKB1LdfQ3Kf6+IWf7HqtGrm4sPGoms/yaqQDvXGGkWeJo1LwnkmupUl2ttO9YM6XVOvolp/RRoa7cfGxjdWRtDBkXfhQ8mR0CYT+IhQBvlQWqw1q83m2n7XWmJYqGAqxtWgZK+BkUF9iWUl15DV8l4FmAaD/XsNpxhMDOTYA9m91/h5hbte0F1axvqF+6NA6noAOeFzeiZoTa9illr31Jma3c/VtjDNSAnawB++xpS/NYj6CFirAb2Pn1f/UgSwicFV4v3z+XRkqC3S8I4x/f/UKkKmNTVfex2zXspupz//10LRZa0UyL8HqD8bRAWnCgFeLunAnxNoRH3h9f8lGSpTjlUb7QtSV60SEIld1Lbi8QxP736UFbVOu4ONgkNWUu1lb6+kCOkKL101QIEMnMNwIoN175HXCMpDRVwt/pPvE+TDfq6Uklh4Y8cuCCbnJR4ARKshSdToeGmdjxrAJZXmmztMW3RbpFGNsBT9pNNsUsFAbWVieD+oU+1iTJq4QInpCdhX8s9h5mG1MSkB4OOpE3rBiGi+rivrNIhAWcUDRfXkioMVbESXICwrqPbVF9tCzVdOtoKsOY+OSwQh8L0wMNF6sIof6So3je3a2IbvCq+SHsJyVItrZptqhEGbArCGytVQZVAc7Z+VEX9IZMUQ+TMIwIBFDek7jZfy/rKM97ISDaBKTVRykFHhtKLNFVZpURDA8dh2eI6WQg+ApPvAVPo+U0nAItKtusfTL/86kvnb3J17uzcvDn61llAemVs06EqBdAZx1TDatE4Bc7QAwnmqUCMQo8CJrPdRa000Fm8d85LEU28duUoxO1H+6tv3x6mV/iFNIRUDmfc9sXt+bcvv/70xx/kxF1vm8skBqktaONTH/2PwkohwvFgCMx31Aotk9gs/RiAyYTBxcp0LC4jZ4clNkbZUtawbuRBIhycq+/Ew/dU0Be8jCd8yr00sfX1Y7unImwjtaY3KFd7j+qLmFNGIMmGKIl0cXJWRzJPYgrgA/i+COm88lnC5Vl4hEL23HwmHmJXrle2t3duBEW0kIZCQCsHDzPdhGvZn2SHoCE+RH0iisprBdH27vbp8+dff/WVugCsJegpXMZ7WXBt6LJ3alPL9IwEKQbZ4m6Xr/s7Nx7yXbVKDzWurv7hv/Nf+dEnn7z44PLo8K04q72dXSjnLdZXbdka6e7YWawnJ//6T/+cQ3d7b/fk4vCTzz747Cef2q6RuUWe4a67kR7CUaYCp1E90Gia7SByz6H7r2m0wj+SNP/8DEj1SgsQ13o7hFeddId3VcRvO45dXl1urj/KBt5+/Or0UBPljF1Zf3W89uovrn/1e+vvtcBuQ1iU/pab8sw47OXOi79+9OLY6l2G8+Xe2bmYBBRjAzftwKhFSSajWPPLa4dnDSVDS11o7NqvqCm0t6YYw+A0y05zhwpJErVisDQLE1defvNy79HuB++/n90yFx4iTmRJKlLOSyWBRZzhZEz1UCLtMEpW3YVQKZQUYVSKlqjTDMWcN7y39/ju1kaoZiGE/x2ydbRtaZVUow799jXHRyKuDJ8qjDMmVtzk+q1eSAy+jAm54hXT9GAFl7gSc2aFh790VU6rpXYqhISMp1szVB9+9B6WWNRSgyW10vprqptWKaZHBAhjfWt7R5DoUuf4O1KzbQHHeUtxIGy2YX0nLMS5UYnys5wYSRhkRe+mGNWVTaMaSpzAiO2B4VA6ldUcO1Y2cu64evIJsUpODdeL0H5Remo62Kt1LdqFKmg8zu+m1h2kRiJ5JZxKsHNx9vj0YvuIbLQNDk1iRqDtm67eW7nay6oCGuWiGvjRamHjsNXz6NdTN313J52Wo9x+JyKjNRbCJgT3FC7x5OnNZL1/sGRcKhM4CpSAGPnqT9wTbuhV2UpagGdccNv7Vb/RoXpkIL0ol39KfWjFjXEoYMkk+PaaF8zBdlUJQTLBM5LRB9g0KxpWYpIJBU6K6QDzRWs19TjpYFp2Wn2mf1niiI+kjpDAmWsEdOLExuayy1xxMZdrMoPYkMQgEKTcbeCkbIhG25FNH8OAMBbVJRoeK7qqYk0mcZbRxt1luwverQknCzlPkxDTTDuccWa9jJeEAoExuCU09YbwhAHZGGrGaqtONne2Vu1JQGEbES6ops1GBdf+VFmlSFQEmoqTEjWZUBgSobbtEpFRqIYp7QihoThSvdGblolb1T2hVVP3dSjB8tPNINZdZOia2uIDtKONx5G62Szgieg81NvBQ4U8Ne7AiCoLQlUcERxwkz8YD8CX+wS2clB2lJJf8eBdul4tKX0+wCjRki9lGJ96MCy4T/2QsqzeTi27X65mAL4HfL/z6G+Cbw/av/0K4BQyBZfGr+D28G9ejSM9zeBI+9234b+ZrjLfwe11mCLlvYD6nagow3Ns63F09ulBtCNP7XXoFVHHbqUNhEpH0PglkRzpzqwHLCRAFC6yJQ0LPLDclsxzWTMOKyUpwdWMuZFFpdX+wOQL+tTXyta7UwKWNB5FlEEOyiD4lSoJaB/ZKHdXzzy5K2/tJl03adJ3yiPjHpgSDAMJZvo4wJVr8lHTs39JDbydJfQoYOk0pBAS8WGCvPalsuzdyecqEq+MucK5zMH1gwY3lG85WtVXd1o5MWK0USBcPmpYcEs/o1pmLnhZkMKCgqJqnnmu2LCqgfUpldaE1HSTZHV1K6t7vPUcfdCk79Zvn6NqrEnNAe8x83H0QrvLUZ0uayHQegdZrC5Npd4+EkMyEerWovElgNvq0oTCHOnK29W7o1Und+JbSGjwxfaubX2Za9h5fgGCpyqgFBOwYwPVLSMPEBYSnFCBSltfPR3VwPVopYdVkTq/g2fntj45Odk+Obl8/eblC6tvM+YJE7GSLUXWOBMRrp71tfEdpY4S3qk0Em1ubz5+9OjCoZUr6zvbd4enh9u7B6tbtzuUuu2Rt/j1bDFxfnZ2QolRt8ZLELxZeUnXfvWb089//cWnP/pY9+P59s76668fYeH1lrNmiQ71FGXfXVW0DiA5a4Q8219IJkJYGgaWLauJkFtuGYllRZVkv5sZ+4rUjH8eAjV3yvDbz2QVX/VMIwh+Kx1RQ8N4WWKwxSHUiq9vTji0bMLvqQ25mhicharLCiIxkQrsjc+Bf383rYLDrJdTNbiRliViShqYb/L7nK1cHHU2p//kg8TMUorN/X1RUvUppidkx3RuovKwSLDeF24ZH+jQika2y6EGY9IldwNbyflIVrY/ffII2Rz3lKBvNhswqCLBSH8/o8yQvflrQHmpnRhxdHT54fs/Egd/fs6utlMlBoOx5hRZphohMdF3cnq6dvv86ox8HH7y0Y9FvX/71VcfvHhP/MjUbkiCqNHEg3l49ZGv1S0R/99fQ7V+xpi+iX03VRuviRo+5QsricedX1d8eUok/TO2qdQtlln5dv/Jp/uP99cfbV9e7WHh+s2nL548/9nznb2r1e21p9f2i199az2Hk5UPz1bOf/TJ3s/e+3T1CZsw2ALSbh81qKeCzRCkGa4dqvB3/60/+PrLg9af2klF4bZI1xAJW26EdQsjP3z//adPHx0dvoRSYWmbBiTPWDRnl4fvv3hhnerB4xc71quniPTW0Ts4yWw36jC9cD+njj5GQBHPiqAr2+nMm2o6yXGvmzEUIoDk0pN5QnD36GB7Y+trKmDt5sPTNw5k6DH1q1TNR/umLvb393/9i183aFHbm+vtrR2N+m79eapy67U0aeM0XXZAOKLJYMt88WxMEJJWCvYxs3B6rBAo9USrQzakg7juDJBPPv1Eaf/6X//LZT/fPJarV+tbZ3d3dli3DO7CUiVVwDItUFm2AWXZEzXSfnzO6yxkqxh2J6i9eO8F003YD6XTSqT2zt53iJnNHNtEW4eSccjxZIVwK4xVZDYvqPnoVNBK1FBNIF3Xt+ckIoySAX/pUBwhuEjFJrUbTA6N6UBoG3mMSHYur3dPdzbPNdALKrTQQRusOo/Wgq6NtysbR6srP1UTJ/CAPmonXgM+uirqIFq9jSdi0/VVmzumV3Qn05WNMEAmEMME6cv+wy/wagEPn94lSKX3DOUNk8A3SL0+ev3ttwZ6NgHFMz2C4ZEUQvaUcL3yzd3K1zoTQ2K56Vz7RpsBkIBuHQ9xxOkn/1dTNDLbhebZ5fWzuzt5tRq61A5XN5YZio4XMLme+Qsa+THf7hyV7QuccgA8bVHnCDXr2wz/jBJxG1JLHX2qke6Q2NC/HWCRLYTTecLIQtGM4WL1poq203xU8UgD8GZopbm0r7oBrXUhnjQPUhPD/A5iK7uftjGIvK2cXHVuPRG/Fucpn56rqZONtp9qTiaZVL2tZTZgZAYLm6kbU6HOuvEw0m1uHu/um9w2C7Fir9S6IiXNZ2UtjA9JtdWPaJf5+2pr4amFtnvonVCDUAzfaXViDgTpbenuJ2bPfJcll94yNmZADvJIAQrIyOFY31DYqqIrtJYcmeBR2SWaff3xObXjJyRCT5LZg8TqC7Jehxzu8yKEJvukX3794DOulbKCysQa98BpQvdXJOi6/jiAtvXzCc++hm1ThurDOKRDpnfzudw8QOjRcp9NMBC+T7ek/2HS5cm7z/uc9/nuE9aA/g3X0rbSkrgVfnLC6m9m8GRqAnsJJsk05KiBCXXOcmVlSVAdE+Np5z6zPocMJH1YVWPwb1TXkuG+zHcFy0BqQqSUSvQxVOtjfihP86vURMnUmtF3KIVmFamvIES9q3UMZr2m7PzDyQARDQPRGSbLm9e6/DJ2lw0KPLGTR6vxGAADcS0qE2E8aSAPRnJJkJdGdiqm+VkZtVIemaXIgAcwhw6rjw5f1/wRrfVtHkeRFAH7AIGgvuiX+kY6FRJeOVmpdU0hZYCkaWUhutJEnSTFQ8NqpK2YMcGbqVCLMaQvUV1Ena2mWFkRYsVgEuij4kkau/XP9sQeMhIoRLQbJkTAcphG4G5pmQPj0QPdwnmUBAp1GDeSDw8WrMfElGscFXdPrC6quJSLbTT5m8DkenDAvYUGQ3jg5WynvLYj4CqM7ulZBlxszVyq013b2doR+cMZ2UK3K2HZorS33n//2ZvDr18fvmpdU2pCHe7xgXtVrzYuNK4gIBONbvCF73Tzo08+daKwmBD+2NOrc2c+5Qt6+Z0Om4S0MuryxNR8x6AEwuWbEAn/Pfvn/8n/59/5r/8XbBm0vc0CebwuQAVwAYeWSYykVnCXKmBB88WZgA1Q6ngyOCIiwrrMX4jQQ7dtpjFd2O4xlde7LvwYcDUgv4CqeiUBoWrWOaoEMUU13LEF4mGHAXf0kI1FyJ/jcDbJqtkSnRmhGVDEwJz1AAGjuyksnsbvSls+vVqwmbIjaW9wCyJqV120A/5ywwmaYaCzhK7sQGL6nYl5cnL4/L2neOStNhiSjSmVhPcJY3vx1I0NGqNcCIOZFQkoRwsEnA385u0b9XFMVVWM1+GXGZq8DsTwV7cuXSWQB3t7p8dHhlj8mgwA/NO+2tXOTpf7e0etClj79S+++Oabb9bWcqvzeR3sbT16tP/C1iLBZyAkhACG7FR86LSUPSQaUi7lL0WH3oKOjIR7rNtaeQCQbFgGnv6aAYHd7LwpwiexuzkT9e7t07W7A9UsKGhO9llfe71zffTBzuVHnzxdW//0SPyPI6tNAYjrWds4u3tu3GLaiikRbXT7KNuoL2sfNVT5yaNH/+i/+I/skIA6F6dMY2F6BgAEV2CYEhsMCBHa2+YRvnAsy9XlhhAgmsFUzPauXW6sv2wgagdoY0kKKR9OnPRoqcCQaZ5UdUTxP7Wl5vFl9EwDME+Hg5PTD1ZANomrpiwxGOL+drcfkS/7Jhh6mwFw5NYsGccRegOcDee3vXnz0uxNmORT9JDOTFzpXRZgzY/DltlkfUCj83oF8jJMRPl0hxIXX+uoB5qWGNfMp1aLYQQnW84I+j/5+MOPv3v56theFh1hoRZVB/7BmZkHtIa6tb/bwt4oL1gwkXa2MFnU4O31qckx7lin/67TZjoIblJYNIWZYBvxnlHF5jKcNmJlUQuPl3ghC+X3EM4gVoHbzohQpCrZ5vTqksEtbyhXtzBB2Qy55pqaevSPxQsbO4RRAZqGFIbh9p7bujzbPTvfu943ZUbA26vsup0KGgdoRDfPOhumc5lqZmoZfbsyCt3eN+YKVMiId+SNYoNG7O/l/KjZ/C3XvJ9US7oqEjQ4pEW1QbMWNhND7bcvD7/96qWBj+5Q7ZyFbKORdgrRvAnR2uqzp08xqi5Fd2WmRR35l7Lnkpqw6r65IfLTqWLc+Y7PvnuD5rXDfDRSmh4f27l1Lx5jY+GLOsE2jEgt2KhLG7NHUNUkYJ5riO557hKadg+ptBGkeluvsBLOysnciHq50KPrUBKG6j3ULTYSyDRsI582iWt/FCCS/BwHlPCl1RoFjGnrTV1wWoFMGpSozTb1pu3fqKlZPNYBAVD9+nsTByniCOwDU7MBAFZ0v72BprPJ68JyGBLPqgdRzVbjTMATBujhFLQ8Z1oRHE+rwHA55KErvZuEMV0vj/LzgTBoMlayyArH6PgXecNwSDB0m55mxGwIM5bMUsiIR6Ul9OEJ/PysfFXH5AEF05CLF0PYwH9/3T+NEm7fXfcpPXYFt88fpijffd4l0xQ9qePQcg1iDz88mgy9nhuwezeJtMRKeHfNqWPvfv0bbu4BLGDC8vLjUv5wF6DfyllpJHCeVTO/4TKlvgPVy7CbOhCjwbBnwPtZ4uELEezHzYe5fTfFeA0LGt/GMczA57uLD6yrWln9dSzXfIiUS3hn+2Nij/49eAAlKFozmZaOop4X5VL+kqfcAU4HxQr5FzovTwZjjW7ja41jEiSmPU2mIbfYKFVLK0Rr5+Zq1NMIF/m2F8JX8kisQuzTJpTZvjb/rR3aZrm5OwiRYQ0cboXPtONn5OBX9Hlz9cH1xbmzjdWxKhXda6S9fmeJozYgNJwPvMgiVWe+5xCuKXNBRAa+/6oEvdzDIVIPp38aaNQgKc5Xyk9uULJy/V5V2/haOhAWLaOVc7k2nRY76O6f6MVvN7+MiTDHnFuB8oIrntzc7FxvfinsuHOdb/fv7k7seZzLeLWdbW7a7K6IEjE2Q0UON977FKjqb1AlnCQdrWC9oQH+xU2HRCpSIKyuJaKtteDkzYoD2G92O4bdHmrpO7RicDxHLhxRhHWWGJkqFpHR7A/xZKq5l4P2aQU5ktgcw+6Qb169bTC1syIQ+eLydONk7dkf/uFmE5TtIZ+DkxIcYxANE5Y+GdNsp5fWcrN+UnlVcwSEbHQeMKY4Vl1hb/gYmcctj0bZVAdTXqCzHT62zi7HStZXNu0uv0a08Rd/8VfUpr3y2GrU19b+oQrYsx4bqxRi+Z9EBYv1qRNHGf8t28BK2A2TsVUCCplJyi9SFk4SfRbE4I+k4Ws8kBfEml01lXLb1ju8s/ZZyilltxY+mPb05Et2Duh3Kzl4nq/cPS7IldSTXIVZiNtpXKc5IFf3sh4wq82RSK9W/BuF1+hQJpsrdsM82Zy/BNPtw+96D9QmkRrsWFzrqx/sbD5eXf0L/M2e04IaMZKWm5fffXP05uSOJ6VGXeOtngaFSLm0VP60DTtzf/D2UEeufcVKHU6MRZA9czX7xge2CXp0sPv6zeuGTHH4SXDWD8McjUOQDJn0MEgQU7Gxty8cZutg7z1LkyQ5PTnZOzgwLGlg7zC8mq1Mt8fHJOp2a8duRZfvPX7hyDnCJ6v4Af1TvfmkI4rhXzHK1la+wsJ+wRBdptUp3k2sDTN33YSXy7saODHLN+pFTobUADtSUyeGdn9B93ab4Uuwhdbq6qnVvo7wutv4hS5/+/wDOyCunX+3dvnk+slfnq3enRpsrjsRYIcjdHP9TKQUH26lTltr0W+IUgvNAUGo/z5sM3rrpK0e0kzFr9zykoaiCiqIam5OEoIEkOfy/CO2+NkpD+Xd9rYByS5zi1qsflVhRNl3ErEUEJwYkRFUg9HG09S8aMZ0K066IB2RIHIppf213GgI+g2FIzmcQb96/mx/3XJkqmll5fDo15cX/4WtRztMQX2EzLbhUchbu6W2CNiQnlv94tRkyOXF1u530EsVVcErOsSwRxtslZrt27N42GH53VVQ70KSYQUHaTBFG4DY8Dc2xkNBFbYd2N49fHNodParX/yGf5MmYEQ2tkwSYFx1bAb91ZdfPX78GDvpBNXnQ9GNOAXM6MyRDpB3zNPW+rbtf0xRNVITONmBfBP20R61sQGJjEhxj7JQwUePHidk3uhF0U2rIzfKo5Ly80qlLDl7rVNICOOeOqldwWCnnT589N6zJ8Lbrpr+mrPBT9c2hf5f7qzdfmVi21FxnKkbm6c1MRCvd5oVX3t8e8sZrCqaQA1zqmvko0RKzZMIRPPFan8acIKwCETv3C2fXvb++z+Plx/zXr2q4qRWGC0DFKOWx+X8/Oj42J5mlD93hpUfI50NonTGWwQVVIZwS7ZWbZlqykSutmS1Z7NlDil+san60+yKYSk11aHbqnB+/vjwdLuTbvkXeCg2MEhva/kI7T4OlDp/qpJImDpHhbV9VOfwU/PNb3VTVxfPYGC6mfhkN69bHN4KsaUquqRIYzctk3Y0gBk+a0Fy6y29xV9J6XSWCLHQjIQYJsLALAFu6ndEa1FSRZk1jrX7HzFoK2AbORDfydbmnybxzuygjxLymuFqlN42KrXHmdQITkYNmwyxytuIrrFcRJdMT2n9EB1huH8GJ/oaWZufdMUPnSgdLTk68o7zVm29ksuLeI5O1FcYmR82Fg5uP2vd1c7QdiIJKz3Jr2U3bq93np53FJFCF4bq9ZAcFHSRO08rUqJ6VqIS4+Suh8n6glyaFX+g2Z7CQMImJFzSBlbKxEwy9R1Ri+gPl/t5fZ8Hf9/5/ksyaE3aHz4PjeD6UPO+w0jh+mXIGTr2ftJ4MIUuaYK4q0qUTg8m3Xzf/1zu/+bnknig9vKhyL+Z8PsnU3q2XDoB5cp8fz3cD4axOFXSdZ8Ee+tEphcZjabb8aweLNakQBHzvmHxZLCt2NepccPSkNPLectsTKAz8UOmj6iBPYqrxHshS2gCR2K1i/5jeFonxMdFRGm649cgPpEiUsM5bB4wB32KDGxSFixVG4HPb7JejG+DkCS6qpATSdvOCDsMcgduPVLu6My0sYrCNIH2Vl5dZ+XUbOSqBdCzEJaJChbFSsgFQAPQvHzV7YkvRVJPwTGymL3J1Z1vgW6YZG2FrEur6gqoC1ePIlyluBQ45GilLB7xmlum0rTnaWU1Db2IdgKUNak6HToOXRrt4Eu2I4/Ht1er+1akmVlsIRQdhabO0bw9pV/s1wo9gfF8HLam0QNZGMULdLvOahTl7dCobc4/Poi2VciE25h+gLncip/wHRV5ffOIJ+KSEc8BzBqrW22s4qijk9MTJZq2wJN6uDpRZK7uNq3nqXaCkbcNdlKVq2er51//5uU3X317fmU7IG44XfiaY4Cfv/dMl6y7FAKRfMSD5BAXEgNsIEbJebdGHAlI954kTJJ0rVw6/CenDi/L6vaZwCjm9qw3xDX3emiGIF2sJwIluyZtePuP//E/+frrrz7+5CP95aPHL+7ufhPfLXtSnaAv5VeKX0W4eckfLxA/BXDfBMgUdFBOBM3q7a71uzsGyE41huDAgWuMw1WVobOnR6Qt7RPYuvrmPFiocXBK1JTaXsYO3GbtrZo1A1Ao0+6G03HgzljskAPDM3hZCnZ5NAKAJIvUDXGSUpREsgjkBg49m7+HhPPTwIUDtRTS4Z+JEbNRxCMWxs2t9Y8//fDt21f/zn/uv+qgetXm68xPBIriI4wSQx06Sjk4OKilGQDlsI2jhtA8qUqZGfCt3d09G7ccvj1Gy+9xZq4NjMHQB5qogcbiMM/ecBzSMbN0sp5MmYmWbR5Ftjoqa020z0vwr/IvWsNgfbBR307T381Td7IHRGvjiC+zf4NuQhZNIP5QAyyaHnSINu/TE/cUjIxsXRadit1npQ7zC/g/rsG6T8mIHFbd3u1bsIFrI8Mem+p7fbElwPnl5cpjywNa5aDAux1TWHv8yze7HaQ8vV0CMZIVZaN04YWJc7IUTo3ZlgjjdmwHpA5oPHgo15izEXV8CUqBMVoHkUORDC/QpsMejbkwohr5h51lkclABI+IP31nj66ohrlgoulOJ0QiZ1WfNoolyl+I6UmKeJT/umM2QIIalvG4s54duWFYaCDrvCvPLdE5PTl1U1voRCcWnmF78qIACpbqRU/GEEWcxVUvpPMgM7FupAyJsnHopLwEqlCwJYAhuNARMhrge++/EIi9vbZ3fHLoEIbkExSVXOqhGRpIDDnEmTmOYG9/m37LP+CEIx6gnbVHT168fnOofk6Wvz273N9vbYYSN9YtNjUKSlu4ENkYlXnnhtffcFUMqA6qQU79E9Rn6oLisLuQF01WG89AmFJQXtMRcOs3k9e52lsHIog0pNevX3/80UfiGq1xv7k5ubk62e+M7NfHZ/aiOrs+utrZ1qsyaM9XDYMbDW1fXdlI/2BMpQdRjlWuEdy5g9HyKJFc/kfcedfvfngRpfy4f+zrIcU9EUd63j1eMpQ7ieKI+fCjD/DzZHvv6M2hreSrmqmReue0hl6mTlcfcXluVBDj62Qvzs+Or67PSblOP+mXnATTyAVAspizYoyBru1YMLYuOTI8A0tc5g5lWZ+WJCQsYTwqb/VmO7Nl+msD+uSjqU/Ni8NDYmAbikzQTtgDoHHf1z18E7OgRtLo0/v+RS0/yHK9DXQX46WCE01fs+rdsJGa9UDLmpFgaal9n7gcRRomhB+IkmoQkhkJK83UUyeWxoewcDOmSSVUsA+tIEvF7slQ7JJBn6+XrkvQx9RtycdTmvHtEGWflQl7ZyRvtS8qjM/OZlslrKd3RgzMramvwU8dHC0ys8E4ywWDJcyVpXxxoNipJ1swrPIDHhxwa2JMj0pYIC9UyQqFBfQBVz2VL7UrMsG8HHNJ9XBz/+R3v0oR/B8mW5jVk+Xxu88SIkoZagY9X+pfxefhA6Bwm3RLGkRJMuZp5lEv76P/+VoC22fis7zr/cM1ie9TeCYFU3vx9T4k+Z3v3LTg8WW6BoHo59bfQAuPni+Pu5mrR8Q7Ze7ibcUFbW7Q3npDBnIDu9iYDXFtpMA+i1NrO1+vWrTZqlrMThPHrzxqUhIxY9BGf1EsPvpLxJXuK6Gu/yAV+iFdl0QU9IzkpIuddWJD+IU8wb7H0BgjGak7h4/7qaGiQ4BI55aCj5C4YPAMnJLom5sPFW4P7+bF+aeqH+JPRbB3MCvIISnzTitP1QJTMx2T427zi7ubs0sGbfasauZSV5cVJ4yktWWN44i3ucn/CmKGQEHhzEI1gk3EVC4bpRJpdl7w6AFUNMwYhCh2rPPKsCPSZPJSbAzxxgBSQTvjgSLY+LyOTBk9r97805Ht5plDF8T1NePmbGBOdyVbGHa73+Dies+GK6YY5LhZF3XD07ytRhCNkQV1t9n/lePYb5wmpsXillz2SzHM3b5tQoBLH4VfORDAIre2t4+MqInnfBS4f3Z9vaepz5ALJYAdInJFOMzB4ZNNwCRQJIUjR+Ece/1wBvPanfNE4Ue3fvLZR1KenZwzKxO5aE1xhGUci5xqn54dk1MkP96hkjeZMrEXkUVYMufN3XYWFZvKEacbzCEJMFEMOat2QrxsaSIN1VZttrb2AeuMEYHYt2c727b32L0wXQTnccEmOZXEzsIvcoubzAs7bzQChyTJHBSy4kiBlceXN992aBff5Y7VtGI6TleuHt1yb18frK4eO8V5Ze1kY4WJfL69/fjZ/oGQhLZzuATQSXZO6jm5vH18IxLp6vH50cl3f3l7c/7icuXrs6Pz4zdn+/Ygt/x4c32HR9VgNo6sHxw8w+MIxx6aEdoQxzskuhd0ZJqK9D0Ie+NW21z6Bg2I7kpW13a+ur18awbFUa8Z1uajY8PG119+9Xf+8A8P3xxp702zTFnRv4rfG6G4KT0+PH66993L01XbohITvY5xl/759vbjjz45fPv2yeP9o+b6G39mTq4f60OGvGEZyEbpCm2nnVqHiGpn9JkU0SRSULYA0qC84AK/0vFcHb3Rxb49PNRxCYrBp4PtP3Ci1vXVITu1mpIm1wK5G3dhnnxcfzTvSmE2QF0mYXVSs6nfkhH9ugZDgmrIJEsdof5TV7WxfmAmCVngTsYpJgNglLu6Pb6+O55oOZOMn3rCZLu5OL3aen/t9MAqzb0tM0X7TnR4uv549faMV3TFosCbv5/QtfPGYFnJ4VwzDMGdNHHTXH7RKsPbSNmYje+g0KMYnf6AH2JCdmv/tbesATDXrj/RT9+tOX+0LqFSFhpVSE2jmmbqeD4Vv/q4I8W2mi1xEZMafNlif46T0KgjqGGpZNpoyof23ZXjm9kuIUgpyU0y1nbs+nN+cnl4dcSodeoXJA1zhdabEACWxafZwp/wVKeuu3NbzTqaBh3GOA5UFjOLiPeAl4TnWwHWZt2QQ6tZeILwqKrcB36Ys7178+Zwd2v3dvv6N7/5dbimafpDr+lJiKX2XbeihmcXl9+8fOms2RfPXtjFeMPS3o3Nl99+dXZ6bJcd1d7f3Lcw08kYTfc126PQKIP22kmSnJTRYZCXofAWjqvd7f1LS4ZISNQ2HNg0L/r1V1/vHu9SBUJf4Ey1qJeJiL39faQ4P7swcuYkevnyO+3lz//szzRGmlU9OVA2BXA82T++SaI2rh4fXL852Hjv4ubLyxOh4mdb+x+cPRZdn7tnnHhJafULZz3ymGgPrEYtFajji+bTRiT0XUMvj6vPuRvxmNc9GDmYLH1cf+iR1TWJH6MCrw72c3IZAtvyte7AHv1S0KI5RxyMnArKqECwllPLhbnb28bwirA8jDN+yIm8DYb53PSals847/kgSb/Zv1094C+nv1dXt1Wyc4zXedoE1OGM5bNADpa8G4bDgmizzWlSaurjUWq0XbPv/Aqkdens8U8mEORN+j2ej/FuUsLB9GBY6dsD6E2vNTSSOT22kPLy05WrC+GK4BGUsUMCJm+qIyxHeqacoUMj8MrzV8RO3r40Dy1M2jlPNTV4BH4hzYJpAg18RSeQ5VYB+nMxa+ITtRCqEHH6Eh7JUJ776sjT/95WMm7WooM0ifALk9LGoHerB6o3XnRyXWrxO1PIeCoqfS5pqPGFRLEeze/LlEKaqi9JWJCLft2H1Sg/ag0Q5PA9EEsQmn4v75abgeXpyPDUYzL2Mdne/XrIvDyQfCD3XdYsjx500gIawHtBMihLEe6maghTm9WJun6niL/1yST8PvGCvM/IPj/u4f8NWF569sPHk77HDyjdw57KhN1gGGQyk+WKT6xVv4gEhlYD1pXf+g+WmgV29K4Iks4xqUadjpIi09gy0bhhCFL9MjTkMaD0GJDBfeLD8L66aKJo6Goewc0DTY3tlDeVDYjHochwUAPWFr1J2ZB35J4OSg2X/4HJ+Gbcxpnk0r8IkJyOfcDENYwvL5O2PszLe3LBWXVN4yqsXlpXQbTh4koFDA6DuVwBrLRyT/vLItGzsxYlzrG7FJ01lMHYlRO3wYBKJ+UwhGpQYJRAQRDhZC09uJNNP9GApGYaBYcqCqxOejfNqE5FA6sm03RsmWBzwTtnu1isloY00+1wE1gqUnLWg9Q8/jToBTVpU0sDkHwJreWXrD0hmO8WBsU/Z1+tWvO6pb6a8Nhd1WCoR3/wbm1umavgAxMIwtQRHnNjemKXfXi9vkWQqkd9fwiij7pHNO2XSNUFNuuyaYVW87b5tKwl1WG9PTqW9ie/95Nnz59xW1mme35tXgK6UU9HBYWFdUujC2Qm+MLLyNR9RUV0NFF7Jr/66RPnrLSkKs2rXgSG6HK6cDlieXBTYfoXJ4D+5V/92c//4Kei6p88eY7gSI0s4nHpH/KrTeiHwcqz2DhAALOuBi9MsmsrU4qGD19SL6rzbtP4afvkwvTW3fXe6ubZ6pU9H88NuhiArZJacwjD+c3KudP19launFSlEAKNGjbbhHoO9tUrYT7Hh29+9f/5J7fXRzw+gud3980I2UH1gOC+sWq08Q1KrW5sr64LO7qsQ4vstGTE6393I1ORyTvsH4XrTvXRITnLH+zIXpKZhHNmCxjfFvTmhocqH9bl2eXJ8xdP/8W/+ucff/zvsdsqhmhnjiuyKpHMaazBM97aO9h7/XpVzMsUID45Vp1fnO7sbTt+deVU0IuCIB3/ShMqIMXS2h7mAjz4wO8nP/30sVzGdWPwcezhRm0xc+GOc3B9Y+folZCi1xq+ekDs/Q+fCXbnxCIchHC0SEO4B2qM/CBReC2Nri9/qUJmdlcYzLM+a8xzTRbCQzrE/UtZ10AezBF2D6+1xnPaOLLUNV5v24kUl0yATA8i05uNvcvNreP1o99svnlhTLe2fn69cyb5+qoNOh8f7++v7lScJlmZFb0gg+E9iHfEmjKPbsWlSIsgyKjuKdre64SXRgj5/J+G41L731zlqAsttJTVu0vVuon+c+s7sCgErnYQm1DI+1KMhLkpVZl7qnQnL4J4D2jtlpvBtOOjR0+sarietao82L/41V8bA0DYEbxOcIcYAORJMQZs+h9RXiphxM5Dn1qjQNqulKq73d4WwpGHMqKYeOz4JxJhwD/IZQ7Zhn8LIQqusyandLFv6oEgNMH1+fmZA7foMsMhgo5L9R21dogEBzpoP20kRwYdX6A2b9jOPo++yTl9GcajqviyRD/ng+YQKXGtngYMA1xicudwzF0PzFcJJtW37mzb2iXHqfsyx4OGNCKOFjY1tQVd1WvBsXkkk5dpNnpC3grlwrCzK01jcs3ERP3Y3ZdXb8StrK0dfvbRTy9fff72O0OGb7d+72dvxDPu3Ww/fkJdj4gqbrmQpaLnIZpWAmZDH4Wrf4yHfuLhBsJejSCOrAyM5a1Pv+B3//OhgJJ4FMMW0Jmgat1/G/Gx/M2YahgTOJ4+krDifGEk/clQsUbe4q6NC1tF53UKSc4rrR8NNW17KYn/EfZD/66ZYlk7yyit1DBCRJSsW6GjIBJCIefGi6yTUO6np2yApWOejj9sqv2Cz0OufiJNfu5m2BZQ31d3BP9dKcHtR/Tsb17UhMnm4AIHApnM1nzU2c+BWZsbrJKjspWmTJi/QIkCw7Jgy0UZKGAkdikRBCDmkncMloUY0+T1ytVtSDIAq2BljeLtu/K9gdrI4hSz4DRVKVOmUEgv/ey0mSkz9jYPuZRfleDoI3YkCf3vWVdiNrBUv7rPax/zutSZhaHqbhoVIEv6STKyibgD6/uPRRT9LmOfPn73WsoYWAD06x6VaD/XQFHufd1/F8C73xUyGDQD6zJbyfd/fy3F9PQe6iD18HZBb+jqUXpwajf1lmH58X1iyY2SXe9guZ2iRVX32CikTJU1RHuXcqmnlrC1dUAO9Bq9IjPTZzSfmvobk81I27T7LFgnqRqrdiYxeAzmTFiO57asPu3Z9A5YXL+XBHjLUZ49lAEID2zbaEu17dXf66f9SSbXrJ4X4sAG+zhkN75Wef8dI7Ry91GtbOPbTMfLD4nZ2tbXQwqIc/bYGLuZQQjm5G6DjzQu307LVncPQ+luj+2CfOZee7WznX1TzH400nThuiZUgzM4Go94iBKZOS/bKkicCV1DT4BmPS4c66E6iTYlKA0c0p6t5DGaGilZuOd9HW4U4OX4iMW4cvc5YOqnrGlVU+I0MRTTKJangOgKlRKJhsVBAUbX4tujFAWFMYjdPqP1NzZe8odmgDl2VKTaxtntys7N2uH6HVfQqZPcWh0lxGjLVu72gjgpUm39dGP1Mc0pNHnTAsRrMTzMsWM7Td5eP+NZY1aJR7++3b66O6KE9SgHa59drX6zs/rB+urrlZunNxvfbqy/v/bom4urn69vqt2OEYluPoPndlOcp73ORU7yOeqnhNezffM7Cqt9tHN8smvWXZyGJBbp/uEf/YGgWNvt2ZKvmBCBImJyzczkM8YslBjOV/uWaw+zxuGIPv1g20hnRNseLFaLMUFwjx3iIVLbPd8QxXYclkKuNQkggj7a6lQksJPi27ff/m//N//HD977zM6AOw6O2rSk4fLy+Pb05KwSGhhPY0L2+NeP84vHtwXfvyElbRjKuFufeM2r9aPjw7qtq9Xjw1fcmQBoC3e3X1WTVJ32VdfqFu6k/eT87Wc/FkLw2J45rLibtTfmbNZuX+G0aYHHe3cfv7/x55uthDMPs//ek9OXF6/efmWHnvPrI0aI/bK4Hr/54tWv/uorfk9icXvxo909oeRmlu7Ek7OEkhXXCGj9zbs2myCxIAvjRvARsNopr7olLyfnl1oDPpozXrW14IWzS88/ePHR8ZHNURhhRLQ2r/X608T1BBPrVEw5+T94tH/RkW9krEnu9a0CSZ3IWxW1mvW7J0/39kWBH54pe+lK68RSWf4v+CbvkVsnIHL94tymE/UFiyOIsZtQiWXfPj89E1H29vC7w8PjnSePDKAe7e69/5HG8dWTJx9hGlxZv9i0mDbTpIhS/7qW/X+mWwE9FbzMVd53R0kh+oRYsqitfATF9e23Gms89Y6z0aCpzR+Nj6PqdaHKdhfhmJTpbHNLmDlRqTyt+/rq0V9/8cs/PTv98dXTR1t/eS72eeWRE5pWr78sYO7Db65+8rPb7YMeQAcE2WAxhadGTMeIoV0mX9UqjwksMmjGpaMdktmZqqrjl7lrxIDTQ/0gaL3Pl63LMM4OXxdNM9XzUSWH8ugWsVKvK85FdsbFIkdJZ1MLi/U4SSTUfwMOnC6DKrliXpmfoRwvb05298VibRyfnK/efOAo+S9+9ZLTm9kqm9aWS2l1dW9/N2ZZ0rS7Q8tfnz8xfba9dUImwSSTRg6bW6LmCkJj91aPYczF+cbV2oVthkwdzDihN0LOxPRbGEoL4WQnoGfLkASrvFZ2dvecdU8okAW1qkvmIwdIpotaNl+FOsKoc7k2hUWA9w72HcAsy8X1OYuTZc503Vg7ABmBNKPG1AYeOIWEZdfpjL0bLpDPWAdQZUGl1LUeJVELDNmFmrvbe2Y5tCEDHN0UD5yO9uzyQjcnsyAxaNUQWrFWxMfG+i5gDC5BSieX6ztbzrj58BvLO7Z+cn13dLlxsbXz7O3ae2uWG709b0735mnu7o3XMIRmDc5f7KaXKPCRlCxJNN6w8n5rB7WnZU6vo1KSEpDaQnKyCItcoA2ge4EL8Iq1fFFiEcEeyD60pQOsrsbkLApCmqq0G09+KIBRY73NkhxRhzj95G3affb+h2wCQJJGWFQNAOPUyGmyf3drBtvQebGRarRTfoWOraOOnpR9ZvCwuYZTjUo5/5eb0Mf2z1DKLFxmeSIkWaB8+m1MMtoiVBZiLBDKCSbItay01cr5R0Ujb9k/nrb54u5qDKeKlJLe1dlxbSzumx4NlVauzz+M0OtfICy9pIzByfKEH9XUV18moLfHSm/YchM5IBhdpAuFeFnFrz5lAc2eiuXLUuidt6JYvW+4Pkb8RHLEXq24+qG8euXxXFhrt7RcgN94A4I8ZROR2DRsfX+PZrFygh/jqgeyL2j0w//7n4r9DPa3m7+ptYzDF87QeXdViSH17cVHUy105Of8AmGl7OV8TKr7O19BuPq0m/bB+/56yDNPJvlSVs+vPpZtUGV9jt2+ULqnAIX3A6B+TxnV/+Gh73k44vFuBqDX75JUzA+S9+L733O3JF26nGi0yMD3iX6Ye+69WqQOer8Frrf30NwFoQpgVp8iI7yLJRRQQh1pfdeV5cxKWklH5sawMEy4yXcZFuw7olYG+U1Ar+2ts4EqakRweDtEoYJZYDN/V6HDVdtwCWAsxMhe1iPzNRrKTea7q0YBAkKBGo1pzAGpsJvCyWp4prwrik6GoXoBMMp7GmDyZ72d1WCloYR91puUgWtowVsrbL64LrBkNEZfgUaBBjYhRcjz20kDGaOUcNMMa/AZWFWBGoJRMjD1qxKWh00hwzeh4JraQho7H7rhiFKCugZK11cbCmx5AClCnTfRauSCfsK9Cb70oPALK4aqDBboRSRBydsrTrDNzcO9lfV9m8Hn0mbniTLm7rra4a9fEV6zsc0OFjWRT39fnhuY2MH9elcEOxtT0y5aXVPXD2Xd7ihKSItI+vz1jWH2zgsw3btZPbOK4G59jym3ZTRh3fDqzt7KM7blydb+nTJaa8EvhZ5GVo7ccqimTR3utrd2cTVTXmHOzbm8eHnTCmCd6N7W3uXpBSocmEjYWHv8+NGrr0/efv0tb9Dh0ZHp2DwLdQbpPiTnCtP/8e2w5NbzRGIZCqnkZpKRXOlShjX4ui7MRiIh47KzOUXJm22ejQsRS2+P8ISornpjZ+/g869++b/5X/+v/if/0/+xca+hAqaLt58uGdWxAn0yD/SWOkFTlrpy7LXND1G0qjVORmTdz5YJZU56XN3bEW7bYrY6Hqjl80JYuOTFzFYyQbNxd3xy9Z/+1V8/PXj6wcfvEele1TZFj1xxAgot+L3f++z/vHq1u/NYoND/8X/3v33vyXt//otfGer94q+/3Fw10yAsWNjxid0eP3j/Y034onwtagbHKIFlzPuYdssRjrWUrgaDKVp8NJxIPyVCWyxNCxmJm4ZI/B1spA2JchZ2f3ku0gzc86+/++r4+EhIjuBsolNXMg4a4JEHX7KKRKE9evTzP/zDP//TP+UWn2bFAUCuZTFTrFQ2HT5Z98Krp+UsTQMFITp/kKt9IBQG3P785z9mHV6dMaObwxFmxLxkG16enxVH4VTkLQHWDsZKKJjQhi7GljW0tswXSxsUtZKyhgfLgDe6iyfJWQoCEfRJyVbzCqnBWnNsRbJBiD7KglRPDzZql9NVAMNJzF9rypR48Ee3b73pNq5I8SK3TzRAxI5U1UlBJ3fb18d3r5jh67f7xfNxVJOHlTfcejfHf7Sx/tOWeFzl7Q7xcGC6wwOCIbFgNTrarbdTKShzTNoNZqepocQ7szKmYIGbAaJmGY4Eu2wgBgvZ1TpmSpugxoX+uegt302fuanXxyxXkb4zdGQhpD+UA6rhnLh5ulIWxjOWGblZL2jFNoo1amNJr97ZSMrCbnGAE9tj3fZ2hruW1cY4q46L7n5lmyQTs6dPnyQgfClmA5il9kprJUMRjOFv+fzmzeHb12SUI9mJ1NiuvcuyYXVBPiEkiwI+NWYtFS1fvXpjtEb4oxh+sT5VUO0jRhTVoufOgASjM4POTk8f7e8rYn9vx3wDecMRcA+eHmB6jBnLq/Y+ExpBaiIvAXSFgimxhiiW4UZW3HGwg7Lg4JeVAjgyjgBLApIJQqvfOTl1FESR8hwlUpqIAIrJiMChenmpvtvWu5gi3Nq0Tkb458vXL+3dvPZMQ3mSwAJ1YbqS68Ox0EYWYq0KspoaxvgRB3WoULgl1Wh0KULS6GNN29eOcCQBULZEpasSP7xGXBKV37lKv8hwVsi8T4KbPOUiUHrUvbs6PH2r4ItLsYzi79db36pI2F9dbW3Sh/BWAvFoM7IoO7wK3RuHx+ytbVjPbjbmesP2cldN6WB2KOF3SlW6fo14+5l1GwWIU468WjqykOTSNZFlxsWIEflzS5cr/sURXMSkFrE2H5xYljHaVch9QMv09PdWhEUsGwdocGvnqNu2zrQpK1QoB7loKEzGPrgEq4aX/xEaJmEpDPuwSiG1d9Nl6J0MNc0ukljmNj9XWSiXEeBklrZyn84CNKdALjAWBvyouJk0Uw8wjbgiynBSJbLvZCaLqAcv+NTW3euhpWqzCmSLXL3ovmU5qUdpjBZQszf02zAIRatQ/Fed+0/wK1qOenFfnt+nWhKVtizvHi83ICpxYeLy7j7VJJ2PKWm5uy/xHZyeTubvX9+X9vB8SYqWc4OAoMWme3R6+gBgCDuAHj7uMwfyfsXVD5IviR4yP2TpezkZgOc+zJXkU1N0BW91xiVOBYbFu5oNubyMRksFuus3Zp8jqK95F2H9S6+MsUvyJBR5aqXp1dWpdBubNidOVJCVMsHF4KQsiVr8bZWdQBEqLmmsawmR4MojVANsjOYCIYJy8iKbIj6XFwwX3T1COVKQ45pV+ZtKbOaOTtJpMJMpRxG6n0dSfYPyncvKr7/5bRJEA5DjVVGqqtNV36Esz4LN5G6tTH37vOMDwTMWjF9tTIgXoyakYZHkc0DeseVmjEx80YdRM+ZkoljI5oim2xBWq64Z3aKj9qoFwrQqZtS6kCZN5Bn6eOuup8rqu/jnOcMVwgYAERg0KSVbczSjFBStJsoyQ3Kjs1xQMxard0g1WK5r3AFuG/I0x9FSMKY1029vfW3Xbofrf2Hb/tWtN0av+pdV4rR2Rs84+nbtbm9t65Q3tgHC9Xurm9/eOQJ2S+y1PX+ObHhzu3a2Zlu4NqI5uFs9XhGG7DjJ1d2VjXbqFKiwdbdxsfqN5cRbRt4QXL3YMsZoFG7q2faDOxv2cVetJvd1S1QAtfs5x+Xq7BBS/dh5Y3Pdrl1aw+rwHR2qbSEz7Zri14sbbhXuOXFM65tcPduPD4+/K/QJvejf0WRg3F4+ZwNcXH0rQhYHZGSsizaRysJgEsjkos9tGLe6dXJ8+lbv0oipnTuMPdp9AkCqzI4LniI4wbArOmH59a++/Tt/uHpyIrom5oziLo4ltYv0Iwmp+1hoHt8axDfWSwhkBcQEiWR1MgAlB7r7lb3ZNFMLqS8hVSMx2aGdDQuQaSzidE17b1jifXb+8uQbHH789CmTJnj2+iyOG5qXTx89ZdM4yEa0BL/5V98c/p2/+0devD2++eqbXzI0OdqfPP+Tz37yxzeXb5F/+/nJ3crxypoN3sk9ORSOwlbI6iMEOEKi0QE3m+SzRuRGpHWbWRHbRJB/cdscCBHVrts7wyLIzdX3BGeJYzl6c/1Pvv5nP//xH/6Df/ifuzw3XARZzziKoUZBubesXym8to8eHezt7FhABv8lpIG7iPXGX5U+yAxtOMdMTEpq2Atuc9eH98+Bur37lqfI3v9WByLs27dvEbW0tzzr9ds6LCOLl29e66i4hzd3d//4j/8t45BdOyzWMEFACisDWUoMslEjorlaGplqg330ATF/MEHzk2BsysUC0KePWVxCwJKA7a+Zg7fmGBMO1nuo0Bx7e3vFotzsMs7OLURc3eLxNfF0dH3Mh1s9gBhtcbXy7Oz68HztD27XPltf/3OxawLk2jLmzplSK3f7x3cb3605LdjM6eUNqzbSpAOaAbvHdb5DmdIZJaXq5tCOjy+RiLhBngVF/ZOCMMfcdGMqVty5PXOZ3plAo8ECP0oUQ9wrbizbiOJau/k0Uqwda9eUQpA83Nx4/fZ4fYsPSGMnLR6x1d4Pl/UzhGPeaBQU8ewWsWovnf2D7bdHFkq9RojNjb/3ycefXV2d2I+TUk4ZJK32/9GQCJBp6o3HzzZef/fWRsHYlhLEm2bjKMbVrd09zcq9yvT25sjsi/J5yXUMdEsvbfxl6xHznLfPq8jm0ejapAx1Dg8PATSEkV2iRbvHYZklqYpZSypT53H5SJpzB5k9a4yXi6idOC8tPxMNmLhrWizUzEVytTQIvUAuHNXZ27VQKpg7Rg6iJtMHET5jsj9iRJwQgITrb/VmyRRZhJ4HLH7pxj677x3AlGvl+kVFWL+nxgXKbxzs7z1+9ITj+uzm+kK4j3MIDjbME9ReqNE8vhSC2Hv04CrKcaw1DM4aZJgoSM2xIinYMHtDYS4mDdoAzCeNkpSVrvvDRMVehSMkfQ7RenV/9btr+R7RnQ/YGt4K3SEnp+dnnzAVzq+/PTp9DdGZkp/C2x3H7PWHut/LlW+MCQ9fnwpfGNaMgHJSgJwlY9rtbJ07Eu86ZcXkv5NHIBzxc0TRaQ57X9+7WWH55K7W79M/obyu4aVnaybesRvoQG42Nkje7pexTRk+0Axxkm+lm2dAKj1pyeNWT3tuVu2m2NpgzytSZkuIb3vb0QT42HF+Qa2bWYhuTfmje7soxjv8Lu5sbh+DfXf3NAyC782d/XQ3tg9Dhp7upMpncKj0sNJIsS9FA7tBaLDYJLSweM8jc63C/5YMDwlMuyXsJGHGRaliqKH+bCJETRZGUZK7Y+XYmWmoodWkBFP/k3/ko72AUFsdtZdwSooHd3fg5svXRYnmIEVf+pAwUtyj0r10/RyaVqhiN76cxwmHtK7lc0k2D37r43d8/wN9crT/Hq5YhVh6JIqM3tgFyOfcLuO47xGaZJH3vsj5uift/aNgLQgPkHxsC/iKUY1+uObhcrt8Prx4eLkkeCBWGWpxkw8CP0wtR0X1141UfS+UHGiBUrspPGv4XhooGHusWdaXE5SFmCOBmHOD6Hq4TPQYaQke4842Z5nTAkVhGonaSCplRb4yTMdKEqfcporT/88KRN2AA/jITQ9HMjTI2sB91xdS/oCoFEgBNwIg8dKy6rTqg700I5sdrK+yc6eJYPqmbnhYl/4mrgITivy82+LlScGt8NDoif1XCufsjRBtLg+EMGGx3YHpJ6f2B+ShpNOnprQ7Hyy555Gc3QZ51+lxFhwyJbhjrCtTTw4ux0LQGCNb3DY0Iz9xVoIs/mgQlNY51SEzvGoahU45fcd7oy6vekLDFWElS6xBqujTGMBeYJzkkL/KsSpxnZhpQQlr2NPR9quN+HjHqJmtL0/u9oZWNhvj0cmu8iEGF3xLEHM1OkoVrEL+dVmAi6nM/hTLr4dkAlFJbAzMyFfAGsNBoLPOhFvqB9BdPasYB+WdrdsUruFUgSdUjX3h68kYBfF2BA/y6NaSAFinfFFCHXQz+Hp0dKKYlvEhPrty//mjR3tPnx4whnlc3r5+e1GQwCxonRaaaNdOSV8SIzbdgUYFmegls2z8Z2SYu0cvhEc5dpT9HbCVg8TApqYRIfIFNzoRFX7XOSfQzZ8xRtL66ZkTaX79v/if/8/+g//2f2caQmO9ip2mA3h1IKtEm3PKnI7RCt8V8559aHQFSy4Y6Q3XBD+YNrk0S4EqaAhQDc1b4x10xUK5CFELpK2lTs3CZOXygqVNoFLCzaGBm2V0c3R0eHZ6trajZlv/+X/0J0ZMAntAPjzf/r/9v/6x4F9icnV1eHzytYAdGDdDoQXVxFQ3tgASfwM4zSFEYaSZOzdHLxgzPVILTSXxbwMlOzpifw0EmpYYalzOEzWQ/eCDD7999VIAFYHMbw1+PCbEtUFd+zTraGF49vf/wT/4Z//knxl6tRVv0kX28I4JGTNEMLfHy1AHepEqO3c8Q34CnZqIS1vb2s7N9pbosptHTx4X+N1geePi4mxv//H5qwtie3Rk5ydEvd7dWvv4k+eGFQleVdWZtRxD9dVzc2uHcKp8aKOSguN0SC32EEFThXlVmH+UgvNgs6SVhSzZv1xXnmSSbFuRXgj6b47l5as3//pP/+Lk5V8zG4sAu717+uhDRgmnodYSsBV7759bBbO6/s2pw6qvDzjIqzhBUvkrB9+/uDvcud47Y6Gj0OwTyFkwxGngxFCWvtZV2bP4RAOzoOLtm7e6alLDwrAKWMXUXQ5YkLJqmc1TbBv9ZnMkgYv08dAh3wdjkzcHdJCRfXTO0KcQwbv1HUbwvsfqGFVXVywKP3jyOP0JiXSEiclnENjenxCp8a3QjlhlCLq9uf38vQ+++M3XPIj48Oq7bz768P3MeuXMhhMsQuqqIasy+ZJub4+PTq4uDEEhTXvUL2TdpwQyzId76UMyl8ZqqpNepU/zAmQqRB28zs8CYgIW/1Il4Geva77Zec5qTfbIisZpTCgjGqt+UYsolIiQpCzzmWRcPzw52tja39zYUbeNPd5bM6K8pHlkawlZdXWC0dsmNBHfSIHoXp2dFaAIF4XubG3NDIStEWiMK4Nwk1ozDTK94kwZVnDxtJSBTYo3eMz9NilUL6omer0KUTgaOmJle3d310yLtQ22vNxmtAkjul2zcZEWkAKT2edQolYB2Uieoq6VZI258Z5QB1+vab2BjYZSBLVZHXAWcIWGWeDmLzGbOw/un02SUrpGWBbip4I8kVc7FYKVsiuI/8Jy7V4leqif9a7N1UneXKQMuzGkMQQVHZrGgOtgUvn5/ZxYeXdm0ki/ZsViaqCqajJw5yrfFPdpkkETI1nwsb5KVUi+xXBKgVPU0MZ8yYWippljHBqqdGVhk3IJSdSqv74n2kKxqZZsQ4cELIpCbmor6wLBqGOxfxpk3lOHSD7AX4qI/dIHvsaLEEjiZyoCfkO+kG2cO46UzPAUgXzEv8lbyRUoTwZYEp8SiK/y6XMibymCOrdzpwHGAsmUtRCk4t15HNGqUagGaUQltntXEQN84fXUBvH8jzuLpETS8A2tAXpPgIE/YhQqD2+Wm35HhYFS+m76K2U38939b//wuFTLx/3ngOrhFHF/M/kXIFVlucLo/u7hJr78sAyITAEP773r/ZKTqTqXtd6e2k/mAfLvZClR+4YuqWXXtHqERByxPuzae/8u2i3XlJwsTXklb/a4Y1wn75Js3uJvkMBNv1PSc3LEfeUmyARPR03pS72XivZzo7B4jFl2dpQ7wdIl5GmqQYyyJXHCixXddHOsTy69nv41iySviXGFJ4liHiNZt8GxkGoRVe1fD86DyDL2dkhIdikIjtFa1+ASMuC7T6EOphSEJqo8nYfgmKDXyEamtfXpOcDTQcvG8DbGSZ/kxRCTmueuF5pM6N7365CVViqKuOLMffpo1ax+aDbLE78ihR0HFstA2FyjFBukpBAdXqJR6XmlZxOBYLdf30ZVBAXCgNjJAWEe2mEIOA8rs7W60Pu0+lazt9EcyeHivHqqb/YGjV/s79gp4Nt7Njyv/Pndk5O7nduNY92QDcUpjjbzoSrvrNQViyM4xtYb6sOrwbl0cX3p9Bl91SU3ycb6M3tlojdXycXNgTkBRZpL3dg42zNvvnrOYqf1DcfsUMOicMd+bew0w2iCd7X2y6O71ZML5xQaHR0zhuweyapeWTuo99z9ZTr24mOCVy72/fra2fHZq5en5+dGULYnPbd9+3/vf/Df/y/8l/5LVkz+nX/79/9P/4dfvfzFzdEXkGK45/BTMmLW8URMdDL0GcL3sFep43SRBpoB5Uvomo9SGo1SiDS1nQoZX02toDq/LMl+n9Tc3L0OzJ0VhFenx9dffv7dF3/5q82rjd//g5/ZcDolOrMHktRPAhYWyiGubKD6nIpejk5MZY+yRLfrExvUiMQVS6XT1mASVnkgTpYzGfsN3U0bVJ9+zGLe3flWn21QJByEfEKQDV7d69e5odSUh0zUWZt9aENX12d4JzTARhp3Qr/WN22rb+to++MZXRodmb9mEFXoKKrooszUQUoqvTC6wTze+MENb5Axly2KEskaPAKaIdrl08QKx2W+WuVjy5O6ofi/+Fd/9d/49/5d1j88yXB0CXidIAKFN+o0V1aEx/bO3um5kNy0f1dOtzovERw2RmRXaJMkGvnCd0gzmMfa1Y0jz4yhP/nkx6fHr188f/7Hf+cPv/ji8/OL6yfPnr09+ec8E9fnlmXaM/v625dfbW5+eHpy+9GPDiiVgwMjStFoYtIa8DMJL4VrbziiWMQ5mm1afqo8vAwp3VgHk13u7eyen/EjGHCw5iNLmieUVarGThXVrRpC3Dh5Q7ukWabSKwa3R1Vw43J79+JEdNMFQ9So4HzXnq3XJ9fX5/Zv6/wJg6Zb65O3H23+werm4+uVz89uTu9WP7iQ4+6Dy1NzFG+2zz++2ttrrM9ULDgwjuHJtVZs+czt5bPHzxNpDcCmgUIFSMPxCdQsjqJq9x49gmrcgHy6MYuRwDKFaAlbyJOsrT0ipEZSjXj4aoKYF0LExUij9dPVTIJXPmwY0G2tTb58qxtm9HZEGjpjAWkQiMF5LN3m9uOc1na/EstHZdLpsBfZv791bascwinx7ao1AZfXZ/5DELO1VsYordtYZS1He2Wf5pclWFqSm6hdJ9MtkL44aWunbFyNXV1MDoiIi000IQA0CUx4LinneJmSZFaRKrMrIPMHrROVffpbh8UKFWgvqoEPaP/xwbfffOuhVyK4DDL0si9fHSHbk8dPLk3xmGC09YxVQ45ENB+grzQKIvZDs5Hl2p9q0TBXF08KJ918468dRW9uqL+j41OSKOZSnumiDG0MC7OS1VT9DCr0pBYvpcG2qPLIr7HkbVL52EHtcetq/GvHpyeM/RcfPOXt1qPFctuhSUReNWg3haHKnwZDEL975+phmqGWi0LpHXpLu7wzQId7SsNjTNr4CmVHGMXGfzWwA/Db18D83UdpZ89CeNhzZoVVpy6Q8O9Wbs5E+9MYlu1Z9KDFz0wU9Yoq3/Dwq6xKGOTWvwCEl3W2sRnI9TWz4rpYkM2Hbt1e2qPiWGqSpMS2ndP+Vw62dgQQIsSF6tUB87lQtiaVRNTQuUMLgwEQtSq7Ylg/ZdCVRl43Z2I67/EgD4TEDTIjWD2QviL+BaG9YkJqZCA96CEfExpG2KwDbWfiPAd5LUOfiimZIrqEmCQ3CFWv0QpIbkehGjlCO2sn9cyfkQs2NVsZCbekCFQ/JKtPcJtXFy4a86qqfrFpcf4yCCuuUvoXd5fbYdF4QlLsdXwLYp5P+tT0aPJIOOZTcuQ2ptZ+jXh9Bb8WnXzFo66+Nr7rxUKXqVwVhp9VDS7x9/N7STG8rR4r15/02UqtkSEpgzIU72u5Hl49PJ6yvVpKVzvd6nv9XHb9Xx4vb9ux03P2tqcwSD/U+3Q/7QKYe3CD37LDpxUd9+nn+x6NdixarqWE+3Lk+zdf92kmwbuE724q+/4HlO6vpTUhy/LkewjhnUIftkxiCmhUXsSbptO29OzjESvL0SYqAJ3L4ZqK1gowdESRtCWIwIQHVqs1gVnAUo6SJb5JNmlpPDhpJm+ieC9mct0/Kk4gkiU16FuUBpiaRxhoOSDHb/ddkvF0ZJv0sP+jjAZdAHR4WhGJG69BaYk9gzsnHVWXZoV8OCbBXiuqesy/tN6Qa1paYquOBQvl+4FAeSPwA9mHgrNwrY7XvESRpoMopDyKqEu15mhUo+bJCVSiWxMJk2ktfmjOaqnV1ngqbiHtYDv0D1Yg+qMdzAyEe9q/c6N0kmuvLXmeMkDKvY8e9KFhD8La/nNt9oqFtZ82/LtaTUc2R1CIDtLAqomVi+mBWx/G7WQ/hTvaLWeYsR3hMGzClM5fYV3f2Xmmrg5OFzedo35mN/M8TFXBlEsKvV9UJQCsJCNELvErXgi67kR3Tx9Vm7zj0PqjP/r9n/3Bz77+8pv/2r/33/w//R//rzpD4SIizhMQrGQ8hGNkmiYffeUO8aGd9yrnqcRmb/IEDp3hrYOyNX5SC3fiZTK7YaGT4VEuiAQW6fLeul13ZuvRJy+e/yf/8p8XSU71b9vXz/it7Kqsn0bhyE+Pqz2rskknulUfxiHn0cgBX6IFFjzluo2cVgveSQV8/ZVqqgAO1a8ULmkBVPNYPyENba1OpW0SuhcCdVrIaxoMj2jw8Gb7OfFn9VFhV7erz14ciHbgLm331YQaHQZkhOsmFe9a2l1S3VPp3CxTdoAoYjohwzOrQTwXS3v77L3nRyeWHF8yi3Q29mpcXzvtkKbT4909gQ35k5o9ywUp6q7m5glkVVUn5TFOGFQkPBlJFTy6wvyUhX0HZgmcJkEooTNtEoUWIsXVUgO0enV+dmKmaP/RHjfq0+fv/epXvxTw8OMXPzm/PP36FzvHb02eXL55c7q+8dRg+MWHT9//6BmrhwOTctjexUoCYfLIzPuaDemd+myOX/9PNU71owLJs5i4CPJ1By21TbuwKxSHzSJ2NdGuhE+TvTy/OTo9NODLBcLEDX2rnHY+Pvhgc+fR/+03/8trDksm+/X161c3z9fWPzi9XrH3lbmIK+GAwqLMq3y5vXn1bOtH+zuOsH5koPB25wM7gL76l/9CYN/u+8/4TBC2GAZFxC5GkgGkNtHqGmgo0hgMSobW7GbBASdnJ/bXujw9FwuFeiNw6RfNAnsTK3RhU4rtVnkt3nDZKHD0jyf4K3iO3bN/sD+HmZGKGSARceVOv5DoMDkylRIfljMfdZHB4DfJQxIMZQ1jsko0ogxzpkI74Ty1QGgGezeHh286PRBfxt5llFjMw28LE5VqakIzcADc3r5KNB82ZscyzyBLino0QhKrfuWrB9ITMT94ZKDm3jDTgAxiWf410qFHzQEL/YqlWqmVADDx2GBLift7+x51dvHBqXmd46NDnZxqGVQ4u8o2wQjoFBRLiO0pUdCRco230ThSJcBhNY0rrlGDUjRX3L7pjT03Np+I5l9d/eSjj7/91hGQcRdXOrZcXeChg1Q/glfzAXP+JppqMM/wAleV5M3qUpgol/2NH//0x+m2GDP7ay2s8rNpUYnSgYNh1INPqI4YjYSUugFSjG0lD+HTN33zzbd7tu6iD3UE8n9/DTFLGx7/2Vd4oYwCsxNOhQZ2OoLJELpMQfZlOn+89Ri5qlRNLpQXStqPhLpdt+6tmEMmFuIFrkQccNd2eK4X8PDu9uTu9hT56hn0RgGhajRztUoQ1bSZHtLQApYsf2q3qZRK67V/ZNtYuSBNjitPN/SkJgRk15u5GpnYq59/p6prhsMhmAAQnKgKQzf+r55fXJ6dnUwqsT3GZCvCzzKRpyweB8tZTHZJTExwHHHoIjDPjk+qQ2QHLLMbxtt7DqHbzlN5u8JV0QBAKUyCGkxFVr+0vS8tKPe/AS2dFqIz8cK2aQDgRzkXEkrFqSjbUC3hbQWCDgpC2qbta1PpVbaripGTrL4oluFXjt5fnNvbmtY192X4xNvYK/I82EieqEzKbpYrgD+8/Aor7yHsCuz3X1P2/aN3IEr2//tSxgLtIVmUdS0fPu9/DWT3EfAB/OD7PRYPEO4xlHhIiQAD8GEAsPVba5AfMP4+8/1d2afsJftUj8xU5jwfLNyVboBM4uUHEHYE6t3ysPf3r3vi/6A+30SWZIyAawzTpaUDyJy2BxAmMQYz5ZJUPG13fFQoJWHh02ZSU+2ylI93oJBtt+WTHZg+s1Om5ASv8u8xH1C9KHEpYohroQvrP6jztl5qNJCXLfvRPzEf4UUxJGQa86jWNOY9tCrd5Nfdtd2ErGL9sp/il/TgpJMiq30T0nomiiZ2mXQ1Dq53S9gp6JuLD/PO3r4di4jdUsMP10E0ukLi5sOe7LxUZ4ogT1W6jPmovBrVUCKjsZlKmDSqyUERVuMoRd0MrlQ2s/jTFuJuWeHAtgNCxgceS6YOcEZWaqdsKcAYYTpBpe6sGTJueiG4aXX1a/7IbKwUCJNzzpotPPE55dZOBWBpoyK+rvcMENZW9am0iaGawfr29QpKPcq6vX3qYdi3VZw7FrxAf0n3NHM9WP7c20c6n6IOhsskxq72wzeaArHz7YFbeXc/lhrKahLrxp2fsR1hGdYp9P3tg939feEBT58/5s24dq7J2i9WHOScONCk6htVVJ9I9L3+dX2psY+3Q2Z0HeYu5JqDKkY7r5ntnVgU/qTyxstYECOYtlsngsOSsigr1+352e3Fyc3x+tmTxxt//eenf+/v/Xzl+ts27INqOjGnLxgPDJZRn+sMy/dWrg7qcpBET4I7gq+uhbvEnObxGjbYnK7XEPbhn0TaxbjoNJ5fS9o/4ZEtwEbnpXuj9G1ZdGU25nbFCVZsoC0Gle13nDRkgk0Rt3f2STzZWH8htOurX3/72Qe/Z6dBcURb1z83jFrZ/kKRP7jgXFGusLgtWMjQb0EGZtkcRHmwEUUlgIm1TPqYw8+fPHr9+kRQyfHpsVMOeBvFNJsY44i2uTtvQiSa5oKiM/zQham0a7YNCDrjSQNRNRX1k/hwqpvLsNKPaR4BokITXyjdqCeBjGhhvLW5//TJc+sDv/z8ywMLkx8/+tnPf04lba18dvz29dNH1999c/XVV1/c3HFev9TtnJ8+++u//M2+Ez7XtxUnhKFhvX15mMZctNy11ulePFoxfNp6iQdxk0F/d26vdzs8xj4bajGLM7SqiMp5Vu9Osj26/FCutY2XjOU3x5cMut0d+5RLsGouUOC2LSYZkI5nuLr8zjzK6sbppbXvN283NaW798Pmyur7Zyu3H23c/mzLKR/nu9fbR+t3e9ubR5frrz79kx9dP78TahuvmnfLo8FtLIRTZ4xsUDhjw8DPxCB7pI1QLbCxBNSgd8+cwenxYRuaUSsaIvmP51Kle2gPssTRGn/wS4W8mealPJwzovAf7R8/fVy8fyErcSGxoYaiBKB1BmWz9t5QSUFoRl5GB7UxCCIyTUA2h5hdHFSzBcUlXtuv3ZnN1ik1FFkERdO06z/4khl+1OLE2E1g5Mbdxxsrz+7WO59B+bMsuBikCmzSYhxYuqTlurllglCoCLK6Ba/GeCu24k3/vKXGAA6ruZJBA4DbW2eQMf31DnoDfn1THc4bxvD333uhhl+uGFu+td2xeSH64/Xro92dJ1mOiEE57j0x7Kl3GGRQrEpncVok3XCIoCZAq86Q0Z4q0fXqu1essplYmkGLBjdDzUQ+7N59NHtze/ke0q6uv/ZcKcONFOHK+is8ubl4b8TgG6ujjt++PXh0sAi0oqf5qG5sCsMICEK8BKTOaS7l1Vl3RZpJEHnr4lcdsXdp5AyLRMi7aelL6gBANWgV8ADPy+XFkur+PjmccdEUs/L67aFjngt+szcDJaA9NVtdH4htkSCqqfag7neujnY+HeAj0g9EKnrNCFyfdWnp0p7D0W27s1QeQPPS6D7OwJowxg2p2TC7tBY3Wt0ZHg1aqqKBRCh1ojKylLl7LKtLjKTRAJtUTGngWZu6JlFhMnRxFx1qJgubhkAU26f1hs4YAe3ik9VLmucLGVypynqiXCk1GoZL89XZEIYoqI0gAc1Y68phav5ZIpMmZPn+OD8Ys+5KlopqHi0c6u7sDKLSNeQBNKIarAVq1es+DY7HKfC0ACC1PvB1n+MeHSQlTPPFSqIPG8uIYYJQkQCWAFlSz4VEYBdLOEKCm+BBSPRBdShplYHv8NfOSJP9QW4WaHHBXTv/lHRan15AbkAn6XwOHB/vgPbg/roHNC8ZHeJxXPPR17z1NfCHXIqsKiPtPksQ1jWJrsFH9MNvlpt5cl+ZSpfMaHEBO+m//7gH8P2DH949VCPE3iV00/38nuKmYcaue/wXCLj6g+yxv2sQHtSD0C/qwMivRwAQFMooCiyU9JA9+FtwyxacBLHbmEgdYOII+jzxU4Eg06tVHtjQS8P2E7yFdgO4ghOmxBhYrZCqJEclqyhXv7yrhKh6zymQ5pXMvan55bfTROq6sig16CGDDPUoGiQ9r0dq2Fk/lDUbJhpGtV8oFvKh36C+YcCUV03Vw5V/S9UiS+maeu5hOBVIUNC2siRIZDwrgEgyRd53aQFcyCHT1GE6g2pGxlxRB1bKeYeULqRZvBqrBL1IBUbeBVgcGX+7hKG+/pbJoaVne/vPoLfkCUKQC8wlfBQWfFYITeDPqIrVHsCAcVcPlZ0kj6LN+dbwV/iYxZB4k86oq8sGCAJoC2Zlvd6xzEIB6FCRRjj1Vl7U0uOvpPQJ4nsYTlzICMXLbcPshmX8Svb7E+C+t7vz/gcf7e0e5GyYufUpp/rLGhHGClEToIa3+lGPQaXZO5ZhVIUapb5U8sy2kFaHpF6TN7n8JSoZKWGZ8DTylZNRKJCExWZTv8enp+dbHxkkMcS9anqHDBGlRR4iplpwFjYfoqVT0EanqCaxrkI69WJaUXPqHgWjhpsqAliXb/9DINHxYz5qlCTLsETeiCrUvxEfFbthOa9T6+1vjct5rbJirHm8EFO3a9EBg6n5lhXre6S0+vcq8ia6dHTAodHHAzKJVnRdXj0kCcWQwEyeG8tUaPBnz57pmh89wZfPf/KzH/2//vH/Z9t2Elvrljj86V/+q7/3d/+ePDy/1u2bLNncgdzIYfXViMBr8sQPRl/KZ7oBFdZ04YbkO/G/qGWmULxoWOX9MuJChP5Ng9LifK86MsI6adRjqRePt7b64YfvCxAyE/5//3/8GbSxgbf46ubcnjDbO08dqyTsgove+FrpukFDl3Y6oqa1RqP8jW8Kd2EyFzGfbos1BkCYF/7Mx5qKx0lbNEyaEypVYOqDPJNFkhLsAo12N4Qi6KvOb4+skzc3qTO2L+GFvXkvdzZXjJapCBEtp4acq3tf3e08Od20kn5X62njtNON9a3TS4dEHF4fn3zF6D8zPVLzKpPaJS7EETaYNTLlZlEs4UYjrYsFOs6WWrCVbfhOpohcghCslBVOqmOTRRMVk4+z6SVxLsHFsMO3h9Gog3iTuqSy5r58W1p6ZbkOG2UBKhNeW/TMc2ydK43B2XmeDjDaaaPArZ2dFy8+am8qKg71uHWMYyHgWLQLRyJYjxSRTTQRGLwy+m0jFoPGnE2sInvdmOxNcOEQO1CyXzV5FSK3xhXcCFDUUqJSScFzvnIdyCxKiihJJ/7HTtaQ5DUHTl8xWldiw6+uLF7ftbsANiq7VvDe4SGzA7LQICftv3J1xG8r9PGi/aUDkpml8sGKyKhBh4Qq8mNKlCzYnZDoILb29tpGD8XWdzeLsQmv0A05ELpfRM83zPMK+6ZMkYY3V3cTBe5zlSYXEtvy4vzJ00eYNTQK4DtggQ7+FDV5B9Ge9aoLJ2WoHcxTBbX3Tj1gI76KhsFgOcnnYwFShV331Xi487PHPYVt4ldTKsdJOyyjJw7mYF5SEFqNEcunaqOdtLYGSdWjcW+6UfeR5gQR7KWakaSTMbVWhg3/EP9peFbXPqXXDCp4KrfgFPxILeC4JiADScxYCN/okHGi7Bo7dVzziyeFuHhltlzzJ8kd5JugVMcFn7KOYkexHnuq4iGTZCbwg0ud61JctVkqMjeU+6J8KKIkBAaJwsCqggrP3qi9dQ1JKZppBzVhVR6+q8NQYDDwMXxE87I1Tx9MlQtu9cqYaVCZollQnlcqs7Cth4FOm7vv10KckNDc6i+zRGppY92VbUgRPjCJfApTOCDDOzD6JX+wPB0aTrY+liJKOnVfiBPy95nvsyxJl08Jg/L9teQsw9z9jfelnFehMBW/Ly8uDkZV+gEDKAyq5Rqsf7uwBc9m2X7n+p1k3799lzKwC3Lz6PsSpV3wWzItbwfefd4hx2RFX4kWaVpw6Em/u8jL0CajKYEkRDV44Mvmz7f45t76TXVJyEUxRn8o+B930+hEaNJPLhJJ22aiAqHpcgfmY8GmEfMF+YE2DnlAsiC7Ajb2b7QM1sAL1eUWcpy9XimCSE2nNQKbQtXQ2WE4poPNloIdyV3/6oFantDBwkzc8ChkUTOCzemT/Wo9ZZBwPvwUMaG3Jj1D6kkEG7JoCpKBALGi2DU8q9fDMie8joUipiKVe91ulqogAn4hKIzlTZ7qA+DhzjUShfgKUP/1rW9q3lUODqCWx+3q1SchuPWlSoZ2fMskqtXEFagjVv0bx9i65U0idrgxlnYqKNyTdU5odcYV/wVNNi0Aa4yBJ+PeSCgMs7RQr9MsK6aFYhKYvRfWbwzQsc18K+t2POCELnKUsWvTT8910hYdnm6snG6vPgFXd0QMNvSOamsgYlefuremZXXraueGreyIVtZABrTjiy8vn7548ujgEZXPcnq0v2M+vb6G17i4bY65jNBImvTRVH3BeggbbSuqNTDGMNw/qgCJmY5JibVCPVmk0pKvqMNUY1E1ZEBjJ6gPJ+RSexE/Vr7iMqfx2cUXRyc7T9cfMR6Mr+BUNWJZNFeWXxOC1Y6EhgOF6EA0YiKiMoeKJeJFrpkNZj7g4Ud9QwLQg65FGFK2eFxH27AVL4qdOv1ASOtf/Omfe8hEPj0RMtFQNbeZvYyu34bG3WaTCc0IcXPemJe+W3/p1IzUdCWMoFeKX5Vcuf1gmy3Fh1SNb1Lr7nOdrrDlNy3zZbPYhdLGTDw35tfs+ppJtLLx5s3Rr3/11Z/8vf8ii5EDuJPLBEXdPJZmle+cYGlQNUjTwFxEmSxIY3KkzlhPYJSJqOsrO5vc1jtvj97KGF7t1K72tY5BGaZ1G7BmJbx+/d3HH36g0TPWWYeM9gzTaH6qU/ruuy+xQxw3wdvZeWw8ubPx8f7Bo+uVr5lp8LSXQDhcXTt/mp17fv0bxgaqto2AIq2laBiAA7VGv6NSgVZDnKUdRqJStptW1cOW26317b0DdNl88/aVNTb7+8/Ob786Pf1KIzo54/Kv9aHB9g5+ffN4297tjRtPj+/Oj99+ufp7/9dv1z948nb/7vHqyhGP98n610dre8dbX1+vb5/d/ogxhNiaW1awiIROjCYK8BjmhWRCM/25Z650ZfyMjrF02K1VajkWm1I9KfAlxdA4ove27jnz0ns5KdiLm7MvRSBEj0RZKu+lmFLqAijG07dnv/nFr0QNOYitUcxmi3aevXgm4F16gWRjuyOv8Z8g9c2zY5FNL1acN2Ky72Lf6IjNgf6Gm0rJbMhB0BFd+GqaQoO7OLVe+Ze7j973XuFvjg/55tuDobpnYTNciHUL97OBYl4mK56Cp54M+2vttNGLEVhKj3s/m5LGIofpq/hcO0UW5hFQGXsa+5iGKmp02g6KFpDYt80wAeA3b9XZoBRbiigbaU+rJIzRN4JRWPU+AVdEGslNHVGeK5prvC1QjyeYa4d7r1+WNWSqHuaqMjjmmtRlKtfokQbhtAjzxHRlY+eN22YTBCNu74w3ZlRjNVNAIpONG7/DbjJ1232NrTL9mzSeI85yJRVVrYL6C5uwCq5rhGzJ6UePg+JaXnd3f+8VyTGIrGllBQJVdhIzSfxEK+1Cn4KAdFwxe3cXHyp9bfMbmRrSQHUCO4fvY27W79d0CZFtgR3/3RDxxiopx6OcEY56pbwm5nRyfiXaCbc8Sz0Myg3Qm27yu97Fp2t0F3IvvzxI/CmxXNolmUlLZRtCc5PdV3qhx1LlIdSA7PdIxebX0wtPUZtfrm4f48S8zJUQOYbBYRjK5BVzmCX2OMM4HgW1iHq5cCml6884/lfWP6cXp4skreN+uvq4VrT5uez9G20AJgGog6qCidFwgKaFWjphqfVYSvQ2XErgqjUx6xtRmBf7WBl36zzfxKx+terJiaupaGSVcYQ+ejKNPCJI0ybqputtgxkOepChkGxdS8tb7udBpBwhGkGqGJXxWVAD3LKfamiuqVBve7CsUDrr/nevAVSyH5bycL8A8Svql0Qd63fUcX6q29yUAuDQhYwaDIAF9BR4n4AcLyl/F4v/X78hsQAvkfwLsyppeRFWvcGZe+DRaCncZy+BGKIANDwv/QInke5hra9ARt0wX5FQlkU95Q+SZMBVmmQBznMbSRYkahTJgvf4jbXN/LBCFJlF2tA5W5Y0sJeSoYf6VDAR75MegkC4zqB/SaZmniQ9QZpykZ7o+aWCNTYtopCEHktmCsBKNYYp8WqWigX2MKioaDWJeNOiwB30J+QmHQRAlZ3iEmhaOdJUHjSYKYqkdAqQrWtRtKw9hEnWQXHkchecnQA8YN6r2rMS+ClS9OBKF7/yQXX4mHz3OajYUdZs1Bnbj7VRH0Mfiju0aG2Ka+AR/+JqmQcGZVc/q3Ny+gzn67HgSO7Kqe2VXSn1m/UFjVuYxvDKjQVfs1x0ba23sQnjXpVFGaogh5v5TRoTUaLF5polkrabVAqKbd80EpC9/3Gu0V3jBTk3Vg4cK3DN2VyLiQA3LW8ERSoLt9qhFWbTZtHXC4IlYpjLkMP4xgbhj/jZCntVqXUz6TzxhapeX+ysbYp1SQMDpTaRMsXTF0WT9snQ8Wu06qw1j7m0pFdmZXeu7dAXt6tzvQ8ixhw4clXQdcXNG+/cQ8kfTNJaOLGzu0PCX716vQMJW7pV+sLJGkX3fZIiFq38hJB9U1EhCKME2X28jmWT3s/Bw3uPgxBWc5UhQVdPVxlTxGhcn313dnT1m19+/dd//pdMU5HM2zscPBfuyKH5h4JMbHIyFoWN0ftvBSFwEawOLyxG6qrAXIPTchuyg4YcEpUWWUKHz9O+enPA1tHJyf7+gWhde/BrFC1u3ts9PT35e3/yJ0+f7Z9dnh8crFnAvbpmixsO3Q4fqJL+qnhV493c3t0+temkrY1GNhK9kMYCaDKotFoj9WacwmQ+QWB1IcqAuv39P/r9H/3os5/+9DM/ZSDzqGR8ZPmlTQXMxnz99SshJfrErKtRVUYvF7c6DOemts0AaF7VS9Wt1yRtnsqSdJJA8eUtXKJyYlg9bE0YLkOLdN24DIZs4VfNJKNmLOlND57fntl7xD5pdqGkJE1kWZf9wXtP3v7mc9PvltULumG7vPnydGfnlIOdM8Hu3ZdHR//s5V/8evenf/fT/cfr9qVyAt5MkDNgbfgreN2Q5dxhEIdsD4fXmXlZxFdVYFdLhEmNLWTjbLWL31MLQrkIJCIv5kRyFvaRddGSAZk2tpBZfu/Jsv5a9zBcZLm3eCDJTMGnJ2OrZGJ1jETPbL10evH27Suq8fl7T7R6u+0y4tnl1JvU4qSz3jT5W3v/fzix6ce4f3l1+vKlY9oeSWsFPLS/fvnt119/e3xy9N3r7z75+NM//MM/gMrZ7YkIasIsQsc0gE1pGrpX5XCNRVMtWromw5C2Fj6n7FRwdMX+/qMTi1YsIN0o/GhsEZVJiVWpiNPlHmHISCqESyvvSdUkpAePHj19+uzbb7+RssAGxzidnkhkqLzb4h2WbfEnQ38MSIKgpo6ZvHW4dna4JmfIUtiPYUcefe6mkoo4Km8IJ5zEAHddHoSeP4S3YZHUMS/2eASPEuA23cYPbR3rxuZ7Hzw3sSB9AGMf3IOwiLJyy1H7un9YwuX2/nEWD7Ao2/MyVGNgwgVKkSyyh9QPryFkjOjVkNLbBfYkC0hP5A6AId/bt44213hEhmmMdiza+eDFs839tdcvT43BSQ93/9j7lZj4LRrSFHfWZ8brsKzaTJEy2ZvVWI/cXmiM2ITC1JmE3FJqUu9egJxa0FH16VZjY5xWr5eUrkrqY+JGamlmVKJL1zQM90sfAh+GAyMEHps8ALOyYklYrUtfue9QXJDFKHQAaqgxtFgsIilrcpEcDgOg8koLVOT0smbeXx0gtmYSeeXGQ1hNxoZI86CqdBuEssvVz6QqMy9J63kfSgLFg8ZaZKbH0roiMMFTWbNriWWkrqsLx2SpQkOm/9ChbcaA0AgFTyY7oUpR638DO389TWKn/EFM5qKSFyzvE03x755UO3VZyOHpYH+fIbj/WdeSZvmcmv0ww4KJx96r39A0Mfazr8Uu7S1qLHTpxQLsAcNJtwDtxd8yAzAvl0J++3Otjckbu8SwxTpYSFdhY/rpQj+VR6S4NP3vL+zuRaX8D89Zcq5Vk2v3ie5fJUM1IwzpEBAMWVfuaHrmsLTjFDUaLtCl59pBTrtphywnSxDXdU0hSNZufhT/+KdN2oJsq02Q7TyhLegiLn7MOllde4vnG6sfZRg6wXcQsJkomxr7FNioUYsdm7vgvMuP4LzaSZMRWVc9htcotxLx92iQGd+rt9Zrcw1/MXZ2415uXdZDOyTYyn7Z++LiA/Xd2P4aupYxysjgmHpd7T7iNWwnuyGQviCdOzWmK+wPyNBSKfiOY2nQBip1UGOTRMNHhWwY9+CXWU3o9gJLaoGNtf1rZRulM95cNeLEczRVIrZQnifSXPiavXiY0zqG7I+MIn3Y+sruNxhA4ocO1iZm03vC75sK4ENisN7t6EPWbn7iDLW77T+FMB8kBjPcFSFyG1X9XNvYWV3/ulMubz6YJ+oBadDsc0OiTPCw32HKnlcz6NjWYttCvdWtz5nqq1fvq+zazldV7fZDVDOs6ITKZTLBWGR13yKAISeGozKkEWabr6BlfGhTX0qztJmiQZXzgRnpZgFsLYeDjx4/EbYxUwXXl2evf/LJR7//o5+cvvyiPTiyrWZzDBOe+NQ0bhxQfQ9giwfhT3s0m28OXQnsNsgQsUKzUve0WmwKNf+LBimqMoEdTU/arZJ4VEzNxrFNnNgHliHuPto5uzw5P39q8+7GUhY/1OuoPbmvg1/E3hZUQrobB7WTDmymKYnip2Rv3l+5stDizX2jruXUBFOJ8+VH1fED0B5BsUc+S9HzPOK7T45/9t72P//LD37x1ZcepKJrC+qvn8PGszsKRKBJqtjGTVZcXahnu0ossHwmrIGb691N2Lgqs2qhY7eZyDbgEj9kNaaAqPU1qxLrAy5Xnj55Zoubx0/3LQPgJP2zP/+n//LEAQab/63/9n/t8upkZe0Iga+vdasGr0kAGqD9FTepiZgLsygaDsdPrFEug3BG15lOlI13DWnCVCOIBoMaOBGcz/69Fx88evzMgGjsvKFSU3COfS3UCp5//Ys/N0qhoqS3NFmDPz8/2X9xvLVrd0Vr0ookYUaBa4Bg2THxsNKzMLT6Jx/NEPIFVPwQbWEDXtAE0ShnSOUuHyNQScLp0evzC6slNPqtF++/4KxYXz+yZ8vPfvaTH33y8cr55Z//6b/Qcq3WeLL75L1nd0evf327+sQuPrbr58Q9OT7Y3rrdOPiU/G2sfWxjsPXbZ3k1BILdXmyuvrW56PXd09v18/W7FwVJzQLBWZxF/Fs7AZOo5Ct+RjsYwleQXfzVdxMv/9DWUvWsqEkat5eq+NSCzO194G5lrRlO9wnkhsWpNbpJq5CMeMZ6o8SYVGu7uT6ziHf19vTq4sjg54rpL4zm/JT7/cX7H0qJ5LRLeI7P+3b9y43dV8ZlIw9aOYlb3zQNZFHjzfXrN4f/+s//1HhSCPhvfn354Xtb2/tHCrYqd3wo4os4CHaamILDcIWS5ImhF7lOPMnd0Qa9nEVUP3epLapurWCxla5to2b2DObRwscQY9ryEGzl9jHNsbp+jjB0B7zabCkz3dKAjf1Hu998ixRaJW4SWZrOdgjiLB/B1lhIlwVic2EsSEgPoQfPCiOCUPJ8sagwSkMQ+EPqtGMTY3bCCSEdBvg6jpjhlzxSSpP6mkUdds0zj+E9LJvx8F4HCTDNYDlpcj7FV5zngZHSv6WrAs/rhaUDxv4qflk1V9L+yliWUtrp39zs7e2Xw/F5XxOLQsuPJU/YzuovxkpPOh+AlT6z5d15NDnmRi0t9n375g2V4GgWXgOR9Ttbu98dHb2/9Z5TzZwww62o11jZeKUs+JgNMM3YTgJGU3lyIjUFP2TW5SqfK838zBZOPXn+8fP3Pzu/eqMNSW/QeHV5XBteM8wUnFkz19DDXymRHnd2Joq0smik5Z/39/90a9kt6DyVv/yIC3J143MFM5CqHWD3rbCKdl1/Ek0m4l9BuIec0bT6LKSIoRKmJvXa8TzRWoSyeo2Fn+8/3gai3Mt79vLuV5piNpRuoDVjABOFVasT4awHhxMuNKDZ+qIOoZlOEkrXMQkIH4iZEhmrruSBR7E5qLuNb2CmbStM2ySAHlI8ohWiWP/Id99T0/R8fWiNAj7aemGZXBk312bm6/eXGkmgiPnTBagL6gxFAJ93C9lK8IPrIVP4VfcI7YpwiDJv50EAPc73P3DvP+fd73wsJSylzWdQ4kzpnJfsWXtvUln9K0X1nAT9mMQ9XCrz8HtSx9mb/AEzT7Rkuk+HWIPiUtDy8AGEDANvcCBgpZm6JqKLiJdgyL1AWeownw/4hE73gMbNBfN3OHpQ167/nX4swU+n1IoqXIF4xljd0Nlnwc3PXtTS8LDpe9Az7IlZHUHd5P1FTABPv2Su6TFbZycPc4sl6/nq5ttBb7QY56XDgEsFBpgRntPozmHmfjqkNlqHgJ5em1ATJEgMIZ2vS3zBrjOIr9d22bTkcxQ0T/MihNl8UuqGF60JEK8P1BplokAoe++7DqjysZoM66XghARSTqEIaU6ZJeQVdqiwSun87OGAWDLl3bEL0Mxc2/S9COf2Sot596zyhbyReW19Z1NsN3dRPWJLQhu09HrZIVvQ6jROxpLukzpYEJNgOIEYEVwnB9+JZGIh0LNLqOvJxho3NYaTlVquRsJfmFrQ3/fzvBo3uqmp57yPuBPm2xgFe5wIdsO5yNjX+js8d/2E0sk3gfcgqlCWttiWbTMOColpUUGQyq74KyfPYgtIUooeR9oGKwD7nbzwtGVhgEUJtTQ3O5viPbMDBCiJodbcPM/az3/y6U8/+myfHbTibCBGP7RVLQzGuI5fTIpsbkwdRmTiFOCkluhjZCIPk2BZ+DuzVPCBQzxPihDdrfGiYzfdlA/8mB4yr9++OjjYdRyYKJF2K1Kh7FYlCrEtJWTrbsOJHoWG1zYZTMPjwJQSsUK08kbAk5/lwbxQ6v3Pii9xrwfkfcY6lXhZzKuBYp3UNNUbG7QIXbHAlwkCI1slOVDBbdTm9HJqj8kPAr+IbNI4JXn/rtB3DxLVSu3BQgiC4X4ekqL2qkRcXV3Pq+E3L1/rimyWY/dGm1rYU+27t98dn7xBUmZHBv54E+qvhk1snZOTU2OqwUer0esAj1Awi7Mh0Fq1rMAYOqXj0IJ2qSJOUvjk0W7jXz3u9TX/ruyaJ/isRuaXKIF//We/1Kqk5OTdO9h8bMnws6effPbZ9o5BwhWiENApknxo6f1IQitxoVHN373PruFMaMQR/+vlIFyuhW7d+r1pQbIVEPaMPTtHBLMJzBnLsBmOnQn1+MkB2lEwxpCffvThBy8+O3fQ7c1GWxrdXH3nJNqLNyefHz86/YOPPngsuvys4Uia2rRB67Ovreg/v7o7EK9lvMMQi3w87Q2to9/gl1B7HKWqjo8oedeoNVwlKoV/pZmqxeJ5U77q1LU2i8I3DRLcb3vdjFL1zhMr+QX95TyWzoSqQXoxLdy87+wxnCN33aHTauvc39OLi8dOr9sugKH25ho52tne41nSrOB1dX36xRe/vL35EFOfPXv+5vXbb19+awpQQczokYa784szc4RtEjVZYCtIz6QlvuN15nXAU5ON7fJiKg+1q7F7wTy06ePHz7b3HgPy+a+/HKZTFA0DhjRVP2V2f2VrUsaGruxsBmNCTVzyENQe28n6Xkzqj3R9dq+nihvBmtx0qgblbS486w2oNJjr7eHbvX0rT7aMhs1ZZeSPYYqT0Z96jGv+J37JVQ9jtZ896XcHJFPqSJoCW7v79ONPv/v2W+OKFy+ec58T0c9//RuD8519LaXmWtGLANzL7TwIsPeh1d9yza8pTl0GgXkrAy1gWipADd4fciU280N236nVqcfkWoA/gL4vZSrU69oC1l8aAYsprdXrJEbJIvTJ46efvXpl/zbiYYkdqEVJKQy3RhnSAHaPMOPXfNFCnOqaXauBU7+4h19nN3c8I3McY52NiV26QpdNSxHIBIPigEv/9CY6/fu+Jr2A3XgPCrMHJ7I6EmJvqks9xWgQ1cRidK6++DwCdV/rkawh1r2sMEJ21na5zjBe8X6SB+UONItmWF6bBwcHSW6UjFqeAF2om5bFaq+g/F6Kb9Jyh7un4ceGg4NkWwi7MDbKuNO5P67n3eKdmaU00SlDIQpJUZrls8Rx8OZFjzeX5SgJYU1kOKcVFKaLCHWU0EkhqjNajrS6R4qGFdKA4VzLMK3/jwyjkGA16mugIiTA1Wm57svxc9LfP51fCRdkshLCyKt8fAOgsnv97noAB8d/0/XD5O/SlNwL8KPIQp3wrK6TaCHVD/L+rQWUuaLvm3Vp7tMN3uE/eIfzfVkidyfRgH6APwgsFasrnSY2uCwQBqN7xJb7wJa5gOB3ZX5/N4jUiBLiTRtpVUkuFa6x9vULK56N3NXrJkrpJjHt6UQufZHROrex8FnoYUKGtvYizuYBwZWRNFc9jK+r03e8lmTj7idB3vl6xgbbKpMVIQF7JaO6HXKIBwmIyprZ1psaX0fSejx10dPlZyl8P6XvZ54Qi/jOSd3W6uOoVL1DygYT2Uo1V9JpY8pfwP725DN9xfXqr3kC1AkQ7d8ublozOCwJ6RUAPnUAP0NYW2raOQOITIuuYoQij6vhvlVvzEQJzHGpRR44FXRXiKuZad6EHIqJKhg1mPomu/Fb3yY5Qzkr2XMeSrjbuYwyxJfpz7R5u6rn5UdGjFeOFquz4OZUyRpv4n6jY6eZWJ/Vwz6cNeh4dWvkmjd61zaeDO0xAcSF0zhPUWrOokqARnHa3js617B0nYV3QwdynCjoyBSA8PNM834i62cJmBYu+PDWwQKtJaC3bza/aVXW3VOMKLtRkpmBmQrM09oE90QnxaLlmoEOl2oDN0EQlre2rxsvHbNmd2/3D370+yvffr2zdbB9d5EpUan9Qz1kLBQBoKxyri9S0KCDJDNVdFBIg0WasG7F22bME5+yxBGJJ/Bjhx6mOm8P7QEtmLxMM7oFTjT602fP8jXeXW2t750dnX97++r5e886iN0cjOLHtmAc0Kv6GGGmK3ePNABNHtMsXICP4UaT1HxXm0Z6CXgl/M1refb9Z/SJS6WfW/XJjumA5J39jQ51WNniXFSP2LCqYwP4lH8cmxTjfLRG4PnWE7qadMSL/xEQpOGRx/1cyp0nU2Bp8S/xu/goGFvfyqgBFnHkEN+by/39nesvTj77+O/+8te/PD78lpt2a/PJt9+9Nlg62N+HJ8hC89IblUFaVy/sFXrJctU68CprKaS9DIeUuMQ8rQePDzZfOuopht5dP0lWNg6lX1t5rrZ3d2/4Ez775Eckigk6rco+kv51sgTdsLn96FdffP7Lzz83+mcP2q3wJ5/9BOY2Cd3YIjG0xjQQbQnluA1UPuWWvCBATarLS9c9XYYB8yAv2r0vc/qzfpBLeqXUd1cWrzuA4+TijJ/YhDl4Q3zTaq39PT62vanV27PVt3XVu5184kCR1X3HdDy7fP3WLmcHVizYbu3u0vDYsRE8y0RYvH6KrbMm1OqvlHR3/amxzerdnvXNjakyj9CxN1HTaDzKu/UwPZ8rJlKH/iIBo/+nLXghh/RxPSClEX0+V3V3ammPRxhDRkNqaoyPAxMbAEe8ZimMpLN4C5JEX0MUQtAC9K11K0lsw3KgjWmM9Q6+kejm6cbKB1drX6KSU91+9Ytf/+qXv3729Mn2zq++/vrrw6NT6k+3RBY2do42d4/XN/eYbvVKndkXeYGCWhNB1JLWLSraPAJ0jMOruJe5a2tDDgSpG2isPPv7GFys88N4MSSZ7FPPhYbZL9MY8kjfu8NylPqh72Bq52q92Zdmbf2ECqJhSJbxsB7R+Kh5ANuOMbzS3GnZCJh3vxHUSIUXTbOiKHXRQG+ID0lCc3f1Iulbv+dCnJEaLxGObWb7toODDz56/8svvtrY3LHPDz/Fk8e/B4e9A4dPk8a7n/38j5z+Ztpem6kCcdDjYXFSMFV9kPBBbkmxvLpPLUNyAb2hZD7sK5U116FDKWWfCdUCfmTMox6Ew/2/9a96vTwGRzPGBd46w7ZZxn12ZgurcQ+zO3CNXwnNVrYPHr+3vvFrKYsuAyIVWKv1raRacgoQtUevDZONsuqEN+wD7mCFerWrq83zi7XzG6e9W4ykq7HqJp+5DcfY4TQVcRrk4lGMMPG9u8goEfDOwxBGdyXUUhZSrDqej6tuc8V8uC1rV3elreEZe8TmmT4N5SHPxtdVn5AHgpbKhlJS2kaPXsMqmcaUy1WzmJkENzW28rGzcBBRyj/KSgYE6EGD6bqW0gZBT9m4Vxc5nrYIbtadj4QQN/YxiPOurJQRKPYPrQEbNvgVvihcUWvmCiJ3kKuYFxUuQSKaipTakxgKnqrBJd7MDH6k1txI9/qGMWMrD/PEYUhXdABW3aInkAFONH0nrd32vHKkerjuH5axV9OqIBpqMzE7IubXor3LGXrL9wOMH3zP++/hvyurasWa9gKqqKlfVFV+bXgUy5S1ICnRYDTo3j8KBBrlDGUQTElLmndZlsosP++zD4AF2jwvSTSvgj7zKboZkzIaeboQ6l35C5zvP0NiMg82A6NcMa4fKrO9vStYkDhWs7wWpARd8685VLfpoVL36du20tz4eZ3JLdEHHeevhbIw9H3WP3MJLQyGLt6SHpsp6ArJvE5Buf4pnLQqjrVdz08kU4PgApwGCJOFieo7CjrBcj9MGIksf+zA7YYDNS1Yp+z0mXogKWXRllLZU/PFc9oaTU8GdY/LWhcRgfsZwCH1fe+iDH0jUPPfbZXEhkoLTGnlJ+ryjh3vca0ROSdaYEnjpZ/yaloI+EDSnoWKt7It5KkNp5JkuK/xEGpeDr6h2oT27NGjQQHSBoWnBjR3q6/v7I0s7LlBTrb62u02/IzPEhtRQM2QKwvkHCQF20XGC9UIkUDPboALjdph9GZl40y36S2K0s2jBwFjce8aqah7bU+F3NyOP4/aGWBgW4Y3IuJt9ZM3CZha9BHxEE0/qm2RkdW3x6/EUvqhiz06er12cvZ0zT42LImRT4mGmUCMwAQry8VlomMgz9Zs7UMSClG6Gm0ytYozUFlPahIMR19kUuCHO/OgDiTmVBtpiGy65hxOtzfHR8cfvv9Ta4W3H++I9F3fvHvy7CmVS/6TggZ1TS/YmYwjqiedlNAr4HUo02YthDBNH6YjLoPU4Ae5v+WCs7cJzqScYvwM4oxmhE23Ls4BXBen3Mv2eqwHtNL6AhHFw0+bXTO/lGbXpREC2jhwaBI0qUO0a8SzF1PiPEhXKIucS3Z8fEw/mDzSae0dPLowrNVBtuzy+uOPP33y+NPPv/hS/B9y3d6dfv7FL//Vn/3zv/9v/31H1eIQ+hO1uZBLY++/UDdPaj7TtNCksTFKa1YsKOfvtSulwHG8GFQlgzCEmjqQyWjTT1NEZ+CY4qtOxio86bd3330jlODzf/z//qfCB9Xs8uLq/ef773/41Jjk4PFjdZe3kb8uih0Gu6FwsjnsiCT9TUOIXEmPn/M538OQ33oy2m7oRRahoH/dXhVekguaGCZmuAN9UGxE5cZ6BdU/PHFqmDFxNqstODffeyS6/btffLN2c+lc16ZL9dLQkrWvKq2JASIea/DRrrOailG+L35BswpoDqoUr3u1PNeFS1lDTk0iZDzwoy+PUpO9n1/lmNeeVjBI3nl0/xF89r7VDmcXsI+vY9q6GX1SEGHyU/pyC9g4Ojx6+uwpZUNZGdjlTmGsFSK1ySuDlcrWsn7+sx+Dxb/4/vsfHB6f/8t/9S/0vsTj7ORoZyfdnRigmpFwimthBaDkZzR2BpXgLnTR0tc5yAtSYpKNeZ26MufIBDy7MHdBjDl3h05hGpQFXoKnpKqyPAPcOD+zpw6Osq1WQ/X7FGAaTE73w5ll7JEFxsPMG4PQaldPJDBpekfbkj569CipsGXBloOdjUCaOFekCs2IJgRGt0xjHBSrugzR9cb8szUwfG0//4Of71FMjrXXLuhbuQf1Zt15KaiwVDA6JQnhXBHDaO+W2iYV/c3z+e6+a/TA/d1IoWQNoMNBOdMj3DcIECLavbhNicEcCBGqkjV1n93jTPiQGxTjHjZi4RuYIWuihO6ZiptM07PtTZsvNVSoXrJPuVVRG8rNY6dknsVMrHeFKMDob86iWLel9cnpa7GK57eFfNlSzpYSF1dGBp2OwthGmNz72gWRSj7CkIsOekPq/JYd6d0AzQwwJplrEgtNyRPjjGk97bgbO4FLpsJ3lxmJqavKhtnQB/7RRCUaZ2T4uKm+FQq0Ng6TUlG21F8Y9DOyeyTNkLJSpCF5wyPthwGHAhBHDONcrWQximuAtq+b8QFFxNbnKUNIBWWbgYacKSU/mF98LGGFJiOK5ZYmhawjG8duJcKTDje5J/P05inoqqkP9I89ON2enCmFlg2Yshh2B7bZieUKVnRZ+uoIHxUGrao2otMzIO6vkqjjSNfySLKFwNFkKuTjXfol5zxfwN/DuW9o979+6+v7vA/lTmmBBycE7iGV8AeJl0J6Nw/nWxbYqZHojpCaX31LNNDu7yePYpbn8QmZSl2h92nmYdAq9vvzycKna9LO17ufc3OP4qCj3IVGfQ1YxgSmxXBS/TFD7G79m16OfaqFxs3rF8DGIs/XXslI6+ucUlaw7Cnv8Jeqp7+rX41cqcHEniCSnUUBWbEADPwnQZmTGtmFLLttMFiBnnsKODA9GW5DVpOYB/VaXmQJPRQ0vsbATaWAH5FVdKNSn17QLN2jW7IsXdjPM+pmiSxaoOvELLaDKAOOtXqaVmYr0AvBrex+snTD0A8W/kdxauOLpD2iehS6eV4VXbHSUxYu71GG9miENFjk/mn4HjXTQXTrAAYxKGVGmPEPNWrIBvamEZpvGiR9ASJo+b93TKY70Vbw983qSxv13F05Bmuv/Y9X967uXvOB8vrXK7Re16JDKoZbMe8axvPWr92Oz0mUQVV06GZcFAFXoE4TNYcQqmoh8FUq5PJH3izev9A3YN44v7ZTUOcA6I18LlTySm9U6H9PBmh8QXK5DEGIGrPv/8vZfzbrtiQJntfW+uir82ZWZVbrhlaIYdBgYIZhxqcEXsALDGmGMmAwYJoW0wMtqrt6qqorxdVHby35/X09+5xzM3N62ljn7PWsFSvCw93Dw8PDQ9nT5vz0m2++dfDo3tFDuVycnGy8PtlbP7Sk0jD5td3c7HNQVHbAlf0aNyt66z30L2GWDos57oDHYlVPoILWBDLElevw2MeC4cuKrCk19GUHnXHEVBXW1k8GwubFOXbxK187fsWcVKXk2F27Imrb+WEX0YwOilNunfPgv+4TlQcIwmzEpHzZfDxPox8TUegxH5TjgkP3uDL31Us/pSj1/YcRe2xmMxJatOhu7d5eOIfr8u5Aj9EyD5w74SxLNuy55FBn2wHdXuzN8U+grdlLSk5OPaxYlxtC56G61mxFBzUnmUlZheP38Mlbj4za2aHl9uBw7/TkzLQiNf5w37Y2/3pr+4frt28aT9/cPzk9/dM/++V/4W//e4bG6gc5m7ozoeXd1Nu3b06Goia8ra0fZEQ4fLeDcB21q0luNhdr0vzvw6Ojtyff5SHefKsOaKhZco7wOj5+jZxnD598/unnp8cnuiHqjhn2i8Gn1/Hiu83/8f/kf7196BjR/LOsiieciJt7zi1q0nBmZmsB1TMDQh5W+uTqM6W4nLMO1674Ej/mvtwSGPPg74tkKRjRcitOdFC10lafcFDrUZsu0kijgk8VTZxFJ5DW29sH1qZubO5enZ9YjQp/a424YT5+9vnR5e7rq7dXbw7v1t+28KVes7kCl/rbdSNvVKvHLQhefy2LdvJZkBxTJpQr41CtkGE3ZZ19Y7fElFw39A86E8MaIaH1Faf+DNFVnYQ50CsIheDNyCTgVl1b73P+BOTrte9NC2E80ZMPHz7K2CWd6T92LeDTA12/szfOghcbiUpU70DfeXKys8c+ewD83cbzo6MHf+mv/lXLgdS1T3Dy6vqHH77+9a+/5iMwzUzPsf57SlWHMwOOvBJ2AyCWb0b2NFQe6o7mt78+PWvBt3dzGpWD77U2OvZeyHdauq5CTOl1uBOgURCbb9OtAZ0AMxnNLc2fZFKQ7V6Y98h8xQetySiGdVaqnEPT24Vszo6YJmJgi2FiJnBuANVr1fdIb6BcC1Cp1PTjcHYgFLa+l9OU3hBUy5CuqQWqvbh7+/b4sy8+MXVE3DRM0ilmkqji6F5hglzkJ8Jc5RGlbtEYm9auPu9hTkKVaTnt2Jl+WBGseRghWBX8tbVM1vf/xusISak9QUx5Bzqo5eHy1H1C9M5gPaYp4RlqsX7euRjMY3TMnKEe+0dpoepuUfM3a3/6x39uigqtz/oc1gdM+ZNfobYlsDsZz8tK51fqsIhp7Y5jktqlQ4utD1FxyCEHkG3ncjje3tgpgTX8+c3WgdWDZhXRyFLOYEz8mhGU6XIkKxBNN+Uuy8zp8owKU32Jk45wwr9Q30w2/Q+6L99HywNpStDDiolNWGRkVqAUpsirITcteTZMYWPamVRjmYrG8saUxks7CWqUWkhZK5vTbtPBDonIjZE3hJzFXvX3xr5smTHWlt+dnztKW0FeOXMwad/PYiu9fuWbKtm1Lsv6Nk8uP8UUlYym50PuFukYApMmMdMUVQKjzJvTkU6IpwOjkZs6lMxIWdJhftVzZAJqSWueH39kofnOAeMdUEF846+Kl5N++Bo+I5z9FqVrZHCeele23ZbA6888O3+6r6uPLKol8YLS8rbEXsCJurx+eA9A4ZOox4lr7WK/tYkrIV9qKDQncbcV0EGrhHMh3L+iWcuqKi+RlkRFWLJZJS+axyXzFbiBcn97n1ldt7iarpIspJYHUXu9T3H/MJFDERtWN1EqU9ewafIuayVdxamAAK1mJrnpvgpc3ZV3EyvGOa84J80YXLG4KrJCoLxXmNWV4ELOUk2zRceQCgMAV0wEODoG5YVv8W4JKHB5CvqAHToKU0/TpmU1OZYI4HdaSYoSZXEndCVfxQ2osGjTQt/nUKimK9ssIGhayC/b8C48gR/9IiR45V+JkPkCfJOwDWz45r1KBEj94vKOkaEgWpBhtnRRgiPL0Fk6VzLUtNQsLZQtCWNJHarJuAo3D9bRavvYAQrupKnvW6cqurWXVKgw9helsMX54XReR8eu3PfpBL0FBi2zO/ncPAE8hILLcqW7lHFtmtfbjRNypw2dUueaGV5kLuR1kM3yD703twfmMdG2ud5nvzAbKkS8JqvyGp5RtgBINmBShUzTjAQZbD15dGTCsMVrZv0c7T2wfz2Df29n/ezipmlPcOVemeLBCfAaw1zbpuNHAGthOECwSkxXXA1BM4j1Zxrrb+S6cipKUweX1lQfFhsZFzNno4SJwPXx21fXl5+f5Zoy3LLZotKri8fPHp2enj1oBYjxa8PWysKMSYW714BPTQlNB7zWZGhsPyH6Tu69+z/Bg98HN7SsynSF+/27OEuxJCfpWP/MPK7taHGH+akc4czNqaVtAWS/vFGm9QTac7MGs0kalVLXklMCWU6FEbwQu39cQmSKCME4eHtreESLZY7NMvOY9Zb3rMlsW5988qkNPM40V1udJvv25M033/2Gx920Pgu8Lec5a4NEM+Vuz8+v5lBdxjcn+Cx6oWLLrozIn605M1q4RVmHSqfmo+JmbO06qGp97a/95b/67de//Nt/62/+9Gc/1V3ku+JWTRFA3jyo250fXrx+ffzWhj78qtjw6PGjX/zlP9S9U7hujMFO/q0e5RadEkmoZTWExoIY07X6GSbB73evifD+QzT4p6lbWzvcahUoh6OSKhr0qly1/JrA7B5zQ47fWOT6EtX8Y7YSPz97dXl8urNr7cvh84u3lwpuHHYNuVEUeusMndYZWSTBT5nvhrsiYctKGE1YSa7wlyNCBu/CBgX3hcp31IV9f6uYqSRvi7zFHjppMYsnfR+HaD+EmC1ij/mi8YlW3c1NUkw7c1qXGLpbKG2WJFNjhnjGQx9mClW9XbZ2qecjVlWZXWFMyxHTTl5DvImROztPHj/99qvn4uxbfc5i3rZRnQ4kAJlcOKfmyVpOI0U4kR1HijJUUqr6rmr9jGbTbHg5Vn/VJalJJbum/g75MWlFJ/olxBufIeZ8p8YWaBD+XsGZgwNBhGx2Zk19gcw8hy1W8O1UO7nEHAVdud9cnXJ4X1ucw0Xt3ABzkRLyDNyZGlT8qQuwCMZIFVASy9M/3wU75tpBJftO36sDM20HASt6JeSvwqtwo2VVaH3AHei9D/C56/6n5KKsQuZ39UkihGFfYzthkVbpmsSBlaw3fwuefpQAhQxa+XKkVLclbAZ+eyvUEDQCo51i9lrD0z33SifDZH9svPjhuU3YXLfGZsu1SqQvgVAs91ozXYOSxhu8gY/zdqvb3DDBTotI0K7yxdRQLfyMXP8TMWVeQkkX7gWo1o/PbokUB2v3fW+FXPEjUjA+LGNfuaS8o3UYo3Kq+cMaHCBykSksHtUYxSTVgTKYT83+lTeGZFbXOb7Ss1SfLBwCtJGA9tfO+jYSe2mtkImO3AIKYu1MBsS9mcYOO7hqBvLF2bkeU3logCA5hojJqoiowUSzQYBmMNAkNvfTLMbFqSw+0yqlHdGb5jFueEeAr0p/WO4RaMT2Omo66BGZ0TCXnPoFnGjv7FCIPdTnRys5jSUfXIWMxN4H30uT9xXEVex5u491/3F57z7SvYCfmEPMByCWmOFfYDVqCRmERJ5E7xCLjSj13hcVyiOa5VL6vroGwPI8wYW9SzeP2UkfAI7Y4AR0xYzJeHYtbc5QlzjvkqwyWhIs4atv9ziUYPDwsPrNnwfX8U5NI7vsBVTMogasmIlzxZ33ywjA+NkBV3NVQ9K4vvUiOFo1dYDgSVPZr34CliQw9yZ/jxLThUuryqASm+O3Ip/6sYRItEIiYMFY4Q0Ir40+k6r1/XCzajk5dJt4oi+VfEXyKtpCS9mk1GsH4kkKg6nBWQN9NKUZmheuMOtLqSRsvtBJzMeS2DR662sNCNRpE9nHZkneqdRBGFEU4p0djbAmPSODmgQO+L5vnLbnzCgOEYYt0MI5dhvoIrNbmK1l7U91RFhONWmHDVqLeUIE2Hsslo0dq5BFEAOHYSwvdNSupLTu9tXry9unpzcmoDMbLJ/YutnYu7ow23FPc9O2MFu/XLOm4foJM6Xp3VVvNZcmKt8la9kpepRDCMxwv7N9jfkGb/FyJtiwZj+b5ojXcDHrYQEvauYiseE7zBSHEn3njnVqfuxNihoKiPWl2Vo7v3hrMJGBaAsdZtHOhimsH50zGm4e7lydPtt3rqD29vLBugNiqda9/Lec4E34IyxcgowHs9IfzhkFoLdXUAwaSVD+yg/7sKcm2VCDDwohoVka9woHA2kuxuvG+SVRbv1xK8bMFaFVr4zQQ8++I5olFQEaby/e7mzt2UsGy4Laluy4xWPKGXQw1SR/ZMs54gH1nEMIHnYV6L79m4Vfw4U48eElMPznLnx5ECIU6XdXRpx4Q+lT9erLu7vDw8NHeUOZ+5lVOgNmgj1kaejdUbzKYqS3Bqndt1bwQPV/rslsuHX+/n1kQZUYMWu7W4Px5ncfv3kLDmsshytuNu7kzObHe19/e3l92rDM9tr33739P/2f/19/7z//N3fbh+v26OEDQBK2xt9Ze/iQzTMus1rb+KM4Md3hUNo5zTuzIK8taqsDcke5Ruv07elf+2/8lf/ef+e/9fNf/EH7TfrMz7/VuaTNrJje+x//y79/u/7SSaiaTGd4P3v6bG/nwFIBh2cxJEz6qPSvdYro5OzRhQt8SMn/iiMLa5Yv78JWX8ncMOyee/dJ3sXzwaYmKoI9WCYwARQLfF7ySjCtYSe0N1d339zd/CLHoqpBKtcsiLWC5+HBo0ePPvr40KyrtVPSTGNYPbBuut36+c0NhyW3n6qt13BAGgwCpME688G/fJxllwJRNFClkd6jquwS/AWhwiOFS7A4C1mwLIKXwX2JXQpx84YrqTRN4VeHD3YPDpTP3fZuh+OOQlLLto9v3ugbNIp4+dG6tY7Ou21/zNvjt2cff1qhNdlgACpZUnn04HBj589DYc2SsyY/WzurkKCgbhMLipSo6T2qY5KzCN++/tiR5+vrL2J29YIah50LnvQ0lZ62divFEhZRt7apbU//jJW8vTqWXhqBzHEwJpqJfDEhjV2gVoD6al9Iy7G0Shy/OSoGWUBmgk8GXMaWQYY8Shb+KraMQRFCS4FX6ysRC9YPrk9OoNB2b2YTWZwlospMDpTXyEFGAVx9mEKpLCJsQOEezt4kK/v7R32ZwuunClMxQXC8IUJW5Ri2q2tYtCSZNDPLubTzfXV/LybDh8kDhMru1u5A229FBjNNrBmohURgiESKWKER/rqCHPBiNste4mZ9dQmhRUdzmo3eVk4ff/z0888/f/Xy5ZtXx9m0F3a42t05ONbjcslmd89pBtMCyJlYEwjdpibb6D0yXCp96sA9rCI3bAd9TFBHKGR+nJX4Qpj6utv6YX17H66KGsiG5fxKpX3JRA6SvOROKRk10LCQGeFTGhFIPbVqDAeWPog8rz6+u3lwd4dFEOIYMnz/NEHYeB5SU0YjU9iVSIygNgAVAs3IqDWiYm8uP7dmlxg1Lcd5RNPg45sxw5wHNWiBIeWNI7DzIJn/qjGRGESG2vdvy8hrjoLBAE9g3xocdXNjVyXJwONOSPaQQKWLqaRwsTDJk0yymuGSSHOi4CCi4wtimIUXX0h6t/2taIVl6hW/iiNGVkSirpPjbfqCIyljZb2XSt9cUrT7JaZoiYIPcPIaPfOy+p2X5dbIFSqWAimLeZIkpAIi5ZJ49bN6uX9rVDxIjYpTaZ+XaM4AnmQydn5ckAAKEQjG2ft8ynpyESUkBtvABcYlldOdvWhs7kPmw+q2hM19gE7wjyIu6Cr3eFPxKN4uGN1TMu/dBCxp34Wsgu6TCJ8IK3a9ey0+gKOJ0BMZyltmTU0cpg6V6iutSXLgUrTQIXullpEEQQ+t/kohBMIhQRyKP9kXsJQLhpHI+9ZgSb6SkQXqklikIW6BDGa8LiSeeZi/QaIasUpJTDvtpaoKxbECMwj6ukgzauQYYmORg5JZAiVJOK/Yz4gzp9s5lnln2C1TiNUMgh4Cmjqms2WF9ACTOfex7jpv03X1eYcHolHLGsgUEZzDAltVCRXJRG1QoCY7tbmeQ+mpMkgG0tzQrl2OEuOJ3ARwN/OQk9O8Vqv/ZFrfHzJ1rWOvVaE56qkHRUkp6vnsXTHcN86v7Udu++y2imkoMeXLXdpiRFaUSg4LA9YQlTBw6DI1Md+BL7H03DO2ADtyMqU7UdOA2p0KIwxaA5Bp0hguw1g8uowaLe2UEzlYGIvz9Ct95phRjiEt4s626RDOkKJtzy+uTs5fvln7lQObrHaDzt3WxdpRxkwmfKDcrDnUAK/vmU7yRrlpdBF2d21JS9xOPPo3elZuIRM16akkJ90OmxjHY9Loav9ptOmMmdBAaZ2enXCrmHzy+vXLJ08f1UQ7WfPyilR88903P/niC4s0gxRYSpGEKHpxFGH+KtkNCuIs5iasqz4hFXrvr3fP5CrcSry65iGicdeVoaMMWmjIUuEXu7i4tkLjqLIjEbfE0afkmtVtyDXcpA0T5ZQGXuAM9GHjAJXlkuPCsnktIO0/4GqBEuMN2/gw7xyQaicT4zaPHj80NYfDjpdXB4kH2E713//w7Q/PP/ujX/zCOcamz6o9taGS15hqf1Y4DDIZR7LT3hDjZVEpNpWEgGZaYa0RHAn1fjc/+eLzP/j5H6iUp8enoDHgSCpXoUri3Ijn3z3/5S9/LUBXyMijTqgJS/aU1GQ6jms0BzqVswxDJibEDiIgt4XrfhPkOP3b10h52K6ka4kxUEStWCXEZlPUaA7y1BUcP4hf11FRBPgpNyeeXR2vOVjXKQqKtD0LVUa+cI7ANlA+rzfX2BEI+lGmIDuZ22qcPdCkjmn1yevqlzFaYTD59eCvFhjnpA9QFIX1os+LMYGEsC++++je4yRZYgyzVnELX0WeRHemw9nvhvmjQBGUWZHGJPrEw3LDlvbIOhbY5DHdGnOoiOLESjiw3Syxt6Zcfk2q2Dx5c8w2xMGwRmfzBxRfT6ZNzLhN+yLUuQJi6lJFVy7Vi3S2u8qesyCPqtci0LH6lvi3sxecMR3naysZFIYLCcOUmBcQV0j3SGjpVYNXVJVS0uesTtUs7F4206YakqqPQJUTYkEIPUD9q4RsyllttBDiu++/o6ksVTE6p3wNLNRbV0cxIT07d8I/6mlYhjkxMpQQBeOk6dYq/LIoS2ncSqt69RyPY4vf4Xsv3hYI97pnInwQukQpYRAmbjwt40U8sgCCp2wqpWAWeTJeMvI+D2qlpVNv3rx58PCBBNK1gVJ9rarF3OKt9lKKZo/p+cWn2Zf58hrt46+xmkk/qfYUPWCmPlKho9OE6VERNUcBNMkixPwlN+LZGsM2O2t2vCEPMwlzxFTZYP7gSLfoNyYhkVXnYcSnFgpAPrAQ6iPFlDkQHasKBDlADT/WaEim2aV0oJm5mxFQi1xzniYi11gVuTqdiYZ6AoAsPBUc6lNe1AQBmEyrTVNOFUYNKI5wpywMn/ipc7aEWEBVLBXHlBMf1pj64ctew69J5iOnEUB4njznuNIwyU4EDXvca7ohfLjL6CDApjR9kqDq5lOGBzwmyzBMVHzvveylwgPJIBQamUQDUvtR+y1+GYgcP7pWP6OZeo0hk0KcMZkm1nyZPO5fl98l9QIN6EEkToRSWU3Y6n7/82MIy9sSz3M0FnH+YkGqMWCDesgtkaZcIn7JZ6DIeCIHZbmK5cLo+xBvqz6H9cUuCe4v/ptBPYgDJyKkvPyy96VfMqXc1yXKO7QXGGHzAbTe4mWeoe7zNSQnTl/6HqzKdok7XJNB4pCJOapscTB73jGlhNvDRwJEWKUa7iSH4INYdlWWGZccSfDKghs4CZ4EWfkEZcS5/D36V8WWUOP/nZCADZVBvjYdVBLhwCyJYZsi6KvYAXUHPQz04M0lMEdQrWYwal21SVykkShOiouGMB0k47UFQNqX6s/UhIEwZm7GO5umjUSHTfRGpsNAGGlWF2Trj75ScSlzsKBlti6yVBL/W/8i0hAjsRrrvFWxDbAwkfdzPjWQVwZpN/OCeeityLBsfsWTbWy2DEkMTk37Akli+FR0MFUumqIZ1cTqUq8AIYfV5bUHPrLvbcm5dvekqal3xxyHGHJ3bfcmWWuxgOPrtiDB16YHORYgbeGvEg7/yp/32jxC58hOA9lXiizuj6hQPpjiUpxppDM3nWiIKfSQjA+L3qsIl1oUpO3f2Crj5vYzvtKZ1giIDRzXLs/vXnz/6m5398Wf/rD9z/7pkzMjwk3e3rzd5tC4aRXK5d3l07R0bjYTm45tMGJvqj2zRJrUyGhiNjFW5RHf0Qa1HRNI0Byj579QCPriVONN+wzqILVfJo5IVocKWVQ3z//19e6j3curR6cnR3tHb4A0VP3w6Ejz1rEv+wdFLCcsaXbHCLVf5CBXN8AvuekYGv3Kdb6cmoDq12A3Ulek1SVw0Q93S32HIoTBSKp7vHXWYyNL/KP2mny1tWWL0qurw9tO1NCO3p7oJSbJ1aBddNsCT4bTbQoWEfIpwruW++rXy5JVaROJidZDsFwk7eDAosn924ODVy9eOmEDTUcPH7148eLRw4NXr6/WrvQEELZ3cnL59dfff/HZlw+O4FD7goBqSw/IT3Jl4R/YBK4qdPfxrd1Fbr4lh70a6apHXY+W0tBFNFXCDphfffXLv/KLL8w92ds7sOrXWmHm44CH5/W//JN/9vLld3K4un5pXZxG7OmTZ9X9CHJ27m6nymaocWyMFhi6otBn5V3hyW8VGs2r53nErnhUZEmWSEuM4aMs5gr4BVF1duk9zMAwOxil5Tq+g90th5J9//w3P3z600+ciKuENvbfnDX1+BPLc7ZuOZl18BguoLZK9W7rbRMqb07TyY0Gqo60elW0Imr0aVAKiR5HvuY5GwNdg3l3MUCVaOjudz72vnqan3Be3kvwAYWpxUq0MKZSuaeg/KjvCziVj3zq0n1vuVj1tBkvTZ4RKcyCpp4twm+vrd1cEq5N86dZ1D5FC1mlEHXh5kGH3L6Z9qvYOjvX47XjVpWUEZ8xtkIW8Cnq+iSDPUKvn9J0N+vfwQnmpo0dv909v9p//vqbg/1D6t1aBmWaCBgnj6yliIZgWIZJmpnrw4TvRo8bL0VNrudUZhTHXndNFziU/3QpUp0QCjRadgxuUDKtmcb8zZ2tb7//7mdf/DSdk0FWHyPBkyYJq2FaynMgu8VmZ4kg9Xb9O74J+eQCeF/S8EwP6RGIHTpLkhUbvEVbX3r43WsVKMbgK/FyfRib6qJZW+R6d/ls7ebRuOA1fFAtNy5y/JdMOMP44ODB/r7/9eSNBaVNNr9l+it2PNZjFxMoYwR6Uvigx262mBLH0ttte6YZAXNcJtZnZoMh7e3lJ/mSN75X6PmYNtYOjh5GknLof2MMuAvy3frJ1for0+vNUrMHlQ23iKc1A0pCdyCPdKw0BCRq/vQtB/a1dLsBHrlYsWLFYCxFVkcZ5h26dTYzDm9/p7xrX+oG6hIaoGbuN+unbDdo+GOebOrHxlD6ERsbLxZrv/ySGBLUIsoWMIQqyZNLVdJ7hU9KwN36ze3W62RoJckMhiSkymEC0NhTU8JLO9eYeLVGThaBQRcgWAWXqHjB9mgBvS3p+OYmP6CqF/LNHacrhaLEsLzqvjIvIDxewlLUf0AiBSpetZRdt/u1wnQyh1TWj/law4qARg5058oGGlM6fpUR2oAa1DysLg8FO0nDTxgsnwCT19SviSC5+kUwQKT9plL0vECZn7KbREtS9+VidfvCH/9b18rfL9RM0/df75NBpwqxgEbGCrHGCiz3+7r76qMH/99d8CglFAUpift47yL8nodY4BoVWaUaPt1nOeCEuCbSZDuPvwVpCXuHywrDflaoDhlhFE6D42BJD05ZiZbeCn78Tiy91eAsmQtLlY4GH4YEZv6VQ+KUZU4EFFzgiUNIB6uSJBxLVzDyEu6lFEMhxVDxi+oKwwRzQXGVxUJGZctuGGByHzqGOMkgMK6CaBhoEMny0FSAK2Q4Sz6rLgHqY1mzJmf2AeXV67ihdJOtIMq7Y+rzMjMECAaJNaCdhqS1as4cl1Ad/+sLmqU66I9Lo2YDpDoYKmQeLGw0uIc0Fg1nJz6OJ6DdD9jyLNScEx07I7xehy1KLx1kGKNUyBkfREXq38cUaR0OhDOwneuRssBQSqeSkrMK7Ol2/Vhn5279jYVhVJ3B0zvnQ+nJU4GNfqjksrfeyJxWvnMJ+VXnRB76FHzRmsqSf64CrXRpIm0zXUSwKyrYSNbRCbfmBLCxaAv/IQMHn1MeU3KpCpz2YrKn6a+2aOeypxWdNkZT4/OTpw9fvHn9H/6T//df/enPv7Dc8eRye+MhJavdsa6JLYSDSd8YjpSrpc8GmNdMN9kxPD8quSIlEl3kp+JwHMr+/vqrt22lvFjAYRUq+KwDsGF7BwVg/soID7SVMtwB+PWvv9rfOXh89OTVq1efP0qrbW5Z+Xr27KNnx8dvDw53JLNBAmLbA7aeTr047UIltADpfIAdcpLVnqwNXh5GLOf1997KvQ/zCxR0MTRstTb2HV0K8Y4XKuPk3Kzpza1zI5Y2xZMk0i/1QFqVoKqMG0brSMQrLCCG/im3YstG+Dz4gVv5kqbJF1NKU//zUDO59vaNZRHXdg3WJF8brHlzosW3em99ywBuhjc4ewe7e0cmTd0c7O0uW/iBADlljW4tur/aCWVAqghVNoPKs2ZDQCKqUamCDxpTEOrjOck6MB9re4OLmXKyrQ8eq9Soynrc2v6n/+JfOUQVmsh11Nf56Yn9cvhZ1UP9RRuaYhGpjJdudclc8YMpMhyAeNLsSveU/e9cVTjhv/O1mhHaqkX7QTVeMe16FSpBGDGz4YbZcfJXEx907tPlue3PGcnpjBa2WjR9qsBs3YtBZVOjD6A2X1WU0Ia8o1VGTw7OquGCckHvL4nT3HD15Opbz+/eogBik/Y+uLclwkSONaUraskxa65VsiXmfJmvRWh4JbMmRVMzAV0FTAHmKOUOaYqCklKckqQOs8WUO/GqT4Z9utyQwK4SqODMqOu2vs1dbmBzc//J490XL15Vy1eIjZQWexgACaoo041IWEFEzK7bF8uSzZu1777XXfXZbKozvhDHAgAMkWQ+tX9PPGjxYqqwHYT1JZ2XSXms7V9fND/BmKEztmsv4gkkV8ioMiglktMtCZWEvP1p6aod0V++fG5vvSU/W/fI3Q4EC/sxoaZiYXlZR07Jh84QGr6rLAQk3i7Cj2tdCQewRalQl9fI6Fuv/XZbaBwCe/2d6z6NmO++CYuUUKuyrmkN7a9l1E0gSoXn5buHn3GvLtjb+5JJbbhmczljWy3kUUmrLNBqrzYNHWKgznF4NQJgTCmbQY2OmepGsWFS7rXNSQ3ONDqkFfqjv/Lzw6N9HoGVwSRN5K4/+fjLX/z1v/72xakDqR8+ffDg4ZE9gPQ2DEI0aJBCy5Ld2iOr9AMjPulKr4B/93jTdvvbp3HAPE7bFxBX/L5+6Ct/kQELDb/WxmoQ7qYdG46ZlafZq/U3M1Tb3QkkNVVaPNZ0bcM0pNBXjxEymwSH6tBFJ5rjRMjbasdpQg76dIijNks7Wk+lVjgjwWig/f7rYmagK5VphZ1wurN7cBiK5gHZGbmGArOzHBRXIpVYQGghSPZdWE3oaWXU6Xzhh3hpmVwMgNNC2lP5Z9bfdg5DbtJEAb8o3U2bYrk8Cc2qMOacnOFkdMklUQJ8fiVKPIX4C79FDoMgvJirKzku+wEijYgCBsYSIwxWohbEcgxscj8/c5+cVkGTYAm9v3+Q3ypoATHYQScklivcJpdJMsj07uNgjR99uI99j8QSgooF0+ykFTw/H/Qz3ge+f0INoKuk9MeyQh9PBC45v4/7n/qEAIPFINkjAoyebcMdZwuFbr+TTe9DTB9XfL/5HNtvN79KGJIJ/wq4u3pMD27sPK80anmH80EZMtP7JG4fFKO+Hqthyf34fX0pSx3pSS3TGsLV5Usv6eDQ8lfXtCB6Qf1RX+VS1embx2pFpeT5He+XkGjjOSOiPYzQq32NwFpECBi0iWJMZjVnHZYBEe59oKV8eCuTV6gyRqbqZsGXe2HMUfgBpImvKR+nYu2cqsDkdvabCQgsI3sQsGrogNY5SWi83i7qMueQfsD3YL1ODDO5QQlt/ZF9Je7u/vTCsZfcA5dnOgPMVqt62nGMcc1Ap355S3P05sJ35XPmFLg142iPZkKVEYc4gqpsXwMgSN0Wbev24yYKrzvSS2cAzf4UxPiQ/N4ZhdfBMFcSYWYwZx0pIdziRp3RfP53Fph5Lr9O6G4+S3dMGU1m8oQZL/olnYffNjfXCA4mvhOMTE75hi+dRFdu/vz6/HbXzjomrWgx7MsG3Zu1r756+T/7X/yvvnvx6s/+2a//R08ffnr406vb72rtTHhQpPVuMPGcKOTNNVvQiUi7e9iTAudakc0QH3pEF3+JDmrDdqQhYfdG8Hyu+FnUcGrZg53Xm3hB8ByuKTNtT8w9u7q8Pfnq6ScOi304vRfGPK15d3F++fbNuTFuG+7PPh4E6F5B1DWSDyGCKa/49fr1Jy3kuHtZsQ1OhPNdRyWWvrtW+kGsuSY+OH4Ro+Rb32FlWNNqtsxofv7y+KPHnzvxg5eYg7PiRzH2X1qna8JoO8y8ffHi+OTNR598YjPM+iFkMNgJh9va6IfVOOEqU8ERU6T4yJ6LV+DaeOfBo7XP7j46OTG75/Ls7NywgCLhob+0ob0DA/Z3r24vf3j+/OTk+mhfm9HB1aqAgpt+iIaMSDHLmOpVs84wSFp/sH6dujLt7cyijnxH6riVHRo2HtPTXZOnb169fX3arDwrTW8vbXfRxjILsLX137z46j/6//4T+kVDLbI29OlPPn327HH6hq3QxDbyo+TqIACursQBpTFUDt3DlYUD6Zb7p+J1zecl9rDm/Xd95M+Ls/nNFBSMFfr+uPCdeZJgUA+XeKAgO3l97WrrDTG6tjv55pnjlRn4dxfPnBBlC9Cb/Z3r9r3d4efGKEmnRHcrAL6IppmZDe+4N2rBGj5Vgki43uGbxHhZtNwKx3Cf4GIlSJXvRFuS9jpRR8x6xMcJmIQj2cENCoK0BZ/2detbtL3Ljjh5pjLNgpw6Wy60BFj0TWaUsVZnr8ajqhnjnh25v8+mwZYCz3n3qSHmF4ZhilW/vAO0aPqOn9gZhWid3oDaJQq5TK0nQhRIJPcnW9wqiztr2G47LII1dnl1enp+fL1+me8VanAqPu62Zsk455Qwbvcv9wgcYlLe0bZ7z1K8TDHOpmlQspXKySkTUom8HO3CsiwjfLHqOJMWTTpC+Vx1b1i/FgDrlme3gWKV515nV19TQcPV8J5MU1b+Yb0gt/gqYPvFyAJQmcK5ciqcIpSwp4letZ63+6TeR87nDlCAS/bbl2BXESbP7isESuHCMxfH0t6Lm43T25s/NACXMPB49BEV/WTN2+dl12D1ztnJ8eGDB2s739GzYGEazlZglL5G+qrV3qolmWodsNlZnsoJffXP44vv/VMKVod8z1htDTwXOX/Z5fXx928sBKtVrhuWY5y1zfW8a3LWNQafvzmmKGwFpRd5riU9c7AEV38LEPDqcn/90DH0QlQrZu9sK6TwjMOXb6RlgTAnqg7rpL2ckaLEk41th3a3sNWkPSMMgy25AdoYft69Cz4SxDCjY2WEdNV60oHb3/mAo0VwTK42HA0gOeTYkP7dumNwEnHxAzn9gMFDCGWScrSroTTXn3Tc6Q41avqsu4GOBP/OTkd9Pg8DICDAbw2Y85hzFhl2sbYmr+KlQXUJXYNlmPbA0vhMytuN78GJwRlvFbDHFvs5Uw8LGENQ0w5PKulEmziCS9IPdViSsFkyQbd4gPcnqylyn6qTS+aFhE+JhCQU/keF9Q6UwN2l1XSEYObuX35RotmLcmCJWZI4Hi6T9vAfBOHyy4EjVGCwlqwnzzAf9PqKmT7N5179Ldcg00hC2BYsQ/dJeh+n3Fdwl98Zi3n/9YOnsJjo78NWOA1+AUqpRY3HrvnpJsI9evNhhQpq76OKcE/fxIDxknqBvYDqy7xHvmf3BTrnCzbjwShCUEkEQ8pHtaJIUFoBLM59TqRjyo3gJqLi0dDUQbhk1Av0JSUyFCwISTL5gpiEyUIeCTFaRq6mEeTprA2frn9R5nPlXEGDVoL45F+XyAgbEuQf5uIJKXTiLAxI0F1LvvM1EK6BurQ8TG7ug/Ci2RJC2KmUUcB2rXLCWgIGTnubLLnEwLnkE5hVpnoMaoNdCdpPvSWM2rBastozPNEwDNIygAKVFnzXit6pAxBgvFAqUWsQlQPFqFgcw98aLQgMp8pT3ZOjgGNbiNAv5US40VgO/BewAT56NmzOBaJ9G3PUpT38Nf3CYKbTZORN6RpqQOCi6yqtnssspWQWCnNeFyh9hw90PLywJ6u1mBn/VDu8Zrhg7ezq7oc3Jxvcute7LOm/9Xf/3t7e9Tc/PP/06ce24Lm9ebm+dnDl+CCO3HWWwcX6zR6jQYPD9G+UHOtudvWnKlbo1mq/43OlKB/sFJ6mQ5uA6Qxk8o94BEwh5rNnmTjR7FxDwYGl+dElUDR2Hvzm6+/+8l/++cs3jgA7UByXx+cfPXnqRKdPPvv04sq5toaWiXT+y9hSlmg32EzJz8VKm/3jfB+3ZTHDU9R/lwuMhajhqaRQPn5rrFzjW//u9dnrtd2b45cXZgTkX23/e53Nje9/+PV3P3yB5/u7e2bqv3n71mKGsMMFNPuLZVWfuPIem/Lzn/RCUiVCMrFORlheTc1fBlqqyO3OYTO+i+tPP/lcR+O756Yk4diFsYLnL7/7/odvnv7RHxDVTk1ThpbyWhbY8bFN3WlgXdfXvtzn9f1MrFKyoaXhTPnWcU6OR5HY74ILioWwaW8PIwDnF6R0oSH38M7u6zev/mf/0//FcorDxen500+f/o2//lfMQeaovL1pOJ4+qJZWqcqjOeK5flNu3sl/bFjKRMD9oyxc7wpqGPX+dfm63Af1aqwKzTMqJgH1lp2hahMvPSi8ZHrQADn05W6TVgzWn9NKkkQLSkzZelUv9+5ClZN+ikh5DfuFzMgSyHUGgFYYqxYTxqHQhaIKa4R9Cenu81DY48Sdsn/3/T5xslsUqaN2eRvtPKJSfOFz+Xb/6D3gw4QeMbpNDrcVtz4hNBWlVbz28aLksn0piSwDSmfTiadNJsmiHc3YzkIcEjvbBo5oqj2bvO5Y9Jz/cVoSXuTL/T2+m0S0hiJsk8aQoIl8gAkqwpqV3Ba81fViKohqXyRQbM0/odXFUibkjHKSc0QEyu9wX8zUsPHbOfqKlFoS7J4WTYspP+nocKXrj8Khm1X/gpVR+lmHrmyMFu6a7+QkDVEtfT6w+nl08GQns3IUL+Sg3ItHgRCsznrPfXPrLJdxAOsBhDk7bBKt4i9QStoVtPurxzKY//eBv/s72c7tXcQp29R+yRXVwiQYvX3zBvGnp6cqvpMNKus5MRe9yuf49O0/+xf//O/+nb+rAnKH3Ws9ThVsIwkp5zjQ4jaecoyOWGyMl+10ubhR5BDOrqSkHn9ta4+dQZqPKjVvomMf9e/FWn/x/NWf/NM/cSimorhwytj5aWCNLp12vnuzjSpBk04xMZ3G7waukU1Ebt4eE6JNHQOyah3VpSPESLNaCgtER6MxXpMPKR8TWHU4tOUqpwLWcuzu7mVb7zS0Pi1LFnMFob6AjuYpMtmMtympw9iKt1IHW4yKSm4F9VJaUpBGXuyERY0LJdb2EaVmRoaHgcUedo2XC8YiBUJSHOypVj/DA+vw3DuOTKeqZP7XoMfyCgx6SaZX8YOrNkExUNWrGjxvobncU3aTdjGDBuJSASNTOQU3gNINM0o/gWUymU2MYgkWRWDaGdD0zeTUDVXzPE8LvJKsgPW4upZoARIwuN1n3PvCG18nIThl+KFiK8o7UPNQzCExdAal4fh9pOX3HtXecgn8u1/3uQ3FFd/lTwrKLxgp9zmvMp4Zwzy51hoLWRDql78/6pZL/2zC3gV4W74JH5qVVsP3TRtQqvpVKbbJcIq/WSZkbuubal3UDh8DOn/TyIkffjOLiyU03xKMWZUofGapmkUn9Y6Zvknn8BFBU3yBGuDXnwKktz0QAnm7+XyiMKQWlaGrblUAP8t3A6FU5Z2+rb+kVtvhniEhNLNUDhQxggh6qMuZi/7zLN3tr5lr1A0I7OFqPQUU8mYiNgtZ7jXSM8wud1YLUxLApSVTXfXmKbLru28NUQep/zPCCxNd6BYhBLc2RO8hRoXDjAnWjGtYQFN7r9d/KR7A6bB6AlE2fJ1ehxEMScfkp+AgjFz/tDcVAHoWu445sPutTzdXn6C29bjAtAkmikzOObpdx0kY2P2TRRZnpyGmu3pe27LWcIR/9AJWwMLU+OCbsD/6ZP32p17Xrr+ozLZ+FYaEA3pN0jbGuqvbyAcxnUdWv/Lik+guevpt+En7hDEPye3x96+/1lQ+ePLw7/3d/9Kp1b8318+fv371+vzhxs7Bx784O7EE8AWNdXu7f3dztLb13FYzt9eP5McpF41bd9YEgDCcHaU5AlVFhnUSgDUVAibUfqz4jyQ0Yw0/01qj+bz6OfZGLKsJOYpFCYLSXr89uzip7Wd+6hsopfXb58+f0/O7e9d8KSRBaeLLnX2yN3n6+bQAXhZyqFP6YC9t7AYXxjGFVuH5t7qWfN69yB0NXdEAKpzjJJLd5ri3lmW/3b39q+j+5Z9+vXa6sb+/8fz1i9dv384Mk2cIsQzu7auzJ08P37x+KdPDg0M8mAqkgBLCBX7l0q4LZeZ5in95aTXCrZVud3/BIwshko0uyBhLOzja186ZrnOz9eTm4tWTJ7dn529/ePlCemtRmFadTbN3cPjw8Oa8pR0Yb3qcprIJMnLKFxAT0OWGmxCWuX3u7AVu5fA0TZXZ+vabSsB6hhYE7r9+c/7i5XHOta3TOGNC68XlL//iX/3D/+gf//Ef/3OglINDtZ4+OXr8+MhxpW9evX1wcGTfpPOOFTt30vnOVltIKtxhMWn6LCZvOslkmmPMjheukFvKf+7z9u49sViFTCQamO+fmDTT3TqfhGbDFIIHSYFnZ0Wvb9m2lMWAzCSl4SZz3s8NGW7f6eNu3279sMkBylZsUHHHbJdqTOnJOUFK5DBS39IAUBN5c3c6DVrXwci7jjcNoRxhRl4hRewHtdAcSAtl9+RVi4eIJdaUSlGFjejCsGdph1G9uJZPQto36T551PQxXUA2vM2imkztJmwZcWqFpz09W6SUgKWBFytCnKsHDw8q/KAR8nUdQrO22kX16mrfQGk7uD0bUDenZ5dFhoToACTIECdI8lzMQK+DNPlXXVPZkUDh6GCxAL3TkcVJX5BKgmiDF959OYRWwtjlNXK895vJq9raJuVyjCf1ADibD6vXZxQRhQwT3Ra1pD6GPk7IWV7FkwgqJaNZMWD42rAhAbV+Wpt08vZk++HDKAifYXRdRc9T1eA9z0OtSCvGpQ38x+bQ6/7+ZwCBMNzE5z4tf0skL119/n3Xj+L/vghVXM2cliMLXT98iv7OfgCPHjyqlVEzc0qEwtnJ+T/6R//o7du3TfcyBX8mmVDYi91f6dWqVhCqTazmampFtpaykSL8qYKsCgXgafJSGsIg2nZhZuDagVORjdqO1Ck+ZoBFFg7R3ro6uzwwJcf5IDS3gaBm+rXR1JS9zGVgtp7z+GY8IcISqQ3W1OZR48PYV1usfumd1HxVyvk0sb1BLog3qsmDZdk5Z5CRuyYaEDfeyhIELdleynDhL13xXVBi0lwL4lGGKaqAJw8ANvdGczOBhkYTFK2/TkadQFTffElQvI0jvwYo8QlVXPN0jk+TJQkUT238yp3o9BUTNIaUBhtCN2nYG6Ir/k4K45kKx7/4hgHpLv8Um20VFEVVhdkErcBPr2zIUlgKr5KJROLqaTgQqHnup4Ic4VzqXS9RX+QidYmyxC+1f6Wtvrtmd53SCFJeicRck3wBMLisgtt/r6tivI9aJgFWwYu6oDYxRLn+fOIPpGzv37pWCE7oAu9dyLuHPvrm/T+jA7CkWKJi9wAVNqi++4b8QXOA+tQvYpfv5RILlvd4NTFWCRaIA/b97YNAj/4P74Fb3gIfZ8ognLJLCeMUxKA4GSfiJUjXi9vX5ZqEw+oFVUk8jLUahytCkV3zKB/qOyFMoac+kRI+yTcok28ZjaUapJHhMFW73iNegFzAJ3a6uKCY+eldLQQnde9ilk4nVeYRlhYPSWm8hZs86XuQfZI4c6FzVWRWnCVH6Gs/ZLa4fmNTeHAfZ2TOWJmUsWFYGLfKD7CpF8HRokzrFN/0wBk1dS1i53A6HpR6KqB0WW9yC8RgPXHVxYFfPydVYwVsFS663aHhOy5e3KzbPZD7FiHDM589TDHAWxZ1BEK38ULNYSODXktLT28YZJVByMCo8BUTaCKKbnKTTn7rBzeOH5u+QkdimdgQGvRk+E+U7pgZFeyfy/WLi5u3b09p/j/+F/8cWOOe+7uHl2tvzi+N179c30XQ4ZWOysZb8yrvrhhzLUTHIVZQMmKq24IppBKLMnFVtF3RoNg1CHmGSIXhknQ6GLBKtCrhtDWgORnjWk7c0d+j1GxjL86e/W2uLk3YBUXbw5LbP9pnHvNoN18lwaH0Kf+R2Fk8ApeybypRXTecGDHksdM1wsd7nvjwo6vXYX+hMPI835OAHu/u/t7f+29+/fzyq1+91LhakPDVt9enlgLfXh0fm0Bv/XXiZKLIs48f7O4evXpx/OLFy/09PXw5jsTIvaJNH7sWMfsRFso5DoY+WkfGiloNjaiaoa3dKsXNztGTx89OL786ODjS6JqNYl4Lfjuk5t/8m39twS4zNrEl2mrhtsnfBtBN+64nRgAAH6zAjPPN/04n5K1PXqrIyXdhpges3Xz77TeJOSnd3L7WJ3v7Vnv+z/7FP/2P/+N/YmekWeN7/fDh4V/+G39FO/j48cODg/2r64vtvS0nDSHTaRgXa+dHBwfTATBlTodmoWhhA9oWdOTpcVUu8xyj3l2rAuk9tsTAeElcCGfaxJA676RggqJea8U5EcmKDE1HCrZxIXkrjRtnUKBWR0DhGETjuDkzxYvWaUnJ1NeKSy4VSWXCOTHSjWPpTOI0H8LGNYW6FOyC/8LBhaKJEF1J43IrybwVG6OLsrriwDDkPmBw8CKWmMOFob+n0bHsCkb/zsXlG30tVcJSEIuobk+OefRpow6RMGcCC96Bpg7LPUWDCv1DA1sYlg/VTC1H9jollv91ti3mgEkapvIOT0ydaBH/ggP8qQCwaCys9c9/Eipcba6mV+FVVWYjMbu1Lw137dvjt3CfyhgfxJ1WAH1LVku5+qQP1u7AWG5dVjMorClnF7lqWbZHdFVrRWSZVhYaDIh3WJiy1RRrYm/R+vb55ZWj7j7++NnhgyMqncWIXixd+Bm88Khsp1jk2Lu3/Ck6Ey2/6oxhUjPR3KaQvIX//fXjVyCmRi1fl3hilJmsgrNcpepv9TofhpWThXD1FBfwASuV0T5pvvv444+M0oCviCFrNI9P5PLy9Ouvvv3JTz41UWr6vSHgwu3yy+hnKVfPa2Gq4Sj0tf9Z/pnfS2OseBppkbNpQsLUFPFVsEb2Wmaaby0WzT9lHKi7zf09a8g4Hi1ZPtNZaI5nlcrY+6VBRhoyeOfU5XCaTuYHd1yJaxdaw67YIOtmUYrUfJnKJBolUmoXlhwxEWQYWibSZE2zFujHnFzRObx0B89jpTAhcXigV3Y0ZAD6PsUhiiI+Oz1LPyC7VSgaZdvLXpvPxLfS4Xv4NhIRI7bPt/ccdS9747GWKGQoMUXknmDFlu6TZZrfFCYI2nGP3ArXXVdAg44U0VZXqLw7u4aYjUE/erdRUzQYzzHmoSAa+UoZ4Ib6tfToKp9airxyVQfg/M09yD7GlingCQ2gCKQi6sNTHDEXlpV2Ar2vwgfkACmSqyiusax6eJdNLz++AlEm9zn7WgGUaYSzgeaT99ItcFcQgnoPeQExcaq5qxjLz48STZDNAQbWcv9R5B+/TNJ30CYznNr5eoIGz1X8FcXR0iyoJcngcf88uP8Is9WXD4ha8Bla4Mf7VDW8R7/CW9jQg++Jhl9VX7mrncnr0mwDKdVSLEFbYARoSWj7tuiPvfWl1PxVYQ9HVxklzXVtFcM3JUzXrZDRbnO4BGCFg6VC1tqLn8yJtrgHYLi8CG/OAtOuSr5hbxje6QyOkMwzNOrijSraVFrTUunr6nCdesebDmkNFMKC4dLaUDnffOHb9vZXAyfEqG0Ldja3X0PUrjvI71LhluaNNZrfqJZINMxPhYRy3QmNm42lFzMoJqT+bNBfcPU2bolGyW86Sa5eem2etT5f05giiQBumKQ5fNgGURWUwcbtH7CPWEfxfGLVJot48/j69oCP2zpddd9qNgclXttGkPv+7iBab2wqd+pgRTuKXJutbhKzjREazTB/Awb7XM7rdpm0EsAAgh3l81Cil2/YUjqWnyKy4vJ7U//zS6aut5gz0TYO+EiaMiMGI0vNCnjz6tvnP/ywt32gilApBw8e3djSZ3f96mTfPui72x+tX9mA6IfK/vbZzZ29EV/c2WLl6lO7rOh71RlwzrHySXQxd8ywhX04nrSQRioq9ZLN2tQYw7LTl1FQbf/g3kg6leqzlcRrJgnbonVQlDzOc/+fnZmt+/bV8Zc/+/L1y9cPH+6fXjuXwFoOMe/evH798NlD49hWeN+tvbJh/fr6M40/tCofitr6wzzzLpze5HWuMjaPUJRCP7zMJq/8eWvE6c+L6IqAyxeu7RD16bODf/+/9Nf/9y/+A6F/52/9nY+fPVatDh4e/C//t/+3P/s3z9fsvG7u1N4XdtLWYYHF2fG5A0rVlZzxMK6uTc4LixYkyookVx8X8tdhaKtYm5/U5mVIVbvFSLb75cg82/56++DlxvG6vfn//M///OT8lISi2ozqV69OzfDeMG/79lLHlDEWPdn06Y/hOuiEV6dMphoT3BGxE28oCdVk6imW4iVOmsP6ydXpkbn19hbd3K/LZm94lpklgC2y1OGsLV4/3Htouu/p27dPHjyyIG9bVjVFSxXUjkK+dYd5bdlqZidD7PKL1Nb2N6sSicr4PtfCneW5ebQFi7kKGK4MZ1TwVFyFRdZwjCbAZ7sF1DIqQU5tjjO8zdKxc/fdVpOatgyaqdH1RDnLd+y4dbt3eWLd6uX22vnWgT7Dg9vNVzfXz3Qibgzi0Xl8zG3GleMCqPIFrcIZnRUCC3ajbhYZGmxXOE8hFoCylYCVIEqm6CcsFbcELoSu7hHvQ2LyPsIKTuA5Ln06OzncWDvc3ntz9OgRcdMv3t/f0Vt2si8dhANqnLzgyWaxQJMCs3axXquVKBeXTx8+ncKPUc7d2zn6Ex/OL2xdYFsXfcgsG90Cnl3xUypV0miv9cjUJ1yyEDzczrrKXBuHCx9z+SLVKVqcDQYY7FrqVN38AjUR0wZFo//pWCpCOzJWjcrnIWuV+7ssx8sJMBxo/apVKFRCMkjA6uonAzH6NpNOm6HfzAaFWhOQyGKtFoLS6kPLCF835fiuiBKrBLHwrO/0SBQu9pnQ+Til0w3EuYIQnCUtT+74NTs5NfKWOKvfSfsu7N0JwQOhiIDgofVXNosDE0s0qk1w6ltG/IIM0pUm9fDVr+3Z8Phg/2h7e//i8lSTLEK8xwv1NNIwMq0Y6mC0GLVt0wCf3Pw2RK4ACqpohtiKFPU12E4LVnf9DoxMcSgFa23t6NFh7fsZh4QIMtJR4VAnOSLLk/9bYdpg18ZxnQEfWshILBU3VDrzYRCjd5IZWVS0wQlzFi5I9Eq1e822VKiCZKIXwqhJnIQObYNSt96AiiD/YgfkCuqDoN63ftNuv1cfQ/ruqpH2u/aOU96Z2uYAVvmYYJVpWGkOzJnMi48PkIVOM85CNzR7BD6t3iPeL+wGzUMbpOKKget6qitMwqXBBzpS0mpPGWLz0MOquTFTAN8hEd9A9guaOyjSRNtQ19rCG81Bk45EK//lIkyD1RI30rvcJ+2qDIMi2iSLvzGh6wM4S8Bv3/8zIgzYD9Lgw5LHoBESiNj+SrQyXeG2xH8PeYVLGP72pw9BB6qJBhN2n+aDCD9+BCvOdUlWjevlPmiYVkBt2Xwt4uA+SEzqCfqd2+/J+XdiT1GWslKda4o0BghYirgiWMrbb4LupXLxb3jlx8P9tYCJhXHYW1ISvPKemEtohjoFwhKN6rkIXcLnmuRVjFzm+KKSUy95l8ekSviaw73EHhkvxAjysGv6KkYW+SSaPTkiC4MqPFCZ2gIHs4yMsLNtROYCc7ZKwQgdOLmaRE4MNQCGE1Mq0KiDMfVG5ajuUwciDHFpg/xPsWlIT1ln5Qy70hNmhVa6CBl2TA0zE310YjnFKMbL4MjalbbKj0cljnB0zFYj9vzHJv+bjeO7L4jKvUryTC+K56yHrW17/SCM+tviB6/Pp4pbrWjicvoshi61nc2r9ktnzCOVQS9rKENWQcxgbm3bsDGFKr0mAEJXziDLNt+mqyRO8kdiwu9erCJsStYQjX0xry9unfy5vW0++dbBgamT2zpWu0+3nu082Nk9tyD55nrf7I+b9e837Zd6/Mm65bnKEW356pTZwWbH+EqINxg03JrcZYO81Frj9y0DUBbTPWtAsyLxlz7kSXLwijOqNuymUCG3mkoLUDGKiOWvnr/4yaefvH3z6u7mCyfvnpy9MUHB1FDNE0n76NNn4mMqP1+dPugZM520JW6qRuZvrMMFJRsrwizm/J5rCY1HlWh/84TPRGhalbvrve21/ZtLJwrdfPbpJz/57NO6vFvrn3786X/yp3+qW0Lz/+Evfvrk8YNz+7JaNWcMiLQ3eK28RqKnMsYEyExAhIZWbIkxmEvUcWMQWar5EhF95r8a4k/UO03JoUTrp8dnX3z2+b/4l39M26sFm05xOzv2/+hgz9gE2HGeubCy1bypzrxXzAJn3GKLboARAR44DMp2i6Ue45J7+mFve9u5bGcXx+YT79pxSJs4E+7NLlaV1Ly6muuXjx8dHu4fWGF/9PBhvjgQR55Bqoqy3rSWhsS2rR6JtuFvPF5dS5iXd5xfvvU6zPBbjRo+TqxJWC0mctWazvng4GdZes54PNdDuXM3bcmBG0kBg31ze88i0NO1i1vH383SGrMkLea/Xrt8++2vHjhV+2b34IFeJVZdXqoJDxzsbKaa49bIVOJZJaB/FlTcy/8d9r3fk/Q7v0PLErokGBgC3gNYwrsvYCp7jxNxBbjnCQzSkvMUQZ5SHCB5L9+8fPbxR/ZDsONI+i1Tq5mCiiVNI5VDEyxgbEaWGTVbzpcwAcwu/9io2JU6J+WWKRxtLaVvcE4k2mVMNz7SiTk5xYlBawpl8Bs5JsosufHB50mRfT0mSmDGl0S2an6Dzjl4e3wyIhINqBx5G7KHtdGW1ufiV2i58blpLIAEyrak62szDSbZk3MqUU8O5LT+VHgkZ6UGdkv/h/oV5eEDU9Qe5JRIoy421nB6KmMlG3NqCVHdlS4VYIaVZy1gYQhyX+L0dSifWO/eBqvYUtV+fxXzPvYqdCldgV0fxl1eB82FxvrTMMygLxQOGy1XHWxVfEWmVXr58uVf/PKXD44efvrxM8pQNKMfw4+gD9oeZNrL0IhhnCk2ztf+5jibZrMcF5xWregI+EJ1nTyT4bZrgBY21aKuyNJKmJ3fGSkND9U1gANewTnT1U53WGrT6XZoqNkLj27Dxap3E+yqC8mzZsVAXAo7TDOGR4l5oklE5TlEdcrQZ63IgoU4wXt3VVC+uOZpkE4qVg+BSX1lwmOUt6pDKRS9vN0XqfYNbulJceiWWl4dm6UDGRYVZXBDX5ZjeWcOwCQE40CWj+GX7KHqhf/p+1WqEhU7PFeQBufUsyglWBE20aadr22qHOKGfNTyhZ3ZFIUNyaVTQSZVPFzi+7igFuYxWEq/XeG/XNHy+y/hJX8X8/fHEjqx5ue3QA2CifGSHXTU0CL2Lq7bitAPYX+Q7wIvoVkIGTo9Fr58szB0CHOKpzh5wZfPq0jvsSsFo9B3flYXniJd9v0Ve9UAgYtRi0hOxNVtye7D+/JhCVmeV5n6+TEaydNQsEQrv6XsBE7WwtXMJHL+T9wFSndZFGuVeH4KngjL23xbIkxxJmeRgagbG+GQ+ibEE0fRR5wWmIvsZO7zClYq5JdhkvZfuDo5Y4yIcK72MB3mXUwGd++X9o8kc/JVOtGQy9yWNo2nTh0GK+1FDiz2yt2YKquTc7t3s6PJObv6M6k0zj5AkiUBGmdVmY6ZErPS/r7MQILlflW0agW+RZKm28Wzbj/1w32Go/kj03hNGW+wPvfsVzDVIJJ4o3d39y/v/gJWgKB4k76SLydmS5LqcoxcuN9umlQ6tTSTrI44ZKCl1dVG8pxpLw+u7g6m7nI1OSBsx94U3Iy3XP5EzpztO1uRtHM8j4hTyGhGayQ6f6AjAravHCto2NlBfea43PDKn6zfHa2tHd+5b5w4MNhmOTK6Ibcbu4xjWyPPCYOo0flXyqO/lrYaESjm28jJ+wMZsEjr4YMH/4P/4f+IGWRfNsW1uXXw2B55//rPrV5xHnwutIsvUb229S8wcv3i8+yIxBJ98NQaNbg7IksLRzlZTsckEbl7mBuVQYoyDeZrstCsK305BVrfsu+2UWAsUqrubLUMRkuib5wf6hzTJw+PZrmbTgJ7Yv3i/EpD/uTJE1iwJi8vTqZjqMhtf8mVbZYqfgNh+48LG+TLUaFrvG82fzVoxYakA07dXH6X3YgLX6E0VETqUj0zYRgxJk2dmGTCoWjxrL1tLq9e67Pt7JqjzCKxZVPjR2xQ8mzk5Pb6k5vLhxEOCMbEurLqtmDQ7+rdN0/+xUm7jVrpm2q+x7X4FSGu7x8cmKHx9NkT6ztZWp988tFX3z4y4nVyenJ9t2s+0jffvvzo8Wcd7DpAm/QDjJ8cQni7sd+Byhp+M3MzaE5P5RQaYwKpYuRcB1WTpSuuX8hQY7Rt7hzsQ+7s/NwUYJ7g09NjeDbYFnnbe7tHF5fnlBQDwPawItTbkIwgVmv0bEwCaS/wtE/N57Kjc7olNCuIuULk/ppPmNZJDnHOY18/iBHSIVD9o1pIWmN9eomX1xfffX/69OOPT07PptU9t9Bl58Hnf/O/81/f3PvZxiUevN3dfXxz9eri1M5NWw+2Hx+e/JOPzvaerf/p/vHG/s6f7t6en95+cWGf4Y2/crZ9enr5+RldsHaQPDtFqyzdKpZU2wo5KEJnL5KWc2DuSRkyK/+u4vd7N3uc39n7HKBKX5F80gd7lby/ijo5eFhxQMg9E5Ct//OxiRSb27/EcQO3zmo4fm3+T4tfT04s3rAR0nRaCGEi1NlYhw8OOtz3+O32+semPdkrZyYY3+1uq0feWjpsapjTr228yxEjkOCEAGqnwx1KWV/kNS0fQpVdRMBy6EnqeEsNaa7rSNHFm2/4H2Jg4xNqq4EJql1W1bOhDoBknlsDqnJSxzHFZkaoULJzxqq+62TmnnXeYmLqhJThBMmq8lcwygTBwLMYNQoOfrC0id8hFT54JoO4VwvhYV7AKdewd2GaJ7NQTMGn3SvysCxsnmSRebVuxLjooaUqOEG2l8nDE/PUrO5C5r6AnhiFzGtfo2W192BRV9eCoVhFufk0U05j0AwamaVJR0sAw5C6+ft///9p8dBnP/nkJz/9g1cvXx/s/sH1mV2CafLAZGANvdTXjO7PKgmOa6u5EK+2Xz9b29q/23oV8EFWEeNsnxBfegrEy9bd7nfr27/ZuPxZsq+cYk1c29892rBRskMSm5Wov8jit+NQJTzauzE3RcJ3Nae1kJrSVuK+Z2v4n8w0PCheXB1PfPM5OeHFMbiNkJxKlZdIDJJ4MwqlQcB5hZQ4AOppDOcmctGqeBW4gip5kuyNbr7+qXPCWz9IW219RUvm5hJDRrqwzUNi8I8DH8lJEFVHzMbzxCacDBEi2kiEgKWHA0S5Il+qqTgwh215T5R5YAzE4nwqJYidZAyhNIzpVvEX2X6gSr7vLj4rzu7XQE7VllvU2VkuE4Wa4lFdOxrrWngyHZcvtf5qHUt4MhnOJFCX9ikit78JwuqKOf+W6z6e3397zOVruX8AHGl7lcvG2ZI+YpmQ5VfRrKJOAX2QqoomxqQVvNjqJarSEaqJ6utEOxOGcQu0vn1wTUbzvsppQJTdKktIrJ4H7/uXhHIw6DbXe0j3Ib/nNyTug9+lXB66JzKrjBXvu7hoJWiVmu/T8CcDoTV9vhEp0e8h3/8GIH6srhRgkYanS/oiEKKBI5X/CewocLG8DtSBV96Lf7cCqurbX2MErQZ8WC56pQI0KBrg2nVmAUmndqsyzErYl3xAhIgnmpwOosc5xXUJGPjqRDmPjE9xQr2+QdMnBrLqmDu5RoEmZJ3jB8lWAUxV3XXwzSDADoxLUwthGF6jfOwIWa/EXPl8SjSgxM0f3dxkV5plrn3TLeHAMHYGN7aK+XkUSHXU8GAb2W/qOtS1SBPKjTDwZ+pkll2Mchsdxu1hzo9axQA2d4E1b0AiZtWjEOIIEwE6XZQg41q/5RJuNZM58BuknmXEyL5IMW1cNO9+03E2u+aXQ5bvFnAo6NzwqxnTTklZ7Fb/A9c5vZFsOjyNEbq+ph6myMLVYknbAOkh7OzvHz4wVdTmjXsHD9Ikazf723sbe5cqF0N3Dhz4XvFZ/E2nK0UKtZnCjaeYLpI6q0cmWAn5gzK24rmykhOmUF9yjw/JSDvFJT7JicQKaXkwr3d39+DU1uzj7pBQOFP66ur8xfMfDNZ/+tmnhgv0cHYPdkeo7AFxcbBjq/vOatUOJgZT0iPXmqg1c4W0hWab8u5CIHGdhQKSh8Jc9xUl7PpzhbeXdzGS2i4o2S9m7YE57efnJ8ru5Oz15c1T08fQ/fa1ruGuRk0Bvz1+fX1zpl9nkETX4/q2OX4DliAtwjkAl1vAY0gy7YLQPEHSCuBYOtl78D2zJhHiZrs8Pra71Mbp25ODo8NHjx47LI0sapB+eNWOQMcnrxyVrXphBAFO3IBSP/AfHHm0vNuPpqSy02oqVM/VIV2zBY96ijA38EXaGX+CVYT9/X2bMl6+ev1qoEpZZ94Sj87KExWE22vDSmsXxpRie0QsVCGzYqIUNFH6JMPrheEr6uPF8OP+fd5Wt1VJ9Em0oPaEsjEIUhyNgNnlyLDSn//5v3nx8vXLl8eb/3rj1Uvml/4M7l0/++Qv/fQX/94btfJmX4u8v8MqfXD15u3F3SvW5dr28e71myPzmNeu968c53a94yi6txf2i7QBvb7Mdnv75t4m/hSWqVPTBViYm8JOAaQMIOavS6h7L++QHo5M4Ls4Cz3KPq26cGv4U9TlGmFYQBQwtC+/KrkOmc4Vk1qBru1t7bbu+ea11TKbO4eH6w8WhqcTiX7GR2Vvh1jDf+mGEQrBZIbtY8GA73u7h/Lwkf/dzHJ4mLGsWBniBhYow4WIsebABS/iYYsAP4SJfsIoIwGtIMAqGopkmZ3Vg92obi2PMTvr8sSibYQAgXXJOYWNvuYxts0L78u1dejqu6pNu3EN2d652hyfKJaY1p1umm5ITEmXJYg+6P4ZePKCimfPnjkFZTClDGbyz+S4ICDdvA2ne/EXn3P/myXW2QUEvEoRncu3fqekK49e+ksm5211m5eBNgGLRKwSFDKPQwhEPkjpZRT3ZFUrmCqNOCVOkdInec8K5Jk4OX35/NWf/ulffPHFT7BZV5yb7LANLQFMvVSrq8stlpqCza9n1tD15h6Phl3Whp+ZzYN/Qzb+wQ7To1GOEOCN5qDRDNnLe90Bf3hFw1SptQ6yMI0Vt7XsxqNVOtuCbDgeVKVQ4yrf5q/qnjdknoEuhwSpqoQGxaednD2IFL3/C7vgAwmtR3zIs5iQlyj8SHQ4JDdxPsttwbrv4q+4O4XpdUphCV/4STK06QCMuVJ7NPZCSGnOEtn+LJQ2xTaWgygzvBy+utcRlK8E4NSopagrmioy5DBl5AEYNOZK7X+Y1gvuI5RX8uJxntzmUQwNZQq7MgaXIo5KAhAM8IOmISDg5dUk22FFdGLFIpr9oiaIHldZlemScZD7+O4q1ruX33lYgZnwkPmdCL8VsMRfwVxexID1JIVNFKzQS9AGybkPghNreZIslEO3p4WQmNFjoSAtkJd3VX6VcNm1NFDk8Ivu9o4ICNsPvy5KZrtD3yfKyDNg3JtKVX8CZL0N32oOcXgFNhAfXNy0ro2zD4KWx7Au0xX0JdBLpbRcC73Lc1SsZGYSFSpfBacKoHaBs8CLB6L/+LoX/GhLHOKQevI+9ygQ5t/CO4jIMKomdKEuAS+hSsqunDo1gAqSn4/vsO+tqlzCSaI+Zeu5Z17IjaCkvESc70stVgHAUK30osdQKHU1SOjYIz7Z7PDTMt/+tjqGMX2DuOeZBDnqqr71OudrR4CpqjIxr5SihmjM5G2vclN9ma8asujx3/sOJ32GD4u/RpF60wpu76rTkM/wyaiPsFBlaTcUg1Wcmts1bkjDpXzZpVVHvcTwsoSiPf5dD0mbyo8KLmpU3NztXNb1sCOQWHtTgkZyparnang8lWG6f6w/irM3j2L4zZN4vvZ0nskt+9/pATj5Q0MBF5+ArCnQHoTw1H0oyECUwZLK4pnmy/8Ny/r03L4/59ube9pomznyE1r1Z/LApl1tDg/XNgwvGKVwGDNL70Cbf7t2wqEDOrORLaj/ZhcOhwRvrT9Fc7of+vHapYjSyZFCPVlwTIuaKyWsqdl6BmlyvGcBKCNFgnsYvLu3Mx0AAJznAA5LDnZrnPh7+4c//PDqwdHR7s7h6fHpwcHh2enVwaEkB5dvT0EN4vUTazXOrYJ8c7K7b27Mw9PjzqaFRzJm/q9MZ0IkLerClzKJv73MVXFNoI89F7x8vRfi243z06tj50FvKuHNo8fPvjg9ean5tBJvJtzvkaCd3aOtjb2Lq7dsj+u7U5y8vW3UpfWJMSsG+FlyD405YfF287ygims4QAQ72boChISbj6jxq1eMxs21z01lvrn7HrC9/e2f/uzTb75/9ekXXz7/j783u+z1q2N2m3Zo0nUimk5yrU0qUR41VzX5Y98nLXLOjrAMwJvK5bvO+WQoA8MZiLi7e3j4wHk+vlrGCRoR1MNZv3tqN7+buzcGrPiNscoErXOHy1WBDKfrCyuhale9EJ7Yc8nntKkwGQTVz5CIOeMRp3rp5/tvbdzpjc3h6slajn6cBzlX/KzHR+47UsgiH9x+cPjgX/7Jvzo5vnn78nVGjkE2U/uvbnZ2fna3/hEWchRvbT690Ntft7+TCe6fnO0/eHn2N86uH+zs/d+2LjBvb+PuaGPzV1vrB4rElKArK04xxerhTaN1SfKwNHaNih6NWdM8wh+qLp9WT8t7VJoIkQzozKfZUpAuzCm6j9/2MzWqCDFt9ZUVV/JCl8tvSiFVtv+GcJokY3zGHH2SY/2JQjdtTrke2BP+AcNLYRDHJnyzeUzr15nLdNgiRSb3f8HIaWsjfLx27sTG0dHDN2/e7u3s1Acw/mP7Ra4HFfeK34MiZcPJnXqkZ6CohUE4bqjQq9HdXC3KOmOQz0L7yI7CNKpybW/XSgw9z9aiGJQlJYvow61STos5W12fxPInTqdbpxboesiPhTnK/2E9/7VXqirtnoKfiUbYQ4lzb3Mf1PfgRLk2DyzL7PDoweNHD20eMHYcJIuTCMbNWIyZZT38JVBIHtYjKz2S0m+LfWSyoZVKxFZQYaxijUXRi2uBsjx5dgV0VdA9T57Lbb5WilPoviwJCp6nioNk3Xy2dn26vv3/8Xlz46G4HrCaqCeHbeJ08c333+hWv3716o/+6C8r7CdPHl3dfjU0Nh9HHclSPH9qTbwWgB5P8Zq0e3mmFuNP7fXm87v2fa6AFrCTRZhjrNhT3PsazxtjbK00qw4TtsFeJrfNAjzafWVQVim0n4+FYpeaPtW7Tln7IvrBQG2BbgC0TDpqLAiNDdu2LGfhba3IurpAc9wcsCMIv+zg42mYFE3iToCgKQqv3rMHSNzTom1/XyblToVYR6QP8rVUob0Ex9/Yr3/ILehRJeIKiPw0GAbX3TAXDgoJeMEljyKuQlMa0oNXtrtQA8qKpoMuXzv2GtlrPVL5qXoZGnb3a11+4+LeTN0lxoDerF9EAzXVT/hvOA0A3tZ6dWyADPtgemMGSB2A/fC3RnmQVHiyjq+9i1mvQa0chAewxGCs9tUJ1ohcYb6M739i9DIfe/i9lyxcy32BvNyXkN9N8i7mEm1JizwW9Vy+x7csEzHWr34yhE5phsryzX2poUIgfr+7JjwSTImHDik9O3frPnRpOeZzObzDwPOSSOpCBwYQBc67/Pq0uiaSwn8fMmnuP//+3yWzhcsfxCiP+08F1xC4Rqj77U9FRG8kZQuXwH2RviFt0r+7LQCXe6Ak820A9QJIaYseW/qyvBKkAlIuXZPRxFkik+IJ9FVdTssGItiTcwj1ffJavgC7lJOqjO6lPVgApyBUMVlBJP0bQSvaU0Mr4Atk+YlAHaRw/NLupihqvNJYXgI/ANRVqBW7+LGMvLN1BqthXdNT1JpBufJj9BhHhvZqe4QockJhnp1LY/sDbvZSbM2iizmkcRuTMaD0Uxa2zo3xtWrzkJAKnnJG2hBYswEpHv2ozdURcj5mGyMnB/kULWSLslwVwJAxHKb+6oTg/AJ72LVElAA8/4teJdfVqc7TspXUUmfEx3Tvk2a0qimMi/dk2Sms+SB2w3ucYdZhazXwEDJxZm/9csdGBJuHjSLsHuczun2o0NJsMTS8tte2d/c3T6apoHLKZbwS09OUrSYfwXDHoljV4pD6UB3eO0FRCV8614C8zej1Qu7u3lRSI7Fa9Eg05+n0xBwGVp3d9AVqz+hi0MjC8x+ea5VtA22SwKy/cuTT9ddffXfwYPcLu+C05wLj4/Telp2mYhgyHMTtcBgGy6mXMlzxNr4lUxXB8tjXK/nrNZo8s7H269/88q/9pT96e3JsCTWrzX8TY8yUubnWJ6Gmd0zrQpmN22ogCGFgBtaU3eAQTFdZTN7u1UciVzlOvLBYfVPY2KsKCHjy7NkP33//9Okzzratzd32dH/+4sHDQ7w4vTj77sW32iR9cDGxKFIrv+BksJEpUBWmTHze1NXj/3ORTnfY9k/MqqaObjM3Mg0z94u0aZKvaqRQfGN0Azu+Pzut65TcWnp4w3SuxSt/FbSzLwMJGNI265xo6fraVTH0NCgMiyZ4Au7Dp5iW4IUx7gNzumpgoY5M6FUKNl731//a3/70s5/+yZ/863/0D/7hzfUxurjnNIDHx4fXF0dru69NdNnZ12tzLFRHcTv8c9uo3MNfXjw5tL5v48KeSvVhbq8f3K3tX95u672huKE97v+plCpzmPs/7oIpLlVD32Yha+5uC77hnkAtCXrzNNcihqvSrvYuclgylyJKFFbRvcTHeZdPulB80qK41KSxhRVhgzhMMPW9PJli+cyrprRpQDORrFfZqlvgharSLzs7UVOAHM22fXZxYTKb8tzfuVMFbStpIx1HARiqC2xDliGVa2T6kanxICnv5AomZbjSSJwahonGMuIKwO5t4wxm9mfLoKFxqlH50gALRqI6+txgl5UnpmUafRXEXbC5uWdhfXYh/WyoVuKeJbG8Wyk11RrNBnDhQDrfvDkOVkfmbZ2dnTYB6f6qMrgqP1o0VvV//nmdloZItSBtd28XGsVVPSxk6VqU3pIsiIKiOZbXcgWrcnGVLLAfXPNyHxbUAvqdy8s8Jxo9D5dEwU8IiaL90n+r5NP81al/82d/Yfb/xx99fHZ28Qd/8NPIMZ11t7MCRahYNVepQBJVqcT6xbi1ayohKnpRWqjvGpxDgtb2j5oY+3e2vsVY/UBTpmf1/zAAxMqm4Xrjlsb2z2ySWWettTdNzV1itat1CDD9tZ3TVC8jAGLELzh48GnhWTTMk58+hc7yRXBXtBcAw5Isz1MuxY914VVxsKBXsZefZE+ILbhZ6DMtLortOEsrHB0OwgUEYURT7w95LWSYnEZMDcnbgC1TwfbBW1f58vg32C0qwNq2TU0oA76DgAhQRv6md1H9gfLVdvpy2o7ek5eQK08pqPp6UW3VkDU/VQnE6FLonGcLcqGTNzNthaPTQfUpwRZTcSu4FenSruCXNK7F8eF6+bkE//9x/WemqmAW4B9EjRCYz335rhCHKG/hHhXLh0m7AClgIi2MGnrEXOJFoCuy8NudLK+C5gOo+kxfFVjNIgEGs6itWFGq1TXR4sWETE+lHN5HWGK+R2iV7se+/4n0O3GmBCa+7wtU6Efs8GIFid6aj+W6QiNCkFSS2NYZBWoTWhaWrXi3CNGPy3Goa9yDvvz1CqvyK8uBtwjV0u4UyyVocCrX0COAuvueh6E4MV9FDJ/lRzSVjSVtjKU6sP0NaY8QoLSwkvgMEklmkYyKpH+kn6rYp3DTSpQ2NZeyUt+cgcDsVk1kOVdFJ93l54Bc3X2Tb5m27/gSE/Kqry0iVraj05gsqrdyj00ZILVL+TfSoYx4vftCG2iTfU373dbtT9av7BBiWjT19WlE2+OfoGTua2Y7udD+ZLxD3hIKTWAAq8F+Rky0Zj429CDf7JytV1XJ64/Cr02sgQYS+2IKDMql9lmhRiggcXsyrJg879qdZubq1VaJjDtRsXb107JGgOzzFZVj4UUJzJRVChjgMLz5osM17/6kKFmG5sXuOcC1uYaltSKMztpqAvD6C/sJ3V4Z59262X5+tWli0IOr9d2acidgWb67u9NBY1Ps4T0VabKesNoarGU7rv/w/Lvj01OduPo+9vHkXWwGSE1pZFQeBo4veDqcc4gynxCT+XjHofX6+69v93YOXr5485Offmnk4uLcesXLRw/vtvf3pDb/gSPvbvc1JW/FRZtP3O1enCkCwsfLe2DlGVYkArF5UejxLx5BcbmGXYmg0hXeqNfwLiZOiSTJmGz1iBGJHZ2SP/4X//rlt2+bfXG9cXz+wt4mRLZppzeb5yd6KFZlXOxsfLmlmZR13Zkpx/synYKRt1Y9j4XfKc752ThbirDPq0RLQEXPY7p+zqD9jSnsZdiO3Hcff/r0+YtXlkzs7xw6qff47enX33z/0dPHtn7MfK8L2vqcaheyhzZssmxSw6E10bhntSVUGU4Zhyv7BmqZHOof7761sOrI8es3zlI6PX57eZHvcG3jBZeZsaz9ff5ykFC024HOFq9sNcNEl3ft+st22trJrw9eVCkUlY66iDvqKtmL/eNJ9TsFlIRjPstvVQhTVmrT7AU0LImtRcc3lLW8XQF5P794qcP4d/7u37i4fPX3/x//SJtZNptrO/v/5KmNU88f327+682zv7Vx+Odb9vva+1dPz//qwdo/fvzmi4P1f7p50VTxTaf86cOsHW/ZfeXujAKw5MSMmAYXt0kypDXkRAs7s01hOuiVuwlcYdXpLsRpyBniiuWPAXR/9Vrg+9+pponmkg6c4PpzBrBYMz7gNZlJmyylZkjRqh2m6s7FOeFhaisFVQwmNseEpzUbtpExLS09FIJ03cYmfy3ABWgLT6krnXHF3Sf56UySNdZ/St1hb2qqBSEWGdenBXuAM8LHzhgY6bQKFHIczEtPKZVL9gyBnvQpc3PiIoE/gHk6VZ1QrOzS6Gps4fbqEVhzzol+poVQFDzkjEwatKwrpwMajyoIBzMDaoQTTnET6XL133gII0t+R0eHu51iZjDBFkK+5O1BeuonpKkOgtkSz97AWLoz1x/rNmxuvaGMHj5+eHF+vrW7Yz6YarRIZNTKL6FPS0xBrUquV/+nmJYyDLMpybl5jg8Fvb9AWOIMVDEWZLBs59utu4ujw2YZaBYxA4sr/WDQrJt/8as/f/HDq2cff/Lv/e2/IzHuW/AgrjghO6AQvnPwAsicP6p8Zxdie/avdo2Q1Fnw1uOs3h0rHWEzTEv+1VawvG8+3v757u0f3K3bDqEswmoa3Y3N06OHG3uvHtjrTv1uRztHYcoF8La2W+zWpGdj41zuapgJhus3uhM43gDb4OyOLDV6aVvP5CkkavOkEO7RY3i1sHekgCDENchUNxpbG2kYxVY5CzFmGMXxOyl0DSJ2SZgxq8APxwaANNPUppyEU7Plp3TTJfEkWyMLItXAKZjvAWLh5OsOW6voYZguJdCkGjJeR3nobGd4XBA9WlUaDGQRJZwUC2ZufC1eM+YSLRbDzP5RaSxIgMHmVzg4KIGaQCaTeKb9qh3HpLImt/cEL5THmER3xQAfu4qD+GHbEvKfcf/RbJdhZDCWK9jvnj98KZPhYWUbI1wyjTe9rE4MKLRSxY+M8yVOaH9wvUNVOjEWTr+L4WHC1fF7kvrWX4BX4JeAXpeEy335qvwq4j5+cC0cEv+3P3wQ50ePYbGK62eyvv++vIgwMjrSJM9QmS+l8r4qqQkkQ4n+EmFSFafoJSrB8GIJDO7EXN3fIVK8JdUKHwWxCPCE99WVvJFDX3QpfZ4avswJdIeDGEEWPkVVeeJtVa0Qu29qgWgRu3Lk+qvfTKhzxzI5gCXldSdYfZKwYWpn01mAcRds57wKvoibZqniAquEKC/aOVpCiQZMys3MpQzyhAyWqYyJNxhV4FIXrzKFRVW5sPlNK7WhsMYq3ufODLNcSv4VH+Z4LndO8tqzcumrKFOLbJXRPOAoGuJXBV5t1m2hkSIDC6SafnxcbwKA2RC++AaVwUuw+l+hC0Sg997SQdKkcgbxnsV0C1JcKv1kHoRioqyUQS+GhKPr43ARBu10/Bi5MN+2Y7jZPAb1t8x9Ot/dWd/aMcj+VjlS4BcWMNsAZOPh5frumcUBG3vXTu3lBjVDxSqObHogpy0NUQgsqM2TnoYluQYVzL7ZzX2I0zz54Rc5OQKvrizya8OR9Yu2Cz3nRLdCEdXcQ3YdgV+b/adq6U3D1QasnSnFCD49OyNN2x1Wyimu2DWHtKSouzZ4tAC37lw58UJ5aO5SQpKxMuXYt+Fht/iSpyquDeemBOKit3AdqjIazF1mmtxYsWB/FDMNIGNfUl9i+8hTOxWyWR2QdOe0MlueC4Y8+Au4CA/s5CPRHXQRBgABAABJREFUqkRCYgkKl/tIie2o8yV+kJoLcaV/pkIhqtGrdk6ydm9357vvX0jgsu/NP/iP/sF//d//rzw8OOTTItLNp+IRUexLLiEQkVvMKF6mTFUVk5A0CC8+YrQoMxjdYL320axiXJbaNuqnr0yRsW6DI7ZGFyT9YgVFiK4tnzFJbANiSkEFNyFHTbeTr8XucdLSEw7pKr0sq4auYX9EC1ton+D3t2Asn4ZH7xlUAmxPV1E4KmiFKGub9OmtOfuQjklzVP0J6+3js4PP/uzr/fOd7UPnEF3cHlxenhjMuPpy7fanByy91zvn60c2z0G7bpF/twfbCvlyj527b2pXo357VwYxmJuZRSPKo4oyE8KrIa6pf1Pk8/R7aVrodC/+1Jsh7Ud03lfjJVIMSCKXlFHb03Ag5QcVc/k2T09HeDMQ9f1Etnmr4brYNKagIaz4nsmi3pJScsm6Nh3PoluHsA68dto55D8W4fHTx2OU3FksVJNcVy31x5SPrRAY+3K66+SnMT01kaGiuhGhuiEpdMZ3M/EVe911EC0n2zRExklkiohqu8o4Gm8d4FV9F+3CMmxCvm3DouLyqfBrz8Y1otRkyLy2oCVDTazIcTSavFw3N06OT2s71jb2DvZ/9rOf6iEPxvRJZQaH9Az7azWhqwcjjVQ9ppmqYXMIS+31gz774jOaqGUWtVIjfkspVGapkpiLqzLP8CqTpcxErmTmelfz+hTjxFvQ8bn3YkX4PPbJs9vkkXN6+6NnH5UT/salYtLutN+b4zdv35wdn7y1WdKDo78btxC/mvFYRbvHoaREJaYZ2G0+lmz0cHZsP82ZrTHbUcrXpocZrp8aWvM47SMoZa2y8bWtv/z+h//w//Ef/L3/yn95UZrpatwvI9rZBMgzzGLTGV+nYxgF2cwzMxaP8Jv0LV1RQ0PV23gBeOJB5IY35SZPDKz1RGd+CqXWG8r9J8RxLHYThlSJJEjzWki1camDvpDM5Yrhk1+UV2K1DqOaB1jMrntBMBKwiT04NN0piRkWTNe6OofHpBnaSaeEM0lfIwR403FLWbZTayOYH6bN6Xwt++l5ZVRYXigy4hMWWOe59q9qEWULwBTMXKEtlnrhtfgJQk9yC3MRY6dygxX0yn5FS1n49KNLfqv3+98fff7/82UFK/L9vc9jXkLp/pqIMTpWTTzkhOdSoEVbMJ6IqOkaovuyvE265XvEeooltW5LnPm0QqQg3yZl9+XbKvu4XgSh7z55m2f4yba3pRw8fxinLx9eCxyQBuaHFL8Tt6UoMp6mVBaAFd7IzarM/Mjn/qXi7upsuYUMCPevaK6+LuIwr57rVzXuUYRJvYAHxxs96OOEawnYMStcwMtSL35/dF8mbiD9gfkFz+HdsmN6CIWdq6guc+zGKqAqr06ekvSNra99mCUqI9UcNxnVsuuqLzAsjc6BFc+Ifu48zYNRXW4nSqGMqK3MOK3V9styvLO+s7JCCFmngkUg/zYgGcgwy8+Yj9nWBNiwydpFiHompHKkRrnNWjCQla7Futncfr5hl+pOJ7QrwKvw5znLEK1pt8lO2sSjFxpg2nvVrsrKaKjidsXk1gkK0lg6DPHZ1P5hVr5YemQ8UJdfyrfZbxERzoN3oIUDgvdT7y0k/lKVHmKDLaY4lWjpl2B3eeFTeY82SIO7ilQSoZxl39xt2+ugdVqHm0cOknz44DG3P6sOj7ctk3t4dPzPP+4Esu3j8/XdtxvbLO5rI/DrO1ZJMn2sf6zZRC0dR3yCPh6+yax6KyT9Dg8LoG8ODneOHh7Y4chiAzv38wu1XSZjjMmeH6vpyM5muH59NiyAOdtr2qehBRdeH//61Gbkb/c//lhHZY+rhTSY7X1yfHf0kGNZW8VDPRqjPb5tQHGoxbCvIYPVMQNZAjBvxnzzh1g58WF4mFBBO1xzbsX+S/NE9dG+Cv2FfZGqGaummF5vUxSLizthaOfR+saBDgDr+vLl6xYi6w3NGhISv7lz8fjJ4e7+xds3b9fWfpKoLnoj6AvcMp5CXspsimq5pZfkXi36IBSniah6urZ/uJcxtbZjI07IE9vLk3NttjOADvf23r59baOgb77+4X/zv/nf/eGXf/C3/vbfevb4KQMPB5LfkQY516SSQm0+ufK5PmFbR2V+1bo0m4K7qU6B2TEd5bW+t/fYYnQSffLqO6eB7e7D8IIf2Vk8a+t8k0YbdAzJ5We314/tNJUEkw0Cuv2tnf/1ME0KBzm/P+2Q5oNGlxzvSV1+f/deDJz6rXgTiF8EoE/0SptrtTzmpKMNbt+cnkNDV4QRGrs/Pnz58/W/8fDg/7ulQ7j1D/SLzjd/9ertm58e/OaT17db19zgljsr1CamYdft5tnF3eXW5qnqr7OMU7PKSNOya1cBRq1cmbUVZFW1LIaelFtCVchCYsHL1afVY/T0POk/YAK2fRY9cy77Ku7qjPaa+VKsQPTmT1VSXrOxp3JsIA992cdZtHs7e4ahisl0JsWDrtq3+fkXn4ignKkOax7aPvzuhM9bT5vdTGLJxcWpWT+7OkkmSTkL/Ppsd33TuShVurBX1ae2Qih3CessVgCYfaQ7kFmcujMSqGwIgz7/zf7emjl99mmyBli64jvNgyDeNKc5mUHg5pksVTHaO/1PX+jTqeAWIV/Zpfhupy1KM3dqxPgMGksIH1fvuh+k89Ip4HdUwfnxOYMMYyQMsaKFMhpt7IBNyvfk1OQ9878evX1zvL75VlOzvX1ys0HtWc0PcP6syzOnRFXetR6D+UooyxTjZzDaKurGmXV19VUgF0lZZsUJQa8iiBzYSBVCWX4WH5SysDRAH0RwlbDhLUPcwsXSpC17PNSMffXrX/2//+F/pLdmiO1g72izs6smq8FT/NSdnKfDANpgUrdMwUw7aHDv/PKMV8FWZttXF1cOb2x/DmqzYyJyHJAZ6YITXTv04f/yf/5/+KOf/8nf/S//l0dN0f/iJMkaYWWuzU3jWTniREkaA9HcCHHAhP4QShe2/Sh4hhCVol3vZgBqnH+Rn1jBmHWeOIfDdEigXED8yNkjl+wSgFDcffXrM87EwYka07qG/30onjD9FjvFEfKA7H5lLwq769i+TN8Ya0qRXUGEjDlnzVce7Ydehbnb+dp5L2sXPy9ccVhqYoVLfgd2vcRiSh9y8o0WtY+PxHKqmqMwN5gNgdtb568XJ/bGZ8CNWU0Ayulj/VEG2HQF8E41IFpxoxY4fafChkD+msl1YcKI+jpFuII0LIBE0lWYv/kyv4UPT3pbYgzHFq98uwP9+PrxbJf5tgBc+CzgHsjtQc+zYw/mTbbzaTUnZSCXNIEoZrzstZ9LtmvnceFIeAvHHUFdq98pxlEhS3CxildU6nueelui3z8ETrzlviRcoiR4Uxh+RP7wEj7xg3Z/BXXJbbkv4avnd6iWkXgfpIPWKpKfpWZGYJmG9iplGC5UF6v8SVViG1UhusK/hEUo+P317rXAeRnGvoswnAI/7WfNflUgGV0Qi63lkaGc5I29S1SrftQKlFdXUJaaBrCwSTVVJRDBHDyT/2qz8mvbdDU/M1z8FtJqSer+VteQn7ehLvHWjhWqa46paus3Qg8b1tyeBY9zXn3VDH6jCusQUC3VJQvaKBcVlgBBbLVL1yJdal2dBGZgo9ae6eZ+/fGMWvyrRYzkBpilHaitLKs6Tw6lSIVFKiZob/NX4EnI9F6J4EBVVYW0MChwcX+YPeWVfDcBKL2pZNKqfXTNrbIE6b4oi9G3bvM37mAID8QyA0iSfqXqQ2lBXEAEs3Q+okMdWyKvXZ1Zu6lTt/Xxp5988tnHdP/Rg6MHD/a1cOzZ2892L3/NY7x3trVzvnN9vnV7aXt5h5xpM6BtiZ3bSCJwwM5cCDkrr1W21NPkxVqFU7v0WGBsSxblFW9Ch8RVvnpe+Sm5Vfc4YG/ONUWm2NLsiyityLllw9hkxnaEugq2oicjFl8dHFkI1ZwMSAzzCbPx+Z27m3N2xsW5AQd58USS8MCRNW2oTGNamMUY790KhvPqNRTjZ9GmSiy+TDxMMgG3JcjubirLsIY5Ajt7m3evG86ytyY881809Wnz7LRBj7RbRRQvFgaVZ9dkfp/pByEkRt7DziWUUAmJhJjDSXl5bACEgZLqJ6kMWcsAjg4f2q9l+8Urk1K0Gva4+uWvfvXZ55988vFHm7e63SCYPKBTjbYEF8AayoxCnSI85M4DTnBtCcj184cL5raS6P2jXevBHQB2+OChgrLSWhnOkR3MT2V7bTnB5cySshBXSaho4EASodUdLJ7F37IfyofGiti1YsU8/9atCKvPg/H715DsbcTeg97/Dk2RWmDzp192rq/MjFcY6vyWrSjPrn+5vvGHlbTCQ6yDDLY2H+5sHtycH7ap7Y6VkvoBltPRem39s7Z70RHbj4zZXVB+up6m7ur2595OhPo3NcsPJMNzeQox14L48rL6sKL+R18DNSwP+77cUzzPq/cVyElf8SWa8b3Ykwo5w04Qck5O33hjdz8rIBYVp6qgVBSzXYCyae1s1Jwvc9xVz3PeYGwzfqW07NIDnO1lVPDLS2dpPbbS1Dw9w2D6enU8V9Z/ukVdgw6eWE6QpS6jVLmxv81cPXBk+elPOm3Q/Ljrtni+auNRHzIrFVZlOWY1Lg85RA+2Rtwa3IO5wcOLK+Onlvg/sBWy+AgSU1nIpQkkOXuq7VnqV1dvjo8h4+Dhj7/86NHBA8OHTCVKXjcVx/AqfkQG8FaCXZvo35JYy6YNWOxuO4l8e5u9ZVdbMTCUkXet6tE8ETYgomtKJTQqji7HJjRcvLb+SPqJWD6ronlXhr5PmU+SieVJYHGLPuHLr+cBH6qywVkUL8pEI2RW5Ldff/vo8WNjg//1/8a/33JVdXpxZo3TKnkZUQ8FAoyvaXLtoFEsbVc7yNXpp3+vL7cPrfreNZFMrYGIRjOHi4HcdOngNjzX598/MNPvytS+4A2+8dPUvk6YwDA9Aca9ebZ2lW3pTxLZCoMcDHp0XA7gsV0NyeZfRG9tJetZBwJIv9MGD1PiBgArOU/sqUK3MqTVlWRS0HO8E3kw7aHnIXiCl1cfu1Rl5X25nJWxtm0WUoaN0/Q6aIVIeE00HGKeIA70hjV81PrB79qGx1rFeHijq3lJ3u17LtMxTUSEX5QgbXKkTEyCwKqENIYo7CYU1tiJMijHyokuLe6JkOYUUTPnw/hBYVLCoAgskymAFX/KXimTAWU3dIaFPONOXFzgLwx4l+0HXOvL4Lsk/ne9r9Cf6LJYriWzXheII9/3wCuWCtE33PQ3L1NchYZwMSrTsB707wG/g3cPbD4sOKyykkIHIBZMRV+RXrywmqv4k6YkS+69v8d2sglp89ohtPSEVkkmYpGjYBIPqJIM3wXbQag3AvQucgkmyepGrfWe3IrEcEm0KqhJMqXlMYuZQChF1d/3JfF7rtyrIcnur/scZ933vMTAWCnG8kdwEj0yTYOXZ4Zs56Hi3DditzxFoEnNOZXkUTbEfd15wItoBYcBJ7xL5EnlB54A8qB/JwrqgjMKhQyXe0XSv662cVTT9LPh0yV5xjoH83h1KFMRRueSeA/mM7QJO+tEHAE+k/dmgJtTPs2OCeXgtAihgfDJiyZq1zOnX52zlsY0qUZJvmcmg5WLdoeIs3c7e/xeW3ZRU++8VzRm3G2ZCkC1tY41X2mrfVCd/ZqIxh7lqDE5997IXlGVWiwxPQOMNEHFh9Wax2mBxKl0pnVcJCB2gNZN4ebhKB248WxuvgE+BSHg3TX1pLKNVlLnx44Z1ZxSBq8cF8jScxxAEx0HdtLZ272xbbu9tstm/ejBs+snn7/atOzh4njj7mxjHyO0wG1k2hQSoIyN0CgpLljz20zDDqUGQ5OlybOnslaqPL5X52fH11dnd9dPLLZ++qg2plksNgPZd1zlJT/6p/uffP/8hQ9XJmbI5PYR4bxdf6PtOTs9ff7i+dPHTywIfrj9gAwQCZr79tZIjbk35KaVi7WJt4dba487aAbGmqBphiELmXAxmRtHEYlPyWxM7c+t3wmavWXu2meGuPxmUhYuDjDaXzRqOAgSQ3r/wfrZK37hTCjMlSX7ib+SiWQPT5usOwxgf+9hHcvUdyjIPmDdVy8Lau8CVgW2IDd4JwuTblDEtFyd9uFpq/aOAdDZ5eXdevhI3/iONWAgv+MpHdazsa/xPtg/YLddnDn0bYslVqvakUmxIcNn5q9pm6uYU/dgWuGOMOjHTLVVy3jKiOIOHrLadg+3/5v//f/2N999/3/9v/9fbKsFiqQNozXnhy/qpZoWlbbLt2JzSxvaCfad/jkU4eTymyRG2jvOxIZe3l/eRPjwAuNdyD0nh6eMArMO7i4/Uq9snkuGbtdObQrR/BOqAN9y9X2xdveHt5v/iR6/1QXVJQbx7R4PwObdo7vNP29hxO3Duw37AptTYpPZNxvbTj/43kS/u/XPFYUhgqttPrpt8+Akukdvqs9C1lJ293St3kbYfvz826QPV+6jfOj7H+oXRqw4lUC8Y0IlSY9lWkCvbgn7vT1zzy5OOYZP3pxu333aONxH3Lr16ZzVRFQVGuNY6WzdPrKNEy+QBuv69gQlZBu1O7udxf7gCf3/dmf3I+c+36z9sLH9oAl1rZ9iguEfPGQ+yk3NrDApZP1emti8rwYc9ve3Pv74qdkz5xfn5uydHp9cOH48A84ZiZQchp6v3xlBatJSShKPo043IJr0WHQWMNpURHsCCdONn2qma4Gi9FwIVK9TRyCAc3Zx9cPz56ojfjx78vEunU7aMy55Zp5Is7H3ZvgaxhoOeorlDN7mzkvSI0De5tUcOTrs88f0FaVk16Q6NeqB/4uyVRBoFnD5Sc2PfnJDMSfMW7VL18FmvlqpWyaun3UjokgbAZ/bh2LdnPWoTmtO4Y5ELbE9Lqn6gnY2d100ZGq2Pv30J0AfHh46jpC2rJXbcq48F4k6ODptBbAauSIZEwXidscsGEsxaN7mubvbOx89/chYghPYzZ7a3tNPa39QO8OW6Vir0mkcLRK76pBDfcdaqTiSmqJI7nb2tSYPbq6MxCoty7Re+96mrlkKNZhwwr+WfyU4xEgJU9XxMUcNKVP2jNcxcaefGRVdKRmZ+DMpt1EyhF+vfYWphAYSw0DxfJvXacKLvmJ69A8nhxFKLqU97kWSc/EZDQWR2lJZwVVrAev2ihS0TFSbjFAg0vUX69fOTBBBLZh5+SpOHRm06f419qXnXO5pGUPWX7R/2P43ZurlnW9bAuiMb9W0S5wAqSLCCNoo3GpjMzCyN3SaMiJyoBlfypIQAZ6QlMPSvvd2Nz5/OdcFGDIFxp2uCHPFkMVigftMlsgf/86+nTjL7Xd9/x98/J3HBfq7YLng79m7dzm4JnSxfHyfoAUv5KCloMgq5o61XsXI5gzpeVzB6KcL5liy5RyVFbQVErfWqxkBWLFA0vk3H2NtWZZH8P3Gzt7ur4DN88RZQifVKsJ7Rq6SfRCvtFPmq0j3MH/0W/z3RvRIYqU4ZVXW/iPLtZBdbP9hmQaJ1sG+zMtuIcXzvAh09e33XJM0rpQdeIRE45ELNthdwZinEPCaQibxBZW4a4CsMFpKSOCSejDEU/9TlNWj8XXHZnVt+B23FxCFRqTezaQPxlAzaUFRdcTwUGfXN86jUgc5LTIDioBVCURVe1kyZjWYY1xnYEF0odTXSVaWIRlnBXh16UIwaww1QIajqK04Val2llFIkCs/2na6HsydzCOV0Nf62DYIFmmgxrC4BjMa2Dbs0md0GdmVk0o//peUWD7KELtvuBYRHPpDaZYBLTyJU3MtD0ONW5FwTn79H372e19I81AMAavnPpZKU9SRoJumYnP8H+7t7pjMwMVuKhSTkiFw7qytB7A9cIDx+aa2F5KmEIQE4iarEJis1EyaEhf8H+j4Co1UFL5RQywSbe/e+WmbinjWup+fnYLkO8MUL/f3dk9PzizXMwf14PDw5JzRySslB8kx0ivLwDzg3B+J493d4dEh315MHnuAdkx/prFrXjR8xlqtSbUJpNHtTOQGcpYOSRwYxq3oGaRDeORCpgnGKEyPTO0wdY+VvJGZNVIYZDejhSlzaibzTraUNNorXuFmQ6W417Ye2h0IYrWyU4sIUbnIfuHeIBDXPCxle/9TYNdguohWyaKwwHhjGUSCy11NLvUpnYewtn/04Omb4+/xOf/sqqe99p/82Z8+fvzo5Pjs6dOnCou8RmKMTICVkfYGbRUbyDV70zAl9CjX9viQ/J+dveHfV7P0eKwKfvzw6V/8m692TC5vSIjxtG7m8cVZCy4313Tizsz32D7c39zcz7/IE1mfbJPpoDQW0U9mEqbh/NC7cOIdXyI5lv3ogvH7d1zpexI3gOBfi0teyHhjL3cHaw721abWKdfq2pT8N7dbX6Mn+2IIs7Hpld0RN85Mid+40VWIydpZcz/AVgvuALl5oF9Q9y+DwBx6bMsXOxhCIv4MHRPgud/75xW6H6C9ChFhqFnEYRVY2H/aNQkGcEQvb8VWdrFAQfKsOuEhiafNGuphxD969PTu+ilT4+amxZSW9jIr6jRfNqeFOE0F1p98e7d2SgDGMbzBuYupypdrnKw4+2L/0LkhdjCUE/tmhFFd9BAyaWMSM2gBsEuTML517E08M3j38MFDi4109Rn+J29PLs6tk2GousahTihZSMymoYnvMjM940t4XVBlqlvbaQx2+rneNKKTAOfjNMsr9aNdCJNwCSeovH37hn+3ToitBSCvMkKZYg5JpZcaEZeQgHV6aqGzSa38PuqRwwf0Kyh7fiLKCzDyYxCTg7zKL2d8YxmnvEMkJQWmnQkwTS9DzxBw8rFzeAAstAI+6A2npni9D+cqR5gM3Pna81yLTprXiTw8L/sJqpai7z/8f/79rV1ngRwwFP/SH/1cb5/VqlTrm3KJpXvKuLQDxGPP/eWbacJszNi+dFq2sZaNq7Ozt7xA+FlrSEqaN2sxmLZifCqDotK5uDxxNLjyadZf12j7hMDk//Wz0zc8bZfXJ9c3lnCkr7A9FU2Zq54VERXK9+DBojUNaI4DRj/k/KsAJzbcsK6iIuBqIGQddmEiZ5MIjA2JmPymzOpWwGT89mKLKvI8oBt+Xgd2PxVcXz1L5X8viVxSly9JDSpJWlHxh5RLi9NEiYWBMaYODbpWsKsBvcOe2kwkyh7ksqu65bNfBFDhgJKyBRPm03am54cQH+s4oJt4xR5mBulnPJmHq39ANn0KZ/HxJPSGgoUdlQEKMDb6FqrnYfU4OIVXfyIssYI3l9f//64B99tJF1l9H4oZk6HI5T5aAw4rEqZIBPqqYOrETLwioG3h8xJS8q7KcOAs93mdDwvFfDxETAP1pe95W0uN8DIo2rKW2ca3gVlB7mepkjN7Xirlapb28JyiZV/ktV03eztBrRElg+61Z90BuMfj3V6nEy72ZL3EEXFy7QRcxC2fQmpBJj4VW2kGjQeLjM9DFCVbE3XuWDPIC1yIuNQrMvQOz+V9glfMfJc0LJcWEHhwknEB5ogP/JFFkz5Ycpbx6edatF6rN3ZDkQfDOBUqUBXSVYpQk7NKW03TV3bOnMOsfs0qQtBYFXIePk3ty6YRPFmOpxUe6lXqedCVr2slBKGJLxefCdnc/V4dMat8Y32vY7rZ3A56bF7zZbM9SrECpSFRp0x2ql1BCUc+rVHtr9ZCt5ghNYPf8WqUfmMf4SIOL6Z87do+u3sa77N3detTG4xE8t1jnLnb+CaOxxqgzJW83dz5Zn3bOuZPYur2921qcP25r8EXUsmExaJkpBzTU/Lhi30zIpVvbLmkCLzb5OABvkJWlaNcA3ERL5eRnM4TnTyWUlIyV585TYvJF7JrOw8fPjSR5vjsBPIZkp1lRSJfvtn4YW39s5NtS2jz0TGmUjot7w7Fhb6RWhgInA5kzBshC51FPEC0KPd298Huz37xs++//87WMWbwbm092dre42VrvajS05biFL+iKZhrxyVt13BMUfpy9Xj1/PlLEwb+6Be/MMbKbfn8hxcff/TMulIM1IWI85W+jN/c3r1Yv3tMYk37J65cUlBWxhqXZCgGVanWrWPx5kzEeB8Ph/OBENks5yL6kkQnqcXRuG1t2jJpd2/z6lT7dmVn8Y31B8SvWTSGy/BwFIS52yaSblvuLLVuC34sslg+Fd/8uH94zbfKanV1ZrO4avEUK1BwW4oeW5Uvw21r81f5+kvKgLt4+PTgq28MHJPhbdu+XOe1Wjs7PfvhhxcHe6a6WIFWJ6pmllFS00og7LC0fX7GELAgoG+yyWiJ9jBp+OL62cadfhS/lOMb35D53bb34T9GLyutSo0rBv73LBexW6Jz+Xb3nTGlSymrcfau6Saxn5Qz9iv1IQXeI+fQl+u11Rf0z7cL/WW+SHksmRLqQwxa+KGgINm94OrhjJE6FPAH1iJ5rURJrumnuq9tcKo9Z658eXX98e0mQzIxwDeHUtksPgckz9zdm+HPpSnrenodesBfvs7QuaACGsFfcx4emxHaltXKOeMmmenf4DeUDeLvMF3h2+cV7vchQ1YERONQ0O/vuZYoixAOwSAlDoWzAqKk5IzduvGs2KQ4W+T7X93++k9/c7H2D589ffZ3Pvp7rBzbwI8mb0QrG33XKvbnjLHr28d2/7fzJ8UorT1zGOesjgtn7p0ZVsKcrauLS8cGMrtHyQ/JSFD7Fj00GxA0fdzO7btf8qTc3P7QvOcWFBj2JJYbZ8d7t1eHV2snSnLTvr6q/92lLgmFJKM4ifrxjtR0MHdmXg8+q2LN3xuJ3dllZT++uVS1X4me2Za8xkRVHf5mlhyfmsRiKGPzk2efPHvykaZEczHydrex/TrBgXapuhuwI0DT66CHFH07IDWCZsOv7X2rIeDGYoUrE198KqjVLChqXIG/hPH/59cWojTeoDzsAQU0ME6PyPe/mtUdddG3usJ3Cn71vvp0HwOg+8f5dUtlrarA7c7WPmT+yT/8FYyfPNn48ic/j14T62MItQcVKUpZz3URGixaSUoIVnAQMCymM2hlhpH1M/OyLHowD+rUoQfOXGeAg8DdkBV78Ux9WevUCCxCXhwfswR3G0/2bIKVXpMeEk9cDnX7fm6cjphGq1M3kUC6DA02qAxVckp8FO+4u8dZllLAWiNxmnMT5zXbCqUlJM2HAdqABT+Lcqz1zwFHHNPzjPXYE1ruw133lY6Im4odK9I+ZHdYkuWzvDZ4UXMuWrIwvBZdhvWW2x61I+bhKXDEVD74bWuTpqHWNcQh/HSBYN4Ej/qiB8qXrbD3Q42SGaw5EFnotU0AOTW8ziKWkPu8XbJetHQiSmbZMwZX4ZGVQQTr+tGqn+LRhlGjEnetcV4Qj40mMsDBqps7I5mUm2HMQA+dsQOapvbBUSc8VoR4tqJIjcIt8/V7/U+/pBm+ieF3eXP/rWuJ8jtfi9g+lu7tYzmJwh9bXUv0fvuCocuFoGR1su2MBa9bv0Fnq1tXMYI3MSbg5qn3BqYLk+z+3yrWQK+oRgoCdH+VegKXrxXesHNCfVy03n3s3/c7+c/t3dfBayFpSOzD/WvwoSGjFTIRKcGkiSk0GvxIFW4MAupznehVFn364PldngPmHRoLtOUuyiqLJMx/invhwGjSPse34kx6lbTF7zCST1qvpykc8SbGkoT8BrkflVxqEs6gUI/VT29yV8pSBGUoAhA8mfnfxx5dEk2w+/LbB6JfWZirIPtiB6jPVTxjwfSu6uVNI+8KL54kMUKpN3FLWrLgheoKSr/li2a1Ri3Xc4RF2rb4nkUYB9WUVMgORLTFIQpIOPjTlQ9qH3QMqDBzqix2Ddn7UtaMDNYBDRVElcs7lMqrv677354H23c/JZ6vg9tgI/rAlFPf0lIL/Jhe3IHQ10Y2DREfHTn2yyKt1BiXj60jNHCXV2c3cG5QeCstS/uld1e73AzMEAtMV8LZr5uGaEG4gBgFC5LAuqf3Dg4e3N78oJ28ODmzNc3N7iU9OOl4jrfXTjcsVNTGf/mTL427PP/hhyjKmJ7m/I4Ve/qX//JfMrnWhF7DBZaCvHzx0qZ41i4XiyOkJdcRTF831UefJMel0XCtERwHyRBNKkdEE71x6OA8YR2JqBz6Q3IlGxJzhcw82yreqribdXNv1tvK/HqHhCte872ylqqW9Vt0SoM0SXAqp3rcqQT8TPAK8hJY5PcB909h4HmVogozIeJ69leHBrmrNmx7++CTj774V2t/OijU27Fwl2VzfPr29Pz44dFnzG+hsscBEpjUTfVnxGhUJ6OpeoP7xBquzRiLKTwmlW23GLjYDKC4Z8a8aTUNRWiltFWLirg7PNz+5NOn3JB4qt1iKtXKw/P2rsMclr73IvJxLt7Gw4UFQ3MELggt3ELSij+KYeHHvMePmv+p3HKbiUwC56OoGtetDacIxd9CW+T83Opk8Wk0YWqCD1zlOy36PLetFAmywZUUDnZmm97cPnBg1+blHl9ze9DkEHRe7mL3LDi5Jz/Vsu7hBPcF8Xn47VuRfB6J8hCUJWiCl9gLiD7NtTyskowmKbhIpVzCyQRBRlXG6914YG+tVOHCbyjSIh/0k8OOC9CpYVk093rbib/m55EHM/vRSKRG+JtghkdML3NLhBwc7ln2bdjJNBe5sA4lUa/lnjrjb85Xim3OilbE6wxKyCVhSShff/E1L4yXhoBsO2Y2T8NoDhdrKvbM99CZzeOzokzyWg1v4hstPNsmbyq15k+s2pp0S/FVDAHTDwBcitfHbwwypGDu1j77/FPzhRhW1DmZrdIMn7NcexJd+8a/21Zvla4RUbatqevW9uyS3g695oI9evhAf4LL1r4TDWVkMTPaKJwAGoKLDVMv1QfY+IRs2Q1FkFzKsChTcL7PNfTev3zwO6V6n2YV1Q/pAl87aBz1n/+zP9a/ev361aNHB7uOl0r7YKfl3XCMjajAKDl4KWFgugkK1+S2Ba1IoUz63IRZB6XpB1aZzV/K6BYZkMibdN2Qc72pSxjARZtOBmwDvWibE1ycmkPnfEDzA1tPriI50tlUT73Btr9QGjqc8YE/X3ud/Qy6pyb3hiHRMo+snXQUMdSaAMOF19A83utnVHoArPQYRAhpeFWiAY5LyytoC83huoRF6QSm64aIouNBTB9S3SpBETM5LGzJwschwk57pq28iDPx41Hus/p8SSNMyiDgogdjojd/GN2NzfovsXE6Sxypn/o5RrR1kEoBcmpan9hby2QalBiqaouxLpDhD/XqS/0ncjhFLoKok62iv9eaQ4k4c8UeuA6Gq6B+grmwYp4/+PJ7HxdoKy5O4t+JtmTkW7IY+G6uyaVH4ZgsGpQLHqym/KJcAU+6Pr3DbADch/uyKqQJvgd9/5JHq7QcQM3lLVXX8tvL3boZomAPQyeX1dPEu9v61UTyueIYREU2vv2F54kuXgS4L2USmqtsSvr+Wr31+V1gYZP3wFqIf/fx/mGEKUZmXvVTRsOnBYd3+XlYgQZXfy6gbrAZ8lYcvAc7aACVhuXgzTUyQI3UJ+DNWxBFLROek2PmfguJWb4m/GW4ICRpz1DNskx1yrdbzK3PO7MtJeVKYVKOOVaW4VTz22ZhtOQKB8pArxpOip9JMejlkapXnHk3Hl+WzN53EaymzUJczYptRpKdgQM8+YG29kClGSIrI8iHq/KcaT/JXWnUnjiTCpFqsWPKTbWGMOy6FhY6ZF1wIEVI+hBKRaDmG6QQ5aohwzI3R5bZ7dVP7byTDsGzy1aSgKOlnGihUcY+9gji3Cao7Mf33ycxlluhXSFT0sUkFCOFVaPumtj2sVkegxv4Cfdt+5vNnf3Lc7uaaH43Hz56Cl8n5ZrboT3LDYFHtz+5Xnt7vWkWhIyahIgcpNUEDBw/ics943CIqhvUfalEoT4x3RuPJkE7G3ePHu29ffkGkjS6Q0hNCc4sYA9cOdSmpYdIsGrWhFmCd7v2mnZc149Pml5B7ttvvvvyiy9gpNRsALK/e4T/bWWolmO4zQSVgl6XIuMTMnFz/TgnE25Q5fV4lGAjP4y+0Of7X6gYTD2GNnZefgJDGmP08PByobqqijjnJb3l8TF3mlwzfja2TxOxBfvmtmz82X/yF0cHDz/93P4q9XuHGzEHmCmZGPOfco3MT4IizPxLSUKr+/B8HmK1r1BCn5pS0bPVbHl+urFhItDD2zXnLti7htVl14mbl69e/+zLn40zb6qSNDYFunCahSG+xLvSq5+U+GbGTnVYhIwi3tg93th8226Na7bBtAESo+iSXYgPrHo1vOXGHFQZCxzMV3cHzl5IZ+a1irFAJJm4Q247x2ARSZTG0iHJs5VFPS7snsynHYTVom7uP02yVVR4jy+ksARXg1lzEj0jnmvmKdsxxl6xFMOpJvH6wvGoH19sGNHdNSIyO2BqkjnhnLv89Hr7Ty/5bG8eW0q8vv4tS3lt4+Xmuo1oXhsINURgduDtukOO0L0nYyUsI1GV3Mg8FlUzehsMV9QNie9ufZyvHt5fhYT2b33qFS0lmRrXvZBeS9HzcvmlbPuSMNya/KMXfPDo7uLrt+snG3u7B8XlkLB1VHVITUgZW52/vvZw0aptpduECvGoZoMAPJS3l+d2gL347rvnLOBahDqWZp9klCN8jGCAmWrTeWCG3142hef2ueqmryiLATg44tfW6/XtN20W6RPu9pk9DxvWf1fxlh/lWUoSWz+d51dLYe6JKj+b2r7Q5x82NGbLDkYSGBJYUfD25DU0tncOnz1+Qs47jpwKCF95xgYGLhRz7qoCLpNgWgSK5N3bi8db6w93dl7x9e/uHf3d/+J/0TFoEXh3YyGN5Mx+h22NzMNUJTD+6QrXpeyNO+nh1G5Ws1bVfkXaUPc+usKTLqJXf1PUy6vHAieP9DssK3fKbJTq6eX1f/Af/F+Z2UdPdj7/8gtdmM46U32J//BFvAXAgtkEDuSBWhWvIVTOrUlbxng3bn7y8OiPHj89V9aGNc7OzxJl7lqqWOY7z7XXqNJr4Mu/PG8Z907j24qgofJw66xoY7xqh11xiAf7/gR76eZpDmemlt6icSS1i82rkGdXN5gQLlVKYSMBqK01i8GgZ9uxzdsNB1pboK8Cy4KEX8EL3solmcZEVrTkEobxFEWlXdgwMNvAsKkPC3f6VkUpwT2fJUiISl0T3/JcRrqFTxV6HUhNE4W6pNH2JLx6XEQe+2w0Vb/XXsnNqTbSihrsYF1BjxqE+9gmJz+93tu52/lO7pZcd4yMcdmavKm6dmOpPrTFE/mEomyMj2n+SD0kUqEkEZeyaeGoIMIz5pvgx4rK6PWhjzqqOA9hz4vuHfIhZUPnEQI/oRVLCnk/YyU2/TteC39/X+SlMq9ymvwmp0Xgd4xse00C47lnjxXt8jpoe6zYKtFQVF7ewTNLpQSefR7AhbpWzz1ut/OkXmNxgtP93WcP5SZo+dTH4iyR3kULfCik2gWGxqCypPS4AnL/bcmrDN+DCPIqvJ/7DwHt8luj+OM09x+LXIT5kVbXePk05JfctUSa8OXjcu/DKrNh6geRSZgcM0KT4CQ0rrukzDrqLeUOq0qGFjMI5SORDNMMju6+EVERFr7JDSxaKskLdH5lYlexBTOZ5BzyAmC8pkcUQ96hZjcNsqJkOMMsD4Rvm2v7jAn817OWmf35+DlGfQe12qEUPKo+cqw6Qke12Nrh09DYWCq56UgmNOoNAqzVuWVzNpfHJe2kroiZpFzIKIZdJm/oqbn5HmJMpAzCMUzG1a7odWlFPEZ9Rk6UZYhHJjZhhaxDsSy7x7aS+SZ0gJdvkQpdFYWH3vv+46uQ+TTBU3knAAsHm5BdIN2nq7ArDsEw67Gs25Ls/PK4M8HGfLdPdvtkWg2yfq3ksKPDQ0u1SAe0Q3nwH8h9Wl3h419U1E3yZXo47hEcZlTn7caDw0d3V98wH3/4/luOyZ2DDf5kWMfxDQ6tk1GtNw8fPnr15jXFS+p4P3Iq0fVXV6YqOX7r++++/ezzz9++fnVwcOhcgMRNnzPOmvqM6dGqk5bum65DZA/qMWVKoZCF2ysK+hzy8wpZz/71moQN6ybKuK63Dg8f1hZUQ3IHRUIOIh5yHkQSu/Xdd9/+6i8e//QPf9JEZ4IXrAqlqx+w8DGIk8PcJ6jgVWi/y1XsVZQJmCiTulCtxlJlWeF5UW/Wnz19xL9rNs7J8YnWxzwga5EtfNfUKl4nsPEZxaLJnzxM25UbCb3JftIx7Ohn+EpeTZwzu+76pCM8XVq2JmawOCBgkk+SzCYj6boGj588sjkWF2BjMsqg/llaABfwwbucF8HwtazAW34CvaDlZ77Na889zKdAvL+KJKQveRD1ipQLWcMWuE2mxmXMVkrFLfKwvfP2ZvftqX5j/VAzEWxqyc7YeLj76gT7rg5Zx1smhdpOinOuMeRH55sHJ5sH51vbp+yBDlZzTHYjHqYAEl60VEdC8p6O9+QsWA+C77F+/xTicy1UJRVD5X1wvwG9v1aAxakmL2DjyAKnUabc8LNk08JrM9mvbpyWbRsfGvbXv/7V/v7Ow0dPsIXVS2xr1DIXcrPiGDNP0iwpzMojvMWpbYqQhTrlZisIW4vyc3zzzZNHRzu7D+FA/Cv9Bcd58Egk/J9edzPEoUelq6SYXHUgZd2bMb9/YN7m1I7cQbk529Uwmguu/HL1Gz1jo9OZZIxXfr/dzZmPs3ohu6pe5eTCOFNfG6PZsOhd/8c0PIdX7B/sC2dvDpfiXaDGeU/JkG6iAUFNyPmZDWE2z4+dJ37z4PFeKG/e/aN//I/N+tvbP3j0+JH2SzOhwQKT7zavfxXpzgImDLy/1ik3+5XZyxTVU1JylOvIf9LipZDC5i1il3fhIwShODF9mKKeyG5xRQCam69ycpyJ/PTZMwO5/h/s7JsnZS5eAqlYUl61VotUlcMgUZFVxhMQOF6/toUWuLe5/vSjJw8en9G0GrazC0YtkTf+sW2Ao6ZdTKWSXiRuXB8WPatyToU0iT+fnu3c7m4smG4xHpZ36MudnmfDRoyC1ExsojMbRw0DaLCYeReCqNFUs5xEw6rnNcM9IfalM6lxmHZDACos83HObVB6bS37wp7IqI3OBQYiMAvPvckyU3wCFqYOS9FS2Oj5kTcgkAMjkuBOBBtwYLSDu71hckxqTmPkw6weinFtiZXhrvW5Y1c4PaMdz4LUEcPp8+YlMURrWJEi9e0jjqr13XNIaTU0YcODwRnk6Y2214KU02ut+RHulT1iB1sdiyueMfPGASgHpIbalGc3rWFaN77EAiVFK/Tgb25epuzvGRSOc61+lpd/93si2TUZ/Hay34V5L4yr6P2g5R5ANC0w+gEa04MfNUvKpTxjcjlO2PK4JHt3H/i023ItuYE9pAdxCbn/7ncF36fVVbFO/DhZfhPwPuXIWIWdlI5kFX/SLxn1unB3AgM7uS6BPUZWge9izvfJaapvX31HZWmGGe9g9qWrtAvE5RUmpRq8JmRuC+AV/cmOyk55OSqx4VcZAN7rcgZoLr3JMQ0CvczgyaQKH7HT+V3lkZh3DSkRNLLXm2qR2PrGyGzwdMIypmMXMz+a2uqHDA/OwoMvmAT3UdaJf6NwHLsIzdrL0F7VVTGmItAcnR6Vs2nUrP2wAdQ+Od1qc+twscNRt7Vx6CzQ9Y23VRBQBnWG5tCu2tTCNcmwnsZOQ3Oj4L3mthR9KYc6SVA10dQQeuYpjksLUR9QwtYCWOsxmsSrD0OiLEN3bCCt9RA9n6P+w2vF0gXgCs3l+4KC5yWJiNFRlHBbXdGWFCzoFnP0A64iAa9Myj3neDh+Y3mc/J1ovru5Y8IDfbrnfCfEiBOJuf63/dbAous+Bx/Wrz+hJO+2v5kPYTD/itEffMq/t0mllM+ZYSYctH+TlWYXb7b3nmpBdywrhNLaraM6x1KhU++ODo5evnqV3G28TRwCcvfmzcmzxzsWD5ydXFqbaNK5KaqHDO+8zHLXJvkFiqp9bO7H+vpxOC04QKSn4Ixuh16lGaOGd8lNlDRCEq1XTtpmCfITFyP+FYpVDJQ6uWNlsvdFarWcb1oLQ8P7RwdWPj796KNQ0nrUUpaFfz3LdiDP7k8+gNOHPodeL5Ndtwl69+ld8CQRe2GrOuRU2lDaMOf+4nrtp3/w+e7RtpOAv/n2N7x61k0yVH744fk33377Bz/7w2wk3eWcV5C1ss8YS6d37ezv2amnJr2hvxodzXwOdc2xTnv2oI+1i5HQmkbNjG5PZYo3Avn44tHlR+u7R7e33zOgdYxlNlapVFXnGKhhnd+oHZoiOWvlnvBC72MUYWa7upO0kalJNDcp7hNprINfr0SNxeeUCzQJg7PtGuklzyqoA89unn19zERVp33d0Shv3BxpJw5uvnx893B7719fM+yvnq3dnd6d+7p1trn+9f7lVxvrDKCck1e6PSc6DUZaqKjqRVWFtlEeizxVMBFxj+P947/td9LcF/7AihqwF2AjH6C+J3eh3OdVbkmaJMw4sSiwTPM51IkxKvz09NQAmkT/uf/c31bIVmgYHEpzrW88++Tpixd/jrjrywdO+DXrYjwgOfizxLbzqxweHLJ2WEfXJw8s5LE3zK6NkWQyfhdCk96tBnFSOi+iHSTVabK2KHJkcIcXjeZpMylrKPQC6rMtvs+I3cBgR8PSucRo2gyS2A4tcdiyBb0KlQfEqm6TghJTgjo8KXdiCGLjCm0tmlaxIPqjp0/1jS9aea4uJJCxtehVXVb7pToz6zsfPHqw7NhjZMvqnc8//7xOi2XRZ0bVMGr9xYvXstvf/QN1an3r10DwRrGMcRuBDGUAPVgtYDtOmxnoKsCv7AofGV/kImoNZnzafbXXUyGh5m9J0bdQlcs8pQfQ2t/E+/a7b/7xP/r/2Lnh7OTis08+ffzo6fHr08NPnHa8ZzJJqYu/RF6AqxWC5DAcCF68xAf2tOlVs7/F1cOP3x4+OueuPzg8YKcSeEkI929+9Q2GGWCRyniqDVKZoI+fPnHExNIiN8+Lvmgd/dXBoalTexenb5wcwhexnvNeXbThm54JYAaeDx+BT2NvmB0M5uXmmvN5IGNuoTgQVW/ZuFe3dTuq3GRnapfxBwSql9pswtFY4tqNHdvon9dVQ+LgfvNpNFv/BvaiwTeys11xoN8EzHMl3kt0ETaRqSe001uLwlIKZu1D/qZRxAYb4TbCk2Ughe6KEKE3V3XJTKMPT/N8qAWAKQi/tfhCoSfxMV50uoU8bmZlRWLbJa/oqZuUcFJ5UpEsT4ucy0cTnpa+4u0CGrdDWPZXBrIaiVZbIjjtJhfMxogQWCShXy8FhlBvIs97wV2+F/Lj60fn/n74aYk9MJf9gj44zVe8MBtwE+PDhD3PtzjiMUQS15CdyAtmC7rFLcZ9ghLH13ui5lUBFq9vS7we81vPVR5B6WU+fxC6BM13cCfKfMWi+Z3Me5qAwff+y/zCLGZOhO6rHBZ0V68T7LZCp1ePGZElzjyrOJbSmPyWzKP6g0Tl4v87xO6h9ntPFTmbl4kWzGBM0PC3qBO2BDLKDdnXggc7byA/HqHSfhDwURDViruDWjoJz87O+AOAZBBnn1EG5K1CnMJASXowqQdFEhZemE3vn3hWaVbfuB7zowKS1AqXSpvTJmAeNDw2kNjRPHAUAZTVJSst+ph5HI0SdDXlERAGSxg2UbkZkFk2zcbjhUiJc06giZ2oY05fqZx1ZICFY8RWxYYFkToMY88xXwYtYAEUR0wfDU3gjfKaOuYjFambE6fDYyWl3sXBi4pjAiVd5BWn+1f8FQ0Seir9u2telpD34SMMAIbjfczV10AWtHpdwHW//z5fIlt6jXPnnDD793cOjixgLR1OKFknOI4t1b4/ub9ixmiUNObgHCBhSw5eloeFnCpwklymPVfe2DOPlC2f3cHBwevXb3WaXrx4aVWAb/UB9LUo+0Ycos4QAXKmIPykEArf2Pj1L3/57PHjl8+/3/rYniQg33708dPMjJrpRHLKC+e5baz7NBUVsNgvrRjZaFMc8Wnhfw8RsGBbRj3fE7qqN8P1CIVMzkX7GD54+PDs5Uuwa/SEM0cIhoQ8qWt3JgycnJ2QMbKx0r6rEhtZmBze31ZZTkB0xl/X/X35naBV4LA8jMO8CjgFxJrfPziaGnWxv2vVnQZ5y5FJMITJ6enZr379m1/8/BcEQG3rNDTle3Orx4VpDtvWWKgyYiKKLdNIRp57F5xueKzavsNYfGNtxm1U7/o8jbqwxBJ/1sLGwb4ZMhzPV7u7TnZjrpU8J0AsDNmhtUJYHnofWfFp8ppbgdEWJ+4LZFK/j3L/VDUqB5d+TMkStcmX3KitlMZs70nqK564u3V4c717leuSB3I64aTDysSznV9fbD5atw8mpUCodtr1R7/n9Pbxy+ut892lY0Fn9U3VaEsSnssVKoN/iCSKg9bqg5/B70MK33/60dM7Yu9DBSxpBczHYA+8+CPkPgXJjDiFmIOSv3ZbKVhZu31ycqw+iObM5o8+evby5ev/y//l/2zVyn/7v/vfY7jw8kB32xhOqt5eSMcmudi6BjQ5dz5WnZ5U+YU9gN68fvL0MfVwuH9gkBD/ZGc2UWYTNDtHjNa9pkPY+jiDifl+lEGdAnyi2A2SUQn6FSxopk/THqr7mgmjD4v3ZsWsftCnWvk1AsD413M4ODRvkBepOevOA5sWRhWo2AEnghCRFf/9Jx8/JdVs888/+8zCZZa6EarguVTXFkKoF2pPE3UePDr67PPPOPhthpyRJlrGaD6mFP3t3en5+a//4lc6MHtH9thRcSyWSJZmUvu2jXdspaD64DyI0LbrUSotaaxo3FcF6Zv8E5Z+F2S6zwuAfVldODZ1YxW5GLBpXHxj4/n3L/+P/4f//W+++oEf5ODJwaPDh/wiPCnq6euXLx49M1Nrsyk9FUMznQZsFIVKYlMnfxhcjt54opURuX365NHh0Z7poHSbA0WOHh45nsV80RKhhfXZ6ezW2G/t77XNAIbWtZNFMWra19v61Y7ZW0q3I8DW7SRHk7DWO50FjXplbdfBQ7DQ13TO3d3DEV6bWDlmwdic7qtVRtu7NzuOjLg5s+eo7X+a/KNbYLvwGu+me1U8qhsikEYwMG3Z+SPe+pNDT/N9Ceq+uuKK0uzYhOm5+oS3QmdkojoQgKwhap+NjmlROakJhSsFX9EO/dMKcULynMhVH4zGEYUYhay40pYFzg5u6YmRQNaPYsAUOfk+GYgov6wZsWAFTIKp8gwgfdoEa4iRDrwmUWjlTFDMvxfe4xJZSVRcWmEe5NXj5LRihh+vA/B9yL/t6V3siPotSNL9VuAC+H01GMhDwLBxie19xNLvhIoUKxfgC4Q4+nuuBHuC331dPfzWCMCSdAWqlwEv7irIj//vgCzRl3jzfB8zoVuiAnCP5JKSNOwVdwXEXKuuvq0I8ZYkTHlULHazKYIYLnuQJzPzPGErRvC2MjDyFvg2tvhA6QD7UrWS+kdYD4Thps+9JIjL48QLrGHuYRtcslR9vvyMUX+3/g0pFoEkrV9/SpI2d3+wuU6GhLS1s+lcypzRXRa3Tse8L4B2NJIWjjONhEgyyTOdqfhVlQmwyg6M+tuSgSutQtiHnwos29ocsW63HUt5a18CKNh7W4jaSPVYAGorGGvRkpfqVnF1GPa2HVxv43WtmsHiQQPTgGpuO8+YlUOMUJX5Cr1ay1R1/snaIQNrNSdClIl+uTWvt84mnIAgIbZdDi39BM2ztFo7uxNQWG1lPcW5SJOvEQIO3HxgSEN0JTEDqhoqwnCtvaSU4G8Q/+E1pbQKiDFzzcMiRu84rtPzEx9bEd/P8hcGXoae+smhhKsh039a7+Xz57bJ27Tx5qYNsu30aYZhxchcE8IWtw7aqRTQjcFDXZwJVkwpp61v53kaujZM7PKhvLX69YtSSJMvq9jb9aat8Q9MIofB/tOnzyy2IxR6oFzUhtatMqbLLq8u+CwfOo347Fg7JPko5Zqxh48etRUJc6FtJbmItOxXRuK39rZ16sbvBYAdkOxC82htzcQPM9R5aGQNo6Gku5epQVnslc9UgqGoFwUbszrleik4cSbS0t01ZdMkAYiRFmKX78aSNwZvIPmJbp89+eTxo4fWKljYoO3AsElOreNW2d05J1vc1VX2zm3AOgtP53mir55EnAj3sd8nnIIBbDKoXugAE4V9+3g/3dOL23htt6K9U4699kEwK/r6+PiEsLd5aFY+TJsOB+DN5SNnPJvicHXKvj9BJhNO1QdRtibKF91ykQ7StrOk5Y81+bKuWap7fblz84WKwBqsH739QvHdgASdPqt/zcVZacX7uXfRt7oWEnqNK0lPVz/w7jdJm5fVp/nezeeJkXQlir2SoTidAVEDqBW0OIHjmfx5rcpd3Ryc2etGBRdEjkQ2wUCdvvhifffx+to3FrhebZ1ypdvs5vbi+vDgxcctB9653ji+vH1yuXVsa9FDEre2fcPVevvxyMlqTuEKrZVILQivKowtwPrasD5ENUyKrn02kxB3uKcuho5IwbFl/uoy7lnaZUpAVPtr/E1l/RrFqlPz7wdGpgJj3KjUlqmP5uL7t3F4dEBZWQieXNvl5+Lhxt1HNzcv05Nr10cP9vDNDBmbx9NEyh80lwcuWx0/AqSY+2o3wv1X++vUgtO4iUedIYYYSWC70BmJWnhgraep8w5TqAYyXsttxmPbdN/AKbWdH2faBUkMV2TdBSJK4sHtET/Mnf2CdN51M6G2aRNIapxoM31tuqUnoKet10Pud48eHurVvH39Wtbq4Omb450Hu02zthzZGn2e2qp+bQ2OkRA5yJ0nyzl5zz56GiYZ8Ay4cGemYkIdXQei7e7+9Gc/+erX39BCa1vfgWNff20T7eVQuEwvrUP94AY1pvpQByl5lEzh+lmuSloQDBrRUoSd97waB5Crq16EymPfPKzd0rIPpNL4pLWF2db+g/2vvv6az9fI7c9//oeO+bswGenq8tHRUdWupaiVBUy8hMews5bS+9XH5Gx95/vkx6tTWhr6u9Jp1Ea3UKTOW7XIpNCt621lJJouzQVD1eqOUXu8ctnfxohnMlUZVb419P4sHjh59fbacTtWITV35q32l2BaK7SzsU+sdTEtCdvY+r4RoMuP7y7tFqoV4pngitDsv2ka6u0XVzdnGzvP77bON04+akyr7mr0a3v5K4wgzYEn18FB2ZynhE3K+m7HaOEUQRQnTjOMcf+M+dW72M0uqJfXmklc+0lqq6/JgtirVVi3P4tRCDYK0cxSMSjDKa2qADNd3HkfhwJnQjqTAGS0Z70Anm4cVFRWuaOe3sim1xGCylLI1R4twYhHuioHXHgGv9Kr6SZjOcgigDBWtrVTgSaFjdSCXoIMjLDqPxEIQtFcHue6f5+gVeQw+T3XxtkSfJ9UFJms4q4Cf+z79zHERdv+dWkXS7WQJd1y11nHc+L1tSjDcYyL0ogNQsHLfTagA88gYZfA4ixRAjqxljyD2OXnXQdgCfmteyW9BFWcie7gPMBX4atn0SaDha1LXmHwDoElzyX5b+UiZbn8DsPeRY7UJf3gE/2BcL8nLybEB+GxZgRCmqrfihUlCMjAWlKvPs3LAijyAt1fFyFXbT2wq/N2JL7EaKW26o9miMtPSBhIPc1MsumNkxCGI9mNjS1U4EgfF0EaXZI/RZvEIbEQ1AqiOhPUGRKAT92UTWVP1/dVU0OcQ0wLVq/aF9HSv0a7OgGqBINFNLuK16mSAKeotDGDOI+dlszuuaJBy7ZsNvN0SE3uonJRe+zpts3xk0Gfj4o07nQu2OVFm+WFInw0ChptPlG6p6lIWDesdPTpzlhYgkJ+ruFxldBDXOth+eYezr30F+vn3stcfV2+3X8VPNGWuKtoH0a+f16E4cMIAzWxGxziX/qGjru2P/PphVFU+7lfXp0QajHwv7vt4GwieGkol15JcUgR7yeK3x6Wl0hbZbGoHDHlMOWC3wEtYqUjHtDcyNrUyhSnTU3eP+AuDCfiYUcIFrOomZU3dwdHR7uvdpeNRBaeAabcX799/fHTh9yRz549efDgQSZFU7OAJiWy0Q55A9NCtEuaVtnlj4SLVjVsa97bvBW4TGaxmY8+SzVXURP8UO4iAkQ7l430mlXLagn+lf0KvbP/7QBq7Do1U4D8f/YHX/71v/7XCFc2aPSjqSLAgCGkoHmYmzST0fCoMojTE30QmKcSL6nukxY86PUQCJe2hN++NiHrqy7tg6OjF69fKEIUKWn41dJhwbTZfEgwlBaDGE8msz79+On5D99IPEoB0kk7ipTI9fUxoi3uzdILl6IYojOswpWbsQiOFo3RyvXYuaEYW89/Ise992TdM0LWA8nPIlDDl0L7G54tjIsAV5GXp7nPM7mLXcO4CjH2laW/CmCYoydf8VAJKBXpdvP81v53SyYJucjZuOtbv9qwOPXy0BB7mx6gb9PhR9eHm39kBsonG491DE7Xji44Le6O7q7O36zvX1iikuAsyIUKBBbIP0Y2jCE5ZQo91xA5T25Vn366z9NSukNxt0iaS9n4Hhy/UT1+G6QN1dRkMHKEU2QJugW4mThkg0R/+tGnp8f/hl6k5r766qsv/nDz/Pzy6OEjfSGpms7dlkcXTpNIzWJLlZPYMCt0D+yAqFeX6qMeFO7jx0cnx28NLNgdmiloTpW+pbEHqnWUqIq8dEsSQDqTsDW1sl10Yrksqpk2jMxRrUtQnrR4zl9k5V1CoMoXkdU0v3bg1KPZMCy8dnFuGfr1Dh//tn2oJCnOV7/5TXqZb2d7+5NnH+09eXxxef31b7766NnH6b7oaKK/OutFe8RLb4WAvquzUKgRq4xi38gQnMOwPkDdG0w/PDx6+vTJ+cWZBrJSmMJGIzd3aRQK+BSR1ylCz5Ew6u9dQfoyz1O+y4ucVg8Tl/kWMSPWPk3BDyg1Itk2sP2P//5/eHZ1+fjpR1//6hvnXB8eHFDZgHCJ/fqrX0q7f/CLw4cP6KaBlXyX6X12yUKQ40ZMoY6NyLTHK7/Y2sGhSp0YlUp5oGfdbHvCxD6gLpKnGmaDQ5cWCJwM8okl6dGeSGhcZ2dzX0ECZ+rdzc1bfGnbfuhcAHHK4S5bUTitZaOvumvMtrXioFtAYCohxumpwzBnvPN2OeQSSSb/jRXdzpewtsnudPYPUkyZ4HQex8aUQro7rBbejRgttUPACJIgHzFVHgqZOLRWw3tgMtZNsKEQTLfPg0WiDF3gknhaBpTXpUJwEpLeM0NocCOdOlAYhXFIj7+cVzO4FSurUbWnbQyVYZVPpRJ34rIU0QtyJVUDij3zPNyVqX+kEP30/LazVqyKpm99TQ4rw4yfakFCN8JJMef0mO/KZsUB2a8408+Pr+T+xyEfvi3xQ3RhbFkvwD6M9ePnVdT7wAXEqlxWgTCs+ixwhSUQ95/mdxLVh32X9ZTofEPUoDEppj7O030+E+e3OwALmIWK+BW7SoCNgfMYjMpw9RiUAdvD0o/Rd9enIWcVWH22GHEfx6/pB64foRG0wAZ0AVzAioDVvtcTpWhTEN4yjZa3Ad/LtL4Z2yKRTMO3ek5LpJDvyfvyM2CK9x61+XAPNMumqcCElCQ3nHq79S0p320HMZu4NVzH26F8fKpYjJSPEojEZI7kNwLOnKvmLBk1SXZBT7oVSlTDoJDFX2ET/xRGtQPv+J04DMSAdkZ/BeKRMrC2qLqtOmXUBC4WajY0Ai1V7RqGoAG0qK/JERfMXAhAcQbLdOEM7wyXpFpnP+EmykZfyfzBo5YnHVXmmxc032SwYiLwNBoaqQaNGbU4jGZJmXR7yzc6bH/Paq9xaTxktNZQl2JaEMlIplmGKes70z8OnCsSXcv9x48hOyE/Ci5080VJ0hupLOgXc+7xcepLbE9hLQWhyUsdZcyZ3LFxABvGGvzwik7z0lA4p+DWht0/FBETQUMYB0YkxV+4GkXNrYww/yNo9N+CKMaOmzAG5wthkZtrsecAnRZv7T04qnc37c/11YURbJu7aW52t/YNA1C6Bwf7b0/4LFPNpMyQ/c3NxTff/Gp38+dPnvAp2oOT2J5/9HEgFpVMUVjvweF0a33LDfv1corXVtykbi+LSLnmQKovOlg3gX3VAYB80oSBQihPcZRyqCci+ELaCZrmYe1qZ3/37eUZKWD8bN5unZ7pVVY3WEC72/t1LVP4Sxmn9CvufvxVkwD0kKR1uacxlH0sLAwdEVTcIi5x3Odt2BFOS+oiQbivylITpOGxAFeBm7c9+YqQXLFdDLXYN7W4S1szOd5tvr6hsjYPLLdQ62aMRc1u1mt8CAsi4USL3FYaTBw0Acay4JbZ5N3nzX3JytxYfyoKbyJ3qbfXb84ebh5w29b1IlJJTvTNBSos7qW9xyVY6IrhE0Hg1KmQYJ98WqRFW0aDa75eP/N0t/EtGLg2BoG5AuAs32GogT+IoPVTvLq5YOrZ9NMTrNpam015fXe9dfWHW+uP1rb+ODuEoWsB8M3m9cXm9qMfeCslxEwb2psiAxwu36y/PHEWKoGxp+HarpBUaeVe4VTvKiOlP2IQrWYtagIWe7FaU10J9eW2sGAU6UpyjAhRXmMPdILslPmShmHCD41XPtZmYnG9uwFRldKBYSoR4a27TVazdRy84KbQOGb77Nwg5rf/7F/+3x8/+/d1s9XRvb3djZtHKtjazUVLQqypaeY9ePUoD/b3TP7RAdBW2Hnr9OzF3j73593b16eMb6sjjTbIMqO/RfCD1HW6AlkKwWT/HobMCCBALRhIF6nRqRH6M5Q1BBt2J2LFequJkMTccZHqXtuSYMsolmiZa2vbewcmme8aDTDAUNdCtk3UuaL393e3fvGLn/38D//w/OTMQIFPLHvObDlzKLx+85boim2gUwk8ePjo4YMDS2BU8NEiS51DBma2l39m1xQD9psjtHe59+olCKa5MAzp0C2DEfUQqiaiuO5/euk5Qrr6nQire58k20puby8+UePuNn+TM2S0093mt1NvvSrf2OHfNCGbf/LH/+ovfv0bQ6baQjtxScj0tOqAgC8m/Y71GcO+uQPgpZwTJb9GHgjpCAuVBfQ0Gtm3xaEjq7FqkD5hMqBf15qHduHkEauIjQfBhCuEp4z4Eb0mANbzIb00/dn17etcJHh6wVI3Zn+KuINtJ3Kfbd8d7G6e7emkXL/auDq823qzffNmY+3F9bVpSyebN4/2b862zg7v1k9ucjqcXJ4/sHBnm9d7/e3t1oPrrTe7Fw+3dy/1V7d2Tm+3H5+ZpmZfVtgRTwoAGWpEgojsuBlKcU4TF4GKZL6KyPip7XBi9PomurTvuQp0UE14Q7pi3aAQOKm3LI3bOLs4E7lKkXV+jJWcjC2QIobV7KZZmh7gayIqJPByG8kIn4oRhH0fiJrGZAwqW7RN2RZTAkVUM9RbCnNqSArElJ8U8EDLuUkP54moQKejrsdPKsN5pCVnlREpri93+VaySejIkRKfdWireQcrAfVxLggUcfg3D5PKe4Fy64u/rvsvy9vv3IvqWmYoLAI3ySWcPKJ7OX8gCb3PoGffxexWFlUUL9dPS7WcV1D0LhzV+E0sH5ewdG81axL/dgdAsGsYWXz0rGRlPvQ8WBVnYi63sPjgtbc+U+X9TlX60ecfv4iSWhd5AVLSSdfrVCBYTOAH6eL0KsnkEqZpuokJR/IuzUCYCj63BczAWuAtGS5gF57Mc4Jz/2lpQXAyiESM0aMiL9+HlV7T2w34Jlx5BfqNvTE6Y7Kncq2KARO9MSXNVVFLyfmb0oikCRAmmXt/AJLfmDF0yS5oapBspzhUlelPUzSz1Zl8B8MSAxktISkufDRVHtSx+TRlpFUWa/rWVTDgZU+BL6Wt9dIItfSgaaw+q12tI50L0gs0tC2DoXAr2gwFpBkZSlRJXQIJhsIyi7QsD1kUGC5LMSxkDt1CJtrqw/sI72LOgzg//rSkuw8bVok4RXAfOAlTHx7KP8muYNwrR/MDmsltxMTiyPxeriLq2bTHQq3/V7/5ise3URHWXNt4N9Gbj0eJLK2C/LIW962oJg91njwEBbhpazy9fv0mI588tOLUcPy1c4qoRxt0mP8z2gpUydkrDIJtRxBoVXjjTi/av4wmdTLAUM8BE2CIf/zps+M3b/7iz//s0eMnf/Nv/fX8SPKdLkztmqlLHJ/rjjjpZJ9k1SLIUG62142uhb6N6kgOmChyxpWYluQmVfFnxC6uj+NErBjnPT7mgtnS1tYb9GGcXrftkZ/q1yRoJExXHReaZMBVAj+6kj7hpZ/a4OPo+glNWioqMbRlgxmwcXS55nlQ8e43OROL2Gd51njLlbPNuo66vi6fmkWlG31xbUsUgQwN7EgJTsk1cSe/l76TjBzgqzcy9S6ADjdQSrK6uz7VS48DvmFQIY6HOm2yGMe6QEM4rdzzScNGtuq5WWpyuWV5n4SD6j0ZC/ILSXMfhgwpC1N6j7T+7u/z2C0oHyRYhY/c9aUWAd9Rl1QbZjd0ByqPHod2cw8Y8OzpdDL26Ae0eEQ7svNrLn4jXxVBKwckYnGKfHh3SWQzLTBNznWJ76737g4P9LT0SzG8slzV89Ad+VoQHRJ8l8ytEp9CWSG9fI2goWihIfmckPCv6KOnpK5gTNT3nFE8Q2gzLWNa9dr8eHYzFwo6ri+roDb1Uq31oW1TODYxg+bJs8eKaZZdsvmY6mZX6+DYuwntGzOeqvYyj63fVXnMu790aLdKrXcByMHanjsEDQjYBVHmcodm6mMEItSHhqSOyqmf0FzNjQvuT/LGqOk0AECMqt7q0EuwSGxEltp/kIGUfUVVb6H6ftnWFfUqZQms2jdFk1F1dnb68OiBfv6R5fjmO11yLmQGmALEUK4ACDzdxW6+vPzoo4+ePH4YahCKwzFz8gY4fTAalLYYSmwS2uYDuzrSM0+HOjJnnSG+YJtATfJVGXmW7/29T4tsRNr8S1BiX1lToC5b+zvqxOLaQSLmRWGsSNm8evX6n/3TP9maLgc79aOPPvnDP/y5+Yd1ZePchqlpP/npl02OGt0lEyVfZV7QGAS9pZJlWSOdxp7vZnDZX1UbaJKPtrisRZhuc8yZKg8X3ixFgPBmOzHMMSCT18KAhIynQEvqxMEDO4/pAaxvWbZxu2aHJDMyse7Bw72bw93Ni92bLfeO6G4jsYPLuzNdaAMEQOU8MPZoCy59V9FMhGum4r43R1k4k/4mt8LJzcYBET+7Nv14n1mAidVoOeabQLGGA9+MQo7bUfgIy0hX3p1hFyqNAucoFNO8gA0HyzUatkgejZYZEX/SxEXy7J6Elh2+yUpmBFBe7jMAmwxtp2KTIFFNVarwvMgNksES7gs0QaFRRngrEZ/cx/lUIgHlldQMBkNLr8ohxIqO6nDJ/PBhIIoreBGJIpV+/hb4ngNR+HL1daLMa7KxPCw/q+ReVugtwe8TrN5/62eBfg9r+bi8RSaqBu7778vTMD/GBd7/oR4X5mWJ8mE+fe4/li3BRY2y2CjEjMdV9GDdp5y4qzRF8x47BqdVpOVnBbR0948z217RlHP154NPPb+7FrAyTUUuYwIir6AX5HHoomMsugpWKjVElmuiJijEUJhee/YEdMN0HkbCilasub/D8sdZrSAOZ4ZjJZrCLBVJ0uBkNKtoST+EqkskFrwREwoi644UjnwNaqRXfavlB0HVn3QJc0KotVTlGh7wURZ8E4nzpA5dKQwGY18VB2ghU4c9rOiZX8nHUql0oDKMmLg1JcDhhHighur0qoGirdR6OK70XiD5auDVtARvIFCAKmH7EqM2KqtOjUjDgqE5wqntnIP3Gl0cCkSGbsQGHSAOV8jfjwAIjGW+9N/aCWW6+XWomfc84hgi83nqbdkWvTDX7z4vnwb91deJuMRdEk3AXWs5VlfKCcA0DMbatQDY9m30MyUZ8XI07dPIo1VrHHiio2mscCankditzrg9N3v89PsXr/mZeH9t3bF++5HdAPeOXjoBR4Nl7F4raOj4o08+dbfkQoNqmN9E2B0OxTwczQR98/b1kcaYFZ5ddVHf7O7KSg1LCV9cHD84eJRo+HJ3B7jNQ/RMLhwEw/A3TYt3bFtzwOFXKwZvJXNxcf3LX/4FE+Pnf+kX9mqwBgCC2/ZzV3ItX7eYYff6whlm4JrtcgFPKlgHLeuF7mWZ6wWkflcdNmNJtW3DmEWNMCbQkly4FHAOr7i6Ymt7+1l9wHC6MR/5xsTYfDNMyof2xN+2X/6MqDTCC19NbbJY1RkdTWRR2/T0aK5YFokgJnJsA3ut76DR15R+BsgU9hLXc8j76SGsQqsq1BKXNU0mI//MDK/z69Z9ApXUjm/JOB0f8NAxUlxNgAy4F5tbeyb1wpmtpdo0nA6+A7C0oA6DO99bN9F5Y/vkDQ8693nj7hpFPmUHh+o7MALwYsPkqKZi+TXNAyl2yuGdxVq0Y3uVfEXLvbj+9m91JrajipyKLfEQH5nLLkATFhHvQK1bIYAn0hVc6p7aR1ulFmIZovNZrW2IbRmy8GcH0gZZjjGnjUgw6vqx2fLm7wowq2n77tShWFtZCN/Fp5vP4jM5CydzYIjS8721y727vSsHnd4+qqSIaQA1vcQfgqlWyqeGP3ljV9XR8nXK9oP7QmuIT7vfuFT0M77lJlUyk8NZ8YBDn+iyeB7hAm/onNwRUpEywesSXz5Vs+9ujy2cur5pK8+9/f3jkxMIPH789PjN8av9t3aONN9vffcVH7v9IzUC9CCXOTM9Ymm+rbvD3c/tjHR99baTEDZt7Lh7dpot/vbNsUEA1nOIbpuDZwVwq0rKtOKp7iRfEYI0wm2sxOYu9j9R619MndULrwXxVbR66NIqtAZ+sU9Pnq5WRCkOOunwcM8Q7O6RaTxnLE9yTyGIzxRzPrF+jYW/P//pX3ry6KHiJKSwDLLL4+2lCmA00yRi67b0g/+r/5X/6unJyeHRES1U1ooZ1iNxyUr72Y+cJVVemz4EvcdPHry2zODqo1h8/W2VH53R53/kvk/ThwkOg4JX7wtOq08KkQ75FrPMrTKUaGKNnc1Ii9wmyUCuvK/1bf7jf/IPDZJQdBA0c+nBwwe2U6bcbi8eQmfLLgBr242xjIMiYYC7Vnms2SmEuS2oDl0kLh1cDRIKqpSkrjUteTe6TDdJZrEIF/yvHGUhUcPFTjzAlRhYOfbPQG42uI30HEO3cf1ge/s7njLDHMZkDzde71tT0ZHaLOfvOml728GK51QqZeO8FwML6+uvSYAT2HQPDK9Bhv6+NRFg/VvVgP7Vvl5tvr6y3E8rc3OydtNIo9iGHcYHkUQYk1D+KnhcTIRid7W3Aq4ia5SQm6NCU3P5SfZyEuVbUUlrdX10LeKVb6OFgXFPGmNWQwHWM3+Z9tj6ddVx2lK1l1lUbRehcldbJU2SPS//J6Six84MsDRDz3IAeXQlpmvxpGIElaVQ4KtUSWNNU0UQHf0TVbkXCPFKy4i3Xr8cVajoLfN4MMRt/zoSV9eEWIvo2vlN96L5mb+rL/t8H3+iFmWuH78VVJJJP7/Lcz77xhwmnCobZOb7qlhWcadcUnv31xSZl8iFU7NdfutaiAngIsvvEApIa0JSoL9zBQwPxSEo3ZcYU4VHTu5D7sEt2azgTGCFdE/t78AvoM9dYveYvNwHTe6TmW9a22qpAhT8Psp7AOEpAhgDp98VjhN7BdSP/6vMxLlPP8jO+we3iSl1MqOpIK3ZKngidsi4eZ23kBKYdhAwqBIzq/HHCmYm1dJNgsm9fEHLogJrNMLAzBZX2GrfVKH0EWBGFtuGgnjP0BUw0pd99yLgCuuCYhwHh8Gs0SsESKQqyrCEwCf9nCA0Rc2XpzAm+Gml6KxHLW5wZR0nwscLDEO4mjcrjIIc2Jq9Ni2tES16TrVS3VijFqQq33AmLVE5ZOAtv+UyURKxuiK+LSHv7xOwRFx9DbPfucpn9eF3vi5Af5REUGybsBLeXx6H9jCtqAzXUtYNd5iYyb+bXkpnpC75R7e3Xpp4YwbmtRWlB6xGdqQlwpT/wb5pmyZ9Ih6/zXY1PG+aBLegoxkvmQXtO8620ofYyvuOA8qXMPAQKSI6Ur47Owec+kp+8SvX9DK4jQvs7SsPfRKOappr8fdZsUEGFHCgbh0WZrDbnIu1o4MH57zuN69/+f/6N//V/9p/4/HuI1ixRSoVOj1bX7fHLo0KShtBTKMX7PH0Tcc0+VKmyVn8wepYt+im+xYjWUl+cBKPxjJGERFiLLWKlMjpnzhrYqYTtODgwVO7ZVmo8IYxjduapdH62lSC6I7500dWEOybZbStsDJntknif8+pcDqhEoOkB4I4eERhj/DxKAjgWmTOJ9Gw01ZLdrDdPzk/NjhT4Wa8JgPK/PzM3kmuxqBBrWOmnGYoORzif9PbcpzJtcm1/LXMeM4+vKpWS4erOsmi2ezD/mHq2YgTmCCqS3YdJUqWC+RWkD8syz5xjJhu89Lzh9d89A2ByCNgUFWFV8FiVrarpPcA/PZ9Mqgg5/KLf5reKbs7u81Msy+mgM4g1W08IYMsXZKMAYYVTSY+WP/+AVE+0zm42T3b0CXauqwndHV+oId51UxkMafMJkcL2h84Le984+3t3oU9QsdMV5iNHjI6KIR6IPjGJqaR4INXdFTFhNV4ifXZGSlfFNQtFIJoXc6ecwzWfc0mmy5Ex5eAwyQCOdMh8mlQZIWRAhweVJGd6JvIt9+ZL+R0hG1976C9HS/evFXR/uW/+OMvfvKFAbePPnmagLnstHNtDUBz86Qk2/ZEcorC6elJOqKN10+2d83YtAhYmStx2+BcGGGTFcL58humG61ZfYG/ytvQFKnesDmmnoLOhgdFu7Hd+d9bs4AEzXzzgIiW6d9F9mCOFIqCX1rHNUkidNUpPuDNg5s2sG7uhdg8BtQMH/Nf/2t/xez/bDtADS9sWShMe4MuQprBQhY9loMj8x5tK/zmCV/7NAmEAQNj6CJiPSVuw9p+E8fURZ0r1QS7i6AM40wVeJTsIr0TfxHW0v/4CoYLPatv89oeR8Zktrd3X795Q0APDmzSne5a6APR3MJ9W4vuOMPilaRU0NMnTxUBcbKV5SZ/h8XRO7whKl6jnSnembkuRv+ja57gna7oJbTFytllLNsZZ7SEe30q6KGsxhR1hLvODxdPAiWNynN2/laBDu0rncAjBixNvLdzhEWXZzxTuotvNp28Y99KNchREoaALLxuEE0R7adWCD/pqbxF12YnLSomQzvxqflQNzQSquvetr1A+Ep81YloY9kDYwfNXrMdWdNuFE5zBKChuFcmdVb1lIu7/CqnKcnpVWIUgTW6ZVnh7tZulKNwaK988ab3kMPQam1iRVCJ95TiWBoYidUJgozLIIVTYH/xPOGY3+ym5TlTXnhuH+Z/TJ1CqsRLS6LAi/OCV7CLtoAvjjfqHoI9Vg7NYlaJevWvnGAO5UU/9FYW/7ZrRdJEEbPXgbHg9y6l8NXXd0EfPAyQ3t8/zNMq77TfqpYM7FXKmBy/3yHYg3wXIFWzVcSBOy9BWaE3+EjdRzGFxvNi3XcAwJmv3V2BDXatsUvsgXSfX2HvM5qye59Q3NXXibX64Pk+g9vdPiwrAVYnqy25LvdJAER4Ki0lrLetmt0nh1Jf/Wknygu/srIXNEJr4BSyXEvCFVarPO6//e5vyVZJpxWRhWpRN7TXiZ8wx5BUMBSIDbGkNg3g1stfWmUPmUQV58hc1EwaoWv61EDV8S2Je0B8iOKpJs0/CSwgwVQP+kqtQM5F5Adaatzc37Tvxtf55n1SWNAC6PrTkNv+buC29A24aUUMT27eGrVfal9KqZGNNfN004nV3XLGY3367lWksBZxFBEgTYgVexx6JS19Z+JEixm/U8GFrV9+sWZb4v03WWsV0IAT3p7lLvGmBsfxSbMqj7KdYljuJfvwNTi/fX0Y4V2qspPRxJ17X9R+jJFhvv93n/oc80IJZkxXHgruFrN4Csv5QABmJNdObZy4lltdNHbhuDC0b+x8ryi5pTSlOMP6b+4Nn6IBaHPtnRPZ0sNy0B5hY0XUzoBjAMcHxs0529Rpm22vRMVPc36wf3h2cQLrFl1q2q0i3Nl5/ea13NNpLUOFFdwrshGJSv/R42dvzUG+uDo9eZmRM3YT04Gq29p9vbb1cmP907tbx0ZaR2ZIgm9Sw1IvrzOmc7V8kUxvKSM5j8z7hfPV53h3u+kM4KZyioO5w2I3IrmUoEkLZkSZ7HKxsc7CBtA2l6K/Wt883dv+/PitTdB1Vm3hjJn0DxNTe5ePR8vKj6418TWpS9fLGGB1RFbNjrAlS1WxlehAVyJJTo4gzyJl9qlxI1XlUGsdfP4zuCLvznHY2/s723Y+NJqfVZrEM/hAsrDHSxVPZ0R+mr6Yi8uNWBsL4fMbgSrG3dbzUlrg0jSYakreMitKZ9C/I3iqS7hXvUzMmgmggySjbWQCDGu5qBloi5fLdf+7ev3RT3BmVzT+nm+B9xqiP4qzvCzBMl4+9hsW9RfCXTGWLWHRFVw3ByabGyv0TMzCReYeByNzxH6GGs67XXbJ3dWXFzePrm/+fOfNswd3f7HvwBBrBlo1/f3W5eb+9hOnApxvPL6xTFEv99bc6zd7Vw/2N344eXv3wmZDMTRlooCwws/YAYt0TSVdKmYEzSXe7Uehvfmq90XWImeo9nv9JAZvvVVIazdPYoNnMUEW5fppqbafl9GQ7jtDpu/afNPsmHX7rxU8my2V6VJBL4y/NcVuZ2/nb/7n/z397pcvXp+eXOZsziCTNleKkrVQh8Z3sOne/trhYzsnnBvkMwt/e48W1JNfs6kUfzwNuWsCtuECxtVqIoqq0QCE+kuRAknJQy2FMN6C3YNzhjtzK94WmJqFIRz852oYSSGk+KfsoKUm7BjE2Ds8VIBgXl++ffXq29urR40Zbr1RuFyt1gTXjuaZ1p246AiDZSRklCF7FGPPLk5HBm4t53VI36PHD+E23zH0nd6MVYN21mcFU4FULBWpeSoOH+FK2PoGMvxTdQY29qElgogBmujLDXn36Vehvg68BajIGl9pDIGe65Ao8BcvXzx98hhfxYPAzHDc0uf4h3//H/zZX/zSSJ0qaknD02cf7e/vj8zBa+Pq9htK++DoS1JepS4syhbdXg7yvf7UbZ3ecw2i4k4jqOg6WJe8aY2baBzVuQwG/0qwAoXliAc324YlGBuPzts/XNHxCFALY2uVjcadFImve/rg7urB+uZz2mvt5mPTjDY3fk3v6UootLu7Yxkq5o2bcwsQoURfpVUcxBHtSh8IIg01/UifDV6JTevo5Di1T5N/Ysz49vbI6BP7l7S41bHOvUWJJvi6Q0oQUKjeXX2mQDb3v/GqjhSir2wt0/quffX1SPd29zNd0rDl53+djZufkbGNzT9f7KLhTZjZAELIzvZrSqtVQAadkgJsajjXLmLtNIsNLQr4PL27/YK9M84jChY+ahzdrl0xY1NWl/Nexbm7+gKVbBtRhnqLDWp94o1GgYx7s3uktmXzN7F8SIWMXw0fqlN6jcxYzylq4jBiHHaV/u9eKx//EL1EWe72J0yCJZSy++Q2v7/n9iPgq9gf7g40eIBWPHayGDfPYLfaEStLUi4DpEJzdZsOwzz2ra8VXB2bBa8JWHBbEnkWyzTg2W3N57kG7Ap7YOUaoCXd6uk+y4Ln03IveTVhwBQ15EasViHvfwLcW4i8B77KJQhLtnOXde1wsPx8eH34vuJWn8u43yEbrxYylwwL7/ow0yXk3X0QW+UVAioviaI8tdYZKCtcpp8LgzQI6UF4gpVWKUoaM5Fyhcv84dKUSy+j64VTyToMxN8kiLRE4KpWoKgfpp7YG47dT6GAyf5mVYuygFM31Ph3WVSLK4icp2JXB8ZyqvzLcb5PS0J1NR+ZhVr7hzQKLNTcAaiZqYpUCAJDaVgytzaKZjDOlmfmjbiiVpOVGwYsz+Hw/6Psv5pt27Y8P2h6s+Zy2+993HUn8+ZNX0UZKopQGREQSEAEoBICVMELH4AIxBPvBB9ABA965YUIAoIPgEIlkKpUVZmVWZk3rzv3Hrv98mtN7/j9/n2MudY+59zMZOy1xxyjj95bb6633rp39IMSrUeb77YmsI/kTtNCJ4mn3IQe51KMzSkZJ08T3rl4IaqpcveLScutiiqlCfTDu1eYlkwJr6Ils/LMnSvQwZmeXQwKto4wOvDgpwOvqLJqIHfSAANBJnWw312XHdwgm8aYTgQ2HcbZEaM91q/EIYBj2EsyxMV0ayUXRShqbRXjb0BPa8rsmi4apbd10B9d34zpysthsU4kpc8GCiJIN1/iaJ7ry5vxnOk0tDekTb0iczpNts2Ls5PH9x5ej69evz2lW58+RTFBcCCBcWzgy6F4LOPGbZU5zIeOvwxiXLRb2FAOry4qYZYiqdjUEx55gEYrs8q+KN8ovOUFpcK7RTdglA4LcZApD1Sh9F7iEjFJOpYXZQAh/mKVi6qaa+SVXOwbddBFtwjOsBOfS9mqI2REK8krMG6NFENY1I4S4tdUi1RE4EPjDN8/k7NprXeRLjWb9ZcaSQj9bg16Fq0XJbHSFLKHLFjLoljQCNGihI+rw0guYkQwuevXoRVxGlINaxc8fRl/ms80AJkush6TWD+b9oQFUypUKmVYq2eev/WmtgIVVMlY96uU1zqunwuk+icwgUtOEag/UifbgzzaTm+jhkaFh83Nhw+OPvjo6fpqyko9VrHgYdD/R5k47bw+v7loNN98POw9hK4pXgiQ6FE8aF2zNGV7tml8PhiPkTmLGtWm2bLRv1rRawj/gF7GWWRXjJqYiLD/c1dy5cX3oFvCVSIRN1hbAZHcgKO6az0jAj9zqT9mkQezqNgVU64eUiA1g6XJxwP7u0g9YkuXBuWLU5+ePHp8cvL28uLyOz/4Lme+9gddvFoyp4OcPDwZRiLwowAoeo/ff/r6+UvSDvcHrtWZ0CRYMXdmuWLNyIRuaTpd4DnTv0jTGXRYpMlOzSzHQSuRI3wEEeRJU2G9nmBDQIi2IudFoW2MJfHZNQBWavGZdHBgAiKkhmCGFp4m/URonVVVp3+IZwNhW6Z8kJ7wRuvBwwe//Zu/+eThQ3dlxq9MQ4JvysYORA6Ao2FAWUXc2/39w/sPmMBOZWHb2xJkEd9Jp5KUll91ku9yQX2GL7aTYSxtFWbBnZ6eMtGRznhmHxm1wEiSIisTK0J/uerf8uYn0GDRxpu3bzxOmFZXu8s0SE4hRshMm8c6kOP11fiP/tW/Or++pi+No744dnd/b486y+XstLXtxaDQwGXi0tsmGgUZvWHCsZ/EQg1kr8WDMHEspcwaCgOrnGbsH4DOw1V1LNW9aZUH7zKz0Z6Mr65vrhgLGowwOGztyoLoikR+mYPUHxwwIExjrb837nQvAw+ItMNXbdbVYLYYUxQruk7EzcrErgqNFeEixgWSfMNa65xQhsmePh0rK+1Z082gmps9qi86fjC+W5qr6JWKpuJYZTgpQLrRB0EQRPvC5GDr+g0ycHBbj984RoMe7TG2TiwsaiTgA3dZ4itPVpSgDi86HKbTQ0fhzACMyAZoTCFkpitzmbSiIAzb4+np8zCWYlclCPpfFwUV56vPoIxxkdlOC3fYRQGQu9NZ05OCbaWrjLqOvF3da7uZF/GBUERruc0/NjcHaPQ3DJR+Yij6v/oCemgliU/e7151SP1bRSmgq7jl5U6qBFRaBR8RUZIbXV6UPEp2ybNkXaApssS2YigxE1DA38lql76GnVZpsqhRoXfWOUmN9X1uzQ3r5ckbZGQVGSehEBXP6j0e3Iv3Tm5qrFET0SQWDX+jdDg67JqV94JpiebdKLl2aVOgEKZI+plclk+N0n2ZXIhoE1L5mmd8a3MPtnSf+N1WTuEXMaLYu1UHpsnX/GYOVjl/lHwNV5fVYDvIF/QNkO9ruZHal32mfc45hfpN6eNx4qTY4MU9xtNq9k61CI5lRSo8UxLSqe/kK6yyUwAoX+hpYRuHOTKB9lGL5n77hXzABrCgjiFragoKMSXKvjgAAcD0xGj22YmIUmJ71kgWHmb4gcVbPhc9ouYABXbn1f5IgD4Z5NkdYIkQLzxCJe0exNifp0DbtF+aiPoDWwCPQV0/2JYlNqC1eY/qAWtAGWy06TXhE2ZCiRjZi/PJXzPwvNnuBRPkYlkPrWm/GGpVp2TK6RC2SsW58N/n0vJ2l1xC63JQy7SI0GhcXz9pr3ysYJUo3A1FGvIQfKsrOKQi4OP60ZodbOAvZzNbu1jHKkDkZK8Mika3DGdDzjjPRTVxxj99dYV2vruVuCPumCXqb4/y6Yw6ezQFGHeh3xrJKHS4ZLUE//1Dzo3GFAPpEUCYWeYkIKNWn0261fFM8KVj8s2bM1RBF2U+BjB9eTbABBi+8qib0RvP5ydvAPBgs311eXnxwUcfsnwOxQUl+i5zgDyagK/g0bamKLUgeqD0WJqGNOmrQTRF1+AhriGn+L5RWR0No4FDXaLgNLJFYPb3wE/GsskFlZUV1ijre0z42W4/w+IP2E8WsphoIsbMe4WChzKgc0YAXf+KBIb6AaJgDFxCLkV7wZQIYDXbLD7cNPfarS/NUNqZctB1Oyksgyg8NSyONSro2LcNbj+4aNX9VJi+w1IN3COsBBnT30Z1THNtRq5IGX7QV6qIQCP1q2hxCDjlENRxf9UfelRRC+bpUWHTuung7PHDB5rr4QtYkDU8tgJEHVpsj7254WgJ6maKHhiRA7WqRXDFqAuMgfNS8I0rgWYHrxw9IwI4G03GfWuSGgZYVN99kq3osyGk443zQ+CJfWVQzZfVbD6/YukHGx/ZXgQpTiFdzqYXjadNRk62R9PFqL0eY+MwcXSnNVrnfXSp9XyxuX6x+sPzDl7kPVxZxg+wj5SaOUSqY3QLMORBYCyAclT/QcfPYFMcL3mqwKWxdSGShBiEQRNhUkdhaYb6NRC4X5bn3LkxjZ2vAEZh0DipRUYIlTkkdFKblwqitjM9D3cVyll2T3lneh6rdGacxD2b/+zLX+wfHVxdMcjA9k1LBv7IOsbAkRFaEk5Q6NCwXJ+enjBaQvvv4vxyMuW8MDzFm2brHkfebXDCLD5xu5nj1+2VXhKMRikgE/fyUsnBBqxGQ5aU4D3bb0CI/GiyPw8jDLbEMEr8oJMKdbOnzmiM+U8DlDMr5hif2fwSgppd1i3c0Ha2WG0Wf/A7f/j06QOn/rsiXzqAg2wQzmJmm4f2MJh32PEWC7NYcKiImZeiSMnLJTPludLJA0++KZ8oE2+2YVhHkbVDtKlADs+ZmsKIJF8+NkH2+BdkIAmgghrxs/c/r9S2iUFOFB/27IJRzLrsHfXevnl57/iIKYusYOA0TMr2cLR3//Hjl2/eID4k9f6z9x48eDCdTPcHo+3ymKLb6l0wIKDzW2NOFqBsSdCQyXl3jrJgiAr6QES1ExZo4Y0Hl65ODjbzJ43eC5lD21nMKewKKgpMtNWrLxunV43+6O31BXPD0LoNM7O4hzaK/azVYbEQYNlQ4qjB0prmm8hxTFc/VT8lBfOD1tLwInsa0hxZQVGCj9RxtAkbm6eInX4cbVv7FVrcWnwYVoEJmLNNKENwDzsNrNmcuUi63DaE0UDqB+b4cUbDgJJhu1DJUvWjRSE1e4iJGExP0eLsNI0VZQdk2IGUWhGFY2u3cK7ow3r7GayczmY67lT+ZqI+wBBbEfZUaBVnlAvMjCyzMmJbIPKG2fgUHisO5xYS3d5ySqLs4Z9NDzbeck1RECKOwfx8ARTrKEaxaP+m80KlloqsO9SmfQnNQIiEQIBjCqiWaSIVs64VArGQWbBKFrz/FZcGqUSJfqouYlcHlk+qk5QmZu8rv7sWoqQgaj7mrv6ZJp9SpxZaq5Wx3RemTbg5VBBMnlS5kbYGXcPByyXzWZWD8Os8fS5gtIF1A6AgZqx85XUXgjBzVVkHZKGgQiJU1tEFeid6eTYg2OeLEQrNvtYJCYVlNS+IzR/qgvH2SkLv/Ccwv4LxqYqQZxUAHSw4SPIOnzoouRuhQlMogeu9fr4bQBWCQhMN/Uo7MvFVffJC5UEUlfQP94Dqwa5JzJCzY9LzZyVLTEGicTTA8VU8JIWCh+XSTeGjKMNntbfJLHBo7KTpBXAy0pvEJuhS4cFomcSFwlVWz8Rrs3uSr4w/K1P6SYAmbWgPHLG1DGLWePjsIk5fA5hQPHBAYBMxiIeZcUsB6m1mouPwu0yW8sk8Fj5S6lk2UgqzELh0lcAG54fmthedVeQpxyjrGAJnvkbHUuyiSYXbQU0jAuAwRwbVD/WvYQYW0eStuhmj/l8HJVWi1qLkN0Tdpix5yZPE9oMc0q4YQs3KD441I8nMoJ0zHSB9cLCIlHykf6F5+vrk6uKKzicso+uK1jRaEL7frexglFuMdZhQfu8B1daw06d50GLjzVHtUiMEW2LqQCGOARlsE6P5oAsYuMj6MOrOxf7+yPqTY4a6rCpesaBNl6bV2mcvy/VmPKHOkM0wW8wBud1cnl8e7R8Nh/2T0xP7zc0ER9xZ8pEIc4iw/nSs2E+ChGjqWA9GffFTFJqw4AkShHA0O3iKmupgZZIYIEoIf+ZtYbDW0NNFMehct2xAqN1P9FGyhwbO34hNufdc/FrKCw4Zta6FVHWVeCsD27aKA4hwCLdP9SfEuQRig/ugL4grT3EkP9C04aL+S5FoAaSUKaQBRamuiMk2pPTHs20Ls4K7e9Mp3h71KAktmXzPARgEuJyRospYGfiDEmWGqR305YKHhc9JtvCE7K29FH1WvkEX+sFmgLCQzMTZviv9PLEEC3r4hIw5X7n8LDvD6J8BKsh7//YrFMFrL103y5pDanA8oUrkWy5Co958UojhKfERLn8hmz19PcAHp4NX+/WYarFanMNFaERz4SjiwG9lC0rs4GZz0e4vmmO8f0oLktHMWVEvDvBbB51DokMQLHRwS+x4FkuUyFzREWXKI0UgqKslcswMUZYgxluogj6xJczyJy2GAKbEUjOtGiFNatREvkiXWQqhJCrpUSRH2/zAvBR+lBbtbSCAwbaNF8whWXbMs+hxuRzuDbAKX37+/Pj4eDAajucTVIQF3GSnkqdhRwacujgYkt1mugbAbNBmEAS7QUO/hxHhSGw8bh4GexgB6oUu89QRHPvQ03WCreZUwU9/9avJJHPPRI1D1PYm0ymsBjcWvaIw0EWJ4sw1R66WWm81XM7AQN5gs+easYERXELrxjeT8/MrxwHoBsZ5wqL1GDm82awOLFIoHDUVzuOa/ggmKW36+4PDg8PzixuqLaZ5HB0dsf0R29BIZ1WWYOXuMvu8ALgSTx0CNgysgSYt/OwVqyycSWm7nRIVKUulCQIkshSakpIYL78UsZKD6s5wzXQ6Je50Ok738/r5l19993vfZUEUfL46P/vkk8/OTy6XC3blciX3g/v32UcNpXNClxvXIHfO0GL3ZtxZGIgqJEd1qeRs1WRm4SkYGCdFC5RRlpgst3RjJT8sBSH4bHtWADQFqQdcQGEbjM9029BU67DwhQUDlHoNY0UUOVL9s6ewlnXV6FxsWe2N0bL6ZUoPP8iLsshqXbSvr0XnXG0yK8vCdMBhEis33OgeUSLxWDxw5UVtTsWL2Qc3drn0fDD6GixQKK0FLEaZddIWHOcFaTkporJB+WC0NHrgG2awkQHKjYVDGWg8Y+Gs8BYzHGzYZfXd3PZ7TvV0zgK5Y4shmFD00vPIAEplSHMTINjNwNXYMi5IPBsHTIgi24geMuEXigdemGaE4cEOkCkHZQ7gwK88+Fz8L6HRzhJPO0Jd+I63RMGh3SRB8F4AcEAaQRzsir4paCkt2li0Dxy/fhmJMP+HUfmtb6SqwOVbQMFb8+IuzJIud/M2YRVc4PqmFQpLffHr7gqqJlJ3iOPHXYQSruCKwO7CJ4R4Qi1X/RuEChr1GoBCYImwXWQ9coKq/PxABrQq+J35XKK2T8k/VJZ37gaUG/wWrUL9O9+LdY4ylK+yyRg13FChgqLVsVj2/FE30M/ErK/iJ6FoRTH0Yi0HOgFE10FRM6iw1EdvAq4u3sGfK6yswvM1+6cSv0KY3wobOgL5i/Gy810BmFE7/RMWQbwBlR6EQITpj+aq3+N+2gCBCmFKDsnwVthezWWAFnOH71yCRRIL8vI9imKz9yvZtgiWWgFtCiabzinC7QACvv1prvgCt9XkPuVn3fqKBBhKBn81TeBciOEbHzY9dJSxF1lGZc+cIutaaCSWNIOhhVxxAB6H4A2PmIryhQKmVadCmnNgIQYOP4ZZSXpOnJgIrbStYQCJsU9C1roIFsuvbHNJFC/Kw0/+1+/ht5RQVi9xJRaB0Qh/4IlXSZIo1atyLVBKBtvFByWx3/1AcOJHXpWCSW8y4afoc8aIiALLoFh5db9czq4RECxkA4R+a4hZsdnGt/Xm/PQcDjBtAIWkp4RJkdCr+tGJggixtThEve79p48PRvvqIRzAbQo+CJtco9Ux2279yVe8L9tXHbpqgIlDSXfk2jPAXDQsj+nn8l9m87s0HIeC7fZWM4+jV17aNX0tXTEulh6uF73hpjecs1no2fkVxhQCWP8R/mhWW03Ksg1CQhCI/iwoKjT/qHKBKO9UbKHzhsb7Hkzi8PIclSEkV7NNbae99fyLPo2K8ISAzjV+NEkYvT8+OmZjQQRuNaZPgOo4p6LZPLacp3A118/Mj9En0Y0QN4zir1lK2unTOqWCxMlkNwwWEFC+UDyi03eESGaN5cNmayzHWleNxhE79283bPyB64YQZ8y+b/UWbNqzXJ7jAg5GEO/aOAiWvE6LntBUkdITPQUFFTmlm3nGdBLTvqXg4AVSQ+uF6wvayUefFa16lERWa/qgl6F/0aP9c59+KpYtUPfbSYB/jJfMbA0bhKQ22a6/syJZFO5c5TzUsnLGphWyEGljwKV0Orhf7TuJoQ51M2K4iJ/gi5qkHNEBJJRZY3r22pYoMNX8/nbWbe5NWf+CgUJW8IbZJ+3mAd5va3HYXOw3Gmd6/4wPuzkbbZkFe9IzCaHf4eA/CvIx0mHWL7N61R7nsmIe0QGcYCTOohpkjdOBKgIepLQAocYSD57FmKOiiKZqfxZCQklFxOqRzO8yzom/9EjCOm8ltsQBhrDQHDwtR8lUZs1RazZtzOdMzsHCOjMtxdeZe8TGk7MF3GidvHn7+P4P1/MDPGJ8oNnNhMG27qC55viXzTHeJJNbyJCtpaz7dcGA/SBn/S4fPnrw6sUrdgnrPXr06uUrfFCbhez+uLf39H1nwtBOwJ11D37OUaP2YnYZpU553GeTqs5osrc/ZIswqxS1EEaz6RfOfU6RY7KPKhehxnyQNcN4NqWZ188CGZWPWUCcvcJEfIDisW4GrVG36enAri6w0dzqc67tYnV6Rt9z5/LiYsABVwPmQ3PQ1d5v/PA3KZtUOlzWHgonWsStYm6UCLOR0rnTqyLC9uZZaz0cHTEP5nI9fUixb2zfFkwt4PYxK6OA4EnQwuGqXpAjcbjUDMwajR8nDvZ6/YcPbq5vpM8KdnFx9rbT2V+ur//lf/Mn/5//+r8e0cRil6/V4Mmjp2wAWhhuk2lz2u93ObuRqUESBEUxw4UGs6jZmWdxIRLBRiAvyitT0FlETE8Wvgbj6gxXgpvWHAXWCGIwDWGCAi02bHb7tD9az7BGKw1y7HNMvcTyN2cimOzFzV7dZ4B022DkAbT6DNSQD6bDWfw276daGOpZzAj52Nx9FM+fJfX6xFiZ9eqxuqAphwz2qMUoYcsZBnjO6Gq7cdBYj7ebQwTKGBJKznL8JSeaMd2ILDmEAksfx1qK/e9FTtBe3AGVIEOE/NBt0Xe7X5SSgpSpv4lv20cNxCRq0u3FkScWaTCkApEK6xRhiergJTXpdv4ethBXHUOuW4LngFzsjSKOalwEZImNH0L+KgQXHC+PeSevYg8loPuCyq41v0+WaXbxEWg+W13FQyxIcYfDMkGB8zFXxYDq7c4PQHaXAHcvPHztG18TUuLkud7pP5Ghq7rywE2uiKePVAYG7D6VqJaMEpT7LscgLw2A4E6sWFEkNJONFaYlelLezTn5oaDGKlHK3RCBEcw9YAI1aRPT1wKOe3kxKU8lXfVRQGJUsAzwJLxNHpCJna8mUB3DA7O2/acnpnGkw9LPUEphYzE6nGKYTIWjE1aVpE4krf15qKbd20lFICVFFTR1lVd5KiQUxAsmoluwNZkJsb1uZOnwqh8dbcqD8QVrC5245A5ncJbsLARv7Ky9qhRzoklRkpGAJFY4GlcMhb4COTDzWDeBeXFs/UsuMyohkqjKtBYya5WjW1k7aK5M2c6QItpLC4AzDufTqVUF00rBlnLlEaRdNzQMDWIHCthRyihbC1PCuu3F3IFv6Cc3TTMPJFTUbIzFSYdbDhO0VGSZrC5L5AzO7lsPcx2qpB4Nnutp3F8b5XBcJmghbJmAXxpOmB1YafNAXHJV7MhrEcztN54qDSnFoKTY3cmF7wVOiFMe5QLBXTQeijoahEyljbsJEyn6kMAULftgbLdwMY92ylGC+A59umroP0HxqhypzM7eMqX1+uzkAo9IXsNVephspMUdJIRelU5rRP8hdTBm0q4SuC9iQZoXtJkwMktfCXzXTQQN3Vxkx9yexYxd/ICFmKaeAuaLEGjg0dU0HOxR1czYnRC+km/aHmG+BYHyMp44ulramahGyRpdCkswp6SjUkkTlEzEBKz8qK5Kq5hGtwmOfsi2IhVLE3wzepTVL5YxvrN4lwOVGJlm2tfQgsMkMv1dlJksXd2Fz+4CAToFq1UEjshrzFNARZRr5SDSltnn4JBvcMW2IqupIQZyAbCZooI9F7ux4wqNmXQuMawB+mTPnT/qWIsE6mjjzv6hDdOsmafNt2zW6cQ9eu8g3pJD7XFzDTS+qicULvZ2BHtHBKSZpjZxaPfSVKCMohUQhijlue1te6Ao6RZ2jQ/52uzhTChi2zUVD5MxB+jHnyhtQhHMXsxwUaaHsWGCxPte3UuYr7K6aFIVT2WqwvgSCKTkqh75nNdCF7gQrmkUKWOho3QG05SymYN7OV2ddzvXzPpnygnjTWqFzMGSzUnX7p22V7MtZx44IkkLgZYDX3GB7mHROs37LFTPnE0LBUOh0I2jr8fAEJTDAHCprz9gOVH4wY67WOlE6TKAFv8J0eWKLKW5ZhAMN2Wjzfik3oTUeSc370krsWLl0kkoQBCIQ71HLenItJ3mPrz2s56dnu3v78MDvjLOxkpTLCs7yj96wGTuOW3XUb83GDLvnO4PzCqTZhjbwaZxLFe2M1J10UvmB3GIH+7LGWkJYhgQ+IwAkBF40uDEnF+cnTO1hnE8eqNJZCnYthhDAFyZclYGYJlcxN5itBPUJXjnBkKZuQMgBaE+QlzMCu6eviTsxfunqmIG02QypxgyjEhHtXViY3Pv0eHjZ/dJRffBycmbo4N7NBrRa+JjJ3i4urzaZ4JJt8fxgpwPgEJTKlAI+QxHFUd1+RbVyleSiwf0ym2/yY6QzPh3lyaLEGjlL1cMuom2JVpokTdp8lYBJfidi2Jpx8VyOZmwqoSKh9pvPma9tXXiZnw9efLkw6MH93/x6S+pRVdrtv15xESsg/1DD1+jsW83BGxmwwurKkwRyiA+5Cq2RfvyBJfTrBIb9axgSCNZbJ0SY7c0VQOKy+CQSxGIYQil2pKDhSYDiwfjv2whjU2mJE0XN5gDsoYFJTLk4egzhZ1JoxiMTv+q1b3EhjkS1WC6DorqMI7T9LUQ4kZFJHNFizvGGnCymEYQn9EOydHe0SSAwxJALoiaAs4kMQ0fpQ7ydLDdeAruYS/lpsUw5Bpfzis7eUTWkUwQKIxS5xyM4YreYBSTgmB2rLJgZ315Cixw7A4Lg8HGiLIVtFXdRCEMlNKE5Ml8MS7YUwxTCoZxCfcdRkhpcvMzSAVRExmHD+EwUZCEH40qDkZObSdoqoPYl4JL0omE2ikC8FMelLQBcOdm5nwJDr8myp3Yt1HvBO4AmwtX/V7exJ3AEOM3C0oVC70s0YlZ2Xm/VAAqYCU234lb1Po2yi6rJKvCE4nENACScUmUPOFcHTNYmYW85lRmw8lCk5oobS2UYb6peBUY1gbATmZvSwYf+atAJ1m5lZAkrT+jM8o7gqDsoSBUQpQTpKOwDVdrzImnACeIriRDLMCqHbF1FMSRsoHm65uqvbn4zN9O2ISalmv5jFuTdrOvFCfzSh76Ls4OBESBIWQAmoXVWIGgc0KQ0/fIsdl5obJZgQnbKFY/8jFEBB/UW/4vMxEowd1XqQNVegqnFYfmG7rIiS4mmx8gYdPWIgoCsIKa51US6/mUB/NSr9FsNZ8om81NEjIxA7uDSQgL8hwYIhZyAFD6wJilJ5FgorRBlSaIR5DEBkh8o903X+yBjCoyMZ7ZkZeaAD4bHCC3m7BogvstEwkhppc4S6DvdVj9C+Svz+wP5CQs0W+TBUJEVOQk7CqiUQtMQ+QmFztQ+Vs0x+YXfddUI8wZvbm4xq/O7ml8p+PWQXPSYTJ/9m///PWLVwzykjZM5mwreh+RuZq3br6gmmfAZnIzxtVjKJw6QWuanGQX6CM52QTfrLkdh2VGJvMRmFQNA9tr9o/oDFgcxhk9+0dHe73MqmJiNg0/XFag0rGPe9FtPTkY7i+Xv0QUdGNr0AUu4OvLq83qqN05YO3c9dWVwSqgq5nVOT1o/qLAamXEYi8yqUthQR1sEQVPUkc6crDwML+SC91KDmXlHxKHieikI8geXccRVyyVtqLInyqDGjiZYYO7Cfm1RMCqIEE8oHVeKh2VVwYT0mzDbV5twJALFS0ZMbHmeHvZab5obu+t+5+35x+1218yO5YNpx01ssDy/GK9/HDd+aqx+Gjd/XI2+3C8/by9/V6n9YpBEpq5rMWVUpoqlERqxg3TDCi40I3MsTvKeL1h5g/NAE5vsG3BqAwOGRNYrXTsw6ZXW+8CFthToAgrW0SNuFyOnZ7RPaOd3tgeUW6cfGKs4lqlC0oqgYOCccETwOaqf325szMJEXZf5CAvdsPvAgsEJVJfik8NSDLKYXQPdB8m7Ut8Gh5MwJ4qrhM6Pmgfzdo3nEtq/zEjR6DL4OuGFhj/Hm/WzA+8cXV4KxYJBYYvvVfL/mzT+QFeZLN5BEkCcy1jESOeJlZUbjPQmZ5TzXwsg6pDNDmnQt1RDM/3DYFCUQ1DQhSSgM4bCOOLV/u1HMibymS4r9ZZJRUZ84EqoYfjTp+Ls5CHw954csMMH5Ha6lBSzClguJh0259e/XR4cHNzzTRuOs/3FidnaMaMyoaWw9zBLlv+Wlr68bUb3b1rXPabk8HR0YdPHk9++fMprXf3TqCvE591w7b0m729DvtXujEABYPDBLAqWId4r4qlcw4vUBs8yVh4e7JoEniSKqVqNTGz7aEbN7UnUkfhZXFwCOQZLbRHlYY/A7WeJo4f3KO7GmdzMlmfvD1/cDyiiX6w/4AagDbPxdlrVr3DSHYMZv0Dji10PWv+/nb1iPHt6Ex4KzfJ4+51y+E6VG6H8YwJv+kOb7qdvcPjw+0h+0cyerQ/GFj1wLMqXiUqkkg3120GqkOMi0H2ZtPlQT8XgyZaLGwrmwpxjtaw95Mf/+RXn7x4TYPm7Vs6DHQUts3vf/87x/f2MZLEZFMjBnD69Eqs2axpMNgbmLulOoUjOSegrEygun4lDQU3ccLyaNuAjFVn2Adps08abUiGVIFB913wh3K8ctoXZEunAc3iZ0we3BucU7NrErEwwuTB+PTF88ciGbJqro9bmwesn/GZhjE9mxs6gHD/p/JADOAZgzsUMSwMpQmNIAxBU5xMw0nzaUvTbYciODpKlxW1seEbDoxnbv1Vo3XfkhvK7KoQF/SYHwE5tYLosQvwJ4hqAQvStUVTFuYgGVJT6rugSOPW4dPUAzQylAKI8QkPxCmopeEUP4FQPJfN4j3rPeWgnsvVIOCTOZDUDkSKLPUj0f2eEkEakKgYSRwaBlQKhpivNeDiPbq1OA4HI0y+RgeYCEsXcgheKiH0Ad/6CpziURnTSOVmqttLIKUQiF8wrH7KewJvb98IDBJyxTi7r3nwUz6L4e2FZAk3CBrMO/cSs8Sqvpe0RiM25gFuvJPFDmoi5hsQEwrMeg1A9LjAvb2rsBVyity3kk4o5Z0ws82XZOAt3DZxAPjRq/rJY8Ak9G7wLQcUEOJDpqiBHj/KLmk72lBLSyaXiRQ0tTg8U13TIxVByzquHQKimpCEgp/C96uPuw+J46v/+Y7bkSJCJFRZNtffKsBkjCUWIQLQJmvbpCwayKMZmZMPBQWxJ7alAfVTqy3fqLpRSC5JlAeb+3adJUuB2JeZRgJF1+ywOoIlPuGRYko4tokpmCajBBEM59hEUrMhEaYltQ/CCEaAkHt81gW0kMkcYvqdWIV2fSVw9lQmCy4XuZutUIHpOAj4YwxLMeXFTO2FKByWLimX9nCf+KKQy8DyRDQeqpcSVMe4fbuNXsICp9yq3JKNYHZR35U04eRfINtDK1INdv1bLBjAZeuPAetsscYaO61EY3ozZnoua0Un1zYelIT22GmRJAeYlXC38/Dho+P7x/gF8jN0x5YJHjgVwX4yb/iN8SIatY2qziK63hB3wVO0uvPx5IrZFMSk24bNQ1acLMt4qz6kotE+oiTWQ8VcSwpYKSNLAL6y8uNrlqXGJpoVXi1jyiiG0S1VCEU94tdnqAIxNDHY+0g0cU2C5BGqCPGbaQqZqCMu1nx+DZOYBqRiOj5LNz8bXIAzA3cgjmNtxsK8vcRWHAJYmCLOVXJVbcwexLPsgtk6e83pk21zn50lFvuL1gGdpEyn3q4Hm8aQM1i3jYG97032nhutt2xd12P952y1P2486K2GN9PuceuIbS77vS/mU6shucbeFAv7sfARaQOwqTtyL7VIspcdaD4NZAZpCEfUtG6woBEfZVSeoy1rjt90txmUgWgIAAFy0APaRcuIycHIllC6i4eYFkxH6j5X2lky/vLrLsPkiO9BnWdFVrM0cCoR7aD6nmhyMn9hNjOMnVsYDXIyyXLYvsLb7W5GbHEP/igLKFpT0sygH21zsuzeW7pfLNLQsGCTcCIa66NG83DZPIZuJ2fhslgexEhpihEqao7ou9klqHwU8VxmIlnGrtMF5eq7P0aQWMktQLyrrLvL5AaWsKJUKhcqpZqhq5QLdtwlC34XC9rqnF87ODg4vDr/khbq4dHhs/ff+9WnnzHr4+GTR7G07Oi/HB30af7NFyvkhq+M0ww4MkG++iGNLiJ9+fwK736ynMEZjDBNAoaZEoHDQDAaI9YWYyUstgHCYAAjvTQhkgsd2wzrwVkwYxYPu2fa7McqqJZsLbC0qUaOpfqIRrmXF2ac7gM40/Z0OcZmV8xNRETbJSu9MBTbx0/usS/wZjVHkOTOSRSnJ28XHDhg3yon5zIcwUx33KnmaJ+Ty8O4wuPwEklDXmEnARb2VFSRRd6VlqKJVJos9IkXiyrYCYJzzDcIsVYKpCIqHgV/51IBIkuFrIjtK3HeaYwzH4tBo2NwPu18/3u/+d/8qz+7uDi31u+09g5GzHJ5/PjJYNhn3JSMOFNhOGQSGgcyYlRzILHC50vJOXQkG3ITyE5nQitMRUziKMMVCvjr+mtraW8RYh8AtoISknF6p6tTI9h3wlkZnu2Fyw5rJFp7rOyQJjP7B24TjJ3uXG7a5wxmyjgW7PrE9pQmsYuEmywtGpwXnmU6IfwHN7Du8iNFZLAdyEC+Ac2pRDB9H1XBxQgR1MLUF9h+ymZKLxH1rBSAhTzJSAQo4BJI3pg4H8SdGBg7K37AhInocEZ4iEFAlQjW4MdDM6be2KHZBAzahJ+AlW9FEFRHEA9TiCgWic6wuTkKkBDg+OxDm54auB90ZJlNQtOQf/ogbdxAD0wCgVRwWGnEpObQtmfKNPHJH1nDEuvQfDTQV+By5ebD7eXnwtbqY3m5jfDXeBLfXHfgl0dRugPAzHyt4otb3m7j8FQDU+ApM4QYVmIrrnLxa7rq/7s5GZg5an73pb7uJCKo+hKI5VkwEZCsTKLyVqevzySTZE6ONHhDrVxdJUX9VgcSuuUIPBJkpV0kGtUr3Zboh29p4iRJohbl4E6hw+lxQYsahJjZTespAfQfV+gr31syC713qGb0N/2OiQYXSSVG3hg1yxgUybV6oJE2SYqz+CIBC6Q1QB7KK/6BW+yAjayqZKTm8YzW0a7Jb0Dj+TnBSa9cuk2hemoxmVdrFevMWQhAXwmPFNVclFoBFFksn6lGrgQgPxrelja+FJtrhsa1m4hYeCGOMmbLTnwaHH6hUdzAM8baEgKYgOIm0t7tgtAYiiJwDCeOPWHOUyecEHkn30ryDr3aNMf1MMJRfnjIZYjxysvulyDgJNCnxt1dcv1WJzetr0YKtuFE0hEKcN79T3xYSvhtwirSO3FtoqQXp/H2/M/Gs0tW9pFiNDpsO7uAAX0OWWm/ff367QvOpHSSlTPyMaMQ3T6hm4vKAQGOevtPnj7ZPzzgGXsFP8VCPIr2lkFwtkkxzGA9K/5YiofJw+Ahl1W2DnLGLkdoIanMsGwwCI4WTjipijYxikCroHnCIcfUbAEGUiqt/JCxOKZX0ENNNJmRhI5u8lMym8UBgkd7KB0iF6XiAR+dGpPpKNhNDG2iE4vZ1Y6MNdiLAHaEnQSa0Ksiw9qjXELbfvEZ+3F/whZDjEK0miyVXo7Hl1RCbIeE3kAj2AcZa55aiW6lU2RXvxd9KW/FSQ6ZK5bRPT7e/9MBSwj2/2Lemjc7N93NpLF32XAXmgVnDsCt7Xay7tzQA9tkrz1mrgz+Yrq+2qd3qfGrTv/jk81ze/VY3N7aX9GlTTI8N2Zf2ABjgyAaY6k+3Gedbn68OKoQ0s7T+koFAjWUBKcJQR8hUCTT4CCeHJLiaCpozWawzGWEWl0InYjV/XbzYbN5Y1WHtAAjN+GnhagwdsfS6uH2R274P7c83H6r01blTJl5eoNjCBiPyE0NsTpvv3FLPY4ZZSjM4YyiVq1H7b2PW/dW66+uZuezzfvbvZPJ8v6893a5fNJpXPfn+50t/dlDfcfmPCxy21ymE6PBGw7C6/RQLbmjMejRrhIyGMApp6/wYHtLSlN2CdAoqZvxDp2cZqz6IubuXcwLgUBU+YSTrypNHirNrAKJYUy/iY2i4bi32RTTyj74JEcBhkNaOtSD2EYK3YDS9Xu/9yPc1uvJDS77Dcf5js9vxjcHI1Y6dt+ens/Gi0OczQPWcaIPaIj76cCH1YZJkbPe6Hq5Pu0uDnC2aCTgW2Ok3fYHx7DduTi7wJXHPpBkOpv32QuyAQ+lA8VKU596RJ2iRQBXccfp/GYqCfisPI2hue6Mm+w6kAaHE6ukjO3jUTY2eekQmVRXl2d6P53rfhe3nmlNe6g0EmLWIJN8dPTBGezbmCP7kzkbjxLdY4Mu3Mnh1dZNaXgWLeGjNYrQq7BfZotyPtwVT0SSPik/aaO4UPtyN4mAeCsQBCJogvwXWswkNYwFyVqP/ajYl2pJhwIouZa32d2jNpuNpxdX5+wLxAjDYjpihx8GCX7/9/+AuTRwmDW4SPPo4D4GlpWrqCC7KWCPS4YiQM6oRHL33nldCAy5IkPlGqREL8euZ6MwalVOemF6HMd0SY7UYNDSsCem5gIP5PCBHWNs+EQj0wE/bZ+uSdiDNs4pIhw1kS6RYwYBtg18D9YDvMfGDs3uhP4BtElMFIIWhpECmEJeDgI48kaVwVfrNTcPxX64DyZKwRo/iuIeGseIBd5ws3XZ6swZNWLev50X9rhnRiuVjm4Il50QpMUEJUfxlw41RDFxFUcCOeI+FJxSmKhepB4+E8i93RwBp8F6J0o2O/TjwOAV8IGWElE3NGxAAFpkO7FVc+xOlbrYPUjA7n5Eqkb7FEd+05hQ6GQg5lf7CoR0H6zft9uhi00jvYfZ4eoBGvaDOb+YNxAQTu5EgkCiKfZMSRAPSOfoNnteRCvyJF481eK1Sk99kVDsFfrdi5By3YYXjyUzF3ZfqzjKSxS4YGwJjM2vH/kVSy7uREwkQmzskYzA2mgqHKLJUkCWT6EDyd7iImMCxkAT+M105VYaAHk3zCvfjehL+bIDVwWrFDUeKd95J7K0GbnkZfl59/r6+92vgUgEqVEVbaEiH11fZ82XsSEgFqjc414JoUAlPilVbv1z9ZuWQyLX5OW3kGA+O1ji7SWcO7wzJv81sobyDD66LDyrZHpcRcMAQClVvcCSvFE1FJUmC8egAEHnILCTQph0GIsZT8DgK+WbOlPxmD6xjQYvUE5MjugCPFM4JBs9xzg6k8dGgiDiQFCWLKEoFJbXTuKCFBlJIpGoVApHEj1rGywokEUOxTyFBclPPLJGyHIIeil3Um9NarEFrGTJHfLnM+hQ2jRrYB/+AsK+UufhykMRkeo8mpT/33rVSn4bw5y4qhTC8KUGINz6xQ9mxtcQm4hV/PwEULkFQhEF5sAZtF99/tUnn/z8+NE9egvYqpk9JPYPR5Czmi1a/b2byTUj6+gCeoCvQC+TFUKzOxr0j+/fPz4+op9JdsBMPSzoFbPC2YqCmnhekYiF3/aqYgcDUmouOQXSHkGFxUJSugxFkfk0ncHi+orlg+DJV/JA+qJSMig8gCSEY89I3FA2bHNmkJ6sfAEp/H7WczLdiCrBkQd0oerFIY7mOgYUEMpTNvPfu/INjyPJBNcsj1yhgQvnvjMc7T98+P7sxXOqgPH1JStUxuPJbHK132crRCy84klpTfEJ8Iij5tBOWAn1e9EHH6wy4Euz+2U2mJ50LDrs7kG1QdsFqgcoLesGMR22f/BtWEAsZzwFub88pneu23447z2Z3jy5mFE+b4icg5uQxYDRALYZOT7aZx0Nq3RZzweeUAUj4DL8gD4EFX2Hp8CV1wqAEg0/tT8ugYYPaILoe7qzO0DSE8r5YA6FhVlwXV5jNwgp69505vgY/TDlX3YZ8xuXAhJPPvLjn3V83hPXb2RuhZhCjCjMnYNHGQTQdBGXLpNNd/MVs4D2Z4cjW1CsBOB4rMFiMGLWAnOhuzS40NvWgvk86iw8h3yaQI2HbC+53uLaFglTM+G1FExSFnkOCpXWVLgq2lqjomK8v0NeeTG0hhJqhFXFA64FmQD+ExZ5J1LCQ3TJmow0a8a0wxsRzKZ0xKr3DOAxuMYq8Ouba1r7bOf/h3/jD/cP9umk/dd/9C+++ooGsMXt4uJqMVg+/+rFD3/r4+EeJyd2beXJeWTORBEWnTJ36Orp0w8vz69LaaIpqP/Cym+c8V53fDNmmYF1gjoDVW6QomXGd1tRMjW2FH8oAhiyWtw4kou1p7CCp6lCLPFtYsEVqxj0ivbGglXAF2xTcH7JIgNQspO6iWfvpDuWdEMl+VKEyNck2DEWIZATcFBnujo4d3DEcBnZVtwNb8PLwlDzTuygXlhZfY70+EzK+LvhMuTJXZTEShP2m1twNl4EVgAaZgqrS2Nq04i+vrmaguR6Os1+Lx32P/YALM6l3tv/f//n/yVtGehgtZVjbsvFwYgN9BQGDOSXIVjkgXdO+4jhGgoy1se6DIKTF6gVOsy4XAkvClVYoM4wrYnBIFdQM8N/yQorxoJAEhliG/BD4Rrw2zQsdSrpENgQm2YbTU3WbyNMooGPCPC5MWi3RzaG6XroXm1aF1neyJcpjoD7FLsrMXhYNVtYwVKbw5tltFgceQha1s3WOMUDWa/pq2KXDoXJCATYNbdDpzdSSN2tlk9+NH50AOH6p4VK6a/kTl6OMZOGLHVLSvFgbJtBVmaqtlB7dL14LMqU9rMNM1cj4FGylJw2JctswIotZTtsgqfHwra5IOfIMxNWdSb4TloQ4mux8GWwNEuIsJkMoNDJ1bMYsPrRXgO6KqwWwWe7ZLoU+12z3wmgYazsEuGwiVdEQw7qWpEihOsW5kWi/Zd8CQLPMNO4v/5SsTRWyiSxDPhrXCS5jV8AJFXC/bKLUAELGoqiUKO9FsV8zVO0l3fFKPAdJAuu6AWzOkmi1DiEUkKS0tRuZ8EldP+z/w8/neeBQ9BtPGOZrIRwR/CoZJC1BYpEEYupw/oC0Hu1v7tPf/mFLsyAX2hAVSIglhWy0QJ5URPjJzEZjgLGFFI0g+qWbjloVjO4i4OuphOX3Xyj8xaXrhAcLMEZfAr+tFPf462e8V8QC7ZVBGNCkSpK84Nna9JUaUyJzYQN0qhAxNcMuyc0rg9VIQixsUMG9WAHA65ASKkDitSVS5+tuXiC77HdfkkWoEXtCUSfoYVnZOBcDnKnMwAI3BSWvafInI+YBUNlOuVivX0RneFdHDDBmTEt0aBOdqRVNfhFtfjmHHdMQz+EUHfba6cG2biI1bbJHZBaAUNNipCpQqie+KYCMuP0mRVT/yUfIZErEcWKJJbEUvACyq+iw9+dy81FATg3yP5mnF3mYvIifb6Sj1dJxYsPtyB46j4XGc4KCPwdCoZwsRZFrhCvJKrA8cVUIQyLxu6QTNv487/4s/PzC9dTrzZ/+x/83e9/7zceP35MF9Ppy9cvPr358z/6cyd6YvrxEdigx2MOWYe9YePwR08eaUoBKf+BqlCwk8kXjMiKUNS45FlFSiGiVgAkKHrgKAuCOcEG1OjMg1dsZT2dsKKfedPLizdv6NtimykIYA9shYFaro8VW/sc6jSR5q+x4wVVsVlDnxjKYFe3KkjPSrt/SS8Vhpg3mx1UZIBA72hMyu6sDwOQ5RtX+yVcMxzI5eJXflbsLDzlc3P9PufvDI6vjo72f/hbP1iup8vJen+0N1vcnF+zKq63XLO/ONvsoD+k1psJN2q5qDfmA1xhmivZ88qj+p8gEjOmz5mr77fah9v1K/fHYqmuTuc10dbNCR7stnHlwtbWia33tsPitnm2g27/Rds94H9x3Jw8XY3nA/ie/eM2U9bPpcsMPiC3ISs88XvZ0CtZgwOFHi5j6LAzlo+gSMUJV6grGVGhSGQ01cIHTsz9tdsCw4XVQg64DrAezwhBS0r7rN3Zj+dHjSplmfuODr/v17IKwqdvv+RR4VR9/5Z4pSDyoawRIqZFgP988BtOhgtdXOPOocWoCEZHjR42n/bX3+90fpJByi87c4zqL10m0JzqyCA/ZqFxILW9+3CCLjT6jReb7g2e8bLDHqjsU2Y9Xaxx5Adg7HYpzjWmISBqRAg8oHSwLQ88Vta8ePNeLl+DvuW1aGKtJUaA55ZjryT02ZzLBZ4oUsCh3czU6c1Z5a80bQNQpBabBXuXXl1f4TevLs4vrq4eP3u6YRkLLbrW+u///b/LzPL/1//t/87uZ7M1u9k+QHZnl5ecE/z40X126Cd3vBR2iaVecmOh1YKe6dHegA24nj7ZAyX63XXJmMZTXNvQYDUi5k68YX4m2kY1kCIK1mybyylslMQm7vty4sJQeKTqyXTT8QCXEFw6yBQL3qMK2W72h7QcaNpZkJ1AP50jC/KRd4hFXiF91JXHGHylw0c8ZoZqU9ek3UsIyFcyWj2Rp+zPQ0z+JbE/XAnxqzwXQwgTXd7Ke37Iy6hqoP/8aAg7azzhTh+8EUJgdrXCmDL0MaWDH8QpfeBBTzwY0kKnVP3rn/8z3Ot+/6DfpZeEcbb13/47fx8/FLvCagG3cMUa0npjD6JN5/7xIdv+QrIuhPqDKqowQUkUCyZ3HgyQOfmEL/r06eMHDynR616vd3DoYhi+AkeOU0GTBzkxkcs2cbPf32OIAFmzF2wAqfkYBh0SqggwQ/YryhvjsfuNzREDlZHpBGVEUrrpljf8ZhYV4VQwjsN6dzwiCkrpQQgbMaNqBEYf3xc1YNMnRwCwdUyLbDC6yKAurkSbPdDwKqitPOAae4XbtF09od+KfnoqHgSFgbLERT7U/ZvZYxBu99/AoJinMIbM7ZhiM4av2EakPX2qqsgEdEn3oNmxTDVa8UN8V02x9dgHh8d0QUQ+Jh3OydtkabEGBRQmglmwfEvHLd0oxLbhhxMB56iw9EgE1Oi/IjUVJw1jKm5iQLcuo/0vtnrhM7eqmSO3Si8qSpVwpQ92MBDx+ahGij0BrL7w5esXuRaC+HC7LvFbIlZfkz4QffKBzil+aOYFvMCSullOQNL/oZp/6r37QuRBTMygmUcB+IkXTrnh0TGrEojX9MSnDitITcSt+kBtgqp75kYJKEWP58CJ72elVSRfkb2jXjjfepXoZKQ0dO9KOSGTpJWVPiQPc/q1gN6FLlgSKd1gSzJKEN0WGEg7ySg4+L707Vk86LsCczTZqoViyTPlEL+XCzTSgcIvGiKsQlMFVxbtUCoPibPDRiTQOD4Zrqkkd3U3qIVYa/m88jkg0Cr0VA7Q5cA3LkZedanhkeNWoEIc9DJwcS856YldPHEIKCHQY48FyokiY39TKC0OqCmjzPTfUD4Ab1YWE8o95oE5/baTnclK3tQuwOeyJPGPP4oRl4zT48IHNH94hennCa/QFgu4QYO+u3EtP2VKqlMdsRO4aRTBdGdaYu0Ss56SfLZlM8EyTYgeh6rKAPMXTZ+xiASCRggJ8unZ8Gl3lZfCsgSqBZWvAPRCtNDqFLep8zlfkjwfvOUh1Zh48k4A/ysIkZhw8671MUcr5ubp2fnz5y8Rzv4h5//s/ff/3X/8P/j3/r3e0M6Mf/Mv/uj07UuqI77idAJYDrOtEtvLIUtqb3ZV0pRKLPGBiZKUrHkj05gPsdBWpSSCGr1HQMK/pDWniRJJNIiV08Rq6ti6WZRr4KZU4+zzLTkYOOmCTVoH0QcVfsnWMD44whP9ATK4KZJgAEbkCfwyAkBLOeh6bBnagNMcPdTNA1AtBXGShCgej+FveOxLSIWstDfIjL4jZi9PJmeT8er+AROp6AI6GPQPNptrFpu+fPny4+99TC8pO4+QFrx1WcwhcpAmIcs4c/WpviiSNoDTc7ZuDn7VarLUb5bW5VCirZIpRIGGIMDH+DSo0vKhlqRDGlOLJ7Tttdbz/ebvbucnzc4v2UZmvWWaEDZlxALw86s3H7aeEA1XGGONuFRpu+fd1wUlsXHtro5qNk0mqxuEx4a/VEbW7qKSj05/VliZJhvZgD4OtI4g2kCdhApZMZe+NnwJGXFLMJCkt6Y/vwaUGO/E+5aYVTLFDkvgqglKBgIBMZwLg9gpHFeDhY1IOKzqtD5vtx+AHVqgtrLvKsZWIGyfhM5TZbJ3Kto6h3LmZ9gpQ620eshA1bJFc4vaO7nBuuhNiEimAqnQqPDLe6KFQ3m9+ynP4ukF0wAIkPIWkHmE33Ucck6sHSSjy1mZwIUrmZJGJEso1pGBvqP7x4yzXY/HjT37F+fLMV1IrP8d7g0p7WxA+fTJ0//ev/8//JM//cmvPv0UU8k+MxcXv+IYJzxL1IyJXjTU8UO0dxye0u2fvDndY4Bg4CpfNsBB5gjemT9gwURv+gXA2BY5l03IFGD0ym6sWGuLgT0N+pAsOmcej0cXm6IixZTAoGLiv+GIhblui9n19JrJduxXlK8bPNGn7z/h2GHOAkhhoz6iAg2UmOs8lxFFRx6i21QTsEbGpTgWacpR/rz8VLK3clHfCUsICUjoa6IYLTECTHAiGxHlWYgElWcfE5BEGlimX9GYcQIV7Wn6XIQJB1onb0++ePGKHqxUl4xsbI6ODkej/cnNpH/QQ2owjgRs4oZPTgE92B/xw9oA+6o0j+koEUkNZTBPnmAjMhJDtAQpJvZMZndUKsyQRQqZk++qulyl5QdhHP+HGOwp0LxhUZ9+8JiVx8ZWOGyzYJ8LxaLbHjnfkj7x7vW2dYkbEPZNbCG4kBc9ElGVhQTxWbVPPOuHBDeRpDHDR2cZeKiLvT/9FEZqA5wKNj4myYgNiqirMe4sX9Flo7/C1lTqKmyTXU+kB2ZVbDFNUESoHFDfHPgiBpyyjsRHXWdB9typ2kiDuDR+0Kn51C48MKZaBBzCwp1hYKbbpRBhTTC6eGjwTdjAIw/yhW2abowGm+HSZPXANasRuM0ncGIG7JJDquV5rKmQwUcY5u2qsHS0wYOQgsypL7VbJI4LhMDkGVGhm9zsL5atxrFVJAMlUNkQz79vv4gA4vn2zSiElE/fntYMypdasxJS8qq+VDFgilrpfzKs8aozTmANqQAlXf5ZjkII6ZRqnWUF/lsRw42uaDFtjz1w6nGA0sq5kyjxuJFdwapoSNgbKMnHCGFhfRe+hADJ/3nJ7zduljUDQ4apilq31/TW2+ZD3mokhlampMwoZGRiH6YatXpmzA5TGM0LHbFjmzg1JwI9zCrUFbwW2WmecwBKMvO33DmIBpDOsoeGLB8hkG37REh23aiOXutHxG52TtBmD+BCeaFB3B26QlfRQBNyS17shSjuTMLmpKTtqYEWYPYvBHs3BqMA2wFgAaUd72RNvtK9T+eh/EixpArD9wfZ+NaKmhfmMfgrqfj6kNziSAKegWCwbgvlN96M7IMCzCDuLIOGlG8qJKJS1Nf0OOEAsh8pYKHGHNccAmA7AVxcwUb384pFZng/2BLK0HMp06JKDHygCaGopRne+6BQDCkKGr55SyC/9PwB1KuE7O4mkn1cVV9+9DPxDKyTNZYfVgBuE/iZc2END2YFVp0k0YsIyU2r0Lm5ufnkl5+wFQb4Y3H+yf/iP/yH/+gfsnqMttXrN69enLziKBrIx9Q5SgPpNE1XUwxkt/khK8+6fWaP2zQqzDb7jIiYf3JFXDxbgXslDNYy1xx7tmbYXSmBFnvMYbeZ+YPZIysiLHFUL97Q4pXZVvNIQlEHcSr+Sx/CJRETuGigAATbLWPPohU6AkBr0TT2FMQ5dbtmZ45SoqgY1BKcDStoJE8uAhKhwiQfhOwFO4NppCnBiYoVb33ZGTAdWQCMITOxGLVkWR5vTM/FUew1u9dnrA+edZgYbbu6ACMfUQ2TzE3gouGVbBPPQuGeM7oC9PqsvrtcDrajlxaDzqlKTscWY9xuDpQOAVjh3CpA0LsP32g78eO631bzvNMY79/7Z/3Ol91he9O9Wk32wHXdmG7ai6+eX/7wNxqDYbqsYIftdibUWurti2JBIa3mmZ0SGAjr3xX9OrQ0QIRxG4qSO0siIDZZN40zX8HagiI1zqbjgY7JLv27BvCKhslLEkIL/TqRrNHDZ+OEF4Ufu8c8bOkxIkLp+7mNdhvJzGSi4Pz1Bj9QQ103/7m3GAdCZ1YuK6c7q2HzWWP2oNn+ld2Va8q5XY9WnSq0HY0kdHsZ8MP/cm/iPbd83b+cM8mi9SEwMTbJjCgUH1wTUEymcq1SGDEi1MjiZoT0QmjYv37xNbG9l+dyt1mi3LgYDeYKbnko8Y2WPMkdnMwKU8YfUzmAhEuJ4uNtMFmfgsbI28VLDkFbvX11Mf94df/BAyb1Tyfjr8bP+93+/fv3/vZ/+w9evflieY1BZBOk/unZzXL50w+fve9xYoz5SIjlG++PkOHhweu3J0Om/bAaFBeeeewMnOCSUB4o8mIe4u3dsbpRwfnqwuu445pqjpJoNifrOYMMxLWW8NiBUASxBJEK9fLc6avrBet/x4vrz375JdVF1Apkmhy9R1t2ya61I6oUsjZ18kbNSK+OaXwsjWSIjuuWEV4EA5f4YAg99HJWQZbvRPCwArdIosNCdLj4SIpA9tXLcGIl3KSBl2gVZOaLC9a4+mQik9KKwjWabMkAZwTYanA2Iyyab1/8m5/8MyzYYrWmo//66nqv++j3f+/34ezBPt38uP7wly2e9hrLYwS+f8wUIK06mANc/pciIFaxp7JDxLkrRDCRnFx274flOtMiT9nR2sTIwDRYRmxCqH+pwu0dkkBYTtsPS8tiaAiH6Uq+dCPSG8caaT6tNvPNcr+5Pdw23wK6zbnOdlTj/TuVALEwMiQqnu9BNwHcwezYNqA4iqCix1Fgnh4+wqX1y9rJNh6/FW4xqY394Ene4lA3+hEbI3peFtNrprPGhQIi5GKjIMBfiWfjXxSt8xUvtFCgks+OhMq0jSdasMRi8Xhxc83ghSrD/Au6CZc9zp2kxSVbnK/Artau+ZZVHDiKhaG7Yb5a0GaAM5X+2NUIAMqCGeP30EFJEWAUnLk/Kguk2LtCXcyhnLwWPiNZSY+Hpj2WXtJTNNQs3CT6txiIljnUcGtWU9jWAU8AZD0GM6KsI4iuAedcFyYTWf5UgSJfn1O2SPf1y2RU0u+X37uxSsjX4guhQAF4i3EeMVbD7PUTLYKbLGDjqcRk7DcvFiLxUc7EymdezbDA81NJQ9QetQZXSq7aykZrzKSgEzo+rU/C89cshWImq/u86rQGcA2WsDuPprgTEBjAIsxOUFCwDKRUVOATX+T87z3AzJyHd+NUUesfIxa+GxKyycGEVen0JdAKsDqdKpjqrORoCi7vVnHBLiHckkWFRqJJipbp3Ssg/M4HMgWGhYuSoEOcIIuK5Onva1DYNh+jgFAp63TczikJuMmusyUOAG5zJkBnjKVa1lt4k2zjT1bAQ9v10/CqtSdwzKzw1Qj0xACLij20ZOy8cyx1qzU6OHAJ1IKhc5II2IKx3bIiil6TBV48DAAv9d1DZAAivSGh1fCgypCH5jAvQv0BAuxg9sQcuwHRnBtAAoomTXyz5gAdZgtAI20TtmcOXIyGrQspxauza9CSjX43mEgDVhRolqcJLmTKzOraPdQB4bgvUdaC6u23X/9ksZBdBSCYlAfuWs2EK84SAQQivBKiEBm8ZTzmj/7Vv3l1+pYaeLme/ei3f/M//J//R4f3jhDVoNd7/dkXZ2enwzYG0BNc/JNcJ4fRGGN50/5otNmcSxqEY80cwSB37Iq58MQXMq1fKx6gT3pQsFy/gbZWA8lq/TPsQyODSoLTiElNH2LYb6Yxm0BFbWEy8Au5mkXDJAg9TF+UQqUJ4fgEXg4YsEsF63Evzy/uHY+ePnnm5qGoXSP7SLiYgYRBUpUVXehJFtx3V5AP80IR36uvvALL5dCt/nLOhvesothyWhkHQtFD1tjO4S1+12y6PH5gWxT4ls+SY4HhvWg+D35O4eEZtuSdanhNu4iG9Se9veNGh7kNxqJosLs2NFdsNhS0FDT/ycxfut9cG2A5ZT5AY/kbg1Vn1Jq219dMyLH4sv9Nu3M5fr1Y3LSaQ/Kz2Rs+gCqZgj8RCtqaPXQaGehXgAPKzh4v1vUkAR+KjLkzrwwPggYC/yC5jHswgAAS9mAgd4SUckL/YOG2ABRmXrn/tS41IxHDJwDUVxgkU0uYuFZfS3y3HWwNO61Lw9msSQq+6Pbv4TLFy6CfD+/+2M641jVMckqx7Uz+aHHhkTCGQbOru9w8xk9xc0OVp/BEmuGQxHuBBNkXBEuAH9QnBCS1Gg3TGjERdjdwjTxLAoNDrpFNsrt2jyZIaAmxnjJEDNAgmu/My0H34xTaFrPhiu+A18iu/Gt0tb29ubrmA9tHvnn1msnV09nJcHDw6PjR8wsm+9BnwT6wzDvf3ozH7DDJmRs4MJhidneiI4DmxKs3byiGTBDCLdnr79HPIwYigBdez+pE+yEB+WvOsSfaTolDt9A3ShPnEKy2DCbMFjPVz2Ot7GctjJR6IaBYOHWT/eN7TPWns1VvJ2XZ02D2OH9sb8MpBllVLLMrjkVTVTSsNQVEU8kT0QoCCqaOLerVVdgoDJJoCel2dlUlryJjiuhYHb/ieoHES0SmaOr4BXZ4E8zsNsa0rjeXF1eXF5eDERshgCqZ4YluxzeXf/wnf8oCe+gbsvR3/3gynX/4nQ/dK5mGeOnxl8nWy2zeygOd0NTdFxdnSHZ0MEI4BIJjNAIstNU63iogyEiIHMEuhx4kAod5tnpFLYgHsrTacOgJN3Kce+ptxUdFKG78uS7Gg0RopuqxCoEY5MzgQIuxIb7i9d5sW1dWF1x0VQCO9qNVCF5NpIu4+Eyt7tHaFi3Q5AEMy3gj2EqLDKXoUnf4mBd6GFGmfYcUWn0w5wX3fdgcgU2ncUSLYEs7NhBlQil1GwaHcZ7jn2AO2HOC4StoVF72eignXHC556Nqll4/uQKjtHioLm+Ig9XJ7uHImcgNupugESZDoEQGqG1wYOgIkTlUS71E4xYFPGlVMQwoLQjyJSuVna8g42BB0oMfeGFOeYifEVdDkQEF0AAlAo+qps0d2Z2MlC+hpAsm4Zv89fO3XUIr38tXY+6u8nH3Wh6EU/+vU5qnYOrU5E6eeat+QLdckU5iGmSowMpF+vKS5Luw3Wc/Bt5tkpJJwkkbNJxIIyZKzqTJo5Odc+wbhm/MWLq9jOkbN/i4S8QDyUMVn/hYiPPByEni17/0qmIHDSXFA46U+tB7URLKjopbYqvGcpUeoKj91n30K0QshBXI4BtMiB38bhERRLX/z22gcfmfWemoFC5UgxOISarm202OVgrKdufLKKXr/ExCECu5XLFgZGp+0agkRVbwyWY1IVZIYQzmAyVvsv8y5QbOW4KkzCKA+xBfcssSRkqdOYkAhZ87f4UmgIIvlQBpAeUHvSt+pAiLo/ZbmQNaFIlrOWGnFGee6FqZYWxPO30PuDlteg7CSj6JrFtdO3qe7gw8KnLy2HFmpwCPCYT+qwiFDKn3Bs7rj7aLQWNwVpAVoeoSOfEXn4gsv87Xr8OMIZjQUcamyqeEJ2H1VHEivZL2eXB5fjAuyssAkQPyvkT3V2TVXwhhK5Pp4uWr159+8Sk1N7ttsNz3f/w/+p8+fe+ZPR/Ordrg9zPzvtccwZ/N+gaMmJrGSg/GmvcO9xkdbu+dWnuGlUU1a/QKzyPq5K+lNVMtKn/OW/MnLQqlBq+5sy+N3Oa4K/z16xvQ6G6WB3xt9ZisoubxTWGGNxY+Kx6uwsqoqSPC2jbqO/yGFpuKsoBtvWBFwXzJ2XFdlmPRMQQEtYLazj4Dpr28tJ4JWDlvLpGSIT6WkEq3EqgpsGObOwzgnMkZG8GvZ3jYB9vFhLULm9aSI0gX087h8IBuB2RDXUT5kVFSAFT0RdS5fFJ7+OMy0zzgVvLrNjNULRI2/f6mOdoMvnIaWzSNdreYChRMaJsCikqIV/SQLh/LAZUo7AUO0/QavV/sLT7Z6x00W8+7bc6UXTc702ZjcHl5fXp6+Z2P9pkajiYzrredsR8obpjLPrarfVbEWsTJ1YLMGA19eIy2+4TqwzB4HukyG4ryMaOmBhn6sixVqdiIyx4dRQdCPP2FIVZCDJBwZWloxYmaF7Lh9kLDmd/JZXD5lDtyskc8x/RqNGxB0WWzQ01NSTYwY0s35JSKEReBypFuzN7mNzbT722bfxbes8p6jwOVxcklhngtEMkb504U/Lqb7tmmO5r3Gosh3X1PGXiBM4LHHRKpaGUesBJIQ1lzhThjRX35JaavsZvB1oAqGj/RgOpeJafF4YckTJ+LcHdXycDXkjg+he4as+rxIBFVY/3ADpvWWWbpbGazyf7+kK14xtfj05PTo3tHqzmO/WK0x7Yq2/0R2rv+3d/74fXNPz87PeGoZOYO0bZ++eLVg/v3Hz56tFgw2ZoFpwumiZ+cXjx88ph9PJ2Hxr5D0wlNAfp1O3364Snzem/wj45h3RE4sjqGvnbrDGwp+/AEgXEMOasuD/YHzSkrK+KJ6b5IcZiGbcImQNaSpcyXFzfM6r6Z3sANVAvicYmZIfrw8f3Ly9Pj/XuYQDQTEdR8ya8FCnD8p71nxy35KxDGykRjx8zyYBLlpG4mFyJZMeUKYjBbePmXyOJXwFSBwuC/ILySVHJ8VN4UOsoqKM2Rx/im3TtAM1mczQR24vz4z//s9OQ8VnrR7Q8ns5tn773/3tNnkMYsrHvHxxgiXHOaSrTcGuuzPluq4YlvaDnMX754893vfzTc24s/TVErhJCx3dhmPn+sdnbe0OrCy9Sm0ajo9tF5R7s10xDLGWtxSYO7w/7wFdPAslhWDrFyg8LtcAHkYH8YKCscqdReMluM8Y7pgIPZGyTIIq6mpy6s508oz2ubBAwIs94Gy8Y4JK7thNIJVTZJlL1o2wIHadREcumEP7JsqjXgLGb6TrCRXmedBbdAbXcZq8y2V+hz61QhlNG2wvW8CyQOBrQwpYnFvGQBp2wWMo6wf8oBNevVPQ5Ez3wnKx0kRl6uVLRBpByxcjaO0OzlCCRxzS0FrbnngMARGrEk4juJzYLkgCAIomw6qAts6QPriNOY6U7AKKdXEUlrlroGbtR1jkfPY06FABxcGhnrnmRs2aabCkOoHglEWZMBPg8xnLScZhZlEKq55EhZFUm+FT8Mqi/x8Uo85VA/luC7n6qQErPReyGjlh94BxuS6QBwSXNCCKuhB2iA74JC+u57zoSR8aQpI58NLWF1CZJJZs8DUOITfucuTgLcMj5QRgAMgCN1BiVCXqug+ktASQABOIGCMRseoGf3Cigj7C7h/VXX1+P4LkrCgWugF3oLb3g345KmhPOZ+BbjZC1O2jrfJM3wfCkPvnAVAPwUZvoumDq26qEpQntYgRCvG+9Bi9tlQxaNg+oolvynF5lyCAAsqRpKScCfp6uPQBEIaOocDIgwfQJ4h0ECSWPOIIbEXouoOzmThmJkpyPug8PzwvFOIUkrNgu2KMFMNMqkg/BKMo2Tcu68O70ehWOTWtsql0QtNNu3UXhpYBmCkLVcpZEdtmf6M/GZpiBsxSGUMDD58SK6fEhhLoytcpP/pFHd5LOoFB4TVD8YIqBcgVu/vPPlNvDOE9n4ZvaK/84XQ3d58SD2olEQ4WuUij4bVk6t5j/9yc8gFjvywYdPf+e3fvjv/Dv/HRw+TSmezmb95NmzR08ez27cio7N5m2WIeW1h/Kyrx+174H7fmrzkK1IyCXFGhSSMSEZPQpKognD5QZmTQMo9ngPOB/Md+UkYKIxO5PZP9PJysN6iqoJTs2hfsNNJzkt0RAFMN/NsTwZz5oU0H5DuOC87m96rb29JnuJck6QazVTw4mfamomQAd7HwyFXPIpFXwBTqzITRUgD/+br4XCdV5UBM5aps3uljcQRJNDbO/duzefXixpD3Tu9Tp9WlO0KFFOk4O5ZtjHcsk8oKq5ERpRqmketDSJiblvdvc/7S45lH5KtUQ5Evf8D3IVHIL8Iwjo7iMhpnCcVs56O9vOnh73esM257u+bvYYAWOghOmyffqyZ/OLxvYD9kqnUwoAMhDnCA8DSbDkDFbi4ko05NrlbaPbDfjcBTxljIyghzLErC2oZ3tFiw9lO3/pXHSXAOva4ApW8FlrEm4byP/CkvJgUB07j+VGFL/na/WcEAMSCM3holxIElkrZupeYtGQt2IGYfkDJWxk8rzRwi8hCu3DMW5mg2lB1p3xQDwsmGhMp6YHYMwOv7CNsQ82DGW79g1nPwhK+mFQCkPJmBBR2ZFlqBSqZ0XfUv0TJSbCT4AqWFcQKpr8wmUW9XXn8TbIvEpK+JoYKnmnzdw0Ov+d8YBkUzpWPQK3+PPD65vpR9/57qdf/PT56+cffvc7X375FR2lHGJ1fXMz6PWZ5UxjYNDfm04WBw8ewDAswGhv5ESh6Y3LsWBli4N42bHXVbxMXRgNWUPUHw0HvU6PWFQUhOPLMmicsqaKWXGwkkLHS42ig8mim0PBAUhkdo0F89hkWpJsK8vEm+JA6L4jJab4s+f9eHbDgWPuRqHrJ3F83BvRgujPx0uOJWYws2iVZU5mwF6tVvEa5VfFVCRHIG/yp0izJCRFLUe0IcwTiMlSJMSHBCQSei5BlZcSrw6vvpK8CN6v6KQ9aNB2eXZB2WJAhvngxShdXowZELi8nmL8mNXIoghaT4jyhz/6oSPUnTbjAZ7TvN0w64nt26g65SU9DqvGfDGfjDnE5YYtnpiUTwM+SFuG1UpLnmQwJ8w7LXYrXTDBem1fvDx5ffKC8s/eBj23nYFwyzJUWVhY37p0OR95SSkQ7c1xxg4zfJaLG+RBhwihMEuvGjY12TNihHagNpwmv2kwE5ikCGvCmoA1XTW2H5jRSEc4WWEmLJUu1DEthpYfzQUgi15TZojGMAF1rVLnEyV5g+8OquxdyzsdKBYr0kqx9+JPWy5E+/YSsC6/ian6qe+YkMplxwkT20CAcy16UMjaTJkEwxi/woC4XtPRJ8jUvtABwUS7+P60dPBTu42lZ4vLh6IuUGznIXihaFxqLcKgaq3bY4gCWlOTqa7S6HdYoC+kUoGUycGBz7hCDGqQebfXdKcMKPUzzReBIhNZIzz5mKfI0D648lpxgs9GMa3qUB78qRlVB1ZfEtFbifL1UDmclAVujGCdBISMXkUwg8AGx8p2whcS815SBHay4UNyNGqNo7V2ArlVCXx/5yIZn26/2oAVgP+r3I3Pq3vy/LrLtp4ISEzy9DFAStoaj+STWx3t10E0S7as4p69IMSGgJJUwDwV/LSNASKLwKFkT+6mLW/Vh3AocJS3H0vCgkKBVlLXMU1/Cy+ZkkTHjZwcoiIpTyo5GgjIRDYNOh9cdJrYEIAy5KIWFiGhqEQLekHQJCSnAGo9cZXY0ogY3cFbnQnWZJJP0KC7kISUF9WXdWAAsREi+aAAWhi4ErN0MzCvlXRaTxIYGfBBljezRI9i9WNk7XlyzXRyShGkjMYopjEtlfwxZWLlygYLG39+B0hKEV9LB4ldm5Yu+x7AzZqHH+4iR669V2ySBoZmAlZRE55yyYr6WUy+dvn5G4HG2fGdZyMV1YNRDI5Lk5ejOiHPF6EUSLmXBJYcjAXTWK9vxp9/+sXhvXuXl5f/8T/9p//oH/5DusbxrSGHGOz7xsFAD46Ovxq/xK5jmtkKBPL5zCQXiD96cI+mQ0zRjhyCWeL1RGzYNwN2IDOgYeHs5NAKwuCoMunQBRAEF1YTYqNZ8Mc0VtZU4VGz6x3b3tm1TKcR3bQIn6n17heOOSMuswQ29xD6qnlBXopJsgGnua8YZY1EFPB1wgauLDPQWJHobjludW88xceu8MgtyiUZMg+I1D1ECXGEmQffuOQe+VVhUQ6KAIRZR2xWo4PZ3mgyd8uf1XTMZh64RGzHSTVgY5Z0qS9VMtlSQHo3M3HwQ3hFtSceTHLjgxMnpJoGxuq3ehz41TpxNKvBKCVhOApKIStWQV+FA7J9JBIOpXpRqq8laLNq/1m/s/nedx7+xfmvLi8+XDbO2t1ni/ZVv/3o9GS6/cGC8Z+CSClKjNXgVbR64yZLDuwBlBk4A432NessaMvzKq9AhBLIsp0s/XQNAGUaexne0oGLLsSBoAfBgZA42RJHHQlPWUIAlJrJhnMpitzL650wHvmSu2WLh+o/IzEKRzRRCdDlRS2Ul3KXdz+Blb2Muix8s2mEYnU2D5uLB432FSaisRlhy9y5giRgqN0CFOedopbMNmFxIe2B3oyGav9qRtOv8RAiwm1rcYUtRlzkAHIFWx5gEwiDCSrPs5+8GYJm8+gIBriRIADqX0O9jCy0u/fyZXc3r+bqie+UQblajovxvG07UDGW7beojN2TzQbz7PG0GRq7ur5+eO/JyYuzP/mjPz0+frBacqAvHf0riiNTMYn8gx9898WLr5YbOcz+OqP9/vXl+f4BxXBq12e7dXR0b7k8Y7417kiTw/wm01FvgKOItuwP+zfTFQtieKYnFc+p0TxBHxqtU+QhS5CKc3Uyw4GNWAbq1WpAJwUcpBfaaVYYH0mDTe2Z3U0sbGHS0mLJ1CUmfmpm3OoG6bD3ZZ8tjpjGYXVBw1U3CrboKBTGAQf1TjEsvAQFxM0zgiYjlUg+Gk+DpWgMyT39R6yOa60POP0XPHdxjZ+rxOTRj7lX0HwmDy0wxk17CN7WcPY9sb8Fi6Am56dkz3CK25uyc/52+uMf/xis0vuBozfYHx0/enifKd3McWIuZm/Ypb+ByeikevjwAUsvkBe50F/WWyKN3v7B3tHhMY666EtZrlBUIdhmnN9AKHXW5GrJKRGfff7F2zPsTOPw8JCaLsUkcWSDHrqDhGZiV3xr8YjxxfX6eYuysurNxrQh5LQWH75bKStPhkk5zB1y59PRanm4brxmow33vN+0J1fNAf70dsJapcGI3j564nX97S8AdUZmYvajKdxgmo4IZUjv2WYtEuSc4faiNZk1OxMOQGRtkkOfMNCefLguiYoWcaaskYIMioQUmNwxsnqiRrPbB+ZamtdPaZg4gUdCTAbfdFsadl3p3JuCcCBTcinaS8xGa8uKL3LQQY83ZT1IvYKswSFsIXMmF2gTDBMIHUn2watUKogAyAsKgSO2flJ5xMNpxmD5yo7R1XsqOUyxx0tvjO8+kCjdoAiVpa7IESbps3F2ZEYuQn8h/dbvJXeShjmwWAaIhTeQCEK+RXcSzmP9m/DdrTrLKEVEQIwGvAfYZudVoHozIz4Qzlv3pXTmW76QXfUSkCV/ozP6hzh9NzYguN+NWZ6/iZQhctIJx7miSslLsH4o4d+85wOZIhKhV/FkcfRBZO4kShQC/P0rroigSi6IW5pDIVkVIDV4xVoi8T3Zl5wLGsnSGGhTUlTJkqZCuwAEavWt+g3jkxfh6BjerQ6Qykl+5lQg3j6r8+SE2okqnEGV7c3nKqXN5qv5AKn4UmitwAqn7ZBQliHDH0tRuMV3NKFmRTAgoh8pJlgcvEULquKXXeUGBpRGCoPYZy2S2IchpLR8BUEgi44FiBz44HqZUsL0CFxwSbufnpXoFvYNI0fJpdTR5Sl2CoA/grACYZUdFc54gBZzEXO+WpGAmizS6PDA+1/jigiC9p3IhQ7Jgd78cK9ETh7lc+BXyU1bx5RHXiUWNoKOu1/+4heXLDSjg2w2/uCDJz/8+DfZ0J8Zt/jWmBIVnXnAB/u/9Qe/t3fvaHp5Tc1AuAP9TP85OqKSYD2XbSOJlCUQLHweiQe52DibCVp/3CHm4tNrRcchSDNjeLmwwcZHhEBdQdc4+jqZzMCHucU47m49LdOwsjiMTUa08SuwX0xjYHHFfD4dX0kf/R5WNWgIxIVIESFbBMHCbur/tn1NkT9gGO5naZ1da9b+oi4OJk1FJZ98VjH4KWwrpUXggCPPmtnK0zfQdLI90h7QwzXg/C870Jrd3ufPP10xganXy6AKUVFvZofaghHUDmPBCBqVug1LDP1s49HvRcli6hom8i9Y6sI0AQsB1asIFzUITJCUECsc/vyaYNfoWlYJazVmD9md4vtHf/M3jl+9bK/fXIwX873JlEnUF9P5/fncKoTuw80y0qSGhUNMa51TrnFzRUFmW+IDzhrL2fQQBTehXLGKBjxBEeSwPEpxgEesO6USCAPEns8+F1gRX8mCXHIVTtVv/orAO1dJRXCBY9ZwzAGiYArVhblmAjhw0Xowm8E1G2hU6tmm88tX3Rer7j6Mlb4Gp/ghEKpM26zAYMacPrNLrlE3tRuzt+KA280zmjzsDwTw0OMd3vEdmAIxVx6B4I+v4BakqmdfAAmjzenO3eh1UP0bWAn269cuIr1z5V27Rw89LjptaIs3BXxGAaRhySbu9N9fXV0fHh7R5qaQsVX/z3/289/+3d8/OGSgCaK2b16f0I1/07zeP6DcH1/R3qFDvbE8uzg9HnGos6WMBQQ3kynDX/TIn7092eMArvsP2V8Wg+pMEtffDzbjCcaRDdVx5vF7ZEqGfuULhYcyJ/EWJpau9vCE2Q9gO2iOb/aG+/PlZsomPwgDjGBWHhABdQH7/wBoOqYBQKPCngo+Mgvo+Pje9dnFwWgfSxIGoKjhLiRpOVUDH0FOkEKNCGE4mCjvHSdNYFJ/EkoPCO00ptMFYOL5XF/viNBkAi93BQeYQJEUOy2MEU43WHB1dn4GUBfvrtgKeY57/NOf/YJj2FliwQmJSIqOp3sc2DHaY4Bl2GdyC+vWZozP7B+Mju4dCthiZz8Og5HI9+BQzppT4XOyrjDNh0KSCgiaoEI9xx7kRvek5OWcNR5OpbRiBbAmOQ0k9RommQz+IAh+wA0jgTiZa+nAomLSbhS7Z8lrdl2ewbSWzuWyeUaVSRuz3ZxOGa5Yj8ezRbs5PhqyJix7XNp/AXwMJvUuTUq8V/MsMBmtoE4BM6YYUlUst8zfp526XbYPbjbN6xXjknScMN8FqrROJpW8PMkleeAt/5WBIjcSNHJwOa4/FYtb5dIo7VN3Udk1KCO68BTuDZsieOBAZ8uRZ0vOlkZvodS5xDR0aCSzA+mSATa2cKV1hgOByVTZ4AU5AcoegqJABQmw5E/f3FYTv3R6FUWSCWBlzyP4yUS+Kk0+pAzIZ2wv7V9GwZQRWZSPgHaBJbKDMKCh8ZpzMqZPDRQr+oFT+JIMhV34In53LyVd66/fjOZV//rwtTSBFP77US0kRkHPdKFIEELegakC3gEm6ALbe5WLNHFp4d693gFFRqausKsQUE5evN4FmIjGvL3E1uJhVHLijwSxJVX7JlHLKuaSyuhEmQj9zknAtyBvn4JEtd7AvIsoIqyCVo2Q591ic16I2i2v5KWXoRUlDXYE4gKfovB+4iovRK8SgGP1wY9+vXMRx+q/4jjqmkTaaFTAuKSmTMIUFEv7gtWlNVxjhv7BpQpAJTXeRFtbb0ZAyl3RAFCzEwFR+KqYRjY++ZXAoIPqRwstA6ywF5/5U8F1nge3iJrCoM9uRgoP8Ot9i5doqoIi4msgWSBCL60HmsdaDK74cDbumWtEWzFLnnGJ8TdxKDnp0O4ie2cRsAMZG3acYMsLOkTtxzIc/KqiBoM0io0FcsEAOv/MB3LlP5cMUmMMSUB1K1/vhlTCgx4jJlkRjdrppX7eTaaW1p8q8HYqrJ58+rMf/8s//uPeYNhaPxsNHv4f/0//h48//gFT5OO3kI3S5zZnTXSz6Rk5Q86c6rB4GsbZeQJJW46HyaR2nctgE8HaBGRvFvxyDDBT1if4+jwtwGs5Z075mg2FYCmWMkUJscAa7B7vcH3LGDddkk7iMhMtHv4lB43t7Y1ohzELFYtHCNZzdAD/N8vVkG52emYUqaMvgGFOfKS7YrMOl24jCsw4X1mciymSBBx02yjWZJE2oUXNkrCwll2HwbFTraYIeyO28BR+k3CzfM/k3Zdljix6dXS8DxmMfS8bS45Tm0+YdN0eT9cffXjEiWloFXC08UUa/nhxerd5shNOFUBQmd2o2456YaxjvVme85vN1QE50rLJzneEY8ptd/PAaDCVR6wH9c++BLZuCjWWrtYCc9QdfUEf22jwJ7/9/dXf3P/Bjz85+6O/OJmtx5vl/enkZjqZ9If4hJ02c1BXh6s5Ht45zbOrq4seU2kbV4iKijWyoSIuNXTE546ZTiiilMAbaiuE2W3Rz4RAHmyWD1bzm3X3gF3zmVVMR6eGw7IMS9mtlZJpOTdh7vKEF5WG0o3de+X96xewd/yqEiQAqOmAz0fKlf+4IjOeGA7CNcWJ5WxjTYvzG8GIqvuDzer9TftzOjdZcbGiM97R4B5s1duzV5uRC0wBXtd0vdnjy4aVM90LVslsoNRqGDOG1nIUw7KxxpGBGkZpREExpohbxESGOUMEFBtSLAXkJoZfk6JSt6IUJgoN+RWlQvvuoYTXd/r+i49rGuc2MMTBcBjNHDxrj4/IHrkUKb7Rul5uFywDmC9Wv/UbP/qzP3/59hXO3HzYH+7v7yPI8fXVo0cP37w96Q8Hy8sLXDCPlWNblNVmfLMY0iaiBDIVbMFZAQ9pubMq4O3p6eP7h/S/np2dI+Zuh+WYDWYgUb4bnSv3Z0dIqkrxHSsJQSp60W0DEeXCj5wNGH3qNyfsvIqVkRO2HjJcrK2jaDgIeH5pj8KKKaFHRNo0z5ltQnqEYYNfLSMyxdXSXXJCMEqEUL54Eal0BOjd8a4+EtUMH/PuOQBKU08dIdME2nbPXa1cLoVgKhF0UitPjuEUKWlaSq4EV5GkmsogIJmJQRf2Ew4NnM9Pb67HWCbmZ+LMAfLP//TPXnCwIGraak5vesv53vHRo8MR+y9xWJ/7W9BpAjvSXe2YoYjDOMsVBkPHC4OQPCVQ95zLmlGMfSax9gJyCaAgcAARslnRqmJgYX4+Zz9jpn7RVddcPwaNTYPVhvJY7tlS5p/bSTU7Zw2OZLH0dx1kktOoib1Iwo6lxZ4PDrq94Wh+wzHGR9vNw1XjFWT0G33gzhdD4nWbo9XWUSMxZGaluUzMxFE7RlEz8OluvGDNWmNlwfCDp9O02WCE8Ba7yzFYwHF9iwYb23vKs1WMdgXdAilZFNrFsH42B4L5oAON8NjvDIohwHPWMnFKclwOBTux8M3V+ws6xHpvBuzxpq22uYDmd9j5x5jgpRSZz8qxis4rYkRd/aKkkxEa0lzN78FETiSgfcEbIUy4Bo40AVH1t0yJWHTT9oAd/HvgtGXMhPENBukhZ03dEXV2uYL1BEnVK9KJRloN2Gy2MaOVRNtGTXUiRE2+OsC/ZARDclkMHeAooeSbD7nJo4yLFs/WlYck36s5WXgbbSJxQoFlTeRr1m4FGjCrvMpPbeFvg5MbpAVGZBOAdSqTizW3b7lKYAHh56TntYTILnoLSjr56/9wUWUllv/5bJiRqpiWY7L0LXXs7QfjlSy9FxoC09R/jSt5GS9goq074HceEsFblUOQrTAytWIPsgWXCqV8uXMrUXYBoaeiMD8SH28DZU0zoDBIsgzXcnolrvlVrMO46JzBCh2cVGlyMDgR3ScBRFeLljvK5weZFwFJuPG5Yu1dPliUD0WOY0ME+uuVErnoRdofgFeOPNmRzT0l0FscLy1OcqQoAoQix1tXH52ZvHNqe6BR0GUgdIC1Vp9MmAqdQU0azpxmwHRLOj8YwPOIk76236oUu4p9tvMCkpzoTJ7sF0rrgCl4AEobHPQ8bsw62OIrWTINLLzyLDPClASFDSW8ipRgb+X9699qGPkOdHXCTPgzATnKUxVYGoMGj00m7o8vTz///DnF+/LsfNu4/9H7H33/+99nMo9cJZk4gTYUNT/56S8uLs81KawTYzkS9gV3gGiA5MLGQS8DwXBGiVRZ8SNfmy02szg/u+4N2M6CCSGO78tiulIwXGoS48h23tNDwivnR759/YaVv7yBdbSISZhixdxWIlPHc2f3YntPXIbIRuacOjmbM8M4tGOfnZSlisk2cMaRVcoNeiHdnG51etKnQnAbafiRpqT8ibkkgWyztiQI60u8gAlT8whk1CbxkqERvcCQSgiSIefB/YfMOyD5ZDIe9fvT8Qw+oggPH93vD7qzuZQqlhq4spHhwpHvyT0v5eYHRalc/Lgd/qS5HmajHRfkJrUZZ64/FbIbTFh4gis6HaySJ7PRWFbDNkLLx0ySaM/vtyavjg4OPnzw8Z9uP+eITiKN9vf295mk6xL3DPoDmGrDRX6sSnS7ETw/52lQoJCfDoaZ0SSmzs/MOqWs7GEvUwHcvxVCdbKJRmxnAbdZv7hlM5BOz2JLDSd2VrphpADBuhAWFvDMVULKcwKqWx1S0gjDqHcvwecKKoqd+hHEmBqGkNkjnHkwGAa2tVlsPmepL/t9sYNptjFB33XnXeGBh8umdc7lai2wNzlladOiDcpCJPwY5wBLHtWKs8ssFzqpoOJfhQKoQewd9HzcoSebfN9FCWMM4iqJSlwhltDcCeTVT9X/oqt6uwYUlbI2xzFy8Q7kuO8qxtpXVAJ3j55TWsftzvjm4tXN9Xy2Oj97y5rwv/W3/ha2DiAMvnFQNBNUDg4O228uOKKKzo5+C0cN8Gyzg0IyrsCMlIPN9gKGURquxzeDfoO+6r2R+0qhrKwUoY5gfhmF2jEgfR2lBUuK0JQNmMlxZh3hSdHMYCo2kxVpbQDkyiTQJFlc2iJMM97nzc0YxQS4Y7Xa3e3eaGCZ7/QZcXRDOXMhGfyv0gsjljm/KmBw0KglAzlc/pcEhcXCAYJGIh/162RBXoXPxUvey4O1IzlXBJaCnvhJGP1X7M3ZbPb8yxeN7gXjHkRmmtRqsb28vDo5OaWhRASMJ+vxDw+OPvrou6s5L+P33nvMZHoQ2hv1Hzy4jzEs4FFWuVrhGVykGuzgwQ5B34sRCtJ6mkVRcbXZBYB6jQ3NWM3PYAriMLnsEjUelBixPVqkXJoiVIUeERnepsE2H4+vD48PiIjGdVhjr+mk78z2ALQst6eLzUl6EXF/Wf+lwVWg7HHanEKelS6ZWYiwb+SGMmCoXRlICGKij8/xZPoiQITzcelbx/w5vbefqX19umCIi8ECjgzgJSIqtHiPEPPwzg1EoR+HntofX991AFl7gO9B49m2kBKlADFE3kdTedOjEIY+OPzBXBBCkYJfHd0RRrkxpEiaVjgRaaqlPQNetFB8xgThp1C1oVFUvLjrjHqwXspuIEjia8oLBOC4YoTYrctjlFB6V3Zx7hvoYGDpn4B1riUAWes4TTFdFzCBatVCHzQRVtduD8DVVx5r/qQGoSRZeUab5F3FQxOoYIWbJTnvSV8Bz6fyJSw3LlgIwCuAzOouiARDaYkkoApY+SlJS4oKTDLN16r6DPDqVsXxzUQFSEmeXJ0CVAKZOwWS3ecRqljcgRYk79BtUqssflFJ5FhWHCPX4jYAUaBVis0g6Y34V1zuO4SQaUsVpMwAmIz188MxNFVwoIBBvvIDRyl+yaTa/ZSZVfZHFhLygaQav92VR2INhZmB792nGjB9HuxowZxr9j8msVeRCn0hpuKkYeWN1pbvqFhRtYwJ0GOHIvZOSENJj5nTRlQgUEm9EitW1Did60LZzDmBCJm8QuWCdlJQVbcZ0qI4EdvCI+H55whscSn4GVyCZpMzS7RBpqcMADOUyoliAYLEwBIBCkTV8zCrApEeMgbv8BfXKxsS5En5cQthuirXdLQ0lj3WrnkVSWN72A9bX0fm0H9Ia59KxFMKoI12Q1hT/LCCNcW2zHsjRS5yrwiqCyVpDDL+7ZUAXmtJ5EuFNRBkbMQNHYXogpJhksYVMokIQZD1L//4T778isWOViqMrf/u3/v4n/xP/oENLXiWjlhSuYXTenMzmV9fXWCU8QKNIHIKFBL1+AUcq+5aETWgYg2xqsyzqSfTOBE2/KZu5v9qzZwDnWs6Z/qeFNNrt6djdnvQD/nVZ5+S12DYnUydINTvddhuiGWE9AjS0YdXQE/joGdnAzgQHzkCHUMMdKkFrIsK7fTZrvbajXvYbuKy9YgR2OYFgw7msAISUE5aIKmWwnfbuhDIV9UDGtrp+9def/My0P+djOeAjohYsYH8j3708b/45/+S6c4Y4kPOj1utR8OD9569z+RasS1yCq6BG1l26V8sVy1FZ8aDBXtnAdo0NMlEfvoHuKzrnudvbBoXYEu3mrUOT6JkPdRs3sByHFIWUqbpCyTYsmpuRk06Dtl9jzHzXnd4QG35irGKZptz3tgIiAOF7o8OerMJO7qwPyDdRZcbVzZTAbaZXc2mmWYH+DSdyVG5ro5dAEt1aE8Y40Uqgtxl3rYFEZYw1eaSA5vb/Xmrwyym/QmDQqvN4VGnT7GhgnUiIAP2zFnHU3hNei6kI6u44Iyk8Xz3jiI89bP7Qki4aHGvHstTrBRATJ52uB4ndIG/p5ToLNB15zgKHfaddQuNeXbYOVg1x+PuBXP6N64DHjaY5L18vGldcUqeW7G3etet5TVbha4POqP5de/+ZW+86Q/UF8ftyYOmgCNp5kzG6ZKz2g7+KeChJZIFUS7mOodrmeJVTgRXH0iNZcDeRB/hD+k6b5IiEAq1vrPYAcucr+EAaVv2C1IXvLYpq3NgbOxt2Xtb68d6Ejb56nY4aRt+45IBhuYf2878g3/8o88/++L1yc2rl6/u3TuaTaaL1YIChpe/P9xzs3JK07pDD/S6eb/VONo0zlm+iUPW7bf3768ur67oxJ3OZu2b/uNt/2DUHF+N3ZB92Kebni4T1MNZl/YnWGJVWNRbi6Q9SQnUFjtyyFnjrAZoTjEB8EERmyIW3BoY5loxaO/RcD1BfDVkwLrYQ4YjoN3xKieLI284QD5FqwAiNLuT/NGPBxwI4MsZjzpHhvEHyDfma1qZVu6J61dKpBAVdg3b3lzjJ3lAmLdfEYgfBFcIx0PVLvG91T/vH1yfnk0G3R6bALEIeDK9+vGP/wyed9l/7WbSbQy27bff+d4PRwfurQRnzs+u3nvv4WQyPTw86PVx98x1s3ikDnbeimmVoxluV4/83HyL8EruKV8039ScZu+tpRk76WnXU/tY4GZrPRwc63Xbq8KknRPj2BoRAHx3wxmYT6+48zQdDKRSZ4kCpz8zA2aBNFwghFZT1LDVIMTUz5vJzXgxW6wX9zds/9+4oDRuN/fYoZZl93TK0aTarFnMQGoswL6VClRwDDnTeaDQ9TldKgF9DCpa2No65UODEzwanDBMvUvfxTV9FkgUnOksB+9gnHq7VFFhlETwT/ncvSyukMnsVhTVyoE2SZ9D5VyZQ8uyHJBHfs3RDWxtMRiIgjS+744Ibfaeh9T3COcUeTSK6XXIAJyoPRkml2upfmwQeTk22NjuIzkrZjqK0MEY14LUxp23mePgWxEWgJkrD5No1BLZlrY4QCeRiEwtSsvajctBviZNLtFfWaoI2wAQYrvBFo5MRJAYW/OGWLtQqYKRptjS4nQIRHLFN9orzxjt4eI4GiI1MP7Y/ucWDueeEDXxgrbRTFDuwiwjuo5gG14gVp9vX/KpCuWZbBgh58ouQD54wVo9Vb9Wu2XyFIzK991zeJcEfpCHftIi5/ItKQ20hFfBgU9atKGCapkt36s4JjB2Uub+9bwKrL/W/RYmmSRL8t6l9GuFhhgWXlnNBqMqoh9CYUGpvpdgQQmlXAEA4SJcw60/Ewtt0KbmswnIKDpQAPClhkV6P/Bdu80DSoiKqbi4AqkqCq4ol2l4IRoKxq+9HEYzqR4HqbECAuErUIFMDN99RUUZ8bL25hN7czDgS1ed2VdUiQYOX/xVe5oDAfXtzpeeHgAcC0yH7g1XSPFmj0UA+kZqayC6PNgJmGFQBhFpgK/Z6o+FS/QEMG1d1QliRKbPLHgloUpCp/aSzQIsjsxLUTCUJVcSADxljDwqBkuob3n1sw/hS/Wcj1WcXRroDNTysSSIugpLIcoH/tRvL2H6ZBw++q4NatOrdHZ6yqwe1nr+zu//8P/8n/6nQC5jrcDHQGmNqEHcgY6VAlMgW2PrYGPrCmyxLfjkbnZkFgSwGlRoNmmCAAuHGShtcCYXEfT+e13OGGJKCaePwRYmseoMbranp2eff/UVlZldeBop7nb8H+wfYIBoULnVAiixPTMTLFAFbE63J5OjrGSqYpinHkFJLla2PfhjaBjvp/Xkvac315firC44vBXNAjWjJTppeeS5UApAA6SlpkiwXoQmjMgmBoI8wN36rd/6bUz8H//pn7Da7eLypN1bPXv66L1nT0Fss8D11ASbY8nSdOUiLELcvftgtFzqmCkG/7bZ3aM69I21qny2NPHMH15Ngaum61r43+JFNUFM9+dwQu0Rk3KoeGaTw70uR/BsphPQpwm7GR3Qz8p4OvJmr6emu8HCahbmkQt7dXetM8IrcpOHQAMonhw7xNBGIK40WPEjDE96Zn9Gh8jkKJdFs+N6WTWRtZtpngFJEmleEL6rtywy9RV5yW5J5D85+JOrCjFTyb+9hAkiVRqZRUnE28Oe0BDVOHkUBIOHsUTMIh6058eDE+cfz444rYgFvnQ9N9n8FOe4s+ecM46pRpFag2mzN+1N2fmn3dtnTsy4y26hnChMj4BlH1TgtywnI8sB4i44VxSoXKIfIiJyXrxuw6uPhEhGdcFwY9y56m/+1s9+rqLhFmPfGMJEiNToEQHl0YEPfAUgM4/FCR4DDjNe9/ts/D+8aJy2W4/fvD7j4Orj+4d//G/+6OH9x6wB/e7HH91c3eDw9/rMuGODV402u+u0tuPe/UMaEs7BoLnZ7TJR/Wxz0WBu0LZxdv720886A8xHs8V2YeBBK57FAKiYVgIXD6YxYmLhjaCCOLFBnEs3pcvECSxtG2c++z/WPCKNfISxJESb4BTDTTzYqsfRhGL6bxgb0LnSJhNXLfSBVLI1rA+v9JiFIA8DtBRs7yWgSpYISRF+8xquW77KJ+OXK2DyufpUIuReQkhqrgnBmjEw6+w7j7dHaOury2vaUefnV+zozw4/rkZdLdmPdbR3yAhVvzdYt9kMlOGm7fc+/qgURZua6kjBGnIonyJjtWFmhttykxMp0OEHyCSB7rsFhvLfGjAGSCxm0rC0+tGDB+Si+YBcwWNkbNmL+Jb+MowEh+ogUDPA2WVWKcb6er46OX/z4Xvp1yueOnHWNM8G2KGMl14xt4eaknLPRDjmx7tzvpYD7Yoo5C3jarQ9KEhoAwhYlMiXKkr7TVUFMqKGSXGEgaoAdWL3XlbqNNcO9eJbo2v8j8CMXcQszcK/c5VX24WUYwGTFZQAwHnAtvSoMMxedS7mCSg8CVRNIC8SmSqReCQFtIAX0FQSGEZk78CPMZfb5kR7Oi1R6zXe+SEW0woBRuoIKinIRTGYq1cqS5wiPH5yQG2Yo8u8BWy8UYQB7EiNPLFGmTFh9knvXRSJXBRDSqQ9hQvviI2zMeltdpUVZzXKf155qZ+SjYHVF39KNJ/qS7JIVkcj07wlKsH8iUZQqJPUgMu7aXdPwg+7S1amC253890985Vnc+AeMFDjgiGBlDOASazyGwT96CiS0/WpyU7MknuSlceUlwI2ud/Bvno3ntn8Fde7Zw4QueJO2Y+oUF7NHS9sDrxi+IRPi5CeMC65EF5wQ2wQXlzqfLx7C2SphemFgtuvzNN6roIBudwBm2j1uQHJERRJSH8Vbx12QrDHzmGvzjkhWY8FJ/G0lY2YGI8S61Amp4cJ2c30nV5r0dp+Qf5uF6FVJKadVVgM/gjWa4EuWwyUfTKykWp712YGqHHxlbf1YDBAe/likB/4zMgzu0qXGbdmjzNKDPLFBaBSsSyHWha4UoEx7glcnTSKujNbzZUy5vT34GATGcEHAnHktvVrWTnYYWcQd0CyY4hJRA06r0XCzMiDx/oCN3kbUmVOfQmu5lYdVn7DxtugOo0wtstnFub2qeAyqiN3pd9YPHPBTyfehOmwh2mdm/mDh4c/MrlVhXHAOTQqWSh69eIlDreQk0lAIlMcO6yk9lfzpm6QEWC8Bwzf1UOYxmFt7CzOvGGsEz2CTi1ZLveGg/FkMhxw1Bclrcuyqsnk+qc//dmL1/R6ZvMd1EbHxVVvWGCAggK4YcJ0ZMlYdjqhAZQQB38ld7v6IhBxop+bM57QOFnAbALGcwfdbZuFczT6Il52S1CKMcUkKFKKCxt6CvdCm+8y0nvNVXgruxLGI5WiM+NBlo6ixu/+wY9++Hs/+OLT5U8/+el7H3x/1OmhSd015xDTUsTx1NpLRA1NwBULfRBomR0OJQaYLWzQ+s9+p7naY+4pad1Lm2EBdNguJXQe78FteejLZylLdBucoUzhSqhD+Z1m9xzBsYXHyqOsDzhQs91lbcC8sT1YTHCY9O4oiqvVxXrVpoWmI2bDdqQrpoApoQKkVba/t+cOgc3+3/27fw+PjpITiohARhQuvEActyxmsDDbsrdSRmDu6DhnLYjH0ZMd9U43NkSGhBFE9Ik+nic+lBGSKihcK71BdazCsySobokbz08NJx62COFoX8jfdMyCBxurRVo7NIP665vFdu+IsfLW5pCzmzk7udE+bW1Z/HfeceeoM/SPDUYYI5w1Procjpu9D0/pT4DfTKWJ3UJG8ttMyBUXF82c45QqapsH2jFVlIuYUSCfPf+1XJkjWxGD6Chi4m5Fg4VXt0NRpRNVGqNnxIAESWpmzll3GoFhIZyaHTRIQogYxINykgPmjm7byc2EHUE5MYoek+X26t69YxKzg+SX4y94Prx3AMg3b99+8cVXmFPU3LLZYfIJHhznAzvXzq0kO639g31Oh2eNfpczwmat6+vpzXo26A1vrq+fPn66f3SICrD/GGoWPkBbXA64gXDYGN42wRmdoagJ1gO1W63Z8bbNzpLYYxko+jJBc5VKB2UNI1xyaq3NWHDvsNulJedFbw8bEclAExb6efM9GFDAiAiP8s3v6G2FXJgZKH4mGhnafKWZDzS/cgdKxVa/V7EDon4mrQwXNvfyVK8rIFBCbJrSaGKdEgt/Z4O9ETOCPv3iswePH2E/KbIko6w8efSb/fbD+fY1E5xePp8cHq7GVxNOdOgxykoDFeUDo+5r9QUKxIH3Kmfmmhd8dndZz9fU3TKjkGIqCsOcg30n4wtsrsVTr5gI8Stx42CzFTg/tDGZaHOP+m+1fUkUFkegeczEoUf/7OSahQTlsB86X8y3xfgt/jE8xBxihw/K8gFcVkYn5+z5g9SxMev7W8aUliPKYJNucFrda8By9vxAc90YbZrT1nq0bt7Q89DlwK/N/obNotaDVZOF7TQvsTM04FmPhDlikKG4w6SUFTIGzMOFsKY8KkyukInSvM9zu/+SmoZSQK8EG0pRfIiC+aZ2ghj7ECnhVKvM8+m+ggHsmkBBazQ+g3gQRCJ0XSFXHJUFjHC6M8ptHLwjbCq6hOhjNpw5RHRfjYQppTqh/5+zud3dVbxS45L/qvEZvgcTI+KisBVKWRenXkFvBzCgMlt3GRXWP1TdxNSWhdkjaGFzHge42V9DBJoiA5sS7bkjvYzR2YRxHQ7NfUrYjm8V71CVu2tfw8nG4j34SEZkdee3es4PNxsbnt2uLpWYZF2eoVC5kNedr4GXqOn7hxzLoFlYAC0UrnSVxApi9bUkyR1oir3OpTwo/zLSZ4IgQNaGSWzKTA1QhEqMoEfcGqkK7wr0LZBd5qJVR94F/rUeTGXqcquSBGlwK6/lJ4WqDqrjEbHCraKt+vAOtNuwwK1I3MEuEAqLCdxlWyczTL7KtsQVHy0kIubHCtDvfpKBfvTPVx/0HY2gOxDxEGZc/igAhJcOe9OZtVUV+o4uEm6WiUnpMq8SSWhOycMFQbGxhJYkkgqQ4kp/FVUdR3IYHjzU++CTaEC04FkcE86DYwUEhRTbLUYRbe7IFd+rJCRYhAsdVKXRITpIPDYo3qhMADfQtlVvll4krp7K+927WCfG3UCfSVG+3XmpHYLwUWaVK3ovoyIFNYlNNU5PT+nAuz4f20/San7v4+/9k//oP2DRA7W1ciMDI4qao+ax7hBmAapwFTpv8F0paD6K9tj+4VO5E8YfHKDzAHs3GNr06vYH7p/gxhRdNkxgZTAHxdLB8vb00xcvX13Tu3h1g8SwPObOnKtOm82nmfDK8ItmkJwdlOg03JikeJnihdV1gBdCi5W0AIsIQEBGuejyIhNrHcRHN6UkYvJUUrx/PSyosU6rmasEjSOgkFs/+lLo9UPEGmb5ouJgUtLdQzSHTjvdAdN+5szOHLTXM7fWc/UC/PQyTYEmLDMv9wqPvJdb0PAmkSK79xfN5R45KgA6p0jrfApaNBadqCaRmYcue0Sd7yQXmLNMqaRWyz3q2cb68XZ9xa55TPJttEc6qdvN+cklrarh/l5vsH95dd2eXOLYUV+zmzgb8kIeU+Jo1zF3HPCHLCA43GeT+AeHh++//3Sx0veCKBlozpRPxqnp83PwRxyCH4PUVn4hK5iF2XwkTRKXeDU7bn9Litt3wP01LkpqlUuZumDtS5Aawk69zAHCc8e1WjbHLarMvfNN715j9ZFawtI9ZmEZhzMA4S2+uw49E4HaPcYDRoyaXLPTKyfKMZGJC9UlFVADWk+dM5Jtrzr6rhuBWnFJeanGilAiZT9w8WwcQZSnPFcxBH8ncthsvFzRGzPevRdgzCounFcRbHg5t4PSgARwRUARJ4DOkdWImQYmttQzja3Xf/z48duT10Rgic3r129fn7xl5h5Ffzad0oSmD4VXW3Ct7YBGujsECwHFYFyObhTW3/LKvBRmaQ973Q+/8/7J6zdImtED1laRaTQluFAUYx4tUGIGk3EPOUkAE0FQe+0yfqahozPIDo6AJv+j29IC2vZe41RprAgHSxfptpg2Mxzt0emAP8scdGLAHFKWhzwDSttOsEaD3GLcKo7KwfKJANMWdPkRA/9qgZSPieHXlPH6zZgEJVPpy3c4IR6pS5CKpknC8X2hpd08OWON1hcvXr780Y9+tOAMDodTVg+OHxzsHfZ7sPMAFTo4oJEwee+9e1SMdu6EOeYSwCK8w4rQ+jm4mTlfc+dDXkTXQpqI8J1e5O5weDhbvnr9+sX3v/MhnWsILbVqyg4tS4igQwm/1nTWgOGSLX/mZLCLm+P5bbrs/IBQoZGKvd/bhwtsksP5IUum2GHMkcCarYbogWDchhH38ZiZ9c0V/idutocKwybmL6odlFf77DKlky2BWO3Hyn3Wljivnt4g9hcjn/Wqcz1zrzHm7LaYR4YGuqYcKJFCoTF0yqxbNsEBQ0OI7OCynFiE2WdpziEaRPe8BRigd+EoZ4dOJUbYOAudHa5gOfpntWPtz9a6HCZGQ4cNhZYTBkniIGm4ne2q2lrtUE2p1UyyZPssukNUBvAgyIE6ZkzRciCyHEyDAULp0mVOstOVKS04PPwTa2yNtOMZAxmuu/ZBJQAWLj8zsrI8AooKaSThVAMcKsXi3FrKwRjzTulE37AUHgS4YOiJJQqOSpFKQZbrXQ2vwupv5Vf6SirekxJHzGIfphsCIrxI2w5uCM97iRWJlK9EC+bCzUOVXfkhDn8lDneTlNg17PJVVHbp6hEA4IFEQVesGGWZGSkxkXFBlYBSjGrMDNhxxLiL97ixS4/3u1dZK/2NPv67Ub7l+Rs0ajHreCKpsQfdih1orZwUyXzxaV4zZZeuTn/7izxMlqR1qCEkoRLEWpHBncuMy9cSiG68iBArFoZd4KKyp2OP6MQv1kErET5jarERFsgAIwfDedZWEEaSlIwE8hwBhft+t2edLgTCK6xjVenOe0RYk/2tKQsxVEWwYiDK/LcKsa7xMckFDCiAWhSNlwIvMylxjrb5R/ExScVrIltaksrQ6luAEk5ZpIdMzJmLiU/RuqL6IZ4k7Sr+JCMsgfVL+Q1IaPQq4KunBJWWtytP6itakJnoxE6ckLv7bInDOC7XX3z+C2zh8+cv6X3AiI7HN//x//pv/52/973FbK5FR0hUQq4Ejb0QA31ogCFIGjYAJEjJ0lsJ3jsuygxqLw4HY+oXdt76fD1/uODE3eElwBnLZqYHdpMFwddX17gO2CNMy8nJDY2My/EFI9p4ivBCdxwgrrjqMPufwQe8Demzc4Lccd9tdWnXyIgwthQBEU1tu0nfGeg5bZSaRpz5F34Yu8wfVaxaIParPmy0z6JK9IRYy5iW9/yT0EJg4f+dXWgAJWMjN1mRy98QTs8VSc0WBtmL1pxvv1i5wfYQ56TTfqBTSGbBGlrZR0IApW+blEXegXr3pTwnF3V3M/ldDmLe9t7YwCQ397vEnUcMdCCh36wc4BfjBjIuSWfnOvRPzBEzTjATqLoTumob7dfN7lWn/2B+fT1bXtOQQPbOFulQe4H9mIm8LjNjFRp7AjbnVHVUbEwZZ4UswOgHAzhlhNrDff3In9qZIGouRti2jD8gaBTHOazWiQwHsLwGLcNpyIx3a8bVCt2IUySiJpbaYK0YctW7Q1ShCeM5CshLYuW9RK/uldRYxYHEKbq0kZQ/KmJxJIQAmMJOP6yHsBNtyOzhzfz3N7PfbXR/0dgcs0CmsT1et87X66MN1nt1r925XC8ftHpXHaa6Dl53+0ebwZKlFLBa/4Y/uSyaljnw4kRPFRRXCdVWOhLoVVHmrwHltdBQJU8g1Ta/3BElmpNiGsAhgIR+NrGJ+FqBMxA8pJyIJTDGDcrtYrVI5ZvOCnGERgbKnimX9PqxrnF1fX2pk8FGnARt9USwavouOGvsuN9ockAYaz2JQ2al+QmOgGD2CPNYXNbRaTNFk22FjkYP53Nmk+/ZbOgPLJlFVUGOC4VQEpQHHLsz8KYn1b5JjY/7qmGUt+6K6cJlecxOVlzuoRRB4jHDZdnCA+BsBtAri6qzy9Px0fHbNyeYC1xrxrxUXHkVjsMG2ZqqRMusqGRGItS8lHuEmUROqkC++MCT/8qrscJsAwoEYyUNkbEPkkMtw7+kYS2HD0bFrgXh+XCv//Y19Vfj9as3X3z5nI09P/3sC/xB+miG/b1n7z1ttC+YE9XpjZgsxAmDMGU0OvSgAPGBEEu4gq+wAnryqPEJOgaVB6OVGHkiMLYLpVjjMHM873jC9l8tNheldQd5RofP1JWqF1aaPNcssGZEkWYxg6xIlo2zciLwGrTpQiaeHNUt1gi5HphDGfuD8eXVbDbcNvbZuJMpKwv6rFmR3j3uN4fLzuF8eHjpSvv9bWvMuXt4MqvtcN2YsrQbc4RtYWctWuZbRuNae2zOSxcLMwq3TLV0vJHZnhu6OvockM5gPi1UV4FYl+sHQ7wko0cSI/3vXBVjGv2XKIRc5Hsqc+2XJvZLJqNVKySBhFVxH0I0jkFdNBlX2hRwBpPCRErWcduugzW2UfnECZRYT0ZIrCnQ/AgOtDhumbn2xkidK07s80PNl+zFVsx4lfWWlpiUEiyafIRq9Xz2GLCd/htKLf1axs1gDa19bDFRtQFKzj+J0q4w08imE8iTKwPEmDN9HBRz8rjbGG77p+Ipq+SayFX3PNY3Ad55zmOJXKKXti95WFpBQmgCTSLI8yRFArLmTfiGI6sCUo55BWB5Lrnd5ulnJZsoIOx7dSWoDqm+o8EJqRWihi2pyRxYMmoHx3SCJSAgcjODXaZ349axKgz+//spCJCmzgiuiUnJMvcarfq3fAoqaAdv9Yc6528JKp+MWCRx+45hVHukrRQTC01wELTh5YbA+F5YLh9KdEPQH2LKvxKcVElnrzAmRiAws3wtQgh9hFVlr86xJBVUjla1uFkMTBsg2nURMlvKeFIHP2sIRgOIL5poRhKKbboAwyaREMmUcsAJ3P/op3YEoBQGHNCSnZHp7S6GkrKkpyl61vcUfbYITCFk9wDa8UIxjhSJodmERB/kHFduQd43rygYv8kxISX09p7AOmGhzSATRB48C6R6SZum+bOf/PTf/hn7x7PTzuzx44f/yf/mP/mt3/rhj37nt5kLxX7ocI3U0XYdWFGWmy2m4MgN4VWYGhzekkC+Qohs5ZnGg/NB6Skh4WIyYfuf3h5Owo32Bc8gDKHGOjg4GAz3X756eT0Zs8SPegOPH0/DnhVKXCYpwj2SUMlx1Jf7MJCNQknm5IQpYyo5I68ddsqjJUn3qq4JDrE9UtRKjobzRCIu+psZiYHnGB52kEDQ4osjLl0Kzh+B2/PoM6RKr3oSUmWuV/Xiz2145EhyoemIqAXyPvaTFoEH4oa54EKzC21c0ckDLiBS8ir5JHmyqYGXPAouKU3RMaIM/tzFc9QWDm2HJ1bJRGc0hN9iWFFZngOVDCyPxKUnewE6280B1m8+Hq1nR7hk0xs2wKEVZRsL7K2xOC2Zsecbtn1ivtzCHltnTLKQwwnWOnBMObTTkcqPWb14e9RM8J8CCsnW9I6AbZkqRpPQKgiPz+qHtgL9sTTy2DMwvea2BqyZg6fUV+rF+7deu3h3vhYxASLiu/NBipWwd8WsYPlH4UWDLNe4Uh88+c56/jyN18WT/qj34PpidIPvSBFnXIQKmtPdlo3+mi6hVRefZ7NiWLxDbXnTPZp293PAD9zIQoKoBRgCGyxygwkQpwIbUuMmIolQHurgu791fLUkdjgJlKcPIYWXuvKTwkKdn4kkoWEIoUWRo5TiBCeSDNc/kSwKtB/tNHfAUo9/umQrqKOH9z752S9urq7avb5WzvkNiJtY7HruugLaCcxvdHt4JnTarNDCpsuw7wLWyRLIdEg6fYIDxeazg/1R+v7hLRoS9PSNFJt/+scotAsY6WkFXcdYWbOy2PTbfWZQlLmIjvg5x4FkFmSpVcCWtjAq2u3WrBQ0us2bTKPHBt1nQadtFIsEMdXf8MgSItaE0QiRd16C8nP9FBRJrKHz8ikc9p5LaIlVXktin2WKUZMiqQCaRMLJFVCWF0wVK65AiCLy5vUbYrHqzLKGpi4XD549Ozq8x6IL4nFOCmcwY9ne/+C94/tHUFb6gFU9cqsAJwe5kxDAiXtewa/gYGCNRSGrsNS1bxTnAdOompwAfUA3ljwPcNMEolYY3DRrzoDDAEoqto3lMNPZhDkuV6cnNObabJZPwzLNR7ZnONy712dyZ4/JkMtWX7NESo4b2HZodbKal6qg02SqJkMALRx9+hmIRFZdPjNaZ2NBG8skf7xbuyxSuWLZcOfYG0c7BF5oB6sm9rp9yEDCqBMSAm0NqQLnyq1Qf/dePsqXRHDCIrQLmOSaMkWNroC5s2ishmACJSihxFDF5Cr/rZZSNdlwpkGAvucDs3bwf4DHV5gqQWg8im0AH0A5l3iRrSBFnBvSJIZKAQb0N/ErCCIoWS979B0LIEOidmlCMw4fsOZIPjJNGMlJOAJjih0Dbo7+bcasL0daDJrRI0BU5Y7eFKLIUIRE7NsvIQd8PpNvxUVdJrPiBwBeIZ5HUwhyBzYPYldfskewXoGfp2/cEkmC+NshWVLdjVsgGE6NxlXyLz9Jmax5Cq5Cg1Uw1gJQISr8JueW8a3LJFpT5XnX9w9tImJaPrWmAZnc/spbzbICMszSXJKFQMwqbz4l26ICycnv8pfwwrJEUHuSzgQV1DzubhWzCtxKYmhu0A8ZiQnxEVlU35cqvcmCmwFhEJmgUdEwU7xzpQluiC6L1bJmg4ubGsIPiWEewXYn85m9ffAS3BWXjzAUY/MU3W7sUU9XTDEaV5fePn+8AYxiACjLKRtCE+Dku5QTvnSYcsiQQeoNYmj7sTL0CVpUmHNM+ezbEyMEimp5sCzAK+IztvnI+SOcZkfA6qF3ZlIKQ9Pg9Ap9nFfNzhB/TcK8hGfxCbhGtWsTOgP6A8PLGJHfo2kQ60OJ7bO07/r+K77JEonih8dErrhhNnrAlDnq1s+//MKu9/RM/MaPfvS//Kf/K6jhAJ040LA7E5qceehknja7+1l3M++RQaRaSAXxeOLWawpZPnsPAuR18vYNm1iTy3r1BZM+NxMcR+v1+WRGHwk9/Q8fPx3tHz5/9eXL1685EJ4jZ9kiAVYtFqy3UV5EZhIo7j/dJPfvPYBjMJ32AL841cxnwDBZENkUghUAnuW0bPfFLCM51pWiJauKrYEH+LXUDexwwjccDOBc0gVDlJCgwJC4DnLvldyUbZIU8vJT90An9M4t0bSxytUdokSDTKiHipLoVcBzmigsWadIMv0fqM5PoyeMNG1mvQPPhMk2ZSr8LLnkIykSAbiSx8/sR43NYWP4X1IB0aADb+fsWmJCIN6twACDUrBHJU1QJKQAAQAASURBVEmAwCvZ0pnrEch0dHOQKkeJbdsny8bocvKW0V7nhritPfGoIVj26/IvkLUnaT6e30w42NUlzIsjJt2uWl9RRKjHERORHIYXSYwkfPSBt5hM2jxWKnyhdJCEH9s/hHgWmxWhYke8XFBg2r/iEvo7UZJEIt+9uq8pqqWqphKXfMq3JYTJwQhowUQkprL+vb/1N//O3/hvMX8FTR66ud7kZ9P9TovJUcfb9uVmc7TqjFfbAzYApZCyt8+6MWRXb4hYdTwO1xZYqdrIQE5DeGwvO3VQOLAASkGqHJMB85ztUMrMHXTBPVTAt5q6SJAoqmd9l69VvwzxK4I1OKpG4uWWx1oDCFEW/vBgYbTzhWdsGRqxur9eHDca53zWj4RhST29GV+cL64ur56998HbU3rQ6elnUgckPmTAqcX5TbTL2+62zApvJwlgP2jYLZk50GRwb8hWiS76px2/x4TMXn/E8mKNVCw+IW6s7tAqXMd5Uk7oA7OOaewTiz5bGqDtRi+HAzJRoTmeXswXNxhlMHEDCFMU76dY53CJUmDRyvKBbOHMmbN7jOtYGKEWU4Uk1BN0NezWaeNfbDLPoTwcvCMH340sYwQhfwTktjbkJbqsSQtU8xE6LfHHJmk7F5+Q4OxvOG6ORNJAeTlng1IDb9k1mCcWxvz0Zz9bTPd77dFs9RJZMU3jwZPHhweHTPUYjgZTzgLoDm9uLg6Pj58+e0IZRZZYSIbaIjxUCDy8xIUMxKhgqPrnEjvJCDuMpuaCHujyiQDd5iVHec3G7KP64ouX3//og1h6XBEjyDR5wJEu91i5vNmeYTaQWxLShFRATx4/6VCt6bW7DYbd3taKjOguXAglkqzW6zWafdB2TjvCa+xhTjN6yZ2+J/pTyv5mQ3SiTU1KnNUeLENZbWczFMA+ma51hAc9a2ca2/aC2B1DZxMtKA8r5jTejCCzKlIGuG99dRFNJklyrvCivMkKP0CCboJrCAG9eh/VZKiK2lpdjqJQnCJ52IHmQmmBSb2DdsvOqAH8cX5yFJCiUSoj9bbJ/l2YRPyHNSvUbIgrkOSM3nqlH6XIKLUYygJoQQi6ypyswIhK5kt7axhNIIrFi1hSibhorjB/1J44ag1D3TElyej8IVPX0MOpMIJynBFLZtjTfmPdNlnJcX7VKAHyU+LmlVsJzzfKGyxRw50XAxMrPxnZ8J28ZJh1on5iYpK6nCcg0ITnXtnwitN1Tr/u12hKLKgEnehGWRWZRGIsb1E8yCcySQzKj48+ROwGe2lTJNt2ZolWoJeIhBvbP6/q586Tmf21L6JqSUxSZZpHMyRIygq2dUbJmhfTVMnKD/cSNeXVb7/+CnEVB4iVHMwuz2KS3BJc55ePVaZGKx+LBSncN0RhIArj1RiakBaoQy+WKxwC+ytLFnHw4TDcjqOD2pNO9bVWAkoKkk1TygPNXIOJLEhLvplYgZlzQnlIhUdGhZmotyuGk47CSc2hmVCmOmdS4SAxd0spsfBWPKPbQlvlYGygm4nIkyppS05+KhFSMoW482uAV/TEqFJSLpMXZS3vQgBMYbOIiV2J7KfkXmJ6zwfp3gUlff0WccBAzNdstuCIRWoseuaO7w/+yX/wP4N7eP8BwvzRLHXAqqgtyUjDQ5eKa5jAACtSuhMKElUGYin2xiSIbxHCcDiE0Qt2ZMON9BwxTg26ODo6ZAYpJ3nB2V/96rMvn3+Ob8EUeeaJ6mQakYaAe81ktr9zskd7AxYt6GEoMkQAGmRnbnh1g+EeJ5S5X5MywsqlhRA0ZBtVMpaFUUPo3NDGCC+xKqCshVZqwgwJ2hnASjpYkIqvEGQSfvPDpyKTSgTyQTEVgEbUHZEFOJdEVZ3Ii3DGo3GmsRwqXpAHmSip1hm4/BGTb0muAApcYXOVV9FBu303r72/aKxGVHDZDAlDqz+XWodvtrtTMFIjk4AXr8oDIGZK1wjtXa/2aJpt1wfLJT18bO2Ih4cXRythQW1L85v5H3QC0Z5lFzv5QAzWhDEwDSZ2zdG3Zw3HgwuRtfjEUluIGyvvDqTkjDxQJPB3kEFaQZguTwZ7qBFpCBUMC6kkLA+7V7H3UhblqUpQAncv7yZASxSZlXRqQhkgKlZwFGyQgU/OPUH7mcOD/Bkb2bTO24tJm/anLgTFl2EtRgDQC50bijX1NNlosnA2O6wDcO8s5J0OQlQoikIygO/kWJAGQoRcaxJRFXakmhhKV7jl586dkIAFelRAJvOZ/6UeLfBLAuLWgr4DIY/pJxVX/qcekSpLL9hTqNAHhQeRbDrZ7TFQw8jPoN/de+/Jm7O3QMC/RF7YNOwEbcXBnpvEszyAnlxi4lPACSSKCeWsFQou81KY18H+MGyywZ6VS47DZiclSqvz+jEsokG+aobiYMYa5wkz0cdirlQ61NA8UbS7C4ehaFrEt5Nqw7XQhXEImjCei4WAzahq6g02YWRNgnvUwDTy1m8jtWUFCD56j9561xAAhjBZ7Xeu/CgtMAlQSxd/8rGwXrsUZABMLkT0MwVJppAbHMXC6fyasmAr5Kob2BVraOJq9flnn2P9zi4uLq6ucJpHB4ezK6aGd+7dP3r06AFd7AdHhzCKfehZGTWZ3nz00fsMlRCesh/EVTFRN5v6XrAEgWBb6Kpok7rbUCEQS/vqflnwnOO9hzezq3sPjqERB93SLmRjoi/2NjNPX8/dEiLHws8M8S2Y/nN9eToccngLs8KY6Ud8Muiw+QQQlhz1uJ2vMGKUR0dxM1d+S5dcYXIcZewRtXC01Uzo8ldEdBzQbIL/TJoRfxffhwyNuNU6eoUvy/4TZOsmv/jVaLmZa+Er2utfQnfcqHhUeOIHmcN/ekSgFayxYhgQnp2NJqcZAWCjT16Y7Lu35wiGyRQIK50we5wjhNnpDAfwzgFgFcO7I6KxzCTkYBfE2uy5+B6BRpurrn3IhOy4+45GgjOqp4HVpDZdA4DPo+EVAasXh5vBBwtmM9jlV7IvnHdsnQ2FnHskwfwHM9iFbacjBN+IZhVnhVEfA904ppVWS300OZIo0i98IWbFRpII1JT8QpnhvnlTgIYkUgmv7oTJLgVqjt4rzEpikwsvwIX2V1ygS5LkWxD6RvzyTYSIW3qtiJPQkBIIJUTd4lPx+60gYnlSgsmFzjL6bsHYZyImyOAgADEFaMlP0nnfMSXR6luVUtlGwoHqx5LWHGrgO7DEDbqJ43eJNs8SaurbJ9++9aoyKMh9LcbyPZFmfj/h1b7UpX+9JNqhZLI6q7u5h5oCE56CXtipgJOdZl9fhQ86gOi0rQFi1ldi6puybRwjiBzPhXaroBy3wc5uDr252IzJI2RC5DDPgVTsKXmhtTHKlibmlqlo1N76H7EElBqs8/YIHXevAAConuitQ5PMPaGYcsIHgZxgRV5iyTxCfCaOK4lxb3dPmH1iOxwInVOsi/SgLetniKHltO8IJMotcCmlSMnUSJO+fPbBVY4G0KcYOfs1n+UcD37N5XP1WH5qOHUo41GQUU6JrmIEuUaD1bXjmwnUsQCUYv7h0w+/+53v2qrRWEgUOMF1CfDHvrxtjkdlcgjn/II1eWj4Yn1LOYWahBS0JA2GMzOYypaeP4YaENj4mgmY2KTmgH3rVs3Xr99cXF5f3FyxKwgdM+3eCKPcZW87hBo3GfazB/no0V6v9Ri488Ur88LQY8oQAcLhxiRh9pwf7DFMwOG/9I2x1b4TWzQkos+sSxinZ0zQ5ohNchzVwCvRiKBgMEk1g2LSSC4XBrR9otdqkGxHc7Sn5SKo5nECSOu/8uzdM5UI0Dr4bHI6mJ1CRoAD1XiJsiutFMsqSmd6oMA4npqrJ97Zs8Wfcgt4YyWeSpGy4vBIYzv5w+16b9v/Z6K4ofKgZlBmADLrzgka2dzsS2OkhfT4VaZbluRSX1ORXVLTer5td7xqLdimBeaUyal00WHx4B21kW4hazpdZgf37SGmMur0JtPlNTBRAAZkGAF3ugVVoq15GRgm2oBgZ1923A29VPQPG+sHm80LZnXDbwTK/H82ZaKtYWdMhy4xcQ218ihX2FEe82UXGIYbVBGI7+moBSSVL9x9gOtbZgyrwHyyY41cWP9ChabWK2/0kzbTisqd0sDTuvForro80j40HzA0wa6rmCfQjrjoFxMG/1Ui8o/vD3ByAWJQL/cgBxoi4okl6IbZl84B0+e/Qb/uMg5boPi57AcVKRMGMAHajrLdm7fCPobZnso1z6wtF5yBbtvoJiSVXOCu/vvQOXezVof78cAIh2zOSG5x9AaF9Hj/3suzt8P+aLqcoVt0LLbaJ3jjHAfR7e8tZxcknI6n7ADbzzagKrRjjOztxCndvdXN/LD/Abxfb87hMxwTC3w0XA2xMrpdjquHLH3cbC8pMhxSQUW70S9czZfs/EN/fmO6XrFclPWekSPJSlNLCMILC6Rmhc5jwidImoYrMlY/2OeVA1MRN4XAz2ChP0epL2UcphS0YVvhSQDKRUCGraXIsyXOlNZEKh10GDu37A84ENqBSSJD1PRmyr5qtmRan4Dk5tpSiarTJ8JsRQ9AoKzKCObNW3NxRvJkfBXvf/3JL37JMPeL5y8//+JziGr1b+ariV7hYHS0f8yELE4XAR126GdaZnfY+I3vfH80Gsk/fEmWVK0YzyqiFeewBRKCP0w3iBcgcHnaA4gV+ScEIuh6oeai2L+U/6zftTCv3p4873b26WaxaScI/FiSChYm24DmtIH2BRIVIiDp52fRvHN5ONeMFssHsylrSKaMAVH10NvMqcwacPaB5dCNBdyg3Fluzi9vbhZz6qPm4R6C3M7XC+abOSCPRWUfWFZ9lPmFKcsWdIyIMk2Dy/Ud0WY0Bzuv2hiDBqVzB9zFl1EFYG/b1LMyp1Cde+HNHWaUj2pqiWeCIkhDes/Ro9aEE0iw59x0NZRgBmGoqGSlEOAD/yAIxO1lx5aiJn60GQgBUgDhUMFAmspAV5d2RqXT2hABQ+3m1UN67hgcwA+nXFiEwAAiXfnNzkhrssGbAjIWHCeKcV1rcPK1bUAWMCQazrgJvS3KFp54qTlgkVJCrkRWN/2jsYrEQc3pAEV3VCCKZ0gTRR9yq7gkvgkhdT6BKL3v6H/vRWFJ+FKAmYVlGQ7YHiFlkYJsCSKEGEqcOq98qW4l37sh5Znwknv1ato751ztQPGAx8XN1lYuECgPZFmHhCAhijjsKvQiG/AqsQmvouejH6Ar3wpFJvwauDrgNrjKkB/zKPcKbPVjqGBhSQU88byV7MLafDdOAhMxMbjdffnW5zsZVWkK6nfC76YzTvl0G2qCksj88rX+WNArQblbPNFXehpZLMiL2khZjbLKAO1IyYOKj/avpRyzQSFG0ZmTkjh7e3u4+0w5JTppdGc1UuoUAXTApKoTlZRTypYPTlW0euix9QctcvLW2ym8Iw/8K8sFtQjALFTgRAjlT6AyF8QAkFT6YoGPZ6To+WIHg9+IlQfpBCUAJ7moVxfRjUQE/5e3gjqvJU71U6e48/vulzpxwO1iiUSzeXl+9V/85/8F+7q8fXP+8Y9+83//v/vfsonE8YPjMvMH5HDcqUBgi3aF2gkbwjx+F6U5uXHs+ZrUW7KCS7q4IjF+MWrm4VeEQ9INY8ayaENlOSb2+eX12enFeHrJUjY8f6YOsxcQE0ZkK0K1x8YFpLB6j+VvfScVUzF6lCSHQrQ5w91z2MhPM4RVArHFnM0H+92+pyvsb8fjKV903GxERgSRuqYs7BVl14FYLsnMzn8NIjELLURLC4caAqp0GRQKVy0CfstjJCxL8y9MkBVeRe+ZD0L1jkUmvoYsoKDTGiACBpBUFCmBWBD0Vl98U524fBKR8lS+i2D1dfBvN5tR9IpP5gVv8JSQoJaVq3i8IcVpolY4fJIEoCgpdgFqtjhrCO5fjZl/xVJLWgNIMupPvWAF32brpTm1NJrQGLIkANHAb+PYHG648b/P7l+BhABPFcV5sugQnMgECbeCwWe0PqPiQZEyyRXfjt+1Sz9wm9hSY+Gk3YrgsCVESD/Qby+5kj+CEsOvPKQYlhAjJw10FlbIaCSEFOSSj0lK7Uad7a6mck2doEolDnPOIQnlkd0VJJ4q5qWISKlwEovCE1Ur2OcxeRmjEiaPyj/lXO6HUgPfvQp1AH3nKqFKjuCStMQQXOCCuCF59a6XLTUh3JIq4f5X/yGAKh9kEBIWMrpAVCwiHot7qGRTRqIjWWZqkS+LNZ88efyGDR0nN9hsbDDjA/g511eX3ehJ4bMeAzK2dS1fWOmLXvTYibDZmkzHgxYdwJhFO8K1jzSLPYINfJg/Jj701bIRrRqE5miX8eGoH5bdPmeGsD+MO2gJ13ZaoT8k5WaG0AzoQn6EgGKSpGsb1dLHj9H8I2ZkR3Sv8BEAMtjnKlJkXMWQSwSzemrqsWRYyA6TuVVou66tXywHcIAdDtZzJ6Jsu5ewyi5/q48G+/nvDYYwDrPW22NDmublxdV8NkZEFxeXszGV2PxnP/vp1TU7bvVmc3bjBQINh87hEftsHR15mC7bWHepLmlycOIvU+5oocksJKHzaTGTmGAcjQgtcqWS/y1BMMJ4hSYewhhZi0WGxTKAaV1sSHpzvb1//xmz+TkdnNaOsivuf2nIkUBAml0UcweTUMoVO8QumBt0c8kOz5yoBX+0A5SzdefevUeDPSQD9WiLXASVCQcaz2e9PsMFHG2gEYcAscF9d85kjoSm5KG3pS6moyctdu8cAGf/PImAZvHE3KngbO1AoHhbHMBWlGVR4UnFGQN+zUUav0RhUmJoTloX0VkOSPZZy8izrKTNQ3ECfmD7Q2Xg1gCdTBBFfuDNCIDKWC5RsVuZQVJk6PRj7hANDPUzxdjdjSyl1mGWWWOLkDei0nTKG7oG1VZyICkAPZjE9XukZZ1My1yvC1WBBmKhnrST+UcMqRIWqYUTn0kQkbj5kiF4GMJDInqrPphnsOLHnInFZXwv0JeiPFc3Xypo/pZXo5vaOLvYu4cq5e1PHfU25E56HwPo9ustzF2YkzJzlVxK+iqoSl3CikR25BrF72FMlbZOzG8ZbEqcMqu77AJkqq9dd6kToFcpSTL67pU3PsHLWgBhwLux/F6wuk37boyw9utBX8sradnLaIfdbl+jkrCiWFDBITBJFIn6MaEVordJinxljl4D+qdPwltSVOpH98RT43HOHP1snP3K9HDVOmUl9Y8UJgdLIkWRMWOAEQYyTgjZNjl121PF6MOQLp4bTWelo+Way+zx3G7POULMfqiipHy1LyF+zXaI5aK8un2eu3hoyd1IrtOZTW4wVvI/fUiUTZKYh1ZGKojbbH1pwMoGBB2x2QakxJAr5aoegE3MsuZ9xXoSxlueK3yVzZ8S+ev3O7sA1XCSpPM8P0QPV4XBf/ufzs5O2UgTy9Pddh4cP/zO979Ly0uLtHHrbocF6ZuwA7XRG1JL4fRPLs9PIZM95ibTCy1u2VIynI+ZU2qCh7UukOJiZMatVKgRYezN+ObybELV9/NffnZyfsaGmBwnz5aA8IklbG5BjCjdHAbXv0NDjs4NjsulFxHk7XjojJssndjucbI9ozz2FltJ6FEfNA9QBuYTawyZnsF+hYPBnHGHJe1AZ6Go/tp8udfsXtLUSxWMf0M/EJaRVKCtbQKAHMNiFgWDGLdhsCaNUhSzpbQjgkT38RuiWTpewd7bVEk0MFN5EaBfrnpbq9K6sOZCycyPlmog8o0o/mcXIKGKuwHJxfx8qF5vH/DMp7/d3Oxtev8V/bae6uq2P/ADw00aOukfkUZioDbEioyVC5tm0FCgW6xDZzzTKlatN8vmdDyj8lk6zAtrSKk/BpwNJ0M5nsMMXnrpWL+xmHZaI4d4lnOqchkVUm3UsB0fax08PcPWNOoE8pRM5tlbSVLNI6jmRaO1z1whV0ysma8MD9Ys7GRY3zLliT1WjpJJWm/8L68SZTD3KsBnC7TiVrJ1RzgefKjmLueNz0CbBd+E6KsNG9WWWKuHYL6cTNCwVvcCIokaBWcSC59LBWxRpG2ZCjVNOcCIpXCDImmKG1IwY45IpS7s7JS0RAOWvU2kKDqgaMwpYPJrJC+ACPedK2kBkS87kFVyYyYsFILtmvM109Sla89XPstXISMafhAN/1RCb5REjjl3JJBXTj9U8SmYGGac8P3R/mIy+53f/m0GEMfj8UF/L76aXS3LORvFsk3k6mZMS3/c77DZFJN4nOxCAacTBfNL6308Zr9fxo0p/+QJ1+nGtM61KaiPQpHGFNAve8Ibg7sgZENVqpgfRq/Egm0k0Tgd5MU1E3gy25usJCIaoKTKqw/tS7nEB7z+FjvHU7J4pCFjvyzWyTmGOIz2ysrq6JO5CQod1yyUt/Ld55QduoM8FANVQTl4oDGDoQMOmOECsg1OxC5Om9YbGMiEblFEAIyqMOi25HiJCXt5Em2xfMvpXXSusL7q9PScHBgf+PnPf84Wyfhi7KAAKzwag9ExzjLY/+jZk8fd/oS5TBivw4OD0N1+8vD3XbXSPdO6WF65CkWOU2nroi5Fy/wYnmYMyoi8lTR+MgElhMLxyhZcNI1mOZby/OwlE3UWS0Z4epwOgRCiuhU4OobwHVnAwLnRapI+cZohLJGZ48wj671PP/ny9e+cf/zD7wMXww6HV8vJ3qhzcHAf7jnmhjTanExuH5DAmfe/wd1HEM7OAFOScGm9grHF0m5r6Hb2C1+hjZH98hVmgL/8KBY2hp0pZzKt9MFJaeGFhEt97mEIrxXDSozIVNaZBLBwGmlun2EDEavBoEVNT2ssTTHydRaDVSK6zsuKqXAskSdE1TI5jV40MBzPVCWshw5Oz335MGZqZhC0H1/tVDTaV8cxtKJWHSC3eMqHVps6Giag5TG5GsPQSfZa7DIVwuwAAzp0qFEwRTBEw0ZQNJzWgz/euWjIQJoIqwmM/FJ5SUL+CsdIX69FzDrYsLR84k5M+a00m6xPI6QUtypfvhPDaKJm5PqVQBL6rcDy6S+7TBsIRio4RB92aQqYQNyFvfvgSG7JMuG3+VaJShbEiH5Zud1GKZBu3/NUiOFTHc7vX4ZAAfKNGBWPTFoAqQw7QAqGhLuPBcjt/Rvgbj9VT3eAfePbnYDIqCBwm3D3/e6Hr2WZ1/AKBS4J8sMNxSJACjCqOAdqGu9oXopZKT0qYgwEESh4fA/E8L9+pJily1FHRLYLBwcuXZIYFVTdmADChNM7ylEd1nPUkPISQ6W1oguKEmd44AcOEGzWk3H8SAwT/3AzMHb0OlNcrCkwUfibXU2YOZO81B+2ILqObOE1pLDVkMOGSFHqCw07ZTE8XIEEfkW54FNY9y13KSO4RCzQElAB95s8xsjAo+FgfzI+/953v/uf/Wf/F0ZK6cQqFTnpiIgjCIN4BObnL15cXJxR3V+cn1FHQSizeQCT7GRw+YehAkesEe8Qq7RwqBj0zYZLbL1w8ulXvd6AfazPzy448hf+MFOS05PYDpnY0u/gKMZvybj2sLe/Z6d+ixEAhgioU4FK7jAcKnA32w32jAw9uQGMwXRkxKg3kqVbjqXE7lsMw2kMQgm6pHKErWJMq4xskTY2GUztp3RRg9T4aoLYQC2nc5RNjEn0Ets8VDdYoa7eDQIpAOH6OwesWvXB9zp3cCHcHhyg4e6oe2SHohsQta8AVjY/af3G/+oiU/II9faWtQY/2az3OaVXZwljTx0gKZp2viZdzLkJoIO+saQ2Dg9LO3bXhzDv+upssexybs5s1uJkbLw3U9tRxPCYTlTH7Z9xC+k5YgNQPB1OtmecmuoWjxb3j6YxJUjw/CeYgx22dOPKI+o+JgdTvPTDaOvBW6LJX8qMsPD7y7gTYciuJ7RCZpCtSfcXnLgL9/ZCoHK1+lLEkpd3GGcS59xEZpXYUlr1EsCETVcUNj0GmAOZibRoCsi11FrmS0S7yLlkIyE7NKRa8NJL8DsfC86mqlIQQHSiipLhXGZIQKzfLdjyrb4Tx8eSpGTNc14FVT5VeZdQVNo2AJHAzEzMtaR3tqWKR46SD0644Dbw2a5c1UWXNGFw1i1B3Gl+n31a8fBoaB4fHb1+85aJl4Ci/ac/w3xIVIHOTw2pkwkdYdP8oRub/dHhzc1YPgC6uz6/OBv03vNwDEdWjWNTH41BOTKSgDTJmMsGIewXWsNuGntdVRyVc0dyNBX0ZVuCuUkr0WydWojxsznieMrKWnRL9xSQxCeOxVWmkAD2Jp2vPJQCoPCLElCOjKubpvBojazwzt3IKisi6K3HELG3Ad0QrLNCl7BanniFiYSM9XZvyBZbk6vLm9liSirBKgvaxrhfZbnFgDHS/f39s9MzCjJtCU9l6PQ+/viHMLLTfIR/TN//8b1jqrCzs7OHDx8wIACjmFxeZAznwVreBH2lk2zki7SZo5/4x1X9+JiIRS8ID/3GFyr2mRaOE0bcQ0ZxWQrUmqJpBa4FC/ZIFxvYYPxJR8HJkiy+sAXPxfXFT37+k9/8nR9geJWM64W2rGF49Oix7GFHAfvjgopWhdTInrxgjdYAbC2e+S7qoYxY4AEGIlrTRjQsoymMRYySinoDFbHgaXK1w9WHChbpb59Kkpp7VXiyF2iy4o3snbOEPqquYBzuYjPRMeJRmZIlbWC4xhEZKA7ysY3NdhvEtoWbCgdNTJGxMUmocKDVGDgx9lOIs5wgzByKiXWfIDwiQslaLKhzJQGOqJ7ewwEiGJhajyKJo0UA+7KS0q43yxONYmlSc+yMK9k53pCaCoHHTIMOsSGMRlQITSKhf/t1N1zMRSRykc/lqjSQ910QH8oz95KqjvxrfxMzGRAlkjMf4EhIAVayr0F/KyT8uW+Es8sKgYv373wo8JBHyQoe01UJomUteZWb8dEuARLCT8K3w3fIvAP03ceSJGHI8E4a4XntqPIxmWiIq2R35jmV2O/cbaU5m997Zop/y0kFfstVQcwPt29eBbs7OJZYzQ1jvpTbwpNCQflyB4paGYihUZVVk5SZz1xQyapzggi2T4a7f6qQOVI9U9I50OKxrxwYXowAQetncXXoBS9pk40gk95Wcuppyg9hIGF+FLPSXwtYpztj43DO9P6JQYSSHH0CTTuuyDulDUg2PXAqiQjkNBWwmBvmMQPKMV+aAXY8sTsLk5vZrtjWOUXWvHPzodHKZKbI0Ln7IbOiuGAZIhJVlKsruwDlLXHlaGXUCtYpB8GdicNL9vE4OzgczZeLZ8+eui6IPTrYeMf5D1Q27O6njTo7PfmX//yf7+0fXd9cQgJ1GBX4hI4udt8w1+K9hrF4uHS3YEB4SD27mT/hw7b5fLVdXZ9fMeg/nVwzY/Xt6VtOsbmaTJlz3ekO18uZq7wYf2wMmNYDtzErh4cP2cWCqQFOaqUFwKg9LjzAwUHjajebNow6pcOWFDQMXBIHuUSjL5nxdJHTZdNosb+oNXzrHBHGOmueS48GRpWL5GQR/iC7yJcKG2eYHHU+yA5TvOy6qQ56iTLAxltxCQIgyyf+3N0XqDqPlqWNtZRiHyt7ZL+8NSPiRRsEp79uDnyo1WGX9O6Dn3Op/pBOZJ5Qwc30dziqfNO/7KzvbdqvN9sDDnCBnQ1GPDZMW3+7Xdxnbvd2eW/TYj3Ag0aHHu7jRvu8sb6/abGT/f6i/+mEDtUO66jHl/PVbIUqavLJgV4qeImfZ0XF3DdypKXbZgkmqg6n5mi+bLHtjGCY3MtET1026ncqPmZzwElEYzOjuUS9cA/panfgB6mnAcigHT1jVJAcF8UEP5qO9vzJjhAqsfKfezIKk8Ks3MISS6KqSlQWksjcvMe75cngArC5eOILO2wIVdWKD8g44Zs13crNt8P2IV2rpKfiDtBICgQs+DobpXiVn61nC7AB6mvhl1yULI6dYi5o3CJZ8CCqFxQBsuSj/QlYE5WvuXPbhSTAt10IMXfPdfQqpIRbUiys0hH4GRuJkSS/Ysh0T9ByyQWyAhWtNVKj/YbEfdN3pf1NGcV32dvrw4X3nj17+fbVaNgbT5mjDwz3nMEVZgEAM+Mbj+w6tstAd1mWUUwtg47ytpjcQdk92D9ikBD/BSqIQEkkMiWVJcfoBQbVhJZjHE27sdlAHfj0TqI0Xa3pPmWTXXDi4t+E+VAdYJZpNUWqZRdUuDXtxdnV3tMBA1nMLERKrgBznZLjUw7V0kRAU9Fu/lOn4NLj5ywfGdZ8K2RhqzWAiycFwlqJIXvYjycgz0CITSDGJWQcyLtzToYcODU2C0D7mBTPPZhMGRbQKVwvDu1e8AQS5MEwy+Z6dsUam8dPn2CN6ecgv6vLczb4Bzg1UW84Hu3vMy+I2TJ0Pz188oCd9ZmQ02y9sbjalRBVylo0seW0A4KqS9zFXtbsAktIvtSBMUbIJBHpH7FPAZIhbs5MnuV6f7R3D/8W7bKXgR8bbHQg62A6SFj8ykCDRe3GIzr0t63TTnuwnnffvrx49fzNk6fPVpsp3QIkRwz/+N//e//P/8f/dTKmvz8WTfWEe1CgbUnVjG9mZRoJoJORL/mRSxQFDYJ/xtQftoPHqEST2PBEbiiWFqPri4FrXbS5ckfjseNHmBTi5Ul4kLwW7wvMNZD5hw5Qi2g9yM7qxK82VrzAiOFzJhdsFo8oNc3uK9JQetIzYxzLBTxzkjJRbQc0108BwzGYIE+ne4vdotlC3M2RrSOgTUzFTZtpGgqp7QoLGCt8VFL7VhQKn9RAkgAxCksIQTIgfNOlUYfBAlkNCGOgjigep9AYcK4CaEkIsLDtfDYPCu/ALqDmtEhI7qRw+UDm9UnA4VjNTTtlZEtihiuJXVLIpHcuyXv3SkggvhN+Z9ZDHf5u2gijyrqOAR6y7fb13Sd9eOvUO1eJW5CvgnnJP15lj6onFeW/7CBNnQwG3jLoDti/1uOvxXOXmhigkKvK8V0G3/myS/PNBzGvUd59LXS88ylZmOU7LDRiolXKGQhiVdLeBVg/34VKqkICxUhlZRl7z621cOcyMkwPLubZ0oUlVaG1B8W2auEARWnAkBOhiIEyCci47hZQABYbTWMcB9eZgSSKnQIstlgJ4rMjKOyNohQ7Y2jCfCG5PqjuafnMloE9ajFqO91iUlMDqAUOCNiZxsHbomkzn+4bXeKOK9WAB+b0isAws7R8FkUik8Ivg7kKDoSJSr6VFCGwDooUbkNKNOGZd+AnKThLyy6L1s9/8sknv/zpfLEc7u3/4e/9DVClmqM6oZizqYZ50h/Dsr7TC2dgsms2HRSaZHs5IJChXc2BqNFLEY7YAMDP27r0gq4ecl+5dGk8e8Mu3W9fv6He/fKzz2n/cJANWFurDWj/0J/E6gvHeen1Q4rMGcBBPDrcPz485Eg3urzwOphcEgTglmUNljoYQN5052WiEdOBWCTAhBU63iazKbpi3V10BVlAXsooCMuTyNRK3cVk4BB+6ajhdiAvSSMaybjxQp4Ijz6VyEJ94AHSCa5kZFAVuPspYbnfCtD8xYX0oUTYoAFjsdfALALyMShE4EE5ORr+zQsrLBp6c+vN6JPx6viyMxm28Jv15JijpfCbHJHDH/UMJUeHHIMM+XbYZ8N+udiccETqanX/cj7m9K+rcXu6YlaD3bLwitFyREAfpHxh5grz8xHLfLruH9ijOtxrcy6b8vGGrjB9hmqYSivzNJhop/8BeQ6Le3EkECijSnRiFmPLmBLTQ5a9DnhamKCGXk8ylUlQYmrJhHUVE4oG5i5bq9DyG+3XS08qWVt/N5oAa5huVQ5eAjdKjIlqbrOEL3APggm3ClV0daSqNJafxIiVD2gyIxptHkFzM73A+DM5lyH1rzrgc6HL53wqobu3Ema829Tlzfvdr7ehJFb5UQ0u6SAamhaEqnwKE8GX3FWkSAdkta8WIOijaGaRRvJIj0V6IomMj87ZHc1el3P5lqsL2vGsPtTEZrIK7TtHFDech0RHpu4OZhCTTu/+cLg/m9EBvx7u9xl4pFXJmnJUGLmDrWWOCw66itUlWYQz2x9VZlaQfaVdNNMTshitwhslOvIKD8GXJ2grBiooQy/Q9FboUBjidt8/PgYw+1b1BkM+kYCmJpomSzQOtE1gBysoGY605pC/WlRgEiGYKWAZ64s9IxyBt7i4vNTmABAGZGoQ+nx9Y90lJ+0Rx+Co2/ujg/HNzcuTN0RL2wdtp+HEGVvqGviwyVaPg1ZYNL1c4PQvZtdv3pyxtLfbYaP8DhMdh/sj2NIf7JM1xWS4Nzg6PCzIQYWEpM4Cbx54i8gNzFWxii+7p/pTfkNUblWw5IsX8TvjGybo2VV0c3PFmqEUT5x7bAqRiQG7lJ9yIXu6B9zPrW2HAW/2FuC4Lo+PD1i19ctPf/nk2WPwpQkHfGrm/qY36OJfwuUYLkofZ4mwJQE+rWyFFpShq1kIadJmzRSpRCSFIj6CIcoXXSpExU6iBcRQbpkGCdIKkOTy4tewo2IC6eCC+Xn3v2wRQ0wqTX1YLbcLKEjlUW6425sNJAlEd/NsK0n7Qn+akDTRWiw0znmuUApguz+YBkz5qYth0UD4AuT0iBHAP/vCYLkvLmWUz+iPcjFi8AXL0GiemN3sgxI+hAz4AQw7tuJBgYoT0mirFaFZjEtyZwe5DJ/JAbT3Vn2m40KlGQM2WJJbYU3JefdSBYtNlSUPeauQLKh6l3/5trub6GvXX/atikoUL3ljnrsUvJW/8v2du2mS7m4DIKpBmrrvXwbXgCXd3TYgf242Vd+t3wuk5vKZedMvWBDJh3wqcar3b/kpCJN2s1fHx4ZNhVthUD2EtgJAU3Vnz9QSmHsF7U4Ij7sZ/DyzcxFxQnwdKWl2CXcPfP7a890EciEcLjdey3jIbrSBr5F8YatvlhMViD2F4GeDOesOmBKJLR/9CruZpak9iHHhNWWAdi7bwrsOFWeEMoQGbrsnZN9qHcI1OhHlzOa14sKeM2BMu8JpeZRiSor8Bw6FAROqE08kFnExI2WP6qTYevqHZDKljM4z9p0EAcu1JLIFNfumg9n7HEazGf5SzEEPbEpt1LH7h/IN9NVyxkdyw1LYEgBE8U4DJ5jULKvwMouULWKUT+GTb3XM8Jksw8zqa2FsSaOtAprxw+DQCw68Y20ny/GLL5la2D1+sv4H/91/dHTv8Oz8Mt3qmGgr4tXieD5d/OLHf87+Pe6O4oI52KURpl7uDlnEiWGH5+nvNxuMm4UBd78/7M8mnO/zY+TCVF86vW5u5jc3b1++euPR9bMR49cD9kpiQxo8dXYN6T1hRIE9IhgaRpIAOj68N+Qkciph2gRUn5w71qf3nd/8U1eYAmQ/22zGAMKmzULhHosCqZkYVt9rLI+b3QtdH8FhVy+da8JDxQQ0Cjco1lh7qBFdr0d+3ACNVWjOCgizZSD1DTSLi3/yT2tOsHGcdVpdpb+/fssvkUuVocKYFD8oQnFEmDoDfuGKyzu0gEpPrMwCdsYWC2QHvzzz/fbyG1v4p6sI292aLX701XLwyeW6N3t/f/TVfvfj9uB5Z/OovXmzXd3bNE4aq6Pm9t52ddBoHTVXB9v2ve16v9k4ZmsgnLFu83i1fvP2qjdZXy2Y6cMxO9kBMzWpM6/QXTv2OPt1cc2UDYsFJ0ijCuwZ6iHQ1M3gnvKWmdZ4Y3D25oqFevbrSxwjJVRsdo3b4MQXsFgTvL5HyadjyRoqjTqrTrSVlT8URk7egDwnp4ajcGjleEuTM1MjEm6VnQ9LjMbXMku+cPAOGyMJFlO+Urpx0ynGIM0/USFXCzL/wU2LWqApCWOwlBPLxEynCpNCFBY+YJN9cnQhY0njXlSMngCm2A7iCDL/E1+GETXW2zi6UH6nLwqEOG7565epos8MyZRR3JeJkvB8E54QVLhkVGASiKPAN4c9HSEhsqMBxCQ0RliSU2qIK8PdvQq5I8fG6j6tokbjNHAfsiFAu3N67/h+6+Z8fzi4bDZpBDCIB8j14mA+WwxHTq9v0E9CO1JHcIG48bqvr29Y04ltYCoOM8I5avSCkwG73b3BXnQhLpoNErzH9Iuy9SSo0YeOwVi73J/tTRgEwJZgYei1wEtmhx+6buCwpEiUvhdpfObNGwqyZbvMwZA93Fq4MJpCZW1kwPI1ETUusEfmiQMzErGT2BA0EAsYaMag+Bq/tXkChE73OXN1SKA6R6PjFMJ7PnkiIYTARusp2xUdFi/fXF9cXpwBrt18BBLYK4cwhQ/0ZMQwwIo58Kub6VUU1aUX7IB8czM5ONpnqOHhw0fDvSEUuCEyPbQUD85JcXAGJsgG9TVlSKRB9vYy/PaNl/CXMBU8isVnOZOrqCePoYyG2JwdivbvHTx4cG//ALvheiPKOQhYbYorxtH61HGVJa076m62zgP22aZ5xanhDB/NFpPuvM32pt/58DtP3+eEWutrwHzno/eH+73xDcvwWHjm7sOt1pydoKy62ZSKswHZJkgxoAwgiHqjvYweUL6ADyMdynYFlG4A40VOn1dwFKNMY0TopR5R/N2X7OXXZCd7WJUZEM3ec6PKt2+//FZmglTf5ZG8R0PUJxoVqIW9k8o+BTmeIQejcMqBHjYxMwvSQSfLIO0DLEWaM2APHxqdlyh9zCABaD7KBmmMUNEzp+LBYnhOQaZXaoXR5Yn/5OUTIPUxeEZYhMMjkAM7GuCxP6zc+oBO/Gb3pVmEM8y2oo3htCuqNRx7YjdnmaJJcpuyZMuErDS6aI3g0ZAFLpmHQoZqC6capcaZRCSlrJQoH70WHxin+Jx1mEpm2vrK7kAbZ3DIWOPv/EZDiHkb3xi7s48S+2s3iz/Re87+8MyBdy46xAhhxULmv9z9FB/+bgOgfCwI+Sy+Uon2yfk09RLghzvEBN0kK3ibrI5wNxrh37yAm6TRkXzOa55qjkkgAfnhgT8EVaJ9A/43Ar6eZUln+gpCUvCsLMixIBK6Cao++jmPBVmjERkgSWcWBdgus9tXgRqTYmNsLouvPzIVHcwni6Z2h9KC6x7o0XazILI2lTJhMjWVuCorlQOnc9AnjMG13hLJqDLf+TN+tDSWwKTUahgvM9XEeeRMqCCWHgACptAyX6HdHI04b7zK2/kPTEbvcBAJiUGe3IxeyqDTPEVJCKWmoOAkJeVQvbRQmndBycdct+/yfacExJVIrqQqj7wU7ifQ7JKm+ljHT7kkrAiGqM35YvM3/vbffPHZ6vWb169ev/iLn/70ez/8AT1gPSw1B0FN6WFrM+r841/8bDLnJBcmRGBk8QmSu30Dy+2UPl0MGlYG/ocW8vZPJjIRn4Vr1NXLObM+OhcX1y9fMevnNW0wql0Orn/0aL/Z2z8/P8uZoexoccyxYmwsz5Sk66vxZHLDtB+gkydip1qDrwjXmeYyH+6xvR7krs7Pz22F6YQ7+5/TA1bLS/DEyaBXWnW6vsYbUc7aMGtXKo/SjSFv+Uc2BhODiapkOeM8FJmNgCDH4SJ6oBGhbCcu0tc7tDQAkCBvv/6qPxfB+AYTydSOFhJ7+QpFbIODeiSGfLYKT5zES9xvyYs4DnbjiIMN/mp7ayOo93p+wgj7/b3rR71Zv7tqs5cOh46xT5w7x0EOseHsCgdD7xcEOHiLeVLNWY/lnqsRXtV806VHcrWhmYcDRO1jFQXbqXgQIgsAer09KnGqDfCER80mw6YDaEHZEFk6ZdEK3+lwpQtv02AqkSUE2jkcCq1hilAcLFgBe9escezSMMSk0vnqUB7i1plTdFLuL8BlkYypGJuQHZ9uOVbHMCHpyaLSfgHkf1QVecd14LsaIoWCL8Ap9UUid8FiJfxepEM8vwEweeTOixYtMKAf55HGZHI3tpATt0rKqyEFDr9+J0JUiycxTZDBv+66ix5xfE2QUEOO5SCKZuGpcbsLrbBI3ksYsrIkUN1T6i07NLPxWZnOrgAEpZtCHwbdJhaSNusBjp4+++Dk9IoJPRi7yXjS7xzQrN876DCHcPDkmRSZDNZ4mhXjBpiOw6MjGuzMciEJfecffvABcB0fwOknHjot6XqWdAGkyLE5FVt7YZ3YGoh/FE5HZdG30kiBfSnd8B8CFEF4UbiqOcHkDgccRcJSJ919+ALJ0ERZtlO5sSDTdquv80p3npJGXUkFlUCSeKnPJkKqKIDhr81EZsQ7BREz5Xx1BxJKoRYNorBEOGLEjjC6ZZFhHdR0yhKJ9d4ecyDVbQhUYFUZabCslhlIFDeu66sbuswPDg+0pZfXe6MRiwqO7t/vDWg+TaGIzhFGAKyF9HfJU2AhOwjX6ir4kkmEn2+VGnxNyYp6840HCAar8oyPfuNOzSuQwSQzPMsALSbFAQ9MloqvshGbR1x/UuHwpo1v5qDHAq6MRq7Bejafnp6f//yTTx4/uU9NSkb0Q98/fnz/3vvTxecaK4aK+t2D5v1Wmy3g2N3IXqBhf4g4jJzDp+mPpjkuzVa+hEVSDjTyP4vuaMRqJKP84Ia0MYXLzYxBTELZpzhTsMAPaUqnLPqWq6jRnQ+Kiwy5oz1IEE3AqWfTWqSOS4CaZQ4bfHJsh/YvNaNE2jyjnYwbrXmxS7LDcpdQ4Jq7aE98HrTSTkbbNLR3rfA0Ulm2nuxQTbKDJMpB5GoGgBQdIqicWGNdouh6xaI1YzVMcoAQLXsa9G5LSiFy3pk9UOCDEF3XzuAbsq04aiEgB9BAG+EoGfNKHtyK0H2z2HHlphJq8iwDQqmv8pEQwkUyV/XrT1Dfxa/y2MEs0Xefy+s37ny3oNWpvpaozjSKfTctHwpk9Jrn3PwuYRVR5TtfDKGkmcJ/d+MYWi5K/8vkViAUmCAWNawj/WW/ZOOK6W+9alS+jtwuPKkqmsQQPHckfSvEOgG/ykfZFfqkToHxWsnsa7D84GWMkr8ZJqi04coIQwLKrWaCctLAU4Ba9mPRBlW/ZSp3G7JkjW3DHUO5cRWIAzaYYHusnU/nZT8xhVkDtGX3GEJYA2r6QMJcY4YsTnQdlhVXuu1YXsuLQIBm2bMwU1wp2UDQmIHWij4tdNiJp2z5QweD+bJFOZbInQ2/YEMaqhTScoGqbg12GHzBHMQonWGIHyz8RLHNIjv5lZagSE5e4TMnLRCW0wCKolUsLT8lemEyKYqcqhiyrLpS4wpPIwUYsrTqY/h4ubj4r/6///p68rzRn63Hq6dPH/CdTqkFM1Jfvfzkz68o+MvNK8botQ9hBWW/0Aac8M07qTzwSKbzjy9mjidN/3Dya12d33z22Zfnl5d4D1Rm7BcxxJK1p8vGbHHDPO/W/fuj43v3kMt6xWALi5I5PbQ53GMyK3uNM03cFXssT8Q6SYiUakHVkTXVT5cOsdHBiC4x+thQbtb9IppW74pIJCcyK/CYbe7aBntEivZrhBmgRgQEKqG4PYv1WxSAs4noq8IbNiOcHP62nEOJqXVvGrOX7ZCpuZTWlKmK4V//qUURtiRVZCYhONwMST1EF7e9m8Bl6APKaKwaB1aDK9oCFmqUQYb5Wl8FEzuwoSX61GTBz+p4a3/o95ZbprF/tGzsbeaPqYda26fQ0GAVg7o3wanbrp+w8GC7pveLgRh6gjvL5SGbP60bl5P2/4+1P/G1bUny87A9D2e+83uvXnXNPbHnrm5TZNOUSNGQSdCkCVOWJRA04H/IBiwYNgRYhg1PEiAa4iSa4tBqSiRNN9Xsoaq7umt687vTmc8+++zB3/eLtfbZ5977qoqE171n7VyZkZGRkZGZkZmRmSdwk44GJYv+1aGRtNHB02M6k6ehWLoGsWWkpJEG/FyxREbt9b4HEHJVBp29JK/7N9dRyuigF2o2mP5b7Tw5kTP7HHZzZHhvQHW+T+WzhM02pczM2VODwwOz3jCAmdVP5VP7Ha5YmHpasPHwaxNTLgKe6sKvUuQn2TceWbOfjEiotwUPnrbU+TS2+qC3NwSRGYIpdoWAV4qqnj5AGE1zQi8jamtlyixSGCID2sBvyBR5+9R6srEVNhEW2s0bhKw7iTbJBcLI+CS7ZoMy4sPBrp22RRYA8pu5fz4EJdRhoUH1R73g8B5mJ1GpnBHQ9Jy9Ioz/aIYdMj5V6GyrVWnHzJqwfINNzgrTdo52fT4ZTV4+W09pGy1iWgpVM6YOGVOgcHCU+2T45Ori5eXi+PL8onf/AVUBJVDlVSVWvityyJvtKEGIy8FihoZ+bHvQG1xezhh7oBKypZz5iHVnV+KplpYBWZPrljYPBFKre/2jw4Mcsp/mNzApBuqyv70Ot8ICbx1E/CHFi8mgIJMA8lRZIAi6UO9Y7EJPIjfch0rZRP0lFKdJI7ONJJAhfGxzxKyQGWvF8siEVo7BTXfwAis4DtCiWYAONtiCmZ3yV1ezF89ezJfXHL3AGch47uxNOAqBdm+8u/P4rceeqHN6f7RzxJUDdGbgpl2zAyR5C5F0tt560co/wb8ztO40dQQQn5R6I8S4i28GSG4+wQxtL1+cvPfeB6RDfworMOFjKzhNKkNdM+dDFLJPR324osHpvWwSshzxZSaZDrRzeX493dlh1ubDjz789Omnn/vc5wBDTHZ2h1/66c//4fvf/eC9iy9/dYeSxt4T7ZcO2qFfD6MTWAHxasXkk8vlKBbLharmEtB6OWO3BoL2iTCLtxHQ1fADazfZspsC2tsDmF+AYMXMXSnUI2eCIzCy4gc9zlJTztnTaHEaO3oIAoMYQAfcM6+WusNFRsWcbmxFoYAsfxo0aoGXEKu901xSKzPQle10YWbLitDD2IYY1h7mQMkDPURaRZelYKVDSJcFLCEEk8jMntBA02Xazzpfw4+tli3omhUzWtRu7/vIORsrYBfk6e6OOKKBo5uQWVIgb1Q4jtVCXAAgIt0rdKYdgZxGxlzU5R4mS1vGhWs620cpokgaL75qJn4TbKG1H/wW1+t0IFs8oubtHD/ZIwGgJaZzw0rCNjb9hbnzBkIs+nnfcBJrkuMnslq3LYnr9ikQ3o6ByGlIFI+POd2kFA9qu54hNvTpG1rK0b6JZZJhSAW3OFuIrd9NUDk2n4m49dVGKZrbL38LqPzvcLkppm3YltoWccP7Fkl5t+9k1thhTBvlTeja+NJSJGyYV/ErEqFOK/LAbgTM4aYtGH3GbRqUOivJ1FwnhyxJpXnFPlQmmJkJQsRJg2qG0FPjHHljVYy4axxiITq8oMHihqTpHoSjGZm4hUtN9LxLzE8ZS3OPmNVs0J9fzwmwMU1+mWUCnKPP3SvAnjU1KauuFhIMS8A873LIfWqK5Ux9dKiflpiqREOZxDB9dMROh8KPzRcmLWC5w8TikZLfuMIlQRpRxLHxSskFblMsCavXht1JJRWI2QOMccn+d7773Y8+eP/Fi2P4+fDwAVdwffThR9juf/rxx8fPni8W+7Pz02Xv3N5NHccRkek6AQFaH1J0cZ8f/hukNXe+5BlsYcpwdn3zR3/47U8/fcaaNwCe2mn7B7+YqmcW2I1KNOu0VCzwcj8oDSacB89gycQzDei6z3DAgRl9BqlU04YNIuy1DyYjDx8/5lQizr2mheLYQYYjrBKgviMgblNeLUmG9n3a28FSCDukcE/hoW+ggZVw0ClZtskyl72tKMfmyXBGMi68uuRp5oCGHTrgAwJS7uKIPODfdpEWryxL/6UMxatbhkS6wGveHHJwWKIaBiFUBL0ErD+7OEVu8zRy4+yywKzEcGJcCgcgeIM6BxpGLkzCwS9EMEsY9rD0NLzhr4McozqSoSC86AJWL7tDl7r6I3oYANmUocSq5QNt72YJYoM9mK67z0HSwWoXQXDrJyoABtmcR85KzgGGGWSK0qVGXJy9XLLPj2xz/WXWrzHA9jwhzfudHKWygByGMrdEtYIzpkJ9QyukZBx/NPywTuIEF92p7JBHeeqr/axfuX3LxjAVZqdeE2CXCRI4U6VCorpMIOnZlQNV5YMDeKM6QCQr0q5WXmToVU9LFaAUGaFFyiYw9DeklCcApGiljySEqJRlggkN7/0Qt+klRoM46cWrIBKmkFXFT79jSNotEwDAlPwRY31W3hzMm80mjBrAtCUKFlt0qLw18xIeWQcBRl+w6lBlUUrvHR4xgHv28lj5W3Y4JxjtHBk6v7g62j9AszUpFAvrmNVzPDqi/T67OsEsZzjmpOAbDgWgiSC/skB2IFjqesoH0oDG4wyG9sfahrLqNB5T8THapDioBmSVFwhSp4inypXsybK9vZ0HDx8xB2Hdt1kz9/Y2xkq3AoViwQyfH3a0U+UChF21Ww3cK8LkkbfmoTFxu5lPdHqZq5xIvGUI+qIfTxqXpINTunBLjBhYBZhMzy/OmEZHk4cf450xS5rMW+F/cYHN5AX7r7jWF2DOQeY0ZJYCuOqEBA4ODsOi3qPHjw4OdsfjM4oNtKS2EYfkK/SYwcY/whMC8DBQqHqXQJCWnA/VRWf6OHhrtwya87ML2tL79x/wNbs+19KHYYsqaOUszaPVguKytVEOQWioKjFq9+XskpMA6ACRrslkj0p+enLyhS++e82WIzqI1eRnfvx/8Hf+zj/8o+9/88e+gskZsTxNiJbdNpqJKZYiLTyzkvJry1jylBPqna1lpK0yjkCbLfPJ25wgA7aEtlyWB+AViJMob3xguJm4E5asmXX+KFo7yus55r7JtLsgmC7hMmzadiHU7IvZ68V0d2fpBnRWy5fnZ+f2SI4qpQe+2RqbS4emtNQqC6x9MDEPBxBq3q7PclrsNfllMobI5pvHDWw9riglHbgNyVE/aJf5In3FVQXJLW3yy7alyYRYiQvVpGCvbP/mkMB22W4RESBOxTJmWma6BvfuybcqZUM2TIpj82VQ8+h3iykx+BRHeSdMxm7giv0N6gooxOUOZL3ueliucJG3MhDsxJPiPAa27q1fGiihX302Pps0YDcYVDSDiI/CuAEQhWk3ySBo1b69ivpH+t6k/xq0VGxY6u28zh/f+iD1b8znzTsSescKyjT822QERoSHjQ9hzPMBw3RjKw7FKj1bn01qehZ+BouwgXGzSRb+ctBo8V+8QYCn22dpbA1ePrY6cXtuxXLFVjC1bJlKPVH7By9y6nwtW2scI4uQ5lldHd1IFDRGFL+bf20DyEz6MGQ9VdJuhqdYmAxXfSDrXG4/Z3mBSX8mI6hVJKtAeQ7drPohKhl4gCELbh9zCH1t92+L7MwS1ZtaR2/J8ATymAHJpFOTnNnk8at8NqtG8Xf9hDkb9kW0UPFu2VgfvCtfATJCyKyCYRKCI+pGTIpzHnvnvffe/2f/zXe7HS6NQeXs/g//7T99dXn6m//0n7p4CW3sxFx+zLwvbIZf0M9vKpEcteW0hzZnbcKkQX67LCAITD6XK+xT2YT0/MUxc/8sBLNtjcg0hVhlaQK5vMdNnpy9wK31bFyjqJlOSwmqU8NvIGh6sBI2SzHq5BwhHCCvXFMW56enV5fo5zS5tLaskl9kYpJWDqX0HiR2+y/BubOzC5CNpr2RsZUf22f1YPBgZOs4h/TcJIIfAkSLhqcFyDdZhi1EtGTNavFUYYGiojBuS8AKQBKBa/mjT/skfXC4loWYP19zNS8m0kok0qJsK2+INgmipkgn2HhXckQnWv7MAympi2a0CYD9sDOz1AJJI/p42Zk676jWJXFNHVlzOhN58cJfxMTJTpMZYMdvvXE5faQ5EviwxfSCzBC0eLCaHwqt6Sq3sTK0oBNFpaetZE9mh11ncFVGWiWpDgzR2f3igvJ8zhh70h3OtOWQoXAeLYp1cHR9en0Wzhm2mTVqNBCkkv8unVfmzWsYEf5KN3OZum/vtfXr1ac5l6nuUigUgISNYJN7uGEUfS102Seqw4W3iLGk8kkz4iCJN1mziiAwALMZtdObMDMGF0BWbQINjnTIT30qqcpY0jIsvjC+fg0MQP3iHQJKq7GdoeiiZeovvqaVyGcT1VaukbmixE672klEgijEszmiwJM9uEvqodow4wAB33Hx34z7n4piC8rZPmjGKHq0a4gF1KZBIE1pkytgxrB+d/JjJ12O7r2CjVQcG2fa/uEYm5+chukiAYZecost5X1OeXq2YGvKcn8+Wz47f3b/4Gg6pjWwCYF/mV8HO40OnFcCV51jDGeOn15esTlpvnjy+LFmYyOu8kX8ECRbKwTQmWmZjERxzJrjWvLG3AeXFnvGAaVOvZZBlD65JF98shWezDjrp/kPsVe0PmQQ6UUiEGQsDG8wmCQJGsjJzvTzP/Z5AGRcFRdZgmgxgltaCHAAAmNJRE8D4ay3GWZli5u8MFJdLh8BTy36xm//wYx5J6s1+zs98ljjmSVX7I0PDg6+8MUfO3724uOnn3z5i19m7MRKCzdl7k6n+4dsuLIQqlzAbDqWJvSEkJAXv5Sc94pAXmDy2xCLhzg2geX2zWMRMKNF44q5Ur/rcu5iiaHmZCdz4fIpkW1UnWhIR0CD+9TNukqRPTJ8lKXu5kJ/UBsd9Sj66/2d3auLiw+//wk68ZSzBPrzX/r5Lx3svPXtP/rOn/zjX2d9B34QlxTCSCRBIfSRy2a0siPjaJEYtI0/pllCgEiMnY2pGA158gkOhyZLijakO14Pj0HWXWCBtj2vbApvftD35C0vCxkKcFP+Ngtkmuabrd7WibQe7nsXwqGj+jOZCDHULM5UYP3ci3cw/TE6Uo+oQCRA/Dl5T0zo5AF/EFZu6btMNdnh0D4Ih7siX3ECR9ySlnabwkibsyl0u1Xpc828ZIQW2QYEs7cUEOGUgp4ZGNsUF7PhHaVJnIgpfGR2Lr0ArQRWKtDN+oy/eUgwLn/5az834QVlIZGVNgXSAhCYeBvT74S2eLOSQASRw9Ct0I27QR2Acgc4mEOJrmYPgBgaawsdhYONOriNFJ/8vvaShALxDZt8hMrLoI2jPAFPWd4GCZ2n8OCsKI3vKz8bjK/457PEoUIabC0xcLildCvmqyk12PGu6G1qBdd650sAUcYzH0bS8YZ0miQNgRC/8mq8q+bAu4rZyDQg9rikYFWArbRrxDKUf+gYtIw47CYQZ/5s6f1PG8Psv5WBMKsE2g0dtT0Ks7jGBtKiApkaoYIGVl6Y+GM1GE2RiJBj+05LQZSkTKvGfwCTJEoDTRv2L8YVQEiqDJiBaaI0NIMLeWI93TkAKjFNISqTfIi4CC4326dcoGy9krwwQmwATSQ+5d/GFoSo5h010yl28sFGNFtiFjq+9Xvf/t733+OknK997Wt/7a//Ly9PTqe7nCaBjsg1PXPMac6uL0FApGoctPg2odR8MdtM8QkP7ZmBdDKZbNPkYvkzY7WaiBzn/PHHH3/vu9+3w0Ppz3xD9Dy1SzxRCjnSmg1kmK6ymj+fX9LQ38ywg4d9jAFSeORQ1pAL9x/ZsEIG6dsPcdYQ48MVcyfw9Yaj91zr5EAhuj00MEuUV2wrNRH2JjIvnyIrLVNp8Woi0Lk/JqHJjbi1hLTwSYpv2cheIVKECsosPClOhzL5nz8DmtpgoZhI84OLL4HqVW8n+yEAseQxMFKo6iCwZPpLmCGJEnr4CiaxRYZ18FB80kZPITri+4E/B2twWBIadSKiAsJZOWSB0R3RX8JDhYXehi7ZboAm333YyEMKGRMFYGSH9IQsOMlCPPP0KKbOkq45xcTiZGggFzjPm53ZTGPOrsaeFYsk9c4vXizXF/BVaWFcAT7vVGDUMGAjNxnEn3xS0DiY2Bpzm5sDO9cTUBSSqUrc3N55ZNH2Y7bf8LRQDXhEJGDwST7zjqISySMb8IzVEIaO3u8jiCxcLabUcLabZn8i5nGsYRCZdkHmmAmfUOAr/aa/5tfiNrQJ91f/+Lz+SukZ0RJVd5dgHrvDoClclVTcAhCUF7GaKADwv/KHwzYhT4GRQBFR2NSV4bLZNc/8MTCmstKEYKHXcce/m9QNEMDG0AbPtmLlLRC9zhklzn1+DqlZORpPWM+5uDxfXg+ODu+h68QonI7VOsrMPceVUEMvzy+RounuyO2uVFK1YRUak7FZhbe2YxBK80JUonS9YqvH9AL3YT3ae0QzhJghg9Bq82s8DM8gi9ZGetMxWJ5oTZ6n6Jma0bEIVbuCxQGDb3CIKxrl+RItm2vFx+Ohsjy7evb0KWQw7UpytCjucqG3cDmLhog04UZaHj6CDVRA0oDACh2OHSsI/RPYDqd2wgP8ycz8esalvscnL52/gAQmm/p9r0pYriCAc5awksJ88qd+4qeYiWLbAKsZNNpokFBKs05xMIgmFRP3L9KWdsTC9ME/lTgfvMq/8TJSINrfhMqWAoBIss7q3cnLcx7sKvf29mER1w5QxMi9MqBQJGOMmvqDK887cjIbfwrR5Bn2e20zrYdSxWVw/Hp42+7EA2Nnl4PJiN1K8+PJj737E3/5r/zZ//3/9n/3/e99/2d/7qevjrkq0ska1odUfLH1cTRrvixqHamerY+ENBAWrnnKD0D5R6FBMmQhphDmR4OpgU2EN7xgSJ78+AKT+H2BRCKiY9j52pxQnRhs2rPIAPlgK4sner6dDzq4zQsEOOEUGqVKQfKd9twzNkAvbxmykkrmJdLCkzLemZCUfpfLwMX4lqrmA8qAmFnyKsFhQKworLw+kRTrmC2NPSxZsmqznu+MZfXzkkpUSIW+Wy44AIDqojx8EG7zmKCUG7UJDQ0bgMaRUKHCzETwK4nyVQiEDa2i4uFd+Yt/vF57CdN64uA/PkVRIXlT3DYSasXnjP1Zu4yDGep4Kg1Zx7OV5lbaDUi1R0hBG7T5LSQbsjb+cdS4qucaevLAu0m0GBGgrbjNrufP6e/se8lmoLZeRvAs2/ZxlzQbYLXC3+AvpArFbYroBjMLvV09EEPgCjjRb1/l6dtJ8aSmiOHYCBKilxSMFFJjCU3PAnu7o6cCc8gYM47ORNLS4w81QEoFUWianJrzzG8ciLoNIbUgMELgpu4h1QXP25JiktN6RKuMLkKJUCdVT1N1AVY5M7KPafU6u1pZ5KIWq4uVnWaIKjEBMeeXE4eabd6sJYTTWUo6DTXtg6LSQUNFI9fSQ3V8YpNq3hfvWOFHniJCSiZoki3LLZEivA2zzpkJ/e+cg2skMVj5SxwlAVMZOjJO4+H4uE8//fj07PhP/zs//4u/9PPkdGd3ulzPOOnbMqEDf6ntkx0/ScAvhlpMQkDV8scI54zzTNUnXTIGmEmp8dFWsGMI7f8bv/dNvgajwfn5FfuL6T9pj1jwBcwrQeXNsjc6pvXnzA9WCejZNQTvcIwgqyQygy3KXCK55GAbFiE9e8RlAYqGiAwV6PSg9eziHAZi7UO3hIZg40YCjBDoWVjfHF8oASzG4A27nXJLmTdDCBtScoe+4zARJoa7csxYbEB00xghyIYLCuSNc5zT+GzqdzQfNeO2kIrv8SBRfcVcjyfEgzrn1SA18dScwHaAgkdWJMz/SLFkRLr4TNeUzBWiBmWLOb/Sbh8hNrsb+xasOR9wP6+Sp1LuOacRGEBVbrgpk1jm0QDWHwjFlNNemeJm6p6b8Th5lSm/m8UlI0eOxEegPKGcCT3tvhwtjqb0MuwCHbEODdNvbjh6tRbEXCpGh2PhBTsh8jecDKfTe+zCWC2vWYEDFgMGS5KRFZSzMUE7n/VqfrAe7iFxUGi3RsVkQ4IDfxiK5yttJqM2VwWT8eLOhkcpTtmytT7Q+ulpSH4woPIXLDDCuixzJMU60Fm81Zlzfo2dNpIBB0br1e7lcnp2vNvvXPSv50dXqx7WpSKU7cEJlCR5+lBw50cyF1mv8Cy4gq93E3nLj1h8xR8aKC+yrzxEnYy3su0jZ5r45YEXBxPr64pBi0SFm2ai+fSnIt2myXc+VFKA5ZPyJr/MfGfKn+KnQJFGJRXuqDLRzqVAxEYMBak73b+czq8edR49e/mM/ZB45SqICabqcywIWCB1RIHpILZAqIjcnHszng7f/dKQa8Vnl92Tk1Nahd2dndDgQhBYqR6SE6WGQ6SYTBhw/PwZS1UIEjtKh1ykRerYGtHsQORysUeTgZ5vRlGrUsUtVx4rPBmEf4Qyf8QwI3mwv7AGyQUVLzJutWRj0njsqtaI48Vml6r+sIP0x5PTlyfo6A8fPWDo21+/TYu06n1CUpBMy1U1NvOwpOCGZlFmcgmFT3sWbgeb7jAcssKz+nAzg7T7Dw9enjyjdsTimmHvgh3PTIvcO3xwsHcA33BD3IP796jXqNGTyXh3lw3AWiJRwNDvlBlwUqEUpEx9dZes+FVdiF/ltC11vuqxDDO5ztKc3ONBGKpwHcnAImr//Ozk/K0nb3/hC29fz6FEFdGCpS0B3JorS5k2YhhvW1EPyJQt3vbdu3vTq8tLLw0/2PXGzHXn/OoGYxY2PUz3dgbT83F/+e//pb/6N/6f//k3f/8P3n707mRvcrmcsWbIeGx183ZvOFn3P7V/Jy1acHNKykxfmLwtlVUZKUXyIaZaadJWnJItxJivSPvgE5asPPMer8EHYJHIH/yEMYIEi/CQge6Ea/A+TpAw2ceoTNbAMksDcYJHfOJWHqwy8JhWTpowu6TQ0x0FKW0I4tLh0DaaxyE7oADiG8FNZyGtSRXU5hc814TTauGiqhBGp5U+DG8UFu1Bev0PXGXgAXVKAc5Jn1UXsgjy1//hKASSLKtfpAk/7VkwDi3+ACU5vFX/+U1FZcNAcU+cBqfApdTcEhTMwR7PrRc7HgFqNG0S4UNgfnks3gbBBie5pZJVeL0L28ZdkCARgZonb+7dqkfk4q89lo3naz9qaSRROArfazB6yFPbleZJPvXOd0tQlaBeG8DXUbbAifnZrw2GAvGz+LvBmCqR0AZlE2UTM9m6k5zMNCP+247JV3JkMNErsMq54D7rvUnrFkC+t0+Tip+qPySLqBVzJA4x5QsJNE1f3p9u3+Pkf1GPukcboN05EqKzzy57OiY1RbPi24bZZp9MEEB1AU7NTrEGpuihW8PhkgI9E9oe42NqFhTZuqV0oQFVFJqsgdQiuyWJIGHmYIjIhwz0Eaf+eEFAsqIPxKONCWCAsyBsvFQ706ep4BWX2MK3+MSYeKLkH6j5TCrlT3w8TZ0oCePFv7zhB5G0ND0/f/+D99k2951vf+cv/aW/+Iu/8Ktc5G4jFfWT5olTEcgIZrlM0tCjQEUpQXlzNuY19PdWnJCTKQczTpI2OUy8kVGioPA9e/qc6T8wYCQKx4+O7kkGIwxvBrA0mMqirjD1lQOd3DZAu8gUIAsUFsNyhpFATOHNVJgF6/tMHFGKzQyfo6pYNN5wWxlrpOzQVauga+YeH8mGEZQuDMxDgPpo0IWxlgo9KCxzQtBeCkNMBVCZs58DgQUaJis6PLK1KfMqF8Ilr2RThzBgTjw+LKp45s3LQLFIQv7bvEQIScKegXQTRbrRtZMkEMpBoQqmJrp5qCdCQQ9vlccXLVEqECvkG6bAdlhhN2zVSRrKNge+OdyrigEK1Gs07WzVtHLQdWJYscu90MP+lIFAdWIyyHk+T7pANZyMd9iDxoGAzuVq6so6D4eGMpwmX0z0uccOI4eryxlDveG4M90ZcAgsA4PpdHR9feWGsyUWF+pAZJ/NPO7SVB9yNw7UOfDDKMvqdcPQ0drW5rpqRFVfmfrZTyDbQmm5fwtu3MQXN39+QUypLXzWxiPIQojhCpuiJzc3+xfXu/3FpP+A6e75bimYyAxsh/v+BKVyYlHwZSFKrGmYmr+BwX37JIN8tiUrGJ+Iu7ppsPEZaptIwaeA1JNfX5VWeSbZBqBxt2lXPBEmaUikgVUmpRu08oPNiBpcqznYVqmGU3XIc0TXrIlbPYXiWU8G490xS0OjZ8+fc9zXYMRmkvXZ+TkLPXwy37++QavGOhkaERHGCBrxMxFzfHyMELiwxxoL88E0CDTs7oS0PZexXPC4uOFYkovLC3YLMTVvs7Lmqu9LyJXLNuvqLACrbFFiadZTj8ISGllCZRf/yWkWIoxEoTjfYUasgzpAzabba1Yk51c7HPuGfDK6GLiIykD3krMlqGOjIYeZctpEv7PAJOZm9cIFLbY3sFuA5S17JxgwyjjcO8uZ+kZvZ12UKW+aynv37nOkJ3ZTyPywx20Gbov68le/cnZy9d573++P+mzKop5pWLXroWSYBF3e3LDZiXWJo/v3mUi6d++I7i271+APuZCtdk18ROrMUAq3aazMYZ6mzNvP1vNWMIgGGqWA2lDQcKZ/eT7nvoH5/Oro3gHHCkwHE04cK4wwV86SGSe5OFMytittWORfKQMfOb244Giycac3n+5x9jMVndl99tZhGzx5/vTZ3uSAfR6D9eR/8hf+/b//3/ztv/l3/85/8L/4q9gaXV6ce2qOskgOcViWPmTc2SrwR5BDBUGQgtpLp2vqdrFACaHoWjwKM3MeuMTD/4AE42e9xLEVBj4FxuStQ/kHGqTEaQuKgpQ8uNBdNBIgJ0kLLrCNBJHAbg4i0teqbFDREXejJy8AEokACFTaqyBAJ6i5Els0FBeCyK0ZJpLpWXcBQO2w9+QXRC6a6GdEFSaI8AE0AfiLERg7ADA4vnJ2DR8bBSXCDgMMvP0FLS0lQTrLq2hsSkZI/AltEBurIgt954l3gCVVhLdIK4rvAFRad2Jvf5jFYnXrW6k3NMYTn9azBWp+K4V8DDwXv3kg2/SN1Na0EAmtBZFwzmOmXIYfCdo85QwQJ9wDXvPreGyAcq5/bKc2XkTGLZDlyVMwW3O9xdmEAWrEctebD2SzM4KSV3CKLLCvFoTpDT8IdIs1BBRwYpWCUtGTXCz7Nwk0SQdUoG2yyvMVCD1TWFCryPmFMCKpJQJ0OeKQxdFmqEOeKwKkIwHqhZIqITAd2V9zJCe/jg9oq7A9EBIqVjezJwIN5AaKT2JkML3Ira7YvZl5NyeZlF0E3ZlLCSKWSOjBk3aHmTA2EdARptgBIkAbm0ucThpRpZQ9Q6U72hI751JjsZfAn56GB1TWNpCJkH/u1mgZKc1J1FTEVO+imwQJM19pAfxyb0CwmnYRTAx9AmbDfXJy9ff+zj84O39+enb1p3/tT/zCz/zq7PJMHDY1xsIOnkaYTHCHFuoyE2hmxXYIIMwZMQH4yEYNIPluj0k8xkuOwLD8ue58+MEHs+vL97733pwz4r1fE9tQ5lDvQcey86zaWyxX6VZp6Tl1mOl5CLhZzDAWoqmx5+hRBJYg+ClwBlz0Mdj5OEWMfSZr5WrntNjZ10tBu69AbjvNzdw3xcJSg/PTsJfuh3zcgw293gkU2iU75kB21JEhjSA86YlBSFGjuabZZeYKliMJ4OEfINiJPlgPUFNYiSINn7CbTHwOCGt0mF1BuC2h9gkkovlxOdoiQoBjnZwiYFcsCTnValEbGzlRVZm/YwmOtF+v8mywAlaPvy4kN2mSLagVBwrQ8+6A6e29qEFgwZfSC3bCMyCiU7lNcYXBdPQ6Vj9WVyhYKC/ri+XOPvp6j8k5IiMq1h74OLTI6ECw+qjewo6rvxqzTXR1iIwzic9+ksWMM1uOOB0e0+/Ls/nTT9jdyAEm2hLsTPsXF6c3N5cMM26uOTbmqLN80B+9p2HU+oA/NvSH+XxbPtTeKKPJa5N5fzashhMb91Y4znBuy6vlXcHDWcLsb5kOIt2Gz4ULa2mWQjij3TVCi4518SVaHodqMK07/Zh9EoPu7txjajiGBt6ABAyUbDrMtlxkPelkrwIFKiI7c9K4Q7KEsBojKCLoR97VBuLPN8P1xlckkq7M1BlQBV/7pjZ5DIZg205qOzh7JKBNmqzTaCMBXd6z0e2cIvOcwUIQCjml60w3G4Vu7gHW7R0bhdE1uvuNt/bSaDD3yRnxGFuyGooWiHqKVs/i5h99+3vvvvOIUxwHbqO95v4t5+lZumX/63w25iB/Lp47PaOVRcyQq+F4R+2Dum2RoMIoulqbpDlAwDiyHHJpGmbXsyknfdEwsC3FtuKcA4E1/GQkj9jAnvUBVNMK2nFwIzv2fqwwM2ujWlZRyA3oNzzSk/wxF8+YhFE0bQuWKtgywU/2vgOJwsoctjcbLLhIkUaE3VWzoVsIbJe4CAVk3tHLzRqj3cuLk/e/M+eEicH0JWuknk7W6zAdc3Cw/9WvfI1xwZylM00P10dHB6jUNK+c9YkFHVVtPJmwYDbZu3e5+ujw6IA87+zuUUpP3nrM9If0W3BwOxUfRyPDaTLIVbUVg4/kYuVPEdrkNOIfKYkAwGT4Q50DQLEt9Q4s9pvw7mqPpRr05iiT6ZY7mGJiwkdjTgrZWkHLTulrsUMpgKhm0ehUaL1B2Ts/vTi97hzd49qWQ2YBuO3TOTS2H3mcBzutgTm7PoeB8z/3Z3716Ytn/+gf/qN//k//P1/4wo/tHx2i0/TGTzsMHuglbMCTPaQwTECJsBz5JMDWzDwoovYI/Nh6mSdZgZsH4PwwMizteYszAXj1JV/Cm0SW89YXsPU/tPVE1uiOrt5msNvjPgGHB6ETrmZWARUD2pRMBBIeLbkZgOEjhLDV3uknSaL1BgAWdj9m6wm1BzgEhjedmSXhB5+MczNpY14ry1YSps8Iytqd43VLZfQJLGD7MYjCMeB1m3mlRdQyxU4dxIoSK+n2wsQNW+RnaDM8LAvbcDqIIBAooMVbwf4CK/uhyQDSsXRYZ+Y3pycJUw9VpTTtwM/dldobfRh4aWhRmsZrD15A8D8Fz25JPMr+JZlp4FeTN0XEr8nHK6HJJm3r1mMK+VTCePKjNJnJZNUMS02BtVEF8ZHV5UqWKl/l0bybFOqnfTex25hbv2JT/IHwfwpgk4ZhJil1PFtYyimzDHj9qezEv6XXVHQbw2qUPFfGhWswmuLt58ZFKP5NYoEokgJLmIQgIUhqZsMjiCZD5aXyGDEQUIAf0sb/qroVqIBGpSOKxYCYogr6Sw3MmXRoctwNBtRqgCEEA2KHGsPehFkKlBRS8AgDgq0GUkqbCx40Xq6YspBJWbKtYEVSQ5iTrIBBAKRBLdXfxlc6dWQOUc6ZAfGkFiQ5z6kxJWJZbEYwgWJt4CNE4jHARwpEUR/1BZAOH4IEaYJ12hQS7sMc2+j3v/Fb3/n2t5l5ZR3lx7/61f4oN4ujqVPXyY/Xu7LgTv+KJdAQxrsHV37K0sz82aCDD+bRwZtbFkk0yLFEUOB+//e//c1v/N79B/c4nRqUoGU9hf6bvhkYzsqjU6Qt2zvY5dy31YUX99AbEkL2R9wohvX/tYo7uD0dAttwTEcw+eK0Vk+ZYR4adRSrICmj+7ny6AMZaHHbBSI/FpPFCNu0IbGhVQWQRymS8BsWFVcUGzBAALxSMxYGYPmI2QC7aXXSbUAkOoR9CaWa8ZsqqQwWU4liUz4pwaZImh9i+VAw5UGaPGl50RXQTxQqKAePO+wcggrJy3kjYevZCIKfkQsC45n45sqApmNRdwkackhG6DbMGl7kQ7YJKQ3yBreSiV+xinL3RGrGaYwBRoNpf7S3nFMWGl+lvMx1unYKlrHbyE33Wczm2ELUgjAYdA50gcdEoTu4YjhDfUIZY+GHEVd3seIao16PE7Q4pZviwhIjPEfD8/w76MIbc5usZLgnGIXJw7BTV8xJPSH/DW7CXwsqjzbmbXywkZrF63DIIoT48CNvmAPLUtoK2JL7M9js3uWwktE1t6dxDw6tiytgsg+xg8OQD4UpgJTKLSm4QoAl0JRYirst0Apt3nfyBcp4+5sHDEEVXuBqUd/GqmADbp8WsIFO4kpFQ6diKDuCDjWDcNZnXBqifnmUk6lbUWAX9Q3FxL0ZNjUpGMIIp2Zh+n/v/oPj8xPwwRKPfeqt7907QGAQKif+MdRJNcCAjCmFEcr+zv7s6qWXXB3sXl7PMK3JjLiCESsSCoFJYU6PHdGwIFcOMd3fQv6QR9KxNUaqIU7dCZpcbTW/+Ahg60oRkSy1g0j0ERKXouWnOCO1IvCMFEygaWnG7AIBSWOpb+fgNSkAUT2QVS7hQgunCWLDLoOQ/pAma815Pgx7HNyw12XSHQ/XmDaxgDpYDW/WMy7wpS3zrDPPhicqcygOcMo0lAvXmTqZTHZfvDhhncOVUi+FtU3d39+D8ow3RvfuH7HHhlbU3DUcMBe49WmlxPwQrk98zTKfCrlOPgqyjWPNqwcYVwmNC7OJTmYYqMzmHL3K0XoX0x06U9sBkkAv5UXbBRr+w1JYhItSoYH1xxIIag00c7LwDQtpVDf2w1GII/LOmPLi4opmnL6AltgdROeYh+3/tb/2Hz57+gkbvb797e//5M98mR3CVrEsFqXXpYKK35ySggQQ6HAPBwFwTo40EGnFAwOkEz4YIFLILDG5gAVUvQhr+aDfq4+JJTyIDbXfIYpZdCRG2cNYpZJPelM4SRUKH8EsqNEJRn23BKQbsYRSahW47deoIpitQqMNKb0cGSIOoWYv+SQFM23iOBTk9NSgToeIV4gkAR5iDYfcyGYnrkoPKuusWIlvivShCCT4QIaXrII1tNuwxqqfSkdzp2IAPcVfSorY8LAVKGIBbsL+gQ1aLaH6jxdPyCpn8ya0eaAqmMPgsKkBF8SgwOXtS7Dyuv0VLkncvhrkd3/aeHd9Q36DlZ6e4qKdYZ4PPeUDIM1QYU/0FB7MgUPa0XZGHxeElDWnT2DVvYVTmowJ48ph6mXfX2hvkzCh5Ng4DfBmnMR3KmuokLrAxGE8vpS+NIv+JJhXgeOxcRh65ynOCwC8RKaC3cI3hRCMgjQhuiJxFfEWXuSwsVkb+TDwm2hKso9vojvLxeFrykzRH//Er+rMN1Kbmu4sfUmLekYEknbBRQGw0VBjPk5rzWkztAHd6VPIXs/etur0n0EP6jz1ATrsElZ7VIJ1ZwY6WjGqAbSkEjtq7HaupN/amSklovQZm7KkjV0dGNBOUHvsNmlPQGBdEB2+1lVTGDyjhq7nWAbzSZeJr5SjlVnf/U9OYLU1WAZs/BpeiySUmDMdvPzVaVACoaDxa30BNiy+033UMwY80yeH9w8nRycn51zgQ70FBZUZINRuGq6g1Cp6vUAzAy+6I8RqW0nLreJLp89QAXMI1weNS7tGy/bk7QcXF+9gXyQ/WeUaeVksSY8mZ64SoCji5aW/67OTlyydc3Q//RzbALg/YTK2L2E99Pp6Jm9oYjT+Z89u7/ySvWF0ONdcvQo5oKJQMSk5OztDq9A8w4ao0ePJN3Mc+Ll0gwbt3MmxBWcHxW/TIFpKCoARccF3eUQJ0A170D+5ZgqcEqVpKwnBvuH5qu9JI6RmZFLK+kDZ9MdDzplKoa2v27dR6kkpMakMCiQqTT7ynCaXwQbEw0wJUmKQnI9tnktlsdRhwVviYS65Lez8gg8kFrwzc0qeeeIvyhIWF3IAAQsd4AXO2Q1rmXJTskP+1WIRf2oRlQrlDzXo3sPd+4+n5++xiuVwRW7bP1BLGKQxUgMbpmOkRkWYYyXa6Z50+6cufLup/sWi85J52emIE1p6H/zhe9y9s7Ozx9lNzz4+OT09xcwofRJydsqgA+6xxoM4uk+eWWcaYC9ghiYTh/imCPk1O81z5yN+FXbXf/NlGYGA73rAjjqBm6Ms4xsAC7pNDZYGCPZwQKFVmy0WbJrx2HvGbbvp/hiwASWD5J3usHZOeTH/wDn9KRKTSbImvyEh0PXpwUo8ITEOiBCTqpLFth3J8KwVBCVQd1He+RJU+M3bOIkw+FRZIQCq+YVMC9k/AFwVcb6cXc+uKrnBybaKYnnhvD6nICkPTsMrd4hD73GvMx0NP5xORlfXE1Z2rtXzuCq6c7w4f/7y+EvvfmF3lxN71eapps4nZIANEpaMqM9cSniwf4D2vZwxr+xiHLWQpMh/v7/DjnbgORUYbZtNo8xBoKB4rJRHkSBF5ALNHvu9Jp8UKgSue2dO8WRTe8sriAc/o8qmmjfcCFugi5aKRVEvJWA2FM7YzjG7z4plLrVFL4MGr5oxHmscNBp0OoxzFzfntP77ewfjyeDZ03MoTPkthztX9grRCtlZHqs2EC5evHhhfYphzO7OHu0qmvaHH34wn+0Ph4cPHvX29rhlcrl7f/HW/V989uxpd/SSQRDJHxzspYzId6ptJt1TfpSIQrN5cOtDvSpIgF6DIKy62IgbgNYC0ZABVPZrroe5ZoNytzM+v+HQiANKkBUblHVX6lxcJfvuzDUmLSxMMRZ7kBBbMJNDbaLwzNigNxgfu/+ClocQieZ3uLO3P9kdX56wHfgFRUDbgja9O9452Nn54Hvfu7q5Pjh6vDt+0ptghsqEQPYy0awEQTJsC9ZZMgfMmVAfAqMokwnLKA4SQlJteSUUgllnQlwZdHDKrbmVeqj197Mfo/oXiGosQGdmbMZx9DujT8gRNNrkIn09RnHyhkOpcbudDO0ACQPYE5CZ3FqOFhwGRZbJN4MHZzBllwyQNeBErtnugn6iNDaP6gNoEFESU/L5qBzgBrnrBlFi4VKGXiTARJynGiCvaDr2MnLah8RIihoJfj+lwVyZU0hwmLSkgpIawp7dF+r+6AVgBo50h+9bFvPPhTXxkYh88RPrle7oo5RUMlB3QzU6bTEUeCOGwSKVybeMlkhoM4vNAwsDUR58NDc5WBYIeyI3aBIr4G1cf3PrcHOfQ+MvDH9kvukP9L+NuEnbhkV60kU3UmNg4m5I3KQuljw0oA2+Dao2aOu3DQPYHPsoUsWeNrD8SVEI07Xg+NVJZQB4G1KggisHYQK279uE9Is+WnANVD5afMX4YCsEW4iadISPM4yqDwtw89zCxTOfZncLZAu2ci6fbVJMVFUJ0XfoXCvmuPGvKhl6jJ4qRDXiX47NwhYE1RDtjlkHCUTs6QPSjNA2gZt5F6IJjjdNCQsIamDWGZkLmUQKCZFHqjQVifpmRZV2q6PAyQjfUEnrSIVzSpvvoEktJgfkIZFEu3nKbXngSowE5bMBCkiwEe5H08AJ72c4kQ4HSllxPz0+Iyto0ou9zt7hdMguOjQvm2Pha33XdQn6JxVlmQKWJQuXaL2ymxfsssmq/hU3LQ/HcRMyYwmfOxA4tXM44nBoxl60rZQJFgEkwekZdJZgxlqCkur3phgKY3rPMYDcMTw6OLq4PuFQP/ayUZrnF6dsttufHGEBzJCEnpV1YVYPQICxvuuq3Gfr2ZWUiNMqlAtJwHnzYitP1p2EA4wpOntbBhTeqmPxMJdYFSTckXtEMV/qL8mZdY2WFNigUjkAZTGeEObqoiTJ5XQ2RjMJvnl8BbUfedqQ9ldQYDIWYXuVEoP8IMDIDNo5B+DcQlowAZc4/Y1ZCcXdvFLellY1DjokSgNc/dwEiS1NZQfYpgVRSpMv224D8Zc5qk9M/DFSW3H2yM6RFggHk8lhZ31KZ6RxHTGh1n03wbbsYxKGpBAdBB7hQ0agl8TRbpZMl6O3YcpFL8fZMNdYgWMwgBwiEtdztg2MssADFcoiKiBoqUyQQQFSuPR3homfVJrcS4SsIQ2f5qc+PvMtN8iq0ESNWxSo/v7YTVptFXzVWWs4/pWPKLgAUB49tqc7OL5haLha7HsUqr12rREFNRjS8chWPJKYv7dPgfkdavIbsIAUrCQaHhJJ1ziNDCTkja+KdCfoDV53ws22T34gnKwrdTA7AoJsUgVUkfGwKaNsmlpjkUARWTAuLquYsdlEtL7huJrl5w8OP/z4o8srj8pJA8I1INwRhkAi/x5KdjNjFhzJdyIcxXdvb+/07BQth7PxP/7oE6zjrYheIsEBRBwX6zoCh67Sdi9ucusfrQyjElaHkPIFIwk+GT5JRYRTyuQZdEmp5SK1FWb9tdJBu61I5aLiImjrZc5AZ9EBgXZbPKMA5idIqHBz0hHqW7YIjzlfge0utLHzm4uXL0+R80ePH7Kf5fLq9AWf/fXx4PSKS9OxjOJYT+oXCdsHuZ0Abnz8ycckT3JUuYvpjL7pxfMzK8h8/Pjxu2+/zZH/7ppgrAmRb7/zVn8yYSkAem08zI4UkQvwIiF8pxAskvgasi05MsRnE9h8pNT1DAaBmB6nOSAVWkGO5No7fNDjesWzC1RIWiyW/rjFhbaAZj89IE09cqJBKNtZ6UXsS00ZVEmL+k3baXvtSi8O2uXz05O9vd3eaA8BOT5+dnp8+uDhvb2dfVRQTl0aMdDpY/mpndXV5TUd6PHxe7v7XyENEVlmJIFogb9yZReALzTjYYdg3nHyL9wIIWYxJEE3Sy1M3YaPDhRbWuXJD3iEyyMecwjyjPNISPZJQKnihDn35e039jX0xLQlzE8RxaM/aeTcgwCV7DWHO+lqGWc65rQvBi/1ggYVfoKZNXQOwDIR2E7CCIAqBN2quQ4TEBZUPxo1UKDG0Mcq4VROl28ZnVJNELzuEosImlhWXegZ+S8J1FJuD+gMmFaDW4xmPV03E/+kwSoca19McpO09QYIi5tEmOxTXwqPw5SGOU2JxKv6yjilM5TWuymRBPmqylthYa3wyVokqYkpbv7iz7tFsvFuvaoKbIqrSDKZPPls47Y0tYH5lYM6hu/f8a6PBjkfgfFsexyw2/ERjGKso5CGUMREn9igk8eW0EhOk5MGaZsrPotc3mBpYhiX0u5xuy0Czvx0BYUAZQ+WFR4cJA43bbCKRBE1gW9wJIQYY9pcrkCvz8IPYojJG5cltP0EZ1pYa0H9kdWG+pCU4mjHeSFjC0dGge2+CHeytxmX3CLYot/KaKlrLR7bdDf9wg2l1hMbjBfVDWd//NSrurAhVvF/QatDKxYuURHBSrVHm+E8FnogxuJMNdnwUVdpnDGlk4v2VnYVoSItzOJd8peuEF9qB/WWBVD7Knoiaj6+HW0uu2vn/5j0Z62g+hrylx0/aaFUd9pCsWshj1lr0h6ONIvv4YhIyJ59cvMUZ+pDngWPMQyQN6QOrbKOeKh0KMHcoz7h1twRRrldD7LDj/rP+vKCJh1lGh9aKddCHfZwFpBdvMMrENGwwAP+cSur3aGwTgJd3rBGzUTz97/7PXJNW8DNNhAAD3sTze5ZC7WBuDp0IX/wEs7SzKCaY1IL3ulwfzrcWw7OWUC30+11pxh30ivmVDtYzLoEuix76riPi+l/EGpWyx1tjCTsPd2BgJ5pw59KUqXPh2vKaaHwrzLUepgytHDYFLVveXhLAD2Vuo6TuBQakxzO4dL4purIV5o5xVmeZgax4bBaEfqGJdtxfpd/m0fY9iOy5kfEMr+lT3rNgqIs6c4kKzq20yw4Jm6Tn5SoCC1I3kNste8+zZwx5AUEWYX/nKzviIIShD8sJS8YkynKwPjwtlGORNlEyL3NcodDEgwztLZwV+b84tmzT9X/5GQx2ukgBDnSpRpDo4EAczxIbgbgA+E4ZAa1u7jfXT/odI7pR6iDiBsBrO2jJUx3p1xVQ5kiexzzySkolCMWBROkBXml8vWKDxQQh6a81V3srPvyOZyQdvPxAx8gBM+bVzKQj5vHlqdW7zzM8QJln6ZeaqEmCr8EpxDwVG75hgucBMtEXRo6jJnlY3cfKI40hDDjiI72vwhEHfZcr6byNydBfUKqet55WjJvPeNDwcB1gaslB289BX/7NoCv22fzsYlyJyy+TVBAK9uUr6qGiQ6eE8yZQipu2UgpCSgRrnrARsSLs19ki/TRDMM85GZ82lmccbYTJXrNybwcBEmbiqnh/IBNJev12fMXL9ar/Z0x566oDKG4U/XgOeP//f2D2Qx1enZ1MTvYOdjbxSjo0gYbs0Wuc50dgmsw9g4BPjkvnuuoGI9jUIZ2NZ+foVM7LykpakZVpBRKBnTki+zjhszAWKQsFOBDfbEuNAWvw2aWtsKj9idjW4dOh0NAUYCYnSWTNFYsbwLwEpt1RrEMZXMZE60aTRRT/9zcOl+8pPY9eDDBOOjk+JxJE4QG5UpLb2eDwOpjY5T805biIL+9OY3PnJ0Ab739zoPHD22i+30OSsaMczJhC+yA8RWxXXyzkKroyG3zWCx6Guhf4x0JKiBzI4/yBBIu6FcP2fc/3QEMseNkxfXi8sXLF7Dk9OQMJebFy+PrGXtC6PVohbHnwXTnnAGf8Wk8+9gyWQvIUU5DavCaoE0rXezRzrjz+XcmQ0789EgxtgScMXOEYrpeXT77pLv7hUMKZGe6owyidI7GP/Nzf+wf/+PfmO7trrlLhKsRxhiqqGKpQFemSARocxH7b100OZUt1t7T/zL3jFAoAELxP50wPzOA7d3JL6dBEO5NtD/oSUpyKTwGVfAVv5fvrLFtuuZ0DVTmTyiNAbMp8JyMI3BqFzcsa7lc4sLRDbsWyYXrYQw1mfIAZybYLQDEnTEYKOjpOJoRnZ0L79gwYRG7WAC76ea0xnSNzdqHbAMP/0kQky1SHa4ZNacjvgaVhLKEtaI+0tyDgSbaSuuL+Rsm2ChPqwq9G3VJ/qH302PLa4Rhzi0VOK4fOXwYeHpkD6qd94MYbtv9nDXZ6MXj8LDchJYGuBXS2v1vWC0jAWzvO0ryBm4cG8jyKVzEaABMucCdw6EcyUHB1Jsw0edpfRpdt/VuKABQa5SMbBKpyZHo/RaNOa6UaTDCq01aTWj4XUBF2YZSAfirdxsWjw0IJVrY+Ykil++0TZuAclQmt6pAiA15ykWeIhxnm+8msfopoMDAOB48+F/uiiE6hYzAeGxF0avJf1BUUCIEmAhNZoomE/jsx3QMLSzlguF+xiu8DgSeiLHrYsywM7+MO/8Ao0F3Sgm1fjzBriAiLfVw0jaIX7sxfNIaEoCLGkGVYVaD7kTzRJIT2JaaCHw2NOidCk1iJsmYnG7HlKeO2jO9Afhgz8g3Wm22LBMJ9cr8pRNgm7LGKlCj/PDOE5zJazwAbp4m3KB4SlTz6Cq/oBFfJSuFLm6gfqFRsfDBedIHkylT4/Q32PfRJJMdMu+UeaZs/KQlkbWaYiY2DRDrfBmhMJqhY6O9IoCBBK0DDfd7339fYpxrR+1mFESmsliYzNNBQl7GCTbbXPtCdKJhoNXZXa33pxwIQxtDI0hs2E2XQ5umwSkTcDRVGZoQ3d5GnqqtUQKl+gd5sk6eG47kl7GfOaLoKRNt6/GVHF6WEY7qgJlT1I1yTxHAFrNh8+qwDz7K7SRq/twYZXBgmprSlkr5+jaeEEFQH61nfuE1qi3UaDgubJJBFQB5WS4L1jzJGjBNqgpJg7eFaH/JBfmXTOpEeroqSjoHDTv5Z0QzToZNtf6aL4VQqWbNB4UJQkbT0c7qkKWU2Q1nFBIKefCO6VsedLrYiZEeK9rwTs0H3YjujOVt6LDLgY5UK3Rr22PWcgY7Y5ZwiETxoUM4U3iztCOyLyZ1p2KtmPCf/tHZf1EgYnR0IDCi9CcXIcO8ts+b2BLoFkDOFCOKm8mJidLQSSBP4+VvMFftIFVTrnA29MNP7i+jJizGPbaZLLENU9rILFmxEDZ4JBVUwc2L1H0ary24eLf+9ZF3xb6NH5A7GAO2AWjwpKS3WLOFsZxt0gE0qzTgVCooVQSBkc8lMZY8LguQHkGNFXAExDU3TfUM50/+WU84UxhDvmuuDU4jgkk/h+NcXc+w8UdTpIaxVbbX5YpoFlEWNLboLyak6OUHvZPf9Yplw8Viz5uwdhyL0gg7nNWonuN9XbRBI6aFR2JouLKyh7jYtFKrNy0BmVCA/J8/s2BfEEpptJ18DRIzHf9qX4jWLHbZ1Gfmg1SUxjAVEdWF4r5ecSRRpBsyoJMpc4e4NLDrGa0nph07Z2enbqrhPmyaOx5rptoVjRLarXmWCNpnEsLuyaU3oN566+3RcIBmfO/w8PDBIV2MewawVtlh2zktIUkxTG/JDlqRtxltqwmpWVx6U6qWsJq/tcwyM9RYsD48t/0XVk9jUa9hKTugr2++/733KG1ohi8ff/Lp/j6TaouzlxeahTCBRNvNqiutM2Vx7UwSeGi2+Q9bKB2Lz17SZNjawXl0733w6XisadPR/SNWGWEpvSHHiU132D/S5wQ5JBLy0DlZJGRX9IALJDH6un55s7oY0+aUJm9/YEbAC7DvZNaM8ijd5iZVMhmLR8KI1jxEMb6iIqwfP/wBJi2C4DxhpuWBjFo7rCVIl8oJQlN4FRg6fPYVhlhaOfo71q/sQ7FFYlDpOrzQlCzZcJqMG4JhHa0u/gwo6HzcdCF2C4iukV4S/lt74TmCZHfNcJ0cMwxgiGveuWBbtpgtBBbBMRpCyJwlXSokD/inpVp3NuNQZta2yQ40QJibvkjN6Q/O+WDoQEQ+5mzbwDRAo1CKiFO8OGbaJEitymCLgWaoCqI8i7tv5rHcDKlG4hEqzvrmU4gEtb8aQW2eFjZlqbAlpOKkiLa+C1kh3iC4dVTUZgCAd8lHMBozYpbfilLiJ1HV16pGwOwteSqE9a44lXZLQdFsSpylChtmJuNBLHksPxI1AB5gh0qgqTVP66hibogTQYrdKPlooLdj6oUVFE+l2L1S8RG5UC0LDed55bPwCF7PaxZdyX5igYnnFrSJ4U+7MhCvDUTR27KVMELc3+1J+YHUKxmDcQ5t6ZKTyyJfTSK1kj4rIomogiHlxrfYVWdpsApZkxzLr+EqRyAynZ/j+e350BcVbEdENhtESTHwtkx48cYbOweggKdSkeqXhWcNgdEI+qVLdqhE4Fd1TrrEEpGZouKkL8pKiAmEVwK8/phcFSzUhLtWO9AYR4+iJ7mle4EwKcd+hmguO9KasBriCqUb+IjEi2YkDU1mWyO4tC6NxGld5Q4BukrmDpyO8DBgW6Fnn764ZkfnDbNjNNMsXBZz6N3o5VS+1QFthNjn9YmNnFPKkkdLQhTaFn6YEeHqdNJkX4Hkg4UonhhO6+Kqt8mrAHAKhyflyWg/PRXUKZvMosF7OWCYnAyMDPABhV0uL6yJ3DoswsEpgmEFJV3UUNpW9jWoC4eHFBYZxUdgepNF5+a+xpqjl5ZsoikJBGKjz5NSBGuobUqtKK83bDBrMjtyiHleQxeF8BDpYJNzsiCzBBU5DqjPF8DxCO0hylRvH/1d2eCdRNz/yHTTEXNxEJ9FAPlmooU4WIOosmFiEVpEk80WdCeMqVm2vkGNWywu5guOVWF9THsLMwK9SAe4EOte7gNeI/ocj0PxMIGEqNDzn3oYIHVheMoegGVvMWFIzKiTetrtsr5PIVGITPwxiUrhdNduCE7P55SY2WAQgRqBCgEvhk/Xg0vZgTvCX4w1v/Jo61k89qO5byH8M8/0to+FG37qV58dFGGUDLMsmqILG2CTvxyiHTsn3CQi8/xDSDmyRHN02NXvXTl31tmzoLqYpxeQNIGdxzKXZJK0TLNzQz9D6k8oHnzsS9u3obijVqcamgMaFipqcsftBwLfPtJ2+ySIl1l9hTtJOJELiHhxyA2JDM1Ekka8DEPgGRzQaOCD5mpeEAJKTzVSG33yDm1mkipJgPWSAKz+2d1JpUWBQIxG5zfLKwbt6CtYk2PGAgLEBHWJk1+QXRTE+dUM3WOIQfTNzYtnz7nne393h83orJRyHOeIoSVLTCTSZS8jYrZAo8YMHY/kYeyFWhk4UkxWU003IbbklrNaIes0Qo4vcqx08R/iyYu5s27SYjkxOuhPMASlgAElvTRsShpqkGkRRw1+hUrE6U9wCzDUP7kN59YcUTrpD64vzq8n3RmTJVyPxowwrSDBWkyi6ctZLLG9uBDkikYsfFjA5gvVf7KzQzaxwUgu1MBGHJNEl2TGIFUK4kgBWvwSEbSWTdDjxdG5lGJ7TCcERiik0vzmu7lLGzMkCw4c4KHlTvmSccuXIQ3rdRjhoMlzJikXq2M6j50W1y5QsPP13JteXP2gwTSifJMe5uA4XO4QdNzIbrMuv9fj3evB6Gw+Y8GGfV+dmzmr9DKQDzTaGAeiNw/QdBGKHBHb+YVf+pn/+/+VQqffmHJfwuCACQ6yD7/hpjlspFcWmCvFtp5yYRceR8ux5LwgZZnlJmVEcTWgeNNi2P7dOoOxQZFIJm+RmAusPFRFhsxrLPqozUyfM9uvEoJ0QZ1dI8XDNyM4iKePo6BhkUq9BYcA2LZQdggKp8wxR4I1AULpKNd6Bst7LBc4vSkT4BtDTabDaOHlMILdm79rkoOP5DnybDRhGb+l1WJNAj0eL5IDg1SQrJEp6hVLXiUzMkb1H8IoSH5wWMX768kz+10yhGwgMDLM3oCfOBveAG26Pnq37rvOJlI4iFsmGCckARmkRg9zgy0Yy1+yZbq3V9G2c1cSH1JvjHqAdpUezSvnYZoFsbXBGzg8ttxm9Rqv7AFo07oTM4SGPJKz2MSYl2ikoVJKTgz7zEe4JL1JP47yLr/gLQSU0C31ujaxGiDS1Ze/eGyxAsiC2UR5haaKwFue5gmu7UjbgUJUmK7XkFb9JGvhTTAJ90OfoGyx8UvMvBPRmpPHn8YJ+0xECSTbDazfuDfQwVpCVBGN0+Q0EmxMeGsNwzv8Awe+QNG0Uw0KM9/4WApJosoZDFkyY0058FYcaw713vpomWgl7MocnUhqXCJKFUlA50bqk5tgDyWvv4xTj/lun7ikMHSKDrh8B31jWwJFpE53QmPBGIn2ga6IyRf7LpoE80tlz8wWOaDp4h5KJmNc+SUCGjQHXMxPPPCaRnu6w8rv8fEpeWT5HitYWjunbyHCRoFs2+SEx1gB0anRapOk1onQR8tIu8R8MyfrcV4rlND6pAQhh75E2vmsfOnQZcfE4nvaJcwJiEDDR4rml0BBoDPz/eKjqXW+wkRpLR23yBJqa8OZYqWT/UoGxWSKNoeucjDpLXBkSqmANcy5pFgLx6YgTNbw23ec7XcFGz8+fCZ9kYTVJkL+nUWmu83SENmK1EMVkZS8RE7UW9y3ruBWJilUIuTiSPKh0kbr6GKMR5hrWrNNRBM/9AV12hYokUA1JBbooQoL5F5ngs0Ws03wSI7KcDo33Gz13UHoKWs/4aAaEt0F/90+TnGRKZmKHdfq0n0fyFqSYNKQSU0Jo0aIkcI1MaeErV+QTvWxIjFYVTLlk2SSMT8t8lRoPX340SUHLEdBGtCKuAltofNb3A04AInLG1exXlTOw4hRgsDKPnWy5t6Y3vo+dbrD/CUsr9KVeaGLX+YCoEFK2ycl2X74S6SEFkj7dfubDItaMm7BNyiIh/erT6EU/rUENylWnCbdoIHQNBtWKxiXh5JQihz1mZJp1R+ZxJ8oqtWVR9NDPclEAPdkyUWahuVqf2+ve9W7iNEIijuH67CXFI49fHCPloR1QOoU5uQodwwPHj1+xOzLyfHx0cEBDKeR0H6ae6n7Cyphbzia3WBqq9kMl4BjHkI/nSqp8KidKznkwgEwcgj1UGxh+j/VPB0ouq6jF7WfEicL1/aIg+IgiKrCXDwSr+B4fBltCnlT6tJSILQxGqKpFFhZp7rYcjIqYFmjM5tfXlyesZehPaWARVGHsyQpFvLpBcA0VLRIEW0571rKxfkV+wqoCqcnp+i+MLYMVuGPUzaSqSgwW0NlI2skLdPzgKpx+aMbH6PcFQLTt6ELW/jhwa14FbDFKb+g1lVZEltcnJ4xAXRxdsX9DPPZDKuT0XiKOu6qquVPy+CZRxgpkRtYQqGTNkc10GLI+PpPAcCC7KIGjDIiupPmFBIApGq7ASxXu/Q4VDrrfowE2ZvbvZpxL/juBYOD+fF8frJc3aes4BgRyY5ZqSfxk17LijbE/PCEK4GyOuVvE5lg6ShM/zrvJooMBIPcRTwtbdo/ssR/iERC+JZoplSkBWCaEfs9ptUBYdSUUQCOUJbqRRTHyJFjWV1rsEaniqahFpOdheWn9gIBYSjLAkMoUEItXCLSIba8AhUDS6iVNlQCohmPBKgejYyCl8cv4NK3mjzFZp+ecicdcdIFk3zVNLQgSzSR+A1apUlPaSv2kiGz0Hzd/hQj621ckbdfOipSYrYvmeMT+nVIsz++Sqr9MGWyUQQ0UbZowKeCNino4C87w1oaFDbRFu76LVzhkeKUlIQxfhHfxCFkg1yA22fbW0K6M9+34XHx7fmpPLOWnIIRlsCiY83Od5yct7NBwI5sHm8zEMpmsYGtRBLvzpmsIbOSL6SF6nZ2vyKK9fYpCjKXv4nflETS3dB8G+XNrkq4woph9Y4Pltaps35I2xZwoMJqAqSwKFKqLfgqhMQz4qaY9OFRsIMssQKRGH6mEvATrYVfGx7RtmmQEh/4R16ZDRJfMo0LkcBUGoeqACYfdhs0DFRJ+elqBsQVPBHjTnRSuPOoY+uRuyAMuxue3Gb3PRmvu/SKLKsH/+35VrP7q/n97pgzdS7o1GxtHZCAiC7ejto+FUtWqzQzBWtm4+gIWHv9zre/y3Et4x2uQH6MrsZpdTQtwzHTvSMasu6AW2C1gEVHoD8bjNEAnLYHr5ziTcsOD9QG9bYR5JdGSm1PKvCpdkTw6nxs72An9v3sk3OKX0TQmIYscmU/DanRVeyBqgEiiGhoFHxCKnFBv7y5ZrxjH60ZCb08QPbTTsY4R4gHJJOQemqHroWsdJi8xN63DrEmFlPazzp9ptOYm6EImcOGHrIowSmoejd06hOCmX3U2dqy427iRC5tqAkcPu0OnuXOCtrOB1C1xqa/4Z+Y8hR+nEHQeG7/CGCY6aI3k2F0lJeOOdf7DH9IxzQBgVdYovNkvqTxMiqCYAsDp6QBtQ+TsS5n9g9nlx9zbSmCJT+h0S6NQRoWdxQAc3suB6/WY7o9pgAZuVllSE6LIA3PctUXWhrdCzOjI2xd7etZmB5MeEOQQwu6EniPJKI6jNKhObHr4E2GK6XJnNwGdMP0kF1hZsDHWzPJhAJEHCuAvIToOoM/MImBK9EFCRv8wWGEEAgH6OrwFUzRUw8mv6wdsQj+CMV/PT1BeHvrK1f2XLltBgKJEKmUhhZ/cIei8kzqSSCUUF3wYXjEcjyYkEBKjYxU3wkW++nugNxVjkK1tFmhtp+kiJA+0rMYkFhN+olniMH6rReP/Bk+Q3rkGIlaR1jtkQ2BgQbqC04igd765sHKFBiV0y6fb2I6zYBcoMoQfzDK9eFYSAWM5gWDIXYkeuzjon9+OZvuzJjbt11gd84N10uNVIip84Pe0eH+5z/37vkFKt8llRIb+yQiJs3bqKLdFYo6a5GhMMWVhgzBC5G2L7QCUkptlo/nZEpJMGcoOfwnI3hgjAf9yBghoKf5YtViwBqP/nCf7wgQsxLo+mj7KLUkygMypndZKkJM+SQys7vIzhkH2HePYQvK1/UV1uRUbs9/i+ZkA6iQ0ySSpTr6E81viTngI9IZDJ7hjzbNtAsT4thYPvryF4WEbQQ7USOTKCZyYeFIfErE8iR5Vqe48QYmfWTbztw/OU0pywXgpbSUNehVOLKGiUNVlLbWYc/iMbh7rm3iOdeojy9szyes142XNwfHL04mU891wPjWxTAtl1A2wSxzKg0/8JGDL2wokrxzBCRryqudiQcouWgg5dBmNxkWsytANvKYcSOvHr/1YP9wuroAuP/86clbbz9idsLNdDywJYyI21ebX9G++ujX+IM/kPXZeL4K/8p3c09t+crNNq0WaSiBm7SdTLPTCtomSCP8kCXpxBCFt43Z+5AeqB5gnDuhxkfB4AfOw8H1+CNs9sm11CKuvMDm7L31jbdPn9a1tH6wBIY7hexn85EKsLp+B873xp/QwgIb4YS7aedJGwFWf/HhHiDQctEOwYp0JqaIi/zbRiMTTNtpEVyTAi7RKk9VCNJRbAHQR4mUtSmpsKINb1kHOE/KgtTzwSu+1rAGG3jysQEghH2wRJwa0uwuiA7WomixpKfbikecFv8GtIK3gIpqBwB55HZYzxdByWTwNMHJY7lxCm3GNx44Nl+tb/tb+S+INlID/IY4IN8O3ES2RQhG38VH6eWr6I4XdCXnbax8J9Y2faLaDhFhw7AGtn42WAxvPwiqVJQEaXpj1Dt43vQBg4uKhvqkb9a2HFvu7USKh1IUmoqwektNgkEueSJMSuIV3Fq6zYr4Ny/C0tTyaW02Y03kyqrxDbqlsiAEMy+GCSBU+6R+JuUGYZA0pAXfBrJ1vP4bigs4TiCgqKGjSY+KARE+dIu7e4dMnHFqBeC2UanPUsEhiEy4obQtFhhmcN8kG/I4gZOLkHrj4fPj4/MzeqV5b4SiwCo92iEr9RdqRN3u4cGhsx6q/mJC7eaWL1oJmiH+7U6naIPMc6AZWAhyQ8ajRaKC07Ckg1DrsTNx0yqPbZScFm/YKrn0ECQyYAGTWSK0dnYMiip8zdBCXptAOvtgIb57FskXY4YZGwYteVss0sLhzUXMcS3QMKjsJGeXg65CDuhtWa2ATNdkU3zYJRFqihH5YummSBs6ZHNb0HrdeRqPKg1R8USYpJr/dp+FvPgE8i0cW847WAsNoeQ70qalmR2/DHTsVYebymHQ5uGnwS0/9EIxUmzoolBjgwb+CHXBOa5Y8MAMQqOmOwXpioojM5aql8sZWo3Gqespqkz6d8gme6hzlC/jS1wQxDwqgaTECFPpQOFQt6GcDONMRl2IKgMB6EYZQwMhTSVAfQ4dTfotQf61z61LmSrfuCBR3gZ8C76NtwXZhIZ1Lb9NwlJGScEaLOUNeSDDSECligU9eMG5VYBhFIQimwimaJVS9vC6LTGJrqf99WvLrZMy0HcTy2rLR0uLBMiuLQg/JTJQDcKGC2LZwi/i+rzrWV+QRyomRBcfvpFXGyhL0ZlCN3UQKkGMSSQL8QDaP4XNCXVVeYVHS2XFj1lhl3dWnfsPHjx7cYy5oKXozs4++wTAwSH6CAzGfmk6UE60TOh1uRm3f3Zx7o5DDm4YU7M56BNDPRwwF20E+yIEiaWCYZe5YrULy44fB64Ijk1MCJc2PymsDPihUysIeSZvFT4F0plaHqYDUK5ZjnTthjCLQ4QisQ4wL6KNJGqouhERoMRmJ1qtSwGuEDn/cHF2znobB6MRC7CbATuGSSE29Mq3MbTHQIwYbAADB1mfVAFk+xlT6RhVs7UMuxoIkbPkAKMbEoV7JGhx++enhPthZfcHVNhWmSlgFH/hrNmka/tKKeFFKjakIBZSllE05JQt2M8+/ODZsxeTg5co/Zy2TGt4enzOwWsU99XVCaMZ93jMvCKEIY1lg1oPT0MDOqw4wUZY5gIgCA5LLimZE8p2cHC4/86DJzeruaNEW3+QW7uNxc30Vh9bG2CJkZkEZxzOTs+494DbAUjEwbmtAUDJZ36SjmmR49bD3JdX+zbOJlZcYij5eQ1Y0K1nG1slAQnFa4IsCpgZ5mfi3qToBO3nkDDFpOqMlUOTTzINx9ze5jSXhWlAdsExFrQxxEsOcyW2E/ZQQpRcx6JgUK6q4nhDgqGhgcTSquKBMwnyK5Lyp0dcX2ddiwQWTqVRenSSCDMioZJvr52ZMuoMKgHkU60LuQJjwlmvQGSAsArwSB7/kDAEVFraP3lmFRLBK4+kR2TbsOBpPggDXxsJyeEJfL0bj0raFinCYHHo5Vdhr2h+Naja31ta2jRufVpXMwDgMyj1LnpbgkPSVqhOa5vFZrUzhi8zJj1bjzS2n3VL2Z2Z+KS07U9om4M4wO6/sCgCBbqcwBooyLSer9n5LskSY3q8iyhS3qROKIFa2DNaYq0AY0WspnB/UPRZnq4tMLH4rrlo/RNaWOqdJG7eBTVrEZVYCYOQlZfsuC+0n/2+xWmiPsU73Pw3laQUNhDYAgWQkHjVj7HNsBWEWIkWSYgUEFGAYM1vk5ruYtkmHdqoid52/7in8oxdEzA5sXnXr9FCY/d2zSSJN5QLx9OVz3Boyh+brPRpYiY00hIx9lPIuge6vpKXxmn0loKmXCJpVSEJk04owgJELdaT2llO5wR9WliqNYobDQoWi8trGt85s043Cw1+uIeFy2xm1+fnl2zYorpTy1f9Uy5P63R3Ee45HSVxriCfqbjezm5vOmYaSCMf2jt0bhs0ND+LhgZk6OQvtoyA0ws5pYfxKM2RM8QUB22YF6nmWLRY3tNDrzj0h3sC7J95zCMOO81M5LOqwLnfdJlsdXKyn2DQ1XwSU/ksStrBMjWn0rJ2/5ldEseDYkDkEibdKD5MIr716PF0nNUVOiE6wsFLe/VrbG0xar+25VItAElpGXSZGnFCUcjKqy0JseJ2fp068kmoZh67DSascW9cthMULf+jSJCyoygUJ+MgDz7bScTN7SIEZT47ALcvZUls4bqdKJnni8lpFkM8bt3WmcieI0TSVs0SzRYF1JJRlA/+TSkWzfB7q+vFdXbhetB6mjVTgHI3zDCrxP5GzE87U5UjWRjNiXoxcHWFUzVYWyKd5RwVjFLjCEeKnw5npO20myC1isYmVasBkmFPMKclUrBDhhzXJIHmQwTCGA84KU3CFkEr9i3p/kKXeSc1GHTLvQ27t2FbtzXYOHmaWHK+wSQa64+sQrBZV1nNP88JL6veR+Rc1UyFlzkzlkF2iZWOiOJL9xxixGnsKkdTCtv5kdx0jW3y8QoNBEXrdOQJZPX9kQrRtPCte0O/wDz5bm4d1s1aWnYODJ76UTC3b2TJVYWgNaNQwaPqIdVFN77IPFFlLPTnv5zDCaFUXziBG/HlBl8nCzHixo6GxS+nhLsoi+ubvUFvfL16Tko2OQOu+DjHaATbQOoiG4nUn/vcCsImAVfnzk8vS7G4ni2xMEf/Z2VMbUnTo7AgdVjZURaQHuaiAdiFQE4eZg7W2f2wEUKRGQsFelX1yYtKpzn1lgMqBaoPwuo15RyWFQ/ruJmm9FNgNFY85JK3kTk5rfOONuzD57Q2LirSwlw9YEyy7H4KzN7Og9nyarFinpKW0vVVGj5aLbKuFXd3sELXgnJbQe+SuLz+mPWQ64ubvd1dlN8Jpw/VnAX3Kq45EofrxOC0jRp5oVighOyYMKN9aYQIxwfaoOOPALo24QWX5CGFjmbmOV2yXo7QUHg8tFiAp0phXcDtxav1ydl73/jWv8LEX7GDZpJbLiYTDvlx0WFx+jJHo+7QWJ0en4QIb2gbTEYm5EMqWAfR5jAnwLYHqz9JQ2v2oTETsGINYXFh7b7/8Ihl5/FkB+GBeMSIkyCgMPMvTEWxBALZ653J6PBwv/8h+5AmF6dXs/Prnb0DzqA2bzIikspv9k8yN5z85kXeNk9z4jtrMjzxTx+NrpJP4zewd2z9Gz9/mj690YsqlulLAlIEHxFD1k/Iwoe0aX32BdmBabxFoCIFNN2uoyRWaS1Ee0tYREeGfFw/ERe7HIOTrCEw4sahAS2qPzdlvEMHl/YfblumPVduQWVfA0zaM8WKzJgq9iCsyo0/pUPs3nyOqZRe57uIDUjV891vhYhAAm8IJDanmdFTMCNGlXFrrzjttcc2CqyN+z1QfeB0aRpkv/mzLpk7UowPmPD3E49kvSqjfhUjEfz0aWLphzv0NXgSv7C0kIEpfSyhnTprcfhxQ0rgpElAOBNvcII8CQRzk2LBtm8gpWDz3A4ANl6NIxQFcxFsFfRJmmlrROQXoq/zDl6+G4/XvA3aegg3I1WFjZMIkTRC8JZbBV9ft3HxrrwXDj6Nm58mBp96wRSop+0IvQWToKRrxgJ/G6mFA2j7AQ8wYTPeha34tA31r+EWm39mJJTikODyahMDooDeiLngCxE4NvQk46/F+AGIXoENz4qShMi9SgscPk3CbfrS+MqTPDWyTnAbISKbkruDbyvyBmf86quR7Pg0BSk9lq3sozq724xK6MZkZlizu8tm2hkXuokex1l8+N77TFmhimHVQ2uPK5NzAy6nvMCGlxtf0M+Ypwm/VX7sLft73NSy6wa9NCTVz9GsUd/wQHkhUQSDdjACRptG8+4dMLSLKAfklu4HIsUKnNPtYnbOAwUeM3GWlSsXmt6GTQScnV9w0iCXiIEVkskebzKvDmpvBrfpraq3pk/CN2xils/xgdwFyS98/Vf++Nd/mXV8HpKAGHtGWkNn+p2QlnfqEPReIQ+l1HYEmIbP/OAO6uZ9G1D+laxwwQa4kfEVT0VusOHnmf0JNlY5xSe0v/VqwPW4+4DOLgG6wczMjLUGB3mh1IqFxQUYYsy8WhR+JDSglhuaOcLC0YQMxRgq5rolMCogjKGW7uuQvx0mcS9XDAM8uoc9nuz5VMGgJEjfTeda8NO1OLvHW+LCP0itcVp47hnuliPzxQokNINiJwv9YYT8R4SKB0V4cZJs3OZDL76Sv0bekr8NxBt5t/FMFKKDBn5h6REtPOnLWlGjaM0oplXfWtNZ7rNVvLMYYTqulZv5UvVX2ARXCyun5eBfMBRCy6iehrr6qbJJNoQ2ylYGWwxNzOanYt6ibxAmMq8moVvfu7FNQcotL4Ctg6ZMNiwpvUTQOHFYSyAJKNwKW9Fp1nnUEjSkYbqaRT+PyEQosGjfnd4bLK5PXnC1HKejWGGPT44P9vYUD8y+kCVc2MUvlmwWYoYZ6eIKMSQBI7ThcD9DQdYHWI2xJFiCxAKIGEiRS1YhkdaMqW2qPzPgLaNCXcpRynKCGeWSCkK/bEOQRmJJGmjSVeC0RZCX7JtvEsWNMs2JtQyj+aItdTeyDVVYUxyDJTR66swOTS7nF5wRSoo0pwqk8utJOBygzzlI6Pc0r8ywXDMpMXd9gLzjzw3Bk50Jky7UGU7D4Vx82AgBjx7f393b89C4GFg6sSFR8IIfx/bcK4aKWJLnBExvAPeYkTFlK6D40zay1LBgIdQC8tw1WwZKiewSfn5y4V4t1n9HEw46pQ25uZlZp8lHxztYqO8cZI+uyEGt56fHqPgabq3kHpU3uxrYnEr6nMoqvFJiGZGIkzVwFUrQJSni8XSoykveLHbJH/aZYmNagbLTi7RoqzG6oiGfX98sOFyIyaZB5/T05OXxs73DXQqiCkA+RA4VP2WwHoqmvlrHVpiiewtbAXeCWyQ/9DexipBIQ0ZiTN/TpVEcdpIYYgFE5ksRVDXPkrJ2U0oaHoiGBy6RefMiKJ0sEoOZHTq/xq5V3B4XxPgNdB6phGBRFPA1aip1kf7Wygg3UhVtgzmSz+UFSDGukq+yz6UDhDkoddkJOZaRhDAhwzm+FAluRsMARJqjHAIBXpp2h7E1MQENUA4ZKQfoCR/IQrFX1lT9uG3rwk8DjHNbAoEr6PYNkA1x4ARvmxkx5mmw4Da/jQyYOAGRh0Qv8E2kJiEjFZa7b6NuCUZjAqRdtc3dzefaNI28jYBEk+sUgAEypSGkcnnzDgXWnHZv2N3nlbn/NpAj+HAWUfVr6aa5SeqS03CxZojXkwKWCf6jSFJUa/QzBMsVVcvC/ph4tu+glct0t64V1LNq7MiDQq9KjBwO3m/gG8g7PyIDkfclN2jDrkQm5Eea+08uRbPBHBxQ0jySz8O3+WsfXCbJZ8bomV9vwuLPZFDKrrEVK9CK0cQT+o5HId96b8/BN24ibJ4tdzlzb3QbXHjytT27EDyRcit+hNczoLImsImycbTIPut3g7kKP5IBNoseKcAucPS0P5gsb67QrWk36FyZy2G7Gy04295owOl0WbznGGMaILd/2W74UJ80lXFbLM31Lg1Nf3xMx3lzpWErZ3ocHpIMczXNWW+0IKSKdLmOqBBSe2yEUk+ROmZzzRQrD+wKddKK45NQXG1dEM0V3QEnFTNbT99JW0QE0iVNDa2Jxy2s8+uMCkgSVYAxjAMDOhobMTVF5dsukixoVURsJiz0U+adCAQAPWN4sLvf741yMhIntIHDrcKRA/pSWlUnF4klWgKlHvmGeOe2N4UgyPbjTpX24bx5ID0J3sKAIQWc6LijcjmeangCKzLhI6GlwoBoC3+cb5r7Nz0CwZNfc4G6bMHxAiV6AN15aBZM6OBK3U9MIIu5Ub7DJw6wXl3QZXT63AKLoQXNPh0D0NxhuhpzuQY4sAMeMWt/OR4dOHAKYvJFU0Avb/Oig4wzSYlawKTwzs31CdgZ3DH76Dq/hmBujs9kHz8H65sdS8jDW9hoi6BSEEw8vdUd7yPDVhNykLZG/2TD7OuCyZRyukEzWWGVx4C0Xnxs86KixqcQUe4gSRrkke5ZGaT4I9Ue+onuhMV2tzs6NTlODZfInVCGnIc+40ke1QySPZUG/6ysrlkdkjRCN2mGvCoCBp/29qpBloXvkoXU5yI84G9+iRnKafGaWX/Bmjn+ilFsuZu0KSbD5kF3hEd4vvNfNpoR1vFsFqzU4bHqimWirCErKBDs1B1cnJ8Jzg6X7NVBXx+Nr1ZXlxNMi71yxMqO+nJydv6QUyBRGL3bi0n+zmjM8S+eEUz9B5LlKiQHXRKbanTNuVU6swY1dW33RioZ9Cpv4KElgWIIYf/5PqXW7Z6ZjeWezO6dAmO9o6aZTdYhKThKysvH0IOSaxmuDPkQBwF1MMDd5dz7O19chjWsU3Ez+AtUU1nFuELRgAVP0eNsbmjBUZ1ZMxpwrrwiggw5gmBufOEa8uXleUZHZodRAMMb2AEUmjSLEEejo7PzM+5qnHTGTHPABnZhsZZyfTnb3eMMnimNGpDwZ3Z1vcftuVNSgauY35H4Yjje6U4dWGmppEke/HFOZMm6bR8jnwUa9N7BEYtw11dzr1fENMumtDu7vpgt+leL2arHNRyc6kYtpciVgksuKGB8z96UmxdsUjg/7v1//8Vv3r9/9ODhQ8SDiu1VaI4QYJmiC+uw+EKPp2GlO6Dlo4KTTa8H4Owg1qPl/Iq71V4+P2ZL2Wg47k47l5dXDIFY1LVQ5axvmp3JdPiLv/IL3/ngu1jHQOjVFfni5CCvYlAUFdHIc6NHxY2vjyXYvNVAcNcTxx1bhjaE339df8ReTZ2YnBX3ccaX5NQcKFMrFH0yZHuC2CtW4+ehhJ0hAKi8ZsiGxf8zUSDJstBVa/wBJx5FYX3Dv/OMcqd1pcQqY8kfTrbdg02oyC3tEGnRM35q6tDH9+QTymK8Zt0NOzdh4SMYKVlkdGiXjwKpAANFKkaSwyDUWowB7Hq1K4FKO/gnxXws1lbzd2S0+iE/8rtowV1f+t+WRYCsXHkqG7ybJznGbXe5ASrgNgqhpcup721sUgjlvxnHU0YEPCRIRnk06byaaKVtgeQhu+bAIg1SqWkcAanoCY13oplck2SAy02QoUqAoXdiNgg2P5vw4It34PN56yctzRcuKgDvENwi4ptiFSiulHWALM5QEv4QK+EVt8VvH5AWPdgAaAoEWEESnKBXXonfIgnYKwA/0mcIErKhPCRusDYBd743aDdRNz6tYxNyl0aDt1CVc8ujjV6/ICFs+92ANoLW/NyN9JlfDUnF0ya3/hT+DRH1+ZlY3hAg4hRoiyNNDy8UZepCj6u76EpojunYqCo4KCtO4qy5dmdhmadKNwoeJmFo9tH2xvOby9k57QHSkwmAJAG59KceSsY5zcqMLYLth3N1URgBV4en+0tjjVBmUkFIRNDTP6wZTkuhR9KFMMufPXYuk7NUjdqfdlTZI2NKL9lzfYGWkVvAaLkUbsgkb9T8qP5cTuS5Ri72m21uFaBDoqHjI22a/Yv7GIZ7u5xlwRQXtSKtKUTTs4NRdRklRcJShVxel61kMZYsECGbbVqqbvHxWU9bDE09soTNhb+2regsxjSX9gVJkpcP70qoRVHeCXv1JTKjSDHdLVzNp7oHObeVb55t1MYJ7jYBYNr8sOoCTXTd/HIWkIf9Bz3lMsy1vkwpDWErqhGTmvLPxWX1MRok4ljc+PmnqZVdEWr89TlTwjAATnv46xxliIzbrSF4kIaGBKQzue7O3CErEKAVKh1WbLGKJeBt89NwiU/i6FvNW+WreFv+mwgBklOGVqQmaoGoR+ZpChf6HFkJDOU9L2FEwqwofY/MI8t0hPYUwRJA3KQClVUKShKBeoDD8gdWed48gSMK3vHzt4HbBtvAbzsqhhlvfVuf9vvu7wYM70BKEZ72I+kcUBUMKuJx5VMW8Lh3w6lXPUvmuBDIzPGHDFArQUSZGygPqMLYz1Nftb67njP5T/Grdmjo3OE4IAYAaqioKFQy95Gj6nA4JuMmysE5akJPTmcMIR4+OCSiMoYCkn3jnIw5XU2ZshhNxpeXHiybDeW2A6n7ZA+qk8dQS/4gk2ZH1CiWtB7sMWBs4XwtoOG5mjBfNFMItQbNSDIkMZ3fvyavfKtZc2Ilc+SOYhyq2biAFLWWmRRXOG2gjGhmnM62RZQQ4bFyoclluMGN5gxmOlyhBauuZ96k7hALDqwXl7OrXW4Um+5o5CEbiQx5XU4XosklaVpORi3nZ2zMuiY1OMr96udnHJW72N09PD0/Hw+nu/vjp5+8YAyFlHIBA6Sen59ybRPXLWN1gwk+KaGJc8E6dZGGkiyzucvRVnd4zQCMkqI5ZhqeTHFF42Tq8UjrGUdQjhgudRjQXbx4DgvX010sr5g4YoGUbCriyADIyX2HU5vIXlolVHYQwqhsIqCJp1lQL0VGuDXu/JSY/elU1XPYGcxZHWG1moS9Gbf3/OmLq4urwc7g5bOXH7z/nS9/9QsQRWMR+UxVUTxLJpsSj8f/H15I9w/GWKGKU1pfJYxsRdbMNx+iULpghS9dOo2oP48zVYlFhFQ1kBkgImqlY2SXnIhhbEBqeUcgvmxmqUIgV8Lwc5RrQcBhIfJnhQbErrNn5wgk58UZM4toVAP8mHCBEhDGTZ1MbZMkBgbSJMHid8wTMPLHxUl4NgkRxcpUiSaLBhirIBqCpKr88JYHm69NwCZYXIU9jvoikcZTVUIc+U7CRaRwGxx+QBZ/eAXhJqj12AZOYJp1onXn7xb2YChqNpGC2EJpH6PyB1en+nY9AYO5K5jacKMF3PwSvkFXeOotQMsXi1ZflYZICCWj1V2sw5mcwo65eNggsyrykGNSdWRsOQPh/5SfuEQeeGkWWf3kl+TaTAuJn9+BvqW2IrTvCnzl3Qb+6/7KEVFJ9m3cQl5E6+v3KrPmtcJQ48Jb+AYm40URJaOV28TeWPYTsvG+G739quDtdyEvFhZhW5S20V79fROFZMKsEDslVV+J+ENouoO85i2MsR2LxtdZIPoLGpz14v7NfF+lzZs75vRYq9WcQgVg52D68vgkszWSQkdt197RmlNTnwEnQDOXc8WMP0qbNxhi/eNUPh1gn1O5abOZ/6G9Tpk4J6R0ZZkWctD7408lgDpbIdoTT0qwL0eueosVFwKQLJ0gc/pO9VvwBEE8jUnm3W1oHCqoKfK/t7y/Xo66o3PbMaC0WaHZonJojLFaHKByYCtELJQ1RwhuGGDMgP2iB3LTyzDbpmpJYqYEcgLVSLVQZ9YczoCZGVntewkEiopGvUhfnqI2OQU0H5vCEF0+shNg471xmP0qJCqxifNoF40zuhU+OCkWSNIhdaIsSOLmK9HaVwURAJQdd5Ypiosw2ckcEJmuJabTHqKhO4JnzQ7ZhvLP5Wk6A05opGho6Omc0Nmc7HQliI4hC9OU/YiTQ2QIJQ5hZsL4lhTFjB5ALsDDwLHfnfS74w4XaUU3oHfnUBEKvJQjeh3Gf9h+w/ju+h7DAY6z1jCIzRgU7eB43b9sM8tv8ZyUbJTqu2GLXIwTGmSbHHztKSBLaYV9PD/OkcMHQcOIihXOOMa1m3Ryk3hLZtrY/vyppxfhwdPjZivmxXft6M19g0Y8fqUrDdb14BPA6VubNFqyLDUfs5PIJIXbvr8BqdJpPgs48EZs4xpa7mTD05AKBsQloC02/TdIBE5CFJnyITEIh2qw6/vhHsBAJQRw+UouErK8R9+2Hr4QnYlEC4EPtAO2D32me6nOxGEed2dn0h8NMP2/KCNttOl+n3nincnu1eUZ84ge2IU9yWDqlgCNyLkTgNshXP2jZiLG4a/TGKQGJIY0qqYISVh1PWenKlSgMlphUXehSeGRrFPFEJr80WUenLrmrq5MJ6DwO0RFK9XYWu4zcoEFyYibdKxUCxoHMk5z5QhlzRVIHHypaIAiWD3QgG9sWkhW3dUXWKCR7GBCyX+nOWjhWOcEFysjlDNjGNLV0GXM/gcq6+Do4J5tKRtlGAxTUxlFoDwzguoP2JclgUzGz9czolBTXFBbXHBCEaPq9erTT86efwojju+9tZ7P0OCZ459x0S4wFtx6fXE52z9iSOJUC2MWmLd3eA8+n52edLlzvTd//OiRlzwSsurOLq/29vYY6jNPD8GffPgJ17wxezLsj7jhGGGe7u+yXGNFhmvIdh64wHoHZDpHgDAt7iODy9VLrJVgBZdD7Ozs0WJwN9z1bPHhBx8f3X9wdG8PaZlM301TjewwIOFhcMUWEc6jO+dspP7oaLzDlchHdGirxSwzBYhsRknKYySfomoe5QTP9r35LEe8f9hrg+sHAFLAlgiJ87Kb4OENqyk5BDI+BRSfBiDewgldNZz4DbnxRraCgQ/FMTUOSATQEWEBx0EiEkrkBibR45HEGsaEyiSBIPBE6B2iR4ir7aYbB41dbROzpd9GpEgohktzUvUTraayoSfJSI3PxlHB+Dhnz6r4h+GQBOWB7DRCddaluyIhwrzX00C1n/7O3/XdsKEquR4N2hCWbzHdfcLilu8JStK3QBVBz1oBCDFNTordUid8WyI6gWoYRJBSwE/RbeYSIQBJpwLiNG5AeYu0iRmGlNvYeLclnrhyP8DFufoUQhwwjreR9BGTAcHROClIfGibGqEyNEDJnzEKMNhBJXThCCCBP+wpSn4Y1I8S3nJN7m7Bb2jYOLYCX3fezcCr4eHclucG5yZFfLbdLWxbZkbYRGoDX/19I4CeYOYnwUnkjYCvYvuh3zIO3Nb09GM0Jljdn5/NLy9Pd3f3CKP3ZRZtsfJwbozt3cXL1h6uJEyXBUXO8mr+mb5nzWbeAfsfrfC0QiwOAGHHx5Y1jwUitZrxopEHAcVFO4ImmvwhaDXHEfXBsmTWiiOQ6bLU2+mvsy4sYqnWJoQpKLlSwqc3/6tNADlB6Jd0LoKTENxQKaG/ZGTBuANPBjPoaHYiijuB3tHupyoFKwAYGrBZ2ZWQVAVJRkWwVdQQqCEbTcBEpQSUMEZkVT0+s6huiy+xXimoRBMheBl1+E6G6TudJqc7hgwbEALaeiiKimc+X0HYeNggyAo4paKDsh5MHODInKUdswj80xmpwEVmChsFKYugSxUGEzBYxPwRWyGY6i5GMqNH8Wi643w91zB5YB87Oz0cJakFK5YY5ImCcRgmQSRgOkybX2lyzMANjYnhI9N7Y4FZEiBFlqVKV0Dr4Go5dAT0K/AiQqpWGuU0lNYPnAnpwV7JkK/mMbDyiofZBcFtVu8AhRn4iNWSlQ3hAjgSSW9bVBARAulXGEg0YrDeQ3TZAO1gRwlMommYhRd66eXRKKQGU9gyRILymGQeadi4iVSMa+DCu41bMGED4+8moiFvEBjzYLK+Kh1Z06aIkxJC2PBsMEm1eU80eWCgNQsv/an+BYt/VS7HxEYQSb1tPsCCqsck8HxxzXjaGjcc7B/dO//eBUh4MIfB9ubTp0/fetTjninS6KNYctguvAKR7QeyESUyh/BwJ4nRDOSf24zRF3sYM1hZNOJBvYZqiJGM1AaJqgfqJakqNV5mjyjTibc9WsEz4CGzln9aDzlmI0cU1QDnQVDStexglXCIqT5iGTUJNdVWBdDwKi0ZurNKmrq7jSXoPXAFIBzh87rDzH02CbA2ohI83WVHTefy/IxzQEmOOXKSOzg6gjwaZ6ZvuFKNiX8mL0aDMU00MzHUT1T7xfkVLZSz7xjWrdYX5xfTnb2TyyV3LFx15+ygmEz3PHnaSsBu3QXXwaNDM8Sa7k1Imkl9SIQzV97ONkE5R7kHMwr62dk5/EPRxzyKBQo2hp2cnLFQwFANu6HLCzRy74Ac7+5EjCgsitzcgS8cUYEHswWK9s9OaM9mWHGqBOx/+uxT+iDWEE5ZxFiA7GLvYJ+x11e+9CW6KfoDRGo8xWDVMc1gOvril782+I1/4mXSHW5LeMFU1HjswcR8+oSp5cwHhONVxb9xEF7+LeAP/N2A3sF9G2WTBOFNpUXKKGKe1CEyzaMY81h5mupZxPIZEguN0ibYJiOJR2yFRwQJDyxf/gahMYzX/pUzEBW1ggSrR8AmLWgUMWnEx9ZNavWScuErKWEI1VtPWzLj+CGcETedlZ6VFUEET6S4nGJrvhMmbJ6CK0rML0/DtpZ78XvlRZdG0i3FRIvuABYxQEMbsslFQ08oKpgWo5Fb99avs4DbIYEhFUF8JQUczD1DyHqHZMMpItmZ418QxSoiwCjrYXSchsX6JqAokM3yvkkkSQFCINmqIjCcKP65RlZPlQ1NYT7p/glu1Bbc8sQoFVFnJVLpGGKYvrz4pOVKj2fBbkgQKKH1fsW/DcS7IvHmP8+bABPQvJqd9R82n+S8cGAvi5M7/MDT2M6yS6FwtrCFnZNr7/pvo497Q9IrIZTR1a1X0q3Ebz11lV+4Y0ItSHncglbQ7fdrriK+wfZaaHm0yF9BtrHv/4xor3tb2Km3TsCwQrTDwZnc2P2ci5t29u8zB8MS9Lx7jaHN7viAdfB7j+/95j/77SuuasLgY8D9rpwXwVw6bXZnNcfKf+/qas6y8vUVil1/duVeMNh3PeN2z7GdG50Gk3Grx4POXrf7VCE1CyYOFXSRdOnp/tKBMrG7eExXc7P6ENWO3VBOdZCwL2KBCz1RYc70VyPyfEOcugj5YaixfsGYIZdRZgKDJNG0GE0ws4XmMTgeeHyKSIG3rGzguA14l9hQPuw94tgNGy/7f3COUO46y/tMevd6n7D6kRkIOjDrshN8qZqkEVQyV6kjvvlsHrwkOT86bp/bok/80KMsbVoMu0bm2aPnok5WCBAOD2RHJSdC2dq+k0CtzHolVbWe/DKAIVOo/vDfdfbsbUjEAgHDzWOz0NdClF/HaepcDgHUu1w0UBDWC67pdTYUfYMZRIqM1ovC9LD+FBmbQ+CwJsYQqrUDKzkcHseWEpUt6F8s5+wQRAXo9w4ZedlqmSl0EZQZdiVhn7WPgJBHCgURsmA9IYXGjM4eSEyMVP7TuEWmzHTUQxhhw0ZOYYiS4bvOv++/IKDOU+LXYipW5d2+8GRtgZnyWMxTMN4fHNZHRAQjXTVKyFaKbOa7FyicziV7+hRW1ayiXxHOuS9VqIApTUnelav+9zRMWX0hQ0o3mrSUCBiwwNeXPha+GQyGBqBKrWJCTko8ZSro7WN+AApX8K2eJgkWQYEEgIxv8BMsTaHL4q8UI9bxNS+0BK2gqtLpv7w+0pdT3qMv4iNbMnpV85UhsM5ksTlhvlgp6XRRcJkpwNg4EnAPqZnPX5xwvOPgCCuU0WBCuTIr4XH72CgyB758SHLdwQkUYisP4t1d+lkEEPzMhmNcxuiUGWIO7Irhn6qntCsXEASl8gMy6pEmIFHd0SwZAET3pzlguAulLjzSulBnqpITlRYGUXV75pQGgQkRcoF4Q7hmPMy8M8cvFMLrOAQk6PEQoa0T42jUXyr1DWeskXmscxhPUO/AuH4KB5z64JiDsx2Arm9eQsJyfvPBB592V/eoQevuy9H0OazwpmQOZudKZRdMvJGdMtnZ37EFnh+u5ijWp1Q3eDzd2+V4zsvZxbp/gRHNcrVHTeYCPo40mMs80LPKwsYedoHS/mvVM+WIpX5vf39/bwe7UDK3Gg2nTz/99OL0XCV+hWXRFH7ASBguxzAlwvxkNORMaMqbK4EZFGHdRVfN5IvSwRZv9/G7PYyFVwZNolk/AweWlSxkEIHmgiUPzLp2H2CJtLg3efD8+XNue/jlP/6rDx49YhToPA6nAtSVC/Cyuz6/OHVV2QPN1m+98+5kunuzdCQpZdUit2VM0nFuCv11RwNKgEX2A58CeAUyn1YMEZAXaWhStVKINT8KX5FXaSSG9BU+IgUyPw0thlXdDELyBvbbGOVqa3Yj2KIt1MKm9QlckpdAkjGggBpKTdxKjbdz/sSiDjTR8eVfPFvmBrAQVB0yYv2RZdxJAK+4wSyGoONlLgCxCW1s94skg/Ce5AcrFeqQb4CNLtVGy2PUrQf8qW4ma2MQ5MJY9YnLnls+uP8qX7cRN1jNfdK4edsseld0RdeTh82sRHVRW3TFP1H6pzJgMuTHSDgbICOa2SoCI5ZHfuoVvlh+yVsBEKIjf7yq9aI80smJjQTCQIMqIikm25U0gaGgeftTj1QaWN1C4wlGUzFBBTcIeetzG5EAIhsqWRKVn/qI8we9NsAbhD8I+jaM3PE0kcx1+9kQEUjcDUT5xvMHvchDGNRkuwXdog2nWP0rZwvT8KW4gWelnXTzEkeLR9h/w6ctka3o/+bINnlRXMCoVoUJj0vddFzDy9n82ctP3nnyNrX/8OE9NPHpdAdTW0A5ge7y/FJTRk1q1JJBQewpM/zD/tga4RktrClfnHNk3Ozi4pKudH6DG81wl1sCJkP6JxCjMtIx05liOiJP4Q1qAXN8BDGT5m1QWDtdXdNZQCEA0TxhL1JH96zJOBKu4sVXJBg2J3k6A9IkR+wfIAhVH5zQSxeuXuY5RSypOxfo+gAjGfoZpseittDdVptnF82YJ/WYKUYPICRrvlUg6O+Bw58cQJ76KgsFZIQ82L+VOIkJL7MGSPJoNOWBV/tYg3zihTOB/EJJxUwlMyM4QFxNC3gAcNoevpmK0Y21QZXIfulNcJIhgjUdN9mh90XNYuqZhf4aXsnHkFCRrOBmhd8kpK8ZgRbb01DsMs3yGhgQkntYzcCAoykAY9em3DcupegGMh5KpqZUNdMyj5rIA20GsAcJJcwK24V46iv0OUxAMOTwcuEZc9csR8Voa9mdqgi4H8AWN5Nr0Gd2ecx30Ep2vuRF6NfbvAnJPwFIowqiyXOFVnATWZwVS5dxkcByVIGLBW2uj94TqYTF6130Os5BggMsNvHAODhqlnm6czIGfwAP64UIQjC1TmnzETk/pFl0xrN53YIXVHBUGM7yKxgxmBj/Nx4RCZFvfDbcUqAIgDfBZlSlQTJ4FBqjEdz48cFmWfQ4ShbtnH/dEfbrorY/Qt+l1rKRd8Si4oqJ6muWD2fXVDRaApDu7u9g8zGZvv399z/BxJxYVExnl69n073pzXVPExsGnZzuj9DTVjnyTDMS2qGHVgzZQ/13dMoUvto/Kibmaox46TCx1Eq7IctNsWGgbvOUCpR8dTxkgL2zmSxAitFrbYjIl1UxOZItVaaO8+bY3ZPhrBZCoRefU1LIZQYPrn9RU1W25QBNRyhhSl4VFnmOZtxZXc44U/cqxzheZgWAMxAYGE1oS/sj90BDN9ybXThfMt5ludWTM6GYOZjLi9lkNKUVZwmO9Qg2A0DwoLMDn60jy+718mp2zOIuN1WTid6Tdxjhe0bzg8P7zuQsOu4eZkGvS0Ec3rt/dHpyMhmPHzy4x+wMujXtBfo6LaerxKfsUV6xZYddOlT4QX9qs8gABlslV2MYyGCMxM0q3gmwWmIgBPtpCLyuAU4wLoJ70f/ZzjGAYClKZcJ6jsURjidlnEaiDEA8KZbhz3zG6jK9EqZFDBAQGPodLqChmWGL0Wg0ffnsBWcW9ScWwoP7B4zLuArahirFvJHtttDxkCaD7zzl2bz5+VGeDZZCSpSK2ETPTyNxomsC/bE+6XX74KtPwZR3pLNxvha6CWywBg4MIrEKFH6+FB5S0y/+SaOgAqozTxy+NjTYnhnkqzwLOBg3UARt3IYA03xX0n6BiLZHXFXdijo/dLnSaJQCqLcsCniAhOGv/V/dnTVyEzEOR+stTKqoOE07uDcIm2wVYbfvJm7ACja4bLfDwNAYZNSvpgD5kfJ6WiZLi60Ku6EbAhPeskYwQm0ZwYyotilKZ0NOIay36Yd9volgXJHzZQnhpjUUCYjnb4tg9CGeEtFkwC/jCKRz60n/1/olhpBp2uNLO1T0JY6J2f6FgzilvPizhfK1NCoq5+3oaCzdk+fXTua5PVP/FtJI3TWL/uQvY8HcVFqJSGJlfJMvvTbPnY+N78aR4FCiuPG1VZgFlMBWzDbxcGxFDUy+8woeMTV39IbmJmoBGKFJdRvlHZh8RFJakIrbfm1+75xLIAx/jXBuYDarBIRRgqDNQ2lisLG7c8jE6ro/Ozmd/4N/+E/+V3/9P+xPMMGY0IWxrsrBHZPR+Nf+9K/9V3/7716cXNAjepQ/PS6H49F7YZy9oLuNcHUesG3g6PCEwyceP77P5i1WBkiK3hdtELtQjObV56rx8xAPLEdQAUHSW1zf0/51/EwNpfM9p5R6HPHB/BaokUAm3+k27I/RmriMmBklpjnZkWZ+6FmJAJjZQb80U/s7e2DGFBh9YjqdMvN0cnLCWROcJgEPXHHW+J9+grJ1DZquK7OJajfjfS60Z8YRqyf7J63eqRj9Y2qqBDv4KQ5jXUA4lxPBz+J8BcjepvLZiqXSCGBiVfJVITflE/aVAOonrjQOxLSKW+UhEhWEEL8dFdGrki5V0dTIB/uTH9uYeBZQgyp4UmPhmid+SgoKjb0sCXCSP2MiraJhHTY9kBdiex97rJIcAhPFRdtC7+4Ih55XFGl+madn7yZzgaDAmhgSXXtR7RUK3Z8Ss9ztl+nQpZHBmRkIFcxsYpnQ7++Tfo8NAOw+cz6SI0FYVKnsc3gTs8hk8RGkUUIIHHQmv9k42UW/sThgRNOWxhHhh0HFKxkjAI0Wtu/Fd96Wi5QALJxZqk5IJhEXfhWdrAOEm0KnBI3goCOxASVjlgWbAVYTpdtSZnSLIRQcZecliHYNDwcVdhF7yVx3+WRxwxXgctlxFP4aoBXDLSjSE3n9WqabmkuJSHuCDM7KSWUFfZegdJaGBCzZFCpBJANDUghEsXkPYEJ5JZICpbd1Kj4VUC0H2z0eSN/qikyIluSxckEfHFke3fE5sRMk9Skd8DHRD1nqe876dz2uhcNg0OcfP3xI7SM2IN7fRUPQuaBmY7Q3u1l//Mmn+zv7CC1iZDoYtrNXh8S7zxV+p5PRF4e0AfCRrUbsIc80PAlSoC7DrBluIWSlasIau0oylRyJoXFBnmwBuXhj26PwIflyxDpePAcsudQ3pQ/x/rLeUycOr7j8gnsGHBKz4gXlYSFrCGi3MAY5qYLDwof97qxecJyPB2OuOx9p3kO7x1HLjCFXq9nNR6Q1wK6G9sspeiYzjimXqzPO8UTdZ9itqFKB57NDJlqWnae0CyjF5H0x/y4D9M7NAxIcTtg3PD04PKACjoc7f+kv/MUTzuzndnbWEhi5OVHSxc7nanZ1ePBTqc7fwpiHxs29wN0VB23i6T3NcItqyiYFrkeER9TqTEs4KOv3r2Y77Cno9s8YehHIKoyzACrjTpfApAyjnEchL9J9ve9hDUPWKLD4osIsuWxmZ4dlHPb8zNZXIOk9fPLkrSefQ/P/yZ/8adYiKHeyw5yUldWz5q5Pjpfj6dhOiQR73D9wyd4GB7kWm4WrzDdPvjZFX563VgYV2sBzLr7R7vStibDpSfMFTCs/OurTO2h5mjsHttLfxN0kFST1glblpMFi4neeihKABiT10/udeDZ0bgCslE3Ou3UnrlYnwb/B2+gnG0uHJMqL+5oAHXwANA9UdeuUJHZUgjZMZXclLUv2JQapqI3ub9hgu4Mr3/h2V95rVGdX6i+YTxNOl76JXbHoR4C6eSDE8MM0Zxkm+k09RJYQRiIRjUB+cGwQC5OWDV9bBT7Bhq8NGufFiWASb5YH78YrmRETpzZ9ZG4rXsDCDVr1OXFpJirEZjKojVQ9R/FI1AlJyRpXrPjJ0Sofo0jH1lNwr3kDYRT+VbppYe3VTTrJF2ox5dOAJCkfm/Tw0r31xqk28yoZidx6Bp148xTlODfeyUrrEeTJUyVT/kl1EyF46hXIW6K2QhonrHoDHRVNkDb01mfjFQxteIPujT9JwxAp/FEiFJZGuOvjDW8wiZCnRCQkNj54blEcoNvXFgmfDXQL/pqrLZDXAspDqRCvydCQYlo7HNH/cMDzeNK/vrlgFZcOjk4eQY3ihr7PvFL3i1/60jd++3dZbqZqcUabNh1zpmOchLFzYu7J9QTuAzt1kmbQPTg4Gk/mDAJIiERq3ZZzYhBGdgrTQaJ3ooIztYQGz3QRTTiTUZ4j49ky6ChqFPaXpEelYxRBnUS/BY4ZehRWfMkJTYEZoWtg1pCpsh5dFz0H55lxjwyGsDQP7rDzYgEaDHqPDudZM09Fj4UHp1zQSxFA9NQgnPRYKAP0j3M0Gvq71LXEFop5O5QNaxQfUAVJ9cjVhq8giIZYxWeZV5kaf6vkDXjtCWQSANiKWJGZRbPqVRIkbdVXbYUHIQUGkbrgt3TwVRFoOpFW/hmOXgIvUdWvLk9vlrvcyrWY3WDii4pECN0zc31OVXKDFXmLokh20D7gMp0/U6uLazR/xneOAyWKtL2C0pJlCEZfj0KWoqGXZl4Yu+EeGg6HDBo/URiJpdwkh+6fzcREZ32Fhlk1gAEKIZJry4+UYKYgo9EhIZKQNXsMmFNcDcfqqZARcMUgLaKJR4GFHvEUz3E3/LfsNq03aeod1og6vBdNMbmNC2YiqXjKYGhr2Cm/kWL0Q3bEoC96V5GazgE644JrARFfT9IDHUmQlheoeQMsxFIGHg2JWQOjV9a0gtKsOCQAPcyyAKVAUZdGU4aIIhOgzPuYlfwJ0uYDt6AhNBXFOCTjtVBBJqzh/JqCn8YNA/xOIvJTMfMxlpJEJCngKaj4yC6AUeSwAyO/aNxFMzDgSPZ7PaZ1L66w1+esGIbNQ4p1MmZGnBU26pnW6uPBZNb1JLKIKHVt8OzZs+GTPm0TSFwAZBTRNAYmb7OAlDGSvaFRck6aGokMNjmy3SK/mruFdxRG5bcyZS7gsz9wxgrEeJVMeg0FpWouyRMAlJK5NpMQQSSoxZ8Wj0UJZtxpcjRljCgxzl1l1dRVQ3a7olCxU4qJCVVX6pazDeyqst2Dsy6X4cPohPGiW4ZpPJEPpZc2ywl4VHNO52cqhtujXGahvmSozfptTGiohbL6ZjAZTsc7bJ3a4Yyfg/1Rf8r5mYPOW8MRKwYeaDZh+eXmhmM1yRKXM3IkqIMTSMs0wHA4Oj2/4Irl8WSCNQ7rsDc39gvm1Dz3OWDZ/fc0fibIUM3rhxFdKFd9X7Kwg5+3XihmOdzp+PlLGE5eNIjCByOlSA7ARJthHdRZcuEvHGAXtJgQZ2f1OQCAa+k5qoEN0xz0OfnqV75ycXZ6c3OgDOSIBphJyR0dPvnog/f/2T/7F3xenJ8zBpjsskbU7DxRIJXtV57XfQTAVzGIPLTO+tz4J3grbBOlCQiSjRtHk1IjYQ2e8q+0toH1qQhNtO3A1p2gisvbr4h1qlebXGBfw/QDkBZyAIKyAJOGxeyjnFI6TWLC6V8RCqB926D4VJXa+ALb/GvIyI9NVgOycfqdD8rXZKrlaZAmzQifLmLbO2zCgqpatooFULjTppHvho7EatMHYONs89w2FIlcGEjZBsBWjnrrDAEP39Iw5hRqFBBOPAXEMUMI2SQPIU2+3OkMaDuHbctoRqGnHWlUhoK8fYWtwSGh3u5GAoznzH8yKRFNJrRtEsUtS/lssgdUKEt4i9y4Db1bfCjb+sZSqgUNniTV+DR46ysU8PKXgDZM5PFEGfhAvqRPaan9oE0dIpOdDidnF47mnVoMzlkgN6SAAE+WRRmnbh59fAqDrtZH92sP9//xsKoAVElOC9LQbF5vcSVwQ1yR9yr++lZOQNljspkJFKY0+FAPFl/z8MUjVOPBD6NSvlzlCOxtQLne5HkXQeC2EG4wNDMEBa3M2COmwUW7OjgcHx6OmK2nO+Xo5b/5X/6tv/w//cs00VzCiKp4hQZvR7XcnYwvnu9f73QmuzbWaNI0+O4dZojO7rBBZ959jirFrBP9yuzSiU67N3bjYakLJDP2aNtKvJoBt7rQl6BsOjFKN8DtAQOOgoOwGrLTdTprRCBI6CAgmgloZpOZIWaVPpoPmjrdwIqzqtVatVXSVoddcR5fvWQWn8FC//KS3XAzZq3oTufzC1cH7L41OrXTtTai4OCDwr+fNfnj6WSXCV06FSZpoQ+LU0tExQNo9zrzq9IoW3irhKUiR2pS9hY/T2SfempD1rjBZDkCADSR75RWI4SlplhKIhEqyNo3CPzPvwqOcYLE9JyxYHq3IkShofOm9KSJEsRNH8nEaHe1j5HWan724uPT/oBlFk/fs9XMTAwKnMSChZhqqCSEioJ24iQulgcM/WA1JzU5VHRlBvWXWg19JgMJMAhP9JPlkoneHeMz/0cyaAHRbdQQPMKPEMaKmp8NmPIdomJ4IAw5UE1R0aASoSC4F6S7PFzMWclx/KaSZ6AHI1qIITc+5gEZhHyKWA5JVhFFkJLvTz0Gt12FnhkHiIA/FcLGNMFmNiWA2Frc0uQYlpwSHx++WJjyZMO32W+JGHWX3Fx07Cxl/xrSqR9SEDwwBjMH9sZzdwan4SA7rKBRE3qdHQzoGLeaLvJiqaF24iI9HliEmDHzVG0+PtVclhg2+afYQrMwieZLmmUDxIaGyGcLkGImOHmmTMMh8x9eMFxD8zO+kQmlSKgpOIbP452Wzeg8jtFRvZUHOJ892kIm1yaT8oIO6jAXXHlsDlmSLDOCajjBRvDy+u13Hnc+YTPo8/EElt6nVvaGnC65xh6E7a5UagmhVVHbtj5eX+449hycYU/iRDwsR3eHeakFtFKy330RavOOsTxDVgxyWfKklvIkA5FMHLQxiisKMaJDa4G0pRCEKT7y41AEvlCxYYZzIi6CYe11ccZ8KjsZNF5BE8V0npwiIniQ8euZZ/UgOleXV9Qe7tBdcboRrYyEiE6LRFZR5/Pd3f2lhy6urthhy/0AhHeoEewPvvAIBFYFeoP9gx3O/h8P0eUxuRlPpxM1cUdEnmJGgRB/ubggIQrFpgstezbbQb/neo7z2dFox/M0uQzdTV9M8Hem09Fg+oKr2bH8tKZaQNRl5R95wCyKA1V3d62D5AWLINCio2ueR/s+Ym/VOW2sy3oY6tBywCTG69g+yXDkoI+lKcb93BtA+VAk3fExV5JR16HNSQluDPAcJAY+84PDw529nZs5I4rp1eXl5z739he+/CVWS+AAZPEwCnIZ8/ryv/2n/xLX4dHh1fnu/aN7Dx8+kZU2QvyXa7dlx+fto1ALsHXynp9GyMP9To1r4/WqP98bmBY2v9u7B6kKaYdMb4i241PvOH/k16uz9S2e0CnyoP3h9GwnuE3nhijIRVuAfUBKqO1nLl5MGvjS1OPv7lZxJd0ku0Vhvg1tHmMpw9uPtRQU3JTCgyYWRMHHZyowH5mDJ7wBNsntYmWWqkmKgJADqdDv7tCs4VhHAyEFeJqXwLFFMen68mnh6qvxWbwl7OCjJlQcpre+eYJAO83TPOljxG9o4ResDfa3PgyWf/lpIaUp2biN8GrswlxojKxIWafiQ3zlvY2jr+FUWfzy1YClhzYw1YMQo1gxW/LK0SIqjApCodmC0i+pE+P2ISKP4O1jxFAQz8SoaPVWACS8vm4j4dEkHlqCT6ZJgT7Jf31u3oQHQo8f+SFhEhLldpRQJHdFGKQF8QqcKd6JVzgCJZ3kq/Bv4X4tivmUhipNP1552hRE1bq3Qd4QxeAkZK+yDXv7GQmIJKDo0O7v/+W/8j/7rX/1+7/1L/8lG8H+8a//o8ePDv/cv/fvYc2JXSpNMy3tuL/z+N13f+3ffesf/YO/P9phZYBlAafbuCxMq3qAaOBRl5058hDP0RQANAbXENBc6JCcD0N9QE01J27Oc86MRwFEg/TCSMhVuWaSSQpRD1xVoENIF0RnhhLLYkJ/hgODFg36mT4drBbsNu4y5U9/RfdJinILbYR7YTgiDotYtVivm6EPdLMawwl5qaKi/PW780s0ktQXEDOHhd7FLKyaiQYofDD5bLUhmT5jjyjI4CJ/ar5BktIGxByV8IhQMajE8CQ/JltlrVZKfOBLdAlpCkt8sEjQSKaKaRiSmMYoSDzT8pBKwcKxTRwlkIrCywEV4YKIk/nnBb0ywWy3uNI8YDDmm+KQn85TUj5qC6jRqEmygdxHVaoCAiHGuFxRynoLozvoabCjxtF7h1pn+BAJDXu864fPIaeqhgRoRktA4TBP2CpyXKJTemhRnLO6wzoDCwv07ugDyZf6mXcLQBSlOGSLovdAoW2zpqQQ8kilrA5CyG7YRRbUPOCkqifJhnMyIv+So4aZKbbIgswFmh/+6wDCiXiKHqlwO6fubNmUt3yAx02dQjOMYrC7wHKNUcDNmEMr7dggh7gAQ4fz3CieILrpza+5QANL+NVoj5EQiuoSg3jCk0T0bPieCmKq8ZVOC5b/SZi3JCosgVEa8wCAu+gzDOZozhVxVeiTr8Qm1NqYBARwAJEkzFC4YSYlg4JA4cNhFN+S4f+KzJDeNiGyCN05011VIYMxdFDGRxppsNqhuYjbVqm53DRIaaL9U6mZ156OmMBeX5xeWuuJKzOsc8cnLw720DtZclzQkOCNApp6s0Z8oAcJoGlg9YrVzMgCZdVQ6u5V2QbtuXINAU/+zXQVv9xILiBXh8cWkFHEFwEXkdUKJP7zpTgJaftGq0KdQb5JYMDmdURbK0cWM4Dy4GAMvBDWjDeYhwCWnFrL2L/LhIWTWtQOVxQZXVNRZKh2RNRHdtLO2GCg/DtmwG5mgW4/HU8PHj/e29l/+PgBDCRXiJVje9sshyNklVppkTEh6aFtqz6NKwNmjhOF/73+yxfPfuu3LlgWHX34ASOCR4+ecIrDiBVAjvdhmAUil0+5x4Oocoo80qjSZDJHwO1g3O3Iofsk4YlArsUOum4FttGGbACNgCtz/HQQGSd4RwJYOMyU8xSQiQwuupSmbIRaG0Jr+v7BIWBPnjxm5wO3H7OR7M/+j/7Mz/7Kz3zyHVRn5Ie5AHdwwTH2ALDs8x//r/83v/Otb3qDwHr1la/+3Ne//os7e+fQbWNAtbMvaaUZcbj7SCe5g02+89cAlEDfhf7X/RJHg5yE6iPv8ozXj4yzidNifCVek4E7WXgF5Ef5lAl54kCYqldxEFjdCvlpggQzT7YDPLwbGuo7nq13PuD0a0/jVSjTbDTVMJD2/qJtoOKADFqFNImVomP4yrY/RUalxxuvNlnrL8QHll/x+Lkpfx1FR1HZIC3UetkN+EWUMMGXSkY9BK7LEstU8aazCroQUa68SXLFLLjwxhTW2mBTgZ/oG17O3zH89v5dYJn1hwJHLbHHkpqgAXFLPWHJF2FNkAqAvoHOOxANK/QHif0lpRySTD+epM7MevmVx8a9gWHVMXRyqgbRmpGcGH0Ev43SuvFpU+C3mNnS3MA0ykzF3bw3DtE28dpk/G3QxvmjvxjFQkZrRSdFTdwisr7KOz6NbV/GsnFjOdlGMableTf/Ru5fEVAYgdk4mqSMFkE1YHuUbNRbGENbCbn1bV0NYHAXpPK9EcMN2IYOgKwAaXY1k3381oM/uf9L9++Nfus3f//Bo72/9/f/yeNH7/7ET32FmRl2wbEmu1xgzdx/+0v9X/tzP/nBBx++//33yOl8gS0+HaWogKEz4DAPeh3Omhh0mJca0PVxlmjEEK0ntw2gfmrsQQtOLHpjxgNMF3kojWbei9VouovFDrNKng3f7+zvjVmXRuPEuGI6Gu/uTfYOD05PRvRG053p5Tkmp64kEAMVk1Mo6TepTaywd8Ycbj0/PcOS1A6JSTVUgfGIausABJsgyGGfwwzTI9SyaLidwRm9H/niDJqbGUvq/dGYwcYNV1E6WcvlOBQmFrOcbrm4YnXaViutiTqVzSRclankzLrsSw63zYc+Im9qZZVOBEb4hECbOl/KEVw3jzxbf3BmGyEIuHhAGhx+JLolXUUcPPjyhSJn+kyHklAUNzUXEHEjDxrHC46sGQ12R8wbDt7mWI9Oj+PBJU+QxCQZiGGasvQwJlbp1FloARta0YJ7T1mImbMPMabPWoOp2hUC9AC0DTbwsfByxW1E7Ai8mcFaNCCoWy32QEEHvZhhwaP5OKe6q9UNOdt8tFyxo3EynmLV64Zf2Ip6hWY5HLy4WeH5+evT64vzK+YGmRrkxI/x3g5bKLG7QQ0I/yAffSA8SztoQcBJfobPbRl9ykgAYjO24bx/OMmstvmXe2iAwNV6iCORGDyo7fiQY7UW4FC9KBM0n+5qADMWy9GcG816V2xI7Iw4SQYkjJ8IYgQL11DENADaWV0P19PuYDZiDeCKe9QuuCv1Zth/v3N+Mpti3qFJhqfQKmBWC1JipUvBoJVGV4KRZC+iwsEyEMeSgvlCx4K9zEYTkUIv0TJhyz/ZpoQiKHyY05JMpdeM6xEZIFBnQMqjDSG6siGoOqED9ch65Jxk+KLUFmd7xy9ekCbM6vSPERpoIEkmCRAAFH7W6NAbWck5t/YxU4zCTwfnQTO0AQ8fHh6sui9evljCSRh9g2Lf42BMDoinEQBYrtKTao2OkndMKTA1wDE0cImzo5gHML9wKHUqHAtD3P5OceFL+e2Z596Z7+W+/twE7CA/KoWDXnLIEMUD8omAyk6ur+eMTUlX7lEpwBXRRUFn+h/rL9sOJI9w0LFGgXUNwEyBs6qAeMA2RhS0VGAHISkoSkCxVoAPq5xqrtQRtwasPcj/EtZxxIJKNSeRTQZvPXl0eHBwwGFHsNlFMPR7h9MhtwoNwm2RHXQQprSS6zS08EQ4B0aMLHBxwigienJy+ezps8N7R9eLq6PDe7t7LLy4qEsBx9wOEsUM0xznoIBrjIcpEiM0xy5z6riJee06icEVRIJkvcURAOhnpc/DnTD+IU1OINWI0OmibodFHvO8WBzdv8coEIaNJ2PkAR4yjuI0omln/V/9nf83g40njx4hDw8e3GeYRcOCOens8vp3fvtf/eZv/cvBZMwdZxw1/e4XJ/v3tEWFDAmmpItyrflrVthswY32B7CId3wa3wpr3yLKU3Db7k1QA1E/5budQptc+9uE3QHc7A1ocW2HljvWBG3wm363KXxT+I/iF9pMr9KsKNvubSQAV5q+rVPNegLwwdNmeDvOG9y1blCtT5NgFHQLDzzVXhEABB42MEK5UYpQR6iBuUskexgIJYbekCaFxiq6bBrKA4Txl/wWRrgWm+dMtjGTRRECOfwI2XIFoEGYn4RJY8GIpyL7nT9eDeq2gTLA2kJmzZwtFiC+fKSpfeIk9/4jWfmll/HyUV+BDgniELB9ypUoje8mjPQ2lOGAhiQsabeoWzz1C8gmCj6VYnxS6Yq2Nor+0r35IWU/6k1e+KjveP6gF2AbsgvOuA3Br0R8HfYVgPq8xVeuouTW942R9AQkSZh8C9QWC9+GFWNlT0XQI9FgcKVTKPQrLIUpeFuI4C6fCt3iQYMkqQHX4k4DGIYn8uaV8E2cpphVs+io3GA6/vEf/+lv/d73P3n+nHO0/y//j//zX/9r/9HP/8Ivnp+fcfQic/qqYoubo/v3P/zwEw5sPtg/HDGxx501nCCqXakWsWzhusZIx14zvQ8TTahK5o/eWrN7zHiQfqb/OFuOyXimq1ivXi/n2LYy94tWx3kUs0tMjOg96CZQGoYsOtPHsWOQ+sHRcliaohWpAayxE91//uzl2dkZe3bpWkiS/vT58/Pj45fcZ4mCaOuAZZFn/DshhIXr+vySYQBZZihAK0J3y+1VKrLoDKpcdmIkcHL8cjaZ0Cm5hxhVh0lrrBoc7KymjyGbU0dgc1VRJyktA9VJvaykllXKW5faCsFVyBsRsMAIFE1T2Ma13xLYqk0XLD6sXIxbJWeQ4U3sKtzCGXzRdaTMGK0QgAd4SwQF0Wnolbs44CTZpfc22AlEwVEOmE+LGRXngnf3D+5rWo3+MWbOtcO2CjILHyg7dJB3v/Bjx79zyrI+6svOzpTCkbF5YCaXmTJf6BRsqGfLAPO1V9fM76Kr2cmz7HB1xaRtn7Ub7Jzd9tfrXV7NELlTxiTozs7zaRKApiGZ6+XsYnZ1cek5oawhLW4m8/nDtx5QOkgVmaCcZIyKBxZKmt6r0skXlJYOu0NgNo60tE3pGXrjlVLo3PBaJDbuSilqFpBINaNH7BbQ1agsmcHlPER2k1/CCTKONQYaFvPGi/UVcnw6hjjOt9nh7gxOhWeMwOk4iOAOwj1f3jtbPZnBiP757r3e9Gq66E2YDl7NLq4OTpbLU6SN0Sdq7iL9HARRJtYFVX+EE6XXoiJbaFr0fzGkIfUUNfQTil0c2bBIzaaasM6wxbzDVSOTPedk+dQH0Pr13bqbiETNII28EwstEGlUOCOE0CeNiQIAvlRaOA8/8WOpqctxvoXIQgGQJDHcQja05+N0eU6RR8Aozp3piIulhpPxwd7h5fXyBSf59tC/AYPswdNPP2HnyeHBFAZRLjAboxOrBc0OGi+p8od5TxZNkGlzYaXxmzRlHRv6XddrnqJbfkAQjNBeBnZBIuO0DnaPWKERdHFxjoCQnKOdQPMCmwmEx8kUGPiXUziLFWHRbM4xOCyMINROWqvaIqh8S5ibr5AIWh4mSsBFmTqR3VkzYKbhAo2UeM21Cu18ttjHUHN/Fzt+RlAa03niFuMKh1WWrrml4BVRCow4irTOCtOGDx5AJmZ78oSxPdaSQzT14d7+kY1AMgR5CIijhAgF+VD+LPDuznRncb1iaN6b9DyPVSWex/0VxHX7MtVPw02xE0Cby5tpewTCIoe7rq7yQzkA4WiQ01qxbiMOwmB7MGeuZ7S3v8dQhMrP4Q0/9ws/TTqP3nnM6sOL58/29vezEti//+DRex98POS+5+mU24s589Xx1ppdW+YXcpENHG96wpAmoGCUcCiq8n1TlE2IQDBDrm7eFaEwEM5TWNufFvMmgQLaADbQiekrctbAbIeVe9tnEwXHZ/lvw8QN4C0Bt6HKTviAV0Mp5YWzPvJLIhW7wbGd5p2AW7Sf5WrBWxS2WT6SoTNMKKD46wU5/KMGWwIWgX9txEAFW2JV1GQgNCvAOIK68kUEfdonbtHGoxymyJPUjBnOtO+sADQsA2Ni2PNTHyYS26fHkn2G4MqUhFQJSA0Rc5N+m7TQeAIRG6Y23Eg1968Pf0lMz9aJK4wztDAbKHqrYp4gMbqxbveME1az+FFdAtlEqC6kwKtIClFwtDCekFpu8lMdLeFJ4vYtQFtK4UZxNaRIzN2nIMOeCkgZwlUDWvqLoSaxgUnGgdmGaoNdiOd5zQqtCdfizYIKRQ3O25SaVPTnDKIkkHi5ySHQTZS7eWkB7WdauitvhbCJlJ+GIQKGHXpuCDKxpoxCILIRoKBJdF/lldUMCiB2jYXhNkhE9YQ2xIjWHZRRa/gdeNjc+i/9lf/xb/y3v/5H35hxJPT/8T/9v/3Zf+fjP/vv/hnm1YZjJmgw/OBWmp233n6yt7/zh3/wR2jPGH/Sl9j7MYvJJxNWw87+AScxM1hwVpijnQlVVJcP6Ub7wxf0EFzu8+D+Qxp/NW80POyGWBujS7QbR9+l12enJBsBGZxcLW5YDEfv9Jh5to6ycZAehKlrVIHF4ur07PL04qLLDCEn0qChzjnqjqNnuhcYyzKVxO3Ep/SU6JEn2hXQ06+XlzkNDwsSDiJkxxvJ0jsxg0FHLzeoC4w0hsODgz203sGI7Nyr6a0cvCeV3e7IW2lhNbxML8scM1ns9p/iRU/qovzibdi9GnyS4iRTdHtqdWDHx06Qh1Tpv2+YgaYAPsHbMGKh0uEePF33n6FQxZPUVGLwb9oN4ErgjSEqnxJcf1BPKg1lwwYItciJ72tY+8Ufe7hcHKB4Hz1gt8P8/kNslJ8wRa3KhR0Dk3Qc4M2wsIfKzq2cR0mRXh7aURXQLbR33tmbzrrz3/vG72BewK1JD588Yl8U9tBKBQf0Q/TqcDR86+gedsxXyMZ42L95jvUOHDsh124h753t7j7E/H93dxe2YpHM8I5Lfw6ODijTb38H9U+r9+HN42H/8d7BjMM+DvcOkQysJ16cvjw8uI8gcVr5YA9lxuOJzCj/nCHOaA11IGqKs8yqr5SRvHemPOwiX/kurj+WtUZXoEu5RB4oVCy2z86O0W5Ko5oiFMMx49Kj/cP7R/tEgi3Omy7HmI/3uwcw7oKN1ZwKNJoszo/PLq72euzLXOzc9PY5f/ZmdNE74aiSEWexY+C+PmZAOVuf3HROR9N7nBvXH02oD6hwDLgZmC+6bGRngA3VKIOQhyBQlHRALG6p72hixc511DZ252MP4X5Kpo2ZSUauHdbyJiMpP2dv8UMTRm2LxCgrPGGFApOeCtOWh/ZSg+dAq+MxhLlirO7YkURJAsFVKmRj/qLfwWdkvz85GUxOY+AhgCmaeHXgDCE43xNtLy0EUwXK2+5kZ0qNsDHhEBsvlOh4JwBM6GNfdeRiw3J+dn61v7uL2q/i60SghDO/IP9tyyhUqwbrd0gDyVL3bQokD02U1OWdtvvstehfyJRg6PTPoFAo+OpaBFXfIe6ME4yv2JDmPWIIoXidwohhPlsAbaCIBFryxkw8JLBlSMMhsoR2zshhxnVbne50+CUQrzqfAg3psA3a0Hd7nfuY53B/LgMAhpHkheaLq69YK4M2mxB47WvOcfv3D/fu3zsaQxmd2SjmAGm9LQQG9qWww+YMdCXGQ5bJlizij7yyekXeVMpph91ZcUyZMry/f/9hHysqCjv6PHEZHlpa1nbIZ+wPZ804g2DMcpim4chRymNvZ+eC4bsC6KjD9p4VWAYPqPyYaWEhGk9YZIkPaVgWGBqxNstGcECZ36cZYQbn8uKCFYDl9d5Br79/OH/x4iV19Xp+Ne3v7B3s/vhP/ASq/8XlOedNcycBMksv9fGHH708/e1f//VfJ63BaIzh0C/90te/8pUvmQ0za1mn3MOA0QdW8tvHD1l065Pv8t32xG3mWq9yN7g2vgltguKuEN+UM29rSfMIdjeiAeh7WFu0D8cG4MxsOjGTiyZog6YF/Tf7fZ2AFo9Zk8TNW/FOC/lqLojR5GVDVMVqAloMG8yNQ2xV74oPt9mDV2LAOxhx1/+2mxSBPirYYBllz+0CCxQ8C6ZNgmAf0EUYkgU+rQrzWgv6SDx2wCEiDRepRmxCHqAAgzh/weZLYrcIbjYBF5YUlDESMVwLXpAmEVMXq+NpYc2nXoLbuEoQJKXXLDiRmabgcVRM3fhCbtKqkDiTQoXmDavwSlDhwl2OzafB8ufuk2BebWxCt0GaHEA6meCDvBhcnElcc5WnEjK/rU95698UdAFWCslUeYSfRCoM+rVsEDTYElRJ38HeRrqN2qbxA343FOFIshV7g6NIqTwCEUq3QbYoKGeLp4FN0uVnXpTzSucWcSH9ATQ2QRWjPoqEwpS3FFLwFEk6BqEUNfnYsK0ihkjBLCtYq4UcEZkN6vd2f/mXf6Vz8+H773/8/OX7/9l//p997ce/8FN/7Gc4jJmukwN/mEl69Nbjn7z/k6yH/+G3/oDzTxBgUGDMTROv8tdnVmm0O5xcXnEjAHPo2oOTLG2y9j70FhyOS1c27F1dnk13uDnS6Vvont04Ydbh1qSIFp0Qx4IMsPoejelTqR3uJHaJ3PHE+TmjgtXHn358jkEqZwrZu1vjvQ8S9ai7pHNitgtPJpKYvstyfbjgLJ9cYGqa3GtVekWkG7vu0InmgLbBEaa9zoFnDWE4xKCGuTIUZHRVukNUHLpu5ztlmpm39voTVcOKrC5A705mmf0iMeaUw3P5YJz6MQ4UWgo4bZJweANQQ6iY0iQJQ2GlLE0lT/22X42XUW34qrhJKwJQUiGoanCve7i/j4qPWsmBgZ6Wjp0ASqgWWUxnDz3fczHDxnc0RtVT5TOe6lOpcWrVFjV2wL2p1/2iGWLnwraA0YQESVwLSbQiNu9ykuP8Eg2JCUK0fIsDQ150ZZRZrYlWb73zFiq8tswwTZ2XfZOs4y8+/OgTDIowA2CVAJ0PWyzQosFwPyjqAHP0J8fnjx49OuMC0pMD1p3QKsCsyLjZm2EGTMCkeB+tjc0C7A+RLh8Khk5ErvgRu5QIsHmzGJglNaoAld9sQe4z0WjJcejAeMQdpywlsQJy/2iPCqP1ORZIMMmTjRB2TSW64z0Mwc+Wnev+6OXy410usV1PZfmI0wB6i8GBd5mxf50dwN3lYA/67k/nWDJN+ruT3QNsH9gZTIIYNQ0ZSjKcQY9yK4ET0VYkOGDF5QOi4ZpaFhng/EQyQvqc0Do7P7vg0FthPC3SfhJNVGGLDCsh/pMJyWrExtrhxC3MqUA1Q0QPCXAE66ZY/Ckr/IlmlTGeHzXSMAH1bPoyuNkkEH6CxbUMkmP8SJODYr13OD4+5oBgRuDIA8BsGcJIvHt9fckC4wXH11/OKFK1ZhhA8wEHqXcM3ywsloaYOVb5NQsmhfDMewM3kcurikNZdLGqly8ASl0cIRoWKwpmJCKuictyPpqw34Bj8gcLiEkwjR4+5AbRSr6cva4MymtHYqI2b2yEQme/wHiJ/JBfPrF+gRi5kRGOH4SpLyOq7shB7z/2lB8Wy2CdKrcF1feMY+bBe08ev33/6IBFOTLL2EbeUuZW8zRYYiY38taYst+HZRE4YmbVBIgEEP9TKgRZ3UijN5wwKw/9/CPxjJqQlJRgRcgghGEt5ctIHkM+hkZY56P6M4pjIEFT4FGhJEGTbi44AYJ72ZQDEsuqL/xxQ8V6h+N9ALOXCT0cnjIeIa5MA9EgMPCnXeEII6bzv/ud9//Uv/0njo6OEBRP+eQu5zkNyAEs+KNvfff/8B//J1edq+efPmfN5Pzy+uGjg5/9uZ/I4DNiEBbAFAoICsz03WfLLwy5E7rlU87b6JtvENRjCk14/VRIvQtcCngSXM4qhULQvrdjx68iK5bNpy6ErPn+N/opnI0UvIahDYU80/KPp02y+bz1qOCGoM8iq8W5xQPFwmcLYT4tOaU3gRYeLrtHU7x98ExzUz7NvDAATbTW0UTJTyFJBKGsLakTFchXfGo2hGpTKPJjBTd5X4FO7IYgFrMgsTAKWJTn21NCxUSFNEEqXhPbCMFsxPilgP1SMQJYdjfAobhejY+pBK+pmISg/Je+DaBhAtIc8IM/NBR8gdy+seBveSMZbcKFsI3SIE4sswhO3DoCHwTmqnEEzoQ3yZQLrzxGNLsp3vIyZOvM3QQbUhyKUkcsFUPeMIp0zV9FFt8bXOWVsEA0M/dNrEpRmO2R9wZTg7DB0STUMFFsIaBymEDgzX0LWM76Kq6Eb3VvMTvTxVsZ8B3o9lUhBBNDDhFKEH/S2TBG3hZyY7UENF6cdP4RcRBGgRoa+CEuWIzaPrpClyXTip+Mnd+c7kxGX/ry3re+8637jx+h7f7Nv/13L8+XP/VTX5twPMvyEqNwVqQ/+uijt99+m3u+PnjvA7pgDvJnbmg5f0AX1RsfI3TMxDOjz0lxy9mc/o/+c71+RplioMssJf3PeDC+Wp1gEku/QhfC9BTXBmMVisUQHcx0ZxcP9HZtQ5kCdSIYE//5i+en3Hfz7PnLly+vMC3h33A6XbEcPRicn59cnF+iR6Au0OnTwcGGaOdn9Ct2b3SZKPSUIKsRkSXoYbsCOkVahGKZbCeP86s5E+Q5rtRtbf5jiZ8XLYWW7hg50MW1JWUwEelH7b2r0NacOo//4m2ZP/g49TEdtmUrdFO8BDPPatn4CsUlGVBrHya5SgGZyhjBxYE0F7YsHGryFi/wZ3GALh8FkbkJS7zSIRkwoAioyHmG6ZANithzMeSh8+14STlaCGSjfND9Xw/WLOmgvQCMHs7Zi6iT9NaoKXDJ2XuGYBolsXDPqaHsoxiPzxYX453DF8dnP/5VpmTUy6Io3nRHx0eP0McZFXCl6AAdlQJjQLheHKhod55y3RsmxZwatXZrL8MIs3x2xlrNgMEheiLrBvDgev7i/OLgaDBBZ9rd3bs4v3ACcm8H5eni8uLk9LQqghLEUTAOTdSdEQAOHmWoqXUQE+Qqe7SKMC/sjJpbLss05aeOA+9R5xGeXmd+cQT7V+yOWHsFVWqK5hOebDpgrwKS2emROcx12NSrwvYhC0jr2X0Eobe+HHPuYedqOLqeTh5hIs2tB1g8LMeIEZtgL9VbexdsCZj07o97O+v11XDJplgOjGQI4jgT6cUCLscjoqLBCqzOWPqAIOzmmf5nr4vGJIgjKrJFjMWNWiBsxLR6zimKaNjcDsuNTapn5JBhAuZulCiz+0QYPFNsYb6jCJ/V/D5oeoPn+Djsy1x1woXhAYvbPKwCdCzhR3xFY5jjAZiJaskSCStyTftEYosjS394rCxqssKFswjv6ma2v7xeHC9frlb7Ozu7pMnoEPCd8fjJ48ff++A9RvE37D6CJbYgq++//97jh2/t7KBHlj0e+27RGtH2X9KIgHk02kdgLUwqekoTBrg8gjizT8OsOqktGbKkeYV+GghkE718sWQZBfM17h6mWRkPzs/OZBcGkLQiVABXVxwjJf/ynQEGADCEjIMCpFA0noyYY2BKZbU6taa6SCSXkH7XCRzynnmS7nJ5cn5yfnqJQg9OzIJgIMMQiBtNR48e379/9IBFVCx/ojOTV0YF6hXsroDht3kwhRQiZETFSRUw21EGAKRa37dlHL6ocqHVdVeulKkSMW7Bds9WguJ1nQQEoHLRgFEEIzSaA64sSMPq/Y9gJpsWCyhyqAOco2Rp9BFMOOye3VVnZ2+XgQ2txHhys7u/R6Ke4ADHaUduOFGNpma9u7f34tknQ/ZvnXKzxOoLjz/3S7/ysz/+E1999OQhhQ7JrKyRt6urSwyEsPj8/W9/c//efU53+PKXvkwH8fZj7nZV8GTB5iS9iKTpVGoKqHTyV67NZxz1sv2NqwVpPiu0Mlrv+CSJCmuwtvG2gvEiiiJWqbfvJt52DN3tyTxJRgG16smvBv7f8EcqILdN7RWEeptMpXY3iTZK42uf0zzGeCU3FRKISst6Jun194ZsbEgKARRXUSJ882zSq28aW6SNXtUqGIQbAMlPmeBDPY/qawmCVBhduOMjLkCb3RcfSUWqsh1lPUIDkapLdDQXnuzCTbgTMPGhcNosiiWeppOuMvQJZsJASl/F2gDmO2kFU4OUCG3AxlGoQUP/Wm6CWs+CCrfzAiZp2lRvcLWo8mtM/sz2KxDAB+1tPOFugeTghqXGlumJcReTsRocYXCTYJvkbcVsEwSAx6/6s0UrjwTcvgptkqx0Q8IthcFxC96Su+2jWwKTGO/NU57tZxMST+VL/ybJJrN+lc8rccqfGGFxm+sGqPD65k8BUpw3CMq/CdU3CQSsRadvRSBsE1OG+V2DT2E2TwNjFsQmFCk2tJUvkdE5BtPh5z//k3/+z09+47/79Q/fe3Z6/PLbf/i9//lf/ctf+/Gfurm5+rEvfAGL7N/+nd9jYfjdz31+Mt55/uzpy6fHdH5go1dAS2MFgNl3uszJZIcuCz0M9Yn+I2qft9cM6RznjCWYgUI+UUvpBphTZ3ldJZ1dlVeohXb6aFfX9Jcvjl+wBrDqzl++vNjbPzg+uzq/nA24rXO9Pnt5zFKD03GykD/Ps+MHPGGL2W6kc6v2Vf7p1qnuqGKuWaMbZNoQJYlOmptuWFhgqR+Nx76dS3ACTHbo8TA3pucL7aB3nYHHti7JNglCkgnzU7TJ9Tx6FFl+4jLcd+hPI5Fg0tWfxoyc1eMXXrZueFQcwHA7CZkgW8WgjLQmLSmzKUNTQRejCycI5XU91o7RDRvcssQZJmjcPHSknOTKzZ3q5iqdmDPS5mBqoQ6PKsX7Gn0IQWGFBtXSvpnOl8PNO4MlB3eMDw/U272PeYKN7r0nTF6iCE2+/e0/Wq3ei+JoEWELzXwtU6qDVZ/RCKU+u7xgMx9jwvWQXRkcvzhAbde6d4kR2MX0yRHz26izsYRxowlRRoPRvaMjpucZedpWJ++qSh4qmPJZrzggHDeTiPgakIVW1Aq4hMajBsI/S1NRxE1hM5LAHLmzYHTUGU7hAOtOTAdzfdXAq63ZhAikFiZkPQYYnnyv7FkGzKcyVY0azPipM7nprW7Gl8z3ozrNep3LIbt+V+51VhdbkkMOhpxjKc+le1h65xgZyHT5ZAkBqDUoaevx3pQSYaIUtsApCoWHQnb63aEdyzQkjJ5GLNhC5laXXP56wRmsCkOAAbQBSaW3gVVhEklEL3wTEKTGsPgUIhXlJMTLEZQcFnveLrkIA4b8swUDBOFEx4bNsRzCM/7BajD0UljRhp0XYCv/2eVToji8lKuksObUf4Z5nDajAWGH0yExE3Ky3wnz1c1wfIAkqHpCa/7TdET24QPHSjLJTEFYHygiFNHMH/EFISGXKOYp/0gyDxlKm0nesHOhrelcLq4IYX8HHCCQHFLa1YQAyogZ/4Y10kDrQS1Q+S5Fn0CkyxBGROyV0hqLwYPzhl7oxRDjZn52dkookNjl80/I7hrrstHuLuuojx4/3mWsw0UJ5C7NI+knFRgboyMJ8L/ZyR8/8N+EQpu+KUc8LTlgiR8fwl2coCpfX2c/MZ8OuD1uwdn6OZtwaOUYAV2eU4Hck0AVoOmm0jhCYI2TaR0bBc5dYGwLA6gIDsHR+yMCnvxGM+O+XuzFWMnt9E9PzrCvoui4n5FuAgnBApPtBMwWYfcPdaR0/8G9d9/9PEU3mY5YwOLyMtKljQI13Pv0o6f/8B/8OuPLi7Nzmpef/pmf+eIX32V50OKxLbeMKSOzmIdc8eufjzL4wx5gFZUfBNaiC2Jz7n/FreJWVNwbuDgAeBPWivZ6chUZxt4+MGgbxXbQLdBnuBpgaLiLpJJpI4WYu153kmzh6rcAG3yJejecrw0uaG8hmghbgYZEOjcwLWyLsP2GiWXoB1mWs+KfREwIoDwFbHCSF6x9rCp8C5nysEz4R8tIhYCGBpldanwafFIPkjYBfD0skNNj8N/MIlcqwKyY5aTC1VkxTcrWx0SXAp8GV0uaTZIp+FeF1EQ0h9JVbVbAY5vXYmgRCE4OmlhU9AAkYpPiFuT2rnPPwGmj6dgCK2R4QIDeG7AE+LUFXMwTmJwUnlfeYigUiRpnQY7eD8Z6iQLEtzANRqt3MBDSpNuWmEmCOwUetIEs+I1zE80ENrcHbIg1VfFu4if65lUhebOjgCLqad+5Dc6HT8lDcXgbGT53UddXkCTihjciamipUGXUp9jSpNPyICHlJ1T+Aq7INRGZsqeUmVN6v3hZSVV4Iij86YnSOzCLMzl9+Gj6J/6tP/XeF/7wv/9n36QD+H/9jb95dPgbX/7S1/6D/+ir3c7sHmba9w7eevR4/vjmD//w97Hs5JCK/vgEJYpOl97Ofo/O3Ks9nYvDQp/VXvps17U51H00ZSIIjUITZ/RN9ofyrDkab3Z1yRkvZwCoUt5wQdglwwAWyw+O7n3w3ntYdpxePz8+PnOWd36JQqAtiaoJaqgzf8xWUYyNPmz+N6KLHkBeI0XWfdz2ld4l3DDK6W28sXCdzW729o44mSQcJJjapMpH7pjjhxgUQTBhZ0GHl5kGDjr9BCkEaYrMJfUqoHWf03Xw5j+PtZIkykcqmlJkHg54SzGhAWg+oTBxKlKj96PWtYBlDWl66EDmPQkFURIIWtVA+KNNxDJbWi+YUO52Ts6wK5nNzpjL76Khom573xcYYAVqN0eFjHpDRgUOgpzZxCDbIcRSQ3cKeM1BJTfY3lzesOZ/SaF/8/d+/6Pvvv+rv/pLjx6/7TkvnfXh0S5r+tCOGOwf7NHTo2Ct1qcY0qwWfUYL7OGeahA2oJdn7hYFjweznk8++vh6djEcH6JNsNB/fTH78IMP9yY7bAa9PD933HCzePr06e505+wlNjkcF35CRJiIsgUHSvjR63vLJxpsT14QEg3PciGHchcgNQWnNxEbpAHtOYtRlKqrKP3+Kaj63FCH7sHoB0V74f21LFUhvCh4FCjrAZ4CxKQ7c86Ld/Dudzjch80qN9M5w4IzDk9faPnPObP9q+6QQRIautta5oPJcnCvs9/bmZ0y4urtXVMJUalvOEv+goUA96EyFGVchIr2YsyJVCLxxBgYry7KYAaNEReDuMybIxKed6R/7yMygqhRN5iRBYQcWkWS9c7gmLzkbnXlArdyDWzvhUquK0i0Y8exBcIo32ZVVNlwLG/R7K3h8cwAo9htECUtQIdNIDyssymneA5e1AYcQqkEaMbo77z7w9OrizPty+fXe7u7nCqGoo/uy2wzgsjiDftTP/7kRb/LkcFjMoAF+AmTxKsXo/5wb3cCTcPJhTP3lTKtC4/n/aKqmlXGU4RqQEWqWf6htJ0agCbyzZ4fOMJwDL07hMsNmi8GZTWAoaW7voZ1TBCwoIECCq9KvyfLRqkqBnb16sKCiybJCXU455FHrCS4RZWlTsvk8urq9PyU/euIOozHsAe5hUs7O/vsdQfLFz7/zt7ePgW9I0Nm+KCg02KmCAB0wIA04qoELZ0UQJsFxPQBzGddEZFOwRIMN4j20lY2cJZiRrkffvghwPAqOj0mWIy5+ux/OD4+QeqJYwVh1aSGzbATFijl2ON5uAJsBoR6i34+WN+n+NjGj8jBYGmwjYVpN7TqDA3wmYwpRxqNnZubM2RAMlb3uAbmcgYZ65/+Yz/1ve9+53D/4PNffJe2HAphDhvAOE54tDNBJP7G3/gvvvHN363yokOZ37D2yBoLU0uyB1rWXU6rs3SVNB8Sf9d39sWV12e+FYkf+Ih5GwBetJ8lDArd7VMfAdmCbOhhVb95jNq6t3/VLQmovns7oNybOBsaXofZOpvfQCG3oDcYmogbrn0WRQ3cD/ppcd5B0Xom4p2QfBhM0XXmlJT0+f3m8oLCTLJIKYD8bx99qvtjCVWhtcrb+pRWmCRGHCYL8sR1LdCTNhWcSl1hJYItAoh1NqtJmDAAPavUAE+Ns7sVE3FNoyFHCpo0EkawJV8VtKFX4O1nQ5OE+DQUil2f8q2mtcIrFeXcYH9uQ3VJkE0itaFBGUBfW49wsL3xaZBthbfOLRR6GakNql+TwStpFbDsa4jCUQm1Gbkb16/XE9h4wZLiRvHG5p0wG3kLqiE/SdyifQWdAYL6FO0tPa1fG1q/2ywriBZOBEkrnNW3SapBUNgL+o3vwIXwYlBQ3Doh048N/cl5gyi4m3Q+E3fih1N0JAXcRpHkYM5P6ytz8ebTRPOTthWfAdsrv7D/NlvZju5/eHJ8esHO2S73wJxeX59fXmGQwXF0h3QWGP48fuutTz56iqkB3f1wNGESzvlUOgBoYMmbY+P7o0WPTtnuFpWJDoa+UFP39er05IS+7fycvbwv6Wcx8tE+fLU8vZhh6sNKOxrZxcU156N/8K1n5+enTPtCsl0rc2mg0EXl5L/qSjJBokm4Kn+YVVmvd/KsEYJqfSo/fW2VLIovNgAMAL76tS/t7e8yDdYfsO+UzszpYWpUTX0BzGI0qrHbkpmDjZDSk4FTZjpZ6FMti1SEsfFLzY1PFZAhFq06XQoBD1Uqi0N/MwckBQutdLSkZ1AVtBCVFt+oBU1AEhKnjnrlEJIUBuTRX/ZfHn/68pQrn5lhRvtBX4EZTOaNbfs8K8VL3EwVBRPlClWesiRvpsKcIPqfZj4UA7tjzy8uKG5P5eku5xezsxfHP/+zP8fMJaXM0UzEQaXisBcyyIXTKBnsr4BV6EIkwxIDZvr3jjhOStOd6YSE1pfnN29jxzLc//77H7AbAEt5pkCZ8oT7e3tT1AxuKbo5PWNN4d79++zMQGXhgTDUBXCiiCAVxQ28HDFZ0BACvfKff+poURrZ58BAQoWG/BVrGeJEU4G3ijEmUxPGgR5mwjvq0RhUMYe4fvb8ObsBMAdHGXL+usuhqP1Jb7kL+PViyjHni/H1LieuLy6Y9R4MrrCDHnYv+hxXz32naDUXLzhNtjfhYiS05S77MZh5ov5cMQftcZkaszDZjCEdRaniib6fYQwUk0dyRJaUEzRIIK0OzOLq6LMX2OG3/BdCKQKcbhE+8SkzGm/llLFCKVUKotxDbmCH9QJQGMsbECUukYURiXUcTRcXX7hJhqEIZbS7s8dx/sVwqkjYW5okY0erOYqhB8mzJZ06NuqxRQRZohyZIUaLRzCYSXjy+C3Oh9qZ3H9x+vzppycooV7/3V1dXc8PHu1DATQ3DFDRhCJaDtKylqD5M67AqD7CwGgWHXEzydHkA5qlOHXEbCVriLW1DQweZZuxkKXjzmBQkVkIVGFG3smwmzLkr3PhQQA9tG2s1DAQpa6QJi0Yq4ksYZFBLLJIkmkLYiJR1AsiMRzc29t9++0n3KQ1ofWZcP/uCtPE8XTkgIYhKPznIUrVfAcaFj2BeSQdtJmet1Ai4VHboSkNSOVM2fdxLkMfsuMuhEWtVNBIQDqmaIUBmx3SAC9JMfsun8ko5PCd8tbQLyMEJYpBFm0wDOmyfsGUipIH5bT5FCXbwwgYU23nDMwG3JZBoe9wYv/F6dn52dXlgGsomfhnJfnR4yf/1p/6Exj9nV+cUaR1KihUQy9WUr/1u7/zL//V72potO6wBf+Xv/6LX/vxL2vWKENStc16ipMXpaIzn/z+oIdI0t9GeQNoi8Vuo32SgJ84eG4D8umrAvJJaOA/A7jCNhHLEYlKq8T3RkxfATLoTkqvh7/qI6rk97WYIWOL6ldjfsZ3Zf2Nebgbo1BXTSm6K6o1rmVg43M3Yr5CdolupGsThVDKxYgpHlOxQBET/rYYlwCCpNQ/hRmYloaGKUlr8yrJEOMWl3UPONE/qVZ0kVEhBPKOsVu0Bts2+VANUneMfxejROAVoOatVFa8vH2xtuDDAjyooD1IjFZRG+jEkhz/4beNJfELvrF/ajLYJJ4g44S8QBdWnfH3s5id0MIukni2aTU0JLeB2+CvWD/6u+Fk2Atdhcd8Wba3qFP/JfuNz61/6/L3NmebSNte26Ce7ESE3BvAjQchY9PaFD8NJ4pz/2DBVZwtd5NAUm1y1IAAqu7RJgzSEtDtIgjG4Kz5jDeMj6FISV+hrJQEkiKpSYZpN+tUEoMQSgaPgTrrU+HUbT/HjBV1EpP7d5/c+/TJW9geHD87OT/7CIi/8V/8zT/+x79+ePAA6wkWh09OTn75l3/hn//Tf/Hy+PnFsfO76HmensEaMR0GqhXdQ4+TPSZcwIWqBInD4eSdz7/7yfsfYdqKLQB2pajaHPaPquNRiszqDSdw5OXxGV3fyfmLi7NLD6bRuMgaJpVkUvscLGXtE+mgy4+3Kqwgme67FRp8zC1IeKMTpWwYJqUkxQb3GtUKt+v1lBL9IZfPa+KCCTZJsRkA5iy5Sef05eVUu5bew4cP2TZLsvRAyoP/xemP+onvGuqYvCq8iJviTqiJ46kOHoMKo/oNbHfxhIPjmR6DjVDNCxWA+LYnCj/k+y9PbHarIMujyW+Spc9HcWTAhK0TG/W0i3jI7AcFheaNGgBbKCYUA4prMb/iFnAUOVbsmdf2tBm0ZfdpA+jlXwgT8SGB47gxj3YX7Gh8fXZKGlLW50IGTGR6nJIpgzSWGrLCo36/u0+PPrvB7p/P5aDzcH7e4RSfo8NDBIUEGWphc93jdPZ+797LF0yOchwkBX3hUOEUAAEAAElEQVTDXHuXjb57WutwpSrGRvOb6Y4XFKAhj3dPOciFa2K5VpcBA6wLT8ImCB08VV0L6+AwA4re6i22Fgx3ji0OeI1Kp3VQSgdADjzhW93Ufe0AoB7BZQgmNaIwOkCpdGSxZgPJFaYbzIriaTnY2VCSC2z276HVebjlJ4Mrl4pWk+7N6nBBdjjFBHavuR2Zoz73GQ0vmd5mppPN6kOuEfNCLA4Qws6CKsOQgIJQaLQaB8ueUSl5hQ15woXQwgMNsq0bvKkUsLL7IDBEVzWyxiN0kTHF3MiGS66jZ2RPqQOjb7yTZMEBg7+cziLYB+9/hBGU8XmCp3HC9fBTbZWE+nBvpOizZIG9TGmSZERhX/bZOSqnNSlhLMi5O4WOQSOniOFDVtgjhFEM9R4G7+30z6ZYzmCc08N25uL6HDY8uL+PZbxEKMGsupC8G2SLYIYZoiFj1raMQNJfJJPJty8Pq08+9EYS1st7DBo7HSxzuJXCUSUsYTYkTEPRJG+wklUqZiS0X1K8iWnhCwsCobH7Byrm/udXJwzmmFCP2p3RAsR4VTDY4BO5G7716O2jI7bl74ELzbi7uMf+iKMjyp5KzSCkDApI2eGh9ZQ8SxVmiffJRG/4kiwqKM3IDZ8TguGAVFl8/pC7tuW3YEko/hY+GQFfsJMVTIC0b+SQXeLSbiBXZedPyfXWj6giq95zloOggvUpLaTYl8BdLyuagTmbdAfjqat5RMXNicpwjUsteKi7ngzFckrn2aeOx/pjjmNe7N/rPXir9/Vf/ZN/8LvfYPcF5Y8RKqCM7JlUoilmzLC7e/R7v/t7/6f/5D+9nHHALvMH8ydPvvRzP/91Tq6LZFabT4ZSvOY4j2VLO/dBK6hyLl7tK8y59ZSrd1BsQ8fNq4mz5bgbZwvBq+lVVOmhAH+Ex7WChqRAb5NzN3qhez283VFwC71JeOPYhCVzbQ43uIArv+13xWlhX1ln2CBseJTOtm4sbiwjCidwLREBqVn/FukWlnLevO0vKwNC2ACWbLdIkGpkMZIQp2RnUqLqeOGg1qRq2limAYQASt1Gz3c9ok670JvZRN766kqNEjJGh0lEgvizORY6aHQY14IGO+hsa5tA06wnYDoJC6TA5SiWBEswJk7gi1A9SaHA9K+n4rcJCXobJkR5NEn4Wcib1Bskb460CbzFU65gq2TqLc7XUr4T/Qd/FHnAiK4Ylwji1Cs0F7ft817J4o+U9CaJIP7hL5PdYldFCLMrBBpSFJJY3q8xoKEa8kycNz+VCYuJR0wttrZgSqgiP5X3QDavu0ko9hHkhkECNei2IoVK/IuKBqYQSRLKDZ0AiHAPBqzAj/78X/iLf+tv/Ze/e/xNYJ8/f/YP/+t/8NZbR7/2p965vDr96OOPv/fe999+8hY3tzMSYEKLCSVOP3fD18JJPiwlsN9gzgz9EVtmcosJL2f9vPf99+aqEZ4e/ezZ8SdPn3FLJkfC7eztH788fvr0BVoeqwIqD1Rp5/Ps19PR0tHQJ9CJcnUlugz6KD1Q9V5oHuQO+DSwOHWE1fKhkRMVAjMvB8LWcJ2+UvYxw4rOMcf+hCuyxMxFTcw2HQ44GETUMEe9eQeNkzOL+tw95iRdkogmJTtFEzWNCOoPKRXp4CMKQlIiIGVvZBNSHQhopqzN0gYX/a7dMCazUmkDJPlgT1TBeJrGp9wgxBEMvCjN0GADxR7H3vOnJ169yqweH569yuE1zAKSX0xZBqgGw+k9OmlWZgDpcVhlhxk7zrwBJX16gxllC3VpZ7y3u7d7enH++3/wTWY9IQPtjSJjBySQzm53BweHuwz8GCty/YIZsfOTK5SHs4HzGfcQgZTvnT3UiQ4n/n/88afnsznmv9fPOctVDYTBxpMnD2H3u5975/T05Atf5KbSJZOUHCLUtMhO6mvKw8RquKxiIj2o3GE0ZceELkp0f/348vJivOt8JWOqwT01YmKFdcRQzIgBPLlFvUCvglj+MvvuXC9egLkmgBesyWIwWdAAndhoMJ3FcImx0IIDf4Ab3BwMp5POwaR3dg6aMYLk7hbU5GvsTTh8Cz3Y9BxlchoTNQbTNHZSKjKscGCbTV1kppNBIXKkZKQwioVyU2lQUVOLQ0lDp8PuQsMk4FW9mwGAQhIfYyggwQDPVUnNeYkVULrBZkVRjIBw8EBuWdrAKKgZAKi+gz8iHgmLXJIYRdzr3Xt4n9AbtpmiM0INo2l2M8jJDnPhrOFk7SXIrVadk1MaEC9kQFe8WXKo/JAdRBwvuxh3pqud509nl5enkMNUPHPVHC21Xu+BKggpPgzoIdEVEhikKsz5WwyuvL5Q1pJf32Qa4kKDtSi5s2qGM05/OyyhBiSQloYhBCKgxDIIRA9Wh1aaUgvH4yGigCcT6XAmRmQMDlFir7mZhDvUUf2ZAccfDJx8g/xfIxShbTri8rfrx4/u704PMGNzj0o0e4sWeyPKWIGEk9Z85MwGAcZa1ikp2Y07BSlBArBIia95JPOZs6/cSnJTMnLG8DQviDHIIiRZ5EmYwsPUj8KPqFD3yvQfw7/KOHuyqZFsJUcUsF9iFavDMB/Wsx1/cXXFmP/BwSFFwfwMujm/18v54eSQewN3WO4YY2LEfSIUwoTaygrh2enxzuHesw+fPv3g+S9//VcODw+fPntKvSbbnhY67w/3J6fHF//13/v7//y//01PTbpZcBbQ2ekJt01eXL7YH0xTeikPaE3u/dU3j9JbLn7kzd1n41OM2wpswTcQW2F3nJXC1tsYm1jl2JBjiB8F3uBpPtoU72Av8g3awvEKxObztcQ2IY3jNiU9UlNDSwVX9AbU8Er8LtZtoI37M2lT7ux5m0dRbcuj9Uu2bXM2MK3rzb82OC10YTN12xySIiRfRi0gP+Vd82WlFxIv9BOlPVH0NE4TGmfL8U3kAqg6RgWtT9+pX0mmsDQxrKPiFXP+gtFxDAvvHya9grQ2S3zLmvX8HWvo4MPQiX8eYFlbgFJR8t9OyBRMflIg+eKsej1NlwQlAtT19isJbTwCmAi3GGrUWKO68g2tLXkbaFiIXRRJsEGtPFtLO8d5dXZNzYjf4v7RXLJRjIwayRzcwE1aeNZMvJkwPHQ15WSUmude3jfnq1LghGuwEaFi6OApb3mEuxBWwF07/oB2L5OgkZr02vhFKe/yzxu3yMvdEOoPcSq1+kjUosKT/rmf4f3Cil/7xFnSUqPnjW1cMUnaW1hy4erT9nM32ASVHn3JcEMFk5LZnzD80FqkgmFVSpfPHa7d2fzs6GD8J/7kr3zjD75x/OKUyarf+Cf//Cd/8uc5p4e+7Bd+4We/860/HA044rB7Pruk++Uga8wzSEeraqcDuVVnzq4+Do64up6Nxjve5NX1kpeT4+PJDlu5UDWX5+erly8+7o0+peu6ud5lti/KAoR6FpDTzw219DsorCDA3IJeF9sSWgQ6LYxi7cDVoEjSbpZ88kdm3ISQbXvmO2joWYG0LKL9wApzjWLAwUVMh7GCQV9DI9EfHc+5lmz++ckUtDekrcnDmmNVHmAHP5+9XFxzf0IMNcBoUco5Z/uY/OTbkYC/RFObkOlpcSwiP4ggCdb2UBSSCMsQjOX0Z1xPi+LgGkTvnlGMZHkHq5h92sj5IIxjmvBUHU8ivGGXejSxWcx5efzMq66wvcX85vCQY/QhU3WWWTsyGIrCu8OQB7J4aUcEPiXEwnA81b/34BDbLY6H+s4fceqLt7rerHscEYgaBQjAVxiCnJzj//QZOj3GQlhKMD2MxoA9zTE2Li+eHz9+hOmHVzsdv9SkHZ2KSx6GNxwBiQpxCWG9LnOKot25t4cdMAcBkSKKCHfGOWGMTp+7JlDFYZM8is4HDwjibmEy0HjGa7l6uj9lHOLsevQowKRVMFLHwADanSJluYNVKXsL9BjLSBjkShaRDv/U1TTvpgxRwFGmmPoHZIw5z3j2cIqF9P7LBTm5uVguPr0+fXuwfLlejLnUs7s67PaP16uDde94uebzsnvzVSpQbzHtLy4we5lxfFaHUPLg6Z9UUY+tis16pAYxlkpIM0/8+SCHiILW+d47y49cTvEphWaKYjUUOP45NtJHyac4CQFWCDtsEAmXzqai4EYtBKfVZnEfz6D2FafKcSDFgRs1Wj6pRyor/z/u/izW1iW578TWPA973me+t+oOVcWqElnF4kyKdFNqqiSxG4SNhifBsGw3bBmw4Vcbhh/84icbtmWg1Wj0g91o2LBsWRIswhAps9hUk6y5WFV3ns49095nz2uel3//iMxvfWsP595LyYba3zn7W/llRkZGRk6RmZGRyKfzOjBKnFMcnHBgvaDXO0Fk5IYvQDjgjdHSQp16mG01NqxEsjOuS+D8yXS6vdVA46w/ZC2AmpJhD+ng+fO9rW26Ee0Y2PkEjg+QYRantfwPsej9SLtP5FjmoMRIhTqnWd2DzXM0s6LKsrLAHINcSOSezUeI9pSFROQsR7hRWqMWICvrl0kZR7LpiyqV6mTSB56DUhxN4Ra78ZTbrzGazNYZxwaIwCxvQR5R/WnWa+wZ0ovu7G5h3RJ6sMNZZgbJvE0zF6aS9EQXRp5mIZpvEUqd0xQRoo10cqEKi27cmfJBBlVwClINVXnyBR5tUlmDUMaNA0oFGJvA6gYxW6kQDeChqJgCzSdNYcydEZHY8JA8a3KiizvoHi8WmK9F85+aqULll+v1ilhwaraq/b6N0ZyP1G0wmlGrFIRZD1uCmoNNJgj9TGixA/Hlr3y9Wntlc2sHDNQXZsBcv9hqNSG73+8XS+y0Z+iKv/vn/+//9D/5x+WNFhWWzuDBy/d+4Re/gX2k9kZLp7BUvKGiiqb0k9RNcck/0sHikr7FPdy2V8DXbEs+Uf4xCHk4VIb9f0CXmnjAaFxL11wvPTa+C1OAlFOPY5BrgrUiTos9UWGER7AgoVCs3PgUiP4EYGAuj0nKWn/WThumk1kHS38lybqnr8rbKVARgGcaZ24gqMAHqBOdeITqlc6lyWYCvvRMXKqxHZiw9g8Gy9kKMvlU0NrHCsYimeRDbVKpWQuBOCOGiioGAuQUSlbkK2htWIoeIPKN1YHJ3lSUTJKuEAZCHKc6fGNuADFGCZEarfAFouUWBYDpD1JsvYGvUMlCfCEPEZNUFUcUqvUqjN7EsBmcu8K3+dMTCC7FrJC4gEJMOUnZ8qDQ4G1sUljiEdwrGMdlMP5KIVe6Maa5Q7QrcUJ0Uk1HuITvBbGSeKkEEmTirz2wC6apFA1V8E/QegQgo0+MF6I7bR7ohRQDrvyqxlnZCpujiUgTWDwsxMiJH6QRmpbTCHRClscMkAltSczLyYgG0HnywsZ/e8KvIsa6JreFJWgDbOKrSIZPAZ49PGKdUqVlcEAiBChb+Nov/NLzp4ff/8H3zQLjAgv8b7391he/cE9Lulnu9N0Y9EfYbJ6PFwzRVN7xCNMmkMj4pSVmtDVQG2A9T0tO2OxEbrKL47e3d7BU0m7t1Gsbh/XOk4MnXaS88YBOZ8wBMXb7bcBipQlM0gZQgUO09pdRTYEVDNsak/VmvJEIy4DDw2BGsyUTSJzGMAn4fEsQIpqW1azuWK8XGKtaRPeCrmpFSbFCDumFSrGAmgaMUUfAch+nmjnnxplmhAKO6qHTLgY6uw25PkhYnIR1/ONXxWKNOvJXMPYPfyPMvrwPltBGYioCsiQddyzViHAFO5yiK5pF5kPpCNpcEbM8lLIoEE8QaxRLtkkqrDOiabKzs8V9zIzRrLki1Su6SQSiX4VPXKJZHvg1D2MmQqmAEZFlKVW2cKQiDcOQhqf5xaDfZeCX9DzPd7uDg6eH0idmNTHHhV8NrjoCI2I97EW1gFEfCqVvQJkVtNyIoX+OIw+5hwG26wIsyZIEon3EjgtpQS7yorxQLZHOGGsEKlMJmpI3xCoIcLpptc50AxDDCEYwFIyxULzDW6K99BosXJyAEmA8rhgJU4BIDTn6pkIrBij1n5ORCGm5/JDLfbnit8BlAV0KLVsdl0qclCgM5jkOAFcwsISsicCDDUvEKtrEhDVU7JxkEGCRbufTfHlZ4aJBBB7PhMrFHvv0tCgcq8bQRrBIsDrBDy1CblLWCi5yoPxU/uERPBE81/itgnCpvsREPUaMRxRt/6i0mZAwEdBiNr/gxlsRrcU5PvHZ6qrFliRKBKRA2iPa+WCQgpDnBtai8bLV7lyQX65VxsiU6jsTUhTnESzZI0Kc3Nzc4bgRh8YpdFFOfUAAn03refUqNjOB81QDlQlMRI0qK1OVljkjRmzQ4zTHL/+0TIgcwLmXb4aFXCofd3UhXur6M5JDZ4kzy2K16k2GGyoIoZJzNTVbE0xHmdSgqUhjYk8NItnCyRWZG+gm7Galtru9xcJHq1nb2NlqNTgUPudKXZthUrSaXhKH4lIj4kNZVE5w4IQq6xGcVj7lZeVqPYJqgGVH5R4egXCKXSsRRq5iGAxv8JMt1W06Gr00UbQ6ASZkdyq21MiYJehRl6jaor5bM38AGg3uIsNSUUPsofbqGIxq1HTWL9q1J7ZGoPUfNO5o2o1CYzycsInHwhDLKc1G887d2+PRYLO9sbm9Ua03yhW25ig7aNE0iOMSG+0NbEz3Ov1me/vgmPX+cRWDRdPpzq0dasc3fulrzCKgEer4F7Jv5K69rPKlfMSF1afx49pPauuNT8AhrhmM8c+c4fuGmIQanWooBuLgKWiD4Ft5Sgi9RGQKfM15Bdla6A0fqUhKJuTMkrZkEw/3Cp8Wy8JvQJvydjDPcXSngldJRU+vpP6V4oJ7iAD105GTXvICs0Zi2EhrVR1WtUNRQw4tmG/FMV9DrvHTR0vDEGANtRIIhR2wGComAMIQsdivyg6HYkQqYnFHJNn8qYU6jCLo05PGbfNuwfKYr/QU5ZxoDNLDW2n5h1b7cF0zA1NfQB1lQcF0f4ni7dnptEBeyZN4K5LNNVc+mrMKUHM473E8jB7yVB17WJl2GJvzCZrFRu5d0xNIdVdEu/I0mCuvUKTKnVeKsKJv8WzmGu/HFUbDGqiymR/sHyqezV89gJix0QaS3D9GDyTcQJi4t3Q++5w4QarE05HcHQp2hVQZipAeN52wWyVKowkxDXS+RdxAvE3/GKaUqO+9BNu0qnFZzbnDSoYhAGOSmFMZGKtQD+Tt5euQ8oRztjRGDYT7uTGqGu2d1udff2m3s8t97CcHF//kH/+Tp1//ub/xN/8G2FnVZXefpTnWfWqN2mDISrCkE6lKLDJsAaMRVK01sPZDkrJ/x2o00BP0nRnmi/NZt1Rr3Pnc7mDWOe6csIA5zx2ybZ7NYEid5gMJtHmta9pGvEZYMYObttGPB6MkV2nAa+yWvCNpSIv5SE+MwgiVaJUgXWkhbckZZUxPMiyp2xYnnAnGWnmwBmZ736gcmUb7fI7yLicsJT8x8oNKt83T9O0mUSwGsf6lMzkqC46+QaI0vEFquM3p7A9DivkIQEwmksgQCe7vfQWZwNPlViZYMj+PAAwoDriqrkLRNWrz8pgexXwB1Nq/gI0sFaS1fUZ7/JFmEKMpVLbvkdqZqmnpXwnSUVi6NukjTX2BxNIw2U48EDYtghpDiAQA4zzFiL62ag0lUsCGEut7gtaJbYy6cL9DCdUvkaoFHKwRIQMi8tSQ6dm1QZKXpr+MDqGhxHyCdVXUxmCsrKprdX9eGw840Mk8AatQGIeROSkJCqiEU+cw4Yp04rcp559bwZEZck0O9BYzCIVO3czAV+AZDhS6IBrzE9QWB1Sngf/8lmJh2Ym3MmnMcPaIJxK/FF0tRUInpKqSWu6ymSqVaJh9ms8UxuMOIlNt3ClPC6PKx1OE2sw5s4hFtqPqlj0z4qilsP8hexnsHkh9nIvRpP6/oQITXUrNF2utTK1gYskAIoqsmOQiOxCmUQPCLLOWJZWSIEU8ZzxwZLg7Qo9Vwdm+nEVuqyCag1kqcuKF4AsROm3pKS3zJ9qWyG5TjDQ3xRUaApWI+BQYh59S9Wor2VzCtMxisv5tlmRQbaJFywQwsi8KHhiGwlCMKrc8ioj4lDXzRZbQK0jQHMBgoyM3H00H+Wzt9JwNItTNqCr0NVCoGqrJH1dLUU+4z4sdACjS7Qe0XNJSPkSTE0yRyWmVRGyjnbAEDr+wy0qdrWGfkroIH5m22HIIukblCfeYsE3ExcS9/vlZF11H1qGVTZYk1L509mkxaS5GmWprcn/vPndGcNFxm4VtOwHFtWAcYEViZo2cGTLc091nkvWLWETTWrumAJDFRhkTLlOZl1qdifIqHZUEpKr+LLbJFaOwl4uXA/khm5QDDKHfpk8T8GxT5Zo7puV6SXnNgFolNd9W95Y7JdFZ5hB+qCITK8scqkaB1euy5sweLsUHK/DHwZwH4sk7un94MAtrtpiMcYMCVlPYRNXZXzE8m+GuX8gZz2b7d+6w1Ycxty9/9Qs7uzvd806tiQFfLvoYoVhJQXO9BgeDWQJgtsj9gD/94Rs/eeMnb73zXiFX6Xd1xfv9O5/b3GseHZ00GmiLhcUXVXirZsq5Z1+/Vs7mo1IWU8xLbJJLXnDTart9Bm2FgGMVUa4kDi3UgGma8layxUeGjheevPlv5SP8BsWLdHgX2SUQJouG00oxAHtUiyJQnhj56tq/h4c1dftQmu77Wd5mX8hZp9oPjZw6EB5jyryGwwkWdgs37LicdYK0hAPF6bSFpvQ09AeqtfKwupfClEQIpWAwDuRBgV+KErmptMQ4KzujmsCkFFWdTQL0/HhIQp7wUxXtm6HKkgtR7UfJhRzjMJ7wjQ9NUuUUH8EkOwCEG1p+lE8eI8JcV15WETzdEMaHx1JEVWXzl6+HuCRgvhZP0O4ICJLYKUSAgEmrnnoScI966e0w8Z2kET1S8QkjbkC67p+CvsGpaMbbG8KDd0JcCszTxWNFnHl5q3JPhVlcfaquqBBWQYYt1ol0HtbdqUQTpyNOPlMOR+/hVsWDU5XIH/PwTwGnqhBfKwIDdBItfq9+FTvE0CDr+N3zMhDfpBPqYCTEgNY+Arr1ChkwOqAWgUxuULFVq81f+pVf5UKmP/nDb21s5dFuffe9t19/7zWssJ2enO7tbQ27/V6WTfMF4zFXtCD2MeaCiHW74XyIrFmu1IazQYnrjooZzPiPR9NShcO1S+z6nXx8xJVfx8dnjLhaeNUOvEZlrdtL5YZxxslVNkzewgehmMHSlh81XEn8p/0wijBW2RCK7TzEXJSPGFqQC4iqJSgMyZ+dnZjUonFMK2Quttjs29ZGSV4jJ6uVyGEIH9YukV2s+nJPluyc6qwzpjOR+I0mr0awT0MRT9KQ9XFtuQIrfLEM0y4VnvVHlm1IJD+OA7SGkAQAAsawJEhiSlb8BuFBRjjjP18s46Lvk0VXApfKyJjrEdT5CKHSwMfjxoTFLE3sRFtIm06QzRnQoPmiVWGhokCmUzQVqQhINVz5XC8UO6isIyNpNiaFEHgs+Z9/uLGuCDMR2LWESATp3mBailMHiObUAdb7OUFeGPaxHYSIx5HxIWZSGPs5TyxM6Hto6uWEqzyFiDzAnNCXUh4iHezCb8XjWRC3jGjLrrKsP70VV9HNjSfYwIJPAJJLMeVPksoOjzz1S+OYF8bVWXmWLaBCQtSczANRv9QkIBqOYc9Ho4USQBJnQrTUEXPxT/OreTW3YPXa0PHjmVPaquL8kIhRoqqmP3ssU/FTUMqGQeLpVUVwlgnrrSwuSVqwyjuQ40Q5Ur0tFaPcosPH5FFuhFIsF1OsWclhj35EgKh1LJ6CKpLsWlKezCoQhfNoCQ4Q+JjdIU0iaKpZovtkNnY4kI2lqXpjkwWnRmPAWSNKmI1HKiO7CVwWgBlZDoXrWyb/LeO6e2RUGov5Sls1Qf0JIKpm0OcUqgVBmBNM17EYj4YcieH2CmLQEXGByXB4QR/S3twgc51TlqJndG6sa3N4iZjSE6QisxOqsyu2uaYL0efVxvbm1matNWaN265uUDJYOMK0LpuSEEUsKqNuTycZui6fSTKXZa7PhFZCvhlRoNpCI5mwxmJZEblqbuI2WK1VKkD5ANCyKp7bTFilQ3MraP5ARdOBBuZV5NT4QJ+mvhYIUuZyFhjOWXsaIQs22tITGjdzJI7ROZMNCEb0966AXTLqNFuKfr6LXZFBt8/KArHgDwROx5pOMYywQDAfnd/a3Xz1lZcf376DXhOCPnbesDKnqT7cY46jxku+1d/S9/70Jw+/970fvfXem9At5c7ZYmu38dLnbm/vbRR0N3uOkyKwhVwT3coTcq3KeeGKJ17tcEWH+xBF7ADeA9IR5Gt8tVhqgmk0Xpsc3spFmLw6AWjJOy3h7UiMEkvPEgaJMMTGGWohfqJLQQHAIivFT/U44KXYSUxHmbzd34EDjOjHGfKuH6MywSCH6LPHgY1ei2WlkOYUAB7g8ElKAUNErxT1Z495Jm45QpD/8I7pq9SVgn+vHKEiGA5FUrh+9cfDp1zUM48Y3ul0BSYsHgS0RQ3xFSgPC2QCEB4+nXf6piUr2P3A4+BWN9zfLckIgjBCFWQhehkcK+5+QoBP+nzp1dkjXDEThp8v3XG7elZu4VY9tiRYA4BdBK7CLY7hW8W+0c/W/i/B2WfaQm16Puqwq30DfV9K20Guvh1MHIG6NZwpaqO/Aa/8w16EI5UG2OU0BWpULX3u65BWa1ZY8Iz4LTwJoScDJ/VnqHfUEVQqSiektZ6kxeUV8mOVVvAa4PSOsUL8GNlrhlLxJ7WPARHWzwhp0EcUp4hpDQI9ORW00o0VLCKJiSkseRxN8onDohoKVSGLZNTnppsbTfQ4uS90OJrmS6WTs84//Ef/+Lf/+m//7Je/en568PzklBFjNBki6DMkYMCBQQIEDFVmUyU76HfYIOao2GQ8vH1np1ndOnr+DJWf/mT89PkhSsEj7vZdbEB/PjdEuF9w0yrCvxaptMysYQ8ZVndM2jCGaA52SSNwl+VRrLWwsFjiYtW6rtFhKY0xUvW+VGbfmW36PiomjCsoBsubjBFTmdVQqhwaxzCCnZm38tlN6ZcoWcmk5mBURhbV7gOnhBdT1JmRYFi0ZnGUFgoqZgKGRqhI1mqVlYtQ3/Rwjy8P9wQHADHemU58rZXqihtp6OpTj8hmcIdk8/TCVjYA0Y8c/jgayT1asJbsiwq/dH/YJyoUWjJGyMgsL8UJzLDaoyjeKQnTWmUUUtPlsG5OxVEqcpR1yVng58+PKAAGcMz8CKHW1BnIZY8S4YLLhXQUnLxyqHXKtAHxhbKDpRLKkSlICVGKyQOSizIi4zwSCXDn0MzmDqjZPuULzZwY4IiIKNO0TqUsxhSPQGngfIhfljGg9OimZDziIxZ5kaNbL8j0Y1+l55EBBisxF1ZZ46NWq9qpIIgmphvrVSgSq5BCqRvFUW63yB7L8ng2by9q55lKLVOsLWe1RQ4LNo1MprecN5b57nLZ5O7j5XJz6f5FTgm35+XxosD0BtSkaPzXBgOfLHmSoE5eMrNW6gkF+HhGjB7uHYNIYAXAY06r8FbS7GwYCiVhIMviIVAAG0LB6yHQ0LIxowCT8lcolX0iU3tgjtUfIyDEsPEGPNY+hYwUJfaSIUpcs8YsdptUVJoP6chQOX+nNzrhDmi2hagkXJKLqFotl2i8aJvgU8kWd7a2B5iJHaoqzaZVVFwuzjrsGG6061QGqrlKgZqnGUJ+PGQ9wpJbYpYHo/UTtrVQLWRqYflUtYm5FLwJtdzeRisfMDfGFH6v10PUZ0bKsVMo7GOGmKO7owWmOskPPRM7E+PhsMCNehzyzWeajfqdO3eazSbCt1TIqMIcEWGVnzSnG9BQ4tYCVRxRCqPIoJoJFXi5hzXLYqUHx8kGqJaTLdW2zJkVipooWbOWHPTyaVvY/yEHKkJvBCBSi1Bx8JhynVbJ6Riz2VP025g1Ma0olrCvRGgGzXt6OO23yHgnTXdfTTvPFde6ZAM7VMPhmFUWmij7MMQFF2nRYNmIUR7UErm5mraIfM5/tjK4oavA/ggk9Ae9zeo2JaFbs7PFL3z5y3fvbR4fHJGNLbShaBqlMhttGXYLMX/FFXs5JvkD9gkh6Y0fv/3G229edEaPHqIuT7pmWGmOZaTdcqXO6kCt3oBGKz7VbDIbWrOVq+oafvA3eUKljPVbvOdJfBO4EJB8ewRBGix5tNQsTdqjTs1FENPvDx+iyB5PJ37ZPTyuMRHpxc4MockZztCClkiAiqSTgXF/fk0mkff1T5K0B6c/3b3ySRKDAHw9J+Y5uQ0Dl4Vn4OCSdmFiBUN588iWq8s8tKAk3NflQv/hvkaQEgKRMOAKbLUQ83EawncSzdIzT8WRd2Af/Qk4JNFxSAd9EwN0HCooIBVBMQMKderaIuQ9s11Q4trC4QoywCoVFbMqusZQf4TbK5ftAMjTAPn11EWPE+ARDEKe+p/AxjCNWCBUEE+gNSJ0T38nKANoOux6t9fTEKY1nvXn8vdaqBKxFG+GIuTTkOJgCXDiWEvu0oelHJhBhJufT0HA5fiR1RFpDI+/8sf9yZiBWAF57NV3xOGYrPSFWAAmq6wg3WUQ6uL5VLlZDVOM+HgCjsGQExD9Ikxsww6lah6bawKxipNEFgGW4uotcHlRkf0HTDjohWk3ezv3fudv/rv/4g++xWo9Y9uzp89+8uPv/cyXXmY7/Pnzw1t7XMpY4ySfrmgZo8mtlSRO6XVOOxhM1HoeR/0mo253dHJ+UMiWHz9+OBrPB6jJSs7JozwrGVAnKQdSiWZ5X/o3LKhhhFIjhpYFTR7SSh5jqp3UJMDUwTXKsRpGelIa4aH/ZMmKacRojMwBLixS02cDBiUEazhV/vWHWjkJ+0qYGxNEkkUQZdERX9SVMhmMTtKp4Fe2u8O4/JJv2wEAgVo9oZSkWrSQGmqKgEB9X/soZT2CIap3ju7FG3TCCEvsJyDyD3B6F7uKY8UtjKnkyKAhNrlAR1ShisOvGaYuaJ8LuURsIYtZsOhg8dScP6EehEwpElkHs8EgjVd6o3PslzMv4rgjWDHPQekgALGqp9MZ9HKs07OwZzKTJaeNGiQxfCajEWyH2boXTmu+jPdCjKoxS4P486Dvg5oEWhecscToEFfkKnkmQUQUd/SnrFml58codJbaF98rvgQfQfkTeuEEyABUoHpUrIqdMIhPhYh38uWf1Sc+Jdn5jtl0Ws53iot+mXXVIicms+iJYakzN11OqdtljCShHc0a/6JApmss+GtloYBkVUMszC6r02JlRB1WAam4lTmRQQ59KLqUhUirlZpRZ7yI1LuPo/BMOmB0KyPJI9Sh/7E0Q4AnYXmOoEYEoA6mehZiClZVJknXnUk+kK0JkxUp7XmoeSuH8wwHZ5kJdPrPEa/blTryepFb6JjuI/ujZjccEwcpG1NCgCF3qonRDywxmT9ot2uwz4xIAkw/s+AsKZsJGOSnaWsaQCvGIr++qG4q08BE+M0HBLHEjOGB6QQxFLlWRxUk207o9tDzn57SRQGF3c9CtcGBFgpd9ojYPtxoYq1qgzMMVeZ4qAGRPeo6991mudgNUT5foswrLJtUUHhj30IS9HyBvSPIooSZeDBJRkSWeK81d4nvyoKW+cVCK3ydeCEWfQG5BqcIYI1Dgv8CBUtNo2RFFxiSZGrATMOM8bPMxEKFideabmm+L30qqW+piOCINgGggrMK7FRAzbg3xBgrqdDo6P9YZaexs4LD1gyE0V+QOj8QwyRHZQcm9cNF38lgM6zXuWBng0ba7V7UYFa1cnLwaNDZLmX3b+3fpgCqVe6KUdfAhg/TDl0mMx7bZYDVg4MnTH/Gi+V3v/sX5RotnYkHOxPMEdjByO/sbnz00Xuvvv6yy3DGGnJh7UPE8Vipqi66Y+XnrAwghOvxH+Oxw7v32pvMCcxrjLlCNHnyF1BdQ4XQEGqEyL0CXftIEBjMWlDi85kd6XQ9f5dRXE32CqUOonrC49mAG/5cig6T1nxC+wrQ/rPCE0Hj73U4kzBvqIEKQRo2jVs41FhUQknqnpTeq+QUiRYieJoN7UkdK08ChcM8Yp+gQEL1T62esACRdBYCYAcgnYa5ZcWFpcC7YgfrxEqR2woFzWMQfMT5hOdJ/aLR5kCX354EbyfBcbn7Muj6t5JlpFGyUnIgUKtHhueTogtYfy94nI4XABAU7hmwJF8MuRaapJw40oklnmtxPsOHqPokBlyHzhO292rtPwFMk4inlTkjC6O76hwrxDwWV3rYeOlNuegd+ONuh3Hvq2+nAX8chpiaY25rbwxz5i8o/uT+xIwK1h/LgdGtxkJ0C7IGI0Q4gMOfQ2/d6aDX7R2VcrdYsH/jJx/+o8IffuG1ezu7t9FhLVVKjCQ6s6W7HrGgw02NNXXxnTF3nw6RxTOc5Bs9fi57eAwqSNgan3VUmOEPYyAdDMdlxijtcIMmA1xWW9HlisYhLRKrNbJACIU0G8aSWqm1zVZ7pSHxaNbG3napNGCJCCMS7EIgHZIKmWJbn7O9qK3yMZZRehbCWblnSU4jp4RJNUPpjfMzzxxw++pycQtP1NgtIZJjbNa1UJIypsxtzrAMqpUbriZifZRHFMAhUejMtzcrDfsKLWiF9epjK9PyNs5bGRi3+RRBrDGioc/MCIhYVCp4E7tUGvHB6elHKNUPC6ReEYI3n6pjiNxa0JXajMZym9UY8AwL36z6PLeyFhoieFrCY8UPSfwCwGMEERs5bMbCvOx+SB0ISnWpExrASBSWpAQOssKpTCy7syvj3R3sZPVTOv9ThCrIkGkhjnLQV6HOjWxDX8sZTB3EQCZipyVXZp7IBozkopz2Xphf2EzPGQMqPcZGObz6WpiyZcEBRnnj4Su47DPxjf6KJhAvUNhmK0a5p8ZYGKpFV2Jmp/tMVpelI1LUcjjByxpGVRe5bWUns0+dslGAHJXRAslkm7ZSTY1FFqsrCXR8VaHrmo1l6jrgzh6JBinxWtVSQATxYwUpA1PyUracbKfV8iEfL+7AAvcVuD2qWMaP8B2DA74IpN81OBWbhFIbJC3nTg4EznYJyuS48RrEvBRVVcRopMZYLTLv2S4/y8wBmClzrn0gou7UQ1xF7yV3XCzT4lDcn4/GE9ol+3UIrwicyNOcxilVy/3RaO/W9ul5F72xjW3MiJ1SB1AiOj27aLdaqjxUGrYQs1kMDyx6tglFC6eA7Ky6SDE2alYdKTV6RTpngzAzj84g0ckCExKkYxa/yQlTAWRQigY5m70sbqho1DbuP7iFuM9iR5UOyg6jM9WzJ6tWi3oP4jCFofkL+tBnFam6cKaf08SZfGlZ4g5y2dPUakUu0y+UqPYsXiCyk2XmRgtdALDc5iwVeufVBupDFAAtt9TcqPW7HE6Yc1MEGxII3xxyKMA7uM7pKpo56/xUKG2BspoPq5H3VSR0htBPvSNFRHBmRlLjZ4kZvUxp9mhNhVLDeinsITpVRfOTDHu2TLqYmfOADQOm0vLXRMZnU7JRu7i46JZr1VyxeNHttAubIKYLaDY3Xv/iK5u/+PODfq9Q4bIA5nvqUWUQgqXb0rJzfjEcDTjy+/TRsx9++zuPPpoUW7WPH/9FtVoHP3MMWA0VWCrbv7V3597LHKWo1xkdoI4Mqd0YyVaG0ppjKBnrw5qBOVIvq5DWENKVP+12YNUM95VLFebK436+Qp8EelexHkFVyeocBcCdvvZFhPjrOgV4gNCTdGxuFTC47/rv5fe6hsVa6HUkJwAeqNRcgyPYFfTkLbCotf/w5HTCjdpkn/Zesw6Ej5Pu73TmiVchFvdSK66lIg6FhqcQ+du34Y0YzFev6OFwwQd4QdPv8OaP/sf2SRxYnZsAebync3eAn95X12dWmMIeS2A6NIEVbI4l4MJDdcxRCK05vXfVRWAhKY9mySYABBEV4ngiCUa4vgyUMAUIKjwGL3asvCxE/tHhoAHnJbiAxn8sOw6A0AKGmJGEnDXwz/oBFifrJhoSgCS9myBvTPpSBMfoqd4Y55MCvHoYTQlhxFFShtkTeSGWhIIEgfsIhz3CoT8rSAPyIAZzhSdwDh3fCrPw6PGpfm0YI5pwh9gr/NYCPhUaUWUYrHkaBl6rqmu1lEUpFmKrGGcEMadpR72JKlVx/P5HbxVyowcvvcx5PbbsWfRn853aXspXzk5Pzy96DA+PHj1D2Qd4VvRZKpX8zSjH4IJL/7WhzehQqdYLhXq5WG20MAFe2bm1NxygVFo4fHaKZY/TY44IL1oNqYBjQ5CHfWS20ancyAGTCccCNHIxJJPrwH4kTG5UtfGO0QskEvY1eKAG4CtsdCUaS5Rh/UfG0fY9qNBL4TCrRkhaEP+B4YOrXJFLWbDT/gCs0N4ovmBQAYRCCFw3Tq7YqFDzurlQjIpQlsKqQRiZ2vKlKsWXgSglDX5JgsE3Qe9JIXAImSCJaT/aA0HFmUkL8oHUb0jGqfK41mMlhOLwR2iUSwMyjtn2qzT2K2hcs8/PTA15QCrw0upHANDMShxj+VVCiYlnOtqrw43jCSUpxV9KR+lTojoYLNlWYr2pHFQrVUVlD2YO5GI0pv5gYLHbbHKuAEGKgqQM+RNtKV44m+RDiD36EUi6fFZB3nY890AonzFayK7i8U+IwanlU32KUwD7mzCED2uPuhbVJpeGBXlHIOitkZlIgsQX0eTrWHKpcxAhiIz8kgS/9mdx7GXo5Ofkrco+eCiGPSIr+RDuGJD+xTMkkQQLtf4sDWjGZWGCk69+jVnm4gvMqlMCMlBxxL+EXc1KVcCJwceQaWEbH51Fr3Bj8gUnY9kL4BI39nVq9RoCKyv60yW2A6bbrY3pRDaDEd+lKW72JdlUzJwPaYHoAilVqs4SZX3uKW+xg0hyqtSoLLAOMWbeqLV8qECUpAGr5RuFosv44rzxWTLRJtMxc1kM+KOQiPVWUDOzpe5pMQGrm+XKvXu3sAja3myyvlDFELIvTas704IgtRgwDFgRhW0EZu8iEOOVLHRz4dftvVazxbYBrQHTBUXdvDGbstydZ7dTW0DMedH64wA3fQ+bSRzWZptBF3UTksV+FHNIWlgBeTvfpg/kjoEZNkQ1YzTu01/R+pixgATCOHMML0SJtv7cqpUVAk2Kbk2Hq0FB36iCpqNgqqU9O5UoHNVJKhWftmmY16JwRUlg8osZhXbzhuym6ta64qDbY7IPNz786EOudGYSwXXeD166ffi0uL27SRM+Ozrf297b3EYKXPidj1QMTvI0223wyEDcaDocsbmXae5uvP0v/qTWbJxeHNPF0l7Y9YUUdhzAvLt/a2MHo2WN8aTDMhOkUcNUo1S9VNP48RqGX9ol/8TDqmDwMW+DBEKovC8M3vaTjpr2d/daguYlJDFi4saL8rOU7ZVQeQl7OkICczXVT+PjlCWkXIkinjkt8SeAeLMIzBQU4dbPOYM9ToI3oLC47mn5t9qoOhWYQfgKElcCGh2e+PoXftGDX8W3EnZQQw4ADdcwK8XQ9fivRfVECQuIlGf7s/7LMBk1FpzAGEZLy+Ljz3+cAnVcsIdHDd5zahCGOa0Tb2e3FSFJTeBEpT7zyAWD1R955ePX+W4pmdtpSr8tZY9v7xtfXt/Q3KJSs7MMHHYpGPI1wlqaYAo2bTRLe8GzSjIF5J7XBgGVpjiJ5J7JZ3DIqi7MqF725zsdwVNK+1wT4ZO8YLS4fc0jxBE5v9fCxGgJnEGtavlaPKs/4ByqAoSY1r14uaxp+EnbL+trCcA6mhgnJnrll8RVnQza3wmIguzjKpK0HqGvHxigxQjQSyih0hiFCSZWojWuqs7S+7MyJ93vfH2KyuZsXp0s5t/94U8Hk2G93H5w9wHm7VhLmwzZPV8W67WP331viJ4HWqXzBmfGsDVheqraK8DSBtsATADy80W7VcVaxi/+8tfa7eajj47aG3VGC21Ql6R/vL3V0jA+k5VA7I2ywE/eEToZsGRHfILBwGG2gMIPew7zIrvdXK2qFS3teTNoWTNboq3LAhWjeK9TpEPOFfpasB5jkR22X5iEL00nNq/ZeECwZHyShCY9ExJi1JaBFmRUqfRKZKAhc1CV5jNQ7wiVVrtiEcbyWOn3q2I5l4F+wQMGCStKC3PZLDLaUn1QL1FUCl511HJlGG0kJFo8UeA1QJQwMkrYYMkcIYi1f8qQbRCOpLILD9VGMUzAu3AkxPZYduRWCuGxFL3v0goiYUDpEB4nuZd9NImrdC8SgLMU9BCyZV/IjPSTFal1LcesJpIXHpQUmA7AVThMvWIjCDVjUYNMgQAIFsl8aG2h0uDyolQ4Rp3mqNds72M8UxpExSKmVJCTZCxFBItUp5/8aGBQ9vVSUSVhBpNkirx5FH97VtNucddznik8h0lkD4yIWVQLfVJLCs8g0xkOJL5Km2MbOVlBlYoKB5xR2+Dk9bKMlMu8E1oVGaM0TIeZ32BdRyaYqOtQzn9LAg+ON6Obpv0l0R8fyEt94ZvQeyVEUYKnRVGx+QNC/xDjEnzqSHisUiR4xVsevfjTf/vDW4zRBzWHTIsHDoq3VRy+PNkkA8Vj+GEbINSCCYU/nY6YSM8mrUIGEz8dFbpWvNFmyXMnFJeHYyOfy7ChiAOjqORgL7JVaPeHw9npELkYCz3IoFq8Xi7OexfNah3yWHxHHkWdx/eR1ISnKikrR883V91q74Xr/PSmUEWoABD9ub9rOW8tl9VFXu0FhOxJLmYyR1spVT/30qvl4uL87AyTUuxguCaMaivFiUoOe2HFSqvN9g7lJ9zUceLTUqBzY6O5vd2m95hxgQA7FcJNheixsbXIoy9ADCYdSN4j6oe1gcx0gVVl6o8muswuwIidHHZYba7J3dJjTTKkjzPT7ekquXlB13KRNuVhFGiSwb4AUSWF0ovQOoYDlslJA+V7TiGrN2MHRq0JMBJCyGejgxxYDPFFe7GseRRopqzrl6olKuy7b5/cunP36dMnqIN+4YtfZHM3txjAwPPx4OzsJQq3XMh+8Quvwv/ZYlK164Hrzdp4WGLvjnWe0Ygp2ki5m00+/vDge3/+w7N+d/de6fDocblaQvmHu5G3NrexMIHWKEPFwbNnGP9hcef+Sw9e/8L+MssN21AmJovV+of1d32SU/vvbjJq0oVLGl7DDYgX+dX+G/B+rs+29VT9AfMx2qzqqflFZCHqVZ8AsUpg5XKK9BZuw2XxL+H0EN5OgBwvfNKj+VXAdPIrKYskvTPBQS9lJw1C3EiNQMzLmRnx2K+9wq6Fw8e3x9LbIxgPpftgqYRyUUWOqdHmKLNshvV7YpWe6k2gv9PZgWdosmhwGK3iy8oZGEzLxuLYEKgCJaqGIX4DwlT/VrDTAqlaonRUCfQTk5dfeKa3FcJ+iBMmGHtkFc12AIK/BXigIvCopCE5fBl2Xurcg9tcAIriBM6rh2AMg36Sx+lLPlOIVn5pl6etUdpS1Kc6BaNSjSUgSChMxw1uD/N3EuEauE/tZYl/ErSndAnqRWReAr3505Ak2REx4v318HhfR22auBtihnhJbMekdxhfryRoiFRhQshNiK9EFDVesATF2F59Ut+raA6SRi8MHs6PWic/6XB9WrVh3kjtzZ2edH/6k3dGE25on1dKle1G62u/8o1/+a0/ylcqb/zk3e2trQefu48A+M4776O4ywHf46MTJP8JV+rMOQa5U9cJM8I1JCBFt9sbxexy0u9stFpf/crPbm9t7N7aYtPg9p19Fu7Pjs8ZPtlev+h0qbkcM13s2ELygms1tRbFw9imPWVUr5mzFBlasEohGU2iaLHIYMWYiZTJw0hTraE4grSp4ZOHcZlhTUIXJeObAbTqQr7R4BbgMiYvEFg18OoG0Ik21aWJI3kOf/5gGwrJ2EiVxBeZpo7O/lZM9zDArdUlpZQGSLmd+aopXjMZ4DnETO741F9AY+j4kE9EGX89QUGynGx9TgzxbhHhVRlhTZSSJSMemiCKwCG5FG1Kz1MTMHASKLAKAkdgoLRDkBzgCkIGRY+gM0JIk/jLm/8ycC/LgEQ0bQqEJjiJnRDLGuUAOsRhKRYjkiDokGNEE3VhWsAlBMlQt+FSmEjHFDRiIhQB7aUo2qBMY4XRaexKuOEZUYt3MN48SbajO/GQQ9gAgV08rEWKFL3lkAwvGPDwq5V7Zw4DldoKP0x0rUkxAYNgOEMskMF9po7kRTVFsx2VIgCGGCACiCa8SkG4LRGvV041QfFJ6DUPgt3DKHeY6FRqBIs35rLQGBjRpX+VltU50S1Ao9SyYSEEWk0ymoU2RCaOOT0pMclyZAB8UOtIH+U2prfUF9VDlQosg6lLnQeeLSfSCypgKizL1VmcAx4NufKNcyAo5dOSW832ycmp1F2YrmPiUzGXvcFFm4s5SI5leOaXTBlRXseeP+rpnEYiQJK0r3A7ReRHsxY+nCcABO5Ic0cPMj11mlV+LJs1G43d3Y3RsMdqPZbFsGLU3mphy5g1AyayZLlcKtNrSUuGtNjR0DyXjNLEzIqoKoDWz6lIJv2jOKbrzZkTL7I67kwQKdoMGc6QJVYapOliCnKqR+wDwDx5svOotX+p3cmHOSWKOqz3Mxlm18B2L2kvONQuaIc262TdggZoSNjQQItGW3CWd8yd6ZJmkqAstMpBrWMKoIrHUv2EdRb289DgxNRSqcjBrcf03nt7t05OT9lKmDJVyJdYxJ/ORlgQ+plXX55PBpsbra9++WeHwx76VCoLOKk9kHznolMpN9DngQkwkcnR+cn5ycnJoDf86OGHp10uCiQTmel8wFGff+d3f+8rX/7ihx9+9B/9R//g4uysWr0DXY1mc//OHuyFEWSWHKiBqF1ZKSpDPKrn7koqZfDwOuqB1jgDmIIpLPDIdx3FGr4IrxRihXe/kOK6J0GG2X+cTotqFFvEtQgGbI0thgW0nsZneIP2ctR0SpfDVpg9JIkeHfbrVHvz9oD4VizVGD3uTtjj4EkAMfxxR/IZ4zrGCOS/HpbOkPuoqzcEoSEDrepgkRI8AdR6VNxWwPYhYIcNqRjkys8jGs4AF3NITNa09IR+T4wJNce89QEd/LMAX2v3GzpZDDIKY8oAkKTgVf/0WkOkUEso9cap3Hm0WD2T/AZopa6ovNHYS5ACFiHdtgwaUUCZzpmnpE+e4L/SPwv+HurvlBZaEtcdK6jrYFahV9f+k/ikl7a34+6r8Ctcn85ls2Gb90fWXo13Je8RJCEOjxU/8LUP/03e+JoOXJa9lwhMTcBpdrjNM7vk3kGVkxWWQfHi+xMeVSGMSjwWHb574HVz1a84GWtobF0/jd5rb3iHhsNcfO0BIxINsfT/4ODxo8cfskldr5T/l/+r/1nn5Gxjd7u4GP7RH/9xt3c4HU3/8J//EYt2w8GI4439PpsAXJqL1v60UMGUW386Oc2MWiTUausAYCVfvr3X3Nr4mVaz3Gxxu0xtNuF+0GqpWu1enJcrTSAZqBqNJmkzOG1tbVKP7XIZxG50dk1GR57S0I6tDWR+lupRIB5xAkHDYRYbFPhjskjnMcGQm+pUXzd/gvAgTR5EV+6/RHHF87jE+HSD43/aJ0DFn3wTABbTyMUwBzwgBqKLluX5mJfRWlpm+rRFLzKQXio7BUA9TyggOfFIvPV9+WFRGIscJMTagy7Ywh17OiUlfErG8fIbHWbLJSBTX8I/BYXW7z0Sciliw2JLFS70njjNUj6gRVvnxl+jIf4hXwEnYqs6HXASF6Yh/NDzSjDRf6QQODlro6d8ft6pV2ujUR+b/Uj5Ei0QkljzL6IuLEEHRWTDuZyOGpnFdjZ7XCiiZoCn+A09zF5Yy4R2G+fRjC9jQX+ePZsMW9jX1CHL4axY1SFRpppIckwZlN8MSllGIzmytrCc7eO7JF9x+QNCQwFAwXRfZCR8U+5Y3QGFdiT4NWwuZiCjix+SEnX0US4lNd2H2EXeVokUE9rJAVnQhIjpChMFsZMqyqQFEUYyMyKbZCDWJkWK/gjQZCY8Ip7UNDWSXCwYmwkEkpz+BNpodEqB1bkvfCTP6VcvL0RVCIyyGGBY27YUPdQgY94DGe4XkYhgHkNnfiRApkRGqGcKlgQuD+AEZGUifx7zVNEy69SyPIykiGddbqI4X3CMhH02rfXdKdKgFhfZTH04Pctwxy668OjdI9YrXrZSLJ1nLpqtSr9nO1qLFvJ9rthfzEpnFxftZhuDPNI/41pgmg47VKUihMBregYpyaiGsU2AtSWyQ1n4I9pEr5d6/kKlQSkv5lw4+9rrr9dRTqpWOQw8GvYLLGU02hQIU9JyvciChtASmy4JnIrEorrWGECmWsKWhHoLTICizS8tG+IyxSWatHcUE+mfuM407j0GCZs/dFHCIGNCbELKRxtiejC5z0aeTBxBMl0aBgk0kbBSICyPrTaYPJuNZTNHhpV9i4ArJqiF4FmiH8VlIPhTJlA9m5h6D/unmP3Jc4ZHm7eQhUoVMMN+jyUUDKGeHD3f3r5V39h6+vRxtlrlYrvnJx+wlzIbFU6OjxtN7DVxDWD2G9/4FQz1Vpm3lTDENITH9LzapKGpMpeYY1mIOz2WTz5+1mhWzs5Pf/+f/v7unTu37z44feMNzlcx12KK//Nf+9kvfOGlSi3/6msv/ff/B//+/+Z//b+dLIa39u/md3d1nQI6U2II3BUP6YvEFCtAq3HeZGLZ+mnMpJyjt+ojTzihpy8x0CuC2gS8DRDWBL2Ou39AwXiqOhPGX+kyBLkihMvD8QRcWNkHTUGjtj2+Bq+zASsfXEKqv0CAU2Hfn/DySGmg4LOmYYGfehDQqq+g68E2Bo9nUB7RbcQHVlgcdSGRD76vEnZOrpLoCfM2bMKvlPQyJy+h4vFdiMTXAlZADh8tZwpeGgrw0KUU5cO7NwpfxKmrFZRjVyX2D/sh2L55WdNRNREN/Klb9k+jkX5XcYsHHi/gUGT9Zbk3w3YAwrchERonIk29ZVGpmcO6G7n4M0pw+uNw8l/7jp83/apwwOa4YmR+V8hxGV3hbUkTxQEUGEEVO7qF9FM+MdEAfunzKpJPSOITgo3ET0zjaqpXfDwdMOFI3legPtkjocWRxAiJd/Tg1/sWeXioqlv48mrqpMjrMz+WujWGF0UN6UaQFJEpZ+SItafIH8ZdtreH/VGnN3jtZ774w2//6NXXHrSa2/vbu1zc83u/93v/9t/+L3/72//5P/2H/8+DgwMg1RK5QLdUZV2MNTpkaVZtWe9B/abe3Lr34M79+63WZq1c3uB0H0qrg15vMUc/B/EBcZcxKb/Rvt3vMWTLMAerpGiYM5DILAe6H6VSs9lgvZ/RnTEStV0MBWpjnXFOi15aS8NKJHbozs8HrPgjviMNsPi/s7N90es+e/aU0VZCKYMGC3IaeMU/+g6TzNA3Z4VM0qr5a2FaIinLkhSQSkyJ6gchhlPLunVLYo/FF06FBzhBednioTSs7IXDMZkjvjzQvkSYxmYiMNPgx9u5cOMZkFha+nDEIaIFmpvI+mcxvPsxNBAKblNNAUwHEClaF+0smqfgGEjZ8wWe+JjLXnSRWv3DXg/ilu5ZM8lXXWcmc3J2VCnfRtipVnRAkP/wE9EH8yiad0mUsUEbyywIOLpIjNu+dAaRXLOwSZ1hkZKbmMQE4xVJsPp7cnJcyi76nc7O7hZFeOvBLrUHG4HEE6VAiwYVQihPscP4o+6cJ+YuoHWOKCB5Vtw0GBB6cRtGysXQCJHWmInlUpg4JXjFtl8lJ3kZFuFS/WHwcRHfOgKHFYAnI5f8LBOWAUMTAyk0y6BVvBgXypRhJWop+w9fjsQ9hVUUGIcCN6yqW2xFWT3GK30qUngEC6j8xDz9J6sQQxXVCqz7KQJuaywqCiNKlOAffvjAJQqklMe6OC0drXKUANmH0hSLcKRPLPfoyC+2d0ZcDlXWhJtzryWKWGr9M8xJZfKtVrtSq7z75kdisVbYaa2aJ46Gk3qV1XTNvBA/6Q0QxamZrEKDeTBEp9DUhSBP5SOeGPmhKYls6NCbFk77n9+5s//5By/fvnW7ZAdyl7Xs0eHk+Pj5/s4+yxQ6/G27PMxAdbcgiw0I2GQQrSV0mdBi1xxe3RFMRD7H7Cb0SOFGdUcw+IsC0SLewFRWtrUXRpB8NY8xcoijGSVReKCa2QOFwN4qBBCNnhmBfjxAu4+9WfQGsWHKJJkZNZOHOYejUMwbyQYaZnZlQYGrezm5wx4A/MBzQSc7n1dq1W6nx8I8SeXZmc1k+2d9bmKGeUdHp/XW1snxBZc8Mj24OD//wXe+jwG3jZ3NwQUTmuXde/fu3dndaG81qtWNrU0SHQ60ik+nj+hPKnTXaAeNhsN6tTkejLkmGZOplWrh/ffe7/R6F+9/CMEcu6jVGTIy+7f3fu7n/goFxykO+u+XH7z8P/2f/y/+4//wHzz6+NHJ+enh0ZOv/uzXd7YbmF2ySbhqgRqCytNqG3XFitSqLnxV8PWPOB8C1UDhtfl4keAMT3RZoUTP1O8l9AFHAFgPFCoPt7RSSNadxLJUFXsd3zrc5a8Yb+V/JX3zMAYZt+zT0lrFSbs8yCNBM//XMPLxgsgr1q/FCpEuZ8y8hV1/4Qmg8dPR8HYQFXp8AqGrQgrVAAKh2jo9gcZEkzSs3A0J2GgODkOECBkzaLUqyT9LOAkNcljysVD1YdEVAqYaP+o55Y+XBXkMvqZ3VBrMhAAQHI//KvJ1j4dG2EiHQ0b6nEXAxOScc4FfeJIbazjMSvWsIEMeXqxh5ok6jPY3GAvWZplOjN4Gs6J1FRBdLwhL40y7Y9TP+qtMLqueoDP3OhazqseM3Pn2whRAlOxLCKkj9rdF9N0Gx2GVK9wkELBa4okdAH153OuIClGSH8HYyQHv5fj0zs/iermktPwtGsivYk77WOWQh1BZO/IPakSOk20PH3306PHDB698aefWw9/4zd+sNnXnU7WRn44yXOj+27/1W83G/n/4f/j7KAipO2bJlmGUqLMZFg3L5fLXv/FFltE+9+CVf+t3fuudn76BjMg4US5jWKPU3miSEqr8/V6PS+O7fWkEMjZxOhjZEs4ByeqXDL/ocBhgfaYEnDamRRFmqiCFra067YfrOdFSHS0Z7DGlWGttVHq9QaVa5ZggB5KR7tkc6PVNs1atjktJOwy6SKUajOdMR5YjbjVGg3syQckXWVSMYDYj6U0DNnKBNhOYQDBT4dommdOZqizEYjUob8OUij3WmOwjqRyEpKqIg/EOEXCpnErPzcuWDJYScGWJeQUiaDVo/K/D5UgtxAjgwjIjiw/4qlXp7LkF3LZuEbIRVZ7jE+URR2BvJW3JCR30kKqW/IXP9AuQR3Ks67MrVCwxQ8sUT2FB92I43mSrAekfEQQaEYy47YriQ7CSXIMUqAlWDnv3WEY/t6ywQChpD6t/GIUCP7eEanWPRctyj2gsdKJ7fW+P2wBQ6eKwOUfAK2gmMEfU3g6koQ0iSZlsmBkTO7GwzD8T3ywBIPgNuVTmmG2k1ngMSKZdxVNFUo7JmGlF+NktCRyqcizTKlAxfJVI2yHk28yACoBQKx/DQvYFrDzxbWg1JcBHe7NKyhucEOLrzTAUr6UBlGGwqP4CkxcLbzKt1IinqFifpEBZHyUlx6tEwaMRzXaD/dNoMWfy8tmsJ+nJaIeEyfyh4muOI6oULuzQLYnfM0pmYuURJQqnOZiAJhl2tidiCsdGhIpK/4mqBihSJfnaKdds/pidAa6S63a62KukqNEFok7QFJkBcqkfxbugh2GvoEiVYKPxTNw1rVz6iE63127W0Raix0DW1hYAGzZSc5c0UKtVQDg+Z9JuBBoLKC5oBa0oJo82H0bOZiLx4N7n5uNZ/+ws16hLv79U3dlsN+494BJfVi3YVGBVAD16acHN2Hs0sVzCvXjDqj3qjlrR0P4Ukx4UcLj2DgVI5gaUhBawmfwaE4rsB3AHLzQymZkAB+eIJC0gWi7WCHSamSsyZlyjPhlynngw6DKvQaKmz2TtfzAY0VkRgR6L21TonOAMPRjNhBNNFNNwPChVqvDEqjUs4dpFDlRU0K6n+WxsZjoy1cCmweL8OMP86vD5+7dv3xsPztFynE4Gzw8O6hsbT58929rdgK3Mdlib5+wBa/wPvrxz9PjpV15/7c7dW+So10Oe72K/QamP2boUW3W6gMUGmXMt0WvSVN9748P3P3xz787tDz48oq1iCIjLgFn4pxfe3t66d+dBvVKXctNizpSAw84P7t/+9d/89X/+z/8Faz1v/PTdt9/5sN1svfTgASZB9/dv1Vvc7y6dulCMVHSfA+Dhdd9CVm5B2qNQykIFpvrJuImTfXXephMRwDymugI9CcqUnED0amiDAnAQByeGGqdiYiVSjd3chk0jeIDCE5e/FSWko1+DV/wbnggbkk2g8OdJQu0r4sKX4mLXwoLFAw+JceTtbkCsbwG7wZivxzX0gjTUqZc8AkqcxuAQap9K1P7iOyDwBP3tgPYWzzw6n9ox4MtLjZRD1JgKpUjtBtoBAuWRhaLJQ2mgAadIkaYGPadeiqeQGEV+8cFfeZGsTn12OoC0YDHJnBArGoBLSDNIXt6JAx6QG4gSE2J1r8mDU/7XPZf8L0NGJPEXFAFxGn+C3bEJSeIihuUEjwR5YLcFXUdUOq/Xhqc9HTE+nmQ66P/77nQ2k9RSzHI/ebjni2hM6qVDXwOaMBB0l4NjGP6eVJKm0/Dit2KlYuK02pVgWot9vW8K5BIAnwE/DvbGqB0cYnv65Hnn9OwvTv8csfiV115G41N2pGeLUm76/jtP+vPFn3/nTzBtx+2niGgohtKhs72MqLacDr/0+it/7bf+Otqfs3nn4Yfv1mvcf6RBlu001n4w1Y+aL4MW1uKGWAsaYM5CQnlhLvsV0gpBVYqzvDaKiDKuVkXdto8tIMyEltAvIi/UYBaNl70e4iAri4y1iB/g5HQhYeigYjWIHeehDIY467zBEtXOA6hvYGxmZOYqsYoET+sK6CcYgRiP2dmQZIeo5wIwDVaXakkFWewSWaFvSTEWNKFpBZ5692AQxLjpCQOYdSTEJ276sYjytD9H4+jTUF6rFNWqHg6yLdEQsVfTAFGmGYtoDwkJOGTEnP4lT8+c1QXVNHGBiDokwRluyrvPhTHlcqffpdR0LHvGgmMfyCpLp8wYmMxxtrHHwQBqKVsBLoogtXMxM8+o3sBIa57zGZQdNQqKkF1Qz6LuQTxjJf5oXMB+zl9IIs9rvXWIsVcOiTIVAxAg2GGKSWSQWOqDjXXKChkNT8iYFZjy6k/MLl/Bzztn8zeR0PwlHQIhfilc00F7UM3A38tfoRGJkEOHCoCIhkyM0zc/8lWVMX+BqiBCXKdPH/LSHoIqpPKkTx7RECMqADdehMIKikUQBuAYeUsqX0UXZIxu+NZfimWPYDyWCGfiBlJHpFIiXSCVbGA1oErWfazy8zIg0Bi9RioFKitAVcoOhDa912kAHEysqR4ASxoszDEGxBGgVr2RrxVQwgETFQAjUujQ7O7s66iJDvMQF2rEVzqSSgUFvjKCNoUDHQispIGb/oPzABgKQErG6IxyIdIDtcEpgvSPvqlapxvJbm5opxK9RFWyXLFRZ9U5zyEFrgseXPRHk8EsM6JKQoLsm+nCCquHpvqv1GdT6MHCFTATDv8OlyxpM7HRYQEuGs8Xh4MeKi2Qh/4MZ5oR8UlnOER21zaADsczkZgxqaMv5X4uOKNrEEDLMj0TDvZQ5rMRC/M0um6nz77EaDRjfsIKBZfs1htNqSfRQLiBcTDAJD/mGZgdSYGePDJ7kWlkFSSzdNys75dy9f5gwISk07s4OHi6Pdtj5R67Xs+4w4vObibOI6bT4e7du3vn3r2f+9lvlAqzIheicWNaroCuFJse7FuyT0uXjujP3I2TP+fn57UK9xXkmJdwWOLnvvH1P/vTP/vWt75VrjTYr7DjELqAmcJgxrez00YPiIkNdFEZYD4ThEGHuxz7ZI1OjCLvdztvvvmTjx6+fev2vf/Sb/9GtYbZBhoI5aZjzkn19Uqs942V/SqsqpL1rZ8Q22qQMKvyE2WVhOMUFvNNAtRagFREDxSgu1ZpXSZfMBEqQYmP+1vgmtt9XvxOx02jStJykvmUgwqi1u9JumsVySH5Th66YmWUJ0kGIP7zmfgk0AHuKpoVhBWI0Bn/Vv5q33zFH+9nrP/VYgRBIURR7UPMt8eiyWVSkwLd37svVaSYZvAPP4ofoBFNElbQKm0dPay5WtoCNMbFCE6e88YId1zMOJ+IzuhlKYm+G55IqYIdAz0+Frjp5MYxqRjVtdPsi3vdYkzPwCrTlhidJCQ4yOrtPjGiEDllaZ/1Ve2YdOrXo6w8Sk/kXum9rUI+lStBt0aERU2dN3gxKnBcje1+12TwMltTuJMzCQlVqcDIreBFitdBpQlJJf4JeVGsWP8cQzqua8itkfKpP4QnYLazCroRkO/S8tUvvvbk0TFLaOdnB616m5690x8+fP/jN3/63ne//50/++73y/n9fLaZK1ywJE/Dmk57lXrj9u7u7/6tf3ur3ag2Kqirlhkj2LpFDi02OVfGqNwfbEwHw07v3f6wh2Y4Mh7bAjIPz9CeQeGHK1EZwqUCxEBGI8JgBYayG60mWwL1epM+v1arMx+gCTA8oBvAOMHEg6t5UCdoNBosnrFyzFlkhs96s3XRw5qkRgpfHbTlfzVKm45oIlGtcUyN5RzVfeMFQRJbGbFNhGHshBKGVVKsQ45subj8ReTZLXGvxIrpqlhjpxPxpYsL6Osei+ICE5i0w7D+JF2PFzqBiSMBJJnoiUxiYw5oNe9aTrhilexoxZFE1Fn6Y/D2AYu8DuhLmMwX+z9MCEUcSLTKjggxZ+BncXs+L1fQvZ7kMyV2UdDXYUV3NB7UufRHZQr/VHpEhHsoGOjkhdY52Y6QepglJ5bDSfXy+p6Xqrq4VEoR0vdF8JgOh0O+sRXLrk692UQ4MIUxyoW5ma1usuqvuJSdCFbe9ITsWU7SbuveLDR5WT6BCTwxf589GEJjKRIgv6iuRFwa/kU00XiwRy79cDSz8XB8Gmb4EjnyEeOtgmkyYwHExofNrdvCGc8kKLLr5evQsOHHB1/jlCBNoV3ymLA7CJNS/OG1IbcxkKL0cGeLRXzxy3ARZ22HBJ7QFreYCy8Xh0pENPNfwNwGIIzFY2VRkxCoUEmEZArHotAo44VsRwUycU0L48iFfFmgyl7MRPKzFoowz/o3HcXW5hYnX5WeTTiRnjlEilXI806feTuq/lQ4ZGLEfZRPapWq5opMKWczTvNovmmHWmVzlkcSr36X86Z+uGfaOad5As2cyS01DrNE9YcfPr77819jpwlpGcpYfWeoZUGAGl2tluobpdPHnP+hcioz3IIntBNmGmwMaA6DIiIT1MEFdwjmy43BkyeHdIsctyWrkrxns3qjxq15xMotd7hepdIcoTBjsjh7IGyIYVGXmxC4VJHLd5ljar456i9yRdoca/DcuML1aFjcynMZL0fi2WYYDGQaq1QcoysFIjZjc8sW82qs6k8m/VqjxvxHOlGlEpuoFEGxMjw5e3an8frp+Qn3/pKB8fx4q711fMYhY65uzB8ePuGG9kq1POp3uHCMUzwcgC40lhho+tVf+eW9/V00MOE0OUUsxzoT3EbJD/LYq2HThiY/6A+5HpiJAcVKbXj88cMf//jH03meXrrR3GHv5KJ3XsQeaJUpQ2l/f4/tVQhsNNuUE1mDY6y/1JuNnTtbXPH++pdee/bk4OTkUEdDysXtzc0vf/nLXMPGxTSsOFFvVNUpBVWhUN2CpOFSh8r7ygMkZQBxPuYmlTYFmCBL+eG06m3wwqHH+h132ufKaWGAeUU3Uh3Co4per4YWBcxUC3QrYAPr05aQ+VmoAVqrJlbinTgCzAt+1M6IaS3U3QA7IY7PGCncgZvY4eErWSN/AWpDSzhoA2nQRXMwUfv6eEaKOn7PAW/a0W0YFa31WzSrP7bbyachF3wqSnSTsoYRp0A3BDMiS+Y0BB7TYzkeWiN7/v5Y0nImmENA6sfissgkmPi4M2KRr1UE93Y2w0kbBoyhFhrBvSwMbcQnBCn3DU7lzApRjMAphKF6XRPDG4cCBKcYFj+kFP3Cp8AuPZ7UJc+//Kfn199/eSx/+Zgh8wkXUpjEm7XniscqNKJxEP9K3glYRBB/QwCfwKaeKx6psKvOmI4VPyfGVtg9xGOsfK9iWPcJbcY8jS5brVONWi6fPz7snAzQkuE+r5c+f/v+vf3HDx//x//B/+lHP/7OZIrl6tZWe3vYwVofYgcqquwOlzfa26++9oVf/MY3vvSVV/q9i3K1OB0XLi7OWAljaEEhBMtxaIV++O4hCqzciopgwMVSbC1j0k72//Ls16M7W5QAztG0MVbexB90Sjc3N0vlKrYr0AtiUGSEY9WqUa/jYOBHsGWQ47r4s/H50fMj3w1gZOUksO73HI9J3VqLCYrWMalroMvAfjYrkNyfV9atNwxg5IWhnPUwRnSJylCgEw6SR6FEcwCkf1o0478wBFY7x67hu8hfY/kVj7VQoA3v5TYpWvFbQ3UtpkACLV94WMBVFGQPzAqJEqRQeyImek0T2Sx3CSU+BogSHoKQWInH8qw4TSmy8VIpY8mzWOHgtdm4KRSH/S66xyzEarlWCg8SqZAeWD1FE2A2RA4zScts/lCyiAtIaY12g+IjCcoRhYuNjc0vf+Wrb7zxhtY+Zxkui0Lh47x7wQkQuwxYFkOkL2RCG/yg5EzwMiZ7b5hkYuUIXIusWQVccgnOZAmTSPnwiGIDFJIQqaNRLoHQHiY4ZAEayLEYqLbjPHP2mlsBPJ64oQmQ8icDFkioFU9MEk/FUq0yaK9pnqzSSWoCihYULFMg9zKUKSQKDI9HTj6j99ovSPSdJE2RgV8ZDzyATMZ1xGUlm2AMvZDFNgoci1Ef8dNmWRRHxZ+1YtCx9Et8YtDoyAOetHew0k4l0A/pdnTi3+z5MMNEKahCNjnkev/+g84bb0MEnEec1UyA3mA26/X7rUbD5oc5mjyooVlzXXUo1KLa6Lyrdi/6lEURa8zhCyEXW5z8395qv/rK6/Vmnc1HJiGsmyPG4GKdWgeOZvRR7HNqqYKVehbaWfgGB/uE9D+Ea6tKNnkyM9RvOLA0n+bRXGLuONUdI7QciluzHx3A5Z5dTYj4g2Y4AQxspo2RffTg4QYwTAxY18iXOBSU4TTycoy+DXdiNFmhH49nFe4Qk3V/JgMTRHByQM8IRyg1NlRYV9duA4Z8mJ0w1Zixpj4oo3AvGwb5887g5Ohi+5bucHz29On5xfnx0eFFt07SWsrJmUlflt2xqZYdvP5zr7/04DXMN9erVdn2yWXZW8iX2e/NLcdLjoQ1cjVWW7AQDU9ZkeG/7CPNZseHB0z2X3nl9e98+7vvvX84nHBkAUVNDnhwNVqW3by7WH/b5ehXr7VRq9YKIzpzNRH+a4/o/LTTaNT+zt/5r58dd998+8e//8/+X/QSqESNZ8Nev8vJbwigp+axKhurmtfL+LX2G0rf/MQo+1bdvuZRNVl/VnAe1avSOkzylU4qkOcYAxZ9xCQSxNHDaqb5wtEY6gSvIVnLd0g64kgoWTkCBkfocLzt0/1iUhYlSenGjnWF+ZJLeIgeka+FEuaYlbJ9xM/EfwWvSXXMZAJmwZQa2bEX39ZBeXIJvwIWS0IERYe2dEPKlqLhdT4L7NIDZgfAocVCf+Rlc0c5LDzgD+H4WQjEgHOmGYlrEbm/+Ro9QKn+6SdGjb+mpaQ7ZT1E+SK2cUS73mYB1/sxhYgfoqX4LEFksysFyd+S0W98DEzpupdwxKB/ld8k9TUkrqHuYddDrIFf+RCdRuClN2vOdy8Du47+decHHIvDGyLleJ0c48HavXeX0V/PJ4snDnoxpCIl+B0kSR2H+ay6n+X0riF4UUE4Eq9FsWS9xt8Q1XeETIMtEOXab8ESgvAFbNAOLaWn3pY0dOarw9Hhcto+eXa4s5k7eHL29/+Df/DBex8xrtH2EAGrjdrTwceLjK7krFdLD+6+/Ld/93fqrY3O+XGnc9Zuc4ELtTTH4V+GPRZ2ON7FgM2O+dYe0iN2NivdzpTFH+4HYLGLwaY/7BCKNR6MY7MSRm1HcYjRAnUPlp3G4wEOhrlej8sWuAlorMWz5eLo+QlDL6M7qWxtbnaLvcmgWinmRuNHZ2dn3UFXqkRklLRt15uMmlhMkjI0hDzb2NhARJa4ADOQ5wSLtIo4oiEa3STUxJczVJ2KC043oA6uu3UFTUPmZl93wcmkrMVV2xlQaOB72CtIbgJOvNcc3qOlEcXgpCOMHgbEPQAkEG4d9rrEN41aYyiigHoMNsrR/8EIvQg0ctQvadUzorLf0IUIQpASJZwO3GAjDhZ7iKTDjrKyqsOaCD1KS+c0FhxfLsNFgPOZbSx/IH5g0cRObmv5myhCrJ5qWa7Umq0mI7eMhJhaNCvE8Hp7b+fnW81nB0+fH3JHbH4+3UBCGvQnA+YP2Tl6z6ZPPERerDDT4BSyCFWOVL4hEyvexYptYTF3DuZtJsSxHFs/KAYaj1RBEv4wQ9TaP6WOllNx1Gg14IdJHUxTNQnJ5KfUFeNSoILIEh4Ns8gQUbALDwoCatXIbLZAi2PvCMaqdJxgZDnNUy2udc/xI+QHSOJKaxxJTjmXeSX85I/DYhpP9Gkp6xcfC9c7Mkv+1z/ODas86PGfLfNn1Bcxm1wYccJSPCEbhtSDLE9hYmDeK9xSv6XUYBv/aGGWFYm/2hnwSaQ0fdjVyWgvbrbJKfHxaFpslLl4lyjc1YUULDvyi2mlWukNu1b9VMORFCkpVp0rJR0yLmS5JRdKUSHDHD4AOMUjSorpYyZn04D5hriRu4BKLSjkcxwVaDc36dK229ssTtMv0N/AYao5Wj7TURbDBEj+eVkYKo/GF9jTJw8IvVgcZjJgsxGKgjYFXtTVLrgVGOmcRWuWH8gjWZbKO9ef6MYw7PIsp5lno3m/VtjGnKb4IIEfUznQuNSRAETrruzz6MwDZHPKt8huG0pKdRnyISW23sbjWrUxyvbmg/PpWIen2TjhdG9u2VPfmMFu8uz4jHPQaOBUt7e2D549haTJHBsJ87POCdujJ++colaH3c9FR/cro9Ijy0nTTLNZqdc3bt+6t8k2br3J0sxk3EPJB4uotXEZdo5GA3IKW1nCn7qGko74zwa9Puv6qE+RCwx9DvvTN9784R98649Pj896k64GrOUmZpFmI+ZPk5cebDFnY4GphK2IQpWxggNg0IzCklYsuHb+zvbye5xVGGztNv6t23+VLv4P/sUfPD84+fN/+Z3zk4uf//mvY1sPyEz+MfVKnbA//CKbxa/gec1PaIOEOOylKns1BmDWBCxGaIxXodRI1hOHYeQ8PtGdAluBu02hFTB1CeU3YkueUX+ioJWmgOO47u1WdBTLQz11xQ4+jAus6uht2QpnCF2PwHzsnKdRlooVsLnPWjaj18CSIF3SwY//jkMHzWPS7HIw9Fj3qCohAEVHSlHHmHDWUfo7gBgHzEfFrdFE0CApPhGTx3fkvb7zI+xGg/XCiuXxAzEE+h5ssDIk6PQjtIqgv9UEIAVhVULJWkIxAHB9W95wkralKi+B8KUoL3wMxeqlWBE+RE1hiFwLIPZDvTEaRIr7807imCOAg9f9V98xKf9NYq17X/O1hucmdNfEe7GXI/LWF90e49NTluKfR01Th9swuR/OdOCLabscqphh7iUs1+JKUR3CPb10qh73Mvbw7YAS4GKU+HtDhOu8lXSIxg80q2+Sh1phNtfY3Mk+OeoOPsKeO6PF/+5///ffeuetOlvLWQ1Uvf7ZdD6s12pHhwdfevX1v/c//O8UcpVev8O60507d7nvlW1c9o5naM8iQ1elmNsoNOfTHqMdw9i0w0kzbnspsScupXJWjYiJLhHGQIuY3GZQ5d4uKi7CgkxTc2iMpUIWsxihGKtQMuF+eI7ocTkokglK+mgosZKHwYpGrXncmfQGHY7BdbE1xKisNizZw9qhsin+028QQfYxuY60Ik0jJFyECW1LIKsh4HELgPb61Yq1Aq61XhbXEO0NIet31vncwFn3Vkqhi1NNULqrInOQ+FYRRAgHcugYHjsTFZD6PEI9SgKg+B4KhCLTy0g7nHVFU1owL4lEFqqxxDqGECv5Egp7LMCYJpfFhhHI3Xk2diZwVOZYdahDCh46vsjW/diOI440LSg3uR8AVrFiyKKimMUcAMMsLCFy/gMaWBNlYoKIg+ijAlouuQmOStBoNp4fnmoDAZpy2fOL0wf37+I/GPardQ6aYzl2ina4iojh33MDgciYotGewBnPiuUDsCRjEUpZttIN4OKHI6ECQLB7Q5fWvPlAn4QVW3LECqyWja0qgkLVRknHP8WV2x4qFoF8Gmqht5bG5gzBanAEWS4ELTBBWEx9Brf8zSmS+LAAeDsz9WdEf1FokYyQEF0/QuVhSih4mOPGlxIL2FQCPAK1AiL7Grnx0K6ApWhvQEzOtohOSEja0kbKQ3cLIXg0ZneOrUKWkDHuOc9OVfQ0YDINQ7SWu6BtU51YXOe2X6RRZnqo8qEeJC/d0bvc2t4aPEObBZooBJ+Q4L0YjIasjqMXBHXWsN0gzwwYtVzRQ9GpFlCgSs8YSkY4gS6aWIjIF54fPtl49WUWI+iOOFRAt4Q2PKbtrcEVuFCEnEAI0bFrKWzI4uofMas/QlAGG7sE6jTQipmMq80q9//CKrLJhEJ05HMou9OnceNZHZM56MxQs23yCBikklVkfaR2ZHi0kgiltqMLNxp3uSShImO4TIYRwUdHzw9qDSyiouQ/7V5ASH4y4q4VzffZwGBzggnDhMu2Czo5wyo7Nkk5CmC5p+gQZnKo8FGQmCpCeQ8TPRhL4Er2u3dQ4bz1+Vdf5ipHrPiTcVb3UemxAma5BnXMEuUoNiLyU/dNa58JGo6NNp3w8r133zs/v7i1f4fzzx+89/CDxx+32i0Z8aeIOQWhR10Hyj9gIPMcF9LVD2WuPua6mCWdg052LZi07HEbwWzKGa78JDv5q7/5V1kq+sf/5J+MR0PsMvUH3c0mm0Iglm4nqat8lT2ref5Wxb30CEQVeP0B/NM8tAWH9Gp9bRTHnUoh5VQEbzbyVItMqHVclgNvOiEnMbale4nMGOZxL70vwV4K9c/QJ1wKC0lFBPEXKKM6QqvVxgxEv/Dr/iFCDEvwJA6xgA/Lhv0GelIAMXKAip9KwEvaCoSi989rYxqRMabRbIkR0+hUZ3dDPEVKgsI9AAmilcPSpgXSXZIDdWciT+H6DDM2A/cgy/Eqr7FSEQOa9Basa4PxqRwaMjkIijMnYAQIgGVDHw6AD5QITNEEoxMLqrLxPHVAaCHxpbixWifxApER5pN/FfP6R/ivS1fQVwLkIU6q0xBPxEaxVBTyNjyX3jHV9bV/B4phyS/el7GswtDoJTSnZWabeTvlSfi6Q5gEGB63qT+9k/KyEF+Dj+vxCpUlKB4HdD6bh4HzWvtwT2CDr/94XHPLIkFSZyIKftNr/+4d1v75UPSIyPjs9RgGyxb14tEHH6G/mi9z6WuvXn/5xz99g414RL5KhR1xrPKzhz2+e//2N7/5W606192jxImx7Gp/0B+P+iW0N3LFTueCzlqHg7EvzeE2RKX5pNlu1qqVnfEmZ4CL7Oxr7VikQwsLZZiAYLA3SXGg4ZqjwLKiwUoa9kEAY4N5ii0gtrY5PYxCESICq3ecTqbAEBG4cH4w6pxeHDI4A82owHG02XBIGiwPUpXUAE2i0aod4myOy6cyHCxG5jBmaDhHWEWnlwbEHIBBmyN5OvoaHnSEOGGMIGCNDEnCLM9kZthOCSvxxlJa/YGyxX/w2juTP9HHtY/I4hF5as3+uF/yiSOACau+0mBym4deJIg4DPd40y8hkWj+o9VFkzUYuq1/EEM9lhJJMCqUR8uxmAmRv1odogOqJsgWrI2yCs5ZXy4BYJYmyYM/VnhJEZX9WrW+yJ2xQZ/Ps3uTw6YKZztRkNB5STsiyZru8dHZ3q1ddmYk/LCEClUsXGaQumRDEHsgSlBLu+fUiU633O0PMSHIpRMbGw2kJ8ooMAqG4VTROJF6Ky/UpikmSphzsL6uX3mGxzK9cofCAUow1ukYc0BhPu5NBu3RcikaJqqt1FNVSsNEVMmIpCPsNCb94BMSFwWKw6+qpUDsbYQisALn0xd12h4nhNt5ADag8I1xUKay3CspPwlgx1uth19qBzhkNiZhEW0/ak2/Hx8g0navlaQwh6RxkK6sOEGUZrt42KQXvQuKkscgeal6KbUQd7YjZ+EYL0HYn0nenPNG3J9TNaTXbrt5tEIxGumNqiChHpsBbLgdU7H6XYTCCha6mOjrqInUhGQnn4pXKhYHQ01BmdSTgPacsO4+ZveAdqwZO6oxsAc5WFs0bFcWkbOpfMYS8pDv4am41Np89u7d27VSneq7pWsK2cPiCgIs4itRLPVg5woxVesOHOjtdDEBhul6jvhy9zjqLDIWqpPGaKPY9oN2w7gveGJ2BercasgOPiIqJjxZ6xiO+pUyajYDuMUmJ7fzdrF8PJv3B9gowwImCvwI90v6N1T8B/0RfGWG0Ot2aVkyAKqs6niNJs5ceoCS5PR8MhySIMZ5WASZYZ0NVk7JGvMA5jUcEmyL/bkuGyiyUaTZjrbOuC0Nw/qYSkPwvnPrq2jabO/n9/Z26EvV+pm9c5dCNjc90aWH1AP4gNjOmdyLCzZoy9R8pUBidDSU2oCj+WyJLEeTYZXrG1vN737vx3/wh39UqtR73T6nsFjbn06HDOY6aZHhqM/klZc/x2yNrgTTpaUSKp0LmSstYN60y8SphgmmXKbbO2W2xR5ZVbfEXGBj6Jd+8RcGw+E/+2e/f/DskGsof+XXNzSXsgoq6ctrIfn1J9Q/VUarhNGfs4iQ7uvo0U9cugzo0dYi8+FQXtU9lvyuPAbpySZ4HEjNU6HeTB2F2oB8VSWF2mOrcpufeiUHEFSQLgyHoQrwQfeB8wP42jvikY8/aTlEW8SSEJSm8PMJHbREahrlWjW0os9pXAbNCDAbXcHbAx076drav9IlGyDEYcCSOsCq0uKtjAVZ6MByZpVJBDh8xJYkHZNMAkQhuEAk6ukgJU1ZLhJ6DdbPncY9AcXSfx71ZMZrZufPzEff5rj00uDiAb4DgFs0R09BiwpHJxwC5isUcPxSaipbsIWUFKJHyKLbENmHXuat4BVp5m2EGwFKx5+VK/rEeIptKC0lhfrXCm7d9eLQddjU1+Voq29c11CXeDngpU8Qy9+5uaLYM6ImsvJL0XDJmeBMHM4TT/HqO4KpblCbYsFH70vYw6ejuT7MfYl/E1DK/8WpGCYHIU6AXY+y/vUiglJhYrCIMPnGG4RyjiQ9fvr0ablaRqAulqv9cZeemvV3LPNzrRM3s9y+u/Nbf/3XSpn6z3zpi+12G7Xd4qTIIlKr2TznBO7p2ebmVqXM2d/s0dFz7DwgD2J2WlvGE+nP5EpFbthhFG9U6ySPyg9B4Ncgv+Dievp5LhGbF7hcXkfruJtmyBFktR+tGGHWgzGdHXZpDEO6ELJ4xhE5zQkYHZm/LLCAkR9qadmKUlIjo4WyKCmCPPJhJ1xZkzODelpMFB8YYakAIODSX10nTHRkX6IbexCIJYHxX8SYPBcYLzaGpqq2aZ/yMugXFk4ENYyK4NDRWz48QklA8FU+oHMNxnJnkIg3gKL2I9GKWOgDobpUKCAj6J4BCDdvw8tL6RlPUh70xkKhfRNd/yo+8qmVNn6wge5jNts2YEdemerUBLJLjbXAer2GnELJ8B+5iJVbi4zNQUQALeKimcwpw/EYImS9RwrQHFXMFxdofSDMULIMRdqQmaHRgZY4R0IbNcyrm3FxbEcRHytCtbLmAVAj8vmzLt0YlLCFYAWGJ2FW4pf4AGGwKnqxi5dzU8gRNGXJUXsffLAPoMmjlT6TFGyWIv9ZMo5BiREL0pSM4hsKefsjTq/g5RJASE4gfK49WgYRJsutuflSgeimZOLp3DQ/FkeQRscahvQHFKU3S9JBSiTE92V+7eFAGm+S4DEpgbz7E+rrWl0PQYYnyYjIAzUszL/08ku40AlBx69epULOUH4x6Y3Vbm28KBLsQVTUwXHkS9QDWc9m5sDiQx69IHqYXqs9GB5T91CZsVh0TDmmo5gT41JvrdBLMJVeDfVfdNtEWKSJScY60kHagbBsvl6ubtabnXMM2Q527tyldjEtZZNToi3rCJx2ZqMlz2miBYpG1TKmh9kCnaDUxpzFlOaLTG9hE10l0jfA9GforaHEwooJXVme29DnzBowm9Ov1Zp0LILh6MJ4Vq1VaFAnRyetNlcOc4ic3cjyweERXewYy/2aXbB+PyD7VH5TkdKxAKsHuh4RjRlmoGp9wyG7qfBHJ+MlZXNRO5jZpaAFZ0tYNdIWB7bOOETdbjRaL33+JaYZe7f2mTnUS/fZWUUliTPB1G2dzGUPolhqNDZ6nDk471JqxgpfBsGyag2eq6aIr7ROREZKTHtjDz98+Pjxs5c//7nd23tvvvFmpzdiCwV+0y/T61rXwe19+f3dnd2dLVb9+5THktPAtXIV0ZAsLpgVFEqb9Lq1crtcrHOx4OnZ8a1bW5hlokA5/PDrv/brR0dH3/ved996+w1M3P7qr/6aqr5KWRUH1ljDDbUw/KhO25M4osfV3yttJxXHnKST8rqKIPgAo7qmJ0SLv0rBU0kajjdwxSDAwxTRk7LOzD2FSXwXjD3+u4oRvD/Dj/VEap6BTqPSPleJWCrudwnztSk7UZcg46cH8k4cSjmJspYKH0lA4nBESSl427apixDFGICvoSIML9WRkJZNuRzcarKFJ9E9EXsrYcOmQ8DhCX58xURU8aJbQAlETFAEO69XOFIREqeS4kOU8vCiN6GjHwmP2Y+P/kaTU2apeZrxJl2f/3lPLVoyxUf2sxbB/J8I4Xxb7sQ+vT7+9T5J4hFt+ka9QLoFxRV0I1Sx1Lr1g/1alodO9U5ZOopRHb/xRhA3Pqumsw5CTEOhxmWsx4FlDwcKXusxki+PGhGs0SaYgMNm7U6f2fIP0d3Hz4dcc54hSSTt8Djycdz27fyR5ypYX3HPQe7Uo+5SgPzxX3g0quDFj2rN8umjRz/5wU+KNZ27BeLjj1gnsDU6RlxMT3Sfv/7Sz//13/gdIpyes06DGuus27l4fvBsb+92tdYE1dnpeT43azS3vvDFr9Tq9WePH/c63SHmPUZd1qGQK2X7cSF10nKxxvCBiM+C38XZBVvarLppTzmz7HZ79O3cHs+O/HIAVglBDEjIlejU6gwcxihZckanVrbrUBaQAkCVGcuwt5wtKrqQLMdxYa1lklPZziLHrB2SdonxnV/GOtJCxMNwB/gRaCXyolus9SoAWTUHp7YDiMnyv+2e2xkAqx8kJ5xBCz8UiRLB3zkbHehti9FrT/QAWk46YpOBzG2AKhEhI2VRZV/yEISS0ApuiCx4nAt1U0QDhJ0MnJrRSHrgoCA5wnoPiaCykorlVBtOQyIJyY47g8akJK7p0mlXkDGHQvWFaxm6x8dHbO8grGu5ET3pibYIEMtRXEa4mXH2cDFB+kCo06xBSWj3gLgjNBUQsrAHxZQhr00c7LWi2sV6rRQ/lkuO/KKYSVJLbMJKCSJ/enK6u9WkB8YoOneXSkIpSbMCgkSVHjHEBn/74mVr/yp0Hmzb8xt2A/gWcHyie6YdAy9HYw3lbTxCCGSNF9Ef9fQKShI16gS5KHJ9koxXQh08Ye+KEybAO1dVS1UGISEhNjr0Cl27fAQRHwUZjHtYfHkx2xSURydCmPPZeKOqCBZKmVpTPPDkHDKNTYmYbR8vc2gTzJq1H77jw6kSEtT+FRVCC8lUKTVUT1jsRiZGKDf4MOyprsX4xD02txIhRYckWGf9S5ipL8mwpjaTQBuKQiSxuE2Jkh3VV6FjojgcTJqNMoIyAifiNgrrrCGgRMSt5BieZ7spu+A8BvXiVFyYV9gYxFYPJSJPGYwCI0prOuZvjZlEOZVL0Bbfi8WFMprLDzoX1WW+Vim22xvM5TiKSigVnuWByXh4fnpBzUQAhcKL846lO9bUALU3atZ0wsqGTjIbzVQNtgfgL0G9AVWavo6Ra7nR2uf6ANojF6ZjYohMagm/UmbBn2t7R/Ps+KI3Go5YtD/pdLgXBctmaF02q20uNxwOSpphLrnkRCuo0LWYsQ/GUdoxVtG0nMGF0zls77JYzvaJbKPBW+7bqNer2xuVvds71XrzVYw419ucvcZ+Gi0L3SOgmMmitTecfkwNZsLQbGG3R6uzdpYiT7Nm1wUwZkKkSwY55stdDVLEWqKmRcUIRUgcMs55nlt3dr7/g+9/+Oij814/g7le2gnDiZWzSTLsx/Y2Go3P3/s6FkIzyyOmJWg36Vwx1lq534AMUtKqBpiL6Far3GI2Ozp8tvjiK7aTo7l3ppz75t/65qPHBw8/fvjOm+/d2n/w8ufva8xiP1L16cqTeFrDUIXTerBVTn4UJwlQ3PBx3UlCwwR7HEoRV5HlufYYsPsYlOO1XtxjGUBITXA4hTsVT17UpHIIdWT2oWYlBxFwxSgr+c3x8E4/gHFs5Y6nREAIlt2/BN5gbsKzplvhsa8kkd5hCGcVSJHHiUxo1c5DpIGWwwwSABYbgPMOHc9kWpR0mUaeofOuzBDTJVkUqqhSwb0CC+cB8CCTobCVEqdHgMqWtF8KfCqCACO1imVfNlrSwDxAhagQw2o/6oTlo8eIcKf89Kli8nIKUNbLhegOapDRGUIkcdhDLEUMkeXltdDh0mR46ilAi3/pdSlhPj8hwqX4n/kT9JfSvC7JS0TET8Xkz4v1E5L2VELMiOBSnOu9V/SFcHngNP/ro6zjXSFI+zuGF8T3aC8ASGMTNTeC3hiwhkEfDum49LYqKn/aAcMkVjP6/fHhc4l3CNUIfCzfE4dxB0X8e3du/3v/tf/mre1GOTd/+NH7d+8+uLW3z/otWp6s785nz4+PDyv1GtL/ZmsLbZxHj58unzz6+OHh00cPK5XC7/1X/73v/ul30fsvF8rHTw/Qr5WNn8lie2cTgZvk2hubve4FYzDDCbsQrEZhPA5pD3FfojhjF4NSHuGAkQtDMSOEBkxDkCdWkdlAZwBDyGy22s0NrrY5rDVrJ6dniGdayFQjtJZHc7ZxVPsBLCqDj8VGLfXBCY12GNewg5Wot7P8zIoa0wNTIqYAuGAri2lC2/hGzk1q9nrRrPxT3Adk/Qkeq6hhAHCPFA6cUO7gKi0VoQrLOhX1ax6UYBcMEgpA6hmlp4OCgR4MnWwgyqiTjXFWUQ2zOET3EvozumBXm4A90iMilrSX2cKfTLl/DTGcYhr2J2h8wUQmabKVYtMMdht0qVuO+sO0iq0bqMXePyiYPxjBmmfhLUOhcBMpjekb5QscGlmUiYQLZA5qVZEKyZ0T2CPn5qRsGdmF/kCTM2Q7scCyImaIbGdKYIV31cqSPau8hvAYkASDBLd1ryGOc4IkoIc7U6l/pMeKLKSiiUK2mBbTamw2ErHaL4gs4evSDn4O7x9OWxKQOIRGI6F4ZTByi0Z9IPrjXtsBcJyrt8WxT0O5+lT0gHIFHVwEaP6jbhem2lsE4CdRS148XoNAqHKKjxOaIBbfTLWdPUPwYGWr3ztqb24Kp7DwSzkyS7TWJ/RUVrVB0zwbVjMVZEjQI2QDrVujZCMfBRX0EDn/o3UxugUSp+jt1Hu2Pxyog1AlFIUAeDKikf9WwUS85UJZWC7rtQbmwvb3t9DlOT09Q50He2Lw9uL8QlZnlgtMDHFogSrKzG84RG9FC+tmNKDIEjyrA5KnWfyfaCOLkwBMcweDMUvs2QWqSnRgbKKOqCjskiFzY5aAHE9mIxoTh2bob2Q/hxtQyDdTLnYesIiowzDIz3Rb3J6ArSHlnheisrR9FkwA2NAjO6xo4A/DmNLnm7U67ZC6yFGZ3d3d/Tu3tra27n3uDkmYbKWtAZKgxyM5pkmcv0BvCF8pZeiBHRSFeAYpWGegtKn2ZFDae7jpS9jLGHMAgLmnyhZaMVpEazh9fqRrzfKLs7NOh/FDq/laZXCB3ib5uZ39HQw6IfqjAsqRL/oHhhj2FthCwyj01naLjrff7UEhnTFWUw6entRqJdUU/qFTxnXRzLNmmJAq/63f/eZ/8n/8T0n/Jz/9i/3bW8zLpScqQ1LKA8wKDx/JE9wEksD1AQ67hiGJHhwWPbhvBExjj+R4uorpKHj7hyohj72VU3cJLGRmHZu+VK/T0QxB6pXCKN+QVApAznW0IdBArUcVId56YrybIuDvVF+fDtE9wLFRsjjsLRI0ltpoKzDN2yM4tR0gfeqRfyxapRdyb3VWkPiZtwFfeSk5Q0LOwOTAtnsPYoXocSLdvfYWYiJRA9eBFMEig4PpLHlBz8nRaJxMEEdLz7Ktbp5GDgB8CDef+kge549hwpvegJev6Bt4ArfucAzZtVnaOkSgds0ze9WKzlr4v5YPY9IlTBOfF6Z8Hcr9E3aIP/bfOXBlfT0VH2cSTd4e9ZKvV5VLkA6zojLUQkfAO3Gs4Vcaq4eggMBrt0IUb+W/gr3qWs3LX5CEUb2yAHAJi6fuyaWQXD0D4D3HTCsBYedBjUJTcLpilofZaP7RD/70u9/9kRLgm0DssqMJjM2H7O291iv3bu1ttbAOUbroXHR7F/TkZ+dnLBftsvh/5zYG2uiL84USy+y7t2/9yf/5H/5nf/qd/nDMOVCsxHz4+JBTcdt7LQ4RtND3r7XBMBnNzy8uWEJmzLh7b3J6dsqAu7G5wSJbr4M/2+WLQW/AdjkG+2kMtJgZxrDRwcVMuERc1qAXLAdyOw7DFOfdWOtiowGCB70uAoT2r1m5N9nCBH1ypAFRgxPXi2J1hDETBXQse+Bj4w26K7a0JiCwI/WZRMFQyDk/Fs9Yl42sDoxXq00XiX+EOpEOWLmFIQAEaP+Uv+H3Hg9K7J9FxEmnx/eqZsU0PBprxiKFP6Fg+Nb6Oqybsha5oEwkGwmTp2A4kw9D7IEWX8l6toD2ZEgYZk9ZF0YtWGZ/WAhFhhOH2aBnwtZkgRYRXzojLJPnCxxnxLAgGYO1aD4g5WCVZD6rYlTUSKDi6GZTSDUtYlSBp/VaqVZtcvSP4iB9ZLBhdtLvzTZaTUSLSrE6HTWXk33dvSDOeL7FOmUsctQzZVlFE4p9Eh77Chlxt3n7q2B27sme4MiOHOKyIaRVQH97Y4s9JkQ9JgAIKyyUqn8OrIbljtPTFFJhiKn6fRFadydcUZjcsPaGOMYphRWUudMvx+aYHKP2IrRDwpdKkwSYRYvBIgaNEIuBN15QpC/gLR+GxT7kF4pWGNJPOLuidqVY/BMK6tEmOzh0FaBV66ERLnUaXlDOJfsI2BU1/vmkmtaIrMrJIJW7JpFIiKxXc3bIUoHb7BRp9ZdMwGxiT8ZzFH6k0CPdK5btaYzZSg0jPBwSZTeG6+c4aNuHj7klB4dgAWTp7nAd3pX2HkkiW0AnSdt8WNxgpRzrAgPly9YdmVLcf3D7c/fvIj2ecp11v3N8elHqdJGnqdrct8WMlykWkq66EZmnZG6irDI1pUbTN2J7BxLYvaSD4z4vbs2l8mMa6PTiHJPHMASh/+CIExH0KXQ/GTbGYIn6U7VSbaeAWAqHmSYuThfTXsgt9HANRiE/z5WFg/BKOVstcvaGhjVcZEaVUqvSyKMnQ8qt1k5rq1qvtZo1NhjgMJnPNVG+Rw+bbo2ZObNr5BdS5agFAv0M46rZIucE8pQqO3gLW4aX+R2ZTpJaG9BcolLjnl8ROt2UQdTMEXxGqYnJzHg5LHC8ajrpd7uo/L3/3vuT+eL50fHR8zPm6PTYTGBUKJj9Z9Kcy2+06pvNNpeCMa8pls9ZVIL/qBv55JlLAHQgaMkFL5zm0kZHsVLZ2v35/9v/4x9hAJoyQp+KBoepVfJAvXnlc6/+wte/9u0//c6jj57+8R/8+e/87b/JuowqPMGUrP/Kvf4oWFI1EAZ2PailgS67IROcGhJVi2/04NUvBE2Eu44kBbmeXPhyepQmBR6EemzVG078stwWnHrkbW2XwjLMpE8J0LTTj0gSlIgU5huekAULdXf6jbdjwGH+ymqCjUTXsfKZBCYh7pO8kd8Uy0Bd/1788izgLzjjAPTLXwEhFxbCx+S+ggpPDSV4DJU4ABxthhjacAoEC5uSQw9APn7SAI+Qoqdrb/kQP1CDtUOLageGFFGh9ghddEQv/BZlkqZJyCvFGJWVngCpH6smotMeK0xc9hsLXzlO4ggySdTieJ6uFLnCLgE6+JU3UI40EJEAJNEvByQQfynH9dicCiH0ZK+HujFBwAO5VtEdW/C5KdIqjkP492VfC3N8ONOOK3itMIPvi9MOSSVVKaK1imXVIR0/TVLKP+W8QsqaR4ifhseNL0/acy1SkldB0KdycSZHcy2WBk+tpLHwM//ow3d/8tM3MEKRRyGfAaqwZN2N4eR/9D/5e68++KvnhwdVDrNNhls7ze3S9tkptvDm2P85Pn2O1MdYy9IcGv+IdP/o//p/376z9e7Dj7FEjbk6Vn7Hg9l773+AGbrMe2xXI9whvnO9TKZWbzJwMwpu7WzsPdg9PDzoDYbPjw6ajWb/orOzu1tntlEqsb+PuAA5550ee9icT6iihsGRgClLdD3sSLNshLSA6SGNo/kyPesQi9EYnCGP6m5NWrKmoRaotUx2EthqIJv6Dw9UWogKQfOY4UtjJv2Gtgj4pRXnUGPn+JwElfSjPiEUStp7rTDWYxjiUFoiz1u9xBWFQC0u69wSvIbfhofrCzni9woATqKTL0jTKUVUpNCcwegI84CkisQogWalbfnQt7n1IwdDkQZyKgnrelz7hQIM8yU8dSLWuk90c0hL6650c7w1YZIdEpJkymaWNJluQYsmAygBIUjpVDY3vOGHhEDhUYGmCCLFVmtDxyozEy0+ApLHvuHk+OQY7YuT0z6XFnGzM0unhTIcUg6onO4I2SCOka9MGED0ELA9CQOiR/KrAUKcCxCWgnYbQAHp0o1AM5DqlUFxDBFW0wI9EVzFE9NM+RtMfFkK8cN/hX7d59ovwVgPE0NNLGCF3bJLyprGW61xhE4JsayCWUGuJRQoSZK28vdKZ0WlubYGTRoOVV4csITEHTV1fYpZSiwEJaiMQgUApltzKXlQYvuFCR7XuqF1hzYgy8khvmq/OGfSHakCCKuxEMX9UrA4O2OmwBERdgxn80qphsza3tzuDQbTKfN82f0kfcVCHl9wpnbQRovMpnHy0vqA+iYxQI9qi7KA2Ksap7SH496oT6/CheCNQQ4NtwEthY4ACjX/KBVlYMco1GI755jLtinKovdcuvgI0kzCOKkyGg8BoNqzmcmcgUasVX12KRdchKKkpZRH8nQ+JtFBEXRBO6I3zJImEX+L+c7WRrNVQ7ivcEyCk8D5RTHHHRsoNzbZhMxlqtVGrtnaKlVzTAOqNWZItWWO4+k0PZ3fZcaCLlJrgysaCSpCA7tVKg0xicMSrGFom7MotUAc4r3S14ab7uBTd2i9HhsRrKTQqeqwAaDGZe0dsMcis785UVgoHp+e3b53/8+//e3D4yN2aMBDH6PpkhoK7xkbESj90//IhhJTQPQ5ZYSB9QAe7jIbnZwcofg3HOgIkFb62SrpD588PpxyjwwmJHJ5eMsSAdMSZnYcWGBNBu3/hw8fPnn65PD5Y+yTokbqrLQivuFlFUAv4wU5ilVC8BbIr3ytHnvJKIgnhEagtKdVXDUAi5UCdiB1jzxCm6BxYL7d1wFT0eX0pHxAMACHTd6JXxLP0XzyW01R+Ikosr2LD9Hkcd3j1FwXYn6eFZzODJCCKEnF/PXpyBNc9qkU1RiogxFOFVL/DAMhSQQAnN5IZohrkyWHiqkYbuFIP5Zny7T2mHjA5tEsuQQ0iWyBDmEqQATwHw9pU4kuVljxCBZ7PD6JWHxFM+yCgRshGxGbwQDisGldbTSV5YulPIJhTYR09J/8NvICu2Nq67E+LUazBWuWcNbjr3+BbZk+U5/sKngygQRBrce77iuB8rgC+TSxtPcST77LmTyKvL5q7ikEpNQCo3aJXqB7JRXBOoEw11xpBALkCJL3WlJqSwYS8K8Be4jgk8wlDstm6ivBeskBtU6C/GMiIZW0D+51CoXbKjy/RCw84aZdBCx1cpKfECW0ePbTn771w+//+Pj4lHVW6iyR6G9/7dd+eX/jbi1fGQw/3L5Tb2/c+fjDDz/68KO9vT2inJ+dPPjc/cGge3p88vnXXzs+5CDAR5Vmm3Ng//D/8k8ZqRhQxrrhBcP/SJCY/MfONctoLGKyqsRieue0f+qbgIcXFx8+PeSuIMYA1twxLHR80ZlkcvVeH8PQrElNKhkOj3KxD7Y5sP/JPAQSZaeDJTEUxlkbnTM6kq0s9wFPFx0NtxqGVlYavXhM1keyRN8fm/RV1iLzLM9x0pehkl/Grun2dLRRrg7ZdM6j8soWwbyRmTcx7ofsJyveatleV3DwAQ+ZHaz0yMW7+KSc0cvLTswnUD3DYrqDcbx5/pnk7OmOpC6z0EIaSTEnkeUIvqIjVaFCAIit/ko61wgMj0YN6UTPZXcvM9sWycXnisoDChtnvN+yzzAGKrrSZ/inrNj157Zm1AeYB7BsD42oSCGuoCyMYg/okQ041Cs0TAzQCiZ3SDoICphpBXy8oCdENjjnDjHWd02exuwhBlGYi4qrTBxYYkdPAiJBvFiyCYAQ1kR1vNcbcQXszlaTbYRs6TxbPCMcXmkel0POkOy7ykzkCF7g5E12YynEX4O+/uXcEAdVPoq61LVliFLIPpy5ZHKDJ9LVcryPgMzN2SSR1Q1h5H6cpLSGfE3n3riq8lW8CObutI+HQAcw+BssdU8xqMgkzDCGJ6XML2K6xzVIcgw1DqmYlx/DuRbBIYRXCRCVNzKsZmYq/cI571xuj3BrRJaKJaDvVDWM6Qq5/1HQNEo+aEVI8EjEaNwMF2eZ5UAz8DyncVRpmMhprshCMCu+KLhoTYJCxhh/CZUz7CFR1miNU6PgP8aj0NspDHLMCZSOFbDeCMIcQKFuICtCsWR9kqb2Ovc0nkok16xJAgfTSGzO1Fg7r7fPT0/OL460xwMAZ2lokFkmIUMlZ7MYHKCimtN1TKYoJeZYeugPR5pILIf0HjYGsfIgenzeaISBBh+w+DRkBAvzOTpYYzUQthhRLk1a27VSocmceG93t9lqiGH6j71O1jWq2OvkZlxs/nATAv8ludv1Gpo+awLNkgf5xYiZbZpgVlPtHcV62TjmKjWKlLZjfRfivmZZdMWamqnWQh6tFaUg7S+RSeU4ywXtFXT5KL7F/FRkjjfI+WR5StLSZposuO3xow8/6I7GnDJ+fPBczEWviIxxPxlthCxnMputzf3dPewOqXXTq2EAlaNZ7OLOuLZ5DupymVlHtZBrFgp9BhRikyG2nDHLyh2UWGOWPiDdiGxD082AHgfXPmTv3L3z0UcfZ8vaq1EV1aPsWAOxr+S1kq8I5lF5GJgqhz3Ud3fqHT3jb/RwO/2c1lNsb0IhcgIpeYNcY3fRvFL+7tSb8fdxaJwRSQj0UEiRv7oeGqCw+eMnJyd3rUobudChBxCBOtQnvi3nHtEzFiNac/7E6NcBJBiM/4aVLNgTEopMdTrTb6Ac1CBl0V+FA7wBOST8ZL/FZDmKXyFe0LzhE0PvQKFK1yayAWGkSkHuBtQi2vCCp7HfsGmgIMlkJ0Ff9t9AdCOyTGp4pfGUFG4lgcOxW6Vwt8IiOG494cc/gk/CcQ+0Yo+0eoVOgX8qp9MNqJP0qeK8EOiT8VzNWEC4Cli5XphWYHiE8byk3zHk+t8bSfXkHVHgzDpF3vblt/LHpeLRj6qYB9yYxIqiBEQOj+VvFYlhW8FGl4fcEBiBwm/Eb3Hih4U5lhR4KjRmIACyAJZaxEY9HMMqh0dHf/pnfzYesb5VoQtHeXVrc+Pv/rf/zm/8xm816xvj6RDr7FwgX6yUXv7858+7xyzS7+/vI769/dYH2HXASNyzj58w+Lz7xpt/8cYHkwU79XYKT/o0GsnYL2ZRjTbE+MEGuuRypEkGClq3FoQYcCeTLnr8jKMMaPPOcIDNyQE36WSzF+c9bEp+4YtfzOX3uhcddM2r1TraqJTQZDiX8dBMnvshkQ841FsplC/6XRaTBmcn0iugHDWAa3gyOZEuRMo/iLO0X+YaDHLGFhWT97xEAjOkIgpI4uElgRQM7N8zJQnlCrgVrboB6ycC79cKQki8ZL1/iKXsvYZ1KRKApE/C7rxyzgOBXnkcf8BLgNVG/1wrUnkZrBHHNoVokFhFZhnUQcp+C19kQYuQCbTiWTVXXXEE8grdh4Q91X0kMxP8BFqcTzKlGibFIVkSksqR47loNSD2M7dj4PeVY9BR1rrNQdcC8IGMBwQRWU+UuM8yf76ClCURE7kqi7ERlj+5Ca6K8dbFuY5v8qlIi1lvgDJC987tLSRSVO6RpTSfVA6hz3IQSFY+kodQuddLJwm9zuEsWENCdFC4FwIslYd/krQsRZUJYaEwUhyM2EWeuw3MnJfAPDz9jpHjr0dIIVD9sGkzIRL91UdZOYYYynkSyf0cfwiPXvJ0tPHtYMoW3BViq/98SBqnCVhd5zNE9EQcnViRsFxe4IBZgOCgxaMexiwRIa/Zbh8eHnITACHCiy0+XRMGIHwlAWmts97rS9r0C9DQ76MPgzZbhdum0FzhxE+91kZ/kDNEFAdyoZaudSJAODEi1qhVqT/QIBvETBJMphKxosaat24IUR9Anez0zmZcplVoZTOV8eQCTGSEuYoaEyBYJ1Ohg5/dQNqTxOej5xeIo2bASn0pyRNFalFMTbThwcPmpM5QqWfTzQFAUJ+pusKDlWQVkA3yyMScWtrc2GhvNMvoRHEuVveMwRPpO9Vq1a9/42scVEAIlqQvYdcmNGRM/RQHJGgIGObiSnVZSeK2OgiuMo8ocH+B2KscWF5UDNitghdmU4i1+GwJltE3QpfyAnvINbmRXtJ8fnJ0TEw0zSSQq+BJl8sFMNSJLdN+c2MDdN///vfy5eoIy6ggVcvXw/YgX2DY2trkYgFpZEn+V46ZUGhJaMSlkLpYg/oA75qbtcHwjKMLqsuquSSlROkM7ZyAYtGTkAAGhXQuCDpmi/55hw4HHUKGqlalqqpqbZFc3PhYQ1El8GoeKrvagOrG+uOBsX0oTDARjl8A4td6zMuwq9CQIHl0GPWrqixCJAbxFp/1BBirIgZlvZ2l6gCkrormEYXhZmJihOt/Le3rgz6lb8QQSXfGQJoxOnLbkFnO7WXZNT9F86yE9G4sSrglXqyyGgsuJESg0aIahEtIna3wSnMD47TCTAaIJQiIL6YoeSdGifiXOKweCF1AZ7YHmHa150wxlIpF0Yc+wwuH6a/rTt9Atko8SSbMbEpmjTX6K9STtVZnyITwUzyevL8/ARygT8Aczx68GJGQMCe+CuS5VHCSDvmy1fo0Zg+8hhrnruFdO1GeSsl13MPZACchSSuCJTsS5hEqDFAqB9ZBn3g0az6puMGi7ZCagqK4RTVAoz+LjaCIPuYu5RGD5OUoI536iu4IxS+AqaRTAYnzGuwKW/NO8SuJt3Ko6lu1Iqc4+GM0mY0nB89OfvKTH7PEdHh0OLyoMu5OF0cs/H/lq3/ld7/5zd/5m7/F5VzPDj/ev3Xr/oO9g8ODk+Onk3YbLe18vvvjn755985+c6PZ6Xd2bu0//OARy2OvvPbqH37rWyzQVWstdga0lsQImC1VG1X2pe0M2QUGPTLloez9sAbEcM96sgR1WTWBMMhD1WbeH2kgpuOvleubhaPDwzfe+eDjJ4+KmNWbzm7dvt1qVUFQa7P7q10MdIa5aBMnJuOYbFwgMaDmakOzr0bBLBhg6BEfZb2+UJJlEmYfOtbJOqUGZlbCWA1glRtJAigtdzN2cx5B52C5I0J6QYjXoWOhA1+VXdAjN56rZKxA1A1RuAYmTy9ova3K6UeToNwpHRR3ZE51x84Bh6TVQ9nKqKFTfOJa7TVUMbZ5B0wGqQFDOVAEj8SYPs4WuxyjW2Y2ZE2x8BwuWP23GHo5hY5Z36oq9k9rKroLGR+bBCwncAiVhlKN2Z30uTWZkpjFWUaTFLR0qJmVqpcmAzCRgu1KW0IEIZz0xtj0Hs9KRVS3EVbYtKmw4AdzmRKw31LgZh/d6gruCjoAjfoORTDPdMfUlRIm0sGqPRvWN0lJhIMW+U9lbAx3L8u8coVneCyP2l8lu7Kus/Y4A4irbgEh1CRs8cUDUFzDS6I/OlDgJG+kahr8ViaiZBIREuW6Z8VdD3XC/O2pXBtRnmAXnOWPkguYbEjTpM5jp9Nc5dqiCeJFjwXr5ZhVrCSqP71NJqHC88AW5EXpwRsVAuBBujbmOysSJIrtqaoFwUDu3KUTmE+b7UlOtwvX0Y/Po8dnUJpdwFci5ErIOnYals1DOgcE7TGWoBqyYMMduzUWnxtVRMxxtbwznfZmmXPVNS3Sk576EWwGYO5GswLxTXsOktFpTiRFWsZKINlqIBq3Vr366tdQTZxMuGS8q2VpdOAFTAzUctSAme1J5kT7J8ulXIvxfNAd9jDqj0V9ifiSoLeFNcsNZQuuOZc4TuNQUYFnMRu30TTMFQf0asXMLRNtL+hEG/U6a+cm6C7L+Tv1AlL+IWdsclnptxnns6g97uztc3oC66EqCceqYFVHYx2dmOYs1MoPH39w0j3d27290XpVK+mlM8DpxEQkkggTpQwXDmB6i9PHKFKN+t0BcwOopUg5dQMKJH7dc6CZnqZGqupkm0v+2OLL9QsZ7gQrMftibf7gvffQzLz74P477z7KllCnprfENpemYFQTjnnUa4XNjZYOcNCFivsolTI7ok+gmPOcQ6A+Ye6Zyvb+mx988YtfqFRL6IVl5lyZjOrSvDtEv6vaaGxSIZh3c8pLVLFpU+CSYy5lmDFb0KZjDo1T7pPR4kJotF7n0m8fc63gQ1NSqFhpj3VhLidEm/EebBUzADmov1WLvB6lfd29Lm/EcDUpSy/WP6UNA5wEytowhs8YyWDUspxSWewJTk88a1YTuRlAEaSvQXw7j5oguNFhyV0b6hYFg/xzLUTaM2FO4vBQVopMshJtynKcgEcmrEl0gRhDocFSUVTTA3s04VW5iGOhzEIMYbb0bICytq+zVXxxskJHpKydEB2Esm+G9PXM6bFYvCwJpamqhX0wvRnH1ZoUy4tFyUo6cQKUn+Tx5J226JmEB/JUgoKI2BwuxBROeTjIyh0ytpaYR3zh25MMCV+F9NRimlfD/5I+Ij4+6bRDARJ0U8KWd0VNHBHPyuuaoBVQypVOOeUdnWkig1+oTapqwUcFbylbPfTaESlZIVi5EkTCcMXbQgO+iCXEWP3cGNFBrke6iu6uSL99eYqXQZRJgVl1pHnRKdMLL7//3e/99I2fSFcH0XfeYnBtbtf+7n/rv/Gbv/7XEMsZPOvNJidsDw+focm5v3trMJ689RaHBKb37t5rt7dOTs63N7efPT44Oz9maP/Ot3/47AkWIaT9yu0uDB/tZhvLDzvbO08fP27v3uMCr9PukMGHEQyJCoVU2h5DGyOxvrVWrYYiqZF/uUwfW9CjHsCNDazULfvDYbEw7/c6YwzeLeZYr+O5/+A+KiXN5gbI+WRljjGPfLK0ryEBjKm2TDKyJoP+v+QFJE3J/SRILDiDqCkhVC7+iMk/o0x4+EMVmExZiHhpHQO/RqzVJi8Iao+CkhphnFcfKB8rBAsiqyQEAcglqnkMY6P+kLGMaYnuQQ7QosMej2xUWZr+MoZ5sZqH8EveUaa0z0M/iBl1Pbb870QAkxDjTiPZUhACbwiszYto9aQsAsIwRmIkBoQAXbJUpbjEJpY80TJSN41UbtIQkpeoJK5M5ojJrAdK/pKelUqXgwAlrIyw5YrGAzLGlJV1Hbbgyc3RxW7YnA7F5zr4pdGRXZyenjx98mi7zXVFCKLsFKmKwCE+jHnOWNHuD54iYu1Zha55hwj8WP5tNchwK7r9eYHiVFlIDIaXGm/48MgW0WD9O3mvJSlcqSeE+c8aoAOlvdwtCsixpyrlHx6Tzz3C9e80mushRNeKVwGepkkJWQUgp9LtRrhTWyLcgI0XMZ5FSuVP36rCoo+aI+Ge+SxHdHo9VL1lT0mza82yBUS1oZlRQ4WYNPm2sR4BkaM+oxG69TPu+q3PGmipUJORMEdDtgGbF12WGCQsqHZLPmZqh9V8NPKH9arJhdiPtwu2gDEpxIpP6ejU0gQtmPnszZ/+BUJ/vz/pdIbMj5kxU82pyKpnJqeSU6RiLuPtjTrsCzBTZaOxWOYQvI4vIYhyuxisYXcUxL0e6+1kS2ziiIIdhqWzxTSn7hws5yp7+3v5QlPTfg7mY3W0gF4ZXdY416qj/bhgEcKMbEpwz82kOk8HOVfLIgOkLYrZVgW9NGVUQFhQIMss/Ze4tKVQnw1mZ0cnkuQXB7ZNwdyBGDy0VrovZg7I4tg8gEsT5t1g1nFgUcu8mpu5EPFZm+cAMsdvdOcXj7ZoyBQ0F/IfvPUxFwRc9M5/5ud+9rwzoFdgygzzaac0VphMdWm32IOpcuxbbMSfHt5mFBwSIBTa6QXIC29iDodcidYtlrRhyOyCs8HoEsmy0AwjAroBDbwcGWa5ajwbax6ezUD5ydEZJDPOEBHlMjgf5WgRfM2jrowHfP4WFeb2T/O3Bu2ASViE0a/Ybo9jCR+f9ANwjCdQPtWK8QpYVoHm53WHKMAIQlXX25LQXI7jkQ2GMgyh6wlepQ+wEO9q2JpPgm/Nl48Ew6WAQOhlAPMmyVUGFE80JD5yyCN5SMJTka8RonBzCAaUHmxOxxOSEXNhRoJJsZzfKmD9Kb46cQPik1B6D8HgJWbKAT0BCz5annRPe/MR8ftsKTsIuJwoeyt2FksCAAve6PWIiiuQ0mNHqrcVdgY8ACuMaEkOV1AvdAntirAXgiaBHodPKPvLPdmoZw8qER4pSDAHtAqwGeqnSsljG6hm1ZeRCafPfX1XIdx+h6+TENK89KOwMDe9a6gdberttEnv38srQeDgleTbHJfS8siObQUY5uhOWdiv8FCH9/cK3l2XsVwOt+/IefsIeOwnib2G3KRA6hkjLUe+RiwcVTexeEBOx/llaaPdfen+3V/9lV/75t/4a/S552fHnB3FMsPe/s7Bs2c/+uEPGo361vYtTH++8+77T589eXDv/vvvnn1w8pAja7//z77VHXTOjs8uel0aCzvQdM307BysQw28c3HOhY7j6UE2P9vZ3rIikmb92XkH7SPGP+mSS5tcqtU4KSWURViOkjyJdjUTitGcBWJWq1hQwhoet8NiwAL928Xy4vjkjNGUiy0lSpuKLuMo58bQaWXMQ36FFxJGlWsaFF9armL+w/IbrQye4K1RiwcoeoLC2SI7xCS9FpbUBE3oIaI0kZGGsfcnYUKw6iHUeQiDeXjTNUyEE+h48fDOBCSKoUHNkqQsTBSAAejDL7CGKZ35KWcPjBQRrLgexxCKQHP42z4cCmdwSLjASQqUMwSLUM7niRimWPAEdkjXSqgcteXDcDl6sql82wIz2UcOgCAxUAeJ55Pt7TYr+QgMGFVBJEIbSMoCEhhVrCSNGhJiHCUiKpka6CCpdgYggFIddCfzFkfBJ2SbC1ML1TIyCokh52EEvVopiWtZpCJuER2Np332kCbD0dnJ4M5+bY4wxgoyStraITLmqHAjS+SyxxgXP8BmJR/ucTPWqdgs3Hkg1sG31UOBOvtJRqKPHvwQdohHTuHrHb3ttIZumcD7yt4CACucFtOYnPYV3msfj6skHBw69EFutRplqlN4mYDmvZ90VdcfT9tXv9LnEMJ62ME6tNezmKCUZAinBWikNF+yT8mYk1eSMeXLSHM48VMwsEPVUE2DioDwyon/cufiVOu2CLKYqLLWQWwm3mFGp7Yo+R/pl/hIhFy/pTMAhkMr3kzgUSbkWpxy4XxyWqyyIqEJA5y3maCERxJlzULHYVWiLGGraqo0pWxGKE7S1KYBdmlOji7y8w0oXGTQZedYS477xMsV7BRx3AOBmPutRygvDWeT4YypBP0S83MMDUm05R9COrLyYjEiS2SBZRQmvJqETDUt4BABx5RQfapWi7du38Uqv52xRXGxifIh22HjyZDFcip/qYhdnXPolClPe8CHSR+UIH/wgx+idWMNRDIzWaBfordUpqh9TLHpQaiXSMnia6HXOT07+hPkeOjTjNqLTPH4p/wXUO/PF4bc48FmS3bJqQlw0CrHM+4k1qKMCiBO4tVylWmVL5Od9z966y/e+B785vTUn/zn/7J72mdAZfJDJKiiO6DUyEIRE2FwWDpFM+ZIoGVRgwkGiLkucHx+QZ1C1mdCSOfP/O709IL8bm1tT0b0rlxvNv7gvYcoSr399juvvPZ52YJbIkehVcU6AVg5AKZLCcg7HT8GyVC+oqyNNfze8JiG9zJIC6qgsCKCQjQnlNzHan0IAKUBBkg+cYVYHhYxvPgX7oVOyiPHNCi3ayIaYVBjvbkiCEjf9rYI5kzJRWglqA1aPb8G40pOsJwCEeJeSR5p1nDHXF5F5sFX/fGxGkY4z+Se/RjtoXOwtCzDbn/SAZdxz8E/LVbipLix2UXlDnJXEuDIE8lTvJG9EnZlWeO3InJuiSnm8juPCTOmGkc1yIRg5ZYrxJ8FzgsDyVqhKYTUzSRIyJJ+nBK9yZZg1NtFbsqbP/LKP/O0YAt3WKFIHoGGD+Cd3uQ7gXqxw6nw942QnkpMa5VEioAb437KgAS5k+LvmD0LVHH4EwLjJ79pHwNOhX2SU3Et/osjevkLWULHDZhVFgQZzpgDA01FvJRWKuQKUsLWoR2xp3AFOgK/COM1keSVSmiVoHoaBqTII8aF/DL/3gfvf/DWB1opz2a5Xufv/Xf/e7/0q7/IeHl2cry1vUd3zH317AkwgGJcf+8We+T9t995987tW/fv33l+ePBnf/Znd2/dXs5Lg27v9t1bb/3RuxwL03Wwple62ca+/zZD+McPH7Zb7Z0d3DnOzLFOZhfryEpMpTxhVQwrGBwh4GZgjWqI7NZkaAeSPxnxtBInwtm5xoMhBLGBsmFliTG2ikXw4ZBDZlgjNT09ouRYoGPtivGYQ6bEVZGrMWtAthcb1gwz2KNo2Ck3LIpiqBTFAwms0MBAxaClvoFRzbV4UTISXUjSWsE2HtN9iIrAcKMZfy+v2I+sSsj6pNWn5RGM+BhJWsKUJU1Sl8ILmXeEqeL3YrV34qv4MU25Auvka1TKg5WLsHhhNcB6InFWMBbHsNnL0akChZaE8g8uzUVAJDk+V9jY3GSttFapMaojwTBvYS2eHQBsoMAuRFMEICwLctoTsQH9ZhZBTS5QKWpKIV0KsLHwiYBFYSF5SLEeKQpmYpmElUt2GJAYkBnQ9OUAMybJMYOen+fZC8Jo+nIxmM4G5VzdWGpjHhRHhoVc8aPcrTMq+EX/EOhFpsHAsq+Y4Ymx+VVPwJ9+VJG0K8Jrhd/8FQ3HNWiClwdeAxIS/HQ/KkZwiJnKCpTrS86r8ROvxHEVJuUDEvV6qiNeYamGiHTWbpRr/lOOOgIBGPESrCoA4w7VzhlqFVjhcqgeSjTUkV/ZGsa0DlIvxn2Q1w1AyIQblDZC0w3YSZGpFFGYFmJ4B7hOt4siEOvKnMShNkp8ZJV4fEH1QWJVVdVcAHLVcDHFk6/WaE5UUgCMKlEC4SSh5kE7Rw7mQrFMG5XA6WiJPcpWe2syGoCcA75UZwz5i5L57Pyiy1W5IIN2bVhh+cf06SdopjN3JVmJzfQ6TJUXnGLBhv323matgsmjTL1S55yRDNqwjk7jXiwb2p1gCQJCdY0ADOHPKzFJi5EyfKol9cli/PzgOXknlL6UWDxWNlZjpaOU53IMxH2MJ9hCvhoOSnRkEE0aiBJt5Fgt1Rbqkc3m074msHiqpOEEt6kACT9IFB94zmqE6NBdw8yappq9ZfPHZ4c//MEPdXJ/MuujSmTHltg4MKp0WAdcGBtrcYKZeSMlncHWBLsHNG4MeWLZC/mdHZI+5wg4512ulDGcWqhUlgt2mNlDPioVPr44Px8MZ51h95133uO48MXFBfu6ZE9XJUzYk6DH4HzaGPK5cIYeZDYdXFwc32puWoaseMmPHitpd4Y3fFPhe5hVA+jVJ97igldc99H3pWcFYZXfI16CufYzQMYIwoxb1KgmWpS15OSpxFQ0OAXrrxR2Jy9EdkTUizU0KegbnI7kSqB7Xwr0pARLgH+svMzT8KT9HHHKRw00QOEbP4KfftJeq5KK6aUAU84Qhx/nEpjVkhybszdhnwpOHwql9hsWtSYpG6we/I33anUWasT6oos1lzXiwYimOLGd4ARN+tPRWVEK0IsJLOFR7ORxJvEOvvysIBOoKw6H+TSQIWo60bT7CuZP4aHZZKAyULCacV6Nnk4tcRNPemOCjnpj8tGTfvNpkOm3rX4BpLaS4LOY173QBhO163gSQKGxFP0d4FY/N+JPYiWoLjsS1BF/BLAZ8HLJZTfr2FmEBuTF2nghL8Ct4l7GE9JhXKdmI8hqOORGVYxof/jwaefsnFO5DJav3tt57ZVXuZeXa2tYe8e8T7vdYgUHybzd2mTEr5RrvR6m9waPHz/cxg5oozXemJ6dnTx/clSqNQaji8Ggg4TIKTTUPjmPWy4j/THCFl595WUu9WSEswvp84P+gBtskBjH01m9xD1ijOSc8UNBVg2DMmQfWWKNllqld++e+DAsAcFCEctaDGe5xe6cU3Y1lq+wDaKDZhwqkBzJhrNWBRlnJ4JWTwtOCS441bcyYi12wVYulUEzQa+dSsc/frxpIunruKcWP93DOwsW1Pi/QIdI3FZ100NKdBQqquQhdFUcAHiAVc7QvD2DWmbTuriyBtUo4yLtGBeQLz2WEvLkQCI/WOQ/ES3+XuKWkGKxRqnkXUUEMVy7+GyDsDApIV7yg9Erx/SWEpBFoLWmo5uA8dIfBcHpbehURtHdrSGCtSq9UWN4IBv/A9vhl5XuxQh5zlhCV6l9DHpV5AimBzpHqGMaSB0IY/o/nSBkYPkHW2csG6qaGElZJAPG+HJhNzNrL/Id/Fm15eFEI1VrOB6cXpxttZsySU89VpEiTZpsRzbEOBUwOTGupXOkrIhP4Ukc8oQNIfveT68Y62DgJe8AWe0RBqHHcykr/o6ZmHAsulcJpVyKaCDpxN3z5rdj9HiCUsExATaFK1UeitOFOJ0due4x7wKrYskj4qMubOIZHVa7LI6BWY6UU/GawRAhXtwWg5ULH+PQK9nhY1k4DlhUEOAQGpUIb37Mi6bHFB8z8IjCmulSPziBoyNA9EuWbECh2AjeU5TPs5k6d4nXa+fnZ0zXKXVVGKxh5jNof2cHWoOn4WezurhKWzgkKFozWAmjA6K3oFmJEiiYo1EmulVHCj3NRTMZbhUr1xuLyazVquiG6YXZesKOTTHP0Vss7WPmcjriPuIRPRB6MdTt+bQ85iwAivR+kRY7bAsUKHWTnRQrsUwwxV5t+9XPf16GRmcsLshiD9MYzaWo6sYWtXgtM0hQVockHqM/47ziSDTkisda7RAHVdRMh2kR6tJUD9QLKbco9GCagKCc1JU8PhkUA/UFpD7Ug5GMCs8ajJit1kiKTL5BRdOz+QBK9hzxV89H2UAv4r5ucGZik110+32sPtDfjjmeq+M4bfBlshdWWkYOsxSCSzIjoe5CrVNbrNIwsu5VR4KYx+iEt+4gw2w0Nksx7AU1nfNeLtN79vzw8dOnxXLdjmBnnz193u+NGy0MsdMxcvPDjA0TjmNxWLpUZoN3jE0pEqYT0V0HuvNRGeMRXevvjFnzC8EOIUCg7FEA/LI4OD2+flYf5nYI+XuYPFfSjkeLb509oAPbFsxqDdv6J5VP6hEfeSLJ1gzNxyqEis++rn8lgTEvV8HScsLKnYZzmt3H3GBVHYQotCHIhzQF5Eget34Z8pUEXaEhevCbSkO+Ic4VCScVg+6tmqD2lGOofa3JcrRmMc7Y6NhxG3OUF48d+E7jAMxACQhgfOMSpGdcMTQDyObFAexbmUcItbju4dCKetNjaXgMgcmVgBtWjxicSigh2Ei6Ce+/Uf5GdeTzZ6YsxYYb4zoHBamOb/VOCv3TILmE/dooSeFYUhSBeXjy6bCICyTXed8YnABfTj0dkLgjmsu/SeR1yMQ7wBPq9NEK1JHoI9897/9nf/hHh+enVN5KrfR3//3/8RdeerAsLrrDi5JuotGY3+/1uNfxzbfefHD/Puu+XJPJrvH25u5oPDg+PmIKsbW9hU7MxcXZj/70O4dHJ6zHoFSDuFZE1RUbQCBh85d93HKtUKhw3FOM5Eh1RTCMEmNunVnmuFBsePpcxiA1ODN8Ij5aS4RuBiezIqKIKKtK+seTjXtUwFEnqN6+fWs4OWT3/OzsXOY+OEeLhE4cBhweHeBTisoxyqkSRbVJjuTBoT5OLBRyVYZjxgwtwOk6T4Zp5FYekiGShi54weji4ygzCp0BwFdDJVAaekkNWPGVGEpIMfk1DPoJDzASSwgBuVY3DdawgIAxDTUCXY0pIlhKRF43PDG6FZujdsxJQChT/xbrAhS04bTrohjgLTntV4iDJhV4HkWQiLFoqxQDFuslJfMpkwgrmhMxMVsWkY0KywtT6kGIk4ES3uI/tzsLJZpSDM+65IvVSSYCRhToYSR8Rqgf5PPoJSMKsMzPBgJShYjEvj7ZaTbamKKaLgZwuqCpizZ/KATsjxyfHN26tTEY95uLGqlof0jVhgIyjlo2LS9WGiRIRvxxh9juvkle5aMP/YZgc8vL+xlFAb+WQsOjmiqf+DKkMXANv6cXg+z3shffPAk99nXdy/GKEhuVtN/NAwmf9kkgE4cy6ozzGm5kmOwZ2EkTUHL6gtF2oBYuKUF7pdgur4hEROEWg4SeyQMr9FRylnE584pSO2ilyw1KLTzTIpSKmhLyrU4MaHxGC4hlbGnzM32VDopdjssSdblepYUXCxVu2sI8fqnE+rVOlKrhhGZIM2Jdnmk8dVUPaYsY8UpF6sVqBDJPGPX7HSYAmBhGt4x+QrZ9pMVYwgjlR4+ennXOaJ7aRmPiNRvDdezuk1vUE8khFRickK4jsHNU9rkgq4qCTrVams0xY0AWWNpX3yaadPRI7ZIzweKLaja0scxOZ2mdnjq8wF8xBKGeGZBmR+KkYGgK3sKky6fFAip/Eeu7ugMBIKgDkDTVZdHNChuPktbUnxmTOK60SVrSP2VDz4wfJ3kAogEag0hZD1zndASlwmXCmAwaTsZ00PTjtHfdHyYhXtMRZY3Zi8R8skOHqTsNoIF9QMR9emOVkE4icM2ZjofR36qwUOxi7lHMjjnZZTepaWKgypInNrSyZsSuRqfHupLYCx26QRlryZl8tUpxoSzYYESo1KVDRVmo84RL9pCL6FSLUbnHAONj9BBb7SFcbtGfBo9wgoGlsMiA7PMSYPDTD48h4hd0sZXIG7d5emnL7Y95x4/wK6pVVw2JE3cJIonrbfba0LSnMF5DtUCcAMueu53SdOwA5jCXA+z7hlxYmKKthydJ4ngx0hRZl9IlhNiMZY7dMZknpU4ZKBf6XaXto7CaT1JbKAyrIyo04qohGDorpBhC+7fHLN5I98iLBj/VekdAMnrwMJenrtDwGJyTIrpEltIK0SwWnhbkMVLOiEO/a3OvVMBn8Ve6Kwv3EclqLpue18bQT/er/MZZptyf/onzOct25Moq+srH0cZ3bOzxN8RI50XcNnZbmMr++vrtUAA57lXaXkhWZCEUGwZyhZkx6EJRpmOmyy/GTeF0qmwGvMpbUh+uzIzXYq6TqOhJDiHFTxqY9QPHTGeNgz4VXc9C9latVOkPRv3OsFyo7G/c/rVf+LnNrcYQddvRhN12hlsOmm1t7+zv76Ef9Nbb73PxJcrZF+edTHFSq7YvOB9wfICGf2aKvk/p7OKEnW+2dInWaNY4FqxeXoMQI55UcKVlxIEwtD+w4DCelavVAXfMoMc5+EA76DKwAXs0eGkZTP0sO+VqfvCUfl1tAt1UCQxokhYwEc1IVqmgGXp2enpqw78002lA+FNSrDGzhMxQl81yk6U8oAX8avLWwJaZHiqy9fpdQLg8U5KHHRgWqAFpzCRZoukaHAa7FivWOsu24PZKhkpRilqKeM6Dkzda78QP/YVxfbavSlFgB19QeilLi+z0ljJWPIJmzVU4Gsv6INdm6kwbYypIJJ0rET2AyuXRzSe+pvu4sgXWoeNjPLPVaOjQeEgJsEJrLAWfRHlzA8fSqmhzerXAiBwW6LSklSRLavSX3tMhCMBkSeRoAMzHS7gGctiF2jM6Uxjw161DMiYoNnD2QGr6HDdEBBJX4aZlQrsC/GfdllPdF0ixWDJEivKZC+IHCt+t7XlzY8IF0+gacLeDRAYkq3JpPJw8eXK0v/nFra3anpbV0CiRmUVqnSoE3KYWldjNEP1WEqSYfkSYWKnHiJHD8mycxP6DfwVSCURXnvC868rj8vjg1tRIsZWOCkr/7CGvPiCplAEqHiQpOYDeAdZxJBYqUhr5nDYB/8qy0Cqqpaiqbl6BngRfCi7tdLC0T3AnAWHQM01X1NbVQ5KGsim1N6RxiKbmWrrUIp97xGQLJ+RIjIALsx3VsMKJ1VrvZuWPJKx2UkDcHPUvyotphTVRpuvZmpEgfDZPoDhhrsRRlMSoJEikFWmnK/4Cq/wZbpotcBkClGhyzqK9zILKVr0mEGrjqgScD0F4nY91n7T035Q7qmu+q0JTVVNaeOI9mY6Zbc5z8xGmRevl87NzJPg+z2h4OjjDBtpkwmJFHsPzyKa5ZYPWi9oRSvT0S0ifda7n5aptrtuuoftf4JYzhFamFJxU4gYwZsSFkp1vob1xsEHK+j4Z4biLZsXqbWCSLTLQQrCyafIJOVGfiZuTCCja0AsBPB9twKZ8+RQU1qgxj7NAw45rymho5MwmG8oUpUb3i1yEIM6HSodpFvt3o014ky2e6K41nR5BxAaeWcGci8HEPvYZsM6pdRIJVRzvpysecjhg2DsfDt97950RR4vNRBO7Kxx4BjPJ6V8OE6g61kHjHo5GRW4E4BSATHWp66WTov9XOsvloFuDC7Vah2rCzcnMQiqoDRW43ozJE9cE5Ll/jEoHr5jcjcb94+dnG+0dTpSVS/UF++S6THrcaDRNhQpM5eUc42yqfuKtaika23BipIzbQyAkhMc7Bj6MMdFfOSCWYHC4r8kPjKT2xSzOAezXYJSmcu86BXJbTN6wDoTm734RpaM3SPqWe0KpVADiSYNS8PdUl7HzI2+f2ThZDmwxwivtk3Y7fBrSfdb9hd9JMJe70++VHJL2pb3C5xueAMhP+hFtTl8S4J/+9tAkjXRMdwOWRIw+qlwprGsgVIZUjJCIWoeNaJSQ1QVHqVCD9vT1JQASNDmAKFIBStKXU+OZfvmz5xJt8lNi9ivA1WNNVOBrvtYx4eOeNqqsElxF/jfZ5Sy4yoj1fK7lAOCQYXMkn2tAn+LjBUmsxQbOu4o13+QjSd8z4W+FemuPxCYVQUEeJ3YH8kkepypNm3UMK7QeV2hFWPBPwyeornUoQho6ulcJWDifLJ9Q7VhcwzGbYNFispSeiK69/JVf+Xe50PH06IzLddGel6hVKD3pnv/gu9+5deularW9udVinX42r4+Gk9nFcP92ZXdzj9szjw7Pnnz09KODHzFgswLFFTjtVpNlGOo9OwB0/DKyaSMQCzkMeDQ47nBhdoHQf3ZxJsmUDXKkSaRemb2R9o41K4kQ3nZYYEI4h1AGD4z8swzFslCFW+i5M6B7ARJb+dL6EDFsMDPJllbJaK2NdY2LiNdCrhLSqGYzCmR6xFuGKY3BMAbbfguuE1DKDJaeomQGlYxxVdnKTpdZnVuVbRDJGOC0B1xgxqnC8EgqLpJOPYIEhRq2IXRwxswFMwftAEhk0fxHS4BQYiUnSOiONSOFzpwOlPiCWqM4UQIlRJd4wfoiZGlMF1+lEQRxqg8iWjQrz0a/ujO6RUs79J9+sE8BJpsQbIM6LEctR1MXSpVyYRkRjgT7JEJAdjikwfSGmOgaiM1KCtGLXf/MIFccLsfI9iQGazGFgjzhnIFQLgvNM/9kMvnw4VPEEVUvNCXQTZhPnh4+vffS/bfffvtzn/s8Oz+3791TRx5IJnuS7SxP4BMv1h68FHb5cS+VjZ5Q98xNyvIVHv5AqTcvcqPKIW576ngDqO2d8Diu5H2Zkghm+Bxr8HKfq3TaeOXLv5Yu4KIkEB3x3fSbTl9FcekJXvIHklwLM9lhBqxMkYgyyhsG8+YjxV7xQtVe/1R71YqMMPFIjInMKxQriNGUZLVS43AtC7f0TBz8QdJXLdVjdEKGJpd0VqjHoK4DmtmwP6mWKqPBRU7GbmqUMzPP3rCPzSiUfLgAWGkiiFKRNAdTUWHTkzZuaOUhwjznhl9NJZcZDQdnZ6csU8jc0BRDQN3ZHLsCxyjVYN1GBvS1l4nyCQvPmrDTp2H4GJF1d2t/c6uJnjqL1/AEgRi7wyiloLiY2/Nl+yWEFctY9uGyM7gmaZg2AUE4sG8DwTLgk+EuQy5Ec+0j1hnVTHQZoqzpYwzAPFh1kG0h0c26vnjC8jxNAmU4+kyzFITELMFdb5NW1XFq/UWTKdoEczkyP+VMF9YPMFjClAnVRx3D5twt0wM7fatZCaXMw/YvvRGzcY4Ik6Ojo2c0ck44qGBEBSCAqrZbEYvdmsxgv4BTOygNqV/VlQhcO8yUQLEgTiTqZmXk/QKHnmn0iFVFVJfYVp2VahW2+IqlGtUDGtg+ZmuCZDpMPUa6M65cqLLxQHlxG6RmX6yDjie1epGDZxs7m2yVkO2whiES7S+89Rkf2OskRw/LT/Kh4kn5qEqH/yAJaFXTAvpVvMsu4RF31FTkUpvFYTE9TL7X4BG0d0WAUW2IZlRcCyxPJaHfFNn2edPLqbgSmqC5EmIeSSxPy4EsN+RJv+v+ymvaJyD1CEkKfPKk4dJuB5OPw11ORKwlVMlbtMAnPK0Pkl+kSg1A0oV8jFyGbFXimHg6C4rn3wkBxLMdAIJ8VdXXqjV7E0qHS73JvRJT41SaSksVAEhDTtcT4/DLWiC6YnRX2EzVLz6avxJlbY6Ff3zW/KMnv5/FX+gW6HXFZ329XL6rPEZ3hF39soegHKTwrMJWrhTpK8/EtQpdaZvBBq2vX8IMZLh1OO4wJEiCIx0rwhjLIzZrTJH56dhOBSFKxALSbnzdU/Xa1/5TtK1ysIq+sk3kCJO3MMTcJXNoq2/4x1JIiEiTeMmtVB1+wqkGo9ajWaW3byCo5ZJrGWFZfheGxfJHP/qDH/zoh5y6bTXbw9mt4Ukd0ZAhmfXU7lm32+vt7u5v79x+8uT4+z/40e7+nUa9PZufffTw8PnTA8bi4+fdzQ1KHBNCJx8dfO+coSKb0VX1i8XO9i5Wgwa9AdMISOLCF/yRwpELNTywI15mje1sdHLEMMbikgRyBHdJdiZWqMlAJMqy0ppl45fRC4o5NMyhL2x0MKDS0XcmXbUo8GrVD6SMqJJLlG+GMu80gZA0oi7C/MEjjQKtXUrEbjMWcZsY9iVgTIlRvSi9ZAnJcEp680Civ6Qo7M8Xqh3QLRdtdkKkk8IH4oDkDPhOG+fkHMMh3rwk6jI0aiU4fxjWg0WcEeStu/gcWFFFP6WZCZmgbCYqHfUSMAUR1scAgUC1UNvjPQhOcUD2Z/D3UreeTURoFIR89T+8JZygTL2BsgLsloescPJoamTJCZM8eAy7oyO6/oEdLIZWbvVm2pwpVnKlGmxj8R6lDuYSkrQ4CMxCPAUIB+lv2ecn+yVdx1BlgTCnW3KR96EBOaQ4GRan415RPYc2dJQOUv58giC10Xr53oOvbt3NHzx6VqpoXZGdAMLz+RpZOes+/PhZa3BxfH7Wu//SnSlnESkrVkDNfrNlS5kUscZj5eGFj5jLGraXhvOAOL7Ird0VPlh0xAfph55wT2+lhb8qEwHGKsig4JRB919idYfAFz2qLoZ+DVJpXbEmJAtUemCSSpZHPdmnfFR/QhGK3FQslWzqm7VV8gWvrfpaDfW6baVmaLxySqJUveARI0SJja8I66eaChg8WHBRw5WodPOomPP2Rn0+71aqQ26E4Nz7ctGixQGP5OqzRCFVBC0ZsFHE5F7L2/NSrapLuXPVHKqGLDJTQNj5mS3KdB8sFQ91JhWCqO0kqw0BYbGpoxqZsSySrCZlJJEiZVqsNjemmMHnFHsl1xuPuWoQg5/Yl88WMJajDonpR7vdoEuqlAobW+1bd/bHg+FGu40ky/YlbR/Zn6MEnFhH0wU1FrQe6fOI1mzVaSG0b5ZOJP7CApKWKCwnvWJlMOAaRjK6sbnN1ijWfpDpgaFLBBmT7GEXKygypku/t1w+o9vULETqMVKl6/d75FM9lRo1FUM85GSsJgnSdWQOpSv2MORg5QQvC7jJkMrXzuyCWTuo8y0E62XuHKEbFU06sSmGlmUagbmWmJApF5mqsL3HdRzqE+GoGMyf+m2rU/KirGk3bGmi60UHz10fIMRWj+pDJiN7SoViZ/Cw2eDQBVWF/patFw5JVzQV5ABxtZ57uuCmYDR6iA5aOoT33v7gC699Cbadn51y8LdSqtF/MKf4ytd+9oOHD+fj9qDH/LHM2WYt+JA4dheJSQmrfuL0+hR+8LruUVuyoBCuyEEew4f/qsOW4QCwhhl1RB7Xp/AUfXW/8IQv448IUkxhQY1UFgiDJKOYPI7WQcxdeOIpGgYPdcjU2+TGG2whWmxgg0TkkoZ7KvGAJfxGn1V4KGAVsRe2IGOsFQnuE9/WqgQvSMe1Ar0UXXhznFyirjEGOHx4k7ZHc7wKFQ34GVXR1zoga8ncjgwIdn4saWFR/y9o/2eSgjd6eRCmLkBpuHuVgPzwVZmZpOBoRF6wAiTkfDgNhkJpXnrcx1qJnAHY6DXCBE6A+5tTn/GJ3vF3DTYC/Rv0m8rJvyJVKSYIkyNOv93TU4E9V1Ne8cyALgFYKH7+XApMPHEkMO6+hNUhV+9PCA7lDFQarUe/6hPQJjivpdKBEpgEsXobfVDV9GsANDMt7moY01McD0Y/+dGPWeLCcMRFb/CLX/vlv/Hv/DW0/WuNxnjAhnXx6NkRG8PNxsaXv/qzb/303WqZzpobN9WvcxYvM+fo2/y8c/HkiW4FQ2cI3Q8t6BRLLz24x+iFMj931Xex19GoV2u6q8u0a/JnJycMk2z4ctqMWJDHcASdjHYMF6JPevmSI8scIShW0QeFQgYnVJXQBRiOJhxANpmbbIkY8smYKtlP+bW8whf9+gKwWimh1vHawpAiuSdtVgMkjEFIZXOa4VgI1Csgv2qTBGmGgZRJiNHGCF6QnhLyypJbfrBBAYYi+IB3lLyjS+QoGSNLVAoxHnha4YgmXDzAaZi2eUSJPUZNHYBCdEDWtE/ryAyF4BXfsevDknDP2D9Cg4CVvCiUsCH2sBhvKataEE7HJFrkKRLMC6eRrV8Rn3rsg6iS++lZlXfkdWMfYgfYEXqw9jEccFcrV/lgKYWxe4bqP5DMtFQCShg0zEUY18XB+aKXzY5RnAADMzOkGpaFIQTOUx1Awmxvo9F8tnzKYQMqm3INu+3U4mDYf/ONH1fLuS9+4Uv7iGLjQb1aReZh7qFcO8OVUbEg4Z2yFTOFZ+KWn4OKiWKQv50tuGMkfnGLX/ZYhoyP5E4+NmGIyfmvwTgJKUQRRnH0R7K89L7yKEQgRqKBhbSC75UIDmlvC3OXoOOTdstv/dsYZgmJbI1gUhRX/QmYLLMeR/2KCf2iTg1BvNNjWAXj3pIRTeQECZO4SqmRzzFRpNHRxKX7x+aPIqkxsBsgDUCqjVKXSh0paBuJtLg3GvuW3GGVybQwwU+Hw3liREhOoxITDpIeYjX1TVWUia9+hYfHKLaCVZ55bN/PdHpGs9HJ2Vn/rMOS/ODRI86ncyKFmkmXh0pKPltstre2t1vtRqPVqM+5KX2xqFUa2PmhqwQReok2fWUHID/PFuqlJra82FtE94uNrlIVI5UQsqAr84mhqCFrqi3iar1RHxwNkObpX9UKOEosi1o0jRp7AoQCeXqGXD4+4yzyHBmX7Qha2IKtWtiFjhNNksqv0oJHINWJXinFkXXaKNE5SE2L5Eu2/GmZ6mlVVhgfgj+AEUjrKlYwqSR9SLSZ6PemXPUxLzMBYDfu/KyDlQamKTCUqQs9pJUXL2O6qgpcNoZrwWM5QCTPoNIjhUD6CmrQbDrKa+GfuQAzBGY4WBEt5LkEjYlOgQNFlVq1glGIi875Sy+9csB5slOOopWYhDArazX63V4HixRUmXIN8xGS8lkIajV3mNfkFuxp0HUwKVL9Uz1Vzs0BWRCmzK49IvfaJxWQigJXrYmu2v61ka/zTCEMVIBXxS+MKxLXo1rSgWoAjXqLsw5281eSqiW2BufZSgBUbCFcv/x5FDWl1eNuD1z5uiv6ivfeyhxFOv5lMhJ8gCbppxCv4gqleB99nPwAKp4oSYpb/wzGZG7zUeNnIcCCxOyYJaFQ/8CPtcRYuCLS0IkHVjqejOLpH5ty5kFES634VEk7TBo++Aito1PakCgP5daiWPIhW+YR5ppJZKCZ0fpDr8bqNQ0rWS2OIf+afqFA7Ijr5Zex3uTvcOk9hMsx4/r0VQxxnftyjJQ2fDblTsDELMMGwVYSSUh0rO9FGHMtKOVvM29m4fdiHP9dwSb+MQmvAFae4hSlo3VL5tZiXcBsZWyMdHam9gcMlkj6jU+Knuhlv1d4tRZrDXQFLzL0ZTR4m4g35+HPEGr9oVZ8tRisu5jmiOwMv+Pl+OT0vVJtMhhOB/0zxGEM/jSaGw8/ftxuscS13bvoHQ6Oy6U8m+kXJ3AAO3llTLMdHXXPu+O/+MlbdOoMOuVSlXvsRwPO5FWw880hTi6BR6dW4xCdNQMbNp73tj949wytX3R+aIDakTCBV6MWLZLFMNbxsACfL+/s7DA8IBqw+9zvM2bNMVKETMDQa02IfCAm2nhjq9gh67RnOgyXwyixXMeHN7U+rQzhgzIDQxcjKF49BrxKGZvH4pwxUEKDugZoVc8h0TncaY9hEK4fJhdSV2DgREGFGIaeXkaKRxZPaIjHCEieEEMoCY3oWjLX4C/7ekAiySiyicUQhc0+2yHHhAVIBaIpixSIoYS4Rh7e+nVKQyUDSXhEjJW9dzSeG2UKHITY7kT+HDEqk9nAV4hDBOsWLba8cCgg9lcWWSzFjzD4ZtjMh+IiU+TF7X2yjkdhIvSTCGM68xemVYZXqhFoZ5E02UIvgoKQLDIbY9SPpUkWgLWITiFQbgiEEm64CqA5+vovf56dor29XSpep981Xk8ys6ZJeNl+H4OL09Eo89Mfv/m5By+hsUYvScaYeTCFIBeWHV7KQ+CcOSwvlg/PlLJLBqmObDGQiLgAeSpExbOiVKetI4aKBiwnOswlNjknLQXEVEuIl5A4BUJvNCiGPZAmNOar8iU1i2aBCglw/hNjGUJtEGlQ8TylAQXmcRNfjyk26An3HwvD2iNU6Qdwy6aRQdFQXW0Ljg5jG6HSGh0wlgUliIdeVFnFMB9jivU3StvbgsoDUhA0MdiDljx63siIXHGFpItEShWxRQotABCHyPxQmFTgyUg9hSxyVbLj/kV/NEDCpz7sVmtsBaqdIlCynYSgCrYpcwM1XLU4KhuHU6h5TCqoY7OGKMx1Y3FAWIs0MDuDef/HDx/jnnLA1Db8mHtTmWr58r3bOxvtDZbbufe6mCtR51iSLnMBWDUzGiy41JzaDvn5PGvkWXYgIBm5HPK50Zb+iZ5Bd+yOF5x85nC8LJkqc+oUISNf4fg7KxqZWrWmE0jGSi4cwCYb1kg5iHx+en56dqZ9A7imu1JYmCBHWs5Hj4YlCfipXsSZq6ohN6v+VEuKTaeT6TPhIm1L/R/9KCzgHAUnE7bI7yR/BnO0ETEdlxt9RP9+v1iqFDjojPB9dHpMXcOkG0v4QklhiIMkQb5gMSXutSe+yROB5JBzD7MFNzaiSDrLapcGT05ZMBNAwwciODLBAYtqdYOdDM2U6FnIV67UaOoKhGpt/Hv/lb/93juPj48PYdqTJ08Ypx4/etys/QzbjaViRWqkCxSopvVqYWe7fnL6fL44ziz2yJHqnrhB6YFVFdJepB885Lr8AKpHP4ptH8Qm86pIeCSNJAmOQAGWPJt+QfKJwyWclY+lksRbjc4JckCd2ATISXIUFp3XKtD803LjSqJI4Ax65Z9QY9jCl9xZk2bjToLlxe8VMRKcNwJ3AkNE+zEWCSo3EiLdRQCXDNC5ha/VCoe2t7wMJ8WkuwuC27CYG5/46OiROhdKYR3ScThkbll6mo7DSK9xVg3KCg+SbIWBRgFeypgvDY3Ca1Tj6XKX+EBa1vkDQLDVqIzuYNZZIiNC/kqOP8uK/0aKk1+BWD8IpMETWehWdSwB/SSHc+yToD59eILPHaL0v1BPQrCz3t+fMQeqUSrC9SflcRmrglLBHi/xANmqRgTU5nc1jsf8LO/LpHjcNfoFknh4wilyqbIsjIks1mgZFhlj6EobjQ1k8929FsMjAw9jKH0u426lWqeTPzw5qtWaX/nKl//4j751ejKiGeYymyzeI4vTIru9/qNHH7MIZYt7urmWJtVo18ulGr24qfNkWPTCYB6trnNxMRpzxS2jCTvCrOtxZJPhiZt0GKdz2L5hkMAo9N72dqNZHw/GRXoGYnL/U7/Lwlive8EACeU2lVC2JFzzSxlaO2ZA0ujIhjKjlIZECGCBn+zS3vhGEkf0V1PmjzZJfDoInTDk4OiMuzALs4xmRN5BaIedvDLOsNaIdC61AxR/MVk9YgV6PB5yWI3xmPS17U4WAFUDt0auPsEc/qKk1M+IEvO2HkXFF3y9X2J+hpYtZJMdaJAyPOfzshhYEtWhtOUIbrHAMQQP+xQcDnuTmtzeYdGHMsry8LakiGvbQeqMcAvKYuFwzPjLx/5CtRKk+K2+Ed1iFl4LlVqDcR0kTAJhJdKUFJrRkdIqPjoYWo6VYKNeVsWhuQ8Ldrrjic0TzgBwC6vWbCW7A5OdIItIjOZQINdDcPQyX7p1587B02MOCmIkBEGEmRLTg0UOOYxMTbqDs1IFu+2bTz76qN3c2L29w/6TREmVLznhrRxpiLnhUQ4BczYL2HimHx6opfKYp3gkhPyYI5SLM8VY7WAeUTXNuRd+PI7x1uEsKU9PsLisvoTo/qME158kjUCF0vHYDurJBCj9CO9VFA627m+JOVqL4UOgeCdxyqas1EwjkuiqOHwimEIAiUhTDmZpuiu0NAxPWe1CsPiCiTqgvb5qpdFqTWuNFrLf+XmHZoaCPNoqItdKghjUFaLQq4xHmJxZYgl+wBLFbMzpUg7c0ifgS7Uh+ekYi/Jls8yFlEpLh1oS5UWySlcdlD+G3JzONgVLzEN1jYVqzHQyocXG/2KB0v7e7hYnUysFqGVZAv2iPicAODqF/Jyvs47OQgBq+qbjjhRPvZ8huRbJHgI1XREi7RyDQrQzKfhDb4aMcHQYPRcmCCjzcz55cdHhKkZqGAsiEEyux31JUeMhWliyxYkKjGZBHFNWWygSxBI8DYyOi1yQqNil/s4KWrKGoH0ShZ/N3PBTjmkUlIWzgsYxGg3gW67cbzXr86mGBhEqk14s2OdqpTqzDagaY/uUciGm6oAxjaRAB61qELRW3kpfMPrUDINS5AA38cg9YGCpVMgLvb66SnpO1vO3d7awecC+h45OM6HiCFpBelyNeuPoiEZdaTXOnzx69Oqrr8ON8Xjy/NlBrVD+8l/5ymIMx8gOgwtF09q/fff50dvoLCGdkTgVMsxFRSS0hdbL182PSF4LVauyyY75rjUh5+Ya9Kf+EJvSDxxTujF5D45AChEda5Q5aARR7MQtxMm3fJOQiCEJFeilJ8Jc8r7uE7w3Q1stVpNX+k5ByIE+zGMVeeVKpeORLAgniCLH1SckcLjUeHlbDUxhjt9UQoNQ3QU61AXqjaLKQ9EdR8wPPobT8Oqlx/p/pQIlyBCeqPy9xw651Co49d/Wgy2av2wm4bQG4j1FeUVCkiRT8XDiDZQ7cNrdbPZ93SsBZqKtswR6SPDKWrKHpN+re9TSvv8a3TfRcJP/DUk7l9K8Mh4GHjmnboh6nTepp+On8RrfjaEqbK9OsWKo0KJAYGiXslBrYHzG30CUp+uevNd8PexTvhO8l+GFNTxWnaAgeKk3FumBMWoE9NZUfq1yYWhyVtQB3WW5ms1u1n/7m78DnDQocvkaUwK2jKfzZrO95CxA/+LxUb5UuDPMvI+Rn2plmOc+1gGntard4eD52REDg7Z1c8VmvYlNbhzojjISsaDT63awnYHaDBIep1tPz8/RkWejm3qZGW9KcM9yrmuGKc/a1u4262ytFvb+OD/GTninN5LUJisQFfRFNrd3ERmHaLuilsqyH08OPNLhUU+NWRosg5TypTJaQ7aBjq061jrVRvmHOCiZUsu6wCGGSohlrOCD0YSrKFF4tXU7qeTOitw6zGioYZRN5hIWJ7IZlhU12OmcwiyDYdR8pspuNSBaFNdqgUY+3rhtFGTo80Jbe2s4xF9FpDeDJKkwR9re35Z9DBI0pWEGdM6/SuncHoF6lFCYooW8OWr/iJUr+hmkdVASfXQAl7PWDPImVmmNU6QGoIghVVuEe/VpAAJ2OhjcpWMgiUEGRJDnlMBsVs7uLqdNVgqRVMiIRHmVMR4oC9FotrEtks1dgIXqh5DEvcJYYV0sh5icFWckvrDng1VArQpSWkgGnB7pD/v37987vTjFbNSTR4+xBsNiMaVQKGbG49yHHzyjHn/w4ePnHz/qtofNjQY8w0aITXVBayQ73/R2l3HJGogYS0rii158qJ147pVhyV/azJEvJWsBxniBJ+hCXOOTewsQl/2kmqFXSItnQeBVXNxOjWOwqIlTDk9NLsdIHolh9LJLTDrUT8uBhQfa+Anw5I4PwdjsjzdR+ccRHSA43wnWkITomO7rG6tHNDLqNVWW+TOFnTvN5BEL90FGFUUQnY7szg1aF6afJKYrIYIkFrvwZ/MCCZaEsRauI6c5DoxwLohLwdGq6XQ6CNyWee4EnMNoZoxqJdL54fyrVg9oJhzGpfOSaiFiejaH9TBgnj8/aNcbOUzNouqSHY+GI2ngLHQoX3NRuymZdE0kVlXM5DrKrx5jDVnHIhDlyloyWcXikNa1C9yqhaNUKd3ev4Pe4/FRd7NdHE77lXqTRqP7Ktj2HU16faYkw3KN7o7aqMbA5id32boiO9zxooJgZFxxuc8aP/cuntDKqep0tiTGXAHJHh06OKfVSiizhROYSDbRq0R3SAv0VkBS+rF/0khUu9Lsi18mF8wHmASAJbfcZJFymj0muiC06q8ZgiCNF5CnGTk3MGTPh4t+LVOFdgz6wzom9JjYr1QahVyFO3w7p+esXkojibiaOcAjTkTvUB7GN31TEVJVWin4f5o9zb9QqlL0sp1E6cMCMqz/rPRzs8KdHvuRlfPaHKV/DPhM2+0mybAWw7oKl8qz2tJqV7/8ldc/99pr777z1tMPnum2+NHs3t2723u7LDrMlhgRpiPjEkn6EKZPlDOrCySlKYetDpD1+ECXtRxf4Wa1OwaYP6Eh2Lx1mo71+2fynt3hFVbH5etYFPLZH497fTzCsFwkCF9Hd10P191Pp5mknDjW8K2SWLlWAJf8+EywMI0mp9EnrP2vYq5cxEijSbu1lk+lADbicak4lQtLTyDuMLSOwqOt3EF2ZT0eUKQ1Chb9fopWFZF/GsWdFI8TUFLRVPpKwjpITu7fximND8DRqSGIUweKKw9VFX6F0k/hKr4GNq/dVpNC96izdrrpQxXe6Y4J+2d4X/JUShrzY6ghA7s9SvzmJwnEkSC4BI6/gyXAEUAeN8WKMP8F//XsOQvcfYULL8qh1VTrmdah0gw1d5qNXvliAVrEdLB4rhJ3ohJM/gn0Oux6utd+JRESFNeCpTwjD/QLHQGBfjQhZlRgLNe2OFQy1nbPO4PuABGa41+NZrPXG3Jy9/nh4dbOLtLp5vZ2v9N59OiE1V1MYnNfO2jodLuj4YcfP/z40UNwMiRx5PfOHtuvmXoZFVONNDxazM5mGCVZvGG/nk0Dhja/45dlXNqFFpA5zlev3793f2d7G71bTiSz9czdAlzAyQY0CJEEORXHQhTCq4YuDgTLZIzlTV0AnYGao1olTrYBkT3Z2OBSs6HEHbLJUMTyvwmUfEVonBI32bUgu4wfC7Y+8MMXbVR4prUyjccMKAgXUqUFDQrHOmuMa4F9jD6EMVzDD225a5gUIeo7FAu3JOzQd8jfyRRj5FYN0Q9JS0ZGpAYeEM7PkQ9kDK3IkVNpFkGKMmkx9cOj2PohHeu9hM4YwU8IE3oF8inWGD1k2aYnIo/EhcHwGHZc4ddTs5D1l/gnehBYqEgk6qrAGnYlJSwyiEQmpOm2I80nC5QXcy9MorOnobTQp0ItA+GAtcXZtDNf9lj1Mz65qMGZP8C4HYz7gzUrQ8uIdf1y8eTBvQfoWT999ATBkRIhPcmCuVl/0Pvg/XcuTs9RCN/dv8ueEnIPSUsEYSXTS1xZU974Cy1CVSHm3phnHqowAoU3gRWqB+YHuP4lPAou55/AQwQXrQlNIsgdwTx5A1Xd8DiRNL7NQ8AxNUVWbMdvDn2KJo+tGETTj0JXGLyKKTq+ljvC/UteiVu58ywLzsY+sIAxp3VfsOpLAarVpCvhn7VrDPhyppW7Y5EyVRVkjkZsWyIzI2KCi+ZJF4KP2gjzB7obWo/MzbPOPRy10atBfOM62GJxPOqCoVmvg1pJi2CKniaAW30Ioj/trMqdXGZQBiKYlXcuekikWAXgdkKE2Py0sNTKhu3/qPmAXqh4Aq88z3orz/bIYcvizO1ZS5AKvlogdjVL+ednZ03Mn+3W57nZgJ5Rxm1lsYoNLdThNzONXrdb6LEkgHa7piU0W6orkx+oZtbLOgW9i2hAA4cTxFxmzQ4DtRbzt9LEk3zOnqbxX8yFcplBQ12e3AoPkr8qMzKz7UDKNq62KGGgckd8eh1ohVhp1KlhShrXdgErIqr6VnNDPVDzJBaeNEbUKdFVWlS4ipgdCzpAdiVU4kxvSlPOVg/ng7P+8dEpmSCGCl+PGjiFD1Y8giexFGTVT14KUrgFS7mrzFRQzKEwpcCpPoEMZbEvBFytOOl2yHWO7pR1Gy5LZsqPoM+Uh06G3YCN9v3llJ650NL0gDMDZeZ+48cf7d2+hQrZdMl0pV2tNqiEnCmCVBxgV9FrqUuUhWeNZPkBdPPjgcRXBeLtmOztzpujfnKIEBrHRFN85AyfqiwJjGVCX9bek8QTR4y//qsIDpJKYh0kppb4GmTA+yL0VzFeA42X2mhALlpw25sMqQ/R414B5tJPrHPRW42YOsHbcUV//Tre4KM0wW+NHrcaCrHUK1uCGpTlsjqMW3CGQPHWHwuKXpLhBcJ4HL0iJRYT6pCNCFwvJ1Ly9XjpD/EAKxhPLOZlhTFB7ZCpT2A8UspPTo8rtKuAieasn+H5jCvxnwHz/29BUyz4VAmrKK1UFdHc69Hci5I1fbhFNTZLQaULIylRFYNwGaCj5itgTscQhk/zKM5NJyVuiJ/kwxyixh4jTc1CS0HzBQMJwr/OjUmZcjZ9/70PtrZ2RgWtx/dP+ww8o8FAR9ZQ1h8N86U+S/tc4cUIxq0BIGTruT8473YubA2+1Gy1EbLr5Rr3+7IgxzBfLFUZoRdI/5MJmqD07+x40xi1ZoPUj4CQ73NV/YMHd/f2b436Iw54jfoDJAgGn9EAI5uZVrvNKHJ8dkRf3qhzFGxRbmI6Oo+lv9EYzRLTc5WYQDtVK9fwrQVu7Z4jd3JDzKyvoVKtjIN4KmjnBp/qSRRHQyc8QU6UIMu4yAjC0nVxqa12hUp6QdhlOGJN3jjH0jVpSLnFhxR9Lec7Vo9OFUk3PhLjxHoYAvUgKOPnXYPgrf6gUQ1xuQKxSAaCGODYIOGOow3G41y5Y8KThluLQaxUFQp47QfL9+TCLdUov2QU8YLH9uKVR6hH6mAaQ3G7hB1oyMx2BSiNdj2ekLuVmNk8MOtG7qdYEgQhEqRZ5lolLJsw5aMiUarzwnOsg1O4KABryLcjuUy0kACIMlueTGd9CFTURWvCrBObftlWLjuQOhCyixaKjWNLbmdD2pBkKV2yGdc8Z5rN6uHhye1b+1SSzvlZpdY8PHzGzayU9XBQPxhftOu1w4Oz7XZuc3O7UD2S5GRzMolDxnDnmXLJHy+s++MuHJJreZFh5Zk/CkNvCURSJJIvj4AMAPptYBGpQBrThMBgWH6lrMfgUH2LZS5sypq2SjAjC6QSMMSKLko4T86KI5GAAcPE0XnpJ0VvaQmXhxoKJrqBOE9Ptcmp8tQtKYOED0Z5QhVr/yLTsq8gx0N94NYC8s5/ag5qL5JOjY0Cl3DGhh6CPrYkmbjK1qNaz2K+iRw8z54hw1PPlGWwqC60qRLZ/CkwmQW64BIDyxw2nXCXSLVc2OnSdyx6EAFCLUNDhubCpEVOhAyhnLXw3Gx7muXIL/WtMMJ2KLWnVBmMhuXiHgYIqF29Th+Zm75LkwjFhyqKgVzYYzkNbn4sAStUZxuTcAoTcGlHcnQVo19o7i+zRcTyTrcD7bNhV90nwjaGO2eTg6cjtjvLnHLHg+lDWXL/nAWM4RDVSnKHmvsUOwdMkrHGozbSk44RqwU0DC7QlZKfpi3jQZM6nC+fm5SvaTNQsJd/7LjyKe6plmn/gAUL5l25IpMQVlvpBskHqOg9JtnZtrheOFcFsK1FcqdpOYjUCdDpkRqVF96AIFdttOn8e/0hG7mmOJk5Oe6gozMZaNeL4lSVJQ4vboSQU9zM5i/wV6tQxYnsVABu/qhjyqMYjEUzuJC/Pcs1c5Uu1LKExNQGf/qErb0MJiJY2OFK39OTk2az8fzwqFkb7+xuctqC5JkZcuU8J4+xGHfvwa2dnb1Bl3Lo/eAH321WN7a3bjdbXNlGvzZ5/PQxveRIJ8RYalBdFX0TO90XVvqNOF4QzCoyv0a8fEWo/6TejLkOhF/xmbeMGOxY4te/6m+StjmQNBKP7MBwO434JgHr3iEPaTockvdaWIIoDZqGsWhAqRJd86zsGVqgAGNsd6fjhCCqN/U/QWkdJ1TFiJZiiGaJJh5ActNe3KUhRvGZVzCLDEKrQ+YlOoTQej21E32DzRBqhcpK3NbpVDmhxyqv2roGfdVr0e9J623oVOkDDgshQRoOfzTy4JIjYZZHtwwaKqE0AH5M9tCHJaT8B4od4IZ3iG6hlpcb4Mw7DfwiuHTYJyJNA///pdvrD7xTp8i/pMxWuXXGKsQr7yrkqsvrnfwNZQBQzxlh0/7R77P8XkfhNfE9mUup4qkRQMQhyiLZs2qFnL3IFyvIK+yxb++2D54+Z2sVOxd0zVw9s1gMi0WuXMl1Ls7bzQbDPktfLNuSI8T0TqcHQgZjjtEib06GoyqWHOpVLnCZjhiy+/V2gx3Zx48fY8dH67Lg4zSctEcYPqfz0fzl1+6zTz+46GJ87+yMOwbOGNVZ/8Kk9s7O7sbGRrPZuntfttIYERk4GDg5P8adnd0u84opt/Ng+oHBjV4fw6BkjS2CIaOvlM656UySriR9CS/a0VPeacZqx/iRCYq8UKs3bfQGEvkbyUs6fiZ20GxLLCKzA4DyjMfWQiak0KRJVQbK1Svwz7sPDed8MDRaUp6iElXlUcIJCf8f8v70SbIlO/DDIiIjIyIjI9faq97+ekGjG0AvAGawELOQM9QYRRNtJMpM/Egzmsn0B0gf9H9IZvqgrxQpUTTJhibacPYBgUH3DNYGeu/3+r1Xe+UaGZGxh36/c+6NiFyqXr3uBiCjblXe8Ot+/Pjx49vx48fdIwYyih6+EX04OhOZl3HZs0fFp5Kbi3A4WAdoaPGR7AtPYDSBwrf4FspcBfIiCTgt2U5FJAY6gw9GDAoKDEQtkPmTTjs+HlmGYAAL3AitcMyZPSmyyxX4Sm1hQgPnMfmlrpEj6oHSIpWs1b516zabRx4+fDYadilMWD2en1bmve5x/8ZNZteO3AgoSm3sfvY8VHTD2k7Aort379+q3Hnzzfdg8ll/8OjhJ8+fn3SpOKc9taA1DJqHt25sn3aPJrMBh5NSNtQC5gDKKWajyIP5jszwAyrrALknOFYnlizJ/MY7xgdxCGwBGGHZG4QHnxZCtC9f/FkLCiHJLyMaCzABMlSsuCLuEgDApDFCjBXfIliGJEigEgKaTEUifApYfsARX5HLwl1GCFBQRukZMbMXDkAduVznserCSGRKEuChraEyQGRFQUC9pbm1NjtnPH3MX+kRKD8iWTGo0OKUDCcSzEH5Y4UNf1fzkJm5v3d8zOZdDp8kDOvVggoqaoiRkA18a2Njeq5UhyV4nZNnW00Qck6x6wu1OhfTttdqrETgiayrvUzBJ0osmGIGIm84ghvFr6EQJ2+ofsTGgx/mIdi33b55c7O9Sf3wCP9mvdftuWDqAQCsPlUhaYwF1AjbeTrSMfgxHSRf8AcZ3UTsJThJCOkccFjBH3WbpJzTMGlCwiZlGEWi+DBzYF4AcghFSwLzeIeAAko5Cs28WXahGFhjYXYL9RLNpgU3OmO75EZnJWDNb8ySkg4OC5i2QEuMKxhJsUYHPhyedukWmTLRGytvWbb0EvAZFBaZWaByWjNUJaDVYAzRT4x4kILZ8bfgYkYjiq2ZiE5dasjo2PmZdTrtyFoFvo0pynWSczqEPdLhwRHs6bf6zKzu3L3zxhsPwMGhqGDn9P/3v/DFo8PuyYvnbEV78YJ7K7v985P5UR9r1WFv+PHHn9SpSk0uZyTNSFvqVh+J5M9HUi864uvii5wFUIknfwsMF0F/hq9VOsoUFuQVhJYwSQ+JLQHCfTn5BY2JsAhefKRjAXQ5dny/OnQZZYEUr4U7HUUyC9+SbFHzFxVnJXCRbIStokvoIhZ12ISo81Qti4jHepolqoP/0dCz4RsagfEZqIgVXaLV2Nm8ig1B8AyHH4EmHbz1Fkv2o3EKUCaa8BndcIF4HFyxUbS80o5K/XrQtchL4Avg9A/nS18JU2C/BFWGFaHzQlfdWoK9jv54FSZnbC87a+hq6GrcZaql67OGvhq+xOrv60O+PFaWYIaXHIyyoqRWczprRugqeERa3jZAUBRFzlnTghAQvQvERsjQ11hvCVyRBK8V+DKZMujK74LEhMzwrLnWcPBGC8Jiks/65M7obFTb6qOdO3rWe/b4aHsbRcz2s+fPOBWTS3RtG9UZh3i++eb9k6NDvhiLp7Nuv98bzYYHB4e0H0zA1yseAs+hziSATpiF6/H8vNc/fXF0iLZeg26V9B6Qj8qfIQqD+gfvvN3BkGNS4QyXBmPQ+Hxvr3P3/v7RwdGd23c4O7KPMVCvh+y4CVql/2kfVLMp+wEajU1mBoigjz+pnZydenMNt9igYPOMuSZjNOo3/8/q3BajCKKlEMUQmY8CcVxkmQLuzEYtjpt2AFa5hWW5XYt8cgRUvp0xr1nfoRQJsEk7UldG+3YcnKgD6HRPxGtHghsn3CZWfOGBW0YqnMXAGYgMx6K6hGP0dpKi0QVm9cdIWTNPnQ91qdQ7/IPal2Ss1CyQ1p+YhGAgjUS8t7WAFJjo6ONJwOxBSuQyZhXztbyf2B65rKrZE0qu93pGBCKJ2H7SiYS2AM4ENE9CbA+1onwes2kQM9b1anvbk7+VpdiJgRS5Vtu/sU8eKMSj45Nu/zhmZ0iDLdb2G5vT8/5grd2WSQBpKoKVEFIKJkAKHNSZ5gYnUM3ZD+CJh5QwpweNzna3t46P2kCSMXR/bJ7kwuDR9GAwbLD9EgsBOBZyjeEWgE/whZzACU/oV0KNdPnhg1wAqlwCR4gWTOQdj5pUACwLm4Yx/DOKTYtf13CUddPTt/BWt4AOvT61TW4bU47zC9RTv2wifGbZZcqizToCjsAjeHhJIOlG/BJ/jD4G+x86ST3C/Yxo5isdmGOIOJDDC7yBpGLIK1jvE9ZoTN2Zv9GE8Y86VkPud3PqfLpZ29zqbDFdo1BYJ5xWEZGpGd78TE1RtkWYRNCdjNn2A3NoxfPJlrbxa6z1YdzO3pB5e5u9on0meuNRf76BJU9WAgoeVJInIbT88bjROGLmMZ93WBhiZ3ArriqnvfQHj2vNLfQVHBdGD+Qk11jJTDO1woTkRnLfsjbIzONPTWHuoBaAHm+rxRVjmOIgsk4n/XM4grTK9INDLNmPyqLH7u529/CAbcntDdQEFW5Pb7uHeczWZjfODlgHq06GSOmWP8Svsd2FS7LX2dDMXJVNLxgHoYVn7y9H4mAMU4n7DVFhzBBkbV90ipjRSaJF7H8YGvI9MwPmDrGAoI6D5hUblyihA7pjfCJLUZTBS0otzYEClkUbugL7drLGm27Bkx2yb5HTkkxNFIsVDkZSzdjn5oIANMDZ6ESkLJTtxAVYcLhEfNipm3/gqtfna0fzKleroZPBNopNIFQG2tfs7Jyrlxkt1qklbpNgq9h4/OL45Oa9u5zousHJpyQUHXO7M+cciHaHMwPaD5892uw0K/3Zv/mDP/jCF778y1979/e/9T+MveJ8VueApoJGoobm3qrOw+aOe3iUeyPJB7THkz/mMrOQvryFSXvxeW0AVHwvQotoi+9rHDlqp5RyOdjoNqcSbaBbSSHDjbXwXDgCV0QI1+or8V0ftgqHexVoibqQT7QfSVzcpaB73hLmFbsCCL3msV3FU6Rgm6QGZadkI730pE8kRf0h7wUPH+FVnbgrY1b/JLponGXdTEZGjeeioOi5zqPaAkCXQ6MGF3USdtMPi8PI7tYzJDKK04/Fc4kyqBaVwVZsLrLWmfARFh7LSJHKCrqEjaQKIKqbKIKUcLz6dQHXJdAMi5xcCvlL+nwVMX9JSb4O2mAor89MXsaRgdkiTewzI1lWoyWtiSRGliztZdCnu4j802SmjFVmCiQXneQtvdAcxaFsDMZYYtM1f+GXv7C5hdA2Pjh4wd7W9iYHr7dR39KE0OE8ePDWwfPDMWPXWY+xGHueDz/+kMVpRnrUeBzaib0NekH1eah2WMLGXmg2Zb02TpumycFc9Ntrg36v3e7cuLO1s7nl2raNdPbhjz/kPI/Pff6LD+7fOzs+41KbVtPkMQAFLb0GijGGlY1mM+QS95xiC8tGYHQ+7D3Y3WkyzCAXHB0enGGXj3JsPOqsrbH47FilQBFcsPmHRKfoT8Lah8AFRkxvqFHWcCREix2n0RGFUYTzyecNTqin4dNcQ3JhUTP6HjzspMIdglHUm+gQkO8cFIXIxI0eo2ZEkJoMIzyabqhLGdw5RRNFndpWNB01rG9Zebd34b+b8IxNPxbRE4d4cBU9UPiB0B5IKCOQZbWEToGYrNER4hDO/JYDedR84vCfPyLJt0hJ8AIu8AEBJvgQ2RFTdLEc8RkDP/5s4UU0HzGyU08QFpguIatR1sByyxJnOjE5IwVkFnyevfjwD775rzrN9vvvvt9CxpACNKBwgJLx2ifSZ3YRViEmRpkCs9Hc5NyPn3z0vMEpiCBiMkYkZoDcJL1W6Q9Paus3nKBgeewEABxKLa4tmBuwJ+Gu/+IRoaFqdSeHamrFDs6pVSVNOSQMuWEaEhnHh197b0jigVe6g3dR7lbTYJww6WMo+Qr4yKURIQNuUlvSG4gEiXfpF9AEKJJnavrAniipKPqMlWlR3IpNRbpSJ13Fu4yZA6TpKvc4xYKPJZxA+ajvRvbzVBxXdWgOlI6tgCqgsZy8p9xJgRlCp9Ph+F46EFo/2SJcuy8ZAwQTOfoElgqojIjL6rzZ8o7Exs0ie3t7L548hacUBdNF7v8gMGXEoIpC4U4oLqBqgIrVJ5Xq/SlzEARoJFm6HWx+UBzATeYXcMlFJ2Y3VnDzn7Wq5DE+5i9YYuO1qAAsQOUdx9Hs7+xuNFjS7DXXN8Fj8xTr9Pi4u89ds2xuGXaPf3zKXhcinvVOtYqvzE77zH9mz48OZZk13JTZYGT3FSZPVGt8N5ob9quV8Ww8bTc3Edm96XY2H5xraMrGA8h3qwQUWzntsF1nK7oycKtWbzJVwTQOpjJVoMbKGJcXjGNVMbZ1AybAc3cjsEtbiyFyoRYVlnm3MGpKG4GRgl8mJy+i+tq5E+T3ovLq5sEv6ovEmRTwRqHUbYwWJcTQeCkPkKw1vLOXKNQ24d03wmayIYdJoHOxrPkGDdWJudGTx48h6vDwgBtpaI8ofKhdG+3N1kaDPd+/9du/ibXq+Wmfc+i+/Wd/9uMPPvqLH/wp7JpwdSDHTETW6eiieZqtfJLq4nvhG0wCIKiSsRLHj++M4Ttdiecv7W2SJfKkoPzK3+v8LkIsvpagr0n5y8DSf0HWIoHXdqxmasnG9L0QVmC0+yufTFyodNmYoy0AEHGjvKK6Uu8Eo4HIxAIHP1lXI6yIlLgMErKoy0lZ8VHELqkofw0VkcFhApQIw7OEWfwGKjToBeE5E3WHdSYcqUcDC6wLqEX86xyvB0XMq5r7Ff3xdZjNV3H6aQZfxbAa7ep5/6/G/1lDV+FLy/vV9JfuVUjlFQrX4smSWoJdcq3GKoEL5vLDbg3wjB+ISD4kssX7Ei6Kf+OyF/iNzFNg1SmL/S1ntA+X7vC++spzmcpTaT8d/hoMJivlSY7MierPJ8MFrYXat945Wms+rdc3R+fnnDXNuMsCN8b9251t9uAibGGni3B8joX+AC0IF7ucq9sajrq93uHRiWe8TSvcGOCGTo6Tq1bOp+edrW0O/j88PEYlyOgERk7NQ22PQgv7X9YX2Oy7u7PPKDQ533r06PGN25U7d+9ubW9xgdTjx8/397lCmGN8tKZlsOAWTOQGxyyHTEZrthYyY9H8gEWH+fb2xiYHS9dQ050dHm1tbfZ67F6gMtQ4L5A5gt2Cw6RiCCyKUQs0jqYxPDNcsVLQQm5ArwCpzAXcEeF4v45hLSoIkNVwc64IJw6hEmRlHplo/VgJS85iQ3SUHC7fiDouW1fWDrPQ7ZIS0hLBz7oa5VX0KjEmauC07v4iVHpg2Gar4HztDHVDARQozE46Ir7JB5cSMWhBbD75LeAgEzfZMYgTNAhGxkGb6WF8JixFBTkZMUiMRAxM2squNCuUfFTkRbanUCcj9nGrOFXqlYeaN4/HG40Wez2ZSuEboh33rGIp1mB7B8v+WixXT+qtBhtGfviDjz/39jvNxpY3njZQB2aaphV/2FeQFo+zRSQjxL7z/jDaE1fFcQCOggPVg+rn6fBb2/0es4fOYHTAfNGdHVquREbdl4qcg6ihbyqEEGaRJ4cYGaB6pbxJDPnF+YRk+5hd25H/4CU5TE8SvvQIUgJHQeFRxAUyKmCUjRU7KYqslhznl9hK9onG1KAiZGiCFO5MoEgEl5OH8MEz/eM3K3uWkeQ4mZQc48Z3yGeJB7RFpTKPTuL4CS9+rTTER0K0ZOscDrbJNAARTYE2mBrYJauBQru+JZ+DvIwKec4vzABtBSTbTgmcEelWSIYkJgO1xovnD7mCkORA7vICduohmFqfoAOBl4LngFhOh4GUOvNALpNmjzin/rOqgNE8doDKsWaavRNGcraQ5CRNoIlPvshx7HyY7MuW2pn59IqPentDjTTHHiBTb25utVpT7jLvbO9Oz0+pHd3TUyzaHz99GlY9tX4PQ/zcEJgZZCcG+NjKohBMvwNF9KiD/kDuVWbDMy5cb+/fvIGCIeiVg4i/LGlQpSGBEmq2OFgMDYuNgE9enHsc2MwSky42TgVD4ABGid55hw4ehT5nsJG7876nCTFFIyjnqqBgOWKtyjls7KDw4AfKjpkDvR19Jocy2OWblBVDTsuR+Oe8ISsCxQSMGlMYJxdT9pebflmtZtsUJnuZKG26UxgXp7WOWakDIxohOmCGFUuoNmyuc9wrWyFIk4UjllY0hWKgkTbmRO7dBycqHY77b2LIzxYyTq+iZrLs8bnPv/v1b3z1D7/5rd//3W8ed5+dn9GVPGfHBT1Le+3G/t4d6qetm8XJ6N/lYtLt7pqgPj2kPMj3M/LsT4AXb4PRf8uMhA2P1VdgKNGtBqT7su5/FU8mKpzszke/0l14Lj6vJaHMXBGfnxX48BTlMvR6V8JkzJQ3yljxq9b/QkJstRD4tVYDEqvVmNN7TD7uK4iCWKHMupe0JevTbd+wuEVBd9yInG2YyIBGJPlHhaT5AxJrNXmWEfCkmOOUIfE/otin4RPui1YkAK1SINBq3s2GXloO6BDcbyLZUa566El4+AWlUY2ExdPGVnS6xvq0JxF/GtT/n4dHbUkeRBm9LjuyDLM0l9WC2IvCfV1MCbdszp8t3mtDf3qFsT2IruQDXxcyE8MiEMoxaFJd5qafR/AcYi2DJq/V6/YHpycMLWidTo5PGJw4sPn45AQBHSEvdIHnKEYR80IhSsNDLGZ1e9LcbHfPuo+e/DDWAMbgolkg/aMeBpLV381NbgjYQKn/9Mlj7ENOjxr7e3v37mNlW9vZ2aFF09kjyXlSBk1aESP0RyH6IQqEjBlN3WNMtfjnSkgOsFAFWKvS/WNuRMfAeIXql86A/6owgx2MiDbUgisIWTRDdZkxuNIjIADgMa2ijsIKP7TcGuOSM6R/4mrGkCpP5ASsT7SDB5sCE7+LUoHT8r3k/QXGFyFFV2CUCDaTlhkCQ2irKQ6SAzcQ5JFzFUNsVeVLjEVFL5MgI0TPf2WHxG8Ew37hyU5EramQdS4QlIPOWEm94Inb7ETaBi4ylmgKkvmAOMBYlGAYV8toXUAcgU1Izqg8p6j5tRzBUIQ9Gxp61LkCaQgkojV6YpZu3MPBGk67waGS7c7GcMrZU9iZsIPTVQ93kSt2mLCU2MHzC7/VMqKSRk2b+ba0rcAUSH0wPB2OOgdH/fPhOx5GRUWSBUwdHB4URKPaqx1WyOII0QE0IHRqmiLuMs/BHKPADtyFS9bhI18ECP74LoKTKfllmFOfCC1QLCETBoKiKJLLIVZFQHwXy9VSr7xFPqgS8iChIRYdK59ZXvImAwAke8IZxA8k4MMvjdevggrxRC7BW+SQKLQxIICEbZFVg/DkQEZamQh54kBJGgbU067FaEsAUgYGmdBg+vzxMt38doOm+IBEK0zBMUFwVWpa293ef9p8URmJP3Il9cwqaaHEp1ZQkdARvHh+QGtg8l/HNM4lGTXOkbRCLS000hc/HCiST1ZkiyjzHkUodUJBNJI3t1WtcYrxpp9Y8w8nh4NDKgy55pZ0tgAh0QILJXQK8NI8k4VichVJqfm2ymKIrwBvCSGzkoYaBfmJKDwbnzLPmcw6Wx3MXWgeZ5x5ho6jWkPPzeoH3RqMRSNOFokCMdbKYLurJ3HEEJyBafAGQgGRFC48YS0gpmqDM+i0SAnj3jH6FMoPoRpdCMgh1LVT+Ybw7UyJFKLUiCOpZp8n3xYCKcBVKpBTA75lma1e2iKyVQ9aaLxUE4ppu7O3ubX57Pnz09MTSCQOlzY8f/78wb27nAiE6Rg8ZJYVS4Kc08DejTAYc8Wggp6Iqz+w5HyBmf/JkfcsrzcxuaApc4ABNNsGZtU3Hrz19/7DG//dP/pHlBR3TIJtcD68+2Bv76YTVPRB0EjFhHgy5D8bhznJ7EG8X9AWeS4yq1uWC7x8jPPze1YxJ9ZVn1X366R5Ff4yrZe/r8OaMC+DzDR4F2wsuQP81eSvQ6/fArJ0BJsjgCJKT95ROvm6TNSCPIKjx7EmUvHyHw3DsrasSkA7BVDG/6gImUpBdvFhBc4qLXhEJSRhyvwm6DJnpFOfc8YOv97iFo9VyaSKxMEVTyLSWViE4xFBi4CVWVFGKd4XdltfpuAC5P+0P66uNrw8vxZY7Vz+zsJe7eWQl0IuFN7oflElBIrCuvC+FPXC52cop4urEBewlB/zsTtfi+c14Iv6l3VvWRdB4Ed2eYmNWg+vGH0ZMhGi6HjZjcU4w7WWaPm4qwspnC7VBWavxHJR/uj4CD0W6wCcHY1tPZcAPzt4zhDOUGVTZm2ZbXrY8GJpOZ12+6fe/sqfaWMIS1dvc7nz4MGdO7dOXhyxcr+3t0u8t95C179J0+WSHd6Un2eH17i6UosRVDg2dZWy0fUrqqumh2JGOg/d8y561dhkEFoRCs4HNcxnkef0gzSkAy2Vh1q+TJDjwQZRxA+8nrXCgXRsOmSE5s5P8sOFCNjd7GDWP8Mq15Mq7UY4Lk9bkiCRuPw6XXB6E3KGnYdYQ8YIJ7r/8sG3dF78Jf8QRKAcZMTiI0RePrF84RyPGdI/NKsaFEoIngW2hcNsVcZ3DKk/AygCjJIRSIPJlIIa8xi2Mk93sdxGIIN4pTH7royRuYhEsl+FsiX1AROBJfs0eiAuh+9F74kALicZxcejyelx78b2Lc5/am9oxk1FQWGJFQdnDkIFVziRLoM6+LlNbjA5Pesi+qxVMPxlWwiXEClKobUmKS9BC3ldqRRx0FpFjeO+Xg8W1Mnlcdz8qnIfI+B6azDs3bjxRRRUVrwxikChcsABJV+cHhPnDyrYIjeQCsyBR9Rn0kK+CIYEW4gJf+RCcAS3ZR/fvFMMknvISDeldu2w5JxfckcWF1j8ghYgAVp74ZfaXKi+bWaJG2WBLw0h4hpKPcadj3I5BJG+/spu+EtUkT9SoCbclAZqoDgChhTxQTvLO+JGTskmcnmlNr1lujXoAd6GAWGmIhuMETnGMN2FkbNubzbZ8cIuJFqB/DMf8DDYIgLREI/Ho2ykj8dFGJ4wWLdwkV2p3qgTIvH67M137v/gRz/gijA3zcb2YkTgIiqrYMh/kLu21t7a8HxKDG8oeNd8OMBSYZyCpjRJIGih1RTUS4j54on8SpdRqX0EVetnuJlGseSws7uD9EoNbDXave4pp4oi8XOoP7cW0HKY8kAM2SG+GUFjQfViIoqNuxOZdcTwWgUdtpMXq5Dyvur/EFfgM9mke6z0zznmmK5kdnSKtoVJaI1LhdlfjHDOMaboyDudrY1WnbNVt7YaMaOmC6LYBWXLLlgQglFvsxMGH2cU7sB2BjWrTrj/hBkV9xDP1iYsBXBuKRJ5TFJYi/C4B6opnRy1XcpRNrAQKgycsJOBKVFcUVDBteAdapE9SzFuS7B4neeoCrGvnip8s3WBfNKya9XbCPBggkSOcuItI1wP8eaIk15vs9WBFR6d7LjgxcPEQ5EUK66QMT/nAhjtN6v7+1v7+7c5yI18MQezmOhbmGk4L5ru3trd2GLmMD0bnKxx8tKsSZHeu/cWx1dwyFgUMXRGsfuKHFnRMmtUkjIsyjLgCKRiAJOPTcrvsvYU3pd+xm8Iv/7JJe/rPkvEy7ArPqTHsyoTXpADlzFf6ip2JKbO/qVQrxMAcbbq8h0sjS9rNvh9gj/pfMVbKLm5esNAwWtLIbhQlEzJbfodnmCHXhSKCPQpybJT4iPh7BUBsg/PeN7wYFDSr5+9VP4W3uXP5I3CVaQmEI9f2c+Gf/gtXpwCdMkX5IuaY8L8XYLgu8hB5CjQCydrAjFvY/71PknBZdL/emn6DKkvW/hniJSgUQxRhjGeFTVgUYtehc/qmSz76y/Aa4suKp5VtMiFQPT1DlyV8zOuv1WqHk9dfGeN+4zLtwaD3b1d1LMbGo3OWbG9ffNWZ3P7W9/sHR0coDFlc+7HHz9knEYRRVOMEYq38vr+zd3Hz544SqiG5EGbxWkXNYxzGGh+9IMfomPbmDMB2NvsqPhHYUPPzPI6jQoS0fJAHgMICBilnIo0OTZucnJ0glbJAc3zQ9YY57QJqHNLDiMig5lDDWINemX6beYCUOPyAb0CGsRonWBnQIp+Q4ptsPggM9e5wkxzWgdCIR0J0VEhmpAdRDR2AKL/C2lG8Su5l6MlbqWfeIq2nF8Fq5dhRSsHkqAihpEtCesP+BQznFewaI5UpuksuUCEYoZDvwYYUMZMBCSX6UbNDX88IlMmIOZC4rHg2XRNKojorF6aeyW/ggwllQJVYhZJ8ZiI1IkiAyNIkjUKD0EHvnEjF3M2LS4SFFmflX13gstm1li0t2k0WM2n1hGr3tlk3qkgwiJ/kFo7OT3C8A7Rb9Za9K4IvoqHBVXJqViIgRYKFbGJA8OpG5wjiRJVawsWS2qoNatPHn241Vp/+837zAutSUj9ZADqSAzLskqFI6ccLfgO2rIQFVuKHACcvE5Oyt6CXXbjyZ/w1F+HnsQI/ge2gomBJ1lo6REzfEQbUfgNmTuwy+f0XeTZhH1MMlgRhWuigScr5EWS+LIkijiSV1IqonRLp7KcUElptggBAiJwBLQpwytgPZvSWDFvtKwtBgFFApQvAaKV6WEa/sQDVLSnyAqvBCYoagg6AXW9nO6r9M9c3UOcyATYqGlK/8B5uUeDE+I9vT7WlKqcIIpAfI4p+VodNYHEBwODYFxJmkklmVKS+c13cI5soBBn15ONfYzM3+cWkvGxGaURajNPtaqu0z7L6uhEEYRoPTBQsSydx0hjVLRgiEVJLHBbpdDQI74KQqUDSKMX7PbZIo+FTAUJ2DM/K3O6Ri40oB9iwuxa6ESq2BJAtkFOHwUMEfvn6vgPD042201W0ewlKly9WJ31hv3zHpM/mt9owvQGa5rp2myNfVsI7VR9pg8kBgWRe9qQdcAyhFZrhNkyZ+TA2Qse0MqPxSjRvB0ryP6cmby3p7ApC5HV0/qbdFLs/GEZxf7Z9k7PvQ79RnWOUWVwYf8IpmI0WKob1Umk7IhotUcjjEU9JYiz4ogO7i7nux29uMnZcp4ObCdv11hjyW5ESeBgFvr3/mf/8Y8ef/J7//p3WfjZ3d/9pa9+ccZBqOTAObwZkWJ/zFKUSvmljyXkOzIXEPnKOAIQHNHS/9I7kZbt7FLgNZ8LtIuwAsPi+7UdiWrxLvKX0V9J82uncDHbCxZ+hviCSmFmsowYLToLIQiV/QloWV1OR5DEsQAKRFETI6woOyPmKFPEoDJfRhYxSSIIsrJnjceb6p/5jaCEK94XfAIqKgXLj1gX+QCAdziEFWmkkJ6R//DDU1A6lAwpmlt17PwjcJQx4vsl9lWQjZUh9F6xO89YP+17kc1Fdn5aTMZLFize+Czw/yxoXycux9UkAa8DfAnGovOR2KJuRG1J75fUpyJGETW+fi6vTy2IZGmRLj8FcSbf4AABAABJREFUi60bkIolnGTEuoG330WhMACrkaIW2i8qZDO4op+ZVdhK22IQfP7s4PjwBKPq/Y0NNep1dKXeCOa2vFr16fPHHOHp+fzDEae4nPbOGM+bSM9rd2rzneHglEXvG3f3v/Od77IrlyGZRFyZ7Xvny9ZWC3l+Phztcajn9vaNG/vQwu3yyLsOJ1wJNDifa2Mw4hPyuRQY8lD1MYBhys+oxuSE3aMom27s7al9ZLhkLHRoVjvIcgGmu9wOg6JL9dNkxpXyDpOAqTZax8rbG8k4YhIBFN8sbPVTmPjUOM6PlXpyF2auIDyJDQgMaY48KvE8nt/BMEZD5huu5vPW064mAm2YyWnBdOYQw29ROngtSgpXwBdhgiLThIjAj5vn8KqOb1fGt6oNTREMcxyFnIibPYoY47v+tOwW0wdIbIJFG4CYSHEvL0pc+HBcXcMAej+JYrSsxh0ClbVnZmmVQJGTCVNUJZ9fvJ3eIUdDJ+4R5yahYGQPMATIH7gWJjo1rm9uNhMh7KKm0UuvVW80G6PKepct3v3jQ2Qk5YDZ/PHjF08fH969tzsbMwOS7ySsmtFjWKmlzi1JDLYq04TuEJOA7Z1N7Bk4m8XSWMOqmCUCZn+N6fD23vaX6o1zFMOYeSGzAIDoQlpkhQoFpUEYi1/7RWUgX/Uj+RXZNBtCUEYQAfeTN5F5AVIipW+nUgHIcU0HAeakQoRGtK0pbCWwu5mp6ixbHRhdN0gi8bXnpBTxiIbUSUTzamgQIR4xmmgECEAwf/hGaEAmLa5CLDyBmlVZbRBDxsFpcVpSUabV+kHgCKrNCwe+7wnLGkJRecRmxiQAsfKEplKt7AMSJBXoxA4icRvbN5/hLlOOfJUflm08Ss+V2eZmk12eRycndDyoA5gGsMUX5tkh0EsgEE9m9DXUBXQEoKco1+Y3qzOOJh4gGgJvZ0CaNiEJg/Ygz3dQI8/1CWnUxJUBKBQqM7ULsOnx6THVFAWH8qXYSIyVGfeys/pA5Qpg/Y0uwygkSIIb9Al4WLv4yZzTsUAMCOFzUCMLTZNVuBmzZclkebVWCRm6vs4NjO3m/YB9jlUM7aW+0aht1NGP06kxox6wGkHXx5rBmCvSWYRpn0+eT+m0mBOQDE2M5Kb71Fz2PygQ1dCFuzzhRBwSSFx5npmVG5HJBoTW2ClBJqabUl3vEjNEfn8hFA0JfKnVuzCC0x3YDIYfS6xs92B7Lqe8bbe3yB2nlzYZLYzrtI0OmNUbjnBweW1+NmIvEy25VhsNOv15s9ZhejLllFTmM3T4qFqwFHKUGbJ9pzY575wd1yuTZ632xuNHL/Zu3WcDFyMICKkMLgpBGOXCLQ2blXsP9jlT6du7fzbqPWcZwoUCSLZpw3S5QJ7kuQ4CyqdwZU0FJL5zjb2Q65awZZwrv9yfTVTh+TGdAs9lwEVQOlaDw+eiDbpIwkq+gCt17avRyuSWawUL1JzUtIAkDwv/hefScTndZQiu1fwvkOBInNlyrR7xne8Ff4v7ks1FETUjgja/Ra6LtcoH/GhHI0RCXQQx+MJj8RaxbWrx2P+En63cRkkN4L+9UWKLt82QbyCpPw4uy1yKM5ut+DjenI/qvJ0kRUCmxJsWK4et6zwiXpDhl+mGbwT7Kigp+oRlGAhWiFuAv9SxoEACl2heCv+ZA5Kazxztf1IRrCPwQVYEj+F0OH3jmWXgx1/J8xmSuwzKt/RmJgrK/aFPFNTaaDDdKQfSoffyBH3kph9/8KPf+Jt/o1VtsemKVWJkdW6x6XZPGTYOXrwYcMkKx/uz/xdRnCPbEKXjKEDOXaDPx4D2+Pjk6cEjLpThFNEGG0BZyh+OWs3GV37lF86O+y+eP79z+9a9Bw/YM8q4x5hti0T/rkmoIyvEMNhDiVtIQ8hj1HTnMWTHwAU8+wTQGSPHAqkwTFZc0WYZmuXyWbu9eT50YCPl6hCRhSHGTCo/OjCRc+JEF4ECO0YIxioywQqElxNhC8BCN3YpjugMZoo7mhY4uBJP0UEUEKQOjAV1O73gZVaIRV8QnRDR8tefAjAr2CKODMjCUKZgIGeDI1ta1Zeblnos1srdeWw6EhF4jOafxFis/opIVLgiBHg9gYO3iL4wwckO6ngGdfLuIJnk2SH6L/CJU5QFehIlF5lYYvYriFXmCWlXB4MzTCIuZaFFL0rHYZ8jGaEFESpKD9F8HvcsoyJsoO1DcoKR5AyMvAeDHgKW4n0Fe2jMM8DGCkD0n7LdVLMahMUHBsctbAXAyeGhWG5QZ9i7ErlndyiHSB0NRmcepWLpQ0CNk2mYuPb6XbgZC0aRY+UzaA6+mQVdZiOISobIxGAPLAnWyKGAETL4BEsSJnnPpwTr6cMnmQwzHn2MFP7WeWtZfAhlfSYM3uNnGI9cjS9/9SMsOFH4BpxkSVI8+StTBS08I02h8tumE6Vvcnjxl+mD2ojInuTResGP/1Kc0ql4h9BMcjSHAh2xJcGn+BVh+oB3xR/y8Y54YEA2VZKGGCRSro948NYbT589Yz82HQ335yJxMpN07oa0yk0+7CFh+N1gzWfKfQM0edaLMIBhQodGuUtpTxDWqZJluwuCImdkhBKJWrQgWm5Dg55kCwrOutTYOfrrqJLF7JakySv9SGQ5m0VwSIaRlWAQ8eV2vCM/wVUbDv/ML82XyZMfNj8rmmcg8ZC+v8SkyuCFyRqtIhoGPq6OooZx0WvG8flefmKPwEwIe0au0EOj77UJ0ZotGbKT3AStRUhfas/Gk9RlmqYaLJIyabbwiGtovGVHnBkKaphPa2R5psG1XFM2b8F2bg8gHs240lyfDL1vkRm4TRf9/9iLz9abTaZnrBvfunmrvdl+9OQR6OnT0c4weHCcJ2uDFCy9dGPCRIiFFLIgNWSWxR247don+oMNagiWgRr+AU4bd/3n3MtS2Pldr29s766/t3Vvo9Gpr78YjLgv7MXe3jbZsBlT5FHNdckCnsggv37rLvz8ufYBALCXPDDbJwr5FWBF7JKE4vPan4R5HUiiLwmzyK97FuiuD74uyrV+l6KXyVFVAOfPdApmRPxPy0CGB5oidv6IzidqcaBNH+DLoAgu8Ed1jQgZx3qMi2pjS8BdAljbS6ShwnDOn0/ECMBoAJFohBGXlsabr2wYZYQkJVaRCSoRERpuwU3M/nWV6sBBWKRQvIyTWFffJcgFv9Dm5tyOGeFKoqtQP0c3OmPpiPnZNTS+OqVyZpkRl9FL/2Xs1VP20/cqzKv9l7h+Lq4gNmpO1oyigMKurlpZzq1fmljmNgto9fwi/PF8We5eiu71AzIB4NHe7fuTtwnWH9GZZ1hUZtwOeFAjpVUMbIbnZ120KkjPDHv982M0ODFKVTl9k1OA2CNA2HA00GxnOu/3Tp89eYLphZdiovREY1PjkH5UsKw7e7fPwckAaas/Yq8wovxU4X4+/cH3f/zeW29+/r13trf2NAwd3sLGs944dVzXIHuA3Q5afDp4RnSGGpR53e4ZwyR7jrGF9QiLWpVTRtstjgZagwwWFoDkoYt38LW52eiRL4Fst1ujyaC9fv/g8KC5OXZr3VRJlEGEcXPOHb3EqJ8plDHS1CvtzW1WEZSQUTKpW5RHSgRMS4gWki1MYapBIvANAIzXR9M978RRmysvo2eJXz+tAVELMsh3dEMBkNVDJ352MUUwv5gMMHQjlQrNyE2aR/OaR+PzP0DpXZBF+AraAkd84l9gDOCoxF7EizeiJ2EWhJsi3I6Y0cBOT0WOAHlRxBfH6qMQA+eIH45EC4Alh5aW8pfoNQQXJBUseice9EqNqUwGPY42B1JDYWRG8kOBokesrj9vbXUB393benb4LGQnD3LEOun49ODG7V02LkoZQnrVtQCld+XpgmgmbEGfqJD4IOC0e8I6A54olGTSeGu+1hqMXvT6T58+1B7B+RqKVMyjsfxReQxmEEK4EpO2+NEmyBt55B+8D45FlkNCihSBzl8ZZj1IIIFxRRSlTJwFteFL7WSOQRGo/neqlO6oYpY1uIKgQAP18ZhSOh1NBCnSg+uWg3CWC6HCSTmpZLUN8gsgmVvaxco2o2YCISHhTEwlGiHiYTUDp0mEGtj7tonvPIbmwCqaMzbrYeSLGMkaUgtqAk2kZGrhZcpSm9/xjpYbPoqwVbS863fu3mbf9mTgaiQTNrCGUAtbrWw1mrdSHbuBZ63W5mDEiZncSDjhpgwc2AKNxufImGJzuh6Z9YIKMgKd0h+pJQui4gfhfDvfj0Dq8HjYxof+IZlCFGRQqXeVgH29DWetlqN4kdXxhHp1gsSKqiETI9MkGoUSrNTTXUSeIW5ziEWJ6Z6013qQjRcZrtW45WDW4HyeAfMgrez6x8fUWXow1kvpIa26VjANcejQXNuEQmPTEnPaxmoSBHICIdVtE0K4Nh1u8JADvkgr8urLmmQ50wN0g3rBiU4C9JT0yezHhaPQ09nYpHXDVFoUBjru2+bC5jzOlRWN0Yh5CqaLG+sdRgSUJrHQOsVAiPW37c0drmqhMGv1Aff+0W57vQFrd+NRpd/joDg2BFOG5B1lAYt4/eH4yfp5hxXZUX+6XmtXm3Lb3mPqai2bpTGPDJ6zLXvQPT2Yjrrs6mFwqK1vMkeYVziJ1TOk/BcVL8qdLMns8gn3nK0X8DLkqxydi5ILDkWDKuGv/GYsvVmkjD0AeevwEhDUiWfpdY0rteDLAPm//LrGtQCgw/O0/pTW0KYv01veTfQ6FFxM42VSinpxEltIQVQ3GiDNy/0Ai3xKekgg/MZjM2GdRP/VnOacOO5jJiQpj7dNpHjY18FH8DnHIQCFKeVGccZDHIpbvtijG5/vhM2OE0/Xn/WGHrHyhCMBA5NDYYTF2Y8iwjuQzfNUzOQqJyA5RAWk4VGrAky3LSqoCfz6mP94VtMOjwJ9hpbvArj8/Kv4vZaOnyXh4OPPguCvKW7QbQFGEb4mEZ9SYGBLiNdmymsDXkvgojCLwTjTL6hY6Q1dF67QwMY3b9746NHHjIfUVPrVra1drtFljZc7uJDgmy3MeDhEoom5BT0sozCWNqc9hK4uaioGHuxT5RY9LiYgHPzP3VWkMqKndi6OXMiOUDrx9kanxUWazCcw9AyFz7SKFIiEylkumHSy8Y9xYXba7SLhQcrZWTeEDwxLGrdv30Lg5vD49iaGOih+OIEHu1LGp5BOtOxBbxcjciwosLXgrN9DzXzj5i0u6kJhyf43LE1azZ1Rnzsmi9KFJ04J/MexG2ieEW54FK9F6Qgbh+6pl4Zb3H3MTmI2F5LZ6ESif3CkVF4HGf99gKWlW+rB0uhgDIxaECpmggODQNF7ECv8UNMTRykLHMrpgqEqZPZBOkDzDsziIqrFaUL0Ogb7RG8TdSAxZ5+Gh8jUO3JSiOVsfLyIQYpBr3H9KrpBAcLDbAqxSIIQMNGb4ktZMz/Dbl9BjekU+3MpFI5HqnA72+FwfMZaDnINsp3JxVQEblGGmHXt79+o/+RD0oMkxAWsnT/+5ON333sTiY6dwqj2mdAZRdaZGtSFql6hkHIiO64C1TgPdLS3vxP0FVMjMsiMworX3gpRUJ6e9rocTeuWdcvF2QgII2dgxi1+336lO7yDDSAvmR2QK7woY8lD/lleJT8TZZZ8FHgmRIxl/As1J4VUoZbpgcSsGT+lVIU8McRbQqU2QfCTiMyLeeQLaVXfwBK/Eiw4ob6zkK0bZl3PROCiGUJqIAm208K51MoWQt2MJMFJueSDOxwShDNowlXQI1UREjD5Snj9Y4qCXct0hqTYbLb7Z+wsUtqm97CrMD9QRWVQ7JvX1jc4NmBNrQQNgpkChG5tbx68OLd+SBlUEcmmSTwnXcXnSur6mGEqamSYxp4zY5eMgKPCSLRVhXUuMHrPbuCRY2LlD9WAfQa1nUfWZSwoT8z4qs5n5QJYFB8+HI9LzQ4MpB+UkieqJYLy0fExinZ6RXKFHxaTmNIg5SFA2QSo9SIxi5Z0MlQqPS9THwhwJiBlYScjGEnZQWWJgIN/oIoZUqAxWK5KEujtZ/hE9A++cN4u66ProLO9qIVpulhLWm7u4XykIWTv7GwhyrMMgDqJ3h2OsBCwgeUS3ULoCOiQB+wWU2Mj+Vxv1h9W1vrzG/v7I6ZxQ+5sqjeJsOZ1YMxFuNDXDQatRmWN3qULC+UnpcDG4nUOfKPL9gQ2uhVm/uv7280mRxpI1Mnxi7ffesA8hTwW7LF0cVpExQ+uT3molMmwxPEy6MQZTQD45VOkHB6vxrCMs+K6NsoqfmDz0zd/10ZYICT0UuRF0M/HcZGKl9Gz6h8klURZIyMH1sAFRfpllKznFAlV1GIJID9WnmU863nxZSrRDxX4C16FdzQHOBeg2ROKLiFNItGv4DU4P6lnTvcnD6Sh8WgBLYnizajCgzBpLj7M0yrKSGbVI+F847uCxzlWCccsBCRXz+kvZ0VLHC9zCUl/EjO50FKn3XwmUKRa6v5XiAh0L5sdrqa1Os97tf/VXLx+3FXMr+8mPyUjF+fLGpt0Iyjzu+C+sHptWLQZsZxbr2ISA08CLALgcPpkKO+X5S4BSt4uaMgZdjHnfnn5lomUdQ9tRKCwKhZh/FipHRii+uLvpbOVcavdfO9zb//Fd7/DOitna6Oz/b0/+P0bOzfefvPt7d2tk6MjdExD+tv5APvP4eCEbZyc9z0auNrOoT8Y6KJ1GXGEone6D7kcGDNe1VTRDtGnY9Wzx5HaO3udzTY6dmR3Bq5a4xh4lOf06ewWdRrA0FavDc9H3IPDN/MBECCXszmM0OOjo41ma3dnB3zsivPGGyA4LJJRiiErBmzyBXYsSskqp/q3WyjAnnN5zJiRlEGRu3K09MHMh6tkuyV7YvRnycSV5QbsQ+bmjlJEgVnlNDsbRjDlCCKEbl42+jjoz9WSEil04Ja+UKQe6mrgZX3WmWKs5sRxvOpH0ZUJGpUK+WRP9HFqkAIBgpdWBxzmrcTj4OchpA7dKZZANK3Xr7KYY/j2u3xIJ4o+y1+6eNA+JkHMKJSftbR2MoRngSyqCDH953+DIsy84OAniQ6GGGj+WPTHZgvTC+QHwxEOqyhrqwP2gLAJoTJYQ0/YRHBhhlXfaLdV7c+nGJKtNdsUGeXJuE95cr4LCsbxGKFzwHYFirgy39bwunESBCWdZgLqJWyyi76wvv4xGw41FmEDyWwE1TCMzQCT6fqz54f6YkaCYAjJCIrsJoS+1B6CFEqVmcytec+mEfnOsiQxEcYPL9MueZXsCdgAKGIVY0mgEjzYKFuQViKKAlZiirdFt4KKpILPekJQCrIJYePVDyKVxTKWUZMiZ0ouT0URhQxHkDHH+9Lv+UI5TY3kRRIpR52crx3QpIBSEIxooqUReNYFHgAHB12KEak8xF8hko2c+9JSO5DikhTiCAiW6Q0c7o64+hDMWhz0rh0QD/0cjQ9R+dbN7aODD5B+h/05R0YxjY/mgy6cBNFgU15UYC74Y4UQqrsU5unJlN6Hvm1vfx/VMguGdhFRXfmxQvimCkiLTonhN/6KluW0ikZhTqvHUa/NaDBETplTt3AQ1XLQTfFM454BuExcVfJWPZBiMEO22OLSarJqSr8Te985DNfubdibnaEUCUAWTc+IAPv4RP0BxtGkbxD5tC5gmkjAPh8V7wOBIom3R5L/Z1SDcEE7ZUQ/Z6Y4Dwdf6eB/tS+HMz+G4WnjJ5bdVkwD7AssVwEDD0F+JLew9plggl+pnHbP6PVo3J12i50I9cacRVoO7KRLH4zRBHPIANodaAOZO7igkI6c456Zf3W48HFWOT4+xrqPpDCzggMnZ5ONdnXYHzVOzxHi3bqDDSbn/3jTZLfPyjNXB/cp7haTI2hyRsLYYSGxD5hLYNhy5FViZ6fd83MGJg5RZRKyM5u15/N+dMLkwKIzy3JK1uVbTvBYmKH7z8/ibQSDPv0JyAQtrPZX0Wfop2NZgchUE4lac4PE/CpqTCbvLApERapLPX34Xvt6mTTyMv+rOC/4LIiH6YszGNOTVdm4VWmFjLKKWkSMaA5tUa8js8EBa6D3DlkR7VhAhdun4llb4ioyWxarn8BawYSKCFZ9KlL0frabvOWpEif/BDlGCmKEzyh4LDCHH6R57wG4heVVtMwSQdSuwBJh4S0YdBRNLyJK2vIx/KJPERYprRCwjJKuVSSXw36q7wsI+ci0830h7KfC/lccKbh3XZqrAZm3Vaj0yXfmmYJeyfyqm3gLZFcxLbEuoi8cy7BXua4Hzxp9Md4K1auE0KRihBE4kWUNLSIzgmEYStWk92Qk72ztcsYEF92zwI516Te/+e/+i//8P2ez3fk5+3EbRycHdMxb222sbRuNTXbVbrQ3Jk8xwdfqg6s5eSOR9bhErHtURZnvUdDKX3mPD6x698239nZ3YRmdMv/NBx1ymLfSTBXfQTGZsuzAVl/8Ueowkg1HfaLgUK28Vt/stNmaTGYQyMPgZNbg7E6HZuURLU9YskbJRNJuUXADwzo3yKTYLgbQsnaPUoqxKlplwbtsoaxmj7RBaKzH3QGsrY8RQareXaogaoeCUm4+xe4UjtKoSShmD7A0KopdTGAMTktnoa8NnkeIvUx2BysFjGdRQuQFXEipSkOUG91Y/DLmagsU+HNEg6KAMWImuihlUtfH9MQhloIAx0D+IYamwUKkUIBJAtESX8aALRmTdyQmOlGTgmiEhyss+XDKx0jxWkY6oyMCR5vInzV2G08otZ3dzue/8KUnTx+/eH6MQi/EI5aVmpMBJ7eAhcoaEkd1fvDigMunyTjRkTKdCUKHcrCbFpLDmZJVN6Q8lH9bWztUCVBpd4ABN8KFfJhyOesYEXNCHUOBqpQlxWD39MMsd3zNk4kYZPb0Kp0GFo9g+ZlRCgZH9IQvgP0AocAlK0WxxBQILYxIJ/CuhCYBRaKBJ9wh2wXNDm/akfuQSsh8QRLf/poQoYm+oEzAaPWRZsQtmen8FcmNOhWPpFu7FH1FYaFTCApdupkPw14IAJu1AGbKOuqEyZoXAf0lNOLjffVZCYl4xKA1UeJc6n3vjbc++ODhdGg7tYyZWTphQ2aFEhaP0DyjYEYf0eQgMmm2mXCd7pBDI+ko3C2LX0wBkh22KamMbF+lRVKDdCt0yNeSFBkhTX4NRNynigZPwANeiyD6ANhFeuw/oXNhDwoboeoYwGPQiA4dP4Rh6y/2TAj3NA8A2NswOz+3yWQpyUfqZJBBwjYvvgyV89kd2AwUYyXGAFBGDy+Tc/0h+qnInQAA+4gu/XArZukTWfPHvGUBe+VdxFDfobmXYHDbN3NylDyQyDOf9Qb9g0NBMfSHsSyL7N7Y1f6HWwgsHLLO3X9cxY3t/nx3d4djGCypXm9vdx9zoKdPnmDJBCLq3Gw2eH7wnOVC+LW13Zz2uDu8YUlXWX7eZBxhsXhaZc/DAJMz1D1xFhCnTTu+MBy4LkEvwbpuq/7OO+8/fXLEgRHjKRPCc/hsYTrRTx1K1M4FL8x6PMmb4iO9ePOdAQuflztk2wKLHy8Hff2QT0eSJK4Suuq+lNKno7sU4Wf7LLmQFPl1iYAFvyKdAKPKJniAJkCUAuVYNgGrKjGW2AowK7HNgyZBIIUeDWjRmvi2WBw+bDoRyTblE6ktHHimd8SQnkV4GVB6AVmvNtjXEmiKJERorPCL1/ILcohjsoEzYMqPJfy1riWSIvhlewCuatOvxYfnKmSuA1yEzCQXCQehpd/yzKLSxxyvui/iuvx1FfKqz+U4r/kdXBV24bgQkXTyWQQXNzOU/vkbYAlSlO9KRREkZr0LZAtHgXWBHAdhV98XU7vwVc68M9IirQKGdBfIy2iZQvm1IDQQFOsJoT8oIhb1PjpHCUf/Cs612YNG/f56a6SFLSfezacPP3l288adeqt3ety9efsebccz2tzp219rcdr0vHfeQ8Km/41tu+wWWPey12b9qHsy4ExrlHbI5KPxu2+/99aDN7cwzuVoTva1uvTNKO/YxfjIigHaX27ZZJiPTcWoc7xUliGAxhL6OA63nt66eRPLH0erGGLZ1hajlMxwdDUfCijsD2Mg4ZNTqDlI+/S0yyIFHEGEQPznZkoSVscovLhAAjDCBLfHD3qo5sZ7O+otaq0+amP2NXBiPbOg9Tmr0li4cvx2NG8H4ZzD2J4ZxpSrwemQBmKHaPsDMKsylLTwwZObg0+Eif4J6vWXFFa/j/THgwFfycqx0zBHd0LAA5DQ+IsuhIPo60RHTElRFItPNxASP/1wEaa9IjZWsN0tEPyn4OoeM5oPRKNZi8h2okblZTKB3Mmkms3CG/+gwEyabbZ5NChbU+Aow1odRSYcmtXYgr3DRcy373Ru3LyBWH7/7l1Eo+fPnrF8xNaOk5MTTIcQDkYTz+/nQH8mgVy4dnhwvLO1SyljFrxWO3VhyNmBu0XhPRxSfYkHT+OIk02pa6Y/rXCbRH9wELIqZx9y6khthOk02WJO6HUBkC3JfAdXFfagmYfMyt7If5F9AshbUaZEJMMmKJOzTGSHPJKQeCencEbBWlj6Fzj5DSSBNiGMlDCCmQJE5MsgnhzQxBRUum7CvBT5zPxrYmKAYSGJQ5Z4UpcMkTS2Isu15+L3QmunzrzJC5GDJAxMXhjTUOaF6NiVZsk6+nITEHcwDGrgEWI2BU2biTPjoYdQV67UxAc+EUtn6OAoNtr5C9/lYxZlWOScdOImhGQThavcVh3eurO7d2P38SN0AR74SOehjsAjKa1tVDLKgF0l5HBjA2uQOd0IUbEDYt5f31SCpFbAn4l2SharJSzmYFdBCWkvnnRL+sJLtvoVJaLb1hF+aqDFWKFNQYjthWrKnHans03PQzKsi7KHgWM512p9ZyyzbfqdGuaObHql2TltIDtJViRhuxJnsh60NnlSV9sd7XeNk3xYh3RKLM8lS3ZHZwFDUOVYPMBbBkVJOL+AW6LSRShBdq0uH1KsRsAvNTL0ssXqELmj2puCJPLP/o4yt/VZPWCD8QnFhI/co/fhxsj1xnyzubm30yA5tPdxxThd+qA1b4Oa/npzYwMcLBbc3N17cXTIQq9JcrPvfFyf3z2i1VbYvLtDH729tTsannqSUHXkvohpi+WE6pzD3xgxaOZSDsru6XmnwwnVTH6qnZ2N3/n3f/vPv/N9ND8cRVGdcz2Cl50j85ERT8WB3lw/h3eQHm9/zEd+rL7xfe3H6IliEWvheG0k1wOqNb8+pLQUuBSaGbrk+Vf/abWxfubjb7I53xfpSZLtkKKy2ZqydgUYofrYImzC0SHzHT35ksu4IjUwWM15OxJGA7NRSIAvIwQAUl+SWJCSYQEWlEeKAT6+r6+7F8QqikgokmYfjy0NP17xKzqC4tNfiAmqpQFPA+JPuNK1ktn0vuadOCPRa0Jf3yuJXH2/Km7CBUThDDpWyUj36jsRAp/PKnDpd+F3AYnvZWC+M+FVoAuxr/tYRLmM7poUyvjXxdEva0lRhUrgld9rkiA0saXj2vcKhmudIPhMT8KXxFxhW1TZSwhjOECf5CEMyMacnIOYC8ywP9yob3Jz0/d/8Oc3bux2j89R2wyG/YbmNHTG9LzYZnbOzj9BdOR86VYLe34XqTmdE8lPPRGGvJykiS69Wr/3xt1f/NIvtFttdTwMikr2amWQIbD/QdpDyMMTtdDRYY8RlCTYOoy07ZmS6pPQH3PmzzZjEhp9pho8WJuAiuFICyQHLY1rQzOFhYCDNPuJTYOdCe4qozhYqkcY8PA4OhOEF273lCUKqSFnY3qzVmd7AmlpKjDjKrQG50k3W1iLmNA6ZkOV+sa8w3wGYdRWH8IAZKD3YqrAN2BUF/7UNSqxkQCJKLM6YEcoPtAJLMk4+Psb9IEt4vLhEoPK/ui3Il92dsASEDrfEAjIlHUz41OKRIwHWI2zpSI60qgKphGV0rejeAWrKCxruW6T9RDDWGAhhYKYQCvfIDdyCk7ZhuARIMaIBKHL5OaI+9zRNu6f9ZhjYd/g6IzddrXN+Ns7O3j69JONjXuHBwfHd7k2ca17OjjrnnLu3/OnLzjzZVvTYYQAChNUyhqsw3zy8JPbX72J+hRaZBnyDdZBjPSSa67xQgsMVUhSJKbMwfEolHZs2HC6EP38FGQzTkgfEYu6EUpcJrh8WUxUm8yyHY8sdgyyOw5eJAey317mXEi5EEiiXPwKRiUri/DwDW/xET+xByLhI44x+R+huHRS4gSK3zqE/EL2mbFKLbpQ7cjdcY0B9MZmyyUtuADNsojjj2AWPBReSTp2XDAljrSZ7gV7wWuRkQgOZECvYFNyj/oMJJJfNiJdtGGnENZeVNpBEG2o+uMf/cSqK5f4TzegbBgfNEaqnTitnpm3zEvkMl+kW3zxS1aLL+Rr1QO0QfS87dY21/0+fvQYSLoIugtPwRGAEsdQ3gYHsZT++lqTibsCtReWz87OevCv3e5gl9Jj9aeHpR9TE+XZYKmZCrKXJBSuCJeYINiKsHjCqbdPFB2N0a0RdAvkeLq9u8PuJmx9EM7VMiosWz+BJkf0XTZLiOcWs/GU2s45ahxroCZEWqz0pGsieBSJYLAEQ4LUCIjuQJZbIUvS+I2Cy2gRRiCij6WJS1wxKwjJngBXLO0BaM2wCzgYGz6ByZ7NKVYUpgikzVdSF9i07SMeiClp5WuzRrY86Y0Tv0bjwXR3ZxdQjo5jOdeFYi72o54CRAeGKMUVfRut9dO61lrGbXCEE632bNjn8H6u/+PUIPqCwYApgwUKS0+7L6bTPrMmVgDYSQR5biKrrXc6XNzWVOskR2bdkz5zCjqW+QyTJ+xGzH1wLPLi55WHeJ/yyIBPATF4FWbV/RpRPwUEbJGVEiw/Mo0LASUAv0l0vle8/wqcq9QmdQWNxc9lEoS3a0yS6RoyY4ItURlqQeJV9I2CUfMSJNxFJU1mZSvCv4QKbyqDSBxAo7z88AEu8IVn+KSvaSW++BGm/AyCQwFwNV9B1RyDP4C1LSsbrKkXCAyi3236nbPS9cfmrbAh05tHqHT93N5BQZHPzHPx8akJFaxIyolqrl5G4CqydCfk4n1tflZjAbl48F/9XPhfccScuPqyGXNptX8lWnhcl8KC3LIEL0RNsorsLfiRIIVvfKT7QtTLH5fAr6PlcpSr3yuxEl+84cZKwDWcZGT1rPtZc+vF3/0HXzg+ufvtP/6TX/u13/7d3/+9Dz/ofeNrWzu7G6ynd3Za5+dUZqThyVn3xcHz512253J2dP0GV2NhiMEZO7fv3X/Mre+Hx5zviUqQsaHTbh8+eXFy56R5hz0CnHrBeKKIpg6Lrp/RCAObShUButflgP9+pbnB0ezRuXMY5w0kkHr9GBUw67yYk3JOhOocx0Wv3nR0RAxA/sOq3CHBcYUDp6VTcwb3BJN1JBjnJ+QwwGI8JPVQZcEaaFK62gYbV/zE8DdjEsHCPQ/42ajKaMS4iISM9gn5Yzw9r893lJPIYGfr87/whTRLRexyWJSsEH5QkjkUWwrSYVr5peRi/qN8bPX2gEgMwJMRMqiwAgBk+Tic+0a9XWviAhvEC6Aej28+Jrd11J9GMuQHPzov0JiWfGAs5SwdH9IjDPc4DzyFDvIlcQCOb0mr+mB+8Ap1uwxn4EarCYyzChDgx0cc8aEnutjb927u397ps2V8eOv5swcPHz2cTs7q9TYTtIOD0y9/5UuIQe3Odr/HJKFydHTEPsLt3c7hYReb4OH5hJNDWAqA3ewtOR8MDg9Pd2/cmE7R+a2zRgHXic4SgasQ5CsYxLfzxxFSYIvFhJ3tTbb97e3vPjt4RvkiOURPv37WGw76m43OTqV+DI/GkyHK4bUKW9o90wasct61iyip4Dr21mYy9mOQpHkPblYmN+Tg2hFFZDnzcFJ+QFJ95LK8wp8C8MBKyAwgiyhc9plQ78uHTxZj9vn1rP30AXJ6w2Bs4m0qVA8oZSrbqjfY7NjizHU34rca2zvbzE6ppaRo+RID5bkiHQcc2VCyLsII6cfLneXOizJdaVR+c/pgmyQlG0KWrxRlLmgeGgi61V7pMBT01e9//0das1jywJPxADedvLJ2omTsRMYZSeR89Q1hII93NhSw56c1CgrJ0Li5UWfvfqP5Ezb9R9ud1V2KMQ3oZuqnWA/xswmGNhxH6en/rkjQF1VOur12p83kiCPpmS0hsdJUOQwTkX0+3heDd9lGmgVxkpd5D7IIkw8SVYCZ1/KbyTlh7HPH+HDQbnJl1+auGgoEVGoUefese9pytXYKf21+cLfeQ+4/Z/s5Z9P2+6x5ZiUIBmTSJBUkAW9a1h7+qHhZX+Cks7tQZMhzKYy2QBpSSeFRB4gaVCPq216oP8lidClYUTac05kwQB2PFaj3aAmmG96kRbgpkhhFGTme19hPZSkCxm4H5HhLmSh24FzD7l6parVHhrh9kS60ywys3+Nq3vHsFsai1inqQUw86IIn3AKOfVRtjVtcqt21LpXZWcnG2nrPPr1axVgI4NbGNkuv5/1eo8WtkfTGm53tvXmNoYG+PPdyML+tzM/V+NBXQx7UPHj77tbuxvxkFve11ytrA7MgA6hUV638g1Gf/mL/jGfsVNadi1bG98Jd3P6ku3jK2lF+v/T3JZr7yuppgRciJ2a9oqCLsFU5J/2XcNaHv64nqShooegtAOtb1KvIQlJWUusvMBFiVUfXbm85emDtK7KRLusl4y8FjXdgDqSpv1DOQVH3qAAtwml8gdO9BxlKuJWZz0g3KEuCrn0Dt/6J9JiPErcIYuRlSCSEpmBcQ0UXHzijzUQy9o/RociLImkiLGCNkwRdoiFRJeqVoJWIK76v4ZTEAEtH8TbxpL5MqUy3QLmALmInjnwLktEL4Nf4WUW/6l6Nukhzmcxq8Ou4P1vMTDDxJlGRLZGUleVSRhN/QJXkREWOGMHK0vvVvyupFQxOn1fHWg29QEMGXOO1GgO3GbZ1OKT6sGL7znufR1f6xV/8ha3N+3/6599/9OHBt/7dN//uf/A15P1b6/tcDQwol1GenWFVMddGX4GCm2C4exJJee273//hcfdk98Y+en3UXOhlNhrt3/jVX0NCQUzjmCCE2FDqo6pcY+2Avpzx0IMmOF2u02EhgjEF42/0Y4wFsxE9e62x0VbGQ6O/2Wb/MQTTBUAwYaELZPBTEYXQgwqKLQCpLKSduSXsXLMiOJGQIQnFCOfQGDYqKhSV45FXGCJu3rrFaXeIOGCqjjh2FKsD9iEwKikaoXtiKFEIqbFZFeUfHFRhubHBRQeY9npvAIhl5ZLTDMByOgZhB9QY04PbWQKEMKwaA7wWBY4oGcuEns5esxjvkFq0XgICCk0k/kX3FhWU+A7dJKdizglYFK3YxGlokBKljegQl2FBsPIdaSkwCuYbhhCM7OIA72TDBMCprAyxri/4KeIiaYpLvnDpz0b73ffev3X3wf/tv/qv+ucQDG526Fa3tjpsJqFiYPRfH7LLEyPpRuSF3NR29naOjo9YlGA4JwKGvyfdF8NBD4c1DK5OcoUnVirEKb2UHT8ILRR8q7359nvvvTg4rLfW2486nAzDaS1IEqiNsULon51trLc3WvPBbMg5I9wggdp4Z2uLncFkm/pGhUW6QSxDRmM9ComFNGR+1rdgIZA8zBm8usBgi9Oy5s9hSX4gi/BpBSU82ENJBETUBKLgG3++fMhBIJblGcQPUYyGg9IhkjN0P2Yt7lvlToz+ORvc4QiVHhEboQ01Ke0otKWpwYUEYjCVpQqZIJU/ZLtAnPVEjHNW0OCkxMYwTfFa3PFNLGek8SJ3tCwFvthkz6RjJDpldXBTuQIZuVP2jbqMh0nrH6SIjUTyR+94ZKLJQJEoJMLFK/gPXffu3rOY8ZtV0AuYd9uXFTZaMCfKcwqH6guumqUOqFDHPsobtWonJ13oaNabLB6e9bEKGZGS4dHanPUEbSQZ6QYxQW7pHeEr1JJXIPGISsGvjYBrE2/cuNnZ2KKLsoDBajtAomUplSPKVFJAFcw/D7HYa1WcJUaypBBdQpRPmayEgCVQlX6yCKRAC4oDDzMAW4J4kuRhttMgcxrJoDCh6rsk4oyZyTnTPNbHKFYO80GEZtGSKxap9nQDQFGLeMP27CdJGzctAkUMxc0RFDa0sK5EZRDUqvExJKi1i8ByzCXEqecs06POq5j4P3zy8M7tN7jWjMscZlZPZ6qbm5tcEkAxQfDe/h7cPD7twgguB+AIaFA9Pzg8OT3t9c45xBk6uICSOjoecUXYs82tlvdRuq7F+vA6eHhotI2m98RxJjO6/36XeyKxPsKe0BrKiAPBWcRy8UJxS71PZCOd8c5yTo/VMBlTPKsgSy9c16dQRnt1aAn1U/0uCF3QmGjS/5LnT5XCZ4tUcMgf25pNj1f4ZhUSXXjqsLUVoUa4wGiDCROJTSMgjRHFmqB6Lh77JBHzKnqV/AgAg2KYFYRoi5gFKSuIAoe0ln5Sn5VeUiNlJgDiiT3aBOXcTi9qeD/jBcV88xXNOlwBAQwn+XB+3htBmh336rPymeCr71XAhTtjAIZj8b4UuoLVfqSEDZojDI5kQhlxiapo7wW+xBOh5Jrfy2ffLtJd4MERsdY/0avYRZChL3k7J6a82hmcWXoJaGT4yh7zC8DXWc8LkDPvsOn3M3N2reMSpNAXH2toyXtCkpGrPhfB82sBxeci8WsAVzUHq+4yVqZjxIuhIi2KtPgJ5Lqpx9GQcAOEnTzK8mqztjEaHI3PDyaz0z/5zu8NRk//4//of9EfnKHx4tg99FjYCp33T7on6Lc4fbGLjI49zdHB4XG3z1Yw1K3j8z7mnu+8+ebdO3c32pwPqoaGQYgxSQlDVaXLwfTmbBFwjOEfO//Y89XeZAMu2lyEabwYlhizEMcZ5Bk+1BA5ckQHEaEhiIObjb8TToFgVsB4gNDHJw7SRLo0YWUjjoO0CqOnQ1q1t5lu8T2vnTiw1o4Jarc+B3YsxRmk2QzcPelx/AijrKMjIztCHlua66JlfOXcumqD7ICNC9TUJYOFcZOeSslHNzkL1ofeDhiFm1ANwm2SCHtmkg3RFlJqinpkjrjoEWVaDMlZvMgQ7oRcVxKkScBLkNsjKX5hjI3uP4QzF1XgJgxHb6qa0JmASQBKx2cZOEJjjICtFvY3GM6vcfsbx2uo1/QsfMUK5x6Il859/A4Zk+Sq3PXLWTqY2MJU6LSMIpcpk3nFDxzPIuVY19EEA26swepPnx6/eH7EHK/fH7Kact7rscoPr8DAgv/J2fHdOzfHo3PO/ZaR413kgeOT7p99+7u/+Vu/pm03szPnHhgSsIiEwIo1mdxwGgnR3saw3p+e99hGYmh1e7v99Omp2k80ypX2eDhle/DXfu398yH7DUZMVjnkqlFrNtCIT7AW6yNFODVFD9lsTUfszMSe5CCMvtY32k2lXqcEcALrlJEFONtEYOl1hxZa/RjtPQsJKjJzihAjBoUSbLR9RT0sOn8IjjHHl8RTKNynaxRtsRxYeNbPbBDc/YwZSeMUZwIymWV/y0ZHiQqhB88Q+LiIFHBrgfYSrg5BDCIdmyMjKqXlvMm6Rx1EnUpCSpBkHg09avTYWaHlm0VdqpatV+RrEothhlCJ0O9ipAEeMoUACDLaVpyEQUNgekxyHAIPWckICbR4MqPmoRhb8Ap/f3wi547bcrkWWzUqrOP1ut3N9nrvBG0/85BzeicqAg9LEZQ+cj50OK9RNsVchMq6HvMZNPHrvf7ZVnu7s40p4zlXChDvfEjeuVPXa8vFQlLKFRZQfuuJV/wQTEgSvigq6JNzroICRe1j4rrHsQKecYkkQCOACVTOWn3GKWVsKpqPB9i1cKAZkxMJhaWRZLTH6nzLxDz/h3RM1vxH6mRXPCTDd0EkLrQMBCOC0xxmNF9u3WKGDE5kfkvC6a49HgSz+5m6QL9lrxsF2241OB6JAl1bG7AYOxqeNerjuOmZqe/JbNZjCskKaK3KzcF0BaCmuKGBjugNrJbW1llWpd+oT0YY+LmLgLLG6qeGVT97r4c3Ob0XmafetDejo6b/RBHx6MmTo8PG7Vu39/d2uscH5JCFW3JB5ljCmtf2UeuMxz/mDFHatS+60zkLJXus+7U65LKmDScXHk/oqjrmkjw26iRArmj31H8nFiqD4BYjSIV1gyH2naPGdIyJIz2zhR58XZRssHj1JZMTJH358NFvdM+f4pZfK8yFMwOFWkT2Iz7TQStBeoE3ccpi4Qcwxbiw6V/EjeSFDIAC+OU/12BeAif1iXrp+5quS5LDtbFWLSlW3ReBkwybdsDELQFRFAsw/M138sfWZjA13jUWOxG6l2gA9jIMZCobY90eLZydLXEtWUcnY4WeHnibjJ1beovW/42HvHiCv+k0cjwFq6JpR3jhHwCiS2SAQ6D9oBFMVMweBlKg9ccBP59IORrvouIZZpYC7IJvJGtSYs74C6SFZxIRaV5fSxbxyvgRcfXjojvh7WQu+l/6XARei59Q/Pn/sliL6J/uSBQFX6+ABz9flcprEbHIBJgW7kVaV30WQa/huIa4BcKF4+V4VqMvwK8l8yqO1bhXQ1cKB8SXYLMe6q+4au2rjbhHfdL+zd/6O//kn/yLZ89ffPKTxz/58KPJ7OzunXuMOdTfRnMLw00ULUgYyMIq8lnvnVc2Oo3z897grLe12eEyyAdv3L93+17v7AyRA1Wrpr3e/MLQfMay/uZWB6lEgVrlKwLYHEMgyGCNmKEV8Z3BjLRwM6g5tOqjQotJhzEYRhBuGdDchNAETLkVXOj8wRZOBkOkW/VAji2Zu2y4yDkGMigrGTk4a1+OCSs6f6wGGvXWmLNpBv1a7SZDHWxhtAEVwhNWRshhpEC69D5uRYgeAYW2TTRFf/sBZFObFgJZdGWki4CueJ+9G7HiKYCsjvYN/GnWbHlEwzSfLmJgpYMamFGPmYx9kL2V8l1ITcKHSQTomVYougFg5kkrVzjgG15kVMFCjdr07t37vf45XSUZsYcNJR/x1P9XYGF6TgfDc9LHrAp5Ymen01kPFWDIMXbJ8oZHYwTlAM6ErSM7oFNcwz5dOQa5cm3G7LGrSo/Do3rwgwicCM7F0mS2tbF5586d7f294XT0wx9+rIAqH7mNYXzWP3E/iRv5MCEAEwO/EhBVxXcwgdJBDsMHnBxdBRSVgYursR2nbsrPyrQ/OH/29NHh4fP25lp7o4mRCmdUeU8BWeIgkTZ3U5gs1RheI19wzxxzzq3tTlQ9c0f+SI46RQREoloF2Xp+UD169vyAAw/bm9QWZiOKpZSaqlBppNwt3CDQmiwScNnKKF3d0fYsODyAL1IBoqyr6LSxMSKD0OMClCY+lXUmT02Fe4QebeMhmiOV1jm+liUPJSFrLLnjByoLaVcuRe0iMQIgwJKBiKAp1MkGBMF4Kt4RRFY0qtEbVNQruYZPFJHJpOmU2ZU95Mq8BaJoFHyIJrIuVnPtp5A+vkEexBgAy6C5Rml7meD8/c9/7kcf/ODF0+fRirsYhm1vbdL24sR/cmpLQSpg6W9zs+MUQWMh6LA3oV1DcK/bxwa9sd44Oe2OPEffx5RI0oTNcn7HTxHKj5lePGU0cmhIFJQyCTdkclolF+uNWNHia87J/oP+KZ0NVQUTf6yS1JODK6FNS14S0zKICgK5USEkhcIq2AF8JAZLLFCSpX5i60IxN1gI5R4VhX2Q0SGYcLQIigMchKBbAYauCU61WEHl9pMRPrSlTc7W5CwDjKbirKT5jb33Tk4Pm20QnJ8c9WZVGMheedYK1oYjzu1BOh9Mhx5pxPW6zBO5dZi6BW2kZM1mKa3GDmxO3WUjGYxhSlznSgBqFukzjpApOHR8ckyvzLRpa3OTY3/JEiMCNZKVByqxhTt0dkrvpIkZfQorbF4yh70lZ7mNWSs+Pz+azbglgE1o9mv2Nk5OgmlUPrYbORFqkVFODjqBsXOES/YAFOtyAi5KE9eF0iUwwpYQBaj4F7GM9IonkBq+cFwL/OrQjH5txNfyvETwapzVjKz6/2W7l+mulEDwMkMWDCkrfMHyIitGCpBoqBBr68bTYTZbUlEqiS0BrJy2uijlIjx/jFiUY+Fv/jNuJFMUX7oFCTA+7byixYfTWNGxUd1NBlLqDwNT4krkZVwCSs1xBohewPzyDgG7Pi3M2PHN7CceIEJYCCBfJFIEXf9DaBBahCYl+ZERTTZgFnhWYRLyqs8isYzL5xWY5Yx2AfxKx3W6/wVNZdvUo1qcUxS8LrOfkFeIMEU8F3heScEKqHFyDvryGCDN9K5CXroVj0ILOiRjEevliAP2SjC1hbiRViZbQKzyecW9mo7p8qyEpkf5LsIL2oypz9zbIvlVYzGdavHJ7Syf++Jbu7v/qz//8z/6sz9++l//N//k67/8xhsP3mYMZgR5cfhsc2cLew7kp/6QYXfEpJxhmDELFf5v/Z2/gYhycsQpLtsc/8wZcIovMWgzzpyxvnt6tMbBmt0uYxXt2BFfSmzVDJmYGtN/s4EPiUe9DmIzDZpQwdRxaoYQggJCIcYRND8XfQeaeIIHdIwIQDBYojxmLASzgwoZVN7LjiYPFjwJUxqDiMRooXqKpOYztMI61mpPHz/DELne5Lhx7ErRwAHK8LJ2dPyc8enzv/AubuROtlDDmdOTro2UO2vR9CtdMbIrhSgxqJ0HJZcR4JMyPL7adoc4pToVMqBWJWKlhvS5tb0jQWSYjFFE0/nJ0emEfZ9YFzhJcL5BPpVHiBnVDrYoIocVgjQoYcR/0pY1Shi0JbZJIE3s7d8Qtlo7Oj7hnHKV4U4YUKGaGnCkPtI0xtOWKEAOAudw12Zj0y3KjM6aaoQEyPbqGcetgpsJWdXLm2prAN+8efvJ8+eICywcccfnt/7gW7/05a+0uEOOid0U437WCjDQGrOvYGNtgy3maDEn075XirImw9be2c2f/LB3dnq+2UbH6MFQ5AVZwdmQjEV+iOKWa4qECH2cSFgZVUl6e7PD2a/mAtlgtLu+vsWuS1auGvt7Yd6jxIWiCUTyKuRcZlLYRaBZR6LiVJn17U3SsnkUcnkkSgFSQlYuN7tvYPnG8ab1d27s313fOKOKsSygDGZhKL9BFbit1qZkJYzRy+KCWeHlKyZ0wIdPDlySpP9wwITkDlw67w3RmHJ5QoNDziXeK9zgAfPlTz7+pHt8mrWC9Qi0s8RWgLfXtI5RJ2xdkRWKg2iWrUp63sJECwEnbtYEzIBkO5FU6BdbZAdf2J51rHeMwLszq59YF0BD/WJ3BPmtHQAuAh5JoM5FvvxKz3hHcPFd+EckNfrOxlmcYiLHctCtuzc/+OADZj+svmA9X612oF/MVj+M7YnMtEct8Ma05R0mpDfdYTid1Q57vbN6Z22zVh+N+5CNfuGcbabOXqB4VxZb03gi63IDdtAEglvhXbyK/BTlShKgAAkzZ+o82vGznj02/ZWtJbpBviwLcbEaQ5eFUI5KHNY4iSRFawl3DFOXptuWee2M6aoJSI2/1CaYh1UPcjxNhjkMUyI+uBiEKgo3eMDMJIBsTFGVz/dBj3kmhYWsT+WlGW7tdOiku2fH29sdzuHlFLX25l6/v3N0evTmgze5gXt3f38+uxMzTLbhcvYxdyx2Xjx/zglqbJ9m+9fZ6enGxhZUdk/OOBTh4PkBeNhMdXx8yGULDz/5ZHd3//vf/Q63tsHbra33jo4O7ty+/d3vfufJ06P1tTl7t5g5cFLQYDTY3ewwZHAHPH0eZ0mTyVnlYDLtkgVWM8YsvXluL7oMuHFK3zuZ7sLleoUlO/jd+OjDx5//wptUDFo7LGKJAb7BcsqeWRFsGAy7JMcEgHFhgy0EzF4mJ3Z61E75GszlFWxOJuvNc+Ejvcp346GlY1zePCVoYcWQuvwMyigr7gu6/0uhK2BJWLxtaEVaQW1GWnkX0a5iDs39pV0BK/HCmRr3q3FX4V4qOawArUpBq+4VkAvOJQzkZ77irT/ZHQo892jvCA7ZnWLjU10GYfRlsanG3sp+THj7AEcva0s8OHNYtR8u+poQoBMg8lVtIKWLOONQsmWimTSIypBEmpiBj0okLTwWUTqN7izcaHZ1EVy++AIZ/5feibzwjHplfiJ6kJVRjVJWOuKvoE2UZQIFbsFLriyTWgBddCwALqG6CHX91yLuhTxdD/t6vsmPBd4yUnrzJZEroTqTayXkhd9FtAu+r/hYQf0KKINeDklIwY4oSdxF5XpFrCJCkebiC8fSq0xzEVqGvfR3Gf0SyLUBS7oT2lrmiAL1jIvUd5Q5w9He7u3dnXvj8SfTyuTf/uE3Ed7eevdtxhF049//ix8w8oRUwe30YzRBSHp3793+3Nvvf+NrX0fYwmCX8yCwMEEMYgxDnEL3g1jx1jtvIo0hzjKu0ZNrxMmFseqxrPUMRZDCuEgsuu6YH0gaVNLR08JDkveT+YDD75SbpDhRQ+NySkCAMC5C4cSoGQ9XgHk5AA8DpJIBwi1dRzQsW7Yijo+itusM7GgmDGMHxSiskg4PDrv97og7b0IyqdY1nGC9m1WCyeRBjLWM7pxXPnzy+KmCWYpNrlcieJEv0tPQQpFLcTPEKTow0g2BQKnDLPMF+/EnU0gJI45AkUikxhDziXtweHB0jIBGn0PMlBegH6FHFhUjB50mayGmkp4WqQAkQxQZGNdzbiJIcVIqZy5VHn30CZID9PAGGEoYWBUTEQ3t+SgIUgOw9uL5i+PjUwtd1T4PFYbcIaq6/gP3gKQ9jAZorjEImbfWN5DcWW/YaG4wS4S/LvloxmN5SFaQCfe4K2lnd6de4/RGrBaQmVT5n/XOwENVsOidNqFnrU+x8WY3BLXU6eKYusppsydnJ4eHhwpgE0yMxiw1dDqbp8dnpAa11LRnT5/GLCXWbqBMIQwJl5yCh6wz1Rl2SW467nS22VgLZZkdqhhVDr6Rf+gVnB/nP5gQtW/dvNPZut1qN1CMkyMntEKbAOxCCw0YGEjBySo/ZtgJi9WYFgNSqwjv5AdfdnmUkTViWuVorICZ3bihJRK8AJvRWe7wgFTlnpPjE6xMMPtGoKL+RCM2kcXAKVKpt9qDXn/t162NuIG01umOtmDBZlxLP2IVb6YN1ANHWZcatgGCixS4+1lFIouMO1eVa02IrGRFIUrUQnOKw08f33zzjj8TJLoTCe58mrDSwsGRrsNALpZhXBWIUplNRBw6xjeg0WO4L18tOcfasHtHzJCDREzFmZ2edYeDIYsAnc1NgOgoSN2q6lINfUFMniXDLEuvpQR5JXH5ay8hhcSRTkmOp1JljsHaVnRWwER8YoMmGrPVzE/7FSNQpmCIrAIgvMTkw5fJEhUBFkGfWQ3dJpMW5Hhi4BZY9Ucu6hEawn8gAeds4k4kksDcCdbTK3K97v7+7lqt9VbzzR53bHFVy3jUaW+yleujRz96cPcBK1/d46POTptzmFm1k1R22kwqmxtbrDG5zrTBOfsdJkVg3t+9QWPfZAwg3fnam288YHXo/p27mGi+/dZbTDOoQuxQpx2xu+btt97+yU8e9oe9P/yjP22us+aG1D7HtJ+cYA9F42UqYtPwINdGp7FO656dM50CMHo2ArTtIcfMZLzQgz7k3jt3YCOHTFO7oIGZAWxvbWxY412urGy0tyajKfolZmL1deaibAOAyZZV1L7gc7A7eR7cLrj/sp+ELEMX8bI2pLf1Ir75vAheRrvudxFrNe6iMlhF/lKe1yfw55f8Ioclly6hTpqyjHznY2uADbCEaqknHjE80oRKBAt+2XsCawuj7hvPv6K1LqAyGpACijSaYlloojDixSd7hCLIWAm0gHUPgB+JKuIW7Rj3El0561r6EBjoeEUaLB++sRJq7DIREK6SoXemkQjijecrnouIC7rSE9NTZkUM2gu7tKt4LkfPxC75Xo32Cp9VclfdESVKZ5V7QTBlu0CIi/+XCOBzCbEAveRYjbbqXoC9jg3cApgUY3ab6fpOVwIs3FcJvWg5l4BLqOWM+XIeV1K+4FwkdcE3P17Gl0yPmDjWzq1RjkdF03APm3rCkzfe3v7tv/v1f/Uv/4fTIzYE/xvsTt/93OcwHUGHtLG5ifBBe1xvcE9n5a17b/6n/+v/lPFpcNZvt+jTJ2y6nIwYYhUKUK+yUoxg1T+fMqyNen0s3umvc10bKhDZreXRLF3FjrPzQM5mNMYE6VIfpnE/fo74U+UtRvfYm5hyT4j4BNNRMGwghIU0FCg1k9UOV6EFCZKQaLeOlYgBRtEkXlFvGtY2eDMCNzGvnc2GyMComeAUsbgTjdRRxynKaV6PCZNSR52xusGaO7uhGabpXMiT8xcAwFWd7fKurJ3AZryCsBQ+bNyV0HUhy1kISCIxoqF0d71CVD5EIpMKjoSTrKIX1U9wM6iAzpdcshwjicimcRTV9FREAxjOEA0vxHGmPZyhjvigYCESH7AIWXyFYEQRRnLnI+/1BYmJmorwSqXOHKUQtOQHo/y9vb2NzSfTPmp+TL/mWH4hFlLczB5q9RPNwTAmhypVlWz+YwkJrR8ZQ4rjWKrqZHowH1R/+J0ffvHzX9AomWjSj1xOgiShlMxMiTcTy08ePhycu8fx5AghHmGOyRcZilxWT8azM+5T5sjw/RvUEDWypGp1Jy1hnHiR+/bGxnp9x0swqPna26DBRfJUzsCHX3AqPPOHITziaa25f+NmhR3N9YGSnUIkgiq3pcIhVlJcOaHgckhCBowykV/mGZ4h9UTJUtWJDPdkIqGeWsM0EgKJpAkc5U0pTWeuJgGJNhgCEM/QC2NhgWg4rqIaJx3rXuCHasRAOIBwjAezEQKs9MlxXJYS2ivLUJeNgh+t2+MLSOuLUMZCpw5BtRMRUJdtWciEzPqY5GvmAWFo3MkvDIqYESvrz/iGGLwHIKgwFdgNWdZfv+weyJr/LBOUgU3aEVrmGaYnD96839nuHB6RNLv25+xb3Wx34F3kzjg2CCsVx0Gub61VT7unk/kZLK1X2pilwGIWp1rUqhpnSZ13ttpoC7SbilOAsgqbrE0VLvFAlU9SFs7wDlfpz/QYzwbs4T5BcscgCgH815v8RLlbjcQDr6i32LoIk51SsF+lJiyprZ+ZGBUTEjHccWcKZpUUDecl4Mfkl3ahgRGebJKvVjz2ngowdTZEJeQkX+82qa4fUy8oGTpJFic2t9r0S0+ePKNR0PGykkZ9QVw+Pj2i5N69/96YM3vZfWsNaIz6J+ubHWym4AEG+Cj792+pVmeVzJOXnUXTHtHUUk1RsjDNcKWLvNh0ZgOuaWaHOLvBaNLY1nH72tbW5jd+/ZcH7OU67/34ox8NB5Qxc3UmEmywOaRibk83m8j+nEFMX9pstdtNJ3gqgxgFvBR8OGaDmEcDb9bYb4Pp0fSP/s0fbW9vfOEXvgBTsMN0joDaZcSYwv3izbU6V4HNf/LBT7onsG5vPKQ/oR2p77BaRj8vn1cK08JaKeayhK/+JtxKTEAu7HhcBC0gr8ebcFHRM5UFWFKWn/le4LxMz/UBn1VzfxnrX/53ZtF0FpmNrGDWpZeejiv2HJlF37ap8MGziBbfhmTzskQJEYN1WRx8OmZFfEICIuQ6QwKG0Ihjl7ioBkYPMhJh4MQLQDHpCmJ0R4rQRVqLPQACJWAiD7hPey1SDPygzXz6FbgCpcleetLDPCQtZCLylj+XgK/5XI1vMMkFfxPjNRF+zl5XMrRgc5EQAMH4JaC8MTAKMaACoID/a/wpSQ0SlvQWOXo1Ry/ELaqVpf3qrCXORVIJ/yoOJOi1pCyDCnxIIYggDvfKc3TN29XKc+7mfef994+PDjHk4OKlDz74GKOOaeWMVWl6fGTfve39X//GrzNsob66//l3+70TD7zjLhj075jhhDEPp0EfHB0iVjMCxVq2CUVaCjrQj/KeFuXQ7h4AzghCSiRIwY8zJRDBVT6hOQWMTcdKm1X2RGJ7kyOuLT94QYhChVokxugQEQBNXwbT4mou+oiQam3YiG0TNGcYqDAmMfIisJIXBhjMlfq9ASmDmjFXMZckZJU23xwoyfIGg7EkoXlnh1zIQ9lXBGJw28tQpArY0cqsw9F7FUXGh9lPz5ClGLOxK0LEjD6NqGSEdFVoBdIUUiISxEAaeeV6IIQq2RJMiOFZaSZ6VWGUREgIBNBDYiQI32CT1NkByFC5JhuXdUXSrRNmAhDO8wlqY6Zk+Tl9suyIrEQuQgZ2iNdoAZmCE0JV+mNgw1ZILGcsWYV+hP36GnsjiU9qw975wZODxCWjKHrZMn327Mmb97mHhQMcwY+EQiKO6EkROYbhLEqAjxPfCSOlARdYjIcoPzmLEOCoAkzJJs8Pn9x94wbCBKp35SSKLPIdIhpikypQu12XniBszFwEOkMpKQMQ7Z0g+Uvd8PY69ilsrFMilp0Sp0fEOlUIlmO9TCRYbhEAEDDOAUDCNNMnAnwRnsUEEI9THKR5EiM7wos96jNRQihnL6wXb/dOz1j9QvIHyOKxckoPNMLD/LEK8GXxChDEWe/4lIJ4pAA6o6IKKzGSklFwBPnI0FYtvkDOnxMPt95OxoMhhi/BO1TsmMmhl22Z50RoEmAwmngkwvwb7lpJzsFMlXyGUpgaAoDSP9hY79rb3Xv+7NAJ07SCjLjFwhi1RtmOu8M1AoFNFDQlCMXBKdsK/YaJsG4U831nbpF9xGl2mpOe1dbs4Ks9TeoOgz4pzWfhSH+5hiteRDQqeeEVkze8ow3CTOkXpUsmZNKphZMpQ/A1AkUa7MT6xY28CvducWWrK6fT+qx5oBQe3qkLloJvrADQcKxTzAFojFTUgTWQf+6GYjKGbO4mHE4vQBm/09lqrLfUI9xdG7KZh42xzcZGrYFs3TvrsqSC0Rfrlkj43JDYbLeYP+/c2IHSzmja7R53tjq4aQKTCaZx9L1mnj9oZJoNz10TJWNRoJDBnIGayPat9tYmee1sb/0n//Af/l/+z/+n/tmJPSoafyad5LVqOTI67K7vU5NAQZdMZtGpsOk9GDAb9gfdtRPuBCAVKCBxbplstpvnngSNlaVdBNyGOXIM1DPO/7377T//rqoamzYHAbkrHZrhF8SQtC/+WytWnghZ+b7kjFpS+K26L4HxuQi9lEBCZjIG6ZIMiKLY/Aoy8x215CVkXos3sf//xHvBgKQmPpc0JwNWCRVARuBHJ5aQQtlwwtNQ+0xgbGz+GO5A52/E9DeKNzgHkF2uTcLwYGyg8jPhbSwZwx8D47sECMSmGB7FK1INdyJO7wDBElfoaBsXI60ieKU7MgcGGzkU+zZBnvgJDVI4+YQxAGKrbd2JDDh/Mk7YOwWbjBUx0xac/gAdP+77eqd7hTWF7t8IS0YIv3zQrnC6ap5W9DKYMu+hva6mhnuJ4RrXPOesBT0FQLB0CVx+yo8iRyuOYmdFnp+dNl6RhyL+RS37EunCtcC48MHxOjPpVfhMMRtytuMyVPSxQyBXCUrv+F3R8S/8k7OZ5WtJC0hC4IbvRcR0XOO1CrEKfpXzUa2z8uUwj5IMgYZTHUI1OPobv/FrP/ru9zkdpdJq/P7v/evD01PXp6v77rc9rzy4/95/8g//VrvZHE6HW1tt1uHR91CdMbrgVHjshRjhuqfHx0enEI65CCOEYjiz57S1GO+oDUWywgp9/YjxADD7fUVqpwTkA9UYURB00GYh9kd0s4cmHs0fZt9FOQhctIyQD2KUR6DjsjMlMpNhtHLUtimBm8Fty1G5dozGl3uOEVrZ1xbSbA2jH8ZIDp1guEUpVVvnontjKr/M3OLGxgDUoIzHjGfQoEkBbZexP+TO6nzXBNeOAUe7DxFEVXCh/My+kxOS5pkDYwvmD0vGfQbI2aTLFIDdqFyKw0LKWa8n4dDJH2ggIQhRvAt85Jrpx3yyK1PWDqMbCaEwosUnUTN9GET6iw4XNd9eGF14IuC8dkQgFJlN0wm+wg8j6RGzDD4Uv8gC0rshwRK+AAgJAF8GbGzWN07OTmuz3fE5ZTqQN0xDZEORe2LCIomZVc97XXSg5EZ1JkITixIk5wQB6y9LBPa4KWJC8TjiE5dvRvfxedtZYf0YEXBw3h2N4FV9c7NNBWbNB9Kpq0jvH/74ISwKdaYMQBBE9oJO8zXZI4G1RpesmzcWnZC/PDCRB9MLioUUnZdASSidsbDAWrrNCYR0i2xaRYFM9skIgg6sQzCm5oBtXsXoSL6RlZDUyTmkwygZTGIWZxR8+shS58WwiSBk6TjuhtrW1BQErOS5zlGM67Pucffjjz+xlbEFpebueSknHrOATNAWZv3AxyTIaSaKH2sFhT8TC0VjY8lu6YQuuaAzJzCw84SPCLTzIVtZSbBCaVc2KC9Od0cXQBCl1uUwLk7GabXAIqb1A/KEs0BuAgrcyOrI+6jGI0ia5IcxqAJMpawSSPgsq92/9+DHP/rxuKfRGpqIyVaKzsx7QBR3mGAcFZuw2azOjpHeGbVNJLROChlyOZf+9ORkb3ubUAXh856lQd1iLgifXScBPrIslzLzzB128KqunWSABEolXNFahvxQZygZeFvIwDFJC04bj8oZ5ywBSAdi/SV/cJk+jUw2kMMVYj2eyOoMEaw4YZVHs8F23p6BTLjI6arYfMYcgRoFzeBHhGbT83jSwOStUm1uNDDtZ2sQ23YHXH/Gggn1gPMMFMfXqqMB8x0nlXTn532MfFye2Gi2mSqycsl6J9SgrBmszZ+9ODw6PFp/0trseKopt7bTve/t7bMdnzUwrqug9lPRmUwHuzjsa8Qknz6fOYbHBjVbMSuGEDfrm1l2iJ2d/Gf/m//se9/7wcPHn3z4wUf9Acaf5IYWBpbp4eEL6l67s+VZcE57OUaMikkIKxtrO+wha3P779rGTvvm/i2mUfQPTBuYFcAKmqUJMZywT8nKVPkff/df/zf/9X/LKUDMLe7f+2XuEuACuaLs4PII+QcqV87vz7C0fdAO4tony3z1fRXMRlFWEiBL5wXAhWfIYHCH84V4AnGBPWircisIz8wp9KXnqs8lgNf6fJ2dAK+FqAQiZ0UGSp+V32gOK986KYzoci7khy4FNtpnUdA8Gcc9OThpS7CYu3iBmty3pwvfgMEGlN2zwXRgKE1nDyYRb0EWrMdtw9WL0KU3bVMo7uOy0bYjhhhMGWBvAjaWUJQRPYd9JC/Rsd6ko3zCzStSKT2v+42x3wDig05XYEwvPbJW2WuQwpLcZXplGmVy/OpMXOITVzwFRBkCiiIuP0uoyGCSUwRH5IJlBariJzEWcVewrDgvRrj4tUg04RexLn0uImVyi8/CscByOeCv/FseUX8tQbLAI2nWklX2RsDFV+Yg3wsmXAS59JWIfS94lRCJ5BL08vNl2ImWxCssSDu1mxak9h25djh78snjP/+zP/3613514ysb3/q332rWNxjsO509Bq1R3zH4rXfe/tt/+3fuv3m/d3rcWtvESJi1+/XGBoYcHASBVkhdphoyE1IQR7WvvrygFxMUIpAuQ6RKMLdzSQOKIkYRhj9iMVqor7WdyGJXiqeMiOsI5YFTgd1Ax+NCqmZgwE1uCMMFPJIW/4U0NYAZ+HTJADsAxI252ieP2WEMYmvBGYp/uiTQkLTRQ+NFHwFVNKDhkAUBCNA4A4jovJxpQDYPwMw4wE7+aLwNRFt+7ePEpowb6UKb1CweshHB6FYfP3qEDp0td5xMH7HYz5rjGb0h3ROP3omHWH5yLjq/nO7nY58RNRCGevCe5Ux6GigpZwLBCMqJH3gTyYSNYMSgSuTZCYWLMYmO1bLRP8CCALlHHAVZ5L+kByHZTHMgTwumwweKj+V4woOfSPQpDxEzisRpYXULRe/xEVyyHSl6ihMRgRMe0Y2aspsryAVSkOfhkA+kBCoWhhBsxcQQAsXzk8cPmRCOME6xRHhTQFppAsipJuzXZB6Y3GO6w1QSeqR8yiISZl4nZA6CoNztsKYP15QRGbR4R/0lX07eyMx777+D0pKawyoEIlwfe4c+hsyYVLEnnZNSw6Y5kJmO2YJR4jQVceqbw2EC6C1//Yp/6rN92Kd5987u3p4n4zhEwS7ihZEb8jO1Kqp9RM2u3dxbKnxBAOUZijR8zBkerorxJqko80hV+iQKAMMkwC+A8M3/QVnEV9S3QF05AfjZ0+dIqLQL7ndjAsCpL+++++7GZpumnc0ONFFng4tqgilHig9c61KUMgFe0lOnsmozAyxWguPp2++880d/9MfTsOhwsjEdNzGFCQpCaJYUs1nxZMzt7e3RkPkXfYNHxcNtnVXsztk6wPlmnHBQQ4LsD6IpaWoY1VLWSE0Qc+G18JId+WT5hJtOIdhreUEAuYJs/mzgTqkUX2IxBylfc3YOQ0MuBwFumWM0+ig+NbmhPdJkbDEYOrLjhbOeXMrg0jcuGd7Apgzhnt0tsc2VaS0rHp6SSSGDhxZEzwzP6EIpbfwpIHozFPtUyXNuyEV9M59ttOzAYQlzfVoQMr2do92p4vVWZ2fADbyD/gcfdEVaqXz5y1/Z3OZKtXVpglVuL2b/CbNwJs8urzBOoOXBE1WQ9czdQbS7CvsYaBjQBp3f+NVf/c32b/2//h//7z//3ndpWaxzcLgQ+8KozzRJZxS0FbroOReJKALSt2+0Nm/fvtfy6CIXBra3t37xl3+xs93udrsWE8sF9TX2X2xsbDLKsArCZfJ/8AffJH1URdDV2W1x9QL0R+2FK1ly173JxitCr4txxW8V/bW45GQ8hMKbaFr5bUMrnmh05cd1v6sRCb/0eV2M6/wW6V0X+NP4JcKkhvfqk5/5Bqxw+LPMdsDb2+AdjKTIolkkdHab+sk4Y8b74ks/2Bd8FVXxH28xLlIGShVJoE8E0h4p52c05/Aq4tAGAoFNLNAHhdEyAq+jy9XHcEm6/Fw8vdWuvP7I/HkqjuQvKDWynbA+SaLdiA/0ELCBQ4LKnFjLJdHHuP7FU8x3xcHcJfGVgX6FO7yXyRe5SwQCEHv0IFCAOH8NjLgJFTCJ63V0/xkprbJKBIvfTGCRjMQVKxhwiUePInGBWPJ098IFYgTDCy5dfHLuu/AnTs77X0frH/mqzjeuSSh4or87PejEzoP4YBVpXUqlyMvKjgvHarUCYijzUubwIv3m1pDAT1AJtYpz5QShq5H1IZmEz+DAZdLUHOqALikPaREZY/7FL3/pD//k24c9DnTn/q9BpY1Nz7TuyISId9Bpt/6X//Dv3rp7o165s93en1Q+hgH25Vy66Ug4xwyU0x75hxwcQgfhykAMJ6aPDM4gH1p/xLhOCztU5C2GRuQaJdagx8HSik2D0TwjmMCAw4Shts6ixPkQU1EgfWWEoB8pQ9sII4b0S94Yl2xFkIV8qrWGOa2unQHFTIEhG0kCCTF3C3DBDNIlQy8JhwyPpLkHHPsOyAuKxTUsWh3CHdgZhAZx6hwUOj2gk1GjRUZtl8g3JMUwRuIIHAVVimWS4BOlYJsGYO0opU3UaYPeRpcbdjicwxCZIe1Q7dntyn9GN1ZgsSId2J+QuuMK/xgQiaf+VQEXDIg7zMGQKThTFel/PqlNESMOUVRzrqskTvZMCRr8iSc6Fz/FJ8eSXNKOJIIg/EwSMgBwwEaAI++IO4oXlechBrJhg5PbsdT1oVgsGlhT91oizuzZ3d+qfMjMszYZbXul2PoJEx52ojMrRKpGPqFemAorLtQfssMaP8hns5t3qp988pCd5EgxHFKkNOGmWBar0BQKMq078cAMGukEoQoBSwLknL2qNat2FFK5NU5+mlMP16ekYFdlsmME1oiSi84glfthrcb6bAyYV48Pjj75+GMqhEWevIuiopQKJuJJmnyBU8bJMnzkLrcO4830g+/pnqFrxxJn4QLu1nYlRidRISeRc7PA3BKbe3HGfCTS0VZLvJaHibBkwhvq+VLTD1B8I8qhDN6TBjXc+uuT0aZ71KwqtybDJdzCHAuQCCPvcVMyU80j/GiL09Hw8PiY+gMHYAw7cz76yUfvvfteQ1tt6ilzZtq1kiEcD96DTOssWBqYJYTGCVkskNC3cIkbdRSRFJI2Ntd39trd3ovJcECl5USZDSaWQarssClo8OMtdBRgtYZZyPkJZ1YiGePPQbdQhFRd5Z6S/b0ba+zrGSNVMo+Arpgqx4wuKmNBS/HDjp2VJ3gU3zKTL0VVOCx/WCykl+Emhyw2KaJUKF30KIiqGrs7lYQ4lP6Izhzbw0H4DU/fhGQA7OH0RzlCySLWM0mYb2vtZBxqPFr/5g7XsLBusMYkgh6yP1QPQj1kLQtmeELQeoPr0jj9KkzvIMurtTGnt8S592trE3G/2z1Zr92jVY7nh5jhoOan/Lhfeui67IQ7+taaHJmFnt0Ltii773/vh1zk0mi0dvdQyO/c2brJDgF6RAikDdbn2AJN2N6DLT4yOrmDIyaHmsY1hHWyRXvsn5/2h7V/73d+43d+52/+4Mcf/Nm3//TxoycsrG40Gx4qN9yanDcZBTyvte4hYxie3r55k/PCjg8PEOhv375NN//d737v5q29rW06BzQXHtHADJO5DGeW/uC7H/7FD7//5PGjne2dp8+f37p1czyojzeYc9nXOoOmLJSFYAm13DYiiSDCZ3U0XCnuz+4EKU++CzaUnwtkhibEwmvhQLdduIl93WMDrQ2lWUkjul/ciW9VBrgurn4X5c+XQf2U/tF7yNjLzyIzNI4FW6KSlJDBFNsLo3AWjeUVuGxhwvq/Or4XDQ+vKLjMuOzAxchV6OnDG2xEBMxHgMkDUXkbQCJODBGW1QGoGRfPlRmIth0fNGBiEUxUkPkn7sDKOyYAARiBAWlWPuUJODFCDs8yQiIQf4k0MJmHwmHBL/Hrsk4XwQFTuiOGMeFsRAosfgl2AX/GS0yLsMQdsBcTiPhFlPwpfa5DegGQjzIj+uMuo14G45ugBLiENv0D4FLsV+O7JonX9QoKlsVktKukCZQNIdCWnI6Pl77KRnOJ9EjQSCuZza8Fpkt5L/0vISq9/S1iXIBI/CUuKpLCq4OXEdYef/Jk0D/7wfe+wy4vxgmuSW21NzD7vXt//3Pvfv323t7dN+5i8MMwxioxIxVpMGIhroyG2lHcunX7xdNnobNHMmBfrRd3kjx1PqVnSSExhzlt7hFXGDKiRcBslWuQE5BG4Y9jIunQB70eYxTYkJIZxgmhj2cI5aXMTT/JCBwnffgROUEPzdDLOM1wQNcAMIN3iJLI94h0nCyxdvvOvU1ui51W0UsxKCPNjDgFezRkRyeUJJ0IDrGCweK7SjjGcxxQzjIG2xsUTaE5WihxTBpjEqTReKJXCXLMV2ZcXsiD4ANv8w6FMbFAOYi3MqgxCSRY5MKaClAp1Rkpk8CTh+zxFkt+44gPMl38hqYNUpGcAh5pzFULMYtAQVUE8QSB6fQdvhkkUQWQIZGYnELgdqqj3YxTJuYqUItqPPbFhrBDgUET/Ac5wuEQeSEuSYWbDNoQAUcjpyzjjzmklDlLGGxEIWuO71ABWqQXWMUVzohSHMnCIkD/vI9yEWlob3/3rN9DVmD+hijS50aoIWehCE9nXzAJ+s0xWfceicicn1YPygEi5TMkZX9MtqJRRxxqgpxho8qIu4aHFLcWQmG0Fvl1rhXyrnjJpdyJ8pRVwV59fKJ6yHzAdcMXwpmeRBXSwIh5C/7OiqN6R3+uZEkll+ZABDEkFGBG1i8qC7FozZZ7BuKbrsQVVSOhBQoYG0fWHbJOjoM2K5mVDhiIkA+w0fkmYjsaDPeMOrNGW0yDevjwIed4sjwYiBTCII7Sdk7lFMKKF7UUd+A09z5aAKkWgAcYeFCZptzmiz64Uj1Uo4+MgCxMjRpzfkCdJg5HoIWZH2UC22ng7KP1NvHhiMSo1ACnToKUqQBVNqRigsgGYbLBMqXzuGBTlmzSsOIOj+IVzJHG0hNHsFzmWiWZj1ghPIoH6pA/W/YQWs4wKZZ9ACGpU9fwWqs2odnOJJBYDe3EiF9FT9/Z6UAgyn5yTfeCdaIcq9FH3aI2cuzZZljhqx+XHvtO+km4AcINrjN3JuHaqXI8q1Ga3A+ZOrClgPv0oAgrm0ar5eoIEvogipATGvpeugF/oIgLznEzGYCp7LDHhpNu8nvstrXXq93Y3Wd6/uabb7FUiy3c/s2bcJL1HzhPMeAmFuSgAjjrMc1Asq/TzuHrl37xS2+9/eajx48nw/4vfePX/tH//f/5+OEUrKg53n73TfaSPX/+nPLgGOTNTeY/c+yR2JzAWuhGq0FmWFximZZ25ooQ4xSbvau1f/bP/vHpkGPZ6Axqt+7c/NVvfO3WvZvc4kI9jYpXVOAouKKKw2xqsE8Upp9lof5sv4kUHOlYRWwxlf6ZCKVd0JMRgDBC/KzGLElKGi+8r4Jd9SmjX/P7mYCviY8XKHgFUeFcQF38Cm/ye40vKJwIR0XOxhAokzUlvG0j2gcepsbP8m3qNsIMCVR4RXg2bsL9EqZEGCgioQI0AwzHI/6Kd34auQApovpF/QvfsTryufMwoeNJRBkFDxqWGuKIS5SgK0/El176P0eVjFMg8GeBzaB8vA5DLBoGFABRkRYACRYJhdOAInDBfpPnD+9MQd0zvfgn8X0J0wKoRHzp9xL4pdArn6vgq24AF5+LbOszfmPhX5IbPC9vCI4UACHSCuCVdC+vCQC+qvt/6Rw6aCnSWk0l3SvJ5Ax7SUYQcymV1RTLqCJa3mGcuciykMJIvgCNJhFoV+JeyEV53lQZfvG3wFVisL7pjm9aF502AybjJqMK1XX94x//6PioOzifffDRx9yXhOINK9tZBSmq8Zu/9Vtf/NwvbHKbYwWdxORs8H1NAJDPU1aYc24L5zRXnj17ilhmw1PnyP4wVaR0ysjiHGqCVBcCHTMHltLY0MapHTGi29CRAhlFHNmgkO2AHhlRqYgNPCkaYOqh9J/tXbQhoxiLfwyE6UOs7GdTGcnwBJiRIgDtHTMA2E0shhZscAHgQknOp3fRHLPjIVomecNaNy0GoYERldEb9ZvHiXgTMOfNgRAB2hFJsdF+BinmkDaGEQqQfCoExCPD8WfGZFXhv9T6Y6ToBcIbPGpY85F3N2SjumFhzLPlBpo934WOViSERqckzihZY1CopmU/y490WJeISx6mP1aZSQA+6P59/CjfJls+uAiKt8n4xNuXbRK/WOkwJxg6r7OfAlOECJhzAEg/UmbIJjL2UztcSVRpnCAUcXJIC9mh02YmUKkfM2fAKhh+cW3c0fHh3dZtImg7oxyJgIUACpelBa5CAdKe9sxOXL2ajdPfKRjQUYtY1EEoiqlp5fToZHd7V62zdcA6DgIoj+KVk0io3PEAQvDgDYxa/tqh2YzsRp2hcspklKXwHcj4FAcO+BvCFJhDtC3macGnYHGUNTyM6YbowCF++Wj5UGfC7ct5FBwj5bSRwH7JnFDZFJeptgixsCHpDBTWDfE4wBhXfuuUtgDQNxy8TLf4Ts/EW60fGUV4ZlVHUa4ZJZEF9tpRJCXzSUZusDF0wulP3JjhofiNtfrjRw9v37rDPhD7BG21UBmTa+VDxF+ygEewlWymgZ/Usn5A/ZBg8kmhoxUfT/a2dyqzD8Gjxt+5gXNHMo5D8ZYiUPngBiFQ0E2B53B06K3AM05Gst4wo8KE5exMYxUqGsfbDJBs0cTLHyZRvMmQHIusrrJFn5Unsl98A8Ycj3JNVTembYjroPSYGjCBkfoJYdQ3r9xmCisAwjCzUFsiEFEzoc1NU2trm2zH5aRN7qa7tfv50y77dJ/a1c24CYuLIFo7O7vRoLCu9FhYE1C4tTZYvrP5i2fPaYDN1gZvrP25bsVcZWLzKh3aVr8DA5kAfPc7A8RoLAzdGuU1HnDLHiy23oCsys0ZlAAK+LSZhHBrmlccV9hF0W4Ne73u2Vnv9u1b9oTsPxhphsdMmKPhuFGbBYfu6Wlte5vTfuABU7WJtzFACsCDt9+47/pp//y9t9+9d2d41j0ZDnfu3LpD6dy4sU+J082edY+h/eT4+Nb6rdqG6iEKjjUQNgCgK2ALOjtNuInv337zj54dnK5xKft4/uu/8Y0Hb91kMwV7mLHfJKeWD3NyVSpRZlFdw53fyl30jtaCn8+TaK/FRRKEYtIamn4B7XX9V9S8BKBICyTpiHpZIvREq2vg4waA9C8QZn4WoCYWskFpT1HYIBQpleh/yt9VLIUcVa5mLDFKUVJV7MTQth6Z2V0Z81Ghv8/CKAEFt/srioeOjtzZOeAddV/ssZtUr+iBB8ad0/pgLZtq6MZJBHM6JFtjCWWkeJLswhuf+CZe4cxPPoKCDDUsHtNTDmcTcFFegXeBLHELWhZwRIuXUfC3YE2tGMr4Lp9w8QqUpefKb6ZCcOAw4CJwMkcsgcl0LiGLtMvgxJwMzQjpk+9IZdUj3BcTvBL8Ko+SpgVxS+CfAStIXsauJf6fyrWKdpU9l/JxCfci9JL/dZ9Fea4GrSa68LeKXBuwgHhdxyLFrEE2Hf64w94D5hgbtdo5Gu11tv7oW392cHjEKM4QPuAISLeg1f8P/8f//cMPP2HcabbRyVGNausbaCgZyKWQznY6ZONva8iBLF2OZQzM0YYBoLYzdDk22zIUC+h9VVMRwECtDAdC2m3KrCqAqb6cxsPKPmbeCIiiS5EtHFGNZEzUegLAamZCr0/bBVU2+qzzpq7pRERTIkGWCHkKKEYyVWJsJRoN65qvQx6qpsRRsBapCxeaT/Bw8RPcCgxuH+BIovXhnH2KxASPdGCc4Hnt66i3kYfRBmb3Eh0AJNgBQHrwUPIWjyNWPGQk+x9hBLQty7qENjSir8QV0pElwaP5igMfm7jczWERKQqmWxD4wiX1siWaUPACKXXGKJKThngWgMW3ABnXdAOa81vRASNqIBkorLB67aEuFC3pAqLUQiRShzloEzvcBdDkRrAhxYGoRATistNauQRR0EUYr/6SWkjyH0IOm26n7c5mb9Bv1RvTFrc3Dwcnp5FF91Ziu4CdhBJi7B3mXjHqWkqQ5s1yl16oC3zQk9U0RGq8SMPcmzMqFqBC6xfie/iAO4WM0KfA0ZLT4AKQP/iex1xGZDXBOiwN/8kNqnr4RGpGwts0i3TBSAbwtEYi0CDRajqiEFlstgjChOYp4uIKFCWe+NLTxOMJeKGDpTiCLjJNQBjQFbiibgQ266uegRO39OsVcjxzkWA1c3kI3N3dZec6x7O+//67lKe6X/iEi4d0nM6ZG7BRBc0RwaC3NjoxqLE3gO4EyR7OzNc//8Uv/tGffof7RjRnH2D7zc5XRFvW6KY0PMiFaBovx4SpJo/9QnRTgCK2WseRYRG4QUWbZdqL5sGJoueKZo7MMwm/8onCAiJgzQH8cqEGylmYhBkNzAJJxZlhvrkexBUStuh64Qa5NH0WNrTwiTppLydDONcSIxyq/nBY54yeeovadnBwQEZYzWBXK7oPpN7+GQbwp80N2hQchjcWQ8wfpAEAVlcHI8Tz4e7+De13FJ2AsOiQ8uECvNraBVkTwf1zX/jc0dEhcwzXCLzcfb0/wnCORRU95JZ1klRYGuV+rTi6rdGYjIdMCbDtOXxxCBUHL17QAO/cvecufTYG1Gvds1MkeDKOB/0ex3y5h4f9w+uc4oAWBI6xYuBUgivjx8N5Z2trvdUCf98rFc5YNyEjTJnQNlVrbO6v0gM8efrk3vqtja0muxN6/T5HtdGg2KS1tbX/77ho4M+/zaIK67Tvff7+e+/dn8zH1huLPFZXKC7aqVXOSYC/Zmvl4fvTin4F+nWc12LMNOz4pIAv3/mTHnxnWPwWNF1CVcAnxMvfokrQRLrAuPp5CfXLsX1aCCnFEx3CpwEXmV+CZexsXEVJASNxcsc+wawk36IjNown3+GMV+Ahjv70LrQIxJD0jGYQCEMwCITLiKA3ToCWv37gmdF1Xq02IjA8TID4zXmPXmXEpXvVB+IyZ8r9UR0jlUgh++aADs/UFhd2/CZYPHl3mh9wqiXX1tS2Fj3UjE0wNHt2NAeAH1ef6O9W98VHKpGq0S4+0dctvAsbenfYfNZngSMjXvq8hO3VoUvggkusvSye1426iKDjOt38sl5cAM0iS69Vtz6RNp78Xg66gGPxsQRcwIejpGcZXkRJ5Nd9LHC+2hEkCmI6VEJHYsZwVG502ghNrUbtD//oO3/x7e9g6a/8jbRRqW512u+88RaGnl/96lc2PZ2t8tEHP9r92tdR7qiUdQsvijfXfVlvpkpi/A9mNkRudposdp+eHDG4M/ghEDNIMxRwUDpmAxwAh0CGSb12v1Y0jQOovhzcoTAexjkQxugelqaMDZ7+5mBOLrJHV7ZwJE9+M/BE/gymefhEU0PHhtO2ZzDadz7cCMgx2PYadBihu0eqQJ9FEv0eoiOnANGyXIIgFsOorDcOv9iG8IEy1jUQhUoPy+PsTtZDsF6eYUaL0g7933S03WrUz8cHbE9shbkCvBKDyviy3xO/rV/k8Y4+wuLxL4fitSPpJzQ8kdAjMrbah/r5xZ9CvFECjHfgKdlkN4r8g8aS0o7/tZN5bWDpywIwOHFKBvkJOUlQiTOoCRIDKCAiMYny4YeZnJHkaGWj1d7f33vy9BlCzmQKP9E0RlcuINYPR5V11L0I+mxc5CBwpCUnYbycB+L0PjHkGB74TNlFLBcGyICFgiQHGgz9UY4ypeyenGKNgCDRO1nXPrhyyASAw4WsUf2t9drmoDc877FDnatSUd5DSclOf6HjANSUiyVLCj6kjsNVAkCCSUAEo7RrV6SjcrLKI0lkiG8QZQ0EofVEa4pgO7986itrREIWCQqocERo+BkCSjycnVK3KDXrPGzAFHYybnK/nvbr+DMD15C9wBVJkEbx5AhjGgESvpF2hpuqTE1ieGd527aYqVrbIya/TtdpIuFhV1FkRDLFXVBLs5lOVANzDDsEz6vf+4vvTkfjuw8ecEwNRQrPyQWJxOoc0rxlCt8Ahpf8IdAHw+lHBmQYAKvBjEvDTzhkiLmgXUGWG/yh12EZMSYJ8ByhU27BFM5mqq93Olt0N9xFaKa4KTc4T43i3DD2orC5FA9MWyy4uM0zSmCFN2R1umPO1k7NdXA48rooF/1kmDVigpEL1onMUKm8UE4zILOxrZbb4vbcJl5reI/ZUEhY0WwiM3OxNvdJa8/NP6R/TuwJIdkNwfVmD0U46g6uw8PqyTUTrJExCULKNpdRCPLekmEJpb7OeVAsk7pfwFkGu3u1AAoCnXfILXhJDrmSj3vRWput/Vv7xD4/H8Beiuzpo6e9k9N+d4g4zl3aHKbE+gBp0Qrh+nr11gTymAg4X9B4Evm+e3p2eHD87NmLjcaDO3fvVjdOW+ttJPjIkBuo4AZiPm1qOOoyNeMqa+bpPEyB9m5wUO/Z5t5m5azX7uxXKzeeP3027u80mrXGRpeCZurCsilnibLgzLFFHHVFVUBHsLd3C9qePXz4B3/wJ9/+9p8yD9nZ3f3ar319e2NjyioAK6/ZZ5TVWWLsPeRalHJOjGxeVv/xHUu0sN2I8PDHItzfYlVfZ/HkGvtV/zI8mszyo3Ql5kgzvaQiPctE4zSboJE2fT8ChbeNxZMEl06+ou3Gd9RCXAVk+PEqMJcJ6F2cvhgQ+BMh3+HxM724i1l8njb5iicoTN1/QkVOg0KqseTYpAyKxmXrMnMRhMRsWV7BnvkTaO7pSXbA6ZX5IyA/E2PkGBxX8USqRbljC2cFAjiSlp6MEqVGXDotZWDUMMnmDC4SElMkEIlcSAn4CIpuIuD4LPOcqPAtEivCX/6T6RFu7vPhd+Fb+EROLvgXRBdR/LkUZyXkJZxagcikxcDf4iMdCbbwv0BFiWI17dVYZfjr/65iev1YP0/IMvufLR/WtGUMq8Pi65IjPxP8p8wtKCKmL6o3QzCjMs2mVut3+48+/uHTp8+/890fn/fHZ1MWbbn0au3NN9/8D/7ev/8rX/8VV3hPjonxhS9+cWur5QAzGbKt0/uh5pwKp3mMC7Tey9NAj37/jTcQhF1JRhQbDI6OjtkQ51Gerovz56jEkM+GAR7leKsqN9fwMEmwL4A8iGMEDMnSMd6xjAwQEwBn0eQH8QthCK7hab+IdIDBj6NpfY3LYRk85W/icxB0IYLcE9cuJSKCCkNZFFzAIqfyQiiZ15vTcQ+lJtgck+RXmtui1UaoHRDJCYkIEXnWx8MT/ElhNERO4zASR92tra3+wSNUYZgGSAISD/JKSPNQEERBnuSAP4iJL13hCAKzTki0MAYE4SWIsMEVX8VTxFYHmOIsYSbBP6V0+SA39ZE3hfxUJrtAs0yiSDiTyOTLpCIW4eTGigSyYF5zb3//2fPnmMtDAvu8mcgpZEePV2RBcGaPVIYalwFz2zHiDlKGiOC7hxsyB5N+ip63DIssQi4g/KEUpBjRFGJ9ThjKRuQkKtD5qIdB8MH3jkDNjILqdn7eZV7aaHUwdGD3sSNFZM7cuzSgmOi0omASflw3ihAQHJJssye3crFEDgEDeORB4oxvhaR2OUM0SkTLdPhKgPhxNFt9Fl9RJQ0kGVGSJHXM7EpN4KM2QquUxgQjaEgugVGIfOTVymfpze8isaCCGKQHkQnO4pU5i6jy2FDbWTB+EVMkMsV0Fa9YPDSeCmRuw6hXGhiyb219+JOPjk+7W9ublAqyL0lb49iq6+m6KolBsYZ5DBoBbxUgt0j5KAWYTtOiTJVqAwjafQ6RtPSnc46daW43ELLBBgDqbd70H+oRIJfNqSwCoLpmJ9LYwgvOIART9ahETi6zGhqLlOyDIgjykwHBKMg04/yZrSj69BIqXObdtLDboTfTBB2MwS1vO0H5gdl9XdMjbtTlEq/JaLR5C8l7A2bS8yHfR6Mzz0gTHIrDBmXyg4TPRVqsdlruszmHlmpn30Z47nAusC0FtQJF71KqFFo4XvzGksbazfqtWG6BMOmI+m3XZDnxp4dEk66/1tMZJw23O3cptLcevPvo4Uff+h//kBONz5kaSUoNy0+WIGbjCYsDTLFoXMxTaNqhGYFy68QJz4ztWIPdW5U333iTCwSYfiCXs7DHTMStOzX0+kOmrJv1NqR6vQMHIrU3K64o47H27MULNE8wCl7SRdDVs25A2dOKzzCr4sS58eD48Jhztriv4Kw/4kTRP/zWvznvc+xp6/S0+6Uvf+H+vdsevkBVZHkz9mXRYoKx5oPMmu1gAT/h8Cd4Ub4tOR6A0yF8+Py8XmCT7UnJKtIymZUUbX2XnyQL30XYwnEZtPgmfBHpJSA/s/cK0eB63eQCbhHVfFBOlk90NAsW0Z5Eac9CPQHC8d0n4udPRDYiEBZ6AIiGoZdPHitAxPbDZHgXCMLn4iuBxVfGjMLwK5FYaQsywgRIlPFcxVnEyIAFYuHt2QoPk1k4l4Qh9aycWXuRxuUXe5qImxRAMYhYH4iqDFIJjcSEv0iE3sWMM5GJpXxWYpVe/qbu/+o5P5Fc4g9btGI9pEgwNNlpebZIA8fqPQB+xv8FAKml5+p7lZalu1h7SY8EXwb+bK5Vci5g+rklk5wG94Wk/FiERKEmL/MtJRfAL7MqYwt28SmpzpOP1x9a66wwDiBWx+m9f/fNf/Wtb/7j7b0bR8cHDLqsw/69v/8fvvXg/oM37yHPolxhXGYYRX56+MlHiL5og+7dv4V1BvqkVmsdFR1GMcPzMYMcWOuzxp37t6mN48Fo9+Ymu9A+/vhjhjGGIWYFLw5ecFkskwHUuD/4wfc5vxrDA9SHZ11OmdD8YzrcdqxrHDMKIlUwZpDRkl7bJM2bTwcz5Y84CUTp0l6C6QQDYVjkl7l2OFi2XMHmCB+2kULyNZzPECC4uGqqIRChbhSccqHtGcsjZHw8bCthtrXgZ7Wfus4cSKVThUNv0J0xvRmzI/F0yu1IrMfj//j4rM/5k6i7kH+3d7YZ4Txc3p4NkZZeCrmT+QZCnNmxMUlm2enwZQ2IovfFn0D48eEfTrmSMXgbUX8efsooIvcjapPxlZmIluK4UfjwMcKlZ9WrcK96ldCRciQKUndewpUJF5vqJWNZtD9HKlLmM4oSLcWbTIeFQHHsCaWMrhNUcVyn5/ygobSwpB5hlx7d6KRvni065zCInHt728fHJxz8MRy0T0+fYi+2sdZmUwF1GJzsOJS5szpWD3t7u/hw6gk0OZkED6VkCs4KpU1qcSF/Mws14fKxmSAzUWQCBBXIaNS9iCRNEsi9FsDUj0XJdGKldCLjZUmVSE07C7nwMXOJG28+FIfUKCvpqsuN6StCbfw36aQ+KhEJ7vqpfb+5iBQBCOfiI1Iwnk/pGzTEN9pxIsIUYy2CJckHj2X8wEsdlnEUHMa2hLFJEy7REF48ezzsb50cHn/+Sw1OzKdQNMkGHJOuwQ4NYbx+5FkttVEcchrHunN8J4jquTRgo+Zqvq3tm+994f0/+nd/3GitObVmKcCaAwvU6HPXAmkhT7eqezBsPD6oczdtnM2FIEvjpUpBD6VL8dGFUb3G81FMOWkVFGWWJlmzrBb5nS9PAYqcR4DhVYxM+EDdT2FwpgF6j9kW9umt5mZ7E3N2imkXY33MaWae5slG4P7JIVuJWDh98/69RrvRPx9AMDtyqewAREV2eZEDfmAdPQdnXnHB1e7+LpMWqGPBCtqkPzQZzqLRj3OJyuSWlNVfWCsoMAT0JgK3uYDH09EtW1ftBRMUi8fuJWbmJBo5pWKRDbJAO7Va1eZsPq7NdypUt8opKWIXRP+E7E4dHEyexN6ruAMdPa/Xujed6qHOZ71i44xFuSePRue9PldwoPIAMUcJrTfc78G9kGjx6RtdIDUud8exawDggUedVmc7O9t0FxTpaNAlG8wx2KBM2WnN5ZFr6+enA67cePLJ027/7NnpIWMER4xy6Be2QL/xG7/9i7/yRQ98irKJJmNvF2VkfY3qyhu+WGw+47u615/irDYe61ME4Iq+AP6oz77ueZXu/yL8ZdsEG0mkk637IjBf5Zp/wFiwllr5LFwEpP8CrAQxT/4JQKWKXz+LfkCMRWgZo/Txt7DdL/YGXIDgI6W+xQmKEZwIl5DL/QlLv1e5rIXSS6/JP36prX7kQGJWIlwU0culHf+Ek/7xSX749ss/H6tx/BJu12mV8FlwMhIKiNx1eUF6DKS180QWEQNHEV10EhTVzIBIlfYmuivP0jfRLQEgKdCSz0AhJNmPsiugTGoZ4TVcybgALNCDM2hMKpcoCmqsguksE7qUZgFHxKBPBJcgVnAWNSxhlv7hWiJaCbjkufh8aRIrcV/pXGB6JdTPHPiKZF4RdE2yJfcjKHOfbz1KVEVBXhO9gEnA1ffLYQ2JVIumkZD4MDqsY0KKWIEuixNUfvmrv/LlL37py1/+RQcWzotcayGIcKsXiwC1Sv1z730e3Vn/vIsqC+XeyckRx0yA5bx3zkiI8c6gxw5alnCphjOGbEZC8LMggIURqj7seTDSYJ8AZvRs9/zSL3451cMYp/Z656gKk0jkeC9VitGbIQ5GKKzbyBfdg3mxy9B6qc7Q6Fe8hFE+9KHN8hCdTJNPBny/BTX7KQSzmDFiyR3rBeYSiO7YJKG/Wmv2Zj3scVGvyZpqhcNktne20GWyS4LjiBBQEVJpTt4YxT7m8ZAle0ZWCg+dGULGWW8AZ3KzHQdT4NjcaiOMiIwxO2VPqYAUKVw8S6eNVQCTDzA+zH9+xe8iluxYPEaj62SYV6QV0FYfyHSm3jSUKzCKcML8LTpJXQtUFxwvCbEbIIgiFzulREEzSLM7gmyyTMKMwLIxGJtwlKDMp9yFGQ9nkqxzxjlaVHpx5PKQNrz4i1pH4aryrCJcMu+KzhJBXHlOZR87JuE5yy0oXOuNShM1aat19+7d0+7J0fHJzRs3XxwcmHXT9ayndqfNPg0PTxSJyCkGaRAzk0zygCP5lOJ1sCaqTLBJrjh1skjIjms/0kQMKp5gSaOShKA8BPuv5FtgKQPx9AlI3KTIW0jp9bGYSAiZDmVoVumYcgBZcDyoJYFAZVRikUaRJMgKMgKdr8vf8IbsZOZ4OxmjRodHMGMRccURDAIuUwUeVTcbPd2x49yJHRv19e3t3ZPpOmXPbL+zuXneO7tx4wZzeyS89eoWjQDxknkhloHbu9tYHalMJ7MEWFW4W6ruecIcxDqatrmfarNz0jugNxqxVjccYjcPf5l8081w9BOtrDevc0bZeHJOA4ZdZsLMyh57j5h7WEgy0QLXFt+TYi1+AAHO8g4+RlbDVZQDbnlE/jJctG72GVXu3bvz1htvUItaGxtf+PznMdOPnHB60Rpt4OTw9JNPRns7N5F7EabpHtvNDXTjVgrl9EAY0yJU4yBB6/HgwR1uAKHpwEOOmJKhMaOmP4Rs2IXlpEumMY0Pyu1IqMn8w5Ne0CkqD9WUOmO9JBjcvKwzlpo5kdWTueux5gWtfBN7JPp/DwgC4/bOruyCdRx4hW0kcyzPZnXK5Dy97qGf3APPplyXW9kFMBodHIzZtQ+3d3a3WP2L5julG2XOxtFciP7oSLje8PGzJ73+fGdrF0tJ6sNkOKKnHToPoadCP+KlZqV2gPXhAYsDz5+9OB/Onr14PpgzbWCtZFJtVD7/xff/xm9+bYChF3vKo21AGVSZQ6t/kVlZUTxZKXwDE4BRvDKDT/6sChFURPhL+FmiN83rHqh5WdB14PplBspQM2+3k96R4FWEV33K6K//G01iiWiZtZehAGIBTibLXg5KMy7vzP0iC3xrgsgTOB2e8Iq/8AGFRj+GW6lBL4DOGNnDZwU62CKmy5WjAIwg4Ytk/PaJtPil/eiUAl7lHgC/eDLO4p2eIo7YRIxfXxG/TEPKww1ABmTM69+x+5ibNQnNlAr0wSEznsxYjVzALWKYWjCyBCos23LWG0SWOSwhSIRQ8+I7mF0EBckG4L0yoyoysjqzXAktZpykCyXVYtYFwiLWxdlz4bkg5WKo3kufy7CLSJ/FseRXESvoLObBnwHRCic/JdaVFOVz8jrfWXmsJ4vaEuHX4l1lQmJOSgK4wY74pad1kiuxGItQulY4cnHj+ODgv/jf/u9+52/9nZOTp2enfRQ36Hg4EZM+endnz6X89QbDrkd1Kz2y/2y0s73HMBrDt1a5jGSIxeq3FAKxTVWVPplPh5jjeM0NV0zGydljL2CaTW7XmUR0XiAc79+6wfERjx8/Y6SpNQd06Y21Ld5jTrPG3CHtf4N2PhETFeBwUW1CPWbvb+V3MGOgQn2ICF7luGrrpj2EbzoLNFxUtNm2bKiewiz8QMHhR2QhcM6ROUDF6EmynDro/t7BAFmh00FCPZ2M2mi0RhyfN0Mm8+wRcDOS3di/2dncOjl+xsI9D+rB7tkABty7dx9RgaF1OJ4NXhx0Oh1GcSkn3aIUzcWlJzIKYVFa0cFlwRmJisBbBJGp6b5feZ5MYIq44FPJxxOwgSjipFfYkPCNrBQCl6IwlauA9+faJ/q/a0Pgg/MKVdSaRrBpE2mGkztGo2OwKt+QZ62ZQSFF2isDP+fYRKrFGGMzakMcAqnUS2lSiuz8o0idV1TGyhlOA4hsKftD2XHsSbPJxAwPLmRmQlmv7k9Gm+f9J/jcvnuHmcCAKR3m6dVbgzPuN2Vthr2IM45jFAlIqTzK8xaivbvEZdkssxpSFDA8karQiuC8jUH8iOzAUz3EOL3sXVeigBJywR5IoiXLhPhcvJ02JADQBufOAlOgZaVoTnkpBZqmUw7oySoSEeMOB/OQIYmLCOG4/CrSh3YQ0Vhv8Z7XD3gFD4IbQQYRwSA7iiz4Ew8ZdqBF/IKdTSbMPfb9M9FC2htSLmvNY7Zmv3i0N9yabu1MOh2kUI3BKvWniLCNCVtKN2DXaDBZ77ACoKEfaOfTm86EZsew3fOFppPtDndhNU/PNtApaGeEmMh5mvM6Uw7gkRGxD2ETwQBzvzDiIsOQASh1CKT2FlXO/SFbsWlY4x+vCmD9oTLz/ix5bU7lukWpM7iIfzj5zNxbwlHiBHBfBEfnf+UXfvEOz/275/0ewgq27+2Nd04OX3TPPmRRhBWMna2Wsi90j4a9bpfSg111Amx4U1YU2SDDXltyxb3jG61tzKfYi0WJ04NJM41Egz0PfmVtDBbRqcHtSu0QN12fJEq/An22L7QzlbXndGDOT6HcuS6E06zCHA5YWp+rKJ6RSnZcdyMdpsWtQZweyo1a67t7TtKYDzDfGntTQJWZG8tR7Nmh7lMorMDAXiYR1VmD+9cw72THM10f8vpZ9/z05JPJrH/r5r29vZvI9FoNse+KfVKT0e72HsmJvFJn0YCulcNObYqQZa+OcRR5mZ91e5ggsW15OkWhxB6fbmVt2qq3mXLs37zzO3/rb9/abzOpogXTi5A1qOJHJixKULaBNYrX3tYqnLYVOoqHnMs+2Xj9swKbAEt54/oI+q5KOyVUkAO2osIV3ngYENUPUqNvK2MsfyNufKadvRYiGRPP6AGsvYUfv/GItHC8NHcRnjlK2Fe+S8wJlOmGO/edpnSqR5JSghWkUuy2r2zm0Oo3JOJHA9UBXOQiqM3RxGkt6OLu5CyJiCUPUxsorPnM7OsAid1zNguCRCrbkxrfcA9Gr94DnckGBCgK+okhtxe7RDI48Ab8pQlARAyYlZfUFsRFriIIevBcwidpAYevYSvEriC76Cziy8IlLljpB/EX7wJuERleF25/gbyQWEZbACdEIgw2Ah08LfAXkaMqrKJdRfBp7lViM73EVOL7tPgFya8L/kp0yYsLHLnIn1fGfmngRYTL4soIl7Jb5GcFWZaYSILR/F5CuAJ7OWgBuYI2xhWqpkXJKSXIQPP63vYtemkULv/lf/l/ffjox1/9pV+6d/8+Ww9Z92WcCmWZQ+lHH360t4ekzlUtHH+BWFblNAmkNYZq0LFji/VdrUAR62iFjK8tJUJMP9CjM+ywKK90yMjkxlkWkderLc4R6kAckega3CfM8TqMmZr/TtJ6GPwooMi1a9ZMJ7jKymPXGcURwSuj6VBRKeo1Mj8r5EQWOOxkQ1tmZ0N2GWSkChTwEQ8tEhx4XI9XaY+5v3MVDhexUbFCwaY5hy6EEkcPRm7ufGUm4NkcTTotFwoIZa2C8bu5sc5/pgRIMkx3oKG5zuEVY8yg0YD2z726MqyfMWrG6NnNCfYO4CWteKIXtLyizGK40pmOBFktxIy3aM0BkOHmzs/IZkYs8dCtIhvxL0fK4AV0KCssyCBiRvqM7+jX6M6pFLAFgRURiQ2+HtjPyM+FPpwvzhgPCd62Gz04vRds6Z513Qy83oBtMJtkmTBgH0BtxFTEPg0ZDlZYKoTrwEkF4HAhbJbRTkZZs0d20uRGpF6P8mxpO4H+EjDueeZo0dHZSffRxw9R/bY6XDtESSkSBaNAK7/yR04FDdKRvuBJlVJJQglecApIzDWs0z6UCCSK8MpTJBSJZrmbpQDlVf6CtShzMPGotw6K4CtQPlF/FetwrxIbKRo50AZdpnDlMZiYyI/C5EwyMxVEAB/8DppW4q84CyItCJy0xJiQ1OL+VjZkNCsb8y/e/tKPf/SD6ZATXSonp0f7N3fr02abUwRoozSp6Zh7Z2nH/X7XM2MRSaUA4hWRzaEkatrPHV5YjLAxPPy0+RHOK28b0dJpvBjjsQQxMqo8saY4azJ/OJWD9Sq05ugUuGEaERzS+e96QdGKog8J4JJjZi9YAgKw5fCKBM8VdWONVfC9cXPv1s1bjx8Pnj07GIwe73JA8nrl9u099ADD/mhzc1uDmcmQ40E5DLe90UGi5pY0OkywQECjTWeC9doEA7lNDrvkJFNV2jxK56YIQYjqdI7e9l1lQ70EK7djMGcGaNF0dsK7VcZjG4KTxrNsItdWdd2WbDjhD5FcdbGjrLqGiXqGGHSGHLSE5r7OLkfaR7W2tblNc4bsoxcvSJl0Fd9rqPbdpc3JRGClV+e4NlLGn4To/hgDTo6w0sd+sso+kL29fZK2u6VbaDSZL1FnSJmF33abFQaWEerj2Yh5Iz6nJ126AwvOQ2YxiNrh0CJqBlulWQv7G7/5q7dvbXsAg2Wq+Vlk0xfURgXQJ8tt8aNPPBFWfsi/5XPho/BOv4uRIijr1DKyLoCvgbwEA8QyoUUFuwh06euVSKmaF8Av4Deti8EB+zqEFkivyeeCHNCUyC+luqQogRdR7HeSS5YUtYFBuKiX1s9FKDDh74t/lGxGM1YAGSkaexBoqxdtSU6Rvp5GLJ/o6oADcNHqIw/2ABdiS4sEFQ/gJW5x2m4uTQASMCP4DrAVzwWCorOJoFpfwNx9HPhXYq04E41Ir1inCUUHkeRzFWDALKlYxMSx6hvIM4PuJYjokoL/pQqTsQwrngDRbSRD8QhmGhHOZvgCPG5IKKJe+AmLuhJ7QZxYr5s9LyNeDc07fZcQP4vLLF2Of3Xnw2WIV3wntkUur4VcMAywC5AZ2feq9aG31vFk4LUIF0gS8xXgKO5sP1FmDBEf/fLXdr/73Z3D7vj509N//i9+75//03/17/3t37r34NZ0WOm0G2+/8zmk2+FwenJ6hmT+e//tP/+Vb/z6D7/3F1/96tefP3uCTvIbv/ZVNFwMH43m1rhyppzHVjxGOPf1uTLAeXe0IQ8BcQKAtpfQta3OiJGNwzN5emfsFOgPh7SIymy4gxnovHLKEM+JMg6NWx2GbWTEqF4MIVrRcvALqj5GYt5cPEyOsAAhUYwEWIWYHmC+j40B8wr0fA6N9iXUTx5sfGPpUNZEz6FwwPZlNtNhXjvxFD8A9m/dQnzHcmk27rCPudEZb29g/NohN4xiVSY3oT2FBKyjcHJwH25yxCDYqjd3djoHJ8eMbb3zQbN5l8lU//xRrz+4eXtf0StG4Ci/IAuXzScKJH2lrawSRZFmofNROCxgdP/5FbFEs/iMBh4ZLOPrY8kjMEyj14AQBlBgTDigEpT3Ak2J+PJvQoZvMhHs4KdkkNtix6XCCYv7zqgYrfFHw4doMR+qPI+Nt6hjUSti9z1vtzcHJ0dIHswYEUlmo51Wk+197L6gm2E2GA9zVQQxcxBKxNktt5/MPmEv6fFJlzUc5CuOI8T+H+srzgV99723Hz15enp8Ols7Ph9zRlDznfcfDKc9DL4g1fPZ7cKSeDMs+dnVh5/sJ+EYcnAigylhFL4Im1wHhggFNfx3PYpIQVpJ7IKHyalAZTYSrZ9CloHhmx8FEOQ5XwWNPLHUQvevDTtVr0g6yYeGXHkoCCiIDNm3TEJEmXgkS7Zi2HSqVqkflikvSVrQFjgXseWSQImLClhb4xhH5uoWMs2IDUOTISQeHjzXdGT6goUwdv5wZCT7Ydhaiik4ZViv3mLkm8wP++cnCL7NdUxQECxn1cZz82y3AT/RdleYJ9y6vTeg/fMfdX+3P2i1ma+TosU18xQdTBehqjI/o+JRFtlyrNYWD5JkDNbTLapOtU7vxJocugilUQtMqCJDiywTEvmDNZlPSh4H01Kq5hAbqft377374I0Hd+50Oq2PfvIjrst9cP8ulbl//vzmjf1WY4tZzcnJKZsU6Lt6ZxygP4A+1O7tzRbqdmfcbGPgSCA0KZVqs13lfCdMnJg20IGgU/cmZ6mCSFmxXm+6yoqehPRdyhhXJmy34BwCLmHBdN9aCDxJaNpG5xaiNuk52RYDbMDbVQVBnTIQZO4pg/WWDAAbxj1UNBjLMb585zwESmyhmP431pjSWAmhi8ti1uvHRwPKjul9v0963MCtzh6W40lRMo2HELYKjA5GhwdHJIah1PbODi2zs9XhXmEWAKo1cj3b3tvjsj4WWF30o66POtPq+nS9d3R4cvsBVzivDYbdnf3tSZ9zJwacG0FeuK+YjVfZGJ3kRCmS/WAav8hCTNhGWd+hjScaWLzzvETbOyzNvZRA4zZnRNbpm8eslk/4KIEkQOm9/F0FXvouXFGXFl/poMgyKZqFVviX5J/LGNX9Q2qUQCJwVZ/q8AbeFK4Y/H4ZhYblE2DhTJmqXAeACbIx3mY/LUTKWAX65WcQeHkPQEl12qp4Wl2hTadwpSzqIFXUPdtJbrC/oD46MrwtCKH5R12NCThVjyIX2KmxuKKAFuwQHCz6Lx4++O9qbTwF7KrFiiFF6CIWDo7Ifaw3ueOnkL0TvQkUEwCcRVx+9F95Ln0WcCsAOgug4DifCYQn/6+PsIx/Cf8y4BWuBX5hSsbpaZJZgxZ5XDgKfIBFkku6MqJlQhBdgxiIFSX0qdQZuYAtEvgZfkrafgYUfwlRL/HgEpFXPz+dhEsFcF0E+VqU1DI4PeOdrdtmmF0gZtZVuvx/8B/9z//se3/xb/7lv6QD7p0d/9N//I+95mU4rddmu3s3uMnrzt03MOv+8ld/CakcrdVHnzx66613/+0f/lvu33x+8HjQH/7Gb//N9sbW00cf3bp9h/bKGIBAzfBAOg7tWObEQxDC/sNPHqIG0/QG8Y2l3sn8+dPnnAiBofb4nI3BHc6uRqfrwvF8/uY775AjhDpOmmMA2tvf86opTEg5OjqUTxh9g4c1a7uVtToDSWqYYqmATsaxzMzzw2jhWjO9KLy0L8JB6wt21LARQhM2ZMfqWg2d1vHxca/eY1cdkixiLZfRIO5g5cTZ3OwIBB/5Uiwkn+ggUf+TTdCZlIvmLGRPZl3aBWddvvHmW8i4DHXsJrZ0IAQRhJmJJVqWqr/ELX7yN8oMfx7aFbxcekS0DLryJmwJGJGzWYKAx2wDEf8Di6iv4LjiAUhAXwnQW07yy3IIov7arO91aZwC6UFP4ynG9+YZtseZlhQSSmAEC9FpLMESAAIAM8Qqej6kIoaGfo87UL0AS6bCKjMU2ZcFsfO7yh3AvfGMq0HBf05apARO7DA4ngTD8e3d3e99/wccs4LW2N3XXAJbn7jV0r2qmkpArvyQbDPgix+ZE0+ZXfsz3P5ZVXgz/KiJjXjAZ3AJYNzEVPwGMkNJQVyRWkYvghJe5EVSOqys1JLwi5pCXeOGK4RXNKbgoeYVWuALWAqyxJ/pZ9H6GVTxmzmdOAVgO7tJBswyOCEDA87yV4TxsYAmhg1AfTStz5troY/2RUEwc75z597TJ89pGO9/4X2OiBk3WuwTZUVorcHMCWNuplD19Q3McRzOqRnOwkEodkcTyh1NwXqtub9366NPnnEcEKcUKbpPp26tQRWh8Xqr5uQ/apZLC0UepAonlEu8RZSyofNzLw5DNqWKCR48T85H3IwF9yPXIJYBSLKgwXM25fyZr/3Kr7z9xjvcF7K3tzM6P+9sbuxsb3XZATRfPzw+JgobgpGj2R3U3tw6Hw05fBMdP7MgZh30Dlx/y4ZmTy6SAHQG7IboT9geMBjVTs6gENqxtYFsQlP6GbPnaNynQ51yIeOELSF0aEynOWCnxsnD3tXFAsFoxilYwNOI0MU4KaXPqiGpkyDCFgIzHRXtgKlvg8Zi8vS/LpXYj2Htw4yKy0/sdLlNGThaTA3unkMGNDlVCDMsmMZkDJslDiziLr/pkLviYc6MI/m5sa7VbGHxBMdAAB50+RwTlGogssZckegsEXPRL+nzH1QHLw6wF2WGRym6x2Njl82+wwlHlI43TusPnz564603n714cno42NztfP87f/zWG7eZfhAX/oki9DuUj+7FO53RvvGLoo3AcBNY+ogh3Eaw+sRvAbqAKr/jt4S84Jn4DIqnQFR+LvyXwdeBleDl7yUs4X0JVXyaeOmfhJQYPv23jJfII/aSIa+MTsxXJrYgDeIoKgV2fn2oHDEDpcnYHi1JkQW2aHjC+T9KuIySwfGVCesh0vAKh6KokRJVggYinEtchf+Fn0AuaDjyt8Ttr2QVQfFTTAAybTHhG3Op4jycKicNQ8dGCQBPI95qohdnV0KO7wv0aacAFaTwE3wLxOTb9YEraaymRzAr48RCBOG5AGvqye6RNFS1lAqoJWB8C8cTJHCfQPwaUH/oG83UBdYL+rJH+ED5MoDP4v+zICqy9FmSuwZ2FUtJzYrf9baDKwDXoNQLVNUL9QSPRP/yuMu0LsKs2r0FlhhgaIreXXXjTvMX5/c7G3/rf/z930Um19h2tI/wValyb8wxpqVHJ9/DyPbPvvNdznX40Yc/Yan7X/zrf8Wwv7HR+NM/+YtbN2799//dP+UUj7//D/4uZvxs8sN61Z28XuDlmI5mh2aPKYg3189mz188Q0TDPpvNmmddTs5BTdhnyDw5pnKe2CdMWBpmC/GMwd7BlOsGWlwvj3k9p2VzWobCC0dMqBTgch/W3bFkDpmAIYdqubXdOTk+RTBhPCRBs0tjsXdg6PeA0dlkG3rm1RPodPwbIL6fIxkAqwH6eMgOYFbtOc8Pk1Sinz+rMQG4cXNe0xb9BrsMWBgnZ8QFMZukGTjZx4zc3x+eYzrF1kTPBQ0b3vPhi26vtlXrPHvyxFOT1urkhZDoknjzj5LKYs3ytQvODku68xEGTqJsU9IpZdEMDfACLn70NreFJGNfhFepIRMDLFazYr9E+rM901/cQLyKaulWz0dEMUsV73ySRldzKRwTgYNaaal1pJjYL8kZspXKmwq0kSDm+Ej8mjZUOEtkHa4hBhFCiWg/RjTKpfKiVvkyZadiATRe4iaAJKMpw0C8dthsnzbmbWz7H7xxVzMz1jO4t653fvvO/o9/+OGjRz9h3zYy2Xg6bq3XT097aEwpL0U/1haoFAU2GRCMDQ/zFZwp+nyBIrdBoDnOXg6/4j+ZgrDo+gQMviwcEUHfZJf+ehXv/Cw8izGCe5oBXj8K9S1TS0ThMUIfbAxbO5okSSk1R7rqvGFP4ORlzVm8bRwSufowVd039bVDg2oshoDN02bKWBeA/TCEV6bBhykU1aaChv6ciwJtQdwEPL6x1kKyf4JgyS1Sp6fnG63G+VHv0UcPT3pn77/7Nj3CWb9LE6hWP1GsrFQ2NjeRGzlZGEGW3aKgRcIHPwgtEcphbfr2ew+Oe92PPvwJ5j70HawEQDeTR4TsWFNi+a3nTBoCzb2N24K0pUTeZQJ4TqHaeuSCJCdUWmCkkgwzOwQjelvDZCfkxbweT2Es34ndWXt99/13v7jVWuekqvW1OTqCN95+A2BTms33drZ7Z1j9tTGPYXe7dwNytcGQE/FpC8x5vemWiTEXWFdCq7C2zqYorsoeOZN14VIzeNavoIc3O2gR2fEFObsFSIGmAT2sJ9DCppNNiK7Wu/SNEA1mc+nEia2xSNb79H6zKn0gOv01xGu2M5E0q6eoMNgwf+v2zc3tLeR1DihD1bLeaCOmo5GHWWhk6EuZbtL62NkMYzzjn2bo9glXEzhCFM0M6hXmJU1uhbdNOQmRzgnXBqiXweopMDCH1/6TUM+0ikZC0Y4PTxgRWAXY2mxzP0NceKAJFyU+nR80O9wSWONesxu3brQ6O597796L5y++9YffOe0PDl+wtefs9v2bQaHlYmXMPx3R4ynh6E5/f/Ij3zXln/BM+OKriJAhgdNohW/i0KN8MqCMZCzcC88SqvjFn2cFycp+zvCnvbO2cOFZgdY/E0hHJBTAymBR7U1hEWPhCJhXv1IqeDXMMvRazHjaQZQ08hlNb8okE4O2jfTXbfOk2RX9roSrAot+zCT4jpSo/dlvYX8BYlcY0LlkMyYKmAaq5KqYF+KZo5IRg8v08U+Wbb+4nYCQqFsllZHMyitJKj1s/UG0OLkwxx9pS+oiUc8BjCf9Snf2vvklNdFDEzH7lySwQJNAy3dw8CIdy8CLrsQcXMyAl0SzbUCDL5zmqXhwRXIGFABFSMRYyVMZnKjK+OVvERpFYmZLpkUhkXCR7RL8wm8BnGnlB+/Fs/Bf+PwlODKRRLwk/jMltIoiIv4UeK7gKMuEgEthUZc+E4HXApdYaT9RM2hOiNObW9tf+ca9v/jed54+PHaknHrzvMcZFsIiJ+SjlOO4Tw64GXbdpecNOM+az3Z3thjGuscHn3vvCx9//JMH91iR1KqVrh/lFBbYyOEMBowKnPfCaEGz+MpXvkIoYxu1Ji4FqJ2cnj785AmjQtx642hDT8GYyMLyzZs3IYJorB0zamv7qwoBpRZb0OIGWWRtLqRUEY9oyPEj1jzG+Fjop0SiUJTS6Ea06c/o9jKha4SMOAWooUGxu+M8l/reg/tcRRljckVNNrfhcD1NZ+vpk6fDMSv16vthEaggFeEMqtTNVuYcdoHogEKOIRlRgDkPWWFRYmurQ3ZByBDntlcmAGHTsdK2pDMbMyUURC+KT5Umw6NlQUDWCx3klEpRFuiFSAtPmyaNNCqP+OlTAwnxEVw4LaToHJYRFslecCRRhdeFj/SDPk0UTAFxHB5SRuj2kBqmbtZTlkIpyEyJXGIhAAYMdZA6uOp0q9M563UJIwccrE6smIopdZBBcyhx6vpYPYgapJIYiwK+FUxgjLzgBPERNwSTBBsyUW8eHJ5wITEqT6aS55PuZNpn/Qa7MhkYbAM98WBh8fAJneagfPQxU1FbYBu1UgAHHooE6RCHyctYvIlG3HSUKFZ/BVh5xL78jGEGH/OMr83TOSYeSE8kQoVjbNWD9MXEuHgFIWFiTMxBi58rqRgbesdaiMy4XZURdJXecEfyZSxRBVdEpKdYi8wyXaZZYd2BiIkBCeXLtB/TbaQ6WIX6GW33RqfBTYJM4lmucRWDdQct+Ef0EMwDkSPhKgVMlnhr8hKNHau5mRp/dNit5toG8agqo5FWIFQLzr9nkw4XD48m4/75EHKyili3JW/BFrH6KaMMIQHot5bqLNnnF8FmzfwTSZEdkutoAZxYCs2SS43kPvrwwzv7ntjPViakmmfPnkeFpONia0GFS9ApspPDEw5Bjv2vkZZaAm7Fmhw+ezGdP0US5m4KpxvYG7KXlWqkOoC5ARY77I9iqYom4BqjPZi9RFybiPQdJpR0LMwuaEZ0Z+vsC2ArF12KF/Vqvu/qClmsYY3DTX91DOsp5rWad3uhfMAkhzz2znuV55XD4yPWVYg4PEMvQ4FwJo/sZ28uOYqCtZShTl/1GWOkew748jQnN0KtMXNQuJ9y7QLNkZa7zg9Z5eAjJD0AKD8QUHuZhDAYkEF+KGTYj8Gnex5YW2Xplg5zMuGMODpicsWc5O79W2++8+Zo2P17f//X2ZD14tnBvNb5//z3/+z4+eMffe97D9687Y4hKy7Fba+AKx9KqvxIr6KIo4QTysZVhBWR/IyI1ABIo/CjMuAdlakEX0khwcvoK78LxCVKwwL3IhE8loEJv4KgdC5BCp+ClPhayYFwi88y8l/Bb7BI6mWW6a1QAc+zQcvLAKEyxHJ3ckJo/0u30QUPMF9FQARRuELZOQBpWdMhAp/YgeVfVCdTiScTyDce4QAEbFkRjBCAoMkYARWpFsWywFXGB03p56/xygmA8USOVyXmUgXSObd+6McTREasIqyEz+B8ywUuJ31coFoJMlL2YPEuQooZJFZukbaJyZNgaVKTyZZEmAPYp2oh2W48CSloCrQiqTSwM1t9AkDyIqUlOBLjJ3ryQHmMB5ajn+Fp+i99ks4MjlQvQ74i7mVQv8skdVyJmjb0qUe/YPGWkBk334F7qUG/Lqn0S2xxduxKzJKSMnRJzZX5/VXUVc+7DXu+lbBkTr7JWlkMQGSyq5ktfV6WVnEKEHELfNaYSIsCxDK22eJkhrOdVufh4JGiewP5+wR7Dnp/rmaloTI6IJE7EmpqykA1rK012Sn74tlhr9u/sfv5x58MPvjR7773/he+/rWvoJ1nwGJplySgm4EcydfUPCFIq24wuGd3NEJa5K4c5AB0/awJKJVWMalvMmPgFPEWxvVNNX8kWudIfnbOcf8raJHT1ZBpQYQaEiA8oZBuAkg3eo53apXmbPox4xCKNQZvskCWpYa+iNtwcdgaGFwx3McWIi521VipznCIKIPp7WjkmgODo3ME9xugPRpVOdvcqRBSBL0R8gpReLt2wOgIbqT83b3t5jkaTYa3GmeBc7wdZ6oSqdG4N+z1SRMhhIFPZaX8gTKLoizC4pfiTpc6aT+QjzVcufiQjeJZbVZZyuZRHILohu5wWOAhXcsNEkf3b2iZWonwym8CBI5lWBmr6KCU5OKUcXZ6cDupWk3kNgVn6hvlyI8SANMAe/Pp2nTv5s7BwTOCESAmo3OvmKughsTWmV9Gd6ocqCPjSPukhs7XXzOh3lEBACklBXHQz1E/P3jjzr/4F/+SiZm7u4mCwVil/pOPHzXQTWK7sNEmjlKXS9HZVUmfyJGLp7sSmWcrBV9MzsYSkJOdSh0jaTlZrRzIhrL4QGlPSICU8+gSbfEZX4vXZE9n/TgJMHkRMaM5NE2Uqgx48Ih/UTkw7cDbyQgzSOK4g86TcYIjkaa1WdFKMqxOuszOkh68vPlYRNyrYDujuYUhUVBavKDDmPng9FsfS6EICV/JxQad9kZzIZlJ9YUK46HLcVCLLRYi3Z17tziys7nRZnb3gx/88Be+8DlLKB5YzKVY54enLPy0tzfQN9s8I0f8zNdc9GGmTWndurP7wYcVjhutrnN05PjsrM+yINlkE/kWp+tiyj3CQiakevIOE6JhBweg1AQjM7DF6SKt0vQjT74yTUEi+VgbrNVOaMX0VAC438MwOhJyiWEbtvLUtzlq6c2dnWcvDlzI8jAfr6ZGAn5+8Bzpn5PPOKmWXoOedOTplpyL33348KPxcJdKPVvrgoFuSnXGpEN7qdVP6F3BQ6Vt1FkkqXJqPim26jfhzHh64B4qzy5iSy6G9BgZvmC5rD60N+5sbNEPc5w/E2/OMUPpP589RdQ263ID8Sv377LOwMUso7WNM+Zm9Ku5duq2HRJq0t25C4us2uWSdyLXqrRdVBuwBpKY1Hs3M73vBCsmKiC7dJjD7JKXWv2YG1ZQCjEzoYOnpVOzAGP+hq0ncwa2PLBN3+rLwMES3NjlgnqTspj1zwZMGqlHp2en6P3ZU/HOe+/evHVrb69jAc2r9+7ffePdz//Jn/7xs8ejv/j2t+/ef+Pt997DTpDphf2CZedf+Q5n8Ur/VZ8C9CK0laDwIUbjE9v76I30JOtZo+JdpCfAMt0EjPcFGSN8lqf3lGAvu22gDL/u18Sg5Lo8Rsh1cfRL+Sd7s9LW/2Wwr+2fXLW94JJ3OPWzt4Et0qmlZHQYcIo+WnYBEcvCOBphMzK6b1CCZdqiFJ8Y521bs1jyj1qsLqbKvb+MoKEIKXs84ROyOrkXHWfSFW/HCwDoUf0Jd/Fb4jZ2RjBg5Sk9k3gDMp/lBACPEsSQzLlgIWoUCRLJhPT2CYeVNgYVokSes4oZ7iePEPGziJpI4g2MiWWGJIpPmlYJGhhyOJN3Mi2ARLiEKWOnrwAljZl2kUgZvPJrepAdmSjILIAj5SjpFfBVZxZTmVCGXPxaQOMd6BYeL3UsIF+C6fqI5uL6kM/iu0CR6C5RnJ8LmEDM1yUofUqY8ldQUVqnpBMAa0Z8EqRP/A+Ufq5GTHcRMSFWgEuPxCVWkuGnilkOS7rolTDhZSTj2Gn2AXBTKmUNEH09flhmR3NGc+yRGsRFAY5wXJ0fvPPO22uNzafPH5+ePGBcGDzvcSa0ALRIlcFxHCR0MJIWgxMys2ecMzrevHl7e2uf7b9s3lXfabNwzN2/uc8WMe+x5xgZkrf+INQgDWBboo1Q1GKU/V7/xTY7pHQQRg3kx1VpyAZTvsWozFcwg4HYzCMKqnNGcHcLL1IhIibD4Z07tz/66CPbKc2H+Jj5j9BHtudY3rIDj1yp8yYpEuIjzrZHVzhbZ7iGGsbyXm/AjjpWB+Dv8xdHaDtn48POBgfYdxm8Y0pFgq7dI+1ZnsWzdEVBwnxGVDxTFlwt6IhQetgeyWoiyZjWGT3iKyiVIYjUZWWiU13WvSL5l/wsqboOwBRIIMqNJRTwMmNUKQiD0ClSBWCK2z5c2EGY8Zbl9nZniMBCADYP3PeJOQFYFDsAxMCA8iUKUg+e5t+qZFZETtEDiCfzN9SQeEehE5cpq2Yx9+7dOz07PzzGwswCYWPC8+fP7t26DeexH+AdXAEtCC+1vjKnwVBqg1T5wFzbCTHinawtA/SkauWQFUARJ17xaTpLr8K1QF3ACSHeSEh+mpgn7VBH4SciLBl0UuQqTowCBf1A8liLyn7cSWPkkXcmnDzki88xByQh/VO7y/wtxoNVKnHzP6gsSDVR2e80z1AKyOlX2MzQRqATpTLHr3JGE/te6EoePnr85Nkz7EY4GgsZd3A+am24oZ+2zm7NWJOReJjLTACcnBdJI0UyJqus8tEqb+ze4pRM7xsIk8L+oL+1dZvqgdTrEVLNSX/Qi0xBWpljMBYZSy+riryxmgBVZEZonKQMePgVQY74CLEcaEuPp1hjg0XnMRrQVDmAypPs16sccAR5TGOJS5d2xmE49CmwlDmB1wieCzxggUJqMHj2OpRYs4yug41OVkUmxbFPtyg3FBwsJTodopcjpdkAMx67GNIRD/PkOooVdQ7I9hSh9QHLH0CYd62NWIHB/l5Vuj0zYMap1tptd2Q5G0Bi7/cOK9Xbd29iTEfepAF7Sxsdl7dTYtzOS0Fav+isIfJ8RIL0b2hsIKGGnZI7uIjpiimaExdgKTUa2XDkkW6WJB0pFyLCGHfcADSnZ2c5otVuVwZkrUp/fs6VwAwinDFKYl4ExoRnbf/mHouoldn49q39nb1NFT3qeliO7nDa8tNHj7gJmC0B733xXQ5GgmDrYRAa5QfFFidZLoozXPlaBPiZIBddAWYLovOxjkSF0BHAWTHkuA+UF46rCWXAK98lmlcCLQKBXmRpSfhq8DLXC9+fwnEtVSSY6Wdopu9bhpSUBTf4KCAtb2cAdlhBOp2VPvRqOpRHhUxPUNH8SkwF2cJEUsDwL3oaex1jFaxfpJUkmQ5eAZ4NrkBlF+dTlGMAFUHC8xQI8uOlbyp1kC6tNLmVSFBoL6oPtPFzMX29F1jlR1SerGT2PP7x+M7YgW4RI7iTOdMvUHl6j/HkRUT2cxljJTnTAjM+ohcqPQqfxBcgy+hLZEY0dkTPBIoUE1vBhiK9tT6tEZv1zJCRIlfpCPRyqgBOYgJ56RMkLslYyVB6lpr1JcjStcCx9CpcGSs/VmbAmasr0MVejmv8l17IfefLr9JlPY06HaGlu8iT7MoiyHd+l1Ejp+zlv/bJnf6Frd4CT4JewHkx9iVIRvwHkuC5SZEc0LKAKhECcSmjcwwbvToPOym5g4cT+g8PDjBDdaFW1aO9rQXq2SyYCdlKkbjwOzr9YPrhi73tvc7WNkcJdbZ33n//rUaLg/C401Fhi04e+d0agr4JuZ+uPa7/BCcDHuibnDSBVT83y2CRg104iwPVWv+sV7/PlVKeAerVMC52NyAP+4HYXjBnY9tGG5kbYhTBGS3YycYQ0t58ym65U3afhtbBPGdNnm0F0V08KMhQSTOWrtfqI9jB4fIMs+dDQ2/c5Grko+7JMZIUQiVDVFi9Dhjt5CQCqGarjHaskKCqjPmDXZ62PRzaQa7Zx8aAi51DjI+MouO15tGjF492d7fRbrHLmmvHsMGANmVH2Drdl0jts6OpFnWGXi8nCRBFoZkV0vc1veHvWuihiegDlshn2SHY6RbgOAjTtoH5SZW0pmwc4ggPjm7ZsyaojS4e8Ce60oPfFDGjthgYJCyD9YmkqR5Sq/rfi5xBjPzNrUPIIuaRARbOIDYh7U0rIzT96ALRlSI1wlBEeZZR5qOdyaiDZINcwNKK+ZnBZ1Kga4G1Wo6Zk+SSQkAsLkUwQCwGcMzU5z7//vd+8IONjfXJORbUWB/c6/b7OzscbF7hHlJ7TpAoyMY0IviafTjnrJutyJ8pWysUsMKPzB2yj1L9u7GhCTLKPi3IKhlHkI+NrHTlb/F21aVgojkDEut/nvqRbhoXlIFat1Nx0vIQItbiZhMXz5y7JuL4LUpfBBE9f3mbfna6kUoG8qZJRii+xbN0SXKJcE49AaV1LJMLmpIwOD+ZbSCAj0aNtXV2v2xsNsac/M8m0rUjtMtUM6d5WxvdwRmLimwL5u7w3pTTIflngwIna3iYFLbnncinbcHuAqNobQjXEEwBYha5d2uz+wGNZQNjQ2x+WFvA5oV1BhYaO7UNVOz9AdfNWj0sFAUFOqXU/IGMjoE3uOGpHMkcw+SiBEpfIDgpiNBkAN0UHIdSvGngtEzO/3t2cPTuG28ePT9gGkNd5EYtlCYHh8cYtCD0I76rBMDMfTRxEYO956yXsvyIWX6YGk4rzAqgzcQH5y3OL200x41mlZ3ACM1oOpq1dXpGar4iPk28csSePDfrMlea5AoG9FEr2ZXLfieqA+r52HfLlbpsuvecAcR1tsZz27prk5XZDi2vNz+HXae9h/Q0HLSwvXkDNnCJHjuz4RraCqy31unmahxLyqYFmikraRo10RPTH2P7yfFmNmb7OW7tAC+Nh2SYK/QwRSIt7vUYAcZJCZMhN6moAWAJUPMeTL+cQTGh0ixqWuPMt2rlJqU5nx9bSGxdqFWPukfYSbJnGlPPdmu7XmfpgD3iWJK5TxnTsiGTRw5ixp+Mx1NW2aJAyypqASZA+S4ALUgba5Z7OPkAmr/xPXu4OFfQzqHEYJ0q4SvlKr1RCoBLCTFpow/PZC8FXfosSfsUiwNiLZpi7CldOZlwBWORZIl05TfPmZx5ytBnfcpsJvJFEpIUPJMxsMohRib9f6t7tybJkiMxr/J+q3v1dWZ6gMUCCwKLFZerfVgzmfigfys96E0mmsxkehOXpIwSF5JA7C5mMDN9ne6uyqqsyrrkTd/nHudkVnX1oLGk0Uynq0/GifDw8Lh7eHh48MHL8iU8ihmXAGYgOqEfeW/A/At8Gi34KFpOjwYQmATLCso3gYx+zKF2Z3EFKlNVLQ1sdHbGEsOJcE0e2Vt4WZVX0CE1STCOcMbvD7zqfNbQJMu/zJc4YvT3s34Mj1IJnwy6BVBDUlxkowIDq3966M1v1a4CwlI1JOHXSegS0F6qKx5dAWoSEZ5vIQN5ADirxJfQAWjkKjw8N9Cl08KNR6yZdsTIHINFPx6HXpz+kZbV4CARQekdkfmOIGCCovg0pwUm4D/pZfT4+yToO0CZkzuen/YJof+E51asLBULqCqT2xhvZy1KCoCIRRR+E9vm+zaCD79KkuVHDHanxGb/YpLkzq+/+Kv/Gqt8zK9cSPnLX/7in/9XfwlzBhRjN0M5tURXZZZggmAqUArE1Mgjt7J1dn7+3Ytvj99xdyOS17dYyfi7X/+fXOIYLUQ2Rs5Yg3b0XyY4Uje6f7LSW9OL6QT7Dz43gMIRsqXOTMY3EUmE7QIoYRlwgRLAdMpeuQr1DTad5eOQI0uZNsUZHdRNRV0cBR7zaFMnGdg4wWQPovGb+cUCwTC782xmoH80PZ9wnNHd8bBOH+UT878CaSxdqNHO5adL/ixI6BERQjLUTuB4kINFF4AOf/GH7JisHaiQkSHSAzMTJMJMLrFiU0HqrArQWZv2M+tO0nDEnz2FTMV/IQM4oISMJ6IGuJ8lbB05kUJSVnrgtlTgt1QzL7WQqO5/m0BSmOHxnZ7pQaBP0Cbv4iYACydtrnNgkSQofHU8aGZkICCZ9GHJOBnJ7hDtSb0CCESEHArJWAVhmwcRIpJM2knWmeeqyV6VuutJs8uLp7RnyaS4EGVyQTXSTVTNWWPAwaNNNplMSCVilWigithZqIlOTOtcOZoFCMTZdtOd0fio0q7xVDGr3wpVAla+JV79WTtiNBWtFcQjo092ouooC/qgxeaSB4SSBGRB7RlXC8oIQVm0nHvSv8erTn/DcYfiKsTp3sdOj8y4z4UPnA9l37CNSJ7q0x4M/RuOWVob29v7w8EIx/uT7//D//VrjIDBQbIpBAZ0WZAcP3+hNqkdhTHBM6PRSmwJKv6jRNfrbf/8539OxdGoQiC84top1kMMSnQ7sorqXbkRnMmUR0p9RY358ivKRGeVrVJ3VWHwyx+Jh4MXZclSnzKnOzMI0PdXXImOahMqfSSCxs1iixMmmrpCGYervmi5V9Op51sYS1nAlMGHTNEd1KpUaV8pO4aMO4yfUUow/VNsBrjCZMToolTjPcWEubVFS0XmwbqixT0r6PD34Imxs3l4dLi3t8Pu6B7qMvv78NZxBKDHngIHfNlqQXbDzgjXCoe4hF03x21Q2pwYyjg4wb7q9JJMksrFhNQR0zjGOpR5qphxjhv9GD/Vzto7fADVRI/CZySk+VHPC056YK2Lm87ZsWATDmQMbs9+9OyLL79k8UCiSIiyKZIQYh1HZ06C7eyyyDubnE0vL1jTcHcYGoBfff0VAyxXJe7u7NCcoNxNKo8ecHRhCMe/v/eQLWK2gJAAfPkjTJXQAWIMjrol7Xii6qxsHJtPVrnvpKcCwMfm4GAdrVpkRQyQzUAkpZ2INp+6BVUem7+3Us6PeNf+taPEuvu9iayiUz9p3fi7DXb3K5Am+N2gT/+mLO4DLj0EWizMKJYqJXxoY/iVh8DofhZwjUykARO/RLUmeSqaI1Rf/DJSNerGV1RWQSApkRrQphCcaokZPyDh16f6za973x+CBEl1ZIk04t0dgDpnGej7B56gHzyR4TLag6FKqsFKFHfnVSnbyKLFFfZrM/1VseRD7hniHfF5iOSImwVe0AVSi8hpvjH/QmRtRtuYUyJG/Uok1bsUBT+icJ0FBhJKhL6d631yPg8nsnbgGLjhsJBY43LFHFEKvgAT39oRZUocznozXdwjWS+g/NwNDcwGV+jWoJ/iilgfW3//0G5DIq8STX2+Yi826OeEhoEJsPm+HdGvDCUj6UiA2+9b5/RrsNpxGzhLu/hl+VSQuZNgED6RouH+p3HJHFPLzdlPfvrlP/vVL/7N3/5tu/HgR1/+i8Xy+529XaYuJmzk9ExgaL8oUlewhEAXfpch3ZEYfo+miMrGi9cv9nb3/uqv/+p/+p//l8l0AujDB0/cXaYRBgSTerQmhEdc/x6nbhVjyTQA1Fw9amHoGilsEK5yLQHzLaYKJh1F19BMK8PwRCTcxKogpi2mLgI8ZMZEpEiYnHEFD2sGG29kEC85zkbrDIHc1nxHPO0JjAvcS7fHKUOO9DWG2xjCcGnCdA23gQrTyfEJuKR1vnV8/B6NZNnZBXhZpTBLMac5tcOsdjpX2CiBOWBdxLqFk74ErKbcaMslAxTg8GJyNhmfMSU//nwbVeZuf4gogRxZNvYJCvEYonDhYe7Nhb/xAb1+wylbZz6sfd4nkG+8M6O+jVjFjP4vFyPWeCI2Orst7lvo4Yu8NpYB4X//S4zxd39w+Apj4tAl7+OVZ5CBF3yRjIbjAporB7F5cmYukIT6HzYLlpD9INV+2AJods9WzWO0EqgC1gDmO/dAWHFFGiRhMZVUHXMiz+ljEIsKhOaPHz26mE7P4HQuzxdb77nq4fri4JobmZA8FhmSymmUnqT7FpEZ9ccHOJpaTmox0pEwsnO0QXYjyXfCBFQgIb9gCwTG9gnCwiVav/Opftd+K27zreOaLqVpdiGLgqPpg5fioxhzfQkGgqOxEC9mAZjVNT5CLSdTzKQjbE0Bn1GyxXvzx3R54t1+V9NcgQTts0M+57OXXAArm6ckGMaQtn6KtEDNdhbDXGDQbKD7QcNHc2P/6GBn6FrZ47S0DxXWEXtjG2BHSilomEi6BP8kLGz10DrYB1hcHewPD/e3TjGtO0MFZQ62dnvKOp0WgmZ5Y9TodR+NT8fz1akdmRbFo344WGMwSNKjNCyT9UPxWnQQaqLRfrPcI9fsPVL4hLADsMWBpPnq+uR00m8NqA3GugWXELTYkNm6mnCAlUNKXHGLdiKbTG5I0hZiVOOULmpsUM0C2Pa/nLXmi7cktVidrJpsdZKEgymXY5AKJgfYTmGI6XZiS6HHODEcn56QH3BQGDezS+QeYD49P2ZMhOoYXDmAfAr/7bKBToOIYnbT77L3MlYO39rqN4YzrnVvslZqN68nnQFnEppY4G13dhnhn3/7ssvNGNDE8gMdfxUaGb6oIMhmA2DKEWNO8sTYQ9mi+akspus2ANsPD1ccG26frvoNLDiPx6e0RgbJ0c6Q8/0ecqBW6eduoy3YUL1sXXAWud3jmm4kIRiMu2HNhJHU+ey81/sRAy07AAySg/42Gxock4ge1Tg/fz+bXbD4YctCQ1Lus1Jl0WvXtZkt8zM91tYUq/ouuviv1uDrjrFsdPCnaUR3K9ZjPmj4RYMgEfKO5DbQ6dzUOEiAznd2pRxjALgTKXcVVlgmAOoH+Z/boXfQGH3zsS1n9/4DgJuR1u7gatCExWc9gtXBljsdlb0sukZQjouugs0cO5y8HBA+peylIQqAISzhIzTcpQ5FWSLZXIQ3GdmSCglVjqcUZXjUV3wGRN4KtZldYgofZGAxiWfdKvzySXgQ4AA8/EqCuO/yhwmn+eRq4I0IJV64b48vGVy9TSPSidQisUwryQTMT3FHVxOgDsm4ib2KFBikxEoyKKHDe5MmBpeqTCUloEqTjBJNfAbx1D5Wcn5JVsyU8VmRVFAm0cYUjdUWmQy3VRmU3UpB2PqJSNWXmazcP/ybefxhmB8OJaE/Fsm98JUnv//EHldh+GF6Pyn0Dippini3/fW2/qN2Cl6YY0S0qN8fvzu2Ny8XXODCtVnMy93+AMkcMwo1f33N3BM8WTQ6soxcCDkd3DmIEJTRTk4vxv/63/3twd7o6ZPPtnd3x+eT/Z0RHKhoebBriCVseTujOvkyV7daSrhW3elMqTm26gxjcmHSYOcbAZc3y4YOEq2dpOXSyRtrEmYh1ULgpJ2rYZA9O4h9Sc1ugEqWzFnSZqlACYpt1ZBDdPNy/P7dsydPsNsDx8HkTYAqJUzPS/bxtU4tQ8L8hTITTncYmALZdmdSxwczJxQMN9NjXoY07ITwZ0yPoRytBM6zEsv5YIhRcPLN7bYQxpVV0wGWOVatvRGXu/lv/dgwraFbPjbWBDKMlMi+fvmUkPjIuCXEzAKaXTJCiEbZCVm/AmMiWr9BEADpgxOP9KtQB5Ulgn7CxLRMxS4QJMroR9Js6SDei7IvceRRrAXl2OpVuAWEm7JB+RvFIRgv+BhZHvyMEyM/NU+bLclngsTJ7yAgCQaaf3CYRw8e/P7b56zcLC6phy74UuqUliUMRSMdPnwGCI7wsCIzpHzbeF0MyC8SibAA4RfI8hQMt/wIippb46ugP/pbxSctiIp1k03a5SJLKFlPC8+1k1SkO8nge/34kR63vDcJXgPf5yIapfEh4RSaZcFCd4FC3A2MJgfxr5HBqyIf+2zosLh9Rx/W7GYTrm17e9TxbMDl92/fPHn8FIYbttkOxWYavDU37i0vXb27xKVyyFoe9McMjnwnWx+PHz7FVhjyBg8dza8nk5Mn208Rlvf7I4wCNRvd0WA4noyjZvLgeLScKITSaqIZlJw6/mWdO/74uIiKhoHbhpctwdqFIK/DmnGWV7W0x589ff3dS7hXJPJMrSz6ierIQDw2KnOpbdmrOcmABJdNv8ABTz/lyDSXXcA7t1YotXD4t9fHxnGP8rFDGKXFMDE+GbOxAAd8dY35Ws0BISthcGbs1PAVoy6bWq4XqAULB/UiqIdIpByZEXZOtlanbLAAgjNUqyQirCc3x+MTbCVjtHRydkGRsptBJqlUdOecCDiJ4bjmYaEbjAJ5RsBlEg2PMDJkgWgXqMGuJuXE+eN5Y8KqhNH6ZHzKaH14dKCyzxx1LyLay1ycwGZz2BczQWjlsTfHwMlVD93u6ffHmkWdLwaDIcsNTD+Dm5u8KD1K8ezsXGUkF4yYHPWiQDZXlAlJkFRFMy0tnU8rzCd/CczWX3lnYL6dFgLSRu6T3xk3o6X/7TchwH88PKBvB+eX74qO6rdGTeAHfnXgP8lxm4Q/DkWJGz9JVvrgpjLT7Y/fYs6+lIF2s4RxmI3AzJrtu/JIn4we8EbRIbwOITNAFBFKHFHYYSMsAkSUzSBipF9iD7gNyBJ2z0/kIXNSRb0HKmgn3JuA030bqGQcgMS3GQp8eJYQbsn7XC9XJHhlRuMdPpSAOS60R9yUNNfJ6siPdMl6+M+nfuPI9HBo4ScCMrSGQ2pUzYImWPxNGmepwKQlqqT4J2AA1/jSYS2gS/eS+IWmqnet46TL7AplpWbuIs27YHe/C2l3vT88fX8XguE9VthlDRqZ/ZjNnLu7DeAqhXMX68aKdsX5hzvB4mFAdSX9X+pJEmpqa0c2tIoKO1JmyeqhKpirkZwNBu0vnz396vf/cbE8/Tf//l8NuKVrwV1gD7wBd4t7djmMu8MchxpOmMJgvmd/mWGfanTDF71uJ8/lFrfncroL7u4ff/vb0/Hkpz/504MHR48espWseRDF9M5TNHHgbV281HxdLjvDs3Z/0UErWOrY60cIxBVkHeSLTM7spMMJxZRnqmBBcoQPeWF+4Lwdcy2enAxkax4zGrCS0MMAAX3M3OFmkmcKm1AQjiXNJosNjhX2sFbBTcCyMbGnEZ3iwdHR82+/xZ6fpy6bHFRAGZft+772hbYQ7cPbH5pA6/UieDMKAaJZdViW8hDmi1WRq4fO8bLxjln/erYcnwxJ+OlnfzbliOoMg+KcakDdBcIi0/aCW+2IoPBKyWj2qo1qzWq88xaBMKV/+UU5OEKRaSWRuBJGn+iDtxMlxsazmRzexIGofOI3MXCWgIDmMcFM3rjTdD1styJs7IKg3t0+jb2i0ARTmk62XUmxPshRhkoiDEbKgyIeFYikZg8s2/b7yI+NraRNGhZ50g8uMmgE2AlqEV7q9cvvaBkcX/FEwZK7p463926arT5tz1arSIkYRgmEBa3u8LDk04+fqFy8zXlznL8RN6ABSBz+JE2iSbAosfys32ICUf0dDuOGI0pDFk8mmuZDdgyjvboEpWmxHkjKAYe2OiKfuP/Qswn+UVgpMVt38UUht9+zYhvtjDDUTX+EKjpia9HGAPzFuTdzwzRGtSy2d0YsgE8QJjT7k4tvMPry4OFqiAY/bKSmQpGbN0+Px/TO9vbA1bNZp95hkelJtFWyrmXMn/z8y1fvvt06R8vmGgOXcIisB4b9IbwwomQOtLRbV6NBj77M9lsUuy28qr7IRVQRuYpuVoWU9sMnCRvFSqGDOGKQU8pcTRR6D6Rwppdrp1+8eIG6PLbqGQC4AZwWT36RBKA8g1ZMc8RhWU4vzLgNgcPCYR7UMygsPGHQR9uIAFqcb2rC1fYaDx4evXnzDsnA6WSGfZ5QLmKJQOGhqMZA5RhJ6iyQkalTNFBOWTO08I+TUF2uDAu7avDHXMkCkYppWN+6sUoLBwkLMNdU3Q4oYNZb2N51mbJYYnKHUbLZfLW7u711s092uxzKZusg5Dt0DJKk4zqc898h2kGDHYKQ5NC/MIbGjW+tJbe/d67aW91+FzsNLGbQ3W9iHAnbvp7j0AhbFCTDMjumymIYBxqzKRa6WAxcoQTWXD7l+EKrPd7ZfcgxYewxYEqh2x412+zrsiOB1VEEBNfULDWwu7PNepJTydlsIatUZN2MOy/19DNe5c2xEmX84Vlaf/wQu/YElChQyFCZcWukdxxE+QPPnfh1GlXM5IoqqLB5fwdjQgJRRbkT/gc/LZicUf4g6F2AW5zMZvoVPlAH51OFRUZiNyCrg6ZSBZXyJYm6pgK6pJluq8FqyzlQp/A5YZELKxRAfEOvhHBOEZQ+HYBr3BGxSiDHZ9HJ6YEvOLFys6+Qt57c+em+jGQi5A5/WGjNeUuCfIIu6a8+dZSP9EqQElyRVoL40SdbbMYyq1FUgTmCY4Bfx0hXVSSFhPAs6d7+2QwxsUJC/sTb0ifN/Cng4ojpMb4LRVSrdcNfiZeB6/eaqISxwZRhdQ1Uu0ACmAOdadWU1eEfOID5T3vWCCLRT0JWx0lyPxrnIxjr6B+NGAF/APkPR94I/Uhy6c3bphWUWuW3gOGiEcn9zX/z33713TfffP2cKe2Lz7744k9+NH5/NhxuM7VwCvf65oITt8x33Ht1dvaOO4BBBh+vlImmIZdJKEOopvK//e755XT+5ZefvXj1AmVR/nZHO433bzHxhpTLFgcosl/eTLVM9PKmyJE42us+QMxYMu6otGJGUKWCULuB6ScFjHOGIBI+ArJVJedB5g/TiUIO5828FAwImfFstXAp8pZ8QyOTGklygplkbHqwVCGOwk1cEmLaZSaDkSUaNvHQjNXeKPoGmAXUEJBcGesmNHSVCzs7skYCJfmwKChmfBAZsqwCFamhzMpRRXiB3d09dsZfv3rJfI45xu3Rbg91JonYaEF82h9LxUaYckz+izi7qoG3YxXw8E5sNitxlcrR4V5NpgS5wQfXHrew3foomJNKQixE3lJkkF/mmXCF98jrXBkJzRkA2Fj1eZTrR2+HvcJhv0csioKvFz6Ttyi7NlWEjIeq5EiAhk1YJCSXHPVWZZgSIEfEAKXNRxqMKAnUcOSXo+C//NVfwKr89je/4VyKhdBYYjEGPa4oWTBYxhk13AVNevlhhkCfHr4t+SrXNCGcUhtFkdDFWdFZx9zAUft96EhqLFL+ZGyxvX51ifzcxogGPHbcLSY5FBGaVZxVJjYJ/RD3P8knC+EO4vSEQphR/lPNlISbAFyBhxUv7dlLIp2HakWQTMe8QRPo4vzi+nSxtfPmzZtHDx7C+aPg10BOvFqdHh/vHz3ghMZgNFRUnPdw2QxUIEHJjk56cHg0GG6fn2PBCUZTHRg6Idc+wBhi2pVdNiBZ/yNHQFMfCnMsiupwnOHJwtVl84jfcPtSJYzitQmHvICGpCsGFfqIi3moigGk8fTZs5M3b+GDWe1wLwr7gYqvXU8iIID5J18QrOzf5tLAAM4lYxdKiRxaxiDtaHd0PkGCvbi6ufrdV79jzYCAnYRIhV5kr2F9g+qLajwwujNk9sjlcbKrhgDCq0XYNmM/iOGala67aCSljSR6NqikGm6bW9ybnkqiPMmIdoF4orfAkMOtm71YWJ5dnC+uGv0uQ+45uxyza00xUPSuMjwEjHTedWgMduzYaovZJYl1KxlabgLs5opKwQyy3P7yBsQX56w0sBdER2YZZ3Ww10eDVozC2k5L/uTU9QmV6eXanEBoM04uBqN+m0sgmhSL6XIwgI7Abi5VxEiwu7/Lyh482eh5U5PmZfO59b2u6QC8A14aggTajxL4VvxNxJW7BthEXgXe95sRqmjV732QH/ol9CemtJG9Oi+fGJV06thGqaPlUF8IK2VUB64LH6/0FdF6aC3Dk8N11tlGDtfw1A2NyRHVPpOYsm74ynj5aRRBgOGPhBIHbz83H1Pk21nBMWoz6K57HXXtuguzUTj2qPUn1kz57CBfr4kwYayJBBg6T5G2gZGzLE40liyQKkjQKgv46Q3JovHtS3eB8HdjYgJJaIqvQgtKYtbAGWXjTTy+8okVz6pe5cRMlxSVwgRPaEHFeMkegqsoaK4oCwIrZPxmMpa19JbySIll5KgC3dCsAtQUAU74ApKY8qN246h9Kmf9W/Tz6u/KoaYalIXm2Ya0PogNMivAT/itCfgE2AS5leJGrFt7Een/g8izjj7M48f8N5LSGbgt6mhReETDirMK3IxohboRhHwHTg02/HC3//VS29XPv/sGvfVnX/wcxrffGQ4HW4vZQ8f+1QK5Ppvv79++O78YE52ey+SiSUDTAj38nrzRyRhl7ute89F4fP4ffv1r5EP/3b/8l4PBoLHCPiYzOGweaTKaK5aSQHfM0QTgaC/zS4vZ7h/+/h9+2f1zTIxDHxMwSYHbFuitMq0rLt/Ny3owN8lcpTysybnhUPiHFBGWanYKJ5oSNXCwmxD8YgMTIviTPVYesHKc040IGtFDAMvsxvSnVFI2H8RnNzePMVHIAgR0zeYE3Shl95SeAkEw4GQWRHiGjBIk6Ctw2w0zH+b8IIw9k9W7d2+Yy3d2dw/2dxHSIRAjRYdHayqqKrqDHSKGsMwGgTwBwy9+UZ8mtxkeQIYC6PydMXTbHckoeVFfyhBKQRjLJNIliug3n4Arvh8kI63RooglIGcJ/A3+n4UTyyeWRxSNrDw6A3BF3NZMMGU13zdO95j0WSrGFUZc7mrqrO76gxH00PzC5L2b/ktk/w4QJhKlYnJRVJYUkcBPHiyv8BcydlR++qc/ubi5/uof/iMHy4mLtPj1q7fYqgKO9VrEASO/cbYEUS5AxCwhIjHYqs3CNFHTNlUDSnr60WgDxk4W0SKyoDr0Id7Gw2f6EFQ/6SNassIKPFS6uS9KBpQ+htmdFWsATF8ZAzp5ka8a+YcIq/QzhQzHXTvS/6PvTdrWQCZL9nlbLPSkrR7WlubYgllR79era0qMhXOj3Zhfwd9jGBTT9u/mN1e7mAHqcR6Gfup1YCi4NLg8uNW8GPeuLqYX189/9tOfdbaRpGt2y02/uN2PoYHRBCP2T54++O7bF7DY8NgcoOckwOtX3w/Uam9zNznCgcXVnPUjTDgmKBktZKU3yidah3Vrr1rsWH30X+qb0mWxsdyRM+3KtipvV+LPwtQM0qkxARD575yfTl49/6bn9lTncsFtxz3FFW34co5As583b1yrUbNYwkl7WXi7M8DILRuLNBC0f+B7v/9+PD7TUgLDH5tUJE1+TQdmGHFBo0eiKMN0FZ9zJJpbCDDQvINNVPR8MJqkFpCcN9sgmGneNmLrFHrnbHCtGtyNKNe8Yt2IQR4LGRtcFAYFKIYlhlN7LCphpyll9ja1snDDyu1qNWuhpsj9yqzG6YQsVEDMxoVtmcGdVZr9hTqnRzuEMnizImWVAndFjXCymYI6P7vY29tXpoCaRLs9Ph6zArFb21e8J44YtBuEO+5waNKtwwbpfDlerq52h/toilFiKFb2O6P5daODMeqtreGod34+c6FJDyOluOMMV900QX/3ofvoG691WB0jg/MTuA3/WtawjnXHdSe1zeh3IH/gs076YzAAmNAfkdgGT1UhJTalriG88nzIjdziHxJwDR6p3yGBwloDJFq+7wJVCRYA5zaf+jNiOITg5RCqo6DVq1hb+jzDiWWP9REBujPGsRcngvCM8Sg6dgBDEa1U7BFH5ATi4/x7D73pV9+CFQ0kY4o9niBBLKQaCwAQFeybkJGNOqSKDDkxK5QYAQSe/K2A+NVDqsMr8xvIC2iVkL8VWLqrkIIjCuh2ThN1lFMBikTKK7AljYnYrBGF/DKGRsfn08HGnERqWR9JaoXK4nHgBEhXwJV3BbL5CcZCZIHejLOJedNdI/o0xw9GTQI/DdH/D6GyOKMEwhkV52eV7wjKKmDSYJ6jhvEbjXZhFBtLz3FentNnmv3+NpWKPBK2Dt4MVoRrOPsjVIZ6b95snbCDz8jtzGnLY65Bmh68sMKoi0vuBb3ARHVv1D/YOxjujF6/eYsdC6iAn6EZqVm7vCamgiWYLejTHLiirJ2dndevX5+enT4aPmKCRajP5MGMFQ0Nmf38u29fXiIVxMYeXC1zo9JHdgy2WSmwwGC+sQ07hUVWzXfF4JmIXCaz4eTsdGe4zUQEBfAAKBYZRUWe1fb2EE0DZjs6K0cC0PafXoyXW5z54+4bbVxj3JO0lPzxL4YpFgyUFZMmmktwBogvXeOSu1Zr0Bsi9mMoAWZ8Nobg7aHTG/K4ERaygy8na9GBXE9km6trC0d0GPzJRXxVYdFbw6e004DBXeGIurewQ+1KQg0SSaISNEaHfBcs+VNwbPjVPuGAqEIHkz2lGpyKKjjwJpQnrQK+BFMlJg8BLpwsAQ+dUAXNLmchkG1SanjS8GC/fGY3MHZgzror2V3nV4LNQmREMtLtAqP2hp9pr5C/coLdW0i5lGDJXRO0FMhAoYrW6mBlEfiOvPBLQYiLX/3NHB4GQn+MxFYQVGVdmOMEM4oLreq5hbPyzN9MqgKtUytJAmNVwOxQLt2G1uJhFClP+xepmrY0AARoEF9Q3E4lvjIpnQmz/q09Poi1jlPi3YawFKwVSaBGKU9E7zBosrwse+l0DTjRG+y4WN+IBbg+YzCkMkbb/bPTs/kcg9FK09F9t8PF1Igeebu3S51QhuScXBFEpyY6AwqNodPq7+0+QOCtmN2GhZTdQzVH+4csJBQkwzt3e/v7h6vJKYZ1yEOcKxF7+ZcTbpZanlciJ4Qrd3bxD6EcfGXpDmMsvqhgW4FVb8kz7jGqkD/qgtO5bDZenI8dj66uEVVQW9jEORj0jsdj1jNk+Xp+iYDg+zfv4clPzy7PJuez1Uz22RKSRQ6uVluohwf7yFgYXTGEw3qY87uovnC2gS0NdN/Z8rQfwXw3vWeNa5ebrWmrzUWH+zSEZeMEZLEwYAiCVSdPXFZAZ2K/qHnB+MgZ7CmLBBRutm5uYO7ZKSXLALjSwVoQPxREeMjREwRA5JfMMhpSEFGEqiWxHOVEAhmizBzo6Kic8kc1EjE9xfL8u+cPUfWkz2CN14GdngzZjsRkmUbtiMkozezSoqxnmOpi/4RUhiMMB7G9wy3RnJHgtj1GBpUe2ZahfLjCezLRBBOSmmjBNuZspqUX6VG11uJ1u9Xe/QIoERCwduiqUBXvGlsJW0MnCsNrmLup3Pv9Megko4Tav/9IvAlfykV5RIWB6qOCP+kBLMnIn+wDt2MGpgJ0H4kGVTB1qvafpIFWID5e/AFbYQp/oGhsOIWvn4r4yi/iRj6rkMAYH4E88CeuKgd0u0iqCq+RV+N88Qjc68DKFSO/H4RrqDhzyDcSdLqBjtovk2C9VVWFWYngKgN8b8DrjCfgArDySlTgJ6Zu/tfhEZZR25wlcDROAAc1U4pYES39A0VGLwnGj0Mfw27MKczKFn7AR2DnVUEKHsuXvwytCcKnPNYggQETzrrsK3yGhrXdcBhTnIkwgnzlZ6LNCHXQH+8op9T/+IjG+ITU1/s8tgTiNGItnjE/zFuh48O1eAmIn1vr8vD5UPaf8B/zrwmvHFmaUBcewdlgS4qvOB2/opbVjYGpZXjdGp+faGo5JgJmN9qDd8hjjF/57QlTdmeL6QoDzQfo/jx6RH13JpOxZ2KZvxEuUalqqzKX2LDgOGerdwj6F5edzuERFt/Oz6YPH+z/7Gd/RuUzebJkAAxO2SYVjY/W60layh+BVQ8W+fzw5pDpBNqAYUrgl4mKicQ7yFrwBF32yN0/RNu15733LF0QejFtuoDlv9kz62jnMo9iRBt2gfkL7oPJCZ0BGKxqTkw76yTQ4Dja4cMH59MLT+p12ufjFjcMYHcEG6Red+OZAec25G3YrmGXHuLgSzzXaE9D+2HBUqm9PNpqN+fNV2jFYN7u9PyESa6xbE5Oz44OD/YeHmAaaIXwElYnJkKIJN/+y2HF73yiDqsK3fC0NOLTN/+rui6flhX/fWJKsPIp74xjKqblt13RCvDjnif9N98ARUxTBElGdR1H5XFxkqVtOwAn8s7h9k5wrofM963OxO0ByIAWtJ+oURjKGAqoCLkiDw1g6ZwGBLkO3JEQ7TXGNF5RxCV9IuZoZAaDlqTHbYQmSsM//tMf/f7rC8LOb77ldrZXr77/4tln8BYmz49xiFWKOxPK/JupyKRvy4Z0aE6RJSkqgcSMWIDEHBPQJTgiJmRx+pP4NjyMnzgiiJSSy1eBih0v2FHLpdFhHaAKuLSWVMyyEho/E21Fywb6cEJ95YUjYSuP8pv+kemKnnuQ0pJsJ2JgPWlU+UEKv7G1sztioU6H4mYNBxTssWKGdcmafDB9Px2fTc8m0x5MMfZ0PBo+Qy0Eru7y5lXzehtW8nd///WP/+QZ9oJMFcxuWoUCid0UszNb28Mu6h/oibAWR34ML4oGy/bQy2doTSPYRm6UY9kEl8zN9/KhGC6z4iIbNHsKKjLZPgN7Nidixhr+ApOYTcwTcBM5h45mXFiLeppR4IdbjZF8bxtxf5MLgLdu5mH4f0YDlUvnarMLFXDQ8en0+tz4tX2w/fK71y+fv1z+futmemoVrVgA22zZNOAEBPb1KWaMZmLmH8XKzz77rAsj7pCE/c0BjuEQO2MN1iIMITEUY2QTQ6JIPfpcrh2DGvr33IAGF87agM5E49iaX21zfhopP4a1OFxEmbTd0F20ulgcxrZy5/xswsHi88nF9PKcswYoZg1Ho/HpKWPpORfnvR+zo5KcgFeq2CdZkLMVqqqPHVWZTYwjsVyPRb6mYOnvnc5yb29venGBIVTGZWy/0k5osrnGdrnAqo+dnAUbJV4/wqLcRYpmlW80YKrFnza3vHC0ujcayv1vLUDCIoElyZyDwxwTb3WPDh5TJrYOiIsqLK21tOBP/LHV0hTszGCxm4ssW0npzYLEUzs2vhK6hIjhh54E24D6wKPE3gC5D99tQu6DKONV6DvImdB/0Hon3kbf34x3D/9QEvmEtAqiu5DxneVTko2RwhEjSMloMYTk4GGusyviEEj9/nAkqMFVzWQ+TMLBxX/xiGKNPaD5jHQN4imAuqLK198BUH36wX/KLcqwnE2N+Ik1MuFGHX71k7EjXiG0BEWAEQmLGAWmjlnRVTAYHCPUJo3GjwgCZXtdx1+7CEmw8FrHWEPgynTCK7qPiSXaEhQAJlJD4giSbkVeI63qgBhJQcwOEX1NQ40Mf92MwfEjms0wY0RXFC4dgmwC5XftFWnU06+B+IAy066B/2jHJlUFa+JYB9zCWXtHcVYUpG8d9p9K1K0UNz5IIHO94feBc514VbBruqLlAECIxnOYHuDpaU+9/uDRw8c7u/vMhGzaw8MzmgscrBzwmJLg9h8UUa+uud/2is1sJWfM2tEcqETYQUfqcKEL+4//+I8vX73a2dn7xa9+ziYBSq3MagzrHhNlvYHaDBFlBd1GIB0OEyNmg1cgQZVHYa5XCyRn2Txg0B89fnQ2PgUA0iEP2THrjfHJOVMVkwv1ENRAh5mV8GhWOHCSEfE0V2fnp8KGEJA5S0ZZCNWXkSnK2XB/z/V0ucT83/z6+mLYVzLNZIaESyVc/sd+BRffKnJGB1Y9IlWcZ+1rNk0QkSnhXq76qEq05Uhcby9WF5Pp7y9/tz3cXrZmnF8EIKmSLAm2ooJUyZXY8lU5gkjDgA+IjVcFY3A8eCjqBDHLocRkGk7mMNlOhcrzItkomHXKFYaN3xp7TWCgDBpDCp6txGplgp9zhQ83oLZuuPdAJEhwTRmJjHLGOZbRe9QWfC7cBlVImaIrBX+AdRiWBik6tCmVfEZs0CQRwaTE18YwACE+5IHjo9hv5GThKQdD4CqQL2pMVkZKxRLac8JJV50rXfFfX5/4FrByy1VaS4RkWpZpCSTLOrMwIkqFDP/8rhwlVPBSufqANVZolInXAKPqlkwUIGTIRRH1yLqJ9Pm2Cqy3rLXA9EMvEgjyzIykCys5ovFJAspH9RMh65cJZrkVaAoSgffkBgU5LriAUeOwKeZcBsjFOeKO+BdOrtUaYyWfkzADLHcO2lwwcjm9QPyMBJlD+2ajsTXaHiJCoKClJb3MpfnlrM3nX365f4gW0He9AV2PQUM1PAzZeDC/02Fdr+B6vhxiAIB+N8P4LNmjfZMLuEnzEuRGni2vKMrsDgQtt7jSawDvPhygwYedHLbwoJCaJgKCbwY2nJzLOD85RRTRnK04ULuzN3z/9pRBY4aazWrr8ZMHv3/+zeVsfnE65qwQlivZ8Oz1t1FT6nb2zk9PV42ro8PdR4cP2SFt9ZoYxcfEPu0+BhlpRGjBKEK+OFXBSs8UsaDP6o+7dZW9K+KnU8Cds0pGBkFnIYPE9NxUlBWNJ4TuDK2eneBYBTSjUObYyJYDKy76w2C4Wh0iiWC05ApeTghwf8v55PR3v/v6zcvnnz/7fHe4g2ylP+LmNQ9G0D0Zh9kuYLS0a0ebxxFrJ0tSLSYuYp8tuJfA0nag2Tp+956oQTkEp/Kh+7pssLBBxDBELlgscEs0hXy4vwtnf7W8OTg88O6QJYsr64xNV85agHBv/+nx8f/b6zpouFJSyCRAabb5gw+PBbn5G54bL9tvfJKVCjbhq7aRwKXFCHPnqaPX/gUPVUDiG8TUcWtHlWQ1TFTfgaqgIQ8VfO1TJ3WPw6aptwlXEfhNp55VVgSqAHR/8nMrEh8ffSKlLIZMyeTjMUvxUUUXtCqrKkxIgcBQZcryJG6+A1PCiIa2x/hg5HyXYGNXGY1A/AWPKAUmPtIrfDLVKjB+M2pWFB6JIUxBGxIevNNB6GaNJh7aMJ5ijjE9Rh0I1atqepFGgQEsgyKK0aIgI+FAUicSAJG0uPPJYTM9E6GlYxhxq3IusOHXfhNhwAbt/trponcQJfMYIIInAeUz4tduHHgkgFmOj6y+Cs/6S58NbIlEMusEKnfQHujwWT/FOzzCbbnjiPgbzmg0QIV/RtoMXSO8xxVx1p1Q9JtPFpg+7DCYdCTvmYqMWDXYjTgZUDxqdNEK0nNN2z3r8g1Ed5yJqkZYhyYJfEbCtiNh/AjYKkJYxrV3RSNA5vUPf//bly9PkL6gafrw8eM///O/ZLSFAYm9IYAOxOCsKVMCFvZyg8favrliYxe5bZykE8BqcRue4RpA4JD0d9qTyQV6Mb/+v3+DNP1of+/qcsqOOgzfw0ePFblpLY7JnmO+7FMzi2t/B+UctIxQOkJMZKjrBPo7e87a4ORAG4zdvL2YTqbAc5SQ9QCqxu5WxzwUBDN10RvIpi3cAcOHMoE0Thpgl3OyzTwU5vaY3HHAtrB6wNAGKukcM4Bb7Y5Af3J6xiW1aDxzJhpNpBCxIaGieITfIneoAoMaRtPehzWbzun23uBsgp7Q1pn2y1tXN2pFM9mNT05+8ctfQAF7BRwPjiuVYXdlOZioYddjYINMu5ZV5BOFGkNN9HdrIPyFwJkv3zl+Ri1kfkP5x4ojRZdpPPMDsWPsNfCXVmDxZN1VmCNY+IJfZz4wWBkXEpmXcTM1o91BVUqAatxNZvmrmwtC5GOaJ8A1lkeyCNgLgnWiYNm0sREljzMfjY6MCUs1hEpocWjPLESikFkRtniAz6r9jvxCiWQbRLllaYGcUybzvd3tZeMYbunmyquO0CijdlDQsrBcADkiGy+wmhAfmV7060CevkBYMsQRVjApwiuj+pFOfY2SvyLHnThx+uBl5ASKd1Btw7Z1B1LiYepFL6ChH2gku9o4DZoDS5RG3j8aNwkkWlPgmR/59gRF/WS6ErR+khDf4X8rVkJKgOH5QIZfEul/PREDd9uX8PFN9Nc5tUkboJxUcrGUuFKKrt++mZ3Rmy8vD56/uNx65HWytAKVeWAPQ8kem/Ovbt4OBns7+9sL7AR4QwjVigB4dXHx/uTdCVULO8jCm3pDNwR+WWu9i8v5git4PTs7bPbYWdgZDVYXqyt0BS0oG0R0fvbo+HaT0/EMNpPtBbNsu51fdL588uOf/fQJJ3PYohhjmeji8tXrl29evLuecRdhSNlRMsJaMScaFFs0dwY7NzNkJdgyYhGLkYCrr9GAefmWZUi/2zvcPTh5v2xt7cwWp41l7+HhzsF2f3//4QjmejgYjyd0Q+TpqyWng2iKC/TdyAzDG6diGIEuL9GmYo1DCaHoxLan6lWq7y9hoC/pZVpaCqaa8XO2hEL2UDMrCBy6XGlCzUB1r7/TpRa2KORrrhng/MjlBb2SP5YHLIrpklv9zsOHnIzZH7N84xj38xevl/NvOfd1cMRzyCYwK1AHSmz7OqSx7cn+HVISuimqXO56Ib63gS8X7ACkIAaVP3ofA6k7fk0MDHEEgnPSHDy45uABrYcFCdu7HJtgaYem0HC4y1loDEazjYqi//ZwH3tCqC4xaoWW0cXr11+124PnL1/++CfPbHj2TdqgA1y0QL/Kc/e78q9+V9y2xIO9IH+yW4bTVoKD+DabEiLM7TQC1vzmLT25Yw+4kD6JMd2+N+lJoILBhARIPHHG0s8goIpWRU5O47Z9wjqM85mQE6MeQi8MHlgqgVpawp1pGaOKFUn5CpA1+bV/OBI6ezkeH0Qu0HdxxIgaqCXL8vMfhBX4Ck/Gq/FG0ZUJzxh1cMBn9YBBPPhUyMKnIE5UEZIQmVJBJBHJp1lrG/HXH2Z1xZ0G4otYEBF+gVmfUAEqYXXSFa7IQQVKaIUnEhN1DO8FddZO1ZYLcJ1w1GL1lXXqV4kbrsBevPipPyMwEqtdxVH/VAQTK6vFd7SbdYjA4nRWAhuvzEF4R6wMTaiNN6A1lnBEXGdaiYp0BKCVbACCVRSRVrgjA1T6La8SsvmTSfkOnPkbAMWvAINZehM8w/2+79mAuS8YvwIRP77yO9+3aN5IgtCNrzpSpJAxw/mf4xXofFV47/5WidjLkDhZNt7++Nv/5zfMhtjlR/+G+1igF9G7LLxVJzorkVGXOQBPOoN6PQeLFUrezdPxe9VJhbVas3YdCWSQnTMQ8CJJwvz0q++//5u/+ZvV9SX3Bx+/HcPxzxbLg4MDGAHmPOYUJFWwwiAhCJ4epg33g8dHw+FI5psrIZle5N48mYBIiU98r5FA3ni9LpMGYsjIVDQwhx7/mPX5H4sXPktemKKYY3dGI5SYYDfg5JmCyIKSe+/OaU8vmOA7auW22qOd/mw1PT+7RpwPEwJDYN6Yz5B7mZ5/jB9ca8Ck6D731VROqNW+WVBE7PP3Z8tLBF9wP1xo+vtvfv/g6AH28s5OzmARUK5isg480YSsmixLS566yDq43YbutilzGU/UrLHMuXGYqq3riE5g/Fou0Oy7QOZPBCYeoweOxBNflU/6g1V4lbOpEE8KwvHB08PAygK2ZhyZ4IT4iqskTBWmgFZBmyPM1D0ribIX150Or16/QQdAwIpOiZPYmqBw8MI/w2wG1WN5SQQlB7dBSlQMbQZFMtQR4DwIu7jgwumbXAAALKiYIpkKjWXAE3UZBWXyhYTEH+FQFdGJG8BiC5e/4fSzPFUCt/zzo8QDUDIiWbzgpmP7QypYYJIfVshkykxQctFng/iSgCVy+7mV1O0gv5Kiqt7JSiLYyGcVR0T8N9zSKsN2ABpk6WHSqtNlVRxtjEGDA66o+sgsup+z3MJkZ7+NVbDLXr/NNgDbPCiKUVtkg5YCEnhFkCBIfvnyRe+E7rbkaOnVBbtpsMhdujk3dmNc8nTM+k27rlwQRgHRxKZXl/32kPRIji0FdM9RFUcVkYEiOrQ2McGsspm5iEzkOODBHOgnH/O//Mt/8Sdf/vjhI/hUtE04rrCLFZ3+YDA9nTewk0PbUVENZpilKWbsr60ETmUoQcewbJcDr5eYKmM1qu7TajDoc2JoNOru7Qz2P3v04NGDxoKFRxgHmM3GY6QDUIKonlaJToxbpjROBBpovMAHY9oAHaE5mkYzxORXFAWmFLiARPVFbZCxIGCrlcFSH4wLeUp5NeV+4a0Fm5KsgJrHZ6xtYMo9vcsopKISBlfVy1v1uzvstNi+WqzW1LHZmrOJsrW9vz1qjG6upgezPTYE3rx9N+Vww/z66PCQXnvFjeww+toKdVx1DcDlyBQ/Szj2GqihXpfzE7DsjHssC8DKCMCkcKWSp6XOSI5SH40E0ilzssokQ1Q0mDhCzYjB8gcyQU5JjM+OhzesXNg58RKYl8+/ev/9+929w05vgKSA25LpAqW9Wrc+9Bed5SO8ssXipPZtp7eeEBnYqK0KO/IGdADq7xONO4aV+KxemVD1ded3M7Xo07fDTXbD59ZnHaAjadBVe2/EqzP7YSAFwZ8ZC/hMgRKL3l6jSJAKeYJ+LK2MVBVwjWLtuE1EphQDpBgdIqKnxS8NysoyQbyTyoguuRWegFx/ZvQIjegBlmhFkQEAxUeVleq3VGV+Cnw7H0FEFVfE4r2vyUSA3ShSycGw+ihpROzMW4ECLJM0ebCC3HrVQU8IZIFDr/JkU06oOqm6trK1AlM/Ys2P+An8daBp4V3Vvk7pCRoFD49I2q8kMinJN550tsxSpENUZ3Kw6F3ntUpQfIk1fDKPomLIi7fuAhJtQHc+INOR0cMRyCLDhkVogua79kgUMkxAOcQEjoI4+KhAa6ziuYmmdkes+ErMUXQQ2fTidOT9+ppEwt2LySDADEuodHC2Hd/ZF3qmzCDW/YJtPvmd8es3ADWqsPVU7qjLEwjqq5UEE9NGOQW6NU7AkrrAGDgBhtMAf7Boqz/71T//+puXGIze3ul98cWPVUOg8TDTRM0z7tMUYOPh6ZFfqQSznHPBzd7e0TWnK5cnsAFMkyBErA1RzlE+MHxMl5xiVM+G0js9Of53//Z/3x0O9nYPh9vo0/bevT0ZbuNCfIiyDXIvDqtxLIyqRG3fiY5SPz+/YNrw3hlU/DmSoHSx0evRH2Ft1RFCVseBXWYMoJlrnCRl6WO8ADSpIqsNxfNI7qxI9XjmF9Pzo/19uqP7BNzWyXTfGkswnxokn3vDJxKsRuP7N+P/7X/91/1O86//6q9b7QGGPWBd6MgsOZj4IQSdDddTTGbo/WDNb4poEH4Ws4VM1RwEgFIf1jCcbfv+9dsHDx5xKG60uwu7gdoA6cj4QR5ltjiw4lvvosPyKhWWjSsKNqr2VuXbFOIJRSY/sv4oEsgiCyojgcqeosyYH5FQKBkt25Il43egxlUhTY8MCHirABRBEiXN4spTgzCr/oXOEYLMy6tzEpTZCtZh0RqLHeaPwlghPPY2NCSO7BZg5aHDWutmiX4CPByxaJoONo4cPJGUxRH0hmw7Eg901i9MJG5aZ7zVJeNYSGdvf/f49KSxOrycnvcH18cnY9ZvLFKScmCjbMFvEZtMFIiZzjI3Yf/bmHD5nzixBoYwu4ZLGoFipLUgypPlKHkVWhyZCKCmXPwjRoRZX/BL0XWgkB4U5mtNVlE5m0NBAXIoHcZvn1TI+d14vCv63icSM6R2JElBWu4YBCklckDpYU4LpJTzkV8UN72RYznzGTa+tlb708npauTNoNzOQZCsXGd0cnq8vG51erPTk692+5/B314vURbvY8GSjuGSLJCfT7BhQ5dpNnc73Jl940pAFUEk5V0OEHSRGwwQHGMjh07HGomDrePF+OjgCB08i4SzNBwkZa+g3eEqW0hKXS+U8sI+PkQ5nNnT6WTs0bVXnz96/Ku/eDwYLrxjGA4aa5gz7Jkux8fvdnf6HPo/P+daXE1YIqlHxEAjQ3VtsIMBUtVXsMGPGZ6rORsRKPt1B53u0fb+oN8d9b8kDZhgxPccgXI3zGUtwgUHLM5BsC5iUGHQYrMCc2Qo5ZM0IgjmCc7QukHhVhqq8R1E4pw54lY7/p9PzjlwpalPjBIvO+ywkUkHSg4cLa5sFZwnQsiOBSEbNkNXqNWx8djFBNDNGUuFk+hOhrrIdNeOsek53Hhjh5t4t0dHjx8fPXmE4daz88n83dtel0XDzmi4wypIPSTGLnY92PikWy6PuDDY9g8iymQ4Ym+UemSZd/7uFG0j8rq4xo4ti4dTmqvVqeafTRdU1A55RJa+tXy4nG0fvz0b/WiXa90uL69Oxidffv6MEmMT78kzLqTfury5PDs94Yo00iV6tN6q3UZnuLet41laaR2cN8Lia8O2G4aD1oyJVdxxnw9DT8CbwK2bcfHIkJzHK3dBXtETUDUGe6kflUftTo9yH3CdXsEVERICGkKn3w5SBg2BTA2A4lnJipx+IqgKJk86S46MKNboveGf5RNdO5LT874n0BJY8AcC3T4RRhqB0G+LMkENTv/0s9lIYKIT0K7IX+e5NXH9uZ+QHHGMHE/E1a9MWDoil4YGEQkfznXCGXnj3YjSjlzUsfwqNEpYPoldf78T7XKI00XqZloZuwKBRAOFqaKZqyA/PRI+AQL2DgKgKiIMsYFGV00acdbIkqokLZpFoDN2JFnhMe0orsCURCSQSVHyOYVLdCbsrJMZNzWeoL4KjShlQi4JZtQsFOEjEp66+VjTEx4RLoUBVyVgXkvMiBelCDzJJqb0yILUHf8jDUAsbTPCO/tB4IhXxk6niRXPQkqhtYCLRmfUTsEU1Ed1BinGS0d2qFLUFblG549MRw4Db0TxRZDeiWxNSEk0wyuwqlLiew1b2lUQGb6QlwOiRPHfLJp8OgCxxPB2ESdAJg65VDKjNkyFbx7k9Ddbv/m7v2My4I4XTruhAIN9DzjbzJt1LVEkoxAIhAzNjN44kEwi9NrbH3G1JNMJ0xZBpBazLMitKwBhCpkqFABvbbGh/37x9smT+T/7+S9QEnn+4tV3L19gJogbPYmIwj/cFqyqqXlhkGcSYCY4n/Dw4ZE2/uXtyFKTyY9taKY7qo4ZRa6SDW8Ea8jJcJMSbdnSIkYUlbmQh7Ja9YTKJtca4IN4FQYLrgI/cGLUj0JBmwg62OpAHulyQnN2cGL9s/Pp4eEQCdU1Or/I2FgtSCnC7BarAgVazFwan4Hrh1P0Kst+b0TOWUKoGA31SA6xwHd1Bc/EIuft928eHj2khmJGlFGw7qJhRylALCno5QOJm0/0fj3MWOYsnHrEGsyqw98ljhiiLhMByEMmB9hdpCWFxFkhtwEDKJIIJ1Sq1nGDSdWEIZXBFsqci4IuMUMOs0K5UzsR2fJXnZe4LHeCk6PG28PRHg2L46HoJQ/YhaqzEtOBSQUZpmdn99vsyldFoI07ephg/OEJesxYDW5efw+/BgOz1bhBivzls2fUD0FGCEB/bRcRkbf5M74Z49dJKwEzyECTJjUBoiFl1BJHb5+kMpyi8okogS7cYEn/oCCcsdAmVYor4pOS+Q36EkukkolDiTETcZVGoKnwFvQf+UmoGvZDR8Qr+CscfEpZphxNLsYKVNZnrsJY13XdECAPyIfxpEfs7x9dvXkNkzu5vhwPz7wZEHOQdHa7s8IC+i/KNYra2dJrrc5OJyzQcXCXLrcMo63O4tDrraxlGy2DDPqEoGD/8HqulTA0ENkc8KoHdadUIYcU2h1O+jT9V5uxthlFHiBhEdhrN/7kx0g60Lq5VN9kNe91MeDDvuDFDkdxp0s6+KC/zShCIigE7u8fYP5/+2hPC5uoPKFhdriPWLo9H3FAaDTqPXv2+bC7t40CPe2YxT/0OYzQmjFJdcmgRH6n06vTyTHq93Hy32HSsQUR+wDlIg5uLhkWZJRhjRH+zy4xg8PorMifUcHxnrU1u1teSU6xY42N074U4NKFj82E3CJ/gAA+UVpSRYct3Y6GlelantF3mAaRpngwY0AFsZUBbSgxUkGsVZ4+fYJ2/uHhIR329YtXDNePHz/BLJsNEaEEi2cMdqEC5LyCDuNicjYhGRSJut2jK85+oHn27oTFUrSQKPFmg41W6pWrHTl9jKCESmCLlCXTsy++YJCcXlw9e7BDM/dE8FZvuOP+MysBLCG9e3My7O+eX3jLBKuUqyuWf3EKxnFHemwR8dgiSa1uw8UzA+1yBQ6PgImZIPz4TFwBYhuLRmN58uc0knETNVF0JD4gasQRbKT6sYvcfuKblCsMEl1hwG8TXJj8rtAIWrCXAGAcWB0d6nLIWJGCwSWxIKNCRw6CgCqQqbkKL/jXVKcHMUspWOISjX+Ukh1KfE7Z/GbRpQ/hfIogkguoOk9iITyLAgAjwlKIIWQfgR8/4CIJ0UBFYgK4zos5L1gAAaJOonJkxAhZhwopTkmMVCIlv/UsRW5OKw+p1QKIgUWT7FVAEhAPWCzGwGrOEG6BHIsrQSwYZ0/NGzLgiGGnD9iSxOwzU+u8Fj9x/MABCNIRPOhOSS+Y2fgLnyCNYgtYgqMQlwx/pHBj5HhWsyf+grkgCLx6iVHixeZ/hArxC5sTgeRi6eCFJd8qqrHEU5oOsaRWROpXVWl6915+ZCb48lndQAmCESwXWc8M/FtzbLsiA8RHpFWkiMVX+mhVybV4VZBbq2vSqqTpEcfMxzCqAHWFJQF4Hu4BkE4hK7p0xx0IaAHqrc49Q2/eIAi06Zgdw/wKnwGIa1oSQijDwJ5tJ9PBnZ6RoGGgWTWQ/QsuxtwHKNjEwmOjT5fvbE3GjSagl2j8lVqjCrQakrhrNRIIr2DlYYYEoB0SkO5McdV+UZGYnYW6lnMC1Ayo3smNLtw4z3FbRPVN7vlCGoKYH2xMCc6ksWDQ0LYJEGRHQCyJ+sbuHgYcEJK1JmOsRHPck6lIK37ECoKj/ctJM2laPmw4IPo9vZj823//f+AJ/rfPv3541nn8YLi7h0SQhMGGeIw4HsNFQmjHobnA07W4j0YbosyGCPBg35H9c06XUqbAODzQabFXQ9+y/Jyh1P1IjSDoJq9Mh7AK9hTOIsNicA4YSzVeZqkaywQGBAm+OcQyOFbMMZrtGgNvJFbt7YPd2eXld9991+99hg2NLe5SgNtHJKmwTq0AtA+oADYRYPqZlhFcUggownMglkwMRoOb2WUwOkyg85fPv3n6+Y+OHhzdzEeXVyodpLIC9HN/sO0FXBahLuuV/3N03yngt3zFgxfUVV+2BQF9IiRc+ML7UpIHkNTYeg3DkeiAtrmZTo43IoqiTozZhKIpASXyKkKEGN2CNMQfcKOu4jCO2f0Fyx8SnU7P2UUJ/IAEbaZoVKqTbkoVYARkds3tE5hyb8l92d/kLZyWcCn3LvTwk+lF0h5QkaKSVaspAP01DQy2d5sDb4W7brSOV40JTQbJJmZPovUSEYpdnAIqhYs93lvtsVhCzYYP0xOdibBsW873oohOhLGMHSJ0+QJVNHijEykya1DJcGOxr9u9l0hxPYRG7OWeiXTOZFWNwhrXREkcZPHrWlSHqMksNtfzKQNF9Qkl6QzYiBo+4c+ZAXza79Y+xs58xFuyE4NvMy5oODghQGD7fWTdpA2lfVOPLeS+Q6qu1Tvp7VzPNV9DNFi+VguxsZ2jycmfyRWngDoLuE/UxLcuZ4vrvtfGkUOk0CQC33sFp83gAFuplf9VFy6ZPgD/2mz29w4eXt+8nXPMgEMjHlHlNC2XeCywdUlCB3v7rCYpN1fms5vell2P5QFrcXnsMjcTifQsYVrYZ4+f7u0+vZieoomnsXtWFfNL+GquLmQVOltc7Oz2GWEwu+/9AyQ8nw23DzGq2dsenLw75gKD85tziqDX48T59qiHad899GPY8yAzCy/5JrE2Z6Npcgj4MYs8X92gY4muD0XQHXD0BdOmHGnicNMM/aPr1QRBu6ugBh0WC2Q8tF7qHxP9WFy4pCdpLZ9pmmsMcWFF6AYdTLcy2s0eMVVF0t4oIyUjjGM2fDcWjS8vMHeGghT1gGUC2H1GAg5u2UMR0GOhh60aOho7C+xQvn1/zLjX7Z7t7O3sHT24nl4eTyiiJ6MBV7lPHJRZgaC+vnrNboAGoltN9k1GaAT1WltXTXSBWLaFJicrtxOSZFTAMBEqRphQHWyzhzPfOzy4RjYwh6rhaP+qiWrVgvrShttoOGIE5ZgXlf7F54//h//+fxyPUQ7cvaFZYUWsNVysrmh6bnuwq+meSel0ja2+bVVehavU4BCQKzPLb7ZnGy0PBVraOM5oqFjAjhB7HM02fEFDZ+Bm+oAXz51HLIDray8JXAnNTI0jd+wNCF/7u2DM43g0CCVte7cLu3QTmCCCibokKkyA5rfoDEpqje13/JTo/MQkZkikIkRowJOuMZOUis4qIRAqe7r1eIduDIGSRMkHHSDHQVOIgdIQUKQNH7kpeR5JRa7vCOGYAgRuSxufuEGr0X0JbRIS8JLkMBPJCxc5dFEhBt+UG0/nBZ94iHTZJ9kGuzRmH5fxdZsIcyX8EiMq5z38YnROh8ERASxEAZHo9CuJ1m4JEycP4wYSjaVqrabDCR8eLUkYJ590izBiIGIwXUYB8pCYjQW5Efd2coEBRh9u33egIE4mnXpHiC/EElm3+MFT6JbwINSCTq5HeqMcAgW8GjS5usqnYA6iklx9xA9tJF46QICpv4ssSppLQUTLisIiOdkyaCHUyTKoMxpL9Qo+QqU06O8KCVdEIsbCV4YMHVLfWXZmE/j4lF5SkA2Nu6ZCoCNYLIoiViKOCOKEdmwzmqg0QzLY1k/QEHFRQDREqQnMbCzGatjNWLolhp+gt+AyblXTBEiShAiZrSrggDLFiBg/JXYSJVKxWAr+FyflEiUTYcY1/YQquVnjIYuiN9hckLo34+rAX7/Ah1a26GNtHagLUiGdRpkkaNSD08ur9pDZaLk8b+w82sVSB3obPIz1TiPmThEUehmmyNzCJw2FIZLnZtHfHhyudmGAJxNWnhr7Q0rniS9KllVCUbclog2GTfS4DMeGBouHeRA4swlm6s6mn33RffoUyRxm/lgDoOtD60MmzJ2U6J9ybdAxyt1oizL4b7V6tAnyGOq+yKra14upy4QmZwPZuXDKh0LLVV8t+iExMzgyQAExf6Dow/HQs7Oz0ZNdDZ7aaugC1iMbEcgvISO247HIzknWa6//XDCZdZygbpjCO07x1wj2NIhE9mFmTdiyoWM4I1MJ6A/AgUMnki/OKYTx8iYXaCJ6nJ5Pwbacda7Or/pPm3Hw2dqsOmsUu8jsMNFQrFSebBdWIv7157pRSoEwEYuBGqP7yO3sl1QcJNJOASnNj/jURaDXj798rHUiBB7rO3x96xO+NTCpMRCg+2SxN5qXV5hWhKlZYnXQaULNBKWa1EVIYm2TSCfF1eYwCSWLfnOLiqb8UWzgYCVxpc5kSyEkTX5HlgmlnCXdNhhECR4ZlrpYLKqMTDtpK+Jl4Qhz1sI9xYYVWIloEwm8UlKSAjF+iTHzzMhpOdivWBfK1UaPMOUKIMATVWAyQobxib+EmkLgFSIegdJhCNhMJRyUpPmTRtJru6gyMbNKD8qEAqFRAreh0mlYIPUrk7n3HTB3Qypk+uvmH3AJminhn3QWbxOkfJi42nTT2FJS/AxDDRvslhrtCnWXa47s9xo3KNmjTX91fPx21O/bF1H2UjkQA1/ePULp0n7kTeEBUelbXKt67kSLUh/cpmdaoQnlIFK8nqJiNAOy2WNDYDadTrlDi2LE2CS9hXEKGuCzqWdWAXR3FioQC20xNSLxt+9c35x2uccMXzsscosGhv0ZGYLbZx3PHXaYr7fnoJl2fn46GvU5BYCxf+T0WAiAGSYmZqtGGKrvsnKY9jvti4sLKo0xi+XEJdaOb66xjkrDR7sJpZjRqI2NHY/+YxesrdyhP5T+WJYz1kJFxysJ3CBg+GWgsRkw+PZaI01k3VzCBSNZwN4/OpAHXCHQ4mpFLIcyo9HnGqxKbAPWG4ZJOV/Th/Z+Hw6bAp1vj4ZsgnGzO0OWhtXcX6AndqhoRRxUnDex4I2dfk4B3HAXO3Z5WC5cdhn6tnYPWFU4cNHYWPUxAHvkww3hBcpSM25DuLrhLHh/tI35L8hjHYW0BXWfaPg0UP6WbC+w6UB7GHQGHjNYNXcPDpCY7BzsdHo9ihRzTDfXF9TJ63ffT6+5wmybVeTO9rDNfo/csu2Nlo4lWX+zTdAOPB5tB8gBnx/biu/6wS1IRl8H6Bf+VXh0NHHhe99TR60c1W9i34wSKMmK0vAAAACgSURBVOMlvoDzHYgpDiebDfDsbwEluKQKI1hA6ZDFiTgJXNDiJUj+D/jMkpDrdKu0AIvhzHE4xpbAT18ltc0SAz6mIgYe04+gKtyhUMyEUF4JydueV8BNo4I2uk/gV3oIZnFKhu8cvgKZYT53PYPrlhshKP65gg2MRosnSwxneqzLiTEoKZFivQNDQNGKgwYRWIrhmSNtAAMJvENKs/H/AWFx+28+Z1iJAAAAAElFTkSuQmCC",
+ "text/plain": [
+ ""
+ ]
+ },
+ "execution_count": 18,
+ "metadata": {},
+ "output_type": "execute_result"
+ }
+ ],
+ "source": [
+ "del pipe\n",
+ "\n",
+ "pipe = DiffusionPipeline.from_pretrained(\n",
+ " model_id, variant=\"fp16\", torch_dtype=torch.float16,\n",
+ ").to(device)\n",
+ "\n",
+ "prompt = \"toy_face of a hacker with a hoodie, pixel art\"\n",
+ "image = pipe(prompt, num_inference_steps=30, generator=torch.manual_seed(0)).images[0]\n",
+ "image"
+ ]
+ }
+ ],
+ "metadata": {
+ "accelerator": "GPU",
+ "colab": {
+ "gpuType": "A100",
+ "machine_shape": "hm",
+ "provenance": []
+ },
+ "kernelspec": {
+ "display_name": "Python 3",
+ "language": "python",
+ "name": "python3"
+ },
+ "language_info": {
+ "codemirror_mode": {
+ "name": "ipython",
+ "version": 3
+ },
+ "file_extension": ".py",
+ "mimetype": "text/x-python",
+ "name": "python",
+ "nbconvert_exporter": "python",
+ "pygments_lexer": "ipython3",
+ "version": "3.11.13"
+ },
+ "widgets": {
+ "application/vnd.jupyter.widget-state+json": {
+ "0027f3aa006d4276983691ad985ce91b": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "017dc44dbe1c4de491e003a1e279a218": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "01b20535e40b47068723073ac6c819ee": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "0204153b17ca4bb0b21fc033393ce9bd": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "031a326124f1496abe1f3bf8de720029": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "FloatProgressModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "FloatProgressModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "ProgressView",
+ "bar_style": "success",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_71ad1e3dbe44437d8df985cfae207dcd",
+ "max": 30,
+ "min": 0,
+ "orientation": "horizontal",
+ "style": "IPY_MODEL_598fa824f517445394d08c37393f9f3d",
+ "value": 30
+ }
+ },
+ "0371aa5607604c06a868deb2a413cb31": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "04846af1def142ffad328d434ba228fe": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "05700817adac4fdda6c95dd00eaeae38": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "05791b70a24a42138755141602399c47": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_5c838962c7854541b61877c6d42481c4",
+ "placeholder": "",
+ "style": "IPY_MODEL_4d54c07dd8e94557b82521772c1a2825",
+ "value": " 17/17 [01:04<00:00, 14.56s/it]"
+ }
+ },
+ "061fcc6e5f3c44c48cde212c1ba515e5": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "071e40d45ad14fc19b1480927d15d2ae": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "07da49088e8d480fad03a2e828357872": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "0805d34df44f451d9b9910dbe5999245": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_babce0e85baf4279ae1d22d64006667f",
+ "placeholder": "",
+ "style": "IPY_MODEL_5cf6cd09cda64d688f4a0f7c511533d0",
+ "value": "vae/config.json: 100%"
+ }
+ },
+ "08fddacdff4b4ae09adb5440fd86ae86": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "09172ff4be4e433483d27b576464d1df": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "0918b23f41e0404e82fccd08cadc6ccf": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "09638c8da74f4dddaf1d5d94dd8ad885": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "097fa44254ea4ecda7c8db995f370afc": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "0b0a85e1133c4ca3ba716e2403511703": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_34fcd527a59748cf832c9efdb954fc0e",
+ "placeholder": "",
+ "style": "IPY_MODEL_fd672cd5ba0c4695be4240707dcf4bf3",
+ "value": " 7/7 [00:01<00:00, 9.61it/s]"
+ }
+ },
+ "0b53b908088648e3b2beadaeba0f5da1": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "FloatProgressModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "FloatProgressModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "ProgressView",
+ "bar_style": "success",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_a3ce5829f8a640e79a19d737663b8474",
+ "max": 565,
+ "min": 0,
+ "orientation": "horizontal",
+ "style": "IPY_MODEL_62afb52a01924566b52f6c2d9ffb76f4",
+ "value": 565
+ }
+ },
+ "0b7ffee735044ece90f010c6771d2d69": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_27671f87d0f3400b89e34bc428daa53c",
+ "IPY_MODEL_33a018bf2ed547caa69f8ca91dcbb112",
+ "IPY_MODEL_a91df5ceea8647d98f4d49701bb00969"
+ ],
+ "layout": "IPY_MODEL_c8555cb30ade40b9bd9a3435d6deeb67"
+ }
+ },
+ "0ba0a0fca31c482bb628a6739d341601": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "0bca833a6aa74ebaa8f69feb738806bf": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_47468a75637d436f849283c295a74ab6",
+ "placeholder": "",
+ "style": "IPY_MODEL_af5003cf40ae4dfaa0660f247598856e",
+ "value": " 170M/170M [00:07<00:00, 22.4MB/s]"
+ }
+ },
+ "0c68c6c65fb94650b15069a25d9e1699": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "0cf822f588244e54b5264176f9611164": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "0d786d8386ba49d0b53a5452d52e722d": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "0e49d820da754da785bec2e5940eb9f6": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_33d459c0fbfe45389abe7eb43d2710a1",
+ "placeholder": "",
+ "style": "IPY_MODEL_dd42a2ff90854b74ba5fde1de26b4e15",
+ "value": "text_encoder/config.json: 100%"
+ }
+ },
+ "0f60c0f123954744ad13b670ca6dce77": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "FloatProgressModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "FloatProgressModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "ProgressView",
+ "bar_style": "success",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_d2ed1988cf8c4bcdb1793b3d5068efed",
+ "max": 1059962,
+ "min": 0,
+ "orientation": "horizontal",
+ "style": "IPY_MODEL_6f113303101b4f448380a878d8900bf6",
+ "value": 1059962
+ }
+ },
+ "10690b309908402289e9891203714199": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "1074a274530e46c5b5a3e43653da43d0": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_5dd09616ba6544c499271054e8d8d2c5",
+ "placeholder": "",
+ "style": "IPY_MODEL_fdb1fd279a0241429e5721ae2e92d217",
+ "value": "toy/adapter_config.json: 100%"
+ }
+ },
+ "10bc970e474a46249e2a5e9e43fec7be": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "13ac509e0d5f42e9bbb6deda62f77923": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "13f5160dd981465890ada8a2cef22d5e": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "153a93d930df4ee396e03f1aaa6f04f1": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_c8e40d44aeac47a78f6502771f1471b7",
+ "IPY_MODEL_270ddad8d7704f929a28c9fbbdabfa26",
+ "IPY_MODEL_e57d317b3dda43bba13ecd4514f776d3"
+ ],
+ "layout": "IPY_MODEL_22b55b5ee1af4ea7b1acfe511b194cd8"
+ }
+ },
+ "157c0c1e85ef40fb99e6cfe0e176be38": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "16e18e872ab64b3f8bfb32f580c3371b": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "17691a346ca5407a99a5e385450c97eb": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "FloatProgressModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "FloatProgressModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "ProgressView",
+ "bar_style": "success",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_bc07cdaad5b64fb3b0e1f8c214bba813",
+ "max": 170461008,
+ "min": 0,
+ "orientation": "horizontal",
+ "style": "IPY_MODEL_9e2e87c131a140a2a37dfdf483d27ced",
+ "value": 170461008
+ }
+ },
+ "17c29bbcbc0c437c9c8bc83e0b085f1a": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "18e3ba4a61784f04b3238cf273c90c3e": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "19679186751b42e3ad2c44ea46c82a9c": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "1971fcd35a564c449b4f437dac46058f": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "FloatProgressModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "FloatProgressModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "ProgressView",
+ "bar_style": "success",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_dc4391fe30694a788134fffdd2a23d1a",
+ "max": 1389382176,
+ "min": 0,
+ "orientation": "horizontal",
+ "style": "IPY_MODEL_cfc6ec59d45d42d187f42061902abbfb",
+ "value": 1389382176
+ }
+ },
+ "1e6c1c848e364ce4841ddcaa1383cfba": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "FloatProgressModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "FloatProgressModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "ProgressView",
+ "bar_style": "success",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_fe19dcea6d9a44d28f077e065f1671c4",
+ "max": 460,
+ "min": 0,
+ "orientation": "horizontal",
+ "style": "IPY_MODEL_08fddacdff4b4ae09adb5440fd86ae86",
+ "value": 460
+ }
+ },
+ "1e8747251a1f4cca970857911d1c4a98": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_dd9666d76af04b72b08f59023eb04ee3",
+ "placeholder": "",
+ "style": "IPY_MODEL_2702528a2ca049fc800ad44c492690ae",
+ "value": "100%"
+ }
+ },
+ "222da37b5af14d60814c65cdd1ea20be": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "22a2ea45880f4b0da47f1b213882dcb0": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_2d7e7e816a63428b8f30471a12b57bc4",
+ "placeholder": "",
+ "style": "IPY_MODEL_e15aab8dd01f4d5582db80e6ad9931fc",
+ "value": " 30/30 [00:07<00:00, 4.07it/s]"
+ }
+ },
+ "22b55b5ee1af4ea7b1acfe511b194cd8": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "22e894ba852e4072a1f63a83b3a98b16": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_95e24bbc8397455fabb724ed3c330511",
+ "IPY_MODEL_d35b3848508c4b6390c243866649439d",
+ "IPY_MODEL_c7cf10df8d7944aeb93947d5f4156c92"
+ ],
+ "layout": "IPY_MODEL_8e3b0b9f26a34ab8a932756b32834fd0"
+ }
+ },
+ "230bd59922e84b90b0a141b3ac1e681b": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_f8e6babf4fdd4c8e80d6dd24ff22d464",
+ "placeholder": "",
+ "style": "IPY_MODEL_5e030e8a026b4513aa954203169f0a27",
+ "value": "text_encoder_2/config.json: 100%"
+ }
+ },
+ "23c0492f021a4b60b1d84b0b82d15378": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_5405d8a1aa1d411b895b0523fb8e4ce7",
+ "placeholder": "",
+ "style": "IPY_MODEL_04846af1def142ffad328d434ba228fe",
+ "value": " 5.12k/5.12k [00:00<00:00, 358kB/s]"
+ }
+ },
+ "2460b9e05b58481e898b139b94532c14": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "24cbd9338ad94801aa11f4dcb2a867cb": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "2671327d35e64f0da670a3a611fd0886": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "2702528a2ca049fc800ad44c492690ae": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "270ddad8d7704f929a28c9fbbdabfa26": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "FloatProgressModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "FloatProgressModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "ProgressView",
+ "bar_style": "success",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_13f5160dd981465890ada8a2cef22d5e",
+ "max": 170461008,
+ "min": 0,
+ "orientation": "horizontal",
+ "style": "IPY_MODEL_cc06ed7338b74ae6a1c563212aeb9f94",
+ "value": 170461008
+ }
+ },
+ "272fceb4e9484b389067080872b1abf9": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "27671f87d0f3400b89e34bc428daa53c": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_b28a2b59aab9478e9ac3ab24a1de6f9a",
+ "placeholder": "",
+ "style": "IPY_MODEL_c08fca70486040069d4f8f1df46a1074",
+ "value": "model_index.json: 100%"
+ }
+ },
+ "28a5059a2cc445d783e94ad5d83a0748": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_faddc146c69545cdaeb81edc8a0cda70",
+ "IPY_MODEL_cd08b99de03c483a965248ff4df752ba",
+ "IPY_MODEL_d37c6ac25fd34a65bf307896443a5063"
+ ],
+ "layout": "IPY_MODEL_66da596ae59d474f8a82a600174adff6"
+ }
+ },
+ "29b67774c6944bc7ab93e7ba0eaf867f": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_0805d34df44f451d9b9910dbe5999245",
+ "IPY_MODEL_2f2c0ea0fc914e7981e34d01751f74d8",
+ "IPY_MODEL_5f52ae61812544f29f774f80fcb7a09c"
+ ],
+ "layout": "IPY_MODEL_ca5dc8342ef946a49d9e67a21f1a67c8"
+ }
+ },
+ "2a0f746d6eab4680b6c44ec5cdbd8fd9": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "2c352a90375443da835eef55b3e63303": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_db8fd6b2687c449fa0600d3e87c96999",
+ "IPY_MODEL_17691a346ca5407a99a5e385450c97eb",
+ "IPY_MODEL_0bca833a6aa74ebaa8f69feb738806bf"
+ ],
+ "layout": "IPY_MODEL_6bdb9b0b68c24b84a748c18ed927a8d3"
+ }
+ },
+ "2c75632d8fdc4458814055172d1d72c3": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "2d7e7e816a63428b8f30471a12b57bc4": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "2db944a049a04426bba181fddb2801b1": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "2e18ce21c01a4a3ca992622957e7d297": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "2ece04bc10934b3cb9d383abfc5ccd6e": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "2ef25bd6dd644347baac12366d7002fd": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "2f016774e7854ef589442734d0bb2f08": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "2f2c0ea0fc914e7981e34d01751f74d8": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "FloatProgressModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "FloatProgressModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "ProgressView",
+ "bar_style": "success",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_f668dd13af6f41d8be358f7db5261c54",
+ "max": 642,
+ "min": 0,
+ "orientation": "horizontal",
+ "style": "IPY_MODEL_8a8ef60b3b72452fb9ccc31052ab3b4f",
+ "value": 642
+ }
+ },
+ "2ffbf400ff1f4cc9b358bb10c6b9d99f": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "30bfac68f4224152b048d6ccf6013c5c": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "31c3a375a2964a06a2473925fe9b197b": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_fc1391aaeaad4eecad967e800a669ec1",
+ "placeholder": "",
+ "style": "IPY_MODEL_272fceb4e9484b389067080872b1abf9",
+ "value": " 7/7 [00:01<00:00, 4.28it/s]"
+ }
+ },
+ "32132ecbe71a4c2c903932513c2a1aa0": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "33a018bf2ed547caa69f8ca91dcbb112": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "FloatProgressModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "FloatProgressModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "ProgressView",
+ "bar_style": "success",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_bab2458ba3f54b229828ad9c8706aba4",
+ "max": 609,
+ "min": 0,
+ "orientation": "horizontal",
+ "style": "IPY_MODEL_2a0f746d6eab4680b6c44ec5cdbd8fd9",
+ "value": 609
+ }
+ },
+ "33d459c0fbfe45389abe7eb43d2710a1": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "34fcd527a59748cf832c9efdb954fc0e": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "355efc45ddaf42498d72d6134a28c87b": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "35c810f4bfe741f091f172cede413950": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "39e4bdf8d621451f984f6e7302fd6961": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "3a017f1d0ebf4a4aab57ac3eb0788774": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "3a0e9adc345f409cbcd79d1bd19219e6": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_89ed71090d5c4366b21d25ad102e7da7",
+ "placeholder": "",
+ "style": "IPY_MODEL_4ab21d7b956e46348ad6f6542fd92c2d",
+ "value": " 30/30 [00:08<00:00, 4.13it/s]"
+ }
+ },
+ "3c222a56d4404863a1dac60f1d03835b": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_30bfac68f4224152b048d6ccf6013c5c",
+ "placeholder": "",
+ "style": "IPY_MODEL_971f59d5f3e04697b3ab3c39ec0fc667",
+ "value": "tokenizer_2/vocab.json: 100%"
+ }
+ },
+ "3e1ec3a51e9b4fbbab489d34640cda90": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_6466eff2786241eeb142f17758894bb2",
+ "placeholder": "",
+ "style": "IPY_MODEL_c181408b9b2b437ca11d584e3d1e94e7",
+ "value": "100%"
+ }
+ },
+ "3e418e46c47841ac9d717a6981807f68": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "3ede828a0374453e9aac9a6695befae3": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "3fe7e7f00ca746cc8cc762da6f365fde": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "40ff502d2d5c40378c25cf84dd3323c8": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_230bd59922e84b90b0a141b3ac1e681b",
+ "IPY_MODEL_6d0f946764444df28cb0da0fd0a408eb",
+ "IPY_MODEL_c995197e66e04874a9f5d34db98b8890"
+ ],
+ "layout": "IPY_MODEL_f2596717405c40e1a39b721386e7a972"
+ }
+ },
+ "414f8301f76043758f69bbfb6960072d": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "FloatProgressModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "FloatProgressModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "ProgressView",
+ "bar_style": "success",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_7ba112dcece64386bdbac6837004891b",
+ "max": 5116,
+ "min": 0,
+ "orientation": "horizontal",
+ "style": "IPY_MODEL_2ffbf400ff1f4cc9b358bb10c6b9d99f",
+ "value": 5116
+ }
+ },
+ "416f31db79fd431fb8dc06e994421b70": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_a6295c7e7630444c9b7425b884ad9707",
+ "placeholder": "",
+ "style": "IPY_MODEL_3ede828a0374453e9aac9a6695befae3",
+ "value": "model.fp16.safetensors: 100%"
+ }
+ },
+ "421b59f4021d4c4d930c51b6b4c7071f": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "42a623abc5d84c0eb7de4e5323bb6546": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "439cf6c6f9e845cea4008e3219454ff4": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "447d29db05384c55a57c5fb1bd121af4": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "460c3c96d1724713b78bddcfc1f3eb97": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "47468a75637d436f849283c295a74ab6": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "484f694f734b4a92a14ecc4d048db0af": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_157c0c1e85ef40fb99e6cfe0e176be38",
+ "placeholder": "",
+ "style": "IPY_MODEL_99717def9b6b4afe8a411a3bb83320c9",
+ "value": " 171M/171M [00:00<00:00, 331MB/s]"
+ }
+ },
+ "486282a4ead148868005c592d74a4ed4": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "48643ea67f2f4762bcd27de1d4cf0fd2": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "48f51c96b7574946bf9542633eb39135": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "490be826ebc14d5ab4e9f0e10ec79d5f": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "491da86a94c44b7c87366b4bb72a3bd1": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "FloatProgressModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "FloatProgressModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "ProgressView",
+ "bar_style": "success",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_490be826ebc14d5ab4e9f0e10ec79d5f",
+ "max": 7,
+ "min": 0,
+ "orientation": "horizontal",
+ "style": "IPY_MODEL_64ea3c5cc12841f59d1acba12deb6a88",
+ "value": 7
+ }
+ },
+ "49bb475a11104e9496f2623e3d5caebd": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "4a4a50a17c014f189b52119901104d79": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "4ab21d7b956e46348ad6f6542fd92c2d": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "4abac6a83641414499f9b6b1514d1695": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "4cae160456c74a5fa761f026d64b2e35": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "4d327c9e91b34c7b84cedd8f9660e9fd": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "4d54c07dd8e94557b82521772c1a2825": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "4e77d8b6cdb94fc68974d27b24cfb3fd": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "FloatProgressModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "FloatProgressModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "ProgressView",
+ "bar_style": "success",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_6a8a634cd3844fa081a4622d224ec940",
+ "max": 246144152,
+ "min": 0,
+ "orientation": "horizontal",
+ "style": "IPY_MODEL_2460b9e05b58481e898b139b94532c14",
+ "value": 246144152
+ }
+ },
+ "4f56214f69034077bafdfdabc1c2aebf": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "4f6e7b21ba0747f19b9d63468861c988": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "4fa4f545258b4d6ca014a4c84ec4b24a": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_993e5303f107468f83dbf51026e64301",
+ "IPY_MODEL_1e6c1c848e364ce4841ddcaa1383cfba",
+ "IPY_MODEL_d432098a941c463599648b156abea24b"
+ ],
+ "layout": "IPY_MODEL_917139ad07a64e0cae89f2beeffae956"
+ }
+ },
+ "4fbaa1bd51bf4b1e90337a435604d2bd": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "5161248cd0384d5887ed231ecd48c82e": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_097fa44254ea4ecda7c8db995f370afc",
+ "placeholder": "",
+ "style": "IPY_MODEL_9fb982789fbc4582bceb356e351db438",
+ "value": "unet/config.json: 100%"
+ }
+ },
+ "5269d405725946b3a657d3a8d7b25885": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "52c7e22284b0468c8bc0c3b1cad047fb": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "5405d8a1aa1d411b895b0523fb8e4ce7": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "54417d8b9c5249d0a028d9e831dd8be6": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "54ab158c643540abb8b3a96c1ae3ecab": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_55130e37444844f88286a87c8d153eba",
+ "IPY_MODEL_7e3048e0fac94dfdaca1bc862ecfce15",
+ "IPY_MODEL_643ba607008547ba9572fa4880a7d0f2"
+ ],
+ "layout": "IPY_MODEL_5738e5d103254c5485856f97d82954ab"
+ }
+ },
+ "550b3ad10fcb422eb66f71ad95988616": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "55130e37444844f88286a87c8d153eba": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_beedc3b275c24432a2e959dcf9dd418d",
+ "placeholder": "",
+ "style": "IPY_MODEL_10690b309908402289e9891203714199",
+ "value": "scheduler/scheduler_config.json: 100%"
+ }
+ },
+ "55177afb435f44898df300143703e4d8": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_7049676db714446b98bba16b5f1b049e",
+ "placeholder": "",
+ "style": "IPY_MODEL_09172ff4be4e433483d27b576464d1df",
+ "value": "tokenizer/tokenizer_config.json: 100%"
+ }
+ },
+ "556730e12d5d4e0ea51a0dd1b5aac331": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_2f016774e7854ef589442734d0bb2f08",
+ "placeholder": "",
+ "style": "IPY_MODEL_a15c3a32bfd347a98c2a50d27cd5b9f9",
+ "value": "diffusion_pytorch_model.fp16.safetensors: 100%"
+ }
+ },
+ "5738e5d103254c5485856f97d82954ab": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "577cc4b4f27941189c62951046db24ec": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "57b491647f1e49cea7ce34774a963936": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "FloatProgressModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "FloatProgressModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "ProgressView",
+ "bar_style": "success",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_c040aa1f65514be28f0ca8ecdd1f69e4",
+ "max": 170543052,
+ "min": 0,
+ "orientation": "horizontal",
+ "style": "IPY_MODEL_eec76868d92f45d7a6db2e232a45e0c2",
+ "value": 170543052
+ }
+ },
+ "584dd148b2344bdc92f1d0850399aed7": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "FloatProgressModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "FloatProgressModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "ProgressView",
+ "bar_style": "success",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_67ef71b6521b47dd90e3dc0fd03016f2",
+ "max": 5135149760,
+ "min": 0,
+ "orientation": "horizontal",
+ "style": "IPY_MODEL_989c54778eb7469fb91e4337d6f49b0b",
+ "value": 5135149760
+ }
+ },
+ "587bd0b90afa450ba82e49cf86ee135d": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_cf42fc299989442f94f4a9df63005ab4",
+ "placeholder": "",
+ "style": "IPY_MODEL_90b9300ba00e41e58170ec5634622985",
+ "value": " 725/725 [00:00<00:00, 55.6kB/s]"
+ }
+ },
+ "598fa824f517445394d08c37393f9f3d": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "5a4c6dc09a1049c0adfca9834b045a25": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "FloatProgressModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "FloatProgressModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "ProgressView",
+ "bar_style": "success",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_fd13a58d6b444a0f955832647f64df12",
+ "max": 472,
+ "min": 0,
+ "orientation": "horizontal",
+ "style": "IPY_MODEL_8d492d53eb7f4225b516a65ef80f24e5",
+ "value": 472
+ }
+ },
+ "5a7d87338ddc45df84080e0096a31631": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "5ab5097f19cf4474945f96741c444d71": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_6d8fdd0303774305ae20dd39e2a1706c",
+ "IPY_MODEL_031a326124f1496abe1f3bf8de720029",
+ "IPY_MODEL_b9feee6f48bd49209e72e5c5e3136f67"
+ ],
+ "layout": "IPY_MODEL_a2d497a2ddb04d8fac8a4c0f8aa7f5dc"
+ }
+ },
+ "5b3bbc663d504fb99318ba186e6b8499": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "5c3d142907404cef8fd624839a166530": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_abaecfe7f39a43bb8fbd655d1a3009f4",
+ "IPY_MODEL_d488374da5e74ec3a5973003590a7d69",
+ "IPY_MODEL_5d8ae9661dce4a1aac8d418d84f3a209"
+ ],
+ "layout": "IPY_MODEL_32132ecbe71a4c2c903932513c2a1aa0"
+ }
+ },
+ "5c838962c7854541b61877c6d42481c4": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "5ceb5c369f974b84ba850c9e81730a0e": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "5cf6cd09cda64d688f4a0f7c511533d0": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "5d8ae9661dce4a1aac8d418d84f3a209": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_887c5eae5b154eccb4a1caa3deef6e94",
+ "placeholder": "",
+ "style": "IPY_MODEL_e87dffe17f1948e9ba794eddb605a908",
+ "value": " 47.3k/47.3k [00:00<00:00, 3.39MB/s]"
+ }
+ },
+ "5dd09616ba6544c499271054e8d8d2c5": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "5e030e8a026b4513aa954203169f0a27": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "5e677518051c43768dbf06243701c817": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_d727913663634e368ade4a7dc64fe74b",
+ "IPY_MODEL_eb73095c804a4272856fe348fa3cb1e9",
+ "IPY_MODEL_7e9b46b10fa24dfea489dfbc150d2a2e"
+ ],
+ "layout": "IPY_MODEL_c8156b0cc68e4b3693dcabc530a4ea9a"
+ }
+ },
+ "5f52ae61812544f29f774f80fcb7a09c": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_7d29b20296aa4e33837b8ad53fc4adba",
+ "placeholder": "",
+ "style": "IPY_MODEL_6a94d1d176b844db96de0c0e3cd67701",
+ "value": " 642/642 [00:00<00:00, 35.8kB/s]"
+ }
+ },
+ "60cc7415644d4e16b88f8fc5896b4b3b": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "60e8e9f8e6ce40dd910ce1a9410b5e24": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "61db57127c5845759360bdf8b29dac2d": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_f46df85f441e4ada831f0e2b142f296a",
+ "placeholder": "",
+ "style": "IPY_MODEL_d4f1dbe4ce244abc987b1089876e080f",
+ "value": "tokenizer_2/tokenizer_config.json: 100%"
+ }
+ },
+ "62afb52a01924566b52f6c2d9ffb76f4": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "64029a1e70e040b49e38d38bd36823fd": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_3e1ec3a51e9b4fbbab489d34640cda90",
+ "IPY_MODEL_ea0910fc31e44597968b2129272cc94d",
+ "IPY_MODEL_3a0e9adc345f409cbcd79d1bd19219e6"
+ ],
+ "layout": "IPY_MODEL_3fe7e7f00ca746cc8cc762da6f365fde"
+ }
+ },
+ "643ba607008547ba9572fa4880a7d0f2": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_2ef25bd6dd644347baac12366d7002fd",
+ "placeholder": "",
+ "style": "IPY_MODEL_0918b23f41e0404e82fccd08cadc6ccf",
+ "value": " 479/479 [00:00<00:00, 40.5kB/s]"
+ }
+ },
+ "6466eff2786241eeb142f17758894bb2": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "64ea3c5cc12841f59d1acba12deb6a88": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "65b15618abfd4e6f9fafd64813e86ace": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_1e8747251a1f4cca970857911d1c4a98",
+ "IPY_MODEL_caa46820018f47abab4a962afe51cc34",
+ "IPY_MODEL_22a2ea45880f4b0da47f1b213882dcb0"
+ ],
+ "layout": "IPY_MODEL_0cf822f588244e54b5264176f9611164"
+ }
+ },
+ "65bf3df199b44763aa223fee96889e17": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_a32666723b0e4b9883a78f56295c4356",
+ "IPY_MODEL_c08373a044204308ac882dd8cf9cdd3e",
+ "IPY_MODEL_fa7876ade8e240fc89a35a1f8c7c7d3c"
+ ],
+ "layout": "IPY_MODEL_de583920d3b54774a486aef4c052e50d"
+ }
+ },
+ "66da596ae59d474f8a82a600174adff6": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "6703a0417c474db5bf261fe8679051e9": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "6715d91c6b62426aa49c344b65bcd8a2": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "FloatProgressModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "FloatProgressModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "ProgressView",
+ "bar_style": "success",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_bd176c410a4e48a382a1b688e77aafcb",
+ "max": 7,
+ "min": 0,
+ "orientation": "horizontal",
+ "style": "IPY_MODEL_6b586ad7a3054c83b14243d69484127f",
+ "value": 7
+ }
+ },
+ "67567eea233b423c8acd62773a4adb30": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_5161248cd0384d5887ed231ecd48c82e",
+ "IPY_MODEL_6f72ea2c284e4e40899375c7b07c517f",
+ "IPY_MODEL_d99a364420454ba5bfd510d1226b94af"
+ ],
+ "layout": "IPY_MODEL_d33c90e8ea0945d397659f6a90cf51b6"
+ }
+ },
+ "67a03631ebc54f99928f0feb18ab38af": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "67b7783351d340d99c44149635b9be84": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_4cae160456c74a5fa761f026d64b2e35",
+ "placeholder": "",
+ "style": "IPY_MODEL_819a26acd18f443882feb129f2c576d6",
+ "value": "tokenizer/vocab.json: 100%"
+ }
+ },
+ "67ef71b6521b47dd90e3dc0fd03016f2": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "683863a313034025ab99fab5810f39c7": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "683db0ff105a47038c350cfc74b88345": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "685797f8907c47ffab4fe7a81ca22e63": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_222da37b5af14d60814c65cdd1ea20be",
+ "placeholder": "",
+ "style": "IPY_MODEL_6a2b5bbd4afe4e0cabe39e95ccf528be",
+ "value": "README.md: 100%"
+ }
+ },
+ "68822f8f861a48859df630fad63f51c1": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "6926c8dd4e4e46d089bb387333691df7": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "FloatProgressModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "FloatProgressModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "ProgressView",
+ "bar_style": "success",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_adf53d97af214cceaae895c8abfbd909",
+ "max": 170461008,
+ "min": 0,
+ "orientation": "horizontal",
+ "style": "IPY_MODEL_9d74948f7bcb498c9295e41e690a0a8d",
+ "value": 170461008
+ }
+ },
+ "6a2b5bbd4afe4e0cabe39e95ccf528be": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "6a8a634cd3844fa081a4622d224ec940": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "6a94d1d176b844db96de0c0e3cd67701": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "6b586ad7a3054c83b14243d69484127f": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "6bdb9b0b68c24b84a748c18ed927a8d3": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "6d0f946764444df28cb0da0fd0a408eb": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "FloatProgressModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "FloatProgressModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "ProgressView",
+ "bar_style": "success",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_f9ca5d4810b34938b6f997ff66a8d541",
+ "max": 575,
+ "min": 0,
+ "orientation": "horizontal",
+ "style": "IPY_MODEL_b418ff1733db4efbab1b00b632b894e2",
+ "value": 575
+ }
+ },
+ "6d492ddabcbe4d65b5d311834865ab92": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "FloatProgressModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "FloatProgressModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "ProgressView",
+ "bar_style": "success",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_ee8407365f5d42d9b98536152c9efe92",
+ "max": 524619,
+ "min": 0,
+ "orientation": "horizontal",
+ "style": "IPY_MODEL_5ceb5c369f974b84ba850c9e81730a0e",
+ "value": 524619
+ }
+ },
+ "6d8fdd0303774305ae20dd39e2a1706c": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_7bb3f4cda33947138c61aac74d952289",
+ "placeholder": "",
+ "style": "IPY_MODEL_d3b73a841e68425994632d0f05cf4f16",
+ "value": "100%"
+ }
+ },
+ "6f113303101b4f448380a878d8900bf6": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "6f6a6cfd50404f1ea09f83e95b04550a": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "6f72ea2c284e4e40899375c7b07c517f": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "FloatProgressModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "FloatProgressModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "ProgressView",
+ "bar_style": "success",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_0204153b17ca4bb0b21fc033393ce9bd",
+ "max": 1680,
+ "min": 0,
+ "orientation": "horizontal",
+ "style": "IPY_MODEL_f02041b1d5e1485bb2ba02b00fc2c242",
+ "value": 1680
+ }
+ },
+ "7049676db714446b98bba16b5f1b049e": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "70849993c0c94ecf87c56e430f06181d": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "713dec1904ce46f6b2d5a9b7e3e0373a": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "71ad1e3dbe44437d8df985cfae207dcd": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "734e9a834ff74b64b17453013208a116": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "75384779c5d540d28afb53a0e318b674": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_7f63b3d80ecb4c3eb837bd0e616e1623",
+ "placeholder": "",
+ "style": "IPY_MODEL_4f6e7b21ba0747f19b9d63468861c988",
+ "value": " 167M/167M [00:07<00:00, 24.0MB/s]"
+ }
+ },
+ "753f64d9069640d985f399a058fc9b5b": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "766567be45eb4db6b8d7a3364566c1dc": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_3c222a56d4404863a1dac60f1d03835b",
+ "IPY_MODEL_db862ffbb44d450db514173df4c7f301",
+ "IPY_MODEL_ddbeb13bb8174fc0b7d5543108d1c4f5"
+ ],
+ "layout": "IPY_MODEL_5b3bbc663d504fb99318ba186e6b8499"
+ }
+ },
+ "76a474e4aab14a5987cf25d1391d578c": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_68822f8f861a48859df630fad63f51c1",
+ "placeholder": "",
+ "style": "IPY_MODEL_2671327d35e64f0da670a3a611fd0886",
+ "value": " 1.39G/1.39G [01:02<00:00, 24.3MB/s]"
+ }
+ },
+ "777c5583820248838f0c39e82362d9e3": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_734e9a834ff74b64b17453013208a116",
+ "placeholder": "",
+ "style": "IPY_MODEL_9784d9210d6e4214b78ab5f8c33e8044",
+ "value": "Loading pipeline components...: 100%"
+ }
+ },
+ "7a52c380a91c4f49bbfde658550248d3": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "7ba112dcece64386bdbac6837004891b": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "7bb3f4cda33947138c61aac74d952289": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "7c6c4dff0a814bc6a7ac677980b45add": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "7d282fda276343c3aff99b001253ecc1": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "7d29b20296aa4e33837b8ad53fc4adba": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "7e3048e0fac94dfdaca1bc862ecfce15": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "FloatProgressModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "FloatProgressModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "ProgressView",
+ "bar_style": "success",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_0c68c6c65fb94650b15069a25d9e1699",
+ "max": 479,
+ "min": 0,
+ "orientation": "horizontal",
+ "style": "IPY_MODEL_ad233dfd52034b9e8c6c2c5b86995717",
+ "value": 479
+ }
+ },
+ "7e9b46b10fa24dfea489dfbc150d2a2e": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_2db944a049a04426bba181fddb2801b1",
+ "placeholder": "",
+ "style": "IPY_MODEL_683863a313034025ab99fab5810f39c7",
+ "value": " 171M/171M [00:00<00:00, 302MB/s]"
+ }
+ },
+ "7f63b3d80ecb4c3eb837bd0e616e1623": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "804e7ee768794bba88aec3137f418868": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_7a52c380a91c4f49bbfde658550248d3",
+ "placeholder": "",
+ "style": "IPY_MODEL_3e418e46c47841ac9d717a6981807f68",
+ "value": " 565/565 [00:00<00:00, 16.6kB/s]"
+ }
+ },
+ "819a26acd18f443882feb129f2c576d6": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "83afce4becac4f37ba916bf1901346ff": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "83f2d1dfaba54da38f0421b69930c3c1": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "85f22e78d47641d19efb6e6d62f6a014": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_d8bbb7402f3e44b2899fc98f02cee87e",
+ "IPY_MODEL_8b41763280a048d485f06682ddc12ca2",
+ "IPY_MODEL_05791b70a24a42138755141602399c47"
+ ],
+ "layout": "IPY_MODEL_753f64d9069640d985f399a058fc9b5b"
+ }
+ },
+ "86cb336c1f684867bd13dae0370b4d36": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "8840288388ae4162884feef9c8e776f7": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_67b7783351d340d99c44149635b9be84",
+ "IPY_MODEL_0f60c0f123954744ad13b670ca6dce77",
+ "IPY_MODEL_dfabe7aa70024d1aa868ef5e6650dc6d"
+ ],
+ "layout": "IPY_MODEL_7d282fda276343c3aff99b001253ecc1"
+ }
+ },
+ "887c5eae5b154eccb4a1caa3deef6e94": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "89ed71090d5c4366b21d25ad102e7da7": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "8a8ef60b3b72452fb9ccc31052ab3b4f": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "8b41763280a048d485f06682ddc12ca2": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "FloatProgressModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "FloatProgressModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "ProgressView",
+ "bar_style": "success",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_9c6ab017f5fb46eda8e3c22e9dd2b838",
+ "max": 17,
+ "min": 0,
+ "orientation": "horizontal",
+ "style": "IPY_MODEL_10bc970e474a46249e2a5e9e43fec7be",
+ "value": 17
+ }
+ },
+ "8b6464ce614c4aa29ac66ecce29b6cbf": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "8b88a1a63cf242de8a68962f50498c72": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_777c5583820248838f0c39e82362d9e3",
+ "IPY_MODEL_491da86a94c44b7c87366b4bb72a3bd1",
+ "IPY_MODEL_31c3a375a2964a06a2473925fe9b197b"
+ ],
+ "layout": "IPY_MODEL_0ba0a0fca31c482bb628a6739d341601"
+ }
+ },
+ "8d492d53eb7f4225b516a65ef80f24e5": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "8e3b0b9f26a34ab8a932756b32834fd0": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "90558769855c4bb08ff2fe4af940c45b": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "FloatProgressModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "FloatProgressModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "ProgressView",
+ "bar_style": "success",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_b79d32186443469d94836b663bf156b5",
+ "max": 167335342,
+ "min": 0,
+ "orientation": "horizontal",
+ "style": "IPY_MODEL_86cb336c1f684867bd13dae0370b4d36",
+ "value": 167335342
+ }
+ },
+ "90b9300ba00e41e58170ec5634622985": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "917139ad07a64e0cae89f2beeffae956": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "955ec2551f8b400dbbdba68d7449de76": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "95e24bbc8397455fabb724ed3c330511": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_b1d427082b9f452eb6546c7d55016b36",
+ "placeholder": "",
+ "style": "IPY_MODEL_061fcc6e5f3c44c48cde212c1ba515e5",
+ "value": "diffusion_pytorch_model.fp16.safetensors: 100%"
+ }
+ },
+ "971f59d5f3e04697b3ab3c39ec0fc667": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "9784d9210d6e4214b78ab5f8c33e8044": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "979c68bd2e224a40b939c27f32c25dac": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "9810873713024e79ae6d338dfeae5876": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "989c54778eb7469fb91e4337d6f49b0b": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "993e5303f107468f83dbf51026e64301": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_83afce4becac4f37ba916bf1901346ff",
+ "placeholder": "",
+ "style": "IPY_MODEL_071e40d45ad14fc19b1480927d15d2ae",
+ "value": "tokenizer_2/special_tokens_map.json: 100%"
+ }
+ },
+ "99717def9b6b4afe8a411a3bb83320c9": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "9a37ffb9810f482b80f245f64947c371": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "9a9da0d0e3d84a19b5d188c9bd6a83bb": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "9ad4192f6f244264aede1b3c8ac3c57a": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_fdb799739700447d8a5198f1f4f9b17f",
+ "placeholder": "",
+ "style": "IPY_MODEL_683db0ff105a47038c350cfc74b88345",
+ "value": "diffusion_pytorch_model.fp16.safetensors: 100%"
+ }
+ },
+ "9c6ab017f5fb46eda8e3c22e9dd2b838": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "9d74948f7bcb498c9295e41e690a0a8d": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "9e2e87c131a140a2a37dfdf483d27ced": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "9fb982789fbc4582bceb356e351db438": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "a0f8a1a3512443ac84799b95da70ca26": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "a15c3a32bfd347a98c2a50d27cd5b9f9": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "a16016987b6145b69caaac6712d72835": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_c82cf8cf90ed4e93bccffcf75881a56d",
+ "IPY_MODEL_5a4c6dc09a1049c0adfca9834b045a25",
+ "IPY_MODEL_c4d83c2b37504473afe63209a178b4cd"
+ ],
+ "layout": "IPY_MODEL_fae9d16daace412492b048b012b8d6dc"
+ }
+ },
+ "a287f197e4fe4f908e3ee0a0e6cb35cf": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "a2d497a2ddb04d8fac8a4c0f8aa7f5dc": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "a32666723b0e4b9883a78f56295c4356": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_979c68bd2e224a40b939c27f32c25dac",
+ "placeholder": "",
+ "style": "IPY_MODEL_0027f3aa006d4276983691ad985ce91b",
+ "value": "Loading pipeline components...: 100%"
+ }
+ },
+ "a3ce5829f8a640e79a19d737663b8474": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "a48d3ad24e9744f7898d1f2c5a696ea2": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "a6295c7e7630444c9b7425b884ad9707": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "a65484354d254516936fcb425917a4b7": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "a6bb8206de044c74a03d1a64c801e742": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "a6f2ce8830734be4b8efe5ca0e14e990": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_de31002ed7fc475c915b4a29253108af",
+ "placeholder": "",
+ "style": "IPY_MODEL_fbf3d268f30344b7864ce691d5bcb1f3",
+ "value": " 47.3k/47.3k [00:00<00:00, 3.74MB/s]"
+ }
+ },
+ "a708db5805424449afa269b714ebb3b3": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_24cbd9338ad94801aa11f4dcb2a867cb",
+ "placeholder": "",
+ "style": "IPY_MODEL_c88fcf0d20154b1fb9b7e8a00116b5e6",
+ "value": "tokenizer/merges.txt: 100%"
+ }
+ },
+ "a7767d5a440f4c819cdb87414f2187ff": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "a91df5ceea8647d98f4d49701bb00969": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_5269d405725946b3a657d3a8d7b25885",
+ "placeholder": "",
+ "style": "IPY_MODEL_b4a697d8335c435ab21219716a1da022",
+ "value": " 609/609 [00:00<00:00, 49.0kB/s]"
+ }
+ },
+ "a9ac3b2188594c19885bcdb9a659ecde": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_a708db5805424449afa269b714ebb3b3",
+ "IPY_MODEL_6d492ddabcbe4d65b5d311834865ab92",
+ "IPY_MODEL_e17e3253c16743a29f09b82d23c3b26d"
+ ],
+ "layout": "IPY_MODEL_e67a69c294334b01974f8bef36f133a0"
+ }
+ },
+ "aae194e7f71f4eba80ffd18f91f083a8": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_9ad4192f6f244264aede1b3c8ac3c57a",
+ "IPY_MODEL_90558769855c4bb08ff2fe4af940c45b",
+ "IPY_MODEL_75384779c5d540d28afb53a0e318b674"
+ ],
+ "layout": "IPY_MODEL_a287f197e4fe4f908e3ee0a0e6cb35cf"
+ }
+ },
+ "ab9c869439a94bddbbc0c6098f4c5b2a": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "FloatProgressModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "FloatProgressModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "ProgressView",
+ "bar_style": "success",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_13ac509e0d5f42e9bbb6deda62f77923",
+ "max": 725,
+ "min": 0,
+ "orientation": "horizontal",
+ "style": "IPY_MODEL_4a4a50a17c014f189b52119901104d79",
+ "value": 725
+ }
+ },
+ "abaecfe7f39a43bb8fbd655d1a3009f4": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_05700817adac4fdda6c95dd00eaeae38",
+ "placeholder": "",
+ "style": "IPY_MODEL_5a7d87338ddc45df84080e0096a31631",
+ "value": "pixel/adapter_config.json: 100%"
+ }
+ },
+ "abf2248c725b4837b5c2babef7f4ff3e": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_d872c3900b8b4275b2224c9ec5e7d78f",
+ "placeholder": "",
+ "style": "IPY_MODEL_4fbaa1bd51bf4b1e90337a435604d2bd",
+ "value": " 170M/170M [00:12<00:00, 18.9MB/s]"
+ }
+ },
+ "ad233dfd52034b9e8c6c2c5b86995717": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "adb2daf9d62f49f8ab1f0144b717d41e": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_bba38c266ceb4f30bb4bc1eaf5e3aa96",
+ "IPY_MODEL_6926c8dd4e4e46d089bb387333691df7",
+ "IPY_MODEL_abf2248c725b4837b5c2babef7f4ff3e"
+ ],
+ "layout": "IPY_MODEL_39e4bdf8d621451f984f6e7302fd6961"
+ }
+ },
+ "adf53d97af214cceaae895c8abfbd909": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "aed53b6480de4dd4bc7463af04840952": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "aef81ec1a7e844f883beba8c5754a8af": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "af5003cf40ae4dfaa0660f247598856e": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "b0abce2d8a2046dba320e788e33e9d66": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "b1d427082b9f452eb6546c7d55016b36": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "b25e822b3f77431fb72b4780067c90d9": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_55177afb435f44898df300143703e4d8",
+ "IPY_MODEL_b79d3f5bd8024451bc7148ba2a5029bd",
+ "IPY_MODEL_eacd646e2b984e60ab603bfc6d631de8"
+ ],
+ "layout": "IPY_MODEL_d158a80f4186411a8a9c335a8d5a888e"
+ }
+ },
+ "b27ac2aaff694dd5999ab2cba91195da": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_556730e12d5d4e0ea51a0dd1b5aac331",
+ "IPY_MODEL_584dd148b2344bdc92f1d0850399aed7",
+ "IPY_MODEL_ccc5bdc185a84901994577ff7f1bc962"
+ ],
+ "layout": "IPY_MODEL_2c75632d8fdc4458814055172d1d72c3"
+ }
+ },
+ "b27c74f0c7bf493fa8bcb4c5b9c9c100": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "b28a2b59aab9478e9ac3ab24a1de6f9a": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "b3eaa188cc2e48d081488eea4ed2971f": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "b418ff1733db4efbab1b00b632b894e2": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "b44f7154c55146a3bf5f4bd9e438086f": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "b4a697d8335c435ab21219716a1da022": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "b600178b161d4a87a0b832a169d7caf2": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "b79d32186443469d94836b663bf156b5": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "b79d3f5bd8024451bc7148ba2a5029bd": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "FloatProgressModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "FloatProgressModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "ProgressView",
+ "bar_style": "success",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_ea257c1c73524141b87ab3c1ef85c908",
+ "max": 737,
+ "min": 0,
+ "orientation": "horizontal",
+ "style": "IPY_MODEL_c474ed5e340146baae6c38f62013afe3",
+ "value": 737
+ }
+ },
+ "b999b3e3af3744a79c0c90657ef37d4e": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_713dec1904ce46f6b2d5a9b7e3e0373a",
+ "placeholder": "",
+ "style": "IPY_MODEL_a6bb8206de044c74a03d1a64c801e742",
+ "value": ""
+ }
+ },
+ "b9feee6f48bd49209e72e5c5e3136f67": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_daad0d12aff8470d990fbbbbe19d5891",
+ "placeholder": "",
+ "style": "IPY_MODEL_16e18e872ab64b3f8bfb32f580c3371b",
+ "value": " 30/30 [00:03<00:00, 8.40it/s]"
+ }
+ },
+ "ba9b002888b448738ba4b127e1046f5d": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "bab2458ba3f54b229828ad9c8706aba4": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "babce0e85baf4279ae1d22d64006667f": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "bba38c266ceb4f30bb4bc1eaf5e3aa96": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_4abac6a83641414499f9b6b1514d1695",
+ "placeholder": "",
+ "style": "IPY_MODEL_bf6e103b43844f17968eadf223a42acb",
+ "value": "adapter_model.safetensors: 100%"
+ }
+ },
+ "bc07cdaad5b64fb3b0e1f8c214bba813": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "bcb3ec98d25b4c138c5e8f84c1e937c6": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "bd176c410a4e48a382a1b688e77aafcb": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "bd2740e191a74558a77a965b4f2d7f28": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_48f51c96b7574946bf9542633eb39135",
+ "placeholder": "",
+ "style": "IPY_MODEL_35c810f4bfe741f091f172cede413950",
+ "value": " 0/0 [00:00<?, ?it/s]"
+ }
+ },
+ "bdfe4e4109a14a41bcd2e1e4242d82bb": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "beedc3b275c24432a2e959dcf9dd418d": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "bf6e103b43844f17968eadf223a42acb": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "c008577d922e436aabb8680ca0d13117": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "c040aa1f65514be28f0ca8ecdd1f69e4": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "c05842ed12c848c68c4a69de9aa742a8": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "c08373a044204308ac882dd8cf9cdd3e": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "FloatProgressModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "FloatProgressModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "ProgressView",
+ "bar_style": "success",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_a0f8a1a3512443ac84799b95da70ca26",
+ "max": 7,
+ "min": 0,
+ "orientation": "horizontal",
+ "style": "IPY_MODEL_e08d739f59874064994212363a307f6e",
+ "value": 7
+ }
+ },
+ "c08fca70486040069d4f8f1df46a1074": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "c181408b9b2b437ca11d584e3d1e94e7": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "c212598c5a8747f783a6efc18816e868": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "c292a598350d4dd4bb9b70aab1320c29": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_cdd8f9b1592842b48e1ffa80f8ec8246",
+ "placeholder": "",
+ "style": "IPY_MODEL_ba9b002888b448738ba4b127e1046f5d",
+ "value": " 246M/246M [00:00<00:00, 345MB/s]"
+ }
+ },
+ "c474ed5e340146baae6c38f62013afe3": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "c4d83c2b37504473afe63209a178b4cd": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_70849993c0c94ecf87c56e430f06181d",
+ "placeholder": "",
+ "style": "IPY_MODEL_e820c557697648378966ed0a073826c8",
+ "value": " 472/472 [00:00<00:00, 10.4kB/s]"
+ }
+ },
+ "c68a5ad3bb664e8785e724085d208e96": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "c6bdeef396174d51af9eee277752bec7": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_685797f8907c47ffab4fe7a81ca22e63",
+ "IPY_MODEL_414f8301f76043758f69bbfb6960072d",
+ "IPY_MODEL_23c0492f021a4b60b1d84b0b82d15378"
+ ],
+ "layout": "IPY_MODEL_550b3ad10fcb422eb66f71ad95988616"
+ }
+ },
+ "c7cf10df8d7944aeb93947d5f4156c92": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_de0b54a59d9f47408d92915ad746cd5e",
+ "placeholder": "",
+ "style": "IPY_MODEL_eb9a5f255fa0447eba6a33e1c30ba166",
+ "value": " 167M/167M [00:08<00:00, 18.9MB/s]"
+ }
+ },
+ "c80901426c87439481078b9da2e0c772": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_416f31db79fd431fb8dc06e994421b70",
+ "IPY_MODEL_1971fcd35a564c449b4f437dac46058f",
+ "IPY_MODEL_76a474e4aab14a5987cf25d1391d578c"
+ ],
+ "layout": "IPY_MODEL_ff3bf3f1873c4b01b0a547dfe02923ce"
+ }
+ },
+ "c8156b0cc68e4b3693dcabc530a4ea9a": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "c82cf8cf90ed4e93bccffcf75881a56d": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_421b59f4021d4c4d930c51b6b4c7071f",
+ "placeholder": "",
+ "style": "IPY_MODEL_60cc7415644d4e16b88f8fc5896b4b3b",
+ "value": "tokenizer/special_tokens_map.json: 100%"
+ }
+ },
+ "c8555cb30ade40b9bd9a3435d6deeb67": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "c88fcf0d20154b1fb9b7e8a00116b5e6": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "c8e40d44aeac47a78f6502771f1471b7": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_a48d3ad24e9744f7898d1f2c5a696ea2",
+ "placeholder": "",
+ "style": "IPY_MODEL_f29673e57d174839a0bde70bfa165715",
+ "value": "adapter_model.safetensors: 100%"
+ }
+ },
+ "c995197e66e04874a9f5d34db98b8890": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_83f2d1dfaba54da38f0421b69930c3c1",
+ "placeholder": "",
+ "style": "IPY_MODEL_577cc4b4f27941189c62951046db24ec",
+ "value": " 575/575 [00:00<00:00, 11.1kB/s]"
+ }
+ },
+ "c9f764b5036042af9f1505e3729cbc32": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_b999b3e3af3744a79c0c90657ef37d4e",
+ "IPY_MODEL_f3baef4fbf4b4ec08480522be921f841",
+ "IPY_MODEL_bd2740e191a74558a77a965b4f2d7f28"
+ ],
+ "layout": "IPY_MODEL_6f6a6cfd50404f1ea09f83e95b04550a"
+ }
+ },
+ "ca5dc8342ef946a49d9e67a21f1a67c8": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "caa46820018f47abab4a962afe51cc34": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "FloatProgressModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "FloatProgressModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "ProgressView",
+ "bar_style": "success",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_aed53b6480de4dd4bc7463af04840952",
+ "max": 30,
+ "min": 0,
+ "orientation": "horizontal",
+ "style": "IPY_MODEL_447d29db05384c55a57c5fb1bd121af4",
+ "value": 30
+ }
+ },
+ "cb89ecd5a8c14051985495da1797a202": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_61db57127c5845759360bdf8b29dac2d",
+ "IPY_MODEL_ab9c869439a94bddbbc0c6098f4c5b2a",
+ "IPY_MODEL_587bd0b90afa450ba82e49cf86ee135d"
+ ],
+ "layout": "IPY_MODEL_955ec2551f8b400dbbdba68d7449de76"
+ }
+ },
+ "cb9a536bc56f4d0ebf285e7f73d4730e": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "cc06ed7338b74ae6a1c563212aeb9f94": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "ccc5bdc185a84901994577ff7f1bc962": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_439cf6c6f9e845cea4008e3219454ff4",
+ "placeholder": "",
+ "style": "IPY_MODEL_460c3c96d1724713b78bddcfc1f3eb97",
+ "value": " 5.14G/5.14G [00:14<00:00, 393MB/s]"
+ }
+ },
+ "cd08b99de03c483a965248ff4df752ba": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "FloatProgressModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "FloatProgressModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "ProgressView",
+ "bar_style": "success",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_c05842ed12c848c68c4a69de9aa742a8",
+ "max": 7,
+ "min": 0,
+ "orientation": "horizontal",
+ "style": "IPY_MODEL_18e3ba4a61784f04b3238cf273c90c3e",
+ "value": 7
+ }
+ },
+ "cdd8f9b1592842b48e1ffa80f8ec8246": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "cf42fc299989442f94f4a9df63005ab4": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "cfc6ec59d45d42d187f42061902abbfb": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "d158a80f4186411a8a9c335a8d5a888e": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "d18c97fe685e4be080125ae770526255": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_e44c018bc76c48cd8738fee5966767ce",
+ "IPY_MODEL_57b491647f1e49cea7ce34774a963936",
+ "IPY_MODEL_484f694f734b4a92a14ecc4d048db0af"
+ ],
+ "layout": "IPY_MODEL_bcb3ec98d25b4c138c5e8f84c1e937c6"
+ }
+ },
+ "d1e4d2fd70e644f986104c998db7e53b": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_f786a0f386f6486083c15e576f6eb3e7",
+ "IPY_MODEL_6715d91c6b62426aa49c344b65bcd8a2",
+ "IPY_MODEL_0b0a85e1133c4ca3ba716e2403511703"
+ ],
+ "layout": "IPY_MODEL_017dc44dbe1c4de491e003a1e279a218"
+ }
+ },
+ "d2cd2572973249baa8e130b5777f4147": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_b27c74f0c7bf493fa8bcb4c5b9c9c100",
+ "placeholder": "",
+ "style": "IPY_MODEL_09638c8da74f4dddaf1d5d94dd8ad885",
+ "value": "model.fp16.safetensors: 100%"
+ }
+ },
+ "d2ed1988cf8c4bcdb1793b3d5068efed": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "d33c90e8ea0945d397659f6a90cf51b6": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "d35b3848508c4b6390c243866649439d": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "FloatProgressModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "FloatProgressModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "ProgressView",
+ "bar_style": "success",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_d70508c304794bc79e80aab136eaf65a",
+ "max": 167335342,
+ "min": 0,
+ "orientation": "horizontal",
+ "style": "IPY_MODEL_01b20535e40b47068723073ac6c819ee",
+ "value": 167335342
+ }
+ },
+ "d37c6ac25fd34a65bf307896443a5063": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_42a623abc5d84c0eb7de4e5323bb6546",
+ "placeholder": "",
+ "style": "IPY_MODEL_a65484354d254516936fcb425917a4b7",
+ "value": " 7/7 [00:01<00:00, 6.68it/s]"
+ }
+ },
+ "d3b73a841e68425994632d0f05cf4f16": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "d432098a941c463599648b156abea24b": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_d62465d39d7e4265832901e9b9707993",
+ "placeholder": "",
+ "style": "IPY_MODEL_4f56214f69034077bafdfdabc1c2aebf",
+ "value": " 460/460 [00:00<00:00, 33.3kB/s]"
+ }
+ },
+ "d488374da5e74ec3a5973003590a7d69": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "FloatProgressModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "FloatProgressModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "ProgressView",
+ "bar_style": "success",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_cb9a536bc56f4d0ebf285e7f73d4730e",
+ "max": 47271,
+ "min": 0,
+ "orientation": "horizontal",
+ "style": "IPY_MODEL_49bb475a11104e9496f2623e3d5caebd",
+ "value": 47271
+ }
+ },
+ "d4baf7891f854c9c9898314633f97356": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "d4f1dbe4ce244abc987b1089876e080f": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "d62465d39d7e4265832901e9b9707993": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "d70508c304794bc79e80aab136eaf65a": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "d727913663634e368ade4a7dc64fe74b": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_d987907f09084d44b452f939aadff65e",
+ "placeholder": "",
+ "style": "IPY_MODEL_e976b994189343f5ba7d762ef92c79e2",
+ "value": "toy_face_sdxl.safetensors: 100%"
+ }
+ },
+ "d74b1c667d42472b865ee1cbefc33a60": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_1074a274530e46c5b5a3e43653da43d0",
+ "IPY_MODEL_dfde3984062442869bc8091bb94f2c36",
+ "IPY_MODEL_a6f2ce8830734be4b8efe5ca0e14e990"
+ ],
+ "layout": "IPY_MODEL_07da49088e8d480fad03a2e828357872"
+ }
+ },
+ "d872c3900b8b4275b2224c9ec5e7d78f": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "d8bbb7402f3e44b2899fc98f02cee87e": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_19679186751b42e3ad2c44ea46c82a9c",
+ "placeholder": "",
+ "style": "IPY_MODEL_d4baf7891f854c9c9898314633f97356",
+ "value": "Fetching 17 files: 100%"
+ }
+ },
+ "d987907f09084d44b452f939aadff65e": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "d99a364420454ba5bfd510d1226b94af": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_4d327c9e91b34c7b84cedd8f9660e9fd",
+ "placeholder": "",
+ "style": "IPY_MODEL_b44f7154c55146a3bf5f4bd9e438086f",
+ "value": " 1.68k/1.68k [00:00<00:00, 126kB/s]"
+ }
+ },
+ "daad0d12aff8470d990fbbbbe19d5891": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "db862ffbb44d450db514173df4c7f301": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "FloatProgressModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "FloatProgressModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "ProgressView",
+ "bar_style": "success",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_fe958df746be4dc1871bd58628697c3c",
+ "max": 1059962,
+ "min": 0,
+ "orientation": "horizontal",
+ "style": "IPY_MODEL_54417d8b9c5249d0a028d9e831dd8be6",
+ "value": 1059962
+ }
+ },
+ "db8fd6b2687c449fa0600d3e87c96999": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_355efc45ddaf42498d72d6134a28c87b",
+ "placeholder": "",
+ "style": "IPY_MODEL_8b6464ce614c4aa29ac66ecce29b6cbf",
+ "value": "adapter_model.safetensors: 100%"
+ }
+ },
+ "dc4391fe30694a788134fffdd2a23d1a": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "dd42a2ff90854b74ba5fde1de26b4e15": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "dd9666d76af04b72b08f59023eb04ee3": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "ddbeb13bb8174fc0b7d5543108d1c4f5": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_9a37ffb9810f482b80f245f64947c371",
+ "placeholder": "",
+ "style": "IPY_MODEL_bdfe4e4109a14a41bcd2e1e4242d82bb",
+ "value": " 1.06M/1.06M [00:00<00:00, 42.3MB/s]"
+ }
+ },
+ "de0b54a59d9f47408d92915ad746cd5e": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "de31002ed7fc475c915b4a29253108af": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "de583920d3b54774a486aef4c052e50d": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "dfabe7aa70024d1aa868ef5e6650dc6d": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_60e8e9f8e6ce40dd910ce1a9410b5e24",
+ "placeholder": "",
+ "style": "IPY_MODEL_6703a0417c474db5bf261fe8679051e9",
+ "value": " 1.06M/1.06M [00:00<00:00, 1.49MB/s]"
+ }
+ },
+ "dfde3984062442869bc8091bb94f2c36": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "FloatProgressModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "FloatProgressModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "ProgressView",
+ "bar_style": "success",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_7c6c4dff0a814bc6a7ac677980b45add",
+ "max": 47271,
+ "min": 0,
+ "orientation": "horizontal",
+ "style": "IPY_MODEL_9a9da0d0e3d84a19b5d188c9bd6a83bb",
+ "value": 47271
+ }
+ },
+ "e08d739f59874064994212363a307f6e": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "e15aab8dd01f4d5582db80e6ad9931fc": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "e17e3253c16743a29f09b82d23c3b26d": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_a7767d5a440f4c819cdb87414f2187ff",
+ "placeholder": "",
+ "style": "IPY_MODEL_f0bc6b14a299445ca705b888b3047064",
+ "value": " 525k/525k [00:00<00:00, 9.01MB/s]"
+ }
+ },
+ "e3a1a5e9f29d4d28b0b9496493dafa21": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "e44c018bc76c48cd8738fee5966767ce": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_b0abce2d8a2046dba320e788e33e9d66",
+ "placeholder": "",
+ "style": "IPY_MODEL_aef81ec1a7e844f883beba8c5754a8af",
+ "value": "pixel-art-xl.safetensors: 100%"
+ }
+ },
+ "e57d317b3dda43bba13ecd4514f776d3": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_3a017f1d0ebf4a4aab57ac3eb0788774",
+ "placeholder": "",
+ "style": "IPY_MODEL_48643ea67f2f4762bcd27de1d4cf0fd2",
+ "value": " 170M/170M [00:07<00:00, 24.6MB/s]"
+ }
+ },
+ "e67a69c294334b01974f8bef36f133a0": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "e820c557697648378966ed0a073826c8": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "e87dffe17f1948e9ba794eddb605a908": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "e976b994189343f5ba7d762ef92c79e2": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "ea0910fc31e44597968b2129272cc94d": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "FloatProgressModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "FloatProgressModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "ProgressView",
+ "bar_style": "success",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_0371aa5607604c06a868deb2a413cb31",
+ "max": 30,
+ "min": 0,
+ "orientation": "horizontal",
+ "style": "IPY_MODEL_c212598c5a8747f783a6efc18816e868",
+ "value": 30
+ }
+ },
+ "ea257c1c73524141b87ab3c1ef85c908": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "eacd646e2b984e60ab603bfc6d631de8": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_2ece04bc10934b3cb9d383abfc5ccd6e",
+ "placeholder": "",
+ "style": "IPY_MODEL_67a03631ebc54f99928f0feb18ab38af",
+ "value": " 737/737 [00:00<00:00, 41.5kB/s]"
+ }
+ },
+ "eb73095c804a4272856fe348fa3cb1e9": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "FloatProgressModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "FloatProgressModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "ProgressView",
+ "bar_style": "success",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_9810873713024e79ae6d338dfeae5876",
+ "max": 170543292,
+ "min": 0,
+ "orientation": "horizontal",
+ "style": "IPY_MODEL_2e18ce21c01a4a3ca992622957e7d297",
+ "value": 170543292
+ }
+ },
+ "eb9a5f255fa0447eba6a33e1c30ba166": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "ee8407365f5d42d9b98536152c9efe92": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "eec76868d92f45d7a6db2e232a45e0c2": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "efd33121bdfc4ce195a07c9ef523a477": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_d2cd2572973249baa8e130b5777f4147",
+ "IPY_MODEL_4e77d8b6cdb94fc68974d27b24cfb3fd",
+ "IPY_MODEL_c292a598350d4dd4bb9b70aab1320c29"
+ ],
+ "layout": "IPY_MODEL_c68a5ad3bb664e8785e724085d208e96"
+ }
+ },
+ "f02041b1d5e1485bb2ba02b00fc2c242": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "f0bc6b14a299445ca705b888b3047064": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "f2596717405c40e1a39b721386e7a972": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "f29673e57d174839a0bde70bfa165715": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "f2c67c29e1224df3b2def5a87eb8d368": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": "20px"
+ }
+ },
+ "f3baef4fbf4b4ec08480522be921f841": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "FloatProgressModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "FloatProgressModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "ProgressView",
+ "bar_style": "success",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_f2c67c29e1224df3b2def5a87eb8d368",
+ "max": 1,
+ "min": 0,
+ "orientation": "horizontal",
+ "style": "IPY_MODEL_486282a4ead148868005c592d74a4ed4",
+ "value": 0
+ }
+ },
+ "f46df85f441e4ada831f0e2b142f296a": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "f668dd13af6f41d8be358f7db5261c54": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "f786a0f386f6486083c15e576f6eb3e7": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_e3a1a5e9f29d4d28b0b9496493dafa21",
+ "placeholder": "",
+ "style": "IPY_MODEL_c008577d922e436aabb8680ca0d13117",
+ "value": "Loading pipeline components...: 100%"
+ }
+ },
+ "f8e6babf4fdd4c8e80d6dd24ff22d464": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "f9ca5d4810b34938b6f997ff66a8d541": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "fa7876ade8e240fc89a35a1f8c7c7d3c": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_52c7e22284b0468c8bc0c3b1cad047fb",
+ "placeholder": "",
+ "style": "IPY_MODEL_17c29bbcbc0c437c9c8bc83e0b085f1a",
+ "value": " 7/7 [00:01<00:00, 6.49it/s]"
+ }
+ },
+ "faddc146c69545cdaeb81edc8a0cda70": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_b600178b161d4a87a0b832a169d7caf2",
+ "placeholder": "",
+ "style": "IPY_MODEL_b3eaa188cc2e48d081488eea4ed2971f",
+ "value": "Loading pipeline components...: 100%"
+ }
+ },
+ "fae9d16daace412492b048b012b8d6dc": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "fbf3d268f30344b7864ce691d5bcb1f3": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "fc1391aaeaad4eecad967e800a669ec1": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "fd0ff16b68b2488d8c31ebe700dee9c9": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_0e49d820da754da785bec2e5940eb9f6",
+ "IPY_MODEL_0b53b908088648e3b2beadaeba0f5da1",
+ "IPY_MODEL_804e7ee768794bba88aec3137f418868"
+ ],
+ "layout": "IPY_MODEL_0d786d8386ba49d0b53a5452d52e722d"
+ }
+ },
+ "fd13a58d6b444a0f955832647f64df12": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "fd672cd5ba0c4695be4240707dcf4bf3": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "fdb1fd279a0241429e5721ae2e92d217": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "fdb799739700447d8a5198f1f4f9b17f": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "fe19dcea6d9a44d28f077e065f1671c4": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "fe958df746be4dc1871bd58628697c3c": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "ff3bf3f1873c4b01b0a547dfe02923ce": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ }
+ }
+ }
+ },
+ "nbformat": 4,
+ "nbformat_minor": 4
+}
diff --git a/peft/examples/multilayer_perceptron/README.md b/peft/examples/multilayer_perceptron/README.md
new file mode 100644
index 0000000000000000000000000000000000000000..fa3b05e2cb5487791ddbea5a3945ef6a0923c04e
--- /dev/null
+++ b/peft/examples/multilayer_perceptron/README.md
@@ -0,0 +1,5 @@
+# Fine-tuning a multilayer perceptron using LoRA and 🤗 PEFT
+
+[](https://colab.research.google.com/github/huggingface/peft/blob/main/examples/multilayer_perceptron/multilayer_perceptron_lora.ipynb)
+
+PEFT supports fine-tuning any type of model as long as the layers being used are supported. The model does not have to be a transformers model, for instance. To demonstrate this, the accompanying notebook `multilayer_perceptron_lora.ipynb` shows how to apply LoRA to a simple multilayer perceptron and use it to train a model to perform a classification task.
diff --git a/peft/examples/multilayer_perceptron/multilayer_perceptron_lora.ipynb b/peft/examples/multilayer_perceptron/multilayer_perceptron_lora.ipynb
new file mode 100644
index 0000000000000000000000000000000000000000..d5ce302e0754a5cf283471b299ec563a05a8a086
--- /dev/null
+++ b/peft/examples/multilayer_perceptron/multilayer_perceptron_lora.ipynb
@@ -0,0 +1,752 @@
+{
+ "cells": [
+ {
+ "cell_type": "markdown",
+ "id": "8e8743c8",
+ "metadata": {},
+ "source": [
+ "# Using PEFT with custom models"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "c42c67e1",
+ "metadata": {},
+ "source": [
+ "`peft` allows us to fine-tune models efficiently with LoRA. In this short notebook, we will demonstrate how to train a simple multilayer perceptron (MLP) using `peft`."
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "ce314af5",
+ "metadata": {},
+ "source": [
+ "## Imports"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "b28b214d",
+ "metadata": {},
+ "source": [
+ "Make sure that you have the latest version of `peft` installed. To ensure that, run this in your Python environment:\n",
+ " \n",
+ " python -m pip install --upgrade peft"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 1,
+ "id": "4d9da3d9",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "import copy\n",
+ "import os\n",
+ "\n",
+ "# ignore bnb warnings\n",
+ "os.environ[\"BITSANDBYTES_NOWELCOME\"] = \"1\""
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 2,
+ "id": "44075f54",
+ "metadata": {},
+ "outputs": [
+ {
+ "name": "stderr",
+ "output_type": "stream",
+ "text": [
+ "/usr/local/lib/python3.11/dist-packages/tqdm/auto.py:21: TqdmWarning: IProgress not found. Please update jupyter and ipywidgets. See https://ipywidgets.readthedocs.io/en/stable/user_install.html\n",
+ " from .autonotebook import tqdm as notebook_tqdm\n"
+ ]
+ }
+ ],
+ "source": [
+ "import peft\n",
+ "import torch\n",
+ "from torch import nn\n",
+ "import torch.nn.functional as F"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 3,
+ "id": "f72acdfb",
+ "metadata": {},
+ "outputs": [
+ {
+ "data": {
+ "text/plain": [
+ ""
+ ]
+ },
+ "execution_count": 3,
+ "metadata": {},
+ "output_type": "execute_result"
+ }
+ ],
+ "source": [
+ "torch.manual_seed(0)"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "2b127a78",
+ "metadata": {},
+ "source": [
+ "## Data"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "f265da76",
+ "metadata": {},
+ "source": [
+ "We will create a toy dataset consisting of random data for a classification task. There is a little bit of signal in the data, so we should expect that the loss of the model can improve during training."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 4,
+ "id": "b355567e",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "X = torch.rand((1000, 20))\n",
+ "y = (X.sum(1) > 10).long()"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 5,
+ "id": "a60a869d",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "n_train = 800\n",
+ "batch_size = 64"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 6,
+ "id": "8859572e",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "train_dataloader = torch.utils.data.DataLoader(\n",
+ " torch.utils.data.TensorDataset(X[:n_train], y[:n_train]),\n",
+ " batch_size=batch_size,\n",
+ " shuffle=True,\n",
+ ")\n",
+ "eval_dataloader = torch.utils.data.DataLoader(\n",
+ " torch.utils.data.TensorDataset(X[n_train:], y[n_train:]),\n",
+ " batch_size=batch_size,\n",
+ ")"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "97bddd2c",
+ "metadata": {},
+ "source": [
+ "## Model"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "db694a58",
+ "metadata": {},
+ "source": [
+ "As a model, we use a simple multilayer perceptron (MLP). For demonstration purposes, we use a very large number of hidden units. This is totally overkill for this task but it helps to demonstrate the advantages of `peft`. In more realistic settings, models will also be quite large on average, so this is not far-fetched."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 7,
+ "id": "1b43cd8f",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "class MLP(nn.Module):\n",
+ " def __init__(self, num_units_hidden=2000):\n",
+ " super().__init__()\n",
+ " self.seq = nn.Sequential(\n",
+ " nn.Linear(20, num_units_hidden),\n",
+ " nn.ReLU(),\n",
+ " nn.Linear(num_units_hidden, num_units_hidden),\n",
+ " nn.ReLU(),\n",
+ " nn.Linear(num_units_hidden, 2),\n",
+ " nn.LogSoftmax(dim=-1),\n",
+ " )\n",
+ "\n",
+ " def forward(self, X):\n",
+ " return self.seq(X)"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "1277bf00",
+ "metadata": {},
+ "source": [
+ "## Training"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "02caf26a",
+ "metadata": {},
+ "source": [
+ "Here are just a few training hyper-parameters and a simple function that performs the training and evaluation loop."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 9,
+ "id": "5d14c0c4",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "lr = 0.002\n",
+ "batch_size = 64\n",
+ "max_epochs = 30\n",
+ "device = torch.accelerator.current_accelerator().type if hasattr(torch, \"accelerator\") else \"cuda\""
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 10,
+ "id": "657d6b3e",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "def train(model, optimizer, criterion, train_dataloader, eval_dataloader, epochs):\n",
+ " for epoch in range(epochs):\n",
+ " model.train()\n",
+ " train_loss = 0\n",
+ " for xb, yb in train_dataloader:\n",
+ " xb = xb.to(device)\n",
+ " yb = yb.to(device)\n",
+ " outputs = model(xb)\n",
+ " loss = criterion(outputs, yb)\n",
+ " train_loss += loss.detach().float()\n",
+ " loss.backward()\n",
+ " optimizer.step()\n",
+ " optimizer.zero_grad()\n",
+ "\n",
+ " model.eval()\n",
+ " eval_loss = 0\n",
+ " for xb, yb in eval_dataloader:\n",
+ " xb = xb.to(device)\n",
+ " yb = yb.to(device)\n",
+ " with torch.no_grad():\n",
+ " outputs = model(xb)\n",
+ " loss = criterion(outputs, yb)\n",
+ " eval_loss += loss.detach().float()\n",
+ "\n",
+ " eval_loss_total = (eval_loss / len(eval_dataloader)).item()\n",
+ " train_loss_total = (train_loss / len(train_dataloader)).item()\n",
+ " print(f\"{epoch=:<2} {train_loss_total=:.4f} {eval_loss_total=:.4f}\")"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "b382dcbe",
+ "metadata": {},
+ "source": [
+ "### Training without peft"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "b40d4873",
+ "metadata": {},
+ "source": [
+ "Let's start without using `peft` to see what we can expect from the model training."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 11,
+ "id": "f059ced4",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "module = MLP().to(device)\n",
+ "optimizer = torch.optim.Adam(module.parameters(), lr=lr)\n",
+ "criterion = nn.CrossEntropyLoss()"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 12,
+ "id": "17698863",
+ "metadata": {},
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "epoch=0 train_loss_total=0.7970 eval_loss_total=0.6472\n",
+ "epoch=1 train_loss_total=0.5597 eval_loss_total=0.4898\n",
+ "epoch=2 train_loss_total=0.3696 eval_loss_total=0.3323\n",
+ "epoch=3 train_loss_total=0.2364 eval_loss_total=0.5454\n",
+ "epoch=4 train_loss_total=0.2428 eval_loss_total=0.2843\n",
+ "epoch=5 train_loss_total=0.1251 eval_loss_total=0.2514\n",
+ "epoch=6 train_loss_total=0.0952 eval_loss_total=0.2068\n",
+ "epoch=7 train_loss_total=0.0831 eval_loss_total=0.2395\n",
+ "epoch=8 train_loss_total=0.0655 eval_loss_total=0.2524\n",
+ "epoch=9 train_loss_total=0.0380 eval_loss_total=0.3650\n",
+ "epoch=10 train_loss_total=0.0363 eval_loss_total=0.3495\n",
+ "epoch=11 train_loss_total=0.0231 eval_loss_total=0.2360\n",
+ "epoch=12 train_loss_total=0.0162 eval_loss_total=0.2276\n",
+ "epoch=13 train_loss_total=0.0094 eval_loss_total=0.2716\n",
+ "epoch=14 train_loss_total=0.0065 eval_loss_total=0.2237\n",
+ "epoch=15 train_loss_total=0.0054 eval_loss_total=0.2366\n",
+ "epoch=16 train_loss_total=0.0035 eval_loss_total=0.2673\n",
+ "epoch=17 train_loss_total=0.0028 eval_loss_total=0.2630\n",
+ "epoch=18 train_loss_total=0.0023 eval_loss_total=0.2835\n",
+ "epoch=19 train_loss_total=0.0021 eval_loss_total=0.2727\n",
+ "epoch=20 train_loss_total=0.0018 eval_loss_total=0.2597\n",
+ "epoch=21 train_loss_total=0.0016 eval_loss_total=0.2553\n",
+ "epoch=22 train_loss_total=0.0014 eval_loss_total=0.2712\n",
+ "epoch=23 train_loss_total=0.0013 eval_loss_total=0.2637\n",
+ "epoch=24 train_loss_total=0.0012 eval_loss_total=0.2733\n",
+ "epoch=25 train_loss_total=0.0011 eval_loss_total=0.2738\n",
+ "epoch=26 train_loss_total=0.0010 eval_loss_total=0.2477\n",
+ "epoch=27 train_loss_total=0.0010 eval_loss_total=0.2584\n",
+ "epoch=28 train_loss_total=0.0009 eval_loss_total=0.2844\n",
+ "epoch=29 train_loss_total=0.0008 eval_loss_total=0.2633\n",
+ "CPU times: user 1.31 s, sys: 236 ms, total: 1.54 s\n",
+ "Wall time: 1.56 s\n"
+ ]
+ }
+ ],
+ "source": [
+ "%time train(module, optimizer, criterion, train_dataloader, eval_dataloader, epochs=max_epochs)"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "4cef0029",
+ "metadata": {},
+ "source": [
+ "Okay, so we got an eval loss of ~0.26, which is much better than random."
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "4f106078",
+ "metadata": {},
+ "source": [
+ "### Training with peft"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "8dd47aa4",
+ "metadata": {},
+ "source": [
+ "Now let's train with `peft`. First we check the names of the modules, so that we can configure `peft` to fine-tune the right modules."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 13,
+ "id": "922db29b",
+ "metadata": {
+ "scrolled": true
+ },
+ "outputs": [
+ {
+ "data": {
+ "text/plain": [
+ "[('', __main__.MLP),\n",
+ " ('seq', torch.nn.modules.container.Sequential),\n",
+ " ('seq.0', torch.nn.modules.linear.Linear),\n",
+ " ('seq.1', torch.nn.modules.activation.ReLU),\n",
+ " ('seq.2', torch.nn.modules.linear.Linear),\n",
+ " ('seq.3', torch.nn.modules.activation.ReLU),\n",
+ " ('seq.4', torch.nn.modules.linear.Linear),\n",
+ " ('seq.5', torch.nn.modules.activation.LogSoftmax)]"
+ ]
+ },
+ "execution_count": 13,
+ "metadata": {},
+ "output_type": "execute_result"
+ }
+ ],
+ "source": [
+ "[(n, type(m)) for n, m in MLP().named_modules()]"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "5efb275d",
+ "metadata": {},
+ "source": [
+ "Next we can define the LoRA config. There is nothing special going on here. We set the LoRA rank to 8 and select the layers `seq.0` and `seq.2` to be used for LoRA fine-tuning. As for `seq.4`, which is the output layer, we set it as `module_to_save`, which means it is also trained but no LoRA is applied."
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "cf2c608d",
+ "metadata": {},
+ "source": [
+ "*Note: Not all layers types can be fine-tuned with LoRA. At the moment, linear layers, embeddings, `Conv2D` and `transformers.pytorch_utils.Conv1D` are supported."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 14,
+ "id": "b342438f",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "config = peft.LoraConfig(\n",
+ " r=8,\n",
+ " target_modules=[\"seq.0\", \"seq.2\"],\n",
+ " modules_to_save=[\"seq.4\"],\n",
+ ")"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "829b4e2d",
+ "metadata": {},
+ "source": [
+ "Now let's create the `peft` model by passing our initial MLP, as well as the config we just defined, to `get_peft_model`."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "id": "602b6658",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "module = MLP().to(device)\n",
+ "module_copy = copy.deepcopy(module) # we keep a copy of the original model for later\n",
+ "peft_model = peft.get_peft_model(module, config)\n",
+ "optimizer = torch.optim.Adam(peft_model.parameters(), lr=lr)\n",
+ "criterion = nn.CrossEntropyLoss()\n",
+ "peft_model.print_trainable_parameters()"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "2103737d",
+ "metadata": {},
+ "source": [
+ "Checking the numbers, we see that only ~1% of parameters are actually trained, which is what we like to see.\n",
+ "\n",
+ "Now let's start the training:"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 16,
+ "id": "9200cbc6",
+ "metadata": {},
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "epoch=0 train_loss_total=0.6695 eval_loss_total=0.6388\n",
+ "epoch=1 train_loss_total=0.5614 eval_loss_total=0.5456\n",
+ "epoch=2 train_loss_total=0.3897 eval_loss_total=0.3035\n",
+ "epoch=3 train_loss_total=0.2529 eval_loss_total=0.2510\n",
+ "epoch=4 train_loss_total=0.1914 eval_loss_total=0.2191\n",
+ "epoch=5 train_loss_total=0.1236 eval_loss_total=0.2586\n",
+ "epoch=6 train_loss_total=0.1076 eval_loss_total=0.3205\n",
+ "epoch=7 train_loss_total=0.1834 eval_loss_total=0.3951\n",
+ "epoch=8 train_loss_total=0.1037 eval_loss_total=0.1646\n",
+ "epoch=9 train_loss_total=0.0724 eval_loss_total=0.1409\n",
+ "epoch=10 train_loss_total=0.0691 eval_loss_total=0.1725\n",
+ "epoch=11 train_loss_total=0.0641 eval_loss_total=0.1423\n",
+ "epoch=12 train_loss_total=0.0382 eval_loss_total=0.1490\n",
+ "epoch=13 train_loss_total=0.0214 eval_loss_total=0.1517\n",
+ "epoch=14 train_loss_total=0.0119 eval_loss_total=0.1717\n",
+ "epoch=15 train_loss_total=0.0060 eval_loss_total=0.2366\n",
+ "epoch=16 train_loss_total=0.0029 eval_loss_total=0.2069\n",
+ "epoch=17 train_loss_total=0.0021 eval_loss_total=0.2082\n",
+ "epoch=18 train_loss_total=0.0016 eval_loss_total=0.2119\n",
+ "epoch=19 train_loss_total=0.0011 eval_loss_total=0.1984\n",
+ "epoch=20 train_loss_total=0.0010 eval_loss_total=0.1821\n",
+ "epoch=21 train_loss_total=0.0009 eval_loss_total=0.1892\n",
+ "epoch=22 train_loss_total=0.0007 eval_loss_total=0.2062\n",
+ "epoch=23 train_loss_total=0.0006 eval_loss_total=0.2408\n",
+ "epoch=24 train_loss_total=0.0006 eval_loss_total=0.2038\n",
+ "epoch=25 train_loss_total=0.0005 eval_loss_total=0.2374\n",
+ "epoch=26 train_loss_total=0.0004 eval_loss_total=0.2139\n",
+ "epoch=27 train_loss_total=0.0004 eval_loss_total=0.2085\n",
+ "epoch=28 train_loss_total=0.0004 eval_loss_total=0.2395\n",
+ "epoch=29 train_loss_total=0.0003 eval_loss_total=0.2100\n",
+ "CPU times: user 1.41 s, sys: 48.9 ms, total: 1.46 s\n",
+ "Wall time: 1.46 s\n"
+ ]
+ }
+ ],
+ "source": [
+ "%time train(peft_model, optimizer, criterion, train_dataloader, eval_dataloader, epochs=max_epochs)"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "20f6f452",
+ "metadata": {},
+ "source": [
+ "In the end, we see that the eval loss is very similar to the one we saw earlier when we trained without `peft`. This is quite nice to see, given that we are training a much smaller number of parameters."
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "fa55d1d4",
+ "metadata": {},
+ "source": [
+ "#### Check which parameters were updated"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "a6e2146b",
+ "metadata": {},
+ "source": [
+ "Finally, just to check that LoRA was applied as expected, we check what original weights were updated what weights stayed the same."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 17,
+ "id": "c7dcde21",
+ "metadata": {},
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "New parameter model.seq.0.lora_A.default.weight | 160 parameters | updated\n",
+ "New parameter model.seq.0.lora_B.default.weight | 16000 parameters | updated\n",
+ "New parameter model.seq.2.lora_A.default.weight | 16000 parameters | updated\n",
+ "New parameter model.seq.2.lora_B.default.weight | 16000 parameters | updated\n"
+ ]
+ }
+ ],
+ "source": [
+ "for name, param in peft_model.base_model.named_parameters():\n",
+ " if \"lora\" not in name:\n",
+ " continue\n",
+ "\n",
+ " print(f\"New parameter {name:<13} | {param.numel():>5} parameters | updated\")"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 25,
+ "id": "022e6c41",
+ "metadata": {},
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "Parameter seq.0.weight | 40000 parameters | not updated\n",
+ "Parameter seq.0.bias | 2000 parameters | not updated\n",
+ "Parameter seq.2.weight | 4000000 parameters | not updated\n",
+ "Parameter seq.2.bias | 2000 parameters | not updated\n",
+ "Parameter seq.4.weight | 4000 parameters | not updated\n",
+ "Parameter seq.4.bias | 2 parameters | not updated\n",
+ "Parameter seq.4.weight | 4000 parameters | updated\n",
+ "Parameter seq.4.bias | 2 parameters | updated\n"
+ ]
+ }
+ ],
+ "source": [
+ "params_before = dict(module_copy.named_parameters())\n",
+ "for name, param in peft_model.base_model.named_parameters():\n",
+ " if \"lora\" in name:\n",
+ " continue\n",
+ "\n",
+ " name_before = (\n",
+ " name.partition(\".\")[-1].replace(\"base_layer.\", \"\").replace(\"original_\", \"\").replace(\"module.\", \"\").replace(\"modules_to_save.default.\", \"\")\n",
+ " )\n",
+ " param_before = params_before[name_before]\n",
+ " if torch.allclose(param, param_before):\n",
+ " print(f\"Parameter {name_before:<13} | {param.numel():>7} parameters | not updated\")\n",
+ " else:\n",
+ " print(f\"Parameter {name_before:<13} | {param.numel():>7} parameters | updated\")"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "4c09b43d",
+ "metadata": {},
+ "source": [
+ "So we can see that apart from the new LoRA weights that were added, only the last layer was updated. Since the LoRA weights and the last layer have comparitively few parameters, this gives us a big boost in efficiency."
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "b46c6198",
+ "metadata": {},
+ "source": [
+ "## Sharing the model through Hugging Face Hub"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "6289e647",
+ "metadata": {},
+ "source": [
+ "### Pushing the model to HF Hub"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "06dcdfa0",
+ "metadata": {},
+ "source": [
+ "With the `peft` model, it is also very easy to push a model the Hugging Face Hub. Below, we demonstrate how it works. It is assumed that you have a valid Hugging Face account and are logged in:"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 26,
+ "id": "1b91a0af",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "user = \"BenjaminB\" # put your user name here\n",
+ "model_name = \"peft-lora-with-custom-model\"\n",
+ "model_id = f\"{user}/{model_name}\""
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "id": "1430fffd",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "peft_model.push_to_hub(model_id);"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "632bd799",
+ "metadata": {},
+ "source": [
+ "As we can see, the adapter size is only 211 kB."
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "4ff78c0c",
+ "metadata": {},
+ "source": [
+ "### Loading the model from HF Hub"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "e5c7e87f",
+ "metadata": {},
+ "source": [
+ "Now, it only takes one step to load the model from HF Hub. To do this, we can use `PeftModel.from_pretrained`, passing our base model and the model ID:"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "id": "ce0fcced",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "loaded = peft.PeftModel.from_pretrained(module_copy, model_id)\n",
+ "type(loaded)"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "cd4b4eac",
+ "metadata": {},
+ "source": [
+ "Let's check that the two models produce the same output:"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "id": "f2cf6ac4",
+ "metadata": {
+ "scrolled": true
+ },
+ "outputs": [],
+ "source": [
+ "y_peft = peft_model(X.to(device))\n",
+ "y_loaded = loaded(X.to(device))\n",
+ "torch.allclose(y_peft, y_loaded)"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "eeeb653f",
+ "metadata": {},
+ "source": [
+ "### Clean up"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "61c60355",
+ "metadata": {},
+ "source": [
+ "Finally, as a clean up step, you may want to delete the repo."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 22,
+ "id": "b747038f",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "from huggingface_hub import delete_repo"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 23,
+ "id": "7e5ab237",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "delete_repo(model_id)"
+ ]
+ }
+ ],
+ "metadata": {
+ "kernelspec": {
+ "display_name": "Python 3",
+ "language": "python",
+ "name": "python3"
+ },
+ "language_info": {
+ "codemirror_mode": {
+ "name": "ipython",
+ "version": 3
+ },
+ "file_extension": ".py",
+ "mimetype": "text/x-python",
+ "name": "python",
+ "nbconvert_exporter": "python",
+ "pygments_lexer": "ipython3",
+ "version": "3.11.13"
+ }
+ },
+ "nbformat": 4,
+ "nbformat_minor": 5
+}
diff --git a/peft/examples/oft_dreambooth/oft_dreambooth_inference.ipynb b/peft/examples/oft_dreambooth/oft_dreambooth_inference.ipynb
new file mode 100644
index 0000000000000000000000000000000000000000..24ed24218c66609b6db8a838415c9641257eb831
--- /dev/null
+++ b/peft/examples/oft_dreambooth/oft_dreambooth_inference.ipynb
@@ -0,0 +1,116 @@
+{
+ "cells": [
+ {
+ "cell_type": "markdown",
+ "id": "acd7b15e",
+ "metadata": {},
+ "source": [
+ "# Dreambooth with OFT\n",
+ "This Notebook assumes that you already ran the train_dreambooth.py script to create your own adapter."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "id": "acab479f",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "from diffusers import DiffusionPipeline\n",
+ "from diffusers.utils import check_min_version, get_logger\n",
+ "from peft import PeftModel\n",
+ "\n",
+ "# Will error if the minimal version of diffusers is not installed. Remove at your own risks.\n",
+ "check_min_version(\"0.10.0.dev0\")\n",
+ "\n",
+ "logger = get_logger(__name__)\n",
+ "\n",
+ "BASE_MODEL_NAME = \"stabilityai/stable-diffusion-2-1-base\"\n",
+ "ADAPTER_MODEL_PATH = \"INSERT MODEL PATH HERE\""
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 15,
+ "metadata": {},
+ "outputs": [
+ {
+ "name": "stderr",
+ "output_type": "stream",
+ "text": [
+ "Loading pipeline components...: 100%|██████████| 6/6 [00:00<00:00, 24.13it/s]\n"
+ ]
+ }
+ ],
+ "source": [
+ "import torch\n",
+ "device = torch.accelerator.current_accelerator().type if hasattr(torch, \"accelerator\") else \"cuda\"\n",
+ "pipe = DiffusionPipeline.from_pretrained(\n",
+ " BASE_MODEL_NAME,\n",
+ ")\n",
+ "pipe.to(device)\n",
+ "pipe.unet = PeftModel.from_pretrained(pipe.unet, ADAPTER_MODEL_PATH + \"/unet\", adapter_name=\"default\")\n",
+ "pipe.text_encoder = PeftModel.from_pretrained(\n",
+ " pipe.text_encoder, ADAPTER_MODEL_PATH + \"/text_encoder\", adapter_name=\"default\"\n",
+ ")"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 16,
+ "metadata": {},
+ "outputs": [
+ {
+ "name": "stderr",
+ "output_type": "stream",
+ "text": [
+ "100%|██████████| 50/50 [00:11<00:00, 4.46it/s]\n"
+ ]
+ },
+ {
+ "data": {
+ "image/jpeg": "/9j/4AAQSkZJRgABAQAAAQABAAD/2wBDAAgGBgcGBQgHBwcJCQgKDBQNDAsLDBkSEw8UHRofHh0aHBwgJC4nICIsIxwcKDcpLDAxNDQ0Hyc5PTgyPC4zNDL/2wBDAQkJCQwLDBgNDRgyIRwhMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjL/wAARCAIAAgADASIAAhEBAxEB/8QAHwAAAQUBAQEBAQEAAAAAAAAAAAECAwQFBgcICQoL/8QAtRAAAgEDAwIEAwUFBAQAAAF9AQIDAAQRBRIhMUEGE1FhByJxFDKBkaEII0KxwRVS0fAkM2JyggkKFhcYGRolJicoKSo0NTY3ODk6Q0RFRkdISUpTVFVWV1hZWmNkZWZnaGlqc3R1dnd4eXqDhIWGh4iJipKTlJWWl5iZmqKjpKWmp6ipqrKztLW2t7i5usLDxMXGx8jJytLT1NXW19jZ2uHi4+Tl5ufo6erx8vP09fb3+Pn6/8QAHwEAAwEBAQEBAQEBAQAAAAAAAAECAwQFBgcICQoL/8QAtREAAgECBAQDBAcFBAQAAQJ3AAECAxEEBSExBhJBUQdhcRMiMoEIFEKRobHBCSMzUvAVYnLRChYkNOEl8RcYGRomJygpKjU2Nzg5OkNERUZHSElKU1RVVldYWVpjZGVmZ2hpanN0dXZ3eHl6goOEhYaHiImKkpOUlZaXmJmaoqOkpaanqKmqsrO0tba3uLm6wsPExcbHyMnK0tPU1dbX2Nna4uPk5ebn6Onq8vP09fb3+Pn6/9oADAMBAAIRAxEAPwDjgeDTZBkZXmmGTApplIzg1xIpIhlXFUHBzxWjK6svvVNx81bQDYiI71XYfNxmrBHWoyDnOeK1AtWeAw5rTdSU6dKoWaDjJrX8sGIYOawluBy2oLiWnaf/AKzmpdUj2yYBAOahsD+8/rWt/dGzpbUfuSTUrjb680y1bKYqdwADkH8K5upJFGVzg0jEtnjFAO1dx4JozuyAfmI4oaLsVcnfxzUqbt3SnLBsXBOT60/ZtAwcetJEsmjHA5FVL04QirsME8q/u43YeoFE+kahNHxbt+Jqk1cahJnG3P8ArPrVi0O0jmrd54b1ZGJFm7D/AGeaqLbXVtjzreWP6rXRzJofK0dDbznYMVciuCetY9oxbHPatGIEdelYSQbGj5mQKytSP7s96vqzbcAVnX/KMcdamK1Gc0wRXL7juB6VdtpTkZH0rOl4uM471oWhGRkZrd7CNq1bKgnrWkhwv1xWdAQoyOKsecF4WuWSKRfVuOOlSRsCP0yazkmBGM4qdZt3WosUXW6DGDULLz1pA5xSbxjNImQ7sSBUDsc9MVNvOM44qvO2CSDTRLGhxyB1o8zjFVGlODjinRszY4q0gRbR/lyaaXHOTUfzDA96ic5bpmqsWOlbj1NZl0ODxV3cORVacAjFXARQgQiXNbtrIAue1YoOH9PatC2kPbiqnG5LRqswCcmsy6bg1O0pIwT0qlM3B7iohTswsViuXwOtSBBxjrTdpyDnAo3YByOPWt7ARTKMHisuZAG4rVlYFeazJchj6ULQCSGIECraRjbj0qvAwzjIx1q/GQ2On4VlJktMgPP4UpHPtip2iIPbn2pGjOQMdsVKZPKQoeRVqKTHTkVCYxj0NOCHAGKHYVrFky5BHQiojJx60YIUHsaT1zxTiWmRyNxioQck5p7Kdxz+FNJH5VuiiCU5564qoQRIe1XXORyMZquyjdjNUMkj+X8RU4OAD2qOIKBtNSYGODUMViSOTB5qYS5wDVQ8t0p6E4wBWbRdiYgAZzUe5vwp0j8YPSoh0AB4qUjNNj3xiq5zuPNTt0HfFRNgHg8nrWkRsZjJwCB9agY4fnOKscEYxnFQyEdBWgi7aNjBxWusgMeMkVhwOABzV7zv3eBWUkFjK1Q7pOOmagsiN1SXzZY4qKyJ3irXwjZ01l93g8Yq2XwADVO0PAJ9OKsOwJzgg+lc73EgZdxzjg0ixkkcc+tKXC/UdKkjYnBFS3YsXyjwMfjViG3jXMko/dR8kf3vakGBUd5IUg2qeAOlRzGtOCbHz69Mh2RqEj/hC8YFVpNanPImJA6jNZYOSdxxnoR2qLcRJvA4B+ZfWqjT5jWU+Q2o/EFyuCXIPpmrsevNJ8s0aSKf7w6Vyk4NpIHXLQSDgt29qsLLvQSIDuH3hVOi1syY1U9zqM6XcsD5IifuVNMfTwAWgcSDuvTFc7FcFjkZBHSr0eoPGoZSSM4PrWTcomnLCZdKlRg8EdqoXgyprZSVL+MbyA+OorK1SGSDKyKQOxxwa1p1FIwqUnDU5ScfvmqzaqQ4GSRVaY5kPfmr9goJ5NdL2MDXgjJAPQVYMYUgkg0+CMFBzxUzKFXpXK3qXokV9uDkn8KnjOOgx60x9u4YpxIXjPWkwRIz7cfSovOyfahjkHH0qvj5uvSpsTJXLyMSBzUU0YJPqaliHTmpTECOR+NK9g6GS0TZ+lTQx5GM1fEH8OMe9SLCCDxiqUhJFQxHb0/Gq8sRQkjJFbXlKqdM1Vni4J7U1MoxzkA4FVLhzjpitKWMBiVP4Vm3KHJyeKuLJuUhzJk9a0YIyyjFUFALDNatoBjJFXJ6C1Aw85wagkTqBWicAEYxiqkyk+xpRkUikVw3HNKqPKQqKWYnGAM1taf4envFNxORb2w6u/f6VqfbdP0sCGxjBOcNI3JNKVdR0NoUXLVmPbeF7uePfOy26d9x5q8ugaBbNm4Zpj6lsCql7qk0ytLubAOF7ZNZxkMrBiw2p97PrWPtJzN1Tpx3OkT+w4APLs4zu4UHvVzy9FZMNZoCR0FclFODISnLHoe34VKkjtn72O7ep9qlxmF6b0Nu/wBBs5ITJYSlXxkxMev0rmiCGKlSMce9aiXxVxtJBB4NV74r9rLY4fk4qoO+5lXpJK6KQUHqMGkxg4Bp8nQkcCot/H1rWxxtCO23AxTWbnkflTsnuBTM5zk1cUNIRulREYIIHXrUm3LDmmnOeOlbooiYZ/CoSo3HI5qdgRn37VCc5OfzpjHJzj3FSquByOtMQENhumO1Sbs9uO1RIAEZVj6GpkjPWmKQc1PGc9O9Zssou27GOaRdwOe1CISeTViNOzcGgyukRnnHYU05ZueBVoqDxUJQZPGPeriF7kOMfd61FIvOc1Ofl4HU96idR2/GtGBFG2G5q6rcD3qjkBhV1eV6cgVDQ0UbwbueAabZgBgBjPepLsZA460y3IVuvSqWwM6G1I2Dd+lTs+DntVK2fCg1Ozgn+lYSWoIQyfvKsxN0xwaoMcOCDip1chR6VEkWaSHKmq2ok8bfSlilHAz24p14u+NGx2rJqxvSM1ISUztJXHNSQQKpDtwBwW9P/rVctl3rsJCyj7uehFKYjCdxXMR++v8Ad/8ArV0U9jOruVbuFY4zC4Gw+nY+tQRQbWG3AYDgnoy1fuI4fJCglkAwp9V9Kpwg7TCx+dDlT6itzEgnjaJlliOVzhqSMsRIhyRjg1cyiYXO8MOnvUOBFIGA4YYFZzgmVCTRLa3LQorA4I4roUkgv7TybkBlYYyP4ffNcplllIH8XGKvWF0Yj5fcHnNcNSLi7o9CnJTVmZms6LPpdxuP7yBjlJB0P1ptgCGBxz6V28L2+oWz21yA0bcYI5B9a5i80qXSr0owLQn7j+orelXU1ZnNXoODujQtzlAP4T+lSuQT34qC1fcn4VZIywOKl6MxSuVyuWpRndirAQcnjNMEZyDRcdrAE3DvmmGPHbk96toCM47ihkwo61NxMjjUqBk5NW0bAwB19arKDkcmpUPr1qWxJk4PAJGKeoHIz0qMEY46Co5JSCT2PFSMmeQLnvmqc8oweeKZJJk4BqszZ4q4oQjYzntWdeYAPKmtNvu9Kzb0ZU/L1rWIWKCAFwR61q2x+XPUVkx8EjsOMVtabazXcyQwKSx/IVrLRXBRbdkWFVnKqq7mPTHWtWDT7fTl+0agBJKOVhHQe5q6EttFgwuHuCPmk9PYVzV9fNM7MGOTxk1x1KjekTtp0FHWRNquty3TbS2I+0Y4ArCkmkaQlASx4Az0ps7hTg8ymp7SIJ+9bnI+73qqdO+rCpUtoh0zyNFHDnO30HeoJEd1W2gJCJ9/nrV+X92mQB5zcIo7Cls4sHcoHP3ye59q7YwSOKU2xLeyZm4XEfQ/X0q3cRtFsTZgkYVRWhaYYHZyQOM9AKbLG8ikrwMfNOev0FVNKwot3McxGMqCwL55Ap9+B5qEcHb0piLhmYE7FP3j3qW4TeVP+zXCviOuf8MzXDdjUZBIGasunJx0qE8DPvXQjjsM25I5NIcYpTzzTPeqQ7DgACDTWAB2+lPUdu5oZcnkYrVAQEHGe9Qt94irDAE+lQMfbvTAWPJAHBp7HOB3pqggcDrT88Y71LQhEOPcg1ZQkAelV0BOatRZxtIrKRRAik8Y4q0i4GSKiQAYqyhJHK8VFzm3I3XaOmM1Wc87SOtaDKGxz1qrKhHUj2rSDLSKbDqPSonBxxVllxnvUZWti0Vdu1gSKtRtyPpULqfalVunTpUSGhtyMrgVDCCGGMe9STt8vANMhz+dNbAa9uPl79Kmwe/SoLZsgDPSrYA9ev6VlIpIrtt5zUisoWiRNwxnJpFjIOO9TIZOr9OavAiW1JB+6azBHuXj72avWf8AGjHhhWUloa03qOjjEjbCMMOR7UrM4cpIfmxgN/e9jUfm+TuWUb4x07EUyS+wpRzvjxw2OlaU3oFWIyQrENshAQ8N/snsaquACCG+Zejeoqaby5B8rbhjjPGfaqefLYL19Ce1bXM4RuyRD56vn5GU5UjtT1Uv8n4j2NQLKIn9M1IXJIIPGe3alzGsqNgfJDfLyOo71EjMXD9Mnn61a80cHaC3cetV7lVHzJnaeBWcopoUG4s1rO6Mboc8tzW+pi1O1MU6gg9PUVw9nMxV45MhkORmujsrv7LErOQSw6VwTi4O6O+MlNWZMdLmtnIVdyjpj0pi9cHjHUVfhuJZwWzt+tU9RUJcAoMbhzWtObluc1WkoaoaACe1KNoOSM1VEwzjIpPPAPHNbcphdM0ECkg9qcwG3OeTVSKQ7wAjHPPC1d8i4kTKwSEDp8tS4sTRWJHoacp4oNndB8NbSA/7tSR2N6wOLWX8Vo9nLsZWGbj6/hUTyKT7Crbabfrub7HNgdwtUZra6XO63lGOvy0vZy7A0Ruy7sg4NRevHNPKSYG6GQemVoCuWChH54Hy1aj5DGk44NVLhc+hrs7fTbOCyRblAZG5PrUx8PaY4EmD+dZzqKD1N4UHLVHBabpFxqN2I4UPX5mPQV2jC20W0+z24yxHzv3NTNLb6ZbtHbDae/qa5TUdReaZk3fezmuadd1HZHbToKmrsZqF+0vGSVJ5rJMz7i+3jPyD1oll81iqnCjGafsfYHxj+4orelT7mVWp2G+SPNVsZfGWPpVmHluByfuj1/8ArUE4iEfG5vvUgIKAnhRwWrrjGxySbY9YW8zzC2QfvN6+w9BU0YT7wcsHPQfw+w/xqoJ1AO4Zzwq5+99amFyIkQTAM3QIo6CtkzFo2rZ4kjMtxKFUfwD+XvVqUS30C70ENv8AwQr1f3NYcM4Zw7Lk54zzt+grV+1vBCCw2bumeppTehUFqUbqMKxRcqR27VDfMYyi7udtTkGSUFyTlu9Z+pMDduAc46VxU9ZM6q2kEiuzHcOaYxY9ec0mTjkZpyLuPNdK0OVEe3nr+FKFOemKsiLgcHPrTzFxyOKLjKoUDrj60n3lOD09amkUYAHSoiMk9K2iyWQsOeBUEh9qtMuDzVWbjp60x9BEye9TBcmq6Ou7irKdj+dRIELGvHNWozx0NQBcHIOM1KAeuayY7EYbA7ZPap4yGHp7VQDksCQauRZOP1pcpkoltQCBVe4AzwKmXGOary5zjtThuW0V+cHnFRtgrz2qQ8nimNkDiugSK0h9OlNTtmnS8DgimRnmkyrA54PpTIyAec1K4x+NMiHzZ9+lJCZqWuSABWgqYAIqlaYGMjrWiSFTpzWMmBDsAJP605FyAep6GmnDDpg+lPi5OB171Fy0xCCDgDGehqeH90wJ5NKFJxkU8qM8cEVDYuazK98mHDdj1qg8iupUr8w5rYmXzrcgdV6VgSlon5+ZemOhFKDszqfvRJNxYAyIAueSKidZFBOcrng06O53BvLQnHUEZzSMQwLIm0kc84roWxlBWZASd27rSifnYOaYwYYHb60ijzG9+xoO1K5OJBkc8ipDKCCMcEdapSxsDhsiqxuZIsBuY81OpnUpl+MN5kcxPX5SK6DTLZrwmRxkA7R7VjabH9qdUQ5B5ArsrFYbdW3I3lnAPPINTyc7sY+05EaFnZrbwhDhl3cH1qS8m0+GNzMAdvZuorA1rxHBYRGFG+Zugz0rjbjU7vU5/wB5Izbjgc11UqEUclSvKR3M2p6KjnbErD+ErUP9tWboPstqoK9cjqa5u1tHJXjOeM1fFpKnKnA65x3rqVOCOdzl0NuCW8uimx0i3HjaP0r2HS9GiXSLeJ2DuFDM4714Gt1NasoVsluRXrvw41yTUbaWB2Y+RjrROnG10EZyvqV/HV6ugPAIGGZl5yORXPeHvGssWpo95J5tqOo29an8eF77X5ZGYlYl2IvpXHCxMUWckEkk+y1neNjazPU9Z+I+jx6bItgN1w/CAqMV5lN4pu5bgkyc454qh9gkmIUg4wSv0qYabhckEgDJx2pxcdjNpki+JZV+U4YnkZHSnp4s2EZiX5e2OtZb2Ljcdgyay7kAOVJ2gDHvTdgWh6NYXkWqQC5LAk8Be9PmjlgXh85Ocelec6XrM2k3SYO5CeR2FegW2oW97B5nmDkZx3zXn4igpHbQruOhh6nes6s4BypyK5+WfOJACXk7e9dHqdk+AYxhW5OT0rmZA0L/AHfn3fKPT3rip0lF2OydW60J4IVRSzj8DUqZXLHp7VDvAzv5fvSK53ZY8eldsVoYcje5MHA4ULk9c0yR1XAzkAcD0qE9eeB1AFRFtxxj6VdyvZpEqsSCcLnPU1N8q7SXO71WoFjkYEZB9qUwsMbI8+9CkYyii9DdGIgRR4b+/wClXYpSdzyMSc/eP9KxWBXAZ291ArRiuQkIjEWM8tU1Ze6KnH3i1AwEhY5wBkE96ypWMsrEHAJyK07l0WEbBjf+lZuz5s9M9vWsqMbK5VaV3YaiknP51ajjAxxSKnr+lTL06Yq5MwHDgGo2OeDT229z1qBmIPBNTHcYyRfY1AcDJqVwWycmogO1dUdiRj8jJ5FVJiACO5q22cEVUm+YcDpVjIEPzCrMbEHPpVVBg4xVpFOOtQxE4YkD5etPByc9fpTVQ8c809VKkjB5rGTLRWVD61PF1680/YRxjj1pwjUHOKTkZpjg+1enNMcZGDThxwM4obnsKcNyuhAV461G4PRTxUzAAc9ajfkH2roJRUkGKiQ/NU0gIHFVyfn60FEjP7dOKROGx2pDyODSr8pz/FUiNO2Yrjvjjirv8AxyazYDg8nFXkbIGDispFJEuQcZ4IqaJQMnPvVcjqQRU6kbfvYrNj5S0hJ/oKVxsOW6+gqFZVUfeG6hpen61nZmcrokSRVYKx4brWJrNuyPuTO01flfnIOKSO4S8RreUjcPun1quV7mtKbWjMe01Ly4xHONhzw4FWZXs2G/7QsjHpxVW7sJLdywP3TkBugpba+DEo9uq9t20HNbxd0OWjuAIeQK+No9Ke6eW2QP3ZHFLcwbWUrgZ5+XpSRSOF2kgikzvo+8iaApuHnY2HvioNU09EAeJ1ZD1xT5XdY9m0E+vpVMyvkrk+4oTKqQZd0NTFl4lJYHjmtPUPED21vJGyfvmHX1rLsWCIwMgVRyCDyKoXcst3dFDtZV6GtKcep5ld62K8azahcF2GWyW564roNM0zzcgAIwGVIqrZ2jRYYREv1znmuu0ezL5lDbX4BUjitpTUFdnPGLkx+m6dCWVguH/jBq/LZYwrITgcD1rYhhSHDDDADGMcimSgOA2Pp7VxSxeuh2Rwuhy1zpquGIHINdf8LYXtLzUY89cEEmsx0ALYHXmuh8GYivp1IGSmfrXRTxHNoZzocupl686TazcEHJVu9Y8kYfbHjhhgn1q3rUvl63dKe78e1QhxuXI4XkY71xVK9pHXCinEVbQKAVXOOAfU96fHZJI7fKcKfmHrViIhlBPRfTvU8anc7cfMcnFJYkHh0ZVzpDFTtVgR6Hp9a5S/spI8rtXOfmbH616NKVkXb9CSe9c9q1ouJDg5/ujtXRSxF3Y56uHtqebX9lJBIMnKtyKm0i6miugkbfeOBuPArc1CxRoU2I5GOrHmubuLdopAUyjA9RXU7NHLseiosAt900vO35jn+Vchqt1ELzNuDg9zUui3cZU/a9z/wqPU+9QakiibcZCFPQbelck4WdzqpSb0IbZGlbhWZj1PpVp1hiGWPz+gqCC8jjG05Cegp1wYiA0XQ9AaNjspwbG+YNrE5GahDZwAealiTzPvMRjsagfAbC4J7gUzWUUi3HAGK7n5rSDR2qMGdAPXPJrJgik8tuAobo2elMNxGq7ZY/Ox0bNNROCpLWxbe9WUgqcJ9KtWMYmcbckZyc+lYceZ5VK4UH+EV1UUQtbJQMCWQc+wrCersXH3Vcq3cnmSkLwF4AqBQCxwafIp3E8+lMXjscg9K2SsrHNJ3dydegqQr+tRqwGAe9OZxis7CQ2Qkmo2IJHpSvLg/QVEWG7j0rRRGKwA57+lQ7CzZJqUkkZJBqM47E/StoCGHheKqyqQAexq0Txiq8hxwelWNIrhDuxVmOMAg81Eg/eVcTGOaiQEqJ68CpRH361Gvr+lTBspkH6isZDRAXXb2xURnwcdqptK3HPFRGY7+aEjLlNEPk/epSSaqJJ8uDVlCSozTSsx30EIYgg4+tRtkggCpm4FRNyeTgd63QkV5ORwfwFV2B3gL+tWW4zxx2qu3BBoKE4z71Ko54H50wcHsRSjPY0gLUQOOcAVZRj2AqihwKsRHJxk5rKRpFlwEE9fwp65Az2qFQcjjPvU6jkD86zKuBG4jsafhgmOTzTQfmwfwqRWyetBnJkbIcGqNx8h3JwwOeK0ie3aqd2mUwOlaRC3UvRKmr2TFeJUGGHrWemjxbmWSQx46hjkVp+FIfOu2QAEk9jiuh1aw8ht1tPaCTHSQg1DvGRqmpROWXTxHHsQKykcYHNZ7RmJ9r55PpXQ2moXguPLnghK5wuw8fjWlfaPBewq6yqJQCSE6A1bjdGtCtySszk/3YiIY8etUniiMoWJS7+gHJqxe2lzbna6H6gdav6JZlYXkcywzFvkcrkYqIp3O7EVY8l4mRJa4UypbtBnhgx6U2G0DDzICCFOCWzzW/5X2i7kDEy7eMHp+NWUsEtkImVwW7IBtrrWh4UryZm2VjMG8ySdRk969A0bTAYYpG6Ac4PX61g6RpCz3yRhVI7Flr0CO2j0+DBZQwrlrvm0OiiuXUaLaMABU71VurZFDFQBx0FTLc/MAGyCevemStvTJ6dzXDOCR1xkzn51PzZ421veEhnU5OMgR9ayLwAyOAM5rd8KRYvWPbbjPpVYeT5rDqr3bnLa/H/wAT26Y4I31VViFH1x+FaniCEf23cjjlqzlRnAxxk4FY103NmtPSKNCxRpGxjNbkVmETcAT65qrZW/lOXU8YAI9K0GfAZQflPANTCn3CU+xDJbRuNoXD9MisS/gaFX3KWJyOK21uUD/fGBx9KW6gSa3LcyegFaxjZ3Rm3dWZ5jeq21gHwAeAetc9cxSEF5OCe3eu4vdPBYkQ7TnuMmsG809WnL7PNB6jJytejSqKxwVYa6HPWDtbXnm7shc4D8jNX9RVtourmVmLjCqgwKW70g7Q0QIbqR2rcj0+bUNLEbTRTTBekzAYH+yO1XOzCjpI4oCVmATODWpbadIy72zwKsW1ksc22RBuU4JHK1o317FbxiOMAHHNYHt0oJK5iXB2Nheg60yCDzpBgc04K00nuenFXoYha/NIHGeuBTTMqrRBcLHHDhnznjC1lzRfONi/hXTJaxzRbowiA8l5OW/KmLp9qjKIT5zscF8U5TsjzuW8rsg0WxRf304wq8hfU1oyP5sjHofT0qxJGqlI0AwnH41AwIIIHBrOKvqTN9CF0+Xjr6VCy/MCatEY61XkPWruY7CAAdfwprnilBGRigrkgClcpEB5PHWggnjvmp/Kz1p2wgcU7jIMfLwOlRNkD3NWWUg57VCwwcYraBJCc1DKoI7ZqwcjNROAOnWtBkA649KsxHgHNVs8471OhA/H9KliLAOKN5U4pFIxwaRgT7VlIpGUxyKQJnnoaewGAacq5AyDQiSSGLkZq4i84HSoIxwMGrcOOe9K5NrjHB6VAw59fUVakGSKgYZzwOK2iBA4y2egx09KquME96tsNvUdagcc4A59aYyMDA6Hml6U7bSqB3FILApOcYq1Eu7nHNV1561dhHAwazkUidVG0YqQKRjPSiNRnGKlCEDmshsaqfNnHPanduRzT1TI602UYUe9MlasYWwAe/QVXnG4dKlIPHGcUkg+QkCqWhpbQdokphuCFJxnnb1rdmsLS8TOGDA/xnJzXLW1wtvdruJGTzjg11K3TpGGSdGi6g4y30NZ1k+hdK17MzbnTLmM7Yz8h79xU1nYTqUcXTbehXPU1DqHiCBIjGDknriq2n6pckeZs+UHqahVGkaummzqDbBoxxvI/ianW2ivqagI/lxJncTxmsWPWTNOIwyrk816Dpxjh0vdkKducnvRGpqOcNLHLLpUdixS0IUE/Mx5P4Vv6d4dnuotxHloeMt1NGnW6Sytfz/cU8A9DXP+MPiQmkj7PanfJ0ATg10xk5HNKKid1b6VDp4YxTp5g4+YYrgvGviu40yUwyAhz91h0+teYXvjvxBdylhfNEOypVG68R6lqEHlXswuEPd1yR+NN0rke1PXvD/iZdTjA3Deo5Bro4pTJGRj6/WvD9CuZkdLuFyHjb94mfvLXp+nawstr5hJVTzg9fpWFWia06htTld0fHLmug8MKEuDgbR657VyKXElwwlZeQdqgeldl4Ztzt3cjCkY/WsaEPfOirL3DltdlLajO+BjzCBWdaSKwD+hPFXtUX/SJDjH7w5FUQqxgbRwD09c0qkLyZUZe6joLa7C5xjk5FQXWoRwjLuQO59KyReeVNvc7VxwK5XxJrLyg2wJQsRyOw7Grp0+ZmM52J7/AMamDU/KgQOjNgsa73RdTaeCJsZVh9MV4JqF41tdhRhipzt9TRJ4l1MBV/tGRMdFj6CuiWHT2MFXtufSjada3cZZNiSHrzWJqmhNbwN5qBkHOVHSvILH4ganpboPtqX0J5ZWQqw+leseF/G1vrlqoc7kfghjyn1rOVNw2NIVFNmP5ESpLEqAkgYOOT7Vn28TW7S2t2E8qQ/umC5YexNdL4gthZv58AHlsc+uKZbWy3VktyMGQdcjPFJVLIv2WtzgNT820ujA6lE/gKjCt9KzRGzsSxyewr0PUrKKa2EckYbYcjPpVE6daRweakQDf0qVUuztU+WJzdquxleFVZ+mCeRWpL9sZD5Zjz3U9aqX7W8LYj/dn1A6UtlMZYxsiI9XJrVSS3OGo5TZOYZpApjTORg5YYzVmztJbVXmm28fcUVUksriQgx+aCDng8VoSxm2tooC25urEnJqZSUtETyuKuVyc5YnFRsR5Y6cUr/MeM1ExK9aZm9RrNxUUnK8UrNhulRt0JzyelOxFhoJA9vWnA9u9MDduxqaNdw46ikxocCCRzTiaNhxil2g4xn8aENkD8HrUDZOCOtWpAM8dBVd1y2c4FbwJISMA8EN79Kik6difap2z35qCTpwMVqNFYjDk55qWPJqJuGwOTU8XOKhgTpzx0xUir15z9aRcA5xUo5HGMCsZFIySoHXqKcORnqDT5IzjkYFCLggAcUXCw9eBnH5VNF0JApY1yRx+FSBSGyBxiouKw0/NjNRkA/KalwM8A8d6jI9eWrqhsZvcrlQNx/Q1Bgk5xVtj8uD8p/nUDLzgk/hTY0REBetKenApxXAJNMbLAbTipGOj3Z64/Cr0XHB6+1UozkCr8Q6GokFyZcgZ6VYQ54J6dajVM4qdVU5rFichyBT3oljyOeBUkY5yAKJVyAaQovUqMvTHI70yQbVI79vepSeCPXrUbnKYHPamnqbmJdvhzjGfpWnpc4IEU0SMp6hmxWfdoBJzjr1q7pcO5hiSPPbNbWTRndpmtPoNtMokttqsecFs1lzx3Fom112L0wOldrY2blB8kJz3UiprnTEmi2SxZGe1c86fY3hVPNYJlivE5zk16lZXbz6ECgw74UHrivPfEWhvpzC4hRjDnn2r0zwhZbvD8Esg+8M4NZODRt7RMyfEesHTNM8uOTO1QCPU/SvEtUjuJ5HvJc4dsctkivo2+0a2mOZLfzscqCOhryrxRoElvLLiIRwSEsy46fSuyirI5Kz5jjRpobToprdS+7hnHOD6EVZttPkWyk8wKI05ZmGMe31qFbS5smDWt3szyV3YI/Cr9vDfTyLLfStcLEdyQDox7dK6edWOfklci08x6dfvE8ed6A/MDlc9q7LTY3upcYIjAGB71Q0zT2vJZbmZC7yn5ieMH0rsNP0pIY1WRSCo+U+tcdaqrHXRou5oWMPKgnpz9RXovh+AxaVI4OQxbn2xxXJaRp8l1KIo0+ZuCfSu+SzbT9IMKMGZUIJPepwsbvmKxMrJRPML8l7tt453E/rWcE+Y5zkNgkd/Stq7t3aRgAcsTyfSoI4iSC2MHnj2qKllJlw+FHPa1DL5ciqCWOApribyRGbzLjdlE+Yj1Fep3lqGgbblmzuyfU9q4PVvDzkyebxHngDsaujNIzqwb2PPF2XWpAyuY0kbBZuwp0+lyR3bxEgY5QngMPUVu3tlb3l0YiBb+Wv3j02+/vUEQvobbyprVb62XiMk4ZPoa7U0zjaaMOa12MoSTd+HOa1/DeoTaRrAjbKrJ8rqf0pEeZJCbXTPKkJxvmO4p9M960NK8MT3tyJJZGklPzN9amdrFQTvoeu/bE1Dw98x3NjNQ+FbwMJ4n6DotV9J8P3sVosb3I2FegHNOj0+TS73eqNsbrzXl1L3PUg00Jrh8uKTB46gelc3/arRoEl5PX6itjXzmxlc5AK9M965mOJbq0iWRsSYyh9aiKKnLQiurhRIzyoGQ8oB1/GprG+kz/o8e8d8VEtiL2Q2lwskZB4YCt6w0y102BljJaQjG4it0rmDkkPhvZI4w8iBf8AZBqrJMZ5C78Z7Cop2DTEHr70qkE9s1pGNkYylckC8Z7AVFInr09amX1PUUkgGDjmi5Nig64bNMKg9eT2qeQc5/SoTzzTuSRhTuxU6AjBHTvUYPzAj0qWP9aB2JMcnA5puCBg5z6VKoz9acYeCT1pXArE4B469qgYe9W2jPf86gcKD710QJIWUhR3NQOpHbNW2UN35qrIMFgcgd62GU2GGOOuani7HIpnLHJHtViJOgIrOQhxOOKUNg8HA9KGXHOaZz1rFlEkiEqQOKrKu1sEc1ekwRkj8KrgDd61NxRY9FUjPep8Lz1wO1MRMAYHBqYjA9qkGQMvfNRMoUjuT3qyy8VCRzgHHFdMNiCu5wcdaiPJOelTMMHGAfeomzvPpVlIjYfJUJPapz91v0qu4OQSMUgY+E4YdzWnAV44zWVERnpWnAxAArOaEXl4Oc8VIHJbpxVcMDhTUgU4xkn2rElllCAaH5BGfwqNWx9aR3zjJxSKitRjAbuPyqMjOccDuKfncw7+lO2Aj0zQaGJeoAxx+tMsSfOxtViD0q1fryepFQWW0SglT+ddEdjOR2Wm4xxE6epDda6C3AkAO98dxWHpkxwBHKgAHIro7Wfj5guPUGpkCEnsI7mJo3AZGGCpFbtpFHY6bBEoACL8tV4pEcDDjHvirsxCxKDnGOMDpWM2bQIUuWyRjg9yOtUr/RLfUEJ8sFj3qO4HzZyzkjjnFWLK6WM7WDZPYdBVQldBJWZwWoeAEaY+WvzlvvZqzpnhGOAMX6n+8ecV29w8crDBHHYd6VokWALxv9TWc6ljSnG7MWy0mO3hZFUbM5zjrV4xRug2nDCnfNIxVCwHrWtpujNI4eXAXGcng1yxUqkrI63y01qRaPdS2N0pCfL0JHU121zdRrYeYxCgjoazrf7HbsFCrx3x1rlfFviDzJDaW4OAOwr06MPZqzPMrTU5aC3EVpOx8m7RXZvuuabJpT26FjGMHoV5FcvbRS3UiO2S27pjtXpunWsUmlrGGBIHrmoqUlLUuFW2hx88aCPJULj+H1qhdWccsJZsM3XbXRahZfZpCWUDnAaseRMsUbAU9/WvPleDO+FpK5xureGorpDIiDg5IXqfrXMPot5DECDwXyxyc57fhXq0MADFMfMRg+9RnTYlm5jyp/StoYhoynRizznTfC8t9MyuXycEAdK9L8P+GPscCGQjK9SRgn8auWdrFbr8qgKP+WeO/qDWgs7LHuDBU9c8/jW3O5bmHKo7Eo8iIhQg44z1p8kVvPECUBPr6VnGQl8nGO2K0oMSRYAXPqKiVilc4bxXahLK4EY42nnFctBpU9xp9sdwTaBlu9eja7ZiePyiAQxwR61lXNvHHAqogUKuMYqILUc5WRgBvJVQCGYcE461VuLg9+KuSoVfIHXrWdccMcmuhJGDdyoXDMSetSrIMADrUDDkADr6VIgOc5PFU9hItxtu6CiTjt0HIpsecADoaeytkYGOKxZZTlBz1qs4IHTHNXZI8n+dQFcknpTTIbK2SCB61YQAEHqabgBuacoK/N2qhlqM4A45qUNkVDGwPSpeAOOlSwInHFVpMAnmrLHcDVWUHJIFb0yCMHnnpVeU5+Xv296n3YG7HHQ1E4IH+0OlbjIFAyMjpVpAR9D0qsG+bPrVmN+ORWcxDmAxgHJqEjBPNTlyV4HOahI5ye1Y3KuTO45HTFQqQX3EUsgLDAzSRxSEAFG59aEjKDLUZ6HH4VKCPTrUaRPtDEEDpT9jhvunmpaNBjgVASwHQYqaRX252nioSjEcA1vT2JZDI2SMD8qhIy2QKsPE542momhkH8LVYJkDYAUtUUijP8qtG2lYZKH6VC9tNj7ppgyBCA3PWr8L8DP6VUFtKrE7CTVuGKXP+rPFZzBFyMKTlgan3YU1BGkoBGw5qTZKRkofSsGmSxST/wDqoI4ximqkmPuGpAjj+A80WZUdB8a5yMVPsG0daijVw33TUxWQD7hqbM0TMfUkxnFZ9uwVxyT7VrahDI4J2HNZEdvMH+42fpXTDYiZ1GmToe+B64rrLFPMA2zpz1yK4vS4pSBhSp9662whl7Bv++afKTex0tvZOQNrx1NfMYlC9WxjiqdrFOWB8uQj6U/VUdYFZgV+tYVo2Vzai7siggMzbmfC/pUptUt9zIjEnv2qrprq8gOeR+VdJJHut9zAAY4qYW5blSXvGPZ75G8w9B1FLdSbmG3qeKmQrEh29PYUWtr5s3muwCj1rkqNydkddNKKuyxYWUSIJZ+W7CteW8KRgErDGR1xUENxDCrkbXkxgcVmyW813ITJLhR2r0MPRsjir19RzXts06rHL5hTnmrEfhu2v5xc7iu/krVa30+JAckE57Ct60n8iAk9AOB3rrUDilUuzL1Tw40cJFjKI2IrmEtdX0y55uS2T8wB4H0rsr6+LqCr4HXGaowRNcy84eMjsOaJU7oIVbMYZL26swrxrLj8CKwJkaKQhgQ3cGuovIxpqLNFnb3WqdxHb6taebEQrgc15mJoNanqYeumY0UuTgfe7E9qusomh3buRxkVmHMUmMDaOpPWrccmxQ4GVPUCuKD6HXJX1K7X/k4ik456+tPWR5Y24IHXNR3VukkgkyMjpntV2zgDjIfLf3T/AErqpu5y1FYrrsGDz9K0bWUdiAO4rMv3KEjgAegqGxmPmjq1KTswirmlqLDzVG7n0FUpoywJOenFSXZlef8AdLuxyeelZV9qTRKVkZd390HJrSlqZVUUNQWNFLMyg/3R1rBnOck//qqS81BpGIVeD3xWcZHZuc10JGJIfvLUyD3qsobPQ1IrFTz0705DRcXoMcfWpckL71VSXgdcelSmQ7Rwfaudo0GzNzwBmqxbsQAaR5f71QNMD1PTpVJGTJTjIp6j16VVWXLc54NXIzxxnmrsUiVQBg4p5GeccUgDYA5NKQ3cGs2NkDDHQ/hVeQe9WW3bfUGqzdMZropmbTI8H04qCQ7SfU96nbOCBmoZFDLWwIqbsHnrVuIgc1WZSGzxxUsRyOepqJoCyXOOnFQkhieuKlK8delQMDnPSsGirHUHT1HG3n6U5bH5uTkHua3xbgZ7U42yMnUAD1rr5Ec/OYQslJx6dKcLPB+bBNapiByBg+9MCANg5BNCpoHUZnNYrjgfhiomskA+7+lbLKCuSOagPf5eKrlQuczPsXzYK8U/+z1bll/Kri4JHH/1qnjfJClDkd6dhczKA0xcZ29KifTVJ+VRW4IyATnmmPExxz1osg5zFGmgdRyfapE09QxwuK2I4+2PqKk8lWGMVPKmPnMdLEA5CipRYLg5HJrUVNo24qVUz2GaXIg5jGGnjGSvA9qX+z1xnbxWz5eB0zzTjEOc9KORBzmKlghbIFONngdK2BAxJzjFHlYU9DQqaH7RmBNYbgeOagGnOrDKLiumWFWIB4PvSG3XkcE1XKiedmLDBtbKqAfpWvbPcJgKwzSiHnP8NSL5keChAocUPmNCKe743O+P9mlvVlns237mx61VW7uFwQCfar8V200DxurAkVjWjeJrSlaRyNrfG11JVYYXPeuwnvzJCm3HK8Y6V57rCmC+bLfNnoTXR6XcmbSI33ZYcD2rzea0Wj0OVOVzUSQylUHU1JqF2lpbCLP3evFM0qNsPcP91OlYniO8ZIXlVyoUZyKmC6lVH0N/QFluUaczhlzlRipNa1WGyIUygk+lctoPjS1GjvOrpFEg5BPzsR3rj9U1m4168lkSQpBnKn1r2qS91Hj1XeR3kPiSDz9yy8kgH2Fb767A1usgmXGOorxuOyOQFmZvXBqyIrlU8mO8cqO2a1szLQ7698RpEJCHVj/CuavaJr0UkqBJxkjJFeRz2t1sHmTytnjORUdnPe6XMs8MzPsGSjdSKTTHZH0Le3MM9iwlcKWXGT2rirK6W01CS3ikZ48/xHisa18Ypd6WWWSPeow0crYIFYOm6o8+rOUkVlB42HIFcuIS5Tqw7aZ6Lexo21kAG7kgVFDITGykgZ4INT23+k2mNwPy9hVEHA6ZboQa8easz14O6J0kQhkbkdqek4thhiG9CD1rIaQq5+YjJ7jiqF5evGTiQqPSiFSxM4XNK+u/MfO44PXFWtNUnDbxiuZt5/OYLu7966ON1trUseTirvfUi1tDXht4XlLfKGPr0qpqOloeT5PP91Oao6Rfy3F8EHPPccV3h00SWwJUE454rpw7uYV1Y8ou9JDMSAfyqKPSgAC2M129/YCJiNp61mNbgEmu9JM4nNowv7OQKMimHT1JJIGO3Fb4iz2pohbcRt/HNDhcFUsYf2BRj5RQbDK9OfStwQcc4P41GYgD/Os/Yl+0MB9N3DlcCqsuk7Gzsyvr6V1aw/NxjPYYp7WgI5AyeuDVqijP2hycOlg+n5Vei04EdxW6tpjGAceuKm+z/LjoKfskP2ph/wBnhR9PahrBgOc+2K2hFhSrY+tL5fYDJpeyQ/anPnTi2OCR9KQ6UmeVz+FdAYucbCKf9nPGQMVSgkL2hzZ0heuzAph0ePacxiumWAHOegpRbqcc07C5zkzo0RH+qpV0iD/nniurNsMcig2iAZI6Ucoc5yZ0iLpsNRto0YOCp+tdcbaPtnjrULW6noMZqeRD9oWGXgGkKBs8ZzUyoSTu6U3yiDkfjWtjEgK4XAFIYs4zwasbDtORn0NMGc4YHjvTsIb5GV6A4qvNHtBOPwq75iiMgAkVVlmV8gKR65pBYoeWS24fKTwM1PApA2jH4VE8nz+mDgCnpOyvhRgdyBQMv7SQMjn0pWjGNw6/yqJJy4znke1Ths/eoERKhBOOTUyqT9aVULSHPTFTIAvfimFiPytwPFOSIqATjAqfKleBikYc8jOfSlYBpQAZHSk27uSBipAmBj1o8rigYzaD0PTtSEDPAxUzIRyOlKkbeg+tICPysgYHHammIA4wc1b25HTFDINo5ouOxTICrlutMG3dnGPrUs8cnl7unpmqok+U56n2oAl8wKQd2KvwXUYIzisouFHz8ntQhG7jJ57UmropOzMvxfYb0+0RKvzdSF5FP8JR/aNPMKHLbvyrcmtjc2xbyyR2XPBq54dszBC0rIqE9BXlyhadj0ozvG5ZnQWdoII1HHWuH8SDfbSr0dhwTXd3m1stk4PUCuS1mJDG5BIY8AEUmrMSdzyPSNJSZ57i6dvL3EAA43GrE+rWlmTHGRjGKXVrhrL7RErbijFuOMVwcsrSSFmJJJz1r1YSSijzZq8jsf8AhIoRjDE9iKRvE0WOB0PHNcXnmin7Rk8iO0HiaJiCwB9z1FK+sQz8Lyx7k1xWaekjKwIPQ0e0Ycp1k+nRalHJMZlikXgOxwG46Vq+DrT7PIQGAcn5sCuXSaa4sktFI3O+8hq9K8NxCKGJ51XzCMBQK567ujooLU7zSMBAAB+PerF5ZhJxKinDDnFQ6ai/Lhgox909a1/MRVZHztx3rzpK56EZanIarujRtoFcvM8ry4ZwR7iug8QDM5CP8voRxWVBDAq+ZLbPgdXj5rmS1Oi+hZ02yDYcbGXqe1T6ld5xEjYwMHFU5bqERhIpHA9c4P8AhUUMaSSZ35P+1Wj2ISNnw2dl/GX3fhXrMdwjWwAPbvXmmkxCORSIwT613to4aEfd6dq2oOxjXVzM1dcgkGufMYJJJzXUak0YjPeucIBY8cV6NF3PPqoiCrgj8aVYwegyPepVA7EH8KehUAD3rcx0IDHu7YqJoy+c8gVfbbjG0nPeq205/pTEMjQccYqVkA9qbuCnB5NNeZQMDpRcABxwTx6VIqKwzwBVEvubI5q2g2gZzzSuMk2jd0zSALuyBz3zT1Q+vHrUm0bMdaQWK7BS2QTxQFLH1PrQ4O/jGO4qVc4zTAYEIGOtKUwuAOak6cDvQyHHegCAHAYHqKUMT1H40rLtPXrTVG7PODQICcn5hn0qMjnpUvltkDNJ5Zz1zTuAbtoBY8ZpWcYJ7VVkbjAwBnvUbXATOWBJPShsEi4rKxwM4pzLz94HiqkcrH7mKmEuSM4z3NK4yOVmXgZqocndkc1dkcAYOAPUVSkkGSBigCJ4jvwvJapIbN+d3SmxklySfl9fSr1vMo+XIZe5oAZHbhecYNWEQdAppGlU85FNSQDd83fAp3BoshCvfj0oKkryOKYZBx6jg0okUHJfii4h6KR8vb3qdV981EHXIPP1pjXAjfGeTRcC267TjHHrTM7eeoqp9uySM9KYZiwHXOelIC20h4GABT43CmqXmYOWOfX2pxuBs+VuPegDQaQE88D2pu8Kw5z7Gsx73Zgd6T7eC5GOnWkUX52LD1FZcsuw/MO/GKtC5B+8RtxVVgJW4C4FACxs0uWPyjFPQSBwI249cdaVY1IAY4PbFWIIt8gUIXbtQwNBWEcI3yEyHgDritIR+VYqcs2eelUSht0BuGVBnhUHJ+tWkl3w5ZsD68YrimryOyL92xTE4kRg/BArD1GDMbGTgdsHBq9cO6XH7s7UHU92rB1e93o6SJlSSMjov1qErsbloeeeK9O3xTTg7AnCsT/rD3rz4wq5wrbW7hvWvTtdvHltY4SoDINw9FHrXA6jbxlgYWJI5YnvXalZHJJ6mZLA8Jw2PwOabgMOODQwIbBpAD6igRIts7NgY/E1I1ssQJeVS3ZUOagAJPANXrS3j+9N2xhR3oA1PD9kbm58yWNmjyAxB6D2r1bRrVIoxvdiin5Wx0ri9FdbaSOPCb3Qqp/vr6H6V1lheRx+XDITsxuHPPXv6VlV2NqT1Owt5IIhkkk+4rRiH2oZYAkDsa56BzdShHQpEehzXR2zLCu7YQ3QMa4mjsTIZLWF1KsisRwQwqhdaLaxb5Ldms5SOHXlW+tJqt49s4uA4A/vfw1Rk8SRzwGN8LgYKHnH/wBao5UmXzM5zU7cxXh+QLKBlkx8rD1Wo7dvLcHByfbipb68W5Od26MNk4OWT3B9PapIYiqRbTuR+VcH7wqJGkWdFpMhJUBsiu4sSnljg1w+mpIpHp65rq7QybAN3GKqlozOrqXb1AyY2g+1YFxAApIGPatpyQM7iTVCZN7fMM130p2OOrG6MoHaPencMBVl7fCnIrOlk8h8YrqTTOVxtuWNwPXdmoZG2LkNk0wXYZecVBOXdTsHIoYkkRS3nJwT9KpyXpJwAd1Vbm2nZ89M9MUQWrgnqxFCGattMAM7eatmfOMjP0qilu64xuzU8aP2BzTAuRXAAwRxVgvkZDAVQSN85bt3qZptvGc0CJAPmJLipdwwMHp2qtG6ucjGQKVTuySckdqAJ2Zs4xjPenGTjaGqBtx+bPSo9xznGDQBZcKR1qHdyVz0qNpsL71H5mSfcUAXVb5QAeaeTjpVMSjAKjnpT0kJXJPNAFGY+aeM470xYVGMjHpUkSjrkkikk3MwJ4NAEoTC8Nk+gpjHD7h07inCM5yB+NKkDDIJzTsBCUJBOSR6VH5Rfr1q2NwBxgYpyOAMkLu96QES2xEXK8VGbZx935RUz3iJJjcMnj2pyTK4x1ouBWMUxXGKVYpdp9cVbEybeW6UwzxnOD+FAFNmlQkZycinRO+/exJz2pkpbzXIA6YFWLOEiMB+G9aAHid2OMYqGQGQjdnPrV14wjAnqaQKowN3ykUAV0UAgN19fWrDMcZAGP1pY8Z6ZPrT3iLj0HtTAoyb2cqvB69aQ+YFw4OKvRwhec9O5oZlTKk5XsaQFJbfco3HBNSrbgLyeR196hmmYAFV+pqoNSPmY/L3ouBfmiKAMT+FRRzYJJyBVc3ksi5Cnb0xUkVuyN87ZXt60rjsaVsrTuoRTjucc11unWSxwYC4b2HNc/pYUEDnFdbaMixjAbHtUyZSRkalbGJWkK8njk8k1z8WpeRJtlI3E4wen+RXVaoGkjbA6c9a4fVI2RmGBk/pXnVZOMj0KcVKJqT3EE8YYODzwB1z/hXM6yjvbSbhhWPHYfjVVrqS2laVckqp+UnrntTbm8lvoGVuG4Gf4R/jWlOaZlODRyGrSFZSr/OSmHZeQx7Ae1cncxxq+MnA5IHY12GoK6SvCoDRgfID1J9TXNPYPguTGzdW+bn8q7LqxytWM54VuCoVQoI61VS0J3NkbAanuWnty8bRspbkHHaq0F08BIHKntRcknjjWMHIHJ6+lXLVQ8oUBWI5UH+KmQn7XH5ew7lGcYq7b2Fzb3CFYy6kbgTxilcLG1p7iOBJZog6yttUjho8e9dFo0ZR5ghLueRu5wPSuftZt0JZxtz1QrwfpXS6ddW9qkaRki4cA89MdzUzsy43OvsIPs8QeYlo3XOO/wCdWdQ1q1s4NrT4UnAya5a58VRx5VmAZTsOPuisGeae+kMcnzAHMeeQwrjmdkFc3L/X7iyndLmEXNlN1T0HqKwr2VSxltHMtsRmNsYb6NT4dSeO3fTr1QyocxydSv0PpVY/6OwaMYJ6r1B96hmiRHDLcCRSg+QHnArrdGTfCYscMd230b1FY1pJFIcyQgHuy9DXRWKIApjJAHTArF7mmx0FhCV5I/PtW7bFFxWVaAEdRnvg9a0o2UY3qRW0I6GM5FyVkZOoqkHXdipnaEodjZP1rMlkZX4JNKba2LhFPc0CFI4Gazry1Emc8e9TRzHjPFE+Wj6Cro1mpWZNaiuW6OdeykV8g1cgjUD5iaWZtxIHBFVfte0fez2r076HmtFuaBe3U/pUMdsN+QM+poW6y+1mU8daf9pVT8oHNFxF1URY8hc1UkkRCcHB9KGuz2jJz3qjOWbOUzQBYFwDgZ4IprxFsYyO+ayhO0cvzE1rQSh4w2c5GKBEls4XIY5P0oeVU6A9etNyi8nv0qORsrgHFMC6kiGPJyc1UuJAD6/QYqsL3y/kYEe9Vp7kO42EkmkMuhhIOMnHNOUZ5GRzSW6tsAPXvVmNF6nmmIm8tSg9O9QzpsGUPHerPmgJwB+NVZpAy4Bx+FAy39mijTPGaheMFeB9KryXhZ9qtnNPgmZhtYcY6UJiZLGFHy8jPrT3jbB5Xb7U0Mgbnk/yqKaTbgg8UCE3cbQvIPGahnjaRslMfTtUMl4yykbMjHUUJfJnByCfXtTGL9lGRuXgmpBFt6HAHWnLMCu4E4AxVGW/CSYYkN2zSAtrCrjk4A9aSSJBgqwyBVeOcSKRuJpxi8w5JPFIB0ax5JJ6n1q2biNIxg8Diq6Warhn5ArO1W4KqVQELj7oFMC7LqCs5VScAc+9Ilwo2j8a4L+2JEuTE7FTnoT2rZs9VjkQENk5xj0p6COzglymalZ9uBuzXOpf7Y8I3J6VLFdMzYPJ6nFIaOhkdSnHXHNZjCSSQgAqegqJb05AfhRVj7Wka5LKc0AK1uxQFx1qE2SbgWAz61I2qIvyABhUH2sSMRwCaAJ1iEbbQOKmaFQuS+W6D2qmknHLksOmKntwz5dlxj1pDNfS1lVgPlIrrLZn8sZRenauRsZ9rDggetdNaTKyZ3g/hUspCX+XXHauR1KLBI6119ywKnuPWuevYySSRXHUjc6qcrI4m9iYHhQMdKzTdy27DcBsXsK6HUIt2dv45rl71JDuAXFc7jY6E09xZrO21iM+S5VscjPNclqPhq9s33wozAHn1rX8x4XDA7WHUitO11hhHib5x61UKjRE6KepyNrcXBuFjv7XzIvu5Ydq2L7TdHtrUPFaRtI33F/rW3/aGns26aHaMY6UhfS5l6hWHTIrf2yMPZM4W6vbyUusECxAcMAvWpbRNWOzaT14zXYMNLjBcEbgPzppvbGGPhgQTn3odRjVIp2VpdMMOFODzx1qzcxwxqm8AyKT16+1V5tY3MVtgVHY5qqheVi7OSxOc1i5yN1BIa0MTTeZKuSxyOe9T3EmwJsYgDpg9DSCIlgzjofWnsqknIyKi5okio8k0n3+X7EVcg34G7qajUqpARTt71eh2nkDk9qTZSRetYt5XAwa6OxgYY9KxrKFiRjt+tdNZoRjKkHHSoS1FJmvaD5QMVoxuUXhgR3zWfA/GOKtCRCMbyPSuhaI53qxtzNGem1T7VTWQtJ/CfpRdq+07WVqpWkjGcKfXpiuapL3jrpx902mgLxgjrTAvy7D1q4xMSLxwRUUhDciiUrO40rqxhX8bRdOhrJ2buM9+tdRIiyqUYDn1rktXilsW+UHYeSa9ChWUlZnBWouLuXUSNkwMZUdajY84Y4Fc6utkSBMjPc1oxTNdxgLkk+tdKZy2NETgN8zkH0qWScdVJaqcEEyfMwB+tWjbhznO04/CncREChIBVT+FXoUAUBV4PfNNt7EcAsDk9av+WkI5wxHTimIqzRbBnGaiQfLhuamu5gwzyMdQKgimUY2nJ9BTAZNbqT0xVQxlJOoAFaErKyY6/jzWbJGAShbjrjvSAvrcogALila9hwdhB9cVQW2yvqcUiWA37g5A9KAC4vZScxkgUtoLieTLsSoq5Fa8ZOMd+KnRUjHDfQUrjMm2813YuCB2rVhLY5PI/WqwuY1tyAACOnFVZL8rjaCc1RJuAnyycANSPEZNoGNp61QjvSyZIOfSn/bBEVwfwosBcks1A9c1l3lkw5AxzWil6JCcnP0qC5fjpx60CKsKyBPmU49qpXdm7EsqkZ55q7DPsbLHj0zV4SxSAFgCfQGhjRi6ZFKJNsgINbhHkkBgCKlQRLgnAFNmKPhWYMB0pAIJAVOSpXFY+pKRA3ljJPtWhIrBcqAT2wahYSSgoqgnoc07DPJdXgupbxnCNlT16VmrqVzathwwx617J/Y8GSZBuc9gOKoXHg+0uWDSRLk0rCPPLXxBeTOsaIzEV3uiLPKqPICpPVauWvhS0tmxFGuevSttLJY0TZ8v0p2Aq3VhuVduMe1Z/8AZU8kmN/y10YjVkwTwKd5fIAUDFIZjQ6UU2s3O3irX2BRhtuattIyybRgg1ZCsADimBn+QI+cDFL5yjPr6Vcc5IXHXpiqzRAyA4osCJYnyFIUfSug0+YhBhFrDidVXDDpVu2dS2UHXqScVMho27iQFfmIzWHdyZYjbk1YmmULgnJ9KzriXZnJ+duntXLNo6IXM67jBBzgGudvYMZIQcd62bqbYSWO5vc1mSXaYIkwSemKwbTN4pnK3kYdtrK30AqqirA+Acqeua3ruMSkmJwo7nFYdxAw3Bj34as7G3NoPO1x8wz6GhFUrg4xUK/c25/GoZwUACtz3NUkQyW58lFK/fZuwrNYqTwuSO3YVKWCoxB6nin26iXOwAOOo9a0sRcfEpWME9fTFXYokYblYj6VDAhDEjoOtTorBt6depFZtFJi7JgR8u4HvUnlyg8Y5pROCAOV+lIs4U/Ly3Y1LRomOWO4ByYVI9c1ftYS/UAfSqMb+cu5gT7A1p2ShNpVSB71DHc27KJVAwDWxE20gZJNZkEwQAMvFW45gzo2MD+E1UUZyNZGD8DhhUTXBQ4OR6mj7u0joe9RzOsgKnAPrVy2JjuQXNyGGQ4GKhspf9LVt2earzxugwPmHf3p9hDIJwwUge9cbu5HdGyidzcJvslcdcViG62OVY1rRvuswo646Vg3cEgkZiMAc4rWcboyhJJ2ZMJwz5xUlzYx6hbFWHOO9ZaSZIOee9bNjKD1xUU5uLNKkFJHE3HhVYpSSDktkYq7Y2X2bCnlR2ru3tFuE3Ac1iXWnvAcBScnqK9enUUkeRUpuLI0EJi5AHFVpY06rIAPQGpliHcHA71Tmto2Ozcc9a2MB0V6qEgMMiob7Xre1Xlyx7jFRmxjX5gcZ5NZ09pFJJgkHJ6ntTAG1iK5b5SRnrSojs+6MkEdalt9FQDcpB+natEWnlKCCSSKAKkSOQAWJ9TUyW4Y5Kkgdz1p8MW2TJOR3FaKtG6jeMY7etMCgieWSG47Cnoj5+VuPpT5OHzjI7CkWUImWbac0xEcpkVT82aiMpH3uvpVp2DJncN2eBVSUMAHAyOgPpSGio0MjjjkDtVeS3kGcjj0q3kIwB5z19qmVN8e3afY5piKSuyRgLkYFZN1rUdvNtZsEnoa6mO2TYflyTxiuS8QeHI769j8vKsDzSYGrpt+JQdpGT3rYUrJHwefT1rI0zREtI0ADE4xW3HCIQqqMn0NAyoumAncxbk54qc2XlY2ufwrRSXAClRjuKmMiKDyD9BQIpLbKI90hY57VBOm1MrkYq88ocYYfLjtUSFZTsdcDtQAkSCaMZIwPSlS32OcZ/GpkhMY4HFTJKqZUjP9KAIxtjODyD39KV36cZUjjFRPlpSEbGasLbEqGLcAUCKh5c7MmiR3HA7VNEEjlKgZNSSwkrwAOKGxlQTbhhRyOtSPcrhfU96rqjqzZ6dCPUVI0Kh1AIAbkZoAaz4524PY1LHLJLGEkbj1qwkEbLtPXFVntmjxtJIoAnjQKRhtwHp2qZ41Ugkgg1WQPj5ePWrDJvRQvPrQNDfJDufSrSWwSPjOagUNGMd/5U6OdjII8nJOKmS0KjuVZJykhyQO2PWqdxcckgln/lWnqNj5QMij5vesCZpd+1Vx6mvMm3c9CCi0UL9iWIwS7VgXStEeOX7n0rpJkEcZJbMh71i3UGw7sE7qzLMr7SUb94TJnoPSkkRJULbdzE5AHam3MTDJz838qox3j2rswJ2HjmrQNCvviBdlwCeBTW+f5yOMYxWmqxX8JK84HArPa3e2YKykqaZJSmi2qMdAaImMcgK9SeKuTQB4sdM+tQmLCIVHzA1pcg0Iyrxhxwx6+9Sk5jGQFxVVTsX5unpUsbKylMnj1qWx2IpVfBVe3OarRRu4IOS4PNTGVo5Om5ScEZ7VZWIKyyJ91u9Qy0XrG2QKC21TjoT1q+reUPnHTnIrHEqx/fbBz3qcXAbhcMvfBqCkrm3BcZxlsj0FaNifMiZSfmjO7n0Nc/Zs+cDoP1rftkxskT7w6j1pphKJr204K+VJ+BplyoTJB4z1FVmYcDOP5immWQ/I3T1olLQUYkZkbzPuk/yq/AeBu+UegNNgiAXPWnLE8j5J4HaudnQnobtjOqjB5qvq8h8st/D6+lMtW8oAccU3WGaSzO0ZBreLujCas7nNLdMZS3G3PatOxvMOMHmueeUQnBIGamt7kbhycj0rCcbM3hO6sejWN0HXqKvSxLKmMDpXHabf4IwR711FrdCRea1pVbGdWlcxr63e3+70rm575obnO3PODXf3UAlX7ornLjSVLk7RmvRp1bnnVKVjnhqTzMUjhbngZ6VOtsuQWIBPOKvyWIgUkEf4Vkz3McL8k5966FJHO0zQBdSqIAOO1T/vHCgcisNNbiU8lcVftdVimbaknPrTuIs+SwcgA4qWOMbiu4/j2pz3aLjAyp6mke4TZlR+Q5oAJlWONi3B9KxJFe4n5b5B2rSlm80j5sgj7vekS2dlyFxTGRbQEBOTgdAaQnHyp90881K0QiViXwazZLllfGcg9KAL6wq2AQAc1ZQDBUfd/vVnrK5buPSp4nlZskH6UCLGWwcHnoCKZHY5czO2WPf0qQZSL5sYpBcAgp3xxQBNEisSM9O9WRCGGTj8Kzo7jAyAc56VOLtsED7w5NAE7W0YORmgokbcE5PX0rMe+mE2w/XPar9mxuQyyNgn1oAfcIDGNn5iqdt55chhx64q24aJhGwyPWpSAqkgj2FAEbyZi+U8rUWZZCGx1HNV2ZxMc8c5q1FNggsMgd8UAUriWSB96g4HQCprXUzKNpUg/wA6tSJFKNwAxjv61UeMRkMiEtQBeWIAeYc5PvTftkaPtY8DioftbGMpsIPSqj2zPICXB54xQBbWRJpsg9KeVUybueOBUMNsUlUJ171Ym3KcKMmgCEzeW+ATnvVpPnX5jx2qtD94tIgz6mmT3BVi2TtoAusoicAE4709ZVT29qyvt+QATTDc5brQI12uVKnJpiTosodfWsj7QWPPAqW3LSPlMH2oa0GmdZKgmiVs5UjisW8tQ33V5HetyJiLOMYwcc1k3cmwnbz61w1Iq52Qk7HNXVoYyWKkj0rHvGZeq/Meg9BXRzy7yy8gn8qx7y238KCT3Oa55RN4yOcuF3AgHdk1jXyfMAO1dBPGySlEH1rKu48uSB0qE7GttDKgvZLWUFSQvcVuWl7BeIQfvDsawZ4fmA/GoY3eCXcDg1qZtHTyQruwBnd0qMW5ycAbRzUthIsxVs5rVS2VuSMZppmb0OdMbmbBHBPFSiJirN7VtS2SsdwA4qB4BHGeKbQ0zGEamRuMg9amkuljQCPopxg024byskDqMVkCfM2OTng1NizRL/aVKAYYdM1PBGyqvPK8n3qjApDo+fu9a24tqlflyetZyRrFl+zCjD5IJ6YrdgYRqM5yfSsOEiN+BweV9q07Z3KjsKgbVzSzuIxye+Kuw2ylNxU/jUFpbsWzwPr1rSRCUKhjx1p2uQ3YgKPgKgpBHMMcY9atx/IeT+FOklJ6Dik4jUisrlDjOTVm7cHTnkcYCjPtVdvMJ4UAVX1syNoU6xybTjkminuOa90831DVd16+Djnikt9Y4Pzc9K5bULjy5nG7LZqvb3pBFdE6d0YU52Z6jpmpjC/NyetdppN+GIG6vG9L1A5XLV2GmasVZeec1wyjys74tSR67CBJEPWq11CUGQKp6HqSzoBkZ9K3JY/MSuujK6OOrGzOJ1OSYhlRMdulcRrFpdMpOSDXpOpQyIW2ICfU1y17bXc25WKxj6da9CGqOCe55TdPdwyHknmrmka5LaTL5uce9d0ug2r8uod+/FSyeGdOeMBkXd7VdjMs6VqlvfwrtIbjpmp7p8ZJXYAOMGsu00qDS3ZoQQeuAasNeoQYnONp4zTCxXi1NIrpfNO0ds962pNWAt96j5R6VzlxpqahLgnB9jirsANlb/Z5WyoGASc0XAqXGuK8rLnFQf2gjY+cHNSSWcEj/KmfUinQaZbAElcDsaBWOhWISDcAAB61JgJgjPzd/SoXuNkeGQkHniqi38rn5YWA6VQjSZWIyzjB6U19kbnamSRjNLuSaFflw9N86OIfO20r60AMWCV5c7cCrSxPhieFHHHenR3gVQzMu09KkS4VxhSHB6AHpQBQ+yB8kBhn17U9YG27Q53DqatpcotwFlXg96ku3hQB4iBn3oAriO4ZFy2APXmpY98cZL4OPalS8IXHXvmrKqkyFlABoAzpJQ7DC/jinj7p+Utu6gdqsKke/b0PvT5jEEBHHtQKxkXNy9scbCVPpSxvNcDO1gMcGrSmJ5MHj0zVtVSNQwKkelAzPCvwrbtx71YiwuMqD9KWeVShwfqemKqRyyAMgP0b1oAvCYi4G1MjuRU+4PNhh8uOKhtXkOFYDnqaknZV4Gc0CFmAVPlwR2rJv3aOFjgH2q3lw4IJ256UzUIgQMrnjpQNHEzam8c5GTxSQa2fNww/Wt06bC+5hGjN6YrJv9AM+BHtRu+O1TqVoWP7Xg2gbwSabBrz21xleVYgVzc2gajBJsjkDjPU1pWvh+8eSFJG+6QeKG3YEj121bztNjdsBioNZN91O0A+ta0K+TYQLjoorH1GRV4DYrz6stTupR0MO4kYNw23FVBdAghep9akupdxIwPrWZJ8vPIHtWady2rFqaCIxED7/c1hX9mUDMOuOKtG5eEMckjtTFu47ohCCCONpocRxkc7JECnQ7h2NULiIInHJzzXT3VkHO5B+NY11ESGXbgilF23Leoun3JRwtdPBcBkHzc1xqAqePvd62bG5KOnOQeD9aq5Djob7yARls8d6z5pwUJJ69KsM2+LPrWRqEu1Ng9abZMUZ97cbpCqn7vNU4oj5mAM55pGVnaTPc1ZjBjcsR0GBTvoUlqWYFwwJ/i4rXhjYsrDnA4rOtoWlK46r2rorGHcoHTByRWL1NNiW3ty6DjpzWxaQov38j2NU4pEh+bsTjntTzclnwrZwe9NRJcjWDmMEKd/oQelWYZSeuRWVCXxluM9fetK2CDnBz9KGSWt+ckc0eZgdB9CaeQSAVU49zUEu/1QH1qHsVEGYk9SBVXWPn0K4UJk7fWptuT8xLYp15GbnSriFAOVwOeaiD942kvdPnvUC32l1JCnJrP3FWFaeuwPZX8sbMc7jgEVnRgSGvTS0POb1NLTrgg11GnXW5lAY8VxsP7uQDB611el2rsisAV9648RFbndQbPRfD2otHIozwT1NemWc6zwAk8145p2YQvXPevRdAvS0SrmuejO0rG1eF1c2L6AMpAGc1z02lb5Czsy+tdPL84FZ9xaF87mAH1r1qcjyJx1ML7NbQjaW6VCyQSfLGwFW7mxthndNj3zXM6lttXYwzk/jWvMZ2NOWyXY3lkE4x1rPj0hpJfnx649Ky4PEUkNwqyD5c9cV22nXcFzahwASfammSzn2hWAYCh3B7cVXuIpLkgqu3HUGty/sNx8yNhxzgGs5GdwYwAuDjPrVCIYoGgtypjBc9DUJtLhUDHgZzjtitaXzFjVZMAdN1QXOcKAWbjnFAEi+ZMdykFRxtqQ2zJ90ZY81owWKxHA+p9qmaaGIZbkAYzTEc7dGSPCENknORWfeRvd2xAmAPQnPStu9uoJ22IRzxkDpVJbO1WNmlztHUZ5NMDnLt7uK1W1hn3seNw7V0Oh2ksVoDLKXfHNRGyt9wECnbnIJFacFpIFGH2sfSlYB8V1E8rxyR5IHBrImvgL0xbWC571siJIXLyHaO+e9Zd7qFiJQDt3Zp2A0vtUEdvnbkkelMh1FkQgKVHaobXUbafCIgb0NTzrHKNw4UdqVgEEouBuZmB9angZCpBbfjpmoYY0wMZKnr7U77H8+5Dkj3oET7I94JwCelSJCV5zk02OASL8uVYdc1G0rwyiJ2JDHtQMlurNyMjGD+tRJBhGGPfI7VY8yXIA+6PWmPIvlkdAeoNAiBJ/srhWyd1TmfzeV4PaqY8p2271x2yea0Le3EaKzlQtMAjCkKWU57027ZJGCpkHHpxTrx1gjLowPHGO9UrGQ3LNlyP9k9qAGRJGj5YjNPnMPlb0AU9M1alt7dF3HkjvmqsJhdvLRg5J/KhgjNjjElzwMg9607RIzdRoq9WpLmJLf51H1q7odu13dhgP3ac5x3rOTsjSGrNm/cQw4PYcVyN/OGJ5rotZ8zBwMjFcfdwyOW+8B615NVtyPUgkomXcNhySWx7VTklyflfmrEwljDHO6suaU5LAce3argZzY6WSTByQfaqM8pznO09iKRpxu5ao2fzAehFbWM7lq01RWIhnyGHRvWpLyEbSyjJNYlxHzkDp0NXbG6knUwu3Pr6VnKJpGRWeEo3bB4pbcFFBHPNTXYKTY7Dv602NV2k45HIqDXdGslyRbkE4IGayruQvweMnrU7OAMnhX4NQYD+uMUxJFeOM7snoDxVyC1aSUMc49KnghLMTjgGr4EcI5wCe/pS3HoiSC2WIA4INLNqS2+0ow3dCCe1YN/q8s0xS2YrGOCfWo7ZFZlaV9x9xVKJm5HRC+87BDEH0PStG3dWAJIrEgKK2UIx9KupJk/Kwxnr0oaEdDBMFGRgfjnNaENxxxXNpOgwzyD8Kv288b4+bIrN6FpHQpM2PvCmM27jP6VDBImBgD25q0znbxgfSpeqHFalc7vU49qmgEjRyIOCRgHvVd5+cHP5VNaTAEnp71jF2kdFvdPGfGGiywajI8s24knk1yUYdJCVGcda7/wAe6Yltq0k0lw7M/wAyrnOK44SxKMEAY6g16sX7p5k1aRpabpq38iNngdRmu2srWOBFVRkAVzfhuFmjMozszxXVIkjDltorzcTN3selh4qxbjGSMAfhXSaHMySKM1z1umzAPJre00HzAQMVzU5e8dE9Ud0F82EFcg1m3ljcyg4lYD2q7ay/6OuTzVtJFbAFexSeh5FWOpxFzol07EtI5U1l3GjpAxM74zwN1ejXCNtJUA1yuvkSW7JPbkjpuA6V0xOV6HG3tnDDgPjHY1q6ZeRRwrF5gAA4rHn05pIiryvsJ+Uk81Pa2P2JlEkgI6gkVaRBsy/aQN8coJ64PcVBF5rqSVyevTpVW4u3WRUjbJ9PSrwkkWNSOR3ApgVReSS3Yhm+6vpWpsj27icDHAqrDpjyyb1PXv6VZns5I1yGyR15oAmOofaBujYA/XrWNdXN3LNtyAT29q1Xs7Y2/mRZAXrnjisWbUYbdjtKkg4zVEj4bN1JbLcnPHrV6G0aQkuxIPPNZya5Ai8uOBUT+I49hIZR9DSQrnTpbxpGM4AFVb7VrXToiWYEgce9chf+NIbW3JMuXx8ozmuKvvFBupjIxJz/AA1VwZ1+reJnl3Ss+yP+EVxsmqXWoXeIQzDPUVb0XQr3xNMJZSY7cdPevRdO8J2emxqnlqzHoancaOb0/UnsbcEwuGIwS3QVr6d4gWechlYqPQcVuPo8Mq+TsTGM5qrZ2cOnuYpI1+f0o1AZday4dUs4nYnr7VqwXLPbBimJMc0y3uLSN9ixZI6kjgUk93AgBRwjDP0NMB0N9MgKrGTzjPrTis0tyjbcLWJL4iggjKvIAc4GK0YNcie1jYSKw9c0XQGpPKqnhsMO1AMbwl3bPpxUafYXBkeQsSM4BpQbV5BsfMeOcHpRcLGBNo0lxetc+a6AdADiryfa3CRbiUXrzW4j28wMYxgd81AbPE5ZZACeozQFigDIJQC+YycAelW2RI2AAwnqtTXFsoj/AHaB3xnrVWKCScDcuwryOe9AFPUpLuM5gj3JnoaZDHdSRhkjEeepFa4EgQCVVJ9TUD3UMKsWIUj+HNFgHRRPKojkBZumc10Fv5Ok2IjL4c8tXN6Vfx3epBYxuVBlvrVu9S51K58qLO3+JvSuLFVeVWR2YanzO7HXPiK2Mmx3GTWXdXUMqM0TBh1ytQ6rpcFrCSBvYdSTXJyXgjJ8mQqVJyM8V5aqyvqel7KNtC3qE74YxDDfzrm7i9+Yg8Y4NXp73zFIc8+lYVxcp5zBsEGu2k0zjqKxI90pQk/pVdbpM5DYz2qrdSBVypzxWO0sjP8ALn6Ct7XMHI6bzN+dp4pgMkEqyKe4rLs7mSNgsgI6YBrchCzrlsEipcSlI0LhPtNus0Y6feAqgpZRg/eXnnvWxp8QT92T8h5qvqNiLeTcoIycj6VlKNmbwndFB5Q4jIB65K1ZRflHXrk1BCAWO5kHPY9a1oYAYjIMDjFS0WmMicQxbmOAetYV9qjTzMgYiMfrU2p3DykxoflU4OKyCoL+3atIQMJz1L0JXOVYfjV1XbjGMe1YokWPGV/GrEU4LZVj9K0aIUjajnCAYHP1q4k+/wC8fyrCiuQ2ck1ZWVjj5/lPYVmy7m7HND/Ecn0FaFtLkZSPb7muVN3HbYJbJ7DvSLqdxK+1WKL6VlPRG1NXPQobiRVGGjH1NWftM0ig/u2+jVwcFxIACW69Nx61p219ICNrDHc1xyqnUqR1DSMPvhgf0qW3nIYZFUtOuXnUByCD3rUS3WJ1ZlJFKOruU9NDiPiQYxFDIEVJccSMK8ttbeS8u1jB+83Jr2f4gGB9FHmIGAJxkdK8n0/5p2lVQgHAAr1aT9w8yqv3h3FosFjbJErjAGDjuasJfMxIjiyPesC2Yo43ZYD1rUhuI3+UP8/pXmVou92elSkrWNSO9mXHyfhXR6LfpJKqOdp44NctG7g5ADetW4rtYpVaRWBHeudOzNmrnrAO21BHp1FZ6aiYpMHkVl6V4mtZLbyppApxwSas2zW9xO7B1Kn1r1qFWFtTzK9KV9Dbg1SKU7ScZ71W1NoZYWyAR35rPutMePEsT/L6Csx5rpQw27sdq7o2eqOCSa3M2a3hN1lZDt/u06W3d1C8ADofaqpiu2u2cYC49Ksyah9kRRNE+w8bwM1dybDzZo8ish6DB4qgdTt7O6MLvhs8itTdFNbt9mlyxHU8VnW+iQW9y11d/vZG5GeaLiNiDUbZ0VFkb64qxe7fIG2QDjOc9aqSvCIlk8pUTpVKSyu71gBORH1wKLjscPrPjBr/AFqK2tpjDahwGKnrWldaJNcyh4pH2MAQfUV5xpVpJc6hErDau8FjXuWmT2qwxLLICI1Aqk7ktHPJ4TLW5LO3+yM9ahm8MRrEdzsGXt613089sLdZ8jaozxUAkhvbYXEMYI75FPQk8e1XQZLmULBbyZXjJFWbX4eXMkCTPKMnqK9UeFVjBSOMM55Y03C2x4bexHI7Ciw0U9L07+zrCO3RQgVclh3q7HJ5sMiqXVhwA1V2+13LliAka8is698SGwkYPDuHQMKNEBas7S+MkiyXGIyflIrQj00wlZJp/MArB0/xEuqPujAjEfbsatSa/BDIpx+8x9zPWhMZpXG15PKSFQjfxd6g1LSoJNLaItscDIYHrVa71z92q+TsR+rGoLuK9niigSZRG2C2TzigR55JoF9fXbLFIdqtjcfSt208E30USs2oSJj+AV3KaZaxWqrHFtPBBHc1JHLI25ZFVZB8q/SlYDKt7OW1tWieQFgMZbqadYWK4kzK6A/w1pxwYV1lbMh5DHnFULuC6CebBIqFemT1otYZbGnzRwlrWUhh0Gea4zVrrVEuHZruYc4ACkCrdr4uv7bUGjurfcF43qKualrNpLb5kR2J5U7eD7UrhYw9O8aXun3EcN22+LoSe1eg2mqWup2SvbyKWxzhq8R1QXN3du1vbSBSeRt6Ve0vTPEdmq3FsjrH1Iz1oUgsep3t9dW6DEBkXHWqs9m1/aCVmKkjGB3qbS5Z5LCNruMl8YZT2q5bIsspQsyqDhFxTbDcreEtIni1GRVYlG7+ldrceVp9qY1H1Pqam06yjsLIsOJH5JrH1eYsDjqQc5rzMTO2p6WGg7HLa7dGQ/KSc9a4W8++QMhQeua6bUpTITuyBnn/AOtXOXfmhpFJO0Dg4rzIO8tT0WrKxmvIXULn7vY9ao3sCsA68HuK0ohH+8LL85HGazLiRhIxPr+VehSXY8+uzOncuACePpXdeBvCkcx+23sW5SPlVh1ql4N8Mtqt+Lq5TFnGc8/xGvUp54LNBCFCqowu0dBXoQjocMnqcR4u8LQkm5tk2EDoorireU20vltkEHvXsF2wmi2sBjHr1rzPxBpwhuWlRcAms5qzLiy5p10JJAM5PfNbd9bJd6awHJVciuDtrgwyZzzXX6PqCT2wRzyTtqLXKTszmIYQlwCVOM4Oa6CRjFagNwG7npVAw+XqUg2/x8fSrOo3KqgiQkbR3rNRuzaUtDKniDO2Cq57jvVOSAL8vGaneZcZBx/Wq7XfJ6fU1ukYXKc6kDJHC9qqNPtYcnB6ValuMsyng/zrNmyTwOaZNy9FccYB/WrIvHKhYyAe7VgeYyk44FXbMy3LrFEjOx7CplGyuXGV3ZGpE+84BLPn7xratLToMbmPJNNstMeBd0qncRn6VqRLLjhSDnHFeXXq30R6dCnZakkNmrAbhuq9b2igkBMDOcUWqYGW+XJ4zW/aW6kDJyPWuLWR17Fez/dOOMfh0rqbIieLDdazFsQBn/Jq/Z7oiFxxW9NOLMKjuc746sS+hzgKSwBIHrXjukW9zHcMWt38nHzEjive/Fke7QbhlBO1cnFeT3Goxx6OI1blhgivXw6vE8uu/euVoT5z+Xu+XNbdtb28ZBC7ie9chpt0XmPI9jXR290VkULxkYrlrw1OqhO6NdyVA28DH50kZlkJG5femtb3EqK7MBiiL9w5VVzLmuJwOxTNFLKJQrSEirFvevC+ItxVTxjvVXe7ckgnsvrVbQtQ+0ST/IN0bYKmhQla6G5rZndWOs3BASVTsPY0y9uijiTAMXYg1HYmKXCyfePX1FbcdhZSJsJ4b9K68NUmnZnHiIQa0Odi1KLcxMZ45xjrToNVjvMkRYX0Ze1aV7aR6fzOAICflcgYrMe4sI5GxOFyPlUDrXrLY8pqzsTxfY3djE0QOOgPepXLxRYMaO3asWLR7Vb1bsO4eU/dU8VuNb4RQXyo/u9aaEyMLa3ESpNhT+gq5BtsU2xkOOwFVnijaDJjB9M9RWPNqot3XcfLI4xjOaYHlXmLZs2F2yA8gjFNn1qd1CrMyjsM16v4t0PQpNMnuryFYJFyQU615XaaLpt5idr1xCGw3y42jPH1pNWFcs2XiDUUtjD5+V/2jWrYeKtVz5EKl1HoMVZh8G6BH80l+5Rh13YxW/pWmaJZwf6NIW5xljTVwMG51PXuWUHgZAxRp/jma2lC32nSSEZB2rXayf2eIVnkZWCjA2nrVee1jnhEtl5aO/PzLk0xFKLXdQ1xPLh097WDGN8hwfyqGXw2LgJ5k+/nkA1Zji1QMzXM0ar/AAY/rUiyTwRpKEDOpwwB600IfBo9jpq/ulO89R1zUtxp9m0yt5YZwOmO9LaXqXAMiDeAfmG3BFXss0h2Fcdc45pqwGDq9lJqNqsELlT3GORinabZSWlzHNLdmVEGGUnnNbLJLCWLj5GB6Csue32OqrE7MTkEGiwGneXKTW/lfdYnKYPIFQQKsMLtC5kdDuLOck1y9/b+J7nUEa2hQ2u7BO7BxXRLpV9LGBBKsDIu7B5Hvk0rgWdPkbU5W5CRA8g8GptT0ZtgENwMryMnIqm0bxwmV5lPHJT5ane8a2t1K7XG3OWOaBlGHw8xYKSD53LH0pt7p01sETy45IkGAp6iq2rte6hbQtYNNbFTuYrzn6VO9tc7YZLmWR5FXIweR9aXULkcVg8VtI0YRmblgeoFWWS2vdMje2uTHIg5QDPNSte/Z2gjKr5cg5cDiqV3MkBGx9u58YTgke1D0Gi9prXBtXe92+ev3WHCkVueHXW/1HYpVinJ44rmJbqVbOM+XyH2+U/LY9a7rwrAY9Ne4aMIX6YHWs5ysi4K7NS/nCZ5A+lclq13w2QPatjUrgcnt39q4vVLjduAxjPTPNeLiJ3Z7NGFkZV7KWOdynd/e7VhXJaQqrFju/h9quXLt5jCMDb6Hqapl1aM4Bzn+LrWFNGs2Z0sbxydflH8qyb9sXK4DFSw3bRk4zzWzKAB8vRuB7V0Xgy1je1vrxo42PmeWrOM7cV6uGjdnmYiVjtNLudMXQrcWy+XBsGFYbTnHeqt7HFcBdpGxOSwbtWXqFrcz3MSIwbIOCvGKhttLuYQTJdNIFOSoHQelehaxwXNKVfLtwyd+FOe1YGpwLcQuGGMA4rQvZL3zF+zuq2q/eVhzWVPP5gbOcLwKymjWLOJvYDbynIz2JpkGoG2mBQ5wOK2dStGueg2j1rBlsDEwyDgdayLZ0MupxuVuVwGK8jPesW51gTzFiThqzGaZc7egPP0qu0DbiAevIqkkJyNFpVfJVzUEkmR8w/GqQZo+Dmn7yV+9xTsTcldzjrketVnlOT60Ek8Dp6VqeHtFfXNVSAnES/NI3tSbSV2OKcnZDNH0C91uTci+Xbr96Vugr0DTtJtNIi8u2QFiMmQj5mrY+yw2ltHbWkYWJF+6o61SMDEgKQcdmryMTipTdlseth8PGKu9yIswyVBOepIxVy3TzGG5T71AqumfMHGcZzVyBVyFQ7DXD1OyxPHZHCsv5H0rTtcZCelRQJ0DcMePr71cRCp3KOnetoIykzTgQFMHtyDSsAhBxTbYBcHseakmQtnIyRXVFaGDeol6i3WmzQvgqyYPFeHeI/D8ysZbFw8ZJBQV7haSgqUdenWvNdV0y30/Ub6Iu/Lb1GeBmvQwj6HDiV1PMIGktbkJICh6GunsrtQQ3BxWPrMSpPkuNw+6PWqtpfFTszjmrq07mdGpynosV8GiGGydtPtH+03ZjGQzLkGuQhuXLcPgDmtTS9TePVbRucF9hri9lqdqqaXO3htiCrcGTGCMViaRay2njG7smICTR+YAR1rtLUxMhZyvmDgH2rG1q3Frrmnamp2AN5Lt7GtqdK2hlOq+htfZzZHzYkLNj5t3ce1aNvebB5jn5T1PpVQyCRiZH2op4PqK53xDqK6dIFRiqTjapzxn3rT2SRl7Rs65tc0bVd+mNeLvb7oPI3VxupWOoJIdN1GeGEkkQSRx4Lr7H0rA0eDTZb+NL2R2MbnCIPkJ9d1egRyWXiGUi1k8+508AGMjIC+gat4GE1qZem262Ecdu1wzyg8EnNX4pvLMrSTAOpzgGnrBHA/mvGqEnnnJ+lNZUkPnQ2iNk/xGtTMr6hrUSQhlRnlI4C96qW8kl26FtPcBhyz1ZlujE6rc20USE8MvODVyK4j8lpjdJg8IAePypIDk38U2ur6gtpDaNegggqSdv510cFvocVvDHeQRqSMtHGvyj2rHjitNJgNvZxKqgYLY5I9zWLd3zOjYfaB2FFwO6Nn4ZuSX3xbOwPFU7iw0klo4JolJ5CA8V51LK5jYo33eeayU1OaO5zHI4z95smhMLHqc2mG0iLARoOqnPymoRqkVmqmd0gdR/Ec7vpXNmSfW9F+yyak0UoIIA7+xrdsdLtLO0iN3GlzNDjdMxJAzVJ3EaJluZShtmQGQZAcZyPWtCN44Yxuh3sxwxHTNQ3DQWcKTyu8zIN0YhH6CsfT9e1y81Utcacltpyn50x8+PWncRuqFF9wwRf4kA4pXvPK1H7PFhVcbssO1W4NR0ZsjeFLfdJHJqpcS6e5MgfdCOHc/wAPsKALn2xpkcQgSFRyGGPyqk91cPdgRYRQuPu5xU0Tx3FoJLNN5HCkelRytcmBgYVD91TgmgCxBZRlS+fnHzMSf6VmSWUzXW/7ZMkOCSvrT4ryCzkRGkdWK7tsnJHqKistdjv9TktYYmAQZHmjAf6UhlOXT4Le5R3vHclMfZyfl59KnWwFq0pyqRLH+8WTkYqtrttqVzfxXNn5PmQdQRgVfskuZYP9Jwxk5Yk7lB+lCEUbm01K8s7SXSdSFoidVZODWhLAy6c7TStHJIm0zAffai7aa0t98jRSiM/ukQYUDvmqV1eWa2iSNM0CspLRyNkKfYUMdii+j3Ftp8e7W5uX3BPKyDVk6FH9pSa8vJZYjjYm3bg1etZY5o4pRvlgI4k/u/hTbu5tLDWYp9QkmYPwPmJVB24FGwI0F0yHUWjjt43kz8uT2rt0hXTdMitYwf3a4zmqnh20RIWu1LMsn3WY9qm1BsjJccVx4ipoddCnqc5rFwfmVD7muUugH59+prd1BizMRhTWLIo3EkEtjvXiTbcj2IqyM17fIYlwygdCOAaoS26gYfnnqB0rWcqWABOQc5PaqF66qGIOW6kVtTMpuxz905EpiAyO1d34SsVh8PweYBmQl2A6muVsYI5hcXkh+WNdqgDqawJIvFVsd9lJO0JyV2HOB6V6+HVlc8mu7s9amDopZJvJQDAyMkVmfaZoHS3B3q/O/wB68tk8S+KYFKTTzgE4O5Krt4k1/btaWUDG0ZTFdTkctmelTTm2uH+1yGUOeAvQVWa5tbmVkhZ2VfbgGvL7jWtTnXZNcPgdsYplpq97Zyb4p256g8g1L1KV0enMIUj5wWPpzis28WF0aNcEnvXPQ+LC6sk0IDH+JaiuNSa4w0TyepIFTyormLFzbIrbBg46+9VpESE7uCMYx6VQe+nJzggrwuKrPLM6s5ZuOxosFy5MyEY4qqFBP3qrM7ZyTmmBmHejlFcvGI54avRPANiItGlu8fPM+38BXlwkf+8a9p8IQmHwpZ4T5ipb865sVpTOrCq8y1K7pg7cMScYb9ajQM75YkqV79alu42HzFGGe/U59qjgUqVxJgEde5rwZbntpaF+C1DqMxkA/jU39nPBhkGRjLev0qS1ABXDD8uTWzAMkAr8tWo3E5WM61hAVgOT1BParcqbU3A9Dmp5bTADxAkjPHrTI8PEysNp549K2hGxhKVyS2k/d9vSpZJQcknPasZLwRsQx+6cUhvgz4DHaTyfSto3MpFue5S0uAzOApHJNcd4vnja/tbkg4dChx0Pua0by6N3crbrjIPJz2rI164tCVgaZSUHA7E+me1deHvzHNXascTqmnoxdgSSoyTXMSL5TAqcH0ruRPbSxI7YkZ84QZGO341k6ppttEWeWXbgZVAua72cLMi0v8Ebzg+tX/teJFljbBQhhWM1nMxLRwyFOudvaoRI6cAke1ZumnqWqjWh7bp2sxTRRzb9wMfQetZ+reJba8tXWEgyg5RT6j2rzfT9durDb5TZUHO012Vhe+F9UVb0zfYb+MfvIHGVc+xqeVlc5r2fjO3a3C3z/Oo5VRzVDU9asNci+zxrIrLyqsK5nXbiy1G7Mton2VwcMF+63uDUCzR2jr/pLSOw+/6VVhKWpoWd9cQmS3RmjZmwBjqPWu28M6nZeEYJjPerPf3xDCJf4fTNcFZu+p6pEluQJegduMmuxs/Df9nam9zewR3EartOxgXYn+79KFEHK51Gm27zuZJrtd85L+UxwFz71OljLBJIMgRk8fNmqVzY6dLHbRu8kLs37qMnkfWrd1qD2FixCLKyngEcj6VpexmMktkhZvMOUxnc38NNisreZViWJULfMGJ6mktbh7qFZLrY7HnDcYFTzxtfRIhLWiIeGjHLCmBwN9rEkgcxI7t32LXOXk+pyt8tjcEf7pp1h4tn025WSJFcHllI6ivU9F1zTNaskuoZEEoGJISBkUkrk3PHnl1SONWktJljHJJU9K2fD+p6Yk4+16fI5zwyqSK7/VtZtIreZUiE5dCihUyM++Ks+GNLhh0m3BhjWY/O+UzihIdyGyt9OuozJHBlT91SmCKfKRGVga1YJKRnBz+ldPHZw43IqgjqMYxUV5Yw3Ft+6keORT8rjtV7EooRQywAifylhGPK38FRVa4Gm3c0zebM06gFvKPykVpjy7WFBqF0lw3/AE0FSzanYWVp5kNsAvQ4QCkMxNasUudPhWKGNI3G7zNwVkA9PenwHTNNsU/eDaRgxyjO41NHq1g8/kwI0zOdxWWM7Yz7E9KvSxRXU0aPawtG/qwyDQxHM2XiRoZpf+JdOkG7EUkYwrD6Vq20F3d3jveXKrbgBooUGT+JqW5t5LP5YYbXyI2JJY/Pj2FVBDJIks+n3yxbiD8y5b3GKQzShsLa6m+1Rsh3nbmTjFPvrOaGZJbeGGRF+7kjP1FYASZ4Tp1zIxRyXMg+UqKfZ31taWq2tvMYWVj8k5Ln6g0XGzeeEXUKCYRiQ9R0z7U2MiLen2dY2Q4Azwfes8XjgA3CeZbL82VHOakttYsr1g6Bi4z8jKRg+/rV3TJZgaubv+10EbTlS3KIuUrpbmyt2giuLuGB0UBvcH3qaJLfy0eR9sx+9gcfhUcs1mgeczBYlUqyNyCfUUrWDzM4amJIHEVgAWk2KAMDHrWnpejy6u6W8sWxFw0hYZBx71i3Gt2cggtlkM0xfbGkYOSx6DivTNMtItJ0tI2GyRhufJz83pWVSfKjWnC7LTRJb26RRAIqLhVHTFc3qt8IwycE/WjVvEiLMLW3AaY981z9yTJNuldmc14+IrX0R61ClbcpXUnmPuyT7VQll7c4PAI7Vek+Zs4UNnGRVXAZW+YYHtXArt6nWypvJhJCD3BrKvV2KWdstJ1HtW7MgjjBX5vUiua1SbY7Y4wPlNd1GNzkqysibTPOe1jt7ZVJMh8zJ/hI9fWtnSLlrZGjntJIUj+VI1bdvPqx7Vh6V5t/pkUNjL5TjPfDE+pJqxZyy23mqbsXc7ApIFIXn69K9imrRPKk7st3k66lcLDNHHDIeVJAAAH9ay9eW3EaWwIO3lWUDJrNuQsskMskkyNI5UoSW3fQ9qf/AGY9y4Bd48AHdv8Auj0qyTJkUzSunkx73+Uu3RQKyrnToQoC7hJnGAODXTnToxO4jZLjJx8o6fU1Ra2uMlvOSMZK5btj0oFY5w6W+fldTxk+1FtHMjsqkBe59K1bmWFXSN3V0UHJTv8AX1p4Fs1qpjRAx6sTwKQ7IoSgEAEhlI6iqkknm8Ffm6BqlaIyb9r5Rec44qMQkITjHPBzwKQNELRtE+0gZPSmmILkFhnNT7mQ5IDk9+wpVjZlcgAADO5qYuUrxwmSZI15LkAYr6AsrVbDQ7aF+FjiUHHXpXkngfRzqviOHcn7qA+Y5Ne0XtuPLZnXJxla8/HVNLHoYKnrdmBNJ5srMvXr81COV28AHPp0p8sfsQcetNVF/iLH+6p714nU9axqWbqOrD5jn1ya37Uh/lHUVy9uXydpABIO3HSt7Tpl2jnAPetqctTOaZqlSWUj5azbp0ivumARzk9a1gQyjJGf51y/iOfyJ45M4UjnNdtr7HI3Y5/Vr8Q6jOof5QeBVRtV2rksc44Fc3qeqxyajPNJKFXOBu6mq8Wqi4nVLVWcjpIRwD7V0RoswlWR0k+qf2Vbea3z3Uw+VMcis3RNOjurie81aOd1Q744gMq9T2OnSyp5kmZrlTyH7g+lbsiMyeQkrw7R8+F4FdlOHKjkqTcjJjhguLhhawHag7HhM9qbDpSOgb907xAmRXGSwp9vol9p10IbnVbcWkh8xixCtn6d666OyuII0axlt5ZmXKqUByPStLmZza6TPNbmRolX5flWHpj3rk5dGtZr2ZLyzNu46ESYU+9dwl/raCaO50sQxMcMEfIf8e1Z0um2t2sby6XKLnJySxYD8aLhY4rUfDUNjYtcfbIVZT8ibtxf8q5toZAoco2w98cV6nd6DbW8R82GRllGR+6+5juKrLphvlS3SJPKjXIEw2kn1xQKx51K0hEYI5AwCOhrR0K2iubsGdlCr0BHDH0rsJPCtjbnzpZGw3BIGVWmNoNjFDNcNPHFBjCFOWJ9hSGkaFvYaNfidWn+ybF3GdMDY3oD2ra0TSbe2hjjtr9rpmXfvc7sHvzWdovh/RmtkW63PArCTDEqHPv610ltqdvA0ttpGnhigx+7XaAD15700DKd1rGjwX8a3zSbW6TKpOaLq3guNRiubKSSSLGT6D61JJf3TRqz6EZ4EO3ywoJT61clWS8tygs2trjGRhsD8hQwY2ImF/3k0RjY/ulUZZ/UVejvZCJPtFq6QbcKGGQa4/UG1i3gEZu40CZ2pEvzEnvW7ouqeIPskcWqWcMiqu2OZXySfpTuDOMs/A2lS3v2aWeYsqeYZI+jewqzp/h7S9Aup79pZt4+WKJuA2fWu0srixBW1h8l2iA5Y4aqs9xLq10IbYWbLuKMHH5gUdSSvb2Eo0zbG8KIrbyYlzkH+HPtV3S7i6smMc00U5c/KqHoK2bLTIoowgDQW4Hz7mHJri9a17QtNvvOExacH7sHt61SE9TsvtAlBKsF5wST3rN1XxTY6NHiWZWdf+WcZzk+9edXfiDWdcd4bKB7e0kJKOQeR9ajh8JT7rdL28ImnOTs+c0NisdLp/iC9129u54baFbeBdwkkHT6etP0fU9a1wzLHaJHZRvt+0S8Af7oqjZeHbSxuZFhub6d43wLfbsXPckntW0ut6jDZSHUreCK1jfcuzowHGAB1+tIZcFlqUUnnRavHM7H5oZ0wr+mMVPcZEcfmacy3agkhG4P61wupfEiK8dkgswCvEchOMVnWXiLWb/WEvmtLm5hUBXEQJ4p3A7m9l1G7mgisru38yUbggI3IPrW1cXMemBJbkhpnwjkqNxrmAl41xHHZ+G5bOL/AFjSXDYbae//ANaui823mcPPDHllxHKx+8w+tCFcrvq+ktK8M10ZXU5iUx7Wz3BPcVdQ2dzC88scZ2Y2CMcn8DRNp1tM0Lukcr7MsGxw3oDVcXlhHJHHdiSERnfycAY96EB0NpcWrIoNs6g45deRWgLbTiSzIgduQdoBrlzrcF7cMbcXFwFBKqq4CfX1pFt4r2x84ao0xgPzLGepPY1V0Kxn65c2Euoywqb4oo+cW69T6A1Wn07RJbCNEt7qNm5lDvkk+/oauy61Ir+Qlo3y/dkUDYT7+9bOh6c2q6jC00qtGmJZkA6H696hstIteFPBmm6Qi6s9v/pTL+7DnO0fT1rR1i7dYS0hAyPlFbl7KsKZ2jPYVwfiPUSqOryZAH5ZrzcRNt2O/DwS1MvSYJL++ub+XYQp2Rj+ZrSdAoYgHnjipNPsxbaZBFHw23J45JNSun+j4A4/r61xOnc7OcxLmIOQqjazHBxzSx2ao7BM7TwSad5u92eMk+VIMgCtEhcAovPXB71MqVilUuY15bNFA7HqBxXn+qyl2chu2DXqs8XmwuCOSMAV49qH/IYay5y0u0gda7MPA5a8ixa+KG0qzit47RZnB3M8g4NaEZbW0GpTWiW0IbKsOAx9MDt71YbTIVzBEsTPGufKlIBI6k1bGpXzwtDYQW+zZgB1wv0Fektjz2ULe80+Mu5kIIykcKLnJqCKdWvRbQFlDfK+xflOex9KsxGVokMkEUPlBmdhHjaT2H19aoSzT3DSLBKsKSJvdlGM49KdwsXbyFLK08u2EMDljuLSdx6e1YyaRPeK/wBquWMjY2bBkEHtV210+1jCTPI1xl8RmZuhxkkg1bk/tWGaB7cRo4OY4jz+J9BRcDLlgj0/zIYtIUu3CysclAPX0zWTPo80wR3xFvbAiIwR/wDWrpL6wvrW/wB93cI8sg3lI3AUg9/wqpLNuuZEf7ROwT5ZyeE9vakKxnxaakcawR7WZjtYucEVn3MFsmFDg7cjYD1rUn0yR3V5JiCoyyhug+tVjp0UbhbVPOcDczE9D6UAinb2TX0jx2SK20ZPmNimppd9dQtIqjYgJY7vSr/2Nbl2RQY5QMtzgcVb03Sbm9v4bWM/LM4TaBwo7k1LdlcqKuz0H4aeH1s9F+1SD95OdxPfb6V0WrMLeBnI3Ac49vat60tE03To4Y0AEaBBgelcf4iuA11BCW/1kgH15ryq15yPTpWiiS2sTJaJLKdpYblA7A02402OKFhubdgkcdK6JbFZ0UY2BcDiqmoxhI5WY7SBtJ9a5fZanQqpi2NmHjidssxGDg1pxWhiYFAWXqR6VYtrZTaRkcFVAOKvLblYc85XkGhUmmDqXJLVt0O0da4r4mXElloZuVA3btgI7E11MNwEvfLzwwyB6VT8a6OuteGru1G3ds8yM+hHNdlFq6uc1ZO2h4BaaPdX6/aGbCk8M4JDH0FdpojWdmyWV4ig+WWDBOjdua1LDV9Hh0JLeAx2yQxAy+YhbfIO1b2irbatpErx29ugkHCg8nHrmvUWx5mzOcN9qiSRyW2ltPZKdzkNhsDqa1tOvodXjmvoIpo0ZtrJKeF/DvUiqy3UgkuBDJAMC3jOcD69Cfao7LVzA8ln5aSkqQolARsUxM0p9NW/kCXVlDIoAIlHJ4pYIL+KR5EktLdT8o7saxIvE0EKypIl9FbrwDFH8qt6E+lNfUEv4iY5ZQ3SSNI9xUHoT6U7oDWmFuZY7O6lO2YYYo361nQWb+HpJvJvp3tnbKrIu7FCynT7GNrmG3RkX91Ng7tvofWtHS9aS7ZIWgWb5d28pjj8aLAQnxPZySLarcSSv0+ZcEn2FU5rSDUbVy0rJMxwpD4LewqabSE16f8AtGeQ2TWxIwiAOPxp6+Fr9ZttvqkHkpiVUlXduPuaGBPbmVbJrc2626kBUkHzGslreLRU8u8iMwdt25Yshvw7VZsLLW7u/mF1tt0iywMQ/dufWrGoWdzF+9ti73LDgyN8n4A0wTMV9bmKXONEma3QqFDj/Vg1agzcpBeLcfZ/LYCVVfbkfSt22gv28qO4eFd6HzQq5Absfeqh0ZIrkyXF5bySqfu7MD/9dKzC4zztS81rjTrq2ktZgfkZSpbHrWraW12yrM0KAnpHExBb2zWJiyN8mot5t2MfulHQHOMACtzUZdbuY1GlQW1tCF5kc5YfQU0DMW70G5vLqO/kvpogmUW3AG5T6ZrTWC9CQCKWGKSM42uRjHv71zN3f+JYrhYLmxneAt88sQz5hrVQXksCFLUwsBkQMhfzPb1BoAiuPDtrcPBcWyzwRTYLyopUsR6+gqG5uLZNAu4VYRzAnG376EfT1qt4jPia5vIrewkQ2M4Gwo+N3HU07Q9GsNMtZZbi8mlvVkKzTMpaNSecA+tFiTLt7C4uNLJudeuEwnyxliu4+nPNMs/D2hpGkwvUllAyy/e2t33V0RsbS6voZbpbRLck+UzNmSRh6CkmiihcG2smhSZvmuYIgxPrkUARIklppSvahpdz7kCnble4C1XsJR4gg2QpPZ3YlxuM21hj2NdAYIYLyK9eSWSKOIghCFHHc+lYUos9b1K3nhlmjuYz9+JM7Qe5pgW9UeGeSKwuZrhbotsBWYAvjqSKtajbxwWcEEUweVUIhVlz5i98GstYtCF5cQpaTapeqfvtnk/XtWp9nje3KTLFatD87x7+UB7Z7CmDOZt9KSI263nhkTRsDhg2DvJ6H2rqrfUnsljtLWwW0QJiWLgY/Gmuvm3lnJZyxzK6nCliVUdzmobzQ2WFUGoytcPkopGVye5HbFAjV1u+s7bT4ru8uXZ8HzBFJgt6DHpXHeJr+21C+stt5d+RheBFtKLj0/rXRN4YghtI52/f6gOFmlP6471Um0vVbi6bMdikTDDzu2JTj26YoA0NPLTWq7JLbjjcrls+mR601bHUzEHuJUkVs5LIMBfQim2j21ggX7M0QjzLvAyZSvZTVNfEY1jUFhi0aafa+/zWyEJP8J9MUXAujULjTo0tbaxkc7cGQDapB6g+1c1JG5uJ7zS5JLYvJsZCCwZh3+ldHMJmeabVtNjtZwcCJJyFcdqHvNOgeK3twJHnUMYVyWJ9A3SiwGctreCP7LGqozjexzvZ27n2HtXqfgvS30zQjLcxotzO29yowMelcJbNbWlyDbxRWhz+/ikJLqfTJNdrDrwuNKXbjeX8sAdKmpohw1ZY1O8JDPkbRxXm/iGdo5LbcOJrlI8/jXbXzbiIs8j1rz3xhcFL7SolwUF2pJ/GuBQ5panfzcsT0FYzkuByuFye3aqt23lRzADkHj0xjmr0rqsITBZmIY+1Zd3L/oMxbgsxA/Kq9krke10Oc0Sf7Vc38Y+X5gw966MFDEDgkofuj0NcL4avU/tmeFieFKn069q7COZVjMjHanABalUpDhULE53W+8HaV5H0rybxWkWl+LIb7gxSjeCOcHua7/WPEMNjbkh0fy+DtOcA153qMTau0Vo5McSEyQzFc7lPYVdKFmRVqXNnTWs55H1NCZI4yC8jfM35VtRvdXM9xdJbQpZhcR9mb/CuPtdHfTwsmn6y0XmSGNm2HnjuK6tF1BDDBMEK53vP/eP90D+tdRz3MmaOeO8RZZkdwciJfuke9S2UFltMuoTo8wckqi8jPQAdOPeuka50azh8toIY7pnGIWOWf3zWNqVlNJ4kF4uJbeKPclsjA5HfPoKLDuVbnT7a8uo0eaFV3ZEjcscdBjpVSR7NJzM93IZDkAr95iO3sParUljNe6nAhtobeBx5qiLrx/CfepIYhczzC2tEuMZ8wtx0/h+tFgTKi2Vte31tKz+Y8n303cIPT6VZmspY7aR7bdArtsy0ed2KfNYvqdlb2NvFBaXZbgZ5A9D710PhKwu4pLqXW2jk8o4g2NxxwTiiwrmXYaLHJZypeiMfu8kqMFjXHTaHLZ3LyxXKtFu4Ut39K9V1oafNGBGhRQ4xJ6n39qwLjQ7SFxG88cIZtwiPVz7GjlEmcjck7/ITyrcsm9mA5/D2rqPh1ZLN4lLblljih3Iw/rUd5YaXaThrmAxDZjcDkE+9bfw9MD+IdRa22iJIAMjoTUVFoVB6neag5igJHGBXmV6ZdQ8XabaRrlzJ5ufQCu+1m5Cxvz0HWuM8JRfavGupXhbcbaELHntmuanSvqdUqltD0E5WNznBzwfWuZ1qcJp7uMnceCa35SxULzleormvE0e3TZkBwFGV/LNZqHv2K57RubFm3moidAYxxWhbDCYPI6YrD0a5VtPspt3LxitwZ39wCeopypWkNVLo5XUJms/EHl7DtHIJ75rofNWSzHqRj8xWL4utyYob1Tgp976VTg1+GHTd8kqjAyMnrWXs3fQvnVtTmGvpLW0k06DTbUutw2XlYfNz156Col01YbO4nunkt3POLeXG8/T0rZTRrLV4jfyQFkdizgJlc/Wks4bGOeW1j8+TavDyjKD2Br0oL3dTgluYj6WltLb3dg9wzOBJ5RJIZvqa2bmze7t2N/pyIzJ1Tl1P1rQvTbabo/2q+lZRHxHHHk7h6GmaLqek3UKywSXWxuTFcHiP/d9avSxLMlxHb6UkZgulRAdxAyG9Mikt7SS709L/AEyKWGfOJAowXA9a0dcmna1m/sqeWaV/3bIRhAp65zVJmurCKP8As67MoePbLA0uTnvg0hPUm0vVPtwW31yy+z+UdkDnkSetbt1olneSXEyxMSqDCp8uPpisAXWr3OlwLHptuojchGlkyV9TUdpPrguJIk1dkJQpnycru+tFwsTy2AtovtE093cW45jtkXkt710Gg6MZrKOdpZkU5IhkOCPqayItT8RxX0UbJZyxqvzzN8uD6Grc9zrFqktzaXENzBMuBDKcc+q+1FwLV9p8VpKFtrkwxglpQ0mAx9q5rUJ3k1O1vpJpr60TrDCMKvvn2qO3sNQ1vxAzahcxzQ25C4jbapYjpV+506wsP9DSadMucW8cgUE+hzQGxpQeIbG7VjD5A2LnMku0j6+tctq+o+dOPs0kUhIycg7PfmtOLT9JVZZZ9LWS6wERFHBz/M1f+x20Fiy/ZJFIXIjiiDfhT1Ao6XcNbaSlwljbxbs4ZpOAP/r1WiuLy8WeOC6+xyzEeWhGQ3rg1ia74XuplSTTpLx43G8wSZAX2Arc0i1TU7S182QtJbECS3YYaPHc98UBcs293q9giq+peW0alVjm5DNWfP4n8RwTGU2ytt4QpzuPt7Vvz6en2mR76MSqx+Qv2H+zVu3jjR4PKtQcAkSTuBgfTtQFzmDPdahfBjarb2uMncTvAHooq5HZWk0MxN4sm1/MWFG+WMY6kdz9aox6VK0kzxalI8xbzykYG9l6kfStu2hUWrztCkQdST8o3yegPtTQitZjQIXE8mnTTXAj3xnGT/vD0qDTL6a5v5nt9OkVXf5rqfhQn91ayNP8ValDfTxXlk0wAMaCJMbE966BrnVJo1jtYks7RogRJK3zL77DTAj1GLTdFtrmbUJiFnB2QZ/1ijkHH1qj4Yv9Q1OG5lhtYrOCRcPOB8yKPQfSrc2hQRNbT6lKLydSGllkO7EXYBe1X4jutPO0hR5LOUDsMbAPb0pAS2lvpWj6bcTR3WyK4yfNlG1nI61iwapNq8roqxT2MQys8cIbB9COp+tWZdKuNSYSatcpfzswjtY0Xag98Vek0VYYxbRBNNy3zGI5ZvYYpdQuNuZP7MsI5LpAkb/cCfIVB6Gp9H1HzFLJcC5zkTBY9oGP9r6VBqTabJs0zU0upCkexVmb5n56imW+mWa6kLWO5uY7YgIltGhCqO5Zu5qgN9tStEvAGUqvkkg539PYdKyLki8gR7mZrWMnKeR8pcf7We1Wrnw3pFlazyW1xcWrzfLvikLEV5tPq88eqrpt/BLd2sTkjahLvRdCR2CXsF9q03l6jNc3EWFVIk2xRp6VZm1BllntLSOexgZPNabA3zH0UVe06OGHTfIttKNv5oDiMkAj3NFrpFrJK9zFIokLAPNJJuOB29qAPNb21vn1JT9kv7izdwXWc5kc+ntXaTXTWdqken6O9o0Ue7a5x5ee5PrVi7ku7K+drLyrzkiOKI8KT3Y+1SXNterNbPdSQvB5fzgcMx9/YUh2PPr231uWWS9klLrGxUFc7m9zXS+CNSvJrZI7nerW0peRZDziti61DSLxsBrnNsm6VLSPIk9Aaoz6dczJ9psrL7BNcdJZpBlh7r6UPXQWxqal4nLbltVRncZJPQCuB1HUhqt1ZMpLm3vgGA7+9WL7SNTtLK4hinjdlIV5Twr57Kf8K5XSdM1fz5LmENCI+WdxhanlSLlNs9a8ReLxp1g81uPMk3CMAeoFc5/wsOxvIlhu42gkKc8fxVzcdrqdzZXds4FxGj7vOyeGPoO5q1pPgWHUZlS4uLoFupeIpj8TTaQrszdP19YNaeVclHfg96q614t1K/unhS4aO3DZVAcGu6l8GafokRZLVnZ33RXEjg+WB32jrRZ6Xo2Z7y3sPtEqhTHcGM7HbvlTyKVkGp5za3V/DdETRyOs7DckinBrsLfStWivUhSBIraQZ8sS7iB/7LXUyBnvQt0sBSRQVmVRyf7vtTZNWtLS5e5ks/JaCIgsMsCTxhhRZDKdrooglSSMM2Dnyy+Yyfc1YW3zdT3N7Gj3EafdDny1OeAKpG8udQi83TvLXBOTtPlEfT1q9aX8c7TOwg3BP3qlgo3Y9PegDGm0CC6ujeDVY7R41/dLuyQx64JqHU/s2mJb2Wm3ct48sy/aZGHDD03US29pPc3lxc2TTRmMGRVfaqkHjYa6e0hinsCsDWggkA3YGGHHTNIDWs9JtZojHDbyxyRrlghDKo74asrxdZ2tho9rfxMbR4JRlhhWdfYd6pJcajDc3FtDdTR27Q+SrJ8yx57k+tWPstjqEkNtdZ1KaG3JkDN8vy/yNVcViGHWrWQwNaGNLpzkSzYPArJ1PxfZZZo3MVyWIZY2ypPqKz73w1p7X6S27TwxsQ3lSHacdwParUfhy0uL66+z6OyWsMeAZHxvJ7jPWi4jS0y9vL60t722UOiH940xwhqaVryN/t2pW5vxkyRm3TIVaq6Tayy7rQxW1tFGu1EL5c+5FakltHo1iLW5u22AcMrfNz/s+lMNjHuYbLWI5bx/tMUCMHWN2z5p9x7V0HhyRNFuZXjgcQyoCXA4ApmnWCBledmvEAPJj24HoRTGWW0spLq7LBSx8qFfSpYJ6m9q2owz2ZdWHzgFR3Gaw/C2pWkWsarErfOgXefWuH1fxElndvJCxdZocBT2aua0fXZtL1Y3hdj5vEoz1ojFJWHKV2fR8F/CiSXE86JHkAMawvGM0UWjly4HmHgjvmvOxrbarGLNpSsRcHnjNWfGPiBbuKG2tPnhtFG5lPUipVNXuV7S6sdj4duDLotsUBIUkDmtu+8SWOn2InurhUj7eua8KufFV9b2VpZWVy0aRFnLL1Oexqjf+IbnUFt45RlIFwAzZ3H1NDgmxKbR7frXivSjpBU3CHz0/djuDXndrqVrJcLDPMXTOW4yAK46KO7vXaSQiNM4DtnH0rodG8JteXTQSuyQ8Bpovnz9BQopD5mz0231jTrO0S5hmiUOvlvCjcMPcVnv4ijuxLZ2Nm8KMCPOI/d5rnbXwT9k1RZ7uYS2cQw275T7YHeugis7V7/zLe7NxAq4aILtRMf3j3NUKxF9sTbZ2yzpI23bPLLzGfdfStHTdL1DUi0tl/x6B8LM4Gwj/ZFYer+E9JvYIbmK/mtLi5QsFYHaw/Crzatf+HtEtbOxAmS3XBQ/KSfUetAHUr4eSOeaSW+L7xhlx8rEe1RzaLYSzRRYiAI+VkG0muOuPG2szWSXP9khUYEBh1BHtU1p4h1t7NbmTRxJcDHkx55kz3Ap6CNi90+LTRsaYxRhiQzcjP1qg8s0U8hnuvMXapt4VGAfUkitS3TVrq0ddQ0y0gJU/IzeZk+47Vhx2a6XHPFHcFwR+7hDgrk9gf8AGkO5HJqWpw3K27WBnhlfqrY5/wAKuXV3q9zEqnT4oQg2RoXyyD8Kig3tAq6pZICkWxZN3X8qIrk6bAvngeWSDHcfeJ+tKwyTSLuSATNaWSNJHJmeB/lZsd1zVy+v7fVkkjm0543JyrSpyD9ai0/S49T1K41KS4DTOv7uJDnAqjqS3OnXsTacX8uQYdZh/queSB3pksnuIPs8MSSatJAzECNI4t+0npWhEJjIiPqcqsnGxV+8R3FFtqNrdXuUkWZ41BY7AgB9ayfEV3JMm2K7tLaQnLhcs30qrgbRvkuGmtHa8fZGZPORduSO2axJLC40uePU9In8m7mO2TzjkMD2NdN4a1kXmnxWbpI8pXDFowOB2q7fWOlalcvbvE7qFxIUXAH/ANeluIkslm+zg6kI9wGVOzOfpWBq/hdLu5ins9TntS+WdCx/D6Va/slLGNGtdbmVRlPKlbcar3M+tWcLTzwx3XlsAnl8kj6UmNCXF8kc0TWOhSXJACtKxEW0HuT6U3fqVzcvcIbW12koYlYNuX+8Ca4y68NXSOqv4ich8LsYnDCsa+8PX0F8tvFqv2gltqmJyxI/Cq1JPSL+9s9Os5rzUr+KWfGEiiIVse4Fc8/ifRpdXjKwz3sEsYMjSkh0YdFWp9P+Hm+0jeeNRdBg3nyS7mAHbFbt3pGlLPFO0m+aJshUjwwYdz2xTATTV1S9vp5rjTksbZ0Aigf5pHHv6VpTIdMtmklZYIieImAGfrVe+8VWNg8dw+LiZY8SFMmSQ9gPTFZdp4h/4Se4aCXTHEUKbppLnJ2+1AEx1KBpYrmxuknfdiSFRhU+hqSBpmv5LqS7t2GCYbbeA3HXnvWTLoX9rQw7Zvs6LMVZrc+WAnoPU1sxeGNDktIbVTsRJNvnyNtlHrg96XUZRTTrP7UNV8+Zrt0yigeYE55AzUN/rF9cSy2iyNaw+WGa7PyqvP3cetdC8dpprGGK5ilVDhISdpx7+tVNfurODSkv9Ssi0ePL8uEhggPc0NWBPUzrPWLiW1ktrae1gjUZW6d/vSdgRUNnquopdmbZaNexArNPIuA+emM9a0lsfDEPhx7q0igWJmEglZxvLewq5YaZFdafHPcWhMnRHnGWI7HFC1B6MlOq6tDeWcSaVHL5kZ85llAB9DzzWdrmq3FnaCW5tbaOQHaYYzu3gnt6GtT7DHAkkkw8y42lFd+34elc7b6LFHqsV9d3El3eSttKI2Y4x2OKALVrqc82niCOyFlDMf3UgxkN6kelF1Akc4a3v0ubyAbQ8kmFB7/L3pl34h0aWT7Ff2127qCJJjGUEnPGMdBUeq3NnqtzaWul6TJPCEBMojKhV9j35oASHUdRMzLsSKO6YgRQJhRgctn3rauIDcaak0XFyU8pZJTkADvisyS31eCDEkMrSGQCCGDqq9DnNXbe4V9QNqlyZ7lBiQsOIR6H0oC5yFlpeqpeNc63bajd2a8K0C5VR9K6KbQWu5xN5UttaBAWiSXPy+hzXWXccy6bGkVykG1WbzN4JZqxjd3UmhqtvdwQyMuZ5uCzY64pAZP2S1GtwmVrlTtxFEIgsaL1yWHUmtLxLJYXWhlJpIrZSuQyTYkyKnl1eOG3j+zywzwKikkjJx6kdawNXuLDWCg1DTVUb/lk8zB8v3FNgY9lM9t5SPql3MjHKQwRbzj03121vbC5ijcReS842MHPzA+3vWOl3DZ3f9neHooVjVfMJaQbdnck9c0w+JbSPU43IbZGP3ZyWHmH09qQyS70W2guxZy3cyfNuUu+UkIPQnsavIYDqzRi381fKzLwNhfsPes+/ubiTU4Ws/LkKYDWgO7Jb+IntiptXurjTbOIXkDyQyqArRLjY3vQMpR3lza3l1FbaUUtzzOxHCH0Wp9Vi0yfU7NdNggjvyAf3gG1uOS1VZpI4rZoRqQneQiRVbmRF7getLFpWj3Mts15DNG8iFhNMdu5h0PFJiNk+F7uSHy4Tb5PO1fujPt6VlXelalpsDrc2cL2y/Jst+shPcemKtjUpoLmztWkkRYs/aJ5OUVe3NR2kt5calNc+YbgxME+0MflRfYU0BHb6df2tl+6ZYyrZEZPy89yO5qq1lr/ADGL/T7a3kYhp44jkt2zW7/a0EGoSfa7oSODstoWAAf34p9/Lf2cK34WV7diGaERrgepzRYDAtfD82kwSNKRfXI4Uy8lvpnpWjcCVra2GpaPMkcMe5rjzNwUn+EAVPB4osL53uLko6QkbUA+Zfr7U+/8QWMqhPtcdu7AmIRHcx+oNAupl2dlp3iGJJ4LeVZI5PmniG07fStk2+mlvs2oxeZNHgQsfmc+mTUOjT2P2RpfMuYzMpaRcAfoKw7zQrG2mtNUj1TUvtEznYioX4B6UDsbuuX8ulTw26W+8yYXzIjlRnuQPSue8QX9/FZvb308DRr/AKo28ZLOPSr8utkmKBzY2sjqyl5kJZSPp3rR0i0vktTMLmGcKDiSRNq5+lAbHm8nhC11CBL2C4mjTnzvNXBX0xVSXwS+2Jo7sbHOdzLgKvqa9Bh0671O9luLuzRljU/Mr4QnsfQ1B5QsbFTqxa5L7j5aE8L7YpdQRwbeGbmzy4uo2hztDIMg/SrNv4bEluoknkEcv3Shxlveu6tJI7228mymEcKKXRSg+VR2PvWfHrtiszWsumNI0bfu8KQFz/F7mmwsc4fAsf2pLV1uInXHmSbeKdB4Pl0+5ZZNO+2BmPlszYXAruoY76C4ieSVnt3+ZYerY9Sfap9RsvPP+kSvs/5ZMGx1osM5GeymadBPYmC1lX5I4/mBx3PpXRaEI7S0ddOtPJcIQZd4+99adHcSNPDZOERIYy7KwzuH1qWPw5Y3XmSW9xeWjTsMFThfwHrU2Giv54ui8c0L3E0a71818Et/hVLSbzULC6ksrW0hu1djK4YbQc/w+9bNpoSWls5W5EpUEedJ1Df4VVtGea2kEt1byXUbk4gTAA9vU0wuV5r7VLud47jS0gRlwrI4bZ7D0q00Lm5Zb9FnUQoElJAYEdfzqHU7rUdKsYprKyim24aSNwC556mpmNzeWRudP0mS0uT8zQzfMre49KCRkyWxlxbWxZSMyStJwo9veid0tby0lFyIQSFBLbiAar3tw1rZxy6rayRM3+rEK9T+NQXFncXWmi2lLPbOfknUYKD+7xzQM6efUDM14yFY2RQAVOWf6VjWmpfaFuBZaUs7H5GfbsH1Oev4VDDZNLZQWW+7tWjzsLJhj9G71J/aN3pOp21tDHLOoQ7zONqk/UUATaPY6vOhN7DZxqrFFdDkP7YqSKwMVu1jLLbwy5JBRslgfY1myW+tRXb3YuANOnUmRozkRfT3plg0fnXEdpqwV7gBY3uFDEP9ewoAv3Xh20h0+NxPdwXBO1Wt2+b8QKjtbuew22+ox3bR/djdIsl/qe1WbefTrSy+0arqSNcRn5vJOVYj0AqzYjTtS0aXV7jzYBKzNHEZS2B/eK0CKW6wa0DiKG2mumP7xnyzY6Y96j0rTtRiuru4niieSQ5iknj4IHSur0HwxpZ02KZlF00h3JLNwyD2XtWvd24t4yrwicDozMFGPf0qrCueamyv40uZQ72F87Z86GUFWX0x2FZ95quq2Vuo0jUmvdg3SbV/i789/pXYX/k+dG62cNwjnYYk+Zl993pUS6RZ2VwtvC8cCq2VTg8nv7miwGLpOr65qdrJdXMVta714d14kI/hA7E1duvFdtAke+3mtzERG5ZcDd7Z6getO1G0t7cNbmYkMGjYzfeGedyD1FVY/D2mWiRS6reXN88YOzz1O1UI70hoLlY4C1kj2ttvGwzH759hU2kyeHtFnS2tY3W7OFl8pd+4/U9M1DOojSWx+0B7gpsaUpuZhj1HQe9U9WtbnR/DKXGlSxyzsMSMrBmI9aok2LjWdl4IrlrbT4SCCqPvmY9uB0rMu7nT7PTli1XVhM2TKkdq2MA9M9yaz9M1O41myeF7S3sYljP2q9IwxHtmrel6N4cuLed7GCPUXtoQZJJmwN3oPc0XA1vDjaVqdkuoLvVl+UebEMyN2x7CsM3MGk65dzSancW9vPgO9vFu3N/dGf51v7pQ1hO10lrBs4sdoCoMYyW9aqXeopZRxQw6d5/Bk2A5Vh2JJoAtm+0nyRd3hhiu428sAtkoD3K9M+9RDR7DVLuC6kafCA4JkAVl7H61yLWX9vXC6pqrwWNiqt+6Q/NIwPTHU1q22qvqIm0rQNDRrZwsbyXLFVHuPegDqDdaPaSQW2oWzgLwrsvIUerdaydY1iy1+C4tNNhkzdgoWQFo02nHB9cVDqYQRNDeagFuISIiYyCpPda6GyvrW10drbTrKNZSd8cIwAx7nNG4MyLPwzpVtoRlSF7r7PtEqSoRtY8ZAp2sXU2lwg210vkqoypY+Yv0FN1Gwv7qI3t3rd1aJGVZoYowec9PeqN9oWkS+XeW1/cSmf7pZiwL9x7UNdguaOm62viYy3FtbkJEQJJZZDuxj0rZ+0vHIkOkWMVxAjASsjhNnrkdTXM6L4DaCKSe51a4gLNuK2hxn61YsLRWuZ7WL7ZClsCst067C4PT8aQzWfTPtdxJf3WqhD5hCQhAFWMex5q8+vadpVlIHvF5GFMeOB9K4vxNc6b4dsIFtZXm1CUfK80m4jnmqek69Y6p5OnvpP2jU5H+QQgYP1phc7+DxDZCAi2hknduWZlOfqfSsFbh21GfUNPW0tHR/wDSI3ORcccD61l3f/CWWV01xe2CR2uf3pgk+Xao4U0+N9S1C1+yaNokMTyv5rzzvgqO5GaBE8uo65d74m0iztLVyd0kbl8+wHvVlriO4jVo9OMJiTezSRk9P89KtWnh+8JXOsmC5VMReWg2Ke/Ws200jxZBciKa9jk0yNvMVmIAY571KGaFpBpf2z7eiNIZVXfHF8vTtisfUGt7zXZJbSQxlPlmtvLDsV9TV/W9E1fVV85NQt7eJSAzxrj9ab/YMVpbC3a/hEgOWuEAL4PoeppsZBFDawb7qy+zLbBSrBk2tK390VW0251DWnlt7W0is1hYEysuVQjsBVh/C2k6dHK97qFxMyP5kSM2Ni92xUN5aXkTfaPD97NJBKpLBhgNx2qQNttMnuFdYY0glkG6SeD7pI7+1QazexaaloNUnupIiqoJiSwPvjFYdnPcWGnPbwanPDcg7yGG5WY/w57Vqpc3mrRiO9voUAADw7AWUevNO47CXWoeG7bSbq5+ybkYqoRB87EfxZ6iszR9b0bXPPUadNBcJGQskmXjA9T71vTaRbW8ihrwlfuBni3Fh2xip9NitdNsZoJIGgt41PmSCP8A1mTxS1Ec7a+FdTa4KXOuxwpJFvWOFN+fTdTLGSGz1MafbtLLKqkvKUPJPUkV01lbR+S1wtyXi8zKSCMqzL/d+lRNcWkF40lvKZpCrOY0xyfc/wBKpIDB1e8j0bT55H0KVmmOTNndj39vwqTTdVOvaQjGOWzhQeWXWT+QPWtiS+kutOiFywlZs77YEMxGeABRbkTxwGLT2giRyqrJHtx6n3pAU47XTrK7tkspWkuGj3OERXLr/tHtVDW3TUljtrC0VPOcCR/LwY8HscVr3cmsJdQ/2fb2MSTPsaZSNzJn0psdo1rczz39+yzM+GSH7kg/pQBgazo8+jalaNY3Mk8UiBZWALbR3wtdLp7AyqPtUsgi+UI0WwKfeqOLiwvZbzRXia3/AImkfdlh2HvXR6Jp8+v6O326Lymmbc6bu/qT2pDY+z1TR47W5zpiG7Vs7GUFpPpmsu01jUNRvJ8WUsVqOGgdMKF9c1NBaabbXctuJ5nkt8oC43FQfQ9xVeT+1y0UOn6iojQHcWTPB9qARTvLwR3BiuLuNbCYFVTGCDRcxywabHbW7pCvIE7nJApizajaTu+qQwXEm/aJWUbSPpVHULS+1B5AsqRQRNjELbiVP8qTlqVykouI5rc21vJELpDjdbDPmEf3qsRWKqkU+p3EypzvJQBd3uavaJqGkabA62scMO1tsgflpH9PpUupatb+INPu9JntlhUkB5Mfc9MGncl3M2US3JsppNTgMIfEqhsDb2LGm3kN7I6Czu4ljc4WQ42xr6VOdBtktYbSC3WSIkb8tncBT20fRpfs6CKVZY32iMSHAHuO9FgTRY06B5SbO3SRpypTewGxh3wetR+WPD5luLrUHJiB2ifkofQVYtdGmhvbi40yeVrgArtJ+Vj9O1aaeHdWlsDBewWkpIyY2bPPrmmkF7Mrw6ZqN5psuoPcW6PMokSEfcwOc/U1mW15LMIrq2gs58uUkRWwUb1HrTdRtfFT2UlmtzbW9rEQvyn9M/TipNGuDq1jOsWn2kT2zGNA7bHdgOSPWgkxL7WGN/LazNNbtu/cqo++e+T6VbkuLqwlGqTai0yzR7DDG25kPT5RVq709o4XnlJUFSRtwVUn29ai0PR2dSbywQ+Qo23OeWB5HHagq5RvNUvLsQ2tlDeaiFPLTJjygeozWpJZeK1iEMy6fFgAjPdPX/eqTVrrVLK8WXSzHcAbRLFuAz+VZ134kvIbjz7u2ZFdsySKdxjUelIDUbTGezSzuLyZnkceU7TcqT/d9KFiazvhbSWk86hvK2zPu3n1qrpOpaZqrz3NmsVxcjGxpm2t+Apl9p3jK6JGnyQRIpyqfxHPvRcNiG10W6tdduJZZp/K5wu3cluf90fzqN9F09dZhlliaWVX374U2xkeuPWs/SJPEMenakVYT6khKSCR9rx/T1ratdNvbzQoplvyl5ImzDpwT6Y9aAQ3yoE1BE0+2ji81900hj3DaPQVg6suoWV09xIwezBJIVsFx6Edq3Jf7Q0iynS5tJ1ZAAGgG7zPXP8AdrOl02S/jWGHdC00O7fIeM++e9AMLTxBaTeXEJJopBgqUft9a7GDxJYSwqmoTyGHGN7kEH61wWgfDm6XU1l18KljGm9RDIP31dFrvgXQ5LYSaXJNp9yy74/Mcsh/CncmxNrF/BpsEV7ot2IkOSLcIWVvwHQ1BpviDS9XMsbwqHAGVeMiRX/2W7U3RrKDQdPCjVLy5kkB83yYlZQ349qvSy25sROqw2bNJtdmj5YevtQiuhS8QaMt9++8xoJ4yHWaWQMfoPrVaxGtzkXGoXOxI0fem0HgjAzngjv7VevL/S7gQs0tvLOR5ayIN+8/7tW47a5t7d5MG9R48CPhRgjpjtSYDNN0+zNlLsR0Vk2FpM7tp/hz6U2RNK0yxkKGOEqnVW3/AIYrNvft97dCBHuFj6KYVwHB6D60lv4ditWNs8qx7+Jd53HPYD0qyCrM8GoaRNG813Ak/KQtEoD/AE7iqmg+G7/RNPlv7qyE5Y/ubYt1P94jvWsmg6fYX0t7f3jTOXCxK53rGR6VoprjXN1cw6TA90YgAzvJgj6UWAx0vbrUfl1rRkhgf5IAQeW7/QfWpdSv4IdLzI8cSkeWmPvIg/i+lLfuNWtUl1KWYAOIxBC+X3Z+6DWwmn2epQyx3W0xRgLIrR8hR2pDOR0vS5xaTX1rCNRu1bdDJJ/q0GP7vc1q2NldQaY11qd6I5EO6SMJtBY9MVqwyqLO7NvLCtqMpbTRrt/MVgJ9quylvKJLgRtkStwhx298UxFXVdNs1ukkFvPvxvZw+dxPJyP60y31fTtPH9oN5wBhaOKFmLCPPc1sQyWP22YS3txPeE73UDaqqO2PSraXui39k4itYJMkmQbMKD6ZpXHYzPD/AIgtdUuIdPtbK5u7okM+6U7AK1btrrRYZ0vLiCGyMmI4IgMjPXaf61laZZWVt4lS906ZbdjGVliQ/pVu70aK78RLFc3LXkrIc246AeoNCYWKaeIVt7iS2ja6urQKGt1U5O49dx9qns9MjvkGoNd3cW351jD7llf6HrirUek2n2KdNNINwRtWIDaQ31qfS/Ck1l4euDq9839ozRsIwj/LAPf3ouAyeOzuLWKS7srW4RpVLB5B5yL3OKax0nRLuc6Np+J243QNmUITyQD0rQ0nRrHS9Die+eCa6YZkuN27iq+o6PY3XlvHuZ7g7oprT5TIPQ+1CGYfii/1e6+yzJZTR6NGw3RoctJ7n3q9aSW3iOOHddvbRKwQQrESQAeAWHSr4tr5bn7BLcQIDFlrcnBIHpVSC1tHtrhIZLjT4IlYA7PvMergn71CQMZf/EDRtGupbNLGe7dDsdmOAPpVi08WyTW++Hw1cR2AO4vL90/hVPT7SF4prvWHtWjZvlmkxmZMcHA6EYqg3jS1W52W1lPetHmMRMxA8sfxAUxEerazqOoXItr+J7W1Uby0OflTtn3q94NijvdSkgSWTbApfN3yGX1HvVaDVrK9adWtZzOx3SAuQsS9s+prU0HULOecCzAiSNsPJcnO72+lJgbeo20EdyMeRKJDllIzJKnf6VlrLA8s0UKPZwpwiqdyMPr2NY2qCS88VTXLzSvAVxEUyoB/2TVvTb2VbOa3tLdpFU7mWTk57/jSbKSKb6b9qnCQyuyRvuChdoUj371I9lo1u9yxjuZJsDfKGyqn61txXTy2xeWSOAtzgLwv1p80dsYnjcrINuZFRSAR70hldNSkt5oYbdGL4GxpvmjI9QfWotX8QQ2y4mkQODtXGSrMfWr+nvFb3UCXSwMJTmN8nYB/Ss7xTrmhkSabHaLeX874RUXAT3zVLYlmYuvx2UdlHJNM6hixZfu5J6D2q3dXSanCqw28sEbt88yLtVT+FZuk/DvUJpoJdReJbaQHMW/5getdpYafbQL5NpuVlXaEdd4474pAYtlpe2WIJqUMd2vKzSDBx6Zrfk0WylRp9Q1G6kiGNojlwpNQHR7DVoS16jNIDkskm3GPbtVqXw9p62Zy0jsf9Wvm8A+pFGwMx7jWNHtY1jtArwxtl5SMtGfT6VmakU8SwM8cbvIrYj8g7R9TVmy0KG1upAUYFyTJlPlYe1XYTZeY0dq8cE3ddvPHSkUjD8+90udLOQ21paImQ6/Md59c11Wj+NLS3sJIbq5AaMZJZQC9ZKxvLBc2kg+1vIdzKq8qB79qxtP8M6TeaxILlJWJyDGTjHHT3NIDWl1O51aW41iwl+zRKpziMFZfT8aT+2tUE4lfTmQXUYxJHzsx1zT9HtoNJimGm3CPbA/6m4GRF6mhZUlv0DtcxRyDeJoRmM+1OwiQSXF3NNbzR27RyJuieXpuqSxhSzg8sxJBIo+by/4qj1WdPs6KsyYVwF2RkhT71T09JNLvXu9RaW5XqmUzgH0FAampa6Zo0UxjkKfaJjvZnXnJqcaRbWNxJcJG25hhkk+ZGx0OPWmi4kuHE89nDFajGN/3j6Zq9/aziZoZbURFBuLHkMP9mqsidSKG6EiJLHANxOAVGADVq50aHUoluNxinX/lpHxWYPEMRkMYgljy+FKrlK1hd+ZGqh9qDnAPWmLYzWaHw2Fe5u54g5yZeqmq93480i5kMUmogxoM5Q4zW1HJbXUDpKokj6GNxkVzGreDdDkljkFkoViRmPt9aQDLjxzp0kQtYZ4TuPyKyZ59c1X0x7e3kn1afUPtVyB+6j8vCoc9qyf+EE02CeKdZmmh3Y8sgg59K02s7MxxwxwXUz2+RJHGMCFT/FjvQMvR3WuOUl1BrOys1k81VVvmemahatd3LKusOAHD/Z4D8zg9aj1S0gu4baGafdCQEiGPmPt9av2GlafY3Rj3iO5Y5JcZbPpntSGiwmnSxwiOG2EJY7SwO/A+vrVa90mITNDJcRrAEwy7huapL3S7m7uoZLTVja2/JMKEYOKrvFa3K3JhdjNGdzuoyd3t7UgLEdhpmni2RYwshAPyRcn6Vpre61ZSMkX2e8hkAx9oG0rz2rnJDqaWUaXTxiV32q8HzNjsuOzU+/v5bS2WcxyTzxKFMBbLgD0Hv3oGWbyW4luHutQtrSORCYwVO36c981WtbWW8WKWZJ/Ngc7WfKlR2x61JcXEGt6SjRmOFmB3LKpLo3/1qhs7GS3tUs76+FzL9+MZztXscj+VKwywmr6zDdG2V4p4MfvBwGPPvRqmpXM8iyxokuxwroAANnvVI6ZJcb/tSRTNbg+VJGxHB9ajmjkh07zmtxIwzhYWyy/4n2o2A0NRjubq3jW1WO3mjT90C4KlfrWPb6l4ovswy29qsUGUVmPbvxWzZz211YwoIYoVTlYpFII+pq5aRWn2/wCyB1gJbdIiqWZ8jt7UAVo7nS20a4huZYvswjHmhDja/wBe1Z2mXdqLFRouqbxnDW90odcdgDWm9jaW8sj3USXEKkJII48B27Z9TzSadpej6bcS26JFF5+GVtoyADyOe9GoXsZklrDAk0l1YRadcBldJYjuBPqMVdOq71W1gvklJjOXlbG32GKsaro81reRPp08U8EinzopjlgPasN9MtZkFzIotxBJsQRghs+n0oA//9k=",
+ "image/png": "iVBORw0KGgoAAAANSUhEUgAAAgAAAAIACAIAAAB7GkOtAAEAAElEQVR4AUT9Z3N0S5Lg+UElEhqPvKq6qrqnZ4di+Ypm/B771ckXu7ZrxuZ0z3R11b33EdBISP7+flCzCSCReU6Eh+vw8BBn+3/5X/5fO7uvL9uvO7t729tb2y9bL6+vW363trZ3tl9ftp6eX16eX1+3d7xvueHb89Pzk39bOzu7Ozt7T5tHZTf3D69qvm77vL2r8Isy20rsVub5GYiXl9ctt8FVTH0/QdkG9HXbS7PbPmypsLO3vbfaWR/s7exu7++v9na3d3crshNKCw6Q2QH14f7pYfN0f/cAgYfH58enFzgDMC297gKwt7M+3F+vV3ur7fV6b3dva3e1jdb1el8TmkQE1ACHzRYMkb2zAzo6X5+ea1ehrW0kwH1vDz3br88ve6uVJp4eH5+fnkJsd+fp8SkGbb8+Pj4iFXmodwN1fYi5W8OCuLLdBZC6jCgAVMWrmK71GPOMPQuNT48vT4/PD3dP3jebp6eH583dwyNSQdzegYA6GLuC3F6w99craPt6cLB/uF6herXawcOd3fDf3t0Cf3dnq8LJo1cYhEf87wtZRLX3SBpZYcbW8xPqnu/x/P7x6voOz++xfRPFifP1dW+l0fVerxiHQo2t9nd3V7v7Byucw9bVOh4SkV+f9kJ2Sm5hVHiu9veh87h52BvRoBIt6Q2kofXyGtS4Oiz1Affg3LdISaCJ5kmZJOfG6+vj0zPRJN4pBNvg7O2qQChROkpIBDCjqKOc86bcG0uqP5eeE/heqhgOve8CktGkTlAdxqk3uKU/FcyaNF8NRDyncr4QNZXtg2tPz8QXmNd0+wnHB9TT0yuho+DpUZvKbT09vVAA+kBFMi5Xd7SxtT7Y3z/Yw9L9Nc7i5PZqlSnRt62dV29br1ncCGDrhQax+EyTZGnc1vMjvcW61wS9eVbHVw09bp529/bGA2RcQypKowBTAEc70ZMO5wD/pwfgUnYM9wHq6etTOj2XI8vnkSDxJTIyTA+Sn1983NpZ4SVMXa3BnAMuubuLV/H25eUpywUlCezBVnXoJ/UdDCSmkf3WKzBuvmDvzusen7Cg/rq9vxrle9nad3Vn+/nhyfubBMHKTRE55WTFW48PHB3q+6wU/GNWPsNr1zt00EsWTHJxJG5Ecm4EbrFitc9v7PBTbAYFWLIo3uPDkwJsaWeP+tGNPKdbiwVhvu+w9iEtRzUiSZXI4eTKWEZfshA0Zn0xtntx2AsAjEmIwQ8MpdnZ3t+GYXwCdGubye2Nkw0S2sfHuI7u7CqS80ogo7Qife01RviGCwXb3sZQbGdO0xBGZCHpev/VxA56Fy1dIK1UJwamAYt4XdKiLxqviYRTO8pAjcdOM0ggxzG0JveleheXXwVYTKQkzPHLS9lsfwEVXrAEXLWweasaLhAYHeAud1fr/XFQmJQ0chUa3NNZ7aFOT6lealH9QPvvc4wbn4LcBfiQWBewEBOPaTaGxBM+wmXg+REaEN+9hiPxa0BWqHLaH7e1XM24ki+tespI6qd8Dit+HQt0kA+6jWdobD08u7vNwyRAfcLW0sHHBr9AQzpO/B0fF5GmYjC5H0bFdijaiJikQFZL96AYbVOExgkrtnb2eAitbzaPyEcpRi8M0g6UX3lm0Nm/wgTEXFRmvYt2DTMHjTBL/rvQfq7jHeNJPKPr4AKDP7D0L9T4d4zqNu+Yovi64O9jyqAsLidMvIzTGDUowjCgCwMGbGDcJRyvqg/a+ZX4i6qqb0FuAFUmVOiTkr64yrCwFFRGXXvuDycFLEQfHTEkFVm0OSUYkQZkMZNpOUIXNJSYDzUFCe/peRKfBlXnwqIBhzWZIqlAabsd3SuugMa4OzWRBeTiAyAYMrWbj6WNDM9Fqgjbrd193iiZRXoIBcEL4eGBgnFZ0IuN3t1ANGOJS5lztGStNc5hVCYHRwf6rPpyK4oUQBrdS1MwPJ4Powghcddi7POZEcQMnQXyul5IUzyqsvZHHCM7BXZ2xTH6NhQBq9V6znia7KBL2MBSaEr98PiAr5ryFp1D8yDVRaXrY5n5RG5Khk3OLTy1xLRTDOwKVbiyjHRsqRow3H59mQJ/d4Yiwj2MAoazexUEBjME/KaK1ZqGXXEJLwetmJUR6XeYCGzjttLdRVpUAaufDLOXPXXRHeSxhxQ37Ug7YQzBPJq7NY+rXYw7KW24ub8QlNQoB8tXdCwdqO0tYVIuA1CcHUENPeHfFewaq3AnlqViCa7eJXzHLYNCBrTSBxhVKisKQU27Clvtjh4VZHUXhbXTZffo1SCQdbpGRYo1yKSGInbLsICQ6pIpTC6p6ogHL0+UN3lTVUwTT23t8qxkvrRaOU3FtFBN/AEie4ODsZxsKHq3X/JxkGTwEZiCqVQHFhrhDrvniJvPYaGQBoaY5DK3ptbY51iv2gEbdGJIUF6StKtQesK9jEpVFWnFOKKXhwfMh1XGXTsQ48OnWjzPsBY0Elas7F90BhiSKpG1KPSpUC57p1rktLVjTLBaCRgFm+HAnwc186A/wswnejHQ4klQnmEnQK1B0L3TYNcDCUS6RmpFAywETinL2BWVowTqchy4Cmd3a7J2ya+uKOmMD9MS+wxrvyDUUEybP1/ydZitre6Bi25CqadcuFyb1YwfKRpPpkZ+odgPaSkJKDgwrIvEYI6xqFDFWE2DFUjNFOvlaiT2ZZAY1BYy3YvhjSbDOgJzQYNENdEWKkCn5+QQx/rKdvI6CWqMRAc+VMEwpdZ21MUmSsXBFDtoXIXiA6hEWqNeLMfz8VqjdgmRFChRJpn9xFEsGm6nolsvev4FJzSqlAxicwzbgc+wGuJ6j4yifjPDJv8pFtqYkeXCcJoAQoFhCdRyY6rnBsZqIqNYCbfH4aI4fla1UtiFPkoIbULLe6UcroXZRJ8vhcwNmjn7uCPqrzImJEm+dBEfGl2oEuSGd6mlcdLTACCQqqRjcSyGa0kvGRVJtotYOsrcnQh0VWnwpprGUo8QrDgGBQIb9ct4LCwcO2IdYCqW1BbOazENqO1hgl41wY2+DE5YGAdcKVDEap94PvrK9kb50haazMziHeQbENADRj7YRF6CwfW9HePRoafvC+5Toz5DCJeU0vKnIR7OMS1SR3xognb6R7X5IwIaHQtCnB4ixjBdGT2t6VRSS3N30Tp9OkgK6DS2dzClVr201D//5TpEHPmIYVi2NIAwa2EhYnbRknTS55VsVXUXhNFYhyTQGVxdx5C+b78Y0FIp3UD+hlozN/qXXS2tI3e6FvgZ6+XoGAZGeWdvSQizG7dCqcg/GoiwykwWu9IDxdKC1BB6WfRCXwajqSQ4TAVyCPN9yB4OoGn4OVwQlecn42GCCyB8YwudWhQxhLRaemxBpO9ZoXChuAaEQMSK4WbuAm5QMow8WB80jBid3N5usLz9iEqIGLzuT/Cb0BuPPG/JCEFXeJPkgo9G0Hx+cykjROqOnEhIdwpEFtn6nhImBxQkGO1G7AKJLtVsnj61H/sIClT1xtu7TxUfopAOgzfwmTXCkFON6UsWlzPKw3ky3cRT6yFMBKltZejwWDWdhhDdcXkYU52J24z5dYHxFfzq1iy8Va6gf0MEOEkGrXE1XYUPk5xhnIK+9wo6gSzEKakMeFoecAsEBfLCYaeaippRi8nWIt5kTKORyhC6C9qbPsaXigxSfHWtpqYSrAZ8ms7moJ8O9gMb/FrciYYAEgpAJgUPfXpcd+AXD/EY4G6n4CGmVKPIfBWZxgwgmIt3DWEBvDA5Uuo2dcdRQIUpECKSYMBSA+qDBuyKz4sTm5AcglHkFTGLDAKb901RXikiOfGKaYwcMrC7URqohLVrrKlaOIVzbBsRxEYxD+p9qF7/yWxXKJN8RvcS2HhxmMrbaZZoshyoYF6uIJ8W/vJ+8snThDfEaGVCFykGnWQowxBe446Cm1rHHZhF26hjlXyIj7BxddTxjQl1NIDwDCmwkhlh4cBCX5GAKjQCw7FHkRD2X2+mbTVGCf2P90ljXHx3tgontThsyFOMpPCInBbOQDRwvoT0XFM+fMLZJ8j1DxuB0ij16kNqr2Lqg3GRFJsHpZHKuJM3vr3RXJFgJvhpMJYvmIRgN2ptgZmwdEK62H2sGcTCyU+8CJ3oDRwomXgy9VGWGZdiO+6W9xivtPfWau0sSMS1EC/yBTBFAgFl2OsdeRlTMEMsVfCjU1Es/SAcqMQjUJJUpaZew9pY2ZeBE6cSGxCuK5pScp1NS7xyuy+l+yKwXFc1k1Pdli5BEnP6nKQFYOIALo9UI7WjWvhn1ir7GGdlfoexxf7MxvBi87CBZ/1hsU7MZeKxP6fCyaIFKAYWmBDkHLFkmoO/i5pexrA7z3o2qNbQYgr5BED90FvprAgOUz1o/xQFwT+NjVZpRWM+5lPGovxD37QSkQMYdSnWkLTYZx2ehiMgYnsBi9WVqV4AYkwDRGVgGJKwy54n3MNOPF3IrFLV5CLiKEZAb8TdZS/FpmSgQXUxfnnN1ULSGJjrmcLh49PIqVSOgilU37s4Vl5BOEBMS4so1OHLG62lINjQoDzdmmLxj9zyXPXH4YmUzGSXDgQ2jZiZAKO1OoXlNVFZVpFaBy9wg2ZEDN+mu5ecJwnWmiL5owtZT8wEvLDKh3Q334MBI9lRmkojDKPj7xAU+SqnMFhXB1zI7kpyznzS0nhaT6BmXxZpAkBXoZXuRd8Q+qSuiZZHIYLLCI9AbYq0mlZEUXiBUHOjWnqMtHEmR1Fdc4u29MH1Ed0wABoQNcOST2uMCNtKBJarHTx8X8pWOCrc11gELhrubk6mRvz2gkiYEPBQ6PIIMwWD5fBVCxHajbkitlFq7pYFYkamFLoUEmn3wB2VyAWS1OiZOykM4aZnUaFDjADojcK7FvEjd3g3QcpwX1/2zEOV5wnNWnVPa4NobQ42g7RP9U1gVmb0gFr3OdwBEFbEkTdujYRV8X34sbyF7ZTIPyz8i9aFnAEMD2ilD15QGmTqp9Fa/A3CtEH9/Wo1YYSny6QGAarzZDyuYAUIEtoSx4PXZImW8baSdatVDMO0LOikPO4q6ddB4h9JoyzCh3wjvb4rubitiWZDc7hQo/U0XmjA7j5ETeq+XB5g6UgtcsfDNfd2i8hJMbWfuGbSoQxefImLQQEjTwFO8q5+fF3C27CFmBAyaxgfEYtgFWFdyqi0+Px0d3u32i+rpArqNFcH86BAPfp4NezKTtN+P5oymhHijNGqZWQ1rwSfVlYqihTw0iqmalhcpheQ/DHDrKEK9L/yg1iuGWuV7qLmsnkAcSvlBD0+AaVJvxWIlt7nN+qDNQoycpzSXRtuKwTBJxOu6X/18K/xh24Bi1Quu1EDKHQxZsWy+Y5R+EcsE9NmerUZ831URLtUqPJkBmVwuzwAJklBa0uggGrCHR5qqTocoIg1V11Vif1FLwqO7xFPOrkh0ItrNZRTHVt844AvWh9sFMzD9spzZfUsgnNcmDPXQ1CLYT6oa7hX2Po4eTl41DZIlLY2/YZt+Lj3pgcFtjUAbX5mgFUxhY9BI/pGMaEZQl33qYYiL2Tq1WpoKFHVxYoFpmpvL+Bib+pe2p0iaVdyhc2Wkp4JZNLhvtIc3OiV5qgfZYm4nnJpNGiDhrtuRbmivahZziUz9LF8dVPHGgkP3wdluLmHgCooN7nlLAXqleui9+GqJp9Xq1Waj5wcSA0BFQB/dete9RNN+vUeUF99gcwbnjBWf3xes5cRhoRp3yeFyWAoDBA0mdjD8wNwqxkZaSpuTyQ4CeSoNGyrgYjSJPRjXI4Ofst72hghIA8+vfdlyDYEGy2Iqsln4GNyyaD2IqKfosfg9Qe1epan2slh5IsjtVAwXio0rWggXP11z5TDamFd7oTvaLFCKpp0y0nsbJfTNokxCRbw/IRmFlIiuzijFRqPE2pkdYQHsoUWmkjdxy2qYdnJBDvSaOaWBLzh5H3QSfMb97L/LsS1mBT+UVeD03FP9J88/WJ6tad8rSbyt7qMPDSHTjeIgcU/k0ELEILod7XaB4H6zbgd3s8wCKNcfJAyP/jkJWOh6yQUSXUGuVGazWPErGkYBzl9mQHrO8I3ZLCy/FVMeHnZP7L8iFaM5r3IgJhhS7umIL8ngMo/KjlTfz6lhzok61YgQNwxfwCrF9rTG6kw+qq1YIVcmI6MqjYM4qp8ULeeK9lDrpxdRCwdZ/CnWvfxp4kixaYr6lsuBznYSS6JOO7jaLJqmYcq1OlgtVbSxQTZK3JGOrxkgbN2CRQYHn8pAyFcCjCUaZ9GyY4iGoZqV5+RlueV1OUtBA1WsLUcx9R9SRxX0pZENKzEpL5mtqNBeJYY0BVKJUehEINSVkxPVlZJ6cuVS2WBybIoWRgO/mpH//y5kGd8ls6tp9kz/VuDVG5YDXBSSM9HR4fkiK5NeNEqLAtdRE6T2lMB9dMDuh7DNLV0cXQOQSM2MlNPUkn8xxfvPogj0sGimKE69RjbyB0rBqXXx8Em0lE6/UGcTgTDn6SM++IHACnYw9OT5YBIg0UdWw2HEnrla6NxjCS9j+PTEOqK1BrvUjOCpjaKaaJSPvYCRLnqY9ZwqzGTNXQaSgD5FtLWrcKjGIUKdKUZ2fg5eJq9I8Ji7lDW9aYesRqXtdRwbkSf7x3TS2IRqn4iT5oDSntE2MWF9dvqRg6Ch5lCmGp5kUoDk8ppgWAEFds7eBQCLNBd/8caamTE7frgjKhcSO2S0/AxvF1ZbFBVryBQuPikzWl2JqYrBff8sQw79DTCdVLmxmVhgooI1lyVpZk3j5qjVK7lLrRSmDCdQazPgSx8TvFeR7q4l9xxfoJxHWXOIiq9BrYuIqei/WDEhUwg/eGCXktwU7NK08hH4vRqwOhfsLIWVl3/givlRXwYGXhH4ohGa80mxD/QJ1qsSMoeR2stP9XH6laTcuMt2+DtMXBYWYERcTxTYAVRS/g0SVPoqNZAAcyCusDx/oOPaYBBI+ZoCWXTkjbnciGh9vqLg5luJSgQX6+3iFlw3dYLYpPfYtXbzc3kihMEZ2cxaBxYtL8IZghPgDut6hW6NzoxHdDkceC2LDd8RKIPWidMeV7UZVF5plQdc+HgosV7iWXr1awdf4RM0Hwt3hmb1C4Gx0RKm58HAlPH8cZPAkNR3Aa2ilO+ckmkfr0qg7Vi9X6+5zgqQcToeOKI81N1n9AaxuUCpgBWF6muWwE1il59RNci9VAfhDzGcjO+l3GundCVPKsltzU6POsiw6wH3VvlKIU+CliKHa7ApFh4G2CqUf+e9vKp6Xr+vSKpOSf+VPBLlHMdfJC9pQlvcZTyURxjVNOuWxKkCgFmNZz2inSTTffZTcsTB5Oo1Eo8zhCGH7BBi/tvv4AY77k1yvsyuSTtj22PS4/jNRYpoNIrJakxpjYrOb27d0CHvIl/xGYwjtpxHKks0SXq2h0R92GY5YPWIa8RZuhz/S/rKFPYaCmCaz/ezsfADDELqPio0ILyNFs+kHLG5zQl24dKAkr9gBq9ispRy2le/KR0Mg1DxQOIaRE+UU4uO4RMvEQF4obPFY+ssOt6xPTb1YX9Q1yYiGbVB7bbEZR6VTAnkjqVik3Hcq8jEg0vJLuWk2EMPi18YTWqsyKM4YnczTpSAxiKd1TNaIB0y826Lg27D1W9v/YzqyFPo8gJrfnJWYUWCx6h7uzur7LRvORCL1RmLZCGVBlHEGFxDYrwzwDQUko0di4/Gpz4a2GRNgHMJaN1sVtXuApdQkYzs23LvDEkZ2BYWNbIgw9Vcmkh1aIOoGBgkV2k7Kbt42S8dac1hdiyQl8sy+hhE905QAiMULArJR7LTV+H5QCp7yPbhL46BG/9P/ZnBcCJPfgLr8WL5DHpCaTSkrQ6vWO9DQRZrI0JQr7pksyVVy3mxtiKjznHxHAGJEezMCVO4pNocbmeimdZKsZfoyX1uXBr1NwiaGjvCRZWZewQnhLABudsuUgLtVLEhAbaj+/qrnZXtOLx6V7+wk3woK2FKGpuLXJdNyfiA0efnrw+8PwH6/UgnwaNd6AP+Loj9lAXOkoqa7aeb8iqM84Ap7ZpXfo50JaSU3yYE8RF/zMiyCQqHMgH5PnQHjE0IoXfaa+M4uNkCLOL6uBPjF0+km9Go25gANTYgEUSxXEZm2NtHYTc6e6+xcWpDDnWNjwadsTQES3eYXeWGUFFBuQGZFT1Xq3wwTSD5NGxZBBOuRswzM0D5qf2GRQX+KAbSzUjmDLopPNDIUyCBEsSgCvvNviNUfwbJDQ/ClCWI69io0wKTFpgpGDNZLcoMf4sg44aAa5hUjPk0ItDswLCLZqhFjSiMIxignfBOgZB2S32WJJZG4oJpONNySNQUoQ4MO9Q1BAIsCT4PFd6j3gX/ZibFW2wmaRDO3VmSdF/IWN6M9UVrnwmkyPM4/sK4RiPj+om+ICHanLfsQkD7rhIdd2m8hI4QwgJZcx+Q0GlXuRClIWw3ckRNS6ZHS0ln4GrYFiqNbpRqVJZg9sIvWZdTdm4o0F4cdmuUyb4pAXjVnGtoDhtCJHa7F98WRzVuA+Cm741IoHVGE4xSEofmilTYQKwU1WzEVRbvYIJpYWJvrhFLt79aSub7EViSSinpLPJ0zY73dAjfOtO860Bi2s+uEKfMMVnK7ceH6Dt3gI0nkpuK85ORCZgLKYeMD/hn1LWa6RdOQIiiu+DkHtxcAwTqJyZ1VJ9xbmhF9rDCtSHfbwOr1mdzkrr5vhBlPSxe2kI96rxis1PvhkG6ZKL2Sq/noKq4xct4DK28chBwQB9khs1rlhKhkWLlg8vM7a47RVGwYB7+LVC/2G3wSbxxurIVaAgusFf7Y6GqD4vnrGmFEBx/SU10GCKFecWCULdCz9jKlaEeI6IU1eGt87HFgUrXqe0astEHUb+JMYPqgK4OrwVqsDG6Lrwt80+ySNp5F987qtXxjNkkpg12hQTfNB81T4rUg6XYiE29O5L/AjBhSdvX/sX873Np6B7zWVtjQqktV0EBaYDie5rxWeux5Ye2CgMgRQr+GNQxUoLsOxzgZ8PVYArQ70X70DpFvPB6rIlWJyLgkNlohoaAQIWw5qG0ZYhvJiDRrpUo7sxOwy7VTc6QkGHFXxQnw1POtRpHRzImhigiKEYnsDWuUcQB4TMpZ9Lk/1CJiy9Tbc6BKIj9SbWbv79LpxruYQw4mjRwvn0JAYPUXUuWkBV2mUOY18twId7Pg7ydVFcemo4ZpnuWk42aq8FsChRuqsigFpT3tWJvdPKmnPTp2LISUtitp9HoLyCHz+H00OZTitdpGpqimHIZzgRjzLeLK/SlUqdS9r4blPXyGFwWvKBNYgRsSh7S336HGMmGQsLHBDFwSc1GG2FylSoZiTXibZCr8pvZsh8fXJPXBTKVMQ/4GtO0aUJ2I89VGleIKgDncFqYXMiRktZEV03wOMPqulKeObqF4ObsGWkl9H6FSVgAPpGXTmG0YF8RLgqyeUqor037N+w6J9L7qAD9OBPFXXGJLqZOrnIPdbAkDLg3nB3l4WEJudOPskBRgUoUqQ5LZTpTwCvE0kn4AJw/6AWSa25xNZYOP68z1OmpPb0a4xNgDHa4Xu2BcBgni+Id7RXiNb1nFm8reXSLflgdNdyL7imBDm9UkwzYMoovPiul9X2Cqhc49hRvNF7kXA52hI59JqkuUWROoKe93ae9iymhmruieyQq9Ti1iZK1KjRQUqOzaZeseNps1nvi/gygFgMt5qrOvSoGaY0hEMO1ntXJ9OnWF0gJfTjCYAT9UWYYloQnhSD0IHp7cDkOtINH5go4LFHPFc2rDDPpxxAYsO+vNnTo+StaEslX0AGsEHm6JIyMITe46t9mMN8uvHyKnWrLxkG5NQy58gdSQ92Y0LhDSy8x4h8SY0SfBJXPQmqrq1GclWvOf9zXQKerRkvFcNWBVdiQzDzTWkvUaXDQJRtD9pgjs9xK98zPlx9WqSZEAIDdAB7hdAIXcyZh2gYk2k/bz9OPOhmXogKQcG7735d807EIEwgsfjZKcL4MHiRMVBKgpY2Riylsz04gx3cgVQzJR2tnkJL0RifTBXTvGbGQSiZxqXkMashXAO1XOSbpmccWJD4llJKZiCayF5HhFFf5LyoQb0X6FJS1OVtuSNZIiJegasS3mY+9VUFdiNO7ddqjMwFecXaEWYywB8qhWE+BWd0oAL9Vi+EhAu+jOQCU8HUQ5lhT7B5mLQh758oo6A1KZR6NycVocwqY1HOZc2hK/7Mj9vhj5UVBYGxpD+TndOOxmJYGhFafaJ9iXoqAgbDoiu6l44VW4BHfoqrPrJcWBVq/oCs+VIC9S5RVNoW/Slg+uPKTDVj0x7Wj0HANqNV2ycQEnikRZma01b31Ibb0lDQoRZPog3Z9RrdUxDPXJx7g0X01AiaKxTjx3EpD1mV5qb3EJgWK4JxZsCMpHCb+xufljswHgI1DaujGPcao/LvQEGbs6lFf5AYOtyK2dz5I3bY+pUwVBmE1AK8PH7zMbQNLbzRg+lg6ZOiDz9ax9mBWNN9Jgqua5ZhSGFrmo9zA8aLEvj8Ik+SI2STIwYRzWP9P+xGzdEQ58HFMmriOsT4ZhBgx8UIyciD62zlGVmmHSlIUVwkNlTkDeFEVUAwVx8BbtvDfysdbwXo9tPDw/66bR/0lDSV1E7SNx/wukrHijsy7vgYf5WJn4x7qKancivErF3cgmYSiNl+RsS+YVOqEk14BZc8UZJNG6Y8tFlXHc80kl0RAz7FOALXIDhzxkEVYsL2rqkH2BAASNNijsn5AhBwsdHx2KjyoLGkBFX3VjxcbzQ6GcfTL9gm9aWkW3mv4qMFZ+hH7wQULuMA/uSC+83VtVlO2ajWxOBu1QAEDOA45HxdXMlI4aylugCBs1Z9C4VaT25pZui4RiH8VBFC/qerMQ7xNceurEkfs8iQ1YH/Gzt9C7U3+OOnfC5SZxrDbbKIZkBGuHQaHqCN1wIFhn5DKpQibGSlQGvCcnR1uUooNmpBJhRDwfE+01vlm/aC62pUhU/gCGhpfYFeb1JyNWDKJFwCjSVqybwUrLuFz8UA7i5QjLdCA0NcdEoFCPBCnKY0SNqK8ndKiGYcq6BlVRJ8IUtoTJncc3XhCc1SygFdZKNhegN+fBusiE05VRqZRa7f+EalFAYhdx/3vZCeqmozu5wePapGvGqMv9J3CnjaVqVAPRrJ7gnWWoYHhLkQ5qdK2IKko0Z+vWzRTQLXzOTfUoFhVD4vTEZ1QoMPQfQb76OrL0VXCs5nRD9Lj4Q2BnOqi8fWYFzXsnBSwRRggod4XJStuWm/WSl8XkoEPKhQ6BOkmU5M6gasuqVdP8SEp/O5kj5kTHiWofqv7hRNXtm5BksRtyud4PE5zfDFNXAkQ8liAJNXBRTmGt1bnHTLUhYcklleIaLoaL7A/1isPWXYWcwMhv/xf2TJ5CAoaNOUFD90xOjNQy76Ddzefum9Bgej2cAms93dA+MSDS1byoUIDTfAp9/PreWIXEnqnBOlbTp0TNFtG3MBwS9oUbcczNMDLBPx47OjFWjK9uPTro0XQmxy1N/km+grIttjgMb1wXp/dw0DngmTUeUgpTrOCbdHajW46GcVxtel9FppgRSy005YVowQSSlRNg2QE3gTWb7PPf8m9gnrJFqnCLl478qUQAZqo9hc1K5pthE4uWs8lchIU3qMX65oq04nB6ZsUANe/lTyNHefaGuXJi/rasK+eCPl9VcnFAmjYOrmjjTvqw+jNN5hHvZu+jA/adKEl4CDQJeGjHySQlpIlSLEPPvoE+THkbri1gz9kaR2bbspjQW4r1owIlvvHcRKKJCoqt3haqaLIay6zGkRohk5TtaTcBeERXy+4UivQWtYByGEhB1gcWnUxz/fS9CDEt8EDFrWZMOWLC58qxQ7YhXaFq2AX7W7T67ZcUKsLWyvn4xJutsgb7cg4OXxwV1szJdBu5g41R24w+HQBTzcx7nGYwSSf6B7jdtbBtl5EC2Yt3jCEJL0eVw0kFqHQRhKGQ0KOWWvvIJk/cvrxlASF7jAjmla5jriBXS9D9t1GgCP9Ek53BI//PyoCk3+XnEwIciLYINzmMxaRIya3W3QMypZLJ9elbCUSkE0YLm1ytXmfHXB0GW+xtTYCpi+Ko+DoAQ3agNWVLcWIJEPPqJAHMg9BX9sY7xcCIDvT2M+BGPAjcRSoeHYUMdZ7ViXD1EI1/wb/sgRsI5CDM4RE7hB0ugMCjWRhgyj/s4CLUFmsIFwhgjSEF0nhc8NCYYm/yDVPfjiPJJc1wrGgOmWX9S5WhsVTdl8RbDLkT22WjgwEZWiymYPDfoSWCoSf5ovstxSr1yYvLMlRZDrJTlgw3cUoHcguwLg0mj9uZajNsn4550UeH9edjR0hKS0qBPYiT6AdBufoYhemO8786x+Yua9h4sDbTlGYss4Qjdek2L5Rk3s80UVDLKSElOmB4L5jkXtMiWOhWKzDsJDssDyeb0qmVtaaGvTcWyPm7u7+43zdWR3XjuopLPhzB6KijvQSjuJeb3//Gjxblxnt0DhUqIYtUthDX/39sWLw4sYW9pGI28OIC2CMWVNf95e3WuAPDQm6poDMf69MaTgN+UGmFsto0mOdVXN+4cc9hXOx43xd5W1hifNyLOrULlg5nfy+03mcIcT5aWKvUZizy+OIXTAwEiQnAePMbNEDY+kGty55ZvP4Vl1clgApXlTMXxc8gcgPaK1lC33v5QMkN+6JWwlNJl0254zBCoLoTiRcafHCwK+UlDX6tgG6Rk0/5++Gz8i129cC8G2t5d+qaWcYgZUbKXt6TEiYdrqrc+VyFJrPgcS6xDCj/im183dZcqEULE6xJirXm99i/ld0fyotK+9ot0rr5G5xeTBhrNvVSrO62P2WxfUghOhZVu9SiYOsrSmNCOOcOG6IsCXUy1UxGg4UIzVPpSoHc9KV6NjaSe75p+0j8kYVLYyplPk2LtjGvJp8/BQ2CUZmLlTt7a2ZmdoSBB4kNxGlpEPvwiskXQ0ahfvVfl6ZfYtZMISQSVzNnwf/sIoV6jM4DNcyTVxQK9z6okhEZJqDJbTZu26nxJgA4WL4galZLkk95cgBnenhyeUeK0JNV2srXFtcF0UHtqhvNwiDs1oMgLm2iKp6BveDo6qoKJCOFHCA1PiLs67Bpg1YWMYIICncioqLZCHgg+So6D6EZX8UwkA07u5yEQWFLpKMuqro1ZohBmCS7ZmFH3tVevTfLoSeyI4DOZ/7Bjzmd4a7xy0kRWEWQF1vmbhRcQJglttMMtiMrDMN5wXBQ/sotZBh1G4DT+5d7WdOOg61Qi7gtSYMKiMdDU0vdCCeVmHpcNrZ/+zpYm130EZD9JUYqP9g33IPz4Ii2IdnNgGpuqTLMOnqdJPWm81Bs5Dp0Q/59XY5ezoFJWGBGv5o90WvwosDo4ONAELTCxIKt9lFYTRwtPm/u7eEajO43x4vL29v7293XTSm7hMNtWZbLOW1tmHJPK4vb9jsWRnA2QaGk+R/GVPuS2f9ZUYrR+qt4D7wsWiHR1sups5De+m5mgm2GyJ/mQZ1cJz2KYjiyT5jfFsTEWftziFpf/OeNIcajJmCclcbDPVIzuqE+MDBDHgXzsuUQva6PCAbqUlvvpQFSgPRXAEKEOnKkrQPVozyS6kLuGmxlWrUApn+AiLcTWta3I5QNDK/2a0cKO/JVTpRrWWvkSl4oU3WlN4SJu1W0KX+ixcUt5a5tFowS80HBOQ+maQPiSFRkwhWlij+GKfEgUNtLszmIZoZlOQOZfRidL6PRKGH4G7gq6Sn3CCqi4k5lCrdhXg0uhywo7rtZosARTrIBbYYFKF8VfJZ/CDmlFk0sWMuPmUoUxA5lYjYzFKOSHOM2a2aiQCIaWR0A9nyBP3uD+t0zuqozWIF4aU2de9Q1FwDy3S88+NRDE6BVPyhwnDgQPutUvIaJrKv3SKT2rsesK32qFEwmhC7ApxGhzukR3fjdEBdDU0R2ZpU/bF4qvrLgEOvDCNky5WFY8zlIxCVSZUIJVjmJxnLA19iC2Zd18jM2XTtk/pBVgv25unDVh42O1eoEdt/EIffzQSDFpYhgsyszPx6UJL1dMA71MGx2otxQKvHiQbgYr3lrJEQOilbH5cAtUXjfXT602NghocWGUu/Z8COIiRS2dVQ9nCGGpNQnwY/GbYdZkIcQ1awcCLARiWAx/mwAkn58ZwagpMU1FsNLeoK/ShMdPuWiTwQknZM4TQOXDqXfUDjUs1xfla9TiKO3qfTlnn9viytr60VEfy+ntmDC5v3UD8miEyTON1wsgi6hFTnmhZJKmr2CtpH8e0CyV1Y0HEumSyNj2iFwAYmrBPCKJQBR/WszrpYbPRwIfTk9Ojk/Pz8yPztE+PDq6W7kBTEGhqVluk2qgEt32lh+IhLyB11C+vTsN2KvP17a1dWcYFN3e3F1fXtzNCgOHui/U/JAFBaVY4InHxNQBByBSCZAVYj5hslnlsSbt9i6QphJeYjzuAAEQNpRYs8LHSOHgBzXh11uN3CDtO+ks3cTUoOf04mK1762uhAW2hQVmBXiZd75P6TJp9qToDHytNA9WrcUDJwLbps7piQ/BxYnFGSIYgwNNWLiRyQW3OmebGAldo12KijKuKcYI5lZhLByGXhU+1N6VNSdGTp8xQU8iKQd8d38d75EAgx/c32ply0C4Pg9d9xUH3dSoQqkxOJPzD6u1L7iQsu5EXjgdpdfdVq92J4rNmv0RC3ZHjJtOQkNFcBbZsqauO4mx2WACaW5icddNYelHN/E0tZPJ1D9Ckpos6my+Lvuols4bH+QyNxArEZsLOyizS7wr8sPNVZhtyuJowVedYahmyoGcNL3aWabWTNjk6t+pdTNxakgCTDvRujXDp84n45THgy+QQmRyDuiXDmSIO6A4o5eV1Q0vXX62AkjpypsIgNAMRoLLqcIGcmNzfuBQ95ahZTONeY1H8JmNartHRzxG9+3CIEZjFmfiqeMxL1gM5kkaMC4SGk8srsZXlfnx5wIopUi0ODFHTdNKCE4DjvfGnrgLcYplk+yatpO8LNLuUjOCpEZ8JqA95gKiLLJqU84hhWAf5FrJQgFGqWg5vP/rPSqEz1zYNx6UKBMA92CLVV543f69hCkiVcEvf6Wtg3GalxnpBnV91l/9Jyex/adwAJsLUVxXlNewK3qKsNnI43nL1kRGxzWxIhIh2Kb/vs47YWUsE25jh72BjwZBHr0O4zuaJ3tCCwl9ejr0ip2EGr7u/6yRLDdiAlmA6kIerTV0BTPZxJZ2AUeqVCsTomhthu6LTGz1IHRa3xVeh8Xlzv94/UBznTM/anHW4s3u8Xv/pl384Oz5Zr8zR7j7d39PZUlcS3KL5iQMBzr7hbjjPPeNCTcYKa+5z2KdHeGQAoJTfu/v7q+tr44OL75cbXx7vLZQ1PqBLPHSenYhsZSpFUFTjyu5q9fioQeuoDKONyi3KJI8IzOJLL1G6OEvLVU5cwUjZRtKjgAIKfnmETQ9AznPVITb3V2ghP1AmqOsxObsPFSJO3xeHyGAlderCXw72rPT3MnoZXcu43rytRhTI53IR428zQwWy1gHo/2AZ4IKWQlawoJ2vklRMa4s+6IEqiO0FvEaMtwhgDm3Hd3dDs/eUHO9jRZoezuHGuAp1K6auP8RKQua6WizI/qY7901xiND0WFin7pYaGgZRS8PvUjfKURuOKagFXF7eB4nKMrvqZvmhko4QVBYdVvVFkQcphWerylP5TF+6nUkGMiXK3JLlcgsFbmV4KUAap97ovZaHByPx2Iybmkg/ZIFokl3fdh5x2+hrwFF55NOvXERBR+MvqUt6CDGxJ99xcLi3bzegySoGsNq1YAGPkk4E11QQ7LTAGLG+7GcbWvHmdZe9HKyhLs5BPucgiwSbRjy8mtZHbcZOMTOfgJHCKh3XsAviCXpUuGxkDiI1R0LdUAzBLAxAo5A52bob15A+nyqMT0ZXCtPSkWp+IMoTr4r5T6XGcxmBt0Cu2mmB9tRqhDoR2Mi+69mLW14jypCcVx8omrsjsuW6bwtKlCEiwMbs1CTu9YpzLhcW2Gmh73yoIJ5O6zOxmUHUN1V9iML2UcYiq7TL5Uw5oCmGVwXfGiQg1d0koQVAbFpuLxztqnpkUwDrk5aAJsk0IwW29DtthCuMp/S0oMHBkiJ1e3gKB2IScTQegLgBJ4XVMfiN2ohZmitEHH4tRrVwcwwgZJQZlmVM8FVXTRcJI0ImGg1gqovSpnPVghaV0neAPHhONzteTxkV61GUqFeuP8NfDGxwC0vNvjw5PMCdh+uNfTmf3p/98PHz5w8fMOXm+kaIrQN4vL8z/YtWhMCNvmIU9U1pGtOkwVi5NGBCrInf/UOuoohvta9HOT08/fHj+cPDw82nGz5doujq9u765sZTcwwRmED+BFhtFOdlXGaUuVI9YETRPGIRNCVQrCgO4mq5Pk4xoVXDnZDIwyWklA1PkZnCTCivy8CtLWehkt/EeJQwJvqbYdaic1qLv3p0dLlZtzF2D3BcXu4Ps+cNai4HQ7PSxhglhId9C4FhnBIm33SQFpJZsoaeGzpU2Iz9zxJbmFcCiLooeUTBrh7VFSjXmlf2hSHeoi4t1WcEPHHHHRrionLaHm0Shi7Vh9gZl7CR6QShAUZ6P2Y1SpXfINRaia8aD580LE0LootaTxFzQpHYtRDXAporAAiZCiE1zhXO4DR/yMm6zi4iKiMaemsl/4TZg9JwbC6OfSMz4aJKi6iGPD2BRfOt+DNRUfCWIX7yJAugG3n7J6onPCTB1vAknBHtaSdPm+P9V88rOjg6XO/tHx7snR6tj0+OFD48OTqQ/eShDe6zNaynp1EIekNbec67e/HN7f3DjaSnNCf4tsztOs4BNamOvscWusQyagiP0SHF9uRSqS5iQzrZhf64QQIZjZ0lyKFc89FCTBBn0VCp7AyFeCxgq/BWuVtYtbCRYMkuNlMBiBPrMDTHkRON/+ynsVK10vyJEuCmyZRYu1132y+ZQ3hcTWhXJTjQQbA7ZDgKmlpWPF3Qfj9uFmOHO2hLXbXpSv19gYiWkESwKU/iDlSxNug0TKcKIlDAVBYI0ELy/2w4slR2FWCN5s4jatiW155q0B2251AYPozG0+bNMjoBhqi8Vft58cZtEe8v1vSaJGneWe6RO+1O7XVcRBzenZnapAaFBZ9YrfkBEq/iUwoCPtA+kOnwIvXCIrfRH9jxFC6MIFEeaSlArMsUYJMvm9aUl0QiQTAHXJz1W5lkpmH4CABDzX5XDxIw8Fhtd+bB0Xr37Ojwjz//LP1zd/n9+vv3p0c203Ds8dEDtx5GeuFomitlBQ4bLX/o5QuHwp0J3vd0AEHV0zxv6QrWBweyXEfHx4qeeaTascNqTgmGzegD7u83dq0Yrxs6saGsiMz2tg+OjqQ+OOycu5b8SBnMS0ClT0NN7ESnuT7kZ9itr0iLtA2fnFQsxAz10jylJjlK8DoXILm04Y2buW98XMymOzG1Pg8wGbCGey1s7SoVxf64Xzoksaaly8aCQtV8kzVSIVHpRaKJDfsMMfEur5oa6AOMZhwWkzx1zqDkPR8fTbyDnJw6MoXdBIwLtppYswkQOTiOQfkNt7XqY3ihy9VIrzOMLK/BxXVNS73VZ6eucN4pGShU97mOXBTz1IkaFY3AeRsFy3pqYUF+Prk0g5yaxZtWBGAYtYeDNzjYK4pxoRFHRwZgBiXwvQu2XTATG5kT90yxQPIeGVCrAAzC8DFTY5SobwjyRhojb0hTm9EbrjM8HWa/dtQ3E+bjkO5GM+TOBbE67mi1c7R7sDp/d3by4cPp/urg+ODg7PRwv5UOc6jO7vbB4RpZjfMt6tMGRCERN5vvleRsxuvx4eJm8+vvv369vLjbeDLeA+Hqs2mvkmxtkQktzHgSNAMXRZVIwpMkPNxY2KE4gked39Qei4d/MQHdSZaYhsvsHDQV1B0qZVZydQu86ld8CmgU9nEMQS5xJzkHtXyrCNERYU4CsASfzFLmlEkVfs0tzrpv06NMpRpMtxZrSeLpRFeWzqBPI/Ba7QUlYGecOIg4WU2AOzdq3NqQwSBNIX1gAgDfVGtIy/QWiEGugOZGsfA9Bs39gbVQMqQBPLxjg/Qc7weGUh0mkwyKVcu6JY58Qd5fA5FeewwjOCGaGJq+mU5o7qV3EyX2JqZUa7I0me+QNpo5XizJziB6MM+zlKLAkPxZUUCTucSytIJsLo1Gh0ekoSj21MC8Yy/2gbVEzXg7Jl9pZqhQlh7yAMFyFHD6jFXjCiNSq3JWL/ePMginxwefz88OV/s3X7/9/re/fPvyBdzW/IBlQowfBAV+FH/eMClfJFmaZpNUvXe27qD2zf30ka/76/3N3fbjl6fDw6Oj4yOHPmpTj3B4eGigcHawPmJpgzq/ry+4XesAHm6dbdSYiR2Dnj0XkbL/hbgJCEoujMPLuPdW82w8zHEv9sew1J8rxshEP2qUs8Mrvsk7TGBj5gbHkl/LUVJw1CCh2eQUJq+lghKlFJh94x6eJCGkeFhQCa9up4vDbSgIDImF6VYA+GCPQtQ8ho6mlrqJn+4o1wQ8FZo+pkm9gbYof2obHlp5lXnm4MBqiUn6OYZRbEO0monwv2NDr/pY5L7ojkLBCfmuRyDfahTSoizRa93Ssp+wLmA4oNdprDA/8XXiRTwglewFIlxwmjGfXUdRmj/ion21+OZbEKG93kdArfhKZu4v+0SS1HxVaAxPxpO91eWooJjLsIYiKsO+S1mJ28ks97d8c4mLk11saDayRgAcHwwpxfUfP5x//vjh8GD/9PDwwzsxzzFVwQBLqYXZSLy9vZE7Wut7rCa6vU+1JSyk1flP0TvVYTiHBw9HdT5Pn3f+/MtPXy++//W33/79r3/7dnVFZTmy1tVZTV1mM1NijTbTISYlcTcNiQSqkKhHUZVPfZnTIrA379r3N8/OrH2bYKh+oPgonnql6znLwmWviTDSvVTHRR6g+CjFpnLxTM3ZT6BIRhbg8afhMnXUi9ERH/y4m2iVqhkga3JspLxC3+LM0mb4Vkhdqkk/FgkqBUctBop7e7uvRFwAAt9qP1QGjfR7KFNP4+4BizujS7EtTH2ttGtjDdoAzRc9GIbSmPAc+t4g1wFIQ7tKmFpqqDA+0zvo4I5+aXw2RWQMcCYzLx5mlnbl93uFgsZpGW+ddGsem0J7QXahJ2ayleKvqi70TRmfwwvC87sgSjwwocSh41IaATLu9QJ4Wg7mcGFaAj8NQHStw43gxJKUlDh4F4Xc1zwcmnDmzkyZvj6fnhx9evdRLujr3369vri4ub7kUjcvT7e3W89WEL2+eoLxuifolp5n3hLFqW/RLPVOtCx5bcrA6l6OoLyTZ8BaJ2rfmtlRU6P3dzcXUqow2veM2PVBfQB9jAsljY50hEdHp4d5grJDt7cXpgru73rQX0SY1huBo6XIIOeHXRHZM8OGc9kB9uTB2VSsign4OuwxcDbx3aMCyqYNb0sTJ+gY2sztNNBS+TqGojNCMvFEUWN1qrCYIJ0BB+bJMG67pVvEeivAqVydZe6osVi3NQGtqQ/zBTlfx+3m2hrVR8MbrPmQMviFXzY7Ag1T4FwdkG7p0CCtZ2ZdwPMvyiAK0KKCemVFx9sOkhJqdaj8uwoQqSVLRwqN2aEJJ1ecGoUoDO5FZ9LBuPz2nz4S+vRf7uOtEvSKSvRTKYxKi6M5TNHvlVnmpvqIr34HuygEo2r4XKdQtakST9waykfQaiYFtM2goU50uhxyrmTR2lix+Ery0RE1zVt1MICVmSB6IvGx+a7zg/cfzg5393749OHju/eH+6333Hra7DzcQ5GQ7m8cb2olzLMlzYT1vLkC++5uwwqorPMEdQIlZS3bGLWTAjg4EN0cvDs+/nB6+uHk7GR9+N/+499/u7hqeiDCUw9VqKQa5KnLx6JCUCRxf3m9l/xmk2UTFrid2qQUsQzNSnD5zQLNxHlH/+Zv8Iu7QiPBJtE4t3DNe/AXMMS8BO4BjKfGU8SkokrjyrvWvQSWqtcecMsrrzR4jISBTL6j+nm5OkNWWb81qyTq20JYMbpSmKlF7sDGz4la6rFkNaUfwqWNGu7HmDDqWosE+sq80rwiP1f7xIpQnK9PEfCHzqVV1nilAwEZ/RhLTX2hHUSXF22iZwGuj8/o8lNGggd2Su0+Pmz0+VDEteFQdq8sOpbvqBsbiK01LTESU4qPIRjxIca/oBqNBWjg1zwc0oHhZ+oLnbnctTKJyVmgXgYYm+BS1DiN4HN8TPgUY6EH4V0LLCvS1AgJTZS+TnhpzDvNolu8PBE0cxwDF9nl4AQ7lEYu1PpMLuZMguZg/XS/+e2vf7WaUwFu+vbarOGjR1LEfp1ffXXLEh5l3sHba2Zs81D2BnL7tnAjTKYVQhIsbS4u/qUe0kc9vGmXhy/2f7o1cm65KEOlgHUHx8er/YPE0VPjj4iLlVl6dHnVYbu870gFdDzefrBaxe4zJ1CmZpwXd+JDfmH45qPiEaxw4qZ600XW45Wwy0mNX3h6aSWqzklMnXMhAL9vY4IhNnrB62mbne+VuSyui8KRES7H1kRdsUwgCRTUpL2L008H8qlJYLRgtKYvxaiFqam6tb9wKk+VmiXOBJkl1crSDnpGL0bKNYMzOiLEmdWAQYapoekIknRRUDOfoROy05H62B081lNWo1UPhUH5E2VwaVqFIIHUV9aqdqM0Jtft04dUwiW9afB6TYihcGAHm0q7+mhsEechDE4UlGtaiCEyV4I8pqalsaWgzWX/e3kfy405DUeGUJKQzC8YqQ5MB1v6XucNAYnBLO1572jXWoZ350c/fv7wno/+cGpuyu5EhwGutuXx7y4vvqMV1gdmA15eLr99B9QWGnO63379Qnqav7+7M3X1+nxUELG/Es70lNnksntXRHNo9kD5s/X+n375OYvb/ctvXy9UoaiH+2srAe3hxwEaudgyhbV7LGaQTVxhsARAw+Vcm9HCSCKJI3kU5FD2FKgAVV4LT/fkblsmzhzGMRZTA0NE2geTFHqPf6RFGt7ni09aHSEBjXk6lzifzk3hWujVFariK1CJO7l6JbSKTnGQG2I1dkzKrr0pBJmCqnSaR1NER9r1VZksy2iv8R9MvFIWfMPSDuqieWggZzeyWDSNjU1d4WtJkdG9BA0XnFWgHlLNSqoRdj5NvWk01qfT0dKoVpM1bI4IPemnx282Mm+Tt1I8o0YkMQiTEGIQzMbuqzcomd9STxuag0dLKHrWFXdhu1GsB9O5lLVEbDUc4hB130LNxqyvHgBgOTxNjsUOLMausNdCah4D5xX4gNTyJCVbVtj6sHwE86hi+gTzvo6ddxHDR7cWi2KuEdrKvILqkeTru7PzdyencmGXFxd3tzd2mjjWEuuIS4c4M6ZbMp0djcaapTUzwEC3O3J7f5utOBNCw9RIx9c6yBT0YfNsAUUBpV1/O0YKjzsPEtzNCjxv3esA6N1qvXJsHo1fre7ADH+x2M7O6Wp1fHogUru3rezx6c7DHyRfaoUd8Hj5D7QM6QK3erscg8MjMSO1jM64GwtjYqYk6IoLRhxcxPA1JpNseTK/5W0TMG3Kh43ZZADUY3QJ8+l0thXHfeEQkwfmYyQM0ne/WKeMdrpbFTA0n2Uk1OxwbjDrhOqtQY0bqSdH5ysJ1REoX181/jsau0B/E/Lo7wwROsto9jpPHVCmXloQsb0PUarngQeaZogMmbE8sdYq/tH6rjWIyB0wwSwiE8puMAks/a0XRFxyL/wIEgh/MI/GEQEWdk/zpXEGD50W7NqJF78SRyvQoRTOUB3Q3EgcDHD9QpgFI7EkrQGZxWkmi9lxHltUKg95slDNHnSDg4cHPvn96dHnH87OTo5Ojtfvz0/PTo6Lhjf319+/Fdc4u+PxgXNvrAnGt3h3e3UF7snpIXQvvl0KgSxkWB+uDWflM+/uKGrLvQxtD4+PhDm6BCsRBJDygSvBzOHRn3780eKGmyvzwpshTART/B9vDFDqaZMKHOM/oSRyryj2wklhQdyOKWgiE3dyP6Mr9fj4oMzoCo1t3SP9U3gqGmfH1BSP/nAaSXOUp6a07Z5PvdRymw1UaHxpwh2Hpfoy2bloAH2Ea6g08qtz0k0uUOLaxDEDEvxko4WICampFgZdcS96yW5o7352upCSUQmi+0otK0sUtThK2Jm0hV6jXwOaJ/KFfYDedEpEDMAMatg6bQ4LR2tzUAO2kEeA3hKSp83LfivSVbTfaZz5oN65b3FZE8sTi2plepoMKstxJ0nkIIgJ8iyYi1Kn/kPX2g0sQzk8QigI0ealPHWtzOKsXJ6ZgxbGm04T5ELJffiOvBA5+AgSp7HJGocGoDlZbBraoyOm1fK4HRk/wX4SyX4C0ravVlE8OtpjJblD5CYEZVyur4Vqj9vPNvQy53ou9nV8aFcv7nms4izrxOLtw6NjcfMdLjuAjgcCdKEP4ZwL8I9bcv3cyTwgoaMfpZCQYoKMO2cBeIWgvYcHw2eGcP106wP5fr+62FvtH50erw9PTh2vvLdrpLC7bY3Sw0YCl9cwTZrHUT3++8Bxy16z5QwnPi9qhw94nGbmqoRfeytmW28lG8tlMsQi04IREAqpQFcpohZv2xIdPU6cT87pfYMAum/V/HS8hYGlj7bBHLmkrJnKuL8ErqvJnyVTQuL9yDvJd6XEaLo0iFIask67i8RTJwqWTHOUKQIIi0aoOi41/0pF1MBeDmKaSWfoNAhL/wRWCCg142fNaSgO7RBQvSI1Mz5D4PiCtMi2PzJtjGtTi23hNEVDJQ1ZRBwPNzi3+H1YHbTCJBrFBMfnj94iIE1fPEHqP74AaRnZJKMCEzMm1Z/G+o1TgFNo0yD+gMpo4wB1aoyOwDmGz0BzRmSqgUnHxcLEILS3quf4/Pz92fFPUj1SM8cd1dB03+2FRZ+PTd3ePQgreoqORZaCvaebm1s5YUsSqDN7x9f7zYOe4fb27uT4yKOE7Cve7QiGl/s7OSL1cjtIZPREtLmT689ZHBydHJ6dfTg9u/vxBxHRlfTR03MPLylgKnRqtfvohM9Ehrh0LD9cRmb0pAwJ1rkeOzCQvIV9IgD8SuTjmn3BlDF00nFtdLVenrJiZHqSS+wd81K48J3/yWUqLdxNBafIFEhSU2xEwWcmohqCQC43Obk/6hcgX+ACBrvoRi0WoC+3XHctdlE3u3Rgmc8s+ze92DOL9FICnvS40aLGqqO9fOoSHgFYp4bXC1r4MNlnLYeTy3ETCzkoyjiaFRfaNzB6MsquNARQQ3NyQ75JgwsDmHGm8toGWpq945HTirFPWMdcAP0CPzDjiHbER2y0fEo62FAN8GFWPFCSp8oiYysWVQlTFj+DL6GVM/GeK1IMCGsks8B2cXh5g2EsY3yKKAdSv/OWxrzaQFF2fnZwMAPCSSQB96X8O0++pPq6ET4YWddmDCKyOZC5f7y7u726rkWXudJZ0YQceKV83m13ZHaPz7gC7t1zp8vtHu3z79eW8Tw/rQ8Mn3vK78HBMXvy0vazc/95I2b5sr3mVCU6li029p2tbX5rQdHD483xkaUaq/vr2yXjIgF7/3ovOQXN3dXB6eGRJOva2MQai6enmyfJWbwTrdtM7CwfYWp+1co+kxY1V78lA895yROjZFGmhl2d3pPVFa4bB9SzFMuim65lOXmSTCzRJTH8gmWdTtPFCpUknFSkRqgmlYmjo2zU16ckmvciK5JKgtSGoirOPwBBMlloo3oiKmBtWRAdHlsdMS/iJcMw0AAYRAnQovDAUnb1+ZOJLZK2YigaJ17vC7JqyRo9BLhQBylp2TiX7mkUKWxlbzLhEUnjAcUBjeXQ9TQVaKwQNtrNE73Fs+M7dIvQSUGVhaO4INitbqJKaWm3tLSsaZ4IjBGVNW4U0lxOZpeni2cYroGpwV6WxpABAZ0xt0CjjcyttAQ2QWikNUtKEraVew+i9R8/vPvh/fsfPn/8eHZK48x07b4+3F5e0yB+X7wPJ6R+//2CsKi0kAVjLy6uFGV5QvTXx+3N99vr22soHZ+c7a33lWGYtxthyANhTmSyd3P9jXdYr9dG/TrGVpNwEW38fNk9OH53fPLt4Mr8ASbE+ESZ5dV6GEd2XkXvV6YOg2km1eUBiXERN7xkCDF6BJpHVQ9SnIazLjC37yTZ7gzjgDw9OL3ya/mrJ2IZ95UKaU/rWBeQcRQxOeZVJeghRAJvHzKI6XHIhNUHyBYKHlWBqOjHC0QEDuAoBcRlgSocCAw3oEKjSNg9tE3azrRTihgNqWKta0HZ9pxOPxMiqg5y+fjUaBBlO3SE0x1inDrW0ECrFQ0tSsJbmuBcXP9cDpWYjPAGrzP3QU1X8neeqGXrtsmvhSOADD5ZSISVbhqWaA5ftRw9xdRvCCCquCkDnrs+xyCMoP9h1J9q8yks/Q0m0awVHPHVX4UCNBbkEj9F9PUKWiTtCk91XibOx9lsTBcxS5bItMkWqpAb52IwewSqErDhElCf1B6LIwFDA0Z/d3Oz2dy7y/5HFepNk6q+wWppq3Gwx6zu2sNbnGv3Ijg62Nk/Oj4Rdlzdfbm630jWSIVuHe8frI6stO9RYDu7m+LlA2muCbpu1vt7RwcHk2pwwptgLaecztuC7sHGMpv7u7oj/YcO8O7WxrEnE8On6/WR+UnL82ihDQmt4W5N395eI4zxpMgrPuC5ohNOHVsgHJyOM02XTrSQyc0ZKpdDWjgZG1O/3E+vbKNPOJXC4A2zacpXTXKoRyywGh03TMvklFYmAHGZR066yTHJ+NJf7jdlBtzHt9dogXbwe9GOdGCimGQ1m/PGEvkMg8KFslk20+TvrA3toKmIghAqyqdqRXvT70MpKQ8JFCdaqC5HAYNCDjwo6Kj79KWbFJZoY4yCwJAd+dOpfDcb4YK7pa9Z7H5KYjEdTBNHSZeGQiIu5RTgFn7pnOb8Lfq+XEQy0rJY3WssVCmGaMLXLFGdsoulO5pqBsq6NYIoJSgkn7N6dDuSMrTrVOh9dvanP/yoA7Cqbb23vbm12Pjq/v7m5vpq83j//ctXLpzRw8cqh9cHC6AlJ1uCXLixvSseMh60rfvqRvnXUyujz8/w/raZrqeby2t8MCAoEHDW28OGbUB5YoNkbiZOBHd3dXWwvbve2T05PLhiWUw/1YoDozqEnHmlr8nLXxT7Q2xsi2c4Vozz4HmNPT+nHnnYSFjk5hTCKiX9qRvfcOttuNkIgLIm6dobYIssvOukgtSbujng+R3raUTlDm5DbkDCLrwbro13JomUiVLoGPxUbhwTDVJ1wPZhhixEPbA1MfCSqkYzsWKviNLscMAdfWRdp+MMknfoIa6P/HgcYGyYBLYPoh8KIUYOWyUVHHq0QE96hVWOIJzcpqJD+Yzvp7AIBVD7jJTIOmZDnADySR6ZmNwrvoitxARgzPKpYVq9x2rLcmEXS7BRRQ3iuPT30nVBA4DsIq8zRAw1wfHN0AEfQ7mBjxeYOqZ8Q94K26b9WfEmpKoEGpJLHzIgfgOPfNYl9zKW1UBohG9i9gE6TfazrPbGx8z4wtjphaZa6sKvmagqYpdfcYIZlkP4+eG+FJAF/dI4MkF3svQP/LVt/Ixjz4FvVze3dybBV4dnp+dHj1ubl21diIfP7D6+3ltSOC5IZkRoogULeQji/u7WesN9C1REcwVKnUWHFag1FNej0OytHRtvCv1d2NsvSLZ2yKyKnsa+zGNB+NZ+nurl5Z7gY763nGD5oacn03NIeHy4E6+NOafO+kSMah5Y9ldd/Gx5Torh1+izZyTV9/uaMpdqTg45JB9SMTcTwgzJG5cqzW/HYhcDHscD4LNXISRO6jJ8IY60C/uTS5Lpnu+BT6OrUbEE7C0VG4nXePIKrkq6OgogUWPsQ5yEmLFQ22wF0uxCWAh2gw1RUKOczMbNUjfYQbRB7gTAGXXWb6VpSqzKmZdAk4qZHil1WdhQ2r+0T92+5T8AyRWJki0G00fizERjIR4Go3i+5D3y3VGQpmlpXikG9k1o0RrcPCfysNkN+Il4Y71rjlBEzKgsONDDBl6nMVDaywAplyjj4fXpYX/v9ehw/6dPH//ww6eW95yfyvI/XH0zo/Visb6gf7SIikjpYNvz810ZWhZKEXdXFPW+0cXKcp6dvQOK2ShodWjR0P7J8T39v7vTEVL7h8etg8OT/cNju9kBKQZF1mrX3kaJHgcpejh3U1p3Gy7BzpeT9dHpwa198LiH0Dw388tvlO2ZoYI+lcDzaDggjiOHBNsC6CVArm8eFXhTQq4FBDrf7ziH0b12XMOlDA3oaRJXpWCeyPd8+KJKJEY36YMLyvrp/3xMOynAYgYpYinQousgB5WuVdjAAvcqMLKriWYspghChD9uVKDUI+dKf3NWaiqJuLfy3cfAxVdRvkbapNpZQArXCdWS0eiwjAKkkSnUYj8KY4m30fLlVu+a0YbrIxwuS7yAWbmJYCz9WU0lhnGRQzY84K5iEGJfrxhNI7P8jDieLVRH0jDBh9iQo594szHe+FkNAINT0+ygF0ZRiLx4FUP5CEMqqGi+7hheMkIK6gwbEFWoRTu7bFQziigxr0Fk+AvJNr4UnS1CmfZxAA/Nb8+MIphiqHFk2DVMa4qjCXd5mLvW1eCaBT8wNqElL0NnD45EvgKuA0KwPF8I2GkxQHGa6/Xm8eX6+na9Pvnw+bOvv/36m3ndi6sbdNhHAyxm2WLDWgXtOxZidD4jR9/ji6OwDqrJCSBZZj5Cul/j14/7ezsPtzc8hVV38tsPl/d23B81Ej9cb72eNS+/ujIh54mUnSPPLxTqGPgkpWQxbGfc+ksd8ygWr4e57qQXuZu8H8Ue3uIIZagwQLRtFB7gNC0JJOQZNnZaatG3e3ktRvT3xXu50pk9Vbw+LfLSTtyK2ODTnoiFD2H9D61IyeJGbzVJyQDlBRNTV5eL/nE3rEkrriVdjVCftL/rtQ/XUVp3+erw4UMWEO5WjHH11Jquh2RkLMOGUmETx8RKTJpxSmFc2hmHue16fxVqIxPLyuAzhhPrJkTD4bAg/BDPkHJBGNq3EAxxtKGxftRlv7iS5HCGuUS9lWO8I+ej+AhFU0+bBBoYj0bf3fGA50m8WAG5LdqX6//HP/3Dp3enBw7f39xcXXy7/vaV46ZsQnKDgI4e2TzkLXZ3jCxtOoHAav8QK283Hh/93PbFnfXGQv2c3g6V5tk3Tl62LJR1OO/2bnN6fnp0enZ9dS0RhBhD2OOjQ9gKmMZHlNsQQZqBeTYIqOs1pl1JaVo6laoJ6q004SHHB5NN3QIM806liLDFJUpHPYyRc32CxfwhaSbBhfdp5YQj8VQ12pmcRzTjJH2bsjEbY8GM2ckY9EwCnL+XSM2EVImyAm4lIwDTe+XTL4aw9CxJWUUdg0Gh7ttvKlDdUIG0W33M0acijWqKpfTusAxuHcJEDeoMDhXXUD604KO9uKmE78gM9KIe9WZ8ZeaoH8WvpX9jxQBpKxzStQYK2gYaDekZ4k0OtTo9DAhgbsSELoHi8iz9Bsr5mOlg6ZOGeIBEwYJf72b8+ZkIEIm4vgxkIJqIwi3e4WA4qN+lGD0A+hyozGY4Cy3NlySpCPb9D6nQItWdAlmcXrgzdMF2wUmAOSOA6I2HHH0RXLmf8kI0afR8/uGaVoVt/sMgdhK3/ia9ALluAAPSZuuV2tUo/9+h0MIrkG9v7g+Pdg8PDhW+vr8vIEg3dk5OTsUqysqsHp2+O3v3/vrGGaDPbGzvYZZ5GLg+tOPh3dkxCnQe6frWlgkDRNmJgxbndZ2fHUMMr2FMkJxH/nXHStNtY/eHp4fDZ6tE917tVLtVbuN4UwvujmzYv9vdu7t7em7gIoN6kGVtXd7JEKG4IFnAvAS1QmQdgW04nFDhiSNf8mUFwenG5NncovBJk/LRodJ+BEU+2ZMP0MMj+GcfaWfeyscRcOrrS6eEGaLMOpQMJyHglbI6j6nnSypRPeDQOZeVqHkta8h1v5rq1yt08sZTJptI3JSWK6xHAdsfpQI/1UqFCseCUe0ZsKsACurcw4uh3E1FIvLvrzTEz3hmWjSqLzWaOocblYDcOKZOSO1D4QjUlj5o3mniwgyxxfQhcQvq2NEbNqmHgMVYmW1GokZ8LdGBgctKtuGRtyxaoBDHyAiA/E1HtG6QK3///t3RDx/f//mnH7yfnx2JZW6+ff/9b3+V6DerxU0fHVNdS33MVfHjLxKUGnNM//WmWSszTMa6j0YBxyfGQdY6pHyrlfVEDYEbbRgv2t6xb6pg5+BkZ3V8efNw+f1qvbezXu8jUnjsvMORiUOFjKEp8wRJKPPJeoXW+KGjh7PWkWK4CCAO0vHGn4zd+B2hTLiRR1KY0A/dndci8lu4pufiO3PoI1y8x4padm1UNw7TBvepcHyCPc6Rfjqd3yWzxNYrNFQn39GEzA//udXGWPRTa2nokndJkRgpaYtONJD3G3GAX+xvaXhzY+nfOEb+xf0xr6SeePuXao/Kad4iSO3xPqmh37RsGtQBDKJVY2py9434I4qupbZ8Vq4EwMZv8zn1yTS66UVotQdpI6LALGoYXwr8fMUHt13W6AJ3VHsinumN63UzG/hW1FfYFTTlQeBTR+cJXjDQjnbJKNYqXPgQo6NZi7G+ERPqF0TCsTu9FoTVQmncyO8I0UzTBXaCqWhRzA88WhpUb5psB4Q2ARsUoSC7Agqo9fL9W4QaCWhxpRR/83t+Vc9083gL/DflSPyhxQqoZmTebe71BqIyJOLDymQvY9ZZOmV3q6jq27fvEkEnp2fWS5gxeMjvczKx2QGgGH5ydLjD0h5uCFiEpUmnyuUrTKyZTJYg2t1tKahga8tTShxhvWbo8kAG/PffLt+dnTpZ4nlv++n2cbX/7HhrqYNj6ajc/vbzxeb+9vp1Z614PQw2pTP4lSdEi+8jHu4+R5rapYcpVzoTD+JoOejxLnEvDsdWhWNcrCKIREqUvvITyS9WDSSXphygYCY5CoNNrWIIJ6btInPHARXK4WpgOoYFejBnNpvR1FkrRyx5ArjBJg3wwtg+ZBAhxMdSMIacBoyqaxvDLQrY3W9tz2K2YUsayvYXNI0jIKD6WhVVn0UmruS/YMbtEkgf+41gNdh+fGmIIzGoG839GyXWzeAA9mM9yhuWaSTuRcWg7srQvNyq/TERJSDs5gT8Ta2pJoiZhsMrA5eSB0UPLj3sgMCX5315xe2tjx/P/+nPv/z55x//8Pm9cw2vLr/+/tf/uLm7kvC/+HYlrbk+PLhxTM/m4bacTF0fn8sP3wjSt+zkPXwwO2VOSXpxfTjhd/lCKiP+c8iPbuPAiYjOzYXjAZXekwu9uLiw9n69OrRSxyIEJ5lY/yUUsrphk8Il8UY8PVNykmpNzucC8JMEHamVgsSfHB3dSLjpTW+0KyXptfCnTEsZv6wT+7qRDPPUS+1ujFaIZIJLizJ21WEygiVjBZI1Cbj31nqAFDOKdnfRsa6o0iTbSItHyhszk8XN+EfbKmvLZyglJi8NI44twdGXTDDHB4EAZWWugOzbvM1V143kBuFBFHK5S2+lgJA4lZWKLJAHp8UaXGi4pHhtFHlEcE3HnHo6qEVp4XAdV3HG3B2z5tSSBo0d00ckXpsRyoND1ntNDq5xaE7xRRUgkp7+z4M+ymVSTzbCbUcWQYLeRGFc4IOiORRhBi5c+gxqgkyESagAKsF0yzU0hoF0dU/ktbh4mEAtBBENjDKz+Ft6l5gjLWscXlXRn7P7bW5UNgriPbDJolrEtYzMU3A9kkcaxJrhRuuEyqEb4VhPaTzVEcRPIn43LC/aukdmz5S3ZvZ+s3ZKjxQw+VHzxye7B/ZX65PTUyki7dzcmiq7EsifHh+r9O37pWWWAvCDk9Ob6+vVwdG941I2jw5ZtHzCISonW9y78w08MKdFhBzB9u4Dpd/eXz883VkPp6HN3Yb7oNs4Us9kF9runsOCLPlIBs9i/1Zn8Oa4RBFbeNSRQpP3aR6i7tNyUEZnA6JeWjzW4Cdx5bSs0UuESSIlyjwzy9hGSBOvJ0y/w1f6MpL0HpOnCr9t0J6y5zpxOP4TXIaQSiwANT5KOF4gcZNtgRiPoaLGl4bricIj5VzUJu/pJy2Chk8A1pbPdWt1DCTsAoQnSCAw4Q/aiH9elSpeXGKzEKdzo0vpbURAoI6wQ29gpmlnY9Kg0Zy3no+SDSM681UVZALL21G95RaYqTw6vZreH6+AR+MPvDmxnJetH0uYaTIR162KCeGWmxsjEgu7a5aIUiOIlKzylXZoP+LL6cnhp3fv/umXn//Tn385XO3cXX39/vXXi+/fvv32++bhXta3fYbsfJJgYvyLq3sYnL03k3R4d3klBSSPTzt++/pdJ3547FCSxpC2QJq4s9rHFBdOnpyd2f0lZXlwdMxJ9pQLC0B39x0V54xezv767kZfS2OL5nkzO1UcxsNJiPepgPZbO1HIzOOkjLGSfqalbUWJKo48a2tMV2RAahPGxE4oICDB6/wI5c2Q86cklb5qwj+CmE7c9bwhOY+U+6rdUqsWntrQY747caZUftO+ltxok+iJkjRyGiFAEPm36fgzhnpy91RRoNomjUSHGwOUZmUymtxPfruYBBHUIt3sp4Ya2sIqJfXCEyERY4pVhUcpFZVI0CgeG0jTzX9Sn7oZNMe4vF1tKLdEaTGhAktbCAavz+PVqVk5nqgan1tbI4nardW0EK5TmY3QLz9DYctToDGq3Kh8oMZuxOBPp1Zum4CaUA1HBivthByNr83pp7WjJch7jWsCKZ70L+DeKhd8LGY6uYBUZFkTWvyI5sU668erHYJ1bFoZfLXAEQewUHfxUMiFAWg5g1xbY5bayBsRyDiucEsvp4MMSPtycx/GqnbRI1ZS1K4MPWOqM1gJ+wX4fO2u7V/yZaudTZuF7RuQKTr68PEjnBjzpbRMmsDSsXV1cXn97sP52lESDS/Mk4mFV5hkHp+iOTexNfTY0cAXoqYEnoVYwjKrteUE6n+kpx9eHKr4+rrZkfwxEHHsxMHzhxNHDP28v/q++/Xb6/OtcaC1pdJA6X58L3sd2QlqtDSe1S9CctJ3CavYrKxVRfEKBoujrHb7/lvsq0w8x33raBhM+j69h08zbGfFOT0mLdAbLRpBQWL8nGJ+vBJhUFLK1DBBwcgcPnwwoTJpSLeSL5Ys2hL6fiuDFPY3ylr9zC0bLtEZdH/ueQobvzH46zLTsdE8bi7X1XRJaoDri1mR1oJOF/MOaQmKQsQnegLp6auqUZ/SJLTW6o7IcVIHkxkeEcKuJgt+fKgVUBh5DsLVGgj2QozqEQNDqUKmhT8+7gpl1OJfAJH8pR3Itnj43enZHz5//qc//uGXHz9tbTbff/3Lv/3bv1x++5IbtgDAsss5hxxAMYHcj9PZdi1YOzs/Oju9c3ynyIAG7e4bFDyWqVrJ8Ag6uEgneypg1At1ha3euX3YcoCEtQlGqOYg9vaPHJNu+Ue2YglQ1feeNlY7W5ZjkBczRm6Ea9H0EzXvUs4MuWkeLviANzGThDCjKQMfOwsvz5ajfIutqyG1qzKZJfVxpQ3RchZY6w7B1OcmzvE5E2qnP25ozms8gTinr8WOfjI0WGiUhuRK+MOSKJjsSgl2dLhcQ2NACEBGPhjmoZV+GuigM+RDhojhA6QL6hZu1lwdiTtjEyktBNhJTGHM2Ee8y0xV9bo8qQZgplqASqqo0KqZGuPbAesDVkde4OdrCBRRwTqjzyzK+FsLTrZKRNOUTxUZAhlM6XCGaHRwWy4GtkgtkkIq5OO+lpg9NgPALQOpTMFS3WYDZE1MuzS8/EZZQKad6yB4ORFMWbauTLEkUW8/uFUfANh6Q4BKGkQGpr5xs/0+jkpNMATgfrYxsxesMWa4nk+v5kghVoW+nOnzoz4FOxiqeCDA1G4CtB7jS1Xl6HnyB2sJOsS/GavprBEmVy4yF/5ggmVB+n4F2OnxycHZyQlRmAp2isbR0dH52fn7d+/YHA5JDcHj9Oj4efV08f3C+T7nZ6uTd+9vri5XBwdYKnfvgWFNDZO/jceyok/2WDblwRoZ22pv/bo6uNzcH+i15Ow7k+u2hRZbOycWCnv63115Koe3f373rocbb3/5b3/99eH6wdBc713+IkaKN/AgyeADdey5C8SWguA44uKQZySUs84F46IVTzqd2SlmbJC18vE0gcCAyTmSAaH6P4pdBJdwG/+lk5rCtoSBZYuHz0bG6tIfl93yL4OvePHG+GvRd1qW6fbM1HSLm8jDvwmyoWuKX6pkv7FyFhhIL0f31YEBTo2A0W25Tu5GF+nU+PxcEftvb02D+bii/VIUQyeiFI2ygMxrIRFOEKulcRPT4FyRl8nU6w3tE7RLxDrT9nKymWDDPEax3LyV9hhSWokx8SYd9oddZnrYiq/6GmPNLKuN5i/OaG77CYXYttBz55fP7//pl19++uHTqf2Ddxe//sdffv/1L19++/Xu5opRgE981g/bmSKPsHa0w5bnm9jteCDkt7/Q2c2PjeGtMNv+enllJ4llo0cnp4xDECBs+Xp5q+kff/yBf7u+ujl7/9F44vYO79jazsnhyfmHd496kesr5mQs4FQTPo0VGHbr1tKKcuXJg0ZE4UiTVoGT/8ybGKpSKf/jfSLGJ5pX0CT6jlX8z+JuithBIGg8S+/ia9pQVxK0xLlciedznzTccnlAqDZ6ot0cwzQEK6ULHBPrOLgp1ZamQYU+SFhNQ1DRVp122pXL4U4pvJ6qsKPuqmQOexJb0NS8ZorL96HEejFNpDgh2zgSK6VvhYBdGwUEmT11EOGokS2Io4WAg117Uz0Hmw9FDBBawFxiY1ZRG5+V1+4o46x4gbAC1MzMXGqllgh3jDzfH36IRUTVfQYihHA/GFqluGO0AW9rJVGQTACmlrJTV/WYQIx1ItMlcO1GhMwqrPx5jXeuZl5Ht4Rm/EiAEx9kHRp0vRq0qDN7M8ClOvii77HUAVQP1Mgg2KMhPg4JNRU9vo5cC27ThHg4TY0kAAVGkznDBEwuMITehEci7C5aH+poHj7TMSb6jqYEHl+OT44PxFbl8lMIXaxjPtWzENO022q9P7kg0YSB8yGuOyPlfGf38uJytX9vT9fB8fHr3c7d5lZjnvUCN8nSLGN7Tx+ko+rxk0f7tiKvT4539w71Lgg7PjSYawQGhe3dJ/PD69cDlySs7ME9tH7v05mtvGawHx+/2j4gVuHna6LoIZmL5Wl7OkXsJbiZSmbXAaUmc1ivAr0aa2JPLBu2KDfL9RY1W5iKeRVIRxZLdZkqpA0tIugbA6kLVcLlYT1Fy3rp6JuMsJ5CIpemKTTBSocTiCRNhnaQjYEzu6J0oyZLe/ARGtOh8XbNpClW45rL4iio8sAMGq7X/tgRiSs3zn0IQEOXcINe81n58SWqSJ2zNH+qYlo/6VcK2J1hBmKxjB3RYi/aub+3T09diXkThfkXW2iad0BGebXTr07TuAf52MK66WL7qztLObugGJiYmVpv86TPen988sOHd//8p59/+fSRTH7/63///vW36+uLmyvp/mKhqLbz9tpqnU5h0x+aqMBJAf7W/qFdK0B/k7W5f5aH9CSKu/uXdx9O1sfn5jRa1nx3fwXU887Z+dnL7srG4MPT8/Xhsa7EGOLwcHXUAYZ2retJW0AXw6WTSVyAwH3VBTTaGycQo6RTi55KJWAPFscIjGXbvTcIwB3MXFQrRnmBUGmMyoIXdo/eJq7YBwrHRyLeEl6snhuuuxDhgelLn+sgZFVaHDEX8jMVCAWtWP9Hx+Aw7gB4HxN41SFME+rcQOuvX2hjtYf58fYmJ9KU2lcmAgdudUOsgZQuXREQ/UVTzYQWsBEjHrUWfXRL719+YoYVud3oiE1hqvH5OnqTModOBA0xg1lvMrAqxjVsjLE+149pKgcXdEjWk2RZqXuGV0esnSoAjLZoGh5pf8G52zCZ1xt3XPGKlDEMJQksoqo6eHePo39kW67O8Jxt4tuyAGUIqlYB6mA7mjKDJjgMcYwtUH59ZQqS1xhERYbOmlpEA74X2rKiyfIo4grzgRR2RIeN8mKTN7RxHjhzzVOJjhiBlvWRzHnAJUtmhDH23SonGlsdrJ42WDXxbRq1e+yQ//3jnvn74CHD++cfzgwK2NDJ7pHM/rE1FeMKPUvGoREf3p05Od1C6aubOwcqNocovs11W0h6o1Uq5sQl+lKad+tp75HEdz1USQmRMKT5OekNvOLMqdSN7TgPj2fnJ88bewvMv90fndn8ebK7/2cj+n/51/92cX9tVXd+RGMNn7MCXJXNwgRSEYDk8/ASd8BvreAGe5s+bTioi87CaVBLiRrf5qKIgmTYL+5WjcDT6eSTpXm5r0zjj2ePhnZNOa0nv1E+GknP+pYNUKjah47uJzhENnJLicd11nelUDU5lSIkPU643E2nSHLAyiblSQu4MRDr9cAE3ntatLSqzcXHUApwacYQoUp65hKHDsUQ6UbZMyOVoC/mrS19lWCNdybz8bytPpj1HNanmcCZZL1WoYp72XlV8yHemuJKOd2PbpzWoF0cklU9j2V9pHXmqhnFpSKduL/aevn8/vwf/+EPf/rpp7O1FaJXX3/79W9/+Y8vX36nswoPzwtFxRByklL8B0envLwlBmIFMz9ne8cWdNqq8tvXq63Vwfb+gTPH+feD4zMrmun81++X350O9Px8fvr+/MOnoteVHWGHty18e7Ik9NDhJEeHtOPu7trYyko0q0ML8Xf2DQLss2B5bAxZJKVDMpajQ3SPnzTENbWAFYQXU+P5qA6mZstdivlpSxF/ClceIn6NM023QE+dUx6aN9F37FRCKAmaWBNjC+iG3SnYlEz5NJjOlI3pckV8FlE1F24AVuegsyKPCYxnQflbSXMaurywGiGmsaleJluQM43QzDxytA91NG+UVEaDNtGQhtf4ME3TZ3ZlJkerXUc6GtCPqKYV7UuvcqBrbCGmQjXcH7yVr3iVBg/tZCHqQAOj4tcUauhEAcd16qNwYBiUnSJnRkkJI7ZS/Kk+EqhpAGIVjtRQjQM+RuLrSHBaYp6UupHVQv2w1e1pdMyvSi7U2dRnjxvRWs3ywDyJWE3/BDO3vHlx8mppNUWAAOwiRRUOsG5zpph4iUguPzGlqUarTDCv4kl9jCzMDewUAQwI3bZvGBWb/MbNcOdYdcLeSzrY9LVeyYEKrcYJO1AiVk+y3vk9UuZPJ6er0/WBmFuNDFlE/vDEoTu3wU+MF9E/2WD2uH45/OHnn20UuL6+g4wTQfcPVLxvju/h8fLWvq2t85NDO41FU5Kw21v3Fo96tIwgYv/g2LYaRUplmC3sib8UFKoeVkOFH0somUjY2z482frp3enef/rHEpPP//XbTXGgA64tksAuUxV1jS1ectCpyW5NAWUtM46SHQ4ENpk2PJWEMEvx6tEhLEC7LlfKJdqQ96dky/+ZgImTo8cUiZC4RxXieQX9zFvuzg/GjOHDcnK+4rNOxoUksyotQ0pTjxg4D1BqUlSdXmRFVWTuoVI3noPNApi1j/lb1QVWzV4o474qgzDYXECWwezFZ6OVoZq+AIKdRdwLbJo/KpRl0tJUEM2aHpUBwIx84QRJ1DcExlyRxFudpZEZlmqpLqgGssmMj+2Ho6BcvN+Pz0M3FWQyOVRIN1jjLzeb3dfHk72d9yen//mf/vyHn37w0JYv//GXy6vfL758ub66cq4DyDaDkKOKDLV9LGUKCPGAb7ve3H27uO8BRUfPV7f3lzfW4/ec0xvqJCV0eLRaH3Jv9qtb+7wRxVtYYH2zRc/S9weHRsAXl5fHx6KLc8sYKAxlJ1eYclUIxWT75xlAi5DLQm45SKtEFpud0QD+RLRxwMP0eliRfGDdKwvFTewdIXKKyWXKEJH7JI7xypQa4n9sim5gl4Zi+QiKwoxP6zwJdfwm6qorRyWmhRTRh3yU5uaFGPBdyXvVqaSC9WGWRxQkja5ptC4Jdn7HKQEagqQ69h1Q6CtG/ecVspRCmTRZtZF/bXs1H56u0DC/WoSkMlNxtDRE5YzGo9WqUvgVZdV7a2GQdQlQ0DFodDOchoigassXkPMVY64saVZCZ5QLUtOWHm+4HzZTbdSUKYaWhurYiiz6PC+YjLQ4p3gXi0MlM3MHAr551QSYmGFLC4MX9SRpWHkpLU4qzHS/XhSI0FRJ9JmbquuMr7Mea4EaEhl0GjQRAjxAqhWv2A/RRgkLTsHM/L2hAJZ+eYQZ4oQBWRQCcxsAMDyvGDU3cgCFCE7pt/9LawwKR+XdOawdM8MCO8shvn+7+OWPfz7fW11cXDrSp0NUtnl8+2WYHAe63j9aWYztUcD61o8/fHj/w0fhmJURPR6so2ASkAcBMF/WZMbA82LETVhuJHF6erLa8kzgjSeJ3W8sN3i2iNvAhGnpp0TpbPDadIKdwY6k2F+/PFzfXb3uHT7/9OHjwfq/iNT+1//9X377fkfoM4No3Mp2tuz0N15hT/xky92whvps70lrWT+VWtJOSyOGz9htL0bGUKedSAkhTibwooFhslRFSjByr8wIs68+JZe0hJzSco31tozCuLk4mjBAWkxFA7SidRk2ZeQ4amQUIyUotV5I5de6C69BoHBtzHq69dQjFr7poX+ZPkQaOKT8vNNUwHt2k0IpP4qSPwomYvyxQfW6VBGNLc4oyG6nNiW4m6cVgZhCoT9ew6TUUZWiotxWpl41IhDftfIK0XQKyWJAage1NmThfMFEKz71elL31hgf7O/98sMP//gPP3/68F6W8a//8d8uv/56dfld+ubJkVn8akk/QQaHyzmaqZqVPweHV+II01bYbQP5+TvpRF7eUgJP/LLe7/b+XkgvZsFvo1L6hs6jkxMpLLjc3Zq87aRlZOkhWiMkuNA1ttyFIiDLaDqLv7VTpZleS6MPOg06ryOa0bXGA71E52y0c9qLMsExw+PXhrc4mcnJVLo1sX+6oKTSaVqi6Kc3xXwTBKiJP7PsSv4GPMXTxxRZpTeHoCOpdozXRglwVbyUnELjrzAn92PYwkdJlsnAMGEN9QNntGp7xB/q4ISJy7yGaaWCEn4/tYJEwq2yhvM62Rd8ekBGA6FUo/R7EAoYUaeRwqECmiWeUd0gRLs6ACoyBjSaAuDyCi3tD1s0iTPUTMSqyRg818fsektxe4dg9MTYGtMphQqA/kDon5fKU2CMs1jrzSCbaahTDh+garNX9GSrWDwG4l+o8vjKKK+N5ORzMU6DY6RVVpNzi1zEDF7ZZEyLqtDAm/Lxb1jVjPt4nUQXcx0zm/JvroFQ61jioze8ns5Gkwlm3qIyhP2LF+wXqqMWdprwp6gzQJO8dT7iaIWalofbc7DvwV3iaIcnlhVqitJismdPwHDIueUUl5eXH95/OH9/fne7ubm50Zpj1p2Ca/SQa6CpExhZcGVtxvHJqQcFO22RC4KR8Kmn7TX8f9BfW2tk641Z5vXxi9G4AXsTvWakbRJ22JZtnHYM4KoZaRb29HS0304cCsRH7x52fKnHDOx5vPDW9ruj8//7f/pHvmX93//6xZFejp9Dh+WkfN5In8Ux4aL8PQPzB4b++OhgoX39bjlD/lVMt8i6iNZPHUPyGb3s1vzoF6CIp/HTpZQh9Ug6fU9ugUkxlGETXfNVqUL7uVAN94yTGwVmpYKDBKdA8KfnGXcg+MsWQOJTBaLJt4hhopUm4xrLUKFqpES0K9iN6KgQFBimnoa9dB2KqKEWTLcKgy/doWajy+HrVqMAmlNR0iCSPqhVN2lINnsSzVdBw6I6a7A64UMNvIa9q/U/3kJcK+Hta2YWhpYmSpU7SFV3l6rjpUZ8sltw5/nHdyefzk7/+LNNXmd315e///Uvv/31P/QSG6590kw8fO5fj1jvYhkx9LFgJewyqDbf66ByY80Wca7WQhaLuvQJHthu/xcBKAYN6/2t5WepRydHVjPTebQaVmYit5uPnz6fn59lMS3VKSeYP8G6py09jJUOjiM8PTzv2cH0Ri5IMs/pYg7UtcTo2fbFjuVTHs251MUmcasciIUQmFWX737cqLfwixm0Z2mlbF5ymmFhLmDknyqpqIzYLJbO9YT6d89eq/G/MGt64GDoqqlD6jJLUXB6lHPR2qKKQh0MpDKGT6OrKfSbVhM8Z1HnV8xD8QCfoQNcJ/c4atdcaS/16n9I10boVnjUww01KUEqJAaILSk51RjlGJjPQjZXKCGF9ZfGALYUZBZxAXVTSd4i5k6H2dEZPkwEV/PVrmKvsUgl08B0HRfqMzDbi5MSN9c7TZ/mX7XRD9b43LHhLg/UpQtlSpwXde3qQP47L8iSxOC9+OuhYaEAUfy79XIYHwU9BSAOZJf963cxnjSTz5mrmTEplqJXMoMdDmdRYEcO7sWl0OijwubZ06LpUF2dZ5/pK0djCpR0SRWa/TVRpaoRgd2/bZKkhm+ugcKbyLWJq7GzM0cPnIko1osN8u+CHaelQ/7nf/gDT3B7c0OVY+P21s3Vzc6p9hs2nr87tSDI0SzmFEAwQ2ATgAk3OwNYJyxp5O3NdYlBCkOKVmwcnjhxUaRqEMLA51jP5tObJHndasj9cPf6vH96ckzCZp7vH1sdJGjbe93cfvtNMuXTybv/5//8zw7t+n//r/9y9/tVijXKHrMb0HgqGXqN2mO+8EUEZIRhabYQSF/I+Gik1rySe6odhxMqzlEe/yliF/+uW5XzvQJvkpm7vtE0QhpFWGRldJXSJr+WjeaA1eJPVRQyFJelB+NDg1qxAZveIME9beN1edWUnCzLy3MxhENDwFEPYLTRELYdkel+qZKoCB5vliEoViNDculgL+H5LF/zHnCtLbSlr75jDm/fAJ+jF+fm9KWRQc1yZ64+FMQuSaxXHKgR9xEZqrEA8rqKHklkYGP3iq7AMt8GmuudT+fv/vzzT5/en+28br789b9ffP367be/GfbdXd3INOKpNvUCQn5jR3qGNebToe9kN+GCwd3h2TkOHh6d6AB6pITzTjgvWxEfnmWB1itL+/UHlAnt9ioeH52eNNe03dPhbaFD2U8//3JwZCaJLj4diA+op8BNTP388PvfjHodnrh1fiZbeeA8oqc7T86+3+vIiA2TbS2DEe2uffFmJhrZiF3wIaY1NyXETF0S1OgJnowHKATGMI3iFzHx2/RPoUUnU7xk2hhi2EkgBXegjZ5UHbyBoW5aAAYqLYRquUGq/OgqyVaoYQPDSlp2YxiX++B6wz3Cq0NKM0OIOOvydSKjjfXW9NQXjlSjTW4UJ4GVni3dx8TrY2DhlmYWNEfdRKKhnr2U2qUFi16aVqpbhtIQAp9cLBT8aJl742sGrYXQea7YaDMsshPIjvpiq2IEoHYo1b+BU2ebsmOOVozpkFoopTApJ2t0zt3hqIpvL+V5exgvNq5+/FWywjQwkP1qNyMtSAOpVW5CO5QL8VRJ2BNngobU4XNzasAiVLmRX02FZ8Ir64fR2gJJfaB8Rqq2vAkq/K/1wQAURUaHGle2D71kTv2iwBKplQZgdKuud/kWrVgXS5gzczLDuzo6NWRWgN68e7dvT69xQFq0L87mJrbevXsnp39xdXnwraw/b8qSm+HJD/RIVZtleojegaOELBCy4/Jp73lOgGDHiCrc2DdHa5DtK6MiQWzgkkwGMFoc5OFkbDyqTawuU8DutSt7Gze3t//2+5fDfY/0ttav/NSjjDCW6Wtyih5xfP7Pv/zEUg4O//2v360NuXWghXMk0Ewkhixz1NDhales1+qBkd142IlB2X8xG1BpeVxPXedN35qHYRKFEW+CwEh3G69ln6OHyafqfgkhpSUeXS2ixBwpRUBoi/sWtKYnBM8PZBXJiGIFvb9KKecjOH69iLaUoc/mSjPGuaeKIl3MWWeOvQkK5rLTNKhdBpUnwvRx8W8Q6wxyB+mzenXBqc+AhXxdIxsKGgHTZRRYuqs7b+eD6SLPjpNeaccItuQrFMsHFDTy6ks/ZJm5kzhb/W2woA+WDcQv/S59FReIdE+P9j+dvfvx04c/fP7wpEP/8rfLb79L9692OtFBYQxs3zjHqvtAfFqB0VYQOYrQ4+Je9hzU0AhJ7O9wt/2N+HNDRSzf39HNO1RKzlAXILa4cUT07V0jmQKI/VIgoqNM2yLb/Q8fPhC9nY94axeLDe1Ert/88uuvl9c3ElA/fv4kSYUN93VLdw2vHh4lj9iI6AblhIdd85J/tPAR99hx/WLGO5kTbY1spz/kl7uOGcmfGPtc2YRCTulAGkGehdSgNevhNdWqUtFkpKB/qhOmz5ptVjoNFPimDdWoi+4RQJ2Jmf2rv6gpgZbHn6Y0GCbK67hTDUbqjQkzkM49TBs1pOXZu8pfKR7WIMTL1HjcdaoUgjki6U002d+zVwjOQIq50px2SEOyutHM+sACIV0nZc2EPMGAtLctkV2Jxo7+12QtdiH0w99YzM+kwsOiRqbHG1zCZhjRFiM1GUDE1hKe9b+/t2+1G1LTOWW0XoS3NB0TQCYhxXU0RhUWzldfqaQ39MBf5AuPOp28MShBIhFyjFzZCXex4y1kC6ydWXFwe0e2JD607jZ8IyRnNxSENwri/cI+V6VrlH4bJeGWE7XqhzwJUTgTZoIgCTrDtKfNxnoeICSmLaQpg7O/T7eYnAO9JUy3TrdfzKM56me9zd1baie0+vzz5//+r//+b//1v/3pT3/6+PHDv377rw+3958+vv/1184Y1cHau0WTbPr1vrm7nSBVgN6ad5wxgm/mYOvAl7vbZDqcb0clUhrRzUxFtt76gG2P1hBbOXAai9iciQc07NskHLbx0YGjx4eHnh7z9HDDe52ff/4v//yHPM3D/dP9pVbKc2UU8fzlcSvntfvqOa8GEPiHbwXVXEmcqOMkSoITDtLOREXZqulDa1eSHkfj20idapF9b2DRz+V/YINMWomwtY44rJ82jcSAg+cSR5yfzLi8aFUgkrDqanG9oI1+NgKfe4ycUatesbzxqIFiVGDCu+AMmFHasKWGk67PIKd6eqXa0hGAlnpEUVO4wBPDEmFEKVAJbdFpaPfLb+iZE1yxguKgFkUpSoeqMOg5SPotB9o0F74GrP2GrzYb5gmeRNP8wuuTI5z//Msv//jLT+ud7dvL79cXXy6//Xbx/cv4Jyf1PooznK/smAbRiUN4SlVAwuoAx822bgzue+Z47T13YJRHCm0c2LzR+toAQ9fXHvse4WuV2pZhgf0CSDxw3Pje2vKTg+MDrkNi5+zcNvYTOoyzZRo7e856YWsBdi4uv1jTfNKj5M8/f/hw8c2cxMXm6soW5VUr7poZ9kqLpLLu78RKkbaza0ICS5MtnPEfJ9OePF3izsFmwOMnxpkRfhVzKOSCYzreqlXSN+JNFfLzKQBDLw7oBiB677Ems2r0qmkJr9Gudl0JkdOsumpANKEi6ZvQUHmwSFX6OGghh2DHv4381cRpLaU9DfnDQHDuOz9N0hCYiKp/2uhssTm9LYLCnZTA1mrOzQOIesY2z+5QVSs1tveItVhjNLqWAIbHOLsi+oGR6qe7Iib0vIFFILLKSyI+fONmM2kvHZ8dooO6Wz5njAIFJfo+HUqCyZzcqnVtTi0IxIzQWF4+J8KcdIZdEMdJJdohibOCUAucsdyfea40Y9xAY6zAQRXpGvLrguZiqR7bNUancE3GoIWHdQetaBSeDLbwHPtnbnC2ridAxZ59VaJAbuxeO/CsTWjUO/A7yWz8V0TRD6+GhfGqh7qXHu2QkCcTWw83pGEuy3yAZREHzlC5vrw+dGruzrZJ4Pef3n/+4ce//Ptfvn37xmb8fv3ylQ89PNiX1ZGd1QDVf/fhvaUFBgHX15ctpT5c31x7LrDAqo6B9z61R/jl2fYa6035x43DXG7u3r07wwPnArGam4tLeLw+bYT8XDZ9enxwFFejhZubB+eV3j/0hBmLqngjQ0hb2rDXSP/d6cf/yz/9USs72//612+X0gCrwxMTGKQb/57KxWM9cdCjWIChlKfZtpQbf4yiRnbUjNIQ+qIFsdIFhZjHInexKOXM0yX2AjcaM96eQjaA0yetd2WZ8wATEOenQYRJTSo9zwUnrGmMJLqWqqagKZLG6Zay4xayLwVI3CvvkGZNJYhX0TtVcyVcIUWdEO1L6pUupHfKsaZFUTO34pKBCbeU0iv9CVFSV24UGVYaMeBrp5mFjxHR8xEcblsBBCzNwBWvp/ujQuDMMBFv6g4pmkEE6j2ZT5TgES4/fvpkmf/ZenX5/XdH+9zfXDjQ39iO/+MTWKRUfunB7a1N/LRQWC5qzwFXJgAog7ZNEfHzxpAOLLm/163uHZ0diiypdZ3kzpPoHyfMRXE3iukNykUeHsn8xCUPe/FoukNHyAmdMDpmHK6dQrtlOYMtYFYfecbYuUdLbr9++/r7t9+/bO6udp4e5HuUoSrYynb8wxbGNRxsVr9zTgpbkY2fw3kCGnc+0UK+sMFBnMUbAk3VtA+CC8AW9qdi4Ax7+7DoQCXTRYXLPaQ+hAsQyUoternlx2vk2WExPi4Zv5zraAKJpY3iLawkfUXVwXVhdLgr5F8xAY1wUd8StIlj3PQxb5y1SPOJVtLpKI4r7gXRX+o7XlHoibzuTUvu6DcRaBnoPMslDOcVOdHtCy4sKmnM1oC1+L55BhDBhJbbKXhIlPjAbDUZIUbUGlIziFx82IRCkkCxmprgAYczmh7Uy8EAp023g44FeO9moaBC01tALXB9LwriwyAsis3TThYlkWdLoCGfi3luJ6dMwnQzoTa+Hv8iY6SR4gE412Oj7FBxYa5k6cCVClV4AVnEiuZ6o5pwye3Wxo3dkqEQTffec7AbxKVLhJOfH5YlgxFCGmA9fs96tzvq6GT/3CFuoufb++ZsD9anrOJ1+8vv3z58/iihYkQiEQQhCZ9vX799+PQOoy6+XbCmzzsfrA5yEjt70zuKiswmGHSrwg0I/COKqUjINgrYY4fD1QgQz9shTMGgKhsrkYf3zJ2EnT/6MA+fZ+f8ijSNbDQ70/8+Xd2+OznU+74aE3AFO3t3374Q8IfT9//X//xHBL7+y7/99eKqxZ9Pua24rTGgvfnBLC2Me8QPgczoUsEs4eLmyHcZ7sk6YBS6CUDPoe4iAs6ZIMAbRU2h/FlHOrQ2jE1ghP4mobwqnWAjBcZk0NDaqz5b51NfQ46TMRhM2ViakqZBKVUY5JavCTlNcim3r+IoG5C5fs0urZvFca+ROy3J9SO4SmnifMjL1C4wOR8tBTGAE4NxuRLuQ6SAomQCDubT8E/0a2u/5qOKf9YUx5f3wSw9ZY4Ph2FkfOChQVKahewkcnyw99PHd//8j3/+dH6+tbm/+v7l2+9/dbJn+uEYkumV5ZesCLD4U53C1p5PZM2O4/vN6yqn5+c0d+8fjSqOLOHvudQ2ih8fwe/q2iIgVO8eO49k10nmrV+AjJhGtjPPIDFCsxELV/FQz5d4NiAwZRWnZQk3DyJ9LDg7O/vh83vd0uXFFycQXV9fG6x4jIzTdkig0VQ5B27MOSlrzOGQ8a9sCS66Dfu60TyRFxmNdmlhvgOQ70qAcbwixdZE4rOyXMeUbK1tUsL8RVjUJ/Ovgy4rls+L5yyswG/SKiNTMN0b6WswCSc3zeTM233OHgTZZQ00iJiwd6dj21OkrsK4i6E/vbtPkOp7TUAVSuOcFMBbLDCCQX+dBCmQOPrTaxs5JXdlJlxo5YWajZ8Aqu26moZIC0fCYobACKS+dWtO45mAV7vdzJ5jQCeG+ahhzi37jcvQSjrjQftXhTDuNq+eHSxrMJpkjveU1z0CrBxWuRjr5xvc5REK8/OaIqAar1Rd5+DigjB0ANcRYEfWXOmR+zBIdVCRzXzaMQaaBkdNGrG1UgXOSQnW3IJ7gIMRua7WpgEB1uUyqu8apGNKnkL7RfsT0KkC9+kFtRB1aKmPkDB1Ysy+AdrKVH1HPKiHCBXXa7gdnx4/v9x5Nh5PfLLKTQuvLuj+718+fPqBpwL3hx9+/H7x9WkjlHs+OT2+ssN+a8cZPVb++AXVMv61ybSt7dttHtypiQ9WVtCJAhAYYL0HxVjK2Vxia6hXewfldNLLHdPFdEHHjGwm6q4ulU9t7YcjvQ4OnJN1dbORy8ctrZkF1HscH+fa6m/sXFjtnqwO/vM//cnq9Jf/4//75frueUPzjgw2Gmgq5mhh3qI4e1mE0SIH+pLcUnma4MqYFk2lBq2SZhFEnAKNBVYWQ9OZ0UJi8DkQRNwzY0v9LyXribO4We2RitfpupVTeJnTPgjQ7RlgZoEjqGX6LJCEU/mKTPssKiMZle2uRvEK1MIaJgMCXhUjNJ1TMwMlSBP3uE4Eg3j16p+6xw7E8y3q8H0aq/+hZe6NeucOhubkUq30j/coCKKtrqTunAXvA7Dao8r1BrLki7pbifv8fHZ69McfP//h8w8/f3zP+wur724vhXbmfsyraqJ5IOe0SftQHqMFq2u4/lKpe8I/jZtjFQ9gGOu3d1dGT9QgJvAsYJd1G8J9inV6fn5ycmZ1/93lJd2Am8VhhY/buz0V/v5BiHN+fiogebhtRsqtopPZYe50OSjLCwEhNfQff/mLY4fc+vHHT553Ye3z890NKhtNZ7Ae0ZdzyKsN+2i5dWZ4FIvpUixmfRQhLUpPjP6XbmIki3GF0GPpMV0FTMTh1h9Uu+9eI6p4HNeDqUZy8L3XZIy6WjSeVler2qMEbf5KNF1xObeWvnf0nOzFeOW0hbb3FeRkUciY48uh5p3cUcO/Xn3PRoB0f1oJUaoS5Ox53P0g4W72ZdKRgkiYq2wamrqGE+7RIh+CjT4U5tvzFagK2xmPerx5bSNwcPg7+UmALHzlZQIz+Lnm1TjU14KPXGXI6vRQVYLF/1R/KPOvWwuu1SQtxfyfvqG2xGBDm8ZTdDjmoR5gg9cxNRIhEEN0WV5L1bREh5CGDBp1QNOZJNzEYRHbsDIeQh7tiSqEsl8U9T4awBEpsnDMBbd8HiOHW0IhVI3IpY+5yrc4bjli1eJ+H14f9zw/28gAyuPUoIIQI1gZG3H5iQdrn53BxlIbQZEu5/zdGVr+9tffL75fnZydHx9Rl733799/+e33i8srT1E6OTlpptHyTU9udZDW9tbl9eX7Wezn0BeRNBEcHR16vpJD2YUpxOphv4DwDC11byW3tZ5cubmp+NqcQYnFxu9kZJkHymiSZ9Uoq9+xGMSGdvt67jzm2x4ok4QtLd2WVTjYffA8efuIP5++f/np45VTiV5++3J5u2cLLQy5DzpUOGpF+bP5j7KCNr3V2eQxY31Md6GFVcmrwIQ3b0ydNqRLhcDTB5fTS0hk5i4kk7Dv+niTVRSPjRUQpLI0AsDWPo2eEWiCnWhaVZ8UAj+INMUHt3UmCoRGogaIL8a0XHGF4lXb2bQ/5gOrfPHABbAVNx7+rhzRQyOjHDe94IxMJlO7bvmQuYgwfCgwSftqcRSSldJkpDQ744sN1iBiGRryWoXSDc3enGDci1E9iaEjOaisfLPcm+3P7w7Wf/zhp3/+05+k4Z8vr64vvt5efG1pkSc/2+xXj/40yz6tC048SaZRTfEtsVjBK+Rv65Irfrb2rDZuWzXMZwHF9VVZ+Mpbg1zqkv5YsnyNEPwvLGNxnb4O6Ms6mtMuI4P6FDmi0xPXPC4Vr/QNFqyqe3H51eYBw4OTw/2Tw72NDSl2KsbS8pJmgBXLGSDfpnqGRTqUNgnBMETZ5Zy9FnNpE6EOf/MwFZNywV+lYD78xNKkkTbWIfuSD3C/YjF8Pi9iWxaZLFIzsKRLiUPpquRecktpFvEImloXkKpzjwDjJzvsxC0zjyIyeHIpBDx+DzopmqqDZKqVw0yVNBGCg3S0DEpowWG1NR7hMcQ9BmQwpufGMZ4fw/nWwhoSAdPj7uqsGjFn/3xl/VsW0Dqknn6umsVVJvT0wPQfEyIvhmhkWFWhaBrWhF7M9xZvK+w/rDNG/rFr0g4F4UZMb1CwaRBtYJjZjzxgAWwvpaIohSd4mMKyBL07LvKi02JN4kp/PsYGcIR+kJ74EQIqUBSt7FqmVLHQUxATYupi3BbGYcT4gLg5JbLE+BlftVkr3obFCSbkGgSwUKjpL8sPMHiM1nviTaLIASTgPqlkhZUYQR7aYp52yXosGN0+OfPIr89X13ffL68lcFf7Z2enp+j49vX66+9fDKGN2jRlsHx7fWOmDA6MBw3WBoFs8xdTm2PHdw729rdMx8Q1efyC+jx1ewvMCGyOj074B+fyzkLvTephzLFvrX5PhSVqc7E0xWePgHT9oJmAgsLD1ZbFGA5ssS533wEAlqNs7mw3PjzwKJA7keyrLPH93qeTw//yT39ImE9/vddF3d94Mo2dQrrsnBJtyWUXuuVGX5qPGl+b+0AIHhFbttoo1s30PXEn9hFGImBsw9921WfqoKWIIxcyylJEIWLM2ZBFbphBAMkAlBpJs3xMIKM2OYWG3N1VdMxYF1XFLhblpN8tfNFQOhMhgXK9ev3BXCqlPLnIaNsJxjxMgh8SUN12RdpZea1OLSDoEROb/111ZVSzalSUPvqn9+DqWesSy2qf9nsqRIk5/XmHG7VQZeWst1ofWxayOw/8aO/Dycl//uMvf/zx53fH63sZlq+/X19eEJkpHCM/63Ou7q64J4NRwHLI+R+hhK18QuFOpyKpBqwQJrVOaGh5z/76sEVGHuTbgT8P1v8I7R1RhcwbE1FX19iIU3KSPEgx4tOLGePj0zMdwmPppCcz2JnPnpOFrnHTk+k8G7Lh6cPTrY0lTkRfrc14fTg7uvr21VG4FDq5Ns9rYNewuLgPtToE4wgrgKT3pnMfLsUJkmrQWrBIdGK+meldQr3RiCwzRzD2OQo2mlFF4AnDT4IoaQNZL2qwSDuxUolu1Qzt25X1BENvqmTXu1HpqahpqKcGuZEFtOr5olwJ0U4tBKURKnplAKOt4TGgujJ4qkS7lHIrREadQCjGFMTNkuFmfZ0B1nLJVgNw7IpNtFqsN3Tg2f/AMrX0NK7WUYk3piGsjkPD5zc21RB8/RsX6SPKS1MibcEakyDlL2ZlZ/W0jbvrV7BRJJ6a1eFBN7bKNmB3nZSLyM+5Zn2qr/KlAYllvNJ41churONq9hnzDXBEs9EUum6k07oaGWw505bW7Vij0KBgGJ3iLPVLSDSOwc1eeF7fOcBDRKPJmP6/cWwsv8UplVQh0alOF6kf2VoFYfWOPr4TMV8drW6yzMGcM1q301e3r+zThrrLrXsIzLXTz7ev7Kw5PX9/cnyC7HqFmw3PKvW/2j+4vLz78tsXo2kpmzk9Yp+9kayBr7b1qSeHR4xdt3F7fbt93FjBcaJtD760dPRYxO3RqsbeHtwBXRMG9ulX5uhQJWsSisfxb3+PUeZ1Wz1p6ff94cHugXGGReD2LYhfXiy7lgF+tdLPqg4HAugsmrfYfj08gsiDbf+6joPz3Z/enWz/4y+a+PffvntS+Cz34UFNGtuTTLtGwmNOGuIosdIrix53CcnCEbLMX5JvGk2tsaUor4fgJHc5Ha0S1N+Vbqwx6Y/8yHB6El/z9hPfEFNNqJjBVdtPF1WtAx8joikWcZcPcF1YLTHFq0I61WDDVKzzCHZWpfIUAiWlW4CZ1U/5fROta0oRBXxP77TSo0n9UHuMbOHTgp3omgdDo2AQ4RNrlV4Ltk4ThAwW1qByK7yci5Q2t4pDs06vBQVgO4VDTM3hrndbHfb5/ck//+GPzvS3hPf2guv/LvMjoLcCgEuVKpSHz3vsOH5ng7dGfoQr2uLPaYIe4uLKyf7OiIJyK+513rGKM61QQ7T72w1dt6RtlG11e3v//eL790uPr1h9/PzZIPPm6nrdQmVLE9ZHzj5xcPSu2dqHr9++vXv/zuF2Vjp8eN/qBimom4tr/Y1w54cffuAvHFj+9HArh7ExWXF1aRXRycmRLWHiFCsgLESzDoniNDBoXQUXs2avhitxg+waAnaUHr0exvNq9RocYnHtLCIq/M6/vjkrvSl9y9wT2DLam3ihrxk9+arhNnnhg8tsD0XW+hk9pW35MD6v0n7JuxyVsJAaNkWvprP5INVMzihQGq45GHpXrKbzN91P9WHDa/Ewo6TjdVIyry5SkukdhoDMhTnPRSyheNiTEmZTIl3PSCg9MxlDTfXiyQFQVpum89uf3SEncSnvBjYPXpew4BNOw4pqTkWdbJULy0KFT1Q+XQzzikSJAtle4TnIady07gacBrMdu/oUHdeveND8oh8cWARStMpBmdskpTkPOY+R4O2vlUiFpMaqRPawD9PxIPg0Laa+4eJWNMAgqx4uRBTMxlEL0vNThAZ/P+w8uoYSXRAJhVnv9ZLIGQgi0frCyOS7zHbEkMgAVvOtgF5iKbO14+HYGE+zLxX1+GBYrpoN8YyEk2abCX5vT7ofM23D+v79+/nZ2cGO9S09/ld/UNynk+vwK09/3L+x3k5C6XWLIaEFGnfXd9QMTuCjxSZMtjvP8HiymAdPWLSDAi3IOxbbw8ninyfGvHd/98CP+I61q4O1SJLnk4GQd4urluI5u26eL5arurYzYMvjO9znfp5ury0M/HR6+vRTLP/bl6/WDQqLeZMYPYYlo9EaVYYwuhiTFo9GBAadfUPHqHjqNJ3vom2KLkJNhgkHe0FVOl6nbC4vnXPXCShfH8SSFWig29xCMGGuSCONGgpaEDI7fO9CY4N6kZRt9JEJyLrLE7rVuA8ENd8UeJSpHIllLWEVQL8KVjoTCFrz5lwEP98BA4OMVsSz9Qe+59bjcL2Q0lpMkQw8FM0lTLC550nulRZEAaXYqJmtGxmcjd/ltoQLq9UP79/9519+/qefPh9svzzcXd5dO93h2sdGgx5RbZrI4M65bjmrWdujf7FO8fGZL8cEyz9pmUW8qX9saSG/EAY1FOp59wHnjK5F/kzd9BKndnN7a1WCs33EGGdn55wsFc2Ad3ZOz47x7/vXb+vjAw063UeK0ihN93BurecPH5n/9aXzQq+PPYnG+GJ/752zJW5vLu4ugJXLBEcAcWT8wd7lpBxUZeGPU0pMq+bQmkqREG2BEp+cqtZ5J0McQ0yBvyduutF6TbLBRVTpb+EDw6EytcmNdK8y9MMVkMcJ5QJSk3he+BeYbgrvDJixQvViMimWAgAqkkeqTp6hl2t5J4DyNjPVBHnoUQ9eoRBg9CUM1R3FQbgaLqfPZDXWXYgyr1AMmYoOqynKYNV3Hbc8Xv2GzA8Swg8jWpvSRU26GxOgks7N6pSZWqkb4Zrr2UAVuMzCHy36AkiTv6GYunkNhWMqsd0fdKEBLT6hZ85gh3abkqxvzKT0yUFI/0vRekHDve4Ov7VC4zKKnG2jzYqGPQv3m530XTXxlbMtUmRgdIlIhQA/82ptmRkm3QEiphVvCkSGqiwxmNk+uMCNsHWZoQbqspNIQ5oPD9AbL6QGVYvlKYbCZlAVxzkPcUlIZInz5OVXSSGMxcL0EcNlbgyGCBe6PYp3dXhz/yTdWSL29fX0/MPp8dmrx11fXtoZ4JAUGn927nSHx5s7By5szs9OjR4uvtlY3/SXxOnxwRH/LWoyH3x7dyMpP8O4VrlgCofFmTN2D+12Bu/9jc7jyYGc5GqgICkE1TQxv2dWgHie33/+eH/p4cT3ojVP6pBirUdLQQrDeU+zwsiOJQIK93RIG0+VoaceHbzZft636P/HD2d1qU+b375etPRY91LSdlSOzjqiWT6wEEzGHBOlGsjU1onmK0aF6RHwLuZDy0BQ1JG40iQHJlQFzmrhMHOoJDpIw/+M581dpmKwn2zKQMiBFi1ztUm+yf+0luduC2QjdFdQmOHVwU/CgdCZjb2ck5FFcc2MnqDGfxgy+XQsssfOgho/VQWsPgh84ZTsTV4YWoWR/pA1/Yj3YA1DEgnxrXAG5LL/mVY9JVHhVsfjSAVSZmdD3VlO1hmCdPLh3nJwrvUff/rwP/3R+T4fV1tPF7/9zaDu7oaOCZofZBE3T/c3dzcO+8En0fN4x5bwG1wkIYeyPW/fPTi/wfMZ+VOhiEOr5CENWQtsEBXpdnKJV4aNSBeU8N+eXUqdfvzhB0sMLFWgXS0BatPi7YzRLUbN0ZO+RQpGUZhNXb59/eoBc9ATFZ0e6QBsMWYb219++8tXOdAvv53KL31+J2fED2iI97L98Y7f5B2kNPcPb57ubFsusC50G7+SB6vXDsHSQfkqtkFyOMmYs+t8eD4tB+tnRmAuJTXkjV/Iy6RCSUeVLvIBkxigmPQuRXPHUSs96kNQlRI0g9W4VwmgQpNe+EwRScnnOpL6cTV8CiVfa0hL85PGBnsSJBlCOIZHrA+XFLgSXjQ69OvFFPfyrzu8dsatCeY59MIOXFHMwEjbYxM+tVeNgpJ/XnhCY8ILbUDDDMSQfePFMK4mVPZ58PZZEY6wS2h1yGX7b+PcMC6Xhwjt8I0Rik7fozw4cUlr1Hi8S1W8CucrGuVj1zx/VYinG5UtDQvJ+KJYVbheat3QJBa7q9PKT4HgY0qeX67vql/zOdjZPK+Nerg39g5vcwmzbcCinxxSjXiDwCCWVqlZOSwDauQKnUnQh5fmHcdjkQxSlCIhM8RBNpGKs7IBxTU26zoS7vHq+krEfnhwYiPb4cuhY1DANttmugxlRuvWadyXHGKM+3fWbTu0R5+wteGleXMmRN7sXGxlr9bjHN3PXMoRORD023fHMetTOtHHurrmpduN7MRQcEtED+elHMzkPe8/OdeX8TvQs/FiXq8HvbJ+wZVV4kkqru8YXJidYGY8Sys6fNzcCYCOD089VwRTiPq3b5et2Oj4zPQDfwsWEJ8YqX75hHxtMq3npOjxPj4J2CRiRNbpiFAuPWDSqWLKScGa6aKwI5raGGtSGPAUWM2Om5YkSLflutiJfgnKgUp9+05ylczdA0QyKSFVSqWbxJtSYPZhFjWEWtblGz0aLfAlZ7+EjPDB3kw28FFTS/zQoskqIBYz/KCxXBM1Dgk4aI6q+Fy3wUGmR265UH/higCIE3ST0GgrPCCjGxdrHextn+6v//DjBzszfn73fn/n+eri6831Vwl/6LUKZ+OJLPpzx4bfYsHe2s7bxkamgpv532sLFxruNiaJJCdTBq2aEmhmGbP398X0sIeciFovDE2nQDH2a1O31zf4ZkmD/mqzuYIb6VANwcT1za2VDqaIPdxUZRMGnfBsqcLp8fXFhTzSyfHh8TFNNwA4/vHzRxH9//G//a9/+4+/unt6enq4b3OHOTy72ayUuLdNMbY0Bf2ULxtVsiUTTFdzX3STmJt65f2Hp0q3zJLqjTvCsDxdAoJzSuW1KFIcJoARQh/zgOSyBIhEEfkuJQ4qqf8uZlSC7ujEukEnSt5QQP6krnupMtJNlJOOhzXupYJpbTh2Xz26O21AB9CKdZM+5r6yu76AGWqT03pTKrWjYfCOSB/USWFSbIzpApACCrKcJqdFrUG164X004KCuf7soLZYgXxfatmXUWgkRbOf0dJ0yGcS1WLbaqEdymNCPTaPP035gwBpXxAWb9A4QorD3YUYjMN0viuoSHbchTEjX9kBB7pcqY2QjR6lM2GjZl4k5vhcAnBBURFXM7tEM5NqeRbXRg98aON1MhNcskd2VXQgJIorIiGUoyk6or3AAoPCGlMRFF8WY+9LsUEP3nKpfmgaRh9hS0pOn7xjvaYjc41odzsk8en56m7z9fffDw83p+/OLfNnknLxq639BN/qDh3UDit7eVofHzkWYufub3ec/kvHj5S7k2TVQRTsm+ctPGwsgnui+JNT+4pllu71DaxYJ4EKm8WMqTtM+vnZ0yebSGOtL89cAx2zx4eMrB06lPNeH2xuHcP1Ooe5WfBn0ptCbFu34cHoNIsjcKqXwcb2njWFHjWg+b3D1eEPzo7efdFj2WPmkcKlSJ8eRMEElJ6hym8qO3zlolpYlsaOBUxk5VvRlrHkeDkkZd7pZjg04ko3GgEU8yTxJFKJFIkImZ//w48SdJRTFf5ML4Rw0biCy6RbCpoKhQ4R4wVIGvKhbsMdQezcdzHHncZPYa5/fnMwNCYzoTnsNNQKhhQtJ1D7aMOmYpBUuF86WvnR8VD3kjOEvUchposFC6nrkAY3vh57iQ2WFpPogGkn38NLvz89/sMPn+zy/Ycff3je3Hy33PPq4tVqH9tlX57uru057El0+gG26AwQkSH5A+XhLZS77MqWp0F4UnWL/huD7u09hAN7Jl5On31k+Cii2g17Z9GhFZw3vP/29qcPH7FY1I7YP//pj8enR//2r//qScLn7z7KE6IUz2ijCOVR8pG6mkXa2Xai1MnJ8bmXeS/PAb65/Pd/+9f/37/8i1z/x48f+f/13uv95VeZH3vBJPnqAKV9wxhHy4nqgYQRHOqMVY34aUKv3GemWOoni0XI+AccrqYCWD8Rxdhu4eXogH6ccYvbkgYF8DkvM06vAoXbU0BLFSJLEHFmIVFTaWlXKJHXeCgKGkpeb65Q7x5aVMGrPmi8lm/hlLaMq2feE9tXF148SF0e0DBKVRaI6ZyuYcFlmmMw2YAi3nt1odhUDzR41EDdWJaYMrqRSk+Y4XMvLUy1NB1C9D9wsWL89lspxlH9SqMsVqhZBJTm54AnsiYVyHZ7OK/xaX++1lRt+bewaDzAOFJ0FbqBKahHCuc/Y4uSffxCRMeYyAc+BQO2DQfGIC7JttJyaX00Bt5ODIPnDFiFXI/iicoL1xtl54GAeWPl3FORBymjHpCxXNcHoGK13NVRqSBoJK6Wmpo1iKbbJE9RyF6skJtWqqzJ3FOzGHsn6yMHrHu07+393esVkzgF38QvtRBWiGWiYX/P07skWXlrpmWG4OYSvamRsW1tGRQ3B/Zwc6kPa7ekNnX458enL+dtmn+428ivGj530ks7A1i1AL8uKqE0dlF701TDav14a+mnLMQS5thIbJT+ag6Zl7MaqDxiWwVfZRKemnJcbbf32Om+B/o3wPYdZLF/yHxxY99Dx5whA6OHR8fV5RsbdPZ0xriHhHpPgCkBzqRrma4RVcqUrTUCTcsStk+iUt7IlVGpbqXoibFptySA8LGYBl8suR6/lcmaruDILn3ysCQic7G6yysFKo4MHVkvExZqQGngTbG6BHczlVTeV3xAiHKuc5IgZItaRpBuoxfMkTWwJjqE50QZwYrArC+7B7B5ukKxxgYgBnquL29ExQSl0Pik0o783q69/q9nRwd/+vmHf/7zL59Ojlcvm9urb44StOzQuR+6eSl/KRfALr5dOXDE/I7FPIZeEkIe8GW/dkd1OqD/6fXy6goavD8N07M7ClDn5SAPuIerYw8428cGxzZ6GN5efBff34re154Ds71zcfFNe/KNdvv6gGDZnk+f3mPW5v5JCGKjmBmIa3tZHFGyb1uAx57qAo7JTHrq+ur777//evX9K9/444+ff/z48e7um1NOWPTKc+lk+V+dW94CaKuKU43JYXK4ibINbTlN70UTKU88GxvFQ+gnGWKi76lIU+rJfkRMaRexz5XFQGO8F1Bq9K7Piwmpy9wBL2gkSOy5iSWk8R2XUukJE3UTI0WazuHQlzBM5MUtk4MFJkgB9T/se1X/f3j/0TZEdDf83W+ee4IDYtFkag0ovclcfA/G0ikA5B5oDIGKLj5smBEHGIYAED+mT4lOcJTLCsMqr+w11+Y6CoADSnwjMTznFGoxDzFUyfhC9MHWA1PK4NRSPAxwleoqFr67mvaHn7ehv6xZHxEQtGVVVLYRhxhzg+YBlLSnZG/xNpIXuoFklEpjVhVhg2N5aW9lfUAoGAzg2/WBFcdBCUwlFjF0J6FVpWAM90ZlBtuE5ENISaJyCm4VdpAH4+Xoyg4zfMfgiub1SqyJ4XOtVtkZirXq0aya5LCFOu8c+Xn/aBWFWa8DNiGTY9h7d69hfsUyUC3dX9/aEqwz+PD+Hfu//NYz9tquLycrQCqnZ42mgYB5s20ghLf8+umxjVw7Hen8bHXgwTZf3ZGKB6cnJ/YYK25hoJDagVzIkC+TbBoRtQXMGb583bir+E+UTbC0U0jG8/nRsaMeLOBEsFp93H+A+fHr9p1ziHVaBiNbJ0eJwTS1SUWt0CYxnM0F+okRqC4mrU37C0jwk3NPcGVRcdZ69tYqTYjE/3TgYiYNIWUK+WbVb9ImuBSKvCej5cSi1ps1qd8oPy+dd5ipTm6fMWufZoBD7sTYjwYz/mVuQF9SZ8YMpAPVpRzEh+rRVgoBpF6corqXL/FXaRTy3dMfpAjo1ID6Wb+AWpKMqgKVbaiLk3S7KBVEDsGV5hTKtvD08UHulJOzRmfcg6ZMzjBy3TXOHq9X74+P/+GHj//8D784382jnK9+//X++tujExR2OybQApur6xugNC38t3UQC/Ojsj0Pj5airdbGlGvKLUBxEsQc3HDG5ZKuUIEaI61MBNqtUmvNxZ6RJefWMwE8U3q9/vDhsxSQFUCEfnb26eTsxGzw1eW1496c5knvri6usUDuEQMkggQx7z+fH6+BWR8dn1hIdH9z++vFt+/fbH+xLujkv/znf3bv7uabiMTcktzp9mY3erm9yWibkTDwpWTNhyd9ks+NEjRmv9lujC/Y49xmTjilydX2wu0kiBMK8Iw5zTLY3R3PkOMaCY+7SyqKTDiKIaKWpGFPD4VcxJvzV1VgAQjd1/K4etJLr7QIbO7D0HlcE4YUA9KYyi3/VQ2vAOVLeEdtgq/vSb0qVKN5IO0EBn1TRZnR3Ny/D2nU+NLQ86Vnc1QLAhM8NIaoDJQwpyamft4t8gepGET6oY94LMQPo2ZIQw80AGAEKw1ppnCkcxqKsHlMIH3VE6qZpdHtmh9GoKD/GZ4P8xcw15YivWPCQps2EtrCl4gkF40tOLvqQ3wqXRvuqvrf4HTiKF1o/MqnT/vjywe+kl1amKUim/Jeu393CIkw6tCRdeJTNycyC/kErWgQaryWInNw5SN0FqGTsJUprF75x78aKGIG9rRNqt0WUeSp3A7t8XAlbtRyujrrvVvxshcK6Yl1e8Ksk9MTK+0uLi7en3ue6mrveu9lYxbWEileOnTsQ+B/5Ep16ykpMx8yTbEyXCacYiLK+MCihd3Vrf7qiUd44Q7hy7ow0E15YaU5Xw6udYEY02B7IhezO+1drHubmeHX48N4LtLEHQe/SPIKDcw1Oi9yveW5Zqvtd6f3djw7shTPbILD0Ia9OUBoY/10qhhKDAlwlII4ysOkn86hNMvX0nfoZaXpQ3LB/lSWHacSybOuHoQRt64RI6VJ0i3TCVmnz0aRPKy1bbxz9yrt3WdQUpX0xYWUrRampKZVVqcunRroBzgzn1XKEBXrfehLDaICgCxs8Io0LKw9/DZkM67BW+BTpcV6xlPQt3jT++hkSYBmz5azSoxqmzOxrpwfeXkwIvt89u6f/uHznzzY5Z0jn4whPcX3i+SPZQFluRy2uXHmmkOU/cJa92q1jMP+7Dt89aCueGqX+OuOp/8arRr8HTYAbSOFeIFaw0334E2nZByB+CNZ+d09WUW9GYU8OT6TlDHCMKtkg7oIQzOyjlTX+T/IN/2Mo5rS+6T6uzvqyPlzFY6Zws/rzaWFob/++jes/vzjD//w8+cPjsK1Eebm1iRZB9dsbl47nPpux1o1wqK6c24urZ/0mlOFAE6oGToeJ1D2kKCS+Bhl7pQhY+v0vCMjkLrNVyZ6ciS0foBIbsTnKiD1H77P+DIdyUXmFYDK8NIT+iDCSzfmsQeUdrvnKaTxNRIc/RKZFtWbTsvrZ7Hd71W7o0c1nSX4TgdySqE4V0MwMt4A5gRzQbPaVQvpv58oRB3Q6mlXjN6AJ/5UQlCevkVtft1AMp+wWJ0Po3aL663NgceQ+FNEFvtABSV6EO2BrvuNF9O5AhbWS/yjgRy1MpougAAuUhcQMa5wcoiLch/g8OZ7Yc6EQFBE/F22xCYlZ6PAQuSIuqhUCT3JbIIUriKOEoMVezS0rmhYMlJcRjga94tqolyYwCyH29Mi5PsFZcGHQhrK+Q6N8fXD+xx4OVlVcvRZ6qhcjiPRdtZeH/L0+kaPZXxc5+dycN4F+x6HapG9o3J3nw9Ozw89YdXzWCy6YzniKU9AYn4OQpGGfX/y/vh0pyU+NzfC8wNR0/OR9XPSKRaAmjGWIsJwedHWPLXK75GPFLYXHHHinjrmSXtWc79I4KxN2zoSjpB7vBLMn1/PTy2yWDUZbEr5tUWiZcnWmL39eLehzyCJqOXVsvbDAxN8Uq315hYLWolk3mtve9mcXfJlZbr4xcQyDllHJWxhoWcHdvkc3j0+XOY8CWt7sy4fcXP/aC1HrpTV1vtOUqiuFrMD1gIv8lQhS2i6GFf5q1S7Cz63sCTPvuipDsylLC23MP6zdCVNZXpCd2IaO0eP+m9iY1NuaIb+6TC0O3oFpECewye1tHtkTPxLvn4Wx0KVxEw0UdO0YVScEIsNahIagKeDDSncNgG4LjECigLz0qtktaEAiQinkH1y3llb86T1UJ+O63YNAmiuVef1u0+bk4Pdj6fH//jHj//08+cfPpzsvNzd2n1xe/n8cH1/fclozPpighSi5fzy/FyvX5zlhOTxyt45zu/IzPERdgkaWKmTaKUJ6bcRwqwC3TF5q0/Pw7r68mq2yWytZURc6cH68Pz8PS5dXl7Yvnh0enp9devJD0g5Oj4Wsvz6t99JxGde5sHq0+s7o9Kz0xMkX3y91A2snFf4+vrbb18E/2LHH37+6Zeffzo52Lt0Uun197Qx/pPKrsFOuScSYdsJiSLIWxiJEoGtKfWtRV8YTobpQy5HSRx1Y5QkX9T1wv5WjlKBQpw5yzOl85c76eVf5mzSobUMSYm/UlIJSQ+q54O6oNVXT4BIkalV6qsPWMukYnM+0LgfynM5+KHHixVPh1ZNYUddw7xy2l0Z7AoE+sQ4aMPftUTJ+ZgT9JmCN36pPvhvcBR4U2OOKpvoZlxrptVHGvpG1KLwKkYv5QPJpYFjUkNLeerA5yaxYTRbAW0VGoDZE7pH6UNb5WFjhftWf51l+JwNVAmPplt2yXdXai34iYojiAHjVLNSY/BmdWJqogEkk/OVSY7AAkCkyy1ftLHg7524qzfWGTL9hokPkuoiZcXdVTAU62qmi05q2e/Sw2eUvmh5tpuRK2SByFvXnir6rWyViww4YZOK6nyQYxwtoBQgSZRkxuiTTPDHy8pRFIlz7vR4ZQEGoJ508biWo+faJ052mOPG4dLkRe2+f78VUiH32tlw379+evf+8PCk7T8COQ9xsbwSt+Hz/CrjhJb4BSVRQEwoMWLYPGfS1nVbRuokLrrhvKinXVMmGZFVqul1a+5GqMbXjT9sAM5z8TtgwkT/tG9dhuVV2PeyJY3AczBIj/A72nmxBEl7e4K/OXSJDjDTfg7XFutZ8GnUYzWiA4mfRaxz7NzWPs6kOYLO+Nbu18KTcjyCvnYDx9lsbMSJOmrpa2y2xItdzWxZ+paamZp+ZHWyo9PnOoIRA9MD0gE4Wx97iC995Otbjq1plf0JHsiY3GlFgY4ajaWaUcKX4KCHYhDz/ASWCrPo8QKNFSGmRUpGImFUTyDXqgexC0xhKIBblKLZ4kR9wmKChVCSPKNDPnMhL/Z8sGeKRXXp2sH61frHz+/O//yHT//4h59+POf9JWOuH26/P941ZW/WyVnLsLPfq1NGeGsPYTZ/45BP6JB+o/Mt55ScnL3XsuNgseZAmn3XzNMgm6oagq6OLMkXHMjfdZCn4OVYYGuxQJmid0cWF3y/uipCdB7n5oFTwUKa9GzAYbHaw/PZ+/OmoyaLmANe6XskGF8dI4Jz//4ff7F3UnDDyf7w6YcPH99jyLKl4Hh9eHq0ehUktH04dmJUBwrUOfZ8YRIAwYuXhKFVpal1Gg182RUC8T3OEq275DrmP45kWF35/CTgfhdXQla8s5JkRsqG6ArVUKPWumMVyLTImQok34aUS/luTlOMpVCBZqWoCW3RgXxrqPg/EYDGyiaJlPsQpvNhXIwabnvR7apxfgqUpM2eFUZ5WvhGX/Ecw3FOgNrKhRGlU/N/IDBAjABMGD4V7EyLwRy++K93IvaQdKWAKxj1oox8aRN6sgQ0m5YYOuBTXAexjjDfl6vMkBaU42z0zsv/2njDTc2uV1jpLnvFCADZXcGXcyvZVUiQXCbC7JUdYZBCgPobKL3VtYwVRXY0+Ap8rMWJ2nORlWbW8d+8hQgrAhI0F4FTZQwG5nTsRR2SoMFRnmsoMpWPnU5hJujDd4w5aQS/AwWB89EXEUJG2BN3n4pmbLKz5PPZAyA5Q4vuTpyvwHt+ufuyPt7oA/QDH969t2YHBTbUSPVc3VzvP/EG9hTvc2q2CNhY6bygjsm1qm/rZn8cJ9LFR9bLOWlXOM8Uoc5ra1tXb76ukBH2Iw7pfmN5TT/ccMqm8iTxd/jLegisSCMpzergyMry1nTpBcwBY5eOhmB4jleTBCvHsHDth9LCt50U/8A2j4+s8OPkt87O3DQGsObQMe4EJ3Z7NU3Ez6dh9r/s7jg5UhZBD5hvyfmz0ESP27hHGeBcbJVPdl2H0Zyty5RmZKiDWFSKlHLvksJ5CetJDcECN4fc6TY8s0kiXaQkT5XP5nB7o5qLSaRGxcejLCmjQSZykdicp5yppbTY25iVukBRPoaeJOAOBB79yj8Y4Igd6mf5Hf7Emn31p+fBV0DL5uMZ7au/KJbSluwJLVJFqs0aJYa5uff0BhjSQS7U8VfOgWaGwLIH6T6cPzDr+/Pnj//w48cfzg73jdZuvj1vbh/vbyz67FQpj07p4QSvlx7JYkO3YFkUbzHQGMODRyrisZTjrmdFyO0820ogKLFJnE6iSAevvUMu3gPr9vZuW7Nzv1pbHXbi2aGmAeTudV631g9Z47C7fXZ2bJ8XC3KoydPDtpkECkZMP/7ykyzg7Du2UJhG7Gxubl1pTcN65RFIv/36O8P59MOno8MTK9MEJV9uryUtjo6sdlub5bCTpZkO8YQ+7XX92jPi2wZicwKDHu1pViNrFeiSufAe58lwHEeOa3z26FW9aTe6SCnGh4zfh9poWqrWACM2x33XtUKiuQEsS0HqRfIXiXmPMjLx8SyCVVFDJ6mIlDL+OoBaG5wotS9+QQhB1QaR4gDg6HFGJuIe755GKTaqiAPC1SXUiTD1eKGytYuPg12uP5o0zwom3ALQb45odJvhu8BxJejxGPgUdoWLw4iuggRx+GRX4QB2zn0wbGf7NOxW9DeMzlLAV6n1JCxtHG4U1WdmYni5IJ31kiNY6mPk+FP/5ys4MShedyV2aBgcF6GVUGeLZiwLqiLqjbkqWrzY1cq77lUjvXpnSXyffbOwtD6sfS/m63Mw7qJUTeXVE/yScbV6hUk4xpME7LKPuYDkWZl4FaMIfvre4lP0QqazKCRqHYcZWS1KCzdqY9oXZ6TCLb87MSd2uDp3tNb25sql+1tZEU9YYpSxYGvLmSsmex88U/Vez9RCphbwbDppy4TwR/0E83OWZ8+WTxl2ewRvCbI8esi1raPeige6593SZXpSxr98gpzulhXanl4jDKTopyenqGdc3Bs3kFt+YYdHpnkd64O70jn2rMm/iDE2153w6akeVtLQdxUZuRl/lo0zMb2ejw+JiVr0GLHG6Nggoio8tGx0LU/1fHbCLT9bS8T+WHOqiEOpIi5DdqGEWGGenHA7oYxwkkSqyAE564ii4RzPTso50znWIjert6AidWl40zIp4N1dFsV3REoKnJgTfdLPfxTGlNOnNibN4qX0VkwtQ2OYrO38CosbY4Y9ZKdvMtDqrpm6xECRDZliQwfwiTZSOeCVVl1D6Z9UzO767PDItlg7NHSXTsU3lS+vh+7Hff68SRqtwcQZndKs1sa/Pzv64fPp6Vqm+Up2/P76u6M9LQEz9WqprmZuN0+SbKZNbRTTm1+1o9bDWTyC8dU+Lx+5d7kdvlM2sl0kOL9a2f0LT/G8FV/yGN5a5tuqBnTtESPWS9z7rJ/QK1BVBF1dXKKZ5zRBZShFc2kOzgMxGYRSCNaGYAgvZC0Qg/729TvVJpSPnz5++vQJFLkjQ1tO9MSGxtWup9I40+Lm5vvN5XeLWF9tHXjucBH4YSo3DT5Dk970Dh+uJp+3GFsWpE3G6FK+oSwyQc/VjJdIkk5yy+GzjQk+upSBw9rGPzALJIgpaTYUppAEmnob9OQs8iaFyAW/dRtlahJxulpQ/FbChXxAInd98FATyBaDeG+g7t5oExK6oUbdC+QnGKh+Y6CB3VigcSG8U0GuZaZd6SL/FFY106uow4+qXR9jXE4DVXGAVYhbz/2DFiEUQU+EEQIfpiVkyUJYQCsxUms1gfIbhWOXQ1Dy4GqQnNHHXEzKADElu8XvKmbF0R9IxVLsMJsr3XpDnYW0JjVPG/n9L7RKgYZvMahAFXJl6QeRBBx2vWpLjdoBsk6OfvdRqFViL3UIO3CUi2Y8BFPIZqjhOgi1p8aArJjqi2Bi7CwYHWkW+inv1kqupnMJOy9nEC3bYLzffNrj09GBneujItKOj08WdO7e3J+9f39+YuH/sTk7Q4Hv3x92b64d6JO9WfkjVF8XvNsFJilE6blpa+W4BjbiKU/2dFoNvzrmFiSChHfcqc1ZQuC9eVBZG6rkSA1I6Y4eAqnFbxI4bDS/abjieIQoJX0DWaN7RBarHcY8MaozWW6vrMOTDrCp2BNfkn2PjmKfZrscMKtCQhTTe4DwQxuc9w/C+f7+8PiETgkSeVshIfUiIR5GF2QJ0up45WHfwn8nx+Wc6F0z2Nk2OVEVysUIMSJjsssxZS3GwWovGkKihEJ5zWSCzYzoEwwLNlONFNQopGkcQa46GARWiSz7ftMNl6CqAyRRu6F80zLIk7PyKc3Vbi5iPwTE0JlCH5QCul4tNehbzj7PwWOylXjngiaU0Cz/MG0vGIm/2x5t34kl/Htnx0c/OP778+dDmzN0h6cnZm/lNdg1EEjQw82ofYtqENLJqVMVVqfH8H7YXHuiy3VTvlb08/63Tc7qvZ1KpRO3WpLkWDi2o4WO2N5h8c+up3ceHArcRPf8v36TsxZneDQp/nLBRgMUwS3hNQo9/wV3rfozbhW/i3CQzGC4CHToo8z+6njsNnCw1fHxMaabfv7y6+9lhzwD1YIFEB3l4Hwqa0uvDR1aE3x2aovYuRVExE2dOlLHWSPzbL7NzdUdfI1pTFDd3UikHjv3YUJDp5SbSJMFaln1xIPQ0AkQQu6sTAhuJw2ugAjoTIn+kkLMekmpNxRNXFSLh2lk36FYSARkgoDq5qMS7ZuDmqVE2ToJj2/h0AJNrrzneAPf8xQDucbGD+R4/KS1uRm3x3+6Vh1VqIhWyhaE72CpZd7e7ZR03NRcHpfcyiUmVzN4FerCvh5/0jjBMML6uRp+AzReYZBSWJXMiblgEAOitVurcl6a07nGq8gJ7ihu+GAEpYVoGmtAgP5WDwAZBl74o620HC21Wi8yd+drBFTGZUxn50mlO03fLET4GudiCAmQAUqM8jpOROhVY9hTYjUOvoEGrCp1b0u3oDKklwKjCMBJAmityyBUTi+tjVx5aKnuvRJ1Tt3JTAcTlQageY6o40SDkTLU7Qz/9E9EpjRVjC0GX4Fm/nWeKUd9mAPWrb4UpniSxspJ+kcP9zs3Yh3D/G2BsOYNvI9lhARfFmTK/+zer9ry64iVsQpo4Hwn986xevoAvlW3z4K3Hpyzz613Bo1uWywJC7gAWscN1TJpCZUiOaaf23K5DsEVO/WNq2FoLuKJQ3zb7ufO7fW93sb+HOhIqzQ20oUgy+Lxh04YJV5uIYMyCyevrfFHk4o8KaaVyoAttD2hgKh1OBw8dvIF1M+ULUWw4HCPl3G07/CXgiyZEiztYIiyPUUTOJ9CpS1qJdum8ygaE8Tqx6ZG3UN1xOtZZh0an6DHIUGe3UXaVGzjpGJxNzXNxsE1UjK077MuQ8URYg9sgjNvQEdiG+Y5SDk5e4kT8GmXMHm+GdLwVhFqNoS9ZPHAeW/0H84FVZ2wn853s/x1yUxNIEgJHYpFtMfrk3f2QZ2elS7TVxwaN/lzeoSBV8bcdG7qVLLVrJGZmo7YfnHyIKd75bC0dnBsHm9ubj2VV3hv/S5/b2NXHME1/ZRFR1tbtEvfsNMBCg5qNaS7v3aKlEX2R8ekpuvgHYsewi6uY54NW0wdz/SCEvdUnjrTN6xjmwKRelib1Z0c8fRk3Sd9Fsvj6+XVd4+3s7bY00yZh6DHvkWqa4EQyKzb3i8LExwFIUKwcqyVUZJh+x4NdukYOOkwuSjjZz9CK9rJY6UEE99gLJ4abJOMQDNW0gf2WfD6hv2MmrrO/r1ZG4LtaVQuC8qZJ+UypgBX5yfWSNyt40h7/8+CFc9z+1XQF5jmvjA2n5mvJO+cFPXN0UCgkAQrFxeXgxxxAxGsirjyd0wodT3A9DxFonWao/S5N2DUHT8DTQDqGfj4PgwkLqu0QysRYNnAGWTAIKl83AjFaGA46rAYn/mGdLT5hbpKGkKOplt8Y9E5stw5YtTm9QkwbknKNWoqvpKo63gAj+oERTuiXYzOjGuU5Qw/suT5VGO4AATfW0cUtqDUlY1x9bV+oqkFPbhpeiyZOkxx4e8QEMCklxXHNQyHqZLRGdC5WomZ7ct7pDMDCYo+RAtqwsL1BIW/POMoAbbOspq6VbDGzYQxU07EeS89kd+4sRBRkwWYqnZdvFbn2E/cCDUkdYR6YSM8iPfwZG2O1+jbMnyL8+yfcvymY7D2zvY8Dlum5W5zyyYxhqmahVu/7txuWQhk1vSRx6cfTnUUBnHTEvCb2w20hEdUozQni4CAluu3G8/JAWCuCx5VTD68v01ZhrMEbW4zJEM9BpwcHWjbiex2AllxhDlSEdK1PI28rpG3RaGtpH/0fImHI0FcJwsZTACTzQDOueDEeGNPqbxNRdGso6WafMzaSQAHJnRyJ6Q8bNcKxQzxtuuSX9tc8/8gYtlk/2MuAjlrJYhh3hM4PZyeVRZFPoBuGKvIQog0AbKNSbsgGVXQb+KkfhiCYkqgbD6Cb7I4dgwYC5gPjZAFIWifG2bsNAjTa0IMxzo9x+G/0KG56V7qOAqPgsX7lCjQOg1kYJlQz5odhWDPkgQ9Yq9KwBpaOEHv6PjsYO+omV7E6sW5qvr+3R6nXIag86RA0RnwTW280W/UjcvHN5H+LGFnX63t46T1Ij7dknFjnfaf6PHYLDxM5HT4G2WU+pfDWa2vb+46SNq5m+u2ncDwRt+BoqedY4cvYKNdV+oIfSA9HcPIRMvCd6IvEKc1hOmg2Zvbm0+fP3MS+ioHTbf13LDg8MC87rv3Z5cX17z89OivVjmLh5z+b/z629VvGPH+4ztDUihbouYxZebZLYDytBkMuru6JUCbFl/u6dSTzWcMmLLRQmYAeSPsUucCkdSMkudbfK5b4q901bnjHE9uaZyj29lu+o6rcrR8bPr1P9xIoJhy6vUWINK5AUAjuwfceJ2kjwMNhTRO1TP7QSBtrb7rU4G+ub54jP6Dn+J4S++nSF1Maw9UKKp1NSUtl96EykKULBD4EBDvu8Ss0u3iTcAEamMfNBYqnCj25OXGdHK0g0+LQYYdmhl2DOLpsg8RycrEKBKpOoZ0VNfwYs+eHlsZk3psRp8jskaybKr72sooJ7JfGolS/MT8XgCngvHUdaX71yVFNFf8gNK5FxuBKhBxswVYeMWr1kvgSPKKEnXzFHk4RPQf+sBge64PqUmhYtqCgftErLfrWtyvEX/iCNdVpkRKoTEfLhfKEiE6konj8ZyvIQwsrWY/iUftUv9Lo4Ng+ZNir3GqwLC41EXop5PQHNWeTcUcJ8RRboL05uZpZ/N0cHpqCbEskSk3cRp6LQ6SZMg/ivZU5/cFucLu7Z1m9p7NGRw6i1/uYlH0JovVb8g+xNsmxFNvO1DCcaRFo4K7VBra/DeqWy7ChgVHr3oUswkKDMMAfLAwvG82fDWh5+SfB0joy1RH8fWNLWA9WkyiyuiAZzM+5OE5YqMOKqYXI3nIYY4z62BFLQ+P8bhJ0K1VjzDTTJ4qQ2VQsifNZrhOd0d7s5/0502DGAZ2YS0Cc9lUFQtztb40SEsnLK+lNjiDvalzM7FFM2TIZmS81KMqE4gD3/iOp3RXno01+mpY5IClFIb6q+kpC42a0vGGMatif8521r3gBPw5D9I090PctAB9aRoqrTOA+xg/q6l6PpQnsgpDJObIwn1PVn9/9v7T/sExQtJpo6fHWydyd2pcY8q02ojJZDGix+/fmSw1N9+Mhrj/3rOg5X14CajoGretq9GLb/cAaIqnkfTTbD69axSW6a6QgOWS/u+OT+cIoO2Np3QVOUAbZSyg2X+qRUbC8/2VtJ5hhunN6dakUos8O5DKDyxktNSSxxSTd/Dc4+ORR0e2asjjxuqaqKInF/H+YNn9S8fvzC09vwgIRJieEXZze33kNMPt3fcf3jnC9Obyinsv49+W0tZ06cuohliqbhv7at/nHlNcD2xIi9P57YSAl2lNciDVmWTPDLM5ZbKT9s4wUNqVo+QVyxaOAmQhmUj2mYkPXwZq7jpfYDShATXJsp8Mb9x2rsZF+q9WsP2kNkD0FpokNCBBr3oaHpqj13lCuixboBE1cB+ymTwVQ9WEPtHZSKXviNOOYfT4qLzOxB7C2To0xGvVP18Tu8bNq+PNdFnTfnmYmtaY1B7LiUGli9Hdtgmqz+8VwdF0Ch6DQgBU2hh1bbOML7xw3jP2R0M/NY8kxfrNrOOeprqHCXRbRZzCETBczppJsvGtwft44U4NjArF8vqqJH+tDPvdATLQCzMD+/aNGOfLsFSSg9BiL/qEDO7U5SzehISmjubROPKKn9QhlqdZ8V+KJ/WZeD8+tKeuBJNgrOhSH5X6xPq8E+3AHP5mqBUQGd2vDg/wtYKdVCFhorOwBmPH7nwP53AGCxfMrPVCB2fHOGRvvBXcjmUXa4k97d1tcJZsdz59+uj8LVZEUjKnhWmIwJSymSGf9oau1MS2h2ywVxlY7qNuoNmqOI8dGXqmorPWJ/T8FwXOjw4Z7POdR800X9oAgsd8bJioCWtB8ETWQSpZMCeP1Mzy/aPz2Q8Oj60V0YGZyCzvb0y53eFftguIIaw6l/qWYDeGkZqm5HoKvYU+w1QmNHR5gjkshlR2NApYJADbRBXjdBUpGGxx0BxGw9Mu4EDSYupbLwcHJjNfckn2oFk7oleSWXZgqTEXwZu4fvb8Fnk53j1bgqG293etYkwpcOz07HSxICxsL1JdqXAklRVkmZcXGlsDbeqbs2Nf0MFCQa4+VeCcjoNUislPm+981hbUW5ZFh8vIiZ/a4O1Ra45Oor6m259ur543Jjxvnzc7707WIvzV0Ypd2gioZ+wJXg+OXBUBW0fQI72k3vKujwL8bfu2rpyT/7qSi9Mfa8xiT2vJLBbQybbt6xktjic8aHywvWUZGn1brz23cb/HQc5qm7MT8xFHJXm0zfmCksGzFic5mQO6N0ElCbl73KHHjgAyXqAzGOgi/luhMHPInknH+dvg4ogqyxZsPX/wDi1LfRx7zhkBibEygLafXF/d4JYM+/v3786OTRG3kM0+ADq6Z6Dp8QRKE4TDUeqDevg23eUlrUvGTUqR8ecSSZsoyJCO58dgXg6wPDkQtMbNYvaEkwLBqFRJWqByeYGcty8TUkNJwdGI8kI5qBwITzhqA0DelWt0Z/STFtU+K0yxVKQYhZ6gqqWvosBuj/pmnV0bFaz9cJfaLKDuMoCd5ixeKQRksE6VH0haF6oan2nWWFOyqNQYpWqEOwjUx2uyhDaty0/6y+cAKjXkBuNXmB2OneVbl5wGFHCnZmDRGoyyUT5iMSh1bhgfD/PnUdp3X2MlRogqYmy+MIJjKWDIJQa2VqSWKWQsUImhwcjAYxeK69PCLUzjIhbFRU1odcSluSAmTOAy1tIHAwOwCBlRL1TDIL6CjOk13+WADxY4FEWAxa1eC7FQEKCN80/ecw8rkyP4JNR/fgeT6/CmI6m3x9+QViFlo5cls+EYEChLQDtn8Xi93nMmqHGbK45Wt7W6sUuSE+LRbfk1iy8gzCBn9B233IHes/MUmK4tl+YISp7LTRdauQLntKCYCLXkRb6TyzZ0KOKAQpcTt5NejBlBG05I52AhfJsTllSgfw8covxTpivDjNGtX201CEhlA/LkYsviFG7WAQ/NJPfMkP31vYd/7T57Oo3V53E6zXvaPTzULRopeAKmtScOHoOdBZF7hgWWbvLTQDrzlDu2XYiBF5wX9RiJ8jI9qZAUKIGviMqz6qSEfgb+EhXGTBI+ZjRbc0Xr7Jc+Oj5CseGcfapMSBAqwUaotim19EWs/bqre7oV8yZ80EnJeGvP1iQraPkBflEb4b9VB6BJamNVVgMCWMz5lz5xal5EoiR8eEir8c280oGSRVuv+gnxbwrbudydxnPCudAWGm/y2YNTTIKevTNbvuXxKbeXFgU7yGe9y9Vv3249He7v3L44h8+pDEYn+kj+lpAejDo9qYc71ru0yBI3X/f4d52LYKIHtHPY2VDihrN1PjZe0BrkkxXFIlH5MLxHeyi/OIzkUP+cN9GMhV/PFnql9liNDR5JzTnRWqkAoUiJooJ6f42E/EoqCleQy8awdF+/Vdqtnci8v46RoIE6e3cKpbsbXH5wBCg9H0ex5fDznL+nxuxtf//9SkrJdTlE29QkGFkalWYiMCmA3+1gZ53w1a2thAbWewKBLA/6jfRy/FxHouU7c4xNJaqbTDPz3DqYjK5JuDzMYgJEJuHM9qm9dio2ulHCB2hfFicFLGszvCeQSoA1GpK7oQlAhKhv81KkBgbI0JuH6+VLtRVVHYLVqqKq4xtHfl3Pb03wMWPSIp6K12jx5fjJkj/K1anEUuaM8r5R7PqPN7cHDr9Vt0DWzIuV5PXGN1ItXSNpUnZ+CfxSGeFaD5Ff1VpLmaEOcIPZ3BYsUVw5QPM+QENO8dDsX23v2RmqK3MhFimd8+tGYnM5ZhLhIBzBOrcE4078HWYNazJE/XnZHHjEeGN6ZQRZXWHHynpVbuBQmI5Usbqy0S93MK8FK2UhU6SvbMMfpGOkwCd+lWSLX64GF4IxgHJJW7CLtpLRrBgiiNC+r8rHbi+E0TmosxnxC2h9LmW+koI3yma9PB0nph90n3G0ONWkZUzd4vzzF09Ppoc9mIVbFn+1WMDN5+eb+yvWTJct/qEMwjgOpux+yjRdL2vxC7N40oSbgnoYtS2GtBATup77V3Tqos5rMjvw18GI+qg/S4c084CDxfr6gKMjp2++OGUClYIRmwz4O8leC4HWRadCIyTu8j+XV6zX0wgsPrRLYddyFMP8LSeEHp0vfTTZ2tigPzBzQYdlbZ5XJ86VkWDa6aj6e8sQsVJfwNciCv6iP6RIenPNZjAlaYTkAnyxJ0JxFWuJkv6cnp6QDVes57CuxvM1T8+tMd+379ohGg5btQDVqNKEp2eNtPJx5ZAmye7N8emhsjJXBjKECDKwOzbhpYIos24eB5yvZ+ZxS1/ym6c0e3bDxaVlNelm6iISfxYFk6oV9JCxTpfDHhWyqYIHt5eqpyGOcDxBeu/Uxtv1yjkZxEoheiAPaYBlyTwH24mZLw9Hlv5wsJ16z63S9Bba97iWZytqYDJT0w7z2b97sDRfwGt9vw0ZhcCpWM3pxTsIEKfplwke3YBMj57L0Wzkzg+IzXlPuUfpfEGJxrnsAzM63IdskGjlyUZxT5M70FUbserbWpi2bfTWRIdlSPUQDNZpEnv7Pj+83tM92aBWOrVRbKU/ZkUeFUDNnPxvnEH17T12uKFnwevJbXG/spLo+ptnjdK3w1NP0fNcbf2cyMiI856lWIogRGKHEND30RNJyBIT8hRUk8XmFHtJkI3yM+zCtSIGHopxwtonsT/j5NWKmtQtf+ZKXseYLVNKWwk1syqMGx+QV0zQIKElF12fwYQ0mG8bOGCP/3Q3d4jX9cdmnwTG3dMWeKU98thqpWBBDqYCfc/V1DzuF0A2BMo/59hAbfjeMEfetSxZnke9vNkgOG5Yzg+4Cd/drAnsY00BWwHXuGmcelhXAoq6GUgVBKjoalj5o3QR0I6E5ppdUdl7iElL1oNMRzRg0DMcCh03opk7r5dAE8yW4RhGNwCfl56oobtW43T/sWA4yfhqoWvxxSsYOba+9x6j5r3bLgSqlSExOGYMGcPDpeDQqFhtlT2YMgkZN8kYZ2ti5O1/TjxnrqmBlES667Kq1KqYs9P04DlM16CCZDUDLtUj8sXZ+ulNgiNPvhpEkBSW2xix08QkNJHLfKgDp42kVd9Au2tSgs6GteZ1OV9C0V9HQPFlGVKBWyyiZpOWI2IR9LIkCYvIqP66Mmiso7DYsa6JbFBhDkdyJOKD8HTnODdNEl8L9wu82RENsDfTPIQBHZws//eMkZud1fERVeRFdGqiRx6M03EAgNxGO4J0kLIuthcfnPLkdwJUq8KPTnfWuhDZxv1j3cTh62Fj+62Dkw0TMfnBb+EhfKEXK9p0zgStVuTqe9AmwNJNFBAx9inV+2xbF3v7fMPniQ7v3p+ffZRL+/Tzp08fwNnevdraO5kF7g2BOFtca0bUGZPPnoJz9fi6++X7rxnV7oNO5uOnww8//HD67ojyUifPqWpwUmbp4Pb28dvF5osHbV3eX1xuLL2XECQtAaa5vRvnqPKWeJbEjlvWSAekXARALZuRkLI0Fq0vXH85qm3Ts1w337yzp3+w1sbTddCntXvHaHP19x6SJfA3xvCBXOR4Gih1BILmGlhYLOCAvSe7uiR7Hk3aNaqig4Xf/vHKJl1SZSpj7OjxXk7W5P1LuRlFQdDJbi3wh9bzs8kd7ph8cd4oIfWgLu1xrGEmZb2aApSeFhdoeLDl1tbx2Sn4+q24TbN1ffO4KweBtPZoHuWICEokXySrSdXaWiwB5nF1uv3Xl4svX2x908F9OD3kojyumknrBh1pJzbzkMgcTsrOdWZCYsgSf83nN0R4M/p8B+/hj/s0FkoxFjeRkc2XPmQ5xpJjeJlNt3IimXOZ8PxJ3ycqHWcTRPfxSO0+InecVR/dC2RQ5756rkHXBQwcf6Ncr8XrMltsAj1vE1oTcqpDTnCGDKhg5HpxVJn+K4mTwjR9ioCxyY125oovLSfLoUw0y+JgGXoA6LnDGspVH5/lX8zCRwowTh8020VGoBETTgpjYD1Giq1VGEccLaJQPvehFTvhyUvnTDmeCB+HEnNyelGhdvPXCgyI+pJddj2colTIVQa4OL5wsmYg77erAwpzc+u+azOWBFDDEdfVJcU2xSdCd7WCIGA/HVESvByHc8dDu+aVgQvEqLG7LmN9LieOT6+AoMEqGXBNLVuEEySU4iyc6Bb3k1tNhZTBDRFNAxNQeNNCY9GskxvDUBbrKzcU+dMOphnYi5REvDyenMn+877yxtoVaGlKaumTQ9X1nuzi9uYGZ47MvVoRTikK7bGi8RFkIFA1FMbKYfBIg9XomfR10Y6nCqNRPt2RC/OtfsPxD/Sh0Ul6Ek9Ym1+x2ZODi0YKZerb2uwxIkJyWeZbj5AsjJIkWB+enBnjy0xvTDx47Pju+mXvkLMh0/YPHJ6aH0mYclnbe062O2vv0oOMmI1pOG0MRHSMHafxcwxgR2rKlWVOcWM3Wo8tUejVbAh/aE7m+5dvcg5Sm8i1q+AP/7jrKSOn5x/tsxPTOk+Y2FjK0bElQwYrpiVvry5+FVo6xd5gzhDh048fPQ3LMUv/t//H//z+08d36w9WIlri8uJBCK2FscDm5S+//v7/+d/+9//6X/+tlS5PpGDY06M0BfMUHSb+VhdXrPjd+Tlrt+HOiJFcRNkSNGyeW8ZVR60+6gD05xuZ/ZcybYen1tXt73rUif13jOaWVEXi1mfqSHXMkrpGW7Jlxgq8txGddIvuxMkL6E1cewdCMnISEpDiplFfz2TTTVq+uz5eedAcDmCcPoratqCvPKF0qEfLpwmUr2xN+haqBsQEIeWxduYyA9Sz9bAgqt+C8kIZa5KEI/S2lozsTMA0weIG+8yZThcuWdSUFcev3z7Q7xKNbcai/pvLlpDRz8fbq2snzb23IM6TDhxf9LDZMS5yyKCZyKLdFZVFmQiCMbNKTp5RNAlHL8fJanPZrTS6jeWYO0F0kSt6W7FNmUfnl8G6awxaAPr/Z+q/lixbkgNN0zmnEYckAwpAURmRuRqZ93+AvuhpqZKpLgAJkpmHBnHO2Xy/Ls+S2eHhvvfaRtTUlJmamhp+SXy/s/FIovjNTzKp3yOuRvApVmESfLw4UzHBszxFYslOyORZHfWpGTAmuMCVHO13wn+se+/HI153I5LiWPV9reV5+aDNAWIgMmCoWKPCyRkN+3aW4PU8pfTUZGo6g1sz/pvq/HXZVQkvRecyXpK2sZFcI+rAXcVRXSMNa2oSP4SCERbTsMfLGOt/sOPregd2LcxQZshQGlietXIhkypFE+Vua3QBiZCgw3SZ29HuyzcBOUWgLCxHnRWbf4m19+FW5v8PiICf4hoP233qgTJj4kcHATCbJfFAQwT3IvQVtxQQbWf49T710UhkpqL4EKbrPe7zLb5GheDRLnjCcdEm+Gv+8R4pRKxiXPsHfOFtwuR4E+uGw1buKWgbojAQoc1SvThFPTOLkO6NTb7HB6Cy3FrOy/OztcXH7fOt7L5cxkI1VsTnpKJrJToZXAz9NSHsteR5IOU8HEKyMFeMaahAiB2LoxGNUde8gIcINoqS5msgVwzb+5rUtf/JZJ9cFi6IMeLskT2Xh3TgV3Fkf/zxRBLsF6JWjrDNTdF9z6tbz9xOm5wPhkdvloCe6r2Vihp1uXwqX5BrqkSWcXmHAiDgesY4SPg64H9tx7Vja+fCDO8ezs6uG9VkJPWtN1xhT6/rcsdw5cqpt7V/enj6/cHpt+7VXN/dwWsi0HlmOpDk5MUBk/fpT3/+8ce//MRvw53tOBLs/PDDz3wg7jH/3d/93dXt7QeXHGBiCowUs4n9uvLLr5/++Mc//Y///n9//npGZrZP8WIzPEe/k00QxbhB30/nzwQWYYQ0rikDWtFyQHLsvCIkZOe/uEHsflozQdr+nlE7i+Ru820bQFj0ZUOA8A7kO7/PBWhxRUn71CE/4JKxrJnMkC0uktsS93eixJ4y4yzNxOjm1DC9DOf8uqllZkfmZ+fCEjZm37jaVADbnpMHsYGvizhivKYk7Hjn/a9uC0CZfMxzx03iQ/sihYe1keW2iSH/gqywgwHqSGbQvKOaleSKTM+LkEmkWaAh7KcbdLV2L31FGchFvm7YwrHYo1NXn+9EQllGPgtDE0+cJmKj5FTlBiJj8IJFU0utmiQYaNLEDtMRobMqKDDfNxsj8Rc7puUDEw2fNPxFLOA77SWLk1PgyKPU+BYxM1LKNyOMkj/xR58xFIngJ7WE+eo8o8YzuPGFKhXUHS9NqtJ7/Y+wqhvf5tLLvZOAhl7Im6r1qZNF/iw9B9iY95pXRYHcDASqrtUiLLJEs629rB6DIxFNGmVhN0A6QmqTSJmEhAmP2Rut7+u2wyYLeprpug782tAK8ZE0aKPZ21Dhe9ZA9KkFgIW5+ZleA944F98XrJIx83UKYgRpjShfzcGoLpK/gFWteZk/fvnCWBtwSO79oDL86imRp4FwPeXCt89EK8zCU/udvlFOx6zLIUet1ksYaSBTsTK12SNcZZR16CsIDtQut5gSbdMy5tEBVNDqA45Ja2R9UCX9YxpourDYDBADGTl4lPGfv0gvCLItd2qEUUL05zaAnDuz5coqjCSIg8MGkTMYOWRKBZnV/rSKcQQqYuguWuJGGUq3BodxwMYOy7QNxZhuzRomC7XxwD5MCMFhHkVFRhdj4xiIjHADHHjgjmp5jRkaJBYB4PglooFd9rZYkYPjQ3nsMnkLck155xMznJ09dibM0Ww8Hgcnp6suHXB8wHDXt17LSkZ7iQdiUm91qdnryt1TZ5SIdRse6zTjq9NAz9fX1/xIK6udG7q6dmLp/uC2I0iyBAtPJ+DIEfE4uVNmT57OcI3Jzt4RUE6OD//D3/+nb3/7B5Awuo1xx9Vr/MolouHcl5DOEmtbzskvl5eQzOGPK5x4OP96TriyxX/48WexQAyT04/HWzsbDsfJi0mw/q9/+uP/+qd//vGXTzq2YQ+qR26RwqvWXErI79xmkxg2uzjPdhq+YK68N6JJV9ckvYw/Ib6DPqtbrlDP0fH28fQoz9bm7pbc2fIf3/BHPa3Y6jBtu7sZtY8QZhW1cifVDkGIv+1jt2Fj1Qd1bxxrDHX7QptuhnQsznExKCd4TLNJkZ7BzVr8XUWSNEdtVlBfC8Oi4k6czfo9lVUy75Ex2SJtztvBinMiauIZz0UdUlFFJskO1nh6Hxl0RjTjpcwwI+qIfyRvtOg4drDnzIDY2ri/v325RAiU1qZQVpAduhiA0dNWyeOOIE9+Q+FPjJJAMdi0H8UNSb6wDpvTZiMPRjiNzDKKkTPDqqqpGAt6je/Bk0Wexai4xZBHvpAoHrRMB3hv8YkZG5kQQ3j5bhiG1MFWClem4eAfDKYtj7SvTiVaHMcpixisV0w/2B4xkSDTTybnIsKqDZlV76vkaVw8bXmygFSvFSLRKhXILdYBh+1BwxjN9ZA8qXmcCDZNvI/HClINazKjZIMmKBLMijY29EC6sLk2iBYDCTe+m1EaWJhreLP4mn1NgT0JPPbl4EPBwW5QDYh6nhH0y/+ASBQpbNg1iPwSR+i2f7oztvqZuQg57wMPC0QWiFQP3nEz+VYjg222eo0uL5DXFRRakPrAWAhPUWp0L6Zl1oA0k9ErA3fQEcbTF0hmmgnLVYnE/W1sRDe0Zu5NKETB4MrPuIJiamZKQAsJYNluSNMLvgLxiMixRzjLsVI2S5Z/SNJtWGsycRDSF9/imkjzJaHQJhnEMwJ8RpgVEPyw7rAc0mYuURUt0p1fbUUyi1IwRUkwNqNoSGRjth6nAJOpFSCICfbC3xGSsXecKmvVUBuvNCOYFlqLRMaCkQcFFc903gRo+IO4fL5f57pXvUNGTk/BgsXB4cn61r6HvJIrm3vr24f7W0crTpQKOiXM3ERY7PZbR0wjKFYUG0/zr5c3j4/n13tHB2D4cnZVkshrm5w3pLY7ysXbrP/6RccEGdcCKHXmLBNM7JH6RwfxoRMABxYWK99/9/0f/u4/fvOb36h7e3Mt2gXBWzwhfFQHm806yfjmDkJn8R7vXDy44r1jtveR/+bqr59+hbmLq3OBkfxxd9dO3u06pPeP//gvP//0+dqeQbfbv0nAL4jXZO6sOQBR9CtjHT+Sg3s7Giz5NtGezf62wk7XrY27MGE+iNfnR04PkwN1p//ht5s7O88Sf0R34i33fCwDBS/T+cuanX6hOyLty/sggj7DG+ozAWXnl/CzJE0WEwUIQqYFgDlBPKKYUiUdsIhf4NacZk1Hcy7ItDbZQag8LvHNHDWCmsii2GKjsDEQCS2yBEEaXcZ7Et0gEHf6oFCxsX4ZGjYcoryMkY7jtTeVssb8Lek8YUC4XNpT+ytPFy9WtDt78lqswyUF4FjKrutguimVl/O2I+xhNQWSFCCjZVNHDZPhGqryKSz/9JhHDUOU+6R1NuXjIIukvLgseAwoSYBRwOy9EUfUyU88kjgz8OH4+R2hRGgeVrYvZ2WQiFE2mQIDCszSW0uezD9g5QkQy+cCAxgBlxZymWY4qgl3NeqNkZEPIxYRzTTRN6MY8GlFrXzK9T59As/QjCqj3pcj6MxqezYjNRNry1JegRADlIY1fWMZhDCh+yCy6I4K8e1sYrYNaLTEdALJaDDCjEbLgy6iwCgyFcwqCBPHoVRxb0sWBLhEnWbCdQNMP/itZWUa7iJhRqSGbjJ4Hmmg0Sr4XqbqKtRLdcMQYW2ITeBUb2zmmzmOkPrGb200GeCDdMUMxgHLWYh4GH5VYswqGIb5YVKTwbbBBvaI0NOZronoUK3dwMQ7g7ca0KbuzADq0kTLbFZXfNVseKdmTWQx1I0TFqMCfAsYm26Wp22e+JKjIoGM00yBDubcABeBRCw5ENjWkLnyWkyiXbxdYXOrfKbO/tQ2f4HFgoDFnZ0SenHxFhlCvUBWWPI3jFp/j30gJk9gBE9seiuOHaOmaaYLiA48Y9TE8UJMmVWZFlBo3zjWdftSzv+YSr/tbTZq2s5AEih1Jt5funi29mEUILmKy8Lsj25t72/tSUFA9DcgmszBXUeWimFnSfP7d374l89fLy9s1ba4ERKDFr58PjMdCyGwd/0Y4P7BYVmGbHvYjc4xo7eTw+Nj889rvL65l5G/f7TlIoWN3TKdsnY2SlmDIqwbosq1Lf4T92R9+Xp+cXljCu64HLKrH3gtRBQ5WsUyeXz6y5cvn5KJsqXKn7O+Ke7z11++Zn67IV2SffGuIvOd0rpHWrY5iquGSlMDp9f3V/Y2dwX+MsTawDH/uCErGW7Dls8JwieOwf3dHTiki2S/QYg8QWsTgGOxZgpf1/bm7D9/DmHG3E+aSeJiRtgGXFTi7CR/MFvENDZACK53Kaeb8Nh87rztBd2aUCgUlYmmkSluKZp46AHdyNLgEe6AZRKbtzBSERxIU7YgzP7iq/FtRBt1YW08lOcFKZBkNphhe9nhEJq7aISOhJQ+RBnSs+NmYDAAiwmb946K7Ql8ZvWIzXp7hYdtgkQHzqo72Nz9EzKirwo/ytDL49Sy1G6RJaN1/rQJlSzXKB44/sEN3CaY0kLRvwaH0xNpi4hINqqAX2xmIB3jaaE+nNtoOny6SIakX00TBXWkUc2SCSSEWUVVKkaXGNXvoVZ4U86at3ZwULe6tndY51TI4paJQ+Rht0pIuuk4dIG7XhJ3yvuns5TGbPMOyFgw1guqagXO8h9HGDMi1iB5AWR4DNjaGV7VNywkZ60GpIlqY4/IkhPAomqL+PeJVM2xkays4iLBTHTiYGlJGRMJZ4RfzETSaalORiIoN8pBlwN61XI3j8UBgnGBkc6sEdB7DQzhOtw0qP7XVnI/Kx72FQ13ISi4Qk9rgthIgdBdU1Xpg36zskGfgqn/eThTXolpsGYjyqV5vYx6aEwzqoYLAMNDCEMfPura+85EJNVpAOLSsimIMpnrMn2uHACp1XpY6kQ3EaTPswoCEfYUD7TB/woMwkcBvgmBzUQinO7sbfBL2P2zVjCAQLXGZz6LwuZh5ffQFsFG/hosuSzXm8bxB0ZtXI1sBq4AueRZ9iCYPUf3jW+ez3ijNtumyuEpyDeFmrCDZaJaITUnUFmEOBQANXqABKsBTMAOsAc4dCitTOknxZu/rLoRCviklRtitjjfd3dtX4oW14oNQDeNcW24IPDq6o6GcGvg509frrl+zEEEZXBOyRlDZCkok8VNjNB6+jchBkMnCZNFEUSBvQR3mdhX4EfaONi1Ofbly5m7R95eD3ILQMTkBQozwU5q1TVDHscZo5WzUKLmCGpcvXl3b8NWWNInNxteXnG4UTPE1pVrsx6e+ILckpP4y5ks0bHsWO2UtkmLvUejwiSXVi4hzh/RFmkvblljy4Mf9uYoK9DkUeAed0r2518+HVBeq6/7kiQJD3LOg6McVGxfly2bPrv3G4J5pOzvNp7O526vXJ9dmScJXG0I0dgRY7d1Oghc8sHjk1MBoGY76U0+kDfwm8EZQebXMdriaEnt7i1BE8gPbiEiZ5EQBBO8WjLnqAWNRHxjs5pueIzOh3fjpERteiIJ5ziIrW9sYRJV6LhJFGM6478ip80vXVtlJwNub5wHQf/sCgTKJ2qZm+7xEZG16Zzvn7PPAYg5/AAKi8FOyY0C0uZM3ayI7LZlIZOTVGR73RQfedNImRcIwNqg8oDPxuFuJSuz+XpmHn3hATZAfkkDv4AeS5Et3ihKtMBkY5466CvtrmpfTyWGVzlSojf/fEveqy9qfXrI8xFgI7ugKKpvMwCBmBo4qt+l1wGgX+WCGm1dzcCsacQNbUY6UDbSUAuDaHri6FpMzagHkJwIyV5d0FcIIVUFyFxGukv6Zy8bS/OUEQ1hffW+hiDduH0tMTkoWnMbAlLxx0/DD/OtrIeuGryRg1ZbjaaOE+vRH4KUIzchXVfVb7j53EP3X6tUI1SoqqBok04Ajaw2myPOIhcKKRaPtAPJ1OfECOP5YRLNPdNQXo20C3xl+fNuPz+URYP0JGhELwCtvaTEn9Lv0h+4BGM+gyBV2fdeWXTUYes7ANRxxvEyGfF6zAiK5Q1yFTadXc+oe322F+n+PDt3RcFQFEQjb/5GYYLgg17RNlUeldlEWe+vPmzsukGeiVROCC9h+HfNIDtufa+l/rZIoPGNMoKMHIM2DLUJKrTjUnjqAaNYBxgR4KEeP+kGsiAW3SNr4zMDfpze4BKclUYWFds2qWdCx+9kkYW0yE9fcXnh0YPDQ8+Y+auMYcGO1jbGUjgKx9nL8SGNJ9LoRdTM9cP5wcmJrxxcIoavbz+dfeKQvxk+4aROq1vQEISEG/lrFvkmWe6kgSPHUCS8cXd/hwPDpF1eCgN6OXo8MEFIl1j5taVD7Pby/P233xxjE0d0udlNFRYz9bfXV59++eXa/QqdLNju9pIn1xrkrrh/uXWvAjFNn0qrQHKzr0kqk20BgQCYk2dnX+Cb5eR2tyhjfzuaGNbNBL53xKzbLFAAvCCjzORXAfjS5AkDSliioEfqnWvt4e7i9XH3c+eNbV0cH9qoONQhNze2JI0ZVA58vEQ+qt1RfAQfarOIYRcLvhVqb44EdnLj5VxLP+rCdvIO259IcB+FIBwGqYlpJdfqNOYAQ3PuEJ4UhL6L8ABk4EmQ5OKQQtTDIEVKXjgtdvLX/netJGhBZpR5QhQ1UPRliVDthGKCVTHmEk7VanRtIvSv2eCyhHp6NjwpTtGW1SJSdnj7QRpyWcbF7JWV6MkelBgikV/Cg0ge+0t2siwUsJ4ZR6m0DrVAV/kEdn2NSR2qF/EyY56RI4P8GcSByUX5JD2VPSY/Ok9nJDtGCKkaOcb4+W1MKZbSqQZICzhMdM+oZ8DYLc5r7GQRfkc2iwjztba8p/xGhbbVHIzz2DdK2lGFw8GXCezvX8FIvNRmMrQuyeaBLIsOBvKlNwvZnMFtkkZkeuurpLIhTSRhSlm7eQFzGCQxibUG1A4j6rUpBWP+10jztPQ8YqGHZDSYR2Eo5qUIEzE6ijwalcYGAU2wb/2esWgwK6Avh0I13XZR42kCND6dqDGkNu15vAynsdV71LPhiiR4mEEuQA68UwH61Ad5Qk2wcpzgs5Y79Nf7ocUEdQaMJSsMmstAhSFzOsRp/sNIIp6NrzAMNoiGBsXWMX1CG7U21F9ps6u2viMR31JmjVhRrcZTENrsaUot5RD33MVFJ1HXQC7kZENM90wNijaz9q6xtw0x+JGXqcM4LFz+B/EZODsfggYjKZKJM96FXGaHwQTYoajwwurJR2uHtZ1lH5e5bzIJlBw4afrmpY1+nyNDY98UOemxrwA6pEwMp1IoMXdbGfm6szydtCt4fHeXnO3ofXf1rfPymwwOZnNQwrobx3Y4LgTqyG9x4RgV98XnT1+/fj5vW9dFJlRgcOYPg1ZCTMdCRk0mahXkY+92oZToWaaYygMUOcmIf2tOuOl943wuc94PE1kzzd2pwwYr3UILNrnTrq9//uHHX3/9keHJZ8XsfnveeJZh++E+DW4189bdmWiNTDVNsGQVry+kAhtpWdlMuZW2WdmBiguJPDy1sc2DtOE+rN7bdRDkzpDP6mZfR7GGJhaK3DFfnB4T44se1r+cfbl/kPnjm/WN7+w6IAU+Oc5AMx91oWlp6ODL6mtrlwfrqQhR+burOz7uTi+DzMNSvBV/SXvu2KFxFKW+zDdq5zcj+LgPI/73jamhtTzsMjuBTiIWhZviksai4qRDO6SoeKzFGJ5SwbRxcpyXUhUgChZGqldrRJZCJEMwqxyzYkJlfWclwXq3CioDOQuhOTRrjvwyKncOXCC6ZztTrxDIX7plXouiebF5T6DaHR/pSVJtUXg4FPa17HAcSKML+ihRCFwtz7D1n9zAcZ5EzgsVKe8fRlfeFGlkhvQuWpSL17FBgRrYeAhS/Rl188fv09jCi2VPg9O+cXKiwIeODDXTBTXVq+/UrUzTqUz48hD50F7uf1A/aOb7pYyP03XVzcgIEwD4CaNV9461G+vPVFk/ppdaxntFrEHkl9dMglW7COKotq9BEZqQZSjJLjBvPvoyVaRPEcRZuotUVQ655cNRVV2EZjxxIFSk+AZG/Wh/gVIT9Rz46vivg/6HhPwNQzjvKIMz/WQx1GY1e+dLkzpvqgeBeoaU0TgjjhUO3Brs1Yh71xQECamXLPfHW8AjA7RRk6ltS4ox0aBRMdLPGpas1kELXhPfGJsiRAZoICk0IwAggDVXQ4OjsKOrOo1kpsc+kmKUiD8a5IIO21yZUKr/LOzNAroZj7SPzbGHayFMXBlcsyoJmrZjZnjZtow+MgB8hOuqtcLOwc5eMv/OcdGYmfMIUYaxhMbs9LQZEH4xZyIgoMGM/VGz9oxAyX5Qg6bsFsMNQgjNpJR8M0934jaoq0kpythVeVwBXI0P9mOt4ltw8s6ffOScP7rZsIGxbRm5v3ewttd+kLWTl0UjVw8u57q9sYvx8PjLn368K3Pk4+W5zADCivZNYi4ma36UaV4Mg26eJalRoA0oBV3ulCapaCjXhHhRh2aUI/keGkoEvSZ8kJvsp59/mRk3ed8fH7pP57klwOqaUJ+//Onfr87PuOf33aZgJ/RuhfOZAkA4x0f7kiXcXN9CVDslzsdyRsvDKke3zHeSH2xJ6y2UtNx3hCTkFWzGJN1ww8E+8/91L8c+W9vanNxItSM8ihD5QnxmBdKHayLApDDzOTYyhO1+WNbAqW0taw5mDtOJidQ1MIx+pMdmOHjb09+1s82SwD3Rb2LlFQTrGpeNhp/l+aF2c/ZyrGHh2JZK8G6rtIAx0RyAp9WAgkYRRkxpmYjO1lzsPAqqpY/gpeh+KB+FRKiVJANQCOiJWCqnCDDg2blu+xc3IL+2YHMMap4OIiAqQeosoooLiydwNnWsxVc/HB2fWD6+vrplyJ3zGOXegWq36aLzXYfSd+hXGLW6AS46MM6MLwcTrZpZPx1pY6zQgnxlRgNtwVN/vo5G4pms+nzOuV8ywCqRFOhP8qwqiCc8I38sMwLKJ1xCFjaWhGpNN4qUSzJBwRE2NTgkGnPNMPsFFf7FbvUzS6LE5pyC0V69JlFUhCgMWo3E0VIvekUzulRGC0sjcWsSo6mr6aRlUlc/vMJL3z6lGzI9E0WaUctQMvBVNpqgpyt8G7PXyow9MAfaEa99UbnEsP+QGKAGaqFUsQg5ewbGlYBm/p/pR3spdgZXvIoEgo7ISbT4iQ5G4Leb1BNjNBoNzp/QotP30VceUkNfy5kUbG0Y3lIttFTG70Rjr6SwFuqdzAByDVbIr8Zq0gSNIx7ZM7Fi7dVqczkQmCIC0YDxnzraUREZYRCN+EgKJQtjgRClUaNvtcs51sCJRW3GKOlVPJE5lXSmc5P4bRuVF81JJYa1GHoM/uoW1fI6okmHJC0XGFBt3CmKfs2VSkSn3kw94cLt04SMLo4URAEykUA5s2L0II9gw0Tc621U0mqm9QRkxgWNoBkAmU9lfuu6MArDjb3d2ShpY2EHMhpsbfC5VJiCW47WqRHxiPLePDo+3j842d59vXKw6vntYHP72HWybFzXQaq18XTpJvH7h6/u/76UyO7q4kLOCEesmCPJCjuHBHoGX/dARKZMZiiCKP4lJl2agJ24sWEDEJbS3GLqnx4sI4u0lgPZTq7r08yUc2QPT6cfjgSMfvlyfnRw8N3HDzLNECJFZKxyu/MAXcDI4ZF9AxE5otGfxbjetAO92orgWdjPDR3sW/HtZVt7uhMs08V35oMgFbLeGd820E11HrBteza7HcpwHvrhqfy5m5vWNPJ1Z1MnPwTBrruiV7Ighj9ea7XNyXFXhMy6bNArr18vzsnn67v7P/zmOyeZj3c3eaC4epx1khNEgjVikQDjXwOFJYfln4wh+Y/bjCL+GfIiPndg1KRIQWiVSDo6AZefi43NprYZ4GYYQ4IoxZEaTwUJidpmLRX/ZXC/pruK5CKOyQuQ5lVGKOrPGoPQmjTTSckMtwgte2NRDgmWmCXpr7XsDxRFR2BbrwjVupw7br2Vh17kFdlvB0Q+DNYwGroTzSR6NfE1oT9tUTkB5/AkVcmisUJAl5uM18wYGSIMAiz6T7bAiGpovSPL+C9SMlbiYZEMC5ioC2/YZUOhBFrkjEFIrjgunZHgSSC+/1LYO41Him1HpT+SLiHPFw0NIhbxE7+HDAIRY8WDKgMkvsukqh6ceBzzhlkV6395MvXUiEM1oAwSCp6ROT22Ea1CE5ijZcYVM4MwlCXNM9aU8KP6aGF+XeIuXPTcq7mhsQO09+gPi4zSac07BYMOENOod9XTXP1lzwYIlOt0gGn8tZ9MrM0gy0yG6MFAI5gRmqEBzZgWzCmQKx2GGu803GpGuRmMMYS/UV2aUAABhk9yK/0UhVkPhlnsoXptWajVP1WxjHlwHWzhW4sZCgrkrI5A2WqYMTGd2vQ7EZ/JUJVsJ3QCVWYgMVMnUcPMDwSGRLaHz3rjWDFSdDT+JXpYnJxNU921kwY/CfcxqEKvnrhIOTA4Da4ui3MXvKis+5s293Yzb1q2y9/DuQmVkSfckNDzuSWYEWAFtp4haR4Jp9Fi8vCUZQcS/VkorMhlZBDLfMLoUICZb7izJgx3Osw/BlBmmo9k1uZTqRfa2XPwl7s2J4GkRO4JF8ixZ0S5GqKINTulZ+c30g0TCLzoiE4oyM3tnWjOX379fC6qXwjOzb3gfksaPh8A28Bgn/rNbF5nXMtmsFrmd1MHKjcqG3hLe/hL/a4UKbiz6dRuqLbTSApymTwaGrYsxoF4bQGy8nZyckAPzbIozpojqVJGvx6y4u0rlFCB4jFcPvoNp6ylJHO02Pt2H3Cp27IsMPAyZ/xagVsiNIlCc21JsL+fcQrTEEyMSXeMHjKqhsNbSCIC2lJDkWm0YgQG4rMqy1LMtChpe0B+V/etX11dp/iFfa4d5sMyJxQMbzJX2JusbnmWrTekK3KUmS1sBtD4jatG22kMf1ZIPvKb24xBAB7xtcYDpnKMdUoDzEmSPMCiUqNlbyIZ9r9p5OGbRCNKYK4RDeEdlq0lMnSaB3OCapD6IjNiZWQQBXjsg5ZmG3YJ34J8u9QGHQ6lF3xxv1guO8tMCyxetZWnTWFGO6CQik4+DBFVGTqGVNYnFpDb6J27wKASM0kn3dZSziwKWCFqyVF6GT6YXpQPEJNJvZIVVs95PvCHZ6Zhvske6svh3NbpoSFDqhchkXiIZpI8I38yGHtWRcjTSG1aTpGEyZuKw6wudWPVNg0hMRJyWkzuAKp2p/i7oEQVUBVuQ2gLJl8EyoxAow3H576dJnxITL6PwvwaE1UKzKY1IaULciUp7YnWprGET+FWINdCUkDPQV2rBlOHtU994GPUWRE15zVWsDZ1kYDoaURt9s2Xw2UsQV9l2Da2DA3f6kdr+h2wQYWIEn5hNHkRBsPhex8mz3eGEGD1HN61RkLU1OKl5woYMxwxhuyKN8ghzfAbjgCgnU5+1btesJzf2SAEN7TkEKfg56iLMRKYAK8Rv/KLBeEgZEBtdzetxDZKJCE5qG94igQk2BpJonzAh4IsK03oERhKLonbPE/50IDgI4RmZhA3N0DYmCD3lx2PSZLyIhAVwgB5JJh7O3uSmu1pTwg0LDnNRE4uArkxo20MCVF1Z2T5A3w2lKQMxPZqrRNITou0nSqQENe0XjFsgDZLsw9CAuBKhTEWMnP7sEkjZOWeJJpNU+hC4qwg3Oyg1NYOznx6uy1+XZa3zc2v3PwPjzK9sFK51c8uqLW7y+tr8fV3ogLvM/Qga0Gi3D36InrlC3NaFRqjCbcTywG3avczQQnDy0YIV4fN14O9XSsSQ7ZyoDW4Swp7v22Tlj4wRjHkrEj5Bw4Pdq+u/n6ei0eSdUc4/h2Ekd07T7mP3D/FS0KmHx7sWMYsgdLyDBmWfW82uoTQPsE5y3jHgbi97ftuTtyQv56X454vqmUZV4i7M994n3Z3ZbyI7ScRKW0xnchuAUOpBwBGwUMYCJNR3MzBcyGxD62bf/z5lzafX56PDnYO91j0O0L+r+6uSThFqTfXsu8cHm1cXYsPphbRoKN24uORHGkLTtW9dtZt0Mi80AkIO+86lRrVN3yCWBx9pYdG1ED4CHRWdrYa7Wq8WZbAilAdOWPRdqQum97oo6yZPtRGv2EQLVTKt+ZAwaRtxhNiIivI5UItZhN4mBGnUInc+3c31wTgbnNsi0Jowx1Msy5te1n+3N05AiFBK+ee5W97XkIOBPq2BdWSWj9kr6aosq55o7cwZfwYMSdYEXYa14VjgpEEHhAfybWYXckYGJHF5yDFAd6on5GXMEuOAJ+EyULSV9+16o2Tez+SQiNmtpo11F9aK4FAtNRoqJyCA5Q1PaflbLn3cFrxxbsY9hHUPieGQAPZtZOsqelgDrlGuQhKzscMIzNfeQOdsWfvAxI4BB9EqZvYbE0kDMDSD4qmTTW17BcOgxjtsJuarZkkhUaOvQ/LoFU08Ka0wU+f9ZrnZ1CniO9DlTrGrlGFlOx3w/IVMWVEOTFqIMyFS0UaX+9Mo7oq18jSS38HEYbhoWG04IXdVr2kWw0Fnn5auCXTDdBAfIgaK9MUocrG2LLXcMMyxiT9ABcSwkmlZ+KYLzWSKKrFFpiihrwVXbFsHgS9piuU7Rwb94CvmwELTrySp0wV9KT7RL5hmbPV8gLx1CJmNXBN8oFr4/baBFqts93D6faOZOpiAQ2MMwZySG2sKQvQuP7f+AUaJP4agihQR0SpWTOcV8peDHtjbOgtWlrcEKeAJDSkXWDLcxuBm2V4Y9N29hvCQS9oI7pZj6URcHM9e9zdNZCFp3fXdqzm7VXYpeS+3909tJg2Y8Yn4YxsO1f3rqgVoFJaTdsYF5cSIlz+27//+ermCkakGDWDBNX+wQGjVYaEhGLuH7SETHixGcGQ0IRKEox9I1pm6eragSRq7U13F7wtqpY47q/ntikFzaMpVZ1iMmqKxk6z4CKqIbrMfzwCgSrLrfNiFoigyWa6UmJ8XfJq3F0Xi8nMl4WGZ1nI5+bq/uGBUVi4WDfsHe7dmPj8oN1pwPdgJWAAploWfa2ZJwFa5twKgxTnGTfji2lNpjczsWcu8NyMMwty66M+GwuImLa/OLswgK2qndB3r6/dzYk+Vh9exIfqyx075v30m7Lv2Sum00TEHq1YaSUi23WwKeIE2PbmCQy7nJOQhcuNdRfLZZ6mfqRXA9jwgFGXHSSB7IdW967ofVnYEmQjA1YdCjtosanHVlT4R42kT7zDz8cVhpwlrhjJiiOGYMXkbKI2jjvjbYede8rZ79vbSJJKjYWlliMxrXgcI1vhMqS/Op5QvlrDuaf5V+83AQix6naXdWecObZCLKjFPtiucpyAVUS4m3pLeUIInfs+dkeztkkwvI+LjMk4y6PlQaYr1dXHUJAjwVJlUQ8eJJH+KgUSRuYXrycndKFs0mwEkGIa7CaCMEZZtowjc3WtQlJ4dhKgjVucWYAkkRFooa5GGguAQNTE+5C8SmBB9siqgVbrhLxv9br0GIidxRETYfliAaCcrb6YKi/UiNVl0NkeYErtJxmnR60k5nx+b3XaDhGQkhG49LW4S8KWThMRuNeX3gE2Za7zYNY6Ngt0NfWk9WQZKPyppB9V8iQon8vF9+RfY2lq/KcORkV33rQp0ef0kpDtpXMYrTMfgm5AJAiUmsej3HtXdYNVevqd1irvm7r2ZaXCOJ4MfgganLYKtbVV04OnZiI5Ck1E0LQDWzNNvk9hpG1GJ/cR+NKVZIVNLwlgbBvgugrfDbhFje5I/9XJyy188E3gG01R4nWHAFwTj27Jawtm85jLOAtu9+jw+OXkQyGg6cA3cTdYMPtpFlWMG8Pxqxnd2WztQHQGajtjBpRvpKhQIqkNomUioEpAZVMx1ptywVkWXnIuLBgRDtaE3wVzcqdvbAuLtIjnEe8CSwke5CTrchI7h6uyAD2eXfNlSQ4gzJPr/8v5l69nXzmmTTVG1Q+02P50WBfyCX93iEAJoZjisf/BvWt1L1NxriFObZqndNAmiLNIEBRtB0xLfzOSb9/xoiwdbkBCJ1IhlbJYRqtTDywOrVn/JggQrPtGbDW8vh5YwAxlucIKDmX4J4xszksBJ6OCZJWCi5jR92uPK8+yda4bMcM68Z1SeRGXZaGT6nQe4KobdXJq08eIf9XpKhPwun1AWHVmgkgTnjSmS/Q5XJ/R7QMR4LcCeje5X8/MVMLo/u6Jy4SatvQSALtVwO+mSKSYRKrOQulEkonxBDZpPYre9TVMUAfhOg2wYh+CrMUIj/dd62MzJwYcvqAPIcIrPojAm+phKpJ9c8298VGCo8Xw52hYk1YMD/qVdL7gr+wL5hu9g6Os3hgUbD4lWhWZqWL7t3CKwxOol2RFWoIVoJ2vydYQ+uDfcUrEMgvZE/dormQdDq6Zy9loRIIdl4qz8gQ2sQDNiO8frgMV+kc2Se/oZCRbM5BAaGg2t6Ry8lWLBoPUSI+98dJwQicJoEQ/fexxLXo6E6R4dmqCIoUxbJaQq5lEzzSk1vxobCgQK/qpQN4PjOTt0jXOG6zrJLioUQJS4wonx0buG6EKxEYs6JVYmv0YZF5D+Ff5pWjzO3jRfnLMp4KyOrIWW5tlPXmMkUaWNfL+69WEh1Kdt0XuQZY7RwIaySCoC/81ljQ1BAyFHgazs08HluKUE/p+NBuoEJJEqhNvgaAP/+Z5j6PTeVWjYatb7Sq341Q74d/TaeevjVGnwKwvRZXBLX6ngPwi1wBYj5oI0vAlCTt7PK9FfMdfyfZUYyySzohPBZXzR82wp9uQntBhjiiAuLBisDCa2agBkHkPy0q3yimfz6RMSWmZ4jDIsbIciw+r7bFL998SynSiHI69FoewyyHwWIohPgf7wIqOz6DhMPMlsTk52WPtdMUrrLBTCSSFH3ekLeunxADiW8YskPmdugVis7WkfGk+eUWjI0F+QxrGk8JwKP/+UVFfmaw98Ra7O1lfQ2NklWj7B2a1z13o6/ARrZasyNONarGjyBqmdI0XgMHn+Xhp4/HewqWIVmlebh8uvn795dPn84tzr3HZv3Ei2ZQkq8FpQWM1JSkeNw6XluzwJqw099dX1Iv7QyQmNox0Q4z4Jk6eF8fV4tZIDhbc3jxxsxCF3BpMdaE+LAsWooz1yKQUAqkxro8YFYY4IJo4CS/t6DJOrBjennjChJ6zneUusy3N83C4t0cTWiU8ra9y6Zh39HRyKEAHIjesNoh3J4MVES26/va4KSua9893/FLwnlfFKsQWhYQ57rPVoWXUKDbEd3B0hLNarhCa4hfLZ1RqHm1jUlwhvDWf8srbL59eri9vLvbPDw73Zcx/2pFJKWJM78uPd3XR+m1tUzJp8rK8bEVDmh/ZSlApxepOghUjehUd9kQv1rqpMtswgWv4iJT2gwjNBcQMIxa2RC74wF+EedkxdBSuVCnZVDRuB3r9xNKxYgxOpIu9Rd28DMlyWpbXpXSVa/uygWxvQQqP2uzTrB1/OAIMFIim4GTjgdONeZf6oot/mTZCzywH5anY3XeKUMTxrE9t2DYHOC/WLDwUQ7mrGUuZzmRrYBlibDZiK0GBVL2SMzpLYiapkgzNDO2fy7tjLS2ysykbV/xjzNqpbPJKmx4yHbG4+Yrs6ccmyhdJCbVqFEKnOqyOYEzQvUMVUkY64Hyig4kwUrEGmhb11U0Cx5BVT4fVcC8ohm3j9bbTu7UVTBU141b1YNO/Ch77PzqqN1rSX12xFHVpQGqHrtAxsmzpoh4GpDoJX8CZgnpJeC/twkHtVxuX+UYHocHIdVNv6kTMI9STHtBL588YKw+bi84JJI02RU2kf3oNCU1n2hUeBjlNSYX7SgnLmHkp1jCrNsUaamXSft55akAemLKxgFCMpz5GusFbRyAOVXrsuXoNvmdpEXTW/Hk4r3mrLnY3BzkrhgDqdDjGN2mOWbFxiSbn0UtfpQ91ExWmqYhyKyhsPqNuAgNkRs3E5uokOiQ7kTONLJDhi/dfvJDNPVEkDGriWEWQEbLFxIWshDpVYjGpf2ChEvzR5jOnX9c5te+hPxpmKAcw6UR4YDl6YRFvTJIRWzXwUEkysOZOJ172Ev4UaGhFzozlf0yZZrZCzDp4Nrb2EodEhCOsaxvK403XCLvh4+xcmvcv1JRBc44bTnaqFX/MLV5R+CXV096MRbG5YSo78kwJ8uRbA0ivcHLMicGf88TW5qFn4ImZhMPysh64+XaLEjSSPQbpwcF12WNSv85DlHfThTY3tyW8bFzRt8ltG4xzLMZ2LuKF6LSZIrLEwU1hE7IJwYRNVDEpbmPHMISjhyjChoM5ZJtiN9svqN8FaqZu5VkeuGdZJI4Odi/Pr7VGdJHrNjriWgKLi+/uTmZ8+e8JXyRC9dqMkAEvzm6XH3qYIDmv6AXGBchfbihC99hsfP+b7zjlyVXW9SUX+TXfyb2JPD60ESIH0Nj+64/yaoqfoVkjAMouQfGmDwG7UjGbewnXCDtzx2tiFUUb2dalYGOv3BJRYSzYWouR2TlWY0fFDVVBf/h8Mi4k6omPhK/GSkin1ANxBwcR9LNPLKHoeSTl0nvBPCidoybaK+QmNoB+bMQMIQ6IfFXNFd1GcTKHsymQiMMfDltIGvgkQTavKTjZtDg0NoWuZHMcP4yFHZoMbIQLlYAAECU3FrmgsM4sPL2JY5Q0gxlylew7HxLrFpM2IeqlLxSi0pWfTj2HiHSpJ9NEPDUgTSNJFW/Uip2NKwlRVY9U7C+EUY0iFJBQijMIFzjrb5R0HxNB/ZhGT4MGJDmLqKLYGJEV4zS6HDTpOBorQ705NeTGm6gf7cIDlomxpL7JA6FA/wfQuvEGuADQuG/ehzZ604Ng9zKoEdQwkgAAJOjTtTrWVrJSE8olgUHd4Ho4rVVS+6EfsgfrCaTQAVU5pgnofA411Svw+lWZINNyGCTawoVH72DPV8GAF5BY7I96FhDCvu4YO5zKeboiG9hrMcpWAQBm0b750CIF0eKrRYIvXUqNg8BgqlBWaif9X5GggKScZ63dF+ia1+HugbJZtyLFx01yKUdQxBw5AaIWzKR8GoD9bgABAABJREFUJzDrHgZhHusvm+tMt+7DwH7aDC2qSkDWlUhYcWsfS/GcCaDxcFBjGb6Z48Ll8OgWHDLC8A7ka7BM03i0olvGvdkvo6IXvZBfJ/zYvTPX8JWoaGPA9kP/cL+07u4Xx+7gKMyFg6XQN5f6SoI5mdWY8S792tpxuPX84npl/a6zxnv7m/vEuXiV56ub6x9+/JGU4/2nQ8r4MtQMiZC7e3hAQPBUMN+k8pF9QVpgeyBbW0e//e23bYxKpNUGwMbx/g66sMsrbZowkS3GN9nMQOT32dxy03hnxdoxDhx5fTw2lHsmRBKV/jOBibNHl+Om81wxUjoKLiaznLlMt5Wm6VEygoPum9q8oa5czcjUdVPww93xybfaJq+pnPHuCC7AYWnBY7nrd7d5tCHow9GRjP6cMDwhtrXN7tG+M320xrMG3ajrbgKzmk4Srsomd4TjtjTXBmL12MKlLbvsJFTpF5ps+3/l6fju3pS7NPpK8NKBPBo7uwcHe47eNTTu+GfH3MyGOUQ5GNUSzVGL+26RJFZ1ZcbNnf1513M6PYuaYjK9ELDIgyjXH4JHA1okbcl5Ah79II0R0d7YnGBmzBYWtCYHhu4xjksxonY+NiYI4c0WwUJ4UL4Pi7xC1XiQ/GBAkgSfMSto5eyJImJZJG+bK47OdVoTh6djskvWuRbFFLBEkBNrBo0WFPvunQBxswClmGUEyRjJmLChjeAYO8+7d2OZNF6eKzCawucZMmkUC8M7FieC/TELOCSuSOEMvzQv3hppyn8pAtvqJXLSIMly3/g9Dl+F+7AUnb4SiD2bF1h0YoJ8qkvtEgzaqmiaaIoGswL1PdAnrBEJJGN5ZZAvhDRLyD0ZDbCAThKrBQVTOAnWYPN/eg6/NZw4jN4UGuHXM0/9NsyZ+aVv+119oX5yH0ZI7IbS/kZ6pF5hJcz7bIINomZquV92Z3QVxSSLtZDMrNPBk4rTMmkFGC36Zv7Ts8aGGGjYBtJImnWVl0KEXsOscN8CoKiDxt1CsYQYjB3fBhFze0xgYOguTdNSNVdIvYSbJtD/2mFBeZMIh5Llf9MCrMhCgRlrWBpL2Ju+1caCtcaZhQQ0+7Mao5ubrQGcNtduKZOyiEgfCd34HV4x8PN2W4NPK/wRjOg2h+0rssbtU3On7u4fHRmN9T5fjnKYKVVVvkngrMrOL1c0fud/dUEzL7sIeWael1sAM9RW3fR+MxWZmpDJAARjM8EXTwkFq23JV10xu/Iv26gSrWpUhAhjEFcbct4ArnnCo5xTjYtOCr2sNcCsyNglZcHzzz/9fHF5zrsh45shi96CFcjjMZ89i0xUqwszKq2NpGl39+27Ws0z6w/29t5e9p6L9+d9exbLsklEyLb/srpnsDFgzOPfExm+IlHwds6GjdX9DvSK6G4xYhb47dtORO58Lmiz9ZjjHU5gOD4wSerJQ3a9+1hsfqb7eS3urBron3Jxsv031vmhKHJHIstM4bqWp3uogD1ilVOIC2v1SVTm2vGeqwqFAfE1U3Era2CWZMLl6bngX+7RQKrXJRzw0dIEyRn4yzPTpy0ZxMFdwxguKt6r43XybcO5q9Ye5a1LXZIQ7k7/4JDAYXvXjum9PMshLQYJBVoK2otQGGJRUWeCS6kHWy5EYAOYHJOXSsRoJjULm+WRo6OoCmZD1ywinniWeZkNRE7iaGxiQyhfQYxCx0BvZWKvZJC3yEkyhqYFfUaiklZZGr2+OO2BFakDrj/+FoTEb2ki0l3pgCfBQZvSm4CLrrDmy1GXc2jdrgBfohwXjy484D3CWzg3JooICRvzhekyvz2IpkiXCngQRP/7VYERKFMyKYOMSbxYHqmYrvHP9y7Ti40D3qzppAKBrMEqqeNn3ls+kRl+gmTkzyKIKlG58AG9mlpg0dFANLveHS9PYFUQ9t7i5RRtIOfKTwpVoHYTiOF3jMvmMpCIp0yb6ahi2X45aKqh79GgLWhQy4IHRZVLNEtihdqMrr5GNlUvZGQ4t75LItYNZM7QlGtUmg4RSTYslDTPitVbsrvxeFc3s1iC7QVjMwXaN/1arcvq2AzxyftaDnrgD3Q1M30NqPCwIGIABG3hx7WRClJngFLTnNVvkEOK2BIHL2sR4Aaiq4jFgHXUUdOn1eJgB5xpTdEE07wGK6ihbewGHkKA7W26odZSIkhdg3pokhakh4mG3CPwQFcQAJFxL5ZxDn+NotcKfopyyfQWB3ZuGT6aZtx3GdS2+9cleNGO9YklP9dnPmFEKUfm41NB1Jwme4d87uiA30AICE1WW20Kbop/JOvMHgpOYHtof83fcTiaX9gxIIsbnIbLc2kaLv4PwyDmvU8AySQgwNz23PXtDalpIOFptCL081AMyRLOr/dXdn9pK7F5K7dnL0+fz5V+eH396adf3FErhvVuDp/LY2YIrWVjdW+A3AIlQbOyQqI5rHV9c0Vo3V1efpDv4mD3jh57eXIbcUng5Vx0kPrpTuJQ4tf8d89XB4CY0LhthbwlX18TJcUalkm5NMIsfyeznCriW3AyAO/pFAVxUrnNxrizICkpxcsz8LZ6fXVJfJY5WmN7mwcHB0iSwSoMZ3/vCBk4gMtxwbVWCfMiWNOeDIWz2l5o6SOeX50vdpg735zppm0OdpgmYjg58Uw+U5txj4h2ZbF+46anLl0Rs91qsRMGyAqbYs/O4fO80Rgv14/7q3uH0iRwm1HnBju5QHV82LUQjlnYcuc55Grqyl6dmWvzTg3k7YHwVcdKOIjcbm/dmGgnb60bIB/5MDgQGmUonBY7kP2TFMJ840W/Iul4Ju5F2NCwMLNnZrC0/hn/6Lf1Q2mXOPaI7PY3iPjdXSROGXR1juPfN5fUB6VosEJ7bb3EEIUcvAetmYWIkKtQEifXxrQ6xAKxNzyHHXFamZoxWcIH56WRYDsIRzCkregYoCpgRMO8fvk2Nm4I2qGPkyYkUnrMXkeYD//t36k/g/Qo6awT7fg2O7KWMhyrrn791F/so/2+V6qEGQaV+BgZPaLLW2wLgRb1teS9pqZTUiwuI3wRcn0FuKZG7owXQt2WCXUO/CoF1/TrL06q134o5vpouMokem1S0o5oLz9ID/wjyJaWKjr1NT3dgTJAZ/yNy6shNpzBUXI1WMZDApZFACbv0pqmamQuMZJusbQNDqLGKzWj6owh+3kQHjjTRZ+Me973ZOCv77Tg8skgRByGVg31TStD422+QlajN8EzH32KkNLto7REFtu+lgx5rNlIY4Y1uNZ+ZUygWXmHc7r0K0SzekiWYJsR0CtV00bjycgJKYHEJEmupUVHX6wSlgXPhb9eEXEBSLNaEf3NH5VXxPnIRHg7X+yyDd5lFgRGaOOCXc/KJkFwsmxox6hQDJ/OuMJ3dzi7sb0PJDVg5DRuVYwRh44wmpUQO5xVStoaOghBTbEo/A5PVJbumrJSt23u7mzsFuIvMwGHbwFz5Gixa+00dZ4IR2J5XNhJKEOyUuiMwo3gJan3ZSmYK15unfYisXVMb8EsNw15lA7gI6ZgMvrcM/nElcKKt0a6ujhjm5POcsI5/EN7HTLCEcXKM00KBNPHdWrm5MlnwgJyRSI1BGzlYvosS5pU7ig7CMl2pr0gx3z9m+4Fc1TAZfY3j3dX4gCoBytFWxrEFufqmnO1ZPDDHWPZvDKwDwQ5GSoufH3gLAGPq+TLHJS/hOHGgH12BQtdGXtQTm6dtAniIwpcWSG5BGmaxW8/HIsCurBB0WnnjmIkNih+ZChdp/obsuHfIamJDsQVcBlTGS+qenx9tg0u2urw5Mi99pxwDjgQhCPJXZYi9ebt1y9fteB09eXlJY1i7u2oW+h1i+Pa6+3DvRnmoclMoj9Nh66Lok0W0Rs5aHhZbD3xF9kagTwfyQlGTbjG+bHauAJ8T0JH9L7VIP9Y8reYqkQKVeipYSVlIIpB2lG1VXaA/erryyvqVpxPDFGwJvTABb0h6FYSPcokWrL5y9ahpOhU2xjk/5sE2QTXcBuiRQbk+zBmfDdcrxV9aiyBEGPGqvMrSJn0pJMCvaqNCuN0KGgsCeMprXrtjhRrAO06pCPUSOIlzTpFMTJv4BjE+C4BEro0BtnJgmkvGAdab8CfpH3/qkVA8prvJn9tqiVgKjU6ICCVCbCG46MyywjMRc3Mg6W3mgVsI01/kEcsZkI/1lFb4xkspahSqKqwXvO9QhvYK+0bNopBQ5dn+YuU0sTSO9iyjesqVZwB+NdGevjenkd4JonYl1CZ1wesMwjINGY0qElWjK9VbNuiNw0LhFnGPjeTOulRTTe8Jrj5AJsOLZfGioxbOQfT5CRv0TvMDTHaFuyj4hq/5mZWDDTwiEqgpwvDgVnxW3stpnCftuu7IfXLb1+BZZpRb1qdYcJ1mjcMgnlpLVwz/A2E4O3ckxXtSFstNkilE92jkVmUwj15VMDdch8vkVQ7+0fyGqj9xsOwsbLNcCUF7u+un27dCbDlLO3Ol73sLKJjbZX4lx89e8rJAY4Y0YGkQjiMELLB5M60/i7vN+ma8eUZXzBEtVlXvx3NJ8oJbB7qnV2H7V92ntv5BG/CQpnyDtC8cpKJbVeFlmUj73MwFRa+uc3uvLZgeXn++uul9xBMpqiHVLis4VWd0w/HW3s7tzeOU2T57x8QqtkBdmFoHNbp7odTO5y3l+dbrw+2uq0EeLof7q4O50J0nv102cO9YX5zvDc7HYR32iimQla8NCKkxEHSoQfb/NYasbWrD7wFFliSUOHu6praMTS6kIZg20Uer/xJr7ts+y03Bj8oLKU9srq/vXHWwYLIVu72+qtr7Im36E/+iYfbtT0P9qDCystC7PA0o15oj/3Mo/3Ng33xRcLDJOGxT8zb5MafnFxmrfjQmOMVcsyj9NS0OPxy9Yh+BxCaof9RXcgvrGfLxet0t5YF6bvfzMrv9uHB0eGzs18vz88f3ZNyfZtcNXzxfooyjCwKW8s3WYbpQnbuoJJNb67Zc6XxGQr2mjtkgN1T7qxy54cnADPmTTuWnh/TRN9WiqmHWEJsZQGbnUuI1NEGF6zlNQaXmY4MSeQgq0SnM3noClpsh4jb508kHXxL97tVweYVW0KcKzAm9kcDMpnum1SSA/ykB4QkXEkCqtNun+Ggb9M2XfQ24YGxFikReBiURO63hyNHGmF26JikiuN4msvM11IjrGTyN1/hyIOo9FnHNZbcMVTfEjV6Dr8QVA2wKJO0HInhk3fJ+pGPyY3oUyMtPpLHySJSpOONVsOeleA9zTpCKp0YheWkGRGWDKoFf6aP9M+7LCHxxkNf64GFwhNxRTtbT4R8LcA2JaZL+jg4+9VaSje9mMkN2LCJHL3CSLhTxGgbgoa03xj97mepl8sIEfWwQRhblgtSG4E5kk7V1g1V8j98h6ylhXAXNCEzodzvpacQFZZIME/9MRhIyRTTeFiIvCA+qmsWJQDQMzmZ3tKlma4U2rXyKOAdqF2xR1AN2lt5ccHDHTdo9yi1exY9AMAqFRWnswIjigjVoTLwAZhS9dX0pIpmAz4vXjpG16SPYQWvotnVo/6UE4Mx0frpmHCYhkDjCJDWNSLy1DCYPO7wkJLSoCyyVLcoUPeZQ8UKpr2+ZzkvIw0vfKi7JPPLMTkr7rsbY58sJwBB7EUdHCGl1hoLsCNGWaytoZtlFG5PQYhn+Ca3ZaS7zYlcWPdsoYYrEgrZk19uWEzEyoNcGjt+89WjD8ddxpvn/e3g6ODrpWQ25Y9DSixceLClQBQwS9tyKbCSg2S7+FEY60wfcLbNq8mUCUyUJ5A4ytmD1grSMK+83G2vvW2vvRJcpZN+Xrl+esmdvL1DTXFryODL8GogLhxjWximKWLW2BLY3rR+0DJJwzNB7PIp2XuURm7DFowyZZ/L54xvODMQx0YiW+9P2+6TEVTz+nwgj+i6eCTkyVEBDOuDjshxLklc1j6yY1AQQWCUtSJR9XT/THNLddDuzfqaq248tkF871p5hx4EDG2sy453fVc4k4x05LFX1x7QIgmBdfsEHo74sgxcJ/EveMa+/ejhtRuAidIHQZNuTaeDHCNzobqM1q0aRdyzLKxkWqJxnKHYDCgJw+nSHcjfLY3RuosYy3gKMbSNmxaEvEKdM8C5BfJfWxEhklwvOV+i7LFZUDKmjHIME5PYpUa+rC3+N5YdfeOHZmELwAek3xQYjGy8pbmNzwU4T6uu6nELEOJF4iHfPo5GnLJ2oxk63Ng7PNreO7joJtASo+sdO4qO42xisZRBOiuto/4DB7sa/ZLfibaQFvP31tADc5FIFpKRXJyXfOurcPMuhGaTQV1KTlWnTBaZQzYSACxdeMxgrMeYEuberXkNxss6nPYiBB0nMQA5RD5QeapxHQ/XMVf7alE4Ay0os5l7H46TK4nuBEqOFZ/fhzZ9Ja2WbtI+XobaFySGQ7KMG3WSjSMnK8j7vw7Lpj5IVWcjaBI0xBTAzW+oHOQAEmWoShg1NICogDcCQh3gNVbKaepxUKhq2gJEl9pSm0Q0Kf6paHYheo7yz8CJZQz7jjLcmficrqLXhtlQ+jv6JHUNjGalNeN4zTQ64w/ggOgjy8eSwpOmaV7wET7rvYPgbLuwnhMjv2fYBZpJStkRQewmxamKwSAsVWZKQXKvGWJKAs4MrtOPM6vqLoCk6MkicJqHOsqBkIOEfx1WMx8Ez8lYmfrVmXnmOYETIW6vssw4OLNHKzxO3J74oNV7np8IgPEuS1rNvRThLWHNbjH4bCp+mj1X6UIBpAMMy2YCNE36LUPBW3s2HlsfbOx6ZgArNl35hoFkJW4QRRcx3DgHuB3kF7aRbOPt5lY4X8YDvnrjS9lwIEqEqjkSIW5bEQ0T67YsMC6T2SLgTVJ9u9Q7uz4aBfNwDlm5UcvF4nZxM433HXrgC+I3aNrM67NcQt1yYClc1t/Vk6PTzRU+EybqrQseD2R53N9+vL0Xk0pRiBj3Oz/K041pmXQ+3f0Nx2hb93k4omXvnRveZoNnJ1iZUF8eIyGOdVoRKrnsmxf/YFaMizMKpJKMEeJBKU72xLMDvm2+muHHWzxT7uzHO5Ld6QHSnJaiKhxCY7eKcUf0djQR+q2LYrj0yGc++WvfcBytuFJZun/3N5prCzGnn4AQnu7IylgRPdKFLIbwEP2oh1QSkuBmNH/69dPNtrWiBGpNGKktdyZrXVb9QDq0c259E9veX9+TXBqh+Aj8gwOC3xlq6mn9KQBcgOPY8iOCoQJt19owCpkoJFAsFWIwOPSw9WqGS0IUt5k0ZE0MKOEMSnRPD/nWnB7sGYLFZ9wsLxOK7dLNR8n/epS6YJ+sOvCMlxAS3Q4AM0CwWLZanca4+X/2rFVxMkUisaDtpdiFNAWCNWsrFcS+iAVMCkPJEHB5GfRw6rvUGrmBESMHtRX2RS8QJqNSGUPfyTn/dQ8G4h7hwrphYgeDah3R2EcuY8giGvLp+sa3ED4yAQyDP6qJUKHR1NcHjMJWssJGakXJDuj1E+RhLojqeRlJQ81AXEbG+5UnoyYG0tROo6vn3mnBEPhv5vnYuyRJKDHmRBZ2jx38Cj/eaIhJEyqQfIOsPhsBuE1SfKMnMzWDbhDkemgDetU9NobMYTTKmb2IYOXmbFsQVKJh+5fGXRpcPmsGoLToMgHRRe+DtioK6QJHQnUzkvYe+JFBK5qlVKAjB+W8VOXPiC6bysyWAbXnCX8eduOCtbkQCYEoQ84BSzFaUANsoICEZASBgMJL6ME/U7A+moyAhL3Gm/5vI4rUMdqAzlIYxAEJAYmubOkT6nEV6bwsWn1CRqGajtDAREM4zYs3TFVRcMwv15cbtG0+W3141rL+8e5GNYrWckW6yr3DA6WODmUP3kWH3aOXv1hySD+dxy1wSFjlfdniHFIyuZDA6IMeSY0Ng37EVExhI2JeSGFvb6CHIXs8vgicJrjl8Bk8Njtp2EyWITJtkPwS110+fl3ZuOGxzaneYkU6Y+kfirFf+LmIjo2Ngz05gkLK1fWFDJ17+zvmnZ2rmxUhjauSHPgR7bTmdnAOF0Gw0sidHEi5ZtPC5TCwrGziO6m3SnTe22pcNTxJAtoCx0iZF/GRRBH2LVrtreVe4VfLBZDEH+LK1BItW26/SL5QUAKVwaNT06cZ0ZxbwcMApgw49JjkbGF63EzJ5si5YctTGI81Eh97Iy8LK8v/gQYAs8g3+l8w6I25yBvountpDJ462QDBbHQyLQ0iKvXtls5ARSJ1zD8HV7qYOGS1AcuJNJkOpIO4u/vhh58M5UQQkChQ07pSHNGewwW723TYrTyC3Z0sK7arEZylsOx5YTfYaCltch+tuiiwMmFYLxaYnEMKnvApewY1t171sm6GuvjSG7PYdYMY0AhiWL89sVfAwayAGpArbCCnjUt+rm8Z7miOkbB/IInGEVshP+RDpzGQuC3wkr/d3IhFoOpKtmEN2/Wmakg5u717cChyUPQU69/yOJ8jVgYPXp5dW3taxpgbuf69RtrE/uYgwYNB09pAx8Cqj48B7fmUTOr74VrbQ81+OzGoXLhRIp39J7gWeS90bqYin0Q/gWrstdgn9D0SCq8DYMRF7A3kJNCICc1Ftll+WqhMYg3/BQYqJd2YHipZ2HlM2iENz7wNT4P/tjCrEwr6WUz4BNsrN+eohRnRaCFukdH7lqt8ddxKZbo0x8VDaiOKmh1RzGwMKL3wyNA3C2g4yYOCwZdmZ8D5wpQIqIaZKkEc1NVstoVLfB57BWFTkUCcF7gbfmBXM/mpHe8tMNtHxMy99A6p1fF2yKtfA1XeDrUG8igPKaqQlCcGaLwwb1p8BR1iT6KJ2hnNUAXigDxo6vStHbQQOCiXnZgp7AnQsgW0NnoZUha4qbhl5GRz4OdJrHcTU5Wgyh+aikAzvbxp6jgIjaN9DeIX3mieKR08kFO/QaZn5YRPDgEx47Ro8rn2caQfATtt8L6+3t7Zt3T/+aQ4cGr4/mF1nSGoBdlmygcn8yP6SrMhNDasrBKo/2WVKyb5FsDZMkBJueU/IW68Jzqrxa2EgqytAyr7n/Bu0xqpEfkJTlXxHtnD9tzZJtWkclu7fdg6PIANtOWfW1/vHiSD22Q+W5qYZjKsCqu2AGVT2Ca2bGPe34hZAmfOXeJZh+HrScz6lktZ9h1GFn3iopsbZxb4XrZswm6viSO6KctAiELmznzNRODx8t0WCcQPZI7TctiPdoBgyewYmzxFeaEwtu2vXAasCI1woVCYKsYoxtg+R5uj1go2TCgHzm3R+cT9xGrdmXrTMnimDfivQeGYwkvZ+1tKm18hJI+6eLq/4j1xrxelwUCmp4zIroKbgGFJVichuuW4y1R8udtwfIFGN+xditv+8K0xRF7d/zlEazVWdI51HEcK7yTTn7Qya/j4mw8fDk9OTw/2LRUuvn6WYvXK5Wi315qg3pEtX52Ud3nYuPpvH7JvV+XQW9864FEDMjeoVZbRkUSoMYE2wiexauAxYfaIkxXLmgpx+2ZhVXRhGcfGz0ZD5KnZjotX136VvOY+2IWze+3GZqwqFMGEU4e31xfPlh9y5wmPSH04z8gp2L4ZbXV4dHpwdGq3/EIMWea3FBoYJQsMGFDjlDAMISIvXAtL/iPvhHsTb66TSMOzCftMlrV8niDvRdQsQqMnoBoD3BOt4Jb24ZVNcJGV9mFwMuJHOPpJxgZvO/MlLprAhxFdCc76VTWex3MpzneVA3Q9AdNXKSFittxWYS4FMHvQtQLno1xafqnto+EZuE/sVEAB0vsZQ6ZqX4z4MdhF6sZPBgyIWKGqTeS08z528tHX2Xg1PdIIVGQesLQ431Y0HRU+AWXkCGHqDwx8ZOgPwAgaduBFQ7DSmohQq2TgK1IHvvW5Vy2YHb99F5e2EniHIlEMCOjRlf9aT5mHzWoOWsghnTE9/NFsYw7LvrYxhY6yONWCluBJjjF/qo0mlGqKZt40Gmz6HyxM876012+tEJ4b/MDsHWDSNGAOFaFpXtonAwYpGlvMgcaeVDcMPapDW+nQZ6Q/IxHykPJYmm2PXtMqTLRFTmgvsmh/bd/pIneay0XBpfD0dHR86DYS3nmEIZJCJjgby8en3OE7zk9lnaLE8DBRWWzhPLlr3ZhIMFzfBHlq1FC4FPhloOqJ+mv5anZAoF6xMWJPrQmsE5xfRTThjbxEqCADNuAjOWXehKq+cuZYmrqWV+j9/cvbhSB2da8k+r+Z/QN3B+DG7KK93X1ismktNMU15aTkvVWbHP37R7nDSUuwCsJx7uD49JSPo1OjsjSD+d52jl1WtrNYSZKA88dQ2swobPP5TlXqpIObjL7h0NGp2ZVUSIRoC1OeuwerrD0GdYKDhLq/1Z1dIKTf8FYcw5PhQBwn9fUkUKlALDRVgq10odQS2WgvD+ImHaqDMAYtKZeUpfNf564yxzhcwFvYJwdB0Td2L1wN3nlNzMjLseFg2euehnckQxb+KTh19/j45ODwmNo6u7gWN8WM2BMXuSl7WomhIlirAcmTuc4xnkRDDjo8PrlK2TJgl2PnwHm6LR42oyZELbNcamMViKhws1sEONrMdIYeX1DaxklbXiSeOZdLGx5FSKIK/emFo7EQJCU/CKnhvhYIaYih1maxTLExNRVk7y3FYUXx/HJ766YCERGYzVrADoyFA+IB+cod1WCWzPuTKFtzgdxm4WXVRYswFYwTF627VG57/8Ba41YaJnYItwQjwgowr8KKg37eCeMbAbQYbBAGFiyN1N4lRp+QKqHBoiO9nFQzlrg3/hzOjll807IGh5IVSIkSwybGE8vm30YqjsHMiEmUbMT41ZfEQ4qFoE3O6C1LJwkTweMu2OsfOCtDUgGQQPOnerqA3aBN2ozAUTQ56XfP9Oz3FI1+Wz2At+VCCsF3uBDaEu2LIyGxt4i0sKhNWEJvIwtVrdl+hp2pUNhJ1hqvPnXmozY1mWNtASF4kmuNlBQDXI3OckafyZoUAIogfOuhTqAGLxiEKatAY2xIlW/syvjYE6M0kPk6YLQ0Y/FLEb8H5f1OW+qsEQRIc9orrCVY3oMyYQhqFnWzfDWdaLn+UgzJ4TDeZNRZaNWgh0E92WJ9au8idCe3rZdmcgjBhgCMvCij9MHog/+Eh8qKB1ILC6VGbpqnKCsSC9wicPFIQx5EYVDz1gcaLRE80BBW1vg42RDWjzcOy/fjdtmHjc0n50t3V944W+ykwe4rO/D5WXIdYlA3EiocutmE14ETx+Et6/jMq1L+gou4EsqyYi9S4KCeBr9xhW9T4xF7mk+GGXvfjgK1vWZRCN0Yw9gVIFlsQtp/JmE3+OaSovLTjQVp91hGUv2td/7gjgXK71S7pOHuPo5GsRlEm1u3EkKvP+wf7Jlm59F2haK8bkkB/c3x4enxHlPLOoBdur0piH59c2dfutL7qzPOqbL1WA29PGAvohSCQGr5K5TFyWEH3gSZ7mzQHTxBxKUZyyFqVuBDFpziC5nn5gSPM+icvOp4B8nM+W59w1jmPrIUI9Y4KqgSVzWQV902QzIYq8ABKaO55ZnqjNTOEOQYS9+YQwwkZ1OUYBlRBJbUEq6Vv81sFZJL5EetxCAn3aMbaPbaLViHJ/yDgnNJCkh6sKdbKE7N4kVrkWfZoa36qm3FbPFkbPxCRCFyiizDMkfUxo2ql1fm6+j0yMWWTkKLwI2TrJhTYY4GKG/ZJybKgAyTBHHuz+rJekfmta1V/bRKEhcGIc7vtlQorp/C4YNaE0gmE1xGkoknN4jBFg9WJNqi5lFhuteG9KNDfY4Qdv73wHSVEs42xsv5lagxTGOA7voqDHRdblGhULJUve3Kt2cBiw1llj04sgMg3cWdfTKe78IjuI1YrEKWaabMEXxvgmbdKaSKWZI0I3mTz7kBDQCnxt/xHTwlkdBFwtVv30BNzDmvYYFuyDEi8gE/MsNMaxWz+nFHsi0bMKEWr+L0mdOEnl6U4Q2zSUeKkurpApEBwQS/+giAmiARTIov/POgD61j/ALnIhc91IHnOmwh01P91kX/UmlN+2J/C0SgsLUcFKmJBg1CFg35n/UWrLnvTBfDphFgXrXVDzb4alAs/IIPk94jMaFhZB8MJi+9lt8eDx70krwYigcrdKSr+pNYD/oZsloJ7vcBKzCDWZ6kAWZuGp6v0lsjaHWRXl9aq+O+UmfaJ2p76xVR9Kr5aQddTplmt9HHHTPTM4hk+kITYVZbemhqIcn0wtICRpq2SjOUGm9Z2CrDrDB/Ry0PSmahMeVs4s3w+wDuRtPUGUsddZosALQ12RQw5IjaBCx/VZSMQqLrxtii5J7zNMuXfJXzjS/5oDzDNi87MU/xrKx8OD48Ojz4cn45QeW3ulq/2aIQ2IIyBOzzn7ID5U7A9VdXUDHBKXaas8ZxAVrjsmjaolbU0KEsIMBpkoH0f+YlHxtEvhoOcLDCHhNtY7M0w3DL+SAMRh58jeRE7ygA1iWhVleuleVwgA2x7Vluhre+OjkpBXbIscN45HR9tWZxkJWf/fnuduNo53CnvHgS3u1ssrjIGisPLYjj3LKBiL1ub690bhSaNWPilCgwgDsgJrZS3DkBjjiMLz4xCx31SIw/37pXJG1OdvgRkFKgIdN4e5urHFbperRgATKWkBQ8YMcu5ddja5rL7jrOa69ZmYHQDknRuQp85SN5P+ckYjhHoymbTMA8v622ipXaoTtNtrRt8g8iVq69VVC9PNgbkFx75f7y/urqcgKWc0uSOlZp6A0mbQnY5Ncbtio/NkoodufeLo4VCuY8P7+wbiN7S99MJttVRQ/r63biSTAD9wzn26hWBUUa+8Xtfd6tDj+s2RPGdqqgXWxGo5MNWKT1n+NjndUwB8J0TaR1I9GhtO9JQaFP+m8fPbGRU2pjY38HUghg7ixERfJbqeZQvHfn+8sNvdsNjms2ppgpNts7aPYmTx9hEsdZxHbJw+EBSpjjYyGNx9xWWaK4W5uwlv8pM2CoY5ZbW8vYkRgAW+yEnS03vW3B4n9hZg6HZuwGfKQRbkYYN9RpyqgR3SJVinM1vwkZ+wI1rdfYE5GNCYdn0oW1l+7G397lqtZcz5KBIafudNabeZuOGpnokzdTIOVg8EqpFNX46F0d6dQ33ta70iPuxvBuaL4wUv8SZe0lBhTSpZ3r1mxSY+3rV6z2KlwWkDYNfIbu+CWhUC8NsX1X/aju+/e/PQ65M4TEJP3STu+LDMYULe4xZl1nLnKJiThuLCMK1RrsqqO24SyonpErgmCYmnFKmjgR7J+Gm59AbXZ7btJn2mFKGgA9xl0DZFWmkDfmRoOBOuaJxzm7+5ZY2fF2xqMxADaNLfo1Tu9oC8xZc9N4J56ig/nUzHnTxwEuECOeNleUiNuWUVkqklLswcY6Qj8iITUQcyjUOA7ill4gDIeDh0FdqGnlCFpq9XVVDKcsOoTUgb0zdnJ5iW8413Zl/i9TWN4bh4JW9tyCW7Jnbg4CnBwUS2JRLgV8zNUlKW93SPlGtAc1QFolfpfprps6ywAhj6Akp73tOIAKCTEE7u1MUT4Bi+PlIADjy0MIoSg3RebpFt8TT9fn53dpQvP4Sk5pGG6pKbZHYy8wUcLkMi03OeU/oN44Q0jPdek0Xx6uX++3Vx4e+GD21bc4enag7NatC+xwE9NWHCe4G51MsrNinZh2ZzrOS7gjnzK88rEsju/IBoAcFOYxDZcqtnihPwZ0U2mQNBdoTKQJBVLynZywb8ks9uLiwEwz+wFtV8CmpFvIH+8M2tejLsx19KAH+F6T6z7KV6Q0TdpMzxJPrFKl3uwWbOOHq1tx7w+Ixcgo+CyBR4H//FhFvHpJHUHukZ4IqDV6F1gKRUXz6AeOadNdgGMdLh23a16vhclDslxA9r2AddRk78fdPZ06oLk0nCXN967ptq/XHIuWz5QnjqfISTfK+NYK5NGdPLgyGMxyzl2YoLrQCC1fAALlz5UoDiBHSUcBEM+W9A/QzWW5s3G4B03c8w4QCg21X+JAsqg2BMCuQWMsDxMh1EAvMBUPik+zA8wl5ohD9zxYPHVcmfkPgfhrkfRmlnnLzTLyANJj84UxfeVT8g224TkpiGJ8SZe3UolPtRR7R4CmxuT4z8zXRTIABFFAEkCBLJ5KacMk5gSMDMZf4Ln19WzxoUHfJjqmIEMGGQ37VxelLTAAKfJIbtRobfZbgzru1e+gbKx90du67bsRQqCr1sAdEsBofoMcTsi9vkqWEjBg17rn3i3/FGPVoWrVbORY/mLJyNzXGrbrrL9w2oKhzUw9VxZYKdLs6/lWO+EGbVgXpiYSXqNbgiJHEIpJQw3IA1xNL2M1opRcO6v+BffIxtEcA/1M37RIcPAbtjgIBeOPy+5CYD6GtqZiFhmwhpkCqyYY7jXrVxMPQmXmmxkA/PnGDykS3UUsEwrIRaCwBlTVAeOcmUAqmnGPodbgtRVtGCWdkYJM25Mn6fumyn+jppXMczAbtU9YH9aH5igc6MmLoA2pzKxRs2hEjFgwNs8AwFoslExjzUhl8fIkfUofj47X1480xqO6R8PITyC3vgMADvSPGUs5EKbrcrwshyQEmIr8Wb8T8mFoGjAyuRhJDpGnUDZ8kXCa+cN9IAEuDCELbNAaR9wmagCS0ZCiAHLfgCxtbLrMvK0NFun55XWMK49NwTv5pjo98MbvIVgldEldCpkkM/hc8kXEGDwq8ccyha+Ke50jnReGCc/kX3m+48pmXDuFS5618080p+j5fooZIabIL0048pyDIXMjk4baUkm0OnD0YO4ZwgDNeEp7PZCqpVa9vXaITvhjCq94D2LMcueJ1WefL6Z329RKvTTiSAI7IHYGzVw7lUcYfp7EqQCBFKNhMDchGQUgaIeECVnmhaT8RVDinfWmCfsRgR2l5nrCcU512O52RGP7aN96aHPl2oG4Z9lexYm5CcW9A5Zd/EaGIHQ+j5/ND9KwjXYzIoByB3APLlPLPCYQ1+7dnbuxenp0jGllfCLpr87sW7ZVRp1x61kdwondVdMRrWKnTp88OzcoP9zdPS3a4bjsyPyoFpyGCjG2Lmb3hGSkKkxCLjJ5IqJSuLbzRCRPjQ5CS1A3aRwYPeJeH20IXV21FWQiMz4oyAjdx5Yh7ClB0kraqEZRQ1f8hQe2k5ydvnYZHndMRlVH3jAsjRHfRVmxuWHgWGAy7jFXT6EbTbwLzdEb6flGmtjIAjNuL7X7XQVClwuuDSUwjRWAM3Sr6ayWENX0ZuDqlGzsQ8/i2UJrCNUEx9KahhPNvku++d+DZFVwq/Deby0grwoHwzKkYMno8rFyNZ/88nippr7yPQq04F/+mSkuW7Jl6rTwTEHUY8IR/ZIrwgVMbvKrTfhgzSjzRx/wSKpDsc9aDMiR4PoY457IHMiiCX03rF7IA8d5qWDEAQQAJTWRAAu+ecWCBuYp/dbYErdeVV2GP3Pg45ByuFR/Wk6YKu1ffbxL1MiX8TV1p49AGLC5fZDpzFlwNLI6z8dg+umKFvIojYmlAkANjFCnEmB+EfWwRmIDMOsqX7L39Vz7NBgq8LbhLkGGuf6NVHOe6NF77tBoJGuDG9ESun3J3Dv8OY0YYGNBN0bqYkxbPNa9QJlCg1zRe0IoOwaF698ur24JgmM5Jne2DfXm8pqNKXmCHVRc4+AVKZZFXGxc1FcmgPu787ONIzuDDEUHizqV9Lr61GlDKMHWFJm1geUrlGXtgYtpPNeC85nkphhlZPAwWaIATqMCJo2Kct4kcDEnA+2W0SCc4+VlV2YCTsanF1fQhkEjhq6klQwBFpp5t/TMcwHb4OGQJyldOcUeZB0eluDZ4uV6mxXIiO0CSGYr78RB1mhRa7pl4TSPxshXyY0MrzlVMj8s9UIuket3o4L3wmtNsuIG7gZEVOOgE8XqZhUGKFyR4URTs2WSNWJHl5tr8ZqaDh3bmES9jF/noy06SHXo849Ysp8NnhQktW4mxRYhi3bI3QKftDHnd0I/BbICqugg4Z8jh141lLJFTiCxF+u0RNa6dJdmEP1w1KI2lpqQ0K4TsIVhcll+vl63TKPgEFm8KD/+ncM+VmkrrgoQLWbn3G01dxdIQGxRNiFxbZd2qM0kQFHsF1LBAwPU4z1kiRPTHEyauBwb0XRRpJFcaod2aPck0d0aAO+PMEoaOv0F822JszZsqTy55FOKO0cULy+vbCdgSRrIooEqRrrhEv9qYqJ6mALSnMRcr2t7+0duPLVu6Bi6I2MRXstUIgAdgsKEM77Cp1GM08AfIXB4gIOUvLMXY3RemaNJA52bHR6kXJrVxcC41f8x3KAAWo0CEUDmUGxCDkHEFwmQnGojXtVRyj8W1Uz4dKTQVAflOGESGWNDJzRSBfW0dPne72Kxxw49CKAKLYAl+ZolzDTxHBXox9NRVJBXef/9DroZEKYcQRW+fI8BYulRe0q2dptMLYg+yKFQ+1kG9eVXPTTCqo+Ii8IBkWCrB02NXlJSDQQQD8zSBCH6dvAExpYQKsRxAUxDoLame9CH0ZKMSNzQAJSIHXSCMwExlglI0FlrVFnGInItNdeAoRIC3bARALEdaNgdWemr1wAchIrXY8NqzddIG86Y9CFl5m00TAKkV7qCQMiUCqFKK9M7mPIzeKg1bQMJECZDoE4tB4wKGDo8TRFV8hukjmYyjY7BhA51wuYhh2ZaaxXGI8F4Moe7aSRFNGvdCiiO6PZcHzkTCIK93ROnWR0Ju5uwwherbV1iTqahrAavt66KwQsOD7DEWlgwqTyxLWw/gOPZiS6Qmb1mFOTp+cIEDQf2w0u+IKsGzbYiIOVzPzgStPbKOGUVu6Wp22wb7rrQ7pdt11Td2I9GBr41oTe33WZuIO4G22FiR6DiwnM72QaUkZ9GA9jr83Y7Adtrhcs/rxyfuudEhNCLzV4JM/e2D1A/fUkWN5a2W0O3SQSZbRGfDEMqhFnzuSEglwg2xjERDJEfbSXTh7T5cA0hWzgPNUOzsQMCBYxrIemI+J/gpW5hJwpvq8BLOfcNJ7vJlISF+zVfROzDszRvjAyS0BxGN6gMDKDW/vpunNA2yS7JhPKjaYOAP3h94pLqzF0Si0R2s+PmxjUVMSWNkIqiX4vUwtYmKU90jIlsIiF6ClUkZi2Zni+vLq0Bvvv2w+9+//sPEk1bh91df/lycSnLBYFrDiIwo4p17UHDCcmrx7bbiLZkJnRAwJMwofxELQMbLZRa78fU+Wqof8OAmfZREAWcZAEGVo4FG0LwS5/av3ZqTlaHLvVdccxN8EHXdlq64UF8aV60J3uE6CmW6ba937qXzEow2PHu4dH1NXUB43xQzSDewrvDMpXzpm5RAjRDTloMlcabkTDRlrUzwqVnMTLbamHsKF7J5mzgnjlCKDFqdbNQvemfrsGU7ecR4a6/kWuVzcrsiekhANDIED+4iIwRvn2lnkbCvgb803A/07BCpjKlTCYQYgSPyYz/YNhDQAe4VyZYHYykNFXUraYqMMSpQ5ya6Agr4I+yQw+SBJSv8Uod5aLgtCevM3aIRxPYKi/Qq5CoHZT6mOyKefyPBMDSTm88NU8zkpPuwA6y+hqGCeKWX9qaX2HKiPUL1FZDCKbWVArK4POq+eD0JMWV1My+yJOcKtW6r3HlK+MCBzVZ2ldQu2yJmYPUQKOoM02FGr+57Wqx6LApH4OqO6JDyTrU8Uxg+Akv8MrQNV6A1YxpjvLBsvTZEKOZ2m0EkMQm8jAqGCACqE9NrR/teQxqbUxVa5G4Rhea8bvZ9m/GaW48C1mqh253I/BgEt3PoqGJ/f39PYkXvv3uu4uNzzeXZ8xZBQ8PCkhkNM3hlVSplbKcBRmDIkbQKKFGXPFarG/cvl5ygIhvMDaEVOQJQCAvlObcI9JgE7AdIhBakmVQLCOutktAqJoE4mTHlSIfT08dCb66PHdPQYt06G69adXRTvCuG4vTXjCgZccFSCwyAGHZI93i98i70KkF8pjT16Xn8pfKnnZ8tHd4aCdb/v9EMEufvG71mnRttgRYIg9bmg60wayZAecGL86bs7JNVwptIs3NhTBDRAoh40bPHsa69KLeF/KL2Mg3zqkWoHaM1U7ZjLOnieYksb4mo5t6E75wfjEeTegQWsHH5oyTp5brwI47jTLeme5OyF3OAsiQn2OAeYQqBFvuOCwZuMEaMLM3ySeoQwXiFhyORhRAySjyoZwEdEikRy/gCcBxz2vOCoEh//B09uzO5S/XF2dXn75KB+SiltM9W0hO/Pk6FsZeLXmoYa4dXJCLgAqIZttUWXdxmbt8nKo2UCPapPOY6Qi4dFHGW8BT7I0rABBnKUddyyliX1chShja4Bdxrkn9BLPI5hmnlumG6uMjdAm2zSl74PpGcHi0ROU7Hz5+c3D8QetTKMiQ97Llq69GnR0XoY4AQkD9xbUeIFnFkbHmNIgSK+9/3zW+QVgGeeBXp4LLwE2rZyOzQ4RXhTwdX2ltamVsyEaQJjYFSZgkSuD3qpcEqV/9SWokDX3hF2LzvsWjL97LJxdGjCygBK9BjrQak1fDqk4zCzyji0bY1nfaKBrWNiI0CRqu/VlzBNT0nWhZNFB+oQErFKk+7ggiL/bXaAq2cTZ7sJqUHO2eHRXIiSMWQXhgvkd5C5YCpB1gtBH8Xm2p1Hd4CNXN/TTZcAw4mat5L1+DRLdZEtAc0urZyHg8vEd2C7vhqUX9osSsqNqxFxc6GzaC83X1B4rG1xuw5VXJ7AB0mnnoI9ha4FKCyFkDlpYUWPCSHewe7S1KlfhD4r20HW6nwzBUW/6amL4deY1RUq96DmbIVleVmRiKK3onM3rVji6wxzLu6tR7qwrT0NQQuzQH3xTTowPGpMTa5dUVo+3bk5MjyR2Pj1X29erbHfm+a5mFk7a2TFa532JzEirpZF1s9c0pf1yYvj3GXXmEuHPM7izj+Qe5dth0bLL8z0AkCmMirA5H3SXAy7tiZ1AyaFgU2MfvrXXMvim/wvrJy86DA2qi1+kG4S4O3EYVYr1tPKUu2qAmWjybZdmqfUqAsEXZtZwWbrOy44o4SdTTk+PTk0M24+HhIddQE4YijBLOwygyUAp4cxNe0j8SmLPCYk9LYoyQRg446RW3TnYB5jbnBV/cONkyVlRquiF+fuY9ZHViGbVwcD+yA+xYa2FISOq39GJCxNp3lGala8Gtl7xELroybzhjIiPaRLVNEwkCmCLrIODqY/cqQLCkDjZ/HfCCaychzJYF0eaa9EcQZq58hSV8aTn4OEftusdlZE1cI0/D1qasQLB0e3WDhMW+InNK7oe//GhPqGRHj4+WOt98+x0t/mF/387G+fnZw8sD4cw9RRPEKcEH50lZHDpeOhGh6/uuKpuTAbMG44UjCbqtkoeyW96gFeXQ9RmdDH8D27CkRJ9mgw+RvOCqd76gqz9sDkF6/NqGIdUqElTqCa4vHj6kLQzJLJhi+yOk/8nHbyxYrVxuyx3OSw1cNlsWfvQ4Yi8MRF7FAo2TsrXXSLnlDjWHJJqemVwe1yZaDUvr5Bp68mEhKVNfsZGX2kigm65kpD/YI0YNTUMoTZv3eHZYP0k4vaRiGoDCKCF5BzfzCUJ0CHnT36ijKbo0qzF9JTYXwaeZWkrUJpd625ATjAO8vlUAIeLXPLqbIfd33gNfgfTSAsgUDXK9e47VDTo4TUT4aRcGRuoxV48v6s6PxpOu0ERP+20QeVJ1H4FHbH6SafA4y4P4csZv9rUQorzQQ8gq5hk36ts4Ijp9V74nEcX0G+z13wjTY6KS5stsHlv8g03155U2A0ULlzCQRZOMbmpDz4jkaaqxDJ48MjQfplN/9ZsnptjwPMrUiW9mpP6g5MSAxs3vMhAg+1d7DRQ6mWAzqatlUwqcoRtUyVZjtESyxqUh9I66lGC01mrDrO5MavtGwTiaZJBliET9gpv0KZqJ+JWx92aPTmAF4XtDrKFr+4kfPpw4139xxRUuSlFjJuvVgXsJ12R4BAH5aggMww4MI8z1VV5Yw3ZGiG1lrd7pMtMC7XNqnKnGulNzkMteALAhRI9Q3lkcM94mZdnSL66uPt/cbB8dcGyJoLTbSF4wjw3cRrX1hkMAYNjb7xQU7Od54cPfz0PilC97UMDM8ZEzDoBN0oPw6JgM7FRlmIl5BomZ5igFXCLN/U43NjtPDP9d5zoZyYi1A6rdnji5Kk0SHdX9wMq4Jj4KowIgnl2NaMj0pjzWKoPx8x2wk4boMg6ZNZpiCwmQMk0TGGiATIqURPxmfj0aJ4+I9XAkK1zXfukWWWqz8FnzxTuCJoQ2ibYQ+2kI3CE6M04b0B2/cgqBY6zIHFph7BJJwAu7ba/VQgkxiDXVA386qgshkWi3DdsOYF7Y9RU6q2dGEw/O/vH2iaMKKkCip9xsWLEFRGMyBiNFgNSuWH2777LCOXKWB0ekllUjac4KISYSvu82orqYpTGjccyAzseR5rfV3opoVL1ZIzJcRARJLsIVZA6tYyyREw50sMzVEghiXVGybVnvrnV+msvxmOL/+MEQnGu7cmG0gVClUEKdILhhvaEKSDW5SWOTHpUsTJ/0job8UdogSYe4ONJLqsVsVYTQvhipAIoEEB4YZPq+9lSIy6sQ7yYko4yIuBaa9jJVYQtFNBA9JPqnunEmG0bpYxs1R5ZqqS58MfD4M4qmXpCZecxUayMBadZZbTXmuFrFATPSTO7FF5k405+qA3PaPEkR5BqPnwLMbwUQPlZWgeRpuH6FJzZJBTwfqKrRyBOQaioxNG9cPmPaYK81zgPihjAZRh1ZpwbhNYOpqUisgkhFgMuciVjk4vTDfgop01UTuzQaFCbF76Rkgyf2lOkAYXolPCc525LFQl6+TJKGJP1P/WUg5Nd8pwtf4JbyUAYRFPnrcGZyv7506UG80BcAQdimFQMm8/rWEOrb/wghITGzaFKAyG4SZDLuHU2Pcsynql0I1JYCiFizjZFanP6CwedGPSZHBTSu9lDaG6/oIEB4pQPBYZ7QcOAWjII7beVxvL64YOTg48e5cxBLPt+wzlvVEzoUw5oEQWLJbURPWk81u9yR20eZ3BJIzPhKKepkVTdGabL9zGgm7U2CTLH254zLdNH/LaJA8PIsh/4d017yYYHkDw8rd7d7DPb9o3ZHMT7kyiv39ibdPVEly8/J7i6MsPsMAJWTTZId8PYc7Lsi/Yn+LeXy6pvQdknKDo92yHCYo5sBZXbt6oGIZyXlVhoyc5vCb7ryYcbtdmX1ZSIoGKM2zyhDlgOcATtkSD5PK7CWN5QBE7ahEh9wL4yIm8wJKEYH2y5+zCLO42jeTInGoqPQlEY0rdFAU4QEEEmt+pA9HPFyMLWgHsGZowmEYpjoJV8G7WxBaC//ziz3QC5zs8sBHp5cKlD4mUVe+x+CliHuPtdf2xZvjgKIrlmzRjBEGl3eb7C5kpOY9QYBYcvtjgzyp23IBbvPqyUp0Oezrz/9fH97DQo7IGOAPIMwjf/6Zq/d4kUk8R6TXSCZ4OI1G8hSi4DQspnBvhxCdq6twx+4hYpF2SULSanGHJQGgqJHpG1K3zLv11fOr2/Pz86ptZiN3VCLL45YKEYFWMM7MQc/vrSOcb79+PhIXBNtd2bv2kjQKLYlJmc5y36nRWDdXODOGHPERZwak8ZR2VtmMA4BVy7rgW9EOFBnFk2aN+YPvIi79/NSJ0Fb+4kUb7Sgl2VK53mSiiqbh8P8Sdgg0ku/kYOZpzkb6pClvpIbFkYph6AiEHyXZTdyzzMDlGTQMKLJxEXKvRkObOKPsA22wbOmFvILqnSZQbxTYlANKEZZ6XCSW6W+FPW/no0XoCll4CYYbTOqpoJ20TKSNHz9BXHWTjBPa2P1YA5ZRBzmjjBwA3w3MGjQXLDkc4dG5D/EngsBgHGrNeDgp3HEloRVno0+Gnl8I0ggUVYcTDACVpGGVVA/wE2nxxDVODI2c55K0JIy6kGqUs+DFGNVIxgqawhACyZQ59XGqH6BIvdpKAJLDTbhGoGrGUtf6KxtLyCBE1e2lzDqLaWMlodKfAlroNOwmuBMCaiqQd0SSIbnnS8CDztoMLEWavWaQOtjkwo4wzZxwQ3E7jbUKDOufQNNyIrFoXJyvEcH7zouc3ho7NLqOCxvi5cc6FCrtDOb9t/K94KLePXhTfS99SRns35YM28vwjRb+9DnGtZrPKd7lqYpzIsX/+Q8giUBqevr925ocSEtrQEXOwdHh3viKu66p3735MNpHvqLGwODBBd9uI1EBmlSyNmF7G63vLokeOI+SWYAtbi1Hnl72D10Wkgmod3T06McDDkOzA/Kaa6NvZMCzSW1RGmRqjmUTWxEJxxGaAeWmwkuuutVvoyHXCcJBqMQ9c8VbelhxhE9oBI6yRDSdJhV1eQSPDstK0SIXSl7BhN3gheiBxgDDtpQbk60NVc+5MOXNmJnALP60SvQAdmqRPRQpiHRY+ODMhUpFAUxXzhbuMv3TRjLnFQFCnBE8T5kWTlEwPWFlTLXeP1tgTgoi1PlXM24fnOJsf0biZjSBejEQF0RgxNl9gQd7rU6xDfojZKABTi8uboRZ+WyTY7ChmLxYWfCWo3V7/i2qRk3Fh1gE4Os1/ktR5WNEFQA19RnR7fEa1LEEGZCwNydX0gW7wtIk/WuC3YsMva2HDgrGZSJ6g7rJ12AioWhiZw2r0Kw4OnAfO12JYEdCslCNi4uzssTHYtZmjqpRGrwF6SQB/s4JR7RvSJgUnZ2q2W3lV0pk3zxF2BArF0xD4E7BlkCR71UL9fHYgAamib7UUZx5KJRb3oWb8fQ80vLRWaNOEEoI99x7sKVQTWsr86sFFDGtKv5RK7J0hMRG0+NhBnuTtpEWb5pxRnjeA7zI7qCTV0N92deYNEUBBIE7L05gKbD5EiFajoBptXaMO+ZM/octVI770NTwle+2JBlpRrZvUguUU706w3eNAcX4Wtq1fFYcHCjr+moiAg4A1UQaqWBciEM9pL+CVxYHVGeqv7foxt0pcarV2NVmf+Bpc1lJKa6cfk+YbQ8JAemxyoomFYw2npWYrr2x1igdsDB9nm7AJaoTUK23GqaC/RLRPiX66MR10DieGmp3r0071WMQWqsOpGg4QTAIsjHR5Hq0ok12rJwHsC0ab0SNaV7ggE9EAK6ox3DQ1+RRa2yfWwidQQuIPKb529lQXTAy6UYxXE9PFzfPp9dXEie454lTCUySNKBNenkHxyRTQlYKHQOdGXNcUqMlU0qOO+Be8Fx4l2eEhfrPZERD1u8DoafJmTgM+5anHmAu0Dl75uWpM4Bh3X7TUpDlpmNvaPjg28+7n388La9fSWwXkw9PcOeeFu9vLy+lJD+Nsd0Qf45dzLiDATmkBdWla3B6bery7sNGxuS7N+vbn97+rK3JRMZcbAluxtLf8yzOUIsJKy0BGSn3QU4yhFhSlCfLUQGg/mVM4PAk5SZurZdzKqxahxh4IhULkypz61CpDrYkVLazKfRiWqTgTbY3iaZ5vHbqONWBkFuqKghQewPFYk/LbE6I0pZUCXkpMPWMnaTrO48oTdNvaUV8e2QB3Mq84i0m4WDwKEcNY49WJDCyRxNao7crcAhJ52BOH+X6HTNMAfRkxD4R6e16GuRRvZFKADAdbvCchYMAhgl8gqZ6dGELCLEcfH0iCQkqUCEe7sHdPpPv35Vx+rKmQO3+ACda4z4RZTkslyDbi4j92cF0IlcE2X7LaW/xnmLKoVrxtNexEwEiXHGJhOaZizQwIQ3NWS3fxTo3VkXCXEQIS4zgeRxACyKl5UEFKHZsPEedbjWZldQg9fejjNupfu3ptndxyB2cxBeSrjrNWNFBDSyIYkGElyj5dEOqJvJgkfpjpEmzX9ciliAPdM3fJxAwqEwF9cPy1e+6rMb1hhH5kZfiSKSNmEZh84H2ACLz1qplq+tjvOgkjMsXf3lWG57rQ6RGVB6bwDorc0279pj9KymxmbcRIStBgW5kS6+CIq+Vb2xZfgBoeejQQJsSItvvlJqjTgKEl+hV5V6DTIqoXKYmVdY6TuTlQtoAc4fbbJHiMi6NGDfw0rDILEKSTR4fsRMILOSe44vaRY/+CKBOGKulheVlAnTQEKlUaVO6jlUatDOUrOVMzLRGn3ofbxTAUggkxszF5g8/0cYMNQEpnbDvAD9nscGrTT00hcRXJDQGDC9KKcGE1jpsE7zjBEDrx15MXm4UU+ATXMgqflTazO3AJkup6smU6+Dw9YlvOu5ALozQOe2BFIAGiL2jNeIsEo4ApyJb4UUJroHUSEYjzCaoDG9l7lcVGhBxxK9a87o7ziDQG0AQ/BUs9Dys8sr4vXkcH8dJ8kvbEG/4kL2e4t49nnRqVsOhXE9b9gS4ObO2i9u3e24Tzytq0dH8vHf2VpY/eo82Zx0b+k5FC5Gg1gp3p8NyESFMK6iZ3a76JCjw6Pvf/Pxb363dXTsqOe6u8q+nolDHyK1POfQ33JcAaopAOt6hFHugbWVs68XcGpJ4XwaGX4vEbRkONuluCBACBFsACtCvwnU/cN97AA9+NrCCb203IKbWMg86m14fiZaEQxEyPAUKeAcq6LmEdlRPlKdmDL6WrpKS5nOUmU42yKO/ocX0F/DrQM92hoRMuUQhiuj0wYIpDu/oJ+vG+lr22oGkje2IHZfSA4WidZLz2fr1jy0F3JrsTRLBkdj0cbL0x3R4BJfANAiJkWo50ZevlDoHBUwU/0UTZY7xUv4Y4/V/QNnp/ev7h6+nl/OObbrhS+ScXEdbrGdjl2ziqVXOz05+vDh43/6j//pd7/59tOf/3z56dena3kmlNacW+dlRZV9R2JwOzkmS/Y9W0LCA1zC6YpOu/fh5L79and5ypbRIgDhsbLZ+yQ35ZF1Aekx+Jv4Ykc6EsZWQE5lX9/f3NzI6Fk8mV10pGBsjqDJFvR4575SYtw1NTYs8Hd1LR9PP1jl8PwTN8SnQbWS31qlJ0jpXFq8W+CPV0aYpKCHN9kRUieZpnyGJQIBFPFUOSpgtnHJHvXHgEwfx0HtHpMCXIJm1lcqac1+xND+HAhITmljhJl0JUiF1s7dV8uh3Q9wwkIt9TTK0SMzAZksyiPJPNvrRbKkIZTJNEl96SBLwqP6RzyJ2bzrkWB0CARtgs5o5pnngwFDSNzNh/7MqwckS8eAEHtyL8KuJ+3j5Zkr5PhXjTjkCreBwsgXPhh2snPZKwolkenEqCoAQjuLKhEcZs3KHCZIELdQMJLcnnqpC6+Kma8EdBVxRN/2szwxokr7B3cV7serYYMptE3ej9l7gOuKJZbNEFj0VW/h7B26vlKXSm4NjtcnbI4+AQpWNiWG2YimG/buKEwk2iqkIYKQI7mVoyKQhXQ9LoomGjFRwgyhCtgRSVivjkdQRnKoXsegaBEHTPiNIVloYTWEBHP6JwdMJJIsi9UblDZrQdHIwVc6rRYtWzdi/AXycLyWphgl1j0mfJNy+enggFPbjImkXv+wuXN0QmorInXyHlzYStMe8YGFybysT+tQqgQKuHYE6Zvi4g39cl1tEqRLEambMVf7lvTd2paX7pLkZvKeHO8cHMj0IkYSo1/c3l6kPBxTeuT017Gjat99t0/0kuZsusuLy250n0zRbqrRjdg/lx6KfnneWf/ug+yXjgCtn0oFKrdaPNVgaAOOEqBelcLIxbnkrZPI7UCyBqxuQmsy3BRhpdAOTblC/CR040A/sEhQN799TaduESxJK+CV57mJ6JSEEMmCUd9rIxY9alhzUuJ1JGLilUJ6qjQJznRgKRFXRBWSiWxe5dpzWo7xbubZS2RKkgvxQGOE12oAixpFX9d6W7DQ+8rmpRZzVeWmj5SO1jf3Dw855W4Y+K4rcxJYMp3rK1vKLerWNluzmZu1tf29TZazZMmUGuoZ79kGr8qvv3761//7n15ub/7mb/7wX//TP/z6px9+/fc/yXo9l8m1tWqpbjBaE2976PAu1STJdVTnUAWyMaDBsDmJzGEnS6cTXKiaDOV4zNIQ6ZTpZnzusGCzI1wZqg5OjuJ/gnNz3f2UhDuM0zoUPs9h90tTD1Y/XD9HR4KVtdDOnu2DPSlUOb6bVzsW8Kll0j/GzwQKa/PHgxh+cDCmZ/JU53n7Ei7kEgMsNQ+hie4Ya5CuRQ+GFWtJ+8mxcDliakqhK8/rE9kUXTB4SQKEh8pBS0WWThFA0iOIIkb40l84iTKnDLRWPrT6N1RauUSYbhICJF4mAPIPAq8FLj3Vn2cDTwBE4YTAiHtrCGZg2kVTCS8Eh3p1k6hJZpquXE96I+jnYZD3xqFFW0lKAAm71pGH/tBRln+d91NS6dR+dIEQFonNtTfcEhZAVLEE3kAfghp2O7MzOBVzihQbN/2ytgdF1dR40AwaliV5kzHliC/cqq1l5EE370DSG63h3hHKWk0GD88nOnWfTZalnplg7gyLZ8tUTMdtRabDEag+Ar8ekZUPhh9IrBmPvFoPTY8z0unur2WmNRFLHBRRR7qCrMGX5Ursy1i5AWpVg8ST9joclhcyLPVNfQLD08EDch4YGmJ01pKZJUO1sM/UBpoaBIQD9cUA7u+LwttxBUwO7nI/XLtZkO/g+aYd4PY35RjYuriUUP+FoHMazI0cQjClUAMYAcbhLbWD+21fu3HDCd17eOtIpugU/qbOL0WWDkHxGTPrjj5+3Dk5vn54/NP/+iO3/fbhAZ8EvxRNAWDbAt999xvKgKxqEe7QNeuUXcMmf105PNy7u77BGDZcd1pMrLvJ5BA4k9YY1TrvyvAnVhiacqFm0CRc/Grk2brQAn8mO2lOv4bWhXTHxd8KOnvRJqSjZUYS6uP7jIKyMGcK6chkDcub2RabvBgOqlrLZ1sR9zBAv+pmtAziRe3hs/RDJNZum/Oki42NFzE8IFocytBmHRCoggzADNYIzD52+UqZZvmHLD9irw26sAw9BJ3e9g7c5vOyf2hEG9e8Py7mtRvgvDeB+npHX1iOHB7vywLISWQ5sLu7i9Al2Lm7KfMGIc6lfuu6uJtrqZZ40v7P/+P/FGX/22+/+Ye/+T37/OLigt48sKi6WXu9f0QuO/slwdjqysttO/jiPvd399kHsy2hLFd+5EDNJBwsqiLyfF25CJiZiEFcMFQJB8gE6oYyaGX2U6j7xycsEAsHJHV5dnnx5YsjG+b69HhfpJHdfnGu4eXZDRbbx0cn2rGitdkFxTCFrePPmC8VZBa8yIi4CU5JOWTg6UhNj8xvx4uBZVLNN2EXxyGizmqZ+JExy1foeC7Im/raGNaP+bT4zl9mkbBeFg2txrSRCIAHDImrk1ag4DNtqrEjAmcvBlLNgFLpmHSMEsBWDfyJrEUaTHcjfubEq6qNENnqJzAagpJTvvcekVho0zud6knzQ2mJ+3obk3csgBoDjxYnThdEjb5WVaujsZ5ro05MmRUQiuwHCN6znrwPTzn+lJoB9DbJNSyY8mwFFkdaFgy8rbZo7Hqu7cpWVY/6RzlhQRM99DgdMMzrOSnRtoPvDUZ5E8zOA7ahRQbVeldF8BjYoR02TDWYG36kEvwhwrQ32KV6Jktr85zcr6z+MfnrqjJoN9wsRNPQZqLaIPAuvALGUAZsA9YDHq4Ti02QLIXCCG80/26DzBhUDNmw7YriHxQMBmotuLXYrzozUaMqpuuRaxAaXZjOcF3Z2ayyAJbLolw0FtLQJbQkDJkAWb/833NoNvp6lYatDAL3n369EErBoc/X5GSwiDq7lB+//fa3v/3elawX55dm/fjgSMz1ytFxDt/jo5ebm/Off7l7ojqe5dNk58kF/Piy7nBVexf6wt5HB6ffffvdf/i7z9c3F/d/ihs2Nk5Ojj99PjOFH/gdPn6AChe2XJ5d2Gv99vTDd999j8SERRovO+B+a9MNICYYSNsuPLm5yQW0MV5g49grezA6MDZxTwJCWN9hXqP39x7DuhNkyMTmKQSR5BVEzU06lAZkBl9UvZADesqHQLSZs9yYbErfoHJ2U2eDo7KFYIZWugmAKzY6NHmdbt0m/VM1yTfihEuN1HJhzgpBTCvZpLf3sNkNDdZUHXrgFrIzyTubX3dWrRPaoK0gm3ULQDvhwNTt8Jn8EqmR57d7ub43ZCt06vj6prQQBsmhj8W6QKELbezB2hbovht+M3E55N6xc7/WgvATvXog33XC4ZtvvvvP//U/fzjYP//02fGRzoJI0Hxzs9MaUoo2Z3YL2rUHgB2NLRdHAheSnm7pEEFGTAMvNyZDSKMn++IMWoFMdXoXZllNDAsh/IwLDqQDihNCNzeZBec3lwJG6P4Sju5sfcMzdbBD/ghpJWbGF2QLoi2HcV/pPL5BSAzuXOpZUTpc5EuyFoRp2xnm8A9o+llk4jBWACIYE4dkzPmsBZPdIzYilsaIaqIR2KL0c0Qjm0TGwnO+823UpLifEb7eJDCS6h7qIQmXJGIt+FVjhFSSObKJ7RVWN1CCMej889A3fT0ANQofx+BmEVU4QzqB6JdiSvldrWkjCBtgduQAmCWr3RaURGm+b5gzVUlgn9hJeia5SNuBKviNP4+3VpvRGkvG9bk+gsB7QJBkySBoqS4JNCZrTDjrmxpWtGbV8z8c9/e9ykDc1+muRtJQKoKEKk37NAGVT5o3VaDEHgxOP+YJz7XLDHxCXUk41nYw1ZrXPKh54EOZAXh5niYkRc0q3tZ5vkBzoyaeoxlSpAae1a3CorJU6H04UIT6jwQBCGqDjAfJgawRvQ1aPDb3ITqkQjf1MoA1WI0AuyDumbnGq5Get00YTPpRL7KDaXO+kM4oPc0h2VCCpCrDv0tujJt7WmgpjpTESd/duQ8LIJ1d5X9oy9TWbsZYzPnp84VM9HcXV3LEb25KH5oZvL19DRgOl5PtzYOPH6wVvSQrFlfILuXK4DRwaCs5g0zERsqtDw3Sykcp2bRcE+tHhxuHB/cd9H90/7gFvTNEtgY4ky7PLxmBH06PodNlJsBBndw7hPXV1bWzvXsyfD7c4TyXzIv6dx3kN998dBDM2bEusxRoMGrQZiJBiBEGvUggsqDq86qY7riNoWet4B3vP2UguNBIxKdBmd7S4wNxNAHRuZKRVBKckYF/RhC23zlb8xDdvWvkUQqcwTAUhZ9cdt/bnB289jSAQKNd17Xbtt3l87ZrUV8iNgvGdwQBbO4H67i7iY5nspLrEzUtLlrCFjHp2B4o1WJxluy/4eO5vpTSWf6PrU3+MJ4kopmXPMobl9/a6ZEcG7fu2rm7Ft7DtMfc3H17Zf4up4L7da6T9Q8np4ff//47RHd1e2NPyEYrleJINrM1fOJyjTLXInUCI9ItU7R0sRxN9/duE2PpU0seYQyQUokEsLhvkmRbfTjjoNmVe9lKzo6JU2m0smuQ42vXCUk7S/izaU+Pj4//5venBwdjslqj3txQYFKodux51w0QEMT6R94gIYqaNipQv9ZJ3q1ZM5nihRHiMP+HUZMGEcEI2R7imLgz72Z0YJmC3JWJF8mzlvKmT3n/Eh31UyPYr3Wfr4TyDpfWfi1p2uRh15g3vI14Ub8mKAgaXaAapZW4nJfNvLzNXrUNzQmQ5r99wZ7FzpX1dhrTR1/PoHU0NRNCA10dVaD++qmFPo0gkkU38tJcuiLtmHPYZ8JzujdGRF33yZk4SFuhlKxp/OFLZAKSiFTDvsmrfh6SwJ5x9GRBQ42GjZjJUjeJaPerjRQGUN307YA7IjRUBna/jFDbuvYxAJaRpKMC2LOR1u8+Mo/CTZzjv6KBUL13eELj/AODLPDmNOOOQwwaqRA10x+BMi+QRbqEhgEmN5D9wPA+Hu9hUAux+bySv9EWKYImGn+A1+egbbilj7qKuIhEzOD4pIhvZVn9EWVDXSoFUdoxZTxT0ltCpsWNBhrdjLOtISCEyFm0AKA5qxfIIAC6tkEBs9NKK0FGaQq+kCiNH3XPTirT1eKek+f0+Pabj9+dX9x8PTv/6dcv+y8vTmaR4LZhj05Wv/nmm++/+83ptx+wrggebmOWwq7bqBz3fHoUvC3jBBYOjUCVb5Knopv3yupwdX39x3/7170PH2CHPLAF5oAxHxRr9/bqFmHxMxzYl8DAQ+0///Cjhwy9FPGrDD/MwaG8DUcBdj8en3z4ePzttx94hZGIvUkrGkYj3UnjCcdMNhaxU6yhx2TKw8o9dQIwfB6phOw25aIxW4K9RhFAKxVvUn1r7kl2jiYxU47slslHKcKGBZrysjeb/QG1Q8MKE0jNGwZyHJ2sbIahdrfVGd+HCRibmWgkVZu1yCFCsGJr6fxqvdLyCP74080veQeTviIfihKyH1BwkHkcYyjKKRBZDKYEyLYIhBhx7mcbk2WFLTy7Sc1CibPnfG3F/Q+G71IXGxIyOggvpU3l/OMECsEbNvgPovK31yOqwAVC33/78Jvvbz99vfr05fbreRvxrhlIC2YuUGkE7p3UpK+vFEY7Cu60KaCKZGntjMTtDvN/+SF9bNhiEEggU8mSLsq5u3m+as7Jb+sAB8HRwAGUWia4/rMUHxtPEtcKFdBzvqUH2YY2j7aQr1lGdSYLjs2ZOSEIqX80YCIGQ/RT7BTPYSEvc+M3RotM/LBMzABWUmYERnoON6GckJwImJcCKg/LmcmFiWsGrgoDzjOhbVOSSFR2msu7U9eTNqmH0xzAIphl71OvqCTwkv5G0Vv/B84pnkla34HRd8vfRI3mvNCbHuuTTvdrKvsd62vRNEybDSXx6FUz/qRkkmDlNajRMX/5a8f+rQzM+gZwWh5r0xv1cKWuYTxTExwNdbALlpyqZjhBnFgMLIuGNtM7d+OLxCPuamNB1U4gRfu+DZ46bSD9Ye/OH/JLRAACUTVQIs4mQrl66Wky0aOgsLrssCl53ZGT2QsqHrlBD0o8YqSV1NMV4EZY/WE2tafFGmYZGpqpyA8IuMTyNDBDqJ5OCdnBRk3HgqlSfrE8xsjAIEkMixBAQmiYX+gxum8AUV5/M9/BrpyG2jIaudNQA5q1PqoFUTIWbL71lLZLx8zwVa6Z6MZvu6PtE4IMkBGrPgkcHx1fxiARSyySsDk4OhKA/+H0VGQ9UXYjWJKz5W2FWW2Jf3RyDC12C1C3ewAYjuiaFOGL5wKWZV7ApnmxZcFnzX3ugNb+h1NVnnZs7/LLSkPt0NetpskUd8zwPdlwMFNfvnx10Z+b37me2apfvpybaoncDg/3m8un5w8fPxBz7iS3h0HWPeL929udvS2G8baTp+jq4V7KeItAtmsmNcd6ngakBEOOrJFqMgnfcz/Akx0OzJYwNK32RSSTgT/3mNvOlUJgEsMxKh0rQP+L/DfSbEAuFOIqG5duKD4kdw0JOabSRDplJeFbK56cDiY2xWwuQ7jhekBKsakzsOxcOqlk1sgmBqyjv9QwrfzGZS/7AoGVOH+KctlVHb7w/O7hPpujZFF5E2yVcha171yyHV4pef/yFdJgpezfWDs63LnnqkIhxrq1fu+GgI48Pz/eXCYkXlZ2yaqjPTTXvcy2rxmuEv67Y3119eT4QDpQ6hrBTKwn/fJq1XX4zfHO73/38jf3goL++X/8z9svZ2GL1KA/xPvfpMLRl7MkJZF7cIKvgJ9svHCTWUtGpmnZBKP5eG4QpTZwmQCBLtaxuYGwy9wnq6sUtIepp91t64lffv7kGBqyzmPUgbmsT1sFdAXmauvp4Y6NQB8zuOKwjHGBxR3X1GZ+jJR4Mgs76ASJ+Y37tASr/kV18VMmS2caMy49VT5JpU0MFrPFw/GaV6LCL+NDXD1k+I6xNTJsabkG1K73qrRk8s+HvugVTrSRfdAlFPryGe/KlYeQ5ssFghGQGRgZLAkXzQZSRZprygfCU8kV8dAT7fYymj6BrXYjUV+UsjQrhQUPNLSJCB03SdzDrrzC6G8a0w9U1Wx6pfn0CiYtMLkWYdLwArzlRF8ndJDydGmQA2YTk+dhhDeR5iFcJgJ16mLrrQXgVMIgX3kzRqb1BsyMoGUaRmA3oH7ivoGm0UVyI2o99RF2ocboLSR5BemPWktx1eagBQGGSSDnsBuk+ZUyMMBRycGThjEiCEkP16XyDTMIiAnUHAWk8w0/01KigynGueZ5AwlaLZm1RlEDTaX6LSBgrjAFcPoIDIUGAPBaELtSr4J/7RI4KG3KaSQW6wGqUaixRJMhWXnPvPEDLyatDo2L/JEiYMctoAUaZCK/vJydX/7l6lxOtu4SvJRHkVkGErhybKS1h4U6ycJrZNv3+vIrNu8ZZbUumLOwDJJax9uHzOudZ6Glcv3fbIs9WS9Jv8QuWwcnp5vHBw4ZP1hjeZ6GdhXwvRNfF18vXEcu0lw8CbQTucZh0Iec+iz354eLs2tTItxHRlIRQBxsQnBsLFAg3X1ChOP1je0b9xvc3Mh9zydg1eHK+NR7JMcRBQXGBKX4pPha0Hpj2jlu0EE3OIofnUO5Jq/uSYLWiIKJKAJEyoXUtYuRdwC2J6wfwYmoGiaaSXvOIvaE8KJYRbISkQVnRKlDLBmsJaHQsQPSv1YswXb3GExsWO4SxnSWg8zsJs/KyfPH7jMu9BhZwkWQIBx4fbSRK1aHUU/oWzXx4xwd7J+dn11fXafkXBR51/m13R3yZ5VP5utnG7kvNAf7+vXNWes1AULGRXk+rHV2WuR/guCFJQ8dTxxKtl5dyvzpl080/sej49ebp1/+9GeoOzg63mPl2FoAVdpnzd2fRnzrSLJTBiXr6UhyTGE07XjIR2R8ZjZ3//7RkbFAGQeQcyFldb5/KNVt0tIBwX0b9Bd6v1beoTzefiFMFIBj4U4CgnR9z22Pbql2sLn1evMxJhAVwMTM3YnK05qIv3k3P8nheHB+JX9xtLmPyM300EYM1ltz22kN86ROsiKe0mTOV/VroXIJG+rUoyliGdMqsFBj3zW3iKG686MpYGovqhh/Bmmk5HBnrIo3LQeoLgsm7U43vkzF09C+16Ayni8te4MOvXyVcBjrNMjfnwUmcMcOiRaJKXABQBdDvAZKEOAOGMrLn3RFqIOiKqeHpnaGewIM8Q1g+vJFgAtkps1bsyR3Q0dgJtGblTjN43CbWxZisogroD+oWWAN/AQuZOgwB+EMHuLMswZ7w1rTZqhTiWHubc89qimFQBPExohyetVrNADO1g7a9i88ZdH3Xa0NJBDP/KmzaaWvNBvQuEH5KjVgNY2qjwGjfHD7ivJs4QIcT6Iz8Q6EjpUAZhuybKuimVV8YAZWRslMBhhqZbSheU5Aj2kwmjQgp3+Dbc5KAqxMnfnUmIxXEUJkJhjM0EHCCK3wPnPABCwDDjvjh8ll59UuQDNyd3N7/uXrs8Cf87PPv/7s3j2T+eXz1y9fv+h+m3BiiElKnHmONF20JZnEDWPcRNKP5K4YjLvHe4GY5tVJgS2RIZwkthhfjnEoE94Sgs/DhbQCivY/Ht4+vrmKwGkAzpjz8+tPX85urm+4cgWi7O/s7DuQajNwY+1a4NHdTTeOc0DvkBiH1gVW/7Ag1MfWwOrK4cnx4W+///b0kAurLewhN8N9u77q/hBjh588a8x8OZOLSrAwfXXRuCCZpolIf3oQUsL6unXBy5MzCbZMKcui/Il04ppDzjt8AnmF9wgnoDyWG9XLzVQaV3imBgEq7i0yiX4iDhyHUWyK8PGgDCSULz6GjgrJKmShcpdf8uMTmOPL1gKEoQ8gIRs0JP/mzU2ZRHcT/2Qz8Z5WIzAsA5jh5ecQqmvr2Mnevncq415d16i1wljftCFLCexvt4vjR0zR2ZdL/plublXTvVr88qq7TtcC5fHl119+5v1AZxicjwUZfT2/uj67enB16M+fjrZ2+WTsEYktfbQqfBQH6CKKZ4fF4Pzm9prnH/LY0jAXl+MYUbM0sYXT3taeE9snB5olgKNDbr3Vt+MSwRauZcqYo2k8K5utDbtHT4xUOCsvkjCvjCEtCqU6ODzZ3dmz1Q3XhBrmhDQVYW9cXgxta/+Rgq35bDvjC7NgyEg1Bh92IeAxSQoBj7VmwpPZxwBOCsRnozsKsKlMrsKejcCbAcbdI3+mnYXPK1vlBMUILt155GP8HXUsz4mYkZ+EZ1IlNaY18kb7Gp+uECBFko+SAZqtmBBoAMsQCEhGgwbVsJgcsz4IA6nRc5yoBjEJg87P5UGNV+Ai+QMkZAqQac/gkzU+DYwejkStKfDQTbQgELH7osDaAqynFGlj8KOdfqNwdAwqu0zJGshtUg3PPCZbvSAfRnuRoSRpTjXj9kuDVhgANFiGFcz1JyUWfMk/dJvA90qXFAHF4Vd2T34meWOKdVmw4NuW9XU4WEt7NUKtjA4PjctXyqRu9FFpzxva2AqJl8pzVSkyWmopADBjNYeBBChzTFhO+yqmM0xBcxk6BzHhCVLMITNWcWOflgdv0UyN6HycX6FnoaGBKr0xelgLU0xvNToQRwFpMi0MTdAA6XCYbKYHb1qzrlMllOtVoM7j09mXr9fnr7fX5+7X5mlnt1mMnpIdhafJHWZgXZ/79GAzkGxfvbq6ZRUKQ2wmNjavL85NBKv/RPplBSgQNiY/956zxSQ3l06HIW7u78yH2Rpp+Hpz6VgSg7uD+Gt2H44Ojw/3jwV47+8KHJWHGEnNHY7mqBDGrndZ3bozIZsv9oXZ+yLBJXwmAeHZmG1sZsRz4jw83DhQQPP4f/fgHNnOy3YC0uaeU3UjiLnEmwIXq08WaAK8uQtJMGYe4bwlNszSppCeX4D5jjQiMmJM6HqETQaGcBiCCUvYVyokCTMoz7Fp1UnGMYY4I2bThfh1l54JaM6wvP3Jjt1JTt1+qVNI4hFf5KbAQebaPihCYJ8I5bdLf3X7YMWTXsqr2ZQCARPY2wABwUAJHR2e2Nw7d4MKZnWPW7v/zg2+bR53Gta6BrSdCHmlYB5EiTIHsuLsAThZdXAMslzqdzdPn92vy3bf/f3vf/+b33x/c3H153/64+P67W9+/zsHuqyFLh+vn29vYZ/gL0o1w8LPStdPwnI0xqp7BpLtX6uBXDaM9pPjTbs1IqOK2C+YxOjgJO6xThXNZL4pAqh8IPY7Cg63qkr6IIQNsdsaNvROf+3vwYAN8InnapWDz0xL284jlCJyp43ccsO11sUYMeRw4vRFIsYKYdrTfrcm2GA1qI3BkAzZYkJJF8dXYhcPATrsuUgJbeIPhYld1DG7mzHg8ho+H/GYuJtViiY0nAFoYqut2/ZI9KlgdkEyvlKRrGfq9ZoGB1plQdiuUpveXjUzpaBAOTKlCpEhQqxi6pk6QyIV1f6ChcREUCS7NBS1B5YuPRwJUisLpyxyHGKTxyGh3wm8lRQA7eLDAqQeAlO/fQ07xH0I0iArCjSUNGbKUa32tKFvQg0QIyZnQoalB5bpZBlfLJMMHbhnGkzGjHO4zM7YplgCwGmi7LEzvenN6ei9IfCHLADXt28Dw2fMMqo/kAbbHutvGZS/87EpNHewRG8O/DW2/G9GPU+Njb85nZRo0EGCdoovk7KgZyqGvCZfE4MMv+YdyBZNnXUPJIUG4zy6+H+cV9ReAkn3Waja8baRZvaKU05GNEAQ5DSuMDlTuHNjVfLt4f7h6vJSdKCgQwWxv0AaJ6ms3U9P9rlked0xYdekuFr20ckAdQgx2Z+cwD2Hc0mE3BpjTcAdsfJM1Dv4WuiN+HGJAlie1AmDzJZdwSNGZHeOFN9zrczT4/klBH3zzYkVRvbvw4u76R1Pery2DXlNB3AGcWgQ9OA0kIcbYT9ieFwMwvVt/2+V6wM2SFnOh2fpLIs/F6jiRuEL+8xuiPn8+ezs7JwD3W7i7d3O8dEBhSNbDqS4QAYZxj14JkvC0jN3MZ9/tETd5bvnsyhcnxXM75QNv77rRps9W6UHu8xVGTXYx+jZggCQLTdZ9CQ2CyPubivGHzPntwYVbilUGLiYO5omzifO3MAjjQ0sCcon6ZQnQ20YUDY5soTm3ttaT3FSbDZTzCO6PDjsrhiupA7BHXdpG9qhAO1It9l7eMIHzxHjfk3HM7qwkth47i4BipOt/yYKy5JiZ5frqfVJ2VV3j0+PPn8+txVvo1hsKPTd3VzbfbXBTXU7YOEuIGFe0PZ4fvMIXhlFSIN8ITnQkBbXIjBCpUml82h+ccS5+x2659zhC3I9ERq1BxN6DBCcNpL5ecwUHJLZu84TcBl1EuVZpBoOtu3C8O8c2/UdS+C4bLVymGxI/EABMCxY5vZYMT2iwlDEznAHUmc0x6vkyzsvx7DpiSQdjUB2YdoMtZS4p5nLJud/+2Fmo71KSY6mrdlV2ZP4L7Ef3/mJ+aiThMCIF9TqU9XafKuAGRvxUcHkTeUxdtQyoqxe/F9aSzPVUiI1czvBVAMWorxn9VuHM0TteNVqBnvQKF0oBFlbc0GnGXUT9I26hjxOPvlNQhGA8yC8jTqkzTOdp5PsSOB0s2EVlIdgoFn/QtkMctZbKhvzdDgF/aJe+tUwZGwkxxrqoj2m35kpvxYTzPf1CMoBrJIzkcv4ZqlmiIMjj0DRBh3VgpQSzFmaM3MhTkH9oyeNOJQaumbEVa/h/lks+D1NGZWnFWnOwBzQQGxGGqJiPuYtbAoZVeymmZzqBHb72BbcOTwGxPrB7qPaliEbOnNsvGzRZLUhK+Q2B3VGNtHtAdhniNCinomioPAwhW+OY7qg1aAvonulRy2pxgeAgpnvaiyIRCzTx7Sqn4aG/dxre/ewKxWEsB8sv77DSF1hQePE2UGzJbH6sDnYtYpMzN09+YLteXq4h9/IGdOrG5n4BY3M7Rzr+1uOdnUBF5IHRjEbBDRTmqDa3LThItMc4emk51zc9OHg4Aj2ugX49fnmiovhkqj69rtvXFhggIrKvuAVDdmalvSxrrUkGhWqzYjd6dsH19yQR/f319dcR5eWFte31z/88Mv513Mi79vvvyNI4ZTccZbZYqJzqk8Pjq6iZPLPFPADNbtIoekQmL9tJjJsReWLXnE5gYT1g2aTBX10RoRq05Hk4xa7e0BJ5orjmO6k/kwOMqJKtMZ+kPSNILLLaXs2a5mfXWBk2Ruk0CNF2fpdsY1DRzoVMpFdb5/g8fmitHgpNpnOEJctb8ry8Prwg1PQhwcO+Umdxwq2joIklGIoVmK7+458vazd3BKqKAQejEYAkzEqwA2TGH553XmTc7vk0y+ikR6cZnaDMA2bgPnXP/7x06+fH+y9b25amtmRPT05+fznH2/OzpwoYR5z0Tjph2gdfUCfSqKrofhCXccObx/RHkOL8rHNMx1Y9OKT9kTv2M22irLV/2i9lkLd3Do+OUKOKK9VWvf/zBYVRfzYWWUih5HScY/dXVA7kgKVxIA5W0SquaG9s2ZbzD2/PdgEyaeHQX3Fcm72MMbMCs7CL8lWk8+JFM+rOQyeuDCamBQTIQtOhOFJDfk0XzexIydGvKq7CD+VpiJzOfbsafJEpbgwjYlngZBNEdRRUQLET98nt6YrxXxOOpNguTNh1Oe4nskc7+fDnAVT9eu/wm12VbOBjArxXYMPLEXmKwWU132/lESFhmnuNK26J4AIGjJtMMCFkx8UiLVSpVzMBhN9j73pb69puV70My00FE3EXaQWfMzg8O0MTP9Jfw0qNVJuhleNCoKosQTJQD7FQltjSkH9VdXbGYiaJ++lFiACgmab4R2dghCyBQBLhFbZi3yaR57W30xHU9Ok1OHMml8+kJn+DAwNDUxZcCZYxar6l9r0akQVRHwho3nSWs8B1J8mqfrVqsFlYxlZqGmkNaK4X+/CQJmeVNq3+bsiooDp0QJvzWbsj35SOlqxDQ0TlEVk0WZvSMtUioIgwQkwcrWALdHasdGrxGEyZpRqnhLbtlK3H7h3c1XIndzRLpEk3kCrhSPZmw/22bPFlQJPHkqHg93f5bipkJESSYbddu8e7+2G8NgmCmcD086tW2cZ0sfHH3b3Dkm9FMLjkxzuhNPezsbe/uGHj0c06fXtHdztsjz3XUdVuscPMhTv8YSnEbrKeFuKyiuzWgawlYfz2/vzi+sWADdXtjF++fWzo60scjEAhB/i2HP5ItfHlnibdl1hplMG0TT6L+Fovh6kP3plosgl11TfIsBk+95phwfOrI2DZ9myBdGbXNICCltD8BDSedOIxIEte+yvOuTFes0fjslX7l4e1rjjLXTgW04bAnS8FjCQXl3dIIiRtbki7Mg1R6RErp5f3f3y65c//+nPUgNhd962P/zht2L37cCIBaY9Lri87p8Onl6pXuY8c4jLbMvWxyo32sr6B9JyryAbarboTTegERxiQOP1rPSN7cvLZ0cIeLGsHuygX11cevw3f/ht43m253/2m29O3RScMnRyhCH++evL/ZODW/spYcrU/q1crestxhhljhSgZZI1PndbWShmKhSdxY5I1qzauabHSWumY/pcsCy42zxfsYGB5ZyEwNLgxUoIgyNtb3ePQ84C7OjEOeEd6yEbAEV9TQgh2kboYRt/WDpgl4lv2F6daQJMvDWL8LgnXnjnNuBhxySbd93PgcP4oLQc1F4ZVQnbnCXArm7s68vkxDSpwQRFXA6r8x2WThRwK3U7Q5RldTnyIV7HpCmBhGO1kiVjRLejjqYUIC0rD4NBUOoRB9NKgv30JkaLd45RQpoZJCAI7lSF38PnHWIYdm9QetMI9CiGvOt74FhqAXpe8GFMZm35NnQG3HStXw1n3bMsl14aosGJQKugNhu+1uu1uj0JH8okEpHBfGIVteXbRsIU8jcNMD01BNi0XEwUQly10o0YTw+VB0Pt+tRH3/dMj/MrNcbaIQkRdWcJyS/PWhxk6dO3JC+LY7quzjiFtVS/qeVmcoE4nC19DLbqMZU4dRKrg4owPXY4Y5gjO9zi3IavfGstiE60MAPUqfW+IyYA5KWvBj9qst6Wr5ueuktMex8QFRzDrXeRkXpRd02E73eERxzZCL1mJn0xRL1MIsIASSQzBDpkohwW4zZ5e3mQWZ+I29/ZPCqskuwpDop44FN72nNZtttC+BY2u6s9Dwk1YVwCBO0S0wTOAeCXV4Y/gUDsGyyPfOy0KdXXHsuObc4CRbaHzhh8/ODijt3dQ2Jb0M7Z1xsCibjaPBX5fUwSJj3XxE1uH50cffvNx/0Ded55+7cO9vdm9mC3OXVeVtc7TwcyB3z9+vXsWvzJ589fzn748Sd5bNpUZBRISfLyen1zaBf697/93mFhbUOG7Q2WL6p2fQwRM8Kn6H5VilgkAsq/31TMplkU4l3WdKlh+c34YrZxNPcXB4t5AolvYSVd/rZq4cPeTDE4brFSamIT4JHe9w52zQmnB6tcvfjmwUFrTPFcCP+Efl5f3W9bYD2+/fr5/MefHZQ++3Jx1VqKm+v2MUfU8Yed/RvMIxcyRxZ6YAtm8rdFgAUcPwYJ9SnvEu85UfLMySTRm5ug7fxfUwaWGLQiUCy5EbhFEiHzeN9c2PJ5fvyHv/tbiQIFhtmF/fzzTyI95dz57vuPMgD+z59/vr4+s31hcSQclQJEkZDVSby9bXTbConY29mSeXztUezrnDJyH+gzriRJfbe5d3TIjZMd9SYFSO47M4b9i8XKOLFfZXfA3o/MFQl2y8Bl5YeiVEFw9GgCi5xQvLtJ4tMYiezm+jcrZAQerEhJVX3lP9U+HDi83efsKk8SQ1lI1YM6jIIe4jC8SI21S59SY5poXHnF8RpRawINmZBVDb2poikypMqYrqLD73F2Um1hWtD65wu1jULRlEjNIr9hYx+WbuqqDEVJ3QBDiqtOzyQfa5CoASEd2u6x2y/I/laWwWd60UOjqfmEGA9XkSNLw97o3kPwJkf8KQi6nc5318VAp735egAKxnDckBOsYdA/y6j68JUvpsVA66sprm/vtUZ2DKIqo6T3QV+V9IvpD3fNI1jnudFCa76j1lOJVbCG0GSq+U/Kt9NmF26UjLqcgHK54P3kLlx4Sw1Mu4NaKMtwE1+gpwXcwXuD/StcfRHPJpD9MkfLOImcxqH//GjGZNytYHq3SObCgRE2izJvZyGhqMpXzZVumwNNp3UKnJlexlgwjhwAEZui3PYhTKu0vTnHG5AyUPnVNwti/V7Uu5YNdliRAKizUANslDjTqavocSR1/uBnzvoDnENKyZpZiJcdWv+3WKDG00YTVlVfNLqv8fX62t7J6r7GEmR3Qs6FaVrf5/onBw2Gf4LgRM6ox7liMoCmSDE3Hk6GJzkcv/140j0AAlY2NjhDboghZrXQl7aawws6gBjhjXv7R6cfv/nt734rRAjSGmYy1AEANmwxGsXjl6KL6eziE16Pw63do/vn1c+Ci86utSO0sqAjh0eB+/wmtFyckZB9m9VEPahIwY3nMtFreUQwDIkDIXdk4uTYcQ764ehYnOlOGmKVQJOX7oDd6iO5by7pADPGHNsouRnXyBAqz57j13ZEHt0qk/5W3thwJlWTtqFgbEJbuLDmOFwE6kiIJA3c84s+x4p/eeD6uXv+y0+//uJWlKvr89sHZ3g7SLC2dn73/MvX662dg93doz234jBxLOi2d6Vq3drZE4JzeXO/n4oEcOmv+Wrkmihr/tb2xfm53ywWuv/ma+snuRi49xwDFHD6eH1nF4FGtQ5AUN+eHu84oPvw+OWXHy5Ehf3+b7Uv+dLvf/ebH14fb87O869w7ka05fkhp8XbELU2WEyYBFB4TDAAax4SHIWGu130a19gf4+/lAVgy4yAP1xx/m/fSgaH4HF6ZGdzBwfhHwp0b49d31qkrNM7dPBb2zx5n2LkpJuVLtJBtrDq7jM0Rxsnhpg4lq0L78Y4vRvmSfyaE8/e2cpXsb+fhGLaAtMm4jWmKauouztLUmbPUrHecFysmBxJWEx5j5p9QqnvkDMN0TVEKQk/QTZqJQS162AbKxGM85T2lYd6BzZVRGoEAGeLnO0b23aE2lxbWRHggMN9g0G1A2SgD13pIomnDNEBxBFRPngQPD33gcD1W6MVijuXj/NtljekeJE8KRUe9PCxDBWQbd0bqrkGQwumyoK79hcUaEfftRZGdBKmMlwXWQkYz3vBgN+thjpLxBxbJLZhk44DcDAHj16ZCuREsr76IW5eTWdlGoiRhC9CTpxDorSNZV/PdOrJUCsxw+4kvQoUxMCVcIkZ5jWYqeFe1fsrrTSi8JOOzVDsn4pLOROmjQX7ie2upEgIt0oeZT8Fq9NCskYbRW9m4jP5AznVO2AjixmVCrPzY4ERItQywmoBJph1SS3pob6tl2GPOE+HwrT/KC+kGIk3RuML02kPwwPGfKzG4WMtJxE8Y487mdhaQ2qsZEtNa4B1blK3C2622TpASC4mPJ/YuL2mzw3Sf3DLYU/O65kPmDrWsYESgvy3iIVzyF6Dfrgn7DmgHEHjDzc38nqaeWBzGGkTd0guKQXQyelH8ebE1tBTdhNkGb+VBe+QSaWY7vg+np+dsYU3nqPD69ud/eM1smN13bnRdoVkPXpdOb+8xoTWExYShxKIkT3yROLkCdgfJR7iiWMgCC8vLmVDy4RHU5iKJBBWN3cPsz1Rjg9saGIn53kZCxxp1py0Sds0IMmuO1TRPImrwc0vrYQg325B8zOHQkE+c+QO9YwUE2RKFc6f8vr6+ezyl7PrX79enN/dy8XhvnN+8Xbktw/cq9vlkP3eZFVjSqdN/ADp/tX9LYhv/f75hphdv+FOeSXx7RN7SNRGD2sHNpPtv0rmzb+HHNAC75DtbLo2qhAVur8zzqL1l+2tn79+5rE2e8o8b64fHe3v/dd/2Nvb+PMf/4WSZEgR/lYRZuehtUYyLEOuCNw04tXd7YswVAu6l10Hz7d59E6OJKCiYpHLk+xRZtCN0atr/Ii2nfP8vL1aR6AZWyoTM+g0gJvs2uFEYGx/ghXGCCMzaZazBfXLDIVQvJlFk/wxe0VDxVYJkbghfo4FkvZJhiTg8AZ6JKuFhmW3qawlAtDc2zFa21mXQiqbrzpZdZgUPsGs0dpaWlksWRaPuSTMxqAL1NxHtFVrFJRAWtZQUkU9/nycm2lLcWrWujUQK9BfL/hRloTdLnNq8qwzlRgtuPNbpnJ7BV/igzY2dIbU2BnJoLTYqBkNJTxn8MWPJGJU0EuwY0TGVxImLBIns3BIG0wxHbZgrVcEIRyZoRtCp5V3eembaREYNRke55UV7EHagpjDX5EIqZWNirfaWm89MYKSZIJd3ehrMJFG0h7rT1thb7ZtNEcLwc5fuwjTXr4Px9N1srBbh3wRElXxrfmjHTiSAy/Ga7J7RSH+VU6b8zwpPxPV9/me8VP94WKeppkiK2e5DCE9kDEfu7QvTIMpWYjEpGK7cFJ0R8SqRF2kaprjJq3US72v51A3BVogW927pTqFnyoJzEB7J7wFTtPVwg3WrMlM3V89XSpnIZNMHVX1BjzFsg5Xzd5fFhz6iJMk02R6A1C+Q2mQszWk581tDJuycVnto1Qudu4UgXnY3s7i6tslcWZodgJRMi4CLV+vlKYMT3GMZk2wClnEmX98fHBi49LZJNTpSm93T1oodN9wvShpmDLL5yI6lQfuW2iWBN4WJhbm4nDI6OaK3JDGJmdyh5bL/tQgzbNhO0579PHb73//t9e3T9d0w+urDUMjY8l/+nK5sfkTseTkgEAV6StTuFyOb2tEZ+gbIWzdwWFhfTDBjU+OGsGZLspv5H6Ck+8IWYbrxLsOSLZIylpT/D3MUQA2NNjbm88i9B9VpwsdYmK5oxlzlq9/4tzhUH0lSYlW2KZesOL9C6gtM86/Xv77n368enq9dBzgwS6EXGl7p3sH518vSgax4QjxFv67fXr98w+fnh7vwI4ibJ/wldnBlqnJobqWX6TJyivr3tY7BWy7vjXf6xPliqoRg0Ap53jR31MhqzZZu6EFt4kLFWn7dC899Hqnwre3//C731meGMvh6cnHkw/S9ds/+enHv8jPaglG54jMhCiTjwUcFpezm255vryJ0YVEdbkxYBwf2rQ3I5/ErbvGSgJkSbPx5E6YHecBVpwsS0KaYS6X1+e7mytLzPsd2sjtj+vHr7xQ2wiMO0upGDDSo2JjAGQQx9XdhCAkBTO24+8sh/z8CmFgDDEyIlWVFqmE2tlSfhJdcWVFFPDWxFkdYRqcajel4iatbHEx5Hifhr2JF423Jn+3bltHWBDEj2kpIk15lZOMJoZisEOVLaIjaRV0RIDQT7boxIPRT+O6GJnAqih2UtNJjRJwjIeqYQdEjQ7IPk43izWtjRa7AzDxnh4cCeIdGHv5kzjJE6RZ1Gl/H+NEKN0lNWpD8xN7gtNHLMGrGhDH75bOUafFyzIqclYrfV9fA7DafTbMBGJDqMOezPPkWtA3UxAEBc2huooomq8l2390hQozf7Ws2PS1TLPfif1QrBJyJvHzEVUSeEHSK79Rg4o4FOgHVXg/0xxk76JZT+FnXlX2RTDPW+TuuYK0ZHQSTIbVxoO+lpFqEGkCwRsLd2K1qZuXzhZYlTV0ELz/nq7rp1VjpWdqBg79YiPfecVnQxwDqzI6pT9SM4HY2i0abHVJLhRapxvfcOn43TfhNTpjJtPlj9D7uHm0J1bSgazt54dbMkUnoQ0qRVox0eknyJ0NTBGiTi4BBj4xTRvA5XowjyS4MTFjHQl9dAeYMdQO9SJL5ZalBguQfHGj0zbo7Gxxndznf753B6SJkQ9UttDf/P63ghUL8G7ehDM+XN7cnn2Vmki4TxsMssJ9+vXT+dmFVXmeqi4+IyJtP1u3bLga/G//YUUE5OcvXzl5cJgFDJHxw0+/JKnf/o4vBG7Fu5OH6FzuGLqQVCGMOSIgTTpSq2yTnVDMlicmeDwdWti6f1q5vLw5+Y5FvCWX8rhzol4zk6mVoo++nYVAt8PykUH+opUUA1MXTiwaOJd0jSy46FGyk9eaB1zZK17Xvp5ff724PrsVhOvuMwkP7IhGj+Lk9w627f0qwOz75ZfPNxfnt7dX4EV+7lV2cYLwXPn0v//++9/85ptWWmy1Kzk+Hr2nA7oGDnmsSrJ2whRitpyviJy6khkM93CamRSLW92hoUnl9/of/+7v2NQF0B5sXz7cXV5e8N+JQHr+/W8YPw6FEG37h5YOqzyBB+S00xM7u0x+ytWevogrNnoH8ZwSoMXv7z5/PUdQhRHnRzAFkatb2aJqxsDdFYJAeCPnb/Ql8yjHTkeY3fZ2uAvHpBo0KoPl30VJfBgjDF9753287IXah5NGMuD3LDPTlaiAh6QA5sYdLOi0gwckGMLWcKXmvcKx1tSqNR/JRwCM4Kz5pLCXL9/dUWPYaiIWSKlZ0CxiRNuAUMFD3SKBERo1ogMNwBzOEqKCoOgI1YACZBaSwMJ4CjKHAQkMbUGhl8YIPTBOM8yb0Q0AStrUSLy5dDLkqk2MWempAmHTdpScfBP2wFRkVKYjq+hrr0GERq08y/o8RvQy6sTKTEYNatIviCSkCbdyo496G1lloCNO67qCBIT2vZ/AFcI/ZALbZKYDlsbABeljMGdDMcv5GsyWguDWRuuCd9kd7So7U4cvatpUBv40bMxA90/LHmR8g4KqSHkYrafA6n8jb6Z6Bex8NYCEgkF9VMaunHEOzOWQCvVqDMKrPefUIqgaHIs8MtVCNKPWMsQa5MgZGmiigtyjQKmENt8/B5iht2yqwUp6kIEPFn3R3iG0nvwrV6WyQTyYiKoQBFgiQBabbAdSkr1dvdw93t6cHuyzA531QgRYjsyiePwQPdngTGt7nk7b2tS9f7AJ7CL222dXcPPhE9nu+gUP2apZITNRsH7ZhuQyXmd3T1gnaz3/ilPFivnLNd79HlLUHEkVKgeoQHuCnTH2enl1++kzYXjtDssvZ+e//Prp0+cv/otSFzPqsFeHDKwnCNOd9gpLJ+GA2NaWnjV4dX3LocBtTcrcXl/96Ydf7It+991v3VtlwiFEugQhJ5QBGWsRSiMCi88KfixUrVFm7HGhU1GtebdEEQmKZbLR7misftdf95CjfJzlc2A9lVQ1zZ8ridomcXj7uVY23eO2JksyR3nj7yzC5hMFsMk6fru6p0+Efb4xe786KPf8atVy+PEjIO7dx/AEqjxURzwtj6/nZ5/+7d/JUrc+3lGAFkMY1VLGyszSzYb9f/jbP/z93//Nd998sOkiw5Jlk31y4VebG7+DatFUiMQ6gcc/Dn9xv+YV8YHKpbZ4LgzY3Q07zIG9AChFKOwVI3DcVgHP3SZv0eH2t9+eismEB7s7MRR52n4jZKwJ37EkIrA4wOSGa3fdQi33rPR/t/vHB9JL8MjRAS3jxIrN4U13yHPLcXuMNHPMWBgr6n1yvdf+pr2b9v1RPV0bGScqhilHMMU+ZGTcxxaxO7FIF+zB3Bsuignit+T8iOZhqTgOf+FITzEMUqGKzNHIm9m2LHVuzJJMiSHj7eSGei0k483+++XfsKEOF6WCrHFhBjUy0F/VM4x6izYwqkeBMzIeD6dItFQDA29VRii2ReqZceWnnbQNGu+VkAKGNtszSJYBFsV5P41gYEUCsE5qvEpx3NJ9wAdYLcybrE3yfSQzfIyrHHo8USMMChgPz8bFZ5TrKbhrPqwvMmkkjL6mE+EkGfCgnPoew5Ix11ZAqBwegBwYmgtan0PifFt5JQy0xVUCLyFuOJU2gw3Bu/fqGiAIK+t/f0aGe1u/vXoMnDBrqCnVuqqvnkxjNdVU1v3AmHGxTFMScOYShyueU7j5yME1QPs6NOay1PF0NZ8tbnxMlxQzoahPEdO8gqF/gQ0yE7A8N5MBFzGm0ZqnaK5m/SCdGXxlFQihlW0ivCN+9FERFMG5mczzvEUAzInWYWtwkojLlFX/8eb6rBwQXw4L41+7ubvdeX7bO2hNmHVWOpHOFvGEIL/zs0uNshZFaBuAId3Kxiwdf/03RHYJyz0ZPpTU6Z6SZjoPgBHWXRQIHg7gx9srIkz1jxI7cNKfHEsIcXPpKgJQPlze3n769OXXr2c39/cWAEz4f/mXf/vhp5++fP1qGBFbo+3lvpUbl0qurv7062ezcLDvVBn+zMfI33BwtH/64YO5vTiT3vTyy9nFrpwyQqZfZGEjsjlpHwUmmldRpDeU39qbm49xOPouSUPozFTkDt7YP9w7/lBiZ5kE5UnKY0Dnto+BevwYvJE2PQiLKBlaRCR4OHDe8qPQE0NtTQbT2OavFcLXr5ecVhYB9IgEGXZh9UJD8AAXdl8GC/7OFy64G2E8zvqSqs9uguR/sUrY7kwsV9WdJe/z69erHz5//j/+r//P9x8//D/+23/8b//lP/32u4/irNSzRyua9uXETWok8B41bSkgpWu3B8jqII8/NJZYYreQ2y4NcmzCyYa1YibYW459FBTMVX3PcuVUoutTeDhhDoejJ5xwfnVjPlwYDxuy7XGAOasx/u+WpI7jOQ5YoJUjzk+lnWMGEOrkolPo7pv0yzpXuj/HSSw+mA57h3uch+KBKTtWCIcMBT8BltjEnrxmhyXH6gImTo3Log60OB+yeZI4Wk5IJe6HgJQxWVHSWEnkCx8dwm4vIJ/kcFR+Y5zIuoPtJMT7XA8vqtuO1zT/LnW0VosxaRa6SlhqOQakwc6RsO0561hrKEf4hcoRyXq5jyx+CBUtREUZ4EkDOAdC5/bGqZuR9y4DUoeL1E0kLCFY8Xz/1I30MBiCI8CTcZ4lNlPHoO0boLZyKmgcOTlSFy7bD5hhZDq3kK+1tDxV5nvlA7ceEpQm2khrLdQuw59PScYSSIxgTehVavCSmNAEGaZgT/wsgg1sM0G+qTHLjNrGYIHaWBqbR81aovSvb9OTPQuIysRkA4w5GK0eDjzroeHxQo8c1XPay/8wUbN6mka8TyYnS8PmfIWoeg0R1EXorLcemxGDSKUYCPT2Uh0UpihRr6WlTPiqm6EXiBhS1UY9MS0HXTPEOo7YwoGqJHeATIeeh7IFAmXeISypX1fR6gGLwkECDoX4j2kipkAQLSYF4+vNi3Ot+9ucP7Me3yAiP8Ho3vGxSWlTUWQeqllZ4bIQoE0BcNaTEtie89e1XQQErw7ZLuhGdP1ClcaW95KITVawpOVqbJ2Fyjj7CU8axu6pYm2xUQDrbNKdLvw4OAI3C5muk5rux595C85++vT53/7857/8+PNPv1oMnLlhhEimSGChpaBXzBdFhIIktWQ41iJt81gNsbXtB3z4uHH64RvIcMD5T3/50Xw5TiXzsWLxtayfrrh/eJJSopTIGyv724cqO6Ck2e3t/XaTi+WQ2tMt5PtM+0h3bALefFazQGP9QTtqhm4+Wt+2WdKOM8Of4Ws3mgnQ5VOMYvNpNk2mxcHDi/xKDxfXdy7wIgkl1L+2Nfq25jYcH0UwgZaaMQ3kxq+/fs2zLyxka+vw5DAvVlFGdiluyZnf/uEP3378KNPGv//rv3/+8uvdgzjSr3D33/7L3//nf/g7VymwkW28313dvP3mN9+enhI8Vvmu4aQJbm+uOWCQbrEftuMfBRryCyIQ+eSetkRqyV7CG+74lXtgXEVvmI1gBLn7nq0ZtnatZsCZIqQk5AcUImzizQoa93p+ltHv4GD74eb+y9XltsOHiSekbQ9AZC2rM+cmQzbC2V5/U/LhDc5NljxRmIMTD2QxQ2cI3ok+aRSHxZWa6wMQvTBI/BtjRyUxWLgsUCGW88xDoMZS1U6ZL/UMoMb/SlSZ1PEgWD1Pi4CSD7PSsZpXR29KJUTUDKXHNgwslXAvMahokipIhk7DE0GvQKSbhISHaDG4jWBQaCxJY1Cym6wnn+dWuspm3iheNqrabCDaH8GFLBty2SmCq05bgib9F3FpGPM8vKnzLlkai2rUAEiG6ZuyYF5WDIWxtV+mQQ3U4xwqRAJ59qu8jC2s0hfQ2Q53g9EqDa2jWXTo+33SjRWss4AI9sV+8q4eA6w5wU65EWofnERoUwQKjQaBb2qlaVE8PMwXo+SBUaUmVs6N0B5lNJU1njU9pBnUrQYCJhkNS42l373prYpBMl94pm5EMx3Db5vA7M3agwiD80XWhB8t1j8w6xSc+WZ8b9rTnd4uRmJNxyY1rnC2YiQxQIXbyDX0eIKWlrHnQHBmomIDWE0E5JD0kNNA7HEbFdwbs2xKCTBncpfChFyMX76e+yws5OPp8enud/wnTzcu17ZzoLdXqRkS+SXKzPYguXjhGYzECC+Po0zE/vgsAx972+sDDggpoQxhrSwsYbSMt6f7Hd6SjJ0cn7keHBcQi2nf0ytDskw18OJaSncPnFNHZ1/+6Z//5f/67//jl69f3NIIewIHOXT4Rsv91IBTpByeZsU/qJL7JXSxmOib+xz9PPwuu//m9Pj73/2+O1OIvz//9Nvffmeh4NDrposGt9oGkEVOZvoZSVHsvF/PUus/S26UNwi24beLq8bu6YhEhn4zi4Zllra/+eAYl06j2OiaULLsVxczCq6SppRzxCkH2xVxf4e2scozV85lhxhe3Qhvk1vMkkty+FN2ZUTeXrMtjAgtGyz8Dd/2ATRz9h+dnojzgSPHivGbb4kIcsIhqaPNrb9Ba7ubHGdOD/z3//Vvv/z6068///z//n/9P6XQcFxO/BWM0U00MT3HFSP3w82hk1XFvnLlQTONYGFEqWHG/d0d2wJWexQqh+c9bBa6Y+Nfxg/ukXxQSVXJP6CdEObXkt73kQ1BCZTxAtlYiuEv2oWt8PAgB+y1uFz71TYddvbWncu2zqAdM3P59cTxoW1rEXvawge4sQ4Prbj5yBom9ThBExCYhPgrU8fRCKKNrhEuNHtXFw9/jAQgKaKW5Qn7b1SInlTx20fY8HUqHIuz6/EaiyIZoqnFINU2oZco0RkKSPZrJ2Hbdg4RgCQ1klTyRakKqCO0EIcmaxa+d1YjX9Y4mma5OJI1ikY6A0wMqwE0ohFPsJYd47YCkwDGXD9gqE4RyYV+9M/HRaCkAPSo0LsoAFUMAmJyBJXmGQLjSNcpo8lxGQwaQxsqRcxjvVWO1FrQmW2n4fKnEHrVtewqRKtdCCPxxA9sTN/hYlBRv+C2e+xzCwoab5Gn4SWZp4C2Eg7eEoQ+hbikGnWr5YbTwBppcrmgw2Xaa04lM+B/iSvIOKaR6jO7/WnmSX/CAkprZNEYmo25ich60Idfpqm3jS2ZO1j2zHfeetqKP2AqqGaYTmTWQwifL7TmbRK63UyvIBRWjOlcgQR6lcFWP41+Xj5OC2DQTb+itjrt8SiVHiMN5SCqUh6nkRpmZ7eUnxnxmwJ2EbxoPJbmkvh7tbjFzAZTl7lh+czclO5RdfkcyDERhw/X12VlYI+SAXJAFC547xYRISlQqvPS8byt7jsHVv5Oa/xGjAQtYPvdOpUr427n8elEANLTI+UA5jhKd7e35D9Rc37p9O61SHlp3WRtk9BY63kjHp9/+uXrL1/O/vzrr//yby4P/tefPn/lq2/cEaslM72DKyAFAlmZ7UURBZFvJAtR0MijrTukM1KWwtjYcoGU7eoSyLuD/uqaB/rh/ul26/5tywUD7qe/OLDrUdLJdzsOnM08R0xZeNwH48BBE8+qh3bqfFmCxFHmRoyDlXnX4xA6BWrYmR9Sa95FTG3v5e/ecqEyF6qczsIqry6B7xwYr5Djuxz/Z5c355e3lhp33eP+dPLxg6kxXn7zvC4obVUaDPMk5GaVW0xcEPMqOoGKh/t//B/Xf/wf/9Pwg402aisFoa18Pn/4X//8JxGYnavaXD3ed7Pv89ezq/39cczNgsZMcujfOvx9d2/HxqFuh8dsIWvYOkCSEAJLyGFh/zubjuEWLrziAvd9GovUwkwWft70Jwc6zPmPXiT/NqncS7dmn+QcdXFv4SiLOHcPB2TRVpV2zlnsmUyx0lMbkkkkJV4li7U2LG01ujLHpnWEgF2VDPHp0ZzT5TWyIrpM4g0PQnvcl7ZQZbjV5IWr2vZuWhvnnQcup3JSDbiEsvAwu/NmtPexJqmyyIpsI1ARXEmwKDD21bWJJO8yASl97pWE0kg9Ult5czLsTl4VMtemAGGJBsAJaN0HVbxshmP3kQ89yc4zKo2m7bz13+f3nqksOFh6m6eNxHgTDoMP1UJRkohA1Vima2jxWTcKJvTrdB7UPGimo54n/XAvnZSQyaZvXIrSBM9dCBN6ILdKS0B6X0JC5cJRn6qxNAruDjO39rE/lBm4cE49gsNMGXmT8y689DggLFO1zEUdhM8QMbAYRFPVo3CnQ2jTXIGPZLp+kuz98aaakWb4W6r7m8hEII3CJ1wKEl8uUzHQL+UroPfwj8AGp6AAYrSCwJ4aESGcggmP/5tSa6qOs08NqWGiGl3Cn59pNHKpmQHL0+ZJsZnsOjOECK2aDQQPLAXGyI6MjH0WazgUFachBkm0DSNGPAwQ2mBnQowK8MuUNV5wEjc3t0JE6IBMHbbq3NYtnc7l2bWY8TzMpDpYx9Bg+zlWxCw7PnTUFFSYt1BObmS/zQU+AVHS85L0JDct6pXSW8tzt8X6Sag9PctD1xkl6ZQpyKcXu5Gfzy9/+fL1x09f/vVf//KPf/xXewCogU+g2W1/cGlck9lbmDG+Bdmof3Y7G71sP7Y00XuiWf4CqSYuqJnDFc4cR9rEuUJOnjf68v7+9vzztUCVqHlnLb9Q4p2GfEbthCa5zxjpbAOvM1Of02u/i1Bsz4LbEM26cWXn5S+i9TjAIBsPd7CCTNAV0aC8SRQxRco4Q0E8OZdL9K9suhtyRyD0/UMLLIRsnSERTkuurP4VQT5i9qkBWNUIM5BIdTNzqwjDG4JoHkvv+sg/hg6kv/IN/Khu41rJs+u7/+8//hGN/Je//1tJts8ur03Etx9PT46PDJaBbU6u5PMAZOFkQHQq+NFDR8jY+m/7u/fXcRmXT26nvR3A604PMZWgXjdXZG8UdsgG0y+McN+DyA1ima2zUrBDjFIsLAQQWDRx7MjugDukhSMzbA04T7bi5ubZ7yUlI3wI3hRfy7PHeLCf3LVfqL8Zz3Yu1dywShLfPpOeEUUMQgcEMboFUFjximvGpCYfllqxFHJgwM4aK3cJMT3slF2XuMCLRcHFAM1tGkWNEQfJlyxpUroz5r2m/AgA7xJAVELiaRHmQOjpVEeBdVaN+N7fYe2kakLanI5saIX3zGUK9mUgicU+qZfgtRCqFQjUFPtk0Aa8YBkM+LsIQCxhuHUIe7jDmxCSQexPJDSvWq3t4WAtwOLS2daqRV9irfAlAhxlRJVthQUcMHQaiQJh+g8gVbXdPIS72As5xLGagMg6qYgee9ryq2EhqlwcA8fgIqi9DIW4SdJFbqGpxtPJKcj0UeZnQr3x90ohtTU2WPcFUxTsI219G9aXKaiz4On1rkX6UjN1kcpbxFrM3GTAWsizGiJBFaNvKu6Rv5kCWYJycwak0fcHtNQEOvNu5rCZHArTo2rzMZiI6ayd2oXAZj0EJ2YQNKKA+wW/U09PyjXmZsO/ZjHArQpFxMq/kpBmeZAqWTUdq7H3hi4tCJ4fVu8wCi8PES5HGreIFfvt5QUnQM5DyV7YKck7Nu2aZI/CdOCYAmhvkInUSozPJ2e4/ApcHPAzJ/kw5Di8eY8YO77ffXJ1MBCdKXBbPKhlsf/w8fTo+AjMct1whfMwXVxesW3/8sNPP/4i0PELLcHjqykd+Z0fIDSbfccIDk0vnAh2RP1cK5Lgu2rMPiF7k4ARqlRA0tMz987nT18Als3ZJaRpMK1Z1pAfsvzYnXWm9nnPWdN9NG3VI2QGJUNWQT27Mh9j8w2hlMenp3unx+3jQixHzd6eVJZZqg+S/DD9bN7Kim06rSroISsupLAuXVJSxMuSSPIH3lQhnqurUtq0eOMq39gHkm0Wqw/21vauwz6vLkuwnrIr3h0+Fl7bWyaWih3CQMhcPpFnhmoTDjfR3ZACqy2WQGaIo+7WVv/tL1/t3xxJ3Xd4tPL1UuJPiOg+tS2rii26/Gpv5yJRHX0auG2Ax6fbYoeI6lZJTzdPd85WdbR4Z0XWaCnkRINZT9ksjm91Y6MC2ZHmkbjZZ1jcsOppf0dMTKTJcJ2DBZXdI8BGt29v5Xg93MNslJ6PJs5lEjEEsWrAtk/fBMg+SIpH87lsyR4RUqD1GVsEM6RyvJEAyRPifTEHEgXLKynK1kkUpKljephJYhB92VKzATsXgtIKHFox7KIeMNnwHxFBm0IlgOMkgOPDCJHwAUu6ZIQfsyH7x3OFkhBJRbq7NYne84qbr/yE93zno7UTP5XjL9EZ6Zavw2+vQU8CMmlLeKvbq6kOAMXGW5V8U7a61pZWI3PyjPlCbSQtrRbzJKukYID7VZ1QvLTjg5+EquFMH8uvkGSc8AdhaAvWqNu6qBGOkwBLOUDORHrpKCLXemOuz6BtLEmlIkxp7O6wQLJ92WKI0G+MjRY4fqripZL/PqnbsxBshMGwvDwNeWG2Sr4IXlM9jbNMnafwRc/qv5UyyNAMXgZnVSd+IFJV39f+NAl+50byMnX1HDRMAoacsfeqaMA0czrsBAAi9+rLkKVCfqWlSR88yZogLMHT2MMT34VGAf9OkY0yGp3xq4ySQm2b2KFZrULBik9IMtdc/Xtc28swvYfcoTTT4J/juzw5ovJSKoYPVBli6BFeHdtWnDnQZf/T6Xw6kkWaFD05IeXFwxCjmy8ll5R8jQoxSpQr5Q9wyNDcSHwxNixDZbqbwwhOwc9e657Z7OjgIv0ZbzmNs9BLF2PiWIKGNmplTaDhFQvUdTN3j5c3V3/5y0//9E9//NPPvwiGgSI4a60ywk5f7jG3zDdR3jBOck6UvN5Fsoz8Qw4Su5Fn7etmncxiSBXHo1w7dmoIqpgtFj1xw8+yvfEq2oSW25Ag1AEcFmakRGiabXRSBCuS08uqPJXOM+w6XLZFkAmjwvh5iyzDfUANiKXYGFehPTHaEQFnEYFifilPit9xCM2XhscOIbkqU86DWKgS/h99cMKMbJXFM0tJr9SFeXHcIQ+7r1qYONCHPh2BlGgObTLVkZN+0M3CPAHsI8sjChyThEBMulBmKytnV3f/8u8/fLQfvu9SMCcqbsnel511nhxOD/cxWI7R/lqzgr65uby52RHyz+1UCCbUu/NZ7rfH+0gOpVkaFs1r8+Jlc+eFW9NVBykAQ4CU9ww8xIribyyL7Re4dsgsnHlU6NB4BekabzoVUJYO4+nItL8tmpwUM0Z8NCzF1MRIwyAoPgTk7OJuW9t6epNOw8QN/4Sk2GrYIxylj9oW9RZFIFzGaFDFogoqYEQjRsoMqISGFqGpdgZuTVlvAMQfAMX7/mqqRpODw8jtPC2SKKjLbDadDCRDxBDrkepqZZUDLGA8QWTQp13vI5BFByS7VMkGDNqW/lMiIbDgRF3tTAtEMfxUjE6sbUMYcdGiJfZJ1tIjYaOfRZjNn4WGAsoJhMHKMlLqqFIhAADv69zEFNeavcwR6+OaKIAIXjWqKFJpHv0hl7VWZyBE0kDybQ1oEMIJ0WnapxDbFPQSO2D1tz6rCw0QOLAaINSrcmifNKuCVU/SZ85lzAJgNb06+iTZatCNaXQMxIeZBhKKJ662siNkw09fAHowiCgiIF0aQ9MRWpsS7/ouJtWer+hcLWgNTbdJ40ssAHJuD0ghuYNnUB0gy8TBizeDmP5od8bvNwZOs4ztH2LnpaBuzQj7BMkNFNHJgBovgVDbTamVTYuEmc/RxETJ7Euy44GsHXhJZ6+4bIlz3tmfQaEIFCGOiba3teP9g9NvPv529fdCQ3JT3IrkJtBurQweXzA/U5gmo2a5ne8wAQDgT7+ElK51ZJwJ35H+sOHHcgHvswtsH/AVXZ59EXYqbTGjAlnph59DPujP5zdcQOeXzsC6ZZDHvDsUHU0EJPLxz3GnExcZn36wQf3l01dHdgenEiHIzOznWdRNqtUNLRaj7iOULrTVwPqhyEd58znfXWIFSqeuZCG+F8nErmd8u2Zwz6BskO4c7rN5Ux0s8Va5W4+ds3txf66QR3QoYQ/KA5QFFb+NY07GBVpKJXoRYmsxdPugP96Ty6trjLMpaVvRnAYbZ+Ab1Q2J9mTbllb16topM7G01g3ICO0yJW1UZO8v5lo+fU4VCojas6hyVI2UNpWlmslARDd8fSXgQap+hVpIwDvznh29ev+y8peff/3+Lz/94ftv3CR55VIXcZfrboDIZrcL4PAHYS+El/2P0navdu5vT0XtW9Vz+Ura54ZiO9Xt3iN3UQD3xSZauq3fP+wdyPHAEWIREHkzEghmMtCygw4zcjkMkKRmQU9W0BAYSGZWu1AvT456UUaz2b7RXQgofWsCDEg/fmP5n5E+/ghrqDwxlhMVi1tnYpfkVRIhK/OvvAnFnoAlga3WoL/N16Wk/sNNfB3/BE4exVxnSRZz2VxRSZGYjxUYrosZfahiuxxEPu3lVLNvGzzd0ZdxrxrK4A6QmCY6YIC3UNRiAgoikgrv8sckxA6AAa//MXLWdZ2Z66Sznkdk4qq/Tq4eIaFRxiZ8QRnySaEZnMoBn1Q2HPSQEPAo8gk3ybAGAiKySsmppRnPoDe9Mejmk0CSyZm2ylEwPR58BhSAif1pFhyNzlhHvtWDD1QSqy1fQGNghifm6ksffx19s+EzIMHT8JFKuNdPaAjdaApj8KuEVxhewNQ7CBCbsTvGaDdnpFPOAaOgYGcGhxIaVPCA0Gq8aWRPUDUhZSGFIRbFlAu8mcBw4UEjG+Fr5qbLwZYi3JuIAPeLms/OHuoY5KpUhx5pTWV9V6kJ7bn2g7BIql7NT1xcmcY4hbyfUaB+f+G9o/etvgbLAZICQHjNjToMK7+1HLmlGjdlJHjmS7Cs7b54TglSJSmtMQYpe5G1JsRTYOfK/oz7wjXir0cOFAm/OzrgG5Wk5friwhkle3lJWTeg4vNxQWuwAYarxg0KqMqUVqA4SMkeSNXct7y9+MOq4fZWJrHPPMgfP3y3z9dhZ7gQ0ydXOX75euYYFPFDmYqzmQW7YeGpBimd5zGL9PBIoqKt7SKp0zVcFjAlL7yT+kzChwcjQnu2NDmZiaoLMS33j24eFuzf3Kxxee9qmQ3PonEIf2tt82Cv61owOzMUjREi4i0KAClQjwNn7+GRQBMRuo+m7HUcOUm7Kos9wZX0bmtH8oudvVLqsQnQoL5G/lmamHmmrNmjl9jPhN7sMebxwBfQSMG+ru/sHJ5u3D9LH7cnI8XmFp17dSkFdH7/4QR9rDh858QFT4iAKVQCDUhxGDjqxJLZIHPtly1cvRSCop5MQfaZzcXT25evV//8L//eweDtbQFR9jxOhOIgBYlEJC8udHdVfgg6DPxQJFQ3C517Hpbj0P9Nuvh+3d6QiSOuhRWzCKU1Ih5sYIBta/fA0KjC5vr+yb2edAsiv7y4YAEA8uHu5fbqhifR/r9qBmVuoMiVAHRVjD8XIwugcjyBfuTKQ1s2BMgakAy/QCqZYt2ZeQjjeRSQGPrPNo1xgjoxBvCsUTIkHTKOoHFBoa6a9SKJNacsFHhiTDGDHtMcKhDZ6o640xm8+w69+wYNrmWbLT16uEiAERitEuLyWHL8SMXxsBoDbFg2EJWvLY0Z+ci6Zs2jAMdUJFviWV99q+voPZPrr68G15hHaaRZHNrHCCppRmBcIxpwUmnv4jBxQd3VBcsq21hr03ijrq1SaxhmwGNBPSw1aaiR+dappQIuLATwqKys+9VSdB4MrnqgNYScSAsdsDgqI4GIA0ffNqUxeiNrLBkA5qOGjDMtCU+AiehEHzVVZKmuVVg0dnOVpBgJhq+C3EeVRyQZW/MVCItkN9/B1ZRGab7tl6/rHo308m6eVOuvXyG9Xk1DA0m01ydU6LGuOB+EgedshIhkpMKLRVDXPqnXluagrcay4wLCJCHe8D7ljSAaC1fN9MgAKloxv30FfCLd9KXNbUCRXmFJMi81WuiMocXvGjJIBidxAMA6pkLbKKtx4Y92+trKe2lz8hWnCey5u92U8OCAg/5UXKiDtaI07Lm1y2QP8+by/OrCCdsnN4jZTtQgTwDmHCKh2yGlCE1WKpCIZAE/FxdndEzpKKVzFIcjxPDl6fjk5KODpiSdzAtuh7+7v7i5Ob++Euz/40+/OMTbbLE/CBOAss3soG5sfPPNN5IOf/lSMpkyEL0J0sy7JYNkc27X0b7r6srxybGzByJn5K80wk+yan794tYaiXGIvMS2yWfG2oXe2XQCwUknKHMNmeNhKEO/pSG2Bk3KljNvb2uL64xGFLTz/+Ppz/trO5bDvhszsDEenInkvRptx5atfPJf8v7fgvMofmxZUaQrkpfkmTHPyPdXC8wGsLH3Wr26a67q6smEb4kMwlZuJmFvkU5WZbSaJOw1S8eKibuN3fa+FI7QNSkQMy6ZYOE13oWShQVtHPtkFv/O/km6U2YMaesxcNBmiFr/SxoJvqj8aP/YNnmv37w1VP7zzz+dnduj5t6moKRQWxzXq9fW0p2KuG3Y8PAl7ZWPEhkQ7fKuMeUZ537+9cMf//Dd8WolrW8DcNkse/2RHX2jyexJUdt8oZMjWTUwNR4wkzfFgJDYubf6d2Z/8oVF5TLmqZqkYqsNnWXWMLjTb9IGK3+dMjSi/AQwVcn28UxEp2SSWOTGOuQzYYoIUXme5si+hHuW2u2qUY+GC4oObVMB0cogx4z6GUciGs9mkBbYNAxA9O2YljJkwiLoov4vekxVQEJJuPZCzLEwcy+OZwBS+myv55AAg9AwO5CpkJbI/ND4TETGeVSf/k5oZom0yoUO3qu4x8CwVJq1WhQxO9XDOsrdQzd+161MewKAS4v/aMRBwandexW6UNO1nNJnjxPAsTH1XcihFovTVeem+qI8OFVQuz0LgBmdiIzuhlH/1bxgBaqhRICCOjs2QzGJA9keChUxq4spmgyHkslYj9XEOIpwQgvRKNplwMBloJ+pActY9mJd8HfL42O21Br9/MMExjO3Tk3Sq9gWiKBn3UaktQh9sw980CiAYV5Mhw0W9kSqSK2wHqYCATjOQJUIUW0BNNWrKHcKsMZvazCaxY4IX83MWdgBTgFkjHTA9UeX0aPdMxgrMxyscqykZbIE1aeMMTutUa0PGzTvE/awyRGf74iQkA6G4a92y6KoHhCwGKia3hdasab+0Thn8A2e3SiII4KDNneMfpE9zoK8TbKKl8A8nbgQhlMhVXdNCO9wJUAwYJ3tLvBcl4HRAWs3soOTNRkCz1+0w9pOwwOiijrAI8nhgeFFEaZ9ksFCXX7x8Vl349rmz2zV9BW4dp9RxXmQrIAtQe0DDAO21NYQv/z68UNHOdpJzPTQE/mOs4vLr+akxn5QthTozev9xThiN0bPggMjDrYVwzvzN7bevBZuHv7bP//L+cXZf/wPf2Ot2acPBi2vwcxpCdburprNSstbxVag3nGbR6vdg9W2SYvEpQEvNLeAjXyIciKS1bFHxoiNWqgBJ8GQBiM6ovnEBT4IbJ8dfuu0RZbb7Fn3Df/KcKjTyIRJthq827q3HzOfgFYyLlzsjTTPsyFfc+UvdGIUejg7+9VBMJ8/cZ+YRTxANOH80x/+8MPlyYkTEOzhYzjGCgqZtOfjMm+86aJP2Ol0l4RHxc1YL0dqwENmzKouE20thz5tK49jndeGM5xpVoDJfvg1i8ZK3DutGmAxivvw6kSXsyVY1hiyAbs7FhJyq9aF0DySIzWr/jpxloiIEvZ29PRtKJJsb2y+ffe9YWFi8vHTR86euhydHIgM0qU6bQ1XCHObPtTCuebatnhiY1vSxyBDk8tIGbHEKAKWwqWpulkQRBvtNxhAOhibRqScw9P0oekYuJ6qjr6kJ1TVyunSQMQ/xUis/GNlFnPjSpq4mIDqRAx6419fMmDjKlLkSRE3EXMCZ9IQQlNdrE0tAdtTrEuE0DsZkxcciU3ZMMMKKKqAynoG9N3OWvivziy9poqfsyFMqmeTPIbZa8wW2aC+PVwXAXwNwQa6x0s8ZCezZSLRose84PiA8BmIhwJJfEav+uE2VMgKRhmGQeWcu8o9NZbs4QmVvQIzBVByWBMYZI7DZP0DILp4vmpLbtRiz/WkAv4Ppsg3S2sWEF1cavOOQFSysmCCGONhNGxGZhRigPQJSMLwMUzAIoIhGTXjbzGTy8ec3TSLNG4sP5H3xdh7Iv8ZmYaHIdXkCvINqaFdTQwk3voV8o6cDDtZldQItI37oVzNsEy4GIGiK4+ELFjCLW01axk7ikhAoEAQRfH6Rn0kIR2y2/bMmoHK9F4Xgi8W6MUbiz1M/ou6dQp6NAAMOcp1ZJBHFORfJiQXJqNjXeUm5EqnSFQ0CCd2Nl9e3sN0RrPm5VjEuhjgYWE9UyPz1Dx0w8LGAywJs1j28hyQE1zyVQFortHVrY1chJNb22UgPF5ScpCT9EwSnSiJi6owtHBmcX8aLmbOxPi0Z7OavfW9g6PTt2/3v50J/8wBJJ3GBu0K9927H5wTwCX+8utvbIOkgc/aVbER5h++e/vHP7z79dcfz86/MA5wujo7S7fkka8uP9xcivc3jw+MFFjjur+zaQshnLMNnMPMxMAGso5PDtGtA1usRt1sT1MdhqbL7Owho8MzRRxsMdIxSV5iBtOtsDy/SjfSZdyQINUHN7WRURbUZ2iZ6maSOjHxadeYB2sFvO+/e28U4qOlwFcO5ymbzNZcnl9+/fp1Rs6RnHE3J3UTdRx58/NPP7dr3vv3+gGSevLHWGb4u0Oy+rsiSiSFYzD+bPAGj1+9egXkj9xqcqEr+PT569czRzOsts7PLr7qm1iagIRlT2k33RW1mRhm9umlPSdUYvCFcCBCZ90I/1ETVnS26WqNdTsVgUtQngMR1/MMWIlk+3uHJi/xhIDn2+qGrD/rwEF873CP5FsMZuBhgkXK6aLdQGywdHCrY2RYBChsxNhRyWKCliGqXbYwXSqHPv6a64CcgEQJFRGnsXFmCWE9/5vKeHpUI0Wqpmzc7PeQiUirM7tpVdbWkWyEyq+ytZvej7VM0qbH4FLBm3ivr7kGLzVk5arfWx6L+M8irWkwY9pjBRZK5FamfH0O8MxzbgMDfXM8gcbwZHL41tIMfoKrXH/fashjWReaKgJigmj9o1DDDFyZlHESQDbvE4gZTJaHjje5q9oVfrnVJgSqWWobYIARCirPsBj3GtemQdajYdRBFLXU0TUf0LrBxpxAs9vGezArIWy4RjciD4NM4eFpyVy6RNosYZomXMzM+scIky3QjOn0hgMe91D+nAREsvBSwrvAfwKlpgwyMuznYnLm6XgXcyJV9asA8ec53xINDpNlrnAXMDR8cyoudFnDLiHKvFzNWIZxLPNfmXGP7ni6LBDrIzesd+OJvFcuwF3FQ2WAe/HuIdHo0DgJTTTCFY4RAfXrw9RPLLxven6RNNsR55G3TFk7gJr88jioU3tmC6xQHsFBijYRHlxqKVYkxOPRIksogZ8xxUAqpJ9uRqghAQZLL681O9YH6AmuPzV5z1z6/UO+YVcSSFedhzi3MujC0fHqhGLBngDt2f4QxfXGG/Yc7zHDY7zRpIgkPhxEsN8xS/rCz09fTf//0lGOombZAaf/lVvIgzNkB3atkSDGbUh9+O3P0jj/8fDv/8O//1uDAcYMUj7dL/HIlk0uD//ww/svn377l//7n5H57/7uf3HWPUH3q1cDOXLIoJqR0m5Ba+tvTo+ceULQxMUOpUBeGHFWVFp+//Bkl9+jhhybAwwlbPCynN8i3rrAvMKu+Z270tf4IHds4bGYvQiWu9h5ML/ecIipsbwzBjVM5QAZGULbKZco29gU/G/vfvh8xvpiry4I9jCgN1fnqFiM3hxHO+o3JCsUkED/v/7b//XHP/7x7/7Tfzl98+Yf/8f/+O3DJ6ksCiVFJ3TGzJk1xN7eoABx++u//Etbg378+NsXeyi5wF7bncfhixcX56vN89XO5cH22fa6nRcO7M1Ai8Anw6UzNC+TtRoJ6BQ4+tixZMw4gcEMzAaWIJ1Zdy5wA+8ONXtyevyNmIloMs9YyOAYZBbFE1fkJ1vqIWRPV2tWAewfWwV4goxZaCIbEtuG9m3Lx9foPBV8jqZRIlKaYZEGYCMYiELvNBA83nxkYZh6fSUUoTgcMpOBleQ+U4RzKbGXN8xEDsx1K5OcGaC8brnKPmnDN+W6n1qjsSDZl0wkKfBU5VIa9S96BBBdGYABaTxQAQHG+QG8SExDYdNzBYg+ewNDl2q52r0zF/73ChoNqTji+AeSuZwvTRjzFnx3VkRDCojUI2YIsnH6fxk21bPAA3VSEfRVVV2eqUK8qg03MrXTcOW5mUji9eLv87gqaD1baEe7uhYeU1keeJCHD5Gl7dUeZ+tfBMJ4V3igQAgkcgpYY2O7eR1H0h4t6I8QTLsyyqAInyFpBPA9QgWRSsAAdhxApElBEDIVggnOE/kJECivlgdxTwGsOvIcEEEmdxvXZrViQ9XHmF5uh33P9q+2XRsQvCVM7J3pHZ57zkbkRNzocZ8B1nOAnAoCOnR7ATU3ABqlRoQAQkw8B1N9hGKxeWnP7/T2WP5iHIq4kA+mpZehw4olHDLF3ENXWBuVsYlaUE0P5ucF+CZVJJGNpSMK/hHLEhIVo7YbYlQDc5T5JdDogMNs08EOMlP4Ki6Zv2cwVaBmgHR755uAaW3DZjIzuJynnwNL1tfM0pHNZwspc30RoJqcs3+wvb9hdOL25rGNgfiZ++fdG9t+7QjtV8enFzcP//R//6mDvIqa9968PZUY/+as2sbvnn/58LN4+vsf/mDayR/+8J38FPbJrkDWvM6PH37+b//wf37485//1//y9//rf/lPf/7x31iS1c7OD9+9MwhhABH8RhVtG/rdd68FvjY5kpu5u3xy0LDZkAhgxBIkRj4EorL9aw9m7nMELpgp6/TzW04CKzNhxJVdzisIj+2vaSX1hvPbDfta3EDgWVKmzfb8TLo102IGokxG9FSUuby52lvfbbpp1l9vxVajNrK2G+v5l08fGMnXJyfv3r6lCD///GeHJm7ukvY1GfMfn9ZOX73+u7/7z/ow/79/+AebpIqpLQ8eDe+8SdkacYBlVq/evUIF2fl//deLWFy3WK7n2fyii73Nm8Ptll7coYEzgGiIiWGNHJKuAihR1cPd5fnZ1fERySEtIKnLNueFRYH1Z+Pg3y7OWYbTTg3QlbCXNupaS7wpkifPupwdFLm9bR7ArHuTVWpUA33tdGSJmoFnB73rrxBrUoiz+kak2JEARhFAUoouqaUao84lgYkBpUDNjAId4xVEveSTubBPVDHv6G26nbalyIpS3KxFikxjc05KsiHNnaV3dY3cdrcAiXlSsWZpicsIRwsWe8aNKDM2SczE9AUmGYhik7YFhs8Zgd9fi/0AjQpT8Lnrc1GN57XOiPsSmRuCpig0xZ2x0Xr5IgHPBg4ILZlM+gpDm52Ls+QQ8J6hwypUxhgUmBhSmmd8pFu1HTGKv6sluLkhDfk/kFLcyRctBjRgluuKeLIUFsSniqAWVA5f/MtEl8oPk3EnbYQUION5gJT9BEFITA1dGJYOSWgwf9405wxdKQf21AaNpq6EHei9qhfD1DqYAqUGVJlOBUG0HJDqKk2kELoIWmPJTEZwoVaszV0iSdXGLR0oI6UFAiXHkcaVSiN1QcdSlRaiSi2HU3VqQkSjNoUhGHm6hpX+8kVEsbq65kOTWqdZc9xqWkNqASZwzPfwMUYql+i7GH/0fGJpTKuKnkI9NqN7BWIF+VVaI66BpPROlZbxRD8BcqimxihWr3SkvoCUdtVgs8vZK2tp2XZRtxVOtoQ8MHA7PU2xv6gWrFQLfRDE6Ev5IrM2nEnYDBkni9vH4Or67vK60W9iF6jW/TpfBQ2bbKFzuMckWnpkb/0m710DZP/AYVUnTvs+fPXWhmgnb999+Hz+7fzm6/l5KHQM/fFXZtXemWICc1SuHpxs+8uvPx8enb777t3uzj4cVjq8Wasvv/7y49X1+enp8d/89V8+3tz+/NOfkBDwpydHb9+e3Mlo396zVOak2BfC/BtZcTkXC1ltcykTweYhg80JQJj52bIGlUyumY1p62dUI0KEVVjcvshi+zvpc9NE149Wx5vmzl9fyDpZyou8GJE0mwJrK066kWVxDDJz+Xh07NgZ+kLI6fUm2PQzrluardN05xhG2TsrJk6PD//ijz9Q4HZ+NtTOgksKOOLm5uq//tf/ys7++3/3v/wf//v//ptT43/68cuXc1DJzWvoxNZ6R4d//OP3b1+/+e3XX//pn/7nx48fknTwPOh8sc9OGL/XB7g6PuQezjesHdkrTm++7w1p0IfRhyD9WrH5qNF+00PxU/cOGNwGG22qGI/OgUjxAc7CBtE8ryBnpBfyoAqDCNfOL7RKQ7eCHBoZMm/2bmudKBlV2TuwwbTjII+OU5+2j+W4OkpTuIAgJDMFIOiIlOvSrRSm1LtNd3vB9XcD0d5k9a68G3dkIYkX+R81qPPkQ+SdWJmC0CW6JlNHo9Kr7FCuMTuGWXmHlxb805hn3V06APioXW9sMLsTjDSjBxuhnJqLTVPsml2KD+HyKF5qo8Sm6BMS2OmQebZyqShQaLWwQgw9C7tT3BI7qT7IBLDVOHYrvR9IK2A3b52tibES2TBKd3k6by8GsIHJEinkzs3BkFmu6d6CI/DHF9WBGODnxlApU8xWZMD4oTJO1ZBB6pEXu4nfqjNLybs7UY3dmca4UgzqWsLPV/r4AoimljHNURUOMAPmKUgnAfUnFqQ9gxatgyEW0KpM0KiqZByWLxRHR5kIyqO1sbyMIPmpcSXy26gcgi4E6LQWverAZeXruzFiRa4e5D9j8/i8dLv2SIRPY1WrKSLU4QJSn7uvDaBNkBKNkbZ/eSNNxE9fPVnbSnlUdZ4cVMsC+a5I8YIaE6nhUq2GLjL691IH5Yk1DYRGB/XnyXpWwepW2jsEsc1nowpkYYLY9EJLhEYBy3kal+tEFGupxlQ0OXCXRKuOwtBcgWEi4hTgnRWLqR+3K2F/c+MwK2fZbn759vj8zdyP1IhAjYsSQ+fgJGTs1SAIl2PYM/1yJf//7MxI58Vv7R0dv5ZH2DBB8eDzrx++/OmnH+0KxxXYSIbHOjk+NA5p2RFY48ydDeNuv559HJ63ZjSZqZNyY47j3//H//iHd9/99G9/+vDLL4cz0HoA1q1Np6VIjjgFR2JFKv/dH98/2nT+7tq+cO1QbzjASBSsjSvY39iRLTsru/VveJTX2tvX9WGgTalk4IxfiA2SN76XIZehvjfF5UI0K/Ng49SovaXT42h00QY10H8yRumEK3tsmg96zw3Y+eHy+sH0JLtw3325NF+KIHz3/sQO3d++3ZirY0SZp7EZDtZ/+WoCZSvO9NjOrr/9t3/4B9t3/93f/f1/+fu/+/4PP9gslXV3hLBpme/evcm0rT18+PTrP/zD/2lbPXaPEcd9qzHevrIowkZz9YNtkvHz+tPx4d7Frv1/rNRIaFZHVkbs8jppiE4kuy93QV6abbWCw6Od4tJQ9YHXQO69XVTtjKErZG+Pg+vDmw17XRAMfsMAHm3tQMpXb/USL5wqJ8TgolrO8ap/1lcbH7DLKEI2z8GsA/aPZhCf35WkTiXFkUeYIJzSpV704MXsRuySeemEy6mKpRqeofPes9DZJd/SnVSusKrUmVfWqIse8jFTqbppbdQzM/2imHTKrdHQRV99oW2ueFJN6aUnq1+5UegsayF/Wu8Cy1O5pHWsoK5GWpn+51AywJWvay5Zl9lUH+gzq9plYaoWrHrrRRe1xSkyzFrIVpkF425+xMwu+VU2jAcYWoVXD8PabWUCdSrLB2QcMxGwyUXlgSOnpgcnbyyJiqIVN6kNkSOz2OXhTTTKSi4mrVk8AIwdY/9rTAkXglRLQ1IwUKHAidVgyuzmhMdwCcl5iQVqQoF67DAW3DfcWcjPkqiGL/PEHa8Qieq9KIumVCCG15vSYIi3/MCEI0jOK5BqNios5tXTKozoS6t9CNDkb9Aukxn5fYUavoe+p6tIibk3Dw9DkDIlCZlq9mm5Fyjw6mKVMckxvACwkllqLwjOhxp+EanaXEByESRD0amy8sxLny2JmM5Z5B+iRu6qqO6QZbMCOmBB7FatKmoJUTLoWgGUJIHC5EkW20m5srUG8SSfCB7zTTtHgHTQjWLLGltHdrI6Otr+/NUYASo9fmsLM8LOJ9ekBMde28ft7ltrsGbGiDDbMd+7j5tPR7bWlKSzPcOKdH/4fMEcvH79Wqrh5vpHU0itRrMy+ej4ULgtkS34NjME7RecPZs1MiRF9Fr8tf03f/EH+0v8+Kf/58OHn3Vhjg73v3v72lzFo9VWe9087dqbTffLnM9jeS37m2ytGL7mit1KnbXFMk45wExijMCvjo53T96fvP3eETnDXll+O2UDwSqHkv1b5v7fl7gnBIAxkdEt3RGhiZtD5LYAMlvJ/Hr9nEPHLGzZN8Jm2jsPl7cmWEq47JjGR1tv7vaPD969e/vL/cfD7w/fv3115nDgD7+Zknpw+JaUWjCBpabNWsRr9+affvqRxTcl9O27dxqwSIKNt6rOhMsvXz79+ad/434Uw38z8A8dqnVglGHrtQMSjvf4pi2HstmWweyvZyvDTdW3VMvC4D1jJIRCZ8WmGgKPVoUZqGsJoG+puOmYpg3prELfR0vJ8Wjz4mJlWYczhRzFc/7ViDBxWY6KtvuJLuXx6clJMzpv7Zbh4DYbmkr+ta5NYs2kSyMJ00C9yww34Sy77irGtqA08Uw4abD/kzEuMwMeaY+xKKNBlpiZtNGSbyaINrAFMwtCCTUya5mR6mElvMM0nareUe2UOz1NWTIMc8cjNGP0KN3xNFKkasEUUChYARfmmal40Jmmau2pw/UmUwSTWZbMOKePo5XsWJYvLDJ4E54mTnUjCg8XtQ/dBYEqEgi2BLGmVUId8nOgKNE3SxflAouVATMOQCWYN20EQgj41WB5GRW3ct6NPAs9lMIZ1HmqF6M4XYdhA8A7sqxV2LUfZYYYYMvIRcIeDuvMsytipSjjelGpQpWoYF6ozExGyZ2KFNny/YQMj1jvxSwCTY3uqtKHrBi0mpDECscrpmroELGxtgnLKyNt1tMnLKXVB+Fh2LDVBcCrCpcXt6wWdnWMcuCgaW5kXFyjvIrjWJK4+KyFQMRFyYWWY+49AzFVwT6ODaI12wcIuATrRfg0Ps+AARE0Wh+/ZKJG8krqXfgLE1eoyVzvcfeLRyxdNzHRBoqqbZbnLIW114EsTBKpJG6NZEV2PPFQTOtTowKutff69IalYye7byB0ul2+1MEKPekXNUNMlizU1GuALkLI85oaT+W2t1YO9b0XXksR3Jvcb2mZFAlZOdg3DVflK+fPyBVpfH9Pgnwl22EJrmVPgkqrSZuy8LxuAx974MDm9auTi3M9iVBm/SFxbe+KN6cGcJ0OKRxmoFEvmX6Q0NDNX399evLm9PUP799dX5z9+OOfDFL+5Q8/sMH2w5P/txORJC37vrJEVzfIYZOfP786trjsiIl4uJ7J78yLiT2bW7zdnR1w9rdP333/6ru/PHjzHvhEyQs8krDIWp4z1sue2bnegtZ75szXEhiTYxShKWNnZjyCkVlHAmSskXthk3gsmUrnYgr4154u35iWJGjZ2zEmc2p45eTUgYsO6bE3KzMpG3dyePxXf/WKy/35z784G81iY32jz18+Gh5oxhe7O+lvH1TLe9Ijkm8D1N3tzdenx29PXu9a9WBH0PUNKzywwMnO74+dl2P/UyPAO87jMcjv8AJU4mvNwMESbdie2pacWM4PIPj0s5PRFJOBkXUwG9vIEFFpvum20x5JnQy0kYZv52Azef/eHlLOg97X63EaTwM2Bo8sL8mGiHyaAGphgFbrc/PFWdQUoClk6Si7MP/Griwxd1LYn9b1MQiy9HeddbUx/9nQMSz0q9V2umedrJAK9k7qyb8qR0e6oSqGREOeLfRN6nsfQzN2d9Harg9AxbVjrVWX+ldYLQV2Y1JcnCDuxciodJK6pSsyPRlrjqC4zA9gMzWeTJ78q26aVjdFDA8+UNUukozN8L/vDFLWlZKFTIAs5iWAQFTdLEO2xT9omerguWyC7hbUKjZU9Bz45mbrolybco1qxN/gCZ+uMpHzzOSRyo7npHMjjcHXKcloKTeWfyLdQdib5zSokVCdZodGPuaFPeorMYL5tBC4rsTg6ZmxPpGLUY0pYaQ5lXqwD8mM57JwuREehxgVRMfvwSaTp4zWvHT0wwqFhliVANJyd3AFumpKmTc0sN1YwBhcRMVL5aOX9mqA1zCIN8XzwcZVc1EqfGGZutvGZPCvodDwq+UXTD0yrVMjjcE8Nk8LyD8QjrxoS5ttTTgKgdgjcSoGXW2MEsJO7YokQFUcZppNZMPJq+YHtnbFoToFqKy/gND0FaGiMHAlYWPuTBaMM4UiH+QC2ouV0bC4LKIjcfPDJF4pdpNHGdAt01skyG/lMVpU2mQys34k6hsCQKxC67V16WAfLAEyumjIV7GobaapuHL9Wi7l9avXgkTDh1Y2OchE9HLy6vj45Oh8dXFsoal8jw0rb27NG4QqS/TD99+9fvWK3l9fnduNwSbTkvuCXlONrC2sE9JmRGysrkDHo9ha3pZZzw9O6I3Wsj/tZgQKFDIasrU6Onnz/R//8uj9H9Z3DxpFkTpzILr+wtVd8xSImlVLUtrbW5afCVrsYgaijknes/Po+tX5BYlz+hbKXkp9tLPEluk38kfIjIDmPGGKSUmWI9iHAV/1OqTJpektgbo6P7u5vjAB57y9+e5OXr9+//YtK/L501fO4O3rnYurC5sFUT+HDQyZ73VJSFfi1qaYzr05ePf6lA9w4LP43iCT5dCH+zuHcjzbWycn+3/x9s3xgQ7QmnGKDkjYcGLBlQMgtdLkzo2tsy/fSKTdQFiZFKL4t6CbWSByLQ5ozlcBwBh629u1gSjrTkMN+VzdOXn+zIIP3gD9D49PzPHlDwUGuM8x8OIsRcGrYwSaLpv9IM/etF4wBBX1a3G2AMiOemVw6sobyRg7T3AwLfjsEk0uE8uUnWGsLsBMlb2NAuRWaGGuJIvROglGpLv9tlBg0ccCvxS3p8ZEpNMDgMaUXartXxXRxuotEVIZpFKKX+mbsmO4fFLEnZI62UxKPDDVsuBzegWVUVmy6IP3AJ8axn66iBH+0CeFfjRLrOxPCqlRdi8jRJpCu9RusYZ7GQYfVRnwA/IUUbv6ExuARp+WjaoFeabpLEkkGDLkE2UUK0VIan2ehVflJzJiaUSQwTgxtYpLJc6srGlbdfkl0AEDaLm4QRhYOIG3jTRpW7oTdZgTiBZ78kINBhR56f6YP1jnBIPQzmDKdIEieNsPmEBijbgPpEgmG26ituweKJvByvQPFXKLBfVewKjN+UNxVyaAH9lSOUBCZxgfQ4I4zieguRmkUCQn8furKlyrTDW5O3RnlH2O61Xh4bDAHG/MLPL2ofYz9tFpYeewoqspg6DXgCTSNf4rAuei0ZugqVHgdtezPZozn+R+ohJHNtq2HjflHdKklICTN4Mzq2eKzMBuCGedMzAOLGeQPgvbM9v3TQ+SMRD2OZhL0PESetDjvCJAjR4K8k+d6Ggsr9nizb6XCj5s1NWMb7sAGxFNVtl7LseMQukmxtZk8HZ9xOAjnQT78RybfoiXjnEkETd2oWCwjXA+7BgC5nDYrStLT+2OIM9sewSTLq2EQrUn2+x/k+R59/oEj2++nR1uHko1GwM4cBjhgU3YtsxqbSDUZtDPNmhbs+URP2ASdPsQtIobITbMMd07fX/y/V8cOk5steLupsdTMIBdmjtY7chw2eNBb0Lc3G79O07X0q3ZdNyJiN+wKXlrvAQhnHuD3Ra7XVwbhTYEat9VnGOO+ShTjI5XB79++Nzozsa6M1tMyTWtdm/b4uQ9C+W+XFkkdvHdD9+LzD9++cU+fQ5xk6k/vjv+27/+2/Obc5kxKzLknegkU9BWrWVBNk6ldfZ5R7110ebD1kP7up0eHb5+bchDcmxlrNie0LoFdqimRJIzI/nJDANv+fPOdgcDxHsxE/Wsa0hV0tmUabERxma1ZoqnPa7PLnP30VLXyjiLqRxfnQ6sU3h+eYlq9LJ+npN/chu7+g/WsT847aDshEuGwFl1bqCxPZEATaAs0xzCp+qLTiXw/bKiFCKzRaoygJwo1ScIE/xl8zxiL9W2WS2Bns6N3RitbGGKi95cqxZs6q6bVTX2gOjX1U5nk41KeVWRMGu+s3DLPddU4UbGfqDTqQOfF0iQL7tW2K7A3KeX+iJjWHqUbpZozSQA0yeMyOZwFsgQCCgvqxOyZIXXrf9UukY3y1PTROKmjtLsQKjjXjon6k4g3bizwiXOBo3BKYyh6KnkP8sXWZA7tRbb1cOsyJDGZ8ZlZj0KaVQ0/obpZFwMLWmol2c5EVhCJTQLbdmjoITX2GWRR+ZM+snlPcNusRSzMpStQs9uxlNdRWEHkrrkFgaKPwj6kMpYJgMiurMKPCJAACbk30id+iN0zrSqQeV/Q7kDIWCGBApEvPka3SP1S2kIZ6WbhYAkATA0IjEAaslO1AO/Wmsq+vgYAF5w9tKU73DnwrqqeCSaJ/1H4TB0YW4Cgi1WL9JFHtejwDw3lGygamAaAXWfuiAhf7DUMPG1WuxyI4YbCnszBFkyrfbgFsVnQou5HLPJ1Nptaf9y6SaBWBF2cyvulks+uLoSmO6YUOhFkNklMQonPc5YTf3acwfxeXu5YL0JNDhiD3b+SrxpM4ZffvpFOGyEYP/oiK7CbhwHilBbiUzK30qiNoXumibsSHHD77T/3MU3axKEAcyYgHi1dYQYH3/7BWg4zvOxnS2lsxtkUbgtaW83n7b3tzZevX2/u1qdffkqwy5NU9b71WHnFdqMfq2jbyQ7xvRfGSktihk53Duw4ZtJn2atOBL9+Oj0/ZHMz96+yKqsDia0Jut+Xa5RYOGAsN2dQ7H0+p0ppCyubovZNfS3/TLpQjMcHZpmcKoQLBaWW1WGaRuFfl5rWYUxE2fNrz9eW2wh2jd39uLChJvXJwcGfPUnOzXz6f77d99JDf3Tf///OxL38FCyZo/ZcJayTS8+f+O3Zknw/s4vP/9qdtLp6xPiaA9X53Tq3zi5wZI2VyS+3rzSJ3DSzEmTYqWD6og08y3docgIuqZ31OI1xJyo/Fn/KGkkU7Y3H12nibQlLR6lppEeERo4KHR6fF8dFfTm9RuZ/r39Y9NnO3/0ecN0WOsL2cyot902G+igxVaGg4HJRyU7horUAEQc6wmTdd6lLiYE2BNYJOiAJtMMC+Yl06O/Gb2mKRPK2NRUdesqZMPsLTobrLa3h2Yzg5AJF2OMPIeIplnRWSG6OdpbnaxN7afzKQ6L5sFR1SyKsf10qdZSxcUuLaqpWoYlm9lbM38U70H1jLFXTCtVmRlQL63P7mmpYurL0gAmCDQRwNkht4IEmm6yM1XbhbIxECj0V/NopfGBsUR1XLWwFCwq9IeUwCtRVpNIqdEgMZSd+UGkJYp110Umeh4pt9HXIHbJnrVqQzv1i4I8iGUtJioDObaZ0AwM2lNG/QqATxuBTprkbQfVWh8KqlD9w0c31DQ5srjSeXjDHaQMBAFJ9POR3AQeO1sbHAM4khKNFrdy3cnupEJiEpYwdJ7LiManPnmv2j6rBI55LFcgpVijUuQpujaDMgurgDobbmEMx/eag/XY6R9+0iX32pEVneRrwjpByavU8jAVUfX3k6ERBT7Ec4Hjv38gRW/CmYBhWHUOcL2jsBOZboKXEgq7k111xb54jLqFGIvEJPoojxQUT3CE7L5BZUOPKMMmlc8qrjnwSyOSMbBoDejKfmQX8iDqMYL32g4M+YCSGC4uCkhhQUX4RDVh5cOgYHsvh7wCzFJU5Df2KK8kDQIsB13J2/iKUMxhW7jAFQYVb8i0kIdfurs9//TZNefS2mJh57s3dtQ/t2Ds8sx4hIotGQPz06YdKtdlXKRL1NuRX8/3r06PZb3397YO3tlV/9YsoPdvjt+8LtF/c2mE3JG/m01N33re3VxBFDYzbrZwWC6gMU4ZaskmqQzxEvPAThhVWoIxFqgpjAcHkhoAznPe3xn/3HSSTiMBQn7y0nTHNCeD5TcxlSwhFbwyLtiYAe1QF9P0RCzGfTxezUEBa6/2d82XfN5eXTpd52Z7/dUh0Tdm7hS1y4svRgmk2e7vri3mfX5njunm3cUVC43eTiYQ22C8880k1VuqbWXWzs6bU3MtTbqy4dzO2zdHb94cmng6fEQH3sfe2hkYc3pbp7xrtlSxp/UT27v7vJjDuAhISFoS0g56fSBmOl68nvi7pdCM9LKR3samMWrCur+63UWm1f4bThEFJBL3bUtYmhuhdQPatSkBSAaZNLKBkiisQOmd1KSo2QfXxoSIAQlj1iN7MaYQqRcFSrFsFzGMXHQsq0dAKKgQw3ZF2f2k0w+dVqca1ONf1pTRGCeklqyRQLOCaRyAAoUC+wCxmg4kRPOtaYa+ktwGpIpzGT8d6Ei6OAcgLmiBB5JptrdGXE15tTG52lNC7gQAbJVFbBkfjWvLthbbTQYtmmRyqkErheWg9GB9ncyL96zEetv/ZVWg4LZXkTx0Q7FnFJFfaYUWwcw7zRyf2eYovGpVMQG32uqqsCeTrlddIjKkKlmaR+F16oAEUGR68Q0RtCoGgGlz4FCArat50YN9MzOfmtIAXz3czZe47BGPG1MSAHRlCA58cUFBfLcxS5E+oLA9F0qmAaeNQOHOPmPhQj5Pz3piT01FWqetlSdHS68SS5ZX9MyBDOBgDokBvc8LEX//GiKLcZ/eRDpMdJVONPM8HkWd6g2kvFH5JdY6gCugsSEIQEN55HIx3CM2w77kjkyTn0E2vxhqXc21KAPGEUsUmesJKC9eQtM0faVlatB7WOOeB7iGdHte0bJqSJNCubFYIonscRE9y5Agam2DuhrQvSRarrR/jkQ40yUrYo/MrXUzzxFT7bkHx4WzHZ0hs+bgkb/4i79q3uj2hoCaKeGKTGdXiQ8S7pIh0Q0LDQHO0rNc0xPLgnY7b9dOds7zZURR18LQ4q+OQ7m+kMF4dXjQTKDbB7G/tL7tWHc2N3gdcf3rk0PH/4LAPhVOf9nbO3Dlu3fHdnOzAN58pnyDGDe/JplIqWwcXZxVP//+3tCHERBmkJs053Jd9M3Gbdu0oFxlSs3WwtdwaAFKp9NoC6mZQhdl4jHF1EY9LhE0992ar1lAQdE3VxL0BWhirxlkddqi1puzAHHZDsLLMh06f8bavt39S0sWtta/W9/84/f3//TP/2aO7fevT/WXnuxYdHWnV2LA1nygb18+Eo3rC4dHMj2E797cIaPrLJZejiVn+j2bT6vvv3/z/rs3M6Nfx4Mjx8f6T/n1ObeALABshN2JwRt8HLaapG8VW1v/WALHn1ybnG7PqMYqZFp5TrqZfdO9sKX22hFu4aEtQj58/ERaj45e2cF7X2pxMiLkjIyVsE69WrPmg8TRWMDCxpI/bnVX2VRoUT7CRm981Voim6XAtLE75IlSzG+K5YZT1XRinExzd49n+eG5mwaWFRb39SRq1wypL+DDT+Y8U5mmkcKMnO41HFU61VZLJiuofExB09zlU1X6pFfXEXhF0AMym17GAshq6znX/ctx1QQLzgQ2VabgCSQNQvs/MWpur+aIzNzFZQaGLVRsmg5mJKSYqsREoCqPH3BSEh4Lhhmmaq/TE6JIm2IJawY2mrDkuEKOPSfZpB2sQCLdWdT+xiOE+9gh6DSCT6o1RnzpvObydo3ji1s1FseWX+X6iRA1PrRFBPU2RoO72Zrl5btGEIwkKRJDaoVlG1YhsQsUkfsr8vWkRohFQhSQHmeR83hwxksGyDN5f/ejSET067t6FUnakp+GhHwAHnRICfjjr5f+Q8/18kTQRyMvsd3wA7LZB/QI5UFb91MiRyQowsUNu2JoClRupgpaQsbFMWvB1UrFmsjU7zgFj7gbW3ogTwBHXgqa8Mo3CM3G6wWfWiN4kMQtsQnOzCNuwAs6pKTN8+ooca54REqya3QSvtwA6jHipvOJFuU32K/C/fFm5GuaZziRqtDMuiNzF1kTgVdC04m49tGNFShv4sqrjdN6mmvPRyeW++cAdkM91guBrztdXNpw5/r64v7B1FI9d2eruLK1ag4l89TJsdTJ0V1fPn+S2efaWNahyaNJ95eXV0wGlbORp5jeVP7vv39n7jzWOZOc4bN2zTwfRp9vn+hTnfLgYtzncoZmhyWtKOJoBKdx4aNDzxLFi4uLx8+fDrdXB4YYVnsoxTyNqWl6+shDqn54eHx/LVgmnwZSdF2eEA7xSJBTNk0LMIG1ONdWkTbVWEV7fLcGIZ9pcj0LbRC6MRs2i+yYNf/UXjgOBrANxqOcDU6tOzf34sux7LCtkqUzPn3+5vTIt69fG3JglJ+MhTw8HLx+tXO4c+ZkHYf0rj/vbu9ZDMbN3TuwzNpve50emP1ZakhiHbVa5WesoLF/akQOEgOIGwrHIqE6AQbQTp0ZSRQnlzV2ZahZEfN6GnzdsBc2lIVwhZ1pBtkjxXqQ5uluXB9Y66BjYLRjzQrnG/F31Bc3tOETJZDMpLdkSt/oxRgnaaxSw+3pntqQi8B4hwKFTVuTwh6jNWqDLKoSygwLPKqc0WcEaEldXsuxW1WKaWPal4eVzPYQTchOLcyZNtReCL0Yk+wjGLMXIyIZkKAiTcEfqvNKdbJS2YegpG4qCtpM6nxLXzITlRoFzwSRKHWXGdYQ+r88GKTz+DyMTkpkO6p8kCew1a37IMfF3L/ccCki6I/Vu6gOZqVc5YADk+ENNSuPl+FVP+2EneF8n5XsFU0WoDWdoZvGPVGB0KPqrK/l60zP9CSANzxwWQGlJgXmyZe2B+lMW4Y/BiIY6tlVkZnDcJquXjoDSeRJijSjmKC+9WEBJoNOJKJRtXoybLA5do7wQKdrGWUtrFvW6CtqxEIvVU/T7s2vkp7F3ViixikUcsr3j/fjToAZTgkIoQA8FCJKPE6aCJjn0RAk7kCLuPK/PDEmda2hrSSyB2un5iIXRDQeh/MoIV1wNCKg8iLN5LqGgnceqgbi+ZKei1ZeiS+FQYT8VECo329BrX55zix/3HBRmdwt8+4d5EMscu39uZvAh6wVvdNl6VARasC+bTkiCg5MIAcPwskPjNRDZnqXQFKOHdEwZOpxrxv3I3YpsCHSV6f6FBICK22MpY0GTEqD9GNooNmcRQeheEnMSCrA6FEEyvvs7Jxvya2hKFvBJDnD1p77yGbnM7NrLs4uzVN89eZk5bT1hyd7Obw5PUFx20PsH7+SjJe3sOMbZIzQphvN2IlLjBkvwI2ZiEoq5XOvni41j6GmLzFWa9trt5urp71Dk0Y3Vy0By42L3G14aYtT0lUu5nBz6/399d7t9dnDzfn9xTc7abQBN4O7ztybhqz701zpchC6FNdrfAC62fIOOuhHkyZmiQEcj5myiGsm0poMl9lNm+vmMTm/l2364w+vDaKbXGYMgDO0cFnOSUrry8fPpoBik2UEduV2gOPR6pR8Oe3XyI35TmAQ9h3v2816NfZn3fQum8dx7pJaaCKEE4aarqtgkr/mGByiKHxpZ7G4tWW6lH28hfvF+/Z9ggtNIGIYSutclM+xtoMgWQpOIYz3GJRrlTgLVUa+g9skeiQsiGi2uNgkM5EzaJl62XkC6eJI+5i6rFQd68Q8Fz2qQOnoRKIE4FKXpNkdxTjmZqTQIgZh0T4y6UY6pAh9S6FoYbFRptyFVLAG0jbfR2x9y8inS9Gj5lNVCWyF6FQKNqYW2NmCKkKmYOlGVqKq06uxMCrvnpoo3pRSj4KepuiVQfQlPE1phugFOlUaAJnx6gWRB3tyKgGfmnEQ6+hxtp4o94TAMxMOBuzHSWBl0XsxwkGpYRQpc/XyRFZ3QXlwSJezWyiSdRI8B7wnNAcCtcOpVVXAnhHLOiDpf2G0gjmlaABQP9P2+JIuB0UGT2IUKRMIGE7RDG2fC6uHqXBxl4SaAJr1n4vgX+qCfdafmNRGjIgkubXEaAQmO42+IFpYBHFQFsrIV2idgyF8AaV4BFtgHePcV1QI1l7qF5QlG15qdafQ0X/mn53PICrljsuAaoxNACbCAyToX6BzOwkGFNNc5V7RKorPR+REgO7CMtRJbK2qPUr2ZTypdaXqZSuxJKIvYHoQDvQsRPgGxn4mxY4jUde0t+BQjfkybja3506/yhAm63rkeeFSvn5r21GLbJ8Q2rv4D4ZsvomjTT8o+5EhiZzBx8I6WBHGdQSgxSOwQ+JK1adF8kiaSc/jI9oYA2RTTQNiS4xZqjMJkhG2UknkJr9vu/qd7dM3r/QGvn3dMdaM7FyD6aoMGam1c9na/bO8jpFeyW49f/Z2r13lDkWqkjG0yRRH8zUpAlEzCslNFYMYOnsQfXPh65JDTMKymRFbtiZabwbT2dbZN+uB946kgvaYE7/lboFM7OiMQdRtw5uH99fnujIPtkG9uSDZJd5EVfGhWJPrZPMZSKdFShCTb7tTIIYOol6UwpE2/7qH/vjJyD7eXdoxe2tfN8U+Szs6AfzW9bXZRGtvj1fFUMbq724tZasjXNiDhkXtxkJO7ITxt3/MKebnTHvdsSHomzennfk4OSm0wCkAojwWEAjS70HJPd8c3FyfqYhEvCGzlXiJou0xykgTifb2Tvdl9qUK99paNtOzJst/9Hwq8XK8u3l4bPqp45GN6nuetUhUyhLYWmOsLmZonCCQFfWnx5PNUPZ3o5Ssj0wR0ga72BU9NiTyLOFRDaOIncTaHzTU5Q4LKqTF3jSoODtfUwlzHwrVadXoV6fmZv0132pl9dDMvgAQVacZtwnxi2eqxgxJCsQypZxAAJrOQ7LhPgaI3Qhc7qzFT9lVCOlV1k761x9I/U1FBL5wAPy1mpqn9dkaj4SpUkUJ4B9C9T4PullV4k5aaWizyETeIp3uqbGpMBndptdjOlTqEVX1QXs68ZazTOjanhYZk25UCHNANC2Edb6nJ2s6I8M4TApo+sMq0B5V1A69GFM4fNV9nSaRZTpPrC3EGs7F8KFAjSUhQWMtGuDLQmg53iTmTP9CvCgXalmryKqOpZ5aLNikBLWeifc7IAKYZbbkLqMP3eGbwuNf4h+EqzIgQ00b86ALfkYa0mDX3Yiw1au3L172Ba8rk8thZjk9siPcilcxGD/cz6tl79B8/FygoU09gECMXQXwNb789ClgtVP4ggKefeFK7KhdrS4w97TymbJhcHzzKqbPNXi4afkOpC1VWGQ0FQyA6hnRMU4WQQSQ+Q7BPNfI8Eq/qMFDV3fXIrhXpyemt+tQN/8MfR8em+ltNIfDkA7wIuSZjG76AMYG44ce6pRvUWOq5aXjKWxhIO1NLVlgnSj/IDkga2lQ4OFhf/9wdqNzjpVzqTbtzzw0fnw4vDW4bGja7HP2yIZFohP42Z8MA4+c2G4qu+z1Y8OTBJSgYj1C2uBO+02GUhFFEasC+/5+Nmd2SAtZe0So22bWMRgbu4cHduWX7rj9+u1xe/95Z2ULzSNT+7nUKonfJryb8iiqt2/Qm5MjKJ9Y6HpxJkFvsy6Lnc0uNYyALwwb92dOgAjY6K9nbUYkFSdoNunekCoxPDg6IAZJkMT6huhh496RTyYXbe++f31MkGgGZ/7Lr5+4ve0/vLWHtqyaKs8vju0BLeHIgZAoDF9fl3I3auGfDd6Mguy9enXSitvdlTlDFiIblSB28QJ9GuvNQDNXEFMDmnDfxKSAsAxPWeqiFneZhMQtrUTiG9tJcP6rVcc0655YZsb9HhyYfGRhg52kiBnDKhhFSDWSRaccp0Eq84s9bX/ke4qQXmQSUrrRBKxIWDONLhDvUZu0Jkq5NAcfpwgRLiVV41i/eiVuAzaDKkD2MemuF8zVq0e/PUmMnUlsi2AX+zB6nSZnBYNHzWCrcd+T8S7hRYLQy7+oNeik+0WkQpzGGueh7oCloMfHUAItC1ZUOnbDEs4G0AvsitbUmmr7Ta1VF34KqqQ6+061NJiFNAsOu0NSIjEeZUiqNbs2VnrgGRyS28wI1DJ8dD+aqtjOSxbGS0Y2Aw2vqW7AVu1LTFdssmSvYoga4KOhFyJkzRHJ9TTO4Gd2Y5kUlIj50VrEy7NGbi17DUH9B9ZYbd0yGOVJUGn2D6nKYYQiw0itAyO2Ad/zhfZUACjjl8CBLDGN7aveBVgN41ZhuKRgnOM5FPN0sqdkQMwPwJKpXt33OIEf11X5hSgxz+NdiEVeKoc1+QpapIMt75SCWePfFEPspZcej39Dj7iJKvGNJwsCl6sfHH5VXd+Q5ap67AyX6TJHZvTxGQA4EDB1KfwoOg/7N8xIebPp0ipaURPa5BFYxIlVXpBUOXqX4O41TknSX+ZdAkPq2/RCaWv2uh/NidKIiXc7DGBVlIMBLHab12Eusrh0ASD6CftmBXNEqOdYiGfLhCTXykwG2KbWosrd5tJIQyjv2Z3tFZA4FYYHwEJ6QTpXASZHi9NznQ9G3MoAQmC1mmesN1XcGZBj5J/2rEQQDWjClg96LFY6W4GVq6/bYWMDjxNumZ5ZvZb4EQR5F+GskdFrezvbooK9XUeW2WCrkUnTKR/gI2q+NvHenkcObPz29eLbF5me64tr851s9o9v1qmZWtPItOMzzQW6vTz/+rX1zNYSOhZmi20UC1th61QVya0GUeLYxEecgTBcUC2j5hh1oGIbyusbJKunTi57+np+sXu8ZysHAJ+8eXXz6uDPv3bqjgD9YP/QVBy9E8aF6bXu4d1333Etjb6YL2vHJrM++Q8pfEkbHtiZiy3wSs4oVCwhDzzV87PVCpbZgRaRWU0yQ8/si4d4I/bElsfkLALO1nfYpCFW38YacnuzKs0+siX6dMZHPDdkZTM6XKzsjTMLG0jnp/PRVINIvBgv4jpKzTkQzdqrc6AUaaEKBbmjKcn+SDjyuZHdYlr88l1U6OaxPTBAie0hKTXOnJBLQTHZZCAzrpm5QlLTFgifYMvtFJGLqBFVg4GyUEcFNZnSZh67O5YArRWhQ6kyi4TLDA3T4ZvY3AVwRtdigUxQiqFlBsS7OkPKf8tgphORlqm+SxpjFmt9THVOAsSK08GsPKUpMet79oP5bnFAaVi16cEwuCFOGnoyw4GQGuFlpP+onm1CucbwGzqziSqy1UoUrIpR26xPN4I42LAF5YCqhbRa6DRztpR6sWAew4BAVEUgI054RnsAAHSBMDJ0F9UA0LAAIRzSTthb33DhBt4W9Q8dK17B+Ki96nCFGHYNsRcvCT4t2t/F1ghpPt8sPgqeIeBUkFd1LVY2B/GFjcw03gW12tTXI0WFTbfqYZb891eeICOcWC3l4alWwHrEY2pKJnyij1HXT+1EkCqq6vkdnuaNKh6B4me3w0/l/WbFGU7XqmAIFj9JWwCHC5qgAxPpDBcGsSrQe7oDXKaongLXoM9DzoHfm/xvR1J54WwknVOOd54siWoKqayB41JoOkfGCwBRwcCra/zsKMbCEMYSUwfbYB7ga2jI7dYAxiiXF5LeVgPxlYcZFehZKe/mBTpZe/PJ5gcelbVmqsiS+bwGVj1i1HhZQCsNYRyLls0WC6xunCrZzbcwf7Z0ZvsZym0T69dazWyW0RANqdigp6bmMmfWqtGfZi8SWWsZzPQ0Bry96ngTeN/6bFyVPzESbqFZTtKS24dvXxzW8uXi6is4vT5/vf2ZGpk+22nD+2/fvP7+veHZQ1ucmthzfXlmRg/Xwr7am+r28qvuC5ljHPkMdrU04fYGeFkveXQGCw7q48OAbf3z/VWDEeT8yCz679/ZzOfb1/Pnvd1FVXhpe0M7S0zXTNaLsTZFysYRRP701LGbDkQ4ELDP7CYDviLNdQku9MoPOmnAHmxN5sHAIlPmRtxCuHzVPSE9Un1JFyuHq4EawWz/hiXXggDJDgPFu7uShPp5Ynw2FHF1HNh3UVfZPbY3GbHJRFkRn6l3kx29U0k/KTqFZeQSq8KkJGhEY3wAyaQMBZDBIXFdYEGOfQMZJ92J4Gm5xxuZ89nzvpeLbYy09kUCjJfyi65k9dLxDAmBNQV2kdmkv6mAdYBStVFI1S4pB/WklZNBmnAvgPvNVeQtJkkRGBhBHjyuecFhlmZ2q/aJLfUI8NhPrtEkAIY4VdvclpBJmUsP8Jrpow8Kj/3N/aS/Y/3pBf0aSPjGgvqSbOuSk+ZRtN8tAVCpOBLjajLNZZ1UFij+L6ZChULTaAB+wzPIhVRZqyijjFuKZ0aKz9EwhNEBaK0DKE0RTM1GirqT0huGxsEG3cYGhER2QyHBRJYldmm7y1lVaR4c8olYqB9L4CzZinnKxqJkQAGwIDJv4os0Qqn8bES8LIJotGSEZ5zQmKKe9CxguUpBj0cjb88Py7TTI9NijMS0omfHxDptSjIx6gAmUdC81lWRsL7wWrPzhPr7n72qh5K7wpR0p66Z7r9wJT5OkAFvLUYF/+PH4iynvIehYZIPmN3WtjLqZe1jWuSIsR4ZEiNeTikG0VcjpWYWhxtyh/Y0omBspLzEUX2e3H4svG2AAFmKv9rqJwUeaiODYPRxV8FegJE3sPaV1KkHJeqebNg/QCrec/mFfv01Ih6hhkRKNs0bYYZ5sRrGxparpE+5EEHi1ZktP++0zsDem+JiHHJ3H6JsyuXTjQXJIn3WP0Fv7ryjjkzikcnhuUwnl2Z52aPC4WdGOIkCnWqz0a2WPnE7VFB/AC0RuNkhyFUvKn2AIcDlMNZ2DuwAR6p39w7lTXYOX63ZYX93tWEHn9U+iWlX9ef2+7TPmkOGv337ZGiTpzEV04b6Vl3huR30HGtsEzX7cX733nwk+0as9g6bzX159k3OSNh0fXthwMDuFAKog+MVDonjHFiZSCIfL8EMhBp3yAVsZNzXDUUfSPpLvTTlaO3JBhgx13jyw6PNQ0/2M7427WFn//pv/ub49Yl+cim/yVXq2DRfy2wgY9s7zsYxnKDRtvcnF7xz63KLytOdZH2YOxwtaOxiVoLYpUTc6fOeBRi36Z2B622nJR+9On1jQ1j1swOt8AIZjSbDOk+8vidR1k58pftyGg+FoeQu/RANWU0KmuRxUpeZthetzWpoJ9EqSgNv/fsGt1IpNogF4A7IbsqCzcQ1u5/5SMbSLLNlZgmufonAKAeTNajnp0W5E1JhD9I0NUglFbeeJZ5H9tECJOSZa/VB5xiBNBGNOJ5MfKI/ipoO9m2zpfIkvPi50zcChWy43ozEdDy/pQ5P9bjZNJUAhsr5v+ZZZV6WF1qKrphBBrJHZGX1nCJtRFhbb1bCrDokK89UYaPe7UJAzaMQPWH00U6dWgOAqd7R0VMNw3LDKTVMMhvarpcGwcCuB4MmkTFQK5Y45JC8NwmaUFa2cfzhehOEpz1tp+wh0T+4WkjrTCU7w2YuQmaxoWQlyIRxYzcSazQmRBpYDoMcSi30IPLaFvZqbSxg9SYVnAU6xPL44UrXQU5AEqlswlSr5nvkRAaMCouggGsSM4AUBwWCRre3JSlAwmGAOILM9eF3jB+LGY2rZ3xXNJzf2D9G0HsCV1zSMIB6i8jr9yqXq+XLotGYJO9jIQECqlZnLILiMhiVY1zrp+tVa7KcZrE18IIN3uOlqGWoOxeaypnuCBPFkztQpmDqDN+X3xyqGyarL+hB2SN0gAkuZ8p02TZnQ4fdIbF13WQ3GJTsKjrBWnMeKFgolmbgyCCyEr7YAUwbgeWlIV/3hb9QqoFfToftv2fzb6/sanZr4mDDoMLy1eExDl2a2L56sg0a+OyepnWeo+ytoembdqvuE8Pm8G5ye++YSWvJt+xob5jz/hpWRnrH6zaaJPmQneXnkF8i0A7Whh3IbykPVnXDEZVHuwfHh6dvzMC3ZQQfIPmyc3zE6z5vGM7c4QGuLq7PL79dO8Xy/KvxYfxp4rq5RhQ+r9rKPluFmpq0f8Q3GZha8Zx8IrJvrSwJ5jBuiqDXDiQmTLeUYGOH+O2mRzIuajBly0zN7c2zK8cx3gnwT45s2a+r/miVm/3S7Gnh8AFVWC9NCB3EIgA38i60eHVSbJ+ZkZOTmdrZowaS7uxe59HX5S+PIzRHsXImREaUPIFeG34mUXjAUOkqTMI8E5aiyeoQmtFaVN2MslaYGAPa3XEw2cnp69dv33ENl9e32N3qNiyWLLstwe2pbH7sAiaaG5hHD3aMYqQm6RobzcI2sZuJpFKLTnfLp3RnFECTgKEJZR+TYyYlxSuqJb7aYNGpfeFhHiNDou/uBfqUD8rtJ8b2NbLt8lgnGl9L+YMok31giMcKuY4ptNK/ArukusaA7IoqU4JsY/oFQb9pWCYrfP1SCYQDf7/+/O9+9aqJoo+lyl793pPvKVUqBkk1Mz/aQUTwAVljU0vPZS4yDiHIIaRm86CSPiqgsdpihQzb83IserCiMBZof2ydgnUOvKquuW6LmVICfF5VEsLjsHumJY3mkA3h6sphZfVlgNqSsOAx2g4JMN5VjFK6vFutxyRU0HBEw61BBLfUUIH6lSEZeGz30KrAN0GpK5c/qnIfSlqMlLBcSFYoEOpxHPJVsxBoqD6E12QAqdo9uAWqQiAcP0EdoxxyK6CNNCAUkspFFrBzDFz0jZuRX0jM/KESNUELzqXi8IEkbFAWGIlBQ1KxS2ASgJEMwOrpRRoWouFiAmlaTM0OIAwacdfzEqfYeSzB8Hzbso0FATBbrSjcAo+Kln2Nxjm24qAOfoESOdOb0xoVgRhf6gFW3WcG0iwRRl9kh34eZjAlZ8bjS2hvm1jIKpkdmYGgzaZ+GWZgmK32FLQ2iCCGbSiYd9QY/8tBFMeKVe9sSxA+aD9LZcX01yGnoEz3zrr586SK0bKNjtZZapF8HRJnqhTjqdyh5PRwbf0K323W+aRncLC16wgt/XZjAGVwrV81Yaml45hihv21vTg9wfEK/li/JJmBtEjKBNCt1XPL0/a2V0d7J6+3HFN7/MoJvXZIaFW0Upt7KCbKxQ67W3/46Oe3z1+/nJ1/dlQWQTYNH5uJSePKa2udoSMb8uq1lcd7h8c7dn62GGxLfzwfUFBvwsbtjvEBe75sOIXz+sLyXUEfpYMih+gQdJl3YzAOxHL8VvvHrVZr57d4hBJQE/7oinEAuji8oYlDUkX4TVve2fV6e+fj569SU7j29v37+g13OtJZjQKv2SXYPFdCJMOEEfAiDJO31jUnjViRZCmf186+on866Xdks3OWTSa+rme8duhEX/s8w9f03KdOeRMDq8b4xphhm/KWiyjckP5pIm8jhPWFFSDQ6YK2xgw0PkcBxlZT23Q7XiX8WFH0SbfAAOR+iFQineHhQFmXRnSVJtMAR82qLqDWcLZZXfAVMSktyDEuoLBAhsFLsbM4UamsQMZp2vBMWqZ1JVKl9MiXoraoleD2jwBkd+YrHavLkt0guNmO7i01aWbsRXVVIwXOARAQcXrGDTYLKlXl6YyjZ+axOt7Bx8C4E1btzUVz5QzFBzw7mS+RNBiXCB0jS91UBVrKiYiRCkYAALl8Wx32yOaHzUnnslPazXplKAQ3lScaKJ5xgywd9FSHwsM+OMcZZ4nVAxvQmKvts1dFFZ5GNBjd3Ebr368vQJuXDkJPTNH+ZS4LOjwM7upC1j4kMQEdUC9sih9eMyNpwFAoShbxhsoCygAbL90clfDupRVPE/epw/Cjla0TnaueyXSreVKBlkDVbiKJU+UxXQBptxv28QSfbcIJPpFLAOb8yAs2qwMkiIEfkg/EL7+bGOPrIF/VwEOu2ojxQQBa33OJNaxlO9kVqCkluhG1eGGrqYYJvUEjO1LU8RlspsGIVEOkUI4P9eRh80MTKzRupk11AHJ6FMw6m+hjdlwLt4+2crnjFHKN9abFaFrdbmMHwLCuWpG7aDmA5a5j6VL/2McFRZfHetTQ98llDlzROg6EC5meHu2jcFgKf8eKJkS8vRZQixadrBKe44/UN6eNP9wzfpg1/HpmH1EISMyg2uBlSNmQPMAYfycBbO7vXJ9fJMSTJ5VNMk5mgHd9Z8VaIafNoXf3T1ev3+4evZLoepAbszXD/YZVYR0AYItrOrhlA+pLO5J++/Lp86cPPkjm3N5ISVmSe22E+fCA4V9dX7GKj+Y7rY4PdGXotVW72QxCa1aOqUQ7NrPDQSi2UgfTWB/rzIw46knc3Ftwm3Nm92xYB5GWvOG+7P/xgaDZEDFLgfw8Lk8g5V4kXT/PNKUdaw+w18U//PEPv374QDVkPCxecCAjzl1ecVS3CcFksQlsB3TeO0BYp6R1Ffy03yIKg8vp9UCRHDS6hjcxloWUgkiFgov4tomftSGm25aPLRbUgp5WkVcyXHheTSXQiiJpqHe1jEJl2KrK9V7Rxa+/3tOdVMEz08usZBdSKMLAOowGZSF8zJDSfChkOLQ7VpM/ZdKCpBgoeCqdOuF94u172kxIJxAEGGqPIjO36WZINEku5VNr7qGLaWVWYAJpYuQ56bk02l+fRWhaLP85hKWPYV7TU48PioEsNANcU9Siu1pVJM2ujZQo2pQ1GCYAHK4LMRnsRxlRLyP/5lnlwPTe2NHmEtwT4cilhqF5pn6IbPJv8VkD8IWD5Xm4xprKgtVixmbEtHa1vFyA10IQ4E7o0Fwdzylb+NmJcbo/ibCOnEw03KJt1EInYwvRMQoDa15VHAFyNUNXdiqU5+VDz1Z5tPIf9PM9WH1XkE1JerC8Xu8y5jNIoDsHD7FqSNxQtCdG2PoPNLWN1dO+b+qZ+1NKnexSDCg8nfhkRMxlrdQu4cmSjRQGDFLTk8DJ6bCyAQ5Zrev0LJF4Hnw4XTZfns0jcQgwdYuy9IExHhK88Bi0I0d3kpBERkmt562yn64UpjabBQYL+xZSj66k7YIySbnRYZIAzPiN3uryBL0kRv4AhDXPj1YgSascbhxCpezP7A+KdUxOVifZ5kiQzjzIi+tryfe9h72Ha6eD8Qgd5KkXMmdf0AqWGwGRKzkkqaTGOIVJcna2kXiRWbKB0oMWsxbr6w6N/fztTOfByOi+46nMg5Rfv7pkHXmCcndTlXFYkEp9uCsFD3phqHEPcZ3gw8aTt1emUArbCTj/qKdlAwnbB9kmDHS2oND0Hjdts53Hjb0NZ5Edvdo9fL21YwZLp4DJmTAarfza3JZ+t0uPcwwdjiIl9fXL529fPl9eSs7oIYzRsCLBlMcD5/FmHGTaaV40l8gFQmvBViJuHRQI8opXX/SyzE4pmKKw9Y7seyGTa+vaB2svJHHLqZI/5+WAXkZIgswczjpbmjTzzxEsoSbsdLM8CqxMu/Myp1aWyln2P/zFD4wxABoqMCqe6pqPn7UnVKaEYisjL++mB6PrzMw3YJJBS60ktKgLR0AgcJCBIeJSkqpk/ZunSnD1onB0QgbMxQn+LIklXfTxmXMSgSI/UhI+gj+COppesVF4iI/MJv0v1mcBITiyg4l5Q41Ehu2AR1KUOhTaWeQvFOJzABfQmX4V+iJFPP2Zyf8sOpvxGk2ClXqAnOHQWmrgBb4yesiWbSljX9o9E5FdQBXXFrhnUFeTjUks1ru7LBwCRZiqBt9YcFJZqNdUrgppiz1Xm7Z6hL5N4DV2IycB0QxCZdwPz9rUcgQI5XzXgJPR4ZOFWAVLkR7wFK24LeNmPnWoUYhu1UcJb0hYi8KICLRCkD0wEE2tQACSGqRPut1uIWnQZrY1HoKTHwueAUHkMZeSLVhn/oxnu4Tz4zVDJSRAPjRFXABwPGjsU8IRVbHeJ9P/UE57oVHgyG1kkgbqGPJCt6nRxaIK8aRWUY345pKyhsVP5Fcxj1QmXJBAS9Xv+1DClajZM5rK2vZAwPCHbahU05Es6Vdn/iAxq8o0nQFON8awVXF/3qJTnQ7VjPsBw/iCLsNN1GF9b21FaDBWYzowqIBALFdwYWLAMH4KhfELfCNZUXMQUXA8ByjMq1AXsHGCBVEcwkID39SGOIB6oeTUlgKkYDFG5ZBLcPGmoFiK1raet3oBuLmX5S+4NytUtjm9zZqovvx+BFKLZx6fr5/yHEYICki8RxHGFgRFl3D1jCsmv9j79/nmUcRbbRgn8W1K/J0lrlSa2cLPwvkLK2CbVHpzaeDBrsQWejm4Brmkr6ztGuonx9yhZLqKpNWfHKhrGyJZl7LJMixGVymxwjSDQ6PX5Cqru3+0uXe8tmv7hFdHx292V8J/R8Cv64JcXTeZblvC/LYVAm3xf3/76bePv/36859//Onzhw9piMR6c/rvhd4GxyM3ZeMszd60fcZq9+BoH18UAXSHy9/dtOnOkbDbsevPj1YaJ2Ao37wuxnfrkZg1WQXuCIjpM5FjxYLLv9vXyEwkFaUy3CL0nVnJ+tEDcbyOggmvq33HVjLDt3fXh3un+q2GynHw+uqKTMgUWfurNTDnRsTogSw+TXkN55EDTMxI86Jdm27mhP80GgeNEjlSxTwl8qvM4FVcKl9Xpz9b5ZlWhnS14QS7sM1YKluHQaRkEdfCgGJVbaS9DdiLjTLQ2QNEqWQRRgaz4RoPJCddn1h7tGzkdoPNjfOJV4Lpb2xisJBvz5V7cSORHSPA4DIQSaXOKoNhWH/UO+2sntR2GEM1/K/CAroMMuD6ViO9AinjGFqskfDjXkaJgatcJiWD0RNil4xcGq2Y62miD/OgW74PkMWT1VtToeijinzy0SPzrM/pLP5oH40aTVEqaoIlAoXN6PxgR1QyVsBwS+hR8AfCtLyWywwhuCbHni4dIczIkwZqeGUq8nmL1Xohy8Bn3QIWVkPYEirjDBiB8jQkckUBz/qXxV9wC6lMJT8z2Rwk7pY6lvgh9+6RmD0jPHMLmEoElWfQnzkbdxUWnhxREQn7WOX4+9JPKt/lUrSbe91VMajYerI9NMpiM1nysEgzrTceBaoaQs0W1+hDcwnVg5DNCLXhmulu7CaYotWApa3WrJHbuOOS+oMbJkNtUkeAilmk/OaSG/GulDTPEKWUhlyIJCYvovbCflwqq7QInKhiOFiHqgANFqxPxNRMi8JzzCO7emkN60F8iIa/CkEqjeOqwIP4bU5gxndTMz3OwTTY7GRBrEUNdsM8OX06Khvx8uOzV49uXyOZGSzQAz++IUBjIiRO+llJ+f0dHobiobw+h6FQwqoF8x3GzNih0/ihbdec0bgvziBspNa+aqJp2fVnRwG0FoF9l66oDwEVUENPu9GI4So92KCy8WW5EqlyYi8YaGdmxqgTfXfNfshd8C9mdh4ebh+cbuyebO+/2jRNZ3PXvHgu6Maxw8ZMVWxnzQ522XYk+qR/RP9fzr45ocXQq4lMKLqTQSurzs4+TN7M+ivbRjRqrXdiwMHZKjjjhEXACPftiqrPY3nWw9Xm7ZnQXC5eAEewmU7bbfBhzhk2j6+pM43Yjrbwj1BkhWyRKuNSiBc9MLVVyJof+5SYNcd/rZEem7ZZ/Fd221xqsuv0MT5ZTsteDhYQyBdYA2Eo2GIx+/g2lG5OKjlJNoorANv2M0Si3oW2CAnuik+0xathJmZxAh5e39ppUpYZn88GM4w5rxm8cJbDkllyP3mrtyMIJZx0SudoEdQsZIKbfhANKKRNpMgDM2kT3r5lRRYjy5VgjnL1bN3iSrhNlVJcempZwiTiNaPLqO6gbeVwysSSaUrV1DPy+kBNi3wMYWavNO55rAgOBO99tBmBckWLtWzabiB5UwHtVTqzK2ZoQetodNIY4Clj1rMvU6cGMwLqzc9NrUEGhsYh5lkGJOsb4lkRj2djuGtdrMgwE37YK7cZf0xP9j1vZL5oQgavJCPO4o8Ki+6mpwl3S+u5g4IzLlXroMh7pLR9A7CmfZyp0r6DLyQGBZdjDmAGFShrm5XsbtxSgaLQHn3kSk230ji0J/6uluqphtih9v51BPdEPwXHXQtv9ieH2TbIWJvJ8BO9VQaKnMGAgl1D2Vr2YO4Q6FjW94lcsoSehC3GLw8FazjH/kpWuIBLu4WWDYgKPuIrUYAiG8lOTTijdQhAimUNKjDnZ5bcEjx5BbWomGH1MVRivHYTpIEeBzXPWuooYw/xRMiEQrMDS0EY/ALbQyHSX/FL9HYH1PSTfaKT1RVQunvUe5xQsuha8jfy7dHoulQ0+CZWEy/roGtWfTNUYbK8GZA+RwEhHSFRlYwEcaBLUgUwfnw89Ai+sCVkSDwR+OtyzfQHb4pN+MUSRzItAGCINzuQy9piA63lB+kJuWFOqmfD3pLa9BDbJkRFWaElQXdclAYszYF8I80CdovF2GQHqJvDY2TYcLCRYfOC1Ny0Ax77JYoxW8mhlEFZD1vax5m3moItSdRTMgy5t3t4vHd0urE62djZ55xYe5NC4Hrm4CsjaSrb2rKnjXMJ9vZl0Z/vrm4629D2cLpEByvQioANOc9WN1lC7LBW4sgBKzpKO9uSNl9FJU8P29uv7uyBdq8RMuPKYwZ1f9/6g6dr+3maf2k43pC+rg/omAEzAtNitLZkr1y/JWGWVjFkSfeTtW4m4PM3kloSMylTHbXYTjIUQI6Eszybk0NMeDNuv68/J3+Fu3ZPwiNjy1axqVHHQwZ/OJsrLQCWxNIQPjFmO+0ibimxNtlfIk3mCR0S6gaQ3ZFM9lPPZ5Y6Pq6bAUU6SQD53n4woUvyDD/RgugT9AxqKleURm8FogWZEwt1AfwJLn0oRNVejCPMaQOdhqpKwFkWQQ2KiyQydmlzd+aXknogXDw26jV1Vgc/NJZaA4NRGpAH0FGg+4V/Hq0SmPZh4t3pGCzJg8DPLLu/VF+haq83M815Z5hiRNWmfhWcwjAcm7BYD02FON2GF4K4mRfMzi4PRQbgT4PqUce45xhRxDa3Kk1aFc0+TEOBSMVS0Tol9MTDEWQMCUB8HZMj+lNVTB3OvGQ1AA7IiQLb4wVZoOdhTQiklEewuFbPosCzGS8sGubo/bLAGhpiWAmco+V/J0uj9RipJcCFoieb74VuU2UhZ7Ozpx2IU4U6W4PLAjMzN0/VZawSZiz7bzKEjwjbxarKZGpbTZmA+aZ0T4BhzLcimdveIYWVSRhtaeMW5XqvCrZ4QieKsPglNQSYWgVJJClL6n+tVnMcUGW/1VNb4akJATiVBgO2kT9Oz4KqmOgGNS1SyReoIiCT5iiuQqpYiFldgJHi5PLqv1UApDVdS8qiq4vqGgxaOyp5AioM2LZOE5T1zIbuQ3RGv9LRn9kIXu2wvtoBh6fYnzJJbNakb/FUT9lscYFvkz1lNIXwSXD9AyZAFeSiFkK4uCr6J5m+0dacHniEBZmpBmkbduM3Hm6ETlbYEjkBvdW5AKgXf3F2xWw4lIzScwBMlZl71mNJ2qOLF2tlGoxp/gzrSnrCvMNruzHfQBNfMYGgUAJrThLCspIkUCuO5T06ePV+5/B0cz8HsLaxa26qPfwfLRtfStAAAQAASURBVH69vsY0iSY9gYuzb2Lrh0cnGRhfNTTipgPZN0wUYi+mtmjhblZxfePk9IQxTZ8erNy6+vL544dfrNAyO+bI+ivHcrGSTuTlEfNXBwfAfbq5XNsH9KWxZJqGwDwJMpmdwxjCMZ2p0z6nRBkCQUZ87pyTXVu+iVtvHL9Rbw8PUb8Re1sricwLX8TarTUuT+WzgfPWxjUd1orcOCyQbwzF+gPSbn6OWeSN7ow99cFiuQYPLLfYhDaZSK7rRCImaXXBG6+K0XZJ2nY6CGdsGUC6qP8AGH1O8w1gkpNPN9IuLU96VTECiDVZ5bE4wIlJib+WSM6iC0l7Us6s1hRU+prqUhxRovdxXKjqwThWdJ89UY3CSZ86Bcj5msbkGctFZ9VZMKlV9RX653YgB6HwgjXjMBeD6CEiuLwkigJotH6BiGT5qloFAJg6KDn6P/CyDWBhHtnExcKMXqfDAKC2WlugyTxVNaMAGhXlA+iMK2pAAbJHRYM0NWxGBbISdtClj5XINKL2iwEKp6w8E20Z4OLcdP5Ug8zZmyx2tiD48Q5J86+4ZVfH7G3kGh4MFiAa5EGgWC9XAJQ5BNlgF6BlEkZcmWONm6SlhRDuMmAVTuuJqisA73LNJOBVVa4m8PTFQjia+uVE0EsOIJ6ixZi12Ac98zdMMmFTZC/qixV0LOTUPhLNlwWRqZdEw7brPqh5g9mDm9hF05wn1DySEqJCChCf0BaY4IVKjXN/zEyMcTfGIA8Y69EMKfoeBYa/YTP4Q20IlqcFhqficoQlD/MAruWEgBZNQr67gZQ2ukXK0bhGM+CmmRgY1A0awH4vrlJKHdF6ZLiA5q0zHUBjB7pXWYOxcGjCg/b8aW3yMMpTLQbYrzvsiXcBfPPn0AHBCFWQcGk4GVNiah4Ie1K4GEyC6VUMHhlgJ3xv4RrsWY116wDQ3n47hcrVYMq/h5z0ssf4k+QCXkPdKAzdpKHuC10DlSFYvRWrvTgUJhCYOGX7ZSmI0EsNkcCCpf2tnQPTPVeHrw+O327a3W3vIBFvZpThUdklC18tjpJiSDrhz1jJg622VltWCojtDw9ZTgPYuw5kEWJ1EmVbK7CnjXsZ7L17+Pzp49mnTyQ0z3Z3++Pa2vv3bw0y2InTEMbR/va7d6erTjuQe9l7PtjfsFnz2uPNRZa4eUCdcbZu44bSbkxl0xXnuDt0Od7Fcfbt8uJKo5WxfOFJbHHbgrg0CM88XgeLs4HCTTWgKtncLjLHvKcYF1WGyT2RmCZP5UqSiiX/2fhuloA/ca5NmsiK1OUe8aRiABmLEyM866ZcVhlptkatOEQHccvoEUG42zT0YRm0kEZiS6JBb5vST/tjK9L/Ghkr18ShDB7ZptheBGDazcIAKTAb+Cl9Wgfd7DVYTcDS+ImTLQZgUpy8ZV+WCWxLYAtOQKpx6irPoYgFdrDM5hJqEhgwmaQCpVQCYDWeDRo7gIT9BCQjBJEGOBP7bEaGxfOaHduujHt9f0HEhyqRYkh5TcTiEiuKCEV8VKTJ4hxteGQcSgoFwLwiCDiz/nWGAgngrozuZyKAgal1y8cEBTyO83JIUU3BpmoPoAi3AL0q7b8Pahg6xxJwaiBY1E82tANgHFBYLYWxYSVp0vS+ak07s4BMT+QZC9XU7WqviR5emDnFXQui3OZQLLtYweEaOShODD+l1O9R78oi1NhBN/mn6FVIsODmPcvf7+A4BgiGQChSyybO3bCOQPn5IIeI3+Rojof2JZRn6ogyt8+3sFJe9aihBjjFmcxQtVa6Sn6vaf4nI100W7GJ5JBVecVzY9nESbyXmqzmbjRqF0fnqex+PIh8MFUg8woziYIq4FaXoAIxQjDhK4pXVpXtAqS5ZBPrfUj1XkrF4xp1peIgVCml1rSAWxo5tpRVk40xNNJs4Topk7KT3XWzxL80cVl5Y5dyHeMixOk2ApDSITNMSJL7uO5oKjloLVLaHhGLtZwtF5CrxkCrzKgx7BxrtWt/zb0Vu2aSPHhSWksTyEI9kOurRMzQgoZp0NOWbUDldNp6xqGyzw9sq0ViYn7DyirPqzmnZPfQyjJzM7f3jrZWh3tHr7Z3jk3wd9MJXNf277SY99pM156hJJkz+ijM1sM47JhGZ8jbS1NLNvIh3w3zGtjds+fxEWCvnbvlJMTbazszf/j1w5ojFDcfr85tE3RmZzpO8/z8k37A0d7q9mDPVhCvbNncGZYs9YYOhAHdyIkyJaJTeriPFSFdo3yzGSpXJ91+zT+V+jVTucxLobNDnk0aZMHzjfRPPhDeSC4l3ZmSRIeJQQvCk6Aw15FGGSWbqOUFKSJD2vTuYKlSv4jvIu9C5DI3Pc+uE616BmAmQFknEuSSRFd+PRUlbDrJ9csnaQ2jVqcS2CKD+tBgLYcXpvUhxB1Mbswil2LP9FFLJFARn0YXtcOrlgbxfQKydpRQ2dgoSpnpAYr7NESRxDo1ZUw1VnK44I1+j8VgtAb+yAY9BXssnZod1D2urnBcFDM1FKv1T29Jq6OkgemD5tAw6+ZVVWNx53JXcJGadlX5NNDnQlZqNcMG0TM3Alolu0srB/Z5pihzYOkOlBvYm7rq90cdHB5dXiqu+bx5PUjWZyoPTBUjenzLG2ho3mQySsmOy2PDh+D6UIxUxGwrx0ZvAoooZuY1uuDkffQ8AwfaQT/4md8WLTJ9WAG2mlYkTgKn5iLYYq2BoErv2iMXZB8ES01MB0oi0CDY9AC89iDpRwX4eetDPlPtBExLHh9qh6xXxIkVCvm3XEn+55EpHFRuRZ+oTjpHaJJ+NbVJfZSOeEKy7GO1dUUzUyRvGbbZo3CaBz3a9UEdwjOyRMOXod5y63VUQUUuaUAuITiTYB/A5U6Pa1VNU02Mzj8ES8SEcM6gIlHWX3T1einupsSM3Lmi5GCqKhRCbI/RbwOyxhinjepYGqn6gRuObERZl6hTATJFoAz3yci7QHiFOvWTi5Va/T+kJ5x4XStBKINUb5oXyat4wbpunReKMf4TRQJZsE4kVzbPOThCaXxQGzNk5lH41JbdEcxs7pG62tnKQoQJ9p9ury7EQsWZWwZE+QXzXhwPeVsmxDW70pses+/Q9dPt1cnmjqh/J8YWHD8Y8rWe1inkEdiGOZs7uGUW0ZXegwUGz0/OJWaiVgeHB69Ot5xqf3DKZukj6g9Yq8UJIMPB0f2nj582b7aNFjuo/eLs7vOnM12QThbbfv52fn57w9pX3/rDzfX5+s2F+VSbKx1ypLo39fPaSHDppMP9pzsjH05gh24JeowinLyj3v7DnTDWkTN1Sb1M4/HVgIDTOpNlRyzwpSW7tGETutFC7Hbquj6C9Cb8OnBGkUngUk8ylGj3kmRiRuLpRP60hHsg5O7UC6FAO02ipTuYSIWSRgSPxwl+o814ZC1kkyPELXmUxcTzV5mvCd1CyIirS3PAKpHPCGUfGsjU+Ihx6pWh8I/1JqSKaM6HBLR3t6f97I1NllyB9oSpzN2dnZ6S/BQFrTQ9KpOzyUxOc2oHuIcS1cBT47glMqABV9JoQo1qGplWl9aH1C7UtNshlkohVGoyipJ90HbkXa76lo0cKgRUODQ1NlB8zBhGnsDNjg6pliazcR4edOsXeKRa6sDl1DXhqTplirmn4sLDCX6ix2DJZFN9I0O5idAyWa4qxwC6MEwOOXAgUjUNraadalgKzLIJQWguRGESqACuczEFKYGiZSgkSvBhK6NxF0KxIHbgwXLuhRwACBytzqdgUm11RAARatkHX8AYcXzDoLKuIepJbPR0+CGGqwNQrsCj9Y0iKJNRlNh5NVNthHpBGsGqKA8fRCFOzVRYYiRxSwqJVMM49bhN5miRpmxyt1FQ614Q45MgBz4ANhcX+cEcIDF+jLF2YlxdZm01yNcr+WP94ZuFqg+2cdeBHCLrhL3aY3Qs9c//iDUEia388iw6rQfmKtKmchFkBEgaecQWWojWNj9giTRAhXuwxWuECcHmlruLitncVljVnAonTuwwQ8kEu8XdOfvRc3zkRIhO7JqDIYEagGyLktbTytEX2ST6KlELAyYKbpfOiawpP+PGuLTzg+nnE9XiqpFTY7OzGHaGVnEhRz/opcFPDqI1BmvPCId7rcxlMbvedm15BhP2ocScy9E+eOzq5tJlxowcOcgGZNu7lnod+t1eHRptuJabKSS8Ihx4gBEdjdiKh72+OrtKEh/bCTHGcW43t/YI6nSXnf2T07eR0EZ1i/VvokBTlWRDv3399n79h/2T/c8f9qToDRHrHlyfO8nsWz2pkTm8av18Xcw1pxvL/pPTtftr1Mb9fZsX7droVLhuwnWCLY7nSIlIs0za9actGSCCnHIAOIfY7gOmzsTDY2sVLq5u15ybdovtMxJIYwRXpfjsos2XzhK8ZoVl7JJNTTf8pnDCnGAig2bbEmeUkNG3Lk4mVmsJYu5HEIzBWwYKhtlyKIwMduEVnhRjNYvMnyuJzJ6zAnY58as2rdOtFGB4skRT2NohLmsayhCvjXJNKaixwNQpLOeWeD5b0jvQ9R/rnPg+RiCkzCaPKRl3Mwe4nDyWUYGBDaqpgrh7vEE2IfSLbF30YtVG+1SJJNmwrMoApIZiONqx5MG6nR8EH4vR/y4s8Hske4UYrB6MJuacptOz1DH4MnJ6YDvo3U6TTOtimIAyH17qGrXuWt270dbwRSliJb1BzTJTkel3U9PTcHEyRK0Q81Fdz4zZQTyKOTQGmqciVjTN0EaoqgqXqkFJmui9wSlXx+nVdFKjt5+ZEHdMpyj3A4SgD87FiEu7ZHHHMNfhE9vW6kJSpXzIFEaLMV9N9QMHMqmmBksXRMasDM8B0e6KtVv9pMhIBLAUIGtJY+AStXDr8lQ9vFmqHeSiyBDHIzmEwBbdN9dTU9Mdk0ouyowMg/VCACCBOpuPFvBMQH0ad9anJKn+XnRXQ7giMNiJsPsM1RQIwaxwKI4UQisCC4A5CT0cDcAoElByylVufUAZWKdNcIivQ9I1QgUnvgEvIx0oiwLdi7tkr0d8UWcSmdTEiaFLdzB+JD4IzRwwtMscOLcrndcIkUF9ls6+YQwuTWODvUSgeZH5xF5IHgDZheqHMtvqTNpcnElSUOLs25e7yQmpZZAwBKppe4FOBMhYS7PosJfCN58HPG3eoPN/F8BRK/ob8OCTHTQmEJmUDTd9K0KmCpYrSL9gGdNvKZqxIR2LPefGbK+klEzxtFhKpgNLMCEJpOwsZJ2iJzvRWQdwcX/z7fISRdRg8PTySmp+/WRt6/WpaT5HN5fXpvEeneyHguxz65K33tuGCDFsvHl1ePr69PHhr/RLbq+v9izD3TswzVLtXNW2LsSh3TRm/6y7nUvESti0JAd1fn3XYS+KZU6aZBWmrIcENXtKtTgphGIaZXCIf/QoGpBLaSge23V5XLAHc/M31jZMBt3YvpGpMqsKnthHCtsR9GXLDOcAWCxq9CjS1sFFjaxWvW91G6PHSoMnZC/HD7jMnxQKDYW9J+pFRsQMq7vDITVyXa08SsJ3R8gRu6RfvRadKoMWY5hQHqaLdmcGCChBBfnowqJ6YxvSw1Qpwz8WLYVTHWQ5AT3R9GACMqJIRO7vrlwAbbrQRuPmk5HTfMgAS0FHSVILMOcDyvBMxwX68AWDBt2kyQldGuVfvOozAH3MW/jucopFy1hj9BtHqYGUD0aqnig9tPIrUbFKqKUySF/b2bxitakp6oujgzLysEssf72umo/OAxQ4p9vk62gzp1JyT5scakDVcARWafFDhjGE4/C0APiitWoLzgTAnSgVOUE7mM4ba5JtDOuwiAK9JnwM9cJPhFQqUqXa4bjAuzwVjePgkMDjtZrRofZDpMxi7iMfB4fcV6XyVm0NbxSrGhO8aPGCciMgoHR9dvxWo0WwkI4XI0+Vi8RjUAlpcUtufBDnvAAwCREiC+6cWizxM1TD25JC7rgXizNYg37z9GxnqNRkxbMhUuDoFlVgBibQIzQe1FfwXETrRm+RzMURhZm5gUOjfln6aDxUAhTX17dqqRrr92jsAE0Bod49vz6gLAcxkUjBUpeIzb1dA5JmBZMsdFOLBxbe9jWIEbTeLiIJ8zCikGMosCYJxvQyGWIplRAjh32bGwoMAJjsfXxijRjoSigBXeWMo1mDOQjuur1WxJ+sv7mO10REc6UUkl1TR7bUUMiGRk5mbA990ZBj2O0TxyrtqkpHgZ1BCGdaqacdNNXWctBy161aMHImXcM+wkKWpIC+zf7KEfErW86Jl/ffJ1CO0r1pfg4VMT/ueY8Z3t22otcYgK3xnUoJL9t4XjUaa03a7aag337U+wc0rxAk/S1LCT1i2/ysMX1yE4gfAR35a67P/ioR5uMub758+HD+9bMlZ2YXOT9B2gc4fKDD4lopdnr66t37O/uDSkTZYu7r5sXZJxqMJRCHgsn6+CPlRqz1lrbNTgLxrCC5v7suHoovWucckVSxOvv4bdgV0y+vWFq+wWLg+w7y3N49Oton3cateepRotSwkRkjbZQj+6EeQp4pHzh8Nu3dqmoT+nhOCT3Y6lhbRnBtZqmdKywUyA/jaLKUNOFFw0gc1a5q02v2Fy7Xl7Z8tXS83TKItQAC5EnehDgeZ4KyewGVSI59SJEnBqnfP0xAGAHWKDLdHI1M2Gu83Sb4Gfd5K1WRUqJadLLpWOnyo+mwZoJyWgFczmNmUq532JHOiJBleieZu7BSJtjmAV9VMWmW7M7odfZNmary5irydcdVOhqOfIlWMqfZIv59ybuoplG5KDDDv4MhtdBAzY2RyG4skvdyJcsAl/pbaOXxeQXqaLN2yff44+CfZgNIyfRoDPuYci69HiR0xL+AU4KFYm6N9Wii7/VYBns+uLldDE9TmLI/CX1yUmAC18Vuht8LHD2Yv43mOSG3FvHwhWHwGXtzBvNSeqwODOqK+gdHMQh2FkbOhgS6GREl+uYSkKwag68fL+0sfyiqgMjFrtgJS9I8Bo81b/OLQaRHWvE7dboWPOoJQ8iIKUwqdGF6D5Gpj0uBYnnd8BiO5NHE57HmPvSq8PymWmgUBbS/GPZkicbWIh2FkofGIcirsm6VHBHNQ4fYi9hU7ZhvuJBYXdz4MbSdFhVUm4+xHIXrckWqZFJLQaYVNPMTpqDXr9OAMuNYwIGVJIf8Ydz0qkuGJp7WJJmTU7pFkIjrBHZiTBtYdsoh5TEuwBL1shBJtEp/OE4lG4ewNLQ5vU/cOPUS1ANArTlLilE/TGrhyV432GaepfNTTMgwssoG8SJHx8e3t4eN/Uob3DzeXDNSzFynuzSOKo1Rj6UljrJU2aknJ9Y60FAXASxH2/vH26tjcx2+XNzKwT+u7d62+6qad4ws+4ct9vG3T44tEZwv338pH5mFdqp2YntpIJQ2rR3Bb27aJMpcz7Z6MmjbfhptnzdzzoT3zaNMWsRbd8L2nZ39g30WqXwdf3jPU1qDJsR42Ny1NZBENaYZSnA2zM05fK3rsUT6AiMW1hAatKpGskFEabBTEMy4rY+McgRyfW2/YTqukyvlwRHV9CCC4Kvwn6Nu1NrhzkelGR3J1kYBrcgTqumh6h6xL/azcwAItUq34z6xKIGDi1kOouMij2tGVlLFgfPKMtCGLoEob4iMtjNyZI0pSUtCLAvIihmZNyBxa26uTT6Yfss4WLnWO5BEjBf1tAa4GE1OaORNyxm8sf7kVmEwjWmKANPnrzdcJzuzEsCZ8Iluo72sr5YFebQb9YqGKUslKu53efWoJ3uMlgRDET/lgW0uKaVObHtgTI1PGYQpTd3AOq8XHVzqpWtJdU/46EcTzEnVtV9Tk/Rc1yL0UjxfupNdhqZiY7FLD6qktoLZRc91QcWVmadwBLjIwS/nk1yuwNJq1I9xvpUz30pnqo1ZyIq4izvQzB9OlbkBsgn9TNlciwA+a6BhO956QoRo0g3PjQXyRaVBD5nEZmi0mDiPQTHA3NKSe0M2hcJ9+BA4kXSsmaDD6axqacvA1o1DKw5WQ14pBWiWSgB1cxgzlB8nGSYZ4qXuam2SbM02aNWnuogeLFCKNhE2XJZMKxrUYBYz7DCBHCAqDCLb/2e3R0BCgb3KE9b9nJ5UvYaREeVR0kWq5hq76n6wLV8HgRxbtY8uu1KsnLjWcZ6+VMAhbmRSX4FndkGqtEaIqkaHgkik0bCIWsO+JAH/gextuRupkvQ4OgIQZSMu4ztUUF3J+XTPcGOLDEcD6/kTIGgkN+PPXJEvZ/RDYXNLogZiZaYhwJoTuB1DjiLxkGOm7YvXGEA7BFi8pM/eAIZchEw3vABFOzmBM0d6ieadurLq+CoeRYLH+AMKwIWtzxoW75cz0iNhQgas7vpFZahRdjFculHQwBWZQrpvfzfbMtunVPzshJbV9sogMGOjQ2Ajt7Obqy9XZvG0M76VwM5kYe1053Q4eBjnERTjaosvsuaZZxVe1l1JGEk/rAvZ420plJt6Eh20a/FXOy6sS+rvkWvht40vhM2QdjTxlTUHFs3aOnR7w9xQzNw6eLJAy8O3F19vnBhze9UYbOH/NgcSx1G7uIerkz3BYWaj1N7VFX6gVaY64pvb1NHKTzZQYqmbtWTV88oBN2jbFo2clOdJC+ISoUTu/m5PL1y1gCutAy6yUSJRLMlrP2xZzWejCjko4XnLTdOlGTFiZm2qUZeIruEj+tDyLRsoGdk2Z8uCM10FfrMth0iXss31UT3BJwGJweRbEFStutM0leItgWPSTweJYkqQco3YMvhKJrvUISWBR3LB3I4qqNtepLf1HzedtdBARMpdXTCqk1CGpLA1L6iCEg7WwBsxEVptl8xwf7ledITsaV8QY7yGRt0zCBwx1iEynruX4ADIaMpYUvJPcoLWh5cMOoKDJFuP7Lx47hxm9SlssogsJbi8R+MAhnJ6rvxorv+43oY8yb060yD/U+3Bb96oSqOqhozaGCbCZEhUGx2hk12q3t5Ru7tqgyKAKBH7MeaacdSNVv1iazxdUmXaAeNYL11pFelKmGMQkbKtKNy+ZBJJdROc3aOZbOiAXuXL8LfqeoAPYx+BWdYi0oMzq1lPEEAhGY1QewjDE7g3N6pJ6Sr2UtJLQ4gJhxGUhSLK4DoqqhXzqwh4EQDWnvIJ6ok8QghbgY4QLoRh7RcYKFMPRAs9MlUUMEwvZwjscZNULIRRtYaQ+cVC90SnLW42qhcvh1LxTbEaQNKI6E4o9DlLGlgemPa67mOOcD5WNOy9e9ojXjEX6ECKvqQ6Cx6Jp1rFexRsCfLLR0VHozQ57PEkPihDw4c5GNGJsjkDY493JgURdzGpFoGvjfpPtCzHJsKnavyiIA3CRRMpJR2TVUc8c0MoMgoE8QixfMuYEmmTYzW2MFXGfX9z93DLklq5jZnDs85XZN16zHTSnfWDQxNIja+qjmrPMsBSKr5SmaJ32UJZxb2VLZ0NJ5hlabdEfmfbzM3j09XR67WdfdtPfP569tuHL+bYXwj8RcrCWQy3ANqydDJGrXdXEix1nmZ3a1HuMKT+6LwyVaJXkMPDFaZS+kgPRj10DGpwL5fIQJZy2Xi43bvfuia7aEW+bNZskdbB9uab14emYlqgoD1u5trmDhtbZ48fb+8u60GX59NVZb31zASkuHOvRl4zY6azcn0jNpt0WVNf+BzuFf2JolF5HTa2u2Fn3VaWV9dNv221wjX9ukO7YSeEe1CRLDFwcHs5KxqMkWu4XLB5As2jzT6ZW8BLlJCjQWVgSAthAISTw7K9dQ0BRcKFjREh6Wv6nO0ijJELbPUd1N/gDreSKc5sMsdpb4KWUV0kNO3qe1a/IMlHzQNWo2qdMc8EKWlKFgkdse49eU3LGkrE0twEKFU/nQaALQJcceAyal3wBCpjLZKDKq3xyg4k5zWSEQifymjBDSWpA9YrCVmtwSlAlN7uyIQgK1oYm9rVUEM+TwInXTO6WXqzUSz6ogn4WccUZDWl4ip/0Xz/B9u0L+NUw9UY9FVe4fkPJCh7LQZErRk1vfhEN1D90xKAsyohSOIzHolB/MNZNyLdtA/V3JoSbGAc0mRSnqugFWph65q1PT4yiFBsbGsj1EHGDWox8DQWkHCrgSEiiPxmgqpbtWoLgZjrmSr1313Bl8cDFNUbCvY55BdmVFYdCz800v1a0WbVDnW6qchcUl25WzcCuP+9pQ+RViw58vMCGscm7UEKayDGpxA+TZ+pZwMeHUA9TVCdLtWsVzaj5In76lMDnJprUtm5OVhxCC9+sjb8VTKqTC2JXSKYrakGdqR6wnBpo3Z6zP+QjpgLCFEANXzp/kT5qYTHM6yt3KSIXkl9rCaXPviksFRY4yVAc7Gp5rctJTCgsmYK5DKzCVRq1/Nvzv92HTRPZgTWzBoUfJoeJB2Mc0vYFPv6idDIR9Skcdm0wnaGgplzk1Zk06VEbnmOZ9si28y0BcOywWb1MKHM76PVqTmF5ESDgyZWg89Inz6EqTLrWwaTy2rqi9mW0+5vPIPJMefXNx+/nF/mFta+dhDZQ/mc9tqEiWBeuCxxYgWyyE7Fk1Kjus1dhKSzg/VN5JQ78AQzsoedrPtwxdexsmM+kjEG19f7u9Vex+kYgjZfU8RMpunW3fWlCaBXT0/GBAyj6yKUYWHdMqmcSgHibKjuELemdaWui7FCurKgT82rKgyczsiGIB3UbY6PmHr8aH90dHBr7FPvmUbG0XIL6rFOoxlAon63EpW2Di793cwcch/cSXukpZhssYIt4GhUJ9nI1Intx1fIt9o6W74M8cTa4lPsG/bjCho0kt8bP2FxtfGWzggWgbcOMGEuoTdyjpuEI9lDgpHgxXC5mE2iIygH3wwCGeTyXXCJXHuEeqVTVKQwPumSiMS62Y1GpclHOqDkCAxNShX9qJAmuglMW5+ghi9zo+vC7Z5Uk0CnWog7EGsoIc5uCSsBSN2CoNR4Q5uyLhWtrWXeZEgGLUYOydMyGDfuZjhNWVKHkoNm6AMrwvyu1D7J2ABkuiC1HlQRS5VDg3S0j01Hn7pT+D6paZpO7eKpn0zekNQlQzgTp/SM6jLdXYqN0FTJjDRELEavZ39vMiqlpAIyxmykMgBi0xRUNrF/MYvlEWDLFns+uGIeSDNDpevwnOZgny+Iwii5rj0PEJ10xmwCa9mlGsqQRPcY0/wizfQZz7sQMaK1//iDjk0qGLupWCDl57OcWa5C0Rgyt/xbCAo+hI9GiZQgYigW5YpL+qfdWEVdiUgmceym510enSwOnmYGjsxKQI3o9U5g1Gn4GF2HQ5aqeNIvAdWAp6PNsAoAC00ThmLAwgM3FauxrvroSk14DU2GFCFUoxVIeGKMR6hvHxDRJF6Lc5HA8wObBhIJ5SeM7XGNLfbTwtypgYmImRWbsZyXZ/F1ZAOBcZ018k/I0ORYkb1xWygbEBaOio5KMSEjcWNrGs6SRZDGFpnu7jB7TlSUpsk7MMfc/iRZMsvtH9FzBIRPaXA5v5XoMLX8yJBQTtrO+wfrO/vmhzoDCSqSINsHh3Jbpp5ePTx/Obs8u76yF9rdlXR/uXt5J6ktdGSYohgbYiBitQ+RoVWEbeiB0UIswXUamutERQ9A0zSbbsVBDlUHv/i8aUyNWsTcE4cF2xNOhen8bZOLvj5dXl7YD2llmw1+zRI4ZsYi4xOoSMo/XZ2LsISZdom+lkRnWeRtDLbY3xTMUgssPjuW22sdskn4zSHgRpElliPgLuOeaUO81dG+TS34R54AF6xRUCuptE1p298Zpr63i0YhWko0gSEeEwbERW9QP9tJD2cntG9Ax+LpJFDwZzEFPXD2IXcY05l4vo8GGV0wBDB0sI2Iaax1IKhmJmiGCLI4hYmpDlnxwWvaJSOpcPC46Lfe2MTG6QguJGC4U33JQPY19+qzhjEoTRc3ifQITR4QI0wOjD2aaHoYdrkzdo+uyxSpjqknasRLI0VOVIB9m4qqTpNJWRZmGhol6OIIfg7K3X4nvaZUGNUgW9LQdyZxzMSYDfpfLKNQVqEpKpQIPO1kPfZTTe75Rnu0Isyq/4Eamg/LxRJR/1HIlBBkY47AGK1z1/6lJmrojT+V1VwrGeghD3otFWaOCFW5RkdqG1LKCHstqzZBjbzlP0EEgHBmQjicUsP1d8DoYibcqZRitx6YnoGVouqM2Mx5BX2ukLx3nIheICAJPqNFIlKZlHD6AmRlSmjRgi+SNhPMMqv8WOI4koPLmfS+eby24lsWVk1DtB4Lag1WjtpIXWGy74McZWa5eQu4Zl00G9HAhJ3BMBioCw4AGpiz5CBX6bBweKsyZKYKBccD+cChKd+UJiQe7gPjmPdq5GpkikXrK6iDP2y0z94rPKyO8ZEkitRDdx/o4RKH4z3OzkBZH6fxEZOeCPHMMK61R5N6I44qvCuJkL3lgRqNCyPXM60PYkXLmHPOLDUsGMwGUYs5pSaaj8OiMEY7JvLbFCzg6Q9Nskin++TK0K/ZDWLZ6AFIDWCc3BCC97JOOCYOeG3XRrtN4Bi55oBCjxK0rMuYclPLtRzoEdfD2YDIZk3Q1l6Zn9XB0e7q2JkDrMuTDMbeLtvE0BkAvr5/kvZp4iRkbVRwcNhaqoNjudxIX5K9w6yMzXbYehCNpx9qaAFhsPfW5pkS2zdtX0ptgMDiZWHKgbD8fA1f5mQz2myHT3ZdllyngY3flUmbybXr1zs3D5eX3+w/xwjvbT8f7a2bzY+Uewev3nyPkuh6d/mthJFRkhLXVhtkBVE3z1cYgJQNFDdiy7Hvdf5iSzkcaLy102i2ea9mz3kIodbW7B+hJ8R2EnqgGhvo2Hfi1e35JQ2pUcJGHlItlt5mf+trl1fYYF+HfB+9wyw2QvrreePOfFtpMHsBmdQ+xt24iGVwdgY1JENbn6T7eII6DsBk5yY4zyYTwyic5Qif+lfJZa2PbU79upKa96GvOIfVeDU+RBZeDcl2kpUctL1IHR84oJmKIB9yk35hCv0k/BWfSkomjDIvbSVUqlaohuYtCJgd9kjr4yNLlvpFfb+eiFYFeYDkCMqLVD0LMO2m7YAkH4XnKUU18jdNcCJTyzDA6HWgqSyRyzCpB6fq1M6nkFEjAro2qpTcvwDvg/uVjDBjV83riWmV7P+QSLERag5PAMql5DuJjM9e6BxZ6Dh1NZFqaDHPMQUEcXFvQleNRmIGuhgfKVrtx5PNGSzI4hsRzbqw/Xl4Aoc8eki5U4LLXgB3kAnRyKnhYTIio7urnix2H8AHc0+okDlMToJgwFUiZrMKcHNPPeCuo1Bk0fPNmvFEedsEC326Eavz7CyizEMSxpBbOhEjQdLeQqE+ubD22yqmfWFlMV3NEmGAegr8vkfZwWXkA+dsmQv/MJgnA3/hgwtB6Q4CgbkoYGnXfywt8OypYdvA6kEXQ1yL7tZcgj9f0R6lyOAylQv7F44DPocBY3+1PYSKRtXRNyJDlnkkoWAQsGGxU11Z4fy6FvGe5rLwzQVvPqE9gCOppxahryotRnVajsj5WizmImKXtMPakzkwop6kr7Gm+n2WvsX29mF8uL+8Yq2dvm7yDiNZ8lkkLzS3OCzb1/x8c1pACUYUTdVwO7Mn1JSDaM5Qte4d7Nnt50C2ZwVinsIiWvZeILp5ZKXU2tmFKSxtTw1tDN5rsqixYmYRg5OfnWcb7LQMQm3WYbEnTR4bVnlnldEGu5jOi6tLDbY0OscZNeGCnvApkanjsbdqGNfzO464sUmytVzEastk0O0Voymyv7z4dH7mkGHLG2/3N06PHO3emPn+/sP9kaWJdxdnjCZ2GveeGVqB6BcRQ6FVTlhM++SUbMTpGGMOZva5TzfQXOP6zh1MJulirNvYiGMG5H9ME+JsSA8lNctvzfJn1BWmtn0AMtRryUInD+SDi2u2U563cRL5EJqTdDMeSJ9ymS26tevDyxxhq9IuLpdeEPsvvzQ5lnykqWHJVXFTw4QJz0g6MV00pa9ZAP/nDy0LnFMNEkbmSBcpGltX3qB+FdgT6xjlhuIQ953PeWkgRU7vYYQ2YXifhrqCiUiaCvhCsEZhxt4FRMLftqlsRxFrmsVvNSeOHacvVcpSmwCWMhUONwBLMJPQpU6KGybFcQGz3BWnwTepYzqYptoFHHNRZjYjBZNA0mKfE/dw644XxdaeyzxSPlWxlKvKJtAlolrqqwiqwhn3oWuON1oyVmPHNSvR1ZQVAwXEUwxHr/T39NwtU3y4XeDMUcQO4s/QAIM/KL04xl0D7I88jXlmEbpxhPKuZmvwb+2v0oEeiRozUETuTKLCK1oU3I0z8wdB7AVb+KMCiyOGUL5Eld4uzE0DB359JmXrTEWD9NL3ApeeHoM1uPVlER3IhndQEmtxWT9zBLeH6/SpBoEU2R7KRQCkjyZFwR4BXGXQUziKkQNB7Kg/ojMOBYayfo+oVzcc62tdDWN3PeXhooMABmh/dZ3KCYyYai4IilBQL8M6xcZ99Iyb8w6HMt8AGf73VGFbXpweBkkRUU4psgY/Kc1lksdSdgITOxCIuCIaP19RSfUsfdlbcp7Zbs+HRJkpZCFnwRc3KVGzf3iQ1FUzBuQ9GDRhazQEIbOdl/CG/7kQX9QkcJcJ3zbPhNLt7tqyE1GlnqOjPSAtKLXeeDLmKdzNvajd/B2uwIOMG/Giyy3hsutD+5smI1nbZmDqEMTWdJP4bTnmlyvZtdhLB09ew4DmRXtmmjhk5NN5L+RP3F5CHAFbTCadMvFbniptL0zD8EVnEImLwSwDraSQIIl8EbSYu7UQQn89m5YFQAefUgwRvb0XGkno3OyGs1Ezf4j+5ffrbBQfxjN8lRdnXK2TcJ7N+ol9HTbtFdTZLw+mim6ZGQfbPUsZihlTTXvPYZwO+spOeXuISimyMXWF9F4kshueTQALMpg8dj15aA+G26sbu+ft7O+crA6vL+yelDmL0dR3Y62xgPtbQ8UowHJ6X34hXsci00uQiuSx/tXxK7s2+ZU0vnlcu7CZ9qXjDxw/YyuK24uLS9+QLoL2AkwiTeYRs5qmC4gifoJ0JFyBYaUimc/af1EgF8b65zWSEQJQ5DRmH4bMlmc9Nm9RTGk/UBMjFPlNXLOIbsqAKFwasOCTfqTJi5awVt0VvRGPVmjR4FLwCBxsKVJlgaCtoc/yP94z/W2NFdRN/VXUw8lmGhye4yxKD8nWCZTqId0bK3WgqZlaDlQwij95DCpcM54pyUyyQy1TSe7zAFEtMo4t9imjWBAp2AiZoZZGyTBdjFTuVSzU+xRA9fyyhVnycgJUle4vNCk6Ykgzm41rpOjwt/bJfxDyGAWNDQuZoBeyypiADHHU3JQJGOHnT9SC/rhRjB1TRHacQcqQvkHPDJlsB/7FcMUpTcXy6pysxfHDCEOoLZuezi4Ykyf4ReocVFX3HW7e/cXUuJoEZSHz7IshRISs+VAhaSMi/GS8Czr/GrsWuWRjI3Il53Lc6JWGKxyECvQ5aJMEoah/Wa3cKb+WiGZyE9MabO46DagXUq3qy0Yr2WCQeUKEVeUkptB7QWRpM5zCpf+xEf4JVzKhrYBUvqAsi+xB1RahBZ9mM2dqhq3q3TWSwogR4O29xx12y1BlCSunupcgZe1jN2FSF9bYklMozvpxXx3+zpIxTxlNYbKZ/81ysZFD1g4Vsv7W4jYZESsLKBje7JP5dVsPlhJhw/XtpX1bs+il8wAqfdA+NTBqVMBGCYLU/X1GUy7RHpnXJmw6iaphOPG1vf7zPU35h3XMiSdW5Ep0W3a6zbNdiTcfpXqctyIA2r2eWUhrD1dr3IM00e7OzPpplJDnRyqg+k8bGe4IxZ06EI1At5SswGKsNydHJjtrBQ2NXvpaHrz9GqL5iBwv1uRHUs0H7tn9YMtKYHn9g3GopBCBMaIsCPODvhYGX38VJFmFcPs5gXq0//TWxqwmM1q7u3qya3Qb5VFDxjSDSkCYbcSzWZUNTp1IFpc75o/+0OmATF2TKr0s5+OYj7pHK0f57ahRr+LV6Qlm0mTbb7PogimhfylQ2pqQI23mc5xlghDXmwrlNHvjBbeUo+6FTfq2VhdXdxZLn13effl6+dvHTwDDUzBIQ1mUNxIoxScp1iAn2UViKkFOSWYGCbWRL+EuqUiPqJuSZHrUk3zE33p7M1umHknGv4m/wOADPE0TFhuVuLuaApAFF7csfxZkuKgBhqkzUQY/D8EPlmBYFCW1Ip7uIkK2K9tfK2nq8qruVLj0qw85RsLjXtQvQb/EgiXPQgEwWgUKGySmJn5kps14zZZuZWtDS06IcpiHGlSj0bDWI5k0cYgH2xh9N9WvZlFm1gwMnsos6Ok2WzlcwiZRpOfd612haWm5R4VUGGj91T0Hnaq1zoekWWjikbkOTl2LCISf6Jt9Dk5eYZ5e39rfORxo9MzvM3zbzia+ZxfKNvJF4DA0t0sw8SCTTJQYClWyFNRgV8X2uCUuUNNSODjloxQQSrFWhh7xHR7CNGziDAk7LYBMrIjPRalxcZCMXQQmfuJmYpSfEGYlKDJUUMvl9MDvYqcGyIRyGlxnhY0rKZGX+/+SjxHBX2JVnys6ew5NfPCUhqKMRGGnJ5Y8cwvnJ1RJ6EkWwXU3kwoYpIFeHbeEI2hThP7XS6i71QV1Jj4q942NS42yIbnibtbj8zjxl3TVi+JeRg57BKbD2hE+cxXworCoWs1LTTeHRI1WRhaIFM8MYRJiQKq2yDX33JzDtj/btx+O6So7FrI2vY/hx3UpG4mHXY4aLZt9aKkUbwDrngW7A61oKdXCNGOtSqVDg3q5K7g6GssCUbQURgiBCSVlvxPtsDl3chu31+uPdsx3dLCz6U3ZHt/axgJpnSgKsnQRgFJAIlczDc+v7kzwkQWy49v63mEkEmrpiHTYja5Faa/iDy6oMPJRRn+OtSnKu7BLz/3D8fHx2gG6JPgME98t5o8qRHnG0eHQegLDrGUIGfXGzRiq+m9exMQ9cn5okZcC5X5K7jFwRF1KTY7IRnV7nQP57fz68e5S53tlrZV+0v2tldcmQeGL3nlhWlqypZcBZQDhgGxUcvDQ0cH7+7tk7+bmptwMv6KoyEzMZI2ZHlIG95FQElNp+/2DXfHN189f2fQxJMiOBXpRBXTNZMGrCdQUYMR5QTzGbfJBK0zpF+Qz4pJIu/pmNt5+sPueDF05ktM3p82FzYkg+dqehWDLEou0mUToY1ID3OLyi9ljunqJscsvcpHmuEWf3POFPHBlUjrRf9GKolbYFKvpjBGxnq6kylLSXslX/7bEHlRk2nFTaEsbKWYrkTecpKlH19ThFuDE/DztIsnVo6vFelACIOYSuqYplCHblmW7PFqbD2BSAUFj0kwte3MtMLIS+rgEPyuFgQweVyRWNj1c6qwkeV3DDdnJNJRdW1BBg8DKBqoJ6NOtH7K06S7i4TL0iQHjhY9RgQS16aJHxjMlPwl55GRV3C64DEBtFBxnRrO/6CmQdVlfYhwP+eET8AbePa7xcCmNn5MuzLduR4DjYZLB7oen+Q3wNFmuaCJnhVJYs+FEp9x+tthvsAAiQ1NX2VV4QxIiyKFF+jzcfUIXdlMxej4ulpi2PmHRCWRRVSbAlapGAPIVzq6o0culOEoBhkxgLwBrZCmW1NUYVkWyMfEAxjqOGllrKJoO2Qrn+7YECEW4QUqeGlYf8atOwoJkYEZ/8aqG8CE35A6UprZ4mhfJwaidWGjdNbVROWweex30AzljAjSsSsh8fmm2cL5f+LjMLJRwycqEcji5GezT4cjCp5MuUuQeGatf+uVFvIJdAayEtYqalan/CE9pG6FQWlpfVcDApKQorCqlwWib2T3K5hHRbakDx2p5yjm6C/CskqT+5qOpLs5OdMwuEDpCZMvcEukdQqaBh1sUygrfXh2dHDvZsIGA1sheWwa8LupnXuVJHkoHSefgFXsdBwECMaRtBHiFwkIOMw6lIggKC+yIr20T5Q/25FbbgZgBHXOO1njz6FhGgb/xUvaf3kiemBNj84TZqA5L6C23h6ccAWIyynUuUqEEL9YFiR/ZfXZ5HF79qEkQWGR7u/7tS32Ex4f9tQPZoDbFyOA+P3OnUvvfbj24qcvg4Ek5LumXU4uiHwxlNE9Fz2t9/9CcJzPwiYfuHsTRHg6siBzX1dUln5Iv3jZs7mmjvnSKza/zxUJhm1W2HWB/d9u+PJs7+g561TBns+lVUzqvbX463awOhmxXJWi1MTTzGqzZF0ku/Ih0hMBiv2e2uEoOjw9eH+wf3loztC1BwPrbjc6San0CK8BoXKcm7N3fzFQgwwBAa3Rp3KHKNZDueGX+qUf/6q8TQaiSs0SeRX6yMI+f5ucwBdEVSr7bF2TPuxtdoA6j8x72HMHqH6lMdhN+ssp14aR9RgoDOUuyadMA047jcOlzn82eAtAYJO463U5xM7UZgu5FCLYsg1iL7PVM0XHBfRdTQObOo6g2gZdn+1AuccVgCS+FyCGsz2oERSLEczNjmAZBXTWp6oiZUGciSCO2xu6z69pvQlNp5LLNmTu/qXjPJX5zyZVp3fXEVRH0fHEAkSOrFWbFQhkS9/K7i8UaBfEQ6DLLAZPt6B/CMUcot7869BXT8pPMbgbUFsRQVQu8BsFs+fCr4C8Is6q6nDMRuHZzgNO+JwgyXkWXdKmYt5O+C4exC3RwRLYxaygWzGgn7oEOqoefktpWSd8UBPHgSrDGLjKH22tGqxbaxaHuz4OVndx6xvrOohl0rMX5WyxNkBcQhiwl80070uTFCOQSMFOzIunqRB5D9gSb5hT+h77DrPmpESjVa86DJZUzjXrK/pfRU7hIoxmK9rdq2kA4hJW6dSNjdujZXq0egIxxmW5fVT2tqmDkPqVKCDzAWXqIQVtQ1mriCEnwhw8oe8qHShVIrq2c9yQDrW//vGb6d67k9oE+GlTdvpf8yYQF63hTUtHHEqlRj3jt8B4GV20Lumn4gaBbqm/dJWch77/B6IsyZGvsPmk7FvbYrMMkDKD8w63N/ZGC4pueVNNESwk+mNWHSZvJkhLbLifPDIGIwVajTo6sn3h1effp6/XD2sXh6e3+8TvnO25TS30EUmO/BImwDqM3o0dqhbFpOj/CahdhkfT+sn4VKUC8jJGjwSxtM6FlppwChR5YQuysSPBK9KO1YS2zg7SObvrBhAHpPD1scmYvxyrgoKHGtfScds+2vhq3MBlJev7q6uLz53OEs9RiyzCZ42Ms5treur3eujw/Y7nYwWYT0kxw2O423XWciL1N03nsSnpnMhs7ligYKDZFf/322hah19emgRpmR1f9HVk6WmlqvomqNqK7u730vvakqgI34kImLAIjiHwdoRR/MeVMtx02iIjNlbgB3T09BPCG0fOTQ9PsrY0FBQK6K4ZrHm6Ln3PPjY9jGaYQFSi0viKbN0owGp/UTMhAQlIsbVcM8WrA98JDZWa6pBLoTwsnONShmlgtbRzvgUQYzQ9mkZLqxTyK782fLboiLAU6zXiz4R+YYVCGKzNX8pMA1ztsCrIiY5CyFJpXGX21g1XFyQqyK6BY/9zjLdpAV034FUpBqYH+AkbN1ZAZQVQtQGTBdbwMxTBtGiClHxAt1J/zEdNxkIKbYe1M0KYBAzoaGIshylinBTWtuWiSVcxO+p/mIEdA12FFp8UpuBD7RKsEsw80K9jIvFpoWtO5AcoR5PbqdxYRMCPODXGONWLi8DBSRlG7iaAqnuyjQu7xfPBS3XC15uIph2n2BMZgQs0EHrIsoX9AZ2/LhwB5yOsCVYqjY8ljhpoAUywKhZLypR3yrZPpVkleZCSpSpauQQyMS64wb1F+6KLUkKl6VOxBE/dKdo3gTLIaXRCudkfvhs6hktvU+yHkHjaKhsAIIsK1ijVsVVKxnsoOZ90FbXm8qooVwRTlGLN8++iEk4lJ5ERhGsW6hnALPHue5gA7rqJpID/rn6tgklLuVVuCUZF5AvYxuf6CEAwgGOAaeprCXlpiJIcVVBmIG7FvdhoQyiY0n1yMQqzKNTXknOiQiByHPfHETUk5egP1doPRrI9cB6J8X/iQilFHEyFz6Tz7pMR8WefWTBmU5XGkgwNBjDLb0hgid62JTVj1SXQLnm6vn++vyo0YQR3GoBtJ5pN0e2w5Ie+Yy9gQbN6wv2hweSlX8cAq2Xxy3WFcJ1JB+1iLm+kEQDbswt1YoEmKditzcA0XDBa0lR+Xq+bzFKz7YpxiWWZsvFflzFjhaWPQdhAynT9Ds34oG/L50ycBt5DnYGWtXNvnFT2Bz+5G07E4Pj4EblyxlMxiNNtAvDplzZycfHvxzdE2umY3d3eXly0COKjvgWDGgI39Tj9Dd9nm2La9s9f1XisVeH8OLA2eYRuI1yK7Q1HWdwgzWRECNw0TbkZs9zCBedZZMLtKZ1phUlfHnkwU3psToO/ewCCLJfTOYCUtbMPkdpyCgNuYSHyRyPZ5l1JDD8+Xt008RQlSQxn3pKksObZ+0HJlfmB3l7SZD5QBmVBG9CqjSCJHA9Ajo4M0VInMkd3am4DM5+vrC2yfPq40WbY13yohHhQI7HP94AwbwYcKAqVtam3oC9M9wr4UGhapZqIK+T3gsUS9UBI6i2aNajKKxlQZYkQMKXCSbLh5o7fEV8sL/FoiMBVQJPMypin341mCTWLuUXAmHZA8xiQ7sGEhRzYIAPgXcKgKdx+zGhnIaAKkDD6Xs77OySZszbmSFW+XnsWIhVFghrHKCOeiyyE4VkAB/AxVkoE0Wley0S/PBUCCotUokZ1AyAYv2ea6yllpdoMqsCOFqpFZGs10tk6ZoFblBy02LBqb7kC2uM0FERzokMo8ZKu8BBcRcH40xKe132fs4j7RmWREFPIy7gvuADIeT5uGzVMkAQ1iho4sEHpyRJZUHE5oVE/Tr2bDHHGS79E975EjH6AggcXjCiJKnjMfaC7J9K3Uy9LNkkKVDgo6x9JcSlJVtSZsXkD3KOGAWgXqdM5YLjmd+3ncSB21ozmMBrg+J18mw+fAup1uxamBqXIMdQqHsqXCRNwZ7akD/J6WUEZbjoFF7UOWe6Ie7yMfU11RSZV5BpXBnv0HVLFCfYAiLc1yPbG/QEYjLKwtlCPldoM5VU4KAoSETP8YRipJ8CXny315B7nLdRJz4Q9GKsXqSV8hKovdGDJeFtfnAGYvBlvoPK2Zkn+9exUimbNANMNRUsLgo5GAWXaoecrb+ibO3wJb2Mj/bO+vVCPv0PUmqUtlmL3QUb1Pm/tHr999/8c/HJy8Ni6gt9/B7kTTJmi3jf2K2U2RfDhjDgCNAkQU13MGaC6Q55u5LebIZEaTMyOiroY27u6ub64E/XhwtX4p+HAmmM0lXr9/Y5xBHV5EHk04V0R17ljh8/4eSaBYjKOBgONXb0TqksBs6YMQ+qZlc2ZqlS2yg5HcB7O3a7INajfHDNUc5GvGrxlrrFJNIHsaFSdTCQ+WmWsHrwwMR3Kwt/tkzPj+0qakj21ZKtiwuky4hKW2eshCmYIisZMNamaB9B/1yh80NXdv+Jge4bM4T2M6h3l58KHvpkUNz8eyYQ/PF5f5IwSRKiuB1+E77FVxFfOyma9CYORtiEgrACd65ClNLDZTN7lL1DRTHI0lRoPanEPHSIdSYjVH1LpvfTVa5MsE2UjdZYqKDhudUicsUDkyzBlqRTDRo6QDKRoVinSxXYhbnGehiK52lfLZbZYXCenC+KSBDEg1WLNokRvoBbvnncz9KIMnqFJmeLRZb4cnLfc3kr/xFGlrHSwDTyuQyC31QFLcXmgFFdwAv5I4AofaNWqKMAShuV5pqgIMoyZVFvH6LyJjjTI87tbEvMbEotBAla2cznqqTOhrRZAweYgeUbO9hO2qBVZ1Sq2qg21VtQcJBuvB/ejkehblIa7ZWJfeGwqIhluiloG6/U5CmAQlRHACKGsEXiniB0qmHhgyoN6T9aamig5wivGJ4kWZZjSzWfBhegDZjmxj4NQJhvaf0aqT4gIuwHCBsQBI8URWah5V0USReSNXPcOgK6P0uMRSXuWX1YneniqFFV35qc5pSnqgYEVSNjc5UjIaoEJYw1tHE+j1+oayYPGKROGtSi/1RuRsru/xskC/lytacR/uhFLNCUABNdvavjdhVhgT/EWi2eQKa3JBM6bno6EL09jZBdwDHSLVr/YgZq43cSZXS/StWaqnLIDMmvQHwtQSQBTu9wnvtLJDRfjWxoeQEig1no8AGiq6gUiZd7UynbmJtqFQWnJHQJ3c2PTfTDj2KXQ1ovDt0/WlbfSfbPiTyCUtdzeXT/fXcuD1W1s4YyDgzkGNZNDeAhlEGMjs7B+QT5v6CPclkYziXsg6t+sBC9AZkCev3zjUC/q2CAJfcVN0KfQ/P7s4c/67IyVFp2XkwWM9Lco/Cl0NcXWaO4qtjHKLmZ91K+DLXjbzvrmpJkrH5fNvrXu9ujy/+HZRSlCO4e6W/UZqE4oaKHEqwEbHzBGmNurpNCSZFHK283TTAS4fv5zdfftwbInCq4Oj1bFp1AiZpEXmgCY9uFhfZ1ZXyRkdYpOInTg0oEt9c33JlPETgxnPF/YiYlBYKRpIyOXHjLd/vb7yOV7PscmMZyZEn6CRmMLk/QOy0AiE/ZnK53A7Elz5TMa0MTmdLssnyLlMsMlAtxTXqT78nKGAHWMo7fT0cGnP6mRDEZ48OwLM6bCz6OWFR6xJpkaZq8oSyFEgto9xH2GujmBK6gscVdZcwOdOTxraJIEKF5LVk602HVYdAIfB6bwWqj7cOTmURngumU/r02HEy3ROEpv2CffFfWayMp3u6bMoUKiYk6B/hX1ZwgkTkxISz3Vncwv1EELLAKD2nvM/sDVuYluHKmRPtJ7aMjD668bfiuXHhUljSKoWGTOe+m09mur1ixaeM3AsYbW2v3NkjhtCMsJsRXI1liKcWIfEJTq7hQiezgSxMJmeCqjQNeqdQQizUopDePgEvZJBWKuRPPYxbxmcYn9XmJKJ8hnqx4YEQwUUdZT0aFgo4KiEicm02yTWNzhN9QV01U8YRLIFAmJq8z6ZS8DmqQMlfULngJuEuOCkZpOOQs/F78FQn01TOQCJ0UyahzSJ9iUfpWJwNiYrM7h3B/6ue5ax0pLyaIEw2ux/RTeMHyqKPpCCffUEvQuEu7kuEdcrprOyrSmP9Orkusu9kAuNTp0EOciVpro+Ff/2rCvqjeRDbp88ktaaExLm5VvzIfxcYZ36s/4DRAFCsAis0REkY3sDHJcU9GH6MgitnOcBOcWRKifRzOgoWvTtWQlHZVbDe904cZAt1JkMU1zqDo+jiNZJKERdYb3L/E66GcygThwDI+VNHcbFaamQbsESYVG67BM5V2hv9351d7N3Zz/7hxvW1o48KcPTY5sy7521UAqrYVC4yyo9NvNHPCiBIMAn+giOnPqabbssWbQp+VAex5CxzI98gd3nrx6vH7aO32wevv6O9jLx6LtpIOLxmYewRaQzvD6Yt/jx49dvX3TRqZ/0EWrPjAZVUhId4Pvffts42z07PjrMIDat0KNrlxfSHk2Lvjy/pIaoLsl+fnYup47qjobnCfbNzrEg2LGRa6b3tL8dCjm/y8bVWtHelRmUpbbK0V+c33RiF63YzVgy1NyDsI8kFZA0fCr/vt/YogGEgiwTXtXhxHaCqK9AkhwUc0crRoEAL2l1p2O+s3sw2iX9bZsk59tcm02UIUxO1M30I5wZVk3bhTyh50TJ+LHNOWZFCzEjF7ircXQvWGUKMJuE5XzK9iVTTEpolYPSpxNh8h28P9/TlEBSlFGQTIBUkRNBIe0AGWtVBjXZydt5c5WWlPbFhaQoecjm6qCaA0cg07GgyAJQOdAsJs27kq1ISqgzDDl0495aF876lvKX0+wLzrGtGega3zRlYO9gGdXXjQkgf+wp6+svRwCMYqaX6llSqfzsuCnrxZ+14q1/KodTk6M8tbuz0u/xPYssJzR22TsRUhQZDNF3J9tAqrsI7/xgUVJ4oJkOE1dscrRywNKIhECKwD33CDAKvKK0YLoYL18TYv0FjbdqlBRVlnYOGi56JtXFE2ZMhTjrtaCQTSvMxcLqHshZO0AxSfXiOLkC8piBMxprwwZ0y/YOd7F8OBbpCV3j88DJYmqQphEtV+OHX/MLNURWlUY4QGdpc2jZtuQvRjN8/WbsPae2QXIsL3a1kSXR4QDo3DADUKm0chWfiIoHTqh6IaXahlsz0YUQe7wwVrvBGi2UgVAtIurzo0knkFXpQhG5KygkmYnMkM9DPgB6Xl3rxvyqtLv9Y5YXcYkhDLRaxIxm3Q0ljUHmxQh409aAUEfMK2dJaCoNoYr0nPd8eyD3GvHiDJVJAGKv/55lEKyGtS9lpJx5aAsM+vUqQPPES/nh6tIgZxwFUUYJglqrEIp1rjdfqCHHVF4sCiyswa3QCXCi2XlVa6stwxV3TzeO6aCTFv5eMn8EC/+JEEN2ccEWp5o4c3Ro30pid2d0gD9EegOW5Df7499MVWpWkuUhpCLTw3zVYRoClQuXY3e0i5Q632Dsz9kwKGPfHpuSfTs7+/Ll6/n5+bez869fvrHmGXthcGOqhvXr5ILBkO/XL19McHZ8y/HxyeHhER4z3J8/fUEhiDHUN1dGHfI8fCdb18jq3V3dkr0DQDsUQOII6V+dHB8eWXKciWxzfN7GbJmL8+vzi3s75X85p5IUHJ8QwposJUortCu/xXxlOJtMi18FWtuziA6uT0YAYA9lcifuodtUR0ivEIqxxhf33wSVRIu3p7wS/2gKx0dzmm6bXIRZGRt3JkEfUob696ybM8Z9L/9TZhx9JxoqvUQsDHcZUDATcm+/3f74bifPmHN109zX8sWGr7htWVKLsZvsnlRrNhJhUBLqClFNo3kzlb5IbcmVBKabHD1VS3qTfRdRzyOdDpX09fRIdXXH966hT3xJOdqDxKE6FgiKqQtuSAmaiDjVid2cg1indnJgWYDtVUOTggVBBNJpqkhWgNMr1tALop4BSDfoTitjCLlCaRdAo00Awwhw0WrGuwo5gWa8MLYs7hAQKsmHTdyUA/Aseix4eJ9Mc1e1kH0AiX5G+dFe+CIJpwkaOKo9YXDKhNSxi0b4C2zPZmrzCXSE5YtGLMFYcx85FreUYtNVaDxDW15aLhrUIlBZ1k6fZE9gNrOYMhg03FyDavczD2P/mgiRoZhgOSuT05EP0POFasOTvYof0tq0lylFQpMIgUv1AIyGS0JZnb3yPcPyYfO0xlJZuKT5lhvzhCAH8HAgxwOkogmxBmC8YyERNC/6xSZnojAdUWasvy6L/ooDTMyUYEdrkln1T5W6im4ljBG0SEBKBDiROE6jOfpUWWQt351AM6SIgL0tKULZYSRaJf7RP5e5oAVCKIVnXiS/qn1fSGtukCOsWifII3ijc6irS5DQaSXP/xJ1LASY+rWjerXOrpYRbyxzzBt3QYhyor4s4hrCiA+1SmIr+hSaJAjQqZX67ANJKJuxyl6xjelGf2XKkuTpC3NV0mXYTT0K/EmRKH7PCZEWPGKLzfO3z2U8r+cIEU2r3DLUBlYLRraODg8O9pnhpnl0kEDdyfRqgolm/oxamYdSkobZI7QgBRU4EcVQ5qs3tmLYu1vftfmDNQJ7R/sK8S6kH36m7nz59tXGc3aiFn/rNFjixCYz3iFCR9eeW/22tcWgsybN0bm8PD46Zkgvzq++fPkMYzOIRC9SP0yn03j5WpQ1KKCTvn1hmZRB2p3V1Yog6QrQXJLGdhweHlpLxTYxxGzn9c3Fl19/u7043zEm7WwY53FaIiORmTeP25aTzYLiDckda9us52Ws9V0pkOB93cKI7S25rzrEhhbkcXlMd4symR1y42S3K7JGCgtUZaImHWHAxOgFn0FCUY8uoR2ZQ2Z7CeGoCa+MOBvgbv11w8bE28BLe2e22gvVeV+RJsOii8pcHx7tOpvYln600ezKWxv42aHCKEEzXqTvZuEGLWD2MzPp6yKm3rVO2JK2sQ9zJYVhIjJpzERmY8ybsnWD4rW3VCC9UXgMAJop74u/hI7YJ8Vsnt4DOF3UfCG7LkGbVVdP80Phw+W2f22D1iqgccoQGP2tTFJwUB+Jx5SOlKYjaU8TlOAUOrAYhwFU3k4lytNn6scAqkHiDE7pcU+1Qq066wdoqT5W5bvo2/ClgYRxNuwPELVSiTDUfo9GMNydGE7JqtRgao7EQ7EC3DhLLypJJtIR94qtpdOK0srIKc9mEToJs6DIVkxLTbfjxsFP4UtFROyO2IIYq5FoRaDwH5OpItUhj6rUznrKJ+BSiY7pfw3IDX3crzUJFxEThhosOOdUY2zmvXHXpAKiyFazAzuwQgr2eAxElTpQScpiUO5R+lM0ispFu8XFXuCt21qxAaziTHgJRNbfqj7zKRvKX6ivsSiiH1oYUs9jxDMRjSpABTS44D+TPoNjLtpuC05uMXxJ3jgBD6CoAn78RhmRQi/QInsUr7asMM65H2LkKyZ4Kc8OmUheL7KcQ+Lnq6jKcKcnq3SqVV281HSFtOZe/jcdKSpxLeAVaOVGhRXBIprkUfER0ikeYl4DK0oQVki5NRAFKbw9TT51KNqgIhh7l2kdv/Z06VwOoQUzLkPy/LQyPY78GoUuGCNNIqlmVbLFxlNRvvz2/h787hmnxmUbh0MRnHGpMIFviNVN/Kq5CGQy6MZ1Bw6aHUENHVop/3NzeWevz00TL9784f3bH77nKKCPAOYbyOw3+VHG5vz8119+/fLJzJ1P8n6EwYAwmZT1h6coHtzS9xol/Szsr798OD454vPYbl6DAkgEEbKCyZIet2gjLjYriFzrEbUwrdPk23Df8ivqvPXNqgKHBr8COseFxXtPRmQPvtp0RSLo5uzp4otO0vq9hXaWlGu64GFHqpU/WN+VCzvPRT3opKewTYxLLuXxDpqPV99oyejY53Vnz5oGwxh35evooJViFx6FXwqLfXV22qy5VSxYFD3blS+y8ljJE11l+hK6xl0NeXOg8j/ElKe3T9OOrfdMiGwsYPuZv2vN987+oVkDD1eKGXB/ckBCYN7SR7YnqcUHDRa9Jo8jt/iosfRz3pkq16nwIn7zcdK82f0Ru3C3QalyuQElC1T8AzlyjMXUinqKv3KkI+2+MMetjTDyD8Gm0CBOEtt0L3xGPKI5wZWTOKln+zUEhVduciy48ql0eiTiqdnQ0HuVU00t0jCxrItEdbHYjC7gFjj1IMi+V2iW7Qnu8EV46I0dD1KtqD2TSXsoLK3XV5vx/Q53GwOv31KfRpYgombWABAreyLtKJbq04SkPe6OK2P/ylkEN3mrrSJRxjcL0DPzNSHoSrBzlwEQUAMp62yagd0B41ZyqlD1jV9CGN8UhJdPWgBZJRgaFiDDp+YMJ1OXa27vkTIVLuTKNJoJzCgOdEBiFgQjNRa4gc46F/dRhiort6QR0uze4AUNcZxXU10ynmAPNxFlIuJz2VXlyUHASgu2x0sjLT6HssbqnZCVIPcMiwtneLQ/2dO9wbVG8+oTLPi4E8eSTi/wilvwRm1qjJt9C4X8E3gjuGchALv0IYIpC+sqVBrCSEL6gJIgFBTI0OVfR5IIJcOMfjpx5WjcrKaYpi5qM9Oq6lsERSK3yLJGCZP++PCzuDjK5NtrzGihvQXGq8SLdCnXoUhJ4T7mdxFH2CTsvX12JAjNytJ7OhQGWtRm9xEZG80WabMLrkh4kcgKCalwWm7psFyEEKF5R3izwRtcX16eXV1u2yCTLcTne6tPb/mA3FDLYbfsbbBvesoyyoomsLNygzmTORHWfzq7vLjbOH6vgIWvNiaTbtf9swSuISXx/sePn3758y+//Pjn0u/nLV4K9ESmBLEXlHUWd2mzLv/dk6gfC9hX7zhuBidfcv7tPDVYZr4hS8eRu6NjYCDFQgTgniPG5RVvUbLo+OgIB3zGSSOr0gfl3Odkdn2Is29nm/areFi72nKwpQXWxmeemVfWU97F7tSpBB60NIG7bHGv0RiNagapEd+2D8gIBns53uVzE2HNoTKzKOK3P4+1r67BU11FlDPfgSymOIkNUSJfCbJ1ChxAv2Kg5MV4fBOm0JMX5HBA8tiyYifztERjjCLMTK5EZyfN0P2Nm86ifzDvsTlGAlwgoazq/WSRoETSkzti44tfvKQ4idKSqWgkbBz/KDYt8Ao1E6kyBgk2fnkSbXBHwtA7CazKYjj1ZSRgRja1TXxwFYDSVi2u8K1uf1XJvLnP5qJipqAwP2FQeepZfWCrTVIUoV70uzKaIZ3KFbZ1rJ4E6Bau02JZ1p7MYQiafW6St8kQwA1jVVdz1m1I4BJgBq6hDRBiy6MuVkrtthbm5XpPDK7RZfS+OyqI9dCOK3hS9tZ3NWlpHHwh8rSkBrh12BzWFFQiOD41iuOFdCSlqQCwS57GCIsHC3uJUftVQXI8g5qZrkJpdSB/sSoRM4VxQ64WoD6DbYQAIriHJi/zWIMxFmammTAkDjdooNS4NF6fvKoRojABK2D6k27GoUgXECpVBavj2XzyoKhYP2N7gTQFo1Ey0XoqH0tuJD1QJ9lDQtcH4SxyRiH6TXWBFnYKLPR9qTAewiM+KE3k4BFNgOc36RtAIJ40ZdBVUVMZhdjKjxEOhAVOAlqcEhWQxd1Aqx/XAh/v6sLTIpZ6DCCtjaoZPENKfW33phVgtphLXSOFU0onXWvaLvKDW2NMGgJYHK/TSsPLhHVPKZihUdO/xmpUR5qJWQ2HGhll0AsgQyhk8t0atvuCaeN4YTvkXUbF7pkMZvsxSJPvru7N43Q2ysWV7fJRSiAcj60427u8vz3cPtqTJKHoJKfYUygzu9DrWwqQzY60cguplBcOAgukDDhIM8byTmYr7Wz98utvV3e/7BwcHb96azYhFv/6y8cPv/326y+/fPj4MUE0A2q/c7JKY6Wl8UtY68OsSCYb5p7juKyiM+tlYDZsiofkPqAP7Jxa4yvTmzueHsMinhb4e52dn//040/u/rt/97dCTopUYv3sqzGABlRvr8+MRH/8+O3jb8e7z4cn9rOzMu6eWyJuCGZdidXnCCklJa2kyevLc7GKqoi6VW9yUABOQqbnXXecMIdXUs+1JDB1IJ/QpqFwUGbdkmgMJCAkh2wlMwm0FFB7fPgw9jIVK63p9LT2ESpQ0x9ITnLnG9ZY729JsaX4VvfYZ6n4dL+VgpaakShTP42TikGoPnHNc9aTc6MEMiAJPwlExiRv/o3Vrf0pUFO4CVrSOlF9EWoP+g5xuM0fOXcF96rVl0yQ/uhdFiK/MQY0tUmtSsWUmEqA5bEYa48IQX6XXpYwofNgmYwWvdhTVUDNccp7BTkgcd+LshB3pAUQolIeLWjdj1AHZuRTPcHV7Fi1Sqbpf7CfoTu2hBI2XBzcgT8q1IPZFIi3Ww4kyHo8ze8sNorMRpayf6Q1wY2ntVMIj7Wp4QS72qtyL8NKL8MZjM2LmwSM/Liqh1LlPOgiKoZvYelYKMZBnfwnSxKH4rhxwvhHbAwUBC/oQVoWZ8zbbBmB5lWRJdpFfXa57Q+DMoYRJzXEwQQWo7kBDxcdYw5ZYWfK2k7hzCAqDQmihAbhUCxRZtwLXHgAHmGYtuxgg9UN7knUFopGHRzNHrOzeBLFYgN80F5cVqn5iut6mImcpqePDMJ7ipezyA4y7/ZV0wlWXiVDcLa9WlUwVJtUH8LUC5vgD6GSg14ZyCm0sFwr02587l58j/TEFAeXklr0vDkFGjH8B8GF9hXkYMBJzGGClSGksRf/mvYRzGXT+2kvaRpXje5sk7b4fnwSsAHQKDRiAoOpWHgXcQca0h7TcypN8BwzmPwxE3Wt4mvBIGRaSnV3v7dlNqSAyNnkO7c7W497O5ZiC1xNMZTeQHNJiSTSilWT7K3DyujtNCDJE0OMiZLyYufNay/SiH8M82r/aHV4DE3Ru7wIdmCxXzAaALDsyEDen/70bx8ubh/X9/dPXp9utZc9c/z589dffv31199+/bc//Wiy6Mnx0cGBGaJrRhPkfyECTYZePenz9Femb2NtONrcOfZgFM2SnDszBpKVBEiS1DxungLZeTtxfRkrXoIcooJGwanD9MN3379983rztRVrt18+fbn49lVOygFhBlAZmYuLm+MV9dsTVFn0z/3UxzTQsWkZsiFXp2+Rsl1zpYbSSVL0nl16MAXYJDNdYewHi2wqvjTYy2TYhkHuyUQmSXzbpNaVSaGtSLDn/0RjhC83X4KpoV2umoyJi28Yf4dejk9KEe2dR8B4zPZHsuZ5zyxbc2ydDWCapLn+QjCjiqkiJe1FQ6lxgiO8Yvko+iJXPiRoTFEOLFckKCNq4PF1nhZI5eAJgnJtPD0GrPGNCW6UIemogF8xg+1NkVKARFYt2WriytzqgzjRiOzykVIxuKZdnNK3s/6xzj2BDwwWTGw4qWiVjRGI0yqCOxKlvmmdFmGZ+Uo1TZz3sJ6E84pZjMyLwRiF+BZGIK8AUSZMQ4SBWfdBveDEhzRX7UVdzXDrfew4LasZdGu2ZHYO133RHn7lO/UOpvetXCj7lxWpi6dHWqv5LQKdhrLpChcfoWZDK40hV8D18RbTmjryEv4FGw1E/FCHQIM+OIPKuVDWm/ecoBXvokqCP4BgSMI0KR1KrnkVZcvqhQ+D4lR8Q3QMggn4Jrk1/GKRQYgMCfl0+oqtgjgSgARzh0bKqWcBVCMLQj0X/Ey33M4Gzed3dOyYePvAo51oCTqEabHJ0VpDRRFxJf5pg7QKmXAO40Fa/GJ/XiOTlAQAuS5PRTeCtghFOrl4laiVAKJJygbmqOZq4oJVUy1WaRIoyVb1LE4Uu1wNojgHrmhBIhcL5QtfLZ6TNldbQpjUkrfIG8C1mu8oos+ILy1Wd1Sdx1P2ZAHCRWlZBBX5PLKdKalgZ/+CNMkCeS3VLy7kUaDP8hgGu3h6s4qKwVFNsXKxsEaaJeJBJxZT6MmlbOwaB+iYQELcXnI7W4fHh9++Fl1Gi3jdMADDpTa48NyIywqnXLo0Mo/7B3uHRxJSzvNlnpSKqtaU8RvL0pP1tYuLix8//Hz1j//PX/67//y//eXfnL4+FXf89vG3f/3Xf/v07evPP/1sqij7am7l4dHRwifkJR7kQfdfkqXMi32QbAbU2lew0Hx5l+EQ2m7uSvdXYHdb1kfLAjv1oDsslWzJ7Y6lMPUCvn378u3b2fX/+MfyPP/5P7E1NhvleeS6tmyPQ15sM7RjTzfwcwNX5gwcHx7WZGo/GlsHssXhW/dtXZBEZfhGdQOpXCWZN67nQ1OD+APJ4hKDmwZ7rZBD3nQpUW0DIBLnCaRVh01XEQLbcnXsgC67CT7gMf3H6Iyx5msL8cyo6QAxuhzTzekwz9V2YLo/szssWCNQT1usDIDWJ0pzNcoslNJ2IkSGl9AbV2FAWYkx1iXiPgReQpWApaJiFk+Jf0eM8ANSjTyzPAR5yQfIY48NVnkUWELCemJVR8XBlaFRKh2p/5leELNkuP50mkWd9LR0PZ+bCuwxP8onAdE1se7HICJSa4UCFkYWqioIWOZKrLlIvdv1RESY+eJ0jiarSrFY1l4RVTkcE2tPyqVnOm7P9SAck203sQhDzUMgXailKYBE2g8xhqRqc2/ujt98AdZXK/XcXJ4GE97XYyW9YysyPmOxr2859My1WkxhGOOYSRq5au1eD9RMUGiix0gjCgI0USuu7Sckl1wNmHN78wzAcZ9cNp8MNZNf3oKooQYrqh4UKQTPwkoTRfaxL4GuzLQd9pSzdsxwAEe9jjoKno9qCx1ZvhndML7jDqEHWknnbbIuy5x6E70N+5rQjbr7i3CQGywKH4oWmeNrdjxtjrLhnosMa8MKj7asJ73Yq2XGwj/oxK4BaW64jacxFszg7mZMi5apKuFBy0QHFcN0BM5X97nv2kSpVNwOBDKtWWoT2lrsg4iZBSmOeckjoC+KqR8mDTSMzMY5tWgxiYNi2aSJTeVdZMkGRS4VuPZA1TlvZm1+yHOL7ONzcEaPtrcDA8B7ziNxIvoBCuMDejwfo4NEPCWDaxDUliGEuUqVkjRgdJpSDVnyJhG0d7uzsokMKkG2hrY2bM22vWk9DqTlDtyhW2V1GDy83N61Sc6+oFNi8VIJRlNi+8aOZ3I+KNU5l0ZUv379+i//8uPazuF3f/kfcJwFlp3407/+9N//+z+a/6OvgP1i/9WBuTrW4AT/EgraQxm2tMVaJ+Sz4YlUIoKKIHDTmCySGvbcPzoUJ0rhWGcLst09k/pvWipc+vFxd2XJriFui4C2j4/3kRfinz9/vL//UT/DmPVf/PGHo8P9y/NdllXy1SQi6XUDtySKgdgQSaOhvsONhW8OxdnYsMu6PXYnpmrynyBTM7xU2eRiUlnab+ffzJLFOjRxi9jLzLUCqmAcfTO5/sAoktLvUCPKRPJN+/je8UqJ+mwdASNF0YRoeaIQ2YJs3WiWPYUzOtK2gASOD8hakVqiw4GwXg1v17EjN5iqCRw0DRcgIFa/P/bKMy4QiVRZtMF0sMC6DrJHiS1Uy7RwGVTDmK/RdhIlwrH+WGviOb0IllKFaRGhom+kxdBovW1IAiAd0QrxJx5AY3GMAKuw4RxzfTDDSMdEewBRP9ralkqdwQaF7CrDlIQDhS4Q3S4WjVFRtxJc6rZu3Z4NeigiXfDw4JXdT90plEI95UqZyYK7fro0noDYKOM7FaakcpGpUwE+PjRW5yaSBkgPpXgxYjpSYCVd6ViGsHsIpjVv+oSuaM4tNY2hHgSyTfxfQNvBg6VUN7wEMn48KtQJwMVsQLpmaxkYmgol3Nc5hS1ND/IMR2TDTvIU54se7rYcqTSd4g6EbplixgbFQyDihSQIW+BHeHWr41YJDI1pxl0tqdXFQS1MNM6+B00NAqHWyFeIz3nQtuLFVdEcJEkDJ5nTn2WBZKvhymUtKE+WQ6mZMCKCcWg8U0HuNOUWAS0sqveEL0hVZlVKQ1J79pZJRAYTYKRCAAPKkGxyNmotDI8twBi56ZKfwQtns5LSI9O/QRktRqgowdbGyVk2GMFATMekGHwpgspsma4nKSITNRxw3Q32HvL1EiIllFSqLs3yvI3mwMFyubbTEoM2K+N3xkvXzLOFBi2GIJDjjGcqWOljG5/N7BxGYnKskAdtrxqZbqkNhZj2WeAd+xE4FwiOZwuicEulO9tW/N5cn0nWPZxfXn79dpa1N0TQFjuEfsfEHrmdfdtIhEM5N5zEgV02+/hEbEMbBLDsi1nbxJCeoCfYhbszozSbbsODP/3rv5qLuH/82snsv374+MsvPzuFa2U2ztvD/cN9dslIHeEge5qRv0A8Xw1NM6lSWIwJO2zTOm+NFU53pIwGYzALiMCW8I9+WBtKKySbSnM65OXavkAjNOsbh4cnyG8h8T//0z//9C//+tMfvn/79vTs0yedg/Mvnx90BdYfjvc2Dlff2XyC6JJoi9psIiDqcKQwzErMMlUaXa3YLz0qMsL6ktih/pqlZ3JgPO3x3o7VDwL3er0N9ReMSu2xvTlL5EUsSTbKo/9Nfez2tGmw+oa87R8aJulkeWcJMIYjuvxQU10nyIBoyUM61NxWkhAl9KR2HUjGMZZVbolGo6CE+mkXIu2uaUnBtuw/saM9CX6WLikdRSg6SZ3r05AVYR0u+KX7lG5UdEzjZG2Jd9I//q8ytUjBys8QV3cApBuwfM4CWBRnamx5nxwULvDkqmVHUot0UOCeeiJLCpJ5qh6df6UZC+TVAmq5C+YEeqw2ilIkgIZPiprxZZC6pmii4lZ95exY+hxS2kyHmwpR067rHo1ZCKksYwJfBky10WSi+ooxTXmHTBPAaISkyah6BdlmGGWISokjAgT7mfqa2aWCZHHCROWpEykySlbGVc4qDqBGgywp6vQ71AKtjIXvv1vswbXgudQPqWz7uiAvHsk226VkGRmOUfBLccdo5kLVIvT2WoDLtMcwYp44+Iq36hoaDJ2LsSfeD3/9L0VMOeNgEhclAaZpMUD6wU7a8Pbh/uruRrgwB+SZ1H9vYgbAZtqFLaxFGEVFoA2HxIsIxTV1xsQig1rELIhHjt5jCrFDwCIXFO6R/Kx0OZwnUWZC3kz/QkdGdwBLbEJIxhLwFABc6OCfCR6dJsjMKpCVVRk3P7zLktYCyZ4uAyAcKju6g6YedzUe46gqFE6rSg9OXB60tatqgFaYdL0M3ibL6K9L3SL4AOmDTxOUuelR8MDApWVXOF+TQi3GrVIxbqEe/Oe5vEXAjNj2uYITyAyXrbFUMlJP5Q553F031f2e/E5629ECE2Whr+6LTTrF/8z/ji0FslWsIR20ZUIdSHprZ7TD09XRK5O1mTA0ZocOHVp7efZwc3/pXBVhuHT8mjnph2/ev/mf//rhH//nP//Tn/58dPJ2y0notjM15NvhBhIXTpdIa7SV2beg3D4HY24kOcmWkMV8ITNnEBnXiv01JBkCkPW125UxgHD+9vXcFROZih83tvYPjSXsMLs3t3GeY5U8Z0HR5+2bt9d7l3/+6acf/+Vf/vmf/ufB/p6F0PovHEVZfmni04Mf3p2yRtmdeqs83J11y0T/+GAVX3hrvt4e0Sa8OnNR99T36aONRXncfJQgaoQWm7D2ikNox6FstApf9j2d6MC1cm7LSGyMpAd0te1U93l0I13NBjayIiXCktXPIiopocXviqYl5RRwlUJlTxkINwCZn04xfaW9iDQ9BN+6T7Ls683x5H7G+PZBiwkjb5Rtb7RK6Wwb2cOi3jSBLC5kZ5RXAmLmjEwnpkiv7jYAGJO1nf3OyfEjrpG2Uns56CTDeegF4G6pr26tp7Ki9SAQMpO1jJ5GbOCHRyhpErSlKJog53FqRNL9JCtTLLIACI2MDgKnuXnG0sfCSBvY6wrEdRvS2wxYetOzqkBk/1NNWE5iABzSmyIuJSLblAvnMvjVQakzO1nd+KeWWg5in8tFzYN97Q5BUSgAgxEt1IxY/AK8iSweM5+MUvZa93KAY7cHWBY+CQnd8bA+sjgNEC2guIO8ESP7ESyJRZrfZy9t6Iu8+J/8qxozhTFyKJYxAVzkqalgjpG9gh0HNJAJZVoCBQ/oQDWUc1I8N0tIlpgCHLGbIlW5B3KnIGojw3IgbrWrD2orAGpRngf9EFE8i5y+oKCnAFW6P5M3rxzyOGHoBJsCga76wPz9Z2D2BiEwJyPoDGUv3+0cUmQ4QUFGqCeV0nNqtkTIR4GIFr9Z8+FqKlKjAB0yx8soQ3arH8/F5A3Qw4rYuT5OKJnIIid9I15ASbZRJkkevVGDNhCjEN6DPtRQF2MMK9aj4Bv5kWfXxIzdPKiHaZligT3UAP3MkGOvgSj8zPcK/ImsJb7cp2399c3F9kcPt6fyyuRkb3//27fzr2dmbF7AXI9EByAWpPMYz7vbBWdz9+B47+jY9piMHP4O0czW1kyEw4c69Zu3kNORIJ/yUfo5QuFff/2wu3+0f3R8uH9wcnxsO34oItvuqu1igljqSE9hPsuh1xk1XlqUzcIyBHyMcFY8S3hM5SBaz1sdURo3sXDXeb4RNINif1B+CDl0I6gTfyB/wg4Ji+W8HDVj6umnTx9k4jFN2mN03i5JWyfOQtB/KHVZcNZaO0T/Paq1JVx8xV/DISWI7OvDepV78DUJLxI3pzbOU+3K2ZS2ww5uHy1tXRZRj0jb3o3uFu+iXJZkTvdxvMduztG76J5InJ+1u5G1DRY6t9S53fHsWbDbGq/tJu8i05jsYj1CSIgJSJNmNF+mx6+Yh57KcrEpckqabDwAa/IByY12XrQGKedL4k3yucFcT/RNPj1RitM9HYQJZhNpiDKIbHgZYEXynR5ZLLc2kmE4ZpEEMSUJw5h+167yRcrgQFWoqXaZbJ7+AyqF7bDFcoKeqrV1dgOYXmBRj/rnG5BSmjRNrTZ8E7VwfvnmNMUKjZBUqKUVUxI5ABDRpguCGUBVxk2IjV5HNE9M/4O101qmLyoF2gBUFgvxl+eIhjuLTIY765CFgF1WniCNe8tfeYkJ8mi98AEuldUWz6jyhaGp82AeA7JeqDLoQh92uON7QzQD2pBisnLVP2IdH6LU2CliOsyIHVXXuyuqCNLg9hR9nyCgGqoZCMjafX9+slKeIv0qXSSnthSadU03bcZiRkfT81UoiMz2QX4GSwHMXqK6u0OsgSAhCQyv5Etp++U2YoasiZuL4xUTOwzLIImCBwwkId0JRoKUcwTMvE11YxfdBKdKFCakw0QrYzuUC0HYYi0Omovv1GKYJnkB7luIKtlixeIgsVx5vR73407oly0a6akhnFZF9n9hWgKSiMibTbCFInUd8jwNmVNExUvVgGQq7EPIoiF7kbuICBBEO/jpR/veDHI8MguKYAVIkBAYn3FwhKVQ1l6lxE/w7qY3syuNv/QjyFy739g52FmdbB9cmsS+tnUlwNKQoL67LUoTtjo/XWXhdXhwdPrmnTFbEm3jNR27Mu4d4dLKWuHL4eGmi1++XN7e3DuW9vOnbwwpQpKj1cHhu+//cPr6LVPnvBW46l6giSkwZ18vaVHjm7aJkE7j8Nh4u+isOmMd28JTj4fQ2PWEpSABhGPyQoLobAo5sbWv7DEUZVfMAnp2ncfatecmNcOaRqvPbzsRYGvr++++Oznavzj7cnn2FSOZBNMSjuzZudfulVapXepG1wMz+XNf1CK3ww0hPWyMmxAefYdWfSFqIRx+jO7onxm5NSHVbmyt3k1ARPSsdyPRdKbeQN1oBj9HwCPFWB5c3krfGAAGddv2Tg2e1bExsNERYHc2+pdkkbtI9PpNiau/oJ0rtnMRk5Th7oJLo8YonNEnSuz+dIALLZOV0ZLszqgHeSKCpvhgNPqgnCYAyv4pqddDFFN/EkuVxljTX58Hx9YiNxgo7FDtKBBUR3jTWRXOlvo+cLIFRp6CNiZSArrDw49HGHXN0CzQQTIMK5YKoxSbptEyJMuPElqJFIuZVkGvdL+C/jFYrk0NsoOa8qT3cTZ07IEWZe70nQofUjq06VLGsJLU3TtroExVqy7wyQIdTSepvkKju7U4TxEKxSqXHWjWTvervI4SK6inG9eBJtKC4xizQkkpz4x/CHkgZ7lwWn4Ye9U/CGik+kvjDO6DarBRtR5El/GO+jkKhscLWVSmRCRR2FORmFohLeB6Tv2Z+KGjD+M5qqGSvYgLIKDmY09weF6RJE2o2BReskyeEXfh0IhUU2itEmrsd7yhkkkVuanNXB87pQZV4IWWBG71/cczQ4rJMhw1USduYUq9RXhlnKwk0a8ckxoAC1ALKAMP9ES+yDz9uUDtZv/rno/Njj/BMZiqE4NcGJZP0aQI3s3ACkY/JBGlokNExGvSOVMqpiICy4vUiKb8JLuKA0R06U7VIHf0JHepVPDHVteIT8/1yruwwgXLRSqgcALEeCDlWq0a8aOCB3AnKAn0oJd0CHIc6HV7R9rQkIVgg0Rc7TuM7+l764ZctxSs/TUNwGIjYztTD26u7x8PTX0xDNtss93V0eHxCcklMwRXhkiojomJpdZr3MAG7lBytiABqbNni4JXx6/f/fFv//1/Ojk9lZxpQzS7ru1usozX8jNGYe3PYy2xoujATth3jqJcWzjKhIkqdeBzA5YXI7uaAY6U6ZdTVK7QRd6wzdQyMXXtnHUjs+bYHP0PWXczcIyj1nNoJ7mnp3fv3z4/nvzyk2MGjC5ccO1W2K1sE40ZsVL3opGqzq4sM1qHFWluL43Tkl0EMHvKztn1bNoaGlPzzkkPshB4jdvWog2HJKxS+Nap8oXu+YQ4TkJTi1XU7eOiiYCTG6GnTZGgeR0NXxqnARkyNP02oZmypKhFf2BbtczZ+2qPr+PlyRLQNW8rFOON+n+FwMKOje0Ho9qyfkK6ohJiQupzzJ5h+kepcZDU62fWwMitkplbilAuITL0FnE01IWey1onq4kxe1VvjkYYwU5b3MmGMW8TBiqfJfXwqA0CpADTmCv5gPmsWEYs1SHVGWyvl3JTp1vpUhWlRZ4KpH6SfHeUD6IBReE6z4XboQssxlTwwOnClrCQJTwir3FW6JnfbU1WhOBGkrexd0EPqgwKIgVTreRstTw9jWD2uPfgSPvTiFSttnsKwK5zOqE2L1fiQdIzkia9CbtpGhHQo+yIh7zm4TxAFojNmeSeMvOwq+rWgMIZAsh4LmiCIHCA0GNeUTWzq4rBLQQis58+4Hm+yBMwnDu17XN1LllCKqjwEophqdn49J7k9aNRRxgyOE2BV0G2Y96xQSUkOAUvqO+l4tyB65nvpV0cugOJ2eQI0PIBJJ4H6RnOF4k39QI2vTIzEaoAESmWz7AMdJf7C/NMdUSKTj6BmlSIdHJ5vwvOInZqYBwj1FCt8kNW5VI/QCYQ1T/NYVsoE6ehDwqUHYsJQQUGpBowAyWysXDGJ1WekE88k4K5NboUs34XXKWBG3p52vrxCyeQJJqkbdWsfnhPlynU/HpOs3XhtMK+CF1BOI6lroA8vKq2nwTNGLV/cHh3fXx5cHZ7yZSaayJXuiaTvru3LRTCPFaGBCPX6ujYhpbCftasHIn9LqdHUmMmYDRdXaKDw+iw9ePjo1eXd+cP509PO8cnr757//3R0REFc2Il6uoRMr1tFDfzei+uzk0cwrxm2ljpsWFLn3Y+gF5CQw1kj0lHAtO1XJucKUnSszQrTSZERrVZj3pZrKXgAAewyUeTmlqmwME66V5VBgf4LrM8//av/+aH969//fWnT7/8Oqmh8lOA3D+0SO5A2G9kFbfItkUHAhAzVhHTcAVOHshc2WR0v62zM/qCemBmYFOxPtIUx/00hv3c8bVAz9vqpJIChscAg3cTf+xXsUtkUgpsxswiAAxcM+49K7R5L0n7xaDyIvG6GeAJlVcmCNfKJLa5NBqVwMrQUyH8py8cwFYb2Mummd+kb9JYCnVjDZXonYAzBbgYcImzmYjzSooKUBo1NaHPHcVHTXI12goYP/Emg4G/zIsbcHDLJcodOWgIkW3ci7Bn7wZ8zRXPE3hP4bPyKGADoT6XIQJEpEwFBh7/Feq2OofIGQ4tjWmKFu0Nlnp6BZca5095XzOJKi2IYvRk/EupwqCYt7lzHkGNZfh6An41hpfqAgysvlRV/AnC2vIYahcyFr/ONUKgWB3V7PEAMOAv7HIJNUzEdjgPb0qKETZaFQ9XbQGECUTqUwO9BurCiBwKeGo7MIg0UUrENcIYYCn1W+Aj8bXdi2fJJESIAV8VBPXlpa4smgth1cUsjqvFM56ifqpIIHOsXWvGegAtrKnXYULj2MBYrKRZLomID/7hZjQBRSj0Nlc1sDQ31ZCb5Ih2J0lksZl8gDBYlBjlJyaC9jiqUDXNgQQMmimnF5DDc4QM1qDtYgQEbBLYxQS0LAraJp/NRE0XFGPSsDLuD/KgAjmok9uFLWNkq6N2a8OHsG7fVf6fzUqa1V35IfT0rKKAJlz8vaamsknLeDa9mXqqSpBYmbp5y0934myN0JxomPXr8lIb9DwC35lagQyZKlQItkr1GwU8NMLaLDBCTykgbdO0+4fmnmwZ0TzOt4jBzy8MncJBSTyPZULpVoqts1MHgv/Xb9ke+z037X62NBZQ6V4sQ6xwCdpmoBZQHx4fbf72FXiM6snJ6as3r5HNowZCcdBBLtZh2XBIsp6JkB/RpwDruMLgb8hTvD7L0tScEYwEdazUgyhcB16hZRIlWEY6BKn/kEmAPbxtLSq34lnCJKLzh8Q6AtrcPrUw+e3ezncyP7YntZMOmunAVWc6hXrPpl1u7D6bt6BSrRIXYQ2VBAC1LKUnP7Z5p13KZheDrBp5tEFLh5rZKroTzaABEmkVh8qYy8NWIE4zPnmrHfOJuJn95Lr5MWailafA7jotszcfhqI19PgLrGbA1CZi5R12GiC42D20793VrmPj+Ho7HpG3NJ8ulk7nKNkm1gXJ4JTvKM9eMikfkI1O48jtRKsjLkm9PgcyCDuypxhRrTwZGmJOjehMk0fuTQkXRgeT++wPGSjI1F76REdtIk0EyXG+RuDohdoZKyXKCARQrXo+yoNF2XExs07C1xcFZ8vgX88mo7+I+vJvZNy97Ac4xsJpC/y8p3RcgGUwNDWdGugwBXBDqWRljEkCRoPqKAwR6902kJBEJJqDoTLgHs304ASR2SVVCIwWJ6epSQuyXTUyaEW0kpO56GAhw5odXNXYcic/iIZjATEsrHAJqPptgc/Gx51cQljAHxLVNvaSLgyCyRxy9G2mqbqb2vQ35iz9isoqlZMDIX6oTSmgVr3xqyz/vIbdJD78eyjgYVVPuS+BhV7dDSwySorz8PpZStXHKmZYCKv2cguTlPRYGYzkQy2D7YtoJXNZfHOXqrc5b7r8kREC0QAI4UtwoynmuCwo7t6QR+vJRtYzV4+u2JPnGNGU3gA5lBeMIOZrtRNnK0FMd1mQCqMcgypBWHXqGLqF97wWsAkXeErL5IaaSOAmxpGFbiQt5CP559kwTZSKIEm/2jKa8JKjLzjyOMi9e2kNfmHt2aXjpdpsf8FL+PsdoQG8dY2LCKptODgCOvrmRri2fUVyjitTHdsgq/J44JjeRrpQURZtD6vMfJeN4SX2ZDkOjtnug4NDY5OHJ693V8f1x2wobauiQZlfls9spGHSFJTBKLKJO2SbTEW9p+fXpyfvv//OjCPWwgRR3uPq0ikw5/aLE+Ga3C6bj1aQkqtJniHHlOIpP7S2fmtGppnw3IbUR/vowbCMCqzJCbgj1LzCj5THajIjDYWBm1s3rYowpmr2k7PqE0FJf/HwzuaXz5+PDsq9n74+tkndzeXt9fbm4/G+ZksVEjAZ/Js7c7EI1vhg8VoLbAmUkNht66HlaGwW0ZLWe0mbfEyevfCibeSsYbPMC6wpvvBGH52WtYmTS7cmw+cxnKvmvGBL00DZaliZ0ivA2P9UpkJnBcasIjFQJRxFG4DDaKjwDbe6TjdXzllnU6NOfWvaktyiv1cknQgz3RlpyshkfRAmNOevmD1JHyerlvltvtmksHTZEhFGJVXK8PAepKkVSVmrzHq+JJEMTweMMkFgJvo1oOtRx0k0mDaO2LqIb4LyKpn5Di8hc/ZbJX4hmdqGLZuDVglwiKehrka74b67mfjuzzvpgY4/F0ZiTCBMXNyFxTjZjBgelE7gk1FBacWn+zLVpJ7UVqMZmVHqmsCAscUMgkfcLvjzig7ZZb49OL0Q2HVvtdxsKM/GlgB3p6kNwPUzFxB+ZoTH7FKz6tPHHk/pLAQmS2NBqFZw1x6oXAuvDNDUoi4sHHVw2cUkEiLTF6sEIzbxI9h7LlKbhurUIWQ2OR10mdGhRbWEVy0PLce7QMsX5lCwTi2DPiaZkNHWktgpSgpMrbQyyN5GdbKkdOKfaTa9sCx3on+NFx53K1hqSMXenbFh2UrBbLm5F0LzZwnvCEbkBVsUjOOASj2GjnDtBYBg61K0acizTqJXyLlXrQk3sPKgCoMWGZDFXaleIEXDKIUnffNBRVXsOx68NDndkcQ+FXJd6zVjmpqN8qE2Mc3wi9VoZF4FyI3DoRxTgoTpjOuDg3fmQzEfWJ+42lhrIZJgW+GhoMeYhC4G6OCy1Oa7ZqGWFiVOqWNre8j3WH/jqra39M4cUS9TWxiyq+3dt+/f8YauGMO3YoQ59pujd+yXEwHtVjJDmkQ54lsSayihaT/6eLuOgoEvy1U2Pp0pIFodHezfrlmxtTpYXeUXWmfh4C97QF+cfb26OjOSbB6L+fKlBGJ3HREPkqIIypRYH3crsCpu0pYNE/ADu0MMthTW9vujppxBFyImTRGGp5Yb23sOp8F8LsBsH2VRwCLb/MHW5r/+ZC+KC4CubEyQKMY7HhrhdST4TXSWT5o5lo066EFVriiYXpMoG1avtl45Nf6qCYNNhsEfrlG3yfYnmkqW/l+m/nNJkyxJ0PSccxqRrHiz6Z3ZHix+NO7/BhYiEMFCVmYEXVXdXSQjMzIinHOC51XzLKx5hPv3mR2iXPXoIQZy0x4jqIL/t5F145l0WSD/aKxg+b4hiCwQ+TF1kOm3/8s4oHcScI3JG2qAHBcgaKUVhzqTtdIlhgg2iEm+KZclxnMQqkH8jCupNYgRBkYYiErBNKKRmGYhY1Z3AIx7dETAIUJpaQ+jNVI6pr+8bowpcTGzDpkQ5gmp49rMl8QASYA2QUXGjDee0Yt2ExcRgss/ujZ6GhzAGSUIlMx8KjMOyNAFkcysOPHC3fRl1Ce7RwB6ls7oY0Fp0fZpIePl63RdANSUdhTJDjRujwijYdqtQg0ng5EaYMSb+PjmyYyF0kc65as2k5PsyFJTqeyKuotN6K72AyYhrWCSkKpO3eAiWliiyjQYUsOvNsSEJEvC009o6xEVGxKNjYthwYC5CG6/YpeGEAeGwRXvjVM1rVHykLx2N6BoVHQPYA/c9Sxk6J+v9t4nmDmWgAxiZdRKB1qG73XYS5IhGJTkRNX2kb0e2St6BZnqdQYgMjRmLlK2fKUTJAmir8npsA0rlA7nqTEb+mirADU8IkUI1F1ER7WkWhcDA8pCIuqRLXFfNAkt3Q9ZaCxMkGf4Cs/FNGVD8aZhbCFndFDAnWGWoYcPAIy2I0b6Av7oYWIUO9ElM518N8KYToAZbaMAvkPQs5pom4mO/VcCGZnzCLswjhhznFmprGpyqULUq5fBo66pmrb4z2Adx19mQ6NZrLZQooACLAMqMVZ+00JSpyLSM9aYwYchjZZBbTsAGbm8vpOOsu6k+eTdvePDYyrOKfbug539k3cO9d/dt2XWeyJtf3vm1oVM2pDwcp6EAbmWRl8brKRgfOfxyeHt48rN0+q79+8fN/YNJKDtNIPLixvLbOiRz58/fXy8b3FLW4itCe7MUSjUNKTlPMA95M8X6oI1xMWsyEKMKNM/+HBv1Ypm/e8ev/jcslenYSKQ3LhxhmdwFDKjtJuenl9efPjrnxnV/+Uf/v7rr47t9z3cY4SLw70Nga0tWEc+Wb7dFiCwcEgo4x87GvtL4VgoZCPFhtOBVhyG2hltQ99svk0MTvAx4e207KgmvAIl52Sxu7OUWuPgXawO4dtzUOOKpaI3171poAWwrau6s9PMNIvsHOqRazMrqa25HIPqlBhhxnBHdYpuwyf6Gcy1SXBUYGQwlbF80/ozg/1X8wBtbcslCHwQNLqRh0QtTmatVBeqzDW6QwdHkkneKBZiZ72QvwDEIU4Dhs7Cb/JXHqHxojlanl7UehHNqKgxawhIZvAVHzu6xxR9m9fGOHHSC0T9nqEe2o1JKSAILgvaY0uR22wDWqzNCAQQIaA17E5SUoo+AVV6zWKkRaxGX1INGCVgoZ6uxD3wdS3KWiAYWcb+aLqWF8QU0e6YO3BWSyEaMS244W92xeVRvCqjD0GOcu5Rs7rTWjTQbICCNyfxVmDIEEfqUTO54ngVFHXAn2cR3JJuUZuQLKBoQn95vDGNOiABgGsTQU6i5QVBNgERWqCWh75rIQTrOIr7E1atUxggQjegoe4+Ujd6CjZoiV8SCwXVWhhWrATunNCaxXRVyCE3OYG8w6FMp6d5vzxIjfuM4EGH6OGgh6gUQRfS+1o5McnbE4JEWYcBgdVTaEgemViDkUbaczHNa4IACdbaf1oc0A3PFBa41d1IbLNYLm42QBZw/G5Qiuh1kVhUO5jy53Uy8UU3u2+IgAlZ+UWU3FzaDBFITSlwLjjbpIk9KJbHixwjQbMgYQRk6DyMB1+ZvbdeRocSMORsniDyogEOwWfiL7IlgtYNK5FvDG7Qtj/TP3gIyx01kwyVMbFI0+7chyMr4p0QdHRq0aeV6XLVPIYxKaTUV7SUCG5OisBUpz5RDzclMtyVRKFv/MbZNWVn2+4APdsWH7zL5dPHH68uzy104QhBDJwZrwxRovAiAGELPWIRPYN3Hg0CdCDdiZRTPC7gT3d9RIdin562lLWB7ZNjO9/OJuFlQW/5T9Nr62utpTFEMeW7vnJiG0DrQfccHC0GEaDTL9SEOEHSWChTtcFX7NNEfNFcrx0w92FNETgs+xfDM/0zfipJ4iyjXXQrOYMLalhP1VGs5gVISTMuL5b8X+X+DCJaevUgHWnvlDaJBIANaPgNRM5xdFDoBsfMhbhE5e0cMM/ssLpeVGlHGC0uDxNF/PO2gzgrjBN+rdoS7PG4DMRC5ApBowzNSCrhCdUipFrgUUZ7NEPKCnRIGYOBFGmcMONtWJymZ6pjSTqC+t3INhaY6oZyjQCqFpuna710dYdOq61aTEwTdRQTY2b2bappRNg2RmEU3fl8BT0T1C5WRFcUT0clOCaE91tdbq1ATTg+3YxJe0sheFhviVsbLaN15t3N+pfkUbhFFr4OqLWW8M3XaNiVYsI40PtWa25NsQVJbSFCljkI+uWOjthFrfa0dv3NE701kleuZSTQX+SOarFVtc5L9dVzj0EZ2r16bRYSlS6lXHoBt1oJA+gGwPKz/hESLwexQW45hIAkRaAYHA668KWrLqoPKl14FnE5PBtpe7mIKNqALrsakwY4tpWDBiLGgaHR4oBuJfTDnHTPCU243gozVaKauhpBFtrVXF0JmaijFVGDXuETU5RNigJrIV9RYbB5ANmeYl4c8iFOmvYyQRBJ2VPL1TOXMwxsNFPIrC2P5OQmZVpgMooQ8lE7axuACVaL9t/4HbT+zQYoJM5qJ2fhD4CRBw0sOGTTJxCXLR9Xte5FSPGlH0jF2lpDPk0O8fusV3SoxZptN4sAFjAlMXXRNJqdDSMZQdWsQ/mZca6NOeKVehpqdIh2wcMnlZG0Enm15S72BTxaBylRzl2yJFvrp4ezrl8/oZ27CcTGZ20QNedZC1qliB1fUqbEnkQNTpiKB81aztEF7K4PN8K3zX1AY61dt17DO0v+bzVAmiLbwJbLHOHT7SDsd/8WXzdKEfexduBCkWiSFCQ7/fcT6yGNrK0gcttcJYoJZzqRrbvFoRutC3r6ZLn/cM2LZW4u1te+fn+IxRPXt6KrkeqWN0pu68BqZpA+bffOev+sHiO9SJqlfl0T2DoousOKHu4cvSZTdOPA6MsrBCJ/Wy1na6G/jI2cp/ETM2hxkLWvdxfXpoYPjpzqtmM2/NNnr4u/Nj6yRAhR9FtvsRrfUL2zVWzMbrMAJ+A0753yckBJPJIUo7YUYNhGdxcxzLKUQ8bg8jYtASPoOtCqfN9YeQafkIw70zGVVQUtA6Fr0bfirQnbMIqyzlX611081C1F1GdSbYXASHd2Y7lwMhtKER0OllZqW+uxrG0uNuVkdQJ97mYUMuCZNn8BByr0oNE+QrVPDdHebP0CjK/pYfBmkIBQe6OkNb0qu8gqRtTFVAYtJjJKnPAcZIJR6AvkN5cT7mHHBy1i+bNwJmRJqf9axFPAzdcgfWNBmC9lRsYLkkgziYYoClZ+gQ5Vx0SH1yBeTR45gsRYFXkMXzMJBE5NWElII2gmaQDUakbdbe/RcB6sT7INE6JBnUoMEdOdBCWzixBd6FP6Z+ge9GODeMv0esFqwE1LJf5rBbiFt+pLzWYFwjk3XY++j7mtB9BGO+NS2pMB4o4SyyLrhhK9YkH3eNnNJWFR+aBMAAqJAdmnIZfbHoav7sAxwKOErz52zxPYRB34RMChmm9ZjYVdJASE1de5gqhPPSpaT+CYxnpEbeZOPFE8GOMPgQgAj4iRW9ojQwGtSSwUKmouW4Nn8Y+WaP4NjwqN7hXbxgMlALFc+b3IOHAEdIFCRartqtU65+KBMid0Dv0UbD7wTYjn/EWQ0RCS2aw7SOuCWgSx9dyo1f5qh45LRrHPxH79cO3JySJ3T7dX+dElWzaHzBgxWbpDiIpYRZjOCFv1Ttob99milRfnLpiJvBFVv+7s4CwxcQYlJefeBb88gFSP423urqVC2NJbQS6bSh0G0TFPb8KNh8kJIvk1XIRw88O+xsVokRT8jbMRPVGZqzgOzZdvbkc2rfe3hkX9pZ6VYfq/3F5ZicTaXl05qG7naNue3V0HQ2wftvNLDdrEo2mBhKiNJlaHWwTERjhkCWxj5cYHL/ZGUNWW7BL0BZEE4/HZW5TtctDU7oGVta3jcbapMRa7b6KjvRd3zeF626Uju09PD4v69/iJcXKl71tgF+4LNrm38Yojz1SBBUD71a32IliwJLez5kRsg5YZfIc3rmdwSY0JuYR9CFgrUJj8KTY0OuEESDKWRDGE1jlmy3s1BkqXg2JhwhuxPUz+p0UCE2s80VI5FcZiMTozAqbhZFcFxNevedh43FVCwp0JMlKfguO82Ft7qdGoHpWodL6ppA0C63sseaN52M39yiyXltyBx1JOVZ8VbBEDYi36lCwV2UDcpVMt++iDBrM5NHesFq1blD18A2NsVEnBrBbdKhkXzNOaRTQZCqRQuASAGsECoNLmhsdF0m2ODXG1sk3FImi/JNWT9rcGtVNuZcXys64MSW33PxrEpQIfVNBNZotalg0YioRoj/pbg5G5nuGW4S6K03VN1nObbbKerokf60jJwRd0yiJOM9LuaBcN2onevHEaAiBN2PAI2Vn8I8dibKu/ZnoVhn+0loSNf4wD0DJJeotJQ6yZS8C07i2WQL+Kg0QDmFSA52OUBKiYJvfVtwqEi3ZCFsXIDmiLFaD+JviUNDGOfWK9lusZwAib4elRyfzJ15OTopxpdngZX4fm4apxm8rqZbmCZHjcZJuu0PsNDPTC1N6KAl8tYozgKy4Fbk2UMRsc4nHtxOOi8R5aJ5zEJ5fFgZiyYe1+0ppd6MyFtwUhycYcx6TN8LWSGk0Y2xooqkgKhkEyN2YrLVBx4MHz9c3968NNJ6AJdFc2n29Xrr5cXn45v3JI5u5huf/9g8PjI7mF9gbYnPXwQD6cUoO4MtdoFy2jfyhjm11JBInwFaTePh4fH94JvVevjQPlKb1N1+sfL87PZbvBwzXZ2DvMiNUxeOgZN32eG0P22O2K8uMtPZl/lZsHS/HuaWDqedKHt3+4T3RIo/k0b/bqGPo7YIBg16siFTLv7bh/CRIzVB0m53SKVa+RcaA0cy12L3ViR5XZ4863KlqiLAJ+k8c4aCWTBCsgJGo4DY087VtKdH97uWooYOkpKbOd18jAgp+Dw6P95oEsFzEQ39jdc5DA08WFqQInGpENC/OSImRllpf1KnGUDChNT8QfTMg9GpvSNtN84wXwWim5nXE0bi6wG1L0wVdUETKQswKfzhYlQNE10SCdCjc11PXzYMI9NCdmVJvoDIH4/ymL4GPJBbKJJIuycCtBUMJoSc7vLasc2K5a6E+mJxR8H11WWPMKB2OmLZAS0MnNsg0AoKdssXrZxmoRFdP4LZcKekTXcU8ai1TM4+F9QOfw6nGYgxRNPcpXKJMNiwTV9zX1HBOBYtIAwTiXR65Uavnk81zREGT42p0pPAVqVHC83ITnjEI0DkKXZobuetRr/UbeoXU6Wy6BFfcAx4boiKvvjGMgRAA/tRNd/W74Z58nPtv+SMWDs/YmsiXUdaGJcYKT/tc0YOMU7o4hz8cNdhDKrOSasjX6YTwHn6CFpN9sfTYF9hhDqia5rEPlI0K9EcI42Pe8C8YMOZoacr/dpWCQUPXFnJx2lBwCZdwQJAJC+2d6K++jBkNkbk5vw9zYHfD1W7P9HoijEdzRIqr3aoi4C0q/NMPOw53t1LWWRc2oEdVn/4JitY5zGmklQhXrfTqZdli/itfe0rmqScwCf8SvlqBqiKbPIskMXlYIpNUCb7WDfWKIpU8V1E7/k41ByQeMpTkqtsAUzXvlHiJVpQgQVyhqFWZCTHpGlOMtFHZm0UVLGoQpbJaKVu7Dpc6lgB5Y8ZYDWR4qLZBbkkVcE5lu7ex6HQwETFAenhyjF1zFp8SBCXcBGPoAEBTMWW1XVnlhPCghYHeY8bQ5UCt/BLM/XnhtjlhDvKyI6MFA5VaGiIcjp0gCjTDJSAXY/IVbl16WPxGkj0rPvbndo+X629eKoW+FF4J44kaMais1oSUgoObIHNr5JHHz7vSIgeilRSsbtoCdvttnYr0P4En5cqO8ghVQvVt4rP9eS0Lbp6OFB3j1/gSroZCvuwRJEqbRutWtcGK+DzcPCZLJAOdmoAmxejg/+9ILjRNfKRkSbMeZxI4z36xSlfyZ0WThKlfTlT9A1wyBwQedJ18+T+DUGHQRLaMOp9K0Yom5mSxiltB/IRCpQ/lJ9RIY0oEhGbAsGAfcrAFyMQXJY1/9yf+wKWoO4Ycxk3Kk0KomA2OOCfFitFO10b/uoMa8JjPBm6BYs4AhfiM6vReoUO+lPe3yJx2UMqyKPbOcITsapwIMKTIXRD7wYmEwZxBSUkbGpdPUrkEneJT9OYGs+0RK63Vu9sU+uxzH9D52LcVxTSw1CEzf3UKFV0cQ9o5uPTJ9fi8Sl2oXYeqKgaJi8cTDbORcvio5Hyl4T6EwfEzhlYwrMFycYlOSLRpsoUPGR3ygoWJMFQG9oEBgOiUo844Ttd1GVhE41kkOVm0mmDwgLtmPUMj6CGpLvs2lpyxM7rv10UaptesmicSLhgUF2m4kiGNJ62nCDw0oJtkAeYvVCCduBV1dFJgEK/iZ7IiVM3fDiRWcudhXr3yLRhaDSIJ1lITRTFkF8LoDbVIzIy93lI53i8XtuWhnw4lzzFBUqL+6GxlYxnW5EFDpB4rxgBto+mCEOqp7+0dqNQ3HCNwxbI4i05ZKcYYER5NBeB5oVunYoU88r+EIBSSliEhiWPtg1q+3vv28GINPZewydMn4uKykvab6E4+Wy/O6oL2+j4hgkinKka4i5YUYALMZb4jMBoUjapBH5oZVTSi7GmpQdhKaP8cWEJT6EypsjB1/tlOlk1lH+fOlolNvcHt3srezsX91yC8fHB+ZEsYh64TB/eKQUMt54cjnaHc8PaKMlPYGTRCygTcy/CwhvFiKggwvnLz3fmGTmlLde7ubX37ibBrFKJ9uusbZRdYokg508/96zY3oF89zF66/Zf//rwV7vFwZKE1FNO0tYoRN8CScXq8lGJabPzLCOT4S8B+deN08J2GvltHObWOiPfOqjezpBN/HdJi3MXXM9I14BlNjR3F3L5d1JsT17fWV40V5ORJ0fXU3wQdhJYnbBwfOa9ChQzVeLi+vL2+82vfF1DMQZcQiXvrCMnWIBaLRghZBmw/AMlt5jdkY3ZS0IeBIERK3sZGECD9k4RoOezWEgQ7ax4+EWHecvTiHyWXCMI3CoUZj1AwbmttVzMdnkhIcJCgJqUD5jYhYM1ld/3XUp1qevERAN4MN7tbTNVhvM5pRFMrEX7SfWEX72UFnYnOec5wnANxIQKavuKSxSb/Efwn7EbCloi4XniOBvKOvnrKYuANsiIAIpgYkXdnYifniE2NKVqtuOAzn7GuJePaDiAzCZVGgXGFAgBISmlGi0CntyarAxYcw8oNtieIY6Br03+fSTWosKEelLI86amW1C4jHrNfW5Ng8ygWMDTGgBDZtrZBhen3N/wWsJDjjHAye6LHXN7T2ZiZwPAUULpLWgWYpGvTRKHOTsZWOdgsfpssGK+X5NQpXEmAoqHx3okgfR71nCDHVFpwt6TNP1YHjunK/4J3M5odHqMYGLbDrjowCrD5bT1EmgmAFLclgAfQS7/2qcf9ioa8xIIsw6I7YZVX6il68+NIUXIjZwh4tQEs9/VMSlxZctay0iHi24TXMoZMzyqsbLO9wfNYv+sJem3xfhA6Ov4EXYG6+gRp6UUmt7C7pqZ83SAZ8oEZpnpGUExj6a7Krai5/NJSiBsAAONgP6NNL9wFv9lCqRwEazECIJNxcQhLEF0CVN3ANqtXRKmAStowA2ESMaXcjoYjPfEvQWYKyu0N0rPB7curB++Pd9eebV2+pMtbaet7Z7aUZ+/tObtgi1HZvvcRzBsnOlN5uzaCAtLX0q7vNC3coxLq3ylgk2rQQugxvTflCVC26DBPbuTzjfNedRQ26N0u+EC0++xmqABNNRqaHUm/PPFWlyAs9cGIKza8qujeUjLRvfNDGNLLWii+hg6SfCzAXJn29SfhoX0nm8fT0RPhvBAhgKyJMpluheXJ86DAMGnZ5eeudkLcdyXlPno8ObYvbWd3efbi9nc0wz16LZoCcejG47e0S4mwfHB+bW5b1spcrM+LVcS/OIt093j84Pnnx9oUzqbDeHpBI+wAfGvogZdbWivW8KEw6LwxqBIyqUOGW30DBEiC+vOGJyKOdzQrfb3ZoqwEIL4FCorw24rH6aYOAKUqAsBU0PgJozPks5E0WCx3wCRERmPywZIRqqJzYk1PVoRiZ7ajgvsrMFBjKN4LNwSJwz9ZSQ7qeo+IDqruo8fAkf7woFgGZJ1g0cw+jsMOuCup4xKhux2iOVU7ys8ls2IyEGC/OGdsr5ugnK4LSBZXrhd2jAcmAy9/ccpawQY87CdLkQhTL8eR0R2HTa3YyQ+lXTQ9razX1r+78qinFar3WigL7wIqOhKZzKWNWoi4MYpa6CmkD+ZF3GqUgCuj7rV29p8KRTpt+Ay/WzNVNNg37qJIGEUJrWgJoosL7eazX4nFxr18AKsvmcf6dC5qBBKqNmWxkQJERGNkVCuwAlbl8bhJsLCE4QyULC8jAkoRz8It7EW1S27BSqM7dzXg5/HlXF+4DX7ODb34/cqT/mWUFyMG88yijAzndKxAiVdBzlpUvJ1tjDVIYoZSHCmjIU9cCCZakhIqWNYr8JGb4BCVoRdP+9KE0l3oLj0VC+RV3YKThzUYVqBji8RtBIh1stFZ3NDJq0pM45OuSR/UUO0OgbRot+UAfLdMH0uGppgZ7XddoTUChFvC/vqCPfMN432Qno7iLAXYprYSbI/PaykkQhwEOMAPbgGPhb0sawcmmPSzLV1I5g0VZbUaCzTL3e3JwtL9pieSN4+29C2aXb9jd37Arqb3DrIx4a+viqjcE2JpkoTawcZi89NKSRMX/RnEPt4kxOyJX3Zz/4vHtxlpZPTw8WN95+STxcXFlTTyC00OIePSmUKBJT+YaHoc5YhDoxbBHOt9j2cLIYUnSPpyfP8tH9xI/tftROAbGUxxKblkBYYB/GMN03V3dmWn59t2JNM76kazXOkTIbctAOyxsg/3e6Y3zQZqwO17CmcwaIiNbDrMzvX1fvAYBVJh8zu7+jqNPHamk5OXlJWdpI8DZ+dVPX37aOr/75a/WfvPr3/727//x/Ozsj3/4w6fPnxEOQ3n3bHaJb24SzJbz0R2vnreUuSwQ6hAVMnDoLW88v3E099AmkOWJFRVklnjggg3nxLJoj6byAgJiO3hMGVAmfdHtbFOkUgq1fF2GHdF8bhPUhrlvZRb+kNlMSz2AxXBCfZBpCl9cSK09SSeARnpxT/ozjdRoKshYaJoZQcGKCKC4jSm/6IKmNYLSbvrRcrrxFg+nrX/T/YqNCGjERQ9sLBctNVCZQBNWnhMcX+u7S1E3B3l/ihXdTH6GFkmbq1vTChsztqQUdNSeR/O0Yq6wRpIkLRoEUrJabqOvmnOjZ/67POyzYpBKORGF5HehWOn/7IYQidoGQqSm3uoJ2gJ7rtFvT1c3imvmzLUYOlcNzw+QkI9scZgRahqCsZ746J8DxDg08DVXuxQLA5+ka4Q3yziAaKul3hsG4AhdHREIeCieVocImehrpn2uxoGQaIBmvk8UWAZTO4ooWAawqY9hynjsDCUZ0YNmpiUY0cMAinmB4TOkwriWIn6t5TPzcAtzozToS9K0799eoTpVaOys5lHGV7rgs8l4xVSBEaiTmBkHuDHNhINig7S/tUOzFJ4hj+I17tK1332N7Rl3AxXfp2pus/4n1ySNhqSajafRPU1wQ+MKI14DLMeBWWDf+T09nRTk6JgO80PajVB6WYKLsMnQjRh1oFXKGv4oxq6AuFM57B1xHsOd9p21jGA3V1dOoXi9uzrYcegbvIs1nOlN4LywxKnN5Xv0FFE6b0OU6OylUIrwi8hK0erOXmNHS0BY0CynwmPxGRBcOzk5Xbm6/stffjw/P4PxUF5lLYZ+bPatn4XKbwQZSiz00BfKTpnRlhGOAcGD6Pv2qzKVjYbLBemUfJEZIip5dmeT1TVqEDyjK0SWXnHew10vRnvY2j5FNX6GyGG5tYGsP1Yb8hw4EcPICPmsaeIVHJg9YoAH2iJXJXDxZ2vbOXFbW+0KQ6d3xk3eLHZzd3h2/tOZs48ez2R/fv/H44NDw47f/u7vDw+Of/9v//bl85cDSadd+9DwaGe2VW/IokqYPNyZj9hqkqI9t/ZevPbCAXuvvTNAFi9dsMsn/ibbQ00AD/rZGFSLHCnJelv9/LHk1/vhcSsfY/onRVmEFwNSuzQJG7ufDGkh04ZQy+ekNN1MJAytuCvPSU2hJP2psbx7DFPBfTIaHIRF6sZ4pd3sLFC22NOJBjLfi3a7qQU1xyqka5SU8V0QzOYkIKs1UvOL6i0mpGBIqwvww5MxNYGlaBFbcjSAAaV+ytZlqQEGQn+Vc1s7irGugIqSzLRn8zQcEEtz0zVh9nycmSJV9FWBaXbxfxGTBzfoolojmvMrfzjEjUEBNn6ayAD2Jf+tHRQpsVVfohUCCZWBZKCSmY94lA97xmgqp7PEsdaRpoC2MdmCBV2MteGoa6KGgeQpStRXGPbbs+o37sCgSDc+3yPPw+5tDtnWGAV1l5VUZkK4PMEE6t3qGRLGElfGYvkwvBSucgD8gfRR0GpAV1n2qcdmDbOyMZAeEruFi/kUG5brkWjk6hNZ33XkHoBRQMvgR5weTte+UgeWUBm09lubS0QvFvQVrUOcIGgLaZKuZYQxfSkxLMddSIWIvtj08WfymsijBBLVH6gq8EbYZfCGO+FEJot/ozq71f/4Sx/Mimsya6Id97VXqQmWqY1bvGO4N97qil4Vm4YaxpVig1qj/tptuOvxAgdTQtKpJ6diNhJ9Hrc3ds1wcn4rz8d7jvLf3qTODuiU8bE2dG9LdTDM8dCWo6xbQunZODFBFiANFqKP/avlrvXViUbCzvaSsV72tF6fXZy8P91fXb+6vWfdrAK131WiQCZE7tGQwpnJoovhYCK70B5eQxZ8GE4MN4ooJo4zFGFxRgd7EMmjl/+xvg8j5OjkKabEh0SCChLpvD5gWUvmtneWnZ5gyIxsni/OLg6cYWeHluM544B65M2L2B+Oj60d8sYE5xK1mQpu6D95jq19SzcTURyUFnPyz7BoZs288HjLJtenp9Ovt//uHzfl+n/66cunT19+/Onj//i3P5wcHv3jP/7u5PT0u1/8kvm8vrw2dPzq69MGVGwpRyvHY4vTuo9P3rQc/vOL/8HfrLsxyOoqDuKm/W5+N1xoke4ylqDhoBGIE56IwIzuMHQOhJAE6EDYl9cHGwJ8m6EVqhrvF5gv6jgmmJKlPvHIPDkDafhEqKhM0b+iI6dRgMoo4VVzNi+39AAJMnvQyYwh0jIw9nAyHhhEIJN2LFPMGoyYmIK70la2gKbBWjDSR0jVIZUgdS3TE316nL7Q31bZL4o5QCX/bhRgz0/WDL6JSteEXxrKcfk60hPrcFyH6fUIod6AVIHEs6c+LqKlr9rJ5nTf9XPbWX+XRjsJwzUAAFRaDvDKLY3Qu4JoaMylvNaM7AJbnagy5enxLIjqJlZEq3Fy0j/zPQtA+TJeVev50uDSCoKDWJtBUJmGJ8q501XeI9JoZfkwFtBzCKcFoNEkQoaolhXTP0gH8zKNdTbeVdPZvmFEZZ2FS1cnv5EZDvah13OTwPCMpO557VKDXJ0BLnrjAdkRxSw8GMiCo3BGI8GjcdgtCCr/hnXwLS3EwZEGHcfLoJwJsQLrUdyAzuyW+FMvNsywFPjhtoQwyVbdhNiC/ojIIJJF1h39cQkW1KobPxPpT/m3njWCaiVK9MhYZp7z2bUa+0cHYNXfpG0yfpmqGOl74lepmJTQ9rsk7EQcKMX0e+xui7RcreEpo6V++lFyuZSuhqxOEcPrxKSgXXBSaazd3sb2/t68gno6QpBdp5MdHUlWGzUIkvSAO7qzQYxJCkWtdpA6TvRGpN7kIoBONkzjeznX3rvdgy2JjyeHD68+Xd/zu998983O4cF//Mef7m7uIW3+U8HM68x5LjyF49+oMULc9251+ZNIkoHWQKjQ7Ug4FJrfKUYOvoeJam2YkJzXNSeiqaWpC3Zwl+He537evT99f3JS5v7+jmIwB/tH+0d7+2yn2IQ57eUvUWlSLdyJl963queWmcpA92CxFqUpXubsHBxlhRHEuxKAK1XE9GrFe3i+/m73q+9+9Yvzq+Pj3//HH//4+3//z9PDI+9IkND//b/9HussFmUyRfbIkrmfc+hQySPYdnYijqYa4Qsdp6uluLJ5DQKS+SlgOsCNTmYusJjxpRZYOxxSNbs4UwBQ4LuEuxZuEaCkpVwr6umtP6lCg1jSOno09iuOZHyVQuWWILLPVRuLbIeIboWxWDZ9VYx+MLpjo1JzzFQmdTcYydrTe3RM5TEJqHBK7svfFolC1PcRuk6ZxH0t6K1Gc/EQB14Kghrj9t6S+EMRBXtSUf3+7cqSRUY3FwnTfv+i+wTg7if2i3wponBhop/pMeeaTKY1VUx5U4GBvKq1jlKJaH/qxtrAQCyE8bCYIY6lTl2VH1iU0Ir/wVYPskmwAPw88ad16DnhrGrwFs4X7A8A7bUoeNdzdq8WPGCxMLivRIeQ5UXWjC2VMr5w99lalRmjgEQ9YjEZhbrULMMRRMrl1LN32kkG5uyRALNkyrZS85b2qVroKZd5fw8d42FEZfKjBuaAeyAOrcWV1V2Zd3RYUpjYGrH4WF6RkCCCuA2GSZvFS2G1yHq4lCr9GwfDrqsb0p1t13SNwHTPAwDkZgvuMsMaixrcqd0p2xYXk8bmzZQso5Kw6qo/0bBUXfAoFf9G+vRWH32OOtoHuArD+YB1BRGgh/iBh0U1T2zhmBCFTtwJnaZY0TZJTHIrXxf14n9WagzZID4iogX7UG8CG920E7Tz/nfED7L2iJZltsQFmJq17nDfCtBiRLbYtiaOsPGgGVDhsNU6+5at7EoYzCkNrToPDm3byUsBWD0631tIsNvZD7e3yCFpTka9Sn5Zr/J4dm/RvOHsH//417Oz89Nvvt7d3//pp8+X1xeGGRsPGzIlRwf7Ft2oFc72mhGt8SpDsxHDN+rFEP+ZIUtzmNmUMEzf1H4RbzYBW6Ef11qZU/bv4MDyns2bXnB/h3S6wIyNtX028O7auRQX37x/71yGVcOS9ZXjg539AycXrbtDJ4g3JeullUaH5vC3DE95Qd7O+TzwdWb1ozVpOw4EAlLg9+4sqTaHxO3sPZvp1aO5FHMolsHyMltbe8fHTQM7JQmF//Pf/8OeC/rA3f7yN7/+4YcP5xdXFoXmdYCU3DROHT3OuKTiTRhI+bAFnVyLWWSDebW518DQIlKOyJgBGSgMYirvM9le1iZlQxoZN2SBphbSwiYvlCqG0Mt4hTgxtE/bI2uzPxkg4l2ukTS78ge+g82YpacaN05rgQhFSOEi96hKv4rO/CG98SFhxkdalMxPNDzNhmMSLjTcboew4BBcWEkRPQFLoDvQqJpvOmg+hMxPLeukJTrLGSzFIOmzlnNvc/ka7HQtHOoI+5bL82gwoZXPo00B7MMYvCi6VIV419BNXZ/Ug0Wy9/aAyqdrfk+biIxE0cSdKEN3f+4ro8HQiNlmfA9Uj/o3jdX6MjKbODwqNb/yKjMeGfGmHjs9LcLliVTPz8+V64EmYjeQW3QmXjL4UvNP7WyMNGaHjAthEIw5PiAiUjX9QDy8G1XpPiF4O7YPiEEJQ424yizhhKlHo9g5rcy0TJ2G4JjS0qRyr0adKgU+ivnbc2LmZxhj+YLoMExCQ4nspzLizSSHuIDErmfDZnSaAQEpB1fcgxt9yKoCRu2KJDL+9auQ322t6bDKrqG3gnFiHqi+1OxmJaW2yAo4uuZDWIf9kHoprYoLeIHtP1xycrNur0gxKZkqlK2JN3IaE6dZdzyqwBBK9KPIIisqImpNKx2dcg4gVbHBR0SoU6GT+zayRmqfZvKwBU5xdjS/PJJcMCq2cwiKS/pr72Dv9f76/POlvI3TArI048IKWTrpr/x4qwjnYPqG97SpY9AyGY1FYmPe3UaC3m7y8uJ9kHfSPgf7Fz98+fD9h5P3X3/37S8ur2+/+fbrL5efTUK4JJR2bLrihra8X/5xp6nWGOfSZlweqw8YgCIj81GggxnpZ3xsHNl0jreVWaWZUSPM9mphMzR3Nnci8IYXwrhM19qekuxpCzXkFU6/eydGkX/f/OrdbqfYAnzFqaUdYLv6cnS0Z7h2dXnj7ArP9EyQS/WZgImGqNsA3xkPRhh5TwpmecyDE6epz6oVROaCHQMHaB7CvfvniGII5oxoRvwf//l/8TKAP//5T3/5/ntbzbx1xx4xtorWkBwLbgVSvXRHlsaqhy1sNVCekMg8YXsAWbHEa/iIRxYvcT8OGTRca85srEugJqYYNjJEaSbcTNKUKSyjV+3SEU23AjqSsiUjo+5qhSUgA1ZTpvrFGy0sJtqt+clc6LgRXgMgLHppZ4lGaO6EcYmz+hkUAsoISUU2KMk6aT/9nY0FnllWMMhk0xTCf2zwT20Hjs8cYoKWlSjwIIWJn2YDwtq2eU1eKlJsl+Y0A5eKRAsugw7pNLsBBxWZrKBqLloV13Lfb3f9JkvLZ7JGJoEKEoSp52a7igW54MxOaYNg+bnu0thbm25WhXCASZ0xPnUxXwHFKOk845dBK+uOFSoDdYjg7xQoAEbJ4AxYfi6e0tAAKnIkLrQUUkO1lHTopDnkGwSiX0B4Usq4IRgfYGBrYm+oEQ4L96OKRgfo6mhznEJkNGyIgsXpKOuJTSudZgzo7jd/YkFWAzgD31y3RluwRBNMK3Z1Bw3Y9AagYQsvHWuKLmV/lhU4we5x7HZlQpFvmAm3IVY2O+szZKjlUjrxZqqpud677An5RA2NVUNL1dK0g4xAqeo+e5STML5q7c1AXVU0gtpAEBSNUoE+QAWYgorwcu76RBq1HH4RvXGYRIonDW6UTS85i0ZIkYqOiU2y1IxcnflxFdGQ7wKr4feIyUJhhRcWox5IcNx6E9BmEccBxxErz73GZEzavNEXICGtrllNNHx5sMNlQ7DpRDFwSkBffv7x6Y4DeFRPbmPPaFf7ZvkKAICJ15EgkHCpeFDWxPsOn73jxQFw+DzamEtx8+bu8fDoiPE05fBf/9s/b+4erqxv3385FzIjMJ8kPWgcKT9OL/dXbb/acLaN5ZVwh9D4j1tzsInfyCMV9hdITCwwqJ37BzbcdpKaExrY4V4gzL77bOyCLrh0e3F5fnHt1VqsP+iL5V+izNdfvf/VL78zBZJEtVQAG5I01NYSzM++2JfLJ2113M/9g/3BWOQV8Emaxfbr5mMd4tZrxWaBPiPi/S6IIl//8uXsHCyHyGVMudM7eZGH4u0+vV4+2Xxto8DL7fXNgbVGR16Tc/Ppx49/+etfTk+Pvv7qq84pcjCfgRhtR2sOh+UDmH3afGAyo6eVjZdc5gYHQdjwp7zHSCHxKUyxO0H3zZFRmHme9CGZYsI9dK1JI4VF3xfclc8I5GsZO4imtP1md9jKdDJZndAN8bXA2YySzAPuuaiDdjj4vtK1najVHm3IWpMM2cLhIBZqmtknroshj/XNrGQL0uMR43Syo6saXimpO5YrLLUfcIHnd16zkUnL/JVx1XQvZ6jKaq9RA1JpBErxpqca0EhYBWxd5gyzaRoUJLjc1Cmmj7a+5Vo8x5mWkmus4QmM39K/mKI6CVfNBSP4j+nIqUxvC+hgJ2WZEXYsJCbqpcE+p3ZjFd3VAYBHBwDJUgUtEikGWvuwWteVxdQPjGdC2FAwK6rF5mFy5rwuUxRDpphbCKHvtGjEZowDphfKce7gh6T2QqIeaYUVjbn00IDCgmRQzH+/uxAdujqZvy9tTLUt3nm3UI+aTPVM3E4BuA2rc275gOij6vCTGJXZUsAHwbRPYZLnJz5LpxuWKY2jrpnxoup6pA018QwGVYz88xaweQbASnkakM+yMIABiZLKucdsuJMXAFAQN2wbete09vxBPWWgNLwZfIe7tUnNmsfuJwrPMifdecA1s7+LfEasQdlvmA0RtZc9V8tXWyNpkqfEHfsGx4aT9ev+CKvuFrlUHF5A4NTZLyhzunGxXl5lP7Qsy9cxZw660sKT3EjH+Cjum3j8hulnUHTW8kJnB+8kIZ01tIWIkbn04JMqXk7uVY4MDkKQdgAUjvk2ssre31w9OAjT8qXPZ5dXNxZ9br7/6t3q5s6Xy+vvv/9wfnUlZeS9wj/++JGlxg2QX19fE2rJpZ3Wh7AS9MjLJBZpG05GoeHZ7DUDZw5TTN3eiOIyVDO7rans5cUlTcjdvVhw8liwKrvdKNccXHuUvPjR638d+Hy0v8dPkO3mhVdWS4sd7JucuLnoVIab6zvyur8rNtpILLTYalqJIFm1dv+CWchlKR5Co7z5ANMbhgUyXczD7eOTjRYsNGZBSBrm8Ohwe3/fPMrFl4sLR1F/OQPJ6fv3/7f/+/8m5OUGuGPwEHW/D72XxvvIzI/Zgkz8nThtzPRwZ38a5hLSnZ0hAyowIgl72jVykjK5S36y/r6Aofi51eVpvEMk2Qwv8ktcSVNyB3+ESoqSj1ZDSDCQwgS5tE9W2BXRJxb0OFuVeniHgSUVzGvyOKav1HzHQUw+JMEEIb5W1TW99p7OO4CNSAeFh0Pip6Ih1yyEK7WdoAFnubJNSK28jNpyKzNiQaRgM0s6/aRZXQAWCy+9htqsn9ZpepGZCpblV7iNHQAknFzwrUQfub9u+abr5cOob8TwP8R0FFokdvm4nCrAtgw5ZTLeupridfXzlc1mRrI5zC8DQVq0ghTA8JOTLBCkDTHiDb/p3oO2WnTqD4PDbzS0Ks43KEGmVMsQLUOiZGYZDNqBPEpFWIYHXjnVbi4Ij5NUE8FBYkicTfIJ4DTHrJJEAIjdV7N6C2N/VlYipKxKhR5JbfYFUJF5ZBP3gFq3QBlbqXHwRUVSi+gxsbNAPdUAdtQ7GD1lkmb5Y84sEWugA4AMYnYZKNFZ3UDXS8YWiN3VQgZMflOWIitsFKCimotNx8isaYeFJXst/gX54K2p1roAKDC7YlUc6sqDdstjSplGxC2NCWnZ2/FkIQdejXAKwFGtOlG4v/NHdQ3M0HjaXcQXKJqK1FOuOggxdl8BFSrGSQxGAGfCAJ/gtFy90F8XmE16OQB8B7mzyZ4fniaiXWFLvHjKu9bfvTvZXTt2Yr9hNI/HmEE+88qwDI21szSMCP4hgBwAfeDjyZsMkTOQ4axYB5zdP3386fNPn84kIE7efXdy+u3r1uYPn8+9APj45Pj91jvPLi4uKSyQvBfeEIZIMBni4vxmTmG0aiRzKAQhd6JV2QbmZ4hwfX3Tgy7vsI2csQxv2b5yMmaoKxnx2Ijc384vf/Utx2NJ5sXR5T//8z/INVx8/mJc0nRGQ6sVB/FbuqmRcaClKRI/X4WBFnRe3sjbsML8pMh2IqubzY3j3e1dpdqjOgsf0OfG6T5bm06WJg2WP/Hjp/t7xsbWotmCd7e3efb5eu265USGAv/4j/8oZvly9sWMHD9hQH53+7DrPQGUnCTp26Ed0k7SK9u7PKhJGtBK5GW2oTj2Pali68VFOUWy3WG3gT4Te5FHCFVstGqVbiHGRLmOyCNFoy1u6pDy7pgCTxqTVqOECYpEIfFXCx3SNSNWCljzZXTJUOnBEfWGaS512fTkFDVYDc98Mwvl67JcgQATrlS9GoEPRlVwQRSiL5cmPcBDhYnLiD8Y+yHmLmzz46pwvK7f+h++u5/nh3bvi868St4MWcZJjI7rnjqDIgMvKJ7Cqg9YFikwBcHXoLxleF2ARB8dcTzT3XgvdyJ44rukByuahgZV0rkANtj2JaPGcS7k4glKUep9aIa2sOVCJtHXwkUijas4NG0l5uYAGFLmWCS7eF7opa5UGEBlKxnqhTh+Z0Eh7PHwDZHCYqV9B0BBwOUDugFbMcV5zw2bIesy+qBIujc6FSWHZeo2uJpLOcEbWLOyY7doSFPBLWAo8ewuAAEb8uOKdTRUGpayj+n2MARPJoKOck46GL76zIVoGbvij1HnIA5ZYXKo/SwEOp81+OpqHgZxJpDiw2JtyQFHnThkihXzHbMaguUsaMN8ayv5wLLwqW4Tl6LjpiIHWKRFAdY/18LIaozvmwEWf574R9KctJIs6ZAsf5yGMS1EAqG0uciqRnyOfY0bpPVLMiqobsVD00/OBitdL61Zz690bz6ETARuZAqqnL0Eb5JHhtd2t/eBQNJ9Pzk52XGKjMPCnr0nd1N0L+cvqi0ctKJPFM3MyZ7P6ilJWn1KsNBLZw/gEC8n/OAGhLr3Buqt0EgaMkSdntOxlwbzounLi+vTd+/gbxk+ZL01vkx/c7kyiniKCDOjM+KQmA/H/dIjtFEj5P2OOmmNHyghRN8iQE9QYEgk2O/Q5pLhBs6Pjy2TlKVy9sXW1q9+9au97X36Yf7ZDLANzDdXF5o4PtzFWVPFpqON6p0TR711hqy8p5g2qjbn0dq2VeszG2H2ThjbW/SM8sU3RTyPXnmAcTwFvvE3zUivrNj5pZj7DPn+Pqmwxv/+7MuXf//D73/9q1/8/T/+3f/8P/+HE+Q+f/lsiwaAKc7+ntkCU81eM/AquSU20oVG7Hgq039375XOdM7b/NY4YNhb1IMmm9vYHikSgoWSZQ8UYEQFtKhevOiWBUcWGiAvPCO4ry3Z6BMXEXU108TMhLIjVYWHQsPUxP8iPcUnA5mI2jxhFZC26jxyUao6YqTyAgVYholzHPdA4NlkGpgfwm9qasx58r4wuMwpiY/7YGmKoj6CLmsYeAWNSchyLdj6HEd6XgQZJAMcvADki6/BXwECl0ULZCHnmPhFx/3WDjCmeBUBy/xRKxIyomtyTw4nfSY/02wDCDj6ms4j+fQbKMDQa1/7t1xJd+Kt4Nxffk+VHkwK18wueaPCypB59+Ee2A1oIonug7JG+h3wIgCJNjTvZEFD+Kkw1rUeUZxWMFO+qORDFkJvQ6yg0QpTBYL+jb1H7RGZUTS36zOSwapWgj5U9c12luwIxzAA4dAxa9a4sDhCqnHxtOO9ApsURCxmgDjODlNoaE0fmdGFjBnZvBRXbE6otCAIIiQhCGvkIe3aBzmpAU606hib8IjuXUbbfVDFL93mLQvba6tOe/lc0lftgqsuJAK+GtF9vPFCAgJNmj3QxeRewrcRW5E+lSMqkM4sgpxY1MtgUf8NY3vZk1wWUgX/0K/oLcLFaHpDAaawzile5zWO+gF+GZdoUElk8xAdIhGAu1PWw9qPZiZBoVZFOgO1ZMUuTUM5e4QlZFdWr28vbJEyhempV6OQ4aI+oDJryFLJ8fLOJnLe5+vz1eWVCQBqgICnp6d7G9a7P11eeaVJQaZjNQ+OjhwyzUHf3j+cXX9saMXx7O19OTv7+PGjPLAoWmRoIriFNPL4gVzMM9xMoFxDLegFyMJpj6NSpd2cb33vQ7wesexPVEkSqKk5AatcT0/fiZqlX3748PEXv/jFP/yXv/vLf/7lw4cfdluc2RSf90LEttgCc8kuS8IMGORZvE3s+ursUuwi9+J8uyg8AHFwzjba398X7tzaFW8xJZdyf2vcbmqFvtzdWtp/L6dknZXhsyOxuSHQn3/+zPjTbtMwBMps+X/+x59OTw7ef3Vycbb2w4cfqOj2sUOjtze2N4oeyCidftmwWhNwlg8BrexobCFiDLRdA+0SprbEzhr/woFRJ8KjEHgVwxqyLtBgcpN+tJ5jUBcjS2ULQmiKRok6056dyUBmBRYVLWrUX5GX2wpSVkIw4/0xAJqdv1iQddDRXI08vfB5qsviGlxO6JYa625E/dmSRMxsSQrc8qfpY0jE2QCpyjJNStxp/bAbDARgNEuNxCZrxgRXGy/V7YJSww0fXMWCC2BN17kqkBZnyik150xnkUhDPbamNnjQEPZjyYqLEKAxjvZIWv/o/gil1uo7Y63DoEToykf5LjAFRRxImhX1e5Q3aHVY6mqMj8JjUZ+8zmcIoaV0EhDaZf9xq0uYmZ8A+QA0QM54RCSUEelEfjXrTz26POyv/yZsUbKzfXTsU0+CZzRy+K595YJybgYA6maZCiqnDQ4ja1dzBQXOoSw5q6XO1zWGCC/PGBmjAQsnREzZLEizjkNVBHAPmYagCJsKB6zWuv9GooBb/oV1fTqvgpt74xwAanlJiSQu0QqV3I7eCWUhw9Ck3v1LdEZYdaE9rVawsU6ufPrN8y8tu+fZUDKvEO7T43SxFDMiDl/3cxstGU44cEbT4PFgCCWKiFnEWDDRcMkbU0lexRqTCYVUXKp0v6GGtK8jHALAj0bIKIvjmVYJKaT9VwWpiC3Dp1FFwZA8yPuOsIu2AZGAG+yvvp7fXJ893ziB7PTQe7FshNqwRCUVNVu7vuGciLG17E6zTQwiSyS0uLi02vMKmjnjlxeHPPz48Scpai+64typjpQCi3NxeeGtvNYgOTWA7Xu4P3OBxfyweVFcaXXm7DtDCkymZqFsIpElwpyoiBX9ylZhTFe6Gtf0MXxnCZhIRRJdQhNDeX1ZlLvdg/3joyOyba0RY40CXkZvKgJxbAQjep+/nFnuyV3t7W051fnHH6+9Jt7+La/bqvFVW5gvb64u+XmDB0OfjlDCBm9PkE6P6C1u5iylRrHEtmqWDizmxJFJov+nHz/tHOx8/d1XXgfA2V2c/UDPDESAeGV2+gHFtn/5q+/+449/+P7Pf/ruF9+A6r/8l3+6ub4U34Tg2sbN/Q1ROjjYH40pRAUV/JcIk4wW73RFmkSZdBOAOcMAKcZsshJe3Nj6aR8QZ0ibFciaqEj2ZiqR+hFKjWguB9DAbMWU9Ayj9ari/H+yYzD7rsc00D57DS32FXBaLGjIRkAh/1TITBsSboKXbS3Bm4YhIShYc85mIegbJtmrGe4XmqbIeKdJLVBTHxabG78HcUilFXPVawa3og0Wo0vGOjvTs8gko6kAiFLPCrqGcGPHRroCAJDEoLxF0/sJpQ9K18w8raPsRkPtubQ9A9mBB2+W2zUPvtx401VKgiAAtRUgya6KtemHDDfmqbzbY0b4sbIdA0oMF0ur0my4i4IDCFoq8/IQ1MascE8N4KUpqKZEg9DizepmAIgTU38oVoPTT0QftJFtIVDShQ16YbbAjJE6WuhbBqM1BkXrMUxn5Uw1ptOc40Ip02jxpEMFJBlKQeg5Scg5LTyzVmGy1qJXS56NDGctfLaSjBAzmjZ0iZ86jQ1l4oBVFnHRkkBfyCiBM3Qk1X/rKOLnBMllQ4aRDMCDE6Y6igRNcjAAfYx0w5ufHWQoB0/nmhUgwE+DaYIRbuNVQSXvkstBgeBiEohF44C4yFUPBgRhxVsRwVcipTXOKcZIq4p5IOjoQrPBESKdCKTMIhM6VDjpHL7CWJnQ1McQvImxjColpF51AY6cDD62mE89NZ5kao73nIbZ2ne5KNbsxpbduwerEgGHRFRWRx6TtasLUaigVCsvTotzgAEceQPxHSwcanZ586UtR84aEOqeX90/XVkDisfy/gJw881ygUXNY7vdKKw232BL8IjSz0wJkfjkP6RGQIepRTwLmkQGHd9KqVzUtLj8zBzcYczuHx0dylDd3Nx66YpY/Ntvv0G9v/71r1+9e7+3v8VpiZGcBYeqXgAgX/n8tHdy/EvdX11e3lw6r+3WYiVrNG2VctidLJYV/hNxosvKw1pm2kgINuhrAS7772VgrXHt7cmPW7tbUiK////+weKrd1+dGm/ZMrH3vMsgmvCQfGKvcenrb796uL/79NMn67L+4Xd/5yUEZ+cOi7vAeoe8StSkWzOphmkiBuCFYpsMkAOFOE6WiXRlSZ0Kbf1RCi9RKaVDjmQ5KHtSamhc8OjRWOnKFHFbaRlhSZp/DCixYhDH7qwnxiP0YyJRKvnVbZkFXEgFrAiYwhrOCJB2zS2qlM3snyZ1QBqZF04UDIyGkmXlzCQVDv688ocdC4hiYUKVcagn+FF3NboUAEKWZiRF4TQrFJIXH5QvqTReWuPVyXQTH2QQYWTNIel3YEx3FSlEVPXtN/1e6v5NN/O4oZPDZHUYIS1kNNAjLLvqyxUkC3AEcimmc1TJNlYslyOQpqIUsyvVfMt5lMNP8ecBg1lr2agQCYeMx2uRGlzf+kSBwB4AWZ0Msu6Zsqz/GIuw1WUWKSQzgiRGDY264ZYKUHH5SkUjPR8uNp18kRI9025oVBAD0T1yFdBXXataKlGQJXrzIm7XcUJa6ll5DXoRi5biQbQbcKpd7DByXAqFANTLXFpbKO6+4nBZiOihWrrIbwkokBSJa0QLQ+Iej8yLRWdWpF4S0LAIrmmQsXS5N4rgDCVtRv4gHUYqCHKAYqZSAQv80uuTUU3kY/PN85yRRytmx1mjgOCZ8aOt3pux2biHRMfgcbcG71HH4ClVEkFA8HGEF7UkKGIHPgG7dJLvRD+ZsBcrBrk81RRLbUaus95MRVi00sIeTyhHB2P4itRaccPZMoRbNLu1t3t8sHtyvLvycHN9/uXu4Zo444dhFcbeXF6ZybdmRuOopF/awjBi++m7960RmsEES2FZkWo9vbj6fH65f3jSRlrvUtkRsa7a//Xxp0/qHx4ewYM8GQsyf9b/NNYJmSS+iUT0nSDWn7iaeQJveu6Jj/icrPRs3PDwSLGlIjKq0FKmdiyvcKwRbXJNG0/rzn7Yt/LntblcQ4/GBNbd3z98+umnk5NDS4Bur15lt9heIwAzbF6fUnqF7X94VNWwCqi6wgPNajjBEj7LG96/7BpyIXfzf7JJjtMw/yaCX3m4vv/y5ezxQy/D/Pa7bx0Q+v2fP8A6n/X64r00eHx8tPfb3/363/7nvxkh/efGn777lp/69uwsl7mzvbe+tWNXtTWpW1lLuwGgJS3hZfTGvhiZlcznJ//mGxoQYzSCdHPEZhFaDMRcIDOoRjfZyTdSW78wdrYwnoTMYkpIYUmWlHEo3ZPSICX3riq+swnjKHQkN4kUybA+ZocQBUkxGQGGuOVeVK+cktEYc494rW2z/Xg3M50JCprWRJZKtbyq9Y3Zk+G637ku30bd0pHu6IsNy3YV8mQ0Jvei5EIMBBnYUo/EyeVXdkuRaU0BjY1s4UKmyYEflLFr3FsG6e3HHx1kr6JgD8hiBadhrfpbdx4OzQGkDG0F7PSfQUvJq9FPYjzmOGBGv2RC4c3sJZZz6RG9fFTXTV0qrNKCTSOAoA+B8OhRlo2Dy1JjXypvtDDbV1C2+mZiNDqbv6LYAu5kvmZzcJqmXidMFaNhSZguCOgg9kecmn/LdHubOXPUwCNH4SnhUn5krwzUze1tTcSoN0I0uY0WzByE486bFUOpYTO0OjecOdAmDoe/DSYm08hE04+2O6ZcUM7rrTgZ6t53b6p6wbuRLWCkfcNTPSyEA0asnzCE2Pm8ULl2QDHMbJmTUN3wCoZanxgBvtoHltBkrPO4u9qlJdxDbSaT3egADG5kbUM+vYNcIBqbGrW1DB/hhu/MCqvhBHApc+8j2bi6uWG+6bFQ0b3klS9i8GOv1lM1LQi0FynXDtgWgRupKy1IVhYuExe8iOLlMfs9ojLa1IT81sHujsUn/h3KdQgWnu4lOj5//sgoW06/t79vqQn6WrGf8wqzdQkNUx5J2Ksc9+He7t6Tt5ucX3Q25fb2F2v8CW8vJV8csN3BHQngxfI3tw+fbLbasp5g4+r6quwSW+iVko0b2kPAakqMiIdBLSvgdxP4NHCELz0DQhda5OYjzs83qA5SjPovSt4AiJWUaImE0jI31wykCVUTqR2/LCl0eESTLi8uQPK73/7m4HD/6vzc+P7g/eG1eYyr67/+9cPJsT0GXgiQJzk5OiEL5np1jnu8tjWf3ochXWOBTtLYZEMZWOKpTYn7zd2tlZu16ys4WuG6cnBy5CVof/zjn/jOvYNdKyANhQxQQEUeEcFprHs7DVaI5IXA//npn//pn/75n//53//jP64uz52svIyZTPm204FbdQpQSMpTbfswLqFTgNKKRLacStGjAGMsHTr4YTfwVMDF2FNuajcbATI/o2gv5oXS3o5YSGAaP7IfTpkuSnPEqAEB5jMP2JTOZr5e5DBt+FeckLbPywiA+vualeRpcoprK875nSQ8sZRAA83DqqAHhwWaJYQFQ6rj9OLPrEdwUyij+jB7epoxAVkc62P3EhSA4Xdq5AI1Lwz0+h1LvShPCjrSoxemVLHK9MoBy44rEtEc8VShxGlsJiODFCNvU2iUjSolhwUlo1U+c1M9GkOUogzWZBYQGUmXsWlutBBQ+8owhpmM+iuaTOC7GbmCjGov1ihbmtnxb2lHe6pMwf4w0bBlr7G2KHWCw14WiCzgwoxa0/zgbDp2WMIIGlM+CZOo5PSqBk/VXDOhqnmOdN59EVgZSrzhURb3b8qnMQfpAsq0nYujb0BEXBWSGqwc58ly86iKRTWaaeE5xYRezYrcQaTlSOF/iOZFPd9gk9wTb2y0y33kd+J0JpvKzc6abHGxCSJmBTrjLLpnbyMT/2I6jAonj3kL19B35jfJjAp2IgnMwNZg076KF9CWVacaGgGIjrS5CJgPizECp0fVKFpnt8chlVtvLDVIhEv3Zz/NuMWMkadvLRsDiS6TBnT0NwIgoEEvwnF+Q8HmPyzJQ38kLMxjaOYtX6ivLVzwHH7cOYlpoY5FJr2NBbmKF3yP/aXWilgRSmlG7UDUf3h4fLjnHDHj++uLi6f76/vbC5laK2YEraty2h2T/Oo1thC8vzJrK3dxR66QQgafAb++uYaj3vOKxo1tC3ja29p9//7rja29T1/Oz89v182lOjynIVTEPzg8VMZB+BYCxWmCClmz7hOk+wpHSsc3zCsPtSqcbpSN3GmOHzKMhmLzApvUiXwu1l97jHVBXMOFtobpkmSztdZkmohSDC5ag4h00NXlxc3V+lenzgL6pRw1Mfjps/X5F6qL9L2zhSBteT2OtyXs7cQ1bxK+f9jcEZSssdTHp73Iq3VPpcQ6Fwjlr65vhDw7O14ucKRz5X/48AElTk+9debwxw+f/vznvx4dIf8u01+OqAUzXv1hWcQaz3F40DKk66urP//lz1y5WWvjALPKDp/wbs4dL7NsDYwN/wy8gQeyowODXlJ1FC4iJ2L0qkNOLeQqeKINrJMfBSNhbiETpjRq02cCnvQpIu5jG8xL0dvUsG6aIox9VnNIPyWlMcM0gyhVKpBA2m8hlIkPBbkdLpNaZyNoHoHBI79HJt+WUaIV/hi+0MhMx2tekC1LjBvQ9IYBdVCV1Ot9Oq3JpHqGzqooO0qQmoyxDqx8D38zmuouOFkJUkfekhjRWGJUR/1x82dr5gPxqA+4Rkdqo/x0qnTU1lF4acD3ITUYzKt7MXvETKST2UneulNebiFXXWofoZQIVNUrvIwYekZpaYrGQbv0GuX8ZIqXhtlt4LhtzCQQYXsdQl7aQipO41ZSyA0WhrDTrFjRgXwCDJWIIZAIDW26EcmsHWud11SuWDbFGz2USotWrHFkGQEX87UQBo3x4UC7tuZJ9ByjL+oTbyIapsMidzdCoJE5V2fgQFLA9XsIk71E1qFdMpbdyjeNA3NIUpyir2y3nhWgycQIGGNQMtkZSifeTAIR3m0tEQwmDUO70AUPdJOCwWJ8RSQBNiqhk3hd5NoSfg5RbJVtz94MNhvxAzUonnBLLaV98wE8Q48ULMYCPTPVSAWEUXoQ4Pc8BUIimB0PPKAqBUbsA4aV0TTA2hzIm/1At8VoKs/FLwpfL9Iv5GMAACnARjIAiqG4E8F9AZpgFuYglIXSFATRlZsQa9v7JLLd33GswNZuK1Ce7mRhrs/vri5MW1ia6eWyTzc31oYj+831ozT13tER+yJm7fi2iP9sv+7Dxtr1tYA9B9AynhfHJu8Z6s9iqE2jlj/84c8X17ffHZ8gHWMqXta92BA/2DPhuMvXdpY5AQ3jLGU2YkvbHddAJprqIM8hMj4eyWCIYpjnzIv488YliModZ66K+yMq9WCT7ePdoWsoLBhDc1MdiCKAZrKd0G9J/d7OvnJfPp+xYAIBuXuz4ohzcnrSwRD6W12/vjU5sborat22mGfVHAZ8hU7v9k48Nh9Mhkf1HP1maGOXcnPf+3sHR8cn9kP8+OMPa5fegmDrnEmUHbhfnl+X/VjzyrAL+xiow6lp6p0W4F6cMYvr7786lff+8cMHEcS//uu//uqXv/n46SOlgwiLaKkkRo8ZY66L+llxopAe+vT6vCFSz6IT0NTcjAsHMONU3EPFgsXUoOAb1ZhUEPMjVIBy5Q3sn3XonFCfn3Ei0k2bY3JRpYZysqt3g3A2QxBHspsdLV+vV9QwfJv+s26EMyJWnYgWI+oBPBtr27evN0aO0MditzTPgFEKo3YuwZ/Y2vAhjvoVwxMGypxVhvEAP24M3hOV43KFtDimn57W4wSmHvVF3+NO0tD+29XdbD/g/S5oaCxSMA0IqjRCUCDPCIYgLNzNNkARRp6PbfLdVXeZX4AZ+9pLMTfLG+vUzdFN74+LO0BJV/Pd9PdtuVGwh29OMIwsOoXneNxxZtkcGlQSBkhq+Q92Opkp1NzIRYXGrDcBiGu58maHlBwECqC633HzZbt8RmdPWalINH5JHlEpWZhEpvjRt6xhvVg41M7Grg6lC4HBpXGnbygZyxZieaJl3FNGn6q3sUIQ09Kx1pCoorjCQ8DMZYaPIXFYDQpLWclHzfQOUdM4BjbiCdfeUZ7tLdotbyCI8Ehvlhvin3+Irl3inRXIOQWGGgmcz+HaL40MPyqOr9EiPBbudwsAPXBuWkspaFBQoVV1G10lKGw01Agb+jFEno2Gxd1EKjLWqVJkRCUJonSN8smrvLzsumbjj4eaJfjOHX7jVHJU+8Ql2aOs2hqxdiCsKRpNu42HIAHuYvjCTHDy2CvgZXJYMGb/wGWGkRlxGIQNvc93pj0RZdcaF6fEG1OVKenNJM+PXMP9zt7BxZdPfpsmlXwAw6dPn4z3tHb6/vTLZ7H8Lf71AqyjrZWr24ura9vAnL5AFCR/QGNiU7T97qt3NEZ+xX3Lcs4u0iK4wCN8I2QKTepsHkdu1pRfdES/R6QDYbETRlUSviReycwoYRMnQCgOSLNmQIyAvrrLHkVbS4D2LKTB1fMv5yY+vv62H9b288eP33//faM1zvn58be//tbcxtHJCVo6FMg8AUYw7KunJ6L+/f2DFlx47/HLi+PtMP39+2MwAN95GPdcxcqrRBmacKTv37/75ptvJ0xY/eHDX70M5+jEyRGHXxwH/cNH7xZgbgwFUmVUd56OafeVFVMUDpE+OX139ukL//fDjz8YUX377Xeffvoo1N7ZzRmSMjMrIdh+by9kkwoxDmt/FnNIBtLWMWdkmbSiCSOntUzTGA8SXGqVmqXsQq3oVlV2g7+tgewCgS243DTXUapHIqNVGXJARu/taWkENhZqZLLh+KjYyhPLl7osLOr4iTdmudf6gJWGpxaz6oaMck56Rw1sBXxqOzVTwwxT4wCfR8vASRGsoH1blbpIzugaRpcg9Uj51CR8PG+8Ema+E5iWw5IIBqHTU8iM9j1RLAO9zu7LSWVXmTgVF6NPx2uoSK6fmkoCqVxWwjlFb2TIM2lKnFfdMTHMlEn+Rt4/C+/AlfhHZgabMoOLudWJtdlZHzAtiS+mI9dofiaaoF7SApInwGeR4UmNWSKL661WZq4Hf9q+ts3QpSdYDLcZsIAY5jl/th1cQ560SBTANod/o/UCxiK7fK8kSsSZgQJ/DM+lJHvKjtqrUsoCHq5IHqMXX5L/HB8l4NLBWMlKaSrSFw44I6VU78T9A2lZ8i6QISPxqoKGxcWKz/SjnBC06113HV3F883ukuZ+Wa+xs52KWJw+WOeLAahUBCxwqIcGImMtkHtzFa2ivvIIbtWoF+5pPJZHuqoFhc9DLDeDClaDeR+I/fIM3ONg9Kib8SM9UCVWTN90zfjJAanaEE6DIv+cgLZXDvF5K6C3vWjmo9TTAnT0msy4GtoDwmAi+QseTh71yGu20McA5Gi4OgWkVekW63+SATpw2ozAv11bVpIZRW7ZrHu08nBLgB4lS16e5PRvrm4uvbrL8TobK5dX19ngne1Hr74iPLaH3VmChuCrjBUusURIemXy9NoaX+Ob0inmCBxQJPa/urll+Fjys7NehXsoDXTo6wMQYCpmxjVxAIKTHeltfYIfphJBwgPaMZrDKZI4+Ee2wla4u8pNz3irdQe7SJFs4IwGkqKU1YwpIsuolM1bXT0/E3df/fK77xh0W6skXmyt5QWd06+KUGj30KTFHU5qguMBkpjl9tak8Y2UtOOjxcDtn2jZ0ir02JSi4ObGmiGzlOiH73+A4C9/9Yv/+l//5Re/+jWDZ6T58YcfLy+v9nd3wQxlS0JXLQadgb84zISEXKljQMkC6eWrj06P4ffhw49yUPJHTmdlqSEcaVJqIucbxWEy+IAWDUeTAoc+RYoOrC4WKfVTnETNkYNkAxyw6DSSPC3lKqKZxjv62yKA+TyLCb0OlOZ2fNRj3WxhsXhL2BQ7yDLTO14804p36uQ9ZnI3+AZMf8cAE3NOaFm21y4NFOs8EQOX4u/CeQrBn6jEBBXFMYpwjOUMY6bW2EBPpTuERMASh7OMox6QBJI5OMIf80dJ/Y44La/I/gSAx40hU1KE0r62nXSg2fXWjiRZLtXAgBgRrwZX2Du/Z1zgF03L9DEMGqmMUlmtxbQkhpMdyVSrNIU5hUY8Y2rS22DyaDGyVgNin2YzRMvVs74PMG4Z3ZGyEB8pGGiCJ6ete92gUQsMJkgcOjIvhbMZ8ax8v12g8U+85fdAH5DLI3B1Dy+zocKb6BdfnC9m7fa8qU7KyleyGGk5H8+j7thBD2bWsboEYawVMlcAAj//RnNAdqepGL4gNxg3NFMSLT3o4YhCgobBPdRTwkhu9JMUL7QzEpjSsbLZv+LlGlOdC9BKw+FIrcfwVVqNJgZIpr1R222m1cKSmSkmqh8gjWuKfzrlmiinUogHr6GiX2v2ypMo/1wa0VuI9CGSpgGTVVNfLOl7Z6HNAjJTP5sA1DhvTZGxhRQq4V2Fm1tiUrBqVQuKWHUWvdjgGVuQFe1PN6/su69ZAjU7lLHVoslD25W94WR310uqdnrLIyg5SXGG3MXKttlfCYMH0aNDZlhwx8Ad7O18+vDB+n2nJ7/7+qvLTz9u7x/Sv59++GFduqOFQxmYK3b99t5R9kNqWfWbL2dXmLO548VFzpc+cJTr+cXn73/4dHL6/t37r//6/YcvXz5bJclbXF1doIEzIZzB//z5AlJW4xB7VjQbsLYqjpPugyv62yplUzYpk7bxm1ykTxExskY5Mb7Yc7tkGgogevdn+yH7QspGHFc6ZEKerS0aK/e3Dz/++KOkPOMuj398cmArcJx9ftrh0lZWzQM70+j46MDZEXAxrXjjeKOrG+uETg+OiYSS5s8z4zd3SQUjNlNun386k9n/YtHPualcHu9G8P7LX/ziX/77//Z/rv4f//N//I+PXgS/s3P67vTu2qT7dRGAjYrSLF4V5kiGsUevO7uY/t3+13DEYlvM+DYLblGAaWXgMVvsT4HJOP2kf7hAABLxGQqQKWqATMzdi1UDnperKTyi2mMJEZEucJbFVp0XI/SRe6z6qEfyrkC2TI4JJyQuFIS75OwzP0UBWieXmDExSqjPgOpqrhZiuZLlwnhiWUqHm8keFc6PWTFNx1FMIKlcapACAmrRL9usWX/++03diERSrSF3wD86RpmUnzi4NonQBIVzNjcIxhcCX11XBepouXSXAQkTjoaomQKJREoVYvitnDvY4QNSQCdgRv5ADpAMyZzCy/hnAbJRLQ1kBFgBmBd7M0cyEHjp06CXHE/rNRFzNGM4sr2AoWGWLanWEYr9fDW26KC9BXwccg5gDocUFTXDwpR5XnLi+9yxA/qRLhpnrWsOisGU0eF9isGAJk4EdLvmiVBhH73KlY1dTwrH5CEm3LNx3NCb/YsmBM19Pzoc0+hrNNJ7hndIPURIerTEtAVJyRxgY0AiGAHYtiAb8BYAa34xtNFArS4cbe18Di+lnX1nITtLQZoGJHYTEQgroIad0zD6dx/ewRTfsx6AdGEGeKAwW0yaS0fGpLbe67dHKjUGRP6gVXHQmcZ+DrcBoZu3ppQZFjSO3BQ0haG2qFVUihv+F/DqxF5QX4c7wQkifSjMANGZoQFVgY1sK9wTM034hsfwFb4EkKlbv5rWSUT8oT9GFV0tHaFMrU+R/i8FBHWz6wU3wlMYPzsRWt7H6nSzjk/3tyTn5f7OcW65orWN88vz4/V3mYQW1+/cmZzebm3ocCFJkyMXlHk72MhZ00tEyPqRg+MDKZGzzyU0vj05Re3Lc7ucHiSCBPh3OxbmAIXPxI+1VuU/9bZhDJ2ugvp1E0fC7KnTh2JGLJ5gcGSHycimmMpxIDLSihlJS4I9gblBz/7eDgpfnl8Z7nil++m3x7Tk7Mu5uYevv3l/fHhAx42QkI0GW6K0d7T3dP58cXn7/t2R3Q87vQSsM/8R35AGh1qRubXmXM+4trZ2cQHFm5EVuweuit9XXj99/Pzjj/8vBf/1X/8f//K//re/+7t/svrzz3/6E4V+3d8182ERFN+Mid4ZlhUTw7X8dw5Lf10xxWIygOnnDsHpgCAHLrH4m9urW07xK0G6SvqZUmog/9PZ3KmOCFyIXzzI4CAWd/Gm++YqpPvoiwIjm4RMQVinseifLm8RUncJWUaIljFZTtAzwjApiP0p02v9exeZU+BeGqiRaVKRMYFLSen8c2IZtxLejJ3/JaMFucXVODMGyoD+1dRUvG+M69ARkXk2KwVUVK2Ghrl9Zp1IKeMe1NBqUUzAu2sIhg7qZotwXyZ2VhCM1dV8UkmiBnEy24i8yeehAGjTsaGeZ1SpwgV87Z8fOTLkRS0gF6ZpTbOZgTEm4xS2Bhz6kyqlqFrOE8wSCb0m3xSaLc146CQwc9stcweYq6gwSJCrvK4CCKnOECG8tIdq7KxBrVG2W+27AW/tMZ75Gs3nFHzSmZphomc3tBcz6qLG5p4ECpx6Pn4/gs7ezloka7iF8c2txcJgXIxalB3yjZXxyNdwQBot6yPbWVgyPA4ezNQpcpMruW+fdUS6qChzWNHs/yRhJsiPSFJM0oK5nyFWChJSgMzutb+X6PYT2Nor1gt+veBZtcADrHAfyZ0AU4PqEKTUNT/RTKPapc0AIjsCd020YL+0oz79V6VWhA8ODIBVks6+NXgEVtTWlqws+IhR9CwfpRmIgIAx0g8GjG3KWiEQEQWxT+qTg/LhyWUjYVwElW7RSkkoECWrMcivTZkDHVErU0cUjPKByziEMjiDobTpMDuS6JtAEiUCZpdytsZxG3Zqiw05gY01DTHfpgAe79t2qgqLiZeyHMYKd8LjL59NUq+vHMH03jaH6xue6+T08MePnwW8cdWLtA72V4TD5RfWHIOmR0nwX/zm1yT0z3/+4cv5mTlkSyzZR9QkIwr4AFZtMoV+E5KW84Kz9WkNBcqVtdJxzUQD9UdXwAM1ErVupHXqaBnxx04Y9/i8zV6NKsm88Ch0cnPzkCTLQLXecuvhd7/93dHx4aePP3748SNDvPLLb+zzMo/BNVr6fnFxdXL8i92Dl/vr22alndS/5+CMg1j68CS0J2Enx4emye1iYN9xxXk+Nn4xZGCW/UcPwoHQ3OH55x//n//7/+5ooN94D/w//BPw0NOxSA6cY6GwB6/sNSNaZiZaUMQd3N8bEhExoO/vp1kk0mw8L1RET1zYCD1BEiEsot3YpbXF/hOQNphmDVBFSoFtdqpnY3SS0YLLzNrSInc5GZtEBFhZAVWIbl6BX1MjbzIq4CMxNl/XrSxO0YmX/TxIEaqZ+Js7XfQuLYZ7HKE21BrQFdI64MUrcZyIUn8Op9sAmKJ+BwxuogqNgA7RtaKhZUUpO1wglDK9mPBr9S0+A0YgSOkgyH9YrdDnAXxkTDOjuqEIifAhVWmH8WK6mUJpQdfKa80HvUqnI5TP2ixNpfIotRCTzhFA6qsucuFDPQwhwImtzruLjEI0yYysgVEP61hFXehLjxpMSMv5YE+Rh0ewwfelr0AdytRzDA30jLrsNRNrKwX+quVptHa8DtNm0i8vGY+pSoxNDGocfHDDDrCGajZKDCGaa+UZgHRiGOW3p8OwSYuvOtYNJ9CudkAGQwoZiONsMvnjkPNVSUXWX3TUJxEHlfEaVUoy/DNjnAeS2rbcEHYosJVP0zzgF84HbQFlA1DGUT3f0Vtrj2sN64AgbA6YrLZj1nMPygMpapYECM/gTK74S1zsA3wVNsoSUb7SPixvFVKO1yMQAhl0zVCIqoqrkJHtMJdY4z2toWVsaO6lmeqQccwDB1wTvduSRUBNXK5awzLuiqU1ure0grluLEwPkZD0a2FY87K96UWDuUB0BbneAy8tKL2GO67o44KJQsiz4pT55gmgJeoQs7mUsZgVD1KstVLqduSJ/+0tGEkTFz9eW0e05qyCNQe1Ce4EffsYJKd99dmpEOTv5PjElrBZGm9z7+b5x+8v726P3n19c/HZmoDtvX12wz6v29uri4sz/Zi8tniM7ygu3tu+4RIuzgHmLBtJKWcGic13t/fAc/nl4u7RAWd7cBLh0iwmO+uddFltymw+g7awSLtNV7YLhmC93pZcZvrtwuXDPCVCWSyTBC2KLMLBS+Sik9YYeYOupgpD1te5qOvbW/t+WXO7FjhWsbFVOl/WPtNJvWvN2tg86myrxHf7E1iHr75+f2hU5O3Be07xfL69uk8yZ9hqxpfQCPutdSXhf/z3P0r6y7LxeSdSWxYZXdyaMnaqKF/78Ycf/vqXv/63//rPv/n1rx29d2HEcHYONEd6CsCQgh2LdNvrwjrcLLBc5Uh2hUe6MIIxZMt4w1xzbPHwuSVAGfQiH/IppuYdkICMIKhCfOsy42qMnrzRnREkExgE3OcGvBmXcjgpqDFW77RMLukDSSVmBNzAuaOjmSkfg05bzF+5kj1LB+xUd8BmVr7wJQFN0VghHziU8tqsDi3l8Q2FCQZdIN+MFU4rpkk3UpaZv6Xp2XV+AmPSKlckkqSnBNDMFGgf3A6RagUal5N6soyavbtrTAwE6BIGsRp4C0rBkbdYnG5U8jlbs/Sd9mSRdQ5uN+E3BbLIimR4imhziDRY4dHywBBhZFlSSnvGmwrSTkkZbqTgsirlb/mAGIe6jCUy1aSWGRTyDzpMB4ROM4aBQdOj5khd8a6n6rNXeNAZrffy1sim24ZdOUzNopTKSiNhDndAU6xuEbIhv+qBCxLxQ/m3FTGgXF6P4mJDtAgEBQ0piUwiIVCFfIBuNRxrm26DCdd0V4ZaefCBZAw6CWqhuGLBqTLoFC4SAXkjj/BhhYYKkEaSxkaEHH1nobE2NbUMGqCJGVGhQUB+0oex8mUig2IMMms8H5Ak9zTH0sVsDeY/XVn7hpxQI78gg7jeQaMJh8YC1Q5/T0cmu7n0BVPNjNEv9sLdn1ubObUiNXeMWsTaO3inPdCycfp7q4gYQB5eAihVjBE27+ejEFzslvcZIdDOsAMvC0kG5VYHMVW0VQYmF2VYXb+G341qjcwz/5vrDq1xWaku/wFHLJjT/zVpc42oceLq1NPR0HeyCnyz4Fn8q3sm+Plh40pSOA1+vru90Lj00oe//snWMcntZcHJ5Yc7p0VbWCSklUmX5yI65AMxI+XKqiy4N2DRP4HPyfGxt8GvHqxuPRAPCLY8yRpcF5DBk122AKnBAe4ZGyYDCIU4ix0kciYxDA2YdZRPd5PP/PEi8jy9YRNuciX8XLdn0MOsWx/MP8iiUGzhlwEKG21SxDiA9lnslDHlYDY3aTNiOSvPKh1Jby1tHx8LAlp3MYN0WFgd9GjBTtnYXpL817/85aePH8/Pz1iZlde/3/j6G54DBz/88IP0y/bRkXyJJUM/ffyk919867SfPSg/Oiju6lIxQibHxP4z7+YYiI1ZdNJVNLOsu0ubSlFb25baFcAZNhT+U+so8dJLF5CGhuEUgsjnYh1FJ4utd1Gp0wB5TLb2gfVGPEGGFXaI7Wbr8pYgTNSSkaNMrDZDJsAvu0IOSlXQiN6tUi8EO7MmJGdfswFKdjM5zorFOHYZDvOUKKX/7o4gM+MtwoEjCU9YCgLfYMC49Hgcs78YlF16wdBy9/5pXqwJTcKDj9lQfRo0Tz6DqEMupQOMOgzjsxXe5YYTrKCzWawkIalQUsdMW91TPHpXvJU6R8xR72gxniMV5oAz/GWf/AVNVtrvQtB01DffXeDnBYO3UMw1o4RM3OvW+tvOXiSqU+hFtwwY1AQ9dVRA3WNtQlD9FsWVDkHDeNaP9K+iOvMJ28zRR5q1NdGNIlp6LKVmmJy+NRsGDR0qlA8YBStLEsCTuSqGJIiD/DCDF2CHTSSOLKKsjvAM0rhSsZqrnRFW1iqu23+i/ccH6dFytZt7OwAocz2wYyyKwAzJAA4kPcbCIaP2rGjjGcBf9r5i49vzW3rzP3iYQgzWTuG5EvGe5c1VWC4FHSlvLGcXgIREaioQaNZvWDvUktkYw1AqCQ4AuxJVbQWgw3nKD0qAlOvN/iahC6khgiekjRlywZnE7u60BEX7M4NSQWVU9GM4jARFl4l4EqCWuEI76AYxvGaw1CFB1kfjmZJDAaYPFfLHGXZH7Zv9KBoyZ2scCHB6gbWySbjgqLidmuWf581rhdJECrH4lZWWu+h7c9eBBZNYG5FFHWBY9PL6YI7UiGrT8NimMKBIwXAiDmoTiZ0eH6Ha7eUZ0JumXln/zz/+4e7h6f03v7Bmz0SouQWHJ9+YvL27vrvpXEydODDOJTshcN/bPSDJnz9/ns0lwo1sEPQmSIIs0jeVXfJms0U1lFbWXaa7U+lyFJI33lVZREFZZli2tt6y+0e7mdPnaOL1i07ffOFOeEElx7uIsx07s2oV5vt3OzZkdda/pM3VORZ/883XMgY2f7Hj1sEKBw6ODx33hjcWK73c38LdIhypGIdWIJXBFEYajpoTfri5YVP0ef75i2OGbi6vid+Hv/6VJf6n//JP796dYmKjor3to8NDGkRkPn/6SdBtHHN8cNiLY7go1i1h7sVq9Gt9O5XDEVjC2dpZ+7/sIbAl47ij9OS7Nm0uQ66NvHOGMmXkYR0KzcRQUKGGJ3HVAMhmikeEGM0k8iAigSidWKZ/KWHh9xhsC0sy9ylBZZQsUsw0G3QYD3hcOvHRi2NZYu9FfvJyjYZQwhij4eSzoF8fqTPdNIzrhu9ElXbUeyMTwmUMqoeeIRpRqEOer0G5l35njzXrF0AVQqKgqKIi4+OnNWhmWsYOWTbsUZ0OBFln/q81BbAP05QvtDIhvvugL12l+FMmolN+1SuRqmIQGBahS1wn4Fsa8VUbBToIydd2MFiwCdPqzTw5qmaq9Z4ZdOXTchtZbP2GYBFwFKtG6KoQyp7mOAVKzM5aXjwShQOwKwrS6jKwlYBJoeIYqBpdCFtTSxMRSK/Y3qn6UhiBnREGwjJKms26Kk6/bMJbBygSKOXsgkxdf5lKcKJsCLeKMaPb+GCKKQDWklzlsxqLsMNDdI02zgxw/1QTPiQQORJt64CXV9LF9rnQQPu+Ks+qRXGeZmiBAv5pnJXxqcMb7G2ZMuPnC7LjOKTbZybN0iARyhrxNa+XpkRB7etbX+gT4yOnKHvJDAgfiiACiXhHtML5MV3jtH9mp/pbMwsybLa4jXdoBKF9kIQNNC2uY3i6FgfscX35Dip9KucrK6a2vthi9dxBZyXkrvNS+aEiMnfsSAKdMF+jpIUxcVMVvPBVw7igd4DMNAEsIyzEmVNLEsReyaAWWWETWKk7UnB19MwnB39u6dwI4PTocHNn58+Or4kTXJLw9/ns6t5OsuvLiwRkY/PKgRBeg/X8LHHEZ1heYGWi+S8um5cV4qMwFJi4k6Pju7srp2b+rKJBO6CuHh3vA8NaScbe0MWCIhS7vrDj+AaVkJCh1L6J8cNDp5Za6hbH8lucdGuCnxjo+xXZRbiXWUAQaZl5Dch6odDD4/uv3/tjkY/V+tZW9mKDMkfRxejnaeN552R3BhQODb22Yujd1++QwtaBq6tzffB/ol8K+dMPP8GRydUQvcfRd7Nq8/zzGZTB8y//8i///b//d0v6/+P3/847yOnfXr86+BMMt3c3ZJ17e3d6SmkI+axQenK0DyFlmb1JGLkQ1nnUJMonBwG9nq3uP78eHp8cHhxJSXAPlgQZ4dFncmEuizAkoslMirp8QKDEjzskOehV3G+xk+FL0//9azTWZxEjFS6zsBiINIP2ZftrK2OXb1GCj2L0snvselahZQcpBTgmONNLApmLwYEiGMcAaY4hkp8ZzAIV4ol0md4u8ztjCjPD5Fd3Oo+J6tVgIxI6pTViTA3N1cOUIdKIXspU81+rDiBp/ilrZp5JlVF5dzJKk8yoSeI5tKrf0TJNpaxsYzHgUDC0w923N78QCuRwiBunxsi4NS0GaM+zig3ThJteBD1NsQHTciFbN1LrEh2LJcwo4yKjg9lzRQ4ULJkwq4liopRacIzAFAGzEmGdQvfTAYD0EIH8AIJOL6AjbhFBkEUoRNErcNJ1vWBeziSEFYAv4FncmO0qIRaQodaxm5DPhvYkwpWWU8AVTsXt0G7kaYDWl4m7NTuxcmv4Mmnx8K1ZEsNh8uIgj92Iq9rS3JhmH92EXszK1xpVNa6BvdJIhkxlRkYDFyLLb4SdK4TKqBgd80RWSdDM2LKUi+Y+F3prkzXROOWmHwkofwag8Yhxq4VGwTUsDk7Nh7Q25rdnml3kGDGTv9wYrUzspq7USMMItlsVy70ijtFrx201tvEPMMHTWgYD82REFQ2DU6A7O5Yfm7wShQ37G6/6v5FuON1fBOWR4ZSv2JlUTJxhalECzeDAZiiegDkhZw3pYDM+lRwIul7v28Qc+ducjNElW8xhWi+tYhL29NCUg4SJM3+ejQkOP/10dVfmwuFFByTevlbBqfCfz7fe6POnM0u17aoVLfhgRaTxgL6tbLn7YPLgEvR79iR4k4yN0IGlXoN61l8+yzjYXjCXw3kMfhETsPf879Pj9rNzBgXj9mokTiV1bCrmgF9aSwOzBmcteWwOySP4GhCao5YzMWbAIDRlP8wNCNvtupJ/x9T9I4ef8itbB5aH7m6btea1DDVs2EpInl7vzO3d3eKM1JX8zcX5lxSbVNAIi3NcGxsWRzn09H88WiR68Ovf/to44Kfvf+S3DEr0w0qeffoMgCYwvMFdAq6l1Run747wzoWzNEtGCG9GxAxrpINmpqfXxANz4lJTK9w369DLvBlTNnnqj45oCh9diae8djIEvE5ytYvmqcFX9ppsopyxPwwK8ciVAgr7wjBkm2XvcnOeiUPrQpMA0KY9KzIBTTwVmarBdiykoNIqlmK4S52JMe0jP/4p+XjjPcbEozMEQTBaWOV0ROOFaJQrlcDuMYLZwYmi0lYfFAv4nEKqSlnT88UabBgTOrDEuzjbOkq0FCPsGKMASFpcMVqhTVdm1syEPlt81UIMd9xXSvn6yjyyNsX1ukMSPNKOm6HDLYxRJW9u0FP/1B3oaOMrcQExEerBWH3NqD5Ggwij6HANfQtKQwYMMc7Diul/wpiG9Ythd5uYB3Amw5xKAhjv0WGwmUxTpSZ3xKm47QtEmAStKqubkAwTpCyDoUvFst3jBgCCLu6GXbXCHOXQJzRYLkKjCvPvhKfy/OXmi8FH7rSvTYXdE23JGaAO8ukQgcEQsVyRIQKSHH8WqgxBlqg8UgIsIsw1LUyFLKSrgbDjoovrrGgZtxQdFwrGCdBkuzVASSBLbCNFV/u8NR4/ZuFgBNBcIC2+rS7D2la1BN7HmnLVRb+SgwqpMEBqwDc3lRLcuY1LWaK7J4JoESZy2Us0+IaRcpPZKLOsAR6jHrB0sDamZ2Tu76aLWXo7Nt98KXYkE2w5zqkBBROhaO4fS58Qx8w02sdkX9ZgySDFlxExITF3BQ8WhwHwH6ZwVY2Dedgg+9juHhSQjO9hhth0dFu2gkqSiACZz9Ovjhwh+umnz46ZUN6SG3MOXiHw+eOFs89Y9vfvv6Xlf/j9nz99+QKag51DK/xterINynFpCIWZrKH5T9hYSVmynrUykUDpJmiFICpjW4rRoq1XG26ZpSj46hDAByl1OifXJOWKObkU1b2KRlEgSfGsrOzu7ePU5YVU/BcJGZuh2cG7mxvYzTqDDN37X7U1jI90Xqjz15xdwVcIpYwgTg5tLG+BEI5enl1wAETw7Oxz0+v2J7fT2B7pZ0dfAAqcnN3/8f/5f//w8Ue7xg5PDs1NnH06M399eLjfjmOMvbmW7Gu+cnXFtuwjx7HuGnnEQUfmJYorFgWIeyBs7wKkdiwgww3JugLLHRvSWTdMHskt9mdk36w08WpUJqjSSo61M00JRElfZkv+RqT44iUN97wsOXU3MbZb7ele11Y86LRRcsUbGRAbaoEWBK5uPJbyed1suYkstKF84b4X3kz6xZsl2O92Y5XlJ3TWUi5Cm7Z40ILOXlYKSPIJUoJG1Bb1YfLIOMFLX5vNMgpkQApJqICHpGJyr4qY9WpM4L5AIcuWM/B8UgVFDK6SvR4VSBcilHN2DWoBk2X2y1X1KJ91ihzd9GhsX+oBbG0MSXpViekD+hWhiqQ8F/NXfkwW15DFA0qMQPCQ7pf/Y26n1ymsxzqf3/4oQpC0hC0KE35qoCJv7ykd8RU001x+kRXzS/laCe5i7wnGeRqjHz8DeVXzdlkKPyGzQN2UemLHRBkqDS08z0xorGKV87vIUEn/kbC7LnkXC6NBPw2CSw0/IMEv4Ai+lCKJimh52uNO1Z1jclEOY9K/yKFNH5aSiC4E1LHvw5Ie1f7SL1M1DSIE/aeTcWugg3zsb1bHD/nJirFacEY0ghKEw1wEYTJrsPmyhkRh18xSRpzdpnw+xLF8Vowf6MhQ8qI6IrlTg7x0057kNsH1hAmaGhHJlZd19jOJBATtEUz3+hD7au90lOcxUGFpxl/SUhPzeoQ+K9OHWZAKSGWW7VEWSTJiHATODKkDjeWK/YBAjQjS75FCWG8pxpkh3MxZNDlY/jLL7/w3J+LRfXOD6W3qMtZEHGguVK86laNAGcIoeeJYSp399cNPdo0h8O3F2Z/+83ux4q9/91tnJZCO6y+fHWe2tbHyzVcnx18dffjw8fLikxWW5gG4o/MvXsB7f3y8jyJB720E260Kp+aQTfh4Spbx5gEzIheJc5zRQ6ExGqbxvQveuqdL2kT38YDb8qJD/LbN2ADCOOT4+JhpduYzM+GIhfPzL2yEOmNSNjgeAyP8sz/OkIMnkJeXVPF24v33u9o3QnEukAkDda/O7p7uD7akfxz7Zrrj5npXJJQUv3z48/fOiP72269ZVekjQFw46yLpWP348dOdnfn3j0YY1HPmcryHedN+Lk758vysRBwBxKNH55c8Puy3WI7ven3hVlrvM0vvtVQGecyI2TFSkEgLLBrvNbQ1UzVhONn1lBlVNmlnNToZaYScOli06Hw945h745cx67PYg9AWUhS0JskaIFEGO2WexyukJ0k4NpCfZFepooPC9jIarXdloixC7WWTWiB1hfyRh9XI/FiYmNWSTzZwadVsM46UwkE23TEO4k80Vv+pkiaoKjQhYigEvhmBGZ1QCcOI5DtQlMhWhgBdRJNF2snDUMwxImQDmVDXwZfO5SlMHnPUQtJFd0M+kR/jOkoXEHNXa0sZXSDqHJNCBISby1bzklQcGG4SWiUT39wPzEKPAicJeR5ONCcZYukWrEoAwMPnjGA/XXrO9HkEo0YMAZdZGSb5grrKggVE5puVzOVqdZRioZ9uGtshzggBOnW/nljBPByuhWjVwFU2wARjYyMHNIFfUzQNmeo7e5q01W31U0HVTZZVvGazni435eCKKXmK8dVGCSzLghVHH3E0pUWfODSNF6prry4IoBb0ocxS0gdCAFoxVvzrZSmttVqsgGZAWI/FhqVca5N1mfGg3xF3yV/lQsoSKrkQhTZBgyATZighIW4VZi75lrGZ0Sd/mQ9Y0IvHGSxA+hQSBSpzRWLo5I3FuNHN5UkkW2xWcaiz+TwKvyF/sCiDBQqbIXe1omGWwaDtANxdH9RSJVLZhEnzW5thXtnsd7zw418eTjF8p7zP65LiWlYYcz2Pg+NK699KH2sDpLsJpSrCOjxIAqFFgRNEFLLf19DIIUFsYhbIGx9ztJMmdoT9lzNxz9dfHRuNXF6f6+Fgz1qX17OffkRLmWsGdmNj5+Trrx2DdnN19u03J3LyBMsRo0y2QBtqets/PPRV1ojDl2uy2fblRkQSU8mPfA8CEidWiaz4wDTRkjBmVWa2TVmhOiys4rGRLWnpSJ9W47076sxnRPTKekRmDI9OjzDi6uKLJPivfvUL25Kt7eHWtGl7MyfXa6se7wBgk270Hh25eXqwzofRwviLsy82mX11eoSSB7t7568fpRxI5u7mDh967Ay5r95//5cPn6zy3Fw3fW1/gIwEyfrqq/cXF+cff/xBUigdFhW2ZIDAtHQbeIppk27pFf2teJbPxSIuASSJ6Ovj3uHh3v5Rgf94emrl38yJCrm0Uea917I4A1ewkTXi/gBCFZwF1GSi94HScIG7p3iHlJVOzJIbzUl6DcFRlCYXaaWpibO8LuprStrXqyosuXxx3kyxDf20QZUeZ+XADgjZTirYP1dQyJEAj4VIvtq7rGgQM1Umx6hnzqSJU3qhVnawXG/agsVsLqvanZl0JI5KJ7Mev12JBJsBMwquVXKrwIiKVIQYyGqO9FSx1DCDQx5h16UlF4sVuFod8hQ9Mxqjp9NXKqIW2CBULQQqBm1vPyAVpiNtPBFpPIr9s+GOJWOdPFK3cGaMfhJch/PLb8TF1ES1wUct/XxFyVBsNZraPuJABmGANxtXHoPQJqqWYSlbuBoWI71Uu1XSIM56jQ0LwYEDfFkAi1PHIM6MrNkCxbo8DRo9cS45gybKF3plaMA4vcDfZZXZ4gZJR2MWrzq6vSWxnKXC4jHhVWSO8EQq86mFOQXI0xbIB33RylAefWNAMwfuq0V89N2zSUPpnEOuSi6kHgv3Vfe7pEdeQZuynfApnb+x2aZAwpHoGxKJHwxz2bLCQeskxDMEKxahDeQigE4ifPOk+K5JupX1zzu64zMmI6zPw7wILiCjVqDPYzG4bWjK9zTgFU3YNS9IWcZ3gOc7Q9mSNUPaJn5ncFQEZjVDq4FqMTVBCx1l8u3+p+AtfzJab8GDIpRW4ynhLFFYdCNSp+GsZOGIcBK+Bhw2G2mBsvMYZFHsaEwJIcl9dEkbWl1sIZLoc+3uBve940VJa0x2mCWsNJqFL0YTax5IhAvnk/3dr799bx3Mlw8/Hr873d89wCGp+5vzs6vLWwtEtzYPP59bE3QlvDnwpvXtbU9gZH2OlE+TNlvrzs3HIkhJ/XtP75dz75wEcJyA9hB5UbkoOSpET5JrkuSUBjfRoYMmpNRPDgW/Auk9b+bd2LBHwe3D4yMa8Fm8LxFuuCWN33F3uuiwIAOgbZPYj49/+c+fhONH+/tfffUOfQmf44ocg2GjmK0UzsC+/OLVYmcO0zaG+N3vfuvtN1a7Hv/myNS004K++uYbZL/0QjXDnLvbMweWrK6/c7YotDtGpWGEKQE9F7068AP1W6g5A15S+trBc+n5rQleEB1QQPMW/J05/o37J5O+qQHBe8n0swZ8CY0uscOIZruy+/2m9UvYIMpfedkTHsE02mk+q1Iv8gJpkorsfi9ycIvYFd1AQ2FCpFDpk4R+cgClBzkVezEc2L61tunIDuzJfDspjkwWBhJI7zlodKuvRaHBBI30lOSn1um4DOP9XbrjEKoM/8S7IFQFs2gQXJLKVXPmxmoyCoE1T4wbihLgqt5ixCjXtJrhqjFdtjay04qo5e2MibVW1zRgVI+mA5I4gWaGHZwocUzH0TDgdTOkGMtcrRSLrQVZxwk3XRdFF6qmXCY1s6Popl+DV1x2R+lpuWQdFPSlwWJYcWEEJmgxRUkNTtwWlBDoVhfkMg7hPiP7IOPt/AcrEEMr+x/XxtRDI8PNCGDv0gQgWUkshnNmvwJZl6AZZapyytYbCrOjEaZQUSdKQ6l2iklLdAbfVNd52/mJV+t2WnMdJ7j3sHYjt0yxqy7u0xORAnxyE26MMqwU5FaznnlX/EOVkAKPRnTHvPc5rkSo6A7AOUSQrYXXrHPfShYT4jBRuRC39UjtD9LG5Ote79s263QDO5hqMOuvJfiWiimC0C9lcKOby+XG4kUzymM662W5Kl6pFAGjOIauVKbBLEdWJp1QhL7BnY4L/EVx+e2lK7V9Zr4FEey54s24kpUabqRpFjebu7ruBDJa5FGLPlEvKewlONqcQUICDVQk7c+QUYhgKnBju+14HFN7bEfq+WsBgBTEInxlGvOJW893G81wOQNGuLdtO5Kg5gl39Yz2mQwRaYmTK6bdIUMocv75J41/+9U7r9O1KlMuX85E1Cy3/7y1Yd8rSFtTa2bZ5BA6ebXk1e3Hjz9qkBvYfHB+y4MJ/HcHJ/IkbP/Wto26nzNuAoyG3Vaw5Q4TyrAt8cqJmsC1x+3+tjWsztG0682RyySgZMvBvt/8pqmXLW+/OdxvKmNv9/Rw3/J/QwRrkagAatjHcCdY+/pUgGDAAjGLc48Otq1mRd3zLz99+enj0dHu/fXqfWv3mXyrbx9/8c1XjrWjSfY2n30+//ZX35kauTiTAlp/9+6dFx4k5l728nDfQW/P5YK8Ws20MwQMkQQsTXjf3ptG2NvdIaJ5dGNTVR6buC7sHVMuAJmUUOw+v7y0H4AE2ADgHY5WETMfNvul05Y5UNdO1sOmzHajKgc7WnFPyHG6QWpS2IkhBRmAsty2Ybna2X4SLSyai5WTnQMqDWFA0kbClJQ5brpJYPwtHWIIkK4UThJQfAGzdjOOzdIlgjRWXz55YATGui5qrj1qi7mtnNbPqIDO6zM9t3GyWVyIJba0I9hGxpdsahtWdjIhqVXQPfW6h8Zzkl/sLU/LjijgLj5Dl6Yoiel+p7TxJ6VTxSfX2KU+6FSLZrnrmLCxZcZKfRtn87p+93xbuTxfBaCWindpK/0SibBIGE3g0ZYqZwOhx6shbsQMdBxwSwuw1AdwEVmbYAFjmpuvilCaHogzq2/AWz6zUCScqfS03u+IWJ8DbW/W5RvGFIQnv80aFBmHpMRvmXQw+Fqsa8Q9iPkVKwt73ywO6qAC4MaN5wDyyXN8hy4gpBP9MmF+a11w6sO0ETYQUGXM4lIw8pNRv7nLWFX4HHraVJy9W2BQht/FEgCQOVpD8LRmMN6RlGL5SV4xrAyl75pg/yYkSYyF7sCWaujebEAzzqd7q15DwpIkjrlZmDFO+ATvZGKxobnbN7x8wrOAnsttOLIfqrvA7PeULRQdksYFQ5yoAXgplUb3jfErDyiNvf2Ts9kVgVGbGTnEbOGD1qfTSEG1UFBMa88qEeHz9IWOYi0pFLK1ubsd+R5etvaNPFpRI+abOcVFpdv/lYFBg0SMH0oikBw8EvSvDy/3NyYDEMr8U2cS9F4cJ0048AcpvZ6nz2tWBXlbMGPlnb6Wz1MMdsv8sBcgirK9VTH/YZj1dHd6ePj8usl5bK48S7NtrjyuOWZmbdWhCM6ZuxYm3HnRScTphDgtdjDv2tHJ8bv3X3kVsTdJHjv/cm3t1ssKLs6ZaL5uWUZGXZCbTzL9+5vf/YbFv7y4hOm3332DXE5YE4mLKm6v71YckWCQ5OQjh2I5JHFve+V5z9T04d6mbQ5eR1CCfnXlet12tq3Xh1v2aYe2rjxd/PTh5fbC2ancrnVIj7dXn24uiIdpAkSW9ydmDkw1v8/9kNVPn77QsW+++4p4SyUZQXktvKiIbzXDwQTZH0G/cUx8QMp2NvfwEyNY5vTQMMaz7E87Lg0msN5FSvDBGxpoNFFGaHEQmSkAlwOk5olAs6ClCgrSkH8cCbE2WDTVbjxhHTZOPvHBz04oaBo/CyCWZFpoQHqr4wwIZzgpIHfxhQkhIGWHTPWk99YTgxGsYloa29hQRVpUbNjRLBxo62GMfWY6SaRK2tK/txTQxGEQxJS6JIB++bln40of4yz9ghFa5POfnkU5Y80cYt26at20UinpBW+BWkvGUGaxj730wlQE49P6eDEQWoG3anRnh5fNNaqoI9diamBInYCt19r3G0gDRb1oGYWbTEUAGPWLzNAaT2s3zlHIUdWJ2HRK7DDIkD01LNWgqG5nOiVCYjdPz1dFYoJQE7VaIQRYQjrgRZBYsJicuN1QPzcWpCrgtxwhIKFUfKSZpGmGGIHhrq8TuCGFZmLXEDKv4JsLsFoYew2yOlOwLrnt+AOEiALfPGXEgZivyqg8Vi+S+IBqUGWGNVA60ZfW5DUS1E8Ugx8a6YUpHz8B5oWK02v8qhR6LrOa88YC5QO6iKaRikLg6EJFgh6AbHFqVMBhR6eQJYO80E1hQXjSBMqlqg91x/bJkqeG7usgKmtfG9ouGM6l9rmWCGOSlTPu46wWrWioF0Rk041LBkcMTIA2pKeW8FzpbHryFK/RyuA9Oviv2zajxQvWoSLbLy2Sg5AyUbwIUA/lPYlSGS2847adsNz7KJsdZezdQSOOIUA0nSRY/igQaejQcpX2a6jNeoQi4YNZzftEvDnSFnPRYR5U+hUydgpQoc1X550LOcswi0QeTZ5qwMjDapSySbm3Na+Y0SJoUMRCfp4Ytzgcu7wfV71yfc+6RROrny+uHu6sDmonADdORkBgTwAcvXVLLWsoWQKLdviw09MTp+dTA8mlrK3XjR1ZTX+bHVyzoPPBytavvnkv1XP3/s4aUzSEhE0DFpwikTOf258MKlYVzR/vBNqmnEwYX37+Ip1+aIv0pFjfnRzA3ytxnMZ88PW7y+01b0JuqKKq2Mi0rI27ZWYMYrz23WH9x6w0ERJadoroMyu/DWv/vCTSI+L2cNtOVB2gSebB8Sf3I+qZPk/Qmx2XW+O5GHckp+k54zRi4RDxpk0iDM/sT6bK7UzkKXcwFq18orsIiOPpNDNVKE7CYlBtYH8rVaT1ZKqpfgNysotQlMamA+JI4n0XMGleJf9mKKCFbMVYAB00BEhg1gunQEjrhCF+96/UELNgpJYxTusaXLREtHeSMZBBVWBXx+FuCe+cXTg4j9KlwiRRyyo6aNLqAAEAAElEQVSO7fGMKUjla0zlxhA8T8KXhZe1a1LflfyniRro/X2pEuRVL4KEqFRPop1XSCkomA/BOUseVKIG6B8wS4Aeh1zQVWWBP4eFLizpHBcq9STiiuYiqS7OoXbc0QimZ2eWcYxeAgb5NBqjMhgdckX/0+ihif4DMRXO2jRkyV6xdQE+N1pNLiBI8UVCGYeOaPNGxw5PT7ExUGODjkbqZQDSMUwyChpNqWHQpiUkUwQk2iF/pVwagGQCompWwbO837iRpUFElrsYaR37D8xSdRZNbzxvIArZCBCTIZP00LZNz4yPO/CIf4b0VFAfRmpWn4N7Rgn+KMBMZ//e2BkuWTbL75bp+PiUrYF2s9Ly2dbGMbIl4hP1vGmUbmECog0L8uSqI4w+DTbhGOeWa8gPS+AZx9YifihR+sP3eBvTh6tajjovNGD50O9hEpLkgTVZR1MhFrtSraolTHG6zxnikaqFwsi+5k2z9rJlzSXKIMfKjl8YptTKuDflk6AmPBJiWC+b6cX+NhmhqrALjquZnUy/GTu+quAjGkZe7eotuHI9AQRMQyDADb20TbrIMhwobY9MBDYRRu/EhrP0Yudg3xyPjqifAi13Q+oWiKCmSVqv9XWEqNMdbMZtPeEBYyVXwBYc2P7+YJcuOzGLBcS29umQ/IaQYiD8Acj5mSN3vDW3fV7bdoJtrB+9O/7l5rcDcQywt9bWX3bq3FrSQiEcI7GPZeLPzzN0uNxLMh4uz1+tzvTym0It729ZX5OtErvAxGsMniw3df4SKs0REaYGUOFg50BKae35nqM4Pj7opfVXVzubdkRv7nOjRhKp94ZVpCkO/exd81L9DrDz3XrZp+tLZxmNO0fFRu4b3qvAFo7Ryo87Dop4kByAMyfkvX8p4jSRKWl4hmtuERztZrDGrOemsbGS7QsiXoQDQ5N6btuP7OnYUsv7maGyD1bcjzZbBSTdkDOYVZRJpSRS0p5wFsAWLxcK6ZrfIbTa4jvRF0TlkJJn0jBlsukc2Iqsk4CAlrW6yFyw3E8qk6qq+7aCtMIF49qRAqTRLn3kjFws+9jrt1rJk7vGE5l7HROtbJc8Ae2brHZGaXKAeGAxTNJYkqDZ0XrJ2iTo/vsaOm7MBzepvyhOX4+vhhQ9TQvkfGj84kcYbgJUeKzPYty0iPpRPBSZtIR2oAg+XYOPBdB+QE8lrcZGrkqyRVHERbYYBO6U1w3d5hgJATYG3oJoRbQjf+AHHqKclL5jDmITPBdTs/Ui7ZfWm06TFx6rOU6qHob6UiZBU5eTb2bYA2WWlKUCvD9GVjgoZgoq17IQuvY8nmggO5pyg5JIY1nJk4dcTjg32Z+ZQx+mPGJNvkz7lSfIHU5j0x1m6yMckp/pFTDsnWLQ87l7ebzmT9CIZdRsqjFjC0+DflyIgvjqswhUj/LYaWaV4nfp/eZb6rw2faoQJDLQI57Up6gfCTSulyqQ8iiVpxwwRpZaOLlE093UvkYXL11fw233Zfn0TZTIIQAGb602joP1CBDJarKasAsKfQaBr8r4QEd5PvT0GNkX7BtMJZ0IEYRBPxTob/ZdCGGjVLPfBMBVyDDvRFPY596uKo3PgiTEiZTV8E6prKT55ZrFf4Ib+bGddBT2a7whIw+z+brlqOf8WS4Brl4P0uAwIrlr+aqzKFgm1GfuxQGjLFkamR1EesCOlRcLRm3E9RLK69t7m7jeSahsbhzu79pX6xhkvsJLBbxwsQyF8OH+XnkKaYOVPLsVqN48jBxA/e7bby0cmtnv143TDkBsa9iLRUef7p86PZQR/nL2+eyLtZWyvek7wqLUzYXNW6yN1y/L96m27YA2dt+IwIuprT8QmMuqWei6V/6JHXpsSPBw5x0JjtrqdTU3V8IsERNGeGk7702IOT/8YkkKnJGA57Rzm7ltq8fttTMhnB/nKKG1dRPaE/k6tqu9G3jJlhgcx9PFwIyOEpKCrXi9iNloA9wtaFHSwqq2ySUbKo4IJBKaTM8m4F30o9EwdvYGUMZiTZ60lK5BTy919+5ljlJezzZgfVuZAM0yO4mZLKr/xs6pjDEYMDBXuGsGr9TlCAOo9KspQLcHFVnsRt7rrRL0znySda1LupnPMsAoOiAZ8bD41H+GRc5C9BvdkJRWtxZtpHRiNYVTV2LQBx/rkQ2qquAIizKzM/HLlRNX4stWuqMRpCivMGsFYTCmDYpZag0SbP/dR0ItB5VWp5sxJ6PR2UD2QKtLMFdh0CmuvYGluoBxhNaiyePlMgv616NQOjKFjFm3ESo4xjUgZuKAUhHDR6o39Ne2lgcQMNBWMoOgzjS0ZC6rkZvAMAuByrg6ht3pNcBoUgGVe+cncus8WBexEO8jfZEvl710Wtw7d6Y1IIVg9hEZEuUZSJo0Ao3W1InVZIfRalaW3eI5TVjPCNDdiJIV0VOQjbXyfYJgrM66DivhnmxZOyZxjyx4qf1YMcwIVcJlQyv+zBgNRC43a59LIP2zdtidxl945YEMCdqGso8gbSSqlk5RzPfGxIg2lOZFOS3TVfXe7vByAhnUjDLOGa40bTuv1+SHWx3kq4il8a8INXGM5YsEjHCkppFPL+nj+Il4Xp/dYoUtg3AmbK5okWZ/k8KAHKpLZw8uvhYUeLKRkvZ1uXQYIxpy4X3TKnpCOC3ovdNWexUgxFEjS7G9ymRre2G4pzQuDsMIVHj0uLk42pk8JcS4hcniEh3km9OzGhMfNT51zKbsPUIJqK3YakWVqTF57fwaIhadaSGKLjEYZphDcEyE0YJ2ri7OpBA2H+4YcpHznjZftw6E3q8vLOnZxdXt/vbF9vrVzYYEywVvwFbKIFuysPIki+8AHFbeHCnnIHUj6HYmBJrYWnV+fm155SfH7X/+ZDYBs8d9tJJqJDdVoRlFmSaKLOAWgK8xvwL59cN9C1yd53P7+uCMz20K50UyHfiPrqtekMMcPe3vasZihhs7CAT5QgpBLiERVUeiEQylm+YvxMGFuJYP65/rwStffM0xWIC4xjImmgQIubBRk3lwrJyIJ9GTipmYV6FFbYj6oiWjC/iI1MQnTcJjktPYnHg3cs2YTsY1F8FS4CetKJrDEXuNSy01ZysbhOuzkt4WZOVifT+9SxKc+iZzIwGjXEWdG47/SMeKaBktwhUCiZXOzOpvq/n6bGOEUNBe8ubsA092iIrOyHpi10S/HGZhGg1mX0fQUSSqtMQgzWOvyCEquY023TILClnUaKJpIvdokJCm21BUsOg9jbPq3115i3obzJANikOvseTZrWYXMhbhGQv6kC6PlQ6I+dEMq0rr0/LRDBtnFsUclRyGmKfkWtkktcpE/Kx9ZmgIO6uERNnoDqeDsq+oSD5YyVHtoCMyTJx+h9HpqdV6bJJ7I0sNfUZS8AHZWw+NFESXeJdM8LYKlJp/48FQIjPk6jegEhoSUl/5IGKx3qIboHTF7tbaOwo/IkJZkR4gLqMweEXDtgvJvI0NKm+I9CV/yEWmkwhl3RLEKMxO5ZLMfZVQCpTsNARbfOmzijiqGAy5D8VQhjExA2V8OBA1P+MKZ4Nurj5bH0qqaAtSc7MWBt/7ZGaGWypQvLHdiatGZt/lDYpKzk7mTlPsZAuiFgHhH3wFMuATQYmPYpyFjFFDsLeIJPhTv8QXNLkiAsRBKuNmUuSDP0g2tT3CdeKocWUhADLPgKEKyEGqIUGRrzFppI3LZdZV02+AzgJhN5VfyJsqFIAmvj7py/jeo1lu24TY1C1iMjyY5UP2jpY450qnTinpuMURhgd8IZTeqVh4OG6EVRGX4hazkXXw8riKPmlx3SpVvuDmBkjgwF7N4KGwxVtuiaZmnfxv/xh13D+8dCrphgNurAbOkQCkmRoLhQ52ty5vbna2r0GlD6qKALCzEgsoxM9Mh7MTLt8dX5l03jKP1+H7VP3sy2fdz8vMHyX90ZmmvT89IKi9fX63PVAGnkYcBhxGK5B1pL8Xv/A9eGBRkGU4x8eHklOOl25lcANGUY6lk9AmlNaFWipj4UASSy9MZ+iYsuKjtrMgqV3mCgWWDXqi+8ODXTMChQtxrZHoNrmeoCorlhjgP+EYEz4DZQtp5NKMhj32i3Q3sacLLrzgw01vs7f1N7bjEY1LHTpmufeplknWZmKXFeNL1CGC+sgS09WMfWt+uHNAs1mTsDOx0+LIceaZWsIZf2E0IltskI6AJ42mdGwHfIOd0LJvAJVz92aSmboQlF+X6yLP1Hi9fHNxehoyhKrVhoy5I90UnGIZgdSPO1rW3PSi5RK5MM3vpIcaMoUjXNN46iAg4F+X5ZVMSMA7HKn1RZmdhFmbI9i0aoKuFMJnIs4keqK7ZfYUSSOmdqtSXiEix1hpevx0rlchSdwM7oDCR3aACaw8YjeF67Z/Dh6/E0sSvAaNnVkrlh9uTWpEq0QCI3QC5OxlxqppwrxHlO1A/pCJQhHaP13gfLzdcd5fK7Z7Pdz+rpAiYOK6miDDVZTE6CYKNDDAUZpxYtgMCVI1xNJpNgtLUFbVjEdfWTroe7+r+hMnY3SgTzYJLPNqPvalBYJzacgXo98oFiMbwRlJxgabWSxxYrUyLZGnqDEm6CI6T3sZtZGRITkhy+inj+w1vEg20AKmzwXarhkLI27kabIBhDHIWiY59HYDuGnptIqAV4omywujuyYpBXTYPcUMqvVVSZLtPbfz8nTwuMCv19SKngKVtqUPdMC/RNO3NGqWZIwPRLFYgRgCa8qE1DvS+zs76WH5yhTPoulVixpawpGHFOBifFWGKvQkIsJXsEEufRvTrE8kg3hNMRW+o43Sb6spGvSMX4z++gWe5luE4D8TKDcx3ZludKe+mImEJ4BFo6V463kGHOQ8DRZAIRDT/rz+uEXDGCUdQsyqUApp3TaSG3qbMyapciyZREd99UJgflg4ZpSF8q0Rd3CmM8u++ta5oUar1rdkfg/3d3pZ8N39u8ejr989nF/dyAvJFGGHDQRPuznFxhmFFPcOZvjyefv0+FiK4ezm7svnn2zIQjrzKY4plZQ0zWAZTyt5vFY7afPGLj2tmwBovtEgsoGz8UeRvu25SGElzy6nuGkVbPqiKYrogB/C13ji5oZakvS09MXhssU+3loDPDYL7YwHhg5jOzAxSYn9iL62owsSeIe6rcTPVRfxxJRtvcw6xTFSjffGOuJEzBj1wKTyulmicRkxspfVYE92S410tor+x8Yu8S1OZqQQeexFEpoRlN9jEsrY3b08NqBhS4RmBmfg93SGsjWSUjasztxpmdjrIOzh1ikv6o0EhmnmEiHlIhmq3c1Vp69trb8aZEicST5TnCz4kCQI+5edGBkeP5O9aYoxtaEbEMrONDJANHdIkSigibgAoOxt0WMxEl6CJmlc7gPx1a03XeUP5mIWIJDFyzDnDHStJCCGCy1NdBOutjfijcKZZevCOzdMeUmCcM4v1DnYutjVsRvC7t6MJlSA5/SFeroATTkZWEBAeyDSkQkijho1gUaQKO4YSXvdrSJt9bnKQ6JCZzBnmhsfNH+mI8DE1MdmOFLeTu2yDJAUF0yAllvTi6ZqLDte5xoCPU8eTxFM4NICnjK0fUfpaJxJaxqzMCtwZzCrnxkcZBfGKTVoiShtEg6HETjW3Y/usjTQKwdS5+hMxoGoJ1BE5eUCOlTUz7gkDoE8HMISdzKdqFh88bfUeSJIK6ZboHuYALUiHIEaAXboJpgojFc1g4EQAALiGtGS1IEXkSgQKqQu1GFTckbX7UKffTIe6Rtk5YiGCDinCmgpIOS16T6qRjPlrB1q/qr1uZRIm4DRIVkBYWtoEjXiXBwx5RlTMlCww+67A5OmelOhpsg5Eo0O7qrqJzrrESfCdDB3A5AsyfAiUilgZSRS+gBCgpM1MfRuZ0j/olewMfUkM99QLbqyOJzoWSNdo3R98T8tp4IhQzbTy5SX6SFCJtxlMyy6v9Y0sllf1KSzVeaNJIi43/wiRWm5AXQ1IzRu0mh15ccP3+/tH3rJ8N7eYSvZmSnzAFubCMYFOwffKaFXt87pvMl3q9nJkbOVnw0We9/fWLHl3ewKfP700ZCHFmzv78HMFIKxiCjZelBET5NtkuD7UNkqCaOrQhB7fVtnmr7v5iNoEYKJjKeYadvnji7S5a3EnTHGnBnXplemEckKD5NFWXR7fxibCU1aJz9ka7hSil1N63ej+s7aTAUTvBhHF0fu89o4MhHjKD4sCtkV6DTCCZKWMXSDP9hQ9DyAx2IrIpOlaZIGV3yt+6RhuEls3C3+sy03GRiLAiAu2U3ybc9qrlkK4tGHUansZx2NNRGeT1NiwgVCxDLzCu8C1ZEdqZ4lGjIIVnVcTisF2oC8b+RnNu5pzYKtFnvoIyOctwILJhR7x1iurpvLCQM+8MFE0wca0dcxg8X4sgJcdzpI7ztWYGKL2ZKStqEOXawrxGVsplkNpI0ssT5Iqdaq1pQvkxIrsmzD0CTWGnI1xlUgA4Pf19EUQVWkjjyLFBTrY23GZQzFeDE6/vPOxAiUrul9Mh+Q7xThRaPBnwGpbaXalsSpjc9ogOfem4HFUPXzYeUkYAFG/bWmO0W0Kjsz4oEIR4PZh8k0Rulpmgli4cJQ1h6F8MhaZm3IqpLr7K/LuyVxh8keuazDLgDzBdGDEdK6BpVPrzEOTbPJhc8mQEbss2tKQoPsomx6j9G5EC/jy6l4hQUI+Rc8oH1WgBgbRqXw7MRjlPJZ44N1ZgfDxIETZzXaLXyfFTLIpjtQAhuI0ksGfbpINHd5mgbaAP2ZuV7q5DVQHQybFeuHFrRkDPzRx6KPJ/tGRfo5Rs9LRhGBYRE8ZMc2EBCYOSFuSXo694xgigMjP9b48UEAjCFECNj6R10FPPR78WEpa9WG8NE59+xHdLoiROZpJGH9TWHrAxG0kWB1tm1yD4h8l1ulywrglUNCqh45Zp4tqyASxil0SO7jmmLWuWImZkuqI3g2UA6Ahyp9XGGCxQqPOtky4sVPCXL/9DhOkoITUr1DS1ZegApIyczEtEE9yrUoyIttRwVgita9rEnkIuqFuwDUS1eEz2KR/cMr2aAtLwsznu3Fwpv7e6teuXX48Mj2358egZwv5jiYAHGOOM0qUHYQ/0Ar6crImEqmNhyiLna+ff/0eER00XgQjPYeEhH6Y2WneF+/sEaXcaGstaW3jHtWWy2pOAbGKk7TyClbgW0z8NjgIUMg/Yn0s+yqWVwRfVxIVuMmZmXWRZ05ABuvvF7Y9gAjQIxLtrHPBwRFKI271NaCvyOYkZqWZdilxlKfble1q6E90CeiWHwFsUL2N6FSLG0QMLbFBCxTq+DZy2g2Z2zSUckGJ49Mbu9ck7anFmaISygDUo4KfsA2NGUwYl8AB4UPjKAmuwMwCBIxEtfTPJX8IHW04dUmmtiOegJ3myXKfhQmU1CMoVk3XqGDIKFhgwInCkGGJ6PZOVSe+XHNPaEycQWhvKbb6AZUONJw7Iw1Q1l3oAR2uKNq6Y9Ac7H0+RItMhrZ0SUdj3nuItmouR77XDHtmcBeoulMDNDcxlzNjrLa5hZDy2pk/fGuwa6uizAboJSsV0D4qy2qbAdGPEXR8gSTuy5RAxK90LMuPRFMJ56Qcv2VsXVgeF1kAZKC/oASJKUiWAzC7I7PdWfUrjQDCfGEqfBneiI1iD/rTIxIgMvThWJlshGsHjTg4EIePZj0xNfsflcUUCCwcpvePd3FvqAkG2V0PHZHmUw/XyQHoFHkhBjhAkzU+XllJ+upJCw1nycc70G3aTclD9awFP+ge/qGFkyhz1FXf8FVJOW3XhKSARFxcJr5ZYB/jhR0jgIW9TlPwVIqJ3MY/DbNQGDhykbiK7zQ2hnr4leS42u9ywYULHABdbN2n1Gu08KYtEoU5SLz9TGbxSTCHPJAhoDkEa7WAq+bwBH0JIdf5Jxq9mf7Tvtk2TIZBSRyC8hh6DB+KCALSdSFvNEOXKApCETwZXNZPJOD6XV9EzXkwHxtTAgTFMFn0jvwPENJI8JeMOgljDwIQjXAh2W695FlYc98ss4VAC73WA3DnYbWWoUaueXoZYKKlCx9ozE11aE18dCLYkTHsd5Bd21CgjK+RGA9GMI/PpyfnVkns7d/IJFJmqW2pTRR3mJRK+JlOl727RjYEj14l9jkW4p/nw4P0haWZn1lf+vAC2ASUyFkE2g+hms8Yy28e0eAj/gkTRixbZix704y0Qb19sQWcW95Da+3rAD79fzshq6aQb5zbL+Dj2TttyjhnKGjv9ijNoa3GCaBH56qqkOt+cB8IL2ZNf6TqCuAn2oZYc6FuN1bwix/fckJl8FgiAqNgSSrTqyQmqktUGRv7adhZfWYwZ2EiOl5qKX+qSJ5LpaG/QgqPfJpOJ8eM5LN3GhH4U7u0a6eKA+GMnWZZgJUAhVhC6KLV3AzYHIIBaGaVww0UNfxdDHqmoSgiZxc053ZKWJj7mNj78b229aGSbvaOQGhzdaHFoKkw3LjizKRGxyhobIwBT36ibT9uBI2CpfuRyEYsDCIiTV4iuLueCq7iy/jhuW12n6UPZlZQ0ozDja9aAjFJTATqqEAZEDSOuPcBky5f+pFf61iGIkqPI13XNdM1FGgCFG6hDNqDk87ZFtgyACo2MztUwcorO+kV9rMRohuCca99XLT2DCdPZF0nO8ZSRquoDV7Y4WIWNYJDTRVrYFCzIrFuMPSARil1INslksWdSFBxwEAsRzI25XFwowcY1kLqcVnKxWB+XP3ydIgGU4jQ/FmJlqxHh3nn18kNYwWNg2Xyi+FJSBqIgcKdvCOPSwHAlZ+AoMRWksZr15Hs9isZEuoZMLPfY3DysWqhGhyMhIw7S9dFGKTOKzmquqy/0YJCSzEbAgojmv197zgyWto7zIIRXgdTCROXIBkNAFmj3bmi0/ERQMbYBczBz8ZVxEFk7zx6lBI0OMqWurHzs/orAyYdWps+vIy+8Jzm1y3BqQTNZCLNsxJnYrUayRqrnqdhdMXmobBaZq8CIsw2geNK6YuUWb1iEjTaXzqoDwt5CObiZ/lxfDKMHngw6KJw4gJXGKbjpQpP5do+GfqLjDYCFwIrSiOCjotMePbJJ+SpIZEpKQq6X6f+4r8RC/pz0IMKd0DvAFJ6616d80TI6te6ilR5oz7SX+z7HYrkCXHhZrL2tnfe9k/bIcxjeIC+CWJJk4GtHvbL7sGvPSp2IQpgHWi0vTMLsnKwjC2hXgZw+KSuyy+DWXYrV+LHAmIU948JRgMnHeDyZ6yQLTYRi08IY92EV9f3xjUkhWqYWkFKRttl+xrHDDDaAluNYlor8yjnGhT7WJ31EV6yU/Zb09knOLraCl2trM3H9j5IqxhEiIqXGJsvWjHZ/U0EbPwKcnDmDYwozhDiK9WL5A2X1UP7N4jW2tEY5iRdMiNMlb4SRZcVIkuiET9Mxpy/AMKEh3Zsw1bMbwTJrGaCJyLsGZxE6lZ+WKB5DLZ4ZyIGbVMToiMr4skgNy9nErrQU2K6jdpKZHlOKO1JxMD3ryQFQFi7pd9rXT5OW5sy1HSxiPtfXlQpwiXNrIPBWRIgX/+5EPfmCG0fXKabFKIIIVcNF8xrswuxYBxP14k92ydMZigotAbWLkQQyvSY2qrIU2+YbmwDqou7bukL3O9M0NJco1QqQl4iHuotugoQ5MrzQk5VTsEzT3S1kJH+RijV7cKr9n7ZaRSpgQB00vOt6hDYzWrndqPuA0J9S+tTMPUxcElWk2cEjcOIFAJ9vAnilFLs3T6726Xxvy8WbAFNVAbossCbTuve/pFpWS2PsZuR2hI6Rv7AdGcGEkD3YTz7FTv36F9ncQ0eWyzKK1HhOTikabvLCwTBhePXNS+PzEqQoCQs1swp7HZNhH6nJKGXkvJ3A+8hy72F8YWAoFWWdVY5iFznIHgybvj3wTwHrUAlEbYjVjSKMJmNqwJuXHgAAgLomc1pBiCGJkwo5a7m16oxNaLg+DY/ASMhsUJhMgHzBLD2sEfvfFDAYhiARWAmXk1uZsx3JhurJmAtKX2GcRIMnhMaXUjiU2hgiI+PBIJhLUh+eEmFiK8Aog/DHWjHxy2ir+4o50v9Lyn8IMUMiQrZeri/hBfbcUYgkyEsR1clAFS1iblQlDGGVWBVspPB22eGxU1VFOKWKYO2iSfqK2M6ujcsrL2kWh4da0XGfav0Kj3t/BZrVVuhpHmWk+Pw46YdwrFnGtk9jjjtvZwG72WU/VVNBpoisuWRn5gZ0s/2tQH1lgmNEHDKpdigDAj+zkgAQSUoZFNIQD7CLvHXVvMQslC926t9J4ANAg9HpRJnfjWZ6MQUb8hCdnwEgJuiSURo5JcUYXiMCbJSB/tDYUTNJkL8mkhdq0sAoaXgByWoiJhFRsSgWZ6EGWCmwxp6WkPk9iEQS8xdeYqwmMWkmG6x5DtK5ky4DAK6TUSOUWimFxI8WUr03iv5sUJokC7QORpofuYCKC4wwo5kVFrUODepF1KxRaskud76/ZZxCxChkYZ3uFhzXy/HI+TefRG+OHABrPojBdTXgTR2hVeABb+uw9RAJX6kWkwr7YqAuYDnw5sb1zbvHl88fblZ4t5uX1dra35AEXcQRDtI451aiPY0CeQjQ8SuujLkmbPwMio4YibdIThoKQe8as4X0CAHMXpgC2yBvxwhMJmSwGufWISg8YAeQrrjA+18Hk6MzzA/2hbooa2lMXE/uFPaQ9Eqt1WQoAvyVgadE8CE4UMWDWFwHSTrSAl+oMjSgoa+G6opNq2DWEcibP8rxOKwjb4WJ5EviJkSONkpC/MjqPVizgq6ZF/PtW7ZIYC2Z6uYkzal5OJ5fIe1gVa9lBmAwKC4wY2rDw5K0E0+zsi79JreU83Q687CXQdTqjLOLXCyVu55aCkg5fhwgy1tOY+0qDyYmjUrpHCShSYdSZQnywYQGAKhDH/95O1rHDXOFUVhgjIUJkxZ+0ajxPUiO3Za33OeK48DfK4n6zQf8ZnTp0z3WdcxFUY9tvJ6dJ6ZIusms9KIlbvAbNmA7nS/ySNb4j+aWwEBT7SjVypVxo0IbvzdiqlKigEDs+0WWu9VkwVKA+bdIJttaNlP4JQckVk3WhsNM6PoLBAQ61MhtpQMlJwX/vkVmM5PFc51qINbfotadFYzmlrsYTpzBShDA023bVuNDOSXQRPecJYEzEJv4rfdVFI0hgFjKz/s0NIo0lDF8Se8FbPb+vEqGZj/eeOZMoU+C5otKl17dnsNmqINcd5Q1GMpRFL7Q39m9yjkH4ngg00RevVRlYuLw1l7qVNOEI7G1c3ns8NrWaezeFiuztXjpBrb7RWYqg97HIIMDAngXUCjugBtEKHF+dO0B9nAdFCwjGL8W1/zRKzu/h0e/V4K8f4cO8F7hw7gwGGVkLMZs7x3VkZlIIs76cSOgOyEy2aWE04Y7ZHETsTMIqCI3GlHBoXKbhtHUE5SKAKrIg9n0pSeQ7yluR4r6cRsGkwr4FsgTy328ZGyoU7UIKa/yisBQDgGansmJuODmVfFrqKzrGr6BNzhsE8E6BYaP0563DHpIeNAM+SMQBGCgE8YrUH2RsCeqWSpmNz0EVmCGb9Etpl5hbkhRLM/swchWh+KqULfkUrV3CBlewttrwe7ycSq/fSp/c3z17W6/yPR9kfpGDAAXfrUcJW8Eu1n4ap+XFHXpE9pB00QBWeZNXSF2+fyL+lUao23JEDIBzFT6TXTfyMkKjVpZILnrmJFuZKBoC1kaa1GC0azAgTmBDGxaQyxwCc0bKUTnMa8IwpQXYLzYh8wGFEBMg6DKn1JHDse/GAJcOzhFdGUPupXMk6/EMAjU0UCMDpFmPcA4TuQJLXy9Ax8UQ42EAuxa4acPs6FRvV6P7xeYNzBSV2kYIMcSplwEDT9BdWKOaPEqyztusmLqN7mAKZGeF/FKjYaLEGM+VRvv1Vk4kmkAUEt693IU0HZq3SeK1SHrEOzwjkPIMSuAkBtWsvs+RrGXmTgI3FaRKDrTziQiPAhpjDhqgD/5qZTQzBOswElWZle6CmRYXRIkFs2iCLGkzoZ92noa/A31Fc8+amieIzlwTBmTjg8lIP+DqBUgy492wlSS5TU3XU7FQSEUH8ThiTDHTLwpICxmWJsBAoZhXI9KexVgKKD5vETCAUHmZ4EIDJ6MwADaJViEWSrrsnL41L4pFLc34XtJETswbNVTTMUmEI0ihb+1rA6JhQiqJUFRkxDaOWwUoDOPcYsxCyJBbsZf8g1z84xZe0fVpK/yNaEuLeQk81kdY8hcMexCCZY8oqlIy/mZHiRCrHp2x71czLunLW0wZSSYwlD77mqJ2dJ9kYwWa8zoBSN92HGVQ0HD3wrtBpvUWWtMiaIR4FTUidNzSCrc0bojzUAae1Twf7HYazjJeR7omNbm8z6Hk3+TKidnN9zXd6Hy9J4IVClfKrTxS8ktfj66uFv/AxEsb2yQ+XK0DAInwNis4eni3bjS+131xX/JvcNAxiZeNtpIvW2OQTwWyk7E709PXp5e55davscEVeKTPCNu814lEaM9NJsFm4HYfiGd+UqRfqUK6RjekHZ3BPi3qiVsMIzaUdPqO7EefjLWPHUGAeGdHmTAqvWQjVwk+JShPaonjngj6bVnVZPpvDS/aCOR8lStCxz7WnrbpIzDBtTJivUWAkKGFAF7MJBibMCEqxK9owKSyrjRxWaWyuPm4JoNekgG7ZfiKiMeQxxzuoaLu0Cey2niwx3l34QnWM7shI2DEUouPcYKKrFvBmqZWYtcGiMizl+rLtFivbZBPX9OKBuoisPa8vxP9xEvjUKCYdyneQS9jVlIt4k26d4ZS+kJZ4EHm2SyMZ1bI3gSKjVoI2sdaGJxFic8eUBpD0EyrDSVs6WpyHTfyvNmNa68EMd/qA5v7qSKs6HKzXLJCbr5Hboxg9LsPf+YdjxaPmAG4BpLNmWmiaWVt+FYB0oiEhrIxz0HEEKDaP8xSETvJdQWA9ZKWTciRWcVVeLYXBmuRjyORvoagyus8WR4hOsPGUvCKa2dY6hYo1dkYJHpPUdC+zmdAQt2cBr7EEmB3w7Wx6i2AqQqD8zcgWYL4h7BGL1vtzE+uQ1P98EElR2HGYLE5ryOKKfhHZQj4X5oPKzaKKzQ0637mIj3f7rwfcKTng/klXSvBQEI2oiNaCxfQBo2FUOmuwiYsRuQu6CZxmPfTjn5gFDmy0zyM8hb3KAPjJWukVdllevDexTgESA7OMeH9aIVrUNkRt6lujbhu1RR9WszJegNU8hDYh444PKSrZbv4DLKQRgYImesafZF+jesz3NOp/whRGRo9yD2KLAnHuqt7Yr4w7kzywJUIYXaxQdeEAiLn5FvzoOywY5k4lYimiifo4YsWX9L9axvTkxz/OpRb45nx8q5tB3pPBXJUWo+fjKBL8KJtDxWU+IhRJcG4ofewrbSlPUOxy0QZjdODIYVBeC6rRiE2d1SA2HziUDfzOAWJF1EV8OR//+Asw+BDUsxBIpTJa8l0tvUivIxHPSiLXbXogY85oRbFHTsFgGmkJT5YyvjdphfUZxxKvBDltKRr2dJRFL9lstZ4fTR3MB3FbDsChQxMYxkpCohAe0gB6nzUzdt/ewX6KhtgiFMELG6A/06GohFwiBdJN6RgITAAbSLHfSUgojTpjjHVl8W6zCKhYuuh1lycwCcCv6TTiFzY1CMzfB3lGtkHOJH+QNgQycZn4xG9c2SJtfNy00uIKPiN3mKVC05U9M+17Ww+Pu8WZa7cPN4UIxUMTqTNcRGwkn5aSIO0ZQ2+0saiY1xvREEyqJwNCbLL+hjmxPPnOpjXSjN6EkK4bSUXs8UYl8EAfRoxLWou3mAMXMJg79osYhtf8T/wUqqhCvNR4d5MlzcTqvdy86GQENZFuKnuaSxCMkqnHiEcDRudTwWpkYMw/y5ZsgD+Y58dXxgGpoifAsDP9z1ajA7iT28XQ1ngKFi4TnSuOQYOIwq8b4tyR/wXH9rDolRJmH1mWGVBEuyxEv4YaAA5zvc6jPDm8kSZ+ZLcDbOKt5g8BrcFEzAzYnD3npsK6V8dvn2m11jCM29SRBIcgbZDAqljb75Ei2pgKraxyBIAXBoKBHMMTEIpp3OVvBkgbY5oHWgD7W36zEqRBjSKUlI0W4WIkntTBpsPpTBGmVNkFU47+4k4cJyKiWXwu8OejDXeMhTte/55lePJi8a0OixkpBxJnsLO13TIpSGb1GlSCbTg6kdPE6RrOUkwO7SZBJz05Cbyem1HPB6xwE7JCUQ9BAkKhNEQSP6xOt8uT8pLsOwB8VSXG0DGz2R1ygDLsfiG0uiBRmUQPnYc2bgVjwbuIBg3jLv6WHABRKQ7/VEdC7ZPNGlFaGBsPGI/88agPSWyGqrQzy9TijfZd00+hft8hxrLxD3qmK3ZBZSELYU3U6h7YiZC8+YwcGnoHkm8mPCPSxg4jm/RnBpxB0fmXiP0oc6xBzpPAbBqmDtkBWZDesTCQqm2EmbwrgEtP4Ttrj143W4YUje1y/RP6RfqQTMJxGW1Z/OSc5Swv5zilcjj6idSty7QmpyjKBq54lj9OgkQ0+orQ7E3WKUlnnMiUp1qYUKr7mp7fkjatXOqzApXoET+ahRuLNojgwkTgcv+OyLaqSnutqnoLOXEpGwfifHcuv8gqe138qMmYy2S02togFOxthGzJvwFBW2mtfXZ0EisP4taQjNJzvEqaBjMomfhvBtZJJkOD6VqdMUaaxK6ly1nVGkHAxJUy/ay+QYXMDxZ01f7qbkTCFBC0VNIwxBIBVrI1N/aRoJjoBA2KbKhDRn5G2wCZ1A3yaTzJg06shmKJ9YgJ9TZPuJEWaYR6Sn476iANnVSJGuEqCdaDyW9nM2I30g478imadekaxSg689WgpChZy6YmuE+RVoc91QWFmROOdRzeDSLp45oI3A8PR5KJBxi0y9YbTgYsaMNutARBSgwEgaiCpiZa6VnxNUiwPkJG6eRCF+B1IXUzjn1NoRBfUJb06xLDiKIHRcSTKqF0sgFRdGl1sYa1qhguxWzhIxRENVFxqAwhEKWBrRMIhHxbsAsp0jEwAEWjoGGEyZ/elVfYb/dJUZh35Z2Xlpk24by5BDdxS++Cu6SXim1sWk2iNJZEoez7CMKs81EyCLUyvMfXKIvtqQHO66mHS3eERdwAX2MjMlCrq897Tzvb53ILa14F5ahgq9MkkBN1p4o+OPhX+EBYrYwwudQCDxvNx4H2Bok6KaLqED5qj1ULdtGqFQIh6BYuAaAkN1vVJtEIZRFGBj1aySEuGaoiUJYMfklOR5YrW3QQds4zaKiB4365X6Dg86hSEPrsJwpbD+cIOkvi9T+Yk/EBIxkBGPiVJOk1klNz9L2YjH1MrCkoRFIRm02CwP4Mw5FeS4ZgCuhcpwi1MAU4vARKE3PBz8s2OWfmH6yiY8mpY9ak/fGNeFkbXRNRfzqLWDK0oYKR6Yv36XIOQ6F4JyB0yHSZoHnBLa6RU42gD4NjbA1Tmog4CIgVM/xrZDDiQNsRrKaLqHMzAExrDIW9CWCIo4U8H3szWGcIsgzutkpN+BmBkreRZ8iS3PyoEcY2ptj8mLXNbZSBRTueeNSE/GZpy9FNyDtmAmCpIxIWTw4Py0rN5E3mHvzEGuI6pFKGD+wXkKEmbLJ8CCmyAcI/tKjPDAJuo3phfMqlTqKicSgYfzMOGzbhptHNPEDTo0xWcpRh5tFxigQ303J3aSbFKMbe6MVwo5t2LQ/JRMFJ4zCayECAsfh/Up3vJxhlFanr+ICkZOgykGRSJ0It9eS0kRenJReI4r7VXM5GMix/2omCdgDcB30zFhCBLSPAfLQVZbtoRmDhXziiez5JQr1RTswbtIn0DPHz4jgZGClFNg27lOzyJAPnInoNh1CSLy2VguOFBbNwZmLXJpb5htEkv7L9ln5YvJBvsZ/pgah4YwYfYgYTZ0k/wdGH1hVgBlXXDSxEt8DETZyg3m5m6gZOBCtWyNbY/ISVEMtP9SExyFVrcKHrtEwe1RkQ6VsyERpzM4+IRIjqHXVsS8mEJGXcSw6ZRrVAvtnkSPMiLEqRAOR3HiUlLa6fx/m+sf7dLaha7JdTjpI51fTqQ5eHYkr1SK1+YeC3W6X6EWNmGkJjYgTWkJmD92LLGBRDaT1KHYMHhYZMETNt1qt0mEHfuKLIC1g4+dW6rwQiifDPZ2aRsEy+y2uAAM8ri2S4acs69YuJtxL9eJNDFmszhLMfHnXKKshW2SUjGyMpTMYQZe2uiSbjlvWne3tGpaGbF4F4CBPKWR2E7E+3Ra9BNsTLnnPgIZ5pGyYDsmAfSKFkZEcH2SDQB3whQKwqmmhAEB4TLLSOCiYG6kb5VDJLkSQrMr9G0BmAdCJ5KIxsjOfKHLjtr1uWDw6hELYfuAmvkAtS3pjls6w6SSSXs6WmCMtSwdlq34IZMPjvJhrTUBKokcXuESDnymBguU4nxbUM01eCm7wztfGW1K2zTXdFME1yzrje+mppKNTJ7FH7oofIK2uglk5HBNESJXGSwNB4WYCohIyvjj2PbFEC6M4coHiWmdEcMilAll1xX7N067nD44bwrHnZJ1THvgRPkFzELIjAcLBPEhbt+IMGYa2Wod+o1ryKwUxFlemUo9BBzFHmaJ/BAT90KuN3GtlIqWaTMim7DBy11ZUHpS6A3WRhOZ/aGCCThNwxM9eQTrjD8IBcNuceU0HqkZv4ADcmAy41yR4v40jap3tDlC4nPbgIkSw/AMrPDNI90j3TJrAzLS62Tz1Rf1KLzT1NOEPcw4u+aAPwhXglYUoItFiuOIBrgRWl0RH3UPCXlsC/jhuIJD4ZdQZSQuDQK9sO9mRdR7sFvw5ysD3RMnGGLIkp/E92Y0eUiRxJbKTlESh17OskDNAy3XG/3ENd5rAH5mQ0DxuAcZRgxIziQzuBeqVL8OdTPVTDB42otbTWDtVG8NCJEujL9I/ONoJEt84JZ3/HOhEMFpcBG1bK0HIYpjQamgO1EUInHGfNkgrwJBUjv83wJ4QjFDhIjJf8UmEGSKCEVcRYlcg+liQ9IT4UvAAJW8xkx2dqmHoYQwGF2zQqJoqaBmVZ49eVnbVd5RZDoHU4+xn6jAkj1I2MMltBh2QDrtb0jYLNhU0dELe0fWq6odjidVCQ8OrSB2RDWGj7NwbxydihOwUwxlCvezt7dkBhv6FALoFID/Ngh1KmcCb+rjXw1NckxTQNK5hFw5EshhbuIyIxWDjlC+BjOX6q19C4WS5jzUvv0Lv2zg5LIaIu1tACj0jWy7ySz91ZJJBamjvWzM01Wtp/WLc5UoO7MlstMMc6BLEr0XwugE5OTsEcwZFRlFo87H1YXbpAhD4RqEwYoxqEwTkhvw/sOzAs1ZBiIoauEYIwmC3KvtJeRbJNkRdNsidzFTlOBmQMDHL5Go2QyvMZ81LvNIIN6VDuFjgBB77EXuyCdLIxJZVSDMMCQpWOidNSiQEcCtjdWUTVohzWzici8bjXxIgKZ8CR+TW44YE7MsSAQ5ksTHMJm5qwEsRcCwRHQawBl4575OVgDDWWqIxO1lx2pRuEpmhFo2lvWWM4jTZGA5aBgGitXgceQGYsytE/e0Uk/IN1OTxgHGyKWgV5p+JQGjT1gNkEB0bHRZF3WpqNCP6Ki079KJUbi19kbIxOIpoil8gVuwVWAaMJJH+SGcnSJNg95BzxZL8VUrCqhYaBnMFored4Fo0n5D2lANhXd50lEM3RRF8opuZYlJyWsn7wytwhkDQPbBupc1fPXvf4zFfIaKLTrfedWUKNXjQ1DZLnRgwfYDkGPsblP7WS1m8UkyYPIKkWZlrRbFNxvhriyUkIgSajHVYRIcbznaBiAL1KARtxjHiZ91i5uj22xZetjQXbUrZlPiJqto/SwU6axkLgtY6M4heaBvDH/xH6vE7rR0I57QIvYQP2QN5+YN154CdgctwJeMxK3lGuXFm2iu5oRFrCfGFt5fVbokJmqvmaAk7wp54jx92ninIhSsDYy0eVSq8FS13Bj5kpC7+zsra74fA+DMMHnGDlGzmFiaNf0lsq2FCiRow7W0SZBPta8eAZ+KNnM0A64hOhq6Oxfo1lVHFtdMADH1KmIotlpQI9JvsjvCkjMx7yCVZh6ZTE4o5hAGzB6bzOl4FI/YY6kbPdQ87ZF4I1/77cB57PIEY4IC4XoJFSMfcBD3BRBQZ425Y1mQxnik3P7eF2DC/cc05V0b78zAwFksIsVPe6FmixBD00ixXkGHoaCaViK5muW/fMFSmvO2pORohD8zmW/9/dOwlC3L2Qjw8Po5YPlt5VngA7q0L6LAU2giPwGxt3r7Up3IdmcllEaUDcjJyj6mP2rneJoAl1zZsayy9xEMAUTyEpu7bzE3QtpYGwxpJjNJpIvJIimkEHB809ZHlxdJBHEMLBAJIHXSSzOgZlBuP/L1KJlm5G0Jl8AKBtYHCHYwj8HvJFivT6xWut4hyQnIecsJG/N8V/lMwxOIwoHhOUpjPow7QeOqNIsd1FSV2Nyhh2r2HFoiwTQ8881IMfLbARaWk1AoxLC+UMhAYfl3Ud6/L74g8XgSAnipEsiIT4/FMb8WgqnQ1lsKBBdiaHzVQXK2UaY1+NqGZB0fUdPdHU2OxMP7EwPFddG2JUejCpoMFrmEVuxx9HZLRQCuw1gh3mYEQ8PEXxwNg4REJd2OT1ixwJlZ4BBnqFDcW3n6V0XNrp7QPBPAz1MEM0zC7ucfVCiSSJhGdK31JAFUlitrZYOHgv6CEImzWUTBggOHxn5oyDX42NRLzusKyF/6xOex0sbbD2ThvWssiD2jr6KHQ3uiOKqKQ1bcGiYWDv2EFGDtG43FtgFmWMUAyWRVdhQe6jAPuV2U8Ic+TIzAoSRF+dI+3oH4RMjUoeiaKOgYaCmyJTh3xv7jjedRd1LbUiU/kJyc5xhGJDxlvogD7DVhpKOygRtWC2WzGVQLQ8NXlFZbqVHUKCAKN06QJogOsrmeMbcFyZ3F8yVyZdv5M8VCSDS3pjK0YJ8C0Kn90GRAAKg+k0SyCjVqxv3Q212nEklTgbzC3iINBgtpQAVUFIPokFDMWGkhsRKv0hF+M0AzbaBlbC2Y8rCkZVsKRTmg23RAwb4y8E159EzOuT7qAwgtA8SrRHoJEuAMQ8nVG9JHdI44QWfeDLasso5vSMqqSoOkflBg7JBIVtOx3KasLTKB6InWAtNyBTqD0I6nHZAdnonkC8vlr3Cx5jvKq4siOqU5LiD2hoWfueGDW5Y2VWoJRE47nkl2hFu/hiy7QYXsuOYmrZXEorMkV4eICSQ68yuYmaPZ8S7s6hKaqRIF5zJNjrVUHPgOJ2RsTnsOnMMjGpM85aC1Nro3+AgUXjJQSECZfg1DPBlNfUbpdCobPFJJPpwxhdl1DpdJwEAjxCrsZjszNu6Ql0hpDdHGGaUDIlQttRffOM6w5GyGCYLwBPH2I6jmgQyoAescEchIFAlhANY3Bx5ogFjXUm+2T7OIIcA9HK6/MpCaI7S0LckFVUig3CgCKvzP0Uw6S6TpxGLG2suydY+hzXSj2UiE6N173FGDSYa9mYd7Y+c+0MUT9EVxG0aOm/OJLySjzrY1J/2UcBMnnJXplq624eWtBEhDoXQ7a4ID1xAXTZEpxPunWPiYAk5KxEJt9S+gIllrEOTL+LijQJRAZjeE0NKTIKqDfwq15OKNXsmdRKHkSsOrhhT6Ou11VbWnMyHViieoOYdgIzJbPmQ/m1VhakXAOn9vIXSCc8ubmBC2kB9PZ2RoE0ldzDrZ9DBwI2VyN6N1Ep2dZ1/lShRfVQj0AyW0bbkQS8UCvWncH3dM7NCO8sbvENABL9M/0A2RZJ35l/50XNZFtlVkZfC9x22op5/reTq0+Nv0r1RHiCGlDFLYgn8b5IHqG14g9DwKoOemPMYtfSf04HWYR2GAbuDA0DkdOQubM+bH3z1mEdJoNe13fk2TqmRYikQun7mfwIclSCauMDOSw8IeLJBf4RdRjy5TrVa4dDmKxIMjAa4H6n4Jx2gKF5SXPcUXHDiZZdgk47EVuMmL3UyGSWhnG+twiCeaMRmKrDOLO7k7UITXJrwJ4i52XMbSdNLED754cOBSPIStSJJuzHP4aa9pgUHSR6m9vOfgBVFoC4LH3hf6qnSbdHwwcRjwFP/nyzBGcESWthYbtgOVO6yvPjlepB6XjmibZgRrQJgA3w2BhR2IfBCmaaKPXalEieConUpzI0h5IBbtjgRhRHx+7NMl4fpmT6k0sYtkTISKlHTCjyWhK4OEO944yljUxOcbyZ55wPOebnoIvXXH3ayoWaz9hdyVS2cTeXJjpkGlAEwhMXpyWa1QUV0HsqnIXqiv3CjFQMeH5tEGk04U6Y7N3tXcPL7BNjV2ohXUXtiF4pQS2mFddlE0zfj6MqBZnsF4PrU2H32X/gqoOyxSOJXGZ56Rj18vzlT7tQLGjDfyzZHH0xa/MTG80mGnMNcSyiRvOc6zDFPcQX2xcaQ9DH+S3ISfg0OSKUgYhHCVAypL3BS/ItHYqPAKm81GfRNGT1UoUlGVroWjA4vMLLVnYTBs0WvmChv6NynSRXriQ3iXGaevDekdcN56oRT92guv4zSA1VRzX0KIhuN2Kqqxc8h3fmO/SAVuBInth6hgeigFU3GZ1wE+CiH4hNjeYPjToUTwYY9fZDPDtdmmMjJ/4nosl883LslE615qwJlgQFigZNYqR4kq2676nCsU+SIXFrQDYTs503R/Dgr2HgkRAPGnraZfFoKQuyZSwIMCP33Bpj/s8u6FuagT7D2CYe5Z0MQMOdcS+2gL8I9qX5NMiQES0JhuKSD3HGr+s7q/vbx0QXWBxYJWhM5tBfIariiW18MLi/Rd7OJEgUJGD9WKZpAJk8O6hZ8rItD7UssYbkBYtJDKNeoxmPRHSEKIr7h4wu0XkvdxZlEktsUVR4jwmU1OBjBqhBDHq6wlLURdZkOCZ2qgX4y06JOA4ON2z9uL6eZSZs09a2FhFK9zCP12UaHp3WsWmFWWuEZFazlVwJlQHGKGOP+lrG1fw81zdLLQp5+qrrMUuZn8fVUj2tQ3p04uyV94nad4LpgVwYkB0LzdklSr21CSkGIE4tboAeZQgzibSbUqC8WmiMAn706KHwQHeoplZPpaSSn0IBwCRj0ZTv5IxxKWMSwZbSdHYgJgYEYcwmLMr80AhUSUqdvdFEQv5apwSseGSBnmH1IRUK6GZuDa5NCJLdJRrUukCEAfWjLaKqXw3YF5JpGt1wmooS5E/BgaYqizgyztiqPCbpVPtsMBMBUHU1xbB6C9ruqkMLdBKlqOJIJJiogPFf65CZ1yCB1q54aputGcvWO5uMp0yGYRW1ZwheHshSwQqA0UtHeMTxqYqMelxwNNGLZHON4UDd9fX9/QNSerd1R+4KriXmOgIoXTAJUQDQcrTEgp+JssyBdvF9xv46QEySd+DF5IdHJ8f97O7vkhReq6BvdFgZF665AfTiBaOQ1vx0HrJvrIsiZTPHeaRCll2uiyq80rMzNjjwaqufQciiif6wJgNfpJ1cQpxfHbnJMzTgxv/SafQ6F45BhFJ1PdJeJiYDOqOEbBM5BBrS14MBDdCan5lV8qZzihsBqYUi3RkKIAYmsAmFQDn+7ItaAapTnbuhUzIGHtUjOUVuaMDMFBre+ezODmKjaC03CkTVGCW1jm7w9tspJR50FMZa+361pimNQxrouTzApABFDzrnXMCebG/ZBdoLGgWSNncJusEDko4Y6vTTVjFxDLRKRW/9sgQF7t44j9JBPa6U0JL4WSn6PPMxjsRZa6H4nB/FhhsLr+2OP2v3SM4h9c6hFvrxBbg/ClKSZG/7IJPKkLHK+p1t+WBWRlrZV8/Ej0kN3AgI4EacVHEDfwhtrqT5xlw7V8pxMmXu4EYiMVFweteaN7FU++ZkiVHIMQMSPEmu7ZAOkkVk22yF5aZVTIMZWc5cVdnZqherWbSDVpaJmDbJ4WAlALBFhstu75mv1ie2ZnT4qwSv9wOjLbmP85CPQ8lZEjkM8wiVjMoaledtKbn6a6cHXr/2evNo32ABAI2RLeJ9GirRBLXfjGF0QLT4V2TRcglWtqlcQDdzQ2nJcqQv9CkiZCLs+egFUOzJSBeISAT8bM/LnV5dX9F6x75eXF7aDqgzHEFzXCSJTnBN5a2BbIkqqpbN5hNwOckP5egf4ujRGsXWcLqTWe8AFfcRZs2rV+Ecg1o3L8Fr2dJMOsLFAXYONdEdt1wkJNQDZM2NbBPu3DCDgAxu0cDimCfnoDjubEN847hyE22AYREUDDQ21Hd2GZ/s9dFiTQs3NAqggv28tIbTUq2GbaG6bod96VQrh+u9QwUaTzKDeAuI0I4nSvrt+/C8jyMsAGVB3pjGeHlqpIdkMaDxssHc7uKIVU08LMtr1rpJDJaLSlFr6qZpTgXdVRzGE+dUJf5J+MuLZJOMBgR3sQTpPEomMyxJAIjRSBfw6o3J4NsPDSZt1/zzLK4PU6ukXU8PN1cshgCrY2HYJ48An0CLOBj+7W2Wf//gwNtoT05PFgdgWBP9Wk6zbyyIe2SLJUJoAKTMWWw07wVVBRQjLkiV3x3ixFQWCYgTWbDJclrwQlyI107sS2nmFkwlkHvoCWVoJGehVi5DxVgGnaFq59XgX2TAvWBxwl2B4FSf2C372xwXUYmnxc0FXDkYxwbKn7Riiny2CVTzQFbUDjY9aYWu4lcVXvJwxYLJVTGXez+LR/gNN/RPJmcourpmYwTZLwAmqiPhCaTMtBhGU0BkdojHhCxli5LVzAvE8ZEDWsQ4sBlAp0zTx5U1XhxoWMABAIkdYazRAbQtrVhGUSLvTtGIrb0ex9rZtIOLlUkXl7XwlzrCQIBv5/jd+gM884f5HjRGn9YYeNPZ9ku5spRDc/5P+0l091oqLnrJrZbM4WbNjIuGBecdYKVYr4aUphcAsS+mYRQbqvmAaqidN/CYQRkBYFSTZ4LL64gnJAgJQZpXHjyK5mOSGjpWMq2Ux9q6w5QcD5yFN3Z+6DS110crtooH5Vte7nkGo186TgIxS/6WXiV2iUrrMlSUWXaafFaotvNGpJtMuZNBMKyX/zaRA76RT5UAh4EVzKwlfqkECJ0ByXBmSZs38gJhyYG1u2e5ZjIlEejQ2Fbdrq1fXl6SLQ3mIPOiifigGy52E2oVcZBbdyPmIzb5m6gCv+ZqO7TGGUgNSjaZynSQFymYQsYOfppT4hUiL2nnMBOR0IJbS+9wiugeiBKyYGQ+zu62ZcE/apJBSqiYONjyc4jHbTixpgiMBUteJv4WTCLwml1jDW7TkcVYWZEy+5zjP0plDiJYFj/7CFhPhL5JWkHPclVwa+v+9o4sMZWkWgF9ZW1lVJm8TORQbbQ+uuSQ9J2s3CudbZqFt7FaMp+mpl16KgXc8e0rbVCk3DkJxGBn8TEXQgyLaAA6AAoCtOefcL4LoHxaloIfTB/6UHldohAgWqLlm8NAeuFGCjcCZzeORoeaKbyysKbGJIBKQFNT+javIDpFAhwNhkRCCGBImIdTFkZDTr7iESls8xwb6TVqz+9Ovzo4kBBMkRYAdXR3f+vQmKur68uLCwOCAlRCPzkQAHNEe/t7TP/+weHO7u7B/v7x8cn+wT4645RwPkhiTVqDvLCH4bgfMg9itzMuQEUHKChQmDBDAdPEPR6WQwexMn7uzOAbd8PIKrk8epdaUx3ZkuMImpSIbLNl6KlM5M+vR3Aywf1E/NFr5iy2r63JjDNZqMrQybGVxKAliVWDRGyb+UzEZv0RFmdbHgZ+o/5sZafGxw0ixlcYQ1FEdWP3FLD9QVfNjbaD6Qn+9JXR0TKVzgVm4QwIyenLvfQvLVXXO2VmUwxLAwXiRK1AJAMA0/qOcW8+JrFqEmjNfm+GQsed99FyQjrT+9fwxEc1oI8YYx/JsVFVffshJ8l5dlk7TXT1BAcy5K5O7HCyc67LGdXrJqgqTC50HctyS4MwHFKrmJ0cIvDWmvQwaLglnaMY3zbawVMqJuPtdAqH23Fv9s5INzUaGpDaaqNH8s4eJaLZmuLw1LTlXvXotZoYqRmdggJGZXBm5OSFImhr9BxsyFq9zDAorKqh58Is+Wex6PMDRPQSSCOzXinRwUAdozSqjZgbDspu12u+npqjJ/HyZwxT2947bISvdTui0Jqg1XGHUDV+TdmzXgXMbt9jSsZkol0nHPRuM8jePQr6qeXu7pqxlrcA2X5jvQKwmW146ZZncvV3omxCHpBFrlILPFBhga4RBKnHy/rWGagERhncHOFnBMsQshhFG/G9GC6oWHjf44fMBHUrZdccD801IOiogrQbSIQX4sgex0tyRRT/DdMxh9Hf2dvNAWK8Rzm+sTRoYEEHyfaC7cy60wu59CxiokSg6EpGX5U8K/PI+ZTzKSa2f6VsvDUCfnOA9BHhvGnCOzmwozdeGAHseg2Sqck949YOrHAZJQWbw1mkLLFijLAOEMV6Gp1H2+yRQLKEplbiWLKTNXc0LipndcAriMTJBmbo0OC6wsMMBB0qVDcKkk2nk04v90UHJs8Sb4qvJfj0qwRfthKBldTnQsfMfYVSzqV9jUZodEksCzOK0tCrlNkc0MEiFIzEWrBpKiO3IFW4ndvY3UOEfDjIiR+mKVZIWpZ/5fLq6vDAi6Rurk9OCgfuO/dG99pROIcqyD84yEySiZ3tA18ODmIGqRyKUJUxH1oLRtilzFpZsRJxxwdjMyCBJFLXem4yyUlx6CmrUUQT5N1JdlFkmBHxNDm1p0LCIWjI+9K1HATqNua1+jTKaiov2AkzqOVDMFG5YBrCqjWOo27wki7Q0clTutOybnKQxeCLxlUX2/dKFtk2IbC+JQ+IlxjqJs9g5nMyBiqIdsQQSAL5YmeJX0EgSZE53PJO+N7X4Vie8rPGXlS8WN1Qw6Edt8XzrZjcoZnE1RPnSegZj3hZON7etlAoOUkxcmoIMVFYmSsUmzGE2WNB0Eyf9oaQNheQyJ09A53IleBAEBqtkAY8Y9AwHGX1HuUSbFpqfSqpXqK8RMVYdiVxizFgQylXEpWoREl6RsItDojspf4EoMtLgWxwpXAW3b+NvMEwWTTkxRM0jsU4pdO8Y34IDxn4iXI9D2P8Fw81G5EPKoWSymDDGFTZpVpDWIlShhe8Cs3kz44tiN4g0IC5sKazvmkez6cP/UHWRG4hFOWwdpf4SMIUQSWHrrH6ngVyAWKGLr2dJTsNrpBBR8jn+YhMasg+qop9VW/qxh3AF0gLQhGgKIBYInm6u31jep1QeO/uy/r9/QWcvSGCtwaVjuslaTdmmh9EoM+JfRZsaIggOgQlPeh0rOQjAbG8iSLUl66wVpkgK7TPTTol73GnxKEGhZV1gcSZmTbGJirN085uTeTJiTV54DFqk4nXTrdyzLCNQwUK+O6DvkhU5ssqx5l2miAsfR9TySUUff5sCDO2kblVU0Hml9yiJvqMrYShNRIjekqFQ7yEn7wTjo/BoGqrTFU5U+g3ut1qZrVY/m1zVr1rp6OgIhObyvs9WaAVpxElMUtgJLD4ZQKruLpu8K6yVpZ1wzkZAAPKBpYbGeIyCElLXPJ0UIB7TwvOudm3C1OX3Odb+fI8xbZhBwowET/tUFV3YnUp74aiOeyHnB43ye8BL5gDOh3iEBDdDe91gZuFwsBLXqIG8YkQ4JPjK1WHVI0emPZlAFG6/+DwQC86cTwR86NTZbSpHUCgpreYixX0BWAnvlr8Sz4mTmyYjG/Ak8DWS2wrNnT1bSKMkkCAHRNUCYhr3PP4kNOiBTyxG5khxRYrjsIIngoZDgdOiUjfxk6prjvVG7rl/syJ9NYQrPBdO8Mv9bWGQeMWBqqALF/cm7JcKWF+UJVO2SzAz2Srl8arG0ZCEKJGlUwLsQCQbXR9ey1IZissyaMkCJFsNhBxmKgVHek7nTOMt6KrZRb1u+VMzvvHXg+pfif0xSAm1UkSja9lha1sNJSZwT1PPKIzVhuscCuyMcwq42m0uKE6KcU7JUdZWTp0JkjRScv+YXP5BflJY3ZSlqohdfGHoQPFR1BQPGx4h3AzXlkWrC+dvvZo3w9TR9/ynl7wXRZOnyKJuLlwBwPo6YQ3GKdgPuy27W9iBoT1WF34ZVdwcaITgYWwINsYwBymilM0ElrnILWVH5rom3g3Ia8d1bWvX1DBd9oLVY0MLIU4ZpONVzLzoVJGAhFeraSiBJ0rRb0lhMw4eaOXyIOR22LX4clTEi1EIUZMjzZHKFJAkpNQgBy/WwvUmihUCLBeUclaaKw1PsSpmmOQq4O+It/nJ7lw2TVKMPN4BabtDoa+gd3K6sHe5vbLqhSQYaPw36l5sKU2uHm/Yu1y/g5oizr6gPx6cfoB+4tamE+hU7hGJ7NiooDaMRotylhA7yHSz4oGeYO37QRVbKiRf0GHdDBm8Q368jlbHxKZo943i0fKRG8GhzUc/nDM8FlxRgCVSnsm7b12N6/wszBU/KWCAzCXyObRSCjZo4ORFcBsyIZx1DKLQLJQv/0zDH2L+MljBiTvk7KTAbRTB3Mp1JjCBMJUWDOKcoQPa+1QqDit7UD88s6DhYNnCTMdSiL85rSSazKFEyVTGsjrwx0geqJua/p4+snthCYi4rGR5kSV6AKcBrhAGIsYy8euDX1CA5Jjvgh6tgNc9JMRpBQ9rEfXSC0Ja0BKSSrAQQyok3ueRUQ55DbKM085lxZp5B5rQ0XtQy74uiPUYIyKC0Wv8FbXoZKY3Zge9LOr2eSvL3qZ8i8H+7Ya1SDDD6bJ5ACsiVNNKqaeOVtPlWf1NGWl61iTNE3jAAKXD3iDSvkpXjaXkARCtcHF+Ig0ORTwogHs0Jsn7iPbhjAeqEKl+5PBKnrlA4oI+oxxs1RG9woEUR5XP1kbWjJ0rfUEtBUjc6NENhmK60rkXiAPMAakeQVt+sg1qW+er6B7NMpNHhB+5Ngwu5sKlkdqrB/aRdwcg+Rq5/oJUaiMZXJILRTUOHlAc5GVVdOJEfslIz/vbznY2by7NU8bIiBDumXNJhHQh1gaQmAEsj9l3EDP2EyngCHQjdd37CpnrWUvvecZAfMejQ0opEgZlKlBObPim7xRIqZDuIAOYS05s78NZKBCDvZVWAtLbzSjRyX9oqk7GITCox0RKyK6sJKtNOwJfS8MWRfMNoUM2DovooWOmg2jlEkAEndSMJpbaGKU0AJBDaaT9CB+tIMpM4Hm+EpuAceUl7todROVpn3DiNR5UUQWA3xAG4iTW0lib7pJvcrbtF2g+Dnfn3lr0IApZaN6a4gjk7zZBFUo0Qh7KmEkwbeySY5GddCYN7q2HnnDep4WW1OPuJrfN63Iu5A3EX8RXKG9Q6CHgaxAg4B1wxFJdvPSXsXhi/RHcq/j3eX4BFRmDRhBtdadA8mVgtfnjHTMTQE32u3Ugf5lV1woDJEsTAEWVEqqTAAZiz3VGCnlypAz0JZYMxluqjJacATCf5MTUMls+hPj/BTITxYOfQSLzVkuSWD2JpkoMNMMorM6KiC/NlVXy4WfXiMRyZsY6Mdn5B1IyAFfNOxGSECUTEYelnSFH2P2/n9M/YlyXNmSpWmCxAxwcL83IrqyW6RK+v3fqiorSzLiDu4kZhBEf/86vCltJEGD2Tl767hUt+7hNCkGPDenjVCGia/5eFxYNqGe+8OieZbFI+pOaMtoChSycBTDzH5v2gQEdc74/HMwNmo6pNlDoj9aNmN7GwqrwwJE8I+XlgIxR3ARiXQgYOKbmrPmmjfiO3RjZ4T5JvkkxTDZXIoMrD6QrkUGoHm3/nXrLCecWkipOGNQTX8l0bwlOMjK6A/pw4jKrF5JqaBTauBnC3mazGGHbLvWBowarilK5PB28Eozy3tzti7guz2WsZjEvs4cPO/ycHAZtH44XjpD6rCYG7OwECoCclUxQKdD1XDJJ5TnW6iItZKXRVZkIEx/q++xBy26nDL61C0UurCkpews9xkUM5PAEw8wHxZEcq410HahKzOYTMzXw3K9T+nU3L53llexKqRvOTTrz0K0QqlE/BE62HsgTbGIzbLulIU5fLiJTqU2BgfKi5ijQdf0FBEnhzccM7+i7dyhZNy0m7T+xVPaW66gcXf7tQP3IULeQFCiaTP80D/O2tex4ye2Y5HNSFTp6OMVdMBW0inHmxKxrOUcleCAU08eLomRsmad6VzMJvo8aTjIXxpmOQGeA1GPrpmdXrKOROD/XAVQuY3POyaNQRjzDzkrBNMesx2MNpyi1gP6mWcc+a9R2RpLu7Q8WDeANh7dITAeSkF5cWoFPaw98yjjTM44KGIbBMcfdnnbpL0MNwCPHaqnByYAVlx+fbtVKJkelRkiSOVbQZ9ZFPRZXdGiHXasA2FW93Sg2IfTGzyKNjs03u9NTobvrinhanmrD2zAVX9I+V4pgFhZ2D6giNmbj2bAPHNrVaO884fggsmmWi6KZbjdqQ3krOTWgJXTCpWeA9ITZSTp5oqs6kFC+4M/CsvGBsQSEvkb5Fml+uHqzIOjJTHMqgQ/rRUKhUDP0yZTpBWGqYPxkOaBdWSdihssFaoOoMhRSjStcmDHhp49bA4I+tztfF/v+RTXDihySjiwb2McaylDhmoIvbyEW2V4GWagpOzSPhYj8izRICYxU/OqgFJDMJpYteFKjHT7KHdxQm+6zFgqb2Ze7K3AkwdkPRlzlW3B5Fx2y9p80g3mc1zheFvUgyc27SOD7SDS1854KYmBvzLcZq4BkA7sC2QkDHof+6YpFCPTpUjMobv4p5ZlSwXh5ICYNOoPQdbxMmgx8RBExkcMfim3LfvNgEJlUI3zoMoHNOTz3s9OFrGQ1HhHMsuce2i1RI57UDaz1tD5iUPEtGAZdepvTziJz8xpxMnG1eZySn3OUPIfY7lEuZJfT4MrkY8+gDW//aCgw5QIwTXEmS/0rJIKfwwlITzbjdXKTu0E1SuqmBdijcTD4d2Y8sZLvlQy3r298hws+m/SEFhWQHSLLxmIRsVxYteRltkh1nyOHFICLlkr3mspyeuMNAnTr8VWreeduZs2M1RmvhkFt9ME+ZodQAF23AiJn94eZ7hHPSHbZsilqGUcv5pjChRPpxs/tGacFzTd7nEeTvETFJvtjDTGmy73mCCa18jZzWURGDv2QL2AG9cy0sjsUBIDEhnngBzdR6y2GEBVSmrgE1LUW+ScMUu+W0uYxd04SxYDl9SIbhhg6ZYe+AHGsSZZE8J6rmODOUPhjoKgNBmAUYIioM59uOxBKiqoaDgBaGISK18+PNYX+hWuYvnEs26eVG5Q6VeyPqJRIitKyHlpA+OhD+0udvbYyKaLOKPFdWLL2wv35OTs1+WVJBdSUvPxR0BxYdVL6SKlpcQjJ9B6dqvIKV0uFbCeJ0BpLkzNaJU5S2yYfy6IPWe9hWASsEZI5tmFZOGpyd4TD4VVE8uUWE7pTaCmwin/sJCkFAeD/JfOe6NsHx5UkpblquuVvjAdq+x9bBHz4z38BwzstuUiWe/0wXZDTbZCac1jbI2SvMAXKtBsv9U2GPWQt7S+OpnnPd4/Pt8/mjyxKBXbDfAFtoK6xCJ3zUEyGJbIspgucQDmEuTcIFDILQrSnpNEnuMlFXjj/nDmYqcp+N/Uk7WeTOH9xIQfMqoaVADvBITYDELscMxA3J63SMdqoqQqgKqkE6JCWHSE7zj1IBCM+7INOr1cxmrEHZ7l9lSUb6MuAWEB8V5Z4egPlHzkiiRo4U8Q1CUo21pzZMp7S12NL40AUAM70tPHRqAk4mvtem/nV0Pf2TgADoaChfyX2KjZf4kGu0HML/QXMNxEpNzFI0ZwHgBNrDzanyLnUH4zqkNHTW0HmcwMoYjHg06sO9MRH3SLT3xuAa+mDuaiBIcbgfowQvODiNIj4zOlRiYoJIJiSYlRdkYePoSURf5fuPlrms4VqMLQrJnciDnnLLVQTdNhfg8UIEPrFSJop/YXbbQ9AUVfGXGOmmwXI/3m65ReZYa4soPI2KosytCVYlSWu0EMHGngW5lLG0h3ZYU+rJQtZf8Ui1K/6I+9IyddY2gnTWk83t1Afh2lif6cERRsO0OTysUtzjd3QT+ykVicYPQVeWWJWuAy7O7UsahtwTPjaLBrGZvIGLYwD1BG8n7Ease+X1re3ohZJlCBR77pF8iCCU7CVPzKftivj0pN+vxJX5ZrGZSl1xTXD+aUWD0znL/92s/x0wj36eHZukwnbElZXMqxO5Uk5EjSZIZ/EiMnLup3wjPkID9/Ajvi6tFysk6rdiTXLm8gMuNJlbFcyepEkFGXpwcxyK61J+VSK83IIMifZzUlXnmXCwfTraVsRQ1lVfsqY8YmqYR7JEFjlQPUcIibsiTQR3GmBMAlVkLB2Taisx8aSMEU/mZVLcvjDVgLMSpOiHm2jzVdFaJRhWkLj7OjktuPJkdsFum4i+cHZ2g6Jb8jaS12B10ilBqMeZYqMgyNnAbcBM6+TLsxer3oOGtg2KAKpdaDmluqqNTc/S/75g23N1U8m/NrMyazjIlmlQNTXFw4OeD8Q0/9fH6QvYsB7m/dsLGD+mdOPShtMEJy8WIgCtucGECJYO+XZbadrLwCv5ZHCjzGAVZ4qp7qykGiSk7izNWrDUYEpprXeXaFH1F+Ca6PSTjnCsGcdPJrWaScL9EHg7rq1LZZip6Q1ypHv+OuKMkmBGwybpDGUF3v/1PnHkjwh3vaNiIcvOHEvWgI8pooNRwmapchOltsLrB1OzOPkmnXaBHbNMCU6RvF9RMSEb4AQTjMnFqIKlM26DEHhvtA6V8H/qAUP6yoAy4tmuOAXNfiOgd5hGhNquck6CAbDXbkZMLPcL3hS6JYUaKSRkGMcnzHkhAtKYM2S7mU1w2+Xq2IcS9LyXGM19glIdsPX0pY8RSksgT4oxHOrz0OFHyZX8ITC56HAJXMGQ6t07zoWDCzLJjceAHLoyf9ojJHOpQ5UPnVcmtbe3ivMjHJ6cb7ib731LX0N4Ah6zpPvYNs7LaUGNu5d0hVuA5BvFAofPin62jgbRLGwabbgDvBhWthbos4K/I0VpWnxBW4CfhrRcd1OkYZGclpdd7fKp09XTJMcbEm3dtdfj0YPfTnJlQgnwZHdYUgfNTaoJsrgh5sYOJoB9kLpTb0y+rQ/UvsSZqNIjgejZr5W91NLRwFZkVbCQ57dlxvUpsxlMLZGGGVrWHNrIIHVb/OVSpJqiv0HAWlqsYxjN3756cHG1LyHEcE2H5qqeGTZRLz/QYGD7y3jMmB5FmjeE4KZNYpVSyXjyCpBT9k3S/B6XikzYoS5IUTdOCK5IjER0FcUmjW2ufV7u0nCubAGvG6pgDs5UHwYFyZRDyjIFHh7KWt6Ya5riSiWiW8X1XHEwv4F9HaIHIDZVMKAeV1WmsQ/C/l6Z4dlqyF4J2J4hk2fm3QUFqSxr1YlGF0ObMKpJnHKU++aTl5RlhuFApRPCBhTcyoYRURbY5qq3OahDADIWbf/3ggKBu7GhkH0HKyvENANnrUKcvdGiusKV69mmu3ktcBQzDF8Q/xC5xd1PD7V7fsTWw0g9UZpKC/qQXREeXU76JwydxT+BEkIbSzfcBRVIu/DEad2TCEPjtfiKkBFpHBYJCMJA8lPrrIRrJwkmoKIitofTCcycRbED9PVIcm05tLdQ+P/jm7+vl+9/BcfUgFjLiKWK5cfBqakxm/pq+WEqjh5I5hQbbLDGf8DW19RsIzoONxIHjbJ8m8Jb+s1i1s+fL6wqEiJQT4LzNGF/HIpgfRy2gxjxukNxDfK3nkMDGRn6Z99sFA6lnL9KogWS20oguZDq5aeJzFNpfTUV02r3EBrXz8/EmAcq/v4LmLN5/fsj0t68xiFB0xdQNTv5KIwWy16eNr4giLdumsnAuXlugNUUzW1moCcX15P1k1PMEPg+wcHjfyfD+TJacV3CIPmiRE49rYl1vlvyvm/GKyD+GpGwCTnRa5Vxidtbn1kIJ129ToPQp3EDydApPwwY27Mk+JVXiGiP/1nWaf2YE/GVg5fEbRgQ1Zo3v9I5woLCimJV/odwUTPf5Sc3ryjwuFCxyDccMFM1+u92KW4IhCMc9DkBDzmzwkMUy6hQTsgtEF0dEijUYpwG5AEHVeRb4gTCt6WzLSsL31EESckUw0OX9d/bIe188aG+Q6yLSlLlRCGqa4CmZKRhkNuXrvnmZVUaPsEOKoGGgu2ZAD6vSzTpDn93wSUE3hGlD2sZfHquSclltSs5/GMJRekPS5zfMm605OHpzfbt2IiIgbHLMK7FWpgABVpXTKtXzmQfebkQFQMqAwtBEJF9+OFWvj+KvvSDThZHYQlk3KqX/aieGrNlK1UYu5oy1tE2C6nXmkAlkFpIBD053pZ1mSDAlHjBjLGZL3qYYeQhmS8yHjblDpQcHXKg1FxISgPLkAKvAK37yiE5vka+JRy/5kaNm3i3Xc3W0/lkg2r8CExKzS/PUr2Nns5qVXiEoOrScH1gq7DdtldupkhUH3inUIG9a32KiFQj5lb+4mNR0RXGvZGoiDXxJwPWKGCNvugME9+sKD9ara9cqoKNuF2cqqFsxGwtrnRFiiUx1jAmkrPhm2JbySermoBgppEju8M2QnHxAzqpvrasxgwRTL8MwKdQEWKgpHbTkBjmCt4XWPYq4+Sw4pnxMfzvTx5eSp+dxe5cYWJM0nXZQFmkYQWUqzVABvkN+4S6B4bJ+8tI8e2TudFiNplwMIHijDtt+pW+bEVAywbH4uk0MZBJAGdA1/7recslIS165i5kOegULFAKTJQuR48Skr7emnBlydbG7w8eG8oV7eFAJj+1cdFfd65/yceJRk76RdZ9ljS1F1ZHhEtPAf2qhCeI8ct4zt8MVuJIFMCzjRIRCjFkMCNKDQwmtvhorMxx6bFrZ0pdRUSDycm8nKffCQtxu74cFoI3drTWeGTcfVhRlzx2tg0wWyMWZhegzB2NNG0wWe98TeA8E8JyAO2NJmnq+b/H5wqwnc5J6FRyMEYcTajUgpfUgz6DnUQ1S5JIxtw14DJS5lHoYycIkq3xHQHMGipvw48bK88aZ3+tPuTmJqJB2jz4oPCkd16A760B2/YYQRvxe7qaWWPGQix0s2jGPWnxqO4Zv+VtJxwUpRM7UGf8Fo7UG0UoMh4AhO+UgMoxLOL/6IEhm0EreJxRKUoxE9eLkDGCjwElt/EmuJjDc8Oc2bgSwl91s/MosZGvoVgkpsd4uODU6CNg4PuzZBDV11Cvv0qzvWvR4bCfbiN1zZi1WSJndQont7vgpr063REEdaElSZ3li3ikpPjlVS8PqgGGSFGUOBd9Y8VizCeyoWTnoOF01UZ2NxYKun85IzX7S6J8ObU4Q7FuOi8enOWS9s710QJkaz8lGWoXC/vIPmFs2CP3cxqW0aDovzXzrlniTcso3dWECMT90Fc8xnpeaW/BBNg/F2Y3n2rpKEu9Aq3IFmRszfqwriv30GPx9N5bYcsKyeMimUBJAq8DVmYWTVhkFqkIA8jle4/vFy4xwARdsKc/kQgdMorS7bWvkVzO2BS0w8UC2Z7oF0l84PzW861527hsP0f+PZBsUMQNeA6oONEU9ixUfblXP/oJkWC+3yA17QRpBATDWNLmzdI0CWJFCjkSvsJhbb5DlxiJV6rEZn5Kl1QyPLim0XF3ct0r+A0iWtrCt/kLZ2VqSqPICUfg0M+7QUhINyBN4NvNVlEefKEEzfnrRayNSsnSy2VtumK2yAppYhZh6VfYTxpOYhbGguJEqcyJeQ28w24MijFZP6LXCzZ02XtOJXyI4oNKavajIoApHsyoe0wAkNj6AAUeOfHOawPVjJ+R+Dx4YU5spS6EpUcl/LyrQPbQZ0pReE5EbdNYxkGGk+PhmDUzYzSG2lwVKEYX2d549dLoeAZ6Qkxy2pz8c9JUtiVFYU0NLFLLMlG27hEeur2Olrhs0olAnwycxUyKXQuG3Rp+t4O2G4X4dHgbpK3pANcBCOZoz1jOR9zFxK1d5+GMCDGLUlFNpjxp9RTHCKjC6IR+RPkMI+VntFmavqSKdigM91nmUOZLhcaDv1TN7Ns/uVCLQPa8gLw1xQI/Aj01L/ylFaHUEc02VezaxyVFzYxm6joPrs5RWTT1qs1CUZS3jH4omSA4CfKGbugx6JGuYNZeMrZ9apuJ7vEb70F7CCGu1zCUkaz57h0fFaSXGsagoqsFVPpDx2gFcIoyft4Q5J1Yh8sRJqcZ7oAgj3ropekJ80NQcf1I4leeiQOndpW0kN+qnZ4J22SZNYdABxwiOGGawQBcDyNsp8O5lHq5EydUD2XMTLBxGRxvzAfyVEQbZwRUXJwvcsqOyoiazn1t+Ji8qJxvjlzc9VcUlzTgVWzAhwSn8FPV1yqHJhTm/i96capcHZBYXCQqPaILGI0A0Cm83VBpG0jFMfPrzfozl0tLfl55u1DEfEKvGgjCWSGw5Pyz0ruJOQid7tpBS2trAvS0lDvYSYuSjWmKjrfIJVrXsyMduoiGxLrer/ZqQ6LIg1NhSYl6ZLkie540q9Ex8U1HQiJZFWIRWVBQB32SXYmffz/4aldoRdnt58uiZoV7hL2LC4juKYtL5YCO+7ubhiq5KxfIbTJeoSF+k5zVobrkt0Sf1unm/e37+o0DQR4YBic6Yc9vEBQw6AwSPTIvPlwe6ok8wPA/TVwnPsS+P7TIJexBLySud1FRYkJrLDmnc5ddeyoz7wp/+X/peuNseGyNkr7fheJKj4Bueoxjd5T1WtvpzH7cHgxJ6h81XA2YJuFaOLq/Imx9Mt5hBcnbq1qC84FP4Jwi6Xj1xXXUnWzY5a3kLoJgZilDL8VipZAKSYnz9s1VTGOSK0Ty7tb95UAdVjZXsMIR4cz/yDqjkwH8nLpgIZD9HxEgZwjGtdPBbxmgPyHhbBsDWYh8KuiA8uiYsQcsjD7qKafy1Im55piURpge+NrtGPCRMYNt6ypjkCm+RqDKSfw64d+3pRxkCThj0UGVpwXOyjoBJQ2QExNLRBh8/LTuay02rprEJGdDZq5oA92dKVuteA9EkA4cLkJ8cVGLSvdX7rgAT96cbFcKm8Zquz03yupZYfmWyaQZFEmsDyptcBlRItul3m9owsL43kzKNxGYvK64qPC25oUyHlmTlX0i5OaJMQwSC/TdGRY2xcwPSeLIN1srlqpskxT6BkASCgr4eyk+o2qxl5O4a0DUMlPo14ePvHJrhaBy26UE6hFYkFmFFOzWgZimbtRDJH9r0Xftd8MMM3ya0yTeIhiP//PyCzpDsI4EJJYo3nKpJf27ZBbTfqpxRGH6iWGtNGtO5qzWaYUlH3+lNr8C8z65JVWn2T/AIC48NMiaIQRw+KG/iT1DaOoMM6kX/aqy+XV8Y1tWUqR/xTpto6C1hZ2UqLBVybuCC9LgnPr619NpQXLQMzOSwHu8IgMyNYJaxqNVhGGSJRR7SiJ2LZmvuOiZYdOc6rHNwWmLFvA4/qIscm/vQea+5O8A01xlMa1VYC2blGCJrE64VwXON/ZkMUvRc1G9++2/htBOmW5Rkd6SGfUmgkKgpJLx4c3UEIKt/lB8STQTc+luAbLifaQ/gsM0dQ4L/ybOSSPY3O0MokCF+gzU8qQOWD6vL047gxxqQp8hfqhTPqIwudvJ40Vc4davaI0CYDLXV6MVV+efkzUlm+AcXOrXOwx71DShyrIHczEYM7mubfP36Yih9+UgmuMdjWLaKNE9KEhjKLdiA5uiGbCRnKC5otlB0assZiMV5Zn8JgzqZ6g1ESKofVTIBt4CT0/3jq4TtyctZhwbW/crps3UkMNmN437w1nhrL2vN7emmtVCcFUmC1MPwSEiWZoq+CaXgiMTFA8Wt7s815lg23jZkvcqPqV1TqlI6nxwdi0VdVUnldYSXFuYbZAATPh4ZjxivSDN6tz0JOmIbpRmUuqwWhscm/7swl7X1o3scSgIq9bFWb/K5HQ4cnrPCAYPKpEeICRNp0RInb8wL0b8g420O8MNyAB6mga1FCd0eoavTfbAPw2ktzKKWNj9sBkrVyw9apK05KC56Ycr67Qmg219Wlojg3/mr9D+VoA4PGA0SKJm5AaOxUFkO4lnGxZS3nMGpCwoZtnFvcwYEkQWSnG7CffSxLNAUIl/xaj1oMYZ34UkeYj2l7oNtg1ZQyYW1bXYXFPLKxx8yqWH2EwTAgPKUQF4N/MxnzFu0gyueZce7fergDBlwkudc183QHWuodb20sAhkLyEJ0COoqofunHbwMPxBS2H3yUOxWYghdLvCX4bNpFqA7gRPwqbNoHs+oKJ7lCEapmgs0gzOVZSJXRMgN2gujd0tX/fSJv66kgjXy645Ek0knh0PrGX32sghapu+LqK3IS6IIBFE7F09JNWJSdwM1d3WjznJbcdToJhqyuo15teyi6Iy7JJO6Sl50UuQ3xxN0SxLkZQ1NaP7558uToTXLbh638+BqBVHijbhrAjKPaoBlPiAv0gVizKF5qXs0P1e9uNkOVq1S5AejWtmk4WZBSB738nK/KbtDw5phOe4ybOJ7+PLTjjJMkR7lQqeSl4a2yNLIuOGYBwZx2+rd3KQSTGIZWSm+F9VlnG4siNrF2OHELe0vbZ9GmRNpkx6HUtamNR2Rkw/dtdv9lp17ke/xiaUrPqgrbHdQ+wJUFao0z/FN3mpBAgTut4+sg2sKqSUJNd3D7k8+3JzekD6lU40X729CBWHsqFjsAT4OOxICHq5uLj3kkhIxRct0QfgesE0+Hy6a+wE+orupejml9uUYLmyZq2CjZp1OTPzHE1fwtTVmRAFY53Y27hnEBBcMHEDJdgKHMZ5hgFQZ3sSIZfFKACsaIX3BrJXpELoQRDRnsjNCcPlmMnIcrdU3yuXwTSc7wMDDyp+ZufrQIW3oqPcZON1nw6uAfPxh0CNQZOknnkjQsX55nft+vMBCB5NInjrl7UEMwGbyycfSCnPBvHRRux/PPoEmk92MRY8ZcWZCub9e2nGfbyGmb4iKkPP/OCBOPuUXX/ibNSMxs9BNhhDk+Vw6IAmfITplNVRkPATG9eA4emAK9flT1g3/toAQHVW2O2csV+V9GNb7Sqas0+gKVndUh5vzc6BqDI04ybeXVtyWGSEOZrfi7YAw6zUjEQf+edekGdmdwUq26/a+qz3VFcdrVZRqVo1Xqy4h3fYAlGn5sDk/G3rzww2lG1NLG1QS60GPvvhV6smL4HB0Ubf5wwYf/qwjq7OZSO6MAIZB2Yd0CIddyh99gqa4VbjgpYMGhNdorwJ4nG8ok0vlrbQcR1Ovj4p5YnZScVMoT+g7HKnMsWEdg1AW3KnQnadGPQ20tcPiasklLB+hw1QKyTvFiaSfLhvEG0XhsGsR4z+/aPxgDbP+DPHLhTFCdLUJoJN5FZrMYQlgUIjU7hB5xuI6zFB9crgEy9FQBW4LOStc1lSeGamjuXCLdJRSr+7KDKq8BWyNHoJ1VtmTb2U/XRO3xrzymuJMct8kJ61kMmb64D7j8HiTqC6J4xuY0iPKU1cbMkN/jCMfMV6+JUh9cxt36N0dlpPCjanbGpYr45tdYMzamCFBVeAJ3eyisnDTvcCFgHR79FI6H29oM8A+QD/FpP0sqgosGggJMT4kIpaRcDAr9DGE2RhRkITPxQJduLhRT7IvCyPw/tZROj/sC3UZ1RZAU8mhITQ/PNouZzLritjFER7QkSGdKNYRjbc3N9nKYwghBogEm4mxrsyhW/ccFnYkhCYhghZ6sbazin4cAduOLkeYBFE05Q8+1JZ+zzzVJHDhoRtst37szHpKxsl1GUVCUPdvXKX5YJFgiK98Cfv8bo/lIc+Mjh06xyJqrDvENF/ppFUgBqW5L+m6MfzBeTcQqSoCg2UlSIVwErJmSGnMiAQHP52v1bJVUwK0UF7mifSdJKsJLm+GQS5VS81T6hJII1Uk0WhrJadip7IJZb4vFXjBmsUgE9IMJi3TVWWxx9PXTkpgSuqUzIzxwJyh6mHcPTrGkiykZpzBxGAjW+qPG5FiyJJzVcJFcckl+WRC+TSIz/rggUwTMGROyYNPlaF3lThKVkllOTebIpwmZZqS1KaueccMPvjP1B2Gt4Gsn/qdUzfro7scIv/KNdiSrWsZcuTkpg4WlDFQZiMan9VKO0CMB6tU1helOgSQHBcFEKcNdKwjzQjIKlmI8MoxZEEP9x2TDf15cZXHjQNubhxtdi7GupgM3UkV2OfXRbjW6lTV1UruUVpXCCWewJ+ossn6PASe+SAsoIG5LdZsWgIXRsGtRGr9oqTvkJef5EuXGoDXBHeAuP4SRNn3nonWo+sU8C1TAwuTRlgwJ1dvaEAspppjcHx8KSXStOuWyEJYqZI0nCv4QmWWqhCgXFvBQToz1oKSSpSS3cWtKN9DETTIGYVGWIEGzWJ/H5JScLywWi4grScLt2X2vLE6YycoEIWOyAnpbvfKrwQjZhNJ+X1GFc3EWJvarwgTOfQwhWsFq/R76omqJuQLRb34rlfw6HeMNkBsGEQyfv/YE2N6hiue2+67jIw+yh0MsStBMA0+EeRtEWpWfOpBJZCzZfvqE/APD2UNnvXXUzvOru03OP8I8Fda7F6f4wPAYCdAwoMO7ADAESrClxwdKgEkZu0eqQ9rcR3VLL4w4AxsbqUxDWUe4TSvJK1swLpB9ZCKp15ZqZZIS/m4R0TcEmOqeXVCeMudeZgr3X1ze/ViBtDxLD1cSe1F5aTmE98EmP9vZosIXcBy5Ulz+eIbsCdwcFcqtyNlACKSlLYUJ5r/Orfb3JJRUmuZmZFsKayt/KfmtDoa2iFJJQE7/F3Kavu6QYA0/xjTsxwHwHjiDQMEBRCstbkWrRPsLNTmO2YsukvgVXlVZl7fZcYOXYDqQh0Fs6KSpN5ICCyI0oUhFIwz/iyraIJk9jUH9YstNTgt7eqP37PURpbkfGGgB54K2dRKfZsBMEXiOujT5GQY5DQiScCZ7Uws0dT2mQ1t7NXspXOAtnGkIBPpgAtaVbVtUoVOgxeT7yyGUJgBJkhEEtSCtE5U7u8HiauuMnsz1IS7BCQQYFazf6HTA10FSaUlL02yENZDoFR7eBwcYJ1gQNQ+Vv1ii8VW9/bQAqu4BPDN6yRDO59R6pDELdrWC+MEZ8EsOGyuYwNTBmlW7+aWmR+1JUhguI3gZObFYOxGqYvMjCX0CVKWGWsPcWQfgjaFToOthBRQ3IlM9FB26T8DI2siiGONiYr/mrht4OA+c+I+Ah/iO1DuIkJrhkuLXip5EMFIDpJJTL59+0MMJQhHF9082+bfSZjdXpVj2ab5gyr43LkiDzvgRDwknJ7UazQXDqrcePwkH+NPJp6VF5ysOTnmJAqPGqQvZPhqdlkT3viQu/oWL9j0rRhAWN64q5TKf5Og61Ow/d+Fa5LceKpAyHIpMHqAv+vrgqyz4/Kvav9SGOUOYpagkBEzmUqKqfy+wJvcDyj1lV8bNmuwvVIQqsTTejFg6N7qGHgW4UeDqzXMORHmGZs1GMdp3ScyEi6JR+LGPuFoXBcFu87wLnn3QicKu7ut1byr9QDAX0cZXiFVLG87q4hVTMud++tthhH9+aTvaku3PwzAG/oQPV0Y7EMkDREctVigqX9JPh9h/hTdV3bUSjAfmzHSIXr1zg2mUCjLZPVT4SjURQ/AQXHzQ3KGxry+lclqzvt8T2bpqo8n4aapl/efd+XF+U9j5BZyN6bxFyMlNudC/iL/YiLzGFukRWGsT3rdpDUrcQfv8jFa2tgU2xoubPSuCL0Nym/AqyDDyTsI3RC5QLXRfSsRKZaG2g4qCDEYL6K204qqSuHkSQKdAVpIuj0yLIE6cNd6nnNFCjKXvQP00F0JZVkFgVTEME+O0ICm2XPcIoyT8lHJWSv9Ra6nx/u772CJKeW1P0z/Ght1lpkb0dS4HiopLjwRjmtIrAhqqjpkJH1CYsYZRlLL6am4XJDdZafcAew8PD4AOVcMkHkLsy+1IdmiduUU4uj0SRyBJ+re4X5PCEB0FS7ZSrprOQllIzhJB3tmAJC0hNEMROHBLuIHzZkeETwzmmoaemHfeOCPJemIMBZodY/y9fmH1yuhQte0aslYU5A9V6THK32wkqebcPT08+K2nRw5vBNHbaW7Mekud442ARVL/CUxzBgYSb33S/4xsyHY5fJz+QFyiss5FWRzlswyG2JUWV4v72hc+NIIDbIcwvMITJ8TqM4ttWYY/6vyQxV0VIFcl92SCRnMzXYqdQSVeU/KmklU28D6FBq5bAwNjWphkCwc/1a1+Ij0aZQEXAowNP1GtumsdZYklgDTaqmBnIP5V8zhl84J/XDiYMw/v3/reAkGfX7x+HTrFqpKIZ0p/8RCCjQspZw5l4hphBVgNOhlEr1UN+ZbvNH00FQSMwg+vNZdOZg/GUmJrozbh/JIkQ2Y+ergnv/HY8wXhHSgHdLUuC505r3X8LGqrmv0Tl6NFf1xK/dI2MVqURXIkzBPVvtPFLrdQNgFjAM3WvZZDE3/pVXGBOPWc3DjbFNDRyAx0tQ7MRI2ihiHgO8T3wbYe0G3qC27LSJNGonC5y5DCQm6qyu4TZwOg3wSJTNVX+mV4c7R0KOHwgf0mXIZBGTiXLwVIS53DRkm8O4RLF8LH/1SuoAdYnYD0bM2F2cUjWe7CEkiLenYYyIKppdZa26/vFQThm7XHvRafvYGpARCgbVDzPeVZ+2IDbjXrMZ0mHRml4kmAcEJhnF27SlRLTK41KnEJpFvssTlhn1d1r6qEj0tG2PhLZwqyPjMWx8knTStWWnncbrbaVNLCdRg6Ih6TKIsOBVkzRRKI+osnafyzP00o0XNZBX9I9lETGh4XIKeKCw4oAqgbMQ6uTVzS6eiCFqT89lHE86nz518R674gjtpj9QJTkAAXtbz5UHlR7z5w4XA2aScX0rleVlrT88NwTy2AvzcfLq1SKJ54xKLckO6KEdoX4F7yx+VYOQ0CcFSFnlhUi9uYvXwNES6MTij5lKi8yO7gtFIyw5fntjPpZMP47sUG426SyclMAn6xbL+Gc8KkuKueSrrgK06ZS2lmImOyHjdytZkSqrnHajcOhElbYuiLqt/CEPk4Xa7NBqmCAZin84oFTO6ZT0hjxClztCm6wp0xczXV89dl0PyIWYRCHDJ1xZHSV9ARIrj7x2gL8BAwGRVhtfKxvRSUpyCw9dmHdpylQPzhORicNXXmVwJi4929F5hZJkq16PlDCNv16blc+JnGTnk5EcyJMO3zSZDGcHsVOpPQawO53oZSObdbKDxJeMMHbT/87HVdxXGt41P38yPL6Kt21mHXsQSll4mxbZCjDIU4nABWoJd/H2wk5zqehBEVpYHLUfTnQA5axDLHNduI3jI1ZHHlhZcnN/f3YtYaTvLFqvoPzTMbfo5JjJfqRDrzxvJnYZDKzIbVrqJIaSijaRC8L7E/mhsaiGi/IJVfttDRM2uEm1rPgx1j4JVaHvZxsZS44iY22gk2XETOmTVfmP1alVqMEuidV0W7Gy75i/Jo92vOEFdHpIsKK8ZRnAAWGUUIz0CtXwwDd3igmwM+qJaXK7CU0BosaYKtSOgcpYsqKoo8Nikrs6qJNYTeqQ8vUPrhjIk7K1P4qiF551gevjN8WFCnpQn9zAZ54glMVTE54pFyM64aJWxut6b1qIpaLfsMqc9NvgEt43uVR80zJnMgls47nouAmUtBKBI7rpirVQRDCmGNKmrURG8AcagRE2jZYsOHzY8VPUqle7sB0QQiGUXYoCjXdAHzLgfp3Mv2+GVJhd1SNEIjBUFXz5Pwq0Fajc8ygEHbsveQixlT3I9NYRVG8SCfU0SS3bgMoSRKyk2UHD2mQGEjVpOnRb2NKkQuSW6/ElraCAiusYaLXOlcBlIlBmXQEDAt7tXYIEYF5B+xlqi69YKj+7byMawgD1bwONM7J+WAHGjsIodtRxzG7Df3h6en8QeqJ8hgZVO7mBjePGyg8+5PHIR40I8rWSwMQRb0qULzI5gj7Vwx48enfPy/O3bn9yhGqZHFNvYXD5KTYRGHcWWZrSaJ+w4gIX+msqOV9us1/5m1PnRDJ0RJfEttHNhLm00KlSXB0YqzbCOwxGK3j9NXeQ42CSR7C1azxvDNdXMBIsEDICuXM1ijfJcLQCo8FouYGyMB2uNnEx6NIMN5mipag++tQTcnHDDDcKW13ujeOSDPCu7t1Ii/TFeFJRunH4KsTzOiTMb56ul4Sw/Ywo5rgHrls9nwQZ8SRunBZdFqWKJqSDq72QLUaQBrhS/REgbW7rDa7CGZeLSISGSk8KB1jRUfw27eq9H8nCfbuaqPdpb4s9HchO5QiOtaYH+BOx4SRW1IZawT/00tx5Mo5Szc8SJNp4IljEOVMmjh7LhteQLN+viyPfrYYODIOPyuq3gMAvV4cKxOjDdpt0NakUC6dX52WP2hHDMmvOrBnrC/r785S9//bd/+3dPxQUo5iuSdw/3KKdgHqxjprIwE96EHQPQgpWm/Kq3ciU1BnBZ8lIG7Soyina9tqgj3nFJDezcVzgiSN/xUwIq79tep1/MNoDpFbeunBDTKuG1vbzhlSs4GkG6YKmidQUG3fRRn+6DNMct7hJINIRkNjOdBIxg5HCb8GCvuAN0Kb8Up65ZecSTMUfli1Vy7QZCGWoqxbLODT7cRAvEuHXoQhNLHSDC9BahVvIbA7ie28gox3Lmyo+XSNZUSBSo+IsLpBEtFtKp0kr2s6C6tGI25QPy1GFD6l4oPnHW29slm7+8ab0HFcSZdRZsLFSoI+wh2tAETjCerMNM4TbfVrqTKDiK2Rkm6l2yNvK0tdSoV4buSVrtKUOfCSMAnf/QtTwsvesgMt1ivadK//Pl0/28CMlNaJ5ZztHEIMgjTEj6fNo5SKIDnMzZkjrOQ5+UkSfoHLkfXnRuENRuKlVSxlllxuNyld+lyx7614CFhhPn4cBk3yIFCCCpIngSMmjq0wNMkidSAw17dlDBFG8/3354SJSWUIkKgFswUH5mzUCUuGdinRwpyCj1QHUqc6W/bnPmiv7bj5aj80kagW0n9n69P53wtXp0j4O1r5nL2R9/fKsc+CKoCOoZlttTCHkB3OXhTmUSrJaJlCCTUqoXUVYsauU/A8/rlVSgfN3mcj12qiM9AkuFkxJddSCixS4qusBII09jHi2U9Gw+0bCzOMIvsVhlp444Nf+SNizqkEAphGVgyD1rZk+Czhud5tVeKBk4xrHwSMzaNeRhXcWJHMwIjb0zWNrOv+fdZESyvhJQDZaO5y+C187VsrK0cbsvNyoiELcpVvmBZgpEcGkPppAl73RxEJ3NEIqZKEafbC0tpasKMoyhoEYsJEBoLEIi43NLb9VF3NY08+AL/ZrJd9051bsF3M++9N9gWoaklBfSFU4CwK7XRxrUAIP012u4hPXSNdHXzrVWWtO9S7bzpGQr5K5h7CbNlBcWByIc64MTSPpQhAnQCzpuRrGHODQOSTS/fmpI9wn7RMHRwzqLQoh4eKiE7d3Xr7//21//KgYo0c4TedUWPIyH+j1y7WCiE+iEIx8FvSw7BudOC4ze++R4RXv2hUAfxCEcISZk83aUSGWsGNEg03JFGFDPO1833wgfk0C3J8WjWVzNvhNfyVduTuN+NsHbofBV4ZZEyL8aDJAjo2FoihngCij/0E2qCAGIlx1gZlHKZ/pdT0il40LLxmJH71hADJG4U6SU44PNhYZYcC/rSV4Ci4Zd5D9/2ShhmsjYNRrunsWXHIORtnMHCS1hzKsnNCioiZqqFFb7XmwqilnPzmqc96oOheg48B2TTxUDEGun+7BNgTIyzod06z9No5n2fTL5ryufl6dFUgEAlHGkOvLI5ZvrTXsGdJrAHbsU9rjxjh90fEVrjZc4u6NGsnXTLaFOyEv6jNvqRJ+YdjKfASHzrgmZnF3edJzEJcadY8lzQ2EScDG0qqK80wCZNNoIpyge3rd8iK+teFMQRQGVEYS+WZgKn/bRLLwyOdwJW+p35H4MJCmFA+UWck7xhe1ShJzLmshn58heW+temeHs7PG+eWPfZ2DJnrenc19hcOhPhGRi8icockwPcRJjNSCTDg7Hrv7U+IOyD7+U2z57QMqNwBz62KhqCm6jI3j+IxfeSYClMibwKdTyRzUA5QADpZIMMY9p4U/AD/b9yLgNiZbUxFcVCKZdFKCVPglGVurIqYk92CJGxuVKaUV5uX/ZZrNEFJpDd5m4A7uJuy+ZksGV97mKDEk0pRYWAhWyldStc2Mfi5saeTGMchpDBMrRpryhtdgMVe/qYETLUg26HW7HmuG4n+KxSZNr24fdkGO1ZvQoCT97+nuPffHMTbpt2M15TF0VHmInxgc/gyd5gSts/ni2UlM6UX2JlVKfX3nZVgYVaDO1oloq8jeTLoAZZuGJX+fQTJPz+oSaiMlHxIgGYvIJUVdDM+ZsI2/l2dnokNw9OsiZaAGol1MiA+LREfFqRYPLFio6WqyKZYkyhGFmDKLAyTX0wtZXnDJD1cuw+kztbYXgTL4+fd8t4R8sYDdwcWwjGM5e397+9vvvhKSS/9uXrx6Ee6v6eHMb3Rufkr8Y6OZMqsRtw+QQIitdu5NgKk/iQJSEyn3IY1XpqM08giDyH+iFMWjL+JjnNilrDa1CAJIvnX6YcJqx+MXE2PEr109tCzPQgcienPgdR5k+8sg1fRwQrCHdD4qrEiDS9z7R06RztHpIUlPc8tBN/qKFAiZ0YAot+IEYi1Clq2nBl0u8LC31O5aZifaZi/b1FepVC2KExSrqJsmZiKtwob7kIXmci9ia8xjZIQsWfJ3udJEWut2v3YNIqRMVJ9QNdzB1mGzmWJwNLCVkw2E6o/Y8o/BHi1zL6poPIESHcrWFkUa1EWI46HFpVpgsHyMxPPITAQAktkIxlZ0+2DxV1cUacNaUGwfILZndJhei8cBUDqIDp1p+aIEZDlS9+qjyi+G8OdAMPWVV9sFqE62bYi0GMHdjs1Us4OcLEdjPEOQ4yUZjnnfoUJ1oOP1JxYhL6oxA2Bj8AdNlAxldIjQnKQg18DKwFjvn7/AkgU1Zgj8hpmuuiwAWrD2PQqZhcm/13oUjo8/uHBZWttFaP+JcHpMtod/r9LII7foUuLEUO4+0t3dbQJsL6OOQQ3qOE+v0Gup3wH5jFwWBk8tWKFk8o4ZhcUEH19SYieX64kZYTjKtgCmTCt5La6rZYGSVsMSJwyGR3vQotIfdB+qvNUFjbrBpKgl5bVBad/p+9M/YfEICDfya8ykKBCRz1H5rZUljJ31LTLjwhr1Sq2Y1dToDyz6H928XlzQZeHIkhpWXUQ2vJyQTnByYnjNh1FHZe0dSZOamOrTvO3OTSoQpPJyu3lZ1G2uyBJxmBzzOCANpGqJML19nApkP5Qp0uZy19jsKlJs2vlW1JkS3c1lFKiwuq+4293fmTQ8SdwFn9OBQwZGkfOlfchfqaOPFgvuqeRxHSzomYg3lHOKVewvQq+wHRIckI5VIZRiYYS3NMHo8kQpai+aO2Re7up2XRP6t8qqIiXdbtybTLH4ok6ZTTWNirOSooCOmQ8xSyIkAyDiWthX6yIXFvlLp+a0JqIvfvn6FLLBGfVHO07hGwm7lwwrtmfRg0U9NcsmwpWgUmvlxtFYWyQdmSHQ9BRQqjzddmbkRmdXNmZUv4K+YTF46lZqjmDRVdNIIsiegFHJsUKCjcmEGz6bz1TqPqwtGd/RbvDY6CTfTBzqbXzlYK6bXmH4ta2SmEUe0K9pye3MDvvXa7bJd3DGz0l6XlbqyuUoNxinW1XhMecewqM22/MCyRE8E6lS/cFMLBKipHCCgqfbl9vS9h88uYFTcPL4daQww16zYqm+hIy60BK1KazBasNFWc6K9wlpySucuTxd69793CENa4OKweGiuUUZvkMhULq6lylyDJ8hTCui9P2r/2bT6roWD8YhyOmvDcPNdriFzyTtzcj/9iypPzw/Ht5y+yLjsHWQwM8xWqnKojnylUb1vq2RaFGnS7LakCzSbYq0SkQSY4Hzyg4LQq+XIBuM5O/7wZGxtZxYHtTBOjy7uIOsWo6I5nnGdzI9EDbmuqFaQu+LUt9Lgh5e7qpTgoFBK3dkIblxdusWBPfj30l5cRzA+GJuK/exHou+NNN6aU/DtMvDHMgRvL0tz5nHpIGPz6PViTkuG4JKiwMPzvcIDoNEBSCYkXc93Y5mrX35QADKOfDU1KsekOBAgwWXsadmAtaNjHEZq76UpvNaoenhGKqte/bMdwnrECYUkRlaP9wSiNh8mNJveUEGQ2P/5kW9dpgsiDjxIj27axWbBrly5koWb2VR6hBsXVySYi5eA0qfjps0wZeBMx4eqUo2/dN1zzCWPDhC19ozZV3Op/FIxuTzSgyIVdzRA5nlZa6ETaz1GdAbtKl9hqfhm8qyy+OEBrolw9hRmSyeskjcCLWWgjA4d7M0xmYTYjV2IqS/Dc/dxgoCIubTbujNct4zCIgWT723DoNowSmtSXa1lZIzk/Pzl7pWFEHWmlrspsrWEV2IktLm9rRouy2M64ilADBJzZFLk2XlvOgWPuVE2p7WATsGKdkoHXUAa/iMXnuICnpWAUEQGGu02642qRQQKDfiCipAxiy7HqD7u2tjsE18Aj/4/YJeadFAR5uL85uqmQb3+s3f/SKRYokl1IK7kK3fRR/bQvDlOqlHW+ww5CMDB0vai34H+Ph3E73+0DL+2dYD0wK4u0j7bBUS41f7bT8vpwFET1KYLdwXWdGqBGTeu+7Cx4ORFDb6l/vUe5uIfVe5zgYGVb/HSsHiFoINmIuAGWnGNkRMfTgleVnfWV2FDQznkXutqJWDGJa3bC9lnbw0kMeZliMG6ngDWMSubx+0fRbmfl4JmOdLwiMEhp80olnCYmKW2IgR6rLL9RapOaoJP+dMx6sF9SjbfXWaBVX+bX7HVqMovAko46og5u06xrWwMeX3vLzcs25eCt/v+8oc9ppbBh6/tJ6W0jwaF3qCAFVAnzXy/u0OGfp1JqzJuJxQg8diY2624+MfrP003wZ3b209JshPUyZOiwgFJrjrcawe5P7JJz9pkP4BASpXrZKwOaj07/+03zBK/IConkQcUXqz+q85dQZbU40806ZHoLUGWOzCdPsvkMZCdUzpui5GNO5BMjcSNMTqCUQU5H3nPrd0FDltT8WGLxJNnNQQ90r1E+9oGB28/fLAcTks3V9efvnxq55HExWmmFpsDH0OtopsqhwJRBLMKwVbXyNEj5ZbXlHNz+CoD6ZSE4XiM6K9oEPC+WxzskLgSiE/X7QOiX0aMaebNhFiBM1ibYZgfm+XCoTYTBOaL053qMZuR/wWhiab5rzzdBb7KtSvQ6ZdMXJDH5VQWDbh2/kt/VoMFUR89ykGxzsa3HCq9RgfGLGToBNnqa1hzo8ry3D4Rf/RAtNCj0Z6lryc9rrmjf5yMVm3bGbA8wYjnmVQFQ5pDQ0+g8WZZZlpHMseFW2U6DXbtgpezFVM7T8VX1fdFF3pjkFkAXppieLeMoQoJczzmMCBXI4CdLiWhYawk7zkR+YVcsxU9ya+oYssdCL+uBE325U9GdfHuSk2GGBkj9dJfdT/KkP+hH/VSREBiOR3iRHDZTeU4am7BV/gsxaV12oIHtEAt2ZybN2Qpoi7L9AFfYMaHJ4XhZMSy3OPSAMjNALpU73CbzogmIz+nc8ONJoE0P0PQ39IdBkCnNe1h1m/f7wq2wp3fhQE5LCpzni3Oy1gKJ43N07BQLwVIkkJOlzHTg3Qqc5mmmEdlD7g5iFxsCEZ9RSJ9gWw8zBK5iDQmYBwNfBdf4FiXBa+ZgmoG6+/yVJ5QvDuaYr7Z74ZgPqZToRpZEWhAI5kqRYkwL2RnlmxHsuDzXzbflTTqc2I5rmTfHAHnEJCeXKk7L9INNW3l8PSUqttZA8Tn24geSehvkg3wuV5GYBm7GBkN8cJWM2SUUCrK1x0pYteGtaSQNyajlJDwQ5D+yG0IF67xFU7iG3RpFYUaEdTNhh40IxPYyUdKDbhDfp6JYRsDNKkK5XYB5WTr2vveEjmzr8YuZNCUNSgwzi7qkIyVdNpzM7JLhCRwkxXmIRoY0g2zNnXZ82Z68BaanVgZZiEMU0ybrKz2A5cWBxEg91EH0jypdAjd26uoILW/tCiUW/J6Y9yN3LKNFHzy8NgzDhGYJ8mFScULI/ll0OOTQ9OsXhWyqNVcj980iEZXpUdgkSXn0LnBoV8UQlaWdqCbKwUwdJMl9ekmyGv0YD3x6++3X/m8a+q4f7oNkGGNmLZVSRDKA6ocuso5zSGD6GugS/hYmZFFKcp1n9FNasyoyYUdboxHzAgbLYvhWv4BEsrwntD6/XA4zG2fpgR3xQaWk0MUsUqnvZB6mFRkUioFJRT2E/Eu4MN+Ym+2R2J+1USyWuAsR7HuFIOWjaMV1byn4kGb7Zxn8qOhU8tSxbOctHYq08jxQ+fKZZO/ZocM8XgYo25c9PJ4d3HikIzOVRCUmRorjHj604pwFTGhPgfK8Sy+kOxAjFYvKf2H6ejvQ4mXrA6fDSWKZryGrquWVQsSst/Ebu99M+idTN01FyqoOju2DZ4Jza9SMVbA3gguw8aKoubDAzxswII7W3MKm1nfnPHCKUruclkDBisjjGvdqjiBEZLPfvPfIWcnwSAQPVkggaaGYpb5fxCR+vw7kghBljCYc2a/v5rKChtvtavFiHVfNeeQgn3h38YUeuVI2ndf6vQtgz9eoUQO3BmpIoChgL06UHKH7bAFbEeCYrXTWzu0qWRfYjizYoZob24EJdrVPIoyThIpHgSIy8EQG+UdSRVPGXN2jzesSz6YG9zynWKEVckdE6+ApS6R2sjP7Tmh7rZ+mRD1hal/xVCN5HWyhKyhLAxUVjUDUBhjLxmC9k0WrBQTldklq4qCxHV4wGBPGwf95KDZCAuF9EmZfkIKMinIuRFtM8se5FRFih+jCzYlhJXFspsNkj7Yx7hH6c6rqYM2XJSi5uZISKcWzSUOhXvlUW3MjE3NMW2aIMAI10P+5qffItNaNblku8YiHk/B1EY5yDeJQ6lShtTuehDz89LAR2w/a3hnDKvqfamStSU7UviI1o48HQWGESYA9FdFQMr7YhFFhia7InAXfLr5YujC29OREB5jWY4I4Fc2ipLb61uibnLWc6WgdoaFIEsbxRKPJ3pAmPEWIyTneWV7Ly3wBgAWcrMEbk8JKWuDntqX/zZ8RKy4lSYIQZKFJFJiqN7IOCdXcso68ymQbfTTpLSMITnSFSNgXr6trezyTc3fS7LPJwN0VnwqPbSXuMVdfBHznm+uq9myH3Zj2UznlHwrfR+3FKhxsyISpt1rTDINMnJnEDZLQV4yFXQT9TpV/H31kEE4kRnTKhwVUqVWHfsAlSC+Q4QEYgPTZjUyrZAldGd09LPRu6fwsgTyblTkD9pAhfZ4Ia8iEJKJ8cwnk6Dt5Dr2+yV74Y3dfMQKaBu4qGzI/H++GxK9PhnNWEwgB6aFzn9r9lWP+k5DGNKoGRfdcUlit7S+h85aiETeWrO7zrZddVXvRaEWEsUO0D0GZDP3PEQvDZg0G7HODeUj86+mkz9ePHvo24KZZpFbMahzbCVjFuM8Plp04BOvFjX1NsTVTv6kweyBNMjNaPX1piITUmZM6ev9/P36moWJiAHY1XURjXe1KQvXpKl6vVyTHrIbLpAFRatLNU2KnIWaQzZKSqtYTQVpKAiNLBg9GChu7t6ocz0xyWlc7OMIKk6FOWGi91pgLukQ/hm2ZyLVmr0KlNV/u4uh13FzgwmDW1GhztPC4h7lIpVLspFEAkMPZFTOrNy2zRRhXPFzpIMbuzCVlJdurousCB2NyMIg7bdzPOhsqJ7PJ2pRckWuTqzttQvj2V2GI2ue/3a7VgdZ2mxk6aV9TSCPeFEFUYrunYK76LiAnFSN/yjH4S0C9iSGDweB+pQochZbyZMEBHMiQtElkeZ1yMw2tPHLQkKXUixCB64o8b5L0m9JGfaiaZmUFkgnR2mB+a8Ak7wORly8+8ipgOWPdrxZRF4gOtyyoaD0g9RCHQDhuvolcs407+XS2gcirYvXf+Gg0XCN9icYTRuhZN/KZCXe5k6t5C5VYr25tAxLWWL1xCNFsBlVjahyExrY7P39XTFeS8ScYiVrVZJKHtvSzPytgLRC48OdkwtXKp0wjgtQUhXRqd4cWDNvDZDSPoLKNzWifLynZFhyatbh5vrWBEMt5EORrYIijy/t24DX3npuhhxmT3iUXFPwjlTSTg4i5GGLSftJOiVlafP4fvXGxoI+kGwmIwajQ/JB9GRFNAVHf/Vld5k9EPq01QwRUIVv3V7eqNU+CmaAr7EQLj2y9MyyZIYnaJzdmDDw5G1rrEDm67UQgo/KvgDxcBDrKNqSmVa1mD2XF5Ehymbb/L9cx20Y6cZQI9p+4Uv6cEmxP0UzgfmpkOBXLkTJ01qhz73SDYF3JsyzmOKSG1fWpo7auKE378nThSyOPv1HwuzZIQt2ethAcf/w/PDQAVMKzEsLW8jBSDEqTTGEhxJCEE7Mk7T2ynT6aSsLzLQa+vmg6CJoVIofsFs+sIFvOBE56B7EzxtIITMSy/2XwrLdgzcuCeFo0FjDR7iShCjImLyxrpDk4b9TbdrD/PCo8PmogmmMfixAYHo0kdjLKqBzRzz9C3ydiMPw2JIAPVmVFieziNdt5pNKsMq8wDcTqqakJTgWhgysrFQupxHmW/HcRM5SfncN93jWr5cmbPAoueSAze8GceSA18a4VTUNc46OkxkhMQvKR4P+vHV15pIKKSCZwBzwapM/mhJUI+aWoBmqytcePcnr7USdvQ0n1zYxF+7ZmGGc7rCdhiA39WtxbuGKSSBM0XzCaktOFQwGl5JiP6x347Lw6kHu3sd+7Jw4bpBfsXNFMgkaD+1pbRqEdAj4eU5GdUnnvw4oLaXIXvXSaC6SMlHXJv0lblyEU2ta1/yqxO1HRwY9PtybB5D2ZMGeOunhajsOzP2UgDwYqF/yxAC+YLdmkYSSCI9qXpPkS2b3wi8ykBMRXI74JdHElXGkLPpGv8vm2M22aZwuNKrHNPMrSW+/mT/TZPxgkwIjwJ2qp+1YgSqNG8FUH8/w8+SiRhbIgHJ8+l3+UBfa7yMV6oZQGi2+EbgUSBRu40VJeTUkRw60pERK1RPTyi4zTfMSaffH+7PUhawhGYCxnl0osSQSz0z+6dU8zYaGVuW5S2pMhK1ZrEQQpPQ6cFYnHF41qWDAxCeW+Tl56kgW9eMB95QZ+Sp4zdwEc1jnPW4xY6tS6xoUigaIklEXERlY1uZo3qb3dAG5yDiLZYJByZiFj1nl8gn1AXlMv9WA12G9Gj8KDwXv2uhHzsGvNu9OiCxkRT5QydraHb34BX0yUdcVLEXuY5GeRFIlQaWkcN7npkSg3qguLUeATtlqBQKXFhMzRULJTEJvqE3qhdCghk2KTIKi6Zk5GcmO2rTPwbGEaukpzsQKAuEFpXVa2XDyMG3ah18y2nGOlwxZfzCd+HpWy7rXPy6170m+yls68L2Ciue5iXzE6mGPBrymc8GB0KaJam92kncWwrMAUORa4QLpFrzhVssoAjWVr9Dq4cfZKg9yEFwkTGMsOB9JffxJ6ZXeYsnXODhk00TmXADws5/Ot1QqbGnBDieHC8ysoJG7kgPNtJoJNuTI60v6mBWOXUvbKILEvJiEmgjKzIvakqyyd/OpQ1/IULW0KR60cL02aoFgOy1PGwfwGEEtlzSUyXiOzKNEB/YiA+udCCIfMKGlW34sn7Dyrlw8cvuvdcMMJlyg3cwT69kMBz5AGf+9mJmLGA3rN1alwrzXQT3BiaL+lUioyZefTozg2wxGa8UlZu6VzE153zjEtkCXo/iTOGpclGNovRvwaPjIsDgwunmXH9WLCtFl9GTm5z72VcaUewXZhkP0lnOl9r2Ys2/kt64BvsXPNjCosYrYPQWsWfTNQyCpe92Ntl+UVNTzS3lxII6wCdsukebIcUaKjQIhGbGZO9M+OrXqc1h79IX3eCtb5xn9QS2CErXy5RJ5OvNyldERETEgukl2PoqfEmifj5JMwntTArhssN9FrsrTNB1VCaFP/cpTF/mknM0LteigJeoxghJXItktBzXuCvmTQY5Ra4VqDQkT/jbM5yg/00PSSO6/QiZBL/DsJwFBEkS4Nc9mx6Fns0Q455zEppFWoexsdNOAMr0Lq/XNlD49bQarZJPboKYRZCvEWq1HMoyYkcVryJoQ0USepMvwd2XlYoVhXIzCrsGYG1xZKtRyEDZpmGzu6/XzZzNSGRsBJzY37XdPeJEn6cRtPmLsmsEvFgyGtIcPbbqDJ+rXr8mPMDu3YJout02ojbC1ExSWYid6BOvllKmkL0tGQC1oNkHmS+J9U/c4PXVo28M//7i+sVyHqLIwGC1FOSSvEXRTD57sEBFCFI4QhEEVTZTqU4RbkAMl1crRiG/pDuPsc5hRHQxSlaQoN7mJMBGAagBN6rp2b30ZAVBCvnuYWQsg6RfT1To03sQw7po5hxppuaJuQce3DUsoqcgRpPZYy9SbgbHjxl8mgT+e3imqiPr2AVaitqxJ7ha+6kavQf/HdoN0ophxQbnLMzyqWHt5hoUyZLg880tZIVJ79alStYtjnZ6/FJHMqra5aPXMeD6qCy24Ql/i7cHC8Ve60w7zqu0atqHFnjVBYMOtxvVVVY4YkH3lJmQJHsWAZd/hlU+YzdIlYlwIFBvytsJWC4bUM0OFj0pJGBMKmTd7E89Dg8UT1wMrwg/YizNwt72Kq8XJR33eEkeP9Rl4VkFNjwalm8B4eJCRmk8pJPiKXUaYAWshoOwt0/ev2G+wc/wemJdD+hJ5yArB2+pNluYhPhhJU9usvLJmFtZj5Bbxs/pm41imu2weFkJqlZC0SbjFocYppSSVbXDMqerrALvcZ1E44At7yjsyOe96Pz9ftuXWKM+UUnXNl5VUIvchlfjkoBNiVF31X60I/FVyNaWFLmRPNZTutSJLRJ6vVs1IRAHNwELjzcW1W57bFBHZQrycnjnj+O70m8OirHH1ROiULyFm+v4Wx9Pz4aWREKWdSJPg6kslMCH6PHYmKpQQSN6cfeVZtdD8U35JYpqN7EmAUPvj083nJIpq8kcDQ4uGdPmFTsgFbRqJrk5oIALNRJKb8Jv0aMWfiOELyn26yiWjEqb4LDhoLJgdZfyHGUg6YMeFSwWFOjNg6ZZO8oUMErrcXqDRgUdEXIPSZqZcZ5joPQ+jKakNNIt6YP289Q4hTciuyCvOxivasgrIpcukhAtAj04jJDXcaB1XCRCpTqbp0DAVc67S6bjbhejkUb50IShTB9INCLQwS6+q486UYhaXGtWK9yvj0fs05oerptwSBeVlMi2GEWYGvJSBGQQ8rcdPwf0sZaPVKDzQx91yfwI3oeJD+JJuJx1+sgXAGow21qMBaJGdI15pfH5EaiR35FvkFsqXA0pleMt+Tbnmn0sEGCG5QdeVYtKyN67rXeTttyr12P4F37pjACVc6QKL7ToTZwIFlTDZbsGOQCIQlRoXSDidPzGqZbYkQlu8+MFy28D38rxTb1m0ezRz//D43QF+9zCNKFppo1JohYs3BEau7+phrgVwby9WUPmfTz9fVBeVk7BD/URz6/07mdUqOMFEHH87M0FnOzirZHlRyoKpaqBkQmlcuzskDwTEBH7QvA089VEJQiOewwq1rMyQBZxgAOsBGuchhxZgsOdq04yObi1vMBzMRMktWAhwLGBjWhpoTQoDyp5bCjybtyBVHDHi2HkPOLNBJIQxKVzgMQKRG71fvZfKcqqHFtFlTnaT6FOjXh2yIpQat7pJ4JDx5SK6IukuQtD8Oxp4SmGnhb4sqdj+U6mCEDVERoIuwUT4XsXG4UNrm/KrtkmkbpJldxs6YmqVj0XaOpuKK+WRK24Lodp0eC3DDN9z1tyyvriuPxv6DvLCaK/8MAVkokFMZrAYigCotyi1zCxphr7pAkntseKxgmemWDw7MiDEZtBkSurZaJPSe+LBrIFPk3oya+AhGFT31KELfc4aCFibh040hXiNyERUvYiTHJJyYYlQAghEThHFIR+yFerxIdZowDjFp0ByJBWQ3OfbbCi7qxSTq5AhIGZhDf8nq770Qd7opiOc6B09mR3KVgcgxNiwtoGm8pN1GyHwaAodWRwL9zqUIMyJsVsE0CfZUYLeyGTjjkzCvcgM3EVBj/Eyzw9CGx/evD4/DD+pAAuhBWyGEkpxhn+KIG8fnELjPDLzwBJhQ+Cqq5SZKVgCb9hSbv7zUfa1rZXIpqjG7qgpSsXFoXFMisoz8KqRfv0ltcglxPwi7XcMXFOcRKfZi8vHr1+++NhqCjYj6CCODTD9JoOIKDepxIA96hV9SY1gxXjfqfcSXxfkVghpggdHRFbISNxS52IAqntwU/GbBMKEFMtHWL+Jnx5c42TmjybHc1LZfDtqWQQv8IzfR48zyDilU+d2AIMxc78k1lw0ri8VbC49FTL2sYvZLqjs6Yw56G2eRbk5P8N5JaPyjicmiTHM+qrQnCtlIa7jNlmAOKo8syV8fcUe45IUsyk9cdA51qVnwSy0+SLM1KJAE7Q1YOV3niKTdCciJqmJIg390aPLlJ6N4chIKnV393B3/+jsAMoFvciQyadr6yYUgg7jxKNlwZoUnzwJhoNTnDxDFlWFaEHL+gD4vHzRCCZsauUYZwKB8wDRBSXlt8fBlHHHUXhQFtMwdxZG0MzC3b36hfUR9wpXIEbM7RBTNTONXVAFXHdM2/Pp80kLN4tIURt2bVYZNB32zRpxwEjlwRkVHdkje3mNiCpCdZSfxCVRHq1s/BGgux41DtQn7zK5HXMi06VfnkLOdtHe3xlKlZu6/kiqcJ7kDZpSgu7zE7f7yz1ozXY5xlqOowPQRs9dWAWGBJDak+csCEIxkxddZBcULbCQOzLJj4CPwLIYXAqKcza3kMHmjaeKRzqYFYVn/UlTiMv4XTPymIf/s0PqylDmMEzKBX6HpDRHCjB0TawZ4YrvNpQpZxdLNAu8PGWOW37+/Fl/KZyW8I57rDGlTufylAkTjZILHlzdnGkVcw/n7uGV+XCZjQbFymED1uWJHlpExaQIWBKWYvHklm9Vd9GZRhsDrcv1PXaMJCxN8aEXAj48i4IVI3EyNy4lacYg9titewqMBkscN9HwIEJhAVyl0p8sg1x/yUo3MC6hHBhMmmRSSIAOMvbapEdZttFjjXmVE7HYZS75SCCvRyruamwUWJsT1ktiaFqIXBa0WtXTrno1C5Ny5zfWZSvCKjgIHkWslVK4lqAF9tAN/D/KX8ymmb21VEXlEvtULTWgHFtGOAdU6hyp0otqN6bIS8l+9NgATTXoqKYDn9upfrgKMjOaZdkEL9nrcwQQJg4W6nDNORSiankDPvK3XTEDLh2PYdI7FKpB5o4ArFApiTMM6Mzi33q2ruXOnqarQ4YUNJeYs1s6rEJVesczGaEThbLeghZzyp5rpSXbadP5+/TN0Wr/3OrYKnToIT0pNuv64BmXFo4nV/tmrEhuM0dpKiGU87rUw4isAdNMf4OMNs0pDKETPgmlQnhF4uUJtNbzVRDYWsFABvGILdzrA9ZZFsMR6K62Nx5Edea8tINZGOqUShszlSc5OE061RkS2om9j80oph81WCfyZk6lwPkfBesjYdVCiIzYl9eAvyp7y2maR+QUPbSr5ZJMT3rAQ7STnTjcTRdCYofxvJ45EsMxgI4BbxIOI1Bg3pSk6ya30i9p9zgBJ8IKxi1hIMxOnGvcm4rTu0yXsXL2SsfqVyevZ/ZGtP6bGTSLG7yyPqu4qvtLtE2EOR/EGjSjGjHsssGf5soMmhZgRpREnusBQSaMfUhB+H24e/Dll89ffv/LX9Kj3CJ0TWh2sOGFSoidYZS4EEzqyx9x9vBoVcTd5d0VZJv8mF6MY0QlTS8CfRUrf/xskA2o2w+sa8To5UASKJpDbb9dpt0v5ShBBpPg/3wuE/SeewN7MyYH5JWtHQaj9nukljm7sK8RN3mDIY2I3I3zG0y1EksvvAKTLgZesdSaM7ohJ8JjHv3hSEkytPFLliIw0iRzjbaIg2Jhq1vIWobtuXR1umTclR2zx2tMQjCjHjNQv1mgP7tfg8+VJbDBDvQba27Xs1t8GBmUuWKR9+mkVQaD7DI7uyUNhCzV9wpJ3cuZiMsZbZv6DvWwBTv03rtSAD/LHrSlbXdSUvTgaGJ2BxZ3ffHVVxE78MIsmiL1Xy/fsSE+BLq0gFSUR3xCS0ReOqIYKsAnLo7GuZGBMnq66Bjdb7TRxdN+ViZLO5wWnUeez5YjL1TVdfib1ZVWtDxtOEyMFF3JpKPzC8N2MpJxedOyV0HHI9jRIwf1gEh+yLbsj9Tx+VN7JnWdNHXVZEzmhKOXH4/CrJymMFwAwmqCcZVcJMXgYuiD5WDLyKJIIFQ26BAkJWyYcKXb2/kEre7uyb/eYJGx/7QA811w2CenGtDFsdviN9xijh0UkGFwkFJ1CbiP9RZNrkWQnwUPwpVZvYZ90NotPmc7IXjmzULw+gGUeGAOW3WfNiBg0RuC8qw273hqxUeOzI4Q6YJkwltZYz6/XCFTs9jdI1xmvdN1muXBUpysQtyKzLyUhErktdymH6EIO6K2NlvC6ndJE/dtV5d0aIb/K4/LolYSzaZR6HtOKj8CySRJ8Bl5GG1YJq7DF/Tm6e5DOjkSfSOlfiPQi4cfPc387u7eRID8gppIg5ckaEjuMEHBwCYGE9x+FxV7WgaDlvLjhl8TOGyTj9Sm8BlGtX4lZPFgAmbAXoncGQtoMcuBQ38ifio7sp5hDFOhOjpyhMElvg3G2Je99WDz/IoBljPRIEOCsz7k+IV9y4vv75hnpvnElnLGJG6CB7suQjYEMGmKnQ4+6Sm5shtvHn9/DOU/NxoAFGrnNULuXj0YWFgx41hVAILLJI6izsP9g5hAQRYleTaRV2cu/P4lG4C9VxdPz2KALzXQwn/GYf4WAJI/gGKXWmPNuTO3OH0Nk3ngsKMwO/mx85CI7SKx0FCGWD03b2jWfkdrNfB3kmLY4FON0E5OQocylIDvGAyVrfg8xCiyMD/tdLHo7MZfv2JSG5LEowaL8IYDOadMzS+Frq2Z8TkJk9Rxr6HTNEryfYIQjSPAr6bEdDoUzuj2hZXCsYYk/braLBJ09KKGPODYo1ATkKqpMz4hk8kINT0GKWvTNjkwmwAw/mozZPJ3ZJCBJqPmCN2GL4YLW+rhQxxVRMqxi0w0p2utJRypg3C9YhppM9iWKXoxDi50uHcQEcK4gQuiB+3oN6LEZxr0wpl/uodK1uMzMpMbOeS8GvvuPVJ7Csx1p8HEioNE4sajFRG89/0Kzw0ZZN60LNoojORgsVj+WX7BVR1QxvgBPFtUn0+4B/35qRMdU4E9vMwGgPmsHSO3Nw2mzLMUKDVlxN3xBvKH8I3gtesGGdiYzXbxt7UvVHaoEtm4FK4d61IupoiMlXKPyQOlGUOz7pIwzkBluLIf1QvyqsLQP/0xFXrRmh1NVXU5dcgHOLgPtLs4TBm8dggmC4XLeUr4CHUzguRSpZE7A1XgoUG/JIjEQUqUGsfGJV7quxq5Lok5FxBcJ2/VLulBfwzcdqJDdnuYk/Y5i3s96ZeRy/sorWg/d2UXumMjCJBYW2QqoS5+uag0q+wEIaxOFzyytT8hf9a/C6BtgVTU4kd0jgB24auCAjkIk37GN0r1mhkZB8BQrFGNOw1ZCyIt5yPJonXtpK9k4OsKIW+ehamUUsIK1/xkWCAP8JbzeiMB5ablBS/gUXcKGBpNiO0SLwJVTW9ibhrHTLvm0dZ15XeoZmOwxScO/LQoqMF1xo76xCCG0KAJy3IkgqmoJHGFbRm9GhTNKpwYEvT8tbdHZbSL9xtuvlVJ9wzp59vNsmnyIHZQgFPSxmjImBQTI39/eujRSYfiPJ4B3cRIHx45Ht+sYavJWaN26twjz04dVn1DVsT08FAapJRn6vj+593d3ffPX77o6OtvXzKMD00OaI95k2RW1Ui9rgOlJM6aikha9tiIrDD1Me6Thr3HyQPgv+/TUS8y4jxswHl3BIoalHEG5RX3syS8MeVYck1LXORKRNlzBjhh3HKi8uiANlOiXCmOgWvnnzgI/kB/HWasmuoWShEwG/is/F0xqqZYums0noZNI9jU3rrOSDioZac5gR+amOploxfX1l8Kuoq5egsUg/KU3V+3AFwa02BOu+77Zp6GFq3zDAASLMlNsWPXbrCat6U2RcbFGLdqQ/son5SKN4wb+1rgXK8nLcPCC1MgTCYeMRn34WBFoJQ0GhJn69pCiiz10EsXIiG1uUmbekShcgTg8LHfmRy5TVAuTNTuYdE+AVwJZp7Xhz04XCetf+/XKInf6dNcsv1HxL4ujwuiJAByHYmhgaRTbpmoF5dTllZStCFHXlikcEf3D+M0lePpiD+UfhpDi+uNS92cUfEXD5xBKEuAL03REQKj0uyFW/Qsh8PTmiH84q4zznCgI7msvgqStFsIy+URTnT49wE95AcbUWE2xLKxaqLs08FlqWwWW/pPtkUDpYjUxLsbIGI5k/AntTBsvxVh8oTs0N2l4RrAKW/RPRFWDWWXlL45G5djgfW2PCM9nisL1GwJfWJkG/6rPuu4I6P4959Qnjxpu+YEofboZMQ44gi6xiXT0q7Zch+yBEIgST1KgOXn21o644eSOUJD3kbtbg4JOgWBkH1FicRpLZ40T24L0IkLsxM8U4yMFJQbTdKp2sCo87dHHTss145C8pjT4VcDREZnb63R7KgMhf8HQHjvTJA7dSAlcPBU6Y5zSeFMBljtCSLyNQxaCCEueRxMXkzXLQAl1k4haabkg+nfjLja+vRFRVksPJR5EYn5JUjgZo0H6SvDxT7i0G+JwahF9vHCMrRrXoDmTz1UR0TISSnfPKAsWB6fEaoBqH/Ytn56fvvhE0lzTDw0XCehBm10nTu3RJ7/gQhDHpsbaLElM8GLUaAz6gwL5DfqBmSbp4TRxebqYq9HjO6o89LHBwOe9h7d3316+b1JAJ60AcnVly9fjBxUIvig2KpH7TB1DTqcR8qBfr3EW6Q1Y49c4y8jFJY2f1SiGV7rwCW99Tlusoyyn2wLUa3RztRoNhQg0fAi2/K+sVmuDq6XchI3mafbPGGX8cG65Fvu2PDi+CQywKggQtw8BG1RYgiTy79Kv6W6PkdSQxC5XJYuW6ChY5x+SD8EYgpJbxk6lMRJsQpNe+E/QFkkKLxqvXXnShQNV/gH8ParcQDzzbsJIfOjRYYauBlLgHvXINqvvtMZpdbsXi4TtaPcQKGfcJ9N8YfqbkEq8/0XiLskJ4eZQNCpVjXTIIy4UJ30GNCSRm3jDvuEzIzQ4BZ/SakByWAdC8BIV2go5dLK/iDSK3VpVmsFnYH2dAdfUmNFdRDF+fVzwG76cwv681A6lHZswEGIuBnXqZ5pGMB7rjZygZHRq+03pZLJTCNSM8iQ3P1Whb+NXA7/z8gaXIWbbw8PbQdzjbw0H3UiZEO0TBl7kzbJM+MzZxAxUlcRJyb1UoUlrF4fOIuH7o5fY9kK/nq3iKHHF2NTGtX0A4lCAvLqb4bN/8IStOYI2RKOfMkNeA3xZsqr7SCQ4rB4fOE9TquGga+2IUm4StjLfXWQFSUJ4a3fCgbaDcHDl+ZSqQo0lTpAmOQdCCKwClXatmSIDZphR857z8KUasB65nJ93vPBac7iRxJnABtG9OBv7cVESxW03ci43KJm7dABf/l1PBIjC1e90229JhQE60p/RE3cqmy1J/BEa58CBF+4haUdAqREDPpBG1nOIjwcpoos6+3H3Z9//vNvf//zn388PTzqQytAAGmF/d3Kc1iVUbwkhb/+RG9LzGwRaJo46adQq/g+VjvqWUQFDrv0JWLN9OSPXMwa4B74pWOjkoZWuKSRGIozYSoZsHElSubEQAzkqi+SnB0JPErv7I6pYPTEYPHu+50Kzbdv34y9+BzLv/y0WdKiQ0J2WRiQtvvFBThqKxbBYsRjF3v/0xndDM/0sm8biiDh57LGxddpnF+U9zMKoz0qNyeESKcKaYYx6MjgSaeg4OzKygJ+aZeJX9rCJSblq0QWYIbtqC3lJxNXAJ+SLqMmevK9+OueFXfTFmWU0g44comyPzba+C0M6L1YAHOnXtrQ1FYHHYHrko1Oqa7mk6yrcNZowM306+l/Ew3PxF2WFLqLQwgRp6byV2sTSgNzjENw3hOqTZ2a1lrmzKu6Hr0gpP1ruGCivqXxkVCe5n323VBD80zMz7CYKPhZVy42yP+wLp7xn4NllqBZBPjPuMZ4QTsCqOVaXEihIvPfqzhDPtWgCzoaB0/ot7KL+aRjOihURKjkCxE0MZ/s6HYk2sCCMFIo5MyN4gXacqZxh9k4JYSKC5U8I5cPtETS/9pPO65JFrSalLZwTRP0m035DMUwDSUF5JwgG+nTdJsX+SUn1DWCsyWK1hiYSuCabhu5aFMOW9mDmuKja7Qla8yishwrXgpKGC/Y+LgBss+9b8Q0crETtWKdqRrH5gEa2D+JSWr4KzOFoR3gIq64Vp1oVXCb7I91RnjTPtX5WQBnaeN0RhJiY3McsOpd6Qvi0XHdwh32tBsJBWKEGWU06EQMM/JBee8GO9pXISa0ijtB28oyBZm9M9ogXO9dvsia7MoGVwidcdJN8k7ACptIqsgrah6w96/r9eAtGXHy9JWONISOxifenW96hqGd2l/Kin8YiyTqktpE2gaizCc1FMAal7l3NlAO6OJjPtwEs/Ow4xIo4H4TbDSisfqpnKVfRoiNmmTYmAmAhwMmgWDBrMLHh3JDDcpiSCaC3FOS2D/QI69KPQHbRCBu6Uvgb0oFBqvut5yx7SCBfBUgU9qiuA+yBPbgWH97AXJc9yg8ntgqjEPjXBs/ZVMYTVqoYokrbZ1Zdvrj5ez10ZDv4/kN9XSwnvycTFMrG1ndrIDNiulF2I9ZlvjDxOr9g/qN1bYRpmplzpr/9Huz90DgQh2RqeKiAFC13TxYzsJGXGBBFylk1Ga5Z+xydtRZEOHFulhjpitjbragJT2K+5rd0k/mgvfc2cXkc3lx/fW3r/TBfhghKoWWiy/WjDVJiXiTONMck7a5snHhx+sSaB8K0myWsgFaEaBJ7xeDpgADQQzXRRuBHDjCQRjPwJSzDjKYqatK8NHCq4gpFfezP4VUqUnP7tRlSUpwwECsL8uQ2J9fq1FZS9Ph3dU3UOJzt0dIAc/Uhw1cL68Pja+Z+6lntj12MGdOt12ODiqCv3oh4bZONCSSKNQTOXpJaMC7HrsGsEBLjUrKmm1iUVGt65w5B0/bySTXLwVLlEFVT+PuwgpU+Z0GKTofiwX2uvhQo0UUsFXXIvzjI2opWJ/FM/dvntyY+7m9LEUUftBr8xlI0HrclRuWrMhbhGnGya5TdTW2fqINPcOQqTSllncRINmvq7l8v4I2N8nYek0gsZJxLCb6kF2tQcLnDkNwBNCxz+uS63JaJlQ9wUd8MinkzOmcrnge1i1Tfr2qHJSptk9TvLUqv6WrW3NFNpm+v3yDgpmQ2/ERZOSP0mVU9UkB0JV1X/Qa8KKEypJix9cgKVorsmvUdbRLaYWFpRrcUHLD0VSRMwC08kY9FrMqbNIFw/WJLpbZZTeZq3WfR5Up8gg22jKP+PGD0qrqIBk3ZMgCWUwCTH7UgfpFCgEpS0+Xmu0b4q2lrAWmsBSCQQMJYxcjWDDfYViSJAJ99+Z3KjUacCtaNIkZEqRxGohdR4N5VJlA2xaHJKi4YPKrvvfCgr8mNtEsJLgdK6lfyYQNCF/mHXYKMeaQFxgSbqiP5LIAxpAlkWPG723GkKgSQ6xNILmtN9rQvhnTMjmySH6HXHDQSFe/RwpBmrzj8+fbz18/O1Xnz+/3AgbfM+5Xe6SU1EF9/guoek+KOmM6pZw+/ihClGVyEZPoxVsLnDyPrgzShKX1SB/PGoZKANqs58rmg43XXz2JE6UGI25OvF6u5T4KqdytJ/hgrh+klx0NJgQU69Okc55T3RqQq8ubokUpRCuRHPbZMDQEbKBJ8Di1JARqV9jpdfl6SfXjzhikCa2OiaZNtSQGMYW+P708Wpr4bNkb6tpbddl2rxIzZ4eoBYrcaZAc6YD5Ew3YMYriOeRC/qqKw+HD5kNy6RpP0oI7Q9dE4bl7GruwfpHppM20m0v0yvIE3uG2HKDeUh6DwXFBjyukTPxWDYhfjBVIO96yl2now1BwlfPHAkvKDVBAqsAuhQa1QacG/aoTdl6GMEpENjwC3JvbBr8ZIDlkDUGgewkErT7PG3xWQTvQk0Gzzox1YxoteMPTxmaWjH/RFFU6whpDx335vOuM8tplx5qbKiHjQ6aHTLwH3bpGKjZBBml6E8LhpJzSOoZI1exxWXHfyV9XjsYuzdds13CPJB7oFwmoJ7tJ8jy0SCS8pYUly9EIaHM7JAVItLM5Er6fVGavdS/pyeP6XTpF0LvM3d3ELLJMIiTjpXPgiJTckrQy5d7FV2gLj5Q7pqZ/GQYsRdiMgR5Y27stf1TjNn27egahXCNZy9oiF2KG5/7CiObzXYsAx6mwWz0qTeLflaa31DeUJSAhemkNzkFrBFFYhTTZMkf/Se9cDSZipqBCXDpbKtm0UCptBEzMpS80gUdM+enX7Dg3aGKJCSOMmZWIaaKmchtEqvEc2aFdq+VoLnY7hjMqF5LTr2P1tIMShBRbKU0Oa/8pcY7VmRzdzvlgC3otwwX2Uo+5GPOHegBI/z48O7tOVY3/sMA8CCcO5DjnF2YfYRmV2tzWSB+zmlNAv76ShF5T9pZT/nD8EXaQpJ28aZZ2SIY7AwOAyPmVk1rh5+Q+a4HezcocuJERoGdgbStDQONeI4MygYwrxjS+Vum3TyiCWnvWlsfHes/T8zIZAavKElDivgzUr3j96ICm669ff/vtt7tv94/f7h5cxk8ePBK6OcyS/bXDCBURM9YgqSJvy3yJTuAzCNKmalajh7Ikn7uLexqW2a9gvtZymafn+3viJweVetVxbl5mSoad+sGOUEryEew9RzR9rVgstTZs1xHCEnXnpH24YXsC101HjSpF+06i2H0a6VICFNTR4GwUf1R3bELzFV8hsqy6xYkOS7ncE6HDAX87FdH3oACEOB2dwHlu6YWZLdcQhyqxGN9T4MtnL6/2dKTqUe0UXo/OATXLXdWYdiKs/QC4LJnG55GxgZXDHoiDNTNF7cH3Ht2VUsWK9ESO2QcAInKq92bp9ka7lEqtHzoVy2WrT1gza9z2ppLYosDB0P2P7yiFehpLsvlUuU++OkcaahTYD8eGgB4Zlgh3ZouL9Zi/tTyuug16Kdkf5Q6N5UbtyH1u7rt1bqJ3o10JdymxuaPk5l5wwGzqndfJmPRuCsExveLbqp1hVBZ6pOpyQPnX3GYUliGyfLJEOXfh4RSWaIvwMeZeRs/qtSHU69GL1S2TrYhJ+ESBSDf61ct9SPI6/FNHGmEKmaJunKN35SjkipXhVHYvYhuoN9nLFAAA1xJq56KN+3yLHm/8pM0SuFFJp1pADxIrzSZecuEgDIVnjoh+4sLf4s3E5hKWoB6tgpwboASGh797DHzsZBKly4636qBzOIX2Yl7hZVHY8IAzW4v2zKZa5IZBopX4nH30SBTntpeqBZhpCDa0J0NH9haY1wD+nZVmX6icUM7VJl5Yidbrq1u2kZ0/VyUIZWYbuOQesGD2njPPe8mjxCJFseS21OUeRdP5ibfiPT/SZt7sGbwyw6y4hSxwMJS1G0EGihrutNYJSnMUpxOuq0iBhayhpluMFC6WHva5T2gjdDAA8Meic5di4MSOlge3EQvHN+fAY/K9RPXT0cRF4O1ADCRkY26yA+PJ4kgkSZVab0rjM6SSknWlqdeLN8fu53d6A9xZFVU1byFcM8UL7UvRAXpLO7TCpUs7WiRGacLK2XV2m+UJ8+4r14vF5bwhBRp/yTS+0WWjuAv8IBhZuzVAFUOD2N6RTPQ01Rxav32EzeBxyAq/dPP89nr/ax+sRIHIqgvrtgpRZDIit4+Mya6jhPTZ6KctFDK4zsYqbjA16TUPyPszn+dHPFqPQWGMSu63s44uLYAydNQVoaCNWRTLzj5cmqXQF4xohop8zDybD/9wdnX7hbi9bwbYTuMEUAFbDmGxVpf6TFf8iLC1SfJV0Y2PgSIZ+A4XXM9Vumr0ydLkgiW+KZKe1TP8dOwwco+R5aydKA6XbVeWrZcch9i16VvrCYGbxbSdgmQkv9MKWINbBHifhAAtSxM6aXMqlwSAyEXQLLyle8yYi4VurRy6stm81aP5S6pjAllPc9zezdoQ4CtER3qqFt3L9kqHA6iMhihalHZQwwiCuTW1VjMpLStzBCbu6KzjsiSdogq4o9I37mKiYm98ME++b43UMvE1kQnyRtNjulhuV7CFfSvlb2YiGuMjL6GWkGL5Y4kMRTGw6HWbDnp4Up7Nt9HTxNRxrV7Giy6SUtKXTbhMPiJ1xLI/1K8L9A/Z/GqYgursoD0RK99jFeJvDxF2vNyQLLEHDXo1yMzW6Kz8Irv3rL+J3QLM5E9irl9+wHb8v58GLvQv/qOhIODT3HYA21U6yBUz1q6Y+oqbVIlLEtCnP6TQlW58I+rCmNaLqUTv8taQGNs2VcF6ZlHMTCt50HCAk+s4QbgFuoMiVAvCxFAqVOLfZiIXEWXi8nLatsPXqjuRABG5jwLbGNnWjo/PEqePDtzoOV9liOoFNvIt+TA2IhCZAoEYFQdUwV74CPPjBofSdl24gJl7gzoO4A0hScLpJG4bVVisYtpMcTYhuBO1S5dCN66dTP0/+dBXuivc6DMQ6Uv3xDnmkO39mnFFt0Ox5EKkrdTGYQBsNqdwsTYb4UUFHc0g/Zrj+EQM6PBjE5VZhs5A+SFv9PNWYqNxuIp+ZmDeRHdExJXRz5SYHJgEu7dWDEtpC7t42hQ6tE5jK10fhgg+iHDlUXYLYKI7uMx681ZkUbhMQtbc1IHg3givTCn3aXo2qWRuGegGqsxFZtnouQ1Lj08PjoBozXqL1qtSNa49PHERWtVPE9lk6Kk34oas2rUsRwxlS0fmUbbi18Y3nC0BEScaLxw1apHj/T328nuLDy3Sx7ws8Nyx0m0J0xwDFGfmsz2dmMy9Omvz4tJs393DEwnK3XWKanIkQ3pGOPwhHJ2tiEStTr2Cd8kGmL683lcumzo4cfIPIFkcVwK1IotAWDrlnNFJncvFVUGxg6yVW8Qrlrk9IuJEA0A6FhMb4bkgbbDhHRmRPZOeh0ObNoPqhndnhobH9ADEkiA6MCpkZ4nh/16UdaQAZSDha+EIgRYItzZf5kUVElzqP4aFfqEMvwYIwX9JempWHerzvqUF8FDDRgZk08NvWXXFdxrFMLOJ1t4fgJf5LmqfPj+KIFlSX1XhkKNVtwomjlKJ7P+H8wMa4co9D1/NOX95UoT5tXSmvLI8bq5Xeq0VNLPMqw+WzbbEKqs2gNiLJWbikb/jyQ5YTdDv9o6Bd8ZSuZksbdLZarwUNiEgGI+uRIXsmOh8Mh4hWYPfJLZPtHMEdB25wA+O2jlYvp1wopNAcXfZ6RcMSHdkhSu0RNySZO0sqMguwzxOx6a0GUOaMqK01TZMb16FNPSPAibV4xpXh1+GiubgjBoSr1tdZF2NRkGpK5oaE+0K51oABUDPOI3wDfqNz/dhjyNPlGSzKQEfMjE20ZSQUQgKiWmuAq0IkLz1akUdL03gZn3KxMV1xtJiPv2dXxmlWjBYVFZzLbzqlWvZZUo87cXj8h51WwkgpEncixuuC2V8gI3IzSNLUdrCQgLkxRyzX9lH0sqvVHp8JBAaPwNQIZYsuMJMVngBQETfHx+On3rULOl5MTlMF5m6S0bEHgsJmAW1EUBEzY0mFAr2Va2rwnUAqPMefsUM5grHXINck5WNgRmdKg1VFs11VdlXGZncdLGS6tv5TDg5aMiLJJqsalwhGpIcnOFAsG1tNEmGCiraiq4Qq6Ghx4c1urLSsQmDjFM7Oj6IDUOxnIUvwmXPBuoiWEaz9RFcn0RoO1Fo0NzTLmZwbnGVGVFNTuDP93ffLQU9ylYp0BjO+kUDBLOIP5Tz+fs5iWkHy9yuYUzIwdBfDZESsMCgg4+vjEPRznghajUhIFiH/frq2QunT8CH2NSAHq/sk3q8l2WdX974ZylCeXtrgjJ63fiZMWGhNWl2gmXgnU38ZFmR/OLHi6MlO2HCIGNyaK8IZan5WJzjuoIUITCtwpCija1FSZ1UkovPRaT1oEdEKeU5Q+zNRl4hELAN8qoHJIHKIYooGRf96bEIaOe8zUJLeZlkwEI6ZVCnMGSi7wbKk0aCx/L4BJjdahYVMcpIq2IE3UfBgQy04eumBOgzn5StDLboVCjBAwJBGXii2doitlGnc4zT7DJn7SjcXyh553JPxXBeHWjmcJkzTenF+nWuHkF5RME/NWBB6cNg3JV8XNqbMnDYogWvozZVa11TdLGlwGUExxboRjuJmi7RNp9STanYV4DgTiXVeQ42RKofHYoCmdwQy4UNlroqMzYY0mkC4QD4R74qAVq0MQlUg2JsWpBVpnKGQIKrmHmXsKpcHHTazd9BN13Q8NCQNYPwHhU+9MoGaTgrZLAV0X2rVUrfnoiSnVLH4uJa2Ojq8E8C5IcPrS7L62oeGWeeCaUSI65t77+K0NuPC3st80mXUWLjFnQU0T1ktacYspISFQ2FQ5w1yrzEgCNvSfaEcO1Q5Ya0cmrEtC6g8XSHQAQd/AgnVI0MZi1I8n70pxKgtUTHYgAD9GSODhaf4gimyK3HVD9AJgwEXpxfn3ZGfhUwF5AsoqUnQQLa8U9miEYDIpBcyCJCpFWG8HXNZBBVNQktnI61QXYzH0WE7FMuXBR/IRllCk2kglYLIJpqjOGw3WKV+bMtSANy7RZqNdAwxNs5mg8zyT7UIyP3lxclTyzqPsKkYDqKlo1HOUNUuyBiWXgTHjm/JpdvIj9r3iWHY6eg7Or08tT8YfZfeZEeDCbY58inn8ClTP3jo4zKPker1x2I5BFanTS5nGT0XNgCi3paqJzF1lrFSGSKkDruRdDyiWPIYpeUPXQl6MvCS+Mbv2CG07pOtY0Kkl2xIdljDFyzTi3hFH9+6/S0Lqxf3GjucJwkgVc+1zoAw830Gn9MDvgWrjunQRzDiLOXZCVKUK5WJaGnxwcVSH5dx3mpDOPiMehXdm/jZEXJdCp8VOjLHympMj1vI/SGmoTQAQcrUD2nQwU0FauXymuaNfQs027TaKN2XLB5g1HISwf49SGDKHMnmYyL5QydUFaql5Mxtpbzy3qr/QJzj2kOuI+Jw6QUTjRD5W4CjDSht2cpNIyohw8fbApR+vcG8Hvd3N6aaHGXbiGVrnsonRuErAA1g6mSizfM18hODYgnplJ9M+vizKzz0BZzpCNMvD61px7RyTjlsB5t+EXW2oK97EbpZhX83CZspJTcIwSrMq6lXE0vvgNThuKhBVg5bWbcJy4g2czFuFunCgg/f6o4J2i6GtdsxYxY5jYDqAsG1CGC0dKfIJX6A/fDSA73Y2lYThlpB20y28CCL/mfQlODbIfE2vydFROcv+zc5IoLYTtpd00NpYD5Z/jEFFGe8kONnLMfC9OZOMhcQOURhLZuXYJo8glWdKFZN7lSzCs02uPDXflJwbw2a3Isu36/JsbhT5UcBMVfANo2wqf7B5choLGER40zsiCkHN2kSSbo/JntcS3TKkyTCAOpoASOSmboS8Lu+b0vz2WdL0/S45vri7bPfji5vXIkvXpQwi6+q72QUODlkE7ZbGFIikjVgX8hRw6rDSs+QnN/Magvq+nKmn68e0wIBT51DEQrj538wzRWWUDGM6stEQWqNjmbBleu9euUeMgZbyRorriEST03r2SL4kgSZ91xaKBLZb905GYKpV/Pa5UsmI7rKV0Eg/z6UuYPwflN24i4hcwp/UgRaWyS9p8GiNzVczBYGDdeROrK7CiVlWT4jwqLkFlFq9Ay1TKBtIoG9A76MiI+9r8IpVORFDrM8arl+TLx+W+m6IbIwyQEAeiZ4rhWcJckbQQAjEgF6jQ49q6pO5rM71mVMnSOkKL8nz7YVUZ1jD4wG7Fphbqz66jg18t1TzpXjm4JBgsEygLngApFUCxHzES2FZQvqyNqKnW4ri2vHZbgHRVUjyJtYi0sZeZ6azWbLonD8lkwW6W+B8UlNR1ovtWQPupmDwQRmbDjAtJRDbHQANN52IVnal46FoCsOvPB99qvs9lIiyHFxQop5nHzpKLkqzLF1YWwsZOr20Xn+wIktA1Mm0kN4H3uV/yjCl2Bkn8iYQWfrqs9r1bnNzQkAZDtoqAmh5BAlxyHQlunhHgfCDFL59tqQ8mx5GBsj1e6u2e3oEl5J+UgQBnOF6o/19sX8vhYQs3png0+jsNcUVQKgHNjfc4zoSZrotZyboFQr77hyp29V48+CY8SST7j14OXdBrXhiEY6Gs+3zsCMDKjk3m69/uEiVNQG3Ez98rD2bvBElG6hg8iEJP6IDq8ADFtmvwQrgQA79UkP/a8hyAHbcP9OkKYD/OvkjassEPjrMbLefzSByyyufB8J3DhEFWglsyNJ9io9rUBkiSuzZdYliVLWv5lCyvhUkUVfdMMLS3NdEiAPzHD2UARkQKjJB1nC9GGAg7br9aXNjfgDR79pH7lxVl/pS2OQZzFmM1dU7zWyBdL2rcmRMuYQ/bgOmoHstmT14TdqrUmoIr5sKdJi+OaSSNBFFnyr27qORVkvoAUNBCb4WppIAD1kvkUPshM1dYRJJz7+vLMfJQ1FZ+uz52ITcSQjixJoxikJkCReVb4ghW6PEBxHlEhj/9xCx0FUdQdMDKCtNb5wPFuEp7xQ7Miau1sAI7CVfzbIyAdD0OZALGsJhDOSDJkAcd67cosCgicJpArGWhAw3JCT+rIeABOpyqmGzbI/biC3HCjZNZaouhLsvIp18//ABO5zNq1hDQRNQfCfuU4FTAZG3kw+n516pmf6GcGGwU0vtSSizyOcXlwdWxIWaocIXLJrW+EA5WXk+WcwrPOy7zqoqMxA6IsAG1JLoix3KSdhHwLRjiAu2U3N+SIdk5J/q5HhzA8KzK5HX+YPLI4H+rOX/cnE/3T59uLFJtnxDuR4DOJVORht0HEKmOEq9MecLt56wqLjCkp+DOrSJZBPhaJz7oXy2AKkg385v3y7pVSG/xWNtH5emys13Y/Msfwq9mQNwEADSTB6hz0oExnbEcyFOwjBzGlIsm3aunT3cMwGiUfL64/nTpmtUKfg8oJHWqX6xBgw+L4Bu0mfPNIcjfAJY7c0L70nycmAzKfhvISkTgLlroh8CEuNNZxA/ksjZTA2RIvjbnJRyTZXCYfB5H9BRSGe2Zt4728vCHXh9NmGih3Id5tDSgTnqCLj4bLZJnbVhSpiJI4lmAMPdz70X5rHYES99LvsnY3yuU6cpHhkycBr+BQ9lH9J/tQkCIgDy1RS88TygfLLFrkUNBmAyDJZbWCfUMeJsDNqTI8w49uSvwPgyPVrtzt83c2QnUdyC4XIDU06CVdSni3DMliQcpAxGUfNK6hBxwiIjFab+NZerVSBZRMhXmUzwOAUXxp1efjo5NEvYiyDkLzRKaZ+PWZyImUZo/V3x7TI0XxQgpsw04b60EqHUNU13rjG7e4N5cbC5mOFyJn0amjfIONQYN8YKPgaEv6kmzjpFKfFn5RUjqpRKjbExsQSNGVc7UMZFEGVUbHLCy7BAuDxBTvhdXQTY1Yo1Bf6cd6XCM7tUvg2EjLHKxXo0v/lStVLYjmSjD2MXARdtfjuhgGrjOlyHCkEAE8PflE5q6udOekzLMPv/326frCOtq/HvjEBloMqGIBZ6p2JDYWwLv1R/DoSsWd80VNjSYZ2EfHgjRf4Gm4PU+UFp0P7/rGAq11UcxUbaJ38CpJQKHNk4YXROEkUWc1sQd8qJ82t89ThkQ5qEktIYz71Z3XkQSkfAKIGvzmMCgsGP+kkgUF/nohlKueGP+gp2nOEu3hENcN9UIavQZtRXexSZiJavrCf3gW+mRrOYIjCVpenJa6K2+fGS++kiqcbC0VswtGs3mWqaoyIQCffAclsdBu3gXoUodiGO/LVOc1Ls03y0uaJtCsezKLDIesN53gmkoZxmEAqIgQj00ve6CwxsIIrSW1BTu3uTji+xcyIFG7HAQdPKzlWkzrxA5k/fuUwXd1OirHzlFiXZpl1kd2/vrBjipzv2RSFja/ZGVEYFKBbrIav1cWYuXJDCGQV1fTnnP4JHAW5xjrTwkq+U1tVY58bbmQX0T7n9ftmoaNnGuzjsa+5MzLHh8vrj339+X0gi+3w5h4yYjtqKy0/k0Awc/LfbM2zLRMYwOJYm0ncJhH5jj5rktLO6T8qCyy7i839KbSnziqmmENb5+MWCxlGSuoOFf7RUGxhaDKPs3YU5FAL52/uboWzm9uqnBkN2ZDX6367dwk71kIArRJsbZ6UJsVXMzVp2AyUTtjKgpbQ0zCGjF+kT1z0mwl57Zi/vwM7hBz+KrJ+TEqoQfVGAjZYewwOueC5LkNKOUghQoud0Cn6gGYtWyF3jkBvblSf2mt1CAj1V0tr7olnUdWzshmeymfndsS7Z27PCNwC6GUF24qI+urY6WsCOKAZQ7QuX0Nhm3HQtV2P/3rmdqbg9Cbvlxcg1sNu+Ccn/iK0RF031Zrhk4tCJHuDe98TpUlOCadoSedcCTrXXx+yJoXFEvvfQ9e3Bhxs9EyJk0VM7xgSuNfzVc8BWqES1CuT3C/CsHNEHB3+kvB4WMDIzz6vAFH7VJ0trJAVVUaQuhGwTE5u56PiS4VHsSDpvi14/aD4Fwoi/RZRcAQKgv3YCXZwoza++qn1SuBJvWp9V388Oyq8pVEJPQXYJPD3ssqpFMU1To7voGr93/7K64gi14QQw7l5iFTnqDYJ8vlPeYxiIVvCSmZvhqm7CG7LGD7TCaIJt1opMiNcxDZauDGWC8tQy2WEDuT2Plc7FDzxpGNIvTFfzw6vVy0fUBWcdQGlSBpA11atJiaNaIux2EPZOsdiXVIoAFlSfEzNdaXZTKAYCcyGrcRQXZcdWJ66UdmFDC20X8eXBrh7zCJ4IiosmpCZqVJ0gjRYmLlhZeG+ZIhUl0j/HaPChiI6CbMJlPNMSPoVmwIWDKxlMggG+BkHnhhGIJdQyULV854rgigL/0RuQzThWIpDbnHVe6GoKIu9DWiZScajWuCkcBZ0V3uJ4ZwpF2O1bgWU4M8IqPBqu2tjg8TkBR4oCN2ibOZf91Xr2laiIwR3xl/2Z8XEM1fSKBnx0o5LBlGby0BShBYVlpQdmVcuAv95FJ5FcqnQBHM0se5HfBtBTAjo7n2ssL9Da3oADW1qi0SodYGasVngq2yscXKTdQ2M9pd2ZtOaBG/Ob443UdXV+yjAlc5kc9lBeR41pOIUnVMt5aMSghUeYAsI7NX5AfKvct8MIUtJkFZxvpPZ8+ESnmUSEQJ+q2UGgbSloUsYXHQSj5Jn4dVGbBUwUmKloyb7Z9WzboSm16YFropEN68qMRmHXWNkUC+mcWQx0m8/JYKMcuIceWKVrJncvDdkszYIQT/2B3dFuezofrb8CcbQxPEkmLxwkRHczjVIeOwD/pKbXBE9xGy3LoBDpGRiziAXCPaZGgekuGiW9nFHICCTE895v9IdDO2y6rKvIPbjGKEoKWh9AyqOjoT9pU7VD0rnEUql7Malxi3oChCfvFWstHCeu3Bu1erhtAuXHgCms/SVLjc9LaICjJqv6zSiuEGRFZD6heA2olDdF2O3Mx3fxC9aAdXScN7v4NoopipNLAgEdbCXg4f7pPW3pWWJio5vj5TbNaa/nvunaxO0OphquSCDtdrMKiR7baoSTmlqitiZJ6NdNqPJgMt5gfQeuG1yAT6VhM5n9mM/esP+hLh7IzSYEitvTL9QjfevYjIbSiyvLo5BVMngexMCPQKmX3bzLO00PSzt35tZuvdeYrZCgQFFUIImAIH5eE11IilZf/If+UtxBXYwQLckTnDIxmfcFSNrJJW8gf0bz2O4/FB3sB9vNhVKmt/X65KlWwA7jPwZnsKZwBxiVkGHi6wLnqDhmoIbLFEuKM0zRamv7TJIwOmILJwJE8EEHkiu/gg5iA/WW0q3jf7gKiO0f2bjZoV88TOnz+tPmHeJX0NHAVyAjDH2AoB6/PyfTWHIm7GAvFMN54Ca7Vymi79gkVNRDFrHqvjeN65qrkXVeXrp0o1zaKEyc1tknKQlFs6OMQtRXd8kKf0zk3lZ3WXu/cbYABVJIYARzVxNMYNRBNbYvcFwfqgSBBOlwX72UA3a/0RRZYRJCVXBwdE5xLS9k5aCfZvbzZPKZ2+vKL3l/sWg5IRHrWfj8gbtFZ9KuaX/oPAmXq01TT4cq333niQBPZ6OpyJp8aUzKZnQsVKI02OJneRCRl5PJ49P0qzGZARQU7Ix7FU8VljjJJaOt5cdHIUoWxCBDWz5WsDjaGRRBQ/JdI8y/QYTZKOO8UCYTRv8ZGsqBe7CjXRS6+zuMjXpTEtdUwUn+Jl2NFEKOyz16wZI7Q4YbOCGimUwV9dWMuRveEribb1ROE0Yy791Zu36de9vi8vrERCz5KuaieU5C0GibthRz6zV/7R6XQdz9SfNNegS3ssy696w3bQ0rPD1ISNpsoZ9FrWtSK1pou6gvxq+vo9KBsYFpcal1pUoyzbVx3uhlxixA1fVWCnAvDnLkSPhuwPJ6hBRqZAU6PKeM2HvgUZvgIv4o4OMD9iu2yX56wsQbw9/NC32sc7OkmtFtkJD2/hP+Bpyf8smxDhiMhkI0IngeL8QsE26PeyBbwl1YYjXmSzxvxIcKQfgjdYMazVMsvjmNVS0lGMZKNdnJhbCvIrsh6uyBkr7eUP0VaMVMOp4uGyn1VoUnBtNlH/C8jwWIJWlGrpUCpjlwUMx8XkwINR7k0yndvqsp/qAaGiFaIkz9zeDTNlLzANVaRNsNzD9RyLTdOagMXq9c8F1Cq0pAoSVTI0eM9znEzboKSZA++xSRL5ZK3JaripTjdEYvGGIxWjkKaR1k6QecCh2CUirBThDT0SSO6wIi8t6xh0/jjpBA5wRAqmZ6IYEajoUro9KnuWUuUqviKFANQDpnLIxKgpevd5XRFduGpe4eT7t+/0e2a8YVepdvBAU4C7dPKHiO3mEsmgnzc0CDtgWk+F25X6ASgnaeg5sGaihuSu5uO4piEdUTDZJt7u5OQ8ySg+9epveNjIA+F0Tc5+AmqJUn6xoljEB5TsvzEzIsmixG8RDnUtMzyw1SzOPREWY1imAS6O2eABslgY1OYv+X4EITmnIFifLDKIKxWAKMwnhjekOKQ2mmmFqz9RC54C0mzQe58logUbrSK3SBgvu4GbKrm1AodBlfTQS/EfKzmxGFML5K2prFfToL7YI28zQKRa+AnX2tUhK7n42HZoRuRXaY1eZCUmEcwDWwl0fnlfxc3OTZlZ87pghMA5IfInj55t6UMa1pQJXN0KnpqTDh5lpfRTcdwT7W1sDGrfX+47REC3xiyU7kMvxklll++muyebUsCFCoLlGwl6T3Zk9rBXxf+DGZxmGXXta5avHgC1CDRfSPHsV4aeqaIZZfRIiroDXTJe6QSZY5TGqKmNCWhQVmRhuxHhugUIDkcnjHPkcHLt+pS8mCvB+d2yaXVNZoD5YVmeSRvzWZndiUIe0oYyCtOeTdoRPZR1WBH1KmkFdl4Ioc4Bq8bnPlkyJenWB8SH3HpZVV1iyvIywsC5BvjpSec3UHsW4LICzgzIvTJ3r2DJM32UCDbpilrGkNktNsbiRkD8Cg91p9lwtkoC+zqml9FDsChbGApEXM/cyE+yaXJdd9hxbwSIeWOqsFH8aKF9DXYGBvvIIBirN2gjFhXHUdvAzRtf6j9g4Y0m+k1z9zl8OCCsfTECPiHQtEbckpp1YCRb3h3dSSO3cBsvylN2e1ovLJ3c6sVFdtLBNTc0eMjZXok7mJSqetLF0xPt1nUhKeGkxP4BeNQ1DnPolZjHFtzrGEISIm96RcfUFKJboy3oQaFXKy5EXIfQclDtloQHBmjm+K0dZH8ruZqnVgGA2Nw9bCt2os20BPWRaAiEDsrWTaDglYM5QaTnjzNsS++4poT6yv6eVrKfOG2YA2qL6ial+Ukr1Eyx6APoSxoSNBYPqsRmqveehI1d/GrzndE3AjpqfZBX3pOlDIoWYIoXmQCxc2f5SirBi8+JlQX40QvWc9kgxnCnz1zAVWOu8Wool7WHm+m4MQakGGRzHK2wKr3g6Or82mZQDVKEAkqeQ24qtWFx1iAfMbzyhpWSjAD/+iQgahS8hvuZs6Ml+Z4u2Ztf/pUCIsVCbzEexxsZOHkAJfkU4qgRnZlIUyOhl5xVeWKWKPECN9US2SefobkGRuWWLafhLnaWgaCqCShrpiRjxkhOOkyEe8gvheH3xNAj5yZtGJmWSmWwRKPlvsuOLeTEl12MLQIV5d96UBlKc14UMF7wnRoQoA4A1s6bHHt4MAlsSeg5d/bwL9Ot4KznCyBkiXmJFFVjE9P6oiYEhYRMUlpi2Af65j3N3umrAV93928pbPwTQ3LupH4rFBAT5mjQJyY+mRmxNOXWWSZS3tMvPcRwuHa6E7bhMLNuoSZs+XF/by1MeAJ3osnahapA1MWlPzy9t+X4/LZnXKBCa6UayEZzy1XkkEs6lcHIo4fubeqXhEWGw/RJjuwQnM8xypwhdKAPGXaWum/z0kxgQ8j2DMELo+OCtj/ACLnDkMDBb77tjjwvQPcXi7QCrX1DYDjQ/laEpHkEYMzn+tMU2vrXDG9o4i6S9Tey8pgcOm2XxDVoiHLmuSEL8/GrNkitVwczZFNzLcpgiKKfIoMjpUSvOqVI18ZqymwEgMhIR3aqWd4lno0XP3wI0Zg2Rgl73QTDidSTCzMTFZGeCSfJo0omqDWmg5NMtDBpCqXMl4YQp1O9qwZiskGh372Qk+oR5l6Y2gI7NLiL8Ays8ItgkW3SJgk0nX+8aXYHdhRSGsuFXtG5VU9a4Huw8tu379psegOVfGjxHrYy1uY+d5MGcERg748/H++fWJBASRvQAwg3Sfkr/hwV257rDXsjMeepfJ/W5HitXaksM9wwHmoHQxZMKXHOH0syGj3nxHwJ24lfiz5HAs2U/6V/02tqwWUoFFBH1GHKyuSeLZTvdhUxx4DYLaRBUdoCvT7Wqa516i56Ws6i+eYWNW83JWquPlyTgL7lRK0Mfxf8NvyiBX8bwJV1ooVtwMwQW7mA7LOeymXZUj30x8cEOsLhOyRl5/smubHixgH9v8+736GS8bnKgrMZynbXxPKYuHCRjipLGJ0cxikxlGB6fsZ1T5L94dnLpWOUK+Vi+ciI9ry7voEvQSODFelQa9yNfVOHvJBlLjXGqPtaS+P/PBl/u5jxydZvz26ImGJiKh2yqn4wsvoJCAIBkpQboR2FdKHWTXiKYx6H8HT/aP6SYWt/JiBbiLBMIgSJ1IjszQ6WL5AC9qCjC3mEC9Jxuwo4GeAGl1ZsMBpFHI2wvEZubR4Iqstcnh4cY/Lj5dpfc5j41n/zCxb4oiNCMsFhAG4PvTSfvJDu/4UYEowGAp4zMiqZHoDaSjzal7xrAfskXPGspYy/Hoo+GfIpm++gSQhH6C1zNxnFyqUa2m1kXK3CsogKijLndUzrbEWghvVG/4ShU4ShWeJPKXILCSWv4aD8euRVKvCHXTjSlKcfeMUm44pnrXzbEKNaBzOJwK14SRSN5ZO587+k+e0vk7w09NgMc5EwlC6BC1sLlWErzyF3+YmnXVanRpD1duFIdmQ5uVqy2bD2v0Ex3zbiz0XL0JMCtTSsrzZCCmkVTn10HHfrs9Sfarzs+fT9KlhxFcnM6ywbIgMV/R46SIiBTyLEV0FVlHU9GnrBacY5puoXGc0CVjLp9IEqaFvJytbM1Id2rCHP61hZXeaZhIWAwgIMYCM+cBmWNCc7IU8i4kQNcVRyoqSzv12rhetN+jN6tUk+opd8oTAGFFZ83wgpUzBayi43vw2qys9PndziKcUS4XZZKFd4NOsxO/TWFh4vl/mJUU7NqxEPIqVB9CQAEDPSyMgx/OPU4LV6jkFVuJ72t7tx4ZJraEEOQXTe+OsPV2SDCb/nrwozjMU8A71otoJK024heckTvMy9xkYO1vXTtQnjuc0R87h+GBl8lvsct8B6DoMRB7Ig7fLMcqB2CBq6CPz8uzXn5PP27sSu88vO7wV+ukDHwtlHI9LcGhIwVc1LizMGMJ+BIcsWFG7mkfW+fbMj+KKdwSYoUXf+Zm7RnW7Lpn6ZOr3D2CA/LTN+dPQ9dW4ilGziugmMXlwFL+FBPlBoRLDMADiWYVaB7BsXoNtXeRHF7aSHYSG5W5iXLTKlY+usdDQqROzW/reBkcNYHGuC8+XtCV+sbvGyIKEP1FAd75px6N1UGQRU+8jriSGRjIypJnCa36QM6vAVL9MMLhFH+16K1PIcQQvvoUBQGpfMDQEBf6/EVEgoYP8aZ2jAF3zeiiTAOf216LCJ2dpmBZo/3Ly75XI+YciVD6gLt4tDijeAFFQ0LVeC/oPtQh0DZkdROWXPzUhf/5K8l48mBfe3+Sowo+SjaTARz3XJqwvp0kdEFRMYUbapplFECoJTIUtAJZMAfyT7RDvNoKpE2VnU4APESfZmGsQr0z+eOvLxzCgkIXho28/b289kpGd/3aXHUObMg+Zfz3+csburHwr1HnrTQubso75LRUlJXi7QpErEKyJ5cHy1Ji1sSTqGZpkwB0/Enu1IwuqnBPpM4GC1uVuqKDh7Q1WGJ0YQqdN8mtdjYzl4g3e4OhxvVgBerevGL1VSqCP7yG4JDEP8c1o1Wq9M3xxf8/SRpaN8CS6WKFXjdj3NeflW9rjUWmZdXs92G7a4vgh/Uhk1L+CygJgpi8DKZxlu452MW1xhisyZY9edbzXlVVaRHTGGCE4MTBU1Lplpuo5xa/9Iyde4rzWeJRMcQWtGL34vUA9lprwA2jW1XA0439e2yQKoREEWgzuZXBDVJ7HHagAN+661PwEIkDQcORwaGCGqDNbIenJ0VxxkKnGAYNorCcQJ/0mtCGuE2PvKAgYZrdx111L1hRDXdgHQuPh5+X5zpbhUlY+c/Tt9ePI9AQhRMhrdiqWX5w6vDQcYF/oNK+QeX798tYGAmpAclkUURGPiiGueENyQl4ApJqSFSYGKW33C7kJgLpwc9IfgQztIk1HWWEtTynqoQPZjIKMnTBmHY0doPmRfBsxXlTjatyPynDj/HT2AkoSS3eQTbIsRpZWqY04Sb81IlDZ5i/uGiTK6CZuQQ+U+8dhRZYYzNm3+zZeTegORnKzlNSUrmQRt+xoihYbFe6/B7YJBJkd+4RVHqxBCIJmHo5K5SwvPVgejH+xv8hBJ4bT9uqnVRNIy4s3CZonlLM6k5B76hqrEY0RlqsajJZXB3bmtg0iCQ2jyoHUCaBBgyNT33tARfuKhjKUCW1DNqhJ/CCc8EA2udUhtXaqFRnTka20xeS4aaP/tRVjoltYyruY7cJZrUZY/4Yz4CnvOpH5pQMXjr7///t0BDa9/kB6KRTL+i18iQgO7JYwocxciyI3Yg1+vVBf67+UCEgWaPmQGRkSGhERB2pl1iwY1yuz1Y9spRCYUS0OePl54pqbqlRP0DHmUlARRGsjN9e0uBjHLRXwDUEuMDB4JT60BeZxaUj/xEe/bTTUKMb5CAgg1h+zEIxx1/O1DBwdQROvWUOJpnWZ6eZZDof+ts84oh9yZmQReP7SGVJwj3okQCd6kmhG6tBmaez6SMdyBdQ2vkUmR/RFvrOhuWW4eoF7NgiAJDVbaezsLHqkvgyccD7gxjsArpNYFWWlCEnh/79nZrfEQFbIv8/6r6WPAij39tFd5G2UHSeSOGpOlTdseKkFoButOKA3ds7eFQypYIMIP3piUrm1JifZ8FRYsF8LbS8UZDZLvBgpO/68OHjr7O19Na02sy18Ls3PjVOlG6VQDCyIU+jZLju3C+F6ZkS84QKqG+MWefgvo5xeN4mfnS+VcJdK4Fd61uPFIHP1uV1e7EIJMVoUYXqs1Jx2IoLxa43pCSSe/Wo+/g30W0liPRR26wH8JddlGD/bjQAV6bWd0vVItwhpcrYSCkumFyBQtnARbmknsXd+1lQuIh+HyC+HnxLoensFltJkQ4sYIJvc+N3cigTz79OkzLkjN0/o80VedlA1Y4Mgqr688nfTTl0+fsY2qHfvxwQq0v/7bX5yZFZaxZ9kfecmtrMaroio9VKyMh4CrueiqHLlT2JGb4wkt0JgKUOYn6eXYyMjeD6ab5yRYv60e5W07P2icL7g+SdqXDOY4hAOoiJs4yFKpdLVRIZuIHZuMCNwlh8QMds0hZEboh8BoKzknUX8OxHUjlbIKecyTZ7Q6EKzTFNBaJyAH9M0AsEY7ZM+IoCLHyYyLTjWgOXTqV+94JfJQibqb6yaclQbWkTsEEOSzxcC/1Z9lgmF27ahxBGNBe4w3CveH3lGPAnHHA1zpHJ7RddBuULXsk3itq3/3DOzwvty2KZdVGskBk5zZxlEJANlpXb95HUTPYwS1XDLcJ0A9JKQoEtizMAIytmdKK+YVOOWl61If/p9zeUwKiQHsHN5KVWL49On285fPt398v3p4sueb/KUcNHTwIkK4O1fMgxGUecSYMISOflgMYZFx84Nt7c4IiI82PQ3WqvdOUVb0McDyWTNfQbMRElOlpucfrT59+rjTgRyi8fHHpVPXToz9nCf6KxnjR4Wf0out49QjMeDU7nRUxuK0rtLirUzJwwncIt3h0nStQNolD3CwwK9b2M2Wgou394fHB2O4mx+3F1fXTI/wTj6qOuoQxwv2lS6FBPtgOEa5jYMPNBLek6Jsv/o5OXVP0asScrG2OOGPwhc0c5KkI+EyPNsbw7pslVlTyOpI2Q/rZKyog1AEOfe340ANsck3bWuUyfiKIsSTjgTLEhrpFl8/OIPw1VKHx59PeGvtfPMHVRiCw4yV0XNjt/D71p/MjGsXwcgFHWhAYs5ftUZs+7FpyTJiBmdgxVxcrFPf8i3t+INdRS7sayLJqMUbhT154L2p4ORh5pJFs3tgqzOXFaL38quvGL0uWJSvUrYQSM2syRbNKlz9GQ3JjihomMTHVj+coMM3tCk0+uGTEC/jCA/cQVXk7sbjnoRmwtx5k4EdL2NNNePi1iJP4BUEYIn2CJGuYSb1/HKNvBrl7QZoQ1ljodT54/Xy5opj+tItG2/Me8Oag9y8iFytVrDXy0oIlU89O1QN058+l5Uk//ef9/dKs/cWg3le6+PDE3+6vf78+fNXhXtKl114+sWNEcHlaSFhsoUumGnrTkidcWVrCYL9ywP4Rp4spSygk0wkWs25ekof5eM8D0e+zRRBSEaeQnyzhDmBkkEbXmYeb9+/N+FloY5Y1tRvTxShfvKuuUaznKP0GM1ZFCKp41dtKWjiXXlIiqhxBHjRhU/Inz59juxcuh77N0iWzG5ABnUprcjUi8mQOxPPPpfHzEDrtNcuga0zCpKoG8EHuIS6hsZb+5RJNe750QaZarlXrqhuhCQ9oVpTB2dbW2wpsN8aioIP+F8B+oNTYLKfyqT8SoRwBwsHAvtDRPFb8QdV5BP7eNx0/Qn0HkNJYkAjkDNsRlbWU8Gryg/DIVtOruTVgOVNrZVwJg16TBZQL6VIBjoIIesTmiRLkQoSbj/deqb5l39+Z1vfrCb5ee+wzczCqzqScpkaHN/X/1ArCQbyfiZl6RJ3blUVNb05NtPeLJ/gyX+QWNKv1GAIwO+0qhmMiRMSltyFNq3UwrKRq3CVQTpZRKJk9mJoi+JSheoiKxK3ZvelRdi+zplBD0rdR35GR+1nptqlOKSMzMOQEi1RsC4BiD4yxc6yxAkDt9PXOxqVK8p8pYlOaCqwgPvwtbFpiUcY722HlKjgMwFv2pdqDKdIKeXhzTg/hjnpliIKmlFoSy8xzADBAr6juMMU5DRVMLqGQvXdsKWHChHiUQiq21+jJ81twbuGhpWCEEEAh5C9HydbMsHu9Z3mhaqqyZRtZkNFPgtewAhBffvUOe/X1zfHcJL9NbtgMyeVuOJsy7lEMEnKC9FbzQrvstTUWy68usEGATmtJAlaHEPe4DZQ5uuZdScc0AsKc8GMay5KLWTrM/Vf4vFhV+7cU9ZRIAzWFfJw3KJybJqxckxqALexQquvxL4Gyz6RVuT1En9vid90VKmU+f12JxWuIl5zuWuiSEkOGyF3wJpHBgr5ZObVpHrgn3bmybaG4cbtECgJcy2hkXFzK/5h1IXM6Xw55k9rYFxT4tlWYKBw7omiv0KXZ0rYNDLNM1n7LW7OhI4Ew1n7SZ6n1zefv/z+F/agt083nz59+kKKhSGPnjj98PXTjcULgKZpq2pAOnekV2GAodeI3EcE6xnYD6+G+JXvmm3ie5wh32jCorlD2VOEQRYSyu69s1o2t9GbgItfGas/JAGK0ClPDs9z4x/f775//fr1ymDj9KP11A2oTAmk0iKHe9FSlv3h1HSjHNlNRKc7667aFqKzDZbtQyb3DrdAaCjrFOH7RmOdKeSixkZ6RI2OcI1yv1NoS8by9/Kp6j95WF6AFTbnP5R11AQKOHFoxhJd3qLnwY3Pdxi7ldRyV7DfOvjYYCeX14bUihjoJQFZTgIw4nEP52yAQY88mszlN8ZnH5wsWUWYUkh/CmU1wmO2p8GqIqUi3gqb5vFjyoeDAngOE50pXesRL7/OGtqYyfTAB8LV3mLLl7h10VI6ojbuYLPjKKLoFMkhQa+cL7dPjQdGW4G6R2nJRRSyLGJRdXh4bD1N51/w3WZjlb0SbvdrIC1m9w3Q+i1sC7xxn/WbELW94NOtB1SctK+iVK4jg6p0uKS6jT/6ZxKWq2VETBQilqcXuklTmcwlpaH0yc6PzhiJJUzVywgGbIslGTMjT00oIOrDNhpb+EOqjLRxsFSnF+GUbTGaOSmZ6Zaa3p4EsJ7qzkGQsAPQP75cymmAetHHaGfCc3tPEKM4nEtNiNo8r85dplg5S2OBNq5ecUetkY32W9hht9vj8/Wt9U6t+hD20GA5FutgQuAGVWGQIINc/VIRn3n7cXNy0zQvq00BpIL5qh9knz9QA8v01eCFeiztuBIGpR33d6JLubOfV9emX7JefiZkPT8+ksVSpJbJOxHWcAEB8B0lWq11JG22g8EZVbgx4p4xKV0Vm84V1LyEq7o+Ub8y+EEPa2zaINmDXKC9hSK6phGeB19Yj5bcFUhYConEJWvmkOlCGxKbQqsTJjYPoevMgr20SKsg8bOHr/1oiJMQOiqOAnzkGlTLOjSZzwwCE0oRqBJPDrA6OxXiAqcuyyKpOtdKGcZS2CPSAy75MF0YhMDmIqi25k3dSfj6gIwKHBVqW0KaOwB6JeOKX/KGy48dJYfXKm/+1/4U3YjSxc6gZSHy4kQ+yVBNTr+0i3nrQYVSr7bFha02JAHTa1vkTq6df3veCUJ2wDWFzmwwStQliCw5A+8vIGthhHyLIfKRomQyT5QSQ6BwsMQB+WfrYUkGmYFqmx3KADBLtomynE8m1SjNJ0RtGQmle5CejPn6+rrqYdBreWKrFB2IY7iNOsNoaCTHkvsde0Fog8kjYnoPm9xIxQ1oPp54BKlGtMYe5FZoYwTqlhx14F19lkejFWzwvYwvheQLrhlPceAC2mdCWqXeOU0Ptk1lVK+e3NQ9gcgrTbQkxapR7hMbQbZVYSUMco7uKSpJNWmuspnwWXU7oggJFtvPFLyd3j180zQgIO3IQp44F6RXF9MsqyxarsXqCnQPlbJVd9uR4FW8YZbZw8JPGmn6p1VMNYIEyrQHJfilXIVZAingLdWtqubORgwWT5XquIFuUHkiSTAOkI9cX57/5fevf/3++J9/fL/99ufZtz/fHuQtyVG/buEuLMXNAI6w4VDGHktEEaDrTaDQlc9FU9736ev1bdtHFXKarQ0vgWIA5N8RkKJFqkXfGKgEdPFswdDL+aNVgDw4uR7+VYI/vSMYvgTcRjlBo2yew8vkmyRLH++tY1652J4Af4Ef6/bi+A5rq/x4vAqQao+mJ5wB8ePEHIr5AE9yKRu+uHY1QOmoeaeQZQZB1IspteolTEKDfCDjaRFdl6lrVEv4Vat8dWKuNSHGAsmwOmQOB0wq+ElCWqZc9YJkWbWJvCzBA4jZRjBUgacCtE/DOO7UHEDGmvBZXEglBLY/wIuB0Cr7znzR1M6phi3cmwhEgG93320puvl0ywDwwT/FuspEXj0z8l0X8O7x/OK33746gEs7lIK3yLIyYXWkhq/ZkrP9Os9ILz6IMdjVkFkzpYfIzKEik9Op9YJklG3c4IrAqfwOnaBpll4tLWh8NT/jZJJHnZKIa2lKyzGY7+2Ap5V0XOz2BoRJijkdI/3WngJEvppwpJU2DRE+XjBT7n6ccdjWf6aCwuy0LQsUX//2LhKi7s6u2xCnBfbHpvROKdYZeUYOc038HFiOaWyTN7FgUulf/buTvfKvkR2REC+nxq1g2DFkwIAJl0jYNZZIiaM08NgAz5aK7gVLSN2YSS+LVa0Fcow7S3C/4CW3StU7GNwcsqGnnwWQ6tsHGUu3yq2ovTUQoSyV9bPWGwRLeXASvY3JGh9TYlX8EiukA1yMiVfyNMy60H8ZnazV0UxvngajHF9IxmSmUcUxLZcPBYttTDnk5osj0aHf0j0BRl5YCLTAYkdclECb1cFVMqMLZLE3MIFSi87IXt8NOkyk4lIoZbk0dXpuWocSiCYc6CWBzJ3a6+Ye+hmCI1LbSMKvvpk3gcHDggc/gmXbwpNw8zL0beWbADCTY7iErnzifzE9KVGhZ5I8PrtAYkw4ICg6qglUjaFHTdW6IW5WHaBSPNPmt80UeLya8C0LNxOyCXwAuFxyXc7gXFMDnanZdHnEElBmB+fxBoxmVVmLj3+Jjri6qB69DPh8MW4Laz7NLBQlnCV4I/uvOCxUuCkzhvwuCu9SubsOwIX3BNl4PeLaa1T/9OFmt/ha+AnxCRYgKBvkSvLXGscvp2r+JBhtDq3/c3Maffnw9GC/zOnV0/mP63a291D1FqSQqvuSG3oo04vZrayNNoYB5iW03vekeEfXVllp3US5KaRenm7SryKtPqM750ugpydcXfpyalOa0w0IixxJqXV6MDp5YS3bc1JDWCcd8acRp2TGddphZSnrGCAfQZnRQrwXmWK5vhTQxjTtpIp8kLdpz9y7VXxpjXPVYI9IJB7TuRs15MMVIiCUxWU5HpWzaLI7xMbEuRlqEO0uw2Q30pxxnJ9aRDD7/v79u9D357c/PfiH7+Z4frSX4e5Pr3/+yWQVAT0VVHb5HPblNyXJLSAoFWKdzBM5etGoyOEUc+GMPIM9nnQQpjNiy46iELfyHCLlbDIOKnGPj3NghUgn+Tn3YGBUbCz9bynqISb2QL455/GilQ1cMgI+UsCAiRaGCuDFSCqcYuwQZHmtN2AEtDikbgyvd3801lnONPfceT7aB6w8w/DNjwaPlBT7Pk+xGvciCV8juOhbSo6z/QBW5aFy1TDEelsfd0UY0f7DfC355Kx+RE/1kIaTiNdDH7m2DcxWyl9jA5ULatHc69fkqqqqW2mli4Ea3fAnMakYbY2WAkXLGDBePsa1SJn7Eb5f/MqdsIZHFj/7/yC/I3QBRmnaKDYJFWcR6vtmsH1Au/7Fhc/sm+KNBC+44TW54KK5QQYgEl1cW/DT6l5tvb7a0nD/Senq6yfC6bMeTseGW+Cgvda3c7BCNpR0QJu8m7CLhEZLk1rVPU3rP4c/hvCNjOmirxzyQpJCHqHRR3e7kkv4EY0FEp9lhvlwsqRov/oI3LsYPUYembqIWbWj4o834MlaD4272F/izqZtu5O8qVfwyEYn0hElJtt6ncPxUWqleV3jAAkcRGTVrKqVESHy03O5CZ0s4k+o6OX/hILrSbWKlrQk4nzVo2B0nRpjh9R6VfjSMsIRAc21lC4U2Zr5DJkrcssxSIxQ3EV2vF1NUBsV9Km4e0QG71fP6kFPd39+//t//tff//N//uNvf39+ePS5gW6DrcMg1EB4WOmEdEl8RkRn4RmfcGUSRIh2lehunC1x8eHGZJ9HsfegOuPpdlByNCEAonSrv/TiHmx3v2uz0Y6+ka5xXam3wwyt4zjx2MiKT+x5ycvqyL2Xhr7cP4b1Ulieu+XoPZZ5qMLQhlDVjZtlcRm9kI5xHpWnkSq1O0ZDjDdLcalk0okpQX4BwOqVIJdkMjBx8XzTkLohS0bZNgKNMYNSHy+WMxtmNMmd5RCVSWdCZ57yb9ssAI7azGYIcgp/D12QpPdNPvgML0qHOuBdDudYiqqFBsWKM2SYZ+4gHddY8cUH6riEoxc+vYodooKTuNXzBCN3iCL3/JNfEHKYCfz//o+//fnHN3e//vjdwcKnnz4xFxQzDsaXr4UDYMvkgaNTLD5rqEUuXlhqDdIE6QIKTseGf5u0KIdtYQmrUbcVMFtkYns1Btl4dbcXZ7x47NcwcGDI5cJt8uVMNM5KKjThr2zLjZkyENcC8dpx6Gt4JgXbLl8kkO9MPhV6+bH4miTW6laqIC/oB8S5N5qxr2WZXwqzrsDZGBLYTvFSaWAu28zcvq7+AEEUOipFMEYvxnsVRRIcY0WwkWC2HRZl6JjlfdSgfZ8fdDKdZQ7ubQqP4yPDBVKZzkqynKjF2LDSWPvIPTshBT1l+gq1SFeNMX4sV24GtQNLwsc81JDTt80EA+v+Ih7Vhc3Qu6/SIUMFvkBk1uvDsJIssko5XQaKJC46mxA8TqpjZR9UUHzP9CV1uzwBYBm/PEtysGAwVHh7/+QJTfCpRQoXPwBJI8WTQOFHEYWNrbVjRBwujMhsbKZo9E3neo+60YvEsfnCdy3oUptddQXNG+3lAzA+n+p/5S0czph1tQFNpkWTGdCmAFx2OLXpCwAf4BtMJRwmzV8ptXU+GsloNC2cigI+hEEO0wThbGpuRdqNgPhXNvDuwctsqPn8iXXyYbiTNNOru2J69mMFpg79UmxHnVDdaC4nTLgxIe5WaKYoAxjq7PMmA7pAb1r5F5s+wHbEyAiIaPlzyhm+bQaBkFqJ26gdSnwHB3/88+H+rlKMR5oYojkxpZIWMrIrakHVgVoYLBmB7Bb1CF7vPy9vIeT7l9vzv3y5/XpzZlrq5tIZap73+2oh3c1Vs+JskpgOzxxDWVwsVquQ7ws6PZ4aDP+46BF0pFZogaRD5QyVmk7kK/oPmisbPb2A1vy2eCwr8LFHmBXfIIuSI1n7ykhVLYppUaQDO0kNy911+KlVKS336ylsOgiI1MeeX5QrGS0Zcjk9ybAFITQflVSPuCdQ+KAdOfqs9V0WL+hlAOUStoxlh1hGFZIM0hVwhRu0ucI31eraw3Rmw6OzA8WfBrzxkFtKlJoQDtcyvHZC+fxV3FtQilDyG35lHCVkoohJierspYOVa1r7D5I80YYRgipCVPvhyfd3d9+/fTMsMK2kDKVSqYhsHNpMQOiPPFIuJqGhwjfsKhtSKnVmqlJGbGaBtLrnAcyfmIjlUMbWfJublmb6hLFqMCTebgaab0RmmygH2GBbB8pKOIVfRwv41Qhz9/+/jMY39FEiLzfSSNjtPwZbobm6P5aD8QZo+VVw5p5+ZLrThFNwm0HB3pweXmGvcYpPUFiPYXFk2+fgIBOfh5yr+uVr3YgzFSOL5z4V8CqZ0OQUUDCIHktiFPw2UJXnSZuIh7vl2YiPsanWlflBP7pAE8hkN8QPOnxUmi5+Sr7KE0oRWYQrERQdTdIZdmQH/mpGtiOfIpglgnxlEwDAghjSGMKntcmNq7iJ6HJypziIwAkrDorT6GIErYdMjlpQ4OFbBBDJegj7Xe1X3XpNGyh0zPXHTlPhj0Lr2YcvEgOjBZxrVoKTk7XXWj/Oj7MfhXQadHM3U9UC1iGM2Oph2rw+nGo8yGP5KCtT6DUOfbEu3mExRLnpAevpSiIaEuYj9I0VknQvy5d48DrH8LV/pfhHRMm9lALlLfPQ0IZSlWWRWmbi0w1EtdHoVq1JvOhUMr9D/R/fv9/Jopym5joCxoWXVkGGlXx0pIFCI1mnOKpLzwOZSQ9AGVrNuvSDPjVYgiJxrS34Ii6BpNEDAwk/TbuxykDWQ0XEkjrnt3Hjw5bOjLNcr7znV66dLuUZDUhOn64tOyjDPft0ffv71988697GqDu64wFwVlzRWQOqOkRH8U/NxMJdZxyRD7uzMvP93YMovn66/MuX66+3518tp1TdM/dvWY5Q4X8bsjgJQiKceWOh8yimosXv6GWi2pYqvdhthVd8LURp5BgZbXgrfewA1PCUuXI0pAn0CNYoTicS/ZBsebOfU1mdHvp0Pf2rOYYIv9bjkRdwS24xZaJzCy9Vv2+ub8mNOREv9yErhqFWUXX95WXnpwVQ2NElsux7kIgIABJcWJTwUGCC9BBXup26j2EcNujl7NSm5CTpwty7OFlcFxifnMDco1EyGx8Wj9ZbrLrT5IxwYZtwQagBuOv058qx4eFkVrPK37065gJjvLdMsCUMllTaAPL1L3/9/d//4z++/v719taovSfXaIfQjrIMJnUN7X3La1ORQwsMaCxRfHhgy8WG+qsKEVT1RARnuEAe6Ne2i0YhnZjKu1RkF5P1X2hECVK5/2Uno3hRs/A4c98F05QLm7oopSLipAUH3BR2VafmlugVJ/c5bAF13UgXe5xYEm/Q/qO5Dc0mGXNZSYpZ+6fVcjgXB2kVkXFZUYIa2xYB310yWlJDQvTws2qOOR2faIbIVIGKGeFm6OCd4gMfw4I8wOCTsQauR18+CXNHa8Fk+XgSqSwawVwVEdgk0so0rSDExjC0pMarAKAvg2RdBXOlk+12jiz+08oKYGrQClWYLwfQf/lKaU25ltXGFb8ipkgwz8kGEyz68GYVCk+RvUtV3FfZwcsSCS4nMEEo3SlRFO21JKMKLMJkKyNffxqQn7x9g4Nfvtx+/nzrUm3yTwQSiKV83eODlBUBKiiOymsVjStdV/kXyLkr4/G/nhYB5IFBagdVAf2q7a7bQibT6Zvt8KF8bXFLbG4gpaOqIYizlmF+iG9Nh+YCkSGZXyKxSNCYrCjFVuB5gzBwSzUM3XBRb61iEgmUXr8/CHUKCHIsV+DGA8+JAKeZdHTlkdok0dReKEthx+hKTDVK0M9G0TtW5AABAABJREFUut1nlDKraoaPOXiPJndn8kHNbHRjEQFjys9s1KXbRF1vpJnJkiF7pDvjDjeHw7EXYa7J7ulhZ09Z1fL50+3/63/7d6dHSf5f//t/sou//PaFt9y3WMTEPpxkAMQJaIoBau8E1kJO+8Cvzh2XfHtx9vunqy83/l4oBDGcUg1/m3F5cQ/xInT2xeZwhJwsp48lCX3md5Q1YTcDpmuzxKmP3KRzeekyXW9Y88VPOyCvtUCSTTsdT6y6vjn8jLKSSvjLzEJFLxiYzxuMnl0CaIzQodqeF8tCnqKYuEJLaObri+VhFFxqszsKd3Dc6dltqg1si9MlxjLulWfewXB36BpP76SnD2OI1m2QYDEkNjW+sV9ZV+ow9TWHLwCoYjM7nv/weM8xssYGWC7KcXXMVtxPrbwdSPW4KZUZjarZ12rG5qf/v3z8hGzMvJ/c+h23CPrzjz8tKkeE2v7nT59/twLg8xf4biWJiNfANc+JSn+ZNg6hBRKP9S2GQnf33//48w/HkOnFqOEk1/7wdCGnKHiwOlAr20KbUIGv2Y2DJjpDEm3k01W6acorlDS9zgfw5MXCqSPVrL5GnYGgvQjBeL6ZvLKusFVrYpC7iMMN2pSjOTohZzWOkVdenXnWyUXo/3L2wn60Xx0m2Ony/PpXRsUCM8ZWmhtf+kVaiQcNMUCtuZAJedEP8EwsvKFz1oxW1Raam6AgHsZoff+gOiCfDUZbWCU11Zpuvc1umL7IyiR642HW4mj+rSefx30JTX9nUN1l4EKJrim6Gj+hBwnlNQ3cGM1gKkqK3i4BS6VylrXZ9Ohno8PSoZytdjUOGzb3IRL4zIRpTuOC4M2XoQaYmWLK/VM07eVjuwo7CRT/XeeM0oK634g+Kf14bS9b83KBhyQIjTNPrXSXy2sQERvY6Qac/JRkax/7+kdUUwVVS/xkWgQekKS+2RERYEDa5FeBzoCJ8QAO1xblkkONkJxSpHViJtTy4Q2sfa6N9bLiZfPVLjYoTRgLSy50r6uEyQb0TCNeIoNXS790y/kJ+/vdT6N7/n72mLwaCFgGNqvwAL0jD4gq1DXyHxony1CJGfuKzcRZxWnltTfLhXXDZ6FvgEnzh0R8Sie/DNINIZofScYlGJr1Z0KbPHC3V9Ie+BCf7oS8YCSfEnU/2Afwv304e3o/vX/y3HU0Ob9M+tDCdmbdKhZh3+X03FCEj2aEbbYx+3N98fXq8uvNxZfry08YVbTPQeVHlnugKGclbv27t7hq6DGdYycdRnEXYTkxRGhmpH3pT5EAzoV3TWANAorW5C6ydRhzq4AsZS+3A1C3lK4W1ENijY2R0AY54tn4YNTjBfTdnF6+Xpk/kMViT+8MWfkkNZ28VAWxDt5LlDh94l0zk4+fP31CB2OmNQscbl5vpMFVwo34e2q8q+KGhUMmVzJFf4GzLl2gF9mwM3HEGCoiA5dTGnHylM5XwI5cvUWMlxKNKhW+JzsrgrQOtTVrIBr2J0QL2/MfopaNKaoH+04ua82TDzw5wcytgCCXhLMdcCHjA+j645wtOjL0uFST4piVfQIammd3pxcO4NW94xI2U8sOXm0uYHTkzUkCuYKq56u+oujysmoJ3mi9REZIlbbuQDM/2Ysc6oDj9DXIZWLayToYOGLpiL7aD+qX8B6DQA0QNOiUrcRzgK4FMqVy917oFraKKJlReTZ41KBr6/HADEZ3PGxHnngpqcdjl3MBU8aokgugSZ/y2tTcw2oMWWxpSZm5GpQndyu6sAyqNuepaKYCAZTyWHjXodxZ0bE1UmZMBXcqqvZDgRY0RHdBj/P4n2U1WmzskiNFkbS0qeDWzxh1kQBMyaN115JfOcaWYyHHktynR3ymWgVSo2ywGaQxhU568jIyIFbpv47EAV00zUFwnCPlYaxluJwEIOqEj+Aun+MutGyKmJU34eFi4qyUzU77KmGV21ZIaQxEoIKuppRNuQZbI5B3YYdw8uwPFq68/PPbNwzJMQwxP3262b6AhIsGtme4zSDT9ckH+YTbjTDDi3AGdcTgrXyWOWcABSTrTCBsNRibF6QpwiFFxZ+bynVQzvJSThJBWZhrDUHlooIJVEroLEEijdBFJv3YECNgQ+nOvvI0JDkWdA0SCxYoMG9JrSDMJj0P+eOh86+PqsSLTBW9QACqdSjfOpZCMTDQtoVkEqBiGRoYV2Zqgp3wt6JcCygy3hMCeOKMOO5JAWoHqrF/jEgoAgMhpzIdVitvpS27LrVeWHAFe+W2Q2FMNAnMLeqjOJxXYl8DPv90df3b58+Pf8WuQfD7//yvf9w/3lteDdCbQ0j9JcKMzNCrKVJdWOTChzpD++P1lcOenVslSLC9rMQXaE5XzhXtSiuTMYyg0I9w8M9xBmYzpIOXMj7lJzjwKo06sbzIqfxVgnCGvRlVcxtixgTiydWs50M1fcZGo9kgcTeDZTYR5W1w8ZcugvRt2oKwaKhosaqTrMCSc8nY8z3LDXwYupCqBdMMk5InglnZZNNJq1n5JuHdWCTKYUiTaBjTnh4je8Aae5MNZCdelFpBhVu30GqcNyQlnCbVEpVtg45M6drSz58hUj5mztgnaWoz18VWRBUfWv2CQCToj26qsexkfBdAB/V99+jVvePhoTwTDS0T7mVZA9Hzao+C+GzzjtP4nJJhKfdHiuygGQsh7h/ufOjiqZ4Gqm/oC+mi2evNrV80jjYsEbhXFwvhyGeqeYCJa6GFOFM1ObkgAMLqEQaUbo4JA+4BzJRoXOBVvn8qvh1yqIWAr+xMs76vh8olNZtVlVpwUN13RZm4LA/gF8lbMU0/uA1hBHCjd4ox2GWz1dmrt97fPwYY2glpSDfIZkbM3S9Q1fpdwgyUdXbiUAe7G1vSkESWxLFCb7DtxwbLrXyF/qDKJ6jF1aiOffpCKKjTEcX43K4/v8hepO3YT0A8uGPZTfB2YNFGkbretMrAsZCHf3ZXysTUrJ+JGuOAkC9Hqtf17r/DLbhVztzMAklOX0TEr/TJVXyDngSc2XoTHeA0tJT0uck1SPUtBAjAmF8hjHn4xm2xZDRmsldZTGHw9NLclv0BbElYQysEujVPXtKvw/LomP3pCF31TlZdfupGqQMvD5+W4ujdry4jt5yIH5Y/xqF23OHX7CeV7ftsI/M4r2CViNJfJZMPghCZSN5FLxZiUp1pwnfR8oqTO72mKZxrI8kSCmsZLEeJpHBVhclSV6kYmht3b00EYZbutyTcTq42FOKHHpHL6tyLRINBImvySbF3a4sLJU0b8KFj3W7siWkuoyop/2yAVphX8N86ZbpmJqVHIWsKk48rLqhe/zzz/FTBDdRkxlMeQQQzGTbJhp7kq7H5UfJv/Y36y5lNzpdOm3If9BCPJf2PT/dSB5CBF5IXIOtSIiQd4ROGko237Lb0pW1sF9RtQwqiSu9XsWRW/VqaZeKU7cjK1ZABJlhuSOch8MhLjyhG1mYysorMSx+tLEL5LM52BatBc05GK1jHYwPolgV6oAS8Ev3dwQILYI0DOHqDp+ENmSWs5z/+ELO/ff8OQr98/eyuQvrZ2aNVkn9+Y0SopEQaoURyknw/2/5Ktz0oqELP/Fs+QSsdOM9OWL4bSOj6k5wkQEa+PJsY/XYkND5nA3IVB+NG+SGEynMbw09bIqFhLMUjGftpiYOV1nICbtBwrdGHnMnv9DY/ZTr23dgx8Jkj+NCxMQ0Gxj5IZN74sW+W6wV79otLJGWaF/YfS96t2zHfdaybzLdd4wDKEMQr7z6TknnLvgmhk5Lfm6+gyAtBwFMy26cTtkakPVCwammsBNiSL9JhN/kjSA2lKjpbr82qfOYWhsAVtZ+fGLJ5hUulJ8Kl5XS49xXX0rIWDBoyGwcqhZbpImTyU25SK03izMzNpYP5I+ToYhZV3lXVtDD23tGbznBFBqq4MbmRp7ubmHKIFdrgjD6Ga4FPUYb1s4NtI0Ik09RfkaIb/VaUguZ0ai97Q5CWA5XbwncLT1GhiUiMbg1zCR7LsPWTrXNFfVbttmUPs6EDkoUBqqxfeVHPVe+E59KuninG5JPEzLyKhzoCHTZw+wFxKikgr8F6OX3ADkRa+9/nhBhnmVoVYuMmDyf8YO4ydqvUs0JO2PG0HtvqTk3oy5tx0WjdBRg+QIVCDYRcr0cPhPUhEwqISlZOHiQ5PIBxMyK7wIRGIyfZA0GXSfmkxyQ0Rn4WSRjVv7Klrm8s73wQskWDCYSzZnbbYViTLQGAARXHmLmOCRFhqMtarj2HvOSYFS3iNHhngdrvEN+euZZamGibiVWx4AozaU5uh32SsPdtRDC58EP18/7hXtEfj0ihVlLiHM7XYqgo8atEkv3UftFgkGHUYKV8KYp4b8xke4GJrytarcrw+kAIbuc8bkYrRwOUFqJIebDMscnWy6DEsC+h03nRLeciUa5HfddXJqEEu3Y2QJL3YolaU9kA82BeSb6YDx0CL5dqSqrd0pXL05c/nv7597/99//r//q//+d//eff//mPb991cVisjpw3ZYEbfYL9arisXRdazrsMjPtrEBIYGNFUcWtYQBi63uAmg3MxkmUvJFyYyA3cGMpliFoP+3hTwEBYmhcfZmO0XPDGGMv0DWylqOwr9bk/hFXoZOJyLvbGTs7brd1Im16tFQXJ9+7qCS2PFsffPdypfxAgGnisxr/98Y3n0qZfQT4oa77j5JXBgFygCigq6/WUuo5p4F0GJpi5tBtzuBqOwXd8KM9UKnljAfrAJ+jQCPPAFRoYKuPJRmU8NLUTnFSW2/+lj3IrpGE48RJNEKllckWWLzVklMsKC9GBSRlND+RrLelyqEGquzXSiOHCObEvEIUbmBkmuedzy/CNiDePk6sWaZuurSYAnZvTgOAMFxWMj1FBAxFFg7ANAVfOOn94ElRYlWascKKVQXYR8yA7nQ9n4A41wI6Sl05eCWSNc0hgvpF2vXSKKXJBeay1ER1QNrG+iMiyMgm9A25vhKxMgOc7zvuiTVu5QGlvgrbzTjtzS+bBYGJFH8eQwiflxa6u0MQES5MbeSfqDvPRBHdlmsQe1aUAjRjWghhMar7sGvSgVHPVXCj25cmV1OIuRGbcBVGDtWarg95pVlqhLcCm0oYQAjFiaEjuAN2Tnn0a6ElkfhauJhzjOdmfbKhIQQw+ZaeAw2pF5sE5OWGFHEEDNWgrPpXVI2xTvjGrViMQ0wRAbE28vfVD68KAmu55uyslgjnTnCyYpYqe0N2IoE9plT6QUBrKjxMFRGK5YUOrRFoSk4LIetAl6PKHu8dHv6LGfJPTK1wAwaUEsgNXwUzPXeSEIQw+SZ6LMxu8rb9+zbqbQGQEFEFHeU/2shEqT65mnNGykawPXSx3CUdvgr/G+F6Mv3GVsDqH7/Bm00WNhnn4jwbJSkxiZTVB+2ZMiPayrEHyhVZd0u+10oAJmNaNzkcUW8lBu50KkNLQrlfCASOkRDOcv7LPKGRVnn+JBDGaZCWaEFQRJbwW1cAlHibhEGF/yeYQKhrIzGeMxiU4xRu1DGLmLqRVBKYzTtp6HlGVwmA09rULqSBYLvD4dPft7m9/+6//53/83//nf/8fHgpJuIR2cXPdQYIMw4kOWHLcr7OmYasxx+uT1Z0ILIRdmf4xFhVrODZC9Gp8AZSUaosBJIAjq1gpRSThT8On3A6/jK5adRoPylg9y2dzp5eCZava4ggLxqzkmSsyM1dmHrjNzIoPVmZJPIwDqmYjY7YD/+mlYtGn29s8WtNvb//jf/w/3//2948f/lBnziCz8J3OLwAoD2zt+/biZZT+ppUOcXrrWWPkud51Bv1lPUAVS4MRRfHGRHXiTxNGJSit0s5DwZVcMMTeezISfX5eesCKDMAqzPem8g4MbSiB1yyoV2otthaoxjYB5IlEzWk7CMi8I2n4ljEyyRa6zDHYyMX5X4jB4M6LqHwyCrIOTaPRkvJsipiEOd7gdAvTKTe3qZmZlhpHCHFLT+ujxzXoV0rj8d5Gdwy3KIkYPoNXAuJ5CESh1XIMTWRiVfSoESuEA9cGbLVbaJnDk7I30lfKUJUiCgJCl0u0BOQEP2rgK3XTxzC71NC3Nob6P21VvmuSjSB1x2OxSVL6A8PKNliGxa5DgHu1plMwupYd7po10TkVYy+XhSg5ohv91w/C0X7KcxFEkRzIPrY82Ik7ooi6oUSRBSgou7Gw0b7TzgjUO2S+tlIkSDpWee5ccg37XWfxtrwn+56n5qvl+XU2oca5EP78LGW/uTJ1rwcVgxLiDNwfqVBqpLrQWUidpSUH2iYvMOQzo6SyC7WrkhTJIG/imUIXWcooDFBkG2poxq6JkKmQI16ynLYCuWcBwI/Shl4Hle6SQvglDWKfMW5lBZEpMfiUg7uS1RSuF4XRG446cNe56iKir10djtlQSt6/1sgbETH3vJ9ppe9m/zTBZtySDEcGnQ94kxwhItfn7Di7A/fUzRA3YcKBG2DvYPDK2GcXTBWDAgD3JtV//vHtz292099t7qs13RytMw467UM+Zb8T91/SNmDCOwYxhU5DMSLhnrRPBWUcvmCuzz/u31v43/YNPoVGPJb/BtiJMWrLS9wb/OjC1FyLSei+B/yV2FJbFwScabbQCS5JUywR5FRriUR3plKLhajy80AJYmHJPtNw5sIJlsijgWTg2YVHm5+dfr8373jqdFIfkihvQVnphjiiWds6ylGUHGz3cYxzA5g9SpkdVh9iMgI1EjCgO8iII9wto+p/WQXD1ncsS8a9yC3zbF8YV+9JyplcalstdtcCl1AjK/TxrFtHokLSkdXouLyeKOcJ/ep85Yvzz58/oddXnrzUXhXUP/ywyclg2goWfu1RZVpwI0KEIVRvOXBYoRGtQCef65/B8SMpS6czlfPImtZPSXwozjYdWEdNGMe+oOJ7Gx3rIPUiVwkkajWouzNTZGyDsA6UcQH/px4tDYWw67ZCcVzTdakePyLr9Lq/du32BE6s1qVc+NVJEle3nz5xV3uMHp8NxNWmmq1jnaRDnITNP+tJZSFMb7Sh5gKJgntJ1gJApl5Bv8wObmBA+3SWavxPlc6V6zjAnvebsIxCVwnRAsmRBI75tMa9MOx+tsWwXEwgWobC2mIcBeGsAg71cvuu9E05OH+dnRyjH8hIsoxRBjT9ayowzc5cBsaCrb4aBiQ/KUiBLd6pOe5KQ8q621muNmzHcpflWZ1tmfV09wy0PopqvhXPiyBoy/dKIioN5uHKkT+l8Jd06oit5rB7AFmcISs6yhHcW+jSi3JaScTyZ8yWzeQOhQOBfJXYciI8tjUUV14KfW2Y7KDdLQCqxV8jgChZaWHmwabCn5jz/BZ6aP+OLNmmPgCLMyKAItCNRVFFewEQER00T/idj8S8mm5dmrkYlippjXtSZPbrhumML/tuXGpiX5AglqWRHlpnx3XQj9Ls/NYhV+lDQBXA8nU3BGAK2eF7SErOv3RBGhW/OiNGSq4C1AlZZ0ayBjfxq04oa6GLVBatWZ0bJBrETk3QQNcUyTy8wpqtIGN42jHicf2CDtKglenrN3n/H3/8+Y9//lP6333VrBlYXtnLOI8HN+Js105tBjxv6ukfXz6ABs6KGEj584mQQjl+wTYNWzgLU1YFYAbcVdpkgrQIHDqQF/XzmLqsHyIwVEiFvJUYpyGjmQYOPizIiSFsLM1JxsMDoqTO9DJjT0MMFC1UxJCgmm9ZkTl+FBmT/ce//cf/8b/fOxvCfrN//HGvSnJ1cWUGbJ4l+bSuuLl0Luij+dSWX8u96QX7HdbXUwT0wxoVmVyc7o/knsMZHkFGI6FIrgXmQ3pvH8R7MbUZZGR3EzaYiP+MlsKHIAK1dZsR8gL1fdRDMLT0x4vZbIxqyFE2RML2VQ5TMc5OmSstlCb+t//Pf3Mo2z//8YcsivYNopk7G9CpK8Kz9jMa6LT8gQbYZnOQ0VBfRMN90c9v/M4gs1WDnWOALhJW6Wg9Yjlcrwr7GUy1ovQJ1D0zMzd9akJO2BLPPzo/j3+SAXTAFzMDC8yNmKzm0LFvj4ncOanBFBDP/qzKRy4iLm4+AYp0Ltig3mGTcGo73d1rWYO0u2nAKptW3Fl2Qsh52raoNTPeQCTLKBnHGgbol4JpnVeQZlBX5qgTO8WeS3U3N8UZ0QBAEaAvgvLCiFkabXA21gzp5LdZpoxR1bLz6ZYCikJF3Yb3WOZIOVWkkWo9MSyfqK2gwUgATBjwUIy7EAODj+vhgJykdN4OXjrr25rVCITRo7YIHSr0vs/l+GmU1/ma/yCBzdCHHrGMAizQlqwHg7NDVqiEWt7oeums8gjXZ6V6szT2UBDZ3tr1t3BF+ykdGMwaxhAjZr3BuisxxcIIAME+D0g41MCOO1nTHSziZMljEGSY3OEK7+795FkeX7948IbFKO8v0qZlXI268V1GkfuDIUXz7EfGJSU3XIK2MKPYKH+YrKnFDWpIT+4lKELjHuJCtyEaboDF1M6N0Ok3PwAMxisnb6je9zoqSZnU/aCA8hoq6GKkmxN+UWNTOWBdFsA2cdSg6uTZ7Go+W4LC4vKFknY96R8FAFEbDfX8lSKzA5FDzUxaEzIoRdpLqNTkYtR5uTpbivLCbiUjWhcYQiLY2RUtPXWUbOdxkoqsRVwQjJFnacA//vln5eKHp4MIw5oDrI27uMQCTBZbUrycAA2II4RCRfjN5oGLZVGQaOFnSkCJyMRQF6qqlQkM9DPxatUYNJIzzQIsMVAkBFCbkP1VegKrQX7GOBuur8lozhJozGrYjRaKOBrTlChUIAICdrM3iQLyJDBszhnv/+3//d8e0H56+bc/vvUM9vOzP77feaSlOGPGwJ9Uu3SLTkVyuHh6cwFJPRsZ9meeH7bTh7dl8JS/wuYOy3S3jzCEd00B/mJhRwYUDQCRi+kl7dCyz9zNbIw72LIrkA8kCgJ+xInpFO/cUtXJELZ4yYeZh8togMQ0xQ1YkwNsyt13WFCPT6e7z5+/6PbPb3fI5phffvv68/2L/vVNZvzLh8yyHM5kwACKVBHGDb2YHB1cXFc5gEiswid8Fl9W01AhLyaXni81JQKroomrc8b0jFwvOTpK9QWrlT06vh+/Tfi3JKCT//I2apTX4K+RnNkhixEsPKhM8Xjv+KOW/RDFlQeJiEI9OK9RJLxCGSl//3ZXoDN5YLd1c7Ab/wMaxJhafH93FpBSZi7Cokg72/PIFxdWHnEVzWmQ0imkA+QsQ/xQdeXhvu1wSPVNaXWKfTe8wmQTwvJaq16Lp4lM4+aRXNMEZfL1oN425OhiCKGvZq0Lkfm5jz3roTjkXqjqJ1LDUO1Jh7ba3yf6JBxSAL6TDKt2MHJZEhPAE/pJcP5ZCZI5qEySXooR/C4sV28woeKBJNZpFKVR7HBqaNGHyovWyrYGrtmXgQbFIAZM2/OcfBguV6R7wikxFZNYzZ4K2Xa8CilGPxHQYlyAFSzmHm7DK+4QRsbLMFt+UF+gKJxm4qUFkJFmRSwJK6vW9fXVpbXJn8y+FH06WiMRxURFVuveGTpxNCWc8PjNgsDS4R6JenViMsBfx5HWdbUIpXpXttZLcdE3yETDgd8lJsJAroqq5l9Ixifoc2OaSFwEphvkh95BFYGhis9WyowRXyIm7EFcU6c9/VR+of1MayLXFmuzfkcDFKljQ51gYIbhP81w6XVXSj4jUQBpDwrJdkoBvKxfHWLCDVUFw9iTY9FOJ0oyJ7KiP025xMCixQMi5NnZH//4829//7sYwGPoV5aoCx1hORZppbZQo8/gWcIR/5vZ9oxMt/RQj3dTU2yePdPbr9U+OsyMAUGRsgbDhPTbXAjp+V7lzM+yO0eSyEDy9pUvqXjz/mAKyiiaob7uYcRbG48polECkvpEKYU0JNFyVQ2rjvcN9NAlYhnb2TWsAZmR9PXzp3/7/S9/+8f3//rHHyxNncp2Vx5u3O35YPkkKjkLrKfbnmeJVGt/uGIrgJYOJ9KqNR0AJ/91gUl+sxlEwBlzbGKXwfOXfi/dSYDZTOlFo704CvhCgHxYYoQ12d5K+btBEbgpBSJPg+0jLX7ymsV+d226QBYFQizs7/wzk2PWlTxanL0iZJ0S4KfPt1QzBaUhibrMg6XxU3+ym6w1Y/OX1klKbAhg3Y7AyoCUE5RCLwKHU4BRS9bZq764lzW2en9ZAgwJwDoKoSwHLBBJ0YUwsVSTzWmFVkmhKTI9Hi3Wm+SdtlRI5d3aZa1AASeM3q3WJ8Bq7fB+pONA09bSWOOkNt3ntrvmTg2HLedCEvoAW+nMVqRpCsv26xSv5ltAChlry4ZjK99kaZb0RYBIMGdrSGV2AfPMA+pjFf9YExcRKUL4hfFEW6LMsUvhrAz5+ZBh+1Tkhjh9xUlC3CUKIRmuk0ZHri9PrVLRhHCfrZQUjLqZApbdCy0bi3RGK6NmIGjwsDdXUGLrN8p6tZxtkYNVF5ID7mvsQl42RUjoNFUdZfZIwWKnUMoyGYhAoYWnx7hG5owEpqvTANLqzmFTzzB5MU78+LndDLgjAZpDeVi0DS/80vBda8Kpfl0TPUZgHu+ycwYAhO9rMRPnQEhieLJFa3KgfzMZn28/G7H5mvPnVqnt6r3nSsKPZFhRbnYm/fAQ3Tbt812tCO1Lk9JT53ZdshiOoU4I0A2kPY2kONscQDWK7H/lshyys4flXikUwLAZMWFuS5VCQjnE2MzJgSRNQfKStcbIubgBPCnaLXClmK0qBpI1KBPAiZdpaLrSEUvlvoFsYYCoGbrW6K7u2hPAJorleH36LoIjs9UXueW7yCdnemfLtVPgg5kkrClz7SzGo4UrdxpoG/EtszoquXr+YbGghTB///vfDEkakgodgMHzRDW17tH747G9Dibi8w6T5Kc20k6cnMgypMDkA0n+8cd3AqQsaXI24x5+3ZhALfZZ4xgBElpmdNyPUcknoWfg2spvcxZQKDHPX0F3GfQAMlXCC59I+CVz5V+oKUzXVEPgDggwo6uElwwRVeAq3uhOgCw8vDkmEuZcmYZsRSxMkUh9/9NTiO5L1MpRWjTI6VCjD7uuNHd+8oNxkOTnz07DO3f2Q+AiGwpbqIdecl9M6Qs79aZLhGcdZWYHCxoFvbSDOsJwT0RuNIOZAPiwNsCX9ceiC97bOmohbe2ZUScQV022+mwFy1szW+yki1mOY6LPrQu/vnQ8sofS0RAZcWvr4LksNMr0n6jj9NzT2Fjg+4WcwHE5PNRYEAuNNFvOa+NXG7vSDZMOszNUbC4MoMzvVOKgC+aQvgmWOKBs/wVUTVLi1rRozSrqtEJJJLYF7OyjR2iZZdDs2TWXdIF1/U9+ugGHLlXn8piwgW96opi1m+mphRAerohZ2uJGLaAYGEGaJNthhhBOnCTYyI7bHTEEXPWmqcpTCPXv4oOt3rtVY2FDayVhX6/S7dZFBF6Jxt+UdfLh0+0nz5YjQnIIWwq/1hfz+sYHNKoF8MOYGALheVOnufBkeURefjNPkFvM4TMWVyZnf0tyi2GEC1I1KJ4cIvKJtZFcwt/8dg/uYRGFB59tkZprmKRAxCsCwg4fVN5tZDddt0fap2RlwfhVD1oxljHQ46Q/nuwTGf3EUVjSnSeI7gBXjWhBzCsRiiS+kohrtoq1T3phk3FXK2ux0Isoai8itTJgJTuDD6sKg7WQjSHxVei5kkIjzXPlGZSKdZ618de//P7v//7XL7f2VdEdjN3x/T+VgRwRIge4kuBfm0yzp/H5RY2DaLVJBx0P9O2O2XMtJBIs7mRL3hg9mhqWKlBSRkJo4SbpEZU/qQeMwnnxRiiA9f6g0MIuozefxeCC4ETgKmqFULwlk7NbvRwtakVYs+XPAl4e/6E6mhCMXwYsUFolx0+kmDRukaKbeCyx9CHI97xxrZngdYX9t/dOBIsYZkSV1ItWHsHo6r+AAbvCHlaWG8IbccCxB01FFLGho3SKyR5TgyoGMhzrfoS5jundPomicLeK5eGQ4HSIqFVTRUW78rJh4zNiJhcW6vYm3V0s6pMT0blX2ouOQaMxVhFwZs9YSAYSSq3ZBgOGKfJLNXTb6DEL74yXGgAQGSMgi6KceZRLEZOMudcB/ZrHsgikYNpI+wdGWBFH0S2dEPPcAYHkyyxVv4nM5g1Lou/uOrvy/oENtIrh/PSPu++slf7MaFGADFRSIHMzbWEn0i0YLbNV/GmjWTVGwHdGX66laUMHlDamJDyN6NI7iS5leJFYeoH8wUUbUdGp62OigyS1UyFCrDUkrSX6YoHC0qxtg/Kso+RVcPB1Sirxcu5XTtEsPS/Awg1orQoCYq3wJMeCElA294AE78nGP9LNjCp4l8mV5RQtziVTHP8oM8AFBq+I53rXGMtfn3YqUVCjnsm+KEpC6aEA6bGzAKCcHsMcOWQb5aQmLJ/k67nMfR5GvkoB1WoQoTeNGnvAfKiPZYDnDSQFvt++/clePULWKT6rYWyl0Ec71PXhtBRLyOtLa/IPDEnP1fphPBhgcqgpJTEQJF6aayzDY8hyhUKegTaThYLeg3T2+9Hvw92DgUDnQTzck0V5uSnsxhP5ZZMFD+enn1iWml321jjfJa3TtWwMB3KQ5icC8UyiwORfxpH8JwQO01E8xQntuIxmYb3f2AtsK7C4dNYL3fBSCinYk3Kl2OK+zC40KJdoaeS23zcGMvdO8NQQgBSzSpZ5JsN2poYjLr79ydxt4rjwhLy//se/OS1DP0Io3twl7HFOCE5/EDkIyOiay83Eb9rRbfqwQYNnpSujO7zPJ+hhbS4rDhUUuapYjgIfkABSMxlZ7ZvzM1qfIwZbmqIX0YALWI5IWme31oY+G7h9vr7+69dPv93azOa5mw/wshhXzlO4E+f1dWF4Tw9nD43DDTis70/6HorVlIbo+PPBR4aY5F42JEhbrwbl0SEG9HBA4F4qmYG0BIxN47U5qTwlE2ItpqNz8+I6AYSyHXSlepb3u67B+i99pWXIn/8GZ/ZVvX6/u3+/bX1zWZ9Y7ZK2BZTKZJhNcR4TQgEcDp2wBXDbYZcvQQNH3jqhtnhEL1bHCMuZdivTWfSpBBTT03WIRCD80H1qdtI0RMTjyUeVVKQyTbj/TeHbck9bQD3b0NBtSXM4JaD0bAxWRcxBls+QMTssmaBGnwk9WrJ0CSHqNkDCuaco54smUhFBLI3yi0IFKzTlaCUktjiV3XMVSYRzlCQRdCpCFKtBlrsVc2yCqMBVeIExvO5ciYV1KXE8dWIlJONMvmXShBS6lv3za1t/yrI1QsMbrJFci6cV/0JryZzt+BaCGKn9DP09xPbbk0fSKlo2FFARkkdYOOj4R0W7r7/dfLktfzRwuLnwHLpnqQgVAiWiTF1FmYxFwYjcmFnSatSVtXuRBRUQcvaPd3BvvHP6s0JwT2JYeYClClAfm28Pj7Iqt3DxN6PgxNUwhRQlXCCHsYnjbImgWE5atsjgoqh5+v78wapd60G/390ROD+GMpbsL68wpUoyLfrleC1/icoqPOgsvVhdFHD9vHpT1Av7fefc6o0euAeJIdhlQgOZu6u6cZvjqAJpW5FIyJkjWoo3MI2+ZIKsouOg2Q2REZHiALSl/wD1wsYEmw97kWFxOlQ3EFB1EMoMT9jerw2iHx+FrR3E6Mm0q1rQBBPJGaTTUV11EnH5Zz5cUsUWCdmL7DRFaWzhh9UVL8/fHArxzRMFwP2d7vBxlNo7JOqhzT0d3te6b4dJf7r84shoA9tTAakRepsdgnySFCqef7aNovFVFfJo0BrO/dVEiDLcdzHUE15VsHdNYpIjy0mIsnp6OULe7lY2BWtE8SfnzwGkYo2EceOJoEdTps0r8bMMSgJ8TI3oqQ3TDJJTKyGRsEWJAuoff/zxt//5XwC+QPZwb+jjSQnW9X/5+kXvKl3YY4fwUSKpWZ/Q10jW28D80lyM07FyT3Zj6RV9LjpWQSITEnYlYpGKPDpZJVcbFUMQ5niR97sHKYw16QTVYtsdALV1eDQGiU+dqmA/baPCH48/nh9M3fJ55UeGY05E9VUQwJORJ1mxY+v6l4jpvUkI/sd6DVSa8ZWVZp2lJRNI27K88fmsI3Dtb2yWljWLX9j3B7gG7sIYDTLe83bh8GyGfNhWJWdOz9xmcCmZazS8CCOFwJ939553bd7lhpni9ln0K40NjQncDCAOhct0d9JsTV/0T6PY6kKWUFJmd34zSkEtlKAgJlRHG/uiNVtnYG1G3Wl2mXpmYIGWMrfBrNEAM7m3QagYvzpSy9I6H8nwCJrQkNszKuLzDw/sL1YjqR/eLywxOz2WaX78aXuWyquvA/58tXSlpH/NOYNA/BkYEm/mSt+lMFlTW17TfyxJU+qz8Uqfg/MSJFV2NUzakFGKnmXOxSHUJGK9KjE2+WvnV/jV/Zwt4bdfr/mKfM7nrTK3bfv03/79r//H//d/v7Mu5fxvCkDST6O0eY87enaTkUgh0VH952e/fXbUd499bzhRBlYWrSkqrkV2i+ZNNmQxMd68I8uKOFcC6YIRRbOgEl8e7/piKyGHSsEoM9jDaTOzrDdfZTL72tClorqN0D1oPNkJBcM1ZjciELMXMhTB1GOur3/7/at0x2zdn+a47++VSIg+D8UIZZUyVnb2s/F9eeEL0IKeZkoJPadoEkURsZW4EVUEqtxq1saV6E62i3YMgtWF827zT4C0tNSzbtJ5yCbT4JOst7UxLHhl/RJDQm9Fzcvp+726s4c03IEe16FGU0TsDwwixzVd6VxWhbwdhUDcHOOHyvfKajkGBoJf40TFmYwvYTU7UvVKJMNwKVU5MQ11oBJnvP/nP5VC/6Hc00N2sy5z3Pee/9d4xNoIh/kWQpsylTymiv8fTf/5JVmS5Geazok5p0GTF+tCdaN7MHNm98MCf/3O2TlzBrQb6ELR5MGcc77Pq15jGRnhbnbtXlVRkZ9QFR0pEXG9UYfIkqZOYX57moycBlpZoRu0W4nYbogELSq9wcawsrrW6Uu3tmqELuB8pSJcUBIYqYkBPV18CYn8nSefLsX5LkkjWgnTZPzgHQPDKVTgEE7SHiBYbBzh+0o8o8MgCAaN24Ce/4h7lbTNxKNpLlwST05Nl+O9ujawtfV1RKsrKq38NF3BTzapkKiwtu8hZqlpDCmg6+nZCmUaUxho4sFI6lnUu/EjHW7zdN6M4APAex6zt5g4wCfN3WBumals2tWVRc0a11a1nxzbLO+ueQCgjjKgc0FefEzun0b2qPySUZgos3JG7SeNEXAOJ9wjoA7hM5WxAlAxY+kZqlocWBJ44uMgKaqjXm+GNukDgPVUyMh0/Bk2X0UUiV2Y2JfHX8mvX8dM4SrdoWJrNCchaRmbDCYBSQcwlFcoL8lxGcYQfLMn0e1i1uyVEvjhFvIOh5UKQO3JBKGUoglWKGy1fHNTOpJWmyGaZyc5psgW8Qc2EdGsBTyv7Lco3a3k4PHRadKUhU46ckdswyNkY8OiWUOuRh4sZYyiDTbrlgM3CFsxb19NdQ6uw8BcCgErE3c9DsF89AFkB2CIX7lG+CtwZOOZ+0CtZxcu+6T/h4ZzAZmCGSmvRqyVSBmjdr8XTnGX5uAN4NMYIjm3wdXleM2yZxkC/h+SEzdji9g+f5h7yFuYmZ9srK3s7+1+PL7w58Px8dHZlbK2iM2Gu74XxjYSwmIka6tLe7tbWyuCC1iBOXbL7sLDIXgqqGJe6GmQwCdfEfZRmvdT1zJeptXeI0odYxIcLn608CVkzYGPxGFafmFchLlBQCc+1vSnrKqgG8+9mILqU2HAbH/eUnTl/iJbMJlKxUWF3CxLJ9YNEVdGsTw9e8byxjcwLBYd+xvAUg+t0GZsWpLlsnWrssCnycqqp7ij/d236qktiP+GuksTDEgpWaMOcb5Akx8Z6s8eY5ZKjIUrsh6RSBwe9KF8sZrBvaEJsLZCqDZkDPBV3MK6Gb0coJcfxWO47Tnssn9Exva0pgwuR5lmapMi7PCWNtqktobN6/0QNw1pceJfP+Q7stOFHavM5S7l5tDKdP61+M7lhb6hB4cHZ2enAWtM8MQxdmqEjdSATyssF1oymAyyA5wOep21hYvuOr47MjGTGdEnTCbdwaFry5XVidezbANKEiugpHYIRQwxfyIQN4l8Op8KdiG3SUJwaikj6V5wjH50vcmC+1IdBACDtxLWPuCJnby8QzTR3kwpW+7yqGqFiOnFaJ4i8gn5rHZ7aosEOiUvAmPA7IipKQWK7mhGHuGLPbdXdf0DMihxcO+OdWhwpXV0MRZnRPg6BRBvTDeXoQMkVK7An0+t0OPTik+TzhIG7BFsVihsrEZcNv6kEkXxnF6/s7myQwEsa+hx7c90J2jrUHPG3QBr1Ld8BCqAueyTktn9QN9lOeWCa2z5vIUnW86zaCvkVPGiAhNjICk1QBN1VnHEzLAzTYO0XpHNegwZ9c5w22iXnPG4qGEn2x5EpkE2vvdjF8Z3ARw6WRwrmt4GZzdXC+enSDQzo6mwjfVqzwslebQw3iOPazzr+bbWmpEkY11ggKcoc6YTDfkvj8IMhdCVePoDctn0iDmcTmeHCemMVVOVSBgrq6vc0kVmau9eB6fmJ1VnTCv6z9S5m94BOb6QUWrc+BAVTQTU/j9TljOvO4X3gyyeXyxVlIPE2yoLGDim2MUch0XcAIBjsVk7yXTFKFRt/h4TnXwL0TiveDJdTc00YscMWi3U71M2u+jfc1ecyplck6do1gbxNxDOrpfLS/lRdCMm27YhS5wyLi4zOKsmqXfW1fETZtqiZHFeHB8dH51fM0t7mOGM+Zi4fO/a6oIGoooHaziZHjfsB4HdYNauqG4RDQivu4bB8N4YWn9Cz7zImjP+23kioOqOfyKTsdR8HeKJWOaLYwrQx6ACOmN5e3cAaQElw0/xWVdtL5qUq9SrasfEnPK5BSoQVEWDX9gtyOvx4wdELN27NIlbZhYhD6YeJnImNVlm+IEOjzYGsNmnoxAQPclorE2Oepvhj/pm3eInwfe4keriuHgIJuzU0zQ5tlF5S3zEttrHZ3PsMMTjh6xVO3UZhaFVrxyZYebnUSoX6JGmYXDjw+eAe3Y7LvGm22VTj20pHlkZvIqBAilFqWKIMdjnYRrq4ICwvhoIGaZw1qI7trus7/Hh0fkxQD45OTvhEUNkVDcZIKeP0sVFEaEMRsYBgku02Q4eMt/QDMAFTFskHymXknWYm5coRnbQr4ccLx8xpMvqEIsc7GtPOuZnHKYwVtZWtxwwhEAzDkBfhhZuA1MQl3op53zxcLt0Z7JGxSogELw0UwYK6BMEF2F89maSBzMlXc9EcwdWVG8ZRIV9iOOnwsX4lEQT+o3Nza3tTTZ3tjlWLvpZwS+xNJBn9B9rCVDHRoqpVQxoddw8wHWLYiBFOeJmLqpX0clEcwzDmMS+pX+5UVdzV5fIYi5jLNzrgtTuEbfN2cpAku6nQzbo0vIb8drK8saa0CIxQvSLaZ1k1KNcndxeHj/cXrKbKFZjoR0J8/zihOoxQvFZIhljC+z7mPzneabQxrhboKanwJ8jopG1MZX8SlyM2x0JueGFToKxxNpdiskOR4CWZdCBlaFzfQBp2Rl+cEsyN6TDGg6zf4AEa7bvI1Ulz1MC7qLwSOHUYzKmWqPCmpJA1FFS5F9jG/q60hqk89ZCezhRPVHH4sNEUu2WUvMVD3eHYRLinhRYGhS7tntdhKfLqCzxn9PTi1Pmzsk50x/hPS27oZX0QnU3G8CRCJJDE8tD6Gc/DlQzcWFDH+FMwBRzZnn0NZcM/62dIyOyU020ZUip5v8xd7uMtBB4Ksy3kdUM5nU4zXY1zqzXfLBUaF4RqqXc3UVcAx0He+EwVzZQjx5AI1IU3MiE4CmAHCYbVyGgks0lasEYquBP+uBxZrH+vrdVflZ4IlZ+8zR7JuQAXj2YmZil/DhZXdp/ubW7vQX+MamMVvp/GggbI6aqKA5r+dVNiLu6IbcfgEg26S2p4NSaWmhuLeY043ubR1fswq680ldM0VolvGmNscSmzRIoZtQ8UNiI2VQk2eEM9pcTGTYj3/l29hapuZIsUSIQz/OGKm7ox2eM9o+VBcSPTgUem2R9RcyQVIEvdibGjfXoqKCzAJFqBZyp+gGmGZn/YGzogpaGk8brBViEcF2zuLxi2RBDY4/m0AY+LAWgCG67KKynx03bQoH63HT7TSwOm90lo95LUbzFmbm5Mi9VGigvystcKGLsnTE4xCVPI7eOyQ3FjNNpbuFOBRY80+hdE38Ef4VrgGDSG0dl3Vmqgjo2pT3Wiffo+PCc8j8+gs5uiADGz/ngiNAK1Qec21hQcVEC0I7zrHUG+OXcOU2wuHCGcjENWXT/uzo7+tRFbdR0GNnFWfb1krLZMJ1CcVtJZcNIfhIfnp5OcGk1Y8SyWskaiZ9EUDJGhIvu77Lz2rxX9cuQTSQtnegFD6Ct6w3Qi8CBA+LbtygeDKGScrQMw6tCnULkLrA8/BMQ0NJaPcK3pOjt2gKikdg1ViDE5DnaDm83zBp+TJQfhpsfBmcMP6xTHm8fhLLDfk/PVnXBMl03Ai64OoyxNGo/NbzLEmzzsYiasI9hSwkNEE0xkGMand21sQrVuRhXjzfnU7fnU/azXxxfnxyo+OXLIxhQJx3iHfOLDmeKX8WIgnUgw8G2VVVquhiIgoJrP2R3lLKLTZCZRazEF7YP7BHmd8sRt0VKoe1bzS/cPQ+VvdO6DDDNE4vaOJBgKq8pKYEkQ4jZYqZJdrEnDwAIkDQqPGhPtGmd0TLzee/kstOHpqexGb2O3DaHoW2TeqoZolulnKxuIUR+Qtrtb6oHhZdDGVhqLkJKhmciOty5g0lmVWEK0G/PquE8Tp2eXR4eH4+TT66pBzuaAIaZmbygZqAahOUH9icMH6GbhNaN2o7oQWN4ikRYbZlKDU1lFCAzveAMTEhWW/UAy/VQIN+iSt/Qxr3IdCqLreSLU3mTtMDI5QRAlWlDnFi7DBBmSbKKAtEHKMqW88cokhaBRB+BLo93N5ksiq5Na0NPkvvhKIkNmaM4wfiqvoJNcPb0TMfMY8KIK50U8jh/dX98JjiIAm3Ekv6dn1lfWd5Tgral2A+WSfyW0qj5OFBmL11dusxy+ApExd+kMIwv737P9I07eanD1EiOk9LR1xNwiVIv3lszk6KehyKIki2hOqgIHo+hk/BJLR2QFy2raFArcTWv/s0SPxqkhn9288Choc7zq8wzFZz31nltBVMimLEwGDNG43KSgB3Z0u7gWdbKM3BriJIjGMc/G5reQ0/jNALGbhGRa5ZiwQYXOyHOWhBh37LELoPgzBq7dtyQ0+9Z19cZjgOlp89Pz+Zs52oAbDeO2ON9FYEjROLERqo6kLoU/QDnMvP4ocW18AZqWjF3rkRFGuYEKhJ765nnAlDwPaJFO4NLsGMVxnUCinFI8901ULg5OQ/3ccDpwSGmjDR1N61J7Onx8fXNpQ/brikmM16C3cwEdZ8r9lM8tZ0HQVAAISyPkQgiETus7yZg1ftVnA8j4cZ6yVqWTbbNckqbDqvmWCXbJyA7IcYj/nAe2cJsQcaqFZEtpALj/mGheSKSmINNzshtZil/SpRbzSNT/1vnM3tZSwAgl0ll84LgiZ4zcqb3Ikc5Pw4zeKpRcKaHp7snAkun3JS/JbeDCTyr+EAYHbfIoNayRuTag9zt2RwIpjoCYWjgBdXE0sBxBiZDEJw1MWLLvrS0drOBt1PoC+yLTuOxC8G82L4UG8YK5EoYZg0JaMOjTlq3Z38Wnl+o1X68PHm4OHq6u7i/Pn64Pr4/P726ODMX1iSA0fZveu48NxrfjFR5hRkjK357fTmS/VYxzngub5wsL+upd6E0yAwAw4DLW5s9MmazINGPWI7AUuFv6I8ytHVqbETSrCODoktI0tAb6JKJmb3cf6aOYn4KJbNUeJ/FANsm+/B4JSNw/ri7tbHksArLR3KcFQReE/VEn0bsfLypGXstC93o6jqOEaVOB7dzJrJR4V0YIehheslkTfSGqq0sFNMDTl6lxK8ClxPlbXfSXdf0Cq5S5U1sjNGwPNa6W1tSxjjEUdaWQhlWYQzYhLp9lYWkzJXPbtQAGWtuULFRlou7jUJ1A4KtKehKwVRnBty46WZK4VluUZbL+GJWRmAyu5xhii1HcriTKRAPjJam9mhDChbYYaVig3w9lcI7Bgvjw2EWKS8QLPzNjRyvoe3BQ8TyHbDhTx9ma7uFlFzFoFyRTBDZ3/GRetLl2Y2N5e2dNYdHeUt14LyB6+P9IAvljAoNPHgAsNmiNw+Ta7DFZLwwlclb+qaf89WvGXCobSkKpJydlZpA7NsVMbvi/PREhLT6eIA0EF7DSxcwyQwfKIgE1Jfq9vHq6aaxzk4rYFschQwLThhxdyS26IyVfAfJhNqGgjG/WRqgPoDBRyLURYYJIgF8tugRj3dDcs3L4w0GYZ83kmByXzQLVogiSfWDgzeqG15YOD1bOfUDGGigdViYLN7AMW0QgQx7zo1MPOXGW8KuPICLlh57jL7z3avyxyDAMkvfIRdKxM8jXmjsKFzhJf0Qa8brsITqtIZDeyJv+RT3gCQ+xlF4BUUopcgRNTrh85Lxf3N5qgjGSV91vjpV5snSEZ4zdYkXnbAUA7WPzt6Qm2uYkYujH/Rksr2zsyWrLtIv3zGS6RANqBZPvb2+0Ai+GFyBY+Y/BSjIjiVMnRYg217CuMjUxjkepVfeW/iJssZnwBqS3AoFX982bzkjCmAAcL+mCEvBDV8h4TR996CZSCNyDzSsw5PZemhMRzH1dPobSaXNKXUj7BRf1XXY0RNROVZrp26mwQDDsMSolqQrR19A/hDCFuoICouPpIdrZld4YWBuzbGydDp6wpwwY65rgQc23dANeJEA+9AFKxOUyfxse/wQlmd3H/fmwzMWEM7eDKvN+rm+vL04ubs4fLw8vjk/fLw5uTo/vr06p24UxXewruMpuBTtlctIGQNfYTuopkMBuljzXMKOI3Dcc5qregFA//hk92uCQUyzp9jXN5gOOQISpI8RkTpNly5FJhQAzyJe8IabGd5H524owjYMZBe7Y78Eb6iaS1A1pC1CgeS07LdkqVMcSK5U+vLKSrc+r+zairob0rkpZ7L8ESlpr1WNkjzRipMlXBOBdCYTQkxj2WiOrybdZ4iEB4McC0ylMdgYtrToBc/1xjnkS6peK0YjlsUMor0ZspEMOCFklKdGG78bYjCgMMLZGA0JsTQ+iQGeER27GUqGhC8EE1UAwx0EYPV6AzPQDD6C/gjgxo1ciYhtxOCHyh/1JIbMPkFe23zNimWkltOV6IGkz09Mruemoc4wmlOrmJv2EF2fmZkQdvYuFoWXaIuTRiTK7GLpSGJMObbzD9PV8u2/2N949+nuz98fHJyeSAFnOnOCsIpLHJhDUPjud2cnV3OPt8v6YAPA64vHu0v7H3AukaEuWQmcPMsBirKoMmjCOyvoDz1tkH60+ggmxMJmYQcIBWCS/FGJ8vnludo1d1ykIcqrFhfuyyFzfJhWQMYBoTGrm3fOMLqZEGrbyTY767h51zUHtLJw2eNZEn2L2q7Qxm5Lhim54vy1ZS+lG2n8Mbb6WHR5ZoruW+KT8pxNrRUf1n2ozJNWLNOQpqcJ8qhZaH16NPpmQdVYxVtWPJPVjsVn0zMLldBedyBMbmAWisXKwvIwDx2r1KrZp5cxIv2rnzOfK8ureA5NbnbYybqW8jGsaOT38QNubn+/jFPVBzRlaTfKjArgSMP32xtB/YMj6d5DG7/HTrebgnnBzF3bvc5lg48Ugxboh27Ts4B8Y33DH+yyubHFHJDLxLMGb0+C9ReinZ07m7EhYDYT2JCMeXtne3tza3mlxAupNkLdLwYoC3YtaWiAqiMsla4fKqw2rWTL3YcPRNQz0snh4IAMG4KJsvbBYPdnoUrhB8nWrBIrcGhRAauxJWCjKav7wDVr5j4tcjYUDiho5krMSjx9ij88i2ZTPECRYB6cPJjYk4M5yBz2JcojAj7quuqmFsoTmQ6fQT0/D93Gb2i9jM+wcATBENFgsxqVV0s//GHsiD9Gki6wDkiEbsClwiX5ik7q1p9f2Of05pT5f3J3c3pzdnR1fqIeNMMwQK7QU30DNgoreIpLy6zQmWvnP0wwfINLbY2IDDOKGKhQymBEvgYGJLMkSFyV9OxH0kWrxaWKkRDNTUmFX9Em7BO7xp0UQVXYQwCzOgm4MEoyz4w3Ly98Apd9cUSrUre413eB79XFHfNPTHjReYjabyyv2GCL5dyR4LayNRxEs+ScFmjvNbN6bHAx4p4yQBl+oFrxYitkAP4hBZ7tYNcR4bmyLje3+sBU/QlcFcuIjpJLUwj3G6ef4sbhKNXiTEgPFoB0s6Ndyk/EPNCizlCeZs1SkAD9+eci3SOaPwr8zNOUoMYwApLPamkiVaayEdMoVGy2B0DN7cNyyvJZ+OX0723qtJugCUbRweIujdBYt2OIp9TYjS634igh1JRACOxzR8YNcg0/1TobYS7diMyN4Rp0JpTFNcWN9RUnYG1vb+/s7hxe3ExfdvJoB4G0+uE7lcjvu3ZO8N0V41ZZKA01N91OB+xAWMgRZdYmzKgRcfEJiYNg0ScErLJTBIw0IToC9NP8Qsxnnqq96f/508XJ+tJkjfknimM1RBVEOsqzY0T8Ar6K5PlemFlwyuMtXwnodsVTBIAIjPyNSOVKPd3yVNRftsXqiH08qrC/cO3CwoqBWwKeGXUKQPycvm+ITUVSDRWGwyzpzDQvjmGNBMSVyXidX16Yu4AIiNvZ2l5fF6xdJ0qm7LEGWZonHaTD4AWeN22bj+VTq/xz8pr9XASDeLi+PTCEeGRTaU7etBvxJwyAdKKjG5kGMhLkkiFYMaH2N/ImnOOPQEF7CzwTCntHHLjvMg5ToBbMjw7DugT9nw4+npwcacUFz3yErSBoVvzVlblVCKTIjA+o4GdldXdnF5pvbW6mA1ZWLZ9gX7bt3FynAkivOx1ncSJbINZs2tZFdIOq2Nre1nfI0xUaUTz22Qa4ghX142vTk3GXALhu5xQ1kAzAR5kmS1r9BS6ip6OncYqiZ9fEZ/VN4rwlcCTTP+7ij5ACaR4mThCd91CVbg+q1BWFCXTyzO/EjT41Em94KB2Zxaqw1TkDd09XD4p2uIjXGMp5Oh7KTOB8GcaAvBqCppL9NpKwz4BjjnKDTAofXc9ckTGSZompw0bFOM2bjdWsJpVjVKwnN06Da9gXr5fqlcqaOG1hZml1ib116bjJh5uzh7sLZzzfXZ2z/e0BMnGCkvVlT/+ymKG0zd3S/MwVtHM3WuJYbF8KbnFpZcOlfCtwLT1MpRtARq4xICmJRqDaWiUyxJM5c6GPPwqab0yZPFNVhVsS6gIvETO7LJM2ygbAMhZuDAEq+ADQxS7YK4kTJOENMGWt3ajYHNyL83GfRIUDVl3HWFXX6QzJm6vpm6uO9Eqzu/e9HreCxZr3lsaGe6QDF6AAzTV0vDWtvtMN/KGB+pj1o6zzcYpPenl7r9HxqWhXpXiWZTAYVjACApS9ZnTukf3evXrbB8EGaSrtAL5zYwg0tRHBfOh6fwqjuHR817+uj12Jcz0E29kEOAwbeYctXlm4ABpyeqCbBDS+dXcz2+YponujiauwBdoQD5lfpsKo7bDHw7RkDth0KX27pzUwwMf2FpgmGwSNhk1DIg1QCCswt8JQbMzGbyUIQ22hVPsccb6D5eYXyOmbt2+u7m2WPq6oVhpXwOT+phJnIdynRxUMUzeXKxLq+TF3TrC1I1E/sSA964rGpc1wR4ZMThXOq+DZE4k4UYxUWSFjyi73gzCOt2KKomOXl2fHhkWD803s+OJFp/xmp+yrkHYQtfNkIeOiBXPMm+ValLWZgyVDYpRGTLOUzc4SxM4ML+3jMHcrandzWRgPx/NGFBCUtTLA+inob0lC3dgX8TyWE6QxtrqENXwMCGXI+602a0cnCuVLl0Iwe4Zev361CRk37ZFwRrLGmix1KMvbsDErRw2X8t6ZGbiidMvFOcmroHF7aztsas96pU3iLbHRInOg0sP4AzUp9u5YQYc3UeSm0qJuRgae7fohjUTUlUG8XwWywVM+p2XIsEn5WOlI5iCIi3PbX09Oj84uzsAy+hBSg6PmKQCBDidFGANegd2rK2s7Ozv7+/vNcd2fjUzyXH4lkp2EIPxlErZPmC0iUgBmCM7EbRifSSGK+kJ/8EqZ9/ampYEZyKloDO1wQx9XFnFZTPXk5JilTuR4UnIhrAX/IQjtxJMIcDj7yvAXefE5dcjYfSRhnk0hoRu4j7KxHVlNUxqSqKukvruVSABLYMB1IZWvk6oSLcmxLf5LWEogMFDzLMlvd07juCOJK9DRzm3kstSe7FnPXE4ezM9c9GIiQhh6ZY1X239WbfzLklUJIdidSveOAcADj2KU0kWK6zTxfrqneMSCmUOcYQcaHT9dnd1dnwnOua/aUvRXp9wmv7hd3qkuC1A7u/1p2jLHFVTm5fUloy6oZB+rE6O2aQFMn6Xm27BfbW+6ZAiFd11D11k21pKb0a39M8RAyIQY13t+oH98TigxI8FqdoTZojHsHqdzWafV91HRQFtkF8lSdRLSkDTaFxV0I3k3pr4QlD3VsNwJWFAslU/9LKITuzOHA/eWNBjRArCRTvJoV5HgwVruWLqPFFhsfBU8i720vUCA60xxPgskBxg2SBfN2s9IVNxgGCQ5La3RAHE4YaHHpFkT3rS2gDnMjWEZoppzFHpsBliMBeDJ0TJTKqMZQacqpVEHUdhr8GH3dK+hdMgaaOOhy+1UQ5nDUmTAn6uHm0sJLEY/Hzvcl6zFm/EZB8RpCs2S0nAfDXLLd43RtmDQ3JlY0LmD+XQlixBBLro6mMLQCGqBH1xpE4b9lYsKA2JubYkny1ubTNjTSyiAZG1oZxoyNPMbsRO9Y6zIz9AZqk+oWTon34yys+oehRWMARVQAPXS3NirlWwB2eG4icOHLnLA1BCPGj2TDGbRDeE+v748LeByszS7OIlHIICUksL36QdJa4bE0gy1wtifbveNm88oJ7PRxcEFGWZwEos0ZY0V7NWq0t2v5cSCwTwrQtu+HIOy/Ld2tRUFsHeS8OWXAx82ldEaFa0k4kucn+MUOJGakvK+tZPr/l5ke2d3b3t7a2dHmGNT1FpM+7mQjzAIyQ4rJWARaBdWUd9vrWCvp6c1pZp92SpiDqaBFHXrCuJ7J3DxvDGauMwMiY0f7Juz5TvprQQI27j/czk8HRvilSxhGmjkhOr02Cw1UMCUqgMQQv7Kb0TK9DxS9S8r4s7IKl1kbkX8T88ttomC742NjbdvXo8JchC3VyZF8+3ZgqyoE95ZICvEzkowi1/JD5NzkS6jdLEwCJnP/CaiY2KGT0kYjW/EH2BXNoqpU4zVQtRRzyYsH+IqyMth95Hbih01L2A/NhKZkNFiG44O7+EZcykJsSm2GlKAeGoGz6fJUvu2ubX9GjgWUpN2HvGrgCIXpPoNCO9vl7gp9pXtaDlHQIUYmYELKI8hU4hvODF+UMsRFlAM05jjvHNnLFdKVBbubnrhbmS9MAUGTIULPUl3EeNZox242V6QTAwBFF6aSd1cz9i6dWOIbJjr+6vz+5tzid8bulWO/R4DpUHXysav0AQYCxmeZs9V893KbVYrIlLBLUjsz+Efy5dFo9KpDpeitvZtQJTY3MSS1WqGWIppPL81FxqXRU6SsuvynFEKR7IsLIJwYnYGqRshNTzsKxiyqHrGcsVdlhx3uK3VhDscxLSyBVA1AzcC6uDWHzIKE0Sn9OoRu4C1NlyTCtg5b7NCrkcOE++K0LZGqpKKOaQ784m5iIO7hPXZqn40wKTFfXSi1jg2u8ZexsQ+FUMB50Tz9/CDm8ShrXMyQycRTaiVq5LkDQmNTvE5/WcBy/1Cf6vmilx7M8HHiJ6SSB3itDgHMYS0VK8OlAkb+3LcCJX8n1Gbfrm/ujgVmECoamzub9pgZXpRh0ZuKswWa3BzKbjq3QoTNN9QsYxbWBtxplSPUqz568X7ZVoThzn2RLjEA1Eba/o3Q9xoMoygq3+REsy15kN7mb1XZRQYgUcMEBEWS1Mu5kKgirGZMsBF9hmlEFPXAnQZ7YzI1qLFZNdg5aJAlHuaO9XAAk7U7xSEsKRoAvcnotjBl7jjAljyCpeXp9YDkVc2Km7Gvog++3C3MP1Q/1tjn35YUAnakGc4u7WxSA1YDSqgew01gMDtMLWC+MGlHs0cUu54LrN5fqr4pdlLdIk5LFW3Kl8rDHF2NnYbPF4M5TRr4yV+I0fohyDgyLy8GIKqYNAUQvpBd/a6Y3fUaNnm1jBx5Ny3VsGcb9JMkKhQatlBjoUBA4uRyCIMNeOQYecKxy4eSEv0RVSKiVm5knLCoLZmZ0+5sS/jQoYYpcfYLGprwtEBzwLKNEMBDURns5aNfLCZ6+DwUAE++E+IFfvHrk6uyBBrA1rd5Kpymayt7u3uvX3DKXy7zurfWJ8sTULVjHoph15oixAEKnaAHMV8Or+UcBM2tCJp2B0lZi7MuchvwsOKGRkJ77sFuWKOFNDSAFVQDKOZZuUlEv3PMl/XF01xpm46xh3QGTH6YPsLWxDI7YBv620wG4vrUKdQDWxVE1WduBANZWnLiUfLH8Ysw76zOMk3TcnO6R0EzYgaKXQlegKW3JdJ0UziBPRBv5fF80RRnrb3XsLbkVYqYdDecToPT7vS/bIZsyY8v+ilhfBAd8OrD3d0hqAHqdW61iOsIPpXgPs4PwvlHWCqm4wcZ3F/rXavT9sc1VKzYe9YBHoCrW1aFAp5WWOcu7uTUc+CJVRjEmi4ZmGRX3owixQDYlwyUOtnUrIgyAZQxOWutUMzwkgRm90L+QXRNcoucmMW/TCcM8KQBLjaVIqYpxZdEzNUBYoRbKGBfv20OOKn+FeVmLdNP5XPYswa4IzCv7Y1if0mowx+rg8QgEttE1VxsJSG9UAS2LETDJtnruu5UEit2igcqMLV/Ymn2dKssRSbXCF2Sqt9fHzcMWyWa4atUVt4KJVhOHjSXxZnHDNlnHA9aEasriPBUshABu923/5K5RTBy571RfdBV2TooYCmatjeNu0QU6WAOH22rkcjTHYwLsenaHknykLT29Sd4X9NQmhj9rkzvx0fjHd4P7SJ3hWZelmK/nFbyIcdaNt2zMACA8zwJf7FKjRSZkdo2z1aEOgJ1sYuH3GZWlCqKYWKKLihuj/4iYo4RBi22Uv/FQCcfmS/GQumF/Mzdn2SSle2K4opQLbTTCTL3+7itpbezQJ0wOfNNFi09Wrt/UPOHSaPN0KKol4ILBYwvzyEsTxlJa2MNU+ZrOFGO+anlU45jpJIsTrA7hKhqc+2Sgo/zyuguxKNmpvXxtUjQShnypIgRIttKEbd7t9L4iVKAalJA2kt5uM8uHL7VhOlGeGlfMFSpYm23TNhwWzOurCsaFuLzz3lULG8aFQd2bRFLQQyO+xR7cKGm4ftzT13JJ5DbPZQSnRBquvhyeo6sMv2C1VAJzgJlzBvcSFr7vSEngDOchqJe4hQAyMvOvlxnoFo1+5NRw2NgARrztZ/mJA9gxNNNRYX+BkFTN5vcVt7RL85Ojk+FLs6PCT2yOODPIYeRzaqw8/YeHiSmXj9+uXnn33+9u3n+3t762sSv3IVNDE9nwnD3kRWZxwmEyXLKJK/xWTY78uLdfWizLDaeG66ZtWA6/jI6kxchZmMGCnHfn0ckplA+4/7kZHM4eGvk7JaKfgKFFKsRGSgkZoE2CkbRa8aMWFS1SR8Rv7dszWfcw4nSMJI1yxbhoyFR8oWkqa5Tl251FzwIrVMYwAc5XasYazsxM58HNGrDjW8X5q2idzEE+9h+vmNqKYS3JBfRQ/6yODHEnhW+0fSRD4u3kwgfDSuKZsnydmaCfPGKJZL0W2Zl05lubl6lNp9vL2sD870Bs+fPOSgwfP2dSko7syZ9a2Nnb093/UcyCukA9h9bIYQ+eIct1+RBFKR55Jn+KTFPPsi+NMP++Ie+2chQfOArJESGezk56oVhN3GfvKxskbZUF3KFncJx3iAiMlFFF8xBXdzC8oEIfzMBreQTwvVBc3PWpSSPb5MgFAVl2JuCyLbDyXyJSpWwd6VJME51oNnVGBO6gCuwycyDuxI66HMEDUI3AkjetZQnu+7vmVtPL1gO0YtZcTeaF40Vdn3JogHEsoBVBUX9BuyZDFZrNgHmw6CsHNhg976WQ3ZJjwbChKFnpWOyVohQSzhCbQZKI8WuU88tMzawA7Li6O4Z75Dk7FGPDAeDdfkXIRL90UhYKXQg/9hnIA1ewWS0f7wKzz3kfcyqdszbxSVdHNdR2KVVRNxEdZTC18gN4B1F2PuO75upq2LYaIwO8HuNcWOscfMzLlNec7A0RFPnRTTJoSxQbdN1zmptMXtg1BW4ypEGfhHAXRAJyvAUCgsqDEfM7wj9RpzUdvqcSIrDvLFqI5HrFSKgCyLdHr6HYkRrpnjXhSiLrHGpmGKqitZWBG3RFsxNVAJrcVjVuaWrKKaBZ2MpEr5jYt3gpkLZ2wyuoNw+5haHPPHg884XLJMnNkaoUUu6Nxz+xlDsuKsBEwNDDo8wBazhYXN7c3t+x0VZfgQM+Bi0Q/fop4JuzhaPJG8QasM/PbZyFRRKRaHTf9sJbD99E0wt7W+lds8uNdNnpYf51Rfjuwz1rfhX4clHLzAEIZ9PlKc432/llbkeyoV4Ay5YzxJQuIEpAEcDBFDbFh1VbQ6cbMpUeqUK1KfnbSbd2z3KH9NKxtzvB4nsz9ZuIUuzWhxMnm5t//lF1+8fvX6xf6+1G873Aq3BY0MjuGFP2SiZH1TdBkz/qMJRnk7sRz60MYnNaH87kv7irMLSCFKiZ/5AA96xwqRPZ/ihkJerM4CIOVzCkzNzkqXHxwc+BqXxazPTk5N1gNUIrHrpK2EhiyAhHzSNz97dnbsfoqTXGxIVo5i93+yK4wXhBd6IiI2KlhvApOGGVlB4FDR1s2d5FjCT2aTFo1NWKbclD73XTeKuKNpFD/Rj2KpVghzewT6Y52kru4CFfoYWM81IPYRa5xYy43N1b1VOqMmIkv1C9J4D3lKnpwec4Qnc1Nr2xv8KXqXSUnUYDc7Fg+vr+5tb2wqO5OJsXLmC+gDHDkxGrTQSmzATq/osR9VCVMS2DRQlBWX2rbrV5jPL+IfGKfIM+j2GONjdXIOAS6whriRImsXdMKPSAiKtGYfzzVNYk6uTYxQ0Sfswe5BzIWiR+kjVoEIwzK1FbzG15jVxe3f62oUJUfYJ4cpPlcjK5RXQ1bfUgrMSbvifIaeiOGEwnZIxOecbdEb/TKLeMiOUrJulwXH5CsOIeR3JqNllwOB5585XibH3DoLUXLoNKPOKDDBvmMIgT8aFR0m0uaBraE3VtFNRFBf/NpdcaYdqK7O7hrh+9n76XIxBX86BJpUVfatHrdlF2S/m6maDEuK8KV91Ep3WKtFV+E69SCojSAokFws5oLws1xZBE3PYRVxDPNkYsD/jNCF8oEbXFYZBaixIOiNySo5fSLC6QNDo+kafGYwDjEAP8IWXG3RfZD6FHlD+LKoQg65SwyOIj98KToSxQTHaTxrgTKWoIWTwXrkunH4C5hVbOVxeZDugf1hIw0tQodXLKjbg4cAAnXS05EO1SlG9DHusPNKAzGlP1ZlKf67PlffPDk7kgnwjjSLsYgGUdpalsxeUSeGJ2CwOj2nJymrr3QiDs9U8gzRGDRMPWNhirAGOR5LTnEwD4CoghGciQDDJKBfOj6LtLKHSeGHd+eHBx9thBIAx6CaBM+uGLyy7PmsQdyTeSRWXMwE3+bEO0WHVh7bTi0NBcXKo1YpvMnqciE7dmmas1gZPdFNUo7FH5IBN4mWIvoSfuenOrLx1dyOBQo9oKZvYuzCyn4IrHz8tytoPMxlbobojm4NVEU9W+kRBD8/M5cj2O8RCJSlH3lgWt/BOcNQmOalqPb58qsvKIDt7d2V5RULV0pv+p7dmYoJBG2fcX3ZEswtnIO9UNlHcSALPWE2BH9n9o4HGKfNu9iPNEAGHDON+iOcMmU7tGl6t3lNPUlMlHHKgboXsxJrsSREhS6hOZ51iRLV8w2tqi+3trZM2Uw9l+IxJA3d0ReH8RLi+Ox9qVrR1fZzqzJUKP0cUiBC5NzL/A2WcA5bvbKTIK5wnjBiFlzwcVucmMwQI0zFpnBBEM8KZXTRW53XqHHpkonTzM1kEFWmzU1SacxavIZpCsWA7Jl23jKCTkbDhuH2XQv+XJwJS00c+oIf2wIhqzpt0wYxJiHLyytCjlJHzVASnjplKFX3VYDRAmDr6/MncU7hqfQ6+ewULEYBDz0Nb1z+MQCLCYTqD/Q0c32rxMJ8Ubf4NcpbJZMy78A00R1cYi1b5bimjzL/qI3KGYlgC+oHpKqj4AXo4SjYNmtbGfwImfFSimkw6hBNf+EZfBR0F44ux0Ao2I9mOtPWYC1rOo2EYLZ/m4/P5uB1XZo9FKh4wTFnaIU5wyl8055hze/USrA21Dixs+20Cl2T2nmT5QAiAOM6H83dMCtqPCv4jHDrZ80oJDlDgxcpAmSCBrlTHtsILYvnsTV7ZjrMJe2f8IMZGapXgSNw2XgZz8bavgraTLN1UmozvB9YVXrsLDNLSYgWTyhbvKGwU1yslkHBfKZMdYRGIjQxgKLCl6Vl8+koLoY8kRH8jODWl38gFVLC85pmAT18QMaKsFkRibSxSeIEUzaBPC7ID/PVHEJ/vqMxm5RrixJVXimAXEisxUn/Y3lQobwKU+c7ZXUL2tx6nBjLjLgJAtsTwtccWZFKAfKJqP+qMeloGRcuhea1aQ190lGVfvUsP1ycPJyflB/H7sOpYwhVCC8YZR5zT9daoUzNL80sLtsJNrd4V7rY3lFtORV2cDSv7tPbK8uiIJAG51mafMa5WdLl/mp4tZ4iXYR+7NgPpgoHdYL8OruK9jtePo5F7h7UQ1pFwsw8BSBAOym2ogRyEBCnAFV/oA0uSNGOnBLiS7NCMJISf5AM+3lh3hBsRMQ/6JCThgZKcsDewadDeEqTkB9Ab6eZivLkDRpmF1eU6bEAzk2DLk7klXSlCQ7/NlnyXlrdEN02LuwM22tbujojzK4EEaiJMAQ5oVSZSZl1LPd+fZiG+C+cEr27v1MB/5apgEXZQmhC2E2CxJhOu6fs4Du/clNL5pBMCg2RUXx4cAz5ruVPGQGC+FmYTIKOumeewvrUMilLOZUWN2cPwtxY3J/mbn/a4SkgUcMNviEaHQDN26Wc0nyyP3kotU03Aq9YR72S2avERRyEpvAJdxvTTs+rdq1zyOL6Fut5Y/5mHthRG4Okck69ikePTF1YpXLu6tLiGZ5rciiJTvUbs3LgjhIVtDMKn2IuzNHGXotpGQQ3gtsRu2NBx8VFPNzR+on6oFCMY0Fdo5PnOODBannO8cFh7VcFfKzfughCDpplFyM3BLdYXdtQjgUZ+X7yBAqBgmWSI2GqslgwoUYR16y5FL9lbWu0PKEuOs6UYfMsE+f6IXDtlxfpUnJL+dh27eLxZzCzkRk+gt4VIWgYKRtwQJjCfzJrArgcSwAcRNvgLKv33dpY4ZTc35+eHHx4907/QCwVWwnqXgtrMAuLNxKSkkPsoPhicGEeTCELaz8AdYblzpgrMiqWeHkjUKj4rjJixRuC7+J++KoSMDtOML8NZPaEc7GLLDGiDNUwUo0l84MAyGsVPNRiU+NYDxM2I/xcEiOzHCcPdRCiWUzuaMGSEWslI+miID5TT/y5kwTSIrwEHR28XA8w2yQSDFQ5Rj3blVYkBKtDTJJJABkxYpq58A6y1m0GLkKHMoUsJwmg2HbRuSuM3XoGdJYTUOSZGpsPKUt3SKWkHiDvLenjOBR88ygmQ4dj20/Oc/VnpNxbWi+TGvEeRouOI5a6wAxZy6aj8Lj5NLixIlhh0RrhSVbZiwYiijTCOTQq4kYJRA6RxI4jAJO8L1/zKUnBKKjWI5EI7VFjGIhktkMT+BOV86flXONGDIdx4HfWr1XD/NglncQfPj8nmGaqMHh5svq0qh/Wsh3w99fnIhX2DUohLCxdL61tzC1Z38WV8k+oktIR4pfAkFS9ZALc2U8qmcFbUiGtm5lGs5BYqTePHg+kkBiHRm2QcGp7ax9uwCVrZcVi+1EQgBmsxRAHJAHfmTIKPJg95u9T41ddoiweZCn5wRJAkzHAxZ69WZjMzq2vr4kjddpDuw6n5gAuFAZtnz59Ojw6/vOf/oyJNEbg3gP94id1Zq0iBfWIZcLDo/f0oXaIEypDk4EDlYGCCdKZr9igs2gBkAncLt1c1WYoRusjhp5lGWsZv48fliar+y9fvNh7qThVcoN+Rg6ZgYEmBRyfYdIYEErJ1slJewUgPnVQtkTlmayOQ9LPbU2qQ5ZlsMT8PD/Tty4g8h7bgFt+hU+3Zw+nHm+cIFtYI255UrSnQInydDY3BVMJR26BQ+wswGUKkYDBAg7NT3M/NWltITqQfWX7Yvvx4YU+/iJ3wwrPtIw6BcTUu8uO+oWXqtZ4CixaMPLpAjBHmZmg9w3GEB2H8+njp5OTE3iIkkaLqUlO+xp2tiVFGFasBvNtI161/CZXhSOziZRLywMLA7tzylPuaWrLowmVnxhWxNhM/IBLLHEZmHYJXlE1XGdeYGAhVKHlpOC9VZybUWzg6Rax64kLsGOxw3piHLCg0qmGcxbeDAx38EMLR/X4hS/FdllYBjEgwhVVkrcWPFP1QuQZoMN3A0fi8jAC6UKsYMbNgizoE14k1JIeJUKtK3p886uv3rx4rSIOovF5f/75B3QAl7QUBDFOZDfDzOA56dwGA2k8OA06JJAgenooQkZBm0jF7X0SzOlZWTVbm3ifnhJdgQP8iwHwFYpO1lasWqZlA1aiyM0pspANXee45TVBLnVIUmViaKMINFUeBYImiMSaMFk3xJm5tsVJgi9EAHLwx8u0jTZtQLuHtu6PeFA0+wmLFj/CZD4dpwY1omEtIZRb0t9Q3+5jdjrSmrkGwiu4x80zI2SAHSJwRz4n2kE5XYo95grGGQdCNUv3VnRIhBZFamA8+9vAaTHNRCYrSmVzUkfV2yJLGPcybv+mX43PDG0SZH1k2FAPdHF5essJ+v0D9BVUq7lAxvXNtcWDo/vTW0Y0OnGSFZbJ9tWspatxnnqMqRUleXQHBs54F+0S7a+8ikZnWMvIWrp8n3bbZnqn/O5t7a8xhcW9UhQ/hI5c1CIqTBAJYzgiJs3nL3/DLX9bSIVwN096fl5DTnea1ROlLlp3azwAW2SmH67uFy9nF1cViC6yL7lutfSWYkNqC0SpgE9wy5qRe9EpKA6O941W7KiDs5L6OHz6cXVhlaVu9QFOphUSNNEizBjYylIyCGoeYv2+L02CN/BT4loDmEKpUPp+8V4FPVwSkxjsVhByRAtaAeRI3SqMk3g4vD784fsff/jp+++++57N+PbzN5rkkDQMBdzwFRnmbntGMLq4HHOREi0b8r8UBZVaMCXwZLXhBrnyrdhajc3fmlCXSab9hE2eJadb0CXYbbAwKWLY7u69ePny5fburnlZE/vlnhnaJN2PxAmKK9K543h0qKEw5hWUhBusb7CLmvS48mFsgohQy/wNNqdIuQfEHFWPhboMovqqLlh5WDURJaZqqvAK5WyUxzTKhO3+WCMKkZ9sMfq+CAASmb15e7kVLkFuIXEXkCkqc3V9hXAGkiP85Ss6UjB+XZ/oomUs0EYBFpPHebrl5yJgLlrBF62loNmHDx/tlghWPBI/BxMzUugfP2pvsbbJ5HXMxMaGYnx46l7MN3xEAN1Hhn2YVn6q1AqIoh4m97lQlm54iOa2SEMAgsTpKSfqKOK3CUhNIHXQqREVvMavQHB1ZWmtk92WKtbVwxWjzc3oz6eoWYzZ/QuBJp41QxY6AgeeiImgTRA25bzyLF7QXAFo9ZpVkJcGIJEdQVg5RcIzJLsfy9TRT30NgFI21sxUwLkFxDb4RwXci/0Xb19//s1XX+2/2HO52CUk1lYEOJzPPl1dGhrowY8Ew2IZk7vCcSQSOCgHiDPwOr8FbOUBIBMi8jxww9Ps8sTlpYiuFbPqXUi6+QuBbTEx/aCwAwkFyL5numShLnFpiRJm3J3C5KD/0aGGZhAruZg0EmlXZeOaVKJkLCFRtugzuisGq29BcQXgoJEGDYBzAJZfXfP8BV/3DYq5u7CnoQWSdjCy2L4ED0a8U3V9fdeCAtNs0eV5WD+O4qXy7xybh6NFz/QAqyvuDH3QzaxAKzvl6HbmIzMTVZ4EB00ou1C6i+0tBIde6uJHApxEmAKI8qnF9DcOFOxL3eXAewgnsJ1HWUbDlgJqYKC4f8zr3viFUdAGOoFBbjLS8DsVgjo1uJole4BvABIYcCrRwypJNe7HR60zcd1E0VAFL9P2DhSqTnhqKsypQD3TpMIjIUOo89cSFkyRKh1K2CBwoojGCLRgAXdLpVVqRIme3bFWcPGMkwj4Of44svXidHZhdWFlbX5pHRIsT0l6PV081ZFNldNAeusaJIzsmEc3VYMx8SY8Kptoc8oQduJUgUrKAVqDMGarmBhlaa3RBYlA4oCdWNnvQI+AkDRjlnoItesvWyFISurubmWlMtswe3pa3X3IkwtAHKYkc66F5n/44Yfvvvvu2++/1Y97d2dPQz6FN1Y+iSO4c/OMV18DVXBAsMG64S32MgG5OLNvIxfB+xndrCqjy6ws1m+IFk/0kPwQbJxB/LxoPDNjtrO7sY9WApCo2MZWEYbChaSIDZKWFi+bUA9D4lR0VIBgVlfTDH8G76hAV7kci5T+rspqYV7kFDogDaj2oj+4cP5GU9JgwMX9Sx704jTh2PRwzXlYKGGKOXBGJZGFSoEOI0U6TPQOlT1FqN0tMQdIBqHDyugpbHN6KO6BMDNwQESkFjnQzSY2hEHMVUW7ds2OWA2bj4SPytdHJ6HSnViRvpG5Pm9DTGH9HO8FDn5VSSSZb+jccNOBfTs7u6qk9l+9omDsxc22sQBVB1HGCyZqHRLAC/jVngAMB0ZoGOKAPygtc0dYY6BNq3tbXrh24sL5A38cu2ARxoJ1tR1sZ3eDVFpW6r30DSPy+pILAM5Bm7Qlg1FMmTFYpDrwtIUAzxe8ZdlaCLjBhyf46J9FbHBEUjhjUcKceGnOIWhbkTGvwz4nMiBKNYyJjN8AA0QmjCU/fcp82d9/+cWXX7797LO9/Rd0FPIYwP7rl7QLYTlZWjg9PtQxC9dBtcxssEZWYD+jXH7AuECami0qgkHwqHjdh1MLE7aDHRIFhcBBsaCVlcXJGRoKRNAmyEWksSJXxVcJCtOylLJWoIp0r5x1UxzeeqopcfMUAh6DLCNQhwyGZ63SS6YEbUlBNn8HepA6JDNN/yczLqirRczOl7CIhgTR6BrY5qsEDVq5CTb2FFeyWIYKsNfsTrcAExZGpVdyyJn4jUT9kjXw5q2kr43gDGwAyldkP/CGxkjtQ8yh4QYQU1lM6MLTJCPoCLuo2OzDsjWN1sz8IwdNB+G9mELwOq/UWSZ+pkdQKLMDf3BMaiBSBGPBYqIGbJksnwnddq9m3Y4jHF89jjAi+hU+9P3MFQWXlKrvy44yTSwXUTd45p6Rk1xPgy2Fj2gCjoNwY1EHNAOkFDZaI7N+v/gunKKb3COLMArZBUHuTN1fSFatl6nrnoB5p+v2Xbro6vTo/vZS2MuppjbYLpyvLa1uzk/WpxfXZPPmH2bsrbi0z1XmvCMFl/GIgVgFyqS0pnG4v610JIR3ecG/ZJEgaCPitzCCne5peckgpo1VKwCjTBUfPEhL+RaLd3bsSRBvVEZvsnWurEyP059LNKwmMgTPWiZfIb8mDyLg4NxP7z98+PDjH/74h+9+/NbmYlwufiSU4ZB1FMjwt4YuHVn7pdVl2w6sNdMNcu/sbsHWTx8+MVqRBAqmoaJ9kVaIz0jvT9ATIU2IvT3hEnN8lMxvbAjzq6LBr64nz+xzXd4cO4j2ZdtGo3NzAL4GALOwhdpZmkOsw/0xGhOYo+QF4A1bY31eD1OIw0VFJUiiCATI8IpGNnkiZC/GydEJOjL9YDFCV2RkLWxbVYEwP7e7uw157BW81DaD/r0kbzoB1EqB9YdR4zrO/zicArXMmu0LCcT1kCsboiVoDfyxd8ZIXLOUI1t5L+VhSMOIM3sQwKaI7WkLXyA17uNdRWaAxhXwVLTLlQzI/INHOZWzUVB7LFbFyrJB2uxWV9spM5Qv4hU1xChDAbfvrtyfGISAYEIyvza9QmcW7ltdFr/Bq9yCp5VFlXRXi7Zlps5pUC6KyCdrcWFhwgO6ujonORlAtsyc6NVxYScpxLoiX1UitdHR5+ZLHRR5GKY286WjFx2SevugyqNAx0iuoXB54gZLtOlClYFpr/C4ShjqNoisZAD4g2+UZZSjlPVdWBSRevny1es3bzY2tqyxeJX15nqsz2y8ePHCYNoGPzYQGbe7uBWd41mMLzAnhl/smelnbZguwG40+WDKeJA/UAe9sR/4F8FjixgPqLUc1FPLAazvWcQMTqJaHpC8UInJJrhDQPbaZS0N/B6oNXzWZf3lvQzIRPHngHeYlR1XWGOoq5y6/CFYlVKnG2C92/BUXDjMc/g8jFd/sTbI1ZDwlMA4+rhH2HxkW2WZsCmizYbrmJSMIJFaj5LvKbJqw6HEjr661BC85qU21sTNpONhkbmyCRmbEdFq+NeUkNd69bwUmM5xkGDekg61ZO0wYUMEoBTzvdMGqAUbkFMzNGb0uLtjYLWyhGKkQNu17uaYp1i6/Yy3dzYF2Eeo30s7qAkBrmL8Vig08hcGllrSs4qPl1lBMQJ0Ih3GkuQQk8tV48i8M6ataE8hJmuoxc6YA5MlRZ8AD2caT+RzQwOaXlsM9xUX9QXuE6dRJTLLf/oCbzBP9dqct32aA794e7EwUfSltnh+6uacDrjFX7otQ6M4alQnp1w6J5ICyFA4welUNCPNtu2F1fU1xB25TGd7iV8J8g8hQSYmGEU4fIHyHWIzmA2iSSi20/CKXgcmnWwxFEaPQQbzElJKraTB/QVD6BurNPfXv/zl53ff/fDjj3LNg/cQJ3rhT1QAcIgJAxCOuSBQx3UU/5vb5CfWStOKPGw6jxh/d3/USRHYc7X89Gz1UzxqRGryWlYyrnKuIQSUiXj56gXrlfdmbQQVBmXh0crG+pphU2emav7WXJGJHLIZWs4WjJ2Iv/R600ozd1Uw/cqiPUfe+UziD+CqFD8JJpFMAOyn/+jFFekDdhSt90Eu9eD7RYoo3BoixRBxLemtCwIDWeRzmdXdD0uLqj/xnM4Kq7Y/5b4sKYlBBwrMgLGfYXgUhi82yqQnh3PXs1MaALfHCsc3ME8a3dlakay2ufUN/jVwSXGi9tnpIupJcXuWNY5wzL12n2mMMaEIrbX3OAomxS4yj9v96yxKIKcsFb7WQxSHLQEP0iTbR/GJE2j+6gRiELm9s8VJjKMyCSNXMge075/Wdre1xaUMk/25So/XNxzCzbgLjESLUfPx5sKJCteXZ3dXp22Qu71UOUpAsJvBYDJ3pnqkTbjwokHMs6qAMufxueoUbMJSYOGxK6dHM4Ab5T7cQKgT+zoLMH9iLEeRDVADrAzXZOm13LUNmbLdl/qHQX86mAJAjUi7lKbXGEpflIAHs0t06z9IDavRKiyQ+lmaWWK+sloyDG/rbgPJXB9GSJyghNXMqq6lHV9DMhz3ysfYt8fSMYFcn8IQtM5SOmns4COMcn6cAK1iXCX3MXsj0mgrFmuAyYww9IcHNTUPef7jNwyZXmSkZmTAXqDaFoGctbt663sCgrGPeYcGV5W/HCkLLa4NzGU3+x7NOZgePnP1CAzUgHHxHUHmt5FuRmj38k0GflFYKqz4jTu0g4+jQIcEv+CEDiBLnNEK78G3NSDpHufOlbT/zd00DKtN8TmkjOFgeZ/1G9GrmSDe9CVmVO4dHfNslxWcgbmgXjkstjI9fyqyRaKpKS5wOsKwZDLlxNuEJWWRB5YfiHcXLRoBslBCTbR/BU9GmXasZPNvln40iDUDqFQvBTF0uWZ1bL/0+rNjma2txC5JRH9Ws7/5M77BbsK5/vi+uJoGguZANcCi28tHhoRojdtXfJK6xF6rfPvJwtT2xtKRbrniqpfqK3TIty89Be/OBegX7aN6kuc7PTlBQPLORqRKrRVxNlBCb6EKZaiGzS183n6bFwVxjdoqUHgEE2VNxPeRgh15b28DZaC5YS+1Q882R1luLzrVfFT5z/3lL3/6+OFnRY0CCwwQxq4ObYfb2yB6c3Mnw3iroAu4RYYMArXMK0tgSJlArDrzuLoq8r5s0AQbMIVu7ZI1dCYRqNEvCXout7HyYXl9XZBdJnpjbW1Fkc+W2g3nns/OOhKbquDiMJAFcDD1gP4Zv2Ic6FlswykvtxpqX3oTOuMUgMV2olHWNtbxQ8YqA6fyMgIRH2B9fI82WO4ZLnE43hWr4YWCI8iSNcyuUL1AejjgFOrok2fKudrCR5SQZvGLk82NTWgPV7BMAQLVWjWk0yfKdl/BUJVq4HeCUO4AseDd4AdDXbgjPIQAV0EkaK6zlIiiXa+ztvwtD2nPAEm6VjiBM3L4PJDOy3iSyWQN1OBaFCVjpXAw90gZX8XcmaGF9LMAbJvY338BDYV2Bg0IedV9IqSPjxMx8M2t9QpVpECVLQ7LjMNLhtmD5i6e+6i+XLOUxvTkpNa1DU7VelylplGFz4O6kVkds+4uz6/OjnTrcvKHxk7ioPY5KiJkdtGTzJmegf+sKI5dXCQBqsWSJstIEaGCCaCRCxbm043sGe9ZeLLnH1yPx6uhorfyp/oW+ZrF3FIb2v8tbm3uMP/fvH1rn7j1k1k2IYLeck/N5GetX6WxhDXPTpZvJ9hh7FhWiI3e1SkDCZYVkQVVXPJajc+sWHGSZk/6zPRV9gVmGpEPBqtbXlxN3J9w+oOK1StJR11rIcwDXaP8WjSRH65BfaQF7lRbVYGPPzPHvUBfjgThcWUWrqkNSkQajoeScQT0HmJ0PaMRqzyndqv6aLhiLFgH0EEESmpY4Pl7rfegn29GSwTJwB8+KU7IaLBMIv5Dk0oDzk8XLag4RxQOxSUn1Lmx9IBqW6jcwQg8NFdAUkRbBLueUmg0UusLGGA0ivpXhFhnCMIEu5/RPHMAgz7nA0hDneYYAbcc76HHIW3Gmv0U1UPCcid3Ly+z5FY1y5YFvrlb5i7P6FizbsWTK2x4caOHNJQuKOML4JstX9FtzNnEsu6UIHIaaZSgnNiYGymCe2yagDEvydCC69ayhoO1YTfB4j8MbeuV1ZgG55dpXplF4F3X5LVIHpi9mAyIY990f8tlE4ATbKfuz/VOnFlUHjAR1oD2R7U4YOvHHlzdUocj9857AA6wt85jd092fiHCxbl6uxXJkuqtFGSKQba3vxymwZ5fnoOdKlrrC9JWg0IuM9OrGyumbdkZDJaMAlHI2c1V202UxtZ5LO4bRljskf6Ym/v5/U8f3/8MVVHEupqYk1lEhXa2916/eruyvjLO4LJHzmTRzDy1ypmYs/WuyFINqCNtDdftHf2NHbMqigkYAdO4XITiP/5jvFtAf8gODlsIpWTrWw4dYxywGZ+E7KUDVcoCUjXLqV5AP3TGunCHu4suAXurxTgigAbQmonGFsCRnOwh4N4wwFxFiXzm/GhiHjtbeXzuI4gaC3DSyeqVbvUMO/KikJ/LXKgECid4pYU3nNlo4tXGzxU1EmuiRXzqrgbOwKKPSJxaMZScmrKPXUiPW8OObXM2XyKS9/x2VBRaI4S4yXQVFI1TYQ3Sr/QK8sJ8lCwyc3V5Uvc+HYl4GFmDnpktWAZSa/TK8D/d3vAXjipLrZZ3Y21DZMxOcgR0nV7ZVodjtHi5+Lhxr2mUboLR4Wl6fWOTjrPopSVtXCi7o+z9muxvra682N3c3du1gh5n8ExpIWMQFx85ve/eNhAGpjUQzL9ir+BR0yUMN3YyltCWlFvWAUDVjAHAOIYxgOb8ICuEhP2EyECy+uR1IpUtrW6fsYOIYH3UNhZb8D0uF5iGJ+ZCz33x5deff/GFHMjIczpqzfOz8qwcfPdduZaEYRsUyAcwCxjgwDndOYxvVYbWAFTlHQ4LffqOszdfrbNbzc3dGh5I6MwANiikipnjtOc8PqdREClMiIXLXGrJi2Fty7k5E0/jWuBWN7POnFFjEXWxICpHOpnWCmb+00OJYiop3IKLuBOIwf1kbvppeZI33OUhODK6YRTq5m3Q8YHJATHiCWCR0dcQ3+XGxergO2FndgORREq/5khnoTGEG7tMGf8EzjGx0yI6XauMxNGkoU4RwRAz6FlLgR61FDS28RSqchVjf1RyczGWZ9dS/waVMA9rxX0ZakZe9MhHNd1GDFDSohi8dfOFUQKEYXR9YRhe3CqVX9fqU/UBk3B1cf5Go86PH0s+UcrUlNyfkam2earMMRwsFVHhXwn2yIjZ2geXfgv7UBQ+WQC2GObi5+BohtrT6uyKEId1AaRhR8NxK9WMSk4rsS8LMeZrrPiqAJHd/rZECGlr3zli1LyhBLOXyDkuUB2kj+jjzNK6gin+tVCUZwiRlVYeWxfRJx2dgUPqSetU+gAjFbSwnjNKDnROgwDmR00Wdl5fYzAhLaHmw+IQkot7FVWbUYw+urlQCa25DXdOsZ6ZVswPigvMZDgggySXHXzLeizPfXz/o3NXEAecWa8BlJa1c8+Jp3C72umLqUtEMUr6VrzYlWYJUbEv5PMt6iV5Gf679wxXmplFjNrspuXJGVyOVivcrfAuCwYzWA8WN+OwlhpOWaVos4KbYXcXqBQUK3WZD1PCtd7UgrlUNypRHOx7KSzKKadheKCGhHfFFYYLUhwNgXCjm6bmK7LstkbbZl0GiVzKzRVA9EV2LsN3THSG3v/w/qMiHEDG0eRi2J4mLs9mx2uk1HoYlJ2DOtsZrN9o6fZ98gzRPgUPRCBMoUgOHX6zQj4EA+rKAUJh9QJcqIoJHsToZ6+nN9Y3ob9QgbbXDuFyG7r5eG1N62wdwFkR8jwA9/rMdor8dFJPBRgTBSArINspJVNW+OVLJUKoZggAAwHdk64V5cbZ4Bdb+xTl2HEGZsQMmDZ8zj5dnNzas7ixsWpDxvrq2pBai0CRBvrk8ME5SnzhWsVpLsjnEzRMUnAXT+VS3+gMemuqPIaSvp/Vja5EzMPFpZiJ52MzdBJyQciATxjPuOggzOwTIRVWs5hFrGByyidRk1EGjvnWK4t7+29//avf/u4ffre7s68+hrbBnWklRhwebuN7pqHLCedkdXXrfkfcQ4CVl+SRYaa1cE/6hhkOlIpugazHLFMIkb5sCxyWyTCmRaCxciWgiO3mZc+qX5QLw/NCfYsrtSSB71auGHhN1Fm4gkv3ZDhdJ37SiBKSxjnyOq2Ml2EaKA0zkMnfijMiDvs0B5daayoUc6wlxVLyOTvJaBO08RpjF+cAc3nqCOvGvgK2HM6J6YQGU67aI5IDp6Q82FUozTOvu9nq4qw6/kk9bXyvpAPdROX3XzvAgRo9GX0Eh8JrASOqJgVGQ6uIaATembV3AMtbosx/+0KDsXSSwfZKqUdbf6XKUNTgi+hmsKZeNbdZWLzy9LmlucXNjY2Vnf31zV2ZJ23AsPz7n8mNJpi3dSNryTgN2sApXWWedH4Ek5CdzfrnEiytLIMvw410aZks5QzJgU5IAOOwMpAU8xeiQGnpEQth2alA2qW8s1lg4CrW1Kxa37bC0JTPawx9OCUCFlYvJUGZLkMhFkuwhjsERfM+6jW1YFdlfRB5swvCiarVVdYJig4Fw3xsx4AC9CwJtRRoqzEPvfXssH4Mhz7iWRK9s7vLJqN+MgW2WB32QgLO2mgiJmjys2CGuQN6yXIWI3HArug9qdy2fXbmXrWF9cApdCDpGwsIi1U4yJUM+DUllqFdM17uWh7bdgm3pv7TNuLPGJOlkUvl/f5iH0HezG187P5GiSGZAR4Whtv9Rk4AcGrKdWSSgX494UHYO14IPsYjIYmMknRCK6Aq8y7Iavcs1NezGUBmjLCl6/e+tr6a128/WqWJbORUt1fGhdJv9+98lV7L48BbYkPZGyiZY0z7ogHbeE1VGCEUM0PjPxwvwru+tqnExvBEQtzTIQUGZpxxIBMGfBq3mF3QqWPgkwtkijC5YJT6BIQlsR6CGMZmzIx6A/XlRQnZ5VvkRBOEIhRSMj60EYQdR0o4toSJ1lm5m0D3x1Jkk0uR7Psbx+gYN3GIwJEiZay7jrfos6Pjgw8f3gsGOWreGO4ed63dELvqnQqgCUmJA8wv0Ccc02HJERxbCa3ok+wvs0Z5qTAgoj/dMUD06tPErmZ5CK2/M3nTHEBe1dzdyg6pdC25RkFjGlWt/sZEaDi2wQpik4pCswaMdCAPQ6CbBVMrQ1RQyYuTYIX8CsuezTKgwcwo0Plg8/YK0P/Nb377q1/93YsXr4iNXfgakg6qXrMJYdAALMMg8hXDkQGXra1tCG+ypWNrnlkE98CCL5bGkwyJGJsIsBgmbe4ji5AxYSmNBybQSbiYwCsFaTltTKloBkpU9U6KFDzAbnGG7kF/FCQP4sSBzKmVgkRMe2hYgCe2zGwaShqDEBNY5c3qNHAqcnkrmsHe2NrQQ9CCn+z4VIp7ErW0l+vEH7zvxkUzMmZ5qyLOgNA1jJ3CSmkIYQrFAnNrywsTFunTHUyjD0psQOwMAuCYmCqCAabdv4i9fXGuEJ7l+guCZbnjJrvAMonYz1VtWnGBSkYjYc15K8KSI0MXIHFETgWYfSZgU+zDeY9mPLXBj8hX8igJUcAAz2bnQbfRI37s51AoIfyCnkoG7KgbK+Gmme0lb6ZUFuO+zvEp71upG7p5FKEL6LVtg540LFOIMqdtcHCDoIpoq84KVVoeKXFiA8ivkFQtacjYYtkqulHrIT+6MplZGCFE2O/xzOClZZTwRVSqclR6BROQKb1WCNLS1ERdYyYFOlIb+g5V54qYxoNOJq+aBqMhlBgimuUPbW1xAmamPjpHKA3qa4uLG1tFv8mZsXthFMYN1DJEGAwe/W3N+KuYLXa/bisZssct0IYnf5PH7yYw11pWPzZuRDiyoJlergcxpGXo5k5dcAAvfM9eK9jN+xRZFjMgIQXMYmKmitDNPcOHtPou9yA0p9rhGdkxseoYh2ahi33FwnDoMn8GYxJaszJPhqS+m0o9zdLATBZqGhCIJ94xU1t4MISbMwCq7alMAOsMsbGcSpmKVOrXwvBJ6gYE5yR2ODLGGtql+qFg1DCEPx/vRfpO706PT08pXRa3UMqLFy/3X+6jKWbBsAQWvhMUoql5jrHBfSiDtrLqJsHGVDNEl8iLCFnQvmHTaJ4awY3YEfOCgd45M4sExB2wIR3DTWP30X6E1zVY1kQIEPpQPwtX6gtBnLIN9WqzKg6MxNTQi19idWkiGuDw083R08HB5OD0tC4iL1+/5rCadV4aoJIjwZCLi+pSqEbTpzGk0mW6YzwTdLbc1urO+rqaensNZmE+idIx8QFoYiMXxG/cLf17QJvnj5pSaEuswzhA4JL2OKtTK0aJLQW12cLVLwVLAYftMs6wbheqoVekIt7JGWwmpfbAnZVnnciwyrNgLGIJNrb3dn/5y9/86le/efHyhen4gopqPI0ICMUXHPyDKxoJ2RN7IwHLD6tWedWeklSmrIUqyco5MDnxGAPHq+LHWSpYBaDyreavWMv0L/VsUhWq2o0k0v+MTZ7OZUTVoabY6W1vxbxsCqZj1M3UMhn2EfpjdXpAyNR0C3kZbYJQYXigPFCxuDk6QnJy6gLSYIjxf1dQDG3aaMykgrAnz15DlbQtgDlZMgB4jZurcUKEqpwCXsrdpjkEUZvfKtvrq9+RvWDyyOLF9AaBZfCKHXgmreg2svfVR1BJnDLRZHMk525gkdX8Uj8AX61AqXTHRil9Ds6YjDnr7sHGdSUdOrh4KADaneSLuKbOWOYV4lb2xRXFmExsP+QYL0zLVVhLFHngHCs4OCVHnu4NSR2Fu6lOu207ao02qOkdbyTXKRFndany6UF6FgXOYlv2/lb/1QjSn2CLGCvdmtcR3Z5NHpX8IjvG9KO2+1gJPhNZtuK5bQ1bxMmOjgoGqETGCgMTxYWp8h3MgfLTLit7eOGRC/gkErJsu+29M5Vvp+ZvHs9vH7nBTwWuYHkJChbA6GIwc3F+ybi0rjDLkAGF+6xOr+3v71nv9bMzWKc4U6JKAtKwsa5rYp1SP9zJmNBog8RSGQtMXovJAL2crVmQVfA3VLFdE4kYi+k/iWBLEVmEd4GjXOfqRBKmcE2xMyqn9Rw1LU546AgqWgJTxtb4CKTFhT3GihoWxvEzQsLiUgb+GwYdfjVi4ArczREMAElFNT72SjxutcFD/tpStmllDKw1otsFmzObdRRoi68GFaKvsJS50IpSJMpgqr2Q76L04LguBTeOj7TGEg0w2d2MW16Ee07BwRvXyCh46LNomYL1bt/z9dWH9+81rXPn7R16XuRtDSlMlIO8sZlAQypRe7EZMuCwGlQ3TWAE4IwfOyMOR8XTzdr0M3yGoJIHw6Yr5YjkJqlbd1Kb5Bmop0XE2Ni1XgqWjI2u31USCrItLhx8Ojg6PaxFh6iX1q/OgWl7KXAqCWEZsjWVVuNTecmwVGq4olIjZrjKDBuIZyF741uYyyAabQb4X+oRLJ30HADZWlt9sbe9viLCSfKh4T0d60HWr8I5G0bbKn95Y29Hu4XVd8nNmvCMsiUBKrwBFmnnOyageNf145zG4zmZCRvxJI4khQIIGpi/afwC916MBvataZA1pR7sRnH3Z18Wpy8vrr1+8fm/+d3vPvvyS2mAUnoIeF2bvwxLfGAz3aUIYeZMAx44BsolBJAgd91ekCJm4CFn19KnuHyRoEMv5ZFoorKfM2e9ivksKVMWLb+/emD+uMVYayNk4KcALFO0z8irXQzYRFKwDbpjRzcthqMuHeFgdpJCDl3FDQif2imIMKOqMkj3rdQgQrmUsY4r8CEd6laFi5HG3xaK99EbKIi32tHjsuC0f4pajVAY3FZ+L1Bj566MIUyxOk+Tpbn15RndWERyuTOKxfj+ldzGmwyUes0z/BFwCOYzAzFb+QPNCzdze0C+b+I675if4g09R5Y8Fj5YMK6JfaqAaFhI9FDK1u3N4nlQWTVimEEVNiA1/vhZHh5y4QPXI7V1i14sCn6VQn7HKvgfn4D3GYW4ArsLZdiADuoyCv2D0x6n1IyOYDPC8b4IvoFwcxatVhoYK0JD49ElbcWB1fqyqGe+tE4wkUFpvQzLGAWqGAiKqY60ZTi7wABJkx7mhQFKRLsK2itP4xmpOsJghoRkbiROzPI3pfvppSc4NL248TB1cnV3eEryWHIkKS+/vUm0hqQpblMoc/dgTyvhMGIi3K+Ttc/fMv4Kt8P354RrjDZqTHzRaJ8LUlJpXOciXYXguIORN11bHgsw+BnAeVkNNNTUriVqYXBTMQ1t/+bt9bdlSQmj7wEXz2GxES0Mgb9JHIAjar6XPD/UEQjiu2OWdVMXdgvQ3TNomOnEZ2vIqRGdQH/yOMRxwaCpAcvJZn72eIk0DgRSA+gf0U9C1DV4nPWvLYVaVXtzPQjRPaHsRSabGruKByRSRsXaPHPv/PqMzIB78jBsscIjIoRCftLl1ttpmlp4IiMzzjfN1E3Js2wdi8BEJEH29/b9DLxkwk1TyAJL3sy5/a0Cx7PzC7xng/FdHaOSRNN0M3/wLsJiS29Dc1jCD4PHgaP8ecLgyaZun9mljXifDt4xdTVa2Nu1sWl/a2OzTg+ehdE8TBDl8aFmSscn1IBsgQMZCUGCIV6O1jCsNFfiW2ZySa9EzvidPhYnJyv7L14gBWZyDXvX3EuTjBgzLjOnVXmdQmIPapcxxIpEtsMpJNDAsFjB/IyjYSvXl2fLULTcRfBobUxDL9NDmBUQmELWqzA9Cw6OT2uvLZBnedp0Dh1u7YzR85AnUdisULKhY4kBlCI+ECiOdQ9qR9yErFkXKCYJx0569ert5198ubP9gpvLLM2bZdB6ML3HLq5YIMTFzkZoxGmBUqwJPJ0kAnmrB3owYlsRb1xkv7wcqbd2nm1SeJxW6Vx7w7pTuTZZmyhK1pBdiDkbnMQz/aED1EfvDHYGMrMwFJoWUTu37150tBTavDYBBicEm3CB7ra/CEkhWmkOb4ErtV6o1kyGE4NnjI3cY8XCMeQsaHuWJ+Mlgx45YraGTmzHEcQu8RY2wwn+cbXDDZSQMbnEdlxU4v7hhl80tzKzsji3afPHoqAoVTF2xmIc1rH51CgYrPoVmRCQ2iX+5lx6X2Anu9uGvqIMkFrFoZXqVBSWzxLQYgbMLaUAhwIGz4XB2FVuZcFkPpOKBmhd8h/E591SEZ0VH8shYi9CJGShEGOyUc48aLYkErEaWeiqY/EsUL347Vuelp1nubgTLqukSrPiKYfZuUSGgw1Gl3hy5XNGbI3dDdcGKZgN+QtH2a/rSKUkmkG8sSikrCqkDdheireBxsX17adD0neh7AMjKwaTbcJjDAfHRGEti20mPF7egXowTxM2wjaMTTmTut8VIbdD2JVyQmCT8UeF0KZDh+N55w+bi5roJelZASMdXLgvhJ+1N7XZsV0ZRsbGoY/zWfzSh8hZMt9/WMWveUhYiDy6AhsNkJHDFkLLJXUH6M1ZDYBqI38FW7GlzroiYnRbUGg7ZbGdRQjLJ7rocusPHuI237P5TKU1b7em/DCMIV3POPpzfq4eNfZDL2iluyQSXo1icvVYuyjEvpaM1fOlwkpoS1EMvsbW1IqBxx74ANuN3Rj2W9kbWCvw4VJoToAtJDvPns7qVypGxETIj7594LhQWltT05WZioRg35uOnEQZT7fYBs/xwVicNcEij4iTOv6FIcBquS00brfeUKHYegODziw4g4xGMesBNWUX8QymxU/jSmqe2q7M1HvNqGXJZWF6CxDBaEYiNphMLZ/F8SgMGZYfVyeOtby53v508ImWENd6/+7ECI8AriCmmrDVI6melWVoVXI474rJf3ttp96Hjx9c781Gxa6yK4Ih9tjBmeJxsrg2+zRfDi8Eu7MdobMzIV6TwENMj/JF4MV+wtIsjPFAh/fdKd6zq8uLDlyuSQh8iZsAoTuFpAWCGHyMIl8v6trk4TUesHbkHIqZOxuWOAVJWEwuRKVhPZ3AQi9fhNQgTrWm0kJ3EoOjLy/PLgbpdKtFZzfLAResINUMYJH312+/+u3vfvfLX/1aLDJOgWXzwnHiAWVcSjU4Lqr4ElxmWuvQFhYit2mjH4TO66FSPGxh8XahfenJA1Avg4g6PJymBhmqENZ1QFnh2dnG6rolpdzwqygIn4Qsu4/pCDTjA9a2n03ZbuJO6NHNfuR4eBQmasIhu8d7QgokyGEGs428T3+Dwy4oChq5/E/W3MWbVI3fG+X4CEFBJxbzRMrB+PMG0qD0EJQ3WWRRC+tNxbKyZfQNZwDzVyNpd8TqZGp3fenljuzvlNY77ZaEWV0xIkXF9wzBTSljgABt0iWY0F3c08BAm6JQ2s5nPi2SYsCZv/Q9lexvuOeOgivmnM5zgxwy/K/vS15EMuKCoa4MPxsACBn1uCUmpVwr35D3WgTHc/cnzo+6OBMUTd0OAsWPvEYrPd6IuzwBB7A46VTG9dCbMLJiQSmJeuQL/FpivKpYPwFwD5amLUrWM9XKcwo4ycGo/o63rTPEnbnKnJpmdEkSnZxdb25zntoBjljX9uHcPi2ssA5owbv7iyuF1Esds5m4uRtSZlaoTlQWU0fRpY0HaYz7et+SHJzArsqcLUxtFGh6PXW9+DTS1Nz5xweZZpV7iK5XmEKP+es2PAFqEzMAzERJpCg8vZi9OtequD2M/CvhCrZL2XZ41BCxSQLtusy7B/WXjClrIdVVFQzAFcsyYLcUh7GIlLph8R8wr9HAu/UZ3SCAjgZzYgDX6lLfvfuZhzQqjQp9KIZ7ZnT8iv6BKrfRVsNVSTj1ghgJhpaxYTVSpSFZuzFbO0sQ+kNR8S9ll7LnhZH1RcJgBrkwd+kQmwiRdryfHf0yH55r81nrKc2qdKXbdTzP2YF3SdrwrEU/EEnYASdjX/6P/QfKZyQMVj/7TJy9JSXuVYg+CJtkAqhDn37UdEFBxhDaxunc0o6itswdoiDcUbE6y18fqzibZaP0St8YEWrunTSbzSMxlcoEFl0TtSztjWC5WDl5Vdrp8gJCMRftUcYV9ObFsh2S9tNdPoOnkBV7nsA8h/4LE01P0IDiQXEvh6Y5RcdtfRsuASPHKomD2b5gnC4T/yCaVn74fxnZGfGUpfMS0F9jMCSXsVGEoVoqqYpPmFQEqzxRmyRSFf6Qcua726aDYByvv20T9EM7hsSpYn8RhuUlpWiMH0LHcrPMxEn8gOCSilJe8acYcvst1Xulqwiih4fxgY6yFLGWtbXNb37x1ddff22juJtYVjzWc/M8MpmtYvKT+TLB+qZPLjwxLnMjQo19ebKTZRlr29HtLRxqy1OaqOnrS43nnvfDpe18kyheXDkcFHtCQP6bvKObMfEWrpdFaogJyOPCoz+1hw1Ybe6WCQypG19HYsTtY1uTC3yGXqZAWtE3jwJMCN+Pr/GKpGCzxK0Q2TcEeVQXQM0aKlAYgkXhZyhVgq2WDyYwmCqB8mGkg71p9T5QJsfgW1+efbGx+Hp7aX9jaUOnABWZRnN1hx9VHXa5CTcYnNN2EKEUeoAFNriAi1t5YoMPOB41fyI8rIGSn/jaH7kQmx7Ez6pYpw98TouCTYtp7PzJUX4EQwKbFgPWooMXJndnMKG6cLKSR048zZCoknS5VdblydEptDFONo0v0uwA1pgxC3RIhRU9i3WQ1ZisqzacNhisOiqxvGhRAzBEnEFEY2J9gnV+4s21c49EuSHX8tIKZowfeW/jRCkrrD3NwoSFvnT3yHJ/Orm8v7ybXtHSDu3gr+De7LwzDEVGbbcztdE4/E6SRIZ33oJrOM3kJz4iQaI18/ZCrdEDq6fXHw6PPn46uLg+eFYVlk+wWhASxyJACrSEpbhUyRWSpykZF7OL86GsGqeBweTQNUdFzFsYD/ER2lmPlPRMVM2oGC0VCAgRBp1AD3JbfwuN6Pb3a6ZqexdptctpzffwsrjEZMk5UwtO9gSeZ1OnxgerEBLUt4+0TimWr9gC/IJEiGzEdEPY2ikfsMVG6CuBrWouC+wSjzY8M/mHnc4Nev5V5tkCLUBrf6szFgzLiQ5DyqpXzOOIR0Er/oN9g9aMPheSSIgKFmDLDLepadGkEMorr7EtJ4roUc1I4TkjX1ylrWcKLTrY3XlPgorCGDqi4LfwTQ8eT8QPyBZf2nzLIVpc4tfnlF0HuMLKhjhZqUvomfJN8qPmXfOGICFjwo1oGIP3Rg5M/fwUJHiLuPE3lTYB/oJCsEHk5373dnJhAZBQPplE97IQqn3FoA9lJA6PTUjbS/DpCDhDkUeVNnZHMxXjNq+9ve03b97QgvVBmp9jGp9tXwglAcVMuiFprqedPAKPQAsWLC8KcfCALio0Xjuc9cblh7FORVEyqmydtXGx/GTYz0gpew94mfzEc/5JLHHYcdDP21bfadkiNjAgPfZYFZYaQ/6o4i+PJp8cUTFQq0cDCr33yjivtCwzhmFebl/JgF+m9l7u/fJXv/nmF7/c238JbjBDIFoCwIIVQ+dvGZU7a13u4fIyYMef5zdRM2DkARjT0tL9LSukNoKYx4vxREJ8F3lym7LYHIHsRMPiwW6qBoMiwcHWuHQn24TcMBFyekTGec05eS6nKwiIVWW3+TTysodtcBpak8GIFWC/h43FCP3gQv/na8V8yFCFRYBMzNnQ2XeYMHzXoDU7KtDEZCxtw3bzEWKR+80AJwAWBdv4HpD0LEvGUl1Znvr67e6XL9ZfbbMbKY0rm5WktVc2JsLvlh7xcvNHGAr4YiZMRQ9wH3H4ZB0XriJUclQjPE+ob2VRbjrjucqyCTfu/IF6eHOJS9RaIGSoNehQ5xgGGaFkU8uD6QvIY4XMSWRyqSBtZfY+hv4WVgVOKT10TU71+b3ktDOwmfJSpW7hB0PHi3GShxlTgeVgtEenoAIVI4UIhhhCZuj7pFayLYD56GxGU5S5HSUVzs4Y4VU6RRZMd4bl1fWHp6Ozk1vCxASwqUFsFrAtt2Nr+ohaeHrULH1tc01oxw6A0bFCFa34pfWbT+Vy7pWw26q/tLQqHLSyAebfvfvp559+sAAilAr2rLZZM6bjBDEFGyCqZ2WHLmB3LGvsPNDspCpibhGZpOBEHK46iNuq3AJPou7IiZbyiTceK/8zayqkcr1xNLzvkK7OhaEmsJ+UB7pjZLDqlDgYdrt8gwOmLgSOOweDbGK+xrQ62T3atYeIQY3d5U2pYdyg8onmcKCUWnykB6MQDvsK6FM4DJNsjkupZlhsI256iZTGakSB0MvpjxoR+22FosA3s1jgTzWOgyQhICGBQBgRWxNe/3pK4gc62gDN2Sf9LSzjhJQpJCMS8xeQ0Fk/dBl8a3MQ+921Vxclz05PTz5++GgiGpG6A17kEvqupZQ1LRIeWiVRJOSiYtNe4eGsJh5wxL6zbMDiMJk65VgAgAnlYEiJBVP5KukE5+uWq3oQyhfKIjJJBTPzqnLyvZftaLYcQ2md4iqOnoY2poo73Y2uIyD0yuambIjDg+ZfvHpBZ7i5aBhpp9jAkT92sR4dnhgDpcr+n0zWIKMUCvoTUz4c5UEi7zXubaukGQrvpmwQYXVjjcGptAeB9U2H+ECFyCejIRbBQCeGZ6VkFJ56WkwBOgrz/i2ZmbmKwhY3pqyfQaZDzhiXFz7HtYqgK4e0WjCLO4AdMb1Z+0lwxDTBHCuXEfr5l1/8/T/82y+/+sZGEosZKe8fFe66GMFZuhyOzHhmhd6ixdUdwEnJ9evoCwazkxHLSr/Wud/OGljAigqmISXf7trUCKu5+Q/rAleratEEEq+vFtdLHoC46TUF8+7e6ee35Q7U23GGBiZSwyIAaaJA2tN6YpxKBkZ6ITwCmMbSdHsUMmNm9yVhGCWrGfJVflNawo/5JrUnEtDvdvzHeCZ4bx0INnRDNrMLRguA2IGD8KP2/v52ZXHqzfrM12/2fv2Lt/sbjrYCtFdXp04Bu5e3YpHQUWNJi235LiWfGEFIJnATyP1SF5KWcu5Ccf8CehVO+kLxMNanYhzrL6+aTJs5IYVdrgDP4q/mmQTF6hEme/Y5xFdrrxYGGqB7C+LCQjbKcpIoHrT3yL9AH5oyAUsWVj0I1qfAkXMuYEFt4vK5aehK60WpUDdMMLv8DNSodwmTxWoWjSC6kRBLoyPZSsatHb2EIYXth6MbT9Jk5Guysv4wvbiyvrWosu7qpH2nqYuN66vzYdOUHrcfTcTXaTdrO6rC1OeIfC5yxCBWqXUKyop0VhdeuD0/OVqcrC+vbe7ZaLm7+eno09HJKbZQiQfN4roOmsOct+/ef7LcG4cbyv+Fw9G30PkIX0BsQo167coiwRIxAk+jJlN8mq5ELsBjriZHx5MLY3A3JrA99FDU+2z1OaEDhgJR4SiBBhdh16ww53ldXnoYE5aqsQbOtrC2vmZux/v7NiTAI+IGCaqAJO0Ls2cn6i5vU0FZwun6ATpxhQIRotD9lZCP/L7nuRXDHO/5WYDCKmYJUM0Zzgm6Ox8fn+pOIf2b0Brr2KkLgEipybNNglqgppbLP5amd+TlsvsMGAbt7DpRIKO+ZljLNeJnqOL8ON5GMNHGi3M4/mntIAzyeASdmVY57uyWAeKK9SQJKtSknvHj4ceD0vi3d+zzvV2Hdq60KHRnJXJDboYUkS2WPkD3QIuHjJUh6lc8dvcVmsxn6oH8TwvMBHjGKspKlpvSNgUf1vR5237WzrpBEJEGTZioh+2dfUtID7mK6pZsJ21S6Djj9PiMOavPklTJsgb8BStvHy4fBI6sMwQmQqTAMA1MAlhexo4KMTpZd1uBpV1xIJkpSleiGQ6VdgN0AqWigaM4oBHhJErRNIOtWhWtyLvZCGwMqfXhs0N6n4eEWVuCMxR4AdAsNrpDgx2M3JZg7gbgTC2g09n1rdX97Iuv/uHv/+kXv/r12voGBpyadlAwCSFYOp8M2vVPrT1hBKwhY4wGTATVwVFr7VK3xXZcFktO5oHD6JI4b5tZu4NUidBDXJPI0TDp8vBXbLwyWEVDyAvkVM/ZLeX7BJVADP3Bolb+nziJLktWuxz6WnDcmxiZdiY7XjAQBIBWw9x9zhLXgqKokSfCU9diRxA20D8dAVB9yUBAW3TLgEhVIlIS4n9XFa1yIbLJtXgIN6b9flsLU1+8WvunX3/25ZvtpTkFiUp9bPm+XJi2Mc+dqfaqJwAznoSZikypdg4cg88AUkL4RLWvXWxMO53cmDni5Wo9xiSgGeWJjW0BIEwogLaeb9S5b2JLkt7tMzfmBhdFUwEhpqJNq5OaR2Kf4shiFbxQNu9ka3Nzd/vq6eTi9PL68rwCDGMk8NkLtK47FURNnvQeKVhiW2gaCfu7iy5JzGK+VMqJ/T6X4ZqLlYIRDtM2rz1hZft5D1YZvflQdAlbbWNjYXVzW9xVJS8+0d5D3FAEpUMPtFr8pBz/+ujsamt3RhiEla1WfXRDEKZc7ryjx/nljXWCdSP/j75+KpjN8mNfIKM0PDjVztpJxCxLor315s1LkQkX0LQmvre3K5L8l798+/333/30409GuLe7R+m0umIPY8+XlCtq46ix374Mij+4CranDvg6+YIETLFucASCvGj3YuqLS37e2twgAgIrFY5K1S4vlzdAWJdX10FVtpzTjkNEdxzQm6OGFKcCJ0ccyhAs8y2ruKp6VuTBNtSlpY8dGM4srHytLlq0iEWXwGGm0e34SeRXwIe9CZrNf2N9ww8iD16+iKOT2doVFYA9lQkS3+3AxbZXCCy1d4IpNMvNmWLLr67rzlbvRprElEZ62cprMRuQeLT6C7tZU8OMC9ZK0pYgmRc6PrsRim2ODo9MEzJgMVyCkDS2O6JsDtDtzciw1t9NLVNi96Rx9NLG+jp0pnjNrqLS0R2IAFC/igdwZMZI+O62xYZSBmoClhbGroUwmRQ36LLiiyXeiJi9j7pkqASYn0/vRnmn/NR4zmBwvfvgcF8CAI5edwHGRz29m6gf2iVvsfMSkO9CsuR4+wRnbO9ur+ysEhOSIPdFGAL0DGV77rmbs6rRUsXkAyQMqOJk5Q/f8nhok3YDWBbN0NDP1Ea0ugBgylhxBZokgQwgxaP5DgCiIiZhIPiRG0wUNM+hinyk0iMlzIBHawossBPYGPY4DKEn1YJt7Lyo6v83v9X1MzrcCxCXztNuEhuDLeNV/rW6sWpSkFDOEyEpYwNBdpOpEhZS0+CMC7sfKx9kK3liU4wtn3zK4q6pPcay+hVUyGoWPc/jhF/aPZgHohCJ1fbXtKmd4uX8Wl+GRh3vyI2YtdJeHbwLeDLqAQ+aSFDHcriRFPv92RpALgrCYEhLTQO8i63BmtGEuX53D6NIF43VkMqq8qm3MTGSplJIC95mZ5ROUA+Tlw6Epqde7Cz+9rONb97sf/NmZ3Xp8fTTBx6/oq1am9m//agGHAdIXY7T7/QxNHE1juhQhkoBbLtbRMVHiykbIkQHFq0p9oOXLvPYkWogWIZTZiLC1R+MZWFQ5aJN2SIos3VNhCWLpt8HpKJYu7mIZEzJ2lV/R3kAKb2J9PnY1eF2Zvn07udPp+fqjUuse6ANK1EpmQ4GaAYBXP6P4x7vF3hT+RA+z5ZvAO2esypq1KXDLZMPCzxSuMMSrfoLOUqJMUDLNbJbTi+uFpbXbPOS3aUuYLQ4w1DqdaXnaBycXn73wwe7y1+92VPnyZsWKMRtRNh8McRcPS2UXbKN6s5Gtlg3vEsxVWeI4Qj8aYyXOv6oo1patPlfn5e/fPuXH378ScYOprHz3v/800/f/8gwlbWyc9u80qD+GV2hFFLw0SEwuxafP8OaYN3dHCYRTs/chNLZt6ZXQFIniRYU6UkrFcGx9uipk7w4mJBFRAVTEaCDSvMkCQG8iFL42FxwMFEnD6Gn6z59Yoq6xiKDIMiqQscgybC7gzCGNtsZXYZN9wRqGb/YvbqDqlAaH0Sz20grR7qnvbg31yTZ3RVoEkyHbSn4gYDUdSIq+q9ktx3MVR8ZGXWiYlVVLJguylfjzDzu2MNWKWp3nPMG1n2dn+F6HMwZGtbfNKsPDhotivuyZg/PtVbqpWhO0+D9GCduo/3MHde7IQU6fTwN9AspMdIrPl2Gf3gUEiIempBjYxeswBPMejsG/WntoB7YU0/iUKqbe0cuA++iNOtbUW3smbAcRsIVyBOembdX4PDoiBIwQsTxNytbxtqndADi0DqeaiSCK+13XUeNiWkyfm4nNx8+ffru229//OHHzz7/TLxIqykrqKsEPwY7iSWGAlgWKPDDrB76wZLOLWGY6mll0xljkPEuUJH02/tAHzw9dAhfNsZoSyBPhUqQlifgJaQgGYBb0dxqCHQaGxGCG/j96UpbOBLDIx7Wn8+m7medTIICotzDjrNTMWN/amZ/79Uvf/l3zghyH7rE0qO21TEkceJhXWc+0oXkBPvRm8hGKYFG7MUQb1vHlc2DtQfAe5A4/a5gvUiMIrfl2yVHoAUqrFbT8SbsM5b4KKMtENcv5tJemvIhvNvZDS4mOGPtdmoYbmOcIBEK0IU45Ub0Cp7BcouUfM2rSvjb/i8SQXpcTTGCSlwUKUaewPOAOCWR6+UiQ0KCkZOkDbyoTYydjVsxbj3uGzUMY1MDZJKuAdnU1MbC1KudpX/47Ze/+/qFHSszd+dmsSqFkHbtHCi3RaVgSLAXoHPqcEIMVaiT7BswF912GQJlEakEn7EUKfqRhrxTKZCFZPBMnBbTwI0CrsPM/EsjM1q8TRHLRwINVySXTaogEalyD48VKaC8sYygG/3GtMPkdt5sresvOGMzqN0mhMlckYIy7s6c0VQpCkxrC81JMRv9ZFLgroPCWFiLhPj5Jj+A9kUvk6EPoEGuGU+9KBZophLMggFpQzm/Uv0aUYYJihmtWt4LVBTmE6xYWpUyPTk/P1JSOTWls5sHbO9tQm3WBTDRFebs9Ors6g6gQVRqtAIordsfriCH8dBaPEn2h+/iMUIhw4fW1dH89O5Pf/6LXzc14lxz8OTCl998LjiMmNU3bu1onj8gWo6NRrFZqv8MXMgClD/zKkv18aKZWiyITy+Bb1ILSS1uu9iXqaA58WFsur27ZbnjJkNJJZr9c2w9Y4d5ktEETxHMPH1CyHkFiMHECA06ir6YTKbWvGO4C3z7W94ONOJ7g2MojcAOw4Ro5Ru6H69uBEbyu49ODsq9O0eFL7C7DbQh9PEo+WKdMXzUsOzs7mgQnQIwepVPdhuWHKzUmroU+UEsxjLz0vUi3dLOFhf7urMxP2y4Nvs0ZVYegz5IOVBR6IEdh1visEOuyAaQgqrUj51ZWIQGil0yGe6dIIDpIbiIgYCASn0qYYj92EDHkeqgrGgCD6Q9jAETCDjzUiRiM49wW6cmXqsIbjPs8gpwQv/NzbV4QoRTzG2eVpNg1xlP6htUKBaynRgTynBe3y0wvWksR4AJ1SxyAJH58ZofIDM2t7NzTSPu7U646fKcbfFb6FxJdSzXN7YZnq5cqlxixcJ7Lm/WJBnpNIu6P+pp4zgdOo8Jyb5QU20nlkNisTC6wnq2f93oqAc12XfyHyjFmR17i3AI6QaDjHsTF3lkCotuYEQIoB7KDv0wbOwNHIKnIFgiTwA3sQz1wj7wyNohqW7l784DGTLJ8oAseTycAGJjQVsVK9G/YgHtp2WwQikDwa/Wvf/aSEVERDmosPK9FgfFwHdHD9DmKyvu7NcRnwxRDRHL4GiQR948yMjGLsJbwMboyZjfV1w74ScQ4koI6hVWxTUDAG+N/7tDrqa5WTA3U7jenbFhcOMDH4FBcQxSY0iNmD4pK18XZXJLyGDxuIWLFc/QX61XWfORlKcnsLQ3KiB1cXU8U5srU7/9fOvXn734xhGZawvHP59MPZwrGRW9Z2HYtBdcri7Gi7NSggws2tGBaEI2z/s4WkkLwr4yvFyp+gmjRN1B4b2WIkZJxxusai4Ptw7GPzjHxQ3QsP3fmOxKYSfpN5Phxd15Zg0zNd0KkpHBUrie8kae+qRNi2RqBLQmq3o/Nf8oUjTdDrv37z7ZpD++EmCl9n0ZdyJROyEK6CO5eeXAUCZ2hhb4biRM89RvNmOchrJk2jxnas0fjvkaQqp+kOvAptLOPIBZe5/gTBv6hCoFSIJmKd+jC2KJZAJVu0nQ/JIgkyVuxy99qyvjqcKSx40twM7tqMzv6UZsTm+C+bATLbQLnVtkYlXFwdobMYa/++33V2pF9ExbXNDvBwiYncgcVEEi8g4mYb3tXV5ugpbp/hoficlJPFhQjiPhuGcUitlbB6azEMon3Z0PDqwpvGtX01OdCAAp8aGCO7gKFSxhrIlMHMXcUH89+/NsQqZK2Xwr6lOonbaoUooZEcozHmJf2EBhjv/8Civda/B+SeunDgrFQo55qQjdg56x8v279333oeuHqqCKUjXuLFlL8dlzkWrY24O2JJzskoNgplw7TnVl2x+qAs85LL6kPTEEivppBLfL50xm/h/1xu5fn1+ltYTRqQ62jtQpVAUIZkFtOBDNzCitw09tk2bBGzrt+nQJRCyifeD8XdDI9TafR6Fz/a2llGV3lfYbDCx1sJptBJs7G1wdfKKtAsShAOaPFbCKFTl+clNcjASmrUUVHPLOca07dJuPqRC15gr7J6vrnCHOIPWA8i5Tripab2CMfXmC82U852RGe1UOQP/+zq5kgIXxLGrii6+/QFLrJaNOE8hjeIQ0PkiXmRfRkepeWHGqgUpLu8yZwTcIyWTmcReJE7+o45so/6UvWGNYhUEYy8xhrGghQhOnxcn3kkXlcXMKoh/bi319s9b5ISlsYk5KISD+hrg2vcNMlOH7V+2YbQgESGvgCP1IOOn79rsf/n//5/8JZNX/sIBCapUoFRTwDyrSdt2IqzEnq/DxXbo6fGfFo4BuX1CM0VCakGYKlN17VCpaUcecLd85KIHczMrDe4lZtU/C12FekEvCBFgq7qxi+qxGvXrcTkiDsY7QFlq0qZDzJ/dAKJVvuj4BmQtA3CezyY3CzWcVYEtnJQNSbTRCQ87OfFYVQRQVrVlBnmwcXVlnXyPxGWRBGdmO2UuhlKfH2Cgo3/t6Z+E3X7767dcv3u6vMZTuzw8W51SLzeufrIKHWabovXzkKNbAFWSdSwlZsCGRAiPsKO+b/HgItg0cDN0eak+nh7Ymq8McqQx0mFXEsBZBZpeUpTtMpH+tIM1kYYe8t6ze5TeZkaUZybA8HZvovSApeHBJX+8GbR8jg3t7e6trOytr61Du8Aj9T5W2a7dDzQakGM8GPSPhinkeS6X4k4QCpkpnhiU5NA4VyOrBrYjQ+PNaKJtmxCqI44oq4Uda/REuWzxpBXeaLpgJ9WDY0sbWvWacM6pRLInKJrAAhZ0HcD/MZaeCr6zK/9zenzrLav5aN8OOzrU+UIvIizjyU+ja8/NjVpVc4ub27sr6OTOE9fn/+Q//Xo+1b//6vYp2tUSGw0p1DCeKDHwOOVOiNuvooCWk7OGoptNaiV8TwaH1hkEYvp1vkRMoKSAMkfS1tAogDnoTAURQb+J2widFnAmR+JHFYpoRJIyGgy0SzipSR+DLCLbvOSO+RLkn9HALBbnIlKUFBKzv9IaMotxsJ6bwZzoshQfWSuBj9F43sjXDkp9U1Q5VjZgatp0MhOER2mxFI5rdvbdffPbZF59ViiNyxtkkAiSb620Eg1EGrlXTAr7dQkG0OWflDYqju4CsXxGFrECBVquODo63vDt6OBnM6nQa/lVShyNgsZsbMABl9HHnKA9ajirxXXVQx1cnhA3QkGnVT3dXjOBLmmtjZpW3y1Y/+PTJhnGOwMz0OnnJpBZcr5e6PZHS6UIK0Yo0eKLIFY60jFDcFCjtN5PX+BcHuN47CkwXnjp1x1G9kzPkOoMypiCUQvhJLH3OX/Y57fj9t9/95Y9/Pj0+uv7ic3EqVUbSv8wCESjLivAEAWVYwrDJ6okz2tp4eXa6qd86KXn9Svmnuo3SEvYH0Po4yn7aghr6gNoxJ5gTgjNSQB0NwKayKNYUKmVAJH+W2B9LXb2NEIE/FqQVdgbDsq7U7bFhU9qocHV7PsKUc44fDvGhIOkbtCGOw+2cfvf+w//9H/+LGtJ/8zsrUFIKWJcMeLCZWaqvc4oskOw5dw+0O+UNrvK61FJw7GzBvfBgVUr2Boo9OvaF6YaNK7iEVnE41hJWMifbZnn5Hv18CF+xgiAye0gMFPoLPYEW/HpyenY3qaYgqS66hR53nEXeCWlqu02JVf5+qohKoXENEwZRSnDQTPJSsoYL3EBItgRLJcPYJ1nQvTfEDVFzFBDVryOCFfrDOPKovsP7viHjBtJ/+Wb9d9+8+s0v3m4sC0NfPFxfTN9fatDJZkG2QPYRwyxEvvNS6AbJhivmJuBPPEpCOV0ly4b+ZCHyt/IvniycSsTaMY0UO8QRLqzRG9aw5qSKgOdtGRljbFR/moLblkfxfUxX0qgXH6+IV3bbApcj4BfXKkiTPwPO6RXPxV2ucVOUE03hm795/eD0a5vhT8+OTs5Ozk6PoA9Rh1KWjjxa1RxbAjv6XtCoSg/F/ewWmxG8S4FaTKOJh5+dAP4J8iIhaGW0u0Rw0BKIY1VVnj8hfgVxRsuJpcnu3OLei1d//PYn0eq20pTDIBNCE/WG0d0BI61INjgBSJ2lcJP6f/KppFX/3WJZGkbc3X46+fTp8Mf3HzxUJbnDXH/xq19+/vkXr1+8+sff/aNU/fHZyc8//yhkuLO7N7dbqIKNizisQHlXKs+msM3NbSiEPyl2paVZT0OnZtJhdFvunaAlecpqtIn5hhFQgblGMzwJq+RiP6gsASxzn33xxccP79lzDKs7hUM2XOWASxwXojH0AevakyEwGrZJyr8DZ5/YDxkhVfuGLZQBEmClBiiSpdze/M1STScziSKralDoVg2f3NKFUJSie6uW1cayqvxLr8fdNZ1gnQsmUb1FZQmSqsi9Ey4XycClGVRDBYDCEGQAN7HEgmw3d2NLs5vxsCkowBwrGlzyMOQLZHOdpMitg79QVtzDcyFXmyyUqGaMYBHpdWncK90SbYkWOPJABrVAgccRDmwjK4W0fjZ42VaNakzDLSkPXgPEAYsgGJSz2QEaj4efCCFzGnQhh3T1sEPIW6tjToTQb+7vhotrS0buu6EvgaUd7drIU6Azxnb2qGYPcJrCjfiGCkPFQtZuJ58+ffB0mynAmb8hvk+5ChnCMzNyFaAf29Rt7+yMoYmgdv9JOjNQqyaXrqKVJbpvKU4eHbpfCt21MYk+KCuAQRIcohN9r68Kd1RdWJgJgOrp5S/uH/1HKrwP7NAaz3lCUSOe7CglAInVIMKKIZrhREDwVAv4DZ0j2HbLL169cRQDKLL5WZDi+OikoA/9YBfc8qqFI2AORjYmtXT+o3RKX6GJ4F7FPjXOTTfVspua0PUFsz9WoBzHjitnYl13kjk3zvq1PT6CDz4tdRXMNd/Wxd/oKbsD6wtEWINsIpu35YkMH5qVT2Y9QBzgihVd0PdUGOaXCHdgpc65dSvTB8JuLFmJgLwtX/ckAkVX+NwcfdkNBuIHsLR4QNtxp9bKrJI8vah//c2Lf/q7L//u65dLszf3ZwcXR5/oi/arFMwhHLVvidC18Sm9CwJQXYdpUolRucvt9+eX5C0bqegl1i45n4Uo+t9u7c60IAYGl0GN7aADzBxOHlmbrKY/UFuoleDLsBqbcjyESgbhDlmmy4ZKhsEFAghGJjquQM9k2UkEakA1IlOf/d1PnyYbextb+4bHQS2czFbSCQ1/z04fnx7hTY8QfZu7AVAsU0on2K2yqZ1UmSagkbFjTD5nOjFtBRIsWooYvpltxgEVpqms7T4qYvJpuGT143Q43bAvqUo3gktaK66s/Z4IOaLSxHjqralzINCrNJmI0JN6fnESgKdKwFoWoLeWaK+l56ePf/yff3bgiq9f6tKxsPjpUJt3vHb79u2bzz77fGt39//4//4f//Jf/1XDCtpkY2NbyAptmUjKTGR5tNDFyV5mTSLgJ5LiF72suUV+xRApHZENs6tNALlzEoBgJ8diAwUz39Pw8hOpjbl/+4//9OMP3+3sfjw+OWJFih/hKmoA3QiOwcX6o4lxtGJr10m3cIovz17OXV5WRduv6Wqh0c78gv7CWECcAehvFjXSFMZQCEQMludEP3CCUDur1ijFJRpWW65WhX1kqwlW0QeW5uM1KfVIYR9kIr3uQEhMsXasozugOn/3xwEmziIzOcWIhucreFrZSDzpjEYm7ihPmkyuPU2oB49Uyfr4JBialMDfaoDv2BkwGs/Ob1r/NaCUc5CQJnBX9hgGH2Q8/4OcHp8dOzrYzLApHnWVgfpPyNhQh6iFmdbbBRABmhdgNmfNyxzZemHzWkGDY2lhkZ+FGcEvdwagIOnjwaf3P793E609AbvhYbhwvxPQiOn80/yT3iRvv3jFRB2KR0sf0uveJFC25UZzDuDr+uMTTsUFbWoMOHZuSruhmTefvX795jWXEDJpqArUAT0lw/lnYJgyrAG5VQLg6NtLSAWBEMsWOAvUPC8UTFAfuJ0LKdjdFppCFTxG8698Tc1fakGRx9kZA1kwOaUr0k3u+EbyCIUIoUU7DZc+e/vl68+/0odtfkmt3d7K6rqnSIYfHR9qJug8AIurm+nC/BloIM8pazA94JhnYlQIY11qrV7T6QV1ymhOIcKtWlGM9lNDk6Xt3U1giiBJlzJaAWVQXCkE2AbeBSQDWhm9LI96EV7NyTNBQoGt/jVX7KAGlDEBpc3ceqcQxsFw4sPgr9bvQ1YLqeA5V2BaSMZQjnAGUOmI9z0wtsmATkop2laW6aPe/Io6R1Yj8f4DYm+uT335cud///tffv12X5D54eJYHMu2ZTZpRSirK+5izPiKIc5sDDxLv5tNeSD0uy0zqpsuA0VtVSBu8ZjSKno8vQDv1AyjgWWp0xaFjTgyvWZtWbFiMmjb1HOiQ6/canDv6hEmhzNX13F+jqSyOaa/sIE8a6l10UQgo2iTAvxbrSRA4q+vbu4tzAPIy3c//zR9cLqxdcHnIHKWNafTFvplQYs1+8KImdkgNlbFpPa9opxADgWP1KkEMxev0ejy7oqCm1Lr1C7XwmkYQUYZMRnxGFa4xIyZDMqBxIzI4/mZiOsI8aj4EhfhE6jXUBi+uXX6w0+OXioy06nj+IgOo8pt+JQny9ki6VZQvvD80xEVApFoUSx0dnLy7ueff37/8dXnr1d2Nr779se//PUHx/F+/933//v/+//1H/7Df9hyHMi81uXrMnhYwiir56tP0RXdbPswraCsxBIyvKAixjNVToB1QExhdBTFtywdbtPq+nppwhk9RAUCxBV45OXoY6H2atCbd3O//uWvd7d3TgjW2SkVodXMpwOYc8AhhVE48IrssF7xqP0FNWRIl3uymzlNxDwxD1kuo+qcrHK2ThGBJ+t4C38QURY5WaFkkQB7g3uKCFeKs2xvbpsDk81SgSpjJRqYRg0ozJWCAYvPXjPLK+XRfnSFXD1xQCRCZ4JZUI/z8VjG1p3wlOJwjIF+TABLSwMhVJqKzZvtT6jjEAPzTom7Yd+hHWRP48og8SKfT7icnxHcB6ZcKmL15ITf82tzcKYxe9+VLN+jYbDnvqyvuYMGE05JBFu3RyYBPKr3kIQ3O3rLyCkAwoak5lL5xoUY5sPHg49/+sMfFb+KS716/Yoe5afTkQcHB0YoOCOvwEkixqIcVtEU0MGcODevXr0yPL+ZLIApvyc+VVa511BgLu7gHVVQcNDGeCX4LGJ1x3JubKFHm6Eq/rnls5cSCsYBs6B/u4BAWn2O75wbCqFUZZMYaT0KAi+1BEH42O+NI60apjy9oMwyQByhWXFFBau8dja73lPwMRE1BQzVSlQZVfHP1t6L3/72d7/6N/9gc7o6PzEFBpTIP2un0ipLcnuJifkmR9enWA4ymhc4q3JjtOaCNQDLPGhxXjNaeyj5oANEkCX9qAqcxqZgjfoIIC7NLpvVxSWn3lyyjGhQEzRXvOIaCgFp+WrwivOHbaxCmcfgOIRFgSI5VvHSkYrI5yF0aN5D1YZF1c0kAPJfWS+4ARHbgpADhIGJEqToFkxX8xEw6F1/oWzaKiMizSFRrKxQu9THrfXZ3/3qzb/55Re/+9Xny7P3VycH+p84rsZBfOdHAOr28FADOGE3JpqDxSR+fF96BrRxoaawTd0ta/M1tpjVpdHZlmILhBplLg1ZJRBdKurjdhWtscasoe7QTLAJvghKqyCuwJqmrJgL3TI+TcqDhyNklf2aoU23YJQyPYJvVeUxBMsES0zQnWLlqclHKS4HIqH6x59+AjnrmztiMZjNAIRaLAGrmwfPK6mo06NoaPcHSkX+pygrLIlIACyNpZyIYyuqYvdyh40rgSX/Q/HOahhSLakNBwpAZxedYGgRADYwmRCt591FeIIMyG4p59ja3oHgJ6cXnw6P7APmOfHzNCwEXwwR9LVeypt4Ttgty8Re0eZnHWdsZxVHIHpp/yrlaiRDhVpdzvTHj5+gFoPGpneMrq8agxgx+TgDsTyHD1ZXAjxjNZHaQ1mELFRwZEbNq6a+FBcGVhn4qJ4S21s1Bp+bkwtwnp9VgWK6YO7Fy5eAUq51+7oakvfvfv7+u+/+/Oc/HRwKZ9vpWo8X085cFQ1X4z9SbR7KGSsbubzsmmdkqShe2nNz0yiHDZ7g+eIIXSyFG1VlOFFypW6OzKN6PVY4BASpOPMnj+TNlEd0pegJhGa0Ih++eC6pDPBAj2ENG4qZTz/FfMCU0pL+Zea03YNmLOjUMSVjzyeTbqBVIQTfMgBL3brgYK/6BDhMp+xh8k7iOwVbxuacn/xOtzandp4cAdXVzfWtnb1Spu2Pz12gPqVhuSgf3n9wSu1kQTZyFGyETLY4NgKjHXFKU+N/aIQgOOIp2VwODqUpZOqPDg+/++67D5/e2WXtMsXPuassLy5UAjsMNxw9PEq3hS83l5lFyh8T8sEsOlIYJHOZmFJ+TA8I1RpV5nxF12WOdHKAKHZtmSmjcRIAk0x4h1HJ1rFUpXnBoZft7BLGiahvSXkP8pFSDCc5NnlSDZWFohsIXYrnaPlOL7W9M2h0L4rByY6d6pwluPqsWxJ69CcV6KaowXZaGEF8Nrd2Xr1+qzT25Pyay1J0XqwsObIHc0pDfvlDksYj/vD+CHfxNR3PCVhZvCur1XIQ+sOjQwlPXZ5EGu3pHudWgDkokDZGKwBgikIk9leopRbdM1QLxDVUpYxY7kw8WOaILVSHMn4jgXGOk5CzvKgrnMtpyMqhdUCOpcGf3iPU3H6AW8zZC4AAMNSkJ5Al/hjEyX5BS/eL1KhBE7oLdR+Tl0tAtswZZIf+VElFEIqSZ6bWN2d+/dWb//Xv/+6Lt3uLGraeHlyfH2m3OrcyB6IHe88+6EEy2CZVq/BDqk4+L61W3Qgn1PFC2IBJRgrEu/JIarPTgJgvBhPyztZra+rybwfTa/gpg2CkFgtjIxSOMs78CIo29gKirAtaAE2H05VjXfkdoY1t0gG1k3tK5acvhCgjwaN8Rq4Yh/XVq9e62F7dfbDRB6RAPjx2+7GOtsO1REGzmFP8JFJBtdCpZW3hRBRW04vBxPihIfJlvjhORH7DEJFXGFo4VVaWCU8ByMc+zZ4dn12ubXEWIPNNZpYEaXEU3kA1WaZjNiyvvZf7Gx/esz9OTs6UcazNr5sWenf2IIZqn3PN/52ciJxc3gunGdzo+JJliSUdCLY2s3pGgdx8xDlf/+LL3/z2t3IA29s7Z0enosND/wmWPsqSbm9tEymmBpDDjZnvo7EYmWX6cIOGyslJNUeo4k1wpsjHeVpsFCpWyxKfIQtGpTuZYFiUSYZqrPzCAAKaxNxb0P/leGVmrq788Y//8+cf3yvIdUSnB5B6rsebz1/XAcdi8kfEldZEVTyyfKaZQ1FmgeF6YXdzYLiRXAPwKQ9BxhxDictiHyJdCDRGujw4v5BYQ1CU8izfEh2iQignA8NXlVKxpGhg+5bBs/C6RvQuWzyzqYqtQmeowSWviiPzqmvdG+byKK8eLwAHVZd7TpULbRVqdZO7ucpyxYhS+v52KjHgSjidIzPfQWbt67y94Yr++OMPP/3049HRAQ9gZw991vE9urH0IZNojWDy5cm5gwQMb297l36uApzN0JGBFUQZ/NDDo3nGaJ2EPm6OvLs7O108ajw4Q879ZAER0QFYll+J0UbJZOV0Nq9pdwOW1MMIqGlrWpeP+MIaJxPgKrkLTXDDq5evELj2xKJbM7MXZ/IuRxLSe7vbqHR74YBAYjjtDs5dvb9Ufg/8Q/GRlaNP6wjkfoVXRuQHaIJ6EGz5IKmnijYyV3EE64ziFofDbhJ83Kx1zviILhhWKdVQtXZINqwYlcVHluZIF4vZZ5/ltbEe6AlBUscfEBNYDGg8HZ0FERXwyNvgcvzM/oCObB9rN3yaTCSJcRumBd/evXv36dN7THL3wnS37JKg1QKgsUsrviuJysPwYsBhMVIqb5HGRV8QOBS2oXF9/FZHW4tu1iA7QMEbjEd9QbAUBuMR38/hVUYY/nx+081ZJJl4ntauQHJHGhJIszL9YiC+bATWzOCwLCBsRH3Bsz0XD7mQrrEQFChi3F8+qdH/+s2L3/7qyy8/318H5jdXGhjxSJDXd+UtCYInLaxJ3k6fHBzzwDlPslnQF2O4itAowvI3d9o1ob/8ePEc+oWy4SM60LYt1kSHzCG7CfuIsKQXBU9EtHCP9KNgCgMc1soYsy409GeF3nXqpMtMHic1RajhH25CbQkM09TjAeRimeaVaUgiGWNg84s7W1tff/GFUSxNtja2N1VOn545JUkZ7u2JKhrRmYhlkEvlOLgFKVrOtGHMilrC255KlTkqejgleMiokZnfbeDlPuxFsF3GFj7+wtXdOWVpZexsPb1QErC7O9GcADMIPbsP3pLYENNwGPXe3s+1Pz4vNqUxQiEajcXoQjm3Eczr/NoOzsRsnVmUNE7bJpKZJPEmRUipbWztTNbXFbp8/sVXw9dX4lVECwYz5IPNLIMImQNBpBDQ5O+uxVrQGCEznMSz2qFV6wfsenR0CPHQE0sWn8ymodQRQBFR5ZFo5PhF8DJiD+cK3ufYnZaA1DGK6DsMsb65zqpytCxV+PkXbxnsH9+9Bz2v3r764svPJWiwNBlQxIZHoRt1jfmzrO6y372Jb59lxi0BGeQSisZhAu7GhCI3ShRwQqZDX8Qy/HfSy8rGCthC4Mug2b9iLG5Ip5nhM6OAbHNGzONj24/VZtmX82wBGzxS3B580mv7VgjM2QzcJ3oPoxRlSq7IyMPamtIUWqWTpAgo1sGmnl7KAYn9o5xIoxv0rv+d3KZ9XTTUmZw69+Pw+IhDIEdf+dGIO8lOkZZPhzvnJ+fKPfe2d8yMrGSJCADTyZoRAY+5DvmkQiRD2Mlm4dcyOeHagrwstSHL5NCflY2Vzd0tpaFlxDp+2jpWy0hp4QY3grhopb6XRlxZ3YfCkuxuUlshNcu2q5QBA08ZywefDre39/ZevrCd4vhIGP1EEH11vWImDIZNVH8SGHRg6WBmQXJWKG9emNXxvyrIZWMdRamO1ICpgijDIh1N3g2sINYIZ4eMHev0iFLsKxxJpsN2RnzlH6RORJjbJ+E3qzzDFwshgH0mZGcVpBg6HZvS6nC36dVR+jlw1hlqdZuQMNu0JZ+FMln54osJH1E9SbzHpith105R2ILUkm9EBa1cY315W1bWoNv75hrT8D+Dj5cumiwrW9BAMGNmaYs9KzGj3Lvb4pqqRcCYqZlp1g/UQoEgHLyR7qRU8Fl9xPAA0ERkwLfvZ/JaEDajum8UAWl4z3YxVChdwFiqkHoY3q6CNt7JQvYkN6yzf/1tFJ2IvFEgD9B/f2v5t1+//eazF8saTd5fzU7frDjR9t7xjnZrOKNKxlshKI9W/pbHmWxDXCkN0zGQi/MrHgD+RfCGTHPYiEv9a9Iw+tpSTdaOWhvp9vxgtcmZUOMUBO3gGTQm41YUpBcCsvJYQiS+y2xZA6ZZJQZhNmZpUoWgguWh7zyUEBQ+xE+XRM9540v5eZXOioOvvnr54ujEumNF9+47FqgVF8+fnS8tzDTWXuz+4m5aU2bQT1XjPsyGv0i2/r3o25zTwJawugkfgC/lozLvDqZIVePC65OLw+PTyxuFUisa1ipAqKRpbLGwmuJ9jFgr7za6stiW5WwAzAzcgPXhydHl+Y0APVlETaS2I6UympSrPAUNEvJDW7MFN3pD7+ysfvH1r+wssLJIcnTwEbUnq2vbO7sbW1uv7Nnc3HwvJPLpE5E3Ew9KInPaWAMsNDVFXmouFLamFwmnN8EC09kFhqzWEf0lrpU5QmGLAmypN9aeKrkYbHv1/OgeCOI9MHc7ezVjO83R8ZEDiOUpjk9P2FwMEGDo8SQOHqmU4d0rHCRmZyfndKhj7ylA5/pCZBIBRjkNfuB+U7ZWi80HlXkjUMTSQ6Q889MT1wB9Rz8TUST1IC+DBbjB76hboFqsB167mazUC2jsJRGI0DEaStslKxLwdFyGVsURuyZuQ047qLTvAgd5G1UGFGvTVhpIPe9MpoI1oL+spIcmgB5BAfkob6wgTAHoGYJwMKs1nO6grqmZz2lpXgpIEC7befHKm0ZrF5rZsUG3N7bevH1jmV2A2DQN8c+Pf3hkd5uPRycE2X7gpVwI7cPcE1iiYEZcr7Cy89whOg9WlAwTbOl+fPd4dHis7qB8o4noIrW+GmBVfFKXU7B+t8w/SEhGTtsjQsDj4xOJLLqH4avIv+ahS8vOCv74/sMgimnow0GK2mBl/y95YCLJCxUvtfQsQ4HmNlvVBEI5LfVKjJBVZMD6yHqyCIXG8/xFJ5QarPJanu5tWBOz0dG+0nL2wRpuAQcECdq6lRqpaG1vFEC26UwbyOVFu3FQS3G1wlxNna/vFdGKN6oApsUfnM6IUUmTBZLQUmI85kv6YIEYBeHUEdp+CDW414TSuqOkejmcQBigGu1iaVjtgDT8hcXWZoCtwUBlwaUif2Nvfbw4xkMEyEwyR/SNuXC10S5jD1OCHaXlzXmoxOEUihgI3SRsZuPOKRGvnDNMkf0eMcAJ1QFinjMqHtYYAGOmWxDmeaGmgfpn1G7XYrPEKRTb21j49Vef/eabz754s3V78mn66UpHbydc0KUUDQoMa8A6zbFj2JKj/KGyTpZBkatr9SedF2lQXLlArLgrLH0SBDVBSQtvFf+xi6tzTmxsFGt+cDgOvC6pAVA0+ZHUkzZKrCoPKSI09kyAa/Zy+cMSJIQSQSqFtFqMVVKR3TW2GihUgc8IKNiYQyVtvbQgM6OTlP1qEpeY8/rMvlHWgC4OlZNhcwErXAYm2II0YiqVbi6WxPrxnEd1xbZ/KF5Q91PKzpiVL2b+NzSPTJFTXeJWgjbSik/T6uw+fjpmXqyub0t8YBJ2v30mjFdXWAJfzet9VDU3v7W5fbRxwgLmhTMyTAJv43/mAEikyMP+RJ//IoF8cvzug1p8bLi/vcXA/+H7H3768WdxGpWOq5Km27sMGiGIT4Tz/XvD++1v/56bocBTSY4JF8ilqjMX6saPewSjGXYF98sjZkj7YepGbCdvmEanmu9uT81yOAdaYVrjObZpFmsXCGr6LAzpUPXEgvs9AEWIQC3Qf/1v/+WH779nC9AH+zt7L1/um+Tv//V/EpI3X749OlxnkUKjZ9PeM3C5LWemrKGlfVuAFc97lLaiU9dtfbahydpRU7Sazp4Ulq+TNh+p7LJWuTyFJgslKQSCCNQ4PUHNuhVzRoIBM/MVBjnsoytCCmYODz5ZNvuwXuy/ZBQI6a5MFwXmZQhFWwZjE5cCZGQa87KF6H+vqXJ4Ps2qYjkosbCWCitY7uqHxbMYmbHs5FE6/au5rz2XI8yNkiUTaSADgACCd5xBsb+Zja3105mp9+8+8Kgxl49ExtyJ90Mr5V4Nl8cH5jHKBrknHkXRcL1jbXtP1hmtiwsI5XH8MMEfNUJaczOAwAXcEcmj9hLSshUaiJ+rjWHrGIAIH14VL2OvCb3gJLzx4uUmLFleFUbkpQZsm5sybJTXqoqG3b0tG5XNVjYyPOhIkALu99fn03fXFgNf1PVQCSbgzkiW7BIWU+qQGUv2cU7VGHl8rPw25TICNDM6ODytBm8eq3lpOhZJEd8ueo9SU25sDLOwsAKZtgTTV9svJPy4/BtPkPze4VqX94vZ4ESQWrX6vBx60eZvXyTEFJPiDxkn7z8s0w5V58J5ZqXaoY31leG92c/RNmtjg48sQa9hKZTERaUaifBLzL/jggUhcaKD/JbL3oxI5uONbZ5Wv3qtPBhRBhHk9gyyumcZYhgLXhMyEOwmhW/oK71559pmZqdcdnIhkGfPA6HTQKLoVrV4kO+LaXgqGoajfmRXD7sVAIE0AwU9DnqTipi6e7W3/eVnrzdXJ3cXp9MPl1a+3fG8P8pvcdaC+iXxnJqtsvlpSpUvHtA8gvxjIQ4Jhxhk+Hl4u3b+my9+kpC7sUhoqFuxvTxkQccHfMaktdyEFF/b3wRJR2qGDzFwgHnpVHcxdRz4dIulm+qYB0q0YYuHZP0KJckVO4K4Rp28ce8PmlmXiA7EQSbBZyQr/y/DuDD/0wWH/mlpJTsv85accFbucT41UafugMxraBXyzOC3BR3BlpmclhfPilaRfMa2Smv/4PK2gFTgRaXTcsg7fALlfWlzE+Zy17Pl9CIZ9yFoL5rBDdcebvXtzdXPP3z/4ed3H969c7QaRauuAsISeWuI0Y6vL+v+BbudF7uwrIL/w3stD+YtBMOOOHx6f/Dx3ZGvsfC++PLrr3/xlYH+/l//8NfvfjAma/MP//hPn3/2ObgmPIDew01RYBN/G2J1gyYwDD7HRrmeOY3ReF90G4ZCFM0rRalo7g8f309OT6WBFRctbG3jMELjI9QUf2WrVufgIacnTl040X/O6S4f330QOSGzVglMA2goLMOJWpzk06VzFjQxF4RGfWrQeidUlu3kOItDoaXy8IKtHlaBI63A3qd2On9lHHGlZhSPSuXR5AQX+SiM1fkVeBEDFOgvIJDNx5AEnzoHJKHFgr0vQ7A0WeKciIMTbEiNTdNyTnAdjVIB05N99kypXNEB+VU0jlh/ebZhj4xhEwMCA5zhC//taU3pkTprm+VEn9p5ZA3YdDvb2+Cnxss5kdIHOBk+zKyVLKokzhg4N3K5jFKV6QossCybFECIFIMPwiNjQdviVQS8PjnB0Ii8trGt47qbu4YoeR57W6NYoGZFFB26ZnNtA0Mdfjp0jiVqSMpJHlxe7tqthiyHB0f0qDs094sLGWAjIZzb2y9k0gi8ooKDg0OuIiecaay5PetpxRZEN+IYKGK+UMEG2a8E24cBIc3Y4S1aRorwiyBTljxZgUQEGYuT0BqSzgxV/0BFKMRM0imetqMdJ0tAgJogeeRCXMKboZJ9m+FgW2jQrPi//T9O9xQc03eIx2bjJivRUIQzr+8nj9BerVcZy0ogdEzc2kYZuoFXNIw/1plwE29hmdwD3JKvxcqEfTLzgZr9/Mk9PhBRr5nzaApWCU+FYWNQpIbwEnxmlvO5wBxdKvog2qbiWVi/Qv4cyBGnSmqKddSZkv3FZfWZr+OBoQszDHCp+yMOGRNLYGC5c8qQYmTBOh/EXaQ9yHa+wdCFA8dAIZ5FJO+O6n3WV6rCF6mN9cn87tba25e7GnzquqdpFjzkhmWmiolwBbVGo2jPtFN7wBPKMq0+UDYkCGiPTNbfw70jjj1XRNeUSHfH+Ti3/KbWvx58PX0l6B/1NMva2ISPOjKyWizphNuDSEwDG/jLi9AB1fgxPuwkM/ZGX7zKP+qHAuHQ1+ezC8LwsMJIh/sEOUm4hFEJZ8DkayzHhNX9BMRHaVA+fVYPo4i/i3FMNmKKpdqAbRzE0YMKobl0RH0QWCaByQ6+pgTP21CWdcMd03UqfzWKC0gF/5E8LbBEU0hH0XGUs7CrdoC2RwtSstzMZHQ14goGgcxcti9hODo43N99sehIAEfTyOhJvhrbMBRmb1TbYfk8VPY5NJLB+vGnnw8PjrWcs0V/rTwiWJu/OT979+OPusj/6+9//91PP33+5Zf8b4bFylalNzrEFfyYvaO8sU0J3pGRHj6JYgEjrPUOgcZtlhXXWBo0VLnj5+MjoeuTqyVVpI8Lc5/2XpwJK8ima9wJ9krKnh4dS11kSB6KRbDi2yjx9s1b+AbyXr1+EWguLwKUl69eUbXUCHmwuqRTrIYaSeQUeIwNGujKc0FS6ujCIT68TUz08CgMzZ4VoPANQsJUzwZ3QM91USb8J6Q7sS1ZfmbGGVhX95cRko7RGVXUNbtNpmIUXeAO1jHXwcwxjbQE6CF+IfA4hZquww5eDFnSAInaCjG/YCTonbY0PpUAPhzneeEsRpR3ICEjhQ2lBKDmzzpDPDycyM1/OEf3tJTKs/bvtdsLlQXBMJJgZXzz/loC+PCDXdfvneFguDjw+OiYuiKNgv4fP35c/ujggfad2cunWhRzWAM0B+Uray+4b8NKvebrLE9eychJO3/73XfW9dXLlxKeYlOcZBr07PT4xeuXL/defP75m/cf5vTKrlyMJNBHczMyvkJjxycMcMHPBVl8f9QHc6eEBd1NyuGCoG9Mpl/Ic+FS+QNBcFtpEgcClrQEonJqsELknci5RJQWtnvhcrbmDbnDBmSyfcxycUVzrYIdOiz3nCjOJUkbuNrfWgcBDVkRSyDbNuwqQY72meMZVonYmvCXp1Fg/H4/DBDH/CxQaQtCV1rIGcaW/syhz6dXdjjIGTAPsCteMqSVxYm4hzVliDAZO6uI2WhSNVRZ5XTQ1sUa7pg/yhYBBrjjs3MJWPHG70CeAccwZYbvvMAKFogEizYvElh0tqBcpkDHtr5iShXU409OEK52BzqSS4fPQZXroAuL3w+hhKs9IHAcqDWUAipISEA/7z/7gq4GWC7KuM2fySuwGBILm2srn73c31xdfiTFF4fyAUKhgpcFO5k87Da4Q71vrHqmoj+Lhzi4TkDcidrhSJ5wHVuVPqysSCxZXf63r6fF8suXlxxsghoWiWwKJKalKmSYXZ4vRW+HGY+B5SYchMcyCczd5WBGxCwKooT/8wyYCflZQw2Yokl19bgzIY0yPiTdRsH4m7V5ijZRqjHrAO6d7Y3Vnxc/HYknO3pojjnSumNgzcZHydC0rr8VrOUaF0EbHUeG8BkMyrVbl/VmFmmh+UcYX3g0each8Lj8HMOHsegElXYyQvClNT2BKmrA2zpnpy4oVV09ipTKmMv/35Aq1ngFcqokuHJlxAkHfYySPAriIjWdp2Xe4hPs5aPDc5AEuSwORb2+Pnn58jUS2W1/fnZydHx6cX6ieoFly84RU2TqGTllUDBmemZnZBaxsdF4KkAmBbOnp9frlxSSOSGgHCS6smdJhMFbjlG3uUM81UPbgWwjD+3oi6fHx5Z28jSZY2PiXpadNKcFEF/96osv3756LZRPQRVuc9RZ0ZjTFy9eLq9pmOPsMUcFIBtEdas8dF24jAANAKWVZ/VYEPa42iLihYJQnpiRTMNi/FoBb1gEfDm22hRCIRBu58gfkpyrm3KelrAmst70OETEKGL9jGs8KncnG8gvhoxmYUimxFjifwjmuFv9exiBFr4VbJlapdZJumhwS/bQM+iL+sXBwxpqsDF+F+aAhBD1Tqjc1ZJ4eROvSBUwit+/e8dyJkLc5LE89dj6se0dP7Op3tjh9+aNQRiK+9ovlmU0Tz+v7uzseKKYGzyxeBI+33//vWYS61sbzlrgcnqTMsizmZvl7XqQ27oMvhweHRy9PDCZTx8PjJyqU9bGtTqV4T0t9sewFCyTfJU9X13n2NQab2YTN+oRcH52c8nMUT1UogRwqXR7uBFbwM0tl35jDlRyHFjIECNn2wj7VIjFnmEex17YwH+0aCZb/jyzminPYFzXHcWnXBmU9BW7w23QlG0VZ6OUWhMHqELPtjjhDgTW4NCJaUuse2EeAAE9uYTEiSBBEtEfT3SdR5zI0Nzc1I9BZ2Zu2KiQ5cNhOUaoIMCh18FB2FMZ3HyHR6Zt0Gms7FRFxiMVUH6eQHl/AHh9zk0n9jA2AWXZhWlHJomwqhah8nhDIE30KnZi17jj0LK8Sd9zt57gOdiAdmeXFfnBaYUg4iEoBESAXtcRCjDoJmG/T92s1gjIH1amftimYh2lU8kyYbBQXPKt9RV1D0vzRf45HTR1ytohGZXq5k9ZTk4cfcxrKyf69EitsqUoYFtJyDhbi7C5ad625izrK74iqqDSQhW8vByqWEmSIb7tW2fXau30b9/kMfKcmTtumtOryylHZugnJDUdfjD6ADXBwmAA78YaHTkeCpRc6kXuiaNpm521DgggbOfm6pLG1TcN0b3blcna3u7W8uJcyHj7uL3/go8QuI4N8/QlFAh0o1grkgegJIZHiT2LSI7MSopNTs2itfOLjkTwyp2sfSkKX7YGwsDMpgvCtbf/YjhJmp3gbcHzqiEMeHgtuMv21QpS7KydTC6Mny6i80ueM4vd2rBGkNECkoCa9eojMKWmaDu39Ir4t/8FZLFy5HtN98CBJ9DcOfGX54p8GNYWC18rdKQq7OCTegSJPlhd1Tm/gLlJuCfFdaXurpe14LG04GIqfmB3Wl/lPiIACIYuBMomMsDLrkU5q2IWw0EZCbmpa8wmyNzxhF9+9YWr7bTEFmQv/exUmo0NLvbG9o4F02GXBiYnkj/F8uhd6zn6Q9i1BIitBmxhP7oPuEd1YSyg6YdsOlQ7v2F6TuZ590swV6pA4AIT+yILQcIZqzJUT45P87KHYDFyhX3UnrL96Qb/0QOOcDLsaDrV+fW6/lhQCsPMmWl+UK01OlHrxC1CnAewUBuGjBMSVx0YB7Z9iERUSksG+HKkKM75ypbBO+QOn8n4MjUN3vTRnu+T6rOv9fy8DROX5xZB3mZ3e5u2pxnMRcLTObhwwJG8OvXvqlboMNWrk5NThxVzzHbspFHxYsfl/Mzh4dFf//yn//bP/0XxIunY3d//xa9+9Q9//w8qRKl0U2sb1Pmp5qnf/fitdggKEd6//0AvytVbMnt9X796iWm++/Z7xpBGHC+VUUuK1FdqHZHRheWsd44ql0fdFtcWtjdW9vd2nJgKoMOaKn31fFNKGO7jpYrqOjiUaBdctuUejpGyqqZIlIjfQAFOKMdiJPCE3m1JK3H/xPLu3ILQD/PQMyXfTAxf3T3YcaMLrcyRcnmgBy/Udj5c3DpTbnPDkNaFYOAFXscjAN3AKjSoXjm8oBJ0MaKQOGqXF7jD/TkxI9h+Z9/iJd17dnqiNEu62GAYDJbacrByQIxiINgLngmDe5u5ufsZu+BVP0N6Mg6yRqpTbZIYFxk3nmWij9WkgAAYliYgBiQqzkt2DYvIf4iTAhAgqnSH5zE2MyIFHBrIpzZdRASHEBxvmVG50BGp7vfK2NN1qBkZuEGEjD8ghjI7vb66uP9iF2Tr3MIj5ruLjIor4iLGD1OYGgpJTfZKrYzEBjnXmSp4BWEj30My5q8ulJzZ8grflQaqvVy+nRV2t1uNtthAStEVYjKRH+KnPlAoJfwQ06oNAZcUoX1CYwU3Ru1TQuTOxAos3s2U9BpgCKxIfAvXboGKgESiGA3gl5LAS8VofZerIhY17Zhowtkh6e1KoXwlomQ0XdiO9Cww/8lnrrEQyDZ7W3UCc5AFV4+qZwp0rsJAY/yFy6Yel8n5aFrubVtZlEW4m8fHt3l/GcsUwMHRJ2irhD+80mtradICIR3Sc7LEKwsBzZkJTDDZDx8+WKv9G3nBFZtcoAs91JIJ4MjQkAGt6zRTeHoSar2mKxhYpCI+fjo4OHua+U4ETbGzAgy5saPjE8KIOGkvwjWnVl6E4OzwEyvxaGf75vVrLfFFWnhxy4srS/OMoPMz5EJvrNQUh4lsvrSI4YBMXK7KEDswEGWbSYOYpanJbQjoMu9omHN3Q3wKAcx411RJkzTA3ou9169ei1dgGSDLhhTZNXi2gh9dA90gMmblwVtiZd9mDiipfmRlIBdsGEcF4gkxARINUqkWinGhyBU6qlZu6y8BHt6r87wkrKoxxWfHp7Ipik8cwbFsZ6wqK6sO++FKkUqXsVUJsT3uirDW3IHew1r4p81nGTjTyTzR16EfFLkDQedLEglrfHMuKKEOJRtf4MiwUUrfTWEZaRHn9bqX5haKZ1ZFbMZJ8eCH0eHmsxsbQNAfEotLBfHffPbWfekbPRte7L346stvZE10tcvUEB5V11Nr5LIpQj3OucEH4Ab1VpbXFJrY7RUAOUvg9Mx4Pnv7GcpEnJsbMZblLcZu5oY5uv8Oh3B7BxGwBjUpdGIHHmZnGrvr3t6L128+V/dpS3aKMDFjNy3bs5bnO/Ww8/LFq335gT1IVsS/vS63SmvtBIb+ZEPpBJwFhFc2Oii1sifI9kv3MeJBcMuas194NE/FkuHdxQ5cm0BMURdeSOa1VU8qQgdOScZa5UALtiPaGywTwrVnF7SKD1MqIcQGMfGZokAVFJUQTZiwFyfUX2WgRB/1Coe0Xn/rQeLIRiI3oqn5nfXjoxZ4KqJFWoxQ8EEneHcct36YAtkKeEaVIpdFpcAwSBWLIj7uzXlqbxO9pKN8cXwjwZ0mC5d4lqBQiSkbEx7YGoHZTA0rQwo2mGex+DwdVDB6B5SzSxEtIz13wDdUxLYjYWBghgjsVzD7N+p6FxpxB7KsusZNo7MwhyK+nY3Jq73dDfaNmin30mMqBLcThdRTHkQC3qrmUgqc5huVgZQFYLzXD4BYxFJsw7VVBPQFY5drEb1LgtaXcRR5QQSzEiIpmK6QRU1ksaz2JaA8jOPumJufVBDR09BWrNdwIZeJJoLyJhp+pCBIpMYBwx4XXTf5OIE+GrTJfiSLxlSNKz3xVCv6aSfotkXMnIQplmUvJ3oYMb9cQ3ErXrDRSR0GfhRqlHtPudvgzT2xB1OSk9ENiEe28zZ0mbkT+X/ScouNm1+FIzIrvbJoELLWe1aZ5Csl233ctwIprTaO3S+o9MvZBXLYMqvXp7Ddfz/9/PPB4YlM6/beDmwU6+e7C6xRMTF0qs2TNKdaVh1B/hW9CMVcXF9SHupdVEtbfS62oYp7q5fbf/Hy17/8DRtI2xOlYD/+8LOMLAYTjd/Z2WL7YgerBgZrhE1/UsK9EJjiQfRON7GI1p1lDBn5tnbsMlBSY1kXlg4ZAyOLQfjnjo8OLn+oFoDSgCbQcumPeicwB1Z2dreZjR4m+Mu2wdwJic0ywo0KwpLwmqhYRPZzgfRZnXLhWI1GbSePxMMAwQ8+Mlow0FcWqnLxn6VGX3cgfqwYH2EAGdO7Mz6L3hIL23Nbl85DbgO6qFEbJYwz+wKaXd9KURY0zXlWLjevKvNuuQYX0N9OfjN1mnkGY0GMPADyIHxvDMZign0X4N3IxZ4YhrLOtCIbeOzp4GnoZ0oDQBBal9rRJaGIhz3oK+1PJijYqelq13x+vr6xsre/J1OF+Tgq4j6oLB/AmKIHScgwJz16NpO8o30HW0C1Cl4X1JjKxwrVffHZV5aA+L189ZLFjkoYTbcG7o8tF6L0e7svjXPPNhXtNJ7qkfDzT+/QYHdn2/ROvjq2/OLkaoqrVGGMOClULwRlOwvTt45Z1fXQyXDLy3wLkTLPUv+jU51UKTObJmj/Shv0WfaQxZ8Sj1iZpsh+y8INkqwp5ubxq/aj2IQhsoepBKzGD6iyiwwADeYa0ar6EVKUMe60qae7S/E0xQoSJemRC22zENaUJmuWUuZVLiaaDzuAbYCzsdZYOxpXTcEmliWhxn/e+ZrXuIUj5COrNj2za30xgmWSKZ4WV6jNFFW+Zh72ZnJ1ngUH1huNmXBCeDXlclT6CdHZvAKkq+SF2p1P6cUuZUTOrSptSOoSH0xWj0wGU/Za0vEgopTZWWjIP1AOuvjL5YjoWxEvcsFJAE4qxk6RXNJeYRL7MWx6ZlDKKPFRAtseySkpD6W7Ev6qPWCXRtUOftNJxCpqU+EJ8IXnVuZRkKjbyAfm7rQ1f23CV3NInFz61vZmGVR9WfQIs4+6RoQVpAGvw9sDE1xc0vjHBot0j2IcUXLjV+wlMtlmySk3h/CeY7AQ9I6JA5Tteco35x0ORcQqGDg4AKCILoaIl0gwYPQUesDX2VFEG1WQG2zxFYWuapZ2efM4o7Ua+Vt0CiOIgkMsCpV+R8cMg7Zt4nwlDAAHqQkX45iQgr9IDoE9zylMaGkv45NtEgwB3pZn4HHkRB9rMV4GVz8knQ/hPGfX6uULSuiANkYV9cCeRcBCErXtOj74eIQruItgmr+w/+q1O+sKQARAi1bHPE4rQN8xMcUkbjc3/eo4EGlFPP7i5crS2orsG66giHdfrDO4f/Ob3/6bv/97Aq5O9PTi4l//x79KGqsv/+qbr50Aa2DikKbpZfomQCJYLnwCagYv5QkBmkwuxUiszAulcaMIeJGMwFy2O+O1IJXoO2N6djL34aMNk4cMBJUkajTdGpRQNwIa23vbUP6nH36iFbEIk4GloxLUg71iFvtfCwEah2cvUsJQ0rNRNB2FR/yN+PSb8Bbhp340m5rfwCNKGwn2p48fZJW1D3IrWkGera/LzXKxqix+UvFt+TI0NB4iacNl86D0zYI25XZgWRBGaHEuhMPDONDCCDB3u7FXgv3o/TB0adlCqigg2obHsdioT5nM0oW/8ZD54kLDo3Jc7F74HhN7DaXNKC1KYKi8JYrXjJDbOW5kIZ99aqaT3W2W7nyoeoW6mMRbG9hmjXBq7Yn0y9vZZqP99NNP+vww8JnwFvKzN599We2X5gQGMoIaNyLR1cheau9ln13nOS9U3ggNpbUrMNWTozAaJKFKd+Z2wIqnKD7SIXSytCJ2gh0ZmsDl9uoKz+NFES2n1CgdkJUSMeYm55nWbMAe4PTsLflTfK0QSy9lfe2h7bCCUMiM8Bo6WIsBa04SFCid1/ywIDekdt6IthC1SGgrk91Xqg40kBMXYbpAkCdSZE+K5oUOznC2F6gSOH6aVZ/A9sGXi4+OjxA/ebxyik2uG/uUqinTCywMoPCeA8HzHPV9kWzwt5YGcxTDuk0qci12XOqhdPiJEwMFFJTbx26KlL1gKrGxuIqfck/UJwPyaTyTOUL8gUeiITlSfyqDbJOnN121yLvV5kg+Q5wTm5OKeXZJZm9oyIjPbtdyUqSEFSZJUVrYA3wZ96r56V8ABJiGWvAmEfYlAEs7uNgsqNc+BGG+5u0arBZgsHHCwksCs3wAv+F65LQuPfBXmWwph7ZTj+nM2PQrsO1RbuHlU6FOul7Yl85h6ApPQH8z8BT5khq2LCpavSGMyGpl89F8ZhGthCiI8yap/4afxLG0/IUFhsn/xN/SbJsdUch9xOKTDtMbHoenmL2Ow8ZJvKENqjDdSFZ+HGudqco5Fcq4ESC6oQMR74afhhjt/7jXAlqjZ6vFNsJvM+c2kXR/fEhgWbg9CsEKlbnEarp3BKTiaXSqHQ5bG68ru7/GlFsXClLwJHcBr9ZJ9Mj+yqNDUuxGArYaG0APhXxSazBUNNVEwJEnQQm0sFCWi0P/+PSj0KtSGh2rOM3iH/jS3BTQCmRtjhpINT9EseyMOhype1GKEulTCt/39/e//uabX/3dbyDTf/5P//X7H34wAw1mwLsTsdj1ojfcBifDLzriW+zuRqPJvzWcJxqoxK2J9E1tjrmL8hdZGpht7OtHDtO1Q+vigvk/2ZiAeUg499/+638+OXJo3L0wNKvq66+/+eKLL95+9jmPAykPD3UwPaC18GvYN1YXrrGmVO1wSYIn2dGboqgLCgO0vbb5SMv/jbWAXJHMxjoyMTm9GXxXcDkrVMySIMAaKSvsPDj4gN0Pjw8A8b6W229e81MoK0EhW0FUoVl5+6F8HXATkowq/HXzBFTbOEqvHlNwV4jFIrfZDl4P+ywdJF1q5VQT4UJE0LfHxl4AKyWyt7fgLAY2fpibe1FFO2x1Q1FtOQVWFZEUD+FpM6fhC+PLlYcKcu6U9wCjlEbtHlVc5BbanEI+Zg8+fPrp53cuoEi8jY2U/fgENWHH6p7iyzU+l4M/379/Z+28HPrGSSdqRcSnlnyKmxUEseuldj+evOM7QhaUv9Iy7IFvPv+J9v75nVXLprKhdW+Ld4UgzBJbRbLEZFzPRSoeeFAqkHnTYne7m+ufvXES56oOh4A/QWWnkEZ80knbF2o/eVhMSyZd6d7pWWFzHoFLLSVdAh3oBt6V0znBAU3FkcFwQBb8GUjmbSIILrJWrIsRAouq/CzesLsEf5hoflb4yeX3xZ29fX2WmCceUrovO3G08q/hO0un2CVk97fQ1NhmzAHVbG6JfkwtzdvvLSg+hxMwuhHIFmIiV/rDsVPIUJGCLr7rlN8ieIPpHgQHSvkVBrPsMQ9jZQBK9gC2ZbTCzeKNnAOPmbUj3/zLHWXp2wGgNJ5+7USDjCuyCM0hbNgqY5y5bzaFPVARhLrYR+aJElGx39NCfqQkMqoLdzCJg0VK0+3cVFt+0f/C3Y+6tAZnPnGozdyUutukXHDB4xg6bBHWlDJzfk9ZAvneYiRIMcc+sSCGsbWza3ODXkC8QkZKVXhra9fX7RdbWq6k8uTxjIdmKPRYg5PL1WlZQ4R2F8sQ3ekdgSdwwqi5EBVRhdVlZoM8ON8IfbcgSAovAXM3mZYIUOkBZtdV6NZxUa5BjxjJgVaqxYTTFJAurpB3YxCtjclP+dnzsjp+IXTGKVgPTLiAvodNMYn4lYV09zRPMZAcF+rXP1JSToTobrTgyEOwzXE9HitYUwhvXkT4/acDlf576gvaZnzzdJote3x+9O2339EEW3s7OXc1L5hX382iLjBkcCs36jXVkG3v7rDZ9eJ3ldXhNSMlW1ZnCwe94koafrK2QSbV9F9cfuAW8/6RVIMGu6XevyvJ91//+V+Ojk54Zq9shn6xx1hR8/PpwwGLSg33+sYeVa1EyCKWyAnp0rOF0Pw3Tmm1DoVu5tbwF8ariObxgYvMPcAHo0otIxtCzP3ww09qxdwCXnz16uvf/fZ3v/zlr3gNrE7HVFrImglE1poEOB5HmQkLQjyliARt1h4gtWDuLFszXdCf/Xn3aMO0B2gMQtvpDKpXgvvLr+o5Wr+Hq6usfpm1x+XvP/5wYHfY6bEQixiIjaCMHdlRDipxhZ5b8gqTiUzGbRCf28E7oNmwBcIRJ+liWS9+PfFxVPeIlIEyzYtWn1bLjRgSKmAUsghDyZeMOLkv1TNawgFTM6UumPmCxp4ASUmF0OyzcYHAzJbjw6OpTQUypfVFFEAHfmY8sd4YcVAJgrBNnybVtIEbIOpTD9XZil5xvbvni6+StOs//OEPP/74YzfJF1lcW1njl9kMKCjkoaI3rCR2ga5U0OkY1U6OPQ9VB6xwOOC86umpeh4sLDnyV8kQ2gubiAtnd04/jnQCE16cdFHZAvTY3tx6Ybf5asXbIBbjMydhHs0uV9A2MIyE79liUwwrv2tLUh9WqRyzTlPZfzdSbMMrog+cwsYDfkRSelqpT92KlAkuLtl3pTQnH1UTTRwESdtrXcW4Ur/qhjquT2+SNb3X8Ye5IODUzBXjaGl1Pctq9AVD8BQtfgfptkfWBekS1UaqXxRuAh+IPZlEduaavBGhxIVUqXABEFEPqoGrCK9HjB4hq4qDhS4jF4kZZAzjUljP4FTwN/m3srOO1azfuImX5GUkjx3yYZiF94//KqepntIo/QDdU3TVnVcIZYWzk2GbyWfmIyRATEe52HeYD0GWN0ulFGrzgTvFz2pqRpMMDyYXRKrH2dsoPii1zgGqfrd+IxYRU1UEyAiJ/sXnRhSqqvBa09jdIOhZ7UaVUTQl5CLLO2s7xJ8ICCbZ3GjWHu/ryysaJrCVDa/pwM0yYTYHpNmlpuUFs4LJUcOFQimw58k3x3Rcc+RZMhxwa+lfEaD7zmcsL/xsrVMqYvU+Qla2hS0Lp6WAZlY2diYO71m0S5GVtrF42rFOlnX2Qg2qpaDL6sUtqmSlFOBR63wuj2RBGyBiRt2RfiDv9BmUzxFNa3KNOPR8GAY6b+WBAAscMEHAxOHxydzCzyivciOum9J0b50Z46PjM7B8LA4ojkpC4elnX30G63VVO/nwzjB4S4pOEpHnjUFzVfsAX5Pl3Qr7yJmui4HNL2msAgvZG44ZtpCh6/XNH//0Jx1G//Ttn99//ITR3r753PaptAtmrj6F1QEHTj8eHMjLgm4EtkxIAZ8pRQBFTmVV8TBFiMg4BcLZzGuQrqwaPgYv63Z2eMpkZOXPKXNXLrK5u72/ty8E8dXXX1OqmlAYOVbzc/t4RDWnOTSP5/o4MJ/t9BmvLCaxeBsF5T2mp0XAoRRW3t7dZqlpFcde5vddbjj2DDosXjiA6uT4f/z3fwWO8ph2S5mGaJpDKz3Lmexs/1evX44Qx6rb0nu0DtehvT9Lclk1S9BqGgMIchN1c7xqf4q2DV5UHptGSSpjPTkkcpZZOKuozOpE1AYJwaWjhfhTes+pqCc6AkGp9OQljvDf8GwomHY5nN2fEn67gumGi5OODWCDuACxzZ5suBVeJlf4CPp7UBmLC27F/A8/fA/xX75+BXSsluop01TORGzAGDh48eIF0u07+/zla1d++PDzx48f6Le55dnOI3u8X3m3srGmYv25cIIJRt2WTjdSBqyvaBzN8KFRXr54Q+Q/HrzXb5w2ZSy023dLR1kHUhLDezEXhQNG57QdsWrloAgEbaRV1D9rI1xvxg6JdNivUq4LVBUiKm793GhwsswhsxbwlGrsLytUoffYBtk+mfmTsrXXvAw6joHsNGzCCGD5QeBGOpVcsos5DSOyLWgjczbR78Ix3kdnF5ru2adhDUUVC9lotnrHGmU/hewexsJgAfAHxHUoAchDHQKTMv6dwHOnYpq94krc6Lms4A6PgiijiVOt0EZvBnJCo7utHywuIYHsRijAZ7aMAiiculOaIgzCm5l9Yu6JgFoIwT9rjYsksFQc5eMXfK+jmU+ZGvB72ECGXDg0i4zTMHRbCmB46NllLk+rFbkmBWAUTGFb7zMmXE9TEOAUCkpbBYUrujaVqbaeUg1F51WHsijr16r8wV4wPb9u2GQP4B4bW4wZlkDJibQF00mqdvg4V5aA2gPCSi1L2+Sx+aJMlTCXGFrDYKh2JnLHTinPly5Vv6vYjiHAjnFUkbfvydtz2S54x5SIaaTyAfGn79YDqiDYQ+11miLzC6BwIlAHPpVYwuUULfEQc5ePHkFgEQ0RR64k283jtna3zm4fVISkRp2ROyVjqOa6PfYyV3jg4X7tYuqi7Tt3ixhD9Nw0ERH9pc18K2UcmFt2lCwhIMJ4M22BUvtLi0J8mUHoQGe/e/8RM1D80kjmJZjB0NzZ23V8q/1MNrm408bGFosAl4omsncvfv4ZMU1GZsVqrjK1VoqOpIHu6k1HVV1e3y1LI4laLMzdHSCV4cxKGj7uTrHgFBSxRN4JCLz/iP9Zfi9fvyAxUGoJ4m9v4QPNKNX+4bQvvvhSEzkBcLvJxF2cc+C76OxndTXojHqPUxabryx4y5thj+GAORQS90ygqi865RkKm+588803bz//QtbReQCoCXrwvcdAq+KY6WZmAWqrCWbS5S7fTtmrVuNAAmNlNSV2CXljg1Ck6Hw+f/70XgPnCezb3u5QX316v//up3/5l3/581//bIlO9l7Yp07rVNGytSnkvr61uf9in/NhGWgISwjpDJQC9BIFozAsEbPdDgD0A9yWyzBYeRAFz8ksYXyRrsF8zse5NFoAPZnskL3Tu9NsJcsCODu6a82kECtEG5Zm2Zug0qRqNid/YG+EF4Bwvu+Ll3vP43kUQltaQRnXgHJeqPmyC9i5DDTob8w0BMvU+j3caL/nQGcnmh5aXevxvGsDmr1581nG/9SUmk49b5Wuv//wAbtLD/DirfcPP/7wP/77f38em6JGDk3LOj0tLM41Il48AME+s4GkWuVrJPIv//2/ffftdwLT9hMagDA3JVYbH+fbOCjYthpZIo/EFLfXNcFkDFFeo9vPzKNmDxmi/pgXj0BMhAkLhcQ7eFQAjlFlDIZE3SqyYXYIiDPlAAzFL5pneAF1e+4BX2l/OMMSZoNaG2zl85EAUOpSkRD7n8LTmPvH9x+//+mnP/75rwsTUSD113bRFzRzN/JDktnsrBhAwX2mZmyIQ2yoxAoxHmviEyfnWHpGgCkAh1bQ3ie7zcV9FRMOrD9ok8ChMzDsrZMLAZS0B8OIxYCTcTO84BNDsuiC/UzyoVCS96GVBfNc4IUn3RkvSWYXqahWtZ3nfvY4d0NDKEJ+OI9oin7JPLcmE3+UQ0ZOa4F+uWK4aMBgF5kwI9THdIEBYWpRanUJTBnK9On20pSNFmlUV5omp4gxLNAqzqAnkgQVm5H1Q95xJrw8PTmfObuarEGIdIfllABoJA+PLCGWKfuHnISSxsJMnl8WUhHl8jtYIVbMT63ADNIX1dXTK5AA8cvG+I0yaq9CHoZfpSwMAAWxQj5r7lt9wACGoBvv06eRg5ZjELOHLmVxNIErfARKbCtNIaqCj+xWZWweXNUSI+7CVAG76AqMf+g0EYcKoRiIml5sazfhEHcHCaYjbpOji+54iL0zEvh0ALa39AXolMHpdN2gaVohvuk7baftI0EQptgokhalcV6XDNDy5If37z9iaSX8G45t2lZP9/Li4hf/93/8Tz/+8L2KAwoMdGqzuSQbbB+JUIyg12Tp7JIxebt4eVm7css6N0uvqAjXIYNuIMzACkfR51rarG6s/+bv/k67yaOTI7COQw0/1oqGAkcSEidvSu8zO+jOeduhBPBMFlWBUryImJjmto4Gr1WPtkO20gmndQkO//CDtqGHtqZCu7l/97/9b65QvSTqAuNPz08hLi5vyWl5zsVddp+gTSuKX3L4SAeS9idbgXfUTlLS0vGniCvKg1ZGPGTk/FDo5OR4b3f/3fuf//rtX+g6sQLWJIkQuJBvINnYoUXUfx//2uZXrlJIfA2oDpYlJU8Y/Z2w1Dsweml3rzPUHMmyNj9rj7h1YjLC9USL2/1EHkRGa3Glhgw6kOT5XXwcIayKuykSf1p3Jk27RlHXRKVMPLe4+Ygyu4ynbEZw1reINx/DmJkp7uFKB8+S2k7frZHn8vNWPUHB85NToTD+hdW6ubz+9q9/EUOAMlgZCDJHaDQLRhUhGbr9oDdGe3dyJkyEWrVBwcYLyC4bKzMvzqhDkDELyGFcnzNJ0FB/DRUd7sG+kwU4PT8R+XKO9tr65DPnfLWL2z5hZ0XeTRbmdjZXdzbXtzdXRtcwaAbP71g+rMv25xevLOaSJNn9QsOxWSjD0J9Gw1KgLDMZ75o74IPO2sFZZd8zDdIlujV/q7HjrcpUO37d0KxJlQGUiKjiAzNXTIKkLCahNh17TOFCL/bza0eTXt78NDWnkk+YIPl/Rnzg4WlwBMWMCPQoVLTQNJyVylORZ3NEKnPp+MRSmjWqZuuKYLBfaguhwp1qh62ZmYBbCynVB5viqXu7pMeCxjyguG2W9yDUfOG0eVmsqm/ZHcrDnNi8GksgCO8+mkigQ0FPksGM8TwQCxY6xyLm3TssDEJPZKAaNENT7wJ4P/NfONhlVfq9t5Gzr4BGqxE39g+6BcotOztu2mpJ3ASe3pZZXJzdWFPRNr5X7Cldw5vIw4GtkEXMngk/q94N6q2tb9Ei+a/5VO2NoSrcCTFHLJ4UTgkaUnbaa8jAwl2XMPfAwPMc3J3HDCKMGyaMnTSzaieMk3loAO7TZGgYrFUISAeXloR+wXVZE2MbGiHFJMVgiD/ZDIPLnZgeW4pzI99vdzMBtxvZ9uT59QmD2kbL/O2ZTscd3hIaTS2vLGphKUIxbpXjQVoH3kMhm09yOPIEXDqWwV+xmSSYGN0YBoeKKhpr83h8LC06xbJkLzuUgq0iNPL6rfTo1//83//l4NNRo21riz4um3v7rziZRP7o2+/EaUxIOZHCB4umLHphbV0sGV85G8AR1Th/dW0iLgqTuLOGLl94w1Zj4s3Zxk4HP1VIsr7+zdff0CVatBM084VJRFvYE5xCRQ8wEdv7TQMdJDxuL2+0ihFjt9x4gnGTSapRssMeqr22ebtMpz/qEuUOGUIqC+f+3b/7X2POKlsu8QTjGut4HFsVkrKRY+vO0OBDYWnFbWiO82JUtO4Cl4CswmotJOYgK+5jekhwfXe9PPKlII8i/cd//Mff//73xaSE+1c1K91g/mdoiTyKBdJouldGgjV2MSFKj89x+a++/etf//rnv/zpr3/US8+zv/r6G2cGLy68ZRgyAXKlGfAFrXV5K//BHAAQBkltsOKNSnCGSsdkMfqwnjAfugooQzh3cAPoR8C8EMLeVE/f2H+hYR08V3kEEwX3eKyQQJm1UKqIGC2dwq1hTtkYyo7VSJgZ6d60X/wPf/zjX/7ynQrfL7/52qYwcU03ZxlbCwMDF9pzCtq8ffP6t//md6z1b7/7q65LWkG9fvsG2RkaUsf4tqz4zQ27uNg3fUD1iwLTGNKGWZsd7/f5119wN3TrteqpiPnZmjBNJAMX/bu9tSaSV2sxW/wIRyGL6+fqz6LUltBCVj2SPrckEHNIrEcFQcgzUIvYV2IsokWm6GlQw0p2RdehKdXr8A0nVSo+0SFZ/zg42T6dWx3TWTHD1qG0xOIqOFtd3zy74jPBmDY+YTZhl+dYwpUWAL2S8OljI87sRWcA4j3mEbpDXAEGoJWROUDWz/kqf/tqGfaQHaIScfpBXf/tncpfxD88/OSQH1MQ/vkbYctph6RmDheE691NXNWD5CvAMNZmomAByjwQHF1PaHqjzGaq3Km97mkBy48eRp6XmfvkbrjUz4YzpjXGaORMg+c5ulZUYlCxKWDmJt9nkB4z4E8MnPyJ2DjZmA/6yOPhCtup3PYfU7PoNnzFkGNsTCvzp+RSOdV32gpUG8RaezgmbGllSZ9RpuoIe1GuRm6py54+u8udSyGcEpgzyaKLuKsKt8pguH1G5DlhtzjG4t3i9Yx8jJvftJrg/TF9XzQrt6aNZlWM+G3GI3OdqQMCiOBuc3J6eao03qke+irrGeXcseWFe+dvqu/a3uZLSJx28lKdeuVBibk4UIaLQVlB6ygQTm34wZtDJ6uOFew9ce67885NH01ZIT71Hzq2QXmU7SJq5EESderzi1hJ4HzmfIrD/OHTJ5Ise/u//C/7f/9v/3H/9Wd/+uMfVU6q/4YwLpubvuQccOhto3qc+US6cQLZk4GisP1fpRf773Eud0R6nMrjWqNzcct7hi+jngQjr459CibVktqKJJ7wxcvXjO+zyzMRY/4ZRqBud/f3zJfIY0LpP8hm57uyLmkureXZQPCY/vB8QXgc07G7U0WZ/ICR8JRYwovXrxjfzskwxlVVbTQnznZfS2aN7YTETO5IbBCZewgh9dw2gkGpgtHgo0UljSl7dGyNyQlHj7VUb1LVd9okxb0zSv3sp3A+iX73jPfjw2MViq8/ewNqDw9V8PQ0Rhy8QFWLC+XwDpblbkN/Ler+03/+j//8z/9M+2F6c1M4pSXOyemRs3I9neDh4JlVhaGEobgqYFS4Snx9nZ4keIiCyXgPikPp32dYSfVkH2l4K0BP1PV3dApERXmMDorhYU+zScprApeMSOyRAwpr2OaI/t333x2enL58/XJlfcWmXOgJm9CX9NNhO/t7iAJo1NKrMREiExOLUtLm86yDyXb7kIUv5jbOKbxNnCm2cXx8LPvthWnt5F5UIVPXz0uU2dmXC2nvLqNO9wvpnbU1HT3b4KdikipGQH0pPv54KMG1/Iuv11++mJuZ3AHjjBBWQtm3DJfndnsPDsSAyRaXKWMpHY4xfX3qGEV73NV0piaBvvoaVggpIzN0v79RGAxQmRZoIK2SJI34Z9j+DPt6wqvkpAZUcxD6Nm0tscOpdwlaYJBFOD+7trLpwJ/9l6+oBzdT020TNVABYrIHGKNCeoYi7oltiS7CEdIwnGnbL/cM5Bl+RbGZQJNoVwHmIu/7j7oYo07a/SF3WHTAp7cDg7LFN++M0SM2tjbZB/5jaJtbMlO1X2MD2O42CqgLcegMRUG2z9ZGpGqHpN/aUs7ARBljgIiGXY9TWqRCT2gZqbw5pMSnGZ5G1GXeGu8jqw+e55hh7CZNuW1hVSmqtFaXPBLdQpxq5bknNgDQmdaT0sKNXMRi2kRcBwvjE6nn+NJ4FSeViFH7KloIfal4brHAnY8AYHMsy13ZrqCvmlj+gtgRne9uwTVPhIIfwyMX7DvRPNEvtpGoC2F7nktQMbt4bZeHHTizVYcjunmLI3EcAYs14lmBCNtXaVzAeHWjaBJmJobsZrZketXR7wvLOogy0LlXskE7n21/+nT61+9/PDk8cfqptBmwFqy2qQP50c/4iCnOM1YCa8ykQ9PNyiUH62S2yi20ha/EFqpaXHwFIn3bJZYSmayXlqfcN8fncPFdWDOMq28/faJ6rv/Dv//3X3/zyy++/IrFprG6LTi//9c/+kGE3ZAV8uuScnR0inMqtB7nrox9r5dcEMsJhegtG5PIOOnGKGofDEWI/+uvvpSu0Ir/4fyRYcy+ZAjyKiyZQC1+1mWAwaeQYfYiP9jIuQYUjKURcXn/7iOUK2DPkKXB2lxV50IhKavrqAK64fjwEDcrgfP6cluRThvjLDWrj8Lj8EkZE2B23/Bb8/4Dqxh1sGKRgDJ4+IWNqESPSWSt8jOfPYu76/xipVEMzJh1dNzA/Sbjb0tLSXFX9/fkPN/IPcgR88epLzdBC6EY5fD7uxrirzju0P4ENvLxwYHtdr//13/9/R/+pzNqjF6lfEcybG15lPY4XCGxPfOG6di4WqBHpyRTE7Ks2K5McoR2SpFOamcCBo5usxMOE0hrIxHRtQYOIqF4KtExqeHA2NU8/UnoVM6nRNCqVAQ9TKTFjvyAvb77/vs//OkPoIIVpVZXUHx5Y9NMTer66UqU8Ms5Z2/tUQLfAO0AAQAASURBVDgkyME1kIWSR1EHrnvw1LJaqXVSuLO7BYe4ynxbe/GCjIVZO1rJJHGlyOAFDqOcEFACgC2QfUQA5CfuQOdiWHz/SENYnYOPH/7y579I9m5tSACck2JtdZFapJTlUwgq8IIRlXfgHmHPeX0yBOSYSB4JhmanBFXtd+QpVLIh4qS7vf0CYoIUmYGWf8Zh82x5faEy5apuBlWJFUwz/kxzv8ioepJnFaAse8wexG22X+lDCQL4qqcHJ0JkQs+vX73df5r++f2n6QNJ7BmwgM2yZHM8gkTsCNdTzyMEh5Lgs5n4v77NMSxSE3jqZ3zFBfjUd/1rIGFqnwyJ799hmrKYDO/20yc3Z4QgFV8SZVSpsdaL6rrARvf0gY0TGAxS8Lf0FefVs49Fk2OnxEhp9myWaSUvbSkY+9EMTmyhChSXQW6z8GLdG603EK/FSNQMHeiPUaYY+qURo6WxlWEaW588F0u7DzTh0uFMPk/JpwqHEgGJMigH7LDNTGkXxhGWKYmtnU26RBFUeyaxPCOpYnarQ+FCqAbn5kidzuwpEVOUH02Iv5TyUtYr9qPTBadjmad7+6z908ClPKgRlmChwnla0KIH/T4RtbdHTPsgklkFkWKktAthEESV2HLl0sr6aDmxrveQhpBHx4Dr6txujCfB4WvpS9zueiNkqRog9iDgaMmZZPwNuyl7ziNwj9wIH51N9kzSoGwQ3WBafNQ1jhYjTqAaBgNhPK6/sqh6rpkdz4tR8uPPH86v/6+Ph8f/9G//8Z/+6R8VW8tl+dDIuQiYWh4StS0AyVDnJ2Un7YoLtFLR9odnhrUYeXBJOoCtri8JtPnsqzdqXt6+/uyXv/yl1BESief84pe/wRJ//MOf/+Vffs+8e/n6zReff2krn7j9h4MDPo1QfhlZIQHHHQzP+//P0n9+N5YlWYIvNSgAkqDW0ukydKSq7qyunjUfZta89+++NR9mja7uqlShPMI1tdYECWr1fvt60SM96SRwce85dsy2bVPWg+twdCB5tKcH2xv+vMvDORGy9cmGPhPuFjyw6XK9CJI1oDlbYM2CU8vD0oZozUijGlC1P/Qiw6geIzAl1A/ppZQLOY328HPaP0KTXo9JRqJRrSlE4Pyg8tUECLUJXh0e7LOEoKW4iahkbx9RNiixUTG0T+wrVy3T3u7pzt1Oezkz03k31vT88sxUEylJtMn46MT87LxHQRuNj4+xBPwpBdMKqYiY9UIlQ/0+2h/PT3tooEEVyLin/AiETmrW3WVFZcWTmxIARLBUenu6i8oUbk0yRB11d88HSafJrk4oA4ZBI/JUPEX5pEvzTtcxFExQVyUX5DvqhsbGNctD3YHqifeYJt/WivYBoghXoudSrNtS00FuiaYTFTuagdGBb+lmc42sTAYL+4e/snUEVPMfODdRioZGzUFXltecy6npqampOb0ivF03EO6U+fMK9yqVKifDTHmk1+Hu2cHuRn+1//mz2baJyYmB/qGBXgPr0s6KBi4e0z6ie1Anero4w1SbwAxGSQffAhFK7acWFORjd3nLFGs6xbsTv+UXZpIwnxfX8UhLigbkGMF0dIHd5DsxNwInWFE2Iaw4mbAUBE6WX6nZ2soGSVqbChRBo66u0fEJsd/h0WNxWyoiESgNUo6O2Tk3bVPsaUxFoftoIsc4iES1NvaZ8uBNpXTLDbuVJM54ZTCr1/nyUxDdHeTcx5gU576wCjn9yXfwK1A09AXHR7EbaFDAHeo9MY844MTerM2Ik3srXuVzAywLswT/Jf/VEQ3Hcnltmd2Gpmc+MKJVfGjYnNxuNH5UbL7L9/nHZ9Xv37lfQp0XeQYeAJYeqWcD3ZJja+z8PfBHyB5NZE4rFCAHEjytH8fCsJrxalKdU+TRIDACwDk2943XKWZKJAIAUqp6LZUllc/yCbmBKhbNWkgYLCuU/0IJYG+YPFMlRGUvxT65Exmk5lgmbKQTzBVnm2vs/hmnaBLVlJ42j6lmmdmQnpT+4XRI9AWTDnhKTCB2bIm40cU1qYUGyh3VUntF3hLjCUpv7Rwe1s4OZJddP5if5fgc7R2urqy6Oc+IlXVjLHA8j8QkEvVFnjhr5OQ0Ybi6CKVFKlU+h9CCRtyGPbbdSKqwY9mVrLy78mu/YSCxBwWuFfe4YbRsPou+f3hycPSPxaWVN+/fjQ6PWy/dFyl3a0KF+miD/EAlC8b4qAS7udDMx8zwOp1vYdlLqZ9FBAqu1wtAyaT2YvBZFd87OTkTFIuUb27TCkyElkvamqT2ENcghdGNv/76Bi6cnJ7sWXjCgZMS5phEWUWld3icnDrdajnAypJMC5esAam1tUoEtQu4Y+olv6KrZevgKkN2F4renslv82sa1vI5A9lGZhwfSnqJoYXKGUk/BKLgjfabeUzWHIXC0oX0BASa2yuaD4RDt/RscoqzCQpw9HhuFdhSHneBPfkOIlG3omogrZPJFdrc3Eoi3MQk8ijX91mPjVLXMQUJdDQ0SOBwIbEEFq6j42KDS3hao/F9EKPPsVJKNjDQX+2tJhPi8tJ1pCS6W2qZq8GHsJFpbNfWLl+iyNoJrPIMTDQVGDqSAxj+iHXIaBpMjpCsZFOEE4ECxviS2k55fiEhJIZeTs724f4RjC5mYCV4OTehqeOGJ8Xl8UFxoEWQwncjE6BkpAkDrpjFGis3Eya4Em4iT9bQ2ubYNDRJMJDAqrCOfsdTn5+eGgCJ+UGGii/xfsKfV/psveLDHGiZSyzi4ZGsecTRwf0De0W8L+qDYiI9vWWiUPClFDULdKnHEMjvPz6uTriyQbVbo8foddEqSfuUgJu0i4Fu7DrlwRHRA8p234QkpOhiqyQj6XrHoNEfpF8a/9WlgyREBgoloF9Xs93ud1DnycEJhYKoRjxKS/YOnXwgVa6AVpWiz2JhC/0DGFP0uY/mWarjy7YaexBzdbu5vkU6pYox0Jx/a8tHIuuO+mfbT/AsHxY12pztibZPGLJQqVFBvilUrl8U//K3B2OsCmuR9c+8pOuG1LRKbk5IKAmiebTH2D925yHtb2+a1J0ETQtLk0nn0CnMtdL1NkbI2fZP++6PDQ1t1fRolLUT6MWOjNugXAKzbJ8/2cRYgeC0fOU+c7cyRxsfAUw5HAJesuGZAHvptqyRIueuEqx6Kdwo5aD1WqFsSjtS9p+MWGohkYmb2zrLRFroHcvKRmgr6bznACd3I3S1KIPP9/zsSoxPOp4WhiupE35lzko4HydapnRTk7OSUk1X8N6ACuvCNBklRrGmjsQ6kpnoEUC9MGi5E01rvCxeOwOUP+LD8IKQ0o2h4Ul4VkFy9wDYramSPKxJA8LUHZycGSPluZHAYe75Xre3+G5+f29fz2foHSUkuVPbXiEpqlBhQUMjAGq0emEO06sD+HPKUDcaf4LQ1vY/tiDWPbYgt01VpWCQBAv5WSX0JiMhLyunOu/8b/+m95eCf7+Ki6A5WIey1mz1Ld5BuFaMxHWjh50iC5C8gMDrIusoDSmkwna0cC63NncHBoYUCCgmSGc3MZiGh6WlJXsHK4+NdcrztnHCGFsb21JEPZqukLIT2TsXdOmC+UmqAtgxNzuNSC88j/SLJj5+eBZX+paxkUAfNyc3ZSOwRU6uUI0s/rY2vafz+Pz14KoUPUFAHF/PhGuLenQm1CMIB6WsHJlgknIezP/ibqWJRzqAOg++8b/eHh+o+YrYtnQXMiHLAp5qcVYlj3gT/0VOSY4L9qDwXWlP63It9f/6ttrjI4ARLiKTlXB/tb/KMklfqtdqe/sxYu4IvvSEugARQafONWkLSFkuPN1h4ewCIFlu5I6hRHrs4aVD4ugwyDxEm0wzCWU1CgWfOfuGf8l1ougPDvbBeOKuaMDIK0VY9pel4mEhoNy/MyPG4jDA4Ip+rZ6nIN8eG/sqDssC5TE5ZufnJ8fHFoXfRebgEa8srGPJ8baqZv0aRyqjBO1P59JfAyODA/2DoFISotSU3t7URE06y7NzTwaHBxg/BkpV3e1VJykNIL255RwGiTY+jg2PzUxMHg33b22s0Sg2QHcEcp/PIvGB0mFmoH6BCZmgYL6AmUSeR/SMTSk6QDiUIDiPpMDFaa5IDxUIPtvh020ciQepyQyJInNcXzqJRddzhB+MPwV5kEbcClCFtvUrgsKkOHRsB9OIW3eExIEle9SKUuceUt9b1bgpitRH3Nww5w45J4DDZU9ZWbZ8aHQEtqUuHX7HQEqDDFovRtMzMySNnbCSZJVq4ClaVsAwlAGE6nz7pkCCpM83jnzUbBjqwF0IgFz76WVDHp/7rP9PNDH8qnlKBtDjQ2TXyJL0LMBy+lPJ6nP03AwunqC6lPv3Sf7O93JsUtgczte2xpYkI5bsx2uxTuSQyi3ikcWjFzbJ+73GGfPZKoBx3GhbYRuWBNd9fqaw9aah0+081E/ODvdRVelxEn8YUZNqGDsTy+dI5h5SM4gdbq+f5fRIvEZS21ipJu7HG4ko9U2wadJcgsViDlwthwWaScm3TuYSh1ylQ2udgHdpUgbNe2ODojS20leQOGtBuahEi6oW93E/grrJIrMmPjEpTvdSNhvAn/oZDC1nBBID2HrdlzCQKYpb23s1zUHb2kF60+JaLzJXHMMhW52r/diJ2NG0oyXMe/g2p4fZu6AxHPDOvi5KgyMi00vyDA0cj62t1RsTG3HoZU7XDUE5chbhPStNxxEPei/SkK3JTGwnynHxYvobJqTC2A+46PD65KTxhCApdurt7SYwcIYHoTOJkvTcU2PAg7hcNmfHR8SnbCs5vxQkOgTeoDQs3fbm1q+lX2l8BcR9fQNj4wn8uoe+3n4gX6TQ91JLjP2A4QoE0KByFmcAjvM8/Mp9QltM0uDIoMiL7fPK1q4MmLJbDjq0BFrldIAJQjdA3/WNLKDa/rEdiuLyeofTFaWaUE4sclR7mDqmVCq0W0pOC3iO/EObA9ZCGn7sXVbKs1Exj6WgHpeCDCnl6kBfV6UbmrCcRNDmEQgqkhj5F0orALhQhS7uE8EilUvuNbVtqSdogPSdF59iz5wQSKE4bw8HB4cCL7bfdo6PjSuPZmyZKCl9eOXf3vymDadKY5OX7XUidLfXgAA2zfHXVMQ/nUJCd35avy5Lb60QUzfAALg9H32sw58OUA93Ci1yeMI4W0RWpGNkdMgxZGw8DUDhHpg3dsLxAsUUeTkCzp7gP7TFIPlDx/T29lkfVgwOdOItGqKZ62NFqQD2Zmtzky8JD5E3VxAaBScRWV1iBgP3qiiGqgM0l1ZBeskx0vYP5vIxGAJkzJk5vFcX+mtD6Ewdup7c6EgqEPX86TyySHhdUYO22yH/dYQGd4TOVGUqPQ3cDDeAxfBG7quu0IFm7H08ZS4wFUY1OmUFdJX+Ads6HqEh0yJf8IO+gOvINHVJawijsaOKt6F43qIiRJlKUp09nGPW0tpFOgi/cCLkSSzVxFNJfWaBZ4xRE6chSiwER1ulv7tX57KTU+6KFGHbnRi+qPL9Y6W3U+Ug/eKZktl5qfcNg6ewoHRWqZ811BkTfhSnEJzcs+wETieAtIz1Fc1YnPQ8nP/F7/JdOoB6TPuQn4W4eDQpyE6l1gaOjR9FT6gd1ZpChWu47ig1wu0w0xuUoP8nc97oOi5NZTCTcSmdk9ALyf1wFiAoJ87H+TTqvzBP1JeDRefkD0BKhfAjWAD8T2cRAKCDDKDHfrt/SjRW+kxHx0OlZqjd1MQKuKS1TqHDbZ4AuzyCxD9cOsdESm5eEZ6e+BFj5tx+UfGP6Y7kyBQWH+kjpckuRP7taYhD2QfxsOyZq8U3MpqNUx/8xyJH7xfuC+oj58hvwRcP65d+QRUmNuKj0roqPSFsAmUaHGsBxZPFF9AUqRg9P6lfHtZOdw9PEA42Vh7j3MI86pNseGSnUtAkbS3QYC2tKhhRhbhIun6gtx9lSkIkkqAiMMPFOX0o1L0OZCf0FerDkKU+2UStrapnrAmZ8Tgk+kpTqQbNnLmn8L7FoveDXG+TPGfBUpzk3wyqHbNJvLqcuoaG3fo+n4gmoWNZN+IL6NuhHJ8gcdixexxzND5mp6E3riWFwQJ9/LT84d1HiT6wsuRGHJ8oN2NI9dEzGF3PpYLCo4EdYpj++HI2bCmVyPeVu8+0+C9bTCW5qWYdQYokaVuDkSmlOsxGEBb63FbRURMThr4YCFOrkWxPaxdgq1j0Iiofu0AoBOFT3J9BM3QcD8C+xvSIBSZ33g9SFQnbonGsFLCZ7veCHdIPe3tF+mw4CAz72apisjxGKBrEJ2LGLeHnjHjSzrQ7giwbXG+OJa2qBTSF4oT4vMtGBR0PCsdM+o61PD5mnTTFVDInHyuqsynJ4GgfsS2ro43GwsITm8VgAYAgqg9yem3qybH6ziT1t3VJ5eQ4y5yzRC1EYXVl/fBw3+oMDmumXyl3lPlr6EzJNrdt1+6QlgfVnV7amWY7SaXpWWg2S5wWofGq6GUPi7nz6Tl4fIVQURSTsEeIfk1SuGKON4GyZXZUXiyvJV5bQ6NcfVEeTmxX1EXJSCX71dmcxh09Az1oJb0QbIe0A8RXFIUG3XXsjSPFldSr0j6ma7QpAVNTk/Nzc7g/xp0mKhSN5Bwn9lqHfDmNmOSiE9wNp49DoGEW0C4c4G/FYmBhlGJkPcHWYIKE2Yu4HueXdygtShQbPhLY0IW0MJY2FzUBd7tPWpWhdAXOpFu1p80XSfMo8ntLSpCOTw84dzoyzXR0jo1NKPcz7QC34JvhUfM9u7lQe9sHVsZZonduAdjEOC54ZjDB2clZpNmiWCorgFq51wCjTnkZp4y+cyCZHM/OONsg98AJo4NQWNakoN08YHRtoeY+OwSBzGAs7OPnQfjKKcOukjhdgVLYyQXKWSsYm1DzkA3Xho50k6qqmkvOUYIdOvFl5fjdTAHUKzxOmQb5JGe4oB0srev5WWEoArl9xSQ5bw40a6RU9dFg6kp/f69Aooor4mZcrfC+67EhllMz2mSpFcSIY5uJywjWoot7VG52MeQ7OBKjku7lZUKeAsDHVFGE8rZ+us2hcSg6xbypiigMYpL840DcXAi9eqUaLv5BQuKdzZU4AfGZKPDEGz7jM4sMjwuFoQsJJXWfWcYWnfZIxVAKBdSmBZfd3CfKm0hSU6nMuwn5c3Je29g53NeSTe+F2lm7STR0Z7Vvfn7u5ctXWpMpucJhP97xfUU+ROP5OllkBMTwyBCvjDawcVFH+sqUpELZ88uwGsoJizmXnA14zjpT++Zjc008o12Acze3tlhqXYbIMx+ec0YMnCmb5e02My8uYp+W1NljvhC8NClHXDWA9bEUlGz2XevbEENybZHNbT2Vcp/BIP197Lmt1QILmCOo+/uHNLBDRcmIDbhqSLaMDoqDJdmPMRgZGwQSOFW+LDeWD79CBwZ79pRr58Lgtga1EoNrwU+OagCTPZXoZImoOplRJICGV0bm6ZTfUpNcOZ0YjkC+wuW139R+7HNCd5mIZhlNI0HPQsYYlzTb8SMyhJrwgPlnUZr70BXuSDMje0zumDtALN1Co76LboISXZGk+MmEalnaFFiSGJXL1sI/fWhCGfzr5gYBkBoyv+WCHXZsAASfworyYhgVdAZRVu/AK2KNYR4GnFny0dTEwf5Bb3+PlkwzMzNmWEKXCbmnQxGf7dBnsb3IBMTMmMTdyUkXiDmLY3KzvLj8+rfX/kXOLBB1T7a8hYLTgh/pGPtBuIRTVBBVeuOCnpnwmVi0DC8v1oOFyGhcQfXgChg5osI203fgz/XVKWsUS62BrQ7MaVyDJkKvP0oau78fPWo7Ij36rTq0lLTSc8Ln0LQ0tGjCojeCV3rAvcM9ioGPRRQ8eDgmzVYpzfJgNFF4nlTqcvtGhoa9LFBR8zu9jCl4LWqdNkfcmY4qd1vaP5zfXpzdXp7dXGpheEXVJ4Pj3hwxCBe8Tg4ibQDt8w1IiAA+4IUWdQFiYHvoDK+xjzgelLbEAS+jvtwGBwmA4+NRAUCflmOmPeJYx9DZp+dv33wYmRh79uIrnQrck4nU6Htl9+PjEzqD2hfPK3hD+Vo3AoKYcVkgCxFHWpxY1oJFIBsjo62UC2UN0/DBkEwAjER/iQIMLWFnhml2QScSLHTkKJDmQq0n99FjWl4Ky63bBbIfLyAoLzMXL/EAsettuPpwNSA03BsoEyAMIruaf/odHOK3zn/+tkaEgOgXs72CuMMKJA3fOY8HQhXaMxFaajEmIYo/f2GWw356s3884Fw5c2QKe5RZZYz0vQx3KZctF2cnjp7FtwV+wZsnyXRg2z3ggvQqEGEuGhrHbaRFgdarenPqygDJZhYbvc3Ih/Qg3OAG88F+4IGk+HgMD+JG1D0wCXYQLGbP7IWw0G0HuTPL5FbjcNvjPIO9jgW9x0n19CCQmwq1HKck95En44MGkN7rWWvmtVUHIOlvaaqipPvHtfWdXaEfc0z0ZRsbn3zy9Nns3Gx/36CTaKy6KoemM7GFJCJSlB7KJOboCgBH2hINxrjf3Z2V6vJVcJACSNS3QtHiYHbT7EKpMSFFcBsx4MsZoUbsM6eRvCmNsAX0l1TrpApHWRVpTjYzHqBQYLaPQuASPTacwnC21dPTw9bQrns7zMO2CtIE/kchdNCc0rUpFvnP0ACl3NfTSw9pOHB4dDqoBri3TFPR1zZfDb9Tp0ePPnGUOvLffrlVqqfS3SUOaN88INkSoSMq6fsfzyyVT2KlBBEOR1kjpAsSXrKJWxNsT3tIl8DNRgmH04GKi9CZg8H5coTwmPwMMurRXc6SUnNOCEm1nZxdQggrWHxSB2rwOFyhQatNUFYZJaE4v6oaa44uMVzXGJYkHqY4wgkprpZeSITTnlkRy+ckgvaDpaHkKaG6pIgAkhnAhg2ICmY2yCh8F1PRUbIKSgfcuTsEQzw/wddbbWNz3a7MzIxLg6KYuuSb6zFZQcbUraw/El12D3Y+vf+0srry5ZdfKg5wbOAdl/L6BF77+7/77vvxySmf65hR946LnbPtUK2xKeEqgb4SToOeM7Ci07NjjeIM8YMMf3DfMC8JeHTnmVDhCIggC7QQHaRE10OHUwpaWGpPZBl4CKSZ2vFjnA7lEEbyTjNxPRVSp27xiazuqYcnENAG1Ka9Ua12vLy4dHPBp2slIkGmDeBJUPlA38jEiLKLEccZ8uRs6bID5Dm6xACPTLOwZWoT6f3rC52hTu8u2YA6Nghs8C7cEAuHRy6AYKEHPFLYWz+M24Gp44jj1hU4c2Y5URIvCAWoj/+hCeX5CFFEIeJDUdPpVazgMydEhAFATtWAVa1f7W6pvT+C/S3U1PT0wrNntD/Xan19Td042aNc7LvPsxSDQwNsaGKfnQp2bms1v08oiNaq39c9HbH2zPdnCbDTXiQndoj8OLSPjdwKoJr1paJ92XSXpZk+qwA2Na6+HUTaGGAJ+Xn+cDAhw4u+RGHByXCqgOPF8XaycVH4bCZSm12hUAl0WuW05e1Fpr0PcFYJmR84yQgC2rpYT8maHXdCyq7AVCcCgeIJKyP2SlPa/EpnqyruBCIwSzolpO4p5yMKvOXh1PDta/5x1ocLSM0mrkp+5DJmKkAwoL8Kv8Lt+JK+Ujeyz+BfHUZoCqtk3WAYN0cZQPexTz7OsSq2LHqG+xWkpPV/HBqSL0OMDNsXAs9O+c7xTtgiNSee1IKoxopxpWP8A0aOLxKrGy6B4Kuo8EtRqu7egY5yD+iws3+4sr4lpx1gYBh8seW8/MmpKXuxsbbKNaCmPGmR7HPpLPqPFecNR6YfG2RVFhbIbOQ2OEPwmKkWscUI0Xpe7Knc887mzsHhIWGBKS2PXzrF7s6wXw1EyJJU88ylubo2qHV5ZRUhEmInDC5TEeDjNVbSRtihMMaou+SMEXL7y+/nMHyObsrQGxqfGsdO+xERhBlsNfXb1d0sqb13YEAYYG1ja2J6ytmX8kCosI5ajDpi0h19isMB1vBigzYaZW213jbc9w1W6VUYKIPTi4Rp8N+Det79g112WLWEnBEMB/V3oK/zwaGjwZ+iCDC8vA1MQMbm0qEAmm+AferfsTk/C+djjxg/W+7cFkcFposg+YGni/1J3WNwwMOpfHNtGO7N8FLLsHuw39O9PjA8VGovm0ulHRCFHvwlFoZT8klp35ovx4giiBjFaRKkQnwLW9Kj7KUjTVOldQyxhk/cl8ZxJJtZY/YlvXkMV6729qVwjD1q1S41z8zsOIcu6tShogiG8yKt1daKmexsbUs3imY5l6VaZTDk1Y6MDD/FGc3Pkyg6umBvtQ6/EX4kVch4Xdse2x+S4NtdiUbOSWr0L7cLjZbLhwgNLhXmgaAxjTwydw+lktfY1zQ3TYYod5SVoNEsl25OESmc4GltZ2fv4FDXhysPPooqaW4eGmLteyQgGfyoqMoSsQEo16Mi7xi6d4ZOjg6ppm7dQ3q6JKPtaELS0TpQ7RkbHZ2fm8VO4Pol1PBAkfupAsMnKEK/Np/6tvH2OjkKKpyvLhS2hQYO/yOxslBEttUZN1HP/aE+PIawHRX2kCajYl2wPPbFsvPfWksqU1NKLYJxVk/Yw345gZIdOBuOcq4oR91FaDcZNY1NMoAJ0+zcjPbfXR29h7qRy53Q7K9ShiJ+/vkXZwzBJpmFvJJDvjCpEw6RC2i7qYZ0lj061W2RyqE29Z+wOmQl4MBYIVUwlxfuQcc9P0kn2tMzcQ5laXCAJ6PxGQbVLHzKIqibtS02pZNyUzbJOvC37TMJSSMi7qtZQ6GaHIKUwVuQsKQGhxe5W3m2IprqGwdV0k0BF+1v4BGxV6FNZrwFSUjEQUuSj2MsbEdaScfeY5kNXQ8CoMeIGUe7QUu/0cGqGBRyzWVl/F2fCbafXtZPMtZO01mktM9GsvEuW5vSswInw/LB45Is9BMIRDXeLj4QL0Tap0wqeJVhsznCOuklcHOlOMA3jicchlH1SvFYmWItiD51vmIgTXpblaUZ8UL4nb7i6sXEcPQzUcEuE8vcTBjjqP7ADE4V7Qmm0BapK2bXUiFwLq0E/Jeh0tsDju/sHNGD65vbzm1SSvSQD2V9I/Yj61qi3erysgtXNWK7l5dRy2bpfRYHKLeXm2gLfS+B0rHCl2xv71hMSXeEKpjgPm0kbITgwXm1R/6MGg+pnEeaUcoXaC05RSGnHxI1nZ2dgV2VoPoggK9+m+4yABTtxQDiRvOQTZlfSztBcjgTwIgIhAoT0mAZEjuJ8Hg7MIQIygFO68U6zSutHGNhYuBoKTmQSCJmEPqVsvAZQ/BMSItLyAJ0k7WT42Se7+wOjw2KbCOkhDmLzmlZYZsLB/v0uBti/epMOzvHR8ftwvnFviIAV6U/7ZHcI+cIfdL9UHZZQ+HVnYrlAjS8/4L0TKzPTVtZCAhGibEnUCA2CStwqhapZVIiygc8BReziakIjlXwLZ5OScLewRHKRvhem2KD0XNuLFywJdou1aJE0Yo5UBgnUT6bSkybmir8Pl9eT7Y8iRvz0b5A6N1tWVj7eDTN8jySUw1Ym17T1zdI7DhTGs/pQLn48aM0OHoWjoK7E+uHQ+7vkUtH+4e27cnTeUVnFiwpR2LgxKe9BPuDZvr5Hezvk23yBziTANZ1dma2a4ArZpp2c6faXFM4DK3uKvMfj7V1jR3qJnBukq2MemjUHfqCKwN3kU1+hq0iMY21qHvGVbCWwx2RhQdaEQzIa28KR0lWGEsax4KlQA7Rzw7JJxbGrR0ze9bN6xlp4s74c0bwUQN9vRyk2+sL6dCDZkb29ooBUOg2iFphq2E065mfNJgY1Xh7fusbsRU5roih9OoEelPxlJ4cVAJpDm4supjRGanxKIYoEFZMj9kfghn4CNBZFM6bsUOyOfmi+ABSQ4TamtthOikyScjVASApgCXYCccFGMrbUfWDWxscHOnrG6YdJqdOOytJatnd2gVJ4rMboiRDH5g1Av3ygjVAfY62jlBzRILe52Bo1XlyeFKwT+E0HFEHD3xoSXd7CdQtxA8haUjA/e2xI0tmXIpSCutrd5KsJ1AZwOPbNKdOw4OkLQJGIBghcaT5DeTBM8bTSh/hFGFSJQ4EuOeYOBqgEkVJleQ0FgOufTp9ZClZqSLjNuWxVLMPcqMomyTXOmXoMVUIOjOl7i4hVmrOVWwCcUEsal87qJWHMY5i1PH3M0/9Jj2NamZ2FrONbUCGrPosa+ASQW1qEcz6TuF6xrqxBswSs665lw5M7iGtiuVWKsjSKbyzJwAAZsq0gAwYoFSpAwJQMESYsaR4hGPREiq9Ijy7gGeXMwKagCfMIWvogVhrP+KEpOiEJWPlik7FRQ2g1+gfpxGK2hXC41skbhcG8eS0vrS2otIKFnVgNFcoW9kQd5Xz+iWzQBG7EmCF0qHHZdnBQEkAwVbdpVKHDNBFDQ+HOpuV27ulnnPW2itt4q7UIqTMZaGGg/SbZZv14IrNXYHxkypepHvYFLHD6ZlpxAN5P1wHFDeFlwPgJMlm9hQ+lJ8BPuW8EEtiA/DDcwy1pWBQnWjnJta4cC4FFxEvezv7ZNKnA0kKxyRyumdAN52+bu62d7adCPSFGWE2lU6zBbr5wjFGhsBbsMu23FV1r1Lb1dAb+j02MjUzxSQxY4kvMvzJ1sX/nHuc0dFhVuHDh3c6S4PImDNqZmx81IkhFfQSN3n18AD2R8drUZD77lCD0dMn7yVO6G0oV616qSRB/iCEkAekMZQL9UeUWAta1ZPKYNna2kb+EAt9Ldvl2mo8Io7U3q4LKC0cNy0RUXSTeKp06TjkxerkdIk7NJ0Fh/DlcBY4GCfQGUYnwcX22mYQJpLKcSBq5MnZ4OjZQ4tIHKldIucKdJOSaMYHLUx9uGBef3OFEdvd23fI3bZTPzZqfG84ItfMiPak0GZzfFAsjWPM4aAa7JU+xMmDYuHM35HTea1JR9Ne5u3ZX2FYXD/Ue2a2sAiBIEy+vAMt5qTr+czYg+RtJNJTM05Emtyg12wkbZW+tEGNjfKdMKijN6OOaMGZdZndouzkqi6/G3WIyhT2S76cLdQoHEKx6wSjTyqMUGlZhrgqxLuuUgveb2p8NNPkme3ifhhv8qRxDGoABs2C6Q96j+vH+Z/IhUIECVA0PtwwzvaIjS+QbRC9hPfEKwVyUEfBAJK+2G4nIWVIpJa6I5Hyw2A5uyF8QHGEFccY+LdUzuRky9iVcRSG1BX8p4EBuCBTgI8YHHB/y6tjDIvNbRgeHvIZgZYNfK8uMXq7ToYiELXa2vpqw1ooG0cPm+mQiMEUWRCAT1gTZ4A8oKCIsCNhD+AuGIWfh9NSLeGHZJKRZV79ypb7LCrXVE4KqSim40CkpNwLCuo/yN0aytfyNxpdpJecuKZN9BMkOH3LMFgxdxA8FNzEDFKp6q7FgRRkqblJxm2AUKyLEYzC8FIUbATYjdcJD++5KE+6NXvnCbnFpWaFLdgaxFVKXzVHE7O50q7j2msgBeuXfC32kGlRh1FPdaHl4rdhDaP6fRDxRe6kQtjCp4+viCwdFlAr2pDkKL3tkHlhcUI/sQY2lbeWOh4yGjvgIpzB4r23Geahj1bdaO64gJ4rWS9OQEZupamDSbn4Kfra6vo0HL/Li9QFB7APrn+v21q7eJ0WyYphtgxQ3T+id7v7+pQBV5TOM92KoZI6S5fwE0q6HO5sa3i+BfwNDw1Nz0w5BVZEfYZTq+qWMMDi4doKFGY3fCONhZqgqWBqqkn1AN3CTPKSvapAexdaMBA2b9fC3TVtq43DEUkMkZ7nIvJcPjcLEcHziYoXyWIezHM0RbHQLDLgLBqtQcAS4FZCj2dRr1Q/37m+0SS/uaX/+vhwf2ffxSfGJwaHh/Ay//pvfzk8OUIeDAwMD44Op1WcVl8+zozbm1uqVW6XKY1MrLpmKrt+eko0WKz93X1qC2udwl4KtlHPtIut7S0PMjMzyYnUOtMu9POZh0ecPSQtLUcFWSa3FGjvpyg7RBLhqaQzosKmMc8fBJtIN4+ZAU9NhyWlwryHVLtF/Z/ZYVDO0sDIZpt8/PCJwM3NzYxPTFGLos+cmp7+fqeIbRYUZnZou5iCTLEhPFYpDovvWVFbhelhuzgHqqJizfFDUFXKvkVXWtuxfP19XqYgXqJRoTF9QulA/vNFff9ojwPt4ugRn0LBC39gxDwp7mFscoIRA5m93k6RPgHqzvY8JsmgK5VuOxAEK8CzXAaggy5TIZGPoC6Zd+yNyIbwEbEACmr1GvZw4cmTMdPb5a3KLblX4KfxXmCPYnuKEsZGzkorspGSYoMxgTcjLOiOjAJuxiyxgLbWlsvu723rtZUiHAgur1AgT4ZsKtsLd0iVkaLR1WYqpA56PSL+1JlhYQyK43ZRP2acBxW99PXi/sQa/dinNaXkE6bX65QTQBFrDX3B8lBT3uX28H3aTxk4To9QctkmJllGE+m+kkhAi2YU9b0YWA40hKtfgvxXIcEWfkDR2R9zrfGnfCrGIikHuvWcC7ZIEk1DU/rf2W809Mi0l4uLM40ah6oj5WpV5ICJcZJks1gB6frYOebj6dOnyrMDhXDBV5fm7XGdqX5cx0NNAwwe8RnMpRSOYCjQ47tSVpoYOOYB4vSciOfDHRbBDYsQkGGJ0NX+Xs/E67HFfCxf1NwxJEKnd5etE1mNk64fU+2UIfRewMp/IFGh0IU9lB2nL6ycH6yRVSq8ZyGPRNGcl2C/JMJTqRSrksDkgYCL/nBM6GXY3Xn2tIwj/MhjsKqOlVf7IHqWU4DtIxVJJ3EGHxt6yqWxkcGeSqf8Dt1I7hOqqd2e1aSPFcodSy59h+nVIPM/mlkyKMm6kqsKF4rkg3Sex5BFCW9gbEPTWe0Cu+i/Iv+DTCICDQnIZtNcskQY47B/xh8maq12i81gzaniDBLwf0yBw0iwAveT/U6+7kMIal2Z2YoPGiCjg+R5sAFWzStODEEUNWxsQWoSJnVJ3X39HJOd9LA836dPuW6cwsFBGfPcax45jSWolmBPcrEuIQ/aQsN/2zI9Ne3+ZcLowcUwMT99/b0tI4OsLBnu7kP7ddO5Z2c1Aqi/99DgwOjwEFc/xOHhoRQ1nMjp8clRWvrsUndasgcFChvUTvyTZnOQBZSJlGYqMs7RxbJM3RKankDY49hDbE9m1dnlICXjOygBPSiwWMpwbQ3LaQv8Ry5x/TJ2VQ45wo1NEwiJD0sf3r39YFYTY4CrJzMdpa7efrPARj0+gafox4ZHWYujsYPZyWnJ+0e1YyTqzNysqzvexIm2pOnIF9+Bp52oX0OjbtIzc1cgdKmlZHNlZgqe+RuN4GWcuYnpUfeVmXZgHmaDMZP+TaewFEobKGQ+pIxBssvg+DDHHqhkQLQ9uiwBsCyKLjJJ+GH3uWmEcGbuyfPnz+k1UsL4md7iIoyydwVQ0GNsDs+beYrf7cwVA1Xu71DAavxEjx1OAUCvYQlw8Thfro2jkD1OFlc+zymzmt7b118l5murcdX0mdMjYWJigspwTgsHmkpu9wCDg+1aIWDRnCtiZOvRZ768klWn5V1c6J+qUgYBH8HU1LjX2WDp8HSGXKk8jV6sRwdr6ytCr17ZPzjMrXMFBk9+HuUCaoNvnlR/6s4OFWESulovwV3ygnvBsOrGgJ0s+rlbJfkA7odD4HZhUlISGBcKJhMWEa58dNqOhdY0e7hnvOO4A0ngFKXCQ0FOSxsG+OT8qBiNnBJMBYroMCHqlHTdXAkBAn9AsgqHdhOEKMf7y4drnU21IjHnbu/0cP/mqu4j85nsIvJAD9fGkBuUT3IbuLLUKgsUVt8TJHMLKLDXcQntTKI5lDu6vxW2izqjSAMWRW80KrWQ1BATEldHJbN07FKlqtHpwNjk9s7htpSm3aPm5lU2PQ+umqZ2tr621jQ1QXIEbA6luBvDcXgMCnAspL1ZwDh8DcpBDkJpgVq6hpynwVZwjKOqizhptkZhMtuMDvN6tpMDYYutmzPmSWJavO32hqYYGBrArsk44rM5+Xw1Ohp5Ah/4v+yF/yWiU5L/ZmIObo7M/AfML0qo5Ch5RLpGoINZYp/cAG4zGhO4QJEWg4gFYKBF6y3HUK6kG5aljXYqwqchFrJ8CJFWmTKqyq98zkBvz4iwR7m98f4SAEQd4RBdhWORDkohFGEBu0PR8xjSBahQl9g/E0s6QDYGywZSpKBUPKqUTen1y/ugcpsAgSDldLNwo7cmirhDKMYLHFhmA3ak130CQp8UeDZa2EeQae/6j51O/XNGuDjXdXEu8CUsmthMbJjqF7jB5OYo1TRcSM+JUmcF97y3tyrdR37JfWMrOpBT2FnukVRd7o5HSAUTCSdXgIe6kF6CCo9rm/wMSR/rfuPTJIL3GbNq2kVRCkHHSNMz8qF5rOlgZ39rc8Nxsp+e7liE6vzck6qnlR/GoYKPFc2Ql0AvwblSGxQIfBAzDV6+ePlydX1FeoLjz4EQT6IqyU0vcxGmlqK71nIGL23xqC5eJhUntg7JxVZJkUgKr96creIlR/tH5M3LNP3n40CS7BfQ/d2330/NzCr+x2jBv/aeM4n6J2x6RIx6sQKjRsGP7uubSejGtvYN9csrSboNXkL48QyYU9kDRoDRZSYZXSzGoIJ1a2dbIufg8LBmwwA3PSMb1U5rv8s8JEtXGkk8X1fS8OC4NjI8tvB8QQsd8Q2bl7zSuK7Oc/wg7zw90cDPxPDHm4Zb2piiBzMga5lq1gj0JtYAka2zZw4DdJvTAgrFKHqh6jPwCqRMD6ngKBXCReserR2YiuQEIIaHR+F0sIgTRUwJFoEi9ZQEX5Y6cRFnVVng4MDl4x714kfGH7YV3cU1O6R+3VabJYLJaFtWTYhVSh8WUogfJHSJaJAMiRQahCraYBQiZ6sIFu8vlLLWctcMQE1QJWkMmuJ2dj19tiAPvSKLIuMMbw/3Dl0FwGMDPLi7Ip44b2eZPp2eGlf15kGD6TNRS3tRBcZysZOAbOs8l7YOcsjkKDl1zDIhy1DlhqT8nymKOTutXp8P9VSalUNeqOOM+y7YqyCIK1CZHAnyfLgFKybHx80/EK9ReaO8J1M6qIzHqxb9mVOLenF/dXp5dnh+cuSqVL/DDyzYkeSc8LVDFYSLgPWcJbgFE0rgAHwPZH1BySy/rgwF5oumFwPIFmtZqi1NVJhfKX5MSUIxLxoU9wH0WsHlKZpXmSy/toO7vb624Ye0xt7u4dnpr4o8uW5wN7B/Vje4TKG1W5Pk3kP5pq3X2en50ZGyBqEXSJYqptkdW19OrIgUxZvQq6DrtaF9xlU52lRxUrxcE1pkgSxuGHuH8yLjSxlkLD2UACXZekCSzPG+nX/iBFWp8sd4aQeOXSAw3ukrKXQWg9Ukd0mxB4ey+0ncamkOPZLrO1pqfO8sK4XF3yX6YpIui0MAw9uaMoHAe8kqe+IA8iegSn4Dl8uNPRjw2948OT5kKngyQzHgTem7UGpQ2cUe2FkW4TzoAbV9la6hjp59gv1j+Bg5XtVN0Zg9s9QE3gLadF2QW+yYWFAWjvGwRFSzm+MmQAz0I9kJB5U893SCtQLMgs3mF4YdVYKQtE4viQBQgkI7cfNg/7sbVZSn55p8OvvxZT9LlM4B4tl0It2oyT8EcaiT8ll9b/9A/d7I6IS+VeG9GOo05e208owNZcrM7GztAfLOPvi7tLwEKsJbYBx1684dLr9yhwlJ1y+gMUtqrzc2NhxZUXtkEs+XqjVvVeAC2QgpsvFE2hrZU8/obGof5P08QGoU8LK9VkszRxItNybKx+rTfoqi7m95kw6Ixw8ryLCAEY09plt5C0jHz9C3wyrxNvBNPBL6B9QGXltauxX5j4+NuLeuckfvYK8eiF99+bVnSVzBxvsqssVOLk7cnhfTUnu724C4Y0Z9+2heJmmhl1Q7A6CMVlft9Ei3gMPj61oGQDks3GdzjJ0LYoBH71hZ8Yys34ipwqoWOsuIy2RYoFXFLkAAn+oIERHDW/RRmpt7MjujswSLwWmSQ0lZOwmwABc47CERR5yid8jt8vKKHgyqHIqsc30akjtEekSg6G5HwldDmuxGQEMuCc506UdIIOIn0aKuTIkw3UCTlREHDQxBTp8pPbsuYqJiY4m+ATyEzq8KxE0aG5nNlH3fqgM4E+JDUlGhAv0sh4ZcRMF5SwRGQm6ya4jRIY/BZckTLQDXqwlguvvwbPQagTWl4eBQophos5RbpxSJLf7uLRZtbHxErZucYpeyDlgm0Yqjw1MGyR3yWT1yaJ/Aq0Yz7gcHqrQ/nOI/7rKVE1zBVtFKSerf2TcRzdXUcEI6jC1twYyjng1BsfxB8lsbvCjju4Gqc0XkjjdlSzvDs7qontYhrd6eyghWdGqS+qAWpJI6jTfnNP55RxvNTETP68cH58eHZ7V9M2u8hqMoPmoTAB6zljjaosuGtekQZxH4rjz+YptpurhUJCR3n2kIfldQxZwUiip/onuCxgvdn21KEXzxyFRG+ITkhNARcodkesntv7k/AsCT6tFVVuhIwxIYlwVULWyyMEM3JX2rGAanA9Ll4uKnfQXx8jqKGRKOOltbYD752jVMAaqUi7K1tuUwpw40WFs3JJ418gtpY0KQLlUZAYQSYTxYEVadat8qKqSIJqeTxMOAN+eZM1odMsmui2IWghG4ASDoex9K01sD3/LZ4x7lMDCODUmWaS8YnmTK8cWTyOCL0rZIPtH3zAbo7RnjUlNvCj7gjiJEb3XpPbcdBl6/qcaHgZ7u8RHEXsX3CAE+SQ5BU0cKB9JkhlV4xBkWjhqvMBqZx+15ZdbYMeLd3sSedYeSgr9UydW0xPCxaPFbU5kRiQpd8YA0l1gO7qioE1RqVLE18hmcB+c88fHPdT+UNM3MPsVrQJrLk2ow6VtAUPaCOVwpCZArra+JCpN7kRsTgRi/pEVJ4Yf17sQt66fYXbYJTaRGRH94FdvDI2OyXYxS4t9Rmj3VZp6cNURcOY+x5Yzc9R186Z5Vv+jErm0yBU11Otgk1p8Ivz5IF9eHeyCOgJmTonN2uDta0nnhlVoc5xS76BSHKM7UsAve4W0bcruMYwBw8D3Ui08nCd1d3fNP5iEz+RkEQIal9QA7PqM9OnFmZnZi0rlTx97B4sKA7oS5JRUYRbk/wDQ9PjA4ROGQ6oEBvTAFqEo0iXkyhS7psxqnZzXm2sKK71H6UlfYSdcHWE6LFvGkiBLrvechlQ6OTmSiJ/bH2CRXIo3ut4rZ8ew3k0PKhTpU/BEzG7S8tEixr2+sw5pTKYGCtMwsOW/xMRCc8itOYTxika5TnQm2aRwAempmmm5iyTkHxMtdkgbrQjNlAKQ+Nvd3ewf7OjZTjjI0mAC5Mp/jCiSENsz3GVXcaRe93vFDKzHg9sCpceRQCvhnZnx0LAkbbLGlcX3/gzD80xkOvmZN8NohHGz/JRaeuaZ4JNiwrpqE2hXqlDWyo06VA3Qnl1y92OEx5ckYyCZurSa6QgpPpQefHHPQhHdd/7L/0mOqNKGClI2RlVdffbnwbIEFvtE8SPEU//jxYWNrg4TprEA9f1r85MxPzExzAuJ+N7fSD06RD/DptctMofFjG1Y/r7C9UphMoBoY6pPZ4cCz0Iw5jUB9gMNERCojp0QoMbr2McVHd6YNNjV3d1WePX1KK1C7rIIIOyeF/UBWWD0xwJODU0ZOBUiZMLQ3oSEQUfGRb84hckv4QL2aiYDwIYB7dvaENyzKjGZL4kBscNB/ntF2ItSlScTl4mzxjGUlFoVslhS+jUfErLM+2vvgsmisZGrLgyhKa2kWZPRdA+77IUNQ1Y15PeUL77LxGoKbBkYttZQu2ss9k9PjJM4maM46OT4dj7rczZuxPPA6+mdnexuwwKPxLA20G58Yl6UDZ7G7kKNFQD25W1tD8VY7u/rF2VJv2CaeHwDc3ExI6FwqkyXDDnuLQ8415SLwJGgVry+0cBI+0cWEn6ryXk+OFKGdGTEZe35OruB3ZrI1lU9hIH3ROs6FdSu2UtA43IRnZgppXIuVo8UUF99DRXoh08vWtYHSDuXFMseqoh6C7Fly/kFcxxgJcf3x4YGpseFuQ+1aMfrNbY3qsFSBga42K84rU0H1eCJrwlDbGabFBzsnUdNOV2Bwp19RXp7apUmJPgE23W2TT5/oFCZwz6mnqg1tBIp5Qh2IsuTqydSMXDD6RYAjSUiMQlJFVf8VRHCp3ZTzggE13fChxm+lGJId1mFMbawIc95eRiWhLA6T3HHCinAFZH2Df23qhDgsLa0qoVqIs4aGt3B61fHh2z1ePugD5pZ43nLGnGIfrZpJZ1wt2TnTs7OzWgZgETyanCvHR4aQk4g2Wl1aXfzwsXZ8zD8Q8pWP7/VXGxJYz08Ojr144elTUTNwAd9CdG1CdUBruQ6BKITVyfkxdUVTAYhQL/LYQYOp4dSGUpEs29BA+eLrs1/sf7G2IIU9EF1TzYo/ROKLV09NTdsMRsCj0X5W0rYAQ4IuNgvLCRpmx+7v+cS8iv29fSHJtG5yMO1swuYYHgUoCulbUfkyAInf9s6OxYFUGCoQr1PiXBEKV76EvylzQ8wja2k6v74/ODiWUIT9l2S4NTlZP385UITEkLg8wUsKjBwUcqdKUwysRkx9mHQzaVh2Uk6HJRCOK0g/KYDX4CoGywEziZCakL0D/nsHFgTYUdVHjcYQpZcEqBX57mi2NCGd+ASOlvPAKw3LnnRfkwYa2Xx34tMImxUtQuykFLLUoC0xAKqH2vWhQByVClInkjQg8b8soUo3BUIjlYgetp0cO58rbfz42NOk+pHZcf1Q9qkHmbO7cVW8rugkKgMKmhDaZep9sagaMJ03n2XssulrNa7SlVnC1iKkUE0X+wvwb2piyg0zA9SXBaT97SMc4SNjum7vxOXl4dpUtKZQD1ekSF56rDedO59cCWsC+iQugjLlRhSLE811e+KwmZrY1dd908BdOFQOCLvRKBb/zEAsMOHuXLVUpbNTZw/+Cv2hm5v+bmCOhX3E+Vzjs47qJ4dnMnOP9+X8+KAM4rVG6c9Frq+YAryyHEdojyYwPyb4rqXFvqBusx2C0oA8E5Twpogttcb7oe8QPwhbtjxxQeoiUXs4jfcjoCiq6bTQwsbjZThwQsFiPacXt6XOnsExQ1YhhBsQHJSmpNDTXha8qefi9kYBL8j+Xf30isBw1KgMsSI0GgxRaBD5EgjZE7ckYhYoAGS2l5C/ICRDziNklTkuWFG3QWXSlVxmqteHyDXwlJ6axMKAvDGNPDxU67nIXWIeXHhcuZ2TE8wiYqhMvgKMOLLugcSGf2BCWtOOlBKPFoj2T8szy8cX8QIf5OeOkl/5PXQZt6Mz1SH0KJXhte7Zs7MRVIhpgoyIfGpIdaCrY3bMbPC+Tqmgd1dFop9ulxzcjGxUeuzR+F72iNzlsMK24cxSTMBIpXqjQa5aGugTdOrDPXuHl4WiTpaziEX6VHRWhPceHXtBqp6+DqmtudUinOiukHwsgQVkF+Pt5GwKu8voKbJr0k6R/XrQKck67B3WdvePTSdKtl+5Gz2WDB0ZMWzi0QmwqPeDS9l47Fylt89pAnNsqMbgk7Rkk7mV5oLgP1FqIWOpHXuRomc2qdIpdMcKO7R66EvHUL4zMzvL62JiEyAsdzHzbW2nAgIDfYNmM2Bo9zUERJs6jEGFIGSYO4+Cgm9dWWPgYbVEa4Aa/hmPGPmW9vrnqF1w1YqSBxJS7C5XG1QcADUsBEmg5QIpRNE93+ER8ZdoEqK7qZV9k/4OyA4PDTolepuybWGD79CASRlg6Rs7G+UYAhS0L2HT1PD4uAZQsu0uBU3s7Z44UyNDg46rSMPG1hbJ5qtNTE2yNPpDwTqgK81p5q4KCRLmBLLA1AgJ393ef//xHeX35ZdfkBlhD+eov1pFDFpw5hDlEnrLHnkAW50YbTzQ2+2tTeSGa4k1wl8eg/YPZ/54b4ShTDsqY/9gZ3V5DV51krkzvE7+BJRBe4Lwzkz0a9GPnNmEUNgAyo4s2QBiQfc03TQq6WT60NXUsZ9bPDJKzwXdpF70Ck53P9arSK8IM+FEoSlkYskM398x/yRZ6kpJsUOa8gsnDgziZ5ADEQn63TmEXgQHGV3nVCUNghjxysXxIQdHe2/fvjcr3EYSQbN0eQkoZQk/lD4vMsOJioGoTjDM6czx7Ht6qh5hbW1DVpDdhV7VGWbniio5nfl8uX+WGYaVhOpLagDT7Q4TPQL6i+IyC+LsojURHnHMpQ7aA9cRYQOx+QFEo1m7zvtDHTKOTEGUboGUdy8ywuq//vQD2PD//V/+59kns2xQegUD7kL3KGEZI1dn1/Xj06O9ulDqnl5Dx/BElaWuCPLTP24v/Wu0d0ZQUYtcEMSro2fv6As2jDCwqaSK2cbhUPGFutG/yJ74lHuoFc0dxy5t0Zq6OkoX1/ojyyjK+aBrKD4HPvUW9kxq0PlV47U5EO7ouLnlnO//3TfPNQ00Z/XDm/eivYotErEsd45NjFFmxu8p4XJjSE8pcRwvUd7nT5+ZDwHOk3Ya1z4j0QSLwOHLmmjYFUF3hNgzhySo38jsNLWg+NpxZURPSZ4bgyd4KVLiomhoqbg3DXLyhGfpZb2QOnSckdZallJpF8Ld6/6dZJzohVZsFlGJgoPL0uYP/s6wXBojmp6YUjRJSMhSkttQQsXm0kNIG69j9L04t9jenpA7m8rwuNLtQ2d748zk8PTEsAEZosGiOLKHAga9jRlWHiF4Q30CzxmSnPRbZIugDN/FiU4Sh7qLwHxutMGfd6QOIMu2GQIhRa04U3oTxTKlcwNmT9VYer63diTNHy7LtFGVYXhcQ8IK1tVzCJJYJTxM0dNGMpjKL/ye0SgiUzeGOSgkEfLmfmCOsTGa8TmuIUsv63CsRdJSC/Zv7+hGJWgOYmFivrTcuLjidsgBs24OGpnaPTgiW2KelXKLQhhryQC0l53fdn64RBeEPgSjiBJUphMNZTk5Qn9fWI1BtTGVXjy2+c+2mCoLeyw8WZDpDROOm7ymJlyQ1zNIkAHeAd6RT6gig9q1aBK1qX4UGZdUyoYv5A2mkQmIKkjbykvZ2Iw/eFJvUZZ4vra8YZudcKBQa1sZrU406nLpk9lheyC50RyAaUNjpX5Z13PCiXPYQdrNje2l5WWCNi3DaWaKFqUEefd8wdSydZYVP01Oz9AltvXp8+eaouLHLFoCS5m7p7y0BPGILTnD9osFpUPdZG+l9/nLl+wE4OtAgGj0kld2qCzGRahdJagFMqDBkqgjzdzqCG7//R9/k3j0dOHp7Ow8n4UMrK2uAf5CoK5Fn8r7RM14uzZtqEYSWeSJuJNYQS5Lu9bhzYZexgBYpsBJDZUko+gkeXejdYi3E+MGpy10QdJlLi+kjtxT6MLrojEexHa6eKu2vN7vsnJF6mcITRbM4Ud1ydhJ98+BfilEXgDpJJ5UmBmOBD0elrrQ3Awpuy2qYUgPxRS5JHalDuwTzmB/f48uAOYJBL0vO59aRF5o2hMHJnmBSRTT5t76+CxoKI0q706wVh2dx3JUMBVaeKJEhD8cM4aT5yH/SVXF/t6RkxRyANZoc37tmv94WsmC9ci8BAS3JAo7KQcUIvP6roZu7L9wp5wHGTMgG2N0rcm+LYYc7m+++fKLf/pPfxyfGCMLupylWjTxgtPbs5OHm7oGD+dm3x7uiDacnhxyCsUkqEJ2mkIC0o17cT1qJJBBox5lirfnTp01T1AuaTzMPpVVUEN8+UB+JsosObXg1IiEnKQJFpYy/dMlZGqgTf96o6DV6bFZCFxbomVF7nRBbUQf3SV61tYmzHuhxbcsQE2B3r5+KyNqeEgTWVESxUH3qqAdVy5z+iDRog268gnWxJCTV6iCTFHxfghWMC04gSR5H0sMvRseGGKDEfo0MgrYecB7CM+6Zb3zvIywaahCfXDt6WXKnUsHGXs2kuN8ONgWoEhjYKRv1YwwYyIKnCBS5B7cJQ0O4rhJ/qsTIeWOUJE89jn+JXqKqwETWtwkv1mkiCWd67b8KFjCspfSbfhz2AyYzr3eaP9Qmp0YnR4f7sSniQc0J3dANq8KNqcEDBRJsxPqqVgtZoVI0SNMMggF+4OxrdKtuRR0gOh09Ix0LPKMAZfKKR/hjC7QVoxUe0yQX+UeU+ROuGrUN10I7okOs4DUfa4ihifUr51q4QzKKlAQIxfcVqP7MilSB5u7R+FfYWbE35nK/RMD3PFREQ/PX5HLLN8hZdI+2q52OzfOiX2kBFzWQbCCPCvl2RRA6QJ5awZUXHYENZ3lwHI2T06PzOOTCK8kgjbDlJiohR6U1kLWXY3jJFM8q36QdrmPg+mZY+n5hcfHh4X3Fg+V7fEyN6A5HRUR86aXH2Sty+ngIA2rjJQh0K7GL/2QEBKxo2MUltBUKH4XpFm8xUcRzQRl9MFFKmGZjmpXQwPiftr3K5WCAq2zvBTlJvJ9eNG0kKs5+J6LW0KOoBNE8cystqezdFDSker9YtNMEQX1xatXxH57d1e/nW4auLNDCwoV8QBTAKgCRkzGUU1vVBtnQDytSyQ0R+jqpjzTJlrukkUHbW16b4/KhnKLpH5nIPedusTHlvbAcxAjyRJ3ep2d/PjD33WW591wIrxmdWmFjRodToMHvQriGXC1T+vdaTFBP1P92Vx/R98DOG1FpnOwYBxncYDC4DNC8Ukxww6M39E01lceMbcD584HlgKl7bWbSWmYPH2PcntX7UtTTDqXHBfkf3luZg6CWV1fgyV5Z46z0+jsCdsapeIxUggmzmG8e08PicfZ5ZADZmrNNA9Q19bW9vTZU5+i6uzdh3fC9lxnycgC0e4yABYGbmkaHrmjSq/vby5PVMw3haNsbBpuatDTGLNJiVNQDEC/mc3DAx7d3ZIJLq0dnY5VFHw+gSUIH0sU9w34EZTOsCQGWQjo2EaGeTzWBfFYcvje5g7qWepZz1BVT7P17S2a3EZ2tDefH5/isTnyr7549j/8j/8ytzCLPlLYldwjTo1TAS+dHLc0XD+YG3tev07WszCmpqEVm0sUJMdrH53cdw0s9dAHKwvXKkjXgccCM8e4CM14NUBihEmD6LJ+EhhoFI6u3SkUT10YvYe/jNTZCa5cc1SM0l9aKTVvwHKpExJ2R4oEurpb28u9cuAyo2x4iLVbXd/gynZ2tc0tTEpsE+oUUpIQRcDYeIoRBxZxbGjC82gSNzQ2opx7Z29HN29aRM/nSvnRi2H5tdXVrY11r0QWWUy7zEgBO1AJ2ZSNh07c2d6zj5guxkZlPUmB+eyCElm3jR5EqrKO0Icloas5KyTP5nITrAkNbu9oKaYR4+EjONoWjTUyVadSzkSgEESUIt2vmlrUMQhJrMBwgqhXe0SivAtEos6SQZ49Iy8wAXmP06TBgey/iVEJG7L12A3GOsSL19gJj8UFwbxlXi0LzLaVqaCuu1odfye9Qn03qopNCuqRyFTqcEcaYrqGJ7IWbsxBU0jweAp+hT1nbu8u3eRVSQKOpLCiRC6cJGJPyK/LVGd9ZrRRaiPB7oeLdnutBIyUEIE2G++FsrQ2d7HNZ8dnGQqEsEyPO+JeAEOO5/TkuAqvyFySx9R2pWOr+0z1CGdGkzHrc3nVP1Bmz+i0jvM6B0dqL6WSEMdjA8BnMSxv+ImHWzBC3sfg0KDddlgE7KwPHpfrT3QJ/f7hAa44DTKYFoY2tvNsy1ihqyteF7GZnX86qkRWqCNdTkMbJGiiqOXqGsxFmuP07KnXW7SDvb3aIzLrSpYglch74BAb5yWRwTfDo2PDI6MWE6ekCnd5aQXCmJbw0tExIvzQ2UU10QbD42NDgyOKgW9vThwPfLsPcCdFdXKP+8ejWBJdgDCtPpoWkpPiUpqfl7XA6ijJadvY2GQvgzxSrqSlSdttc8hnitELiLRbFSeHl8bHR2XVkEmySuvWmSfFvbeXlS6LhgiwQc5KcyOfhJYkrKQRXLNe8AnfDk0pXevwYPfmeo72nJ+fxf+wKuZh2QXpNGI6tDyla3AVnS5kEwPwmIi/btJ3lyhLIse6Rs/DI0qPg3vgisQF00aDWmGA/CThX1Gpe4HB7JlPIdd6wXq/4+eMWYjCtVAM1SveD5LI/kbHmhK3uraONDBdhM+FzBejvilJgCsdH2SKJm1FKTs9Ek7iPwfaJiTAZkonF1F8+vyp8Mjw8Cjq0BV4auAS/w4+5TwYwmj1l5c+bW1vkAN5R+7NDTviypJ0mfFonpJIeafgqs8qpz5XSKOF6IRe7ChJbeXmq/t3pBgpZ5EDDFbtnZ/bLfMvhV33NdBQyXx6KrCokTlXhNQiLJhedhJKL3e1Dw327ifL8GxmeuJ/+f/8T3/6pz9CMpasLf3bqZfzh6vzpkeTp+wdTHhFX9hj+ggJwExKVHLYxEDwNEJ3UeclQ3ugwhRSFr9qEoL+DBUTgKHK5CZpCCoihNgInwFyimwy320gfwKO1FYyXqK+LCwh9jq6yYvFAOFgFalgJQN1Sc+2y31swd6ybfv7x47rzOwTeyFfe2VlVWhJTyRYXvrZ+MgEIil6HDxnO5VTMgLVPohMLimezTqzOrt7uywope8kyKnI7TVL7qyIBgGJ/D+q3FYy7bJH9CaBJdhjPI9bJUg0Pi/Qjs/OTrPZ9lT4h4Of4UunknQdeDrWDqQEnaLzoYCOoAXYRYZ5EKgnPyQnhJxRdP3YThi8UGrWiy34LPPuhLGhmb1FQJ3lIAAqAtht8CuqkBK+vytXO6ZkoY8MMsvypzvBnqLglpeAIbIgmj8VUiEZzJc+r2maSwXrXp3Gps71TSZoCvOjv5LL34rmiTC4+9YWnfrzLh9ox+LQgKPJ12fRkxyV76SimyyWiBAdxApLnw25LYeJHIpnWkCb7njH93C+2s7rJyd7R7WdA3/XbXzYL3ef+BEXx3tLQ2NjA6NjOV/lToreI9MILJNF6OvvMPWBChaMjVOpo21vNxxNEoTy6EbJdA4Xli9EVpuKgUxId6hl9K1urPmVxHEfAqMEiVd6mBR6f29/zw5Cb57rvF5jDhlc1sszrq2tiV4qBxUx5lQPDA47lYQX1VM7PnLlWAynoqUNseUZEH1CSoRQOjhDLiC3+GkRh7Gw8FTsU7IN+6IAEwSSbErLCfACK+IgQoMDvdWWsTGCSkqdBV/a3dtQDzXaPAKGylLxSRQIq7azu6bhnQU27Gh2ckZ5EyT62FdEEze3u3sumGrXhLQdXctIaXNh2QxBfrsJP9PnTgzSaX19y1nxL3yG+DNu3DfSJ2VZK+pwfiHwNJW0KH0DVdnWUINBK8wJRtWtK43Z2trRzlethM7yjopSYbz5x/cfeJA299PaBk6W8ZTLdHl47BBYYplCinqj3nlVLeQxwW3MEIQjbGKJ6Vz6A+5268yXS8WzU5jQrvllOo1Inl1bW/dKtritvRtxxmbheiDtA6mvwrTVKixTY5aOjv/+978z6XSNHLLyb13zT57Mzc+pBxMOqpaqQp2SLFULh3pOBZAUIJJxurG2qR4EtHRXuv3ptSd9aFr3NMhBIUbCZck7cgpYi31zyvf2VWRoueP0QW28Lfglqu7hEa40wcrGZkqi9o/JtgbuZTRpxKrjG+/50aIl46noaN/ZEweTVZCiSi/DW2iFm5vq+UYGI/lcu8K4Gu4yNjjw3XffCme++fi+o3Zoh3wi+tQhVRmk28PC3Ny3330jtGFLb6/q+mzcaq1ZP0GdND9KJ72X7nBm2FgmoqBZ6hOT44NjI4JTpLkljSpxaOCnJGBRXHSBsyzb2937HFpIJOBRV1fKSexc4gjexslx/OxsFBzgfG/cgkeU6ElZ8LHhB5M6GrTvIkt8sWSdNMg2MzE4/jV29vD0QgS40tvlCtia8ys5VyYDn1Cwjmv94gwHMjs33bXfjgWQNEWtX5wl0ZavZgGxXmfHip/vRAXYWoqVm7hjJNj2tqiM3jDDo8Mk3ocqz7MbpoaeK7u7fNhXbyYhWCtZqr2rM3bv+raz1PHi+Qu9/Ky85K7J2SlZsIsfP13cm86hj4h86nPHhJWx1d5YmLeEyGUUyx7BzNJZULjT67fMD+MBFdpyW5woUwSAM3Xf2M5yKBEA5pNKCzbTowyrH2q+Sgeb+ihsYp1xws03dyP9vbOTClf7VReIwnR0tcGBFKIF7QwY1zlREF4nqL4zUXHpPUZZtTTpqukBZYD4XKao5ZqBjv9hQThYThnp4h7al6LEmSnCnRDS5FzwVISWUPTZz+SGxsbDbcSA/SfrjivAxwcKnSQACE4JBccvB2jaefr7R2er67uJAYil8MIYoaL1UKwiN7HI7gUm+HZdjfJ5BuWxSCOhvHoSom+RcJFMmHhU7SPjYzbFoe6p9ZBeOldKCxMLxuIb6F8+AQLW8RHeB7OInrNs00UdoRBy5XzxGGhzHk+lx/Wd+7Sr40CoLm16yrQ1f/r4CfpeXFnCf/YfnohKuGMPhjLCFgjLw6qfqS8glStL8zItHYPJEcKRyqOodlYpHPmd9DVDa1ehCtkErkwm8Q2jlXE6x1rp48vK6kokSVIupqGPSvYHBlHWXQzt8aFJ9KrhFEm0D/T1JeSg8O3kXgsytR1Cxxq+Mley7bVA0PtSOgl42WwCVyNwmZBxehomK1oH8HsdIFYWVz9+fH96diT/gFHRGH9wYLi51BoMvUdrHmN9lX8JZbc8mXtib0bkUTWhX66++uJrwIN2QzPpPtTTs8ZuYEg0z0F36qCpvEIsjvndNKzjUg2eDlXYwhZXpWVsA1eUxxAD4IuVTjY36J1mYQp0oAeeAIx03XSFWqbuwSawiIUQVALnUXib62urovOXlwy+eeZ0N9qEAbANLAFhhV6YuHjupL6pGfc/OjGmidvaBmJwQ7j1Y++7sdGRmZnpkeHhwN7Mn5I9kiLvBwydWvKzmoUIWRQ6/aLov0YtUAglyoP/cXuk0wOk0jk0PEwI3n14g/n//vvvnz57xr8TjldlR51BpZyG4bExujME1wOVirvrAkLpU2SqExKSpE0nODFSvvYD9UGbcH0byjHXwKbsHc6urdo/OjaiIO6H8RFK4fU7ksdV5iHe9J9UmVXEEp8UC9XX1/PFi2cz81NodVy1DHy8v+iJgYQPt+dmvkgrRxnQp9pHH+8drG1suqWuSm9HV3fYvoLdp6wpe/8F1OrK21X2Brk6AagyhOKcaefCOw+/bMib+DsVEicgjWANsAa8mtWWeCXbwcJh/BMLxklw8qHlAFpLooGikioBRt+rY0p6mHQAGH9vb0mDI8JAX8AQKVy4NegjuYlDA0M2C74baBoAuykheeASqDFs5I3Z3lGnd4F+hdWapGVwXoQKvJK+1RGXEkFlywLk3skXk8nrqPPcvZ7BhmZ41mTFZsHZ7gpbyPzQlcg4qXUUB8lKLDE5NsibTCAwdB6+U3ho5jRr54OVX4aIUO34WRYBRu3YkjAZD1dozqdAFM4Ew5meM6YnClAxPZfwvoRfvRcSSqEWeW7JxfWuDCArTY6akjBc7e6C5GkbC3J1plS16KLVLI32AvHoc+mkM4CL+9Kth4KvMpII44wvg8ql37kfRJz9ss+4LJ1hJPMJD3QIsxRNfgLPdSiLBTDq+tGni95/rkeGaTgT0ZThQEJPea4CJjcz73dXBbuVJFFhqUYJ/WfGbtfqtL/zaUF4YVIT0VZF2AOH5ttchx8GqCLB3a1HcMZJnzZnTq5VwpYMDw9OzcwUiLDk+HM//JD0OuBMHTjiLygF+rVHtoGyJsM6CVFBGCEwMT+VQlr0H0O1SfwA2u0XDSA5ZWR4xCmbMz93amZpaRlpQtidceKhI6lFlHFc6erh1RIDFpP5wdjSCaBhoiZKOhoble9G+0DHpTY+K8E4bjkGVgRP4CNxhRA7SZwjCG7GOUi+JX+6yHHJDoJMohEKhlKylTTBU82PxHj1cYOb6V7EibAmIVGBtLmuJ11NZgptrESW5ZZPCIdZDWqLYklaCb+gM6EyMTAnTFAWHJI1i3FC/APfaysbCqrctTPPMfr4cWl7e1/flZfl3i5yz1OenJh48nTOXEPXNYKciydNdWJiau7JvOKsxU8fPn74QCpm5uZ4zcqQ9TgbHhtxTniXDwPcUBMdROR6ObMCxfaA3bbiIXDJV3LvhKSjvi0Iew6rOPyE+gpP9CjmfKhUmgHY391ZX1snrhQ3sZS9CxXu7expOiR8wUMk1nad86VAg/a3Ul7pGG/vbzMBgjSAG46MqfEI+CBiKFCsmhcTTrGJJz95sqA0Y2Vl+UA/vLZWWV0QhxBCAoD2TWCzsYEjQo1ax29GvxkZGXRZmhGHA0nhOoOUzFO9uTmuHY+Oj2vJqeYKvhJU5llT9OCqM8DgcbsoBGM43GE80OhUJDUAng6XfqLW7HybU2ZOtz0tGRqkUH15Zem8r3ra3ctiOk6Ogfoh6SGyLoQfp0aNDh3hV8OT1w+heqBCPSfFf42ycCmRZfnkMjnkWjFVblb148j4BJ1vr2Udgv8JGksqKTpBce0FmsL2sMpX0WjC0Qw2wyY1Nt63cEVoH93UpKwVONHJUZeQD6O45YHKIYSRm+7P9aanONLk0nmwOzJTLAY1JBHNxRy2xaUlvzH+5dyhFC4w3E2BotSDh1u9fTigX7x8NTw+IqYnh4QqJ0KAm4zInu6qNGW6xKniSXo8mgLUVoXphqmHoqXHdfddN84wXGrRz8oaMquOCAzu4pI4nHPav2DeJbylzW7zTtPS4hLz5ZjBBbaJ6uTUe3KhNuxThLhF2q5skV5bKCluXx8q9ai8fRkEeJ60KOANQ2dBo6GkpdgGY5eI30VRdE0D4g0YMEoBIaboP/FWRlbVC6Op80Rr43B/7/jwYE+3BXcAuckhdq0nmAQoUfv8MyvM80Bf8CTtTkcYS6x3K86mt4+vS/CMiEyag5PrNpwFDWyJItcHZVN0+SuZecW1KXG8qVJtpsrR2qy3IlM7R1rJG7KIUxhjY1BJCfCKIqdMLU8WSNzLmPXHk4ODGj9ZyhoeqsXsobSLwOL4Imkgx73LGGBDJ8tIOhZmkwRF9Tc2IHkAdinqcrhhAowQKy+HlTxgOD7n+YjGA1JuQ5OYnJois85BhDDpAXqPMrH1PHvuBS3MxlsS203jkhzKEfHCk8gjiDAreStncKHZtXj3UPyJfcoNaZDNKuNRO2LPCBBEfmLJEz5lnOwcIhEEV7RMKoiWDtVUs6fgy4lS6BRE9WuI0Do/PzQ6BK5yqlikiqZnya+7B1o+fVrcO9zf29tW3wKdQLwOHJQHu3AFbaUaNEYGuKLlqF9sx9MnT9kexSgCvLJh7YWSLomqHiEHk6kP9Gmg8awJN9ED/vFPf3KSoRNuKXRLAETUPQJE6eaZNIdRUI8L2zIzt8DBfP3TTzolw02QBaeUP1I0Qb0RB8e6Cd/JmdVwRxjm2ctXT6bnaD1OEfMC5OlY13jXOj88PH2fAjkQTAicC+aQYNDIN8gfYoEKSd/gBEuJKcxExG6wiA+3Am7GvG3vbHIJ6dezkxqPnnl98fz5F1+88pAMpWdjFZSQ0Mgzs/PPnj6Zm50bHZv8DG04PrIqXwy84JGpTNjb3j062Bc82d11JTmLWiwo1bF913JIZvum7VO6JT9Ev7tPDiWiDUHsQwtz1Xx4sMMeoSAYbeZKcTVv3eLCL9wUOgI6V0bob0qBv+t5NR93/46LzXbscWtcYPLaoUnsAyTYQSHr3wBL4WKP0sqRgXLiWlaWlz99XFxcWbYrvd29f/vr344P98od7TMzUxPjo/zx66J9RZxtKTEdpekxtYfTsMijAivsBIulkFWo02HuKsFjV+ehrflLjh5vg/7orla1QB0aHaN8KBsqSdJVqk41i6CXW0tX54JbCWTA154FFnVmeMCqriWbOLzoAApOTI8q0lHPojnhkIg0+NBHWFZDn0T86CsLogmEnnMxiLlmvG9DtwXZFMgkbHixf3AipOOcyyshG4ClYvfdnUenq6j5qjqiTjJog92xEb5va9dB5GF1ZXllbUXchds0PDIMEHx4/x6+knw1PDTMQYhTiVfPlNf20YlRuRD2iTFGIjlU1FpgGMStsKjcxeCBL3xNGtwqOp+eXb6/hOCrc7pbTLhHfTVHjV3xyBafL+Ic6i4g5SNYpLmNGJADJJLXqKYiQhQ8o5XYwIOhb/7w6I8pTR2HMCMklgY/PNi/PNPMIP1IdJseGR24FqY/OLQhqB8NYHQAVVIswZ2cJD4ZCBUbQ4poJVCBL6iowhMN5MEHyS1XO2spDqA3qPwxd8ioJ8UzxDdDIwxaui/rwq0XolCyjWfLBQS567Y5pho+04RIta6BPxmOZsnxOWzBLbADzooHExqNnwB/sI/IODt8CG05EBUON4XgywgBfvD03Iz+Y0xH2u/cYa47gAVQlw9pdhNzZmEdbVXckKkWsJYORyEt/vUvv7iOQ/Ts2bPJ6Sl6EOVFy4ujCvARHEt9ySA2NTm2ZAMOswWOmNeg5niEhQV6FDfEyTC6vCw2lLWmlPFJPgjQYdTDJrW34sQ1r0Cv3cmvMH3lfl/vL3cCbVhUXZpTwh7wk9Io7+LNWCUfx3VoSAE7A81y56DEtmv2nqqWTm0FqfgDrJisIQbZyIp6DcceSufcjIFST7UqfwagFFAcnxyll12ZIyjiwXL6IBoM30AJv6y8cvo9DhfcvSin0GeU3GkLAbcCQH7O+1kNet5VEDA/B+T0JeJVqymQkmVODVB6AmMMlWNFec7PzfMwGLc0KwxLc3Ozt7U7JAA/06GA1kmgpO2xpCfeK0PNH8fwEI/izvSD5eNql6yHjBaGBZ3NpvOVJHJI9Ulb87j6zpt/spa9OnmVytxSXmpHt/mfLVgtrb5k6dL+zr+FhtogDjthUZEABrT84Z/+wHRvbW0xmqAfnvf77373n//856nJaYaESXdbOmGSu7LeZ9eS2gQrVf2NDQ0M8HZJBmhgEcm36gkzRu2QJAcUiOxf+FEB8PRsqH8LFD+Gvmttxpzsale/t0dIHF0TuHRWAiFZCcjOi201YgoUxP3iIMmKXaFHFOmwxe6fcrxula+Xc+uVtSZ5CyggU3rka6fK5vK07hs9IC6O6m/evOO40GxJwp0x2AQOusRx2hcIGIOMxxFUkPyo8geJMz0xPjTYD3Y88MOBE/krd2J0DzY27egBBDdkBzM6mLZ1iu/wg3hDtLBSYUgjZDqsLvdUs5pbkq24+p5jROToI+x71ExhqzkeyF86nVzHp0kqp+IXqsl8KGqlWRvq6AHpNi3aXSTTPxkd9h1HUVyhWNISn4gaY16tMQqIFVDM523xNBQSp7fJOUA3MzX97fff8vk+vv8oc84hYcnsYDiHG29UuK728JxydxT1BdY2DhIHx04ejjQYY/7lq4BClJegIpaP2q0O9B/u7sP+rAt5IJ/sA2tNlff2V0lseBI5WrSpMotGwjNBT6KfgjHTfaVD6NVtIDS72ruUCxyeHlpBnkRCQS2tipQF/IEMFhM4ptQIao5p4etxRsO6GMaCwCm1T07MSFg04eSv//aXs+bWgcGqzFRevCQDDst6ZnaeDw1Uh0e0oHCuG5PCmpWjxh/AQrbLBkEymi6kEoQD3c5K6ao5KKREXCVv1gwxvEhIvLVBfN4gOaxeitq4hLg2VpuVFqTVJJ4mhKwTi9NlQWA84QIsZUNHhWvZLEtBFj+72HjDSRYnAGMS9qU9ER9sKLFzX6q9CIz4NTkiHn7lCInQi8rSDPWTc/hU8iHBga1QpujTWq2OzkUSSDePj95TkTlniUAVZ0QbodXV1bdv3sIH3AspOhgbeQp2B1viGHIOMA0aeIAORJccyluiDGNZi6YRSA7qy0m3BSg4eMvjY0mlNli65oZVsIzyghrdsaxN5hpvhnJwkhoeV7ludB2kKF5985A0G635k8fEnepMfoccYlCI/pOtKTTFvRbwxGzQwlqTshMKBQhzohTM9t3D0vIiNScNKylyxjoO9hm3QMboN7Dy44f35MuHanmc0zDSplqoct8tuGUdtL92dl+++EL/SlbNbnIWqTI7q8GwdBX75axCJwN9A+RzsxwowxlyKJxiidTuf2pqwkQ0+pw2NASCLmAvYfKUoSwuLvVWeVHdw+PDyMQg89BWiiwG+LNnwLwOcVKWqCLG+ep6aWWJrDu0Ut4BOuIpk5cY8VCsI0DhQPIfe/VjrTCEXTTwhQ6UfKiLxKR8RD35iLGbDqpy5z1zgI4P5Lxj2agaL3N6x8ZGX7x4JuPD0U2ez/WVQ/LyxcuFJ0///M//jPnRy4GPhsqn+mENnQyQBfxIgoVbVPQd+qylCY8sMsHdJkkjg8O8wl9++vn16anDvLa2gsOfm5sfmx5vb5QQ1gvvyifRe/Jg/whuoztoGbnsMI7cHZ373r57R4+oisBEC6I0CjtXUCrXnAJ2za/wd24mpGFS66KcATQ6jo9pcey9f6M1UlkqrbjUzLeVM0DRa7X66ouXjhmrOS2C3ZErSNUSafDGofFhzWaP9/eh/pm56cGRIWcxEbir63QrkAv8GN9Cq29BYGRR0jZIvd5PUouS83XXy/sC4bGQFEmRPRWooiinta1HjdW5CSE9tDEdT7DcdswVvNhVVijWlE4Ppc9PE6gYr4VdT2I1Not2IQp3gv0sSvL5sP3MK9WkSzvPq/GuURMDgJHJ4bHEsBgQ48Cgd0W6yBFJEISnLednx5+/eI6y8D3NC/6wX5C7GL4fnj7WnCJPNa7oeWwUvsaNkhmEjMIZxzOWUJn0dZMfwjgcQWV6JH5ze8NkBd4ALCINjtMMinpk4HHMHOGOkkxBCIce/MPvf++c6x9p9TQJkDFN77saKOCpbQqPFklI9fMa5Ksw+ZCd8QDQ2b7Y2sERkG5d2V2HSJg3+ZRJ/A+d4hy6K/FpfV24GjbdHkLdzNKAyn43r9mc1F7dCFT9iEWFM7PUiRG7AkXparCXq8M1UVp4FQEGzV702dYeJ+klorh+3iCV3YYKCabxBkRqbiufobnUgK1N9x3gXV0ZGMSbaxehEsK189hrRx4EjhriyeGjWjoQFMhFboXddhMkKCMD3Bg9l5m6ac4YX9DjxcmInydz7dnzp3Nzc3yfrbV1mBUvDOOzuGf1KxcfHaPTKkgJFCiZr1ZJ9DDKxtZQmpS031pbKkUkDxb2URbWY6Rnw+kJUoF6FROyOJR+fLqMZJDldWqFrZXsIXwJyO+CZJCW8prtjU1+A8zqISDiOC5xKyGMG++C6uLuKJsTnnRUWlu1itnd2tH9++uvvh4dG3NOEfdIMFuJVpCrLRMQHmW3OEBF1COlv/aUj0se5IVSIOljmBiPIG2jdRSORpvTAyQKNf3Nd9+mNthsONOKiG8yCNKG5+QI/pYJZXn85oLs2XHPLmplhX1uWnxkFDBzpf1tJxV9fXXe3t01Mz0FGn5cfJ+OJMJ0eI+M7E0LGeyifjA+wgeJkvJZYDYEWgsOubM80N05zC7xWbi9VickGvBFcfQ3SssXn/GooA1/HLlzWDvhZRQ5Xrz9lk6hJznRfK2rS63NYsoA8cbUwglVw0qe3JISLQ9TO6ttrG94jYO9vbOlTQcz5VzAufaS3yoXMaREgoqPEq1e//yaVgJg//SnP4lnKPXS8JniSWTzeI8dFoYwxEcPQq0hnHm3IcbWJnQVZdqyvrr6269vLQ+kz4e7uL6UL2JmAO/JohjBjI9RggTcP3v53BmjCRTacQ+dKyRDeoqr90h7qXOhc90rOQ3yLWStdle1F1VSkP472LDjg2MOYN9ID56aMDmcjFbh/jOAV6IzykfFnpUikQb+RPiPywvWFuUyNDKsO9OQiHxzs2FYREp0vqO7c319FayQ4e1Bajt7esxOTo2rvNPMLw0l7T866VE/uIckHjWYyKriLCEMuozWwbQhc4+MWsvM4R4xIvepzkD/nCJ33AKH1fZbTbWsmqZJ5IpICR0AcVC8s0BB0+8wKgeRsyg8FQ9GdxgbrMVbIFQy5hrNs0rLe+CwsaRwOZyVLZViZMBYosOggRSnEEIJgcgBHcUyiWs5pcJl7LGDwSmVJkGBsRJ6EdII6ktsq2GcL54/s9p//dvfgAPzwQtgjsUSbm1AvJor6S4Ojw/WV9c5P/L4XJDO3Fhf15Klq7MyPDokKQuAlXhHE31O7VU6J4NbclQxAECLtFtHMeUGrY0mvqB19P5FN//4D9z0kfQPHhIOToIDQZUj5JjACpQRuslxSlZ4+nlEC5IElDpA5xH84KqjSNZ/vMd6/fbrb3d3P+JtnSa6BiyNB7y6qt8D7139x+jM9Oz0hIluGc9QZDpQDBRyKDsUkDm62izcSD42RvzYz4F/n5MEntQqsMfCV/RjqbWjTAHVDFaXFMQb8BpRUxgybnqnYd3OLHxDHWN+YG37LiINdtCDDkKcBQns7S0KNYyJkLkk5zy7nwl9N8IV0keJq/oRqeTCK6h4ckgI2IFKJcN2dJ/3Bbzv7+3cXuAqk3Yo/mLRJbd42YcPH0WnEDLJ7O2v2ve9PWjteHAIg/EkGqqhcXpumjjYIOmU4nRO99LHJbX0FKsx65rqMg1sPG2ZDJGi/2qp3g7cJEL38CCbBKQT5xfgE9JzrsUHMESQqVwMOxXXrzPdt2TXNww3+SnVz6Uwdebd2/e//vo6LKmzxRrzpXhWbZdIWjVXwhU4As+kSpnhYQSpIZJtka0LaogGtx2pkJIR09Q8NTllTegB/DB71WFuJYHu6+NTT05OM/Ue32MAfLvbB7cPW+6em6sj8qsvvsRqMMM/v/7l199+tXlz80+GRnWTrrTphSpHPDxHQLPzrO7BIsPZ6T+uKUVHe/m6axd5omLOBKoEzKtSTJxf6YHnKoUUu7ATznB3X89U94SAJIrbh9F9qKKARcVFV5mQBfvYEb4JNeFJKFf2nIkC3wixkEtfr8BaD0YaIuAbij9g9/C/9AWY4JnRStQooteuSNpPBtj5hW2ONFYyfVQjlrxd/QhwpwWG9u6oFi625NOh4ecvXmAGsgdpKCZdpQ6BDvYOAlA2SXtbjmRD4xjfDf0hpucidnlpcRlsh9qIkScSDZd95Y6YdLrGursNvUdke7LJGEa+1SA1+rnfOvc74WswCbwJh9HTw7NDVnBfTEbVTovzUwzp02mTFb66VtrEOMXIPmpNeopUYKJsFZUmmRVOoYCcfCugOS0khQJyHzrzsRloDp0eQCO8JLud0ZX6u1Vwdq2mz4syEfqFZ4pWqMjoDrck0keODWhoebi55FhcqB4w411iyIV9oS9soEohurVvYEiSD0EBBzM2kMAGkMYq51uwKPgxVXvywaF48CAtwDISQIHXg/ofEV6ayO4AOzEMeJPWVjrev3kSSFYIFeSkYNAMrS2nvgcTc1XwsBiESxOxHgqmBwZH6FNi6who4uREqdsQ1iBdzpmb6+zt6K8OerCjDgVxDZNTvIVxRO5XX37lM3wujUBBA8sCDpxQZBfvdANVt7VVZPtok9tj4A+HxKKNj01wEWwESof+sqHAFIog26Ti9zIzWn2sigFBJoEB8mYNVpWWrK2j7/0Wp8xBtHFAgBPuIlbXR14XrXV4mZre8eL5+yyqjiO0GxxK2fqeow3bMRZyEA6uD2h1u0PSaLDyQMzqwbkUXqF72QG3fToVT5p/LuW65/bqFCLysIw68K1VFkyIpKEp3LdiZrSYXpIAkL9j1zss831m30g+ubwFNKS+mKmudSkHTpiTXS+22Bw7Pfc7fWh2RlbSg1bNKjMcAsIgrNMWnHCfTBvViugUXSgKf/GhXUEeJJlEBoIgB5EMhU/UklyFV29Px/nBpbK8l8+ezkwCNKSun5KVB+n2ADtnHGwn0qZOyQLhXYks0v6Okg2VfEWr2s7oBB5wEW+3UFaWQ6DTsHugs2yI92K3OSCWuxhAvu/4sAckgedK89Ba1gi0Z+ntmjV88uyZUqydrS0ioc5LrgXjZ2gTd90xwqOH3uLsR5zSHUc6JruCYNjZ3f746aPSHK+Xs+J/ZklK2afQaMWRiRFJme7cgGsqC1HORVMJSmsRBkb6w9t3sm5hlInJMabOidb1yMVl9zsaGxvbFPrQyNg5WvJejMT8pTZqRHY175OEo2FkTNMV79+9W11ZoUDoHz1HDbep9g2goG0O5oP5lFAvd2b502LhBieGY0mdYnLCBFlDz5UCxozXTnRWLSY+n/i1SLlFq4Wvh2vay461RAjYIXJkxtU5FGtBro7Oj4m3jembA30riRlIODurO06UIJ7U8Rda5miLJIuSsSKelqpJm5e9g53tLftxJFlAkQNf+WAfRUGHFKU0bMmtMSDUiNxbSO2+S6Wb5MwTVV0CF86DUgtJSoo8Qdrk0nZ1QfuWWCTObbue7GDryzLBoTrmS8KVSSqOKL0MTGPwaWFN61SKAX3OSBhSbzw4wmlUB7B7YuuJYEP8gwORbi6IUyAxyfMTUKpeOwuom/RAKNQuC69NBSHGu8kDUdaEatednwZ1n6b2BIOnWbGSyU4Oyu7uFvKayqU7hGtIcE9JL1esQostkrB/e8nLO/cudQrOlex1ule+INrCoZNeMzA+bhBovKWita89MkWWoGGHFJOrcGM/DPY6l3ByWQd2/LEL1NCAqoEUJ8NwLEI406i+tOHlBbWw35Bpcvt1qYuTD93rd6liyIvvNOyl4s3oSP6b9pBYvxQAJ7ZgqrdXMo/JlhYNSClAm1wGPIJBDqIjqEQBbDws3zrlxA/GmXVUe9PQ0a8oYfgrQbwskYk6HZQyfiw5WPJbjk2+M7w3pbb+0+HZWVUob2zgwdk+/4wch9ttS/3nyccTTdDhdM1VLK8261ZJPYbJz1xPpBwMxXq5zs7WLlKe9+kBuEtmbDoe2g35EFqPt5FAsaHSBVMngCcYwzwjHtEcccgaG202KoBZCIOmYYzCWoEQlM29Dlr3RJA28WLmChMQ4MCnaGiSi9gCeGjqoC9eLTkR6AK/oFk8rWiC/VB1NtzbIwnbY2JWpKVrk0sWo3Gjfoqoifs21EgtJcsMUhc5Wlb+TnvK1jaMgQKERJpYXClqtzJtNON0lgPh88RScZuxWE55e4wBuRcb0GpFXkD6Nkr7S7pU0eFGVZH4wZ14D75IRJufRzXcF2Qe1CEe494k2/MVoNrZed1rxvePP83PTP7X//yfVfapNnDaN1Y25azqrzU+ZrxHbCH1YotlT8pwJvwsNM2wvrYpr9cGlQf6bcTp6Y5pvZvrTYejR+OcIyCP//5geB+2uh01JI9GCrckDPE2mS9uhg6hcFxcIbI2Z8SARBJmOkHOGgumqHCob0B0VzEpcMmcmL1qXKL9IiRi1IAf6A6VyoAHVml7SYzl9jLCVjAj7evbW40w+Otf/26uJXxJrY+MDvMIHRbIfVO2glZrHko/4Du5yFqcPWgUKg4vtCcYiyj25Jnl0mcEYReX0R8tdgjz8fEpgOhJrI810dbXD1UMcM68psiPOhEKfur8cwq0XRsb601jnw79/e0hFQdsvn//loVDZ5n9yz9yNdcUaAEaKD0z7kEtJ0vZk7pXqzcyIbwy0gLvQJ3kT9uOAxgNp4mmUCWgVwj6U8js3FBDKvvIaj5ZWPj226+rfUMW+vjk0DlwesVkWNHkvRbNDxRqViVloiO1J+0SBmn0kW/e/KZdDx/Z2SHLdiupaZ1sbw9dnETmckVtpRQ7MJ9cKrTDnc3MzsnDC6hsePjxh58Undkt1gizRKrifwnxdHaq7QTNeELMEqdE5k/6YBi00uDM1J1hTBrFJnODrTKxEhBmgbZW1nZ3LNEe4MB9I4gwXXrcmWClSU2nxL602Ha38sor1XSV8XrSCeERLxfE4nHBoAbhPUy0qA44wOtX3HRcS8WyZgeyU6jajc1NMtrboqIdAa1iFYcO0vE9jagF3Ot6qvQmwXwA88is0lA4leqAkbltktFoWSB0cn6mkj740QahYmVr8bZk3ZtGmeGOV56XWkxepQTsu7sLKpIBlojXBWh3IX8ZAHrn81Gh8OF8HoCUQovW1k5w2ylc4AEZgihuEwiS+tnaTs9T8GmS0qhIwlsa9H+Bi0mzkDJCU86JF0AAIhmUCGSN4uccCbR7H6Pjpugti6+oYmZuXsMMA1/oSlZD0NgCmNhnWwsA3UyoUI6CXRaBxKBBWGUKhE7fXt2SJKoYGDG+u7UVN6iliS8omRrrDZchQEdHxywyLki94Oz0NDrREUV62jE+NXXBMcUL09zW+f3iEhESpXcdyT8SsdkjYVVGTj4g/CVq4G7duYfi4NIphMcHOZ8xrrI+rhT3l4f6o7bgBvEnbARLL/+K1qhh1VpbdavlUlOXVv7koSYqyRRIBGC0/ZBFVeOS7B25TD3do8P9JkNQ1+mkhTjW3TUq7tKJxbnhklD4VI7ub0lfB67NYJFXa+8pDx0Pe3tBEJF6VyvWx2tMWzqP4W5tlwTgjAAQojitJTEfuY9ApfC5YpxECFkU4Ee9iIabICTh/0woAS2eKygSSyYCkIsIYMhQzYRrlsweTYxNLC5t9vdUxN/wlkuLKxt7u8oKIMGPn5aF0BxWm0j6QVF3APw6mWe1NGbPyK1SJgGLTzpo4DzsD8ZRqahOJZ92A6ymlAAa6pyTCmSr05n/+gs4d2tjU/kVRhxTkS1IYJbqL5M6wFGYc3tzexrVMjXN73Hm9fISuTlXOiN94vpaHiXXk3iY6CrDUvRVMiRNJWfm2+9Hce5s3y2f/vR8bX1Z6gFcRkUwM//v//OvsD9NnVxbZWvdVdEppJEda9CcvG9wZmpWaB3hbbi8Rm8KgFX8UEEqs2SmGF+OJZ9sC3oGeC04SZM4TwHeijrKO2hNPwUJ65bFWafsNJsgkHgLyakXjWIdh5+WFn99/dveNnx5SmwoUhpPupoDRYHT55Ll3JKwk6ALapDx5pNRZUuL68+fLzAA/UCDmbKivXQuzcK35FmA/bBhfJYU1yG2TAG3+K20S3PtBHTkHGrrnKbTII80O7m9Dwrt2jHfAiEcQ3cpxIvE/eXnnxYXFyWekmCMkNhAc0u51nzKTHF3oRF+k+GORQqtidD9jJhkD8fYrUvb+PX1r7xs2l++NqaFfpPXMTY6bB7l9tY2Hb0nZ3PHzKA60Cf8KVuAWIL5KkbsLo1lXRQZdnxaVKSmJIrTLw7h9hg4aEKoQraf25Cs7Smy7qW22el51ESA191dbqyvFz711B7Bhak/MFArgq7HruuHBLRJT7E4Kru0jTMFbNrwT3Ue+CiYR3m5eCNPllByRzomJqyEnLBNVQu1YxH17d3ND+cXmC77gzTcPdqHIgnTsF7w5S4wdbh/kNAwKgZu+1XOHxPiG3co5456QCNoeKDyNnuosRRRl0ylYxIeIrSSkAEB9wiPV0AlHd0GxSNCAgdLnTQLDifBQKWtNLpkp9Y2y+Ic4K/ktPhPwSS15cTQj7I9CqSusy2G08/JsKZPiLJQH7GLytbEgskOIqiYSsjJ4D8hfxBRBEbVBe5u3yE4OqTpmlsmsKJAw7FOTzV9Z9Os5uBoH4JWy13p6aqdKRzb7evtM6kI5EF3WkhHhXDSfXqkAP7UHuI++Q+34FvFLtH+n9UV8djdVlyTRoe9LT1WQLSHqGDzZ+cnmU24x+aqlUKM0gi0v5Nm+sfq8vLqytLo6Dhvg60FqfDmsrydTNgQRGKkyRjNSE5sCxcX2ouTlU16kDXiZJceSzAmmZQ0JdXD1jCY1oimK7X2yKRg87n7X3z5XIRbeqNJDPAH886NDInGuKqxuNNxyGgaRs0kBiUaUv8rujzA9bYSiudMIavZEp7+Fd+9fhWORkSizUh2ytpkVg6BIH6bMm7SwiPhXCCvfICAtUXGdOu/J9otY//2QlBHd1uPkclovIjkQlkoY7x1y1SSgk4ji8F6NyznqycLMtmuNOjdZJsfbBYL9PLVVwjh337+dXFxGeYYGOqnUF0wlg+RcnO/t7dDcyEDcV/wkyGGdsqJsJ+8p8OTAwrneOVEwF8tHtXEa4xG9t47CV2GJsru7UygXhJxY+Pc7OzwwLiZ3oCza+Ax8TbSCNFu23tbWEA7K4Gqs0n5ii3rktPFz2NCLJmBAX64vLIC7vb39s0/feLAstyUOy3g0fmapMXsAeZf0zblmetrW+/ev9tNTPUQof98fGRmboav4sX4N/RGHDaulsclDUwZdXbtmLAOXdBSkjIe5HG1Lzx93jcwECBY0q22bFnJFVjklSh7ogjCir9KkOX37W6sCw3jGAAOpNPK6srWpgqAi9HxEaBKcBXhAkBTjPLENHGgu84u1azsgXekb2R89BmS7uXTD+/eAfpiPrd6Ggmg2NWBPvDBlkfdA3q554dmj6p2jsX2xSUSVdsXuzebxmFmbbs6P6NCECnqyAE+PlTHa8CvY7B3cIgIswGiNKhlStLajYwkgoHAAfa5SM454l4mObcSRuAvS8lwdGn/vd0DSd/IWI7q3Py8bFl0GwuW4LUCxZZG7dXEarwGdKc7uHLWOnX5jFMyQI1GSR5zcRRvTJBY39rhcECawbwhGTPMYWJiUkzS00kgwHNE3jPcVVylWU2cK1sLthCPZsWdc5uHRgBe6rU60OAEcBr0BcAzsB9uHj43nhS0kUtKHVtPZvnFqxf6B+UsMaVq3y6umAfOiYiNg7Wzub34YUk4xP14OhCp4OTU6DbIb+ur9EwSu+6y28bxwYY4CkedAYgOOq03aRbf1mo+MDeI6vFbXD2GmlIvl/SraaeIKe0ARrY8+jtp/p8JHKn/MiyK3JJMf2U5uQEqWEB4cb40/xKqwUqJEzhhEsIT8tHQs+S0CEiKPloQ2pAZ8PYHP0A8a8Jg4kLIIpWgosoZ66YbAD0vVuL4q+xzPER303vReMgMWkiFGl+TjuNOGfpoKw84c8dHMkO0YUmBWIZvjCgpkn1IS2Jj6COK0gnxc0aO8+6WVEI6urYVrS+B2OY6GPZRPJsxhMY9EczJHRFsnH+6gMJOS6vjUwdGpEc3CEvrW06VfAzuCGOK0oFRUDKYWbqJnJCKxnKXazJmoEZrR9JLgprTIC9oicB7UkbOc9klZAWxH5uYgGRPjrnCerY0CGQahaJBpV4OMrefifGMDWvokf6xonlMRTR+qhYcT/ZVJJ5DJmx3ga4BzuyqRm/pthJsDnk4TbgMO8FCNzQby56NccNqetUDPGoNQW23tLuCn5NYq4c3oYvdKYvi9CWMbFBHujypXKEhdaUXkOywk9ESNjWfSQMzGc1qQ8gqd0R782dP5pfWVn59++nHH/4xPD5Zu7pFYztVsYQND+fXYgAwOzZf8rQPbBLnuLRddSMt9SHnF7vNJPZIugf1lAtIk3CLfiK8h8Uh8AIEWhTv7O9YTJQD3/qX1yrmFGQYl4KtaoMYOC1sCM8eBIn709ay8HSBPCQh/FLjBFR459XBAXDIE8Hi4oG9LtV9vdX93YPFpUUmkfcnFqOZMxVM9qANDMHklNiJ/I5btIRYEdt3+KI2NT3388+vhYtcmQviAQF2MSlOtMMrAGAEm6wEzjcMocVkd1V3tsm+wf6o2Sgd/GEZwJSlAnpaZAfcPiJ6iDyiAta8KXk3Vik9Ore2NukxKo61t3eWR+bP/OwMt4kf6WXqnhY/fUTqkkNMFbZHMhDnFT6FtvH+BI81Jfzw5X//17+27O/s4AYlsaQPSYswcWYrk7n9o4PlxWU8JuCJJ+Aaj42Oq1wAnF0CjojH3JsMLSFBGwDHHUjMOT4y/0Rlk4xMUnl+lX5b3AKNv/wT+wHlpWAnz9s3PjZOmhxRYnZ8vKfmE3YBoX/64cfaSd2Rtj4IrK+//FoPAJpc8cj0zAycRVpA+//+//43qZxcG2icISWaHtnpkuYg7EyH+wl0JnqJBfZNuNSGR3ZFZwsODKsDJOqEIeWJQleFwLSIl5InDC+HaGtn09VUivkX9OYPrJFGMqXy8KC0x+B6P63hzo5PpgxrvtWCs0bB+SNWgfPxJeXABCtKkz9r6eA+UVztBE6ujWw+dRgBBXF3fphTAWI49hSHF5g37HH2d/Zp+WHlzoMDIGr99NjEVkfCsgjbhlpRniNPkMYqAsJYAx+dgv+bm52dA+4BSYJYE1lypJvaRC2U+/DxRRekaWI7UMnSPb0h01uV7xoig5a5RH0Y+fHQrF176yVi3+9C9VNCzcwJ42FyRpvgiPMQBzk54XdsqkNIN4XhVgeXstI7WaiaNOKCQHQ1qAwbLYQQUPzp0KnnmBmfXNvYWF5dtqdccuWj1px3SMmiRHa2dhQG7p3umSAC3QsXK0sx/RRX69Szr/FpOf4Q2WN6OB8eH3HaMKVkgBPJrggU+b/hIUZawuWAlVHTDpToHz47/2R6Znqof6i3p0/KBxmQ9zU42CfNhqOpggXqFKXUj1dPTw3R6EHFXHw4MScMAHCHhqaZ+c4UKZnB3lHWagw5Oj6d7rMbegWK5IBHOSxoq8eUTAdQh7Q0063z4frcmEvpv/BmtLL/GdOmDRUJILUQv/Yk1GFd4W524Ow82EYixkOjaZ8IUssgICH9Nl5BKq8T/OUR8KKuTGRm1RQACydB96RdFZPeTJiitBVSi9koQNCoXpSxcnF2JIUhDY9gVMKAjblh0WKyFMBYugYXYD7KtCTWk/6dqU7Xx1b2p+5Vv/zy2+vXP31aW2+v9GlCoH5jX7Heh3fQiBQGJlDE0rZgqTpbu2afzIxPTXD3Vff98OMP8msXFp5RbZer5rdIHrypXwRWooVmpycpcQDnzdkbHhkf8fPpXlpUJAzYagqrBLd38dNSqXNH/hVe/mx3n3mWAsQHBqrOTgPMpWAfbxoXvMUmVQ+tNmx3XyoZHTCkVbXU3bnZ+f2dXQniR3tHVb2/2lqLoFFduK4y1MPZVC3CIjs1lLdGOKqIbCdSnicKKLtJqPHGMTOWlU1Am3a09TR0D3UOg6xOQeYgSDltSHjVbfNIpF1BySwurMph5QJ5C8EQJuG9vf/4Bp+j8wSPgcxL5iHk5WbB2pJWD1IQeWnEm44VM6ODW6cmnAVxSpYbHhIkh4wtu3JF/X5EfsX4CIyuCmiSUECCImpJYXb2UT8mZgFt7UhL6PQiF5bLhTVDkID8xC+UCEIzMZbEt5AzlpVJ+fEfPy4vLyJRpNHjvIgsmMmRcFqkbyapv69PHi4AzgngGaF9mDhmShMPkNsO8a2cRgCb2HHE9NJkuCgCplnyJdfbas3MzVqvN29/QzHF/bfMkhmwsQEkqPlQP7wnnouTo5aKjRmZmJRZp87QypnpobZwdn5eXQM7yfxIESHZi/VPID9KB77zWAzvyvIqACF4Apft7vEuE2QD8RgDZ5hlIqzMg2engllpbv7u2x0tBotp0bbqqqurn68jfihStLS0+MPf/769s8sEPnv6DKTyLCzJ6ck165H8y9bWFy9e0WVIKK6LjsqunBKKy3MR5rmZaYuWJ3VS0+8wcJDVBQ89O40KYLP5IgA8E731WQPUcLIu9ZzoMkG0y2qzEvYO1YKF5D8ZaEaFUxj4GcdbRLClPUSQ4JcsImvVATnQLhLKpXvrpyiX/6FRea4MdHdC37nnMIqiZ2BmUkLhxYw6gKLBfzF5MmorXd8hLtyqRkm1pNAgJ4/MRSRgIPvk5AzgzEUg9MCBI4GVhmQpOeSqqBc3ky6QacAu2nckvsMDxZfLLdWBXleQP4dB5WcQetFfraoVy9A7wn1+Ih0A7BCEpP2Jqxw0iEcpCXuALUvNuSFg5xecy+3dvWEZgZWkn4bxa2uD/lBGz0HI7opGJcgrH3J/kZl0XGdODCqjdpTicLQ4leQkQ7Ld1V67ZlGIlqMOr2iFp9kXn8EzwlnSY9Fk/sUkWDemonewx/Qo4u7gcMcEgbngyK2o8o5SRuL5JDm7yjDvG45OLvaOzgZHBts6KioRi2SLa+6aPQJ58T8AmSvz3poVhlPvmdX+aFvPb+7bOTdN6n6j4lMbzMwYdCzM80CPiPeEmYk5y9+NF+fmqZkfcoH4Q1JbzFb5wnzHFpWe9834AwF/pGijAsDLkjiKcGKlc+d06/q0ub+jCwewtblnkKr1FB09PjhCO4SsGBkWM+AXWAHuKmmQcyWZkjh++vSJOZft7cRJ0DupSxY3JuXD+Wnt2fNnUAbCcnRkZHJscmZ2ljGzfW/fvyUAILwAN7pAnOPP//znp0PD6bx+k07gUDlnkcCJ/RA9eQTUqHYd9kIHpSbrVwy0Q7hxGlSZIGqpzmxos/FkJ0LCxIM0Ma6XQlNnZ7xnNpUH5uDzJKgpbiV2xZcABx3EZXQ1ccS0FytJJSsZ+YfvEsPjWHO2uCleTl9xp6D+RzmQD3ewjpiH47x/dEi+JdfSKtocyzodGBqib52kUO5Peql7RhQAUqyB06L8wAQYVwiBTR4bHnv6dMHTEUsEF7GjdthCTADhSITbYMieKtCp2rxFI2Itjum7HGm4suHBInotwW0vlxLQ7e29vpWgevHmt9/40eRQGJr+Il/WyIK6nLRLgYjtrQ3P4xiwj5ZD2iUFrvsEn0t9v1aUCnRdynbEjCWQrqeVgQZNHAK61Y1yi2DHZwvPhodG3CYlzjn49ddfGRVWSyCbZZJdaSSZtX716qXmbfKxwEmld9yf0E0SIR7iwPYPDhql++zpi4npSZ61gIxWcaqQxyYnxASsjAJ1Es9lUYlupVjvZ8+eU5F8wNXV5fXVTTssnjw7O2e1+WDWAX1LAdwcpRkRHxAhhu5mBlgOP6EprC1N55WeADkG6JFRr4wWhE8vL969EanfJhH8RJYcdhXnlF5CU7Q+b8EjWT9K/+LgMpQIhXp3+er5swQnMYYa6KFkyF38xNTnYBXtvBWHzaUznh2lRwV4wonQz8Y5Hew3Mtu4eQzAo0gtz4R4gfDoA9pfocDnbp22LADS+b8+gw2lH2EyuqQ23jfoG2CraEwiC+4B1XJHqDWrjXtOpiidJkdUEzM5iJapyE8VJmQ+yQCUxKZ4TTFsIi3J+LkJjuwdADu2fr1xA3wBDl51v/RUQFAC0LcPUJst9phX1wl+KjiWarl/tOdcQd/YA13OYTDGXnIj0d3Z3ERS4YIcRXyUWs1lnaVPdX8yraJuLNT0xJTgyvr6yhKQ2FEqP+txccFAMUggfWN9a2l5RdYTqvTkJL1fNOO1RsB4uVpR0yTSS7WhbgSQjAEgqIgvdsXBO5X0SWn7Ueh52TeYes4Vdoah9+AeKmN43ZnHR0oghfzHKaTpJPIC6U2Pt/xhxo9VcKagTlEaXkh0fhIT8fq2VK4/2K3rhxQgcdGLSt9DmymmPf1a42tcC2+5DcOXJa5L1KSD6kI5acLaTHEw09pJ8AYwfox6kb2ZNCLsJT2M+0KTZ0BhuQIioFOgfjhDYtiF2pobXRprbhqK1x02ppoYWmUQoOjnw74zZM66wubegUpvvXvmycsnL74odXRvbe/09GYrr+6uePA//vDDwf6uug07bukpbsecwjGVC1qC5VkCBc9ff/OtB6cS8PUERlsX4ImeAQuQGDiAweogUFwkAZY8nVgOI8o/ZWKFQB0c+f1mWyo8kC3SUenUQHjoln44o0B45CNto0X2Yw9ICk9ALjocL0YBNiOC4FbHVsRVqem7N+8kiKsq3z/YX9/cmp43flLdz5WkTw9lx0V3eTCwqtHE7oHiRjXxp6l+NAd1YcUQU2/evsMmvfr6JYpF7KWFE8UFeywS6pziJp3HsPdn6esiw/iizlbVNo5VTYWRq7ORR7JpYFBhEsSLzTYSRwmtH/YPAuTiVSpL6hQZ4pcESLriaPQP9U/NTKo5UIBMMwDsErE217d1pqOZsc0RmjGco9bBTmqpxdU/vP8gVX9iYhwYHzBTqbucT+zpWV5e+uHHn5aXl8VhgOL2LsEtLlVSOKB+hDjNy/BVh4QMUsXHAdeJDt2RvTdB9+TYvVpW59Gi+2F49iKM6Hx4PbQmj/avf/nr119/LdfIM4D8q2trNMXZxZnbg49c0/xMz4AKYOgk7Tvwcg8kD7z64gX7BlHy10huMpH6Bxbmn6ACSCn5hF+ine7vhAV18NLNzXbLr6qffaJ8oU7eHGplbXXz7W9v0L4MvsDR7v4upP7suZmFMU6gnyOcoHfDozmFXk+LAolOMktg7rMVW1tfxWqzddSfs+IpSCR1jTeUShXIubP1+vUvUqF5VA68lSNh3CzsCfUHYjiK2FJhRg5ZpbnzyfwC1QDFxcibpinpElECi6ZhNRySSWpZwws5ZKF8nX/A7vJGp+Wb8Q65VeVbc5qMlNROhVUGJ9X0IH/aO4G9InVKxmSHhSV6acsZCor5F01GJbRC/1htHwSWFxUxOOB4sj4J80S5UVJFkb9aNOxRZkxSKygq5t9Coa1u92sK1Xt6+1Rj2QIxG0FezCwLTQFirjmFfESZXXg2jDBijWH4XK4ioEp1qeegpY4NuDHL6fpGDPDlyxcYxTfv3vKSMiX8QcT7GsasaGMOGUmRQvWmELGzaAKh2d+g1yx9XAQYld2BzEuLn9hs1kIW3Pq6CoJN7gyLyCoz2n7ovmwvHs9xTb4/PCnJjQ28bfYm74WB6Agg06rbG14jX4TlICZMDuVIqHQJFLgSSnNGaBY86n5yMQoSVVO/BAoTSyeizhSulRQlwVyrnSZK/JrcUgfIX/jB/tjQmJ6HJpG0hxZoVMENI4UIIoZ0l8Y+CjPcAUl5UBx6fiVNgECo9hD1xSSFIxJNFqKJr5xSbX1cWIQO5E78BKy01g76/LDYJIsv1dVlrgYzgvwT05BcVlS1e6HadRrgc3a/vvxGQmqxcqn3Y39CjrfPnz756ttv+Y841VFFf03N8r+RqPuNgrqXr3/9VV8EUNSHOyZQICWuXumAHm837mJQagYnAGxHmBio++LFc8zIp48fyQP4PDI0yhqDEavLK8SRI0oPRIO1tWhxALFL+sJ949MkGFMakhIjDPLl+6oEkg2oVPvU31jY+o8/c+hdTe6DfA1uJS2ctIlunRgASwXFJ0TUOWXJLi53jLBk55gYK8Qp59sBkZYchmxFqigUvbzAY/d2VytjFUgFsyIBcn1zDSCQhOSwSHIT7xXPA20pfSgE4x8t3wBzdOMV0x6OD1gUgpUgXHKISNHKF6VA1Vf7uto7vUvcm1bhm1DCABMTAiXjKugBmH3uZJZfjsCH/VVRSSKCHZgY2IWNJL1Mr77OfIB0Nv/zv/yZbTRpTGc7RDYLnA+qVh1NYmDDJianDTMBV4WmrS0eLc4rrEIEEvJCHT6ybFNT45ZEqhZuXfwEi40O83kMg5Ud4K739rJR2m4kyCkAaHxHt2bglejWm9uN5Q2UDooN14mtpfVYFbYUI0q8YuEfH8SW6SfrQU1wvSEpmbx2XX6/+gtFwj4x2I0C0khPK83mRjGGtQ2Nf6XfMEWZsSZ9m5dELjG2iAhcMAiPbfnlx59kHx/s70HlQqtArn4SUmhIjNXwtGhYt0qt84fUZZAzTT2x9ZKr6Dwqj1/pHKGJ7A2Kh8VJcnrd2LWugbsBHoZd1Arc0st+IT2WFKIR3zaOpr2tc3d32ygUep/7JqeFjhsdGpHMzpJzgbE9PACHPDhQvTmmSCWwz/A9+oV+krrPcYOHGfxU/YpBQutekh5tTihenjuSZsT38SUZkSKHWoJz+935rUl+UguddM4AMuHGMgGP5nfeN6bSWH+LZBkh+qE/CkouSRAt/zX+MEVFfSYvJLDAgE/gEXRwlJpanPxHQSr+kyA55eh1YlBAMcXnQiyKkouepgLX3CYJhDRTrlJBpHVd7F6CRoiXU3xAvW55mQeaaHlp8c2vbwVmZ6bjF7KB1L1wjLwIq9o32Dc0MmigBT1XuiixwYC/3BX76JacXifHWTX5jZbnfQvuEE/RY7E2TbIU2rhPPBOMrzgRSFxaPkayEXg2FMOTxrHpQ0AzYEmRVu0yrA93j90exCepUtEEF8iWJJWWAgXtiqCREy5hEeq3ESq6oWAB+MyY7ZcbXpEnQ4WHi4/zoMEezWxv/U1Z6833yNvJCB9Qta2M1NONSWpCGCOHIok9RkBgqXgP5MH4gSQOwfluUsU7gJCgCXqxoSVlp1zE+xtZr3FEHGDoQxTNkCnuwGOTyDyNipvVKALmhU6uL+sGFnlhfDK139JFi6YfWEDYVkBJkRTujj4xwXx2Zgoo1h1a0bu38PUdWNupBlj6Jk1EYOFgWmRiFGfda76bjAnx2PhVPT3gtkik4Vkpr2tqGBwdvL0cYuV8FrFGH4FTBM5xxpn4RlTJq31h/zjQv7z+bV3jh5Oada32aK9/k8myD3a/Lzby9g40sGvAimjN6PCo8IGor3xF1Zf4KO0JNrY26ydn5BCEfTL/pBhA0izXnHBiJnn2svIRAFKHceuSWUL16Vzw8SMSQv0bM3NydvTp0/7Hjx8xCszIwtOnL14tTE/PioF5cEQWWoqSxSCxi1wulG/24OFWNY+WRzz+1nKnnpn9U1M9fT1OFjOmXMY+G4RnUxkGal2aDCTq3SKRsu25DqghmJKPYpF9oyO0eABhAwydVrvu4pnRklHnpY3KegtLMlWabKw0ClXhbb/7/vdYbCoWnKTZHU7pZNwcCEuYhdHTqszhZF35OCRfez/X4qYBGEpBHAM0EdRDoK0FbZ9EZh0Wq70acKs/XEkUS2RM7jKccq8UYXZmxru40JbFJo0MpzBNjRKA5SIvnmtop6X9kY8WnLAlBS4rJdOO2TBCqHYKLLjJpb/8lU353bffg1qwtkAEO4oLphQgeoBXmhRtSYkoUld/gA5jBibHp5zmrNjNdT09h6sCYMyvqoX+vqFZE0LqZ4uLnxQji3iDeyhBJ5LOxSaDddK0Rgb5M6KCZzXjBiTIGmHaVYYKwdVYu/M6wn5n+wZwUNFKUIBczCtVAiC4xvzC/IsvXpk8Qp2hQSFLjLnOSD//8HpoZODps3nb7HAnjww4pACslAVVoIACurlUjY2fxRhg0OBxuA/cdpYP5bhe3UCwFJAgogSrBG2aW4XsRImhWqgQ4kYXkUdpHY96cAGXqCSTbSQCRVCua3pDtVW8l1OsbVQ8jYZ4SwLhai7DT2RuiD4ZeKPrpBbpnNbefHF7CkYIAGiTB2C3t29dhRzKhM7qQGnS1C21b26UB3OvQV76eTHY9nJ3Z+enn38Bpa0h+gkbq92+Ewk06ToGiBX9bVAUrWbd4UblKVOcDj5JY5xUG8lzWN/ZhtwEQqg1iNJKSTzvtXdXQUPCnipanLYvXr2s9Haf1875pkkMrfYwqywbFZYpEJ3psY46D8xpeJQfzOS4QxmqHAUFRFbC0RCshk+9CAtMTdOYbl7SOoPEcuDulfoQQq09aajdrT2UFNGymUn3VubT0ny8U0MHlNrJfI/nQqpRx9Ix6Hh+ub0I28zVlmuFn0rJ7uNJ/ZpXLEja29apBAUzwyGzgvg494pHRUHYR26Y4pIMHhC88UOZuLIg/SePiKrXLSCcL24gHaL4dk7jfyQCYaXxfYykSgJ1JOUEnziHnstqAJV4TkCEGWZe7LkSLX6RvzX+sE1YZEn6h/v7V/fNq1t7qFT+U3Kz9JviqsvfM1016c2j6mz5x0Fs8Q5H+GG6cuO1qXLPLSAjEwH1BKR1dstAGdHRVsRVcp3Xy0Dx4OF5DjD7NypvwLKkJuqMVDRLYD4DiW7v4TmZco4w2hCdq7wKQUMLU7s0EE1FiYNiTIJTTKNRPvsdXXqU+QmP4cmTJ/gGl+JqYPqdEYCd9melaCQ2CcBNT81WQ10OtRviK7EW0Q+4iAvdXpWIDrnPwjutFvkgaU2vN71D6iKYLlQ4IecXqvighmh+aXcSnT98OGAQDEcy7J7gkgt+sHwTqUpgDQOQkp8r0zhY9Ey0pvSJiz4clK19cc9hBFTP7G3t/LhDtgm8l3C8jDYHSeGFzPX66rsvlOLrfe3wmjPnnugpro8WWmhKzLjl5pGRctXYXHUkJqk3f9cjIS5A/qPa0cd3H1iwuelZmVwJeUhBS0MSxX5VOJKi8SQ05ur6CqKHB3Cws0u2QJXN1Y2dtW2iX788c08cgmzA/u7S4qJwktRa4RoNTql41gV64SsZ3Qd/7Q8MLS6/xyfoJ0djimD//W9/BUxE8OX/EQgkJo0g2YmFC09ltuf9DQmkBcQlOIZOviUrNZZAD74Yyuvpwvz7Dx+bVhojl7WuhWc4pNlP7xdxbTiugcsBywpEQx9ivKCE4hTGBk613yRAignzyzwAGsi7rY0tp9LxleJpk+imjY0rGkFJF++GQYVPO7oOBW4+fVj0yOou4AkQVeaJuQjsB4dpfHRCD8kUeYkXKf0SFnREuFR+kpymGIXib7CREJCQHE1w5CTJSDo/dwjtQmdhhkqq9jXpiX4w18ivdAzQpicKglUOwxsmQBDBTKfT80vckRnfDSjjzopIIqXA34opEghQSa8zFz6CQVCBRBveSz3MKGBo0CCq6ziljTYU+mD1axp4XF1hfnB2rARToZkNx78gUWCx1P3DDesburetuhrIw3IBNWBjfHZ6qvFRKxgKLkOD9Ti8utTfZr5P+emMjEdSQ2s4wJx6zitR3EyBSNKoLfvk+IR4jGCAYyZBypX7VBPoFdjWerR/vH+wNzE5NTI5DmWAV4A/VUJn4cbtLDvNBNgIRt6OQxt3DTfOnivT1JSjZDoekKCUXIVxSdPNZP6CMkVuWBe7JgfDXbmmsBf3UXYUdOQeZAYLJ1GUqu4oU8jXQoml8vcpfZybU+1/3CrRL46Xlh4pDddJQor94QlvoNI7YAxA+JzM+HK39/wCgk1NC+8gmCk4TwTJ+WBPBeSgD7l5/AD6Gt2n+4++asb5xLhc3jKtPosTR5jpct97naoOUWvbp2WKUSiu5vp8AiDGodBPTag76MNrjTxqaegsl16/fY8Y7xmZ1vTx4Kh2uJs8EcS91KgjBV+drXq/eTuJBTlws52d3f39+MAOah1VjS1YXl7jAYn/y2GmJlpv2thCkIJXbWtqF2dbO9vQB9cwTCMtsaMZ12HyjzvQ/T39Q4N6IKalY72+ub4ODSLRfv/7P/A7k+VRStbyZ3/CLnCzSAL9hhNjeKh1JDa6ksrS2YVloJxTb5Q+4X08G5JDbr0+vnd6xPpKBrDN5c37+edCwsamsnSyh8eJoZGh1Y0NZ/CX1z8fHx4wgTgreFHbSdKlr5G/sTcOBV7Ezin4wy2xEAyD87a6tqyXDzDkwxxvE619nvN/sy2+wKLfTgyM6Q5EfaGVJD7wzOQO4UtGkv7XqgEGVHqwDYxiFvbpHBxBT3UQv01Ry71s+bi43NWt5QfXTazmymSagUITAVmMcLig/j7Gn9ORU/HQ4Ccy4YShpe1SxOwAaMq5cDj5KXyui44SQonpti6p1S7qsUAEFRxOBQNDlaytrm1tb7LP1Lr1qpR7pbGjfacmpkn+wf578TpPwljxvoEH8JmpTeusVHLuswdMa4dW3roSpTbtXLMWdvIz20P1OTjYbgjrOj2I6s6T0wWFMOPqpLVC5WgjWCXDOPaGkygRWl9fe/niuaFrOohJxfHn7Ztf3dWkYr75uUzHy4RLBZTaSancOTVjk2JirupKoGO3M2CaoschWnEJheLqDjMFjUOQ4MQRQWLSHa9efVXYvlp3X7Wk0txIzscHiWrlUYXKKoSd+UYrPDI+rKGKcJlzjIdtN7Q1Ohr7r7hBH+aw/Q33TQg4wNyjgTvOLBoUKqzZbnksmeekk4ymC3WEBPeZBpf1YXBqunviKcL2NJmNfn96Zj3odZeRBXRxpRb/PP1BvbCtSwrQ7cWZ7A8vdgXKBjlDfRjRKxnWQdXJwesgW/WoDH8geqeUoUdNGKrGa0jVkLZydbWL2iqVdLAJMwuEdGkK1A9PYxRZJYhbzz7dY0T2FvRb7RuQ0yZlgjXlCJNWWQOMK06PCy9uPD6BPOw0Ycb5mZiaYpsFqI7YVNxWpTw+Oa4JO0jIFR0eGHBQADSha1q7O9Rj294eyv4U7LJs9g4el2mThiWyG+1xe8lZMqHgcyQj0f6SzMLznuYqWtY/heMIpEI5Cjf9Om4MpWlnvEFJeoGcwhYwL3AqMnF1oVUUXghNQcZtey9YQAOZP6/66XBf2qLPURyrIpcifaSni05wqBs9BC/tqx25NDvedj82AfL8m66eyujkhJGQBMaaS9sJfof3mjWha7s1lSihIRaIeDSo6HV4GSJRYfusbkCDCTtOnPgfSjYewwkkrss3QDI6OJx/EC2pGfEbM+dH542kDDyK7nRAl9YtPum94piiSRRm8vqGWgCH2XLh2uZKvx6CCCSKabp/hjfvcpSsJjbYC0sjG8dkVg1c+nqHfKw7JDMWgfdp6eK6SrwczSmDjE36emzS+OAc9gKD9AZ3K8IAPpHtXF5bFkQcuhjxve2nQ1BYvFHWjwMtzqvVsLRj6eneClIkf6Nw02Wi4ElpXj6ZZP8iE6kJMwOI0WbEWUOot+/erq9IvW/73e/+QOtBA7gvK1h6bNOKk5VEkgdNXl5R0zZAapzEeJ6LiB2chF2k4tZXVhXDbo5tTE5PMCTUJ9MCIsjNCR8ugO8rnfOvuDgMmzjiF1+89DPan6iIwwoYQYV4CMwqaLS1AeJc2ClROFunDmNufmF8akrcQqdk5K2O4ongoqq6dHBRXop73P/4YQl+4jRjz3QKsOItr3/4bXBsSD0MWEpXmrvmr46Bwcw/6+zY2NxqaSwp52aW0VnvP77D5UKB0tIhI1Mg4VBJoqyfRVlZXcahtbcaJ8llVpjqmxVFECCv0S6MvDMP13hkorV7qHZXSxydMruwQ84tv5urzka5Y7lDGGrTWVEoL16+mJ2fZUgccsfpzds3f/nbX4xCiKZ4sgBZYJKHBo15m9amFX7AbWnkLZJjz8Ry2RIHT3gA7FJBh4ExhhAJx9JfdF+o81RjrB2/P/ITiLUb5ukD9ctLy3b3u9/9XphRza9MAMoONSEeRQyD2lRmj448jgxyUwK17uImFw1PtAzqkv1pO8kp0TeZ0iBQUS7xHz13Tk6L1vOPzT1V89DnCzN5KxqhMoCwMJxUdf9Ar7yCahX9x4oEh8afSAjiUl9zeV8Oqi/+u5MDETv+Tjs9BeBc75ueF92MLBb6QxHj9JtNPSJz+g4+nHIUcP1I6sZkhD96f9hq7SKOPpuNdNIBFU08JCJ8T6ZSjZ/v0w/r7lFrcdSB/yg1D8gnYB+Zc2qBWmQ2YMOCXGrTp0zZdtPaFobNxKa6GY09NU0aLMjIrIzQCUv07h9vOUZwnC5P345/g7Z1/lzUY9H4/AOexPbBjnlEFIHlIRswGn6ExuE587pIES6Y6LtIX2ef5DmgobvaowRwe2NDjx0ZW8oJORSpL9NKViLpRXKTWMWOSpewltuztDxwGtrhB9OAfUdh2KCSkVErrRMvFYNGLdq/IkElZRGHsIVpBCeUl1KptP5mv5mrhnMZtm24TSaZdrdbjhWFQsnSfVQS1TM5Nh5XAHNdNBZEJ5Bw5L9UIX0ibDqgSpXbIZZcACiEm5aJvAEdwru6ZXp4XLy9YAw6HWynk8ktPrBRu8ezk6IcmokCvCI8+Lubh2bjm7l94fIb+GH3Ak20uF0zhyPa3xfSvYC3NpadYzIJg0zitlL57tYcghKeSpzBI3vexHsaLhha2+5nVqezpf3J7PzlQ1P3wNDtIyTa/cVLo+DH9alQOmnyPLViy+yFTGCWzIIQYPEdO+iA2FZb8Of/8s8SuIMJNO14uGck9K50MDNstFFHBNguno68LG4ivSaXh0OpeeDlxGXTsILTjsGBx2p3VfN7zI8We/aXqjV0RIcYEWPorbGfmYjDZ0+5S8xG9e5WMgCJcpC9pLWrVSgZdyRNG7DTUcUqYzN40NClZVHLKHIbXHJnilyY3i5D2dIHkIU+3dzcgJycUGPjoMnwivBKW4tuz6ZT91Z5jH1m1vogTJbWHvRDlG9dBPsg2R/dXTrCEhLzRJPqMjGmY38Ah/bXajeuw2f6LDOMORM//vyz+hgNR8cHJ/Gu2y1bDC1RpM+pFELuP9F114l2ck9NWgwZXtTcW+lsGZgcffX1F/oCgUF008SERDeg9jSop711a12F5JmQGgRCB7168dIJ9MHEBvB59+4tmptTD1Lt7B1u/f0fPljqoe5AjmhHe1wbG8yJQG5Q9x6SneCIOcFMMNyNB19bWrWmjHL6IqmxbO9QASBl05fxabIRVI6I7eDfgQsuv0ExH9+/x14zoeg54JqrLjIOPh8fT66trjOYC0+fIRwlBcHFAms0I+q/sR4BT3aXLdjeRgpZ6PXVDdrHamIhR0bGRTg4Spxcfrpmvl6v1PvTp4/QvWqCgf4hD2jDYAQPoBsao004PBSXivcK8XEPrTIbhihDrMi6seBWydEfGRuHNKEn5l/sCIzlkDIkGCqpRNCo1/OCMUsebVSL9MFBJzdEhBSOa6Q/Q5PQpTBLB8JFaJXoJQcgtwQ8whIyROTui8/ia3j61zatuY05hUeT8607rCFcchVF772bXoHupPIrja6pSZbkja1PRmilr4crwo+Wjd8lvcTVQ7mqhhJSvsNUZs8zWVA6gcN1j7ZKqZBsleBH84lOZQc3nHAjqv2DQ9KNKB9KyOpRrBrDUd6OsCVip5PGc38r+z7qGEEn3t6gIubY03IUJKEemR68v0Ot01qyKdDxsjaAI1YUIpSdRGYgMv/hE65WVm2zDHim3vwfeMpK2ttomVrNmeeTQfeFw+5A8lDvAC7FGO4cUKCLCSqB4VkaTqArNbi0GmdOjWRPd9zffivhQTyqUBZQhi8VePT/iKDkNBXzFbhgSUbUEd656u7GQpqo4V1u7b5yjw6CS7abtuTP6MRDTYpK0ry+OGkAPYTE3Pqbcqa46We+Gyuspu64xqNtVlFMq6Jt76/FKmMbbCbPknXRoc7bcswzebTj9rHlMt2aEnyQzsWccOWEXmLCC6aJjKUe6sHoX+1a4gkI0iQQzONT2p2kkY6+oWHBRiyCJK80/3aR3KHgguZI9L5yaDsiP9naS3monB2e6QIg/MwBFTYTmR8cGulQ2dTQSittb8ldiefJTed6XJ5fVyf6R31YWt9oFtRJ02GPSVilASep69RNW6f5WekDxuzIfQALumw6gXh4lMFJu/kpQ4svRWVInJeCiNjiyguPd5VKaGEW7m9//Ss30QVhJX6YA952RQwpsABwDtyThSfadnkjZeJOnFb1IlqPSKxybXPVyUDgmWwLSEii7qNW1dDXJQ3gJtkPF3eH0kOUGWFK55/MTWFnpmfsqBodUS4JIPWzw929bZKg6GF8fIJVUzyLcwD9SIJ8pcbGPjtDobBPAsQ+UZYBhSMTYnN9A5dgioCXammMi0vLmaNj/USTNyHx1oxCrdEPjoiPTjxArQMia4ErJgVEVwGalsUE/nCxJa7B0xcLtHHktV0/Uu2ZzjXwE4lWQ/H+/XveTbl8dniwy7uZn5/mPDknsAwvZe9wT9MJrAv/6btvvufM+rF7AYuAejlP2UiMW4vGOFPQoSxgRl5BAHvQPjo6NTulnzqT8OHD+//7//5/tOOxImwV1fDxw0cNGp1Sregcobe/vl1eXBRvM384MA38GRoGXqA8SYHgc0trd1DV8Ym+IrSwZvqSt5AwMlOF48rlQQjRliCmvNgFuagyL1kv9WuC5LCGYchz87OcPqNBnCIJealSbk1LogQPQPuz057aKbcUXUPd9PfPcxqVC0iZ5b4J/UkfQnSKjaOMwHVhZ+8VbW6/bM9FTkH7jucvnimAoAUwPCw/VtGyv/3tPWhDJff0VycnxyUgiiHLPoxvC+nIWNSNhZ5Pda8nrmtuwuPhFjjgdC8ui2EuHPZM+JN/D9lxpJ1xhUlGF0gTJND0vHi4Ba5f1kR7HXHJWTgceU08IadJ4hILIfZX9BmTw6NkPKVVwC1xRxakoAjCNc0Mp4yBjkkISe0QkkWucaqnr1PspGSyreN84/1HHNtCmUXrIw8nZxduk2kEcvUkubzYJUgiMmo1vv72G1FBDL5VOjs7cbJTWCeXhppqbKK1nSt+6+T0JM+dE+IGcFHEYe7JHK4FRvnt9Rsu3fzcHK1nLygjCJFmB1NkK21sbxIacQUFlgSDMuRqwN2shaQy1dvDpluMjnPhiROFDnnIMNYkQlY0YRNSNqOKaD6bfT4yNY5YsWumZMnIZbk31jYCAppbVKSr8BATmpziPJea681qbOVKgiCbm7t8dtq03NPlPkEZD1vuGoHMVffGxtN8cqRwHVe8tUByWtXRw9OjWUD3qPgW7OKlZdT2mzeQlgp9g446e47wp+boXqQ0BU0/8cIsdsHmIE7FaWJFbKdoPQbPN13GhYUDpLT5ko3J8I1XYMVEkhXH6hItOCxa4GrovY5yjx7AVVkdsqek4aGIYH9BDanA0utkHgVVtrUXnSpkDjeLYbV2agR3I1yBeSZ8M/Pzs/Mz1JNdxk7RufIvLAVjj+cBGdEvIbHIVVOKlVh3B2BE7Le3B18BmXE6OAcamSUP0NSKy2sgUh6H5b75+99B827Hu9LNnaWtK9WuIjazIwIszLuwMEfTC9J6SCUIDqPtZgXjO2HA+MoPt5wozrrOP4G3jyZcHdmmwYE52JITBIj4kpDF3pmP4baPDkRkj9Ch1Ku7JQm6znFH6EO7plAAoBGd4kEKGyC1TtNQgKfYDiZxQA8O9wDcuRmdTrqMH4Abuvp5ywNgBjvG1Mn7ACmIla5KMYFtWiieym7a3VOQeIsmffXypQmqQtbcPuqOdqX9Xr360sBjcU9hxeSKwIsG3hjw1V8yjEGozCEDLDhGU7PTSixbOps77i+CiTwZyTMnXcRDg3UZ09Lw3Rzj2Yea5T8MDMKPEBQ+xMKxNx61aL7YSiODtNx6gtvBWDsAKoCEqov2zrZ1e2uXTmQG9AFgls0qoEnRYHgb6XYry+vueHFlyWknVjwDR3FifBzdBsg7BIhIsRSowfGmrqen53b2d11HViCFAgUwyJAYK2r5Bvu1VGvVl2pra8cJCSV6py3aIwupAcCbvT3eACpNfJK20n13Pl2GTPJSSXGO0hmbyBAimx2C+PaGUUROSepQIw7Xy1Zz7JGcfmi5iDLQESD1+OCj9Q+Zm5mFB5c/pe82aQiSajSzjDLvgBUsC0ejb3CAbTs9SQ4vzSwAAB3PTuP8J3xEErn5+zmfxFVD06vGByn/lAKjfOVRKQ7gDJil47yG9ldrSy96C50bzhc0STcYZxhgt9K8giAd/wyWzyRYZUExIYGWIhU6QHgAINF8GQYqnaDvyWhRAuYDUrioOUGhLFIhJAMmGaIu5vPTNKbNJ9A4mT3rCW2XLHWBhIt6186efqLjE5MHx8IMKfsEa0NWadhyfPLTjz+i3eU5oF8VW3kcbmkY/wKnqzVhdJiMiekJPhNXjzS6Je4DK25fbASHWqyFOYeyGbWZ6TmTAxgYEpEwe00nn3WJ1UOShQcGAX3ktOlHI+MjqDbZ3KAPFa9KHNCDtsypwBk6IXaK10AVvl/8SEjUoGgZNTg87JBKGHOqSZ0Wa86wgnnizR8iqH2DdwhSsifAUe3TYCcTd/0NbOUg9PRwGxDCaBUpro4PJ3p/b0syfcpxTd411iLZP/eCOz7Uf+gOPIxtsYf4d5H5fTzhxXUvP2R4DByRHSCXMbeCbk4MX68w+jx8IZtCKnFyUkXTjy+1IKLBpomlvphJsEtR8fJT42REElxHRikhYPcxy46MD+WMIpGKdgOaO+n8IYXvxkt1/JCdQLrFkdWdIYUEp1j4SndVUFe7m7ZyVcia0zk+NoM5w47COtw7qkcahf8H5shApJpN4kwV9LcfQvdUx8b6mtDyytqybHLZOGpF8aUWhvx4TPzR3s4eeFRfkJurTk149VDVh6xyLrgiL7cjtLSyskRImCs9d6mvJ0/mpRLgOciQBmrUsVPPG9OD7NmL5wRma3ODouMv8iL6+8zCSr8mUsdToYklg/CCGA8DdXNUOzvOz6TDPtLRus9K75ZqjIySt61rDlIEOrF3ploxDIK3HgplxxuweIIZ9Dgl8HRuQSQM7LBrMD7zoL8alSUNPX1iSgEQy0tLP6pXUMYPIlzrrXIlYiHthcKzsATEdhRpx0mqxlFLeSH2tL/sBolP4qakhGl1oOPutDQbWqXXTE+vpq3tEvKEa5rUwcOw4iQ8WScQ9wTR0LyMhkQoy29dxB2hEjeH5JE0JQSh6zJEVpBCSjUVRlZBofbWdqDp00fNO3epJ16VILVFhFKuTq8a+xvZadpTaF5sTK9Y7t7806eSXtjTsyIAIGwIgJsCwubQ2sRURMdu4emx2MCCCj3hJLeHy7PWKEW8PBxtFWT48DyoCVgP8UJ0KPE0FDPz4PFhRXVo/QSJNL+wAOanuYrI2M3lytKiNJeMsOjrQzFzEayDCVMkc6SPPBgxOeRXxJS7J3/A6UAwUIl+MzMz8+4tBfog3+TZs5c8aO/99vtvZk9m5C9BjjKpUMYcPQaL62yb4TQHVUHTNExUqUA0V8Z/nCS0QIAoZD4TLelMoIQ1xzLxkd1FKId5VelXUl6bWCH1QKHyHhx4dLzMFGfe8ZAUK+dDKBN5HKoChCSnUnuzkqGqM+ebFgjJDAnSNTSOktSiOYQMkAs9Z2ieePr0BYxDi8GYdtMtIShCdCcnyWf74EaxpEcFJr50isFIydc/v+RfH5ycycTAHtgXWUjJP5QoguNwOT0ZS5m6R4O+ffcboZSIBd+pTkS54OM/LS417OzzO3XOQJdKDPVZnFZeHWlGndFW79+819V1aXmJxeXH8CChLQaDPQB/1CMofaDGhBAc2gsNia5v+rWEHxgQ/weNaORx1sITNQAH6QjL75DrYpV1ZEH6+yH8ql4E+DGPCMRRlmJ6LuLFMcJ32aOTMUrsCCzVX2QcUnVCdAw9qVl0/goeNWRGr7be7Xxl3YDbm0VG+fqe2BQ8dZQntUMNnVwqtI99sGUIGawMA0DMaGfBGFnWmDkheuMtDFt7OftkeGRMyBT/FitORsJGShBm7JktqrtBc2/7IeqbZtGPrfjB5tZOw0vJhvyewj9g6vkzmSWZmHOTLDIJxAktQQkuSKrIVeBA3EgWK62cDEoQOiaJrZc3Wgs2t3ZoTJTK5QaWBhqLOemp9t82tZ+cE1qtt0ZMfOwwq3Zji2sFi6q5UQIhqhC/hypU9tjQhO0QPu3q6Dy9O7UyMN7ThSdv3r/DpItXQ2l4UWRlKoeR/Yg/o6icwfPL169fU3BUB/iFatE9FPLjlxMtWN4DgHoMtk8RgSAzoIPQjiCQPBScAcqRyYc8lleWLCGCBQScF3vLliVXm++IclGihejLcJgPnzCuZpw1Nv4RLSPhQ/II5akXqfRiyFKEdnpKl4pZMAV1WbgNDm6qN+nMZNAYut7dLcygAwoPY0KooyV9iHFHyA+LL9GEKUo5h5Tt+ybSw4c+BpMNTzQR2jFWgGKQasMjwdPdIx9R5Og7O5oQk5nNzXWFFCNDNJzGpV0kIw12T46zGj1qJfs4BSTQlTUSbnFKjjbWTar77e1vOBw0FBKK0iSy8mr+5V/+69dffQMDc0O0GGWf6UFS9vHdp83tTZBcFdXThWfsuRNFwTkYF03ICk3zuxvH1ItiDPESTSJ7DpL3vnr5Sjcez2lZr8/SFNeSPW97Tlvza0SsFcUIyOBVpITyDCkYdBNV7lAFCt3ey82wXmxy5jRVurlwst8a0Ng5Ccq+dsSrxdYYQwSuPE60A5+dUymeg96B0AUbuBeSRCkwAQBcEIXBLCFt//HDD1qXfO5cLebC7KWcVUKBoOjFlYg8qeXuOMFYYzaG70imeAQAtJBRrfZvakph57Qk6DPaezjxAZkzl5dwh/F4JGZtZUOsxylQ8cgtyIpdXjJf6X6Oebu+Hhkb8hM50UcHTQYKjA71a2h3vCc4cdTwcGP0CAukVWWRIh4cR8Pz0smFTFHrI+HERuhXIPQR8C/UaVPbqXozoZx5OD6ZhbQhkO5NdIBmXrJRL25lSSUfX8WTwBnQWhARV1XhL1O/VRtwM3ALtBKigDqPAYmmwFsbMBd/QMY6cdo/pAu6yj3IDwtLASWyV+lu1mBO+/PubuFkQFmZ5+GxcbyHwC/k66jPtM3w/z5++qDzLQ1eNmsUzpcbB6hep87AgSDrFpMZIHLCNtQrqOVUw+hMqXJyABdlr/mSXeDjgw4q//sHBwiJknIohEX0dieCV26dHTZusvkEE+MT8ucw3X4LFXLP2SELpsk79MAFdH4QqcTSGeSyKCZnkyi4xFQkQTBqPQKN7YQKg0WAU7c50B9aM4OUlWU1Uw1AhlAq4cHWsLx+yKwKS5AT1Jbt8g0rUBx/GgBCp6C5hIj5hHZk8dLMwioqq+VQkgHCkPd+tsZOWnCAK6kUbueHHe8e38nXZ+RbStKfb3bkw1zS8oKCPgyK8mZR/XtlISZg61ZjN3koPotpD6rQL5qwaBsn+cQI3AMxFeNpW63h9V1X4TqcX/EXYCKapLF+WDtQ2takmc9geaA1/Uju5NjI/+zueVVV8BjPKXEndFdzRnqoMO9okzEv/slpePHyuS2RAu/3IpryD/nuRicQD8WxtKFzJwRM9lXb4u3YLyzF3//2d+byiy9ffvnVl9SEAwVxf/zwQd2PKXhKFAWQZZMsLTcTbOfda9gAHIOTSXk6v5IdqH5pflgEkqbSCuARb2P/ZGEIZwoGwMBmgc3MTr5/9/6nH3+KyentRkisLK04itgI6JBm4EriKhHL/BqPzUj7FMfEEWTyVJgCJ5wJo4mxDoaSMocugk6z2V4MiHF2wR2Fq8nUom+Hhsanpxf29lfXVrW68wgIVGDMVRX8+Ab4cDVajjcD4Znw6PNC21Sr5IqOImZMoMR9KwOIg3ouKy9esRFbK8enDZ/JsaUIcHtU/8Vlrv7kydOvvv7S1+zcHGkmmklWa0uylPbLGxtJiiAfCwsLNCo7ib0BBlFJtBhGmN16Nv4MAYzO9mTIKNrcWtDhK2ur3G0D/AgW38IZwHugSKyR1qYYcPZStAQW9qhygba2tyF3Xpt5ODhWlsmjStVgDyy6EwyaOWyAP4ihlcXNxdXTZ8++/nqMakDeUVlsDyYVBby9vSNBEG1ls+XFOboSmVwExh+bHNUI3mZwuNykl2lU6fZYhQJ3nB4fophOnz976Q6VKSSq3Nj097fvVtdXJSwL8cPYXA0hDWEuF/z6669IJCQuFu3FklK+/vIbRot2Qc4AYqsr654L+UqLiYs4MzSRccrdqkwbWxSVKehElgxKO2ttFMCQjVAWKO1ul4N2d3UPzUjByyQQ5xQGE+K7SaoudASB43AQQ7JGATkkpqAAUyEXk8NHz6B14Fy+PGhOOxTjRYA4WIGWI1jN14a46uav7XxyUFKxCWvE7lAlntOhpC+kJfo/5STpfUIHwsT3Ozow7+zKovEaVLX1PEy5Q4Wf5A4gdEEOtyedSAWJHimkyOqBzqJY+EAZ+P/63/8NprP8E+OTwCgk7jSiyPFIEHXttL5raLv4m4adiNT9Q4vHeE/NPsFY/fzLr6AeKM3Uyamir32cYTJ8CJmS1ceqiURbW7unF6doL7crnZzn0WmYqAb4CYRcdVYqs3MLRNF6qzWLb9Vs7itl2gxDMELUGa3hGMs6os18DQ4PXF9cu9WYgbY2OalaFjqEnGNREdLF6jIqqp5Ib7nSwZaRf8QF9AaRW1OePhzj+IQko28Tc3EQ4XlZQCL5VF+LBE78nuYMndfI7j5cinuz3W1N+EEVAFC9HCQJiNysTGxHbWNsin/gl0QIPGAZYyOh3iZm/i+/MrPaXJxFyDvUCFMZDIqd4sF4Oo9jkbkH7eYtKLKSrFzuIZhgfrggzqgZJi7LH23SbO5ma+do9+jEyMmRqcH+nn4aLc3iWto9vrOGH3OaPJcLQmgeU/JDYboeYll7y8PDwCX/4/btm/fvP759+eKVMkluinkMsgFpCek7GH/3AmLyG/D4aBdT/8RshXMYDwkFc5ezGibt7h6gZNwAHeAEkyjo0xmR8eVl4Mj0tJyOQXiIYpE8CixT0O/eveNf4msBTp6EZC1syfDwoI4y4DTEVjDSDby2jKH78F5iwsSYIr7Kx4+fmEGhvZmpSSw3oVI/rbIjrKydtsBNjQohBXtxOxw1lIAT7zX8hg+Ln2geupFRF5+gC2lqtyTiAnGK3A6pJRsZ0e7ZKWOiAH/uTEImRmbNTPkVQiyd5x359KtXCJYUSoqekrevOmpYagpc/r0+24pkGSe/tSzV3gqbAOf2zS886e2vbm6uwbWjw0lAef78BapOUg1MhPHneaPhcNl0nC0cGh6hZEkjIC0c6gGAERKJKEB8+2DP4Ox9+eVX2AzZi2ygXC4qTHcdpDmEIkPJIbk7kDrinSpvr3iGKreI9Mb65uLyMpXAwIA5nKPPjRNsm6Oe6uueHnrfEjg5BJP2JJ2146Pdtj187sT41OzcLPsp/4emcw4hCJYJOfjNN1/rvB0N6Bc6CyWtUEb5uDWSzAqu/P4Pf/rzP/8XjjyFjnT2FFZ8eXHp7Zs3AJG8xdGxkcP9o59//gnKk2Ora+lf/yIntapqTK86zJV8ISkrDiHBd4pkjzCbGfWIw8KCJ1jwwOahO7g1Hz4uw5h6joKKGIOBgWEADuAQXICvAfBjRXPHR+1mS+mcdXOnPTKQwHCBC9hH2l00FogD9xxa2UHGKjuMnzv6REGoFvakEgS1UiuGH1H67JaVL5SC9/LDOymFNJFLSRlM6rYbEZScCbFxnQacc1t0ZhZHZrpi+NFDjARILfOVutIughKjpxRkXqn0kZR3ouucTjfCHtub5nWNjE7MDY+z0D39fXA6Z1/GyohUsZ4ynKnxn9VwTnw86dKrRSEMD82JVVJBcTA/2uQpfkGTkhzMLNPunBBu6GR2LiZLAFf5BUaegUI5at/0w88/6quBKoGGnBqZeW6TufJKLEKxk2Og4mmjwU/dZmaGJ2tqmp6ZhVqEvLAEMkaE2UXmcUGUuGwPFD07B4QhPzFeYm6cZi658kLBC9sNx/EXpTZxSvSHEVcWE3G2uaQujnf2Dm5C6F3B8IsrPGW7GfRlKcuGUqWgl0qG4G19jlOsSAOKhuCg77l1mn4wUWpi+VJacOLSEIZeSLi0YHRZpWhebYNJhS229Sn3peNd3Z2kQPSOQwY1iN5E/avYgwDl1CWzIMkBXuY1HlNhQlvEwbwKNQRsEPKqp7PSI6OJmyib+OEYbGzqxVS3t3IGRF4MUjT6U72ytH2jhrJ15KTZuulZm4qq5ZVlwA4g1WCVnmppTtWeBZIbMjoxgvnAzGif8Nub3xDc2xvbyyufUEWdFac8TU/RbbbevX3OgIPJACNgS4VtkTrMXDcx9vPzCxJQaBu8AneRpdcAan5uloixByRexoqXcW60DLI12B4KyhDHb7/+RoCPKGLNRWI03yeHTxbmQ4GrY1CS1tL05Vcv0eACpa9f/8yL+t13v4ujfHUlzZ25woiQFn8sduKvWBttmUNAqEvBv5073bSrMyrIDOYirt+/fWenKWFgwjYVs+b5Yc2QqNzlSrWbiLMHNsZdwL6y+01Aq53GRE3Qv+NjHGXXtYxUtKfjUMmhUCxEieHn+R7IAzHHrGQinSGIEZNIts5ye4tqr2++fvnnP//Z2fvpxx/418+fP6PIAG1g9oe//6Anz+jEmKPumYk18UySz9ikzA3AzRpt7W7eX+XoUriayOkapE4fM6uX/VLHEvHE6tLaEnwwZaA+511vCWFrB54HAl9nCzolDTzw/bfutz5+1HpuEXai37neSH/u4dT0lIsQILn8SjwEmht6Go4PTjbXt/APQ4PDSv7cixjT1PQENMRHE+btqVY84IcPH7T4EKKQOZFCWn69SQZW1JIp43Yqrm6YeB3cHBHhEZvHaPs1U8lKM/s8LCeGYf/hhx+8Hw2pWFzURJBASo/tQedZ3KfPn8CtTCB7k7CHbmtKl6s6W3TQovXL083dzX//979ohmxFSJWurabnEgsJVwCOJ3VxecCONXtuKJxNVQzf2dZ0eHoCnCeeKM4T/7zx6OQMYBMNlmKhXjfJaAyduKFm8iY9cd71lFYBWcR6lVFZT3YFAeQZ8UV0R8CtfEn9KTOxK9FfJ8SBh1BwkjSGSAMIy9QVJS10tUYxXNR2ueTmjhB6i4NxUCyANTk8Rg5k9uP59c3BxgYtBdHPTM6+//heiqzOTdj/teWVuJjnFxxSWY3O8/ry6u7WzhdffqmkVrBKtO+Pf/wnj+ImGSk2gPxSieY+/vzTrwznwbHCjnMNGOhxR+677srKyorTVdZWTqZz/wAqHDpxDp03ENfyplWpArSdi7W1dWDFSVOLhAcUGUZQcLYhFVrhcP/YebZrgCEFQTCSstRmPGEPx5edRhbVT9WXmiiJ4pLCCEQnqREQkbArn48EOOimG2bWdFRturypVkS2EQ+fatbgxdYFNe2PWlohKF6TGorImu5vCQQLBWA7GFwVF6iPz7xAU/Jxr9X639kLlg+/j1dCucHoRupIG0q/aHY7wfME8O2uLYZ/ky/D3MojtrWUcasEmzpPdlzT1kZUPueBk+B2iGobQ5pLSB6Kk0cQEndJulfCA26xVUpX10lvMzZWTV+jWHS77NGH2mXjOQ2oUd3d1v6xgFRje+Skv9IjsICNvLoxFMRVm5xB51u89vKCxa3SRzyfLs3n9e/PrAtTXHZfv0ZG/wZXWW2zX1bWl4aGBubn52AvtATWzpGkT1FCSr3YFSN2//hPv8foylGWwJ0WADS3EapVhfl9WiIhJBES09NTwwPDVmNqbNKTOfoA6F5tFwHgiZNueXbKdRsaygwSShsNhz5mM0QZ5QgSKgxt+MDeXn2iuNoNo6NW3Zp3l3uWVlbwotOzk8K/cqNpD+FAB+fj0ZLBjrIvXF0Nm/MudQcS139YgBHA0osD3SdAkgSbwUG0MO+EgXROZdbFE29t0av4oHI4kkk+LZCvZAbgdXp8cnHpE95saXGZm6bPOZJNHEWco7u5hSoTEWF5eIWQpE9HlMDBkrmGx0f4jidHRygT7fBIZsun3963NzfOP3lCcoQr6RHkGu1PiQnkwgjf//53Mo7lwvtD1mUFCF0I9Rlx+cM//oERe/p84Xff/QGbhB9sGmvMoW1pA7t8PHh/cX35cJpgJLUrTcic25Wl5Y8fPzAY2Cu+pt/xv+wQ/86ziafvbGvGuQ/mTyiFnZ3LeR2CyQbp3ANH6PyKQ4Mw0cvz/dv3aBkPjKoiYVqNUKMyTBAElDKN5szrPk+bj03oyzjkQFpccRiJTLKmxF2tC3nnxNk2IJ2+BgosPWxE4ZoYTiuJwlgBuv6XH3/W2ZxszWQEjyq5za6mzj/8/g+yC1yBEJimMDU54WYVEEIfEhX0OASgaGYGQJCAeMGJlLFZjbqPffnlF7AJvPPXv/zNmWe6fS4hQI+k3NyaaSUtEitciG/JMSK6ssuMjD9LcqBGj8nYQfYkYUOkqSjpMdBDyodcT7k6afuM1/FOjj/09ABlgocheDEE6aFGrfjP0XLEOQAZARhVoe9h2c0IPhEmgBv94OapHqnHHIXTk0MLxdfgOIs4UXw4AT1FAlQvdX3AptxOzsx8+fXX6C2Nzhkgyo56PRN3Pw1n6g/AJuAPvVKaac7Q3+eM8Vgu2y/k1ZkvJBEToLZ6HNOPi4sbaeh9L3MUXjPDCxQwmBrpp0ZPIjJo4ocMPxBXr3eiBauJfdUfH1r0Dt7e2QsTcHsPBDx5NuewYVeePH82NjWhJHVtdYMPSg3LnQjvNzSkUFJSpu7ZOB8HxhG29t4PzKURQsHsYyhJlNW1w+SH0res6D7ZRLjXrs72Fy9fwrbm2sqcZtEkgCEB5NcJYyp8DMV7c6eDMjzD8HOTaWssXOKuqexNPAZ+JMYMAj/MbiZoELuUtvxFBJdut5tIBk1h0yxBgFE7ifyMlWl6EANR9+s6bBsC0FIT68Q4pKKacIkvbnhUxC/SQEIKfyIPJq0UVZNrmv8WDMSIlhSd+Ln6XOEEqkU1xn3DWUNzx9W99GQ0AQVe3z2sqZRv7eiTVyPaYwzJ5ESLFdNhZXN5xYJOTE5Qq7SVwYcqq4+Or4UlqT8BJFacSNDvchIYV/qOPGggjxpCVsB29DajZJEpJdyLdI/hiRGtDtXQwLTHO5HIcm+F7lJ+pPCK5SCtVsHaIruFNigo+4W3RP9yB7P4A6Z2V+muHJGkjqkXK2m86Fa1F9EVzRYDs+m0fKb4f0jMViah/tVuj5bAkulfIteIvyJPTMzfOTqpXYwNB0DbN/1gBNtoKlhZt2AvoOLsIRkDKxO+rtVkzFO8TjUBAzWg5QIJMGTNL199ITFGJz4BhO7bCk0oBRwslg0ovpjsouVFHsP33373p//8T+Jne3uHHSVTNGQTlfiazgIeKZQXM9VTcbeQLhfZhvKnBRWclBbpuUC6aiyErBtiPaUQsUuEhI7QSR+eQkW9e689Q510YM4FACBxXZZoN/jdOn7WfTxinXM09sNwffv1dzrvy/0/XNHLYt/5F+j49rvvSO0nXY72DjSBkOWJeLGjFOjMzKyseW4BFZxMpNY2H/3999/L0RRD12ZPjIGr+fU3X8GnoWWWl4S2JfMF1pvSly5OFZ9LSTkz/ojeCHJh8WiQFy9ekEaRPWE/dJPD7yiBmfANCy/jXkQIgeDe/Jz9ABu1aNA8QMBRHtHC3ILQ5U8//ZBUXfhQStDwsO2sLn5yPr777vuvv/4CVGfSXPPnn34mEHJePwNqhRE8J/FilklOi7DAP/2n/2RL6FaDCmQ64sSKKoH2s4ODn374hYgoApSgQ7up9err7YYyGHCpjegXgB1GB/EIkQBXHDJO/N19UbF1p/gXvwvcQyaQkgKeRGm159F0pej0EOhJsdgtfyUdVHjwQcut5CjcW5BEPdkFyoD2aetUU4b6dwRu2+SeqiHE81AkEJ3mmtpeL626AsaY9qQAtJrSM4OP0dqqP0cnHfPx04oEQX3PXrx8Rb9ATNFmxcAA5rUmGbezMjkxzSHVvEFCNiyD4Pzw7r1SRASTFBEcxurGmno9TqdeA8pBZOD87vvvYbrt3Y03b18L7+tkAD2wr+7ot9dvHeyJmQnVw+rsRFyATLwkY8+ovXj1yi7wP7QjdlAXnjwVwcKxyjoCFdvaTD++4/8hZJIxbBiy/LHDQ/nmlLOMfumJ3A7bypDQFmctdarKwhE81WEUB+NsaRHTqeCR+J9qOzJ1TR8ZkEcZ+ZKwpLEwKSNpEkI9lxyh5qZ2Pf1IIz3tIsyC+HrGM4gSuAK8Eyse6t4iY6hx/Nkqgn57DWwBh97HbCi4A/JLHbAIUchkt3xM0o3I6S3GyfdMezqJazqdzq9JGOJFAhMxL/KPlBQnqdUFRU/JCUck0y9sK9aik3K6udHQR+rPfeO5tM+DkzoXSn+m08ubOr8otQ49iD4p6Wdn76i2L6WQlLscB8a+2gu2DWgZLT7pytvbmxiwi51zuMKpp0n8lyT9l6/U4WhTh30XB1ZuKDvOzatvtjv43nJ3fUlU4OJsrGOirUH5SN2ACdFRv01z6fOEqeX3NR24f3cdzhC7wnhIHsAL2UksmqiDAcJMEa1C0cnwoS6LTst33E3ehogHj8z2iQZDik6KOTbg/0/SuXY2UVKKXy4vDODdPagdsEk86BsMrEMiFnh63N8E0w/RNiSNhO/v3y4tLnkrWgK1PmgkQXsLrFDKNB7pTMlVpbV5GIIchAR8RB1zZEXI4EJbjTt57Ba21wk+c0T8Fpvsw1ev1g2D/Obbb3VaLXf3whYauPL4qPikmMsx70W1NRNJDvdyrQbi0JaOofwKBEyLvOn2jtZPHz75GOy8VBKKjIIAkyXRcFX+27/+qzwnlfZK4lBDjIamWvf355CUnFbVNz5G0RJm/uDgHS9MSS7SygcTOvJmS2gv55550GZHbpvpNii9jCzwEAjfStnQTk2V+Rxv3r4BkcT6+qf6n8zPkwDXOdvSFPJS0YCyOtKvazevn8EGt/XdjkJp1lU8M1pRSW5PdM75THo6YtVEs8FkcFJc+aIHM7/QCcBWBL6hldww7NHUJPTq7kRKTeFZ+fjXv+tFMzs7/cc//ifb/r//b//bv//7v1NR6BrxW33/MdpGEbgi8xMeQM/RtVU3L/3g7W9vCYLmE7JAvNxrRHEYDMaMDyi+L6UKEefZdQdaWlrx6YIrQBub6lc6U3a2oYyuVfKova1WumTnM4odIwMcTEddLwBHDSwAlqmchpYH2RfCUgfHNbkmrZ06xXM4HvQPTLg36d46gN5YbPgJTCjicLYGd9sp3ymExn2yBikb3xLlAvqxK0ytAgpJQXXpfR0d6bhwuesonkPvi5+Wt7d3P2MN+cPMc+X0xHrqGIjd0hjbpnu5TD4C+PTpUwC5XtMTmPsu9yDK3sDenbst6EbsRCIZnatsd21FIH8DFSHt0kEhuJ/H9Uip1koaLACCOAfytfmIzrxD9vvf/07exOvXvxi0wB1xulSi+mil908WnurcsLu9Z/WGE74Z5fnpef7DP36Am+hEoFhqB+TbLzXYBJKMVzOVW5G2+S0Dp8M1KWF6dPOT6G72ySNRoEw0moZPUDCErcKJelog7uV3SLbjdI8MDmvzQLD5cZtJmFjjg3ICyP/2/i5PCvUns0SklY1hqIoaPYUjt1IGlKAKeTM51p+VTnTHfFn1H6bCtGutoUrIuW0Vdyl2SntOTmxaW0k3Yf4lCBABxj35ozdqp0FVhCK/sc3e2nxGI0Zd8numgQrnPOqmxBmS0l9kgKIPmRoJnBJAXdRM0FLwHaAR+rBJI6SunmrL3uHFUY2ISgVQZ5wGcjpFtLb3j3RNz87LPwTKZeuhdKob62Iq+ACbwsMO8LC7JIznkTB1k5hkuI5Ult3CcnTj48DQ+FhINvaAkWABNf7S0ocN1pvAz8EVjvjW2S7CanxEOw35itM0gIMMNSD9k3pweEjt8so8FTl23NJGQo6T4+Cf9YusZAfVdKXjixVkJOLAWQod0uvnXNWAXX3MkrBwRwuBBTrH0YeWbHhgJBtUIE0m10jRu54HCpPbI28emEBPoXAhy/HRMaKOwpJ+8vHTJ5Wnpj2RnNbmo6Z6U/LzfZxJomYVqBwhJJodyuCw1Ca/thhIte8mBewx3jwYiW1qpGROQ6tOuKwHjeIbDo4w5z/+9AP7gchzX3SO6KyziXiE90XI5ayvr16v7q8ufVqUcCjkyU4AJEQxvg855HFyeTwAT8epY7vEvQUZWC2dfLBhLoi92tyKIzY9rfm+bnnmk5RevnzuvtHhsJt197T//C//hZWjyLS0oP3BZWEnKldbFZwFK2/s9c111ac6pS7C3bWWu3tb//jHj9ZIDtTC0yfGCQT0PT6Ik6jOlZkqxvvXf/s3TLVkYSIOTsZmHxxzJulith3EUN4N7xMDbKNRPmISLgLxuRmmHs1GwiApvVMsEKhFLKLs0jPLreEODWNqabxqJAF7ZsXU69ejY+ItP/zwt//1//e/Stiiqjhw4k4w0mD/0PjkpEVksTEP1H66zYj0H9dUrEDezA0VJ+NT35s//OFPX33z1fjYJEfISMI4ZV1lW8XjWfr0SaoN4lToVGAHCQAcQSBwR6m5dWx0kLlVDSx7LeSjGV7398jWDHjB1DqU/sn1AznOTJ++ElusGEuEP3bu9VxqbGYMdGwEKW/r148dUk7v0o314ADJND0j8bHNmDCHypqAkpp0fg4F2FN2zk+07pPWn8FMD6GwOF5GyGkprmngZR0SSW9waPTqtkED3Jb1Ld6go47u1DnDMeOiyvkpEqsexEjo4PGmcXoTJ8EYyIpjDJhJvZvYXcfW48gaQN4YCmTyESgNqcHOy0sr4tIdFVXyDb+9/skpkQ/gZVLzaF7r/9ubt2Tsv/7L//iH7/+oXYaMe8qNoZEVwynUl4mlZx7okafPugjkztE+ohmoft62IMHPBAvcluvb+vcf3plL9fTJgmwCzEGAqvrENN24VdbAlzdhozrYjy9yzzfXTWRPqszW1vo//vEP1QYSUnEXYGZGXQjDKQF5TFK1Lr7bW5uYH0YLo4hIFY0Ns6TXpilposEdmZ/Ou6BOs19qwlK3w20zvyHK05ZCTpCgU806Axk0Z2o1tLe+vGTfZZPemhkttOZUCypIHVU/0Vxq0epTqYZUpYe0HQV4cSask1EGEmwJEnNCqzbecw6YwGAlvo4/RXJhO2eOiiiXMyGnSf5Xa0mP6VoaMJsAquX4nQQVAiz1C1k7MDzISAMB/AYnyDxO/SExLdhZ8kDhGktDNdtBsH5ja8tMcrw2Ehj+AywQvBhOHh7EJr0HrRQ11doUHkyopFGop4OXpJ+BHRGTu+hBUfYKVhtWShSjz0DMxgGuXv3ilH6zcH4u0guRIItcgS2TVML20xRv3r6FG1gddYga51M4BUBpwi4QRSqfloD00U1pRHF/u7j6ibVUuoWTPDrcEp2i8ZXjcrslMqgc4raKR0Kr2Dsd/KjpllaAVuCmSymD/+cEU/ECk5a3OAjyJ09l78gEebrwlDEge549Bi+h0Yx4hA5ZF1Jq/fE/FH3HbYecKmhG0vzDk/TW/D//j/9LmvvkxCy8394umjjgbGCRwixpv9bajjLi74kJ0+pAFla29//P0l8+yXol6YJvZmQkMzMzbhRTqaqrq+2M2Ryb+2H+zLExGxu41n1PdVcJtrQxmZmZIRLvz0OjrqMjbWVGvO9avtwff/xxX25qE1ViUp0pzSqPqjOHoW3A1DMRjkwqgFUfGhoitVCEgu6b6ustBLmrGMLG4llkaMSjtfKUKyIdQEnZn2YGDSpjNYwXQeMPkSfSGXO89fMZjwMUjcfk9wj+nung+EChjrgiBm90duJbRHiI2JZaQVsOm8P13pO2z+vLJA301TOpdAPfRBy9TLHsEiWASOnpYR8E9sSlWSh5ofO+ca1EDCJVBwZ1+btIF/Lu07ggJlbxo6wNPQtLiZzqDf/tv/1Pghk6XJV7Zma2o6OTQsCf8zI8kQgkyBFtMaktkHJrk2VLb3t7ITs8+O3s9PSnT5+8IB+qQhgT50tLUCA6AGFy1okQox+1Dv7BpNY9Fklmk+MS+SqEn9pt0HFJqMWk8wvOx92PWv7p+x19XE26/uS9bna3GfOhyfgIfnkWoK0mGywj5MgFmNl5lcrPcVDjqin3CJq3JQ/1wObuWQdNSRbPPxBpMDcoEKFk9ZwuJ8QOpjc6s+hWmn+7sr6xsLRCxewI4YisD7Ghwf6shY/mNU4Jvzc2WFtnV1wyHiWJBK2L0bCrdhBSNmIBxyXddyyBIx8Da9ua6emZje0NOJ3uSJymKhHHgRT3ckRluKKcSNSJYw9sjx06J8Y9tbY0czSSwoO3B0pnlt2GujeluraSBhz7oRdUBUwBSQywYmEcLqZH60eh6LGwtLCnr1N1ETgwthLPjdoyGhZKSoODy9bmVl7FcYBbbSWggEoRk8ofDMEtuTO7QjV0fx+8Usd2ryfyypUdtIBMV20WkLLvRgvrYFrfWkM+f/bZ5yb9oFNkmt7lyQ09LivIpcS/RaE/KTeArLmhDopxHdFcTUjzgAWy2mQPeD1LrdSA3hF0/yD0GCSnGfdoeiPzqbJMTg71MG4KjecSOBc/AP12Nq3o0TgazeGyBxGFeUSdUKghN9LzFe2Bj6mLa/tug3V/GQ+iVdhcKQVCHp/ZA2yZOUZOGS/IG+WnyyF5HHO65SKq06D0SbYp/xqOSoF9cF12oetdRqPwBHaojqoKSOqVQl0ly+n4uuFnz6VH//X3v2vLsvWKseE0Cfyqq7AImKLdo30vaeNy8xuwGpqYvDjuHgLg4xwrkCUqbQpaJqWbXc9N1VYDhYwNE6jVDnEpv/c8+Df7K+bxvK798sNmirQ0tED6cSvZ4QHDJht72HigU6LNAyj9iSIzfyhfB77QwtbH7AfvVt9UDz1QEDFX939RWMHHXf09xe7EzlIscQEqRYCcjNg3Eg5tEDhD1RrLblWxMYx2fXUVHOQMKeIActE3An36It8gpQU1FwK7iykvp9sFgV2dHpIdysDwdwoGyID3v3/49dc3SzUrhJfOCPdBFu4bZX/x8GlTLCvplgTLxj69/6TJprahWuRPToyPb+9uHuwebUdmcYanVqqSfXsf6tO2dFebz7i6PrbiPK/PQoxKw6Fy8+mAd1uuvcL/7IHIpl/38uocQBE2Q4ItE9GUmJHZ3dWVvu1eDerSRKSxsVFaGWENE6JUi4/rHxyQGuvshcTXVta9nmwDRyo7YY/iR4SW6enJyQnS1y8//7JvZIAh+172VF7p7pEqrMLy5Qr8YeMNGFE0Hx5+7tQatSGrkk8R0kEoXJdUixCJfn2of8ihxfMKy2p9kCn+v66lVknSgVeXQtMTEgrRjE76D6Q4JDTIwBFI+Gn004f3bwXqwf5+THTUjc9dSuW+g+3DowO4LS/LDePnH99/ODjYQ3MRjPKtVkl6TEuOoZEuMCxwwwsiDey1HFca63Ng243N9draKkkPlsA5dFskl6aSI0NUVMEsh/s/PgY03Q6ye3DMtGsaGgqKSpXrjH1T5eM8dvePVI2yE0Ls5ezCEt7JLCrLblJUjRRSe33GI4U+b+SISjNBE8EYxlQLwXfyHbwSQLC+sX2A3E3FbaagqWpyjBDAUjHCyOOstP6yi5zkzTZeVDSQfLHum2vACn2q6Ky7rajoEqZXekHKYmZx0tFkv7uve1Pd23lDzukLUkBUeaMX8Ehuk6Yd6M3q6WjtbGqJwpJ96e7pQY+SrltefjaUsXc3zAPLoZ+or7ePPZQWlRVeFLJNhxZAExbTd5cXNVTVdLe1rm3oRLlPXV2JJ0xL1qKn3/wPEYiqy8wPLQj0BeK3kpilM8wgQi/PyjDO3WerdUa+ZJLltVRa2G5pb7aDeYU5tub00YV1h/JXEU/yNDMxbXkRtfhx01bkyoJRXoE5HBmyh4OjQ0Gi4l4F09rIRNVsTIGIvFSKodoKYArP6ur4R9iF4QVxHw4kWsTRfVIZ/8PzEPUiPpV6RL7Q6Rr4kR4EJBIH+4JtD7odS5C6LebLM1LGTNP+B7uFXORtePw7HBCoj59hCkIRFZ8+dMmKW2QUSt0RLMNU/Q+JmRaVqLpFkVkxADNNexn/uTKTWwSbBSrcwM7lnmf1IE6Z08peoEDmTYviyi6jHjEkVFscCEuyBLhftK3r4Hf39z2M3wXeGooateto0OHvfIXdFA8kQ3hdMJGXQ1FABk/Hx0qA2CI7LgLZOBUeTQ7FNZWaWtipSKFWBn3riqF4t2Y9nX1S9sm5UQpvq+QJoS6xYXbhEu0krZG3WY3488sbLRv2iytwDIEGgmDSV8GY/hLlwqtsb27xbGqc2fnmcRIs3bm4mQ/mQzwhh4lNAnRlct6XnUtT9rf2j84EHhex5XV19vJ7yK5AWeH6JYQytpAdCtyDfQPkTTSUPhnbYYQ/okz1tKu3M2MhQ7IialJGWQEUtwyZQaLFVA4kQJ5B3yIMxDwMaJBBs+fku7dvkZD0hW7CwxZ5W4paVgN2iaIEWv7iFi03oh9bjQdwdNPVJhdiSMT0JhwDwnI0vlhdGgtierMjKFaJNlyDDMCUJmISrML+/g4OZPTjR41g/IKqW2V5ZUNDU1dHm9wZ7+bzdWF4a7HBAomZ9thsIt6ErEKk9fQ4RKe6YMdIIvMdntRlGxprwQE/bETd7tw21y8zY+/nl9G1oi7nnxUc9J0Ctlh4O2nwhG8Jpe79/WHMhb9jW/hfqg9mtDez57eAEcl+fn6W4XRzc5daO3wdHAHXUyuD0tghbz38bKi1vc2I2P/6xz9mZqeRfNyElXR4LYsR1JMT41rG21vb3YQE/chvAlwXkvSWEMvrMbYr/b19jNO9SAi+K4dSscd9WBDR0VFZRwUtKXdgyP/l2ZUkH5UEWSBRCGkN6pLpu3RbFnfz+CDjlNsauBAmHlNWTI+2eBfoCHnrysr61u6uKjq7OTk/iQCQrmTW1e9yfEA0iaq8m5Njf6CoM6MByEfhBs20i2pB4AlmGd1hzr3kSRXLn3E09to54WcEFXm34834VB38H5wO1pWYthnTybNYmsFilt6Z8T/+WvOUQCJpdXj8V5/vESRVwoScz/mX1Xa0dRgI6NevruF6EfpeEgWyqwnZX0wgPQl9Jy54dnbqfioMw16zFhaIqNFVwCNQdsOG6km2b+zDJ4QMCbKDQ0S3f7DLHegVt57n55Na6okbJcZcZlwJq7xm0mrmk5kG4nOwO9xMQwO+GHugjm27/aTIvrWzpSaETLi5vFLRocxxQEiBVctQoATgaDEKmfzcJCaEduVKthSVmdSZG1UyIxjnuY0n3RyavsAH4tfkre1RU+EOhq2n2/7f6eTMlERkI47MtcbgGf0UpWBY2/l0L7KpfNgboUICga5x+sRoDxDcjRgSNQYHELHvzoAnrL2ebe4jhEPGKFEmmCB/sM+nt7S0+FL/VZx2NnE1R2eYq+wL7R6pW67Qbe0ciDmcTEK5gcMi63QNQIwk29jU2euPODPLS7YIHlGL8URkiC9evVJb0uP+9v07V0Vx1tj2mInV1uKd4XF1JhXjltZmfVjyd2m3m1/N3/Z4aT4k3zHRImf4mK910nlM7+eNEKDwL9wdArkCAU/BKLogvaBKkvsR/CSBrzk3nIy4o3cMGaZ2VVpSzKHJhehosALHGg4jYpT7Q3aimVmZ2uqrRD4W6V/LtZYGUmEvn796oSCKEJ6YmqDqJpMJvYlpO0KRc15S4nu9HcOGcrQXA/U2QroJ6TbWN7uZkr2lro9IWoEGp1Z8daQYORBFWWPQkINWlF+sjdnni+P2BemS3u5cU/OcLJhbQ7u00m+FjlBen68BJYNISU7j3UldM58wHOYd1ecXFQWbDW7rrDMDTRyW0DFpgVFq5t340Ji3caE84paDvIKqYnOY7QrkJaSsbW7YaXmarRJePCWT5x2JYQf6B5ubmsUltw+dHl7EKK7aCiGLkhTDhckxfN/hxw65snJgYOD5i2e67UhlvBjNjND82eevcX8MLrTSD6nFufnVtfWogyVzvvnuq8raaqno9ua2PQUWnnd32G1akQIqgNyctfUTuwteKrm8//BB4y8hiq4F1VoREpEiKspdBElYbGz001ppydL8gpJOdD/UKiZr5b8wvyM6+LMSe9ua17bf/PZGDV13qvZg1XZ+xIhKn/D82XPFPedNWW1tb3Vra4OlK4IFksvNIUgA9blFBJ7n7O7uoTQ4Sh3pQqJzcDmyIVAMQqjlgQIU50QNxyHNytTQYV7NpUBrgh53qx2CBsh44621bZfRQceaaNmQHrDSwhLSwcOLk92DAwtCp+SyhPTcVoWNJCyvcgUyP1YmDqglTnTvpNQWs/MyxcKVtVArwRdKS+gUuN7xdv75Gq8vfVCKODo4RtRIfbTRAoa0y+HoHTKNQ4TjlItpclaJUtTyF9RiXsKrVy+pePn7w/09412tqjZ68imHDTpxLO/y75/yuOZcUAhtar9iEuf6ipMMfFhhRoVE59owx2CUjxIbzi+jxMfwrq9XLi5OletR+QRtPtbmQi99A72Qky5NiBJAgRkRypbr5PDEpiDiBHUwVve8GqkCL/uvb2zyIi4aEhcFgOvbet4MJPc6KkArN0uRyrjywXIGys6iFZHXGhHlnkLxCZpMXd1aN87JHVLK6MoqyBH86NLZEtVn4eU5WgAPHmg0PSwe4VN6hYKF1Uqyqs12ckNsycNtxsHpIZERYSLYy6vy8spFcRE1Rc41BeqlLmhtEEpfSGoElFV9MD34iUhJ4gr3KWaeSi3FPAgavJYYSC7xH7YPiwXlAHN8IQoIZCURC2oihxpYk8qNpg+lYzVmY343NramZ6fcUUHwJsMADmAm7nt7e4MyGB8JwbiB0IurgIALaIe1VZnZhTgd4EGbgChz7cIG8/qPoQUdsFaYIw5WOvyyVvaoue5sHcgtooPFO0esUvlISOV1F4FKJL99vb1aNemPaJ9YmiZYOoQ74kNfAXrTOD08KYB5BmuQzAScE97OfqFQSuKGSB44+2Av83DP2oaemPH4DOhZLFHcWpxb+u3tb3AMdl29Eyg0nEZ1BO3uB4w7Roq4tBVy916AJT7IARBLADmyLTazpLPhJqUiWF9Tr6NF38CS5t5zKnAUd0hyxaRUzBw1ofexqExkxBKnDrYZ8qEWJZTmZ89e9vUPhgLl+pIQZOdhWyUDZnLK1Nvw88AKfp5LMYKE7s459RYS6HSZAINtZOQ5t97c1MLMBCH/3WoCxPLj4MBNfbm7lf0c7R2yAacJ2MrV16Yr6OvvvpBdkh+o0HAWMcKmvBJhYqYNdQe8ACqYaO3echPLFDnBv1rSyaJ80x08U0t/X2NLo6sZaQERR3/+8cfW5hY0uiOj3O3kILz6B/qJkH7+6Z/v372X7TsGnph5ajlubnbFWkW6AJsp/RHWPJwWXJINkAhZoRtTt4K/ywywYzU19SiOxvpG7QxScJaqq1AkFO+xDZYJGUxfSIXtGHBjoOjI4LBwxxrQpy7bwRTALawNdYIuUNsXRcFJm2rmFGaW2sTwIbm28AtoaC7d2dve3NgW+TV5sUgyTRmorEWdnHjr48cPSHVnQ47z1VffBuh4Ci2gMWshCDs6IN2VXSkFi/yrSyu+COpsbGx5WllRd0CLq2fcFd4hg+Fcij16YL6poKD/6OSQrEhXkeCKHQG29xnDoTqkHqOoqGH3iotzlbBPL8/Q+lTvsmzFEmKAGF/i4sf8PApI9RjJVrArNj58WKK0qJR8KGqXl4atozJi4hUfIZygNfj34A3pdjgsc3vOr9raqp0Q+gH/VaRE6N3HKMlMSyfVs4PsDCsoejnMopJEKpx4ZmYMaTw8CPhPRF1dbTavuOVh6KAVhB15xsg26AXsg5NgwdMls0IgyxpKgDxGcJ2PmAEdasoYZ97XqRI4zVJmSxZteGgotHbohruYOu6/Sn5xidh/kwjhhsWlRSBGHUw7Cadvgtjb97+vr60RL0lnQ1jtwoSbGwEy3LZ6eDLL2K+t9fUAmOEzReGHtOdKPF1lAsm1tZWtzU2+GoQ/OboyCJq3EqLa2lstZowBz8tDqKofCFFkpdCucR2kdFZNIEEiOW25+U1VddWmvFoHrajSXIeNs9/fP/F+hl4gftRn/CEtjwQBdo75X1cG2uilioMZKTSmNIsCCCfpIuWYLL8wP+fUDg4NGdhLAxZkt2U/PJDXYvzJTgy9oP+HHShVlBTktQhl3WGiiOtFzHIQVCcnp4w3sN3ncTFhVu7q6sXNlTOOr+MB8hV4L69UL9KE0r1iu84bnPaJCe8AfklJzG3ML4AG3K5kDa2nB3U1DjmJnifKFhBVpF+an9/Z2ae84KnBW6IGv+IqkMnTCQ9sxszIyxG3fLPZNOUdA8nhUV9t+yEsRqI/nje0RRaELbnrl9M8O1NWJ/LWCZNkhEyD6zQjQASfm51HN8H0rvvOOyzwCczDs0lz5eKq0xI7QxpK7u7kDMIeT8SDg1zGSYkxvJBJwGnrS3AIJcJ2K3dXvLSyzP7n5mda2zuUjkGKirsqk5mjI9cGR5flvQzAmuPKUL5cMpctTXQWGqJvUeBRlbSqj7AaOC0CqZdYNzUDSSQ2Bppkm3wpJwkUcCNiAIuSVtKIi/2XlycOhTBACOcIi7huGhejLatcQC0DKQenq6UFefgohl04a0lZ1eToJGQqeauodMN1hscSb1taswzhuUpdcdbWESqx8HBRYY2ratz5UiW1B6ZIG/Ha7idTpubjmppbSSBwAejvp0RMzeYmxJKVlYXffnurZcJIPGQ3fgAjxPvz9fQKckpfYZPE+2fPXsAuPnx+aXJ5bWV0fBRRrpRREh2DSbSi0qJUIwbRuuaWYll58/7J/Y8yIJmOlZWqSzadZBVF+kKsq7zkTAZ4c7A4v4xwdgbilsS8/O7eruraMjS9/J3v4Kx5Het1cLS3MLvkPLpd0rHhyAeH+r/7/ltdafCdup+fUSCCaKbGJsbGxmrrq40M1netcM9A+dU8KDG/ICoHyujm2ZaVM4KLe7MrkiXyu7iwlPz/BPBvqItBCNKjwNSJDAoTZ0OTSkl5cWI9A/HHtzrV0cZcXAaSIyK1zDiZfromhmLmeMylxRVJG1fOlDfWVzn9GDXV0KBVdXdrWwCI0NKkYhQ7z0/qK5Tc+GGsolMBZTs8mEdhxZYFw5NGu3oUjYaTCqAsaRzJjCKTyHTMTIcL3oP87suvviT0WpxbUNcBtgJepRvZCINODYZQOjCOirQw45GULYrbNI3XNwbQy6t1TwfRdG3y9gmzDcu+upYXcjFaBkRmyB14sjBra6tx5UVevgYo/Xeer6enVxOPYZvgAMxCyUXFcHBwMjU5qadEKyYEJKWw74L06sqKT1bRm1ucnXR7wMTU2saK8KEbmbnIImQ02udvjfBElJ0eCjm43ZuLy0iJAS3GWRCpIScnuhhozKfElZ8Y/GBTNJFEMocMkYFy/b7acaXqTMvY80rLinD9uDywXZ1WYbn0UXexlg65Q0qS75TA3hc355Fg5Odt7OyC0jIAIx9cnyknjNkvoSJdtXSKh+oTKCnPZv6vuK3iF+pdN5FdnpFLTc3OIXpcbFZVra6Tz9phCHBHJEgXkN0KYElFjKQRliJ0TZ1p9fRaa3ycMLKxvj1LnbyyCvKrhZCMrqyv2USAV0pi/8QJKnuRnqkonNpB4dzjUjE4LJq5VLp4aq/AawtLnHsc9tYmBVv5E9VGtnmGDxkoJqiitCyO7djSEhcEKMBG8m/Azn+Sy3LuHJ0dARzxbxwcPtFnqEx7JNkRKaZ3wUDioDjaUC7fI7tcdxj/yaVj+AxYXcKBAGDUStM0YBubaz/99IthbcPDw2YbGzUPS0P4Yg/FFxVTsqCAPe/t7JYVF+tC2FrfxA/bWjFA/Ha0ZQNOCRRbVlQODmp3HRufJOvY3N3RDSPqoB+Uhbx65DpRH4j/K6+scmwdELkI2IfqJyiiZafFB/85a0fPX846P0ZcAihw6EMDg7AFl0jhg4sD9eimbKW4S+16suPSLeFc2nRgSJudPuzrM2lYyIFFBSc0FAox6BMvkJ9A6bjfwn81xzKj4D65a1L/hpawW7MWkETTU9Pmz7Sbl9nc1NbahrUoNgCksECfH27au3HTQCBppgfwNfQGICHg7H34Ojzmwty8U6Q3wdWdjoFrPx1j/RdgjhovNkxWbhvsZfpkJQkYZPoshtuyk4hxp2tmyr2PbxiZPNvwJ7UfhB3Ru8Oi/wBZYXvWVjZZp6UB5TwnXyO6mgL0RxqhtBB9tjU1E5NjYAhZlTBofqwoEkkQ0Zs2vJPjifExgmVTJG2Po66Q638CG4IelVadFYPkFW2EN9V3Eh3FbhuP3pVhoAiVqdwfjQiSefHLdkXhi3GITNgR6iZpaX1BAxPBDtGMulTIzW3Lq8uku4Cn0jeQKP6DbIsri0YShuLw5kYPQUl6FqZLf3ya3fKOZyUKjyn9L3IdTwhlG3JgvjQXy/cJCVQqnJ24Yt0kqmVFZUK9qOZ3L81KUcp7esSBOGBa0e2UD+Z6wHl4ipfHN3C7dFMRv11TXFLq/jVHGprX5IFKGOjvN8yDAxLwzMiUePUN9Lu+DUqQb6SbOUqcW0FCoY1J8IYWh9LJXax6cw0611HBuGEl3gRx73XqGrR6lpJwOwlmKPqTAClHR34YkigvL8FQbe5uqaLTrn35xZc9bf1yChhdb0FDQz1tprKwZN2Tzy3Mu2jbtwuZWsZ0YRsIk5WRzQ7f/PIrSsYFZjgw8FYPxFD/4IvnL9Q2lOJB3ehB5TwSGZSpDoj8CRVLkMtayLAsFHkGjCIZF6d7B3rJWRXQ+FYUUGFJET5kEzmyvuEUgEoWgd+RAzt4IApZKg+lEQlGIY7ytNYG1FdUUcI3sBDxkZseAqrPA5SmX9zY0lJwXnGTMpsIxNs/OhDFXaOtt0x2TlxLCdPb16W8Zq6RrfScOtqRQjuG75GWxn0P7vjM10ZwfnTizxSMPC82DOaV6glOHt7M7YnRT8pLKs/Hh6d1l5cEg8urFBhruEScsDGFrEPHPF212BN8Rlx9GhYp0qczI/O95TY60kPhrdpEa2BTwgsHVncjo1kaJXEDaLRP1ghFimEoRtOTcCYtTeaPbRLTSjjVReRMgY6Js+/N86iRSEEqnDW1gkIr9xXJh8s5SkrEGlMxWK8iE/O1E5y+AIz3BnzT90K7MSymzuzuSAUead4kF2CrWxhFrMmJif/z//y/fNfi8gKmMYJ2gTu9S3ikWJyYMgLfV4is6Gs0mtNq5AEtqFTeDjvd/Kfg7X8uwwMdhGG4hl9CaUYpIoYwUZpcSoBtmO91lOyyeGnijNjE11mfcOJZdC4xhgD/cf8QtWKemt/XNIWBsRQy1HhNHTaqE8XFopowqYmK0tSv87TL9ytWyctyMu7Qfff7BwNXmpsbVCu9hIqXxIK/8wPpdCfkG7YRVOEQ2Hlyb+dQYZB9Kss4Y6Nj4/rfQmhlPbQPI8uLilEiDi0fkdbnrOC13dgnKsjRhH0jyby2lF+Oz6wsKEQpV2Wy6r3K4vCaXt9/+etfzCNYXd1Qy21ubHLYgCxMC3msqHBz6bIXepbjn//5K0U+16oXjpqjpa1ZqcSue+eI/xiJ7DzYgm5yj4o0rVfjsxBBEirXf+MiWxtbNCkX6X/Lzhr98PH339/xvK9ef4YZV7Grr691Pv1ukGjBuadUmpz/04xTI5yIIZEk66sOwEXoTGpouplClZj3B3blv2SsmxsJ7h7DYAyGH4BMpcak3IC2KH16fiIRjutrDg+1DqCDtQvqRfAPapLei+INaoFhGZkNRm4IV/rUl2YXgFihqra+kkyCNpn81LvTQkB25nX7GUic/ckv1F63d/fOTk4UiMJ3w/NCAGTlKN5fcRb2m8zf10mJNDRqrahvamx3v10MSnInrekxsijSYJMI9EYW4VazyrPqG6rFA9Cqt7f/xctXwo+aDbTLjIYGB267u2Hi5qYGnxmKkNtbQ2oVCdiiWMt2LSYDkNbobjfTzV9GdmsrkuWITwAZPEXaKH9nXqs4fJLkPWLn4FWtZ0VNxbFBOtgWLiEdlnRScmfqyR4YH01ZoO/G2uIAfbtdgfX0k3tZCj8kj83F2Mwtrs1Oz+Om+B2m8vb9e4l5NfleWWla7h1VmSaHJONpwdSpu1tEn4ZoHwHjc3I9vd19fX0VpaX4QMU3f3c9pM1SEpASCr0hYklk3J3fRbYU/AZ4LYswyg3Jlin4pTMhDSjmWu973wZ3rjY00l0wj3qXWBUW6LfngKgqtDuwz7T2PQ+muz5LYecVvi+udzOObQeCJXNPhXTPwl5B0JhA6HKlVINOHOGTc+MT3DOXyj7Gid0YZk3+62LjwpKKLDef3D8cH5njZ4o0C3YjsE1DncsJjhcSSx8+fRr/9NHxsTigZTRCHAThaZSmhSBIVpXXUwhfIAghG7BJeCat5EOYmcfkWNm/YCZmezDVRAsCgiBk/ID+Dj2hzj7b8K9yAk5tbWUtQG5PqXKlkSe20AryN8b2oVKVCIkdZdjgPhLYZO+dHMWhE44oeaHp4SFoN33IcDVqIpi0YITkmfIwASMnWaPC5Bk4I3AQYSgqQJzAuLgFGHlU0VdB7rtvvx1Ngz95LZ4HtazCCriQAp5WVbloDM9MDVldUelriguKBVoVCMlorhlJ0XZ6R/3hpeRY4gBkIK4ADU1NjezB/6kWgsy6048P9sWeutoGlnAyNaXBxa5JpUwpkS5Kc2E1GYM1IaskMeBn5ufmlEvX1laUNzhrb2r2DFfjjPgu74UTg9wc3Jq6amGITsQVtTUvqlsblR+WCcUdoCCLjw43t7cKKWdEi0SWpoEgr1x1WVjCk4dM4fwmtBzm14YTyiYoyP3s88+ZclOTbKDYSYKnML9AVYTx+objo4O5+Xldl9yf6faabMFJeihULCgkw/LjHp1PkRaI7f4rxYXTjCn+7PMvNtZWZ2fnU6kCLpWJS6YEUkeFAN9iSTAltvQ2ooJPMCmhq7fHGGFCezmvhu9wlxoa7+4UXvg7rRM2SFV2qL+fDOvUffS5xrWXuHMStIDfKR7d7yGz+eyzz/Vtxa40NbJFWXvTxQWpCfgg5BBiqtG5Gt63zM5Mz83M8CzKQQgNLdvSGlUfqXnk2Ol4I+e3WP2D/d7LlojPIKcIQdFmR6XBWpw0hYHkyDHkm1LzwuIsgNPe0jY/q64xp5hp1FSMfCAbPTmBnnIasgUa0y96+3rbO1okdA7dw/kJDiFcki+OexFOPSE7k4GCGMqvlleNEUGkyCZ/xCD5Mc8jP0i7RXRtrn+12fRACiS8lGTRfBJ/KNcOkioRFlxUUoBmhNirq13rVuv2SUM9tS+2t3dhNqSisuh0du5KZF2OuV1d3RjMmenp39+8wSWoLvhm1gZliO7yfdIA/DKv4S8/Cd0r3FyeXszbkTNNjLfQBmmH8/P+w0fZPbtnrb5PN7+15f1xlCCqCLqzvRnJx9AwDAVeOO7KvMranCAeD1ZA7yiWokDgFeHfR0WLGTIVnxMdj1Sz141N9bI+UMsIWzfDQzDgFBuzjC1Nbbk/FvLFVAYCavDF+bkoLwdV/JqZnOL1UBxISz2fuFhg5fj4dHZ+4cYdDwUF3DrY5oGV/iC0iorQSbNtNxfpeVEWyp5f0PIEITl6zIPIgtnxXko14TUolKpy44xk0vAg6MJB0+EYHn6/aILQxe7BDiPhGU9P6QV4n6SGhgfairOj7Z3N65vyiHyP2giMKorNNy0+Ozufjsi9usT2snZdKnaTIDhde3iUweP3ZL0O49LyQmhfhEzIIZl1cnZ8PX0TxO/1pW2VtMEE0gunO4ww5r1jdNV3E44AN2o2bfBdj8YPZtdW1ZjlDv6Y+mD974pi3BPu1GZGtbwB7EUIHkmBMJMqIggGn2W1aR+M88SPm3cSw22al49PjxVCrbnMWPZD64ze5Ar5X2dQcCVNhO34f6kIDOBk2W49MUoLajz+zrBBnChgkJzqyC2w5tg+RoXNzo7i5KWCTT65cI0xa1lJ5sGnB+4mDjwKg+cWIw8oLyOqFDMcOnkbZGOaNKSv2u+tAYbrLDz5jnQ2mL3CArVSEcAvAi9CGsGZeO/JyVWoSPziH+Agv6uTu5WsiKAUzPrYHWQR3qrKGg0gkCStxDipY2dTcsnjO1Bgnyd0BKAWVLPiga1X44G1Ini7P7mgsL2lnQ8BZyURXPTq+rKHVHS2cV5Kp5i+FMcTThY7mVHcUapq0drRgXKUsBv7I6JiyYF9Qiix6ASKhGiKCitrqlEx6xv6cdj/CdUEBSDRztrmuvCiGIgKsHyK2m5LUH5xjb3yAHGRbeYfHXgqHVXNP7ItFBEK/uKiGFgQA7yqzgKiftjqq6++tp82j4S0vaXVUrr90R6D0AKW84NgdSSGBgcrK2p4Og3TLg/RUO6EO3eQKVMjYE9kVOQmcz//7DVGuKKsyiBGEgMH0KrJF4OIZBKKqCUlpGDESE4Xcn93x6CuK26MK1PwQTuKmX4yLeEqqcqUwx66hNb60F1dPVzxMuA/Y0pm1xDAQbUWraa6kiLQDrHEze2NiYmP5FavXr5qaWvhfD2zxfEVR4fRk81fAOm8nv/r6OxQLWA0lnFzfW2fLPnde3auhcdbk7g4FbwYl55uBHvwlPCXDJRJB5Xjs9KD3hwBtQHDfVGQvsiIhQsXoakqKjxGJSpRrwurtrGmvspxipQwK2GUppm6zo+Dvbm54y30TX748DvCxHiTV89fEONz9J8+fLy6OXdLX21lLYMBeHUc0pZNTUyKoLbsy1dfSBrt59z8rI3i0KQ+Yi0DcLGAA58eRJy5vrHlyPp12nF3EhcWGYiWp7qjaIbvVig2LRLWM2Zc94ZZ0KIOh3twYILsNKWQM8zu5Uf0LUC2WcvOB/0u9kx057k46/Y25ahqTLGJDN99/Z1BiRVVZbyktJqCwy1/8l1lcwwwkCEPg3JAYO4etuBpQB+8CX0I3UhjU53EC1ZQJFTbEj8IsSnJunoqHA3pPnwnYWKXVlp2L5+0s9hbsz8gQX1dOvXiYvYnbdvXaGo0Gicr10R/uf/HblBMGsaFUgSHxYkAapGH3WhyJuXld/B+vAb4FqorF9KeHKlsM0KH38rwaHwEn0LQgXAWQggQzJrHI6hPUnMY5KXdT7xnXRwiS8c+4e3tPfCpiErQQfoQrAYmnVXn58G83L1hIY66EyceI1ElVZR4wfoaCukGlaNjK25iNi3fyMgz9gPgC2yyPSB2f+8wnirIGL2slbQY+qtZOwooEtOrSy04So9oVpdvOD6EwiPPnyPi0YNiqkiB+mAPXI6bceFQfAOm1oUZTIu3QZR7CIfRWQM1bBnsMDQ8JBgfLhxaOqvEkj18dWXI8Mg0u3q6MJpKwXAkDOTMqPAAaryhpBky42RB3rHjY4bAMLgUiyDDA+9Q1JRU8iE2QGDmdHNHgLbEQspLqtTT16esajYiHsRvOa08A121rqCPYx8Ut37805/VOGXbChRWHt2I9bK8vJMeFPvLD0jywKCG5ob2zrYwBotXUgS6cZ9OrsdT+9Ttj4qg8dP4eOvuae5YeTDtqFWNuQUZD1NpaKyz1NIpS6fqv5Yh4oYkCL0hqSXxMr/KY+QWlBRYByseFKRbRDMT1OhBnKF+09OY6YLQOA4A10zUzAjAdkAA2GejIT5tbsZz6Qr2BsPPhm2PnL2jq50c0MNhkSRoMiZGid32Rep4ftFK+YKqyprbKozhVV6J0NjpOx1RD6mUpIAxOTmpowHdnIPBP780zgNNQ+Mh2Vc2Ya02fn5qyt9BiTQHdYOtur698S8qxraWZmZiYpy5KDjDOsK233JGwAG2pZALRFh3u6LexxuyOdIP1VejuqEDAynRzbINU6tFaVhDiiotgKQEUejAynFeAglEKeRYKDGWK+QydIe6Pc5MfvIs5fsYB2hKmXmNlsOfRj/mY2RnWUkYQdsLDysbVZL5x8//pDsRVamtYjRQXpHHamnOFfOkb1ZyanKaubM5maqJ4bprpmYmlWj5fxGL0MKOaESkA/b57G/R2FjAKT+PKB1+4ohdJwWpgScxlvIhA/ulhO0QohEgdPGA3WyubUATwFq61F+KCxZCMELet6m+2R2pLKGnv7e81OB+DNyxBUQuF2UUcUnCJxPEWlLXcE9mioAcSoV25PY++2xnB8PJYXV0dg8MDcn4ZTwUNTyUXtlkXEUeXe84G1tpm8wiFP6N98EChZB41b3tUESkzB48ShQ8FOd6e0vO5HTyKTbLodKqoyCMq0wmqgVyJTKrIa0heWZCi4ZUrKxWV9UR26EXyFdEFB4N5iLl3WM9AADMzUlEQVS5UTuZX1hymMxSxEACU+ebF8F1ZD7FePLWtt7+Xv2qfCRmzzrbUwooggJHmlYEno29oAiCEXITt+ZWXl6IBM58yK/OLrG6LFbZgBgHsKB72dned/5xzXyKk3x2EN34nKmIAbI4c+FZdN9lZ8FMIRZwSG/iMj7IsSjuoaviah1MQIDTxqia4oVY9ZPoTY/HNQv3hkawQC6A1+MAgH0OHnDy1IgIh9fGSRnjiHOQDFq7gClJuZQgiLdyyw63qmcgB4x0QJ8LxjAHxoZDpLzggIKtSmR3dTx0drQJMTub2+WVJmNE1pU4SyiuajdTArB0axurwA1VtD8ROEF11KhqEL8ZuP7qmlNxllFSVg/QMQ649OLCCCAfpQ6AkoprEVGWcZmw9ArGy64oJx84P9jbdtGboqCrIlU/W9wx2xz3TXnBl69egW4iG88IEQpzlixNioYNgH/xXx8MSdJ3n049XCSQ6yQGByW35m34K3DM+DygXtEYWJHHGOpk5XlSAZt0A4/NTXsmUKC9LcWVI3xspT5eSQMzcFgBN9onUZklC5XmN3ijvf2KRnW14mJFmsXFFYhEkkMrLHILihLNq0uT/Qs1RIVK0CCAG5epFGP5ZBOMRScpg1OglijIgaTNjEfRRX4sl1IL0ya1kFo8vdg4Wz904cm5AcA2GLkpPhBL4Zv8mn9xvNPfVypTtlKQvyATIaGmViSQ32MSIFCf6OcZE/oibk43ZMS8XPqKmyt5On/HfTAIBqeqRApGIfvxw6hVcE7M/Gpv6+KoeFLkPlfo3Iq3wIVnUkCWYamvfvb6Mw0pIhAn4ozpBHHZgEeSyMs8PDOpqOI4cYSeCxAOCYfqUdCTTJkFpixot1ivw5Md12MJomABo7/QtwcMSZGsI4NwfkQpIhAFLK5ERQ8XMPRsGHGM0AgmNP1XmuHl5WQS2WAA2O4VRJRATDSg0ex+aiPVQ6xPjJ6vVjWVkuseylfVgHM5Vk1WFs0RtXogz8LComoD+bzJE75KQs2/mIzhrpiQfh8fQ3aMTFNPjJUPRVa2T5bhCkMn+cdGmkRxJ5GwIF0d0YKnCOd0iDHRDfyUQXRLGsi+1zbWp8YnCPbO8wvP0zS9h68o7fLtepp8cktzs5qdSq1oiC/2MX//H3/HYKLlLW9vR09dVW0o1A1ZlL7sHRVk57uZiPdfWFiYnp5q6+jEnILSljcgW26eoiFB1+Lyig+BeemUHVSyUJvColQ00PcSZIecylQgb+7QMVBHd2DEOGU9OOKDvEO9y5mqasl/cYBOoFIKEk+YJHbiHRhPFSFCUQkCKJyCK7ATmdX1Vb59a2MjxonFzPRzwBDa7W7tMJ1pY3NrfW1TBYQHFG+sVWhYy4IZM0YCdWuug2rGV59/LYTYU8fsD+YXgHAQhDdhyJsK6Hy9M2mMhbdwkjjo9bUNqJlyyjkCekQsB885N9tBho6NFP+8rCQM6UE+CVpC1raF92egBFDipQdzNsMP5gZTbCdZGaGxDcXsczEOv/hCfOzAkqK6lwoPgyk1DQnPgzsSsfhuvUesl/Myt5CD8KamkMXUc6uj7zemiOqkFQmQzsYJCSIx/ztCAKnP4z08ye8wD/Ym3FRWlloZN2jLOKCB5uYmwWhnaxMg8u/sWdaIeo06UEHR/OI8i6X5caJtsDdycuqiKNKgY07CJL7iCXFHLmeVlbMQayWTIzQn8Csqdz97FY6XO/OmGE8+vrungxfCFLENLMKRu5LKy4i/0E3U3qyL1OLmeYof+Pbb7+1gZCvZudQoVtgnOxK+iDwXHpVbRMoi7Xt45KlAeBBQWhQg7Z5OxBgoofPOi1KFMktFLMOJHdv1rW3FG72K9TXRhCUGex1uR/mUSdAIaLqx0rR3QFt/d5mptBIyc/zBR6thhQf6BhQvQWSvBsTIXGUhoKqSi2KNNmglBEJtc9tSqZjvz7GEUKqqCqXlE2iclpYw/na8xC5wBFyiRY5iYLo1B8pXvvYWNBpxP0Jlre5UykMH0Ggfs7z21QoIprJSWfJcr2Ra0NdFX3ITxMgsOM2oZiJngWiWwKcjRgQW/+D2FZvB8+Lz0tniBbPTBMFGN7c2jh4pT/M4CGm1HJDzogsGGCFcGJsFI5osqnPLAC2EbBpRA5ZSG5xdQAExEkDspQZjgMFLxATEGBCshWV7a8PLU2fLNsRM4n10gaf67bffRkc/QBkAuzHiBcUFnKyNR8wR8NmViooyL6VVWJRWyJU5wnTsmz0F7cxY0tNx6YuSt1l17XWISmMAZJTNLW32xkmR0AFZfCj0LXWI8GYzi4QcVbV9HtFZ9RXYdqwXKETnwNT8DE0LfIG44Ask+xIgmankE/cn6yclYmd6HZ8/G3H1DYbu+Ix8KF9vIUfszoN0T4PZpcTqPiYF7w2PDDknEpoVV7Yd0gInVZu9FlduI+Q6ounD7a4eRb7A78BQOHRBkNoVQ//5F5/JrmR/6k9e3LGHnhxCjfrSW0cLtInZKRYkFAiuiS7Y2rqLpLKhXlkPYBGwTbawLJ6HWYdLz3PtRjvQvbK8qBBRW9e4trZMlmKb3O+Irt3Y3OY+ONDr3KvgRhqao+rO7WY8qv/b8YObg9nZOcD5s9evDI3QeWejURDIsfqGJuQVVthp9PPwGsg8eT+l7leZnozE7DHmVO2siM/F83355ZdKRAK5QOJEUCUov7gAxLOVlOmeLgvtaXW1MJCb7xbS282dTRQM96SWIIdODzJ58fLFi2D485I0BxIRQcKv2CyEpBn3PL5EgJDaIktYmbrSrvjN4KlLJTQqB/aR3UZralLiqHc9G6frUMcUULX83AKuR/7EI4tPIocmTCkp9I3XgdO9LNTCQmEU3UPpzDvDr8jnEGihmbr24Zm4eLBJxDUkiJzXCDa8vuoIwZvVq6hS/SOlNzA5roTlX/h0ztg/+2GlTdjF5nI64L4PjwaWRKb+EMIVNDRk4AAqrZnkZFQG/G5WBzQkgPlqHCMGHDPp/zllIiir4EB8Arn6thC0teW77s5OVZd52e6eTkK7GBl9dLyxvSnwy3EZre5QAYzJCd6CiyPNh3DCoiCsqc0Af93Z3iHwAN3ycqqxdNexmZrVdy13iCb8ErGmJ9RtyrSVeYNTraiwRvCB4AegsRy/a6HQ15A1V2BujRqSt/bP3sjpRgNEtcA1iJcZnBhIjWySyBLdmVSowNPQ2KTHH2sN5UXZLTMpp/QRNXo5c3OjAaVS38xTHReml3ArFVeXmzKptwN3niA/vFYftcioP+9OAQi9ibueHE0P2XhIv6p3C8/W2dMpNadQKyoMPRW1CNmorCKm8RwdM1eVUTapgihaKxOKm/CuTkMIgBdK3VwJDJo4aQAQIshBMVXh3X49H3melf0sWUItk5OAa0O+bh7O6ZlBcYha2ISTFMwNBmDfOFwnGS+hpg9uyI4l2EKlHMepUCwi2+ImcMHTM2aym1woXbr3KyKq+xDWN9bx+NCBgEF+67zRVjow8mXPWlZss0M4cXTwyI9w+vyLv6AeICI/pwAbbiewEz6T+kcQthYh181KTOJ/jo4cc0aPnBUAgG5VR8V6+iLkvoVmKM4hmfD6pscIn2W4O9mi0OIPgRT8FRvWva3GIkQxYu5j5MWIy0sFKqQANCJc2dna2vqo/SSycFxcJ1Qkvzb/GUbwynr7AAosakeHYRj9RcUFh0f7yC6pq9hgqBHd9eTk9PLiEkGegqRinbdmGUab9ff2mxXhX/YPdxPuXktmFuUW6/udGB13/zjfbbUMm7QO8glEz0YM9VtxmKHRvEeirpi8RNwLiQhsis98JadglTyMOOUMTE1OgBusRYHX/jq9SnyiCB2nASbTk5PSUguFq5VAsGzeB8eNlRRl1TBAP0n63vEeHbHwQzqdc58nc9852HfpoGk/XKdvxxFJHZxhu6u5hhO0IRAKENfZ2skRU0nxR1JrlsAQ1SE9KxSq3oWENWBganySVZhD1djQ5N4hmgfPg2yRuskjuaramlrm5MhBbeCqL8Vlbay5jXjHOquSuuBIesS7KUUGJVqey4kYpeufGXB3dye9z5RrPsn/Ty83NncwTgrs/K+nFbPFPLIlMhXnyqC3t+9/o2BhRXyHBBcYYhE4Lt3fTr5nMz2Xx5H8OYS8NuSVxphZxpkYDa0aHGEWOSAIRLiNRgqZf7COudkuagMSlZkouGA8dDZMEOJO+v+44Mcu4GSQvPA5u7NpIoJmOPPmgqZTqDCD6cYdYTjluFeHY405ZXxPlGEfM9xQJHRJFGj5/LZ/ZvPQDEtw0FA8aRmqx5ED5cBDoBXA5GuEECyb2g89JqvAyOLzQV2DlXht6MfrcEbguZhaXxfX9lHLsD03BflqQRdaJ2jhbiASW7V7uOvUUNdAe7735OwIxTnYP4D2xOGAX+2tbVGPdncVZP3HiNCD/TdvfuHqnEneA9T1Udj+IGm3trxUTDGolY/S4+om8+0U6gfCRmVVKWzOUfoTJ1R+bwiupA1C508FFZFGzQ9GZMYUGZCNgAS6aUfwkIAjXanlxVhysofJrDQnDB5FBytfMTgySKfg1KxtrCkcwjHCzNnxqaR3b3PX7CzJt4ioqqbLPTyvEK6ufhkKFDPG+Ri6G4R2WOztPRdKKesVpicmeDlVSYw3sphb1tog3yXD29y40Y2kn0sT/cHhmeYqLBlsqbahlQ87phqqqpxdUmZXOSI8leHH9fV1fCbmU+3WGfS1rCXIOj04NpMM1ETpyqoy8JoHklL5r77PUkqpIuW8lwqYMq89O313BIV7XgJHpsv8j5TE2YO5YJa7zbvFhUXeX+zq7+uThREfexQEKC8PgYYNlZWBioxYQg0S+ss//4HOpMZORWt7uy8FoABJRx3i9ivitqHwNpv3QVmqAsXB4C2ivHx2sLs/MzW5uDSfrhZWxJCj9CVzfizyXIqW+3uKGeEKQUH0bSaEh5dzsQOH0kcxL+McnED56UB/f1dXh3DPTbS1trvHU/RSYZcM4YedGOsjPQfWBF5xjrnLGBwbmha8LvesVdhHy438z8+DnB4Sm+R1vaBwQuKlJqxgIcfELA/0D9Bxcppo6GOT5u7v4X05KbfukgY/n/GQhWRvb24HxvHX4NDG6prwjk6xnXpYDLt1aJGz8AJijVSRZtQzcyu0uXi5lrZWb/Qf//EfW9sbvCrwCGWUFqcqq13LF7tsDLWD+vHjJ8MQeRB/P4iZaJXAI0/nYKA+QF04jV8jKckty4u0Xa56vCNLJWRiSw6VNMpiIhIJ1ajCpOFsml4bfV9i5mJ3e9nLl47cxNQ4doLLtkhi9e7BHoDFG8KGgwMDnn9hZtbRlYn29vaZxkbpZDdh5+D3M56EGXBbJo9cNrWfZfp1S8FZC4dcOQ7di8/OzrDnNDlbZ7cry5LPnz/nN3V9+9cYVn5wtLu9/e79e/fXqmyZMqSSyTJ9INzjqKv4pe8dVHYquM11C3l0I6vRQ4ISwe6ubngCBTE9Myvq22glxt7u3u+++5aQI6STKKOSEtUjF5aJZ0f7R/C5arZXARc8sMdAisIf6KaDvX21d3Zup/TQeTvRiG/m8vlmLl8FwL9aT8dBa7BT5mxKXBFRCsy3TymzkMCCsEkIU7Z5rsj8VIjSTNBeAwrHoEOIkTK9BRMwb1m/ejCElhQsJeT1z7yv7xS3+F85nfK7OpNYaL+0jNloZcn2zlZlRIQYL9nT3aMKpUYlRWAPGGu34DlxHgzlBn8I8Pk1eeTUaiqQGbLIAA2Rw8ATQv9W+sPsxNbO3tinUYiH4/NUJui5bNV5oenmHITNF89fSdI1BGQ+JoS9jGKzgdWQo4YEDPH+yj9cnxh/tb0lPADvICwBOsPr7uzinTk77yUXl9Pw8s5OdOM3NUp6raeX5axhR5vDhAQ6oIcZQBjiuv44+aIwAHHzoTIe7yWiWi1xHYq1lXJBP2+69cLScjp7SMLkvX39kpggn6RZbnXWxPeIekoA1upqPP7wyDMew1Qx9sbX6Z+wv9Kj7u4uk5Lgej8vf0IPWnkDPXa39n66+Fl+4M8xhIg6eqpcvD+V8M4+4rpb43tXlwKA+mXGTVSqY1jQPY7/iVLEcjnIUjfhwHeBKyFfI0rzQN6T3JhMRT4nkgBjth/0lVbL2TUSqqgpSiAxmAhQwvt7Z/aBA6Uy5FD8iXIKisrZ6+7t1i4ho+AFHFYYnOeNn3ncltWLBAIj/MEPKt24rYSxIu5lmnAuIGN9qVbAB3UevlXyCyN4K4qahfklOQkWDIiQG0McdXXVl5fNXtjeqPKTHqOGNR8p8XG4MmKoxws5zMaIkr4yPiIBCQ3EIdSZbm/mMJsTxsId9w4UlKHzNs2VpGA0W4TmlraH7eKObZUJEOCzfAoc1rvBBsAlFCqA4LFFU9ERhWVhpWNOFBjHm7vnwClmcGoGIraHp9aQi3z4+IFXclrmZ+fZK9W/Z/DhODewEIQPuJFfKNP32LZA3rq8uijUqTLxDLYbXcleO7t6Boj0U7czczM+VkxSsK+sqIa28H2ry2vjY6N6qlFl6nWICOm6L8I/egUr7PlDwkyZZ4yXYd1b61PTs9qwuHX0kS0eeTZkMXWl5jeSF5YK6sCDohPJiT0iMPZptkzoEjCQjdJB5L5DYsgayl5KxMmUlbq5tEiNjCyQ//IhkrqHXZKfff8qHVbq5+oILTWyCie43cXFOYhBgZXNuchB0sBVpfvqtQ5Fzx2gtLe/v7G2zkJsq7CjZclbHJ4cZT7ElSa6I0INvbWJWXcadbESVp7yzgRGRyfoSgeM928oBmERftX8oH1k2wgxJwf509nb7ShKuKMYfR20MijX0GxhC6vNWA/x2KHJV3J8WgzMnm/h5kyg0njlFzwBDtnq4c1AhMDg0UcpZz1bX1llWgyG7IRGDkMig4C9nEjniPNik8yG21cz8J80Q90nQxPMriIqcN1wUMxmfUQjSO1ZnRxOXs69Sh0cakDPIqejY6Xzy0IYEouSBXowS8Cz+CRxRpYP8+YR0lfXSp5M3eQTOTU4gKQVObC/v3V5dsNL+vO8itza9OQj3ZFYBbQcgRDUD7I41LBjdnG2UkKjWm1DvR2EOdc2llxJdVyYt7e/ZTKeT66pr60sqcbOOCXu7o6eAxeKcp8ZGuB3sNucrWKYTAgaswiCt2dWcSRws1Ne3bMAAWb96qz2dk6eyKYYQ/QGIcEiTtx9y0OexgjNTOaO8JHXKf6BvXG1XFwwJ1qxzMZ4dJOdyFcGznORhtEUlZbI5BSfci9DlGWpKQviZvIS1RR/HWNKoBn2jGVSqaLDhvTZlbk4jipLkC8GRZaXr9BLAgdiGsHlNL148VrmJyeQbrqycXMzjwYEd7C9ucPG4FfQ0ObyvV5fVoGH6GxvBzjIF//xj3+qLXlH74uqVUecnaOPuJCZAQ3B+W5ucegWze7To3GF+hObG13P2kqtyWiP70+EIvHMK5sRl6ypRO2JaU96/2yz9XfGXDfMeA+lSKYO3MGATsypxghJPSs3b4cJquC1tLWpLCDuj7NPvDzD1UYxMzf7X//1n47Es+fPnBwFufn52b///T8lhtK33p4+RQgJg8hoXZRDcUVOnQDM0WPDUbYagwmwqLV4Vf+nnViEEqgQTQhzo2Oix9TcW1eyaQM50+Vb9M3X31L6Inasu9RMcPaf/CQ6QJ7LzfH1cp+4GDOGfR/9kbgIpIwAN7qwsCzhADD5FK9PhWk1XU0ls4EaLvsvB7OGpb1moUDHjqiC2/TkjFXu7u7gEfhuMtuCkkLlJpcXsQn5Cq+H8ceE8HS2XirDSYEZTF/vJNXzpw+f7A4ex7ubPMxN4KaMrMK6cJTgvPQTI2kOHMrS58tFZIKG8WEk4UHNlUEbDQ3W1si+G4FTZ4Y3l2wRP3ETBlfRBYOZ+DeQ+ZuvvtHfhKzQTYrAYR9y89sUE3O1xREk/pe//uvS0qJs0cjJp8dtuM9fkN3QyEhLkzpKBs/iXRAssktNJAI/1TM5jAUkiTOX2HmRS3FbNhcLrOGFYMRShLVUVIJXQDd3bwUaW1rFsF9/+RVYgxHFOb/ilJrvRjdcX9+wers8MTZh3ULAA6ZosHh4BKc4CN/BKqSJYDgjtJsQjXzZaBxITZpopRwzcVrpRUswWbPt5ui5YxFCaVGFgOYeBWknujt7hCuAILDSrVuGogzgL1uvhGCKIfvZv92TKaLRSsoyIVyUPdcjlLZmt7rOgTGbZsoF70e71g7hALciB+FiDExEarFJgUpsw+QIbMf7h4xTH/ny4gpD5S6hSJ4ieuUSJHPFsJjddPinJqcYv9yIvfP2sgrEjogrHIAXDjAo78H8PKRlN/0l0PLFBCO0OrCnN+I33bDkXXg91xGjzuAA0V0IsVb01yKJ2KfUt7a6jghSF0UPClTOsq/AqPlwKlILgrVgkBY5hPVxJUY1Nbdqp4OQnjgr2pmhr/u03nOis6Qa3s45xBjzqlgsYAjYZxjiWf7SAhvGbrvNCJln+wRs5ir3Jddhm77XLSUGfKyur9VV1dvrAHOchfFN9a7Dy5AqmwQogCF2OMS4Hdu86zh5MTdbHsjDCrqAqcXEAsmHgC1rm5+XpQyDJ/FRFt+vO2sAwbt373/79Y3f7eg0TSS0Q2xVKIVTTccLT0ItrSKdrhb4Lc0BHkmeh/S3R7oF+dCBgSH+wHNjexR1BQx4F2ZVK3J8WKOxCA1N0dZKzOYU2KB0bu1ebsHa3IpLmZzyPmDKsJGK7L+ikly4DoPoJ9JVlku7AHVBxyRxfowGz2PPz8+MfvrE7G0Nh2O/KMmRBahjclmykQQFWVr7zsKZovDmZ5Le0fR5PWPLi8tra6sqb8TdevzSN2Mkfvjhx/qmBlMm6J0xIaxKCm4RXccBsTNl24NggRr6+/pFC/Pzfvn1TUPjCn7KG6pETUxNjo1NWAU1NVUamQg70/bFfD1lAApB0kC7y7OUeaKZmQ5zT0eXzHRs7BMFpyoSPY8dglNounAdUgX1Q+WlzY1NvriflKijA8eNCVEQvkpdBpXsmnJ9DMf746N6mx8d1+GhEbgVZMLT6RFbX9kgsDW9TsUYZ8qdsWkGylwoE8Rnfg0Kxf6vBi/8qEj19t3vEYS2dsFkBCJ/fXCw65MJUXQkqdbKlDE/qCSdlg6M+SfPXzwX6TUW9fR0q9aoXrgP+Q944nDZ+JODY0FAw8HwyLBVZRCiOrmIgsqlAUFPmYRrTNA4Iwldz2Bf7ppxp+vGGhSVFhFlGupgqhq/o8UsSuu3TP8SscDaNAHI8iTI4uLnX3yB+/Kf/Lw4zciQ14IfHo0XkL0hTGFAiTMppXRnZGTYIaQ7IvSStXhk5BJJmDwBkGGyAXXNtClRCYjRGoZBEam78qy7p/vk+Mi0V6hWZAKvxAp6XwDdXcKQOEgC3jq0U1PT6+sub6g0XTUvJ1+8JoYGOxxR45nhYpk7QXSIbVwpUcD1U4/YjZvyauGgoNBN9GenyA0r09rZhhQfmxxzRO0UDA49SM/RhM763eFhteFttVVzcwuiu0IcqWVXRzv6Aq7jsxRoJQ3qFh7Mt9ByIDMVMDvbOkDm+bkZX2QsCuwiM+AT4cjjgxOnUShHLOQW5SFqAneb4Ze6LDVgix/SF+meRPcjFzh5SXdFAfgyOablfpx2zX6tLcJojEjJiCHMLMGJWN/ccaNLbQxDrHNRgYaF0/NjF+nwuoIWSOtjCdUceKVyxLEqBUCmD/ZSLiVwqawIbLp7MBgupcnPPT85A1DAQ1k4K1WJEP/4X3GCx4UyEKHpAQlthAludQkOyhSarZgRawd9QtVJpfMCP8lDbKjbGb0U5Yl7d6/XNpRGfLLpOkgYZNJThrto4n4bdycIy+KMBQRyNtY3mev3f/mBX9PjtLSimm0WETwx47jFRQvO6mMURYy+MDbQaLbmymhSgQmMn16YX8x8CA2IoMV78BvyDH+taDpYWZW5shOi8qhpEBQnstXD0PQEY6oX8tRQ/m6ZovFU1derHit3BxpsN9aIr0NpcCOEWDy9jw2EcXW+uLBEA9Tb24vJFZh5YVpVvDSEDahBUXJgcjvBRDlTlskOeGRZoMPiL6dvczPEyogHi4I+pd/TNmgZl5aW4taZdHaS5ktNqC6uqq5VYPeNbsVgiD7R4zEJIcRi6btCEEHS2mmBFVobxBF3ql3XmiP65xbmVpbXkHIBL/Rj5uUGcZ2f099HYj2U9TIxNT49MT7pqZgukGKsr7hoRwxlSo6NfkrmJdfXiaGCemb6MEXnX9oV0HFrvoAtukRF9VlCEeOn9NPKcBsaOWL6is29A1pq8371vsoYZKAOP6LcQQX8IVaFfi5jYAC33v3ixQtpC0RgARCFXL9+GbsumxMwaZjwHl5VondycUwaKEzBUzc3DrxqosuMssuwHqRaBa4WuEDiKsQx+zSASnh5Vou/kvKgdBDxECIc6p5hHQPPX7wcHhwy30raq9kIX2TDuAkxjPzGBCDthiIZbYlcz0g7qbmqL38BBJqtT1KN3wC9eRgnRO2+f6AfwLH9NthSSLqxbMxSzsYdMH0CFcBhfHzS8LsQI7e1884QsLQDB8PXS2PhK31MrIH/heJRTEb3wG6ACdGCmWSWArqTQePXoNS6ppjsIYjT8NnCN2/eTk1O//72dwGDwEsXBQ8lMpmv55xACsKJdFJtH5SW7rl+0oJ89sUr1LZCbmATLRVV1aI4xMYciUP4F4OcmLjXXF5e8TX+wbbC1Ihi+I5d1mXXOVfOoWNmnTkd8AoxBXzZHT4dtyj+gYEHe4dK6+pjToKzEVjxPgpfLG11dZWzZgKYRlm54fq3kbVdsYSgf87POjo6evu7ISd0WVr5yLlHTcXXVQ5WyjkETpNLPEZrRzswMPnbFITFzGgBIVQCbv6OuQgkajYo/hcv1LGD9cZHE8V2G2uRHRd86tiwBS6ZAm9BKUASrLMOCvUeUiIiNDY3tEBYgpkcOxrrbPZ1DJfn5flafBF3hqo6uZManSZ3ElyMlDEjqfGF2CnP63gvx1Kyj7szZ+LVi5ckJWoIFs27AECHK6vKg6ZDUDtc31431dR1dbefX5IyVFr509Mn8VcVFBHGBxmmUlVb1dfdi/TYMSZie5eGxwPLGAQzUhDZgLc2zEAlwKqqKsOVVAmVlWWM1sG5ODkn7rSb8hqjXzTDAd0wtXekXwQ5nEQcMkqWrSqcIFiQk9AYYMHyEWGXITY5p7Ygqi4tEF+Muqgyp8GH886WSyS+SaO9aIoudgGhgFLAAFiBWCJPko5IENHFYo+xoDIbg8eNdVVVlCtbXpxw6sYgB5VPV1pey5H9THFRgiMWsRAmaQFM9X2KwiKDKNzhLXhMQDwsnzELCEGk+jlFr9JSLRfYha0tEwCv8/IzsIJeBzWHvTaMAEEI9OgwRbCSvKMrOrsNsaj1+g4yhyuL8ouVcQkkC08wZYjK78JDzh2bgf8k9Lg72YDXDFo9wNa5a6OmZqeZMUqSY6RzYV2cHgxBMiThRwSJ3sAO+sX5w2EwexCh4aSplgx6Yx1qEB58slpI2hnqYpGzFgHxcWZz8ypMyby7QRVyWbIu+XTgg6YGIkZswdXpJS7ll19+1mxi9SHRGNdxc9vR1ZJ0cgik6fPSNZmWF8+fyXqeDw/L/V2Ghmfn9GnGXO5Y13wfAPn2PnLVxwfZjZTX6AlZmG7Dm2kKoHFUfjCnZqk/PmoTk9No6+gm+uvt4W5tj9hgQe09BwFlw6q2mR1ZF+5OwXD3Ys8gq7GPn+SCTlRIpo0brDSSoQjc4DR9gSvM7KUACImIqEhY5Qwm7lg6YmCivMZFSsaBSankHC2NLRDoJtJuFwqL+aiWcWhoxIVRimt7hwf8i8wSl7W6vKLqONg/iKl3YoV97J4b3/RGuQLevQ0uTjaWwIrbSzwdVOs4cetuJjHkAPFjA+rrqxQw8RhGEolG/CDCKvypML2yzqZFJgQtbZysJTzJ7SV5BYLUwDiSAH5ZixDPy8nyaGDadQK+KIU3XaUIG0tOcVlG556O4AEeFmbn93dNABxEyDixABQDoj9E67FOr2Bm58LC/Lu3HyhwvBegJrsSaz0YhM7PEfVvbx+q01hCmyJP0n9vZIWd5aOJn7XUgh6OJLcCZsE4Hg94dEZZ+UNRcWtz88Xp+ezULDZpcHAIFealnVIaHnjCv+JMJJrcls+fmZlx7FknsQA1uDuCJBBcBjmHS81lMyuLKwrU33/3vdjsBWEOTgFSMytIacdzS2KCJ3EXgthbZviakaLXcIBTqhrvPkKdLe5+1OTgrHnbSHZjRkI2xZvExa+sr67//uvb9tZmpF+hK+xzr4E3ywJz+BAyAZXb5sYGbsyYEK9pzQx2plKlT5U5tbS38PiQta108oFTSYvqrnjABtTMPA+YpvweU+Sys6jeL07Qqpcu/9Tkq2VPhJD4ymbRgHMzc/6+tbdNUJFPyi2VuL4ky2dxnkiasLqxytVKVdGYXCviu6OjDXJU7+HWpfA4J+bBT12euQYOeIh+dwQifEMVLiPB88C2rqQhrFLVR0N5I44VNwgeid/ciknrWvdtDS/m+Jv1Yq+RJ0gCu09Q++bNGwNNlUwcRq8vTRUGpE3cWXGZ/tBKKdfV1arGXZofiI3pgsmotjSdHRcSUIjicpUPnj0b8fmeU2iMGnQiZioQQbiLHF1mGKGFZcwN6qu8UExpLUCgXbmGmSVwrg93HHdjUQNPIm2VJ3kMyMlxormjuJZvSQ94WIyWGEkPJsW3MJcGr6rkpG4s+NLyEi+k8iTfVYqzYrgd9IaX9Q8WSs2dtwEgwudqNHfPcNwUQo1yxpitAKhnB321p/XrwBaPZ4muFFpKKNTrge6zq3MVPkJn02Uk0LpeHJnCIsr9gmsXpx8ckoNAIboxnLHmlnYCIQ+sQVr1M6JzSZFGNsyBDcTecDuiGmaPGJdyBJxnbDhkr+n9jSP1UTKnV69fkmAgfVQ5FUbCbd7f/vbLGxzswJDmgxLg2f+eEndJPcdkFZyvqG6GVF19ja6NlaUlNVI41Hkwv8k/wuoEsLG+cTW26YQH3FlI0t2jFBdQaBQkVnVW/R5mVRvFTeZlxrNnz//2t7+JqxFst7fIZIApBwwglj1ZXH9JixQutjStUMNsKdyfmXjkfFNcdnS0aFoRtI27WlpAzgJnt9tbe+b3gtifv/4SJNempNCqFilQsHHWWZ1Xq7oguZO5w8Vff/0tuAERTM9GgxW3gUlwaAYGh3MKcn/56RcDZ4As/IYp3iKHx+cHL5dB0VOOBh9FNF5SUkD5gIYyoSA7Ede28J5sUdWEiEWjI9TADqTusrkmqsloSJGPZjjkaBzGLfawAydc9jM+MeGAARTeSNyipVMClYFeXnfqoJEKiOogmAldKiuUnUAlkjQCTvIJLmDWdbXVMBUH5GxMT8zs7W+TA8XdlsFI31aUqfiVqDQipr2C+k+6NG1yA+VMljqK1BgQJjdE7FB0m9ZAVoFSk6F7Cw8D2rMKheVIpVkxKZspeC4zKlJ2S7iQhPWYS2MEkENFJcC58Lz+E6P8+OEd4yNhUw8QhwBtq4EHQ6r4NBSZpRNLOBG9C8wG+GA/2NWoiKzLmvfERfN+5+dnsGFytfJSqq0kJ47t/yNZRkwLGDyvuM7R2mth9cuvvuaLlBO4LU8ibYcPzNRkFU6vghBrkUg25NUpbgsMXn9jOysaxErKMEh+THUBI4F0wn/GwU4LWKFsSlmTgnhG4y3xy4oIzFhSLyUXgOB14RCGYFSYDb2HNorHgJOAm/X1Ze8H4vlndWZqcOhMCsggdc5nPKCVQzJQUFTUnNtKPYDcUvDEaOMEhH9LQQMt/0MAsiV/t2L2CIiOKvmZWS0p32UoGDEf94oB0OxYaBRIdtyHjvy01NJWLByM1VjboD///rbFswnYIqVlcgY1zXAWusZ5HIYBoNojiYHgcXsft5kbnEdjjQez484A1QaySMeRd/G9zo4YQxgq/oELVpujVKdReuHsgigPqizIdKYbQ/Hi6iHXCxuTGVX3Q+KiTIIWhedmeYNRGSgvmYf1dr7cCCk8CCrCmxMFg3P/YpDf5ZqtrVl+PDINEqYBYJXEI9wuXZ13erEwT3xh95QWXPlwawgoA+Z5eA8OELvAtCWacnRHG6DhtRwE/s0fGrPhn8Xp7FvV2hiRwAC8o9G2Dj76wG8xEobkP6laW0ZYxzGxehyAoBjUEL3T/Z0SgKtVdXR6ff+g2uE4OHqjnyZDv9BYNzQ43NTYgnp1QJRCI4SEcte9vrYu4qN9Z+S6T/BWHCxCYvzTmGS0sR66axGZfK+Od2wN9tuzuX+XEQfonF8+PNkHGTupoZI5BEXKEXpjEb8ISCdUBrAt4+PP3GEPIpErWJqZqWn2ahIyo5H+Q5FuXAk1TXaWt7SUVjmmqJsDFS2OhVracNz++Q/VkINq6byMyURIYdy6G5qAUMXJ+nozV0NwxpLk6We315aY9+Tj3PN3d38t+FWjq13geXu/tDxvJL1sBkPHSdFYmFvnVLtfAK3nNBregugww5LjLisvKLktJbQOeHBnNGB1W2dr1FeX19HNrM0EG3MFHHLraNyBic/oY2mBI90KT3k4fEhdreC37tbZi3P22tneCTwA6Vuba2guMaW9qdn30iNI+rhaJQqNCF4HFMX0oZJ6+twYU2JVjf0Rklz+trm+9Wl0jLkojPdVVRo1GtfP30a2iD+hy+RffTX3qr56fXmOxcq8T7BRYjzQyGU4jhOPQIBhxpF7kZiamkBhnqb2JzoE+Jr4Fbq36ro28KGRvRUUZ1Rk3jSYdYHVOMGKBJOQzFJPxnhAxqaJMGg1m9mZbX0M2rbTarOzNHeUGK4eph9lXl5TTV1o54m8JvyOmsNu4kO5HKa5ve7elHVsg8Og7qeGJVkBJtwuBJyDVzaIgxNa1s3PMaQhGnxC9SwUxRMryF9fsTqECZ84Nz0L7PAV2ztbRui9/Pz1sxfPqUES2QWedv/iAInEjnk9EYqTpBr49PGjgVTcQV//gKnd/LjAAJrZ6MuLY+kO3R7XKa818Mp/wVR4pI6eTvcMy3EFS/60sLzAhWC0Hbwqe0b6WXmd3qlUFtk7gGyp+7r6m+scpVY2Ix6rddPi8FPCFzmpNNS34prNwuII1MZ1uXtONTABiU3CI/5BlsbvCPysCHHEHxEvSXQEcsYsPvk0XOve7naMd19eUxgTX1hCXW09G+A4TL4BESkWeIiYSxN3K1XpOVQZs3RxYQZcdXe/vrFmSQ0CA8MddVXc8B1ZGQZpCI2ARV11PRZCUQWPgRkHcs2G9ff4ZNcUHxxKSR2BqKPkZJeeK0oVDwz131274f1C0uBDTsinL4nxI6UGifBWGF22isEjQXKFERwj8MCD/FdpBj33k4TDX2wV2KMOq7pJoWSlznqpBBKDyuyy2fY8hnq1Z+BtvIGwZENyMk0jln1KjQJXKarzG2KeeON0S6oiKpjDVVWpryWpfPWUMTU9qZ4BmvR09vLIq6tLKDLu2MgW/D5BLlzr13kkkCIu0XR7ucN3d7+8tAxwgAL21PpAy7bSowLHFlftWpkGyYHS8Of+K4fj/PpFIQS74ENAEP0l9ghXEzlSIcXgw9k1FKKHpsKsN8ZPCo+WkgrYWSdF8gEySlDYowOuVoH352NtgkYk/Z7HJ4csB/0QsBeZ6art+tq+wX4jdkFy2V7/wGDz1Rnpo6V2giwOaQs7m5qaMMDcbPmm1iaF3l9++ZkPqa6KmwySP/30E8ZGtPFkDJe/Ey09hHtPZ6GVmFJ9h5lxrhxkwchHSwsYk6RDfkKMIVEgdu7t62PECERxbHtLmDUBo8LRx4E4gWgvZKiNtP0SKvns1uYGgpsHsaOaZgHGypqqjIfOnKwccBXW17fJNmb3Zp1jZ0AY8GPmehjUOjg0oBA6PbPIFPr6BurrPImtyoyO5bjjKOax2FdCGt+Vk79vfaFygWvOTYHHR6SispmhoeGegT5wW0u3Gqx2VvEwXRJogHnxVFwMZoaL3NzYQiM6e/W1hVy82oB2ZTDQWPa3796a1yH5JfehJXFnpN9iS/JWG4+XdPB2ErvIaEf0xz/9GRLCOcj12Pfy2nKQEqaQZ+VoBXSiJJEezy0mYriQbrqVIjpalnfzsc4hhdylsptZNHSxASL2RRosJxLZwbN90X1QW6d06lhC06pb7BK8kq2CqHZKVJdU8o8u2nRUATh7odosKMo9+WVfpCqoQ81eqZNRZ8hs1Qzxv2KwKq6LCgDSYFcQndGFG3IaiR+lB6fDo4H8uhmMnuPpLGNQt6lH50FuyMX7savb64qyMiCLeQSDpE/n4NzfpQtuBga7HjPMrik4P7mQqyH6JTWOnEOl6Qk4sjT07PJ4kAKrZwidoi6PxikEaPKXevSTzo99JzY8QnkVnw5xqEwQX0nvwEbAMHA+BVJ+LiNkdXietKOxVtmmRgPaZFkQmJ/kNST4p5kulQwldXlJuU1SIzXd4vL4DCKDzvBacmWJEQhmneOt702FNMha6l/FFAUSWYYYjMuS6+BzQVG5vP85Wag55xO/63N5veMjg09OfaCxKu6aN8sW5De3Qn8f8oHkxldQB9yVV/D28jlzNSym4kQQO3k5cL3jbnSHcfAimf0Fb1mpE0p6BN3LyZQxVW69pj3SDwZx0gvIOaj10tR8ykupPVVWVxgNEuq4pyeiCJHPXHE+VHxNZq1Mz5xNT84i/QM3ZAu6coNzHlDO3dnVzYbtHRI3FZ1ZVe50YgO+DqnLP0A/FgtkhGwo8dWibASIoLLuS7c36QKuuDzio8enuKqXBfHpVtsKBO1z5vZ5fMy1gncaUz45O3ghBUsKkanJme0dxrZ+WnTKDjkZbArqDxaUFmBXfKE2e7mF1EEqC19VGIibL1O8cBCwQx8/fdKqCVrZKdSf8XkUOJJIvOXzl8+ZATkmRkGGas35PdlKJGeEiJTHx8cqMdIF3Dh/CABB2EYaWnPVXXyHZgV11FevPlM2dnLVI701G+Na7b5zV2xQaLrfnj/gJ6XjEiQlMlVcOYHPF+bVHQf6BoEVfsO6AZES08tdxNIO45SaM/C//u1fV5ZW/rf//X8b/zShdhG1PfcBpW4hwv/2v/zbxvJ2cvtgj4Mgj0WYZCSyKCyhOWcbo+KaSF8iyqVjXcLf/QWmOIH8oKk1oOvc7NzY+LhXxSDDqGCd7WyoV1xyJM0pvJmcnKIx96q0MZ9GR+UTTc06ROIaYeipIFd+qtxEmlxYeOW6eve3XRo//3ivMlZAdKI6Z2W5Nf0m6tJN7a3V1Q1NzW2wumuJsK6uIGb6XJ2pBYI8gRDvL8O1l1CDRFUy6KrWipISZmOs3+ODjKmgsqbWxPfcoiJdtFj1ne09bWu8WFtLh1HwmlKdUvGcuklgsAHOGM9qtl19Xa26wtHc0drm6vT8DJuwFBhApIcI57KWX+d/NQzpxcvXZr1Q++go+frrrzg/EYJnsTf8OBGYjNsgKS9t75UQSO85VseMCOf6KmQ5Nl6EV7ziF2TEgACkjNyVdpD9uEJaMZDuUH+j4q0eBfvS2zeg40b8hvGR729/+51gUWBOywENAtuXuvkOrTcSch7ESeIRhkdGJKGqYVhoaMv0Su252EyX6EK+FoGPRuLJM/h82+HZsGLlpQifrMOTuJKTfh4n9Nuvv81Mz3SYBqVF44FY89S8JecT6yWzsjWcQuIwIWVZWVieRzvkF/T39wE55yfrqAzXmSlyOnIhQU5fGFJaWar1Rm2QzYCHqtDKJf5VrslbLC4wvVnuU83ZRYzcZ1BeKddkZocxK8fHGJKCsoLS6vJazZOYOv6U7N9yWUPpi7J8hnLJbdwmiDcXosQA5X20BpzqX/2pPJUlYImODpcl79geaCaRJlWVYRwc/ovZiyUm4xwc7gKh4URiqvDR9GRKE8bLVy8EZmESEKb9Bud0fM3OzCqw8wdUtL7LgY94cHCo6oMZQFuBuvUNNWVlhSoQNXW1RGXmsNJZiATkdupS5eoyZRXeUaqqC3RxcRlYiVlprpi/oPMJUpg/MofPsfUhLe2t0IO7/yBHSA/bJ4oEKeQsmZWSlUDPCl2woCPvPOoHBEBVdKSSBq4E8X0a0404dL3N/IiZjBwWCElar1rIHxm9yec+Zj60d1SXVJU/JIK0FIC5VLQtXsZJB/AdojDCtLTU/gZHZLRQaRlCy6YJMOy858lVft0d3Z2b9EMbG4h1BDLnyC9FEdQIW8aXTDrs/n+kELJLe/Lc7LYWoJHhERrGdGEiD5WgVdCGImBjqTD4KYEtYDg7VGnwsnyRY8Xs/V9aoR73RPkc6IGnlKbgfuUx/DKAIlGen5suyM1RHEbrmt8FXGo/Qp0o3cl9IT81bICQNyAb5tiEOlyIupozt7GuB4LQ6Mm+f/76JS0AJB2ToPb3gYx0WaXMZH/xCXYU1/wdq+xXkFoE1OB4VWmNcogLsgQwXt4yMgARCA1oymWMirm5EVt5q6c7NyfGhRMeO3RT/gnvc3ZGFvHNd98w1M7O3prKxqTLaQ2ZFfSsjt21W5ZWZsSmAS7WlU5nsuy1tcaBa9/w8h2h0y+3WxJxhSN5g85YG2mR6czg7ubCFgyApxEb5QyOtGhvCiuwYkYOVAVFJgsk5hm2GGsHDZn2ZKEMKR/9NNrU0vDi+UtrClC4if3zL1+1d3ZYIEZAuSi4WaE//fC9ywAAfvH56OgMVuJlJExBnt3f8W5KpkAEAFhdWZHzmIGwry7X+pSrt9BmUDKqxIF4cAFwgT1QPMEWYN0ISOy634XO8tx+WB431UFKkWzCg3Edzf78vPwj81//9rcguKO706JXy47XUmu1He3CgZvOMIhGpTgtTrhB/LytJ7w7vSMFWVicR/LCyxqXpqcm0W7Php9LLBGvR4fmzd5bED6ariKKugRqkD/KKzsJ4yCopT5IGDkyTkNsouAWgOm2mKyhknNz87CPjNHrIHAlAZCpL7KAJ2u0+qdME6yDX/w5XZWvQAMC9VoQXcINZZPSq0RRNmg9U75YWVmjJxvo79cn+MvPvxBW8AKaKpXacOiJ0szTI7eAwZ65jBIWFmDkbSYf6SqBWbQ1AKwOL7jd09PDyWpYcyDl/g42oh8WAztUYZCYzuP+/qHQ6BKV2Zk595nATfYIf8qcDADgu4VVFCaHEuXatIBVuwtLA4Kaamq2L3VNbFK7u4FWyuk1ZWxgr8WHSaM2I6PJyPDufJuslpvTTOTQSZDbKtoUIQU5uijtDhgh3tuRi9697FzlkwA2FeUQhmghabPvXuoPKYiJgVILR9qZVNYytk9t1rFj6jIddaA0lWSdHuEAtVyPgUcyvTA/WSg2kzOYfcjgDWJC9EjRXO1twW0f1b8KKofLs/NoEaXIZHOyNTrxvH7RgNTz7GxLgV43xMl3kEydiyTnZ9qXuFiX4sGvMi5y9C3y9C38QLSGCm9QtWpEeWVSbTRgrPs+6X+KKUczHUDbZxG0I/FA1Nh+/jj7GMlJygDjq5uBmR4mPbV/u6cnboaU8kjoyZ4UpNxWnJNXSOg5OTWJPzFo8puvvhIIeXlgHrKJgmHaWoBu8vkY+Hl+bje/SV27fqutrdkrsyi3F/gKhxqFYCNUjPBmWE0rIK/CQ2StB9pDmxC+Czw4YSycqoJcWYS26RAdk25ubZH0I0Ak33JQT46d5u6jhJBuN4ER0u2iXEQCTyXBojsYHByQyQl3KD41ACcL4abeoA3e8nmF77//Hqb2KsDHQ0bk0OIKlbqnbe/oqK1t0H6gA1mjTF9vPzdCFhPfngcrnEvRaH6yz+RhGXrcpAs+UNj2dVCyt/OXHoWZ6XmsV8Ty5lYPj3FAjbJQtVSTSjnnMNTCfM3zDNwHsrrf3vzy8cOYQdZqsTQsHCN3PTg42NjQ8vikpiGBLEv+6YcfeWHJIOINkWevKV7ETNSE2EvHCas6D7ye5AvP6yOkYHpp1D3Ymcd1NYqOGV2swoCcnd90TyHs47kFZ/GeueC7mSnuwlNOTcyYeKwHUw1A5Rod5qThHPoHBkR1L49MUYI3CYPQSMbU0tHWOzCoJiNYW3pBO6CLgc+lNa0tnSzSOYTQxS3bD3Ia76oA5cx7Iyx2bUuj8g1BztbKGtWjwl0y1zTdk+vdXYmoOdgGRZjV7j7d09S5WehiKFTOuThgf3SIONLct5IUS2VJwqSyoYAnh1VSB9vhAszG8dmxWTdff/uVntipsSnYFiEo0QUwqUQsnf9L3iQlgG/f/j43N9fa3srL62H2+k6gEoUHvji83NhcF58Hu4bT9woXPt49GpkLuQBOMXTY9ZlIZw1Lu1sMWh2K+IGlTM/Pkj+BLdJ2/lGmYg6Ste/v6XfzzP7+tpIdOsOkfg7ID3ABo2OjQJ9WICwROCN/bL1pxV04h+gcsZbrdF0i2MsH8Rlyi321F4JxM3lOztzrK+AJ3ielRwK/Cl5NfR19+qdPo2JhY1MDpAg92Hflk8rqY/2it493qImW1tdcs41jKqycQNB2Q+uIHTgjdAU3N3yQ3LasuFTa4X1Z84kLFHc1ZN3BUzAI2lnA5kbNFuJ/IRVHp76mv6W+5fri2ovrymmobwaOaMYUMIuKDbCsjBzLlz7o61mT8rjYihIY+KXmAlMMHri+uz2PW8tIZw0+Mu74yqmGbADqZyPPKssqaYHys/OrXfziGGjDTd8pD0DIO72CCgG8bLQGIgtmpIVXeMRu1dbXsQEUipZmHWpYMimdpE2eLWZbJavtVAO2toNPV+AHPsi0pR2Red/flUR7YEGP0kV58dX5+fb6JtfDmwvqPgp8gY6dTYXnyooyQ9+R++l2uUMs9/rKivYLqKito82Zc9lWVV1l9VNtxDC8nEl8pkVWlhmvtnq5CmGh7LWu0r7jXXlt60EEITZ4SHvqO4wKUq8S/Ky5BjqUi7WA7VSpYVVn3PQi3gBw4TQ0Ertvi+FAACPPhs0PR0H4H1cBy6O2JEyiO0jHGNgeskUFDVsIKaIE+VCfwkgyE0Zbu8PgXMKtRA0BeGUFKlkyE0UxeTBoWvRV95KowX0Qqk3kqR1kg3kYg+RPMOadkT9en9bAk4D8TF3F28O4N1DIxNSZr0Gw75Hk6yShsj1QGjJDvVbXqXs3Ah8Su4PjoxoQxDro18vP8+HiOp3wz29+Gh+fUIzt6e5jqLIOrs2FTy9euM3JP0KeZksogJ2r+WsTM7DPQEmx5/L8CkHNaYDr3lH2479KcxUXqaV3dvYEQkCJBpJvBPYVC1lI1NthweoY4CEFofnhe2lkOTqwyeW44LGXhKUEEKDl8GgXIgR2k5QezqHzjKZUe7FAAXvzcrX4HnV2VlVNwR3SRrjSiQ19IvTo/rbaOh7Qi1kXLJjNtjEcBOIbXOJtFxYXFYohfQ+hAiYtlddIEiRVE2O/TEyMejJHyEIoVdXVN0K/aqSeLFV/bW/yzQjT72qeTGsbZbd2wdXldeyQEKJ0b9ZAxI5oS8708qwH6OCmL68KJarIHGcTKaYCpjJufNLEp9Hx9+9WlxaBR35cyoKrk7sRr5mMpT5ppothSfxpLR9WU0uBIRZaU/XGNPC8NgUPU88P4taFZe8+/Ow5JhK6Z8y6Q9fXtyyaaYW0B29+/gUJY1XZroWSm8s5JGVMZH1j86dffhI7hTqcKb0fjdFnn39uTSXs5mSsrq5NTEyxXX1KalDEmjv7RultSsjKqvSMFkOy1pDpa9cUUeA1OEIh8fj8VMz+I0SpemFsg8NVVb+9zrpRy9Fbw0rws1LSXK9G80Nw6d+QzmIeJyPqszl9gyxAOYQGFHAj6uju6vSQNlHZn/F5gNLCiOjmoTowllkFhXjAP8iglDppUhWo1TzQCzYIpzy+Mjk1MyP8OFyIJ48S63Z3m3uRe11zA6UuLi2pieox4aA1PfBBbKOl1YWITSTZ0qPJqWkCX2ymZaDOJKdju2RaHlIlg6AQfS+fcg6NO6YjEi/xznImSFjAlh27j5J2nUmgg8QYwgO+hmUjiHEzpDJaQgrzTRumFd6S0kWvPqlPR72KlDBJi+0ITc/MvH/3rqenazA1qG6pXA9EW089GQKyECBPBU30cywuoTHtlEvNDkSyurpAu+0gc1O9rkDBxswABy28bHoIuU3EeWp7doLEy+jTKTLFs9xZY4KMmQ5bfGBFboRx5+FT4ulw7wiloMlAFkSZI8zg8Rob3JrZ5VbY5eVFNRthW+kb5ASLwsPeuYutQT25rU23Wlx1ApZKDsE4Y/dDcyISKbFqj4+JnreR9eYZCaOtR9YXHAjZFY8vlUHN2Eq/YMUYnlNvUIh/UB4W/dBNVHzcQihHMjK6u3uNUibfRPikh0saIlmedZEVbdXn516zqaEyMCzBzp1qeXR5uUACZyCv7eiCoKNA4uyreCmvQv18t59SkcIbOWtCp8wy5FvoAerqi4uE2UhFxfCaAoXjo4AKpIJPXoGj1GylUurPkaiuPPLz8fjpxi4Zc01dHQ5Tgo6mg7LFeGfZqccJCFyODDIZ+Ybd+p//+39XePCcaAkRV04MR1g3zVU//fMfiIRvv/tWPAlv7q9zlwWd+urGBpeii0YZ4r1dtybWXzTVOWtMCO5Bcsa20xAhoD3KyI50dfeAkD///BPNhUVo7+gGH73X2dmlgJ3u2IhtFHH9OpmJqCmz9+s4Vdm2r8PW+gox8vhgSTpI2sPgk8d7OKk7b+WEa9vhFCQdMUa1rMIoEeyt17u8OvSheC4efHBgyAY4bNg4v2Xp2QcUq9Pl8PaIa2M0Ctw6nv03bIX8W55iUeQQ9nX/YMehxV0Iyw6YUKxWa46rSRfyss3NRdmcnwf2+YL+viFxkhXxUGCCcRkcnGpNdWWZnhIgTUquEiKQ6oIJY0tQbmDt7tCmgJvNphRREgPNZE/UimZ0sHJ14/7BgcayFjzX5o5RzGoqCgAujGyWlyG7gzJzdt2am22CGzlB6AgBcHUX3K6GW4FXTYKTYhgaxEzKcHI4cbLL+ZlZ6N4Lkjpw07RFkkc/j5tGHiBgKUbU8V+/fl1SIdAUQS48rx3kfHf3d+sajZd53tbSqhvL6d3Q532kR1ESX26uEDVkZWGZQpMzD5FxLkr0+FlJG3djBhkIUFKKQ0yqA5unNvbp0+ryAiVWeWlVdtYN4oi3slzyXKjSKgBKpp45sbykAK8RUUg28CM42dMxaoSvvvjCzSdylDlckN3d2YJxuKfFpajANzc2il6MhKtd2Vh14Nn051+8ckeYBN9d5AoniILT88uxT2NKlEg0gnwnHMZWN8JGy2h4HGogiYtbTwkKGQ+TI+/JL5qvKqOd0/nxwE/ZbqID7P/K+qqKE4Nm2dSbvX3d/f2Dto8ywgi1h+MHT0jFbw7r4tIcm3NNo0ng5p2o3pL7wadA3F2zVPXGrRyzc/MUI0iVWl1+Dvb52dTMtM4AfJQeFX9C97G4sOjYSEfsrxcM3ef5teCHUbkvfkhm33CIzAAeED6hyd9/fzsxPmXLXUKCPAwPwj2cXHkpxJ3qtLMtrbGtBq9qs8cexyBR9GZOgvmF+uP8Uo2huRWBUQMvUubwbj4QM8Zfy8/gJ8pHej5IAlJ2mNmrSOdmBp3H6A7/JplGvbrDlTCMwxVjnEFVD6U7rSaec29Hn+pjXWO1+/zEDx/e3duBR/Z4jknkFhlPzS2NDgKzlzuaiNrU2pp9GxPTrF5Q2wRWYLxmC9XL1B1V0vE5ifAhiR3/yLFZJU8S/lPWfnVtdp5+q/b2jghs/JVhduUxIoVjYorZNiZPh1TGzv6eeKmswg6x2xw3lCnHEgnQWn7NP/s710/mEMKEEs201jlSdtB4a4egeR8SFCdcTZF4zABAJTf+lWIKZ+ubvSAX75pUxxlM4RoVGsVXBwEUk1oZ4+mWN36fAzNkxXmxDpAlkm1tae328aG3vw/TEgras2zHcHfflJor2hsb5HYmg32ePX+uCM91WJC0Tz/5/bffcQw//OXHllaFnCqmaFl4wvBZD/eIeDiGr7diXBZEpc4nCWBufKcaHtJSdug5teJiONXM5Qdek6+yDZ5c2PZekjae1kAqpXK3QOkIMj6SOBXDLC1ggFyH2h6Sg5NMbu/t1NSWO8Cco+9AwIkzMJfrmCVcfk427KMxGDg1rXGSWV5YusR3yzw4QbGLDUg/DVYjWWFSHLHWVoENrDs7iaFaKhCoZLV4i0iQ8Pnnn2Mz+HqTJ5A/+GUrJWNwtAiBvbZGCduJzPfm8jjYO8c9oFwalHpxfjAxoeosknsiVivh2jDMfXcXYQeGE+8UU6kUFijqghAEQdxld/8A4p6yaGZ+wXNDW8ZrCTUzKMC5RUDs6x++faZ8VF4pbgHI4SZ0C/Om7kiRY6Z0f5wQzFB22hirpPBAYawIlplFaOi+jUKCQjGZZX/51ZeWBwgDGRwMcFIBXBiWrL16/Yq8kvMy+MHdswZIKIi5iu/JPKyyYsdETHj16vMoqx4cjn76919//Vk0+utf/zo0NEiNqqrM6yEMojPg6VGRJn3s7zH+UIxAT2XhAzkHnwPo6PsAcGygyoGWEIcEVIyEGqTHrRYVK51xBMwCL46y8IEYGzhOMIbcsZp4Bqd9ampidmaeBgLQKCqIMXa+zKLx8qgSlWEsLZ+OQhfuWttaHAzcMr8W7oFK+M74BPgUCZDFFc7MzCEVnVt1LWBemt9sbmh2EjSmZ5fWqla5mvvk3SdioebWmDjCsGyiYQwKpz//8ycbJA0AFGAQ9JEyjwkfzhLcBHLaBa+DZzfRT6eMho+i4oGizEINr3wfWsKrp6/zy1uYn6V+kTXidpfzFgcuBjWB4TWUSTbW7olusUMQrvhnH3Ut+CKDboRz+nowkLWGetJV3XE7q8XI9A/4aSieokasGuwdcv2eS6H5T9f/ka7Jx4ml+Dsw0AwMaWigt/wCzKWUXPHDJrrksLaDmKuW9TmixrSkPciVYSBJh1zNk7wY12MqX3YetMy5QoUSFtyIbMax5dQse1XCnt5RPYFuoFj4UZWVhoagUzItF7u+tKHqbch9ZQZ4vqyyLC/7WsCTV8mBhC7h1PO5dcay+iipQGGx6u4DHonv5jEhJDU5p4+Lob7QycjdG7Qm4SAdlDGz/BgysKfLZ4cnwchzF1g7rJHaDy0THEnm76QLgYIBvNV8dqZ5nquBMIE/WfcffIMFd50GtG6FUZE+GaZXv1UuC5afp3iKm2EUewxu4k+4ckQrYsyyWFz0iR+RwloN0lZG3tOXgIu9PmG3nFE4wcgJ070ZT/ySDhHna2zUBZFHXCLvLxvjozhoixxtCuc6bMGiLfxcfqF1SBmcGdWviyuyb3kq16SiSQeRduUKUY8OoPo5xQ11Jn/FAwSPk5uVkZOZZ3ZfpmH4RE053KAVA7g0fEl9rC23KRt79myYeoLNpNkhFQQYJjp4uJTsnGSPnpvaOn7JrwAlOv85CjwEUE6dofM88tEs0y1jKqo1Hx0dT64vr9+J0MbK3FwiAV++eAGoTk1P/eMfP3ltWyUu9vf3v3z5EhFGv8Ud2JAgMDj+dC8oYY1EjI16KydftwisTaEBtnD3NgNBKZBaPlGEGEvMACtAoPGxMVHItunbcpDsN+BRUX6M1RHHfAK+lVHGtO6mBgmUepJ1mZmdd1+uxEd3kjhvaQhP4DVpmghp9jOowQ8qJ1K/6HM+MQ2+rLRehGltXQGdzs4Xl1e1tm1pojs80sfMNxmkoA1Yd1v4QfFKNmQAr4vx4nJEtxElVaWITITfdKpYhOjQwcEZeTAnGe0bdKfiXSJL5zOQyDvLQlBhTNBftsdigeeOn6RMUMalmXThqPgK8Z3HIXRBmzBla35ydCYY4H+MU1D5hsjLy8hgCmln1/ZdEnRl9erqamITcnMAf3GUK2FzqEwQG6cJ1FMEwX26MJygT58+8qEuP9GXAK+xQiwTha5sjNPnRunbGZbX3F1dwyQ4hIyGQwFUiU2VdqUdTeBoTTXrtCm8lVVqa+mkE11ZXZZKNza19A30IXbFZuvnllen1Io5KgBp9KkVFwuEHs0P+zFtF4PDg5T2egDN5KlpqNXxMDs/e3R8IBsQ9tRmVjfX9GmrAHud4E3NvdSanpdnm5xMYnncmssVtne2QUXnnL6JK1tVMVxeFQhdAOv+NQ+sRgrf2BddRXRTskne5yHjPjs/x+xSXByoayPsA2ESUO6cCN7BgVgaG9bZKrQoDGxebfgTAUnPNjDPcrDq9kaJng4A5oib5u6eFNzSd5zElIW7E1R+jvaF6po6oQjTI7vFMISiTCyhaVHSzDeUKXFw8CjPxWkiWn2FOg3y3QGmFwAmWKTMWxtBjJnLCa2hKz/vW+6QJMwMS6CbAQl+dnkKaBuaTtsjulsV/wl5CRJSaALdCkmRjh9fJjNQxuofV2uLKzGpLfORJTukPs39ZAI9c4XbjDc4yQlkygn4GdGCM5UcaAkS+aQUxzdHwieyRfe7J/ec2qfhJ9SiQy1UUKaIjmqh2LY/6k9YX0Vgo9TsLEvDJTIYUyIAx+AlAJPSUrQeIGJn5Z12R1qQ6+wY8ERnKBWoqX1I3QucfsxvCSfAjdm3WdlJHp6lRP9KJWNByMRxJssx3MWCYJbAC+VQ659OwjIR/IlGV0pcnB3zMWdAZ1bqdnF+QUEe5pZUqW7CbcsrS9OTU1wizkXslL/KG0yHoAmUiCwvsbeSoYGBxpFGYUyxgTcoLCyZm5/jWFXM9RGbBw5PpE/xJsWUsis7gGjVQatq3L1IeF1mawQ8piiXkk2i8mBW1m7xmwd6WbLB4CAm7G6oiBOtFYGPkF4K4P6Z+J2fY+eGhSzMzo2OfXLi3ITo4HPCCgNAOUICB2Dlq2pL3WCdbGmjFH4qqCp80facwtcKRu13ZVlUijukystMdyGZV4PlEVRJ/KY9BnbETxHen7ASLkPo43AdAEgZifnp/UfOmhdW/+Ea2ZZE1eYpBKnEmkYJEsAXptZEHhAZShGJkq2iBJHtBtOi6PSUOeDQPHtuphuWQMbN4OZnzIaaV4Eh2+JNEEy86ov+54aJhwvf2z86PSLMEIcysx4RF0aM5eR2GoxNZSQ3iYlfxSXm1Qv10vN6cumYS2rXMtGamFwvjimWeB4cn9i/y8s+aFqbia3xY+Z93Z2Y//OkkYTUh2GxP/CNCTI1yYft8aiuRlxaWoQscJfSAyZr3UUCW6usQNKv+nd+dSEHd8LDDkJGVuEA/xE8sMP4zBfPXzhp9vJgf+f3t29MjxkcGjkBbPbdrHQnBaZ3dby33BZUXAw6Ydgjet0peVVbVQyAblXjtLhvl0pGsEm3j0JVkndnyVPZVtmnh4f24AITi9QV7JcjLq9zitR4JPLdnd0R8rOzXMyEZAxZRYzh3S0oNkugQdaF6fLzPB10hP3TG1E2P0/TKUvQCSUCMR6OO3iYwiIlCkfIlyiYw1D/4z/+M65fTmb5fXOiMAmCpdkSxDakL8vLq8qZjpQX++mf/3TqBCpPq5cO8m2C6BOZ0Jnlt3owkrEi+tF8Gnt79fo1H+ABlhaW0uEc52PE9JLwCLuktTrbdgRZYYq6fgcqUqwU8Ykhxr4OCvZfHV2XZnMc//H//XdJuBIRC1HXBv0MOsA1yUv/yBetG5TAIAVv8ZKXF7HwruhN/yyumDEZ4I5he6x79zSd+gp19aKTItWm3Cxv3eobVcI5I04Z/HeAdXHYZW5LHzB6mpzd5qQrhFAkJU+e6WBSCqBPw5cpGth6fQH+FRqAYzwepC+FJVfCQzLOxAOA8gSmKqqvLC2LtUplyto0QNOT41YYawHKaAzkKdLJTZ6KaPQyFeYjrKU6nmd5aSEI8RyDxHIBBbJAuwbVSmmY4uzCHMWtGXzOslOv4Zb9K2bKSGgHYGgj9VgmG2b/gDwnJQyuLi8jtb2yI0MiB4/rUuJzO7q7QvV4eqpsg0az4+2tC8KDD+eFlHny7uOmtrbONqQHKgb5LnFnJ3Q442MTIqSnGh4eZoNWQH4z9mkcAJIEE5IqZFpnVxY3mlKuPX5vd/TT2NsP713nQG43NDIsrnN6/g41GT6ogTzUsYXFWnDLS8qIf7yvAZFWJT3JrlpmQDXgS50CLKiheZgGjFna+crKMtTDqUgcDTlrdNLdXnu83v4efaTwhvMoQMJA8tSRkSH3+ZydHsHEszNTvDxbxegidlwRJOi6B8jVsdwpAndyYhwd9v79W2mSjDBdF+lWN5atq1PoP7VWIrGvGPv4kVH/f/7X/z40PJhEBNBCNLW2YCQwj7vLe4C55unvUCLPnlG/wAiKM7onIMfgnrTaR5pt5PQ9yce6kV6PGdC3JMLsbn7HPHenC6nPp1pukpjzp3PukqbVwgkS8lCPgkVA8kh/jZdYXKAA23Gi5C+Vf65IlCfpnX/8048Bc7Kz9ZFI5BlidBSWFA8M95vSDlx09nS5qUNrGmIBdJXYUoKadUImb663CcZEQZYPmlMbce9pdOaYbFNZrVKnNsvCAGR/eR2IQJVMvuJNwVUvAySKagoYjSKfC14a6joKCiERY+aODo5NiCMmg6eQJwCd13T4VbBi/25vf3/35v3v78EJ4VM9xEc5IbbfWfXKaFMDG+QEIf85OdX0pEyk4uL54a9gb11Sn5cbU+Hb3TZcQYP8n3//H3MzC/ePqT//+UfJk2orP8W/OxJLi4uM0tQuzRn1dY2YEN5NbPNFKhuciNKlXE0ckthhuv2Pi6db4CudXs4fWJYHADuwg1Y71qwsyYEyQTN69rKiR1/jgXWhRSNsdWxEMv88MTaJT/zhxx8oyUvKylm8jIrwSQ3ZdkCmytQUAwoeUHOwjW4jenxww5REgeBBXZeaRWbw5VefhUZAgug0IkzRIBdnJlNZCioagIjZ6MnysppjuQx8ke1CoJsZ3tbcSouF/OdckCeMCifw8vVLbG8aw9bwsLv5uY3N9LVevFKhCIrmOai2zKTDz7huwPFWvbekZBu/v3m7u7U7MNBPb8f2dIEAEAVXhWnbuPMWUjdnTwNZ7VONaMcl4SStmIenv4RwmYSgyfD8Ic0S+h21DPKQeVBbRe8Vjxv30wp2F07QzsaOQ2GQn2t/uPiLDLeERveJqMwRm/jGSTXdtqCEUS6wBAgFEgr0Up/N1Q0xu/krmt5mUFSnqt23eiYMot4Bfzq/1P4tkoLIZ+T5My3WjhJI4fxDXdPj0yLeq1cve3u7IVaqdlxilApLdDmtrofG8Ul67TTZuJPz4+xUXHpqrDyBHBEPqSuJYEtjpDuIlT9yYk1ijoktc2mF000fgKAwQtnplOtTlIqyBgQ5PiZRelSYV/Dz2Le79C1bttCXasHGHaINRFxxCDnOMgtUfTe3wF4eyZXgza5kSM9oYplIacFD4uLb8TO+XTurwwgZnLoZImG57lGUILaYxE58skONv8L4RTpygcqmKA0ekt/nMcwx07oFCmjQ9Qh/lDYFHniRZRlPoPRCcClrB2vkLtFPnpfHk8xMT0LALY2tW7suC9tQMPcYUlsZT3dXD22eyGoN45IYk6MSWhEgAffdX/phBo/nNPmWmTn98JAw2NHZpkY5Pz87O7XmugXXrh3s7grwCIayci2ZSDViGbNqSui04SQWroxkqaE0oZSVkTiPjY6LQLZVHd5WYodOF5bUw+6juxddksyQ0ah1WFlBiWrTI0rKlHylWhCJP0UUMBqQ0xkDcKJIYF7+5iYm9Isvv6qurYT6sboN9bWYzc7OdqcdTJa5gxiGNTJThMNd8Z2LA+FhrOtp6PayyLTBas8Ejf5t+G9kwmLJ9PQkD9XR1U32YJSsWSg8NbLYu3pcUqqu9i6rrCNGMoGFR80TcxpM47/yd4TJql76SjDmbR1d1soM/bOTY29UXFbZ2dOnOCM1SaSzfnjHn8sZeSv7obpIWYHfYCIOM81iGX3F3b3rkEw4ZWo0aqpkhJXsmN4WtkWIOTxsCM4SCRBQMhSo+d/+9m+GL2IVpHQ4KHYiSEh6eCatLKwG1YOKYUkIRPstKN4a52zYnjsar/XvGFt9Bg/Gcc3LN2/vH/+4VvDRgMvJohlBWvS9CjB3z7VJsRw8ujRrrpgvnHHuZneYRARuUDHyGmhiSbqEiYCargmtAZnyPjGr7oIAUvnLmMcs6gSZ5hrx/xrhLKFpVSgldIFiWF1ge3ZKEoacZFvqC0//+V+KyTYO+29Wp4fnpIAiFhltDa6Wo0y/jTulo/yTHzw17tRf+kmcmbvre4LVm9KoTWl2SRCENDe4ed46jI6O0bGYdEmnyBzhTUUUgjZGaKg0K4IqdEsauYHDUT+UMmvAd8gtpiOE5USqe0jUDSYQLZkiZ3R9dpAu2VpnseR64sy2LC0qhe9ofV1JeN/YIAj9IfPgiXyXT5ianJLuKHoDKHUNyHkH7NEQ3PGJyZW1ZdST8hhHYHG49phQUQQtVohAVF4Z+Q8UWeanmGrlCl5QDtCQyIoTeAAem8gOLgZsUaFAbQiRZQBn5+KpfNobYfYcac7Uez3exemVbQuNsjq2QY5ifgZZsIiu0aJ/aHhre31lYcWYAt2CWvykMtU19RVVpXCPjGFrY4e0Fx7HInpSpwYmVXnzVAp7SiM+E6Mb9zbsH4im5kaLnd5b7uJQ0JNw9FqOnr0YETZOTi7y2HwqZYCNtVJQHJuc0EJjCJH0mpNinlJWZLbBkYSFPJS4u3QZkaa5qSF9IsxxyZ6amkK2QNCdRV0SAnydH8N0oz7ED5+vcq7DkJkp+USPQ9jDLWi1SR1weaHaBOxrr9E3w9QJffX8sTHz2NWNeA8f5S9raOudCBvtFCg4+6Cj4305Ckzr1Rw2J0v5ZWTkhdNksr/TGs6KHNPFNQ9PsNDQ8PP+vgExBppSyEUD+qK0liyhnAg9g+cNNc2oaStMicsG+AbgT9wHxoMnzMhyOgUAxBpRhlo0R68ECNLBDGySZg9EsC8QIUDJlE1Fy883AxgY2l+YnQQZv/r265a29pPblCtjDaLHRugO08Sj7x9tYKnR1LQtNhpVTq8ocGLUVdm9K+fT1t7iZJtEnCwsLbL0m2vb6WKvWlame9r+qJWZQ/IUlxRleGjbCY+YlvLxw0eMKoRMMUK9/vr1K73RvGFrS5N6lvMpkQE/+XH+nQYAv4FO1aCIV1Huo7LiDnwXIOlb9H+7wYB5ffvDd8N9zyW+f////TsxDCs01UCSGKKUggLeWeJ8cGquCBfqHuOA+27bVpDhcOEsRS0UDTSBl3wKEJ2am51Z39qwhb5OWxCJiMM08uy5no6RZ8/wm9dnpuLskkR5ETdFeRIpjugmIvpA6846vfvi/DykxhN5KYkRR0YhEMo85f/8Ak4NVqLKAF5kPF9+8WVHe5eEuqy4/G9/+ze0ElE/fiBiL270/JwX9go8SxqtunQ0EwmMmZHgG6wIIbJpfIiXkhorafAFUTloasAZ0Fb6ltnpaSDFwkL3uBeTuQ0AKassFeQcS4vjV5wQrty54i9sqDCDyZFqp13PuXdh0K7eBg3MRxgefuFguafX68AVzBpmUVfgy5RkTUMqKs6fnprWWxWilwgA53wNYd7z189hH3jf/HShwldDQDYLQ2KXnTomT2svKaQqAUxw5Zgw7Mfa+orzrKNFu4ATYjgJ7w/zyrc4Tee8p7cHqYVdaevo1FkkbQn5Xm4e2PgZ9VRxCXMSbkUvBLjTpSgmiSTfBlmsgy+1F5CscGo1LCPwwWWgEZqam7GuTrs4RBcoinhsRA0eD1Qv6lP95gLOASBUgEQHLnFEudelVVRJdltX59CzZ4P9/dS6eHmdpMID7/zixYjeToBAmQoWhrzU6wBGmm6ZsUPAVg3FMt0TP4AbpKZ1ozgPq1tQXQxwObk4paz3K6S0opQgwx1gsJ1VGbbZNQ/5FAfR7hDWuLPDJzY21/X397J1l3QenOw7L62t7YzScaZXwNFV1xFMV0FGSdxsZobxfuxcVYAZSJOlgq7RMko2HjtGABiLVAE2IqaUw8zUwv3iN3ysTVfwML0VqwLvAIdOJZiovsK/y95kfYR52G1NJQo8Il63IQp9vdW1dR6YUyNKVZhRmu7q6JLAfXj/uzEqy0vlepp0D9hEN0MojCWT3U6KssH9ttsK7pXE5GryM2yVs+mM8OBcm0fl3TDV+I3Z2Vlwra25GRSwd2rR6BQggMzBiaPtlH7p2Ukn/4/SfAdbdK+Ktoyc7Z2NoNFpTGI62ZMXRwGBgz293exE8cEng49DA8PiA88rGWEnnLKZQVQ6WDWQSIYaOZ+i1M2tk8XddbY2Dgz26GUROCanJ9i/h0dK0/TRMVL9EbCT8BdduSimmpqAwfAzjFmoNnKGJIjWnvkjJ7QVSLr9MfjYUNcwODKwv7U9FwLok7mZaWoOeCIrJ1HT4AYF3SdxeRdP6BUCd166M/JB6u9idFaKk5DZvH71Cusrd2zvMVWhyZiOJAyOcGcMxaVFMKBCE1LLaRHiAEyT0rnC6NtwNWBRAY8GenhWJQvSnXhGRdujQ4n2Sx9dV+uUCt7YHImbPgYsigM5NpqtnOAH5FOcHZEfX21lwQGGYRG1/+kyN5uRPBHtKLfiQeRI3hDLL8J7HqfFt4DOzidfXFVVRj6olugH5JX8suq5MlfkpK3KR2W6zL3C7MKMizTnl5fQz0zW47pFfGV9U4tkWVGx4T1Sh7HJSdpqgneei1/gOkFXD8nLEHSPj41aAA4lBlE0NrIn50SFIIJDJpDuPJ5jtJmFAIn7YhlUz36AasLplwahQPy6egaXzGisKvkK/wW8RFJSIqHmakzVjyuOvV26Bo4LCl2msVYwtWaur7/+mgjnw6cPsPnO/q7jjT4EUvp7e8UzMUzN3APhzW0Bc+MlnRN3Hzp1IjHi9SqBtXugMFRXE2Z8rAOj9ay8rBIuuMy8VJBIXd5ltJiaE8NGBN3hoeHQFB0fexKlpp3dI1mF1MVYC+kXAyCdlvhgabUpY5wZM6/a2oY8UeQw0DRTcpHmcI4j5Jf54XMBIHV/A6QEU7S+MT016S5iuy/Z56wFwfGp0a6proGhkf7+Hvli4RefK4fYdwfMYspgCnILkg1JsRBHjBMw8gg4xdRLQRg69CqQImShfh4iRiNIp0i+DIi9kI2loBBxAiNFQAw+FKLPXMCQmX12feLn4V4nkcLGf4WVMMsMiV/A+ZIPUnC5dDU0X6WlAC5VomX0VPyjN3LIQ1/oQlUXo6RuTBnBwwIZ9OYkIuIx9AL5kxVNTE4ZDK6NrqA4v/WpmUUhVXwdFYuGhbyC3MAQleVn58f+kGSbYFpKfZ9hJrZ0MFcgFFT0hZWVuJr7vqzyVGOmUKEJ9nb/Pk6ByzNcA3t1s398hE68i+EXtw6abEwHL+84PDwoeF+fn+uE6Oxo0+rhLnUJt6gTzu7I5Vl6Svs1H6C5XKa9u7c/Pj4OXNv6rl637OZdnrkd4YL98NDxeG7awT6dn/IexpO1dXSUVSlW56QqqGcLsUqmALA4d9zR9bracW5+VoeA1M2ICJPXiM3Ulh1ZWRFn4zQxJCJa0NB8Yp7L/MHJ8UluCPMON3hHT2UOfciF8/MwjdQrX3z2uboO/2wmw7dfFwW18OBWHIPFYnbA7UMKFZnOg0N1TSpDlkb3SF+k8KZ6yEjMEZIg2lPnCCe8OLe4W7bj1OtrJNjFW5J4u2AKpszOSgRdk18EKyAPwwuQCD48tgvCqo+ZRpneCO3gpsPusW29kgoyw8S9/KtLBx8bUHFA85ajc4JCTECKGS1kV7f3Ti75gCIWupgXM5pAFsiAUcoqMGiay4tpQ4129vZjhFp1tewT9lIh4FuQEIH2Liiko1pW2VzFSywvuT5I+3FPR2e34of+ADkH7KWJxR6BGHAi4U2mJMmZxDRhbORMIXDaVmozkimmzio1aCMeHB6gWHDk+Kmt3e0PH95LV4UseIFoUpPBxMSESKg1VAyA7Pyf+5H4JjNzFO5Cb5YeuMhBGOMFOTI5nvr/+N//Dy6ej/jxxz97n/RvRase+ky5GHgUA0Fv7tWh5e3FdkTPXS65XUR1LpiVgIH+k15E55PwbGV5PX9tzSWfTn5La4ciD66DUFV7M/c9PDLwp29/NGCKfM9xkubx0gH60yVQEn6d2DqW3UDCe/JBaFyT7vXRgd4RqE4POBFqBhXyL7/8mj1JPpgOWO0NNQpKfO8eka15HP7R6qGgBdkJU8p3uHKVn811WuFtmSnJmgV0wvlKzaWq1LyF65K0+Poxx4SDVl3e1WuWnfP6889kAFArIxaZxGzF+PPjCxvY0NgEn7ip3H+qqqi2VguzCxLqu+s7ztFoCUstteT4nRkE187u2f76fmbmsttR0LJ3+bdEZRNT0VgrKx0aGIRQXK/KtrHAN6kaJq6blBcYHpHnuWK00Mpz8eK6Qg6A5iDAaAIh0hBIIeKsqapGO1AAyo5J6c23UcWyzqKL9tHj0yMnimuAraQ4UmNVHx5btJTLa2GFHzm7TgNls3PIIfh0OZ9aBuKLNJvZiADCgHoaCQoQZ+9QhTCVDEmKKRPCWsDjykjBGzzcWX80ruo0kzdA0Ywda9VV1GlZNDDPz82SDxMCeQsPBovgFSypY2mJ5AxAxtbujvMsPNQ31+tsgIWP9k9mp2bAFFMCeQ3YxWhAlYlEcXZlVY0ADNISa7oXmhxQ0oZKQl0CnsgcK2a2dn1NndMheTL/bm1rixHCVbmJrOszl6vsuQRX4cQOqqQUEMrn5xKWnOg2jiET93y2UrkrpLOukspFopHwxpERTUlYo3Kbl+c8Cq4ovd2cuLaMVkSFJjvmvesYr7NutA/qhKo0hdmFeLb7hzYnAt8l6YFUBLaqijLu3ffmNhDjNDkOMLjZRGJM6vJKnOME5+fmtMvpfeW7sWQ4LzQA4+YND/cOeCXKXnNb8R2tpiAU5ltGVkfGSLVBmY3qW1ldQ0iT6vf2uT6kVIOv3myjT5w49K9jpUIghCMkvaYcSPB+/bo5CnINDQP9MZBYTEVEKwxXllU9JTOU60hXuTXR2qp6ViHG69hNqN8/y73UWp2I0wuT/nKNqWe9AjZQSWPS2tisv2lidGx5cVEF2FJD6BYQGqajcB2Fio6+PzO9LXVwpO5KyS9xc70c1PeK62pLWPrl1WUWrkH15s5vXLAZJZyLY7ckHUWGU0n7n30rF3jQNu1qIEpLe3umeRt1iD50rQA35Rb46ZnJ9WWyPdThATGSegivrQ4hBRTYxQwVMhcqyB+slb3TTgmss0Au/9sfvglXmcIcnCqfaGtlWi6wS+K8WKR5AyqGNKfSFjHEESXkZze4OVQAoRIiAt4JrVJxiXoFGpH6Fbsn9/HpF+cZatBanDh9QnJZkdMWmcgV48hRcQWdmKU6npwLw1BSYiICGdM+nQlfqahwdj6qPGGzlXAlECbm818aHM3ndTkmaZdm18GBgTRXi++FqR8XlmYlAWAYEI1UtQfl5aUiPDPloBeXPOHe4PDQN9996zoQ3STt7Z2SAPthrM75lUkGkaTLi1ua20wVRHbDj75afBXtGBt6CbWHGJXiRRHy7NTfOVz/Glob14SubxDXtZ6fff3VN/Lf2FQTRXLUlwpAOQ04Aqfzyisd6wS5vuCuGZlr3pSVGHcoC29uABBJ6/nlmS1RI5KgOQN609TOecyD3cOSwrL9o73x8VG8TW1dtUNl4BTIJakSMDR8cpfmW0hQ2LHMw2Q0KAZS1t3NIPh6IQeOo8MJHYeCg8JUTtL+2Av0lf+a6rt+8exVW3s3N87PsoyK3nKVAOXl6dlpAu2olVdUNDaFQM3dPuZJqdJDi6CiX8dR4BOBlIKWmBDnnBhEBVf7i+5C34qKUVnZBneP1+YRqMDkRmilaCi5f9AGL5eSSgHaHByEElcdjwwjpn04VGFTuBshhDWzcmsYK+klvZvTHErlOhqwmObEPqjM5Vx5OU4p7bMa5tjYh4XFZbFKXiiB8yrIWTgAFhGcQBy5M174w8cPfMR333yvs4xL9b6BzhIZAnRjsgnbo6PB/9HnnR2doruYQbBGvQUZ/RllRWUYJdmGgjoHRzKg5ua08cjQT3dX38l5CNQkE0TV/lK0barHZafneiay2rs6lEl1862mVswIQBMqk8iWkLhbGzEM1XwclXMaawVhgOxwfw/84onWXS98eTO7ME9SLB23tYKxmRzwOxeJW7AvLJMzRbkoTR0e7JG0UZshsJBUCv5KeiTCZDMVVSUUieQrdhqlDreKWPyjhmgXa9fVN7S1dcrw5HxgKWSmaA+4CIWXt1cgHfHo1OSk8jUhk211gkRdYw28iNKcl19cXBK/eTZlKg5BbQvZZXoX6IrRzpE+abSemqGfVpvBkUalwzG51IR/p3AtJYXB9CTiAiV5UGB7BYKwA2MBDMENzAwiTF2m+B1aIGnrfTQGuM8q1+Zy3BozoxVhc6um1n0kHdbEJjggPKxf58dovbSw2GWIEmhzy+XAYL8OdwHKXZCuT/buxUVljY1PgqsszQLyBuCvfIWUSIrAdzvL9shJDA337R0YRDuLSHTjuiyf10IlSXEig9dcfW8YjU6tXEhEmuK/Khbir2zc/qGrg489m628PD81pUkclWEI58AB47x9uN91ccvKum9xuhOI2Zz8wooCyAP3ABSibwAXsdMrM2N3w9W11HtgzhmOcQyvry9cUJXk15Q0cQWwlaf/7IvPUb3vfnsnQSAhAGY8PSWsAIBd4WeVSS0uUAtMPX/5oqsLS3s+OT4FMS0ll0QeQ6AikdSFlelrCpubWr/7/nt9TOg8EQLwdEj9J3g/WN10U7GsU5lYOm8FBXm/roToo1ZWVuBiq8Pr+RZUVHPTIfRhVKDz/ObnN/7Tn378E2JRaV6SBU1bGlhSEsBBIFI93r/85V8gHS0VMHX8FRf8hlbVp7kpk1LTjEm1CBY/NTVO+6AGAAJrORGogDkGtLi44JzQ2k9OTXoM/o590yEYsGXT9MQqYjfUU0Pmiwp6eRhr5mpmFGP3D9Q5CGB5Fv4ItSq/gLuAdnpNh4uoz4QZ55DelITOP6jvu8BBwUO+qWuUecnLwSuuxGL6OqdIM39pRcnSyoIHsFl9HR00MG9/e4d7+/Krr/r6+qWfk5NTSKzhkWHmopPWlrkqSAD2SNbH7ghhbm9W2oHlxTzsh2owGkr5wV90g/NziysrCzNz09Km/qEBgcpsRS8IEXtfuY5s1A/PTM86qASOw8PDUgxWLvaLrJyIMy0PZdASYeFhaWXJW/jGppYmHNRGXB1649hQrMPxNHNOjRNoAK/qbntb5+KiNYHgrzHm9ssCYvF8NT2rhKC5tdXIEDEjxns1RMMt+hWcD/ek1peTdMzyC2IQI0NHLzA5ObueEtECY4MeEiPb2jucfnGUN+c6rf/Lz16Fizk/V9myC5NTExih1uY2rBqPKgZv723DPYKTTl1SY5yhM2LXEHb4aOMhenr6mSiUOj0zZRONePIurc3txNqkR+pkyCKr5yITTAXYqhSJxjFVQveL626U8rhIPwmSK0+/fPVM0chhkmIeHeyZviNoGdMq7GFTlTeCTzw/E6VaW5uGno34dUUOAVIVXKO/5IO61NATl274n/4eNZ56Y80LCrUaFKUuD06PyP5Fta3DfDcMuxjHdZ3kpP4PusdCcLJi0crSqluRWLIhWLwzI1f3shqCMTJQVq/UYfUcQ+eOl7GkxQSgOUltBDGHdWuLegpU96Xob3o/n4nnBoP8pIkj0MKzl8+BOQlrZHipFIDICfg7DAr186pcI0LIJCUHEz8LpEqMOMNgaB9D3bi5uU6syEGFcrdAvTdXNmpfvItB5dMz0zysDzEx3k9ubazzVaxamIfpQUNUyebmdlStj6ILRP0GCnzx/JXZ1Ez6Zg2DlJt6dMWee2cJnnMdE2iacCYar4xjcldUSVnauWVwbmwM+++gOwtJ17hmZngFVBHpDMabNfJXqpJ6A1W/5P32Sw6QpmTLbR+mmu5Lhzb7n9nfUanu63UV4UhdVTVr0emJaXCBqMoTqkZSi6rl1p1LYFqlR94mKxUbVLiANmt1nntO+YLJJOJABprVwZ9fn18nZyamGhprnZa+HsiuAx096967rW1AlSoG94KOhMoBisi4NzaoRUHmvv5+rKUxBxzxL7/8srW9YUsi9aujeCt1KqyFqg6A5vB4bo3O42Pj4qFT5Iml8D4wWHnNjgVxCQ6pol9RuJNTgWbe5+P797SGHlWQlNd3dXQzR2VSp4ElyUUgql9//UkMwCeIn1YqhDhXl+hOlPH33/8gyLsfw7dQQKLqoE77pOEr5sJyqfv7yEf3N6kBdnV08C+Lc3N8KBGRkA5WE/VzSVweYteh8lv//OdPII8MSaohYJsp1N/Xb+lgefQ6L8/QV1fXhVJVhABT1aYkVKKn3PMlMqkBAiOceBzdwwN0sMzU/3lapAX+1PKuri6jy7HFfByyzp6JnXhQGkGFMremiZqcGr51eWUV88j7+BXOVOIlTDoAgfevrnb29my84RZgowMpBMJWF9cXq2sxzkF88yeS/f4Bd/b0calSAbVs8hKIOGY/nr4DzXApGjWETAaE/LFsENwhT2LOflUNQC2JliWg1HBHMjZJngCpGs8LiIj5dTlMmbaHbMkuuPPIprMEASNu7i6t0KtsazgCURFkwka6yo44z3kG+Z0yqAUBpdGG/2VFMAcj1MBnzJD0winysUq7XKoUG3zxwEK1pzLZJg7tTVwxzwKxCgAmY+ak7BRbFTLNNUOI+xxLGm7o9JRJi81HBs64LLcYBX++u+OqogUQQdOWK7P05POVyoHuzb25Lm+obVCetVlWmHCFGg0pgcyNSUaUVIkst33uHy67GmF4aETOhHDVbAF1hhM/PoGsxaqzpzPUaLo5GVud8XCX9DmkiWYMmWLeYnh6eSkoS+PiL/ftSCV523T1m/D6vKS0/MXzES/z/MWL9u5O9d4YSJn/IC1WVeCkkFrK6UyFuok7sCBW3lEVmB06c8camptdDH37cCtm62xA7LCiu5TevVoYXwjHMvJoMtqWvX3tCs6U3EkBFjjLrcjl8og15JdMAsstnoVoMJBvJurVEZuZnebW6cKHh0ckaAxAHdEWyJjtoC5lHab4cYwoaOI4CGaoY+bq8VAC0jiIUGiPekMZDyuu5UmDEHSwrTSBkzGHlaXpD1VfkZrA4/gUloNwEb9FM+vJE3AgBo4BCWgAvoU1IqacdMpjiBaYwJZYWNAbyy3YNJU3MualhXkViMvLGz9L7YLIF164b65PCLTT/pWxWfZUpPfkG3QW8RfXn1eUe352eXt2C1UIP1LPUKclMLGGZFCCnHD1HIXn56woyXW9ba27dNpFHQWqkpITiYjxOa5vQ8GobKvqc9+iHRWTrkDsApkNVT7BGDqadkqWLDihEvSXsDEcrNTQkFHez63dgGcagufrJXQBy7NXL5O7a5uZD7et7e3wvgV1t62aO1ZHeUS1rauvmzJQvV1A03smWU7Pt+vREODkUDGvriCE1iF3zOPIyDAFETyCPiPYsr5YFBbDI//2+29v3vwOGmPflCMoQFQTOHMMmCDpwx0/RB7yFOeOXFJXVH9AGogWdZW13d3dBDa2hCVF2fzJfSMGiPpz1fYrBaX4o4doBdKmwZPZZ0yugRuaKqyybeZ543+ZGV7D8HTjBmMGnClRRwc8svrqy5cvP//qC6nDxfFZGiOrjoDqt3hbpSRAWyp6feEKrXtGKT4rxvo/h9PHOh5uA3ceABo6CtlMt6HHpTBFJBOjox/ZN+qc95G8kUhiLxzmg6NDgMiVF2sbK6opPk6ebpHt64u4Bivf6RV7uB4nM3s7e301GHCz18dGx4hGkI8mAZA6zM3Mq+BZRpIejHqw/G7ELS7hO1SQPCSwQc+wOL8Ilgox1laYN8aHq3KSpXPYdq9M54N8dB68uTeSIA8OvOA1JLOBV3KynFizpNGeo2PjHk/skkWRCsg6IU0umHQPoBGE8e8Ci+INsyMgNmeI2aVz1WDPVAiI4p1bMBAzKkHhE5VYnHzCRT7UMSbe5HBhAkYMlykOMS3OyDFjAGKwdJiDMM2SR3aYCX/1K8jLSYwUEkFNGTotU1AKeXmwLRjht8ALfYt+0YU3UatIXQF0WD7hFpbEY/z90yfBrL62wcIqI/HXfkw2jMJl1S1tTRoUTltOtnc23ZfgtHLNxXslsfWpVMwfQJ5gqjX0JjIHBs1773UlpIsW9JFR0Qjkiiui41lG3PmXuo2bm2RR9HnsRIiS8qfMKr1N0ReCOIaMA6dROec57u8M9za0lgGn1Wt01BfuYRsaHGBvUR6LS0D39VjJbOSIbN24NDmW0g89QWFufktDCzajrqaus1slsAKqkRQiPDx2RUkFcayFkBk01MQd2rwbeUhpUQlwozm0b6DfCSVdWF5eu6eZcnnR3U1BdqGGpaWVVUVgiWZbV3fxYaX5BSvra8mdpKNKwoBGHh+bxAcqnvGVoE9OfrYHBk0ITeWj/oQ7ttr0EUEbPCU4MqcSxJFP1DbWtXV1oFxsujyVn+WdL5JZ5MHyQgEeGKIj0nbngVHKVlXdnnnTnpC9GTGPXcSj681++fKFAwjKaJbOOAv86zRNTk/xV6CPvEFsVCvH47FqZJ+3Hno+YpCBMSdv376zvweHrWh96ITdyg4R8Sqc4uiz58NMV3LvT50g74Kkhq6cC9jTOx6cHKIQsY5K1kr6NJ8UuzJPRFZ5Rc0P3/3w5ZevoUnBwx1H0vr94314Tv3JLDDnWoXAbjpcaKHNJTfjurMzv7unu6amnk4X5HcbCgmGn0FuK7aAVPXV9SVffs3F8SGC5enppXTEwffWiCzpJx9WXIxiv0+aKYmX9ALR93d4xM3J4iWdHLrOOooaZAV0Q3Oxurrq8AC8TrI/MYVA3YxqBWQjCOFbaUAxTSobcA34CTLznvHJ+4eaG8V2hSx+E7gT+cE9WNWx9PmUZIhjWHt8cnxhbh7i4yZsCRDa3dE18mwEYAH0nGRfzcXPzsy44UGaZnUk+4Su8noTCaPe4NaRTOPMirhORQ+rY8afk48fAPlVXxm9R5WcKNb5n7DsEBosYzpbDEA9PgBtZKAm6/P+qvaJxK4WWOwf+NDeYeZEgxqazECVJnRjD/e8sGeDCDxG34D4/gT8iupgL+iB6Q6B0/bmSZQc9zXckcNCn7IWZgpKv/39LXzBuH07+5YHCK4OD4PG+rEqagcZtwCqg1EwlpBaRto4RHeUUvPzHYblea00cR+kMhqHwg3V1Nz7QGvonY1XlntZdqkVxxQpkSu8qypDbJbWp6JuYViRSaBVjwaCsBwmIw2NDAlLmzubkhimbIPo/DbX1t8evEdnYSocSy5D/Z8aVTIH9ylyqhkwNWFYo6moYMdVuvhc3HxLW69m4Ci7mwKLJVcH1BDvCqSsZAzEyy9KXcQkMl8E8ZHiyA2kdI76xdmVMCCJ9sdyl6j/398zUYYazXSPTzqhJBPinEEUPpR6UQiEp3jJ/HqdNYi0GADJiUkRfCMOBi6xemc3Z5gpX+pj3UT06dMn5jEwEINyRILevn6CCAnjQ8ZdFKiq66RrclwRSz3IKXX1gqOugYswhkJGjUiqJ13zhlepC7IOd/e8fG1WyrlAo1gaJYu45Tx0wA6nZecFIGKAwIkoLiyQHPjioJjSEB73mZ5tEBe+k3YoTqBhZfoQtwTcZR4uO3LbnVNtosbxRYhAGMbq8grDlhbDxdhd+joWVVtVmzGk/F5TUUU16CqOxLGZS4fnhcV5hY0mWeEQXFDs7dwo26ksDMA5OZh6bxTH8/5R6kFao7zhDLJY+yUwAxzIB+sKEcr/1t2PvZc+vzonMh7S9WEt/TpU7vUbhj+KwT4GcFSpEGztYH1Bjgycjd2URPo0AQ87qkhgkI7A6aiwU/agGuRQWDre0yOJHoaegYkbm+pYJ84ENkxqyw9aJb5MtauxvUE1SOgKeoBa76pYqYl5S9+dBiaq902Y9ySgKv0VKRaExz4VilgIyfU6zbt+GCEtK4Y2l8dtPDXOUXB04BXzznjiCdKOKJuFyPiBnmB4c4LjZXhxO2vIygX4qBu4Zun47iSM/+GR5/z6y+/++td/efZs2IJoAEHDKAwY//7u7Yd//uM/KXK9+DdfffXysxfZiRzVQWm0aUsyj9vrW70UNtOGozHXlqNrT/vU+cnp+uq6UgCuJQTxN0FkYVBZO60UuyWKhfzMx/UW3Fzy2atnarynZjFpWK2uEvGUXHB6hbUFBB6anlQSnHNn0osxPmhIoNNq7ELUg90DnZyff/6Fmxr9DAzFLvkciN4RI1Sg07PhHAQu/vWrz9i6M2l9vQCdjyB/d9cI5kD9PhzVTltNesRJMSZpDo5VCXdgeMDbyvj0lK1trC8tLJs9Ejdl39yip3R1IfL8vAeAIJrJsaHC05g9RxLAupR1bL/kbmZGtWxRqkUEooqA5xG9uQADkx0WxUPKgaCPqXH07xjqfXEmK6yvww630qLgiPsH+jl3IZUBcXOuKxGW6fcxGPYJxYye0kviM5Fa3k7mxHwQtd43rX66cO+eMoTgwZPyyFI2qke3Fqu2+RlEhFdQSBerOBr5gV6QP6gqQgIN+Ohy0unegT7JoB+w37yeZGitxxgLPmRr9NOo0EiEYeAiSCgFoXLkEngdjAcJHcfG6TjkCCoeWS7CEUix9a0IG8h03e1m+0Bnz0aec/oyWf9ZbIsrpR4ezVl085paboQot0ijerV60ekrLhcVitO9PT0ry0t6O/yAAq0eYkoP3yb/kgviAUorYKJDXiCzUv99hQ8X232yHiKW6jRaCsHbzAi8jdM+GHMla7RTUFVaYSefYQNr+CnZiedH+GIS+SDHdHZ22j0Tysj+k1Actcpo90s5ApE03JNp0NgVuHZ8a8Ng4SfXpSUeEhbQrUSk4kQQNovYQd8pzG38i34UVk0O65zrsnXOOVaNXWAQAwC3LZ6aEJ/CCxCH9vf3W3yadClTbirbAkEGvJ9ONQwyXsKxVKSryq325zbaMYE6qa1U2py+0sIiWYux24DL8vpa5ZWbos1Lj8E1xeXFrGlhYdkmKtsggiHburpGT8gF5uQekIK4Aq9RKTJhqMm6zMlpdy7USElVIV+No/IkYYZeDS/Bv7NVKnKL7LzwzLRnLpspuC1mNvygP6mtrqd9cnawdu5GU2lXwTI+C5yQgGZn57lm06AbN6aJCnsHR5ysVlOASWuAGaxSfDEA2vGalmgjrok/d8WR8BskmI7CvX05Mf1FGGHUx1wJECum2AsnoY/+8V//wII6sN4aT4Lx4OzAFucrPTsoi32C2EJLU2N9VPhycr2LfbQs1Aq62JgTRAvYXW5cBCF+d4fm5ce8fhRm84F0c0eVbe8OXd+UGeO52GRLW0tzewtMPDU57UZYrE5HR7SnaFJhlg48KaoXjBTw7kGWY9qdtf3uu+/Vt5xBBx9VzlzBDS7iD5UE+T8cAvs60eZKYr9evHj145//hKsAhX0CTyjp4flqK2teP3/p9g+TBxn2v/zLn12Ca6SjhBWtbPWODot5YDKhi6vT/r5B3AnXzLtSFjBjQRc4hQspYiFRRHvtbbWqhbfjeVKR52liSL1/+wFES3a2d69sOPAHkinen6/0JsM11ZpjWI/Vt6poR68kCQjQFNd4ibGHwptR3SPDI/p+kW4wJu5VJoJDxDohxxsfH6ZnZ4ydl61oDmZebsgEGrkKX+TGmKeSIMUkFogLXhXqF5TYAWtVS6itHeEBwVAwZGl+wWxuz4BxZtmoQK3zjv3LFy+Hnw3Zg6XFZZBOvHVEfQVbQgt4HLSvzWZ/6Xwi06thtG2w7XE8sPzOw/bepnXRxxhzTdTinjIdP/ZBG46j/3+rfLU1XCSyGDROZ1sJwX9iYlJVjT/SMq7OGaRzXC+XusrBAPAXWJf5xcX51PUF9YC34n8Y4u+/vUWqHp4eQRlEeC80EQ0NpwPGqXZ2z8Zk5d0CHsIdA+Dz+Xpi0672djtNMcLBRdcIqBAcpot8643EUEqRGjjiAgAbbe9os6EolDTRAWne+lyei1qRA9MBTz3GkoQaUNRK4g3F+Og7vo/hZTTu5CsmzscPyOUvrx11VSpBS8bT1tZCn6cT1apywTA+VT7zgEY5J/zjWnmpedhRIezsNtnU0qlCSwd5B54ILRNlt+JSvIN81ivYeoau5Lsn5crIbO/oyMrMThODJ7QD0Jm7cGOyWlkFukaeAeIxOZgdlpcixJTKK6J28O7KhiqCGSjEF8jxfJfCjLo8N+ov3Sf6lhE+MhUCeWDcV/O8QgUjkTe43k/zp3xCHqaBHVXID6IZ5VUaXHCyWQmD6VXsEvyRIo3hPALWh9Exkozy7NyW9g4XlnoGqSGca1Oci7nZaXe8616UGYBTPsrLKvLgu9LdeSnX44De6CayGMy1Oq36v2gBNd/dEHREUo7K19mL+BLanWplCQyPT9MOMrO5g3PAL0EnkmDyVj3PPIKPinLi/b11sKFYO5p8vYfuaLYRaiGAgaNq/iDbQI6pcEZP3KNrKu70nFtbk5Z4Zbuv9CXSSuO4YBTT4NCgf7XRJmZbRWfHp5lYELR7Spu62cUHxtRABjaabQOXUqXRj6Mc7pdfftPT2y2cS9eWchdUg9TR/ToA5O5goIFlO30SAgcw4ykE7BwWToa5WnYDqvgfxl9WUdqW2Yab3SzeRJHBi+zQdwm3XKHsPG99VXnWgYrgkpnBacA7ZjNwNVyKpbNiXLMCbkl5CUpHWdVmqYByxxoSpZ/KNk11sqsCTRtWT/OpXxP78QfOoL563exWGdaEX0Wvrb1tCHV0dDTky+4ia2zg7sVatSvMAbwPR3Z0dMkclMYJE1zUZdQCpCg60oCFY9TvchWXc8ScsQrDVl2mwj6r7TVZ1PzConzOnnpJDJXeBu8F71JmYrdwWWxM9YrcgM1aQxVTXpmQBPqoyNH557rcYkn5Iw+bdgVnx+fRHORH+X3f6jm8jFTLYE6wmruURvI+nDHQYXVWnlaC+vYBiWgPNuXq9WevFUbUgeUjAixmwOn667/+K8wP8z4fed7SckJ0ZVPNJuWmHTkdNZCyv/hWJAD+2lfHEFfS4NublaU1u6jSMPxsxHP6EJT9h4/vFUi5ctkcMIQiV1DCyfT19vFW0+MTyBZQgqWurq1YKUc6ip9ELU9Pwoa81YkfGKAU7g3FRQI1HwQS0ArxvXv3kfiVzpvR1FTXRdlncVlUBzQa8fYNjaBxiFseHy0lrpw1o62D3+Acj8/00GFO1OjR1pp4Qacou19m8IhzBpqurBBwINuUkT0P/+tqwIMTs0r49KF//cufSUR8IGCO3FTL5ewcXkvMieBMOXG9MO726nJFaku7M2B8ijW5TCksPwpyjNUdBrwkj1BWXtHXN6CAK9hoOARakeZyn6d7Ot8MQAdzJLlRU2Jk90Wuks9zvL2XLwL6dJMxHLKc6Bcn1dA/ET3JKVd+IROT05Om6lMmsP7cZH5pUV5zQxMFDABrcSwXl0FWJMNDRzi09XVJDu385OT85BBZScMHMxpmSo/DZl1vfHd7hNADsoxq0LZG+0FKqi7qtFSVUbvejE8QZa3BRI6w9AsS58EZDM4nAnaxsaZ5liumgW7vtHa0ggss5yJiedycDrjYaD1wjjgPJ44KbyxC343xwsyGR2AelhreBPmVXmlOUtdXrDuo/7w8ek3+K0x3fkk66IzIOLIyEmrpZIVGnvCefpjt6fDo6jIxrxvh4/UorJwOhIBeaPPQzXtwdJHsTQ3NenNkHnIRJiQZdbytlRseIH2eRWSQCsTIz7jC2hiAG3stfRUjC/IKh589w/WbTSvMMw/HnN9xlGERuyCd9Wnj42NyKfHdT5Ksr61swlgWVzhxOpxbmZD1BwvianZj1EI0K3zkRCsTH3yKe7Qq7m5TOpLO3pNQHx6H7DJGKD4obGc21DVRarmUg6MQGC8vrsVSn9PW2s70YV76te2SbdeZgY+SWukXL0kzbe+konhLiaY2T4YNecgmVR8Zqi0Tq2A4G6qsiAGLeYutTZZ9aHhY6qfjg/2X6uFPR2Tbx50pZnS0tTtzFhCCgQ8w1MqnWATEzpvffjd9ge6I8l3DPL9sZiE5OPISAQ9+CoSuBK+preID1boA0Hcf3v/88y/LSys1ldU//PjCMC4C3N9+eUPGqvVE6LXOfKDDDoRZZsKZ9q5zc8msHe5DHv4QxNsVqUVXZ4fLDfHDNHUBxitqkEDGXcS1nbLSs7hNWpjBzxhYJFCR6IhVShToR4smz/BbnlQbl61SKjnc3YcvQSjMuUERaAAfRbJ1ePw4PzsnANhBrhVkydfyXVG6sbY5v7TgV/hzW6ApxIKrLQG4d7dFwp6JVUl3L6hKW4ullRUxf6C/H4jT6W4wVniemirogLE6osq2ggFk6gkc16iSNzY6+UrBb379FSgLCHxzY4Qc1RCKZnZ6TvwwFZ2L4eXhWd8CpL179561MbzB/gGG7oTbLdjW+7gCRZ1KuR94RGpzxCauXKeuQBJPggnETraBQErW5F9xv7OC7dM/fvpZftLd3cnErTskKKrJVdGdpmrob4AB/RYAxQs4DxwjSCfBCQB1dcMobT8h5tT0zF9+/MvQ4KCX2jvY00PPHNV4rd3NdZbH0y0Nb6qe5WRndvf04qNdeiXD6u8fdAIwd/IDKMn5Zw1oEJ1ukDzVvkEPOTc5If27vT++OPPJw4NDf/rxh2+//17dRisM6gmTqzeN/uHdu3c4XPKe7m7NE4H1HGxByLk1jc3DpPMwV7bK3I8VZRGeChnAuD1ytCqqqkE6PcVra2teBAooURIxlivtmCjKDdIRy5UfJENoVAcfOSN4qxb4MdoebL5uAIt/cXFKOM9VoxR8qUzOcBnFbc4XwaKGQZIRjN/W5uXZpY12+RqYbOpLa2uHYCNgYzNYZWXVHuWYEX6OKNbLmHVlbVvhoiH0AqPHnPrL1qApwTTrLNXgFMA6rodn1/TgS9mYDJ3vYAkK2hbZSrI6a47YEQ+onBOPxTYNb/vhwydZAcUL/67ag7fkGij0cQsCZ/o85DFXZLfMDvnOlpwl5ag/SGfuVS4FcfOwIW2OPkGA8k7Wz8ZceEl8zNdjw/EDuC8HW4ZydXZ1W5wySA5WfXAJRJqB9damKBmQExg2jnXwAJwIFpvhOU32q8z9GeKBCwuDpVUy0WqqimtcxKG6hRKaroIoA5ydiZV0OCay1TUkDM/wlxEgViZnbnb3cF8sFAxQ9qxazm191LeampvxfjsHO497kmCesxzXLpbyuozTupUY7wps4cLOLjR8+Wei8orKUmoVLKgwAG+iL+I5dfeZ/Koj0f2IMcvdtNGYUUw2+aA755GMWLpw6/kFId2aZn6oyij0qhK7QUXmj+NV45W90Y/6TCHZjL/Ipioq+XH8jFgFPBvPKUFhuDl10Z+v7AGm3NxcKJMKe7yQIgi7JuKErC0sl0KtZgF5eeEcsnahrDYa+SI3apEpEVBDhCF4VDgGHpbIhaLGSMS4SD3XA0j7PDmh4NvfP2h16unpip6PLCNkhr23zRKeleNjUBKBb3FhfWctA1Ot4rv5WYyIjRK98LE+0INxILgM2RVVD+B/vX1NVs6r+iLX21luYlPNNeGSMk3ZywO7uTtcN9fD4FnpzvamEAjR1lS6W6mDBzO0SehnRk6K14cpNS7wayGf2SKfOYT5rFitDuq9QxM4DFTm0i11dNugWGi1ZccOr44LadpP//y5rqGKxfgykVPnlJwzzS/54hv1WBbrsdzLgX6VijnPPkLw98NKswK7Qo1TIbyncX1Qlr/+8iuMxjpFSLmJfA01w6c7qxy6JEOYjrlFzndc4lMtKvDF9hXa0s7jkCOFZuZnWYOUAnH88ttX9hvJ641JCMShzS2AIuAGO06PbFRntlAS5lAyYDIwZI5NW3a2QKKOWpCPU66UQDmFsW5ZipLKTfT17h5yM1gp0kVyUFZVqhZqfaS3DpIknGN1evGu8CkjM4ZFfPYuGjGC8hJ8VWDWV7Sz2uDBoWGoUDt07FlV1UB/n94TtWhn3rJwBLaB5aFW//rjj/09vYZXz8/MOOc0EhluND06mZqcMmaGd3BUKKmU0OWkkoOf//GTqOQIEuAGcgRmHx7smowK+2EXwEywjt83/QORuHuwC6SIrNh5xiNkKQe57NBO4dyEMXQcI1C1Yg0CiZ9E5hBiKxjsHUQ3H78mNkuD/JgMhukYdGAHRVn8HXmoB2DBHLFjWddQI0QpXTp+3G5zY7NS3kpU0DaxsYQx+G45kJUH0uoeSWxLcDDFpJzGspa6jKlOJzNfn5eZizhWXmM/kkJUPg+L2qY4yHg0OfzIMor9tthYU3ybWiu0zvlLJjwz7KPQRpipXOVWPGLNRHuWgiNbLUq59xk9nVR8CZp4b58gWqh2Yp1kjiNW0iF2B7oE6+oCj5QuCeIDBYmdP+BnPL+fkECIOcrdqkQPiufumy1zlTwcjNtUe9epJ16mrfEWblAhZ4RIBg5LKPKCIocMmK9UXbSGZhhxq/QXESICJUSuwsdyeWnWJXFiEOb2DlOXaujl80i8o6hpwImqKEYABabgLtNBl+Q/5eN3Lo6P6Yc0IwElnX09WY85XLmTa0k9Z5BAUc/QKyU9jisouASlgmSuXjE1qKOS0gc0iH4fkccp88AkY36XE5QEi2juz46CRoyfzPEDKD7t6CJk+v/cy+Qjg17TYWvkqvpHbU1DSWF56u56bGxMnwDiyCfTdwg/ULNyY1tLm5KSqkBMo6muxTEc7O4jvnV4uNAKzGB4VoYISuLidKTUVSxPOjLZOM8QCS8KKEsDRDF5mHsIyqsrXU2jG4AHw0yAUG5FILwXFB0K3tyCkIcgbBUm0XGqlxn3T//6l79qZzPd8pd//ordctycZd5cNFLVN3ltbOwTPCGQAH+8JW4zXGJZaWsokpMOi7m8OjoRgOJ3diKXcM4DM123UzMfkbT9sk3jNE/oqdzvonkSJjguOa5vqhd6OUbPTCrqEJnQDJwR2poFZPdl2PNzH5Ep8g9MKZmZJ5estLW2ItZEDlNDoS5DMlDRrrfyjkyIHt3J5cCdNdfyiBByStxRtBlpJ9Cd/PL1ixecTbEpRdm7O3G/DPgvv4h3zs7GfkvDLS+lXWWqEnnnfMpisWs+QkbGmn0cKEeBwLm8f/cBcrS7OCJ2wFOzbIJv8jbJpsSQ0duSKPtkhkDe+jqJK8tr0IH4T2eOj3O2EWcvnrd++ZVbCdupg3yJM6CEwnClO7J4bA9sxnZJQgnYLahXgFCgfHTw45NejBNZBXrTekKurlI3F1sxBQeIMaeFwIFoF6I3R9ihdBwLPSP8i8liBAYLs0uobVPEJd3mU5C880HCA4eu5Gos4g0l3/r9P/75Cy/cM9Bj51S37HTg965Oqne0vudyHhztgOqJLKgZJsNH2Ym1tRWKK/UM0Z4W6Keff9It4cNdcoT0sLzcrhMSD7O9PT0zS+3U3d8jtkqq0NaCJeAcGkFpfkmJY5Ae6ZGBaxJpHCS4GDRTWuSPxHKKfX/tHbgFEwS+ckbhIb9ofmBfb29DQzM7dnWAd8QnDwxU8tgCAzZZbs7rmUIjhqlWRbuVFht4+/oG8DZ9xFHE5NgCjsAkHn2seAlgHyfgGcQGw5gJB4FZUmORBvDnbgAnRTOAyCFER4ZjNfXs4Z6MhLt0VaxfxNH51/HxT3pl8TB2UKqLqe/v7091tDED8AeCW9tRbl/1D+Te4U1LSzXEyWC4N5GAZAX7AS4jHFgXB8TJ878wjK4oPsQiD/UPelnNFsItiqyupgGJj8c7ml+EZTQ0kQiTG4rK3b3dLleCpzg4YNlQB0dAuOUk8FTMzKRKewIeq2dw+tEqdXWFD9zcXPNbEn+nDC/vKZ1wbJIjBj95L8uCiYDvWHgYoenoVXGvt8dQdVPngbmAPlJ3YZbOw7oD6UkXE0EQcL6ZyenLtsgf4CFTi9XPOQvlvu9/+JOp3SFtRuzcuqTlWhjgvBwEubJyknMKOlCFmYTiWlWszdXyipjGEauxgBp8PabQSubs5MZ4n8pyF4A5PqrfeLyD3T0JGUePj/bK9ptdWfy62gbaf9mqRNZhVFdfXJo3kZsuxKgcliAzEPixE2zPIXK6mb2I+HjzICUDc6yJEwTDMSqIhK9AYoA4fI6TbuMsfiRJN7cYcNlh9FDHdLagx81u7WjHRtY7X0C2r7NZWnF8l3yXPhN6oHQA7+SFeJjImLNxNa6NjIEKqH9Qj/dzfCSBTJpgwenwr/IAjDFPi0LwaT5Z9YQ7s7zKTnYW45ruL0mhbP2MxfFnJBLAFhWA0Ok19etcZzLDG5xC4Kera8dcndztylIHmyv4iaQ2jR7XXTgeCURmLV4RSuNnPIYrqYD7osK8TolnQ31XR6veJoV6Ll7jEdd/eHQ6PT0l6TYaQOkiVsalGgXO7+3m2mbyL//2g2tRsWed3dFPyxB99/Pnz7h+59/Xi2k2xiYZ0unA42coKTHy+ByZDhDkLf7gxWJx7fTFRUNP41fffKF/WCCB63kKewkUx1q3N4P/ziFa2g9bjmjzi1YFYolH/4ycMEncpoofX3/9jWIMbu7jhw/v3r21tTbG3yEk7o/61zPApyYT+DEsk8TF88fhKSzw7TJWIwedRCIWbROYUHQnu6ioNuG4tLmhxRkDExx7wme6hfXVlU8fPiiUUbjjJe9TutVzpV4WemJ8fPTTR3pnh0x1IezSNMrHh/zSwqW5RSN3qmqqWDkfpGGSfxSTMMhGXxGNSVaQGCAP+l7Cy6BMYKWUAPaP9ne//uprg1wPjvdnpmc05YPoDXVoljIDEuBQKk5xQmMIr0S7acyD+y6ZjhIiMSLvDwh7DJslfeGPQCQoVEtKmh612YmF+UP4FWYzEwnsleepByg3OT9ALOQBs+se8ruciaXDM1iWioZmQQufQ2OnZK/oQjhk2Xf3t8/VHTRAUkYaNYMor63WuqJ9JHVrRn+GLfYxCFlOGKlvDA9rw/aKVF5BCMQhADICOZ/JfB0a6ywT5IyURunmPIBI5qUQjy4TlOzLkwh2DbVxQtiSEIusBtC9MOiUfMjEkXkS3tkCYNx1HDgzmJKizGLjpMc/jSNnyJ48FvyVaQR0QYn+YXmgJWVIWunJAaJZOCPTzCVKfLWoo5MDfVu+0RJBczyFwixGvqG+cXj4meecmZ5Wi/B2YgOIh1bGU0FtlhpSsQKhF3Lz4iW6WfP9I67PqAM986gGpYJnw88yKiqgTkhcZqTtlswB/rDOkQFYhVsXRVRaLKKcQrNWXFqS/gt+FKQBXlkCGKeGISpAAhpNbCsjRI3m5hUSbtCzVdSGB1F5v3tI4fmkKZILKgAZlXMByfAmDhGipPAWE5aNWULlE27pULV0zj1szguEJre8yInV585yru5KVFdT1FSPD3Tr4g0KA69SKI0yBjEuIjfc5JxDDGFB6s4VKC5xgnlFMie908CSjjbBBiJhdax2bWVV8yntJu5RUQKk5WdEqf2dAw3sQJgMQAXixasXxg9jKSUajM3nSxp29na5F++uCgjn+mcksDPCKdfUEBcXO84CAGvhHJ4ST5gfrbtLy0ughTSO85EviutpoVrSeEdTLWTbqusqB94+vkWJeMvkuL2nTji6vD+3HxKSfTDjyalJyDnGV1AhCscOVV6eu0ZWTYmnFXTToiIKFOMqobq6oZFBe6XwrM9OiglG0VMhplg7ivv++toNHCyKATAMAllNPyGiiyujH9c3Vx0JcJnshRYcnsN8sEmZ/dr6sr2Wo8gD5G3EWgxMnwmOWiw5PRlbW1rlx2yOgUWUAizfHTFRcUk80injdRvUigNGQi2hrnN1cjm8D4txrz5a8FR04jtiZZNZXJszjBIV29UJhSknYfTjJyRU1l2ipLgMUGWrALJagv+EZJB1azLQ0Ds4MChNduAZE8jj/W0V3kauE/RIWZmB+xy3uvGr15+BCVitn37+ZWJyAoeAPFFDF6V4RgFT/oXd83c0HPwCGsgqoAzfJdFWk/O0Ws9C4FhBUlUguQUGQTCXFoDYvJJgKGZIh03eiInE6+sKetCfaMc3wWidtd0EPEfnh//x7/+uovKXv/worjBpCh8JT/p6ppL8ZH5fTz+5kVPr+JnDZZCE4vvCosNcypJ0Lsoo7ZzVAELZnwFrhCVWVYOo4GQ+8PuP79++/d3lB9w41xa1RK0fwS9fyPXYegggy1UFQqevrISLYP/OFtWjA/8HgSMhd2K9Mrxp+7l7/sipmxgb9Z/YN6KDaoI0E66UL6PIeE1B2pfKyaQjOss1HPpn7Jbddywh7oamevVMkN9e6H6SDYd0xxB5KP7ukQ9ykpWxIualK8/wL6djbICdkorBpEQovMZOUI4cdZ6qbG1VXaImk3MHeQRXaldmSORznHHMyj1VQaIIOFhZXdWAiACFTiQTF+unygyCgfOglxSOxnhkckXJTJ/LsgMiBQKIESuSavk1B3fnVsZbHHRpRXX11VWdJ9EQKmUMsIbO0fNxdZOR9YTYVRjRsy1+mZOqrZR+wzlXzlVzQioyTlkaYlA5kC+YmjSuqtC0L8ybA8yJOz+2W50AeUVaE7nBg2kwx8oiJGkIJakJh0UtR6fB7AmxnEywIHiGUp0NdhK9i80IFQ1MRh7jpQi0zfEBHbju3AKsN6IjS/nQyhsgUKodGq1PilBaqmio05quBnlemVHpxzCr6jFmzKIpXN+h5ikTcgAB34wMWJVXtHyZ6XzoRmoSqIImqhirRgHYEPKE27hfu7TCbUsFfAIYJ344qvyasfv6L2m3nAWIl3ZA3gMsmpal4JdGfrdkRV4HdjYPDvLA87gkEHcR2eRNKj2eCOjnig+Mv4XfMQQEID7f+lg+hDOD6e/rR0iIQ5+9/swxsCA2EYTyeOCRzzdUw1r5AdkS6pIT4xPwagCNzkEWjskEN9GkNpQfxNM+0QukGRY8sw4tTL3TlJnMlMpxvlJ5qRiVhM4vdB8HxRPq7ha9BAwrBjAxNoCVDlWwEyRELzSJmE2AQq3t19FZl1JkVeY03EZRaoJBovAtfIW4i4RAYGgFVcaVerJnnHOaXGRRj55E3HINe1HxoLByZxD7xRmbSRfPiwxA6evtsSOOteRSQ8PS4vzS0gJ/rh2R0YoEOBJWIbTwrroQ2Vh0w9zeuFJQUnJxdiZcJ2lS3fPpLsiQO9wp5ETeD8VjSCP7SCZBdBuMbWAQ3hPNi/xxQl3oLGcEx9TEJGi8APJU3kcj6DBjWqgkkTLAGsjvAzF20CKSDieDa/WTrAIbo6bL4zMBOyS04PptoZOLETWNWYUZgtYjpzAIfZMD26o0H4W+fGCF8dB3d3gW4gEQTkoIrcjO/uvv/wkmWwf4KLcAtal+eKmMLpdZNmng+GxlfpHjUx+WUCsZ8SIu5pLGubLZ/gH72GEXQN6ksvKz82g/eGFW55mFYoNk/UeviTyMarbBmRXVe4dUVFGmd9yEq4uTEwO4VLHVS/Q96teAg1QmLCbsJrHFRZidP79IJTg9NvqRuwcN7KdCH/DFBfPgFAsvnr/g7vFC7IOXUbYyJWxr8xxTayW9KWPyA3YknVGpWp1xSQB1pTbw6ipz16fdtnEjJ4ibhkwXUcC0ksIcZR42j0KwIX3Rua5s8lBNsHu5yZnpXSCFGlKc9UZGzgHFExPjssiBwUEFId0Pgo1RU+yhyY43Nwjm7MyBv3NtAChhLwoKHEVpIbhq2el36ZEoVxCu0gXUkDXk9aiDnGY/r9nKZcgEUXX0c1nId/+nH6rUxAV3xco7jg4PHImn6gx5wPHVMe9Wel+OewE04AnF66rqqL6KTz7cFFVTA2ARRDZnYSUJT/EVnrCxvl44uL2/Prm8fri5hdf0CR3uHpKQWf/G+iaH4HRfyn/gYxXGPbCZa4CuMJDMzFFKWVtbJZqKRjyXkje12AKuFaATFA2Comx39swgwlApuug5UMClTXr12Qg/ZQzJm1/fv/v9jSuoaL4C5J4csSX+Wg1ccikPwBo4MtaEfBOt6j8Z1eCExrto2iigGXXReUIITxYZVes+xYL0eBVtHwVAq+XnLNBo2Y8ZQciA+QGWUwIV+otyKZlU9sckxK1HLNt7iRksTDVSbIeLpdoQJaSVng5JDhHKS26RtoR3VsHwiz7w7DAuWObg3NSMWgEg5VhBamAjsxJFZSXCAGMAAeka+wd7o7HAqtVVpa7v3NSZSl0a8gx+MV0frvDmgCMu9DgUZudj6lFPUf2sbeCm1RIcz9k5Ms0T2by0zMOq+CRzNcQ1Qsq+2tnx+tmFObwEGiqQZfYlp6zjhBfy2LwFfOCwaO6hUoVLZ2dnIT+1RpLn+gZh4F6u7EZrl0EJY8wJ9kW5oGSkkY4hZGa7Vd3li8r1FCl7+4ci/e5O3IdoF27IorKzbajsByIEdv18Ovwc6cYHT+EVn4Os5p3o6Fg1yOn2JwRtUL4FBeKT+5IxMeQMsB3MilS4PM+NT8sxACv7IHLAE0hdZ5IPc69DTXnV2cXJ6sbGh08fn0x1LSgUMoeGRpSjDF94qLqnOOdUI1DtxwgNRIIk1STXJFwAILhES8QA4pA5kbXdpFTwCWBtKarG0HyO3nGUcUxOTtMtSRGQ1OAbDlEA84nsifRTwxcdkVAxPj7OwfHR3gAzy7YQ+l6GKFNwg8plEz4QQ9LRBeZv8iOshsNShzQK2IpYzcxTTQExR1pFAc/c2d0B6TvbLkghmYsGDefZ9WnJnIszA/OEehVZvE0+tmFhcZEumjwfG2C2zfLCkhOFX9O+dHZ0tLQ0T+B4+3grd5P9QVDoQinOXsleXXU9yRDRKiJt834N4hDbooL9+PDp44exj5/YtEBqyJd6lyQmyyh/wyISboS42QjhzV5tbdXrV68hBQ6RtVEF2FrDPh1LpCpvos7nJ8Xs+dkZhpKXl+29bTpfJkfGAv0///f/rXpjgIF4CReaZMxkdDwZQq/6MjY6ii8yf4kQFcMIlYBO8gnohqKAUyAwlxgJjF7cSpLwyoshDQ4JDuXQfQmLB0kEAEedpO+rb75CbWm405kEhWGTXUwEDxIhuCDbCXEMdBvsXG3Pzs7EYSgtj/JJugXfM/hvPJdj76wVJ4uhV7U3PIZeFZUA/p234kFcskpSjP6ZnZ5R2MTUlVVWNTW1gS1gkoXllLAniC+6ANDhj1rx7cPN1OyEXMep4/4kmqSTTNlKyiiITrbWt+2gnkRJm4UCYRwVqQCrU3AaHHpmIiPkyz2lh6UTXGpI3IDEaTDgPlVjjBYLd80hjhvnqVOV5eMcPLZ8HOz17UrH+ASZjaPrLRSuZVSgJQNzE+fp3hGaghdzHwmyvjA3N+Twe3tKStEXGaNqywuaGvDyXG5Bbq4hFXwJZKCeP5fmRlra2nLRMPk5FblVEU9cIAEnF+S7BbC8sjoNmyQHV4K9o0nf70IsiR7EVlSakbiz+KSbHjojWaJiJ2snbnm4urm7uo07ljMyCY81p+UJw/bFSeBdog5sAE3qHlTidzjTiM00PMqOAPjDkz9k6lIZkcBsWhAUtPS/dGjXgYHcOLI47Pzy9JxTowIQtX0yUSVPyjKFB0Aq1wVKQbcXe3jm55X9ZCyp0cStsjEkDY2faXE19ssVN06iCKquAYMSMsHaPnBm9mh3d5FOzcor7FrSNDB3+xvyTzJWlHWbxDT6FY9HYiCBEOG8OymDCoGD6Tc4dG6AIfkuDwNPOB0UawDHpcJXc9yo/uHjRzxOfUOT+9qjOAvruBvrHDS52cvcl1MKeGgPPl1aRlwP2wnPckdRudigoVQK0+Bo+J9OFVZHB4FGBk8DDtmkO9iItPLeeXT8SbAQDy7ghIcwz3ygD5e/xFtE8zCiO4627ISfkVVQsIeaA3JFoR8fgnnkQ6Y2OD4lOEPXaqKOwcODA1tWTm9XUoQVsO/wvLehf/cItuPVZ89nJ6ej/gOnALyK0QEcXF+QVuYpY/IpgjnPbo8xdOYDjI3//3u6z+Y2syMLwABzAEACzGImxag4sjTZI4/DflhX7db+y93aH+H9sGWPJ2okMYpBzAHMBBhBcJ/GVK3GdskaCnjfe/t2nz59uu9bhVCDXHItWUV4fyg8cehWf3Ii0jR3uUCXkR+1ZOit8AyqxA48zb4AAI3SgBovgcoj6ZEwuqzKYCg+xZkXPEUURKJ1dLDFbcS9VZRYEFZZbRHb4EKDTfhW3iSukD48JiLiFBAsWEhphPf0tH5Za1QspsXlnCYx8IA0zqCLWxdARChFAijaDQ0NPZ5wR9hzn4MkV7rCtWjx/jC/aDYOM5IoNaXUOVlZE6GnT5DkNaYbIkcTwDrbW1pzIqbqFofF3eMuGzONekGR3ZLQl6VXYhhdGBDqhFhh4M7PKzs7rM6GBKKnywS9LN8hHWTK8g7Pz4yYb0yS2NhUErA43tHdL+bG/O1//sZ3izfYIUluMOFJlYy4pAnP2NXb48MNJ2CyCBwL+Hj6ExHxp59+JBjJZnJ+v7iwAJWEFMXd3wf5aCWtrVX8+HiwioIz07w960L2o59/WnCYVOTsEeNlms6cOofpb70Pbista9XAuFuFK6RcRomlSUe1K7dIx6qrKIzX1jdBHsYApeqS0ONgTczrND85qNqzAtIUhRcsRLEI5dkUZi0ZIo8B2dzlKwOwX6E3tF7WvHLTgKNKXaPW7WA48/WjtRqmTg5Pq8uKrs2X50kY1voY7A1GxfSI2hquE7xVgce9+mTKK5wk2KFqnd/b9Se0fMCOZZ+fXSyV5hqaYjaqT+PxvAudogE7XJg3Ef8sHCjNNtz6ILFTFFcF4FWxDREOQ0BkqMA10xP+nXlrSEfQ0dat2fCgcMRFuoG510XToyPuGah09ZU6JKDlMtWHw0m2xJl7bz1uasL8AiCID7EMuAWO1W94XXwUSpvN+2OVEskUiqC1tchFOkW8O//LgemsotVBWJsy7hcCHfnJOvGBKkAWtqWpFT/DJXkwDo5mTABgfgr10hovG+KOYnFpb0kK5UwFM1xTy3pRlJaOV6346DLyRNiwXHbKn/M1kgFmQ6J9eV0MFghQqrrHHCgtVFRYpSdPH2HAIFb41Hc7ZYvz81ALEG13IWMxRvquE4wbhcHNvIPw5JQxF++i4LAgi3jt+OsymJLm39h960+7bTeNPQDKqUXk055WL6S/ItnlZpQh70oJea8EAtZWqomXrQw+IB7V9tbQpUvrTEZx35YjEQauisVopdSBTz5AHWt+BJE000VFOMhTRna35Tj60yPiwOi/9iIaMEIIMDQAcglvupo9sOuV+CMK9bb6tu7Oh5CfYiuiUhxDk0AzjY2pmnrVkdJ+PkZwmpysByXT0Wk0yPrHjwAcisVKEnQwraCV0Hk3tw8Ge4cfjko3tB9rVJKXzM7PkWXDPxIvBKxdlnD7LBuj7T1upal8X8a6S3t5cxGPQUh+lf4lo6JcKP80EyXuxRwP9Oz5J94TH22++clOpc2stpZoxWRdjcscKFQO+3OAr159KkT76w6hfM1vWHSFO2vRcQPiCU4ggJRC+gWJC1kckzmaGmuxkA65ewcZCnQM2fERcmPbBhTbepnE/NyiTzZandMUwzy5TktqdBYM2IrzDMAqIBlYlggnnTJlJQJARRHvf12l/PLFJ19/9QVIBSAjJZWwINb52Xlz2WRZnlkJ2nlwb6ddEUz9V7EBhBRVgMaOjknXiqllaETgIOQcDE6I+sff/9eiOWYOBsgERAiEfBid1tbODgg5Hb8enasG4M2a0TK9PBpIhdtVTqA0PXLjTN4W3kVyoGUpfQ8bEqTjNI1s30aRlW7STVk42E75Uj1uT548GXs4oQPIAeBJta5U3yfJiUQXrJRhZB1tT1HFH9dJxMwibhWSATakFqeyvbUleyJtUu9qb+k0ZlJ6Mje3oLooi+JQ9na2K40Cqc8++yxhkG1Uj4vhkisJvokAILFE1VLLFZwBfKv/qOvSIHN2dkpV1F1DUvhXv3s1PjWhi3bXyNIYyWO2yZkkio+2az4ZmNU8VBlgcuXMy5XVdySkHAqNmVNN4tIgx2hohBJGK2WhYybrmh2VtxhVpuaJfMes0LUXTCsEpvQ6+ATVoGRLUpkHWS+Jdm4pPVZXFmy0KSuqI1b7orDq0e+PVC8Q7nH3AC1NTOuMW3ndI1YmfBChg4BKp3iWjY+bXlyS6lYs3T2M2S8hx/FRWhJuJcRdBsdOTevOA8VUBUy8QaBKbX0+puWbb14rvqVa00RtqkPVBrrFFF4jQ04vC9fmHBhpK63hkUAGxLWXYpDeFEIULfi+kzx0nIfokWqAjmoBp4BJ8Mz2moMSjfidADQoDNpZl3PKUM0lThEKmxQHmF8xUQQsgM8PoAF+C7sa2OsTgmgzG2CrM7OzlIhiJwAh+vovNy1sMGlhgMNXYBQ81HUjI7wiyw5Oy4fIDkmHiIL0PknuxTOxIVhnQWsgh8QXR3WuGJe2sb5mp0AN/9ZcSJvIwSOW3XMAsLPk4HmsW6c6Vqco76OUg1mjryPaFi343uA3bkpgjfBjociZ685Obw89VQmHrjtLREHukUBFwf/4wKqYWsHbSIkUdf0vdpLREhbKzzREPX76zHDMxH1chylIqH7BndYTMQcKC9ZUcBCzrA5iEKI8Z4xmOzjkMmTS5BssWeahnAOleUFBSwVK5UnO7i2M+mEnDhQuS20V7PZpbA/LqvPEAaHx4VT3d7Z++uln3k/R0kmBS7gj15VwEXaj6TRTl0rFDRnd3baVqvW8cBID0TTBBF7UrnFNpCSpUnpcWNQaeVNjRIyUDji1lQxOxYNfw3HPzcz6jUNmpaQknthyGN48GFf+ajpZQGtoJpIi4C5U1UJYUlVjKoaNRHvFfIIGI8ujPglTG2i1OL9ghxixHMJDjI2N84DAizoBY2V5shs1PbFEBdj1GlYxxB61dYIBW2A0XjK4sEJhy0Sg5WUhhMCLF4P9VWBknwjfqE5TTVhCY1WODpBadDIQMrS5sbW+v70nn2VznMtNkVbvLug4Yxvkh/vKUOWjY437iyBteCLM75WmXMpszE0d1kvaiJkRFKGNjvaSwgBOHJKlXEo1tcgTkQDWULIivEu7RCN0vCWVNxDb+Tk+lE2wS68jz5X0+ShaFCCFoIJTNvPSoAhsgw4v8WBkbJTeUaoBT3EWMLL068//8pegpIuniBoRii9TRHFbzvOnzzReaF/aW9yHGEyS8wOsXHS0TawHx+q0APVK2RZKckCow7vpquenEBp3N3dEmaaxfVxdknz4ZCujXZKdyYoM+WG7L373HFJTpQiuulRiGBX5XS2uDHiPJluD0m7Mk6h1XJ0lOhahE6oAYZj1b80EhFx+QK8K6bs/09wUPcapZq7TssukpVySKp6eCARI55tkFahYiT/CWn4glx4eGrEdMXqjrobAGX8C33FAltQYED6I31lfX5UM42r7RwbtgclISCqEj5Z35A+Q5joqyytZAItMy1GXEzJrDejW/NhKW3WrQVZiDUO5dq58i4vXzl20tqhVwFzlA4423UjwAplZEQ9fia8tXtYEQAcPpI7KZOKO4wafjaNwqZZv1yS9n4+LJ60T1CJsU04ag1BTH1NYWgzWaqpdXlzZO7i0cekmc42SqtOcL12stSKRUP2FfaE/SbM73xkJp3xZuHSUpFzel+3y5iIovyQRaYmEhhDoBlDFPJAgl2KIgh+LgaxwvcULVFxxPTwj1yQ++1fpMhEWhDsNzYCcCo5OsWAcN1XpFlZELhSEASCMPNze+eVpOR6O9VRqdnYM5cO//SMD4sTy0tJZXF7o2V0MtcmluEYTaFNZUZHFbiA1HXxJ2t7OPmDKxjyJAhh7872cFeW4c+s5nVCRyG+c0NWVNX5J5i36ojwlxCpYStbFq6IkwUd29/ZUspxa+ECXEqLOU625V3J3Fz5kN7CF74rMC3ivOGYwVygS+T6urPT3D4jk/hX8quf9Iu47S7lkxFFC5W8Uir/+8g4Lm23NcMtOGejJYXq25Q/R2EWQY/vAVuKYV5+9AiCCrD4+BqwdKLGEj8JJkifYiGAAI0OvATpFHLsgXgJAQfrV1pl8Jw46axXAVD0+OdXa1qoY7u/fbLJcb1mWbWPEUS8Dvb1zc3O6f3gwUgiTAoynpNjWtgZXiZQCWjVcSVhq3DxHEBD75JSnUq/ziB7UMcbT4dE4KYXONzjo2RlH0RACt667Upxkm+OL9LBYsMEoPZ4XAiPh5jtZJAU3YRlf6YspgZEqL19+Kh9ni6MPx+IqknIZ6hQJzOcy7V3KCWQ5Nsrf3tqYs+3NbeeNi+Q0JdbwHprMO4CcH5aXZt7PiVVc2N5uyD+wh1998aWTAuGSZGBfVOcePOg6Pz6jmoLBYI3VpVUZqyKtyCxaoj41pIhqix+WZNkB+tIZLIpn8wO8j82QRgmzNKz6aYEdZ9jFD/YAsnv56SDi4s0vb7CFMF1XZ49WYa0ilemGRX8Xgw9Gmb/+8hUW++Dtm3fgdldXx9dff0VcUKlPKDMWaAQz6Swcw2RNF3j67AU2GBKXeTRcFGfez3zy4oWCvAA50Ayx9vhku+0GF+vMXZrkPjc3T/Lx7OlTsUScAxcZFiKbg3K0lMgcO9HcXkCjQKK14k14AZ+gnGvUw7u373/8/oelxUVg3iHhiFdWP6jJ25SIyseoeQPgyE+ISGKaOXQJWMmVuBvr5ECG90xljNbxAzJC5feKDKkKjtNwwJA8Fr+v7NTGOaUVAuLAwEeOXwhAqpNqcOI97yAhc5cT5xVfEZfK5mgzWDrvRnnikEC+2nV7yTOzOUoVPyg7PjlWfUmCJpJ0BIjOKb7Dw5VA9MK5h1E5CAJXKRWdcmNaqguOIO9QOT9oeUC2JIqI03ClrxXJHOAId3Smt9fOCFUCqpOhXre3ST6cW+QDqCD2S1U5c/gjoFVjuH7p0vrWduOv7+GkyekJsEC928Q9Isjj41NOATnAd3M73WaPdPeCph6DPsfBsbmcu92RqEWbxemxUGERMNe+nhJfmou496xVUZMwsZGE7ZoHkSL4w/vbe2yNvkcuTVyPgmE6ZTtQMb9V4xXZrKqvtuz8JnAjXeAH4Q8Egj8En0FDd2fyv9AMyjR4jPFxCAyv7MushvZjR4kLg46JYvEe5nnAf6UST17LdPWsOTu2yGMgNHSDepqh4QHJCEWmhI8MBmT2oGAER4JGMwnLocBkug+DehBwEQP4Kh+GqaMHcE0jbohHtCDsR2+twCwVhlEwdXw6gCgZ0sltO3QcSxPYWLI5sbm2sTifd9DwdIavzM7MOJiZTLQT4/GtnoQYgMTgkxGOT0z29BYWZ+Z+/eWt4XQPR0b7+yNvozG1LGzqtliUX+LtMTB67PH84fHM0Kw26z7rvFhqMUP1XuwX6fncts42Um/baoP29vf4GZ9APIYI4t8YCYrx+PwEdRyJTnvno6mux4+eGPLB1GW9n372qTDPp7uukliL33OD0ohaND1S8VzaTTrtDFr/rCCvPlBbP/FwTCsZFOrGQeIFDwO3YiPSZpBch1Q17oaGgsyfNqnGm/uLfQO90lJRlCwX5tL/jgxxJpmIX2zaFFkdLo+fPIY1JBn4RywYhCEqChv8BTvDVEZfz+H+9pb+nVO7znkxAqGZMRFdeFDaDGeG3aoqsxW+GIHFMvymwri2wAv8Gn6fs3bqQH6n67bFbbR1Cu4Ks4ZYwFkjw0Oy2kqJFXXbJCwzlGwS2ZeCFYQNKhFI2ZQs6NXJr+yKW+/zUuyJ8Qmqm+Da9g+EivqaBjAH9eFYmt/tM5GtfsE1agROiIcx5U0gsVYK8S9efDIxMSYzjWvn8ruk28PDg+ZLU6jSBRGKxJVBsFgyaUabJd3a2DDFXr7pMSyYyIedN+5YKKYlN8eCVwU3cKNggHHkWjlITVDAbunad0lkS3rQQPW+fpHbqeNQnFg99/+PPSkTRkaH29u72y7ahDogGrWlbGNiYqRQ2Pa9fWIrwN/RAjYdY9e8mPyqvEHEIM+AMUFjg1DaBZqmJniqNiOb7vDXpV+uCsEZghjWkwQLB8We4BPbJ6GSNYvBQD2STWoMOXJMdARDg/0OjnXQUOIPcffGZ6IwkBh+ODRWsAbvFvett1319gRpFFTSodcUWmgE2FJbdRJEoLN3ukbGRjBFABFFsBi0s7OHc4PZGV23Cp4OtZrqrh7KsRG0BkcPBTpmjDDGDARAOVWnPc4fw4wAlHlzELA5P2YJUo7BSsgH5R4HyfIKY+I9vgvvDAAq9ohVMXA/pnTkTK2BYDTZaQjI5ozEaObstKeAKQgfp8Ox+vXNe4MvvaFjLJng2dVLyjljuJy9mGTHD5p7pgIoMZUfwmQiutiMb9zZ2laqqdyPfUCzgE9w16OTX2npr2PJ/q7ADCqJi1CS88VDOaembEdCdou81s2nvB/F3vv7RkkhoB/VxegduZX9wMJodymUh+E6iTt58yr3rQcbE612yO6bE5cEOKHkK65qUGTykFfcEAk145dceBd1Pj5I8JCbQnh+FHcxOGKMVZQ3ymUN4XV4cJAZPDdyx9ZYImCRA8JQO/X0KqXcjXEywqoXMUvY3l3IMc6LkJUha0KO6uPs7Ozi4rwsmUeVmrAh4iuPZ2dZkg0K3UPJ+HeTN12bg31y7VUkECY5Y9/V14V2MEjRGH3naKsNGCEuB3LYlfGtLU2a/4v28Xg7ey7wqAuJeKmEdsh2tvUM9B7lj/Uo5Hf3o4ZamdEfvbPNzeTCbAl1AS+gHDq7Y3SoLFa4Ghkf5uLBCDMyKA6odODLOBclUQcXJwmrl3ljUkiX3Cm9sLCoR8SOU+l4MG1Gz5+9cKxof9khCQBHh/dXVxekf2MRjHF0eP1TPD25cOtZS1Z8ok7d2tnDS1mlp0+fEKdhKaKU484Z09YQNc0x46W5J9GtJo6PtoMip5KdU7e1uUvy95vQHp+BpOrr1n5Wpa+BdMR+q+yMTjwUeBVOlZ4jHkDaSvANdcRDvIkzaWuVTAbaB1+9+gwpILxL+iTycvo79ciE+/A6VJ6Zmv466Yhg++T5U0sDm4dvgIkuA6qIFooq0IqfZKeV0pBevoEnj544k4HRQpN3q1LphxUY8dGyJ6oDtejgc+6Eh9ByUCa6WkN8FodFODDZ1k1NTag4HOzmhTorS10uVvpXlzcm6yqTO49pSj65qgzJiRgfe/iH19++/uMfHGaVD8ks5s/kQilRzCoIIQTilteI4YyszTl36pCC33z7miJAVyH1PaxJJhNnQFJ3dW2rhk18zHU4nPItbzo0MtzV0wsNPX/5CcwofriIxnUsdxelohhgYntlKllFhuvSK/Lti7dv36fSazbb98JWkEhceNCZc3LQ1mzUZ3pB/lpdwTtC36xzfn7OlF3Jb5AwvlhnRows7QHAeSM5MvfKamUwOztWjACpVk1YysgiAQXIPRIBTuQqwBqKkxeWeHp5pmklWIUrJDX4EHqyK2Vd1Ty1PDXvSqoU3txX8xHRiHDLZVj78+BnoyQaGYYRJjpeKQocDgfMzIjSPRYFVLdyF8YYYMvEP6JDO6Km2tPXGwg37nKC7JCe0HGtA+nBqM/f/fru8mpb8k97pv+TPBulI7Ohs1S9EjBCd3tfsoLKTlEnDBX/KT8VjWNJE2EP+H1By1/HcRHbJ5K1bJjTpK3StKEegfQTPJaXTQXfp9X94fufbHqU3Ixh8dxyhRS+K0hkKQufi/Z11ZWDahC/AyXrQaqyHZbLszfW1RN0i/qqIdI+/tUj4Z1YI7fomWXJAqe1RQYJXey/WDBK/dBxFMqSKTfBhvwBayTY/yalt2VSZ/0nUT9x/+ilmRklKyBWCXhSXm+qeTHcojs+yUkvr2Bnj2cKejlzZ8pxXXV9ua/srelkcq1uV5VmsahDhqGLEKVmsywCpzw4MIIeiNShcnPh+ISrqZKSVAeUDsciYM8Ayu6ejphI6CKwTFpt9urciOPaNvlUg5KMXhZXIahg9TjVHjUUqx3twIark0ANWbuUVCYh1Nmg2fcztuBBT8/XX32lDuTKK6nA5NQ47CVcMTYUN9twwytYrU2sS/OY4WDle3if1IJfUut255kgYY1AHJib16LI8fMMmPmurW3wxWoSgpa/bjqtvRQxHQ0VEFUl2RgRIMjPl9jlk/Nj6gyWgxzljlTCeH3Zif2W/WJBDSIT0SEJkQb2XVld9WmK9r6TlMCEQ+Bb0kNOInI2l5P2Yu9kP9fp8i/TU5rYLdneP//x95lf3hrbAZ3YU9IMIN1SR99yU+OUkT83t9X3d8TvraeFNqKIq+K59BCwhEwNpWGQ3F90DF4mkC1Qp/Br7ZBWWhtGxwyDE41VnxkJGlHcqoMC1E7lQVwHKxfSsb4MNVRKw5BvixFiIqrVkaxBe3wkk2dn9NpQHtRuEG6cmbxbB4+cTxCb5+KRrTWjr5ze+hhlE8cDmnHLuYE5A4J/VMPMY1JUiQ43aXg1O/BpzYZOG9Yh7feC1277PIR3evoepETF7gcUFJ6qzdDbZI3+JmVM3QYQ5PraCrxTcZQKP02DbTm26IExlbAzvMKafV9358jrb//w8tNXNg/3pU5obLfjh/lhDa5c8GPyRO2BuGWfrMsBJHRuJSXeS1LCtUWuE53fdb5d6DZsRKqtdm2r7CU6dWR4zA84yQZIjI6Obe5s/Pd//tf8zKLtCHCEc4m6a7Cm9EL2gpBf89R3//wOO0pVzeysG2KBr/xgOunKiiUnMokOFBwQKvT0lIHK0FNkpqlW+quzE9SChTGftYm4230JDiGfrsBlGXAJKG87EiKQnegfVLcPbi7retUGgjXKtminCm4x5gtxQ1ZPBLxWCLy5zuQyiULSTun3Pi1eUNVYSWjxNnkDQlrk0HovLNAsEcYFWezGIaq4bGyBr3QDBGbJdssdmYestrk25bHC3SfIJ3Imi/FZu5Ll+hOnBQQRndQb6huicw0nK+yxT+BdSQb/NDw6LJVx5rk809EMjOJDGbOKjh/zvlX3eNiE14N4GBKrA1ngO75ACJPXY134HWsjWEbG3NgoAeIa+IuU0kQaA9ngNcUynvbwzBhE7R8Bz8N9aDs6Pwe/dGMa9cUDC/kAAd2XYwIdoem7DPaK3jf35HhpN1VwpHpX5Do3boc3ag0/ytq5KnVN0njJpsApSIvF4G2QZ2XZhudqMEYMQUDfxW86aG7NDZdUFW10Pg364N/9YkyyC8EA9lJa813QG5AbWUWijAkG7zUV+400Re1C55HibWNdQjKkSGDV7K+opICJusm2Z/FjHAQZhcTITpmdZdYkuPblF1/585rqfOLkyPs6FxVnAsITA8s4cwq5Cq58lDPu1cRhngH7L1oLoqT6npaEFFSKjjbH2GQLiK6uKteY5ZlABtSHg+ZfUW34KwzV1ABUoZCzvbflIikkidis3KiD9MPSB+ytvrOBoX4vi+yCgznxnI4B9y0UzlAoww8fYi/Yj42X4sjp7QeCzoWikozQ9hwfi2RSfM3Y6ArY3wRm0AQV5O0AUxEO5JNeo/KsOgLAYefi/VvEkUEdFGeR4A6N2IXnz54PuogiqBQh50Yaq8xdPnTPQR1vIFVXKvRqnEZ3m1S2za6h9TKTaYNKLs8KuqPsIMa1So26OsGt1Vc3tGRi8kKmJ63hs+Y4fybZgdttGE5Abq7KDiA4CLLgGJth+yuXM7FvdRs+V/xhZrItLga6p65TINYqjYTSt+VGN8jFS6Yyt1qgT9TQOnLciZQfgoA3VRdl32OTY8qSyUQJ7gZI+VfLo46mLiTeKBGzeLhPFAnVqhm5NX0+bXtjU62D3JBFNGGwxOo7DG/RKTLCCA0ly8MRG/8HWTqx+4e7BlWGcC2qSvLcjMNhrcNqW1sNwoL0mSz46SFLMhQ38JnF4Tbt6zvD2aM/o3h+e50RJIQoR0+Y8bhKK2bITE9NvX79jXTELQWsBDwZH5+EA9QMzZkwBYHJwrx3NUEp6jzy1yHKze2tSska6VVkl0SxYAj6UQIWXGnOUMwqrYka3JfeLsJK/QODxiiaB+C48ddID6q1s3Qhq4VifJy9w/tKxksrK3//7jsmMoCYpqQ2PULx9PTQUUHdKMzsuDeuEJe0IEmhQLeLiE+OMaCkUCtZNwsIgvGHYlI4VtEgEKjbrDT76A4+07+gz0h+I9zYNBeRorxAM4mr8CZ51WXE8zEQoYvrZLKSMPvFAfEZLgh0rgcGhnl59c8j1V3SOldstmVhenZMGWy5AfnZ2Znvv/+HdMh3mf33SJ1pcJDxoFyZivFBHKGiEM/L4ao+I1kdU8NT+Dtfbqy8IkSVW/c0Pd3d6qMhDhI/Amc1xEUxF2fRwoZg8X9Zsi4z1nK4tydMCDa8ITvwwhwdM6Yi51OwsT7BpZusUnXUGeND8QF+2WLYCpjgN7210qjkicEDswXzUwyYitvWeqFg8cPnwIAwtV+G0Ziihtj0MIaviDpmFJIxSsChIsys/pjj/AFnQXft6yRh1FKoNsGXMBcX52yL0P7Rbc5lYNMYoU8Q2Mp3rW7RoaLhOTofdPe390l9/AnPhWve3TYU6dg3Cu4yy8EYkNnEcTtr7Ny3i7USNOHPxvHmLIpDwPZ4RWrF0uVdQ8lt8zX15SbMME9rL+ob1VpdG1FjD1p5fVcE56Elk3PUXLWMl63ozNx7/JQIBENgXzlZPTfyarpKKIMHtLByF5lES852y8yDngqZ7M0ttoQ4kpxBS1BL1oFAIulnTsjIJenQ536IXlQNXcfoECUkkaQYONXPP/+cuQbWOTtTESzf3mv1klpxH0yUxEgHiSlA7oMjoHBdNJ2CMAFgYdD5ChIabwhbqME3NMmMzSyK28VRcPwGjh5oMCPSofmNfQK5xG6ZnP5KHewMhp3LI48PDvX4AETTU9OQmSgCklYKGAa6RHM7mo56U5+m/zAkdJPCRa5DRkLIjwLMBxd6f/d+/p1grxSBOwKeZFtSQN1zql3WFZBRvoKlpqenLbtRuMyjKcMeyptb207I1KPHVsyCaWj3kzXXidtsR0tv4YErhtRPTXppSDdp6CJMBFhgce1+1BuYwbXCGnCHoaOlNitYLkwmMDM7w/SJCmye2593tnZMM3cxycTohIew6NjPW/yR5j1ylNubhfkF8kQXkwLmxsczHWeBT9WgDNfLtVULUGAjo4jOYW4LAwC8w0o4HDUdZKSY7BJLLLkWDOEOKDjYyDNojoMFd7T3uHz3unStyCYWpzVCGHwd7RCtujEEUmQTumPv8MBx0uIr38df04a7foGL+fGHH2lALZnXjCnhiaTWB8ns+va2KV8MLijrlsw3r79B0NP2Wsrl1TXCONUYn+wzOzpz8kDnkFoEmjV6JL+XXzpZsvFsUfzQg2eMgevXG5prMfsSWHjHjSW2mIU2VNf2DQzrFUP7ri1/VMQ2hRqQgV43Hd/1DR2e3/75jzHXRKpOJ5ffoxTf39/++eefN7c3EQWWWtDOprNCFeBu/gICZH3bDXYnFg1IccDPLwvmHiwvflBmefr0GbAucmgO394pyWddjRtUW1IDXcHT9gx1aSHREs1jX59QP98RdiJ2rq/0CQKjxoSoWiXsFF0Q+3NPnDRTXHQedFaZt8y4cWK89sXFKT0YtaXrKci0D88P1dw6+3ocSFVEY1DNgN3YXjNGm+MbmxgzKsNlc5pL1CrEXYETF4wz4dSMrANTAD8iObhPEqQfUl4CMbijpCVH2Ux9a3K6wmc0NyFwCEqJLYhEMUr2XTB2KpAfkDaUAMc1tzT5K2I/O+HZJR/YDH7fS4Lkas4xFqUyTIw3rrD2F5JubAPaCzwEgEx/dHSx3sBn6M1Kd9IyzhReZBUCqo4oaNVaHckOiXHT5hK3cg0aqTY/mkIoDeNHi0HL3MEqZ7qlIE0hH+BgcpSpPJLI5PHgvhNooK9bNVqGBIZzSY6QKWfJ1oQStJyG6DZGB8YdKSYc3aOJAmbyI6Xb9bWNdEvKGrbH3WSHgjS+HkzyvkhnK0NNSMTt25GuDqY4Q9KsWyBZzTq46SjC1YW8tnlnc9deq1QLhkdbDvWdXk75Lg/pNfhQV7epkeMV9vdXRAgSwadPXuyZjbmb11+ob4VMU/WCYt24FspgV9Fy9jZXwqG4pchkndX/xHj8G6TI73tUDwnxg4yVN4qrxQkrnFw7BUuLCZwvNsmFfnGf5EnL2srqx+VVZwr/Q9Wi7CGaHh7fMWa/t1+elk9zzuyDSFmtyayq2laIhcZF9jxotyA///gLlaBXyGSpRaPGHoIIGvUbA6kakeexQTdX5np2dXfw13DGw/HRdGvqp+9PsOIinPE552fGGXmTJEehs0QkTTW0UBVur2+tfljW0sExKicMDI2A/CoW25tEa1cPx8cPj/Nry2vRKdx+XdcQfSeEv2QpoI8Z3faAwiDVlOMedF146dbp9F2yLNgf7Or3ybf3tEtwSR7s/vrKJmanxn3oam1u1e0bHnIG1N+rG2omH09DKBtrq5I1EdWpoOSyQx5atuKTJFD8C8DODsyk+uhSQzfPwU2Hh22aRNNYaZ6y1SBfo3V/mJvPtrcJa3J2SptUpvH3335FXyrkolNENo61p3tApdQYd/IY5xmNKxdBU4jIiglOiMfg4qef8gV9lYzpkv1xNI1RobLiejW9T/bZ899Z0PmFWTya6206y65ua8NnINyv70sQE6UHjw+D+DodiOjLqraaZDNlzok5Krtbe5cmxhZOh0cGEVKEZFLsd29/hY/K4CRBWOGSsnh6csKiFU7M1t8WljPplGYQWjiKLjnIUX8fR2/AABrh/BzvdLaxscr4ZUv/+td/F8DAruZ04/TjccxMcypj2pkUXseQGvzdRTnb3q24VDy7/Ot//BuUHbKO0tXh+okr6fXo5bf3lmdXXn3+0kq+efPWBLGrq+LGxzW+70FXjyKe1iNU5tgAddVDhWsn38HbODi+vrtSOp4YHzu7OM+v7AoeRl9gdhwe/8SA15Oid+Ty8BscLv3+6eGRpVCzTTXGRC1TjFH2/J0Mz4Hp7ut2m7jc/zbh2hDSmoQiEvzrqkT4rrc/oqPKNuDvsHGf3MX5iWmgm3xMb39MtcvX6APQFL15tL0Pi20Q6q6uUP5gnezaUO/A46kn3b2d6AtZCBWTcIKXU8allMZ0gAXwoCwqWVMXRS43CyZDgb72cdnHRqaaTteX6/gL2MI4EBV9gUIAII4SFIU9mQ6sZ5qAoYmc2nXxKuoeddWlwo3EyJ6SIQKf8LXtFufKGFFtsVp8zWJUKWlNTz9+xFEy44aTJio9ZZ5Qpl4UkXim3EY62Lo9O/POOl8WVfL7si2uTT9YWV6UGbgJbvrxpM6ticlhGDsogmRIKpk3WO1JrLlYvrK0LEc1TJcyDWWsWbLuvq76kg416had3e1QnjdRW3JCeUYWkt87fPnZ5yiGqclJJ4zBUyXbNamZTwcmh4b7FBhJHlgXdrhWl6mO88so5twmSzCZMyhI6G5THvDsEmieK+Lltbn8CSDAql8V+KB6lTny2dp6TiJaXWWIkhV1NZCRbMEI2NqG2uYWfV7R1wrBaIB9NP3k91++lqEuLsyTfVKtWEOMmIOHYnXLGHc0ODKiQ29ubhZY0g67u6k2fUkZYanNhOi96+M/yUwVKY7NLW9sUonUGerBZKUdxQ5iITNHPYyTqF303ft53UU4jfcXM/1DA8+ePZGr4GXMy3DFLCTvqP/lT3+R0kkjKl1amORyqGxjkDsRvZhdODnKq91/WFwECERBq4FUgQ5hUywTd6Tkhn64Ld8YaihNpC6h5LXs6KDr4s0XX37p4iiLahQEsYARyfZUr+Lx4UYoeR6O28CGhub3795QykgREH8ooLOTokYWKSaRt1FCW3tbKoiDJlA1NOZ3j5ozKdN6NHIawaSz0DS+Mpx7di5hMqCBLVclau5qqrK5DpinfyRunHVBtE4/1WnDoYXq/wNo/ZO3Pjs37wAAAABJRU5ErkJggg==",
+ "text/plain": [
+ ""
+ ]
+ },
+ "execution_count": 16,
+ "metadata": {},
+ "output_type": "execute_result"
+ }
+ ],
+ "source": [
+ "prompt = \"A photo of a sks dog\"\n",
+ "image = pipe(\n",
+ " prompt,\n",
+ " num_inference_steps=50,\n",
+ " height=512,\n",
+ " width=512,\n",
+ ").images[0]\n",
+ "image"
+ ]
+ }
+ ],
+ "metadata": {
+ "kernelspec": {
+ "display_name": "Python 3",
+ "language": "python",
+ "name": "python3"
+ },
+ "language_info": {
+ "codemirror_mode": {
+ "name": "ipython",
+ "version": 3
+ },
+ "file_extension": ".py",
+ "mimetype": "text/x-python",
+ "name": "python",
+ "nbconvert_exporter": "python",
+ "pygments_lexer": "ipython3",
+ "version": "3.11.13"
+ }
+ },
+ "nbformat": 4,
+ "nbformat_minor": 5
+}
diff --git a/peft/examples/oft_dreambooth/train_dreambooth.py b/peft/examples/oft_dreambooth/train_dreambooth.py
new file mode 100644
index 0000000000000000000000000000000000000000..60c87cb036d1c50ea9f8b81d2de1841807ca09e0
--- /dev/null
+++ b/peft/examples/oft_dreambooth/train_dreambooth.py
@@ -0,0 +1,1115 @@
+import argparse
+import gc
+import hashlib
+import itertools
+import logging
+import math
+import os
+import threading
+import warnings
+from contextlib import nullcontext
+from pathlib import Path
+
+import datasets
+import diffusers
+import numpy as np
+import psutil
+import torch
+import torch.nn.functional as F
+import torch.utils.checkpoint
+import transformers
+from accelerate import Accelerator
+from accelerate.logging import get_logger
+from accelerate.utils import set_seed
+from diffusers import (
+ AutoencoderKL,
+ DDPMScheduler,
+ DiffusionPipeline,
+ DPMSolverMultistepScheduler,
+ UNet2DConditionModel,
+)
+from diffusers.optimization import get_scheduler
+from diffusers.utils import check_min_version
+from diffusers.utils.import_utils import is_xformers_available
+from huggingface_hub import HfApi
+from PIL import Image
+from torch.utils.data import Dataset
+from torchvision import transforms
+from tqdm.auto import tqdm
+from transformers import AutoTokenizer, PretrainedConfig
+
+from peft import get_peft_model
+from peft.tuners.oft.config import OFTConfig
+
+
+# Will error if the minimal version of diffusers is not installed. Remove at your own risks.
+check_min_version("0.10.0.dev0")
+
+logger = get_logger(__name__)
+
+UNET_TARGET_MODULES = ["to_q", "to_v", "query", "value"] # , "ff.net.0.proj"]
+TEXT_ENCODER_TARGET_MODULES = ["q_proj", "v_proj"]
+
+
+def import_model_class_from_model_name_or_path(pretrained_model_name_or_path: str, revision: str):
+ text_encoder_config = PretrainedConfig.from_pretrained(
+ pretrained_model_name_or_path,
+ subfolder="text_encoder",
+ revision=revision,
+ )
+ model_class = text_encoder_config.architectures[0]
+
+ if model_class == "CLIPTextModel":
+ from transformers import CLIPTextModel
+
+ return CLIPTextModel
+ elif model_class == "RobertaSeriesModelWithTransformation":
+ from diffusers.pipelines.alt_diffusion.modeling_roberta_series import RobertaSeriesModelWithTransformation
+
+ return RobertaSeriesModelWithTransformation
+ else:
+ raise ValueError(f"{model_class} is not supported.")
+
+
+def parse_args(input_args=None):
+ parser = argparse.ArgumentParser(description="Simple example of a training script.")
+ parser.add_argument(
+ "--pretrained_model_name_or_path",
+ type=str,
+ default=None,
+ required=True,
+ help="Path to pretrained model or model identifier from huggingface.co/models.",
+ )
+ parser.add_argument(
+ "--revision",
+ type=str,
+ default=None,
+ required=False,
+ help="Revision of pretrained model identifier from huggingface.co/models.",
+ )
+ parser.add_argument(
+ "--tokenizer_name",
+ type=str,
+ default=None,
+ help="Pretrained tokenizer name or path if not the same as model_name",
+ )
+ parser.add_argument(
+ "--instance_data_dir",
+ type=str,
+ default=None,
+ required=True,
+ help="A folder containing the training data of instance images.",
+ )
+ parser.add_argument(
+ "--class_data_dir",
+ type=str,
+ default=None,
+ required=False,
+ help="A folder containing the training data of class images.",
+ )
+ parser.add_argument(
+ "--instance_prompt",
+ type=str,
+ default=None,
+ required=True,
+ help="The prompt with identifier specifying the instance",
+ )
+ parser.add_argument(
+ "--class_prompt",
+ type=str,
+ default=None,
+ help="The prompt to specify images in the same class as provided instance images.",
+ )
+ parser.add_argument(
+ "--with_prior_preservation",
+ default=False,
+ action="store_true",
+ help="Flag to add prior preservation loss.",
+ )
+ parser.add_argument("--prior_loss_weight", type=float, default=1.0, help="The weight of prior preservation loss.")
+ parser.add_argument(
+ "--num_class_images",
+ type=int,
+ default=100,
+ help=(
+ "Minimal class images for prior preservation loss. If there are not enough images already present in"
+ " class_data_dir, additional images will be sampled with class_prompt."
+ ),
+ )
+ parser.add_argument(
+ "--validation_prompt",
+ type=str,
+ default=None,
+ help="A prompt that is used during validation to verify that the model is learning.",
+ )
+ parser.add_argument(
+ "--num_validation_images",
+ type=int,
+ default=4,
+ help="Number of images that should be generated during validation with `validation_prompt`.",
+ )
+ parser.add_argument(
+ "--validation_steps",
+ type=int,
+ default=100,
+ help=(
+ "Run dreambooth validation every X steps. Dreambooth validation consists of running the prompt"
+ " `args.validation_prompt` multiple times: `args.num_validation_images`."
+ ),
+ )
+ parser.add_argument(
+ "--output_dir",
+ type=str,
+ default="text-inversion-model",
+ help="The output directory where the model predictions and checkpoints will be written.",
+ )
+ parser.add_argument("--seed", type=int, default=None, help="A seed for reproducible training.")
+ parser.add_argument(
+ "--resolution",
+ type=int,
+ default=512,
+ help=(
+ "The resolution for input images, all the images in the train/validation dataset will be resized to this"
+ " resolution"
+ ),
+ )
+ parser.add_argument(
+ "--center_crop", action="store_true", help="Whether to center crop images before resizing to resolution"
+ )
+ parser.add_argument("--train_text_encoder", action="store_true", help="Whether to train the text encoder")
+
+ # oft args
+ parser.add_argument("--use_oft", action="store_true", help="Whether to use OFT for parameter efficient tuning")
+ parser.add_argument("--oft_r", type=int, default=0, help="OFT rank, only used if use_oft is True")
+ parser.add_argument("--oft_block_size", type=int, default=32, help="OFT block size, only used if use_oft is True")
+ parser.add_argument("--oft_dropout", type=float, default=0.0, help="OFT dropout, only used if use_oft is True")
+ parser.add_argument(
+ "--oft_use_coft", action="store_true", help="Using constrained OFT, only used if use_oft is True"
+ )
+ parser.add_argument(
+ "--oft_eps",
+ type=float,
+ default=0.0,
+ help="The control strength of COFT. Only has an effect if `oft_use_coft` is set to True.",
+ )
+
+ parser.add_argument(
+ "--oft_text_encoder_r",
+ type=int,
+ default=0,
+ help="OFT rank for text encoder, only used if `use_oft` and `train_text_encoder` are True",
+ )
+ parser.add_argument(
+ "--oft_text_encoder_block_size",
+ type=int,
+ default=32,
+ help="OFT block size for text encoder, only used if `use_oft` and `train_text_encoder` are True",
+ )
+ parser.add_argument(
+ "--oft_text_encoder_dropout",
+ type=float,
+ default=0.0,
+ help="OFT dropout for text encoder, only used if `use_oft` and `train_text_encoder` are True",
+ )
+ parser.add_argument(
+ "--oft_text_encoder_use_coft",
+ action="store_true",
+ help="Using constrained OFT on the text encoder, only used if use_oft is True",
+ )
+ parser.add_argument(
+ "--oft_text_encoder_eps",
+ type=float,
+ default=0.0,
+ help="The control strength of COFT on the text encoder. Only has an effect if `oft_text_encoder_use_coft` is set to True.",
+ )
+
+ parser.add_argument(
+ "--num_dataloader_workers", type=int, default=1, help="Num of workers for the training dataloader."
+ )
+
+ parser.add_argument(
+ "--no_tracemalloc",
+ default=False,
+ action="store_true",
+ help="Flag to stop memory allocation tracing during training. This could speed up training on Windows.",
+ )
+
+ parser.add_argument(
+ "--train_batch_size", type=int, default=4, help="Batch size (per device) for the training dataloader."
+ )
+ parser.add_argument(
+ "--sample_batch_size", type=int, default=4, help="Batch size (per device) for sampling images."
+ )
+ parser.add_argument("--num_train_epochs", type=int, default=1)
+ parser.add_argument(
+ "--max_train_steps",
+ type=int,
+ default=None,
+ help="Total number of training steps to perform. If provided, overrides num_train_epochs.",
+ )
+ parser.add_argument(
+ "--checkpointing_steps",
+ type=int,
+ default=500,
+ help=(
+ "Save a checkpoint of the training state every X updates. These checkpoints can be used both as final"
+ " checkpoints in case they are better than the last checkpoint, and are also suitable for resuming"
+ " training using `--resume_from_checkpoint`."
+ ),
+ )
+ parser.add_argument(
+ "--resume_from_checkpoint",
+ type=str,
+ default=None,
+ help=(
+ "Whether training should be resumed from a previous checkpoint. Use a path saved by"
+ ' `--checkpointing_steps`, or `"latest"` to automatically select the last available checkpoint.'
+ ),
+ )
+ parser.add_argument(
+ "--gradient_accumulation_steps",
+ type=int,
+ default=1,
+ help="Number of updates steps to accumulate before performing a backward/update pass.",
+ )
+ parser.add_argument(
+ "--gradient_checkpointing",
+ action="store_true",
+ help="Whether or not to use gradient checkpointing to save memory at the expense of slower backward pass.",
+ )
+ parser.add_argument(
+ "--learning_rate",
+ type=float,
+ default=5e-6,
+ help="Initial learning rate (after the potential warmup period) to use.",
+ )
+ parser.add_argument(
+ "--scale_lr",
+ action="store_true",
+ default=False,
+ help="Scale the learning rate by the number of accelerators, gradient accumulation steps, and batch size.",
+ )
+ parser.add_argument(
+ "--lr_scheduler",
+ type=str,
+ default="constant",
+ help=(
+ 'The scheduler type to use. Choose between ["linear", "cosine", "cosine_with_restarts", "polynomial",'
+ ' "constant", "constant_with_warmup"]'
+ ),
+ )
+ parser.add_argument(
+ "--lr_warmup_steps", type=int, default=500, help="Number of steps for the warmup in the lr scheduler."
+ )
+ parser.add_argument(
+ "--lr_num_cycles",
+ type=int,
+ default=1,
+ help="Number of hard resets of the lr in cosine_with_restarts scheduler.",
+ )
+ parser.add_argument("--lr_power", type=float, default=1.0, help="Power factor of the polynomial scheduler.")
+ parser.add_argument(
+ "--use_8bit_adam", action="store_true", help="Whether or not to use 8-bit Adam from bitsandbytes."
+ )
+ parser.add_argument("--adam_beta1", type=float, default=0.9, help="The beta1 parameter for the Adam optimizer.")
+ parser.add_argument("--adam_beta2", type=float, default=0.999, help="The beta2 parameter for the Adam optimizer.")
+ parser.add_argument("--adam_weight_decay", type=float, default=1e-2, help="Weight decay to use.")
+ parser.add_argument("--adam_epsilon", type=float, default=1e-08, help="Epsilon value for the Adam optimizer")
+ parser.add_argument("--max_grad_norm", default=1.0, type=float, help="Max gradient norm.")
+ parser.add_argument("--push_to_hub", action="store_true", help="Whether or not to push the model to the Hub.")
+ parser.add_argument("--hub_token", type=str, default=None, help="The token to use to push to the Model Hub.")
+ parser.add_argument(
+ "--hub_model_id",
+ type=str,
+ default=None,
+ help="The name of the repository to keep in sync with the local `output_dir`.",
+ )
+ parser.add_argument(
+ "--logging_dir",
+ type=str,
+ default="logs",
+ help=(
+ "[TensorBoard](https://www.tensorflow.org/tensorboard) log directory. Will default to"
+ " *output_dir/runs/**CURRENT_DATETIME_HOSTNAME***."
+ ),
+ )
+ parser.add_argument(
+ "--allow_tf32",
+ action="store_true",
+ help=(
+ "Whether or not to allow TF32 on Ampere GPUs. Can be used to speed up training. For more information, see"
+ " https://pytorch.org/docs/stable/notes/cuda.html#tensorfloat-32-tf32-on-ampere-devices"
+ ),
+ )
+ parser.add_argument(
+ "--report_to",
+ type=str,
+ default="tensorboard",
+ help=(
+ 'The integration to report the results and logs to. Supported platforms are `"tensorboard"`'
+ ' (default), `"wandb"` and `"comet_ml"`. Use `"all"` to report to all integrations.'
+ ),
+ )
+ parser.add_argument(
+ "--wandb_key",
+ type=str,
+ default=None,
+ help=("If report to option is set to wandb, api-key for wandb used for login to wandb "),
+ )
+ parser.add_argument(
+ "--wandb_project_name",
+ type=str,
+ default=None,
+ help=("If report to option is set to wandb, project name in wandb for log tracking "),
+ )
+ parser.add_argument(
+ "--mixed_precision",
+ type=str,
+ default=None,
+ choices=["no", "fp16", "bf16"],
+ help=(
+ "Whether to use mixed precision. Choose between fp16 and bf16 (bfloat16). Bf16 requires PyTorch >="
+ " 1.10.and an Nvidia Ampere GPU or Intel XPU. Default to the value of accelerate config of the current system or the"
+ " flag passed with the `accelerate.launch` command. Use this argument to override the accelerate config."
+ ),
+ )
+ parser.add_argument(
+ "--prior_generation_precision",
+ type=str,
+ default=None,
+ choices=["no", "fp32", "fp16", "bf16"],
+ help=(
+ "Choose prior generation precision between fp32, fp16 and bf16 (bfloat16). Bf16 requires PyTorch >="
+ " 1.10.and an Nvidia Ampere GPU or Intel XPU. Default to fp16 if a GPU/XPU is available else fp32."
+ ),
+ )
+ parser.add_argument("--local_rank", type=int, default=-1, help="For distributed training: local_rank")
+ parser.add_argument(
+ "--enable_xformers_memory_efficient_attention", action="store_true", help="Whether or not to use xformers."
+ )
+
+ if input_args is not None:
+ args = parser.parse_args(input_args)
+ else:
+ args = parser.parse_args()
+
+ env_local_rank = int(os.environ.get("LOCAL_RANK", -1))
+ if env_local_rank != -1 and env_local_rank != args.local_rank:
+ args.local_rank = env_local_rank
+
+ if args.with_prior_preservation:
+ if args.class_data_dir is None:
+ raise ValueError("You must specify a data directory for class images.")
+ if args.class_prompt is None:
+ raise ValueError("You must specify prompt for class images.")
+ else:
+ # logger is not available yet
+ if args.class_data_dir is not None:
+ warnings.warn("You need not use --class_data_dir without --with_prior_preservation.")
+ if args.class_prompt is not None:
+ warnings.warn("You need not use --class_prompt without --with_prior_preservation.")
+
+ return args
+
+
+# Converting Bytes to Megabytes
+def b2mb(x):
+ return int(x / 2**20)
+
+
+# This context manager is used to track the peak memory usage of the process
+class TorchTracemalloc:
+ def __enter__(self):
+ self.device_type = torch.accelerator.current_accelerator().type if hasattr(torch, "accelerator") else "cuda"
+ self.device_module = getattr(torch, self.device_type, torch.cuda)
+ gc.collect()
+ self.device_module.empty_cache()
+ self.device_module.reset_peak_memory_stats() # reset the peak gauge to zero
+ self.begin = self.device_module.memory_allocated()
+ self.process = psutil.Process()
+
+ self.cpu_begin = self.cpu_mem_used()
+ self.peak_monitoring = True
+ peak_monitor_thread = threading.Thread(target=self.peak_monitor_func)
+ peak_monitor_thread.daemon = True
+ peak_monitor_thread.start()
+ return self
+
+ def cpu_mem_used(self):
+ """get resident set size memory for the current process"""
+ return self.process.memory_info().rss
+
+ def peak_monitor_func(self):
+ self.cpu_peak = -1
+
+ while True:
+ self.cpu_peak = max(self.cpu_mem_used(), self.cpu_peak)
+
+ # can't sleep or will not catch the peak right (this comment is here on purpose)
+ # time.sleep(0.001) # 1msec
+
+ if not self.peak_monitoring:
+ break
+
+ def __exit__(self, *exc):
+ self.peak_monitoring = False
+
+ gc.collect()
+ self.device_module.empty_cache()
+ self.end = self.device_module.memory_allocated()
+ self.peak = self.device_module.max_memory_allocated()
+ self.used = b2mb(self.end - self.begin)
+ self.peaked = b2mb(self.peak - self.begin)
+
+ self.cpu_end = self.cpu_mem_used()
+ self.cpu_used = b2mb(self.cpu_end - self.cpu_begin)
+ self.cpu_peaked = b2mb(self.cpu_peak - self.cpu_begin)
+ # print(f"delta used/peak {self.used:4d}/{self.peaked:4d}")
+
+
+class DreamBoothDataset(Dataset):
+ """
+ A dataset to prepare the instance and class images with the prompts for fine-tuning the model.
+ It pre-processes the images and the tokenizes prompts.
+ """
+
+ def __init__(
+ self,
+ instance_data_root,
+ instance_prompt,
+ tokenizer,
+ class_data_root=None,
+ class_prompt=None,
+ size=512,
+ center_crop=False,
+ ):
+ self.size = size
+ self.center_crop = center_crop
+ self.tokenizer = tokenizer
+
+ self.instance_data_root = Path(instance_data_root)
+ if not self.instance_data_root.exists():
+ raise ValueError("Instance images root doesn't exists.")
+
+ self.instance_images_path = list(Path(instance_data_root).iterdir())
+ self.num_instance_images = len(self.instance_images_path)
+ self.instance_prompt = instance_prompt
+ self._length = self.num_instance_images
+
+ if class_data_root is not None:
+ self.class_data_root = Path(class_data_root)
+ self.class_data_root.mkdir(parents=True, exist_ok=True)
+ self.class_images_path = list(self.class_data_root.iterdir())
+ self.num_class_images = len(self.class_images_path)
+ self._length = max(self.num_class_images, self.num_instance_images)
+ self.class_prompt = class_prompt
+ else:
+ self.class_data_root = None
+
+ self.image_transforms = transforms.Compose(
+ [
+ transforms.Resize(size, interpolation=transforms.InterpolationMode.BILINEAR),
+ transforms.CenterCrop(size) if center_crop else transforms.RandomCrop(size),
+ transforms.ToTensor(),
+ transforms.Normalize([0.5], [0.5]),
+ ]
+ )
+
+ def __len__(self):
+ return self._length
+
+ def __getitem__(self, index):
+ example = {}
+ instance_image = Image.open(self.instance_images_path[index % self.num_instance_images])
+ if not instance_image.mode == "RGB":
+ instance_image = instance_image.convert("RGB")
+ example["instance_images"] = self.image_transforms(instance_image)
+ example["instance_prompt_ids"] = self.tokenizer(
+ self.instance_prompt,
+ truncation=True,
+ padding="max_length",
+ max_length=self.tokenizer.model_max_length,
+ return_tensors="pt",
+ ).input_ids
+
+ if self.class_data_root:
+ class_image = Image.open(self.class_images_path[index % self.num_class_images])
+ if not class_image.mode == "RGB":
+ class_image = class_image.convert("RGB")
+ example["class_images"] = self.image_transforms(class_image)
+ example["class_prompt_ids"] = self.tokenizer(
+ self.class_prompt,
+ truncation=True,
+ padding="max_length",
+ max_length=self.tokenizer.model_max_length,
+ return_tensors="pt",
+ ).input_ids
+
+ return example
+
+
+def collate_fn(examples, with_prior_preservation=False):
+ input_ids = [example["instance_prompt_ids"] for example in examples]
+ pixel_values = [example["instance_images"] for example in examples]
+
+ # Concat class and instance examples for prior preservation.
+ # We do this to avoid doing two forward passes.
+ if with_prior_preservation:
+ input_ids += [example["class_prompt_ids"] for example in examples]
+ pixel_values += [example["class_images"] for example in examples]
+
+ pixel_values = torch.stack(pixel_values)
+ pixel_values = pixel_values.to(memory_format=torch.contiguous_format).float()
+
+ input_ids = torch.cat(input_ids, dim=0)
+
+ batch = {
+ "input_ids": input_ids,
+ "pixel_values": pixel_values,
+ }
+ return batch
+
+
+class PromptDataset(Dataset):
+ "A simple dataset to prepare the prompts to generate class images on multiple accelerators."
+
+ def __init__(self, prompt, num_samples):
+ self.prompt = prompt
+ self.num_samples = num_samples
+
+ def __len__(self):
+ return self.num_samples
+
+ def __getitem__(self, index):
+ example = {}
+ example["prompt"] = self.prompt
+ example["index"] = index
+ return example
+
+
+def main(args):
+ logging_dir = Path(args.output_dir, args.logging_dir)
+
+ accelerator = Accelerator(
+ gradient_accumulation_steps=args.gradient_accumulation_steps,
+ mixed_precision=args.mixed_precision,
+ log_with=args.report_to,
+ project_dir=logging_dir,
+ )
+ if args.report_to == "wandb":
+ import wandb
+
+ wandb.login(key=args.wandb_key)
+ wandb.init(project=args.wandb_project_name)
+ # Currently, it's not possible to do gradient accumulation when training two models with accelerate.accumulate
+ # This will be enabled soon in accelerate. For now, we don't allow gradient accumulation when training two models.
+ # TODO (patil-suraj): Remove this check when gradient accumulation with two models is enabled in accelerate.
+ if args.train_text_encoder and args.gradient_accumulation_steps > 1 and accelerator.num_processes > 1:
+ raise ValueError(
+ "Gradient accumulation is not supported when training the text encoder in distributed training. "
+ "Please set gradient_accumulation_steps to 1. This feature will be supported in the future."
+ )
+
+ # Make one log on every process with the configuration for debugging.
+ logging.basicConfig(
+ format="%(asctime)s - %(levelname)s - %(name)s - %(message)s",
+ datefmt="%m/%d/%Y %H:%M:%S",
+ level=logging.INFO,
+ )
+ logger.info(accelerator.state, main_process_only=False)
+ if accelerator.is_local_main_process:
+ datasets.utils.logging.set_verbosity_warning()
+ transformers.utils.logging.set_verbosity_warning()
+ diffusers.utils.logging.set_verbosity_info()
+ else:
+ datasets.utils.logging.set_verbosity_error()
+ transformers.utils.logging.set_verbosity_error()
+ diffusers.utils.logging.set_verbosity_error()
+
+ # If passed along, set the training seed now.
+ if args.seed is not None:
+ set_seed(args.seed)
+
+ # Generate class images if prior preservation is enabled.
+ if args.with_prior_preservation:
+ class_images_dir = Path(args.class_data_dir)
+ if not class_images_dir.exists():
+ class_images_dir.mkdir(parents=True)
+ cur_class_images = len(list(class_images_dir.iterdir()))
+
+ if cur_class_images < args.num_class_images:
+ torch_dtype = torch.float16 if accelerator.device.type in ["cuda", "xpu"] else torch.float32
+ if args.prior_generation_precision == "fp32":
+ torch_dtype = torch.float32
+ elif args.prior_generation_precision == "fp16":
+ torch_dtype = torch.float16
+ elif args.prior_generation_precision == "bf16":
+ torch_dtype = torch.bfloat16
+ pipeline = DiffusionPipeline.from_pretrained(
+ args.pretrained_model_name_or_path,
+ torch_dtype=torch_dtype,
+ safety_checker=None,
+ revision=args.revision,
+ )
+ pipeline.set_progress_bar_config(disable=True)
+
+ num_new_images = args.num_class_images - cur_class_images
+ logger.info(f"Number of class images to sample: {num_new_images}.")
+
+ sample_dataset = PromptDataset(args.class_prompt, num_new_images)
+ sample_dataloader = torch.utils.data.DataLoader(sample_dataset, batch_size=args.sample_batch_size)
+
+ sample_dataloader = accelerator.prepare(sample_dataloader)
+ pipeline.to(accelerator.device)
+
+ for example in tqdm(
+ sample_dataloader, desc="Generating class images", disable=not accelerator.is_local_main_process
+ ):
+ images = pipeline(example["prompt"]).images
+
+ for i, image in enumerate(images):
+ hash_image = hashlib.sha1(image.tobytes()).hexdigest()
+ image_filename = class_images_dir / f"{example['index'][i] + cur_class_images}-{hash_image}.jpg"
+ image.save(image_filename)
+
+ del pipeline
+ if torch.cuda.is_available():
+ torch.cuda.empty_cache()
+ elif torch.xpu.is_available():
+ torch.xpu.empty_cache()
+
+ # Handle the repository creation
+ if accelerator.is_main_process:
+ if args.push_to_hub:
+ api = HfApi(token=args.hub_token)
+
+ # Create repo (repo_name from args or inferred)
+ repo_name = args.hub_model_id
+ if repo_name is None:
+ repo_name = Path(args.output_dir).absolute().name
+ repo_id = api.create_repo(repo_name, exist_ok=True).repo_id
+
+ with open(os.path.join(args.output_dir, ".gitignore"), "w+") as gitignore:
+ if "step_*" not in gitignore:
+ gitignore.write("step_*\n")
+ if "epoch_*" not in gitignore:
+ gitignore.write("epoch_*\n")
+ elif args.output_dir is not None:
+ os.makedirs(args.output_dir, exist_ok=True)
+
+ # Load the tokenizer
+ if args.tokenizer_name:
+ tokenizer = AutoTokenizer.from_pretrained(args.tokenizer_name, revision=args.revision, use_fast=False)
+ elif args.pretrained_model_name_or_path:
+ tokenizer = AutoTokenizer.from_pretrained(
+ args.pretrained_model_name_or_path,
+ subfolder="tokenizer",
+ revision=args.revision,
+ use_fast=False,
+ )
+
+ # import correct text encoder class
+ text_encoder_cls = import_model_class_from_model_name_or_path(args.pretrained_model_name_or_path, args.revision)
+
+ # Load scheduler and models
+ noise_scheduler = DDPMScheduler(
+ beta_start=0.00085,
+ beta_end=0.012,
+ beta_schedule="scaled_linear",
+ num_train_timesteps=1000,
+ ) # DDPMScheduler.from_pretrained(args.pretrained_model_name_or_path, subfolder="scheduler")
+ text_encoder = text_encoder_cls.from_pretrained(
+ args.pretrained_model_name_or_path, subfolder="text_encoder", revision=args.revision
+ )
+ vae = AutoencoderKL.from_pretrained(args.pretrained_model_name_or_path, subfolder="vae", revision=args.revision)
+ unet = UNet2DConditionModel.from_pretrained(
+ args.pretrained_model_name_or_path, subfolder="unet", revision=args.revision
+ )
+
+ if args.use_oft:
+ config = OFTConfig(
+ r=args.oft_r,
+ oft_block_size=args.oft_block_size,
+ target_modules=UNET_TARGET_MODULES,
+ module_dropout=args.oft_dropout,
+ init_weights=True,
+ coft=args.oft_use_coft,
+ eps=args.oft_eps,
+ )
+ unet = get_peft_model(unet, config)
+ unet.print_trainable_parameters()
+ print(unet)
+
+ vae.requires_grad_(False)
+ if not args.train_text_encoder:
+ text_encoder.requires_grad_(False)
+ elif args.train_text_encoder and args.use_oft:
+ config = OFTConfig(
+ r=args.oft_text_encoder_r,
+ oft_block_size=args.oft_text_encoder_block_size,
+ target_modules=TEXT_ENCODER_TARGET_MODULES,
+ module_dropout=args.oft_text_encoder_dropout,
+ init_weights=True,
+ coft=args.oft_text_encoder_use_coft,
+ eps=args.oft_text_encoder_eps,
+ )
+ text_encoder = get_peft_model(text_encoder, config)
+ text_encoder.print_trainable_parameters()
+ print(text_encoder)
+
+ if args.enable_xformers_memory_efficient_attention:
+ if accelerator.device.type == "xpu":
+ logger.warn("XPU hasn't support xformers yet, ignore it.")
+ elif is_xformers_available():
+ unet.enable_xformers_memory_efficient_attention()
+ else:
+ raise ValueError("xformers is not available. Make sure it is installed correctly")
+
+ if args.gradient_checkpointing:
+ unet.enable_gradient_checkpointing()
+ # below fails when using oft so commenting it out
+ if args.train_text_encoder and not args.use_oft:
+ text_encoder.gradient_checkpointing_enable()
+
+ # Enable TF32 for faster training on Ampere GPUs,
+ # cf https://pytorch.org/docs/stable/notes/cuda.html#tensorfloat-32-tf32-on-ampere-devices
+ if args.allow_tf32 and torch.cuda.is_available():
+ torch.backends.cuda.matmul.allow_tf32 = True
+
+ if args.scale_lr:
+ args.learning_rate = (
+ args.learning_rate * args.gradient_accumulation_steps * args.train_batch_size * accelerator.num_processes
+ )
+
+ # Use 8-bit Adam for lower memory usage or to fine-tune the model in 16GB accelerators
+ if args.use_8bit_adam:
+ try:
+ import bitsandbytes as bnb
+ except ImportError:
+ raise ImportError(
+ "To use 8-bit Adam, please install the bitsandbytes library: `pip install bitsandbytes`."
+ )
+
+ optimizer_class = bnb.optim.AdamW8bit
+ else:
+ optimizer_class = torch.optim.AdamW
+
+ # Optimizer creation
+ params_to_optimize = (
+ itertools.chain(unet.parameters(), text_encoder.parameters()) if args.train_text_encoder else unet.parameters()
+ )
+ optimizer = optimizer_class(
+ params_to_optimize,
+ lr=args.learning_rate,
+ betas=(args.adam_beta1, args.adam_beta2),
+ weight_decay=args.adam_weight_decay,
+ eps=args.adam_epsilon,
+ )
+
+ # Dataset and DataLoaders creation:
+ train_dataset = DreamBoothDataset(
+ instance_data_root=args.instance_data_dir,
+ instance_prompt=args.instance_prompt,
+ class_data_root=args.class_data_dir if args.with_prior_preservation else None,
+ class_prompt=args.class_prompt,
+ tokenizer=tokenizer,
+ size=args.resolution,
+ center_crop=args.center_crop,
+ )
+
+ train_dataloader = torch.utils.data.DataLoader(
+ train_dataset,
+ batch_size=args.train_batch_size,
+ shuffle=True,
+ collate_fn=lambda examples: collate_fn(examples, args.with_prior_preservation),
+ num_workers=args.num_dataloader_workers,
+ )
+
+ # Scheduler and math around the number of training steps.
+ overrode_max_train_steps = False
+ num_update_steps_per_epoch = math.ceil(len(train_dataloader) / args.gradient_accumulation_steps)
+ if args.max_train_steps is None:
+ args.max_train_steps = args.num_train_epochs * num_update_steps_per_epoch
+ overrode_max_train_steps = True
+
+ lr_scheduler = get_scheduler(
+ args.lr_scheduler,
+ optimizer=optimizer,
+ num_warmup_steps=args.lr_warmup_steps * args.gradient_accumulation_steps,
+ num_training_steps=args.max_train_steps * args.gradient_accumulation_steps,
+ num_cycles=args.lr_num_cycles,
+ power=args.lr_power,
+ )
+
+ # Prepare everything with our `accelerator`.
+ if args.train_text_encoder:
+ unet, text_encoder, optimizer, train_dataloader, lr_scheduler = accelerator.prepare(
+ unet, text_encoder, optimizer, train_dataloader, lr_scheduler
+ )
+ else:
+ unet, optimizer, train_dataloader, lr_scheduler = accelerator.prepare(
+ unet, optimizer, train_dataloader, lr_scheduler
+ )
+
+ # For mixed precision training we cast the text_encoder and vae weights to half-precision
+ # as these models are only used for inference, keeping weights in full precision is not required.
+ weight_dtype = torch.float32
+ if accelerator.mixed_precision == "fp16":
+ weight_dtype = torch.float16
+ elif accelerator.mixed_precision == "bf16":
+ weight_dtype = torch.bfloat16
+
+ # Move vae and text_encoder to device and cast to weight_dtype
+ vae.to(accelerator.device, dtype=weight_dtype)
+ if not args.train_text_encoder:
+ text_encoder.to(accelerator.device, dtype=weight_dtype)
+
+ # We need to recalculate our total training steps as the size of the training dataloader may have changed.
+ num_update_steps_per_epoch = math.ceil(len(train_dataloader) / args.gradient_accumulation_steps)
+ if overrode_max_train_steps:
+ args.max_train_steps = args.num_train_epochs * num_update_steps_per_epoch
+ # Afterwards we recalculate our number of training epochs
+ args.num_train_epochs = math.ceil(args.max_train_steps / num_update_steps_per_epoch)
+
+ # We need to initialize the trackers we use, and also store our configuration.
+ # The trackers initializes automatically on the main process.
+ if accelerator.is_main_process:
+ accelerator.init_trackers("dreambooth", config=vars(args))
+
+ # Train!
+ total_batch_size = args.train_batch_size * accelerator.num_processes * args.gradient_accumulation_steps
+
+ logger.info("***** Running training *****")
+ logger.info(f" Num examples = {len(train_dataset)}")
+ logger.info(f" Num batches each epoch = {len(train_dataloader)}")
+ logger.info(f" Num Epochs = {args.num_train_epochs}")
+ logger.info(f" Instantaneous batch size per device = {args.train_batch_size}")
+ logger.info(f" Total train batch size (w. parallel, distributed & accumulation) = {total_batch_size}")
+ logger.info(f" Gradient Accumulation steps = {args.gradient_accumulation_steps}")
+ logger.info(f" Total optimization steps = {args.max_train_steps}")
+ global_step = 0
+ first_epoch = 0
+
+ # Potentially load in the weights and states from a previous save
+ if args.resume_from_checkpoint:
+ if args.resume_from_checkpoint != "latest":
+ path = os.path.basename(args.resume_from_checkpoint)
+ else:
+ # Get the mos recent checkpoint
+ dirs = os.listdir(args.output_dir)
+ dirs = [d for d in dirs if d.startswith("checkpoint")]
+ dirs = sorted(dirs, key=lambda x: int(x.split("-")[1]))
+ path = dirs[-1]
+ accelerator.print(f"Resuming from checkpoint {path}")
+ accelerator.load_state(os.path.join(args.output_dir, path))
+ global_step = int(path.split("-")[1])
+
+ resume_global_step = global_step * args.gradient_accumulation_steps
+ first_epoch = resume_global_step // num_update_steps_per_epoch
+ resume_step = resume_global_step % num_update_steps_per_epoch
+
+ # Only show the progress bar once on each machine.
+ progress_bar = tqdm(range(global_step, args.max_train_steps), disable=not accelerator.is_local_main_process)
+ progress_bar.set_description("Steps")
+
+ for epoch in range(first_epoch, args.num_train_epochs):
+ unet.train()
+ if args.train_text_encoder:
+ text_encoder.train()
+ with TorchTracemalloc() if not args.no_tracemalloc else nullcontext() as tracemalloc:
+ for step, batch in enumerate(train_dataloader):
+ # Skip steps until we reach the resumed step
+ if args.resume_from_checkpoint and epoch == first_epoch and step < resume_step:
+ if step % args.gradient_accumulation_steps == 0:
+ progress_bar.update(1)
+ if args.report_to == "wandb":
+ accelerator.print(progress_bar)
+ continue
+
+ with accelerator.accumulate(unet):
+ # Convert images to latent space
+ latents = vae.encode(batch["pixel_values"].to(dtype=weight_dtype)).latent_dist.sample()
+ latents = latents * 0.18215
+
+ # Sample noise that we'll add to the latents
+ noise = torch.randn_like(latents)
+ bsz = latents.shape[0]
+ # Sample a random timestep for each image
+ timesteps = torch.randint(
+ 0, noise_scheduler.config.num_train_timesteps, (bsz,), device=latents.device
+ )
+ timesteps = timesteps.long()
+
+ # Add noise to the latents according to the noise magnitude at each timestep
+ # (this is the forward diffusion process)
+ noisy_latents = noise_scheduler.add_noise(latents, noise, timesteps)
+
+ # Get the text embedding for conditioning
+ encoder_hidden_states = text_encoder(batch["input_ids"])[0]
+
+ # Predict the noise residual
+ model_pred = unet(noisy_latents, timesteps, encoder_hidden_states).sample
+
+ # Get the target for loss depending on the prediction type
+ if noise_scheduler.config.prediction_type == "epsilon":
+ target = noise
+ elif noise_scheduler.config.prediction_type == "v_prediction":
+ target = noise_scheduler.get_velocity(latents, noise, timesteps)
+ else:
+ raise ValueError(f"Unknown prediction type {noise_scheduler.config.prediction_type}")
+
+ if args.with_prior_preservation:
+ # Chunk the noise and model_pred into two parts and compute the loss on each part separately.
+ model_pred, model_pred_prior = torch.chunk(model_pred, 2, dim=0)
+ target, target_prior = torch.chunk(target, 2, dim=0)
+
+ # Compute instance loss
+ loss = F.mse_loss(model_pred.float(), target.float(), reduction="mean")
+
+ # Compute prior loss
+ prior_loss = F.mse_loss(model_pred_prior.float(), target_prior.float(), reduction="mean")
+
+ # Add the prior loss to the instance loss.
+ loss = loss + args.prior_loss_weight * prior_loss
+ else:
+ loss = F.mse_loss(model_pred.float(), target.float(), reduction="mean")
+
+ accelerator.backward(loss)
+ if accelerator.sync_gradients:
+ params_to_clip = (
+ itertools.chain(unet.parameters(), text_encoder.parameters())
+ if args.train_text_encoder
+ else unet.parameters()
+ )
+ accelerator.clip_grad_norm_(params_to_clip, args.max_grad_norm)
+ optimizer.step()
+ lr_scheduler.step()
+ optimizer.zero_grad()
+
+ # Checks if the accelerator has performed an optimization step behind the scenes
+ if accelerator.sync_gradients:
+ progress_bar.update(1)
+ if args.report_to == "wandb":
+ accelerator.print(progress_bar)
+ global_step += 1
+
+ logs = {"loss": loss.detach().item(), "lr": lr_scheduler.get_last_lr()[0]}
+ progress_bar.set_postfix(**logs)
+ accelerator.log(logs, step=global_step)
+
+ if (
+ args.validation_prompt is not None
+ and (step + num_update_steps_per_epoch * epoch) % args.validation_steps == 0
+ ):
+ logger.info(
+ f"Running validation... \n Generating {args.num_validation_images} images with prompt:"
+ f" {args.validation_prompt}."
+ )
+ # create pipeline
+ pipeline = DiffusionPipeline.from_pretrained(
+ args.pretrained_model_name_or_path,
+ safety_checker=None,
+ revision=args.revision,
+ )
+ # set `keep_fp32_wrapper` to True because we do not want to remove
+ # mixed precision hooks while we are still training
+ pipeline.unet = accelerator.unwrap_model(unet, keep_fp32_wrapper=True)
+ pipeline.text_encoder = accelerator.unwrap_model(text_encoder, keep_fp32_wrapper=True)
+ pipeline.scheduler = DPMSolverMultistepScheduler.from_config(pipeline.scheduler.config)
+ pipeline = pipeline.to(accelerator.device)
+ pipeline.set_progress_bar_config(disable=True)
+
+ # run inference
+ if args.seed is not None:
+ generator = torch.Generator(device=accelerator.device).manual_seed(args.seed)
+ else:
+ generator = None
+ images = []
+ for _ in range(args.num_validation_images):
+ image = pipeline(args.validation_prompt, num_inference_steps=25, generator=generator).images[0]
+ images.append(image)
+
+ for tracker in accelerator.trackers:
+ if tracker.name == "tensorboard":
+ np_images = np.stack([np.asarray(img) for img in images])
+ tracker.writer.add_images("validation", np_images, epoch, dataformats="NHWC")
+ if tracker.name == "wandb":
+ import wandb
+
+ tracker.log(
+ {
+ "validation": [
+ wandb.Image(image, caption=f"{i}: {args.validation_prompt}")
+ for i, image in enumerate(images)
+ ]
+ }
+ )
+
+ del pipeline
+ if torch.cuda.is_available():
+ torch.cuda.empty_cache()
+ elif torch.xpu.is_available():
+ torch.xpu.empty_cache()
+
+ if global_step >= args.max_train_steps:
+ break
+
+ # Printing the accelerator memory usage details such as allocated memory, peak memory, and total memory usage
+ if not args.no_tracemalloc:
+ accelerator.print(
+ f"{accelerator.device.type.upper()} Memory before entering the train : {b2mb(tracemalloc.begin)}"
+ )
+ accelerator.print(
+ f"{accelerator.device.type.upper()} Memory consumed at the end of the train (end-begin): {tracemalloc.used}"
+ )
+ accelerator.print(
+ f"{accelerator.device.type.upper()} Peak Memory consumed during the train (max-begin): {tracemalloc.peaked}"
+ )
+ accelerator.print(
+ f"{accelerator.device.type.upper()} Total Peak Memory consumed during the train (max): {tracemalloc.peaked + b2mb(tracemalloc.begin)}"
+ )
+
+ accelerator.print(f"CPU Memory before entering the train : {b2mb(tracemalloc.cpu_begin)}")
+ accelerator.print(f"CPU Memory consumed at the end of the train (end-begin): {tracemalloc.cpu_used}")
+ accelerator.print(f"CPU Peak Memory consumed during the train (max-begin): {tracemalloc.cpu_peaked}")
+ accelerator.print(
+ f"CPU Total Peak Memory consumed during the train (max): {tracemalloc.cpu_peaked + b2mb(tracemalloc.cpu_begin)}"
+ )
+
+ # Create the pipeline using using the trained modules and save it.
+ accelerator.wait_for_everyone()
+ if accelerator.is_main_process:
+ if args.use_oft:
+ unwarpped_unet = accelerator.unwrap_model(unet)
+ unwarpped_unet.save_pretrained(
+ os.path.join(args.output_dir, "unet"), state_dict=accelerator.get_state_dict(unet)
+ )
+ if args.train_text_encoder:
+ unwarpped_text_encoder = accelerator.unwrap_model(text_encoder)
+ unwarpped_text_encoder.save_pretrained(
+ os.path.join(args.output_dir, "text_encoder"),
+ state_dict=accelerator.get_state_dict(text_encoder),
+ )
+ else:
+ pipeline = DiffusionPipeline.from_pretrained(
+ args.pretrained_model_name_or_path,
+ unet=accelerator.unwrap_model(unet),
+ text_encoder=accelerator.unwrap_model(text_encoder),
+ revision=args.revision,
+ )
+ pipeline.save_pretrained(args.output_dir)
+
+ if args.push_to_hub:
+ api.upload_folder(
+ repo_id=repo_id,
+ folder_path=args.output_dir,
+ commit_message="End of training",
+ run_as_future=True,
+ )
+
+ accelerator.end_training()
+
+
+if __name__ == "__main__":
+ args = parse_args()
+ main(args)
diff --git a/peft/examples/olora_finetuning/README.md b/peft/examples/olora_finetuning/README.md
new file mode 100644
index 0000000000000000000000000000000000000000..5e5e9b197ca4ddb186c21b84a432e1ea3083022c
--- /dev/null
+++ b/peft/examples/olora_finetuning/README.md
@@ -0,0 +1,96 @@
+# OLoRA: Orthonormal Low Rank Adaptation of Large Language Models
+
+## Introduction
+[OLoRA](https://huggingface.co/papers/2406.01775) is a novel approach that leverages orthonormal low rank adaptation through QR decomposition. Unlike the default LoRA implementation, OLoRA decomposes original weights into their $\mathbf{Q}$ and $\mathbf{R}$ parts, and then uses the first `rank` rows of $\mathbf{R}$ and the first `rank` columns of $\mathbf{Q}$ to initialize $\mathbf{A}$ and $\mathbf{B}$, respectively. This results in significantly faster convergence, more stable training, and superior performance.
+
+## Quick start
+```python
+import torch
+from peft import LoraConfig, get_peft_model
+from transformers import AutoTokenizer, AutoModelForCausalLM
+from trl import SFTConfig, SFTTrainer
+from datasets import load_dataset
+
+model = AutoModelForCausalLM.from_pretrained("facebook/opt-350m", torch_dtype=torch.bfloat16, device_map="auto")
+tokenizer = AutoTokenizer.from_pretrained("facebook/opt-350m")
+dataset = load_dataset("imdb", split="train[:1%]")
+lora_config = LoraConfig(
+ init_lora_weights="olora"
+)
+peft_model = get_peft_model(model, lora_config)
+training_args = SFTConfig(dataset_text_field="text", max_seq_length=128)
+trainer = SFTTrainer(
+ model=peft_model,
+ train_dataset=dataset,
+ processing_class=tokenizer,
+)
+trainer.train()
+peft_model.save_pretrained("olora-opt-350m")
+```
+
+There is no additional change needed to your standard LoRA procedure, except for specifying `init_lora_weights = "olora"` option in your lora configuration.
+
+Additionally you can refer to olora finetuning script.
+Run the script simply by running:
+```bash
+python3 examples/olora_finetuning/olora_finetuning.py --base_model facebook/opt-350m
+```
+OLoRA also supports quantization. To use 4-bit quantization try:
+```bash
+python3 examples/olora_finetuning/olora_finetuning.py --base_model facebook/opt-350m --quantize
+```
+or you can just pass a quantized model without the quantize flag.
+
+If you want to run DDP by [accelerate](https://huggingface.co/docs/accelerate/en/index), please run `accelerate config` to set your ddp config, and run:
+```bash
+accelerate launch examples/olora_finetuning/olora_finetuning.py --base_model facebook/opt-350m
+```
+please add `--device_map cpu` if you want to run finetune on CPU.
+
+If you want to train a quantized model like AWQ and GPTQ which do not support olora init method, please pass `--init_lora_weights gaussian`. For example:
+```bash
+python3 examples/olora_finetuning/olora_finetuning.py --base_model hugging-quants/Meta-Llama-3.1-8B-Instruct-AWQ-INT4 --init_lora_weights gaussian
+
+```
+
+
+## Use the model
+You can load and use the model as any other 🤗 PEFT model
+```python
+from peft import PeftModel
+model = AutoModelForCausalLM.from_pretrained("facebook/opt-350m")
+tokenizer = AutoTokenizer.from_pretrained("facebook/opt-350m")
+olora_model = PeftModel.from_pretrained(model, "olora-opt-350m")
+```
+
+## OLoRA and LoRA
+OLoRA differs from LoRA in that it mutates the original weights. To utilize multiple adapters simultaneously, you can leverage the `path_initial_model_for_weight_conversion` option. Below is a simple template illustrating how to convert OLoRA to conventional LoRA:
+```python
+base_model = AutoModel.from_pretrained("facebook/opt-350m")
+olora_config = LoraConfig(
+ ...
+ init_lora_weights = "olora" # Initialize the model with OLoRA
+)
+olora_model = get_peft_model(base_model, olora_config)
+init_path =
+olora_model.save_pretrained(init_path) # Save the model *before* performing any training
+
+# Train the model
+train(olora_model) # Your training loop
+
+#Save the model after training
+olora_model.save_pretrained(output_dir, path_initial_model_for_weight_conversion=init_path)
+```
+After completing training, you can save and convert your OLoRA model to a conventional LoRA model by setting `path_initial_model_for_weight_conversion` to `init_path`, that is the path of your untrained OLoRA model. This conversion enables you to use multiple adapters with your LoRA model. Note that this conversion is not supported if `rslora` is used in combination with `rank_pattern` or `alpha_pattern`.
+
+## Citation
+```
+@misc{büyükakyüz2024olora,
+ title={OLoRA: Orthonormal Low-Rank Adaptation of Large Language Models},
+ author={Kerim Büyükakyüz},
+ year={2024},
+ eprint={2406.01775},
+ archivePrefix={arXiv},
+ primaryClass={cs.CL}
+}
+```
diff --git a/peft/examples/olora_finetuning/olora_finetuning.py b/peft/examples/olora_finetuning/olora_finetuning.py
new file mode 100644
index 0000000000000000000000000000000000000000..e3d41f3c07b553c6413d2c329961d603d4637316
--- /dev/null
+++ b/peft/examples/olora_finetuning/olora_finetuning.py
@@ -0,0 +1,199 @@
+# Copyright 2024-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+
+import os
+from typing import Optional
+
+import torch
+import transformers
+from datasets import load_dataset
+from transformers import AutoModelForCausalLM, AutoTokenizer, BitsAndBytesConfig, set_seed
+
+from peft import (
+ LoraConfig,
+ get_peft_model,
+)
+
+
+def train(
+ base_model: str = "path/to/model",
+ data_path: str = "yahma/alpaca-cleaned",
+ output_dir: str = "olora",
+ batch_size: int = 16,
+ num_epochs: int = 1,
+ learning_rate: float = 3e-4,
+ cutoff_len: int = 256,
+ val_set_size: int = 16,
+ quantize: bool = False,
+ eval_step: int = 100,
+ save_step: int = 100,
+ device_map: str = "auto",
+ lora_r: int = 32,
+ lora_alpha: int = 16,
+ lora_dropout: float = 0.05,
+ lora_target_modules: list[str] = None,
+ torch_dtype: str = "float16",
+ init_lora_weights="olora",
+ seed: Optional[int] = None,
+):
+ # Set device_map to the right place when enabling DDP.
+ world_size = int(os.environ.get("WORLD_SIZE", 0)) or int(os.environ.get("PMI_SIZE", 0))
+ if world_size > 1 and device_map != "cpu":
+ from accelerate import Accelerator
+
+ device_map = {"": Accelerator().process_index}
+ # Set seed
+ if seed is not None:
+ set_seed(seed)
+ model_kwargs = {"torch_dtype": getattr(torch, torch_dtype), "device_map": device_map}
+ if quantize:
+ model_kwargs["quantization_config"] = BitsAndBytesConfig(
+ load_in_4bit=True,
+ bnb_4bit_compute_dtype=torch.bfloat16,
+ bnb_4bit_use_double_quant=True,
+ bnb_4bit_quant_type="nf4",
+ )
+ model = AutoModelForCausalLM.from_pretrained(base_model, **model_kwargs)
+
+ tokenizer = AutoTokenizer.from_pretrained(base_model, trust_remote_code=True)
+ # For some tokenizer with no pad token like llama
+ if tokenizer.pad_token is None:
+ tokenizer.pad_token = tokenizer.eos_token
+
+ def tokenize(prompt, add_eos_token=True):
+ result = tokenizer(
+ prompt,
+ truncation=True,
+ max_length=cutoff_len,
+ padding=False,
+ return_tensors=None,
+ )
+ if (
+ result["input_ids"][-1] != tokenizer.eos_token_id
+ and len(result["input_ids"]) < cutoff_len
+ and add_eos_token
+ ):
+ result["input_ids"].append(tokenizer.eos_token_id)
+ result["attention_mask"].append(1)
+
+ result["labels"] = result["input_ids"].copy()
+
+ return result
+
+ def generate_and_tokenize_prompt(example):
+ full_prompt = generate_prompt(example)
+ tokenized_full_prompt = tokenize(full_prompt)
+ return tokenized_full_prompt
+
+ config = LoraConfig(
+ r=lora_r,
+ lora_alpha=lora_alpha,
+ target_modules=lora_target_modules,
+ lora_dropout=lora_dropout,
+ bias="none",
+ task_type="CAUSAL_LM",
+ init_lora_weights=init_lora_weights,
+ )
+ model = get_peft_model(model, config)
+
+ data = load_dataset(data_path)
+
+ train_val = data["train"].train_test_split(test_size=val_set_size, shuffle=True, seed=42)
+ train_data = train_val["train"].shuffle().map(generate_and_tokenize_prompt)
+ val_data = train_val["test"].shuffle().map(generate_and_tokenize_prompt)
+
+ trainer = transformers.Trainer(
+ model=model,
+ train_dataset=train_data,
+ eval_dataset=val_data,
+ args=transformers.TrainingArguments(
+ per_device_train_batch_size=batch_size,
+ warmup_steps=100,
+ num_train_epochs=num_epochs,
+ learning_rate=learning_rate,
+ logging_steps=100,
+ optim="adamw_torch",
+ eval_strategy="steps",
+ save_strategy="steps",
+ eval_steps=eval_step,
+ save_steps=save_step,
+ output_dir=output_dir,
+ save_total_limit=3,
+ load_best_model_at_end=True,
+ ddp_find_unused_parameters=False if world_size > 1 else None,
+ ),
+ data_collator=transformers.DataCollatorForSeq2Seq(
+ tokenizer, pad_to_multiple_of=8, return_tensors="pt", padding=True
+ ),
+ )
+ trainer.train()
+ model.save_pretrained(output_dir)
+
+
+def generate_prompt(example):
+ return f"""Below is an instruction that describes a task. Write a response that appropriately completes the request.
+ ### Instruction:
+ {example["instruction"]}
+ ### Response:
+ {example["output"]}"""
+
+
+if __name__ == "__main__":
+ import argparse
+
+ parser = argparse.ArgumentParser()
+ parser.add_argument("--base_model", type=str, default="path/to/model")
+ parser.add_argument("--data_path", type=str, default="yahma/alpaca-cleaned")
+ parser.add_argument("--output_dir", type=str, default="olora")
+ parser.add_argument("--batch_size", type=int, default=16)
+ parser.add_argument("--num_epochs", type=int, default=1)
+ parser.add_argument("--learning_rate", type=float, default=3e-4)
+ parser.add_argument("--cutoff_len", type=int, default=256)
+ parser.add_argument("--val_set_size", type=int, default=16)
+ parser.add_argument("--quantize", action="store_true")
+ parser.add_argument("--eval_step", type=int, default=100)
+ parser.add_argument("--save_step", type=int, default=100)
+ parser.add_argument("--device_map", type=str, default="auto")
+ parser.add_argument("--lora_r", type=int, default=32)
+ parser.add_argument("--lora_alpha", type=int, default=16)
+ parser.add_argument("--lora_dropout", type=float, default=0.05)
+ parser.add_argument("--lora_target_modules", type=str, default=None)
+ parser.add_argument("--torch_dtype", type=str, default="float16")
+ parser.add_argument("--init_lora_weights", type=str, default="olora")
+ parser.add_argument("--seed", type=int, default=None)
+
+ args = parser.parse_args()
+
+ train(
+ base_model=args.base_model,
+ data_path=args.data_path,
+ output_dir=args.output_dir,
+ batch_size=args.batch_size,
+ num_epochs=args.num_epochs,
+ learning_rate=args.learning_rate,
+ cutoff_len=args.cutoff_len,
+ val_set_size=args.val_set_size,
+ quantize=args.quantize,
+ eval_step=args.eval_step,
+ save_step=args.save_step,
+ device_map=args.device_map,
+ lora_r=args.lora_r,
+ lora_alpha=args.lora_alpha,
+ lora_dropout=args.lora_dropout,
+ lora_target_modules=args.lora_target_modules,
+ torch_dtype=args.torch_dtype,
+ init_lora_weights=args.init_lora_weights,
+ seed=args.seed,
+ )
diff --git a/peft/examples/pissa_finetuning/README.md b/peft/examples/pissa_finetuning/README.md
new file mode 100644
index 0000000000000000000000000000000000000000..4960dd500dedfc178c711ba87a2747f9220c66a9
--- /dev/null
+++ b/peft/examples/pissa_finetuning/README.md
@@ -0,0 +1,131 @@
+# PiSSA: Principal Singular values and Singular vectors Adaptation
+## Introduction ([Paper](https://huggingface.co/papers/2404.02948), [code](https://github.com/GraphPKU/PiSSA))
+PiSSA represents a matrix $W\in\mathbb{R}^{m\times n}$ within the model by the product of two trainable matrices $A \in \mathbb{R}^{m\times r}$ and $B \in \mathbb{R}^{r\times n}$, where $r \ll \min(m, n)$, plus a residual matrix $W^{res}\in\mathbb{R}^{m\times n}$ for error correction. Singular value decomposition (SVD) is employed to factorize $W$, and the principal singular values and vectors of $W$ are utilized to initialize $A$ and $B$. The residual singular values and vectors initialize the residual matrix $W^{res}$, which keeps frozen during fine-tuning. This straightforward modification allows PiSSA to converge more rapidly than LoRA and ultimately attain superior performance. Moreover, PiSSA reduces the quantization error compared to QLoRA, leading to further enhancements.
+
+## Quick Start
+```python
+import torch
+from peft import LoraConfig, get_peft_model
+from transformers import AutoTokenizer, AutoModelForCausalLM
+from trl import SFTConfig, SFTTrainer
+from datasets import load_dataset
+
+model = AutoModelForCausalLM.from_pretrained("meta-llama/Llama-2-7b-hf", torch_dtype=torch.bfloat16, device_map="auto")
+tokenizer = AutoTokenizer.from_pretrained("meta-llama/Llama-2-7b-hf")
+tokenizer.pad_token_id = tokenizer.eos_token_id
+lora_config = LoraConfig(
+ # init_lora_weights="pissa", # Configure the initialization method to "pissa", which may take several minutes to execute SVD on the pre-trained model.
+ init_lora_weights="pissa_niter_4", # Initialize the PiSSA with fast SVD, which completes in just a few seconds.
+)
+peft_model = get_peft_model(model, lora_config)
+
+peft_model.print_trainable_parameters()
+
+dataset = load_dataset("imdb", split="train[:1%]")
+
+training_args = SFTConfig(dataset_text_field="text", max_seq_length=128)
+trainer = SFTTrainer(
+ model=peft_model,
+ args=training_args,
+ train_dataset=dataset,
+ processing_class=tokenizer,
+)
+trainer.train()
+peft_model.save_pretrained("pissa-llama-2-7b")
+```
+When utilizing fast SVD, reducing the rank and the number of iterations decreases the time required. However, this approach leads to higher errors in the computed matrices $A$ and $B$. To preserve the model's initial capabilities, we calculate the residual matrix by $W^{res} = W - BA$. Even with potential errors in $A$ and $B$, the sum of $W^{res}$ and $BA$ accurately equals $W$.
+
+
+To utilize the fine-tuned PiSSA modules, simply run the following command:
+```python
+import torch
+from peft import PeftModel
+from transformers import AutoModelForCausalLM
+
+model = AutoModelForCausalLM.from_pretrained(
+ "meta-llama/Llama-2-7b-hf", torch_dtype=torch.bfloat16, device_map="auto"
+)
+# Performs SVD again to initialize the residual model and loads the state_dict of the fine-tuned PiSSA modules.
+peft_model = PeftModel.from_pretrained(model, "pissa-llama-2-7b")
+```
+
+## Advanced Usage
+
+### Access the preprocessed models
+We recommend downloading decomposed models directly from the [Hugging Face Collections](https://huggingface.co/collections/fxmeng/pissa-661ce700721235e542a5d7a8) instead of performing SVD every time.
+If the existing models do not meet your needs, apply PiSSA initialization to a pre-trained model and store the decomposed model locally:
+```bash
+python preprocess.py \
+ --base_model_name_or_path meta-llama/Llama-2-7b-hf \
+ --init_lora_weights pissa \
+ --output_dir pissa-llama-2-7b-r32-alpha-32 \
+ --lora_r 32 \
+ --lora_alpha 32 \
+ --lora_dropout 0 \
+ --bits bf16
+```
+
+### Convert PiSSA to LoRA
+The main advantage of PiSSA is concentrated during the training phase. For a trained PiSSA adapter, we recommend converting it equivalently to the LoRA adapter for using and sharing.
+```python
+# The fine-tuned matrices $A$ and $B$ in PiSSA adapter is saved and should be combined with the residual model.
+peft_model.save_pretrained(output_dir)
+# Given the matrices $A_0$ and $B_0$, initialized by PiSSA and untrained, and the trained matrices $A$ and $B$,
+# we can convert these to LoRA by setting $\Delta W = A \times B - A_0 \times B_0 = [A \mid A_0] \times [B \mid -B_0]^T = A'B'$.
+peft_model.save_pretrained(output_dir, path_initial_model_for_weight_conversion="pissa_init")
+
+```
+This conversion enables the loading of LoRA on top of a standard base model:
+
+```python
+import torch
+from peft import PeftModel
+from transformers import AutoModelForCausalLM
+
+model = AutoModelForCausalLM.from_pretrained(
+ "meta-llama/Llama-2-7b-hf", torch_dtype=torch.bfloat16, device_map="auto"
+)
+# No SVD is performed during this step, and the base model remains unaltered.
+peft_model = PeftModel.from_pretrained(model, "pissa-llama-2-7b-lora")
+```
+Utilizing the converted LoRA does not require modifying the parameters of the base model. When multiple converted LoRAs are needed simultaneously, each adapter operates independently without interference, allowing for the adapters to be freely deleted or added.
+
+Note that this conversion is not supported if `rslora` is used in combination with `rank_pattern` or `alpha_pattern`.
+
+### Fine-tune in 4-bit or 8-bit
+If quantization fine-tuning is desired, it is necessary to first decompose the original model at full precision and then reload the residual model in either 4-bit or 8-bit configurations.
+```shell
+python pissa_finetuning.py \
+ --residual_model_name_or_path fxmeng/pissa-llama-2-7b-r16-alpha-16 \
+ --output_dir output/pissa-llama-2-7b-r16-alpha-16-metamath-10k \
+ --bits nf4 \
+ --data_path meta-math/MetaMathQA \
+ --dataset_split train[:100000] \
+ --dataset_field query response \
+ --bf16 True \
+ --num_train_epochs 1 \
+ --per_device_train_batch_size 32 \
+ --gradient_accumulation_steps 4 \
+ --save_strategy "steps" \
+ --save_steps 1000 \
+ --save_total_limit 1 \
+ --logging_steps 1 \
+ --learning_rate 2e-5 \
+ --weight_decay 0. \
+ --warmup_ratio 0.03 \
+ --tf32 True \
+ --report_to none \
+ --convert_pissa_to_lora
+```
+
+This approach ensures the preservation of high-frequency, out-of-distribution parameters in the low-rank PiSSA modules, resulting in reduced quantization errors during the quantization of the residual model.
+
+## Citation
+```
+@article{meng2024pissa,
+ title={PiSSA: Principal Singular Values and Singular Vectors Adaptation of Large Language Models},
+ author={Meng, Fanxu and Wang, Zhaohui and Zhang, Muhan},
+ journal={arXiv preprint arXiv:2404.02948},
+ year={2024}
+}
+```
diff --git a/peft/examples/pissa_finetuning/pissa_finetuning.py b/peft/examples/pissa_finetuning/pissa_finetuning.py
new file mode 100644
index 0000000000000000000000000000000000000000..36d4ba04f01b0388cafd6af10ed7cb726eeb2dec
--- /dev/null
+++ b/peft/examples/pissa_finetuning/pissa_finetuning.py
@@ -0,0 +1,150 @@
+# Copyright 2023-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+import os
+from dataclasses import dataclass, field
+from typing import Optional
+
+import torch
+from datasets import load_dataset
+from transformers import AutoModelForCausalLM, AutoTokenizer, BitsAndBytesConfig, HfArgumentParser
+from trl import SFTConfig, SFTTrainer
+
+from peft import LoraConfig, PeftModel, get_peft_model, prepare_model_for_kbit_training
+
+
+@dataclass
+class ScriptArguments(SFTConfig):
+ # model configs
+ base_model_name_or_path: Optional[str] = field(
+ default=None, metadata={"help": "The name or path of the fp32/16 base model."}
+ )
+ residual_model_name_or_path: Optional[str] = field(
+ default=None,
+ metadata={
+ "help": "The name or path of the fp32/16 residual model. (`['fxmeng/pissa-llama-2-7b-r16-alpha-16']`)"
+ },
+ )
+ bits: str = field(default="fp32", metadata={"help": "(`['fp4', 'nf4', 'int8', 'bf16', 'fp16', fp32]`)"})
+ init_lora_weights: str = field(default="pissa", metadata={"help": "(`['gaussian', 'pissa', 'pissa_niter_4']`)"})
+ lora_r: int = field(default=16)
+ lora_alpha: int = field(default=16)
+ lora_dropout: float = field(default=0)
+ convert_pissa_to_lora: bool = field(default=False)
+ merge_and_save: bool = field(default=False)
+ # dataset configs
+ data_path: str = field(default="imdb", metadata={"help": "Path to the training data."})
+ dataset_split: str = field(default="train[:1%]", metadata={"help": "(`['train', 'test', 'eval']`):"})
+ dataset_field: list[str] = field(default=None, metadata={"help": "Fields of dataset input and output."})
+
+
+parser = HfArgumentParser(ScriptArguments)
+script_args = parser.parse_args_into_dataclasses()[0]
+print(script_args)
+
+print(f"Load pre-processed residual model in {script_args.bits} bits.")
+if script_args.bits in ["nf4", "fp4", "int8"]:
+ quantization_config = BitsAndBytesConfig(
+ load_in_4bit=(script_args.bits == "nf4" or script_args.bits == "fp4"),
+ load_in_8bit=script_args.bits == "int8",
+ bnb_4bit_quant_type=script_args.bits,
+ bnb_4bit_use_double_quant=True,
+ bnb_4bit_compute_dtype=torch.bfloat16,
+ )
+ res_model = AutoModelForCausalLM.from_pretrained(
+ script_args.residual_model_name_or_path, quantization_config=quantization_config, low_cpu_mem_usage=True
+ )
+ res_model = prepare_model_for_kbit_training(res_model)
+ print("Wrapping the residual model with PiSSA.")
+ peft_model = PeftModel.from_pretrained(
+ res_model, script_args.residual_model_name_or_path, subfolder="pissa_init", is_trainable=True
+ )
+ tokenizer = AutoTokenizer.from_pretrained(script_args.residual_model_name_or_path)
+
+elif script_args.residual_model_name_or_path is not None:
+ res_model = AutoModelForCausalLM.from_pretrained(
+ script_args.residual_model_name_or_path,
+ torch_dtype=(
+ torch.float16
+ if script_args.bits == "fp16"
+ else (torch.bfloat16 if script_args.bits == "bf16" else torch.float32)
+ ),
+ device_map="auto",
+ )
+ print("Wrapping the residual model with PiSSA.")
+ peft_model = PeftModel.from_pretrained(
+ res_model, script_args.residual_model_name_or_path, subfolder="pissa_init", is_trainable=True
+ )
+ tokenizer = AutoTokenizer.from_pretrained(script_args.residual_model_name_or_path)
+
+elif script_args.base_model_name_or_path is not None:
+ print(
+ f"No available pre-processed model, manually initialize a PiSSA using {script_args.base_model_name_or_path}."
+ )
+ model = AutoModelForCausalLM.from_pretrained(
+ script_args.base_model_name_or_path,
+ torch_dtype=(
+ torch.float16
+ if script_args.bits == "fp16"
+ else (torch.bfloat16 if script_args.bits == "bf16" else torch.float32)
+ ),
+ device_map="auto",
+ )
+ tokenizer = AutoTokenizer.from_pretrained(script_args.base_model_name_or_path)
+ tokenizer.pad_token_id = tokenizer.eos_token_id
+ lora_config = LoraConfig(
+ r=script_args.lora_r,
+ lora_alpha=script_args.lora_alpha,
+ init_lora_weights=script_args.init_lora_weights,
+ lora_dropout=script_args.lora_dropout,
+ target_modules=["q_proj", "o_proj", "k_proj", "v_proj", "gate_proj", "up_proj", "down_proj"],
+ bias="none",
+ task_type="CAUSAL_LM",
+ )
+ peft_model = get_peft_model(model, lora_config)
+
+print(peft_model)
+peft_model.print_trainable_parameters()
+
+print(f"Training PiSSA with trl on the {script_args.data_path}[{script_args.dataset_split}] dataset.")
+dataset = load_dataset(script_args.data_path, split=script_args.dataset_split)
+dataset = dataset.map(
+ lambda example: {
+ "text": f"### USER: {example[script_args.dataset_field[0]]}\n### ASSISTANT: {example[script_args.dataset_field[1]]}"
+ }
+)
+
+trainer = SFTTrainer(
+ model=peft_model,
+ args=script_args,
+ train_dataset=dataset,
+ processing_class=tokenizer,
+)
+trainer.train()
+trainer.save_state()
+############################## Upon training completion, convert and save PiSSA in LoRA format ##############################
+if script_args.convert_pissa_to_lora:
+ peft_model.save_pretrained(
+ os.path.join(script_args.output_dir, "pissa_lora"),
+ path_initial_model_for_weight_conversion=os.path.join(script_args.residual_model_name_or_path, "pissa_init"),
+ )
+else:
+ peft_model.save_pretrained(
+ os.path.join(script_args.output_dir, "pissa_ft"),
+ )
+
+if script_args.merge_and_save:
+ model = peft_model.merge_and_unload()
+ model.save_pretrained(os.path.join(script_args.output_dir, "pissa_merged"))
+ tokenizer.save_pretrained(os.path.join(script_args.output_dir, "pissa_merged"))
diff --git a/peft/examples/pissa_finetuning/preprocess.py b/peft/examples/pissa_finetuning/preprocess.py
new file mode 100644
index 0000000000000000000000000000000000000000..57eed4420c68388dd944aaaf99e8354764da9194
--- /dev/null
+++ b/peft/examples/pissa_finetuning/preprocess.py
@@ -0,0 +1,69 @@
+# Copyright 2023-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+import argparse
+import os
+
+import torch
+from transformers import AutoModelForCausalLM, AutoTokenizer
+
+from peft import LoraConfig, get_peft_model
+
+
+parser = argparse.ArgumentParser(description="Merge Adapter to Base Model")
+parser.add_argument(
+ "--base_model_name_or_path",
+ help="The name or path of the fp32/16 base model.",
+)
+parser.add_argument("--output_dir", type=str, help="The directory to save the PiSSA model.")
+parser.add_argument("--bits", type=str, default="bf16", choices=["bf16", "fp16", "fp32"])
+parser.add_argument(
+ "--init_lora_weights", type=str, default="pissa", help="(`['pissa', 'pissa_niter_[number of iters]']`)"
+)
+parser.add_argument("--lora_r", type=int, default=128)
+parser.add_argument("--lora_alpha", type=int, default=128)
+parser.add_argument("--lora_dropout", type=int, default=0)
+script_args = parser.parse_args()
+print(script_args)
+
+model = AutoModelForCausalLM.from_pretrained(
+ script_args.base_model_name_or_path,
+ torch_dtype=(
+ torch.float16
+ if script_args.bits == "fp16"
+ else (torch.bfloat16 if script_args.bits == "bf16" else torch.float32)
+ ),
+ device_map="auto",
+)
+tokenizer = AutoTokenizer.from_pretrained(script_args.base_model_name_or_path)
+tokenizer.pad_token_id = tokenizer.eos_token_id
+lora_config = LoraConfig(
+ r=script_args.lora_r,
+ lora_alpha=script_args.lora_alpha,
+ init_lora_weights=script_args.init_lora_weights,
+ lora_dropout=script_args.lora_dropout,
+ target_modules=["q_proj", "o_proj", "k_proj", "v_proj", "gate_proj", "up_proj", "down_proj"],
+ bias="none",
+ task_type="CAUSAL_LM",
+)
+peft_model = get_peft_model(model, lora_config)
+
+# Save PiSSA modules:
+peft_model.peft_config["default"].init_lora_weights = True
+peft_model.save_pretrained(os.path.join(script_args.output_dir, "pissa_init"))
+# Save residual model:
+peft_model = peft_model.unload()
+peft_model.save_pretrained(script_args.output_dir)
+# Save the tokenizer:
+tokenizer.save_pretrained(script_args.output_dir)
diff --git a/peft/examples/poly/peft_poly_seq2seq_with_generate.ipynb b/peft/examples/poly/peft_poly_seq2seq_with_generate.ipynb
new file mode 100644
index 0000000000000000000000000000000000000000..d6768d01fc0730a357a14e4bdce96889efee028f
--- /dev/null
+++ b/peft/examples/poly/peft_poly_seq2seq_with_generate.ipynb
@@ -0,0 +1,14776 @@
+{
+ "cells": [
+ {
+ "cell_type": "code",
+ "execution_count": 1,
+ "id": "2edec24d8563b583",
+ "metadata": {
+ "collapsed": false,
+ "execution": {
+ "shell.execute_reply.end": "2023-12-22T03:34:15.998083Z",
+ "shell.execute_reply.started": "2023-12-22T03:34:15.994854Z",
+ "to_execute": "2023-12-22T03:34:15.875Z"
+ },
+ "libroFormatter": "formatter-string"
+ },
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "env: CUDA_VISIBLE_DEVICES=0 # force using CUDA GPU device 0\n",
+ "env: ZE_AFFINITY_MASK=0 # force using Intel XPU device 0\n",
+ "env: TOKENIZERS_PARALLELISM=false\n"
+ ]
+ }
+ ],
+ "source": [
+ "%env CUDA_VISIBLE_DEVICES=0 # force using CUDA GPU device 0\n",
+ "%env ZE_AFFINITY_MASK=0 # force using Intel XPU device 0\n",
+ "%env TOKENIZERS_PARALLELISM=false"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "95b4cfd741795038",
+ "metadata": {
+ "id": "95b4cfd741795038",
+ "libroFormatter": "formatter-string"
+ },
+ "source": [
+ "## Initialize PolyModel"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "id": "1a5c7a99-5208-4d22-ac15-bacebe1b52f9",
+ "metadata": {
+ "execution": {
+ "shell.execute_reply.end": "2023-12-22T03:34:29.137789Z",
+ "shell.execute_reply.started": "2023-12-22T03:34:18.146604Z",
+ "to_execute": "2023-12-22T03:34:18.025Z"
+ },
+ "id": "1a5c7a99-5208-4d22-ac15-bacebe1b52f9",
+ "libroFormatter": "formatter-string"
+ },
+ "outputs": [],
+ "source": [
+ "import torch\n",
+ "from transformers import (\n",
+ " AutoModelForSeq2SeqLM,\n",
+ " AutoTokenizer,\n",
+ " default_data_collator,\n",
+ " Seq2SeqTrainingArguments,\n",
+ " Seq2SeqTrainer,\n",
+ ")\n",
+ "from datasets import load_dataset, concatenate_datasets\n",
+ "from peft import PolyConfig, get_peft_model, TaskType, PeftModel, PeftConfig\n",
+ "\n",
+ "model_name_or_path = \"google/flan-t5-xl\"\n",
+ "\n",
+ "r = 8 # rank of lora in poly\n",
+ "n_tasks = 4 # number of tasks\n",
+ "n_skills = 2 # number of skills (loras)\n",
+ "n_splits = 4 # number of heads\n",
+ "\n",
+ "batch_size = 8\n",
+ "lr = 5e-5\n",
+ "num_epochs = 8"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 3,
+ "id": "89a1d2c6-0d35-4254-b9fb-035a426d86ae",
+ "metadata": {
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 241,
+ "referenced_widgets": [
+ "dc5d4672fcd149239cfe1a837094ce53",
+ "eded01d7629e4a4faad592e8e20a3ca3",
+ "5d1e94d40f514faaa5819096f167d29c",
+ "f98f73664a974ae7804e494425fbe20d",
+ "1c0bd751a3294b8ea0cf828866169121",
+ "6c3ed2de06fe40c09315ff72d43d5c8c",
+ "2e3d6b5d46db4295829002fc311a9c74",
+ "5ff0d4da7342457089f0961b189307f4",
+ "a08c4e6628bd440fb31eebbb2693f327",
+ "379357ab63f5479fad469c181b054bb0",
+ "f860e1c3467348f0802b733fbef45c15",
+ "567e165c27a4494bbf4810ecb7de40cf",
+ "015fd47fdbdf47c5a619eff218052b45",
+ "ec33a4325b6f4dcfb8a9fa4c80a5c704",
+ "3241189c875a471ab0831f0f4411d2d3",
+ "268fe971a0bc45c6b7c37586e0f9da49",
+ "8851d4a04cb9410c849b6606a812c52b",
+ "3b5ab7d9f27944d8ae1b172231c9c6fc",
+ "85f57b44dbe442a4952c65e1db4c1176",
+ "3f173a7293cd4ff8a54da8c8174cfb43",
+ "40ac1e38c100435fbe95b669c69a31c5",
+ "a634013728be457ba590aa333908addd",
+ "376242d1cfd74c88aaeaa76a6813d855",
+ "a17443b5713d4b60aeb85da3adce6cf2",
+ "91f821fb888046b6a2f8ade2cc58db2d",
+ "4bea407148e846babefdc88eff8a9131",
+ "26a75e6f6628472b91f3214505afa935",
+ "c7c0b0fd45dc448eb9456f58e36fb3bb",
+ "a14f26db56d04b8b840a9ce366e913e6",
+ "09fa4b156f174dbcacdf976f2b39a280",
+ "c9ca89486def4220967599e5b159b980",
+ "558b98eb76654045a5eae24170a5dc9c",
+ "7edf2ac4dd264843a7838a0130668757",
+ "c3aa97f46a60409091dc4d33a946c6d3",
+ "e6315c5d217b4922b461c9ac22528e62",
+ "04c34c92e4374c50bd0636c72953a8ba",
+ "32a6ac79c27e47c1a4b32098bfe25807",
+ "bb99715a25d94422b0048de94f2fe563",
+ "637bbd213f3345178742523d055993e6",
+ "6113f1920c5743aa8f2c6cc9739029e1",
+ "24bbd7b810b34c4c9baeed628961c64b",
+ "1c63e99470824a3aa0f98a94862733d5",
+ "98c677014f1a48ac804cec0714a22172",
+ "a4097270b9b947b0ad0b3b5d217eecc0",
+ "8eaed8cbbf1943328dc80fc43bd5b97c",
+ "6b1972a032af41de9bf99a6582c53f39",
+ "b4eb16a8153048ea9aa5c9d43b44820c",
+ "9bd66a63faf9416d9e774a5d8221c5f5",
+ "40b859a2fd68457db691bb5e7eb23591",
+ "533151b377d64d3484772b3173dab306",
+ "2cd302d306e3440dac4b70fc46741544",
+ "41b36d52e98249b1b506d369d2d8e994",
+ "ac83130fdd374b7c8f41e0f8f011ecae",
+ "66b0e949143e46faab77458a49a9fe1a",
+ "abd34fa3e94c49869ea7cf514dba6d1d",
+ "8ffe87ece7e54294a160540fbbbe124b",
+ "9c3c68da285449958a3d8745bbc50305",
+ "ae517eef5a004b16b4ae34cdf2aa851e",
+ "08a572aefb63488d8125ae3b881c0729",
+ "f2131e286f704514a61b5af0785dde8b",
+ "43d9b3de4a6949f787d9733d1ae4d18e",
+ "06716294f2244cc48f78af918cc063f2",
+ "e69b0005e91a478297d17e4089cda650",
+ "f92f9afc2c694f0cbcdf4ebcca98221e",
+ "7ffe5fd0a64c40cebc784eca83154069",
+ "d622b006621e4110a157fb4cb43c9762",
+ "874e05e0b861466ba57a08d8f5a5b7ee",
+ "8ebe69a07de64c3cb6dfd6433e222186",
+ "2aceeebfd0dc42fcbbc1b3a7e1f54c56",
+ "93c6f7c0d1ba49a295ae60a73bf509a9",
+ "6c3ebb812cfd493bb954a6b1d7455c72",
+ "a27edbdb4c824979b1b56e8fbd867595",
+ "5bdf79c178074ebf8757936190bc37b3",
+ "3c076081fd7942e184f8d4f171a17e1c",
+ "0a03bee83ddf4ad297bfdc9b4de3b075",
+ "6f59ae0a20cf4cc5859925e3259291a7",
+ "49ac9897f49843fd8c5fed4bcdfdbb56"
+ ]
+ },
+ "execution": {
+ "shell.execute_reply.end": "2023-12-22T03:35:33.229420Z",
+ "shell.execute_reply.started": "2023-12-22T03:34:37.266443Z",
+ "to_execute": "2023-12-22T03:34:37.242Z"
+ },
+ "id": "89a1d2c6-0d35-4254-b9fb-035a426d86ae",
+ "libroFormatter": "formatter-string",
+ "outputId": "fc90c2cc-9cab-40ed-bf4a-d76bec85b72f"
+ },
+ "outputs": [
+ {
+ "name": "stderr",
+ "output_type": "stream",
+ "text": [
+ "Loading checkpoint shards: 100%|██████████| 2/2 [00:00<00:00, 22.43it/s]\n"
+ ]
+ }
+ ],
+ "source": [
+ "tokenizer = AutoTokenizer.from_pretrained(model_name_or_path, trust_remote_code=True)\n",
+ "base_model = AutoModelForSeq2SeqLM.from_pretrained(model_name_or_path, trust_remote_code=True)"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 4,
+ "id": "29d701a4-7a4f-4eae-84bd-9e3a02b7ffca",
+ "metadata": {
+ "colab": {
+ "base_uri": "https://localhost:8080/"
+ },
+ "execution": {
+ "shell.execute_reply.end": "2023-12-22T03:35:33.396336Z",
+ "shell.execute_reply.started": "2023-12-22T03:35:33.250286Z",
+ "to_execute": "2023-12-22T03:35:33.272Z"
+ },
+ "id": "29d701a4-7a4f-4eae-84bd-9e3a02b7ffca",
+ "libroFormatter": "formatter-string",
+ "outputId": "63898f68-926e-40c4-ca13-ffd1df32fcce"
+ },
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "trainable params: 9,441,792 || all params: 2,859,198,976 || trainable%: 0.3302\n"
+ ]
+ }
+ ],
+ "source": [
+ "peft_config = PolyConfig(\n",
+ " task_type=TaskType.SEQ_2_SEQ_LM,\n",
+ " poly_type=\"poly\",\n",
+ " r=r,\n",
+ " n_tasks=n_tasks,\n",
+ " n_skills=n_skills,\n",
+ " n_splits=n_splits,\n",
+ ")\n",
+ "\n",
+ "model = get_peft_model(base_model, peft_config)\n",
+ "model.print_trainable_parameters()"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "aa695c2d-cf9c-432c-ab74-7e89f816ba13",
+ "metadata": {
+ "id": "aa695c2d-cf9c-432c-ab74-7e89f816ba13",
+ "libroFormatter": "formatter-string"
+ },
+ "source": [
+ "## Prepare datasets\n",
+ "\n",
+ "For this example, we selected four `SuperGLUE` benchmark datasets: `boolq`, `multirc`, `rte`, and `wic`, each with a training set of 1,000 examples and an evaluation set of 100 examples."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 5,
+ "id": "d0b36e7eff50657c",
+ "metadata": {
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 1000,
+ "referenced_widgets": [
+ "d6250bff76d7454a8216572ab28e4a72",
+ "384d10ea2a354f24bae33c3a1d564b82",
+ "a2deecc9aa3d42d381d78199f6e29d1c",
+ "17fc618034bf4aadaef811b0e7c80eed",
+ "6757bc0834fc4e69b7b588ae6de14ec9",
+ "b9ec517b4b084d548525ac41381ef69e",
+ "6f3679fe9b60498da864bda9ba6d899e",
+ "ef16f8bac38044c3b6a092caf5da320b",
+ "19e50ecdda3b493184611d97724ac1fc",
+ "c2ed87d5599a467bba084cddb9e40713",
+ "2cfc492ab0ed454dbf2c4da18cd24d02",
+ "91e6e0685a4c4d26b6154d3ed18418eb",
+ "ba1864322c0d49fd915e9dcc2469ef6f",
+ "67b108def57749edb2564b3e507959a3",
+ "c04a17f40c974f378c60858473f49fd0",
+ "4189c6e9c59e44d3a776b49c38cc8f06",
+ "7550307b4e894844b8d032df7eea6d82",
+ "bcf20733fb504a71be5cf0455928b587",
+ "cc6c1b2d4fcb4ffea016a139738e1ead",
+ "6bd3da08b5074e81bffbfe6d92b8ce8b",
+ "03d340641a414362b0356e8178148d9a",
+ "61fec3b2596c4803924ed1fb087d52d1",
+ "4fc54c5844aa44f2b335824c3544a334",
+ "736443c7e26642379ca66ed3e5dd34cb",
+ "3c3d747638004a08a898cff7c6f59acc",
+ "1cb2dcb242334f46b7f195929dd1f341",
+ "f577bbac4eab439b9ccea0a49eb99d86",
+ "8822d3a8fa794fc0addb5885a862d205",
+ "10436da727ec45c8a5e8b783696636d5",
+ "0622e1de75f34da590f241232613cf5e",
+ "5b868029728541dc9da977312da38cf0",
+ "33add0384c36462ab44fe3e0b03f63c7",
+ "e227fb95b00b4af8b82286c75db84611",
+ "54d4afa42e9346578c0a1a193ee8caea",
+ "2918f1fd9e104c09967d698e11728785",
+ "170853712c0c4a8d997696f74090d7c6",
+ "fcdb61acbf0d470f881ba8f283360e0f",
+ "4803c9aece3346488295338254217aff",
+ "d725549ca34a4d54ae684e7e4741be29",
+ "d94392afd01246ff942af838a995379e",
+ "7eaee1cd25d0442092846922cdd6c413",
+ "483b9c219aa94ea1952e3534a02395aa",
+ "10d7a41588744be1b29678b4a9dfdd27",
+ "c4fce7e5a2b44835ab8723e0022d1e50",
+ "ba3a7258734b4edb86b8eef074d65222",
+ "4b3dc87d00ed42b0956d0bfa39bd466f",
+ "2c5eaf38e66d492d8661852cacc4e527",
+ "b7f169f931074d1283cbfe912f11ba98",
+ "e86771ea303a4b1b86ecf5128f3ea421",
+ "b3a18689eefa4660997034094df0df04",
+ "91cb4404dd794d22b2bbaf31eee207b5",
+ "d8594695c03e4fb7965dcbe04074d4eb",
+ "f972a2e10dde405c8aec8f7cd1be4317",
+ "6c9a5a39cb4841ba8a0b93283be0cac2",
+ "2deb046362ed4570a3f550f4f288529e",
+ "2cdddd0398e045a6a13124bf6fd85506",
+ "a1f5618e59d148409d6ccf4bfffca2fa",
+ "c870763add1745d9acfc2762f468c984",
+ "be70aecc5b294c4c93b0dcc09d6d1cb3",
+ "37b18b2ae9504b6c91066798a19a1319",
+ "b17eef10573f44689ce6add6231eaa19",
+ "3e8f08e000f248b59331d2430bbc8e3c",
+ "d8886d5af17f4468a26554831c9c05f1",
+ "b1cad4191755493893bbb46dcf27e03b",
+ "589120da6f464686bbeff0d44643d17d",
+ "ea89ea173ff3482c8a9c91dfb15946b2",
+ "b38693117df44071b7baaf123215ea60",
+ "9d716c9e43e04a6c9496620633ca28be",
+ "4de322f2413f44bcb03d41dcc8ff1963",
+ "3087335b98964b9eb4da474487ca4864",
+ "c010fad90578489cbfeb0764e3a11286",
+ "627f32f04b544b4db834b79645f36733",
+ "7d39222af2474a68b0db99f407ccf380",
+ "775687d3962242d6aff3feb0627754a9",
+ "92bb9917ab194a1eb1dc6fc5c4c4195d",
+ "43717a0ae4c043f9947d8fd844d71997",
+ "3f0008931054433c838a6633ca1347e6",
+ "da0dfe11648d4ae8a70852ce1fac87b0",
+ "29ad37e81b7f44a9aafa982b52f05a7a",
+ "bb468a6fe3f04692a211d5519aec455a",
+ "b1ad08dbe61b4064985ecdaa119870d8",
+ "d91093e80b814a018edaabe49f529ef5",
+ "1e3f013edc6341a0837af33ff4866d0b",
+ "1ed6f4595ec540729d776a81db96c403",
+ "cd7371ff8504454292559c18adb76645",
+ "d4994c6d7fa240d0ac6bb31f5c835192",
+ "ee1a9269b6c843e28cc49f3b5f17da96",
+ "a12a6638b2a54e88a020be42c139646e",
+ "2f2dc993705b447aa771cf0cc13c3b1d",
+ "69dffb139cab46b1b93bef960f702655",
+ "e7dc30a09a64401393e43618b51059de",
+ "75c397c506a04d0d9ca62e8d7f990813",
+ "eb7e509acfea4e1bb2f59b2fde11603d",
+ "b75a3d92aaa64a3098c6e1aabbc50856",
+ "3b056671c3fd41aeb4d6da821d562b95",
+ "9ac87f9e5b7847aaa90e3208ad405c23",
+ "cb21cadacb294854b304af8df2157299",
+ "30b3667258174beaa01322ffa055759b",
+ "48cb432d95dc49deae6077fb5c76bec3",
+ "763eec2b33234fd5ac192f25489b2844",
+ "f7fde1c95e3946659c6208fc52c254e9",
+ "6e1cdd75ae2246278c80f8e5d4e340b7",
+ "6af159109303490eab7192815fce0d6b",
+ "315575253cb9433d81f7d26770907f29",
+ "daf61ecd65bd41d9829e8a1872b82f33",
+ "54823295494d441fb9f26a70fb2c3973",
+ "df13aabfde0140d68db8b5a69759091c",
+ "cadbbc94bfd24daa933bb7d188dcdf92",
+ "f271a7dc607b4c05b02f6c5621203bd6",
+ "4e60ffab53dd4aba9e094098ed5297e6",
+ "a91dd2c07c51483eb326d010a82e2920",
+ "4188c097387a408dae680f67bd97752b",
+ "2a6cf3f2b4c349a9adc26351c2f0b222",
+ "8efe1cb67f30446a8fdaaf96782e843d",
+ "bdecbe50f693451b87bd331fd9e684ba",
+ "ff00f4c2c63a467098b119ae2259f529",
+ "d6754db1364144e69e3ab320aa1faeb9",
+ "9f1feddbe0d449a0b93fc5b1027e4319",
+ "1507ea5f89534b10856b99488ed5da65",
+ "f69205c589cf42829eea248f378a1436",
+ "85843fd6df264d25a4642cbeee260459",
+ "c2a415c28fe0418bb6032d4b91efbb07",
+ "b02796bf6e5547cf9418d109ad772537",
+ "de7a527901014a6b8abf6b714bd09535",
+ "143eaab6e65f4c8eb7a4314cadf323ba",
+ "e0603f00ceb2468692a36abd7bafaba8",
+ "8abf122ed835496aa09945ba8edd4688",
+ "663b9bd2f1af4df4b757624f53c2f2b8",
+ "c352adea84b043db8d43eb1c36d4bd4f",
+ "8fda102684834d21b4efbb472823ced9",
+ "ee7eccaca57b4460becfe0d5d5afb3f9",
+ "554a1ef44aea4ff484f0944878bb58a2",
+ "8ae15293ec5e4296a625087e7d965249",
+ "db067e50373840b19d6925deb950a20a",
+ "ab409caa3be24c18becaf9146b1ae69c",
+ "63236709413940f59d2622f2927c8d55",
+ "3e6d67d246e54fa497f4398e3aeddb00",
+ "118967bdd4a348858cc7572d36c1b736",
+ "8cc3c0558720400e9ed89170883f6370",
+ "59ee159eec154095a368efceb9d1e042",
+ "f78c80dd733d48a687d8a47bfc792ea4",
+ "9da9d7eb9a97495194a3ac4a2786e1de",
+ "3f1d345037604e01911ef344f3b51742",
+ "eeff19b29a6a4c6d9ae34e365c78c310",
+ "a098c442cc8149a5aa562c86fc64528e",
+ "badae7117ab644ffa80d099c17397329",
+ "13ccc23d506248d5b66ffe7732ead149",
+ "16938b11881741af8e6633094a4402dc",
+ "8d796692add94119a4e9fdc6530a6878",
+ "9202902fd37446cda1678c0d83e0c641",
+ "2cd168e5e3c4481ba151aa8a655e7ce8",
+ "f773b949a9cf46ca9fd56476398a3191",
+ "c6a00e1b00684bb7930fb27d6499932e",
+ "4395227decf642f7b8fbc6616f9ec826",
+ "205a7844670249bf83d468fe3af0e139",
+ "28a78fb894a4413e960c1e40d7df8173",
+ "46bd38ac919e4e66a72226c1f0da67d6",
+ "9557a05279544cd8a5f2ba4d3429f576",
+ "2e0e7f437b5d4e4086b38ee6da51dc4f",
+ "73a0ea365433404babb83a2d1caa9c66",
+ "855a155046904aaa9b91b01dd6a86088",
+ "d49e405525ec467bb7a69a9aaedf82d9",
+ "b8ccdebb7b11490e8222ff79ecfc9a33",
+ "9edc1d5792644f79bc04d853b13dac46",
+ "1b78ff7e32254777abe2c802b6879b9c",
+ "32168837680e41eaad4e5e4cdf09877d",
+ "319bf5c6332f41958974d9c3af87a382",
+ "c1e065fa36344f509e7863c3ec0428b8",
+ "5b9510c694a24afbb1c8318fea1a1bc5",
+ "f12d118a6b3f46b580fbe2018f4cf5e9",
+ "726e82f2b6c94e8eb5620c18872aabb6",
+ "12bb708857e84e5b893ca3e9ff176082",
+ "53acddb088564a73aef61618797bfe85",
+ "fb208f3792174ac2bdfb077450b2218f",
+ "0fa8ddd8da924c089221611c98e7da6e",
+ "b4a5fdee693d455686507306da804b17",
+ "045c5ac6981440c996ac7dda054fc112",
+ "f6a6f03ea7f140189a277742ff7082f8",
+ "ecff5b6dfb784c96b69d1a39b7acb171",
+ "43a32f261eaf42af978a6bf98502b1fc",
+ "8b7bb3fb502f4c3185709d6c40638d70",
+ "bf1d0b17974049c6ac5653ac18f1169c",
+ "32672cb3395045bcb9c2d370032356cc",
+ "4728eddf9fcc49d68d71a30379f08335",
+ "8676e2232dc242c39d4f19b0eea90dff",
+ "167e67c018e441d8baab4127b25773c6",
+ "88405a75b92743e589f424ee8c4d4d79",
+ "b5e3536d816c45488bb83336eaa5d53f",
+ "b9bed2c861df4c019ab4fff46b11a1a3",
+ "35bf380a7c6243859a459560288ffe49",
+ "b65af12dbf9143778412adb7b4c0bfdd",
+ "cb2433a0096845468b26c4bbde625ed8",
+ "8d4df1cf62d2427b8e850b031164ff97",
+ "0fd8ca256b8b49e1906a2a8e21156164",
+ "9801a82eda354815b6b3abbc8d1e0140",
+ "b10768b6bc654da8b822b4878889639b",
+ "c56ea889f51848e4aed83bcc46c83395",
+ "c75508086f6f4406a0aa9ce5a391e0ee",
+ "d92dbe59ace74f598efc7fbedb4c5ee6",
+ "675c937cf0ef4bf582f4bf90df6fa28e",
+ "e1cf760846bd4ba988c29665a6593220",
+ "768735ea9663429ba9f24efd86682f71",
+ "4d2a10e9307a47f4a1cbf512380c65bc",
+ "e8738d4181b04545a0418c1dd5b6b1b5",
+ "2aab7297963040f1900f0bc1f24e7b2a",
+ "8182a23b5be640cc8a48c09a4ed9585c",
+ "c3e198ae77684d61bf5fc30a35d8fc11",
+ "aaa71d52156549a4b8d7aad390497ac3",
+ "6387cbc474144e59aac5e3b42e714887",
+ "efc4f9ade28a4bb2a67c0ae4ceecbf28",
+ "7c105cfe1f344bf7896c7ddc0fcdc322",
+ "c1f71dcbe98f4ee9847af6b800979e06",
+ "e12dbfa20e9d40448366c9528c1a2c02",
+ "b3d7aad60442432e96c8c8bd3ead8427",
+ "0d40464e81fe4c06ac3400204116f243",
+ "69a0d832b77e47b8a2adcf47efe3f7ab",
+ "947f13ea22654b4ca6fca7ebed29d64e",
+ "45becb2c72714dfcb721b3a20a92d28f",
+ "4ddb5f1d8260448981c67308bcedecbf",
+ "d43db93804c24908bb6d75f26b640199",
+ "71d656fe70004c6db5d23d86bc6b108b",
+ "9f2ecadf1f3f4e399aad1882f2fe9b00",
+ "8826a0177e334508932a43563d2ae97d",
+ "f9ecbb00f95548d5b0c5cad345b1e38a",
+ "ac78d9726bc541df9907425442d3a51a",
+ "854937001e534695b08ee25f6e443962",
+ "06b21316e1ef41c9b7c9d943a9ff91ec",
+ "d38618d4c0e64b7baa61c0eca47427e5",
+ "86e235a532f347c781d6654c3ac25ba3",
+ "1727de01c47144b2958babfb91e887cb",
+ "5ac310c605f64948ad744bc1f196441d",
+ "32c1cc0d5327462d9175c74b91d67c4d",
+ "910d8a34abaa4f92a899dd4f5ab03d74",
+ "fbd92ad5a793482aac5570387e917188",
+ "ac81634b0e0946d690fb7d8ad7aed911",
+ "01097fb41b9c4cbf91300e049d9f3617",
+ "abeae554ecff4bb0ad8c38fa2829f706",
+ "a2d84cfc801f4657bade62d42be7046f",
+ "06a2114630234393bc0f07b3a64455f8",
+ "c6f31bcf48de4d9fbc7f2a2d9984b247",
+ "d5eace6b280e446ead2d1517801e4612",
+ "e29da03f6e474f1ca97ecfa6cd09658c",
+ "35bfe48a1b744262a8ea68bf5b5d495d",
+ "eed4b0b927824444aa8d875281cca1c4",
+ "e77316215dbe41daa8e89d8b2cc0f032",
+ "11c60d67f2204518b007ef47c801fbff",
+ "da21830428b54f76aa31b03efce202b9",
+ "a90285006dda4eb8a3e77964294a76ea",
+ "8164a08b9b3f49288963539305eadabe",
+ "591e6dc92b5c44418260cf659c5807cf",
+ "2bd3c665eb784f149dc21853103e8ff0",
+ "1ff4bcdb97294287ae8f3e9f2dc6bafa",
+ "bc265b1f822348469e3c8df0ea608abb",
+ "3635aa8a2cee484b945ddf7379ff4102",
+ "94ce06b3df27425eb8ae1a0aade4244d",
+ "e8ab0bcb4d7f4a298b2b3555d866a11f",
+ "5570fad8913d4bb495681b5e1dbe3950",
+ "47735f6c830149db965660d6b2f200d7",
+ "61d980530bf0408c8e2ed9a7997ba615",
+ "8a9f0a924d53496c8a8f228738ec140d",
+ "60ab33e3e0d84395a1269604f0fae91f",
+ "64d829532bb94214b805c2de4cf529cc",
+ "438c02b8134e45d5b2760b2e1f72f004",
+ "0f09296d37ee44b89871fa22cdd0127f",
+ "0fd475cb9e064d10a8ed031957cf2044",
+ "d1d2687d51a4442d8555ed4071837da4",
+ "0d80cc1f4fcc49d59e3a80862678fd86",
+ "9e556858d4a44b5bbc3e3af87d138a55",
+ "d86eb0ba47884ab081128a8761e9654b",
+ "620e2fa48504435a85d95c2d4b264b6e",
+ "af9af54477cc4972bf0f0a99c1344974",
+ "0b5d06cb83334b53a91c929f8e308543",
+ "8b9f3c47205d474b97efc6e9c6fb5f68",
+ "b63d8ddcad7745f3b4d7e683d23f393a",
+ "b83993ef787047cb9a31652fdd7f9ee7",
+ "f4ee33b4a2d145bab3c5c2e14c73a3f8",
+ "bebb055c0ac14d59a8b617399d60e602",
+ "888e04dcb56f4c43954d49d3e392ab25",
+ "6058ac7bc0b345ee8f5d2f631b7b6940",
+ "ec94298c63ab4b0e83c074a9d2ed4fc9",
+ "0d56de85d9244f38a8a0b3d84ee5d7da",
+ "b0053efc5ecc411f902fcf3b19cd362e",
+ "1d69552268b74bfb824c4f783e362949",
+ "de35e43c6aea490b917084a93c4571fb",
+ "8fdc7615fa0b412283eb3beb36b97872",
+ "d5542140ebd34dfaa8c66f2f3e48fe92",
+ "9eaafbfddcec4cdb998770d2cefc8fb7",
+ "a9e2ae7f987b4d9d9636c3963530d8ed",
+ "283159e7918540efa39d255f475dd984",
+ "2f5aa471e247475691da674db1d8514c",
+ "c67e91be78c74ba9b816e40dd5c181ae",
+ "d02de13e2d7843298e61b8f47d8dee33",
+ "76d9a70692e34521a609b337755d9901",
+ "8a1465ca8728490dba4fd79730ea6a30",
+ "3d563f4f9d28464788cab663cc814cf4",
+ "6fe391246afa49e08eec5793a97690db",
+ "47cc4883459449af8f9b35cd74b84002",
+ "69da0360a8ae4737b6e1af2e790f2b85",
+ "d7cc01fb605b4dd58cac287c36b6afea",
+ "638f9ac5607b42d3a467295cb8f7c50d",
+ "8e885a254c6f4311a3774d816e5ef5ac",
+ "580addd60f83499386b626c6440c6fca",
+ "6bb5cbb9ce7645c4ad45cdf056af0445",
+ "2e3ea9571d364a40aa9917a6f49b45f7",
+ "665f8e9a73b94639aa42743d16726a96",
+ "34a2309f1b78432ab51a87c964946da8",
+ "078db166712a4daba8e99ccdf44eb16f",
+ "dde4b35063b64a28a2fd5412eb9474f0",
+ "4d9c96f9caa54ac69dbee2755cfd804d",
+ "aa9d3e82fed541cca0fffe35b55aaabf",
+ "3221446fbbc24420a923884c67e0b87c",
+ "abf0151dabeb49eab089f921c8f364b5",
+ "488797401b9e419ab393ad5b2438039e",
+ "4394b231af2f4e1499a308c93b0ff951",
+ "4f1a59e4dff4470fb123ab315ded6e4f",
+ "5ead730bc1c34a28b5b046ae270d04e6",
+ "13b77ec58e65475b95d0041f90639e9a",
+ "deb2a67f32e64ebf87758c3ace7916e8",
+ "c594b48ac5b347f78c099d581dc4cd96",
+ "68fd129101844ab18b2b107778873d54",
+ "d7e07795e63c4ab78ca92961ba089b07",
+ "d3450ca5684b4a5680c114d29a7ce8f5",
+ "61ed075433b94feda586eec035251768",
+ "c46be587d0fe4ef0b364f822f5ff903d",
+ "c7f7e4ee797749c0939c9a3926937b41",
+ "2a4d28248796477994a17db0fb8485dc",
+ "0dbdea008e964ad887f112336be78449",
+ "47977de9d961442682805f37f7217387",
+ "241f6ce34fd242ca9a46f8232a9fb838",
+ "846eac2286dd4d6991f80b6ae03ce804",
+ "72858c26d6154ef3b8f90ffb0339781e",
+ "4085f5c89ca94a31b346452cd8009dad",
+ "47c175c19d6b4268a2ade2966327de78",
+ "f3dc7118a9fa4b188cc3a9aaf366b125",
+ "9f07e155db5a473abdd7b7ae0617e770",
+ "05feab0298c54df4a2372152d4f3a891",
+ "abeb4c3be90344469c004e29465e1580",
+ "540e6158656d412591a5442eb89d1e65",
+ "51a0e1eb84eb4dd6a95f30268541ccbc",
+ "fe7d093f30854ee1b66f080c5b8fb68b",
+ "880e13da115f4e2e9d413b75b0eecdcb"
+ ]
+ },
+ "execution": {
+ "shell.execute_reply.end": "2023-12-22T03:35:36.853391Z",
+ "shell.execute_reply.started": "2023-12-22T03:35:33.398019Z",
+ "to_execute": "2023-12-22T03:35:33.384Z"
+ },
+ "id": "d0b36e7eff50657c",
+ "libroFormatter": "formatter-string",
+ "outputId": "4198784f-15c6-4812-f96a-c3f62914dbbb",
+ "tags": []
+ },
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "boolq example: \n",
+ "{'input': 'Persian language -- Persian (/ˈpɜːrʒən, -ʃən/), also known by its endonym Farsi (فارسی fārsi (fɒːɾˈsiː) ( listen)), is one of the Western Iranian languages within the Indo-Iranian branch of the Indo-European language family. It is primarily spoken in Iran, Afghanistan (officially known as Dari since 1958), and Tajikistan (officially known as Tajiki since the Soviet era), and some other regions which historically were Persianate societies and considered part of Greater Iran. It is written in the Persian alphabet, a modified variant of the Arabic script, which itself evolved from the Aramaic alphabet.\\nQuestion: do iran and afghanistan speak the same language\\nA. Yes\\nB. No\\nAnswer:', 'output': 'A', 'task_name': 'boolq'}\n",
+ "multirc example: \n",
+ "{'input': 'While this process moved along, diplomacy continued its rounds. Direct pressure on the Taliban had proved unsuccessful. As one NSC staff note put it, \"Under the Taliban, Afghanistan is not so much a state sponsor of terrorism as it is a state sponsored by terrorists.\" In early 2000, the United States began a high-level effort to persuade Pakistan to use its influence over the Taliban. In January 2000, Assistant Secretary of State Karl Inderfurth and the State Department\\'s counterterrorism coordinator, Michael Sheehan, met with General Musharraf in Islamabad, dangling before him the possibility of a presidential visit in March as a reward for Pakistani cooperation. Such a visit was coveted by Musharraf, partly as a sign of his government\\'s legitimacy. He told the two envoys that he would meet with Mullah Omar and press him on Bin Laden. They left, however, reporting to Washington that Pakistan was unlikely in fact to do anything,\" given what it sees as the benefits of Taliban control of Afghanistan.\" President Clinton was scheduled to travel to India. The State Department felt that he should not visit India without also visiting Pakistan. The Secret Service and the CIA, however, warned in the strongest terms that visiting Pakistan would risk the President\\'s life. Counterterrorism officials also argued that Pakistan had not done enough to merit a presidential visit. But President Clinton insisted on including Pakistan in the itinerary for his trip to South Asia. His one-day stopover on March 25, 2000, was the first time a U.S. president had been there since 1969. At his meeting with Musharraf and others, President Clinton concentrated on tensions between Pakistan and India and the dangers of nuclear proliferation, but also discussed Bin Laden. President Clinton told us that when he pulled Musharraf aside for a brief, one-on-one meeting, he pleaded with the general for help regarding Bin Laden.\" I offered him the moon when I went to see him, in terms of better relations with the United States, if he\\'d help us get Bin Laden and deal with another issue or two.\" The U.S. effort continued. \\nQuestion: What did the high-level effort to persuade Pakistan include?\\nAnswer: Children, Gerd, or Dorian Popa\\nIs it true?\\nA. Yes\\nB. No\\nAnswer:', 'output': 'B', 'task_name': 'multirc'}\n",
+ "rte example: \n",
+ "{'input': 'No Weapons of Mass Destruction Found in Iraq Yet.\\nWeapons of Mass Destruction Found in Iraq.\\nIs the sentence below entailed by the sentence above?\\nA. Yes\\nB. No\\nAnswer:', 'output': 'B', 'task_name': 'rte'}\n",
+ "wic example: \n",
+ "{'input': \"Sentence 1: Do you want to come over to my place later?\\nSentence 2: A political system with no place for the less prominent groups.\\nAre 'place' in the above two sentences the same?\\nA. Yes\\nB. No\\nAnswer:\", 'output': 'B', 'task_name': 'wic'}\n"
+ ]
+ }
+ ],
+ "source": [
+ "# boolq\n",
+ "boolq_dataset = (\n",
+ " load_dataset(\"super_glue\", \"boolq\")\n",
+ " .map(\n",
+ " lambda x: {\n",
+ " \"input\": f\"{x['passage']}\\nQuestion: {x['question']}\\nA. Yes\\nB. No\\nAnswer:\",\n",
+ " # 0 - False\n",
+ " # 1 - True\n",
+ " \"output\": [\"B\", \"A\"][int(x[\"label\"])],\n",
+ " \"task_name\": \"boolq\",\n",
+ " }\n",
+ " )\n",
+ " .select_columns([\"input\", \"output\", \"task_name\"])\n",
+ ")\n",
+ "print(\"boolq example: \")\n",
+ "print(boolq_dataset[\"train\"][0])\n",
+ "\n",
+ "# multirc\n",
+ "multirc_dataset = (\n",
+ " load_dataset(\"super_glue\", \"multirc\")\n",
+ " .map(\n",
+ " lambda x: {\n",
+ " \"input\": (\n",
+ " f\"{x['paragraph']}\\nQuestion: {x['question']}\\nAnswer: {x['answer']}\\nIs it\"\n",
+ " \" true?\\nA. Yes\\nB. No\\nAnswer:\"\n",
+ " ),\n",
+ " # 0 - False\n",
+ " # 1 - True\n",
+ " \"output\": [\"B\", \"A\"][int(x[\"label\"])],\n",
+ " \"task_name\": \"multirc\",\n",
+ " }\n",
+ " )\n",
+ " .select_columns([\"input\", \"output\", \"task_name\"])\n",
+ ")\n",
+ "print(\"multirc example: \")\n",
+ "print(multirc_dataset[\"train\"][0])\n",
+ "\n",
+ "# rte\n",
+ "rte_dataset = (\n",
+ " load_dataset(\"super_glue\", \"rte\")\n",
+ " .map(\n",
+ " lambda x: {\n",
+ " \"input\": (\n",
+ " f\"{x['premise']}\\n{x['hypothesis']}\\nIs the sentence below entailed by the\"\n",
+ " \" sentence above?\\nA. Yes\\nB. No\\nAnswer:\"\n",
+ " ),\n",
+ " # 0 - entailment\n",
+ " # 1 - not_entailment\n",
+ " \"output\": [\"A\", \"B\"][int(x[\"label\"])],\n",
+ " \"task_name\": \"rte\",\n",
+ " }\n",
+ " )\n",
+ " .select_columns([\"input\", \"output\", \"task_name\"])\n",
+ ")\n",
+ "print(\"rte example: \")\n",
+ "print(rte_dataset[\"train\"][0])\n",
+ "\n",
+ "# wic\n",
+ "wic_dataset = (\n",
+ " load_dataset(\"super_glue\", \"wic\")\n",
+ " .map(\n",
+ " lambda x: {\n",
+ " \"input\": (\n",
+ " f\"Sentence 1: {x['sentence1']}\\nSentence 2: {x['sentence2']}\\nAre '{x['word']}'\"\n",
+ " \" in the above two sentences the same?\\nA. Yes\\nB. No\\nAnswer:\"\n",
+ " ),\n",
+ " # 0 - False\n",
+ " # 1 - True\n",
+ " \"output\": [\"B\", \"A\"][int(x[\"label\"])],\n",
+ " \"task_name\": \"wic\",\n",
+ " }\n",
+ " )\n",
+ " .select_columns([\"input\", \"output\", \"task_name\"])\n",
+ ")\n",
+ "print(\"wic example: \")\n",
+ "print(wic_dataset[\"train\"][0])"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 6,
+ "id": "9fca2225-aaee-47aa-957a-5f8ed3177cdb",
+ "metadata": {
+ "execution": {
+ "shell.execute_reply.end": "2023-12-22T03:35:36.858952Z",
+ "shell.execute_reply.started": "2023-12-22T03:35:36.855329Z",
+ "to_execute": "2023-12-22T03:35:36.819Z"
+ },
+ "id": "9fca2225-aaee-47aa-957a-5f8ed3177cdb",
+ "libroFormatter": "formatter-string"
+ },
+ "outputs": [],
+ "source": [
+ "# define a task2id map\n",
+ "TASK2ID = {\n",
+ " \"boolq\": 0,\n",
+ " \"multirc\": 1,\n",
+ " \"rte\": 2,\n",
+ " \"wic\": 3,\n",
+ "}\n",
+ "\n",
+ "\n",
+ "def tokenize(examples):\n",
+ " inputs, targets = examples[\"input\"], examples[\"output\"]\n",
+ " features = tokenizer(inputs, max_length=512, padding=\"max_length\", truncation=True, return_tensors=\"pt\")\n",
+ " labels = tokenizer(targets, max_length=2, padding=\"max_length\", truncation=True, return_tensors=\"pt\")\n",
+ " labels = labels[\"input_ids\"]\n",
+ " labels[labels == tokenizer.pad_token_id] = -100\n",
+ " features[\"labels\"] = labels\n",
+ " features[\"task_ids\"] = torch.tensor([[TASK2ID[t]] for t in examples[\"task_name\"]]).long()\n",
+ " return features"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 7,
+ "id": "0bf6c31c-73cd-4eed-931b-0cad5d7290fb",
+ "metadata": {
+ "execution": {
+ "shell.execute_reply.end": "2023-12-22T03:35:36.929414Z",
+ "shell.execute_reply.started": "2023-12-22T03:35:36.860477Z",
+ "to_execute": "2023-12-22T03:35:36.849Z"
+ },
+ "id": "0bf6c31c-73cd-4eed-931b-0cad5d7290fb",
+ "libroFormatter": "formatter-string",
+ "tags": []
+ },
+ "outputs": [],
+ "source": [
+ "def get_superglue_dataset(\n",
+ " split=\"train\",\n",
+ " n_samples=500,\n",
+ "):\n",
+ " ds = concatenate_datasets(\n",
+ " [\n",
+ " boolq_dataset[split].shuffle().select(range(n_samples)),\n",
+ " multirc_dataset[split].shuffle().select(range(n_samples)),\n",
+ " rte_dataset[split].shuffle().select(range(n_samples)),\n",
+ " wic_dataset[split].shuffle().select(range(n_samples)),\n",
+ " ]\n",
+ " )\n",
+ " ds = ds.map(\n",
+ " tokenize,\n",
+ " batched=True,\n",
+ " remove_columns=[\"input\", \"output\", \"task_name\"],\n",
+ " load_from_cache_file=False,\n",
+ " )\n",
+ " return ds"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "oNvh2WGlLo4z",
+ "metadata": {
+ "id": "oNvh2WGlLo4z",
+ "libroFormatter": "formatter-string"
+ },
+ "source": [
+ "As a toy example, we only select 1,000 from each subdataset for training and 100 each for eval."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 8,
+ "id": "1bf88dd1a6aaa6a5",
+ "metadata": {
+ "collapsed": false,
+ "execution": {
+ "shell.execute_reply.end": "2023-12-22T03:35:44.953151Z",
+ "shell.execute_reply.started": "2023-12-22T03:35:37.023791Z",
+ "to_execute": "2023-12-22T03:35:37.009Z"
+ },
+ "libroFormatter": "formatter-string"
+ },
+ "outputs": [
+ {
+ "name": "stderr",
+ "output_type": "stream",
+ "text": [
+ "Map: 0%| | 0/4000 [00:00 **Note:** The current implementation differs from the original QA-LoRA paper's approach.
+
+While the QA-LoRA paper describes a direct weight modification technique using "beta shift" to modify quantized weights without full dequantization, this implementation uses a different approach:
+
+1. The quantized model is first dequantized to full precision
+2. The QALoRA adapter weights are then merged with the dequantized model
+3. The merged model must be re-quantized if quantization is still desired
+
+
+### Memory Considerations
+
+This process requires significant memory (enough to hold the full dequantized model) and additional computation for the re-quantization step. For large models, this may not be possible on consumer hardware.
+
+For most use cases, we recommend keeping the base quantized model and the QALoRA adapter separate, loading them with `PeftModel.from_pretrained()` as shown in the usage example above. This approach maintains the memory efficiency benefits of quantization throughout the deployment pipeline.
+
+
+## Citation
+```
+@article{dettmers2023qlora,
+ title={QLoRA: Efficient Finetuning of Quantized LLMs},
+ author={Dettmers, Tim and Pagnoni, Artidoro and Holtzman, Ari and Zettlemoyer, Luke},
+ journal={arXiv preprint arXiv:2305.14314},
+ year={2023}
+}
+
+@article{xu2023qalora,
+ title={QA-LoRA: Quantization-Aware Low-Rank Adaptation of Large Language Models},
+ author={Xu, Yuhui and Liu, Lingxi and Rao, Longhui and Zhao, Teng and Xiong, Zhiwei and Gao, Mingkui},
+ journal={arXiv preprint arXiv:2309.14717},
+ year={2023}
+}
+```
diff --git a/peft/examples/qalora_finetuning/qalora_gptq_finetuning.py b/peft/examples/qalora_finetuning/qalora_gptq_finetuning.py
new file mode 100644
index 0000000000000000000000000000000000000000..7a39d264531f99b97c8854466b06a9b2979ce2a9
--- /dev/null
+++ b/peft/examples/qalora_finetuning/qalora_gptq_finetuning.py
@@ -0,0 +1,357 @@
+#!/usr/bin/env python3
+"""
+Training script for fine-tuning language models with QALoRA using GPTQ quantization.
+This script supports cached quantization to avoid repeating expensive quantization processes.
+"""
+
+import argparse
+import os
+
+import torch
+from datasets import load_dataset
+from transformers import (
+ AutoModelForCausalLM,
+ AutoTokenizer,
+ DataCollatorForLanguageModeling,
+ GPTQConfig,
+ Trainer,
+ TrainingArguments,
+)
+
+from peft import LoraConfig, get_peft_model
+
+
+def load_or_quantize_model(
+ base_model: str, tokenizer, bits: int = 4, cache_dir: str = "./quantized_models"
+) -> AutoModelForCausalLM:
+ """
+ Load a pre-quantized model from cache or quantize and cache a new one.
+ Automatically detects if the model is already GPTQ-quantized.
+
+ Args:
+ base_model: Model identifier or path
+ tokenizer: Tokenizer for the model
+ bits: Bit-width for quantization (default: 4)
+ cache_dir: Directory to store quantized models
+
+ Returns:
+ The loaded (quantized) model
+ """
+ # First, check if the model is already GPTQ-quantized by trying to load it
+ print(f"Checking if {base_model} is already GPTQ-quantized...")
+ try:
+ # Try to load the model and check if it has GPTQ quantization
+ test_model = AutoModelForCausalLM.from_pretrained(
+ base_model,
+ device_map="auto",
+ torch_dtype=torch.float16,
+ trust_remote_code=True, # Some GPTQ models might need this
+ )
+
+ # Check if the model has GPTQ quantization attributes
+ has_gptq = False
+ for module in test_model.modules():
+ if hasattr(module, "qweight") or hasattr(module, "qzeros") or "gptq" in str(type(module)).lower():
+ has_gptq = True
+ break
+
+ if has_gptq:
+ print(f"✅ Model {base_model} is already GPTQ-quantized. Using directly.")
+ return test_model
+ else:
+ print(f"Model {base_model} is not GPTQ-quantized. Will quantize it.")
+ # Clean up the test model to free memory
+ del test_model
+ if torch.cuda.is_available():
+ torch.cuda.empty_cache()
+ elif torch.xpu.is_available():
+ torch.xpu.empty_cache()
+
+ except Exception as e:
+ print(f"Could not load model {base_model} directly: {e}")
+ print("Will attempt to quantize it...")
+
+ # If we get here, the model needs to be quantized
+ os.makedirs(cache_dir, exist_ok=True)
+ model_id = base_model.replace("/", "_").replace("\\", "_") # Handle Windows paths too
+ quantized_model_path = os.path.join(cache_dir, f"{model_id}_gptq_{bits}bit")
+
+ # Check if we already have a cached quantized version
+ if os.path.exists(quantized_model_path) and os.path.exists(os.path.join(quantized_model_path, "config.json")):
+ print(f"Loading pre-quantized model from cache: {quantized_model_path}")
+ return AutoModelForCausalLM.from_pretrained(quantized_model_path, device_map="auto")
+
+ print(f"Quantizing model and saving to cache: {quantized_model_path}")
+
+ # Configure GPTQ for first-time quantization
+ gptq_config = GPTQConfig(
+ bits=bits,
+ dataset="c4",
+ tokenizer=tokenizer,
+ group_size=128,
+ desc_act=False,
+ sym=False,
+ )
+
+ # Load and quantize the model
+ model = AutoModelForCausalLM.from_pretrained(
+ base_model, device_map="auto", quantization_config=gptq_config, torch_dtype=torch.float16
+ )
+
+ # Save the quantized model to cache
+ print(f"Saving quantized model to {quantized_model_path}")
+ model.save_pretrained(quantized_model_path)
+ tokenizer.save_pretrained(quantized_model_path)
+
+ return model
+
+
+def tokenize_and_preprocess(examples, tokenizer, max_length: int = 128):
+ """
+ Tokenize text data and prepare it for language modeling.
+
+ Args:
+ examples: Dataset examples with 'text' field
+ tokenizer: Tokenizer to use
+ max_length: Maximum sequence length
+
+ Returns:
+ Processed examples with input_ids and labels
+ """
+ # Tokenize the text with truncation and padding
+ tokenized_output = tokenizer(examples["text"], truncation=True, padding="max_length", max_length=max_length)
+
+ # Preprocess labels (set pad tokens to -100 for loss masking)
+ labels = tokenized_output["input_ids"].copy()
+ labels = [[-100 if token == tokenizer.pad_token_id else token for token in seq] for seq in labels]
+ tokenized_output["labels"] = labels
+
+ return tokenized_output
+
+
+def train_model(
+ base_model: str,
+ data_path: str,
+ data_split: str,
+ output_dir: str,
+ batch_size: int,
+ num_epochs: int,
+ learning_rate: float,
+ cutoff_len: int,
+ use_qalora: bool,
+ eval_step: int,
+ save_step: int,
+ device: str,
+ lora_r: int,
+ lora_alpha: int,
+ lora_dropout: float,
+ lora_target_modules: str,
+ push_to_hub: bool,
+ qalora_group_size: int,
+ bits: int,
+) -> None:
+ """
+ Train a model with QALoRA and GPTQ quantization.
+
+ Args:
+ base_model: Base model to fine-tune
+ data_path: Dataset path
+ output_dir: Directory to save model outputs
+ batch_size: Training batch size
+ num_epochs: Number of training epochs
+ learning_rate: Learning rate
+ cutoff_len: Maximum sequence length
+ val_set_size: Validation set size
+ use_dora: Whether to use DoRA
+ use_qalora: Whether to use QALoRA
+ quantize: Whether to use quantization
+ eval_step: Steps between evaluations
+ save_step: Steps between saving checkpoints
+ device: Device to use (cuda:0, xpu:0, etc.)
+ lora_r: LoRA rank
+ lora_alpha: LoRA alpha
+ lora_dropout: LoRA dropout rate
+ lora_target_modules: Target modules for LoRA
+ push_to_hub: Whether to push to Hugging Face Hub
+ """
+ os.environ["TOKENIZERS_PARALLELISM"] = "false"
+ hf_token = os.getenv("HF_TOKEN")
+ device = torch.device(device)
+ print(f"Using device: {device}")
+
+ # Load tokenizer
+ tokenizer = AutoTokenizer.from_pretrained(base_model, token=hf_token)
+ if tokenizer.pad_token is None:
+ tokenizer.pad_token = tokenizer.eos_token
+
+ # Load or quantize model
+ model = load_or_quantize_model(base_model, tokenizer, bits=bits)
+
+ # Configure LoRA
+ target_modules = (
+ lora_target_modules.split(",")
+ if lora_target_modules
+ else ["q_proj", "k_proj", "v_proj", "o_proj", "gate_proj", "up_proj", "down_proj"]
+ )
+
+ print("use_qalora", use_qalora)
+ lora_config = LoraConfig(
+ task_type="CAUSAL_LM",
+ use_qalora=use_qalora,
+ qalora_group_size=qalora_group_size,
+ r=lora_r,
+ lora_alpha=lora_alpha,
+ target_modules=target_modules,
+ lora_dropout=lora_dropout,
+ bias="none",
+ )
+
+ # Get PEFT model with adapters
+ model = get_peft_model(model, lora_config)
+
+ model.print_trainable_parameters()
+
+ # Move model to device if not already there
+ if not hasattr(model, "device") or model.device.type != device.type:
+ model = model.to(device)
+
+ # Load and prepare dataset
+ dataset = load_dataset(data_path, data_split)
+
+ tokenized_datasets = {
+ "train": dataset["train"].map(
+ lambda x: tokenize_and_preprocess(x, tokenizer, max_length=cutoff_len),
+ batched=True,
+ remove_columns=["text"],
+ load_from_cache_file=True,
+ ),
+ "test": dataset["test"].map(
+ lambda x: tokenize_and_preprocess(x, tokenizer, max_length=cutoff_len),
+ batched=True,
+ remove_columns=["text"],
+ load_from_cache_file=True,
+ ),
+ }
+
+ # Data collator for language modeling
+ data_collator = DataCollatorForLanguageModeling(tokenizer, mlm=False)
+
+ # Configure training arguments
+ training_args = TrainingArguments(
+ output_dir=output_dir,
+ num_train_epochs=num_epochs,
+ per_device_train_batch_size=batch_size,
+ per_device_eval_batch_size=batch_size,
+ warmup_steps=100,
+ weight_decay=0.01,
+ logging_dir="./logs",
+ logging_steps=eval_step,
+ save_steps=save_step,
+ save_total_limit=2,
+ push_to_hub=push_to_hub,
+ gradient_accumulation_steps=16,
+ fp16=True,
+ learning_rate=learning_rate,
+ hub_token=hf_token,
+ label_names=["labels"],
+ )
+
+ # Clear accelerator cache to free memory
+ if torch.cuda.is_available():
+ torch.cuda.empty_cache()
+ elif torch.xpu.is_available():
+ torch.xpu.empty_cache()
+
+ # Initialize trainer
+ trainer = Trainer(
+ model=model,
+ args=training_args,
+ train_dataset=tokenized_datasets["train"],
+ eval_dataset=tokenized_datasets["test"],
+ data_collator=data_collator,
+ )
+
+ # Start training
+ print("\nStarting training...")
+ trainer.train()
+
+ # Save the final model
+ if push_to_hub:
+ trainer.push_to_hub(commit_message="Fine-tuned model with QALoRA")
+
+ # Always save locally
+ model.save_pretrained(output_dir)
+ tokenizer.save_pretrained(output_dir)
+ print(f"\nTraining complete. Model saved to {output_dir}")
+
+
+if __name__ == "__main__":
+ parser = argparse.ArgumentParser(description="Fine-tune LLMs with QALoRA and GPTQ quantization")
+
+ # Model and dataset parameters
+ parser.add_argument("--base_model", type=str, default="TheBloke/Llama-2-7b-GPTQ", help="Base model path or name")
+ parser.add_argument(
+ "--data_path", type=str, default="timdettmers/openassistant-guanaco", help="Dataset path or name"
+ )
+ parser.add_argument("--data_split", type=str, default="", help="Dataset path or name")
+
+ parser.add_argument(
+ "--output_dir", type=str, default="./qalora_output", help="Output directory for the fine-tuned model"
+ )
+ parser.add_argument("--bits", type=int, default=4, help="Init quantization bits")
+
+ # Training parameters
+ parser.add_argument("--batch_size", type=int, default=4, help="Batch size")
+ parser.add_argument("--num_epochs", type=int, default=1, help="Number of training epochs")
+ parser.add_argument("--learning_rate", type=float, default=3e-4, help="Learning rate")
+ parser.add_argument("--cutoff_len", type=int, default=128, help="Max sequence length")
+
+ # Adapter configuration
+ parser.add_argument("--use_qalora", action="store_true", help="Apply QALoRA")
+ parser.add_argument("--qalora_group_size", type=int, default=32, help="LoRA rank")
+ parser.add_argument("--lora_r", type=int, default=8, help="LoRA rank")
+ parser.add_argument("--lora_alpha", type=int, default=16, help="LoRA alpha")
+ parser.add_argument("--lora_dropout", type=float, default=0.05, help="LoRA dropout rate")
+ parser.add_argument(
+ "--lora_target_modules", type=str, default=None, help="Comma-separated list of target modules for LoRA"
+ )
+
+ # Training process options
+ parser.add_argument("--eval_step", type=int, default=100, help="Evaluation step interval")
+ parser.add_argument("--save_step", type=int, default=500, help="Save step interval")
+ parser.add_argument("--device", type=str, default="auto", help="Device to use for training")
+
+ # Hugging Face Hub options
+ parser.add_argument("--push_to_hub", action="store_true", help="Whether to push the model to Hugging Face Hub")
+
+ args = parser.parse_args()
+
+ device = args.device
+ if args.device == "auto":
+ device = torch.accelerator.current_accelerator().type if hasattr(torch, "accelerator") else "cuda"
+
+ # If use_qalora isn't explicitly set in args but passed to train_model
+ if not args.use_qalora:
+ args.use_qalora = True # Default to True as in the original code
+
+ train_model(
+ base_model=args.base_model,
+ data_path=args.data_path,
+ data_split=args.data_split,
+ output_dir=args.output_dir,
+ batch_size=args.batch_size,
+ num_epochs=args.num_epochs,
+ learning_rate=args.learning_rate,
+ cutoff_len=args.cutoff_len,
+ use_qalora=args.use_qalora,
+ eval_step=args.eval_step,
+ save_step=args.save_step,
+ device=device,
+ lora_r=args.lora_r,
+ lora_alpha=args.lora_alpha,
+ lora_dropout=args.lora_dropout,
+ lora_target_modules=args.lora_target_modules,
+ push_to_hub=args.push_to_hub,
+ qalora_group_size=args.qalora_group_size,
+ bits=args.bits,
+ )
diff --git a/peft/examples/randlora_finetuning/README.md b/peft/examples/randlora_finetuning/README.md
new file mode 100644
index 0000000000000000000000000000000000000000..fa9d2d61de529445a81c5ab7183951d01dbca26e
--- /dev/null
+++ b/peft/examples/randlora_finetuning/README.md
@@ -0,0 +1,112 @@
+# RandLora: Full-rank parameter-efficient fine-tuning of large models
+
+## Introduction
+[RandLora](https://huggingface.co/papers/2502.00987) is a parameter-efficient fine-tuning technique that is similar to LoRA and VeRA but performs full rank updates to improve performance. RandLora can be particulary usefull when adapting large model to hard tasks that require complex updates while preserving the parameter efficiency of LoRA. The full rank update of RandLora is acheived by linearly scaling random bases. The random bases are a collection of multiple low rank matrices such that the summation of their ranks if greater or equal to the full rank of the parameter matrices. The trainable parameters of RandLora are two diagonal matrices (vectors) that get multiplied with the right hand low rank random bases, in a similar way to VeRA's update. To maintain low memory usage, RandLora uses a custom function that prevents storing unnecessary bases in memory for backpropagation.
+
+## Quick start
+```python
+import torch
+from peft import RandLoraConfig, get_peft_model
+from transformers import AutoTokenizer, AutoModelForCausalLM, Trainer
+from datasets import load_dataset
+
+model = AutoModelForCausalLM.from_pretrained("huggyllama/llama-7b", device_map="auto")
+tokenizer = AutoTokenizer.from_pretrained("huggyllama/llama-7b")
+dataset = load_dataset("timdettmers/openassistant-guanaco", split="train")
+randlora_config = RandLoraConfig()
+
+peft_model = get_peft_model(model, lora_config)
+trainer = transformers.Trainer(
+ model=peft_model,
+ train_dataset=dataset,
+ dataset_text_field="text",
+ max_seq_length=2048,
+ processing_class=tokenizer,
+)
+trainer.train()
+peft_model.save_pretrained("randlora-llama-7b")
+```
+
+There is no additional change needed to your standard PEFT training procedure, simply swap your `LoraConfig` for a `RandLoraConfig`. Note however that RandLora's trainable parameter count is **inversely proportional** to the rank parameter `r`. Lower `r` to increase and increase it to reduce trainable parameters of RandLora.
+
+Run the finetuning script simply by running:
+```bash
+python examples/randlora_finetuning/randlora_finetuning.py --base_model meta-llama/Meta-Llama-3-8B --data_path timdettmers/openassistant-guanaco
+```
+This 👆🏻 by default will load the model in peft set up with RandLora config. Now if you wanna quickly compare it with Lora, all you need to do is to input ` --use_lora` in the command line and reduce `--randlora_alpha` to 2x the rank. So same above example would be 👇🏻;
+
+```bash
+python examples/randlora_finetuning/randlora_finetuning.py --base_model meta-llama/Meta-Llama-3-8B --data_path timdettmers/openassistant-guanaco --use_lora --rank 32 --randlora_alpha 64
+```
+
+RandLora can be made to use sparse or very sparse random bases. These sparse matrices can help reduce overfitting. Add `--very_sparse` to run with very sparse matrices or `--sparse` for sparse matrices:
+
+```bash
+python examples/randlora_finetuning/randlora_finetuning.py --base_model meta-llama/Meta-Llama-3-8B --sparse
+```
+
+RandLora also supports quantization. To use 4-bit quantization try:
+
+```bash
+python examples/randlora_finetuning/randlora_finetuning.py --base_model meta-llama/Meta-Llama-3-8B --quantize
+```
+
+By default the RandLora layers are the key and value layers of LLama model. Adding adapters on more layers will increase memory usage. If you wish to choose a different set of layers for RandLora to be applied on, you can simply define it using:
+```bash
+python examples/randlora_finetuning/randlora_finetuning.py --randlora_target_modules "q_proj,k_proj,v_proj"
+```
+
+### Full example of the script
+```bash
+python randlora_finetuning.py \
+ --base_model "PATH_TO_MODEL" \
+ --data_path "PATH_TO_DATASET" \
+ --output_dir "PATH_TO_OUTPUT_DIR" \
+ --batch_size 1 \
+ --num_epochs 3 \
+ --learning_rate 3e-4 \
+ --cutoff_len 512 \
+ --val_set_size 500 \
+ --quantize \
+ --eval_step 10 \
+ --save_step 100 \
+ --device "auto" \
+ --rank 32 \
+ --randlora_alpha 640 \
+ --randlora_dropout 0.05 \
+ --randlora_target_modules "k_proj,v_proj" \
+ --hub_model_id "YOUR_HF_REPO" \
+ --push_to_hub
+```
+
+## RandLora vs. LoRA
+RandLora differs from LoRA and other related low rank approximation algorithms by chanllenging the low rank paradigm. RandLora adapters learn **full-rank** updates as the [paper](https://huggingface.co/papers/2502.00987) shows that the low rank constraint of LoRA can constrain performance gains as trainable parameters increase (with higher ranks). As a result, using RandLora is specifically recommended for difficult tasks that are underfit by LoRA. RandLoRA however also often improves performance for common tasks. If increasing LoRA's rank improves performance for your task, RandLora will most likely outperform.
+
+RandLora is expected to increase performance over LoRA for equivalent amounts of trainable parameters, mostly for larger equivalent amounts (> LoRA rank 4).
+
+RandLora's performance increase comes with two limitations:
+
+1. Performance is dependent on using a large `randlora_alpha` scaling parameter (usually 20x the basis rank). This large parameter can sometimes make training the update unstable, reduce the learning rate or the scaling parameter if this is the case.
+
+2. Increase training time over LoRA when using very low RandLora basis ranks.
+
+## RandLora vs. VeRA
+RandLora shares similarities with VeRA in that both algorithms use random basis combinations to address some of LoRA's limitations. The limitations addressed by each algorithm is however different.
+VeRA aims to reduce trainable parameters beyond rank 1 LoRAs while RandLoRA reduces the performance limitation due to the low rank of the update as the trainable parameter count increases.
+
+RandLora is expected to:
+
+1. Improve performance over VeRA when more trainable parameters are required (hard tasks)
+
+2. Reduce memory usage over VeRA thanks to RandLora's random base sharing strategy
+
+
+## Citation
+```
+@inproceedings{2025_ICLR_RandLoRA,
+ title="{RandLoRA: Full rank parameter-efficient fine-tuning of large models}",
+ author="Albert, Paul and Zhang, Frederic Z. and Saratchandran, Hemanth and Rodriguez-Opazo, Cristian and van den Hengel, Anton and Abbasnejad, Ehsan",
+ booktitle="{International Conference on Learning Representations (ICLR)}",
+ year="2025"
+}
+```
diff --git a/peft/examples/randlora_finetuning/qrandlora_finetuning.ipynb b/peft/examples/randlora_finetuning/qrandlora_finetuning.ipynb
new file mode 100644
index 0000000000000000000000000000000000000000..887cf1f516975c7cbf2d78e04bd524e83abc111d
--- /dev/null
+++ b/peft/examples/randlora_finetuning/qrandlora_finetuning.ipynb
@@ -0,0 +1,8100 @@
+{
+ "cells": [
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "CV_gQs58bsvM"
+ },
+ "source": [
+ "# Fine-tuning [Llama3-8b](https://huggingface.co/meta-llama/Meta-Llama-3-8B) on [timdettmers/openassistant-guanaco](https://huggingface.co/datasets/timdettmers/openassistant-guanaco) Dataset using QRandLora (quantized RandLora) on T4 Free Colab GPU."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "colab": {
+ "base_uri": "https://localhost:8080/"
+ },
+ "id": "FuXIFTFapAMI",
+ "outputId": "b95d8260-65bd-405f-f1e2-8d353aa46814"
+ },
+ "outputs": [],
+ "source": [
+ "# Install the libraries\n",
+ "!pip install -q -U bitsandbytes\n",
+ "!pip install -q -U git+https://github.com/huggingface/transformers.git\n",
+ "!pip install -q -U git+https://github.com/huggingface/peft.git\n",
+ "!pip install -q -U git+https://github.com/huggingface/accelerate.git\n",
+ "!pip install -q datasets"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 145,
+ "referenced_widgets": [
+ "8cc86330c2af436c9af314e8c04c8c2b",
+ "e25f9ca445b14e3f8397779df071dfb4",
+ "8365680c634a44aa880317e36fa5e46e",
+ "0c4ac7c3db0b431397cc812f7c9e785c",
+ "c84f542c863043dea8a3675fa153e78d",
+ "b3b3f4ddd4ed4d938c923887939a0440",
+ "35186465f87341f683affb9399661540",
+ "791df472db174df69b8c9f0e200af254",
+ "6bb9c7182d2a464ea21809e59043562a",
+ "31c574113731403b88edc5bb0798bc6d",
+ "3b8bc5b9392e45758813a1db9db824a9",
+ "90661b333d6f496ca606b3046622660e",
+ "5f551f9b217e44cf8b5433f314b3844b",
+ "d2d81cc8296c4b10bf80b86c0a3302d3",
+ "7e3a386e672f4748882211227b7721a9",
+ "57f251691b4c453896b2508c431dfc2f",
+ "4bdb196cd1494f809829651ec5b6cbf8",
+ "7cd50bcc8fcc4b83abcda6d3604bd4cc",
+ "7a00aa4a97a34da39cc052c6926dbe13",
+ "14c73d88df9e46e3bbb6690fdb48ad07",
+ "0e2beab611114239b6ee48a3cbb09c49",
+ "006b78b5191b4fb888d98bdf6c20ec1e",
+ "5f6ffa1d929443a5bd9c7c550f0690f0",
+ "668a7f88506148a9ba2b48920afc028f",
+ "57b0096985ab44aea342e52795c4f999",
+ "a4c404e420cc4ce781ce569f9ab3f987",
+ "ee4e4af964ec4dd597cb04a90f0697f9",
+ "974e3687f18a4e1a975969b880d086aa",
+ "93a50117ece543d4857ba02505dc4514",
+ "71a3a56edbdb45669d382fef4b097e1b",
+ "53f287d4927541d08e2ae7d4d0b3c396",
+ "afa442ab223b46cb82569438c0047823"
+ ]
+ },
+ "id": "wAAPv5CRmg7e",
+ "outputId": "687f979a-04c1-4160-d71c-4de8ecdb07d9"
+ },
+ "outputs": [],
+ "source": [
+ "# Required when training models/data that are gated on HuggingFace, and required for pushing models to HuggingFace\n",
+ "from huggingface_hub import notebook_login\n",
+ "\n",
+ "notebook_login()"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "MJ-5idQwzvg-"
+ },
+ "source": [
+ "### Loading the model and its tokenizer in quantized setup!\n"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 546,
+ "referenced_widgets": [
+ "5924b266e95a42039634a334ff561a82",
+ "eadeec171e7b4c0f9e26964f031cfb71",
+ "feae525923d5407bb69a922954c474f7",
+ "00371a48e64c45cd97020a78b710e64c",
+ "156f95b0012449e8a0c604e6e03bf35f",
+ "de3757d6125a4c07b502dd60816bafec",
+ "8c4d6f4eea3742289a2604e66b0c6182",
+ "bac377ed96ae4e8db9b298bb623888ec",
+ "02d6cc4c2717434c895798601bda7c86",
+ "3f9fa554747743f8a86b40a4f7530617",
+ "ffe561df8772443ebf40a3b8b656079f",
+ "800e9453214848b69bc4c6ca2d5e8f79",
+ "6b0ec8d5f7294d44a5fa15d8ef12471e",
+ "7d3a7be9ed6f48988a2c4a1a4a2271cf",
+ "c40f583823574e40b6b29d4914143c0e",
+ "a4368e6da8f046aaa32f3152b7d333d1",
+ "8ea89e52123643268857285e0e1db1c0",
+ "a8514e34378d47a28fbf0831a14ede8f",
+ "f86b969ef69b48119619e1a424b50460",
+ "7725e9d443e249ada02e5ac7056d00db",
+ "f81756eb9e554899b0778311f2c407c4",
+ "3b614b9712874fac990d2c557b0791a6",
+ "43d12a98d90a4bf7a96c033172c646e2",
+ "c35b16156253402f90a432f3f07c2e0a",
+ "1ae1d2702da5483a85504f59939ffa39",
+ "1b2abf90003e4165a3293acd6a5ea9ff",
+ "3e45aea9f7444a4db885c4cca4c9c4ff",
+ "6b6ed29053ec4aaa8fc5526a35f17c2b",
+ "e69cd88ccbae4bb7b238fa112a60f0f9",
+ "8cd63d3908e4411c9fcb42bc32c8dd16",
+ "64624b26145b42db82f7afc36c32e117",
+ "cffdf12fbe97462ab74e88ccca943aeb",
+ "bcaf4c81ba9d437bb6223dbb22d011ed",
+ "8800c351b6da450eace0c3890d36c8d7",
+ "7037c32dfce84e70ac86537dbbc6a495",
+ "31c10fa464e24f97b379675a204a09b5",
+ "6149752353fe4f9cbb7b26bcc25199a9",
+ "0b145e421f4840f2872c29256b49f168",
+ "0f4c664612364dc89acf78eb1c740980",
+ "0f60f9aa76b941809e013ffcae83604a",
+ "1d27ab2bc6ae463a806292b68b7891f8",
+ "2a57bb48e1c6475abba242994a79d44a",
+ "6cb8065803724d80b82b06dc95ded91e",
+ "8301c6302df54bbc9f15295f11cec208",
+ "0aad2d9d1cba40cbb64308ede3242ed7",
+ "0711e28e06a440c2a241acbc1f90d1e8",
+ "77704d2e27e94cd3a0c5f6b5ceeffd1c",
+ "3b82b8d41b134bec9bd77ed8d4f00eb4",
+ "25fef90e209f4b14a73f3e39d226d913",
+ "f4ca7b63d7d749ff83a848e250f03ec1",
+ "8c149bc655a34fe5b91853c66db458a9",
+ "0f54e8fda93144f6a95493e6ec535e9d",
+ "880124db7dc04aaea09edd75e1ec7921",
+ "14bf612f6ad7416c8ddd6085c72eee0e",
+ "f7e59b47f9b74523843f37268212d566",
+ "a34b3fd5859a441f89cbe7f6e6df9da9",
+ "8f5b8c513b164dab9e0892422163c483",
+ "5b2a671976fa446db408d58a215b8249",
+ "c934919f617447cfb9226929e7a68d79",
+ "124a70bfad434c5c946f611c04a91c8f",
+ "cd11fb7d54bb43ae821f2272d075a1b3",
+ "fbc6a2834c5442fbb6667f1b3612bb5b",
+ "63899ac621ff4e9cb8e215d5ab63bef8",
+ "6b2b59d2b62b4f7da8c60ff783138397",
+ "c27e8ce031884a90b41d8220b1870bc4",
+ "88024cd312ee42c2925ebfbe52077780",
+ "cf6d1be81b6c4ffc81ce8fdabfc5ad28",
+ "07e0aed682fd4cc88fa75c0592dc04a7",
+ "67b4473eb8a44a96ba34983762ab38fa",
+ "c7e06fd82f7f4f9fb81c68e8758f2de1",
+ "3d9d8278667d496aaea1eaaa4d24ae93",
+ "47944ad8cadf4a57b170193c46d4389c",
+ "db05b25cb38140bdb21e6f3b7fde7e66",
+ "6f474268da0f4337a2ccecc1ca2098a1",
+ "c2ceccfdb59b4336a24003cd6bc2403d",
+ "a8999d04e4114693bb6be358bdbe9b83",
+ "2540d57e3bf545e3812da1ee72b85fc8",
+ "c56d8289513441688f9bc5f4b52d60a0",
+ "a53b4776f95f4dd38197193e6c5f649e",
+ "b4ba435f6d1c448f99b533bc6df32e76",
+ "42eb041021214110a860924d28d73409",
+ "17c797e08bd2493fa685918129415309",
+ "aea74071600f483b9e6de1a61743c03a",
+ "21bf14b771c14d2dab9e98a326302e14",
+ "35c2c635c2024bcda3265bf95d330f63",
+ "ec014d847e394a309b6a82c30a6fdfc5",
+ "4c369386ba5f4862b11a50e50130663b",
+ "bbdf3bb657e64fc2b0a90e78e8886480",
+ "d7ef74cf4a914ad38a69c84c34fff393",
+ "8d0f1d547c384094b10aa00a3ede3c06",
+ "9bdebf06b6874bbb88404f4ad14e1dbc",
+ "a2249f364b914662b54045a1f8d6dfd1",
+ "7504986b8d8d4d0da58ad79e80a81948",
+ "082b6990ce5e4812adc0ad6a7b376dac",
+ "610e1ddfb7a44d51a54ebea6dad3a5f0",
+ "5f60910d1e744432bdf87518f0f45874",
+ "2ab86b3fbd49488bb02f8205a572e752",
+ "9f13437a44b8434b9cc3afab998e8d3c",
+ "8a7c82dcbd414b24b67ccfbc562b2e38",
+ "d1508f5cde9a43d8abc26dd2d0c34dbd",
+ "9a0b012915c54abeb100f466fa99d303",
+ "99529129d7f0435da0fdcfc9803a2f11",
+ "5b56ac3009714a5a84dd8749db4a7bce",
+ "546b76a22f1046cd856a8fa2f9ff2d9f",
+ "fffbf696c07744fc8e3d81ab51dc9c90",
+ "a153cc3ca0cc45c18a941bd57e363ec3",
+ "5a8ac674153248999007a713299b2644",
+ "1f82a5685eef4b47a2dbf7618362907c",
+ "51b3af446ace409dbcdf5de499552061",
+ "9a12124915994b70a71ebd64b99e93e9",
+ "57f87d4780634d36ae8159d987c22993",
+ "58ea619f81bf42ddb8b166db3deb0e86",
+ "8bb83ae3229e4f38b1733f92f536fad0",
+ "5c0104210ee34ca8a072ee5121f424a1",
+ "34e381adbd9242759b57f2a305c5d2e3",
+ "e4e1a4338c5e46b3ba5a3bb960da7107",
+ "9a5072b8d16d4a1eb0652da61bda0ac8",
+ "1f75d85e6c7e4eb6a91b03f0c8adb644",
+ "9da33f07ea354b5798e85298e132b017",
+ "604582e8cbff4dc9876551a3307b5b77",
+ "a98165ee656643ad85ac9ea1447cc775",
+ "5cf4a57d21a545029b6448258a5ebd84",
+ "0d2ae3466a3447c58e23ccd2b3733deb",
+ "ba7f32c41f9247ec9d4c40e6396b55a9",
+ "ea1bdb5f2da64332960bccd967a84b4a",
+ "b08631e4cffa445c912da0c8eac2ef23",
+ "921a1a037f7b47f8b57d1da8192a437a",
+ "892ff4e2f0e44c23bc5c2be7547cf0bd",
+ "4c8e98294bd240a6869cb199caee66e1",
+ "4e1f5423311b4dc0930c21c9ad5a88f5",
+ "347540dc03d34e65b7ffbb0f5fc569aa",
+ "7243d8e2e1cc4043a2ee310eabd0ac09"
+ ]
+ },
+ "id": "E0Nl5mWL0k2T",
+ "outputId": "a942d9b0-1f38-4a9b-ea20-e55bd7593920"
+ },
+ "outputs": [],
+ "source": [
+ "# setting up the config for 4-bit quantization of QRandLora\n",
+ "import torch\n",
+ "from transformers import AutoTokenizer, AutoModelForCausalLM, BitsAndBytesConfig\n",
+ "\n",
+ "model_id = \"meta-llama/Meta-Llama-3-8B\"\n",
+ "bnb_config = BitsAndBytesConfig(\n",
+ " load_in_4bit=True, bnb_4bit_use_double_quant=True, bnb_4bit_quant_type=\"nf4\", bnb_4bit_compute_dtype=torch.bfloat16\n",
+ ")\n",
+ "\n",
+ "tokenizer = AutoTokenizer.from_pretrained(model_id)\n",
+ "model = AutoModelForCausalLM.from_pretrained(model_id, quantization_config=bnb_config, device_map={\"\": 0})"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "id": "Xpx2Fq-icX56"
+ },
+ "outputs": [],
+ "source": [
+ "print(model)"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "Mp2gMi1ZzGET"
+ },
+ "source": [
+ "#### Prepare model for PEFT fine-tuning"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 2,
+ "metadata": {
+ "id": "a9EUEDAl0ss3"
+ },
+ "outputs": [],
+ "source": [
+ "from peft import prepare_model_for_kbit_training\n",
+ "\n",
+ "model.gradient_checkpointing_enable()\n",
+ "model = prepare_model_for_kbit_training(model)"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 3,
+ "metadata": {
+ "id": "gkIcwsSU01EB"
+ },
+ "outputs": [],
+ "source": [
+ "def print_trainable_parameters(model):\n",
+ " \"\"\"\n",
+ " Prints the number of trainable parameters in the model.\n",
+ " \"\"\"\n",
+ " trainable_params = 0\n",
+ " all_param = 0\n",
+ " for _, param in model.named_parameters():\n",
+ " all_param += param.numel()\n",
+ " if param.requires_grad:\n",
+ " trainable_params += param.numel()\n",
+ " print(\n",
+ " f\"trainable params: {trainable_params} || all params: {all_param} || trainable%: {100 * trainable_params / all_param}\"\n",
+ " )"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "HVTAJuKyM0gX"
+ },
+ "source": [
+ "### Setup `RandLoraConfig`"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "colab": {
+ "base_uri": "https://localhost:8080/"
+ },
+ "id": "Ybeyl20n3dYH",
+ "outputId": "ea35ec70-13e4-4f23-9481-1b33b1b06dec"
+ },
+ "outputs": [],
+ "source": [
+ "from peft import RandLoraConfig, get_peft_model\n",
+ "\n",
+ "config = RandLoraConfig(\n",
+ " r=32,\n",
+ " randlora_alpha=640,\n",
+ " target_modules=[\n",
+ " \"q_proj\",\n",
+ " \"k_proj\",\n",
+ " \"v_proj\",\n",
+ " \"o_proj\",\n",
+ " \"gate_proj\",\n",
+ " \"up_proj\",\n",
+ " \"down_proj\",\n",
+ " ], # parameters specific to llama\n",
+ " randlora_dropout=0.05,\n",
+ " bias=\"none\",\n",
+ " task_type=\"CAUSAL_LM\",\n",
+ ")\n",
+ "\n",
+ "model = get_peft_model(model, config)\n",
+ "print_trainable_parameters(model)"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "colab": {
+ "base_uri": "https://localhost:8080/"
+ },
+ "id": "Ybeyl20n3dYH",
+ "outputId": "ea35ec70-13e4-4f23-9481-1b33b1b06dec"
+ },
+ "outputs": [],
+ "source": [
+ "print(model)"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "FCc64bfnmd3j"
+ },
+ "source": [
+ "## Step 2) Fine-tuning process 💥\n"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 277,
+ "referenced_widgets": [
+ "b2a19b6092c44b20886987b30f1bf48a",
+ "1f0efc167b3744b38ff832b71d529318",
+ "a06b2bd0236249999adffa44e53cf80e",
+ "23012118a7314a3f838870a2aee9ec90",
+ "dcff079d850c423a83eb70105b816ee4",
+ "64911f0e52e74067a1a986c5edfc7f59",
+ "b4a274fc9e324b80bf559c4dbd05e319",
+ "5fb4a4ef8afe4ea4af6655faea17f354",
+ "b1a03a5e9bae46129830daeeb23bf6ff",
+ "e297072ab5d64815b90bc89d22503378",
+ "67fbabb9082c4241b8f937b24e0cdd03",
+ "b1de7b283eeb41828e8093e60c83f2c4",
+ "bb640a5c858349d29c13ce5629e72f22",
+ "37523a6cac1047e9a261698212d47737",
+ "661f76474252493caae8f7d6aa8f99b7",
+ "849cdc1912aa4df4b0c721a8c63ca0f9",
+ "5962e77eea5a4d88ba6dbc5e9f51c709",
+ "f07c8a6ec12f46ea9e32a2208e70bccd",
+ "191caf3a38eb4191a35f623ce25238f9",
+ "30b74bd2db8d40d08408013cebcd7661",
+ "83c355e1418140a5bbad11bf0646b332",
+ "84d6d2a6afcd423f9b609cbb2d10f00e",
+ "51180cce01564821a170d1d4b8a9a918",
+ "03dd6c24f6d94fe7ab85b79d6f6cbeaf",
+ "f2ab2fa803e94328a237e84cd4ea0027",
+ "1bd0a270c7ee409c970763398e54fc36",
+ "e92b30d0b4234af6b5a33bff989b1b45",
+ "cc5ce633746949ed98418cae9f68afe3",
+ "4b1f795c4c004cacbf3660d935e52995",
+ "5690d92586494b9187147f32fa708405",
+ "317cda72329c4043ab0b224b46b259d3",
+ "076357d4bb9943bdaa1d6846897786af",
+ "7b3e136fc9e74a699497a947006f4f1d",
+ "7e2e097c703a4a0d8556733a0739469c",
+ "e0fd6d00f0ba4e59bdaa5779556ec4ea",
+ "cd318c6bfc8e421a9bfcdab16be5eaa7",
+ "4bc1fd9d480a4799954c69031c071b30",
+ "25fc6aaf37fc49fa822df29236bf2f90",
+ "7ac8e88f29f04b859f592a003d39836b",
+ "0ec2643d9fd44785addb37d9ecd23989",
+ "d10ba011d05045b18bbfeb9660e4d9d3",
+ "e56c22f77c884caaacfafd48dfa51a55",
+ "068eb104d5d346b1897f8cbe9860d267",
+ "b621c6a8c0e9440fa840d75a1b1b02fc",
+ "434fe18d50a14920b30fd2d0650297ac",
+ "353bf45a4bbc46d6a798175f152399cb",
+ "bfcbfe4184774fd3a8320f4f0e1baf54",
+ "99c5c846cc5e43429905f071670b4310",
+ "8d988c86648244788f6dc5aa0fea38fd",
+ "740604526cc44cd58b811827d4787d96",
+ "2558c2dd7d394ecf9fc67a69ce8fc97a",
+ "a2a7b715b16a41a288209dee1de5d2d1",
+ "bf77e5aaab0547f7b2beb015687552ef",
+ "a2c543008f444cf49972a4f35c32b8e3",
+ "bb7b8a9e42f6478f851236685a1392d6",
+ "9cfaf17064bc49a5aded0fc53dd7cd7f",
+ "ede66e196fa9482498f58dcdffd494a2",
+ "a26cc7fea1a64d7bac1769d33cc74e28",
+ "c2f24a8930be4b70b4bbbcf5d908b01d",
+ "1f59dd66813f419999336e59a3efc56a",
+ "026072374b7d47c194707a50f5c99099",
+ "63ac7dafeb27446cb30aaddf4cd27c9f",
+ "854e35df771f470b82a59f878a2a6a46",
+ "d1cbe0ab9379453588eb438d13fd272d",
+ "b0b7457a8b47496483da1506fb2505b3",
+ "c7dc386d978a44ff885763ecec94dc38",
+ "4a7c8dfd88db4bc893da2bced0560d47",
+ "27a587021d854b79a279a510a55f9d73",
+ "4227474e986546d1a7d31dce35a2410c",
+ "1561cd47c42e46368677d34e7b7084cd",
+ "8b9e961c837a464fb7a8c44756dc41e7",
+ "d4092198673141d3b4a824d629d73f64",
+ "d3cbfd564fe8485ba7afdb1cc54abed3",
+ "7e51e8e0612e46b1a3403d448b39aa50",
+ "061c45266c484ff6807dcaf4722fd73b",
+ "04188e0cec0542818894ebc6a534fb51",
+ "4a13203d132b45beadf140c02dc8a566"
+ ]
+ },
+ "id": "s6f4z8EYmcJ6",
+ "outputId": "8ece7a1a-cf27-4602-c70b-ce4f3d7e11bf"
+ },
+ "outputs": [],
+ "source": [
+ "# Load the dataset from HF\n",
+ "from datasets import load_dataset\n",
+ "\n",
+ "data = load_dataset(\"timdettmers/openassistant-guanaco\")\n",
+ "data = data.map(lambda samples: tokenizer(samples[\"text\"]), batched=True)"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "_0MOtwf3zdZp"
+ },
+ "source": [
+ "## Training\n",
+ "\n",
+ "For the sake of the demo, we just ran it for 10 steps just to showcase how to use this integration with existing tools on the HF ecosystem."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 498
+ },
+ "id": "jq0nX33BmfaC",
+ "outputId": "94e17005-065b-48ab-9192-e3ab55c0c292"
+ },
+ "outputs": [],
+ "source": [
+ "import transformers\n",
+ "\n",
+ "tokenizer.pad_token = tokenizer.eos_token\n",
+ "\n",
+ "trainer = transformers.Trainer(\n",
+ " model=model,\n",
+ " train_dataset=data[\"train\"],\n",
+ " args=transformers.TrainingArguments(\n",
+ " per_device_train_batch_size=1,\n",
+ " gradient_accumulation_steps=4,\n",
+ " warmup_steps=2,\n",
+ " max_steps=10,\n",
+ " learning_rate=2e-4,\n",
+ " fp16=True,\n",
+ " logging_steps=1,\n",
+ " output_dir=\"path/to/your/HF/repo\", # change it to your desired repo!\n",
+ " optim=\"paged_adamw_8bit\",\n",
+ " label_names=[\"labels\"],\n",
+ " ),\n",
+ " data_collator=transformers.DataCollatorForLanguageModeling(tokenizer, mlm=False),\n",
+ ")\n",
+ "model.config.use_cache = False # silence the warnings. Please re-enable for inference!\n",
+ "trainer.train()"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "Mr3rLrHwqhf6"
+ },
+ "source": [
+ "## Usage Example"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "id": "9mrOJ9l8SMHv"
+ },
+ "outputs": [],
+ "source": [
+ "model.config.use_cache = True\n",
+ "model.eval();"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 122
+ },
+ "id": "AM6FNOFzqKfI",
+ "outputId": "fdbe28b1-e440-45d3-bd6d-c15e744ad23d"
+ },
+ "outputs": [],
+ "source": [
+ "from transformers import GenerationConfig\n",
+ "\n",
+ "max_new_tokens = 120\n",
+ "top_p = 0.9\n",
+ "temperature = 0.7\n",
+ "user_question = \"What is the purpose of quantization in LLMs?\"\n",
+ "\n",
+ "\n",
+ "prompt = (\n",
+ " \"A chat between a curious human and an artificial intelligence assistant. \"\n",
+ " \"The assistant gives helpful, detailed, and polite answers to the user's questions. \"\n",
+ " \"### Human: {user_question}\"\n",
+ " \"### Assistant: \"\n",
+ ")\n",
+ "\n",
+ "\n",
+ "def generate(model, user_question, max_new_tokens=max_new_tokens, top_p=top_p, temperature=temperature):\n",
+ " device = torch.accelerator.current_accelerator().type if hasattr(torch, \"accelerator\") else \"cuda\"\n",
+ " inputs = tokenizer(prompt.format(user_question=user_question), return_tensors=\"pt\").to(device)\n",
+ "\n",
+ " outputs = model.generate(\n",
+ " **inputs,\n",
+ " generation_config=GenerationConfig(\n",
+ " do_sample=True,\n",
+ " max_new_tokens=max_new_tokens,\n",
+ " top_p=top_p,\n",
+ " temperature=temperature,\n",
+ " ),\n",
+ " )\n",
+ "\n",
+ " text = tokenizer.decode(outputs[0], skip_special_tokens=True)\n",
+ " # print(text)\n",
+ " return text\n",
+ "\n",
+ "\n",
+ "generate(model, user_question)"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "id": "T5t_gl2_f5OO"
+ },
+ "outputs": [],
+ "source": [
+ "# trainer.push_to_hub()"
+ ]
+ }
+ ],
+ "metadata": {
+ "accelerator": "GPU",
+ "colab": {
+ "gpuType": "T4",
+ "provenance": []
+ },
+ "gpuClass": "standard",
+ "kernelspec": {
+ "display_name": "Python 3",
+ "language": "python",
+ "name": "python3"
+ },
+ "language_info": {
+ "codemirror_mode": {
+ "name": "ipython",
+ "version": 3
+ },
+ "file_extension": ".py",
+ "mimetype": "text/x-python",
+ "name": "python",
+ "nbconvert_exporter": "python",
+ "pygments_lexer": "ipython3",
+ "version": "3.11.13"
+ },
+ "widgets": {
+ "application/vnd.jupyter.widget-state+json": {
+ "00371a48e64c45cd97020a78b710e64c": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_3f9fa554747743f8a86b40a4f7530617",
+ "placeholder": "",
+ "style": "IPY_MODEL_ffe561df8772443ebf40a3b8b656079f",
+ "value": " 50.6k/50.6k [00:00<00:00, 3.65MB/s]"
+ }
+ },
+ "006b78b5191b4fb888d98bdf6c20ec1e": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "LabelModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "LabelModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "LabelView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_ee4e4af964ec4dd597cb04a90f0697f9",
+ "placeholder": "",
+ "style": "IPY_MODEL_974e3687f18a4e1a975969b880d086aa",
+ "value": "Your token has been saved in your configured git credential helpers (store)."
+ }
+ },
+ "026072374b7d47c194707a50f5c99099": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "02d6cc4c2717434c895798601bda7c86": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "03dd6c24f6d94fe7ab85b79d6f6cbeaf": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_cc5ce633746949ed98418cae9f68afe3",
+ "placeholder": "",
+ "style": "IPY_MODEL_4b1f795c4c004cacbf3660d935e52995",
+ "value": "Downloading data: 100%"
+ }
+ },
+ "04188e0cec0542818894ebc6a534fb51": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "061c45266c484ff6807dcaf4722fd73b": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "068eb104d5d346b1897f8cbe9860d267": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "0711e28e06a440c2a241acbc1f90d1e8": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_f4ca7b63d7d749ff83a848e250f03ec1",
+ "placeholder": "",
+ "style": "IPY_MODEL_8c149bc655a34fe5b91853c66db458a9",
+ "value": "model.safetensors.index.json: 100%"
+ }
+ },
+ "076357d4bb9943bdaa1d6846897786af": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "07e0aed682fd4cc88fa75c0592dc04a7": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_47944ad8cadf4a57b170193c46d4389c",
+ "placeholder": "",
+ "style": "IPY_MODEL_db05b25cb38140bdb21e6f3b7fde7e66",
+ "value": "model-00001-of-00004.safetensors: 100%"
+ }
+ },
+ "082b6990ce5e4812adc0ad6a7b376dac": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "0aad2d9d1cba40cbb64308ede3242ed7": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_0711e28e06a440c2a241acbc1f90d1e8",
+ "IPY_MODEL_77704d2e27e94cd3a0c5f6b5ceeffd1c",
+ "IPY_MODEL_3b82b8d41b134bec9bd77ed8d4f00eb4"
+ ],
+ "layout": "IPY_MODEL_25fef90e209f4b14a73f3e39d226d913"
+ }
+ },
+ "0b145e421f4840f2872c29256b49f168": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "0c4ac7c3db0b431397cc812f7c9e785c": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "CheckboxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "CheckboxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "CheckboxView",
+ "description": "Add token as git credential?",
+ "description_tooltip": null,
+ "disabled": false,
+ "indent": true,
+ "layout": "IPY_MODEL_90661b333d6f496ca606b3046622660e",
+ "style": "IPY_MODEL_5f551f9b217e44cf8b5433f314b3844b",
+ "value": true
+ }
+ },
+ "0d2ae3466a3447c58e23ccd2b3733deb": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_921a1a037f7b47f8b57d1da8192a437a",
+ "placeholder": "",
+ "style": "IPY_MODEL_892ff4e2f0e44c23bc5c2be7547cf0bd",
+ "value": "generation_config.json: 100%"
+ }
+ },
+ "0e2beab611114239b6ee48a3cbb09c49": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "LabelModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "LabelModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "LabelView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_57b0096985ab44aea342e52795c4f999",
+ "placeholder": "",
+ "style": "IPY_MODEL_a4c404e420cc4ce781ce569f9ab3f987",
+ "value": "Token is valid (permission: write)."
+ }
+ },
+ "0ec2643d9fd44785addb37d9ecd23989": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "0f4c664612364dc89acf78eb1c740980": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "0f54e8fda93144f6a95493e6ec535e9d": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "0f60f9aa76b941809e013ffcae83604a": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "124a70bfad434c5c946f611c04a91c8f": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "14bf612f6ad7416c8ddd6085c72eee0e": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "14c73d88df9e46e3bbb6690fdb48ad07": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "1561cd47c42e46368677d34e7b7084cd": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_04188e0cec0542818894ebc6a534fb51",
+ "placeholder": "",
+ "style": "IPY_MODEL_4a13203d132b45beadf140c02dc8a566",
+ "value": " 518/518 [00:00<00:00, 976.36 examples/s]"
+ }
+ },
+ "156f95b0012449e8a0c604e6e03bf35f": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "17c797e08bd2493fa685918129415309": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "191caf3a38eb4191a35f623ce25238f9": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "1ae1d2702da5483a85504f59939ffa39": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "FloatProgressModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "FloatProgressModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "ProgressView",
+ "bar_style": "success",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_8cd63d3908e4411c9fcb42bc32c8dd16",
+ "max": 73,
+ "min": 0,
+ "orientation": "horizontal",
+ "style": "IPY_MODEL_64624b26145b42db82f7afc36c32e117",
+ "value": 73
+ }
+ },
+ "1b2abf90003e4165a3293acd6a5ea9ff": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_cffdf12fbe97462ab74e88ccca943aeb",
+ "placeholder": "",
+ "style": "IPY_MODEL_bcaf4c81ba9d437bb6223dbb22d011ed",
+ "value": " 73.0/73.0 [00:00<00:00, 4.75kB/s]"
+ }
+ },
+ "1bd0a270c7ee409c970763398e54fc36": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_076357d4bb9943bdaa1d6846897786af",
+ "placeholder": "",
+ "style": "IPY_MODEL_7b3e136fc9e74a699497a947006f4f1d",
+ "value": " 1.11M/1.11M [00:00<00:00, 8.23MB/s]"
+ }
+ },
+ "1d27ab2bc6ae463a806292b68b7891f8": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "1f0efc167b3744b38ff832b71d529318": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_64911f0e52e74067a1a986c5edfc7f59",
+ "placeholder": "",
+ "style": "IPY_MODEL_b4a274fc9e324b80bf559c4dbd05e319",
+ "value": "Downloading readme: 100%"
+ }
+ },
+ "1f59dd66813f419999336e59a3efc56a": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "1f75d85e6c7e4eb6a91b03f0c8adb644": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "1f82a5685eef4b47a2dbf7618362907c": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "21bf14b771c14d2dab9e98a326302e14": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "23012118a7314a3f838870a2aee9ec90": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_e297072ab5d64815b90bc89d22503378",
+ "placeholder": "",
+ "style": "IPY_MODEL_67fbabb9082c4241b8f937b24e0cdd03",
+ "value": " 395/395 [00:00<00:00, 16.6kB/s]"
+ }
+ },
+ "2540d57e3bf545e3812da1ee72b85fc8": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "2558c2dd7d394ecf9fc67a69ce8fc97a": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "25fc6aaf37fc49fa822df29236bf2f90": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "25fef90e209f4b14a73f3e39d226d913": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "27a587021d854b79a279a510a55f9d73": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_d4092198673141d3b4a824d629d73f64",
+ "placeholder": "",
+ "style": "IPY_MODEL_d3cbfd564fe8485ba7afdb1cc54abed3",
+ "value": "Map: 100%"
+ }
+ },
+ "2a57bb48e1c6475abba242994a79d44a": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "2ab86b3fbd49488bb02f8205a572e752": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "30b74bd2db8d40d08408013cebcd7661": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "317cda72329c4043ab0b224b46b259d3": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "31c10fa464e24f97b379675a204a09b5": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "FloatProgressModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "FloatProgressModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "ProgressView",
+ "bar_style": "success",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_1d27ab2bc6ae463a806292b68b7891f8",
+ "max": 654,
+ "min": 0,
+ "orientation": "horizontal",
+ "style": "IPY_MODEL_2a57bb48e1c6475abba242994a79d44a",
+ "value": 654
+ }
+ },
+ "31c574113731403b88edc5bb0798bc6d": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "347540dc03d34e65b7ffbb0f5fc569aa": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "34e381adbd9242759b57f2a305c5d2e3": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "35186465f87341f683affb9399661540": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": "center",
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": "flex",
+ "flex": null,
+ "flex_flow": "column",
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": "50%"
+ }
+ },
+ "353bf45a4bbc46d6a798175f152399cb": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_740604526cc44cd58b811827d4787d96",
+ "placeholder": "",
+ "style": "IPY_MODEL_2558c2dd7d394ecf9fc67a69ce8fc97a",
+ "value": "Generating test split: 100%"
+ }
+ },
+ "35c2c635c2024bcda3265bf95d330f63": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "37523a6cac1047e9a261698212d47737": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "FloatProgressModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "FloatProgressModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "ProgressView",
+ "bar_style": "success",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_191caf3a38eb4191a35f623ce25238f9",
+ "max": 20877686,
+ "min": 0,
+ "orientation": "horizontal",
+ "style": "IPY_MODEL_30b74bd2db8d40d08408013cebcd7661",
+ "value": 20877686
+ }
+ },
+ "3b614b9712874fac990d2c557b0791a6": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "3b82b8d41b134bec9bd77ed8d4f00eb4": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_14bf612f6ad7416c8ddd6085c72eee0e",
+ "placeholder": "",
+ "style": "IPY_MODEL_f7e59b47f9b74523843f37268212d566",
+ "value": " 23.9k/23.9k [00:00<00:00, 1.51MB/s]"
+ }
+ },
+ "3b8bc5b9392e45758813a1db9db824a9": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "3d9d8278667d496aaea1eaaa4d24ae93": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "3e45aea9f7444a4db885c4cca4c9c4ff": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "3f9fa554747743f8a86b40a4f7530617": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "4227474e986546d1a7d31dce35a2410c": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "FloatProgressModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "FloatProgressModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "ProgressView",
+ "bar_style": "success",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_7e51e8e0612e46b1a3403d448b39aa50",
+ "max": 518,
+ "min": 0,
+ "orientation": "horizontal",
+ "style": "IPY_MODEL_061c45266c484ff6807dcaf4722fd73b",
+ "value": 518
+ }
+ },
+ "42eb041021214110a860924d28d73409": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_4c369386ba5f4862b11a50e50130663b",
+ "placeholder": "",
+ "style": "IPY_MODEL_bbdf3bb657e64fc2b0a90e78e8886480",
+ "value": " 5.00G/5.00G [00:24<00:00, 249MB/s]"
+ }
+ },
+ "434fe18d50a14920b30fd2d0650297ac": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_353bf45a4bbc46d6a798175f152399cb",
+ "IPY_MODEL_bfcbfe4184774fd3a8320f4f0e1baf54",
+ "IPY_MODEL_99c5c846cc5e43429905f071670b4310"
+ ],
+ "layout": "IPY_MODEL_8d988c86648244788f6dc5aa0fea38fd"
+ }
+ },
+ "43d12a98d90a4bf7a96c033172c646e2": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_c35b16156253402f90a432f3f07c2e0a",
+ "IPY_MODEL_1ae1d2702da5483a85504f59939ffa39",
+ "IPY_MODEL_1b2abf90003e4165a3293acd6a5ea9ff"
+ ],
+ "layout": "IPY_MODEL_3e45aea9f7444a4db885c4cca4c9c4ff"
+ }
+ },
+ "47944ad8cadf4a57b170193c46d4389c": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "4a13203d132b45beadf140c02dc8a566": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "4a7c8dfd88db4bc893da2bced0560d47": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_27a587021d854b79a279a510a55f9d73",
+ "IPY_MODEL_4227474e986546d1a7d31dce35a2410c",
+ "IPY_MODEL_1561cd47c42e46368677d34e7b7084cd"
+ ],
+ "layout": "IPY_MODEL_8b9e961c837a464fb7a8c44756dc41e7"
+ }
+ },
+ "4b1f795c4c004cacbf3660d935e52995": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "4bc1fd9d480a4799954c69031c071b30": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_068eb104d5d346b1897f8cbe9860d267",
+ "placeholder": "",
+ "style": "IPY_MODEL_b621c6a8c0e9440fa840d75a1b1b02fc",
+ "value": " 9846/9846 [00:00<00:00, 38881.08 examples/s]"
+ }
+ },
+ "4bdb196cd1494f809829651ec5b6cbf8": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "4c369386ba5f4862b11a50e50130663b": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "4c8e98294bd240a6869cb199caee66e1": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "4e1f5423311b4dc0930c21c9ad5a88f5": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "51180cce01564821a170d1d4b8a9a918": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_03dd6c24f6d94fe7ab85b79d6f6cbeaf",
+ "IPY_MODEL_f2ab2fa803e94328a237e84cd4ea0027",
+ "IPY_MODEL_1bd0a270c7ee409c970763398e54fc36"
+ ],
+ "layout": "IPY_MODEL_e92b30d0b4234af6b5a33bff989b1b45"
+ }
+ },
+ "51b3af446ace409dbcdf5de499552061": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "53f287d4927541d08e2ae7d4d0b3c396": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "546b76a22f1046cd856a8fa2f9ff2d9f": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "5690d92586494b9187147f32fa708405": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "57b0096985ab44aea342e52795c4f999": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "57f251691b4c453896b2508c431dfc2f": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "57f87d4780634d36ae8159d987c22993": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_58ea619f81bf42ddb8b166db3deb0e86",
+ "IPY_MODEL_8bb83ae3229e4f38b1733f92f536fad0",
+ "IPY_MODEL_5c0104210ee34ca8a072ee5121f424a1"
+ ],
+ "layout": "IPY_MODEL_34e381adbd9242759b57f2a305c5d2e3"
+ }
+ },
+ "58ea619f81bf42ddb8b166db3deb0e86": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_e4e1a4338c5e46b3ba5a3bb960da7107",
+ "placeholder": "",
+ "style": "IPY_MODEL_9a5072b8d16d4a1eb0652da61bda0ac8",
+ "value": "Loading checkpoint shards: 100%"
+ }
+ },
+ "5924b266e95a42039634a334ff561a82": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_eadeec171e7b4c0f9e26964f031cfb71",
+ "IPY_MODEL_feae525923d5407bb69a922954c474f7",
+ "IPY_MODEL_00371a48e64c45cd97020a78b710e64c"
+ ],
+ "layout": "IPY_MODEL_156f95b0012449e8a0c604e6e03bf35f"
+ }
+ },
+ "5962e77eea5a4d88ba6dbc5e9f51c709": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "5a8ac674153248999007a713299b2644": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "5b2a671976fa446db408d58a215b8249": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "FloatProgressModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "FloatProgressModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "ProgressView",
+ "bar_style": "success",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_63899ac621ff4e9cb8e215d5ab63bef8",
+ "max": 4,
+ "min": 0,
+ "orientation": "horizontal",
+ "style": "IPY_MODEL_6b2b59d2b62b4f7da8c60ff783138397",
+ "value": 4
+ }
+ },
+ "5b56ac3009714a5a84dd8749db4a7bce": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_51b3af446ace409dbcdf5de499552061",
+ "placeholder": "",
+ "style": "IPY_MODEL_9a12124915994b70a71ebd64b99e93e9",
+ "value": " 1.17G/1.17G [00:09<00:00, 45.8MB/s]"
+ }
+ },
+ "5c0104210ee34ca8a072ee5121f424a1": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_604582e8cbff4dc9876551a3307b5b77",
+ "placeholder": "",
+ "style": "IPY_MODEL_a98165ee656643ad85ac9ea1447cc775",
+ "value": " 4/4 [01:13<00:00, 15.74s/it]"
+ }
+ },
+ "5cf4a57d21a545029b6448258a5ebd84": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_0d2ae3466a3447c58e23ccd2b3733deb",
+ "IPY_MODEL_ba7f32c41f9247ec9d4c40e6396b55a9",
+ "IPY_MODEL_ea1bdb5f2da64332960bccd967a84b4a"
+ ],
+ "layout": "IPY_MODEL_b08631e4cffa445c912da0c8eac2ef23"
+ }
+ },
+ "5f551f9b217e44cf8b5433f314b3844b": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "5f60910d1e744432bdf87518f0f45874": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "5f6ffa1d929443a5bd9c7c550f0690f0": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "LabelModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "LabelModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "LabelView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_93a50117ece543d4857ba02505dc4514",
+ "placeholder": "",
+ "style": "IPY_MODEL_71a3a56edbdb45669d382fef4b097e1b",
+ "value": "Your token has been saved to /root/.cache/huggingface/token"
+ }
+ },
+ "5fb4a4ef8afe4ea4af6655faea17f354": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "604582e8cbff4dc9876551a3307b5b77": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "610e1ddfb7a44d51a54ebea6dad3a5f0": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "6149752353fe4f9cbb7b26bcc25199a9": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_6cb8065803724d80b82b06dc95ded91e",
+ "placeholder": "",
+ "style": "IPY_MODEL_8301c6302df54bbc9f15295f11cec208",
+ "value": " 654/654 [00:00<00:00, 46.9kB/s]"
+ }
+ },
+ "63899ac621ff4e9cb8e215d5ab63bef8": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "63ac7dafeb27446cb30aaddf4cd27c9f": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "64624b26145b42db82f7afc36c32e117": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "64911f0e52e74067a1a986c5edfc7f59": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "661f76474252493caae8f7d6aa8f99b7": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_83c355e1418140a5bbad11bf0646b332",
+ "placeholder": "",
+ "style": "IPY_MODEL_84d6d2a6afcd423f9b609cbb2d10f00e",
+ "value": " 20.9M/20.9M [00:00<00:00, 44.7MB/s]"
+ }
+ },
+ "668a7f88506148a9ba2b48920afc028f": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "LabelModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "LabelModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "LabelView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_53f287d4927541d08e2ae7d4d0b3c396",
+ "placeholder": "",
+ "style": "IPY_MODEL_afa442ab223b46cb82569438c0047823",
+ "value": "Login successful"
+ }
+ },
+ "67b4473eb8a44a96ba34983762ab38fa": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "FloatProgressModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "FloatProgressModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "ProgressView",
+ "bar_style": "success",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_6f474268da0f4337a2ccecc1ca2098a1",
+ "max": 4976698672,
+ "min": 0,
+ "orientation": "horizontal",
+ "style": "IPY_MODEL_c2ceccfdb59b4336a24003cd6bc2403d",
+ "value": 4976698672
+ }
+ },
+ "67fbabb9082c4241b8f937b24e0cdd03": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "6b0ec8d5f7294d44a5fa15d8ef12471e": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_8ea89e52123643268857285e0e1db1c0",
+ "placeholder": "",
+ "style": "IPY_MODEL_a8514e34378d47a28fbf0831a14ede8f",
+ "value": "tokenizer.json: 100%"
+ }
+ },
+ "6b2b59d2b62b4f7da8c60ff783138397": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "6b6ed29053ec4aaa8fc5526a35f17c2b": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "6bb9c7182d2a464ea21809e59043562a": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "6cb8065803724d80b82b06dc95ded91e": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "6f474268da0f4337a2ccecc1ca2098a1": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "7037c32dfce84e70ac86537dbbc6a495": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_0f4c664612364dc89acf78eb1c740980",
+ "placeholder": "",
+ "style": "IPY_MODEL_0f60f9aa76b941809e013ffcae83604a",
+ "value": "config.json: 100%"
+ }
+ },
+ "71a3a56edbdb45669d382fef4b097e1b": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "7243d8e2e1cc4043a2ee310eabd0ac09": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "740604526cc44cd58b811827d4787d96": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "7504986b8d8d4d0da58ad79e80a81948": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "7725e9d443e249ada02e5ac7056d00db": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "77704d2e27e94cd3a0c5f6b5ceeffd1c": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "FloatProgressModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "FloatProgressModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "ProgressView",
+ "bar_style": "success",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_0f54e8fda93144f6a95493e6ec535e9d",
+ "max": 23950,
+ "min": 0,
+ "orientation": "horizontal",
+ "style": "IPY_MODEL_880124db7dc04aaea09edd75e1ec7921",
+ "value": 23950
+ }
+ },
+ "791df472db174df69b8c9f0e200af254": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "7a00aa4a97a34da39cc052c6926dbe13": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "7ac8e88f29f04b859f592a003d39836b": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "7b3e136fc9e74a699497a947006f4f1d": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "7cd50bcc8fcc4b83abcda6d3604bd4cc": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "LabelModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "LabelModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "LabelView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_7a00aa4a97a34da39cc052c6926dbe13",
+ "placeholder": "",
+ "style": "IPY_MODEL_14c73d88df9e46e3bbb6690fdb48ad07",
+ "value": "Connecting..."
+ }
+ },
+ "7d3a7be9ed6f48988a2c4a1a4a2271cf": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "FloatProgressModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "FloatProgressModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "ProgressView",
+ "bar_style": "success",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_f86b969ef69b48119619e1a424b50460",
+ "max": 9085698,
+ "min": 0,
+ "orientation": "horizontal",
+ "style": "IPY_MODEL_7725e9d443e249ada02e5ac7056d00db",
+ "value": 9085698
+ }
+ },
+ "7e2e097c703a4a0d8556733a0739469c": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_e0fd6d00f0ba4e59bdaa5779556ec4ea",
+ "IPY_MODEL_cd318c6bfc8e421a9bfcdab16be5eaa7",
+ "IPY_MODEL_4bc1fd9d480a4799954c69031c071b30"
+ ],
+ "layout": "IPY_MODEL_25fc6aaf37fc49fa822df29236bf2f90"
+ }
+ },
+ "7e3a386e672f4748882211227b7721a9": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ButtonStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ButtonStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "button_color": null,
+ "font_weight": ""
+ }
+ },
+ "7e51e8e0612e46b1a3403d448b39aa50": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "800e9453214848b69bc4c6ca2d5e8f79": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_6b0ec8d5f7294d44a5fa15d8ef12471e",
+ "IPY_MODEL_7d3a7be9ed6f48988a2c4a1a4a2271cf",
+ "IPY_MODEL_c40f583823574e40b6b29d4914143c0e"
+ ],
+ "layout": "IPY_MODEL_a4368e6da8f046aaa32f3152b7d333d1"
+ }
+ },
+ "8301c6302df54bbc9f15295f11cec208": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "8365680c634a44aa880317e36fa5e46e": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "PasswordModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "PasswordModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "PasswordView",
+ "continuous_update": true,
+ "description": "Token:",
+ "description_tooltip": null,
+ "disabled": false,
+ "layout": "IPY_MODEL_31c574113731403b88edc5bb0798bc6d",
+ "placeholder": "",
+ "style": "IPY_MODEL_3b8bc5b9392e45758813a1db9db824a9",
+ "value": ""
+ }
+ },
+ "83c355e1418140a5bbad11bf0646b332": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "849cdc1912aa4df4b0c721a8c63ca0f9": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "84d6d2a6afcd423f9b609cbb2d10f00e": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "854e35df771f470b82a59f878a2a6a46": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "8800c351b6da450eace0c3890d36c8d7": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_7037c32dfce84e70ac86537dbbc6a495",
+ "IPY_MODEL_31c10fa464e24f97b379675a204a09b5",
+ "IPY_MODEL_6149752353fe4f9cbb7b26bcc25199a9"
+ ],
+ "layout": "IPY_MODEL_0b145e421f4840f2872c29256b49f168"
+ }
+ },
+ "880124db7dc04aaea09edd75e1ec7921": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "88024cd312ee42c2925ebfbe52077780": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "892ff4e2f0e44c23bc5c2be7547cf0bd": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "8a7c82dcbd414b24b67ccfbc562b2e38": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "8b9e961c837a464fb7a8c44756dc41e7": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "8bb83ae3229e4f38b1733f92f536fad0": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "FloatProgressModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "FloatProgressModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "ProgressView",
+ "bar_style": "success",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_1f75d85e6c7e4eb6a91b03f0c8adb644",
+ "max": 4,
+ "min": 0,
+ "orientation": "horizontal",
+ "style": "IPY_MODEL_9da33f07ea354b5798e85298e132b017",
+ "value": 4
+ }
+ },
+ "8c149bc655a34fe5b91853c66db458a9": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "8c4d6f4eea3742289a2604e66b0c6182": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "8cc86330c2af436c9af314e8c04c8c2b": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "VBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "VBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "VBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_0e2beab611114239b6ee48a3cbb09c49",
+ "IPY_MODEL_006b78b5191b4fb888d98bdf6c20ec1e",
+ "IPY_MODEL_5f6ffa1d929443a5bd9c7c550f0690f0",
+ "IPY_MODEL_668a7f88506148a9ba2b48920afc028f"
+ ],
+ "layout": "IPY_MODEL_35186465f87341f683affb9399661540"
+ }
+ },
+ "8cd63d3908e4411c9fcb42bc32c8dd16": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "8d0f1d547c384094b10aa00a3ede3c06": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_082b6990ce5e4812adc0ad6a7b376dac",
+ "placeholder": "",
+ "style": "IPY_MODEL_610e1ddfb7a44d51a54ebea6dad3a5f0",
+ "value": "model-00003-of-00004.safetensors: 100%"
+ }
+ },
+ "8d988c86648244788f6dc5aa0fea38fd": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "8ea89e52123643268857285e0e1db1c0": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "8f5b8c513b164dab9e0892422163c483": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_cd11fb7d54bb43ae821f2272d075a1b3",
+ "placeholder": "",
+ "style": "IPY_MODEL_fbc6a2834c5442fbb6667f1b3612bb5b",
+ "value": "Downloading shards: 100%"
+ }
+ },
+ "90661b333d6f496ca606b3046622660e": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "921a1a037f7b47f8b57d1da8192a437a": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "93a50117ece543d4857ba02505dc4514": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "974e3687f18a4e1a975969b880d086aa": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "99529129d7f0435da0fdcfc9803a2f11": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "FloatProgressModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "FloatProgressModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "ProgressView",
+ "bar_style": "success",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_5a8ac674153248999007a713299b2644",
+ "max": 1168138808,
+ "min": 0,
+ "orientation": "horizontal",
+ "style": "IPY_MODEL_1f82a5685eef4b47a2dbf7618362907c",
+ "value": 1168138808
+ }
+ },
+ "99c5c846cc5e43429905f071670b4310": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_a2c543008f444cf49972a4f35c32b8e3",
+ "placeholder": "",
+ "style": "IPY_MODEL_bb7b8a9e42f6478f851236685a1392d6",
+ "value": " 518/518 [00:00<00:00, 13408.85 examples/s]"
+ }
+ },
+ "9a0b012915c54abeb100f466fa99d303": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_fffbf696c07744fc8e3d81ab51dc9c90",
+ "placeholder": "",
+ "style": "IPY_MODEL_a153cc3ca0cc45c18a941bd57e363ec3",
+ "value": "model-00004-of-00004.safetensors: 100%"
+ }
+ },
+ "9a12124915994b70a71ebd64b99e93e9": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "9a5072b8d16d4a1eb0652da61bda0ac8": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "9bdebf06b6874bbb88404f4ad14e1dbc": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "FloatProgressModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "FloatProgressModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "ProgressView",
+ "bar_style": "success",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_5f60910d1e744432bdf87518f0f45874",
+ "max": 4915916176,
+ "min": 0,
+ "orientation": "horizontal",
+ "style": "IPY_MODEL_2ab86b3fbd49488bb02f8205a572e752",
+ "value": 4915916176
+ }
+ },
+ "9cfaf17064bc49a5aded0fc53dd7cd7f": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_ede66e196fa9482498f58dcdffd494a2",
+ "IPY_MODEL_a26cc7fea1a64d7bac1769d33cc74e28",
+ "IPY_MODEL_c2f24a8930be4b70b4bbbcf5d908b01d"
+ ],
+ "layout": "IPY_MODEL_1f59dd66813f419999336e59a3efc56a"
+ }
+ },
+ "9da33f07ea354b5798e85298e132b017": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "9f13437a44b8434b9cc3afab998e8d3c": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "a06b2bd0236249999adffa44e53cf80e": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "FloatProgressModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "FloatProgressModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "ProgressView",
+ "bar_style": "success",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_5fb4a4ef8afe4ea4af6655faea17f354",
+ "max": 395,
+ "min": 0,
+ "orientation": "horizontal",
+ "style": "IPY_MODEL_b1a03a5e9bae46129830daeeb23bf6ff",
+ "value": 395
+ }
+ },
+ "a153cc3ca0cc45c18a941bd57e363ec3": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "a2249f364b914662b54045a1f8d6dfd1": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_9f13437a44b8434b9cc3afab998e8d3c",
+ "placeholder": "",
+ "style": "IPY_MODEL_8a7c82dcbd414b24b67ccfbc562b2e38",
+ "value": " 4.92G/4.92G [00:32<00:00, 171MB/s]"
+ }
+ },
+ "a26cc7fea1a64d7bac1769d33cc74e28": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "FloatProgressModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "FloatProgressModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "ProgressView",
+ "bar_style": "success",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_854e35df771f470b82a59f878a2a6a46",
+ "max": 9846,
+ "min": 0,
+ "orientation": "horizontal",
+ "style": "IPY_MODEL_d1cbe0ab9379453588eb438d13fd272d",
+ "value": 9846
+ }
+ },
+ "a2a7b715b16a41a288209dee1de5d2d1": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "a2c543008f444cf49972a4f35c32b8e3": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "a34b3fd5859a441f89cbe7f6e6df9da9": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_8f5b8c513b164dab9e0892422163c483",
+ "IPY_MODEL_5b2a671976fa446db408d58a215b8249",
+ "IPY_MODEL_c934919f617447cfb9226929e7a68d79"
+ ],
+ "layout": "IPY_MODEL_124a70bfad434c5c946f611c04a91c8f"
+ }
+ },
+ "a4368e6da8f046aaa32f3152b7d333d1": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "a4c404e420cc4ce781ce569f9ab3f987": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "a53b4776f95f4dd38197193e6c5f649e": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_aea74071600f483b9e6de1a61743c03a",
+ "placeholder": "",
+ "style": "IPY_MODEL_21bf14b771c14d2dab9e98a326302e14",
+ "value": "model-00002-of-00004.safetensors: 100%"
+ }
+ },
+ "a8514e34378d47a28fbf0831a14ede8f": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "a8999d04e4114693bb6be358bdbe9b83": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "a98165ee656643ad85ac9ea1447cc775": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "aea74071600f483b9e6de1a61743c03a": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "afa442ab223b46cb82569438c0047823": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "b08631e4cffa445c912da0c8eac2ef23": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "b0b7457a8b47496483da1506fb2505b3": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "b1a03a5e9bae46129830daeeb23bf6ff": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "b1de7b283eeb41828e8093e60c83f2c4": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_bb640a5c858349d29c13ce5629e72f22",
+ "IPY_MODEL_37523a6cac1047e9a261698212d47737",
+ "IPY_MODEL_661f76474252493caae8f7d6aa8f99b7"
+ ],
+ "layout": "IPY_MODEL_849cdc1912aa4df4b0c721a8c63ca0f9"
+ }
+ },
+ "b2a19b6092c44b20886987b30f1bf48a": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_1f0efc167b3744b38ff832b71d529318",
+ "IPY_MODEL_a06b2bd0236249999adffa44e53cf80e",
+ "IPY_MODEL_23012118a7314a3f838870a2aee9ec90"
+ ],
+ "layout": "IPY_MODEL_dcff079d850c423a83eb70105b816ee4"
+ }
+ },
+ "b3b3f4ddd4ed4d938c923887939a0440": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_57f251691b4c453896b2508c431dfc2f",
+ "placeholder": "",
+ "style": "IPY_MODEL_4bdb196cd1494f809829651ec5b6cbf8",
+ "value": "\nPro Tip: If you don't already have one, you can create a dedicated\n'notebooks' token with 'write' access, that you can then easily reuse for all\nnotebooks. "
+ }
+ },
+ "b4a274fc9e324b80bf559c4dbd05e319": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "b4ba435f6d1c448f99b533bc6df32e76": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "FloatProgressModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "FloatProgressModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "ProgressView",
+ "bar_style": "success",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_35c2c635c2024bcda3265bf95d330f63",
+ "max": 4999802720,
+ "min": 0,
+ "orientation": "horizontal",
+ "style": "IPY_MODEL_ec014d847e394a309b6a82c30a6fdfc5",
+ "value": 4999802720
+ }
+ },
+ "b621c6a8c0e9440fa840d75a1b1b02fc": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "ba7f32c41f9247ec9d4c40e6396b55a9": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "FloatProgressModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "FloatProgressModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "ProgressView",
+ "bar_style": "success",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_4c8e98294bd240a6869cb199caee66e1",
+ "max": 177,
+ "min": 0,
+ "orientation": "horizontal",
+ "style": "IPY_MODEL_4e1f5423311b4dc0930c21c9ad5a88f5",
+ "value": 177
+ }
+ },
+ "bac377ed96ae4e8db9b298bb623888ec": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "bb640a5c858349d29c13ce5629e72f22": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_5962e77eea5a4d88ba6dbc5e9f51c709",
+ "placeholder": "",
+ "style": "IPY_MODEL_f07c8a6ec12f46ea9e32a2208e70bccd",
+ "value": "Downloading data: 100%"
+ }
+ },
+ "bb7b8a9e42f6478f851236685a1392d6": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "bbdf3bb657e64fc2b0a90e78e8886480": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "bcaf4c81ba9d437bb6223dbb22d011ed": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "bf77e5aaab0547f7b2beb015687552ef": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "bfcbfe4184774fd3a8320f4f0e1baf54": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "FloatProgressModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "FloatProgressModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "ProgressView",
+ "bar_style": "success",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_a2a7b715b16a41a288209dee1de5d2d1",
+ "max": 518,
+ "min": 0,
+ "orientation": "horizontal",
+ "style": "IPY_MODEL_bf77e5aaab0547f7b2beb015687552ef",
+ "value": 518
+ }
+ },
+ "c27e8ce031884a90b41d8220b1870bc4": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "c2ceccfdb59b4336a24003cd6bc2403d": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "c2f24a8930be4b70b4bbbcf5d908b01d": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_b0b7457a8b47496483da1506fb2505b3",
+ "placeholder": "",
+ "style": "IPY_MODEL_c7dc386d978a44ff885763ecec94dc38",
+ "value": " 9846/9846 [00:09<00:00, 1066.17 examples/s]"
+ }
+ },
+ "c35b16156253402f90a432f3f07c2e0a": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_6b6ed29053ec4aaa8fc5526a35f17c2b",
+ "placeholder": "",
+ "style": "IPY_MODEL_e69cd88ccbae4bb7b238fa112a60f0f9",
+ "value": "special_tokens_map.json: 100%"
+ }
+ },
+ "c40f583823574e40b6b29d4914143c0e": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_f81756eb9e554899b0778311f2c407c4",
+ "placeholder": "",
+ "style": "IPY_MODEL_3b614b9712874fac990d2c557b0791a6",
+ "value": " 9.09M/9.09M [00:00<00:00, 19.3MB/s]"
+ }
+ },
+ "c56d8289513441688f9bc5f4b52d60a0": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_a53b4776f95f4dd38197193e6c5f649e",
+ "IPY_MODEL_b4ba435f6d1c448f99b533bc6df32e76",
+ "IPY_MODEL_42eb041021214110a860924d28d73409"
+ ],
+ "layout": "IPY_MODEL_17c797e08bd2493fa685918129415309"
+ }
+ },
+ "c7dc386d978a44ff885763ecec94dc38": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "c7e06fd82f7f4f9fb81c68e8758f2de1": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_a8999d04e4114693bb6be358bdbe9b83",
+ "placeholder": "",
+ "style": "IPY_MODEL_2540d57e3bf545e3812da1ee72b85fc8",
+ "value": " 4.98G/4.98G [00:34<00:00, 232MB/s]"
+ }
+ },
+ "c84f542c863043dea8a3675fa153e78d": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ButtonModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ButtonModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "ButtonView",
+ "button_style": "",
+ "description": "Login",
+ "disabled": false,
+ "icon": "",
+ "layout": "IPY_MODEL_d2d81cc8296c4b10bf80b86c0a3302d3",
+ "style": "IPY_MODEL_7e3a386e672f4748882211227b7721a9",
+ "tooltip": ""
+ }
+ },
+ "c934919f617447cfb9226929e7a68d79": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_c27e8ce031884a90b41d8220b1870bc4",
+ "placeholder": "",
+ "style": "IPY_MODEL_88024cd312ee42c2925ebfbe52077780",
+ "value": " 4/4 [01:41<00:00, 22.30s/it]"
+ }
+ },
+ "cc5ce633746949ed98418cae9f68afe3": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "cd11fb7d54bb43ae821f2272d075a1b3": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "cd318c6bfc8e421a9bfcdab16be5eaa7": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "FloatProgressModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "FloatProgressModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "ProgressView",
+ "bar_style": "success",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_d10ba011d05045b18bbfeb9660e4d9d3",
+ "max": 9846,
+ "min": 0,
+ "orientation": "horizontal",
+ "style": "IPY_MODEL_e56c22f77c884caaacfafd48dfa51a55",
+ "value": 9846
+ }
+ },
+ "cf6d1be81b6c4ffc81ce8fdabfc5ad28": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_07e0aed682fd4cc88fa75c0592dc04a7",
+ "IPY_MODEL_67b4473eb8a44a96ba34983762ab38fa",
+ "IPY_MODEL_c7e06fd82f7f4f9fb81c68e8758f2de1"
+ ],
+ "layout": "IPY_MODEL_3d9d8278667d496aaea1eaaa4d24ae93"
+ }
+ },
+ "cffdf12fbe97462ab74e88ccca943aeb": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "d10ba011d05045b18bbfeb9660e4d9d3": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "d1508f5cde9a43d8abc26dd2d0c34dbd": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_9a0b012915c54abeb100f466fa99d303",
+ "IPY_MODEL_99529129d7f0435da0fdcfc9803a2f11",
+ "IPY_MODEL_5b56ac3009714a5a84dd8749db4a7bce"
+ ],
+ "layout": "IPY_MODEL_546b76a22f1046cd856a8fa2f9ff2d9f"
+ }
+ },
+ "d1cbe0ab9379453588eb438d13fd272d": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "d2d81cc8296c4b10bf80b86c0a3302d3": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "d3cbfd564fe8485ba7afdb1cc54abed3": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "d4092198673141d3b4a824d629d73f64": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "d7ef74cf4a914ad38a69c84c34fff393": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_8d0f1d547c384094b10aa00a3ede3c06",
+ "IPY_MODEL_9bdebf06b6874bbb88404f4ad14e1dbc",
+ "IPY_MODEL_a2249f364b914662b54045a1f8d6dfd1"
+ ],
+ "layout": "IPY_MODEL_7504986b8d8d4d0da58ad79e80a81948"
+ }
+ },
+ "db05b25cb38140bdb21e6f3b7fde7e66": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "dcff079d850c423a83eb70105b816ee4": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "de3757d6125a4c07b502dd60816bafec": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "e0fd6d00f0ba4e59bdaa5779556ec4ea": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_7ac8e88f29f04b859f592a003d39836b",
+ "placeholder": "",
+ "style": "IPY_MODEL_0ec2643d9fd44785addb37d9ecd23989",
+ "value": "Generating train split: 100%"
+ }
+ },
+ "e25f9ca445b14e3f8397779df071dfb4": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_791df472db174df69b8c9f0e200af254",
+ "placeholder": "",
+ "style": "IPY_MODEL_6bb9c7182d2a464ea21809e59043562a",
+ "value": "
Copy a token from your Hugging Face\ntokens page and paste it below.
Immediately click login after copying\nyour token or it might be stored in plain text in this notebook file. "
+ }
+ },
+ "e297072ab5d64815b90bc89d22503378": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "e4e1a4338c5e46b3ba5a3bb960da7107": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "e56c22f77c884caaacfafd48dfa51a55": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "e69cd88ccbae4bb7b238fa112a60f0f9": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "e92b30d0b4234af6b5a33bff989b1b45": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "ea1bdb5f2da64332960bccd967a84b4a": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_347540dc03d34e65b7ffbb0f5fc569aa",
+ "placeholder": "",
+ "style": "IPY_MODEL_7243d8e2e1cc4043a2ee310eabd0ac09",
+ "value": " 177/177 [00:00<00:00, 11.4kB/s]"
+ }
+ },
+ "eadeec171e7b4c0f9e26964f031cfb71": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_de3757d6125a4c07b502dd60816bafec",
+ "placeholder": "",
+ "style": "IPY_MODEL_8c4d6f4eea3742289a2604e66b0c6182",
+ "value": "tokenizer_config.json: 100%"
+ }
+ },
+ "ec014d847e394a309b6a82c30a6fdfc5": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": ""
+ }
+ },
+ "ede66e196fa9482498f58dcdffd494a2": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_026072374b7d47c194707a50f5c99099",
+ "placeholder": "",
+ "style": "IPY_MODEL_63ac7dafeb27446cb30aaddf4cd27c9f",
+ "value": "Map: 100%"
+ }
+ },
+ "ee4e4af964ec4dd597cb04a90f0697f9": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "f07c8a6ec12f46ea9e32a2208e70bccd": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "f2ab2fa803e94328a237e84cd4ea0027": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "FloatProgressModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "FloatProgressModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "ProgressView",
+ "bar_style": "success",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_5690d92586494b9187147f32fa708405",
+ "max": 1105272,
+ "min": 0,
+ "orientation": "horizontal",
+ "style": "IPY_MODEL_317cda72329c4043ab0b224b46b259d3",
+ "value": 1105272
+ }
+ },
+ "f4ca7b63d7d749ff83a848e250f03ec1": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "f7e59b47f9b74523843f37268212d566": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "f81756eb9e554899b0778311f2c407c4": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "f86b969ef69b48119619e1a424b50460": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "fbc6a2834c5442fbb6667f1b3612bb5b": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "feae525923d5407bb69a922954c474f7": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "FloatProgressModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "FloatProgressModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "ProgressView",
+ "bar_style": "success",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_bac377ed96ae4e8db9b298bb623888ec",
+ "max": 50566,
+ "min": 0,
+ "orientation": "horizontal",
+ "style": "IPY_MODEL_02d6cc4c2717434c895798601bda7c86",
+ "value": 50566
+ }
+ },
+ "ffe561df8772443ebf40a3b8b656079f": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "fffbf696c07744fc8e3d81ab51dc9c90": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ }
+ }
+ }
+ },
+ "nbformat": 4,
+ "nbformat_minor": 4
+}
diff --git a/peft/examples/randlora_finetuning/randlora_finetuning.py b/peft/examples/randlora_finetuning/randlora_finetuning.py
new file mode 100644
index 0000000000000000000000000000000000000000..d6b4d8a24ad86e595b03bdda956265d98855cf47
--- /dev/null
+++ b/peft/examples/randlora_finetuning/randlora_finetuning.py
@@ -0,0 +1,230 @@
+# This script is based on examples/dora_finetuning/dora_finetuning.py
+import os
+
+import torch
+from datasets import load_dataset
+from transformers import (
+ AutoModelForCausalLM,
+ AutoTokenizer,
+ BitsAndBytesConfig,
+ DataCollatorForLanguageModeling,
+ Trainer,
+ TrainingArguments,
+)
+
+from peft import LoraConfig, RandLoraConfig, get_peft_model, prepare_model_for_kbit_training
+
+
+def train_model(
+ base_model: str,
+ data_path: str,
+ output_dir: str,
+ batch_size: int,
+ num_epochs: int,
+ learning_rate: float,
+ cutoff_len: int,
+ val_set_size: int,
+ use_lora: bool,
+ quantize: bool,
+ eval_step: int,
+ save_step: int,
+ device: str,
+ rank: int,
+ randlora_alpha: int,
+ randlora_dropout: float,
+ randlora_target_modules: str,
+ hub_model_id: str,
+ push_to_hub: bool,
+ sparse: bool,
+ very_sparse: bool,
+):
+ os.environ["TOKENIZERS_PARALLELISM"] = "false"
+ hf_token = os.getenv("HF_TOKEN")
+
+ # Setup device
+ device = torch.device(device)
+ print(f"Using device: {device}")
+
+ # load tokenizer
+ tokenizer = AutoTokenizer.from_pretrained(base_model, token=hf_token)
+
+ # Compute type
+ device_type = device.type
+ device_module = getattr(torch, device_type, torch.cuda)
+ bf16_suppotrted = device_module.is_available() and device_module.is_bf16_supported()
+ torch_dtype = torch.bfloat16 if bf16_suppotrted else torch.float16
+
+ # QRandLora (quantized randlora): IF YOU WANNA QUANTIZE THE MODEL
+ if quantize:
+ model = AutoModelForCausalLM.from_pretrained(
+ base_model,
+ token=hf_token,
+ quantization_config=BitsAndBytesConfig(
+ load_in_4bit=True,
+ bnb_4bit_compute_dtype=torch.bfloat16 if bf16_suppotrted else torch.float16,
+ bnb_4bit_use_double_quant=True,
+ bnb_4bit_quant_type="nf4",
+ ),
+ torch_dtype=torch_dtype,
+ )
+ # setup for quantized training
+ model = prepare_model_for_kbit_training(model, use_gradient_checkpointing=True)
+ else:
+ model = AutoModelForCausalLM.from_pretrained(
+ base_model,
+ torch_dtype=torch_dtype,
+ token=hf_token,
+ )
+ # LoRa config for the PEFT model
+ if use_lora:
+ peft_config = LoraConfig(
+ r=rank, # Rank of matrix
+ lora_alpha=randlora_alpha,
+ target_modules=(randlora_target_modules.split(",") if randlora_target_modules else ["k_proj", "v_proj"]),
+ lora_dropout=randlora_dropout,
+ bias="none",
+ )
+ else:
+ peft_config = RandLoraConfig(
+ r=rank, # Rank of random bases
+ randlora_alpha=randlora_alpha,
+ target_modules=(randlora_target_modules.split(",") if randlora_target_modules else ["k_proj", "v_proj"]),
+ randlora_dropout=randlora_dropout,
+ bias="none",
+ sparse=sparse,
+ very_sparse=very_sparse,
+ )
+
+ # get the peft model with RandLora config
+ model = get_peft_model(model, peft_config)
+
+ model.to(device) # MODEL TO ACCELERATOR
+ tokenizer.pad_token = tokenizer.eos_token
+
+ # Load the dataset
+ dataset = load_dataset(data_path)
+
+ def tokenize_function(examples):
+ inputs = tokenizer(examples["text"], padding="max_length", truncation=True, max_length=cutoff_len)
+ inputs["labels"] = inputs["input_ids"].copy() # setting labels for a language modeling task
+ return inputs
+
+ # Tokenize the dataset and prepare for training
+ tokenized_datasets = dataset.map(tokenize_function, batched=True, remove_columns=dataset["train"].column_names)
+
+ # Data collator to dynamically pad the batched examples
+ data_collator = DataCollatorForLanguageModeling(tokenizer, mlm=False)
+
+ # Compute the total amount of training step for warmup
+ max_steps = int((len(dataset) // batch_size) * num_epochs)
+
+ # Define training arguments
+ training_args = TrainingArguments(
+ output_dir=output_dir,
+ num_train_epochs=num_epochs,
+ per_device_train_batch_size=batch_size,
+ per_device_eval_batch_size=batch_size,
+ warmup_steps=int(max_steps * 0.1), # 10% of total trainig steps
+ weight_decay=0.01,
+ logging_dir="./logs",
+ logging_steps=eval_step,
+ save_steps=save_step,
+ save_total_limit=2,
+ push_to_hub=push_to_hub,
+ hub_model_id=hub_model_id,
+ gradient_accumulation_steps=16
+ // batch_size, # Maintaining a minimum batch size of 16 post accumulation is recommended to ensure good performance
+ learning_rate=learning_rate,
+ hub_token=hf_token,
+ label_names=["labels"],
+ )
+
+ # Clear accelerator cache to free memory
+ device_module.empty_cache()
+
+ # Initialize the Trainer
+ trainer = Trainer(
+ model=model,
+ args=training_args,
+ train_dataset=tokenized_datasets["train"],
+ eval_dataset=tokenized_datasets["test"],
+ data_collator=data_collator,
+ )
+
+ # Start model training
+ trainer.train()
+
+ # Save and push the trained model and tokenizer
+ if push_to_hub:
+ # Push the main model to the hub
+ trainer.push_to_hub(commit_message="Fine-tuned model")
+
+ # Save the model and tokenizer locally
+ model.save_pretrained(output_dir)
+ tokenizer.save_pretrained(output_dir)
+
+
+if __name__ == "__main__":
+ import argparse
+
+ parser = argparse.ArgumentParser(description="Fine-tune LLaMA with DoRA and PEFT")
+ parser.add_argument("--base_model", type=str, default="huggyllama/llama-7b", help="Base model path or name")
+ parser.add_argument(
+ "--data_path", type=str, default="timdettmers/openassistant-guanaco", help="Dataset path or name"
+ )
+ parser.add_argument(
+ "--output_dir", type=str, default="path/to/output", help="Output directory for the fine-tuned model"
+ )
+ parser.add_argument("--batch_size", type=int, default=1, help="Batch size")
+ parser.add_argument("--num_epochs", type=int, default=1, help="Number of training epochs")
+ parser.add_argument("--learning_rate", type=float, default=3e-4, help="Learning rate")
+ parser.add_argument("--cutoff_len", type=int, default=512, help="Cutoff length for tokenization")
+ parser.add_argument("--val_set_size", type=int, default=500, help="Validation set size")
+ parser.add_argument("--use_lora", action="store_true", help="Apply Lora instead of RandLora")
+ parser.add_argument("--quantize", action="store_true", help="Use quantization")
+ parser.add_argument("--eval_step", type=int, default=10, help="Evaluation step interval")
+ parser.add_argument("--save_step", type=int, default=100, help="Save step interval")
+ parser.add_argument("--device", type=str, default="auto", help="Device to use for training")
+ parser.add_argument("--rank", type=int, default=32, help="RandLora basis rank")
+ parser.add_argument("--randlora_alpha", type=int, default=640, help="RandLora alpha")
+ parser.add_argument("--randlora_dropout", type=float, default=0.05, help="RandLora dropout rate")
+ parser.add_argument(
+ "--randlora_target_modules", type=str, default=None, help="Comma-separated list of target modules for RandLora"
+ )
+ parser.add_argument("--sparse", action="store_true", help="Use sparse matrix multiplication")
+ parser.add_argument("--very_sparse", action="store_true", help="Use very sparse matrix multiplication")
+ parser.add_argument(
+ "--hub_model_id",
+ type=str,
+ default="path/to/repo",
+ help="Repository name to push the model on the Hugging Face Hub",
+ )
+ parser.add_argument("--push_to_hub", action="store_true", help="Whether to push the model to Hugging Face Hub")
+ args = parser.parse_args()
+
+ if args.device == "auto":
+ args.device = torch.accelerator.current_accelerator().type if hasattr(torch, "accelerator") else "cuda"
+
+ train_model(
+ base_model=args.base_model,
+ data_path=args.data_path,
+ output_dir=args.output_dir,
+ batch_size=args.batch_size,
+ num_epochs=args.num_epochs,
+ learning_rate=args.learning_rate,
+ cutoff_len=args.cutoff_len,
+ val_set_size=args.val_set_size,
+ use_lora=args.use_lora,
+ quantize=args.quantize,
+ eval_step=args.eval_step,
+ save_step=args.save_step,
+ device=args.device,
+ rank=args.rank,
+ randlora_alpha=args.randlora_alpha,
+ randlora_dropout=args.randlora_dropout,
+ randlora_target_modules=args.randlora_target_modules,
+ hub_model_id=args.hub_model_id,
+ push_to_hub=args.push_to_hub,
+ sparse=args.sparse,
+ very_sparse=args.very_sparse,
+ )
diff --git a/peft/examples/road_finetuning/README.md b/peft/examples/road_finetuning/README.md
new file mode 100644
index 0000000000000000000000000000000000000000..b9ce14017cf8dbd06e3d8d142416352ff514c7c0
--- /dev/null
+++ b/peft/examples/road_finetuning/README.md
@@ -0,0 +1,88 @@
+# RoAd: 3-in-1: 2D Rotary Adaptation for Efficient Finetuning, Efficient Batching and Composability
+
+
+## Introduction
+
+[RoAd](https://arxiv.org/pdf/2409.00119) is a novel method that adapts LLMs using simple 2D rotations. It is highly parameter-efficient,
+achieving strong performance with less than 0.1% trainable parameters.
+RoAd also supports efficient serving of mixed-adapter requests within a batch, incurring only element-wise computation overhead rather than costly batch matrix multiplications.
+Additionally, it improves model interpretability through structured and composable transformations.
+
+## Quick start
+```python
+import torch
+from peft import RoadConfig, get_peft_model
+from transformers import AutoTokenizer, AutoModelForCausalLM, Trainer
+from datasets import load_dataset
+
+model = AutoModelForCausalLM.from_pretrained("huggyllama/llama-7b", device_map="cuda")
+tokenizer = AutoTokenizer.from_pretrained("huggyllama/llama-7b")
+dataset = load_dataset("timdettmers/openassistant-guanaco", split="train")
+road_config = RoadConfig(
+ variant="1",
+)
+peft_model = get_peft_model(model, road_config)
+trainer = transformers.Trainer(
+ model=peft_model,
+ train_dataset=dataset,
+ dataset_text_field="text",
+ max_seq_length=2048,
+ tokenizer=tokenizer,
+)
+trainer.train()
+peft_model.save_pretrained("road-llama-3-8b")
+```
+
+RoAd requires a higher learning rate compared to LoRa and similar approaches, set it to around 1e-3.
+
+Run the finetuning script simply by running:
+
+```bash
+python examples/road_finetuning/road_finetuning.py --base_model meta-llama/Meta-Llama-3-8B --data_path timdettmers/openassistant-guanaco
+```
+
+RoAd also supports quantization. To use 4-bit quantization try:
+
+```bash
+python examples/road_finetuning/road_finetuning.py --base_model meta-llama/Meta-Llama-3-8B --quantize
+```
+
+### Full example of the script
+```bash
+python road_finetuning.py \
+ --base_model "PATH_TO_MODEL" \
+ --data_path "PATH_TO_DATASET" \
+ --output_dir "PATH_TO_OUTPUT_DIR" \
+ --batch_size 1 \
+ --num_epochs 3 \
+ --learning_rate 1e-3 \
+ --cutoff_len 512 \
+ --val_set_size 500 \
+ --quantize \
+ --eval_step 10 \
+ --save_step 100 \
+ --device "cuda:0" \
+ --variant 1 \
+ --road_target_modules "q_proj,k_proj,v_proj,o_proj" \
+ --hub_model_id "YOUR_HF_REPO" \
+ --push_to_hub
+```
+## Use the model on 🤗
+You can load and use the model as any other 🤗 models.
+```python
+from transformers import AutoModel
+model = AutoModel.from_pretrained("ppetrushkov/llama-2-7b-sql-road-test")
+```
+
+
+## Citation
+```
+@inproceedings{
+ liao2024in,
+ title={3-in-1: 2D Rotary Adaptation for Efficient Finetuning, Efficient Batching and Composability},
+ author={Baohao Liao and Christof Monz},
+ booktitle={The Thirty-eighth Annual Conference on Neural Information Processing Systems},
+ year={2024},
+ url={https://openreview.net/forum?id=rYjYwuM6yH}
+}
+```
diff --git a/peft/examples/road_finetuning/road_finetuning.py b/peft/examples/road_finetuning/road_finetuning.py
new file mode 100644
index 0000000000000000000000000000000000000000..0469785db44a15f622962bc3da8447390c511290
--- /dev/null
+++ b/peft/examples/road_finetuning/road_finetuning.py
@@ -0,0 +1,203 @@
+# Copyright 2025-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+import os
+
+import torch
+from datasets import load_dataset
+from transformers import (
+ AutoModelForCausalLM,
+ AutoTokenizer,
+ BitsAndBytesConfig,
+ DataCollatorForLanguageModeling,
+ Trainer,
+ TrainingArguments,
+)
+
+from peft import RoadConfig, get_peft_model, prepare_model_for_kbit_training
+
+
+def train_model(
+ base_model: str,
+ data_path: str,
+ output_dir: str,
+ batch_size: int,
+ num_epochs: int,
+ learning_rate: float,
+ cutoff_len: int,
+ val_set_size: int,
+ quantize: bool,
+ eval_step: int,
+ save_step: int,
+ device: str,
+ variant: str,
+ road_target_modules: str,
+ hub_model_id: str,
+ push_to_hub: bool,
+):
+ os.environ["TOKENIZERS_PARALLELISM"] = "false"
+ hf_token = os.getenv("HF_TOKEN")
+
+ # Setup device
+ device = torch.device(device)
+ print(f"Using device: {device}")
+
+ # load tokenizer
+ tokenizer = AutoTokenizer.from_pretrained(base_model, token=hf_token)
+
+ # IF YOU WANNA QUANTIZE THE MODEL
+ if quantize:
+ model = AutoModelForCausalLM.from_pretrained(
+ base_model,
+ token=hf_token,
+ quantization_config=BitsAndBytesConfig(
+ load_in_4bit=True,
+ bnb_4bit_compute_dtype=(
+ torch.bfloat16 if torch.cuda.is_available() and torch.cuda.is_bf16_supported() else torch.float16
+ ),
+ bnb_4bit_use_double_quant=True,
+ bnb_4bit_quant_type="nf4",
+ ),
+ )
+ # setup for quantized training
+ model = prepare_model_for_kbit_training(model, use_gradient_checkpointing=True)
+ else:
+ model = AutoModelForCausalLM.from_pretrained(base_model, token=hf_token, device_map="auto")
+ # RoAd config for the PEFT model
+ road_config = RoadConfig(
+ variant=variant, # Rank of matrix
+ target_modules=(
+ road_target_modules.split(",")
+ if road_target_modules
+ else ["q_proj", "k_proj", "v_proj", "o_proj", "gate_proj", "up_proj", "down_proj"]
+ ),
+ )
+
+ # get the peft model with RoAd config
+ model = get_peft_model(model, road_config)
+
+ model.to(device) # MODEL TO GPU/CUDA
+ tokenizer.pad_token = tokenizer.eos_token
+
+ # Load the dataset
+ dataset = load_dataset(data_path)
+
+ def tokenize_function(examples):
+ inputs = tokenizer(examples["text"], padding="max_length", truncation=True, max_length=cutoff_len)
+ inputs["labels"] = inputs["input_ids"].copy() # setting labels for a language modeling task
+ return inputs
+
+ # Tokenize the dataset and prepare for training
+ tokenized_datasets = dataset.map(tokenize_function, batched=True, remove_columns=dataset["train"].column_names)
+
+ # Data collator to dynamically pad the batched examples
+ data_collator = DataCollatorForLanguageModeling(tokenizer, mlm=False)
+
+ # Define training arguments
+ training_args = TrainingArguments(
+ output_dir=output_dir,
+ num_train_epochs=num_epochs,
+ per_device_train_batch_size=batch_size,
+ per_device_eval_batch_size=batch_size,
+ warmup_steps=100,
+ weight_decay=0.01,
+ logging_dir="./logs",
+ logging_steps=eval_step,
+ save_steps=save_step,
+ save_total_limit=2,
+ push_to_hub=push_to_hub,
+ hub_model_id=hub_model_id,
+ gradient_accumulation_steps=16,
+ fp16=True,
+ learning_rate=learning_rate,
+ hub_token=hf_token,
+ )
+
+ # Clear CUDA cache to free memory
+ torch.cuda.empty_cache()
+
+ # Initialize the Trainer
+ trainer = Trainer(
+ model=model,
+ args=training_args,
+ train_dataset=tokenized_datasets["train"],
+ eval_dataset=tokenized_datasets["test"],
+ data_collator=data_collator,
+ )
+
+ # Start model training
+ trainer.train()
+
+ # Save and push the trained model and tokenizer
+ if push_to_hub:
+ # Push the main model to the hub
+ trainer.push_to_hub(commit_message="Fine-tuned model")
+
+ # Save the model and tokenizer locally
+ model.save_pretrained(output_dir)
+ tokenizer.save_pretrained(output_dir)
+
+
+if __name__ == "__main__":
+ import argparse
+
+ parser = argparse.ArgumentParser(description="Fine-tune LLaMA with DoRA and PEFT")
+ parser.add_argument("--base_model", type=str, default="huggyllama/llama-7b", help="Base model path or name")
+ parser.add_argument(
+ "--data_path", type=str, default="timdettmers/openassistant-guanaco", help="Dataset path or name"
+ )
+ parser.add_argument(
+ "--output_dir", type=str, default="path/to/output", help="Output directory for the fine-tuned model"
+ )
+ parser.add_argument("--batch_size", type=int, default=1, help="Batch size")
+ parser.add_argument("--num_epochs", type=int, default=1, help="Number of training epochs")
+ parser.add_argument("--learning_rate", type=float, default=3e-3, help="Learning rate")
+ parser.add_argument("--cutoff_len", type=int, default=512, help="Cutoff length for tokenization")
+ parser.add_argument("--val_set_size", type=int, default=500, help="Validation set size")
+ parser.add_argument("--quantize", action="store_true", help="Use quantization")
+ parser.add_argument("--eval_step", type=int, default=10, help="Evaluation step interval")
+ parser.add_argument("--save_step", type=int, default=100, help="Save step interval")
+ parser.add_argument("--device", type=str, default="cuda:0", help="Device to use for training")
+ parser.add_argument(
+ "--variant", type=str, default="road_1", choices=["road_1", "road_2", "road_4"], help="RoAD variant"
+ )
+ parser.add_argument(
+ "--road_target_modules", type=str, default=None, help="Comma-separated list of target modules for RoAd"
+ )
+ parser.add_argument(
+ "--hub_model_id",
+ type=str,
+ default="path/to/repo",
+ help="Repository name to push the model on the Hugging Face Hub",
+ )
+ parser.add_argument("--push_to_hub", action="store_true", help="Whether to push the model to Hugging Face Hub")
+ args = parser.parse_args()
+ train_model(
+ base_model=args.base_model,
+ data_path=args.data_path,
+ output_dir=args.output_dir,
+ batch_size=args.batch_size,
+ num_epochs=args.num_epochs,
+ learning_rate=args.learning_rate,
+ cutoff_len=args.cutoff_len,
+ val_set_size=args.val_set_size,
+ quantize=args.quantize,
+ eval_step=args.eval_step,
+ save_step=args.save_step,
+ device=args.device,
+ variant=args.variant,
+ road_target_modules=args.road_target_modules,
+ hub_model_id=args.hub_model_id,
+ push_to_hub=args.push_to_hub,
+ )
diff --git a/peft/examples/semantic_segmentation/README.md b/peft/examples/semantic_segmentation/README.md
new file mode 100644
index 0000000000000000000000000000000000000000..fa23cb02cd6cca1f6e2595e0091dbd912c655ece
--- /dev/null
+++ b/peft/examples/semantic_segmentation/README.md
@@ -0,0 +1,7 @@
+# Fine-tuning for semantic segmentation using LoRA and 🤗 PEFT
+
+[](https://colab.research.google.com/github/huggingface/peft/blob/main/examples/semantic_segmentation/semantic_segmentation_peft_lora.ipynb)
+
+We provide a notebook (`semantic_segmentation_peft_lora.ipynb`) where we learn how to use [LoRA](https://huggingface.co/papers/2106.09685) from 🤗 PEFT to fine-tune an semantic segmentation by ONLY using **14%%** of the original trainable parameters of the model.
+
+LoRA adds low-rank "update matrices" to certain blocks in the underlying model (in this case the attention blocks) and ONLY trains those matrices during fine-tuning. During inference, these update matrices are _merged_ with the original model parameters. For more details, check out the [original LoRA paper](https://huggingface.co/papers/2106.09685).
diff --git a/peft/examples/semantic_segmentation/semantic_segmentation_peft_lora.ipynb b/peft/examples/semantic_segmentation/semantic_segmentation_peft_lora.ipynb
new file mode 100644
index 0000000000000000000000000000000000000000..e21503279d32fa25fc2fef95bef29c38d8431ac9
--- /dev/null
+++ b/peft/examples/semantic_segmentation/semantic_segmentation_peft_lora.ipynb
@@ -0,0 +1,1556 @@
+{
+ "cells": [
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "JAeWcsvLF2_6"
+ },
+ "source": [
+ "## Introduction\n",
+ "\n",
+ "In this notebook, we will learn how to use [LoRA](https://huggingface.co/papers/2106.09685) from 🤗 PEFT to fine-tune a SegFormer model variant for semantic segmentation by ONLY using **14%** of the original trainable parameters of the model. \n",
+ "\n",
+ "LoRA adds low-rank \"update matrices\" to certain blocks in the underlying model (in this case the attention blocks) and ONLY trains those matrices during fine-tuning. During inference, these update matrices are _merged_ with the original model parameters. For more details, check out the [original LoRA paper](https://huggingface.co/papers/2106.09685). \n",
+ "\n",
+ "Let's get started by installing the dependencies. "
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "lveGHtBcGNyc"
+ },
+ "source": [
+ "## Install dependencies\n",
+ "\n",
+ "Here we're installing `peft` from source to ensure we have access to all the bleeding edge features of `peft`. "
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "colab": {
+ "base_uri": "https://localhost:8080/"
+ },
+ "id": "lbYTKXv4ZTwg",
+ "outputId": "5a033ebd-6bbd-4bf4-802c-a1bac6a48a07"
+ },
+ "outputs": [],
+ "source": [
+ "!pip install transformers accelerate evaluate datasets==3.6.0 git+https://github.com/huggingface/peft -q"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "B0fmCvTsGPah"
+ },
+ "source": [
+ "## Authentication\n",
+ "\n",
+ "We will share our fine-tuned model at the end of training. So, to do that we just authenticate using our 🤗 token. This token is available from [here](https://huggingface.co/settings/tokens). If you don't have a 🤗 account already, we highly encourage you to do so; it's free!"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 331,
+ "referenced_widgets": [
+ "f2a722f371904cce80dc1c087b153ad6",
+ "6c88a55a635b4c9f946a1aa838d69f20",
+ "6c6d19cd893e4d82bae9972fa10c6d74",
+ "fc48ee28c2e44f1daa03149c8004c314",
+ "cb4053f102fc4207a1c9513f81ad6415",
+ "0dcc5a2866a349e0843673bef499dc66",
+ "b7431f99d93b4e9b8c8177ac4a7b4070",
+ "14ac809ba0bc4cd5bcd51f83105947b0",
+ "e7393e78f41b496495982490b72ef2a3",
+ "42a7b8268d8945b5bbe9d3f20bc8840c",
+ "554b55f29a5e4d5a81608d912d3635e8",
+ "3f69c7b15e5e48039777e4b6b1a51f53",
+ "5bcfe3da0ffb41ccbb9404ac35ae8945",
+ "21bf954f54db41e6ba78f76195721614",
+ "f83dd354396e4aa3acd214a6fd98efb2",
+ "24fde588dc1a49a397e379cda320ed71",
+ "9746875e74b845daab06619393b4d46b"
+ ]
+ },
+ "id": "OYhwMOj5ZTwm",
+ "outputId": "ff2d4cc4-4363-4093-8bdc-763761cbe3ef"
+ },
+ "outputs": [],
+ "source": [
+ "from huggingface_hub import notebook_login\n",
+ "\n",
+ "notebook_login()"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "B9Cu7j_QGVbH"
+ },
+ "source": [
+ "## Load a dataset\n",
+ "\n",
+ "We're only loading the first 150 instances from the training set of the [SceneParse150 dataset](https://huggingface.co/datasets/scene_parse_150) to keep this example runtime short. "
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 26,
+ "metadata": {
+ "colab": {
+ "base_uri": "https://localhost:8080/"
+ },
+ "id": "sGJWDwtHZTwn",
+ "outputId": "260c874e-1844-42ba-9dc2-0f727e2930cc"
+ },
+ "outputs": [],
+ "source": [
+ "from datasets import load_dataset\n",
+ "\n",
+ "ds = load_dataset(\"scene_parse_150\", split=\"train[:150]\")"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "RpSPx8EHGeLM"
+ },
+ "source": [
+ "## Prepare train and test splits"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 27,
+ "metadata": {
+ "id": "ydWKIqCUZTwo"
+ },
+ "outputs": [],
+ "source": [
+ "ds = ds.train_test_split(test_size=0.1)\n",
+ "train_ds = ds[\"train\"]\n",
+ "test_ds = ds[\"test\"]"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "yHtqAQ2WGhlR"
+ },
+ "source": [
+ "## Prepare label mappers\n",
+ "\n",
+ "We create two dictionaries:\n",
+ "\n",
+ "* `label2id`: maps the semantic classes of the dataset to integer ids.\n",
+ "* `id2label`: `label2id` reversed. "
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 28,
+ "metadata": {
+ "colab": {
+ "base_uri": "https://localhost:8080/"
+ },
+ "id": "Hu8Y4dEIZTwq",
+ "outputId": "eba72235-c1a7-4c95-8c89-5ef5588d6581"
+ },
+ "outputs": [],
+ "source": [
+ "import json\n",
+ "from huggingface_hub import hf_hub_download\n",
+ "\n",
+ "repo_id = \"huggingface/label-files\"\n",
+ "filename = \"ade20k-id2label.json\"\n",
+ "id2label = json.load(open(hf_hub_download(repo_id=repo_id, filename=filename, repo_type=\"dataset\"), \"r\"))\n",
+ "id2label = {int(k): v for k, v in id2label.items()}\n",
+ "label2id = {v: k for k, v in id2label.items()}\n",
+ "num_labels = len(id2label)"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "5V8nhdt0HBsk"
+ },
+ "source": [
+ "## Prepare datasets for training and evaluation"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 29,
+ "metadata": {
+ "colab": {
+ "base_uri": "https://localhost:8080/"
+ },
+ "id": "fNi_TKYpZTwq",
+ "outputId": "a28647b4-0deb-49cc-a1b8-c4a2ab99bb4d"
+ },
+ "outputs": [
+ {
+ "name": "stderr",
+ "output_type": "stream",
+ "text": [
+ "/usr/local/lib/python3.11/dist-packages/transformers/image_processing_base.py:412: UserWarning: The following named arguments are not valid for `SegformerImageProcessor.__init__` and were ignored: 'reduce_labels'\n",
+ " image_processor = cls(**image_processor_dict)\n"
+ ]
+ }
+ ],
+ "source": [
+ "from transformers import AutoImageProcessor\n",
+ "\n",
+ "checkpoint = \"nvidia/mit-b0\"\n",
+ "image_processor = AutoImageProcessor.from_pretrained(checkpoint, do_reduce_labels=True)"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 30,
+ "metadata": {
+ "id": "JAjiYzklZTwr"
+ },
+ "outputs": [],
+ "source": [
+ "from torchvision.transforms import ColorJitter\n",
+ "\n",
+ "jitter = ColorJitter(brightness=0.25, contrast=0.25, saturation=0.25, hue=0.1)"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 31,
+ "metadata": {
+ "id": "_HaS12U0ZTwr"
+ },
+ "outputs": [],
+ "source": [
+ "from PIL import Image\n",
+ "import numpy as np\n",
+ "\n",
+ "\n",
+ "def handle_grayscale_image(image):\n",
+ " np_image = np.array(image)\n",
+ " if np_image.ndim == 2:\n",
+ " tiled_image = np.tile(np.expand_dims(np_image, -1), 3)\n",
+ " return Image.fromarray(tiled_image)\n",
+ " else:\n",
+ " return Image.fromarray(np_image)\n",
+ "\n",
+ "\n",
+ "def train_transforms(example_batch):\n",
+ " images = [jitter(handle_grayscale_image(x)) for x in example_batch[\"image\"]]\n",
+ " labels = [x for x in example_batch[\"annotation\"]]\n",
+ " inputs = image_processor(images, labels)\n",
+ " return inputs\n",
+ "\n",
+ "\n",
+ "def val_transforms(example_batch):\n",
+ " images = [handle_grayscale_image(x) for x in example_batch[\"image\"]]\n",
+ " labels = [x for x in example_batch[\"annotation\"]]\n",
+ " inputs = image_processor(images, labels)\n",
+ " return inputs"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 32,
+ "metadata": {
+ "id": "Qyjsvup2ZTws"
+ },
+ "outputs": [],
+ "source": [
+ "train_ds.set_transform(train_transforms)\n",
+ "test_ds.set_transform(val_transforms)"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "Lu8RjicxHJiO"
+ },
+ "source": [
+ "## Evaluation function\n",
+ "\n",
+ "Including a metric during training is often helpful for evaluating your model’s performance. You can quickly load a evaluation method with the [🤗 Evaluate](https://huggingface.co/docs/evaluate/index) library. For this task, load the [mean Intersection over Union (IoU)](https://huggingface.co/spaces/evaluate-metric/accuracy) metric (see the 🤗 Evaluate [quick tour](https://huggingface.co/docs/evaluate/a_quick_tour) to learn more about how to load and compute a metric):"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 33,
+ "metadata": {
+ "id": "TMSnlebfZTwt"
+ },
+ "outputs": [
+ {
+ "name": "stderr",
+ "output_type": "stream",
+ "text": [
+ "Downloading builder script: 12.9kB [00:00, 34.2MB/s]\n"
+ ]
+ }
+ ],
+ "source": [
+ "import torch\n",
+ "from torch import nn\n",
+ "import evaluate\n",
+ "\n",
+ "metric = evaluate.load(\"mean_iou\")\n",
+ "\n",
+ "\n",
+ "def compute_metrics(eval_pred):\n",
+ " with torch.no_grad():\n",
+ " logits, labels = eval_pred\n",
+ " logits_tensor = torch.from_numpy(logits)\n",
+ " # scale the logits to the size of the label\n",
+ " logits_tensor = nn.functional.interpolate(\n",
+ " logits_tensor,\n",
+ " size=labels.shape[-2:],\n",
+ " mode=\"bilinear\",\n",
+ " align_corners=False,\n",
+ " ).argmax(dim=1)\n",
+ "\n",
+ " pred_labels = logits_tensor.detach().cpu().numpy()\n",
+ " # currently using _compute instead of compute\n",
+ " # see this issue for more info: https://github.com/huggingface/evaluate/pull/328#issuecomment-1286866576\n",
+ " metrics = metric._compute(\n",
+ " predictions=pred_labels,\n",
+ " references=labels,\n",
+ " num_labels=len(id2label),\n",
+ " ignore_index=0,\n",
+ " reduce_labels=image_processor.do_reduce_labels,\n",
+ " )\n",
+ "\n",
+ " # add per category metrics as individual key-value pairs\n",
+ " per_category_accuracy = metrics.pop(\"per_category_accuracy\").tolist()\n",
+ " per_category_iou = metrics.pop(\"per_category_iou\").tolist()\n",
+ "\n",
+ " metrics.update({f\"accuracy_{id2label[i]}\": v for i, v in enumerate(per_category_accuracy)})\n",
+ " metrics.update({f\"iou_{id2label[i]}\": v for i, v in enumerate(per_category_iou)})\n",
+ "\n",
+ " return metrics"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "r304cnpxHxp5"
+ },
+ "source": [
+ "## Load a base model\n",
+ "\n",
+ "For this example, we use the [SegFormer B0 variant](https://huggingface.co/nvidia/mit-b0). "
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 34,
+ "metadata": {
+ "id": "Krvppe44a_7y"
+ },
+ "outputs": [],
+ "source": [
+ "def print_trainable_parameters(model):\n",
+ " \"\"\"\n",
+ " Prints the number of trainable parameters in the model.\n",
+ " \"\"\"\n",
+ " trainable_params = 0\n",
+ " all_param = 0\n",
+ " for _, param in model.named_parameters():\n",
+ " all_param += param.numel()\n",
+ " if param.requires_grad:\n",
+ " trainable_params += param.numel()\n",
+ " print(\n",
+ " f\"trainable params: {trainable_params} || all params: {all_param} || trainable%: {100 * trainable_params / all_param:.2f}\"\n",
+ " )"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "q_Wwl_ewID9I"
+ },
+ "source": [
+ "We pass the `label2id` and `id2label` dictionaries to let the `AutoModelForSemanticSegmentation` class know that we're interested in a custom base model where the decoder head should be randomly initialized w.r.t our custom dataset. Note, however, that the rest of the model parameters are pre-trained and will be fine-tuned in a regular transfer learning setup.\n",
+ "\n",
+ "We also notice that the 100% parameters in the `model` are trainable. "
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 35,
+ "metadata": {
+ "colab": {
+ "base_uri": "https://localhost:8080/"
+ },
+ "id": "kcdLdvIlZTwt",
+ "outputId": "a6b71dce-905e-4389-dcf6-46b43e769fcc"
+ },
+ "outputs": [
+ {
+ "name": "stderr",
+ "output_type": "stream",
+ "text": [
+ "Some weights of SegformerForSemanticSegmentation were not initialized from the model checkpoint at nvidia/mit-b0 and are newly initialized: ['decode_head.batch_norm.bias', 'decode_head.batch_norm.num_batches_tracked', 'decode_head.batch_norm.running_mean', 'decode_head.batch_norm.running_var', 'decode_head.batch_norm.weight', 'decode_head.classifier.bias', 'decode_head.classifier.weight', 'decode_head.linear_c.0.proj.bias', 'decode_head.linear_c.0.proj.weight', 'decode_head.linear_c.1.proj.bias', 'decode_head.linear_c.1.proj.weight', 'decode_head.linear_c.2.proj.bias', 'decode_head.linear_c.2.proj.weight', 'decode_head.linear_c.3.proj.bias', 'decode_head.linear_c.3.proj.weight', 'decode_head.linear_fuse.weight']\n",
+ "You should probably TRAIN this model on a down-stream task to be able to use it for predictions and inference.\n"
+ ]
+ },
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "trainable params: 3752694 || all params: 3752694 || trainable%: 100.00\n"
+ ]
+ }
+ ],
+ "source": [
+ "from transformers import AutoModelForSemanticSegmentation, TrainingArguments, Trainer\n",
+ "\n",
+ "model = AutoModelForSemanticSegmentation.from_pretrained(\n",
+ " checkpoint, id2label=id2label, label2id=label2id, ignore_mismatched_sizes=True\n",
+ ")\n",
+ "print_trainable_parameters(model)"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "4yhyYVTCInF0"
+ },
+ "source": [
+ "## Wrap `model` as a `PeftModel` for LoRA training\n",
+ "\n",
+ "This involves two steps:\n",
+ "\n",
+ "* Defining a config with `LoraConfig`\n",
+ "* Wrapping the original `model` with `get_peft_model()` with the config defined in the step above. "
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 36,
+ "metadata": {
+ "colab": {
+ "base_uri": "https://localhost:8080/"
+ },
+ "id": "YPg4W5eFB__n",
+ "outputId": "9995eb44-1c30-43e7-cc4e-691ecb1b1878"
+ },
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "trainable params: 566422 || all params: 4317068 || trainable%: 13.12\n"
+ ]
+ }
+ ],
+ "source": [
+ "from peft import LoraConfig, get_peft_model\n",
+ "\n",
+ "config = LoraConfig(\n",
+ " r=32,\n",
+ " lora_alpha=32,\n",
+ " target_modules=[\"query\", \"value\"],\n",
+ " lora_dropout=0.1,\n",
+ " bias=\"lora_only\",\n",
+ " modules_to_save=[\"decode_head\"],\n",
+ ")\n",
+ "lora_model = get_peft_model(model, config)\n",
+ "print_trainable_parameters(lora_model)"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "4M3wYekOI95X"
+ },
+ "source": [
+ " Let's unpack what's going on here. \n",
+ "\n",
+ "In order for LoRA to take effect, we need to specify the target modules to `LoraConfig` so that `PeftModel` knows which modules inside our model needs to be amended with LoRA matrices. In this case, we're only interested in targetting the query and value matrices of the attention blocks of the base model. Since the parameters corresponding to these matrices are \"named\" with `query` and `value` respectively, we specify them accordingly in the `target_modules` argument of `LoraConfig`. \n",
+ "\n",
+ "We also specify `modules_to_save`. After we wrap our base model `model` with `PeftModel` along with the `config`, we get a new model where only the LoRA parameters are trainable (so-called \"update matrices\") while the pre-trained parameters are kept frozen. These include the parameters of the randomly initialized classifier parameters too. This is NOT we want when fine-tuning the base model on our custom dataset. To ensure that the classifier parameters are also trained, we specify `modules_to_save`. This also ensures that these modules are serialized alongside the LoRA trainable parameters when using utilities like `save_pretrained()` and `push_to_hub()`. \n",
+ "\n",
+ "Regarding the other parameters:\n",
+ "\n",
+ "* `r`: The dimension used by the LoRA update matrices.\n",
+ "* `alpha`: Scaling factor.\n",
+ "* `bias`: Specifying if the `bias` parameters should be trained. `lora_only` denotes only the LoRA `bias` parameters will be trained. \n",
+ "\n",
+ "`r` and `alpha` together control the total number of final trainable parameters when using LoRA giving us the flexbility to balance a trade-off between end performance and compute efficiency.\n"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "XTF68xfjJEci"
+ },
+ "source": [
+ "We can also how many parameters we're actually training. Since we're interested in performing **parameter-efficient fine-tuning**, we should expect to notice a less number of trainable parameters from the `lora_model` in comparison to the original `model` which is indeed the case here. \n",
+ "\n",
+ "For sanity, let's also manually verify the modules that are actually trainable in `lora_model`. "
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "colab": {
+ "base_uri": "https://localhost:8080/"
+ },
+ "id": "PUe1Gzvd1PEP",
+ "outputId": "7b8ba17f-01fd-4ab4-d703-9a0c01cff31b"
+ },
+ "outputs": [],
+ "source": [
+ "for name, param in lora_model.named_parameters():\n",
+ " if param.requires_grad:\n",
+ " print(name, param.shape)"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {},
+ "source": [
+ "We can confirm that only the LoRA parameters appended to the attention blocks and the `decode_head` parameters are trainable."
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "rX75AyI7JYVC"
+ },
+ "source": [
+ "## Train!\n",
+ "\n",
+ "This is a two-step process: \n",
+ "\n",
+ "1. Define your training hyperparameters in [TrainingArguments](https://huggingface.co/docs/transformers/v4.26.0/en/main_classes/trainer#transformers.TrainingArguments). It is important you don’t remove unused columns because this’ll drop the image column. Without the image column, you can’t create `pixel_values`. Set `remove_unused_columns=False` to prevent this behavior! The only other required parameter is output_dir which specifies where to save your model. At the end of each epoch, the `Trainer` will evaluate the IoU metric and save the training checkpoint.\n",
+ "2. Pass the training arguments to [Trainer](https://huggingface.co/docs/transformers/v4.26.0/en/main_classes/trainer#transformers.Trainer) along with the model, dataset, tokenizer, data collator, and `compute_metrics` function.\n",
+ "3. Call `train()` to finetune your model.\n",
+ "\n",
+ "\n",
+ "**Note** that This example is meant to walk you through the workflow when using PEFT for semantic segmentation. We didn't perform extensive hyperparameter tuning to achieve optimal results. "
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 1000
+ },
+ "id": "K6HVcNkDZTwu",
+ "outputId": "1b28a072-0e16-4b1a-ec32-d78e93630ef3"
+ },
+ "outputs": [],
+ "source": [
+ "model_name = checkpoint.split(\"/\")[-1]\n",
+ "\n",
+ "training_args = TrainingArguments(\n",
+ " output_dir=f\"{model_name}-scene-parse-150-lora\",\n",
+ " learning_rate=5e-4,\n",
+ " num_train_epochs=50,\n",
+ " per_device_train_batch_size=4,\n",
+ " per_device_eval_batch_size=2,\n",
+ " save_total_limit=3,\n",
+ " eval_strategy=\"epoch\",\n",
+ " save_strategy=\"epoch\",\n",
+ " logging_steps=5,\n",
+ " remove_unused_columns=False,\n",
+ " push_to_hub=True,\n",
+ " label_names=[\"labels\"],\n",
+ ")\n",
+ "\n",
+ "trainer = Trainer(\n",
+ " model=lora_model,\n",
+ " args=training_args,\n",
+ " train_dataset=train_ds,\n",
+ " eval_dataset=test_ds,\n",
+ " compute_metrics=compute_metrics,\n",
+ ")\n",
+ "\n",
+ "trainer.train()"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "dacaBLE6KLdu"
+ },
+ "source": [
+ "## Saving the model and inference \n",
+ "\n",
+ "Here we use the `save_pretrained()` method of the `lora_model` to save the *LoRA-only parameters* locally. However, you can also use thr `push_to_hub()` method to upload these parameters directly to the Hugging Face Hub (as shown [here](https://colab.research.google.com/github/huggingface/peft/blob/main/examples/image_classification/image_classification_peft_lora.ipynb)). "
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 40,
+ "metadata": {
+ "id": "pvkLkrQo-6l6"
+ },
+ "outputs": [],
+ "source": [
+ "model_id = \"segformer-scene-parse-150-lora\"\n",
+ "lora_model.save_pretrained(model_id)"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "Ur8n41kBK4uj"
+ },
+ "source": [
+ "We can see that the LoRA-only parameters are just **2.2 MB in size**! This greatly improves the portability when using very large models. "
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "colab": {
+ "base_uri": "https://localhost:8080/"
+ },
+ "id": "grzLeOT-__ht",
+ "outputId": "1ce26a27-2f38-43f3-9454-8ba11f2cfc59"
+ },
+ "outputs": [],
+ "source": [
+ "!ls -lh {model_id}"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "KFYC6Z3FLB5F"
+ },
+ "source": [
+ "Let's now prepare our `inference_model` and run an inference. "
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "colab": {
+ "base_uri": "https://localhost:8080/"
+ },
+ "id": "T7zeMQTaACur",
+ "outputId": "762b7fbc-07d4-4572-f107-c836e3e7928a"
+ },
+ "outputs": [],
+ "source": [
+ "from peft import PeftConfig, PeftModel\n",
+ "\n",
+ "config = PeftConfig.from_pretrained(model_id)\n",
+ "model = AutoModelForSemanticSegmentation.from_pretrained(\n",
+ " checkpoint, id2label=id2label, label2id=label2id, ignore_mismatched_sizes=True\n",
+ ")\n",
+ "# Load the Lora model\n",
+ "inference_model = PeftModel.from_pretrained(model, model_id)"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "2L1R0LDWLImd"
+ },
+ "source": [
+ "Fetch an image."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 43,
+ "metadata": {
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 444
+ },
+ "id": "lwjRvZOmA7Hh",
+ "outputId": "44ab267d-e2b9-4bda-a52b-91968eabce29"
+ },
+ "outputs": [
+ {
+ "data": {
+ "image/jpeg": "/9j/4AAQSkZJRgABAQAAAQABAAD/2wBDAAgGBgcGBQgHBwcJCQgKDBQNDAsLDBkSEw8UHRofHh0aHBwgJC4nICIsIxwcKDcpLDAxNDQ0Hyc5PTgyPC4zNDL/2wBDAQkJCQwLDBgNDRgyIRwhMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjL/wAARCAGrAoADASIAAhEBAxEB/8QAHwAAAQUBAQEBAQEAAAAAAAAAAAECAwQFBgcICQoL/8QAtRAAAgEDAwIEAwUFBAQAAAF9AQIDAAQRBRIhMUEGE1FhByJxFDKBkaEII0KxwRVS0fAkM2JyggkKFhcYGRolJicoKSo0NTY3ODk6Q0RFRkdISUpTVFVWV1hZWmNkZWZnaGlqc3R1dnd4eXqDhIWGh4iJipKTlJWWl5iZmqKjpKWmp6ipqrKztLW2t7i5usLDxMXGx8jJytLT1NXW19jZ2uHi4+Tl5ufo6erx8vP09fb3+Pn6/8QAHwEAAwEBAQEBAQEBAQAAAAAAAAECAwQFBgcICQoL/8QAtREAAgECBAQDBAcFBAQAAQJ3AAECAxEEBSExBhJBUQdhcRMiMoEIFEKRobHBCSMzUvAVYnLRChYkNOEl8RcYGRomJygpKjU2Nzg5OkNERUZHSElKU1RVVldYWVpjZGVmZ2hpanN0dXZ3eHl6goOEhYaHiImKkpOUlZaXmJmaoqOkpaanqKmqsrO0tba3uLm6wsPExcbHyMnK0tPU1dbX2Nna4uPk5ebn6Onq8vP09fb3+Pn6/9oADAMBAAIRAxEAPwD2LFFGaTNMQYptOzSUANIpCKWkoGNNIacaaaAG0lONNoAKSikoAKKSigBaM03NGaAHZpc0zNLmgB2aXNMzS5oAdmlzTM0ZoAkBozTM0ZoAkzS5qPNLmgB+aXNMzRmgQ/NLmmZozQMkzRmmZozQBJmjNR5pc0CH5ozTM0uaAH5ozTM0ZoAfmjNMzRmgB+aM03NJmgB+aM0zNGaAH5pM0zdRmgB2aTNNzSZoAeTSZpmaTNAD80mabmkzQMdmkzTc0maAHZpCabmkzQA7NJmmk0hagB2aTNMzRmkApNJmkzSE0ALTc0hamlqAFJpCaaWpuaAFJpCaaWppNADiaaTTSaaTQApNNJoJphNACk0wmgmmk0ABNMJoJphNAxSaYTQTTTSuAhNRtTjTTRcDtw9G6sq11zS7zAt7+BmP8JbafyNX85GRyPWmmnsDTW5Nuo3VDupN9MRNmo3njQ4ZuabvqGeESncDtb19aQEv2qE/x4+tPEit91gfxrJlSSP7yHHqORVX7QoOVb8jTA6DNITWPFqZQgMdw9O9am7IBHekA40hNJmm5oGOzSZpuaM0AOzRmmZozQA/NGaZmjNAD80ZpmaM0CH5pc1HmjdQBJmjNMzRmgCTNLmos0u6gCXNGaj3UuaAJM0ZqPNLmgB+aXNR5ozQBJmjNMzRuoAkzRupmaM0AP3Uu6o80ZoAkzS5qLNLuoAfmjNMzRuoAfmkzTM0ZoAfmjNMyewzQcjqCKAHZpM03NJmgB2aM0zNGaAHZpM03NJmgB2aTNNLU3dQA8tTd1NzSZoAdmjNMzSbqAH5pC1RlqQtQA8tTS1MLUhNIBxamlqaTSE0DHFqaWppNITQApNNJpCaaTQA4mmlqQmmk0AKTTSaQmkJpXACaaTRmkoGJSEUtJRcBuKTaafSgUrgReWaPJJqbbRwKAPOygParFtfXtmc213NF7K5A/Km7aTbXkJtbHqtJ7mzb+MdZgxvljnHpIgz+YxWpb+Pu11YEf7UT/0NciVppWtY16i6mTowfQ9Gt/GGj3GA07Qse0qEfqOK1Ib+0uP9TdQyf7rg15Ey4FRbdpypIPqOK2ji5dUZSwy6M9n3H1pjBG+8in6ivKLXW9UsyPJvZcD+FjuH61rQeN9Si/18MEw9gVNbLEwe5m8PNbHfqsSnKxID7CpPMrkbfxzYycXFvNCfUfMK1LfxBpV1gR3sQJ7Odp/WtVVg9mZunJbo2vMo3CqqyB13IwYeoOaXeaq5FizupN1V/MpfNphYn3Ubqg8yjzKAJt1G6od9G+gCbdRuqHdRuoETbqN1Q76XdQBNuo3VFupd1AEu6l3VFupd1AEuaM1Fuo3UATbqN1RbqN1AEuaXNRbqXNAEmaXNRBqXNAiTNLmos0u6mBJmjdUe6jdQBJuozUe6jdSAkzRuqPdSbqAJN1G6o91JmgZTmur1WKgMvuozmn2z3juDIzBO+7vVndRmlYCTdSbqjzRupgSbqQtUe6kzQA/dSbqbmkzQA/NJmmbqbuoAkzSFqjLU0mgCQtTd1MzSE0AP3U0tTSaTNADi1ITTc0hNIBxNITTSaaWouMcTSZppNJmi4Ck0hNJmkzSuAE0maDSUXASkNLRSuMSkpaMUXAbRT9tAWlcdhuKcFp2AKUc0rhYTHpShKeq1IBRcDzikxS0Yryz1BMUmKSR1jRnbhVGTUgt7h7P7WkZaHGSR2p2JbS3IH61HjJp4kSRA6sCCM0EhRmmG5FtFJtp2QelLjigREUppjB7VNikxQMSGe4tm3QTyRn/YYitKHxPrEH/LyJB6SKDWaRSEU1KS2ZLjF7o6S38bzLxc2at7xtj+dakHi7S5uHeSE+jrx+YrhStNKVosRUXmZuhBnqEGoWlyMwXUUn+64qfca8l2YORwfarUGpX9qf3F3MvtuyPyNarFd0Q8P2Z6hvpfM964K38XajFxMsU49xtP6VpQ+MrZgBPayxn1QhhWqxEH1MnRmuh1fmU7zKxIPEGl3HC3aoT2kG2tFJEkG6ORXHqpzWqmnszNxa3LQel31XyRS7qYrFjdTt9Vw9LvoCxY3Uu+q++l30xFjdRuqENS7qAJt1LmoQ1LuoAl3U7NQhqXdQIl3Uu6od1G6gCbdRuqHdRvoAm3Ubqh30u+i4Eu6jdUO6jdRcCbdRuqLdS7qAJM0ZqPdSbqAJN1G6o91GaAH7qM1Huo30ASZpM1HvpN1AEm6kzUe6k3UASZpCaZupM0AOJpM03NIWpDHZpM03NITRcB2aQmm5pM0XAcTSZpM0maBik0maMim5pXAXNGaQmkzSuAuaTNJRRcYUUUUrgGKMUZozRcAxS4pM0FgKVxjqQmmbs0A0rhYdTgaZkUoNK4yZTUgqq1xDEP3kqJ9WqtJrllHwrNIf8AYWjmS3CxxmKQ07FGK809IgmTfGynoRiiXxJqFvof9lQ2yYA2mRTjeO2alIzULxA9qpMiUVLcoWGoTWFntubWGYqkgUovzAlSAD6jJr0TwUbS8tXCRxyItvCHyoOGwciuDkg+U8V2Pw0tobcayYXDqzwkkHodpyK3ou8zGpGy0OjuPCui3By1msbHvGStZlx4Dsn/ANRdTRnsGAaun3EAE84NLuw34V0unF7owVSS6nB3HgO+XmC6gkHowKmsufwtrNvnNkzj1jYNXqAYNjHelDcnBqHQiy1Xl1PG5rS6gOJraaP/AHkIqD/OK9q3Z2hgDnrmuM+IRsLTTrSWWEozzFd8K/N07+1ZTo8qumaRr3eqOIpMVGl1p8vEeoBT6SriphEzcxSQzD/YcVhY050MIppFSNHKn3oXHuBmo/MToTg+4xSKuhCtNK1JkHoQfpSEUhkRUUqM8R3RuyH1U4p+KTFAy7Br2q233Lt2A/hk+YfrWnB4zul4uLWKQeqEqa54ikxVKrOOzIdOL6HaweL9Ok4lWWE+65H6VqW+q2F0Mw3kLH0LYP615qRTSorVYqa3M3h49D1gE4z1HqKN1eWw3d3bHMFzLH/uua04PFOqwYDukwH99efzFaxxcXujN4eXQ9A304PXHweNFOBcWbD1MbZ/Q1pQeJ9KnwDOYj6SKRW0a1N7MydKS6G+HpweqUF1BcLmGeOQf7DA1NuIrRMixYDUu6q2+gSU7isWd1Luqt5lLvouFixvo31X30u+i4E26l3VBuo30AT76XfUG+jfRcLE+6jdUO6jdQIm3Uu6od1G6lcCXdRuqLcKQtQBLmmk1HvpC9AEm6k31Huo3UXAk30bqhzRmgCXdRu96h3Ub6LjJt1JuqLdRvpXAlzSZqPfSbqLgSZpM0zdSbqLjH7qTNM3UhalcCTNJmojJSGSgCbNG4VXMlJvoAnLCjfUG8etJ5oHekMn3UbqreeKY95Gn3pFX6mlcLFzdRvxWY+q269GZ/8AdFVn1pj/AKuED3Y1LmkVys2y/pSE45YgD3rnX1K7k/5abR/sjFV3Z5Dl3Zj7ms3VRSidHJf2sX351+i81Vk1uBf9XE7n34rE204LUOox8qL8mtXL/wCrRE/DJqpJd3U3+sncj0BwKZtpcVLk2OyGBOcnk1IFpQKcBUjKOKTFPpMVidg3FNK1JikIpgQMnFdn8P0C2OoEADMy9B7VyJHFdn4FGNNvf+uw/wDQa3ofGY1vgZ0xHy0Y7+1OA+WgDg12nCMjWoUJ3SL78VajXiquD9pYepoYyTGJVHbbXJ/EiFZNOsCRyJm/9BrsNv75fpXKfEIj7FYL6ysf0rKr8DLp/EjzN7JGHKg/UVXOmRZyq7T/ALPFbG0GkKCuM7bIykhu4P8AU3cy+xbIqYX+pIMP5Mw/20xV/wAsU0xCk2LkRRbUAf8AW6cM+sTYpgv7Xu9zD7Mu4VdaEelRtbKf4aVxcnZkaXMMn+ru4HPo3ymrNrDNdSvGqDcsbSAq2QcDOKpSWETdUB+orMNvc22oOto7RK42lgeg700kxPmRuuHSVomikEikhl2nIx1pFw65ByKTTta1jSJWkicXO8MCJucFupFJbeaUZ5god2LEL0GalpFxbvqKRRipSKTFQWRYpNtS4pCKAIitNKVNtpCKQEIUqcqSp9QcVcg1nU7X/V3suB2Y7h+tVyKQimpNbMlpPc3IPGF7HxPBFMPUfKa0ofGNi+BNBPEfUYYVx5FNK1tHEVF1M3Rgz0W31zTbnHlXkWT/AAudp/WrwfcMqQR6g5FeVFBT4p7i2bME8kZ/2WIrWOLfVGbw/ZnqW+l8yvPoPE+qwYDSrMP+mi5P5itGHxmOBcWZHqY3/oa2jiYMzdGSOx82jzKwYPE+lzYBnMR9JFI/WtGK7guBmGaOQf7LA1qpxlszNwa3L2+l3+9VC5FHm1VxWLe/3pfMqn5tHm0CLvmUb6p+ZThJ70AWt9JvquJKPMFAWJ99G6oPMFJvoCxPuo3VX30b6VwsWN1JuqDfR5lFwJ91JuqAyU3zfei4FjdSbqrmUUwzUgLe+k8yqZmJ70xn3daALzShfvMB9TVO51aC1++JCfZcD86r+SFyY2KZ/GlKBl2yMWHoelFx2KU/iK4f5bS3TPq+SaWy1HWmfM0KSRnswxj6Yq3vtrcYHlp9KjfUYl+7ub6Ck5JAomj5wZQSpRu4zmk8z3rIfUnP3IwPqaha7nf+PA9uKh1EVys22mA6n86ge+hTrIPw5rGO5vvMT9TQFqHV7Fchovqa/wACsfrxVd7+dvugKPzqvilxUucmPlQNLM/3pGP40wCpMUYqL3HYbjikxTiQKVY5JD8kbt9BQAgFOFWI9NvH/wCWe0f7RxU66Q6jMs6j2UZo5WBRxSOyRqWdgqjqScCqHiG4OnOFhuCqbow5KZYKxIJFc/I+rG5hkuoDe2qH5UHG73IpWA6+KWOVd0bq49VOaeKoWCg4kS1+zAqAUz1PrWgKQxRThSCnCgClikIp1GKxR2DcU0in4pCKoBjDiuz8Df8AILu/+u//ALKK41h1rsvA3/INvR/02H/oNbUPjMq3wM6delLjg0i07tXccA6MfLVUj/SjVtB8tVZBi6HvSaBFgD94Kp6npcWprGJrQXCJn8M1eQfMat2g+Vz71UYqUrMmUnGN0cVP4P01s/6PPCf9lj/Ws+XwVbk/ur2RfZ0B/lXpuKhEaNPLuRTnHUVo8PB9DOOJqI8rl8GXif6m5gk+uVNUpfDOrRf8uu8eqMDXsDWVs3WFfw4qJtLtj03r9GrKWDg9jWONktzxWbTryE/vbSZfqhqqyFeCCPrXuDaUP4J2HswzVWfQRMMOkEo/2kFZSwPZmqxq6o8X2g1GbdPNL859M8V6VrPhnT0sLphapFNGhZWjJGCK89x2rjq0nTdmddKoqiuiDYKNtSkU3FYmozFJinkVXvneGzlkQ4YDg0krsHoS4pCK5SXxFqVpLtYRTLjIJUg498VNF4xU/wCusz9Y3zWzw9RGSrQOkxSEVkx+KNNf75kiP+0lXItW06f/AFd5ET6FsfzrN05rdFqcXsyyRTcU5WVxlGVh7HNLtqCiMimkVKRSEUARYpCtSEUhFAiErTStTEU0igCAoKaAVOVJB9RxU5WmstMRPDrOp22BHeSkDsx3D9a0IfF96mBNBDKPUZU1ikVGRWkak1syHCL3R1sHi+yfAnhmiPqPmFacGs6fc4EV3ET6Mdp/WvPSKYVFaxxM1uZujF7HqAkyMjkeopfOrzGK4ubc5gnkj/3WIq/D4k1OHhpElH/TRf6itViY9UZui+h6AJacJM1x0PjBeBcWjA9zG2f0NX4fEunzf8vHln0kUitVVg+pDpyXQ6EyoDguoPpmlEydA65+tYym2nJeKRW3HJ8t85p6pEjhtpJHTcc4q7kWNfzKQyj1rP8AtHvR549aLhYv+ZSeZVHz6RrgKOWA+ppXHYvGT3ppes1r+Jf48/QVC2o5+4h/E1LmkHKaxkppesg3s7dCF+gqIs7nLOW+pqXVXQrlNdrqJOsi/hzULajGPuqzfpWeFpQtQ6jHyotNfyt91VX9ahaWWT70jfSmgYpalybHZDQtPC01nRBlmCj3OKrSavYQ/euUz6A5/lUjLmKUCsSbxPZp9wO34Bf51UfxNLIcQW+foC38qAudNijIHU1zH23Wrj7kLqD7BaT+zNVuf9bMqg+rFqAOikvbaL78yD8apza/ZRdGZ/8AdWs+Pw4T/rbmQ/7gC1Zj8O2CnLRGQ+rsTTsIqy+LEBxDDk+7f0FbHhO8Os306XkLBFQFAFKg88896IrC3hH7uFF+i1q6IuzU+B1Q9Ka3A2UtoIm+S3Qc46ZqXLjIAwPapMEsfrSlCQ9aBcrkMwOT6EUrjPU9c0/bhAKZJxtpAcn4stknm0+QKxKlg+0ZODj+tSRx/IuR2FX775pk9garheKxe5YiringUAUtIQopwpBSigCpikxTqSsjsG4op1IRTEMYV2Hgf/jwvf8ArsP/AEGuRI4rrvBB/wBBvR/01H8q2o/GZ1fgZ06089KYtSHpXacDHp0qpPxcqatr92ql1/rVpsS3LMfUmr1iMxufeqMRyua0dPH7hj/tVcPiJn8JNtqJV/fyfQVZIqMD98/0Fb3OewmKTFSYpMUXFYZijFPxRincVjn9bXNveD/pk38q8eI5P1r2XWlzFdj1iP8AKvHCPmP1ry8b8SPUwXwsjIpuKkPWm1wnaMIqrqXGnzf7tXDVTUh/xL5/92iO6E9jK0ZB9puQQCPLTr9TVmWDTZyRLbRE+6CoNGH+kTn1iX+ZrtrTwXFfaZDd4O6VA3BrvnKxyQhzdTh5NB0mUfLHsz/cciqcvhS0f/VXMi+zANXfS+B2SQFQQB1GK6Dw3oEFpp81reW8M5ExZTIgJAIHc1Krdi5UUlc8XPha7hObe8X82X+VIbTxFajMc8jKPSQN/OvepPCehz9bFUPrGzL/ACNcR4p0q20fU/s9p5nlNCHw7biCSf8ACnz33Rla2zOS0G7u7oXKXbh3iZQCBjqM1Ffa7LYytutlkiDbchsEU7w+P9J1H/rov/oNNCK+p4dQymZuCM9jWShF1GmtDZykqaaYyLxXYv8A6yKZPwyKtx67pkvS7RT6OCKnbQra5XcNORweMovP6VQuPC1lzmGeE+xP9abpUn5E89RGmk8EwzHNG/8AusDTyK5qTwtFnMN4yn/aUf0pn9i6vb/8e99kdsSEVLw66SH7d9UdMRTWFY+ky6iuoG2vpd/7ssBwccgda2iKwnBwdmbRlzK5Vn3AfLUH22yis5EuFuRemUbGUAoE78etXmXNVp7YSbeBwaItdRSTa0Ibq7s4GjEVyJA4JyylcDOBn69aYtzGwyCD9CDUv2aMLtCjFQPYQsc+WAfUVV4k2kSeYh6N+fFB5qubV4/9XNIvtnI/WlsYppdYtIGZSJJlUnb6n2ppJ7Cba3RIcUwgV6bd+FtGuGb/AEXyjnrExX9KyZ/Alu7H7Neyp7OoYf0p8jDmRww3IcoxU+oOKtRaxqMAAS6cj0f5v50t1YSW29vMiljV/LLo4PzYzjHWqZFSm4jsmbEXiu6j/wBdBHIPVSVNba6i8iKyoBuGeTmuGkHy11tv/qIv90fyraFST3ZjOKRcNxO/WQj2HFNAzySSfemrTxxVNkigU8YrEl1kpcbMqAJCrIEYsij+I9sGuqtbS1mtYp1LSK6hsk+opDKQIHelZ1jjaRjtRRlmPQVrrBFGMrEg/Co9StlutJuIXGUdOQOKLBY56TXtPj/5bbv90ZqlJ4phyRDC7n6/4Zq1BoNhGoP2dWPq3NX47OCPASJF+gxQIwP7Z1W5P+j2bKPXZ/jS+Rr9z96URg/7WP5V0wjA7U4Lii4WOYXw1cStuuL1j9Bn+dW4vDFov+sMkn+83+Fboxn3pwHsfxFA7GZFo1jD9y2jz6kZq4lvGg+VQPoKnxV6z0m6vYw8YXBOAOSTQk27ITstzOCD0pdgrpYfB2oSY3I4/AL/ADq/D4ElP+tdV+r5/lWqoVH0M3Vgupxm0CgYJ45+lehw+B7VceZIp+iZ/nVtfDVhbzQKA5DE56DPHtWiwsurIeIj0PNlglYfLE5/4DV3SbeaK+3Om0FSOTXpqaPp8fS1jP8Avc/zqprsEMOl5jijTDj7qgVTwqSvcUa/M0rHPRx5XNOMfBqWAZipzjg1nymtzPdeRUE33qtOP3mKpzH5jUstGRdD98p9qiAqa4/1w/3aiFcz3LYYooopiFFOFNFOFAFXFJTqKyOwbijFOAoxTEMbpXVeBz+4vl/21P6GuWIrp/BJwL9fdD/OtqPxmdX4GdYtPPSmLT+9dqOBjx92qd199auHpVK6++tD2Ety1D/qRWlYki3/AOBVmRf6oVqWQ/0YfU1pT+Iip8JY3VEr/wCkOP8AZFSYqJf+PqT/AHB/WtjEmzRxSYooELSYoooAxtYHyXI/6ZH+VeMsMO31Ne0av924/wCuR/lXjL/6x/8AeNebjd0elgtmRmmmnd6SuE7RtVdRH/Evn/3TVs1V1H/kHT/7hoW4PYy9HybqbP8AzyX+Zr2rw+P+Kc07kf6ha8P05itw5U9Yh/M13mmeL9Os9ItoJTMZYkCuFTv+dd0nZnGo3R6Nge1RFFEpIxk9a5KDxTaXAysF0BnGSoH9a1I7xZWACSDPc4qHOI/ZSRuDA7ivO/HvOvIP+nZf5tXZqoOPm6+1cp4o0w3GrFzcQoBbD7zcnrTTu9CWrHnPh8YuNS/66r/KnRr/AMTJPUzt/I0aB/x9al/11X+VaGjQRXHiS2jndUjM0mWPH8JpL+Iy3/DR0OnQq2njfleGO4depqZInS2l27i+MhvQf413GkaRY/2WgVo5Fyw3A9eamOl2cX3V/AE0SpMuNaNrEK2Fnc20fn2kEmUB+eMHtXO+KdC0y00Sa6trKOKZWUBkyOrDPHSuoaV4wAq8AY5rnvF08j+HplJAy6dPrU7GWp5WgI8RHP8Az7n/ANCFaRFZ0Q/4n/8A27n/ANCFaRFZVviN6fwjMVd0XTTq+s21iAx81iDt64AJ/pVMiuk8AD/iuNO+r/8AoDUqUVKaTCo3GDaL918N50yY5ZVH+3Ef6Vj3HgfUos7Hhf2zg/rXvxODUMyI7xB0VhuPUZ7GvTeEps89Yqa3PnS48NatACWs3YDunP8AKoNG0y5j8U6d51vIg89SdykdK+jZdMsZvv2sZ+gx/Ks2/wBCsYbZ7iJHV4xuHzZH61lLCJaplrFN6NHHSxkSke9QlSwkTJGUYVqTx/vT9aohf3zD2NYtGqZ4ukCIxIUbvWnEVIRhm+pphrmOghk+7XWwDEEf+6P5VycnSuuiH7mP/dH8q0pmcyQCpAKatPFaGZG8SnJ2jJ74rftkCWMAAxiKsRuldAi4tbX3gFNAPMZ2pgdasS2rSWsqKMsUwKeiAiKt7REH9qQZGRu7/SqUbuxMpWVzkoPDt9KAFj/JSa0IfBmoyYzHIP8AgIH8zXqPTpSGutYaCOV15Hntv4GnaQrIVBXGd0nr9K1IfAsC/wCslT/gKZ/nXUp/x8Tf8B/lUlaKlBdCHVm+phw+FNOi6+Y34hf5VyPjKxt7DVYY7aPYrQhjyTk5NelV5549/wCQ3CP+mA/maiukqbsXRbc9TlK7fwwMC3GOslcT3rufDA+a3/3zXLh/jN63wHZmkp2KTFekcNhMVBKP9Kt/+BfyqxioZB/pUH0agLEmKyvEf/IJ/wC2i1r4rK8SD/iTsf8AbX+dTP4WXTXvowLXmM1JJ0qKx5Q/Wp5eBXJ0OrqZrf641Sl+81XGP796pSH731rGRqjLuP8AWj/dqOpJyDMcdgM1HXO9zQSiikpkiinCmCnA0ARdqbS5pM/nWR2Du1JRmg1QhpqzpXiez8NTTNeRTOk4AXygDgj1yfeqpNc/4i6Q/U1pT+JGdT4Wegp8T/D5wSl6o/65D/GrCfErw2xBMl0v1gNeMgCnDG3Brr5mcnIj2wfEXw0/H2uYfWBqrTePfDM0m1dTVSD/ABoy/wBK8hUDbWReYEjEetUnfQlxS1PpK11vSZ7dDDqdm4PpMv8AjXS2JV7KN0YMrDIZTkGvklcfZ4TjvX1T4Xt/svhLSIf7tpH+qg1tTWrZlUXumrioV/4+3/3B/M1NUI/4/H/65j+ZrQxJsUYpcUUxCYoxS0mKAMfV/wDlt/1yP8q8YlH71/8AeNez6yCEuDjpCf5GvGZf9c/+8a83G7o9HB7MiPWkpaQ1wnaIaq6j/wAg+f8A3DVomquof8g+f/cNC3B7GLZDF0w/6Yj+Zr0fSvA+l6poVldyNcRzTRBmaOTHP5V51ZD/AE1/+uK/zNdppvjTUNMsILJbS2lihXYpO4Ej3rtmtTjTa2Ogg8EpbNmLUZ2XsHRTj8sVqQ6PJGMGcN7kYrnE+Ik/PmaVGR/szkfzFTL8SLUf6zS7gf7sin/Cs+SDd2X7Wpa1zqBbSIB0OK43xXuGslG6/Zgf1atSL4haS4G+2vE/4Ap/ka53xFrVpqusrdWhk8n7OI23ptOcn/GnypbEcze5xfh8f6Vqf/XVf5Vb08f8T2DH/PZx/wCOmq2gjF3qQ/6ar/6DV7SY9/iCEf8ATd//AEE0f8vJFv8Aho9Z8OnGiQ5/vN/6Ea0pJFUZbpVfw+YE0aGNpYw4LZUsM/eNaMlvFKCCEcHt1quV2MnJX1OfvtShiXO4VyOv6n9psWiDDBdePxrvp9EsJv8AWWcR/wCA4rl/Fmg6dY6I91b24jlEiAEMehPPFZOEr3ZsqlPlslqeaxf8h4/9e5/9CFaRqhGP+J9n/p2/9mrQNRV+Iun8IzFdJ4AH/Fb6d9X/APQGrna6TwCP+K3076v/AOgGnR/iR9RVf4b9D3Ijmo3H7yL/AHj/ACNTY5pjj54/qf5GvaueRYWqmp/8g24/3f61cqnqf/IMn/3f61MtmOO6OOuR+9NUQP35rQuv9cfpVFR++P0NcMkdkTxdh87f7x/nTDUjffb/AHj/ADphrhOwhk6V10P+pj/3R/KuRk6V10X+pj/3R/KtKZlMlFPFMFSCtDMRvu10mMWll/1xFc43SulP/HjYH/piKcQLif8ALL6Vv6GM6hAf9s/yrATqvsK6HQh/ptt7sf5VvDdGM9mddikNOpK7jkIYx+/m/wCA/wAqlxUcY/fzfVf5VJTBB3rznx7/AMh2If8ATBf5mvR6838eH/ifp7QL/M1hX/hs2ofGcv3Fd74YHzQf7xrgu4+tegeGB80H1aubD/GbVvhOuopcUlegcYVA5P2uEf7Lf0qeoH/4/Yv9xv6UATVleIlzo0n+8v8AOtasvxCM6NL/ALy/zqZ/CyofEjm7Do31qxN0NV9PHXiprmWJM7pUXjuwFcq2OjqZjn94xqlKflY0641XToSxkv7VevWVf8awbvxdoFvG2/VIGIHRMsf0rKSbNk0Tyn9630FNqFbuK7HnwkmOQAqSMZGKeGrntqXcdSUUZoELSim0tAENJmm5NGazOweDSE0mfajPFMQdq5/xCeIef4jW+eK5/wAR58qI/wC1WtP4jKp8JiD7w/GgdcUL1pM9a6TnLAHGKx9QOJiK10bKg1i3zbrhjVw3JnsKTi3gH+1X1JpWpTDSLJSifLAg4H+yK+YCgb7In96QD86+tlt7aOCNBCmFUDge1bQ2MqmxVGpt3jWgX/74yFOq7cZqz5NsesQFRSW8BuYVUYU7sgHrxVamOgDUk7xn86cNRi7o1SGxt/7p/OmmwgP94fjRqHujRqdvnBDj/gNZ174y0PT53guLphMn3o1jYkVpf2dCf4n/ADry/wAd2q23iOUIThokOT9KyrVJQjdGlOEZysR+JfEBv/HOnX9hd3I0tLVo7hCGVdxDdV79RXNyyAuzHIBOckVoLGcD6VDdKRBIf9mvKnXdR6nqU6Ps1oUs0E0xTwKaXOTUWLuPLVFcoZrWSNSNzLgZrh9Q1zU4r6RI7p1AYgAYwOahXxJq6/8ALxn6oP8ACulYWbV0zneIjsy/e+HNau5/M+0QAAYVVJGBVYeHPEEf3ZgfpKaaPFerr/HGfrGKePGOpAcpCfqn/wBetrVl2Mr0n3GnTfE8fTzD9Jc/1o2+KIusMx/I1IvjS9H3oID+B/xqVfG0/wDFaRfgxo/e/wAqC1Luyr9v8RRfetZvxipf+Ei1mIEPaHHfMRq8vjXP3rMfg5/wqZfGMLfetGH0f/61K8+sAtDpIk8L3DXTX87RmMu6nae3FOl8QQaFqkVwyedJHOz+UG25GCOTjjrSJ4stP+feQZ9CKf8A29p0x+eAknuyKaztLncnHc0vFx5VI01+K+myf63SJFP+zKD/ADFOk+JWhzLxbXcTexX/ABrKN/osn3reP8YhTSPD8n3rWHn/AKZ1V11iyOX+8i9/wntln9zfX0X/AAI/0NE3jaK8gME+r3EkJIJSXcRkdKzTY+GpOsEQ+m4VGdG8Nv0IX6SEUXh2Ycsu6LtncwXesmW3lEifZgMj13VqGsjTrPSdMleS1uQC67SGlBFaQurc9J4j/wADFY1FeV0jaDsrMkrpPAH/ACO+n/V//QDXMCRG+66t9Dmul8BSJH4208u6qMvyTj+A0UdKi9Qq/Az3bvTH+/H9f6Go3vbWPBe6gXPTdIBmuem8UIPGlroaLC8Elm901yJR8rBtoTHTvnrXr3PJsdPVPVP+QZP9B/OrSukmdjq2Ou05rmfiFdT2PgHV7m2laKZIlKOpwVO9RRLYcdzMux++/CqSA+d+B/lXjbeOPEsMmRqkkmf+eqq39Klg+IfiNXBNxA2ePmgFckoPc6ouxVb77fU/zpjU8knk9TyaYa887SGTpXXRf6lP90fyrkZOlddF/qk/3R/KrpmUyVakHSoxTxWhmDdK6fH/ABLdPP8A0yFcwelcnq/i7Xbe5NpFfFIYWKIAi8D64q4RuxN2PXkHP410uhKftltx6n9K+Z5vFOvy5V9Wuseivt/lXc/CfULyfx3p63N9PIhjlJEkpI+4fU10RjZoxm9GfRVIaa1xADzNGP8AgYqM3toOtzD/AN9iuo5x0f8ArpvqP5VJVJNRsllmLXUQBYY59hSNrGnL1uk/AGi6Cxerzbx2f+Ki/wC2Kf1ruP7e07GROW+imvPfF97Dfa88sBJQRquSMc1hiGuQ2or3jCH3h9a9C8MD54Po1eeD74+td3od2tnDBMyFgAeBXPh/iNKyvE7Y0lYb+JVA+W1J+r1H/wAJI56WgH1bNd3Mjm5Wb9Qt/wAfqf8AXM/zFYp8Q3J+7bJ+pqM6zfNLvWBdwXGAhNHOg5GdJXH/ABSnmtfh1qc0ErxSr5e10OCPnHerratqx+7Dj6RGuJ+KF9rEngq5SdHW3eRA+Y8DrxzRzIqEXzI8Wg1C+ncmW9uXz/elY/1p0rMw+Z2b6sTVSyPzYqy9c8tzojsUWUYY49aqsMgj8KvSDANVoE8y7ij/AL0ij9aaFI9W08bLKBP7qKP0rQU1SgG1FHoKtrXEzVbEmaKbmlBqRjhS0zNLuoAr7qAc1EGpQ9QdRMDSEmmbu9G6mApbisLxC2Y4hn+KtrOQawPEJPkwn/pp/StKfxGdT4TJXqaYetCk4NIx5FdJzkqkhfbNY1zzIT71qSFvsz4PNZE4yFwa0p7kTNKBC99pqY+9cIP1FfWDdcelfKuiKZPEmhJjOb2MY/4EK+sAu9ycfjVxdkTNXX9eRXyahk4uYPq38qu+Vt53AehqOSPNxbhscljn8KrmMuVAHI6Gl81valdFVj8wI74PSjZj+JQKfMHKAlb1ry3xzN5/iOcZzsVU/T/69eoF1jVnYgKoyT7V4rql4b/U7i5J/wBbIWH0zxXNiZXjY2w8bTuWVClBz2qG5QNbyr3Kmo1kPrSFy3fqK8dRdz13NNGNGflFIT81KymOVl9DTc/NW5ged6mP+JjJ/vt/Oq3QZPrVrU+dRl/32/nVZyApz616sPhR5sviYh5pjDmuh0DwhqXiHRrrVLKa1S3tZRFJ58hQ5wD6e4rK1TSNR0e4EeoWzwlhlGPKOPVWHBp3V7BZ2uUcA00gUA80BXkYLGrOx7KMmgAUVKq+36VCDyc9RUytxQwJUx0wPyq1Emf4VqorVqaXaXmqT+Rp9rLdTjqkKFiPrjpUsEIkHU+Wh5x1NOMGP+WSfgxq9f6dfaTJ9nv7Oa1k9JExk+x6GqpmwuDwelSMhK9vLX/vqonT/YI+jVO54GO1RO+V+tMCsV/2W/OmFP8AeFTM2DmmMapEs1PD3y3chySdhHP1rvvA8C3njrTYJGYIS5+U88ITXAeHz/pMn+7/AFFegfD9wvxB0wk45fn/AIA1cdX+OvkdUP4T+Z1vxY0qC10XTnQszG6K/NjptP8AhXn2nQDyG+Udc9K7n4x6kputJsFfJVXncemcKP5GuL02UfZ2PvSxMvfdisPH3Fc7/wCHuj/b7PUnWcwkSIvA9if61N8QPDd1aeB9UnGqSPHEis0RBww3DjrS/DG7H2nU7XzApZUlA9cZB/mK3/iIxb4c6584P+jf+zCuqhJezRzVov2rPl+c5waYmcpTpfuUkY+ZPrVS2Bbm72FMNONNNeSzsIZOldchwiD/AGRXIydK6xT8q/QVrTImTqaeDUQNSA1oZjjXnGu/8hS4/wCuhr0YmvN9aOdSuf8Ars1bUdyZbGeTzXoHwz0xNW8ZWVq8rRr5bvuUc8LXnwOSK9S+Dv8AyP1scE4tpenbiuh9DJ7M9lfwla28MkguZWZVJG7AGaqaLpi3emwy30UsN0QfMjUggYOODXWK++UoYzjOMnGDTjPHGMKpKjuo4FVJIiNzFt9AspIyzeafmYfe7A1ONA08fwOfq9W7eQtESuMF2P8A48akDsOuKq8RcsyoND07p5J/77NeYa+ix65dRoMIr4Ar1suc8HFeRa8c65eZ6+YawrtOOhtSi1qzP/iH1rutDC7LIMoZc8g964Rfvr9a7/Qh81kKxo7lVNjrRFb44hQf8AFOCRj7qJ+AFNySaPyrrU2ZOmiQYHYD8KI1/fyH1Apgb3NSQupkfpniqU7kOnYSRiGxXn3xllK/D6RP79zGP5n+ld9fXNvZ20lxOcBRnrya8r+L+tWd94MtoIJB5r3StszyAAabmkrDpwfNc8KsvvtmrT1Vs/8AWNVl+KwlubR2K0x4NM0wbtYtR/01FLP0p+irv1y1H+3mjoxSPUI/uirCniq0farANcbNUSZoBpoNGaQx2aM0maTNICkGpwNQhqepqTpJM0ufWmUtMBc1ia6A0Kf71bGcA1ja2P8AR1P+1Vw3InsYi8PgUOeaap/eUjn5jXSc5LgNFt71izMA+B0B4rbHyxliOgrDmGJSK0p7kTNzw+2zxToDHP8Ax+Rk/wDfQr6mkkzE8gYqM46c18weE1DeNfDgYjBvE6/Wvpm6t4JGlMs5wqnC5Axn0P8ASneyJlt/XkWFhaYAB8/LzkYNZ8joL2O23OSjcsfWpLfTpIpI7tLiaQBPunGcelSXdkk95CTKxL5BwcdBn86abM2x9w3kTpCSQ7jOQtLcTJapG0gZw/TYM1EunLcMJhJN5i/9NOKsxafDGqbAUKZx8x49aWvYZCWivbQq8WYpQVZG7j0NZp8L+HnI3aXAcnA27v6GtK6lt7JlheNySMjb0JzU9qIfswuBFtZuoHr60uW+6HzW2OB1XwnpySamYYfK2p+7CscR8dua8oU3e8j7XLgfSvVPE+r67Z3t+LfT7aeCVflfLKV5VcNz715tDFJtPnKofPIXoK4q3LF6I66DclqEW/GXkLn1NP8A46XbtpP46wudFjz3U/8AkITf9dG/nVOTmNquar/yEZv+uhqnIco1erD4UebP4mehfBnVpY7+80iSMvabkvyQeFZDt5+u4fior2rXPB2i+IrVoL22BDD7yHaQfXjvXgHwmm8vxfcRf89bGTA91Kv/AOymvpiJ8nrUySb1Ku0lY8V174HmImTR9QOP+edwP6iuU0jw1r3hTxfYT3+nyLDvKidBvj5UjqOn419MSrvSsLWrRpdGvYxwTGxB9wM/0qZXUWgjLVHn2ueFNH8QAzm0EdyUBeSL5Wz6+9eb6l4LutN1g2D3kCptDrLKGA2npkAE+1em2t2sdxC5bKuvr/n1qt45tkku9MvEXiSJo2PuMEfzrjp1ZRTszrdOMmrnOeH/AIf6cUmvtW1KC8s1j+RI5vIXf/tkncB7Ac10sHiHw9omkNptjaJLHyTFaBoo2Y/xNITuYiuSNsuScAjuDUUtuMMO2Kl4qUjZYSMTvDql1qehW2pOkjWwTZmVPvFeAxPRuR1q9L4B0nVdPjuJLJTLcIJvOhdo5NzDPOSVPX0FefWN1dwaXGysz+RKYU75TAYKR0PU4rq9J+IOq2FvHb3NpFdW6ABCPkdR6f5FbU2lJu5yVE9rHC+IfCt9or+ZDm8tWJCyRrll9mUZx+HFc/ZW1/qUxitLG4mZeW2ofl+vpXp6eJYTq926IY7e4fzAko+4x6/rmtLU9KGqaJNJa7lnRfNgKZB3Dt+NWq7Ts0T7JPW551YeBvEeozBf7Olt4z1lnUgD8Op/Kpv+EPjsZ5l1vU4IFVSEjtj5krN2yvYdevNbUcOvmJYJtSktVcbfLuLzYee23JI/Ksh7LyJXjYESIxVwTnBBwaieIklsbQw0ZPe5b0zRLC2t57i3kkmDgrGznBQjnDD1re+H8Y/4T3TXbldz/wDoDVg6fL9nuNjf6qYbH9j2P5/zrpvASlPHenxj7ytJ/wCgNWSk5TUmVKHInE9E1zwNoPiHVpb6/a8WbaiExzYUADgAEf5zWU3w10q1ujFBeXX2fyt4BkUnJbHXHpXom13B+YZJycY5Nec3Hia2uvHv2VL3UGsjAEZ0iPkmQP03Y6cjpx712yhDqjhU5rqbej+D9P0LUlvYLq4ZxmPEjAqwI74H0qL4jOD8Pta2up/cAbR/vCuujtJokZVYYY5rnfHVk58B68z8n7G5wD6c/wBKtQUVZIXNJvVny5JwppYvvp9RTZe9Pg5dPrSl8JotzaNRmnmmGvMOwieusX7q/QVyT9R9a61eg+laUzKZKDTwaiBp4NaEDz0rznWB/wATC7/67GvRSa851fnULv8A66mtaO5MtjOQ/OK9T+EB2+NFPzbhayY2jPpXlkf3xXq3wbAPjoDeU/0WTkde1bz6GXRn0DFZ4O6U5PZR0q2AAMAcVnaos39jXQgnaKVYSUlHJBAzmvOJNY8RrpzyJqkok3gKz4wPrxTc1F2sTa6uelpbDYTEdhLMSOx5NQyztA+14ZD67eRWX4X1WSbS2bULgM4YFWY/eG0HI/HNa9vd2d/LMkO2QxnDsB39Knmg3ZPUpNma3iS0QndbXuQcH9wa811eQS6tcyDOGckZ969auLJo4tyEELzXkWqHOp3H++azqpqOppBpvQqof3i/Wu7027hsIbW5uCREgyxAzXBp/rV+tegaPbx3KQQyrGVMRP7xcqDjgkVFHdhU0Ronxnouf9dJn2jNKPFmkFflknPv5Rp/9m2seq2VutlZPA8TNI4gUbj2x6Vu/YLTGPssP/fArdRkzP2iOePizSu5nx7xGue1XxdevcLHosBAmPMjryAOOnauu16wtF0uSVbK0eRCCokQY61g6nDDa6p5ENtBFCsathEAIOB+lDjJBzrYyGj1G+iX7fdM/OSinA/GuK+JcaR6XZYHPnH+Vd+H88RSQzLt3Mske3nHY5rzj4m3800sNo6jy4nJVgPUVMY9RxlrY83tP9Y31qy5Oaq2p/eH61YkOMmqluUtivcdBVnw4m7X4f8AZBP6VWmOVq/4VG7XCfSM0n8LE9z0OPtU4qCOphXIzVD6M0lFIYuaXNNzSZoAzQ3rUqsKqq9PDe9SdJbD0bs1XDcU4PTESMcCsfWj/ohPoRWozZ71lawc2TnHSqh8RM9jCRsyfhSFvmqOFvnFKSN/411HMWyf3TfSsGV8yk+tbczBbVz/ALNYBOZKumRM6Hw+ks/inQYoTiVrlQpz0Oa+ihG8V3bCdpUjjkBLBN+frjp9a+cfD5YeKtBKStC32uMCRDgrlgMivoLxt4sn8Ny21va2sUk8yGQzSjgAHHQdTWdSCdmDSdrmw+oXcNwzIGlXccDadvNU47m7CF5nCTGQuGwWAPTP0rkR4v8AGdxbCeKCFYWwVkEIAx9SataN4s15vElppesxR5lbCjywjAkHHTgioUGndti5U3Y7lLyWK6Mj7XjdBkR5wDiud07XNUufFbma7zpq30tqsBiC7QIlbJbvyTXUfb0tVP2tcS5OEjGSR9K5FEuLPVEvo4wkDX8l1Knm7i25NpwMccY74rRRlvcS5b2OuvbqeGEMsayHOFKnNV59aFjoVzqVzakJbQtKVUjLbRyAO3SpbfUoNRjMdrcbJs5ZTjev4Ht71dlj82FkeNX3KVKt0IPUGn7120xW7nyd4k8Raj4g1V767vnYyHcsauQkYPIUdOnA/CrnhnUJbuCeKd2keJhhmOSQfetvxr4A0/S/ETxWurR2sLhXS2uJMyDcwXCeoGePYVn6XpselxvAhLNu+dz1Y1z1mnCzOqh8Whot0qMn5qcxqMnmuRHUzgNV/wCQjP8A9dDVFjw3tV3VT/xMrn/fNUH6PXq0/hR5s/iZ0Hw5mnh+IuktbqH3OyyA9PLKHefwXJ/CvpvTboXVjBPtZfMQN69q+c/hHj/hP4iVRgLS4JDd/wB2a+gPDxJ0SxLAcwIePpSk/eSGl7tzdU5HXNV7pA0LoehBBqwvSorgZQimxHjuHjtVUjDwSGM/gSP6Va14Pc+Fbe4bO6Ccc+xyP8KdqkXlX2qRBcBLjePxAP8AU1NcKJ/BN8gwGjAf8iK8tq0rHdB6XORPIzULjin5+QUxyNprA7yfSU87SdYhTcJYDDdpjuASjD/x9T+FVkUyLIJ5trL8zHOMDsKteFy58URWythLyCa3ceoaMkfqFqlFG5RQ6hi2C5c4wPXHrXZD4UedVVpscIHckFwExwCeDTN08b4Wd8s2dqykdvrU2yD7QT5vJXAXHpUKqpiIMjod2AzLzWiZk0NEbKxATa3UkNzj1pVkaR5HbqzFvzpWijDOqOnzDKryOPrTmB671cA9QegqKivE1oStMaRuXHrXYeAJGfxxpU4UEuJEcH+8EOf8a5DqK3PB+qro/iezuJE3xhycZxgkEZ/I1lSfvK5viI3i2j6BmvLa3V1YhSCoZVHI3HArx3UfCeup4u0/Qv7QiW0EJK3AlIby/MOPl6lgo+mR1rtr3xXpKO09zLp0eSoZ5Lkc4PAP415jqvxF0+T4qWerCKKS0tIfshuFYsFJJO4c84PH516MoOerPKTcT3uxuYpoWWPdiBjE27rla81+KXjC+s4zoenWcNzBqNo6vKSxYZ4O0D2IqxJ8Q9KthKLa+stxYswiDOCx6k4PWuJ1fxZY6v4p0kzzRRW8MciM6xFAAw9/oKd5JWCMerPObuwmtbOKecFTKWAXHpj/ABqK25dD716BrFzoF/Y6ZAWtZJor4QyiNyS8PTdnrjpzW3f+GfDEOi3c1tZQrNFAzxsJG4YDjvUSl7prFannZpjUu7I6imE1wHURt1H1rrAen0rkmPzL9RXVZq6ZnMlBp6moQaeDWhBKTxXnmrH/AE26/wCuprv2bitaXwjoU+lRXMtgGmmQO7b25Y/jWlN2ZLVzxmE5kX613fw+XUZvFJXSrhoLwW8rIyjO7C528+ta0HgPQZ7lfluI+eiS/wCNdZ4d8LaZ4Vv49X08TyXEalQs0mVIYYOQBW0pX1RCXQ9Si8648PR+ZlppLVd2eCWK81ysumJPaeV0UnPPSn2/xAhnZ41az8yI7ZE8zlT71MviKwmXDWkBz/zzuMVfMnZpkcr2MSW2layENsbxXDCBdkAMZVl6hj0Iyf8APNdN4Wt49Ngks/tMk06Aeb5nBX+6FHTGM896r6ZrVvYhgLcNnJLCQE+34YrQfXrKUkvby5AwpGM/nmsFSSqc63K521yyNK6+1SgfZJ44iPvB03Zrx7VCf7Vud2CfMOcetegz6u7SkwmRF2n5iOc9jxXnN+xOoTknJ3nNTUm5XTVi4JLYii/1yfWvRfD8QnlgjOcNEQcfSvOoj++T616R4fmitpoHmcIvlYy3TtRR3FU2OiTTUju4bgM+YUKKpxg5NaVVV1CzbpdQ/wDfYp32y12lvtEWB1O8V2JJbGBFqFjFqFo1tMW2EgnacHg5rA13TgJ2vAG3swiAzkY2j/Cl1fxnb2JMVnby3c3QEKQgP17/AIU3StRu9Qti95Fgk7uOAp9AKibRaj3MOOMWceyRsDJOW4ryn4iXIl1PYrBkyWGDweK9s1a2hmCblyBIgOR1ya8V+KVnHp+vlFVUBZ+AMAdP8aUdmCXvHB2n+tqxL0NVbNl8w8ip5GB796UtzSOxFJytaPhLnWZD/wBM/wCtZ0mMGr3hNsa4R/ejNJ/CxPc9DjqYGoUFSiuM1HZozTSaM0DHZpM03NGaAMVG9akDe9U0fjNTB+Kk6CwHp4aq4anBqAJi1Z+qnNjL/u1b3UkSxy3lvHKoeN5VVlPQgnpVLcTV1Y46OQB+TTmdRJ19691/4RvQYyQNHs+AD/qhViPRtHUrt0uyHH/PBf8ACuq9zk2PBrmZRasARyKy4oJ5z+6glkJ/uITX0ncWOnx2xKWNqpx2hX/CsSJkR22KqjdjAGKpPlJerPJdO0nV7fU9Lum0u8CRXCOWMLYwGBr2v4ota3Vrp11BKrukjRkqc/KRn+Yqwb63MUayXEasOoLDivOPFfjG4uJ7WxNsYbRLkiSU8h8cLg44oeqaDXQ7XQi+qeCZLfzAjxrJAGxnAI9PbNcs2q3V5pGjayJiby1Y20kjct5iHKk/gRUmh+IZNFjmjW2M8cpDDDYANUJ9SMlvNbLbRxRSy+ZjcOGyT/JiPoB6U7qxNnzXO60zxXHewzXF1GRdKVWWMZBDdzn0xgj603UtYe5ik2OoEZ6D+NT0I964rT9SvrPxHai8TZp86pbOypuYgfdbHcjpkc4rpL2PS1himia4V92zekDDIJ5yD1OKcr21Gkug7Sr+5uNYiNqxNweSV4KepP8An2r0o6tKCp8luOo3DBrx4NrE2pu+gsbSBF8oeaAXY55JyOM8cVS1+L4hQWaTw6o8jBvmSIYyMd6qFOT6MmclFXbRB8VdVsrzxjBOCHe3iQyJ5meQ2dv1wP1qnBcw3a+fAwaNySOensfeuGujfwyuLlZBKxJbKjrSaVNew3SMXKIWyQG4P1rCvSvfU3oztbQ79qiZgKxjqkg6zpThq6AfOAR6rXDys6+ZHMasf+Jlc/75rOZuWq9qjbruabBCO2QTW74L8BXnjBprkzi1sYm2tMV3M7eij+vvXpw0gjz5L3iD4assXjyxdn2hYp2I/vYif5fxr6S8O2j2+iWUUjlmSFQSR7V5/pfwv0nQ7iO8s5ru4uTmAGXBVFcbXcgYxhSce+K9NgkitYEiQySBVABbqaltN3K1UbFwZUc4qrPJgGopLt2PyoRVKWSdmxgAHv6UnISicLrbs2u6kCvy7EwfX5afZNHNoOoRFTt+ztu6ehqW40u8a5vJpLQ/v35YjnbjA/T+dNm0y9XQb6DT7CZ55k8tAW2jB75J+tcFm53sdd0onBpIDEp9hUUsoGea2R4I8SbAPssCADGDMKjk8B+I8FhDA59FmGaj2Ur7HX7aFtzI0q+Nn4k025VSzRXCMFHU89Px6VoX9ittq1/D5uYop5FXdycbj/KkTwH4oS7t5o7aBHjlVlLy5AIIPOO1aWo6PqWpeIr24tNOutskzMUaPA5OScnHGcke1dEYtRsclWScroxv3CLCsjB27OFGM1HtjCb5Zj5gQhgmOM+ldHF4D1t48BbaFeyu+SPyBqJvh94gWctH9jIb75808/8AjvSqszK6MFXhY7CCEAG18g7hSsbYFyrEkNjkfdJH8q6qH4Z3skTLdalGikYAijJI/EkVaHw0YZxq0gJ6/uRz+tVysV0cHLcLBIUYrke/Wn28s00qNbQySsrAgRoW7+1el6P4JXS5WaW4S6jbqktsnX1zyfwrehsFgTbCiJjoFUKP0rNUNbm7xN1ax4r4l8H67cXkk2labPNbyndJGVAwfUA9qxZPD/iuyuFvJNBuldcYZLfI/IDFe8z3eoppl5KmmSLdW4LLGSHWRfVSDz9ODVfT/FME9rE9zA0UjLk+Wd4/Ot1WjTSTZgqU6l3FXPHdI8caroUUto+jWYaWRpGNxbsG3Hr3FVNf8TXevvBJf29vEIQQgihKjn6k5r6AN/p95A4DwzHHCSED/wBCripZUPiK5nFtaSQxqsARowyNjr16+madTF2W+gqWEcpaRszx8tJEY3FvKrfeRvLI+hFW5tZ1lw8E015zw0bHbx6EV6t4hi06bS4b7TrWCznhf/SIVQAMp6MPUAgfnT9T1CPV1ttTuoLS7tb9SYzcQKShHDJv4b5TnGD0IqfaRa5lqU6couz0Z45sumh8wJxnG0yfN+XpU+mli29mPKnjPvXdXGkaNMtwzWktmiHCSwzEqw+j5/nVW28H6YI90OtTJuHyrLa5GOvVW/pWcp80WhpWdznifmX6iustoxPcxxGdIA7Aea4yF9zWbeeGJrd4zBfWtyrOB8pZCPc7hwPxroBY6bApNxdTzv8A3YFCj8Gbk/lUQVtxyd9iNZrnQZXsNUs7S+c5dXZmG9D0KEdKqSXP744spYk9BIHI/MA1sx6kmnzudNi+zylAFkkPnSqvopIwo78CoNZ1M39xDLOubjy9sspABkIPBPvjj8KmbcVeLNaShOXLJFF2hMeUnU/7LAqa6i41Kyt/DsErXMZSOJFbacnPpjrmuLu3aJFaNFbnBBOKg8+3kAWUFCR0IqYVZtXsXOhTTtextJ4kWKfdDZyyKDwXcRj+p/SobvxBqt6hj+1PbwkYaOE43D3PX8sVQVYzwjqfxp2MVnOrNm0KFNeZLpirb3XloAFkU5+o7/zrYwKxredIZVZsYzjJ7U+78QW0GRCDK3r0FbUruJy4iNp6GuFx0Jp4dx0dh+JrH0XU5dSFwZAg2EbQo7GtXNXsYEwuLhR8s8o/4GaYWLEsxJJ6k96ZmlzRcBwJUgjqK0E13UUUKJQQBgZUVnZozQm1sFjWHiK/HXyj9Up6+JLofehhP4EVj5pKrnl3Fyo3R4mk/itIz9GNOHidc82ZH0esCkp+0l3DkR0R8SwsMNbyj/geaWK5tdWM8sluJCowfOUMf1rnO1amh/8AHtefh/KmqknoxcqRPp+kaRNJIZNMtGx6xCnS+HdCbJOk2nXtGKk0s4MuaslsrWlxJGNN4W0CQEHSrcf7oI/rWPJ4X0jTpvtVnbGKUZAIckflXWP9wmsq/wD9VWcm7FpGcFxS040wmsUUBpKCabmmIXNITSGkzTEc6rVMrVTRqmVqg6CyGpwaq4al3UAWN1Ij7bqAjr5q/wAxUO+mNJseN/Rwf1prcD2KVtr/AFFCPwD6VXmlyY27MoNET/IRXUmcrRNqEu2zJrjJrplkIzyWrqNUfGnNz2rimbfeqPemSYM1xcaXeTGSQkqd5zyGHWq/iLX117S4rIW5tkVtzkSZ3/pV/wAWbI9a8pgAJIlYE9+2K5ARpsJxyM0+dxVl1HGCm7voKjBIliEsjKowAXP+NKoUHcIhkd8ZqnArySShZmjAPQfSp/sLsObiVh/vGs5SSerNEr7I2E8RanE0DLPhoB+7YoCR+dMn8S6rN/rb+QjOeoFMhOnR2iwnQoJplG1p5rmQlie4AIArNGmw7ipUZBpOourGovoi6fEuoxsSmpzKzdSsuM/rUMniC7k5l1K5f2MzGkSxhQ/dBxQtqm5sxgAYo9strsfs3vYqtqKnnLsfoTVmxttS1RZG0/T7q5WM4do04U+hNSosQblR16AdKRFQlxyFx0B61PtI9h8j7lCWa6hneKS1dJEO1lYDINJDPLLPskXYMZrQAUKFArPLf8TAY/u1UZKV9BOLVtStqwcMkCZYscBfU1774St4tE0Kz02IACJAHI/ic8sfzrwyBPtHirTojyPPQn8DmvZNNv1LgMeSxNbL4EYy+JndQTrMwHGf5VaCDdhCfzrC0+XClieeAPqa1Y5flZs+wpCLihui4b68U4oO/X2qCC4qzHKp5NMkb5Cnktj60C3xyOfyFTBweTye1SbQOBwe59KdguU/IfPAH5UNBIeoUD8qvAH1496TZz0/GiwXM/yQOoBPr1pTbqe/58VfMakck/jTTbg9MGlyhco/Zufl7ehpfIcDnOPcVbNtjtSeU46Z/OiwXKhjx2/IUnl+zfjV0CQDGAfqKMEnmM/gadguUthHTIpQHP8AdP4VcEanPyMKRoFHVlH1OP50WAxPEE15aeH765tCY7mGIyRsBnBHPTuOted3N/Ys1tfWUHkW12uZI1B2xTfxAex5r1DUooJtLu4GlX95C64DeqmvE9J1+80q3e08qK5sJG3S20q9/VWHKn6Vx4uLdkztwc7NuO6OgMiHGCDn2pw2t2odNnlTQgSW86CSJz94qex9weDTGZsZKYP1rymmnY9qLUldDmwQQcEehHWlt7eC50LUtHj2pIP9LsgV+5KPvBfqo6eoquxYZNUptQitpYy5dXzwV7GtqMpKXunPiIQlD3hLOKS5tsXm2T/aJ+Uilmlt/wBwkCLKjOUbaDwO+KqwLbtfyTfa3bcuFV0OF5+tXIdMlS32W11G2STgkr1/Cu2x5dmLsiWIhEkkZfuhjz9M1FL9muYVZBKm7K4xyp+lXbfTUtoiJNjSOcvt7mo3sbfc5gJaUL9xuCfpQgaZEiW8IUylpHA2hjHyR6dahAhkt5HCNtJ+QngEHoRnoe1Gy1gkVGd0kZtoUAnYf8KJFgA2i4Uxo2JQV3ZzTJ1Rl37M1kTHkMoz+Iqs4juLZJk3bnGcsKuXsccbMkbFlYdxWbp04MMtqXAeNiAM44PSpprlbRvVlzJSK7F0PB49qcbqTnLnp61LcIVB3L36jtVM4HbrW5gPlnJCnPPf3qJ5AVOKa+TTNvemI6Dwi/7y7X/ZU/rXT153aa5e+HkmurEW7O2FYTwrICuffp+FWovije/8vOiaXL6lFkjP6Nj9KpUXPVMxlU5Xax3eaXNcinxJ010Il0GWJscNDeZGfoy/1qOH4iWTn95ZTJ9CDUyoTQ41Ys7LNLmubh8caLKQHkli/wB9P8K2LLVtL1B9ltqdmWxnDzqn/oRFR7OfYrnjvcu5pKmktZYoTMxiMX99JUYfoagpOLjugUlLVMWkzSZpKkoUmtbRAfsV0e24D9KxyeK19E/5B90c/wAf9KqO4Fyz4DY71Y3ZqtbH5yOwFTKeDWhIP/qzWTfn91WqxzGax9RP7tfqKiWxSKhNMJpSaaTWSGBNJmkJpKoQZppNBNNJpiOXRuBipQ1VkIAGOlShqk3JwaduqENS7qQybdUU5xGT6UZpkxzGaBHqkU/m2Fo4PWIH9BViJ/kJrH0ubzNEsTn/AJYgfpV+GTgDPWulGEtyTWHxp1cch3X6fhXV6y3/ABKia5K0+bUF+oq0QUfiBCVv7GUd4SPyP/164sbv3nsxr0P4gRjydPkPYuv6CvPH4lmHqR/KlLYqmVbVsTzc9cda0ftSKg+YZ4rHQ/v5Aqbnz61NiZcYgQ/UE1M4Ju7LhJpaF83sfl9ec5qMXgLMQGY57Cr9vDpiWSS3OpzpcuvMFvYBtp9NzEA/hWYy3vH+ksF9uKz5YormbJheygHbBJkn0pjXdwxI8sAe5qubWeRsPO5z6mnPYRooLMxOKLU0F5jWlnByZY1/4FT7dL67dhbLJMR18mNnx+QpxsIggOOcd6t2rzWsbRW9xPDHJgukcpUMcdwOtPnghcsjNkaSN2SVpldTgqUwQfxqGJ8XYyG6dWNasy5UnGSTnJ5NZTPuvfXAqoTUrilG1jR0MRt4ys2l+6m5sZxnCmvUE09i3nWMyuM58pzg/geleMi7NprkNwDgIwz9O/6V6hp1+Vj3K2cf4/8A163t7qMG/eZ2ljdSRReVcRtFIDnDDGa27ecGADOQe/4VS0rUkngRGCsCo4YZ61qjTbSSMmItCScfKePyrPUvQaku0/jViOUtCpHXNUpLK8gYFAJkz1Xr+VLFPsQI/wAjBjweKExWNUSlZAp6f/Wqz533R3JNZjShmPPPB/Sp9/7xeeRVpktGksgJ+lTBhgVmRy4P41aEo25zVXJsW/vUvlqe1V1l5qRZcjNAEwQ54JFeZ+IfjNYaDr17o39kTTz2kpiaR5QiMR6YBOK9MWQV8o/Ek/8AFy9fYf8AP0T+gp9QO6vfjzqByLXSbKL0Ll5D/MVz178avFc+fLuYoR6RQov8wTXm7kscU3ypD/Cfyp2QXOquviV4pu8+bq1yQe3nMB+QIFZ6+L9fMoeK+cPnggAn9c1hmB/YfjTo4mDhcgEngniri7bEy97Rm3ea54nvE3XOo6i6N281tp/AcVu6bcefZws0gWUKFdWGCCOua4+3ubyzIa3nmiI6GNyP5VG9/dTTtNLMzyMcs5PJrPEU/axSvqXh6nspPTQ9i0u6iufD0unG4/061l861Cnl1J+Yfz4+lXra4We3HzbmH514zb6xd2zq6SyBlOQc5x+ddVY+NYFdXlVUkPMjBSoY+uBkA15tbBztdanp0MZBSs9md464T5uD6VzetwFkEy5+Q5OD2q3B4m068AIuRn0xn+VLLdWlwpUTxHPYtg/lXLGE6crtHXOcKkbJnOR3LAbiDuboASf8mtK1ubmEB5MoP4UZsE/h/jWY9v5VxJH5m0L8y8ZJHtUsXAYngD1Neho1c8xpp2Z1FvqiyqAzcjqMVYMzTnqFXqPWuWgl3hmEjbE6ugz+vSrf2psrtdx/vHk1DiNM2rgeehCuY5hwHFV/IuY4mkMRllYgOIzjI9ef5Uy3kDc7if8Ae6UXMT3EiSRTOkidUHRx/jQJojvbZRamRmKsgwRmuftCE1eVdgYSIDz7Vt4kZXXbg5OCwz7jNc9qiXFrrNs0cSl2P3QeD6imlqLm92xcvxkkAEGs7aw5NashEyZZHVgOVI5rJdirkA456HrVoTEI5pMc0hdWpA+MCqJK+oRNLZyqgyxHSubVHx0rqS5yc9qxJYtkrAeucVvSeljGoupT2jjdHj8KURoegP51bCdOKCOOg59q1uZWKxjUnGTQbZSpIYZxnFWAi+lNUFt3fAoAn8Pp/wATq2/66L/OvYSeTXk+hr/xOrT/AK6D+deqsea5MR8RtS2FJpM03NGawNRSeDW1on/IKuT/ANNP6VhMeK29EP8AxKLn/rp/SqjuBatz87mpY2yre1V4D96n27ZjlPpViJC37r61j6keIx/tVqlv3INZGpfwfWplsNFUmkNJmkJrNDA00mgmmk0xATTSaXNNNMRySnipFNQKakU1LNiYGnA1EDxTgaQy/p1jLqd9FZwFBLJkLvOB0z1rYvvBl5Z6dc3Mt3aHyELsiMWb+VUfCjY8UWH/AF0I/Q11mpeHrexsNcu4BLFJcxs0n704Y9elb06alG7Mqs3F2RX0Rv8AiQWTDvHWnE+CprE8OPu8K2Y5+XIyfqa1Y2wV9zTQpblnWT/xKWrk7Bv9PQ+9dXrH/ILauRsTi6Q+9WjMu+OFEmjW74+5OP1BrzOclZ29wK9R8ToZvC8rd0ZW/WvLrvIlP+7j9aGOG5St2Av5D9K0jLltuQOKyUCC4kZ5Cp44Ck1J5kGc/vnP5VM4czuXGVkaDTKWUbhge9LLdwDq+celTWmgXl5ZJfLDaQwPna91epHnHHQnNZZFxuKpbwjBIyOal0orcr2jLBvo8KQCTnsKY920n3I2NReReP8AedUH+yAKP7PcqC0zH8TRamgvNkr3E7LyqLx1ZgKgNzKGAM0eewXn+VL9gQdSTxmtCwu7vRxMLC5a3MoG9lVSxx6EjI/Cnemg94ynu2yUaR+OwXGPzpluQbpThuc8t3rTuCZnaeVzLK5y7uclvqazS+bxAOKuMk07Ilppq5n33N3J9a0NM8QXmmuBu82LoUY9vY1nXIJuH4PJ4qEqQcEYNdMfhSOaXxM9d8M+NrCdER5RBMPl2yHHfIwfzr1HTtTSa23BgVwCD7gjNfKG0iuk0Dxlq2gFkimMts4w0MhyPw9DWcqfVFxn0Z9PW11w+W6cfrVmRYLkKksavhR1rybw58SrDUCqXD/Z5mxlXPBI75r0Syv1mc4IO6I7SOc45/lWe2jKt1Rfk02Js+RKyHoA3I4qB0uYGBljOBxvXkVMtxlSwPQ8/lVoXBSXrxkiiy6BdlFLhWXOe4qcSsRn3IqVobScZeMKx/iTg0f2cNh8q4PXo4o1FoKk/HPXipklBBwaqNbXUQy0e4A9UOahWba+Dkexo5rD5TYSXKmvlz4ign4ia5nvcf8Asor6ThuNreor5u+I4H/CxNawcjzgc/8AARVRd2S1Y45jh+KlmlZT0XJJySMmq7feqS46r9TWpI0zSNwXOMdBxUaH5xn1pf4ST34FNXr+NUSyznaOCRSnDYJVT9RTD0oB4pCJAqEcqR9KDAh4U/nTQTkE0/JH40DImt2U5A/KniW5QAeYxA7E5FSbs9DzTlfIwQD7kUg5h0WqXEXVVYdO4q8uvo6qs0LEA55Oc1nEIRyp+tN8lWzg4+tS4RfQpTaOmPieG4CIYljRRhVQ4A/CraX0M2ChT6muMa0bGRyPbmmBXibIJUjuDUOjHoWq0j0Nbg7QUlBHoOladvL5xCkhWHIxwa8xhv7mJXUSlsrgbuce4967HwvcySaOZpn3yrIwRnOT24+lY1KXKrmsKnM7G1eOUC3HaPJYY+8SMCs27m3mAI4adZAVUj7owcn8qsyXwZsnoRyK6PQvCGi6ppa3gFwkj5R9sx6g9s9KiKHI4ya7kfIDgMPTvWXIRIzEZ35ya9SPw30ovlbi8A9NwP8ASpF+HWiqfme6f6yY/kKpITkeS56EkD1oyOpYfnXsC+BPDy8GyMh/25GP9alHgrQQfl0y2H+8pP8AWqJueMttJGMnNFto/wDadyqxyTLK7Bfli3r9eDmvbE8LaRFkrp9oB/1yFWoLGC2Xy4IY417KigCmpNbCauePz/DfX4yTE9tOPUOVP6is2bwf4it87tNkf3jYN/I17z5WB0A/SjauMYFV7Rk8iPnWbTdRtc+fYXMXH8UTCs5ZApbPHsa+ndgYYrPvdC0u9U/bbC2mB6l4xn8+tUqvdC9meI+DbeO98T2ULEhWlUEj617XL4WQk+VdEezKDXL3Hg/Q7TUo7zRzJbXETbmSNtyfr0/A1oR6lqER4uHI9zms5zg3qiowki5L4YvU/wBXJE4+pFU5dG1GLrbMw/2CDVuPxDfIcMsb/UYq0nigj/W2zf8AAWz/ADqbU31H76OelgmiB8yGRfqpFa+iHOj3AHXzP6VpJ4ksZBhw6f7yf4VD/aFlIZ/KmiUEZxnGaHBLVMabb1RDbNw+ewzTrI5tJD6saLYq0MuCrYGRg5qSxCnTySB1qblWGk5hUVk6n1j+ta5I8kHjvWbc2txekLBHvZTkgHHFS9UO1jOzTSanlsLyL/WWso99pNVmyvDAg+9TsICaTNJmkzQApNNJpM0hNMRx6cACpQagU1KDUM2JgaUGowadmkMmjlkhkWSJ2R15DKcEUT3M8wJlmlf/AHnJqLNIx+U07sDtPC5LeGh/sysP1rWVuY/c1i+D2J8P3Q6hZW/DIFbRAEtsvqRmt47GMty5qx/4lEh9q4+2O2UH0NddqhzpM47rXJ28eSPc1ojPqbmsRNL4Yu0UZbyc4+nNeTXeCEf1zXtFzFjSpfTyTwPpXkWsQIiR3EJBgm+ZcdiRzSbGtGYUZH285Gcgda1SEweAKxy+y7LY/hFSvcTSNwCPwpVIOTTLjNIv+VF8zADPrSqwVM5x1qikF1IOpA96etg5PzuahwXVl8z6IuGeMIdzjnrURvIlQgNk+wqNra3jHzv+tV5JrROhFEYRe1wcmSvf5HyqTxiojdTt0jP41ENQiU/Im76Cka8nk+5Bj61qqfkZufmS+ZcsCOAKh2sJ0LMCfanxrPIcOQB6ClnhEM0eCcbSTV8tieZMs65H5sWmiCMv/oylygz82TkfWq1/aQJbwi3812CDzN4x83fFdbpVsh0+DdnlR2p11pST5wtNVLaGbhrc86PXHT60YPeukvdBYEnaeO4rHlspISQ6/L69q0UkybMqAc5HBrpNB8a6zoE8bwzmVEIIRzkcVheSV5xkU9Yw3Sk2Uj3Dw/8AEzStULx3B+yS9Qrnj6A13sVzHMsbxSB4ySVZTkEcGvlQRVs6T4k1jRZFazvJFVedjHKn8KzcV0KUu59NIxVMZyQxFTGciItk/Kc/ga8m0P4rwT7YtVgMDn/lrHyufXHUV6NYaja6rarPazxyKwwSrZqdUVY3YLtuOe9WD5FwQJY1Y461hRT+Xwe3WraXGeQafN3JsW5NKjf5oJCh64PIr5o+JETw/EPV0k27t6529PuLX0zBcc8183fFHB+JGrlTwWQ/+OLQkk7oTb6nAHljUk/JX6mou5qSft9TW5LIick+nakXr+NAoXr+NMlkxNOGMU3qMUq9KQiTHOad2FNFOHSkMKXAFGOM0o5PWgBdpJ46UpjZev8AhT1IUdKcD2H6UARBiG4JFTK++CUNydhIyuT+dBVGBOBmo05V+f4TQBUjGSfpXX+GyiaO+QCwkY8t0rlY1+evUfh74TXVNKW/uSPs/msFUDliPX1rOrqjSm7O5jWukatqsmLG1Jj6CSQ4H1r0zwnoN3ounNFcziR3bdtX7q10VraQQRiOJAoHpU5ULzzj6VjYu7K+wgdD+FJnK4O4NVjzFzjPPvTGdS2OnvQBW2N1TNNLuDyATVso6/eUOh7r1FQtEpGVY/jSKIlKM+WyDjB9KsAJwAR7VXk8qI4aUE+g5P5ComkdSfKQger/AOFF7BYuGJWySeapvPBExRsFh2QZJqIHzS3mSs+VzjoPyFQbgExHhSPTik2OxLJezE7YoAnoXP8AQVVl+f8A18jSEjp0X8qJZv3gye1VXc5P0wKQEcjBd4UfLjtVIe4FMvZpIWj3EKJZFUA8Z9aXdz60hilVPY0u0HrTgSOoo3rnkUrDGiMD+GmPEjDBA/KpieODimAgHmlYCmbKIk/Lt/3Tj+VPjiuIU2RX1ykf93fkfrVpiPWmBFIPegBqXN1Emzzt6+9W9N1c2crNMuQ3detVTECcjimtFuFNNoGkzqYvEVi/3nKH/aX/AAqwL3T7njfBJnsSP61xDRle9REEVoqr6kezR3L6Xpk/W2j+qjH8qqS+GdPk+40kZ9n/AMa5WK4ljJ8uZ1+jEVaTWNQhAAnLD/aGafPB7onkfRmnJ4SP/LK7P/Akz/I1Rm8M38f3TE/0bH86lj8SXQxvSJvpkVbj8TDH7yGRf91s0fu2Fpo8kU1IGFeqWXgfQoEXzLYSt6ySs38uK3LXRtHtMGGxtkI7rCv8zS+ry6sftkeMQW1zcnEFtNL/ALkZP8q1rfwpr9zjZpk6g95MIP1r2RJYI1wEOP8AewP0ofW7S0ALG1Qju2Cf1zVfVl1YvbN7I8wtvh3rc3Mr2sP1csf0FasHwtlIzc6i2O4jh/qTXWXPjO0TIN2W9olx/LFZc/jOAj93BLIf9o4p+zpLcXPUZVsfD0Xh55rOGV5UnQsfMIJyPpUvlq15boVGGUcVlXOuXNzcLOsUahRwCSf1qJtZvDOkyJbjYuACCazk1fQ0V7anQ6wAuk3RAGcAZxXGC4hgmQSuFyRgdzVy71XUb62e2lmjWNj8xjjwfzJrLFjHHyBlj1Y8k07isdBN4ktY7MxbHlbbggYx0ryL7Rci1a0nidY45S0bMMYBzxXdPFz9KwfEMW20MmOjCmpdBNa3OXM0cUuXBPHHFPF+38FuzfUYq9punm/8wqfukCtNfD5H3ifyq/d6ivJbHPNeXzjCqkY/OovLu5fvzH8BXZw+Ho+rD86vw6NFHgCMHijngtkK0nuzgU0uSTG4SNn1NXItAcjIiA+td0NPWM/dAz7VZislPGKTqsfs+5xcPh84G44+gq/D4cjOOGNdfHYIBzkn2oMRU4U8elQ6jGoI56HQYkP+rAPvUOoeFftk0bpcCJVXBATOfpXVJGR1FL5bHOB0qedlcqM210+O2to4skiNQMkdaurDEOo4x6VOIRjkHmpA6ou3Znn0pXHYzZ7SGXjaPyrEvtEDgsiHn8a6wqrHKr1pGtwVPUj0oUrCcbnl95o7wsdgKnrgjg1lPCVfBBR/516rdaak6nKjNc3qOgk5/d5H0raNQzcDjAxXhxx6ipBhhkVcuNOlgY7csvcHrVHyxk7CVPcVrdMgcVFXtN1jUNHmEtlcvGc8gHg/WqG/acOMe/an9RxSGeoaJ8UI5NseqoY36eYoyD9a9C03VrW/iWa1uEdD/dOa+bSvFWbHUr7TZRJZ3MkTD+6eKlxTKUj6nt3DgHOPRhXzz8TQw+IWqbsZynT/AHFre8OfFa7spUi1SJZoTwxx1Fcz461C01bxheXti5e3lVCpJz/AARQlZiZxHc1JP0H1P9KjP3jUk33R9f6CtyOhDSKefxpcUJjcM5xnnFMlk2CelOwQKYHBPBp4YnrSEPH1pwPYUzg+1OxigY8H1pD0pufWlHSkA8HgVJuyoH86iBIpwNAx+cA+9JGeG552kU006Lq30NAgjX5q9y+F84TwbDHkD9/IefrXh8Y+ava/htbsfCUL8Y82Tv71lUehpBXZ3itu+4Bk9T6Uwo4bOC341GVccRo5I75Cj/H9KUmfGGkVAf7vzH8//rVlc0sSrJhSCu0j24qvLdxPjadzA8hBu/lxQUjJ+fMh9ZDn9Ka8gAwuMdsUrjsK9xKVARVjX1f5j+Q/xqs4DEebI7nPrgfpS+cBwRzURZSTu6ZpNjSJNyoCqKoHsKpzTH5ueRwBT3lJ6VTkV+So4Pc9qTGgR33+2BRhiNoGSTngVn6jr2l6NHvu7kF+0cfJJridW+IN7d7otOiFrEf4jyxpqLYm0jt9RvrTTUMt9dJCg6Dqx/CuM1P4gMS0ek24Uf8APaYZP4CuOmkmupTLcSvLIerOcmkCVqoJbmbk3sa+j3t3f+I7aW6uJJnLE/MeOnpXegkHoK4HwyqSa5HsYEoDnHbiu+AcY3LxUz3HC5JuJ4zS7j3FM2g9jTl3DryKzNADMnbNPBVqQcjg0mB0P50WAk2rTNo7c0mGHAJOKTJJHalYCTtzTXC470bmHWml/WiwXIWQH7v60wqwP3f8KsbxjpRuB+6R9KVgK5QHkjH0pVUAf/XqVjntVaQnOQKLAJIB7U3LBaCRxkc0FsdKLAXW8WXbAeXHGg9xk1A3iDVJCc3RUdgigVhoWPO3ipkyTnNauUu5KSLrXd1OcyTSP9WNMwxOeT+NNTIWpFkAGDk1Iw2HPI5pQpDDg0glO/FS845x+dIYm1ge3PalwQelHQjiplJJ4HFICPHHSkWMnk5qfkdhSbx2GaAIBEMn5Tk1Uv8ASrfULcwyl1XI+51rUBpPlByBnFFwsZVholppsb+Qr5c5Jds1eEJP/wBargG8etP24OBgGi7CxS8gjrmnAbSO2KtNDIRwRmj7Pxz+NK47EOAw9/enpGc/4mpBHngj6VIIztyBRcYwsQCo4+lIkYzk7qlQDqQT7VMm1QD/ADpAQhRu+6MfWpgVXqKV42JAOAPrTSccAdOtIYrMvXt6VEsZdsKuKc3JDdu9TRFicAAH1oAYwwQg4b1xxTc+WfnQmrS7W4IGfepYePl6/WmIolkcYC4/CoprEyx9Rz0rWZF5GB+VRhcgjac/SgLHIX+hCTJ5z61y9/oTIxzGcjow616lLAzHpVKfT0dSHUexq4zaIcDx2e2mtyd67k/vAfzFV9mOYmx7dq9H1HQupUZrlb3RSrF0Xy39uh/Ct4zuZONjCEmDhxtP6GnU+WOSH5ZkwD36g1F5ZHMZ49D0qtGId+FKBxTBJghWBU+hqQHigDKI+Y0TPu4A981Mke9mLK5A/u/40uETn92n1+c/4VoiWUwrt91SfoKUKQeSPzq2X835UjlnPvwPyFQOHVsOFQ+g/wDrVRDGYxTkYg0zI+tLnmgC0FJGRyKBxToRtXrU2FbqKi5ViLtzQBk8Gn+WR905+tNII6jFO4WDkUZpwJxjqPegYNACZ/8Ar1JHxu6dKjIwM9RUkZyDnrigB8f3q9x+GzFfB1sPWWTn8a8Oj+9Xtfw6wPCdsMk/O5x/wKsauxpT3O0MpUEk4FQNNxkVFPKyg8YXHeq+cYyTj0rG5rYmkclwd/tUPn5yFGe1DwyyDIG1PU8Vl3niHRNERheXavJ18tDkmkrtjNRN7O2ASaiuZILWMyXVzHEg9WFee6t8S57hWh0218qM8bn/AMK427vbzUX33lw8vsTwPoK0VN9SHNI9N1Lx7o+n7ltc3Uv+zyPz6Vw+r+M9Y1YlRL9mh7JF1/E1iBFHanbBVqCRDm2QYLMWYlmPUk5NOAxVhIC/StOz09RgshB/vHr+VNsSKdppk9yQcbE/vH/Cr+qaTDaeHbqRFJkCj5yeeo/KtONZIP8AVjefeqOuTSPot0sgZSU6EY71F9UaKOhm/D9f9OlbAyFPWvQNju4w/wBBjiuC8BLumuDnHHX8a9DiV1AKgke4rOs/fZdFe6CmUfKy596eN+MlM/Sp0lU9VKkeop2zIyprK5rZFfAb6+hoMR64PNS7Qzcjn1704DHT9afMyeVFbZtPB5pCTjDDmrLOc42g0x1+XITPtTUhOJW3c88UpGRShlY4ZCp+lKEB6dKq6J5WMK49xTCvPapwvXmonTnIPNMRHllPt3pj881KeBzUZGT1/CgRWYsM8jFNJPUAirJA5GM1HJHkcdaLAZcTKDgnNWVZDgZx+NUowQOABUv3uBimBc2qOj59c0g2ryGyPaooxzlgCPapwD2GR9KQw3Atnk81OvGSw+lNUY6r2qVQW6dvUUACMcdhUynA5z+FR4BI6Z7571MCewFIY0hmPTH1qRY8DApFYk9DUoXdjJNIBuxSevPtS+WGAxTtu0ZA5pRMFx05pDG7GXpnFOVB1GaczluADSj5Rzx7UAODFSBg/WpQcDmoiCMZNTxpG4IwTQMjMqg4C8imh2duB94dPSrKrGMnb81Kh4yoxzzSAhWEgZPHbk0oXc2cjafUVayGxnkGmNHsBIyc0ANaLIwDnHamCLcDnrUqruYZ4PQ80rRlSOc/WkMgERAweop0eQf8KlbK8YH1oye/GPSgBDw23GM9qGG3BAxTjzyvJ+lIQc8gfSgBVdyQWxjPPNTEsfurUKqWYufpmrkahF+Zs+9AFd1fg4xTTG5G7APtirDp5g+XJpBGV4Jx6ZNAFCWJMfORj0681l3mlJOTtVfpXQSRKO4/CmCNC3yjnHWjmsHLc88vtFZQw2bl7giuautHaMloDj/YPSvYprBZATJ909xWVfaLbupaOPI7kVarpEugzyGRHjws8ZX2bpUZUrzH09Ca7u90WPawK5XptIzXG6hbC0unhTIXGRntW8KnMZTg4mUV7FuPQUb40HEQJ9XOf0pOelbVroiOV8xHdj69K1cktzNK5iPPNKNoLED+FBgfpUBRlI3LjNehWfhqXbmNQv0FYfifSTpzwswGWJBI71MaqbsN03a5zMcLSBip6UhDIfnBrT0+wmltXmVCYw2Cw7U57c4wRkVbnrYSp3VytC6uMA8+lT1Xks+codppnmzQHDjI9aWj2CzW5cFLUEdyj45wfQ1KGpALsHbimEN1P50/dzSZp3FYjqSM8N9KQ4PUc0qfLkZzkd6dwsSR/e/CvbPh1G7+FbbYyn5n4zz9414pCPn/AArcg16+stMSyspGt+peVT8xye3pWc1fQqDsz2rV76y01PN1G9ihUcbVYZNclqPxP062Urpdm00g48x+n615jI8sxDTTSykd5HLH9aQKKlU0U6nY29W8Za7rLnzbtoYj0jh+UVheWWYsxLMepJyTT8YpQatWRDbe4irjtTwBTTIAcDk+gqzBYT3A3N8i+/ehuwWK5IzgZJ9BVuCxnkwSAq/rWjBpyxYVF3Me5HNa1tp7ceYCBU8w7GXbWIUgIvzeta9rpkhIYnNatvpsa4OBWpDahB8oqXMpRKMFn5agSKPyqe40iy1C1aCeENG4wQDiroi5wOvpUixfNz8pqHItRMLSfB9jpDytZtKN/UOc/lWpJDNGu0ocDptGa0ViZeTID+FSlowPmiJ96hq+rLi+XRGEJUDAbgfUZxUgPnnao5HvWr9ntrjrGhPv1prabEvzIWQ+g5FTyMvnRnlWVcfPn3Gaac4ww/KrjW84+6QfY8fzqNkZVzKhX1JGKmzQ7pkCqBxilKMvQn8aJIzjCycH3qAeasmOSPegdhzAMcEZqPDK+AMCpvmI9agZhISsRwn8TD+QoFsRMzSS4Q4RerDufSlLEZJwKk2qq7V4AqNos4I5rRKxk3cYeajYbSCCMelPMbjtx1NNMe4nI/GqJImbd0FJx1xzTjHjuQaQREfxdqYGKBzU8UWRnHFMTAbHWrS8gBMACgBybEx8vNTLISx+XgdOaiEROMsAM9qlTZHwTntQMnD4Byoz0p4c4wFGD6Uz5mGFQ/WnoqoOnPpSAYIwQWwR/WpYwMZKgUvmcYCgj3p8fPJIB9M0hiiPJyMg/wA6fukDcDgdaQPkj0pWmPbv2x1pAOySRjmnpEQcnFMgR2yW4H6GrSkdDQMb5ZxgNio1XDZzkD1qVlywxnpTcbVzjikApXdyDmpEwp9Ae1MQEDofwpWZn4CnGccUDJCqg8dO1OjITquQfamKceuR37VISNvJ6/pSAm3gD5untSMxYgU1QGHr+PWpU2njv6UAQ7G3dge3NPMRbAPalkz15x3pUc9/0pDBocDGeKaVAAyD+NW1IK/40jxq64Jx70AUgxPcAZxUiwsee2PWnGJhgYH1FNbeM7QeP1oAk4BUA/kKnCbx8uPrVRScf/W61YjmcDJA29OKAJdjLxnJ9azzeEXDo8bYHGR1q9uZuP0pksKTdMCQD7w/rSle2hUWk9Sqs6SPtU81M5c4BJjHt3qnLbFCcqUcc8HOR6ihDK3Cylj6GsLs6FboTMZThMb19M0sbBZGD7VX0PSnICsZJcBvaqVyR5oy/B6kUXHZE1zpkN180aqCe4NeY+OdP+w6jbtt/wBYpH1wf/r16lbNH5Y2s2709ao69otj4gtlgvI5FlTJjmj6qT/P6VrSnyyuzGpC8bI8S0i2+2axbQEZDPyPpzXqsOlxQja4XdjNTaN4D0nRZVuxcTTTr0eUgYz6AVqyLGpOyM8frWlarzPQilScVqVbW3KAFXQZ7Gs3xd4ei1+yhSG5it7iNt2WBKkYxjjpWpKknJEmU64xjFRbfTOPSsIzcXdGrgpKzMbRvDJ0jTPs73EczlizOoIHPaql54dhm3MF8o5+8o4P4V0IQNnY7fQmpMKYyrMPxqvau9xezSVkec33h65twXVPNiH8Sjp9RWNJbYByM16wYQATGxwaybzR7fUCS0IRx/GnBNbQr9zKVI8wls1Y5X5T+lQETW/Xla7W88NTxKWgImUfw9GFYMtsVO0qQ3cHtXTGrcwlTMtLhG4Pyn3qXNOlskYnjafaqpimg6fMtaXT2M3FosZpQagSdTw3ympgMjNAizbnL/hVrg1Utf8AWH6VapMQ4CncYqPdjpzVq30+a5AdiI4/VqlyQ7FVnXOBkn2qeCwuZgGZdinvW9aaXbREYX5z0Y9/6VpxafKzfKpAPcj+lS5FJGNb6bHCoITc57mte102Rxkj8B1/+tWva2G3h05xyfWtWGwCneuN3pms3IpRMi108BsFcD3Fa8VuiAAAH8Kt+UxQ7lBHqOtNUDdioci1Eja3YndgY9BTo4mj5ORVtURj94g1KbUjq2aRRXVScE9qfJDvIOcA1MkRjOSARUq7SxypoQFZYynGSRTxG7dOnt1qdk3AEjFNVWB45NUIjEW1ScYP0pqyuDjHFW1fCkMCKibYx4HNMRG05X76HHtQkyMMDBHoad3wP1qNlRTlkGaABrK2mz8m3/dOKik03C/u5AfZxj9asIR1Xr6VVubxnHlRH5ejSA/oKTURpszJN7M0ajCjhm/oKNu1Qo4Ue1TEDgZGMVGwU/dYVKVht3ISuW46emKQYGc808gcdj7UFR1zj61RJC3PIyOelNyTnORjuakYEHk4pjqe3IpgM2bmH9aQxgccZo2KW/Sn7cr14FAjBVc/N8vTipEVsAg4oQhSAefQntT+TyRj+tMByqx5bpVlHCbcMqjviq4yRjjFTpbk8sx9sUDJTMSCRkj1pybifmUgdc0m3ZjngdsdamRQevH4UgG5UZI3MR2p0Ubn5iCB71YRAAdqjFJI5LYAI96QxGVd4GcClWQZOVzSIVLEleV9aeUDNuXOP50gJUZ3POAPSpgNo96qx+YPvfKv61aQqQTzn0oGPAPfgGl2gLxQGyuSCOehoBAUsQcikAojJHQZFIylece3HrSq7biAD9RUmwlQSD7gmgZXBLfKQfcmnYOQAOMdTUphAB9T05pignjOB09aQCq5JwnY9egqUMN/BA59KjRB90k8mplYLhQq5znpzQMeTx9PakWNAc5yabux657HHFOVVI5IPGKAJFx6Ux3ZuMfTFKQFX7x6496UEIchRn1pAIDsyWyTjjmmhmYdeOmMVNu39vbkcUKB2xwKAGAcc5J+nWnHcDtOORSEqCDx7ZqRcNwO449aABAuOOOxpyrycfhSEIOOmBSh8cKCfw6UAJOokUKwGB0I6is+WLyXAfp13r3+vpWhkAZJBPtxThGJAckMD2Pp9KmUblxlymesTuQY3BB96mayilx52SwHUcUr2/kcxAlepA5K/wCNL9p3qowCvr6/SsWrbmyd9iCW3WFl2lsH3qxH83UH2J7VJ5kTFSqHI61MzGRcKmMd6dhlGSEIS7HcKoXCbzuGAB71cnQAZ2EHPrVCZHPJGBUtlJEasU4cimSSxY4yD7UpUn723PtSizLruVwPrQKxGsaPyd3tjrUqWjSKTglR6nmkjRIxl2yfSp4rqOI/cOTxwaAKr2/lsdjZB6g0fc6fexwMdanmbz5d6EjHcimKSSd6jB7mi4WMya1aY7kyCeorJvtPW5+SWNWb1xgj8a6+CDLnapaM9Qe1Ok0sTsSiKI+7gdPw6mrjJ9CJRXU8wuvD8qZMXzD+6eDVBNGvJpdqwsnGcuNor11NGto4xJvEhBwXXDKPqp5FUpdPZWJ2jy88FfnjP9RXRGo+pzyj2PNP+Eetx/rQXl6nHBH4d6p3mnPbxFxhkH8Q4I+or0K605TnICqTxnlfwPauf1myZLC4yp4TPz8/ka2jO5i4nIW5xL+FacGmzXWHzsjPIJ6fpWTCf3n4V2+k2jy2MGzc3yjIxjH0NXN2M4q5Wi0+GIDEZaQfxN3+hFaFvYtMB8rKRwSev5jrWzaab8wLjnvxwfrXQW9jGUyUGR7Vk5GiRz1rpe0A8ZHJrcit4wiluo9KviKNUwFHFN+zg8jjPpUORaiLAIjwVxU5hTHyioFjaPnqKsw4x97FTcdiFIpUY4AI9KlaHdyyD6Va2qy9Dn1FQuGB9aBlYwkNx0qdJdoAIJ96fGrt1HFTqhb5SMU0hNkCXKFuVHFTboXHHWla1VudoB+lH2TA6/gRT1FoIRuUjbSxogGMEUqxshIJNDjC/N+lUAwxKAfmzn1qJof4lJp4UY+ViT6GnFzs5XBo0AourI3XJ9KR0d2Aq1uLH5v5VVuJhgxqSQPvMO/tUgRSzHJijyFA+Z/U+gqu6/LgVJkdOtIeTjFAFRw/Tb27U3GMDrxyKsydMEZJ9ajwByFA9sUAQZGe4zxio2DY4xge1WAgJBxz9KaUDMctTERkZUEEH3pjqVXg5p7oFUkk9ajywbJB6fnTAZuxnHB7UGQkcgZpcblGcZFNVT5mCePWgDKVAB1zTiMcZXmmKxJ5BX6UqjccjOfSmIchZTuH6irMcrdBUWQQVBP9BUsGepGMc5oGThJOTyD6+lLkckktjtTPNMpIwcdxjrUhGGANIB8UhJDMfbAqQgk5B/WmoFAyAOPQUolUnO3JFIY4AhuTge9PMmFGCBxyRTAxZslQR3ApSS3G3afQdaQCbwecdD61aRDtDE5z0z2qqEUMCSOPeraumwDOR60DFAJ7EnNWBlQBt+tRRYxlRkn1FTLktjdz3pDGkNHjsPWnBi2Mk4FOfI64oUqUJB5HpQA5VyRgfjmhoevQE+lLGwU845p5ctnHH0pARbG654xzT0A4JHOenanADuCv1FKUBIY8jsM0DHhBJwdu0HinbeSoXPvmoACGIUnbUynb0oAGjPBIHHv0qI7hlipPPpU7MJFAbpmmmBs5D5BoAi81iSduD0pwBGCOg6qKCmwcDP8An3p6MGPTPpikBHtDHJAB7CnodrYx17+lDct7+uKciK3zZJ59KAFMRYAKtRlTGQDyMYPapwQDtJAI5FISJBu4Bx3FAEPyg8cn0J6VKrfJk9R1FOYfKCcY6/SmbuMrhiepoAcAFOQM56mq89sH+ZMB88g9G+vp9an3naSDwRTAxZuuKTSeg02tihJcS27AAYHcHnFSR375DA5HsavtDFKhV+cdCB0rKms2t5GeMZB6AHIP0rGUXE6ITUty7uF0CHkK57VDLZIFPzZPqKrW8hd8Hk9xV5nkVPlAHsTU7lmW0ZjPT9KsxFWQBgM9BzTZjI/QY9ear7GPAYkj1qRj3gO7DKfbFRCIg4UHPvU6SNEeJDnoB1qzbpNdyMCVBX7y9GP0FNaidkUvKcOpBHvtNaNpbvMCFjGV6luP0qeGygVm8v5znPXbIlWNon27iXZT1+7Iv+NaKHczc+w2Kytsk5Mjd1+4R9BUd1LjgK0qr3HyyJ/jV4BXX5j5yDgkLh1pzwqwzgXEft95fxrS3Yzv3MAzFn83lh/z1iHzD/eWpYAsg85GABPMkPT/AIEtWprYFjLGpcDgsp2yL9fWqcghhDXDzBEBwZkO1gf9oVJW4t9Yxv8AvQMbhzJGMqf94Vy3iG2W00y4WZli3xNjnKtx2Hard34qeIMLQb5FODNjCuPcVyOoSXF5HK8rGViDjPYe1XF6idPTU4BJyr7gO3SvavDMttcabapC6M6xKGUdQceleHr97FegaeJLZIZY2ZHUDDDgjiuuvokctGHM2errYnAOP0qVICpGM49K5jS/Gk8W1L6Lz16eYnDY9x3rr7K/sdQj3200bZ5K5+b8q5tzZwcdxvkRsMkVGYAGO1quGPLHAI9aQxgDJHTvQSVjbMy53D3FKiqowYzgd6tqUI9alUBjhQv0NNIVyupjcYAKketOAVT0BPrTpEzwOD7VGiyBssOBTAkyM+lOyBznFMkTeMhcH2qBlfNO9hWLPJOQc/SnCRVPJGaqgsoyCRTkkVuHHPrTTCxMzoeelQORJ0NLJyNq8iq5iZRuA6UmwSHj5D0z7Uv3sAjHvVYyOx+lJNcHZsjXB/ibPNK47D7iRFUohGc/MapkrgrxSM429Dn3FNLBVyOR7daQBgZ9O1JtB5z+FKWB6AUjfMck49xQAx0y3U/QUzI3EKefQ05iQOHwajYsMkgfhTELwOCMfjwab8pXrxUe5m4259MU9DkdMA0ADISnQn0qB4epzjnoasMG3f06U0kg4xjPWmIqNGw9MDjil2Bl74PoanbHINN2cHjGO9MDn0yRgDH+1UyoCwXANNjjZ2+XOPXsKuQKqEnrnr70xEZi29OCf1qSKIhhzgelS549SDiopmGMbjnHAB60hj2bYCUxn3poPzYzkHr3qIEnnGB3zUiKSfbGaQEzMoAyM+wp8au4yq7eec0xM4zkEj1GCfpU67shR/KgYr5VSvU98HFMwAwwCARgHNAi5OSATxinrDv4GwDHfOKQxmzBUn5gOwqbcuVIJ3fWkKrGeQSaNmCTgUhk0TlWxgY45qxHOgIABBxyTVIMD8zHavYj+VWFbyye/GOlICd3LLkZPsRimK23Ixz2ApFdMkHB9amIPVeh6AmgBiEDJOCDyeatqUC5PGenvVcqqrkAGkRj3UgEdfSgZdIXAywz14owJAOSQR2qrudMk56dF6mn+aRlc49cCgRZACDGcA1HnsBxnmkEpA4GcHk01mfGPxz3xQMRmIcbQTz3qTLbM7vw9qiO7aMYyO1IpO0DOSPWkBJvb73P5U2N8KSpxiguTHghRnsTSBgOBwB+VAEysp+Zsk9MVKWGw7Rgd/eq0OXz3XqMVIOWbjB7ZoAY21iu0kY5PqakXGPlPPpUb5DDC9e44pOqkAD6EdaQycIwCljj2NSEgAheg/nVdpnwMdAORQGODkZz97vTAl83AKbsk0vDZOBtHOaiCqzE8Hb09qcQSASynHbFAD3bEe2PIPYjtQoDghgDnrSfMRgdKVQOV6Z4oAqPbmNi8bZX1xyPr6/WqxZlkw+7/eJ61rjKtx2NRtbo7cKACfmXHX3HpWUqfY1hU6My2becY5J6irNvaySL5pVTF/ERyR+FX2tFjxLaPj3Pf61FFKjTnyyLe6H3lP3XqVCz1K57rQUaQqRmVl8yE8iRDhk/CmPAWTex8+Jek8fEifUd6tQ3TneIR5c4+/EejfSpIjHPKrRbYbhfvxngNWll0Iu+pSJKRh5X82L+GdOGT61K1x8gaYh0H3Z4+o+oqWa23OTDIIJerRP916qgKkhEA8m4/ihb7rfSk9AViUz4ZTMxAP3LiPp+NStd+Sw+0ZU/wzp0P1rBvtbtdMzwd5JElsOQPf2rlLzWLq8VoDKfIJyIR0X/ABoTZahfc6vWfFdrACtsBNdKceavC4/rXG3lzcX8zTXD72Jzjoo+gqsSS6jGF7CncdeQB60y0ktgKjHX8KQLg8YOOlPZg+QOMUzeGJB3DceBQOxRbRdLe6WY2zqwOSinCk+uKvvsOFUkCkZN7HkjjnHWpFQjJAycd6bk3uJQitkRCI4ODkA9KBLJGwdCUdTkFTgipAxBwpAI7ih8E5BBNK47HRad44uoNkd/CZ07ug+Yf4112na1Y6quLadSxH+rbhh+FeWmPnJOCfypq745FZWKuvIZTyD7GqUjOVJM9g2EN6U5oTj1/pXA6X4zvLZhHfA3EOPv5+df8fxrrdO1yz1FSsFwN/8AcfhqpNGMqckXgpQ8/rUnmqO9VZGbOQeKiD85YZ96fNYjlNQYK8HmosbSfeq8XBU5OKst7HNUncm1hGjDL/Wq7xMOF5B9KmEmOGFMd8ZK0MCDcI/vHp60LmQ5VgPalYs4wyjB7moZZAqmOI8dCfWlcdhkzKcxrkjuw7+1Vm5wNpA7CnblzjgEUhJ3UhkZcZGVA9zSDYcnI9BTyM8MKh2FQcNgepFIQ4r8vzcetMZOmD3pSx4y3Pp14pwYEY7Y6mmBCen3jkU0kA7SevapHweAVzTG4zk/hTEN2Ic8AYOaYq7SGzmkZTluwPPNIsZVTyCR0x0oAPu8g8N0AFBdiApC/XNIy85PJ+tNPKnqRjHNMQhc4w3A9elIH3Ntzk47GmsXTADArTXPOdvUc47UwM2KVEUA8E9j0FSm6UKGVAWHH4VRHVvqKkT7g/3qYi0Zyw+U1H1cAg5/nTsDYFxxnpSJ0NIZIqge5+tSk9i3A/ixkVC3KjPrVhP9SG78c0ASIAGwoyQcA1MgO4D+HGCcdaRP9eF7Y6VJ3X8KQyPYckkdf0pUdueBgHG7NTbRhuKr9z9f60hk4QYOG/XJpGVdgKkHr71A/RfqasH5gc80gGLlcc5J6KalIYxkg5/CmJ/DS9l+n9aBkscfy5OSB274qZCFUEk8dCKanT/gNRr80q55pATbldlwOnY9CaCwAPzA4/WgqMHioW+//ujj2oAmMxbAUnpnipRhgCWyRSIoyOO9SIo83pQMIwQxfAGfU5pCSpJUkZ6se9SlRxx2FNPzRc880gGqobhtuCe9NeMg/u1+bpTl+aM7ueaSLqW7880AKoXcSwJ55H9KHZRwQvI/OmglVkwccU2D5kfdz0/rQMnXCqNp9z3NO5b+Ij39agk+Vgo4GOlPbqPwoESgEDJOQP507ghgF5xniiPrUkqjDNjn1oAiEe1SwIA79jQFDg54GaYpPlnntToPuL9KBgpHAAGexqUBCp3c5/SoV7/UVO/3F/GkA/MYU4ORjr61Hk4GVJPUexqHuT7/ANKeOg+p/lTAerPu5HHqetSA45wQD0FJGBkHHPFSH7n4UCGKzDodh9SM5/xqO4t47qNSSqy9gDk8dxTo/mC55pZFGw8UmroadmUWLbhHdZVwcRzrUzSsJFjuTskx+7nXv9athFmik8wBuD1rn2upv7Mn+f7q8cDioas7GsfeNO/1SGK1MeqMsbgfI6clvpXIaj4jvLuLyIRshHRj/rD+NYErtNKXkYs27qT71Zi+bap5GOlM1UUiLbjaME55LE08IAC4/Cmnqv0P86iiY8cmgZOxYAbcEdfegfOMjOB0wKhP+sH1p7/I3y8fT6UDEMe0/Kdwzzx1pyqN3IO7oAOKmgUbxx2qNlHp/EaBAwO7djnHGTUT5c4QEkcnIp0DHeOaJPlTjjigBCcrjABPUCmqcKQo4Hb1pX6tTYvvt/stx7UATB/lAYfNnOTSMxbjYCPSmS/6yov4/wAqAuTnl+OMDvTWaQHMZ2kEH6UiO29lycYPFO7L9aANqy8U39nhJwLmLAyG4b8D/jXWafrem6mgWKXZN3ik4I/xrzlfnYbuetNZF8t2wM8c/jTuZygmeuxZQHOCvvUoZfXmuL8Jahd3GotazXDvCq8Kxzj8etdWzHaOe1WmYSjZkrSqo56+lMR/m5H50w89abfMVCqpwvPFO5NhJ7vzFKxD5B1YdTVU5yT1HpTplCyLgYpr9RSAbkN2HXqKQ53devY0qUknb8aYhxHJOaYxBBBBH04p4+Z8nnimvyzUAVpVGRhQWx1NM5Bxjb9TVjaGPIzTJfu0AQclh90nPI701R83JOf0ph+4fr/WpUYtEWJycnn8qAH5+QjGD2OKgDZBO7dntTz0NJ3H0piIpGX5hjDe5qIl1BGNwPWpj8z880kfegRFs3HnjHb1FNaMAZ5z0GOhq5tGRx2qGT7ppgf/2Q==",
+ "image/png": "iVBORw0KGgoAAAANSUhEUgAAAoAAAAGrCAIAAADfLLEcAAEAAElEQVR4Aez9+ZNkSZLfifl9xplXXX3OTPcAAxCLwSwGQy73F5IiFPKv4B+1/8X+wJUlVwTCU5YQyO5ihwtgljN9TE93V9eRlXecHn47P1/V99SfP38WEZ4VmVXVHZaRz9XU1NTU1A6169mr//bTz2pVrl6vV6Fry+WyEr9arSrxtRzvBEEW/L8mPhiWUk/hS2ThTdGn8BHxlkDk97tC7wKH2Ck9BEEpXyl8opbUUvTVtbCWpk/U25J4a++u9OuYt4JS+bpV5G8xUao+7IoP/XjEVPS1JvL+ZI0xKBXxrvCR3C3lTKe7CFZFIE2ftZhbprtr/xzplvinymVX+shjiX8Kn+Kfok/hU3zqeQdUkidFvyv/FB8vF0KdIIBGJPB+gCjXUnIpfIns3vueNeDV5T0nep/cH5oGvivV7JuS812nm+J/j/eWeFd62G7X788Ah4kNwKUJbwDbUt5j3r8Gos4F8P5luE/xD0EDUcEC+HbmOsQL4P3IGckFcLfpBtsAnH94A7jHFzUfagngev0U4wbc2tXspehLQkQCTu+hwAGk8BHx9wxI6efbmc0onQDuSv58Bejbme97qW6rgVR92BUf6UXEACJoA/h2LEEj0vVypkLfGh8RA9hQy02eVKzAbwPOsoQvebf1sE1QySfkLdGXvG/NP8kn74BKBCXvjemm6FP4yG8JeE8zYO/HSTsAlyO8AZTku/d+IxrYrkbfiBj3if6BaOC7Ut++KTnfdbop/vd4b4B3pYft5pycAUeSpTi7WkronVURgGfRGwTgU+mWxPjOeb9D+fIiRuAA7rBc8gHod64A7wXe0ECqPu+KLzKNuAEUQzP4m54BI0aIF8C2nKmgr4OPuAFsp5vCpKIU8QEH4NzCCxAwQQEHsE1flCfIAtimLwYFHMA2fYp/MUrAAgodUBEfMAwDDmA73WJQwAABX8OnKHOr6HlH8Lat9YRS+Hckxj3bW2qAOhSm14FbRrwnu9fAW2sgeq4A3prVO40Y4gXwTpML5pFcABF0J0CwDcDZhjeAPyx8PXvrR9m3VzJyILPkudfMtghS+ExtOQFkonzfS9AuRTzv+/dQxbcKKDW2b5Vs98L8Hmvgu1Lxvik533W6Kf73eG90d6WHaMJ3NgNOmdLUe2kpfIpPSFwCGo1sDOGqSSkoYqUIdsUHw+8okMpv6N8JUmRvn+vEe7ephEKeUoop+hLZjd4Un1S6KYYp+hT/FJ9d8d9Uuql87YpP9QMpPqn3wlP07xof5eUJRXKlfgkyD0rlN/iUgGDo+O3iLqUbBBHRgRS+lBxkTr9YVL+vnKKPfJXkCfpb4kPOiOiARwe+JZ9S9PCm+KTw+YS1nG6KPoUPAQLwnN6ZAQ6+98C9Bu41cK+BPygNRLdbynXgAygRfE1vim3gA/CEwhvA9fiUeBE9gBKfUsQSWYR+F/Bagi7Ima0wh2HOgRvx60wblNHfG+DQyz1wr4F7DZQ1UOh6ykH3ftdAqCgA8AFvA3elt0rO28jAXCNtpcCVcga32wBvl+I2528nn0r97IpsRW5LMVP4Etm9t6SBe72VFPI1vTGw/Jp8UtHfNf9Uuu8af1f1cFc+Kfq7wqf0dlf8d+UT8kTEACqDtkODrBK4kT4IAgg+gQnAg8IbwDa+FLTNE0zQBJBCfn18JLENuGy3xeen6Ev0JW9B4KyH2CbwdL/m834G/DUVeB/9XgP3GvhD10Bl71yJvFtNVSZRiSTdXfEpUVN83iKJFKvvCj6lotvj72fAt9fVrSij6tyK+p7oJg286xnqu+Z/U/7eVfhd1cNd+aTo7wqf0tdd8d+VT1GeiHsboBjxGjhY3YYmiLcBj357fFCW0nV8hAZQJAtkALumvk1fZBVwANv0SXnyGTAEER0g4BK+Vlt/fChoAAqHxbwLiY6kBIQ3JNqgv58Bh17ugXsN3GugrIHodEoBhQ6oFPIH6g1FOVDyopTA3K2Cgu0t0y3RhzApfBA4sE3mmKgP2wSpiL8f+JJ+dvW+p/eAdxXrnv5eA/cauNfAd04DYX5c8vAG8I5yVOIf3gCulyfIArheziALoET/h4YvZf/23lZ7fsW9kKtG9n5dvdZcGTjPZ96resFIrxq1/GaQW6axWlW/T9ZsNikk3h7jiYObj6Hq9SawY4pPpw8yTx2C5XLusD/jLdMAikwUPV+CKOFL7+15qOiL3AtwEBRwAgvKKoXs6M3lLEXz0ikh8SbItwkzTIxYSxS78klrqFpz9aRGS4Jk3uz6merACmxK/lR+K1gYanc+1flN8U/Jk6pXSfrl9hpXKs3r8Ml0U5FSyaYUtyM+pc2UnHeFDz0HQwfCW9JHvP9awpe8he6oFJJ5U+nGEmgIEIDHDK8Drjee4Q0C6Lfxni7iZfQ5EFJG9Aywcgw+0e9E8TpZxIp8ZZQ53RpvF0KFAKu8Ppf4hDwlPo1V4aaqPNdr4hwT8sTn7ENRThx3VDqw9uZ2MO+4PF4t5CzhF6vMHmV0ecGHAMUFaJCtpVO4XupNEjaO2BFPedOg7Gh9i4oowf6id4hFqMPLZYXBprTm8w1D69wKpVhin3mL/KspNrG70m/Gvvfda+BeA78PGoh+IID3k6tILgBPN7wBfEvwJbWUxIvQG/ElgpL39nyC0oEUnxLZthfL8tZxt7mlMKTSWuZTKhmzlQysGWBSx1Q3VvUYCqSYvCUeA0yKSpQUC8OEIkyQa4Fn4D298OYjqgoxPG4wqaDYRO1Kvxn73vcHrYGoPH/QWvjuZz7KsQSE9x1lMfhvAdlSwxY+E+T94+8kxW0m12A8q9sEb4e/vgSxLJ5QAJX0IUxl6DbSDRaxHAjmrXlNS75yLPa5ObRFwqUtV+Q3SzvF2zxTgoYcDih9s6XNps6FAeN8ecdhlqCDxjE8AwOQck5GqAPZysAWdYks6LcIM0TQpwjeET5rju+I+z3b75oG7qoevms+Kf4pfKocUvR3hS+mGzwBAi4SAKfwJbLw3oY+aAxYt/hNfLBcyxAEHhbeAO4QHzwDeDvmxAoOAaSQ2/iIsg0k5Km2AG6GnAlwAOktNmdffoY5KweYP0Lh73BrYSvN7smWs7HEFHq1nJVs3wZZueeKWMU7SJHKBQPvjpSK28Ygm83rBIXAhQvgelmDLIDr6e9D7zVwr4HfMw1E2w/g/WQwkgvA0w1vAN8sntRDkgDeQqSIG4AzuSv+1/CJhEoA5saFCaBEEF43TOENoF48MhXYNNBamIXKjJiZ5QbqJQIWWmY424MWbLvCG2ey0nwjZFu5HuQ5xJq6C7K5nf7CPLuDDIAokWH3Bn3pEFakWwSCGCDfMy+GCw6aIlxEliJcE1SivFuvFdfdsrzn9h3WwF3Vw3fNJ8U/hU8VSYr+rvCebnDbBkqCBUEJn/JeTx+hAdAzwSq8ATj/8AbwfvB3lUqIHYBzvj3/YsSAA6jiUz1hc3sEfRFQ9GryWiPfNvUkCs9EBKMIKxZAy5aaSUXRZHrt1DIAXv4zHshYZwiQOSYLeMsf7C6TXY5WzWYzgFCZG2Dkw2FrHeDZbrcDDtsM5kYDHJwDuF7iIAvgevr70HsNoIG7qi1U6Xt9foMaiHIsAeF9R7IF/y0g62+38Jkg7xkf9fNrprsd3TE27VPWtgk8w18bn00pM/Wtf5SzXIZ16uvwTSj0sIleTxRT+IjoQHYRBwnjz5N/H12AG+CpOcwwXgQwGZQ6koRzb6fTcbvLZnCr1eKJsxilnFZ74VYdkMDuSp9gc4++18C9Br57GojmH8D7yUMkF4CnG94Avll8aKMkz674iB5AcChl8B3hS2zNAN3KUkBZiuve6/EeWny25tMJftm2ZlPPWk3z0uUSI1dbrhb8K5gu3gKuNVIjiEp5QFbTY1Cxu9jf8XgMEcmROJIwH3Z5eJI0k2Mc5nkymUQOoYTeo3Q6iogx5hmiElcJ20vGAHgdAwFI51N6pvDBs0Sf8u5Kn+KTwt+qdqQivwN8Kr8Ux52kluLvBXr7JHblk+Kf4nN7SZwyxSeFT+kzRZ+SP1XPd5W/RB/JpeTZFV/iH95d+WwL5hxSfHbVT4pPCFwCgr4EpOS0hUjxKNEHW8dHaArv/HmWKMNb4rMrfSrd6/G7yhPcAgj5HeNiA5fKMfAl+uBTog98zMgD4wCWxIFQVI4vEWZe+BcpQ55Wv92WiWMpeDqlkbfaMmbtVgvT6ETe8pEbt6zpJo7qFHbEYn1JqN/vkwrGFS8MgLmIA1k9Oce4oYVGAuQ2lYVrBIO63W6yOo0553ljJwWHu5F+x8zek99r4PdAAzQ3cuHPaIlgaFaROw8N77cECAkD+GYFCzECcHnCG8At8aXslKJH6HcBr7pUkHNdta7BRwZvBuw0UxXZRkJVBBW429d2KIPYAX+2WvUZc91ai5d8mloIXi6msyn5xxZzPVaYNKhdKQXVVAhUharOGEYf5r1ezzlfXV2RNtH7/a6kMEda/PKEGGsNDIFjHElcm0VrIRsDrKGDOTi7nCG2xyV66hBWleS/zzjXz3YO0dg28i0wKf4pVneVbor/rviU/N+UnCl5Uvnalf5GPtsZd0wk5MA2WYrz+8GXxCNRxwT+HYmR4h/4bcAl2cJn/WcJj55LmMjIHxo+Mv6egajqASBAES7KU8QX4dbl6Ru3W76ku2qs2tyHVa8tbK5I4VOccrpjUVbNz2cVWd8EVxtgYsENUUi32+0C+06wz7yxoEgFEsOJ9eWJ1xMiCg7Yn/zaBH6OCYcGiz4YDJyhEYoybDaYlDSk5fxLzxS+RBbeXekj4i2BailvGfme7A9eA29dP4nocf1ZHJqrWVlbRrseuq3mXfHbHBzzdfhEXICASwm9T3ykFUApj4Zft/ggCwD6gAOoYrLOZZAF8C2jz/Ib4gVQLedaPes8vgcotz5hhgKonsAEfUm21ocPD8ghx5Ans9l8wi/HoptYxXanR5uyA8rsBRNds0/eQUoZ4JhilhLA/G1hhMBYYjhduSwgY4b9OPTJyRmhpOcO2I0xhhkYenfA7iRQ7txU88QY7+3tkQRMICMc8RzO493/3mvgXgM3a4BWQ/OBzhtRwKkBsRPczPc9UoRIAbzHxCuSCjECcKLwBnA9ntCgDOD6KEEWwO8Hvefi3Tyr7ZenZTZFrSMAvUu0i2udvHjW7fXYi+0MutyDPZ0v50sumqbVYR0zY27c/ZbKdZGXUimVaCE0OUTBKGIssa+afNvBZrzHx00sMSez2PTFS9I09Rhuw5aEcDGp5TUkjwsZSOy07xaTI4hN8rUseOMS7TXWIHiWMO5N4SuJQe5Kn+KTwldLmaK+x99rYFMDu9ZPb0HEiogO0NZgrAZlDafU0DbTlC+il4JS+BJZeFP0KbxHjNBtIDiXKN8pPiVGFV4tvgq/FjAV+p3E1+1bAGZ5JH8ADoU3ANZkd3Mpg7pbz1qs8AEbYJJdK1KUC1St/+r//F8eHh4+efzhoyePDw6P+3v73cF+r9s7PbtYNdu1Bi/8tJgTc18Hr9xiklPvAReZbqZenbEwrghNXLzEwtDu7++zFs2c2G0wxtjttDd4aDwhnu4gBvBQnji8kIEPvYQ8SuuO3mMOnt9RwLW0Lfy20rZpboNJ8U/Fvat0U/x3xafk/6bk3FWeFP2ueqBBeRQy7nn3J02VJDwVBxz20F1TeXf0LhX8S0B431HSKf6B3wZcki181n+W8KHnEj6y84eGj4y/ZyAKwoHwlsTw4ig+IcDbevHVV/z94he/aNRbvcHw+PGTjz7+5PjhBx997/uNVq3V0xu3dSB9Jaox51NF1fa0lNzNXho2nJm8AmAs3R7TqrG7PJm/spULHi+Oee2zZ8/IG45QHICnERNfOJAfvGwAcxLLLTGYoFRkGeB7d6+Bew3cVgPeZXjb8XbnMC2XIBztjrbmDu9t+b5fuhAsgPebfjm1ECMApwhvANfjg2+J/g8WHxl/zwCN4voUo4AciGf9v/g//XNWmtn5XTDFXdU5e8Vm6YIt2m5vuHf46PEHTz7+5NGTD4+PHwyG+xi2N7UHpMSEmIbHrZHsCreYKDdb0xkM2nZRZYN7unhfCT+U3dmlJ+bt1qXcliYwvICcGUkE0dEvBuDLem055zUkWvqCKfFEFnuqBWqa/Vmt7XEZQCBep9ftdHoArKozYiAmImaJ2m97lb1P7Mh4wi3gIpDSbAhcJAZu7NgFpfiU2IZXOXqXLpXfVJop+hQ+xSeFp9NPBVXiU/pMyZMqrhQ9JVyZbpq+kry8OVIgql4iS+WrEHEDTMqzo43s9ho+PmZoy7qUj3fB0MR44kgIY0zatEwGyo16d0OO3LOr/Hm8285cU/zvCh/6DIYBuKjhdSC8kZESWQofER2IKUMJH9EdH6HN/OM6JXxJ/qBP8Ql8CWDE5Zh3xH+5qPjsbFGGVLpFGuDtDOZiV/fzpehrb34Z8xqzCYViHWhyhqpwRjhgWorHK9G36k2spU1r6426THEWu1mrn528efnq1d/94ufd3mDv4Ojw8Gg4HH70j/4V09O9vQNOG/c77cVyNV/OFtNpr9WZL8azeV2zZCyw1q7Zu20Ohj1rp3osocaZDfFGizQSCMJc6Ml0nvWJZoCXtSU2GEuMbcXU1pYdO+G80LK1ucMmh8WyJWjem2o2eIdZV3NYN7bU942jx0z1tZsKvffda+BeA6EBzjM6zGAX++ozXUarwN54edLcaOy0O553tULmidK0S0AI9o0AKXlS+F2FTPG5EV9KKOi/Jr4UPbzvmn8k9C0HZLzMFYGACUFReENdHlQkaDV53xcD1tK3f7nmyg0wc9hGk2gN2ttsMZ9cXsym4/M3r7mh49/+j/8zBvjg+Ojhw8cP2Td+/MHR8YP+cL+x6vQb7b1+p9HkRd7aZDadjEcY3edvlgyWu31mpF1e0yUtM8XcbDWT5BhIsrBYzyoyWRl3+EeZskPU2FOuAMHCMt5uN+odTHLdJpudVocoGHU9caYQZXmej9RMQfFYJkY0RaUEsQTMu4Ai8lp8ifAGb4p/Ktp3fRSR0nMyvwn9p+i/K/h0ud9NCSf576hPDLAvQvjRSPaDNJK2dwqwuDg3yQCc3mCAzhC+sgiS8lRSF5AR0YHwFkgEpvAlsrf2Bv9twHmW8OEtpXgjPghyoDwEcTztKCco5/2u8CXJw/uu+UdC32Yg+rESwNQzxHZF+dPJSsRQtkAxI5XpVcvBx6kysRiPLjF1g167wdRT7yPpqwnzq/EPnjzktsjxm6e/efa7X69WnW5/ONxn8/jh4yeDwd7R8cOjB48ODo5kcTutere+7D2mxV5NJ+dnb9jqJYVWq2PTVL4DQYpKy6pYJvd8piVit5JMeIHNkHICDNimtaAgyKplrTEZyZuPRCxQNdJ7DbKW8fUAcSshsoASh5y8XLlvgQ+SWwFRm29FnenqlrT3ZDdrIK9HN1PmFLvHyGPe7vcd89/RAF9eXFFFcRo326dTaIl4GVUz6p3PsgMcq45gFr84m1WZTaJU4m+DjLgAAZcipvAlsvCm6FP4iAgQNAF4aHgBAi5GLMa9Bh9xDVjrbROfMSgh45BpCR/J7YqPiA5sRw9MiuB6fIn/t82LQawUqWBw4piRgBiAmloU1/Xj9sVjGZyxbdlOrU0fLR1Wnu0Dhat+r0M7W85ni9nUTl5xEKvWbtZHrz9noWnQ7Ax7WO7GajmujWfjq5Nff/Up6WNce/3B4eHx8aOHTJIZEbee/EmX95xwww7mlmXomQ5LsZc7ZT7L+jDvGTFtZRlasuLL79gsZ1unLjW9JTI7zVHPGpMZ+cHc8sSxN+00rrdsgaAwKl9m93lss682zGW6e/+9Bv6QNMBSMyNvHM1OS1ndrlrZagWGhWgAlMHeMO2bJ0F3qBtnDsMA7pD5W7AKMQJwJuEN4C2YEyWiB3Aj/6AM4PooQRbA9fQeuv2M6AFczyfIAtjm+X4wdqhoh6QS9lfnm6K2r29X1LpsZqQ8lPw64BNCT9gx/mxhZUvisPbMxFFnoZYcYlK4WfbMyDUWs1aTpqg7LmZcIM1xKIz0fLl3cMjS1OTq8uz85cnz333xG9qjrtcYDz85Pj7+8KNPPvjgg/2jI7aTG61Ovdnq9tvYfgywXgbm5JfNbhG3YZNfkymziEubs2K5MdWIurInCkAAzd1bbUNKUTLLeoMZkIn8Ol8xKoGSDJXym3kThj/Zo2zpzfkkuFenCXbXGrkr/2TC9wGmgd31uXuM3VT9jvkn6m1KRsbQo5H2kjC3GF2f/gJ790G3glXmhQUcNpj2zluBlax2refOJGJtA6VUgqCET3lT9Cl8Sp4UPsXnenyEBkAPQRLhDaCYr0ACxMzkmlhF+hSfIr4I+6qk7I9LFYCjwhuARw5vAEWmG/B6mXMDvfZ4BYtqZhzXoQEFQWDeBvB6vh3T8REaQOjWowQ+BbAEXTElbNaWl2enzHRpXZysoJlhJjUbXi4HXewi5lKfRmgu6/1Ofa/fqzfbZ2cXkO33+GggZ6U4I837CePlmC3k1lcnTz/71f9vvlp2O/3jhw+ffPgxK9Wf/PCP6g2O7LWarU6z3eHoFFaZ4cN8qkswpVR2oPXDoHqhqTZpY5tNWsPb4WgZXZOf+zWsZ7ElZytCEQmw8lkXxrJWfcquOEJx3eXP6plxSdE58c6/u/JZ52TnpL4VEaIi3lKaXfWzK/9binHnZOl8VZfwrvlK8t/RALOzSyeA8y+muAFGGA6CuPXVQNs+hQKSRFPppvA3KjYiOhDeUsQUfle9ldiGN/hvA05Twoc3OJTIUviImANZfci9mTGOfJXwsU+3hbeOMG3Lt+hLApa9Kfpd8WW+3xF/6L8E+EVPjiwGBUz+iqH2xYWNJu9Gq36wv89CsXZe2dsxpTDn5ZMNjIO1XGxzUeJxXxY0fBJhyIzWZp98zYHXmYjRbPBX764uMbLNbpP93/Hs/OTp2cmzzzDs/+GvB7wz1B9yvPoYe7x/eMxYm5a8t/fEUtPstmG3nOjVplWDrw7aijdGlRVxmjoElPVqlglP62clWnlr1dt4NEjX1Nllj50pvI6xRAqPqDcFnMA7XVQr8b733mvg26+BOhfl8Q6CbQHr0hvsLkNzWr0bZofx8lYgf5UD+rfOZLTKAN6a1Z1EDDECcLbhDeDtkovoAdySf4k+Ur8rfDAsAe+afym5b8CbXIOW4TFTugGwQgDSV41zAjciQQba16WF0SEsM5davzWXWRyuxwDDlnCtpa3acCtOHbOki3nEvvHSgUVmZsp2kM82WarGOjueWIPlmDfHsJZc59Fu1ZctKGmts/HJ2dWq9qZW/4LbtthD6g66vNbU6Xz4yZ8x6GbVerh/wIay3jJudthbnvHGoVJR5rC0WHjsu96cqrG1nNlUagMT4YluC9EtHyTD+KGu16KkKa8rvb7jNWN2jM99HY5s3gikZsy78tmVXlsCuzirIrtESNDeFR8VyS7urtJN6dm1GakEsKucqfqwS16vo03Jn4qTos/mQVvRUvlVe6OtNRqa53Zoa5lz/gxzcTlOv2k+1Smn5EzxKaZ1G/it+UdEB1LeG2UoRY8KVsKX+BTINtpLAZ/1AyU+0TuU8MHf8XgD8KAUfUTMyPxQbI6N+Qldb47TbwG/lsgIwlskL8B+/raAKIHOOSpTKd0CcXVCnCQq0KzB0EZo2AEsigPFJ9GKp53FJbiafEEM4HD0D+71J/H0Bv1OblG3KExKTeH6OpIbcL+TE8UwPeUpIy3GndWV1o0ZGIgA7TJnZum60e7qtBf3TrO5pMXt+eXlqDmq1z/7zVdY4r3hwf7hwdHRg2O97PSYDWYujGaNmo//AsAWK85cnPch2JXCi/pw5EqvHusbDC02rsgzMKe4AXw2T6seXV5ADwZif/oOMdHBbzubRm+j6Wmq6X3JuyrCPe7bqwGvPMgXwLdX1nvJ3r0GojcIwNMseW8UJEWfwt/IsERQwccGTMJnNirvpswb+ADW+SrRl1IKb84vEL9PQNjFIlCEyWx4r884ZNuU2xjNgJ1R9qPFZd9j5XDy0qbFtiVr5QrlSvNbGz3pN5sKC7L3n2R0jZwCNsacnWYpWFNUVq91SYhNn1kq5qsPvO/EW8Odpswwxpi1a2IN+QrTbHTx6vLN888/b3BWq7e3f8ClXB99/L0mrxMP9/aG+8P9PSCOXRJ5al8tZEaOccXJKs/G8Bn0dFwTp81oTl7Laerds+NjHgQZGJ44jLFyseW4hGsLJ0SKftcZaiXza5DFQxbXkN0HlTRAiZcw7qXoAQgtAZXE1yA9+jUEtw66mx7uruSJpawt+av1SZewRSlESp4UvpLJWyBT/FP4SCIIrgGCuBLYjuhkKXwlk2uQKT6V+G2kY6Lmk1DQXJPodz0o1Q9EvoLAAT/VTGgJH/QlIIuV9zZ4HZPiwK5u3pDyX9lKszrs9frktpiGdmbzRikg3ju2DWBPV+icG986UtrGAtPMdR+cUMbc1hfzLIgpra0oMznGTe2qM27mWDRW+j7i5fhscnH+uvX5r37GUa82p6jZNsYdP+DBSZDDD/6YvShedGJ9jMt4Fq3VfKaN6fnsknEEhtneodLMuNttYe45uO3ZIa2wvsDFPBbhjfX3QgBxC741uK2xddhdQPcG+C60uOZB0VNZvQIEsA6ugJJVpYL2bVB3w/+aKl0p1K70lUxA7sonRZ/C75puik8KX+QfNAEUM1hEFmOV4CALwAnCG0ApYomsMhRkRHcgak8JX4xeGVSJLMZyOMhKQSl8iey9edcWaDNJVmw3EZmvgA3rJcDeKnKanMSMhee3mIrDef+vuBhBs4MZTFnByMgCSC5BMx1MGiVjASvRZKIZLau6uaRr/LKu14Rwkoy7pu29JiBuliYP2h3WAWvmjdlMdHb1psWls1xrx9tOnSY0ttY7b7Ygu1pcjk7PX58/bzxts3HM1VrNw8c/593EPdarDx/wf7h/2OsNuq12l+iabzfYAp4uZktNhJm+N2abLwJLS7YWnTKofJvR5S89iVXCuDcvgMrAu0AWasRt2KXylZrB34bn7xnNdt+RKtzfs4zfZ6dSA1EfAgiywAQQQZVAkAXgZOENoDL6jciIHsA1/IMmgOAfmAAiaAuo7g/DFmzRB8KNQmYaArsFpPhvEWaIGxmmIpbx0eoDgCLgSs2AdIIgiyhg3BWTAePeANZL0EHnC9C8BOyYkkWJF5mxjM5MMriltwiSSYBmFeAXjfXBDUwpi9qYBKZxjRp3gACyaCxC06LYHA/7+DHNTGLn3B3NvFgR6lyvBTvS5HUmrSlzKGs8ZmX52cUZmeGsFse4BhzfOjjCBnf7g+PHj5kts3bNWetOQ1de84oxy8yNlS6LtyTioQ8gx+jBMlF4pPZ688FHgVTgqlltmEtkb+1NDosSHMlkZUgKX0n8e4wMPVCLHA4gketqfSaI3wJ9N/wjX7eUYFf6FNtd+aToU/hd003xSeGdf4QGUEw3kAEUQ7fhIAvgNqmUaLbZBibYAtDFVuJL3CJKvjqp8EAGEKwCSAWl8GFpgsP7AVLpXt87R6wAtqX1nPqzSJbBbvzwmCM6v/F0bo5xJAbYG3xmbjGquoySwshORSt23iUI36jpDmeSdy4GGK0lLLGMg8sH5Sw3wGCgM2MK6/rVNN7HbWK03EFfm1xCJJPMzTsYTNaOtWvbvDh9yaSNm6uZ9SqJ+rLZYFN52WzpigC+jcTc+OLkqxdcV93uNrido9nh28a84HR4/IAzXHzqeO/wiCXrq6m2b7kxQHxYarePIfJ0rwTYdARtIjJfKLEUqtHFLi7FJ8UjYU9T5OtGVaKIAirhf1+9KT27HgjdBnZSxd3pc7f6kxLyruRJ8Unpc1d5UvxTfHbFp/in8ME/CByI/JbwQZ8CUvQpfIpPCp/iU8KXvHBzzFvnKyXPtxwf+U3JGQQ5gJ6yJulAeCs5eKw8rqxvwE4fXgfsSLNCMDOZDS7wdeO8ts0EYUN5YrtCDgOyrVIZX4m7ZB7oBKtGD3rBHGfC6SYqPKt6S2xdCEIVZIvQHSbJ8OAgmM1JjY1mw0d7zIz51BJu0WBGzKeMSUNfd5hzLJoPECIW81h2l2fsHU/11vFkfPnm5QteFOb4NOvSbB0Ph3sP/+gvWLJmqry3t8fdPdhdZBDXhKFFyErnuasKspFIVcA97lurAUozqqID31pR7wV7DxqI1h1AKdEUvkQW3hR9Ch8Rbwmk+JTw4Q2gxD+FL5H9vnqj7QcQCnEgnkGQUgUE19BEEDPgbI/WGWlWaBbErmx0y5+/52c+DCMkWn32Ka9F0+Kw7K6fn1aAL0MD9OcyyW5c2YQVkbZm9T4SIOvJHpE3lTDehE1qA/DbbuoTUVKXiGu3WsjvTADYY+/Wa92mLDrTb/By/E5fTc9qXN/18tOfcZ8I69VMi48ePOSDTkePHw+GByvdw8Udme0Vx6rrjbn2jHV+url86Pyx+VoesPfImMpPZmO9C0Z66IN9We1ta2wynLBIT9Y8oyoDxhM8YWXieTYAGarwWI6a+/JsOlgUZ+TF+7Gb9hEpI1dBSM+2YqF7T2AZ3qwsIDnjf5R3ABw6Nyblh4SqcrzRVYVeJ1MKlWruwq0Fvh039hIqCVMDrMLWQ5717LeaT/ZxkMo0qpF3o4dq3sKua1SRJiU9tbRI9tZwik2KfwqfEmBX+lT5pvjkm3FZ1xFkfkhHzchzGPnM1eaKDfUmjojk0Wl6lsMC/Ub1CnzowdMNeWJHq4QP+jKH6Hk9nbXYIlwT5xAbes7KEdYJB+8KILt5cCskBC6F3Ph93xI9y6QlzPXe1FsqqYysWnnON/nSTzvCM0Jv7t5m/n3iXD+G5ihy1s/QtwtjT0XhGo7Mb2vL6r4cI6y5IDBfzICz0Lf7wZa4vCwu+85wtrB9LTuyavQ+aRZphbg5h1QBe7h309AAOCUGzAGe4SCeLyaref3sanR++ubZ0y85P83suNXuf/+HP+augW5vb7C3z9cV+8PBsNtvDHpnb67gyevEsrIyeEsGDeS239YlYjL4XJXJGvhs6dfT7/f2bfncCgOTnR3iwutG2ssxz1U2msj32wNNQnnBK1HH+1thfnWoqinrABZAHUSQjDFveGUtCohg757RALArx3XlLO+f9xr4Q9aAt4ttDaTw25R3i0mlm8KnUt+VPsXnDw3/1nojYqlf3cZUKvNuDDCsw+LeOIBxc+I224QWAmvh5qSUjUqhN5D5+KKUYT/l6wrlGQC3VXPomtntdDG3terxdNRc1BuvXzzFzLJ/3OkPOKG9t8c3Fgfc0PXx936CLeeyLraNG802No2ZIOMj3mnmaDU8WPTWpnK73e8NoZmcXWyIZx4yJXmqBneN5XpKK1q7CCbbf88YZfYXH2aUt7MydG5cxdZVqPEBgRslkA+NMusbcXcFXIEVsdbibAQm6Teo3t6TqiepdHelf3vJyjETCiqTvbX/3fJP6TMl7q70KT4p/B3yD1YBeKLhDSAlzN3iI7kA3k6eiB7A3cr5HedWvWIkC5bPegO4TU4h9r4lAGJVwOvO36dK/ky+hmST0ar0/buBEZKx0Swt7wi0wRvha0Az45xkjTXIM+AzttTSZWqJCUGdG0yKinOejiwGLa4uEI+0+kTkVSXsmZaIa+PpmEXi+fh8cl6/qDVfNFlz5RBY41e//Fu2igf7e1zLdcRJrv1jLgPptbrt7oArvWaLGjaYi0RWfARmzpcRuRdES7WkqERZ38zFm07mVWpptAsfh4hBjHJUdSUb+tuoPqZPfUpK9Bt2VxhzoZNincgDd/gNPuU4iTJN0pfj37E/Ic56SfCO07uZXUqim2PejuLd8t+1HHelT+Uxxeeu8JFuMHQg+rESPuhLQN5pl9DJ+hZsyxFyfxDk8mQBJXxOnvy9JX2QJRltBqToU/hSj7XJrMKX95cVQZWoKlMjwhSfVGsJ+beBynSdzLt34AA46GSpa+tAsnmQ7od2NqxUCooV8p1nwGFFNqyFM4/JVyGX2F1811hfW4XOLJYkywTNOd70W5zpOm3ktRg1kNxFDZwJaDvFWieurfY7Xc1r7TUnFIq9X870KfKn519giVmcZoKL6R0OeMdpr93qf/DhJx0u6do/GgwP9zpd3qXCxPLdigU3e7l+acrzOrNt2+fWLNm3N0wVYSxXXBwScppUmYWNu0ZzWTOqWWEUk02Gs22ojGeuv4zPcqU9/sg+sFedSLQEuD5LSLypAVDDl8S3IiTp72hveCvBe8S9BnbWQLSFAJxFeAPYmfVbRYjkAng7eSJ6AElxqgb6SWIFFDr3DboUfoPoG/eUutOSPKjL+88ASgQlr8jMYgWQE/gmsk745guf0ed7Chk+aYCLXXbOVL9hIPOOXkh4h/pLOczsgKjkgsy9PEkIk2Vb1foCUhWJaJPyKDBz0KAI9wQQER0z7Ok9YJy+2GDvO2mfFvN5dQ4la8ncYEmo9nExVbXVRw8GbPHOZuPZxWh0+uIlXz/ke0u19u8Ojtudwd6QF5weMjk+2OdrTvutbqfRGUoMS4KnVoz1nQp42taxTnEpzHIqIA5ByFNwIX+Wnzwo3nKCo232SsHwFL0+EBUazuN5BOWJoKy65Mwqf/OIpUDjUMLh1RLCLi7ytUukHWhT0rzrdNMipiRKx9gt5N3y31Vvu9Kn8pric1f4YrrBE2DdgKjb+MwFUIyVBUWD2wwr8imGpPAZjbdT7zBMgNwiKDzECKDIOYfXPW6QBZDTrH9vkGdNmEEpVin8FoMbENFd30CXBye6paS9SOW3KH/AAeSprX8JclGLAMF2CMoui8wtpTPJfWGPEVwmOWmA10klIIYKJVtb9K67Za9SkmyjqkpuMJv6w7jxwbPKBFMFU2QQuriGw2gyzVmtayr0/Z4uDEEAHHzUEO1vOh3j5xPH7VaNzyXy6aYGnzvk7ePZxWR8cfHq6Zd8nqLTw/ru7x/ynvFHf/KPWIVud7kcc8A3nnqtTqPbXtWbV+OpGV2UpOs4XftIoJQ2nYduobPF5+LbUlK45188lJ3imUAVgWUl2HvWwlsJbMtTSbZGbgu6DquAduZfwUOovBDLwbvy35W+nN7N/urT5jfHezcUKb2lUttVPyn6XdO9K3lSfAIfAgfgQeENIKK8UyCSC+Dt5InoAbxTsb8zzJMz/qwflrqsU82AdP8mQp+t5UBWUkyvhOePqV1+OlZh3lk7VTYhfgsDnHEpmtuydfUk7Em2spwVkAEGE70Nkg8SIvT2ABlGX7k6lKDDFRza2c1cPkQwMpkupsM8dY00fGKaWeONJs3PfZ7H+8irmV5pmqPKldlh3mZuYUTnk/Ozy9PPifu3P/sb9oz1lePjY+4A4V2nwWAPg3x4fMRryrzgpIlqtiEvSzwtL+E2JEcmj5tq868fWuL2ya6AFeezXcG87kRUlWvcVhaqd+XwVNSvoWeleO/uNfB7pwFvGtvZSuG3Ke8Wk0o3hU+lvit9is/b46OLvyWLopG6TZRsA26bdFdGGxxuqTfISt1pZlboZuGnUPpbdcuGp/uFXF7NlMwKJA1wSgLbKOW1GR3rFTN/w9dOAhMExl+sxFYhAF7ugOSwcAYbPVFEVtgLFFnu5oVDSUWVRFYhtKzJlkhItz4F0iJBAZ2DjXwJeqXPNFk2tWTMbZZYtQZ7svBsalHaC7Dly+LsCturPmaJ9f6PRdT3yTXMMa/zbU1aq9nFxcuzi5efs3vc4sJq7qVutR88fKy7QI6wyke86dTlHSftCtfmzYOQDG4sIsvay8jPdApMX69gbLHegmWgQChmlhtE/MAXK+TLxQyrz7BBO6/4bKmZUKkipsymN1OOiskkz1Mu/po+XYegAyDDRaqAuYws4CKwjljEsmyeVwZHp8gikssZZAEop1XOiy3IAkjRV/EQLqmfRIRIKBFeRqfod5UzxSeFT+UrhS/Lnft3pc/jlX9TfFJ6SNGn8OX0cn+K/413v0dCDug++2tdTlbdfCJqsA2MA35wJJBRrEn6+F6v9V/W6BU7RR8TtFvLWd3uQsJvCZDKL119MadBFoBr2K2Y6a06v1EQpfzChyBz2GD6acqdkljyYSE/v2ymT6bTXDNpgEt8w9s0y+teEsMBa55thpYXfJwxiVLFmTG6kcDkOyUAhkNRzAFA79z0Y9K713w31NqgvD2Qfc9YilGCJE4TQk8mhl6FMpNuJ7JtHuwXc0KqrzpoNIf9Ix4eCoaRBK8jySLmz9Vep0/GuccDtnzsuDGb1RZjrtX44jcvMdS4Tq+PHX748OHxwwd8WrH++Cdcr9lqdfz0NNdfz+bj2XLVabctOcRBj5IOg43r1DvYMDdjyMLASpP2RX060leePBc2CuLKMo2+vIMAj0D+vI2ulCPj5rFuE2UnmmAbwPXRgyyAu6W/ntvXC921Du9KnzWfryfkfexbaYDq53QBXB/tlmTXM3kPod8VOb++KjynN+YXAutL6QQT7TGanQF0w05PzwyACaCvpus2JB10nd1JE14rlDBnqkUg5nJnA+zfEBQDc5pN21QYEyRboPnZklkvdherDIm8udqIJRDzb78ucYQ6FXI7GU8IsiiZaXEDI0IPEoe8SXj0G58YzIym3mLGCMwVGzZlxPhKO4S70ZICufCyxilifhGGULKDfkXU9KGNBIQl+WHoobFwm9sw68Ti6JUpCBOp7yPW9to97tGc8LHi08urs5evvvwNLw0zh10c/6TT7x0eHj548ODo6Hif+zL7w2anzZ6xitB0OJvOeWuZ6BKjsW9atfLWFyZ0JQt3W0tyjSoyzTA/lGDkrmm69lBTqchywNAbD4LcX1T+BsWmJ+g30Tf4gnkA10cIsgBS9C59kAWQon/3+LX+b5PW7vrcjX9Kht3Trea0K58U/V3hq6XcHRvybAMpZrenTHF4CzwVvjJWCLMdGkEBbNN8ezGJPd1tPXjuvG8nO5HZADyP9H8e14FtPiVVED2nF9C1LU7H8CQUh02ZcZbInHp1S956a1mKaucstsO0gWkL2prjsT7CJRUNti1X09kUi8tnFfhCEVc4Nu0yRa6EbgDbNioWBHEymXwyWEjDmOlBik7jTxcAfNA64JROvC3kNZhidCyXVm1leEFnYxPFlQ22FWoBSC0Mi74CtEWro1pmd8Gy+A7M5BiUOCyndsiLFYE6n47g1mrFEbf5hO8/dAcdviiBdzqbTSaT+WT+ZvrrRr31pt1+1ucCLjm+5sTpreOjh8yVB4MB33Tq9+DTdrtbm82x6TKtYmtG2b55zBxauvMxhSRBY4Wz1qZYhedAVg/EZ8MFAYDraiN4yxP0WyFJhFRlYgSQJLWAIAvgGnqV1Y78r+F2F0Eqltu73fW5G/+UJLunW81pVz4p+rvCV0tZaAhlgryBlPEFf8hmwA363yQucNkEg2wTLUHLGPOn6BP2d93wt7hZX1JQSIqzR6RtbXG4HpHxv54oQhPZjfBtoFoeOoEgLeZofb4nT8npnCaLFV0fNGYug1UARXpgjwjgcDxzeibGmg2bKWR6mqEhSxrgPGb51xc/iYk9gKNbX25hvJpOsBRcJTWf1aaTyZT0lnrDtV9npqdPDxGFWytsbZeJpM/N18zNEmrWZlZMeMAI9uzxdAC8A0WaIL4eaPgeiZlYp8yZSCuwNa+2AByP/TXra8JIJKyvrKoujtaE2I9AITlUqmrk2Y6TZZvcMKV0wKMwXkhiLqv1eu2MN/b6vPHU67e0pDxlBfn87PXp09cqI05ZN7mHizeP9w+P9o8O9/cOuRqTXd52uz3sP1LeXZ/LGsMdbgKRjBJXC9JacRB7Ls3memuGXhsNIM8sOfXcl58sYoBy9VrGydm6IMrUDDi2UYbJOGyFIljIEIEpYid41/QhxtcBaA6J6NXauz7LCVbfYXRKP9uF+63NZIgagImaKncFBmUA6dxV1xPG2ekolSEpeVJ4MQnxAqhk/Z1DenYiUwLydlrZACFwfADXZznIAhiPJ3Rx1kPrCI5PdznJMxzwMSFNWpdLJl/MRtls1KeFkga4Uj5Jgx3huC3dPFPhtjr6yWR8enGOCersceB30F71W+MxZ4iurq4ux1e1Bl/jZY+z5T0v80IJYVYwhIYVomTOe/2tfFfKAzJhR7bi54iWXsvN6rqbRuVJNlMr9cBwzAiM9bKpYYRZNtlYnGIzXc5SFivQwbPetkMZ2hwWUs4MWK8/xLYxUpkvpihfaHON5piCGjYaw7ZaGmMUldFydfHi1WW98epLjV2aXAPS7w/6e8yMjx5/n685DfrD3lCT47ZmyX3uyCRVlhXmyxrXcmW3f9gll+26Tn1Hcp5oJSaCAiDWjQre5hzRK4Ggh7PDAVTSBzLIAoigIpCp1cYQO/EvMnkLOPJVjptfzV3GJ+r5FtlNCKu0NxHdHJ6U/+aoGxQpPrviN5gWPO+ajzXvQnqbYKQeAG1rk6TCF8QBbBMlg/KOohTlzugLfINnAIXA9wTunnS1/p1PPAOg0ynlhP4EDATbgCh9tbEUZ4M+m644Y+ZI8MHY2dKwdlv14ktteXV1jtGdziZYRSwjz+l0yuwpaYC3UswQsAbydQjvCkeT8euTN5iI/XqtP+SF2D0OZI3GV8+fP796Nj15feIxMQtkktg858sFYmqcYA4Mzg2wnyl0XfAMAMIiDD1ens7h9k/NgN3E2jqtEmY+CTPLkzxmjw1tY08zwOzrWpZt8VdiY4CbHJq25ocYlhGfvLd0fxZi2XOhWJbNs/OLRrPeZokAK2qzQBHwhvHiXMvV0Og8YgPzqeull/UHjw8x09PZnKWF2Wh0ecVHIWSMP/3sCwwwE2Juqx7uHQwPDgcHh93eEGNcazF1ZrjD6S14aYcfRryGHMohOdehpXyz6m6jYVgF/9sATh+cA7g+bpAFkKJ3aYIsgBT9XeHTethNP7vLczf80/JXS4RiKwNSfHbFVzIHeVd8UvxT+Ei3BCTUsGZTol8HvBsoktuVfUQMYFcO3yp6zwXPcIgH7K9oqluwkVMAWkLMD1IF4FFS+YKbt4IAoMQAe4pmX7VAybSLU7mvXr1gysutEpPJ1XQ25tJEQqDc2QAzkyVZjCVpe/LsZV5eXjY6ShjbcPzo4d7BPulgb0/Pzp6efeHTX3IseqwDNmY+58sG657DRM5nwMqv8VYL9ySEuiPHhwrhRNK8AeQzW/NraVzTYE3u2WNlmg6VQvw1GwTP5r+MIIRmHNFABaxI1/XtY5lqt0TL1dgBPZko85FDm+v0uMiDF4RYMGaNXtF0Tg2nT0PYWgQfdcDxNhTvLdU79fM3L1hC5jWmYae1bDftUBUUy1lzDouTN5evX71gyltrtbr9QbMz+OCjj7r9/SFL1ge85qQ3j9sdXXXNzZtoVxnLn0rlpm5jJ2LJvaNz/kQK4HoGQRbA3dJfz+0+9F4DrgGqXwm4pWYi4i3p35rsayb0NaO/tdh3HtEzwjMcSQg2K8tvZR+4jVeMKufRt+lHl2MsLtZ3PNY092p8icVl6ov1tSVopn+8E9PoYg9affp/dglTCWTJugQhB8YCI899UJM51mTG54Gb7VZ3OOAlmOHDh53jw8be8KM/+Qnnip+OLqdffnHePlwuu4P9Ryevn2O8sH//y7/6y3/zb/7N6Vev/9Vf/a9Xy9bp2fhf/MV/Vm90x1fzF69ev/7tvx/jri45pdRs1DstnfCViVtx5YSOeTGxYySxWs515Isz2asjJs+5eIwLZB61zi1K5VnZYN/WZt6QNRZDKJh8sx1NzjFh/GnxlrmnVg5a9pYUVlZ3RELfyi7GyLShH1lbzKZ9xUgmOAvyGzVIyv0mksweiYDRrw6Mt5DavHYHNJlpHsLByBQvA5a1RleHqrj1gzXpNb5W25uNit7VdFWbvgHz6unPeJKBTqfDMgTHqg8ODli4nn3yE566JrPT49aOmV5zYpmaXWLuvmbCzfEulIHU0iW16s34XOMCc1kl09JFnR3olUpcDi+jCtKCoL6SPBo+ymlYpmvIgVCf8CoO6hwPrcTUalet7CIUeRgJ+Ca6yyDVolzpV0nbikJjNXavp6AEfaXBo+cjiaCv2ckDeU3tAYh8F2cRKyLEss1WWFbuJTyH40sY96b4q6ZWuRS9n7qriOEFUhFQjUrlK2tB25FS/PM9tnKMrIZkNTwqvOreLs5PWlTEyPmXg9YvYWyEJPXpPcYGrXmMf5RlADpyUeUig9RlwjW8N0d7qyK3/qEyoLb5tbSchmF7Dm782t7XBsY9BXkqQkFVZ2Ob1to1aGcYbOkwtmnBaANvF9dafx2u1BAyrxecnuo06tOV9FOsFdYDyyLgvNeXrszLnG/R0uUKiq4uwt7S4WFHho0EYyKRIXDXrTeymeFyDkYmjDmVHbxVB8iS6HLOFJQ1ytFoBDA9faEZlTkJoLVo+6qPvtcuBxPbaVz4GamdZ8Cw8NxYFpV10sAkY4kP9vf/+Ec/Hhzsn52cfvX82VdfPp1cjZnpdjudH3zyvX/+z/7s5M2rX//DL7ki6k//9E9/+Yt/ePz4MfanP5jjbXeGnE9itfXNj4/JyfnZ2enpm8vz08vL8/EV10eOMA5c4UCGNQEnR622bAS91ZSbmZdoFKlkmzXflwKgo5KgapFBp1VfLcky/6am6C1eDmsTQ69O4V21210i6Gu/ur9ZE1z7crNbDdPcWz1QN8WwHbWED28AHiW8RWCbGxgZSOWQa6tnp6enFxcXz549I9evf/5bliX2WKxmanz06Oj44eHxo8PB4Xgy507rXpN3sfjm9IqFbj6RTLU5+vAR+jM7O5VqVGNkUimKZl0b+VIn13GqGvEnm2s0WGSI7aidvS4FIWEw19qBmUzvMErjPbPQVE3twqtFWeUSc7Uui6GCpeykQ1eCUs5cptoMn2P5JcAkXAOFwHvwG9NAVmDfWPrrhL89kqxl+g5C3vTuVPCS3c14l1q0vN7MvXPN+wTwGCb1PEbANIr4CEnHRVcuaUUpEnopdRHMANS9qeMCL5Oh/kWAdzmYHDu/hP3pqn9d2rHX+YLZLXdrjMcj5rnMF/UxeDM9QwyMuSxRJSzn2TDmAgPY3QDL+LNPqWS8C6ZD7nW6JxdnZ29O2GXGqD3/8ulvfvubkxevZiO+8nf1fHT5y1/87M///D/ps0DNBY2HhwhNX49hGF3NR+MxhpDeGnbsHz/+Z3+uqyhwk9HV5cXl6GJ0cc7WNfacs8LM6Mejy8n0CrazyWw+nxx2PAsojj9mcV1uhyR7zPplY2VDWDDXry+7H+XvabHv6m8AM8MmaS8zhFfBYTfYx9YApzG1ElN4ySXwheoTpjcAZxFeAV4S24CTbuO9phHL9G9VymqK0yMzeCyorYGwGL6q73NK7vKK9Yca4yR2itk7PmJK/OFH32t1OcF1MBzsd7i3etBZDfWq+KurU8WyW8LtRSpVHpLroTeMomvKRzka6WgqTShEZnG1UJGNO2WYGYyWB/y6z2TtVIXqmnPARAsOhGhKBAuGSjYXtF10gpQKrC2q6IPHGm/HnZwmkAEE/dcEXILbM8ll3iHG7UmhZHSzE/2uxLvLn0whWAUg+Qu1NxlzI6A6v0k+1eTJdKllG6nlniT/nOAd/X5T6dJwqnNkeKSKluWUKTmTKzTV3DUXKofEilfWP9A/Q0MPoPW2IEYAHFaWHtwsqIqYvhACzaKgNCvIvhy9FhMM/quvl9WQgwxYnb66fXVoGeeJSLWLi7GZXDHHxdxykBaYNVq6Wc5VwRByzUyaTciMlXeJxg6G676LVDKZHdCqY5bSrX/UU5oueDJlYY6LZT09r/39L34Jj0cfPHn55vWLFy9evTl99vTp62fn7Pmen7y6OHnFsuiDh0esZP7yZz9nk/Lo6KhWH119/oLvDO01eyyNNpqdl+cjpGa9VMd7Hzx5uGSiqkntn86nkxEG+fzy/Gx0AXB2fn6OIZ+enDL6QCmYbFSEABhgpry8QauJLgMF7ICZkGZ7oCHM1UTFokyb9NK7hkU8VXisRZiKGqsFG6hUhtQKGUqtVBjJGWv9inNUmgQeNlKjcQvAaKvxnm5QBkDBq+pgvvwGSuvaCJ2uLL8a8bE1cTG5eH324kteWPrs1z/n1WFM8HBfQyKurd7fO2Aa3RwcwMG27RkV2pb1+JKbuUCiNcsN+dI1mJ02Yxg+MsESOSMZ8qDLX8xmSzMsVysX0Xg8SzQGW+HJfDL0pihpAJxbVi31GIEaT25gGEsxR45lLlezwk15Tq9I7ucJHPpXwB25SPiW/FySWxIb2W4p5PrZJYVdaHeVP0Uf+C1gt/x6hdnOQbAtB+3IPsUnhS8nl/tT9LvjrR3lbOM3xWdn/QTHTSBvg5tY81UmXYmEfNf66V3zZqqVRai+gkS9qwAQzIRXv9r1oS8imiO1Z0ZXXLM7qiZs64khVxz58q11m3ahkXjBAIPL6ypmpJnJXIzMvjAhlInB6NoenKbCkBMXi05fyHqf8akvRhPSwuF1jOcFTGQqYICdZ8DWo5IhsxnGlDV1Dvw8evDw2Yvnf/P//fd8u37MeibHrkeXz5+/ai26jx4+7PaaTNZfP39+cfLw7z/6EPN89OAR8tHR804Uf61Omwlao9maLLRGz96kRiALUmPWxcGt2vDgoD08Hj5k8Vgqxt6wzc344+rkxXQ8YsWVdVdWrbHNTJ3RERi9jzOnnNj05jiTWyZOJiE8OO3w8kMqeLX0OVexyXgrc/TdMlgqw2ZxzzJ0mARczWjWizkAjxDeAMADl9hF3G28R/QokEVcNOnEIN1l3rEGNFqv53hem3xzkwe1a7UcTa6Wy/MVm8cMd/SaE47d/Ic/+kfsIjN84VOLDII6baa+mD1d6K3vPqhFoRreYJvyIKFu69iSo9Iy86Ya8uUn1Kko9mdL1F5pLJeN+VUhUzRP50ljULCaiX5kaLOmawvRnk3NkmGr9qN1aaP3WIqkGDgb0AgouNBSAfeWINXiLWPeLlqKfyoLiS3j2yX23qmoKp5mACkRUnpQ0Ve5lH6qaK/F+cZHBUkmeUVINSpFvyu+mvu7xiYLyEowQreBkmBbfVspvOxV53yt81VlI1FN0NfOcUiFKHI2PRQCe8zd/ta9attS516pJIuZ+kO6Q3d0OF5zZrMpVU7TXJZZc4d3ZWjbkmOmIRPe1hStSXfoRhdDBZKo2DESpafFiyOVXDSJhRekYwLAm5wBE8epy09bgtaOHZ0tG9TW62EzuUQRi3h6fn7x+mTCfRPzeXu5eswn+vY+GA77B4d7XCPx+Re/4+zuX/+7f3f65jW3TLBJeXE1ZyGZ7LGyzkTqajbnG7veC6sFsqWr+averHp+ckEe2P/G0rSaXd5ubTX7jf7y0aMjJERazIpW5C8uWbXmsPeXn3/GcsEVM+bLy8nYtse5HWShF2W1SmG5gi2fNGoxdtHeo0aamsrpXBDZovBkYIyw4lFUYjEYC+KxtL1g0aUrc+ENQOi8woF0ngFErBIer3NwAn+iHJDhIuiw30WT4DGZPME32UBY1fb29lidV52T4RzzntrZlUKfvnxO1eRjipzbYl7MvvHewUG3w0T5gEULvrLIa1QIwKk+rb7M5py01sE+jnLBB1ArO1RqxKHyw1BNwFoDT2WVs3Q8q5wrwmnWi0uZGbYIyO+qMB8tzau4suXr1U7lzEXp+s8Bx9/6mRfMZgTX4SbuTn0mcxXHlDzV+CoOjqs2YOuKuBlz1/ym6Iv4gA1Qu9t2vni4jd8Z48cAt6IVKtJGWMi2gbUqXMJc792Vz13RI2mlYCn+lcQgk/T5ADQIAqhkVS1NJentkMXkgG0t06Wl01bna2ywlXRLrMfRpdMZyYJ4iQ/b2WuZTMFYR2ZGi6nCAJ2dncmI2hkaNnfp3Bzf0tofrm4Lfrqfnz4Tyh4fmbWLNTisS/equRz9DFaRLWUztDyLogbSc+le4J1nwMS01UCdmlUCWhjUfin2/8H+IcvRmL16fQ/pEYslzX7v6OLijAlUq9Z5dHR43m69ePZVr9PBjH766W/GM07t8nGCfY5SM+tFaxwmo+/OpLcOlyuT2/UGt0L57IhufsyGt96Dov9tPD87hRWTtm6Hy0aGg8NHR/Mplvun//ifaSyDNT7TiaSLcyzxBbK9+PxXxGVVAQklJCeqUcN80W33bAWaAkWhKjbWWbU2nfXyrrfbPGU8XPUBeLTwBgAemCf0JcCjbOPJfgQVAVMIPNYjLw+dT88JwjFcQlHtJmsA+uLT6PJMKVJfNB7UiEPnEDj1zUHpxXhyenr55tnzz1mSaLM4wak3vubEzjGfkTh68ODw4BhN93kbud06G3FfCMe5OKFF+eg9Zhs4kTGqljD854AeasxahhYdyg412zDFfk0nWTtSd+IdtMw2AmuES+FkDhsceLcrpKZ0jHIDyKN83V9U9HVZXBt/Z/47i7NbhJ3luTZ3BAZDB8JbipfCl8hu9ibKK8mfGlTlUvRqRO/SpdJ9l2mKdzJd02eEBpCSh3loKqgav/Fm7DputGgdKynIsNkfquxs1rtUv6Z+AFMCOaeM3HCyYarTUjhNz660p8svdpcf4vqwj7RwzHTpKpsyrLGvZx0p57SxPtgFm20zd4OAuSGWF8vFlmkxX2KU22PHuxfYgZ0NMMeIixyZ+3ifx940a5iDdre5rLF+qcXhqwmfo+cscZu3VVe1i/NTBh2PHhyx1/rw4ePPv3rxs7/9u3m9+6M//jMmVtIb83RmtR2bwmsEowUB5qyL6aJmB7kxitKlAjSjx5pgd1s9KQVDiknlxD7TVn0JotHCRNeb/eHBYP/4kSLOdTwYhpPJv0TXjHdYsD45OTk/P+WVJ8ZClxfn9RX3LE8pP+hZZpBGVXpFfd4Me/u1iBUxb8SXCMIbQEkCr4uOhAa1OCwtmeNVJH7xioMdLNabyItpVyM41SBb05NVpK5qjrqYsA6vl7r1Rhc1l3P+08Ws8eXvTjDXjHTa2F1GTPv7g/0DCu7D7/1U4x/YtbqY8xYrDNzmpRPmMxRJXeHJSomPYxjdsEJdygJe05QPRCDMejQEJsg9SGoaUO4sE1k2tSiUnWD0Cp3pnKx59AC2E73HfIMaKNbbb0SMlADv2J7untfEgGB3RrvFSOkHGwWjCA3Am9tuaVxHvTa9ovKznNYXqNPKBSB11t4UTtcXexOM5Xm9VW9hMPxXJ6gejyVmu3nq4vQrOkNZYMyBnS7yLPR6HeNGJJKm96DbMktENwiHpU7S0LsyF8bq8MR407fZdVfZtBh+0NA/OkMYuYs+GW9oKQD7/G1OWvnrpBEB6bCgOFvWBM3oQKuN/W6PLVcm5rx0hMR8Ta/LKy5oa7nwazC7LTRSn8+mbC2yrj4Y9F6+fPnbz561e4fQE4Y1HV3N+GwEGkVoulgO7GB/mbi1W3Wdr/ZVVt1KxdhEy8a62Iu0tfZA4Wj1XbrXZVK8v4vd5/0a3nWVKeW1JaZyCNQ7PqIA+K88IN5iBufF7Gp0eT4dXbx6/sXZ6auvPv/0/M2rvV6fNW0EIY+hRETFedzQSQAoUGZN1UI04HHOAdsf6nW8eyELvAOEApTw4fVQCALwWE4QZCSKI4jPKKFIFIpAGDosFtvrrDGrgqOtbHwKpSPYBfcZZ2Opyz8Yf8iC8mCXgdgsPHOLy8n4/PULt4y1/t//kpfQuCYTo3x8/ODw+OHe/nG/12ecyXbBstai8qNgTC/byRTxeCypXAPknDTQDEIiLdWaERihpmNC5Dorf/2OQZGkRR4tda/mECtfOK4a8cNZpvCavV8NOtQagGhNt0UAuNIVYxUJXKoixuHgXApCqBLmevpmqsNNCERxVvJPIW0fvSJwqxpmNDfKH1XOgZQeIskSvfenERpAXlCByABtVe3itLlU5VJy0tlWka9rTik0pTfqcInSvcniTTGq5FJAlvTprZ7wEj7yW8IHpxI+vEHggL03WMLJG/SeUDzp/yuorYevxJf1bx0ULZ7OzLsFdffWkNXBaRN0pp+8i6a4XfNXozNMLGYSp1dmOPdiJeL3CljSS71o6q/nkgqv+eLLp5dkSDVH67sYD1Ik0BqyttiwK9M20xR37HHYnI3VQkdE3vE6nFGalkqYnWfAXv31VKY1TzJQh7BtbUC2h65Xb6xovko2EN/nkZq1K6e2Ddjlsw0dm/XyDmunz9XU7NSyJM5+JIw12ECttWWbe0N4eVo3cvJ6rjhiXtG3ltyxx9g5jvxgg636oi5+2Y0kDYRTSUlALSNLIMv/eIrgLea3tiWvuTmCtJb7w6PHs8nlk+99D6H+w//0P/yb//b/efryDRZhT68HW15dJPhyoMuc1zllMm88oJliK5BBidF4XJ5cQMnTiXmiJIc5Q+f4CA0vQDiYRSqBvA1Q+P4xGUEjKMubBDqCQV6NrHbJn++ZkR5lh8r18vSKvQoe5ImsKopOrJl7/ew3yMb4RuvbXY7Da5O42ep9/P0fDDHFR497wz0ti2gcOmEQtVg9IiOsbIgRRpdhUbfdb/bPL7nCU8sephy9QGb6YxeH8rPKkOuTMRUpw1BS1G3hvGYHp/114TxDmXz5D2xDh0UgD7//fRsNRJ0M4HouTnZL4utZ3YeigdBkAJVIQqPOlwhS+JR6iwkVaTwJZ+48i5yLlA4zC9pGgqFf9iR4mtNMib4Ho0LnYxcQ0MLVqVtvVuNrNpqm8ekBjv5yDwZXSdhMl2E9x4J44lhzhgn9FyyYiWTpZnMP94EURwicrQFu6zJy/WxEKeC3QIu+hc34b+B3NsAbsfEwZLAeGVslS2fzdLMumrmT57kmzBpJUAUYYfBaJxdbob+94bA7bA37Lzut9t5geDVZ8iZRf9C9uHyDGjSb5VVcqV1WW8MurhSSqSKMPtoYypaguPU5MowzpSqjQdW0FCHV1A/za3dKEHG0WmAqWs0OOrKirWlJgdlVbcHcfdhr8jmJx189HRw+OKu9IR1eN44sEwWnkYG5Il62RDPwOoYoQuFPPcOhCo8VceGCstwgOx8Jkzs4hDfgAHKqW/3qlWY5HTOmEsqMoiHTE0hVxqxWZYbLxn2oEHIKjmECFjBr5yvdHkb9VcuBWtxqtaM99hw4lc6xfd1ZPb3Q4Al7/dVn/8A5rqPDBwd85Hj/kFVrjn1xJqDTO2LGzKo1xcKizZiTc5cjOPAqskqOXWRy3qCSSM84TlsjJ6XnA4NcLbr7hdQx5dhgA8iXtdG1FkGvHRFxZGqNKvRfRaTDJcogSLCP8DJQKNVyUKVfVXsXtyu9WsYujlpQSY4yHb8NVNKniCP6NbG+TtCu/HelT8mW4pOrrRwvSX9TeUVEB2xgmjF3zPX4iE6cIn1ZvvAnMlDis+6sEh8jCQIietzsydB+w85Zm11x/SLNXJEQky1HbKv3qycjnXHByurYFKdC7TUhKUF9m3VvWAKtABIXRz8f9d+7AtEYZ7zAlpylImrcRn7XvUdwIa7Icocni1gAPLASv7ZeOYebfk2hyKa5r7OkY1fXZwuByK81To1iwPDE9mnZU2IimxB06y12Avu9J0ePv3z6RlNRzWPthLNNB1EfcWGCKHCW7bXhEpE1ATaNGKwHaSAGRloeS8AQUorryKboGvbIZjBpWiyYdtHTs3eAASAtLiejdFlb5arLxXzM3VvT5eqTH/74yfRD3m+qX6mAiUUZU7zuwLCaaglKBzIUKltB2lWVacJDMZJdfnWHJhyUf21x4qRkSUuZ5y9ug/GALFgk0pfjA7CoFna7h838qdLkPrdPGgtRm1GJVi14GicAc3W99EXCeGRhpWFJRkVBk1oLMjwFbLYctapEWK8me07LmEnxuIX68uT52Zunn5JMm2MB+/sHPFeDT7DEhw8ecl8mc2VO7fd7XSbP4ynrHxrBaK3D9q+x8wsuD7ELyRBGZ+LkspaExXd5fUlKBK5w3WtT4VyBPEWWa7WC7iaU9LKLs6R2iLCrQd2VnpLZQRpptZrcdehhAQdQHUe1yepVQSk3RimxKkQthSS8O0agLicYJRSRoE7xSWk/VY6pJfpisqFDA2I8KpIIcvrwBnA93kOLz2u0EDyjiRGReVgx+hqGyMUjWr4cCJg1b0Jx9JuyAnRcNa6B0AKZtm8xtTheydWlVKOLE2OQpQKl3pRhuVPXOIiZZNAsTo6U1DevHbEyrzoPh9U9BhKgSL+OGTRrlEGB3wacsoT/GjNg+m6bnUrAvFNTHll8pjbZn6TH0JGjLBukLpNM993utD968sGHT55zdoxrq1eNLnxYpOQ7u0S23p2TW7QGRjoslrLYyPxIc2k2AbV8qbS1OsoXcX2uBI5yVMIkkjs/8uP2UKWs2d+S93CIzSSQz/NSPZijc6UEJa1Xmbgmos5UTldpY0G6g+7+oe6HQiIr+6zwMca8KhaGmUNKbEdLau5q1lJ3JgJzYptt6wZHoiMUQTivMTaU0HtjjnR8PB1JFGcbQBDfEsiWlGUdEUslIQ0lexnMsskjMlsjUmkqXwhgRpfWoAxYVlTpJ1cXJomyzUvUNs5RdWBBgP0VBlZomG9TTs5ej09fETrvfM4VHsx3OcDVH+wdHh5xvnrv8KjJFWa8z85pLr5FYTvBVpCr84lNuNGgDWLXufbqJ1kgUPtyOfld0xSgyIUHS5+F0AowL6xSUGrLNa/hJXLqffamYimAylPCuDf7XnVlWCVy427tSopNpIZcO7hcqxVRIigAiFL5KsZ3en/qTcbdnPelt49TzV99RZVLFPut8lXF7x3iQu0BkFjoP5CZnvOMlfAhXwofBA4kxrcbVBusEnvAIWcxJq1SH62xXDDr0ekp3eePW5ycviEKE1x/cYijuXgJYPmSJm8zvpUN0emaZLZp3l61sBnOz/iw71W41yHrjyUC6iF1QbgcUNQcZwHxyEx7+APgGj/gYBWAE4Q3gN1nwHlSYkHnrGVmOkBZWXIo0Xli8cAqQK8/s2trXST6YqbaxGrSlbMaycSTL+oxEzId6VN9aJUDzwyI4AMEI4hxHKbiOggMMAdwsJAWSnJYizqLn5rI2VFYRUT/3P8sY+GO5pcrCxuB/lfsJXPLFW+s8jFkicKmr1ZZ+XT9dNLvNff3elx++e/+x/9+Nh198MHj/Z7emNILsL2ensPB8GCfvDP+QjBGYmw84OySFI3ITAHa49TrYbMplO58gVqqMkOip+0TazJuFQRxvUq53NADEET0AOTl/y5OmTZTaoAVCdFz68MgJmeWM67rGBkSaetARWkrCOq1EURGDovu8ihifTnkGw9yYQJ14BkDfTW60vUnDcqNi9JU6UEScVQfwXt+cTo5Xb5Z1r5i97jDYfn+4ycftrvD7BuLw31OWve6fTQ/7UrbloRS15vc9kaBL0GDN/14JxsyOPnG02X2p6s02G7Q3eSxMrmJaCM8NLyJTTBC4xt0N3k8RzdRFcIT6RYoNkBq5YZ/0xOpbwObhGtfmXJneXbTD5VmnXYBCjEKuOvAXelTvBLiqG5XRknhnThCC4BC3BvI4LwrPiIGUC2lpVhMLmBf4YvoAUTrA3DnQZyrpRe1JWXds2Rf7qM31Yf87HCtFsfoD+g/2/zH3GnfKubZkk69hV7B0OxNHbvx1UYK1om+I+9MhC7ADiKJkVtn51C5x83Gf0GJBBmh/RQPOQZNACXm4HeeAdN1m8nIpcslVv5yWQWBtyoFwLavrRNiOLWgjGGhv0a3Xz39gneBHj75AVdJTxe8aUQHTWvXndcwQF2a5MpEMFjljw/zMoPLDrl6YtoZnM0hxbBLII1qmYHL4lKEbs9IXmbZlzc5DNXkVNecdXReNIKtlmU50EU1YRa7mCl3iwbvDj97+iV3Xo5H5xz8xQyw4KyXrAYDhgu6Mard5h5NomI8uEVqz2ynJ7e8OAWI9WoAHKaV7YnQPjUHnphYgMbWqU7Y4iDm6fU4AOew01PTfZSSN28/gUU2C26jBs3QpNI1ffJrdBpfYTbNwSrTNYEKNp9SYG2CCCxPyEI/efBwzswXN+EMtO+j20iocUam+y2+W9zSysZiwhBmfHX6s6efttp9vTfe39eF1Xtar+aqzP0f/7npX8M1ALO7UgtKpgB9eOCCadDA+CrPaY7MfqF3rQZeAucaDmQACBlwEUiwL5KU4A1dR1hKTtdpkN0IpPgkI+6agZvoQwAHwpsUIK+NGeVN/K/hc5uglDwpfIrnrvRpPtUhKf4pfHAJAgdQZwkDJRjqcyW+2ASKBKXGEslhAAMuAsQtRvdE9SxePVuI4PIQhYYZTl4uxOB78daFsrHLvh/2mF6L5khj5alRvfZ0ceohR5Nznnj8SQo+qZA377KE9C6vyUUF3l+5KBiBLDthxxTP+zVDrQ32RjdpFDbryI1eIW8GIoCjAih5Hb+zAYaLrFQxF5Gel7FmmeoiSYAnquGZdUIWiwVZAl+/evXZ588+f/rmxz/+Myixoyw2aHJjKoFQNzuQTcWWPbaXj2QIHKUVT4JJYsHLvzZhs0lwlknMaP6iEbpnlYvSgiW8OHBFWclwy1Koy8ZczDho3aj32dZdzs7PLimAjz7+4PK8ywBqYh935ANNr169Qk6sJjaAp1tl7DG2IqwyeL4CSErKsqZrGsrxxHEhF08ZJHaebTsZMhjOpSdfRLf3cFSxVJmI7gQOAL+d06EqJZQ3S3HdrEqEFmwEywxKSKqX2nVZJ+NGhpxEssrqJb+WygwbAqvENOCkiMSBS8lIGWyXFQQb5xGFdsXnjtHDfDbiqLx9qqrLFTMcSj8cDmgb2OrRxZuL09cvOdTPUnW7/fIXz7DEXP/x8OHDBw8e8P4xSxEYYktRCoRtqMtssMSvdC5zEAdQSXyPdA2sC3pTI2gPRIQGsElV9gVZAGWKe/8uGgg1loCSF5aOuT0+JQVNuDLI8cVUHFZHUuWYgKkfsMNTrCDi9a6yO9dbJNYHynbQA/BeBe2aGbDQ9DDWoVlXqoE+3z2H3qKoQjIHkyS6l95uF4LCrobWrFndoJ1PqZJHXZUTWKgoi2TlLpMw6yfXNOGl21w7+Kw9BSjwySVoV18hSga2uASy6HL+yraZR/XalLfTYFmnmrbSg/PekKai2pXVezzHnUF7tuh9MPjBxx9fjM5n3eEZpnDQrl1d+DlidoSRgeuV7BVWbjxiscEHcerXOSWrCXWtPmsNmPfOF3oZSeWjHlmvlmr/wM436dItkLpmTPOw1/PasM+eb202GYFkO5ItexYs6q0uGxCsePClw/Fourwcf7w/7LArvXeoMjTntlPMZ/PR6dlotTqhHLyWdDlDLYPROThkpRqb4Yd+2e1kqYQj153DI5NN9YPKZOvW7Gew26yKiINnc66ax1vLOMwddh6GrMwT0QmIu2rrXD5eO9mmKkUUvXSu2shHFdvwxAPAmUD4dFYdBNZCDfdHzmfGsT2xr1ZQxVCMDWqs1torQM0Wh6Hk4KZnXg8ZthgarWvQphIwp1QdysO9Kqs+5HVy4i8+QYCcc+2ps76eRdfolipLpsbaQNbl0rqfLeM6r308erY4Xc2/qD9vtl7bxyO6wwPuxPzej37MXHmwd8C91dwPwtt6xCaPl3PWIzgYoJG6homqNTLweumKF/V0+qzOfaTSpNHvNc+UBXNEl/MM6biZdOty6no0G0Bsb+l6vrkNzCnzCFk8spRDeaOQVqVf8FoRMhcj2q0FkSz2WpIMkePn+l7ytiMf20gwOkpX5chdFZqpR6rDrab3fG2zKvEPIax73CZPYjjtVxlW4l+gKReIB6Xo+bx2IW4BTOgnpedCzA2Qz7V50jzDQQHMU62GMrKBvtp1ozHjLcx8HA8NY1nHcy5Um2KdPkhOrNCfABDEEUqYUP2dD08QzlzVTX53ebHa2wRqDla91YVrHcs+vhKVEvFycn2txhz9rf3ylMGbL+z1S9oMPYZY6U48+Oy31LdYFnRGmb6Ing4En9JRRKQzPnTcOgzDvVOcusyNJaGwoKHCx8fwIYXezlWTN8VBIAmVOcW1TGrSID/8rQsznpDR8Qu/5dSjWmeuztfe6AWD67ElKpfpEP4omSdl4jxyaUO0TMc5PvNGgiV81mtE8NcE4I6wMCkC8sgJzX9TV40P8DSa8+Z4oZVG7u5gH5dO2CKGDMSBmz8DuQ04a8cDmzeLRdnzBlBEkce6VKk0d4R6LJ7SfV0Lzji+DaGlc04FeykbvTFUYTAbo3ioUjgrKb4QKTc6OXU+cKCFDAasWGvJ+tHjB2JuDtvMTA4mcF5wS8WCDy1qL5lZI08OevFKG0vfEkw2ss4QwiTq2MViIOptbhmRVNoRITrH0uDNZ6H1zi6Dnjk2/oqc8o7tdMQpJsyoaiHZg2B6NaIZ8PYtHLSBYjVXZliMc4NAmDkwLmeOuJvfYBtAJAdAioHnYxB6iViH8ZZ8FhrtLC/OyMk//OY37V6/v7e/x3Xj+QWZLEXMuRWTXWfOZrR0TJ3PTkz5+gTLJJyO5CgBCx5qkerGbBOgOb7MRtwqHRvAmQDa49eOkVbU1a/hCGebZL4sGjxVLSlW/z0H1qmg2MynvDiNEKbdrFvLliai3eYR1lEDI0AqqHIa1VY5slOFvsd9wxqggYcEVPKAKS+8jqGsaaH0CQCXi0v6DD+DwvdqqE5q78slvQrfST89Odd7BFwSOxxSY9V76JVXdVDuYKjxJ+1a9adUVeRlCyhksORlsmSmpnztR+LRKYqJwuSlA+EJc8644NRAbHgNQDPA1pvRpNvKZOB7PCLW/Mc6K/uSKQhP1HiqgeQu2k2OuPlXrAp8QqUlILzVHOmryQ5qR41oPufJRUbrczx0AtJCodSqee2CvTMD7GKh6zJg2jFk1qsKdlPXqjE5JVcITOZVQja9gkA0BRdeC1FQEeOEEeShsEUYFErFxv45PanQ7ypFnaTW0MwF9lGT9MvHj1p1qjuu02HexPBTSo8UoQf2p8tMgSG5hDduXGcJzGtq+irT+fmZbVvSup49/YKGZCYZqzzQ6JUDv8xx9RKOnv3lUBd0aZgohleX+gyWWtRkwsclVhMZVJy+ymtbyG7LhcIstDT31X1SfJu51+NEmO4DaTYn3E2GpW02dR/WatHtdfnwFMa512mjGcwGdlklZurUj3Z6s/ZArj2bAbieb/l0pVURS5mW6gYQlBHkGJYz6BCUcW5DozgYc3A7GssDLe7Yujh5PXr1+isWyFmoohviK5ZHT36MBvb3Djkrx0Yym/S6GaTN4vaUUTOzcgpK2x0TTmZLgIO9ISl62bFCYImqxLkBW3gGL9RM62YYAWjVQYtgcjK6ua5sWySQArIOBrJmNmMzu2toUzAsNUYvMFE0ITZXmBx7zdMq5HY4OdpGgkmXSyU5JZXCVwegtMoIaXwleRKZYJ81yWS0rYCkPHmZlmKk6Etk4U3TV9sY2iNF5o4yomeggfPkGKPDDJHpEDTE52378Ywv2QAwA2A0//HHH3/wwQfUf2r+5FIXGVGPIMaQMOWkLsY6jg8BQ0jrd7MqQSxktriqsUxEeILRIDY36GDqi8K+qabUVs1oDIwEsV8Mdmla2rvNsjO7OI3k4JWNQXkVxQYcHmSJZlQOBwaAWP4MPiWgSFwKur2XLhdil8pTlO5RHG/ZFBxBlNHt2d5ImVyCTsdUwVQ6l5ugAIDJgw7n2MwdvLwMf1gO1bd0MLrKj9y6y8p4E8X58CwmB77oBc71I3TAHh21YkGDD0Cm4qxuiTOUWr82BwwB002sI5/vay6WXZsBi7XVViIYoUYMtCSaCVd6eShPgvaNFaF2+TStQI5DfC+fn5B3ChRLSdPyJ/7+0b4bZtqPJcqmRh8xugMtLiE90dEVlpgn3tVkytI8qJVduYW0fpbLU29yx0m7w4tZg+E+uaCV1rp9PlaJAZZIao+MD5bDbh99WwvTkJU+Jx+CoFxVRJLm6Tp0ABjgLly08416EpwjUcdwGbXpjVrE5Sm69INz40jHChd1F3vMCFxjt+nkfHJCdXvx6iXrBWiSqz9w+4dHXAPS7XF2/VDXWPcHzI6ZDdOs6CLI5tV8zBPlYGZJkWvO2HWiRBj5KMtaEGERTQXhfUo/78xEbbPVtSXWcv6Wy04NSslul21tzAmjJQeATtbVaYtXFWKzdQSFl2B43xpIsM9qyDbbVLpp/Drv29y2MbvKs83BMUl53rEB9iMWnrpOvORtjQoITE9E7+AVnic1kItoJqMJtpYPynCDPSu3fHGVPoHaqGZQq3Ghvb7uenB4fKQTEo8fPaJvwSmuOdKiIjt/r4WuAXvS3anrA+bpzkPpfYtIgjCxOHaInIwGY+y1UcgkGKObLQhq6i5YnRVvu1h7UVNiX1Z9CPNpGPsrHkpCQeYyQDg594p3wetw8VmOnkcs0hThoC8igVEprd4diZK1kgDQuDDb+BKrnbx3NgMm1e28IbGQ/JcTif6rSLRyRg1jBkxdUbYB6VgxZrY96XkgTsbBMp+xcEb29FDxlsvTyWGYQIALbRqZ5ty+Q0CQJxSUzsSsGg/tH/b5SpKROR9YlRhGXA/iVDP8NY+u6zuAtBOGhNRFTgVbJ24zXGzq6OpqodWiVxenpgfpIFOF7YEzS8aPIWFUy2TuoHnkCdWvZIZzq3xFXec/CTHrhZjkTk6Zdbd+8IMfHD948NvPP+fqKWwHi9GcMmM6N8MeNPRCFyMN7dfo4LK2KW0Ii74oGRlgAjzXAYC8KwfPEivSQgkgPVEPdTI+rQFS80WtfrGGqyJjQ5cvXlKBbJe81ehy8lEXj3OMj49A8DWn8cX88uTLl/6OE8e82mzBP+C9Y5sZc95rTxsfPW0NLNp8/pJOgTtQOamOYqdjvutJb0FKOk+vtWo2i1krIDH+eBfRxPN5TG48dH+A5LKgLHfWg+mEvSFzSuSXkuW1EMMXFv6vOTVqfG77IDuVpNvKryRbI9dNZI0TVGg7GwEJvCtog9I8CfJtwm8pJqVnamOlxFqyLbggQz80WwbNNARaMRaXY5s06suZRt5ugFkV0+KWTS7ZlqL2ingyP786v7rgNvsrDDAE1O3hnvb1YE4rpzrStnjJQ8mWWx4tSjVXYmR/spp0B4zTqSp0A/xHNqYV8gHad3Nlb3Ez3YYBiBJoOJhh4tJUSYfOxW7spWF6fvUkjMQyhDUWONKyaA4Ccqd0cq8DRMwDt36t7RiZaAJY0zmrnCGteh1UgDgMRFysEv072cF5IJ83AiAIh7ZxDgRBgcfbgHc5A/b0TcvSZgaQc5PeNGBa5kFmuHifXTmZY2nEsqwTbHic3LkBl7QPxoOCIKf3KiIfiRMKEMydxtVXjBisICAhOzggeaDU1B3HYRxPkaeutIIqcx5XHlUqbIhxyMtXeWH7tt3kO4lOiTleLnu0HyyovdOmqFeWc5ATvp14fiGfCU9rRHqfi2ODWaPGMSg4aGp+xsIq2z612jERfThMc2UniKPaLFJNFvNWb/jwg487g1/xEhUfYiQuE+yrKzUYor85Pe93ukzFKH7dRGbZ9JYBqAyZ9gJwr+fiaz+z4oM5acHNAYedeciAV++M41CKpFLroU9BbD49aQMaVpN1nl2UGhvV+0PeM1t2F9xRSZ+j6cPVVe2q1jh7+SUFxIKepsd8AdMch+UOPvzHrD1osbrXHbQ5ldBksYA2x9tl8J+yjrEYw0vVoanFwBUX8sipWfoMWGvLJoBhsroHTIXgyTTB8B7ob82bevOJhwXYFr1Da1breECW/Q1M7nF5ct9d/6a4p+RJ4VNy7UpvjaOC2a58UvQ2PtqBf5JPohypv3D32s7TATAscWE7NZ6mldqhKu8o+IwASVC3MYWMxlmb891VpsKMN3kZdm+fr9v0Br1s/YxPxfF5melUMyuYE9ctorKUDV8F5oNFDLOmsI7ycSEmkX2XDh/6VuWlMbDApDsPcJCNzy7E0ladDKelNZIQDjtqxt6yJVurv/URHIsXSWWHOpUyVF6s0ob1CZk8+U9oKUesf4tBAQNInioXNKVAekXvT4hIW/fBDcRchwylRM8d+aVoUnxKbG/03tkM2AVCyBJghQDO0ap8qoG2PGI9lDBkSWuJrMJjlnORiQC33Jf9Gh9FiVDn65gi7BhU6ZQkAYCWqW5B7PRSrG2sgo96QJB2hPlB/3mmFFFzRSXPBeAeXUSWiqHrfIhA2bEtYaysDJw5briEAGm67CzopJ/uryBkrFquEsVpST6LuBpNxmx2ji4nfMZRAjIbs1SOuodsT2Iz3GGhzR7rO7+d3oBN385gqPbX6x8/fvLgyQeHvd7f/vxnl5PTwXzAEhZt9bDXV+td1dqcOWKfCZmY22kkqobkUrnmEc8BkLs64iaiCA9bJwigSB9IUVoDhpmPh1wJEDPilq5smYu9MvAaHrE4f3VGKPNW5hLsFKNyG5ajveYcq8zO72h8cXE6Omm87mjp5fxnv94b7nOkjhedDvaP+Mbi3v5BvzeYzs9ZAelis1X8un1Ew2N20gtV0o6f+GuHpIysqry21+t596Zb0IOFqRKxecZNMKYgq0/apjEfi9qFBBxlT0ug4F+Du9EX9bzmYVWx6A24mruVYNAUgbScRao1vCt9Qj2qUWumt4BS9HdlgGnUlVLQs4MndRwV2AGeGGBML/ci0DYBiE6VZsCHB3pKDadLFqnqVO5a/eHxA7oiKnC3rQ0XKCEj1v7hAZTEpVNx5iCpqFDmqtsQTMswUh1tH6cnNhPRSIPuS52SdsBspmuXTy3H2aEka4m22pcf0nL77cZYvHQV0aLdyqYfVu15ZKlLKHNIiwSexwJGWcYLHwBJdZNzeqgCuCnGRjha8r4XTaIrUvTxECc3wVBqINXJmEgQu8I3WLyV584MsKceygoAPDAOyXmWVAnG61mTzVkdwWolTolflzlxz0vRk4sStVqiRHHAuJDTY1lEFTNBRpUlZKGannc42G9ZIBTAarMI+YYEXotitUe9qswzSzIANBV7T0erQOYWh3v7Rq8mF4UNaMeZOWHUqdmpXcaQIuDVAhZCbU1VbUANQY6IJ2enXlHgRrXADPN9Xp8oswDFIUimdqwtUGV4EerBo0f/6i/+fDSbvH79GhoU/OTRQ45svHj27LNPf8cWN8v+bGLDinQxxCwdAePIPqk7/C6ewT8AT8W9PPG6AI2mviJlVkq9A4MUWgrCcYZDd13SSTGDt6Jjco9jLqDpMu1bvZteu2fhAnZs+LKY3Gs2uOoSFlpn4Gg0V68s56PJ2eXrL35HdhstVhH4egT7xx9+/Alr1IO9o/5gyKeOeQ0O9aP5eXZIKh8oeq3IuhWQgc+AbACRdX56+8ruB+Aki896UbjmDTUSkGOkZb9bD0lc7arxrsPqGN8qrK/U34FIu1bXBH0CfQcCGgvsE0WpiiTblrVsMKwbc+zk4cNjbvphwRkzzKbv1dXlYHBIqLUFvVvImUqth7H43KzzBVhtVGEYbCznlmMq3lohJkq2boy5VseVvTajOlZwNCP8JGBC0bpoKFjuBYN19UM+CTZbbl+6qQ162SFBE4mouvyeuLCkynHimjapjpD6TQUnyMb0nmDUyQByQeh71Ai+vntrPlKXZiJyKBz9c4DmzZs3S65H7Pe5dglH1xpjHYrv60sLB83PKhmZfitDboXcjm4JydxaDdCJdaoRfSDZgyMDQI7IXPK0qapbSpfNTSM0VCyeeHEuBIBeLbGyh9id1wzsDSM3XAy1vB4zM4KA6gax8wFomzWFuMtFWVbdJdtizI0P+tps7ogXSQCAtrQUHEB8PCCMGdUbGLY2tJTkmIK2XXcMrApvnThPW2clDXXJvNnq3oW9h0ardbIxh3E1Y9akGSON3kaXY/Y+qTesbbPGCtnx0cOHj578T//+Pz796vkXnz89O734oz/6ox/96EefffbZ9773vf/FP/mz3/32t//Df/ff/+xv/45jWdwcspzMyAB1ixOWzW5mg0MqZS/tnCwdnmkmyAKIKK5JfwYSsgxjlkllzFRYO1KYXjatVXxWAqYWzNaS4yGNbquL7bXmz35UFJB07nthvgOHUdZEU+8E1/ZaU8oDVVOzmOEur8YnV2/e1Bqf//rvOGDHosKejrc8PH74gK8d6xBXX6emqYocpbYKqUZbb7Y5tGVDGM1QkIzXtH1Bo9lW9aauZdWPVHndyfb5wOOsk4IlVVJ56XR9j9kD9fR8rv2bkDRzFy7agjOLRJnGgAlvAIi7U7J+4Gg7Cl30NvItMCFYKi669SAHUvRqp+acLGIFfWAc0MzSmj/ecGCgxws3Kok/PfTsRANoYDoojZ7ZD+nZiHC+oM/BpnI774R/g+FZ/wxLfDVdQsNlrhBjeonVauv0hpWXbdhJgWoO9AozzvabweP7NmoFJpme3FdU2NM1dCYsL2oAEcrtyupR5NjNhSHqUpdFK9NqMbNtay/Z3fLiWSg4bWOZenmowihIkfhzMfDLZUVApdf3EqoGm9kikanU4/AkdzjkFIu8HB2P6UcVOKdxAmjQe46RBNa2QOsKZKa2KJMn5cIYiAPk7NyhfOjZ2YPm888//+Uvf8kQBM3v9dosSNDNQonXJ8eUAsSwxTkQXkfeHn/HM+Bi8uQkvNvAtsRBs50lMHDzZ5BdAxQpiejO2V4fq0gD7I4ocHAYAC9wik85QNXUcKqgWq4WByGy+tRhmIrRsIkvQb5JSAPl/g03wJlV1scjCOdUhU1YqTsarApFhefJIQwORWgDaTJrty5+99tPP//8SwZxk7PTX/ziZy9eajRHteM+KYZyzznYNRwyfOY4NQ2Oldy27QTrkFG2u5nlj5zCPJXZ2+N35bOm58uE5vRBDtOcyYMGpTK1YelT3YTtaIC2kSljnExsjUg0D7aWTWeCFwsOS89X1y5e0DCe7X2VhRLhgOB0sphNGrPL+ujN01df0OLU9zFuOvrgTxkIo8P9w0N6RGLx3VE+xcF5GLpuZjS8eazKYgtZtOrTiwueNF3WsAhQ9zbRoTzeO0MGHQnVDN4qhFUqroDx/MbT5UxVuV3LJsWH6kSKERqAZSarAyCvFyZk/lYBLjMiFYGAbylq0JcAt6bOnCAP5YlJMF9WPkXVOaz2a1uJeIEhposv8vEWyqogIzz6fRyDSNiawMum+hMx57UFS0hoVeLcyIF0SuG5v0cNRW/wcQrUHqSm1aQmo3ejZLJrfOhNMF363Lrsulh4xciSo4oY23go1FwJH+icwDZocqz/EuTZ2UQXfCjHfQ5komZZU4FqlxbR7aJEMhgEKI2IBKFa4tpsSz++vM9ci4KjFTPE4Rj5V199BT0riHifP3/+6aefYp6ZqzBpuTx9TXvXPMcOoqsUeKtzqlczCmK+PXj3BphMuhYc0DOvEyEmSJTDM1dvhKy7AEc5hSlabCMCQKQCbE4xACwigXLOhHoGHq/TiSYgA9yLTk2tGrE6K7x2sEDhzk1xVa6ZJJFEAJ6intkIMWswVlFcHmgzwQC8AKg4zhYMxgCkUsytMkvPHsWeWgYwenHWBU9qKA3MKbb32fTZmEs2Z/Mvv/xyNBpTaZYXJ5fnl1+tnvL2wuPHj7/38Uecn/j1r36FPeZFZewtR8Lo/zkILCNUcMUse+qFwB3AEh9X4DXxS/RByR6vVyRty9vQ3/dNZVszCDGxolmVpqDcrGq4sy6vLH0oBekUi/TZkonmxVz0ito1Ie732trC0kiaj12xD3YxsxnAp5+/YBzDC072qeNDfWNxuG8fdjrgWGpr2MXaT+jhaOH0dNPR8fCB5Wi6mvLSFP1mnSteeFt7MtYWAz0uT+Uxuqd23mFFzg2wmrmJMt9GmVWEl1FZcmV05s+0s25Hwme6KkS5nkmBcA2momx3Dus4u0Ap/kUeTlN8FkMdptkFMniWohTxbjuJAtLx8XQgCNAt7uj4QKbPjJ/eSB/bCHixoFIpvlVLungufeHgJYXeaQ+9u/IksNqYFJ4cIbCezqVl3J6JzTt0MBGJqq66MojBYEIA5MkOgSoIfGOan2XR8hJ2SmdJ9cNKEk5D2zwJ6/r8jIOCMkcvtF1jq4xT1h8Wqro4EHeDGBFyzhu/5AU/AuM8wClRmHtBh5UliGwq63nPCQal8kSljIaxr7y7Bc8vvviC6S9kPB89esQg++XLl6w/01V+//vfxwCfvhowRWY74Ne//jU8SYvxtAOe7td8Jg2wZ6+Ke7WCnNK1Q9wAHA9G3Z10RE+HIgUINjO8nYoFmRHK1R00Fk8yOCB+mRPg+CAGUIlZjZQ1zd06jps6i+CBVmqqUkbPXEg8cSa3ALh5mg4ExgHbcFHFLVQswRArsoljADqgStUb9poyozUIcNgMXwL2vDjSP+6UReYgrkZ6okdURn5YC7jz5gE1gwUujlJS0SaXo+lkdrh/wGHGTz7+kMp3dnby2/PT6XiE8TjnBp3z8/HF5fHRIfarZW/dUx1JHR15QjyRgVQc4PkWLqIHIEWmXZAF4O1fXtUZ5ZrYSCkP//Hnv+Is47yWX+mIXgVroP+KiSBsnvaHrWg0cdApdnoDzDAL2iy9Wl+kqQwvAlNPmYLD5NE+exOT81dfvHn2GZyZ2w729jlAzXvGvON09OABN3PZfLfTH3CSlBfDNM+g0+NlcLZL6Adq7FLwqnmb85XcBC4BfRQlKVm7zpdATWCvM4CeEQM2H5r77+JIYhfyrLRcY678XTlkyVnBVSRtS6YV+AQq728TwQm0S05gABRKJS3F7figdCDoS3j33ubpetvrDebcEptffayuXH0FFzzqPbdwmQx8UM2+qKYxNo5kdN6YZspGjCwffh2Wkm6VHQDeDFK3gGnP95hZXQaDySfUopuhlUHS4gs3LRIvL1MGn7ChhqiDMRm83Xlz84a0XX/UY+UcLFLxYa0mR5hu3aLHiDOrYjlJXj+RNUfpN/g7wNMB2lQ4MmKdNsQ1BrgQqPHG+oEd1eReAPpJrO/vfvf5q1dvfvnLX9ET/uVf/uXz5y+/+OIphpmiYTCEei4uRl9++dVyesnMGGXCCueJ+rMo3lvDSQP8dhyRzBUXgOvOi7OExOvaNiAr14CzMJOjCLtgYKKEIhTAXdDgpeyCEg16qQaZEah0oXGkqq9t0mSS5/XNKYXMawxAltkCkC8BZc3YJeFplCSeC6PJlmj0iSd1+xDoL3gik6IgPw+sSi7hoC2DodsnNLLVzhowjZK9GZ2oYneZmZ/dxsX3/D756OPa+IQKpEzNpozjPv3Nr0mUjZDpZMybSDh0wvCAebAU4MbfqnuWtYKeIy+3B1xs6AO4Pm6QrQFbEjc1qOgEoBaH1HPI651yJnBewBkZS3V5T4uBVcRo+VIwytUysObKVqxguB7bu6EMzoY7TIfFqNkcsX3FyyCLTh3byo1nl69Hl43my2e8pqSV6haXcvV62OLj42PGOp3OAUrmbBeHbMgUF4Cwc485Zp1PSTH3pgLY+j/HtSCQgJ5BAwKW5FXurgywqoGlGDI4QM0BD+ySBFAly3U457NNgXa3kddg3s4AwzA0GUBlKiFnkDng+BLyGrYazVY5FqWcCYuZWALnAMa7eF/hdGTWC3FMRrVCXQA1hSDNCHQSgiJh6VXGFXMrYl1XvuT1YbgJKSc8jg5D+01aikbdHOVHHSgEhtR+axQmqgTTpEAl4pMVaxRexawfpNvZnLBaPD3gFXBh7sGpTt8S8lAv682+cZ0+DPw0xpqT6wo/QxPPF093TsQaYo4QI1vrpJLWh8MDlGlNL3tBCw7guz3lDCtL86RjZHkZ+Kc//Sn6Z+UZY8yIiNUCVhDZA6b9DrsNrDV8jOcQxWKkfZy0lvJrQEkDTHoJtil8VsWJiEaIm3FQPXHbBkHGUkHGBkDwlgukA85wi0pJeGwH7CluDtCn4CIuSBSXvV5uvJyMJxHQrAAVYWaAzZtLXOibimJAE5kNoEiglpNVTVhlsnk197hz7puGuUaxcoqbHdBHafKBpMnxNB9nHJhGYTG1b8iq7LK5ogtnCRojzv3R3IE87fU5HtRpdtnheHCwv+QqRM3AZlw/cbCnN5FGkytuqOaixgMO++6zwMURDOUZw8StjXrdJi++ACTH7i6iB2A8snxs8wuyAKCp86UMl8dWEaQFZyDNC0JsJ3A8GpQXLOpzfeajCpWE9th9kmxk3Hmb33QWTLDJaJMtWzE3bRDkDszZ5RvvOnVwjyNvNYY9uthkOuHE9XQ+mV5dLt9wsO5LXgHnMrX2hx9+jD2WpvcP+yxW9xn2DLHUvH65qFP26p5YmdaNcBzcqnGUTJ2ykOYc4Em1FHbL7WqAaRFbPIQgtWvwHuo11tpFkr6SyY38U7G28dVSbtNtYlz+Yh6L8CbtOmtBA+DOKYFLQIkD3qApBdHRo0BKgSeOUO+jgIni9hIkXvBujy1p+jHsqOqKVkxqXFXLq0osrLCCzU6HtnXhTCXxiyMiUV4AsEMjzJcVkcL3cb9agrUevv/mYvAEkT/UH5KYe10e51kwtBsVySgVI5LO6C2ZvAv0UH+SGecQUdyr7BI3ng7YMEJBCOYY59/Sd4G1Yk9bY/zLE4fqmMXS26NAHLIRBQ7E5XVrFgMwosB8jwAzzJErHHF5F5EnlNypwIo0m8HMWB4f70GJJeb0DLvycIYPPIsylLK8kzdpgHfi4sSeT+AAtpmonFC4pnZyggqulCsIShhnbhGzVMQlcxkjfKoI5tAX6jNMdlhOHsmQOWeIl4IV3s5ae1WmGpC6zY1EbpRZEsWfyIAD4RWNjSUzYuMALJaa9Roh6TIEBbZLPAQB02iWLERbiihKUdb1mouebBYvk00j5V1VbV+ybdxtc7pnfzCkclyNxp0eBvgBMXtdlkx1kpvxNmeI2Kbcn06po3zki0ExC7BMjfU2D+LpjQEzcLnaybXkeVsX0QOAk2tym6XymCcXgMg4e2XjDwFSRRYVs6ds0yDB+jKyh5jplZVVXCna0Z5uHlsRHb+MzzrlnQfFTkqsEarLyh3R3X3w6BB9UkMm00todNaal9ebbRb+uOWjw0uZHSwoK8k6tM/C36///m+IyJVcTV1XPdw/fHBw9JBt4+PHH9S5U6WtGbO9HsUlokhVZ1sY+hAvT38tcGAcWItYCkh4aQ6JkAxN6g45EO0iYnlJ3cgn6K8HtnN6A30iOMWnqMygAQi4xC/wJcC9JSRxA+N8QnvBtkTAwA4aHHh0SCVxApqkY9wLARyc0Mm0iaGVLQ75zTlpzGvDmGEY2HfeYKOVZ+IO83vvLa497KtBzOpIk4bujioZSeSSRy9HRcQWWs2yjloE2puSSBUz4KxzyqpNbladq8WISbPNxWxOsmG8gxTAs88znCPxAiCD21efg+LtdQ6B1aGZw4LSAZJH50ksb61Mc7G7apK1K5AcxeKAKtNfOJycTP7mb/6GTV+8H330EdGZpbAT7DPdh4f6rh1dJU83z3AmORh6El/zeZcGGFHIj2uqKJaQVpzboWCCcjtiBDmwHX2bIBgChAsyMAEHTwcidQB35CaIwRDXn4EsAgQVvbeHMcAkJM4+9bSpMC/5MV5AayxUw8osrlhCxmlaAH15hLqlI8ssPrNuozePaYHUDCoQkakxTLyoZ+0Gl9rwUUS+9aErnhgiUlFbfNXHDhTwZOjBqxDkjm8kUke5QxP+nlkl+fXcrnyq6DVHpNzQkGRRVWL+D8bGMeCE17x9Q1LhhfHtVYBsGqwFEeEt3AjyZXePbwonkCu0e+jXnVtiZMNdnr+xLozbUDgg06OI+NwhBpYhE/MRNMjZKysTmKi2HRzoxhVKihtJz88mp2dvVp9/qk9+8DlO7hg9fHh0/Ojg+AFTZDaNKbt2fZBJaHXVYTgEAFx0LnYRcz1MFioJyKnjg8ABqEOeIpCSp5I5yGCbInhHeJczpA0g8luZbikWNCVMkU8xa4F3ZHgD0JlHu2HD0w1T4fJgSzwtvL5ryzTX4TnfJ5qphTKsYxmMJkxJqovg2CHTwLZf7MMdrfnSNw2b9WbqhwpWX5szo0s/hizUbJ5yfGyXpyisAkQ3JsFyo0sPFHks1Le8Ivmvbdt4prKnrLg7JAg4xyV+XRhJljsIATF+iET/BhC2FnX1OsfIhstS0rIAeVPT9YgAxokVBQxzazrP3kFitZnzz3A7ONALSMxumQ1jZaGnGQJ7WdQXY6a/wHSVOOeJIffkvv6TfrvAa60yOMcgQnkjD56YpltVLgicMCdnfpHvdup7C5pU8qdeVHtfKGrFQSGuO+UFbvTGZwM4lateFu2RjvpZxKDSSACcUuehPteWbdnQaKpCS3A2CXSmJtM740s+3sVMZDVlCrVqUmH5lOhysmofT1UlGyRWZ/xIZ84ppNqsx//paK87eM78cVzrHvxgtFw+PT199CDriJFWVxEqCaTXe6AAStaagUkjCbGElL4A6i81RpdN8f6A9hVIDrGRXk9XJy9Dr/Yg9lrCaNYiSr+qP2Rb3EWbVyMd0fJBqBRp2jFuXNhytddr0D4ZVA8POXnA+8On+wNmZ76k6afJ1uOtRqen3WOpuMWtH0C6PARTYbpVItIxTw4cZyq1hHiILHtyiNJWuAyT1xg8NF3PoGArLMs1Po5H6Bmh8DfY1UIQutVDCoSOfe59ATkmw6sSBQsPLz+dYE2Wk3s8w0swz906smeO5Ob2STLOxIHJVrmNRfsIdWg10HziI/Ug8wLCnm41kDfS1UuVyq8OZ/czPiJfXr5cXawuni8v6/UX9uVKFs3oDh798V8OubL6QIvVq3qbKTYfYOKw9pTRE9+i0PdBeO1JWxC2pNNszPX1G9+91wBfyrOaxwDOrrynCL2/wEuFrNdfSx4GdtZSFFOTIcXCaRnEISlcI7+rmvSvOmiKgx4AcjCex2x0mJcoozyJY845iS7iKuKGwx7lCW78QhTRN4B8oLBBnVePElLepr1XjdR+ajinVKGZc9kAfYTH53c38HQQJrw9EVXZ5pkD1AIwipELnDHWPDVHoivPDTRiJxtBqGtaTQycrtOglcty6IKOzNay1nJ56vI4fxpzR31Qnpy6B2s6yGGAvV/rMZR8DuXbMOAkPGY7C2K0aAgFbLh8ErmBROiNQ1XrQI6LuYSgAgC+nMhwqg9U7cvoyS91ktc0mBgwrGALBiPH27bjqwmdOL2sO8wtBDQKGLJczFMjVJ9j2KYhveJ0NefIBiqDNQkw5WBuyvQDB0w2G80WGC5IYJkazMO9B9xK9Pjg4V/+83/xX//X/xU3n/zkR5+o3R3294ecn9GX0g56WoimkEiL1z5dWms7iCB3jQEm1DPpQHiznOfKCfy6Rw6KSoAIyFEZVIks0isxiUUt3I1JifON0ZWQVes8xYwBXmFyR5eBKMpM3mt4MP0Kfc5gOPzkBz/kQ7MUNqOk18+/RN00CC5Oon/TSVa+b79ccOaVzoq2xMwS1hhz78YWSwobi4tPmzXT5Ww84gWABScBqAu0P2s76DLr0WAujzm7gUNSShIdj6S9wkengryR8SObjIfegsB86RUMtp4BGlWNhWhiqOKyKs26Vt7v5Lnf7TdvMlksBMt1hpQKLBswLaaDlv12SgTFTweAzMZFXnXhXlI2facPsjEUSCJampZHo994SBtvWw+LjG7JJ8gCcCbhDSCFh6CYbsCM4skIpU8nQsGx7aT+ol7/u8/+H/3ekOMhXIo53GN0erR/dMxUGdPLIS9NdDotLlzhTDWvcKu31p6iKgmV0bogOrsOd4EwjKQXY8LAmJEvnZAWTor3QbaEsjLQvUeyGWYACN8ocL15rbdCrfap78CrHPALUl55KLQMj49+ytMiXwrddGJFIlaCTuCYTSr5nKb4dBrF38X5iIQYtFWP5zxVczdTcYUEUoDajvKYRwmp1lkjF+jBcsGD9qo2ThSatUVU686nmzK0fb7pJSUQyhM+igPASwr0F9QHDe3t8wZwZpHZO2iLAj+pXT+5C28AeUj17y3JiBxZDkbXx/X67BGJG9EPDw+ookw/xmNtWlM9zBjrYiImnQw637w5wQZT/9EYE9Dj/QNoqLqQYRdhyxMMPbBLAmcY8oSDmo+uihWGULo7pxHeHDJ7hQTv8tPKnLlunz06Iq4be0LdQe9RaDgExdIaoc7cWRExeAb+LYCbDTAJR2IOXJ9MiV5eq8QGSAswcfh6PqVQj1hC4gUfTwtVbS6SGcFadxr4S3XWbNQG1MpA4GeSyFJhuzP46JMfPvnwe3wQkHrDlAajxp1wfCnhiv8cTr88n3Nr68kbFhYxxzLDlCJDLOpNg9fqVMm414J3exg/Sb800ZVeDNWaDv0ddcJqz8pO0PMNANeqnvmkhEgT7Lo1VImo8xdy4DVj0XjG1EhPaNkniJpKlaMiuu3Hy54ji89RcYl7G6c0bnbrbjrrm/Mo5FSgGdiMyEwpuUBS5MzmFyJSodhAnDQbGsXICUG/I1D0hYS+Xj0UQ3OuOsAAsoDNH1O+BC4BTnV7vMZOKsFMrwFQLs6Z2gKBlx2hnXpnOT0/fXn55uVXVEh2iFma7vaGH37E1ZjcWr3P1Vy6ghDL2uewSXs0kc0ThwX3eNHz8L1n3VPOJ581QGN9i+7J3gklCciwj6Rrztq+V0UStpWSculrEqyuDUeUeAKotuYmTcE5Ad/dghlp8cR5SkHgXp4EgTSScppOHE+ndGKeOrFe5YKsFKh1N3NBgFAgEIHnJlIYU5IIcB4aNIWFjWxaDI2+WZDRKtOUgtdxYjGS9PzaKJoykq/NUBMKtVScvwTM17cWWCjiY31ZYbaSyhcS8qkqcS2hckGU8Na5OWH5WaYsh2/4kcHpi08ovLIBFNSiiPRv+tlyLPMSBUvGlCB0TlzomQHzGu7FxeWPfvgnXNVHz3Z4cKQ1y7yxkDSO6DjkcUcVJxHp0Kws1RAAblCSCk9CofRQIkKJc7x5Fxh+puO6S2d//8WLZwx0fZLtaREXMsuHbDOHy4E9uiHXj0AGsA67NVS6ijIrY4suGNF5kkAAmoOlXZAFsF0hJK5X2jSfVAhxFd3r8hqWvgIPmKWuyWJIS08or47ugMuH7OKh6ZnKnduCx+rDuDamT3fU5kBTn06m0V7OB8vlMTWSctXBQ4zjjE+DzadjfQPsAtt8xsCKD9mp1K/e8LxiOKcX8mZKlfmfPvPJzUcYe70yr0kwHxu2a6AX9j1aBDaZTds2guZAsjC2PEX9kXT8ILbsr5xlTRlXTCsg5kfc5oKP+mOhWgnNK5PFKTwgK/jWoHHXrY+Gkqm36WuMaSxEXZh3DHQy2cgUDFG85mpgYPEljKWT6Vtz/PVqGCQW6LSKIKnkyw8Zar6vpF1aMhWAqNMuyAJw2vAGkGmzihU0rsYAgsnt8b5KUaKHIZWEosF5r+HyKCHDk5DNbqlndFOno3rzxZe/ZfuebzRxOSYHQvQGxfBA6xx7h3QfXJnJ+jXq12Ui1NIlH/M4R3l8xok6xwoK6WCSSevy0np2W0chFfo3xo7oXEPJvPSybFqxNFbaMpCDNKt17vdn1k3LQ9HpIyXZqXV4mm4p0ahpcNSfULmRRgNFdgHDynVCjCJASwiaDSBRnylCJ4vwjJthHc4xkoQGytMx5ABA/YVVQsUwLpiPjCkIbZl5CPmHXOLxzFcUyOqGJeOrvoS6+Y1v16MMBlSKy1cQtIFgxYIKpIVoelKvp2UBIUIJ7yTJZ5EJRDnLanonjuQAOAeWc5AAOUwuy3J6EKYTgDrJtTQcHOMtLCa7TGwYgHKGkdVgauYf/9GfcgaKLpOtl0u9CKRtb7RBPaaZkIo1FB0/djxeMdeDCi95wAtDV2Ur3YrrIymwufO2VpvPaDUMd5iiYIlfvqzTlDjhHPnPyVWWRDHGWU4jqJhxkB43gGB1G+CGGTBMveIakKj6hXSCLAACga2c1Z2pkr2VE5NoGHmeg5N1DlEbKBlWMk0vNoUirkfPuxiVFr2OVRm1OvYdsHAM3merxtV0dsEtRqwKMldtNRcLLWvoc8VtrlCRGe2omSwefNSl09I518kUS8yTKkUVubx6pcHdBavXfDr7bHx1aQabz1VzqlbfzmNxCjOEHeP2C1y33oUf77+ZoZJgMlJ0iAzEmFxrcY8pO9kghhqobwAjEpn07CsG7xPnuyBeO+nhvZF3Cnu0Tu/PVEFIjIxxkdxh6yulUlea6ApL0HrFp0BnICQqcQmbpegrzNK5/8+iZD9Wcg47vX8OjDy6N4DNaGVfkAXgFOENoByz4Iem4BMYMtweDxNcRAyAPSpnSE+BA+9By8kVsyrW31p8hqLD9E0WFKPA1sJiNp6MTy5eS8tan7PVufbeI4wyW2gHB4ec5OK0Jh/nYC2Oq0xRO2fQtKmlV1XGE7Mandb6zAFFwAePVdxsdCGDcqUsW9FYWWvwtZ4Bi2BLJ44hjx7bL46gEub10HPmvK0fMEphs1wr3rZjyABH10kRQFfbxGCccjuIZQAPNflElgFFPtYpYRah5DC7MzGGEltAZoCzpGlcGZ6fRf51IPogjXNU3M6BBSk6BLoF07/uH0X4yaWdgbCmIkpdgwM5zYgL6Vg30yPnYLWC85Y5wwCcf3gDAG/jBw+veEJpJSGeDlQQGQoCnIc6EF5XtXsdhsxX4Migdzs8gXGjUfY948vLi/F4hDZAEgsbPBzuM3TUuUN7MRejzL0gmsnYnSG0ANhCSUUC9t6VuC6S1y7JYMM+vFDiVcOxiMAgfXQLHN7pSF8vpiwY8WgUu7eHPeZ5dTWCBuZGm2UcL0w8xRI+kCXAvbd/XjcDduWScADwpcqkuAdZAE4vA2MZ48e58US3KT7X4ItacDivJJaU1VVLHa1lYyJLK2MpmIrnAqnWW17YtaQcmQrwdqbs8LLRHXJc65LP2Nea7cERtoxd3MmidkW7U9lxhGaxOuNCBg6z8iGjXovvX++rvEnmUe37CKB2hx3mZuarSy6f4v7fN69f8GGNydXlmE8MjjkpMNYkSLNqPjCrGDbXlW1WzZGmSEs9JBCt0zLLgSDuTrIOgoGx1bxocVQ7r1g8XTPUW7phLU1WuaJaNsLV10QRW4+pYBK18sL6KpD/qEz53agPJi4iCW+5AhBtdiBFPk7b8aSbMDbwFBPvFDXSEB5tCO8SgjBvVnMgTkpOmLkUfSW+UH/y+Ju/xPIUA4hUboM3rW0I72LABIDCwjnGuT04GjAVsF5syoCOxC20cbi3JzugvkOXBnMfADaZdzhfnrPE13pOT9Pmvv4hNpij1axRf/DRR3wHgvVr1kXYFOZLWIwWYaVRnYZxtlZqd22SLulxllsiqVh8zYK5tIrGapty7IoqqUtxs3qo8oSK1ECGI0V3YIwge3jniIe8FPEBk1Ng4jomAFBBUwTWBEUssJFH6M1ANgPOTazsVLZp5WaYQrMUNCwGGLCFpNEyuuXBQEdP8PamqfBukNRrLLU20Lbv31Cr0Rz/0YOpeclrMmZ5OSxEGUhX4qO6Z60s116o0YGSl1gbWsZf5YqxbkPvSvOnjpXkznKtbJMIhpMs0ueRcXfAYPikEwTKPX1mvpyLAPBgigINBphrcakGcIZSCrFQF9KZQ0wFj6x4kEsBkq4PmCTA44IS2LkBQKYw4+xVjqShZATAK7+EHh0dGrEMuScEsce6xlsMcuKI7kE3Pq+bAbu4t+d7S3plLMvjjeIlCSItFy+edOFiLyXmFVd2oqxKrwoWy0XRUgbzXDqdVr/1YO94j/tQ2KVrtN5cTlg11TCMaSqrdfUuAE1OM0st9a0uWXPjEgbMHqmqomjQxAfsWroQ6aB3BJ59hPn3f8KlC7wyzyjwkpVrrDJjQOz0i89/R9XRFIWR4mzMfVVLnb9d9jiWTX3lFDChnLCVmKroPh+RGazr/AHLjIiD2VYtZDXMOlmZsdxxkzGxtp3UVOmyorGfqoJSv0wC2ejFuu0yHxQuUUnCCmINCGk5yDbO6Ot9bsGoRzITzUuKEtQ7yUonwUcBCVeZLrQpfCUb1w/ylwAnvj0+U+dWGrR/F4knFQZHQrjJXHuBdNskwcFYDqN40NnJSw60U8p4+dKxnQ1Rj0OtXKy0+jIeLc/fqP62O71Gq/v3P9d3KvcPeO346PDgeMiVK7qzuvvm9RmxYMKiDsqmt9fLbIz/zK5ozzcbEsHajFDeVlWULBt5vbCShQ9emoYVnRUcFLZdR5XGuZYgc4fXnXvp/gC8h91SjzfhDE0sIH82EqdwPXSbT91WsPJONRvrFMkQIYubpeLbH5ZiZnoJX+hoVcaFEYxrRk+tgrmV1VxXziZ/Og5JqMrHKh5PO59c77ez7RVnxt2RNHGbB1urUV9BHBtDE5GAvJ2iK5jgHCh5A58LaaRVj+2IVVTCuVri6QA1k/xSuGTT8wsMhndneYIh4/RsPIHB8M0nUsRR5YpR6BzPzy/BUMO5aop1aW7FwBszaaoH0d0BY56dCWIAuHjA/lqX22APUmK5rjxr4HGw4gklghF+yf11jQavG52cvkZa8FYhZYDBO3/xyVkVeVbCRaSne5vndQaY+DDN6+5tuDm9tdFNchOuAr9JdVvfZlZRlvS1dm6D5S/gMcP+t6ZbQzBUdWm06dLa3eH+wyfLens0nmAPDjt8M1Gn+CikpX87iBN37PIycqeh6EV4JmsyuZQaJYchpoayl4xVZrah3V8OwNNH8dpSo9fhOqr9h4c0bGqtvTv/p3/2F6xiM368GnHA63w8umBnGRv8+uULLqkBIJQTr1Q0f7HBhuEapZMfOgJm71qkXdkpQbpSKzKtVtM10AP6LGad0Z0hGLkVVExd+pFbX9et3uJaVyEMqCSQo1c2EEGp9pqHZOOAeM3D7KvPLVAHN4p4rLzZ27qrd18EWD3cof6k6FN4iVzlgj4ApwpvANfjgzfN22EaPHGBnUN0EBZKpekQRhAaUPfG15N0a4rovUsCoJQ1e5qPOIvFq93coaXT+Wxl8FheTS/H44uz18+fotpWh49f6dUm1r0//ugn9GVcjskiNgH0ZjMm3CTA2o9WHdwA+8hLzceHRAB0SzxxLraIfbSk4Z69LWfizSdaQqSx4KiBtAj6NRwRI49wcCRPOlzjWn6QZ48ST6fYeM2mECnXawFloNqnks6qX6Z/Tt3nnayWA0w2j8mwAy0bGRkz26wdANtekamGj1ofxaLCqNWef/WUZ2RNh8pNFJNTdtSoHFDRM0V0JE9KT0Woma/6LHp+TDmWQgQmIYBvMQtjLoCSt4T30GueN9KTC8+I263wvnpzCoYipkt0B6yuxnLtZIBYTMZ4CMB3jd3uUqConOLm5DM1EP0/fPj4ww8/pEIdHT6CEgxL0PCi/4QP/SnVg+k2ovb6fVIBEhF+c9BItrk+TAQMzjGwctizH0jPCEGIjbVlms4g4OjoB4NXPT63QLJWSzVQyBkan7zCOzdnHnAAsA14J2Dde5aiIXeOEetIQEufuzjXhRo4+rEOVZyNB0FsmTP2oUgur2Zkm/lffsZIabgMnjSwA86wGGTiUAbIqaNKHpFycrx70T61RByYc9m7Q/QZ7LXxpAEQigxXvNuhNlEfXU2WLSaY7P5yEaJmxsxoO0P1FDYTpeORMJPRFcsXyMxeAgN/fXoI0zui9tGEaE1czoB9lpnVBZiktlyNefHYZq52VrkH5YLXErq8cFLfq9ce21xZhhYDP7pYca/DlEXri8vzU9w5n1Lgq1hnLxGDCQ9XWNGFE8z7zB88PIIE1VGHXEvoB/uvOUt+6Mk15k/XCc9tpwUwHJvQuSbhgmqZfqnjIT/qVestrTTq5fRmZ0iKAPQs6IkGJu90QutBG6jaVcbuDHiKeDk5Vz0wp3QYoRCm7h1bLix9EtEoJbVpvI3sA+CQyWu1AgCv5NxyN+KDSRY1Z1PGb3L2UHAl/ilJAu9WKrzBlfwCg3fneJgvs/yqD4JCIxSdK5Ey6fttPKRiJpQQ2iKHnWFDjUBlnHtuojy9qM6JFQ2G/C2K5fzq/GR0/uY55firX/wD3R9XU7NnzLcjDh9wYfURvSKnb7G1imjF4HbXBnraM87E1oRV6z4YbKKAtUEW40xlxc8b16cT7hhiPoSxZ18ajpOrMRyQn+U+MshQk5EmEWg1ELCPkzHf/IF+E5H5SLoSD2dcBJEiDq/Wj8zloWbeUN1Cn6xXCCKac6+tiIuGAmI0olpJEdJotaFr07spIwy/99FWKfI7GYw/5zZEDD9ScK5U2xwQHjIxlKhoVz9OjaQAXitMr7L+0qpkEYnkMWfcNLx2ZOCdbLpYr6w4xunRp0fPOl/LO1kG7xmn6/DeA87OnCFUbmR5iUifVtPasn09yVnx9NR9WomNFMFYdz3CkyAcX9DGzuG4/pbLgehm6SJICACrjWykb7A+h0ybhxX1BAFCKmjoXsDz9FpBdEd6QtQoG1PqdRInIDqyQeYYAPAgBRie6MjG1i8jKj55ZGSa01uG1P9AAAfxsdec3BvPIgCMc2kBiGWIDAhvEHhoPJMGOCjeDiDhSFJCZJVczEKmIucgLiJ3h6mjcLLemZ7cHKrOOoqcXUEWFYehqYWZ4rAFut1X14JrVmZrpOsYtBJvUBw6ZebQG3LDVGfv6JDLpfp7Q1gt56oHlOVC566soc745DtT2bHO9GHOs7kvK01WyewsFi8P0iFzcIYxH1OjRmfFxSxojfpxTMun4fOtbe0JLk6e/Qa2vBDFOezV5Or09bOXz778zWdfPjraNymVfc8optRHPHm+9YtKgqCI34Ath+pW6UX0uU27bkvR3KRjSlvkxD6ROWqoaQ363b1Oc8AWN/vdLNS3mPbrdQu0hQlQNm21HmB+2OmVBPD6QPN2GfCq4TJ+xu40GmdX2iN0JE+akNPT9jZkTnggLiUXqbxPfIgRQMjr2QlhNFST0w2l6mKtEoCjpmoRVC1J5QsRpSK6lTpcVia8w8ZoGFqdt6y57CI1ixKl4kJYG89OGWaOr16dvXn65ZcMQXU3Gldpfu+HP+JUV39vj2tAeIENSgwOy9OzRcc7LyREVBa4cb12n17PTTXtC6kIckf1pox8HCYaDQQ03aS88BIEZ++F6f6oORBIrC3nneAWmoSy6l0Kgn8uQt6QjSIG9NRBIZjFmmGz+pPZeGk2d4OOJl1kVjf4qMPnP2vE7GVemA1maUtYF4MUvW8xQExQv4yvHlknXiKQSbfhu6IYF4pJ9BuOEsuQmBavGzzRFU8ctKgOAElwhrPU9Ul5lZ3TFAHXs1N6RIcZBtFZua1FJzi3oJxPNt5ijqjAcMBxygCYKFASiycwGGDIKF8EpmSpADis5sOHj9SWdYGGjqQAQAMG2ciNsZKxzPjPubGrYkCGDNDjXBiH/UnccIF3THgDKPLJWW3UlqAEgEnQAxeD7hC+ewMccjsg0TPtKUuI7rkC9i4Br2M8z0F8y0xqGyu3nZYWSWRNWpNbc4zGwr5qUC88xazNFi31qFEy1s1qsJi49unSJIThBbjLGgb3cYg3ZyaYG9oATC8bUWb26jxDKNUZRuuqwHSVOsGqa25YTNb2iY5Ze0ueLzHhGl2LhO8s6It16jex5AjCNUyabjb6fMWj3q21a8uffviBjnpMLpfTUbs2vzx58Q8/+59//Yu/VfdqPTZSeh+lzKkOZXIbbHkpVKwsrPCT9/CK7OVCJlVCOFOFxOFGt9n89OyCVvrVqQ700+Ss1emqCMa5bT4IMdeSBv0RSsGWu4PHfHGOqMZODya6NG2Avf1j0dj3W/RrU23KqNuVwcYhowMOk52C1BVgKr/vGe9yInMJcK9niufa62v7oGQ8LY8qWfJvF75A6T5+TI3ZuTfRe33FFrMKjQHHKtMQwKI62V/ntjfIDuvpQpnJkgXRKyxoo/7y5efU4j63VO8f7h9xfcIxi9bY2nb30D4q0SM633FiSsQZBsTp9PqMT1XNbZSnUZMGAc0uH31qHO3tyzx4b96qa07TaMjWUrL0sLLhdmcvTYAmgezbTjmucrTkKjT5VDbVpeThcMDZxXpFC+fBS87eWp+g9ikTaw7OLIMBmq1ROzXrQlPV8SLaMyGUlM5J8bCxoM4peNJ5haTdmISUEOlm5Q4mM/OZ/NBYEYoUYMtp+SNzpIhIPN04eVWhIDzY8QRh22hx4CG2FiRtu87BYGgdzzOQwL/85S/dmnqWeeLlSWUIGD7B6sWrE1LEkZY7juPj/f73f4AAdAU23e0BwAECgpBTEbLxhqQmXQtSvxDlCdKDANyJNHfbGOOZPXIq/YKC2DFK1RyYIqwWYc7je6jDoJ0SHg74M/Ae8a6eSQMcqZbrR1VtCWk858QNwIOMW5ZnMCKwACcrEQe32wO0/FzVMLdJm6XiNtiKmQTN7upaKSVoQbY+qj5M9YCcqdfSopPEs/8y75ti6GpCOR2Fpolp7MYQ0FZhfSinKRo0mndorIdkTBlrtSGfAzMTYt0QEhARsgl3aVLpmeFqm5lDWHpdgV6pzutONBX+yYoT0zsR3irh2k5OUqqGsy3I6+SshD/76svp5an6IHWHWXejeY9VIoQV4GrPAWWhysWoyLKPMtRvkyO0iiZgrexrRU6f5eIYxWgx+PLLE77Jxy00+7zR3mWEq57ik48+pEHSzfZ72XU26iDQh3W4vkyHqOokWHJfrs6vNIORtlCX/mUNhnvqSNDV5blwqWnAVeJnuO38wtz58AQOAq824Q0gRe8JBFkASbylFdwcCBnCCx+H0QChOdsMUBiCahzp5Zfhqa/6KEVGr1fVFK4aTh7xqUJEgfpeAHfhGg1HB9QJElV2hdfwGPFNp6ej05MXT3n7DgPpfeje0U/5zjEr1fTgehG50ej19T7x+SXLyCRPBVWiOv9nJdUcDhjP6rZxDt00OYsoYmflsyWIrfOt8ylHlnRS5ejacK0Wn1pDqnLOB+bhVLPQqi29EkMM2c3lSaPl5IQ+Y2UmSlLI1kKP43u6BQ6ZYSaXmBPLrjQGE7GxnkFNnQBzzlx+C17j8xk2eMrHQ4tPj54/r6vYrjriUkAhJ4AbUQCGDxln20OlBbr37OKCbNLJsA6Bo/EypACD0SbXAMTNBZCEEIB3YwwQaQ3scy8UKFNwd8A0bbVucxS3pwg3YhHXvcYha8ueFpJGigAqQejV0+lPKsxHUxCW/sST8V42wse3LgKYy2+uyN8EUB5dkpxsPURwYsXLCtR4FjgHQZHt14STBvjt+CI8GSNuAA5TVz1fnu1AAjg9AE4062rguJufioVjzJidZaAAsBY2Vs2HYKSSJYTxKFw/S1wbO9MJ0UFpcYrRrZb/aDMs3uHPh6JZCbs4dhUvn6PjPSV2y/SuOa/rLXy3TnGgUp2FH7NfUwj1EqRExQrZzqdvnfF9X2vYfaiYN7PPRGOg5qsuqv6z1KNhOEjtlqwW46sL+pS27brWRovjvta+eWW0ztUh2lOx7ok5tETQdhS37Hi6LgYCZHoQusLJ7uJyKtOtUDQP5AJQs1HL0YEsMnf84Y/mzRejxfOL0YTPA3HKRBsoq9qnX56RY2Y+w75eePftH1rpo4MeqqA7w1JzsSITEamjtmKz28oCFdH+1B0yz7frIbTE6g4Cdzki+QtZZX6/ETyJlgQN2bbxXiusSnjJmcKpTkZakF/GGBzfNFQIKajyCrAfVWMIoEe3oqRTsQA+viGLiY7p5bxfVZnOtBJNde7ojK7uueQE1/kbKt6Lr8b09Swa+z4eV2NycJQ3nbR7ry5eJpZkdWbCHO+WwIEgyprU1avaHh4duuuBUFXm3BEpBzd+nXgD5R7ErnJFniQRrt/Nurgcowk3M9rLszMwamK8JyCnI7s4Go4nzZPmQydvXowK6kN3UpkURsu2XPCJMaeXUBS0lbUoZObzcs9/VQLGkV/BGiPlYfJWOLRsKfpkca06FIujKfEkGmkhD5SYQ3KBccXWumPcQ5CfUgbwzgQaiHG8hwtcxLsQcIAzhaimavNaN7QPHn1AWqSLIxQnOeyEs0eEmwOefQgAzIFelx0pqrKaQwy8wtCxFPRBLIKy2Js/pJghLHVgZ8WzCAcyAOU5d8ZB9DgnyGArG0cauOYZlMHwawJJA1xIaZ03JbbpKyZPvhRe6PuMPO8SjLQUCs61YYHrfLr3Nk+Xk6ecpmeq9yYJJeRvla1HlCKxDFCF7E47CtzrhJZJaRo0G4ZhMKBlQIH1aucG2ISxuu7Fw4u7mCDNV5gT84kimqjGfvqoq8wgRPpznVCLfH7g9Uuf3qUpW6lzsS9VyGaNmjTzoqD9ydqqYdintqma0WAa9Y8mo/Mmbw9fnS3mI17j59Q275tcXZzqFUI7opJZX+Ofa6NcLindOr0KmehIn3VAio6cSCU8GdNklv/tN1er/v7jD9r7p2fMgy8Z3bCpTXa4tZPvB4xmy5PLq8YrNv8YnciK7w85f9vihnX6dGwzb6p2uTCz2Xh4fMRbYOjEljK7WotHi/V5T5fUZ86V4E9Y5ejyr+u8mHEoit4gMLxyWSIoeYMAPC68AVyHN3V5LGQIoAhHdJDsMjhbqz0eopwyS7WVEPU7IjCTCn7OtzRUSurMAVT0FJm6f+2tKEiMQFoEDm01dahNHOwZALMiVXtzfEl1r9NvNHS8jkOsVGq+8352vnqzWDy1V+yanfYHH37Mi3b9wZ5GV3abAQcVa5ij3iE8w9kIUtuKYOiyvdQoQclr9sNhvCXn+ikh8WpBKOGIEk6Ulkdt+sjQRlOSoQUxurowe2Dalp5cIQvbR/LqH8zkzRy6pZuQy6qft2hInSAAjeTXNlhWxAmo4ZZSNvESvOHKtRrz6XKgrmBCDIwrXvLCM8ug9RKff6m76wm1ia4ewJQCs1Vl0hzRnRtxeQXICwLYAZonJfX9738fgLEXBtiXQ9wA23dbJDGceMJZnnxP2pGwcm4wdAK8xFDVzCPCXHVTc3eNG2R+GUDwcVB9zVOt1R0c8PIML7A7hFRR6oxDrkwTCUqi4DIWph8XLJ5EdJqIW6R3OXlCH9ycwGOBdFbu/TrPpAF+C6YhVgDBBAxqUbdhTgSmICsVob5OfsR67SgwKdeRPA3I9CWYP5qQtWIL8s1fmxAokr7PS3maqBzcZvxZrSINxHXeVG8D16mEMNbuW21qh2JgxLxO32dQe9UpFWqRlzmVBK9VFQlt68a6Ty06FroEeFHpsVlMsjOViVZuPKvxfhSVtVbv1BdXEy3fIq0t+9DtMm5wOnsqg1aHXL3KXiRcICuBIsujR5EREXyTVws4ZKXOhTGGsncx4bxYny/bzpaXfHVCBarvVkw4fKFNbqaxtDAW9lim50u3y+XrCz7/w4lwLAHnzfiiX7PDwKGx2u/38LJ9vDfoH3DZ4mDI2nW7PZyMT5Wu9d0AIWoRDiSAy1mZX6K8f7zL6VKFeAAhf4jkuWigJssFHYsBZJmVDeWciqj+Rg47CyRt8Pktfqkz8qBfK19Weej8VR2MFT2JKrSlxNKjCNXbmlE2lRL3wfHhwvdBuNnNprD0vGidtyYpdfTPpueC72axQsPkarz6+fMvKT/dSk1JaYWDG7h69Kr73/9PeYreOHvG8eJIF+d9H3j1nuYcX3qGfsp4b7olLOZO/DN+ztmfs6sLRnLANBnmu8wAhRcTmUJG0CQEYH04tZ4WnR36IwW1Ai3VKzEj46F8uRNWZeOlIAK8KilrPYpkkOG1Xe4EWvxWkB6brmR6MwrEJqJrz7MnQ2WNkZalq+lz54b21Zs30GNXpHFrNZQQGKIQEXPO1NbnxM7twydP6Gp84xYAh6Gl6K30xQEh0RhPZ+IWy5MADi9soYFnPD0WXhz0ps51icMfMaEXB4Wbs8FN7tGvx7V09HD68Aqj+VJZm2BcEku8/CDInRIw56kAOqkDZAXACl/oUqhTfv1ntXV5a76S2CtsgYVEj3wUclIguWPQUlTBCKhwa+SagjqNxjNii6tax/91w/CZpZNQMxe1xpTvztARqiZRTfWnGwCx6TJ8OuSFncw6UIar3qVCTA9gNLBiJZaaikNvvtvKGJy1Hx/hSjwbA/Lriu0Nm/WTLjd7MDqtLdRFkqQO61jXAEPVLauU6lvyDEV0F/7G5zY9XJFEk2xe2dUrZZnjMA4Xgo0nOuwy4LqH/T3sLjewP3vx2qbC3BTGi6jcbJ2l2ezt6UJtrLK+bzrlVjANTFa1F6srFI1t55aJXrfGze0DviXRav3geE5bZbqMo5sABgkvNHZNLrbld+JvHL8tABhkQ5uZhGZiNUikltjwSUM3WVArAH7kES0zXp706/Lw1BK0jKodAkCXbBhQdaQl6qHzpwLTvYKBjqcXoV+4cXl2CTXHVLtDFRWnEOivuRzmYNilsCZchEkVrTd4g6TOFTH15t6wpzfT5wteb7o4PyEXukex0bj8zYjdYo4m2L6DdgkpOEqNTt+queq5iE1skiCtnRxjtUp6b0EwxKl6mVMlWVxBb9mXKlAfwxRTW/DBizYQDC1Sx6UZF6/4nM9Mk1pUU/UjyFWKbQz6HAjOGZ8cz2/KrTsZE2ZNhkX0YkKBMa8F5vwjWSxaU+IgFdom1ygBGqa/0ADDQbbUtn4g4OpjSsfLhZeEaFCkQqhzAKAcSYunwy4AXpxW7wqOtFxL0AA4vfMBA+BPgihwN2eOQTDDKIAODxlkkvUWnBiGc1bhdQAxAuO6xutsC6IlwRIlcYPU2bq1quRZJI5YXwfg8+tqkJlbS5IpzvDr+oQ31WLWkmX5yXhxd/eyjoWg1jMD0hBGhojCYPCiLoMiYi6lv4beWuHwkZBEzuLnkA89CVI7ULlKQhzv7ChpSxTWfBzSo+rDQwvel9XcEsuo5U8aGMedfTmX7kTT4DrXTdKkYIi1tLT1EgL7uk0+z8PLGbKg6xwXFcGkFxu6bDAF5YPDVB92Yb076SC6hLAMRG1FVGKY6M6QcwbyXTEIR+bttyFbJO4kIsu1UmteTo77tdOpPjO7aHVGZK2/3+b7HhxbGk9aizFv76AQFs+ntAjNLdfyG6MbHuPOuL6ki2ESxe4h83vSMVXVuKmV1aIpCqUfZnbEWJkb/vemJxyZ4jz21fzsL/7Tvzh+cOS7Ta9fv6R3GHHp1+jCV8PGnDDj8pL+hcqOYQN7SH2afU+Lqzpsxip9fVZrjJd1ljqXp6v5KyYr8//w2YSPYXe6s2Fvtjec77PeiWXmqxPDATdz89KINqGYUmt0wAvbzXHzlNO3jFKarNFNx1Tu1WzV7Q9GV9Nmt8eaxHQ5Xi6uWo1Fu0WBL8/V58pRQygjzsPSYVHmzO5UgOiQYpaTT++wNNmttyVNne/RSAo8NZoeRPbSjB0YO2HPb20w1+tVbkrV8YteFkCFrgD+eY0mpoBZg492yLnVpOpSBB5rOpuyHcdiwzk3qc11dR9rEPv1Du+I87XUia5Sm9K3Su2jkeRhDKhRpRoL/IwpzPz0rEy84/R2GTTNHlM/3o3NJtY0VRpMu8ahYA25uJbaHOu59osGVK+YH2KR6bkVr6Y5UOfir8fn9a++pHzZPOTVzyEHqzvtwQcff8yzzwmuFvsLWu8xw1BfNJ6gRmnSenB9RIxdQ4rH7SjzPzsUqXmrDbn22nZWwLpg1OmOuFzin0fRcSokoRXgZFXMAfOrBanMmzVNaUE6Ej1PzocomqmGp4EWkbf6yTt+m9xLWk/Cqo3z5AneNUTrcNlAegXzAPZjczIrFaWAE2PooTGvzAkWFCt1cX5GgbK5g6MdAat+2qf3oLEkqLEOKPpidEooadK+uBONu9C6nR5rFdx6oUpu68kaxbLhb7uzFIbRa+7vgKSh3jIKlqN66gVl/rQ2w3imtu8EtB0XFRLGeb61IR7ZdUCmO7YwWmON11hbVr+qcqEy62XOdm2qS9hYcFiRVGufVxd5VXPKl3Do6hFeqaiSeveuZiC83bWtg3hqNoapqb2gc9Ri+Teh7GIkagf3lKEdKjKdrMyN9vwnXP6g1YLpFeaGEkV7TA8Yp1gtIE1WLvUkJ6ovuX6kDCtfB1wJDt/mGfQOhFejuffjSNJ7q/eTnKdSyu1tkiYKzisjgPdelREV6o1QMeTwZrW4MsI7Q3rS/rw+EWhopdfTFENFb/5t5vDBcaiHaSsNRcvTvLTCa8HWQTx8/IC+hss1vR/hqSu9FosvXr4Goh/h7vWJXTF2heGYMOVVF6/jadgyuuE+AJfYNaeTV/QyXJ7NN1SePz8hKQQixX6v1u/UhwM2knvsJXPIi6mWBtHDOU2NTz8OGrX9Zpeeaa6PMs8bnS59uZosx4bYZ+I15rnu6OalVHuPkcardseogM6Jyx45/KaxuGURwUgUDRCbDoRypn/ALHPyCPNN6+aHl0ZV/Py3FgshUaU5jLZZODZlGXdAqYZecGCcknieCoFKNutevRtf8pbXatw4OTvn9CqLveQWPUHJQXTORbGYoJu/642Xr98wm+FDH7YuI2ujJM3R//I7no2cOf0Rvb1S0U3dNteRzMy8ybfVYxffxCOiS1UCPB9iZAR42TYgvlsEzuePx5OTN2ew/8UvfqmrMfcPDw4fcv8Gr5Oyf4yoE66UabAloWGoOswZkXRoiKEGOYchdQFtc7GUKT8zVNQfr1Exw9Ngwx2Dn3xQJalyY+yiFp8hcwmADWSOdBgvQnhaSAXsyoSGvWWn5OnO4yIelB7diYEV186sgSlKAoxJIFNslrvzMStINEIsFIKDP0m7Y5ibJ6hfGIIHOH7wwCa6fOZUN2AwBNLslmkGlc8ccwun9OjMU1xglwckNXxTOG1m4Gh2PP3rZABGyUBaUuHNcqRahQ/Hr3LPGp1Mb2PVsbEsrKjnjHLoDbCHNA3ePOSMOU/INQJSE3LR1k/YeXKwdaxhlIoHkZIIvJGaPOCvccYtK+IimeOLmHcNvycDTMaycnFV5qX0rrMH/9AphYTzFEFSTBEEshAoEgUZbZHG48aTKNuhqozv0pFiMVH3Bmbt3aqLBHn2A7heTCMTSQCV9HwggmklQ1me+lhEhw9I8a4K41NaEoasyxEOGSHrfehEPvreD+nIuE+HzgXHN3rYlaS3en1yhiG0WZwM9IShsDkdM1f3J6PJBJeJvhbLGrUL3quYrS7fjFavRrIgJEYf3qgdPGkOWvW9duP7j4//6MMnzAIoJe6z4euPTBsxk402d4f02t1Bc7XX6GM223T8zO11Dta6AGbhGgHrmkbsiGYbOqBnDlXMRtkerYvHUBwnCc0cUmfovcCoGsieeYUjAc03URLMWPJwAllc0UAqR++Kx+0d3uh2kQwpXr0+GU30tcyPf/DDjz/55KsXz//hN7/GUu7V23sHrYvROQu/jEYmb97wvUKi221TzjqXQolg45Ujt2YYNYSUnEpVTVSkdIqaXmSCoYpcQG8QYgImYy2f2CmaOaaqaMnO22lSzBSECamYN1pMcE5fL09OztCl7rW2Zc8nH/8xFoIDeb2hDMZg0BrUdZXE1WTM09RLfTFTZksOl1MuxLDXA4TVa0KQkT5I0sUxR4rCwmuhWaN0LxhHhncbgCDnrKw5gdstj8uTFAlqNbOLL4DBREQyFRhHEopjzEaBuq1loQJDi8UlhzjwPKHxiEbOIQpNeS08MqsMMn/FoTEWk92pVutdKV2pCMA4EgIk10a3SQssLx5zpEIm2R9yr1EJVN1w4ymfamxEwc/XsWCiEHMGW7gxJp6v7xCYkTEQoVAoO8ywghnAsqTT0Ne6GG8RSxKstOjIwK1RZwHMHXl0oJCQwEACQGOjxSwtMJZCnrTHTDwhdm4R7pgMWcxzULwDQCW0E9vdqDN9Zc01y5uNYt5DBslaKXfUOVW7TVfCZLEUk7aXLEtiOXOnz2JZDjfZ3+DjdZEbKDaDI1GyYYlq7InbpDKxLaNO73kEDqBEH17jqYzjFNcgZ6Ig9dYKcj56dhqrdhPTOa2xtjtnxM6fvwOj9XuaLx5v3NpDxCSz48S3afuroewEWwHeudJ38fULzmzGahtTZLqeMz4ygLPDXHRFHEJjBscJJDabteqkxWsu8ZZMJIJB+s1nCzYx+fhPq3728Ycf8a4TH6ChZU9my+cXlydnlyzOsw/a7bVZZGP2XFt10R6Tbj7PrNmfFqpgyn7b2AwliWE3scV6MYpUjls9+iQrM2mpkNPMMGs91hatITZttTWw1yqyOhQ7ySyFZLqEhTm8Uqb1ObJu6srVESuHrIojVaPJ6aiHT578b/63/7uf/uN/9H/7f/2/f/vlU66RfNQf8uZPu8M3eepn5xcsw11c6spAOmWlb61bnPMiaxTewfOk9VSCMh4CTSLXKF6tFuZMSgChmdiKlzudGGMlwTYZmL5yrbXnRlunDeZzrDrYpM7YNhvP37zEYLB0wm4xt1UzOWaerI1q+mXGNPpQnV36n00CF1xdbSll/bQGY+qpMwNslQ2hVD4qS93LmbUvR4J3oPgMpADmeBHFyk9efUhlKavWyU9sYETszz4muOZJoh4dy+pqd+YuDIX56e8+46kxprmwrG56CULmiEhcP5WNcUUbqrf2DUrgR48ekRDZB3anXgBVsHdGJLNesIIh5p7/RFRJag1eDs5ZzbM1ece4qLKkWnh1vZU7luZKe+pZiwYypxquZZPMWQps3UgtTa7DtzOivLOoZOkExNsaA3w4Q0ivwOLFbMqfVou4b4j0zTkfZwpMdnh6qOsZL8Lq6Wq37tppMlESP9C48/AsunnAu2YAxDvB4a7Q72kGjLien2Lduqs8XM8nUzSdtjmIpW6TJwsyjAnmCBtYSVx1nCnmCi8wEbVhkhFSjHbEu4gRycSUwI53GSI0APCWwayyBj4FiI/lRBGNaJuzM2SNiXvTVzPdWM92O9tEM753xLK0J2jbnW5vkBLffKTXJ7A0cKXRQoXFIm4fc8gq9P7eYnmcdxzqjLCa9E2649Ic/dpkqqMlbO5gMrSJxATVJ1xWBocP+Dxk4/zl+XTBnnB/qm2eGtOK0XJ1Op48O73kxo8rzbn57krnYG//cHBMv6rv9g1YPuelKI3NkZAZGqN27mBWw9dVIXwPQ1Muzp0jdCgc2dVTaatVBkxHoahd6giybnTBZpcCgkDGWbEMRUR+pYq8pqGY6IAdSRZhSVfLDOji8uqr5y+HD16enV92e3tPPvr+f/KTn/7H//gff/CDH/A+yd/8zd9gdy/GdO7cgKz3bt0+eXcmMWq1A7tZzDUcTwy9fzdaKWU9b1ZhtBNsLhcwaxPhJSMmZ0bPeysEgYE56lJ/C0sWITh0I8PA5iMapltXjcV7MTudT1bjSw7urRpPzRR3+6x3fPzxx0zl2dKQkHMdG4EYpoyoiKhZmjlLSAMjjBDzLC8XvBpISUT+snbquSCSA6knHCKoSIwYniLGjNrnlg9KSyVirAH4YGGprj6g9CcY7hqDAwYYJs7TZSbII7uXp5fdo4csKeteFGwwx6ZwboyJ6/RlAWT3suEUAhMXx7KH9xDOvJgvvbhguTCkylqdo2pntaJ06FSOpxSlzVhSxKPlG2FV3CC9GunrQz1OWTKS0gIZVZmhkpo9S+7s93KMVamQKmtTDKRpcixzqbvQwEPDCEJFYNWSKiBAkpl0SKJ5tcoFGuEVkgMWcfvhHJwe/mqrBScO5gIoBL4T8M5mwOV6kEtrOZHWIqPAVkQ5xbv8VVq5TpHQXSQYQWAsSI3VYqgYVYvkQvCItwaMNwRkUDygFovd3G4RlETBSUDqUV5TCREGpww4lPWMeMijExQYlEFFNWf0ggzDw343leEMRWPthabug3F2QE9PzzhsQc9ONDpcnMVfHjcfAOAlLlPLrB9p1EenpzQ6OHCunGNVTH741gQrZN/ff2JFow6dnktP6/G//PJLejEtYhccmI8//CPuoT57+QuWnbkjlCkXJULHrM/GsTrZ7bXq/eVi8ub0zexk2j87H9Q1INAuY5uZcWfQp89n3bpxcMAhrwYwx4Z4L6PFFV9dCHnv6kxP0ySXgSMSJ9Ix0e2OltRQhGYPtq/mNYGZa6Z2mSVmbzLYPgEAr9qV9wGMSkzxVmxigpY0FVD/2eDraVdk49nzl/+X/+u/3vu3/93rNyfno8vz0eSDg+Pzi9HB4TFBJ6fnvf4QGR4+esI3VilJvd9mPabrUJJ0dWjF112UETRtk0T6P/DqvNWLyhFov4pqgNpICcDryAgiD2QJhVDAqoHiSNEzcWSmo94GNHN63caqs5f1/T3phyPGKJIi4hXWq0u+INs4PBiQcY7QU+CoUzsPujEzk071Kavz1AjVJV510wFwf63FBHf5kcFl5pnnSACU/nQ8XgeyMvA4eX7xSUnck4Xc9gIuG+5Uakqf76UgAda0OKkF8/nnn/N0tqrVVv+xo+dnZ8RyB1vwHsqLXLQd5qnYV5wbWoaGfMHKZcmyY4WCphBDKrDoRHQmeFleIFH0wX+iqO540zOv91QMKeEJAU9IMv6mKFOXdLDWmgfnT7TgphdrC8s1nSwwkVTHNSpe6pYeInGWjMrGNpUfxQJDA9BJt1af5WNOh7FjwOdkaHltbgeoN68ktXdpyp0n63nh6QAEAQBDozjmkCcDLHWPvv3MaUTsoQE4N48tsu3IhkGARMhu6PcxAyYXIazlKHy7yfrW1ErU9KUCzBVX1G0gi0lI97Z4UkQWYWJRQWiZ/DlAqPe9RbIMTmSajraC+FpUUXII8ZYwpdiEegYDKBGUvEYmnNjm6irRwDDjyTBFk1CZYOYgdnKaw9NsC/NxPL5IMZMWeb+FXT+aU315OTuhs8A5c9qrOohmY8jiHpTcv0E8dc2WgDo9X3KUH3tE564Oe1X/yR//iA4O26dk9D7GXJPjyeTV61mHT0VwyHauaTjzZDVxJMO+8E53r3u0f9Aeci6rc3Y2WjXa53x1StMlZlHq33kXgy2peDIh5nVkNtfoEO2WzeYfPzyQvP4drQZXT1BFkBBB0AKCkwkdq1c/ZI6TX3QKkhi8LknVHMDMCAqQ5QC2RTnKSBEiIvHQjKyvOoM61462esNVe/Tm/PyrV6e64Kxeu/riq//mX/9r+l+GGr/61a9evuEythdYAg4Wsw1IAu5gK2Ngf6cXF7DFaUNdTudKEZjhCcpd6J0w5iomulliJDQhXbYsIDBOF14ATKgNRD1lNzwq65Mz0uV6cMZmmiuxcku7QYzTi1ekjommgmBj+RwZO/ZopN2scUMLQx8isReBEvnzWuHZ4akKxc2lWqnm7icpXAJozCGHV89MZINBOdIozVd+EL+MMj+sqFWoEZkxkCTKMaiXL18iG0h0rhMN5oCh5L4wAAaHTG0dE9FROpZYn72wd7QwunDjxS2eWFxCJb3lC5hzjMAqMLOjwC6eDuWZI3UczGkFINo97k7HNLIfIy+OoRVxpCvPmS3OYJc9lDtDnaHzlQ21nSMh1b3Zb5ame2Qysn1lQfR4MG7w8TUAEExIfSsFGqTV54QoOxW1eght2bAQxrs3w8GUe/P1CoNeH2l1D5rs/utMll4/0bCVvsTejHI5Kb8AgCWKxrmUdV7AVrLWWLys13gRbzpXI0+nLwYaUginKQa9C/h9GOCQW3lLdOhBc+dA6DErP0sgkPhcJHuqXAlSaKHppkTKKDOG+lHEHTNYrNuphIp4JZG7ECCAPKT8C8FOmlcqVRXY8BsBHKxQ/8dxR9aTeEmQ1cIpr56tWC5kv6/BNye4a5euXB2IpOK8Ft0Kd26ESGqazG7oNmR3tSrFYS69jsLXxBgkL+0KQ+RRe6Z3tHaIPeV1C+vBe61Oo9Ob91ZcOsgB4cuLi35rSffNS4WYXiZXsnyrNpdy6uNU0xVLy1x1zEY0H8qbzVe6MV6vPWh6S++h/opNM+7iZjF9slroxA8CcFL3nH6eLPyGDeYO5nCwP9zjkwO6LqTTgh2zZyWkHoncow8bmCjHMrfizSRNcwTshE1vsyCVplSxqW4QINEMarEZClP3zvTiis76qNnkMxhcqd1hqbbZHJ2e/ehHT7744ouvvrpg25e+/vnz1Wj0DGnpviSbXWYEpReAdovNyDNzX83mdb7UZYaWrOicNtqXQC62FZh9zSCvPFGLRIHbxjPIsOhZKPIs0eNKb3V7hy5rYVNDnUlfMfBSKipWveJCX75g1R8JpmNu/OAlQmjNIsgqaYjA52RlcGRdMDmmJdlyM8PSpNItOOWo4LUWmvtdeCnf2qwDGh1tOg9Ff0TGhPT62M498vXm9emv/v7XrPdvkme+zz77zCNiVn1GS0EAU3OwsprkmguLi/kkFEcxkT3iIg+8IABwhxe8O2w9XsdbC1I1wctbB2iJqMhqLQ6QINutIQdUYYgIyI2rtG6OGCjeiOVHAsfrSRVxxWpDoisN8ZYnWF7qVCBIbgeaijfapuFyykNDVEne3z9iANxtMpTlwrsOA3EWuhga845BU99rIaU518rPat3LKQ1eq9XuiAvgTwfIeCCBM6RTO2W2ZlmuBDnJxi+scOSBpzKx6Qy5iXo3vjy7t+Z+o2SuGn/CVZWJcuGfKoWSsfxqYYQ2RCWEEhp6lkt7fSUlCNHFgehbFODRn0LNasAQJ591YSRkBEqFvtWHl1RAi6QK7WR0mV4Vnd7aPfOK9YwWSlL2p8QwR3uxMbFkgqElWi5LheGKFdox2XOjg9gIqfKgLVopIeSF0TIKpi9wqZAIfC6hC5h14jnStGTCo40q9lm+PH88pW6xzTjTH1LJUShawsFBByhWcw4aYYSXkzEXyw6bndl03Fmy+dm8GF+wpsgrRhwz5vgNkl+O7bNlSkdrrzCRbcBUdLtnlxeHxwf/8q/+6rPPP3/xmomRPr8z4wPL5Fl9sxHTIbEWjHFuNS4uzrn5g0kCX+jhZcfZctJpLPlSwNXZKR1Dm43pqwteg6bjZ9t4yHHo2YSrEjHM7OgizT/66U/JztnJp6iC2TNbzKiEGQgZxDCzH6wJoaaz3mUpsxC8ONfXZmrLy1rtklVrFp57OlfGxRRsznW4aFOzmm4Pe8mTPpfXqPhYI2e++8Pu82dPh12d/WUo4NXPFesF4cWn9QQ5NKzBHEjMNT0n0yhd29lr9XivsdXkoBX7wvo4woyDz3r16I//+AOIqRVHR3TmWhHlycLAaEQ7Q3VkDZPc7A33UCEzS3a9vSKRHUYdLKSenJwSRK6ZDkOJ43vpl69e09fDCi/0XotJCIxkyx06BIPb39PFHWQAlULAyoHtbjI4yRoYuWIeZItHVFYqTV7lLJv2Lqcv4TPK2VuqV+dbDm0mmvTrxOVVHWknHNpZV3uSUAAFlQN6TQjH1jiSshFLBnEcW+PQOCoia0jIk6kqGMlMlbY6SWadmCcYNOx5pcsiCu9es9P+7KuvmMlJgblDS9AT9/Hjx0SBEkfnhsMLHsAFlqC5I0cEuQ8YJgEzuoW38pBvQjslSCj9yQ+heHH2Pi4wtZjxjZTr2ugMejDSbokoqVwsxqi22EX2WS9hRtWLtYVl0jgNi6umD4/sZ7SQ/KRN+pzJZz+XrRKGwnuH3HwnY3z86DHyCzg+pugvddpZ7wFr1LlqMGpgosxBvd6ge9BnYal3tKebX06efnV5cjLsMAmmCGyuzOsK1sOoirDupQk0IinX5pSY0rPxinJlGkC2nEAZCLwj8ToHAGopT8bOKJv9iwLnYCAghd8g+hqenQ3wLdNSIa2VlYwEjTvr4ZNkdxtAitvJCZm362JyWX8Iyooei2SUZpiIAKfiH2TrClBkcw0cVeoamo0gr2RR1QACdjp5d+a6kcSNnkiRhSe9HMuiIq1Q7xIALjHDTDB5c4gB/5z7Jum42S3TRzDqfOYOjalhMDnWq43M0ujZm89fPseUH/3oe//yX/yLv/qrf3k51Ss3l6PRi89/q2Z8ecWK38nZ6dkpNxO8wjDz9i+9JvNa2h0T6v1+ly9UsA6p1yRqc6wli2Kk2lzOmbjSCTMAqPHtvaXuFtnrdR4/OPzBJx+wS9xocVpYX6vlc+N0xJPxjLQ4SMz7teCVGa3d1lnGo7dC6uPHD3li4LT/u5pfLfjgPKZj+eLNGV0NG4OMyZgs0QfRsOkdPnzQ4v0a+pInj49R1WB4yO42r9jQF2Ld6Y7YB1X3puVoDTIY3ahFUAD0bcBMm1mrXaHDNp2ljFSz0Z+1l3yNusZogmXpISnR6Ss9LREsMZUc2OX9ZpNTlhjJxdPM+YvXp/B2e+wWwu9C0nLoYkjnTsdEFL18amXzv/8//B8x8Jzw4nYz7BZvN2GrYMVxZSg5uA4hSRORbXL2z8fjMzBwHg73vQOlh1R1kgFeO+sehGHP3KZTNByd0WMyBSFzYw7AaRlFoYwy+UNLwPwaN+ckGLy74F8gMGOGMJhelICWGGahJWwDOUJsRMUiAvDEsiIwX2KEAAcyHHgcSNekq5RQlKZVcvtcARzCgYGbRydiJqyNV9pqLXlHYwm5F5VS5DZrAGt2U5MEGvKa3imdm5WPxS88CKJiioBIoQ/5V4wYGFFQSHYsnSJBKu0Ps3CjVKCgqjP00gkp2nGdU98kD9ooxUL0jJs6WipHpWSaASBtnEJnsks1prrz5BTCxcUlbWlR79fb/RZ3vzfag3Z3rzcY9vZ436zTIyJX2Hf00bPGikN588vz1azBoBQdz1kvsXruTyVLRaCRsyhNU8xzpW4GcVCUKVNkVc60WhXwrcHdvQGmOD3bDui5ldtt5HvTFBWXJqHkVOsyV0od8VSym3JLZusYC4Cii9hqsPPSckyVs6gVARu9RUX4FsrELqYI7L2DkxaDtiJ/XQTMrc6v+fj4Ay1oIdDGIthglMfNzsdMTx8ccV87S8HqrEeXKJBrb7CCdGEcbNZBEsbC9r3C2urBCZf+jEez6Whw8IBFLLaImDP85Hv/isQoNfo+Di/LRPIt4vn8N59+xrcQ6Vh/9Q+/saE6S80ckMFqYqOw9OzNa71Mk3V2aVk4Y77I5hJmS13UhDWwfk/dLjuGWp0d9h8eDRl6Q8uscTJmaa0+ma3YVh5dcpB1oiPY6lUmp+cjzRE1kpZDNvoH+imMIBJOWBSdzjHAmdVhae6cicgZXdvDw6/6zEH/rIn5pyPXQWCWAXXfmLY24YPcznCtXJCSX50MVl2Uql4rbpNipZbM2aKezIY7UxQfJtIdWGDwAiAVDo3hUOPwgWZ+TPXYnbzipdrLKQfmKFS2NZnoDvZ6JKhSrtf5qPrRo0f/+M/+KcTombxjfTHGjISwwRyCA7NcjZjccz80oykm9sTCHLEicnmlo204BhmyzS2ulOaQlAQkLc9mDqgL4pCOpljW5dsPwqv0sAT2D69eb6LPXbfaoiVet9WiSYax0mIOyhgOJTDHZQzx6tUr8MjGtJgn68k80QyhqIgLXfA6QQB4tZ+iyRb8tJfPe1OPHz358Y/+iMNh1CKb6OoeGHKK3SViViQ+h7NoIOXsWOI2fwRwJM+S83ggASLIdcjTCzrwCaC+d3DgX/LWxJfPjKFOFpEarfH4hAoKZ2tijPcQQ2uW3PLNYNIHVuSLDJMvMr5sf+RZ01gQUmqw9vZb7DtxJziaYFBSa131F4tPfvhD1NJ4dKThKH8rHa+UAojIP17+VYWHA9sJbT6FzvsFUy649wu4LBueX/JYzHhk0JFimPetopSS5MA5vhgacb89wJ0ZYPJMrjy3ln/rU9TIlFmFohQb04nQVAaxaUm/AFC9B71YYrK+JnC5aEG6ixZt2XJ5FUWSWnaAs3yZ0JY/i7pjHtTB7OLWCblkJow3wkzyAjcJafov4N4ShJWVkaKLrTkAtoJol9Zna8wqW6iJnWiODvf5xhHbuGzAYj+5k5JZ4yUXFuoO4flYxu2KDtnnDQeHg8Yz3umdvnn92i7d0NtNXPn05uzUZxKMsqFk+Dxk22q1+tN//E/4JO2nn3721bNnmAebUOp8k+ZOdCYmIDKoe7Cugnm47lMiDxy1XXJ29Wo+HbHe3G0yw2W/WmdtGUXQSfEiUpu7PGptJTTsLR8cYz4RWF+FnM9P7e1kv7MIo4wp4sMz2Dd6J2wMVKYCxhj86XQ0kzjeH6bLw2rvcQCZ9VetHLcRQMuyZoNZXPeJn+RFcvuJEOldtY5LC/w0KYpZ8vY1vRjL7MyMvSys8alPYxoBOSMW2FAu7MVRQhj8JWab+bGu2m4PujqohkVmY5y5DvMeYIwFppSrqZCWS0P5mBU3WTLggJLXdPcOjh9/0PjYPrODHigUDDPzKi4ldscUGczV+Ipul/uecKTO+66IMboccYSNmk5+KSMw0Y5Aad8xLy9yQSiVtmBpqSM+fbb+1WoXKkJNkXGvb17xMmQWheFRm+1YziRTSRAMqahFCM9rTh988AFiYDKJQo4IlX6mWj8PBwEOr5TAuoJrmbNO7faDBw8++eQTDDAwM0J4EgqHcG6olB0rUrzAslrmAr/tLQaROl53WUyTIYRxJIk6wLt3phx81CXrdU0A6iKD3vlirAvfatyrqSVdBgwzrmRlRsutlVojZ25KXnps4lIPqTs2guVXQwo4Isq8+QB6UnfHFbxEYweecQxzX2+qXMdGu/jg4+9jjE+1hk79tmm1arLEhPkVE12dx+LYoPaWaBSanTPfpuAJoXIboGwAW4VwwBViGCis43HZnLXYWwMqrLioBC3Ui9JIvi2POzPAniHKyTMZgKsDBWRAriYvUZDQK0q0Jmf0zp5eU2kLVkxZqhLAHFJlDoGs1GR3RCo5i4AKmR4LA5T9kQVg0TmrrWcKH01yK0YC4RJGIF7qPU/HeKiaz13r1DjDVAl5KgD2zq+OQ2EWuALAWw0NiyM0/eHg4ePH7LliabBCV5faHdzjdBOFzmX/zErGE848IzytnsVMru5h1fXwcJ9dMy7CGvMGUaPeGx54vmiV2m3CMaLWV6F0CmkwHLLCyqu+vPhKE+4O+rWTK85Jk6Q1eS0GY0pZSOOsDLNGhvDqcHVkp8G7Rvy1ZjrBjP2Bhpk5HRPzSoJns0uKUx748jZMg4mdDNgHvX2eZATxNR0fj3x2xewQ74h/tmNqBHR5zNr1rcqjIw6hcF/uvNvbl7VHIWjK1OjVAn1qMoABxdkJF7qWbMpnBavqJwNE98lrG3Sh9GlchK5fxXBHlfVawGoAowZCjDs4VVVNuhvnl5dMbDh3yzCAjpH9YTfAU/bBbBTSQPEMSlZcvj383kff49ARV0vrJajRFSWFFeElrX5/QA/bGQwfD4ZPPv4EAcyck+n5f/t//2+g+fLp5xejM02lGjXWezkVIGXS8VpzIqsCyJFsBF2tMg1G4uupjUVZU47Ea/4vPXDcZ8WhgorGRWTPc85EvJDfWJlF/O1vf4uR+MlPfvL06VNm8LwzjUgIic2gKBk2EQNhHCCpTBjxy1RIKDN7WRrf/MbPgRV2EOlH7NiUKHPZ3NBGkwRPKjgAac+WoI33xoOg8EsJuaN48fhfjpMaONcvrxEq6TyGjvObk3WSEuV4cuUcd13wejv3nPT6BzQKdRtU78H3EVXS2ktifoQKYTTjt4aAaW5hZPl0t03uG72HmF5UwV2XPPWjU9wShi0YTuwhCx8i1eH/VnvO2QUGmjrQbGdlaIyWE1RsulQrZU2coZ8OZVK3qbQaxsihhKIegF3DgXQgvB6rGBF6j+JBRTiIv3HgzgxwUUGe1VCQmohaEe1OlRsnYgOkobUzMsO/u4enltXcXIZicsgmJyGFZnBOFCNYA3g9P4TGn7cC9Re7uFwTt45jPYvL6IJZq86qrQm+ZlXyrgPuCIK/7oLWBQj64dohO7ZkU5ZmY3C49+iDh5rxYOIWM5aasVnzhnYQZWu4SoMNRJ6ojG64030wfXh6dUnPgg3jVVA2ellpXXTZo5VDr/QS6iqsy3v++oQOlAsm6XA42TvjjScmtqxO85WqekP7q3wot9HWm7AYYBkI+sgOhohvN8GL9KeLaWNea1xoisZuNYwRjLNODA2YvNKpaFOMu+IXVzKY5uAyvexLEKRg47DfPBru+yicaaRbZRnm7KZibb6evGTpdd7vNs9fPhtdMu+fc1K8yUIvFUf1SjZJG23GRXWNbpO6xT/TCxi0Kz/rnzJLWoRlxUEHxLG+ar7qYzWLl/mSotxxpofsuNhgSEU8a7Unh0NSozwkLe9O2Tka9YOa/Te5lpcxSY+etz55sH/8w49/0Gr3uaqel5TgBg+eXH5ML89mtuxt/rEdrZFTLs3Vv/pf/WdMhRkeMeShHE/P3sj60zdrfIORIb+Mj/StCpPIJMZeSglIBxbYEmLjXvlFdN7kpnojgk7K2FK10OaIk+XZ2lHGLQuTemscrsPo/pN/8k/+8i//8q//+q85Ls4SNIvPrF4wf6U6UEZe9OQFkah+PN0R3XXIEwfSKQHwEhdHueiJ/OYc5onPmXhEvKKDcqFT00FvdUAx1xg8JrmwwquMlbzXhwypzwlYqCeyftqGiCoJKEmsYuc/zavV4fz2/tHDxx8P+kdYyplMNavHdrispRPLmkDgWB1uth4O97G4fOvMFpUHzG7N0Lb08Q3LKzLaIIRzcvpiBwsMKIf6Rh5HukmWZRStx3A20SoNoylW36k8NCWKn6qLeJTmlD2YGlexzMfL6ZhBEANd+DNFtim45cImQngZ1lOHPNekDggyO7rmMuXKIROoy3y56tzz7XvemQEma5HtALbzS5B0tamdUNY2/Z1jVJHz1LeZm3gu4ToQv0cJYB1WgLK4+SCjEHL3oImYsQWm0uMpIu88SZgXx0+RHOaFcyWYXnbGaA80LV0MyQYsC8jDwf7xEWcnWFim8c2GzHLZf9WSJt0/H1HWRIXVTxrkYsUpaBCzlxxznbKRyNR2yMZTr3d2lR0goggwhDq0NNPiars/4OtG9CsrW+5k7ROufDMP6+uDAACux+CdUtYLEcisVgcpmUZjqrG+bPUyAfxgcIT22GxmLQ2TdDG6xIAy7+K7T5yxUotn0w7DTx/G2xONRbfFOjIigaeTYS0dSjV1uirm03ynySbKPd2/Za7+ww8uzrnsiQkht2qOWAHF2JO38cUJBeY10XRL3rJCjMqmjk5mk+6U1GWSAensEZizXmibLk/zf4yB268sTU+YSFrjYzneGXpgfTyBD30t9p/zrEzsOGUMV41aFnU+uMMNGXSNk8vJ2ekpH7J61XyNZSKur9wCU0D0s6SLwgEI0pSIf3Za+PWLzxgF8VGmf/pP/ylvoP7b/8+/ubg8o3Q4lKSOVeML6yjISaYimxarcpEfjQesohEGZ7PBRGMQp/M9TcVZxpK7Z8ifEEtb286F//nPf47dZSH69evLRuMFWWDH98c//rHGcLae7HlRC8oLzlkR6g4+GCRHonZKwI9Dc10MMBgVojlofNwDhiCPAoCDLFvkcGzhqaQrncyPnAcGT5LYjgKZDrWp4K3SeBwbwmkc2m3393h77qDdGTCwZMGJu7fP60PmseSl19eHI7uclOoPtbzc1dIKO8XaUtLhLD7zzceysJXZe8nwNqlsWt+oM9rmcLvZ12XzvLHkQtrljMY2veJKV0w6BpfFJNadTAHchMW6g8YJtS5zb33WjD90uOR4ojUEckFN93kFGP6g1YjC82QYmWqmADnmul9XYKjxOtL3G3aXBhjJUdB2JoW0el0Z6vm1WKHcd6iDonhWnBRtVPGkANdI/g5lTbNGHlx0FoI3nQWXkZskO/ssFakLFynShrAEWF+ZPYdJts4OIps8Op9sM1L6J9q09h15h2PGRHU84egFRzOgpaVqA5IzUu3O+WRMJ0UZQTlmb/X8fNU7Vl7oynRH1np2IhswX/I2Dn+Hh3wYkdbdYfC+uriwnpr+m/bNKR56bT4Fg61g2medv8wW0mBQunwwZvxyRAfENZT0TDISDd5MaDJZ5yj0dHbFkjInkDiuxPEvem3MLcexrQph3dUdYOFsSlcbnV3poIrNJDSosKkAdpJ3WcmdbZQzaWZVrzOfXfJxJ+tlFsSWBcscoCZ4mvAWOlyVokym/qxLRK8AGucwC+Y1aySARP8LDgHwEcTiHr/I7I7LLsAzzdAKL1/sRC0zZsKs9sKUY+OskzNVGrB4vj84ODo4HB4cMFlkvsWsns4OJprP8q1MAygXkgCDvBCA/PWvf421Y7EX28YW4JfPvoLh0YOH49GlycPqto7I4dT7qpOlAyU7yoplArnwK4MmIzSsMUnYxBK0WF3jKOQ/+ZM/Qaqf/eznjx49/M//8/8/e//9bFuS5fdhx/tzrr/Pljdtqs00ZrrHAIMxGIATAIckhpSCQyNQJhRBBqWggoFQUFQgFFLoD5CJQAR+EH5QkCIgISgOBxCAGXT3mJ6e7pl21dVd1WWfN9ff4/3R57vW3nn3Pfec+0y9V1UzUr779smdO3PlypUr18pc6T4La12/fp0+AQuyqHq4wbUj4eDPTVxWIuHIq0NWeLy6ygOJ444+JZztQIgM2T0CkD2tWMGWEBKOB4urhz/Sk7Q4cgyp6KAGP5+Cn+s2YaGki151LpyuSKKnyKXP8GFjZX1r60J67VmB1boBdXAFyQ6t6aMJ6U8bYNVUrNFRlorvWdh4VNFQqN0eh7kqX51rRq8QS88sywo1KMpImLrVzgF1sCgH572ADHMxbKKUgufONNZW9jv0vlNFXW4RXCgynmQxQwQ8IU4IDCHLkoSYH7tnqQIOZZhH8aSuT32ZK2pIDnPDAbRRCUS1q8h5fL5iu6CRdIeIYPXjpaxFU/3JWQs3H1VrQR6ujh4xkbEMnCQDiElbBWzs1GzdAZPbiInNPNeUtSjY72yLCBghDoQVabWSCCalr5ZnQS0CEjMmb3ZCXwRGPxFagKJNkj33EMCmkpoIWTFkhJ4nOXnCeycvCR/SJfF24qWtnrwkfBy3jNCivUA6ZgIZq3GziGZOskU27jCtR/tAlFBk1AFbbwEPeXCQBTD+xGPJBXcuPDu2hq3RLGUZM3tDA5E3led2BGQvSoULxLBCcuAUl+6sFZ/BaAkhC+NJFmsevWVZhzh4Kp+trY1ra+2B9gZh1GKFkinXnkzCNa07ooastsUZZIQuxbJ7PJtyFmSJuw1LBczUGImNJZSjEddIrGKi2jMcT1XNl2d9dhpp1yCW68J0ymYZHU41HaQyKEVmYTuM0aiicboz5FyslGzIsIOsb+NCdr3HLputlcZwfJzqtInHSq/uXp96yU+GjVRqvVjP1Ndl8dUBA/lMY50ZRFYCtzlDq92+d+8ei8nwMBe4e39nbVUzZM39g6tXr7JACYWezR/nK9yK3MpnjodqCh1UMCzHmV/Owdp6A635r/pJ5+iPiDbMTbvteZpnrpHjRGbDajFjY/Rhmk2dtZXD9oBFo/QlEPlQUA2A/yIWQm6C2JN939nXWgIBBDUzG5CGiDLgcU5RnnFwppTNMPal99Lcb8M6GCynuVFtrZSvcYWUrsQDIpBJCAhasgt82IxpQKzy3NLEiiTGiO+98+53vvl1zBzQ/1/8zr+wzVDsmiqz3tqLRwnVyVABVVq9WL+NoqrtgxUtkS9MHqRL7LVSttKIebZOF6ZFrd3VkExc681GT1caag5yqlyecTvNlMabW+scmYJOgEPgQL5+/vNfYA6bcXu12qBfxcpuDQHZ2KYV3SNxqeCyXVWGDvWxxPaY5lEwMzamk2NBAzrIPqpkW9hHkBrMwRBXeIlXMJdQIh4wqQhGQcGIb2X1VGwwnU7TrZNaxPYznWg6QEJEaUUIG/yRLFe5iFji5BguMGHLU7ZYseO0y1h72AOQmw3v33xvvZGbjY+nk1Yxn+qRkXXO7DnF3M8f7FQpVtIzXT2SztZnpQYH0vSrm6PVSywIoKg48oJyFMDbO1AU4FTGF3skLxc5pi1oUyZnUKh04ziwpKrttdMys+WqXJm8Rmyio4ywOXuOOBAsNS6wsJ/WPuQepNmkUqO7SOkZcY8Rr6oF9e2w4siyDWtQKNaPaBYEOSO7myju/RsJTLGPxAX8j189CjCge0CYYFha5924CJI/hCDMY/6hqFDMyKFIxm1x7If4JdeHiHUSZakCPony1HxqJBJFcmRir4+G/RNEzZAwVCKfqgC8Ysabz8pwntdqCoxb/lwCle5JOOCcBXU25ElktQAGGXkNhRxhayOFqCadSj2KBnNOoWoFNloKcOkiK74pePWIWEVV1DlNLBBSZ4i2yM4hSSV0i9o2meshzSHOOXFSMLwTc3GvhZiGpBBTS1bLjhjP59KQvmTJlaWj3oCxUfvoiGj06ImNpC7Rl6hVO4P+3dt3fuqVT3M8BcoGQQ80IpMvQhw1zPwiQ2ZmQNmVwr23x60m9uahBo2RO0H4jA9QREoEUxDwtMJbqXSUNVKMfkkRG3ueTcv0JVEU5UqdbiXbgDAHI8c1McfUHJuMRVqd+YU6MfsoEkhGYw63Bh4ijGVwDMzGDO1lHdAIj+zoA6PkCEUPIemYOBAaCdYFSQUh/MwBEFIwCoQC+LFL0/9gXjWfVx1pEtFOnzhTOlXE6fImiv4Q3iRKyehnw0GAQDBhKYKq3rqnlJjcQZVwVaU5QiiT1lXZkBim41VfyCBBARQx6ehYoVn5iFQXNWx9gjrGRi7qCS2rLr0Sok41w4r2h77dHvMkHEsjHpQZNosNW3t/qvVVLVhnnF1gkoLj3YQbeaVyDbq0dPKZUrVJG86PQqv0G/VVTn7JTkZ7d67Bouwtp4dJNqqcRc4UGA+hJGdtlNdFcT9smMAvcfCYNb4ln/9/L/jjV8DeksWmH6uj+cWdAXnV7aJjZH31ZXh5AvAntnpXSfm5LM1TCHd2V6My9xRyiEAC3n3yxIVF7E7QCCgHc0SI0BBV5GRKJLaNqIlExzdgyAdtPLB+NqoV/UsHHaILmtKYlJBAsVZL28XZOAGwbrsVfHdaT0ugaegYz+iT/XhMSSCcdQair5z6xBwwU8CcRYwRBlGn3rrUA0oFgViqlhrVGgOF4VGfga8GSZQY0chqYPZt6ByGommgsS7wKepcJC6i2NnZ+e3f/m1GxqnimnMI4Y6s0SfQz1SRvVmmSZTd770KyU1OHUYok+1klmeVS2N1u762cbS7z/F905xUrxS2+gUsdBGGrDxHPzIIwZ4MDmgd/qbpDh0HVDK6Fg2k3UGy2+j+XQLLRcaaukSwVipucMNDo7Z7rEVDVAd17wUAE9PKKk/M/FoW7l/BEEcc1D4eEduihYJZMZVj8IRPSQ9fcQvFgoUrbvB4wvAaPISDIa+U1DtMARm6XNQdGIInSHoSRZY5Gae91Brwi9PE9qKnOQZu1DjpKCIGsGJlldiUVnlpZTSCgOkJxqzaUU051aGB8HRy6B2ShgsmMAAb21Q3OBmrxJEy9KpoH1YPpJX1KZoUQLFrKJjJl8rc9lyolgtltmdXGQ7XWcxM76Hf6RzdbR/dYWDOXE8uOx2i1Bc5SkER3Hmb8ZDQgCKO9G+LIERhSyKorcIjfKXdxn/4l0Sfz8AbN0+R/QSn+Wh/8d7NoL+oWCLEIufsuOjLkrDFYBTZQYk34VobTzxsdS3J6sMHU2p3akdqvZLEC8FaNLELDvyNbeRfVoRldFOSRW5ZfFNKfJRQCE7v5gjhN4Q/QU8AK4+hbBnKFDTVNQqSs56dIqj3giKzJVASSjINyazEbsC4uN7kMHi6OVKDWAzcSCKN5VAXWneLaHOxxEBYKtw0OeT2rDXwsAUiKFTpCLfe+TcjUyi+KsYkKQIImDre2BxxGWiweYIM2YHEwKbKpQucXIVoG44OmwdsnlhfXWUe9OD4gI3LLFDRNYjWO2AhFwM+5nfZsoRW1silWGTlNjBrjVqr0yIimys5qyKgkfQITak0heENHnUhKJi6EvCSDIHSABzmly9ySgkevGwQYUnpMy996upzLx4eqE/Q7bW7XFXY077kIYZ4Vr0xf8CeXrb/iFxaoJzJV9l5xECQqmEuDrxUR0yfaAm1BsdQEyrxf9jvMQrW/mEMzuaEIXiq4yKM+eWwbY0d+SrrnQ6pIA5azT08oTNPIqs2zYSohFZOK6/g4DmnvVg0xcER2V3wz3nmXonsIXRBPFMyJxBMeMWhkh1DormL4VMQEOdQc+gRIcxY1nsVQIUlKRsBePlrDzBZi7sFXMQDmGzs0JOY7GBTP42NtVL1OooyV2INlE8Ps4VJa7KIl4FzhhBTG3LLbPuhZ6dVy5pVubC6RV+PE9uwpmAD59gpTOEsl2AaqFpI91oa31Pp6Uk/n2Fl4SCVq3lBlj29+NBhWYTzw8luYQTAEh6+4sERqB+C+Qhd1GIVgCdugguBiey48E0w/oK6j3ME7CRV64QbdKXQJ4LKXvcSRGp+56GkOKZ9wd/9HwGTBCqRtSNHSNIlcVCc80qQjPtQfjLyZoHHE8yBtzbGXJKEk8SY9qoShnZE1PCq09vdaVAlEksSmP4kmFGZzZ0xm4ROZfpHMJxFfQ8wcdWcYxhSIdhEddaslLEKG5NCUYTkSSsOn0iuUI+JWZAxA1igSukN0AOwjROpTqddGetQJCpXh3ZhUeSu8EIB3ePrUKAtclFHA2mCGUTZ9ZRusuCZmXgONu/3WFhSK7LtWfkEhOc89ilCBoD2lbbAL3u7Ynu65hTpurATlim5HPZnVrAOZqmNy89sXX3x0ss1RupaK9bDRo7rslyMZedHh/sal/e6bLZmzRv9CRwqE5u6BsIs4WaULMVBjUJD1uVo7p+zpXXm02SAcmJozyfGgqpHG8jC79LB1IwqVsgKZ5VPjRc66GhGO4eLT2rUZxzRvJjBcyZKFEAEcwLvQSTE+VsIDB6PE16Dx/FRSrPBEE4I3QOFxI2XtCE+gbySDc79/tUVthY4iAZM5jOihmjF8YxrqmSXgCsYG0M3FC0qkwXGUpsaYIuA+BUrm73fHLH4mJ4RwLnNQ/MM0zSLk7c4No596WyuLWk1MouSpXFzuRUmpG23Pcua7G4K6mc6mA7RYFxCovrudqlZVhFznRgr1J0O5z/V2WKYvqiCzk94/tdAw6QnYmr10NV2caaM1eQVImJbiH7lRPOQJqqXk4rwOH+Rnk9/BLycWl5PcAOOpU+h2paneIpfyD24ZDahESYD8ROOg4mD41Vx7DEX+TFeQWZhKlTM2fCAefAgUc5G+5AhjpJloWKGvJC/NCf/Shb4Eb3IDja48KRy9UmrUbT2TTuCzAk/G/b6a7SegqSMunSwNCpIQyg2HiqCiuON1aPrTQ1Yn+j9oNYRi5qFDmgEjyfgFQdAf1U68Ob4xD6LchmDoEqZC5Rc5qirjoaSA6bZUPDHR61MvsOhIrVag60sOsLR1ukgviYZaVddEZBmbxQLugrVeo3BCyKYQ5PBDrWIQo9GkRojKnPxjUl4FzRA4NXxEVIa+RKR9VHqxCjcXrEia0aYI4q4dwoT9HRSWdnKlmrtMX2C7Ixjdmu6KFGKUUZMVujo3DFmcxkf97ptHeN8rO1Ak+Gx1qD3ekjtGbswdUMUuzBHKG1xchqdwWiZTUdZTmxgxtnUBgZtERnEGVBLbdv2WShACjC0QaXIiW0WRUWgWrSVVBgZ2VVqayAqb+whjteqPKcd0cxFofjdFzy8Br/FjCLMhSczMBTEIahC+iLEBFVHJqTSlC4meHX7/OxJ1Z60qNQ2zGOK3Ma+rBWvrXCVwDZr2/2rxdTBLbATawKY26Ajqi4DvUn6klBxll67/BzdFBQno92LzFmUyjDPSmMtX9L2KhtDq/mI0JyYOkntNNtS0qSkhWhwznCb7g76XDg6YnBcMc9uQNYzaU3oMudUciJ4xRHiQmtZkrPhJDkbeDYk5CVWFgPraRUmr/KN0wTfOXAfMtMY5J+n349zBOxkhSECN3yMlBNTmAOHyGO8GdrnWdyclcPzbISnEQJuASX3BLSfRnYBJrkEf9KD0MEhY9AWHkc/NC/ZpjFBS2ojTnwMLA/C68RJHdo0sH61uVROIkQgJe3EHHgApzdZsPBEESQLXYASKLkaaV8hcAZZgsDTQEVi10N0QC4bjgslVBE2QCyyLG9qdXpodyyByn7ANWlcKsG67dxRpmnrimRoRYEBTRgajoQgVcFeim3W7vVZ7axrXykKUlIkkvP8oyfvLv6CJ/FZejgycSgbYlJIaJwfag9HicMyt6++tHbh0rhF60HhsaODo0tYJc0pm0N2aFUr6/RiiqlZnbyFIfuVRN7h+JCtmZ1Oq9tp9VhHq/stDnllIIbtGvSJOUgfC6Vcqcu6Vp/gFBBwkFoVHalEWU8pDySVDpMRHxT5ZGNlK5Gqwx2pyBo/MQUh9uBf5oiz7JOHhwjBszDc8/VPqiqnuC06UzkSLvqEoqPrR6nhVCZgbQMSy64UmREsh8owCcDC7HyRgxfX0/lBYYvIjH1Vchzq10a69U31RdCvmEM4UZW7p7TQj95JsYHx+/6e7BOXLl2EhN3+FMt913Zj2Sjd6t1Ln05V6jU0F+EwQ1JpUeFabAfjs9h3OOqMWsX0gKsz2ZC+kG6OnT9DoXkNJ2dF0EMeC6FQd0vCSc4nIAOA//5HB4RuRDINzYo9S8scX8RF1qxCHMGMai2E/cXxfCIU8CeKvtS3V6+x6dKadpx5uiMenpD2bDK+ng0k5JwkC+MvS2LYLmftZbA+dLjnS8Z4kGeoCKQ9UBF8OCZ0GV0RwHQiE6bsOJAxOnbWWCMFi3IkMkoCbSKYyDqZR9l1hZolgRRwPNhliDdDrMVgTn5pqiQ5eU/4kDW88dUrwiuLQCbb0B2M1YWttuFqXM1y03q1quWq6XS9scIJlyjj7GRaa6xIFGpEghg26Jjy7EpGxC6blznRAPshg04GRYwHQZqBCkDIKImY5a7kFniKMUyhRaoXpaiuiOUjncddMZyHwH4VTi1orF95/uWNi5c30g3wl+KEetK/XL3YRSJzfwJ7K5m37ulUIvUVID76O1PZLJZnxY3pBQwMmJi5I6Pb5sYJhHynxUFkHc7NuH9XFy2sbF7OV1aHvQHI48jF1jGZWmWIx8ayHCeWQAiKJssnZcERzSmM3xCP+ijuJ9C/+uv5T4EDBkmWx7MYCz6HcDyOP9UGbo4ebdHVJJ9CTKCAm0JYj6JBMAYOVK4dlco+IxCh0wF/w5darsw8bJG/UvWyT/9L0dqVSoyM6XhhgvaMYWUV2e0GmUxvokocsE1ex7apdpm057gxCiqG96LYjxoKe5ZYjW7cT8Oiv2nqSWzK3nZ24VAK9DrZsSXHT0I5VlUvcIEOobx4gn9BgicXRP1RFJXJTT1ixWhRZsjEmdxfH55DQvI/v56lChhGXFgqbVcz55UXqvB8qvFVxHfGMklNnbCIBQGI4KNjyAzScbfL5VgLMyWQjFgrggcetFd1UUGSuTI8EvnWfsjFXfweverHIjjCHipRYTv9iIzcgL+9WTKS4KwC1nLSzVxGIDq9pKLJse2ETZDm52oRbJKL6eb5CqvTzvA6HXTumzZixs41PpBBBsy5qBb5IvsallWjFR63HALSM3I0eBLT8wkhp7Klpryijdp8opqISc4a0tKiZAczacsO69GoaNvzkdrMR7KyBMsn5NvduXfrZp21JJJ9yl/JGcApoRY7S73BZQTaN4VICyrcpLxJ8BxaWxl6oIzMsrFyxY1NN3LgA7iRaaUs2+/RURNouGRZlIst5gIyZ35w5V6/1QTC5uYmMXOpKvCY+t3c3EZv1SolzLPsNCEuplhGsTAn02u4cq2xubU9IdqIIQsHWojaHABFXhBffl0ENGN4KRvjoMsyGiijiyLGGnoSjQKBjPBBzXMQiUQrxeHPfhJIQ37vyDC8UUJpYppIke2NDMRZoEbfgM3fbGZm2A4FzWAPN6ZKNVkYNF5iqME2U/bDjAadZuvGtetwKYQ67h+CKioZGzRTxXR4JukqV1RxZWK+sbUOLSaTZ15ugnmjVmmOMqwFonB5zN7m7BoncaCmk6VaYCPOW+BMLTaBay8TRNDabx32y5Zs1RSkc3tvonwnXqOHiqggJIScWEI/5jxfnv7qT4umCMGT/Jr0E4G0wsRaewwtBa+66qL9gp6Hg6q2l1oTVoihAATCKQ7r4Jh+KFUrNoU+e+GlFy5sXxqWnw9oiPGirUcp6IqiodocjmSXGtSErhtth1BGxFQbeFW4eVrNI6JBLCYjFQUKoMGTfo6tVIUZoI9ZHqYpjC4UhCzYr0cZOcyCBdPAEuJGMJA39EBNVSZkkAiTSc7OcMajxRYJ5/GV+jTBQ5Rl4UQAPrddcJYamEBbngFaSI4HhEAtz/JKDueCEmzJmurGKobzaiVUAbsM0hO1K4llAYH+ni9PWo81GO27EG04DM5MO1YomS4skSrbSsfqBpNU6C2llQjiSUMAW+qUt/EEE1cE3/J8qIfjczbqsvCFpCD5Mv1yFvKpkGXgTkVa9GIJjTWs8VAVYByQxiN++TjcY5fo40D2E5Sn1Z21d+N4rt1FgNEkRv0e7YoBA1tUeZOEQbCh8PJa2SSjmklnmoUOwmK7flmDAMbJOpbdpAYJAMnFaEhZ2prCACe/Lq/jfMdKte6SkQlMKALvnMM9KAZ6S5y9SKtDTwgT66kwJETDNjYvrK2uDfpdTvYoVLhmoIYepaELEx3lZUJP6tNmu8EGuaD8JL3Al3GTIUb3wf4xtrHTvih4Ol1xdvdCLas5Sx61ixBHolGkwmhH5wWPio9TYZHD6AkOCuabdU9AEYf4QWPzAZnO+IpLISltOlfeHEwvXbqESEpXpQ598U6v09bwt99FE7ebR+wnTnNEIedPlFYwyXNwcLbSSPUPVEKpdapaW2aZxRcSeCAIHSI7q0A9KtkGiCbHV/c89tNyAIhK9eGhLUTDs3DgLoLkF1UpFseaR71AF9kQzbo+Uyiu2wjZwFWuF6u1IesVDEUUpHpJZpeHMoyxCRZN9M8rRxHhcEhG/8ufsJC2vamYRDrRhbxr8ZXcSaC/P/bzKZHR8XFinsVtjg/mXs/GPz9ERYjIsjiiNEich9dpiBdeAeJ1yqdQ7+FriP9UPWTn1fE4CthTgl/wPAyuRBYveirL3ikFKnRzPPxc2j5MJk8sjooWV+QTA/oXFZD0HtoK+ayDHXhD/dAxR2VwpoC27dgGJJ1zzwCanRKSUky9IukknGSYZs9Mty2aS/qJ7rAEkl1sanII3kGWiYF4mp84aF9GXFhDObKZiCx4kWVUCmiBQ+WgDmdcLGAciBpeWVlhqDrudoul/Mb2RQaIHJeodc7IWp2zoS4zZnGGwiQBcyy2uANmSFM674txMLt3/JP1tdUJIKEzMyufuOyJcHrkSua8TgxzvAZWN3/ULpShBK7W7CicUslsJJ+sdtAgSiZUUHf6O+3YDsxSaWkCgbEVbKhtOjVaVcXYIdfjG6OkKn/11NYFZ3LM/xzrxRXNg36b8zc5t6vL3cyD3t5x75LujaBeVFUc9uSIa0WQVompQqKRmlFVUc2BFL+nUXsCbwYzUO5DAXQ8/RkA6VXz9fpPReDsYR4Kq5qg4FildQ4W9wBzS2NqKBEqnIw53ePGI4EVgUhmEfSOF0ZWFUEdqygdoKUaVhSJwTk3TRUExGjJQ/DtZyF1QX8ueXjlk9KedgTOM1Ac4Wzk+MviX8fNeFcdNDw8iSo7gEggtMXDpxEkCjgYGvpABNo8MeF8nBIZEH96CIFn3fmfPHlIRXUiOngqD3NzEULMp+Ehw1AcPI+sgAOuZz0L0SUaNPTqxEf2RJPHnngQUpJZFi7kFkL5SAJBJnLGMIYnvkfDCAgfCbKflEwoL9rARRT1KFXE/t8Ji4ePWHlrB0WlWBaEXCMmI0UOZ0QlQ1XGSoSgw7jLQclZx0n7Q8SoQ6bjGGmPRBgOTNArCxnqCKKZavmnhrMaaqPp0Xp5lh5jbOJwuyUKGJRwXHTr1icGxJwoyZ0BrWMpfuzLGZQS5vsC54tOCqDFKZ6oYGSirSNDmoA+/4tDdh9xbRqwNLIfpXWZkr3JA/I4BCtf4QNiJusJ3ImDo5TRjzUM/Mb+9lWDWG8NegUZ08aCCZ34YkQKmtgOGoTiBid6WpYyc9JLYKk2t1eMxmxO6jI7iITX+amQXpGEiPE3QzJd2J5qpFPbmAbHXB3ZbDKDcHCwl6bDYfWrRqpZY9CTVdBUkaBoyBedJWXB9jAUnswDeEFWkNuTAWpQgAzf8QwwhTv0p0TGkvpqkhoPMynM+I5mWP0x/gsl7Du6zJYqMgChClyLOlR9ilH2aOE1ZIpH4BQtjpr4FpSW2F+kh/3BzyrOFJuzHPPHD+lURGl8OYFxRB8y8SNG8zzE9TRmsZocPVJ5rKyiNLVwGgdK5PnwKYmhEp2mkLW1E5xCQqcJHywkapXxq+IDCreQ4Pr8FJzjZpkKq+B5ZAXsuHl6/MFzPs5Ec9JZfHnxmF9jHeSXi+PzgTzVr47MU83iLypwxBM7jlwii7do37PJ9vZWvcKFRl7LTJHa6FBLIBFirD7R6lLkCU7nDBSyXKvrVcDBQQChi4qO1FW8HL1o4xBED+FAJzuSsFmIBiTVWa5yekFjdU2nUE2z945vLKQzg11M0ORGjoABeKPR2Nraqq1scopFtlxhCzBrebkyhtlZuoT03MHHlD42Qh1cwYoyBvMsObDF2swc6ZoFoWQIJ2aS0N45eha6OoJ7kWPz40IGs8CoOQDIMTfxGAkHE14YLaV9bXM00pc/zPzuMeikMx0scYXDz3G6OpWJ4ThEVnOHahyeiGPwRT78oZvtTGrVgaWa0PeQaT6bKuUqmfoMIz9iU6vEsV2kR3xRWdlWYwuV1C3SHLDZG5CjnocGiHIA9KcgP5YzMIJB4T4kqIX5O3zxknWSKBkeAkVcqVWKYE9T0nyCIUUMDdKk61gHyPpC9oYRkaiudD0jDDTqYJ6MLb1aIz5Q80j+WT2LXnLxrwodOeFhE8hkAetJ+8IfmvPwCGJmd+LWODROferXi0yQle7Upw//4sBFDZFOT/csgxwzuxRz5KzQlOWEDHFiB6VPsfMi8+ae+FW61iiqeOaPEyReCXchYJgq+7mYJ2metI+MQlnc88gK2JM5YsEfPGcRtk8iHB4avnuoInzO+tACR+Pm00dGiLN4ekgoiOrGWDyEzCVZhuqjxp8D++fu1aU3pXb5JelgCz73d3be+NHr93fu8on6xQLMfCNEK/Q62GkRZ1znwnXejDawBpcqrIHaRHwABClDEgJRmSzlyFZWteuDT4yrga4hALykU6Orlcb29uSFF15q1NdWVtdR2Sw9/fG1xQqYrHGQl6xJizriuh5cKVvOHLOWdaVYb8wKXYzaHCNFByI7K2GYVRLpXt04wAQov1rX7ZMmGqSDkPiYEB1kKQ9RDEEtmqEbkaGvQXFwyZrVK3+GD/7QLtRKJKjVOOy7D3+R5YRrkGPlpxPAJaoEah5RF+0KkP0JXakH0lNMEqNcOH4M2rG0CNOEPnFuMJxNGAdE6BkJc4ur1XMsm8akz24qVlOzSWlrBYJD/hwGcNucjF/oW03h0YBYcKWb9AGnV3NJfxz2+L8xbCvG44M5SUkRcAY2wtkQNgJCIWhGWfyzGTm0zon9SxrCkQp9rD/vgSg9dWA/pIAohiXMSqAjHKGtc0NFMgSvrNxecZZbXC6bSg5Y5uj2yVRN7dsQGK8hS9UJuLFQiGw5h7dTHrDyDFQoL5rJ5LPaLk5m2cQvj/SrLGIHKcRu0FE58cWfTh8LVZgcEa04JwNWJY0/uZ+AZImJf5ITMRLOKcOT+MAIr0RBHCGCaKgcmwID4POvidRP3ksWoYzBQzaPrIADag6F1+AJn+Y8RAh1nyyqJ5T6NSn+QDhzYJ/4qyPA03hF4MUVcbt44tn9xQAIH7NoMcnfRjedi8TtQPzB4pzpg6GY9cCQ9kJBkVlyldG5wzpIL8/ic5sWY4zB6iiM0yTJFnNF7jLTyLjPeDWrewe0EhuRlk1xaUKGu5JwnKOLkiYvRI81RknPhc4tzzM7mkitbjzmYGcS9jIlOgcbFy7UUJ8ZNn7amqJ0lqVJGsowXPbrEjXliw7iOjmNoYEgNmEyWKEaB8MsBFqUaFByFg0xljnnKrwuTYKHJBSTfyEcmSTtKeWHxFU+aF880Xww2lN7suTskCaiauhOEkhoCgKTPCiyDpuFYSrCVgEFQGTdAKC/kRLiUNhY8e2GuAn2/HI+3eC44VqFjTOUSzoYhWEr8EES4PEc8EkpKUVSB+s1Fg7A99eT2A/ns1SSHo+X/JxMAIiL6/FEk4Gq1OZpR0wVQQW3TqKIwV09utwK55WFxxCVvCCydSTxarGeQmI5YhuIeFEV2R+fObIVQIqWdHzG2TwxvSo4QP0trdDWAi6NgJ3XyQvHTADIeJIkkDk/BRHM5HM+2zjFsvD4+9lfih/+rMtIRt47O4kLhmEfsGGhOI4PkUiushhVT9LECOtTwvkrzzkPUTwkxE2+4qftM3eEMCloIYo2FNIuAg4h1RP3kLXnEjxk8fgK2PF7SLyJdop4TlPVAMjIPfHS/v8BfjQUkFJEOyYqkbrGceE5Rz2wI4VFx41MA2Qk4guFrdU6bZDR7erqKuuS0YsMeZmv5PJE1CFn+ZGWyJKNyBwmbdkoxKjQhI23WO0TSae7rTbnMh4cHN65zSB7j1vEGQHfu3t/WalZ84zjgmLSkunhUfPatWv3799vzjRyxYINMjRLgLOUjGMYkIfSrYwb7bADO9QLLNLFxEX06C8OCPQxDl1q6UYZqjkyUtcNyUwpOTTP+UkMrbALmF+pThqFhpg2HGfIZcNNAyHJJWFFCBC0IosGrs48STH0I2LGbPOjo0Cvg/4Q5OXM7syo1wYYq6j0BRXNjZvqS+g8YV2rx3H+7HKF2lzhMBhynFZq1cYwKsV5StQKciJJk2V8PL8D9LRJ/+NBW5YKyEng+EVKqdp5ByVhYF+aNbGlM1CaiQrRxePaXkhJtEi4yWIRaisydxDTYkeqysai+C0VD0WPFatsPTjxlNIIGqpLOljBPFRJ8j60S5b0oRM9bERvm+JJ9z1cuhBXdH9ol2gaC9KEr8HjkcKrOqTxYklrIFi2plTuAlhPOggc5uijoyg9yJ+OJU/3nEWAocbC+OKcRS6dHiCFOGqS5XwSF+pg6pD3GYOQaZ/733jPpjuZaYfD1OgK9q1X4nQBHnnhx2Eo8CGAxKJk0wR5SptAYti0DU2DStS5tkxuWUeKWDpwlWUUHBevZatckZtjUQ84II/gFG5cHc84wQCeRnyly5gw06nyiKPui1qZONRiIXqyWt161jHAQMaVuUOHVT/TIVexM1Qq5pGAZ+MqhPwWf3jEUKQlspN7e5gyhW8YfNKLQ3VBImhF5pSeU42FBsMZzmywaaFQm8HziNmqIs4WgDCWFXORENU7YjvujBVKrBqacMIhHc1iuTCdFDmVif2JZc4aLrHJtjxuz2rVej1dKvQn+UGrnpvVSvlSYdIYNXXd+4h5SP5Qk/nUYDwbDirVia6xz3CoBZtfqRYGwlqMW6tWhoPjan406e1yJuCk1+aq3/TsID2ppifM5lJ85BW3BLO+gN01mfGAm+a4P4BrY0awA9ceptLN6ay/1deyrKvpF4tHIJkbmurkoD+EsGpSc7k+VrRmV+UYygABAABJREFUO5320nXMzdMM+zw5j7k/y/BkudaIEDQ3WTA8GYxYF6ZTKkmjkaJ4k3VKjJ/ohVBJaEj1IYyepurFG+CDSE012Xs8HZUmgxKdj1RunCr2s3XO6afbkJt0y+leNdXiBuDOrD6alTuZivE6rUp/tn5LFQto/aFaOWIE9h5zRCFHjWB7SPVKK4SgtqkomqGYhXlxjjYsldvsb84X6fJQ9CID5+FotVhity/zyDS+CScQx/rEBuDaJT1KDXSolM0uI9RklGBjZb+HWYJN9PzRSDkPhEOhIIUwUzlF16C2aGIihPQYPTFDm+4BBJLJnO6EKRqY2qJp7jsa5VEGo5/xPAAjcpqPR/SVjLhK2TIQdQEsNIz+NvYgtcSIVtWpDlhFzwUHsAG3FPXH6W6mgmyCV5gOxjzAbYvIhUo+0+VCQPiCix3TBa4WVHYJZ2gBTb9BSTIk9ihqsogt7TLXhcLIq5AUGRT8JwqJLilUgIcku7XkjfMmOXacts1hIdQKE9FFOk6oZl3XLVkooxIiTWU38JrBYeU2h63ikekbgahjrJEimtQ5QSDkjsepmww5309eOquGrb0ciTkZVSorNrce9RSQRXFPEcYDEscJCEVoNxmxym88LaRHeQqjsuioidkwPx3msPdTclWxZkEoDN1aGEEHfJrRjfKlp5z8pa8ZJJD2x1t0dtNBLfEleFHjCA91bGBR7m1E11LN6lcTQOOe6szRWDBajXll2VNMucjF8ee/nfChfVkWLST7sCPgAOhRPYyNYHNSQQB63/mGzjbi8L7pUMs7HBqfKIA4STSWw6OhkfUj0EP8sVrVFLDOXGXIAd3hY6Jx5Qjn/zBCUUumoqC9bImTDGt6TFcJWtzVxc9B9ZrnIiZuSKvS5aiyiNoe00ct3SckPuX6uDBh/LWGBbNU7rTb7EpqH3HeYYe99l9+7QuD2eSImwPG2UoRjZShvY6H09xYF6FTJdaYULd0SFVBJng18KDVIXuoMdWf2ZBt8A2PqNYWFpTiBwqQxEnhgSTBEcIT/qAx+qviy4orh8gw/hOXqFkb2yD/EYckRRTwlTGyxkEMdzVc58FJkChXhPWAmCzLHiqTJ+NCWbwIc0BB3Aq0QHQujD+X/CFfAeWEgiRzSZLozX36BL4GbB8Ptw+Z3DMV057Q85ERSfI8lfIYTT3wzCPnfSaB2o+xunmih8V6MF5OTD0fo7Go10YvzrPiB00vRBwb9dai/EUf/sKnMyX4eAI+NgXMAlRK3Gp36d2jgOu2h7LXG3KPpglDFCeiTb0PBB9/0tZWwwqNTPYQecqJS5AWkUc90HWmI2tCM8WVaowDXQPT8eOMK4QoQADljvqmT4WwlFzlgHtfDcSqn0JBB+tpgoy+0aPv0/p46vFUrsbKcNpH4agZdCPORyaaiDKOZ1i5deHSpQtbvQ77SrFl9ppHR+xKevvWTWYk6bqv1MoXNlYvbKxMucgFxdXscnl8kWP8mP7Ns/2DvcEaqlFt1qbUOqliRim6EYha5sgPTBTaZqOasrN7T5iZ2HOOSheW5vgk1jHu0oV84quTfq5FIUgEVMO2P3JnGAEq3FWvYQvKlulTHbSpEyBtnng4sQ1RHCUN1qNOj+51NDacQ+XDvYKeA0h4FGCN4xRoL2syPE56KtoDXwzOGYJKdyhQX/98KuOz5XKpvYwg/tVTqdAxBZbFXxZOUk++LMLDhDsEUHKsSPLhYT5MvsviBEzw0LLCK2gtS+JfAiXxuH9Z/MXhZsBU+7XRGQ/+4dR5lxVAztXzCUoeSpORtFLsU/nGtoo41tP9PZFZTzefM9AZAWPCPW62S/U1RqdMGU5zlWm7x/oWJ4fTCz8DIxyVGsJddLoe5Qx5WYo1ApH51ybs6BGluG6blavMr2Nsw3SEKc40NHZNLcFFNev0emylmsMDEihgbCIHDLx2QBqWEll3OOnv0eYGHMkzxX3qAULdnOeEN+K+p5yza984E5NKDF4z6dpK49XXPvOXvvgFgsYYk7llaGDX5Q2xFre5AGDYbXFKVio1YFdSZ9znICqtQOZkZszU3GGQK2IuU5VxDR9VoO0v6GPqGeMEtlQNjGk4qGCs7ehgsQgVKcPkggZPIHUcKCPimCNEvyz65Vc61huvKOdeHSSgNS/S/AyISZgdD9Rvm4wyowEW8smgT19Pxv4+d8QNWOw0HrBVNDfscO/QSCfjL0AnptaiX7IITkJVBZLzuMETkvIlqNg4licLUSJPMub8t4d4t8050IfmKXtBjAlUPem7zIHxODzdM/f14311rMLzgcjAJsTxgpx9PjB5iOBpw2uAKU8iNOlPBC/2Om6CEDjgTEQ+nThjqjNRPmyAmtJpR47nA/XvJ4g9KP5ZaLJCWw8dQYQypd1q1tysWhYOr8p8xhfCaeh0DRxI/Ks3sD6N6gPQPovGY4d8bApY00WcOsSpPJXq7u5u+ebNVKHWG00LZS2KwUERnshVBq6sxBkO+hZsD7NDInEZ92SYrvKlKRLTGn8xTURalDRyEXkoK7/dpanBC3eGr5bKpVypzEoTjv5nghKpS3yW4iLHZ0POp07lU5z9W+CB9MvZZMpjk/djSOjc7CLS+PnpKmLVEWqJzYqxQ03Bzvfu73KpH/NdEHCQ0pnJHIvIjeKNWoPxIn8YJzjujytnmbql5RwcHKitsL2S0S2ri5mW05wpc1Y65cFFi1qWVK9EPqZrWokUoo2AIbSi6YsI4K/ymeMVPHl6S0v6rV3yhd4yQ2GVAj/6maiMdEVGCzG/9D9dNfzZsaa8J1xc3xuk+z1xWa/DlYQ2r8WMK7NL9BJo+E+sJYeChKKZh0fkKLQh73SADPzRFGSPkGnIOxFx5If/hcJM0YX4oAE9ZO+wtRG88sJXi+Y4njxDqk+gx7E0zB+qjsQ5VoyT4lnBH6NoRrM4/0T/6ZFAkd7jgxjOGU2BD93cDYNHyvOhIjs+QulcJ0wtihPCn94wz0135iMyw2d5bZ0abE5D1nBMOlgZ0OxtfBbhRYh8DNHMWRzTz3qViIjcRzUO/tgUMPdIo4BRkzs7O99+/c1R7neHqDzunSnpLgF3Eu6xY9EsXlYbYUb2MC2a5Yj8UhWSYQhl6IrdklVZpCEh20yxgjI2smMedMUp200LuTz20GymVGSli87P14iKJ8K8zoRlvc7tJkzaoZiRXAzkHoNH43YRV+QT/30AYz/x/B4AUEQKi3/iuChgzqwv1apcmUAVMBGv24G4sm02O8IwC2nzOZZ1DsaMZyeshKN2ylvbjEOxYaC+UOHajJTlbKxsqtd0qN6AMHGo2jgy2hYQYO/llSyIE1qy+WNUEr8OwaN5fPgEVOm0afgrxSsVa853FiHWbFSsLOg0KN8sa0ZgGy046826/Umngxpm6/Ck30cLYxsHGQ6SBwgZsenJdjUlkHiQN5QCj8oUFyuks3C9uQeJg+Nh0sbEioXg035VfdDSWf6w5PB2okuV7iGderTKzhb2qrvl2lcgsWHw1eEk5JcFeCol/OS5OdweiKQktY2Tkgndv7BwJtkXfFmYkVMoSaakfwGUiDP0ZVlGC1N54Dlon5Pq/E/JcjlKD8yFUtufR7Sn+hHGvudnlviKOcr/NPwVNaTY3THepfvvcWUPtBpUV1Stmg9a+QEK6tTTUrRIz9wp0hMYrQiJvj7pn49NAWv8ayPgdKEyunlv/3i/O85UGmsf7N5FtuJCb8jrh12bqFvCeRLiutniyERMCIMlPiG19dSF4VMUMJKTXPxIh0qZuznzP/tLf3OFnTCTOlfMaZEoOl6X3ZR29w5zhdXaCosOUxzaxxJtqoz5ZmA/aZo/FXhOJdHBHJ5HY+THRcrztdTiYIl642+UEXeu9bhklwEUTYSF/nbDOUs42fYLu9vS5rxObJLiS3WpK2HPWBqDB9fCc0YHfSeqSLoQFyGo051oMjNuPeeZ7XKshLQdflIHVUCggJnDgyOCRfO36BOsYpczueGEnjJKNnKeVgWyhFwpgbWE6wom/SYLKDkDM9UbTLrdcas97vbHowEKWrfbp9MdYpUmvaFuAWRJ5pNqv+CdLFRcNJNYMW1inF2uhbcn4lHlCoc4L4jtIXGA56LAs86RPxv+MYYspOfD4EPC4B4m/gPjxHz6wIgLIsDVhPKETQ0rMexCF3DGsyzOwoQPGejwHR9lYe4h8/K0ej66Aqb12x/54aG9IbdFAnqcrnuBClMGLWoYuqFLKEr5nnJJBk76T0V6gi8fmwKGLiyLZQSTrzRY/8zlVZ0Ws4SDaqmIWETREgFZyHACAci/rfU1lKXqyAQun/DASuhP8R8cqNXOWjvFcJi9E2yDZJqZLJjd1VeNkrWS61/+wXe2WPtzcWN9rcZom2F0sVAtFtmWevGzn+c84PVKg0BqJqPThkjG0Qx/rpyTCJTN89SR1xkN5KXJFxFNpLInt5dLr6JEITpTtepvqoFMuGUXE29mguGZP6KRkApK56E3JltN93IPzWjI8Ra6SLjKAYlUs9cgGpJEmK85yJKdQtQ1lwLKSGz1m2z2wuNEB9ubgHhMJxFPeRhksyfC0hqxWMcnMzclUR9G7VOp4EN278NLHA+F/TyNtbk/GMNdne6o25kORox2+yx9ns1aLM6ajjvDUV/62IWA5/9hn8LWnCEe+R8INE70wIiLI4RMqTyXcTzpJ2GqUALVNcItGiI7Yp4kkXAx5I899JHwhAeg+BMs1BME9XiUBIEPyRvJfA3aCcT4FQ5JxjrPb4kflqsDIGvRtDJraGpugmDTSWq2VJqmnhyqZoftq4kLY92F2UmrBPhP2yM953mAbMiMQNQVIeg5D/cQnsiqhfFDWo+fhBY+JT0OEEPxcbeHxmU3EePUCUZkrojEcQWN9VyQt97X1hk9tHPQkl1a66WQiZpT10G12CttxCxdYPJSZ1vqfCWEvxdE5kONb2a9YW9/n+VZnTu3p302wyh39kCupNKl/+J/+xlUMhA6rWFltSDrpuYFF1aSmiJoC1PrJfCKH5SS8wiEBBeTOQQ8wAPhF8eAieykRjorJVTbpM8yJcb6joAKGTlxHYF0YRyORwgwwyvRCfQnHsilOKBr5Q4Ph2rEtc+kN0fxIT5VwZI6COLUphqpNZKgd5mGH45HVDQ1sL9/UF/bJpz9mN69ASAYWmF9Cl9rKZhOUMfKaNwfHGo2wLfJS1WjMemdoRmZcQDHDPt4uTpPXGFGaaqASqfmSAKC3HjLWBl7ht87IpSMpYmPEyYgqlts2X/IxX3sN56xxZdAkkvr0hEgUyzl42mTldzcVj84YK6XnXPTTh/ty/B31mfoqwmn406nWK92ppPj46N0qVTfWGcDMqA0V5Ips9SfDaWAzGs+BJjRiUCBwqK5VRlJ3Hk1xH6ViOVsWHQ6w2G2Fl+yS+1FPKp6JHJ4spxQu9TZMMoOeB27x+kcnCFhc+dWwV7HDp/ODI4GZBAoTcR+UIIbKuh5aITPCYpAIUPbPkm9QUP2AUMm9oNTTHhSUBY5R2zBlyif+S+OFaWx8imScFrWGuOCE80zCtm59OCVtPFXSRHYgFdYxfmEVwLxO6PxiiOCCmhZMwggbnjFA0yPQ4Rz3Bw+0BnAnpDSuVyibsRmSSjxC3EEQTYaW/1g1etRlcQcEeQ8omGlSRWcDIFax+D9I+JSPDCfDNkfn4GRYtmQzPgx/QC39QaROcoy0kEF4ADKws0Fip7ClVBIEYpArqCKkNciEJq+bYpBpGAKww9wKOYrKohGx5hqsyRTphwxdHq9cB47jYRPJKTYOeaw6CzLmDmWWJGEyPNCK+8dDNm9UExzph7HGJQ6nRbUEPurz60MYXt+0MRkLc8ZpzIscg+M7xFCtKUjYGLgQjZ4eF2U40OFKe0SjOfShxwJd78/PfcQgseJjkfOlpl4DsaWWswMORHqlMGWKFC9snwyAUlCHMOvyEmFUze6KdY5WwAfv6xzBXrCr6DmEIVk7J5wHsbxi/nrTE6gEIdJVJm8k8pXy0+lOJABGUd7GA5G3CfDDYDs1aEqjbrCXknoRE3TlUqZUOoI8aRJYwbAyKnZsLpSIxrth6V0HGBDb4cJSKaKOduhwGkJtb6u8mYMixIgF92/K70L2LMuGY4fBwPoqK1ctlii+1el34AMwEZOWhMHSGgdzcUhWeVqpdaok8Ws8Ix6DP3hBAXMKrNOf9IfghE7rA5bbbY4p3o9DpFqDfpHh81ypmLdmbO4PE4ICIdkSX8IXObxyCeJl8U7LzxZDvz0HkxCJZMwbvgIhw7JnB/DH/Hg6ZQWKDr514huInskDgLZFyY/DWzxW4CQ/EwOH0K4nkB6bKxOQHwcvgSdJZyR2DwJdIcf7Un3DpmsjiAqPur/SblCOg1rLSqbTdXBQPnnc/R3WU1rL3RJNFpjRozAao0jVZBJDMyUFy2a/TGmbsXhyBxvZFByAYc/BeIsVcBxH00l83zBCSeT3SM6pTIYeCJYyyGE7M56PJGH8/RKUh8hcpFIoK2wAhUstUYah0LWXC71qsN1iKtAuRTjHXaTqGeUznGOf71SB1OMa4ytvD2cmj1YjvNH+cXLSo5xqUVRUfjJuUeqL5TfCTIxDigt9pUNBsP93T2thuOMHutx1ypVxrY0BnEXelespT4mQ8w2R0uqZjQiKeUKNv8r28a94x3qkUD8GrupWlWxOtajXGbIxejfBpfFEgPhAodLa/wa82yMUPxrn/RQ/ZuDJTVvTduW2gUvTWKQQ7FUpHkzeuez7XSe5QpFnTOZlwFcxzwxqmZASWw81kMfcvzVDBP7mJN13njrzYM/+3a+wGyw8o7zjfF4Er/AdDB4IGHyNQk+hCcDH8svvSsVe8quDnhVoufy5PJ6LAQfK9Ec5qEIagVWb0AVeQ04X0MEAuR/3JYX4ATPo6IPgiCGc0yQcu5fCIdcHNPHzm4h2CcV6FjxlMee3jzNqxDaOJyH6KCjjSWTIT5NVeWVHcxUEo2YFSOwoupLJ6CzwsdAceqXjtbLFor8TUZtg+G3ewkgU2Fo94iMWgcCAGFxDjGfVKmBownUheAIFxaOSyziFXlJfI98FpTBFxx5DCAenIIWuQAnmTsR/ZWEwU8Ir6w7NWc/MnXIrkGfhgz4Ti0i6NU11+w8eZI84kQHSDdHO8dmKa2Brq0AHNVAN4ondfwYrcuKuKhgjxjm6C1MJPKZ8zh4pc+ekAOaQzrjWVZjorwnivuMkHs26A7+7Fvffu/tdxha5tmUbQ7Fdml9E/j0QAngU6VcQ2vSZV1bacAUVizKYwdczLiGYbbaYARs/WJeMNjZcgpaHwqeRe1HR9RVrtttsgOXyfoio9g0ijxC1aGRHSEhkFdv2yADGrXqChzDEBdDqziE5qyTk4sctKHROPvQlGuEGeqHEa865PqT5TrDHcI2/c3O4DLteDrhTOpKrXrj/v1Bf4QCBgcML8Z2joVhEtHYKf0IzwAiAKCsZGGMfQKHaMqXJqAw/6oUMWFOYj7Yp1Zz1qGM1dGxrEXeoIPPRv1khjjmjpvwN4KGwOCxoonCyAL87gK1eX2M0pHIE7on5PUYoIRY3GBJLv9yjGLkT/Ix9BcnSII9SfAUfEYKZ04hGHKYQ8BHwGq5TPdysGZGNirmKUf9npoq3M4wFx9ye8ryjFE2X0QmYhPDbAZMINOfpr++UuM8WqxryBQFklCjXkksGF2DNagIForgPHGCUUBNHuKfen/cl6Uj4LkMeHW3BJ8H5E9aivtweEcjKiIn68PIAQSUJU//EzzF8Y6O4Ed6SNsvbOoT3YoqFuZpVtroq+YlOHzDOk+8QkiGx9g1uZluZWVNa+e4EzabGhFXiHwSnVeESGpOg7YnOJljMEWw2OO5LHtaHWls5JVFVRAT4nFBIOdtHOzt02RoPDwjkBOpVRSd3fWL8tWaO76uNNZQh5isGTHLlXUXISG5lToP4gGEXWSYjvAoSdwG6isN7EjkjhEYyIDCb7w2j7KH2lcbawt6rtflMGdgoUZZQq+OlwzcLHnWvDSH5sJw2qGgzpitxy7ZGcJkhF7WTULabg7TkC9D4yyr/gQsm0P7MhKm5923WVHP1J/zaD3c+1xaXknHfxBDnktsGD8oGgEeaNKYb6Bvfxbv4bI7FSviBcKsScjO7NUNqb2dhFfnmlOpP8kvTlWecWOKZI7qFy6l62R0xm98ra8Woq+UK+rhPEoJz3JmBPJRgChrdbxksYkwOY3n+cAsRy/I+RE/oq8BHzwqzxmnJoXZKy6v5oAwRuGGwxyrN8x4RcNnjYQJE421+l3d4qX1JKzuNAkjKZHtpbJDLXRgf6AmTNDaiHpgMcGPKnSJKoXhfobNxvFPkQ5LR8DQwrOFGiF/ApOvIRxPiJ8MxC9i6rOC8TpQec5tqhZBeQWweNxPoGCZw6+eKYJF7GjnSkr4EwFxjxxVbdJRJ65C1a/RXKJSAZmBj2yHRCZsyhQgN7QTkwAm+Dnm8PEU8LJyJbB23B/wXAYntHkniGhifPkAcA/92QjyCPUlqkJgoevSKpLOKyur1XKRngEAeXJIFChIiRZq6rri9IXbaTvoPNrA7sEejc87ExIr8XajVLFKKiZ6cahk1DJDZ9Qw+8IZP2N/brVa5Iy2bHe6aqXm5oobAkUuIRsdr0arS7OaV0VAr5cYETOM7nIYy3TKoZjGt5jKZTCXttXsE4v7tIdBjJOltx01HwKIl6NwLPFIzUCzwvA+z2UUWW2TMhdw4A0IUeiH+PGyBABzr4R7yNnwkOQRPKrjeQfkZDkso6ctr+ZxeOx3MV8Se6sUQqxQCJUFFcQnd56p/C7XHgsJS652syirh4V4tgjLUpKdJJ25EMdaQ3g75fkwWJ0CtORlDv4cYp4oWToEhitgPknXWj+b8VJ/0GE9Fcnxs0+B+S38A42AtTCTyCzDogF3e70jc6P+LqKDzrpmgWW6Rm2jLOQsU4SYN084wXYrLWB8RYzjW6LEg9wTbw/2Lh0BA8iwijBzuAp8MMzFMYSxIbcMdU8mhRlFE7uEepJx0NvFKRw4SEnwDDjfEery26S7ZhrxyxlN9A2ixrSLs/FGlEG+5yss/yE5FWzX26gqFpflYwxFx1AgeAunnp0Wukb99CeLFblENRJ7lsH3akqSisaw5zcBaxE6R47pFAshnM5gLjZ80wWu3rCxLG0AyOwZU03Z+TXGedLP9KCm2bJqKp0a9Dq9TmsvHutjTXKVzIkuaGIi06jQ0DrUzPgnYBte3cPTnRNwc3OLE7vQn2qT+SKrrnSoCwYuNCpsYyyHSZwItEjozpyuezgak0ZPqeEubMzN5hFj6EKRZfRiQy6vyYxS7eNmqrACJnGe+hXQx3UBjoMAlphUfC2aeUb2jDIwxpff8o2e0bcP+3Oiax34h4X3MaV3koqO5rwsEFNUVcNSuL3ps796iF4fSwEDMsAR0Md1YGh4egc4wvMcYMlMk/5zknw0nxwZnnIiqpwER7wUixD1rWlYNH+dBqMmqLipVKVeYyDr5/MMuXQMbTvmdJze3bt3GfJ225wf0US2oHw5bxGD3Csvbrz22ms1XXSdp/sOAbkvlYxU31FrElmB7SGPVcOPQLbzFDBgNBYxzPA7OT6E9BBaAZpelriYFqdkSogbILjHhrIMgYWl1Ygi8hacJWReQCMwpCgK2Or35EE4VSsThLfBeCGcJfzEPegcUGTxpilg6QRTx08JUch4PuR43jeKZa1CHRcWPGux4kwHSXJXY6oYsXi5yrSoaViGraxnxMmCrptrVTCUnoIZYZolgzCOs1FHI5PndNBQd7IVizP5wmQwY2KS05zUStOK5i6JvCEWhXvdkwTPoD/Y399/9913bd6IQ1vKbErLFvKFcokIIGWZSy+z0QY/aACWm8/QyTx9Rw5zSlyJCJZgNRiwN6nLwR0M1jnqpR0j8yF/k/gDau71fOAe2bn7/JiP+hXI4o9F4+NHBfURx0/yxjlZJ+mM312IL23xJFwQXA8PbGGSRyoUZXn47D6amKCE1Rh5FhHa1LD8mYw66Nr910enDnrsPcTbH/b6t+/f4hNtnx45/V2eOKxi3Tab9Yb0zkf9Ac2Ylouk6fdnG6sqNcZORAUamnlhbgHgExEIh4Au0OT5SMiTs4nRBeSlG0CoOvcxHsS0vkEkkSGLIsSfET0OxZkgsMIgXdD8E7KSqMpMc7PoOE5eoMMySxdGOYz0pVmK69vYIqk1yJDD1CGWBN3dWGTpmhktAeDOMyJvcuHiOlCgUwSVEd+ECBPMyBm2vXC15JC7WXUz+UQbyhjWZGct3c06LaZnlekky1n6YIFQvXTlwqA34FQOTrRsd3vqFLGR2PqYUXb2E8qFuZIDLTu9Qb1Ww/TB4l3WyraGQ+5VCvFDZELgLJ7JEI+WsQkMBk8UDcVKIDTiD9FPuZy6SSU4YJJypKsbb73/Tv94f6tR/unPvZoZocCYH21wLDEX1DK0ZCcMVx/TtxvGl+t5duFJdu73ivYnIbMUu3rscG3biOwUgCuhKWd5YgZiXYNOs2IDbqaQKtZmk8NibhOaN6r5H/34h2+/zWrkEvZ7rLB0W3UOB5O9bPQxixBEXalqWTC5q77iJ0ubjX0IAC1iqxXICyl0sLKmHKlbkIGTZMOg5lTdIDXEHp1nMxH3eRTSw16zNLrQ7GfLRJp0U6nDfJFNQaMSlz0PivX+cXlaLnVbK/XyzuGtfKrNurtWqn7x6pWdvXtwHY4eA70C8mVwLl6KTpSVWcYQ5gSuitQwButSyYfgZhJXR7a2sdHpdzCUay6jUuqytp7ZazaqZ7mEeDCb9gt5FlR3IWGpkBmPdOeWxq5qBWxc5lIvHX+9MmAnsgrdZU6ZXiPLwCbsjipmxgVYqJuq9LKFLou7MsXSJFsbpTp5gMgBiqfXKk9ow5Y7eJHJbBCmALoYkf3I9FssIvNg0U5kUqVSBTZEsl0Y48pkhNF/zEEjmOPzVTZyIhBTzLNxiAr7feENJm+4upkz5vIcxyn6M/eTGkwqVTaSqfGp3rlIQz0kiEZLkoHebE/O/xG+Z9uClSN6QG18AgebmEDmlSTeFpw3PKr7+YDHXQTC4lNme1VCt6/oHE0bPs2mXGY81mnk7FZn6To8qm0sjKI4NH6ayWN60b4XGqK2SWglACghw0CHiqXPl9Vm00jshTznPY5xhDfpuTKce6PTWh+AtIKotvKAzfTzCeN3jHJYWGB3yOHrfRkDAmFWLnIDyN1J6rBc4uKPPjbVbLqcnnEkAG2FOiVPkEWS8D/H6TBw7Syf7c7G3dRMywWL00FmVGVNobk5PJ1qMQ4nv8sPOoA6EmDdQY+te1xEyqVnkHOSGpIBJjH+KAGVgHmSlTj4aWLg2W8zCVXZqF69++7XqsXy3uwYW1SnddzvdjhgDjk2HvbHnNvQ6cByqMz+QLoW7TvgZDrmtvoj4qve7UYd7gCGc3r9vqqG0/RyNXbkq1efRcvQuvt5xr7lYpeVWcNZnpuRp9kJ9xGzIcaaj5hN+5poLqCrqg0Vd0IC8z0wXIDUHvXELYu/dATsyR74BG7I45xszsIhIc5aqXutgSRVzdk0FkLskGPweFw+LUl0EhySeK4hIet+imVu3qYKUoUZwg6hQy2oyZ0kTvg0ajOTCL/A5KnrAUiBkj/tohwNt7OwWFgkgch/awg+9QwInfnvScRaBlFDPvoKjAVnezv3//F/819/79t/9OyFzf/N/+o/5Xb6nRGSVsNNOhqwIBKC4aekGOJmufMsTn8XDSkZ+MCE6ssY0qwwTE911S0iA3sQGoJ1DPQas/V1lP7h4fHd/eb+0SCTHqSzLXYKUAQVHLHFqmI7wUBJOQ4j01Sw9UlRDHjcobT4SgiYu8Ov4mAQVqo4iUIAxKsQpNuhA7VoSgDkWkN2MA0K9A/o1Qwm6J5MEasyN18xP1uusW14OivlyjWk3XiWb/fGXEqMKKTSC9r7zx/lU2l5DIY9mBNZTJvnio4BUkBnPU+aRx2Ixif8PHFOQ9Qw6/iQCyjm7e3tW7duDdrNYqMx0fkNOhIGVQLnSgBLKaJcjaySWsg6/vBQIAI9/HSdfOxvJoySWFDqqOsWN7pIvSUjfSL9trjD0DcWlQHTPKeQdU1HpZiutsYp3jAHW8pgI78q68Ey5xTkR32RCDJn/SbxiRolT9o1z/irotgnj/ygp3A3F0GNi/Hgwjw4xoK8lUvo49t3lGghXSzT56nVCuns7eu3/tXXv3Zwd+eD5nVaHIfI0R4wOZWxnqlYOl1HhjWBMfsZbdA8Lj1UFyZSkCDmpQ97oj4J8UbqnwREzGvQxAgnCiX6FNHGEH3Kj8dXwAHvpMexJeSBaBNHwisipvtlfIx6ImfSQzvCPK+QIyGEuwspeFV4LMiIbM6IboEewaHxSXWaSiE6mWTUqrdctjfsCy4nKE0njHUccsglgu89TK4ZQB+oDYvHuCqCnziCoWHJgID45hk+uUeQUWoS/DQoVmwLb/6DVI1Lnugo8tDoQd0C+waJJvTT8+nx3s7t/Z27tQzHMPU5rnE05oxHTsYXUaW/WZqPORQiL+nKAs/KDtgTj/xoUJiTUtgIGHyiaOx4BbCUhHrr6OfZtJea6sKj44PDe/fu7Rxx/CKjVxJkWKSozrCYXCPV9EhCT51Kut4FXZ5BeuwQ8lAq1dfsxt4eHm9Orph5xVVzKCiF2y0bUtgMjwlH26F4I4WNhUlqWgDZm8RtgPSJwGWcznPyk1hqkuu1B8fcisjlhowa+90W5uNCdfPKS+WONCi1AwFN17KbF0U7WqvX0SjjcUHd7UyGcUNPu3zHbGSGxLoCkU6XzRSrlLNZ9+C4f7QHF4HG8f3bhGzWStVy/u5xmgXcs1SB5QUMKzPpIpXJqnvGlepi85QG0DwC1plYmlIQ98YBRqiP62EVp8yNwlHTpoCBN/BrzCUnqffnziGA1QBl5lFd8OpFUHk1eooKxKtCzCX90een80N+EcUFX/xgowJOg2JIaeskFMgLPVKGlTGui5Bx5GlNp0Cem2QRmEcNc70pQoJx5LCtFItwkNZPsRoTkdsf3Ll99923flK6pJ17NHOkXLlUqJU0RUuTpxkCiCJEAwKTi8RkBOxCAxkh4P4iYkQ9Y0sSZYsfea4Q8ubvjCOcrx6c9J+J+MQClipgobjIgTjBjmVAEQ/Oo897zmOJRRk8KAz4TkGe7s6mIBw0eQqtyCkWXn0yTxxOiD5xKRPz9jRATN4DhpJUJDf2oDDsXDTPyJ9ExuMVychIkocTm9huwv3BLMOzrrHHUV7+RxK36JryiIMtY3v4bik1dr5xQkiaDgEmSvQgbIRmls5juIi+4dadPFdGZSe1Qmp7rVotZbC7drpNrGUY+7CXUS4WFYu/BEmvKt5yFyK4R60abEkoBaEOABjxSSsG1TGgy2TvjP/HGIW6P3nvfW4SPDhgcKk8spwlZ90GKRQlDmNKLvRVUTvDaM87MHGE+BNzruKbs4iRKG+NGTHL8YVVT+6xgF2eNLQQAnGYpH3+2W3IwdHMqSw22vIo44PNbGllPVUcp3LVYn0NK36j220N0nd2WpXWUaTFta1XhmUHyOwRg29u72BPsC2+rgwq0tDjbhsN7XNOCAUcr0wIN2p1FHOpUCSE+SfYgD578+g4m72Sz1Un2uuATSKHJqaS1YhkmfChDPSUGmZIj80iIoF+kv4QHDRc8Fht6btVgBFKb+JL4y2JLP9T8KM6F1YiuIlPecjCcvGKg0FBhc6QmNVxeNQ8PvL4xnaQF3ZCttvTOR4iimZ8ooQ6zFyFNTKqi2FxxLXGt3xioV5E5IcvgprPor9lENQO+cZ/YWWxvGZ5im0cH8OJarbeOow1tzRDFWR1ZunVaKxL7KCX5bwwHMhLHcWyrInj0chSIeTOjznCKT1P2lWfMySHQzF9qUDzZzEHZrDBTCflIRSwMNHc+gx+afapGRFIitM4wOxPJuMEl5LhaHGEuxr2V6OJcuXVMtd6DjurRyM9KOCOaETgqdc4pl5j9RHFezo/SxXw+dk50sQJHo8fFSOWqucAocy4iHgJ/7ImrMgx2GSmHp7MyEJOgolsDsCQmPCoMuJwVTaO+mYuQRp3OuFoQXSdbiVMzQac2WtJlDJ2nh3VSUVK/rJGoKlVvvgJ5GscMfolZFl4yRYNqUlKuRgfIRE0IBoyR1JkVpxXrSADF6zSozyDulR/tZxdreYzE24CYBlBZ3Nj5c41Og0MO+FO+IklurpHGZQmI6ZCF7pAz1MeLryFGnFfVQrBeFwl4sBHmjsBtCAmAouFGfO+a51MflpqcAIVuWr+jOGjpAAdCOKqvckx8wNYoTEgaVwFRCPE28ywrQM0/BNoK9wciiywBCpL88ByaoQWORJA+KEwCbtv/SiXHnI9IMZ6rnbGmEVvmxmg3jh1yLVFoFTlMMzJnd3D/8c//n93Bq1nmIszvatDQWynEzcXA+fixYsApLmiR3klO7c5p+EKOQwCtsGwVHIMUMngVqwUc+VJqtMBJmnR4oVUnbPG2fzP0J+6TKWLaCwmEqERdUVJqDTRS5S2YlvxTj8ijk0EGhFIBzz+RyTRd48KXaGTnoQE/evRFOsRneYUldgIjg/2kgynBBwGhumBbhbDdw9+RNAfcXSIrD6lUV09BpWK5sWGEziLWrZP4jIKpQ8KV7HTLNXQces46p4JcIZRztsxyZXyYRy0UzuJ/qAZfq/9ZakZ7FKHIKOGZ04/wj6qeAoF4vYt0tanQEUtxsJcxsQFVJAZ5N0jYqi857sYiQWxRFAJsuhP4MDNwYoPRV4Hz4i2P6LcLCthBk4l4WJvhjEc4WyiEp3L+el0f4uSgRi/tMvfq0vsFzmXLfGLIcSL1xFP/4CHGkQq8p2G7As2acuhN080Sxo9TlIlQ5+af6kCnkMrICBOFcVU+ODx15M4cZEExBgjfEp6RKP43f0CGKeNv0S/imCf/MlrcB4j4EN4JCvsA+HmnLeEjUU4qTxHEOGL0OTaAI9AM6OkKD1dh2dwPLuQnCqkOmNQ00FP5iAcHOduLr7HPPts0b68XBJocpi+KWu9WmTqsTfmTp3BZMgtxq1287jX74wHwwtbm51Wc7WSef7KVimb7ncOB/lJp3U44/5j8Kf3oIlTgQKwA4+RWvwb4uChyFQZqt4bPWozqiSK5nSlDBqjZ+u1cia9Udt6HlIAl+ARayJ0B7MaWn84kJ7CSuuOFRS2J/j27ki5eB82+ibSTbSdTFYjZLn/GfIajyPpcEYk85ifmQEqxgPFiHbSDZ+PB9eqLKSjEH6DL0Mz5hVkxsiur6+n8nVsF7fv3D8+OupxlPNwZidFSvVZO414g6ZKR4K5W1gCZ6pdLQX0KDSOEP/kJ4QQgp4mgjdvSse9CyX6MtPSCCO9rAUD1vhwjgi9IxiKKWsIpjl6AcWLFBaryWaRlF98TbqT5pIMfcp+YSXyejbmcXorECe24Adewx9He8o4PQZ4KB2pXqM4RJd+BW8NgvUH44v4Fkg9q2mrJaiGvOxqmcwSODdSZLWvx0DkkZNElFcLC/mBKnYmOm4YzcES5nHOMePTwhxUVVY7RKZM/GmZ48KoTzrQsUY1n+BPFrZkBprqyJtpBrsRzQQM7Th3VQh0lnjAlkxZZyylKkke09cwmaY05unrBrJAF6HOK47qcXnipSYcD1V2MgK2wntkT0UEJYypgt/DeZ51IdrZT48UslQBnwMlYBk8yciONyHBk/wa/HyFiEh3d+ZX7xJqhzgf0uMEBYhhIrB4nHBRrvEPn5CnalFGdE+oj0jFk1YGpxsQQ0sLa/hKCzUpqmPRYGssxdaJU5S4vTh3UDRLJz5wjz8nPY2zpajUiJQz6z8A02lm7t669sH7PznYvcMi2hlr/bqst28y8lpdabBhOTNqvfrcBZbqXn/3xz/ptm1mgyyUG3kNedhQrVxcPglsGKiUhpF7mCYlmPYpVYFPpXRGnLDyyvpHE+Z0IRVjvWw9XxsOfIwockkuaIoXBJiltRDTtWY18tfUa1oyTcvCvoSzEbNWM8mQYOF4kuG3mpHC1leUsZ44GqqSstjKsSOQSXb+VjOpWolhKiexj3PTMYZvlWE6aR4zQcvdvYO95rU33v6gyXrildRmLbd7oIrDWVWquFQoTZXqYiUsBz5nOHtS04LiHNxuRyrby8LTEop8gXmghhOEEPT0hUK1Ui3VSropqM6ENl2N2ZT5LaYrSAWFgYyQsek7UV2C0Z0wxxF42lm1WExQPP3pKbxRZIgOYHmUq5Ya0lNCRopkUl3Swcg2qYKTxvIUUHkskFJOC6gEVbVCmMZmf1Qwg12UK+GUAfZVkUR8tQ5i6uQHapN+l6Q4qpildTIy+aD5sTB7lERzpQAzKSjjFHWZ6TaYXSXSxQaZ79K1Ln0sxOsHYlBlfMJj88GPggdxI/ZblEoUA671CzwaHJJAIJmG5TKIf/3R2mfMB7MwW+ftjLO2a0iLLo3faPCs/jRGB5aaPzsTzDFitgao0gSn5uRC3tg14Y+aKhVHZODAF0l88AuapZrzz0V7sq+Po4AdP4pxDipGmnO+S5ISB4fH/dQFxAskWJjYkySzxk+gR8bjn3gG7PyrnufhK6YkDg6PJLBEKkI3lRlFAppPYq/YsVoXtBViWgGVooT5BMMnsCIRe3EMQpze65sxU6UCHGYR0T+WPfnKtre9vnb7+tt3bly7fe0npXxqrVFmpdVKKbVSW6Gn0Gq2XryygXhA57A4f5pFpvs1d5KWUm9cHaTlu8NysXKS5XJfwI0DlYll9mKak7CkzVEqSmkNnTkYrUVCDLPeMMMtdLNujsNQuLyX+W+7JxH5RGeChuJ1IBEdr5CCQsPhkQQHfwXR3NYe6zOpVPyYH5wlyL9V3CQQZaurDkYTTBRQirEvZeR6E3WcwY21GGMmx/u8TjtDLL2t5riSZffRpKgVT4zMU5srtd07mujfO2qneqmNSootYwe3xqmKigjRvHrhAuawo2lsyqDhuB0mafwgevh1mS7FDG0KYfiLecEKvsAsDTIQnwHx/tHdRj11YWut22uxOUu7H1JjJpc5mwR1ZsoNj0kuYYDDz9+5zCo9HRypPKE/PSFP4jgcPP7qqc6HHMBGHol+99JPcNyEJxoLuyC0glk1fERFoQakCT55zpUNyig5CGaVoJFFhbJetnngFtHK7RAUj0DKqIcNfzUZoQvVmItxp/jJunjIwisv+yO+U8yfC5LT9Oj0KB4VYbHwLHR89E98nwMHEP8UNUl7DYELoS0LJNUyxydYg6f/EQ2PMx/+ObSnnDXIgptspsDRdtpPoTsE2Ws0rRk9JYIlE4jAJ3ZR0LTVX1JlKFxfrZQswsLvjnCrLSFIiKRJ1KYkIjwQaP5pnkZKFDkiEyd+e7q/81rh4XPzIoUSktCRhgr4k1/xu0PcxD0iERFrAEMpWi9yio5Jjztz2JasdcW6MAdo9Il4uh8IngUhnoXLaLe1JjP1aNQRHuJ4NKrSGJhZBx2kQDWYR1tK8BPzmWeeQcqzEICxCONyLtnhfsLRmAspVRycI+BPfwUx8qXXxsiUEE44YzFSCZV0ptYJCYGCFUPDQ3FAQJcAEYOsScv64Flm/2D3uatXrm9vdA9ra3Vu+UHRDqe5VH7a41KP6lqVe3dgMczVpK3kV6ADoExRTbgOALNrt9Pn/BdmQ0HSy+g4EA2nzrs5Q0GJ+SqXKTPdstJYpz+AEhGV2IqazzP+RhKDYCZdSrOOCpkrycy2HjUY2JUrFaxcKCHVlOeIBwdUaGXQ0V+qF/zJJy8aM+NISM+enrkMDHKTjE5XNoVNpx8lXZIYYqE1MGjgLpWYMY+ip2ZtOg90BdiDOGYHUh7LhPop6fGw8/zl9Y2Veqs36FGvk6mWO08nR2l2r4puOGhlv+oJYUhntheh4IjLijy2QXZWHTLli3DxFWv2SiDY8wf/cAAPXEO3YsJ9DBlOy0vduHlY1SlboDxZWWscH+4gdDC/SSpppAINwVGcBt0oJsSQ+NJoWf0pVsNJ4Kh3ohkLRdMmYw1g+E/ZIS+BVLTREKgzeiu8wo39Xo8V40i5LtcVM6uWK3hNEF/MZ10A6po9l+zdJE61XOr1u5wigjQEGQ7VRPZhqmBSm1EglAEZVEIuPdHRdKUMRyJwBmexWBgOuQWKdpxjRx/9D9KSHSxmtQruQjvpPFxMdK5TQksrZOXmYztkPuDBeYwQz0P0JJ02F5Ef5IY2moYsFMv1BtdUtyhPuVSlummOnMKSYv92Njfh4ODhkPO9x4PuaNC9cfMaFGOD8P2D5tr25c9+4Wc7k0Exow6rMo4L6FlT8ICof4qeaH4YdNDn9hF6ziwwgMWoSsw5Hn8Of8gI0takIngwgno92KCHMFqnWMgPOq0yrW8K/RVHqNCO4Rf16SVTCKRG6qUV8duEjRFq+xStmi8mukxOQMlMSx6JcQOmh0NGICiPOBf3+JP1KuKUYb9Rr8JOLKpQq9coRuJFXXbTnWQPrCHz6KzY6PVLkD6bO9zfZdIXaebDHc8OUjg1QEm8HZVMYzYiBPsPKBGCIzIf8KA4uJ1FSex8Hu4SpTaQ0levXoU5kW+1ahVSiEutxVjxVEDnRhhO/nOdY0gUx9CfvIZw94RXMdwi98gKOOQ0By3kNBe+7NXiR22GOLy6kwxb7ogzh0Ccbp5ky8KBrYqxXAIopMaLL7747LPPcngHW1jZosJgioY4GA1zMzswIYCLGRE41DRP9CfnsiC461zZrXM8IqMCKbwcc54EpMgrUPpzIcEPMnxS0KrhKWuPYVd2vmQ4Umo8TE0G8BpinI8MC2E3WcGIqAgIY3gUGz5gWS0lWYkDQeDjCYUNWNn3E7r562hS3Ds43Dm412l3EanlclUKmFuDajUgYBuHkVCiUuk28hsre3WJ0Jg83RGC2PJwYWjMxyuo9LpHICA/zlo/v45hQCz5mrNZWsNNeoWoqD1cuajtCibN6LRRF47+rFKu8KrBC9nqoFKIhJ5N1StSQit1zFnqs/CHCke/dbRdQXyoFozT9QrURoZWig5GghBiX6XkqOX7Pe6ll8EcYe0OPyGUQqkVh3vvZQxH+ACJuWpKyetgiAg4YhxcLaXZsIyKVN2AqpXfaCk69JtcKs5qbaYCgClyQvzMLK8ZY2jOBIERjUwRoNp3RgAwsqyvjoqgNOlMpVjqDvrtXheJwz4OtOmFCxcAQIGs56S8lL8RkwTkwrsTEQ8nHXzzm998/513n728RiAgITg8UK9Xa+UKkQf9nkwgMn1m6J8Vub5RG0vUZXFqUCyH5sl5KsNPgLMB5Qz10On179y5MxhODo+bnXZvOIHne+lxH2tKezBq9Yatdueo1WS9BYQc9TowPMO1Uq3ODrfPfOkr/9bxfgYFztykRIEK5mX0p+nNk9KG4iN6YBb/oIqyiucVfxICNPQkVK5TzobsigNhs7NxqYze0v0kBgRGYZqFaZ1JqrjYqAkPhCzgOnShGnEm02fvZcIJvv3BXo4VqWA8zwVsMTOF6IS6n5gwpLrOOvZOY0zWLoIaalNXeQKQHgTdNpZiMnOkQwK0oFRTOxM2/42Hs/LR4QH+qKiAMwcF3FHmOGzxL2g8kL2IA98GhBcDetxQ8ATyY6ReqoCXgVsW7pTiKx7HI3gWosVX72mFyA7B9MXCFBF/842YjoYn4RkS+CeeAIeJPXL4ioeExiEilnMkIfShtra2qitVcmefJmINmYICLk7GeTvIIpmRZ0cqHFnAeQeZI9oUN+vxF/o5Hi0gECB40woNjB27ikPvjsGR97zSbCZCgw4LqTxiAtx0AxdTn/yNhvliWmcmSb+ykZaDeAwPlCQNChkNZWRm0HBa+gU6iP31B3s4mfDI7xTS2Ms/RuLyzs7BO+/farU6zVaXmdRipTwaWhxZGhm/imYYu3lqrRjbCao6q5l39RW0HVdeQhqNmsJMU3uoIZquKpUiEVlRceofR7zrnuSzODz0mqIgflio5I/wp7naqDAyTKHKnDHol6hEGh+zMYwwWcJm+4eHZKvuUhazNIMKNitLp65yCJuRQCu/qTyUnbFToaGpAZwpfUHG8TqurLgHv9SzOUJkPbMQ19M8cYTs93U6Sr/XHo0GK6t1svLuGqeDkKFGM+pUSCAKC7t4nPH8jIN7ON4LB+r0MwzXLGIMdUf5bfhrp1az2E23vuCIS3YGBKgsKZgMBujIbCFb6Y/65M5y7+P2MXduOhvwZNBFM/EkIOljfYBolDOZfPDBB1/96lfTk7aYSyJVU3RaK272qnKZwTTZSvTj5fqqUlnH3zOqAII+mChwlMji43MQw0ucRCH9/gfXv/f9NzjTsNMe7B9yhB2cwvzIuJDVCapszmfv+tQ602nbfbBWrxq3sdJx1GeGh2XtLJ4v0+s+4Q1qB+fZhLpI5oqfq65RrXQK0UgYL9CBUk60LLanSbJFOsjh8ERHic3FGmq4xFHHN5Vjeimfoa+jnhizojmOHsOiog6k3NkCUyPiMWUALHrSMrqhqzF7EF8VbAlD2hn76a0sPOWYJbPfCiMDc2RFIWBx3kgFt7PogkOqhuyxx/oyHfXbebUBN+3Rj+W+UJ1kw9pIdnmSdEofl3NuZoNRuj/64Q++32k30dmssDCAJ3okxmvxryPuOCRjWHhEBsNXnUjJ0pgznZieRMlD+ZNQHsJP2oBDgorzKc9i6DGWKuB5AOE95rAQ4J6ARzJcgeIbETWEE2hShYCo0AowursnxEx6wic8ocBEgOd49UCPY0/JSjzeDJJw8Hs/CA+VwZNoSBb5wYKbeTR+FFiEtDKS2UqIzlUQos3TcqJogdOD2WVSbwSAfPKvZz1k584jaCkCOtPksPrmWrwwpYfLhUz51HB1ZV07U2c97UvSkjVUK3Zo1kOp4RNT0yjCmmKYXY2mFWGqVYKmg6licEevEMnZmmLxKtqYxKaY+rNa4SQ5zodCYLMQOjuCJJMsx0UhgnVuHNmPGIBRp7SgKeuLgXi4H02RAtvrxVq4/BRGPQVv+UQ1NEtZ9aAVaArYn4RwdvTC8GdKrRCu5cyksillq0RVEJAMGg8ySw/Yb6Sc9eqDctAG50JuZIipVmXBRqxBMPoHk2OqQ9iZM7+4gmNn8avezUWfIUhXCtWdpGfUpc5MSidz7UmAh9k19CVSklNsUe7VCgqfETKXL7HvWVuyVE3mjJwgR92K13jCiaoVtlZTAVZh4moJMfUSwIHYGJmj9PxgoFBKkJ6yap7OUKNaf+fdt998881XXnmFbyyhH3MwH2jH1U104Ij3lYMqC4nO8IXBFZ/Qpi8+8wzylG3uOE7YPTpqKevpTMeTwGokUxWzFkATRox9vrBpNa5RkPRBhKfQ+ngc5DUFpiYip5lsUXxr68LO7uHtW3fZm8ZUC30RtsTAMhx6iEJk7Z2KgVrTJjRWX0y7/V6l5OvhxTwUzXrEnBGKFhNn0fu1DKIHfSZVUOyCX5oHI4H9kaXqwkbE4EBcj8YzeEY6KVFmjwydbVMetFmzkFkUEgMRm5kGtJSL+oizjH9BizAQxhFGedxupOMrMyOECYH+laeYyzpiNDQP5BWW4OmvZvMwHlREOcKpZe+R8KQnSiCqDvww0rAvE9JgKGH1aORs+MtZ661OW0j3h539ozu3bnD2pAShOQAG5yHLnuRCTCeX4sSqJcT3CMShRMhSnh5ZqWKC4zcihUQnHvt08jrnOwFldU3k8+PPJed1sb3ibLwQAhGDf87jeQeckqg4FYgfAvEEuedJkl/nIIdX0gT4Hgg+hNBYTgOJWOQkD4vtr9QBbyQkFU8CqRj1+mVIoSOHKpPsENvRWGxuBuA4zwUPMVkKREJLjnZjQYqWUxJmXxXB8hJz4D+pXdU5rUkR3KFrYQRa2ARlQBDf1IimZSRAaliqcsQ/BzvrUjuOS5xw+SUHUUnS2vpLTpvQ+E8ah3z4RStLQZItbRn57pkbMiAWIyPcvOAhBPj4cVpzDBJM+LE3gDlRDpOilRRyfcRSxNy62MLaoaYwJ7VVpfDyQhJNV8nchEFSLd+0Cg+Fm2ufLJpAxIEqskM1+PbNG2AMhakdHB53P+o1LVwTw/6HtiCEdoT898hIyZDETeWSnfrDaVzOKIPZTzORQV+ohSmKhR1FvMNZtE/aKg5Kqiz4GePwFc+cQ14YcVWDwZbocQjBOTWChzVroFDgX5FPmlHGYs2xnjqm2ajoaaL4s0yBNaEa+9LBgSzChDLQhWARn3gE8S3G1JI3lDpkJQLyjiAg4OeJH7faWB1NRq126+/9vb/3e7/3e3//7//9T3/601sbW20EPblrLbMcsEVPUmGap39TKg37PbYv16tVsoCwrGAzSwoY0fejQYhJid9oqANBKNProIRdXL0ZDhqbRCNyr24if+yOKqXEQsP4FPRBmg5Et9vjnHgYlRUHnQ7Tl4zWUuv1Oqcz6VQ5VgZw3ztNmgHbZMTdHEXOqq1U6TqNsrOSNo1jBc6RymucJ/QkE6OrKsX9yjfhZDPO6m4P/uiZ0WWSR6SX/HEIHj2CxguSQPMO2jcucSUWA9Uso06dt6wvNDgWJ9J2YQPNSZ91rildIOCnf7ab3UVkTXtHgEMaOBfBOR6TEIB4Wdzjz0GPMeqJ87LzDrfQA4NXSU4qEAFTdiXS8xWPaJSBsrG5MRGJWXDU7bhWqeVKBU7k15IIWormVOQA685fz3kGDImfjObU8xA+URwo5gpYQuG0s7RC61EdCT2j4HlUCEsVsOG0AJpk6SIXCjyXUAQifoI6RHAg9snki3wPLn+AjMfj46GaISgeXMALf1AwyXBDJFp1RThAeOJohNYOreL1kEUFZmDyEDhCzpxGWOaAI9mkPOwrzYgcuRmAOWNO3DfnZQzkElBzAmCM7a9AoIHxzXqJ0muwPQvGRuzzIRrL0jR4hTi0UjavcCQW63qkf5kjpOj4gQcigoNlSl0KJaPFop/QwSFfz+7skwhA4OmOZsc5JP3xqM3tIj1OckT8ZlifouPKJQaYYyaKugigBbSemdDpNOAHAiMrVWQ6zZ4pwEIX3nRMkkXm6dwvGsgplbtsLjKFQQCbBAcGaSfIJ48sojF4MziEIHp4AgaZr6GvLUzlvX/3ELVsI1MNJXHo3Ux2mkfYsW6ID0iddL7IIVe5MhNVhYIOjyQvEIsdOUm1IygJwU/JePrXWiE22RFkpfCnyx3KYsGJTz1EG1wieyMiWef+ZJg41Eo92ThdLyChRCe5Spb7DzBNIvUZ2Wh/miLGpRYOdsY8/Ql1GS05YfjVIXFnQ+L7u/dZFdioceuL1pdubGywIg+j36VLV8gq/JEC8zY8w5w2M+Ycvct2EFkL2cVmIpWBr/hTOlujQQyKTgcG06Rl6pnikIVUAuu7ilQWB3cKLRUwrm48jton5wn5bMhOvxlGlrahFMxkaypBqjdDeeAbyqzKl81f5aaWOfmsO5D5FMcV0tyc5aXzZ2AJ2McL60VPUIAlV9QXnAdEj0JrEs2IY3JLrRlnr0yM0vmWfNMYUr03KUjWXzGMnA5ad+/d6Q+6utWB7ywcKeRQj4BzdgoesiGrqMlRs8xJ9KedHp047iLQIscor3iYS+7OzxRHxY4dMcGayI63EloDx8NJ7FoVqMZufVxUMOsfpxzPVwA79Zmdh73No3uHOiKgj5Sgx66eLM8JC8pYfuDAHaVkXh4+9/TmRjQ8ycjRq7VQBwV+cyPgmCQq/hzY8HrOJ7IgGhGCx19D2ofxyIK2MN6yjM+Jz6eHx0ZwkDvmqF/3KHCJC/iczYIQXEiHHzjGwwvUj39VAtMZHo2myDvqQPwNChgm1Y9DNiHcxVUOHv4MGMKZFkhssRbtBQ+Rzd4lXJw1A4MGj1jRPiuSGgZfNPso/Yl8pi3Km2U5YVFdY5+pQctKCDIC8UlWWrcMqFqEBTwwgIB4eJnp7HI0EsjIdKWd+VAB0CqgswvfDQfew59QseqrNWqlSpFppexklkdDZNk5kytUqkfHLaGlCiIziy7JNCvHcoYg93rxJqY3UWEoHiEm+oADM0DSD45M0qMBP+EWzcOdYrtsV5KTqlY/xbNmK22BnK33Y30gld+jYSecFdCzGPKtEw8xUvQi8houcwGQskGSYRUuZEdoraP4hCMTMmLDSCxiaUCIWpFAG9j2mskN2sLEnIc49+K3tPqQDN8sNmAqksiiDM8ZWIY+RgFlRxdCCUV++VF4zEVO+eNUTyWgO6KDf5nuY8hDgCqAbVfDIQqg3J8Mcxp5oH0hF4u74WfAgABrGsi33W3jX1tbQ0MzYltfXQcV7K2wOXhqCY+Ipu4mqYBZzpeFPOesWKcWyJwLRp7YI7EmMsaSZFaPccraGZiNukGdkDX50mi4XNXLDkxCeJILTzBR4T5JjuNFdTsQRgns6ygiLZejtRVKVUivDrgKqaZtzZN6iIvDKI/5KrZL1Kt17S6kOoim8krmEF9J4uL7a3gS3mntQ6LDQ56QRPAhO7XDtbUkd0d14PDzlYG64ql+RUmwYK0VW+tYLzzut2/fvg3+ZS7/4sg+OMR2IpxPZtfNwGeZFTcK1W0NhLcquhvkCBwgkOVCOFhjaIMnJYp9DGDUur1/YBwo/DkHlj9ryQkbvQi0vtqQMb4/gGtK5cpKo0bh8jRjy9egnkiJZcg4nkpjlFyGtuMIK0JnnkQORUv6Q+BDegDryYPnnITEWfh16Qh4YWwCl2G8LINlcBwU0JLunMhzn0J2eIKfOO63sFPhITmh5DgXkyYB62AZ5MniIqpI9SThof6+R3bI3ioIYXwQMJfQhPtsVxJclczL/Xw9gWPc6zB5MopBptLUpE+R0jIjM0njhz6y/4fDiIvTMdPBWtvC7hnEu3OpJuCkdM3ZdkR8dBbM2gYQlfGE0QwPL0LI2sJOVSgQOMGqy0pHXVUtlYOyJdPucFCuskFPPKR+E5nYUcY0xhJXMojs/MnibVlIXbFNhUZBBHXdJaDtC0lNmZ0gFvNluEUKHCyXCLFxnksXLERP1R2VAmSoLO2EXrRl2IziIAuvvREqR1dAUHWmrbS+ibFGj8sZM5jxSSpTLhILqUvrb+arKhBoWL25rqUSOCggi7nB+hqUAOxNtaTKdk8HCTQ61zWJyhRH7bsnhPhrjWvUpMGwXNIbkWUS2gFKxkcbLsAYCH6eJATVOl2s3CBbHHKkJfKC2w91lyJ2DiOUeGAwaLbHk979a9euHTRT3XSffj3J2WWxt7eHHAcsihMHixIfsJubm0QGDWI2Vjex60BFVkevrK5zXQSmDQaxHPLU7nAUq5Sldwrhatwoq8k8SmD1B2yykgMUJKMcmBhhfPaGO+PzySng8S0ttPrEOUa6tPicDdyYO8J6RdVwj2yxWoJoOkWN7g7tSyxA7VCESLlCn15/cnh4eOvOLa4tzE80jUVaHB53lJbuERTAERKehHMLLVXDsfPHx8ckARpEpqKdQCGye5SQ6ScbiNM50DEgIihxlY6dUbADmo+Lp1lxNx70WTmSSq4JcKCJJ6mpIA3rsV1kC2qaNgI+ieI1jbzCxB1Le2Uat0FYmHBJodMdTVganEGLr6Ak+7wtOZ6w6owGqFkydd9x2uepSZU0cSAqy2dKmfzRnfv/sljsHDVTMjBFTuSL5UMcdt6vkDReI5X8px0hanfmTn9xqTUX9lCvCzN6qJRxJO6NkSA466zXcjbYpL4Fewn9SYBXGJ6IZJAC2lG/tE7NrJ1qhHxSFTLgCxqE+rQaBaAzH6CMVqJjBBOf+YFpXkVghEh8QiAuwpheOvtKmJTtp2bcJ4edY2Y3wZkZUAbIcXHIBTc0m0G1eH/Yy5UL+WZvNVOclHL7416DFabD2dG4e1SY5qaT1VGGqJ5XnGOkGGhWNB8hoP0bmIaw6mhBPzY5R5unlSmSR5xLlYDjzKEnFhsgSlnRxDWmUyxKwpwhG9VY94Gxhg7uaDholHPNzrAyrbJFkQhTTJTYVPmvRp4qFQssrwVUjhEgq7RymfyQ2TmWv0IhQAqXWCOTh7JxPKEtZXE/wqYyGZY105dnu2CzP0yr1cO2kxynV3BHGF1vTLqc1KgbUyGnpDegBIQ5QorggwaA59kOJKf12zy1TkSZ2n2+/MZ1aoxBBP9qCRJfmWs0AeHo8QFOUkyZHNTULZWNgw04r2zhRO+zlogdNxgBTHIiXVkyxkQZd0YhBTRwBnlsvHTP86MumTrLneJADPHqaESOWlTp0ukOO4JiJ2zjtOy/EN6xI4p7D9N1ERsC0EmTJ9JkIxvrE80bhv3Ku54eN8fZSeVSt3d8pTb6q5+qrpa7/eF+X6YIlpBUMt321mTcTbfu3Xkns7a5fzxcKU9Hnf3ytPPO137nD373d7jpmg4EQpAeRr5UvLSx8fJr1ff/+f/1vQn3bWca4/5Bd5Bb2RqXNn7z7/zPR/lGV+daaztvo6qtWozwquUyN4OVcxx/z41wFBE5CTHGrF1TPxM6aEkNioSOgW6+4qwSDA4oalZwDdENtrqCUbQk8hQLqnZ1s1bICQLB8AioORna5REl8dmffDRnGjUjcA212e+ey9GfoII8eSAvKZN+A3nqMWa7mbhOGSD1ob8Wa1g3V6cQo2bBn5lHTnlD/swyPRb9U09qLLRrm3bVokh2RUD90qDVLddqmIYOb9/8nX/831x65lnWYKJr0aBQjrEsHVO6JrQY6MRGgEFPK5Kw3DNsJQ6lGKeqHLp4qVFrH+6DOXPtzDbMevqq8psDWVqVvdETrBEN1Oi9gaX+MKPQmrKpHjvBUulSoWR3FrAXe0VmEosCUUhAF5oKU9E4ZpnWaBXCzescFzQa9gr5ysb2ynC2hcSSdDBHVup28GMnyav/IbGs1Wdx1yuSb4QTV0/rOGJ/Rh4yzYEOXltdrVRKiFwqq5yRCR3WYVEnhn3+YE9hRp91xDZyri9jsR+irzpAUGOWyOpMSjgHjWJZi/98tHOqXuMXpt1QMqpInR5Eo3Ixq53znFiAMhDNmTeYdBqr1UK5m5nVqHKjqMQiok5tnN3YZkhT05H4tSbrloDMqXYdZyt2iv2kwPkTTzSNbYEPfjzyCHgOJHiAP4EJhCJ/FOKa2JIpJMYbPxYKRCW0dkcI7qQgczmd++pppUli+MnohmFEL8eWr0kPK1xCKWBW0ylRhIUAk8Dd79EiNIwmAPRXzytkN5cWbkMiYb+DFGbc4ztUYqQ7ZKaHZagORMnF7aG3ZKoBdQf/i+ci7Y4UQbVQgqjvHqsBAU3UVCishweUiBP8cwjr05mvIY6R7CRtAHLiQSAYkiFrPAElogVQ+JPhiTw9TpQL7cqTAAZP7I86uaKUOjamgAXdZqEsmobGJjXsjVU20VmyvCJlcHhAAOeY+NNfYdSiLe8UyDga0PjKJ6UxT8TQzo02hUF8nEwIsQJmiEFkBeopCBYl1Z2MevR2uEDJBJgHkhfCnb4PnILpkYUw3WwBuc94lwsbuWkJalTz1ZW11XKpUmIaV6NW+lATNsrYaqGiumqozGy6NOHkEU2YG8xxq9fklsbBcNpqHwNZiwzQPBgMOr133/vAc1/2dJx54lz84FkW+fHCDbYz3jxkZZpg7zn453+di/wwrwCEN+jWoClplagZxtCYHNZrDaqb2iEEiyval7qQYDOjGi2aVCVu8pmVbSV8f5xRcs17wkEs8kLX0IiJbB0y50zTeqogXLSu099YIY+yoeCzSb3W4Bq0YyKIT9xgJhUZCYIzRQI9oIEb+NAPZRTOEoELFy4V61vKxuZBSGQDAPF/bO6SlkIeBkoPKZIxvxLJI3WFI4m9SiD5J8LwgCyg5GQLU2ERTry4IFMi/ckOb5EsYgwwhqO2ZmELHgIc5372s38lHAjuzsZZGBISLvx6NpD4wD8b/sCQpduQAgbL4IYs3RPiz3n0NYyKDB1CVBvSlkwPRsLKAkXKR3VCz6SeCSy0p7QPlFAe5ubxN6NiCCQaXAs7KgR0fAetVRicYeOnxViRBWxJHGOo6EmGni9Pz4LiORri+0VOK0vVH2cAKeOziMU4g33A9IsHAy0JwQM0k/IAAaypHDLXfDF+VDdl0CtOLZixHUDkaG22iVdYKZnRxD3uDxiFTyEEDzHDUxFOk9S/njQlN6XEcTwhqUCdlNiMPaan8lwck5CFB4aE/gr155KEaI4zJA8heDxQ+cb171+d/oDSmixTPzz5VKmueB2JXL7S5qSXk4QWQcQ4SSpHyfPw5Poc8yGsiCNcIYkepStgR9LAGHylEo5E5omgZN093VLwsToXWBzjECqYcwy0EAh7TyHLuiqulzjskgGr44vlSrFWbfCJobt2sWMkSWWZVKM0dhiChKiXHVIMuRCilgcf7J+dzrA3HJWKld6wOR4OGFR1BkOGMshEspj2j5P9AyFqzrHiKbwTLv7+YX+TlQ54a+UnFW0hYk5c0p98nQu3uA9+kIrqnYtHILUJbXlSPwzI6nbgl8wMHMsqctNpQdeWVhoNXtrNI9ZIwU61WgOlBukxxDJGZmt8qrAObbl3j7Tk4jMFKHX8FBlH7VjV68FroVyxYD0kcqQikRZTrmBpH+8BGWRsuoc+lURZJG7mCmBU4qu3AgqCjZAt3cxNdLWWDvKqiErEj0wGsr3bm+wWMLKCNKeDKSAas6lBy0U7jx1dUIdLBdC++QOKwu3SvogBRgh8lERQXog+cEE4yGIvwScHkTUJYo5Siw5kpnpZ7OY+CYTiJlFQQifjYhAWSjIj8jlRFnwKqYJnQaTlQecpYMcmKo3JYuAkX0OWeHCei3vCqyeJX6PmGqhDuLvlGD7UF4BI3qGFJPFkvkmCTZKecFtYisUBxpKjimkzsCBY8UoEvBiDpX2pNefLM1jAFjAfwYoZ/ymBGok5I0hMFS2ojsLP/JCPuJZlT+xNAVfx34Tlz0OW6ndaqgUKhpHF5pjJVrxOaxMPa0oYhL1jieh06wkeGgvSlvZme0iiqjmTc1SbKnJcv8TBH97cx5Mm4BwdQhxapGCEpHKhDxFxvrVpE5zqep9oX8PFgXheDgcc/NU9Hmgh8ob4wY88jANPlQ4qEU49Qig8UE5JVFeKJrrRO7FWjZ8QbnSUPNJiIg0OHCafgKCERgh/Rq+2WAy/O8eWp0MjpsMhBEcc7TA1p3eIFAtIGVqsNYnh4DiLzBOjHHsnORoGYY/ZlThSyRz7UCqzgJqleTkbGbMG6NVXX93+1KcP+9lxr1nNjDZK6d0PfsL2ytx0yBJpkgBe3TIWo0ITZCAcqCkhxt4sPkqtb26yUCs/zBa5UGY47nd7nKySHVeRdrzr2O3hkPNYtuuaYfEiBDoI5di5II3fopge/8M8k3l5cwYauTgyya/4LVy5eTivwRNx46OgorKIdFHr8LZAtQIDVvGx2qVLl770pS+tbm7RvvhULjBhNMXUzIEk7OK6fv2DP/nGH7/6qZc///nPr9TrTC2DI5VCrR0Osvfu3aNnwwA08Kom1I0BHM1QOr36YSCaP7U3Wr1E16SJnSOnkz5xYm/n6uXkB0lnUeLDG4gYcRXz/fiUi4apah8IE/EoDUCw1ObVu3dngolJhkWOzoJFRV+Cjl5cEGisb+zNjDqDZ0Dzxj/AAxZxy8icSUT2BDsFknQI+SSrOATOec4mT4YAAecUmEvor0QmQvJJOK+4ZfEJJ4lHC55l8RcCIXCpCToActBz6fkaskxG8FQhrSMXt19jaL7pswvGCKpDgDrnEGgOgYWvEWyAu89oB3B3joYLO6Gg6qdXy1oqbQJW3kon7ezcDG01XbiY/hryOodJxtufi3hMMEB2+As9c5hLWUppMw2MHYlBsBo+LZ0zAJj96ndsDSSBbIEYDdmVpKkgWJyTX7UzxLHWBKe6l6ZcxOKYy7TolxUm2ZS1F6dHMusQElB1bKGVRzvrCcn9kxLSXNWOvLxKSOokQH3S1qGouikYiAc4Fj/KLqQCOH5/zsW0fKP6CMqS6ITbJ7UHfzHI8kIqfaNHw/SvFY2HqtocIQhBxhCekYSZ9cCI4FrZwz1h5DeTm2PrTw9f9kQAhWjJETCrYAJw4Rc7lqxgZ6TyqGuwAB8wEVo2MEb6s3yMEIrP8DefzdermUlhbYXjSWfdGtdkUQVGIYZk2OgZCLOmkHlcdCvdEpIivbW0a5K9cuXK88+92EkVuhPZPykyq6yZ40dho0j29w/f+PFb3/72tzGvUvxQBPzgkiRIjPiT//VclDX/zSXzIECFjdnVPxEYUs19SqZ9GL/BP2nLDFjRYYwAyRJxwanCP/VTP9VY2aCufBkEx9QxuciVk0dHB/d3dr7xJ99Cvf3sV36+tr6BdYIxgYaqhWIuXWT1U7ZYYb013SmQVN1zg4f1Aq2U0oGWu5VbIgEX7emne8Q0ASuhqC8EjnMpfgRIlMZin32EDoTtHNNAGeMHPYNadQUccEZL9GKmYBwO8ggU4DB8VfbWzOFM08siuyU58TAIoKVJEFmLcwQsEgyrgmgpCHCk3RGsQIqcLzgFE80OR8Ig/vYQvyq1OeLyGz8XSBVx+BIzZDIfATkjxJIRkn4iOx2CJ/n1YfxLR8Ak9vLgIY+QwUJPyCnEDGnl0T9zoBv9grd8fHVnwcoojuoBD/skIY7OF/IT7g1wk+mJwKs/ZbuNNQcVQ+sybcrRfEKH0kqnEln7fAKrJIHBpKx+UtvQmg6aBKuTrN34nIgX0xJE3sVQFMMbGCQWZ8Ly1sPVqJoDzbsc629ogyQMzI5La52sMwMsIxotJ3SKESsqmlEADYPh0USGLNiGyYJH+OSeCEJMJV6TIf7iIcQHqIbeEWwV0ysvmcTBGi2j3OcyOotTlCTGOUDzmP7KU6o/Bhl7VO2MQP1V/gTfYusjXI3QDAN4cEQolatoNT6JBzKcjK+Vw2G4ABBeebqHaJigg/OMeAIHgYUnfAoen9uLPkEkMZdIpg6T1SwvCC5CcIQgUiX6gAbzxU6IMYrVbtRcKZcf9jQHSXwt288UOt0+50MUtEd0ilS18561QVyHO2g7uJYe4aF2tM4fscrKqeGM0ViWmxI5RzIVrTMU4TgqpM+2lnK9vsIQrdPp1euwZFTHQtEceIGqOz7KY8jbbxzpw/06KCdAICsgPWt/eg743ROSBM9joGDQxMw4hyzC2UlPWk0lC4pqEG5hGbnicF+acQg2A/rrGdYq5zhBtnbp8lVW/tzb3UPow1Rss+F4k+nRcXrlSpfjAnRIagoPX4HpByxbnuFhONiFNBEa5MSfDmSl1Y84nk71bRYnIKC7wIKaCOnPeoAj3jYjjQaotpWj327iEQQ5X+pFqYik2x1IQlUHRiQmW+hFXjVpS6EslSliSOMCaEMPUksuiAoUwlnZZoICQefghKTkBiWXQUaTyjOIY+AiExSpk450ydcH+i0fNSxielqAU0bcOWmJqaKddsuyDpGTnpDdaRjnvS1VwJ7xWYQ8Dw8PeRNISEiSDJffemeKY+QgRPQUN6CyNAzFWaAeXp3nobzomxMXFpDFOIYVIiZLoZgseouqQ2yHnMIEhEcjBFbKqo8njkZSwyjevQ2ggkca2rhCTxlZ7KliLTA1C/h8zcaQrF2xuw9UlLMaEevGJYaHGLO0iUUDIE7OoZ2n8sXRtKfZXpZiaDkGS+6EBBGctyi62iHk5LyJqKVJUp/vRPYEfkm/JyQkclFFi8aqM8hlnUqtFj3tiO9gw9O7xjPWPsbO4/AWPP5FgM2ZR4QjgocEf4gjksWOaM5LFiAEfYBBYo6v4CtUmlPAxCEJn/xr8KCw+eRf/UlaPCzCCYGerSdBcRLunwCI81cWyXg0vYJHrIB9DphPqvO4BEQhhLQUA3sGDj8hnoULa/ZHEeKDYEQwextBlR2cqXGfZbYohlopUynkOAjaeqQIRg5uYi7YWx9IStmjp4GpvMgNaCaPyZvpTXQ64RQWh8dQOsUeBOIcJQFxXxziXz/809EDjhAQJUQZPU0dJr+e9RMtBD4GJpaZMko6emnjMf0fMZgM9O7Sw1SmzFJbNzixmARy6IToxsq/++/+1tHRIZ2YLvb8fg9zRVE3yk97lAPjhh39TEvVLaK5TLdL3UWrbR3zgD/qyQlAY1cXX/YvKU+VUTziutMkKYF8W+ICI/Ed4F5tVDEweUNFKiVriU11whIFLR4Uq/BBZLfvvPaY0VBVRJoML+n1LhWuPR02BRihYaWgwSkL4igafvLHA+YCSjOB+9JsfVSdmT1QoKy6iU/WYE5MS33eQ7VmLkSaewU8Lnyd8xCZr8knEex1LuLJq0eOoy2FfJJgkS8aLpz9lITO1znUw9dkQo8TPuHxr8GTjAxZafpSFrEjmmIup1EyedJPvjiqjbp1F4GyFz5Rff4kQFIMbuEev2hBk5lqORkBjqA7KZR9VkS6XF1ah3jmqXDVFwwL+xJNf4SFEY9yDHQzGXIGxkmA5mwV2TezYotGAWNy5qT9LgwossANxuUsesxOc0zdEEaOyh/D4nTCFgesWOSDiKXjivRW1+LcHt9J9gmfo01A8PhHXuUs3CvWiQwWUAlREHSw04FmJmQERq2JiUfSEplUFnLyBL4XcKHHc+dpmYc3rV7xEMDHHhEcioSYeNzRouEy/EQI/pCpA4VWsAQOD4LWh5h88miBksNBtFxT7GsuzkTAA0zPiyci26PxSUIsVsB0+zy+atcC+SEEuwVdGpXBsNVHwkViGRxRA8O0hrl5uzKB40g6Bh2aayUuSoIFzQyRORef477YisaVIjms0OzWRT5qN8gslWfScjbrqkSwPIdrUClUn5ZYqw9heGmaED/nbbEHBETwG0ZRWbxEjmEUbsh7iH/9CJ6OVTKjsyHJr4/kBxRMRxLzSG6Yi3p4+OFAtrqYHsHWJPMEROuNBkfHBxjwL1y8CIVXGmsENqW6C7ROLWGnPQM1KyMw6k5jAemwFKe+zqHn+ZLQxAx9XbEJjcqRwgO1VamGIVBBNHDpHKjw6hFAiYM2nYFtGz2ggGvgkR80EUbnzWOZCX0fko37aRbAYVsiT3BTfiZwlbWaFdoXRiMMUHr4H6BNiCqqSVdxk/zS1jAVmSJ2OdiO+TUSnjRz8nYKeHbns1aISeRz3PlAPKFAeZ/jHEDxJyI/DMw4+oJfv1X+VLE9lldVEroXUn0m65X4K5GJSbQgj+YyERxkjFUStCcmCZXWLIHcRlLiFhVb2e/LDehZOgRi4vAT2YF7CH4cgf4KfD57HB2Yy8IVDmfr9zudLgCZAmMEAsNhrZEygLG0XTdbKtSQYggsTiTH3nf1mcscaj/JjtiEZgfxogJJnOF2QY5rc1J4FjQ8Bhk+PPK99rzisDIRgZiIOzw4MHcM/ZVy8Upy4uDxMvKJu1c4ww9uBgI9TrY5YBGfjTkcNX3n9i06CxxmBIWYCqTbPaukMZcTGesWvUR0vx2IoayYT6IqMJDSH6dLQHnppXPcT6Ggs+soP5QRrQwx0ICGjkPA0xGjukAPvIgZ8AcCAy+da2OFsd5O1D6AXCzkoCQXMfKRww+bR4ccyKy9FpwjRqtSJ1s1CDSMnwZcxHFMPAue8ACgyAgXAokGv/EkOeFCyZZ6gn8i2gmeimACIkCQNLDkYQRs3CSDAQQh067uKZIlMBBEvGLYUstE4xVoRAA4McmXhB6f16hccRPwQoXIpOWWDgIdeQQPoxens2/n4BOEppR4cKAK3binoTMacekfIdhmRoPjIrvV0/kupC4WW60jjJ+gxB6kxgpz/6mVSo5NRI1K8b2339H+b7bnsi6aihQ3aDKZ/+ojsVUX7swVjnsDFgRxlARWbsjCyAqLNmIQsVMtlrk2gmuSqG7OKoLnsHh6GUGGTEEejxFfzUqN2Bu02qCKhnOCe3FOnhHLqzoexgFHNYKcENtA/BOGmUvuWXi+fCJ+eOIh3Vx8fyU+Zk9qsFSuDbmYdzpC1wAKp1LyR2uyJkJMBmZUOp849IJtv0CgInilF9W3s6A5A4P7SYhJ3qwnZ4kWJLp08WKjVmOJ9IWLW0wPk0TUGufvzm4zQcDCt9Valb3aIMEaLmezgKqXgldflCx1JVucGoPmFNBabG7tcxCHmpVVBLukMpyio3u0LNDaHEQTQWBIcAsSgBDuPIa14P+i5pijgtNKrZaYCFbvjXysy0jPT4Sgf8YzbYu3acaqZtLpV4nIhxEDq+gZUxkHsMmec1pYaa9hLcvsaVTCxIQfLKMLg3Ni41K5eLy3B3gGG5VyqdnTxnEBtOZgT2KZfjEzG/DdEchXMYlXuo3lkDkoENWM+EeiG5IzkqGrQnM2yqgbgcfh001QrRmJAlgyJ8Rfo2hn+Mq/hudctBAePCFCCHFPNALms2cZPP7Zk3lRQwQPTH6aA5p8VTSAJ4PMT7i1KX+EN6vxmPSKYjWBJ1BkDhL0hpaOIWTFwY60K48muJaDPqCX1GWMOhBq3ZYQvoQXVVuc2aG1L7Ln6bJzoDKza1rOclddUS9ShXYYOs1A9cppp7q6EDWqisRybXoksuPRkMUSEzvz3WrRajYqF356zoIDM6PhMCppOllSY9zvdZrHnDMHf5Bc4eahtDb1q04arVFpnVesnIy/NQT3uRU6zZTZ8zNC+MNJOkfG5KtIlnAGYT5EmJs4Ro6ggGFuOrGMeLk8dTjodbleTUdJ5fgqMcfK24L2R1I10ZE/CfjupTeDhzIKVNy0rNJMCp40AOVrFXcKxBzOfItDItZD/EFGAskCeQQQVB27vGr1Cp/IlEDQwxEBwRRYyLMjoWrROgfJjAnHgSep8IRPC/0WyOMkmsefC/HXuUCRwoYkZATt+QqqmJBgSsYsiLPULH+wvwt3akhBXfgiL++ABLQgY2rKPYKswmpzZhaX+sp+SvXoBBtoRtdCp4USDUkp4Mo0kfrEC1mc76Kfky9PxjdXfICeDfHAhQgQORl+Nu3ZkPPxhnuJAM2dB+AWamQyG+bzNTXESc5PGmH9GszD+RooLbSl1i6DCQS1ji0NWyvj0IWmwAiHadSKYUtrv44zzyAwmY0QBGQcylE9WYYz+LRWTht6jJUsfkhxfjlOfVU+UmhoVklJ/VHdsNdUR96KVxyq2aVdiHMyF6ksW02HGzjpae5uxXynnil7q7gUnZtjQFK7pHRQC1dhMnWNE9EYEk1ZlEC2XHDOGmjWJ2AcGHPWECU8hd/pF+WbaDtJ/+mI0ZtKZy2Fd/xqOCd0XZjiJBDgCyMvCz9J+Yg+detIQmZzngAnfIpDFtCItJ48jpP4tTLzda48hMBJSsV/c3ioHq9b0keBCc8cBM+D9gAUiKu0MvFI+zIgo0weIYLODx0feJeS2upBWYSsH+QKmBe6UMDhBB+WKg5yJpeoNrWgiER8xc94Eq5CZIOvHSKoDjNdTP4AritOQMh6i7RGksDKmKpk41ZhNQ/kAB09YvAOUix6VUPDIpjGnpw+bh3v7+1wvyaLOjh6AY2MSEWhsnyDcoiz6BTTXEQv2rD1ENlJbAoY+KpO2dTV+RXTm+5RmJXFC+5+R4Pn3GsIx5OkPH5zUpZQU2NfpiC5RHk8KucZgg+rjLvLRQZYFJrz/bBplbkpuVpDrnPY4cJcPBCw5OW4qVrNFXQJRIQAObqdivhWDuFIIl48rYWrsjycZxxvxniRbha61kaDUuo+Ami2jpCYQMZRpzw50xHkOT+Z/AXIHPi4E0cYnvEXZeExQ+7u8az9GSLjCSHBkwxMxgx+YpIFT7IWolQ34ssMGxx6RpeNXePTdu/u7VtaOMNpSOqkwR2InwDD8gXOhE1OdDfSh7v3ht1Oj3uMCjVuvMByAm+yPnfGLqg8h3AqAyny6CzuEzhnfWCVyOfs96cS4tQAdPB4NuH1lMe+EQJJAja8ugsheAjhkYgVfaSMVAE0JwISI+qxTaaDrs2mq81Ddd10y7VbNAhM/8AiBS1Ro1dBhcDMx2PJZcEmxgnedSEBWl0az1ZEi5txPMnP/FoESkRqHy1JJhJ3CEkUFvu98eicQUkXNLPU1wnHRnjHPwYvKjuY4otChFX0RyC71kyuOJ28tRFIJ8AkDcHCw5zwk+q1IY0yh2WQA8gm1LAgaVwBPlPkgzqN+EzwaiTMoeEMcWA5ik83RfIKRvT4EfgP+UMZkxDUaswlAxf6ldDoJCp5dVi88Bo8C5M/aqAUMNnwJGXwJKGcyU8xPf5CTzKtIuif/fFiBfMIEiiWr4cJoEkZ9bvMEaJAywuP02IuRDE0sj2VxAUl6xwsXOk8bQCrrG2+QcktCzQlXwUFPiYrcQ9L6jVxSWoXfnw1PuKXAAaaYkRi4+EP3qHXRyoknJR43k2aBsfOAUZReXbk7pjAD8RXErrVWtwoNUrDkpU1nTnY3zs42JsMByx75Qx80KTZA4F7wlG7mj6x2JBLzI605MwdNQ7docY7sPHTXSaVE4R8lVdMUsfh7NMjnA1fGAJAlndifOYKOwnrWbbbalWK2f5sVK+WyTE7zvYoeb+LwZ+FJ5wsGLZFATDgg8dLR+5g6ySCPgTSf/aYMbnEezhS83QIAQ4xQyBew9mLDEm1wBhckIXAJxoo0TupN6oIU/ptHI9AIFoZ50TjlQjkiwcXsPJcCDH4AR9/09MjewSe7klGFsLObjEQT+Vxgt/TenL3i/n83agnONMh8o3zrzp7+/fv3tIaAO6JUldMlvyTtEpoEpqxMuOv1Oz46AAFXCitIDHFwjoQRrPA2AI1D8gkjHQ5lqRlNouArDzk5e5U6Id7EfJGHxXZiB1CyAvYvAaPxwivwROl9MgnNCdYzhF0D0l4N78+kTfFCiUQz5i1CX7AwRjs82JvEFO/lsRC1XtkLYgmShjnyYYLnurCA0YKkseMcR4VRJOGHe3yDOklxgQY7SRs5NyjJxjkNSZBLDHCoD0LpqQX8a17JCEqZ41Eyk/d1UWOOGeDCYStCbcCC0vr21mzAqtk8ePENmetF2XqIFVEeoBDpn/QsEhNGjENWpDT6TKGPcptYy2s2nR1UdOMYDISnByKSYYTzjsYc6cT97+pIx/ndPpX+Ft1i4rWfgFulD8dL37jk0onDpLzKuNJWeMop36Jw7tycVaJPR7/bLjHPwUiejkP/tn4squchUV+FJJPnrEnS6KYDD8bM5mNUqnpy+EPbIDfWPwkrkIIi8kqv7k5T/IVNHDEc0/04y/kJI9oTmloMIqlzpZWE4tTTf+BvOGvvNQM4HLJf/XGlDI7ZdGBKzBgYbkkkLlU9CuBJCFzbNe2mZh+MR85U1c6j+x8LE405DuOEDAXaDFBlDswCRSayDxsVnZokYzes8m9e3d6dgpHiAOXi1vRsHLKWWsOBUHNRj1zGowMRxLuau6M1dQVkHZxg2qSdPiDM4DRYy6Q3I26ySiqRzLzmNPRkMOUO83DZ69eWatXs5wKz0GJLTSucOG6z7XG6mAya3W6KD8uDQCQEpvDY/D1AqGgDK8QyossaqL8rLF5XkTzT/aqVAYqgqZ3cxaIz+rUQigElQIdcOVigTlUIGP0xjzOElVORWDSmgg+qU9y91NZ+B0f0OM1YEs4DtiEEI6HCPhx+AnBeQR/GhZ6nARan89DYnpEEbxdzCUUZA2E5FSvtpwQQ19m2i9w4FW2cGvnTvvoEAEtluPYLAx9dMLE0aDiZx7LLkKPhr1IjFyYset2jre3rwzTuf6A0y8Z9WoaBfCsfiAtkwpaOLfEeVnDc74OlqR6+OBQfDxBeoTkCjRSB49/Cq/BE8ITHsEjQnD+KRHBvlhdeS58goosmIIZ/CQyGhRkpJXBsr1eh5uF+MSojvhqv2I3+tPq2ujIYxs3q/7gf663GI/yhI91tDVSifrSQj3r0Bs9hV7w6OYQtWeYQl1tddPZQwskSTGJIHDlv1Sn1oQQZbELABXfnIf4awgUsZ3cp8CI39wxbjVEeMPGouzAA3xkF5fmNcEjK50EEg6Wo6sxnmg3ea7ISm9sBt2jg320bjGXXV9ZZeFpp33MLdTqGJ9ZiRblaj9AAGAISfpDYPDYVxXRo1E7VAkEB7EQ56yHyCQhPHg8TngNnrNpHy8kMkGTOODqHnIKEE/nelJ/ROATLsQ869G3EOd01ZJRcMmEBPLqT/cYgBNhHXLEwwiFLEISPNAaF3AiBLpTEYgt8UiMgwWqeoiAloJPlJclEy9jSubd1jqqndjSHk/iedECAwQiKg6zREwf0v5wIDakxamb64zF4QcWrAyA4A7/cDhistRWcuhYK93BMx522517t28hQ7FFC4IlQQIgbxnXUhiUsNZkUCipOfEUBl7uNwEsrUEDYMoJztgUCzpnFfS8pIDCBQL66yM9La0eJtllFQDn6vb2f/R3/sMvff61bvPw7p3b/W77D/7gD959/9rNW61me29lYwWLbl9LdLVULSAAtp41gUATDc1gjpoEZwpOXM68NU8UgRAimwscG6pawPjEE8ju4cX96Fq2t+LouGBkJgvy0mtmxr00OHiAV57MDRMBvzSXQQOg4wCGzs3JjBy+4+9+UiXT8ho5ww4/ya3e9OvOA6NPcWD4RDiQecWDY6WJRrhujWTKlrFWZvruT95iSrfKBAhLikxzwu2gYTrYtqtprmZWZP6QAQHfUrP7d+9sv/p5rq+AGuCDBYWeIy1KS7G1uCFbdGY+jc/CN0dv4afHDgRbCkxyeWK1gD+QIng8TngNnjhtlDjAwRPcHHqER1UcCwqPAExqnycRoDz8qWWGHKKnGwZb7WaLfqOMJ0VxEbPsQpgOPcYfOnl9zbygAOAuKic95fBIOkX0eJQHSoxVwKE/Ru6GvzGJ9DIzoyhgGrBO4VHXGsjMeWmkKcVsIswMd+LNudKcvALTwEYh/poMsQ8qYCSeTkSlCbQYEswH5rwhXzQkF0qMVtC7lEO3PmiEjqiiLfPBhrfAZAIO+gi/yfhg5+7N69fQtWuNlUqWXVzD5sE+vUHukkaMGT3izBK/QsyYIRHmjJEMOPFDcGqMFFahJp/NmrVMAVt8VYfi6zcAX8pvJ5md8i2uA0fjVER7iRQwxfMYwZNMEAItSYRQElYycjIcv9Dhc9xs5r4COThHnNcADb/HD57wyT2eFr87YhNCO4HX+8OR+FTTJpHuUWSbE40xUoZEZgqQY1GBAJ68SxJhV9IoQ7ljKmImlzkdIiDOEGiOErBZckBygpBn9PnQfAh3STaCbCWt97lormhrxL1j68mViuy0rGNENJiTHjWDDtRZb9Db3bl/7+5d0GUyaSTrrg4EQeIym0L2tGsRhv+GMrkanqhc9HG0mUR62nChzQNfRTcXPP7qdJv75Ih5IE9DW0+ysfiEIYMoAbSY7e0d8I4YeuXFF3/+Z788HQ2+950/Pdzf+9L/4j998ydvf/Xrf/Anf/qdvfvHlcagUKmbwAmA5fG8LAthCK1wQAZnpBnI24SXFhx5ZKNZQEMQRIYEdwXkvcTxqway+BGaLNTEwzEUHGZ04cKFn/25L7/11luvv/76/fv3NUa3TFdWVohDrfH0msJPXqpQG30SblkLZ1HGormHEE/in6hmPElHZJwLXDzh01m/4sURgCkBZ6UikHXtmNC1cm3KlR3d3Kj9+g++xwJmBhnY9jTgILK6fnKsdrCZRE3B2SY1lhqgYsfvvv3257/yi6liVUaciSY3CtCSs+Gkn6XJow5pQPGMx/CJioDfXs9E+nABFBYqOx3kT1S3vUaMTSbhNXiSOSvQWjQeKs2e+o4n+JPx5/wUTZS0sSy8BGfyZAVbuVQaljk/VPqV5omrlkv0lCeDHj1p9SM5wM6QZpUR64zQWox9tTFAI0jZ2ZD3fCc4OLgp4WdmRyZtDTdtXh/kwZraNW2p+kX/SQ/T3wLcOUrYeTWATnis4qRoZTTXi/jFvivwBBvxtloiwxzW27DiFIMhvCyUJAlputgXtXEAiQNiyEcio3vFSFqyNui0jnfu3b118wYz5QOOnxxCpck7P3mrfXwE9ZTjQI+FDrySNZX0n43vX5VEglYmaHdnY4YQoqnoCUbyT8vCQ8IP49GwDLcsDw/nSZyAnPs90NOG5Lw+qgNs5JSDyn/26Xkln8lcQrh7IDQQqH4emJLFoOas9cG18IYHqFBERgH7cEcR1E3LpjDhwfXSb+hOKQMckSWlbOcJfm+BwjiuM9ccnBiJlKfhAZklPzwJJ4SW6TFJS/Zg5Y1ZbGrDa00ra3XFDKnqF7uWzOSlCwVNxZoSKqCQGP5w/Bb6ngKonZg6FkwEJngTwbQvp+apURo1yJoIAQF/BZOzjmgeGDwhjie3cB4m3FPpixc2uu1mp6NuBJg3D/d/8L3v3rp1i5MOv/zlL//cL/yVr/7+H/63v/3P3r12g6vZsNkxqAqQ8QSUoAPOP1EjnGDAScU8v/fdHzi2niO6ISQPeHqEgGcIN484CkddcAZvu5O6fKH6y7/8y7/+67/OWb7b29v0yaH2Bx988MMf/pCTF99++22GLJyVDw5UEM4R8x4AGdG5AwEcfoeMB+eBhOAJT8I9Tnj61/AaxzyJJjgm++ZiKpxMo9YRDcIgeDmXZeDbbR9+8MH7YAvTibO4OQldinEwZn5RVotP6cowecj0bm6UHly/fu24eVSopHWyBIxND4OlQcOx7mi3mRdWZiVRnfOfLd1chA/zCr7nJBcpztCW+MvCAygDG1Ebv73qo3u8HtWqopCTeuEThHU2oJfGLEa5WNZmGh14kuaVBX7qFw1YNzkoldMsMueVFkznnuNRUD8aC3e72qjDQkvaKmYMOjqoXw1f6bZHaIAJuQozo4D6jfqioYRWYvKmgmuY4QTwmCYHDMSSx0JyJQKVv171X346bUYGgUsoYPplJoy0t1dCCE1MGnAasZONUQT91BnHyanPQcsBSQ1j+D6ZcKgQhjHO6dzb3z083K+XKyhgxr6d46P3331vd3eXUpmYTeSmzCMnvLzSjR5GHJNpcYTzf0nukjAUamF8wCqjM25Z+JmIjxzADlTlR67O78FDrysCZgiFcOgLBbRi48SJIZD9RpSIlYNfTAZwk1DenOmmEULl6ErUdBbhAVM2yvlOt8cwcJypOD7IDkiGcuJJxQAQRyCYEIKfaDxZfKtIpt5oHkPki80m8lQfEaOtxhram4RipZGkMwN6eWoqTOHQM8JYxLQOBqJ8gZT9Xi8/nA4m+U6dnfOpSpclUfRYCemhRMmO+LQd/Byf3hz3ovHlrNQ6Pnr37dsXtfv+kI4uWIHSjPvfQCybLtfSw0kTtEVGV12xsskUOVWDGeDReNYvZyu5UvHg4N7Xvva7g1GXpVndvoYvYH84ZDdqdq816DTvMG6jYzCFVqMhxsKVeo2dP3RZ6XlCKpkXMQOluA1YbYkK1ooI+ukYu222MkLDxAzUPKl3kGODIKZ36MI+BGBpzzfLu5iF0hk5oC454Apfq8wQ2mP2/bU7Iy52YcfWxtql9954u9ce/N2/+3fv7ty6dvP64c231lZnv/7Ln/vWHzXffevOcJBqVSVDsKTTowF5BvkcDcGIl62npUqNXbnlfHrSPS7kB//5f/4fXdhY2fvNn/+zb3/rq1/7vds3ZKCCZRjc1Vaq+93J6vazO4ctjqRnD/ew166VCpweMF3RLd9sKET5dNqtaqVILjt37lbKuU4n9ekXNv/L/+J//Wt/7Vfv3Lr5vW9+DVPzL/3CX7lwYf0gffxzr238ys/8zdu3P/9Hf/yNq1de3Nh+5v/2D//RfrOfLVZz5fpxp19prLBOpniwT7cAVPeODg9b7fpKA9oeHR+x+9NNu5hLGCah0qh6tHhjnIXyumUWtrWjG3qzEcPwSjnfo/ufnnb7nQuXtpvcn8O2jOGwWNxMDXrrmTY3IVTrG51UsTWrb2Q4d7+XGTaxNw9nuWG2Mk1V89Px+qw1O7hdeuaZr/5//umN997c3tpsDXqTNHf6YpNQI6EuS/UKV7f3+92tjY3j48NJpcpZie3DFlqku3f99ut/8tkv/+XJYTObK9EPZRWNToTgZKdus9ven02bsyn7mGngPlCDm/FIiGGKxDyjtUazESQes3RLu024jDiWG9ZC1Y8154vpvM2GJx7uaAYccZG7sKcMPDJ+ItzhTPhDm/JgY3JUh1qbq5xhJXFI7k88ISOFycX5ssFXjc7C7EED9CZIQ0BK4OiccT0UzV8DwCyLN5nAYukQYoHWz6Ge9EbUCMslM4SlRoPRpFrNdnq7mUK5fXiTimb02x2luFuQLmaql0m3s9V6LZexS+lzBZWIIXKxVFtZ7d057I92bt/br9VLK9XiDAtzlpNVuiybBktaaiZbTGXgXl0aOByM8zV6VNr+hDUGbHwkQF+7W0wfTPpj5v/L5c7xHrfxVgulfk8JjJZD3exCd4qcZRsus3AlPS1h/Ga5AMWjolmuMRt3Mnm1FIoHUSCaTV1JYmej6VgqRDdUQkPRlM17dh2n6oYUzPgyarClZLAudqPdvV2MA1y8O+4PiuXSeNCfzo7bB00UM0KXPYq3rl/bZa3+qJ2vbSJV4NBqo9LDVKDdzFpwoxEEMLWclPqW6QtbjXa2izFAUf0CGEKTLJp/Y1GbnfGugRane06HSKWoA4FcZwfwUDJs0ucCzhXuGZm0xVrmnCEEM3o/YREC/asVOfISC58/LTxisOhz/MPcY+w99esEPBVkLw8YAYcEZLwMhMeJShEnILInOSlK/Ml/DVr0EX/kbGdLMuIcWP9EYDIO/ii5jWjdj2qk/WgEYB04AonEK4zCwY7wJX7antuK3U9FwQBaSmErLbrdwaTVY+M5okrBNiSifWHfwyG7WazCoa+khb3EjNMxYo6xE9ybtxNTyRRUWeNMHCDQkGI2Vj5CCWhCJFXKl/IZVkuNBu322urGL/7iL9kZWJyGJTsj+lVZTNS32Fj9IiO2t978MXEvbG6sVCvdTvu9d6/T0YZJgckEMF0U0US91TQnrTh9EDfK1UbbhDyqU22eTuP406tlQz/nlXz1q1/9jX/zN37wgx+8+sqnuJ788tVnLz1z9fj46Nr19+kof+mnh9PJt374/fsqtAGSWFHvT/uWqaVs3k4DVTUJYRzmBnBeX2/88q/8leefvfyjH/3o+vWbN+7s3L6f2tvtjPOpg707jfoGDXIy7LABatg7rtcKSD/OILlz43qlWrq4vX375vVRf7a5Vlpfa/zGv/bT/9P/8d/5/Odee/utN99/9+3de3cZ7+7euvWf/Mf/s1dffvl7P/jmmz/6cblS+sLnPre1efm4Pfr8Zz8znBTavfH+cYdJYqoX+n/qxZdI1evf3rhwkZ4Qa7ypmtWVdSqJE31n3OXLVB+W6lyeqwObLe2BFs1z7MgaDzpdpmvz5ZJEFYp8fYXpwvuj4c7tu6x+4g5zJObe7j0CUxyIwcq5QZ/ZCe6NY6kAXAKDmY2E6tVCBxgSzTGd1Ec7+9/54RvH7S7jozK6ZDCocaBBt4u5vFRtNLsSSkxwH3YGx50hNxFWKpxZVGr1x/1h871rNz/zxXHtwsVJb6gzQ6bp0bQPBRm50GNIowyMqUKDO9v0rK4+tofY0trRHAbLwueiLXtVMU+zOyE4iRMjCE+YgdbJFjuUBAdxDFCRWFsLxVKxnC9ivSqwHIs+F3MBSmGpeK9xO9JqvVwrIzGYPB6P+7AccQBOX2amDYeYMUbsnJBtrkx3f4jUp9+jKVdTLRr5cqGk3UCsDnCMEnRYSAovI1wKAxEBHHjCPzAPlr8UZ2MqHYKD7OVokbzBfDyJ7PH9E08UssZPcSI0NgpdGr7RoJswHA7KnArAsZqTyfHh0f7hQa+/w3Q5uXOuwd7O/Z1791m2iURFPkMSjmijMDQZHOQkx3Nq5ERZCkt7A8SyBHE4cQHrLg77BP0unQMOOHoBeA2e8CnpoXbDK6XF788QeNYTUcV+opqWxcI6O9biydFdEhohvPpT4ZYRMIBAndhBSXhTiCc6qtpeIZ7RV/AjFVYk7RQ3/SeZxvcYIH4aVW6MISXVpzn0OpPuAKVKINBoZkTQaWss2ipkWwyJ8jXJKXZrsA8fq7UtIOp2fLrX+uymm2E+IGDVNL6NuN2ooZLXynlsVnAwh0F0Oei5S0dy/af/0le4SZ2+J+NKNTqyMe2qVOn+7Td+mM5W6e19+uWXOa7o5gcfHOy3UCpCT5xp25hEUK36qxZlP6CxwfS8Wr4n1PPXh3yKUOLmU9EpAiThnKavf+1rh3fukMXV554tVyuH94/Wt9Y3SkX09qWLV77ylZ/78pd/9rvf/rNvvPt++7h5uLPTPOiwIwaDdJ6tCfkyoovFKmg6DO4rVe4w14XznOpXXS1efebSxlptdbXy6isv3t8//NHb1958/05/Wrh+5whdNeQMsGF/pcpijnatsbF/uA+pr1zc2NvdvX/z2i/+7Ff+xl//1ZdeeG57fa1ULGxvrf349e+89eabX/rC5//tv/2vf/Due/+X/9P/+cev/yCTHbUO9xlxsEipWqnfvPE+NwX/9V/75a/8/K/WV7Zu3t39/T/8xvffeP0N3I9+VF9d2bpyiTVlO/v7FIAzhY47h6yfo8eTL2vSQVOqHDJY0Pkeo36HZTcMgRDKxZUCPNTt9w6OjzDRs9C9czy9tL3Vbh0jlUadXmY03t5aRRKVitntjauf+dTzn3rxcnPv1uG9awhyY9SoZWnMxSWy1GnpYqbbfvblz/7b//46AhDzx87OvUqpAOdglalWStzMwxjl+eefpa9ZW68OOI24WK6tVPKjdGmWa2KZGU5XasWJlhdwP/yoM+LwSfqLaZ1WaH04ax/i2/lu7ylG+KhfoAYokWvwOAbhNXjOwQwIuFAu/A4wfka8DigzpEUNR0lsPUFv1F3PlzFLIGroY+fyXHJU42itfJG9W8DS3QZhjE7XiyFfpjxbWeGmizon8qGZepzLR+PO0P2Cc7SFG2iILFBCNdFvYyKZ7OgKRapGk8daaE2HXzOrNpYnOSN1/N5H1q8ZDU4kspEAAYXjK6KMrWisbvGYZkI2MUquXtk2cQpIHWSgWTlEkRaU8uCMDSKJZBbTN2qC0WTQJVajUUMc3Lt3+4Pr1+/v7rTb3eH4EKELggxs+90O1sFGrb65ts5BXBCD1sPKPzgZGYWYNDQXP0DVVK5+5R5aAQMOAgKfsi8G/bGGSgE7PzmiKlrC8Yk3j+OeqIYScea8noTAKG2smAPkOANBJk5wxkVSwB6TZ3CeBa9zec29OiixI8yO7MMSiKlWdRWRHkUI/nxmhEp1hKwpIvH7HPCoFfNwGkcbaJUsSoujd1GuDMs08OUgJw5xI22+vMGix6JMTN0BZ6dxKC8GPLRcHvuUDTV90ws6kdwYEzNpp04A8QOSag1azZFjlyx40ndmoISY5RQpjCf9LjZytg5rGolUPi5UK8Tel19ZXb9Cu6ivXESvFitH9frW6tohKDJKhkreqQQ4OaanHTycREMPgbWI6hfYzlo+iZxialGRyuCTNbU5oi5+pRRKxUlyxXy72WsUc7dv3/wn/+SfvPbZz9LhgPL1xiodE3hrbesCtkoKsLlx6ZVXP/fz7ebO/bvvvfX2u2/95Pp713d2do+PJYvYkF9rrFzY2sT0Nmgf37nTfv/9d0v5lwfTgzojtlSqhiX42e2rz3HNzJVXPrP/9T/+7u7B0WRwyOmJuSL3nQ/bk8nunZ3+ODXuMFmgcn35K5/53/+Xf/cvfemn/vD3v/7db32DKaeN1RXstK88x/B8q72/e+vaOz/9+c8e7t7f2bsxGrcH3WZmOqgWCgc7O1euvHS0t/eP/qv/OyboT3/2i3/tl/7Kr/3qX337vXf/0X/9j1ix9d4HHyBEV1YbkHvIeFETsQOqlxMWJJtsLMHCJzpQhVqZCYtOrz/pd4gAxRB/HIB689oHa/XGaNi7/d77DK3/nd/8m1cuX2Iy7IWXXnzzzR9hK37m6sXPv/ap7bXqbHC4c3Pgh4XIKErF8d+YjBHXhHMzVrb/1v/gt2q1OvVnJ0L3S0ys5HK7N29gw/vGH/4Rg+mf/cpXuFuaqcpKo9jtchhrkVMccgVs/uPK2naL4ZuMp6yjyXAgKrBpJ6zxHczS1TP1763S6v/Mt6cf4ELA2U+sHgsozzm8Bs8yniaCxwkJ9Sq2WdwMCKevTr9EjVa9WY3hBvRXWhowYgsrsfhKIqAM/cyUHTq7QJUDvP5hDs2ls5xMQ/esn9MEU4rTbMapjI7cwekgH8JUG+p8Y8FSIamTNJrP5YhGwHT6udsQxxDZWrqWBThxlBfDCjV1FSc4wMA2tH59dFmEEBy1DDNQi7sKJhGKJe25VNffKCwU8Mm4xy1JZrWzHUdGLVrnlHDWhcNve/d33vvg/Tfe/DFH39AR4RghiAbjra021je3EERFDs0qsGwN5BgiYGIRKws8Esiy5stZp1Jgf9Z4yQoVVRURFwst4Wr9JGJ7YaHSWbCPHXIOqo8EUybos7BA3aHwyf3Bswy6A4nKLG5T72xZ5AA8pCK+O4hlVObLCQPxKSTBEz7h90+KTXwDAQQqlD6kB9qHCBRJpRPMGRiFk50PUvGQT542VMlgdM5khqXZVGstytiLpMQzw6E1EVYazzY21mgmHfYAdtpsKFV4rsqZhqW81u8AlmMOmSSlw8grdU8WnACIAxQi2OYIWd4147wrXmnPXJvOWBpGpB3pGrhqTR1Cxu20MaMJWDPZxP1I2eLq1uUX6cpW6qvsU1rfuPLCi5/d2z3SKIrzdDBYYWJUj8/u/+GoACWUMsbhB6qK84hOSaTaldZrw6iI4YrlGNyuownnf/gP/+H/8f/wv2POfXd3b/vqJaZ2OBWC3vtgkuqx/bFQvvDMc5vlPMaoL33uC/dv3/rgvWtvv/3ue+/dvL979N71W7aql/34qXo5hW2MTgkT3cP2cX+wyhKXUjF9fNTiCOV6Jf/ZTz3/7PPP/fgn137/G39yuLc/6rNYPfXMBa6Sn/1rX/5Fbp7BSl+rlH7zN3/z2Yvr/+K/+3/+4R/8/qUL268+e+XFF567eukSnfHv/MkfffOb37x39/bW1pXp5JnLly9OZ/1rNzqsZ4KGWDXYH/zrv/a3uOvm2s179/f3X//+cbVRZ6z9n/1n/8vf/eq/wt7+wbUbe3s7VC/CsdsfVKt8xWiCSZCpLC09B06vO+gdH0vt1UrMl7MGh77I5Qv0AdZ7zXa32dw73N+olF557YV/79/4N5+5evlHr/+wm+pV8pOdvfsI4qPDnfSIizK1DFCSUMIZBYlYlBlGNTKd3tw/rFaHrGpu7jcbjTpLfNbXLsHUVG9560q1VF67fJt6v/DCZzhaPF8qbT6zdXBwpNVwmKdXN2/d3mmOUq1Wj8kUsUeORQCYorGfD7CocuedMQzVfjJMfETGeSrRjQkjTnaW9myWhZ+PRBICMQEiXvc/eyEQ9cb0gVoV0iUPIeVYVzIdYIJVT505oGypKGXLHWXjMRZkAxUBonWoyXFGLGe0M9MN7vlcIVdvoFZnU4w9HBKHDSKb4wg/s8nRDbcZ3xIMxrCBYYRsIHZSHuYyFjy2O0JTmOnwVLMgy3SM6pXmFW1UEP1Is0nKCS7dCNt1iVAiLrMcqHvEZvTnsUlLG6+UhTrOKSHZigajg8nchNZg+2hb+fCfv3xm99a9a9evf3Dj+vvvv793sK9eSbUIXSDO2pputyyXdC66kWCMpKQjKQuBAGmmX7jFozVHZOFT8QACAvrx7BdEFClMThELD4KXRuQJF8T++IIiE7TKEavMpIdwL4B7hKeXWr5TzksbgiLiWHIPPAmx94gdYmgkd+csEyITNwonyCInnwEyNUc0G+yK3LSSSXxrjSWjahmOoAvonCoH4vv6Vj6g/8zaedifjvPTfArrJ1vSEP2snelhHB7C0fAryhVLCRWJvYUktK9mp72/v89V0ohaPldqVYY/TIgSB6tyt6eJQ2qdHS+abqnYOYjZLIr56PiQTwBBL/abR+yRrZYv04qkPu1aApq4Leig70a/U9e18kqhGHwzDzjh0PWpMOyOiMCqK93vzSoStgCwBE2Tdxy3QHu3062LVeZaIho6uZye7n/4J2SkoejJT8JBvtXV6qDVQeb/+J1r779/7ad/+kuMKBkSFKpljPV0CmhWWNRLWVbopPaaOwzzG/SH69Xnnnn2C1/4qd29w8Nm9/Ufv/XW2+98//vfvXvnIAWwfAr7MxNRTJ62mkfDfpbtHFpRNRi1usPZMPXSsy9dvnhp2Gsyaizlss9d3v5rv/iX0bL3WylO1UDV7d6/f/PtHzbvfbC5tvbv/e1/nerDVP7OW29+/Z/9NlcX3Ll5a39/jyM4fvj66++8/eav/Y1ffPnV5565+tz1Gx/s7DBrNW41O3TUEbosrNvYusRY5+DoaH//+E//7I8/9cqLzz535etf//pXv/Y1llCxmCaXLd2/f6tYKFNf3ATS6o3pbK02VlZqHLSlQ6ePDne52qper37+tU+z7OsLn3/t3q2bb73+xnTY/5kvfOHCxnqq1/zmV3/E/oxrB7fYH/Xyc1e4Ceve3ZujXmarUa3WKpj4NPDhmEO6aMzs01pZ0zgYbl99AUY6kNvPVWrcFMwOvG6rXatVZrnKjBVk1Q22zGSK9Um2MkzlW0NWsRVZFJaplDiHMpUvkery6oXj9jG1o47alO00jLsY2GkuAxe3UdU+fnvOs0GCI56ul9xBiTySHs9yWfhChFSw2CER8BKNZyhsMhV5IQD8TCcaKUdJMLyjCbd6w2fXP03LpcsL6UzHSoFKBQb7Lx5pC4BbIBv9AS1b2yybYyiIUmOY2Mnl+0z59/ptrgAfDDvMxDKFD8z2zi6bKpiJYkYDGAglWhP9MRTKALPKiDO8x5ymDIZIPySEDzzIi9r0lsonMkQogadFk8Q7ps91vX/7zh2u8yBwzhHf1VUUntgj1Z1yiJWIT4eQ8qgnaA5JCAuSkHXO/PFppdbY3t6s1MqseFhdbbhUBH9Z6vMluJehvbokNp5GIOOABITzXRzH2GB5dMcKUKAKU1McVdCTc4B9IsCWzgFTAPLw0gbPOVmGmMQJyMmzhKZ8SroA2QMdiMPkiSM8xEl6+MQrlackrLRTZ06KlnYCj3tMq1wKI56x3uJJEl413HEHZ8K2xEbYs2ig256xtHEmBcY9NIDVWNZmdxiJYI6mqbB4laRkSitgRkeTcESwiWH/CtvJvpKmATOI4ToU+Rk2Y2OkGcAWOdrQaMB2e5iEVXpaiMGCJBmXWMeq9Ugc/qwOcrvNK2Op7cuX+yyPLpbToww7a1ntwUQS53doPY5OYaWPqnOqyU1lxyRkS5mgCjSBMJIFJifAA4LZwMYIy1vUZEWch3EGQSIbvPOVcqfVW6/kNzc3EQPNo9YzWNS5AZVDhmlWqpo8VmY6NXRH1PZGEI27vQvrm2uVRuPyOPXCK6/89f7g7t3b3/zG17/zzd9/68e7t+7c/uLnP0NHhy5OazxkAMCuoc319f2jzt5h+2jv/qUrz3325Zf279zUvofm4df/xX9fLZcPemlU5l/75V/5yq/+ZYbU5WIJg++bb/zoj77/PWiOtj443F9fWWGy6sr2GlVTq6/cun396LjNWV3V2mp9bf3uvZ1ssbx31MQqjmVQ6+TTE1Qss7bYh99563VqY7NR+9u/8Te21mr//T/9nWsf3KNpMwWWLvWYRSil0isrle3tC5cvX6Xf/8Gt71c2VrY2LzyDu3qVzhaT8v3DnY1K/t/69V9ZbzR279z84J033nrjDfZHcvp3Pz/ut3ZffvXVZ557djxc7bQO0YMwXrvbgs1MkqCC88yqiefHw53dPSri7v17krAI6Wqm0+0z75JhPX0ekZ1ioMunSQah14BJ6KvVuAps/zCVK+4dHe8fHTW7/fX1TViF9iIdou1KuosCRoV54QSx7OLG9zBs8uTj0EKc94LH8wivwfOQeTs0PU21RIrLEgNK+tMUEms8YGRUJ/skaJJ0srFqlKpap6YmxZ/2VWiqiSah5boiHX9aWcyfIsgRxBJrznXnMCw60PA1vap6tdSY9rvIKKlUutIMk6mQ8ejW9RuwP7cJ0cRZY9DnehP1/jMvvPA89RUwxxDFP5b/oYeFrvDmv5y/0U5d9JE9vXPODjm8dXDUapZGHROPenhkQzGqd0/Ck0B3I65PUIMWVyAwcKTiM9qXjsSLL77I7Sa1BtM4BQxRGHvyFdkGWBFNTJZeF7OM++HHYqfFgmQdAAidMGZ71gY5IpNAJ5x9Up5ETQQ/wAtY6EAqL/4DYn8cnx+wChr8reQPRo1oHllFdgbwp9XW2fRE85j+KelPJgesu4XRCOQr+ZFcDARzS8tgkdFmcEI8lQOkJvBYV0idQeJQK9QMEIgJl8xGPYxAWt5gvIi2gmnraw2SEMJEWmqcZtUpBkA4Dg6TfmPhNCMr61uh7PijN4pVqFRGFuo4ai7exl+u5A+PdrmUoVpvEFKpFlZGVVDAuJ3usUiH6eUeOwnR71z2zXJ6FsHs7B/QPSzAuaxWKKBr5UF8d5hsxDaLluXUQJZsaBkxFq+hHeMLAjrrWPJSjQLOZi4PJEGZialY/YrwrH+QsDXaiUg0qUj/6m2xI5VanjmIxi9PTuTZP2hfWNXmMTTfL/zCL3z/h9/v6VSHzHGzjTSS0M/lOI1SQ/VSdZxu00dg7SRyB/lBKsyhbHxh0rJRLl68cuG11175d/723/zDr/6z1KDDRp1KIVsuVuiT9NrcT9EusCWoXOHylerq1tr6xsX19f7xcSWfWauu3r91I1OvYPXfH/X+6X97792XX/nUpz7F8Rrf/tY32QHMNANdJdT/q89eRnRyRBG1hnp7/870s5//7L//P/qfcJ3rcXMvV63sHHZu3Li7tX01V6r22+Mc49pimqsrR5wXP0sd7txi9MMFDoB65YWL/8H/8N/Y3dnn8gZWaO/s7B0fdSDCX/6FX/qZn/lyrdqg23R1+9eRN9QdXAS5RDFNBXP8XvN7f/qn/933/+y9t95aqZU5RbJerTx3dSNfL71348YbHBLJSpVGtdPcw2SCmGJaHTsdPT/QRmyrV4Om5JI7XStXunsnxYAbrTns9TG/M+ZgZzOdITKl1HAaOHd6Xa6r6017cB03wK+sbfC1Ui6jS3qdtkyjQ/ZxcK/DZIbpgoUz07EWSnwinVhxkWBZFv54hXBoPEkObaEF9IBomXyRhX6Qt8E2Mvo68LIYGTWCAZlGheCQzZrmgbVMfe4IWQ1A2SI7Y80i2lTVx2YfLLV039l+xIC3XK6sIlim0zVGwOMJyz/HV//qKtzV7vVRwMwNoIBxlH1n5z6YwFo0HZLaPcOm8l3MJQqsNs4kkVawaKsuFxHSfnos3B4N0ZprBYk7nDrK5iQVsaHZkBFkyALDCxBAHmdfVVr8MpPYwlWeF8qXW6wlhFbpNDv4L1+5SANBqNIFx2YHi8GEgKKPiLjC3s4GSQQthIngYrYTmg9whqDiCAMe9iPvGedl8WD85I47E+vjD4gUMCgGXN0DTfGE8OCH7h5h7hmGm8lwklO9nsSpwNNNDkRT5dHLswhWnegvNIPiuyMynoAJHneEk9zjYHKBDQXWHOMxh8wTitvZAyCsOQAaBMoIBgLVmd1RSxyk28XPXLxy5RJZwS6NYpUxxfffenewVtqs1Vg130uPtra3aX5INJ4vvfTK9qWLQGAGBwMm0tQP8Ydax80m9VwuaCSBCXQwbDP8oycwmfZnqcJ7779142b++eefRyHtH9yDs1mYyvPOB++P+kOs2sNRV5sAp7Oj5n6xUoX/d/Z2Oc9rY2NLm03ZwMx5HFqXmmEPQ7t33CgVEZmYvmurVb6yaDuTGnLYKvZDOtXMa2udJLLaGk+gJDTBfw4vQlXocHRwDIlohMyIspeaOqclSkVzV4S1FCc+T6CZBGF5GjPBA6R/q9XZvLwNbVmoS26wEf1cXVhOdbCfGJKonHy3HXl5LAxZ/rPsDfWArNncqBVz27/1W7/1nW/+4e2b76VrjYP9ZrVYaB11KNyge2dj8yISjiO9sfKvN1YubV84uHu7dXhUYQcIXR4WRfUZ0O796f1b3/2TPwBDCazBsFEtZ6r0mbjnETg03Vm/0x4xNT0rv/Typ3/wozf/+e/+zoVLmxcuX0wXKtuXnymWV2/e2/vsa186anYODo/pr7B+hO7dFz/76j/4B/9ga2vjpZdeuri2lp/WLrFoO/tC63OfQqtVynW2YH1w7dbv/L/+q1qtAbf0rnUYOq++8EJ2nIfZCqXi/tHB97//fboFzHCMR721OiuWuys1pC/Lzw4y+cZKKc/q5T/62u99+ed/7tkrV27fugGtqAsMNTYlgdSeZAopDNqpenW70Ng/2r+0tc40G4ONTiFbtbU56TXuoq3RSMii2Kisr9Xv37vF3s5yefV470BDpdH44trGxuqaNrgjCtEYwwE6mOO0OCf60oWt565eTLMrpqBVCzCA5LRWaVFx1vGyrXrWg6V7qqkTmpjFjOSD0lgjVYJzHYDVtbMjVhhfwhcwOeWlHcE/asUMzenEZVlwpP1Rj+RAzOMLH+HHG2HMq+pEJxzAUST6Qm8aTRjLdOJY5mor2G6RGxSTBer0dFFItNxamVUaGLDYJkSfik3cGLFIrc1j+UqV4Z6gj7tsAKbfJKvaiA3HpWyGrluDTjIHfbIXftgd79072rywygFTLMZsd9rIAbpqTIJRaDa2Yaxm9/DaFh04ZnPYk9Gn/6aNf9nM2z858tEw/S6wxsamXgI7/y1naI+o9S6zlVe2NXqEjbUSeTOqBrv1zY1x8z4mYa5kp4BEICYZQfyXX36ZjFxcWJdechjn8pO6pkt3eHRw9+5d+rhYmBGDn/70p5mVa3A9y0oDucTiRO2vAqI5Gj6ygCtXJ9rkzUbqOixVrzaGXTYvM+jn8vISfWSwIjqU5wk+phxUJbzip7JMa0eq1xCOGIII4MbiNLoAjDt4JS54coADqoC2QIjDIRUOv5VOMe094lvCT/dhTsL59EDnuZyN5jmeDX/ACJgEpFwG9Cy4B4YswyOZxbI4AXgSJU/IE+cLjeiBwoK8ipKnHYG6hsTHuKyCh8VyGSoelVNZX3/vxvvT8dFasbR9YevO1MzL3Xb3/qTd0XoHpCfA9g4PmLghOi2ByQw4VQai/pAQ6puRVnrC3r4xkWFQ+n1EaLdXWi1WZsEdTAd22DQoqTiaHhzsgkAV3VJQi0KhTFj1DGuhrNBQ5dx2HsXPQZhq3oxzADWcaFKaxd01zaxU2TZy2Nxt79+fzgbrG/Vhp8kBeIxdkGVM5flqWV16JvaN/tRPlxMvGn14dSp5CM/FEk40tzRzD0hKv1b2hllKB/2wULwgg4GcMlMiMtdQwb1sY5B1zjLSiQeMINT7RcJDDa4VAKA1DNR0lrbJ2ZH0m4jH8iImwzBeqbOvEmHny9fZJLS+dXzvvna2arE5Vn6OtqeboP48jZ+jE5jmnFV0GTBEEFbe1adPhsU/y4bb6ne//8O17fVafe1Pv/OD1Rs3Pv2Z1158+cXD1uCo3bu3t1cu1ZFTaHHGiUiARim3tVY/2Lm3Wi3WS5lt5ni1NJXjfzorpUqfS59m6csb1ZvvDN5547sMly/Men/c0xwBGgTHFibOirl27X2qWLtNEOgZzjbgGIappg+wVg4H69Vyf9BjsHD/3r0XX3qJeQcGrjLgaa0KtUPJREoRmPF+alrHOJLLcu0MY1Yt4eOKnsysVq2++97byMc//eY3mVQ+2tuBOS9fvry+uqblrNQW6wXGnPPCQRoD5JzgwZnw5bDPkI5d1Tb1IoG40KmRCotTzhE7FfSUX5KiIJnVXLiwfQh3Dv4wNn17apAOJAKR5n9wfNBj1UUvs7FJjZUY3GqAPBnduvnejevXqFPm0uFkdqlhDWPvGTYMqvL4UM9yiWX2zzBGZKdvdVJWk83rsLZsbiWbXcWqpF3g4wH9ucHhbXok9L4Ra7oFIVMwRcZgGrWovzBylEfd3VNOs9HmAE6+mGJopKyOZD7kZ65+GbJsrxThbWQTNjPaCHIMocj0NvO2UING6DSh9avpzNihkacjCD8POF1mNGq2WgeHeyywokOD3eXOnVswHnKP6Z5+t7e6snbUPEZMYjCg+K12F06j+9If91YLJdZosrQFPQ1VQQ+pDKbLaupsOCGnNWVUUv+x+BGDUgQvxakYn4yXpXPAoRgBdYoU/I+BvOhlENxjIlhgRBsTKAthEjkZPvea/ASvMwespwSDUHXncZTQcsFjnKRuDo44VD/9WSQ9MeGbYxbRFCYrz26ynwDbzwGHa3S570epdDTB3h7xmYzkXgGYleSlchXOIZBOFtFooeqI2TkJjAgVAe1aKLzyyiseSC6wo4CZpuEACfbR1Op1cqHnkC+xpYbJO7YdTxlm0dql+NNZFkXT1lhUy66bg15zNO5x6GylXFircETS0ebmaq/fmox6nPmCZMckoPWFuhSMBb/iQvLSMxA9rkqFmvNP4TUOPvmlaBCMCEa0k3B8NJ5hu8eYlv41ggmy0KRFLmQ6PWAIj1mczEVs+q9aw8HwWPP1wTFQZlSHlpqxioRwxhJ0SkpoXLZFEkyniZ4BVjTmYo3I0Wknqyv5y5euvv/WWyhcFsFhgS1j2VLJyXuCMqcPTy8Yyrc5UhsRo9G4GIGhFWqKw5xQRW+++SZDkC//3JeO24f7zYMfv/WTu7uHe3vt23cOXn7lxude+8LzL76ggVea6JlqpfLSiy9e++C9O7fSjDUvX7pIv2rE6ZXVQrlUPTg45oDwZy6/0G01d3fuHh/cv1QrYhNhXTQ4YAS+3zrCUsnUAeu6WdfD5kosjSzwptPFXDXwp4Physbm/YMj5Pb9W3cwaDNKaB03tc84rYGmNxhVBmO4Yb/Z24cgsP1g0kRJQHleWd13vL8z6rU5dOvb3/rGn3579sUvfpH5ue2tFboyyHJ6RpM+mraDzEWM0g1ilxorELR7gP11jDdRBY06yxFP1fQn6cX4UAwbPI5deD3lsW+EJFoAbyeyRYQ910Fh69HS+dOkjpOajYucFAZ/wdwcHwDrcTvkvbs3/uXv/o4meGzGvrGyVqrV0UP3d/fp7Vy5+DlGimR34eIWiz45TqVchb25o5D2MMSGw3AZRPiPeECqjLoHcD4VzMCR9jzhSDo+YVYjMLE2ylWvL/FwlTzXX0YWUdfMzXJiCB5WQWIovnX79o1b+2trGxe3to8ODt5+75211XUk1eb2JUzEaifRBk75TOerGcKrLOHm4DR2KhXK9R6H+GUKl69cZdR79/7O/nGTFdoarU61O0CilX36w/HRceu9a9fYZH/12efYL99nU0C7AxP2OvxGAhaqkqNVzEnVzFVLqCmP5pVoImUuohjDv5KEyrOES8HOJ/6o3qWAwSwg6p6Qe7K0cbQHcGpIu9ADfM+CJwAlTsRq5rUE/tXThpi84g+vxHZ/Mhy/w3FLhVFc5A4xLZXi8MnDYUSpiSjhDLXKps/2zl4qP17ZZolOeWOaPWZRBIMEDEtsldTwrkC3jsWtmW5Xg41s/tlnn8X8gu7BVoxm7bfvEwedRC7ARyCSChxQJzg8OKZ6AMgnhDIaCdMpo7RCKY0JL18qcyYmSY5bh1iG2FpYYT4OMtnAFOTv3L/2rT/5k9/75/8M6b/RqLz26gvvvvGDuzfeP7h/q5RJN6rFarHBMgeNyqS0JJopoDuSx97H+QVzqAkMK0TEyhCQrcj9aQ+7d3+UYtxfW6lxzJNmKJmHlr4DC/BHJ5IUqUFLkHQysaI1Y7qLGx3tA3YzoKHLET5ILvUiZPHTAYgMjqkEMlMtsAbcKo7pTGYEAIZdg24Uh02xEJl9UaQhGnGwpvIKGMaIzDgx2QxEujXAlME0N33hmau5u9PXv/ud55+/uLG20h91rt+6CebAY8n097//+tf+1e+9+uqrzz3/7DPPXGHWoNXuSdYUSnSM7ty5Q7lY70a3Y2NtnVKYeUNHi3zmM6/cvX+Hg6zbPV4LdKHoSlAl7BjGNHyxcpE5YFYG5HPpXruF2oUIo940X2FtzpRVfNjSuR+n2WreuXnnpVdeYY8Q3cBhhpl+oS/aibGZRIQkM5gNUwwDWFGtyIFiVj+TzKsvv8hEcq1SXF9f/Y2/9etYwsGZFbccu0rd0KNEFmvWB0ZhBT0U5cAZM0GUC6yeK64yVjZlsJBXlIcwOeGoD8ldC3M5G6hsrcHyxO+ZeuDi8FjLKrJha5EFBBcS4jdQUbh9PPWgG6cz1pjAhM5mgqaxl3XuMaaNAgdZiiHJIp9trNTYHLixtob5BhXZWKmura+xH+/azRuceFzIbr7w3GXERZ6rHGZtjoOkv00bZROtFBv2ai1DkVDEKkKF5ssNkKQBqT3Dx+zjtdN2yUyV6I6TmdWtxKxxgj+MYqwelYKInFhQxq4Nz7GYYTZjyuzdd9/F1p0rVbZms9v3dr/57e+wcvDClWdXGhzq4tZ4p7DLW7rzqGXMXZyAa2PtdGr/uPXmO+/R6n/lV3750sVKszv4yU9+wgFhL73wfK3RAAg7gQ+Pj1g2SAOn1NxKurF9iT3rTGYfHrd2797rHh+zgprxPiwtYRUtnBXaIAkdoiKeriwLpLT6VVQTSvIkXPTJwAJZwJPQEzGfoDdkOgdzWbh6W2e/JduSf02GzIF++FcHxRMdaTJETO8KOAmECO5Cprx6BPfw5JPH8TqQqLXYBMKpqDe9mrPySW3g4iDNFqhXaQ6/tvIVCgwi2TxaefXl7cJkN9U97BxwgmqtsorphoiYmjlqVcOpPGbnjqwuNMfRiB1GTP5hombwSqPp97BxavtGsajrQSXsxqyOZmKIQBBQR4zhnZQArYtZ0nRBlqtpptXW2KWeLrJahoyODlu0QZbRlIs6C0Gncth+Hiw8m2urLK+9fePdd3+0M+kcv/6db7X3d2j1nHFIlxlZTHyIAIWxZLMYSiU3B/zY+8i/Sut/GsmeJMeyxAshrPLiOAEmhC5cvnDz7k2kgTVSvsgmyuIhXvFzyDTx7RPjBgapUF8nu2NfY2ABIAYRbLXEIrqxsck6Js7ELnFEMUCyKTrLmPVanVYZoZFjpxZbGnIc6Mj4kasO1Vln+Em+0Jctm4wpmTNELPKf/Y7cyyjnE11afAcafClmpttrtVt3DsddJNL+uNupUieslel2irkS0Zt7997stT74yQ8ZnbC356c/+6ka08n5ynDU2z9ug0+tWqGmKRK2ZfYK06lrdztbly58+jOf+bPvfCe/uoWCBA+UNPZuSnkfI8vNW1cubXfag9WVKoMgDL5MDbLSq1qo0McYdfs1mGqmA0pvXr916cozmCJbxVaWtWN2+ww1IVEsactuUQQqRnfYynYfY33maM7hkPENG5MQeS+99EKVgw9TE87Z5uSQXKqez+mmRRkXoRZ6XsJbB3hI5nOE6oyl/hyKieWg1ulPG7JEL3XiCnNkz68/l8Z+ch/I1/MKHocdXoMnhCc8QpUIOPeEXgQw4wJ59FNP4kM3nswJ0ZmucPp3KsfiIpoYG/d1D6mWOU5ffuHFL33xpzDGFjlGm0VP9IbVCGacWI7OXl+rMGF0cHR7NDmuF1bYccT54iyt0H4k+kAsr26PMjBKbVVD4eGYJR7kSHNG+8+ynE7GdZld9qQxpQqq8ANfwQBe5r+2X5xC+eQF+xxCTGIhqwkjGJIVna9+5tMsoUCmUfUc+pcrVtY2t8u1BgtBORvcEiO0XIBY/apd0nulobHWVBOtsEmbs60PjtkvgB2Q5WkkRQ7wdGs5d3vCWpdXVl5+5SJx2GJgNnxN39GoDw4PD3Z2Ea0ght2OljLrMMkmR7nCM+nRN3NEkKg19KAEYZ4kfBV9jE9czn9kzOkIPOQzMkET25hPxZjzBLy9eAnZ+1BZBGjLYhPBHRGUxekMAk3xBH8U0yDGqU+A0EjgMIiuSf8zDiCwFI7BFw7VgEplAYP1+Lhbu1fp9lMbGHeRgH2Wux4OmwwdaDmc34L5ib4vtmKWGmFoLbHJMltgAQFLeXKFEgcCM8LIpIvsjO/3WICsXUYcg4UihtnAD73A4NiWH3PxKmcdSgfgGAy3u4N7O4fkXq1q5hgkWUfAIqFadVouSmP1uroNAoS7/falC5d/5a/+0ptvrHzrj77O5mTO4HnmM5/Nc/NDJsWE8v+Xuf8Otm1JD8O+k8/eZ+99crr53RfnxXlvcgIwA2BIgGAAgxkkUaIFy6UqlSxbxSqXHP50SeWyKZsSJVISqLIlSCQIgiBmEAYEMDPAxDeDefNyvDmdHHc80b+ve591z00PMwi0+p67dq9encOX+uuv02UABEDKCX2KrGty1HV+Y4iT09H8uiiH5H73vI2wj2LGr4R3jsztj0GaO9sL8/X0XL9+9dOf+XjY5AoCXWAQHQAWZW19DT7JJq0WjbJ2QnYXcIuZAQ3YC2aXBL0/cNnO6PhkbXxid+sKkxIg2OBQz9YmwdVwvbV1ODR40B5o7TT2DvdqY1WGFcMEBjSGeWzHoEeZUFNPP/LAfMD70gEjmg5kb90nKYia4Jb3mhs9rkMYGzl/en7z9YXevTZT8pfefv2h809UqpXm4I77FhsbS52E6FqbQ792Y8Hhig2lEWHYvhpsEgZOT445KQKQzU3hJXpbnX1a6yfOnJ2Yn3/n1iJ1WePeOzQ8Nzt9hnro3Mzs5OTvf/l3b1y52LOnmkO7O2FU/6B3Z1B+A30NhuzHyp3dA2o+11eY1Fy1GVEqlduN2GInMjGZKOTRiCbgH3R5SVAtIW+I7gw9qbBmuLG1pe3vXrzwL371X66uLmNHPvbxjzAZNj9eM5R0nY26vjFO4D7/YMmMJRhng5qAIa4lHHKFJLHFA1yaSdLdjlCs4gek+JMJjnmYkP1xT876/uFpwudaSpIrnDy365Nrnp7afTv8uC9oetaY9XyI52NJcog7pJge1KHDI4FHocThkdrkxBSDUGW7D+WR6thYNtxBAdMBnX42o0IAQaKxMjlF+AXf7LY7G3ay3GKyucEea+9YdabcQ4FukGLXAFUP+M72r01oBxeHOkg9ACLJQlQgFh1nUaG8TP3M+Aq5a7lmeZv1hTC3ILwi7x4++3Be7y4qIi4ujdTK7Mnsu8Ng19XYKeOYJcl1B3o4tGRt3FCoZHtzoFwZnZ6ZJ54iMqG0jRyfmERxblOs2tvbMu13Ww2AS3G2n0+cOOEsgTroRqTe0GDJYgTuGPKk3qYhoe2iwBieKDWPV7weGxVpc4hnWtkpZozbHSOX4uQcAqMldJBkcLk1f2rP41U9XsiDwh+4B5zb6Zlzkb7wH8/3B/HnrIoa8IQ/ZeyT3+M5x6fkjnsKvy/8OT4PZzhz58YTNRq0ZiIYE695V/Uk9FXRkUOij1BeHIbRKd/aSK1T7yzdWhweHHOgNTQmelZyDmAbMSCq15wDZ2lyUbyiPWhiQXLylCGuyoQ7LIXISGXgZuabBEUOdHHZW6SLr5jeuLZPJshFij0gdSpCnfu33WXTivoEzw2RUnWNuzXSpkgYNjTpQ1USLzw/Oz/07PP7jfqHn3vqsNU+e2J6+dYNxg4p1GgX9ggPGI0NeW9uQXcu5pdc4e6HH+wn+i39FRnmdPqfMk8s7N3Ybb5x40bS4wCIkk6FuhiUMJcd48ofCz6GwEDFilNH0jW1tP0JtzjAXOLb7223tsdGR0bKlYWFrX1q3tgDV+UdWKrtQ0pCwyUERme3rWjYl9Hp9cUWJrhaHurvwEAwijzTkR0SMwqoYWfRsEdxqmq0jA86TSVmxka2BvZvLa7tNrbYQ1lbvVUuj01UhpduXJmbPxgbnZp6+Iwp1mnXnbJwVme5sfvelRvl0iCr3cH1b26T7KEXkBG04ku1MfyljSyyOFTdcy986M3qe889+6x9NYaxSdLXl1fcwkbR+tnnP7x4a2nvoL/cSy64M+wCHKeOOxh3dEMfwXBw8H3947WxhVuL5gNYjp5CpHDKNbjIO+xVuX/UZjA6B1hDWJJ9UCwzqVgU+Xt/7//xla98udHcVr1f+41ff+W1l//t//XfmZ/5aByTSbMiNov1S2KgrAmkJPrHViPCyBhVRqcGhquELz/YBPnXF6uYvYUnl128Fp7jdYrABHR4Ak/FUyu70OZ4zPf3S2KFwsfOyLniqn+gZqK5Ujxm1B5Bfmy1dJoMyBBF9aPaUU52BswKxwjK5Up9Y3W4NHrqzHSjvlTfNqUbZNtrq6uw0dWrNzbWWjOTZ8Zq4z0HuzjM2JeP7eCYu0gt1DYu0fQOeRrcq0F3ukzb5jD+4y7DHNPGTggw5dNWY4v0pN5oT0/MjoSm4cxcvTVSGbOtRsyWEHOgw7tdMCHMnkPjWNgeR/VqY1OIQaQEIgE9guYA/VjlDCq8N8TOtp+BBQcRd3bdkkm5MA6H6EAg0iv4CRhKYmKDm3cXd/R+70gJicC7++AoQfqNCFqSXMDDOz7+L+KlS8qpqPqpUeE5Xrv7Bh6P8Mf359KLfHLHFa/v4wFPQVPJdTK8mscjKhxh4bTp3uQimMeG3OQwNSnRdEo9zXr7YGOTRE/glRvvtdbWK8390tQpMZ0ClUnKrpeuzcxMGHG184G2oyajDrGNkeAXU4aimVGmFrYtKFQKL7iKUqXThhXwaIOhc0Hsc4hR3nMNgejlssMJE41kyFA7qtVx9bLRaHbayjRxhgaGWWc3a8+cOv3e2++oIXD/7LN0a5559/VXrV6Ls9XBIYVdYpuOIGiAaiY7gte+7X7wjr2d5k6fHI5nAg3oRwtoBxfb0+MckeVtZQUWDAog86MGwQgl9fOgcm/v80SXxhjhWO0u2VsasBvOTrx0dmllvl3faDZr+0NhsKDdaVqr+M5evTk0TAVVAdMj46Pjte0NauTUULunKTBzNu4JWS2+qG5kF804Ki1+M/iyCzV/ambxFkSz+8Sj569cvwTXfvDppzcbHcIMF/ntO1Xi7sX9HWa4ANDqyYdcZcjaQFKOG2i221vbG/XGFhUnH4kNWWIZK1W0x1myj3/q05/6Mz9FXvLm229/+WvfaLF+sLxUHRp+5vHHf/yTn4I3Uf9spuBYh/rpAcSJbrIEVEhnd8/tHFYjxYIrC9cJXcbH4xwF1lbLiHb4Q6xAucwlSKGgCwcQdQLou0yXk7r8T7/wTwDrv/iXf5bJkWvXrn3ow8+7nIKRrxB5gHLWROr1gOyIpRRApBg7fPvYcVskrmwYgT6o1t05/v+LeDOkeuDeqjwovIgpQmp5BCR/8eUP8QSSYI8uaDly4DiNGzP8sM8tt6WxctZON8vS4SLroI88jFYder3CVEel6jrL1bWNxsJifXPh3Pn5s6fnGs31S5fX7TWN1kZI2uxkvf3OW43N/Vplki2+mK729EtlnKRVkJoa+EOGoY5nI/+o9VqRHUlG8OQPcGg4ChOq7TB4iUpntQruba3Ut1u7UCaY5oQuXIq22242KxiNEDTfATpzgaFGoRr9PahOE2mrvkW7anN7C7GAQlATZ/ZQvKOj4/u9O1ubtKS3VdVzr2dhpDquDmaZGUtpzQInyS+z81bF25T2O1acQrpNkFVUID0f0KYI7kZT06MOEZjnxvG0Qrg/LLP3KedP61OIsXIzispFu4NqSA3SI3miF55kYkljUqxuU7P/eJcVjaeL6muAu5gfCrHMYz9vZ7djH4BmE1Gb3MBfIg2jGIA6TnPRZ0F6x4s/VYrpHtACRxXUqyQJ7VIedNNkgCLKJHGeFMuFQrOXRhJHFkdep9AwXSCtPA7GaOeRy1Z6SvUeRyD7+ne2BhbfXP9O/15f67DeM9RXm6oBatcv3hyvTD31wodrA8+uLi+yjMFmX7vpQtY64s7VltVyhWlCFpgxJ3g+Ko+LS2snTpwaYex4CD5ePjxolocno2cCBe+QB/cNNjEssZ/b12kyClEat3vT20z7KT095+bHHeyHRSx1fOC1GztklY6wEngtrzQswv5+8qzRgf2Lz37wya99+avf+oO3vvG1b/6TX/zSres35qYmHj5zAtdXLtd6Dutuch3ugzCgeJo9UQczOzH8MYrkX2lE9KoeNY7Rnzo0vaDmcVM7fY489uHqEquV7gIWTzsA68iIGBTKhO4G8WptZmAdX6zUKrbGr6y1Vtu9EyfPIXhtqLPZRzjv+CMDEDhCOibV/WZMHnMh5gNu2FEku5BxTLIaF1f09bRccNA/NnHm1trG5Jnnd7/9xYHBkaEQje5Up06BfF5wnsOHO/3NtTE4b3Pl3MT4zTd2Bu1y7Zd3BztMfsS6JHVIT1vhzvDGAVMCQ+0PgYJp4T5DRhdZrXLM94rLpa6sbn/06Y8NTC84VdYpzR7sbruyd29jo9lyV27N7QXNziGj1o3Vt8YpMPe0HzoVZ53VertRX96oj2/131y92um8S87mBDCUifcR4b1XX9qqb7N6EGYHoegxF0QNLmxtff21l3dHhvc6zdqIOTGw3lqrDQ+6VqfVV9tzPsr811n2ttubU9WhmxffPPnRD40wCl4epK/S2Ns9ffLU1n7v2GHfVjOEModtsJ4p4r4wA9O3t7O9uHHrnT/7459hdfqt114eqB2OtpfXli7v1vrfvfj1xz7wFBCK2sPuOKGN/mSqaNcFOX3E+zsONW1urFEMGimTJdiQhFbIO/uMikmYYHIYNWFi7Gg+pOkU0gyiySTa1uy01ItnCgiIkQckh/OHJ20RpJkQX1PMeGQIE0MVG33eYsqZpjFp7+dy2pwqf89+/ciT0BUVYsx+AAR5tVGoyET7O8NupO5jQkMcfzs6y2muONt7aJ+DbAxN57oPim6Nxo7Tv86t9u8N79Zt94wfkK2W2ZCJY3JsR/b3jIeu4d7uUOXcVvsWkEYnYLAyxQ466Q5ynJnSWqNVXht8ZPbkreuvj9T26gtvjZ6fWXzvzVcvX3vhoz9afuR8n/PsgbB7KqNjDWoDJZIW94x06OyXgvHsHRlhH3ygvla95Gxe68CuAWSJQ7BkbTe7EVMnpbY7kmZ9EaSN2M+nfNBorg6Uau5BoKsYwuJ9qvI0DdY2FvdGz5497Cwv33hzvPyB6uCJgYPGkC1dyzOwQ0ypbpdrpqaYpIPlgZ4WCV99vX7zvVfth/e3N+3I7dRXRkp7Cwu3dvbCkoHJNTw8wURgtVKbmJ7QvXSfbcQFhzJUXl/Z6O0ts6azubbJpuVev7vgtvYOmVAFBWIsQsU82ORwAf8NW9ovsYiDAAHTk6xR3fBbJpLw7MQzV4F/CVttt+O42XGIJFxXUe8QHwqKyLF7HtAvcogyk6OZEvCyi+BAi274n85PHNmUc1He8VKKwMJTfC2mO0/+2m3GD1bdHLnIrfDclUkRjSc7MXnyU7nZXyTPnhyY21V8iuTxEpdw9dtghPldOphcfbtJQlIaGxydJz8coNLc2G6zvjRSYl6xUR3fbLaWm61bw+57b265RrtUniuVD9Y3rt64cWFzuz49NxqnXfqJQNGz1k4Apr2d1lp9/fCg49YTGcVVsjZJSv3N+ga+5PLFd7G2Tz7z3FitvLu9i6DtGQInnNOH0PSn7dS9Rx55yMbc1uY6OezEeMUmizPBUAjVmF/5xX/6e1/9+ksvvXz1yk0qYQz/Xi8Pv/P64ER14NEzs+dPT9TGxnr3tsOSDio1icBzS+965i7pdkz6dtx/V+T7vopvcmM2jQWm3ExiW4cfd854JlY2rE6mU8FFcgwcvziWjEcOj9cj52Meu7xsLCGkGD96mV+JXkMAiH7fYqCjtD8QEnvhAhH4laN1VOR8V6OUczwk5azEXUS6+33xiHan8PG459XVrQ61YbfN286q151iRNohtjQBfhWonmolByS8KSSQbT9qaAZXblThlTVKy5RjAyQRM9JS5ttaW0Uz8Ye4PC1Atc21ir3zIDTRudQAgjjm5GNajtVGm8txCm7gIADu6PgEZZ2ZmbGAS4d7w2UtZzk17FNyb7z15tnT88Qw128ufP9733PVsZq/+vqbZz/0k63mdnlkLETWkXFAHhngaWgSMcDauz9E1ww6b7Ub7GrVJkJjP1G/0fOx05Kl31EvA55HMGBIcmmRHb38a/jVaepzvKD7hmioOMfHPScJhAwwpAwyieodMA4y9U5nshkvXYHaJxF56+03v/7lL+PnXPD77NPPEvpAUoYtbgvvsF6zE6veUNLC33XXWYj2SU1IFCpD0+Vq5ebSgov5Gs1OdZyMY/5Xf+2L7i1ZXFxafGuhNPbQw49/emx0ZrO5Ux4ZovjOhC0VAcgL9wLNoAf6KwhfF0iaj8QeARYMIlYlmJwHjIBvnLlKMEzIkcY0CN7hEuUs5tKY+LBTEa0OBiAuKbqfC8oZrxEH2eQmF8uQRU7Y0AxhmdNVMTbIpDRVzFN8beugkbs99XN0tAkf+23OMPWGaWsda7lZO1RxkDlNJ97/pF20PLkfPGO1leIHj/9HjhnQUUm5vFzk8WeRbxGYe1N4TlVEKMLv9RyPExP+aI6I2cWK8kp1SMshZlD6dJ8uyAk8c/z8LPI/7gnAZqQLF+Wm/+ZzInZCD4BSCvOq7Z2lhdXJ/tGe9d5ab9UmWGuruXB9+XC+98lHn+7s3mx2rnZ22kMdXFS7f7iW7kXoXd24cnC44iTnzt6izVoH3Le3ri6vvPehZz7h+F4YX2tu4SEmRodRVK4pJKp59dXX/8k/+cWzZ87durXsdOljjz5khoLLSEpIpmeAcedDUmbaVnBtvb41OX2ybC/YBcWOELRMTOeXhi+/9dZ/8w//0fr65rXrt8pDVbOcjhjGZOHaxU69tzx4MFEbGJooh63HAxKskcbdkKTbSbknix7Lr/qzCLmvp5vqKJbXEDCknXgEuGB33Lqv/sknzi+3ttTNKWiwRwS6wYGxwjiXQgIQIEG5eDkqlEdw5JkucYRu4QzIzBofHQ1Mb7zwZBatQ6tYrY2DQ+YogUX43ljKX8cdDt2GQDKUW25IUYqQ4+Gx54rs6m0jHRiswMPJ0MZVIOClm/YATs7PmipSIaID4CV7TwpCUKsnJAtqsB0E1vAgrCFjgFERsZGvOa1tIgBdYRsaJyefsDd1eBBCOUDKPgj9z9QRuScDIwZZEx3rLFns/MOOfX1u+XV+dGB9KxDnfs92sxG7GPYzhlBm2By9iWzbYXlNZ6PoHJ16+dVXT58+eePWwuo6w5ZhGNrULcfhdeXRm6Gh5r5BKoKBgFTMJYbj1cnNjZXD/dL+fru+uXH61Lw9S6iC3hfCkSKg4ci9oZS0kHWmpCiF292eO/yP/5Tv0dSI6pks8UzTJhpwBCILz/HAu/xFZUTOMyIxTAEffIJ6u/GDpEgT2sSMj7mrgqajhgn/hZYlSxT7Oy+++K21jdhtef6Tn2ETjfoIYyl2gmIbZueArVnDSlhNoGTu9PXsOR1WYbh9v2dq4tTy5vrMVPnmytrFC9+fmxl+693XL11ZwO9++SvfevaFz3zuRz+XJP8s0u65onpsfESWqKr6Vn1l8WZjewO3zSglKZ3pF0cLuB5nocgnjEFIK+7rUmPMSi53JoFUmFMNkMsWjMO8u0x/Ixmd49jpr+AitDoafpeLVRwkY/CIlnatOqb5qA3nMmx0m/M6yhqJdUQpBN+NBE8uUHRe92HMJKY8Z61ZR2h31cMUx35364fTOcjtyrkdfwrnhESDfxgnVU5SeH6Y1D903ACOx0sqqns88HiuwvPrXRGOhx+PX/jvjSBEZjk8lxsjRcEu79ulgvJXmUTcI5df78w5Yvuee5vH0HrmOJHOx3ixrBRFekpMSagmOslZ6Lw8/NBj7X1KTAc2UCvu8enfGgqzSoPLa+80WcNyB4i928M95Fq7fcuZzvfeu0BQbLN2feOK/T5i8O16++rV6yO9YaKyvuky6vpQ/26l1Ds1PYMqrlaHFm5e/o0v/PJf+St/bXNtfW150sEQ9WnSTNjfcRuo80rkfC0qOo0te8OtpjsKWYIe7emhcGGTdc9m4d7u5q/88i+tLC5UKq7OnaVntLG66T68zWZDoWDmBstYqxv0ePFlrmawGdjzvhRl6qIM1/7waRrdCDXqv0T/6k0B4AzpOjWlIL4hhkbz17/wqx94/D+ksjQzO24pxmj6T5yddhaKtHloimfkmlwaqsDBkBYOw2FoCr2BYhVDjyUR1+h3RWYcBiKMT01a+YhoGaQWRa6Fv/AUZWWPcB41oz3HVgrDepDxc88998obbyrdHZNAg4siwCkwBykwNkTNJEwgRSqMAp4RzMD6hCA6WAFbuWHKMR37Dg2v5CSXG+YglHSit2iM97MZ5Cod9AgpgH16wA68x/DidsKMXnRZkqd5JUzTd729ttqUopnb7U2CT1BSCLOCB8OHzi6X2DCNkttxV4hLO8bHPvzRj/6D/+L//eEPf/jipcvLq2snTp2+cu3GZz/72ZNnTroyM3gmmmU0bvvT9jOdn06TGoHe/e3f+o03Xn+1ubXhYoxbN66TfIK3Q6URdaamjmC1sDQ5+vloygTvF31y9O7lT86lXozsosQjgWEeOyGFJxeYX3Nk/pQklBK7q/+ohsK7vK9+MNdCcAypBO6SpcENlJymh5Ccp8kGeCD+WImVnbu8KAkyT7u6togLlY6htNg7D7Wp/eGRwd4dViGDV6Y4Fds50FAIafa3NltnTs0tL1373J/9c+feO/kHL36ZpdtnPvgJSLfV7vnxn/ipuUcef++1N90zMlqddugIsYW4os+ws72/uVJfcVVXu2XO0ZPCaxob5t9NQGvLik/7LLkn7n5GxCSvCpmys4DJcBA1Uoa3NBABsfeQfevpubn5UqmSZulx7BsYN+eI/oiz49GzoV85MTX5wedeGJ+wTEyqw+nJGYckt6YmkbPWI5kJepR2pFUgOZgcyh7GBZWSDCTE2Ur0Y2DfoFk7HW05Xu7drbjve6rM7dkoH05zi8g5pHi9rycadDTW/JJ4jZxvZ3PfdD9o4IMyun0M6a6c1ECa/Dz+yTB6zfXL4TnrooDjn4qEkVVuT2pUkTA3LycRJyZJUprh54pw8XNI9hTZJs8dy76IZrADciQnMPaCA5qFZWAa8Y5fgKrovt02q86lybFpxwMowrCFtLWzPTk2+finn5ged5XHaMVBgFoJiUZJiPSm0ybxpRjBUuU6rWfmYOxOhPCkjM2xV3l+f8c6HCNtwubs7SBYl4YoCMdx4eHycN8zzzz+c//u337xm99mQnVrbWmyfGrHIaadpstocbp08pmwtNQJGO2IX79+IfbFe/qIRienpxvbS7/1r37zv//5f0xoRYheLVPidx4xLMxReW47P2i7o90TklKnZNlx3G71NNweG1P/Xld0FE/xNfnv6M/iUzEWYucYOQfh9MJ3kgIFTAEHv/jii7DjpYsXXMMY15CFKhmhAAjDzARa4kidLe1UHZUeODqPV1GQEOvWmf2bN28Qjw27SjdY6uBM8uCyjBKDOdhhK4prMHSX5ok650yKrIoQxQksntE6IbjbwcGltW12CT7zmc9AwFAZMCFPLAI/IVuZAe6RquufLcxUepyYwvUSfXg9dMjbAbNSmC4qVUJGDR/DktGiPnvyjir1lNgHRky1KM/3lUdr2wyc4ZddKnmwT73HVni6DhpwdKMzqgViiK0IWA3tiOMn1lxeXHEDwOCW4x4tymrLq+ul2tRez7aNV90L+DqpjNkygVT8b/wb/8bXv/mNte1tVx7dWGD56ObE2Nh//H/8TzrlgdXN1bC+WnIeKR1eYtD4cJdeN2sca8urX/7d3/rNL36RRacR50RC/h8GdcfGa5jpME2MQ2q7BS+WKjLB5Ay8q65pfUNR0aV/Ei5PjKPpEcvfqMYzTT6eYnCzpygzJykCM9wpInejHdUzOhfISUxhoAU6zIqI3CObKMoIhIOzrDlTV3Bobz7z7JM/8RM/8Yv/7Jcc9x8OUYRZqUdwfPtE99YhmTM2cMCpwKG4dcRVK6avBdtT663vNKvw1MlTHz5/+sSp+d/50q89/tTHTJXnX/h4+dTDm9dvsSRltncam+XqWKfhhE9sEExUx4fOnj9h5yJOOhxcv3JZo9JcVlWwDkwyER/IPoqUHTGTVmhS8KlRv0jpbXx8anR0gtUBvDDkSNp0tNBTBxw9tAIOjd6Pg1FhatYaoeTR3N4kIfCNCjcbb4zJ6086CbXpGuVQh+0kQCNGd1oelPz74/CI9csOlie/HoCzkRZHRf1AvxLKWVSeIkGUlQgOnuyKT+/vOZ6bhO8f+U/ka1cUIK+iAbkSGqAGd1XIq+YWBRdfjycvvhYNSPl0gyXJkeM3zfsELUXpdqIIue94ssspj97iV8ix+PE9Aru17b4mKNmNHD9xeNIkAEA0WWqEmPVgJveN1SYfPf+4MwX7fXv0mAYOB1tb7cXtW72NnhPnx6qlsU5pb5f10gbAhwSGyeM0wFOPf+jWwnJleHJ0ZAYn09nG4gw9fPIcFDQ5P19dZwzngEVflxpubYYGAX2tWzeukdSdPTl3YXLs4jvvtOobPT1zjtC02mxfuY6m1fCvHX8mqLsNMVGWRJDVlEEO6levvP3/+e//4dTY6I986pM2gLccgO+09Ro+JqQ94ehkHqyvb1N0HKqR1kLpiNTokAc5/RLDcDT6snhQzBwnOjLFSDHjjWoZrLO7S2bLwOLByBDbkHPg0dKthcb5U8A84BU0rp7tdyn9PqNNUdMoKOfULRA+y7yj9/Q1xhQOdjji0uWrDOUIhPBi3TrfFOrVIVunK46yEW1sYuLajZth5zuwQuTA5ayPqhxvAr0WTyHxNbUJYfCdF1/8a//mvw2ebm83YZ9aZZwCDnxjsyIEa0MljGwuLuesPnQ4lQ6CbG3VM4NuvBj7M+KcSRhHv5noShJsqYAsIhcaMGgyYnOIQGvIfIB13EHIZg4Z1ofOIAWQ0ne7wWFjlaTY/nR1bBK8G9psRz/QThx0s29D/geuQ3RwqwrYtV2H7mbjiamJf/Df/PzVC+/8zm9/efbkzs/9e/++i6oo9qxtrNkjGB+ffPyxp/r1XDAKFL2blTLT4vvNxtYUCDpWqY1MW53GkZZDuTTizgaWPVz2HPvv6UY8CEZH2qhOo6Wr/8RQb+7bPDTG0AB151z64CWP7HFPTnJ8WHNyzzwLIosgZrq5RQ/LJ6ToeN9oZuheEPhHspCceUWvR5ycNRtzjNyhnoJvi21L5O8HPvD4ifmZGH2nyOAlR70ttjiY5EjOiOWcNi7ifgcFoI3QPA6n04OemTvzi//z/9edK+fPzX/7G7/XbhwsLDUdVLt5c6O8eaFcmYyLEGiHtZqrCxvVoYdB4r6B/SEbHSPTE71jzJ/521pbZmAgVJWjmH7i7jj3d4ztyxUvnuqpOeHAvDQzPaV1gC4O4jrjx2pVKL2b8GEYUr4pbQE+uuMbCkqJKDHb4/yb9prwTfbMQckOIQob2Ac7g9gKhwktFoOCHD8ax7BhYoHYM8GuxOZHkh6ZUUoMAwAIjQdsmRUNudcTte2OU5qMKYZALk8VAYXn3uQ5pIh83ONT9MSfhJPtfbMJaFh8EIkT4pkHLPs9uRzteDYCxeyGJ08RctxzPH/+KCMiR1q/OYOcf8yJ9J4iRMzjmee0xZMnpxJN5YrIOYmsjlKnT16iabHPL1OCaBt1oJjnaG3izOmH+suHW62N1k4dfF9aWH7rzbevDF57dr1VmR1ElrW2yJESl7YbJMvgcG1qfKbdcNR+EgCsb9vGoA7cPGhuzM4PHnhvNs1cR96A74Zb+ZKVc1p/m+sb6yvrJOAVe3HDwyzd9JX6S04BUNTusXuJfd7aK7uLe3CntO/Yy5OPP+YAKBk1+tvhpWWbQGutd995a/EWJY7DMCRbjh3IUrWyvbkx3Lu/xnbINia6OcKoLKaMYi359h/mouuOxvf9494V0yttNltHMiDSJHwzI/7aX/lZlv/398LQZikpp8BHriW20+NChXQ+2bjBHncUleebUQuWKs0rmXNzJ08d9n3PeBlPmF6ecUVODOYhHOkZi7a3130JJgEQJCTPijtyf/CLrKLovZ1SqR9mwhawSArJkGiUBnqb9e3dTmtyeha4YcnZFiCmsBQ8Ty46yBvFeUVqgEGyUh/YFi4EskPxarfFSPWOYdgL2fLkZFUN9xhqoeFpo8BxDKen7ByShKabZFGKgdUSvRjYLRjh2E6ojVTWnWJaX586+dDIGqZhd2x0Ath3gSXNQhdnLd66+fgTjzXq9UtXrjhy4qIjmHVyavZv/51/15QenZh2MXBrs64jWdBkduHhhx91T6Y7mu3CUIu9fnWxVq02t9dPzE+7a4clmtAkbO1Q6rZkWAKZmBwzjQ2iSwJ0v3MBID94bayCjAUCbR6hTv+EnF6SU37mLJM/oBBPHuLCU0Qohr74FB15z9xOWUVVE7UW4CBEN4GJg4VVQGi/xSZAzjie6xsbBpNmhtUKoeA4Z2cnP/8TP/bOzS2XCvQNskjq1IGNrT2HeU6ePHXt+sVYErG/bj6Y7o63I6VIMjrXF2+NTk2/d+2Gjfy4nqpW/uCHf2R2eua73/3u0tKF8w8/9vgHaq3VlfIonVBKx7HwCWFCp5kwK0i1XcrEDDGbR+7VRgnZHXNPUswflmgeMAI6QasDwJqjJpQaxUqD9FxZFMsKRYig1FJQMQ4LPcAlxpIxDmrGkksXYvZOs4HqsAc8MToGJiEwdSlbdWyJd5I9IoRl3H6sxjZokM3tg+3YtIntMYHmFbmWvGTxIJ2VB1SnOxliQI8GK1p6Z+x7J8Cd37tvMskxC899o/3JBt7mgIt8Y5COcFsReNuTZnOuYjT7KGYR8qDW5sj5eTu35Cua7a3IJ3uOx7w3hxRy1PEpqpAUmHTtjujXIhOftA0ZC47Yq4nJ5Oh432B1ZKy1t038Yn5QfnjsoUcfO/WovTZk5QH7MKDr1LSdM9o0hCStHdC5guOZHH1oemoOQh06HJ6bm6lvujS9uTGwRSKIVC4NOYMwbJJpHboZ8rBxe/bMI7OzJ2anl5VV32g0t949mGHKo7dSdSQOPi1RYsBWMW5lla0sryPKqSZub23DMla4TeF2X/vKpcsDxFvgQU9/s1lfa6wwjthuNcqQQyAjf7aNUJeW3J1YruiIH96jFXoru+OpXak3TH0ssWhE8wj+z3/+J7/9rd9zrgieRA47ZcX2rCNnljdhKRZKVmnxx5Ofk2GEAHqBgCOQPwbr4GB8YhpLQctI6eCZFmqir54Qgzf8n751eQuRRk6Vk/O/jxNH/iIAX0h48ALKtLtgU+rUibjZ1FEjNxnAuDvtpqtz7QvcvLW4ur5xYpaZtKqiQQ1qo9tOQCbBq5ljXjmIBXkmPmkPVo669QKx5b0Gk7drJNTuVlDn9SZEGKxSAoph4xdcDOgfG6lmKGjiGVgNJaySPJTpMV4ba+tnHnlStpv1ut01HUR0zCTnyvLC1WtXTp46QX4YcI0cJ+DcXnV89vU334W2n3rqqWdf+AiibXJ6kqzSNFbfQx0bEFlBe2+9+fpj5x9qNxuj1QrOhlns8+fPTU1OvvnORdNyfGJyUg+rhzmXnKNIGq6SMXTRkbhG/n9Nzti9zyjf9yt8mp1f9T16c8geExwNiZDYeo/+D4l6yNV1TgRlB/U2GttOkTmfRmYg8odfeL7Tf7USZ/8cco/oLHYjxaq16b39K+gY8mnzGU6HYliTp0YNITle+OFPfPxDzz6Hjf7ei99mY6UyMUfn+eOf+tyXvvSvvvXid8+ce6SEbti0dJi82HRvxsFBiwadldHjhL/FHYuRNWU205plJDxcyHALYYl7QR4wCHk1xfoiGIdjzUyTRPMsrX7rSCPNGRan84ZLbJekwc1Nz8/IGhmBGma7S1qCNyUSgZkX9CDED6bW1UZOauILGC8q2zHv7zgDcrjX7DR2G3U6Lnaut7dMtKA8UeUqZilB//Q6eFTjeJF/NH+xuiUv5knheZ887ztz3if+H/9TaEHnWqpfrmIGhcezVi2v+Um4lmPmyDmaT1Ll2udoRXKTpggpPJE29lLiFAeJjzvmfTInOnthCEq4CBkQe+UBYXN4/iTzIjxlElMSEStcZCEZ7cXGb/oTnuvsKxp2vDIKXLK7S/YiRWm42js6MXI47PjsbmfVTQlM7+7stzEr5ZFROjAgaJjS2LV7N1irxtrsdYnd6oaNNJO4MjhB33hlaeX82UeA7/JkHFeY6BsEVXE54+Mn3ByyE/pBaMz+HYbknNsvjVkwZ57+EBh5UJthg9qBJaueuHt4dthsHhouU1OdmtgZrtSIBWmhTpw9ge362//Gv/P/+s/+n08//fQrr71ODk6fFgIeHRsv23UZ7FtZWLGkiAr1pDoQikHeaE9On0Tnh2gtfoSEJw1r7hxB+TV0ktIOii4KeX2oLDpLgSkPOBQDl2LKMOfpYsTYFGTmBnu7f/j5z3/O3Sf6CsuOQjAQNraHR8bZ34HM0MTQUh6LfAyJP5V7iCRSVso8tlfTggxUbZ07qb+2ukF1RYQYWZvuQ4NAT8ZJdsSZQHHolm07c1nD76pn0Uye7M+F8ousPTmJU2c3rl3HHf7Mz/zMyy+/xKr09saGmAyt6E+Hi+BgOC86drBvfWOVmslobRxQ1lE6DdWgzg6SgWLiqwMkSsIpw9SHpl7cy+TQsH5DAE6wrGEnQ+FMBTU3VaXsHCkiYpBNyoR0M2uuknELiBHcx6cQFq8uLZ49febd68vbW1vl8al+gDm68JApGAY3TszNu2l1a6vRbO9CDBvray9+53tvvfXW5lbj2ede+NznPre1s+W4ESA87B8CrtXsde8DVgif1W6Nj9ZOzM22m3VD8PD580yIlEeGn/zAU1QWLlx4t1Ie1v9WNOzL/MjczLRLGmmQEXOgDfp7a1PTEz17jWj70VTh0V7P3POFp3j1Vf+kDUwr3X1C3B75jQrkhFaoUeAP8apFdTd7I8tw4ngW2RZ+3c4Pifp05JBbcYOFshgxU7ixVktIxQj2DtsaT/sb1klgp6g/GIW8aq00w7zVwAA0HPyfM6aN+ic/9kn3ecex4V6sZA9xvbWAC2RXJ5SudmKDX7uCtZbfgaOGDIPTVWy9+c57506feuq5D7EjQzMewKPX9xd/9q8tL8RMw/em25z3B0Yckmg0W+thUprcpYGwG+4ZnWLBg6UWt7WopN5jHM5uruOVsXdx1BupS3RMOK2gSAjx4kA1k0pds01ZBIZ3TCPYfnHAA8QoWlaeOUleGvz6IUUwG2N5QrCK0auyMhkYEmpvbdhFsT+ilY40nZw/4ZP1Qlug0ezdObDFRyxXoqTJAFy1Nukc+duX3mttU9QKG6hRYiLwlaiqIQSiwqaT05imJRaAPVUszilEuSZtYJeAaT6FVew0yuF3p5f5g0RmSMFxqUQcO5HsErkgX47miYQxN9L8zPPE611O8hySI+enkCL8rvhFhLvCH/TaJTeKZLmXPaNFXeDY7fpuqccmeq5EkVaE7C8yESIfgboIfRi/okSsYAC0zNjLz38uevOotfetbv7qGdkcOa/h5HFnpxyPcxQ3fp3GI5nF2pIaGyRw/+WXX/n1f/LP/txf+jMjk9PnJ0Z3G9tgGnOEPUMjPQPlnk4jmBM0QCmOcrqWtrndoEtTnZ3uYZcBtTc4tLPGFMzqzMRYZWqspzrkcpygoYMTChOnRMysXBLBLK/UV9ca64ubfb1lWLW1sFyem29st/QQAG6jD5uIowt77Ovtysio6+9sHjkuMjigxMPh8anP/thP/P5vf/VXv/h1puJoHm7Vm0xgkYaxAdJp7YP6s7MlEtQALrHYTeu4ZbZwD+qTIgLP8Tjh706/41Hu8JvcsUM5RJ0DLdWmEUaYdv7cmddf+84wm1wO0dopTC6AWWR3e+zuyOielzyww+Wam3pZpkSrkUdomjvMYSVwENkeHZYcMxco8Q6K6lh778kyAmKyHD15ABYaqlBhm2mYTuetN9782Cc/BVStr6xiLgkuICF6nCz7hLXezg4xg9boGY5iDtSVatK/srKqInSyOABXVhxGEz8UsEXDqbxArgcHCJHGdp0xonqzDQkgLcFBe2E7dN01TP9kldyjnlcEYpUNcewFezAb6+sOu+DXg+Pcw1Y0VWB2eurZp5+Zm7H73nti/vQjDz/GRMzOKNi3w1LgxtbBE08+OzYx46Dvbs/B88+9gLSsbzWW6kuEhMOjA+16/blnnxmtVKnI3bxenpyc1DM4Iyw8yoO5tY9+9MP6B0n3ve99X/X14fmHzk5N1FBaQPhg/6HNY4fdN9fXZ2qSdjtZF93lzyER4wEuRThq+QPiHA8WPw/o8UD+Ijzxr9bi8e8Adc/62qr7VFDb6G8QmGFRYnluu02iHMdkTWykgJPVKLQkf4lzt8hwB7IpSWkp6rk6f2KnvTtU0mYoNmENZFOwA+VTc6f3D5guJxUC/vfZUN2zA9PZM3uMoIscTp86OzM9G4tUbw2NbK2vjVZHekqVKUKSsXEkr/njdpA5CQYPyxUM7/b6ZhvD6bxQ88oFW1uidKG0RoYYwkyJ2h5vauHPk1ZdIC5l6jRkIg2x2/TMHb0eL+KYWskT3acTI4Sad1Quts/t5lLpgHcP2s1SrUpF+9rSLXslNqcBBLBfjxgIdKfNOBdN6/dqq+MSiNmZkzPTp3y/dvnaXpIRalcUlIhOnoC4oWR95I7RT2lsU31kjUJK6CDNge5kS3553HaiZTR0/NNx/+2oD/DJ4QFf/rjBXS1otSnKyH6vOSS/5upGUKIoi9dcfoQfVTHHL+oVYCo+BdqNXjAkqTcLVCt+7uYiqyItT8o4HrnE4slz5GKimPKiFglTifFWeIpPqCdRAxew/0coGpf+rjtOgMav7VSqEyOD1THqzj319saNW5urGzSJSRrrDpiHPKp3fWtzY3MThEWlUrE6MXvijIU0MUkeMzS0s19f6D8sMQ5MC6O/MloeYHCGqS41tGFz+NFPfGZyYu7d965cePutlVUy7HZ5boAYan191TbcQI3YZ/fq5euLN22gHn7kI5+APWOHjoS8MhGE5+HQQ088+3f/7t9dXv1PsDtrG24FDjmnDZm46/OgZ3J66KGzp+lX4lapjRH3MqdwVydEh6SVdm/P3BUz91iKf3tuFN1YeEAp9/kQ4hoCQx0UaWmIGBPHQAptEaKTu+uK8BgF8wAAUWRYePL4jlRq45PTVy7ROR9Ez7LI7aAWsg42E8HMSecaApqEae6t+nEErPLZyVPMnHNMljQxcv4RvssgkktdQn7+rW99i/1IMOL1V185eWLG2V7CflQFN7ATtMQQHSqGwHR3pp17DxhtNvMwOzhhOBhvFVzr3h4sC4Y+98wTa65ZcoglFOIoL4e+jtxIR5wnoWhXU3HiCx2FkqFf6miStdKtbECiWDxCnFZCf5QcPFvtGarOP3Q6+AMo0X1bg8MzdPnGpmDM9bXNk3Onx8dmxsdmAVuc2fzcqYfPn3nuuedPnznHamB1svzMB55FDGCg2XUgwtH8uK91p9PeDsy6sLDAKuHmdsOVOKxpfvZHPgMfOyFN3rO+tvGd73yH0c2f/umfnnH0K9gghwhscu4Dywu3bvzWb31p9cabeiZ3cu7nYgh4hOTA7HkffxHhQR65HR/KItpd4THfj034XBmBTzzxxI/8yPzUZBzyZj7W1naD1eytxuLmBi4/iCQHEup1mBgSIgaAd6fGxyDXamWYPOyhs+egYZsLYX0d/QTpOm3DFqpdkiHlHbhWCGkX858znPQQmU7dPfiDS98BcE6fPD09Ma3+9pt0ikU+Oj5G4CSuk90lGfb2VTodX5fXXifdGhw63Npe3a5vGguTaHn5VrPl1DvanbGnELpQHVMFiwFRGAUedU6UnlzuK8+AlUf4zJcwaneHSxUWHqLH2G7wEYGSs+VHUdD9t1GM746N87AgSwA0tHDl0q2bN3TX4OmTY6PT/f2juhPAlzLh397SztBeKcxQm/yYBMSHVbZ0g9WawEFHmD6GKqp4Z6WEZAwqZloQGbB3Ix+1KZCAoHhNDSyykjYnF5IDI8Yxd9frsS/hTYXe4bkrwh/ntYuAjw/YcX+R9fHAokLFV54i8HjMiJBWXXxNniKJEOg4xifo0dTpCaIFHZecTsl5emZP7qYivMgqJ495lbo19/VRolSxY91tcTFIMzxUgwjEMXmqo+PPPvf87NyJxu4mFELgc/m9C6+99Orbr7zNEtZOf1xP1Gg22V0cro7gmyma4nKAPqGvK/Sw5+yJUy88+9xjD5+wHm7d3MAnsUU1X2LusoQrDMMxPf1rKyvDldGPfPxT5x95mP3Y737ne+++d2nusSfcMlZjT8eFe+q9wzpheXZmnrApjLof9rfryhoerI4eQDsMth3sPvnJj/9X//Af/vzP//yv/+aX9g827f+NDJaeeuY8G0ZzE2Oz0+P4QtozNG1t8vijX6h/cgfmHjvyR/cmf/IcDUGOnIbr/VB1zqp4Rt0TcU1RaQ+NsrbSrDOUjZuw40OFk4QrDgRDQaHtez93fOzy9xjOZLPOxcC4E7OF/TIccCD6OFFrsQebgr+gpmJ73gXhOwkvpkbd0eR7C5RzDgz+EqUD9fXEZc9vvf6GT/Ozs/zqXxoanJieQqXdunWrs38wPTUzFKQUJDs4GkbRwokPsJL8ow/y8tdSIkpwin6KUpxHwgrjJqi8OMkWLuSuccInBt1xjINeR2yxMPRWRFBc7D3mhRComHau6obCNKS7v9Vsbm8QNy7dvFYbHd9hyuCgtb1dd2DaUkq3WPZfeOcCSE7HhwD8pZdeddHNF774GxOTU1GxoFtYuGQNJDbpGVakGOhOYt2hLrVa9fXXX4eNHHi2/3JyYuKdN15+49VX9MYHnnhqbnZWQ+x6zM/OAM0Of5PIpquZ98lRNzdWr9+4avND/sc7PDW4iyyFe81fj3uO4txOFyFHtEfyJJjcDeyCC2+5rAhOrngtPILTx9urIEXuxdmfO3d+bn62GfffNe1zS2JGPT77kCllgkkQ2sfpvGxIVnt6xsZqyJTqCNOP5BXtyxcvdd58a7A66R5QJyNC2Mm4RakMCZuT1RpKK2ybUNlzAhESd2qR2udYqdozsj9Hq2Bzq7PTOn/2vHLa7twcLDlVZ6Kw7MMM36DjA9jkAacMz8T9gwR2O/uIbiuoUh5136Xj98ZLnTk5ON5HRyJ3fO4WTy71d/ZEp+Uxy9LemK4hXxvOXXf0NGMDB4dixJGTEK2X35g93cf1o0twwyMjcPCNixfeeeety5cuUv2zXwNAUgPN08OKR0mwRmIPWIiuMJEcLLBqsnBY946w7Jucbof11VW77Gmre9Q7OcNxVJfub6SIBnWdycF3JwLudo4MZJtzTrHvyClSva+TPH+/13PfdEW0+369NzD2gO+thFxyYPGp8BwvIAfmkPwsoikph6QtiSg3fdLa+PU/ndRAt6HAAuOKzKkMeqpIK5rA4vW4X+C9LkWITHJ35yEUTXgulB9Hw6pGEvWFiUG0v1Lo/fc782nTc7Dn1e9/7wv/8lcvvX3BfvTM+GRfyf5KXPFhu8TWLEzCIhwWwSR1Ey0B5sqtxYuX3nGU4+knHsUoUOJyWhSFWHGzrD0tSopxiHCf4cq3L1wAKV977bWdVhOriC9qLS1udPZPnD7BYGRjfQmiJxZzvVdoKnR2hktEfGFulu6VecwYlo3PxtbS6Q888ekf+QwWGhBxPuTalauf+sTHltlMMMtjr9o5/f0SoQ9VRbU8mmA64Wgu3dFzRShP0eE5Rnw6Sn5HmmMvCHBvMYuMXRpdx6KwC9Bi3M6WCKwYjrhzPgb4WNL386oJB2GQIIyMkP2GfBirhQUkrYJ90ft0lQP7hqHEA7xIQMljE0ZyBWbHXxQmJH/KIegnQj5ZgAWkZzfXNwnYHLyGUPGoao78QjDduLk4NFI5eer0MMkvi+JjLkF0O0JosMtHBJAlwOL+PmXofPRIBHmaY8CN47vMCeNt7DNubrKb0jh7+pSLacgTTXjb5+ahzf99J28dBlKngCUE1wmCBYVKnY3sO7SlbVg2GF27fPk73/wmbL1p533/kDwm7vkA7AgKhsuUGxyFUZmvfuVry0urInzpN//Vhz70oc9+9rMrS4t6QLfZkJscHWsN1x0XGa+M2ffVwwacrnqlWtNFcMnM3PwrL33z6tVrM47OnD5XqYzUqmTX28iR+RN0xWMsdtyd3GmOj7JZ5jTabhijTu54nxcdruj8tfB0Yx/9CBflQV+PYuUVHWMq5vGCitfjnpSqC0aEc0Ko5ceA9A/U97btPoZyfpzjPWQs1le9GPbLnMtxM+/omKlFj98QEyPHUbrS8PpW48p7F82NwSojJexnjzFrTKBgNiWGAlxj6962A47Y7gy5iZOwFKj6Wv0tHDAqjlL9tqP6rYZqoOnnZ+dMFSylyGHzGbu8s0NpqTRS2tjYUlv2qWhi2GMpl/pqo5Mbq3Wrg7wnaFpNMinRcRZZTJ67u0WIyLnhPJL4DyOSf7Du5ysX3RgC3e5KETn7ebgcQSr7//rGn9vDrr779rVrVy5eePfGjesg6tlzp+V2Y+HG+sYKyzk1Ir04dWKBHDTDwkYP3neENuJG3VShckGtz0kBF2/r+VT90PnIBWXk2vULPeJoj4UISx8E3c+lOncjyFzfegYwToJ0KeLbUXH3y+COsNwDggrPHZ//GC/BAXO5KrmA49U6/imXUoTwFCF3VaCIExkmyjU8R/FzZN0RU8a/gPHRFyJEUJpA+TWnygk9s8vJj96Ofo/o45THHQg4ik0dnRNiKJNWy65L8EBG1BFGJ7QJtrcPBl2ot//K66+9/uYbk5Xx0Snm8UskURgZiguh4tuwJWQzLu7cqm/RTjxwxxhFaLSuk0fXry+cPX2+PMoonNu4IN/+bXtrjdbGVnOdfb+V1VPnztSoBTLsenjwzLMfYMHq9772e85Xbq0vzJ2aGZ8er4w4gbq9t71NL5KAp4K/GOqzJeyPkgzgV6qUWttL1957d+7kic9+7nOddtvhzr//n/+9kydP4GUa62vu5nEjO4Vty71nH0NIIeQ2JZv7U3/rtRiZIxedmMYg/Uao9/CnmBE1vv8hTmVLPTvu3nHCCjjD/NGzQPPG1o/BTUjablEyZnWfrIoR9y0XJyQCe/tovAEgTp9SevPV6iUwBT4AHjgG0PcEJgnxCLsIg+/NXYaFy1+LVyuTygzl1cEB58LizKIhICLDoExNjgKO0LxqzM7NlSoJoe60JFGHqAbt9rjAKeR+ayskHyw1EgjHvrQVH83GwQ8Mjg6O4sxxKBiqkC8yv9tsuLDh0DngXXcAOxt8SKXbrMByBSmftsAKUZAKy4cRgyEcKwUllpX2DjZXVy5fujA1Nzcx/7ASR6ZrZA3whh1N9jL7ZoZIkhkw+dKvf4navvpsbG791pd+u1oZffqJD6hkm1XJ+vZSc0m2HbfqsZHv8Dgt7mZjZXlNs1Alaxubk/XGT/7kT/7SL/3S2tqKTpaPsqyISpWt01CO0o2x2GyWOu7ad0gqYK8yV1idi4EQTYTjr9lfjELXc/ecTFMvTUbxYwqKdwRAeXMREZZc8Vp4uiny50gcLgUesG2CYdRkZAewAz47f8/TPxTML+OOdsv9D/KLjZt6YLvJ8QlJNFw/IEX2xnZmZ2ZurF5Az/fjVisVeJzum9FCDhLLIBSDA4yrK2hDGjwd0jdYKR+099YXVwacI9rdgb1QyijN69evxTbSgWPflq/LeMM+805rd2yitLW9RlxCxYLFKiJeBrOGBl11gF1IvErs6SiLmgHoKU6AdD2QW9pt+hEC1iLVQLIajhwhj5L44YrY4bFmRYGTQyszf9E/OoVJBFtguN433njj1sINo0LRIehDQiTG2JjkpBA2GIcSgVYaN3CzOYOEZqNGtweQPzxEnmYKVWcGN5zGpVwqbTZTUbEMwuVyeXKqqHNUKrkc8cgbvzFBun/ikyQFrZHE6aao7ynDmABFzkX+2XPvM+XaDS78hef949/79d6Qu0dLzXLu0YDUfq9FYHiO8igCBdxVoeOfoNiUIksVzJLU090u6PaFbuKkujcrOd/lchyBeUi6A5O6XUWMbQIIWdKXSj72UAR4GqJZerbUStkkKpdtgVlgp0fOHrgixcVz2jvQX50Yc5fB1WvXxmonTsyfGZ2aiIPDbFnZ8oLhBh2qGXZTgt3c5Rs33JbieqPdTl//1OnxPURrucdF7Z3mqnO/2w3baWjYJ598cntjk6rGE48+snTzxtqqu2B7Rmr21ZYdGVxYmnjuuWcmpieJLkmshkbHdrfoRQeQo3uDz4MKHSe1BcVYzeV337aWrYFmq85EsELsIgP7sU9zsBeKmkEV2xYOkJ3Bnu4quqHw5441FMWn7Cki3BV+31f9j5j2ScfrXgss4BMXYthQog4m78j94DnLKjsqKFSi9IlhZReLyjxGhKhOCYq24K1ejv3lkE6Dcsml+txustc8T3JFcpz8lH60NrniUqHhfvyNTHTs3EkbqCGRNsqH7f1KXNc2Sn0UQGE2N56DIToybVxQWKlVAXHCCTSaPME4EAbgFmHY5gLzQMNDtPHWt9z00uOWOohcqsiEDSwHPxh6tMdXrRBVa2PSRgk0HMMScoPY1Ladz9Swuplkg05cAu1Gmkb0yvLph55lH4IcL/Yseijoulnk1vjE1JXrN37v976ytLSiEVNTExgppshVqfK3/m04hTHUddsEm9uyxfuG4fKtLe1ttBvLqytEOOXKyKuvvbG0vHp2dsQ9E7Dy9Nx31tdwbC1aaQ5MP/bwI2Hi2mk45/kOd7DFesMkdBheJx+N3v1XdDEK2XPvUzfeG1iE+Cp/r4UnfypeC0+RJEfOz/jq1GlSL0K/gTyqbUaRfNAeau41qOGavJhEKhTWuQPdqCX9o9CQRVGvaLvdG3Fdd5maK7huXL986fLF2dmzU9On42p69JObxMIaO5gRWkuBYnFffU772AAYLs2fZCprqDxUqbq5vtEzSA2QhcsalWlEPiaYxhZ7LcBUxZ5Xix7lhKmnWIRBo+kszzoBBq0F7TBLowxEST9wDX9b7rcJbi1NneQ39tpiUECGRHYAGXbKqKpQBkzBAYGT69rJkdRs0WNEN9Yaj1Wm1Ycb69+ntvrq90m59Nuoe1CSVofNafPHCXmTbXJyvFwJAYyTRpaGMmNRpL0JecqHfMBkBhzEUTetoAThGUAkXVACftlo0nUShXmUdLohRD3anFCwfOCS5JJGZMDK3NojX5qE4qt5RE5YP09MIYXLWRSv7+PJWYlQeN4n8g/+KUYrWnWEd73y58BcUvGp60k0xfECjlfoeFZ35mMs/cWECAozSkkTIgDNHe54zsf9cs4uB/Lz5OexkAjwX3fL9ihCeApnDk1hNUdKq5ub/HYkHVqylsyCnZ5dKs2jE2HBGKAhmquOjfYdVs6eeeKp556FLOlhrWyuX7t5zfR9/oMfc/hnfGTya5tfbjP/WKdSQz5Np7SfveD1jc2bS8sLjggPl6Znp+dOzC+vLo2PMizXBOBI8CggUCBcWliwut2S5IrZ19946ezZsx/9xMfnTpx1nnSoOrmHNYFEWXqCa6IBccxgp7n20GOPfetrX/vir3/h1Vde/YX/4X9cW1k7OTs1UWFk3ziGcMn0pcdJPZH8p3O0fZL66o6uyH1S9CFPHrKir34QD+5NNGnBDnua+o2xBmyFpZUnfc5fzuqVuLrUlAdnXdRHFKms0jDiCbmCBbSIE5dpcXqVv0UbyG8njrGJrNAMf/Lr8UJytvkpJk92cgA3ZKVriP0VR0T8sCOxDz1UGXEPBGTUCtHcgBsFUfc7tf5gm5zbAFMAZZwTOYqC7H61XFiYTv1iEhIadnUV8x31scGJTC6QXzYAVOjT/QatJhPCzD+O9PWMDiHhiF8o4jZrw+YddwdZFO89PaR2tjAwFmYD2At3Li/c+srvfvX69etx60adudT+mzcWv/LV35+Ymh4eKb/y2iunTp5GCML3G1uatfnGG2/9o3/0j9xfGWL22ZmJ0VpYm1TUIQtlROwVKABv58ZlR5VefPG7AN5gZ8X5LtJN+s9IybNnH5qenr5w4QLwWXbQlWDGmhnsZYXGfCc8gBNUNVqQXB4CXe0t+4uQ46/H/SIff72v/94Mc7R7w4/ndtwvfkCJnriTALSvHwb7ixx3pEiwWbHr3sy+vYF9O1AIWvMiBB5mMAQ8UBkhld7vuBJ47+bq0te+/tVXX7126vSpD33401PT8+ROdBNIO3WLPWBKWSwNDJJNDJQJtRutg5OnT6yur+y7O3O8zIo8c7axZcMiQWzQO9Q+TD04bEztI2fdyEClsbZ/2OjsbNHJcsAQX2zsHevJ9bTYqVrG2oeJIO4HO5OQ9gubujTxUZmdhUXyRvsahiaARkh/gmVUjRwCZ3kpDQf5q3MASe5gfcWKe+T8w0hr09V9wM6BQLphbJKdzVoFZEPt6SudQ+Z86OrCtCdDi1Af5trJ1ie9LcQaCQTvoHCzub/nWs2aYdIoaw45PRhmt2JxClQHTysj+zMCDqCSEUGaXz5l9BI/Cbfkryk8T8Lbs+uuOfngnrv9Jed++/2P7RuIYw9cXiGpeQLyAAjmyfUtPBmBFlUvPLkmES13wJFnN3WQh1608xFXLQQmjmzwoUJb+61kZnDvsNzpbG70DJ6OckMynVjwMM5nrUTN5EzGYtcj3t0qGDOl31qhUBq5mvLkHrb7VYFSrhBn0GJGUgIwvbAiBMlubRtngn53mHLjzmB/05iY+S4x6O2rlfZLrvs7PfHI4O5gJXQR6iwFba2TN26cOjm0vLVGndXJ5fkzk1/6yq8/8dyjH/3wh2ZW5g9tvVUYBhx6/cJbf24fFp5e2Vx57dWbpC7nzpy1dbez1ZqYHKlNDO7uAK/D/Z3W9Fh5Fdpc3oAwektz7j9cqfdWxs5fX97Z+L3XfvLzp+bn5uk0ucxIG/HjlDtoJZh/B737g+OnQLidg6ny8Pzc2OpOfXNot2fBbSqPPNJ2jGVodK9cbrjQNzp4d32n3TMQ+iNZMBOQNnoxhjR+4rc7gGZvvB8etkZsWtIMimlu1JwC3j8M4RcV3X33wMQ4xIl9ixgFrtNdP0T46XivQ8kj/T2vvfrSxvoymnjwcDgsFh9oA1oYWR+yWrule+7W5TTLI0rPcDmJmEhY3UIe8w+CSX+YxHZzcrxy5tTM5vrCzCSdkd2+EnVjx7gY7hnpGT7Y2qmPD82zbzw1N49BY9azVqNQE2cw6aCFwhaIaeXTYorzgSafngGrFKN8N6ePLmytD1SH92wE77XoQl2/du2zP/75selTTEPbCjblGO7Za63vdhqg1aqpgaUNzdTDod3DDWzQ/pIdr539MIHA8sDm9jbxLyH2idlZzKJbrg574vQRLRt3swccb2yD77ZgU32Co397bc1I2Hhu9LpNdUuNKaEyPe54D+6GCM3eoO5e3l5z5zEagwKCo9mdlWsjM5Wll9+8/PbFm2vbo1NnBmrT15c2mNx65+J7D5996AOPPOrA026r+fZb746MTz7x3McfOv9Iqzr4ztvvVk+f+/F/5+cqjpPuEAaOU9gexYIN9E8O9194+aVf/2f/89rixV63w7c7iDgbCTELaOsMHbz89nuzcyOPDJzZ3lnuH6qYGVvbuxPl0c7W7vKbt/pXeq51xpjNJorYbtbBFkaVrE/EAeniTqM1WkFCbQ4NdE7NuXYM+bvT2h9MRiSCfzcjwrgWOUov6xKDdMGcDKLjbTsWkYVgB9z3e9rgNemlmah7m840u5KM8sZwBf3L9uoOQZDxTdhGb++6rAwLKucAPMH72v4FPrDuYc4T/Gk0gJTQKDfZdlv7zZKCyFODsXT3Hxt2+63KgSvLdspMv8NSpd5alTo6tfmNN99885V/8UvUND8yNTQytHeKeHj9ojuRTHX3KzPMTvhjZwEMDdAHrx4etAd2ry/EtM8CUr/AmDFmYSsHJiyYEWGwKGQw23m/dmAgzk0mHCkcOWWGuL8UqRcmpPqrPJ0d9wviOEm+49Ssea4dMqdK4tpgtFGZvW/ampK5XYYdNq3qD/IxgAE1LiecAsZ2nXDOjoLish93f1gbo8AqhpDh0cnx5MmvQmjWb2+via8OUQ2eODDMBdRfXrHl0T8/du7WhVujg9Xencapucpu4+Av/uznGPlloWFjfXU9rAraW2NaICxAkKjJRP6YfkhdG+VFahS8RsLHe4dR5yggzIkeGi+sADjfH+RRKKePqKeV6Vbvzo7LYfsPt2XIRT4yMVNBAf7i+ETkBsVEnlzAu/u5osl3fWSO7K6Qu15zwiL5HUpY3Wqlyhk+rznecU+Oczw8h+RihBcRivAsNMgNiYTJxxP+5HIEXiMWUgaZJARsAFKcbjWKIm73Tuivx2Q14Pl8VDdDYhZbgyHSEDe51KFIRNsx0DK2hqcT9iIcIgj6zgFf8ALEo18T8LTDsACcE6bGUYtkyK6ca7PF0c9OR0WOv/ALv4AJOumahJnppevX7daaH++98krpkWeWl5awoI+cP2enbT+S9F6+fPnkiXlrwOpfY+BqbSkOC/YPrC4tjdY2GxsrD5+ZI+izIVWbnfjeN7/66OOPP/bY42bGAbbIpHOXjo0l4Htw8NbqKhOJropzl/v66vLsRHWn0RgfqzHNg5txHt/NSwxqurzdTgwsFPzIA1wxUvm71+jtNOO6IxP+2xMwvoYznYtJFqs1wNxuKFm4TYdNxFs3F8mjXNa2Wd+ewVAg6ykZJ2eTEmw0v5Rl1I4QcKjhJcVTu1nh5BkOxRQiKTpJAaQCTkmMAgIuaYfSei4jol38FBrpwHRlpDoxMXXQWIrjYpoR22IBAgJ5BHeAa45plcsAigMZe3JxUoLOc9gN2GnuXr10WWXhyKtXr+JH4iizAyFlas9T9e1N3ACWF/EuQ8S76QEZSyg+/gDs4BGH4zdzqKsowWvoiOk7M83FDMktLy+bM1hn8w25pqqC98PkISiblHmCfozL4WnUgfwsKZnleiTtshzaYaPG8/ATj1y6tbh9bal5uBhWY/oPmY2cnZ3+9Cc/1WxsX758MabDwWF1aGiqWpubmNjs23vsiScff+rZT3/wgxOzJ1thz2CQgS04rzrYj+7cvPYeZYNOrTQzO42BI9wh/2Pu2Fywg903OWK1vvv2O7aQ6WozXrHX6EB6tjrajgpsNzt9g+tb64ShcUK972Btc0M6pBL+ZqcF1Q3R598dYHYfZrUfaSMTbaQviRbNrqN5ddhLumDvP/rZ4PfKwbCHeId5TP3mFrwnHnv8sY9+1ARYWFqmtVHfXAvloGFmbiouATPkDi6LzCBTsFIIcnR6uggXKDcibaWynVGu9G7VdYEJZbteCzCgvkJM6XxOqJ3vtPt3Bnown0iZFs3lnfZC78HWxgYxLPfsWG12ZnhPKxjoqG+NTEyzL9bcsSMemI+Liahp0TpNDEJToLG2rvgtAuPpjVAtBUYqKcKf4DCYwBOLJbkUHEvSvozJIwchnmadQBOSFXkejvw7r6TcHBDPHLMGlK8aSbDsYiu0SrA/CVd6BrbLDswxKPKJsTnyeM3nkYqQ7EnFpVGMuIlPMmmEorjr7aPmOGOXjGno2cPDN157NSilvf2TJ+cffezcWK1qdVKwv76wqmh11txYaCxcJr7ZVokFlWslVY6jqsyz6kCvqA+75poJefPLyqkt6v0ul4tBSLqTdhxA41SvNASpqV79HiHc/PFP66nhd2XdRcBRg1yP9N2rQc2x+XlyBB79krPI4XdlVwQWnsgk4VyewHBpRKXKlEV8TSGYrcQqx3lHI6FsayZ9TV7jLgTAFhyTOaVK2JoFdP2H1BOIngWz1ZwLUjGYHtn7jWmteDGBS+9mKmaCfMdoERERGQkKsNdzcOLUyTMPnXv1+zerDImD4Yf712/cWl5dPf/Y48Os4O/tM8h7w5G3GzfoTv9bf/Nv2dW7+u5FM4sR5l/7zd/44E/0odNj3XZa8htn2L5UtlUIWrodhzRKiSAI4I/EZtXy2oVXSWPWbr7nUoWx4eH2+s2B6ui7r3zn/PyUOgbjbj6xRu26nVp7gKZRtYwanBitnDkxf2VkeHp8FBN85sSs1u+167v7u6UBUZ2tAzSYqMUTRBdoffq77UkDHj0Zc+/2tAAHjybo0VTRKSLkOOkZMRJ27MbMCNi8gK0cToZ6z5w8QVxZdysEM++UlJySBmti5Xdd2umMMc61isoll8ZZbazRwL7xuqdrzQp7RNTKgGDDGQYE9gGfAfQ8yM9WWKd0gOsdHBmuHdRXwVPdRRid5kucAzO5MD0YgmAlAcGwwAcBmyYBeSx3e3NuMyhVJ4Z2mUq+Ttfp4YfOf/nLX7aeByrDhowqW7VaYsSRapPxNTVjgoVSPQaO6mwdwgAEDBlC3VcQgljcBrODyxqrJrRhlYe4Fy3wM3WsoWHIQBvJltNGYX+bYSnbkwj//iH8mNmciA/UBz0AskfbYRGIdYOKiLKN7kB5aPbk9NjiwtXFzYXNOnvBgab3D770m1+sho7hrovPKcLsN7bfe/31havXp05jOvZdat1eWKDoPDo8om/iyub9dmN1fXVzffHmpYH+XbqCrZ3G5kZD3SyBEnG5EaBsVKoanZXFZfcmmdF6tjxcJjTvNKlWOMo+arcTu2nnsFQeNr62eEJqQoLChrQ22OGLqRDDLVDnQwEwugEz1BkCxGwNhwwZNJQ6LDhbhwsajVuLS831m61mc/Kp2vz01ImZaeTLR57/4Kc/+uFvffs7VC5sWm+tLTiJgCZjBaYMx0Y5+N34kakmu1sxZW9rYxgx3nS4DdzASRF4jlacOgC+A1KH+WYnZ4iREUA9i1cvuWhPf771ykvf+fY311Z2T54c+cSTTx2sLo6OT5DHNHdJZ1drk9PISQJsF10keoL0NM1yjQ0KMOjBqEasuqiFKZFfIZt41wexGDPoi4CMfnLlRU6rJB6wUaJp4yFc34LM/KHRpxyFp1IMFgc1vfvu27QVKASYP2hZbYehg1gcHZV5Qu6RPHuEgJM5PAo4Fu4ge87Z1zSA3eYUdcueKD65oUMsKBe9YVqGaF0rcoWR1rbXKPZZSXiNvVAGdAxErTRQDVmbQdrmmjg4x0UzE/y3iLRLDcbGKzK0pZJY39AIMXy+slWH5iO1aoYF9214nPUu6rchT8z9n6r1r/OhUbm4wuM1lLC4jFZ5NOm+dSo+8RS53BXZa/5aeMSMkEiRoHZwITEfBUY2KavE7KZOyTjY+1ERaasvTaXUZSoZgyc7KzY5MYVQVJJVAFa7LzEVDcY+PYkQL4QKX2Bii1we4rNGarzdnU1TD0Hlqjh3c1y7eSPwvwN8nbZ7dU6fOfO9F38fywnMtdjhONy28k8//Cg1qI6LcprtsbGJ1dX1K1euGWMXERL6weo47tffeOtWa+/P/JmfsrBe+d53P/aRj5LNLi0uMGVf31q7ce0qwzuhnd/T44AmGFsY/ZMAAQAASURBVIyM3Vq+US2fXF64ZgW6gqZT3xgbGYqZ5kL7w1LYO46tQidNGXts9tRdQDht52W8Wh2rlOem3JXkyoew/YbvWbp53S3qY5PjIziAZjtUimI3R2kPdHeNVI5LZpbGKJ5G4+hoQx7K4FQIesKEVBpGORgCi2T/0G2Iru3rqY1P0P0GlcqVaux/0eSO25fDoaFwIZJk64kKMDzCbcTH1EjgJamSJdQbm8hskTilc9hmN8/RLNaLNYnZ2wOsDqEmFFPBN1JvcRbTFa0zM/ONlUsQrZGHyBIrDEOrs9ENjyfolHCwCYMp2h8mLYxTnXGaBzr0zVaYXdUPPf/Bf3X6NKhptw0do9GBXwljDxuELvhvUIkcOtqSANzKyjK+f9qdEOZYvW5k0y4XmwoBsMAFqN4Q2zmTD8YuSL0Tc6xJxsw93K9WR0xvIlUgmFo0KSncBWKFxDxsHuw4C8dGx4FJhp+lZkCu2+oY/NJs7eTDp591J/SLL797uTU41KIopOeYtxyMS7Si5bGrSGTdaNlnW79x3Ubv+qWrr3zt6ywIygoSUqV6PRSyQuhNUrrXGVMfd2wMMHG1ahScD9bS1vYGfDA4PLDf3hsYqURVevsrw2HM+NAi2N3vkEbsbVMdwtrgP1TDJZQEIKhPY2w5UxAMwcHALlmOc9FCQOSgzAMs6DnUEsIrkJQOVC5FIT0BM1L8dme8tb54bZkYcmt+9cp777z83RfVikmNE7Nzj56an62NTI0MbmyU2q1QbA5HbWLXnWAJKMA8OhMsCHCg55w22KZrRt1Sb5Nmb3bQyWWK6WHBaofNwr7y0Eh5eHC8Mjw6Mnz1zeXvvPrSIkCx56zwfOm0ObG/u75uGxN9gzIzqdY31ztMe1obMQETnNKsmDuBV8Esg870o8Yec134Jo5A4CyeASZjsnIAQPzEa9dpVvaZgRk9+1oEBqCNJZUhZIQHYgsTAzv7W9HPSoCAOZkEVFktIkcy/clljwmZi4jYJj2OgU7GYIjK8ychPNmlKX07K4GREeCLwkvOGoy5TPQfVaCfOMAYOawZDv7sBKVA8OAu1oyA6UmQP8vH5AS9PTn0Z865qCHzL9389XpiDq1Z2rUoM7JA0je5M5vq5N52fWt1e8uGdk571zNn8sd/as37Z1JEyJ4YBt2Un1IWrzkXn+7yGEshRXhO4qnxOcccPz9F03cp/OiRplk3lbBU24COsSMXz4CQCWOHpDMulgmYaQJHVmngY3gMZKLxfAVhJEz7LHFPdFrPkWkwHYF7JcxeLQnpg4u3hiDyFMNcgDmoDJBXBK2OkCcxLpXcJCMliZZzIk4AuW0IviRcdT0728oUKH/qp/7cP/7H//hKuGvT004LT0DMog2Vdt5+49WxysjHP/7x3v2d8dHq9vrKG6+85HywE28EkvvLWKtzpNxUl7O0hL32W8tLp849ZONweW0VQHBc+IUXPrywuBxs+mDc50XTJ09Ktd7Yu4W1dRLAKRTHGPYcbOjve+kPvvvCCy/gN5gYRLy3UMdsU/Q509lh3E6q1KWpr6NvsyeFxhB0XUTi0iROECAPXETjcqTb/vwR1EnmC2gCt1zp3j546NGT5x46//Wv/f7Zc+cnZ+cq1XFrjuxSh4PFnlCRkUjTCp6MiQcmxLgb5MT48phjyQVnYqAtT1es4nuwgGRnEITtKla2WOKzZ+cqNrsHmD2ybacfWEYGVZgHk53aBcy1cx5QDkSMuRUUXPz1JaAZiU0/2m0OTdVJa9u7FF2+9c2v/+jnfnxufmbFrtXBgd1Z99/YVpi2JdxfNnzATdDatppAJvv8yZBHZaQ0NmpvEgpPEIoR8ZJDLSFNDVl0f7+zxXAwptmsA00o16qXfFQO+vesVSqDDbaVhDXhJvnYmAwLSq6cGmahATkC5cOB1Ox7UAuA2vBoeahnaGKmM05R/zqdsR7nxUvJbgLrih3QVs9vt6LfaMMwRr25Otxre76zsrZEv69Uq6AqkHHVns5gtR9VA2KHha5Dgpe4m3OU0cp63SCERVRLMQyrmHJIiZHD6oCzYdvNva3mFrZK9Q5bO+O7G0ABptKJVU0adM7YTTgETKZBzJZQP8azaay94YRvYiUngUdGHL7E3BIjeGbDS+4dsu+hR0+eeuSRx96ZGH711Vcdvr/EMlrHsiMyfw/CI6KUDoqgWQJ5u/w4DZMDBTMwOOCuUxs7O/U2GaX7O5tOcI04D7i/x/wV0K2A8kg6YXjgchF3RIX4+urC5dVbC2tLi4qZm5okS5hG9DnxnPT1cNWwY8dxipBbHMTtHS55rm+V0zHwkAib3THtAifyIKb4TYNoYWpj4gu7fjXks5rQCBEU/nim9ZJ8KUlehp6ZY86pRMu4RziYl8osMgkMBM+Vy2jHpKUYwoAQL4frwVDGWGSQkELijTPts+euJ3irkorLz+zhtw7ELAIzbva63xuctCsccLoCHbJKVDeBUNh7B9boorKOZWZapIAWe+dRdEK03cwt5ExCUYtJAEdBUXf/dbslligSfaAgMynXO/G+TTSGOYsqch8b2rdSibsxihZF/NuTrgj+U/REtZMrPNFr2QnKodqTahbBQgp/ES177vqa0woUP/uzRz/lmIrW3PSpGxIvvKlPgeDbODj1bWyXKF0U5iWONg69xWwSHjwVGOUWMNeJmxEGSYJMUIXEP00Ioi5XZ4aMSSrQKqo3EteXC6S6QEqqdEKSW4sLhGax6t2plywnOKxJmAP17R8Omz6sLkPtcSoF8dzunDlzxuxxxuOdd9/95Mc+eub02Tdfe80x0HKlNtN7+OI3vz4zOY4d2lpfvX79hjV56+b10vB5S3R5eRMuP3X6xEPnzl++cskNrxhbl7OyiN8/Orm+urHW2qK5Wpk8uU02CQQmFYMQ/+mn1F+klBO1gIkQtl4BAmx8vv32VfPblekMJtgMY7XOGWbUfXNrXcL7utT1KUe+Y470yttdSY5918N53DArejcksWhrT8Nt6tshL41UF5eWJ2Zm3WBvJhE7OVAB1wIS4oTMNk2SVESgXoPpo4EyFrF+wqaPt9D2DYwceur2LkyBtFZyVQ56yJWMiHXq7GulOukcD0ylW4JSoVEa4t7gd2Qe8xkej2mZwjwSbk4FHjhSEqaYD3qdvjyEeey5tZtvvf7aj/zoj1ZKw3WKvr1sfE7A0yw9qQcRmcYinqBVxVnPWZ8TcjUWQqKMdPSQmgwea3Jqxj2yALMZiOvLO8FU7NFWy8tL4ucMb95clC2cMdLfTyUq2Emgjui+J2EDvbB7yP6us2btUDFilau33mzZ8idsWF5fXNto2Tp5eq/v7bevNxoBw1n0KNPCDSQXWg6tzh7Tqf6Syo1NWDgL3dHugWsZOe21EcjuSF9s+OpRhG9/H6meTtts7NGI3qzbTAW+rUcoQRIinDbhNFEmO/v4TcvCUACCI51QcqpN9Jx/dB6sXlhc2tpiX8QAxhgEIxXXtgcYN5JqF7hYdsnFuB85IkarGqVCXGoB22OaP3Hqk5/69CceOfGVr3zlpZe+Z5q4KvGRh867iHNtdXnu5CREqKcdD3KpYnvx+obxGB489/jHaNE7RzZaLY8fDjc6Q5sNwpQdcqbZiTHEx+oyURktdLdIhGWb3i2KGUsWbGNzB66YqA6cmJ6cOTOPKmGurN9eeMP9jz3k8lDKgN4qDaJ4KCLoUduVBDXViSn8vRs0Mn41AXVt4F7vae3kJsa0NwRHrkBg+jz49IR+PfGGhf8oYaSKFZIOGvhqvGLI0vwOhWj1M8WjOEUYMZFDAhITPwFUUWI3JtgarbiNqkU+qo4ot1FDEchjUXKKisFSCdxQvB4SoMSH5FSpcFaosLS7TBIZmhyBVmNVRgO0enJ8jB13q8xGz9b2JiLTEQIZwpd4CRRSLP6A+QB4AgdRcvDMnFIGbGR3D1wEKuE0k2OGLspJ7U/MWmz5hTgmGLs/RacCf2juRRyeO2SU+YOnhsklP/Nr/iQke3IZx1/vilB8Mkp5VFOE8Oslyb0Wo81vlPQWzpT8y2u4xAlZqrvOsx85wuWAsJGDgYyObvfuxIG4A+cF4k7q2AtIznUwKRGJZTSFglI+0HZQ7nflC3v56F/HAnyyiNa3Nshvmbii6rKeLOPaoXOmPKoz0M8eTXV8h6XDZE0l5g3ga3NidXnl5Zdf/YnPfm5mfu6tN9+w5Tk4OWhfamNl+Xe+9JtMZLCNgdw215wAvnb5ivMaJoEN4LFxmzEhe+BWWz1D48PXL90cq411+stKefZjP0Y2zWZCMIBYvZAIB5jyFL93Y8UBqpe+93KrvYecq7fxQf07Bz0XrlzDDYeCroPDpRpwwDBt71Bmf/Nw3fGUVR4FfRj1OHJEy3Ql0ieDlJBxnlKKTuDDYk64kHZn5JA6OThIGXhdX9+0QW4g4BIi2jj9ZzZJmkZLi8iLReNSbulB8iBp1MK1oHEzaKyhWGzx59g/uaiTwHvUhQMmBDgLQpoZvYT1PeL6xqozskkTIJTsYAhQLPA3tjXUO01bKSNXmQcpE1mnTWDgUTDQ0Kg3k8itf3117dEPPAUugX10lUl2oNsw49tzuLK2Wi1Pmo7qGuy7W9dbbR488PTklDkvJsoMBwaCEmgHL9vuOGo5eGLAbkVsAwffFyOqYWgInLGG6ysMnOrZGD6kqecW5/ag/REHn9JuqakNHvVr087+IYMZsa3aM0AdAfHvwJf91lMnZ56YmPvkpyvrGw2EAbugNIaMEHMijrg0W7vL65uuMJRuf6XeOOwQZ4f5aRqI+/u14REKwQg7t7jSmg/pbMVqguBtsxGi9IzVYiNnqxHUUrBvuquvZ2o0lOGCdxxkNgLHnQx925Nr7FqNs3MzZ84S4JNh9paGNtzCzki1TOzeR8+liWO567GYCseczknAIAbL/gWK2CjF+did3cXFJdc6PTU79olP/Sgtom9+8+uNK9en2UZ2U8VQSbfb7hkbmSrNTGk49WrKifbjr77zCtNgllPYxrHpbm9i/8CR+YWL61dPzs7Nn5gux4boxcuX3vzON+i9z7gVtH/g3MTo+ENjZOsEzvYe+p3B3eswQTnIRFYoaQemIuGE7IdHZgiiqJA3HGYlJ9lxUBtJ2glAl2hLjU0wMHoPLWn1aO49DbfPEgisCL/L47UISV0UPchThMfcTg5VUERISUAOkSOmpVrET2XF2qWuxM+JlOLnN/KVpG+cEhQJvVE2S5HNwFxOPIVUnZg/ct0scoZMx5nwwdZyLhxJS5G8xBQNnYnhWpWYn/bACEkedNvajoWQcwqwkJrpFbg37VQgZJ9BooQs2tfQ5IqeRuGgHPW6XS6IN3ZVTHaiKcTQzi7jOagz+8HNibQDWNRQ/OxPjTgW/Kfm1ZajEsMTvVn0+/FvAvPrvR5JfDoennMswo97cvtA1RwHOZMBcHSYTJDOgLg6WI7pL0gjuecnORUNkaRlkEk8yA+GNUIqbUB4KVJ6oeQDpAL3rts0lSHpuJGSGbnYias5SAfGuSwaZBw9Re1uZrxaGSsPs2NAjXNtc3Nq9uSLf/CiC+7HJyZ6DhnF2jYzKOYSd5bK1Ru3FivJLHtrbc0ylhXmxnFzCPj1V1+LnaS4wnAEqDUnJkZHf+wzn/mlX/rnqxBtlcFCSUMN4OLFtXPnzuHXKey4yc7kCPZocpK2weUbN1CCi5eue/38pz81MjZFwxf0I+oLuAaUQyWJsNNVG42d7/3By1/4lS+ubdRHBntZ8qUp6Eim+0RfefPCVmvn2Scfr43NuCYY7AeSiqG5y5MH1/Mu15UTpLGwDuI1M+Bp0DMbGmsvFmysE7Oe0I8BWINCkrmwvHz5yjU2O5kp1lfkh4CVgyQkQQQJIaZIEyEKDcSXkKzR7l5BkFBx7AAGspe9v/247aenVh2kThRKaYfUca1G26Iks/t96T5y+7Oka+5Fa+/g/mzsBikC0AYpESU6zJ9bGfaoolBlyxs5cEhyOEzOgI5YXa/Xppi+wlM2nnjicUNpgGxyoclsEJJ0OdJNVXVrvS0O8suQwT2WtMHlj67o6+Mn9jfnfELRWyMXLlwkLzFDQEYHpMmtDYSYOcTrxsZm2i+uymoTvqR2QK6758QwZc6wvSCyyb9TbxLEjo5PVmcn5p0kPXWaUbVTp04dVnrdd2RPfKu5P1By0fs8CsMthEx2jqar400e/PLi+tatpTWb9BtXF997752VpVtOi928cYkdLOyvHoehaCfYd1HFequ9tt482HGqqmfqxPTzz32QfP76pWv1jU3srUFCl3z6059+79J7715+D1TrZ/h0OJmcYOt4eByExLtcusBcTAz6xFiV5HVrfQNAAS4hU+ARfCdsjFVvXhnvgEpdUKh/DJAJb9LHnbGmz3AZJ+iyxZXV9a3HH1b0sx/88Kuvv33t+pX+obYdn9LI6Plzp/bq263NVawqJOvivVGGYg8ONxMdv7u7vdUhJ4cC+wEUVAb1xle/8bU3hgax0bTq3n3ttY333j1dGn5obiroNnOMYj9ZNZtrcUK3f4Qeugra33F4wuaCw/us8pDRQ5yHKKf+9UaDgpm0JumWw1F33WmPlg1WuEtz6Ji8HnVQ9phUqeFpeaSg1CcBnIvIOYJXnyw3s4Lzyg8wCuRMxeP55LQ5SfAawR5HcvGhM/0wbG8joYRIfOSRQyXMz8W4ZBcgN5ZjkI7COXmamdnjKcPb4xffI0L87LtPxtBquRfK/XogmjxWY9vEeTxqO2YcK2zDUCYXSVK5UVhyKpD28IPlFaiFcvZFuJhE6CFgiFpiiCNna9urGRjsmJLj8579AlYLB3q7G9JRxv9fXa68KoQtklwTreL0afaIkT2eRVVzoNcisPDECKXwnLXw7MFgCIdrUybxzNIYiFQSMJqemqS4QztM9GrWm2GNSOFqYp8jhmA/rjSPyO42cPoyQTpxQjzV11er1ARibwFKEJGJIltRBhKaFFMchgWwINCxyQqZDM/M1sCacskF2c7Gs34+e+KEUwgu9zp17qwVjiIrnTgl+dWLS+dOnVjdbMU5yMNDxgee/eBz9Bnqm9uUPlgCoifpKNN777zlahSZK2ZtY4Mo66/+1b/67rvvEWf95E/8GSC72dcGggFx9DUtA7V987XXp+em4WMwBTqZHK1Mjo/3nDixurw2Uam6LhhjNDYON/e6eYk6KS4j6d44/Lf2z37l19989fvr9d2J2dOlvsPa6ATmzA4H2Tiy4Oqt9Z7ei6fnpipD/SAEC7T9rvIOZzjSL0/gThRuQXHHAonAWJsxsjCLEUHQ2N1kxgrfTxmiNlojmUNiUhAbrpbWVlq1EcYbR25ubrmGkSEh99uuLNdnZ8bMKO2iIg6GVkqldMnQXu9gbNUYgaxjpT+9qoaVAhyqQCsukAi+R/JYPIE4IVqge49+05tvvUIH+tHzs/XNLRfWvvve61AgVayxynQsN9pUffv15pableOK1137rGW427EFTAmGyxGMmEsuz2PwHkZSHlEYvq93oN7Y4e8Z6K2OsvlXp+XlqxoYJnVQnZuL1J7HKv1lA1qtjV5dvVVzLtvWlWdpeKxvXFtw3CgwchEa4Oae8MnpKVsApB08SPNgyUMfIbYAwZvtbcc+yxSqxibGTVGaB7WxUSFw9ubu3mYr9mDHT52enhwP1J64B5m4+XjuxIkpsv1KFYnjbI9Ksl1gn3RosDo4UbIdu7a8Fpay3NE7NNTabTvYDN3ZIahOjj46N+OQYukjg5/v+xk0Ci2t5vbqxury6uL1rfUVCJt56u9/73sX3ruEWLWvgbQyY+tOCXf2NjZXR0bH3LM0PzN79cIll279X/8v/+eeidHf/Ke/8Av/9H+ALi9cvqCnDarbN0O609PT3rEjy3Z32U4B2qLT7rFZrTl7uwyDlA1fo7FmHCxpgAb2CIk3jTAjSU8nzihUiTRo9duNpRyLBjEtrYIvf/1bW+1Y3RvNnaHq+I//2Z95/oPPPXz2VO94tWd1+b/5v/+nCIIK9UnjvBuHiJxOCKVfm5AxycnzQ//DgkEH9FEgaPVcXV26mmbdw+OjNguGu5IzRBIxvOkHnwWDFRgb+mZnlloGKo883kQZAgF2UfkOHIZpqoESK5RMnoxUx51DCiIvrbWgoGRldQFN9BiSjrFpg1YzvAbRuHvKL7mYn4U7WrZFQNcTk4lgOUuEU94JTodURoygmrlY6F1BI3gsVoQEsxjyw/gWkWUUkfOTJyclTgx/cj6Rb4Q3IkbCcJFV9sUzi83Cl0oOT3I20bQ3AZbIwbqPJ/nK9qYBDSK1j23tvNaCdwq8ELeoyRsECvwMPqTxYf49to9BDPg2tSLQrqXqqVTO/AvSLTg0C47hPHDbRCejCpI3GZrDE7v6M1xK5ZnfIn32HYXf/tCNcedPjnZnWH67fz5F/t1IR8UF5S6o+OyVv3gej328yBzB18KTYxavhUc4tuleByBiF2IAglwhR9jFU37g8SdOPPOh0JUHf+0XssBikjBwXypRYkonPgcAFLmZr5w4gzZvQ9wPBqu6JXLILpJs07HasO2XjKEbewA56DcuwCq1Ulex4jHBWRV05dxAyf1i2qOs5nZbWe4kYdivPDKB8qKltbq85Lgkc0G4MHOAhvOrr3z/b/2Nv+mumI996EMMWm3u77ls2D2BrO9+/vN/9u///b//a7/2a//B/+4/olJ78cIlJmXPnjkzMTXuTPD161dRrq5VQXY0ttYmh0eq5J17++enq62lqxdWbgKvV15/ecAtobFf1aaDfXNxiW0jQOjW0vp2C1p0v2ZwlGFMCStxuLeBxGeW7rDv2vLG4srqSN/hqdmJs6dPsM+su/TNXUMQVneSy1/TrA2EY+8tdHD1uyRdgp33EAdDVOSQnZkDKJ47M014gGObqA02605hkMjVZYVYoQ7267/xxes3b1RHayAp1Et8GsyvPIOZjg0g61AnWmIcuRzgAHyjTnS13g2qPna/sEm7PZ3tVnuzUiFlnSXKwEnKwL002FOG9JrtBujK2lRlt72wsnDl5rXzcd0KLW3TxuIjhgJpYl/TrNBGPJCcaR3EAo0uB+9HGNvuHbAJPLTfcnqhhWL3gb0ns4iF6enp2dXVZUwta792nJxAdSsHvthZIIKKEYfCIhsKU9DDoWkzNjrBeNDWZvSGI2o3by0RSerJYKWp2O7urq1ukKaO1sbFJ8E1KZnQSmdhgvjYZRt6oH96/uzzzz//2COP0DqAtKrVGkkyD9Rklods291Quzu6TBfLx/JxSsuWAy0EpWxh9zbWXVyBT1MxJ1TcnYOhI2Te6jQQJW6TGyr1TVTn5k/NHOye32s2Lrz1OmuptLRXby5OVMp/7nOfZZeNaP3N9qHTvbal2Tb9/S9/RZ/MzlNKc3NA5/f/+S8+/eQjf+8/+7/19e8vry1cuPj27/zOb7/1+vUEN3dIjmOptggEHQnqn5qAevepw8TFVvs9201yWmZT7TEzsmhQekionHRn68bt87bGl5dXrQIXQpQrw0gmUi0nuGJcxia+/d3vLa4so/D+8l/+Wb3Uamx+97U3htBnZ07+pf/VX//Kr3+xtb42MlIm4kf3hzFQU6qnlzq1CUZpwWp3CRA8b8oBTWYA2GCGOCPo87DJgeVNEqC8ZJI0JjOwCbskcKbCGbPRoY+Tk0i4ftUt942gioIxsPEeAhZjEw5hEghT+rExaL4tSBzwzdOENGNTWbdxXi76X8eT0aL7ugRm7/flCAHf9e0eCJO/i50xUihBc9FrIWCIO0fiy91wSc9ErKPcrHYuEgZu7eKp+yS7E8ukBJFI6T9UnxblRuJj7kHhx6L8Eb1dBFykDvCUkJ+Q3PKi7MKTP+VXcd4//Ohz6tbYDJQ6/ptzIBfSKm1aHDg5MDox8cLzz888+SzKBSRSjcQKo4LjlIs16WnbSSqfJMtz10ipgCAg1aeOu3ubiGAnCrAysUMW6F2RIf4JkZGtAJIi28oDAYLjGtSYDoTZ/cPtzc1ytbK9sf2V3/md3/vK79ktGD1zwkID0QhB3L4AfKADXKBlX3NifHR2cqI8OMAE5WuvvDw3O00teXJstH90/He/8rXHHntsevbkK6+/8S9/5VfBbhywtoxUR8gMVdvSB0IZpARS56r9zzzz2Mbq2i/90i87/f9KdXR72/UPJSIAp0QcvcBBXrx67dLVq85LAOiLO+PNrc1BW1IlO8MdQnKVg10g1FAIJrPboq7TcAqRBsrk1F69tV4MJU/hcGzGruhGLGEsDVxPkhuStsGXERAfIDPqbWh62tiHM1PjLh7A0DPRODLc26jvjtUGyPFoV4FoP/qZTwFztL61N2cetLHtwnQwI0pEBuEMkN4BEEOMbDSNoAhBADtyRBwdSPMQGRUswm5neXWZhtSJk3NGGfO0ubmOXzz/8KNUVwlXh+3/In/GRuWS7p2pUr3FndhKghjxYohmOxV52oQWUbAB0TIYC3KIiUCtHHPkFppKb9XplGbz5q1bdAgePv/oG2+/oTI2tpVLzcrATc+GxRU8a/R52gxWSQ7HZgaiBeW/ub0ljumKURupjapGCwJLIhyB6lsb31lZJ2wOp+1MA/qqcziHiBGFq5evvoHRPHfuE5/4hLnUpnAVO7TQAmQaM98ZKN1LoFcdrm3VGwPDDuiOb2w3V5cX6frV3Fk7MGjrmW1eK2LbPl8cE7Wf0TM5NRUb6zA43s0pIksj1s3eM888QzV6e3WVFHeqNFRfvHFpY/XZp55++vyTlLCc4nX55u9+qbm6ujk7PXPlyiXo8PXXX/7G1//VyRPTt25ceurpxz7+sQ999JnH2/tjlMuu3rh048Y1ImLGTJYW11CRzhkkYa1V3OfMlTYeuvhnoMedJ9q+Tc9ru7G6wZIJVcchFxDpbTZAbNYYKbIBNA2bjab3yTOnn3zmacKDJ59+ujJa+ye//M+vXL509eK750+d/OhzT/70j39W7K3m9eF+V7/vWJ44Xg23xIFyLJWx1w3WF3X3sFtu4gX97Uj5IHgXJ//NFw6WBfcTro0FFpM4QpLN5RipDMisJsgWjo3FErYn7RHDZ6GcgjyNg9qxxJCfgRFMQw5lRipmepgwtdEQ84qcQOhdmKJ4fQDCK1byD+opkFFUJgPh5Mm4P3nveORodwR5SQD87sB4D6B+HweOZRRsousZlHERNQBOyEeLlNFSXZF6IyTJqfsjz0RDdaNJlCPkwqSJHNNHnW0o1NBiilQx2il1qnaUltM84FlkW3hyxOK18Dwggz9KcGiLmiU5aUys1BTPDBqEcHfVQ0iOVnjuSn48vNsJ3V7OHRXdElaozHCLIzYtCPmbzq3iCEPWCj/ZHEvEo5iYBi7y9D+VpPTYIvJuTVB4teMXSC3YX8g1x6IOY3tOPpY6nVBySIrveCtoNw4fkVb3YiJxkkB0kKv2XFdXV2b65hv1ulvHL7578eMf+eDU5Myt1XWbOkSiZCYLN2/E0opzn7sw0MMPPfQH33mRDZdvf+sbp06dgLTglHJtcnF1/fuv/UtiZNpb3/7Od//CX/gLpZFKeXcPYCI3Jw//yIdfUNZLL23TW/700w/Zbvn+0uLqtavUxJwoRAygEpiSPugb7Bwe2E2Na0Ibh80OLmhjv/IECFEu0QiJDVIdaNbhbVjkZ9YD4ioP9TsH7EgFymFjq97XaeTR8TzqvwggqM2dr/+zA9CxBGE1HneH6KCqEqAh4JHR8xQfkg0Wpu3ATO9TT5x95qmnP/Lx504ySVAuo5BANHL1/+q//C/c2f7BDz6LibQjYN8zFi36NdiAPufkZRugKOkx8kOU5lOcscfyhgG5AD0hgOKMc1/v6sqaXUATIhCd20Sbuzbi6fba6nVNoVuk8B6N5s71hUW6vlvuTWK6wf0ADEftEnKYD8inkBdCkPKGg4mfwUZYDOrdZYRjpAS7rG1soXVsY9y4dfiL//yXf+Yv/exP//RPv/XuOxp+Yv6k6WQvXybOiTEAlaxKxBWn+ioOyfT26c/a2LiZCWfoimBuXMjRtsES1dZp8hkbc01WdXIKKz8B/qZ+DsU6LdcfuYdX29v6TSCB9vTM3OTcibJLf4nPkia5EmknSCiCRRG62Xv2tXvCoMzemh3cserw22+8/uI3fu9HP/nhkyem5mamGb3X+S4eoXBJBL1F8OsaRAesSX20nD1C1kz6elcWFjZuLbz16vfZmpoa7t+4euHG5sbB6o3+hcXp2flTp840e4cfP3viG9evHexXN7a2Xnr5ez/2uc/+g//yP7c9D125lO7Ke28RGFZnH6MQAMU+/ZQb7z++sb7lNsOVZXdE1xcXVq0alomsIQIM1geRELeutpnx1yIC6KHyYKUWN2roEA0yW6jIUuFwplMFoGSddubkGfP8ey+9/N3vfdfJQJa23Gr32NNP7zXr7125ik51QgrxgWomPSavaneWErIEz2O20FhmGXRgaJfmWtjCJe82a1naAFnwvoO7IThODuUesk9dB64A3VZB1qo1n8SNOPEwIoHXTTiXOpO49VJaHmIUV2viJOOACyQtymiOOeamoFXzY41+xg6a9byTEeVsSzKmQWTZdSn7rv94+NH3B//eHRuQTZuAKUUXkid/N+Kd5T443z/yl4RmU+pAo0U2hQ+u1Np4pj/14QrUK35OJDD8ARnC5TgxPIGMIgT2jedRvikH2DkWfiiyAPLxfKDL+fucPNFR3ZCjDO+McPT13vy6OOruD0Xyuz50EbC5bv0XkXi8FlGLcCHHoxURcuTj0fKn45kUkbMH+ACksKT09QMRu2eXyYOtei2wQKoMaMkAUrpdK50lj3GCrwNQx8kJuhFRmZ29NouuZrrSQ+iY9O2As5yJ5RHrIKHGZJbR5XiNuFKW4mbQTkhX20uWycCVd9758u99LWR2/f3vvPW2yjS2m9ev3nBxJZnSXnv31q0bVhF9SosHUw6kUtuzyef6PRBna2OV9qPj3m23J4zUllbfZCcImL509SYNkQ995GOLt24sLU1OTIxjPmx7IA9OnZj7+Ec/2tOq/4tf/c2333irb7B64uSZZOQIw9g/Nn/eflrIxMbGxsH03teWaQDZag1DUM7+azAVAwI127x9u/19cHMn9J7dLAw32fxC79OwabGpq8O7A3RsDDp0vs3Ojo6iDhOIJCiVvj7nT/WviPoTv5spfeFh3CcZkQE9Hn907qf/7E/9xGd/ojpSnZkpq7Pt5/PY/DNn4B47C2gO523oXjm+q7tCUaI/9DwNUG/YHeo6SFgpeQFRxAgpU+wFJns3dG+o1w6XmpuHjfaunfHtxg6LB26XojMZxg/cGbC7P3gwNDY+g1K5dO3Wa6+/c/3WFu4mrisNy2hBBpN9h/bLQeyJ0kB1mClEjChxpzcJHBju22kRBjSh7sMDKNtR7pFR3T/4/VdetW/pkK/tUHbjmboy4jjarW3qZmC7O1ujukmpWV/1U3d3ZY1ZvboWMal2UVPX7Y8+/jTu2Vkj1qEhEk+vws0lzzxL87AEvUElb4xIvGWei2Yab+JqGzv8lakJX8WUxGLRmSgMEP9Lv/8l7PsHnnz2Ix/5mL4kjFm4+k6lb/fX/9n/+OwHHn7+mScVWrI1UqkQDGg78xoxGaJkMqj2XnN3azUEGjQDRylh7+3MjAxNDDsW3J4YHWwvXV7e3Op9+NGztSEX3PzUj378lT/4dru1OTpa+cKvf+E/+t//B5/41CdXlm9SCiO+aNU3ZsamDyuVS5fevXrt8uTU2OOPPwprlsulM2dqzz7jDK3j4mNT0xNIxqXl67cWrq6sLnRasYguXboEN2vT+uaWZjL4poJPPPbIM888R9ytV5eXVxZuXtexv/e7v+1Zb7dXbX/MTD355BOSuwH+zNzsbnP7xe/9Ac7exQXV4eBojWB/Xyko7DDJ7KbE9sp6vYnyHxianpp1csiuSsx9FotBCSCarASGTi4kNUm6llkI+9Op/70FsoZU4xFLKECl3rRWUFqmeNz+W9LQGospLMG1286g1dmORVEFDnZzVL1u8EwJ8xgvDp7FkEaG2RWe+74exXoAO4eDL2J0PfdHPFF5LhjG+7kjxunub2Gs+/7uQR/wVxmV5CwDI2aowpOaGl+haemRPBaov1SC/k/yy6B4zHEqezw5K4va8IiWCw18ES703GIQ80KJ7A1WUADZ/SE4WKQ0xBG58OSUxWvhyeF//GcgYMMvXy6akJx8hXu9q4AcJwfmyPyF5/7hqTOOejz3VzylMv9s9YNE7NRbB2gWhQI6kCKMCyKLwxpdxrhEd16jjxNCldbmlndaFbgCKDvqlo575swhDAnhEEcgQoYcl/vZdcACxyrDfu27wItNoSQEB6+ZnXWl2sra1VhLO3u12pii6HSxwovt6+/YtWrcajSBXpWEcoJlcS9hGApuY0TYJKQtQtlrp7+83WiePH1OBZvbdapbv/wvfuXpp5++eXPBorX2nFmMS6lXV2/euvnSS3+wvXnw0juLpZH5D376KTJvC9K5dBuSdK+GqjW1J38vX716c7+yt7RAuFlq2fFzVLXdRx+zuWUzD0Ky8KHkSplOI4EXTRGHiPfAlFrZKfiY8Zz+KZ7Zk3s77EulTzpTOEaHUUZ+/WDWixMfWSYqDy8sutuu59FHZ3/u537uRz/16TOnzgKabkhz5TFVh/LwuMvev/CFL5yYn8MOsDQCpRtcVoVgYgsD3DQkdhEUlxaJSZHng2IdzsCYBuOdSIiYilCmfYTFa+1yeQyVQ7mC/D9MOtDxcWqose8IbMPtsxdvYp0uXbtBbZwJs6fPuaclbkvAJwYZktaf4uQGq2kVuAlzu4HP/XlQHZG4+KAtDSfnwvHHDq084/KravVX/6f/iaKTHmBuBbHo4DVG3GVZqgGP4lPhY6jRJzloKK4OCFZzCMMrAgLHNjl5UtEcKkdWgTeTlr5PqW9D1CS5VF5NKrZA/GHXgUY9okR/CqICFoAFqg/T+7hg924NH1YPzj1+7lf/5Re/8s3f/4uL137yx3/ixOzYWzv191797rnpGsPWe4vXl9cXQtmVPJpea2//5KMf0M8kpRh00yyOGVF9aLZeeOLxGxffba+vTFeGJqkZNVYrJRrRrbHe3puvfvNwa+nkw4898cwLTz925t2rN+hyXb566evf/tbP/vW//t//t//wwuWbe53tqTE62ux5hX4GFUlMpYM6G6srrqtAl7qouFwZ11gETS3Ms/bBzTNz0+MTpywKbaeQ8e47F37nd34Hg2h/92/+zb+5ubHhPC5NCxGMFKd7p0dHENlTU9MWIj1kt2TQvBuv1RZXFqsDfZcuLbsvkBlCRq1rg/0SVl3/YP4OWCU0z8OOk/NcTjgtbrVZcC65+Ng+vPPUZGIxW3rGLBlTPjkUIfYRiDA/aYMlVi2wrumE9M2YC8GPDraXYWrZVwkdqx3Hw9hAjsm5bjdia8vBB7tXaHoQ6WA4thjS0Af3zHXL6uKSjHvU+Mhzf/RpydzfQVTpQxe/3o70gHzsvt2O8wP4ulu598TUinvCUgAp0xECTgq5KV487AtFBL6MIgMHh6Ah3O3cki+6C1pIQEmSkC0fFQfqp2JioXOJKiLGC9YBROlCmGh77pB7uiUljmocZXjcH4HHmlXE4Sn8Rxkc/ebqHL0Vvw+KH4xjdqLy5CdPakyR/LYnxyn6qPDkGMVr4ZFpfIoc4ydFy6UEcCd78yVgPaVCnBsIDB4dY8d9slOjc+FjU9J8xX2GsycZ6pNhoseg2eiBl2RiUxf446xVV7QaNheFYBpDzmkQaE3Xat5jMTvQwhCBerGL23G0Nw7uA4vWCQC3ubpMBXSsUplwtrfPiVaXglXQA0naFOrZslI6G3tTkxPLy4tApMs8SMM6w5RU22SMFj8JNqsUl69e+W//u59vNRuVMohMbWfYVT00e9fWV5YXF5Z35/b6J8fmzozOzdHknj1xGg4uV2ub7Q7Fsw5ebXBgvnb68eGZKQYH1jcnbr61ubrEYuVeq7/Th0N2+hAtAqIOpUt62BDeZbRyqDcQMFqd2C13v34+7vIACUm9mWTCSZ+QZR+B8Io2t3fswIasGD6HTeUzMVEFGbG/xogZMAAFuIM/9NtIpbS8sAhd2E3U+ZBZ8HD6ncoNmjawC0vo1obRN3DdtaEaCfuGRANBY6uOBESGYJxWKbE8Mv7ccx+y0Q556jomONFm1qMhnnSwjM374ZH502enTpx74SOfhjWHSFrDznYcjgJR7XCmVmdTIbF7CgkhLEiMzQEMyhTjifY/2i3KVgtLS/ZT6Rc/8tjjX/7ylx2TcH6UKtD5hx4599CZzMWOjIXesgmgkuabakjOc+r0WSPO76tG6YGofLncdP1gAAcqKKbPAM3lkWpN9WBifaJuooHd4sSWLoMVnZ7J+UkRzFBVh8uUsHBzQelUrdIyCelOtCSIiZ6P/sjHn/3oBy+9e/mq41/XL/7Ihz9c2vnR5bde+sCZ2dMwXc9uY3k5Dkq5rcfFA7397qKmOjZSG6+NT41CgWOT8+fO7p8+5aaES2++vlffOPnI2bnxkd3N1tBBc2a8tHV4sNjaXr30BmqPEtxHnvvA6vb2qgM/O61f/KV//vyHXnji6edeYs+1ViMubu/sN5pLkMfEWG1kJG7U0iGGUgdAq3MDJdJyPXP1uu6v18ZdilzvH5yCkKxKh4nQczQNnzn5zMc+9rFvfOMbELAuNb1RPK7yJN1B6VYpVfUNNrZDzt/XLrGE1Wk1ltrbaLRQ2y8N7m43q6POUxEDWadDWX8hqJlSBWk1OjbcR/YzVFqwu9xXItm382WSkpqYMNxB6A/gIg1I6K0Tr1OXj71iFy0BP7gue5OE0WZ1cvY0jL9dsJ5+404pGgPe2O3f2GzcanYob5pZjkaGxW/jjJKnBAfOyFw/cCZSngM5tz+5J2B5DNncxr7HAqMwWCqUNH8IFxP2vu4BH9wWF6UE+oxkJnz8wr6GCCCI+kANSUoRH8xqncMTLkEnr8VK0VeJHsqfc5QMTALbpiYX9McRYRFtzxne1fbbmRz3peGI+HeNS/FaeI6n+iP7uwj4fdIrL/fI8YKPB97ur1TpIvLx8HvztzKjWw+6+szQHhFeKiIGkif5u2Qgv9yOZ5i+347ptRikHBMcHOg4khToJMHJOI5mqTfW1rEYncYmLOXYvLIgiV2n/g56x8fG5ueDX1k/c/q173/v+qUr9KQGa8GdWDMhUx0cJn6G4cUBQIGV+va2cQdn33rjNQpW1Jsnz590m4OCwPerly/T3/FKv5RCJLxL6H5ifoZdaIzQ2OiIa3CaYx+7ePEiC9MnKrM4iP7K+OrW1rnTJ5jTPRwestnYWxmZqs09NXmq3m7eWl458e7g9WuX1xeut7YGGwxO7jRNWdvS6JKQ3rjjnd2pfjcyoEHaays77UMm+jIj2+2iouuAG1jEMyLA5KqIDArOEy4f2XNbfIOp+rAsQWOns7PtpMwHPvCB0NYh4U9jBIC3t+LiMLz+WjL491f+ys+ykg0sEktE5gAVPKKLnZVkQbFa3iUBDM2X7vzuEq6Z1Ua8x8VEEoYaC6fo06fPzM/OXbtypVIeDun99Bw6xCdc7OT0rA3Ctc363OnTTDWFXmsYTKbDHJKP4Fpi5J0pssccl1Hu2X8wZez+xu1JDEnXavjsTlTVJWqlkZGZufm5U/2UdfGv1Gs/9omPU1k3sx575FHD/dD5s6yY2e1Ik4280QQgHQl7jjywNWCK8RZTuycmJkWD+fLdWSKonBB9pVHimFF5nmuLcH7jKA4LPko3351loqobpfT0TE9Mm04yCTmB0+EiA1qAWG/v2sYyqy2PP/WY6g1Qje40zpya/7m/82/+s//uv67tzI1NT44N9df6KoNDZUkJ993njmlcW99whVfvcAWpx7B1tGinbRv4sfPnR0cGt9eWKr37rfr64EG50T58aO5kp3/o8vLN3/71Xz3xxDPsotCDW1haHJ+YWl3b+Kk//+dffPHFyxcvbIyP0f866HdNZGlu5mFq45hDOPXa1ZsOENSqKNUZauTqnNtroB0GJkcXgr/XLUIcf2L2+6tf/apMHNFG15rGCFyWgU3L8dpou7Fx8uy5zWvX3HZzMNBiHfahh4L0Ybh/e3nJJNlYbiIHt0x9BJAMR6rwH216rBu1bDsvTIkRVY5PzdonbjMQVQ89x1g40CPyr7WVOjlMJsL9JYQnYs6RtcBngdXUPuTPoTUYDgqJabaHqY5BBNVaO45Quwaqic6DmjU2aXOZf3G6DuGimQYd9o1qORFEEB3wJNbpn4qL1ZZd4ckIKQJ1RffjD/gTrbyve9AHhQaCteDNQD8BjcKje6I+iTHrZqgqJgN3vAAdyOWQ7LszQhE5cuNCkpp9x5+pEx4gbj8er+svSrzr24PC74r2g79S3YtDe4SzSDuEipSJlDBneKG93CORYSz/EI1FX6QuuMMTMe4fnimR3CeSdDvHBNernQPKoqXVxkZpouoAzGpza+JgkOTMwb++fnpLoXzoNC/aFzeQhKkqEZtvuDULmdio1xmPuESWHImWzZ5bBWlUO8KCr2UL6nDnoGWbLzSuYyW0d1sb60sX3n3LlegUJKcnJsvjk6uN/aHxkwPjc7WnHmPplW7z+OrN9f3hlWb7u29eurYehifn5mZ6ekGGbevEH0s3YJAMsfBWEY/ra2zyAhpPjpybd3HdeO0mSLC+dHZu7IUPPvnomVknOVoknLudNVcmtJoOi1CbqS9vTBzeOj+wU3e17K0L/XvN4cP2icGB+sWXQWqsp/vn20w0NTYPGnXaRyd2925d+k0opULJ9mC3QhoX9pVjONQh9k/3WtJZ0gm+92PN9vZnAFdmKnr3WgNxVh2P6egW8aNLKLKGEu4Mmmq7lBF1GfhWNLyqqwZYvW35xn5NUCrt3fbP/NiPnJ+Zqa8tkcT29O1utzcGhkap0CDpgwjo37l4cxF8GSyPyMZeKKRiIM0cO/Hc4Y4bEcJuMvClzpxso+L5eScVFYSPCIc9t+qHfRPnQ1GYvh290+o5T3wriBVSkdro0jbepAp6wkgsIzoEG3/JsURL9MwbqVOGkWd6VSzCoHd0GgXhZMpSkDCDpifFMVUdGCvL++wTT4sWp0ZKQxdurR32uO1R3QNSZ6raNCS3CBhaobgebngoxiIsPMp2oOJsWF44AB1PIOJ0PUMG4GKGeCc13wxH/8SeYrJ3TzNKR8HoKddeu5WqLX4kUf8jz1j/02ikiem5W+uL1fGJTTLwwbGzP/54/3de+qdf/62P957/yMMPDWxs7q4uPHPq/Mba0uFEpMw2Ww8o7W0FrSOEQYaPnWS1SBEhFurYPCtPbtntHhtcbW6LMM3AdF9j5+1vPT/UOn9m8BsrcdrgW1/8hU988oVnP/zCSxevXFzafOqZ558e3swIZms1Dhky7tkb+ygHtZH+7c2b9PXck7KyestK6axtLd26hbUtjY1RSNtCraw36JjViJcG+1r2eRnODAYRlRnnwlEtxLnl0ergNuHzZHN7BQM9PjC6t7y9s7m5sL/q6rqbq+vzs4/gO68u7+CbkXIHjYWQOe2ZeTuj6O/91UZrZ2RkfqBaWaf32XTWeGDosNLPzKRjUT37Cz2osqCWYuLCx8npcKSA0VMNJ4C92uflN8lRc7t9IW87iLloCoRchIZI7lU9aXAlTLLsSHk4NLveQr8OsNLedunzQKmzV7cpbgomvB6jLAWAFlx1HNg94uSOPqTfLqxO/jsew4RSpod1g/aNp92dWDXaAcwbX1Wxj+vJz9HB8+SVRLV4IklS5I7iJTxKwi9JJ+mUpC8/0KOXlC7jePMWv5U6hFTaNh9K24ZArX9ohAo6fYz2XslouKgYOqL7E3OR2ZaQJBEyONtlEqpd2vpVT9VKFaBHovLahPT2OUTwTpTHjWQR1wnzXpydv05gmzCCrfBwKbdcnfSund0cU34xbtnds6eeoycwchTn9q9xv/1yP99RuUoJ160NX/6Qxil9OXrcN1xgjll4cvTitfAcZfPA3yKfmNzpdLuoRaB8oiePHuGJYei65O/WJAel7/GwNnBCMgy4nxRN5c85lYsqx2K5VddrNcR8NVuMkH614pjPOMGne3ZtPjlJaVBsv7piaG15EurCCppMktH2JDMjLO1h5banDKxSYOaAnmtXL1M7dUuARWmriyU+nNjqytJ777zdbtapzahMB0bd3Iz7CgNnXKUqQgkIfI4LTQeGiOnsJCHq6aC5r8TuU5yDiNUUxxNHBlaiecnpJa3jeDTXE2NHP1rDt+tdTHwY6iVxCQ8y3r1J6mxq7QSrqVvYQNIc1h9dPJ5WnSmPfUxHtEAxVuFAFtlKjoJ54bnHnA3Vz/oWNFQFkZUnhF80hDy/+njq2/wUftwxB3j8VZzspJKJZwzSUVqfuqN/1N6cVjguJ4V1H0W4URDUzTRNJJ+8qpvwnLlqC8n+OAScnAhKL2BuESen6hYTdni6eDwnF26OiZwzkQPHnz2+2l30VFzOIXs8daAnlxPmZ7ymQA/558x98goVHX2545fx0RiM3bY5vLfTZt+qXl/ptGp/7a/81ZlK79KF1x0EenhiQrffWF6uIKrsgEZdUia4QjA69uLjPeBkFIW2iMomPaOAyLlFdC18w9yzYTRc7f3sZz755tWb77zx+sqF9376z3z+rfcuvvrupbWVhcXhulUQEzs5OnHTc7PjU5PGSy+ZzagKr+IoguFVQiZ752zAhbXIMEUSKngmk61izeJnYt180+36OXYNbGTQwRsZOXXmNOV22brVUQhKVT4gyLUb11m+I8Dwqu0ntAUXwcY7vEjnne11vbW5Odzr/qYYJeMe2MgqIykPg9XRTHUTn+PnDIEF65nDeXIDVcwVI/nVJ6+SeJVtTpjTFv54DWWiMJboVBKLYPxGQFdjHwIFWIWBd/3F3QQpfh6q43nc7c8xc6jsuIRE01Pux6L7KmvicHK7yD3qE1WNSkh1O6H6BbkQPROxggqIOhWzMwJ/CKdz7oqtl4QIzy4VHlGO997Rp260HD8i/QBO2sj+jtbfTpa+3n4tfD9seJHwB/Tcm3+IoHPiokfy64PCi8g5glRFTJ+K18ITnRCueHaLS4ExU8WMyLBN4ibTFOyOs5ytYvOTJ8EEICnNh0gc4MnXEAklF2UkJ9AyyBIeeQpXilUn3LLZcJwXucpixUE/a/lbjd3Baqd/dGZ0brQ2MToxOdrY2txaWVpfXkByj470zpfCjKUrBsCn2JIbsvaSUvW+C+bCRbmxv0HeRLPLceFbVw4760s3rUb7ykTr77z+fbRecMptCrSsLPTjFdmtVNkAVSFojGWIkAsbXskIBul8YIJoYGh4hG4zkjAUwqyELm8X5VoSsXiiu4Lb77i3L/Yg5WxjKxgoxvpbHYJg+jAs7yMMwkrRYW/TVV8jo6jBYLlCdr0fPGPYljeCoRRNcgbYhYGNZBBHMwf7Dn7kR34EByNcKPRMLKeflaVjPQ0iOChmDkks+O2Vo4bZ6XxxFJFd9ksrTxF4hBeZCAk6ODn+XEqOhl/iyX7xs5NcyH3jB1hPVT1eW5GRaUd1CXaniCNazlygzHPOEXJEs4qQmy+QVFv+4tAp9cjxu0mKCSteqlt+isOT43ge80T9c5yiIV4xk8fipASpsU7c+CXzp8Fneux2yt/51mu/9ivf/8/+0//TyfG/8Ru/9D8uvvPm3viEe5zqC0tMsu7vb8hNyZE5lGsBRaOsEed20hecRBHm6I5zcdH8OC4MY+CNaICNDAyVa2XaxK3L13/zX/7zf+s//I9/5ic/d/Xq5Zdff6U8gwYs2bHGgGaiwawwJ3Vy7iIec8N6VBh6bnnIJjdRT2zS28qhOWfyi2+7h7KYHvak80gkgySlCFnqKeODRbD9oReofJhMbufUP/KcPHHCZjPCO6yfbsax7DhjRVvTSYH9pnI0WjUcxR0vjfU44YCsCVZxD/8atk1t1rIdl+ZzfkZPHU0qHsmjSmkC56xcRSoTC1lMDVGH3N6cKnVod0KKL0+7RlaIRe1Et8uQ2VSNe7uDgwtIlVyeMekZ4C6/5k8ZaUZQllam0G5gjoF55IGAuzg4IVchuT5WU8QOfe8Y9AjnhYwDfvmY4UnECII8UkV4TI/bcPmO4iKLP8xpeI5SeLzmzsydLFzf+C/wuBMtfeo+7spEaA75QZ7HIxf+5MndEHn8YOE/SGn3j3Nn/t04gYC1ufhW+B8ULl0Rp/DkzIrXwhPh3W7KneV5u9fSxO7ODCNhZpvBqVyBEY2flNACCU+avgHiuFRefItzFcHI5rCciXyssez4ffLMCNja4AZLtCf3KdP6hPts7K3tXr70aG1qp7TZGuxrbmz07rWnxyqjD512FWhjo85IZr+dTDQygAVxJ1O34EXIDoPghL+iKkEqRCUH1pfaG0sQW7QFN9FOlg7o5VLtRjbgcpXLyKJVDB2ubFxLx6Acf4x8cLoypPY1Uh7RQGRy8Kq0iqQhuCUH36VKEx0QPZL6RHN5ADWwVKvtepJblqqSHzqXaG/KCtKDnb0WQTT9TPikc9AHmDkbFBfbCKQyGlqitrp6htVswHX3IdKJJll4hmZ37+TclA1gPUkwUK6UoeFSmSmPuBdIfTgd4qtC0+B073ONXkngrAiP8TwCZD6lpN3mgGvZCSwa2GXHUrYyKfLJwF3Mo0RdSg6YznUuYub6ZASfMogKFAXBDkf+TDoEklFlOyM54V3P2M9LlZFKk/lzE7yKWRRaeIxIziE3KkcTUhAoOVWO74n8KEK8ZickiyJ4cnHZ4+kShXJppMOSqk3Evv7ZqUnGOL/6u7/zG7/81E//hZ/8yIc+9KVLF9++fLHy2JOd/oGlTrMnlILTojNdjWxs33ilHReO30s8E/w1wWPakfolpzKaiIckKNRFI/09n3j+2Vdff+nS9198/rkPjRzuDu02VlbDKqeNcRY/KHsFctUDfuJoVrCq3lmicOMQAzVsjEw8Ppa1x0Py74CukQkO2JkpIxCLAmalyaSrJY+FTKuvx13IzcxnyzgEUUSaaN9GozY66iR6RtWY7zMPndt/bwtOQvVSfkdCWGuyam3tzdq+GmH+ruKIeIeiVBhNC+SaTr/n5gbYyePl6ZNnHo7UD9FHPMrl8qecTEwheW7kmDlVdJnx1X9ZurDv3qgduz+h2BVIUN8GNAkkiOVI/Cf0CGBEWHLRzjwu4UkwMkt347XrApXzJkQb8OmIB8wI2wDKJJ5pmSqOGngMaso3noqOV880D4MHVpR/8ep/f0/IhO91uaX3hkdhqVVFhOwx2XiyX6rsT3Mw1mb2CNRpOc/jMe9TyoODcs65iOJ5ryflHxW9u6CY8+HuDs+h9zyPot/94d7kOSRE0MW3IlFein9S4UW2d3mK/Hl0tInL6QN/QXInIZwkMVQmBkAXW3YQagyP8EgTE9d4dWGiAC4WRNbwkm9aVJ5CPMWkS0X269guBUiQotx/CBttrK186Yv/wt1BwLr10N5cbm+vD0C6nf3Z8VHF4c8TfqU9kHxubGiHjWWKkVF8HOwAjqNWDPyk0pKtgwGXCzumG4BDxRDknnkRJ5hGGtZhZlgqOxWZGRlAGcc63a1vLCuXHm+cZA0VIksBbu5pHTrp4QsXS0I+YZ3n8GArnRZ1QzyAZWcLxEBzhBx7uMomBxsMugCPPsDArvh9g9t0UVgxDCi8NxK3ObgpPBTGhzHi0f2BUAOI0OpMvCndK2wN9sKFa0x6hXkN/HV/YGKgkIsGJiCV2Jcu1NASzidV5WSr/4WIaUTy01chZInRpiNXxEdz5ITFM3+KuiUnOZd7WICaiMAjMMfMTxnnQOEpXdQhSkPdpJgCDaRsIQlJzIQifs48JwS/c3JP0STJrwVCzeE+ydszZuiRn+cPdXclz5lIpVfvm7bR3KKATjDDCtx2vTE0NX5iduahEyd+4wtf+NAHzp6cP+Gawu997cL1qZmJSm37sG8sTnqF0xxrIurHyRoZl+oJCURIChPM3GZCMTsEJBorhBi5zQ5buWSBjJX658dGVq5cOP/CBz/46JmdzZWt+oa05oyJoSeVwulA3K2hCQScTigwU8PDMVdtipNF59bpLTIq6PmRx57Q5ExmMdrjCgWHiM9VXDtUlaFeitnJUWBIDrm4OLx44fIlxuzGxsedGbPkHPYbO0Cj7A8Nu08MTosdBKedNV0twkBP2K6yz5MGvVyirsB0pprIv+iB/JoLFa4tuR+yHz0rRENEyPNHuFfJebhuu/KLOWbHJ8n7aGQxOiQ/WDLJIUzXoxkbx1mjGuGSSDzjyxwgmvEKnOjfUf7dT87fxFiGC+ybntmfIqdAqDV9SrE8Ehi5HT+KQhd7RsSYExEh14b8A7w8SvhD/B7vhyJZDtRpXO7eos+zJ/dZji9C9hRxinzu60mZ651u/+c491ajCHlQhPcPv2/R7xNYFFd4uiLoPF1yyuzPMe4NL3IvPhWe48n5u+HdKZI7Ig1rkUXM84xGw1M4CcOZAcGEJUAW39KqwEDhiY72aYTCRp6GR4rssR44heRXT6/AvRDLjzqVVevONpYTyKbsuQLxjuXanN3FFVKzGeyvDPTOTtSGHNmzl1uvy0EeiRaMSRDqjEnRSSgGMi08gNhRBZKkMDWrJp6WF4VpSgQiKB0o4UlZRVfweHJOyObq7SZcGiWllkJI5mUcTdQTSk9GyuWwEws4qiGmV2k9OehWi3io4zoCA4nY0xSttVtnsYFweWTYBX49zT31dyVM6HwQfcsI1xon8tS/b0jVCfxsvenOXARQoqJO9nzwgx9UolONcWtYAjFIAiwLRRQ1VFWBnFRe9bOKeVWfIjDW2dFKE40/x+TnCgRTpOIJf4oWZhI4I5ec+OB7Shf9ENEQErx0XI4QcAGbpMgxi/g5JGcV/Z3qGZ0oRqLXfWJEJcePxkE9qV1CfBIxt67IUIjd9PxV9OzpvibYlYsonj7l0nIdujHVM2UuUEh2hb/on6Mv3V+6im6Uc3PhaGV0sDrivBblhpHhYTZtvvn7X3vhmcfjWoVy5cKthXNnhmojtep+WJhSggqES+gkUSGpvaExl6VMUTVlJFXy0A0TJ067AeTWkxld35yqlBauXS4f9K3duNRz/fJP/+gnL73+8tj0Q6ailrLAYibBuy5egOcQKDhdeC9Kt5Mch917Vzc2IGpLQ6epC3xqjGMm73TeeOMNSwD14KvlI60Rx782OiGKj/5PNZdbxG+12Gl1+8Xi8pLbMBnLxNGqPAPp5cOerXa7cjiIF0Ruopj1pCP6Czdvju8PjB7GjgzpgkaZzM4/o8pSr3QJxDxkslJQt8fTj/D8KcvJJclfRVO37HKc3I3Z76mgRPSheyOW0oPdDIyYpk0XKtwuKpJYpCrQ/RQrM3kjZXhseXQ/xYcI9ZsiJV/XH+MmbkrCk/0ppnUTGRz9RXn+BKZZ2G110lsWmr8lz52PXM87w9LbUX5eijg8usUXT7DCuOuJnFZPCswuJ8n+oodzNE/hhf/9PYrLTjSeInLyRybF1/zpeHgAlSNXpC08R19u/x6LfjuQ73iSws/TRcBi5PYc/5YzuCu8CMwxfS2S5EzuDu/WKDfDs9uenFC3ZlekKmoSBYGMjGG588uARROiLBITwTm5VyjY/xQ3XnJuZnYkT80WYgFzeQlZ1cZ7ZXmJHCxwsIV50Le5ulIbm6Bsbf2RNofaYK8rWJiJtzIp9Xi3bRJH13CqFMeTCZCAAsH1xlzCIoel2VhR+4RjYQaZE+6pGvC0PGyaColaBaTtMlJM/5Jly7g/Xf3rKxgEHtnoAg1SC9JaVZ1g63t2BtfE0SiNTchXlXVIz/h4eXVlU4T5+TEHouzAATQAnwsKL118Z3VpsTIcdjlAK5i+f6jaBgecqmLfMUqMJoBPoQhczqg05oMS4WKnQeZmpljOUyVgqTQUXG9cpmTHEfZNuqCpK1KbE4OYqxfjkYZGz+dvPGwYqb/MhVh72QmXVdGunDCnDUAA9hvldIxfh+Q+CTXJ5OQTtT9ajeoWCfN0SYH5qyrxSJFf8zNKpCifEKomcEXN+XN8SRSRyxISMzHBQ2lzbrm2mekpsi2a0GVlVMk/w2MbIX1T/9wPktzhuQ1NBd92Cb/Hay4ip/LKnnC73mZdUTfUpsZ3tuOmarTYcO/ut7/2jZ72dq02PDk//+67FyDeyclpIh99biZGq4O6is1XIanTzOOw/elfvvlXW4MCI59Jk62X6W0g/OCAAtV2fbOGKVd2q7Nyre+Vb3z1uY989Mz02NU9tiDDnBxnBnI58zAKvbQEHdOogE3VX7iNfEKnmNlH9DElC0TCuXLpzTfeZm2bWhabJ2Jm49vms9Niul3D1V8q/42Uyn/rxW+fP3/e3VMqLLLD3Kb62YfO7V18jxoXtUJrMrhJepMMvAz13VrrDFW2nHoQGMqVzp2nzs09nAc9l5KnRB7r/NWTy0Psax4Rr9GleU1a8knkJlrxNSUKKGLhABcJYhDoDeypXHzzCPIm6cLluBlfJjY0fU641tAk6rgb5fhPZEOZyzNlGHv6CTJGHKXGT3i67oigUGhw/UkzS8VkDvWarzmPo9hdsH30+sP/xgRL7rhH55gnxpf62l1fixLE4c+p+O/2FPEe4CmKKzLJEYvwwvNHC39AsQ8MLorLnph12eX33NqjsPi9b7jAol+OJ3lQ+PEMsz9lG71ZuBwO0KZJEsPvU3om+i8gXyIYA+XGmATHk7bucw45/l255cVjVXB58FrtpltsCLKckHcXgwzwgc4aOvboCGboKBEm7VA9CVv97Em13CMT2C7PD1g0ZF8Dg7GSka7hBpmFpNkbRJxSGJoWphrWf7poIDAlwBv6nymcKotoea0GBGlEfHOeX5LIIc3IontztwQXmhToBw6DA4hrqcN1kZAAHMbWamt8tOfP/9mf+PN//s8TF6MwALgrCwvf+P3DV512PdyvMToRFw/0D1ZGWFtyexpLFA3GwtAgup0WCvO81a6Wsu5XJaWHxumpU2oFAVfZmGaustnUa6ldIVEPBgLwSEo0OTCg9pFTt1TVWO9R8USR5EaJor05PI9UTp5DpIq0jvkcrUD1yV0nsvZ6iilJzi2/Wsz5NT+lLVwOyYXKipMEhSeCT54OaBW1k4+Y2YmoptkvPBKF6KXrpPWqPrkgryLIPFc1MG5yYmfPXa85W88cniuTX/OnHC7DnH9+yi17WP031mq+trLe1+qhdn/+4YcePn9u6dq7LCDS9Rs9OfvkU0/fcsEve1Ckx+4Hc/OE8QvmFrSNco0+Ks6/ROtkXawoNhWBbjTYNkCoF7gtkHntOKQ2PT62tLI4Oz6+f7jBmMV3v/YVlyd+5qMf+s9/5beoRzETBs9JrgmmjXlIJmz/ghKfDuQQiEg6T4Ya0UyaAzebGxZAtrzxxBNPrKytWhG+6slAvSUHt2uGwWtuu3nILrnchEtuorJbqTgK1b5cuHQxrJQPUw6Pe2EpSlF60jb61246G6wH580iVxi0s0JpeJBmEXmlazpz29VHQeomQi6UJw9EngP85Gc5Wv6Uo0nCEz2YqLTsEYGH4kXAit4g/DvMDzhP1+Mq0YgSEjR9HrHyoHhJjG98TZLxOJskjpnkCaXm+JEshaQlFtRh3gf2m9jf+I3Y6Tfnn7053LgHCx6JE/ZVVhSfAsDY8IaTbTeH/P5He+ZOkDZ5Yhj1Xu7AnKFwgXdlLiSH3/frXZGP5XMbONw3jsBUjft8/GHD75PF+wYV+YeoUMzoiTTVilRmWBHOc1fLRc5ZFJ4i4V0ecCKFRG5p8JMnwWvX9g2FoZ+QSjHMa8UC5bJ1d0noRe7SJySYClrSaXicm2j4K7JSoxaZJaGSY4YWp9dcn7xa5KNdeZFYw4rg98laZbKJYV2yKJel2GOSOTQ8Wh3Zbdd3tneySVim0xnSUx8MX3Mv5I8OzY9Ph01gWBKoZbXaulQNhZowLYfXdh2fUCZhXRhDZsJQlZaWmqRetZomhMV8H/VFXj1CdEwIig8dcEOrEoe7Pi7QW8CnQRYYOvB6bgVIof6qqkpDvavdOAkTiCB67rqnHxk3HC9/+2vvvfaSQJALMGr3hs352YlKKZYgzDGgSuTQfYP9AXJCA9MBjL0+hzucUxoiNQyOEFmxsbEKojXa9dX1dYZEdHK7ERYqRkrDAY0Tuy+ywfJUQxHUkD+jRv48LrkJ1phsDURsZqeZphUCPbOLfjxaZjyccE86t3oyN58AE6VCxUzrFARy2FtIcWMZU9uRRMwc4pkTyjkTQT5lJ1zMHD+2Do5crqqnAJsHoh196f4Kcc2sJxeou9MFsl5jZI67wFJhdAJV45nbIpdcAR4VlqrIn180T2rzAvNrkUqI/Iv4MsmVFEJTeKWxxrhV3LzrxCzGyg1dQUshKzuw25NPPl2dnBgcG//+G2+4cnFmoI9mAIoz4d/90bDNxvgoTnTIbEAmQrEws6rpoyTdjNPlKFHx3erAMlTU2mHe3V1XpxARTY6OblpKfX3f/4Pvnjl79rFHnzD0NnNu3HhXJfGvMTSDgw4ThbLggSuDSnOzJzTWPNlY33AUlyFoZkEReQ7cw2eNrW20oxZUyiN4WbZQLDQolsyWwXPXjCI4KHCZAJycoV7z4fHHH4+rSvb3XY1lxqqDS43ffvfdx8cmDwaGCK5pfpToPzKCRp88xL49LLePTrRcdmKnm/KDnVmsuUPIMtF7+lwmZqyqyp8/hxejqfOjaenQQR7HPF45ra9cHimenEoEgMlSUb4TGG4WPe/c+GgZMxDEoGJD4Bc6mOJHcRQkDUiSUrCVqd9FMk1iGzvuFyGPCAvJAQpDVyTmj0P/cuDCn5ysuLwIePLEU1qulWMXCblGDX1iOYdLucbcjlwU0/0Nf4GQ4+WYU9Sxt2PeWNfxKn8PnqKvOnG8G1SM02WeCs+10tsF6NAQCXN4LsJrDvQqPOV9rLhjXhmaqKJJYqoYd1Pu2Pc7vEX1uqG50j98e9Uu55Brm593lHTnyx3sQq5rfhbRchapfkVYdGIOKTy3v/1gvpzt8bhC8hTPgZFzzMg0USLIkojetnjMSHs5OZoxyE78I2/85vyPP3OFja5yDHBYBOwb3GXQrq/PJZ1bq228IRUsEmEXlQUeDGkq6TB7dbt1wtlN9vdsbHVwybBjvdGMMVKZJK9RTZPJJLRd6rl7GILoydkKW1fyYkHJaRG1UoeYFqmlEtoK63cwMpwvhg5SstoDBw/tHDijhCW24ijkRme40Wawf7Y8mukJAFwlQXL5R/JESMn5kDpsPdgC1EP/YXsEu97XU4aGic/jK5RldcbBJ7oyNr5d+B77Uge7ruWTDUCTuzFXUiebUCauGewTYsQYIeItpSgLokqiNoG+poZE6zLYEsjvqTLyyXGCgDpahJE+OSXmQM/oiGMu4E/E99DMQGnam3oxDpJGaHLCwSuVTF+76fnT95g2qUoZ33sLJ5IMQGaeHCKyhokk5xyYi8hPcXiAyKPId/zK33tO5Vl4ArKH2mD0TapPZCKm+DwJLJqruTOjE4x8MXuPFnNE03s5/24HHBURG5tkFbAbkcy+zX4SG8ZO+rGha9cb77719msvv/aJv/qXf+Sv/Y3qV77yG//qty81tgiBx2dmWvZHSwxUDmxvbbAbGXflxhkq/KBDaAC6IuWMFvMTYueYPCi1hLrCGy7mfGyvhBnYA1hTsvrWDk7XqVkCZwzu3MwMGbSWO/EDBMqETjOAq41mhWhO/0Ko8Ov01JTNDoQdhEr/zflsh2rZSYR43AoM4ypUwsnxCWhyezMk7YgSWDE0DV1oaIP5aJtJX+lqPSDb9sIq0sGui+5BdpvAyO5y+bBaoRTNtGXbNc+WcwhCDg8365uV8qR+VlaezHmkDFYeu9TqLgJQqEAxC5cT5qeYwqOPkssez5HRCYSCizbHp+c+9ukf++m/+JfsIrM5olM0RNf52mTo3HHnmCY97Y2F0Ox0ZH8XExy6nsQVzQ7DMHEwMgYgZh0elmA7iouTDMmpnm0riyKySVnFmo1l2MVaInPuxtRdnDZHVsY35kG06SiZEJsQOVc53NbK7gb9YT9FP6Q8u7HVLsrozvzwRYVTl6pVvN/TeznE8w8rML4fj3bcn9PeG/JHC8+p7n3+4PmHnC032FNGxWuRaRFehPDkJMc9x78e9we6DFc8u91XVJEnd6neN9FtRMJi5haX0sUYmYIxPxB6aZycBGLECRqOP5vCKTCyORpFabO/eKY6RLUZ+AsmgbF47G8IdLTaaqx0NoDeXgossZumuLilbNCVOXaydtsHbVO52erfgbJaEDBkFEgs7ZbIM4tJAVml7O61fvRHP/P5z3+ehA1Ah7qsK1cy/PzP/7xZbsVmbJRrGJjzgPwtSGkLC33ul6kENdATVnd7MITS7k63LnhI0SoDfQwz4er7ew4G4xYKLjBqXzmQHBjkE36FLrfLjdzI7lrcuLBhgElWfeJQZywvIkWIPchmwmcdzhdPRAKqP6qmLF0nN10P0mGFwb5gOChOA4vySCJocXZw6kkF2thpmvqLIKaGS94dxDSv+MUxtmqch6N46sMiJj+X2hXEb4gPU3Ih8i/SZk8RU3Llyr/gFHOqHCEXlP2e+ZPKc3nUBObw/Kl45oTHn8bw+GvhL+rfDUnT3JxlnFxVY3yP2P0cQVtyBfKzyMf4yEpgEcIvJGMgHk5Ls/OJgWNoxYzBC2BwD/c7rjuyY//udy9XqxWW1371V77wBy+/8vwnPvn4c8/+x/+Hv/v1//a/ZstzaMSlu1U5EXdESU4hxUUmbujFbYXdapMDPAeVSV6UaL4gpVRL3JgZPGZn7A6EYW27vg430R9wE9RodWZzPY6/A+Vu3pyamNRwM0EIpq3Taje2XfobexYmqCy3NzZZsIIpYWvCZ70L40pCdE0xmmkbc4lwY6RUVqjOga1df2RNuZGzOloTGGr/rTinZB6SxFgAaysrDgXHrQ+12m6pchgnfSCjXXI2LZXEgWmRqStuj25Xx8dVJo1RDJNpIAInhIt6pnmbP0VXHLniqzg5SfEUUrhiXuUQVoAwzZMzM/bTf/NLv/ON771CSe3UmXNuiUKskwI8/sxHCCUoSBOkaZr7qY11Y3t7bW3VZUruCmNQr7G9OcyKlEEJOQbhhJ4xAFHCdmtdVTOlGQR9SNPiTSa+BprVNFNFM1OFVuss8qYpoE8o2eECEsEF4nRdEnQnWCxA1B8aAR9lFL+5iwpPMc2Lrit6NeqZ+v94BwrMr8fzSfl3w5P/Pg/xc6FBYxyVmjxHlEWqW075vuH3yfyuoDvzv/3xvuEBBUSJ8TiqVvF6PPC+/uOBt8u50/cgBGwq54ip3OgFU8Ris2HTM8zqnVmBto6KBYbMW7ABiYixQlIRghdoI1QFiplyxzIQJzv5c5FPAuuYMRADmK63mqQvkBFBDjo+baoesJgYRhPpTPYN7gcaDgY8iP8+Zi9hU/u9LD+zPdTGjMYucOq6mOjJKWKoNH5ibobtRtahXeeAxg92ub5t8xRSEyFd+pfU7ol/oRgWcKJmcZwRUsNAAwKq0EM7Cnhz5hKjDNYx5dN7gGrYaYd2NcAoaYgI4yAUppk0OdEsdMSYoY/jTyGn1QP7TkyG8QhYU05BcKI5gv8NUlf9YxT4g7ZJvJQ+VZ28XOEzMSBgcA0s8Lo3GCxyRIHVE2LIOE9B8omVnxCwOHpYJlyBNaMyoEA6NyKa5JJweXR8jX5ILofnp69c9udOzvmIKBMhPEI4HmUpl1+SFBaB/J7ZHc9ZiFdNKwKjpGNOuLf8zB5+RRT+IgKPyhSvRSohmpzrE21PLn/F5+VX1SgmT1Qp6h7O11xnfjkggIoQdYA/cv1drE1FPM6JM3bGTLPdxYHh2dOn3ns58JhT3etrK1/78ut/8PLrH/nMZz766U9/6BOf/OpXvnz55uLp+Zn29mbPXufUzFSj2XI8JnWmjExDUyKB5WAMrTCLDkkXay0mUNTnkIIDGzKOjKNCCU2RegQjVPbwwtAbFAIhw6zUwdScc3EGkTUywjPWNtqOBebDns3NLawq/ArvwgthPCY5mBsNp+FwLWXJWOzk/Ay4Npqycr2iZWXJ1EZrnVIHVjNL9YnRd0RYV8fZYaaka7WJmbm4YWq7b7euEU4khSRZT+qtZtOdRVteqaQZwKAeSe+TpKeYPBHz6K4qfk315KIX0rxCvObX4pk9eez4C5fHa2Zqkg1PO82of0KCl998e31ztx+FnUw8mtRawdbYybn506dPT09OnT45jpQ/cWLu7CNPuw9G+ctLCzevXX/3nbcsZ/sn1kACGvoGLOutjZxUoh7WLustCc5jIoml8oaPTp0v4gB+fAOV0WhIjLglFMICZvxgdftWcgk0HJYPIn6GFSIn/w/6SL3UXUdFmiKT3EvH+yr3cF4y+ZlTFUm8pjxj8YbnKNMi8CigO0ZFwuy56zVncpSkm2d+7cZPQP54tCKHo1R3/BZf7/Ucz7bI8A5ocjwnnVJkUYQLLFIWgTw5/HhI4deJyZ+exjlB/Jwk5++Zx1RMi8oC4IkhseCDuOtC2BxJneBgH2MyJQdcFGVlTw6XSeGERIbZoX+HzXL2cTdp3s1MTZl6hzvs5YSExiw07+IsHdKendQeNmKJpoleQerB0Vqlr5f9iaE9ZwiBKGRBLL+oaJwBjlJ61uubX/nyb//ub/1mIvNDzmapQ94Oa9qJVpTVQiQXMiN0q0LpcyXI5oBx5BnSpEMFEyoGwU+a6O6WA1cIU9bYdw8fETIhE0KA0169ASSAW0SIcCEn0FoMubOVlCypWlcWG5ydMJVahkUPwFQve4lgyNcyw/GwQsk6YUi2Er2cUAb2F0i0h5JWc5wSgbqJ6q1eHLdO1q+5z7WVJ9eBx6ei54tXQCHHLzAWj5CcT15+OUI356AawllqgQBCMgqI7ikL5ZEPgZC/BiiJI55xeNfsyGMhlay6Li3XqFKakAKVFQq/yQRFKiGVIn1yOYQ3t6IbamgSC+WrkJwgxxQtAiM4wnN8HrKWHCEHRm7p3bZfDs81KZ4EBDmt2uUuEs1X2CjnkJ/i5BJ7d+NGaNRU0GKDA7TaAfPS6Bgjqa3GFtLt1PzJyYmdxc2NF7/+7VdfeeM/+ff/zgeef+FbX/v95fWNyiA7Km4C24ckjQsAnhylXCfLjUgSb5fN7Bhi4FjVkYIGlQJDky1f07G/r7Xf03Sm1Qphra1v8OTMqYmxSZWEONUZw0ofSlXxc5BubpHoNJNhZWtkapLt9fHRWs3wRYuMHdywuzcxOg6dCjGZmyVyFtbXXY+0IRoNLxdry42zjCDjkbMhoYnM+3qx3WdPn9G95q0daPcN73WGrWFHGg5abJ4TMumnQyKAwf6GbCUMg1kwk8sRbLLY5k5zQ9G5CF2tUARodMLRyArkvzdEYBHOoz9TQDxykkqpb2ujZZuoOj41NzHpjsiN7UsEEXENVqwrhPcBsfPilVsvvfhSJBskKYjdFtN/bmb6obPnJibGbAUs3LqBBYAmkS7UMipl8vuguWsTw8ZRV6BOUGBhaY8lsaRw7nJV4xXYNPB83DWGHNmO4QxcPMBqqsuT3Y0+jA82JZpk3UY7oFMSE3ZxXZ6+UbMf1EXlj7quSCMkuTzlAshzvuanzj/ewzlVzieHC8keMVOSKCKFdDMpohUxcyZFVnd57no9ntyn4rXw5PgPehbRCs+D8g+55fFIR83o5nz89bjf5+K18HTT3PWT4dQRFFVa/n680BwChloP3FGfmhWhdYzIiykCXwVuCsBD/myp3ptDfD1yMimcMEWop9EmpnTnOr4HpQuIzARhCHaHPdjApjJ2HgiCCrbQFUl44wZVCExAmI8Oq5GsMbtTxeEcHLAkZGZdriXvx5Qq41Sftl2kWh2ZnZ6EruyxseNYG7afFWeDTW62qSQiwIv1OVCydacYSCMEwpoF+R04/ARDpj9cGjOB+D2Y045cWtVWmPpmAAFqZCZLB/FEnvCZZcWOrnt1+l3DHrKqyDY2hNTaEnRPFGYp7OAwu6GtdEEPHIcIdkajAvRE4xLVhGvRdRoiR3thIBEEPXhAGsDodXc0dXVeSaKJgL0zmlzuc1nl1+w5PmHycMW4JPl8HinRiiED/YxFhMAHIY9Qq1AMgDnhZKS6zov+A7nd9tcfVwmJw3nNpXtyMRmiQ3VvmgyWvLaSPOx01bjUQbSYJjFTuqAzqtdFiOHlQj6bqsefPcWTp/Dnr14LZYX4FuKK+OX0cDcHA5E6Wh2FExHkcPUhV/YUKMTGrWe0IgkSskcI4WxvXD5/2IE3hzFwDefkRsbHNxvNmcihz9VfOJ2JkbGaC4AHBr7wpS/9b/83/x7q861XX56fnVCftY2tiktN8mCbDCEUUiJPvAQTBPQiy4QnGGf5RVf29VNBI1jebLvfoO1Sgz7LqjzS3wyazASA2OxlqrH6ez196hREAkPoXG23zE0Vg37oFhC3BydVJqQbxtpX/yFs+7oiSDLucu5RuyP7G6tro2NxyGp3kAS9urqxzrS7+XnuoYcsJnekZGwK6w82BhVB3N3eG+5Bmjq5bJq4syitAnWAoUYqLHLv1rc2J2Zm4CNlEVkf7oS+Ve7koGcTRZuHwFPCPAqeXtPo3EYbQrgcJ3v4U1j3IVV9fZkdvtFKzXR25+n68pohL40MsAsU6hEAjNUVTAWaPpiCXXDHVUyW8+7O9aWNxZVN4rdQ6YzZFBonCLzyMDSrC2MDaG8ImBqiv0a9Di2CmXZPFHAX2nDUJKleu64mFpVD/4xa7fbbp9A/ccGMM4f7rV0kCMZ6D4Vvk8t8DLrXH4iS2qL9x1v0A/pzd4nMU/hTR0V3FS7nluMU0QQajuKTyMUnnuipqJJHgYNz3HhG6J3r9Hj106cYoBynSHY83Oy/MzzeRFCNIvy453hWhb/w5JjFK0+wLLlJOcfitci0CC9CeHKS457jX+/wd1ucmxE9dcfXbuOjMXrZdLcsefJCFag+gZGAcj8hJQmQlJ4+dkFjEchTuJSw+8glqjNnJikKRHB77m6jtb3d6N1tTZezQC8Ai8KxwfuZG006D1jP2A1jFosEVuHQ8m6DQSnLIqAUnlV/mNQhqyawqk6Mjgz07pL+DbqkuGeXPUsGAtstBSHCd3DYiFOCI1Wxxg72xw/36c14PbTWotjUBgqb0cJ+l3j0jfRWFdW2TUthud9pXTedx86i5pEmKfrArQr61XmRtEEDiDvsG0i3Dx8fLCR0an0nZjK2b+WrUXEbUggZzGhQFqeNo5FlIIYMd/SWD/pKvwXCCATsKuW4dYqNkkDALhlkQTqhBOBVtAC7zSaYGGA0QU+tEMErl/z3mbtKFMczj1R+zX6jpaXc8QgKMkOEqKfI4I4I4geVkOazCEI8OeE5Z/4iZvpy+5M4csuRi/g8XBEzvxpuHhkWLr/CLN0I6cfX/EqScTy8yC2zNcczyaVDMzmt12h2GmU5YP7yq4Znl1/ri86w9nd2241QMN9zA9Uw46NDA2MT46WdVr4ZDDB1q3G9s7u1tvHK5q1L164//tTTzr6bjaNjY5sriy7KJVRB5UVVgd90R46zMgiW/d52QsjRvWZsINTAECxC9zcPDpGwjc7eVqPjbqSewU519PBgfdO4mzPwn95GD3lClo4hmRWwBOerwOzvOyjreUliBpgDxCrJIgfcacLIhJAD0rRD7N6kw1OnJSS5rbuqeWRkbWPd8WLnhnXI+MTE9ubm8toqZDM1M43/Fk14eexUbDW3MJ17prXpbUprik4Wc2O17SbEElXwimrsqedOI7YeFe0ZnZHWQp66eey6w3QMBOcQkQsnRFvyaxE/v46OlHDncUnn/t7IyNj8zPRW/VoTgbATazSWaawPkykvW8iZJTLIGgCKo48I5VKlTNxQ39yAGnEonR0EBnDVMtONXIPdXKKQkOzgLSh5xi3hbgJ1QKvmvtVx981MOB792Ac+cPLM6TBd0miGHQIdT02cbtvKysbSrcbWxv5um0QMAEArBhhIYFMT2JMvmvmDeHRgWoJ3xBWYQa0VyX+vE1svZMcfE+NoQd2R0e2lfVdwvN6V5EGvf8zw+xScgopsC0+OWbxmT5cD1lTvnvdml+Pd9amIXHjuTfj+ISnbO4oToqPNy+N5RrQUnipg7O/YO1REHhvPu5yEx11RmbyuEN2gAM3mtfX13p3m+NxU9EAas26qoPlDWDMEK5qBsCsMtN8J/olAyJ1ZwDWpGyEPPsMmcKwc1OvherNhvpfjSjv0aZCzrU6z2Uj3w8tDJ4epg4Sqg0fr33EvBDRIhAc0YOEMQUi2wx69OttX02ZX6mFV6YQHMhp2FW6cjgCJAhDbUeP6XN/WTE2LlS8CusCrDLEqYb8TatU6NQ5qIQiAYAmiepZWAjSx4YM2MA2obRmFWGaxpPvjOJYSgEi1AonsP+8SCbBuD5z19RYIWHxdB2LCgkrmyT0pXIYSykE4v+fxoeHPcaIh98zAfAQih0srpoZzEJgiZOuTGsoz6uaWxmPHgUQOyJ6cJGKKJjC7HC6f468ClZKf4mcn1ZE3Bp3LaYtnDsn5iJk9+dmfzMjcG0EpRczbmfMlGlDOvLncXIp2SZLbiDvUUv7IpFnqKQ2t7TY3ezp9lf6t7dWe3XK9yb6jU2ENpwwrpuPAEOyMMZqfmd3srPze137/b/+tv372/EOvfPdbZ2ZDVVjmZlaYuDFf05/yo9yC/Agpib+oacwgaoxDw+62ReeZTj1uUEDDhTZ0z8jgUMeOCTYZQYdntlu8026Ebe209dvZcbM0IiMPB41nug2QdB5HzUFc+lQeZrSNJErAAcmzQ02uS6JUNT8/j40VnyVL4fRFsqaVJMtLS9ayzeBAM2NjOlxa2abjZMFS6sxDLGKypGdqm4m2qGW11W5Vx1dHOiOmjxaX+muZ+ozFlfh1WeUQnmj/neObX6Or0ldPzmsOj9hH8XOgu8BD/js8SE1sd6cZ9MD+IaWOUtmeDtGy6IE4Y5PHimE/IFtkQ1kjkBDwbn1CAkeeQUjESrKkoWsJUlnseSnIGu5ph8k+N5/194IMvReuLZO9B1HO2F9laP7MKTpfVAlOPv6ovj19Yn5uagrE2V7fXLi1vL6ycPbUCUAvTfbY+FJUJs/0a27jH/OpktzxlRSDrdqJ8fAptSYeKWJ07/u4lNX7fH/gpwcl/GHDH1TAH5oP28D59AgQgwyKTo6xNT3zlMoZR3fwpUmWnl50TfHkkcTzPi6sih933WhxvIYMxF3vicHFXpUqPc3OWmt1Y+jE6Z16g+YPfT9ixWAJQw4SWDD+q0yW0WgcpGcPj1ZVoIq+0C+Iy+N3rHy26EAc0hWnGWIYEZGEjQdsKaMfy2OjfeXDvQlXpLRaFEbqW/WegerWIasUPZV+F7syH9/o62+MDewtH4ztINMGO432/vjB4LDL/lp1KHiop7cyOAx3Yj7tmwRBt3fIBv1YH0qy6ZqCYdo9cbNxyzIm27HZ2+kdshp03E4yiaXHiAhH+pdZtzepcQQwSRwJjiGIq8KNQG8NWOzr2GWDSFACpMp7JYas0MiSxNW0/qjfELgOOuBr0IJm3XWSBDZPfGG9t3qw12YjdoiCNvmCy5L7DwbLh624D3jf3hjTX5CXiilPjWxBHbBJaasXkTFgRA7HJmvbza2d/Wa/rbk91+uRvg8Ao/Xt7bH+cZgAIsSOwGTAmZ7mJ4RXVR6QC60T3Z+kGphjJ4mgfvOJHqoFrmOCm6JH7WJ2jHkPTRyVV1DgaeFhWaxcZnnbFRr6LlBsuaxI9zmDRHbvGPBXAZ2mnyWBEvSI2Yw7iPWcZqYCQLOY4pnaSDMnvVF2D3Apmqf4vNSAsl+QAJ+SeKEbrTRcE5KmfxxtiQuqAj0fOgbD6KNh2t6qQ3gOoekBGZZLAUGEe/XUFVnNyEjlciXPzis3ktZfKqLP1Xzrq5s3l1bWN+pXbt3aau9sNB1XJ0PsGSyXJmfnJqdnpk/NsNh2uFc9PCjtrjRWr29//Z1vblx9u754eKI2aaNgq7nBuFlpZDjsSfbsD+/MXL6w/uaF9bmHn99578Z3rt04MzV54OLint1hRrKM8cGO897NoZ1dB9QHewdXDV8oLlAkiJ0K10NjSM293dYIs5E9B5u047ebJp8x3aMANTSLLGq0O6US/ax+O81aV7aLU98Y3B5k85lxq6aN66zZ1NlisM1ERZ/qGd1kfODg3eZWcMn7B+MTlcmJskF3LfbmejMIBZpV7gwtD0PAjgNOleawrcJL1Yo+wSfGgd9OOxS7RkacjNrZ3yQad5y8o+kHVWjEmJq9wEZtZHByZHOr0zM6NFitjm416832rostdIKVBnAYMrukVrZEgBWEFgqIsSzNNlOJyMA061J4EX7kYv4lJjv2PNIk1DprlCuNT5FxYHf7h6ivD4tQGamRxO21gyALtYZYzHrYLSp43gNaz5GXzkH8H8N96MlcmtoALlA13C1kOPQmOQgZbIgZlWa1bezgooFPk3a/tXP97UtXDy6Jd/j730PxhxLn/kGt3FMt98xNj/7YZz460tfoOdgB1KImIegNuJ3a3gXgub35GQU+wFllqpA/dhsiTSCUcOaGsbNyGVoQh8feGqBhucT2CXaH7jpOQ+dn2kQCfASRX+rexKzcLjjlGJ2gySLGaIWCKosIsdkvXIQArl13e7wiAF2ZXYwj/51fu9/u85N7ID/jc6bQ7xPx/kEx749/uSu73FMiFJ7jkd8n/K5of+hrroZS9FqeMTFxgkuwsFPpNkKOuVzPYwFpcuQpkp73RsiRc0GeBiaHpGKwpMkVaeMtBtJsUCUOcrDUJIHzQarwGEvYPyYDajQgqpUKEAkP4O7gUPRtkDVAVjoKEUm6OMBXiw+Rn4jyYHvwxmHuBj2iFCVHi9JEjekbjGzUyEZXSAiAcjEUnVys7GRUBOaKWCZflu2Is3HgQMiui+adD4XbxZTW1TRrbkOi2BXU9x4kpJs5hQKHISAn92NjiXQzJQEha9VR21fr6xiG0GUl0hTftHaey6ph9VKZIaJOFx5bO+nAdGYu5dH9S0sxKIwoLLnsV09OpYUJKQJVNft57BLretFyHCFFDjnOXa+RS3KaXGQrwGsRnj6l7k2J8ydeHk0WrUh4lye9Rl2QdCIrARrQG8JjA3LQ2TOX38WZqM3NdTMNJUHgKU8RoqkuqB8dzb1gapHb57OzWNtbl644ZnPt6o2bN12U2yBdRHkxWFiu1uzWx3bgcJnxhoFSeWNrm1x34StfXV5evXr1+tKthZ3tDfdOVg871cPmYyfGTk/M1UaqbefccFZsvUHRpD69e9euXl38//H2X82WJcme2He0FimrsrJ0d7W4qu8dPQAMBMwwY+QYzfg2TyS/DQ1v5ANpNOMDh/wC88YXChAghiDBAXD1bS1Kp848Wiv+/u57r9x5sqq7uufeidy5TqxYHh4eHh7uoePJ5/fevvX973/3X//lf7f/5OHvv/+uIVGjLptL2XZrGY+2nYkOky3hQ2xWrYRNttMT0uT1L2e6lZSyUQdHJyYxl65m9o4eWQCodHb2tk1Mbt7YEOn51gs8wqKZ+XOdV9nEXzbSxGQXsa/hdkk16TU2lKSqsNQXNADomrgwu+oVP1loEGyzMWSf3rz/lmFnjDVYDUBXWHHg+fF+7Q92hmtJZyjW9rfoslLMgqx5rag52Kxlc6yGeSKf2iEAQgUU8as+CdEQGPeqUFXASMzELYivftTXFvLBLAW+VX7GqQi4YalSelhiU7SkAQyS07S1Rek0mlf8Pg0UCpxwsknVp9LA3ATKOx5TIeM6l/BG3mhfIu8IRUN7YZ6E+Y1+8JXxVwC/IZLOhZjtmUTVIZOYhbySRr28Hvh6yOuxvknI1+H55uExwO0m4xA7gSjw7PAJz4gw4Q3Tnsno34T0IW6n4gkDp0aRePVa4sjQZmfk/Gm7NcgiygCHTiZw5F6W0Dhk9LfT8mwnLXhUTp/5U8essapeWqZ6NcOjXmISfcr4cIF55K1GYtFD+xhwq4lVXQNLlE3iOKfpynqtTLvamtnnwU3rLccsnmmWZ9XJlebcXBYQSVnerk4dt8t0G67LGqzcSZNaYohv3lVF6dMaD+7WWYixr7SUlAewBFQtlq8ZyyfiUsGsRYq+aN3hSgb9DwcOaUumaaCH4YaGqYVlfTfzRJe674a/ddpYXZrPIjV9SLSB1IhwvdIbd9+kKF88eWhB76VZ8GIUlZflpJrsl5c4aTTPkmts9ZQ0c87jB7iW0uaJRhHCnqI5S95GJRY7hsQwrKdScTzbT7O6zXCdjMjsDHOQhvCoOCr7GclXLAEfO2l0eVUWXqrCLvrQ85ob4PsLGCHdPhs+DR5caX/JQ+xPxUqLu1vxjEds5sxMhvhWV29O3SY3+WnD1z3K+spGAv7Nv/lv9M+sIeLMVubMshqJnat2RSYPXKc3r4fkdqzLk7Orpy+2lLADkzzdtuHoKCugqE9bZUt7Z117SY9RnGNi9eDB8UdvrbG3mv8riywiQ3Lqwsmd/e2FuYtHDz794Nv333jz5re+/d4vf/ijJ8+e3raG9sKM/sySecNZq8kzVRJ266VUFlMltACUGQblEJh8ta52yWqKo6upvSzktSp6aXUF66QFwgJca4OKXc4dWzKUbI5WCBtp3BvZjx492VzWSpHTyFXVtSz6LeajWetDn1twZJsfKo2+hmfOGVqrybAOJ/XsDEcTRbzFSTCQUCaeEOYQmuVlrLSvXF8xTRriaImxO7ZLdrySYpvYLi4PJaJVnKRLWryOkk5Jp2rEhSdd9FGSeRlJQj62Ey6wvwoZgZWRSxWpZgzepkuX6NrdafPFBVXxOxUsbkDVfq9cwxb4iBL+jAcWMQCkzvVrN2LY4A6BkocC8TWUxaXKD2/xFZ5++tQRh8BJD/9v6wZsIibtcgLbvY5NuMDXv3Z4I6ivL+kc4K/F6ij9VeKvp/UNQ17F8zLSbxU+6gWKgwue7eEfSh3i/tQpVImNWNbAwnlepv/b+CYj8tOiWnbEPeMn9ZqZKbJJf9XxbPxcpwg4/vFreV8qYl8nyW6ihnzJnW6cQB5I2AsqM1GqiGVIsQhHSRY2MbCjKpBWv2VLUfqzTGt0U6ZXTdWcu3w3c7xS1W3AvsyKpVbZUuSAdGmw2T4RFaPH3aQFOn1srquqgVpvjXEZUfmixXlHre90ssfCt5M+bjKNJZX1ztnV4oK8Vz82CWX4Omo/xu4U8W3w6WqbmE1BWdll4NyxtE4DcFxw0ZfmDso1vvX5wwqELkytbDjR7yZ19q1vfWtve/3Fk0cvnuuhPTX+duPOHacIHR7sMZaON1lZzlpWA1wybVEl45l5A+vKM2ssN6e5spGIyUjGQpGXkm2nXOS2AqtMq1WEBpAMMJj+CsBa1tDmg7HSFoAUnoIaFTdDJI2BMzCLBYPnhCsqUvdeKqn+2vD87Rleh7iGVfkr6UBhc8Fku+rqak6TwGxtSKNoxkh3Pvvsyy8+sX5KL01nlaHlcI/NELnzTgI5SPr1RS1iqqJP6esBH/dZJNbkp8VGTWYXWiRI303X8HzfUhs3QxIZEyMZ3DV6f2FV61QO+jbxcnyy5pBTU42WIR3tW0pw8+byj3/853/wx9/dvPH2f/qf/acPP/3EbfSXc6sMjoXNJnLcDCQXy1NL8zNXB/hsCDqD7TnHsTpREeaM+mgzzsyZlHFK1fL+qXYoAZB19wnK3fr6qoGRrb09pswYiSEBxsTpNyzB8bHZ1n2dTvB7u85tvbDSSDgOJIly3rNP4TBLsbTbsEiLRJqa5+F79tPPG2RW8CwuQ/vLn/38nfffM/zA4i4tLvXuL2DPtrfSnrBFzbzJ3IIJ5NPDo5PqDLLCutIsurJb2d83gk3uze5UgaTbPXZKO65k6KVBRUZTMkiX5IZAniG8AxsYnlEKac3IbtU1EiXjLbZMMzYYclBRCHytckDSgLDYM9qWNgQOnqE/MoTwcNLFGTkqAkJn6ozFn633gjRc9dr4Q/z1WhM8Q6Ze9+Tza05KDekpCc92yrBhk/CEG399GTSE8AzEi8XfnxoDvzgd9jLyuJYNIQ3m9ZrnFSIG6K/3XIs+IMS1jvQ6wFeGR7u1axT8Ddevg789A7OADdkeAq8B/8bXIS0YOK9kovsBqipxgEF4l1QDe45ccVAZWKwxBHWReLZnHD7KUVA1wlrIow0uJAKnGuiD1deOkjTRM84AmLjqh8t3qg3jm8LORCxnXZZz/CgVw6iGuCSiktnxDpj2YndZ0Nzc12tcmOSsZ0oTG6ieCY/knB3pLfswOtz4XnotIJOECogqhWPbZbuiN4FN7dZuFlLrlIKkrHRrsytQX2RaT8oxz44vObOTw/oO82x057aVlzpKJ2G4rocx6oWZ7MVamZ9z7gEapOVHw5pNf/z46Tv3butzbKx8cO/Nu0YUnz7forZ2Dw7fu3vj5Pjq8IDWsy8xLE1P7zR7SzLbxJ3nBkVBxk1pB8MG+CILpnfS6S9nfLFNLOhwdVy1ClI1i9EdsaUMcMLDmSivJCF2lhTEVYc7SfRr9Ek0Z72mXVWlWnlr1jHfifWqU9qvBkQeRiGFAEAnkSmFuGwT+tM//XOX6D1+xMQ6jXjHKOjDhw81S3CYQyr1p0TgkT9DCE28jHMFwuJYUKURJmMj/WRY1Kwp4+OUjUMLGuw401jRfMqygRPFs5ZT0rPswFQdYup3QdTMqJsNXF5ZX527XF2cNrF7rlLNzt5/69bT588ePjh4/uLx9/7wu9b+LK6vkrQYPKsorPizF7yWCZJWSg5tGQCOLYoM4rIgBsI0PcZrt2KATFlDfXJk0fLRk70c2JKdRdZAzJ4jmMt2NUk4DMuKf8eD5ISN7CG3dtAlXRwM0BT5+CzZK8PUVixkNtCh3NnhHYfRuTTBSADelUXR5TXSwBIz5w6K2pud/eCDDyD8yU9+sru/5ywLQi4LjqexT9ZGZesDjT+nfZ0GxGXGV65igJcP9tc0Pq1ttKCsetvwl/il6CH0mnJOtzkhwVAqiD++DizBngwRPiDp8OCRto5FWsVdrUtlBLJmYVLyCal6r00fGznIMyTtEJlUX3MKAnC7/gieBzwGTqLSakHMqNoEafI1uAExVD7kOcpvvvTrpCehX+UmIo6QNFSHTyYnpF0D9KcB2CfUehXegZ4dmJAKA9CaYxJghLTonwxvv69D4O/gGaIPnmtof2N4lJ0MNNwAPYRAN/jbg14e4YAHz+9AeotCIxnwIMZ8mArsoCXpDPTwNJ0DJDI6MLI5Fo4OqYDAdxJNW0f0FCiEFtAD9hqFGJuZMcPAVAOcN2hLWbsTwghYUq+U0hHXHzDfqUdRtl+R65fYCHCSSVzN9oi0dqZOHxxRP5yNt7qiGVw/nzoJw4V1FTrJ/gsspWRisdviMqU1IqinkbMOovyi/0L5pgODiv+e7SqDM2+8mWODOMl6CuwcORLI8DOttQTp1cXOcWZ2U3cd2mCpl7HpkwsLny4tKqPOczNaTFpZJbxKnwYeuuzh47ON5cU7N9bfee/d997/0BbMzz5/8OjpEzrXEhmKOib16oIqhLtMJuvoB1mWV2Q5y4V1vHT3YHSRn83JnQtwEuocDJXCpyoVCCCvMsm4vFMzE6nsMgWf2UERFSVwnhYAAPjWfvG9erZnCMz7OLEGGJ5gGjgwE67DhwDwxWczC3P/+l//63/1r/5PJiI2ndS0stYLdHV/FbRtJpzG1eVRVvxyGGuwh91lZSSlbA062w3nWH7+NFZq7EfWjo/dUh11XM+sWDOFkemEFPH02SG+TS3ruC0sX+oHs41nxxenF/tnp18+eXHv5urtzZtXZ3tEbHV93WkwhrXZqrdXlv76r3747e9938zDOx988Msf/Xh1MYdHmgFeToas93NNbvbtzOlmZ4Vtpg/ouWau0pBxRtMoipHTpfnZjZXFU3uhjvYtY715+xa7KI8Hhw6My1K7HJxuQ955Nia9cXvTlhijJVtbL8wHT99a1yYjs8s27vUyOpmbyh29gIVgFCSeKfC6FgnTTJS0H6nWdbUZZrNbDJgWfHMipsbtB9/9CKNSxeYNwC8aHdpngzOsTcpT/bVZa7lV9QXrwFeYEQ+Dp+LuIkZMSepolDhjO2MF1TLTkINgDJ7+OryGGJJYwki2NW5M37gOI40T9buZnwY8CCgzfTUZt4mRa586vPEPqQzy3wDDV1GwUS4ACOTxlMEoNmKUFuqoJgof4U/6ScXT18E/0NMhDTAEXvOMat1EqFgV8aV697Hp5Bl/fRlhCKlYIzL6c3/q8CFuv0IYT5E9Ait9PgA3fJeEwPD7t3Gv4UnkJFSpNKYBZvC8Hj4ywEP+QbS/44yyUYEjLJWxAWaIeC2NTuk3PodUGg/haAOs12ayzetLiscC11E8W9QGgGS9nPD+1K+eDTOQ6pWEMRWeaqDGORB+Lq3+SKfurn5TrHKjEkUZZQFHpqeNXZmRNOOr35VOHs1fW4Oc1XxO+xUmBilmDmoAkMBEL6j0qkDPa5atjxqTVmhTJRBWZ/Kiyj6pTtonCFP/y6G4PUNmyzNtFUzvwZVa2evUNE35O7c2Xzw7Oj2c2lieWl3ODKy2zfzC7KkllpmolvhleE3BZnYzLQMhGkAaHJmDq74jVWQcD/4vj/fpTb29lfV1VyR99/u///STH3cU/ZLDvX2tGfUczcdnhzkcj+uhO1iNbGc8LTPE4WaGGGqgXFdAQTPh7nIMi6OgkKIVpL/e2aeq0nvu7i+ba1A721VlRwlEF6O5rAJMcXiSpMsBE4KBzbHh2V+jewq4ueopfPC3ZwiJ5+XXV98W0tM9ONSFTXLsLnbFDpUCFYJIjsorrYcTu1XKi6s31iEqQ3tsmcCs016oXRnSFst6v7nVxXnFAbnGH0kgndpHmdjIUqT5ezftCZg/nV7YP5vdNZScY0otJ7JS6+LBi/2bD59d3l2fPTsm5a78OrRC4ehk1lb1zbUf/+QXi//X//Kj73zn9lvvPrVYeW8/kpOO4dTG3LzrP6qDdmVmwWLU7JDAVT+zGwpI6bgR0jpdSvzibG0hR0tYN/z02QGDWIKc5VGWPTCgeJhJjfML5ym+/dZ9R1AZNI7pvby6d/fN/eOdzvuBIWVDx4ZRVEPuKpuJ6yaRFAcGesZm1urfvGbYo6SkarFerPF/4crAgvkf/OAHJk2YZPd82xmRSSbE16Y+3DOog8l5X3Aq3qwX8sXGq9w5NrrSCg3lmp5xYRdtwsWuXrBwqEag4z8BBlJy1V87xNPmRPJd8urlcmlhQbvInNSzF1smF7pLTAOlDoxc1otxIThFELJLM4WS+jL5HINN9FhG/Cx6WgKFtIsZznD3KxjgHCf96/4OuR48XwfdAJ4QD8CDp7IwSlHgED5g68DJp09NpEA86caEwH717PZNh+R17MQaXl/3jKF+u79fh+cbhr8cr+gsDc+O7zlktT1N3RD+2xH7a6Hh5NTb1lCRcQLHFWdxFwH19hJLvk7w9+WH8r3+CQbOR8+2EwQxRy+qC1SbT2NPwtsYZwl8PlVZW0sZZaBn6gS/TERaaeSSUUc28xh5Y5udcGtwi3ZhqYtmueCyoUZudL6d9abaV49WKleL677CLwRh/ALRRknxqzCdqXSAigLXJraHMurq5Bnd4lirc5fizbz//ntMI+1jPgzOLz/91Y/+5i8+/sXPjGzOz7n8B1v1tmn2hXOdAlt5GcGaT0374Hzqxpr5spzPosNmHnF3d9/v5Gj/4uRwY3XRGSNSp+wMU7gCz5TeP/pH/4ilMd1pIQyPT4hPs6auyOVv+sc0s7G4kExFd44KFP3RJhmmrBLnT1mkneTvqLwSmFiaNGW2F0o2+NOXiQoVDjh2uEoooxjxJzwGnydJxNUrL3y+JomAJLmSgUq9sQmcJMBrF1OQRG0Fa+LDVIuDbt10Q19G9ZWOvGMpIYKqi7JLk6LvhAgMAAU9JI1zB8527nW/1VlhKo7GFyDqQ2oZNgGWGC2v5g6D2ZMXN2/dWb/91uWiawEvtxy3cXI8f3V2b3Ppwc/+6ovn+8Z2l65OXAV9eXx1sL97a+n23uHe9O7ZwcHMf/n/+u+f7Z1+9NG3v//H/+jf/jf/Jk2fowNTBleLS/rCqwaW3VzigrDalSMLhjGISlhmyOfUADhGZkDcQUyby/MHC9P2Ii8tbsg+YObTyLnjJpeXVt66d986PurXnLbxeYdPpbLM55IG1YE/c+Y1EWMtFOFUD7L3pAZLcGDqJMwkVGG7mlVlhode06rDlOlp51mqw/gpXYNbmmiiWGh9qCOu7WfilzTMXujsWqPlKIxFAway0Q2avvBDQ3DqQulAqxA5SdS2wQiG10hMYFJJRS2R8fZbOuMJpRnU3mkVbW5mbXVZOmqQNRkZbahBn8EA9y6+FqGxYkyK6PGU8ZalSSIEgr8WIi4nvIcWSmRHIPzlRqLeaCej819DOHz9uvCvBPiNwB1rEuyaf/L1daqufZ2kIZ+iSK67r4tyHe43vX8dnt8YPkf6AY3LYFRykbAJxSf1fuVpjF6/DvU1Ur8ObMAAoOp2+ovqGPkgKLoODlVXGciZfafu7GYyQDawbqd2MgyET0hXFfpTCCcEBtg8VcghL0LAe4XWJ8rLpObWixfOdj+9iMrQgn7y8IGe1q2bm+6FoHYwRwu1drVm67EG9bnBMCt/51R83RSLOQzBTbu1VO1EztHZqRE7Zkm4JGTHTUKe/CqSQ1kphVagyUlVkoPLKCB0uh1TRs5CcgbQ+EGiyisLK7udWd3w0lB6FT6yB1mrrKwg1skw6Pv73//u/+R//M8Bu2bVLUxbTx8c7u2sLy/pXbK0M1OnBputSZ1aWjtLhydJ12B5ZMC459HpiVE//dyWWEQ+ePjwjbu3eVyVtro051YWh/G6g2bx7Hxh8ezhw1P6zmWu7733Hs0LTAnaVGMGVC9HOcKPz7LPw9EwYJCXFk4sYdKlS2VG9HBJ77xmDlsVtk3EoZzmtJjbo+lP/Srct91FLCHpk2VUX2HZoDxS5VaCx3KEdRnnwKSYfq2PcmQl1hgFtWpFmG8cPIPrEJ+E9JMnXe4KCYLAe4tHSZiM3N8/NXZjtMDQJtokfeikogLwKn3FGk99SiyuZNhQYPzl6GcTCe3PBET5xPM3k6617IuZNKrhlNSHz3cXn+8tPz9cunlv9da997/1Hbfq3ru9OX26+9M7N372Z//tD3/1ZGNxas3pWG4TmZ89njuemVtyvMrKxvL0+cnPf/Fo//jq2x++d+fdb/3ih3/+xe72H334/u2VBUeau6bxrbt3iG6aGe2KXjnGzWWGEzmodzmYNe/H++tzV+/e3ni6c56LkA1onJ0YQcEBUZU7UUQ/W6kiW3rsNKcYMidyLMyp4Gkcyd351fH0ucsxVJNc2m0D+/Go/mYbkXlqI0+HuT4S0qF0MvTicuIcG2D7cbQH2YNNocODReqvG4FOjw7XHJo8k035d+69RUpTr82Bzs4c710+c4TW2jpqF69y5ra45IpHWkoPTp/kgriplfw+8XAC+dspVlR59msDAB4VdGEDgfzG4UCby0xIza0sL7lxbPfwyNyBrdL0hJMh4bGfPPxPBXmZ4vAKgPMqISkSLW5EykRrsknCn4ESIdA2VcLdZb7sWtQsTKFTalauJFbOISekUhnQDjVoCPn1nqQSBZXygsdz7EY1bvw6+ttpgR+iwC9Q1q5BCgcj7w3Zr4or2czQWGgWpRMFJm1livPCBydu+0FOeJLU6HUM2iFD+Dj4a/825gF/5+t16KyLQ3HDNfYhDmghw6dvEv56Al8XMpmTST9GE46B3bjWHOwMoIGnlteGQSJOxu20OqS+jJjY4eJyHctTrlWzzrtnwwzPRgJembVYY1Ku79XbBUwordTOzCwcGOgKX8uVwsxbm6uicOq8UW7yLbqJ0oy5cek1m8CK63ydTC8KGeqDdL0SNomgLgTLLzOh6V99ak1ywRKaqwsZeYK1TNr62pImwp/96X/7w7/5M0OgKONubaycOVd96lwlX5h19M+MYxvcQXzqMDwLoc31OV2hHCaUo1YzL6QBgn1KAuVaJLaR5kyjTJdpnLi7Ys4coZVnh4dpKFBDcqrz4enV9KfOhw4xephVyo4qhBydLn6vDOaR3EWRJYpzG2pVTrWoYlXTLhRFxFS01NyxFgiLFEqWCdS88FgS2MbaJN2FKALH3x7PZlQn2p987deO0s8GmwwZ4gZ+8sOrfhFlKP/HiXYRD68DJUIKeATJ/5Keyma/0qYGHDsR4/rmM+Du5hd/DpnJcOTU6eXM0dbe8dbx1K8eTM39cMpFfQtz3/vw/taDj/e29+xkcnjG3mkGVx3f+dnOE0gWV9yHvTxj/HXRcW6Oj37yT/7BD+j9x5/9/ONnjw/2t79157aemR27M46X5LRFXf2c4QaCmfGWRZf2puHIiJAMh6ekq6z7urA3dZotb3PLK6tOJNYw1QayMyjVNhJs4Z0j1yAxGKtIyFRsGwEIl3IAi0UJWSymDafoNcLSYyzF3WBqYeip0tTOAaBZRs4NJGgICnf3tnXmRJEQ+uQQLrXv7q3bNttlvnp2xumbINNNv5o+3d6lwwmWxdgw3L//ztnBLmKkBad0axguzQgSjjbAXXC0klpLhrsoQ/xYVQIOfWPXxeetBaPsgvzEsJH9anlEoRl69yPaSbSMjaYhVJp8I/UcIQkyeIRgDkiuXqO+suzE3m0rPMeuU+ynT2OKQslAJGivXEcaPGMcla/KnZDXvw5gv94j6V8P8E2+NpJrqDpTk9ETMhrqmgz+Rv5ryIc4v234EPE3el4a4E5jYPHwes3TjAR2LfxrUxoX7esAjaGfvnbSpLxdixcrwAPGs2HiMQ4JujD71G4ynQ6ZTLGBK9KIchLMdWUjjo18EmdHlyqYjBpbV7y8zIwQVdtW19c3xeKMpAayaovqov5DggAmhOE5r01VaHOZDbiqXBkrboGU7OmF1dN5BRO1lJ5aehiwLpjnVCdz8V+MnETk3bEBlI6TeJstISDMSXt2c33ZZJyUz4/PHNm6vpzDCnJ8yGyO13AwEeVxChlNcnF0Me0452y/FZli1JZI4s4ZZJsdjxmbWgb4/PzLLx++9+7bel70I7WldDyNTvpuEs5JHEuXF4cnx+4wQ5jF3lSmSbi7K2/SWTjgyYlCwVmve779QjKlN3PEtFxYMk3tyF1W1pwt6hV5pZLql2GMziMbDBqYnIYRWfZlqlhrNxPZycuomRyASdd885QcxzPpQHr1HD7Bw9/hPg3hDTY0oCvKBKbC0Oj7k2dpvUgvF5IjybIgRZ9GfVyfGkv/1ZDL5xobaOPb4QwgMGJKHEyux5KpG7r4gLMUwWBIobHk7dAVlJd/8T98OXVyYI5hxond5keUljMI56Zur6wbYNEtdz7k9KEJlOPPnrxY/OUnnz968gff//Cd7//R6Ys3XXpgpZLjwg1KzJ6mFags0GmdAn2h+0k83KknRJOUKFoSsaAv6y7t2Zlba3M7OxdH1hTNzWtG2rV8Yn/ezKwJEfxIU1IN6rX6Ydb01nYOvVpdy0lq7NvxoQtEDBuf3755M8MWaQJenR7H+MEfya+BMOFo0KmpPOehOeJUaUhQ6Ig0vVvczlbs5RVrsxSEqzyPTvazpfjq0nZk6xgWV5bn3MOYdV5T2pHb27vvvOMktdGc4lDu0gl+rgoQJXmtOWAw7HSSf1VOhAMX2IU7FLEQSLyGlyo6+jEh/gv6xS2n6ZGT5Vy54rPGNm6PRhEGbJDjYcnSIDnB2CGoHSgfPOKqiWB4gDWMr/wDDE/pnlE1aRI7Sj1TFoOH/3d2jXOIPrwOnuETzxDI066/NtmTIUOsBP5OBjjxyg2ea6/fMHyg5Jt4YoCHMugEPIUMT1j6dUTNxOtk+DdJbBIGfm4ypP0El+ki5f21oEb0NICQzK+WFDYBk3gafpDOyU+A23WguqqB3LUrSqGIASCVRqIUA68iVAudFfam+mSdcYyE8Wd0xPhxdueGvBmLi4GHe/Dfu/eGpjdzQR188qsvfI8FMWwHZR3Bo/K2MW5OdL8AMSB1dKJuMplatbFKBHMcf9dkyyNWgaQYdDIEbqw6btelbPNG1xGAWh3QldUFfV1dyvNcyNbbnLKkNvNrU7RN1iqjSSosmT4nhIakk9M0KkKwXStGAt1VJldMqRzr0tp5Sotb3Hu2pikwBcBvcTFzeVgqC8bzcz7g2gbCkO30iV6XtH+44xWeUmRJrgpCoWawwdJgJ/kLbCcX+ttG9ccB0VdVChjPITgzvUbSHcOU99Z61beOtu8OsmfFGkUu9kKYCEk2Jd6vMA/OJ4HXXoUo20DnU2mH0Vu1oXxNhuJEhAE9LYpJqDTv8LWHlPt18gkwr5MqJF3FJJdiKw1+nnUL8OdnmDWHeJugYZVjDNJhdCrM1OkRKw/egIcQE6npOs+tbMcCACLJGbtR0jkf5Pjyv/7/ffJka/f3vvfBhh1pOydPzo7fvnnj7dt3LdaTF+uw0mawwguioDUTnJ6oVlJkp1bOZxnh7OXtjTXrr3JHlfVgxiTOla/VAlZfO+tYvuQBy+FEWkwRw4xL+3sHnhJaXFq4c+cN4ygxtcVDTbeydsqQQU4LgHQZeJIYBwvTAkZlOdjdc/OAbUhEziUNkAtc3twkeCqgSlHnQtsmffHw8SOymz4uCVfNc3Db5ePHT27c+OLNzbVog7QTul+u/ZFUkpYhHS2LuvBDrOokx/pKyJNDfz+HEJ52HQ6nbFYISNBMrLZnRMX1CbYLssCWQ8Qq1ncZNxM+YAY2+FUW/knXAmYCTOBAySRAUzIg6dckNbjEu57cJAb+jn4t8Ne8jkR3HLGjV9JBxTXOl54Kngwc/DLY/qZXlKFy8TflPHFfb4Dz8SvdOLwAwoSGHKCHiIOn0QyvY/ghxlcmcz0wAtSkD+ggGuEa0zREGjI5hLRnEsO1T1/3OqRyDSDWrIagGb4hOZ4hW0XbiDLhQxngGFSNdkBewEkBZDt1QBS1SuVUUb1eg2kkYLIrMXN+6YSZcdPbYOiyFUIb2lGl+Rj1H3WnOlZ9QuWL3al//s//3j/7Z//Z/fv307RftsPg5MWz5//5f/6/klCa4hk+jUlxqqBarYq1JvK1KNTrrRGw+VwXQ2n2yBKqkvC0LUP2RFKmMq6VneyjyWznRbo7mcqxFPfF8S4GGQGUN00D5xBavKqmM6rStUzXPhanS0uR6ozGj/molgT9fdnbmcI0bTPtINrNeUPLrq5zRnYmtl3DcDHnKH6nD15Nbe9ML6+sZSpVb8DJTazCxZUxQZ6sZHGcLOOg/728+saixSYzh0fbjLEVW5Zr4YwEjQfKaVo2I0cJxVExqBoVUDIafc3WloqoAh1XkpAacaHKsGMkAw0vCidOFOiEqHe4JzDhDVP8Hz3aHkidA9Au8LVFpOCh9d41P60hME1beaJVU9qaNdDH8jB8mQ/LbwIyLxPOcDGHpvSLGiwVIaVJ9UcCc0ZLBgMiJVzS4M4MghhDqJFdZX06M68AskPuuMYkyaejygnb3vE20XXB5YUjzmu9z0zu4pz+wz/53vnV0c8+27JveOHsaOH06Onz008fHtx/523T8jlkxZTqCqLIa8wWM5EZiaNDoxzay0UqCVjcuFw4soSwZthdGbiwvDo1u6if6MAqVCJILzn3j2Q7nzejug7gKtO76PT0pczaLGe1BNkguc51LzGQaZ1+YzdnJjlkuvOuqFIQJcQIIKjzU1d6vW2DiZnSxTTpHhxnURh4U0XrSzfX9w/3Dg9csERsJeQGVGvVz/amPv3k86UPUm0N6xCYtB3Two4GCPHVXxQuUcGwSVS45+DyaewGf8sYsjsEyRUymt+voYw02mG2AIJu0ERPNcpQ9EVWpH2Vg60lFc52LeEvkx9Ldcfur9IF3BH5uchjOWDt8ZxMMPDjinbt0yTYr/HD0F8Hz68B/rpP4qLW10kklYPkaDKWV8XzSh4mP/9a/4Bq8DT48Dp4fn34r03klY81z1GsHzBKYzIZTO/X9gx5vRb+CtZv9jKJtmPASeZUOU/iKTCklMQQfzLXIdGyXsavADp6exKh3GQgP+ScWD560f7VKheuFIX0V88hRNpeI7hG41L0Mbpa5dH1M3O2/ldnSFxqxfdAhKTZ89u3by2vLD589OXPf/LTTz/9+PHDR1aF3Ly1SVOQIltuZVGK1B+Xqq9DwqXPCYPGfc8/nS/kOlhdVEaQTcpR8Lk7kBkUHKtJBeQKQboQVbRNzm2/PF2yCCjm+XJ1WfD0rmm8qStn3es+VI/I9o3Y8jQZUFNdd2iqEZAOZXODxsncm/aNSb+5XAB399a6fo6xwNXZrIRaqg4r/bWze3HjZqwsFKysRak8i0uzehhBkgm/XNyOx7JmHdWNxRv0rGVZeudUJDNMufFQdoarFQpPCkhGa2yGJITBVPHV6ex5dJ+1t3XgWJcUzkRI5FRXuKaKU6DJT6nLQjUKSemMnXAOjKmDDvMKyeCkO8ALHGDSihnJEnhJJpbUwI9x529HaUq8Qj587STkukPGuEdRltzHwdmrBWttRwlvS9TQo1IQQj+MYqm4p8+f9DWCyZwTNAzKl4xoMmJIj8tk+sAtWlNzh2eXM2sOxVKs0wfaN0WD/MjGl//2r5fWl9bXFjaW5t5YX7m3dksT1c6kv/74qaVL66srpoRXllzzpThzsfvx0Z5J1fml9eVlZ/hr3QUbt+LYajtuldH0laV/azc2d49On269SOEoF42JnHvKRa1gQTFKj15g5oOIVqYqTnKrByfLdkS38cBDssCghj3VPU0FLsda2vLEa4DZBDArbtE1MePf39qpxFKChPPi4mj51vKdN+7Cw9zj7ZPFFxfbJ8YOlpczGEPUtQidfC66dFVZYokk1l3+pKyxiLCSbhmKMEw6nyZf0dxOIOBkKf3ptH1T6QhPVTwV0od0gmfnThV8dl2nVawHrJlCRDPWJu1UWpESQngTnvdqRBcAJJSFJ/z5MuHBsaZWIOc1NLzqIgdjl69juS1sSYpnQpAFfBOXiJOuUQyIhleeuMoj+H5LwIS/A4UgcwAYAgdIjflo6a9yjfArvkxkbIAJ5gnQ4W3w9MfhlWegfyLer/NmgS4542RpQNey4rXzOelpgl4P/7pEBrTXAAair4WjRyUMVbXaQpVGDGDPdhCyv8qHDEWMxiU1Jn/8Pi65Jl6swXXSnWtfJaFmD7VUCACu2cEOSCWBusTWkeo3G3tilWusaEovI50fJ15VVby6fOPNjf/P//f//X/7v/8XZ8eZ911dZSFNg+VEGynOY7O6XnYOPaHNS3k6UUk5Z8GKJcczzNL10LLWdoZArzXuUKD5hJfRwJeywbZXTF8a+TMvDE6vnu7IYNmRi3OmZpcsFrZiq24l1F2TZLbaxqIxMTofUsheC4o7beqoCR5DYRonTh6mwZcWlp3o9OF7by/kZtAL3RMwqFVGEB86ktjamTqayNRv77DM4Vs1x7lklDPnRliDarLbv/OFHEY0427X2zdvIdLwoCsHWgjT0nAWaW1iSWFd5dZY6kgBAZCiiMoqgcVtT042lJVPXPEwxdeFmLxOQAIQ11e4K2oe1Duwdkl0rJs6otfGBqA9Q7gv0PcwCU8LaoNho7RAJkoM9viZCuUTrAYh4oZ0efpVnruKsf885rc95c8WYRBGYFNIJIF/fo4JYRdZEd1mO4RypbqxffviXJdkfFNMOlvhuqfd6l+DxvrjGGbuwXwwK27MAiEOr9QRvKD5V7YPzx88fPGrqxfrU1O3l2d1Nt+8f3Nh/mhpYV8xsjxmqHXS5qctpnMj0cLaqttp3XwdNllDp7JqQW+472htZUvTb2fbMZnudDI4vHnnFhZhVPYT6QWTtFwAf7G2sWY4hBjg1cbqmo4+PpA6TUNVUnlpO1TE8AdXdVd5hnJsYRAChvn0PNzdo0CMbKsF5kG2js9urtxkQcXVtjs82veV32Eg+thWmOkxb73YJWZvvHH37p03T/eeS5e8pT+tDmRhVJyEoolUnDKWRZJkM28ylJ3Xwc8jVj9bZiQqxLNfC7IEg5m9dJmZA/KMOPnoxOpUGYonBV+tjcbcCPkhkS4PJ1Acrl+h/UoHrJ2vosPO40mQGj7Rx0Yr3jH9/fV3fkq0U+AZcA7+wTOJvwMnQzqiPHbgkFOQ7RpgiCIwNe13colbfCjPSxTD6+Dpb8Pr4HkZ5xv4RgdxKJJmuiiNaCiDa54h1a8M/wYpvgSRECTX6CbZ7VLXx7LVHs92KYiqEnkdt5gGwhrmZTKv+jpFMLLM8TBjsDVUZ4o/iFPlo6nVRn1yiswd9KKoxsxwbLaGe5QkPZvBT1nx9fDKNqe5O3duUWxmnnb39oyo3b93m+JgfQFAQxEV1iy4cKdhJ80WRn9BJXcUaDZsROCotLSJiZOf5VTVBWGnVbs0kWmFKIYCSIuZPbSySoN9an1jav3W0vaBRV51tUGZA/VuaZlqXjjcyakgwUFWsygmAuABmAeFKuel5TNZ9ePQoi36yNoQHTOdHIQKFxuwdbB+LGNxyYKptOTqmXOtfbIIGnLdCOGW8jIABixhoN0kYamqOT9+rFpYeJ5xx0uLZrMMZ2E+Edc3N4SENQZdmWE90DJskuaEc7EzVWQV1mU3eg7hHctru44r0AQAv0Dk8Uw+C9tIMIZYDewVU8UgfRUrSrBhGhU8/doIx/4SKUF1NdA4MJBC+ul+TD6ctSmH9a0FZsia0dkNAGtk64oL90xHEIvL6ZPjI6uXjS2sLFgpaF52fnbKQMHZzvNTTIHVyHQu+GA+Mv8wM+WkMj53JUxpT1LACzjuQLTZhaWD/SOlmqWGmuNnp1tHMFw8+PkTArq8NLW+PGMj+Pra8saKtGbPDk+3dvbOTuwbdnDVleM12M4ll2QtrC8uLd/YWN/e2beS2XUNi+sbbpzVqWt+eqbM3MJ1dHh8cvizTx4RA0uiTNm89cabiHNutoisIfuLLVqvwMRS7dhUUdsw64lGRGv3mqfMR7AMw4C5uiJOOrLuD77c2sUeEtWp5HJkh76WEdX+A28wRkLahyvLa/bXrbx5U1U92M/50hLNKVxQO+P61BWpnEhpbNIGwn3rch+Kj0esLkpPzivXADxYPgA3QMNk4KtsPYSZ5kAuSDseLlMLhujBMKqq/sYF+zhFr9WpDuKOMnhCcznhwCD3yTMsmwC+5q+PeYg6IBwCv6GnyWsk3zDK62CNZEDVAF7bDa88Ql6P/tuGfB2S3zb8N6arA6ApHB1fk1m4nBKlVnSTRMb0ViTliZeKb9df8nw1wy/DCy4TPW4FX109ObI48ch2N8UvxJ3bhh/NXpr2IPF6R5GeaVfjre7tbl+cpSra5kDGSTSzZNOJZ85/5DJ+S9HkmtLu07Fn0YampgzA8eQG6UxYyg3jUrtIjVcRcWO02flqRcbx4cHb79z/i7/8UxXSaXdWrUhgdnXpxPl55xeLiytpKetwXiyuzq9bNHp1djm/drQ0dz4/e2BDj3OZgq9Op682ZZoyVjrdFp4j3o1RXSzMHN1YRc/Z3NFj85wIwxx5983JRBnLNg1ca1hxkSXQwaTGZy71MFZcyaRHSGteZeFzzudJXvDCWbVO0OnVnGn1BpNhaqMC53vGrjeUT258mZ06PJ49u5h/fniYmxKknmMPHE5ke6ZTmGVrZf/kMJf+mpDDLcu4lnHzbGp+aXfH0QVTVJJBS2cD7+4Y9Fv90U++fOfeG/fuLD3dylkHW/vnC6u39o+P16/Onz56/P3vffdXv/j5+vzU0k0j7ZcrF2snhyfWjdtvuni14MyG5fmFp8+er9xfkSTnuPz9k3MHLq2tbx7q2124N3ztne+8ZbXu9rNnC3s7Ok97u1tmsJ2eOT99m+HWt84ZUVfTB1vPqWL3O5ios6f56NTCbE2jBZtJ9fNP9crrhAccKr2Z0ZRls+MLC1Wg2VhFABQ67VlHFR/w+GSMn4rHRgXklIYStmyhMXRATxHOsv1Oa8wQqPKKuMbuJzum2adPrtymE9s2R2trj7iOIpx13RQz6RfSS/dlQHl6+o0bb9rf1TZAipJoMpwFiVTkiVSSXsvpWavdHMySupll0obYro6uHDlpBR0Cz1xs7YA1JHGX045zXly4mWkOmDOgRC4NyEwda/0tbif1dmfOB5+KEcqNXedH5lQ47UPi41boHIUltcupfRCJfTm9dTQ7c4Q2qehcrqw4cfNNp45L4GTn5OxZGk/Ly4+wURd3amF1YWX2WPU72rN66407txyaJding6P9yvshRMszl9/77nfM2or74lluYNTaur2+yMJfuO0JazNlkkNbcpY0mVyYtsve1FEUVFplylOXnidjCgwL46LBTKGoatp4N5fM8h7Nnh2szK/vvXj68PHTSmvq0ePnlJKWzltvv22R4r/9tz/cvLWWLr9q7vSxFTvqFpUznZKCw3NoZfP4UMOYk6hMaXk4GjREVvNLiaEzxca2VYPDJ9VT+6nwoNLp8EqM8LhuiXSlGW1yRj0mcs4QdX0GTYZ/Zqasn6Atp9fWw97a3yyD5ITaIHmzi2mLWAWZtMjy2K6fHDuMrNqjZV/Jkr6BKkCM8IpawCJXwKg1Idv2ivMDnLUKj7ZZXXeZ95K91ig6zZ1aJqouyX0mQACTi3D5TvjcrnKaboDW6Fla2MrXU+EQ9+SMm3F0j3ZkLrXLspe0CKXrMDIHGqgc88cu05qdPZyZO3Kg26wD3PbBF3oFqtEWfvJgsHkAouWIQK+qfDHbFNd57uVO2zLjeXQbwSD4zksP2emgEBrt1VwPQ5qvZrJIbeQKuZheFVMCa9mmEISPYOpAw3ypkInw8ff6W7mOb/B8Hfy1cBr2Ffd6AkIGpK+A1svXfR3ClX3HIgow6U4pGAs3SnoululQ2/ANzWY3Ttb7NLAUO1GBsp6yxJ9i0UCDT/k6Dox/zKaG6ZDBH+jKi9KF3JPKU5faT8ImIUfS00HN1nRDJaa0JCR21FDrAWjJmqoWj/LPJqnohUzaknnD1VmIk7gFQrcT7GCBD1tUVem0vhbhyvVLbKrKSY50hKJlyJTX/FTBaJkQkW1/gWF8L6dWVteQl1pd/U6fvKqtZ4Tu6EzrR3OauoGNBrCYdVd76AQMXoRx/pdm0TWKv13yO/abGzs93N15vnbz1oaOhS0cskE1sBPWs1hioxwZEdVj58Xzz7/8goJerZsEWbss1dVegkv/1+SwNoWjO9PBy2Q/equChf+KwwSelo3pw5t1lezO3nNTd4fZnXKMRoiK95ljdjejiN2NH3M0ohI+1EA65sDpyQnhmi2Dv0JqIG7Ic+W8o4TgRFe2o/HkjPlf1dleVZBqdFXexIFKZYdmwIQMLkJTrnGOMTtibBdnok7ca1txQNGzWdOtCWWBk00phKH2s/ER1VHcIYEkGydc6jz9rLDIFYT4iWOhrXpOJNZ2nY7S8B3Xs2N5NrWeHego54bp+gEQVb4+ffoMSZDD6ZWkyYtXq6RJlMkN0c5IKPnPnRznDx8/t57IvLWDLqwkczmCbesrq0s/+M5HDKEkcm7Ls23I0ZyalfXO6aZRG50vqSQtB3NOO09Ta15lSFmz6KIsLDKe8mt6embqOOv/LSzAT3Lo6+bmTbTpB3fba2lm9uQ0Y9EGwbWBFMFbb61DTq0LxAR+ogLYGrBOPUvcalnA0OxCs9Sn7aQuDnjlACdQ/a+y60DPDqynYiJSSiT2IfxmtDQr3ZHsZMy5udqF1Q2+i/2D3akMZKRQsiCzR+y0L2oYoNPzlYYw1iRpTmcCNp9Qy6bGJJUIaTGaZwcoYUKMJ5aaZMU8g58MqDB2qs1Wa8dIXWYwYIZbmgFezNCWd9u7lCzk1nVSZ+IzcsLNRwRclQhYVBwmlo/1DaVIkXGNKfNQ6qwFIaAR4HouqkkPQ6/iKnNokdV2AGTccxwQKe0QnsGllVQww7NgXor0APkbPRL6SpivC/9KYIFfB/96eAyw0Ndz1ajr0yiVa2DD6+CZiDLiGrRLhobOciearyltk5RLy6SZSyPR1XjntrXkZh5f94+c0/RSWMFAToZ80gbm5xKzwvlT/NXc68DhOQE4hMUjHElVr/NKZdBThEmIPoLPCS06M/vaKqeKPE3Y5CnFX7Ywr51KSXRamWJDlR5QrIJzoiOY2deT43/m2dVYs9Q6rVCxozFhO7G0qyp86rzmoSiiXRh9DrH+azqGmKxpjWi+2DpsrReexKnqNMXF3sFO0NeP0EZ5zeaoDle42457fuQ43BgLecpFdaZvF9GTkw5Y/7OLA/IfQjEzu5LiwoyqQD3IgNSd3Z39XQu6Fx2bx+jeuXdvbWOdadK/2tnfd/7Ri+3dbPdM696ph4cW7tBgF5d7qxubehVKy86UqAqLqDUyctiImWL1Mfc4dXYUjlVYLq7R8FfDJbq+nzszZmd3p6f36SqdObmx69jIIbbR0K2VcH7UenOMIoq1RNJjNTlunD8/i4SwiYbGl5zonYquXaNXE/2Tsi5ui8sPWubD+2oLC5A0XvuU666iOX2lrzIyEaU27h+0BFW5REJCWwp55BoD3npvRZ9CqnlNjPK1DbCvsqPHr4CR6xXUy7hVOiOME8LciQ5PaDlgnRx/p4Wgdg0Z8kvOPRt48iuYDDyN9ANV/jKu5qbpZj9hfnS5sV8ViqSfZMtTVh7oyRuamM9Qtw7SCVNpIPliykXXZG2FuV5dXVtY2TQhzQoeu7drccV4HBeR0q8pV+9pOZUnE8IIYt7KwhEkxznrkDpf/Ri4xobTo2REvdZqkSlGF1VadXJhphmHZVdc/OfIgaTXN4ntjW0Xil1OrRtcKJ77Wq0+p4oaH4yNR0Cq3mwd1l3Iw7q2ymWwvUqlWc0Tgqush8LiKWYyhqVQ2N7skSP+uRhRYTJvB0dndk+vrjsWO92DPfdclX5QpSkv0dGDfvNhsFWWR4cZSD3OCTkFFm/tlBJlbjbDfiaiyvLXIk5LH8DRRdGItrCpAroIGjOa1m7TuG/M5eJMyz1bsFXxDJBGJ1wt9i2uyVykK4nVwJ5BB1/1Bjx6BiWZn5pacRObY0GpetKo5imvtAMujXvJub6Jn43qutxmvDQPGXYYkpH0ogl/1GPqWiojEZUw6Qmf21Neb14zowc4dCblwQXD2E34k6FXXCFJYFf84VuF523wDJ++0jOADZ4GG14Hj/A0q8PCiafQQCRLVUYVewDozInSYIOnoEbwDdwAntpOGj2ECVNddWfX/tGp7QSrTBH1nM2plw5CMgA2dXV8buyjozdVigJ9ImaZUJHUaKNAy7WK7NT72WA+8pR/RGq/dk3up1rK9TCgr10gPOKSA46AM635pfAVbeaxioC0cImI4s/0sK6ZIXL9JJo/UWIsI7Y1jChWDZEAKP5IhjR2+3Jq6qCO1qvm6ALrbR+J6mC9TFIxKJ1mI33hFr/MyyahEu/0datdIvsMsP2ZvvoBBlOFg6oQdjqvrpLv3MHgqjs6cmltwX1s9nc61zraBKWskAzaSyvRQUM3Nz2DLptGUx8uLw4OTz755HNHGbyzs/PeB+8fGQqeX3DuwsrmxtPHDzZebOv/KOszY/05hOjs8sgxWIuX67Ux9PjIkCEbfHF6kqbypd4NTjvOV2bDcAlhbNkKDQNtlpl799/FaXcLsa8+0afUqCK7PDhcOMsBn6UuM4ag1MK0tOgVi9HOsh1pkmND+Mh280fp1atSRYrRAK3xKn3dgJS9UG0e2iUmVLGr9dFS4WzNPyuGFFIUEBVS9ikyw2RIZ8IRYBow4juuLA2Azv4EtqzAmb5aTRqUanHgM5zVDEubqM5ak4wsj9BPpAIPgCFN+LnGj1dJuKp2c6ZfRzdkVMQO6egi8oDkWrR4hET11Sd54RFFYEWMfu/AlNzFlRFCZlSbz4ouRDHJTKOrfhaZ4JmpGxtrWZo6ldHACOqZqRMHn0795d/8vA0e5GSM1cHJGL0aww3DVSUinjihcM5axjoJxO6p6HvV/NQ0cbpxvkIFg0pNAj2Rt394KK+GZyDRKhPIk4OXYzqZbdYr59VI/eGjh28oaAXP9GfMM+l6ZjCYlFbe+z5jxESbRSBM92Q6Q7peMxijD5q16ggPtaN1ysW01KNYLHY01Sz4o2WLudMzTnhdWdu4dXvjxs0N7QADJC+29mTa3j106qCIbbQO/UvWhS8tZUAoA1pSzao0aSVtzhaz7ijnwI2YcCnISDwR3HBJn5bJQ59PGjrIIvHTM/amLSwtr9994+333v+eESsn5JwcZtLbgOXpsdPfY/hPr/YkkpHdckQ1vQmG1vJ9LvUh4pHWU5n4s91MhSTLJdZp0EoWbSVY1ivMX1mycIGg2csTNhg0bFxSqdaMJ38krFnVzCyYZLyUsyoeIsYu8jlCMw6S2fI2EuU8DsCQfBklSwWU0pb+GOUI0ShiIF9D/TIRuH4D/BC9PS+HoL3LzvB5wNkhyeqEK+CEDJ7+OLwOHkVISyojUu5KMBp5cWmF5jdMm4uzLfgwkLWkibq0tbP9dHufuHXcTpFfhvKIL64T9d6lkkneAuivLwHG7yI2qhKYFCTZIEkCSbPqSqd3LCHtvCqHEYJKeMidChphoJrsAGoaQhuRz6BZ5p8UbQxh6obljETRVHX6oYup5GOkafG00/GJEF1pxOee4OPaaaOu0BYAKBi1GrXILolMLzZaPcNKSUKxUCUaxNVA96n7vpF/iEWZW96QGEFXEcuQGBFyFamlzJblGIELFmdWsM9IHRFYVryzXM/YSjf1aL+umPFzZd7x6c7u4e6PfvTo8dPbawt6D+6DXV5dN0J84C7hc2vATm/f3NTbYGBQjsM3LNRi9s6sKGFjTdbo3ZrRruEztTGjZqVBLmo4ZO4inSYtAkveLlcYTmuMqAbZWVs/Nm1svM6ApZ605ddYTLlwemApTT2tZrOCy9UPCiO/lL4+JZnVHOpXRRjNGsuPn0ObxlyXdLnKO/WCy7E5mEO7IF7ljJzY6gx/gsOv1Ohqq1Rfuf2MwlwSeNWBFaBMuU4FArFZDa+aLbR5YGq5A0/gZOE3ORQ1SOMMheVgGBwAJSK4k/AU0mAYCAyTcEMIT8fS7huit0cUGdBVid6sXn66NjEoorC7aWenyag5fXq+l4UNOUFDG4OoWoeo0jGPklZYO3tkb09yhTlWTSFasiALy05mDFtTkxozqRVuXYHeaA7iqNqHN1pRAGJIqomuzsw6lcuYqRZ9+qzZ1QaA34o/pY8DFhhs3NhErdFvF0fqHzs0RDhNpV5Zna16SStELi1aBZWh6AwpK9CiVI01Ql46iYEW1GwUpXnL04HCJ51ANS/N8dK0hCmyQ5xmLZlcsajLgPkbb95DjxUQGG9R2E9++nMmMGNOe3s8R4cm79KJX1+XRBjO0KMz1OKy+aasVQ8/ZVkgTvGzkmdqS6ZIUvQIYIMBKGybLvDX8krKKiv45txzdvvNe+9pRlRj2Jr6UxvMIoTZUH3x7OAzXlXbFnCNAJzxCtKOiWS5WEFAoohyh83l+lJudcscsNA0S9LgJs/pSBjWzBidnuuZ7ZbEyeJBt3Chv0veMygqM/LjVQ7712nxw6PFr6rHwnvmYF3FgfjqOzX3Mw7ZsCFiskSu+YM2kEnfY/har3kbPMOnr/QMYIOnwYbXwfO1Q9AguiDH9XqcdjVwmpRwaoKm4XXw+Kq01bb94yMLXeRt88atf/BP/oO1jRtrZmWWFpdXV1IRawXjn//lnz/Z2j/Y+1KBNbmNvNkg0CD0ZLiQBE4Q0F87b57tGQI7hLhI0JN0tgGGpCGFcAPxHUh0StBHyFR0Ra1u2CWFSm8+J8qMExjTCs4Ei0fMotU2aQTqHV9NzV9eZY+EdLVRI8hj506ZgJyRm8w/kWlNE1O3nR7N3OQ1jaQCD6hN6l+tcjqVLKBZeuCRUfRHgjkZ9zyIdWMTnUjgwnSdyFqlYBHH0nqWSmdgyOm8Z1cuK6/o1wU0ePyybOr8xMKpHPWQocWoqanHj5/uPDOS/5h+sKTu7p3bjh6xW1SZssGa8DUtOO98QY1p+FVXB/WwYSynoTK+GgA5Vcm6z5G2Room1GhNoM4mFl0rqtn2KhVZY+3mrVU2eHVtgxk2SRZVYNvoqVGHnMivyaIA5D2CoXBoHTyv9pYy8Ql32M+wS/VOQ7cau/irNGdN+NWUh309hgLKzoa9qiJ6oKVCsr4vwzEZ367Bt9Ik+j0xG93qD/ODO/wfC09I6jLN17GfNuSUu1wLHEQRTNKtjAgkLB1riNiego9qG74OAOLCIJyTRPJbTm/RX2DX0BKkIW7yMbbNGX6Rh3LIaI+QleXq8dSnRq6MYJ6b3zQl0iHGEpQ0Fuv32ZWkvmDK/IybiMAGWIoW6WlsJbPR0Wdug1p2KeHC3IYVliRTHUouLHUy2JxxbcMtlY9WuviC03hlnYORmFqMBFk6ftlfhtrOqWoFTktRp7ONGTmVS6IBklUD4Ct7PGf/HpfxfwYsfU5DGxnvypXOGt7N1Wr0l23AqKKnq17kqtk+hHc2B96y9PIqMIJuYDDDbBoTaTpvPX/84OFnDx99TrZR7oKTd+7f/Y//w/8IbSqXPjGHeH4Efvrpp2pTSK1mbsbUs7lAaz8EdHIW3ETs1F+V4MRFKRjuU+jFHOY7xq00jJa4upjqEhlnhp1p58w7PfkM8dMz8pWqdHl56/0NNJNYNZpL06Tujdh+8SJMynKxLFuv8Eyf0+2ipglPnEuka3WfVq0qVsoNU7PPQw0yAp5JOOQlylgty0ALnsCQPlF9kjkVt3+JlOzGJJvEyTcurJhwkw2j/lQcSn0cQ5XF74iFcPgwqr/gOqFxhFf+RleM3QA2ePrL8MpT7aPKMKK9D9mTzeFVtK/0TwZOwkyGs0t+lt5oLRGR5fWb3/ro+x98+zuu/jB2a0pQwyx3kMzN7x+df/bo2WZMVKoNSkLMmDFwthM49qaQOkv9FD68NszwOgB0lMh9dsXE9ackVlrPczJWmmwjx9yKTYuna8t+EGAaRv0MsZYQRMTUebKDQtYC7ejXwjNye3VykHtauJolIcwxxhHlWpXX1VXn0VoKqdeSpZARYnJ/TE3shLAZy4nR3PCe/Ia4OztII/e6m4eHBzyARd9HkLppWo6ym8/PsnNryI/OVMhsyszAq0P9kaXLVZ2GIrs5iZjUHbnQMTk12Jdzj1SVjpjxVfXt7PD8J7/47PnW1u9956PP1lffe+etN+7cZoX39w9dAXtneZml5NhddlgTmzlEnvbLhYaQWYjjU7dCWMnJqLcpki9qMXUgB+XPnTivOr0EJxOfIp2WZBnvvPnm8sH+yuEa+9vOSoOL4yN22CmgKcHL5I2q8DPJHANTXWF1PNVd7R8NNkWcsM5TiXgqGQRgaZBoQaa9U8uCUtmjgRNaFSWd+FjnOFovrf6aky4RAmGwsb6VWPKJ51M7BdelFmQhIFOqneSVGYIsNSj7XzKpXAo4GLpgKsqo4dgYPNszSlJTY2xEO+l+DoGSAC/jHUveE7+cT5WdylIt/pIPylKbA3w7Vy0gqWW4UxQVbc6I7nzJoLZdpogzSkmCFxlEkKrMoWs8cpNHsmIUWtHoeqbEDSfab3DmxuLTQyv4Zy2tYlNjTF30aQKTHbCQH1nEIMmNWOqtdhaZXIhKD9+MtCfmjDOrj2W55omc376+f3Tce44JhapjHAW8wXCCZ3W0IksfqvrWkBNvc7s8xrNPz4+UCDANa1njNBDkNEXFEleixbxYC2xpPndIk5qE0F8jHB1FiE9EiDlE7Q3D9LoHTtJxn8Xx4fMXM59+9vP7995WjW/eWL9z+wacwVB6AxMYZt1i2WGV2eZedPaLT7+EU35VzDQa0v7UYT1jjBGWNoQ/MpiZ9OoJpC19lv7uqF06Uk1aPIoqKiwmOY2gmrGNKS/FqbxWl1eRE9n1ePudDyFWr1GlPmpzhwBr6588s/QKTIw73Mb28DF3emjw5S9daohJEWQaz3G/OQe3kJawpM6ly2yJmbqpfkQjDR6QiVq1zFI/mqwaywPXRyI2fo/MRKv8WiftfIeLp2MU/Ch8LHW/Fkc+fh38tfDfPATduEjMZJKwXAvpr6+Ha1uuLK1q1JoNcm3f7t7R8xdbKzd3Dk5OX+zuPn+xbbXn3Tft+rtt8GNt8/bl7h4k3GRyk/7hU0GNICcDB0oaAN39tV99HSgn0JzXa25ITngNZxKdDqudvxDpB2VbUI66zXhVepVZ3Q8os2ATLjp6OsY+Bq5ccS4iozqoCraC+Ko3aFCNoWUdVS36iPgKR15GkfJtZHSvTs50FhmCDMCeZbIMJNf5Cimpn0z4TA71W16+tbls8fLu9o51RVraqrpkHerj1jMTY5n9unCKxjFCnETozjrkDdl/6Zm+2t55sTQ3bU9zqZcrp29gAHSsDoLl5enzvampX0no/XfeeP+dd/74B3+o622g73bNO6iTlJenS3hQaFnaheqPVAtRKdxiiuZHmgrGSI2Hn2eNCQVQV+RcmNYzXa2loDhoFfFMiqofdgnfXnBl3mmroSRxvCNic0NC7TBwCORpf8OwriptdAht2BonPQMlWz3dUgYp/DZm+KvCR4Qyk5wKWjY2jW6thULcyNP0iuS9lD2xJl3sTQ1Ee5b6jgCwbwY48DPKOhoAURGP6MBxBcxrXDBzGVAs16+87YnklOuvrev5hcLA8fcTfMMMGIS3XyydoHaQdWA/W+REZIo8BQImjUurS3guSnhO58Y2abS4ISS7wuazIjqdP1liRtGisaEHdXB2AEn6SHa6s8fuRT4+82fpjJDGArOhCMDk+Rz7HMFVR7TToihTXhc3Ntcd8UWcjNLS/gbwHd+ZVlfOrlqy3l6ilpy7sFAf1BgvbG5XefLsha29GAHs7t03n29vWV4NkgErjsWO2mPdddBksHqu4sqyEHm01cXqphRUmdLmQ1fzUFtOIAcbB9CSNMGw1ugqr2Ff/Xu3Pz0zu8s5d0xffP3G5gcf5GLvucslscBB2Dgv6xZOVWl1cW5t6dbbb97xVRKdrvs+WUF3eDt9b8uqSPd5p898+Ktf/UrjwerF6ByLqlSu7k/MWriuFxDF45CfOS0QZcJKlr7SaGaXK2WKkqTZXzfKlz8Rf1mvdhWPKlLj+SMJHGX5W6n4rPLhsenkXDl1dHyQ7Vz7e84ssEb+/GouJ6tmWH5OM6RuXC+Wvaq34e/QzqzXDlH18lPTUFPzwaPI3lND2/neI9Jh1Ddxjfx1yK8Lfx2yQ74OfgiPFhheMFP2hhx+JdKI+xhmiAtDx3o9iu7W7t724vwy1mv1qJGHVl5NzTx9tvW//z/8H3/0859+9N3v/Mt/+S/f+eDDjMLWCkOio3YRUiOK2+wxITUeqRtdTb9IP61P5ZVQdroIaPlGQInLaKghlNKNNSYz0IYSNVAdIBYOxDGYI66v8DNIh44XODtf37jRNsNBAlkJ6pe6l44idW0AyXLLMkVpZQrSw1cnJWSjIuSPHj0ljkg1fLq+vgK/WuFptF1GSKSatryWMx3PDbfWiF+Tjd4uDvYm/rQ4L2wicpxtM1l3s6lFcOda7U4uYyPmtvbO795c/hf/4l/84Ac/0FM06fX86MV//V/9P//Nf/Vf7G1dbG6oIStGIvaPLhbWFk3YOcPKbao5XSsLlwwvO9peTY7cpk1caOEvXU1vhhifJl0NIFXTY3rq2fMdsT7+7Mknnz75+ONP7r15R9tcPf/Whx8ozdPTA+30m7dvLMwvOWnBPQ2O4NBspx4cwmB1HpXFBusrSxfxhNGn9ZUNfoESxU98bkVDlSkvgQ4XFOIkB6cPCnn+8KHyhbYxR6XVQndljcNYx3Ioen7Mx8CFxfTkhNDyvnL8ptMsFUIG0VHwFsFkA0XXlCjOGh7PGujMUpuajBW8ULiKLJOsBu3gSS9/jFNCgwva2nHUafEnF5RIKeiokRbsqovwi0hMJNEqCLTALnSUd9HAMLhGKBb8nv3aX4UYpuXvr175k99qhgrkIB9e4Tfwy8Q1KsBNG0vILE7ioRZITHhhazstzrnqFv7ZDC1K0AkdhlnwUQbttum4DrC+nFnhT3bSr8mY7PGh/b85G5LC75aNqrS87GDpNWZ3+eLKKnh7CmpZYpa+45/GpK6228C09Pm/+Oxj53NBaqaD8ISWuCmtNCpGT5cpePDo4eXFc/SQsbX1dbdZf/HFF1qldRpJCOqGqPEU/UdljgkM9ux6D9STupGqJF1QS0K5c62jklg5/PQX09oFrbYIg1cXKTq6RHTcZkCsVXOD5/sfvHv/7bcJM3sI2JoJmMQNDCJYKVwxGe626avoB4XFgUz+bNm9mnP/+PT0yv17t6a/977CLzua5gGxf/zoySeffPbFFw+ePVX/Xjh/zPXVGiTqt23Cpty3t5/Oz2rjfvfhg4+dSQaz04SUqAEMQ9vKUopGpjG8ZHZs3dJwukqFLVeU5JGevSbYonn96eWNqxux1lUQ2U98sbuztbe9dW5t1+Xs8dn00saNw719Q2TOAJQdl89VA2vW1mgszSLqc3tWs8ieR/0k2iZTdGIcTKRzbMGfKq0Bz1TosKh6yTPpKYd7rQRQZQWSZ+SzpALJQOTLqGL7q3IITGYqdtg7OJDtH38dvow8kF8P+rXvqQntYBwjHwfV3wofpTr5YQj/SlKGr1EVal0cr1qmuDNUcHB8rmRM6T19vv3nf/lXLMAvfvnxk6fP11WpmttfUG7lmhlNQec/KVYPYJKeb+IXEd9B8nCwETJPXENcggpLPGP9pXeVTtlZroGxW8qgFmE8n53ShquCzCBbD0xO197/bLJREzTn5uXOikz6aEF9vXV7E3zXN+jIBO1MUBbW1gtPKrDXs7p5DZG7u1ZvlqCnf5YfJ2Sp9Fn8mSGVASSHTZKCQQ/jvffv/+CPf//evTt//ud//tOf/vTZ7oPtrRcm7Dbf1s426eVArqmNzSVcMGekglpkpHz8SiRho1D4Y3UxIUKc4jNkFK/V1O1Ex7+MCUm+glKyfCEnJf3Y4Mbertr+4x/99D/5H/2H//Sf/GOnJBlk/eyLR/SLHSfm3WKeVdSpy8P9A0ssjw+yXpYt0/AwDWhoRKZQpYyqNJK22siJ1QXET017RlnU6QjWreCD8wVpHE4rij3moSDEwnYIlYLomOZV4fJXcWjVUbOZCNNB66YGNsDMAchTJdfiyOB1mlpps0d5RjGFkhBVhVFyhVpwxZvf7tFZE6dSTqPht4v/KnTnVFiIK03d371yKJ98bTDhgwevR69jOAwUi2u2VLMjSLpQVF5+laRaDGFJh0cucLfGOZtHESB9SN2tBMIQ+x0rzofDKYQIoalha4DNLxydbEUe9k43Nx3FsK1aslgMp1HPzz/7RCfLcRLvv/3mP/2Hf/Luu+8vzGQoaPPmrR0b8EJDhCSUV7sWHoY2TbQjA0hTbhORF9L4/JNPb65m0RZIzxigGn8i+/odLYT0dvOk2dJCBaH2AbniUa9h04uVKWLDdWCH3759V55k0Ct4T2s3hcA2v5iD0EtFhL2ccEd/9lcAHNuR8tBwrOa+hBoMsSjhtACrCReZrOJVfbCRXbr61vv3v/fR+8jRD3ZK9ueff+H5cPfFz37y088+e+ECrc0b0+srCwd7z376oz9LF8V24Cwpd710xht0HuRleeMezEnX/zoLwSv3/OmL/GGu3Uca5ZZ+RUJWkRF5YjFxVd20Js/Wjdt37y8srpjcttzDtLiFZaYkDYcoJvnlKunRdJtAjGonnAMgsxBmGDtNvjSDKWeqtynDRmsRouwtQHOQQAx59MmpOzfC/5FDZBKrnfcd1K+eXovwIeBvwfM6wpEB9kF6ncJr/lHCQ3hjGeCv0TUJ1lkiNlXzyIFRW2yjpWfM4f3H//F/8r0/+IHq9+a9exsbm2ZodECbrZGkLubURTogjB0SCgG/yQA3kUMUHiEcCSAfPEJ4StzTX1EQ+TyOkDTLGTxn5FLiiNaFClTGTWy8AUtbGEFSS0kcbGheXblFUJaXM8YFgMfKRqwlK90lAuOOVE1lT9rKOLy0SBhnhIv4URZ+DnmCwK+LhTLi8QPcXC32SKRrYO4murG5trR4/PGvfvm/+9/+r2VzZ4fUTi2tTTnSZ3NVBZpzHod+uAqyvrG6ve/wm2g72kaOSCpB1jRNKzvczS/YZZmZzQR3DG3lSZSeXAngSGiab4aSatwHa/ZPMqlpbdajpz+l2p49e/GtD9+Hbf74bHWNAZ4zWD119USh53ZbZ3Pp9Rwe2FisNZQFIC7bcfaGM7QMNWQHhS6i7lHaQtqqmMDhGITFz5cre73PO7JwZRVFAHSd6VlmGLy4CNMIyNqDsmqiuzQ5dpL407exEREUi7S1A5Q0bRt9i+9XVlmZnAv/U+5mpMILmzHnrV8jnBGLVNrwrTxgf5cKLDuSiGZJNzuuUyysv91jTNIrRQSzJCDqrwNGqQjpQH4w/TqZeocMMAS+lGG6Yo3Hp76/tin3CpMUG0meYV4c2xrnIJolNxiliivPUJAwTn2k/7NQvsLSHFJs1vdYuzN9eKzVlJ7b9NbGzTuK+JPPt+02pdtXl7bMGzv5Umvu9NgR1DuOVI/yqdIPdXMaW2kY//2///dz99L62v7eISFmb+7de2vPSoVjt4OcZ+dNnYqajMhnnRrhD+QcNWVwzkC4kDfvvkE+qZEs3641h147+8nH2GFRO83BzpHXIK6RXX6xrGAioqTc5rgSxzJglXTHhQxmTxh4BPazQ/rVILFXQuQ1lbM21OGpg72qN+yU91PthPffv/fhh/fBuEfFRPinn338V3/1F3/+Z3/65WfPbm0ufO/Dt3de7Phqch2FyZ854bKsC8v7QjBQljHDgxcZmw6jV2x0e6qPY8nTruVO6qAPuRMLmFEEP5Ud1MpyVMuUHk5qncTc1bJsn6PCIlC0rjV3Iqr4Vg+lv6FVl+PLDZWrqcYAclmbA7vUXwOU5RgYUhNxJHWYiYCmNknP28O8rF3XTIOQi9yV4y++BQ1PVfQW1pd2p8J/90cnIf7g4c8iLH/GqeYbfwV+TfirprrJGTA2nkYypOSVk0iF5L4OHQiLAj767ve+lbQvCTORfvL4gcLULcayjjJg69fG0GjZdHwstAK+2vkKwzUkapeQRighdUYZG4jJSRET6LpU4FVhRIk+LIVoLjaFNj3jbJ2gjlxp9aVQs+DbgX2HlmhdOiSfaIqoS+vMCst1ARwe7otBjBiWNM2yViL3K7SDwG8pI3jxCK9uhO7VKN8RSm6qm5YhNulnKpE0T99c39i8sSFFw7wINB1291bOuV1kX6wqsqBUI7NO9MxIoN39IpHcOBZYXzgmjl5MCuX8QTMXQNWa5FbXdkRuerkZpR7Ek7TGHmc6J85phNis9a7h+9NfPXrw+P/ynW99+NG3P7QM3uDu2vqK+kHHuQDYamK1RUEcHO4YeTO0gJyQphafmJwOM1Kze87K5cZ2NaftsBKQtJzqxijWdjYlu3tyqETaMPCsb26ubWzglXLUAMIffs8eZWFgLXbiIFFenvGn9xZhYBLCo6gxPEAjPz5VxUWib6XmJGotox2iEpWiVpS4zTwQY3b9Fn9TJjhZXYyONi6T3wIJGoaiLHoSl4c1lM1riIRzQ6D0k6kKSZlW8nlGYvwrVy9pFKnNBdDB+iJMw6hZSDzipEsrptmEiQ3mmb6t/Xnz4SelUAAqg/ZfKIGznOgpndAWNT0143ZpEmaZ1eKU4csf/eyXBMkX80RZjrjglJi95dkrbdGz44MHn3+xeuue6JpukpY4U6wxTf0Y+DHx8ff+4T8gWS+2txgTYKyokU2Ku8VDKzkpVj8vR79VhahOnmqfshZlVKnHGZYX2azcpYlB0tpV6sn7hhNmyjWYyiebAtI6jJNZ7YNgFujdKomBEeUJZ0YlkwIJLxCJAdUozlQnJySV1T/AaV5atJFV0JVyhhc0KCOu7OLFxbv37n7ng3f+6T/445/9R//kpz/5kSWcOy+eGEOqNlJugjHGoKmLJjhPnx6ijfpOFXPoST0E0IfhVJa+xSrnSxldy8i7lZ4NCXodlcnM1yzkBFOm1azTrKln6iJ95FMNeAXtn+kDnjT7zY3p7miXsJnKPmMRyWv/UqhVVbV6ZC+jeVHANhRnQDFWvGfr03/DatkNCfjDhRtIqfJqsOJwMSmyFgbgX3yvuUT9Kvc1wS9Bh4jteWUIGkldeC/Bi0qvXxnegQNGYPxDYHs8BVZO9CLVhJGAdqckO2HSPHV+ssXSVlGku+M9nUULKMLS5LPFsQ1QYyN4wCbpvObviJOBHZEa7yREJygas54mWV8he0xzCo2+n5k2HE6e7ty67exMEWOtqzEPpwLUqaLSLeP3aXZqVYcPAhWPzs8ykWkWd2pzc2pvP+So/+o1lUKD+MricmBK72chvjaxsRQVTwWvYxMkMtHRpDwm1u+kgZhTr4n34d7WscYzu6c1akjMugc1Z/o8a2FoNRcUZb/H1On+8dX+7sHF/BJZzWgaZY+RJD0/zG8FGKp8M4tU73QKya/qrnaTfvbBym+DAeAqvGbJCdBIuVszaS+Cb7omYtiE8qOf/PLzBw/X1jfe/9XHH3744Xvv3GN0nQvM/srv1Mbq4dGRvJ+6VJHQX56bxpMFm5Ulow7aytUqptR4ij58KXlDZ6u5yIkuGG2U0YQeWMYto3yzt+6sqvDgRVRp2WNKlmf/2fNxHc4AtRrreDYEdCAegI8Ms//hgckow9cscxFQxljiTh1eW90gSDDExqWXaeDERvGvrqVwfp2rPFXXpXT66LVU6tdF+fXhzSIwnffXEXZIIxlqQQP3q0/t8WwnhObtKJgvsGHwn91gWDGrv2bisoSlX30nag0vIkd0dddyUFJ6MQ5+H6VlLa2q1a3T9IXTHoms4bARVGhXllcVyH6WUF0try0d7x8vzmWF7b4VWIvTt2ZXlLsS1/hFKoYSbOUSS3VlGvPieO/ks88+u//Oe8axNzdv0ANEyAql7tVZvogDldl0AnlSssax04TgUsbgEeDQ6M5Os1E4Ivm7knagZ2c/uajBMBkXktdqWwCg8TyzSrKcrxHXy3O2rON6ijUgnMQ/APBYT93V03PkavAqndlyEkU/4lm4k1M795ZP9vYPXes9c/X23bvrS39ix5OOw+72i5BdKRbZ1tQh2FB2KpFFEY4UY9LxKKlczTwwXKFVkoGAdrY1pzqsbtysbGYwP0OFjHRIyUy40+B0f82CzZrazZn4WaWZw/IqUXF5xOWkwM+FpHI87WrR+kv1aJqsw9NcQC5KU1IZ/TqxD9N08lwuNYGvEBuJizpVCmarOiR1vSuLzJLWgY0V7d/xgbbGMHhe2Yb06rfIH7ih7ncczBh56utAUEGGU5OeMcKyo11SWEJElWON2xA7asvqCmv/mI01iyB6ydzhYYY9FnLqGzIYDksQJykZt8N/C/ZAlSIcSzw/vhMWZkDPtGsCgnmUO2B+SfuewFqcCkosNFvIae1GEGavqaEdxZyGVUZxD3eOz6c+ePeNjY01HHJssi320vzrv/nLuflnqqdFMJ7yUhsvpxx/hTFeCQyw3hOpluJKGeMYgxh5lKfH4I6EmHBJ46OHmQ/PqakTexhIlUFZWwB2tnfYaL9oP/BzLlV1DboqzVS4Tk5dWdx1aRKMJi4de4lutStzM1nCWsohgidr0mj60i/P7KekE8ClXAiwlclFf/hVIGojn07+ohVnRpJN5VqQurJgherj54d+DsR/8PDRk4++/d79N22uuGfT0q2NqhvWlB7n/pfjw63nz0wVnx4fKiCjmLY/XelTc2nNWxTlIB/U64+Gaal1Fm26uylrvGNHEdfqkk41zIZUpRx21cq+xQWrPhfPVqJK7qysGm1Mmaai+ssdnx5VN3HUwY3STx+OcdEUyAhOuhJ0uaec0gq1VyXVVUIVFk/5iyvhzDd1VZoKLopYnCjK8aDxN0UxhmtU18gouvIYQ5UsFdH9Sax2DZO+ONCqhvmL4+RHrkfxAqvKxKXbZjIv/GkHHhKB6XkkKAHVb5S55I7TIPfMN53BGqxOfhm2uvgo/Z6xrSpw6Zo3yprmvaNjZbqyvgH++PjA9LFLPcBmJmsu0x90rhEgp6YB0GODm0cJRsKvppdX1zTCmGfLMBHpU5YLHB9vrI0MapNt8JbWCJ2J1NnJrG19DcMOD/ZG9HcuikrhUs/ncsltZVusHMkZIQkvvCZu9SUW57JNiBPROu0RTEYOwv5CU42AiphYYw//4AJctc/HlxGTiG2EdQh/sUVcSafzOje3/3zH8LtLLVkgE0Y7z14wVPjhTG2NbzLdCSEiXemp6aW5rK3LoL42TVsnBlWOAum0gZO9k62dLaowo1icKytpeiVlol06yysmwzLoSH2pacbi2HWzzSbPsrzqeP5sPoeGSqE51rkYZMDr4DrXXnk8tdL8ogvKJYQJLxUtRR16fK0v0eH4rO3HY+Z7eiYjZ51EG+YgrLpc4V9dhZstndbk86uKZfJ7/ENcnjSv/JFSQ/1G/yRARxkwDJ8Gj08we+UCpszaltTWOm1Ugevrq5pKDpRTwBkNrR5Es6OlPMFtEwpbJwegcXr99a6zFgrKeR1C4Gf+OR4Onv7a/n5tDbi/e2y50tFBWkluDsEt0FUhS+CrZqpPsXmLcx999O7/4n/5P/+TP/kTxemGHPXaROSXDz4noJqd2hUUPT1ACuFYr5thK30UpCDYGEmr2E77yMy3xMKYkV7LuSZCsmHd8i/Dt+JcIMYVhPbdiWjyeGMtuwos+H/2bOqtm+xWhv80LV2ekz6rFt/s4rSlh5keo5Ziq4Rnm6VjWR2hb5uwo+G09yWj4DJzk96zTbW5ykS1K+0bYhkKESVPgr2S23SLS5ZshTIqa4Ph0YGNRhZb0ttGNCS0d3Txq08+39ne+sX62rtvv/l73/vo/lt3meJM3Z2cLiwu2Df15PFDlzGwxzXjayHqMQ1ixpY0KXptd0+1CAWyTH75lZQS1oRWuzPK2NqtBA9XTy8c5RgDjGvpEnFAZmfuvvFGpvtqAJDppZENKsLGvNMxsJb0sccxw3CGUSM50R5JWy3Mv8pyXEiCtYShU4cHeb+VKwzRHZw8dqacFsf/O+C5FgXyaPQyij41ToFcBecxGcXrZLoDDA/t2ZD8jQFk8CTHxYOqIJFOHM/oHx3tEzU9+nX0OsO/C5EBzl0RRh6pR11SXTTTCtCWUg0lnDaWmViSee5Mc5sRssUoqyPXl23VPTUA6iiY6fND7WOr75ayMK/mHcr6it4WRUfZqhwEmK9JmRYrpLi+efPkaFe4jABuE5LXS0dCLglNoP+V06bfKtwGFtghEMps1e7gEdgsqnij0YKG6fDIGaaQrnQQq5Wgf2IXRBnI3eNtYO06VqfS/G/8HQImHqNdlWI/E7HO/dCqJFF2o/TuXbJK7O0NunPjtl0nv/jJT/f39wzDr60v31xf0wywdYUm7qxp8fLEJYv7oTZ1X29BBZq3EhFhziFN+9tKCiVOg2UmIfScHzoCbfp0f2b3xdP0fv3i3EO6mdb8xYlsXx7tX2yuGu84OzpwaEJlU1TcRoAk8fD6b1wUWboimaYuBCdeBLKUA/UV5mvKO9WE2hO4ve2IsbRyZF+bw3/j3mqZ6WEF1APUMUMqdzn4/nYd2hphe16ObwgVJNHX0/u68G8IKfo40eJUpaBx2uM5VFvYceyghjMjrrZulPIZyZ/CoIQIvBnWUn1JsxCOHq/T0CEvkxxDDCGdR6886onkitV5gM2z3tvvMglTFW7N8i3TJlmKkHFyNI8SAl/TVOkZGESzm2927mBn/y/+9M/++q//8onO3sMHWpZ37tywR139mLM4etHwXRZuGH6fP45u4uy9SycgDbMoHZZLdazJoHS89HS7hptFYcYknZ0RRpyiuzThcuqE/ihmumjq2VNctP6LJZ463M+4rqWGnlmIdTmzd3phc+D07GpZTjgoxAicwQEsyZKLuctFXcrzaSc3Uqe0v+HrXNogmZRV0h2cccFMAoZlCiiU8XmsrC7vH+zTbG6JXZpZYp+ELi/OHJ6kwlBWL57vP3267/Sfna1nmxsr/8E//kdpwVo+unhLGkcHexSinczmgqSlC6xyqK9JINUkDQG/ZpzAdJVcZlGUKVk1yqfmmPKFVjNfIFRt0nwCJtyVtvxgJLe2tkIs3aADZmd3y5OOouk0mECCB5al3rI6Wq7LO2KG/hPIThEwh039OvDqm3iaqqaZpqCBxKK0vkncbwLTtFUZpaQkJ1YnGma+mpBXn9rVx1aO8cIzGdJI5NfI+5CEiGWuwgdyVXKmAZVVAim+UqL6WzKrYnELFhwtLALmjBjCKQk6258OxA/lbDyCBl9Y0vqZMgTNBFrCeXKwUwMfM5pQZ4fb7gMlJj2CLRbp7nLPTE8WNFzoAZsqAiyc0EesLTdwMFa690k3SXdXV05nsmWxw0kTgn3t176EoAoq+qTzDgDBALgR+8aq1WCZQPSDbA4Yl0Kc+eskGbRmOqu/XUksL600knAgzYgoBxELMsiTRrkuugxBJ1FJ+ASbYFkyVL4WDNlUlbG6km0NnPOffPazg8M9u3LVPgc2MM+k3jYtq1fUNKl0a2JIyAaoduFXCvbcJBdqRg2RMn59SGeb6xrBSn3X9hFS2aezzr/89BMWMTurz8+eLs5urK8ZLTMmkRN/ai1b94u6u+wpJTRwPCnQcvFUG1fn+cJpgglPX0K+UhD2Jmga11SjHrBzERxN8s4770ECQIkzwIq1h6afPXsiuiZ4meTYb2A4SQ03e/92n40cTv2zg64AJBO75ZKCUYKEzueC6zLGvtAQHZ/y5UYiGF96SiOB6/Dxc2r7fGnaFfD0Ed6cH9zb3Dx68Dcvsv48B6p5ZsNmbQbFfcrvcs0ddbtb24/uvOn8fQtqOhXMzJwTtuBrUiS9ZnyMIGRDXhZXYxj657So3f2hZxeSegcv8JCcvIlB9t25UrcRKwajIkxqyuMiZ1DQGKYuDndO9k+PjKDqas1dbGYO1f7Rw30bIxaWL5fm3VJ8vLwRrHjhp06HaRcO/p06WLza3f7l//lf/W+MURpttsaTnG04DXr/yfrUuYWT81fHBqxNejgmznjUyswaUUCA6m4pJV1AJmzRsZ7Exqdzs5e13EPWZAcPl2ZeWKWWDGVc1AxrLha1E8dxqoJ0AvVr1+2hNeNl2tTio8Xs5oo0WkFYiiy75+yprvs7nT51Ma9jLKGpIxtrDLquLN15697v33/7b37yk6dbuycG1HHhavEsZ1nPrK7f3HBm2c62jfTzl46QZJRTQ9PSdOdJr2hKskg6WXWMFTpPDunBKsap4xP3iWZK19qq5t6TvakXP3uiFfRwd/67nx2+8cadN++oJO8cnk//6V9+8Sd/8o9/8hf/D3XY+ngLx04PI6vGGZaX5ra3HuPbjVs3Ncyev3hux/POzpZzOabt4zpJ/8lu4xyc6fxxubaQeS4HcbGvTjPc3trGECbZnX97y2vYaCboNAeWUVqLpq1cbj+78RZhUBa6AqQ0o9OU39n57WJdTPdSRNCaMNI/u+C4zcONVR24c3N2ZF35Uv+uEs7QqoJjAvAknZFknDJRI8irJ0GlffHDW1CNVXObc80q0amDRPsqF+aXA+ZvPzvQc/D0J6+ZbYsgjfRLhiyiqUo5Jn1+XcwkGqzTLg+kF+IdOcEZHbgwplwpewZylBICMjIZ7dhJp2JonloSUXcGJKV8qF8SglpjzzrXUop6VOW0ATc2bmB+6UTrac7s10GSjbwL50400y7UGsvJ0rPZL2tc6WRlefZkDy8vKBPjG66jdg+PbRcn8hBSsTqNZh1Bfsr96dPnno8fPvSzlwkX3JRtr+tRNETzhAznbJbEdV5OVTc5HXEmf9MjMCMlkBJIrPoxpHktG0z7tyr3tZ1RGqgQYttChHB51as2njrdK4upXtoAA9Mn1vSdrUFp7e7qhlJ+TQmYNsbQUpICm7azs2fyRb81GDwhr3a9C6EjtF7tvtDysBVYE2TdxuGVmRtr676KpRK42OJy1tGEVXlFblfqlNctvp60TNrt5TISfXWlknr6JMUO71dH3YUtZVzGPIg8OaESskhYndG7e5T2Ll5tP3nkK0gyICOaZS2fyMvOLsetZHwubLBD4uTibO80N7JYurrgEKO1RUPslrjqIU3PLVgNYJQkG/3nbxzaDjW9Prs0u3UWOvU1phbdWzG9fHPGfmcyfOvDKOFISPWNGSO1ngQe7z7QyEgNTFtBZacj9I4vTOqpl+kS0L8Gd1LoeZ5fLKG/wJIL/IgwRHNnzL5STvpASD0uhpsFl1j9Ib7XnE8D2OTH3xguVrsWAqX+wx/+8Msvv9za2kqeiumhbtyuUWP7dSCGp+j9agIQM0AOhL0e0mAwp/C56sUBQ1uvORTG74FOLhYMZmsFTrPUIA09c6ROUM7qPhPDV1b1q5Y4WKIINAcHGI8kL9OsbK0FVjGcHR/MTLijGtKUj+hW14hOciKNXv+hgTfibqD3auqYZp+as3TLZfV1Vo4RJbIbnZnZK/UZL9K3ihpMW9T6lfQEr2aPzICiovJHZ4CXbNIrl/neiiVbBC3N6LRGwwz0tINN9XLKwbesS7l7d+ZnP8OQ5ZWF0+oHnx4e2X6hyA5dqzAzs7q8Yo+8xRzMiBSKddIjbDr0kk0hjvCmgEZe4eKqsQgt+lJ2pEDmfvazn1EK5iPu3rr90Ucf2c5roZZDc5brFA5tY7bTXl4D4yqFfSJeqa3DA+ci5WwNHVCoLI7bPz9EpKp76YCdJOzBpclvRfrJSZpxaPOKEpCXc2nppy5lRE29xCkqNARTAQw5+5FWfOQzVXRuf+vqxDiAdrOhNYUxpc0nXTfrIc+ghm52kM9BmI6dWKPMv/oHTQLy7MQURBVW+FMUllobMXbMv1dRTLw1tomAYOtXHg6A5yTAv6O/sL5MArbGP6QiRW5IRYl0iCdmcv21w4EJEVeJ4AAP20Dn2sKn7yKE68a6grqWDcCS0T4iG+m+OE7HYdNLqXHKWWdOEmCIjSSUiLTM9bq5mjQ8ePTok88+I9haYzH+dEF1m8E3SQPNPgrs8MksgOuMJEu1rEQWgEmow1EOVUUdRffqEzq9n89nKgqFwHga2PoNABUlvJqMzsg3WvSUecoeMNJbiYelmzc2+SFnSzzFBemJHkaF1tWI8YnRItucmuFrpzI8ZaFj+dROKu2hspu28ZfkZfgqsP1FVUpfpoYQnsEvvDGI3gSjlufWrTeQpxw1QDmF7okekwVoVus5hYVjTSGlyL+0uqeLnzVDRIi5NKN5doApUjEAZ9ZPxVZj4V/bvNEpYpJX/szupQmVEce52cXVlWWlgE5fpXt59m2E2ZXGIptJPK7roZxZYKla6XF6NWKmPDEiOep7juPN/+Ja5lDAEVNczFRdDAGXQd0RdxJz7JA05naC6jV4Bk8DDq+D5yvDSziQkiEXjMBNPRW/FlBxxapeDZmLnTk4okAr56mQo2ZdZSePdsCKd5HsxtDh8jSE8Pcnz2ZoxzJiWpESKIRTfmJB6CEw1GT8EBP8tG8IaBQz3D76pFDVaMcroYJlDVRmTxGvlThjC4Rjiw0Zc+lzZjwkW09NXUk4LTet9Fgfqz99osHrFMl0X08upp0BZOPe5cyiLblHWlqpO1kamt57xtSS4vKZDrnjYjPhoaGQAyHc7RerliYlvT3qvqTPlWSyurJyRwTyiRnXoZLd0Ju2QElJuq0Bw3xzsTc2NnVVZV/nAgIlhw9v3HnbUfhbz54jR/XXgDDZarBBKs3TlpE26S2NI0EaVd7wsPpDQKp0YmQyqpFkr6a++OIzqD5fXjEpZWnMi61n2hx/+L23dvdzsqwTyRbqFEN8VuP8cl4gxmYiKsfvqSecOtOeFKtKlP2jaW60+XS/mtls5QieQuYzdy5Rd0OlQVrkKv/ixGWNhJlBz/b0SEJVSKf/MfYHR1rHxpxt77dDwtli+ita30QieSxO1iBYJPQVB4+vndDwoV5TWDzUSudC6xp5DZm20oiVQ6SXHgj7ZfA0qn52xGvRh9fB8xLdN/OFieUGDO0RjgyuRQ5Ih2P4AC+ktScPJxywKDyKrwM9+TOenJ3fuTGwYWiwVmsDGKnjN37tSLSGXHfRgo5yzqWM0ZUW5LB5Ig97oeVhktVlBomHTu8UPQeawfdrUyiK1yGDjZPl5OHAeEqFh5PugGpAEoC6rLNs7siSQWiHOeM/wJcEjhCmoVxkIDUANRhfIbGpnLRSEYqBULGywGSZ/KdHS+5rWeujR4/AyLu4GpRtwxL3NCxSOiC5kF495sEPGyewn1QSDF49B0+/enIFPq7w0e0jf4ePkBR/Bniezh2ETaFXWehCEYhC+WrDrA1BP4gis9zNjXVMWDxY3lveM+hlvixq+mrGcYsxdSzq/IIJLL/o8ykzX0/QAHknIRlIWtUXA8JJk1zJBoOE3/OuC5paWp3auHU3pRcFYxLu/OhgPwMv5qjcCHNoA7mWnlXWlpUlW6YJue4T95oe6WBZkEcd0abpPctaCpUTp7nJM/k6+AdPgw2vg+frwqPzpYcbxTHnWmiNASYf6OD421H9ACGkQfFaIBOQ3JTzDafaP47xihwUJQnhErccz9Bg5ofEJXy+8GcrUUIs9DfLa+WOMRdDkSb3dGrIORRBZRbWkxihJfTFkWNHMEgrDRuJNZWdoo4rI8mpmMXzAiMuNRYxHokZS7OWu6W7jLPPaRz5xR7awHJqyqmya9WX0qzBDrPEAOQg54HQ+VRK939PsuIyuQZWzEaptyAEGokqUweNBVOkiw6TBemGdBxK2WgckBjqyXwn8sJJ312zzWOcykTVH//RH64uL//ob3744sljp7qSQnO0FpZJqdOLR6rFlZclF4nKr13IellLvSUAnVoafFbg7JwdfPb5J0+ePvr8i09/8YtfnP/P/hmOUyVuY5qZHc0LGnIzLJBqdnK+ruGrOazNxJqmXws9ctKu52LfjRLJ/5RmluKLXLHBDiCwkitC2IahdF6YyKWuZN+C8VcnsHSxRkG4fmPm0lrspdWLVVNpp1b57O8dOOUjRuLxs+fO3UW/IbIa7CcEaWgle686CDvw9U8AW8jTJqny9xrir+N4iXFAcs3TZPdzgB5ghPg0hP8OnqEyXovbBLc89KemIcUw4YANb01VlVFidDjlyy5WO8lCvJRCAwDmHxLlV+CqNI2tTewkB5qVKEe3udry7LSuHbyiHJ0BrZisFYKWuiRQjPrtu3ccRA/GqRq+ugPBOGzjD+ZxAwiyyEONi9LdUu/sAEgbuxzy2nkDgHLwgxsINurF/jEZVmuDh011FyX6J2WuAuEMWU5+SxmU3ixKKCeQlYoDvLJkH1WV+5A6sigZZE4b1FdOD9JYQlsvIzRGFOSa2CPMV2zhaZyiIKaz7OkVzQP97RGioeDZeexnv6IKDD/Xnn4y7l8T/hK+Y0kUQvibHoFCOlAIdnW+EMYzpOIwS/jV65PDq9M5w912OaWfRMuxurSEZX1EhP6W95ydUgqi9JubWHEwbX8OTzwbLRo6aZj3Q37Wa3Yupp0LFHBnnt/CBrnWRy6XoReEPf3yS88YZhOJdqSQYSOFF3V+ODxxsTLZ/wSnlkf+jBk3UDAZ0h99GgJRObwOHoFfGR7NXkqkmmJhehez7vxkcvyo7FLkkRkhKBN3wMwjuvASwbIwY1FomAGyMQ+BTXmY5SZtaEudRaWWfux2Ij7KVbhRQ001OttyFpq7JeAECw0cI8mUSclAxhZ8klySSEybVdOwkZYaxCagIZv7qsPXqjjYFECcZxYax+51ohCNhWBmAU75jXKpehkr5XfoCKa0ZzQC5IaKT0chf30NN8rcqpRlcb06PqD9lHj1pxVHLLvLSLyq/JZkSEUuYnajOMy36fbNHh64Q9LNcfrr6Wi/ff+e/UJEx3WDe/Ozx3hx7vitQ1evFtF0Rdo6ciXL/tMevDgtpPhd4akqFHECOdwuk53viOz2txcrWJ1e9fz51oMHD/Z2n+sNv/feO3U7232dc7TvbO87SprHCSfUio6/TDkqVoaUJuEp9AhIQTjtH4XSVbZEQH8ga7qrExzSaq5L2TF0SiT8twQ1IwSj7gIPbLHxabDMWCEt9tzS6tzS8qJh501TlYeUu+OErL8LS0tEteDCj+JG+APthBvBvBLyCjDo/F6LOBHjFe+Af/C88vm1lybsteDfImDA8JUp+sr51B4FzaDCLiQlMu7oCMHYDgfJ0/CeLIen0kz/ZjHmamQtAMVF2BnEDE1FgRlhtq8upUb37aunJw7EOSPDC7fv6jCZ+RJOMDjl6AAs6wwcHv69733vg29/y6uIGq86TI19eA65Iz8Cox/GLvKA4HHJ+tSxOoPtF70xtMdTKoZaM/Vf8p9nmhARYOInrnzRDxUiLZU9Xws4qfOntlMc2YplyGU0go1LQW5fe45ePTRg69k0C6frVCIwbeaZXnhE9wnTPaVbSSeJ9gsEM+kC3LJdodcAfBI8PNtTgOr4gCYw/WoMYAitQPgChzkDZh7E5EN54CQtmi+TpXB6uAcmPMkEmkqHJ+hQkSliy3zPjlx0uKUbeGkcOU2flSyoVHYjZ7U5plo9k6vKo4VVPN2IsKboWVjd4Mmaz+jYoFZiikuK8XFzZjymF6o7C+D+vXd9ipzV+s02zhL/5JNPkpd0LUfO/kwhNaxRnOj0BqZ4DTVVPIPn2us3CXdnZSmvVrVBUOzKAJ3MeIeEq+SigrNapSTJJzyKiSqH1oqSFwDJTDHIs11wlRu9jokfB4/QSit49CKt6zU1q2W0tm78Cscoz2YwGLEkUeV5bN+4OYW8VLq4XwR7j5aMU2G8pbqwLeO+Fxse0xpcgnOUi/QCMZNzOIhEe6YWDSO7slD0pFj5qqSSD9W1HfKybd01bjl7rSmpE1/GHVwTYJy0VClJJlUpZauAjNSnLN/I0uq8ZMzHCG3YbmmKComXWRR0mTNmlRcLrJdwcjQ1b0mBm0pf7G5urP/i5z9hdZ8/fWRNkbWKxnDdyn5hZ1IVBJzNW+zlUsmLjVo1PjVjPS3xTPLhVv6IwjFXOo7wRJ+m05pPyLZQ78/+6kebm5//5Be/evvevT/6oz9yyRJdrBsjcyura2SZ9dXMtNTRcmvTvPMrMa7hdFHFjHYSOqyoUjeMQlv4Jk0cVVMWVlr2SBRAsTQRNMPTTPSuOMzUh07J6De7sxmNWW8dCrMUd22RGYZ2ffP2862D5bUVm0mNCJInZr45HNCxS2ar+JA3duNv9VdBCwcUro0hO1YFXH8AHoIGf3uG1wGgPb8G2zXI3+p1MlFJ4LboPO36FYxXT68Nj3XA+DmfhHsKIT+shUAMEejZjpVSGC3gZIQNjvhUY5bWLbSkmHgZZNTNmH/uGq+t7YPDIz2/zRs3tQPY3bfeessxWBbuWWogxKQM5IBJftPTJI0qY1VJ4UVjjFxT6BXYAM8/0O8T4ieR8LezapKNOK6JD/CMoqFiT3nWeG5jnCWk7UhsHZVXeRxxBodIh3YnkVbJpIVXhmE4Rvdo/wBJKIdAw4XJidUZL2VSX2qktOdHgrAWY4Ry5EElLlZorOCkkKaiPf1Ua3hed41hCIfqWohPk4G+em349jQ8CvsVAeogNgrnBHLyhUKOv+Ou2T+c7YLGhTs8Otxcm4ldI/s5Hc2NW8dHW09Pd7ZfQKjHQ/XhiXJftS8512otS8UyzBIqVV6ZZp2MtCRx6SSvMeVIyo7MmqoHEWVWKro6RCMZPjvcBQ/QWQuLBgwjz9lLevuNt2XNVcnHB9l9rqRoLaz+dYuwYJfzIXmedr9VOKOfwy/SztP1Dk8hQUqzlD/8MtZSh7ViobNT4Od8SoaTgXAG8zv1RBm79g/hg8f3prxDhlxIBQMzwug+hSz5jZ69cXPDRjFtZNU/Q8+1yyfNYetxYgFjEeAhj+NCR06ks8KyvKm+JxdGvezwlUoI0DqX8JUl2bEGRprJyVl6yPMxd7WeziK9+bPVQJUSEWtCkuCJzeakpPmhWmmdZMVWulb5NT086XhFLwmUpXCs+BZWL2ZQKxhqFl5wdVhLAwpLm7HyBaTBVNrHjx9rAaytLOtL5BbXVEWrxY5+9cufYhmimGdHuk5trljGv5vFB8ly4eGN85qCHpneSt3nclWvm/iQFYJZ3SnbGLIWPV8zI0VikilCbuOgW1uePtv7/IsH7u14+vTZO2/ft5gAsntvvCmy+qDzospcLRlVc/aCVbU0mEFclGWdIXYQPqOLdJaFF0aEXPnO3vsKfm65ug74q9ayCtn/pxRY35G8Ybu0lIuvHJnJ1cSSOHdTEMKhtw3j6tatOzrliOlskiIzEVkhWeLagcNTpgf/4OlAC62FaBf2GEwzNkX7mxy2N0h7hleBMA+vPK+nPnz9TYm88n2I1Z7JpyTwqpOeTI6/3YCoGn8vKYdElsGwhZ5tDHjAD8mN4yqXtJmTjDWty8unV4e8OitXTnPUK6GDZ2f2dvaWVpbvvGG/tztP71rSxcPuwt/dayVLq5s7jJUq7dT4Jcc1MTwDDeABeG3XADLbr0NcHp+49vg6xJIpzmvHGgC8ctKSBHg1SGOYp8nw5KCBk0fzwpOlLD2eBRA4yd1Y3xCRGyLC1k4GpdVO3MaT2ciyZ+Cl7gnA18E/jpG/wrnJkIYXMngazGtDomQSfojeqffrEAiSKvZJdjy9NuUA0OMVWp7BeXWkWaJbIWuptaMKQmNscLQKTWjljTacYWgdqIMgnFtZMqh8uD+1HSzZ6ekJz61btx1S3YtLyIbp5NVa6vXcNocMc+CXtqBr72xQqdrYG5qzJ83KvfkcdVQD+DMXSyjnUJ5ijnRhdXosi7MueVpdX799p3gIZeiRtj+Trj6MAvlf+x7YCr8e8SvDjSHBUG2KNLvwSFyvVFVjRgCuFrczPh/2lYOtPuXBJywJj93k69f5x7Cjv4VVyzRC1tsJeeaW5vWorKwzTjUamwaeGeAscWKHyhIgvK1JbcHoTqeJ4rQtUqgZG2ZdIzQpK0FyNOf2csdHmafMwREGSRcdQ6XJa2WVzTiIAeaI1WWbl5RP9QhlUe22IxG84syEdSr+SOawG/POL/aTHw07O/5snEkDJqJEDNTZfMErDBv1oORhZIADVEKcpJ1r79ygmmeyWFKixeMkpGx+/tOfaiG9/dabVmO5X53+2rhxK43ro9zoR0tpRGvLufdNT/l4v8/EQLl8ZAQpFioneVXLMbr0ZYEiTx337CLLU2VJe2LaJJ3oImml+V5sT2c0e3mwx3Gep2e/+NXHGgdvOBH01s0vPv3sH/z9PzGw1tfOaICQKGTDSfQlkUrQLaFiID8ANUIz1McSAxWDuq4evDSzMwevwr2RbZ5VXrXUXN9K/Bj1ywNbspaMH5CiGrP3KQPb0yd2P9VKXHlR7C3nDrrtnKLnGzqSlNZqaE7/W3R+7hviGcA6okQnQyZpgHPy6+Snb+K/hrZfPdEMc0RtrM0bmw5Hf22V6gmSI+fCBzckDYCBLC2R7Ouy+KS/4uwIwhBdUGJTuQiLoHKvkT1IRl+nV5cs3XA50tbungUCLO67777rTDrWNxOBJZlqnwGQqqrTOkQSCgYH8/U4ZNWjJgZt7RkoF9IZ9CRR7W/9W/QEnGn07HzxCG/X2EQBz/lEaBlOBHCCAcApHJ2iQIEwgfF3voPi4mA3Y8011LwvAH9kzbPa4aphxjo9xWJ3oQIsOZAchE0Sv/W9HQKyKAoMSjpRYIMTzs9iDSGveEZMGoWNeWZRcMTsdYeZUhyS5qkM9miWxEdSJBAxnTQ/vnUsWevisIgjTewSZmqj1G9qcRrfPQsGl8ngrKjKDLethT5H4YbE1OJMGztD/sVzljhnUmuLOVI8SwRW8XNx84bmHBqw0R8wNGvsuupJ1YTRpy5xksGWpRxSXBpZgwA2J+5JVAhAhCjBkF1dZq9oSN645CAdkQiKJ5iOxn/NAb4W0q8dcfg0gJWQJ3iQtsGfhDvpCf0iabm1cEBlIzTsDA1rt4AtcV0S6G7aSNiAKoElXpXJrA8sha4TMsoRSGlBbjH5+uoaxpjOzGBDOS1jM3mfffyJqvDu2/f3draOTk7v3r61t71jEiYjDdHnhiMc65gayp66r9gwV8aK7XD0Ht5KZE6fLW6qttNldaKpUk89XmvnrtSaTCdwYzZaPCBacy/YyqkLogpU3srGLx2zvE+vVBcr/joQIHXG/qWxCFYDIChCrgZFqAu7AlWNa3LAyXQ97cqI8IHVOMZeLLW4N9w4PLQQWptQlm2tE39lyddVmoLpdbsrzcEvotYLbPw0jtWYsiXzhFqIFLluxTcM6+IyxHbJQnKWN3SOu478zuhOIB4JNFRiTNyreD7tOt1jf9+EioN8f/zjH3/no299/3vfMaJ4Y30dOjrI5TZlry02zGQbYNpH1wcH0IAtJvu3tp+natnQnY1JhqZHNRypwKQlN2qcJi8i1CYVQgdDXEnMzGWOubWHy8/gVL8wmLrzsdtDDAcDbOxa6/NwPwqOgzYZLo9n++t1pKFCm8Lq5nY+JBwDPb+6yvlQrAtVY8UESbuOCMDX4dnwTcNk+ECMuPztBuQNfy3WiLDKTuMXiwdD2jPCUn+EMxWicDhM0jiBHPhI5Eg9RRI6nAZEjHAIBGrzCeehCD1HLDOAajOBzX65AWD27Mhs/MnB4fHq0qK1R9blLK+t/t4f/gkFwgYbcKZSQHZd6FSaVPikLySDk3X8rSSk3imieQBu+kPA2Fmf3WACUevJNc3CO66QxsCDYMMbXe86oleNUEM4fuBxhqaDgTQ4XM0RlaoCahSkwlFDbSHRzqAbCbYtNndu3hJFpsyjcX2MZTyjc9kyPAuYI/NSVE+FYC8/GJBZKFRHAktdFnpoFKOSk7Fr+j0RNjwnPQ2AaWK0v59arWNWjf52eOmKhgx7S34DMHCs8XT6ADo7HQiMR1oykk5JKfZ8qnZRKcawUSzUQGj/DcjQZlQMExV01maPi7Wql2/MKa3r1lm9IQeTNJ3zK0ssdFhtn9PahpFrpjmXZFuxq6By7JLxsEhmBCYXw0ffSsQ0e/XOIgNcZ54Hw00OeG38o2rgBYohtL9NPr/u69eFT8b9Sr+IXxmOBjkhJa3Bdex6dhNwZSRGpR1ImRm/BZsQjie8KNev/WwAUki21Kka4HV3goxHZRj60EA2hZIz1WrHFCR2lDlFKtH9VBNVhdmuCmOAQ19WqaZhk3W2SgAN50c2x464HVWuTHxil9TwNMsCFecTMCQvTO2HMP+qa1gpRW6UsxwTlnEWREjWljIrO8pppDUuyz6T5ba4EgmvmjNT53OLUtfUz2RmSPGAHmGZn0YDa6IlI39kFGGkQ9MkPbzcv6eRIcfafdiu75uFwMTTGL41S+Ghi4m0PTQFSH0ukrBYtAi5uHIQRlJKgplPMiWiw5yMX4y2XXV+8iVm2EO2ZCxtpknX2QecahJY3sDv5pLBA0uffvKTn9y5c+u9d9/9vd/7vQ8//MAqLYQbyHUEmLK+ecMiqeMHX35pkEO5i5v2KwZYUlHWDokGRNh3tMXiZj2XSqsHkMZEFWCKs+py0tVlyxi0wkB5hBFMCjoNooxKGbQIeysftTRuMjN/l/4mpVMYM+1vM71rOCXXKfZzSKkKdCSYonjtT5jvlfMasRg7qk0gsAHP+Es0WsN3iIg8mfwpfee1VljUosmrKXsbN9ZWPnjfhQK3j472NKzevHv32x99eOvtdxU9G2wCopVy46Q6mrB+CmxH0V8LES4EMUPWmn5P4b4B8AlyT5WI7uIaplGF7ELi1ZZjMNVBzWhNxxURPYyfFqETqPCK6DqTVaD63iuZGV3wEoEEfLUpR71DVoO6tOUq+JcypSUJDg38YnE8k2SDFCjEIJa0AMs4GA0djnkW0jCenE/DswJGgR0+hCAM2n4dfRpP5QiUnGeoGcMMkIDb9afhGdDXgKUioidXI/Em+Eqv0UhIrXz5BAbRqCkNgwO8kCVf+TJC649/RjhF9Smj1pGs+ONOciTn1T6lNzv7TP9YjyVqeSb6xE3Jy6t6yqyzIrMLWaKz88sYLWLolmEO6yzLz1Rl2NhuBJDz98sBHktIYg7+hhNn0jMR5SvC++s3eUpoAOMfXtFMaXKLSzkmRg+ywcLu8dgIGIGjZo66UdEBNKn9lZ+O7ECE8kSgtVrmZrobikEaUALhwdA33nrji8+OCTrMRlezwAgf2TZ/WPqaHmZFqVVnTB24C02Tydy/tVE2w7JwRFYLKA2sOK3VEoBo+7z6U1/wEmHQNmGL8+QebSl0YSDzNVObSdb/CEgwyGLNG9WcV4N5Qpqv6S6NDoCTd4Xd1c8nAy4VkqaCV8jlV0KmLfjDz4vj86szmcww+LDNH0BGm9mibIaL2JmQm3PM07TJjjPr/eeohszaXjh35vLKeILf2YK1Vxn7ygoImc0veWfzvMLgPbmqTIUPwqv7iBXMYX3kK4hUnLhEqr/1IQSGFVMWYOdwS6sZzB18/Oknv/z4k08/+8zS1n/4D/4+3UTb7u+n1a9YNRtSipVZCXHNHGyJP7vwM56veLEopZD+h7Fv3GoaQrpqZDV1smDkQ7lkCjl11VV1qfFeJrpW8MOc9vA4F52Hv7tnl2zjR+SY8r+FBL8SlcCuYsPXTtSTdHnK/vAcqBLSfrEGB1JgP/trl85kj6eBfeVpGM8xNgIVU0oDish4WJG+uLSiHfbBh++/e/+t22+/x5x03xcYmEYi+kBDY2sa5MsnTmC7Ad6r8H7t7HtKHk6fhHfjvmPpPzSkZ7uGsdakFQ6Cm1cNb1Ocad256YxYSoVBdBATzC+ebkukk3BQpPmyzqkRO5CcJi2lJAkwINVOgfz92sg94fRVhfXsXDTaw7MskqVsEayyWB+Eh1LxOhm3MSRiuhlx/B71G8pC8Mh2+FoAtN+oQYNCKQ7P/tp4CjYyk/jjIuYZ/MK5AQwkfwPQZUFb+xZKyTZ5ge0oMAIYoug0BFdSKch4FN9Yq8YM+4WSfi7WbtnS3ee1dojuj7V5+nCL8mR62V22l58zDLFy+80o2PFarSprelRvDdrGya4U7cWNl8Pr9TlfhrwJ6Wx0oNfEK7jXwzv6Vz1fivLk18IQZIURjDyP0LcAqYELFgiX0HRyMsP5KpATKM8aFqJ59VQuvhbO5ILzysVXlZy/IcEIVe/Dtsts0jIUacpz6/nzF8+eSYV2JcEMD9vKLAZ7Ok4zhvvVOdrZjmsdJqWp9pli6EaC4svaq3aJMxJHybFPnrGxaQfEe0K+AAEAAElEQVSUFQxpM6sLIwOM8LH9pdwZqgyKQJC2QiYfpRqZs2MZmvSmI+tcnkjsfFm1hW+qmcEwhIl0PG0INEyWXZaFtISFc3NuALOdRk5lc3omW+VCVilQ3LAwE2Oy1im5CX8IzXnOF8n6IM3wXOdZR1+gPnXd4Zbzqn0d6umC7cvMxoHE5MplF0ryA61nspO6O1JnQrKgqeRegnxdsf1ptskx2rwWE0XMij6Kw65cqHQcnjx77niXv/nJT//iz//8Bz/4wR//8R8bdXR2VulbO/UuHJvBEtPFYVe1USqz8yfnfdJZV49wLGmneo+afXkN8xRKhZ/X3J6hYnxMs9lToyAjXZHO6lfJTvIASZD9e3KdZieGmMnXf0cKmvOTSAbkxahIoK+e7QbIAUzIqMRfgyQ6Dd9xReEZMEx+4vfJKsDAxAx40zqs2j09ZfbBDVpGRO7dvXvvvbe+/a337t9/i9yur6x65kLKGq9QSo0nqMb2oENUTYF0ikenKyGuwcitwA7x5MfkIKnqptKxYTq+LH3EcnGRGeu4JWxVRSqnRtqSSiUBtw8AaBI2Lx4j1OmMWixrD2BOF5+5mLV8J1mYy9VtkEvrxLGsJyeELSe7UhwUU5QHoR3xuVDlIaGmFsEwtwEWcaDNIi4YUC4txEtUzVV3Bg605+VrGeDKwcvHANNpde4EBqKOVwqAUguF3S5N8Y1j8YBTmQLulEdI4ik3+JtmYajlByB3SU6MsCA4/JqARB1jgMj3hq/wV/YxV0kmuOyuWK1gKFwhkUwNiEEnRDumYyF85ozJzwx67lkG0HRKxSHXRCVD0/pwNfuuoyyAfFobgnIusmRiGS66NEmXa9KHnA+BnZFOYARagtiQ18IHgN/o6eRej46t6MYyHkhKHNPzENJOFK6/Csd1/pZj5QBGGABxxzES0sUg85SitxyhzKDmoEcqE3zazlb0WB5pXaEBnVgwh3XMzenoSsDMLsFj9lg4AqJ8shpRry2sJznVCs80f64M8sY1xVHPcTE8ISlriuNqvCoeJ7ckD36JRPIcrVFeaZBJMyjVvpVQ7HAMc+ZmxlkeNabEPD7KUH2BOf2qPNAJkT09NSfNGllmfdNeS9Pb6jP7fXFsdv7IiCpBMIYKcxYC1u4FFPrRWsSOMNEIGeyzQmjRUSDztk3JUdg+m3kptdcIVl7d++boGR6jwDlkHhvxqcoFlZG4kQGWBc1pYYBTTcdLNJVWATYXGd7AVKn5i6uj8IXZTAw7+DmFI9wEtuGHo+OTTz5//mzrb/76Rx988MF3vvOdD7/1vg7x4uLC1tZOGePUbaWnMDFfvo4soaitR2OJiuQoYV+DtlzST3Bep87r6uiMWVlPp4iMVBCC9OBFwVhPiiHRGYsRsYn7d+pa4ENeE1k19G8xxcbcCCfTGpIrPuXhaz99ashJMiZDgPk0ZnvicgNAv3p29C4OT7VNSAWnsgAo25M5QtL9ztvvff8Pft8VW2+/bafRm0g4S0eOMvEMYcC5/iMtrgkonEnryqKeMeUNMHwCSVY5IZAoa3iQ0oWuCtAhBN7oC0updnR0sQAID/FXVzdWN/gBe8p9TGvaxCHLlMqhq3kd+XSeKwtJkiuxN9duiS7R7qRWopEu+DMVVgzsXPRkOnXf6U4+gXGQDJnl4cAUwqTeWrdzwR579VWsAU/h0AIelUh/QifXnyafEHY4BgsvqIB1OJxSn4TvtAI5ruCTX/nR2TADKoFC9B5CZYawSllVtIxnjfE3dQEs35gqUctF4jqbnYvRazROOaWLc40tzyjhOAvbQkmGzUZKGHqZdqGakr48PUy/KhnPKUuZzyvjS7NmC1SWRGc5gsBICTz17BS72iSNgdbBAwJdw+vgGcX8yj/jzv21j+JKAjI/f/Nj1GoWUyH5JLfxlNyIy+8pMJQVyxqh8NSJchknLtefeH3lvCaZqioEl+HBFqn17LKoaq9lXwzwrVs3WZPnT5/tbG83AdLLyqZYay0f/VF/Mjyp0RqaEea/Z9JSVGZNLT5KnWS92G9Viz8klCCy//LttX4ymAHPotbuIkKjSezJ0quxLLDuHWvKjGUdn4os40e171btRTbrZpNqsc4Sryqayim0uYaijLrDnHEADZw2V+pt9EZTEJGpBmeUU/q41mKUSKDALyuEUcBgaUfUKE3aE6LIxvz0fI3jW7qvuqb5b1dwXHXBz6YsVNaqPtjPWTBw4b+kkeCk5LALhTr0dglNOOHjOpKCq1fmt4aMRp8ApAfTrjiQITWirNMhV8rxxvK6JvzPn3/8+Sef//iHP3z//ff/8A//8Nvf/pBaPF88nVld04sQQdwWj9kZa8qyYkvTW6KNBGPDqJRpBI+nqzlWz154JT2KSME78RnfzQrnjFU2GGDkLBGZ4VjiMbF/h3+7Okh08PxdJAY/tJ3ENfzJ8Ngpjv4KUljDe2rreLYbYAAQy0lsjaZLv8OF8Lx89jiEcilPwUtIH+4YKtcq/L2/9/du3d5g1Mi6jqSBkkRXDkRa4Si9/M2+tVG6RVOTxNv7+OOpROFvAYhoj51PxEM4R/CkC14tMH5LAj3bgBVto0fDN5hYusicegGlumz9oli9k4hiAdxO1k0AB7KO4iobyRSFk5G3YnUlgJ4oH5h9GpxM+drZ7MDOlKd0fQWvfweV0pGLjs7PQgAYIvKI3q8UW3uGrz5JpQEGsCFp6Q80tKeBQTZwewS2a/vbn4YkeHwd0p2MWJsEE1WhpqYWmV61xjtW6+emUcgkhxBZqUcFlqnpbHZO8xROV9ClGeFKsycuglQMzGd6LHpXEw+FUWu3NnP5DbmGnKuZX2tGzvf3dhiJ4xqbdiNKowIXbsLDx/N1/kmASZhr4YXg9cdLxr36bUhxYK5SDDEcOSYBRCFNm/1DEZPzMsDCATQqHnOVnjkUeBye7Cc7yZRY5U+V6zxHztJaUi4BiCvWPnz4UPd3dc3s0S0rpSWgEJlmYl1AOolZqtQTAFWZSwcoIXxPzZ53uBS+r9Y4Q+qPa3fS10y7LACZgu3zG6RrhDvLO7Mo/XIZ/aqSn0V4jjC9cBuJbUJGuNP3Ns/szBsVpmEu92YMbeFSWg9jNsiJGpicajZXRfJIdRKQjbzpisXpA+OiZw20pG8raXHTSmslcm4gOdqESwsDyWli+loNU7mHwMaG7GmeYYNJ2MLVpTW/fmeLqbSyUNNJLh+dP9VKnJ1z/IzSNERfSLNmVbIteKatI6M5HjIDHj6kWENpuRBIsj1bVFCaRWFd9ODpoxy/nsqTJkY6Fudnz3aO7a2/e/eGHO3tHvzVX/6N9dKG1P7hP8zc8Pvvv6eZtbwyWoUornKyIkbcpKKQX5IU9oSPNcpX/fCknK2GZXRRwtSogFFUtNhRVpAmj+XS4ihhbmr/PTwlO2bUUKH+1pKt8uhSSDnC28/XExhoGGCKH688Olbj7A+TsfrrEGF4BSOwZZaUdPjwJOX8BvqsA3Bc/+HRLml02MHGcqxXS5fCHOB95e90feVagWh/8nfqACIAVZV8Lah8Et7AnowVJKp7Q2puEgOQrNqgcIZEeQzzggegUhweZR/R3t6OWJub6+CtzF9YyGIxJAOASkubGmxUYjHtEmWVM/VbBli6nbjqwG8VrlR8AsahVmDTLByezlo/fRIivFeoOWYZ5s6L1BvGV55mlKcoQtoJH3vzt+GHwI4ihQGmP00CdJSO65koVdk7/Bp84xlo4EF8dlCKMm6NVVOrTGIt+4Au21jiMrToj6zQaTBjUSImhEqL7RQopJPOiGdep3YODnmAUYzNmR4DoAcrmWDOWiD6kqaisR0LHKZWrvUngznrtjbdNyyG3apSPnN1Dh2fJK43Z5omWNs1EeO3l38r/HodePn5G/texxMWGHcvA5wWXzUWmlmA20HfnBKuIeqVh/O16fcs3lbhtK8+CWVXQCK9eoyRSKkQ8cePn7157/HbC29rb7Yo428kuJYKw5sf9YzvzqJ0DNPKWjb9V/8sdm/aoiYGeGazBpmrqGLuEo+K1rHNkVRKUg83iadHXUJzeMz2sMN1N5LjLtjgzCjbxAJCNbK92Nla2cjWBvegGqZQICKt8FT8NMb1RCvTKfyQE+lM4TqCopiWaIxgLCkj7XtoizUrSB3xjIKp0ViRxrkO5cyFYym6t8COMqElVSVRzmttO22l2YV97an5xf/0Qd2dfHJiyDrNapykuIy3GZ2zQYiimVsNl9pJHodRIa6cVzVo8W6qkiH86+L2DN8i9ynxkF2neknRcJ6sWjc2t7C4lsbQlXE8OIFhkXQPDz/RwHKepbO0fv/3f8+2JTa4SxnlpTFTvK1cQkwdCZL8MrxG280GdI2KClMOmlQpR0PXqb0WwdS2q8IjduQwxJZKas+/zyfO/HtIrtkroWvJNaM6cOADMMU0UAUGqz05FqXB+lXEEteIBCfQ6xCYTxEQGXyZSV85grS0PL9p1fuNGyZJa/1dGtMney/xK7xUnIpqdEos+FEFawxdjaVFT9PQ5drTpDZYJRUKmzyBzKy4YFT5scAnMkvmK3jAHVcUfuFqgWdE9CrGVaNB01CrMdGctDZ2aIPz4NzuvgSqQVIxfqN7CqHRaoFwSt1fUftVG7k9A4WduriI4e9XXzv7ffCF+g6D1sDTp0/t2OYB38D97Ix7drgkGg9P+yeBvy6kwyUNuEu2kQzPpBL1mBJpN3zyys8hgL8Lzmsstny1RFTPRCCGKOY2kGlWd/PZuB0ksdip0cEVjTzKSJC0Ayyw1I4AR7qACTPJWDW60+l1ckupXbHCVnGDKYI6fXwimdZaWTYb9AretgkJR+/KOZ1tCUv35VxUu5p0k3zlkFIsPyRFd3Wt2YIExkGfZMiuf9UdGbcEUJhP+pfF3FET7JYugz5OnbciuqMQSZX6B9Jh2RE5+izzOHS9/vrF9Nx7dpDYlfrgy6cfffid9YW59Tk7s87nT/fdXGnM0rpbXbnLuVUEulzrjXu5RN0ATg7dXrxwTqgWafa41divtRFW9hMv3NGeXJLQ6UndODY7v7hi7/D+ydmesavFOxezaz/+2eNbdz6cX3HvytLp0dTGytppXWSkVbPmfkAHCZwfLFwduIxWb9OSI2OQOe0pzLBAzn1HludoEMiC2p0ZV0Kgn2qQp85vpqhdcT+rsWTishiScr24WscEtai4MRf7y2kktbwpBCoiPdRwVUorliVXbe/XzNKWq02EYKpdz1CV82U2BQ9JwOgcfdIsSckVpKca3dhycrhzMMvCn+h4m7qamdqzeXVpIXek4KJYpN2Rqoao0qkvhUhUqhbQU64DPncvhWKkwaykPLk8tzjaNUkzG0tHTtJyTPKZXu/F3IJrReYpYRuhrS/RcnFKHlOfFqxDya4c6rjITlPHx+aR5wweLChAmRhlhfxx1XxHlRphiJHWJDb2IeRW2cueNpsyhl4A2BeJzWVNZvUup1bm5/7y57/46edffPCjHxuUNj3sZAYN/w2HPSg/+zDJz1UOys/48uWZkos8m+LWMrHTFMvKZOS+qhqXPrs6ujxzosqcrYFuTcdPW39dXGWDuEuZLdKYmXJa2OzO7B5BpVVqyHQ8YaHyYRvIk7O1jfW9sz2bOMMo9WBc0br8FVCy4//XuAF++D4UXDhWrj/x8iBk9Fr8KdWVAJLYcpKa/ZIGDa3EQkZTwt8y4HUAawDpCkw7rlwHenIw1tBMmOi1BV4lAG8MI0qghK1Z3F/5tZBgwlhfedQpIdOnI/qjISk0Lb+qINMri0c22rnO1nVD8zl5X4M3tcNJk+VCR7RTCES5pKG19Ehy/CFSEs4PONyX0NrKumeD+To4IRx8BLWpItyGTdBBXoDVcE5aiBsbm2pHD805M5KTkCRePN+GWU/35t0burtCqAefXPgV+23EyCW2tSMI1yVkuody8VdmbHZ2Od9Vbkl3vl6OppFH9hIS9ACGOQfVM8k58k8+0yyu4bqUoDx6CogpqGa2FM9m7z599OjjH/9yd/vFF198enJ8/gf377lF1wAB5GFLNJA2smfqY+4fjatSoPrh656cg1cLfz87OX6l7JkIyAnjjRYEjywT62im2nmhMDsKcwA+sgloJKIJSEbKAciEXPVDBLjsSNT6ErNZaCIaEWE/wMlzytpfjoJN6IQbvWpFl0OglMOmkpBV/nRcizx/28rSRJHZsnfVmqxISe9sZmOUUkUPUHreF0SZGig1XHSCza6W3GJbcyElkclyeFJZjXGNHgeUkHjiVqr91fmZONHjwrCPQP1LpS9WuF3Ovti8zi3qj2GMjOt9g8rxDkiPqUqGcywvE3p2uXPwQt7mNtbUC0tsNpx7v7zsp+5RjqxUsMYAZPix1xzC0PxkidPHqhEZ9ZaHhKGZvCKrae7kcA8N2iXOIhPrzt1b5NhhoS7tWnz7viskJQKDWMmJZplKFhM4tbQ4r8gpJZ075gBTauwLZ8OflJVFObJDWCMp8qXHzfRemgxVXl7t9YZWhUqv1wXgh08QbyW1VGAIRo/pKWecRmuT/dL7spCUdDYTaPMLb0A5njTKSvOVbAsIS0UB6eCOAJSU4GE7r+3RcLEpy2ZyIVy1tYPfV5gRJi7n1bNZh43tB6AWacEByyS1sTJdD534LBC/2D9Ig70iZlaZPFv/Bf/cbIaO8VamFRYkoJzHavlU48ciSVAoyIDBJESRn1yEpDoAGz6x0qUPU7ou0uyR2wbjuebk1Cc4v/jiC5PEv/rVr9w37IKH+3dvOnKEJfZJom7AW1lc8EpjlrgSG9nU4LtcdIyo2lGlANjCCnRKRS7YTiMiqG0nWFrVtrxGxd/mK7ZfQzcZgoDhtXnSr6WkXsYT2F8929PfRsApuBHAyzjF5AH5ZPjr/gE/ke8onUr4NxbgjtWvYBqseTvACBRC3ghiA/h0Lf8dkK90mLIuDaQaNLwUCZ4CggQxbUHhHL42GXqEQy58gkcUT6uUFbRuq2fH1axPZ3F/jydHHlWVMXRiRQm0lcQxawrYtdZiwWYkyWwISrLjKO3ZNEfSjGTYtMmrGauO8IAh7PC0a5o1nKNXqgJKTl8kDdDSnwM/QcIprY6ig2AElJaFNbcDUeA5A3md+kSSI4n/4sf/ncGhTz7+pdtxdrefu/eMwlnb2HDxbawjXmosxkwqL8lTZUGCYE4qHHraI3xwvrbfwTftB5M4Y+crb8Pw9Ne8tvXpD1/1nIzlu4iJVKiGT0JQ1bEH2trT8B1lEl4pi4JpnK8po7rSsVH1p87pgFn0xjB4AIs1JNThneLwFF34AEM9p4WSZTLyUL/2Y3mCy7VkB4C6qVtKRvTpHswvgFRQ5AxSgtdUgixwXZCcR63ZFMoSmgE8bU47QmhaZ0jtHUdeIc/qqMXlhYtlBm5tZVXo1s6u+kC10Yei0uCzuRwKGTkK1Ym+2rmdk5Y/SQAj+vS7EK6JwVMekspRvhnDYZz0vZ1qFJUaO6HB+OzZ+c9//vPleccDx+n2NQZxYWBNq9JoSeQmQkq324aOdlJYJaIC3B2oI3+pP2kGx21o1lMT/TMXBuiGVR+fYBAN/Y22G9pBMoRFiOcUe5BJaiGqhqe72O1P3msoOO14lJfD3OrtZzGIcfDKdx5BNzezqqtYLq9jBw8vbrghBMKjg5hPq8Ggv5Oj+qJNqjQjxCCHdoyIXVgA2t8GePZSdGsNuIvz+Vxd7GI4K6OXj06OXBl4nq6GAQLDHLMrujJMnS54nbmjmOfTv1HPqcckXWtStH3CKF+qARLEbfmsWrCLe1SXWXbT6ml+BfV4aBrNaEvghMerVMiGiS7jbJ9//rmrlpzI/90P3jMi/fY7912tWFP+aVUsnRnMThMk9bg6KAKJAI5ZBI4HUOXUuswqaEqartPsyxYs0J1u4v77dZ3u8AxLU1PihsD4x5W6vrx8AG73CjAe+vc1Rvpl5G/gg6Qd2MHTfk9JD35f+ZuTQy4EpiiiVWMOq506ilVkR2PSIsCUgpaZA+jSVFLoJT9gCJDiA6Ag6QeoOiGfxC0BS02R9OAAcA355Zdfknm2lkYSvdZMnRtJXl1egYHVZM8iIjm6Jwg//vhXhIOHSLepXqmbEWrpRnVpqv0KP4JFlCiP4bphdRitkwYxC5YBRHokHV6KUxTLEs5BGqeprmQ/0yeju2u0QAi95k17OBeGzpyurW4YccIBE25HZ2fPGN1PPnn06MkPf/ZQq2L/YNfGw7T4a1qneDhiQ5qhIxFKZUNqcI9rVhg0Lq8OHEWrPyDRBLyL17Ng8w2TGrICAzN6zSzBV7gq+oQnawXdz069w4cnT/TFWPKHsgas5dPhobtcvxbWEWYh/cqjBAc/zxClAz0nAcBLS2BT21/b3+GN2ZNrVAZ10wsZ0JU/FSArc8bO1/byMFRixoKcZ8WN8KEyKDwL6OQcGEFUnNz5pb5sxlVrfZEMjSgWEvswt7Rk/G5lxZWcJmx0Ru/d+x6Vd+LK88P907Pz/UMdqenjs4yuVLrJIUU5d2GMN1trDCGplUKkK6I+mGvSPaFCg/lBqasDVRMY/XmWMJ1ny8FXVg357btSXU5s3ndm9dTU8ye7n69/9tbdN8KQaoKowKqgyiKb6jIJzUBhGhoyiW9uncSN0dYj+d3RGdS1TSPA8LepL02Q8CGmDFNTomGtBVvppU5PO0kFbeVSCjylMVI8gZ9QCB0i1xhCF4xVxpRmtVgyxCjjUjDkysmRTjG63GgriZdKGYWLCw6K2rh964YVejTS2toSpt1/84YTwbRRJiuhuJLzrExEKDt1JLkxWKAQXqnHO+dig7mVFQc9ns0vHi8dLx3WCtUiA6x7HOYoI1rscHFR5bftS+vbuvzq8DeS5DFcJz+nWR6lEKUoc3k6od7sdD6rty2l5JAnHGsiESOW18FDCUIiFgDywGO0w6kIe8+f37r16Tvv3M/9dG/edTWWttH++fH6tD6xApCQSfwen1Ls0ZpwNm1KwSLbEhAHg9Tdn6MhzVAeAq530hL+uzmJlhwlS5MYpDLxJZ/6tbPfrwNMPlWt7K8DDDD+4bV4m0QCP05t+NrA+fxVTpR24HmAePK3wDQS+Nv5qjJ6dnjDD1j7tUWLX5RAZvXkuPEpWhqpyik2qSqmuRRXbKt+R6pANgCVAm0kOglkoMWg9Qm0XNCMpWV/f08kJcuJDJigMoTjtr79iq55jYOTUCEJKlFAWk6VgwRevHBLJnFSHwEsLTu9Jng6X6qVjLCdXmWFiy4hlnpC5YgMbMJLh1iin1m3nCjrTNsMq5V+v5ruXrgKwWCH+IxzxrlRAJrspTQ9hOuMrvoyO7O+uWlsydHunz/40sE1H3/88YMHj3Z29s6nM9pnYvnGJsk/NS8EETCj6ipZ9FWmTdMJLlZHKeKYhPpZaeYhg83DyWd/bUh55JGWQDCdxwbowPZXabb3lefEWq5ReA3toqNeU9fivJSAv2qA0zqXmTy1m+OvPhWaUxRFWGadon4VfQRSoI6T1hEx6PRahDuJBkh6rbEr3QbrOQgylapTG1s8fapndFpTWjSE9FEPWHBlJBgDMqE5hIzzGE8OFOzZjhRBaM0YIZsvhQykMHDp8Zhw9UXI9nFMo7bjsqvabjoaYZ25pQHfff8DA303b9xe39zQxyWpAuX28CCTGQf7e1989unh/q41heuLK9jiPotMFxfOoj4jWvCLx6MI+bmQMzGCio8CoW0AHNcA1lZl2mdOz47Ozrd39w5P3ab+VN6Wl4jR1JdfPrTwiXz3IQ8m4SFJ0bHB9gFbOAFFzG+MAB9xR7Cmqrj4u+Na4RKBZqSB0hr9z7ZjlGBFuViSJmnm4qhmsqJEKkdGs3E0cgQeTCxuvIXUnMdSLs/CK09Y8iyzVO3uiF1VlVAXP7t4NhoMCKoJLuGcwoDWELSLfn1SHOyuLWw9CqfiSUW43AFLMlV5qLmKFZYiuPZFZ3GCQAFpBcVqTbuXVGnRYVNLWcmulYDk6BSzxDVRoYspOcf27uZursO06E4zNaoBIpbOcFid0cJKpWynjVj62dGMJrc08CqrJWZthpuB0fuIET54+PvVszMSSrTUjo9/cXi8ZFT6iy/ef/+x3Ur05s0bm6Rxe3ffSEzuGNYW8F/Lma2Y1fySw9hgqMKHkloeq2o6pJLuGhMCBP5duMbsOZmCpL0XAaFNuv1sAhq0C7FDJmH4B1yDpwJTskNI45x8bVSvPxvGs6P3U00CKZAbUA34O7xh0Dl4hIPhBHqSL8qtJgOEd8UPVv9FYX00mRmkLCHQND7PSU+giJISV+4EgOwFOUVMrjJDSNOOi8zEbSUnrXYKX4iRM0m3JoFQWr5W4c/75AAQRzQT1/XVVVuhNjbWdSrBEBvjzBJtLQGDIxo6m0mljEXnq8dZBPZkOfJK+HNzaU4DMPCbtZw13iSns1dmi+kFNIQhVdAR1BJIZ4GZCRJo6NAKA20AvHj8xK3Iz52h/vNfMr0P9g8OQ//yyrJli8ynnfxUmYbyfI6/JenG0MNkvPE5zdvwXcoLr/VQ4QmGamEMxLRHeH/tLHemgo4eq32DPCDDinEu6m9BvPqQOwGNZ3gmevHwVdiXbwPyIYkGF95uIC/yUPIjvD1CuDHgSPaGV2Xa/peYx8k2BuECJv3j7y/lH0wOlZZieC1d/YnyJ6fFeCajBLsQlYjuHWSomdeD9HePVgEr9SRWx+G6OKG7U47KvPHO9x1PSqc7DP3Grdv6WHq86oA5UU+tMyyQd/1GLddLp0nUDEqGmw0JOv50ytIDK/8Wz/djSOSBTM+chkcoM+LK9ip7ZeibX3vS+O2aVhMkBFMNoG5V0DkpXV26H9Qq44Ojk+29fQ2dF9tbjtHRS7XtaGdnamXhhSbl0kLNC9bqTUnYq3d85fB+c/hJ8TiLizEhRnd4hi25/SmlRWI4WVQDK49haH0aVRt+zhh8MU2c8FWICVlVKRh0Jml9Y0bVxy3waS+FNvjBCGR/WbgwpJaYCBn7AeBPetoDPUMs0+fEixhtbqzevXOTKvHKIBlWAN+qSqCIsPnUFYw/VNa4GbAIKFXHdROlMkgtaJgpJepCHdc1QJiIRonjS5PARJKz58/Rt7Ka9oSDoxmwE5NfCiMT3BkKy4i4Sx1rS6LU21VS2hnVvGOCtdOjG8K7pJC8h4f9mkQnnIQ6O3LHYQUmnB1m38jJ6ZPdvYPPv/zCFYfvOsfhzTfvv5UlWnVDmT1LQe7Yf39yYkmtDpOEhiZBM2inKABrWVIrx0fWFtXIEIiiaoKEv0Nv5b05kFSuvXbCAz39dQDjKWKTTZ4hbnkiToMbMAwh1zwDnmvhLFALIZydBP7zq46eHPiO20kAJl0N6RO/EA5cVFbyh7kV0Uo5hrZGJiIkbM/0hUZtlpdMT9EoBjAylJTx2awRcwyAa+HQE5xZQZA+UBnhpK9hCwddwVyT/8gMu2tL285OtfxydZIGGaHZs/Dz4uLp8+ekyAzxB++9B74yUjcr+GaV2al1JskvkdC1Ih5W2nnRPKjAZnjVoNSheJoPiV3aXyhQnOpfVaSA0AwKuTnTwPz4Y4mJYcibt1elpc2rI/H5lw+3tnd/9JOfPnry7MsHD3f2D4At1iqzRK/64qnHbN7MQp5kAZ9x0Gc1sAdNwu9w28cm0sd876Cxv/6OyjGgRZJnslwWrnM9vHb0hvScxNyofvOzGwTSEr2gG4m2VcftFKXOxT8eiuCNPJV+A1lfsjiA84oY8qnEhU8S6RUeACJOhndaHe4JrEN42vXrkNwAk3F/LrjS74r5jdGN0/Lyyyffxx7BGQqWFTKdWLp4Wfkzc//++0srJu+t/stWgJt3DGTeJpcHU1mcotHZ9Q3xhlIcL7W8fhuLVJs6ksi8qmuGgnB1acqNrU4XtHTQ4Rh13qMOp7ZBac+aoteDYpi7kzcaVKplCyGsTIVnWFt1mAhqoqaPNTWFsPXFpfO9i62dbSPHp2ZXzBZn1GFmaXH21o2MI50e2xW37KS3FBi5VGNqQY1yOcm4EQFlwt16EfHHKi0zv8wIlkKZXrkNPoLta5eCKcPRsFLWatXXFGoaO1qCK+n3c+nP1Ugnfy6XbAlwqijq1LZiDvgszC0XRNVK8sdSVQavw7sLLO/9qp8uFge8WDKy3GlYZVTG4u1Yxgv81iM8OrI/h3bA4VBjcXSGvrrJxfKMBmeCTs8hwkzTYXpqjmZNwqvKakPDQ35IV1h6arphBoMI98L81PnCucWaB3ZGa0XiG9YXX5YydEYxGlE4dddD5N+SrcypjShPiZTtVxbdRkl6WabctbCVVwqJAznpwQ2vONDhcArB2KmlNEQgNhxneviLzx8YoHvjzt3vf/+75kTevn/f2Sw0rIj4HBG8TDcoA3s5kSBzDfIIj4UtwuGEudNNWb30j8N+17/XspP6V+kI71Q8B49E2v96agOer/vUAJXfRjhkZ8TSIcXXMQwhDdOoJuFfD+koTW2X7yQSwuNVLJ9CTZTsqOMo3Gs//U3tSQs6G3BdJM1s0icUmHhtawGnHlWh8/Nw0AqEv12wZd4qJ7tJWuEKT6JXV/q1NufQSC7EpFLAAIbh29/+tlJvuaqIJyZyxb1956Ymh3WlkJBn/4lpGgdzGVEzrwunKsiVNs1KDyEiyiEA8F7hFwQ5F3LLhRWimhOrfTVeuQHAytKMNdndfnnx8PHTTz/9/Gc//+UDvhcvjnWSrL1fXFheXaOvrFDR4KbimeqaPcQHV7cs8Esawpav4kmpKgp3TG2R/VLwvCLNs12yNnY5iV0spVbTRjzJNrVQQw4KLmWX6h9P/oy27Y7jj/+2JIzfAhngCRnoT5Lu1PspsAIiP+3B+Y7VGCaRJMulakDyyJGQxtNg/AOeqI5KvT9Npt4JdcTBD9UA3586oh6wMe6Y3rwnXX/CSjTEAEujXstTr3M55XJ1Y12P9s7dnN24efNWerq3bi4tpxOg+4tKDTEu2HJiX04lqZUrxky1AxntWQMjPlYfL7YZf0k1uT/Y39o/2GMY9Ui41bJP+s07Z1kWi3vQAtYJRZLesIFhxGKdyjXYKXlov0q0s6N7uwUVNeoIsOPdPcntHexT737YYsx/aX7uD77/PXaauTV2pN3w8MEDixdxyhalLonTiyN7ZsquRhxvbSyPmyBRyzJCjpDk5EpZTcblLnJY7fVswE1gGjXVuIy/4F1zRXE7skOICkgE+JHGLAep1kHsS3E+wptJjJGjK0rQfYzgRGL0nuPAZ8i01I2YzTHPVAQTOqJdTh+dHGLI8vpKcf5EfbDEbXXlBtWifCEBjw5fgUMOJ1fpvJR72Yuj+tSvmN6uGNl+TudUC3LOMLTtFpYWW5kF58FhyvFk7USPQqvI9FZKUwNmdo3SMZGqpA4tnbfiKfcrWTASlnemOiPgedI6GhvUphBtzZCQNHaTIfSjV5ky9I05kkPAwmyGBHGQUZVjGvPpk+fbW7ufffH5O/ff/u53v/utb33gJncSmPF5dyEfHPYcihaFAuaaRSGo6iflGYSjypmC+7tzlVDpyVFyXT6jkK9Mt2nzBHoNoD8NgeOyvs5VYNzr0YeI7QEzhPB3CYqVyCNGxWyUah8AI5teGnmDdRTsDXA+JXpUFp9XRrYssq9pCNINivnixH4w29TAzy2uCeC63D0FtnmDYXBDotYtpbFYE4FolhalJPqf/un/4Ale6buCk9GCCoDj3pS38KI2QzxUmxpBmWgNCEd1hotLXMGw6iW7pUiqDyPp5KgAfNJjF9JCRUqt4IydhSXzMhl0BhxFUms74KdRqpXuDMqQdKyfcHzmZPQvHj74OJd2fvHo8VP9D2bZzsvV5XksO7Ugx8Isd4yurlvMZZxNhyeZrFEBmaIBXDsa9UVGItdRHOmNRYN4LU89m3hkNK+G1wGmOePZrsOBKQJPgQpuKFwhlUj+XnMqvZBGIkp7hAwI2x9SQ12a2vkT5x3Hxp4yZxRV5WSUmq+hxKlF+geFE0nRM1o5YTWXBH3R7atR+RzbUDQEnGcgY2zoE8Dfr4Ao44IPHTD5EhqMZJxeGPLM4lm9WiulmheoN05IwJaWbDvKAIvu7Bt37+lBvvnu+4RvOQNukULFGaGRGOM0PbV7MnV6cKzHyoBY7k7Dv7GyDhtJIhz6wYgosi7pOEq2Sj1jgBw8kCxO7YMh9PpjomhyfjlzecNJ1vJYRzf7ijUuDVHklPXi0ubByam6yFaZR/Hj1whlPrfLATY8eP/eW2jQt15ZWFR5DYnXeGfOtzBBs7qypAOn03Z0cMwPTNK0synA4zrHGHnIX1tdVtmRnUYGvhtrDT/Tz1MpIgvTbHlCVDT0RjtgUBvISxe5W3+kXZ6Z0Vj/OvRxdjmtqiqhHM9shDmWjJ2VP20frmqpSggmKZRqSBolu0GOFcqyNiQYXuPIJ8gSIMRWS4VwlWHGPXE9dfqx1LyYV6Y3mH2yh9LVticZXg+fayYJTqhQhbeQu08t4kHLWd2m3ZDB/rg6rEJJBxVHDUV4q6bU+Vl2HLtT93x1ZTlxjdkuW683bTpef4I8qobmWmdMFs9auuIcjyx1cZLl+uYdCWlISTQL5abrvofqoxARcRUr00hlSBQnCQnKAXPNsQTWJ5Cdd+h4vFa4YlI3MhCJNY6KEyg7uzunvzr59PmLbQvj7Rh2sjTnwAQjdUbrkQeGVV5ftxFl/+GDx2ch84p2Ptg/dKeqvSf377/zy19+bBBe8sVbiFs5pCARb1mEPAojDKS/SiZFjDZu9Gfsbwze5GtQduUfNdKDvBICyYEJksLWT4EJyarU8kx8Et6Bg0eU5pKBJ4HcJKoBoVjXImr9Nbxw5PVXT9hazvm5Lp1G+zpmIQMYD7BUhBLg7AGN690t5NxaX21Eidap5yXTWQBa25cN7dg6JCK5lSF+F+DyK3okNElFTJRjtwroByV7bF/u4WGWWtWNCCDv3r5DxjjYZKTzktV5YVSTpN4WGzPiBX2u9NYc6NsIgMXqXZwurtyQd4DJdRQ0DGnj2gfcDO9nZT+qlY617EuGeUTUPlb+EV0n81WDcnGZ0GUlNmX44sX2/ulUX5X9yaef2yLFZOCd66GorOijaP3opLAw51HE0stUZ19YZ7BrN8ZTGmXrk98QHHMcZcV5bdd+5EGCQm7yq4iVlzwSrZyIXj29eQZ76UCvdBkOd1XtcJBwJn458M2iSiq9mcYjbsxo4e/HKFwiKRfthxhnHRNoAlzPhmmcQlrGfOXhhEvFs10T2SGAmzzE+Oq1XcMIEc7P03Q2hoaBXyD8PHO7+6YT9HW0epZX1pcNIVsYxWK9914WSZm6ZX2X7A6qxfSez2scFrqji+lDx5dmNNpgpbNebdZlqrOlMiubORP85jysBc4x5Tko1QYQC/f1cOhNmy+R0SR2v7ZJ3Np9zjK5TFuv3EAfUVVAxyeHkkY0E60poSurEYowaW1t74soadpQng2qWIVomEgtkluBIqJFrfMKEjqeFABpNCckJD23mqdMSWN9F0N4lFZKYsSl0gDA95wiqSAdixgsAgOWOZqgXajtRQEoxtuqojMaA3nlmAtjQ9n75398ZQCml2s7KUpK7Iw1wxOGVm8YDmPLqErKRUmOHSjpEQqQYZYWETPq5BWv2Cag/MDwENUNL2TSBUvhkVJ7KsCjBLaadfyiSAfPGEXfsJEnVBkcrqpFpzRaeAKcWh1nBEyW0x4KJRH/dOU1P1WuDKpgoFNmsq4p9xsumJdIo9LwoV635W+GAZSZQtw5SvlCouZUXvDa8HQ0ha8t/QSMJ6RfXa2tjlY5dk0QEWM9h9dxNgPMr9fUcwGJXr8KTMeKGiJLBh6fPH1uEM8ClgxKv/POrds3eEgfbtB9WqXE7MmTJzo921s7VLaSzO6zszMwL/ZHQ+JDur+bRxbSxKs8yriq7b3aECnfzsuAuTnWr9c+dbXvwMln0H+VA9Ng/RGY135+Ffh1Sr4SRmAj+bqvvya8k06NmwAKZ6rKsMvBHJNmyCnzlxvra6k/1afEt6wPLrEnP1BhoCYr+SAeWnOK7NmjR2SJg8dHLfVu3mW0dqw0RYRQFDAtMqmgAgVTBi+Jq7FiMCWxBBiYiGKNlEphaNKFSTQLI2ovA2zeuCikEmAAllYlQWtQYgQtXe4D/ResKTXI9+jR4+dbL/76R7+wnGJ7J8db5rggF5qlSkZHJE6NFxB4NMqB/3Q01aFlnACsKKuDDxowyaUsylM0CZcHiw3wmitqU9PxpPUSfzuZamD0C0nWiwPCvQLmBHLNTz1xbOf31RNwe4ANiXZ4x4qGKwdsAODxtV8brP1gouIL5xACQHBnXOAQsWBDG88APOkR3q4Dh7hDIE9HnyS+gYX3p7nf/6N/rHf79v13NfNJG5OpvShCir084Gw3Ojq9dDmWJbGnS2lt5VvcghkFf7yaWYg0z+UmnP2D46fPtllZ/tPT3YGPBTB3c311an11b+8geDQUKXjKOE1CtE2v37yh77t9tHtsG9LRvsqh82PRvl4aiYQzjVJ7ADISm029B4eR08ScntZotamcA8Akt1VW05KF8Wa7MS9SS5J0xlkMLGCzv1p8FvLOXdrkNLJnpfM1+nLyQ+4SzlzNqaWMERGnc0BANoMzvai49boQIgy0ADItuVCa71c5xEPjG5xXVHUPWEMjJVH9ErF8SmmXbWWlgkf0MqiQ+3IyunUnRcDGV5opZ68hSTubVYJg5MKYZk5DCm6PRIW3E9KvEMTiV0KNgF8g5B3oObgRQG4NjoOB8xViPzpHRH0DmjFpwtsFoXUZ853VZAunF6fzcyfzC9kw7dSV2Vz6YIBM5c8cnn6hUeLzHCoJsdJXSSWEGHw0czLnDkQui2kyXiRp2UlfvdxA5/DanuGJWn6UqeUdVwj2N18MC1m9Y+395eGhYRi3DlspTaLMBZp2sYH4jUy/3Lp37837776jZ0waDo+z4BZOlci1tFqcoXPqb8cAF29HZaltjXZyUfijpLjOToGFD4PrrPUrPwbyA+Pa089rYA3vibeDv2H62dGHT4NHOIABOf/w2jANwD94hrjf0KMORsJGpUZTpydRElgzL0zIpQUHzB2BmNXiJzAcmKaqPWyMyskvg/wKS0uLAtFIxtX0H2pYpfUAsFYjgIestdSNclG1KkLP1IU65GUldpyjazPGQm7RmMsPKlDs7IsphDH2L8tlbFGIdAZ4TFFRqhajpNU15dRcY810yvrqujEoIzF2tRuA+eTzz2xtZ4Y/f/QCw2Ez1RfiZ1VD9NR6ReIT+Uaf0aaRkCALPFLpYl0CDV8gkqaXUepLFGSxunoCBmBfGsJkbuxE4ZWuHOE2DwezlozYAEsMUm4VS0jIVHbARKzA6jJqs2f9tVhBLjw0aNdTDeWwLHMNFZ7hnDENwJKRcjyg2i/1+gWXELJZz8k6khA0p0hKk3TEJgyRRVvC+IuqEeZKDXkAuqSHcOmHYFR03IEwSAZs5bma+xf/039JX5C2FrWAVuyMdYxHD3LZW81MEk1L+CPO5ZAIy9mptX5nDx88FQaJ8mvna4YoTdf2WpUI+rGOjkyKRZd148XMYB2Gny5DZG7/qWrw/OmTp08escFugjd9SBfHdM3OsqxW/B8e59g2lMCztWXiNnN7kut0EekmMpni4SSnh8Qy4R4YXTDAnHzG2rVkmDGyHNLTbGQsfbqvmIUe86qkk3/B7tVlZ1m6+NZw9IKuf5IDB3Ikb4mymYZ1MDeLRsdglAU1wkzaJU2W8IlfmeZEy1AjCQgJS6Lzy2/wILfSSGg5raHms6xpuhadic0SZQ4hkwHBl/qfwh4LX6TnugtcOR8KOC/poRcwzB0h3dWS3Xw2qpZ9/bF83lCSmdAyihHesbJGj8F2ryn8cdKdxGVWr7EeYoUHLLHofKq31VddPTQ4sAhTraV5480V5dvjgTmKIFQpfI2qwjA3ez6XFljXf0mQEFRhTmgr+QwZtY3Y13bJyDhHOa4AheMvNbOQOi+jopMiYzuNYffA4A01va+/e/fup/feekPL9a233vzu7s5HH33khCNmWM+YfIqIAFKnOowQf+M/XRYhaUxToqbjkQKVp9R4FqjMvP63cfrOS8AmXDNkssiHjwN8pzWR4mSSI/BrwEIH+AHhNc8QpcP7dTItIf2aT1+R5jV8r7yyWt6LOWIyeKl0sGnDei/lE8ngISg+bayvT8YH6aMnEdJ8f/TooScycNLgnzIk30rNV/IjXCGeWLx0dgaAZeA6Oc8MfUdDjGwn6xuTMerbmpATW/Z4QkjKLEp59oQqSjiZypIxTqUSQLtJVxVWxSQn3FCW5LRNF9NJkaFZA4ur62uoQ5DWnvmRT7/43MDMF19++fz5loygdmX1ZucxFKZbGfGWrsCSbczC/NTxdtQvG5v2gWZCWVDAFIup9EC27jNSyszUGR2+jqO+tCVCWt6QLaEG4BncEGXwdCl4RWSDwZxsRg3GDZ/aA38HFsdEGsUawvtrYlb7D1in5bU9/RRx8pW/Q4KxXIfwdl46v6NvE3EngQeSxO3kOtZk0k1VJz2Jbe4kJ/1a+UdVhjIsEHnOVKNrhGvwlixiSxPkaZ8IhcZWdojVUqREkAHhyFPOfsrCP/6mxoJ/kJLXUUqPbU6rwKnDVzsvHmWGpFbiMbRUG9VJgHZePAVcs5OnOcfYNp2TA3O6vf0Gu08sUy5HTLlbmze8kV2uyi9tVe0JvRbhmaRhTo3qLGQGRdaMM8WMXGZxHrm7GG8TUHOkqvlAw+n/AsZWlcO0o78YsLQwv7G2qu0pd8UToKEUZMSmh46np5ccylE1TVqcb2xJMlRTfepBl1aPWAvU8Knc5JFGQdxItsi8l8KvBThSHA7qEtL5DT9LuuChLaQBHmAlEcvHCWnP5LNLxJNrGGBNWL9KQgg3fBUy1DGQKfSSUZkLZvW8foUSGWxzCK5GRr4LF53k8MPdsaI+iznMsH6H5SyaHcdzOsM5GDkLUJSdgwVO7d0MKhJC35EfbYAaHQgnqmUW2mRFKhZ/IY9gCPGZkwsF4VNnBwGDJ5RVC1/UhNf4fldQ0YFlBq3UHzzQkgeLbo6PnxFXo9Mbm2tffnlra3db/9g1D0bdgRGwmZkcPw48+P+OnXxNptBZ83w99WSnSqHhGxLBXtt/DVWDdWDHbcivBGvg158D8JDENc/rUX59yAQlMu5NneFR8FldKK7x1RorLbGsMTPaQHO/m0SWhSgstgokm2rMzziG6oxOIs2ZcvO0CsR0MR7Cr66ZZ01nq34JLKZFxZFo5jNdWRzPTJMix2N1IXRmcjotjGZCVabUAkknlk9wRab8vCczBNU6FmpQOEwII6CSc67cMru4lNX4O3v7TO/PfvmLp0+ff/b5l0+ePT0+qmmg3AK/FMUm6SrrdBWnMxgAbaoDftUMruYcGsI6htPJ9daIzV0AUwnUM01wIQYbk5XKBrCYYrBmnrtHLOhVJwkBnVPPoj+vXRg+BVPjm5DYhvRJvjwhUc2LJ76kNPOnPAIBcP0Kvp1CCnXJy+jZVFdrqEis6AWQV13y9vezsfXTVziFe5VcuwFsErIBhufgCf7iqicHQ8dqzJ5eJ52Q2KbF2qdLHOU+klAUOx2K5+jkeP9wT+HB5SlkemElACVhzAvNyIToBx1uvaByCevCzNSyY5Kdkc9Z5T+rZ3Ny7EzUI+sMGNp9J5DaYmSfEQHN0VWM8NmJnZjAiL7jGTQFSYMbizM/SNYLKK3ddApnNzBaf8lAsRODz06X51bEatqCq3pLMqLKAUgOx4PJXkH6VGzp2gt7kWn1ZJZNlhzo71ulHXmSZS+qU1ZU6VCbcnaKeoiMes0cM/zKq7idBzE1gqMURW8byVOFmopHrMGIjpIOl/bSVe5s4AR6TSHFLEUtpi1QjtUnGKJ4y6DC2Mmeqt9WLfU04+PJQhoYNUpTSFIxOkbR6qWkJOYq9Qp8jBuHXYo4i5jKPgooelRLIEkH3vyrYY8adUCSez2UexIaiVfku5CB65zBJ/uJriiNoI2yqbuidC6V9ezpfI6JLp4kLQJlKiiXG1CFF07fmFpeWQLneUwic+Nb6l0ot+MzxBchKckri8TEgo2lVD7UrsJSFkKKxsp7+RAZmos5/Sm9YRKecrjKds+qh+e1qhlHklxoS9dWj9xEya45363nOw6N+eILJtmhBz5BJa2VOuDM/qsR5m/8p6kCXtSNo9UoHKqUK0JaUoxP+jyIzRj0ZQaHkPaIDjk59OQETj6HVx6QHWUysEMmPw0wk57GORkyROxPTYbAEapX8vl6vK8IGZKYoD+L2w04q/Uq6fTlmVYt3cHo3HzzHqP76cefeOKVr+bsLclUlAgQYkTnOOewzrkkfWFtfX83YO3grzLPQ4gnOWvKGwCGdkQdy+hHOgBAGargpyfTLi4Tq+jiK+mqD/nS2ZMQyem0JAG5ELUgVC1veGpnKrgX2zuWGljb/MXDR599+oWBwAO72NOyNzCZA61E1PJsOtGuZgQ/iU4Xgr+3QUpUvY8w+Fi6Noe7MrCamvq+mTJzu2q6xOPlEbS9SFEHFmmP9N5AeXsGziTXJVo8aFZF+/X15yQPfW0MqOJ8msTD36/AuIZpdlG3HTj5HIBf90TLjSW/ozRM4/SEtgH4fULJJNiAsMMn4wIbvnbEzkVj7k+eg2v4uQ8++g42Kf4nL563+qg7KY3AEN/0ZWFhOLTFHJqIR+dn4Y6Bei6HpJ1cnbqSa/oqB66lgE4uXSHkFEYm98iZo2f7x9uelKbVD6cnLsg50umlV3PPbQZ+Iwe1ksj615xBoYNHbFxIKInTMz1xtkfZ2Mxn8ZP+qiYc4Ykd0OGAee5qHvJ4spwikzeeXA9FdiZDa7nkxTJXJZjxqjC7mJaGhRpruDnXLTls0nAPIhBXBYAJ8KgFq46fdp27pYllhsUVXm4kLvzOD+kKgFdcc194NgpXZ1ctlmp/hd8l8WAAGBaQkOZ0NzEBZFStBAKdikNIhIMBHi9EFAv7hPPIn+fIpdE8BqvJ6Q7vhPo5yBkPdnnC4Nm6I6lX3j3Bc3INwLPDeeDkD3NC2mDm4SjXvJEFOCsXKVg3DdVRprCGJKMv1drQQBfHuBc8C3OWimZDWm+MYEelSwzxP9MOmQNLH1mhI4GMGF0upYGA4JyvBgrC2okLkWdlIg8w7W9Pjfxk6jfkRHeMYMyFiVUD+RUkF0ikWnUZskiEsrs4PMhR+87SfPLkMZN8++4d4y4rK0tVaVokRrUX8n9Hh6zwHn2ZbYlfERB7VbExd6Y8Q2ZlY3gOScugwujXymyyLIqQLkGeDumvXvvrADzE7fB+nXxeCx/wgGnMk57JiL+bv5PzZK1IvApqe4a5e+JrNMtByJ9++qny0s199913u6eryIgES4xRIhJgssTRGFiaJn9EMX+QRAZaffVrEwksslHMSXiqRVx9jakLVd2Ok+cyupFAPn96jUJeug6MONyYU5H0WWviTLzgmZk90HU5tMB5Rzvvl7/65PMHD110nR4exclCW4Rh68F0Fl2TCkcOQoUqXYvgpCu0fNP6H4XQniXto9QNYMr4wf4uzba5vtLnRUOEV5kGQl2sbvfKzE5Nq0hNamgbi8cQkpxXeLJXlrj1RHE6VDWkZ31sYWxYIh0JoUj6HQx42DyFhIHlhq/tabnlL5wJa4/n4BqyX+EawtvTUYhB47/2HBAKvxbRa9PG42u4PzmX36lWcr4OeCaRCJ9zKKguQs8By0zgYgnOWE+yIISxAadH4chusjg/syowJ0WEVfDqbWgVne2eHJneO7LE2e9wX19XuVp0OLM8OoktK/Izvm/cN+0vU7TaVPSZstBIEi6DEjIabTuQijTjXjeFn41zLHpuxwtthCdiELmUed0bUXiIC0dwlRNVGIGrWUBfReR4AKDZcUv8CsGzWZocl/MXqhjfOjcj/lRAbkSbagktAbFSw7JgrOxRpmHYgGe+LnsXt9CHn+0knfSocVLNHhd5PMu16EnesMmrHoqOLyikeAWfKOXoGD61LJircgqGtuxaFqBZH6E4ZFaKIaBGxSmT4HnNiQhMME+7RAnmhPD7JOfNOq8dIkpAavaXB2T6Ya1yEo63VS62hKlPGZALSnQXmWmhx2ym+nnKGAHqjM6uzy/ZKGxkQXFnOXTWq2buzYV9lGP1ODN6YS9uPc+ntqcAMHVp1+fUjigYWZcEUom04g6m6gpj6vp6FBNiPCc97Y88lBiUZiCeuePIJytXlfiQ92TKto2cwmGQ3JiN5KK/AD9//t/feeOuDgrN3u1TMGj4W1yE1Zqj2d5lhzBd7s4T9tNUQvpT53TIb/JcbjKkIT051I5BXvkL3td++sDfz0k8r0R49eUaWKN6FeS3exsomcSs7BS0qjWSWGJge6FiOD+3tjRSVNcfecomp6NsyRVeQaJMxUIEmRFCiLx2ow21CalaNrmYC0BnxCcHKTC5kAipwDBoRGTNv8IsPJJTCTnMsTLchdkCGZmMYolC19CPopBEznO2Dn/Hic07z5+9ePjksU29Xzqf4NzhMUulm7MmVO/UfKAGfM1cO1gpOpDgq5Sw0QFV9aje5DGaNpa3F2GlJqpZR4eH29u2pZysr1bvRX/r6lL9yXxc+KFPAGVdgD0hJ83/4Qmg6A9LeYoZeehTdAhUXtsPIAxp7VAC5lNjUDrC+xN/CBhjG+IG79gpnAGgPZ4cYCA8Y8CRv7TqCKC/5mW8LxmwiFykpFLnb4B+em20k+FD1jo6SJ4JkRgxpMMnsfHP3dLWk2qpm9il3PSX5bX4aexWCeucQEctk0bnZ1ydfnF2mEUxxtw8qR5Sgnc8kuTx5NDHZfT31AzJZV1oEBklALEuclUtDiIhSR8K2LrFmeWVDH27iqE40LKo2bWonRfqAh2NQ0TgztvFiXuDiuHkLhXDRllDttWS0knuRFUkKbDfOmQp6vPcQaR3PVp2j2BqVB0wwisLs06Ecber6jztgOgZV9QmqSvq1qLddHClYltWclEJD0+e2ZkMQo4dpR4I//FG5TCWxL6FP5oI1W6Qk3TnVWCjsWpLJnOTUavL28OfxgkSIrJyHYFOUyD7mDKmjeDQrGmdUu9xa9mtH1InekhNVZMt9W5DeB05HfTqo/drAWcJG+Se+noKI8T4YWYNp4OcX87MBddsGZJA/OBqdQE2KBWTTKF/qFcwt5O1HGyxkBYI9ecgMh2ac8d4rKw6H3N/TgvDAfTWF+CSLU3zi5s3HCZge5tNF8rO8j6jj86WPsnuIf3C7CFZXHMcV5ZlHR+ebO0eCWER43SWqmKjdqbadsqHxISfuWWY0tDQpMEURG1xj67gavBlfukk2+YqQLeimlP1cvX8mW7EmrKVToFHKy8YJTLBUfCRwJJimtl9FEd2ui8v7J8caVpdnhDdqEu99cIWRmPU/5+0P2myM1nSBD0APg+YAhFxh7yVQ1V1FasoUiJNabIpveCCXFEo3DR35A/oJf8hhUIuKcJNVzU762bemzfvGANmB+DucDj4vPqeYziByCxWsg0OO2pqqmpqarN99tlXWPnPPCyrqlTooRGrvM3rSlNiLSmPEWaDcTBpWaw9nl/9abbiSwxoGaVyzxvh8I1agCo5uwNJZBUoDFGCZipTWyOQk06WXOME/S5fKRdfP7zjXC3RCoZy7L8ZEXX7tky6d5s5UJYFeVfQOQ18ZI155G7yn/yZyuVSVwOFaaxvn+byvcMTL0EmLf30jKN4GTrK6OJEjFa1EZkQdz/Yg3O9gdnVG6eu9I4arAsL8hzKaKdHyXRcVfG1tI8eiByeHWeRnNLz/sRsxqg386nNmB3LjOiaEOHc6d1ceyDL1qx242yMeXZsED26f5y2m8dyd95eX714+c4jXm8T/fe//IPNc9/vMkwSeHD0xcGJiazMZrab7lRfMW9e6CDumDncfe7Dwceu+L17mO0ndZVJbCje8Zwnrw6P5Y7uP/7617/6ndz//ctMDNxe4P6wj3vvdb97t6/cC3Hz+tWeK5O8PWwQ9Sjl1vMOnxT1OdqHbDjFOvmp55KDXAAgj/kEPZwCCZmf0zMADJunO97awZJvY4ftbD61FtllDhXqp3EhsLhXK7IlcXjkIX8WYBNNThr5ze3RVJEmkRTH+YWehpE2vPkLo4bRBYnIDKVcVXJFKRitPGAwbriyMdmc9y1F6eJGk6wiFJ/LHCABem8AJ3WVkk4BgLOJAo8kqg5BfWIVJQfY9+JojijNGSdsrGTc4bsxwsu4F+9eW2dk91gZzED74vu/TubHMVC1J1cjATeY5LcufdQEpYdsi04zg6+rWjBRaO5irRz+6BlFS7Pl2PzCIxAAFFVKPt2w1BW5VSAiWRMy0GiFTLfcLGDs/NfSbr4RYDv0jg8Yes6S5jKHsfGCpYixfhWOJpu+uep8UixjVBfBE4MRS4pvvigVRs16uyoVZPQil57V1nsIMJzYsM80n84cjGC5lmL0hWmwXOTA8EfMD7zFW/XKNYrPilb0VtSAEetejopYFqie1R9ZY4sEz/x+U1i1QHNRdgLRSLHVQFDXEa6DLGpHmIsx9V+xnnmiS0MV3OXlqeQscy4uXh0adGdzQg01QcTrPPb9r86teMrlJML1vVzfobjrS2R0yEtuSUsHfHRi5ayxzhjMXK2rP6hptcDyCVnwjwHFtRs/wXb76d/RK405y2j6mJtAYLLHuLU2TJtw09AaSKAq9+O0FqZy0ADqGE2gYhdvpPwj7WspgABcv/IJXLHFNJjdg6FE8J8Q+wOWbSveaDmMrZ9NpZUHC6CTj8W+ACWYEbg0uu9NmZqIpWNdDsEu/OPg7XXOZ1hBpkXlzTc9VXqSUvK5sb8CSM30tG0ot9MaLTLGzA2XIZ3uHPsyYI5Sk5jx1xTTDOFUizbAeJ/SXEK3//z5s7/7ra3mX/lakcNi371OdyQJE4jpo1I9ZG6VPMkLlqC9Q31APmB44+r7vNSQ93wPDl9fGNhSiG4wfPjoa4elDcDfPb/4eHezM0Rh8usMwGq+/GkRTf3OnitBsmCBUQqIWyhUUamITdFsrVQAkmYdkEpD5szbU0zw2T50HKw1Ji0Nf+zMmV5krOVm/5zmZHZUJ9OkrU9+B5nUAoSaGzGT9DYcoesvc5wdRxrNFyJyxsHUrAqrsdDtqXaJSyZqIXEtCZtcT1zt0yh+WuK4/etM9O5c6m08T5urhXL374dbWy5s7TF/RyMMM1588JU5Aokof4uBr7+DrEL84tHgKhIMKFy/mHJNzKfYqsjniFq8gktCWRq1CJYc6i4CsctppRqYILEAPkpBVYpT0cHOo+XOr58k70+efCVr9qxc0P/VV1/qtdPUZT/1Lf1gfT+yB14KNEVBAL9pNbnSICbKPKqUJRNVzVeuAcuhIQcNXq5FkvY/asOgFFv6ZtPtm8iGPLotUc31Shq+CgBEEchHD1mWSqio+lUD3ISQocHYmlDJ5UVQB3mTKWlcBZasPgw8WEGAm8o8sbcM8RL14ZVPHVxe7TtLMN8odOiGdrqy09NsYDhHbxvm5asXOhFjsBSzbJpaqyYrQYopUCeoAW1LtD3SRY3TFdzcZrVk1jfLSpY0CK4xeJTeluYmsPND7Z3QD4h3Y5A1mxTb5Lo/IdLs4mFGI2X2qLGgxS85AIbdsG/rOS6YpUNTEZRQi6Ypbh4NThLblPPLIIt3F1hyKrw+goXfBSJoVFjIihJcjLvCwRutpvKAS1mFP6MUxX2GXMG0yu1mADJBikRgNt/iUI56m/6xoiJxx0Va1ris4WMhxmCnkQmxBzA2FJunPJSMufAZNdCoRebCqeqJmrXwNIRsbY0L5Urd0vzg+OzcvQn2e4+y3nVc5vLCLVkvX138/k9//LW7yH/zW88yfBMwV2wd3ae2bsf6oJN+eSFQ8UfbuNSOQnw1fMZHH3DJSySWcmq7rwLbTvDh0UePHz958qVB+dZCP+eeN5x0n/4vnuSShJnE9QdLfAI9Bba1IKGDW1e2pb3cOZxTbyohCTJnIO16cbJp4U+Tljjb0TatKEagtFVxqq4kOvY1ts0sFNk0zDZ5ZPjh5biPQcdmggFcxqPhnE/t1cCxbd0ksQ1sFagasEkogU0FgEmwSrSqbGsXZKUA1J7CLcrSs0BrVKN2famI4jbJbcdjJVj1GlUyjPvffft3KpAeynLBQWUTf3EspEfz5FXZ2ZXbHMuK5VKzm15VQcwRSqfCu7FodMh8SGXcqPqCxZer0ob+06paWhUOX/l4YZYc8GdiV1SF87mmVRg3ABk/NWlbDGAYKaqCPcnltU5WOz9/AClWD85XHasVf/FWcsXm0pBxu8gNJcVtjNgPm2qfqjYPXBdlM1vfKFI5y2/Gmzq4XGLljmJcKeGLaa6LrExRFQIJXvQLLqY+9qayiwRDcouGQagq9TZd6nFqFBv+g2JnkAl3hJjwfzIIfeYPm6ph7MkrZLceS6ldkfk+Jzy93/PuyLNhH4/Q833wmEwHmXu43XJ7oHQOr595Fc45v9yJQQfdljr89t2b05OzPLkNZqMhvGrvVeP0bpOFe/esHtKHks+uzePaU90EN2bbhHZ/KM7B1K+VCg8SPuQwseDW6egoJJS42SAtsEU0xFwBeNty2+D9rCQ+oX7YTGRKlAKNPztS28Q3if6DQjYqfSLZJNTkmovdFH+sxsrULtlnMBrFUl56cg2yyUqieJSQ20H2MzGfjIBY9bOvbXKNiHVhMIJXiyAKsiIADfK5OQjPzoYHfQvjqqNTL21tZbNxXjq6dcCe2GxB3fWILlUwM/Ks28byZDpy6TtLk2gWizLV1O+f560NT1IcLrS/6CpWj1BMKZ1q/vvf/+GXf/MrQ6/1cerkcd432Ts62xg291ynngjar5TE4C32P1U5yQ1+BjHNKKdAMkb6+errnzz50pW+5+479ElQ37sxRNt5fjsbZxnx4pJEhnC7MSaquZk+R2eMhXOS2reQvdp+zF7dbZMjbhg78Bex8UnEPoO8Co9qW+3dVDyFbgToOqYSUIfG+nYY+XMqy7OIrJGNwSYJ4swBJuORppcYk7SOhr28CMQ2OMLBmymgYhC13KJnN/DCTxKb4IJbixSNHJZyhG/qHowgOcg4QYyLF9dKq1x8NPt/+zf/wU84toseuwvKxhkpTdVdkKqOzQcTo5JZHpdfcFsJooEEYCq0BEQCNuUziVWb0ix4sWDncImS6Gf4ljQC+KYLRlkM5HLFVD4uQP1iNJyU0hTONK55KjfP5uC1II3l1HuDh0eP7j8w6F68eTWf6FTRctbMreVeHmb/JkcmN/Kn/kTupwokKojx6bxUDc9wid3Vtvj68I3aTUiUdteoXeJmsGmB60pg1dc6UWmijJT8dnOQNSbiJiS45JQFhjNcNV1+JRMCyCXv04GWeGpLDkBhWfRgnU658pxzm5aEqirKRV+yKsl3I4kqIXUXblwf5M5UtVFV9V1IJxCUyFX2qH2mlBIuKLv3F+c/f/ki32f1ioZX3ZSgmnn/7Dz1KrkmMo/5pWu1QA646tGZm9jMw7qdWZvs+oh3gz+GV+4AtcnkqOCGvFFQEnKQjArqdaySnnPjdIlT2RMUteAC1BixOfP2A9GLfeiWDmjK4jUDJIJ1C0Y5CW3SF1vMVt7nv4seZeM29NtnwJ8z/CPhz9RAVQxp3BK+yP4RMZsdJmRMqrYYoCzxlLKVbIqslXaZ1wBr32/rmCbWmRrrfIDaqn1rJSoMnGquVoslmUvP4fR+zngpNd9cyvaoLimaK8e80ePcBSvoghnT9M7DjrmUaiz85tIDQWcMrXmuPRbxpQSr3ufPXxp6bTo6umr1c3aea/bpPc9VZrwx1GQmkM4kFX1eqwOPMtts5MzjnbNjA/ytFz9dGXy0f+Qeki8ef+kbsA8f+XiMMxPvCPBC5clJjrCg6SYLs+Fti86g5rJ9B2JsPMEZvnN9kGHTvpGrrWd3ynbpnK5iGS4lFTNPN6o+ppfaVKRbV1BPX0f42CkFxEKNzhi8dc2GhfvKDwZCHSAKuSLypghRonWDaRD503i29DFO2rWkd2pOYrfKAJkuMsc1ZSBGbskpsMGkYW6i0ItaXD8gGzwMYjqQWbg0fHVywZXQ4P7T7/+kh+L0Pb3Hl/KqF0Ey7YDWXR/4Mf3ILkvc8dFDnIkdtepX1i5cXeFluLHLD+cYqDR0rUKQaFqiseMMtM0JeMpvk/9S1l9iPwPI/IxsJVdKsbtmAkuCowAC9rI84ntLcChzyGkY8yXOfyTpqFf2JtEU65dlwUtCRyZckoasj52pSxOdtg4mxypmzFjCARwkLvHg5qXsxjvcouDDPa5RMMXzd13JSkNUkwOg5+A5CitZwlwRgMCsmUMDqe9QnZzRQwxTB24S8zJ3ZXzyRVUagbCIySQEr8chTGQuaALsNExeELeo9a0kxSBrdz66CDdn6mwFWiLYUt4/efzwzPUpbinl3PHy3nWpM7JKxTSTTxf6Wx8Hc53+2rMXEiSKkg5iJS027vOGuclII5dP7c/g2mohAaEZsmYQRopOjJGYh24VMOJ5099uuCnMqLhW2rWdaCZeSe/ET1ob7vyIQhZ/BkhWnvQ2tQXBRvtPKeAJowlbYreKg7epbPTtT/Xh613DNm5LmcAu3Nj6VZ61o9tGZGbYigABDPzU2cwzAN2i35VQuDWn9Ni17cVeQBQHFsu13RVDMgfJFz9/eVrpEklLL+tahwft4vpT09QO5ebBWpvCDIx5lilBua9AyvQgnnNWPWlFcrZtrq+fv36lY/HuuPeKHK1yidXvf//HZ89fqglaztmDB67BQPzWK5hGnZzPspRnjLzsMMpn4CcnpoiqMRHfSj2+juvG08R5C+D0+MwFDw/OHz964FzEzYe3Vm6OMqnh5FrMG6nao5WReEOA2/o862EFBzL7kgrD0ES7VAO9XqC9UIC2XGpI5jRW2fc8aSZna08UqMaec4mv9sYiYg0n2m3G0/m8Cl5cEhjLRxF0fEFOAilWheL1xUxIwREburSY0k32B6V7m0LJSI+AvzFOFAu1/zBjujA0lfqtbwtTSn53XOAxLhp5LyZSti65s6Kd+X3hxkDSWScDyUHyIQFD7+D7/EHGEjOzszS0V5cs5twhhkneocR9rz3k1hV54ApUaIOFtyrl1yEsyXA1HII6mJIJiuKTkIqWYoorASApbZf8Re7yIiCnfgXWJ2nxrliMaVfjduSL76In20zqgrsm8kD8/aV25X0WoiiACctyxSzJlcm3ZVB4UTaIEob0CcavQWaLhuGnQfcBSexq+2hToQOPZfhgBTRyUgsBMEs+oDSQoopn0FIuMrFcg8hKuYDPYinZ2kZyKREwiNExQ6BectJCo0drjkQRrp2jh+cERTUWmWBT4RPLFahYsVjwFn/n5rL1UywJEiHhwFfH9++duIn86MA06foqsyUH+V1Z+urdtW3n48ePzs9OX1+cWmQ4Kf3uzZW3g6ZNGn9WcqlqTvqTLK05e7eZQ0SnKXHKaPbxty6T73/ENVOfRUIWs/3dxMtFkwg+E4KQyXelC0y7q0gPvzYT2XRU25JFLxqmEuEFV+yCAZsk56fpyjJXGlbF1dLZpSxc9iUEJSeqPkBUYwvI1IqqhM+CRS6/9E0dTAh6waXeogSI+kFmduIStalNESKGkK2FE1ySdYUqmNgqXOIqyTcj8tgUQBcHhYZSSZmRexqaprdvt2XerZfczBqzoo2onHu12NVtukjwjkdXUTbL41yy8eplrk5TG9/cfvCpmL/927/1vUtbNRTzstrx2RmbZsx2+8KNb8Q5dexZmIqcb8hU+XluJaHcaTX2gU+UjI6/9T7cnp6cPnrw5NH9xw5k5fIBe3ce17z3zbdz75s6YPj20gWGeax2fnzP15Nm6rBNZebrkrFLnhP+fdrt/LnBmzLub3d3znZSLkn5bkkVrsFZCQ0HIEWvmg5ubghBoHjopCGrgHiHOE0+NlT6eeQTnP8ZrjPCc/dytW1mm5kNiJJrkWyzUhw5KQg0Ydi2XzDdIm1btZaqkFz1bKyoxi6AhiWI5iNTkCs9n0NMTlmol7MpUTqIpiA3fXQ95EM/MeLt2h2h1v87ciBXOpvsOh9aROdRJZexYdKjimnYVIltTR+dmtQamAWraPF6aUqwb7VpLL9u9IsJxOKSwnqOgqVck8imVZeen8xN8X/miyKZrzEAyju0GxvNc4TAEuU3UenSX1CKi12XbQPz8tJHI1CVvXwZbGoHKohrQnzu4O6sVBDuuCo5xZZ+IfqIHQWsF4FFlGMjZ2dLHwtXPE3Au5QUEIzpti7yt46qBUXuAvRvsKKWTw64ll9IAHo+FnLQcB2APc2iQA89LS59nPUlPWEowOeqdtWov2u6bAnu5WmuKLRWFGKNjTdZ5ga0k0KChwC+IX7v5vbkaN83lOwyXu5fX+1fHR96cHDkTeLDtwbjHLayVn708Nz13V6jtLXnfNZI8Qa7sW0vc/B5f0DItravLPoQk1EcI+XlzkG82keOt0B+q/kupnCNs0uAcgepwH/AxCAIOOWGjG78ANuGkJXTOMrol92zL1bBMwJBYLwAVD+QuxMoAUSSGWK+54+kkgnmJ8XZMavYHe4NWMYGENcJAopEQMIiWwACcP1d+nItH42kOUBdg8XwSWArqha/7VeXgA0gNsunTuLla+ZwEbJlYADBuXg+O1uxwMx3W76zkLWGzU4qE0nUTF26hi5aEasacxKb27jbs2RI8kU3xLNUU5Ec/8s3aZj25cvXGcmdWnh37T0iR5p9LMFntX7z7Z/IIRmXW9tUbFqZ9/l2gisKbg17riY8ORVhMobSFmTUVlvmZDXh2aSZh7WT8+lMdozhfvKTo9MzH7Y7sSh1uZH8O49298GD+wrt7RtD/r3jg+P9PX93313mznkvWakNZEw6ybIHwO648c02qY3lsw3ADlmOzXqcGsn1OHi/NKzx+ZzYOrKqf9bEmvi4jDB5AzSuvN1exOhjM3l0PhWdBG01Qxf7HjCUk9O6Cccuk3TfACShCUmFKyyWlfjLUVIUP5bccViq7eJNoluHUB9URjiUfMFmVuyWME2sjKIAXGOJheH0kDBF4oLnkHkNKYsYudbPeUszCbhyymVPc2Wg+mr6Qo2UYw4UpjZU46YtWKADkihuN4EZeUMCXw2qxCiZrArWiNGImzd0l6IVlYq4HecqfwnBEenbnnGXsXgJFag/E8lQ64UWV8p7PjDqIhgCTXbJSdd2+7GXuVdbUUyZGVxqzoYdJZWWM3veTU4sB4O3TrC8RLVJt0OUhCAaAGliyxj+kVBAD9y0ViroGwVfoPkaHfd88bf0yJqiJBDog3a5YBBwynGXDB57fbEAXBXY5IoENxfVX0bIh9QMTGIAGBsFX5aKAkuOM+CBO42TBDXQk6Me6olK45UFb/E5KuWr0da1xlKwLRZvbno54vrg/ZHPKe0dvj82BhuWM+13bvKLR8rw/rNnz42vLmKTIVpxPowoCW9mS0XSWogpF9jGtcsJ6NnOjiYsWT3R6/oERclUcyRKXpqdZf9i+BKqNfpanJJsubhGVabCOzwAvy7NfPTwixKY4NPBQzvLpqs8b0OY6V5jEdeq5hpVYPkFqP0ZRjBcqerOmOX2CMbhNG410nwFQZ18raxlbr5tXJmKRI2UJuVJ22YzZ4WJZwhPGMmkG0eavHOIWWxL/OkXgYRKDNsgDLhCoseMzaK2Wd60909StpBUEOfZh9va52PhKhUTSxqvOkRdZ94Nrca5947TK0RRnX9sJ4hu9kNsvMkOq+3fuUV5Hp2OfQzoR/nyGx2ndK5uP+bDa2cPTg+d09/3LeHb7576QNH3yctH3+h9Z4f5l3/7a6Pv69cXMdo8+LCpLREbH+lcs+unZHVI0/1mwbh5c9x+rH1wOqiDM+gkq3rI2UyNelLxw4BWtjKrDj/I12Dc2SsD0r+1wPIVmVwJc6BxvUXgxZab/Y/XV7n6Q3kxgvmGnsPQ5vm3RXeuQtoeFJBnjcwyzb6eWSt30Po6hduiIYGGmlaUk+mc/U6noVqpLb7/rVFfWnPn7XyVRMMxNBpHFL2qEWPjy0+AW3vgPnTGMX/Sy+qPsfMuMgJCZ8qSKN1nYnTjYwT26YqxE2afDxj6TZfIUHXOfgMwNpbmxSfFrYOhvii+p/WljE5TRSHbuOCLLL4wa2AvjEBC6LniBesWDXNsVkLyu7HDNDFVpYUrY5FnDT17dyaJZc7PtAq+ePaVXpWWHkz1G6qNQqWH51IXdzJQjRHgnfgkU2SDS2aFLFFSXGQrUQD5K7ibEOOXvn7lDKVK06qQmjMmS27Ya5ey6uFSBsVXeH3EptJTAyifvzqUrKhReGwZrtnGFJxjIgyFcnYuMl9NtzUKwA9turyYYoIbgX4GE4NzUmd/mMKCg45nAIaPYjPUtfhLKS0OcYVW4JJcLrFcKWEKFFNRpYeXFoLlrDhhSlm/BK2IuCA5QKt9YewA0gDwUfvu+xxzUe3yx7zKJtxm0FqcQcYw7Knwu8P9Ll69Z5nHnC4sMVv0+Q/9Rsa8j//8L/7CQtjhLC97GGER67Cck3aTZHVWzsZIiXfnQ58rGVZFSfPuB3qUfHn1ujrXpFV4KS8Y5bZFJdh3keXIiC/GU0QXxEnq0MUyU4iidIuUka7R+p2L0q+vvQDq7ZRVplYzXt9kEMvzTTYzV4sAk4/qX7+m28X8GG7DwszJBRZA/cFF/xVsuy4GskAzSDL6yi8jmH7I2imXWEsRlNDSZHEh2MUjgGk92cVDcov9HwRSi9w3MUc3chf0jPfhyggVJx7jygIYplF8wUnEod/sSM0zXeNDhg2OMhxyt9OjlBVq5uC81erpQ4yiLt5e3zqZdPPh1cWFY81/+Mb33J7+7nd/mI8l5NWSPVf3kLI3d79vkksD4cjksuEKv/kJzGUQ23WfnoCk4PAaJYyAqhCn/ph7uiD93v7JnYPcOZi7fQy/7gAqo9Hx2j6ROnYXQLABM11THnm1K7AquOM4Rd73cdZs3r8SoUWaH+RzOvO+VXWu3cjnFHyDVTbPUmZuef3WlNfTZWeMMiMcQ2aFU+U3rT2BpM6tBz7Wg+kxTSQMrB/nNVeFqStIXTV/lObUfPbc9m+VLxhgrDo9Z/aqM4gxZCRsXMnqb3GbagDJUTU/w0KxwFvXYLmQAcRE+3RovKTSDEJMERFFQuLgR3YsgcuNMcnGiNgzJGYuxhZuTxEd0UmYbQBT7ZBHStOuj4BTm7dJhgUNB7BpuEsG+Q+SoRwd2CkDMwdT1yCuJQdQgl2yEn8WtUtWONub4xZlAeW5pFXDlLCtpw8ZwEQ1FkYQS+rc1glyLYl+VCosyBgwdo5LlzQNhpzS51jFtruBAbfXQCxYHSJnawrIbYKbXzTUiOSZp/M59LuuMptipZWmvHxRo+BmSghGBl81+JUPgCS5vmCdU9BFFg+unk0RzUoaQfSGYJnYRz2NP15W/FUvrR2SQRB5jdPe42zCMIQ/3cIkYPGQJ23IslVz5D6QY0Omwen2o3fn7l37nMO+a0ftt+oU/ej37j08PzcYnJ9fvHr9xja1OTv65q66mZLP9ULJoyWFzhQBxZoLWatlChS5i6FMs8BfTrdonm8rkl0ZwCFPHXck5DBqPhQhTJT5ikeDVMqHntJhuV3/yHcPEaQE9+75hg+yqDIFhLcGz6PvnfpJcoSv1rStM7HntmgaC1NXgexcOYsXwFmEFygxGP0k8qmFitqhCUHHtmpY4qZSslq7MPxir+alX/WhQf4iK+NnfnnRYLTatbKTI6bznAHrFEHGG0lPgVrW0Dl4LBx2Jp0Jd0ZlO3/IOkBXAcPcPICznkyJGPKMdrmwxV4td+M1zht7FY5WOdVsq9m1ke6xevHi5fWHG6tT5aheS88xqGpesWBAa/LGoNPlfsrddsGwGUHTr/jvHFYuJ7C1Y4mZGjI9sOyYkw4JRPIVjIOGTtG+1zremvH7HqLV8AczVJP+sMXX4limx1eUiG5LwPq5JlBv/dMnpSL6POvozOck0RJsdpLkVIYF2DEmmIZ89DHV7IgIloVfORHHbesSWiFG81QqOTrc7L/OpMlT1k1Hdz2H/gjDR29A9Ml9junZRl6mYARsEhqdk9COKyWCKtkcQQKywh5X9vrFlECOBOE57DjgV1DUIElKqxHFQS7fA4AEuHSEOdKRUphPQmXQnqxnvidyCvYHxsJVVfirW5dMkQWameRkXHNYVfjLNTYCN9xBVD6/QDEVRU5FLcmVQGCBdiiFf0Azx6A2ZGOp0FjRbg8rJa3Wiel4K46fv63wZHvkVD726Dpdie66mRqpKUIlxG+PqSIOYTqdlYVtLf/B8FYhn1IcU+OSL35jSRDkC+oOlkAEXMUWbrB2WGQ0xCgKnqtMwQpslGDJrAPgF2W5+GO2ZYaIguSmx0mNBEOiqK8aLYwk4EM9qTShqvEJbs2c+mf8ynHIxs0jOnAm6nMrp07E8QXX5VHVQHZ5tXdwfeOM9L2rO95KuXj9Zu/g8Ex3ZcPw/IG+0pd9Z5mrRSuWdhARLgcmafpZmrCu0tNlUN6N1PQ8O8/7zXUrs5ODFArVuJUdAAsMJnVKHTgZBQCW70Z36+OLFy8yb0gj01bv3p91MCUNwBhF2VN952rOq6yiGHcSTSp1hgVAk66PbGkiqsosTDrT7OP9oPtbZBW1K40mJCzXSoWMxficqAJ8jJa7DdY4RRazdNhFtj5Xfsn4ghJC/2M9F81nADn2J7QCgH6MemYraFIlpkTtSQII5CtQZGKZIbGWFRlwLPB8DTBlnfcNbdRvFs3qBp1ColYcHztscGbo7fPR710S+e6dJ/TffPfdt99+/4c//ZF79vzF81cvDw+ODz2N3fcMZa7n8DBTmU592LVw1Jhm2BxpILtODUowl1CkyCbKW8d7hl5N7NiD3k2WNeSMBEf78mhXRPbuuhzD20iXtqzvOkqR+eSdu4cqtweP877lHDgeiWp9EhmDZ8vZt4c9/TUOSDELMW8jmGf4Gs49l6e2sERxYJF4W46AhSlsBxzGmTLPbppEzpbNKF6C0KtC8wNjgrTwQoH99/q6fs9ExZLYRgekbjU8eSZcTfhmByTpEOFHSDQnOgIiOdZDriARLK6J2rBM5UlMsox3FBMM/z/kRJHWmJJVeBXY5diNBSOofJ9p22zBoY64aJjOmCAXu2TyMQ+AKd8MyE1l7UonrhV6yV00xWwyM8WDkexWbmR1S9r2EPHYDvOYUmzsMQ4GC5APvwgqYQVbIQR3HRqz3HIt9gJUInMJLFfoZ6s5ZmCLKUpRbJA9jm3BTPloH4YAHPNYY6LIDNFoSx+dQq3UXkysoL4Az64ry8IIgifRqaWTcbycKPhKKFeJSy9Kjiy+GhzjbUZZvIIIaFI8f/EuUQtDwqLHMolvvMVI2i796qAXLwZwTjNutz1Lzxf1WS4gCUQ/874Yn31pUbzRy2M9/YrlBRp2J+Lu4VG28Oc6s6uD99YzhmEWJtyXhXWgOeOSi7CMt/f0X0rWR3G++86604CdHgRGr0pWRGaXS0VVZJlN5x2U2YrU26KUu2ZH6p+5ZYfqb/REoNLpKPXduvCOu1bhCGLVeVLuzJqhjgJWS0xhuHV2zLIYkDdZt2mwCCvSZ4tIUypMWl2D8LtBMDzrZVN+jmlmZ37VaRVsLBnzDhkgkSmvzZSRqooeNvWG5jepV6H6zJ8JImL4+iWoPosYUFf9Y4etK1dDW6rNb5JLPv4BR45C4ZSObhYlCSmy3F2VNtKqXrGTkenisG37a0LhHWSeqpi3gNLGbfilahiKXGthx+JEIfYZ8LOnL7y4+8vf/sHmxG9//zvjrmHY1zLn0wh3Do/OTAfuHXpl7oMiJDyTqpOT63e57nTTk8yeZDKTU7KxZNz2t6E0gFhYMeOLQ21wffDggYmiDNrOVW18g0uVlsTt+wvk7tC44zISaTvubHP49vrs3Mo1X2pKhg3IrXubNNKxSAfeM3KnKnxh9tB3hFWQWm/q35wGu718n9cyY5FxuZZKcuMqTNAomQKdsQ/tJJV+Zhgln7bTUlbv+kfAdHJ5ysSJjRu9IjalmaNtyf+8iaaMOOXVkbTK6E+Tu2kRYkmkeMwXATEcr1d/SCKStl1okpwGwi++NYQKwiNg4y2yaDfTDkkvJAyZ4RpXmgar1WgRNQSL2e9nCaC45C+jbk7Nyaa9iVAphNl2ZueJ3wwqYRjlmnwT29W1sEa+qw2WBlUaBCNjk8PKsQUNv4G3RhEcW8eYZWnSgvLPrytXYfQAmF0XTM6cJUWyFiA4tcXsMFyceVO3jzXIIWvxVdWoAV/JQ85QqMbFSHEREpenX35g0LS3jJVbcdK6zFhRUgYu+ysotfex5zDNxA00lSHz2JTJOMQcSk7XA2aNlqvUS6PfryZoEEC2shoGBJdVcVUUApRNgkwwdmSf1TNBJch/Ox0KXiyCfI4QPQNk1SiyfrWqWLEl4C9NqiG/+vQ1tnB5HpWH59ETPd0yut5M7Z/NfCRJYj9zGjFOtqCp0wMa+fSN7+569kVVq6VsOTKCdYJxzrBqiHX3HsWwkBLNkla2KNnS0Ny1nX1F+/010crXEG8qbTUvhm9ZNj2Fy71nmZsldXbhrq4/Hh/t+yC8V1CkmI7UCbF37569fyGWYtZrS4ga0pCK0RzV1NLyURRklKwrzBe12BeAhs4bQ7UubuNaIqK44hCD1a8Gy7hSoXDxi75BuQMg40fWuIUpDVyB0vAJr2RqFChN5Szk4voxsOpPiGdaWU1630Zz1/ICE14MMxLVFNHDe6t8Ek316P5/6pJvHWZHxGL6jnfeXr18+vT75zaZ//CHP/zyd9++fv3qxauXqUK3aZuOQptGqbeSmCcPdwmyOpOq4Vn300xJlxnA+oDUsE82icFn2J1cbjuWOR8ioATtijrA/JZalPRwVR3zS5RCsQOQNet02ZTRP87nKz6YK/i8AImZzX20AeMGkTlzO4mMNwNkWk3ml9eX1wHnhJCB2UAc/+7H128uqLpJOsm3e4wA+I0TIGwGbxW5SDILMEtdWXYZwR4LqDtT9RQSMFqRbfan15Rjefcpm6wS8+W3zeEsi56U0naRk4wrZfWKaQ1mcbE26aKkvpuouGKS+tZFwuQoY+Gnokk0O9dF6rgGG6UTakI7SLpkEh/mjZVUeCXDz7SCTrTfPISPQGNR2nuO++YwwizsZBvvsG9rxI5amHbS27S9pteEP4sVpeRKUF5wadaOAUyj+AWKAbMOB4ABYARwBeq3gyiNKMCCERReAALNTzGUd8RHLDJIfpMDcElpBn5RdYKNQtYqOyTxKrDBBSODwQtTybuUREE2SpUqgWDTMuerDoIFSt8gYsCSJursNNdNcCuDaDiSmaidVFPBKCihOrzwfHhDgoF8Fy+qDgHhopoumHBImOL5HMwkG/XqEJRXbGE+J4igQvheEYJxpqOxG4KtQK1adisw0tD7tx1jPG89OLjZP/C+0s3HizfZPzzVapkiH3ciCuOXX37BDraC5/Czi/WFen6b3YwlyUuWwpnqxzlqWg3ZilmkRQcYTmyB5UvCosQAn7dL8w5G3vpgN5X/z37xVYbhqytb4YZbmjRrDm9XFMJJMJ710ddff42e2qSh190zlT9UKzlAhRRTuH6E7Bi8lEUueJfrxzBimYUH1F/yAXXwMtJYZMvBsKogYNfBMCO/RUaI2JqClUovCGjULu9ncBUgTUI+kep7tggiNlsMcZVcv/V5iZUEV4EAD0oNvcqoYwY84fZOvJH47OnLP/7RZvPT7759/qc/feNM37cXaUS09VmFY1MzdUoW5KPl6dpl3zXzqo8bY2Y/48Hher2NWKvsjL5bl+A/6GoiJjHEyIve+Pr9FQ2tem2IS52G1FArDs/UxvmCVQyo2jpbdXzn7tHFK/HTobnUVVlkjydbIBo3oPJrJXRQqdvGjIwT5OinlB0/W75MhKZ6gmtGtoqVp2OptJYI0fIE439heEHmCXLrNgQoZ4IyY47Ep9jSBJNBtYQwmbJMz5NhQg5c1BNXlfgchalR4QXADUoN8TbNze/CRNDWicMb+m35bGOSFrgCwbvSsCyy0kzKGw8mAseHYjGw3f7srTgborpJEYpjcAVgwaHnUZWwxcxjrzBs4WKW0KpS5KIpctcnX5D8hZw0N56PrVaCvO2KilbTUGWSW/IrjagCK6iKlKZ+WSbFzQwdfikAQF9rlpLfWPjCpefvBrG0LgLaDGzxLR1IaOrlRcMtCcgESeMgwURBgolquqKmAWx6T8GWOJq68oLTYLbVbomiwOlJBoymRaaoatVho8k1FfjmBbL4Jl1p5domG9PBCzbXlQxTRyBHCDIOUHzoBw+Arz8kdxwDXurhJZYval6zzPy7Y3CJ5QFxyHz91Pe8ZiYBE7V9adD62H0Jou/d5NQIMu82+Oyd5cvNhzfvvAaag0umFPrZl6++tWI5OnpsE3h//6X7s9KDZzFxZaDUJroFAjMPB2+/+CIDts6U674mUbVDdfvMn5HSMJzXsU5Pz61eDJ/GXTuWpWRExtkakL5Zk1HdozIsjkZz+0eH+no0ksbetmOlgsyCDH3rMv/Hhv1MHxmB4XPSRQ8YCcDPC+Uz3t2g3n9kpN8npzB/O1HZSFtpNZVdCU0au1yA6yMD1C8BuE5wl/0zuLE0iXGm7avhXB+gkYBAFMeG7M+2i0VspUmatWXNDRZ44bstYVb0u9/97tWrt3//m9/+zd/86ps/PVUIMi258/tfE2i1lXriyZpFsCP49rHtpTlJPBseKhz5Ok414M7q9owlm3Jrj/Gj0Xd74JmeHN3Yqe3CAPxnX/9ZZM4MpjaktljHBorXDHTqebCdgXj/qyePfPKBni9evDIn+fBewWWzXB60F6IrWZaVp90XW+3HOWimURjRVRSNS7O7PT45HytmZygKTf1hBzrUjJBVgM+R0EIhFrFUCOTnCdK20x5AGikFn1vP4LxTJ/NoN0U/O52gcVIhx7TmxCP2mQrTqipRyp9CGU0UQaaorTojNx63Um9w+bQVVZektrDfRQOQBZR1oqQ1mdKWN1SQuOH5UBXTuEZVdt7wSj3QiKz94SZFT7J7kyqhRCx+sSZUMix74G2SsT4Hg3g5QU4fh9h4y37kIOuugLIXW4UqX9FITPuoBE9cvGIxMmIEjPCCjQU0S+2hGWKJqjSxKGnIlbF41bJWyyMKNqq4TD1umlzTch+NSDqsFHfkpIRcRFyB1bClTilFUwwabumg39zuwWw018AR6A2qAmkUg5GQujUPI9M1c8TCqf2EEC4OWSscGAasvaQMZmYKQ0iD1nZaJjIYSRS5FAM0Xak0O7tRKwlj1aixsRZRdRK6/ZDORcnpdCDBuNzQXHoEMKY8Cs/dPgh0fKlpecKqNFOs0o0c73+bbs9+e5QSM48D1k5snwhUvRQotpzEyGBpHu91+eGNhnOtgS3EUxXvxetXEj8+8rXPvALkiZh3Qa737727TN+K4MH9vPurA7FV4O/toys9VN4CenN9Z+/D4e2xq384D8jcTZBO95Wnywfnp2fnp1nVvbt8Y4j1PRu3Dkm6dpZNVZuq+jeP/5SdWTvgxcvXeQztRsOsmWqZyUan2drhPXf57p2enFvZOIQl74Z5jxgl5FBPMjxntVIfSHfAl03vpBviNCc1VstlTOeAo3OcdiYkOlVLlLcm2S5EaUzRUeLcWC86q7PxoDdu9UdM3jY78dtoy6ThpVGUen252XIknUtJxbkZKhMspuazItRYKXFSh9/Ky28rEiDRU+FhWkW9fxvGMYVpmdjUBXeI7vn8rY/xnXo77fT41Nt3Pruhzl3nm3feZXAcL98NzBb+wd0j8zPv6sytUmZD9lrP59adlODeGc0AvhjgMfwfvnn293/Ioaq//fWvvnn6zOr3rdN9BqbTM9WOwKO77+7OFQvXd+fVmtkosQneYSiXRsTmabC5z4wtt/ccUDxZnV1ov9pBsjpFEnRynWOVvtQAnjzecRGVTzQ4LOC6Ah9sCFmKKXJkwStpqtnHe07Q5zAav5VQNAmvrJjPv5SxL+4/UQTPnz67e/rxrUq052n3nXc+L3bPdVeuhdh3bswH0e/5Iu3RnTN7594wutJwNLSU5rs5M5Sr17f9qnLhJCdWQoSrrnzFCmPqmVdr8rLcVNTsV4nObQkMkwLMl+ZV057wv3M1V/9iTClvrZH6mcrFsVIGGhDfS8lXZKuAPqrs3tCOxHokbzaLd3QrfxLJCTv0cR8uPFrOA2plcas65G1G9dqmtnZEO0pTLBZPzVTGmdBQgINpHmE0zJhgXGP58NywJlPMor4Xj1GwZkFDFFbIHDRfcgGFUaCu3PIIioJfT0mrSn3WF1W3GEdYZiJtdWUvTaMqH4aQOvDUm8TDlKUZKIyg8gHF69yWHMhwjp5lX0FRHEqDW5FLTxkEl56Phg+DHqVg4eKLrCj+AkqG3jQMO+OCxZaXj2DI4zWq/qq4JW4qovTy7FbTgUsslj0rikxIvuTwVvNGtWghBQ2QfHkUrI8SIyQHCeYAS2DxMJUJ4D4rYhhkGE2wmjtBwNCGcVlg4RtrDrFqFGIw4hqhvJVcGK/YhRFcjk0IxM4vDZ8+nnW1ZniQKnMW1k6emkkdHfmG4XvXEuUVpb104jqpmBdmjoCln7xz59wM896+ZdCrl4aSG/Rv3rwW5Ypc9Jk9eE780VZwpttN2mBJgnSzRp/arvBbBPD0JJaeHBYDcMhSjjyaZtjyQJpkThJnh+c2Jt3l5fqkV7bF37zpB6MtZjBMlzqlVgMptciYqkUf4HYTk/hGptef8h0vHZiwn3ubsVzRt/xj5//prvldcujMCa56yybFtD5IfRH//wTC+A+R6yczwZ2unBBBlArXHOX4wZmyMHXyZ9lq8166it1fDr4dneZU87EH8Q42Z69o7+6ps1S/+8Mf/+43v/nN737vVPM33z31Md0LX/9wjHiuwLOyTC50/a4MnPMxLPhD92nRQuaU2qY30zLoxlGDv5tlerb3a2z0n3aXuuoZdG6VzLNeQ4scYJeimQgayoD5xg2vraFRkUJpbrTpSA1gD8Ticll03rF6f/Ozn/3M7PzvXly9uzDEMuAlAozk3FzdHJm0zp2alPHFFXO4NisPiGE46vGrf1MHAyZykzvJeThOYA5QzKVanuVoHKbZugrMtLPwz/HtGINzk84nR1rl802XBetQbMEkt3RgAiZiLtI27WD0GVttajka5mNImjgU8ubVGwOws3X59lRKRC5jyZRZJH9SYGlSgKEKED7yx/6ZJtZOiaRkaYgCR+x0m41qLrIcbGYWkQhuEQFKU4xVRAlwweOS4SUBzegdH7K8JStNeSsfjSjwxmqTUDuT3UQrsNKqA7/AigLUNYrfqkx40134Mha/WAAwC7lLDCm4kT6FXYEp5m1md5NojmAwlgtmCYRfcAFymq6gWCwAfmG1nEMgO8XXVmKbUI0vSpDTy9dHVrElIBC+wotpkJzd1CuHz4nisJSrfqP4giQg6MqbkjBShxG7q3ATKj1/tyMWxdGnhVWxaJaDEcuvg0cPXn74B9NcSF2/w9fD6JFZMcLnyZxh0kffkNXZrju6OaLw5YcLymvcM0CG3vWV3PHRiQPMz++5Nv9t8vX+Wq/hvnomaXVoukpPX0f/jK2z/8nPSOt1qFiCLimpOuisg7JFlmrZjtLTRolaHYm1Jn/5/R9Mmlkpbl4d9t1YnZc3kSouQtJ9bZt3ZlY7bupPwrMz4dc4wcvjvCQaNn/RY8YyYFTMzxq7w/3/t5MpGn7mSOvmTdNKctsKqWr/g2khKFn9f5BmFyl3VjqzkOqsLof21G43pokyL3L7itmMUjJq+vv5z3+u6up5yWfpt+/e+TCRBxCXl7eeDvzHv/0b3+X97un3F2+9yGbsTk3yCu/xaYZzlrNayuGZWHXT0ZEzFm6pK6IAHPz8IvsUlLtBbjDNI6SaBgXgAATO7Rp5VjID6nTLaQRp6XnahWImu/aZ/RkoK5aB6ZaKNQ5s0QzMmZ6bvEfnXhefPP/Lv/zz//iHP7169cJM88nDBx6vSKUSpEhhG+1O5epUJKeZSNelzNi5kkndUMSxIbhRVR4xmg+z4pcljQMe0peitA5fSJE/RjSLyFM7uwSZGsrBZoG0pDUhfsVG5vQz1WGqd0gEZ1m+eVExxDmNN21RqnetdqPe0KekVBWDujaOy8G5VWtJiuZTRWdqEOE/dtPkMwvZmIXEGSmqFXoKJLkfFnSKYDCLbNNNCy9UYT6JRS4YcDCn8kXFlFMkgCS+HW/QcFIqEgyoX7UapAfrxDLjIMGQtqAXBj24Gi8hgDpRCLKfOVniV0KDU4EqaVNXKm0VHg1hlsNF7EqueMGabEneSJzeswktygKaCDlgLHw0ZVlBSJgS119yAE0Inp5cCdh5sajrFVjJCMpegkoghFNFKN+vlJQYTYl3uWhbUzS5lehKBQtXHSBrJQAuvoTELoGAMhZYfmkEVXo+IZy04CsHUDe6RyYAJYBAQBMSBHMzvpYjGLGkNWkZp4QeAa31QHb+rlSzvBKar7TmtcxDO242quxI3n9wliM71Mq9HFk06Vq11TlSk5nB2fGJp8YTm6NPvlNZw5pEV0kJccZsChT2cpQuy5nYuzfZWs9+l3nlnHY03sgvT09HTntVjJdv31mOGIDpLLfbjAAyjfOcwsrFADNZZ5MSxIZuy9dFxlImnfP8OAaU3MZOTI04Bu80+Sbjb8ouT0fHMV6IZ81gGtAktj7Bqcz/+a4yNwWz/cEujxUCh6b+f1osGgTLL/AjFhqmIbOkyhhLXl7qbN0z4bNZvtjx/lJxq7xK4t7Z8bmnu13sesBvvHJvi6fqrssw6PoskQft//GXv3mR+zSeecZkkWTn4/zkjPmybeDdN5udhhTVM3W4t9X2GXzyvatbN5hZtfhPsT40l3V2yrjlXK70hfq+6RKbne6I5HH0rGjVFu9FMYKOyhhh91Uhch6cxR+HRmYROPnMxOSwtD9Ds0qhdqSG+NasD84eHj58eP/nP//pn/2rf+lglQ935vqwOx99GMDXJIyOxidG064kZikstdQkWwofsnukNhE+JUJ+TDGh2AVyi0kpe/Sguql+6E2LReazrox4qZlBG4Ay2qmcOf1gKN6+Lox+15ktCRIoI/VTzbm5KAOm1TTmnmYSspBn+sCP/Ym3z+4liP09T6PeXLx7c/mOxVzfLUf2nHBoCZn0zqSwtv5UcFttfoxJKtP/IJEPfhLeURUGAUaupigBnwKZcVT4wlYcUm7F0hLsRXQA+rYofoWibDKEAMoFroQiF8GKhWmiUmyiS6CoyqwvuOuWQF0efIUAqgygSjahMhamZWn4XKP4TXcX2VipNy3qIdtl2SVeclSqSkOPEQ1NuF3GpTxKxbSUL1BGA4xGMi1qM4+rkJqdVtxKtKlUn0WQouVmITYJRbxYbuWlcpYoEkRVDr/46lOWlWIF8pf90a+MwEulciAFwWXpSkheCEcjFrCEVEJTXNIqBztXOfUrBIwyudq6kM3eryh3FeQR0D3tiz666dT2g71cE73/fl4+PjjR0VxdHVxeHr7LAeN01jl/+PHesV1nn049OzEu2mHuxR1Xl2/znZrt7QcZXNPryMK1VVGOiM4IR5fpblSA2RMbzSUdp/vVDX2460jz6/dZfyNOt2Ei7ns484iLTRDmysq8kqTDn4FR32EykbVyKrx8y2nKKNpmHqO0hZI0mXjGZbGmX9N1jmLv0zL0n/sexnRAtyqyLowCmShQb8Oo01DDppOrpP8sf3N3NFoFnjKnWhjnlghajzy7fmMJaW7f+wvNZw73ZFOldApPIMt2S6Vxn6vmdcoMEZwRaR5/spC3gJhWQ1Tm7mAxrjCRQdFjgFcXr7xB5ymvsfZP333rYwmcZ/8vX+cGUE3ko8JQyvu+zed5cOyTrY281WTZe1dEBg8d+scZgOkkn5ss0zS1Gq61PmX+yaqpw4NJPlT1OjltZluO1g+envCNFkSlEbMUNi+uTO1Oy3YEcSbZmdGNy/HgnBzcPANWHYy4gh0uDaWjpjH0w1WP1Hz8+PXDh7RLtVJh33tJz6mC7Je8fvEytS7DUSTmNMyMKFmlbhvv3PBmW//91Tyopn+ylFwnIQZJtlNRU+jMZXfbDMHmk67UPCldn7M2aqfaEHOhTJ0u+2fS5AKGE8tiIz5BrPmZhPyKzfbOIGtYnR3RMFgSqz++t+9C7DlUcfcL3644OXMve740mYMS6S3YGlmVx8VNCgHw78Kx7TzAguSqWOkbHHTMImpbJaJJ8ZDhFyiq/IJFNihJsbvM018E2ZIATLb6jCr6YUTTNFRi3UFhlPB8QTO2plIfHhdHFMyuqwJYAFzJKgTSCgPMYak+AGT84uvDFLAtU6Aq8XeDJSs7n1vsDZaeXyMUWZrlN7Y5qhrIdvX5YaLJOGLIJgfgDFRKt1ZiQDRtmQAJkSYKRrDCLdEKNCE+dk7TIq0s/CaxAMHlilRepd/Fw0gOQaMA0gWjKRdAkNsNgusaW7hyaM5Rr/kSVYEAQpbYxS47Fb6SADSPjWKiJT+53ho8BWUr2vfU4KwB3BjmoInFhhXqHBW5fWcZbOwxKrKY26ludA1eBlUgrOVxrM4nXRrOAweYT55++53t6tuby75gOoOmgth3xkei2q3r7+9pa7I3VXqNGM0atVvWPR09VpRfmVBro/b1h7wu3FrZ2men0UgMk5qL1IJ4U2d16ip5GhTz645dmiGbulZjkfcvsfQv/YrjJUNGgWmozvzo+GQ6Uw0ajPXS9aBSCILz5mcq2z/JtYCwjDUiVs74TChqlXJj+QbVf1D+yMnIMFXK+Gv4yQgcrZLrmkDtl29whGgtZ/fPHz9+cnqYXc3MJz7c+hY9g6f3P8yqzoj77dPv3YLi7a/vnj31jPfbb7999uJ5rz3x/s3Jowcu0ZBAdMtGpW1tbTNHA1RxBaVgPdIUq8qlkW4nuKH/kZML+PqNVH6p41PhWYNuHALtwnTPOo+ebdosNtUivdnkNwOLIVa7F2VySBGUMFHJrRn8dAsJxqnVnOrCdLcVku5ety25FgX6vEj73ke3P6g8ZyfHxuoPV+ry1fmDR93Pod7N7d3c5xr34eFJ8oGfLxF+y7e5gJdmmssoA35/8y5qxJmppBVz+g7ZrJyZUGa/SJDDq2zRJCDf84c5X0sb16aqNIQiKvPRT05vx0ql5E+6qR+09JegewJsPpug2gbP6w8n+c7SVfbPpYlVqQ/lvHov3WqyJLZiTBALpxD5sg+ABvAptHxpDvkGWbJqDL+57bMMSMliO0FARSxZFTTvqYddsA6ZVLuIgVlc1anKQa6oAvAF+KRRqwkVD8lVFJ+rPoWT/NY5nVAk+vIuCUhEVU7EjdvybX636M2sagULEEUxMDk1y2IvfqW1FGuK8CtpAK4KqV9MRZFN1LLVYixQs4Clrsq2WkPCCJKmTZAjaAAWqz02CUgy+flowZgXHhmXNjv5gucoUwcpqAFg5CCxlAteosWAi+fDUKOx5Sp9RRUuIxoOvUl99ZcQgia0hFfmro+FtGIQo6wcAORy8l7KPpMWqzdSJy1qWzPPzu5rq7d5q8lHOL1cnM15ZD6X5lyWXtTNCc7NXh/5JsxehmCPDXW9FlBzYnnP1rNDtb4SNl+60/N6omzRawGUqXNuHtJv2OqjLV2UhL2vZNkzyPxI1WOojrf0mP7XsJ0hM81t05vbCzx9kMdpnl93yzbVSEHkdTJDzYFtO+nd2dwYnaiRzRROgrpBWuG6itBlbB89Kso0I4/BMn53Pcz3LpY5KztS/cZWpM5clx3tafGjN2GMdlH2n+yUC56InNYNbkkpyuJH7Vaq/9wEsFSPGY0L/sCvTCllEmTC5P/HOw/uP9k8Psh58md/+3e//s1v//7p85dONVvvvr64UHrRyuWLZw80jYtrt7hAwGRq4LkioxpyJ0dRPhHd0Z0ZQXNUPYZmo9LkPQrTGn6rO/hTe2+OVAAE3RjP4YPZYhyWTX7nDoa0Pmkp32zMzFGpLM97L/VonPX4tlsAZGMjtY5n8+ODNMwirG21uxYqGkm7O10RZ+WXKUtyd5NK7NGMATgzjHF5+S2t756t2nfu86jmlCSBFKLyaFetcom0gd/MIG8/p5/Zu0opj5PxtF9OXtzmGc3mYp1sI2UQSH6j+TKW8NYtvEThFo25sCDNI+OH1QwlV0Z+gEwIbs19PW2SQabWFr1jls3wnEqkUFjoR8n2Nvi3KvzgN+qOqzLARjd34AgaV/wiWEBpNt9iK5aKxfLT9WyzKhbM1pwvVW00Gwx8dVVC2JUumiUHILbso0xsB0glGAduWmi4lToAY2PBojreLCGQxXtEMqwbD7ImaP8+VJ9sgT192zhRgtWWLnq94ptoE+KLWnAJmiMjX2MXQfVpUOrIStmEEFeZklUUn7VENbhL2Ta2TK02t0KT3KRxkd+G0UT5slP8JB4D2pADYyEcL1cyjPBLJZSFEQBEUQmw8Ks+wHCE1NETca0HaCw1wAgECamoAvArUwjAnCgbbk2uXJVT9sJLCAkoWQO+OgCkWBvqbTk0MkKyx2paOWJ7oLfZFU6vhA19DL+3//j+ganLu3cqfJb4Ht86rHK5f/nq4jXL6Wrs4Fouy4ZFhub6z36eCzG8TJxN6dc+XPjW6y1Wy8cnxzqA9jBZXE6u4aVIGYnyrTWTl/R/ezpaGKKqLQZHVg/v7b95o36y+x2Ht72Z7OxMS8QtDtSO6u+lYhWcFTpJnjSHXNc5byDNoKPVuYtbDYx5bWDv3Th7PWsDjwyiSSYWKQYvhh3dNQBruK41pHNE7iyCB/NP8+Rvl2GVGqCFxQfLeHRIhdnsSO1y/WMwxpiPltktrEstZXlLNNvZL15dPH/+UqHfd3TNbcmHh98/9W73a/vMf/z2m1/96lf/41//9W9+9zvfw/KW1+W1Fy9T8dzX0oNvuQWFNVSXvUwro6SZXOwei41xmCeGV31QGS+d40mWFcDWjQXkTKEHNWvQAWoZNVDGe6BpZsNakCL2vd7KzKuXyZA0YjA6RPw0JctTy2P0x7ZxdB1zVZV5Rl3Ne3p23PE1xcvdeZ+RNUknD7deL6JrSsAVfdb0GsGt89/OUsIYcS00STu7/zAPZnPL1v6+o2q2DqYOo3nx+7+ZCWLGY2LFowfQatILu84v+Z5G5t332GJcUp2hhDksqGOc2E3FCDh/nzqcUpJcR/5wbzQhr8EUx0AjTaJxWPhoouIkHSGRfdd7DT7VbLr69RdPXPs6bxlcOw6f7FQhDWRaK8srJY9coX/sqgAuifMFd2mSWnK3ceDPCBrL3zcdoOtYjTE/jYvNHgFiC9fud24+nVqE2SaR07DNeTFYAPXZrhrAWACBacznSoMMTAcS3C5ubNArQVYfqrMExkpe/mIvwMdeGE2VESRHck1xJdcUBRc9+ZBlxFv2YkqGskavTDCashdobCXDL1d2tipGkEMmU7Ta20sBNzkW0KpXrsuig2DAJsHnEGDnwNSuHF/OAWCBJAQLfcivnpAdqpsWsqYiiAAjaVVMELJw9SxMYAuoLPwGiWpCTZePPubeTuBQEl4fYKaPXq3TLaLUhdXyGNE0LX7lAMrYJCqW37w3C2AYBFi4ea+6NQEmr5+SwCHI1P+OuYJLcn3/nKmzrDEGHzh1krvqUxwHuT7hxmXxx/sPXBzoU0PzBvsd83s55a7evJaut3UP75F9/Pby/tNnL555l+PtpbWSu7a8bSG3mi4tiSdW6hTDlXn63KhrTGe+JJ4tVjmYUXTGlAPfkduzT3DoBpVzH2b3frEvJt07YDHvJ1/4WKEV93tfM7RyPbp0ze/kTk4Z3rkZX72xOSd33jemjrX+8WHOBttu96ArWZSc1UKuAzO5eP9GlbnO3smJBf40x2xdZqkwvViUSydGf1rWSRAGXGDSD2YDJDub4l4EoZfRTE8291qjNtLkGeV8kb4lqIwqhK8O84nCi3I2eiNB2KgtJpuD06fKe2gcr7v58Nd//deWvV7a+cmTL1hOef3NL39jkuR01e//+AdjsDPtFjo+x+FE1elhLG5S5GvLxDruJEWjEp+pyMxKbj42wlT6JsUoip35sqvdmMTGnIKbITJRk/0MXnnljJXnVE8q3pwvsGxtNtUHNV+3yYHlVykAmFrK5FSU1CBEqS+ibHJkAWuHQxnnCqWcGzYGlx2j3WOxFYL4zr7+NuvglKAy97nyq3TaEsqX8NykltNaykX5JF2OKeycpBLMONSimUzJ/t2f/vwXehK1kQOo3vZXkun38z7hvBGgTeVluyR0cziNjCnlrQJlX4r6E6wKCLLaNpY2Mi+rk+XM46ViP0ojH5P8wEOprKEUQ/wZleubHzMsyfQnCgww3L549fb49Fy3Y8/DJlaK+F6mDtlYkg2PwsFpu6l4ygTSYMRXWOQkv7P0YnAA/dGLrZu8ZHwEFDMWjUdIinDmA3z25+NNJQBRVHQNUU5BgKiKq0S+hPlcycqCrNIBdY3lS2PRiNoVWxrI1IbppMSyNridslTESlGwNIJi+QXAmjSfKzGgsYqhNPDgBmFkssqXjG7lLQAG1FUUxtLzOUE5AtSCaBbBbrrgEiPYdfAVLrZw7QbZILELLmMt9lkxiyKBj7gsCGjCQfKrABq1BA2Ag1djBBFzaLimAlmHrHjBpoILUikU3yCfBDQaEjJRMAXAS1SJ4WGa0zY5mAYRVzFjHQy3LICmUfxdoHhylg4wRSJTVcCiOEFbrhyMfjnCPb7TCtxZMD9Mklt652HodXZgvaSpw3Ng+uP9U/d4HL27SifelnZ172M+TRz7afBoPx4cHXiH9Ozk6IsnV999/8Ja0zEWPYqtQWnF1tuZTTSJinJEGSFvHF1HStYj2T12A77HUYy8f+7M6pxUtQqzQHXw1v62HaC9Ow9OjyyI0dzcPM/++N6Nk8zm7WRn+Ttb0HnJMTvj762WnGvN+VUdqyR5BpMZWmORlH+U0nqy6rln09oupTKyOHeu1CZkFNa00LaMmoUWrtzJXDI0tWUXADe4ACyF/0G/Eti0kpsKSh0WTJGtEpDJexagP3CGYzYk4f0HXzrw9MAH+PZ++/s//ubXv/7lL3/57//D3yrr1N7ss1tWupA0Nsydz/TyxzI2QANXz8/l7ySWijQ8Mt5hMhstUNRW3Vgr0bTJCi+9NmewaV2lpfpnviP13Io2Z6zAQ2OfOn8ZKsM0GU9/nBnA+EyezlNyWGxr1Ym1Yp+xOelO6W37t5SdJyNjxDwh1kR9K0wa86V3MyGzbrOY9qj0nNxLI3UmhyKMglITiGoyiNH/e+9vjk8Ojk/OHk4lautIjZp5vCDDWkgbJRwgo6gSGQ02fYJaSWULZilP15V1Asn81kgSpLIxwXQOMHUxzPQk8s4UHMnblXS0z//Z8PfrPasc5pijrEZfTdgt1gbgo5NzqxMVQi+VPLF4MwfK8YI4e/6aVS2MAjCUn1a6MBQO5egwTDt9ztSHiJ7mw6cn+tqhgMwK8jcbCI1D2pQArRnFLB+Ah19XQ7R5sFGTrKjloylcYAVr7rIsP8XgPvE5hgBmPoYTTEX4YTMuCzUWUHiRkd+0SvBJhynCktVHIK2achdDYIOVXDKUAI59CsAgW84qY6WLAG+dLACQpeLMXAcjpwQrDRc8AmTwJRaER8AOTQJ+iS2mxjEhFaxkALLlluQKEeTawQEWGQCjpPnwFSItDrKUDdZHD08mAKZ+AcbftY8o7HXqSSmrKmSD5OAV/Cx1sRzkrkOGvVH82q1agQGItSLqzQnIaSqZ5qlF0RmBzm2Uz0fc9+58OHDPe96h3Ptg9bl/5/T9nv5Rr0ArlVBLfnvlzHLmvw+OfeQwF1RdWibp9/NQLXc4UOn1xaUtULve1p0ZwZTazCYBlIxWrQ52tSWV06TeznTFx/5x7jfafA3p5p4OK49erV50g/c+XufJrM/AydHx4YP5GO3b1xcvHVi1tZ6vOMxaNvvP2T2135ghOSetDUxC1ieRlOe8mVjklZ3JeJbmTL55PPzhzuVb9VardzuQU96bboHaeswqT/9kYVxheCHwLiCjgtzCL3jQn3slW9VgSU7RbesGmMOZxFXPNBnVJhV1xAV4e/n2wf3zR0++UPd++Td/84ff/eHXv/rVt398dfzAt+DdonJCmoUsOaZJtqsjPAvoVD+VRLUbUZCb/i0DYpDJTogaL5zNWQG1aPSZa4q3asc+oc3OR/ofZPTxLBVB6h/D3rpc7cBxJ9+l7OSVSibP2JSWP/ZWUhtiS7e1xZwStLexccikorbPAJzCTflOQ9soM0M57WikLTir5TyZOdYYkoqiDah33r15n8wjyktWTg76xbLnexLamPX6NK5MDOhJ8m2ehGycoNzVIdNS9EJahjautK5sf3/84K16jHLo3ILfMU4aQpU3fTCXUK2mNMlw+DTjSFia3HZgTmUdt2Hcrtk00U2lHMtvCmq2WunDWH2lyhMlGyF4T8/Por22pyo5666xzIQkU9SRIDJmnEJkVC+qwXPNLK0aBExeNmvZxsJMXpI7GMHmYhSPV4xYqRS52Q9pWPRyjAEuT0nry1VpsHSQJg5xDVS1EDQNPreELOEA7CuqWipI+B4lWPqJUpwoq8+SUJmC029u0Els60jghBYLGEaBFeA3R5LgkMFwn9GvdFeKpSnL4tplrASYXZZdW6kWjUWghx9NM6I0rdphV6VWcWRVeGkoSE7ZNWYsTXFRivUYtJIlWsYGqzkfF/lNjo9lyWlsg40Sy8ETUrgpggsg4wrzF4yFWxgAFnpWGoB6ZDYvjSpLJaMXVcvAEGvMq9qLJQnHTY9pOlv5Xtvw7Zd51i4BvPpDDSHjkHz4+3DtPdp8hTODHgUs6PO0iXJ8SbgpyxM3f+8PM2Z7XuStpDcHPkezZyTOPN7/O/s//+onTw9fWVC6vsqSkqgMt7qtqVBkTf6nmg10enrgRkEPDiygk/ftjPut132Js/FjYzz9at7AIYpCcqTDcheTOxaVpSi7xm/HTHmurFws5KzpxbqL8dpDnKRtLzDTeQ1OGrGiTOQ8+I0F/WyQO15qDkU/u8Mfrxzg8uWo7Nq1OA5HMcK5GHdswudg+JJYQOBZBW76IeEQjAmy9P8H3GY8m1QIktEcybGTcZDHLkmGBCgrfknnu35uZZKbzeg7VvFcM7HdZvy73/z9//jv/8P3335nif+Tnz3eO/Me6thBWA+TE0L2QbK3WcUSm/hNVdQaSj/D2SeFo0ZG6hAnSyMzqDmSTgD+UGdo4fsOPUmZm4JtPDhAYDmonB998QXDgkjQZ4ZgpI29gwfoKzg1nL9n1NzucjGIKmzMioRs4Tg3n+rPbBKdVauJV3SMtpa7tKJiXF74ya9VsJSj5KY3MBkJfkYc1cPsQgNCcGxrNtdUpaVIqLdGpigO0joyN53Dh4myqzDLdDOdk9M8YNJjGyY4zefira+G4EvfPkcYqGfemi3ZXPtsvW3SkeptqjeTxEwRNj1S23sYx8GzWP3ITKOe2TYNEQm3UALkNSddIvlY8unviwv29A3Hq/0c42YWcmbCI3epyXWiAFthAZAVs9JVRvCcdArw0VCGT2rp+QhwcQB5QbDoZagSclBlMUxZJtXGfeYji5spoShgE6iZ1JWV2K5mkMMWYkCTg2SdRVbNGkxxzIKP3yxJaykJXq70U7LBNZXP/OazsVOI93LXwo4jpGpjXMQw8IJNgv+ZI0AlQ0DDpSQajE2FNMEKXCqtZEUtGEsJyg4vs5x6A084zC69YOmX2g2qFsjqqj9/BG1mlMi28VFMdazk9gIoBTkpIqtwQJF4YZoQHw0JALGtjuByVQ7i6o+gRgA0Ci8A8ZJQgBxCFhK9IIey/q4CyODr4BcXSj1YeFOAtJdQBkIZylg2OjoCHLws6MuywNM28pxzVJUdvV0aEm69TKbyN+mXDOPkpmVnW9dRBbcYHpscm+a7o5B/c+eegz8XJ0cX7955ZUPHZbxTya/ftb6lN8RNGb/+n993bOvw/qlLjtx8EGUNjQCfWSfeHqMLsjz7BeuxKOQIq7sQdau6IAchX5vBu3LBJ9qYIm8TWv4qJPk137p7drTvM+xk5t3RDDQZ5lqYJhLpoI3utrjNO4QtBCxW5rA000jDk+U9w7DLgRXWzY2i4cDMUsuQnGxsqwe4rrHgH0dtST7/dSSbVdLXb0dofSMN3Xssawo3tcVoZmoRoQoqe7Z1U2gb2EzGBuN/+Pf/g+2B1y8vXFp15KTb2fmL63cowjsVSelmXuMBgYWT8tDDSj6CAgOcHme2jdAf/VhEDvGnMdheYWSMkwSFjbsZnlLJFU+2Er1bZHKgaqF68uVjUlEiGJo0BE4UAzuPwNKKxuA74693GGJ49i9ZHhMM6IYZ6ZYxg1jcqJ0tgjzA7wXUo5J6kn8mKzmknxGTAZIit8dO9MmwLdKgHbwmF+2N2d4NznicmslIkrnxHnL0T3VKOptm6kuLWW7m+ybyO3MLPaRO4M3Fc1wxS/oEHyf24NTRtmuPUyZPmSaYHdAzQlnTM/K5tSodyFSF6DZFY1IzT/6nbROpMmgP8xYMndG05JLlMW8mZB9vDb0qBs1Oz13DcnR9m/4tt3Ep8aifiRYMX5NqQnxFM/JSzxmZ336yCaGHlKOStWjqeyiMpq68iEuvIGFw8Qtj2fR6S8TiBKCr28ibH70FJIklANCM06GDtxz5FeRILnsTLhKseMDIqFK3YelHZ6a7h1d9i+c3RcCucz9rg02F3xT5TWsRN1iyhVxAlRELoN4K0hNNeReyXCvFcpXRdrmky7LkCDJR2SG50izJBYpMuxxXJOHwTCHI4S0M3+CuGjBVFRkZfK2i6lWIWOyQ9Im4bVVYQowZGKstYniMfFyVDMYFJpwPLgawMBULX7dLD1MWArkGJbEmBIu4vEvPldaSiYsT3BVFZCiT9Rz40RNq3mMU7dcIxSjvtds87pz9Pkdg0ddWfo1XBm8ySQbf3vWqzgcPYq1kbUYhsy7TZi1AVFzy77qn/n12IV3tQRVPXlU7iZoO6Uo9YH5zmZachfKmf0xTVz90ypZEhh8X0kpI59zzaMdnjs5k49EoayjO1QqzCPbQ7eKNqyNsGt+zeWm/fA6/mAVKyX7AvhHo7NBLnO/c1SSDBm86G9wsavSvFDCOyViOciuCuS/DSCSvh7dZTtshdA7l0ltZrJV+NgeevKl0ea1P1Lpvshqb8qrNmVe+ONJW0QAaLKYEuzQL8xlAWrQaV95iIBdeuuptjy5ItcSN5dPaFwO80etOseODo/PT+3nZ5Opm/3RzeJNYTgn6BIdLCNXz6W+zGKqsiAInuNVkze6VYIwXPBkFmv9cuEzG5ilmxl0VzFgzpjLLca/4ST4amG8Vbqa2MgKuGalEmqCs1QfUlcDrPPCJMldUJadmzsIX3FGUhOAzgkSVCQUBw6oqm81nuVQrgmz0ZjzvGY45/YBDdc4QN617egBNyBMOM9Ds0mpYivrmbi7jVBnswwDGIDGsD0EQTYIbszdIbWj/4PzBA7EZY209GZKvvQFkZeyUlinQjW+ZkRnObGVk/W3dTazSl/3YcqqZaCvayNn2NsuGMUoqOC953tD0uMA89zUAU9e9m6xqh/x2vs6U2hX62HhYRue0jgiqEBYDz/vVm2xGy23fTklkn1KsLM+ke3X7VkjUGsWkXnPJFIwgH7yZ2JJbR2I4pjMtwIfkSpCDYtvESkAPjnGHKuwoF+9KuBg0BaSNCwxTzRoFVXx9BE13EZdl+fP0ROiTkkuNYLcOe111a1qlhAHQp0FlA+ZXK7FlJAlBiRcAKRbx8hcBZBMXBeiQhnFXDhj9SrG86JcmFQKPEp6jG7jlt5CNKhfiBukP4zBt5xCfCcfLlYXf2CVhN++llCJlqg+MJBrkl6vS+BW1Zk4oKwG+AJ98PSC/pq4oeKJKUwzeVS7Y60oALnE14QtC0ispbtUDN+iZ3PSufR0nzT7Hm7wSjNHlDnlzQlrZsMrZxlTyMOqSrUSNhkZED9ntm+3fPcrj35wFSreLSd/mLzmafUFq6ap0lXJrKTQqjQXGi62y/rzjEaDyscAhgc30ZqdnufzIsWcdm9H59Ghfn20prFMg0yeSFMGJAfLmQ04ss9MNc8UYfJP9r7766suH5+/fXrx5+Sw3C1rt+Hd714dhfHTGaG2NLkfyiwOX6UdmGtmbTg68A+XhryPJzl3kbZSxYmYY0pFLWX7vDkJ/WY21ekzS2y5v2/dFoXEx+7ZAC28ifvgjdQgEdS1TGBWgUYASxHTjBDNMJvObJCRFPS8dnZ2csX1GG7nDeHD34u3rPlGlM4GGPonhlVzkjAXBxg6LBRj7ou3NhyBk8xAhnwyI4bb0mUONC0F6jLm6ZZbOScVDAEWo3uS0laf7ecqQRHW5Pl04QnCjA2cwmw1nGtZBNorwyJrxumtWXNvRFxUyQjZjuVxnuyMl3B5pxo+smHFYsXaHLMake60KznqHIVXK3OqVeUb65TEBdNRQjVRSswonwz3ZtcWSzQqjcb7JO3qq7N6ay2t1WuvMQWb+OwX37s0FGuva1F5fenzwQEZ0TL///W9TiPkifYxgyoJZ20M2MiOZwGRyrMEyC6Z2DbVoosGsDEXR3oBprHX+KxvdjrzNJyajm1WQF/THxQ7cpisTmvo2aQlQLJZWZDMhIDPIGapwm0NUK0gucrbVmP6x3zhRfvnVnF+Yv9wmt40rdeOou4hIR1Ch0hZc+V94QPF8rngSiq8oEkSBAewiJwCianR4GD4a+NoLe9MCcJWzC+BdSPikPakTFYZxpKHZBEaBsvBLjEBRCQIwKic+J6hrK55PwohP7qSLgJJDGA9BacQW5hffpBeSEJnaJj0VXkrjSslHAFGWUkoLhm6NbRR4iQWjFAQURg/Db2mC6SMolnyU4LIDOPhdAnATBSiv3YRQln4hCV9OLDyuWhKloFj4pQkD0qHJQepAFzv6xYsRV81VX5BDIAolRo4ESARpMhl/jS6z5ZDsJhy7fVpD5OEZelGOWMkaZQx7H/by3q/Cz2LKKOxZ7Nzqh4B86tNw/8prSgrC+z9SOjjVbPcOTu/uXbzLXh1KOkzW0qN/uDYrZecUnORkhcpZx8wK2Cu+JwZe5TMLpnTWXjk6PTKQO9ZlzHejk4WsOT4OC4u8VXL3ngqpO4t9mTQnnaWTve4vnzz5Zz/7+uri1bd3by8sBB00MsOYZX6eb+fGg5xCssE39pBohi92pLas2PvU1VDWoO+yj3ypMWe47+SMuwwYv3W67rG8541877DlNRL4bb4+AUWGZ+sWzRbxg1/mQqA0W6DixlCfaMRy7F9gtnw/xS6IPgaqVqTjg0xdfDKOMBuPJDN/qkvrjAQ2rYZI2NpyScroHqfWTEy2+AeAN0JteTdc6tUk2u9vZsPZEVKDSMZdH7g860mraUezojo9PSNBwm3I6J0DUPTsUJeUxwFGUTrSPa04WkUvfU6qurJdTWaWp8gdes9TxU4Isjqc0dvONnjw5lbp3JpEgDQEc7zUkZlJxkgKRBbyL1ePCduLvmf81aBV+hz2v7wxvLV12LsC5JWe6X/soO+pZVv39dlPgfSJoZL45Zj345//+V9GyWxHO73+3gkpzqBpLpmcbXstvBUrlZGTTFAeEhlfkE0A/FiDfQb+4zd/MpPExbzZeZ4H0oLvUqiMud3GIGt6OZUD2FGeGNMOMjnJS0jSlS+nMqJtNNGqikwQDQkKlD+mjp7wdeAGlw/AstmfLBbpJBqv9SNZmj690smd451KIoWkIlFI3+U/Mj6FiMKLfjoiJZFDQIKDybpHKswhKJUwT/fXFKuGsVAOYURVIIzgUm+UigfpvQzSahH0kMjIAS96ZMUnatveRqOYdSK9x3yCi9Ohel5Ty+JSOnxBrjqUTKKCdYQsGulWMjKxuMRykPxFBk6N/PDh7dsLRuCKGQWSnFhwkeRgBBOiPoG5Jr3Sku4uBnG56Fn50totU1s68OQ0CVEAQUCyOm2gqbQySUgQnlbFrCRKLFhMVUIDX5X4YLGQ4LZYclrKRpSKreRqUhYaHh9mKzVRBgsDyLSyzEtl0FT0yvdDr+0Qn6f/dcLu/eWdN+kolWP+UtgZtcxmHVSeder+Uc6MIEg2bj+8kimTVqUm716SvL1+994MV6HrffyztXbI18Hl+2x3Dp+eHNwevb29eP3eV9w+3Jzs354lZ/ce3r19fnt98MXJ73/5xjjqca03ij1h0x/odeTi6u3FKR0/XL+9uPOv/vnDP79/vO8J7N5t3jU6ONGUWGv/9ub8jnsk9w4/vDv5cHjqwOy+z6nm4v3v37z5y3/2V7///sUDX719eP/NzZ3Th0dv312fn95evLrz4Oz6i4e3Bx+ff/Hk8C+//udPv/3mD7/93ZvXPiZ76SnZ3v6xjaI8f/vw8a379rNayLsmzMna+inTH1fyOT/FRLrPYxcUHqoJuuzbq3dpd2N/v+mdry/vuLnfWVcPy11hwakWpUG2d5tnrnHbhSQw66tpvxOh/+tvfPuQDSwCQopRPoDWHLEb/F0nmMfiKV8rdhNhKzFWzoNu/aIvFuF/48KmEw/C39+98i6nAWajQFKRoTmgNCmmF5JKhfNv5hkzIKNtNNeONjnxPGNwU6M0nBnT3+85NufBqK8Lq9jeLzrw9Q42UR/5jhPY19cipKLau07NGCNHRsQTD+p1mGnZH2+v33pKbPHtZbO0VnvL08Bl1Ibv6BbV8uByXNRzw8q2P9GNhk1B3DU6vrWFYo8k27x5zDdP+m49EG9G8eyl40/rSy/tI73RJ4malUa+S58tcR1IyFpYm50UPSPa89TWe8Zv33UKR0ETwn014tqxZ8Knj1KJNSjGMZwz3IyjoqzwXR9C63YOgGev3yVRuzyHZ/eOXfT2/uDBV2rji+9+GzKnKLInHakJfrj2GCht3szTIQ/6Qc6QefPh6uzBfebKB9o1jbMzD5qfv3r94d7R2ePHp2f3fU4jj6JyG63+447PniCevlKpRx2eNAxM4Fa5ZMbQPgOqfsDXzQUNRUrfh0jpc5YH2JudhvQi07cn5wc+76GL00mpUXr4zVxBLobsU1UX1aJMv086oQWK5bfeb+rBtrtH2W0H+BVFFcQkVBUARwKfZqIWMVilnPiM3AACG1sWXFhgSgZWJGg41be6NdjUwRItPeIqIJU6sU1riS09v+pVIB+GkEUM5gjhp6C3eQFIpWQGNrEVBQ+WI2rTAcEiq3A+/YvkyxThTVTB7wpZ9KQVrtgG8Upo0axUluYraTScIOGNXTRS/4wRDYd+AZVTCcVrzDVIg2BALVDeEmMswA4LQADPl24n+xhhaqumBcMtUUtDj0iDTFFo/um6Reki5GJWsdkiVtsZ5f3sOO3lkGO6eIrIUoSDXDhgnq6QTfWdzHx3kb5pNPRuEYygBADEAtJXnuQjDZyCJkQxuUKEM1FxMcrl/r2ro/0PV1cOG5u/I1P4ZhLnd8y4Dy98RUZ+Xdl/ePB2Tp82O+TT8+z4jg/RWCC5actTXle5OW9koZIeJ/U8nfU83NvUEOOnV0P+1b/45zf3Ds0w9Oz3z0/1Ql6NMhHPWaNcR3Dv3N1aR/sW9LKvcv2bf/2vfFD46fMXL1/7hHw6Ca0qz46ZTUF4eJ25i9NjH+VUfl+/eaf7VVA68TEgM8Qgx4dnjIM4FldDxKV/iRlnCR0LpzKHPIwdI9iZC+0UPWDXdUEJszsS7xL8GJZKBYoC/5igsSXbJS4llTN2zgCzwWzUY7zOwjdVNLsBW/mA1J48I8gAJ4/KEQw5D3qnK5jRcm6H9LnouVhDebqX26rrKje5KC+TZiZ6f5lvPzx4mAl0G7XuQuG2g8yJgPlIkaikxOXE1L3TbbVk/iomp/DVpP6yDPyo3/4nGRXVWFHYwc0SRg6G2AL8lOOYBaMgFm5Y0lRR8p1uW2qgRxCDjMX4uFYQwKEp0Fh+3WIUlARLyDf45OifqW43eVK8dYLXZlYGBROLnAwnkDJ55fj9e7b1I930vodHCpnNOU9zeoyN8Jzm5k3F1kirQFWlRjUULD6Uk2s+pHh4GW8sAEEV4BdeGYyV5goXxJDN40qixPVLgGazf1sRfNGlWIZb2hRQOURxDSIGcDCSbzYarJyV0jClgGHK1Sg+RkkXL6omJqoCR/zGTGJ3HS4ZJlnhIVYeuBBgqXAElQNIzZ5940pAUBrBps7nGkvCAopv1vh1kIDyLkpA502VXGll14PTsNUdgLI27MBMFJYmij6a7fYCEyw93hJULB8XfylT9fiQUmmWBZGVEr4KlIVsZKKWD0DDVYfiBRfBwsM0uWL4BeCr7cJM4pvGXCRGaizF2GFXPpoSaGhE7d3L9AvBHOfIHpwZra/9GYiti3OsVV/ueVIWO6O2NRcGo4HcsWQCskmC7+TevDN2zRMHgqGcmbo2moyThBdg4FMJfasuMcb7HM7ME969vUcnRzfu5js5vLo8sXF2/faNNY3npr5U9MFa+XDvweNHb75/RX+i9g8PPrx9b3UWLRybsirZv/PF45MnT57k1v39u7agT6zIbTobgOmsDtzNo5BMoOcCh2QZs48q5jNwhz/7yVcfD07+9O1TB5gvb+48Or/79lUW+r6b43uuZ8eHV69fWCQ4XK3PevTogcH1yeXN89dvnr+48EJIvig/dY/YQ2v7e3lupxLryyzxs1DsK7F5Om6VqNJYwx06h5bB4MpzVhuGDBnlMtDmsd31PXdpp/OMcUjMZudyQ9kef+reGnlrbPu5G+A/8ZPsT4UswC/xAnZ5h/KTUEF6lh1ZhuGpCgw8Ihu1GYM3YmcGgYWbJKb8QTkOnIxzeU666a7dtZ7PJ9hw7sUaSnIYzc2uDK3GCxnPpyRzLm/f6GsAQADJXArd4kVN05mKZb/YUV3O0BuakG27siYdzDijU3I0rlFaE2Az2KRPSFxp6uPdpS+MSuzUggApxHGVCQ8JrvDKEb8AUWi4CgeUfdevhPrwkih7MSTj5eRd7P7Rwwyux6paLoHQpc8Ed/Y4P368vL69vM6FBxmGHJw4Ob778drNM/KdfayPH5149hqCJBSKykgffcw8Xs6zfKkoICmSzKGHGXNunoVRCWYpCaZX87hyKhaWkALgZiRWYK7YJqZHz18CkQnWLXo0rS4b0rCOW3QriH/jbOiN0nyxRHASlg0+e0F2BN1GZd5EYO0eHbc9b9k3So2uMMhgAE2FkAZJBmx0mKTRcOiLrBzCC7RcsdfWKMH8sc8ntSNiojAWbnJVnk/4wiAQ5MNIV2wys1NHQzDJL3YYMJ8Tg33RF2Pa1nnDIlj0MOBarzD22kEQXFeLmfRVz9Eo3cMKktBESynIrTJquo0iENC0qkaFwCwCeNIaCw8mjb+Sq5DqVmJR2ItZlEv+SnSlu5uEF2pltcLD4n+2pG+th9+7H/ntm3xG7dDbnhnRzo7337x7HZKxOeqWtDL74JMv5GRfKDdOGP2opM1fzR3IaaZrDqTQHTaZxi97YH+KwTJwHr+7yOd2zyPT20NfTMgzN1cQ5HNmrrDwpHTPu4Z//P5VLUMmB7bQVK8d2CfuwYPzBw/v6y7sL3vY4Smwk/OWsCGLKeXVXD29vdDV9Tu9xd17V67MO3+49/jB+f7R+VePzh+f3/nDd3cuXua8ycPjO48dsr1zu2+UtmEzm3NXuXYgTyLPHxzdf/Tw/MHrZy9euRro7bWYt2qL6njsc/R7B27HdcGlgcBA7kTZPP3KhWAUyWjr+uB7Vu22Tw+c+DbVmM8m574IsUYre2mKIE8e534ms4noj8ccGLu/TIFaYTJ/ks1d1/a4i9mFV7kvoCX6GU0KeseVuIicIYrb1M9Mw2JpDpXEi09bFtLaNhGNyrQp9daZca+ylL4NHDID597eqfvJtp8ONHba3tK9ayH+ciZeqVsuf3yP2C3NdlCUKStwJBDsvwSsfUeY0RtK9Iz9sdmtUSi1Yvvgkw7DOMzJwUjYNi5BM9NWuaawk51N/2NAT8LDGD8Pyzeu+Og844dEV9cE2fw6vYx66ZCWNh0CZGFAhZdGc6v0IsnhKr/0UqEwDICfF54UkhF03ybR7AtNL2uamxY4zuQyQ64Zr+rqu6K+c5jl3+2ri5dv31yaDp7ff5CBc7PxyyImTNlFW0pKehcWlPTSc8ELQ2fw1rDJoK6jsbu8MMVXvhzBgBss/a4P/49uQYuTDFc7Fl7iqBKpkw1IsTCMo8AEwU0boG6BCdnlhS8Gsq7yg9zOtuRZkcNgV4odeCCbw7KXi7QKNOshDbxSn5h41RC+d4ciq/L8xu4KBNfhAiwNV34B8KRxaBAIQgp6+FPhghzhDVZ/xPTnc8UDmlbVWPhVwCUjucCuv5LAVVgsOWAAB2+fBoaTStNqVIOlAQOKYUPE1XxXzoLLvoKI6SbYfFUOuDWhxHwEHGK9VVsguGojLmaRVUi1qh3KXn9iDajvjb6vXz2/Y7p8dHD35vjeyanlg6DEmh7KZNmf80NXn15jcFOkR09N1Ad5iTWS6DlVM7B0OXWv+UJmZdc/sa47zKoqj6PdK5SPTVmde5XXOvfGW8FXH71zgkw3qvv66DByDjBlXLNKtF2tYM5tP+cuJHcR+8ZSFoyeMJsQEOiY6cebJG16wCh5+j0jRCYwruzyxcN5Bv5v/+Vf/p//2//Dr/7+93/607dfPL7/xcMHf/bznz16cOrsmHPAua7i+v2TLx5loL3KA0h18uuvfPn0sZc+LCCePXvhG3yupL++ukgj2997eHhy895rISqPoSw1E2UqUd6u0XgzCM1/wwRVZC1rwJx8m7eHZxi2ELeNf+cyL5ZkvsV1gFG/lUCMPIeJxpfCOAPcf3IVHEvutBQ8MFyByvhP+x3taDRj9Ay3MwdInQinB4uRthnBNxvwyXmqxNRYJajEdW7KQKFkKpqlrQ3nHLA6se0wDnJG33zlQjVxUbilm23n45PDRw++yML3o8fnVz5LXP2ZVN126k7Rc97r7Z5zlNmswuXdPTFp+JNmZxKbzhZ76vYPXXgnN37FLhf0GI2cxsBUprPMaohYfrnAGD+TUGJ+3iWYdOks8RIDtPcK4S/hZKaKTOrlQklI5cPXYeFKaWosfTIi3CROlYp2987vPzKAYkRmMNbyXSbviMOJ5zN7ORj18vWrjr4+/6AFuaFJ65nCzTt+fYiVMfjDZqe9uaYAmRxgtIjygMYCZoc+1Ybaze8yFE0KN4pBQp8p3sZ66EnjF2ha/Dpk8JthvDwiAAsWRFHpFSEqqk1Ria3GwxH9BCuBXwcDT9FGQQ53Shp+0RTZdFMOQ1+xSXFbNmBqLB9AQmObUFUFl4bYwkwDwy3Nm/TyRaXMttkf2ngwEixZkaXh2wIifAgoFVey+iVu6lVDptDQsGKRwYN3M1tkJTQWASFoICeRzfuygvBoyi64Uix7MVjkCyWHQLBkjeXD8xe+NIIk1xdbZ80EwwmK3aKTLpjfBqkloAGjaWbrtwhouywg6Sof5eYha2VWw6UJRmRxBsep3DkLfHf/3cVr698bY1IObNy8dXAqL5x8tBNImtT5NJGcKVtuPipWvrLIcOCXrBAZQRNjgM0mMT5ZCwDvs0M5K5ER6dZpGR0lgfpXHaXqmzFF56Da6C/u7b29ur38YE7+8dGDcxaCcnTEcgSsIwEY8ZnKwlHX7Lnvk8cutTT62uZmWFcMynG+eW6kzorKN+cM7TIq6ZTbPVvhBJB28/bi/vHRf/Nf/bv/6r/8d5ZlRlvrKmRvXz23JeAzEWCbcu+ur6yHFYfjNAZ3CpsUSMNNBKcnXz9+dObbfN9+972Nab1IzptJbu6mNgxbQqcLzNhlhZzK4BUUqrGLRd39uVvqzbvLwzyJ7xItV1riUk8tTlQRu6gKLlvrcXqug7kbOZWNeVvQkZ+Z0ib04x/ahnqqboHxP8dAokQGGLfpARuokC2s5DbDTJKe6pRcDbISVK5kl8vrvHGKSFVViTymVTQmLNqU41R9du7A74xEUmCC1BxB3bVCP1TOuSo8H1ORFWWROdXoicJYbsvAjMbQGxu1mGP4mfykcqXA7KXKggoggegxjlYwxadybGPRgOEbVaCMZdEatAk0RKVpqBWzZye2ZPB1FdUN8yUhq4jU/rhF1mAxu/BSspSCHaRLw4bUoMBSmLYoPcopPQPMXxqNkpr34oZ+b//k1LTx6Oz+IyZ9+/IP5kZGX1vPrs989OgLRFaCaZ+Kbipb7DDTrbS2nRV5U6zm1KgRGlw6q+Hg6lnNBVFyLYvqjyCJ2Dmb0+ClFMWJ4hDvSo5KQ7/Zgi7D8sVJpswqB6AYBIUBNKiWMIIISilYoMRrABDksPDRVH6B4sGc+wCoW2nwTWUJF4VGsCwRMkcVYDjE8IAqoHianGBja7WQjgT+pBmviS48OXXFFCZtBRm0yS0Jglzq6A+HOpIxikJZdnA0H5e7lkZnoeIbJL8qNelGNTvF8CE5lPC6huJLs3QoHhIlH55YrkE+Lsi6wiUDUwlcV22RlaaMYA4BPAJ+xVZ5RS8hsaIKKJHaBxcaMEAURnCT2PUjverp0l0asem88nIN2aR7dEn2HMNyjUQ2EDMij0NMsuzPh2ycNM4EKx3kOB/cquQDp17Nk9OveICb+WgVwAtz1TpucXx17TFeMug9Hl2nkcUVPJ1EWkzl+p7353qno7uevGbSfuuKaT2sR6NWke4Tei9KOzEWPnpwZgj2gorJuyOyl64l0Mg9udXm3LOVJfGmemfprHDU8ByQdl5D/va+f/rNy4t3vgTrG/Ms7GKnDz5p5H6Dd2/lIfdazTEQn4XwjPnBQ7sCRxrJuzz5fjfT+Vyufvbk/uOHZz/56vF3T58/e/byzdtLJnA5pUfZe3bSvX2SjtBcw2sq8Q3NyivXieTVl+jkFusPd/ZvD24P57Stx8M+5aeTEcmG2oYXvG4/7N0c9M1Oj+jgGSD1bXfRm77jH3GtVyIXsAhhuBUEKNXaDXnx2+CGagWXeRdlgQo0oyBKRW2zYgS5le2HDx445Gauw3qmgDCpIQZUd4rNFk6ylnXbHArPJ4Y+PrAT+sCzhqzPNL8ckjs6unKsfBxm9U0dM+Jnm8QLPs40aETJmQal3rON4/k/GIBxkUZDgIxV1HBsPJMe+NbhndjYJ+qmr04KgmWY4oocUTAbY80PJBYOICoVAFe02rhKqF/iwqJJg+FkHxIjV6tWjmCVRCCJwhhz2Wh0ykLb2URRk9i8epu309NszQKZ5ez8zNB08/aZa55dCuty7fv3H7qJK0NmKjBC+ZGjVMhY2EbGuBG48arkkG5ys2JXvgpgLRkW2i6WpTkCWSs7mgWUYCN9+yO2SW9WwKX+zG9KKYGxggSw17AAxPUrq2lXaFMpgeQhF32zIcoKkum5prLS0nFAdn6EmBMF01TAXOWLAmzmj9PRt2gjdOiHO9VOm6GG4pcomqpUUeDJ36dpXeVXeb74BUtObDXh7zppkcwppSUTMbhkK9GS1SCiBGlbsZDNryCt4Gv5iB07wMsFf7ldHX4MIytj1cOLhljm5SAFm6mlZxXD2Kj6kGsujIucqlp/JYGrUQCaw++KFeTkpaYguUCVscJuliGLrybZ680aJZbntseEPjr9eHP19r2LMZwU8vlAxWgc9Cnf1+9qYfLz0cEpfbBUamdv3djCqhnFGlvFcpIjv/QoTaupAajxbedi4byj4ygma3j2O3ry04XaNLbZ6OGyy509R8n3E9xOQLGr3K+sYe55lXLeoTg/OfTNTU9cBfN05b2Byv2WjpLdNU7f7uW7aSoqtOWuVeKRJVc32V64M8tnJW+8F0Xam9cXbz58ODu+T1HdY26WPjl5++7iwi3VrvjImylOSKu/B4YUnZIvThiuKXvlscT1jZ26Lx7/2c9++vUf//T9N3/67o/ffK+is8Bc1Zdxkq1tFHjmq3aaHzAfC8mJrWdPmo3rNv8M1Tk0lPLJU0+TyXt7875m7kGWjxvvl+7dvTbyOn9UO/+T/BbKLgvMj5EtvpKpIyXgw6Qef3JrkNYjmwakJ5E58SXmmyFOLc2GqtFRBYjb8+1JN42d3b+fHWdR5ouyx+yJzOEpZeC1LrKyVlZejx7lMNFbHx7O+Xmr5bzpi9Fr3nwpWqGxduo6q7OeuZVQBp6UAhi9SMrwsZS4vqB0my1wmxUfHHlTjqVcWSvxiAqIkgOYA6DkikzcjiNTiCZce1HPgBevqBIAKq1ApY3UTdctFiUhbNIG1a4YjeCIj0c9zSaiUoh38lnEpJ+tBQ96R6B5YRL15sHby7R0r8Fnc+jw+MHDhzTM9Wc+6W3abRPK2hm3Qplpt5vw1FJ2W/oTKEUOoP/ZxYdvHJlT0LEVNzqkl9CfNCMwgnhVCZnyGdFSVhofWTHUBnOQK+loI7BENwE+haZujVGGh6JSev8uilYDQLqkkaDDkm00ghwCMumEAMw1FfkR2yiqrFiM9BPVYhbksETWFB7hzUZVJXBD4AnNVn8YxMQShR4NYr6MoIFvsAALooFnNZnVwMDLTbLxEFeOvBAbtSYVwcJYkJEsCDY6LV7AEkhO6UlrTuVd0pqrIHYOcbXll77CmyJpKFshxIqCRwlPlKiywwBIg0HmdJJYNIwgy/CCCgumKVZtLMsVL4iGI4ffhADwu/ogXuWOsjACTurSAuDlVxR6pqtA+pTM8NbiWM0DUEr7uFJspnBpvp6s2fs0hp3fv2/N9vb1a2NC9gf3YworY4XGlpH88cPFxStm9qagQdJWdTKVwTjyqCdz1qe4OCg6SDevAGmoPhNrFLnevJKOkUHhja2e5HkdyFUUMqs5Z9F48zEbYh/fHe5lFPTA9W9+/f3Jfaeu3lpCOU59/6FLIql556vHR4/v3//5T55cvHiWW1Q/3riq7ODe8SwQc5/Gx3wN4o7cWGh5mvvuzRuV8/3dO0yUR5Cz2spw9+H6xPuc+qn3uevSEOj5M2rFrhN3w77s2MRUJQ1+ro/1wpNFrM+zyUfWSDL8wTvP9zyB/PM/+/pnP/n6z93i+OL1n779/unTl263ZnIjjUeUL95cxSTmr5K8Mocw9O6f7PsiRQ61zX6+SbCN6uPbI5a8++qC9dWtHF5TC6dfp9Cdl88vPO9S4IyPz+wD0VSuTecj1ymecWAK1lepAJwYfp+aTZ0MvvQkkRmiuA1jAyY5BarLwFPzs/c6lB4PZNGUNiJWl26xpNKrCXOThgaUZ72OsyGgNAL1xIXHeT5uXXvmHev0cjS7/yDEFNCuGdYO87RTH2zwEur7o7Os2zwigeSwS468pJuLblLhu38wYzOsjuzD8UHuJwj9qCebSraZLWZM8alD1+bIYZZRNrVaRoxE7Tc0PZEVMql/GshHqU8TfVzkc/DJ5ziM6xkwyVwJ0LR7XMQtLEng43N4uYoVZCLE7Mbn0JOGwMUOYqO/biffUUkqDKK+OV0B/+bNa/NdExrvRXqt69nzl978PjvPMy9nCRXq3seDXO+aWWEkjT+7E6ODyWd1o3mit9ulFCMBsj786JtK1WyWHlm5UuIjED71ZxxKk/uKkkFRKgpRMgiAT8WZkXuxxMqVWL+p4pFDZYYHzDUBACQYgJHc6oFXsPjKCc92/wEQy25HBWRLsya36+valoTYfrrFpsWvI6pAGPNgLKkvJ5YTQ3m+WHpWph7Tc7FiGIjyaCQhs5C7joQGqy3hAK5IQVyTzsYrPlyTU8BnLF1BFkmf5WbA2NRyscnQzBsAaIppXmjL6Y4JhxElyJc0lnJVjfrFoKnmpeQL8kkoGZgDR/nxAeUtTX3KwNchqxC++oCgNILIVhRieMI74oJhBAkvXDlgTr2ELwEaQsQCDCcgGW2Qplm5+MD1+2tXDVn26SUvXr7wTitjEWG2a+uqTZtAJW7779mzZ5sV/KjUFAnhDuazMIUlx1xLW0GJcrVzs5anopnHpLkqi3zP2/jkXR2Poy8vHz558G//zX/xq9/83fff/z9fXLzfu/c+Hyx6c+fjWyvUOz//8s5f/Pyn5z5omEs5DPRHPjqQ3d7c05tM5fHc0Ym+xkalF3wMXOnXknz6r1jdjH9e4Y/CVLljYL6gJ6eTGgOCorO27kUiG8is7s/U2MBrYexWgfduv0DkdiMdM3F2um8+fvnEy8kPnnzx2JvDHg8/f/by1Zu3b9+/krscDLvrm4n5PrGFH8tfXV5rl0raTEjf76OxHzOP1NA+ekeZoezw09pBrYwh9KaQQdICfg42dUSfHPE2tS5K7zRkETIFk4z+T3BMtpUwNovAiFVDaASVVPKsMIbiXGapZDmwymNAzUvbp17HvaeEFQcLeMLgKb6PM0PaIXCu0wvA4M7flKFVpb7HYtiaOHs2ltLWu9JR0u9zqnxdpKyALx1Dt2hTXnPqXLpZE+dv1fmULzdqfxojP7MKRhiFHX/qeTu3dIMKSJGPG5LJ6rYxoh/xn/oEhAqx8rdcCQ3ZAjY9Sc21GrVgpZWdnCUBwErFa0QU49DDNCpGHlXZaVJLHTDOpGXs7TnxoCoBTG20tWfPnz5//ty02zaPY9OtYyPH/SybRQibVRkmDTDfR1mKVXMlujRE0tj68EtC5azYUu76lBfUaCutOeWPkE1RNrM1UUVt9jEEFlt5dKy1KWpGrB0lYK+Pz6FvBppA06uQMlYOkwFgSlZe0hQAjHTFlqCAeTqgZPwS8ItpBprKhn4Oye3SN5ZZyyUtfQGYDtzCV3mMTb1pVaVd31iwGySHQ0wUoFGfAQtZfCVLpSnyYeqjpF4zQiA8jChKqpqCYgkRBc+BIQVnDMjEQhA74kY1RT5kWXTZRRJbenixbFKBJUNTt4Irtvjq9knsSGsuECyuYvgo6cmXqLQWpllD39wt/QEtJpSNxU4yfJ6oGiey/Ih90o3dU44+DHjv4Pj0PN3VXVfOOiRscfzoxBZwEjWINb/6uOxLpYGGkkoc4Zyggxr8gWera/ukCiZJWyXlswckpSDmGFN21dI6Nnf7eexJXA64OjZlG9mE7n/5X/67L7744t//h//h//X//uWbF/lczk+/vPMv/uLnf/mLn/+Lv/pnP/vJE6etfIQ4h3WMSB66ZDWQDRWS317JilcZ3zn2bCczumbssjg+zkFtA9qs1XK/ceJyjwek4Z+2albIU0+ytM9NV8mbHyO7LXNdOk3TH2fJZ2DIzjRCVc4HHQ5OT7wq88XD++f3zz1fO37x/KVu7uVs19urybBi3Zfrm+75ygx75nGzU2dsFDPOSvP2jvtFdLnvfWTpZh76WIybMxibZxjWEBnyQz45/CGP7rmxaYuGLxfLCe46qewG/7NhzS3lrvTylx41QSMijWRcHjyAJa3KqDZeJPOitrfFPGsUqca+efvaqSs02l2fdIAZh6oqqeuv7E4Pu4qU45wZu/cPjCISUHvVJXxTYCZz5i4pV5Uvmb9jn+NwarS8qw5U9JMyNGrvOmlJdPkFdgnECmotBcAAWknOw1QZERy3XWsOQRIs47ZPK1HpKx9GcskLpwZtiynBGnOaFRrJxabb/g3AlYy/C1MKpv4SEv3TzBVMiO0egellJkqk/sGobesL8Oq11e9LRWMwNhFFbranMs+WDKuqkxnpq3OU2OqvjdUyYrlG8dujbvK4jRqCDU3zNTHx5HTxAoonOcaeSUazBl42RFMhu/RZ/5W5/m4cWDFw7UDHOh+9yU8KeCXT/ggZzHKVJggoI2lcc1idFnGDYgmhT8nAAOz1l8ByLRbxjSKZa4ow7c13RYmFvHz3Dg2dOYDkiIKvHdAL8isHjEwU3hLAN+kmWn9Xw+pQGsSlR/aZGREQKNbbNPxRZ7NPThkOEhe/QBXDUi7sYsH8piXdAssXtWIhSUDTrGHU6UNWfmWCYcC7EspSroVHOb1M+hpDhVhObIkBCCpnYWgCbpDPGsXUb5bBdaxBIOHkzAot8rUx4wd/szjY239rvHU9hXuVzx8YGbyW8PrF8+vbG+PgoTd9To9t22bWvH/v4fHDpkg+9fgGEBU5Yn13b55vtaCDGYe+lFWJJgiy/TOXHLm4VFA+0EbkPacf33n8efnutQuhf/GzL//FP//L/+Kv/vzLx+e+rKpD/zM3aHzxyNtSvnaXk7C3To/lyj+jqf7Zdqe0JJ0qL0eG53wkMcviaKWvnpdfFDAL2ApH2ZEZ4uH5Wa7Jv8nXkanKPtEqrx2nHKmGnOx0Y9lK+Hh0dmppqueyMs1esQ/sJYcf3715ma8N3ztAff9k/+BnT6yJyfzTU1d4XLx8+SoPzq81z4wkFi+2qQH0yWvAXnTNZowJisfCXsSQJ9ncu83GtO/emDfcvnELSKZS+c6Ss+HMZnAzU8r586ktfArz6cTV7LtFUMw/1WfJYZGqXOqiEwIyT8o5g68HAWnvjkSpcj//+c9b0CYyUWzfnqhzBnmOo0VqsaNSWNs7Hh3m3lp/YkWRYOjtkebcxDjIyBGXssg62yafL1Y6Y4BOMTk25UO63hybyUGecaqgzNDSazmGd6cjBdNnISN6COA7mWBAGkIqQamr5XzB8dM2ARz6y6vN+i8ipvlDcql+G/ppL5NbYj1sKEF9QoYvxizAB4utz5gpztFn+WKR1S8XeKi0bs9bZD+R/keMMvK5zPfvPavx6rzNIRtaL549xfDY10duHMvqmJ3mNEYjMrkjkF81wGTxydnNftUQpeDEIl5+AbqUkb+IwYQgrkMJwyGAB0hXxosBAxYNmIOsNGQxEEGwC6jeKIqpXD58zkWOawK4ANna3Y6XFU0gXoQsCOCKSeLjiqxMviAJaBwU4XMVWDIcgvLGTJwkYDZRs4IBYymmfmWCEaffHIFqbUXxl7RiRlXgxlIYFwYSvFxsMGmFeutgtuBGsV1lRCFIr7edIsgOgUSxHgC+GFyIYagqipJgUQgAMoIAbJ6Od8UaTcGVxud2U8dYmdWwSdSv2EWMoPhSlrEwmSsWnm4cTE2Ki6jyLk3kl0ODF3GD1gpNDlJ2iMLIyWPZ4cFNC5cnj2CTXIZQloYWTvTRPlPYDtUNudHCEHp8dGpX9c7b599dX1yoJA8fPsw9F3Phrc8cSF1aan2kzbqH5tLNx32NcTav8+7tdBaWnMlrXF4jskDUiecxmtsmD6+p6fXE6dGkQgLJZgKGvneXFw5sOCn7/t17ryg/eXT23/4f//fzpaJji07Pc23d3ly+MYrS9d3lm+v3/TTbjPQf3ShFzPtHj+97ccWJagsswZiGAa0gc0xH+1boOWRNN4rorOfoN8OISnHEjPNjuWpVCp+/dkvhzJVeBgXGTLem0LzIa1xBkjco9MZvLJLl6/Q4f6Sd3j93UNsnzV88f/X81UsX5l9evrWipZSb/2IB7xZbf7uvQ1LOLtw4UD3XC0zVNc6as0iIGlK8cq+RRXCXOHNrkKPXmPyp7Iq7lYd0pdPqx+daN+qL/c93tEiN4bYdUUDH28ZOAPNwufAQyj6z5xRfPHos16yOzCpZlJWomub4lbW8Qulln3q8+2fn/Kvrt5KwTlYaht68eNUhyqbCrIY9xqM/Q7e+eXM48rOM8bSWCbI/vLKYZbmN6NTSdNAzfCdSo+CGbNOWp15szDA5CgyYVaNfLpR+pKt0GXaTqc2MJFEI1LHavKkUCVYW/AgdB79x20OgxdOqwNJnSxfhHCEwhRcAyQj8OrGN4tuvn7wyntyTajppquhMhkp+x+7Q90+/tfOMxakd5nZwXKOI/A+0TQNJjde9K7xxTWLynjK1F7YSBVR/gCgyGrWCkDqJhS9Qn9GQgdHIS9n5TmnUFMsyaMCL4LMUY+UVB6gGo65QdMIAWR/gAruS0UCstKsKv3qEbXQSO1HpmisQhoTSF+Zz6EvDVyEEi+dX3QbVieXKhfL6/eYGqNLA1FGGNMgqDymoLs7T+7lCYHp5ykiiyi+ZMIibNDnFw2xlRz0wyXXFl0BP3kT5MItdS65KWNDTpGRaPdiA2hRXBhGjpBjiyqFPXWViF6w08NIBXAcDqFYAwaUtI0sIEmbRNEU+sdLlSlCaSigxTDUBdEDFJRdVrOylhERDFJ+rSnxaIWgSDaYrn0lGicEdfnwyV1+kLdK16nreQ5Bv8TmMTKQncxeXrv3zVs7hw6OvHHn6/vvvfVfl4PoqXeTZ6eXbt14SNNjnfsVNTU7SLCBpZ2UoXLNDVgeqVp8Gm3e5o1LGjwxcRpE8/9abQXJkWCo5tGWo0mYpo3c+ODx2Duvm0DTCfY53vEHrW74eodoN9h1gD42NZnSwAlI2mrpjCVKgjOsZZLf60IHzmLB7koqcQTR6jFad174JkfE0RjaTyMLa2WQNPnRc4lRxBGYalpsSgNVjsUSieWqpQ87OnHqf2vaw/VOHpQ8yDbI/bvX94Pzs0YP7P/nJTwzD33z39Pvvn756/SaPQmnAGccdBp4aQfOb3P4f45ArU16hyqtUH+96Wq8jFT8TMQNQZhEKJKv1zZZjciSnyci2w6J2HVXFglOn/ymO7FlKVds24SSkyBSx81UdevXmWqIie/PKTkbWQypG6kzW9+kuDL0WsOzrW5E6d5THuULbz7SjyYyFr9E3yn9wGjHPOHOQbZ5Hype2AG+aYQ5052jTvbDCNJwo42yR5wLJZjIps0onnbtcYye2lgHAmCuEaJzYAnzvFW/hTXNDVgI+p9y3wGb8QI+GTP4CKA+uqEFvCNhuhGx4KVMyepas0orks3NheElw1b/EK6oJ8VVG9T4tfva67T4rAQ9Lzk/PdJLPXzx98eK5jCkvx9y87u4YvnqPMQ+CPe5MZY/sMWF0bnJsZnIC70znUkBGMEIia6a2xLFwpMR0G/0b5K+oCq+EitqFK6piyyIWwK0osRmuRdRvdNOoQWF2S10UZvT8AjB4W0v44OLVKlEoTTAJaXEOUzwYsSVYlILwK10wyiL5JJQdLJVKKH0FFiO22ekWa5EqARZR8tLsjGKZbpceGQfJLfngXSS84Gc6kFCacmGpMiXmV2B9QbGrZmPUwiGXg+EQcwA6p9FuHcsAm2LVGPLNJnkp+UU2m8hYinyMVawyiWreRaEvQX1BxLUwFsjPXOkRcKIqp/pUQwSCTTHdylQhfuEWtyCCagsgB4YjLaPaHE0nTRIwCHIowx6qXkkvRLhVpF5f333HyBRFcDoNJZMPvnhycHJ68cq1i1Yr+jUbfB9yRY4bfyIl9VPXSKyneuDcH8k+fdCbfBsbDIU+RZ8k8vTXvqUHnI5cORHtiaZ3m3LyOaTqGAlVmxVPT05f3LiO57VLGu6f3Pdu4vff/PGrRz87zmLU+vne/ZPjy3dvrSONn4qWBMzmE2PhdK9M5I4fu5iyI1ZVIRyhrgeNosxqjKkMKtJltLxtK0ofndNnXka2Ds626f7ma1qzRCbJmWQGT/25fOdGpzijuPeIbiyuyfnoELVXobxNnmHjMFsKzH7PhxuevX7vBWSr4jPvsbpW4vT+o0ePvXn5zXffy6BFe+oS42oH+VqGfELk6ii9AgkVLnVq0c4gIo8Yjd9Kn1Uz3VaumceY2SgdJZ7H4RQgLew7fkj/ic7wWQ7ZH2nj+ajivX0fX7audbbWMFpT6yjcU8ZcALMNyXlryLfcHz9+/N233zKO6SZi48NIiX9/Pi8YE/u8fE9hGeFscth9SS5kJc6g2zv4HH2Plezki8ukRz+pB7Yxrc3niXxCqd6sx9/soDa5mHorkRqQNEzhTnMDc5psLaaziVLt25l+63DtOhknk4PcEE/ng1wQEsBHUAEemdSVgErlKntZykUrNCUoC3yRMch2yzemG1caS3jVQLLTUpMZYkx7TFaVyDunFz0EntPBMzQ6BMjYqcP2e7gok0c3qV0zjwlychCAqwIAaVY3SkJOZNibr40y8/JIZO5ouCgL1DIklIV50II/YaYTgyw9PAeu2M1+b5lLUYXaOSJtcBH0PTCpKrmK4GNEiUUyomAWezrGaU7wlUYgeplHXF+wqaDx6YsSVBl+kxaFuPOpEpPGESLIfUYP07pFEw6ZYlNrbfsBNA81AAuZnCSIqoQmh72YBVCguQPsZrA6VA149GVZfsXSfGIy6GIhRNDs23syCCgDw1UyYqqSuSuWnjKCADFX5QlZTWiyEqtW843Aea8TFyRisWCUABJg+I0qjAtQCShL/xlNkxbFoS97GbFUrChK0q3BSpD3HtPfrTzV02CGt3AVIAFAHb9GQY5xWU5yZjHO4r559xaXpuTVW8sRg9qby7e3txdPHn/Ber/73e/cj/P44SOdpvHTyo98Tz7v2araJkTDi6uLpbPkwBJin82Yl2RjqIXPMaa41Hadp2mhQnQPtYC9WUebf/GLX4h2UR4t/+U//8vn37x2/ljyF28v3196Tdfbu6/sdqKxXSkrcqXDzYhqcHLSZw5SsaJUa1s71baqrc6wMG66FVbJM8KUna/zZYpgo26GMiNuCyLEKWgRWVGN/rkOwtYrFxtm8TsfJVTgPvfAtF5jjkQbDBJPGsbi+3eOzWQ8TXfQzc658Ul+L594zWPP7UPPXr40JcnKW9WdYjL6UzC9kQWcZG3na1l+7KxYnWQ9mKfgGhOL5STyrSKz4axDzGpYlpCrp2fzlcdNHreDQdT7J7oOwORsRG22BvLig9dzPadQFqIY+eKNj2pcn5+kwnhsr9zVVXeKOUYgNz/96dcpoY5D84g9jVAznI/BdLOUauYZMW0e7zt6piKliUHWxRTjUgYslIqMOF+AVt+KjM2m8EuJvfjlx9RbV5pFCRDDn4TSilftpSp4gsE3I4gVClfFVPuKQlZzNVj6kjny1N6jCW0VSaLgkZ8s11VsUp1GhKYASj0AeLGXN3hr3lRTj4JTAyWahyZ7937z979+9yYvKz5+/BDyjQ8OfvigEN9cpt5LTnUicD9zWhOZ7ClKbmYjEBuVRskUwUouNONCNE4URzgH8O730hnATfynhRBG+hQZxsw7N04UqGIxAlYqYFGQd/+7/9N/015S5RNOhnv4ZfpxQTwcJZElOEdXyr9NKGnIPwK8+j4+14yFY5sZchYjwDBDQlNHIhbXNH6Rn4qTHFFNq/jqUzxbN6ESJEvjDLFgDgtEGdF4wFZ6viACSfMF0XBLOAxYPDJ4wVqj2aE8TF3lo4kOs4U7jJG8GAErWHq8BC77ICgXSy5jwiz1GtsOmqEMZsWQA9ZF4iKERJgCyOhZzKiWnOJCAL/yDoNGQcDb9aom9UVxYFGVg2sUTFqiykV4R1BBDp4+agIW9GJhcOnKLTgWe5KbOYE8IhYkEzGAQ6YVYSeweNlUrAiKx4tMFAeWFudD9Gh8o9Bg9+rFs7cXF96CPT10YeSHqzevfUDYCJAOMbcqZjJ0tbeu6ky62eYlckZBlc5zWfPuvnpIOIKD0wdNC7zr6E9PmGaT2oRDXucwcMZQ+NqBdGMUIdT26JTdZIcFYnt1chocAMGGBtuYdzIa+zSqvgklvOQUqCQgWzcqATHJdWhQemOqRV9jylQViO22yyC8YgWxmDdw5jq6ozxmvrtnCu6V5qOTc0+MX76+cJfW02fP3f6BWAY+vE8BcVVPilIXxS9yKYYA/PbOPcdZX3tTy6MGI/Us8L0x/NAnJtgnj7FTncAJKvqskjerDRr6AiBVETgEJ1YRWB1Jy+PsBA/2zuYztK1LDrgZbh1QNy3rnEktvb56R0LXwfScI2PKwofh881XPbjXjTJaz9vA5snEmghLEZeuzstGYJq09MEcVelQuPkd9ScL82nz0iup5kW6zR2Aoy12TlpeVxNVUX0BT2qaqFkCy4Q9m6vstJk3X84WK5aKAkiLQ8NBFuCL4k72N5twS22p1xEuUxx2cOltVYilG3p4SNWJY42mWMnoy9VuoYlWQvNCrCA8UdibWRiMNQuySTyPLMyEVBJR3NITixT5yCCbNQSAaggvSGZThNTQ7ETUGsgQSAughtOzyaEnkyujD5NW+YWMEnNOpWKrD5oqIJXiy46SWCk2ll+HHgGnvm4UajJLCdkmqHSLhxKaILbi+Ssxm/KS4SQJLz9RM/YSiluUlSYKkij4KDI1hny1GzwciSWQj5iNikc/YsMFziWq7cu2JoBfThSHnoMklsUrnKWWAlJZMEosJYYUpHBZAKIKlyzSx5UdVy0At0yBkmsUsuRxrMFn5NyysKNhpaFHRgK3RAEIsW9GDQCCOjRE6S/kSBRelAsYGZtCwVVN+Opi1QBzyAr8YwOwilEFcNVJAiALGAGUqRyAYOmL51c+40u3OaJMXTWE5GAQ88HVh0/UwhO+uFBywxdieCqRVl6d5t2PDwXev/NE2OrNcvxQN+UKxyzH8tKSVfH7jydnhGTKrTH4nnmYk/rx4VzkMkO+RA2ihFuyKRixYPQAbqWIrBhtCoAARhLKBVBVk9l5ZBvric8T0I0TULf0nxVSCYWJMpajw1VHICCYm5gdWQ0Or+lxomDalyFoGmWpHIrRhWSxVXhJQFB8JfM5uWAv890eoTJzMLz5wMP9hw+//vrr758+8+j95cVrW/6VT0KBZPPDrbXmCIg1OFHJmrXwvezrHntWnhvKmMvId+fM9xRnm9E+OWLFp2o3jxmTx1XJwny7xNONWq2/kzUWsFdw8OFAcXOSMO56CkAII7x48UyOvGvkzLPLVsyxnPTmR86TRzOY5mBpzqbNhKaWNPqyp+S1WKlPjUu5JB/jyARXpZTzuKVhFVZOAI4a7IJl8RZTJBhjpOWU77aSbGRlkqIdkRR95oT1PPNM/fdcu+mCpYKDfPqnqk8zbNJ8TiwFKnVpuxuFd2Wq9C5RoyFYVNmjw7ZXhG+6FQIvWFf25rd47KUvQdUgVokj6wSI2l5uME+qGlWyokov9WrSFCuKho2tfFxouDQiVWq0ai5Kxu84iKbC0UDyqwyADelAflmwQ1YrmKbOJ6HBSgCTgBj7ose16IMVqFzMpVsZwC+q1ADEZsGC8FyCWyUwYq+KrIZYcMom3IiXroQvmVWlcviVWfpKJoRDJqr4iNs6SEkIEQiuK2OTgFlyKh8xBerEklz56MEcsjqUI3DTopqKKAAfF7/0TXdLn1AlAIqsT1WpSFqw7LoJtlqmg+cqHFmF8CErCqA4CYFcSUPCLAJwMSSUUlQJGrWCS0iyPXaAySHM0b9+MNtgBRLOwfMrv8JJUIlVcfQyVT1FAWBar7DoJZFNxdg8H2IKjnBkXKVVPl8UXsIRNEU0UXcwJUYjKBbN3lFm4gyr95SQnvedG6Bub8ygH9paPP/C89eL1y+t62zUuELHSJV3U2yFZhAew07PqUfWBdDT6Vi7DYRXvuNJFCjc1EeXjT6isLQxMwKXJ9VTIs2LWKMAarx5A3heEqU/LYz78G7eaiwkB8ZYsaPCpvbWvDBoxKJBCa5iNWZ56zcKZT93GMW2mxaiuBYTAviYYkpNEDv7y5EqZiVvLz+PxM1UbJghnjNeZ75p/OVj12s+evPgxQuLfeJTzx1bl1nD1sejvKaVHPuX7XYjG8HJmiNpUiT/iy8eHc/kcr6pZm39GlJ1aikYbzjv7N3xZeiMwZsuiIYcCcrLqtcRZTJNoTySqNo3VznfZKH8cPusNwnf+fjHP/5RVbR6lHdJmK5NxjfX9knXCbqIdgun7M/7QihVXNzqI2JBUVkE77ikPuUV3nEod92nifM0TyTUI4rDWEoAycW8f7ep9nnYGbcZLxWQxuE4w1ynYOMmRkjSHiekvmR+oNugmkpEtgnDsMdDmeo3DkHxeMM+sQgosLK18Im9ktKcP/AkwV5Spqu3IMIyd/eg3QawFOZxNnlNpY23cpLMdgorIVFoAITDA2Rc0VNAK+7oi0aBDF80/LHDVScKUL/0gthhaudOeaVYmqg9bad6VpOqBI+GwVdZMAhppVmpDM3GpJA0x97Y2lZQYaljP9YfWS4KJ6LJS6nSNSBWEL3yAGiwmWmqTUAUQG1O5zJ357Z5Q05UygYvXxAjuMH6MCjrUue8Qjg0iOsarD5YBH+Mh6x8UbVXE4XnNoImdXcyiKorMb809WkCExXHidyCsUb1jNAdsQgE6y/rVyy8tETxmwUAJLgSAByxaPCKbSrNRdnhITmx1x+z5SgWy4qFr+VLCQ9oRgivTEhJ1FVCZZascGj8/6ETBaExkMkJksmvzoWJFVT51AE06OtLmhNUzZoQv+IrByOAj55fRhjZATe2afFLQ0Kd2AovgVhBM0o3/73Np3e9LJvuKq+XHB08dT3dhw+2Uq1/7dedOkXpOiKt5ebK49SobPMlOiiwiLcVeeCcc741eHq6nZiS7xh00+3kCYyYthw1EPA5yhdgkAIo2crWN3oY60IYDiUkbFlqKDSNxVH6Si7M50RR2BMyLBx2aXGiwOghMxJunyXREIvNdVzw9B++zOei147yTRQNp/8RnO4vNM61ZQDOO0X6FZ9C8gRXN5+8P7p/9PD88Ogw7+oYDvlsmDe6prLYRzQhV3XyzQcFl3Nt2ct1kRmFjX+WsPfPH4Dd8cshzGtb7hp7/2mApE8G362riWJDV20eeII9o04eoI7zWPzy3V/++V88sDt3fo6MWE8TPIBQUf/iL/7CeSgb+GPYed0ozx4OFcSRQ3Tznvc8iPfCmwFSqnm6yBRantGhz9pp650wZWkUMuEz0gWz7UCqRTK7dUYmtUeI8TZKTklhoVKzA8+YXAmUWobevG0tfpDT9DL6tqDzmHmybFi0YJ4pSHkRqJ6ZW+bTmXFlGZW0UKXgiV+SRb+iqoCKVHr4Yd3o4yEe/aPKuCakpVb/bUbzW7EKASG7wSCGlHfwSm5RVqDYPg4w9Hrf16yLJoRXq0rYJppf1ZhwAEbCweQQLrjSbRJNVCRiBMQWKL2ahp1DxgHEcrbA+A02ig/T9h6KiQ3n8DaIpnYTBFOGfJi6IuGxZDnbnG9jN6vsha9+DaLJB7jHLfqyI+DElB4gh1zWFaNE9R7WzUgALgurMfFGoCncToWg+vQDm6OMFV7K2hpmN11RTMPJcHPI51oeKM3iq/Bn+lMGplFVsurhbbBR/DIWv+irwy7jigKIrY8AwC87PGnRata1RVb/UrYPpTyk/HKO2pa4PuOIreZ8XPVRAtgf5jMnFSkiqIbVBw0kZ+ZaVXfxYKnUNZbw0n9inMeQglRqbQNTG31ZBAFtqAAS6ABJrLwUQyYMDTkEZVwwTGGMKMUuV+EJGg8igsI3tmf1tmaFVrJ/9os/f/H86Yvn3mG49cXAB+ePrU190JCddFtZfdIuo+JmAvTo4WOq0p8w03wHZhLvyfE8MxtT2H7XlaQ5qCPT/CWvo7mTr6GN/af1pi+QwTHXHNAcUiu/DX4+XrTsucoludgWCqAman6X5QVrMUDt2XQhGWqRYUfAhzw+yTNaBzasu/RuSzFLTQQcSXJN2mz8eu05dc8wn3szp3ZlCexE1uW1OzXv7uWt1stcTpk9D5J/+tUTYt+cH9k2dI31u7det3KI7MOD+/fZ0R36l94cNOTnCk+Dyp2vv/5Kh2uSZAv64mJzsgbSeGzT4rtnT43l+uLq78bHt47DZ068xoPkkhUyNqvVytv3BWZhqvKzhnd7C5CgL3Iajnr5ZMWbV75WxGk0cmq2YjFrv+TaQ+xxKYg5CuAXrBYNkE9mVRmVIt3hdapulNj2fmPDjXox6BgfDQduMYHRF8NuQ5UyEsvnYFqCSTaPJkLuf4onLgVkIZp6ODWLbVv0tUMTheE0JAIzhm0TJZ2sdBbq1dRGQFsWIKns+El46+DXM1F4DhdW2TIzEWyvAEmvrf6bmXSJixdlSkdaXcVPvtInKD4l8s033zj+5jScuoEL+5Z8o2G5iAKI3aWBXNLAXAkAVsCcWAkB4DnBGapCSZrgimI3mBUENN12rWWX9CJoBouH5EpfvERFQfKrVQpShptG1SpFGzwMN3IiCCwvlQguho+lvRVRzUMThidH2k0eZdOGrxAAeshqM3SblUHlY9dgOs2BIb++nJSgjEvDpks4/IpaqSTdsUiLmc9VkyUBDZi/AATSWgRNQix8kbtR3a4sy9KQJpWAqyVdsySNeTlkgAiUQSohbkNqFuAhMcJzrMQmWBq0emD85HbqWdXjNxbxEl6FBVG2AhWDuDTL38WD4fkElmCS2vTvkCWAbFqyxlGYWH5rlygEKLlS8isWsczq9BAv+VWejwwBfOVgbwbhm8diiiQBnq+7NGmxwrHNi90Q6+0FTwGtky5evfT5vXdX713imC/5bK5Q1n2kO4tKeZ82eznOF1ARzpg9h7NS+Z1abpaliLhq8NcMlz6Vo1DGyGnqnOWeSbko+njuuFVYV5rZPQl1+dTiSA5Bukxxut07bESyFEtce2KBpE+TEKWliOLAnFxQg0NWO1OaBWWbcgDlRCbXqly4fQNKf7iaRIa2A3mvAD34vApFLAV9BWnf5x5SaO9uL514O3p0+vDBKWVev3nrhJXbO165Q//evnv0XC+i8/3iyRf6VtrZrz71CNiLT+/zcpbD7abciojp7rsS8+xML+zihRevXzluTZPmi79RdX6EPMM9zpZGJhY5afXIQau8X/TquZu8Xj1//pQRrIN9lEn6CsvJMU8A7Gk/cufk6almh5ijM3/b1mJA9Vsi2ZL2Cm/uh1AEqoXqnhebPtzmtaKpF+qIY9z+9rMk3nVmbvPqHO0N8y1o8c1Og7HdlCM/Aqc1oRHiM5RqRY3pztNl5a0b1TEnzzfPpEyT8KqveFGCU3OA7bu29bbyI4rzk0IeeEJwhHOr3NEvF5bJWmnKCEagygHKLtgomrAkuI5MAGSkjFaCZcGrDkMyvtHXeYLe367I4Ps8COVyTZSvWHGRyW2S2fZvu/pgbNIu5gGTqWRh2lLS2LdOFLDEZDaIBcxfMuGXzBJXQPTYalKbwCOGLC+uugYzXgqjIAVQX5ZE8+s2HPNThYqvCCzlImqZGEby0x1k8YqyjGB4lApGthskbZlDwy4BlhJgBHAAXGUUO8n+wGteGjXKJjuChetjh1n6g5dbLIDFyBLSRQ9JPnxTAZS+PiHF0BPAwTTLeLHAswZiNUwGVTI0kMwvWHpBDiN6DmOzXMrqoD8y+rJzifnpX+f1HsgyVpklFrLyKwGew/iZ/iuIfcG7APalG4GCHDl8wabehKgNaLo1ghQrClkBscbdwpWDEhK8FK4mWJocAvQVhQaMuBKaLmUCDMqJKhXIi7+5g+jDx7dvL32rJiez9u599803F289W7M7vee4oCrBgK1lmAkxAFvV6UsVssqakvR6hGEwbrO1Faptu6rB+fThCiCdjGTVm2FrVKV8zk1tDmW4l2oz/0vTsTy83RwSxIhm2YGoGqFWhW9UzdIqHc2GRRSYGtSTL1k2vsGofmrOsG7Y6VmLkYMXCzKFgrJw6qr3nBRv7hnKkS70uCLftxX6IYHMBW9PDnJqSXJ/evEm2Z+XDz8c+6DQkQHOebe//c3fu0jMQPT+g1c7zr7+6U8fPHqkQX/zhz+amrx59VKK5/ePH9w719s+f+E17rc+mMg5dYj+5KkLQL5X+X2lSercppgDZRP2oeWsG0POToyQWZvu3Xl/eeW2EwfECHTAytLXW6S3H/Io0aD6b/7Nv4a8ziftvL+bt3sZwao9V0BPlUZmjjJ4HZmPamTozRaJ669Tt7fjXKpkugs2XXVbXjj42qqA4kCmnrUIINEggOTEgusEF6ASgbUwsuAxCRp9JeZJCiNkljbbqsSOJt6ujm5skLfMfOsjaNX4087fCIycAZJxblTe6ANfaSPwU48Hb18pbFMHyhjp9jJuNovOTSRJNLdvv7+xDIHokTIvX375MEOfhgMjSj204aF7NItS+mjUxiZXen5Z+NhVOUCFJ9fbVlb5SoRD1iACZl7EALFlAXMoBSu/QU0GLwdZSjR0EMuvaxQ8oBL4nLyUoDILw2/YJiOb756WUxxANGDpsTDlzFi0namhjNbjKIqyxMWjF0Nz2mu6HACmsQzHEVUtRQGYw70mAGSiSFMkGDUDAJr68Gg2ZB5ybB2ugqIAEopC40gT5AgpUE3ATUgq5YUpLwAr+rrGriQqBEGB5TdHlcBvuk2CVsiaBeYSq2c0309Otk8sUMKzQ5MW5GoNeGSiCGE6vHQWpYJylKwOyOoExaIkCoZPVGn4ldNgo/h1kIAVVVjS2MF80vgywpFTsZCS48pOn2aqLOWlMKSoCgEjFiSnyfErBxdRyEoJhl+xBURVt0YJNlFi0c9e9IydeTaoHu6/0SO7zvj2zpOvvkKgN//m6fPzPYtvA7ORz20Zk5xjQvubZz/Ty8YU6Pn5as22wki6qcNzqqhgs0YKDK2Ui14QXAwCp362UVdKpZ0ZBemM2JDmeohaQIrNSOnrQ4qtq1imq/BGgY24tTMyKZZ4Gdl2EsySvLKAABeZoiwQBSvn48VbSI4k5caMkkhO7zpPxy43gIm1L3zrpvWffPlYLt6ZTPismYWxL+meHbm/43/x+N+54EOztPlgwDw+OcPgU05fffnYHrXdZjeI3Xl95/zswWm+rH5fF4zy5cvnWj/FfKlJeemaLd6ZNgp9GoGZ+sObN+/O3apxdm7In8eeKmZ2Vr795o8y8uWTx3Kt0Wlunit4ru/xrzeYfHnC6K5nEqt/6TCsFgjKW7ofWnrnOw+sfdvYDRv57KAcK1Qli4g5ogz7hIMiKoo9E1eczkxlhsdlZEZsYZEPCWbnxoIh6yJtS6kuJ8DgqVFTFcmk3jxcp3NSnqZnaI4ediPydP3DXErphezgInZadMVGh2mD0WAOlKFZUWiXMmHecZEzAuFAqlxr3SKpEP4n57rvcYrDL7wsk89VCB9SUE0WZbak+uncjL7wCh3X7i50NRBVRsGKwg7mi1KHOcFUgumgkt6MNfa8YCqET/iKwshVveqGQD1U/fSiJEMuvCjExfDB5FRgkWA6gOEjd9sS4Xe59tVO1U4a1FJBKSQo/xhUX0jU1WkrMSpCVhB6NPyOprjAEgbQmLPJU6AaYBQkARlDQ8LwV0IeG9GYNCqhbK6kpZ1g4VA2aVxRe+4KLp7CkM2OJAS5RVydqxuxu05Uc4GYBLz80tOBcFyQYASCorDz4QUhBZuvhSk7v9JoIlOCVQkMULqSqoaVXLi8CyacEJI5WaYbVwXQQPK5dPdjOrGE00fFNanHC48AsvooXzWboQSVgij68Oljjw47WL4AVR4Zh71pQbaAKANflSQhFgtLVib5kLVejYOY5ApHRiAYO18UYj4JhKMvb/UUJIdYSAQSEsQILwiO0HGMYOiFGVE2dPMQ2OLl/c21L8iZzXkzhc3Q6tk8yDRCZNvz462FlnSVtIunfMimajCUpZG3BNs0ktY9L86mBtJBmRvsago24apz61Lz8ub1q9rNWkSSNZFrp1NoGdfzoLquuXAsqMITVASksMxcH5ihYPr5ae50iROHXorgpk7VGGHKjmSpizWk0ZOG3oMXq1a0p8OS9j4lhVIUuzu1JFFcHuImrRHVZiUt8i8v+26M/sXWzmYXBD0J796+YXBnkB1Dz03dHq7v7Zs++2qyXW/j7k/cn/zeKueNazgP9+/60BDFfv6zn/z0J1+9fPH6xauXl8/eIjx/+IDxbTtTtc6DZqu5DwcumlZP0rVx9GEoFyD7wISzdu7rdwRPWSsf1ePhk8eMJ68GcqkwgrfLUMrC11981bVBpbDDZCS1C6Vb0thKVMbdu/ceHNxXL2JMX0RGaTmsrJFmsNtYXsVUf6cKq3teE0o/hmy52JGszbPXjeb0R9ao5qXVABzFpjlM7KZH8gRcpTFxOzlL49IniTUu46Ien0n4yqJBJVL5/Dr0xCJAxp2cb57F0rNqTLIRWEpBylQaZD44tHWlLEE7gcLoObAUdZoka6efJEwUpFhqoFS1OBXy22+/RQmWQqPa8JVXW3pTrPCk4T3p05yJARDIB7fCS46QKLBtlWJHbGqOjCCAKUHscJLTDNj5nCgOvToDyTUoqpZROQFNSxJ0JlYQsimi1JoqipyqJ7ZZkG7Vi11kTwRUc460KsIwq6i6MujLylxBRfLp18QQR/dpGDD60naU6EvAlBW7JOwCDLFJaIpNWhVFbMn4xSQNNporgbAQG81mBNKEZB5SXiTKfHwwBy6AEgGxtZp0K5lMAJomhwBvo4rBWDkNElKHEXFrsShImJbcElKWxTjV69O+cfEl5gtWDaIA0kXvmSZ9wNUKWSmZFI0SNFNBbyiVOjL4KoasGMjqRj6gQZIF0cycIIsh0sTCtJKRXGllEcthYWp4ylQfcmDUTp1maeClC0bWFPnckoaFk24TxS4JjunUTEixTYsceLwAeDDhTWXhT49OM6pt+6M2NDnLFw6m55Wdg7mC4/zR4+Pz+9/+3V8TdXh8uqdrnjrszUqOWKlozULqMGOoUXj1D80I9Tg0Ja6S5aIMSrpRI/VTp5ujYfnuEHof3Mzh4FgjB2hhts5m9WY6Qk7Zt1H5HbN97iErikDpYqQJWNJVprFUrU1sJAMgqzaAZLGCRO1KEIT36g/fgWl0ilDpsIW9ZsiHDx4wjpwqa8UncavV9P0mxTeOK99z9/XDx1/cf/jYEvjXv/2dq6ZevngWW5+fe3/4w8cHkr58e/GU+/al71l94Q6zJ4989cE7SM+++z66+cLU4clXT764efhIzfcFWCzMxFDVnF/nES2FqeHEu31rD7LSoX9z8eTLr7qZKdYQbnjSpf7kyyetbCm11Mo0hNrNNMnD3tZqpePZES1CcbtvFzcmmtewDLyZTynf/dSTEGybfAuiGFFcDS4JSLIRcGB4jr3Q0AdmyOOVfTC4/E3MrHE9WXG7ncLVdiMTEv3m1aC7J/fPyaQnB8DWdAOnwil3CC+TZugmv6nDTAKbYQzMGtWheD4JXC5Dn5w2F3y8hSN32zxRlrFC4BclPKRqw5eKjCN+8eKFWgRTrhJX2i5cabt+By9cTaKaEMtVVKNW7MfLPAdkvWoID+Z2LbYrf+FRcrg4gHSrGGI2hCFkqQqApwO/KqEBU4aPuABRmwW7sB42rWuWGi2VSsTQsoya+tzpMqrErkQ0hHCQkgzluGL4ZOrC4CQvoeJLs+tnN3Bc9UZcV5pmrAQEUsNRmhI0SrqyUF6+oESRcWDOVBk7XgpjJLbSNskMBuNKFIy3NCWucJiV7iJGUGKYJblFKOmKxdik6cl5c1Gw6gliVDXRqJfoCRErWLFga6AKF1VHclDbZgCJno9FNjlBrgTwMGwCg2BxVQjM1TQwsZUDw5W9WWguKl8UCfwqWZllRMyJ5WDqI4AsAQx4GbPETUjUSkW1rFlE7cpBsBJlKyyCyWy+EM/Fd26Il3MxFvoZPTPRPMzhq1k3pIUc/OIv/6prwTvXeVfPRTnonr94oZs28hMy3eRMeu5+zBd/txMCaWmEEk0pzhRBFrgaoWYXa8lFjduD6CD4/mpujEoLzOcI6DPOvbU56oqmHVNzKo9iwRyYX+HLn4iYt+aSOk1oWDX4omShOpeGYtwSC6aVKHYuEr0g3gIE2njgLKXVp3vGN1dV371rVLvInvAb+wEmXWcPYjfOQWXJkeC8lWpmA8OpF5Off/FXf/Hsxavvvn/2/NXrb//40jDsTNyXT758d2K+pUO0GPpw9e61k13GvyePH2cZ/z6b4W78+PDelkQ6Tba37b3rWiuaTZSe8l7b2r/NZoZrnO8eH1mu5xHycQ5euJ2QFY/2c0oLi4VsTlZtGma+8Jgse3A6ThY0kchv67/z4eDDXZ+r0KqiQJrP7C+n0LK7YRicWmdqZUw0dud/Ht1OlIF/CGVj0z1Ki3D2x95SGKkbqsichtNCmeHVwt9gm3tcphOItlL1srUaoBXmN69CmV4CnTPHunESyoNxecn0DzEdUswkoGi64LoGi4cR5AAMwu/l4ck/u/jZRgqO8Ubt2aKfPiu7VkiS9PgVGDkzaCkmFc/Qqw2qLVZBxaMvpUQX+64EMAJkNSCyuiYkViWUBYXOARBzgAWjX8SARvHBJeYvgoVZgKpOeUFp4aJGFZAcJLj+aoPwKLmyFCA/6/3GVYmqyxfkUNevRGyC0oukcQg4IL+UkmynCQmTjuZHwxJ1K6S8Fb7gWmGXgBRi+ZB1YPTN8ygSBeooz3WMB2hN1QSAnhzIjsqCrQGlqbTSENXktlIzWsDU0aGJlpjfPC7dkC1pAEL4UiEEjcLjV7KK0rREgavqUnslVIAQL4SIrTQ+h2XpprrXtqUhuRW0wikAb9iQ/bJUB/7KjoEHjeRkAVIUrYxMkDBLn8K72Vw1nnDE0qqEshSGX2QrtpL1iShZprzKhYYqEr953PUp1mCFY+HA3NXbbFNLRWl7ppu/PD7LRm/O7/tm0XFkUpJlAD998rUt0o8vXgi65pB5c0T4dl+ncJbDsfes5t68vbD8YgRKzmBhUzufwtUZ5SmuPtUSd5a3Wjwd4hlebRdaAM92pYRY0gwhy9/pelzENZTocg8ya7QsXjtntDM1aRHw5YiPLJmcnqWAjpVwDgFXmITGNsggMBuj7TlEpKOeraPxiczWuC/OjBo2Xf1hxCI5Hxvw1uuBDYDNHqyak00OH0RKQX+8m82DA/XKFVkXrkl6+fbVl19++fNf/DO+Y27Pn738/vkzW/2/dQjr8ODJF4+++vLLN75P5e6p1y/fXLw6f+ATFYdHP/nKi0zZf37z1hByNAejNdZ3764k5ECWeuEQVZ83y0g2FtKxJFOU5BwsV0A+nOBFI2emaGvcffzowXfPXzEZmztobWXc0vD6mb5+hjFLvTHgtgmw4JhLzTe2GdYUjPMEmStJllWckZcoWLMTmYvBti56TAHxWa+OtBGYEEJRfHAtLAqg9jJmo/gFSpbvNnO5JXvPY11nmtRmTAor43yqXyQbYL1/hdDnQ8I4Xc7EJSOUd2MHfIVXfm6fyUp3sxaqJlUVgZZIrOBy5dWNRf7UDZjWGeYFrMqGYFOXtGhHAbauAvkQiEkGy7geCUZjV6+Sr638prLl/oHyRS6BAA4vRxn2JLxB/ia/29VCc1T6ykEgCF/KwtuoaMvp0IonvLyIP6MXlHrpSQOghKRDhVcZyGafnyGhcei6rIbh0rq2z5AFS5OMzYm7lXATq0RIAEXXADwJx3AAQuDRC9ZAiInlKh8AgxYBhxIXTFnAnOxxAHgOI1GCaLC308cLqTWiBIjSMSEuvoNf8ZBNHSNiQQCZHGJikXmmAC4eMWTxkFwlVMMhdogsbYO0pVLzZWiUffTwHJrtYJNy4kiDBNRXFjCClFlaAVz3A0lmxRaWwaZYIZUgSlCdrpwGKVCBlSnIEbViiQJD1gg1C5jMCpfNCqyPF8ABkC05S2alEQj4zEGWt8JXbJG7iomC3MWAZYFfs5PQWGOkpDnBdMtTB8R6r9Q8O5c0+Xp8xhLvjFoMH3/z/TM99dc/v+8g7rNn37++vrh/dvbw8SNBOwWXb5S/7jzfuHUN5Xs7OG7inQpGJuFclZciPLiqLm3fvbsoUhtSLxU6Fms0PhqS0FOVK6AkqM43AAIg46Y4SsbHRmbdtS8G7oy+aOERqG8oRXF0g69NDHdZk7mByy3H8/3aiqVYDu9k5pDPr6a/4TSEfEjRV0OO7l3dM6rpFgz1Slo9OTg6cQTDWeJnT19I5fGTL/7qX/7r15e5PNqZc2tdp6m8a3Ryfl/q//2//w8vnj3/8PHpwwePHz1xHfNjix6Hqnw/IwbJh0nO/uz8p+6Xfv36wmBs0nN0cmZ0PJuvBGoOL15opIptNqCnacR+A2SovHvXF+t+8pOvjDaXby7evnnjkueLi3sGXRk3H9MhGHRl2ZpUnfFkzGiaXMwpL5YmiuksULOsm8qevRPL2JSwsK4vLYX5WyCZx9iK9D2erUsltc0xVZFBpnPxhqwmHJDDODsdm3qCHSufpdusktIUX0WGvovMHGlOuuNSK5xayO0cM1vk9Q4QBe7KcwKlxUdWaXxJwBQZ9uk24X3yuDSiRscoOYSfPJjldvOCUdlNj6qhpYefKrPpBFQlf01xyWoSgq2WqpM6wFcKokjjS0v2+eSvdItcZhFcMguIkimuLYuPZuVIbLNZTEpnjN+ECvObXGMb1FEUKWuApYBYaZHJoecATXSXRnLwGPXD6MdWCWInMA4WUcWBAYLwJSWrmAoSVNT8iqgvqgmsIBapVg+iahFktERDMotTCFlZEIMrNnV4a1wsxYsipBngC4oiWaz+DIYEQfKXHEmUBQYxVzKpI+sUAQs8aYjFgps0vymSYAuLBNriKoEomJoVXGIAyZxnsNWwAuGrlSBpYK6al5dM0nbTRSCIuEkINl3IOvR4lwJlR4+skkVxaCBpzpdBGJRJfnpPvmAdsQA+CTVFaSqhGC1EkKvkxQgj13y8HDwdEOsxl0x4yDBvD4KVXbCA5Kw40QC4Moqtzk2RAeHFRspMFksJTwE0TeX0MGcIaig13+qu9C6EsGxyjQDrWz5Vph08H/Q2FO8fHB1adeUA1Gv3sr///vtH98/14G5l0h/bdvUOqHXh5cVrczEGqRqEcNKlgyzzBaUOU0eN62w5e3CQnjTU05ULVEmDAMNVQx0IoK9eNFaQhMa2dGpbwhf++etXlIEvkg6Km49LWgD4AmQi8zkKBByCMtaMMoWAI5mPC57zeUT3HVqVWl3Dr48nPnj0hV39d69fK3v7ySdn5w8ffXn/4aOf/vmfK0q9qoH5t7/97dXNB7dAf/XVV//r//p/9dvf/f43v/nN82ffW/jev+9qyPtf/OLPvn/tBLRXhS9Mj2wx2OP3Au/tg7vffPMdtS/eGZ5vDeSnxyevXrzWFKhXN8ah0Bz09QTNd0durl6/fOUZtWz6zqDFl6vQjLpUh6F8bon6+MEUzWFptUbuIOdusuRXciTLYeRn6I0zyqbaOQGu44ubxM1UWnUNX9uPecDUkQMgvMFhqLBKjq9cuEbVT9FM5WmwypCQ/RUNcxK3+iaWEtnXMQBb9mYNPFeNQQ3R+3ll3f7GRn/VlxB1S0XNBvWwY8t4EefjYPylTIine+liSdIwQxgagGGRDlVDbCyTa8IyGqmtY8JNZ44PcbNDCEfzkRDVFArYXC0n22eZQYKao3RQwpSyMHoOMlImtsFi+Bx6TmzsMzt/BeqLQlNuviCaCW66IEEOMbICfATbviS8TWVyGq6kNw6XWHgdkXJsigg4LI1lMfDibayolHqTLPVKQ5CNyl/kaFOdIrciylW4pQJGucQ2yUqArKJ8GG4FARXlNSR4cAp5WsjkMR58M1OCsqNpEiRwkMV3BYC+DhLANxHGwkycVIjFzhfLb8fUKNIQLCOM+OSrAPomV7+JNrZp4eWkhRLQlZkgV3yJxYduW5ykIaAAX3ESw8JgxwAAiENJREFUBeBPn7kZkgU5lJVQTQS55gVQmcg6OJVeLCdH1QESWdUjqkGC0ZQesukK1g6lJx+mbkSmuxfF5yqqwCA2TaL0BDZ1UXj5GGE6qlVIFaAYO+ymIrYELaalJyGIOcQd+AsLjuwUvV7eAkh33MLVrVnPGWudEiLHZQ2Gaq+Selx44bqsp089SfNuo6WLI9Rz0+7sKdtBHldNkuQUbrMJKSgvLb4iHaOWz2Zzw5tt6zb1HNkTxWIabz5t6saPnYkO/cVOLlJRm1aTaJTYGrOSt6KSHB0gSwZQDcpo3dkCwljeclU4xZocoGTx39/cOfBC0eHR2YktfKWlJ//Tn/6klz84Ov6rv/wXrrfwiV9Hqf4/v/wbEz5L3J/97Gd/9ud/4QKN3//+9x4Df/fdd574Pnrw8P6//Z/rZN2xoNt9/vTKKvf4iwf39h5qlfBWvVI7OT47f/DgJz/5iQvF7jx9/urN2xkEVUAvJB36TvNnTj2itLyoQkb9Y1dSe7vIqe/cGXl4Zde2U/OZ32wzGPukFLq+3JG4mZzlcUU+0Tgxm7PoyiqDnGEmV1xYtX/qAyuWJZkazGhgvMUUgI8bJpiAP3QT/WkMqASb/IompbMZfTsNyopKPZprwVLJ8ZZMo9lKVrWaQBCRkMpGN0gRUg9GZ7B0FuTKw56h2zZnOarzNSR5n09SbToup7nUeHbbshMevizZ7bRsn32TtpsQCifm1A2KSUtQrCT4KAEwgMqsD7PUA2xztMmk2LraoXJgiGpGwAWKKbwkC8KvKMGtC8kub/VUf9qRroSQyQhXRqJoshWymU+IRQZZmfqxzcS5dKKlRKLRi/RWXBh0TYZEcjFzSzQADTz2GqXZAMPow1vXSSCn7GoPVwkVtQSWt4omma2rZD5ppSm7mZrUuQYBYttBS0IusBQJEHRIpApDUglxeSu2lPAUqNNpN7klBw1HVHnhG1VgGUqwBgRIEYyrSf9Q1Y3dSNOD8KWLGCwXeAXZAMAHa/5l/8xnB7z62QqRd50aJVVxvljsBHKjfhb9gMrng2tpr1HKAmckIxA9PAkwAImWTFTlUJWjWJPoeM8vfWmwRPMpGv7KPjLyq0OzSSzF8NLflIWvKpZFFDmiBDGKxQuJkXp0IFbUzZtrx5ngG8xdGgraCZqZdhBuBLJysO1cs3jKmKY312N4SGkj1CEd4/Cv//avv3hw/9HDB+77c1LXvcR2Lw3hb7wMOk663EpXLmocGJKpioq2x7MDAaYGv9bjy1quEZ62PYVi2zdZ00gWcQWWpdkJwVigQAXyOXg+fLkEiQVTrHhyKGyIh+FqNMjyTm4ShaWY1pDzY80tq0z5Oj0767u8bgwxMXFeyja+LTrXiunMjZpHJyduMPrN3/39r3/1dz/1Bd2vv37yxZc6f8Ptf/zrX6qQntFaEPNhOHXM2KzmnFlAP3zozaRnz168uXC26+L8vm9n5MWi09cXMpILsj5kPjoZ3HQ+zSxk8eQb5h24Ojs9dCuWvV+SD5wZjtk/Hs6NNbHAbJ9Yf+PKOYGtg48NfSBjzGjWZbubMeBhEGuFud1FS/QsdjPly9mxMWeHtzSimr26lRHvAmwmcMva6EtZLkEOQZEYHe0qPYMDRA4uxeFpgZo+lOEK8Wx1FlgSCjAFgBocgGtCVvDl3fXFIqscvqg6CqxHMGxVxWgC4FCO4E09bxKq2cJXVH2jr9lSG7K20MpGyaXeLvFKfWm1MIDK/4yRqOKrEjI2h2Eyqi4ugKAo+pCwhOAKcfrtPJYuGQCmUbjShGfLsGXXMgUjKAsAI38BglUDkMpG8v/1//K/FVhuEo1HdNOrfjAYuOP9zWstpWFfjlBRpQQDKhCNWi15saQBxKZVzHdqxXLwkTvdiqA2J2MAZYMejAVQSsQcmPymosU0yN8FmhYMQBUhB4tUev16KRkLhvymgqw0HXsmZwcm1DSRqChc6PmlBOCtE4tGrJpUO8Bw4FZQUQAOGRpJN5ZtyKFk81V6Mg080i0ZTcqIxoEV9AAO2RJIWnMKA2g9KMxncwRkGo9LZqsTwMFzSweYWkPqKiU5gro2QphFECV6qfMp0FPoiJtxlLIgs94raLp8lJNUCpGQJoemStaAfLGc2BoQI6SVawlETabb4+R+nKZFCAKwWKuo8vIFJcEvOxtWOPlc9eHfHng5xXOG9zrcYxk9OM569/bm8O69b/70hzcXL3IX7fH+5dUbtybp0x/unxLlun5iDeQkOPGSbcBcFmj/MgsBCXlXtKW2d5mhIznNmyu3knJ2mGFdaDH4dPdyhoUjzX1YhUmTCy7qjqMImTLO2hCi8L58nxmMoDYGDzNROXVGDphPbTTWrYIfvMISlzegZIGRHdP2ULem05fO0fFwZRv2zp3nVypwXo6Ibl0XWogeHVrieu1IFrwylJ40d+h7L+nB6e21ha9bq+T08OTYsEptyXz3NJcLvn6b232NzWipiubm46Fbf//4x9/bJPV9QJdpuJLj22+/89mMk7P7+7YsTh/4vqBXiv/07ff/t//7/+Pi5R2dyM3H/WsPa1VsJ7gO7h18fH907+Z/97/5r3/+1WOXWkrXGs3pMIPW8Q9ubhrjjDU8hUgJebSw2b1PVOxzs5kpUo+Ta0bgawUr2BrFpKLmOFQo8bZEzBUUhCjz3gofITE+AhWj7JAVGOR23qOeVBRGDuVNElkulJodUT2bldoXN6N6Il17kQlrJXePetAt9HYyG00IF/XuvW354LlJJk+b4zIHSJ1VxGqWWAUE4/xEIrcLA3DIpqaBASgxQApye3fyZiOMLoiD1wupw5Abgllg4GI02YeUcXJayZkdBn5023iE1Anrg4rd4ja/uEAhGG0bhFHlIOnf5glDGW6sFA8lgmS6vcd8P5itqiGtsJSmhSUKfWGArr29JQwJYhEXKKMkljQ0nR7GoBW6fESQJMI0DTBHSgUVL4pjMrLgabkkbOmTE04QJZ8J0gENPMI2AmGkyFXOblZxkQDPl0Qlo0xa003AgLkiAdVKsEnXQGSqXpWApqkL1omtHNnByKGBxAvfYAnqw0iFQ1YMuABMkSSTAAY0X8XwS6BzrmR+9WkelSJptWqjsAh+mKuIKkpay6FP7PY4JeGqe5FgjhB1DgZvywvvShqMV5RE+URJrllDI6pZKwsMRyYkoMgSVzH0OWW6NSBRaCSKpgqstKpYeZFVAXrCgJmuXE2FEA6ea/vBThSHsnhCBMGVXHZwMWVHA8MR63Ji/RSy2UjbbAh5icOS98lXX7pB+sWz79yg5ZGwEzxGqZhYmTpyku2VA4vmea6Ww5yau0d2UpY8/aP6/v7JnTxKEGumKN0NzJ4WX9PXUKxTixYfmZPLz+vzJEtA9rWIXQYxNjZTGtjkaWr1fNmpQZTZC5TIjKoKwaKOASSXjifOmv2eqxxrwMyY73i0ac6ap6ePfv6V8fX5y5eyrTc09Bq72cHK1WNga9mTs1M1zYj79CncN/+zX/zc3A6jmZMXel2tYMR98PChL+924QvpSbCh0TFpz4Zv7x7/4he/cFTKMPzs+dOXr/ICmE8V2ZL47unzP/7p2zv7L3MXpRH77Nx3D99dvLcVYw+VQWQ4RZnXgfI9YFvcapebqa3XqeQ7kgam/f9vZ3fWq1mypAk5duwde55jzunkUFlFV3UXrboBCXHBBUiIf8AFSKivuQAJ8Zf4HYBacNEg1HXmczIzMoaMac/zFDxm7/d57pMnT6HCFOHb3NzsNfNhua/la/imP75SLdAbzjkdMWTk0yM9EiYn09o27aAoTLpDSq07q0ZgSgmd10SBUJNGLSDGgHbISDYqUlRjrmlYYdh2DHVRNXqNVnnsm7jxKwQM56082VGLeeKRZte8lBx0VeWqo3YSUlz0QV/IIfFRDl8mBdfxcFb7xw3REZbn3jMrnYZNRVQQY2AHJGFnuNJ3R1EjID2iyGjjhVw8QIIQQ8IGLuFwFKGUF4axlY2J1BRMyF2mrOjD4RGviI5sgsSkazA98uu1WO7Elr4b5uRxUcOsqy9FlGFilAY/fIqUmhS5jm10qA1iixKqFsNUKwxiAEIWM4QYNlIoUgGFGZIgEmLi6U9BJv7SBJAtwCrvvDgmcOgr1TRSu03pvLRIMLtiFVKQbwdQ00tG27RRgCRODYFXqqpwwCJPc6R2qWzS9sthrTqsaqKZvkbGjnAox3UQBJNhnSAJ4UhDYogcgwiDTygMOIlTilLBoR8EcoY0ZRWFZ1twLVcvpbGNSVKlmAaeNAXXUVMvpcIGSIcw3oOTrCKEz3SgiIkuSzMGXBqiGQYaRpY+d3EkWjzDIPNLhxDRlyWPISZQsomcITU40QEbijujKJgjAJoM6XCX+op/dBCo6DMPTip+7Sahmva3i2e9NBzyEqWmnZlzO3Nhaf7tm1cv37xdXVu2qfrhuJ7a1YH1k08X57M+2ujVkNqYrAPHI0GJx4cNZz4sGJqekhVPhXRde/5KaaYdBNA9wLCOkQSm+tTCJ04S1MrFsFUvIKBYeRLKpYkx6szSk71tUqMLaVlqZTPtGrB+gaGkPcdpE2oV8Ic5z0HZzHBUBrwB6j7nwc6upoa0uu6tnvsULI1O822l7O69t41svfTlLHdqLMGucb/55puSrK/bDXYlWhvNR0d7+/uWW1erdUG8tmpttqgjzbK29cTy6pqY3x/mZqk7O9d/zh4319bN294NO/Ko9OGRXyn0TndT5uJ6lLy+S1OXbD5IVUOlZpXr+jUFD455AssPBNfomY6x6p+aQwqldOoJ48kJvQoS1tV/v2aj+jTRYDS1hkqL0UxRt95kqlSKLI7cZWiZSITUfd1jI8vGrRdPqAUWGlvZEITy3d4zv3V31MBAnFdab/9OdFjrbUJ5OyGYiqT/JNSGnywbJCHKVHiUkvwINh1+U1EBOn1Ji0SfJMQq9TU/hA+sAGDSkU0jaIc+DipRmjpOQslh0O0WCUMKMU8aecCliALS3BQQTBQ5ZXHiR9EwJy+rPnHX+BQEJsLYkscKM1Grn/OuxpSNbbqMlcGQoniJi9FfihArgCguaCYbcIC15sVZREGhlKEW7aRx4ztBdEBHBxMTA5oETy2leJIEADz4Ssnx/OIjTFZKP1th4VNhvNrGOwWEDyO1asedlDzxMNHNAdFeKCaR3OZJEjNfQeaLBI4WYOgCZ1A0Y56UCU1q0rRkUlkKSVNfafClkXBE2QVH8OlHR4oMaBKUCKWJMOYUgsZFzLOlo5tNZIoyOEydrDSFCDGoscuWJvCAtJ/ilTLEDIqOLEfodpZQtvelCkCWeZoiIAKLMFWIa/WiQ0FWPIqCnNJgUgBITjhs4yIKgZWGaALUnqkU2ATAnBWeAkyl6VxWJHGhXW3AGmIlrDd3PRjVR5of6rk8V7i+seUYPDs/Pzo73zk63raFaM+5n+U/O63TeRGC9ZILhHiU+vSGrWzzsfWjfNUnG3PZym9tZvoWcdeuzs0xHX+9w31+OvlwQeqblAJSykUWSE4VSevzxG4f12cY+oSmRnHVTlWLC3UMtc46Ibg81g5lXm+xuHisfRGYxs/Nh3nb0j5EIVy+kKgufFvavvCKnyuo59c0cf1wQX88wVXvm/fv9vZ3vFlkZXU57Mnm73/3G8uwopX1NVelnqWyAFtrXR27Twxn++GDjz/+2O1hO9XuxzuNcWrSDbj45ZdfCoMm8tGrhz5P+eChG9Avf3i9d3Bsw1qD1qFWnxeuhlEjQZ4b7B98XXJeZ+ubKx/K8mq1l4b6k5UugmsM1VHuzkKPUo+9zzi57PYppJ6FfTPRK9t1k7dUNVsZTI8y2Qwq7tIjJBiUHax0otW3txpqbXDfJl5zWE8iMDDcnJ660LxcwNRf8TVgA16pC/ZbVDF1VOk7UThEaGGiBTMg0rof0usUE3H2waR22u7WXOQl9snBW6pZygt8ev3MtnYN25hmahhntalgiLvZAbJaMrWvpmHiyKoY7kyep2FrItLdmZnBkoRSI3zpp3a9vg6J5k3RaDpq0ayDq5vYEMJQiI5s+ChIQ4Q9iutkHaO5WOkCci5uU/AtdwzJZZlQRiSxjT4JnODDw0SnVG+FFBcVdxNbpZObo3EQuBSMgBpkAqTI2K20Qxn6GF7BRnniof8Ixl9o0gwOoaOBkCIIWoGCVBGheQFDThjbEUmYeK++bmpv5Qi4VDfHlnkQyOlYk2QVyUZBSt8cFI94+HSkAjAeMHQQJq2Midq00av1KcBPvYYmCc0hDAhJopXqOMo5CDFBiD5lmqFRZLh3VDXbDnCaFrbIpbJV565Cqsl8oMWFrJi1kpQEkSBWEDhlgleKj0RKKI2yIln7mAGPDoTIIWtPFHNCpPERfQj0R2wkiGbMHaX4mIuBMApJK9aZGddYzCMJbCJPGFJFWjUNG1iYhIqYR8LEL9iV3/qSxmQf223Bej60Pim05A7ZsU8pLa18/Xf/8s2b1989++ZD+2Xi24zuh+XCC6BPXAW2rhU03d3zG9+Z1hcuq6bHfI/o8k7BAixFNYd13clNCDmj0VaE0tRdqj1FiyKhHB1TZn9N3JPAcE25mfXqOjeahYP7U2IuMlMy/1HY3N7W2b6YcXxyZjHv9478wtHi11/+C4cGfUujddSFsnvG7i/Ysvaos4tdj0O/evH9999945IXff7VlzaTX758ufP995ZYm8xb29tu7nomwHc2XDcbqEcbfh14jRDC/sX1Rb03fGK0+dkmyJ88/Wh7Y/P58xdeeX+x/9yD1vbDP378aHlhcWtl7ffn72b8RH19DroqaIw7obu8OV9ZXLIBUEuCHYd6DM97B/U9LM2gF5AzjiKPTId6I9ftA3Ng/Z5SCmuBKdJl0epcNREEjU+eTiEnRBrNODRWPQZwPV/TF6HWZU5TVte1/0oIcx8dziC2tzG7kyfx8GLpA1iMXukZxoQEn+OKsCT9fxK4yGvkW/diJUycfz3o9Xfe2tIIrSa43Ezu9btaD1zd1BP8JIYy6dZwxgaJuPz2ESQq0XYdJ62RinDNRLNUlfur3SQ0M4bZkpOEgAxSBIGcpHy0Fyl9thiYEU6tJ5qZCgYOJiCJXBZskNO8BmHCSxGh7DCPi0n21slKnAZKmnjERjNVwwg5jri+DZj4maBWC+tLpm0/VOND1tiNMP7IU5mLk7p5Hj4YUYshydAkb4XJKjIU2Ka9SOgk5UWjiFIRK1GlRdJeUpKAD3dhUtt2NFnqaCLxS2OS0gQgZRK/kaeChhGPmWvw8UhydVETJR0SVklJgMvGu2wAZZlEX4riQhpDavikSgmTHfI0DvBUnxw1UkFhTNdpfDqY8Pw6jGkCtBqFUZQWSAqwponuO0WJfIAHLaU0ZfnKqAoOWCb0k2oiJGvKTy3YohEqqxAhJvoAy6T7N1HFJI2GTzyU8YQxjMkwVDSQucMn2thyoZqEsqEoJ9rUGgLCi9zT1j1H6eOatTWwHxBwWSlM86fJe+7enHpenF/ML69+/tVfX757bTqyQtfdLakJxgtMpmaDrZ+I4VjHelPD1ERwXb9EUENabQRbuB3/yvxKafRIy/3IEW318q2RliwQwtQFk14g9BTytfaoaMVb63dwgGOqO6pRGerTqrVPUVTj3PVwg18anBWjg42Wnx7yGpQTEQteXe8u1V40fTvCnr7jCPkBQZ8tOj0+8eUN28j1w0MLC1tbG44RV73v377Zff/uyePHbsR+9dVXFFwHf/fs2c7urkthmLnp6+xKkS1lq/X9R/WhZtfNfoLl3Zu3bhh7Nqr3tDc+/+wzH8t693ZHnVxKefnJ459+9NArUbV13J/E1ZrVDtaEyztus5+dHF+vL3rNQVQ6xba0e5j3VupZiiJLWG3P9g6e4/HygmQyTmr/thdmk38v1NVsPRonbdjHOyGYasTpQC2J++WovxAuq9lzDZRjB9892VeBvctiwWPOb1n1lgw+EnVhLI33cpMFyYV1DZsaFSRSRAdyZ2siml571s9PKWqaHOM1jO/UBUab9RxS5nXwIj9cUW5Qj17jiG1tj9T4qZ2VqOViGm8qlJZ6k2gTsOFBHh4zKmUDIhN7NUyfwSjVjNEMSABhYkgURSdeUkoui9JlstBK2K03DNmiKEtjywRp7RoG/bqakBx63QMlVJo5Jy5YoZgDw5NLAy7F08cwVPFCbwRygnR9TAQZ/URODSwawroGj2pSECFKQxLtSPDkgygX3nRBwigilHZU062elsQqJokMGjVNEKdS2Sg0arWyLEM6MZcOZYwdpOhHjVWQMbfDZkVejd6/HxLlYOIHURPAbUfho4CPiUY3oLmIPIMvfMwV0eRuVHMgDEDhUTMqhoROWoNt9FMLKYqaBSdFiYQ+nKrX9Dw6sPSDpggfWGkBNUGTFXlwpLJxIR0uoAUwRcHEq1fUbBwYcCCDEDk+bSIbWNn4jTtCUGILICHNOAUbHfoUZIOglDwpiUOIidgo6Isw5PGSkIYyeYriUTCsEKtaJSeDc7IpIuvIdjfw/MKjm/eWV5ddt73bqdeIP/3six07ltd1W9cU5YlWaxYMV4cek3W3wtVzz6a1pLkbpyFtz3X/QK1u4hoBv3dn8uEOmrrdYZQ0cZZ590Kqk4okpVBhTx+q74nQOlq9AL/Q+sSMcttWOShNl/dYnJfWeUMtyzYoZ2/mlVq+Z49Pz01mHnBeWVvfvl/rotXYIv3Hl6+Ze/beJrPfyl1dXXMipwqubi2iiry2YGXd2Fx770PPOzt//OMfbS8/evzYPw8B2ky2z+zSWetZcR8/rXeTLMbZf3ZWt7B1H7KPWN25ry8ujn150meBT07vbz/8+NGT+5sPXDh/9+zlzut3fj/pcHdfvSZV679ey7NaqMzB3v7zZ99fHe8/vL/5+OEDA9ACXB+eqJ9DnZnvt+2r1jkuWMw68GpiYVuNVo+K10irW//T8T9x1O2owZGWb+U2LGMnVosy9SNFzsq08uycUWsOqrM5gl7OKxg6jHu49t/JMkYeQL7IB1+VC9W9hckcS0BHauT2aCmNLKUdYyUqW9ImPVsR3hpI5aLvRCiP3FBqlbbq1bf2+evk+9ywKLV+wbeTymqm9mVd0mq15dI3o7lKu6lOfPPk3ohZuH5vDbGKIzEYq3iSVPnHAOBPH5ttlDoPUDoOiqHPtmLrIsJQB/ajl+6xmlWqV3qZlOJJhhc6JLKZavAJZsTm0FAaK17YAkHU2Mr+qCnTpZHHJAqUMdLgUwgUyWQBxt0m2mkjDO0c2IyRs0sBUZYqTc0xtylQUXPgxZ+sRUKRqRPRZ6tIBRRBTqnZLcHFHN9uJ1sQI8jhbmGxFsKEEUBpJJoJSPDp88Xv3flJwykaMWBM4pHg4yU4eowECSMKUqHKxil8+hQw4Smg8FItSTNnoCmSDn0hgUqo5ebHY2yCmdYj54WhBae1Jt1ZkiaOyGVB4dNlbG/3HZ4uNR6l+AQpi1ILCNQYykaYdnNZk2GXbpKqV3nsAxJUlAEiIAOHPM1FAoFmHA0vhBSUxlZpXGDopEgpXyQYgFIkgNQoFcHTMd40qZkdGmSEUQXxk2NkgxNAzybXjuvkKDMp1LHh+snUbT+Uyev3O/ru4ZOP3ar89vnLhyur5yenfpbu0pTrKRuPIHhFxjeQDw8X52b9jJ236MyBwq35q1+f5QgmKDF7auhe3Z+t02SRJAZpV6hawPFFGaV9wpOndjSRWsiKSlPUhjl8P3h8945rOtN+V3rubE5lJyej6msamesHzXykkT5BfdOqbo+6pzSH//jTx17D9fsHTkgu8xt7d8jvfPzJZy55LaKv37yzalo71+zIr61qz4O9HfvK+/v1VokN4Fzmvnn7/uDwkNSFrP1nl8LZu3727BkQCG4AuzFsxT2oL1Ee7u7ueCnCwu6l3y9/8bkLWb+DtPPuvS5c8lrxvfn9mw8+jfL6zXvb1PvvT+s7PXUEuFSuZ84NZE3n6svy+frVD2+//+bB1sbXf/1VnQM8+cj9+/O5G4ewNqFWDV5DvgYA/SI9kFXHVNj3/r2mCD1UqlPS4OkLReyglbWh3r8UqUeUGunksfXdEqtva9bYopnhqt3Ss9TSyxOc6ZwwXGNY2aOMhHJM6GP6CJ6sdtSUZmw7KCkYGIhbbZOQegerRg5N4xvCpAodbzkSo1W1H+gz+uym8Ffrq0O8VteKopDVlze6vdeiFRyQowphoBUVlLW8XkPKkz1GLLHqI7xgEAmrEBfkAhMjiSLMj6H2gZwwktLBoGjKTis+edy66jr1kllIMAZDeD2CJgfm9DYwBGgBZN5PSdX4AR40TIhh4ieHg2/55Dy4219Visj5zbRGLkso7NL/H//b/0IqE72YkWQKSygpjcKHy8mLoTTjWGtioGMYYtIiphKHK3cCVURfEU3XEw5F7yRQRqmqNNnT4yOaqTAJp6xy/IBlDgrhyZEFIE0cZThKSXjHUwsleDpnJ6fho6ZUlyMu4lcpQwh8KXVFQxPPlg6PGHJVI0eyDBErasyV4pMNEwnNkCw1xMrOGStqePgoygEkZ0JTSk4zD+ngUYRJ6bDFC0nfSSNRkTgSecCB3G4xjqIgZY4gh9dxjhwpiSkyVqNUbCWZvocdQ0IKUk0KmTBqUlkkBrH1yK8VKK5TlEHMHKUlxRydBJ+jBW+VpUBNbE6u8RD4wvCL4QWyUuNe1mBg0ifi9YgTBAS59O9OPszigsVpFUNrkJuSAF3WTCiXSoC4OHq71KPFget70X484M711fzdGT85q+MNfY8/1zs8FUF13M3yqvpyxJZMClOz5YSGxJtMQ0jt+qrevUbU0g7J4tMpbEkCSOLeo6rZkSGh46cm/JguxsRHi6aTiVqpuklhnlwce3aMHJysSB+6LP3oYxe+fgjL8uyK8/3uPhs7xPWa0KxPicyZju0b++1eC5hWcvr5YHu7pmy/wOD6dm/fkHOZ5y7s1oN6bclaaG3WFxZCC7PWpvDq1avaZL57l8TVcD0Rvby8f1G/ZmjFFq9Hrh4/fMSXdZqmOc1d42fPnn///GWf5Fz52Nb/8cIvzjvhmLH/UPuP7rHfufJ9rI8eLP3VJ4/n71x4fl3f+Y2Hf/2v/+EXX3xx/7MnPF6e1auPhsHm5raGqtjm7vGrMQnFSaixNIgfLTbMtI9OETYoJdQ0YKiatLP6DnlSgNwcIGUespMvy69D3H9Qhd+ED85PUoaKEIaiUuC86z/EI8KQR01RFUzpR7R6XoqPyUFNLacFwgYrCQ67Vrt77cc5eupw/kGhDzG/fFVHqKlV8xJSVgnxaJCejap2cIIJB4I2dLghvCal3O6uvCU+jbHqNfgEPAkjoCz7mFVEPhTCGOTxyKlSmiomte5FoarTROiv7uaOiVJZQgxD9ape68E/upJCPGKqvaa385jXx1e6y5IGJGnMoak7K1nVBwAqaLfV8LcR4kgYk63UNM2ImHZCFEGwkhKaOKgZu4Ggicph96g4EEkAqxd9LqclFGTJgVi92u5PEoDIiTN9OoGVFmKPNjw5PppqXnQvHzSooyIxaD6kJGqEnKZ16BhSJOhPfPd2KH3CYYWPJgmnADW0NLFp69QxUPgA0hzINIMQSZADSx+JSl1TmqpJqbFShegkJRE8PgpMqI0UE7SkNBOzYIZ5EAJOmDgDwlwpoSz8oIUJjlTfgUVK2Splggx0vGZBYlaE6NOUUkYDKibRHwhR413pbeVAkVAIDQll5oR6JJiKaJILg+vUhdBcEF5/0VQa74riLikdX8vS8BYVE4tshddfb6ZgNeowql6Li6umJXqzCzMra5vek7k8O/1weeFLTr6AvH9w6Cp0Y7Ue/7FMWa4y5hMDkATAOygXIvX86E3dhFOE+ErwFU/XQprjvA+lGvxRo5kGdCSaLI1OEsG4qDX5ui5zwuQjX36XV21kkb/Vie5zq8XKiqXIT/CenpzvHx69/cdfPnn6sVdtCVfWtu4tuR371n6yn2Zy6e9Xz91YtRjf/7DlwSjr6/HhvgB9GNL3s7e2/HjgfV9yVnnn1h6/cm79V3/9Nd566cErxLuV2FNXigwYCD4T/fqHHyzA9z/6ZNXZ0cM5m8/uIh/t73n7aHl5defN23e2tHf3To4vrJAk3mfSLN1OWkrz9T7DpOXuOBO3Xs37jUEnPnduzo+P/vj739kV/8X+l59++qngl+cXXHDvvHnN6dbaula121AH4PSItoaI0/mKhs3w4E6ronQfOaKTUgzKN6NdlOOdcVXv9C3b7uJu91Zzie6vUtvswRz9iyExMFpxMjtFWer9LgpIqCg8nNp54qre1C2aNEu5z8wgdGtnnexapIQcBeGbkEurKyU1ymsPH1CfJNS5TT3vpQlq9UXYOjh49L84HotNUBA61A+uqlRZtCYBEoebAaCvCSkX0HRuYYKckEGmLG3gmgy1swNHFkUtjDTmFVffrkqDkNfuxy1ilRxkOqyGJIBp5+hUTK2giDyakUijk4U/7jIeIq8DfLoSMaSgNEUDPIyYg4wJrGxIlX9c3qfC+svyNvptXIFqXP7SFlKOQ9Q4COHhcFCTWlfSwT8mwcyb0Ym7WBXmdNAOpxTgD/C0FH3KSBGF6EiFDXy0JqsoDLUcb8xJmGN0FX3hxSMJRpG0YPvntMrTkHQw6kIzylqDcrJgg1MxTUdDJEMnRawwgU1R1IIT5GhKKSPg+RJWNFMaXq2jI6sR1Cj1osNKkb6Qchfk+B1e6MQvcyajspgcJOpLB8XpwHE1E5M4ylGEtwBEAlY8AxAO/du+mNCkIzyMoihHRxocrvHUZHVWMKMvDYG63Q5wtENgXf4my3Bgxko8fb/KXOr1Imfulqp6fopjLac/qRkRJud6WHreRcm12c+gWVjxvM/S6ezh+cnJ6kYNI1DX52duAFr3Cq0+OzMZG3iUKlTX9Ef8SaZNOjng+YoO+eg1aqmyUrXoeCbbic55BJcji75ga//j5s7B0XFVs+7v1rbiZFUwy99duLg+vvHlrsUlF5zmvNpFth18fGS9Pjq5qBeKtu/7AJWPb1jd/YTRydGxachau+LbFvkl3Z6bHdD7e4cXS1f62k8x+A3BDc8t//AiwWh5b/cK23bX0cGhh6Wtvp5d96izVsvsrGTnl79+/OiBTemlze13FxfvfO/q1WuvPb149v3L12/8RoMfelhcXrWpYBBp4bqrPmkqreIgrav7+mO70wep717356fqgvtwd69eQN5///r777/44guf7lp33l8j0T1wpyG19dWbBx49r30jrQcx8w8d7Y80NdKSiqTkGYEpKrn/TQWLLLR9F9a7XRPzfrKv+qHNre+gFEkDjkdleosySttksjBHYWJSz/iVPkODlHCYOvSTld7cuci1uFKHAkyd4nzDYVSlTXajIcuaYwqtH662+rownoZUv5QcX9JSnB6SIOTYM6Rtq8Tw4MUAsG/mzTCXhFq5azFBox+/hGiEjYkkzdtOCjYKspklhhqmouW9Y4takHO8w4lC6TQ4JvyA5TFqJEOf8tDUpwZwDsOgZQBIqUkR5XjE/HmNohbM6NOhCU2NpPV9QcVIAY2RKsPrLtopba067KllkyFBB4icPqsoBIeJCuAx5EoDRRLYYCYlRPRvh0GilDLq8kqiD43QT3uSYJJVhCGBg0H8Rt/xRm6DS4qGF7WQNSeGARV9Cpg6VltZVlFgo0M/OryQRC3uopAUSEopoFhFQjn65CPUFOmXwA7bhCclGZiDj3xUSsdF33QnZvpxhIkOj/ikA4QEDb/4KGcYQEic5JiQg23KTqangpicINeCKowQIWREf3gcDJ22m1wjklMj5JRJioJDEqGoyGmiCNVUL8uSRye8LBDmcZ3ZdlJUIOWgbn/5HLOlqn6g111Qz4C6ZVgbJvU5Ik1R9w0t1UKqx0OrgX2mrm9ZeYPNVrjrwW2zT/12vWXX4VUN4ueA+BUq17W0+/23KSUqgXE6QvLTugmSVhdNTkosFeQAh5VStLpaO1JC6rdF7tKu3cPrm9P9Az9f7NuakN3bZWtldYG7vLnt0tY1qB8CnLm354eG7DQ/ePyRq8P9o/qopDMVt3gtuI8fPhT5zt5BIZzYnD70c0VWUL9Y4YcVVJOy9c19YD9ACLyK1rcWlhc8eOVNJO1/f3PLomt1vtzatqVsSL96+dKB5qTNc1uyzJ9982z37Tv3Fbc3N3xjwAtJL5+/cOWk+ewbUzbVgPLo9NnZuc51SlMHJeqeN2hqafMjK7Y9hXvj0403cJxgLNyb8w7x6f7h79/v/vDt91989eVXX33tjaiF5aX6flm1ZTWmL0f6WQ5tWLfJa7qbzIQZUfyk2WXp4wdVDEqnQnu0KYIpwk4rRONXmiwFi394KcDpwKjpmCSaFVnPNqKy5cBKkf8qSEMQBmovu3VuOPnXZ3uF6TbIdIYswIIsc1feGkZbVcSOg3I+m+hpGJl1nLnvayrrF4cUswJQJh2YYlA5FpmEWqdaLEsvc93q7Appseqvqsqk3ZSiDPXspOLhANF1SHezKq9Top8sedpBNoA5/C2P5IgF+dB37hgMRRVBtycJjxVEzwYQyCnAJJn6rHgKsSkTfkqnsvoLJ7asxEahfJQX1j8STUJ5aiMNTuRzjrcoyScgDMrEmnaJJR+hCFnFMcZBIlBMqqcdEbXoUIt7QsgRKk2YKQqvKM3aIUy6Ld6BYCigYSgej9GDoh8htZyAO4aHfpzeNlQ0/AKRNSCiMKJlVVVo8MTDJGHQV4SG3yGJOaiBPxg6SBErQmnQSJAiwgSjSHvKIkWyUYhJaU+F4aUZKCMLJ5GYuMNLh9UA7Igq4Sh8rJJNGqscMAOKcnzZ6YphQCiwQvpaGqexooDJAhm1gGhGDHmUDQDIeEJFaaJAVYtPB5X6qkUkQ8iQPMMMQg7vqMGnho98FM31PTCn/OLWDKpVE44nmPt3Xmurs659zZtsy3x2Yd6ptVneLOYJSep+JIhH461mWq3SFXBr3Ms5eYfNWDB5prmMIK7xF+d1vADsSa1CFbnKXt6dnIAOiXag5hDDaIdkaTJXl/QXt/U8mO+Ef7jrNp/ZedkV9oxPQXkaQMdbn5Z8G3nm3pxL1Xt+bmijpsij49Oj43MjZMme+cLS4+XatDBzuQVr99gyaef204+fcmGWcLUqPTk60APViTPus/pM2IqKI+8H+0kG8u2NRVvNGgSCz3RYjC3MPhL59ddfk9h2ttJX8De1R+Km7+bimu3o7//47UttenOz8+7t3s57v4O0vLqyYCfL9ez8wvG5t8DqHUV79nUuZFWpzd4+ldFh+sczGX4RcXFh9vrGB7Dq2POlyZsFz6VvLK36rPTl0ckffvWbF98929i6/9nnv/j0s8/Wt7a9SOb8qj/w5obyrF9rEPbJ6aEWDqXLND7CQw0pTVGpTbgaw9NS4Uyv2Gq5LK2pqS6vHmQkBRteqTZRfUzwpPjq36u6q1rCqWEbZaVpaEtvoU8wGTXCZD4MDtRCq3OzamQHQqZ6pXqT2zraJgcupHpUTZGotSXcjsRKWSe1gSp/Ta1W/g1XyEaCQWJo6SxejAcKP0upO8PGnKQ0A0seksVIFQ0JPscyEENz4FPAE4pEPDEMAomsFI2mJqEsTQwDhw55oKxYw7Ct/2RWia+Y4zs7CZgVhFQnTFzjBS/VBSSTawgc1QSNB5QWvG2fmigCbZFLNQAZtRqabdwoRdRkMU6IApv+AMKQxOEXwNspfWd5UsIQPo5EFTlYpJQEeRBVlrtIos9EhGootp4Pa6rilNynKCfQ/afBCi3g0kb98SrNmT4EFBcUwpAEhyQBqCDCBwoOZtAwJ4+OYFDvCE3iH8qQB87wktLTs3qqKL6SyiZ+LlAMUwsmap1IyNFACxPDwSfLCo50ZCF0G9R2CF7Y0gD6LVhCEgMGafa0s0sfIEGOJLweGSAkQNSCJltyDCIEKItSyl1IGCQMrQdKoVFmEjlGABQMSIBM6BDSp5CASeI3jsTmMQIqrVYXvA7f/r3gvpVHXP/6XQR+zIL1vaR63bauFuxFexhopj7l4Jnbg/2d/b0dLxF7ecns747l6cnp0nzdcus3fVVzMma6LlU1tVchCrW9WnvbmnFfNmGrXetU4ISpDkaoqkMHzXLl4DUG53pz/vrcMkXF8WzRslBtbm375rJfefLbup5PPvz2uccsXAyvbWxpQ4J64ujA9zF2HZJ6zbqr9Vzdeh747ev6krPssvOvxYWj+p2iw72+gH706AmRHw5cWj73TJN7vX438I7npQ8v4QOBZvV9/+ZtuagfWq7O8pFnE4JHrljoKdfNV+cXXmf64cVzc7dV2YmL3lpbXvH+9cVsDV1tohE8NaJvrg8PVD8EULPVhaFvLfUX5ik7yfIMuh7xLLAdDVOatvS7GWY7NxWOq398QHPn+fPnf/X136xtb24/eCQGd1l0Zl26uZ0/nanhZsCk8cUAH/EbCQZpe53jXEgyDaz+9mtIetzN2hreOjqArutjmDRCqQ4d4HwhQhL9OtUpC3wIqkB626aGt0Mw8jYxUit4UUy0uy7Mr27M2wVOLYdMLc0aqt92LeUZg7/OOXsM1tlO45S6J7MIa0O9rr4nh7+aJSpPQ9KkZzTx3tNaReVnTsi7BSqYMu42bLW6vYV0scFgABAaPLdjHnwGfGwJMXEnDRFi4oiX0Z4JL34zlqhhIgkgHrHVMkpBycY1hdvIcdHqpaB0KESfAoqCosFjKAxYvqL/J++zRpsZvcHTo40El1YQvZaiFjnN8IledtK1vWFLM7WFg1EaQMq8MEwc0gRNP1FSgE9OZ7RXAoMPJxQccsrkwWHitJ5CEAKIJxn6P/Gr++ORDn0IiF8jA0OiNB7hhJSKFo4iaQyDz4RODOM9VUh4cR0vWpdh5PRREGIVTenQiS8SmklTJFVkNBPyFRx8egozjXrS8T/BpxAiD8li4EjjAgIXUkVDYqbGI/I+mioAZDqLHA9BGvPElpSQThS0MwZ+oCjIIn3KUBgZSCTJUkBxQULOy5Ak5rQVW+Ak1KJ/uxbivDub83QXEfV2i6exzGumIPXuS+K+wqjZHMbNRX/sQjh2o91NcynnG1oXH65WljeXV5xT+jm7s/opIhfiC/O+e+wSXgDOBsRmu1oT8Y5csIrHmE0LcEdIc3Z28oWsVCH1CgJJKsiMcgydz2iZumvtGrpG64V9V3vjEvpq5CQ035J0MSaM1/tH59fXfl/IfVYb1Pf7DoUTJ2utC1/XLvV88qYVcBF/4fcB39Vzy37hb211w02+m5UVcg93udCpX6QQLRfzC65ynXmJ82Sv7gE7mrY2Nj399GBr24Wvld7DWXaJ7Ty7PvYFD0ugbWo3ht8/+8EQciVuHKiTExEgznNUh19nPm4LGFleKVajo3r2031NrVJUTWRsyuo4/+tpM68tuF3s+ydXUpqnB0fV2ou2xpe8JHZ2VQ9df/OHP54cn91/8uijz04ePH7kATqt5BMZIvehEq6Ba16GiJdy1CSkMCTUdIfZ6k+LJsdXAqRA05g1Y2Uk2/AmibyLyhFYpOIk4QllkQCCD8TPfDRfOl37hq5zZQfL5NzOIytKpyaTlcC4JYm7eE/r1XCqXe0JaXY3f6slC71vVtfhJsK5OjOKfPreMMDERlmcstDCODODiI8kCtJQnGlq5trkVgX7ALu1IsBkkpRVeNkgaP8STrMRJqXpQBMAwhOGj62U36GZBq95YDq/KYpV65S5LGIIVoriHWyySWVzkh1wKXl4Z7HB4YV38jROXSOmIGmAOIs8xtKYaazL0/piLU9QgJIDcjSmNWUhKMJQc8DToQyBPDpxL9uVqiSuw1x5eqUnWWn6BhTSQNS6hjXESZKSCCDKYgaOJzQIeGelp0kU2cSTupMFJySGKVt/2dLhlL5sYAlDPNKXphaplDpSRoSBCiYJhUGK0mgppRw0DB3K5Jh4xJAPHMxtWltZjSPKt/EJgyPlS2lCHfjJgqIQhKGPGTz9QJFETQoNaYdE0uqTA8OJztAc8WC0vFpo8Hjk3UiQNTWn7sPLqB2cBJn2STZq0jQgRhjSoNFPwMLD0FEahiTIGQaKwKYrgx/klhuZtQb3DbPJsddPtPYCrD08G+vRYk8P9Gi3vLKtx6g8GnR3/ubqzMvE33z7rZdj11fWPBx8dLAH1pav33LYe/VD4oGvPaRiqEhcutYgmc5T/cEOsIpSF6WJX5acFUxQ5ClSd4zFTgXrFrAniSzDvcnvYamt+w/2Dny4Ys86d3R6ZjPZqz9e6l3e/mBFfPXq9YubG2vtw/tbxjyoTz771GPMVsp3798cHtVXrtDGw4euX92p3d/ZFcb21oO1fgPYVTYQd53t2rqcXiG1APcrYavzl+4xu8DVSq6DZ+/NucTUWR7gcgM47wFvrW+oiLeSLMDz53WkOCAcsIuLNVdY4A0Sm6B+OWthcdnpwpmfeO67jC7Q/UCio7DvgNbpxSB1cfF09/LYYdr/6marw8DxrOmsze4ue1LIiY+nrN1NdXW+f3L04vUbZxaeAfvk0099pNp1tu+V8QVWarjqDiGpeyQaCilKp+gR13cR6qNp4cS8HuDr/upBWh0HjVpJp0cZKEIpihADhzJwyrJ4VMK61DZlValzJmkdq02l0fSnO2rVtm3yI06GFSNVUDqufeO30h53Ks2TbKKrm79N9TjfLUqoPGNyoOF1d2qKN4omIXbFB58GBBmwWGnw0dQkowgDXHq7rRK/1QzmJLhubVm24omvgEgjgQME0aGA4RSRU5ClGcCk3nvnSGmOPo6oISb49JEstACGGTyQ8Am+TWsBJmeLZv6H/+Y/HxqKK7ReHjJRBjrVC/TaUn3QgCW1OmJ6fZW1BsMVlpRVKtyVEX/NIIlAKcN4TK0osyIBa9a2RVwRtE5ZZpTcqd8Xoy+SzLwJprzY6+l2B4JIqIFynpuLYIFRNg64huY94yCw4i4VUZStD0ISagLgEflRtdQRSADVhZwXEjwTfjUFEzxJYpNW9NPdgrRPqp9WnbTSnRkzDqcwgTBPNfkKWton4CSmPJjAI6FMQYRp3jilhoGpgvl5V8p0opaQGFJgxW9aJn596ZdCagEHsVVByqkjNeAk1FSKkA5eSi4Y+lKzsBQyIkFhEnBiY5IukxWbIn7Fo7PYAjcI/aI6hgIE0TJRRGeMT3ISRUgAlxe1VhGCuh1VstwBpwaTJN4TeQXaB4bBg2ByShMUBRI8/YwrvUMhDUUoeIBtV4bBESHlx2vnviyBc5PSdWW9LeMTH/07OXqHjieAXPfV9xb6yNe/XvW+uDzzrpMKu2UsznwjgjtPAFv2dIjLXGstQS8BJqY6pN1/s0Yvr65b+R4//chRatP4/e7O4cExF/2+0NasB4r7nUWrqmeoNJpvTtVd225eTyTZlc72vj1ktDa75KMj4jRK/fJQftHIjwPauLFh6+lpe4xuoNYl8tqawXBxti8mC61PS9pS9hTWxvKqoN3KObQu7+56adhzzpZeZ8f68cNiHbNCSvepkdZGGl/Dasnw6Szt/L/8uz++euV2+51HW7VRasvf216fPLnz9//q7xa9iFynRH1e4ydsfSLaaDmteTx9BEQfcRGJbEZOht9nn33mYelP/+7vyOtRPM1r2XGIOw3zXqnvH7jHXA921atKBeX27MXF6mU9xOoECCYCmNMsRa7m1Ys7A9shldLrfm+YyWR96deTNIAIHT0lTVqDubLnd3vtd7LRk3z23Ks9L5329UxVPyxRC54HwWvEzuQWT52rIXFWbXq6L/C7k6MD39dHl75+xlbYdKLfVai3WukgYd9Or06PSXrg1TGrBw1yBzsdPFKqvqoPkNAtASl9BB8ffApd5doqo6mjhUEhWyAYOCSJXDAZCYQJlQRfB1pL8Ey4oB98sHwFJMg8IkJF5MYqZYdteHJZlCCZZPjt7h0kZllEmQ5HvISSFQ+mQahUkNJgAlQEkJAkmqkanBrfMmoSG6pDIw7ikryAGzSNhSfU1kCR4OjHXBE+aorK7JYET+ggT2RRE0OGUX1RfRp6bBWVfSMkJF6QUkUofkm0ryppXwwhfFbRVClFoqVPqIhEGhDBp1coUwspCgKoct/9TahUygWreB8BMCeRMgxIXLDV31KGShE+RW6+YCKMBBqikFBjNYoIgSA6wZHyRR6cUS9CEr++QhlI1DCRMx/41FA8qhd+4MeWMkbrDXA6AAnDhJfFIEImKH6jE6E0MQiDPqKWwZOjV1SK0l94L5hS0HpSsaWbgCR45ngpzFBgCROGIgMMkUNgNfRjS05zal0dFFuaeISpKk3Hm6UXWrIAxWllsomadV0RoZQhHfyzZ7/zkwP1qwPvd9yC3Vjx1mudariC5JRavX8pBPNJvwFj49oTYT5UWS8bE1/XuNXDGqdWX1+h0Bd3a6vGCx+ekjm33dufInEz3nNIrk010Q9v3p6c+T3jRy58Nza3rXY+y+zJKnPl/MailRLZC15eWrI2Wyw9c2X5UTUv/OozLUAz5ygf7pVrK7FV1prtgph84fDAk9Iu8e9vbZ+enwE52j/w0LJGqCV1cdH3NBbuzu28f1+fq3ROsLjk01cvv/v+t7/9ra9cWTlU3OWmQ/60n7lNp6TRNEt6SkoSnjBt+x//wz+ozouX3+++uzg5r43Xjx5YgJ8smLk1oeURlkZzsl5fVPQKzeRKBRRSGMBqzx6BsjpRvf7whz9oJa9CeWXZC1SqfHZpD75vXviyR32b0w89mDWu+xTIZ0i9b+3ucg2PydUWzm5JL/BOqSoQrwKpgjmtBxEJXyRdx5qIeG/KiKpxWE/eW/OL6gApRMdZtcSt2aOOvB/HfGVo9kMLXAzYCqAJyGTQOifq6UIqEgo3zlRuHU2CMeARkNvmwazwpke3vsabxp2ckWf2DjifGCGRJ3WAJwDyQAHnS5YvOhSiPBRk8dQioTMocgpK1QFOlOMXj7ltTh+RiAFhQPFISBNPmJW4FUszvjBGKR2kaMSsFK80JBsoQmfjEUaSOZO58ZaaavYUJZ3cOVAmCCLFtKVZMNQNehBTzxmfne21lrNoUlCU+gSUBCBiqEOVkuPJb9eEhBwlygl+OyOMXyDkUpK0nXKuRUiB0BinoEhKgjIUZIVEM1CpXRQIUSKBTF9ls2YHKm1EmVpMAjJScmHAZEsYAkgORxYjZUsNphRPASVO6UTNey3TOlJDYFNfOojhgFIKQZYc3+WFQych4ZNVmqpBUxqig4lCkKmRkIPFUDZtRbmRKlGKaKZqYCngSehHGDVysKDiPeCjKJEzJw8gZVndFI/QSBRlPARNSsHwJXeoKwpCwgBOIWhgUdwlJQcYHfqIQjo3cjyKIxKlQRuGbCMUG55OdiaoIYAqZcGzBqcWFBATZGywuvPg8cmpjxKc+jkBX5sy6XlD1+Lq8rGugxcXXN2apn24yjxrrF/1ryR5kKiC1fj9GroLLK8z8ej6eMYzYz44MeOB3+rKyxsfAxL2rKeqvE+kByztvmDxzvu7XtE7O31w/9Hnn3/u5uuLVy/tu965rJeNbAu76pWuLq322rz74vvnnreykbu6uv7k4SMTaz1Ztbt3NndsqrUaqc36xsbsnLoeH70/tkJvbNUTW/aWbVp6jdgNn/29s5WF2fO5Ey/73ncveWXVcuu5J1/VcOvn+XfPfnj5Sovll4u6CSfnNxpcXVCaThsqlU3PpuMUyT5eW320+tVnD7e9KHx4sLe2svzx08feL67n0t0Qdm3qrWeXm3UNa8d2ckLMKUAIMIEDxEQoq6cMg5xznP37f3y1+eL1kyePP3q6ub01t1A/0ejAvvb4kj1tR9Bd19MuG+fO69y50BKn2I1Fml0FPelDK8zqiHDuYkxwkWpSSO0qrVUWgkPGYaURehBWmAp7ATMwpgd7rZ4sVLHO13o/up3RjoEHCWKlikoIO53MGLJ9x+Onc1oaWZgNVsnEdR9ZCZuwKkKn+8XAdiAY+YiC+dMRCh+vVTGl2VRX9E0wK4DpxJgDKpq6I1m2FKing0ZzjQEAJDhJmQ93XVIuEEPH4+AxiYcXfR3beMwErpRJApYGKmpcq5RpBwhfrMgTJCv8SCO0kJOEUprgBz4hF6kgzMnpQKqhgF7MEkeysSFBU/AeKAq6WQGlNG4Ih5oglZKnAqmM1CEdW65l8eqG8PESEKlYoWkCfIiJbDx6IDVtLatUGhypLDS2hKkwTb+CkiAjJEd0pDEUJ56LoI2wMUwQhj5laIiLxKaIidIYhpdNG2LSyOSsIKRNFDOUJR/R4iOhU/H1yhEoC56i+JKmmpgRcAzJMRXMZGarqGRpIoBphAj5RYRMHEv4hNrimjUSD2FsZRUltvgtR00DlmYkSSkgpQmPr0SYlI7SoUkNVaB95y86Ks4X3qHu4E8wFGLb8IWvLQl5SZFSQsqONM2OzxmDABQl+AGSLJ2gSUnUlEKISeJXNJWVL2jpF+HFSim57Kdf/NV33/zh/dt9l4A+wPRhpq6qHBMWNb3aaLVQuESqkGZrf0wA/S2H2kyFA0SPwa+PNpvWry6cJM16LGl5xQ//zCwseZBG6emle6XXa2vLjz/+ePvRI78jZGX99ptn79/tehjKyvr5Z7/wYNTO8Z7r9Tev3pwenfoss7uqTx499mCBy0qPB7uQtaZam9dXV0RnO2pn7/3JGZv6RaPt7QfrG75I5dayb2Qdv3/71sa056Z9QssHoq3Zik4Pjwy5+rXIJRe4d9+eX7x68cJ2tNVXV/mmlb5zzuG56Bw1biPfblU8UmutkY4LL9UXJFd7OyJ59PTpJxtr9kOc4yy5S+HTuWcn9Wkxd56v/aBCbRJYEMm9LmbcGV9ZEXqU6SInedqszpXxfBkdznvpv/3h1e47yYvt7x48efr0yccfbT+47+PXoP3clWfkObg6u7AUlyFru7oGbwVdfwVeT4KZJXyPo5bdejCMlMTQUStnT4xSy/JtsHmgrzbJNY8OF2qNzEIT9HRnW4vVQwn12d3L3hfH1hNZxg/o0izQMilJUbVhssYPIUeyrTI51gjRbH1CowkOAOFY32sdKHI2I5CKpRyUwJeucAx0n0ND05kxHFwkshXFNIZy5xADMT2g0oOElG/3rzBIYksHT4cwjirKKR/byAdOFIJQQbe7lBIi/MjGixQpCrJSTOv+qEwIyjwnJMoFMSWaBg85wivFRCcLU0IKpvZnlytsynhy1cfI1gLMElzyCtJhlEhQ6kONhKZSKWEZ97Vah1HuI2GCCY5UbJFQCEVfbw0XATc/6kgvnrMiYUWfI/p4EQZfqSxbJACf0sUoogZT/TEMbbJ185VEKQnD0uzhGEmqRgGTIMkxw6ksE5LEjB+xBRws89Qly6rhSB9RUCRsxFzVhpdRWrE5wZ4uBtC4iPdc85GIIci8KKKg1iihJjxqKSLEIy7wSPuFqZhayIQkE32EbGMuNWkMYZqUMkDxYIQqGAqCSTsPcAx5XEtBSWMi5ZQ+BSkejipg6GgEqWwYOrGCQNn1XnSKn570xFFggQRWSDQHvlL6QDAoarKRBIF+qiOLFJEgfBhoKNECiY4UTy7gdL1FJcJhGGVOD07OPv7sy/sPn77zmPHh0frK6trmkt/006ZuIZ6cHLtzV/gL1jtvQFVlTVm+AuIvnY62nuvNLzR5/Ks/L/lhZW1+aWX1/v2HLohtDNhFtj/s21Fraye17bzhSWav2Dx0xekhrF/+8pcWWssw2ji/7y6sq2QXfK9evHRh6pEoN6eXf/G5O3kuWF0KU6jr4/X1J48f3rn3wVtDFlcXuCpr8Vu2oby0sLMzZ7nd23nna9h+Zt3F9KIoV1Yd1dR8nWvnhzces/rtr35taVeNOv3xalEPHpOR4aeJKtsfyjQgZEebWwTow1GqSeuxIMtLLVXXy1riaP/y7MSTYya2D+eea75wqmJZ8Bi0Q7/e7a211yBzGXiXGyAYgyG9ViOgH6Mj16NXFzbEf5wBPKvl2sAX7394+eL582dbv7//V19//ennv1jb2KyhX0fHh2uf3LqpFybn7rl09jABoWOqXpsVqV3p6v16c7wqZZ9CRVyW06l+tMNEs8mCx7JU6updRc1Czs3qMBlUc1Ytw/2PtHKlWu3WI78Na+iWsJ+lL6YEkzlNxXmTlWqcCqZnyB7OddlD3iY1qjFRpibLhcGZ0hTVK3a9nOh9OKY1OpRRuWynCQwO8j3ymKcUJkApUiqVRUwodDrZEmellCQU5AgZEuKlwcJQTimG8gAnxEvDjDjp8Duqr28ZImrxlZREETXyeIGmKARNFqUUYHYCtEyIOStEh0nACWWlJDVWgkVErxqjw4oSIQp6SqUBooBXFEqWLeHgMbqbwgBJhX/iIgoiVh/mQWBCYo6TJkJohGy1CJowcxUPYguHTtRuN41SOOS89454RRgTcgskQw3HEQaxVVpAPT4SklJZpS2uj31Tw8evgSgeWZcXGMRKtCRhSPANX/iKpMinJSuq6RM9GGp8ITr0peGlonLRo+7RJwkgeZTjQpY8qamHEFEYlGwU8JQBxpcb6GCDHIWU4lUhrkkwUkKahd4UhHhRhCFOjaQkskMOjW0agaEiWaXkGgRleTu+mJyQQcvRTs3iQYFVwo45vl1X3fEUZAEOtfhKSCnCc5eQwLb5ZLTjAxt9aBgI1OIUnwgDQojwaBjiz86v61cKlla3Hs74oQOjzfhanF+01WyQ9ei+cmFOx06k3hZPhVH7qPVgtLRq6iajR7c8Vu0t9rvzLoF7X/Tu7sHh0saWf+vbDww8y7C75HV5enruUtUDnF99vbZ1f9tPI1hBvQhk0tx69MAiilzvWhqdFrgidyuX5OH9Bx5+tpBT9pTUyfGxpWjz/oYfHJvbu2d1/vb7b9+9e+P+6EM72ttbPjW1e+fDwf7hs4N9LzX19vXq4637L168+PaP31rjUd1UPaufE7acay6kcq7ncspSNdVY02NKc+kLKXHaoQsnRxyecP763LX76U09tEgToNRXqec8izUOlnpnzCa93q0ZOl2ToZte4wVDnm69PQB8/sNPa9TzTGc+zHnse5Z+5Pg3v/61q2EvLH30yadOZeZW6oIvK+uNS+0mtwlcopLnXr6B74ktLqy8vgzKoQPR9Gppr9iampmMmbr1Uwv45EBWhBxATPzpf1lqfdLFYLDFXsc+/LaYjFUSwG0oKWo/dWirqTD7Q5Ol0KO9mhqf+MNLZTUIBa09KHLKDjKlmt0WSGClzqi0J52Kp8GloRrGUxcYCjAFEzkT2WqlPk7jLiBRFkzMaaIhpImXCrTqNZ2FokwSZSk+VPZNdKImhaCUd06R8i6smS1yJ2nkUeNFxVPkQiuwhBiGKoU8ixk5tbiTQshwpRz9lNKsSwQuWUYvFSNkM6IcRaV2py5WFNEJKc10zATJpg5J6XATPkV0ZEfNU0pNF0otSCQYgUYiy9Dki2HFO54EtbsaQDSlihAm5pQFhiyxhKhc1xMvP8ZDB04kUoaxFSFlRBZHkIdyGjFO8dRYySJrQ/zSb4C6wxTXspQHPlixcYRBSvGsKAhYT+MpKLp9tQoKwcmFdaySpRlAOEh2MHhWkBE+Vo1UTYpIko1ODMkxUrBcpEbqSEifXJDkeBR3w0vQCAGGl1JmRQIkJhDI8SQYyEzQMBkKrBKPomBKE0BMpOIUh1SoslGDieFCM6YWiSFCEow0DDWlUs0rBZJekIqQu9gGPO2Ap4mGo2TJhTo7v/T23a6u8Ebs9qOl/feeiD6qacfVUz+XZ0tZwxhlAqiqNY6j3nTryHRxZTPThxW96WQy9kbv+sb9mbkF93f9ZtHuu52lizsPH875zaGPN33a+dTyuWu/u8m9262NtQcuhB8+dCPWAmxp9IC1ldIq4rOUutFnp9TUdyIttzaNrLgucI/2l+qSeuf9zts3j+9+bK7xFWdx+a7G6dnJu7dvNIQ1e9kzx1ub7m1TPt7f880Ft4sP7i588803fhXYKq6tPIp1t99UtsxrZy1iWTIZKdKYdR2s1bqD+u9k4sNnPGhDfNK0qpMvLwm7EPWrGVY0q6xGq4vMixqWpooMj+Kr6Uj6hIa0h5l+VCQSlC4DTiieHgLXfupKYF7mdjysLy/5qonPl9jNd0H86MlTX820EvvFJ1f8ajHv/v3cZJjVW7o9U9U62ZhS3arOBiR8AXDtKrjj7IAq8v4Hpy6Ri6KWtPL3lqLq9rJQEZkkjL0BHoYJoXpFIbXD1+hqUkqosnKYgNTRaXOhxh5V6pPdvuL0lx0IHmrFd2DU4VCP6PezkHDijsfUDiYCnpGcLGsELDFI07NShooiiRCmViUp793veGoAtSE++qN0IAdKFsWEPrXYAscLEn5sUxRH0gQTHenAwRuiOe8HpeKGhtIBxRYf7xhVFiorJBscPAVpAguvKMHUdB84+TQfiYAIY5koA0fBAkaTfQ3Tnn9lbzujj+JbGsdDCByJMidQSukwR+kwRST0o4nXlIrMAqLCaI50RnDmzE3TxTsgkUsbtRKY2i6Vcm4Lc1DqIquhOU2V2ZLguXMaIJUNWsBBCYMCZFYU8ITIkRlbaWqtaBBJTKCpBdrf3SOBoIiQJpDcMOACKc2WnVJZPAk1NRIMBI4w5ECQooQ66ab+fdOElOApyMYXp+ExSmMrjZwkpaBEBZxcp1PgN1khYaDFdVxIxRNzacBTRF82EuAYhtDSCHiUAKQUMrrY9nC7dHySSEkQc2pMCBHGNxeDABAJOy5EiGeSgBXhh1ARCc1UhF/xiyqYhCQUDJLcYpBFafzEEMBErggT/ujk3G8J4P1UkL0LP3bvW8QHO+8Xffpw8a6bLnZQ3b+0EXp9XsPA9yMSML7uHvo2giDuLdy9vDm9uPywfzgzt7Sx7abkhmsvY+jyzj1r6u7+gcc1lxbm7TyriznS27sXvtLcvybpetXzRGIQ/PsebwZPLnn9zNGLF9/78SP3Uyl75nxjdc3KrQouea3j33zzh4cPH7tPXD/iu7RMeHRw/PL5c6ecq57N8rrwowVXjbue8T442n+/++rb58BRrQ39bWHtnKbQXFrSlaKupECYnlLfdCWmmrWJgr90JvlePPC+UGm7yptR+sKhDNOdK0quPErftWuvG3U1aWwYIaa/fhzalq03uOpG6lyd0fglJ2EA0fCiQmxL83LG2YGeEozhsjg/s7m+6gnrQ2co+3u/3N357a9/oyn83NOXX37pVMa3HXVS9T5P3e0GZd357ZNyy2p1Y0+YGWNL06HLpKxydNx68jFtNdLZm3tVBc8JAKoRMaZ1H8qo2880o5zm4kVdKFaNeurngReVrUrWzeTJA7O0CC6Mnm6jBCOlCaQPMb8pUgeJftTKmVYMEZt/kA0SUOlHvJaEJga26XFZVld5XqwjUTRKEzMdIJqaUxK0tDh56jhZaUKiCRY+/VGESa0hoFEUNfoo1SFB9KklxUDGB59m4o/aQI5OgozQBKJxNEJDTpYqaKpGomg4Iol3TDVg+8KnZaiBrfeAa+qanhgCUoxItLVmhWhRyWMvsks+QDBt6BFcXEZOmErypHvMiiSqR2cokOBTnwpiulbhx2tICZ2EaxOHYJiIShr8mNslSsW4UNrjpmZ/LvCpNgUmghG/b77jKQcEPkApfRR5hKmUkSMAEgEoFUmNqp6v4UPuOs6Z/uhnFKZUVjxSWXVxbYGHg7hG0Jjn930V4X+SxpwaOZ4h3qwrhUlfAGJTKgYEkzDjgzKnSHtGWTVp0gmaylIGRYcwjYA5Oj6AwJ1ShvGuFK/i5DFhDoecWphEC83Q1A4UEh4rsKwQhlxKyAsmYbNFFJRKB6ZaXF1Us5MTckctoaY7CEdUOh09uP+EX2qKAsVWVOYIJhSY60TI4nQWmOYiFLOLNsqaVG8yB0KNRJAQEgB3hCmKCwqIAhASrQGTmhbj0Y8OqaZJwyM+vcd8teit2YV7Pzz/nnubyxtrSw4A66WfcGDlvYfTY8ddvVXvQtUyWcNvZtZXFK1xtpfvzS95x/f+w8ceDfem6+v9Y68Tm5M89mRf2KNe9WLS8cn7t689rezXr825Pj3h6tbR4OJsZ/fQIqqyW9sbjx48VBd7135K0APShpUqUHYDeHmlHnOj9ruXfzREXS9/8vQTDevhKb/mfbhXv7zozvFHT58+3H6oGX/zq1/94z/+I5DZm3o+VgtrCu3mVCDDw4YtX8gCrF+0SeTWPUI8fR5TpBSCJsVoE1FpTGgUNpfqiWXvPil1YlKjqF6Qq8EG2VvTSm0Ck+slaBbZdlsukFalqVTXpNfoZ5xEzXkDgR0J8ZCI0lElWx3aL1x4/ddOvqX8b/76X/z93//9x3/7N2DLkS8IuVDswxNvhSdU6/59pPJuDVWdO7522aSwshOqy3GRqJSUnL5aE1odMcImoU4iEh+ujh3FgDRkr/89AunSp9NeJhNyxdMrfZBNihSs4tohjaAco9O7bWvwx53DgVO97ITs4qw+pIN4pA8BGurwJj2b+EnQZf9eODVCjlCF0USIYg4QT8e5TgaPw5OyUnJdrwXSCITBhyFOzST7E2JCWYoSBuXy3VfSul41DYPq025zpdwZFYQi6eiqR3i3T0VnqAEkR2DFya/mknInSE3klRqwoNiS8wgtjDRQzOmAkp35n//Nf9WBVa0UMCv4phhTdUQlMjo3fU9OefHTuVI2bQQUg1JKgWl4EVOT0kGxxRC2YNJS2YImEQnCJLxk0weEMKXQPM+C1xPU6IhTVgBgg1yVnK79nNavhU4pOklZpb4KI0moFiNWcUchaBREopUpk2iinA/qDMrRjw6QSDBAgnMbv7+wOqk7nRBYvvAYJnxxQaJeXkRJs4BNqBRUv54c6TYBTiHCiq0/0UCSLg+srLGSCIFHGThMqwTJQFAUQJMOBFUW1ahg1IRBiKcJXzCIRHZUgQ4FyIoSAzSlIuRCUSqoKJUiUarIqsEdNUWYEHnMuQiRpOje3JIi5jEZAchGotR4pgAwAzU6UeCdAqKAFFETM3BZ8VMjjFPK5BTinZAEMY+mo9qusasyJsAsEHjQfmbAe6s2eN229YsBnndynmQVrAnu3nz9CIFOUeObOn+ysno1iHe/nWABPjo+s4/pCtjDyj4PeXHnrq5x6qC1NnqhrQ8xmmhm+zdZ/R66Hzg6P/HKk7XcmfTZ6UW52d9PHxlNRo6LZ9eke/apd3dViD/Kpl1h7F8cvulfULBzvL25ZTvbc7y73i16+07N+8uFd7jwtBfMaofLH09cuNDZ1Y42nKc7SdYhjaaVCLXYwvS9/7SkyDFweHe2BEAMNAnx0tWlmlip2dGqtr5TW3HW4/W1TW9xdUdU+/toBnD6N+eTLxwpCqXv0rNwEDkgckLHi1HhQCavXrtXGzxWs3o2opdh065rXrEpxS89euBq+Ouv/8YM4EuZ55cXNY8vLvtpqdqhmNPT8xhoYH3nZL6ngQqsXmGtdghNgqtn7SYzW+I5uegrVzNh3SGuj5KrnArmjSMLMGHvtE+nNcHV+KxDcoo8wRRDFmBFXVo+f3ILeRKnNr2s3SaO0lygVNnSJfwExlb8UlAkFcZUEr/tZMYZ0TQM5ZODlKHWIGeY/qWcUqdQJIpEIk2pIt4FYyQEjSEQQbJXShjzkWbMpIW7sqWA8I5KR7FuAkgBT44ZtZBNYLzbIFFUTTetLASlaR98xdD7snS0jzqxQoTlr2NLRdK23AU82ck5PnRK4BAboCDUQZRSEtrJen9xNEF8JBvb8ENhFKU5gFBjhYbmEAbBYcy1phm2GPqJMMKqVjdlTH7Cy9I3bSkFri4kGUlALs/ryEEVRFOyad/gRx6eobUKjuEoMOOGpgOPJHOxLB7xgkcJGEiQWWG0gEiYU6OQIgx5+JES0glBI088Ey+9VUPCO0mK6MgyRIQJMiE5wOgkBpgJj75SJiSKWCU2cmM8alWTJtkoJBIBl5vpiGcehViRR4FT/BSjajEUBmw6RRFiRc4kvKwI0WWfp0dYek3xGJ5VKpKmkFVKkhN5OqPrKYCVKkV8xUTdk9WtCR6INmSbKggDTxnyECbaUanRwkwQOaKsd/VAC7SAXU4VvJk1l99cWeU8V3XsNxwOjhfnfYFjafv+4qFfLvJex5y9wXPvuR6dmQAO7BLWI07rm8urGz7N8+bde1ex1jZhr27cX1ladFp5egZp9/jowOnF8uK830a3hvkRBTGcvT6zg2rre21mw2fGth3VS0vv3fh98+by6tz17uzsA/jO3bne36+fF7x8/2bjasPavLm2du/J3N7inh828i3JmeubJ4+euko+Pz757o/fPXv2zJWpZ6B4cYnnAxhqlB5xGSW8kiO/9Nc/KpC26XSSjAYfQu0GQWuTYNL4+EjqMlORXeSeFTWkC18NXe9y6a7uJu4wRq2hIOG/U2g1olxIc6GVpOTAeoCXtxa4KKyfVDKLVOS2pcHfmdVBtWDefLAH0Ctrfant/dHB+tzM//1/7vuppc+/+OJv//Zv3SE+Ojl97X1rJ/pXPkht//faOlzxu4Cug6C6vuK4Paf3t695UzXx+N8xV41q4a37sPWQAFv3nO/42ohsPSFQqP6rxrQKtb3AXJwBqSr0N7TSpFAqgiat4a8ObZ3yjeHSDEBJY1l+TXoMcyjVRFpvJUyeFmbLtdKkbAObtKCaKIRPmgOQDswYph3w3STXy0urGAr02VosVcQhHLSkigaR4Ic83hlyhMcEajQpRhE5iiO2dKTJRkFKYgCnYWUjGX61BoTYxlyRSaCvL2q1HrCxdcxRC580gdXTaCwzSSnAJw5RgkOEsAZRYBljfIdY2dhiGBrc9OGIEkMt5reRI6cvVgqs4oiOYGQh9wlFzUfOLg13ykHAxJyJr94kywTFEUCXBbIYJlykvaRbG+uEKAFjYkIHTqCkowVNxCIBQl9rCIYJJlUbVrLkaY0gA2FFmDAMZY7oR5hS2UxeqU4UBiZbFE0gYPWiKwm+CPki0VaQqWmr+MVDCCAJBgWE66wrdEBp0hwGSsMU/lVt2XFHiBIwX+mUuCBESoMsBVhupkeRUlCE9FFwCFN3aRqKF2oUGEoHSBj6amqyko2kPUxOWRIAKEwo8SzMrwSKi3QKOUc0azRPL/eZUEurJrxYSYOmQSJRiuIaiHbAR5g0RZSjllDxmDRaq01Gl+uTuuXmvv7JybbvYGwuM/eU8snx+f3tTTdrnTgK+9Ku8s2M5db9YZEcv9s5ObuwRnoX1xNVJvT373ftYL88OVnzYHNf264u1S8Auhj1i4HHfaPk/n0eNhTCc15r19Y7wZZl930JxWa/1FPKjhR71hdXlxsbax9/+vH9h/dfv35lga+vJe/vc2rMP334aHVx6dWLH/Z3D7w5ag/3jUXm7Vuf0KoFbn3dFbZqcjS/WF+rsPoCJHGfsS/S6naJrO+NOCrSYknrWTNjyYjVYrZY3Uet5/aL8a9/WcGrhjXpX9ePHXtIrT7q6N6qF3H1vVqYHtzeYa83YUKrZXN61OfGhiIIzOOIr/zjSW/om4qhyQce03E2I+ti3TPMtSXtC2TexKtpzZJgc1R1vDy9vrpW3eMHl23j7+3uvX3zxVdfuUHgJ5bsVDPz0x1XZ36CqN5JspjW0BFpexTopCmEoI08uS1ALqsWk49vWFpF7tAXUg8vW9w1n6C66qVcH/FQGUz/7erjUtcMYDzzQaXX9XU4qrVfYhbPoBRJs/9BbszXeOwtgWQDhac20jAkIdlQd0dZkI8YFGlARSj64fmig5c6VONaVn11NAlDQunEjTm2T/IioakUYaJMDirtgEd4RRQg0CTBIxWMU6ViIydBfqbzJwiF0o9TiIphshiA+OqaRk4YbEmQ+VkqS4dyXFel5BNfzBKECJQFOgp0RsUwcaYoVkpRjdQOiKdkVcAKHscjxATBkM5PXNBxwJPT4UVKgkQvpGFIgqcG+cwPTXe1NZws2JCVJuA0yVPEJB1DGLXUBR9wJoOJglWKFY8YMbgmgKCmwangOpgoSxM8HHyKwjPnK/gpkoVjNhwe6ROiMFxAo+MAIOTdcnV1Vo0vy4oCwlOIXykX4VUZY5aiD4SaFKWUIUY2DUVHFo2Y8YmcDtuslAk1KROUh12DRp8mAmL8KA0a/ZhQQMm29eTgp6YKFdz06b+hZvanCZMCwneY9Vg/KyQbXyqCIJCoexBiG3NVKPfTSYqasGUHM4pEmPrCwQOJrzK+dfCTy47q0Ek2OpMwTOKmyq5oQbkIqt/3uWMP2ds0J6dnS/cWnzz91GevHZunFzfbK5sz5yfe3ZvzXq1fw104u3t8dHrHG0x7qm8Xc31zw/c0DJudvfow5Ns3r66vPEt8bcbsD0LdsWru7+5qE6HXd6eXl3why5bs8fGJXzm4uLy5WLpa8QWs9bWllSVfmXj39rVvUb58/UPdLp2tX1Z/+PiRinsG+ujk8I4PP8zM+Dqj+9F4z1E/+/aZSL7/7pmL2ocPHmsaK9LuyWF9E2Np5eSy7sJ4gbdWh64vxkWqaqO0mJaBmbbSX1Uwbbo0uFKYiujj0WBc8jr0dYLec2RnPxagrq+b7NUjtPWxl6l9kPJiod+qMADijibCJ6XfJpOjtXgPV9fwKRK5BcrD5y5inZGQWOwzMdpyqItjF8T9zXl4e2/evH7x/Nm33/zLf/n3X3z15b2lRYvuvB7wMpIt6HpQ+9I9e8938Y5USgyGNl4qKM5tEQvbJzb62K1QncEYMv5W2xn8edDrzod7vgfuqyx1IZwvVtcIozBtyWLKvpr6xzZsjElCoZqlTkVKOVJRddVnDQO9bAKXjtbjYopfnTJowCaGkQ6GAmVZFMZFGtj0/ihSmnmyRm8TQ0IHY5iY4CmoGpVqtSnBIYyv6FMYQpGjUZcoVANNJz0SvDmBVUqlCEIYfiCEN//EbYJv7CryRf/hJZpJ1ctUBpy+VpXG0eQCl42GlqoY0voCRTG+7cNDWOQ0FZFjEEbQGMIWVAIQqRT9NIS06zupsz+pUsxlWeHFihGuRz8ITfHO61Ph4Mc1TaWZQyELWzYxY+hL4cS7/taLTI4O9m8HGX0SVQ6gkDCILbkDWySgElUAtSDAKNAJySI4spjRPXgSjoAgAUchvJSvKJMPnt8UMTdMKYw60klHkii1Q24i/uijj/ChVAEaxhU2cwQtEjqCkZKMkQ1Tac1iTYoQlhzRB0WBVSSKKBAyIZFNR0jp0CSJX9mUxoQ+HbYJJpg0MdLgDxPI1vROJ96jQEI5faffIZMEKqnAELmUCWU1lVXaJYUWdxknEYoqvjAJMjFT5iseoxk1aWhgDoYJW2Q0abKMhlKur0SYNDmYPT24dN2zsLW0sr4sVt9Svrz68MZjVq6XFhYp2EbXwSs+lLG2ZgfYIv38+ffrBweWw9W1jSeP5jfX17777ruj3d2zw0M7yeSPHmzaQPTyrQ62EAvbgr1Wz1X5ISNtf+HlJXeRTi/OXQk7vgwbF757+9svn7/Yc7/45FD2vt8Qfrg1O3/Xqn+1V9+s8klna8m7N++84OtOsXHq0F68Z2Zc7A3QGgk6T6/4ZcZqhH5DSCPUhVr/s6CmcbStZtES9Qivi8DJOdvkhFIpoumcW8fh0014Qp1iTqqrwNrULjXrkxe0nJkUZn3PwjjgvL4s5stVnijXvxqhJ6Lq+vLb+Ekrwh4SI3VnkJpR44mvPhx7G2NRP24zsSSJpKbIvn1oTlilf3XjqWyPYi8sLs1cXv3+17/6w+9+8+Sjj3wu27NyzmaWF9cdIW5XXjhcnIv1h0EMBAeBKpbrilpDVi0dZHjdV8VmsKql8vrcqL+lXMPZDNCX03X1XAUTqvmjFAukCSLs1BpfpwzTQyAmOQOIf6aOAMeTdiZRWbd9tV6bTz3U72UXBTPNiCcJMh4jDf2knScofVRCjiadDAmldY4ynUxSCjljgBo+8QCXRZyxojlCEvzIKkoYJBEO8yDoRwzhZOdpurlIKAyDx5Y7w7jAkCfrUIqQBOERBiCFeBHeiEpRRduahHQQpqZLljLi5tI8heipc2NWEtUwipggQjyCy5AEQ8gwwdG3dKWD8XQQfTriu20eBEXUHHhxLR5MomocFj8SzfLdj31Dk1VGHw8NOeCl5B1sdWpMCEmGPIijSDawmKEJUxhWXEKwzElyYMc18+BIUzqqoCilEACmv+nwEomHsPAJNa7xcFLxhF0N1y2sYe3HUaDJddzBp0wCNhNNACmQeIoHg1gFE0/OSqvShAkn1anTtKW6TAxycGKlRoRsCQWTooBQQCQUUMLjItmg4ePXuYtGgEBetWomVcYP2wRM4qlLKXAuAoWBoCNgkqTWFPA1+m8KmXkiAYhH6b5EFS+Emgtal0+eFVJEJwQBAxkNSZyS0OQIM1I6SqMQQ0UubMTotmKr6TkfI6ol4ujkzAWu92Q9W3twdHZ9cT3n4sjT0e93fV15dXmxL5+u7/qNec/+3K17wHs79ZDUu3dvhf3gwblV2Rd4nz66/7Z3nt/d1C/gbm7dX11emnn40HF0en5J3w1dDxDZidYCNmttgOtxrWd5hmNx1xtmn+un166D93Z3zLlKvfjr3saDR48u+uJ7b2fvh5c/PH/2/Q8/vDES1N33s1wdHR3tWAIMHl/WVGWA7lF6SivNKJvWkLUMW3iqKZusvml2s32Y0vlTIkET2N78r5Hj+1d1OV3ANWB8+8J+s5M801dtxdb66y7qvAeynMfcuWccjH6Jax3BOOM5fGH1NTHGBSueifjM/AY7XhibW+ueX9Oq9aR1/+IQoSPofP9geXVle33NvSENa4vi2DbMHTtDhwtLfhTy9cN3jx89fmrPf2ll2adLvEYLHzGP33r3qS5DaxLrBSVLrmXYLfUrmb6HW4cAtratHYJ+C8vxmP3nKu6ayVYzT3YBR63VRvEkO7kj/uO4VSQSxHviaUc1DxsG6qMokmhqGFCCoKz9UVVmEkEdC+TRb3FNTSS3Kcq3xwYJzJDVByZ9rtUxgJRhgpIiIVGIPmeDj8eqTMc8UejOjU5cw6fQ7Vho8Z4iclaUZfHGm7UNH3NpvJOYx4ZJAk5WzAXak2T0gwaKAnBpeHIx1L3MeKrjsy/1SKGTw0XDjJosMyh0pCRKI3cdpu2Uajg9R+iwRLwkggYrc8gorUkt4QYKGrlIZLkwR9AH4rKSBD+ImmpIfZ5OJKotRVWlPpPA84hPhLyoFDVPrODhBDB+SaiFFA0GD4chNTEwz7RVHdNdJY1tAsPTSQUjrwgbJC0JGaAmSpxKKQMJTSLo0awvUhEpKASZYf0m2vQBpYDYFTcXQ6CT4EdTA6SDyCmMDgIFVi0EIwBqGplVgqFPHpMRWGoROf0hT73aSa1nGGGMUgwFKXOl/BobWjJCcmFEh0JAuEA0yVMUHULIdHjHZxDjGVJWRE0F/XhBQpWSJDw4dNgyjBq5bEJKd2Q4wYGpiAkEPEkoPGGyFDCEoQhjwgsEEowxWFc3A0fTtar7uJ6EdqXjJq99Rb8i5FSJvgPP/qvLw+UFTyjPe9/ksn6Vsd4G1NFCtduxu7uDMaeT+HIGX1rEyZMbunivAt+/X88we2TaxqkRawBbhn15w6AyVOiovs9Ouol7cLjvyxs6wd3i7oqZnffeCn5j18nltFV/88GyLzn//ne/s5arXS3VDsyd3XzxR1XqXd9Tr0fXG5Dwry+PHXVVd7Nn94Xaa6uMvV4ee6DWDnEdKfPLNTFBvk3aAVq30+S0kmQKUl1pfhKGS3CjeObeYr521e95VRffs2tca3HdTvZGF00UNF7iTpuEGV0DHw9c42TkTIdHHSP6wLY3OYJGQs2Y8UPHdo29lOW8StaZk2tcre1tjvOzUxv1Pje29eC5j4B+9PHHPrPtFx1EMh08FZTzMVHBJDSmwFpn+wSgDlskqnz9ytDT0WWS54P6CaxOMhTrBkc9a19opdbWhuuPzVvnJz0Uk9IZlQ2m6ocMMJRmV1QBtWEWPjokYmaeePQXBR7jVxpyMkZIGVEYpBnx03aoZk9rO43SjJQ1uNSISlYpwKEPU3isVICaSIJPQUhSVqm+ojiVxZBzHXMmiAIoKXy2Mac5SoMjS4inhqGG5wiaNOaKsliQKI1+zBOPgGUdC6zwlGf++//6P1NJax4p+3iNe8cqbQcwdLwmZlPnnx0BHTTcpPkoQKAQHaWjIShHLjgMtFSVPqth6OYNE0URClRslPUHPsqyhKIyGS0t1qcq0PAb16qTViDnmi1SZCsxymKjgKoa3dw8ck2nDrY2USlNJZjYMgma0kwomLhTlCo4NrPAaFyO0qqKOBI2/FSBoSqgNC98mtw5j6GA1ykYsPDZxjXA3DNO0414opC6AOGabVXYU2NLk4etKPOeZucdvtazvc9K54qZAltjUYpnyzWoHIfpFLBKyUVOUmp9441QHUUlckFqQCsDZcL4VQTHabXfqMcQioQLDDRQ+ICI7Se1AyjIgRzvQALOELFKc135VnKvtYTqyEsaBzgcalEevrz2yR1iTgE4Ryho9EWIFIElXFvdIgwUNZGDsvhpEAxwHlVTtyq1gJkTKcc7nPiS0hk8pzARBWNf62l207tF1JpGqku9Jeyb9yc+/HiwY1fAK0z2L3/x+aebG9scCc3q+/rteyAPHz/2oJbf53W7VBe/230HUHj2qD01NL9YB7KKWEQtwD4v4STAGcDHTz/SUA4GnwQxCE+989R3YX/9//x7tRO/aJWn4vgw1TQ90ZAIQ/XzEU01wvOi0fA8iiTNRV/fMaeg9bxBhKjRQUpHW8myHaOFeWCl9IU3Gpz3aILF8BsrLkbMeIDaR9siConZIMlIJgHoC1/igUAfGh6C1os+Hj65LBKGfWaaI2yYKBFS5k4pCWXx+4LHF//qP3Ro1La8iXhxwRrrF6vcifV64aXregOBmXb2vmefya/fW4MGpH8Iq569uvRwV+/AmXvq+TFH0AcrdB2tTkFOrs8wiGtUxU23eYLoSJfu1UyrvpymIkJNEw1DaviJ2lzd0qIfF2Equj7wZTlKkSCRiUXKJE55qbD6tQspzaptC1u9jlCaYnCAsNJ0wKN2O42tlEJ6E4/YQiPERDLSRCW+4NyWMyHkTgyYmBsMyCMU5Jg0kVIMNWMpQuFlXAnYmPSa2BhmXBha9MkZ4knighUeQn1BIhVWQCOUaBIWBRGQC4vEB+dG3TCIA6kmS+jxQUIf8UGClAZQkeyoUhfWMFVK/+ToMMrDI0MukFLdHEBZcgePvhM5inc6imSp4UNxoRZcezGSJnfwE09b1/qNoa8IYShgrGaK2A58QoaEgU20UkKpycpBK86A84jIpUyGFca4kY4Ix6A3ZLV5lsZgUmMuACGBQiRIwKnUiA1DLkXUpIaFpqAGCgk+FXdbnTA1ZSJmLgDGimECYxKnaRya5b6R8cism6mQGpM0lBU9hsZiMGW1CVgTsZScPu9K+UVAgow3llpW7cYw8jFgSJRCYC4A2UhAocAyEQw5iaqJKuOcYdCkwpDWmJse5NAoBE0p2+Cn0QQgsDRa2oQOBWkiwdORhaATMbIn5/XpD8QkyFwA0RoYJoicMhLP7rv3ftze3Vkdzp01YWW5fuvez98q9ViQPnQZaov14MB3JPdsOdr+1RqrG+tuj5oE9KwV9P72Qz8XiFxFezpa80oNqvuPHTB1fQnEKLcMW7nd63UN9+TRI8uwl339+sIfd/eeffedS+Gzw3oHT/zqKACUsEnCkIhcFTDqYq6STYtRiI52cKgyUUQiRaU8vWekNZhEGSM8CvQpRBMCfQqK+IqhouFXKRqS+AqU+JEi5iG8ohCJZq6K9Vm144Uyc6VSmOS88Nsqkyleb6Y0gIowUQCO1IitsCMUMN6GxA//9t/66WXf0/YTUoWQiau/k+pky89TWl6d+9C3R+JB6w+nk/eE7tb3wn33T2Q1/ilANmLKWXx0+6dBRjCl061keplqVXW4liIf3VQX0RZvuPoW2tERZUIgmkIaBCZl5ddR+gCUpoJSlB6hz4ui0uxRnVIgSFFSjOMxRVJWzHNwaWe2vDvpUYRP/ZTGVnaAwKEjFT9N8gSMx6BExSSY+tSRNsKLeXTYqj4Tyul6aphRSo6Y0ETi4RqT+IMpDMdj1EgApgoZPIkqgCpYwXDBZvgICnu4tGPsyBEWCTUK8Zo4widVCpSVIvpSOHwoxTAclPiiQw3RQVzgxRWFxBchcBVWDUISPPM0+uQksEcJ7xRGdWJLyDX81EJ1Eg85JnIm+juYhJETakE8OTUMQFAdct1Iw5Rq104RNSQAKUOtQZmcI5FbBoAgQjoY5tTwKoI3afJIOX2DVxR3bTdZqoMQd3RSxJwhYoJnlajw6kvIUXQYslIq/uEaiAlaSifBYEKgUhFWeOZSmhiYauq3XaWy6X2HLlj7mZYB8SQSthRk+fUiCkaDKCIXRjCBpOKpUQKODjlhwgbOPCYiDL6UJIbS1F1KiDCsoik76oVR5ApYUYga89F9lGW5y0jDMHGVghFSShODbAKmj5E1vwQndY/TpDE03mgiJuQwE3DGJyuVo+nUyd6vz2P4QqT3e+uBWI/kzty4F+qy2K8Hvnm/s9xfqlpdWX/8ePng4PCtl412dyH41di6FPYpru1t3eHUR+qXD6/W1y3MukDR5bJf9KsvZPm6kjePrbhuM1qqfTYaT9+1mGYRFf2KZzqnCDhVG82rFqqcOqqUUikJq1QwPCEiCWMAaHwuqBk8dLQ2X3EkC58EpX3SCzEh0dRSUN1iNR7gsEKJBNRoW2qRkwyiH1sxEObLdOEhYJgwVBRkPDlHJFznAyMRxiOepv5NC6RINdWO5MPSyq8OD304bPvBg//gb//F46dPbFZbdJfWfHf6yhezbZl4ext+jm3PXOlzMbhA88iZfndQeRha+9Tg7fvDdbRXI9eAr4+ITwe5eJQkHcIhwYRXEdUUpwgtwEJNzNIKuA95mqmvuo3qCzKawaEpi9IL0R9+0zgjq0b4ZGmmFMNcMAifziLBZPgNkBhK03fxGE2GzNVFNmpVz7F29sCTZYLoQFBlEgxHhKXdBKceJ5z2dfTFwEr7A6cVXhF5TQv9pjVeGACRIoNBPJQBZsTi6ZQkB4ADTEHqzyYVtmYQGvpUTdCEsragUyuOByUUamG4wUDjQCqCQXSiFhA8HaWg+JWubm5wlFJFmHiBg6ej5lKGFYylxUcKpkMkygGkkIowh68IKbI2kCNyEmpAgEOjhiFBiUHj5FMGlAPLhDCG0SQPFBOwHiLN1aRSRTThm45jRZMLNEIizxwhAAiKpDYwKSQMKZB4Ufe8hzCcUkNgRzCKSEaEeJiJUMpdNPV4wkjYImcSwyjDURQhnrJUFgOBfjqCsgqGKKgFgkNBFmHohMdoCqWywA1KKcBgEsKXJssLvqrc+gFUJEuY0tRFSg6cjnIg4ROteISHHwQhOAXV4THEIzpCQkx4H/VKVI6FuzN1rUaTjpScd1YQyMPLwo9QO9MUsFExAJXiEf3yemvg0QfVh2vVlI7d0joS7866J+wegkd+fPJOh3vnR9X2do/29w4vzq8+PJzxpJVnnu1SipNJLnnzKvDTR4890Pn26u0Pz1+crB/6DUFXV9QWZu/5IOX68or3rV0N//rb73549cq6aydZ6eb6hmezMUgkBk+6skOuRB3J01bVau7LzteeR6qAoZBSTBXngq+rr+7QFu7UlWWg6JBETYsFXB0dINLoE2KkiYF3+gITIYks16P3FdEUgAaPuSJM2v82ID7KQU5R0sgZKsKH4SgBeCgSr0hKf+gIAz8kDNWIztn5hbMfQfiV6Bcvv3/46JF3lj7/6kvfXrl7ZS4qVNe+6vChPnh9tji3ZDu6WuVygn937splFmSnTf1rFDVROG3SeER5b15DEBb1DWYPP2feqJD899iaJ790X1/Zy9dNBy/F9W6ZIA3C0pzOYGXRXaPIFpBoMOkROmmHCrvHfDntnmVCTb/IYqR0qqxbSZdFgRXSRzQhiyGA+JB2QzZsEoN0ECg6sumjdL3RAooJWEFm+EWTmsklsCSKEgwJp4JkIkVxodQCKJvSgFCOu1as4YcUJWxvanMtmxphqIGNDqEJkARI1coFmArbLqOBSFMHZsrwMZPqHk3G3i+EKBVf0jB47qkxSVjQMCTSaAJPrZLmjIaQAltdnl07X5zhCw6iGSs6bpzASTzANXEa9+S4hvU4PulDEyfNVIGyLNtYZdIffhUxR9wxkY05ZQyrAUiSAMDSNCBkUdRIUi/ZSISEAQuBiSwF+rKB4lR2xBnviVyQdh0TErUECUQXeGo0+PQDFRw6iVmaSJLaXeQFkad2MdeAw/XACRTl2wx9tnGXKkhHVqipKRCGCTX75ySIJjQg+OrTi+qsBBlkWVbUEIWESoiJO6V4ynAQISgpEPLwdCJfXlqOMK2HBxscjCwCJQVV9bqpM+XyfWtBVUSoNNVJafQ9SawoYwDOiDxdzEQfaZMEw9BPEeIFgyDwSwdjgYSTYBKPLPIBZ13jhp8wZRVtbG4+vHfv1asXvnW1ZditLHvQxlSrFXW5F311sTeCjTPj0mGCast6d9c6uruz49PN2utB/Ujwhmh//9tvDnf3z/zSnp/7feSLERsLs3PHM3d/88tf7bjwffkyvw4y7zdOZq58hUu0YlAR9XJgqkvOF9OAihAdWTpKZfGpsviHXIcSIgp4KZ6J84k0JuW0sJScTiRR1npRU4Vgxh0QRWJzkRHXSiFQi3ftLGBFo5RCdBgCIafMBL6Osx+glBwfprR7Pqzop2MPE/nS3brXwBfCQJOiOmfqcQ6KJgkvehbrnJ45BRsYxweHfrLxu2++/fzLLx49ffLko6eULIde2qazolJ+MdaRrr+tt/VkdH2/yle1XAy3n0Tx4wGrUumy1Jf3ELQQg9EUJLOLNd86YC0EbNMa0YQvi+IDjjr60mKlTRTwFHhkS6aOsoQQZKXDXLYDnhy/5PEy0DAowWMA6hEMvzQFGcAgB0qabLyUfeszJAnRwVCbpD2VydKMsDulepzrARucgrPn1Zopipyyzo13PCKPI8/IihyyprCowVSEeAlDnrFNjaSmLfYiRmlEqizTH0rh0msv1RB2mjUEinvpyA4dPiKUQhs6Q0himjDENSu/sg4SlCZISLHiGpOhLDykNJ2EUZosCSalvGhrEshCwiBCUSEmSgOYLmFFM3FS4I6cWqKFIEse5ZjT4U46aGQzUKAhJhRU01To9IIOgsAd8GQpMCFEvCRa7S9CCrxTIJSmdtQCIqsUToq0Hiawg0kVhAFhgCtFbE1bCFpKqdGHj0FpChKRqIvxwIRyzCmwUiQMDDmGMjnG5KK+8Q4wJlISIKzKQZPSRCJ+PFtigFLKJJRjKIaBkJhlY56oBlQCS4MAzDCgQ4FJCDgmKV+KKIgk3tUdnzAij21qigebiuCTDcOcfjwGP+OBPPFAIKdsVMRXqgmNIXKjjznyPowD0cHKhI6V12WrKH1R0oOHnn07Oz+1afzw0RPfZby+ee8t4rfv3h2fnGxu+O3ddSurFmNr5/nVq1fceQhrfXXjr7/8yv7K0cHhFfvjEzvMlmq//vurX/3KRxbVyw8cVZv71QB0cuohI1EJ2FBJm8BEeFGlCmpERxZRY66y2lAtGNJML1T1mkgix3g5R6ksWybS6OPpyiqigMhlMbzzyHVS7sgFSxJlhh1jBTkipIxoDliliJAOEq2sg5BKPefk41c9SGrP1wJzcT2949qfzJhOPqwgMAQLRDBSWcdLNWPTkGuWlcVlj7nVHsPMnScPHjqc3u2893kTG/7eyf7yr76yDC84y5uvw9mRf3lmrZ3U9INJqE6MJlNH1aV+xdCLd95tq+jEgNKYSjEiSdORk6CENBhxGqJaj7I2Fyp9WSc0dDRjNAMFbcGb391H0vY2SVixDXFBOhwFIekoAgUzUREGjYRHwrjDAIxEO9NBlCMkxwheqqmRGIzz2GpqDEk6SNUQkxpq7VdR8KXk4gkyNBKOWtE7YjXwSJRSS+rIgkYYokkfPzSTBSUMjshd+Aq1Jtw+jpgQUphsSZMSUSVKJUmCAhdDroZ0yAWBSKRRTio+DFzEij4JCoIi1KaV0EncAQGbJvZrRYpua0JQ4URIWc25hilaCJmXI0mj0FFKgpQaSekbyolqgGMIK9wOBo9YhVHKhSYnCR+PvKD0q9gSv7T8tS2n5EAI02ianm10pMKIx8QZ2JioJnMLcBoECB0mCRVPzkvikcXIUkjMFUFn44Uw2xuRBySYnDJP/MEXEknMoy+LEmrkspRZgRKn2vnNAFBagxANZV5kWSVU8ngZOHEHkHlWIzyTRE449GkC4YstebIkUeAIE0fMKSTIdBM5hZhQi6aUEMV7QgIYCWZUJL0cOWVkPaOPoZYqSDl1pIElZ0tfKTUx2EfEDCJHUaCpUrIQEIaaE9OaEH0Tq3aS66iu7NmZB6q8nmLP2Ps/Z8dHpl6f+j+fOfeLhr7UMTN3r99WOhUeKDOYA3593QPPdjbr93rfv33nRdPNzetHvh09v7jv3/7+q++fu9RSRIEL+I7Yuq72Fo+n9G38qst0gOlu4alRYlZl8ctKKadBKJATVkP3oUpOKIVPQlkqG2KYWUmDpIikLJui020zmU80svEffPJYMeHCQsI1IhShaGHoPkUYUCmKsjRdcNuRAFgFnEK8R4EyhhANJlkpzaSjiCQ4DFGaLmPpYG/f6ZFvmdXj3yentpettRsffbJ/cPD749/Z/3/85Mmnv/jM89J1yu77lVZdT945lDTdrO9y6dv6daauU627SMq1t5/xqisiQ7JPfuK/xrl2aF2aAiYBRHNmZ3dntKQ4C60plZKFXOC9EMpGOUJp1FhEQoFEFsMEDRwSJIviQoofUGG6vBLKJDoFyWrP20UBp0AOR1QNX0euImnACTHUpEiRNMjQWA1D46o8TedzpZQL39PpTQxlI7ythg8sk+hk7cfDvD1rMR/HO0hh1Hgbjc6eSEAOCQQUJfTBKzWOEwflKKQ++LRFwoUmMguJAy/IUWNLjnfMx8RMQQKWpomYeRolFQsO5MzRKkBOmHYshNnJpf3t6kFQeSaUQ2BJGrxOIyAkEsgUpOIhNOg1SNqRkMSEgREw20wisnRGOwQ/gOIxzqNPWbSWf8RXslFOAEzAhg8mXpDksmZGpSHVIUSywlDKjWyqnKx4lJIo4gUjS8e+hpQk5sN1hFk20lwQlJLEkBARApTqytsu4PNLaAG2BSoqhuqrmpBV2YQYcJgR0q8wenOPDvAgSBEE5oj39jw5IeWIXyk05tQACikpHJRgpHh7p8yV6n2GYfBCpcBQOiqoNO0JeQjTVtQSxmhPWYBeygU1qgaBnF9VlgJRFwjkMfRjOOSDKEBGhhCiPBBYyfpG9OLSYv3M0bU3bc5dnhhujhE/v+A7G9pn//VrH4/c2lj76MnT1Tk/kXQxO7ewtb3s7p9Xe72e5OD1WUiaEt/08Iln93Et23Y7r/20zkV95nd9ZdUd32fffvf69Ws9SHl5YfI2bcUzvYmlmvsW+z4joZPWS7OkgqnLqJ2sJlCkVRE5qxja5FQ7pNZqWppNXsIJVIRpnzSFYyFtK6UDhy1YpdQShlRUkHQKHqxU2A5kfA55thkJqQh9ZExSCBSFFMmmFCBH5AlyaMomwqhJozOUZZGsUBOMLDW8GMS27geN79Vsppn6/mQP6avL7a1NIfl1LC95v3r54pNPPrEM+zb4yupG3erlt1bOatw63b266XFVC7F1NQuwd5B4MT/yUp5unaoq8A6b4AWTKmTeoa9fUnddM+pOTpi6E6bKGqf0T+o2BD4VVBpAWWrwVRMFQRoQRYMicbyIETFRFOFoK4ahUaRPBzgrLgIIp9erSVRqQROlXjXgptuxXOgXBwbkVGp4B6VINgMgrsPT5zcDiU7qC2oc7yQIAjXE1kDFiEovywbHfC4SgUkzNUVz5n/67/5LcERQ0igZPQmOdk2y04/1s784KSCaePK4wfAqiA5msgB0PHX2p5QzRTA5khUTc0XakTA6zPny3IEsBeYBZMsEMSFkojThCcODCnEEn5yyIiRIdWaCVyQrVPj6WmtyEQVoidwrm3AoS/mKo8JpW8hpYikepXHNZVYaahyRgBIsnkfNKBg8Ex6ZYGiSIzxlMYzaYRB5qkPHxZA44RtMQjKnVAc5+KaTe+KEDCp84k99gSM/RceQXHiyiYGJwODwiFfq4OcRiNuHstTIZUWOME7btSeTRCgSdSd3H4sEQz+jQpNCkyZOze5ZXFWQ5cIrj1yPHg8aZRKEoSNOMaC0JB0kVPUK4XWlGgFnklpIqd1c1vBAeMoYCqogeOFxUVhdO6WYs/MjhpzKUkgA/DJUqQTANhVU6iEsVi40BcBEDJo3zUIHk3srWkBLKnUhq3cYIt75QhwJSTUhxJYw7XP3xicLff53rr8eXL+bo4uoGVdaWf18VKuOByVeDr6+fvrRlxrBYeELTZ7WIj8/OX6/884nSF1micF3G4XlC39i9pMBHq59/fKVGjltYqguIvGwlfBURKWAd9vXHIfuzt+jAEeNDEU6nMdKVFqpK1QJniT72KmUFKmmirOVAlF3muQaCv7h8VHagVMgGrwPorpxY8woIsHTjC+uh8cEQB/ZwpWSUEBxwYpTKXBhK2Wb2sWdUprw1VHVPB7lI51iY4IwoOKOvmCoYTgiV8rcw3FhlHKhSGqHOYbAOWWSAabU9hYQQlbuuwJ3jcWXVONc3tT1z9Ky77IsANFW/9F/8p8+evLY7QOj+VLX+wKnb5R+uHG7IPUFrnKeseIXZ7BwjUdchCHhEWlzVhpWlSnrFPUQA7WC6S6goC5MQkDIKchC8AWUNIhUdvBKc+SSgJUCIdGkbFWZR1AaBJGomlKEp8w8jnjHhA9DAZltEg8+paKKQrVYn/7CEZLa6RfnLtoTGbqGus5N7XQqhEANv3BIBEySkAQJityPlDHs4TAZRcM2ONQYSslJHGhpPSaycGBiKEhRzCFTgPxjQ6fg/zNVt8QN63bcMRwOko3vCJPGVlpjruPGY0Yl8SSJD4j+SB20y8/GppScCVJJKUfx9bP6Qxgd+pGkvVKjQE2Qh8EtZljdkhXb8kkT/6QIvtLhFA9fZSvWaa/chlVx8hzwNFM1jWBHEbIsikcMhUTOBAiKsJSayAPCJHzqm9Khr5Q8I1UReYKMnIvoh4FDmQSDCNOJgkzYhMylwaEJx4aaqmEoM1EUIvlnUWDHEAICDSV4UCRJI/9ngf8TyvwGdhJ3e0kwP2tFLY0mVBSdxPaz+pq0lLxs0J/Matv6qHE/5uqDwJpbo9Xngm/8LNGNXyGsT4+Ydd0dtHxS9GOGHtfxsQ73rzxWZHe6LoZn5k7u+Lj0xdsXr7z4q03MTe4gwq+He7oj1IL3nACKMIeer0P8bJx6OaMu3UofSPif1RcbwPQOTeZZ9rqClfA++NFokcSRFLIIlYbS7NDAalsK5LLUIiT/2WAIBZOBikm/sCX5S/p/Sc6RkETCFp/TsgT2syZuANNPXYSrP+3507SCCsNnvdwI8JkhUdn6cNj/7//r//b06dNPPvvUL2p4Q8Q74h6H9jVvjixnDNWxq1wHGkZDEuJRxqYciRObljkRd35c7xq12uRLQY1QjXbLdjIxktwmrXQ7G759/YxcaZqUAp6tiqOOpJIBpSg0hLqeRDp0/lmMkwCuM94CFaf/LBDKOkuzIObTGOvvXxpaGbEUYpIs/i/5/f+zAKeNRJCYjBvkcIqP1DOx4kccKY1cWFrHWs4QL42m2noAgQ4GEeotCtJ05J9XQykhL1FjK8vwzzUj+fMiJoRxR0cWVHCkDq+fQKWI8CdQQ/4T/WQzFGJFs4ZhL8BpH1CEiELStIlaCwyPFDlsFlZWW/HHoQknAccwUBGmTfCE4RMAPkegLGKYUgx5lHkkROYCOiKJXFZdyEVOGIaCUnLREgJRGmTy4EuL6W9ZU4ty4qT5z6XgJzawCUYauo0WCZ3bwvBi+3PhPy2BpspVkSYMEEIV+UuGdFJNTRrlnw0m5pqwSnnoZ34YGiYWYM0161O/H+r6oy53/LVqznmtpXrG24GuHH2mYWlhdvF6/sP1xW9fvXTB6/pscX5pY3XdN5N9efLl988Pd+qbGw49O5Z+bAlagtcjmPSLSDRsLdyO05Pjn60X5cjTv3AQSV53+XOTHOxagBpb1RE3yqdVCeGkSVVYtis+OfbJZaVg2SpF5asvLqWy0cekheNCdf48kkhUzihFzF1uMmcoHk39l0x+Vs4jXyh+oY1LlJ/VP/c7jR3VJGwt0gea717pkbSPr90p9ZydE637WxvHh/v/1797fWd27unHH3t1+OPPP9vcfPrm/Tud425V+fbKd07Q6hJ2MqVnuNco6rZaXqxNF6dcUg/fiaGq3J9kEafuEL80FcGnhX+2Cj8p+qeV08LRUan0o+xwlCKYiAJ5nCbb4qoKtZ8N5i8Js103aeQePHFqoPwlk5+Va6gYKk0wMJG2+ln9jENFGHWJMsO/pP//AsKIhZVioLldAAAAAElFTkSuQmCC",
+ "text/plain": [
+ ""
+ ]
+ },
+ "execution_count": 43,
+ "metadata": {},
+ "output_type": "execute_result"
+ }
+ ],
+ "source": [
+ "import requests\n",
+ "\n",
+ "url = \"https://huggingface.co/datasets/huggingface/documentation-images/resolve/main/semantic-seg-image.png\"\n",
+ "image = Image.open(requests.get(url, stream=True).raw)\n",
+ "image"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "kdK_bGhsLKKE"
+ },
+ "source": [
+ "Preprocess the image."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "colab": {
+ "base_uri": "https://localhost:8080/"
+ },
+ "id": "G0z-3R-PBKc9",
+ "outputId": "56c91198-0116-4c2c-fc63-147dc7431b89"
+ },
+ "outputs": [],
+ "source": [
+ "# prepare image for the model\n",
+ "encoding = image_processor(image.convert(\"RGB\"), return_tensors=\"pt\")\n",
+ "print(encoding.pixel_values.shape)"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "hJRijta4LLu9"
+ },
+ "source": [
+ "Run an inference. "
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 45,
+ "metadata": {
+ "id": "z1p-QDoiBP56"
+ },
+ "outputs": [],
+ "source": [
+ "with torch.no_grad():\n",
+ " outputs = inference_model(pixel_values=encoding.pixel_values)\n",
+ " logits = outputs.logits\n",
+ "\n",
+ "upsampled_logits = nn.functional.interpolate(\n",
+ " logits,\n",
+ " size=image.size[::-1],\n",
+ " mode=\"bilinear\",\n",
+ " align_corners=False,\n",
+ ")\n",
+ "\n",
+ "pred_seg = upsampled_logits.argmax(dim=1)[0]"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "gmYIcfL4LNtj"
+ },
+ "source": [
+ "Visualize the results.\n",
+ "\n",
+ "We need a color palette to visualize the results. Here, we use [one provided by the TensorFlow Model Garden repository](https://github.com/tensorflow/models/blob/3f1ca33afe3c1631b733ea7e40c294273b9e406d/research/deeplab/utils/get_dataset_colormap.py#L51)."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 46,
+ "metadata": {
+ "id": "jy5c6vmzBqzC"
+ },
+ "outputs": [],
+ "source": [
+ "def ade_palette():\n",
+ " \"\"\"Creates a label colormap used in ADE20K segmentation benchmark.\n",
+ " Returns:\n",
+ " A colormap for visualizing segmentation results.\n",
+ " \"\"\"\n",
+ " return np.asarray(\n",
+ " [\n",
+ " [0, 0, 0],\n",
+ " [120, 120, 120],\n",
+ " [180, 120, 120],\n",
+ " [6, 230, 230],\n",
+ " [80, 50, 50],\n",
+ " [4, 200, 3],\n",
+ " [120, 120, 80],\n",
+ " [140, 140, 140],\n",
+ " [204, 5, 255],\n",
+ " [230, 230, 230],\n",
+ " [4, 250, 7],\n",
+ " [224, 5, 255],\n",
+ " [235, 255, 7],\n",
+ " [150, 5, 61],\n",
+ " [120, 120, 70],\n",
+ " [8, 255, 51],\n",
+ " [255, 6, 82],\n",
+ " [143, 255, 140],\n",
+ " [204, 255, 4],\n",
+ " [255, 51, 7],\n",
+ " [204, 70, 3],\n",
+ " [0, 102, 200],\n",
+ " [61, 230, 250],\n",
+ " [255, 6, 51],\n",
+ " [11, 102, 255],\n",
+ " [255, 7, 71],\n",
+ " [255, 9, 224],\n",
+ " [9, 7, 230],\n",
+ " [220, 220, 220],\n",
+ " [255, 9, 92],\n",
+ " [112, 9, 255],\n",
+ " [8, 255, 214],\n",
+ " [7, 255, 224],\n",
+ " [255, 184, 6],\n",
+ " [10, 255, 71],\n",
+ " [255, 41, 10],\n",
+ " [7, 255, 255],\n",
+ " [224, 255, 8],\n",
+ " [102, 8, 255],\n",
+ " [255, 61, 6],\n",
+ " [255, 194, 7],\n",
+ " [255, 122, 8],\n",
+ " [0, 255, 20],\n",
+ " [255, 8, 41],\n",
+ " [255, 5, 153],\n",
+ " [6, 51, 255],\n",
+ " [235, 12, 255],\n",
+ " [160, 150, 20],\n",
+ " [0, 163, 255],\n",
+ " [140, 140, 140],\n",
+ " [250, 10, 15],\n",
+ " [20, 255, 0],\n",
+ " [31, 255, 0],\n",
+ " [255, 31, 0],\n",
+ " [255, 224, 0],\n",
+ " [153, 255, 0],\n",
+ " [0, 0, 255],\n",
+ " [255, 71, 0],\n",
+ " [0, 235, 255],\n",
+ " [0, 173, 255],\n",
+ " [31, 0, 255],\n",
+ " [11, 200, 200],\n",
+ " [255, 82, 0],\n",
+ " [0, 255, 245],\n",
+ " [0, 61, 255],\n",
+ " [0, 255, 112],\n",
+ " [0, 255, 133],\n",
+ " [255, 0, 0],\n",
+ " [255, 163, 0],\n",
+ " [255, 102, 0],\n",
+ " [194, 255, 0],\n",
+ " [0, 143, 255],\n",
+ " [51, 255, 0],\n",
+ " [0, 82, 255],\n",
+ " [0, 255, 41],\n",
+ " [0, 255, 173],\n",
+ " [10, 0, 255],\n",
+ " [173, 255, 0],\n",
+ " [0, 255, 153],\n",
+ " [255, 92, 0],\n",
+ " [255, 0, 255],\n",
+ " [255, 0, 245],\n",
+ " [255, 0, 102],\n",
+ " [255, 173, 0],\n",
+ " [255, 0, 20],\n",
+ " [255, 184, 184],\n",
+ " [0, 31, 255],\n",
+ " [0, 255, 61],\n",
+ " [0, 71, 255],\n",
+ " [255, 0, 204],\n",
+ " [0, 255, 194],\n",
+ " [0, 255, 82],\n",
+ " [0, 10, 255],\n",
+ " [0, 112, 255],\n",
+ " [51, 0, 255],\n",
+ " [0, 194, 255],\n",
+ " [0, 122, 255],\n",
+ " [0, 255, 163],\n",
+ " [255, 153, 0],\n",
+ " [0, 255, 10],\n",
+ " [255, 112, 0],\n",
+ " [143, 255, 0],\n",
+ " [82, 0, 255],\n",
+ " [163, 255, 0],\n",
+ " [255, 235, 0],\n",
+ " [8, 184, 170],\n",
+ " [133, 0, 255],\n",
+ " [0, 255, 92],\n",
+ " [184, 0, 255],\n",
+ " [255, 0, 31],\n",
+ " [0, 184, 255],\n",
+ " [0, 214, 255],\n",
+ " [255, 0, 112],\n",
+ " [92, 255, 0],\n",
+ " [0, 224, 255],\n",
+ " [112, 224, 255],\n",
+ " [70, 184, 160],\n",
+ " [163, 0, 255],\n",
+ " [153, 0, 255],\n",
+ " [71, 255, 0],\n",
+ " [255, 0, 163],\n",
+ " [255, 204, 0],\n",
+ " [255, 0, 143],\n",
+ " [0, 255, 235],\n",
+ " [133, 255, 0],\n",
+ " [255, 0, 235],\n",
+ " [245, 0, 255],\n",
+ " [255, 0, 122],\n",
+ " [255, 245, 0],\n",
+ " [10, 190, 212],\n",
+ " [214, 255, 0],\n",
+ " [0, 204, 255],\n",
+ " [20, 0, 255],\n",
+ " [255, 255, 0],\n",
+ " [0, 153, 255],\n",
+ " [0, 41, 255],\n",
+ " [0, 255, 204],\n",
+ " [41, 0, 255],\n",
+ " [41, 255, 0],\n",
+ " [173, 0, 255],\n",
+ " [0, 245, 255],\n",
+ " [71, 0, 255],\n",
+ " [122, 0, 255],\n",
+ " [0, 255, 184],\n",
+ " [0, 92, 255],\n",
+ " [184, 255, 0],\n",
+ " [0, 133, 255],\n",
+ " [255, 214, 0],\n",
+ " [25, 194, 194],\n",
+ " [102, 255, 0],\n",
+ " [92, 0, 255],\n",
+ " ]\n",
+ " )"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 47,
+ "metadata": {
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 595
+ },
+ "id": "3KJFvgENBih0",
+ "outputId": "63d42e4f-3867-4d33-8ac0-83bebf8819ca"
+ },
+ "outputs": [
+ {
+ "data": {
+ "image/png": "iVBORw0KGgoAAAANSUhEUgAABLoAAAMyCAYAAABq3KhbAAAAOnRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjEwLjUsIGh0dHBzOi8vbWF0cGxvdGxpYi5vcmcvWftoOwAAAAlwSFlzAAAPYQAAD2EBqD+naQABAABJREFUeJzs/UuwLUtaHgh+v3vE2vuc+8wkM2+STyQQkAlClEAklIm2bjVqijKTmUwMZAxkMpnaagQDpTQQEyFGDKWBxEwmtbW1TA+znklFVSmrTFJTPKqgqgtEJiKRSJJ8P+695957ztlrhftfA397eMSKx3ru7d+9+6y1Ivwd7h7un3/+OzEzo6KioqKioqKioqKioqKioqKi4sohzp2AioqKioqKioqKioqKioqKioqKQ6ASXRUVFRUVFRUVFRUVFRUVFRUV9wKV6KqoqKioqKioqKioqKioqKiouBeoRFdFRUVFRUVFRUVFRUVFRUVFxb1AJboqKioqKioqKioqKioqKioqKu4FKtFVUVFRUVFRUVFRUVFRUVFRUXEvUImuioqKioqKioqKioqKioqKiop7gUp0VVRUVFRUVFRUVFRUVFRUVFTcC1Siq6KioqKioqKioqKioqKioqLiXqASXRUVFRUVFRUVFRUVFRUVFRUV9wJnJbr+4T/8h/i2b/s23N7e4hOf+AR+/dd//ZzJqaioqKioqKioqKioqKioqKi4YpyN6Prn//yf45Of/CR+7ud+Dr/5m7+JP/Wn/hR+/Md/HF/96lfPlaSKioqKioqKioqKioqKioqKiisGMTOfI+JPfOIT+DN/5s/gH/yDfwAA0Frjwx/+MH7mZ34Gf/tv/+1Rv1prfPGLX8RLL70EIjpFcisqKioqKioqKioqKioqKioqzgBmxltvvYUPfOADEGJcs9WcKE0JttstfuM3fgM/+7M/668JIfBjP/Zj+JVf+ZWe+7u7O9zd3fnfX/jCF/Dxj3/8JGmtqKioqKioqKioqKioqKioqDg/Pv/5z+NDH/rQqJuzEF1f//rXoZTCa6+9llx/7bXX8JnPfKbn/hd+4Rfw8z//873r/89P/TfYvLCZFOf73vw2/LGv/Gn84ft+C19+12dnp3mp8O3ggrksvLHQc61b4nZfumKl3KninIsziBEXx3gW3eRKnEEseRZ95n1QhRby4K6srXqrSueKyvYc+az1vaLisnCmTQ57cTHpWpGO5eOnC8h7IQ0HT9XCAHlNSpbObSaEc+jyWdUGzpTP/eOwCeEdMs4J5TDoYqnfAX9T5oeTntrSujcnzinz4Cl1rOBksP1OycSkKIuR7nc7xc2A21lxRuU2VBYMTvzvnu7wr//qv8ZLL71UDjTCWYiuufjZn/1ZfPKTn/S/nzx5gg9/+MPYvLDBzYs3k8K47R7h8eMXcfvCo8l+YlSi63hxXtPg55rSuhpnmBA/lIn/wWOsRNdqVKKroqLiYgilDBeTrisjug5WaichupaSMddHAC2K8z4SXVPCq0TXnkgfBtE1hzxa6u9iiK5SeAX/U8xXnYXoes973gMpJb7yla8k17/yla/g/e9/f8/9zc0Nbm4mklMMvPvtD2LTPUouv/zsPYvTe8lYPJl1leNSBk8VFRXL4dpx1OnXll1RUVFx3bgYguuh4hQE1zXj0AvYl4qF9WANaXSOOM9Bjh2SqDo4wTXFzUKCy1yeUrYHJLgm+p1FyO1zc+bO4CxE12azwQ/8wA/gU5/6FP7iX/yLAIyB+U996lP46Z/+6VVhEwt86+vfiVeevq9/7zzr54cFUbFREfbXpaKbgfAqKioqKioqKioqKioqKmahzi0rLgBn27r4yU9+En/1r/5V/OAP/iB+6Id+CH//7/99vPPOO/hrf+2vTQ7j2776X+DRO4+Ta8SER9uX7wepNYQV5FQluyom4xxbQ8+xjfCK89kLpaDsWvsc16R1btke4kksPYl3TdxL69A56vtD6evricwPG+dQQq2NM6+zR83DobZy3dM4B4M7YhzLt3YuD+HQ20mPWT5rcLZ85u+hQ29VPFScU8Ne4ffg+Zzi90D+lm/JNB99sz4H3v43TeK139/CrZVz1GOrtlovwNmIrr/8l/8yvva1r+Hv/J2/gy9/+cv4/u//fvzSL/1Sz0D9GN7/5rfj8e7F8s2BMS6xAGkBJn0mAynzMUhOAUlD62VnYHviaHgVFRVXA9eOi4RXbdMVFRUVV4e6XfHycKkETsB503L55XMYLN+6do7tchdKcM0J+55ttzzHdsKDbkMcCO9QcR4DZzVG/9M//dOrtyrOxWtvfDtefef9+Nx7/w+88+ibJ427oqKioqKioqKioqKioqLigeP+8cEXhas4dfGQaNUNCATJ8iTxEdFBVucGjc5PMSo/ov6q7auihHPVi2veRjgHq/OZb3Fxl5OLnNxbHNWaE6/OULZL+9s1KV2az3PU94ei9KuqmIolOGe9mRP32dL5UE9dTAJdoXhZEO5eb5cY5yUa8V+Q11EfE+rB0Dt+TIV0jjhHo1zob5/fufk8qxptJL9TlGHDbkqXeI+ndWqrsS2Ro6qrM6T1EHhwRNeX3vUf8ZVX/xN28vm5k1JRUVFRUVFRUVFRUVFRcW9wdmKzogJXTnS99ejr6B49neXn6c2b2Lbz/AArDBwfeNVtr7Jr1HPf6HzfQF5FRcXFo2R0HiM2uyoqKioqrh5VqXhmXKJS6QJS4HGR5XMEHNIW1YXa+DqH3axz2Ac7h12x49rNmlKGY3EtUeutjXOKO57gpo+rJro+/cF/j5sXb2b5YbqXXe501BMWKyoqKioqKioqKioqKioeAFbRdycIb8w9D5yktx9XTXSx0GChz52M42NEiTX2zEfVX5Xsqqi4fgwouyoqKioq7g+qkuvyUJ/IOB5K+VykjbQDx7fK7xls7K15Jqcu21WnEU4hAea4neCm+C4amoLMSV/sfijtNHB/BGK604qzok5kKyoqKioqKioqKioqKioqKkZx1Yqua8Hakxdn+z3QaWv3FVe1+lJxL7GmPhQp76xeHrK+rTk5cfGpgtdG7C/tF86RzytShiy1jVlRcQ4F1DXGObeFXd346VLGbDPe0VOeSW6S5+Sj/mPX9SknyY+4PYcSqBcWr9LqLInQfJRuFdxNCnIgjtl+5zzPvQFPsAd1ojzOD9xd5nluBtwO1zAercyHPuH3UG6OgUp0nQhLBuznqBRFJWGW9sWT17E497y4rmdqVlFRUVFRUVFR8eCxZLxMfo9QP7hSFIN3zovZhN1czCW4Rsp1clrOMVk/JFl7ZUbop+CatjcebZti0eGl2uQ6xBObHkbdulhRUVFRUVFRUVFRUVFRUVFx1bjPJNc8VEVXRUVFRUVFRUXFRaEaYK+4WhxINbRGXXPpOJT656DKpYnlusbv/sBnKNVWup3k98gqsKVbT69JsTao5FqY0TXKsPnv1XOTXOtQFV0VFRUVFRUVFRUVFRUVFRXrcQ/I2Irrx4NTdNUVwooHgyus6+cwzn1om3NHBdHJ10TWlM/i53niZ0K4/3VvbUznMAxf39fjuBbbn9eEazQovyru2R5Ob0vn2uIsBjcjjuK7aEwh5u9dz/ukH+AKBdxa/0uN2e+L8xgHISzJ57Hyd4A485o+RW11EHXbkfz1/U5XcvVUWnOUXBMK96G++6uiq6KiouJa8EBfVMdGLdWKioqKiutFfYtVXB9qra04Nh6coquioqKioqKioqKiouKYWGQPaKnC5BpxzxRKB8XaOK+onM5h4+s8KsDSpal24Yqe9/t74AvkVdFVUVFRUVFRUVFRUVFRUVFRUXEvcNWKLmZ+8ExlRcUQrrFlnMNe1jlsM63BqctoTfksTus5nkmte6M4x7v2HHbBrgn3ffxzbfm7Rvtec1vYqtiOYbPoEuMcDXi/EoQGrk/1fxIcqa7PsmU2w+1ef2v8rrUvtie8pfnseVkYzrHLeapNuim2z071bGfFOSbeHFFpjSq9Bk11RTcG014o2+zS+NBrTt1b2goO179cNdFVUVFRUVFRUVFRUVFxsZhBUCXX1xi8viJcihHyNX4P9RTWkmmTDLxfECE4xc3i7Y/nJvKmEFJ7A9zvJg2PBxzuJ7juI+rWxYqKioqKioqKioqKiooHiwcw76+oeFCoiq6KioqKioqKioqKiooT4NyqoYvHfTNCvgaHjHONhGep3xVxPpR8Ls3oVEP2PX8PpiOpiq6KioqKioqKioqKioqKioqK0+EBkU7nwHUrupin05Kj1h0vGAehXTn6F+UyoPgrlZ3tMZC416gp0XB+itcPl/eDBzsW4EXVsYtKzAVipE4eOdqlOG1qaZXxe16Uz3VxLsWytK7B8rp3dSbaF9aDq2mba5N5jjhPiPVJPWFmV0e1IIBzxLnU52rRwjnKZ1qAvN/JitCxsD+7oIY+YZxetnc0MfjSlb1+B40WHdZfr49eLMGZ6C53OH2eMRaFb4MDjhIj5Gse5kjsUWz2cmaHbVI7mTK3mzb/o97lKfWu5A8jc9zJF9e7WZr2udH2whv3tDfOyRiyQVbGVRNdghUEKwDondpA0bfcRFsZFzh14HkPM0FcHr0CGGe6GOzJroMjP8rBdwqX8DKf0Vmc9DSwSyib+4pzle0F9jdFPKQZ/KmfyUNq1/e9HjykdnLfcY5yvbZneY1ldMLzJR/MvqDJrM0KF0vL8pCEDHC48cGEdC0leiYnYTKbty6e/QkpXDr0c5vihlMSZkYSKKZ3hvwtncZP2Jg4xc2w38NiCpE1FOcUf0vzedVEVwxijkpwiPTa15ley+RzApgTBVXGl5fdA3Bl4JrO0defiADW+51NuDiVMJ/U0PZkIggEp+V2Tc26lE6soqKioqKi4nKw9D1/Qg3YAXCAOAmDk+hroqWORUWMbnpZrORaQXCdxU7SfilEacw/pQ3ypZCfo+kw8+BDpDWdd0+oB2t2Dsz0O/Qs5/Slsd8xf0NJm1RnJrgru5lDZOY+p9TvUoy8P4aBmwl9M5iu1M2cZ3VviK46qy+gR3JN8LKU8OPlrHJFRUVFRUVFRUVFRUVFRUXFIXDVRFeysS8VJMFtWaT8fsTG+K8n3YZ2fHBEcCU5Ixq3kxVCyH3mEaxL4IGxdCVpXZwlye1Ro6yoqKh4UDhHl3oO+3AVFRVHRm4HaKmbe4p0R8MK5dsJTkLMZydL1UBz/E1xeynpWOP3UMqzU+Rpsb/BnU0L/Z6xswg2tQ+UiKvo+AhzBDlXTnSR3VmbXDSg9Oeo8PRCB7aH2KlcpKxKxB7HssP0/j6hqw92KOyBuKbGMQsrXpbL4xy6/JA6nvMhENbnTMU8XNNkOrd/OAdL87kmzqV4KM/kHKhlO44l5XM9JYqLHWOVsCqliydeZ8A50npp5TM2Fl1DKCz2uQJHaGPTthXOIMWWbmXccxDWaHgHIlGo8F445Xa7U8Z17PCW+D/Ycyw6Kl2axHoNXD7ijHNgj/HBCa8TIjEpPjChM26mbRfNceVE11A9W2Kj6xJxlvXspEP3RNmUbZALJwjX9UwqKioqKioqKioqLgBnI5Lr6L3iusB9ecw9xArT7Yc7GvFicN1EFxPYnQnf07IGbdI9e2aTUGrIkwg/6v9kwG95JEQr3sz7y3dICp6/mA/R8xxTKTYYZ+nSQ6xxFRUVFRUVFRUXiHOMD68I8xVYexa/D6TemopL3dJ3CDXVOeNeG9451F+T/a3ZjXOCuR/1dldxfLOYDgKBaUU6VmVh/UR+WC+T7k8rKSyHcN1EF6KdisU9eoWtdRXjYJ6+dYOijY77tgyWFGHOD/UbdEVFRUVFRUVFRUVFRcV14WJOmqy4B8g5ggdCdAGB42PAq7gSRIIvjj0V3MSBUuYobBs9ISHDSczzESmvzMfIPvdYecU6BJGHtS+upTj0ysOkeFakeQ6bvzJrVSE2EVdUTNdkY2mNfaWl+TyHTaeH8kzOgVq241hUPldUB64npTiPbaZz1LnFHq+3fOaoj1bFeOLnedDYDmhMfqm/fX69mOWKlU6H8HuIcA5ti+zS8tN3MHarOLHbH+eR5n45CNSPa0DZtTKiBV5OO8Z7MIouhykd4kOGKx/OCa/Si4m5v6uQgt0uX7ny3/tQUn/RMVpoRUVFRUVFRUVFRUVFRUXFFFgrRWdPQ+Fq5uaBEF3x1sUcgfF3aq4hl4zSdtby7vMLqAFzwCbXhrwKJNdcogtkuNp9JJcgd+rDuBIs98drlWtxWIM3jvfcTsXmV1RUVDwInPE9u+qU0QOmo6KiYj3m2IEa2uVwrzFHidVzO9HvUntdA36nPJlDK4L685brVpMdyi7ZIdRe5VP3gLmTqOB3pr+TKLkO89z78hBOb2DdOISZTrpxrYTh+B+gja4Uw5nmQRdjFa90L6FwToB1DYMzoou1BjNDMw+/6AeILiDknIh610AEjpRfbMkxwzQOqL9iRdcDGVNUVFRUVFRUVFRUXC/qoL3iGFhTr2qdNLiucpii4MrdziHjrpzoIhQNbA3g1DTVuRCz5o7k0o7ksp89VZe355Wx7k7HGBFW/ha8FxCRUXTF2xytf68Gs/coJ8GO2SbPsSp3XX1MRUVFRUVFRcX9xgJ7UA8NB1VkHVjJNQX3+fTFS0zHpca5CkuTe6xsFqz8HMvwz3o110K7vBNUXIm7h6LoSggbOGKl5DB8MWTXyJGdg57PaU9qRYfm1FyW5OoRXRbBAG9mhj9Sf+XkGEffQQQhRM+WlyO1hBB9osuSaGHDYwEjlXnMIOWwii84WGLkffHL5Rz15sreLUvhs3lFLPY1GRNflFLX/pe2l3Nop1c8k1OndlXtWXpAwJo4r6i+n9TY9op2srZElzzPq5uwTEXUJlblcPH44Ay49LTGC7Yrwzl1+V7K81ycjjWE4IGM0o/56ckbTtAvjcUxdm/OFqul8R/S79J8LoObWy5Lz7KyXdYfnGMO5+O8p6/dGD3T3QfEdRNdWoO19qqh3hY7585VF+akYUR0zWhLo96XU2JZDXeEklIKiEguR3Q5N8mni62wdZHi+8hUY+YCtNY+nJ7fTNHl1F+Ase1FlLldgMkl9QA6jYqKs6KgAK2oqMhwRe3k3pJcFfcaD6LWzm2bJfdX0g9VVFQcE0N9yTH7h0hok20oS9MT3Z/R5V010QVnjp6zbYmlDjshZnjw3lAsLpJDsfPTsEJhUDCcWFJyefe9qEfoVb/NkZMjGrzB+4J/lx4hhCHMhAjXBYGszo4BiDgPY6sLE57FmB6vvtYrKo6IK5rEV1ScDbWdHBXFEUTPZMODoEMuBvGiaQ/1WazGqrI9kCJrjb+peCjk+zVtU1yOZTorYKgKrcj76M6wuf6u6RmMIWFZAIwdInCYOA41NLpqokuSgAAZ4ooBzTqQUQQIEZRKJCyR4skeutdMR6zaIiHQSAlNZP60hub0JEbAFUefIIs/Y8TkFQBopYLiyzmyKi9/3SnwlAqKLkFW1WXSypYMc+F6xV5FRUVFRUVFxSEwNjqv5GPFfcK9mXBXVFRUTMdVE10AQFRQdIEBJrCz/+SUQRQRXdGSUmI83V2+dqOV0Yql2w4ohDBlQjnpFxUHAURiXEllPw9l40NrDtsaXdhEgNZlBd0c4itWmfUDmhpKRcVBsbQfubYauzifawbldYJ6FKx599UnMo5zjCuuYSyzL42xyYrkGmbapRkKu+IoSMp7ylj7oZA0h7abNkNlFb9z5ynCeOTXmL+BKKa4uSLD7qeyrXWoOA8d3jS/hXq6THxYDOusWPMiuZisHPttGMKfYpSeCLOSdNVEF5GGSDIczJrHSiQj9Ar0jN8Sd48nRMkWPSJIKS3BR4BSgNbeflfs3tnQAgWi0PvLjUXG941n/5us/5I/H5/1r5mhAU/IkTVqL932RvtbuHuHKqSKiitDXzxcUVFRUVFRUXFqXMxMvOICcV1bJyvuK66a6DLG6JVV/VCBt8osMtF4o8sbZXGV7+QNd2V8kaF+BhJD8EwEtiqvxLh8lseg9spIq/w0m8geV0J2jYDz78yA1sb+liXKiBnCplUA4XTHLP7E7kOu5Mos3Bm3S1fPFvg7Q39/lpMez4kHkt2znEi4EOc4dfEcJ1o+hGeyBtdUPufANZzCeokpzNX3JdtPlLufHPj8HC8uo3O0ycUej5PWMSXQqhgPrZK6xDhnjLOH/BT76FG13Z7UTlCTTWqbB1Q1lWwXL8UhSZxLUn0lB7adJF25gGKaO4O8zk5Thu2hAio8yuO2YdPda8Z5437XDCGvmujSux1UJyDstjy4k/0iN7HEje3Zgfva3+W0gQOkJFKu+RMPrVIqNlAfG5JPbXYh/W7DGrLdNddYfz4wjdOinRun8JIy+HPPe094Q1iqjHlw5FFFRUVFRcWlI194szjtAUIVFRUVFReLOoU7Ei73PXvVRFfbSmwaAbcd0ZM2AIzdrrBdERQ+hRBwdr0MsaN95eehh7XQdv161n+h/wFW3qm7YrJLM5tBIjO0ZiitExXX2KqLG0S661rryPGIqioKj/L1oXylKbPVxVobg/URwUkwK1KO13TPtqT6qqioqKioqLhSxGOLAdWPV7Ln45/EUeEInitQ1107piiMKuZjlSpqhj2vKWEv0/PsD3dveBdqN+vQ4d0/u2KDd6b4nhHeQ8EhCiAXsuT3c3ZgpvGs0bAPh+smuhqJRgr/W2kAmlPCC7DMh7PvRP4aOTLMk1zuXyoPmrC86pxSyNwTc7oW75RatkY5u13kVFTMYFYpOcScbCMsxmMJpiLJlYWVfBYSPDQA4jiNQkBb8qtt24Tk6nkthTd6YyJm+j+LEuyBdPRJO7/nIOCq3uBLt6yt2cp1jm1y17D1zKGWz+XharZ2nus5uvIpLJ4NLpDNCG/W2GEM59gmtxSXkNap5Mqa98Fij1cc5wLyaXSOM4UcWeBv6nbJoflY6u2wBM6hyJ4hRek5DM1fShkl/ibtI8wXM9wCBY+42RfaqXG9Y6BzDk8Gq9iM4rxqomu3vUNzQyBBECTQCAKLsDVRM4O53zhOTTqcuno7XhVARGClJFf8SXawyFqjaQwhyJa00lp71ZcLy3pMT0ickTabsPA7T1sWpnPj0kBKATDKPNk0EEhJt+mJWIjr7a8qrhxx266oqKg4Ge4TWZlMtPoLmxUnwH2qT2fG+Sb39Rk+VBxG2cZ7BrUHYDmK/k49iq7t5Jy4aqKr223RddJsX5PS2nISxmY6ALIG6o2qyNrnAvqrggVrVJSrupjhQpmDodXGBSFMR25wccBNQg4xW7tXHAzVRwSZCYhHO7fenUzBxf4yZ9dMuG47JTnD+XG81l/ul2PFGaaRbjTVkFcJtb+qWIO1g4NrUX44LF3xW2OMfrHPikE8tHp7aiwt3yXleo0Ew0iaBw/LWRt2rbOHx5ztcZHbK6yxi3BoJdgclVXyzp0U3kBqZzzjKVuGJ5F4V7Sd8FKVXKcIb9RfUGeU/U4Jf0Z49xvr8zz++ivYxz7Q67L/uAr9Cc+rg1dNdP3R5/8Qj195hKZpsdls0LYbyKZB07ZG7SMbQ37JBkSAEIROKWilAbI6IPd0iBBvfnNEi+dq+tTXdJyS5LLxxUTR0Na+UuhSCEgRSC5hT2UUQkAze4UXR9sUdbRNsZSWXpwF4ott2ARAC5EOcuLw8/BsWkgIVFTcexS2EFdUVFQ8ZPgeMRsH+IWv3uImHugEqKKiYgyHJoUqKh4OLnNuctVE1/Pnz4GW0TQNdrsd2naLpmnQtBsIIdBuNhBCQtrfQkpo7VRJQcJoTmYMtFAguXjxIqHHuTpNZ7siO4nSr36OrZBGE2lHdAHGzoorF43ohZArruKw8mRF6fO/A+NlvmqdGpHldLNpYv7OKrrMs6pbECoqKioqKu4D9ipBctI/tyNK/cXLYvh1cntyTFFyVSzDqrKdo7o7hL+h4Fb4XRznGdRW14SzqNEWe3wYz+S0mKLkmk92letHLmrJ7z0QRdfTd97Bju8AWMWVVWXJpoEQAptHj9A0DR49egzZtGjbDW5ubtFuNlbMRSBrzN6d0OPteDH8SY6JtOsKQRHRFauinBIrtrWlNQNQ/reQEoCpKLHyqvS37TqvyrIB+HCSz1Iao/RprT1xZi8aso4IguyhAkIkJ0c6Oxt7m1hVw1RUVFRUVFw/8jFFZjs0PxU6WZRDWNBcv6JZUXHhqPW7oqLiAeKqia4GW0hWCPbs3KBHAiSgaAfIBnfqDkJK7JoWu3ZjtzYam15O/SXbFoIEhGzsAEkkSi/DH/ZJkuF3B/mdkexlS7HiaArhQiDW+5xEiRly1KeAzGmLqZd8w6Pj+EDOnSlh4VRiwpSRIHMIgNZNsqWxmLBYwuXit+Enu7I4Wo11z0MQpBDm+QgJIdxzCltQw/NwirBQ5sE0l/u2cHWiGvi6TFxN8S5N6Oi5SBeKpcTyijJabO9oYZQLcA6TV77vWxT5fPuUAbR8RfccJ0Qu8rX0XbIGa8iZNc/zdKDoS8iqHacQgcgYlTD/x6QWhwASxXgY9ETDC2PzI3YDseKk0Avon6cId4CTkx/T4zxgug6exYUBTvV2rnrn4x0Jp3eLCx3m1HSk/dfq+si9L+U4y55GL+2JcNjfkEhibxwDDhaWj+kGw7xrFRakYa9Z5Pxm9HvI76T31wV0xReRhiMhtbHn/9njsHx537w6D2LO+OWqia5HeIoWVtVjrzEAKICZwDugA9D5LW0EWIP1TbOBlBI3t7do2ha3jx6jaVvc3NyiaVo0TeOVYYIEGAJ3uEmGh4Yq0WGQ5EDCUUK2L4+plngTIZKRXH/oyXaw1a8AfYtbsa+MWOLCtTQV6fVY7u8YqCxu6W1huE/GTStNXrUdarIGs1F7warBWLvyYnsNUCB0/uAAqyQTpqyMisuot0gQhJD2uyG4pJQ+F76kIrKrlD1Hfy3Z6HjqEzuvD7V8joc+YV2RY039O2XZrm0npyYQ16DW2+PgYfS1wppTzQ+jAURQeRPgKS7njswYzI/RokVDs4YZKfjB0NB+XBJcXSumMF1nqD9nURWdq6/NceZnMsg2zInzkOnLiaI5YWfP5FDJOjTHuCpd+4i0eYTeXrJpURqmo9iK8rnzHL8ldxPDqzgOKBGQDO/g6t0j9jvMhtz6X/anmtEtXzXR5YcptgWb4bTdwhYvBVow4A4VhFYdtFbQrCHuJJ7f3UHKxpBcbQspG7RtY2x8SQmSLejmJa8sEv6ERwKJSAXlYwJgB1iCDPEGaO8mWTyJ7IM5JRhAEGBLKLGX2nvpvYsjElDFq+YUSaM4usbmyyBR1ieL7Bdi/xGqcUaAuXClyyBBa6O6gie2wkDSra4qIkiIAiMctjySJRwpUnH5LZlRVpyKaxAPsBe8pul7xT5cF2lwTTuFryipFRUPBHYAbAdNbgxkoKE1gckpFaIxUmTXMzGB4BCPH+zv3BboKXEwKuWebk9bUz6raS4b+ZyyTZQKZ3gmg+VVuDFNYDfsqD/TmJCOJOgV5eOmJ/1LRYylNQ9nOMpl+ZwXR//CBC1aL448rVPTuaZ85qA8ml0eCydykcsY0Z116fXARTAluJKb/rWUDONC/R4LJDZLMAXXTXTZzMZb3qyQPWpAcWHYwmFAaQVmxna38324sf0k0TQtZNOgbVtIKa266waPX5EQ0vxJ2UBKCdk0RrtFzl6UiVvb1UNiWBWZU0dpz+cELimol2wqzb/CKpvYiqSygZzNsI+3X0A+19aNyyj1apUf8jGMAisPhw2xFbiomKlzFJ2IBF7muoz3ImaJZO9GgElYJ5kbGzghJbjidC1dBbsWddbSgUBU8qfDOYv0Mt5rR8epB85zXig5FtfdMzBk93WSWDEPD6UWLMrnmVRAXDLh4Bf93E/2n049ru3BNoBbPwyLZ+7TqbvcgtqqidYF9yGHStsl5/EYmJLfSzBifvqwXHs7VHgzMBDclDF90c2UPCz0twrFKBfmcSC8SX4fVpOvyDC4g6x42b1bp4Q8ha7FjPDKuGqiKy5QQ2wFZRTBkEOB9ArqHyIAmsAEsGGQzIBJazAzOmYo1UF1O7uNTgL0Dl5/8jaIzOmNbmvjxqm/7AmPrbP51TTeYDppEVJABOmUTwTPP2ttxPOsTcIZgO6AO3AYlAm7lU+IZNAWOKSwkpmsaJbkp9mlXIuWOg7fKCK5YjZ+kGejsLXRi9Xi+7CDTnLKtTTAJNxkBdbdL8U8/SV9n1FeLamoqKioqJiJMxEcShsTCLlqw43XtDvAxpJbJqlhUdDZ8HSkVp4LYQ/dkUJAAqvJroqKU+OhkY8lrCKAKioqVmPMpNI5cd1E1w5mmxyAogCSC5P9FibXXqUEwJ2uaGVWWisQa7DWdpDUQTNw1z0FQUBIQ2TJpsHNZgMpG2xubtDIBre3j4waTLcQUoKlhCBpVwwlQAQhnTJJwBmAJ2I/aOPoTzGsDQq7BTBegXR2stitYsJL8If3u1oPWXmFVdH4V3IR6Z2BPd+c3ku2BgzA5cuVA9iQkOChfeWcfl/67jphmzzLQKRU/48e5XkGEqVqex9xbUqnpek9y3aPK9pneY7y4XMYhr+qCdw1pfU64JVZrJP2GSu2tNZQSluboGHs5MYUfvwkwjYJtyhIRNBEfkgohPDjwvswKR7rJ66JHLm0tK5Jz6U9kyVxpmZSDhfu3rgGTa5MVCFN3P83qe0vVFtNwpywF+ZzaR4n+624ahQZglxpUrg0PkqcrgI95HDzqoku/u8Z3ES7kaPCS0VLgS7R36vA3w6/wielVUfFpJEJDaydBN4MiF642fidcqx30HdbPL17agZGwoXX+i2NQkoIIbGxZJiUxrh9a3+3mxZCmC2QxgYVQYpoMEcSLFq4QZkjwTq1A8DO5rvJIQXFmPkgXw7DVa+0O5pHXlA8/IvTL2UCbCgVGvnT2gfvelVruJ6JbcUwHtIr103OKioqLgkPqRc6LZTSULqDXf0CgIjQ0tCajSLem3QIcnAvKAesep+MWQmGUYlZhbwmhhBmbGfW2nhwUl1RUXEeGBtMx22Xl0HiXEIaToGHks+HARqVVpzvWV810YXXAcgSO5gXdvT7dftH5joJq6gSADYAXgCCUVK2qjC2KirzW4MBt3poB1hQJkytFBQJiEb6EwJ1tzPklyW6VGeILvfZeFJMQAhpNjkKAgTDPKKYruJARnmbWzDG7knku1oHymMYAzTVDL9LPKa0pEEpveUY5ufSqBPOoVSpqKioqKiomAZmHcZZ0UKc1vHv+F1uCDGyvFgY04QL+bu/9z4/tRR6JS5N8XSfcAn2t86FY9onO0jcU5VcE92cXck1GOXh8lmVXOfCGXYpHCGAfWH2XqUTt9vsm1Ln9+dMwa+b6NqDkv0o+jRA/9FcNYbjVXDz7QD+y9TOF2B3RzJD3T01d8hst2scQQa71Q4AswKgANWBO4ICsHv2jo3DHINNlgBzhu4b2RqVV9MY9ZewRu6bFnTzoiHAyNr7EgJtQzZ37gRHkxftKhQTNCu4xMY0mTuV0hks84bqfQkVjL7OwtBmw5x4jH5xvEUlnJo5VpG9a17BIFeyqqKioqKi4mKhNUMpHexwsbPDBavIMqosg1ThHwzUA/HYxo3hhEj/6gJWRUVFRcW1Y+2bbK5/iv6dHdeRX7tXTXTFoqYcfZLL0j2KjPqKw2Xv5nUAf2AVXp6aIauYYpA25BERgd4N0KsCzrxpWFN0K4Zx2mLbEjBGVImglVF7dXKLTm0hpUS3dcbsJUhugDtlDaVaA/iWHDMnMloDZfGpQvZfe1ijvxKXQzDen5ZXXlbDpToOjq3O98ogxOzT54yp+U2+kS2NEluZx0fDN0d1YUtXovwRmjOxXPK21OMBfF9yZBkeyBylnrp4HFzTCvyS8lmbu+X2ssqLH1NwDrtgFQM4U/twZBZzGBf0SSzYE7jDwC52k4bnwiwTXWuq3KX2IZd6ut8pcMz0HstW13WEtV7tVXqPHVrJFbslLjfug57EONHveLhjgZSv55rWZT4P628aDt0+L6t/OucIZj3ZtT715HacAfA8TEkptvfFG9kFo3lj4KsmuqYiLmJhlUxwXAVFHeuXAf5K2GdKFHtmQDmiS0D+GQK9C8agQzSo0s4QvLchAWOvSwjvRunO2tsy9vRdmP5ERfvJ1EA1j9A0Ddq2xc3NLdq2xe0je22zsSc7SmPQXRjijbwcKt7sGLLhysJ009FLILozFZx8j6m1vPQLv/1XsbhFjum5xj3ychp5VEVWUVFRURFQ+8uKZWBmv6DH3EFrjZg4ZWZobRfL3Agm2cqYGXPwB/sQpAzK+pjsMmEcP28VFRXzcQo7XQ8ey9emZuJ+k1wBl5quw2Fdizxue76nRBf1vrlhkNY6JSqICrRMZNzBDZqYEcTxDHxR+0CNKp6BR4D4DoAkACYEH1ZuzyZkSYi2FObTAA1isqovBncSne7A3RZqdwchJJ6+8xaEEGja1n9KaU6BDAbvbyxZFkv6ndLKEmEEBKte5Mmv3hgxb6NUvtxfiRmvvP4x8Ihbjr/0e1/C0KB0vGPhhaIsH+cp37NX1EfWUxePj1Ornaotu4oHgdXsxgr/p2wnV8biSCl88WitQQRrgH6fmQWjBPOjOktwGULLEF1u+6K75zDVrsil4py2le47jmmz69JPXRxSSC4Nb7k/Hv2ZXhoOt+hmYjLW+F2GLHA3DxuLc9TNnsSOzpFq3zEd11lWU8buiRsnosmraRLMWJjle+VkxCqk/bhuoosEkmN1EvQJEQDQ1taD4ZoIJIQnu8JDCwZPYym8sNZNCQx8QYO/GGxFAAC9m4A/LiAaa0zeKqu6XQdW2vJLFNmCiDRUVu1luDV7KhAYrLfQABTMKYuaA5UghYSUEu3NDdrNBpvNDdp2g6Zp8PjFFyFl69NgFGoiyXOSDrJbNW06Uk7JpTORg2X3srKPyLKEq8rdMqzB/5RV63NmruxHNyMO3qHsmiHZFr6Ql3s97YTmgeA6XyMVFRX3B7UXOgaIDNElBFmCy31qaC082RVOXPQ+vWrLhBPGP7FqXgiKSC66Ng6wh0peHQ/VKP16N6fAvMXW/YTZJL8Hz/qU8j5u+If1V3FVGJimjk9fy3WDMW1b4rSpsVu0mjeVvm6iawGkEBA9OwyReiuzv5S6s4MqOJPuaUnz2wz8OwUWFBFIBGJASAD/hQC9GKJMu2TzzYq9zDZLMBjKq7CkDdItZDIUWCnsnndQ2+fYSkN8kZB468kb/tRHCOHtfHnVl5RomtZL9wPxJSCo7bNRLnE9tVwQEpt0U+FufL2PfV1nX58XngtbWVifbhtrBbWzrqioqKiouHyYd7kz0UAk7JZFXSC4rA+KB8RBseUIrtiNw1xFekVFRcX1oc5/HgSWvr7W+LvQqnXviK69zyiRqBe0dhwIpxw88N3jjoH/bO6aLYOBDKMbAr4bwC0FkiuOt6FEnEYANBgEZexugQBhCB0tTDKVHeTproN2pBoJqyZrzKDOyvNl00A2ErJp0bYbSNmg3bQQwhBeRGRIQNmCGhHKwBmGL24xjAnDQol5BRePtoFUp9UPJ94mOPR8Of0nQTHuXOKF8ZWgXEm2aIveUiP2A2nYh7NsIzxLR8dni/qajKZf0zbCS1kdPjaWPpNVRpDj+IccFc6IXljrCrFO9UorDOBfGU6Yz7UxLamxh2jPMVllbHeJHtEVCK5gmD5WccVbFPuqfZdW/21xOufi0P3dfes/L6V8LsH4/Fg4+8nbQ4NXdV1j6SsS2IVvNhXxj+Ew860YA24nve2SKI9RzsMzpr0+FyVnqqdD5/XUfdU19Y1jaZ0j5qDRn/2QKXGzaJQ6Y5fi4O7EGUGO4d4RXQHj1ErJ+WghUmxza9jNYCg7Bv49AMnRCQQRfhDAh9JLAgBBhQRq8ylhFV82OgbZbY8Mp07TqoNmQHmiKqjMhDPCKow9L9E0nuhq2ltsbl9AY920rTsFsvH2LJx9LyKRNAjNkXqL81LOX1ExmYbeqQxDxeitcmg3iE18TdxWSBDkakjB8bEWdtcasb8enuLkuKZXV0XFuZC3k5U90sQYF8aw5sCQinuEsmJrKaFUSaCKqbimLXsPAcd/X51pgbgHO5e7OFw7yXV/saRdlP2c4aiHoa2SY2zbg9m6OLpRM+0SPY3CunctD6Os5rLhRXwMFz3kKw3RlzfchZA2d59eB/BSPwvEDNwCeOT8hK16MbkTG1c39vPZ/oUuU9s4tTKrm0pIq/pqQIIgSKDpFJQGGrsNUqnO2AFT9oRHKcMKqRAQJIKdMw458/kqlGWZhJyge3S2w9Iisnn0sqzRl2FCiEUX/OquvZDUnGns2QSs7D7WWM+vqKh40Bhb9ul1Ed7w5CE6j1NMTyruJ8okV0XFEqw1vL4mvFPi0Okqtbnz5p2jf8v3yhhXGE/L0WU881I3eKHV8WSY8mpYXEQrPZ7qreVMHyXXxtwfiO7igYhKZBWFL+HWwMMbIrvmjAOum+g6OaYV7JjgdtDP/w7g/8gvagjegb6HgD8dq8mchTBHljHMKY/uN8GaoYB2RJclg0xHqMyn6mA+HGFIeP70KTQ/AUkJIQhNs4EUAu1mAykF2vYGsmnQthu0bYumbb2tLwh7hqMQfrsleTLSpFjDEHAxQaVZJKso/a0D+WEBYctk13XmileZkS+X5HABG6+LQCsNjYj0zBtNHUxXVFRUVFRUVFRUVFRUVFwdHiDRNUE5NOAv2XFYWBgYDrXASOb057bgi9kour4B0OfsCoYA8D6Ablw4aayxViwmw0BGlMQU3HhxmZdBGVmYEb0xNBMUA5oIWisIIaB2HUQjsWss0dU0aFpj60s2TVB3+WO7jc0wbxDWJsaY8+ewdTHLQ1Ke7Kx4uXSyz7rjoyhkE+YEyfCcHcllCL8Q+hza8jArJcvqnq8ys8k3jp5xxTFwjlXNU9t1WqOguNQV7xLuvb21Ulxua3t+eczPCXE9teeKsPKZ1mcyjmvq806NS7BxdYg4zvGMr1lhNgeT8jl2dfTV2J8vTQ29Bzr767HiQWJA+ZTQDLlwoxTKfjcHQ67kmuTlcAm6V0TXnCI0mKG9otLdfCsdDQS79IHZ0x0/x8Af2isNQD9BwPsMaZISRJa84cgQqw+HIncxmeSIHEMiCTT2iEgNaEApBWbG9rkNzxJXQkpI2UBKQ3AJKfH48QvmZCR72qNsGnPSo3cjIGWbGIcFGQJRZ2VkkmOJN8vWsGavSnPplkL2GpHJn07yxRnRJag/WZwjz142KV62hWfpxp+H8g5+KPmsqDg4qh2sioqKC8d9IHAqKioeIOhAlm8qFuOqia6eia6Ed8pueD+RqqZgFN67zGqmoZCozDgkTktuhjfNEspb9YKz4NfuOgR+j4EvxYosAt7DoA/GWi7298jlhXyIIU4iHwRbxZenixjQEXfnCSRNdsuhBmsBrTqQENBdZ43EWvtdEdHVWDLMqL8EGmcXTAiQ3Jg/f2KS2XcpErkWgwVbY7IxxaeT8nFKMSTlCmc/31eYWMewj+DKB1nxiU5zsXRKyStPbLzfOJ/50HuvAloR35o4z4GHoM6LfRVVWwMKr3Phuk5dvI60rk3lokWXq3qOp8c1lc81pXUfluTl1Pm/lBMnj4116er7nRfcfv+Fg4gnhbMEy4viMp/tg8cAdbAXTINPdHzoSOP3iwovF2fvy6TED4uEYqmG4yLiefhQOHkDnBRbEddNdGVKpXE5lmNDokLfU1HKoVDBDSe/Sn7Hup9QITOFkSPX4vg1wJ8OIZrTChn4HoA+ENdR9vUrbONzzCAj37jnyS4QtDPYT1HJkXkRabaJUIDWJjxlw3qmnc0rAllj9U711TTms725MZ+W8JJCotk8gtyYrZGCgsF7io4EZwBMluSyJy4adZcKNIftFDJaypZxdLS4I/VcOIW3ytxjj/chsac223MluSbhDJzKObYDVlQsQV5TSzW3SCzVujoBtX+uqLhkrCV4LnW74vnCO1xYsw4JwMhkGFOGyutIsWMSXP3wloZ77Lp6mfXoqHEuViks9x6EJ8Mo3o81IvNjHb5UCLC3P26MRBuiXsbyORDenKxdNdG1DBHpddAwjwWB4fQ60oaBLwD4t8GlgAhu3gXg+6zbpAPNqijDEEdaARSMyQtXC524jLNVf6cYi08uZA0oglIdNBGUJa22z40dr0ZKvw2yaW/RbG79dkan+mqb1mx3bBp7yqOE8GSVSHaTsteHEgQ7EixWt5FPolFknZY7CtTigrpStxdVVFScC7X/qaioqLhq3E8l1+zYThjXWlSS6zi4pjqwHHXEFvCAiK5YUbO8CpR89nZAFhfFJ+lee96ZytxlrNxiIuANgN8I90W0r5PfD+BjZDkzBqQLMtIXcRQeM4gDmUTOuLsLLxbIRamVFBFMzrYWA9r5AUF1W4AIOyFtcISm3aLZ3Hnj9e3GGLdXm41Rg7Ubb+cLniAzJztCmPLxlJ1ToTGgyRjzNyl0WxwdMyaK5TqElBJc0FGyIeMW1TyXoflRBv8PAqfL6NrtfNdkGL4aoz8ezm6MPgRonOSXp/gdRW+9bxbmH8BRsRfVGP0orqnPAq4rvZeqqjpUuOdWfQ29F46Rrr7JleMhtTmMbKjndmbMD29eGia5mp2WKeFNdn2AeMdfudfT19xHlNVbww9sAjXRqzRFpf+c9Ph7/d128eF4e1FUci0bDz4gosuCaEVbPXUjJ7BXZvXB0Te2ZEjQa5H1z8A3AP5vDevEDOD7CPTHyrkRgtCQ8OSd28piVFpRm+DomkkqNk0DROm1duAjv9bGFhhQyqrDgJ3aYXf3LGwvtKc0NjLY9ZKyMcbtpTFqL6RRebWbm6D2EgIkJQSZkx+FbxSRLtKSdkSujFxas8Z+wpf4XqxJQp0nXhyYeZVtprrtseJ6sG5hqaKiogK4LkLv4eC0z8S8TebGOcf9yO6Zg4Q/Jx21vt8XHGIEVEdRy3HVRNfYPs1eFxEvLC+cKPbZUS5en5iiQVfxqkVuSyt2yN4NLMkV71wnkHOzBfhrwQ+9DvC7gzqLXoTnpyj6i9VLPiyw/+4/fXLjFJjTFNnfMaWlYcgzDW38M4MVA6Tt9kN4pZcW0ii7up055dERXUJCNuZ0R62tbS/ReDfm5EdDloHIEF9sFG3E40b6nNomtpvmCLrc3RwEwdwaJdAyf+cYHx7yaNh98IrKBzIQrsboj4NrMka/FJMVWwWF1wpd33LfV9WmryOta1N5yhp7iDZ5DX1QJXHGcdm2qs6v5Frj5tKR5qGcnyl2s6ba1hpy1+9HpvqtuE+YPbdZ8fqZYzO1uNtsKOD4sLXZqSqnZzCbNKzkmmZjveB2Jq6a6JqGNYOcScK/2TEPTR7604GUOkr9x/86Qiysd2g9nFb+LQCftpE9BvD/EMALNkbWAFRoCIFFgN8kaIko8uItAQagdltvzsXZ93JHY1Likk0qyW4kJQ2QALPZXqi1BgPoutA4DGklIIQhr4iMwXpYJZdsGjRNg6Zp0fgtj2YLZNtukhMfSQhozVAsopMeKfnuy+qQby7uP+Fj4wxRnh4PIY8VFUdAbTqHQp3hVFRUVFRUVFRcEq6b6CpKuvbsJqXSgHSITIrvcUI7MY9NEGLf1LsznMJ8ryz1bZT0+adAdlkCKgQzsH7fEdBF/r/AoEd2BZ8ZpBl41Si98lMCyeeAo9xZ3ZblwGKiiKLtjYlGwJFlcAXJIEt8Cbfl0sdt4mPW5qREsvcJgFbQJKBZQSsF1Snsui4yYi/RNpbo2rSQ9qRHJTZgajzBJe1Jj84gvk+/V3gtt6t0KCyK/qHMYuuMvaJiEYpNx3U2V6CGqaioqJiCh6Lkug9Yns8p/uYowyaE9jAeScUKLBlJjdkoHVZQhf1Y/QBHlFwDqv7ZGFNt5dcmRFFUco1t5yvguomuMyJXYh0qrH5448SdI6J6aYiN2I9oGvk5A/+evR0tAQ2wBj5BwMf7CrN+cE6hBbRSJne0s+/FTm8WiEIfkm+UNkHC3XW0H0W2vuwfMxjKXtcAAKUIW+fPkX+WtJLWnlfTtpBCQkqJ9vEraG4eQ0qjCGvsyY7uU0Z5EUJcDNk1B9eT0oqKioqKioqKioqKiorZqAuTRdwzoouSb0XtFpeulzYNxveizwFyMXZpLJ2HbYSl2OJwgm6JerSViAmtKDBHHHmfxGAOxFaa/3KOSz+YCZoF8EUAOg6FgMcA/XGjMgt34m8ZBRaEX8aFu+CUZwO56T2LpIA5nCfAgO5J3II9MJN+AnEHkIDWW/NJAlop7J6/AxLCGOCXrSXDGnPCo4wN31u1FxniLHnOjlr2SXbKuFCwgRuT6B/RiZD3gT7KnGQZFBb9+pb8SssOxlbb3iUnSzg6AjKvb2O0WZ5sTXImyRZt0B3qqPNTd4pulnTytCfQwcgAS7ImYQ1E0fd+Yhpy1SEca+KsdOsgFhbPumKd4zGLaPEYamSFsWIFTlymnHycPuJFWLo4tSzOdd3ddbSRtXk8Vt+1d4gzFs6hn9vRH+WQYiP/fYY6daA4R98agxOrOaH3PY3HecKyXBjVepqjP8/sTQUOjVMPhc8UwKGz2Re3RFfdXHlpKqj41fvfz7Rk97P58fTSyMJPEjO9RA9OdP3dv/t38fM///PJte/6ru/CZz7zGQDA8+fP8Tf/5t/EP/tn/wx3d3f48R//cfziL/4iXnvttdlxmXP1hk8lHBIylevpnpdo7nNfZR84rn0slpzoIQDCypjyPrZvCJ/8PD+/x6WOynFiObGgBTQI+DzMX4z3AfRthH6Ri4F5dEYiDHIYUdmOvNkoC44Rn0nJ9v90NG5OeLTfO0DZ67u7d8BCGuKICFIE1VfTtGjaFpvNDdq2RXt7Y7Y2Nht4m2POwL01eB9Ir0BasXt2Nm3EzUAhlBuzu6KZkW8hzaRxcPbO0rcSodHT3lLO6CHZzpIQFHn7TrnJazqzRHmL8DDYxl00vhi7K9wn3144uZqmqnS9pFAsX+HeLV0IPf8dHuTZF1qGO74jxnkJGZ+Okx6g4P6Z2U6AdcU6z9tAfZ6Nc03gr6funRLLn+J1EDEpTp3mayyjuViex+Mq4veHPTSWWZqqQ/cwU9pYMU7ufRl2uyQNhUt+6OmGOUd4tvvGZuU4y7medLWw7sluID+Cw79p7CL9bH/HaZvHepPyosXp9Th5rIRVY+FReqj43BbU2bwpFJJbnhkNzbXs1SQgHg58kv9lOIqi63u+53vwb/7NvwmRNCGav/E3/gb+1b/6V/iX//Jf4pVXXsFP//RP4y/9pb+EX/7lXz5GUq4b5xgzjRG0bwH4ZaS1XQD4HgDvPnK6CohfA85mFzn5GJlr/nfkxvxgQGt7MiSBlQYRQakddva0x+fWxpdsG5CQVuElcXNzC5CwJztKowqTDYiC+oukAMGowKQwJvh1Z+yMmbSHf93L1RBknq7yORM2jcZ59Cb2WXOrpEb5ZWz6mzsNGTJv32qUu+tsz3F2b6yrySnXxZg1UFo6CY9zc11ETEVFRUVFRUVFRUVFRcV+HIXoapoG73//+3vX33zzTfyjf/SP8E//6T/Fn/tzfw4A8I//8T/Gxz72Mfzqr/4qfviHf/gYyTkvBoQ4fYXIQaPpYZ/AMHY3OPl/DuD3Cx4+AvDLLoIsFkEgienoLae4y4RBVRP6ax8JyRWTXtH9oH5iuEMqtYIhsYhAVvElpAQsidU0LbTSIEH2miG43AmPTdOAhICE+XRbDYkIGhrM5PkqxOQV4rph0ubFHlYw5g0TRoovQrQSo616j9naRWMgs5vWqwMFcqlfNxdU0qwuFEMoLlNMJLsocus+kvSm4aQpCWQi9e7tSQMXv6ZJo76Lc61cAeX0TIaTJ86OdHmU5wIvUFc5nFINdi5cj33CK6x8i/EQ8nhaXE89X4f7lM9peSmMde5PEazGVCVXz0k1yF9RMQEr1HZ7L56mPURT0ujiuErL2bdeHWkv4uk4CtH1e7/3e/jABz6A29tb/MiP/Ah+4Rd+AR/5yEfwG7/xG9jtdvixH/sx7/a7v/u78ZGPfAS/8iu/Mkh03d3d4e7uzv9+8uTJMZJ9Ukwlni4+TgbwvzDw/x+4/3EA37EvkOUpKxFcg8quKM1SCMAamQccOWRtfrECMxn1FQFaGeKrI8KOBO6ePYXb8khCGCWXN2bfeqP2ZA3fEwkIIbDZPLbEGMFtfzRfCYDdAulFZ5GyyxE5lsRy/BwnvQ6BBNAQeSP8AMCd9iqy6YWaEm9REqZ4Rm67aqD7m5emEe/9AdoQydVPETMV+uf9vek1beM5yw7CfTLAioqj4aFUvuvpgyoqjoVKelRUVDxM3Pe+7zDjuIMTXZ/4xCfwT/7JP8F3fdd34Utf+hJ+/ud/Hj/6oz+K3/7t38aXv/xlbDYbvPrqq4mf1157DV/+8pcHw/yFX/iFnt2va8HQY/JD8Zlj8smqrMitJz28gunA04A3R+59k8FP9sR2A9CmQFgBqWqrpIqhQHYlhNYIyWW3v/vgYwVTYiOK3TmR2p4tYFRZqusC0WVJK9EZQqtrWggKpzcKabc2WptesmntlkejGCMiCEuWEZFJa2Ts3ynsGO6oAg7kV5RwIgYx+TBcnmdSXAmWq5C4TKwkzDynvx3Bt1Q8Nj1liY8yxTqlUSYPIL1TkGvSCrXQobDmec6FI5rXqKROjWL/MhFL87nMGP15Tn9dtSp3cjwUsut+o5IY+3HqMrqkZ3J4Jddh8rY4lIUeD77wNhBcHs9kgxFV9TUTpxtPHCLeihNi4CHny/urRz/JQUT5/Nxezt2XJlSxAW+K3PZCKKWY0svJnHF6Dg9OdP3ET/yE//593/d9+MQnPoGPfvSj+Bf/4l/g0aNHi8L82Z/9WXzyk5/0v588eYIPf/jDq9M6D2urzfALYnAL1Eici7ujveKpA+u+PgPgs3vC+5MAvnfF9qhRJ9mWR+dHawAqyamAPeXScWXOLTHc02AwFGurrnLtldHt3GmUEVnlFF8w30X7OoRsIKUA2RMehWzQNi2apkEjG8imhbCnPhIJf9IjCWm6LiY4+/LGFpd7oZM1fh+RYT7PmUIr2wJZKkincFuCfcbrTQSTL86KeW7EPSJ0clqua0BwalXXcLlWOCytQaul4BUVFRUVFSvxMJYTrmusV1FxNhy0Qzhcz3KUrYsxXn31VXznd34nPvvZz+LP//k/j+12izfeeCNRdX3lK18p2vRyuLm5wc3NzWESdMQJwvgWreG7k8QAh+CfEkVNHnykA1tYRsUVlJ39G8M3AXwh26rXAvS+lM0dVE143qbPHBcn3AywPTUvVk6N8D4hKjYnPXo9DwVD8JSdHslEAAufJMUaEOS3MypljN3rtkUnDdHlbH3JpvVbHt3vkFFhcysixVek2OFAdFF+VCVKVYmdt+zqvgpXLiiKlINz4PRzhaTtTQd7eeR+/0kzoOFVsGiD45RgkZdHrOI65OLiUpJj6Qrn4vgW1oM1cV4L6tC5oqKiYhmWvsuOreS6FyiOmZaW931Rcp2jfpw6znOoxE8e5WrMTTL3vqzBtDnOwTFgh2sKr+X2W5mPWGSRqrmGw6HCt3EfOY5OdL399tv4/d//ffyVv/JX8AM/8ANo2xaf+tSn8JM/+ZMAgN/93d/FH/7hH+JHfuRHjp2Ui8QcDQofWGxVxCniyPFZ9I3cvwvAfw1gc5wo48aXNhhO3MQ2sRwaYYgm/1ycwsqzdGF7IbPyv++6p9DMEEICIKPsIgEpG0gprTH7FkQSsrGKLtGgaVrc3t6CRHBjPjdhWyRglF7sPjkQcT15qOt0wqCAuTCU8Z1a0lXtgacA97gZwpI3HxvbapO6yozi4ymkyrDm8nrWMx/G2mtFRUVFRUVFxfWiEq/3BWYeiZMOvy9rpD8u9pmP+eEcnOj6W3/rb+Ev/IW/gI9+9KP44he/iJ/7uZ+DlBI/9VM/hVdeeQV//a//dXzyk5/Eu9/9brz88sv4mZ/5GfzIj/zIxZ+4eGj+Z/Ledut4aJFibpoi3RaSDW3+BvW2xU7B6lUUzj6fAfg0AMnJ5bJXe/e9AL2WqWoGtqXF9rCKYVnyym0vppgIYp2J42xJRvuP4/vuVysI2m8jZIC12VipGJ3ujMqr21mCSwKwRFjTYre9gxDSGrrfGKKr3YSTHu02R5MI82fSLhI6Ju9y3HZM1xuH++5OqPlpGxhoEZyU4iyMqavG4Km1guc833kOxlp2yU+4tGe7Y5SXg27hW9URLfAY768/Fc5BtgPrTl1cat/rskYko7gumydnqkQnx0PI42lxXfV8Oe6P2mZ/XFPe8sHfQWI/oa/D+J4XYjoCLro4sbIqje5wce+fgRwHuRnbaXgYfde1Yekwb3Qmld0Kcx0+yLJ2MYyCsmt4nkTeS09LUMpWUXCQzT/8/BaYk8ODE11/9Ed/hJ/6qZ/CN77xDbz3ve/Fn/2zfxa/+qu/ive+970AgL/39/4ehBD4yZ/8Sdzd3eHHf/zH8Yu/+IuHTsYglle4QgADFS29GLayzU3PUBWf0pX13jGUKlf68UbNpKTumYDF241ifsBNNp8B+A0uuhm8+H0Av7Y/HgIghNn61wfZjiKYf4+3N4IZWuvEPVnj8YnRfxcRglpq0wgwOfUXg7W2n8ZkWKCT0j8hrO0ur+gyWx7b9hZSSmw2N5DSKL2kbCCkIcTg7IMl/MvQs3Wxx/XAlkBUhWNyaKx+TrHTlbqggZ51IrJBwRjB5e/b7Y6hrexPcxpuyswl9T+puocZfJAlnZaGt6h98joCaC7OacT+tGSVHT4v4h6XpXPtxOO6tpPWAf99wUMhnioOg1J96Q8tBkZBV1vVDphwP25dFs/9I1DPUykOQVbMj/FcOGVOVxpqnz0O4uxzCebOpw7zLHNhRNI57C2G4RmZE1AkJpN6AZYIrfja9OdAfIWjiCdPnuCVV17BT/zAR9HKEllxeHjVyFyia8DtFD8c//ktZmmApac3+EjHIqNQgU9eJSasxEx66b4bwHsHMtl7VgokGPQnAbxcoEWYwZ8F8KWMVngFoO8lOI7Mn2+YkByZossmvhNsiC6O4kgIEYIL2JBw7lRHAYKw9+01EISQVvHVQAqz3bGRjSe7SAhsHj+27ox6zRnIF0T+pEd4O16BXNPsCM9U3peukRaeFgMEPakL6j9SmjyZzv2qEbcDKbXk5HiK8khdMZmDAdK+5xREwJo4Fvs9McFBWZ07abxL/c4sI7fqtjSuJc/yYRFdFfcBVzg8vRrcP0JiPI7TEl3LAloe/2HLdY4ts/y9eQ7S6Zhxcpj9nQ42ygVv+ZWRnguV6Br2OeCPSz/TGdqhSrUczsA4vXAtjB3Tz7jvIMq5nD7RFYezfWeL/9dP/DO8+eabePnll8eSf3wbXQ8eM8iw0r2Ddj2lwCiN+yxdXdReuKeqsNqZQuH03H7T/u0FgzWDpQZ9GwGPwvXE1Rc18B8zr+8n0MdCvH2aNZMWgc3uL4Lf/kgIhHjIV7yVMiK07H4+rZUJmgFlj3s0+Sdru0skRJeUAkJKQADCnuBIRBDSbosU7r6AcKSaIHhmnWHtXqX5cSo3526I951aj3LOPwxY9nfRvThGOM6h0CYtTBQjdoOf4Nul/ZiEwEM4ca+e2DiOh1AHKioqKuZgDdlR+dR9qAVUcUycun4tiW/NLHkRazneMXltygkWD9Ioo6sTM5UnkfIb+yQ/kZsFvGElui4YZ1hHeDgQRpHDvwagdRfT6TU9kX57m8frAP9S6LSMkigmg3KiC8D3EOiPG+JKBlcJfNv12yLtSYqOe2Jy9Jfnwhxt5k451LsdtjskCq0nb71p7HdJZ9+rNYRYY054lEKibVuQJcpM+Ma9bKSjGf0nkt+h3OI86MTtMIbKYOj3OMoEafl+Tq+5a3Oo5ko0VFRUVFRUVFRUVFwHls6qZxA7FR5D5BgNuhkJZ+Gje3BE12ph54hCKydWp0ybh6bfqYspqV6Ws3NtE0pQ4IYChktosUkwjsJ9vZeUNOY8ji2Ar/a1S55VLxH33wrwe2EVU4XICOZ0yU3/Jnu205JalHUU7jgPNsRXbF+NASjdAQhKLtU0kE0D1bRQXQspJbQy9r/cSY9mO6QEuA0Ks+iT/KdLBWcPY+qDGZK8R3Xe2z3zjgrB0GDb9NRlkAz68NkHT1nQMa23Ly95pHS85eFoe3F0ccBt4dqCdPHK/CxSZtG0VapDq756mwlLEuyBOBevqi3uw06/BPJQtpGdY1voOXBKVeA1ls+1YJ2S6Tqey6p0OrMfB0rLQCSFKI8T43hRHDOXXPg5bPX1eCkYiu+cdfnS2tGlpWcPTjkHXVU0o5PVYbhtPAuSMW0rdu5pTgwDWLpF00/doi2HA26T8XRvXpMpuTzT5dUfk1P24IiupfDkQeEkl3zA6Dr+eFvU2KCy9Lgo/sI04GrZvDreLhd4rmgL1rV1kovgtgjm4OxbicW3qip3z/I85r3vGntUhp8G8NmBqFwb/n4AH7Ph+vbNgWxLOi4OaQsiq+JzExCWLOsA1WGn7tDdEe4iG11CCsCd9EgEQYSmbdG0G0jZgIRA2xoybLNpQdYgPoQAWYP3IUsEjXaZuJed5SLh28s+nRYAQPeHP0n7SQIxDcYNREkE9VvSUefvM5pICufnCB/yBV48vuTIOEuc2e9zE/EVFRUV9wzXQnJdJw5dticksGb7PfUL+tT19hztpLbNe4VSM+k94v4zH+2i79G4OMz9HPmVih6IKDLZEUs5pqESXTOxT19VJIko8uOP5wSCvSPHY2Qki1XNcP7c4y/MPbJrykotZeEUxSIHgj+NcHXgk2iPCcFkKqEShm5SgWum1HnOdWAHowSLLroUeH/fINAXEREs7JPKCevCiX+0AN4DaywsX3EjCAqkWKhjVgFGGsaoulFoMRmiSxOBtYZWyhiyFwJqZwzcq84QXk3bGrtg1ui9EGSNCRJYyqAAQ1wfvazK9Pux+iw5vdC4STu1Edi2ZI5jHiCEOaqDcaPz3BaHso+u502J2ZFdhZUd14biDvvQpE2PeEojoJCI+/MiLDKYWTkfM94jxLloUbDa5ToRlr6nzjE5qXWiouKYGB8bH7vNV8JjEqZ0g0unC/mXQjj1KVUMI60dh+5H+lV/4rxpL0YlOD03sYo1JabMuDk5YdEQHNF8zYlHhhqym9Asy1clumYgaEzKhT2ohKIw+Yz5CqZ00pTrdYxSaOJAlgqT6iU4VBu5cJTO3cgVPK4xxsyHIyc9wcV5CH1SJw00j8S6+V1Yw/cRy7Lvk9icNPlfEXDDWYzmtxRNROCwtZ8VGB0GQBqm/pC1DyYEdt0W2+eclJNRfzWe6GraBpu2RdtuIBuJpmkhZAPcGBUYKFJmFbZtGnKJzQmPLvxENTXM1hg7/a5FkjWoD2hvqD8q95gEzsgsrdhuBx1DJgtL6kVFRUVF7QsqKioqKioqHiJi0itbgLfEV3QBMSFCgiBEfLRbf76Y/OR5wplKdE2EJ7kS1tFSCoPqn5T0cMbDORhegmM13Ql7bBU3McXAsYqjZwjMpizhBIbTNYU3GyLX7pvUnXtyneQDKediGqYpZgLHjzb2AE7baKQKIc4Ik5hGYiCVggUGO6VUMjnSUwC/yyAJnz53nyVBfJRBt6ZeMblTIjmJIXixRJdmS+0Exl3b7X6aGSw6sFbQnYDaSeykUXsJKUFCAjcKJJzSyxq2F9LaCbPbJYVRfwmipL4ZwiuW0rCvx8y2LGxa2D4givU1HCvXECmg0vIMDwUZBhpIT8Blyz9yTtkpoP5pFOrDYkXQEL+WqclK6TlofBPBe0nEqcmIlGrhor10nH7p2HFGC2Ah+LEt7ves/52CZSq2deXUP/l3qr9V0S7CGpHfQ6xPU7C2XM5h4+2Uz/Kh1Zt+dvv5P3yRnCKOilkolP/DMPNyH7Hmuc2TD/rZ1t4oeVYb95vDkuQU5qALwV9h4Ot5yDx50GGokjDviq4CNwx8GwAZ8RoJEZaHU3rvaExFJbpmwZ58R4YAyI1Xw29rsq799q2U1PI0l/0nGRglZFd4uEXBoLtHUbyRQe9SfRysolZhQ0kaMr8LtiAmBukOtoXxUKDCz4xWcuodCtJLTj30CEbEP2MiMlEGxR3AkEHPQEWl5xxGROk7DP71mFCI3G0Y4r0auEUi+GM27uOcujrnghDWhperg87QvdYKUIDCFuaAR/J/TASQBG6eA6KBkAJSmhMeN5sNmqZB2xoD+JvNxhJhDUgY/1obdZfJcNipTQSwNmnQWvv6E28jSwm7uMOkhOwqkVyR4HIQxTqb8WSDg56k/zaelgyQ3FbIInnEffLsICQT0+Jwils35wUQkpG0ugkP7MLj9N1Bfj3ZwnuA0cqV49TvimB7cR56Y4GToPyenuTzDHXrct77x8Wp8/kQjNED69Kaj9wOgf1bkA4X37G3Ta6pBouWItY8y4V9F/vZ14I4bQhpeEMRXU+bSnHGdJ806uX05HjVGxr/c/o5FwPilnK0udsl0dkwPs/g/z0Ek1N3eTqcOMKJD8rpsH5fBvBBAmQIVWtlgzXzhrDtMUlc9KMSXceFtYtFoDAx79VF95AMUxlRE97mlu92me1knTwXEmgHTiuNI6Fie15uL2xSCSLiYkqWAu/8QLBg1TXz1Re7FKQ77pcl0fqcQZHCHLjuiDLtiRtO7mXoAP2bGnQbgmAA+DCBPhrlgR0RFofDYNaWxAqkbZ58ttsEXZ1kaHR3zwASXtG1kxK75w2kFNbAfTBuL5vWy1aN2ksG1ZeUNn4R2gURmC0x6D5BEBn5ZTKXUHlRokPZjQ+aRu4tJH8YbJRWS15AeV8w8/4S8FDdmuh3VXqWR30dcZ4jfxWjWHf2wqnfnivaJvNJya5rIlQeCq7pmaxWvKFkrGJFeHuTcxkk1CWEf2ic53ycifXn2gqzYhaG696Rnvs56tPXAf5dBr62x11WGNnscXzs/wzAr7FnoNK9SE5MBG/yphjS80p0DWJp/+gNrZXkHwMkl4N2RECkvGIbpvlkCMAKwjIWk9kwpCTihAynM/LsklFsmH7+36MuTk92LZv3L95iEoVQvErJ3QE3RRmQa+r2s8R7DSU5Dqf4wHKKbRj+rgL4PzMC8207jw2AD0XaJo78EQPCqgltomLVVpJkZrBmKMugaa3BYChs4alba6erkxKSCLJtIaRE2wRbXyQEhCS0jVF9sd32SGgAEhCNBBDi90QxuVSTP3nR3/eFSradxYR0TH6JXnkmTSJpQynRt0j8QRHZNRfeb3YxQfQwD9GQB9Sde735fmxZIsrty14aIBkPRvKdI85SMgbK/SEovc4xCT/mgSwVDwPXRB49HKwkyYrep4S5vi6cklBbhnOsRMWfS/2vT0F68cDP4dyPtWICYrHJHjf51rwY8a6nSdFmE/w8uClhJMGxmSK65L0O4DOZm6Gwe2RXmNvwyFyEtgA+G/nqTazcLiEeNj++nd5IHhzRtRa9ldBsX2l8zxFcbruVaKS3xQU2ihmzJQtQbKgFN58yU3SCTLY1AoKECY+QTO6dn1UdJEcV895jaDU8FCD1rkzFgLJrjHzw9+JYI9LMUKH2Xmy0jwuBxuw49XLK/wmgrxedA+8D8IOxB6fWQnlNi6I6Kg1pJIUwqisGGNpUK9VBAdDqDgCwJWery5zQSESQTWNPcjSfbbuBkMKe8Cj99aD+cgScgBSbUI4xyejJZEvMIZ2MEDSCUi4ujLjsQ5ieW2NaNrhJ3wvz/ca/x8I52EBpWYKPoS6rqDgmzqEUqKioqJiPh8yEnI/kqqi4d9gC+BUG3jY/+dmyYPzOHgDxEnBsWoniuZnxBQAQ0u7c6SmIHAnGfg5nZheMndpNTlsluubAjoTjiTJH1xOnCA/eEV6OnvAPXhNIAKzYq1B8eFE4ziaYQNjCZW+Y8KJwSyuKPQK4xIh51dlhFifGVAfnttUVKIxS/LznfZhq7no7RouxOfcMLjRy/7XHYmRkV4kZL7JnnIcegicC3gH4adGLqSNvAyT695kYeBTS6XYGOrWTY94lua7IPGPtyDKwtXfvhOAE7U/aIKhOGNLKElqq2xn1V9dAiAayaSCltGSYhCBhtz1KkBS+XZltvDEr5dLYf1BBOMRJs0pt7jg7VX27d4u4piGOdQI4+5HXYf/rQDP2NU2Ue8zcNMSHIJTu9W5Fz/AYOGacRdNve55dVY3sw/Ly4RVt8/RYRyXXelTGOcrlmp7FNaUVgO8O1qd6eGw9xe16lMNc/zgWBmAXZs9hkH1xnGvGM8V18YFnsjwaAFf0ClqJcxnzL8/99vsysPOrfDDeuxbdG2mkVB4ERqGmsYdg84l9kpKyH+fmDobgAoA7AF8F+Emho8wC4N7ldAIcJynMXiPTTKU0xfNJH44ziaPtb21FQ8FetOq6gdz1UYmuqXCz4JzUilRQ3ii3VXEppdApBW9HCIAURrniTsDTWps/+yBVp8AAOtVBgABrEFxKGSpMZP8rNsTtiKrRNpyzH0iZ2Osa6C8FI+eO+y4CUo3V8gIq7/Of0uFS9jkcQ8+niGShA97jjpG/CuBfAeFkRMukaw28yMD/HeBbQwbqEmEKApEzKmimYtLG7U5JNL6cPxW+7TQUMzpXq4UAgSCE/S4EpJCQkerLnfa4uXkMImFPdjQkmGzsyY9Smi2UwigqpRSAVZS5uMM24tJnlNbAJC2eZj6IJrYCD0UNdmXTxSvDmtK9/3WvoqKiYj3OMZpZ1rdf0wmJdYx4TCytB0ueyuHq3EHrxKcZ/OmI2EpUXKP0WiFVwaVfpI1M3RBRdo+dE3gqjBlK7YI4SCswMzrVGfM4SkGzglaBK9lut5iKh0l0LVE7xKyrrx/pQ45va2YoS3aZhx7YBhIEQWby7rY1Kq0ta2ltHWlj6F6pcBIBCZEqyhgIx3eGyMP2yiGGgwdILp60I2uKWmsKxuzwTPO/9IVn/ecRx8U6Fm8UxphoJakd1L8afnIggnoxZb+S54pomWko1ew7Fo6DjDMQx6UAvGN+MoXDEqwgC/gKQDdmWyK9wMDL/TjddkBHx/blqtZqGAdT58xGCRacBTZfKwCaTN0XApoIWjbeYL0QEkoj2tZoVF9N24CEQCMbS3gZe2DSEl9w24iTxEXLC759ITSZwGvbfE1oMCUcaFWcCyefHDJ80LoV26W2yKYoqI56+uKR44z40v697Nk9BJtcOQ6iGllYbMUV1gvFKjrvgRijfyj5nItrSut5UC6f5Ta7TpGOB4IleT90eZV2zxw4iopLA0e2oTPbUoOqLkvsDLXj6Dv1J2jJd07clELI7rjE7AB8IzjlbzLw9oTaOqoa6w+xYqJrMC1+55iXGUBrBaXUANGlLdGlobUyqi7W6Kqi60ggoKxfdTfJE01KK+y6HXY7s/2KhEALBltFl5ASTdM42QuUUlBagZ4/R9cp7OwD3u06aG2NiUsJYWUmHDUqEU0M3RG6AyJBuBl7TG7Fnw9hKcHJKQPKXU3/TrhKya+pETu2aHAePxAgRX+xo9KDouyrigJMAx4iagFY4jUw70QEekbAv40Y+o8T8ENZx8yAwNb+FJac63eLVitmCS/jvJENhGysksrIVB1h7Azfa2VIso6MokqQAIPQ0TuB6LLbGxu71bFpjI2vZrMx2x6tzS/35whk+BMeRTj8AZTUl1BmhNRW2n3FGTqEB9AHVRwTdbpRUVFRUVFRcQqMk1zLxyRrxjIRQfYGA/8DG8JrbbAjMKckusXgSEDDDM3G4j377Yf2NzM6y5Ww5Ta0Vpbg6qzfQIK5v65Tk9NVia6J8MSGlds5A92pGwO3ddFtX4QQEHaKTMxWVRIUJySEYSy1glIawA5CCmil0VlFlzO+7RHNt711IQ6Viq0iJSEaBki6RNGF4TaQ29aK03PJNrlKcGqjPnL2vOzT3Q3/xj5zmjHq7OLTBiJHjEgZlJRlRHIl3FyJ/HLhRisOiQAlJsHSOsFx9YZ9ZsyIVyGYYU5ydDXuawD9TpbclkEfAajxNBb6+2FTwsvvR2cNrSL6zdZfYeu4P20RoT2Sz5lRQxoJLENrgtYKQgjsdjuzrXF7Z4zaN1bhJSQaa/DebGsUENGWSLe90ZNgtlyYHdFpSbC87nOvtI839c7qTJmYXRH8AcI4CApLSP5U0GOxYueIs5SMQn9bUVFRUXE6nF7JVcYFDaNPDi58uwRcVmoqjouY1MoJrkxMYN3Ei+Wj47gJQ7wp4TAz8Hn2BubxNoN3gJuSTUEqvigru3Jod0Aeay9YYO3saxkzTlppMLTfzcZWqeVILYb1AwZbP7nogkGQMxpdJbpmgCJFl+MTyBm99gwBrE0ja6dLa5DWnjgAAEFklCZt6w1sG1mehlLG7fO759DUeXlej+hy0TFBC20mXhHb6ViaqeKIhIR6AIqKstatr+wab0tpQY27T+/0d7wxhs9RjWOIvxeIrp77Pg2X3B/w7kgd45V9BxQJt4AvMsQXDQHl92O/CIjXGGgMSebqle5Fb/dwk/B9p9IdFEd26CzRJP2pHWQ7PZ8sGxSDyBBrZuuv6ruBJauczS5h/m5vb9E0DYRTfbUbq7ZsIaUlxWC3DTtyzRm7twXRe+6F7Yyxm3vetCoqKioqKioqjoBKK1VcF8r2mY8aIfh3GPijE0bJsKQWADhyKwh+lFbRFsWg1nKG5lNhRCS5cSIMQZ4HMX/TWbsHSnTt6Si55IZgTQ/ZLVNWZYJAAIRHw2FS7exqEUG0LeRmA7FpQU0Laho0Nze4ubmBttK+Z7udmRRLCSUkOtGAIcEsQKIByQaq21k7XDZlDNzebPDo0SO8/fZb2D6/g952ICHw0osvW6PiBK0ZSjMe3T7GZnPjiRWlNLRm7LoOSm2hts/gT4u0tsMCowtLRHjuAfGpZIYgycrO++eUAPB+BQgiUvIUnk/JHheZsg7M+pCbDJalzM5P9L+SLilRRME/Z/PpVEXCh5CoeDj9TqJDTKkX1WJFtszmLWFLygqpfpC6fzd/PENBJMyMyx0XnTjKj++A7jdk1LNwKC8B0McBvBKxwpH6zSujKDyTXpIiVWJcBJJdJwlIZGUff1EEYpsXInTdM2gikJAAEaTdyiilDH9Nk5z0KIQAZANqHxk7YWRPfvRbH0MmvEoyenymvqR1j+OHQNF3V6co2P3z7ca3xdhfnmkD4dLFob0kzSxulpQHNO2FkiS7WIeHr8UxarsddTLiOpGQtxPbCANUyCMN5qVkt6xcL4fcRJ3I3uSFTuiMA/zVo7R5AayJjmPp50ysE82t8LzY64o6cZb6NDejnH0uiO+UNhSLY8eJTobXnY6IJWVz+igBrGicfPq6fuqmlc4J53tfnN6BcfdUr0uw0DbvMevt4dttv84Woy/2I/3TwSfGePJqS5YUKdyZGsJEn+nVqXZn41F6GkC+kB2Np6N7dopqbF+Tm0GFOU8/2DhlPOTKu03wVQCfdSv8BHo9Tno8T04Sbj7iT07vh2GwuaF1ILGMGsuJaxi6cwblI3MzHLuP1FmeQQnx+5PaXVr93NP+1mznWQDph0R0LWjQuZd+NS5XbAa87XdXIXy1ZE63VomgHoE93U1ICdE0EE0DaiRISsi2RXtzY+bgWkO2G1DXQVvD24oaMAkAAq1oANkYRhRufyqbNDUSty88xjvPn6HDc2xVB6ElXt4YhQrYbIXkTqN9/DIevfCitUNEUJ1Vkm236O6eejUaaQ3NnanMdj+tIbK89aVkXkvRt1DG1tZTTHZZj8Sw9p5M/sh37sF3KN/oqWTb/4JyiHtb8FDyY5hEwBNUcXBR11aoW85Yf6ghLowwOY9TD8T9nsvrHmTxJh2avzfQUdPoz96d0ZWGiDAIHWDh2cQp2gLqs7LXOQIwRfURAl4ayoFNEwf3U5o3MUPum1zEZRht7dZbnbxmd4A/cdIRXW3b+k93ndoNwMrb3xPUQJAEkbREkbADB/OCca3HUHvx26NkopJgZXKI3zQMDQXXbow7Zy+tOLKJ5MZGkQbPuHm7f5zWgNBy3WBJ9d+NA3WQ4jj7iRn4XnbLtKedJEGENPs+ujekKBBTGe8UyK6sHqJE/g2/RTjbIp4+mgH2jAtOejdPPw1OknBSHmcV1bXK67otoqd8RmckPmdiXamsyecJSa6pcY91kSfcnjxkHHkfVpXOqkd53vo+58kcNqU08iuNcUntYV5zfvQyLDVjQn6CtTjq68CU4hktw+soIDf67Kd2z0Pm7Etpt1PvW5jzDI7D4gh6tziLOh3TUnIpzDfDSJSymPMxZfyLI1durMpRsjj1qgF8E+BPa0Nykd0ZEyU1pC/MwWHnEm5e766HA+0QhCscbzU0iiyn1jIH6Gno3XOwnVs4O8sAhy2NLgpHVlmhgLsWHGAYbEpO8EMiui4EofIFNt2clBi2djVNg81mgxdfeAGyadC05hS43XaH7W6Lruvw9Ok7uLu7g1bGGBsRrGJE4PbmBo9ub/Hyyy+BwNh1O3S7Ds+fP0XbNGjbFi+88AKEEHj7LXN03u3NDaRswExoNKPrNF588QW8+NLLEKIBQFDaMK+dUlDbZ9g9e2Rkhkpj1+2gtUa32/rKzdqdfqADCcaBBHON203GTWGI0FgRVXQQoCUCQ0VZJWc4kjF8Ri9KSumWZMouwnOAJRyc+3RRqDTpjLbIRX+OVOifjpFOksExZVABANAA/y8M3NjfY+/pGwA/QsALx02SECmhEturcx24UsqTX+5TC4mdfNsrvGTTQApp7e5JtO3GbIWULYRVhUlrB8wZY0Ss/oJ98dkXmWJt3HnDjQySEm0rs3KLtir3ytPVRUa3s6e35qQWOTtpK+tpaVyAoXnbvpj23B+sN/kAJm+jOYMcX7oe0qCioqKiYipq315RcZkoLUIeGsuZ0eCzRy8VEca75EUxzr5v3288aE9dzDlZEa8z+NcZeMs5C2HGXEQY5LuJrTvULsx53J9S5hCzcAKiMcPEWtstiGa3l1FrOTELQ7BGULe5cNN5AEXE1qnszlaiawE4/cc85JjUcUoLiiqYuQpBhEZKSOlsc5lK5cmunbHL5WR+oU4ahlYIgZvNxuxX3QoQCNut8EqTpmnsaXMCzGRUZFKG7UrSEG5GndIYVVfTAiCzn3Z3g+5R6yf5u10HpTo8f/o2lFLodjtopSybq6CtEX13ggLgSCQGk1WbOaIJnNg083oL38bTxu7WqLxSzlPSYQJbbv7kZaLxtbB+YPw5iqPcAcXPN7pDVs0WU+WlRESkeWIofGmffqR3Qbxhc248yXmEA/564X8zujkW1y2At7IViAye65TG/dihB0sOS4g7fufO/SkQdkJ5MltKQ2TJtoUUAmrTQcoGutVoGnOSZCMBIdiIG0GAYBAig/eOKAfAxDDmGLV9H2oQhF39yIhfzzLFL8qYwHNSYgAkojoZVosoctsbfGRMchCKUXbfN1LfH4YynfFCS5fGhp1FxzzbBIX05/XG5dcT6mP1vZ/mtG5QtD27lK/0XrzKl1fDvAeLt4FHF4tuTw3iGc+w7/lwCTkylqkNskHkXN8LyvZ6SjSgZ9ZgD84s4lmI8ffVqM+ryO8hEjmvvq89yGjRVq7reBgXgFpOZ0FkQ7eHK6u7Az1m4edAQ07l9yPE0nhc6eaZ/FohxHwLoxte2n+oOBcNY8+gLmM/fiiSXNF4lhjAc/idKfwEwJfC70RgEU2Xg2KLkrlDmOM4Ykt7O1rGlpb53lnxjdLKb0tkO7dIy4wL1S+a6yPmRsbmZv3rS3mxSnTNRaQAYAy/DAnGLo4UEjvVGXXUbotm10Br9rK7brfD9m6Ld54+xd12i+fPnqHbddCdMn/K/O0AvCUFum4LIV6xRBWhaSQ2mw1urK2vt99+G12n7NYkQ4AJIcxJdLayKrYnGgCQbYv3fdfH0NzcWBmhhkA4ylMphe7uDl/47d/C9tkzdGoHrYyyS6lAdGmtcPf8uT8W1Gx/VNGfVX8pZRoIW+PhmiEJkCKqwTFJ5AvUqqicSst2DiafLjeRZ1gD6ASjJHL7hm0jbHvKsTiqsJeaYdKXhux+pR1GmvZ4c6dxu/jVc4J3VlwUc6M7Cid/B+B/ZOQ7PUuTfX4XQP83AtrDJyMmuuK2ziSA1nbrHaCxxQ6WsPK2vgzxLGTjlV1CCtzePPIENJGAtIbwpbCnsBJBSrOtmJvQRStmdGrbI//Ci034+Xb+QpB+62JppShXTIbPeFXI2fQrv5hiAtr9JCyqWX7hYCYYZhSQbX8upsGnb2bagucFCUzjOTdxdX9xjnK1JO9pFigrKipmIFcVVBwK9R12FJSZmiPjTO/NE4Y6uwuYQXIVnUUkk3+kjreCG6u6Mam92iPGQlievPo1gL9iFo5I2/mwzNzreBwPb0sr2NAyJosCmcVeoaUtueUOyQsqL5dvDvmy43w7Iy+l3LoNxFZMeJ0CleiagwLJldRrO/8xE03y+0/Juu12O+zutrh7/hxKtdDM2G63uLvbYru9w267g7KKLtV1UJ05ocBNPLd3zwHWuL29gVIKgswJczGUUtjtttCaIRvC41degWxbdJ3GbqdAdzvcvPQybl56CUK2aDY3aG5v0Gxu7NYshiDl2eZGa8i2xYvf8h7s7u6gtVGbaaWg7Ofd22+h224hZAO2Wx79Hl4VTlrQHG99DAbqDCkUTgfMiYV4Whk+XUMTMDqtQgPrzXXJKsos8ZQQF6UHnqstouvslDUcVwvv0qcv8kM8FM9xMC8qqz7BiM2uPf6SK7nYJimJEpOZgQE8nZgECeDLAJoZRMpLBLzofkZpH+h54z3r3n1kAN8FaxadCNAaREb1KEUHJXaG3BIC0BpCNp7oapoGQjSQ9pohp61xe3uQhD+1lZ0m0fYzJtX2f5cPMmmjgjpoIG8+/5zSso4YdqtAROTLgpPHGC1l+fLIiaSJNcspQfenPCyEJSND8i93Xzb5yhuCc0+RJ5GmI83empwn08aGVGEwEPxFDSOPDnk7KjLsZwMvVGWZ999pZ5lr1BjL5fTLO/ilZXsxlWMi5teD/gLWsbFODFGaEE1zd57Z7fz4VotFsoWa48ONJ08Y5UKs6rewNI/L4hxTuhwdC6I818LSovdJNOby4US3sgiK3pfg1CXkxpuHDbMwsErlCNlQlNO6zJmPrL+idECXxO1HheRmgVEG4+7d++vnvlRbvFLsLQBvA/wmg96J/Ed1xYcYmT4B28PlONjYigku92nEJ/Y+IqPydu4Rx+BILjffK+5GiMortis8ntty3vulNL1dVaJrJgarp5/HOYKDIEnY7Ulm4vvO28b+FoPRti02NzfYdR12nVF17boOd1tjq+v502fodgrbZztHq6HbPocQAt3uzvhvW0gp0G5aPwl+9vQp3nryBEQSN48f40Pf+73YPHqMbdfh+bMt3nn6HO9972t4+ZVX0TQbc9ocyNrZErZiW3s+ZE6REze3eP/3fK+/5hq/Y4W//OnfwdNvvm5+u6NElYLqdlb11XmVWdftoLTCbrezbjW466C7zjdEbY8d9RLJRBoZ2HFn9yzcyZ6Ma3yeTQ+MBFnVmffBQD67Tn71Wpt7zrFpQ/LXAGd+MPgrndU2BWdZ3FmIcyya0psAPrXPVfZG/X7zVyK54o64NEhhNoce6Ixc9dSQNickMgDsCDuQfemZGiEbaUllYU9mbezpjq3fety2G7sVORjAZyEB2UDYRiDcSgqFdPn0aW22PvaIxqEnRIDbmhnlW2s2ykhL7ASSKzaSSWmwyZbG+C0/EZ6MLt0b9GTiKN1P9egDvnOPpcHSQJyz713HpOtQmEFxHia+B1O2DyWjDymfJ20pJ4zrfFE+FCwVQq+IEddDqVTswzmeyPF7vCnjuAHnwPTBRCyacHFZFo+IvXArDS4NO9nWl1yLvnyawZ9hkEoFIYx0/A8AeteZ8bsOZJZm9jusjAF5p+Ryc2NHcHESrVNhCcsJpLa/EBLc9WerPTthZ8BVE13nKzaDlAhJv3tFlxBopNEUslbodoyn7zxF0zTYbndQ2pBAu90OqlPY7nboVIfddgvVGSLJGbwmQRCCDEHUdbhTykyAmcFSYvPqq3j01tt4DIJsWjx+8UXI1hrD1gySwtGwZlIrJYRw9ruEncAStCds3H8wW6oAb4LHOBEgrfH43e9Fc/vYa3tUtJf32Ztv4vlbb6G1jHHXmVMcd51VdikN3e0M0WVZ5q7rzDbLnfnUKhBeTjbpUqjtZLrIvlM4fcL9jil99zOQYOEhJhPfEsmVzZ1NH8WJUoRyt454m4lBKevccCZ02kPEznx/SSFkl0YIgJK/KX5V+XLu3+NrAH4XYazmH5yhI4kAfAsB7+0H5dRVlJ364clOT6y6uE0krl1BMzQ7koqgaAclBMROorO2+3at2c7YNmY7oxQC1GxA7Q2ECH0LkbHDR57wIk9ACd8qgsKwWCS+UTOcIiUMmn0PEHmMysnnNCa7YtI5blP90iqBoHsKrHIgpUpSzqtzTj2VWRRUL84Ced67X7oX+fOdZiFOjF8eUvkcpjc4Edz46Z5PbFapG1asZNTtWJeL4dfmYdvCOltSa/xeU+W7pv7nXJRDxVGwmAvMyZPh+2ujOh8oGyWuxbDd5rh0+kOrbCF8rE8dUWP5qOKvfo4axe9G1xlhFMbw1uNTgD8fGDL+OoO3QWWlneJKh99OecWd8rum+p/akFvWdq8fM0eTfMdLebFItrA+Xk5ZfpLPpDCDj72DmeW15KqJrpMibifRpIgo0vRE5KYgePmi2Zok8Oz5c+iuw27bQUhzUptTLrntfjtr++r5szs7TxIQUmLTbkAClugCFCvc7bbG/lbXAU2Lx6+9hpeYoV58EZvNDW4fPYJoGsNr2S1Qjr11ygzDzlryCwSGgGZh82FOjnAiLkqYLjtpJIEXv/WDICK0jfFnxGWmEX3zDz6H1z//ebiG7huoO5KUGWq3NWSXte/VdaYMttutsRFmlWGq64K9L8D63fm2ZviEiHxwhKNttH5vMBOYBByl56fHmUyY3ZccJZIrdur1uHknkBmcuhI4Bc/6gLD3TezlvodGJgPH5wF8nqOteg4c/v1+Br136JkxoIPyMdQ1E5KkQLcwG2UUwe5gt/We7b3QrVBQeUlhSfLGt9P25hE2j1/0JJe02xybtrV2vVKlWEI+cZyzLLdUsEPmyoUaOMP2yTgAsfuIeknUXEMvpgkvtH1VYGwSOWR7a9CGEqP4wqbMTe9i7KecJ+LBWxVHw5UN92sdqTgLrqydPAQcYy/XXixmYg6aiooID6hoD/nqGy62dG7XS0Ox2e15CCPDv54J6PiwtnjXRDxv6A1PCXjCUP+zBnfGbyCrnCmgSK1lVVpaazvpcONzN++OfpfKIyajWAAUzLWkHFRYGI/nC+5OIKyc37zEl6zs9Z/anEW+SnTNQV6yMRtSKHQiM0UkKaGFQNtIKEVQ9mhOZRVLxnC7YVlJMwQTNo0EQaARG8hGopENmsZMgKUUADOea4X20SO88oFvBT1+hCdvvolnz55ht9tBysaTRVozdp1KTnP0f1aXAcfuEoOEjJjmkB/25E3E6JmWCgaw7TKFCxO+HR/Fu8VHwnzbySrJNEbNjM/K/4zf589ZdpmhlfnslEmv6oLhe2Wvub+758/9nmLNbn+xM3jvCDHtsgeOGqiMmnufXEmJy/AZXBYFLL5YOJSX93CmGY1P17BCpbxiFL6On2PSR0l1wk7hsieQot+SumX/gkrqJG+/8fMq+fkjgLe2TkuAPk7erheQHqDQJ8o4KjH2KyYCsPa3REJ2wX6aU8mU2VrLhE53fiWlUx3udluvFpWysQdStJ7wkvZEVyGlNWxvVV/W5hfcb/sdzoagJXodKefJr+hl5+wNJHYHrG9vs4qzOp699EIZlXRXNiWjJNl+JDsV80c+Rtj2KkJwa4cowy/XON+U+RuoZ8MXk0gjt8Pt9yR4IIPvs5y2tjDKuRYV12F9uVzHqYvLIx1Pb+H92bs0P+5znQ4491meD8vSeRYV6uIoj1VnjxPv8jjHXqbTvJ4ai+tRVkjDa3uHyVgypDshDvpYRgIrkjuJFzeuzQPh3KEJIx7mZnPilPAJBFNwlk6sGewPcePfYeCJHYu/rdG90xk30Z/bjmgIL/a7nsL8PgxD47xSKf4kc3akK0qVIJqogCM/0TxIeK1aFuecSjWwaLyiXl430eWVSDNwgE6BXdx2f4+ffgRjOSZ5cKytIbwa2QBQUHpnSReVyAkBUzkFgNZuK2ybG0hhyK2mlXYia2xp7XZbtLe3eOG974W42eDtt9/G9u7OkkGGGOqs4mnXWfYXgc/l+Jtnewkk3R7cvKPlrH6bCbjLf6fMTdfABQgf5PfjT9J7e6QQC7aNF1BQ+CK+lhVyMJpnjNmbLYw7ZWx8OeJLysYfh2qM5Hfo3GmQztaX0mBoX8aJVHPCa0j4vCY1wFN+YXMkR//2y28pDv/e6aumpsWRU30j/gr9aP+Q3QmDlh5JV/A3nQOb1/6/xvDVsgX4owA9st24AKQ9jjOsarhWZesFRVv7LPFJANwOYoCidger7grtIj/sQnc78PbOklWGMBPCGbOX2GxujF2vtoVsmkTh1bYb408am3xE0mzrpUDeaAaYraaOAQ30+wGXHcdpxbWdI3rPrQQVxgjBTRxocMV2W+diRGOOnvHrkWD7R0UXCNdRqbbt93tx5v1CHF7mdOx9xsPhnAJLjOqeaxK+BufI5yoD+CfHmkn13HxeX/3po5yHtMqszefpy2nZARN8nke6hJRbm87r4qDnR3kfmuaRsZzkyn8XSPJlIc+I9AQwk+mDBjieC97TBUUT3J6jiNjJhCD53CZ/nwshgMKBaX7boRO7dBr6Pyrwl9na09LY7XYmX+zmBrFh+ZzgYrNQDcs/uP+icb7I0uZcx3a5PDmV7/TICTH/jy+ZnqJrOvIy3OdmevjXTXSdG9mTCFOd7LetJK1sjK0dkCdxICXA8BU3MKrm5DUpN3BG3smGRZY0uGlb3GyMUXow47lVN0khIMhsN3r69CmElOi0mciaLU8NmrbxNn7YbelxDUi5LVlZfpOJbThtwW6SMvbCkFVFIcAciJV0QmBcfkx/O97P7/ISTqNEsayyhCEJ7B7kf6d+A/9ZfwFs9yK/+NIr1h6YDuRe19nPnTGAb5VzqlO+3Lvtc+huGxRmEVse0smh22Nb9gRftgCgwclzd3cCq12a0FdcAvL3WK97jhuAAvBrADb293sB/tPavgsCURVegG7Dn3lrMLE5/ZdhVl/AgRiPmJkg+ku1GsxstkOSALM9iVV3UAC6rXmR3T0Vvt9wNv3IKrk2mxtjq08aUkxao/dSmk9nBwxW/QUCJMgeL9zBKb9CsZg+w6lBXRtxLd30Ka5llDqSOO+c3joQSjEPu40ZfAz45IX3huKsqLg21Fp7CByWJLiiZ3KWpPK8l0FFRcWVY6yjWXKPE1FLn25J/TlVVSCEtBncx+otNlsR9X9WUL/tth4y9Fc78HPjTmuGUp1PQpCoxFEG8skspLvZZ2pdl/z1OFd2/uq4BzeJ8WP3dIk6+I92N7i5QW4eZgaWL/RNQyW65iCbk5V5oFAZOH7wzGbyyYRGaGuMGr4qimgroSONSEhIIaE0oJijSmuUGO3NDVqr4lBs1EzOVo+bgG93W5CSJj4SIDLbnYRwshLK8sVhwh7btCmoNwhRPoFkMtxogU0n0Sjpvcf7eeOK/Spexiv8CASrVIHbXiVCmxPG/+/S5/A6v21IJxjSyUs4rXF7pYxNryfd2+h0Z4gurdGpzm9z3ApCtxOeJVfOmJ9T2NltlBQRXlbjEtmWZuSdTSihwFrERXiOrSalHU9BgzbSMRX8TfXbc5P2rombEsaM0g/LbkcwtQOO6mVCVDOsuita0XgHfktlQuC6htEQ6MblIUqzP1TBuY/qCcVj8kCgOWWVIZLcy9KUkl3AgQJsGyLzUjOyLxAJKNVBCLMFWrgTHltDcmm1gZAS3JgtlbKx6SGy7z6XIrc6FPIUUdhJURMYZp9/oYgx5YktJ4wKVW1ZuNEK13Co/fBcifh6WnA+OJxiPvpLv6JiGa6IULlgVCVMxf1CrdCDWFw0nHQUxWDGOpKrG0NMGxXuc5OORXPyaehHXlzZvcRdnyyK/cXBxsIJgjL3n2mwSg3D668qdH/QGbGFM71jRSeIdnvZGMppIz8kD+mM5kolgs7NRh15ltIAjuTinr9ky6a34RU4gCnvt9IYd7jKlt1WG11HBE9oj5RvObLkirSno0khIKwySwhjbN6fhKCMXSkpJAQJX/kYgGATttp1kLcbvPad34X29hbt7Q06pSAE4WZjZqHP77bYbbd48uabIBLQkNjc3OL20QuGDLN2gtKEG9s9JKJG43k6M9k1sshA3oFhVCbWbpDz9v43XsAP/MFr2GyFtZ3l4rCNj8LJcYIJzCJ0T7b8lCMY4CbOwI/iB/HD9P3wJxy6CIlBEkBjCKYddvj/qv8RX+FvQOtc5snQagetg72vXbeDVhrb3c4awO+88Xtj8E+DveG/znYEZktkTF+5jWsC7Bn1nnKn4jKxp+eM1X7iywD9knnChix1pxDCNx5+P4F+1LVfazOO2djNEoEETwXN/ReZfWfZeyrUNRG8hFe73Y7sLiizSfdZtw1UFQmQNMovEnaroxDG1pd0xu2NMfx28whte+ttfZEUtl7LkDjYrsCPzdinxXzGFt4Cwd9/hca5PhyGyOU9T3thWpb6q6ioqKiouCZUkusoqMW6ENH8tHhv6Pa+AueeQIOiewwYlRaQkFhuoVipO+htB/0/afDXg40t1gy91eDnOplfOLLIzJFjxcHwwWA9w/Fu4uDH5Novijv3ZOfjLg538Jgh1ziaEpXt0zpxjpvECHcI1oXhuomuMLM6VYQI1Gl6OZ7eJAv4FCZ2bhIsiKBhSS4hIOyEkSEMm8VhO6DzK3ylhJ1QE9rbGzSbjTcuLZ2BaavG0MzGRhcInTayqKa9AeskhTadoSiLU08KSg1D9nK44YqBAyusSONZs8MzaQmCqOGaMgjKk0d3Ao/uhG+QMc+cFD2Ax3gUyjKeKsdMNoCOOnwI34oGLb6ivwkFBdbSEg4M1tJuyzIdjtiZbY6y7aCUO/kx2DrTWoOjUyEBbbeUKvPHGmBjR8yx8ERuP3TYGDVNfTLWIQ+g9NAYpZIcDzsWHq1oW0uUYqkT94QP1L4Lstq4rVJ2fS86AG+5KmvCjg1SMgh0C/BXACZLP8WRETLWPMopAfQqzDbJEGR4YUXXvNLYEkfEHBFn0dPXoQ4SaYAFtNAgYequEk71JdB1O0N0kYBSGkppv81ZSGmJ8gaIlKFBJE3mxFmf3pDVJLecGZ2PVoQQXx8BR//4ovWPOe6nI8P3o3U6qx9Ovh09p6EalK6buduF2hUR98WU9KvpJBx9aLEwXcC6fmTJwvSaIcG6E2aX+ltWuFMW3Y6DFflc5HdtJstv2VOh/Gi54Oa0aVtnV25N5VvRHyyOjRdHu7hvXRDfmmpgxgMnrEOHfukMJL30puyp+otD3P3+Zo2NF4BX1LtVL7Ihv3tfqCvSu1RFllT68XlDaRSWhsXlZ9qPMAQbj7GTG5E7NyXjkM5g9sYQWsluoOcM/bq2426G6nbgXQf9DQ1+3flxuzLsIngxeWaAn1BdI8VcklTEB3m5Xjud74Q4KOrWEzdZGa16c1D8fV6dWVrFrpvoOiUGC7hgmpsIFJE+koQxvm6cG3ILAEt7iRlCGMmfpMY58/8IImtEmv1vIawyjODtdzkbWZoZQgpAa9xtt+g6hXee3uHxiztASOy6nU+LOXhNhIGWbYAhEfC1i2z8nriKGGSydrRcOXzp5bfwlY+9bYKMOl0pZVKcDOB7vvAt+PgXvmWg9YRT4bz9n+hO6AJ0kmTBEv8V/Vl8E2/i/y3+Nd7hZ1aN4jK+sfML09FstMubK/awlZTdKY6W0Oq6HdgSYLvtHXa7LbrdHVTX4dnTd6C6Dp2+g4Cxd6SsWi8qytFBQv6OSmvYzI4hCTd7rpGDueFeJUpyWWDygCKW6RJMO4trYx4Kfx3gX9Jhq6slYGIbvsWYJYA/D+D9/eQP2dT1m56pX7UYgBBpXAwNuJMdlekPgnHhEIhsWoh2Y4n2/ITHBm3bomlbNE2DptkY+2C2jWv/RhW2fAjuBFQdv9iJICAhhCXoTdJ8UsxHRKhHXxyB6EJz7gQxzHEYWVkUmgDAENDRE4zfxM419SP3I4JMGZs4HGtXQ4PsJUzXkdvvwnStnzOctl9avnV0TU6XMog4/nMvRnoOv8dF6RVw2qK93LIp4/Qkl8HStrmW1DsR1iwu8tKUXlvduwxMIcmWG6N345lT4lwrJzOIqZ5TS31FBFQP2RjSzQEJgDO3M9bXe8sdMLt52G8xtLah/UFodseP1sAfaehPaa90ItYANOwOxl5ayXIGPoFJerj3vZzcnMIquC3MD1wmGQw25rmN+GZC7TNJHQq04P5M08xKdKHE5Pafhn9VJpPW3tTWVCQ7AGXAVF5faeLvzgv7e8kA2xrmYRCI0grsFF2GYCK47tStRjuFFxPBqR45sgvkTmEw1w255ebsTGxmmUnnkDY0E2XYEEQJDRWyqCRn6jFYsz1p+X79xWf47PveKHYAL961eP+bL/YEOS42ir7FySQiSEhINGaC7eyHsSk9z+vZpsrRWaw+dbZQyBGVVhFGUhqZquogpESz2UCrG29kfHt3h+1umxz7yqwN4ZnQdK5ODdBMa0koS+QRZzWVcmcRQRv7G2gHAAqn6SUPZ3L6cq+LMERg7UNBlVgMp3g/qe19HsT9UAW3gxFZaID/EKAnmZtXAHpfxlKS6w9KKewHbR/uwHihP6BQClCsPdGl1A6CBLrOGLXfNS1kI+0pj401hG+2RQtr88sYxpcQJOHUX4Ji216ubcKSYQ38sQ6OzOrlJCbZbVti3xMG4j7rUhNlXRpUFi71b9n4vGLM9zv5DMP1rWlhjrXxtZhyYmTF8XG/S/2aJ8TltB9TANMP+5rLr+KicZaqdaBIB4IZJYmKHNNgQOHr8ErhvPhH/E32OwGzQ8k7nXwcwIWxonezMs1LOtMxL36OwWG4lU4Ck6/FUXYyZAzmZNJl0zAm9NsGmcHQ4bcZiEZbDq3heNbQX1DQb9jD5ayiC99k8DaeeMULqWkmfVp6D6bPXDuSDihNS/K5er7dMCfBxp9XOobMxpfBUcFjMbQs7NGoD45KdK3CRAac/MYiU3cdkeB8E+BlHgnJENRMblJl5lTuuNCwxxawBuvtTMwZcxfCGMF3k0qC2TYoSNp+w9is4hA5zEzbJ7dAtLCNNxikTzuPuHQ4+l2aFAKff9db+Ny737JuOJlzf+SbL+H9T160CXFkVpjaa5++fiMHAHPio9OiuW6CoTn8ppx8jAgfI7OzRuklIMBocAOwgtYKG2gQNASMdBUEvPPOO3jy9tvG3pruAiEpdNCYOLLBMvmxjTPkk+ycAE2eROF67F5r9GpoiVjLeh4SBZVKr87mDJr1m4V+sO2HF4S9xJV35VpJ/2hhj37zAn6rX7T0XQy8N2FivXcXU2wPK94eR4lLQyOVX7spVLe1yjVbhynue5ydL2EPzzCG74kkpJR49PgFSGlIsLbZoG2N0XuSMqvSjNhAv6lWjb/nbPb5cojTYLdUku0bd8otmdnexw9gXP5yqhmR+xC++fRXkjIZup6HUy7R0AdVVFRUVFRUVFwr1i4WDI+iOXyWSK6c08MUAoVhrG3YBd/oz5inYW+32RuFt9sLYrduvKq1Bv+2hv49O34tFIYfkZeIrL15d9+XMENL/d0/VKJrNZziqkCmA4bAYMduoVjvKPrHk1yubcORSHYa63iSboc3/vDz2Lz4Al567X3GHhSEmZQSQUqABLsTTSGFhCRjX0cIgUZKKHtPs6GLhJBGhWQJGyMkE54485m0ZFN+okOJbc/JLgDobhq89aF3g4UhoDQBiggvfekNbN56nvh//YU7/K8f/XKYlGaFLCLyy/zv6SsQgDts8SI+iBt03j8DUDC2jNwkOWGv7fe3v/51PH/yBMJ2UuRvM8Dk7asJYkhBYK3Q3jxC23WQTQsmAndhS5m2yq4knphESOpDlIuhVShf7ojSF+c+CmePNteTDIiJ1iipWdkUboystlDSb6+a5E/klo8PS67GpJMnU9y/cVmVqCWODipIr5fAXwXwazoJt++yv/LCLQEfJ9AjDhcRvYCR8OwpRL4B0PZKbMg7rTVIE1gRYO3umU+BbreFEAKyadA0LdqmNVshpYCUDcjaKDR9kowILGnCgDXa78kh+Pbr7RqosCWYQUFyHZ1kaTjyyMBnVDb+n4hddwdv5IqsEkI7iUkzG3dWmOV6MR8lOyx5ez2GrZZzqMTW2xE6TZyD3OeRcUxF0hBo3/vo8DGu9B/SO1xehZ6UDxdvGu489/cKK7M4qMgZ9bQu0kVxrolvYSEtra3n6ENKmKLIAmBf1wW3nP8svCcH2nTidkZ59OI4ZFkueDC9oiqE4a/Eczp/57CVYd+71KyXjw3qOfsMP8kyW+V3r5vTpDalGZF9LHvfHVbmiS3llFxmfMsdg3+HgXccyRWFCwZ/Nd65FC2jZgvSo4WwFyGM4WFYiLvkby6W+uwnb2nPdLjBVCW6ZmHio48n+WaWNWl+YziqIbdp3KwV3vrKV/Do7lW89Nr74FRj7hQ4Icz0VEBAaxh7XkJYlZf5Y21s2zgezpE+AIyBHXJMdETI2LS4HZcpAVV6WbDPD5MJS91IPPnwu6ClsEQXQRNw++QZNu/cJfl86/EOn370zSTcuFsUUWcdS0xNH2juPcJreBSlhzkjuqw6JSbzGMD22XM8f/sdk2/TI8Npw4wSS0BKghRAI4UhujYbNNsbiKaBQHo0rGaV9cWcfI+NmYffPFpvAtlI3uA3+W2zSF8EwVNSno7cQv4ZESLsytNVFl8oUV78NlrOq6uPqxd//Lvgp2iUfsT9KcGeKcmIDdc4xn2j9yA8Bvx+k8HfgKO8s9AKo0H37ZaBPw7gxrlND3OIfbD7Yr1LeyqGryPuPe8GEqygE9teVsHGwBawWxgbY8NLtmjbFkJKr+5qmhZSSjRNY7c4CkC0IGIIYVIqrLrQ2+PS5uhlhjvNlaEtWW0Is35Fc92w28bbOxa5NyArbHEslLHrsxNZumsHg/WZM7tt6zE2oDwUQbXucIplWJL2KQTlweO0LfKUk0aesghyhFjPQ64tqQdjCS0RW3mcKwmSvf3HmNvT4fRxL49wiKjYH9uaOBd7nY3QdS2L9JSPkgvfDhPwCDljf4weVjSSHO7b3Mi8TshLMcpDl4H5OAbVHviXoTTPzEueyPxhFaOKxmjaCTjyDnhPtLGf4nw5UmxFqix3wJj77U8/VMoruhzRxWy2IPJnNPD1nMwaSlP/+4DrkfBSz6PvIhr9eSAsCbVAeU0KpuxozTC2El2nQj6njbYYettZjk9K+Y4kiF51pzAIdMEKRFuL2g2EaHB7s0XbNPEc1k78jD0vkDFw74zRAaYT8NP4Qi0LE149OhBlAG/8sffg7pXH5sTJVkL77ZQBb370PXj7W18tRRK6xaw8vAQ1cus8xGqLmyfP8K7/9LUkb2bvdzCOH3djrBkvvvZ+3L76LpPmbodvfu4PoLZbwBmWB9ApDa2ATnVgraE0g4TAo8cvQGsFpZQ/rZF05/26vd9h1SH+g+lkI5JQCNF7WRC5CVa0aS1e3rCZGupGk+sJqWlKgSN38ecQhgZp99LQ/aJeN36x9TqEzO3+l9/ke1sAv4yotx8e4NBLBPohAtrUrSPA2JE07KsJ4NRSduDBEFEF0+Buh051ULjDne1rpLXj1TSNIbzaBlJIQ2rJR4BoPfnVtBujDLMnPMIS8pIAiLCN0ZBxKnSEyNRvbtXN9RcETxg61WZSovGgxbpK3TiSLC/GkZYyVAXuMc44h7/neECVqOIouBQ1T0WEFSTX6XsDxul6+P4CVsUhsfBZDg4nOf3Mrrt/zbCRio81nqvmkbpFzhBSug0RzFBaAWxPQjQDRCjVeXvKJjkMfovBv6aBXbRAYhfvSQP0FpIFYEpSF9KUjxn9GLnirLhuostOek6DAttcIB4SHzxwMbBHvjG5OCh3ms2lUrsyMa/hDDJb+1l2+1DbNGANNE1j7OgkCob+9ppSrvtZpXCdeVR6qqWAkgJ3Lz/G02950Ru1Dnl0+SBsX7pBkJ1E+eR0xcSrmMh856EOFaF+sCCom8ZPchVraDakFIEg3D5OGw4zo330CM3tLaQQUNst5ObGpEV33hg9b1qoVoJIg1mBu0dAI9CoLfR2C/nsGZQSluiCIbo4Jbri1QOtTbqgyXffg88mIhf8CleJEczYUuKgP/GGHpOSjUhMp0FxyjCv5nLuOPu9YhiScz/JLUfmct/90KLOHpS3Dc5F//kMioSCi/AtSCOzMEtpMx1C/PLsR1GIVAP4cqEzKbl/FwNPEYguYiS8FQflCsngzvOjiNRNZOs3YNWjxh8D6GAUlEpKCCnQ7VqjOpUSkCoiuiRa3UEKgcZudySrTPUKLgRbhSo0AJvdSN2Y9yWO7XIfve4jDGf69vNce0utfpXLtd/frcEsCjRaSFmLJa3FD0MXeE769kVY1r6Xbl3s6yyPjJNvJeXs81QYHl9MQ6GXHA2OJ7hZkIqxfnfv9cMjpOdc9Wiul9jq5Ews6rz2jcAeOg5AchW8jz5jLruZpOwqdSNz4z+U3z04ZovspTDpmJalf3CZdmBu1h8dhTEvZS7dOC5PG7stiNb+rTMNE6uytFZgxdDPlSHGLPmlVWdDN/M+fgPA5xnY5jNdNzaP5splTg7J2Deanx+im432+4QQo3lb6jZN01wMBLskhHBleIC6P7Sik4h1nIDrJrruA/L2G//ute0Suwa4UxkNd2a20wgiYxD65hEa0eHZozsI2ZoQtIZSCiABb4eC2di7YSDMbOMJtzNO7nlwnxLNcTNM9TtPPvQuPPnAu9DdmBMLncYiPqUxEFXwhJ37Od7vOsLLTojCbLuHu1ce4Ys/8G1urgvNCpo1hBBotx3e9x++BLlVEQmlfd+stYZoGrz/u7/bdq4ab3/tq3j9c58D//D3gr7v201uWIHffB189xz8xjfB/+H3gU/9GoQgQAg0dBNzmj7vsbzW7Bc3x9aalYh0hYKdH4T94prhybm8eBqk3YF/lVhiwG9ZjUjj2FDjYK8+Ii+/lwqui8BQuc4bnIzwicATBv67wFZqVkjsysX4IIH+SxkGAhkJ2VMYciC6XPtSnYLqgO7uuW/7LFqwNXJPjuAiY/BeWDLMbXncbDZm62O7AZGAsxNGEOaMZBKQZF+KVKjLtstQOt2S1dumO1aYS8e2S1nhyUwXHXa2fuJmHWj2JThtYk1azzElvgKS4iBxPoR3yonLdi1/eHKsSOxDqUIPAgsf5hXVgbMklZcTl3rhOEMQ7PjMJsGmg02gABjakVGRK2bGbrdN5k+G3Eq3HWqtwa8z9P+kgZ0Jzx3ilsyXFOz9bL7kbL1SiYjL3QeSq7+oIbD2iZ6qTlxRM5mMSnStQUZa5DdGxxHeLwGxTZm4lvnv0Wl3/pv9dGw3hRVwIkAIZ7NGGOPPkRLCxxMlha1fM7eLiCMQ4iaekFwJIRdNCqOOS7UNdo/bpBy49y8QjPC7cNjb03EqkjjBU6f8viilQPd4YyfaDK0FmLVRkDQC25dvIXYK0PAG+V0encFsKa1ZbtZgqYDuKfC+dwHvfsXYFGIFFh30M4lt9wz6lRfA733FqtgAEm6bKIBtB/raG26hEgDZ52Ond1qAmSFsJ24kuPAEV+jYbXrCEkqPOEzLJ7pnp2ci+eYfSPaEXHmGmth/pkiIyvLz4fhHci0hRgbaVkyQnhsmiUNpiQ6OiJwNHTE8NT7fEgbZ4OHSz1dqOGpjPl0KwJMQpqnvA+G/ANBXC2SQ788Y2BDwSnTqLIXugsmRthb29FdGZwcqAqQJne5AJKA724cJCd3sIKQAq84QX93O9nVt2LbtDNx7Q/em7zPdGvm6TCCjNnPJj/LTq4bMSR30isjRR9gvv7QdzkWBZC6+g+wzPNCoZbFx7hUT6mWGoPMB6cS4VpCCg0OBI+PkPSEN9WHHjXStKnHY+5S2tBZT4mCATqwIBHBytmth4a5959th9Mw4rwgL10yM16Wd88IIp8ZfuMz5t2Q4uT9BzsZbz+2MvJTGsMfC7FfuUhWiI7kWt88yhpLvr0dzXD8nYfhFfGfCxSvnvRuG6jroHYNfNyIB9ra12C/OMmvwGwx+g4GOQ+T+bKhoVm3bUG846w826s94UrdcKAiO/lb07vkEeOTnetDa1KahDS3CHslfCZXomoijDQfygOPfft5vCayeo+jEQIpObIQhZ6SUEJIgWKBpWwjRQDYyYdAJgCBhFUXuogkvKLriJp6RXYCxfUPmxDNnK8fBNfHgN6JK3LvKTXZt+pNGVphkm84o4tFd5z40IUd2ORoUEDP0psHXvvdD8J2stidxWPfSEV3OKDZrsP4g0H0vRCshBKFpBFgTtOrw/PlzfP3rX4N+5Qb6x38Qm80G7aZBK4Qnu+hL3wD98/8BtOv8llJ3SACi7Z2OdHRSXACRLNecCqKUOS3EfYYjcNPRT1AR6+R3KEqKfsdpiIov1u/636HCll4UMfF2SUTVGoz3B+kdx0WXBhHzJo3Ue92auET0vR///lCHn4ghZmXi2uNrAP67gic7UFFagT5EoD8nrboKQV0l4kqStmVFDA0FwBDPrM3invKKxmCXS1hbX0JKCClxc/PIENOyQWOvNU1rT5ptIYSEaBvTBv22R4IWDfLzJbMsIVFU+sYDJId4VCTw/fxJi+fkEeLk2xZxpon46Yv2XJGeHqfO5nka51nwMHJZcZ9w1Dpb2pHh5gxLsWBFjRFOOQSyLYfc/+3/YOY7+LqG/iVlbGshJsPcuJuM9Q1t5yp2+OnmdjHhNpz8dBY7Cb0JwljZTGMXztt/TYv9PKr2/bhqosvW2ZNg9PENLefGifNcQOaYkbawiJzwJBfyLRymC2Ry9rgiQsK2c9NnaXS7zmwPUgpE0p5sZsgW9sSTDc+HHzQ+JgX9UmbvJs2wo992j1o8f/UR7l68QZ+i82eP+SwHBVlkVL03b+/3RsXTAhGkpq7sklPObMWhSKrLkgBru4oJYOGcE9gweNDC2UEjMEmAGMYitguULfHUYbfbQnUdFGuAFVgTOmiQNkb/aSMhvuODoG+8CfFHX7MkFyWklyEPI0LJbs00W7TYHDogjC02c9KmhFvtcOo86U4XYCQvCURufBnEdTIq06TIYxtFBBAHW0hu52hx9d0HveCFEfn3cZfczETp6OWpCK1jLAzOvg67nSpcSWON2sOg/5EJeJSmsRfUIIljuSgTSlx3TJwNJPAOQL9PdnDh2huVFUjvAvAeANBZeijJJrv2ZklpJgKzglbm5FPTz0lL9AvIxhBchugSkG3rjdu701a5fQwWjbf1lZ/KSECwU+cvwA6W5lTAfBlgPjipS+W441N6DqNQISw9hW5N9EtOWQvxnnbQdXqya9oA+dA4aYwHj6wcYH+ryeExJY7LnCYcDhz9u8DjurjnNs7DS/uOjkUpXpjNaKl7WQAT01HeBTDf/9gi6yQbX1P95X6Xjk+xsApOUXUVia6lEQJBGOFDC2EOzY8BQGtvMD42x2JMt+hAdLEGf1VDv+4WGa3a6wkDd+wPUYvHZ35JnsLivRk26qSMksdDWThjWS5e5OK98tXo7iDLVvA54HTZYuuIn4SXmODepXU0GUPj1TE/U+Iex1UTXafGkmHlFD+Jm7jDiEiFaNoCyzCYCZmItuJoBPfMUErj7u4OXafQ7TpI4SZ4EoIENBxxYgkmdqnpbxVI+isiANoM6zlOWVBrPXv1Mb728Q+YvdvcS3063UvcxMRRv/BK5GZf0RXH0icKTZ/HIOFSDUBrhG13YcKSqJmCJMqqotiUny0HZg3Vdeh2Ozx//twQXV0H1e3Qto3PIxGBJEH8X/4U6Ld+H+LT/8kr8Bprh0g2jSG8rK21tm39ioSZiIsg5GlcmtJyYADotsnRuv4o3fgFEivA2JFVA3aZfAHCE3KO7HKqw/Ssu/uJEsl1+qlL3pKKzPpIGiaN5Ibe2pF3Tr/D1I22bYEnAP/PRiGpraFQZi5H/ScF6FsI4A4g7fsmZ3jeb6VmM1hhhg3TBKc149lTU/uEPcFRCAkhG9umrLLLfzZ2i6NA8yJBtDeJUkz47yLqG5CSW75LOOWk6BwTsFJFuGRcW3qX4Bx5vL7J/3WglmvFOpynx7ueervO5uOJwbzoeYZh2ITRaD7HY527mBFx2E3Um4fo/tzEe1MK6JypiuAmPaTLzlV+V0P/VpRG6pdPILWiRcrMkQlX2SCCbesspMGsjj2TMiHlymXE48kwsUYdyt7FhURVia5DovTA2KkBcqdWkRAxyGE7TETKJLUgJXBA7CeABLMbSNuJoOo6Y3dm26HrFJ4/v4OQDR7FUWhLbPg/dkKJLLbsxD1m+E3O5Fwa7G5avPWhd+PupRvve3Bxgxy3wgBreBtR2dw8DsGfuAhHyBQ60Xgbp9sOmSwtRIRZ3FlyNAl37pkBYbd2ivS5OGPuzBpamWNrAYYQhJubDTopoKSx7SWIvMHG2MYW3vMK8KN/CvTZPwJ97ksQVtHltkuS3c7olF5+iyORd+tsiInQw/s8SSkB4eVpXtGVGsFPr8ESCMYAvvGqOZBl4PBMlFLhmdj4JYeyjcsrfn4xWZDaRHIUUoHhtHm4HHBSVXvNf0Fa962XDGpGfPn0CS5/ZTChe9DLR/wMAbcgxVG8BPL1x9UZI7IM7aYX5lcA/DoAAehgoA++NkTbZt1mQWIC3wD4mIDcmHbDtnWbvpHBWtmTdhSICJ3cwtnwEraN6S3AsvUG75vGnALpTquVdhukb2/ZKMsdAnJ65JH2B1UnHLNU3Gucs/NdE/cw2X/MNjsc9kW9xCoqzouB5lBSS/WuFPxOUfLOsQs2ye8xmjQv0ySz9Zv8zsLtuY8we3iYzWvi7/H2w/wPAPBlBfr9rvykOS1r8VVjbsKPCdkrO8xHb7dPmr54ZpvMRwjJeC7MB7Mv+aSmsMBrh7gZ8oBL94ee9D6/w17GPU4NcE78E/KRX50cbt/fnHFtJbpmYul8O/iLQogmimVWOaG1ADjpLblZow2KwwTSuldKQWmNXcfoOoW77Rabm9s08WzYdttv5LeAZA0kTpuNn6PfNm/dTYs3P/xusHTW/oapAE4upYnIgo78pClKOk2ETs2RW/GnzxWHYEPfFU+sY0cE1trY8WH2ZJO5JQCYTlyxs5Vl4t5sWggBKHuApSHEqN/hv+tF8A9+DPzmW8Dv/QEc1ePUJHDxRYRW0zR+Ei6Etb9mlV/kCDIytKGQmd0hX8QciC/3h0B0mfqjTP0A4NW+rI2BaFd3XFgR/NOJuACyahxhCyOuvknyemTvcEsbHQbta6Cuo8xepiWibd+ronR/icInhDOUDypE5inf4QAHkpK9smcjJi3Dh6eQE6LU3TKPn1KiyLn5BsDfYMPLmsYNt72W4xiIANhth2DgRQL+BAG3ZGyA2S3I2tZvrZUhmf2RrwSQsCSX+X73XENTg6Yx2x43mw0a2Rj7em2LpmmsnUOBxpHOQvg8p9sjbKZGiEWbPeQlP/4cohpSDJt6AfR2FCAu9uHY+tWsEFDP1fw6OI6xgdM+f0sw41lkUTgSefF8Z0mSC/Xn6AgV95QRLsomFyvfpJnsdLdDXpe6PPHjNHGeONI10S3qDlY2zsuQYuzHhJlfOSszyidWNqe+p4WTDzqIQCPd/GDRx210ML7S+yq/trhSDCZnb5TLowlhDjn205fBl35472ePywyN+s9wSvJzAiuxI6y0tyccL6yDGfiyhvjfuiiBYRE0UWZZMsrswjGFqnU07k08xXmI54fsnZhD2aLi2bN1MP2dj9TT5edMU5G4m48wZzUJdR+luYCLn52LkfFXaaxGhdsD9WjxGKsf1Sn8VaJrMlKDw3PKO580T+67OPAtnDtic/X5W2/jy5/+DF5497fgpddeM5M3AK2QkBAQQqORAuJG4oXbR3j86BGEIHSqg4aAFoSO3VSZwNb6cyAo4lZLCI3aJcz41K3EN//Ea9i9eAsI2OkeQyS556QUnR6GSVhlm5skZqRacsW68cSMDmo0F6onVeKGmxJinV0taUgkKdLaSGMNoRZIo3gOaWxkGSJPs2GACIYA0kpDdxrcKUgGNk0DIluysokUbAjkkmbwD/1J8B//MPS/+03gj77q3cDKd7XW0DaZXUZ8mW1awZh9rDqRrd2eJcP1+M/ZKHLzf/tkQawhORAVOTHmFF9Glhy2kYHtC8itRsVqO9YRyWFeaE7dk7Qtnx6n/nF1gBDv408mesmjTutcXn+KfbVtaP4wBR3qEyyh4dV+TkEJ4Z9hjkBI22dF5jTPpC+IX15ZEKGqZi/pXkwoxD/1hdpvZ6XQh/zsi2X4PoNKdyncBcvMfcGxC+IZA/9WAbJfJQimnK31OtCrBPwAAGtvzxjkA27VFgwB7GwdeCbQkQBLiZ10qkpDdImmNXYOrfJrc3NrbR8KSNFYY/hO9SVCeu2n+9ZB+utpH9YvlND/m1yxrYdp3wzvtreIacdFkjokDksoDo7S0VtxwGHHnb2Jz6pBTfHJT/A8fGvecHOa6zVzmeVDRo47ipNgzfB2WVJ5RaSHmtSujXeOl3UTiOXxnsbj6esP0pfCMs8LcdpnmY+UA7LJcskFpz/in7GdSheaG5sxRUp/xGMv9u8CvzCcjPLMPQEA9jT4eBhkFsnMmDGb4/v3un/PJYkdLYHelTIKY55k1wFnZRm/bOP3MBsbk/tm50NJKRqV218f3UmFMZIxb1Ro0dMCmRFQci+Mtdk/22DnN5xM33U7ONtZYQxg3f8HDf58ND/jMNPD2wAJ9mPqwOTkTz0dV3DiZk+5UFxzUKwg/baRCzxCepLxzcAY5ZBIniWnpFxC0EX9nJ+/Irudfct7DTsjL5ZmmkvuXblkXDfRNVe/Bix+Wy6juFyFSxtr/4VUTpNxGxlUdwqlyI/adXj6+htobx8l8UgSIGKwm2s1EpumRds0YbudEGB4e9LJ2yOeZAQjxNEk3f0mQDUC6qbB83c/Rvf4xt4PL758Op2WoM1fxLBz1phtIvolFpMBEYkQDKRH3ZTthP2Kg+20NYKpqzRcDvmIJpRuiu7INDPh9FfDhFUzBAGNFPYFwtCQxn8u7xUMfu1bwO95F9T/9rtgEQgUP/lNZMHmkrIEkSO33OQ7tmskVGu2P1oVilOBme1YRjnm/UcvAiIJQrrqEZ6PVcnEqzTMIEd8QdkiDC9KZo6Meds6YV94MflJ0Z+wzx1RefsG5J9RNDzKm2as9IueoEsHR378fTsQ4GhA4OuAve7bRnl8EycAQLChh2iAREjHMUTZ4MnH78Jx5aaTPi9vX8V0DHVZyeBtCMteZswDz8TdH4zCFWYYYAyvtll0AL6YEtlxsInv5ww8Q+/NJ7XpBdnuuGarCuuccosIUlrSuG3hbHvpdgPBnbUFJgBr+F5wY/osIc2n7d9S4lak9QEIQtnQccGP3l1XEOeMbT8U5TQo4Pplaf7Ph4xp3+psDiZg9y5LEtdzE+elMJ6aDN8/TPDXa/ZguIWgQfdRu8+RDvOmjxeWWoDpldVEuMWkJT6Bwjt2CiY+k543nl0FXHQrxtTLxnrrcI44F2K8i97vcTEWxLiw/ljfC32ty+elTAN7XfmeOdDQ3VIzdO+q2C5sIE/SFwBRIex4oE5hQdGZHcl7YkLEb9ixj47y0y/z8GZMe8uxMsjuDY7tSr/tPCC+H5VNOdhCBOVXK1B6N2fxOwGAGzeEN2Famv45ublGMuaAte3L4OLWQx3mJwyod3bQqmDjiwB8lYE/tD99Vjl8iLCwPVyuLmnR730NzL7oh+rEXkweWNPetCw9jXAuXeHGfsYMUTYOiosueQ7pqG4sK+m9Uo9Q9j24nXMCaPA5TA/juomuBwNTWQPpNd5UCYbQAMwEWmsGaZjtN9bmjBACLAgaBNIrXukEvP4dr+HZu16Aum2XhrIYrkwARH09l8myxJ/7N3bD0Z/7Pd7BCb810qxKCWlt/wgJQdor7Aiuy6UkXcm2S6khNxvwZhMNHOzkNCLy3JYwZ0g+Tq552QAKCiCC2u1sUp2yKKjB3FZHtxVLNtKTZE0j0bRNmJQnWygJUra9AZMnEZUKaWYrX7aGyN12SLdix1ob0tHmgzidSfmSjtIeq9k8ARYRIqkSJDxPb1/MDqCczSjAvNR19PJ3PsFItqQSANFIwOaLE8dZHbFJUNlAQUjRy2NvIF9qkJcycr5mvA7gl/qTGAIBtwTxfwXwYkwWAcwKmm27IwJ3O9+eAAK/+YYnukRi8F6iaY3dr6Y1WyGllLadGTWt6w8IhMZuo4zrhrZ9mTvUIwzbHcnlfgPxTML1b2YtKPQ5SlkFqp9fUOQ9IkCSPsq1bUfGslkhQER+ORLbqTABaxuQwc7xxWDq227uW3ExI7MIy2M7bTorKiqOC9M9D2kx9iMekwqRLnDGC7NuYdP9VlDmHRCNzXI7lu7kXGfnFTC9j5ACWptDs7pdZ8bRVj3vbNQ2beuJFhM37JY1ILyPzHfAnCll8pN+ZqU1r3CiReb98G9e65Xt4G6AEBjqhnuTPDcgicaycOOYjMLzadWJ95iC7FN+7jlsfRi5OCCYOEnrADqG/mUNfD2E5peSCWZhcRCX+h6a84483vvUH4aEqPy9og5j7KmZ94Ojqjc8l12yeHVNqETXiRFPv8NFe3WgMyWgr2J1bDWHqU98z6yIEIQwpyMSh5dRTwnneKJ48jMh9eq2RXfTYPviDbrHmzDZyfO29yUR9+r9uEM7TZnn4IOgEZ0sGN8sgKMXT/g3dBzGP/t5Y8KbRKkK99MJJQn7B2GuIyW6slD864eEAL3nXeC3noG//jp41yVuXQcnSFgFVTwJRe9lHOwbhfxqhHQqpYwqRRqj3EoHoktzk0xiky2RFAZD7j4Av1WUpNl25k5bEUIYsktokCJowSBljhTWFOXBpjd+Bv4ZO0WY/WME8sskwsnE+48q6egz23aeFEsGFo4Y4KgMQ2Dxa81SbLFn842ihMSPxRFrHPtP00xROuL0Dhqiv8fIT/JZDQXgCQr9A4PuAHyDgOfwY7R4SzRDmwMpXmWwDH2oZoCEAimCUAokhDmkgQQa1UFIiVZ1luhqIBuz0GBObYhPdzQEmFOQAaHvEV5lOJy1mAazOUJew9K+jNKKXAwzus+Feu4+XRSFMd9Qksdqsz/Bd89jHyoSdg9wIPTiVc5c0LDb/PIyLddKZIqHOTCv5fm+J73Oj4BFUS5M5yolz+I4VwawAEtr7Dme/5py4ejfE0VpvNNp4yzMBJaFU3jAuS1cH1XygjDK5WDHlnr+vfofZgFRK4bS2iyOAn6cCWsPUyJagBECYTDmRt5R3uNF4ySt4T2X22vaUxKFbzmy8XxmfDZE138fmTQHq57Jfc7bWURS9Uir2FMcOkeX2L8vAjkWEsgAWJkDe5Ixj7vfMfgNtrZ6dSBawGZM9TqAN+PyigmWEij6dt/HtYfpMOMdN2vGw4EEzsv9LB37SVCJrktGUes76Dj5FlZXBAQZA8/5XnvfYXK05l7oc4fw5IPvwpMPvwtapCqE4STSNHexlz03w4mK0cvU7kf0EmgXUP6eHkqPDy/lK4pJcCSPIMCquaRTS0GbcgeDrJRYZ4xlMK5o8ed/GPz2U/D/578Ff/2N3qjSb3UEoLVVFnmSKCW8GIFsYgQ3bmXMZd2RVrFKSgjydr3Mti239VF6NVhi78sqUYgAYYkukuEVJqPnA8C/UOP0aaWMjTOXTutGW9UXIgVVojQDINwwL1tZTP6MgzDuIbctDdDanRoAnydjF80cRhAqA5mVEk9MELxuJSKdhTRl6uyWsdbJysx0pO36IZJdJ8MdA//WEUrFUSlwy8CPE/BKcCNIgGFUf7udGbDf3T2DI0yDHT1rK89+b29fghBW5eVOemzM6Y6NVYa5OkbeQn/UjiLWii1hbuoh7ISAoeP6Q4S2sSS0H+eGvi4oY30rs/5cX2muOTI6dcvRJY4YkRkvlAylVrJ+aDbmI0wDloR6TQP25N04y9/sV/hq3N/h93lR4KTvKWoN2od4bDa0cFoaUwmS6Cm6sjCVMmYuzKexY9t1HbZ3d/6etlKs1iqgHz16hLZtcXtz401vOKudipR9twSai9042O8Q8LewdtQUF8O0vi94GJ7ChXej7r1L3e34ZPth/znClvbCdkPub0M0UdvdFd22nNonDP7v2dhDzdPBANRD6UvOgB6/TGHeGxW6N9rvKqkGksV8xPU3Y1XjX/ewu6xE1ywsaMp5z1hQYPGAW2OvxU1vyb9QOKx3g+2EYvfsGd7+2tdw+9JLaG8f2f7HkQj9PhTMYOLRV8CQ5LF7tMHzVx5h+9ItdCN7/mLPTolTDDhfdemFMXo3RZzf0M+nq2ruWvSOJJccTqc5ZkAfT/g8DV5Mp13PSrfXQZidSKzhNvSIsXwywG0D2rT+CcdL6D7ZdjBB1pYXuQRHK/xuXg7hnr+2eQ/EknvJ9bdSMpQClFZ+ZU4JBRIEpUQ44dFt1YxX8YTZAukm+aZsou2aEeFEIJAIK1PGnTbqFbCxIccc2QHLDx5weWW/YBa2JYZDCSixARBsZhFgTtQEoGyYAvZ0Tbi2Z+0rkSUz2WxhM+GnduVcuwKC3Qj7WPxEODzO/G0SKcWiuonIaXHif2jF09lRYKRRqqMFn4W2Oc2ta/kMdFkfbP91qaItwH/IwGN7hQjuOEd2/woAHyRgw7bNkR18G6LbrHoLaAgIMsSWOc2xgbBby5umtXb0Gjj7YKCgyDX0qvstfF/FDAj73ojOkvD5jAdHoR7GW0BsriMyGPFg3dVFV0zRSJ7jeuoqPg0vFvSeTOFRBdsWNOSk5GmPSx64PWXrz8B9Ns9jlRpoAZba/hhqZ1PARSPJR8TCpC5+Fise4TniXIWhpnBhKL8zjxznyvhoQTtZF+fI5HXwR3ox9OHhPeGoKzOOisd0wasfU9oBtlmoNARWpzrz2XXWbIUhv3bbbWLj1cTPdtsj0O120J0yJJd9R1I0ngyvILfgRFBu7Ja/94v1Z4hEGkZO9MfxlNSu/eFHXM6cuUsdh76ds4/oehJBujXRk1r2lENT1vFYOiM332bwF6IOIS6bZzBK912eH5f3eEEtzWsvrIK/qYtEpxrvLrJfeQS4eZpvd3G6ovbnfvu2mrt54KhE12QsqzFTxmhjbsw8IiO7/IA6TLaevvE6nr7xOt77HX8C7e1jqyQxqwV+0h3NSEK/Ov/V+vxdj/H1j33rbH+L29xAp0MgQ2TFL1xHenBMCJbSEQgMBO/JZ55w6rmMOhXLhTmD8FIIELRROIFg/iWMlUJMOw7WCSJzaoln6IbBIDRxvmJFlX8JBgVVbHTSrbSZKMlFndj4AuW2skz+m00bKVli9Zf7tJN9O3ByWx6FLK8quhW/5MjieIBkV/LYMZiW7PQ1W7miCmq1OF/xS1NbgtLtH2SrppE2L8yM7bNn5lkKq/4iggb78rIF3CtzCDfr7zEQQ0/bIn65XcO0ZC3Ge81YxXkI2BbhfwWjqBEx6lKlAPrNmPiJB5eWELsB6L8GcOOcaDArsII/+YNB4LutJa/siY3S2PaLbSk27QZSSrStPVRCSMimQdO0cNS5ENIqEyPVF4y9kpwY7ljBHd86tHLvSGin0HTl3SfD4oKxw+tspZgYMALPE464spXO7ObALx50s//6vnvHwpo4Xf2+bPhxyuUn9frAS4v2IbyD7jOyPrDwLk3sNZY+nUPt1FTaq7bcX9d1/s+puJLxph27xfVvZyLB3fPnkFJi027s+7C170SB29tbv4vAL/xYlskp8eMxQrl+T6/DU1Vc+4ckKZk4RHqFeK1BeRd+NH8zHwxHankXvmw1YMf4OroWj6GZ0xMz8VWG+LfZEDPnVXplcf865kshuRy8yRoIQMRklh3HuQfW68xrP+1w1UTXOG1QRk9dtCjWORFmFnwmKLz8rSjGZHHI9zjsOyWn7AoeQnTuFMJYbeSUOgQz/9ZR2obm0t1ti7c+8Cq2L92O5zdhncnbEcvz6VZe4vKJVWRJxxqt4KRLSXn8xk9QZrkTXIaT7JdikpWIfPLX9xZWd4JiKLaDZkgcd991VAKlNyLbAJkZuNkAP/J9wFe+Af7NzwCdSh2PVHz/0oqqQshmmJxKCDMBF9KTXloHI/KNlHYg4oKLysS/Xxma07QRGePrJOJtW2YSLkRMjMW2HOBXK2LbDiQcexi2E/pXupt4R0SXS7sbADijpayDTQEGQ+lQ/jmZ575LFfK12WyM0f629dsoXZ11p3cCbnuZLSVHDvhSC3bFvI2x6HHaShvSkBSqf7oYwpSVrmVblZa9LJcPFvLB4PTwxwbsY249Ad1zGgaWnF4J39ktJETPd0fA7wjQI+898cUMQAL83Qw8BgAFaAXFHZgIuhPopIQgAdk0lgRrbPsxRJdsWmuw17hx1/2WWk9URX0SAAEJa8ouUeY4QixtX0EV6dub9yJ835eVlm/L0WpK9mz21I3oxVcmorIwcl7L9f9ZuQ9H5PxlfWc+AaGhcKw3Xrp5sVT3jo9lbXuchD4K1kR55JX/iooiOIxB53tdS2D3v6Y/x8cI4X2RKtDd2CccHsTolDLXLIHSdR2UVlCdMkouS3Bpa4eLYRXxUXxR7LAvVChttjmyVX+ZP7P4A8Bu95dmB4GUtgtNF8BylVG+6DOnLJNF6kxFFa16hfuR03TBvT/Iy4covmwckeWFCWFXgzOJ4cavnrQC+/Guu2bGweE3MwO/r0HfzMrizb0F4lOXpnl+fZ3yphwb064jowrzuyRfc/NzzHdimCP5sZi7ZdulmQZxMjxx9SXwAG4c1n9+fTXeFNL2unDVRNc1YahZFom3mPwix91YFZdfUeHEvzutLg0tVGrXUBKyKyKTyDnEgBFBAtRtgycf/RZ7WhhCvCP5dZP+wXvuGqV3Y7FA7ij2H+XCw83HBkkuCn/xlrq+xf8B2P6DiENkLi2FgYJ5bBQUF4OTdKNQ400L+Wc+Dv7i16B/6/cArfsvhqwQi4OjjERN7FQBAISdwNotgoIScosEBRtafnUokkO7lSIdXrIAwFr5STZgCVZ7Cg9FCrDwZ+KL7X65bZFm25YEBEUreP3nARVsYbkJu1eCqc6vYjliwr08lbUDJjP7WZ17lkKgbWGVNq0/aTFWuDBsPbPHY/vBIcXkQfwkwos+Gea5dsq565FnnOG+bGWcQlBN9VPy19+6SL7g4xXXWK+VhIdQzj5sIoAFSAH4jzpd/c7mH7xhiG9j8OOwtYBZo3NjMLLtpQk2uhxp3Diiy5JhTbsxNr/ajd3m0QQlpTRtiYSwYcrQt/oyINu2YdtQTHi58nP5DRkyW3PS/szVf18ecIOwiL0aqMdpO2FLYA2+OQu/yP8oP7XStaixZe0ubW8pcVZMFcea3GnwA+uF2wFP38r3GRk+dGw4eSbX9p2nXFA4B86T1OWRDvcFR4tyOVm1qmyjwWgBposbiMCNUUGJKQpYP862VrwVUWttDMlzUNnHii7311Pgw70nwmKJazKGv7GLlEr7ON2ft4tq34NCCGjWwYh9lJdgmiMpAOtgrAyHLsUv8cyd/83Jb6+aLvWb0bDBIVk8ys2NRISi5tjGrY4IL/YkmB+/+A0EOhTB5xj4TyaaYICjNOkaQKka9fz13/VzCK7890H7yIHp1P6LJRTaXT68nBdgL5i4bvtge3Wsnyw/lkkIL4oWMYNP6jeUe4NKdF0yEvIlsss14uXJl76MZ2+8iXd/+CNoHz1OJlt5B2ImVxS3gkDiRO50K/D6d7yG7Qsbc+rYnCzgME1mTqxJH8PBrlmcoOEtjZGjCRGY96aZ4CQdMZGdCHLEfJS3UpogDcvhiEFmGPUXuQlqHymFkm7VZHJbXMfhiRkiCNsdODs+BAIL+8J0L1pvXN1Ozm2F4ehFr8jTsL4+aWVfxF2XJSDkzG9ppEgJJsiv3AUSLCLMbI4bT5ASIAQEgpF95hbwJF20bZMZqlNg1pCyATOw222NHQlH+GkNkICQDdqbWzPYkq1ZHRMCis1gLDmVEkbV5lVyNj+dUoCyxF80uMte646lLTyr09sAehiISC77M+M1Utcx1yoFZNwvuwGmI6wcovAYDGwJ9GsEunHkMht7hp5A1WAJ4AcU+BWAlSGVNBHU1qoHfTsx9vKklHZ7o9niIWXjyS5zT0JuXrTG8MN24rAAYvLuN3FGaSa37RbwaYzbfzpINgEZkp+QHHPeK9Vyz7ZkUBj7nkQK557sxUWxL53XcjrRqaioODTqO9NhSAmdbzmPSRWllVdWedMR7O5FfhH8uLjc4mWyO4Ajcsb3u3bXiQyKfyEI0pm8kNYciHBH/7A3z0I6jP38+DcinNKh1IqOmofeK8NhCl/ebnwR8uy2GsbhuPcBa4buFMIYOn4+6QFU8fV4HA4w8DbA/yvbPaGBZMQ30nRmyTwgpsxCHgKWveRjwhlAr52W3MQxDpV9XO04apdpBbg/A5PrJrqIZo8ShxRIx8LgVslMbQPExG/K3vr5AvLf8bZA42D7zjvYPXuGV771A2gLk2mnNHJL84GuMNeoUNFZCDx79wvoHm2KediHvU8oymBSXCHRaTilTtlma8qWpjEDiIFMzNmsEE9fDYJeWVDs1k0EObsf5c3ctkSVe9nB2q/yRFnw6d26qsLpbzdbE+i/u5LsJGUb+zevdBe1WyEjS4yafeFOidIvC7ZpMhNhc133Xsz9tMS2IDx5JAOJJOxgJxBLjjSSQSHm7IfZsnNlQFaNJaI0EMwpirJpzMBNKShosFIhSzZM2TQgzRBSgjV5QlJpbZ8VjHF9RrTyxp5kdtdI9g9w8O0yfg695hXb5xvHoewMLA1n+erbOMmcv/TH3AxtY8hRVG1lyUi7JddOHKETEUBwbTGO3zfSEIhi0Jd00rZF0j4AtAC+k4ENhcGIyQwA8u8EurH27nybsLa+pLTbGsP2xoalJcKsDTDZmBNCBQHewD3su8C8vxgwfLtNK8PYpINr376wQv11K4de9Vp4ViNP2Yc3ndiNHlimtB1CMWQu18A8qFJuaODOOMj2r0vby3x/a4ZAyatoWQgn83YuldTVqLM4+Zjv8YQ4R5GuWlRayqcsfyjld9wEAoNAyeKf34ZolVue4FLZiX2IiC73Do2IstQEBcLOcGZoHcbDBEpsv8YEmYzHfG58WBgD9NtcvPBUKo+xAu6P5QMHwAMuywRYb64QpTclr1KigTVDdR0c0RXnx38ywHc63O8RFQDeZuDzDNzFxZbNPSn8ShRlcb5W9vmXRpnsTdEhE+yneOsCHSK5St9NfKmwIp6nxU5D/TP30rpwP3DdRNdDhe+MspmYq6NOmcVsCKTChDkQEQgtwE1qhiNdkNZsZDy39Yy4zyf9XtWUyzyjIPyklFwpTE9PP7jhSXlMW7gymFuCdhqdxD3oLjoBEIA1WhgmquZ9yYVP9mUcE2WaOZA9NhI3FYZVTfnIo3SAAQlLgrmJfyRbdzatwgoUfP7cSiHs/c7ZJttFz8nWfbfl0a3ibURrVF9uy6PbukUCUkYqMJt+953I2EwTjVF0aQaE1pDRSY+iaUGywWZzAwZwc3sLZkYrBJ4/f467XecHJQ2bEyd3O3M8jdlCZlR5WitoW6bCrloSACkCuRkoxwkj1HuLcbLrGCjFNiSh7yljsyO7zTUObj0v5ggxEyPrWN3o6jPgbLgBAH6NjD2vAvPCDEAC+LMa/G5Ad8YGirLx7mKy2KpD1Ztvg0h4g/dt26JpW0hpDP46W1/C2QUjs6KuYQzqw9qhEjYNxDDHPLq+mAHyq9b2c/RRFjrphDzL7+0Lx5b9IQdp7NKQvW8LzuZHu8xX8HtaRK+LioqKY2BNsx5om36crLPfdp4Qq7Y61ZnPXee3KsYLg+Z/E9HO+iulwY1fe4QXALLvGAf33ZzmTdb+JHm7pzHatg3v1UTNEi+g5gQYJ4qvvHTGwIzMXmNO/nBwCADE4R1P7s1hXoTOXpbW2hrmj09BjE4V9+PvfAwSPvkNAP+O/UmIYZkp+qIAKDLq8GwQ4YkN964GAdRfhE0DrTgHpii5YpKazWp75M7MdVIxQS+W6PN+PfBKdB0ZgyvBKaVadOsummoXSBw3rQAQFGODKxSe/ZrEKOfTDfW4xe7R/C2LaaDjfnuLCL2U5GH0SYCc5EokzLYI/AuXSrq1aD7jPwYov+TZFZ2EkN1kkNA/brrHwKelz7aDKk7CM7otfbvFwce5C+nh6LO/4hBUSGmIZpYTT9pLWXZDE7YqMLYG+GOlS590s7WUwwvYW/6y7uJVNTeAcKRXZxVWRAShwpZHIQzxJRIVWKxcsWG4AQbgCTOzhTHYEhPOEGpjNkreti2U1pDbLbRWNt2BmCQ4osucpMfOvhcMkehN69vMuPUX/xz8A0prQGx/4lKxXFGWkhtj+dwXxxT1V+R6+CoNu/N1MiN04roZ+4ooIfSeK8O2L9vPM4C3wr3ENdnIJYBvmqDIthOy9ZAJ0GQOhuBXCGgJO2YQCWjdQCkJrXboOkd0WdVXawgvf9KjbOD7Dte6Ka6pFNYzks7U5XK4bMtPZfhOGf3wk3lJ4iIPu/8u2R9P/jDc7aUDxHx7zTy/y3G/BrPXjcvuz8+PB1I+h8ymGyshIk/s9ZzoCurcCEUyX4N1NEbJ/LkdCfGL05uYiIguNy5ySEw/WKLLjedyeHtc2S3/jo/yHV0YGQOMF/pQL+nnFi6uWFEVjXG1W9RFpIazpx56YgI6jA85hEFbBt4OqbBDBBPLmwBeZyCzBuJTTfFz4SQjbsEi0SC4z9nq4uHx6Jxh4JTx3NHHvYUk9LbDnhilPPcXW9mrL509O8uaJirJuI3F7dOb+EkGcfcHlei6IvS3Lc2cELj5szN0HJEWgbyg0D8S8M3veA3P3v0CuBlg+o+FBW3NN1Tbht32Pr/ND/HULJ84kn8hw/uZkozCM/Dyag6/2W6lQ18JlXtPlWb2mRQ6tn2pSgY0cZR2Mo2os4vDYwDSysbzROaKlWQFzb73BZAQUYgGJYz0M4Qb2c6yd7STd8d2IPI/4xBbvfMDiRzuKGpnw0hKdzod+W2QbdMCRFBaQRCZrYyaQVqDpABJ4U+129zcYNO2ePerr2Lz5ptgALvdDkqpYBcMJvzbmxu0bYubmxtst1vsdjs8e+ep2Q5A2mx3hD2ds9TECBHZNZcAqJgGSshv13YM8kEyu4Wy0E/6Ju36D0MmFQfi7E5KYkjbpyakjFU02mNwowTFo1Tn3PQr9Cum7/MEsxt8u4AlQD9GwGtkB+AEpbZQAO4o7u/tgMgSXu1mY063ki02Nxu0m42x6SUEmmYT2hIIAhJujsOsbfq0TYPMKb3Ct6SkMnIs7w/XIg8jH9xxwV2JHMvCPPkYsfYFFRX78cDaiR8bZWOlaBwVTuLjMAkGIKRRx3PTQDWNUXR1HTRr7Ha7YHDeKrmEbNAIGZE+PhF+gdAvOIpw8jYAP+n2B6fEBxXF41Y7P3H3/K6AKH/J+zoMdEuFs+d3sTjN2D1yGogt975jX+6O1ALsKZRKBbcIflz5DxFxjRTAlwH9/wuEWpICRkpy+TiCk1gBZr+lv6MdH8fBlDHr/SNWjoWYlHJwbbTrOjx//tzXOdam3rnDiTZ2PNe2rR3XyWjRP60Xl76QPheV6Dox5qwfBz9kbSL1A0pW+uM+xXEYjsxgMwkzW1hsGuykx/XhxgaT63ytIkAKaDshK3ZH+bKAy9+MPQ5xR+s75n5Wcx/Wvdu3j2SikXcGwWffILx7aQ1NxpKrSQfDMYfjX/aWmvKT3pCvAVUdBb9J1I54LJBcUxUzg64yRaHf0lkon9IMzhe363jtlUAHFB5k5CKn3wKNEwYxzr6ZFmE7Y4/kYjOhV85mmBsEJYMf81tpBbKDvGDPy6i3lN0mqW28ctf59CmloZTG3Z0xdNB1Cv8ne38Wc9uynQWC34iYc/3d7s4+/bnn3Mb2Nff6usN2YoydCQhXgp2qwmCV5BIPCCQsIRkJ8YCEhIWwkJCABzAPIPECqLCqnqCUykqrECaTotIYbNxcc23fxuf2p9/9/ps1Z8Soh4gRMSJmzNX9/27PHuf8e601Z/TNiDG+GDHCGgPn8o6cPgoGIDlP3d/fx/7eHg4ODnB6eophuYR3DsNywDgM8AwQHCjuttTgpEEYYOwzgAuU4/BpWpRyVS62TquA4ghNlUNV89JKvkQVTiyoMkKWwfRpRAG8a+hdQlWAW1WkuggEFI5miwAKiKNvAHyPYYJ3LWUZDGQHkB7cE/zrDF44EDycsbBmCJZfy7M4Tg26ro+AV5+OOYbbHeORXMXvpgawGRQvAUVpw7g9sQ5bSm3F1bwpQbF2P6hUJtbVZbysiqAKp3qVZCl8mHPxPHntBprPLPcXmmfTYHqDPJtD5CHzxvPl9vTw8a3oAVdbgxLbx929cFM5k1WB1uTJq581w6jNx2LTr5GftvZv+flJoJL36RMAvHMgAJ4InmRDJ/N58aFFlG/btnKLduFXNRTCiAxmSPngkvbLtU1yYqqbtEGTO8f45cId5MI6TExfMfspr0eqvyxaJYgotyP6+DzfQu6di7eSl0AXdP8gFuxtAMdRXxDB4h0Eq66iLeapWAGbuhSvDFtusl8UPW5AVuNGzup9ey2pXeUUUUKQFFZ9YaRxXbi0gJ6zOZJYOnp19DCVi5TOC2AYAqh1dnaKYRixXJ4liy5KeQUfe8MwgNlDjjIaU3twpnOu748vPQO6nkCqxUUCwhHGCC4lU+EIbHkGyCMeQwl+i4BgMeM5ONf2AJwPQJfYpISJvUE5qtmR53g5qZtprDFHXcci066QN3DkIGtfK8twrCcyK2EWxRrCmeun70gAg5xxDkHzUTwytdIWbhCED2kSkNp8G7kpFaVR5zkq2pLWt19MsMyzlRaQFGSJky5CqMvDioFPFPD2wa3gM82od5yeIz7PFt3TtF0EvLj4jLuXYinmGZ7HJCSFJb1ccHRdrA3A1WJvD8ZY3Ll7F8yM09NTeOdwsneCs7MlxtHh4GAfi8UCly5dAhHh/vF9GGNweHiIw8NDXD46wsnJCc5OTwEAJycnuH3zVrie28cxLFaA6pI6Y8ONRfreupq2tfZ7/Olhl3/VLJnCTQlvFGArgV3ycE7wJhAxSj8YPAmjjbnm0hFxuKU7ZRAaGaX59TDzLHyOW8SLv48I+J8c2BCGcZnfCZJDckFE2CXs+gW6rsOiX6Dr+/A97hwa24UbHq3cfpoVMR++oISnIgAYG1csOnX5chhKcRNvYJ3S1KJu0lCSHik+0IK1FHPPPKhKlxi1m8SV9Mhl/x0V/3NNzXqDZoNGmM2wEbd+9Cj44M5ZPoE8+wGP4RbItIn7jUZC69NeJ+humd4mG5GbAF/CM0WGSc94Gn8YBnjn0o18QibK/cFnqWx2U5mH6A6Il/+ESoS843Gozlo45zAYbdkVstdHDsUvafK3ZdVFQc324XI9nWstkeeq5+spg0vVcrI6jpI33ThW8qf4Q5K/EvgqAJFUr9Vlpc8y+Gs5/+mm8/q66o332Xqtir9RLu14j8GitgNR9WuN0FALWnUaNVtJakWQWwS86jpbjBkgX2DV9wsQEcbxDMz56GFIp9RBl8sllssl7ty5E/zqjWPSibtoQemcB5GH9w7O2WgoEQC1oHvkwudNyqcL8Hqiga6kcGxBT0vfpQ0ImQBqJ3o+9KYLcInyr8q7BjtWyguzM2h9mfTCm3JJyTUlj3JR23iBq8q6LlpqqEYZRA8VbCif5yvLWWWSmO3lI+B/+D7QN94Df+73V5a33inYrPCtgqg+ajFyeRcyaxVElUMdQYqDShbverSm7iJxap2tNUQxDyf4OIVJ95xFy0Q9HkqwKwNl6V1MW26C9D4Ie/pmSCKCcwbLs7O48ASnrCcnx1h2PSwRju/fx717dzGOAxaLBRgMay3GccRisUDf9+ijpddyuQwmw8Ymc/5YswwOcq5Za9ElNMZQ0fybW/s9bHpYANwm1m5FmPAEqyZn4TdNvU+wF+XDdpwspMrJTYUPJxnxadIDoHLazVAB0KbUUXwT2Zp1IAAEP7WYYUmLQEsCPgtgkZ/p0oIMqCfg0w68T2A3whmD0aqbHKOjYbIGxnToFkfx1iy5QYtAJis/eRbEXFjVIbVpnJ+FSJ1vngSQFCnP0fIgWRcoq9hqDWJmwCk4jabjIPwyZfRJJ8Wd/E2nXgtw25IelSxzHvaS52N7zWztKBd7Nynv6cL5NAnmTz1tAj41wu1mYXXOgbFJGVaEaYFqK0GuavnYZN3Mm3/z7733IGOCsq34IMdP4ZWTDU6vXEpQPNrufVCU4xpjqPKxJTdla/5LJZfLczlx86pNdBtOapTTyUm0w8RFkKpXhWUYAO0MPh1B5Ng2o5dISDFYLLu8So8hGzgBOGjIAvcY+CKDXC4MM4DbuYx5lVt1idVkEclfN+DRc9JO27xhTYLNDLdYKHbUy2raVsasVZlWfC7GI828axEV6RbuYSo9Q+aNAMgAsFwuC6BL+xmW44nHx8fJbQoRYS+6Sum6DmAPAgd3E1TqiMyc4jCbVN7ipEOzqSvZaOMu3jVeGZe2HONCTzTQ9dTQYwqhTsZRq5zVs5aKd/G0ZXsp/tQ+mrdjKWSFXZFcndfEsaEGt+rqXD4C/fD3gj/7ReB33kyPW8z4opx/66fTFGcArqI8kblH4JWLpEPrT0Aujk7qG2ApV59CXilKXPVBYcLPSklXRZUwoxvhvPKXEMEs7znuhLi44ABkDJg9Tk5O0HUW8A6nJye4f/8eRjeiX/YAIRxjtB24Y/Rdj76LZ+JlwYq7nckZK5dHM4smA5KguImQX5tEP6NNqQF0rWJmxcYCoTV9J1Fmcq2ftCGAdsz5WZ/9DOr8jZoNuQaUwmMJ4HNavI7jyec4fEDgNwJg5bAM4JchGBMtBuQYrgmWX4v9ITi5j8d7u65DJ1ZfxqbCEZDszQLgVyJyXs0PFsZCKMAsggEhH0/W/mBqcDMrMzlda2wW9Cvro3pOamL4aEkx2yFNSuvB1g6AHx09KNbSArnm89bC7+PUdruVZZVK/9jSRRd1FaB03rzmxsgmgNsmYaqw4ht2Lr1ZoKtm/jyTVxUuWXw0iqxdkvj4fWLRFb406pP5vuRjrc23boNiWooHi+KOnM0E76lRJ0x/t2QhRsWW9cyZFL8EFiYicmGFxeFCIaib67xqF6cBLJ1DJaGmMscFLYFjKsx9AL/JwKhAhWbDtKXwB0vl2GiBjpnWle3hlb8GkVq0ypp41bozB/7oOHV8fdxQ0tDppKPA3qPruuJiBjl6KECXzDltGSm+uO7fv5/AMfEFfHBwgL3FAsOwBHuf3Kl471JYAbq0Y3qi7I5n2l5PNj0Duh57Ov9gS1PuMR23U8WOio+1NCMMFAj2BOCq8uBcjvw5VSbliSDkAnZle4QZEeg8CKBIDBUi/yCJRHHXwlQBLlWBASC2h1HSSKmX5HJn8WB6nIWTkCAhUFhhAepmR3A89qhXndLBZiWKSFEBBKf7njkcIXQeZ94Dzifzf44LzugcvAsC0HJYojMGGAcMw4hxdKDTJdwYFpDOdthbLOCdw/HhAbwb4VxYlM5OT3F2doblsIRzY7odxRtutOnqo8NPL20G9TwamnKJ8nkrrP6NKt4m+WnaVXgUvygtViScSwNBIR8JY0wGw3gE8J880Mn7cA06f3KE+5iB95FLEoFhcHwyFLePBl92Aejq+q7w8WWSMGeS1aNYA4Q5YfKuO0SA9IhMAAwHgsGis0igOxiUdt3FYjTUJqRtUtvIXQCoBNOy1ad9zcQ7dctFbrw8WTQdx5X+/SGkx5XnPenEDx0zaLpuiEWZPK+ALe0vtU5v1RDpOgu2Jt7eJw7nNfn0rDgGCaQNgRZpR9V6w4AQfHARmfQbKmx4JnloKYyrejRkyqbUprYbCqCuCi/6QHyuj7ani1IE4EIAtMQaqzxOptrcT51HFBJugWuInA7w7zHwtaofziJwNqnro6Ynh/nO6T8XpxfpjZSpDFZvmGtdMMSJGmTxLM8dAZrEGkuArWEY0qUP4zimT3EiL/LQ6elp9M11BgDJP/DBwQEODw+xt7eHYRluet/f3wMAjOOIYRhwenqarMeERL57fMbixdIzoGsrujhG0MQ9LsiyqwZmFO6wQwqt13HislqKZyy7Ns2uVCLCJ+mfjTRnWN0kdD4uVyoVNZAVThbGcDLvBe1u1Cgh4XX21Q6A9k2Q8TXK4WcqmA7tGQPTBablvSuEod1oRaZK6JhzSt+WGaeq4CoK43KaUmh/DahlN/et/hbFtb4fMo8dKp4X3zk4TGUA5FxQkUkdh4oRZCEaI5A1jiNgCEvEG/R8cHTPI4POCM6MQDQ5Pjs9TYvh6ckJzs7OMAzLtIh59vFCCZ7OnVSOAm3ciB4GGLotbWJtVh9neBh5Tmld2AxycfxZcJKi31YDVZOcqApaJohaeFpVrXxUvCz3/O46ozwLqPhYEusJ7Bj4BsAQ8CjGfo5AL/nCMtODsPQjqDOwezYecbQY+2UW3qxNTu3l05ABdT0MDIgskKyzAhrCTPmYMThe4S71BozpQsWSruLj7zzPdL8FQS9YlNWcZqJyzfbrLvMtXDSzi1HSo5vdFzU3pzVIlnprc8x9ONlNf9QK204d01bsn2aarekqEGS3Kabxh5jMTEJzYWaDN15MsK1pOnMAmF63J3yoGuhUrDecACefNkW9ilcCW7LBlmRiykJ4Yo/VWizybna5EKx4IfJtSyaNAIAGo/IGtKr4NGLxmcsk9SwPhxZpF5a/Pofw+fIggMu2AOIaojc4MtBF0oaqTRjx+ZiDppVP2uJ9AF+uGdQG8g9vwmWbWuSGcVbRKnlTyxR1vjvy3YfArssLZ1obyNXcKsqUjyDKWCkty8vvYQ4jjXvRAbWcIW5QxjFcemWMSf62zs6W8RKIkN/p6Wn0pyWO5AlnZ2fJJ5c+2qit5tm7aNG1iDJR8Pcrn632ecxUhgujZ0DXxvQIhKdkVlM/l39WaTmyaNLaoCuLsFu0zdKZOauQNu83SXQDAYQwvZJ1AjgVD9vlamWulxpRuuQ3VWGa/TlXTxXu8No1PPfd343b3/wm7rz91hw2daGUbNQqhg9u+wzQCn8G8Vp9qwEYmiSfPygt9snqixGV6FJwZCKAOK29JVCVd1+8eiyCmY2OWckYGOMwLC2YAUM+5+niDqkLyvKi78MRLQK6vgctFvG2OcLoRgxuxDgMWJ6dYhyWabdluQxWXMuzZViklksQUTAtZo7tp5ydx7qnUVXX/RldGO3csudikDXg9eD7Vltl1phawQlJnomll9w6pRwKI5eYAeB3Gfhy/BUDWRAWZIE3APrvHNg5DCNjOIspRMHNGhscJnddOAIpoFcEwayx6BeLbP2lr6InQpd+h+uykzKTFJds4ZCstqJyR2TArI8/5pbwUs+s81R8Kn/ZTHFvvTzHIHrEmM4zquhcU/jDyNu3qPOuWliUCR6YI/tG2FXHH1e+Y54y5o2IYE2QY8SnlvGlk3QBtjhq3yIvZXkjtpARXogEgrU3VrM1bboMq7G2QPHiNkDSaoz6MyfF0YeRBrPShoeX+uqbEENEr58DAHwucgKfphvsIIYxdZkj32YAv8Lg9+pKx0XmuBWvpqn0cT62fp7YD5kHPeD1ayODAC4+wnelL0rvBCuseBNiAn8BuYVGyyOFLEHB2tJaE0Em4PT0FMzLeHP7AOc87t27j9PTEwxDcCj/3HPPwTmHk5NTjKPDOJ4koFaOHwbQmaIMEwC009N486IbQWA4108suMqjlU+/EPHhA7rObRt/zviTXZkGa5nsxDfeTRaUMKHsYoGuX8DImV8qNxBq4byVf13Di2qxVHJt/VWBP3X3UOtF2QSN3CogBCXIVe6EVdFS9Cq/Jj8QZkdJiAiLK1dhOGMUG42/EN84RneyxGJkLI6OsHd0hL1Ll6ahGfDjiDGasU4XzbrBVqFrFL+Fnb5usYCJZ7xTZlWc+omJwsjy5HSavmqDZil0USmXIxdNKYbqq4lBii6sfhXej+KHHIsyRPBpcUJphacATEK4rcQSYIjTkawEDLjQ/957DGCcnJyk8/XBMsxhHMa0u9g6MpCHCE+bG/nY7Dq6iDP2D8Iq7FH4EVufZ7Z0Ko9CoI17t5hkGlrcDjP/EGIlxHXQyYMqtepRs3oVn8t8WD+mpBDW2etiaHtOmcpJNzsBcFIpJnGe4BKAG0opCZJjmN0W8NfCsUXnxujry2Dswm5lHwEv58fk6ys4tTfR0arc7GWizy9R4lQfMoIFURNX8pAjkZnHtBpPt5buYyUQN4eXKGStdzMywCbUGpcPnHYubYitBuzUciS9yXkl65ZGMaoXE/+Xj4h25WszNX3qaRPg6AIymeSzEWA1d0SqjYCtDrNBfTIYtF08Ic2zS5lXzapgKgImAkfH9Pl4IhUyEQBQQ0apjz5KHvUozjNSnuh1NUEICiPT4cq0aiua/JkBvWTl6wPAxb60aiuPo3NmQpyfFsoRAPIAbnH4LGrLYdPkJkA3W50kt0lu0IFVX03RtpWR53LekjaJNV331gXdiIp1YXvZVrup2SCzNNZyt1frmpJrCmkg6S5hjoTju0gWVUCw2iKUl+B0nU3O5Jk5+ictN+sESBO9QOScruvSqRL5zKAVwRhO75bLAQAFQNc7EAHL5QBjSkf37fbLlmhPG334gK6niqZC57WPvI7LL70EilfYlyFKZroVL30MSTv8jKwlvcmgyjRODlO/A7hItQ5FigtUUnpcl/U10EXC2zY0Af3pgJd/82swQ2BOl195GZdefmkaloH7Nz7Au5///GRx2S7XEhRiAp574w1ceinm2QC5Jt/il9Pbt/H27/4u2PtchkqRrpJYXdgV+hURwQqQQUoYiosHU7RL4ZAQx3JkvTa8M3FhM5RVJkTQCkC8rtfi8OAgOPV2QwCxui73ufdwcBj9CD863B/vpXKmm1VcOH4anNMj7fSEuswoPGnCPqMHQ5tKZeuQpAuOqQOcW/FrojwzeU04H7j40gbCSmUFYSIaB/oGgHcBy4ju4gN/Zu/BzwH4Hxm+d/AjIk/VgqQFTLD6IhKAK/x1fbjoYRF9fvV9DyILY7oYjmDj9y7tfoZixYtWo3LkVPm1yG8qFU2vH8JEGMDUh8umNLE23jgeHgFPeCSZPjG0O8iVFftn9OBpF5BrE3BrbfrrC7YjMZzndCRRU30RR5ENcwKEarBrAnA1QWdW7zRQsBoQl+IoeCPJPaHd1U2PHNeKCG65cSgBK2W1lq13pwCXMbIRkvPmIm9VJ/3gPoBf8uGzRUMVd0N6cFx0nSC9ih4yD4py+nlpG1cdpT5cKyAynikv76mcBp1yCC9yiBV5JL4rbxoNupQxSKc+WOkUi2il3nUdTk5Okn8uay0uX76cSnZ2doaTkxMFdMkbj3FkHB8fpzDi3L4zAXQ7PT2LYz8rEdbmI8hy+VZuR3rqwK5nQNfDptJsIDyKn5tM00LhaEQyNvhzSidNisBlEWbBA2q/amU5wS0u0mIulbP0AZDKQTwpZLbaaQFZkfGQ8sNEmZFNlLZZEqagfyErb4jKSyrshm0iwTzj4OYxFndPYQYH4wMCQ+pmjpoWBwe49MILWTCIZLbqjmq5Z8bi8BC26+TBJHyrrZiB7mAfhy+8gHDFLZKgoskNA05v315vhSJFIwVU6i6uHhWfebBk6xNKuGR8n3s9+OiS3czwXPx4WRMsszrbgeAB+HS7kLRGWExCP4n/Lo51J+SdHwLQRX9F1tq8CEquFWCgHcLq34+bH65tqF2HzWbgReZJEFynnNfzjG5avgabXa/saPa1ap7yfBheEWbyDhnAbrwqyzThW+2DP6m3knlO+Ef7YWF24BHxOnXZ7YzZeYCPAXyVwZ1We+K/hsGvAbRH0YdKmCcuztFgAWbgxnyzozUWXbfIgqhVDu8NwYQt2ARmyRaJ3AjbqN2EAq9PcPgkZlGLViNX+ew0j6mV9oMmwu63HLbbkye7HzE0ZeV3GqkoUXykx2A72sOgnUCOit8/DNqI9zyUAsjPFfV/AE2zkVXWjmDXeawKdx0/aYNWr21ZYCimxaTLk98tpAWwAOBnLCunrj+yNKw/lRiWniVXHw2gSh9HRGEBHG9H1P0S5at8PDO/0HJgkL+4iEMjwN/kuDZNKhfoFMAxg5fl401pXfiWylS22ra0NseVrx4eO8iyyKr1b7VP11Ke22gdVcJachSSpwlExhB9I6gCFAGrbIVl4lFhGy9kMNENihHZSdJU9aj/RB+Qi3rk9kU5nqjfy0ZeeF9UJoUXEM1aC+5C2YZhiGCaTeUM6VrVfrru65vwSaNnQNfjTpFTl9ZLq9Z9NbuUABmtkbfP/CGM+pX1WZe/8KnGrlU7eGZg61i6mHBvElY0xMIcekcyo8f1z7+N/v5y4zh7ly/j5U99KpRka6BrprwbmRBPgzEB3dEhXvrUt0eQSwlJKvDpnTt467f/G+A2sIaoB8ka4CEHKQ4sgqPylA8fSahwdM0aAzDQ2WwKL2NrIdYjXRdmY0akkoBmjYE1QN/Z6MDewHkP5x26rgtpxc9F30ObKEspPWcEhGO5zNO4+szSgwW7WtnF+wRnyrKOViBRa/KdJPEgiQAf7ak0zakwmgyZySt99GyiEKp54V3gY1lINJmnGgAnBPz/UAFwcZdxAeDHASwI+thj+ozlEaHNGIPOdtjfP4CxQdCztoOxFn2/gDHiByzswBpjQUngM8HKC3oEZhiLinrltpMjDhkc35aaquf6WLtFOyedJ9Nd4j4itGpH2h3geLLq+STS1iAVV7/XxJsNuwWdCyBrbJ63qHinrLgEKArlQAKgWnGzDyKVv4RIYBNP3iYZR5zhKwssfQRR/IwxKj9jsVwbQzmUJbwsQinJ75TD2nMs4Vvtz3njeianXcWz+XitF7tksnmc7VLfJPRF1WFKNbC1DdBFUDeFxjU7AVeyEU1Gfc/jPdwOTcWz7H6knA3JRUMCbn06diiWWWJp2Pc9+r7HYrHA/fv3o6+t03TE0VqLxWKRPoXk1sblcpnmiITnvoO1oWzGGHjfRzAtWDZam4GuNCeeUj3jQwd0PSabV5nDbbA4iQJQHqqr08uZqINX01RXDeQ5JlHFybszDZRjjhr56immXydkuYo/V3L9Rqxi6haXM9MCimWlSpWCdDqNssa0dZV1NzLUgsycjtGV4ssKhZIZl965Eyy5lm42RpN0Qer+ajbcLGo0m87EEXyxyNetLmNQpVPpOd3+Pq599I3UoMc3b+Ls7t2qeLp/WvVAmCCsHC3qV/JE5hCXYwWy0PkAAVhr03jyHK7jFuVcdlyIEH3+UJTrstUXyKQdIO99UMK9h2WbbpOTBTUAXHkxleaR75vQg7bsOu/Ct72/hR1Bo3PkmY8NVfHSuN6uLHXuqy0VEnNvJMDTd6loBSo0CcNl4OJHLbKzSqCxLAFAcathXZ1m7ZQF4sJUYoZSWgSsKtaqOCeZGVgC+ByDDvPR9MCFKJfRAvTtDBwC8A4OHqcnYTdUrLrIGHS2DzuwEeiyXQ9ru2jpFeen7RCcboRjjpANFJJjj7leJSCmeNxOtFvEOWuoB0UtUHPzuC3LtXpN0fmE76UCP60v18ppS79+zOmRFnPLzB+YD7RVoNPM++2S3xLoqt4/CMBrIwf5GyXFhYycxVu9zqFg7LUkl2RcXl36QuYgNYOVDCyKfgmWiYUWguLvPbLFlv7OYM8xrQx0CZmygqi/UapQ2Rr8DoO/7lDIkmcABkzbTf/gIPC1esrUYYuf7bacFr2tG83DeevHzLy2tYriSpwasHq1cW5apllXh+kGY2t92fRZ4Zdu5rshC6JOgVVB/jbKMivI6FlWBwTcMoUMoC2ipEyTPzAQT4CIxVX2qbVMuoDUx7lgnXX//v20Cc7M6TZFqQ8zJ6DLWpvSlg3FxaJDZwOIJpf7iGWYdpci5Q9tIHLVE7JwbkgfOqDrUZEGdcoXVCw+2yesAY5tMn6IJGUUBqF3jXKgVtA2myywD3U7YPwTX0ytBATwkiCFQMCKyTelgNVUMrdYjomgVCckNwoGAeDo7ds4/ODeisrnupc/55XinagJcKzScKn62gIsyvrbg31c+9hHITt03jmc3VN1ZzSH77QFuYmDaZEugb8VYCqLmEE4smijdQcZCo4hySdlWRYMKYSJHvA5glqFA0oBsKITyGSmTAbGZqBL74qWfjLQGDsrxIYHDHjtSo+n4/m5eC2+FJ/MJpX5zNQ3Xw1+NEaxOkpRv5rLshgDcUptolhpuGDmRf5aBREfDuvXqpqPEzqbj/KK4MfxdizvM8wYImRAiZmDfPi5qMQZk+ZrwVV6AK8zcBj6yY0eg5OLMDJYRVYc1wcLr65fwHZ9FAADiL3Y34cxAewKfCD6BSMOvsJinbKCFy1GGQFE33I5P8+0CGvYw53vQSDebZHZBeSapFGM4pmJohaNBwbKrKCNwItnFGgd0CTPuMEnd8pulQyzfdjZ8aXG3qrxsHLjess8jYqWZG2VzPRon8puBSBW5K0mZ11Erdhri63iSKKAWZ7h/ajqk8NAWe0KOKCLJM6+p3WoJczyB7/D8L/mUlhd75qnFT8J7R5MQr4OOoXMsgU1zYSdvptdqzekXUCydgkqPeoBstM5q/B1z4Tqvpz4nIu/DXXBh2cBdFECf7R1+PqTQtpqS2QaAWeVBTpGSOMJyDWOYwF0hXgB6BoGh/v3j9H3Hfb29hJAlTfbQ5nCTe4B6NJO6okIe30AtERv0WkYY1S98qyhqHg8ZmrEuekZ0PWM8MQDuDUfasvP2wZZQQ3ASpkmbJsuM+PS27dx9N5dLO7WNxU+edQ0MmCU6E1Dhrz88svYv3oFQLhF8uZXvgq3DMeeqAYfVUwBpoqnrPo4d00DdguKsAiBxhCIg+UVwcERFebDlEAtTm6qDVG45bShdxkyIEspnLSB9n1R4oX5tiPZ2QQQLctSkGd04VTALYrqEdN6tkmH1GlvGu/B0xxOUDwT5UKP1+p7M21mjOOAuu2MAZjDcYHc8jI/BOgKYdIc1pZgWqEYAPxnAHvyhGHrWlgG/qADXyWMowdc8F1BxigwK1h5peOMxkZn98Hqy8bbH63tgsNZa1NZw4bLM4hjO2rPgYYx8Uzs1S3+KECuZ7QFbS0oPZBSPBB66GOPE4yUNk6bCjpR2mieI4rhVNL5u/B8ZaWFBERVtx6m41rCt7PVFqmUAxeoACMSpbt2iK+vB6lfxfRGAL/O4DtVxNvV7euzrEOANgmn/e1WaXLxS/W7BroeNu0Ojj1J65cGoWpgKh81zKBVCheBLvkd1vDyu7RhBlyBFgMqjydOJalQDoZnA2aXLtFxzmEYBozjCGsthiFcsGCtQddlh/ACgol/LgGrJO/FYgFmTr67NBliGAL6fpGAvFznGjSMs/AJ4rHb0BMOdM0pJ8B52MsKzHjrVDcZODz5UuYYMdb4u9xIaJtZl8x2luXqtar1vELxW6dsasioCfxzGUwDaxzfyRl4ZXujtl3KxEtgIAZFbCvZcKJcicqCWYEu0yrP7c+UxOktxWQ9RNCQxswFUy4xp0qlZxjP2LtzisN3w7G9lTcTVlWZhmkw42YdJB0WyWb6kuvW0KLJKpJWaUZWv5MkAQKwuHSEvUuXAABuWOLOW28HoIcQBKeJL680eKZCneQ3gyfoRV1KGww14nwjgDmIVLI4mWjJEcAnjnq5HG2SsccFACBKcD7XH257m/Zfnt9QcSfzew7vK8XRZohdaLdrqhsk262qbO1SChfYhabCcuZt3AqiitbgYSrsWmCcG2FWMXZ5vuLomQZq11GrfPVdHSlMbQXUwvLqtOI41uY2iaM1+KmmcMU7p3merA2UdVZimU2wK/LWuJlQ8iAKzPebZZ76wjAGAxbgTwLY53hjkYujLObXG8AqCy6T/XpZ26HvF+j6Mdyw2oUdUsMdslBt4/FlPc4oVwe67Ln8beultmv7ZttOYqrnm7DpTcLpKMLjNo6w06tmm7R+FfyxUZ/JerWJuHgO9rnSvUQrr6peD1TPmCR+vtx2iy1r/rpQtVCqnm+YxVaB5pcH9ZSmsvIGWcwP5RUpbVuHyEcInIHiLcrKes2dWezykcSYt7bUigq/52DJFcCtCHZFSxWG3AjpAVDFo1Hkn0XS2oUJ0lpb0MiQi3MxMPjrDHygU4/Rq0pOl63IMdTazapw69pzwt+BaAWntDGqQ6xKb5dZRiuSrWSrhvxR8N6GWL2SZ6WFp8GMSayfS+5dSl560E4HIpGRgZ6BLVC6ZEY+5TSFNeGiJ6NuXDbUgUzXrEvZDuWx21Y1NZ8Kz/RYy5t0IjsZMmBwYVHlncMYb1sEwo2I3mffYFZZY1lrYU3QS3TZgssVJF0kJhxEm75P+gdSvNaC1wLrng56woGuh0kXpPDN0Zay47zMUq2uHJUpDtYli64HgeBdWGzSXjSH41tUF0ZnVM+PokRrKtHgfdkanQO/TchDYBBGdOMm3+YElhBx3PjhiDhp5sT56AkBoLCrxOgBWHg1ySMXjJmG9omnUeKfz9XlcMOFRbD+cX4EOwfnAM8Gpj8EOBisOjfCO4e+t+m4mzD0wxt38dyX3kO3HOHQFdie2DqIkhcYWbv1J2xLyWbpaT1GYluLUCGWREQIpuU8vYdssvBU7xgEA5OXU5bn8TN4cI/DYX5O2a7Hy5/6NDj63jq+cQM3vvKVcjHhoFS0fb/kNbw1Kim98HEnBTCe4KO5MRiwXQgZ1g6GpejMoYttTmZag9hJc0JMGIOm8VYVVi+WjSCrqb0wz89Nmvmeya/IuP1mnQixjjzStbFraJM8yjHcbhdGN3lT89nmEYTKIm9Ve+xC2wgepQC7gl2vijdfEEwXg0YCreKavnrd4uZcDd2pCGzjlzKL6ThhQLvsC7ieZ9B/BNBlGwEt8tP3EejjBIxlOUcCHBEGMuFGYzKw8faisFscHd4vDtAfXAnWnyR+wCjtHIPCJRdeFZ7jMc10fJNIZ66NhHObFYCjz2sSgNL6QdaNqnGEx6e650swJJ/gLwcqV5MVz3x9Zmxb1gHLrFZyeMlx/ejzsLV61shr/nlrXq+jiRPudSZmzFUrtpXNukXWTZ2LpgvL4zwJUWvOttq3oVzuVIy50bPByNhG8SuCNqX0XRLamPL6xFkJb6anFNsYk4p3rN5yssjiKPMWf26MGxk5dpCtNO9WgJJq4rYqsX52tqQn/hLCEfdYCCqsuVZxh/qtWL2UIf2OfRL0B2qsW5vE3XX8tK6QFKLZnwzAeeH12VKZdFhqpAGk8eC8A4GSrydWsnrXW4CC7umZ4R2XySL7ywJFfdSEEw4CXCUn8iD0i7606EpAlzqqSJJ6li9KySK7mknVjKc22PmkD4R1PViIMZBAqaA4xZT04p52tUNdO2thqYuWWx6LbgE6AF64fh13797Fe++8A9sFEGt/scDBooftOvSdxd5CjhxG8CuVmZOVlt4E1O5T8jgW3SsXTw8CHe5ppCcb6Ko1/K0iKtqqb7fNcIPENwgiua4Nqmcxpyke0iAkE06u4gTeQii2L+bST8JyDlqjxNu0EscIknQCL6RMkwS5+JC6pZ1zwoyAEsqY3kgFWD2nIPgTsi+mAgqgnHyAdeQvkKFwy1fX7yXhNxxyc4HxgNGdLkEuMND+/oD+3hkIlBWdWFZtCVYWJHdw2eICH60bJTFsw6pNmlCnvaovW+9q3yn6GKH+rCl1WVzo+oODVMTx7AyLo6O0cA6np/DOIShmrBKkaVqtssZCFMFix4YychLQxHeTsJvCT9BEMGsJT1NqWqBtEq6oQCvC9OsqXyMzI6AMuo4dNFJKi+581DW0KuYcXNKK2W6n1lOqjkkUu9wzOZ6vjqspgNubpl7XeqrcbVTWjYZbbP8NMgghTf2gCrO6ZNXUnh/XrTzybgpwJ8evVgLQDQBXuIzXAXwpHwdiR/BEYBeOQ7AcZTbhZlVPsuPaofPi8L6LArdVlSDVeDUHp2lTcPksq6dcrLvpJthY/GK/p1BQ8k6z/J4b55lnN0ainuOaBwvToCnQNj2yPb9WNefxzDBhoOmurFzrVdgVPLEpOWy5062B28nFF5yfbQKTb5Xvw9iRP0cWPPmSH7RFtvqhtNu6cDmshG/JRWU0EQo2WDPWtTPrsbd6vVpPmzd4e4Va910sruR56Vdr6nNI/flx0haFGDcp4AYrakPmoepHYjVLBu4BuMmBh7cCbUBl+tO1tJnYxkvz9j2f+MK2UdeykxVrLSMBSZIAK31P8+x5uTSubdGkMK1DnOd33jMLa4rcVpxPPVCSsa0V/1nlEUSA0MUbEHPc/GeSKxPRBzhO7Ty+kXhw5ptp05w5gVzpT+rF2fBgtqHnxnmcaIaCtdmi34OhcMsiAFCHWGcTAb4I9FGwwUgKmhg+pOwory3IRgtNpUfkhUqw2mGYzlBj/k4Zweap1ZN/hzSebKDrGT0jQezn9P6Lm71zBUBgyB36Hjg4OkLXL9DFc9FEhHEc4dyI5fIUdHKGl3/3m7DHZ8HXk/cg00XeJUcfs5ABDs43uy4qSqKhKIZdiHMTBifm4sIpK8bBHHaroql5eBRuEbSkWGlksASTma36ECZKqG6aScEYVYQpqTrXnPHw6lXsf+d3xmAe7/ze53F865aq6mpFuZ0rxSYheMo3ojBztHjkBA6HBVZ88phmas9oOyqG4dYxd9W26lxJfT6jDy39FgP/Ta8XBLwC0B8nwGRBOPgcC0JpEk6J4E6WGG7fgzUWxkSHrzb4+Aq/g3+vrgs7tdZa2K4HkQELEGhsPB5tKyEcSdgO1hXhjQjkotRle2ytakbFIfJtqd84hl1/Q3HNkJ30GL5Q1BMq1poj1bMKKyxCbjnF8orx9M3POUDqwcsrjwGtAiSLhxvy+MfyuE1L3qmV31K20m/ajrjLcPWxKrNWNtHrpsDXIZ1hHFJatQN5H4+eax4oW7jE62wtHzC9A/D/zsFP4zNKPD5vKORX5bH6KQUL5F71f74dEEDSD2rn7vpEhVywZK2Fcw7eDwnsGl24CTm4I8m+pxZd7S9LA1Ym+sc1FdAla2K7LuLTthizojPFdhKwyyuLRDCDzHQOsUoj+wmVqasRvBZF6zW1vorP3729Bfb2FlgsFsXeF5nod5jUn6La4T5zBh/1hVnPKNAzoKtB51GjdspPDdZWWQA0jlLPlJLmX21PjP1bxyBmnD53BLYPRsGvi7vOimEq0M+lug1poWF+h0ph6EVIub2j7xcgGMhNHmQI9vYxzP0lxgHAmcGV/gBmL9ySwd6DFz7cQpYceHKwVoqLTWofVcQk9HAuVWC6VFS9vn7eQFvKKUWfGORFpQgLQBm12g0oWqnuB+VXTpKH+C7JFmd1D3kq9LaULgHRaXSwtmM2OLh6BUTA6e07YOdUqiFeuc7TdLdfK3UIlnhaEcyf5cIu/Vxqgo8frRz9ialslsLGFoLA6kvg6kJx+1UUoecDA5P+zk/rcVmlo+fGiqI+DrRqXdgk7oOy7pjlv5usO40wG/Hzxpidi1f0OLVHbyGgAuHI4lits3cAfAUlPyIALwE4KNvXswu+9yLPBnsYZ+CdAxmD0Q4wxgaQKwr4xnYwJnwGv2DhKGS42MLECzby4ZHkTzGC8yz8em6yJ2svRjjLmW2P9VEFcZibWiaxNr0mCnPOdaaiU6gCuRp9QtrZ7Rbrs6x1K0SeFpH+0hoEc2ATADlevu4msIsGpi5qzm6ezjny2ykqN+f5bFIz63ar7+bSaF1sOxdxJQ/aIs/0VmNZBdBAVcH0jKtSXQGKZqvflpUNx/+zIl5uOIY/7xneu1SOpNAjAx61BWa2Km2Uq13YZh02CnOLwbd0+pn38vsMnOP+poeBBewMap+ncPUQmug0jTJxviEcyOUuNn8wLbcGfwQ0EoBsGMZ4i6FJt/0F9SIYB1hj0q3MAnJJHmKZJTJ3/k5FXnWFA+iDbE2W6iKWWTG4ss7SRDLWJZGQAJiyzpd8SlOprZa6ItSvaJRgDGRVN4aS3y1jTAIWbTo+q9ojlievo9I309xyH/GKMbTt4HqyUbOtga7/8B/+A/7+3//7+LVf+zW89dZb+Nf/+l/jJ37iJ9J7Zsbf+lt/C//sn/0z3Lp1Cz/8wz+Mf/JP/gk++clPpjA3btzAX/krfwX/8//8P8MYg5/8yZ/EP/pH/wiXoiPqZ3QeurgBSQxce/N9uL0Ob33/xzEeLi4s7bV5X1g9ZrWADZ9B4zsplDBL5uhcnCysJeztH6BfeOz7wNSMNXjunVNc/sZpVK4M/PWXw0IwBgeE4xh8ePl45Wx4tgyKjHNwbsQwDEnRYC+aSKlsJRNgVW8fFRzEN+IzIOz+QSlxAAxg1ILgZQcnAVQlpJDANq9bj9MtgyTKUQKdSm11ss57v0LQLG/quf76R+CGl/DNz34Ww/GYyzSJt2IcEeK5/3z80bKtrOSQrx0W82lRgpRQ8OGmWShhi/Db59jKYQXk0QhBK8I9+fQgwa7HnUpeNTPitCAbSbcX3QDwS1WcDsD/CPA+V3FMdBPpAe/h3IixhuuJ0o2Owk+MsTg4PIrfu3z9t9zuaGxYR4wAX8qJrQec9w2FidK6FNaL+JkaJPsxCT9rJQh5rZmMn4YFxyqFLe1+E8C0Mmg7vvoyB3rMPyjKsAsVxw6furlUApdbR90p2jlArh1pbq3YPo8t1jlaZekkcyv+KsaV+p5AMi3RlVkS5bcGVIF6+oSAtlhHtM7Jc9x5lwGOKIdJnLpcm7pduDB6E8B/zT89ePWG2oecssXdduS9T+DR9BghoP051vnl460u6TTOBbDr4OAQe3s9Dg4OgsUXgkVTMApAXiOqpKdH66gAdvJmvY6bf7dArhRCgVwaMDMzMpOsiS2LrukMmVaCY3ltcqAPGFgsFgv0fY+u6zAMSzjn0KPL1mwVkDY9sVOCj2LZFY4ytiWfD4PRcE1bA13379/H93zP9+Av/sW/iD/7Z//s5P3f+3t/Dz//8z+Pf/Ev/gU+8YlP4Gd/9mfxJ//kn8TnPvc57O/vAwD+3J/7c3jrrbfwb//tv8UwDPgLf+Ev4Kd/+qfxC7/wC+ev0S5U6t9zjx58Maod/DbYIwM9hmGZSHqH5SJHckPAbJVqC+uDtBOVmMoMrEX1j1Vp04pwpP6QkPjZ7GYFaCX0IgjvAd2PzJ4BkAnIu2HsHy9x6eYx9u+PsDY7ZCbvYZhhbAdmhnXBsgvso7kvw7tw3Sx7nwAw2VnzzgX03/n8Cc5OQRMjZrCvLA+ikBB1n1wjBe7I0ZXJ1c5z4KBRaRVXvTFWfmPJT+Urjo+bMconxhhcfeUVLO8f495774G9XAOdLQdSj1OdQgWJGILxwZwYzGBlvqx3lbQlRC7zw6GL50UtoKfei9pkzrWIV4RYX5OpmrAKtFqRy7ru4fTPNMdzWFRdJF2UZdc6Dro6IfU9za2yxbhgKDEMrw8zl94k3qblULLg7AipmY+E9X4iwBZz3AP4IoHeUeVigF4AzOva6XKG3ZlzOHYe7B3YELz4+vIuglldOtKQgK/OxmcdyBhYI0JwFGTjsYZkaUqxPSgcy2YGWJzlci6zHPsI4yPzAZkORbtRbmNZ67KFLhSA1WpxJZFwEyZbTyvG/TznKhLYKJsk80lhJ9nPrH9zqRVrhfrdBDiqQlwYrQCWGlNq4zTPwRInfHkmrSaspJXVIrB+0pDe5xaD5tjaoHINAGiSxoTPcRUiTciSVPGJpgG08WWOEviIzM8gl0Z5UQFdCcTy+fihfOZuzSgBqRxUgZSsuGL8rJKxV4TBCQNfQPap/pZ612jWXWjbMj9sCSBtJM+slUVYFSZtPm+X2SyVR/+yz6oMbEWg1DnI0XrvPZbLZRqLi8UeiMJRxUXfgxE2i7su6D/sXB53rarK5Sgsa5vqE7G+Up/NhpHflbWarme9eomf6HVUa56lHsUKjM4gVJpflI8xjmMIZYxFZzv0fR/0kXX5J/lQxAHJY7rebq+utCM8aWDZ1kDXj/3Yj+HHfuzHmu+YGf/wH/5D/M2/+Tfxp//0nwYA/Mt/+S/x8ssv49/8m3+Dn/qpn8Lv/M7v4Bd/8RfxX/7Lf8EP/MAPAAD+8T/+x/jxH/9x/IN/8A/w2muvbVyWKONVhdi8LpOgkpje1d08uSa1zDw3jlMEXc1uH+eB1wIDCrALur1r5tT4Pu049Se/VwmgmfFoaskb5UKfw3AUnLxWYgAg3vAIAvbuD7j+lZvhXbfImdiwOFiE8dAhCnCMvIuWdtiCvyjnXDra6MYR3juMowP7fDWtDuNlEXLZxDftRsQ/OXOvmzYw+NAPZEzEsGQZisy5ErSCjqM6h91EiGvvMFUCHGbGihKsdQxrLa699hrO7t3D/Q9ugFndBjaVqKo8SwXMEIENQNQVuehdpWJHKL7cdtpdjMCUl9PZpVjtdtVgQxkm/YhJTxnqNI/pRKTJl0aRpTyT2NMc6/5rj541rb+JPrZKUJcgKyyjLgro3Gpd2DFeS27ehppgkySMBu8G8s1RjTCz6W2QdhMwQ5lc24G6JKjLkd8Vu7UqDJl4rTkD+ILmInEe/gEAb7Ssq6IqyYg8OT7zYXVhBpZnJyGlaOlF8UITYw1s18fd7x5WfH0ZsTDtQPHYgzEGZC0I4k8w5pNlaqW0AGNaE6TF9LFCaR99XDvUNZ6oB4MzX0l5aL5Z8xZZ3/SzecrtG9bAJp9LgdZxlFakkqhgBLWfybl65eRax3jT0I+8uDypVilcAiDsvECsaYPm47bStzHtEi8Vc0V5V5V1ZXnkYypX1OvafJ155vtcaRqCSc5kgzymJDKYDsqTf6e8lL2LvkWzrFf7WyoAC1WO0i2RzDmglhHkFACwbgavCaMAswk4cwzgNwEsN8hgR5qqELWkX7yMbbFDPo0xMKcPNeNtMMWmWbQLOnvsWrGgbN1bWhwGEMslPcOlzXdOlmACdDnnsFwuY5oGl44ugQD0XQBvOD7vui5Yf3lfVKIFQq07Mt4M02qESt+crPlV/NxGbV5Z50H1cwp6FHz0iRkturzLv40JbbFchlg2/u77vljLq5nYqloZSm221SUtLePmajOltrj7GIMPkS7UR9ebb76Jt99+Gz/6oz+anl29ehU/+IM/iF/+5V/GT/3UT+GXf/mXce3atQRyAcCP/uiPwhiDX/mVX8Gf+TN/5iKL9JRRsY/69NKmymMTz5o+LM1v1+S7SnhLCiOrMoaddR+vkR0947n3GD/8Hxm3O4evH40QJ4vM5W1X2fkigkURksqRlSpm2B5YAGqHLoJZYwS+3Aj20fzclzsvozsLVmEc/IA5N8aFySVgLPhnUBZhMX8G4JJ2EpeBdJwxPBJ+mfkmwWgTZwlYCJqsGG0JfqT8dT9OdIiyj/u9A7z4yU+mRejee+/j+MYH8/2o8muZ5ieBDu0hkZxyPgEMfjN6mHBde+HV1JzWF0blOAz/tg+9PqMnmbafm+JEt0laEG89+4YH/ztkBY4ItEfA9xnQQQhjSHG7BIIEx7lBsfBgF1aAYTwD4maDlCsAYBrY6qOfr+C/MDi8N+i7LoUNvk3E/1dcBwtNmgSDSmw+WXylZ9qrIoEU59OgjWrJUmuIvD7z2hYgWn+R9AkGcsxqmk3uhy36ey5oWnZy/VOUbQFtKROhUb5KaZKG3hU0P88y9DBBLqDSJi+Q5/LsDyinPLsm2Pi9LgyrNqJJ1noKUv1CpZHnoE/zEozkViJZsoDhR594ibzLqcijCGLJ0KyzlLKZmbaSMtfg1HmIAPw2gPfi7yWCz8RntBOtM66oQSFtteXc1GpLAC3npsBWHdYYGz+DNpMtjQle4jKDKEpdMS3tG6yuQwvk0puPeiNfhxFDikn7QI3cKq30TKVR5KviklhTq3iJj2udU4HNuq3DPAzuDMRlgfc+rfHi2D/rZdNKrFqXHqwc/WTRhQJdb7/9NgDg5ZdfLp6//PLL6d3bb7+Nl156qSxE1+H69espTE1nZ2c4OztLv+/cuXMh5S2EteLFHOBxfsV2+2MoUXCW5Yzqp40dAzy6Ab7Ssf42da93hDVanY5thp+sw21WysZPimbxqaUnYet8sqUEwSP4TOnOgMu3GH/gtxlfvw5841spMcSRSjmeQLBMsIhXyZICWJQgEc525zHJ0ZSXTXReL1ZcyaE9YzAeHj4CXS4tJm4cMUa/X2IZ5kYX08kO8AvrL+IgaDEjnIORHfbM5MOmdSg/k66oFvjjbyrf6RZmAc8gfcHVYFZCY3xu+g6Xnn8hHUcdTk5xcvt2NtBMptGq7zAHcuV+LcGuvEClMhYK44a0q4KAPDK3idHmBNT43pK6t+F4VRu2Hxfh5wwx5nwLTGlN6dYWXgZIoxB1yK359na0a/oP83jlHLDLLTOUBvYxSW/G0rBY0+b0rUbciSVHax1X1m3NLPR8VmBHBiXa7cy3GbjJwQdi5Pc4JNCnKUlZaVQbpFPhHCoDIB59j+xOW38BwBgvNzE23MwY/D/2AeyKQFc46mDg1U2P1liwtTCW1YUeSH4GpWCyr5LKQVmpLnWALvsolJnaALpyy2mFJX0rnkvDsAIAq9adPkpxdI4bcKuKtUzwtbqbZ/X9DbccU1U3AFqYG5cOrSfiqlKYzoVUluaz7XjHuTlNHF9zCW1c9g3DBhlClNT65WyjVAklwaSKwu3vaXNQRc8asfp3ToTQ1vdAefQQcNFChJWS713YzNSJFxYd9dquRalYKQKQLtaGUqSL+cGJZxTp1TVwADd0dF2uNGffAvDVdtg6kw1m0hbUWpjKn+cZ75sC5Lus36uszGuQRoNSAJpO54NvLTmCKG5UfPIb7H1+p+PpZ11HqhyyFpZlCDci+nDTeQWY1fXQ5deO6us2aB5FXAF2Tdqs/t7IS7+flEXyb1gGspLR6lNMBCSn9GkDK/afXJCVZrBSSDgrSm0ZME3bubpv5y9zPuzFzcQHSU/ErYt/9+/+Xfztv/23t4ixqvF37ZjHp0M3VQOfDlrXl21vPhfaPk1TYxMZTvjNxDg8YfzJ/1eHa+97GOfxys0r+OOfPQyMyBB+7Vs/wPtXzqICFRSZV29fwvd87aWMmYggIQJLJTDlDXnKzuflmSrfr3/sHXzz6n3sYUwCE4PTTY+ePfwYLLrCTo2Hjzs2HBe3cRyAaAnmJUwExcpFj1Oxp4JnyLc+ttGCWrL2IoIgV2+r35Rje/X88iuv4PD69ZDf6PDuF7+A8Wx6Nc/crpE+4lN2vexQPY6zTwZPPfpn0KS1adXpbhZ6M1pXlosVZTeh2krwGT3JdDFjZ892e7sAAQAASURBVFOQCwgXVtiOEl9nMHDG4F8aABOAK0mTvpOAb40cm4AuHjlMeXIAbZiR+CvYhfCyu+sJ4zjAQXwHEs6M3FQVHNjbrk+3OskRSBstwBb7+5CbHg2pW4Ip80W9BMmGQ1acBY4On161GGurXwDBBxgVzLQ8PlLyKC5iz3CD6uFFc4zgA00pClR+ByLARNIGm2vg6bhrBSL4OVRgDaX81e9GoMYznnnxlNFUJNki8CYJTIExY4KimvxgFUHis+go1WvEFgwXj3LJPCosZ6Is56M8FzYgQ8wa/C9X8WI0V+NU5UUEw0C2VKkHdRwzBS+cGfS/C+AL7cbmNJ/i+7vtJD7MtKnbm/r5OAZzOH0DYutPW2KlEyAR6BJAqrREaoNKGlQbxyGtWwLYLM/OsFycBeCs64qLUFppzFELtJqT4TcCtyqrK8+cNoJUoPy1ET89pxkJMm22RR0sAtUx09TG4qvLGIMhXlIGQnRXYAuQK+Q5X79c92cyrdCFAl2vvPIKAOCdd97Bq6++mp6/8847+N7v/d4U5t133y3ijeOIGzdupPg1/Y2/8Tfw1/7aX0u/79y5gzfeeANT9V7/XDHQZ3YiisczE2Xb40qrUPdV74uCraJd9NgtiZjRnSwBIriDfn0EbL6TEUM36zpdtrl6w5OwAn21ci8YkyItXuf39bjKYy0DIFHQZaA7HbF33+Pl9y2u3DQYjcO+t9g7Do4Y2QBXT4+xXFAUYkJ+V4/38dz9g5xbQoyyMJHMXBHGnzHhM/tPibd4qEa4dnqIewce9/dO4Y26VURZa7ENi1oGuvIRRutG2HEJxKOQPjrDd7K741wAy9L5erUD6Um0oyTopcpJ2CYoE+cXBbBLx6Xim4Z1RBzL/WUXe7CLvaCAjSMWh0dxAQuO/N1yWYhv2pnj/ESqdkB2tKC5ePhGz4XYdlUuXD9LoGNzlhSfDQ67shQ70URhLdu2rT9KXTHpskIEL/p2Tf4bdOkuPhe3oU0Evrl4G5fnogahKFgtJVuDAZNoZZhV6W0Ut4rXXMdr4byMOgmzEcilheASxwmsznOw8srmUoFuAHg+BCIikFVrzwLAoSojpeSQlEzkNSQ4pA/Cc5CNI/BlCG4c4+2NFrYbYExwcm+NjbhTvPmRbALHsvAfrXMRFYKUbVCupVRimFPCUrGkXIljzaFJRZzcrnVfNCJzbqC1In3d4VHRruPotX9WhmkzpLWkAahZ68hd5j5K67JZS7Pm4x34V5vtbkaKLyhsp1GWLeqwwjosZcp1u/Dk3/yqCkfxs2QWxfdpOvW4zDKQyBlBXBJZMMt6zjkkeSrGycebVTywSk/W6ixL16pQ+VvJZEWpo1Qlk7clpjHAJwDOypdcZ3SDgRUeJBgbWtsUVrZrg5+LtjXQ34U2PdFSipu80SeACYgln2Kh1QK8QjwZe0jjLI/DqcVVq2wC3GigS3x6SV61rFL4a1bP6jzkvXxfeWyv9W6vBy4fIWkSst5FHYaiYkfWAsen4OPT2Txq3WFWwGw8T5bS4VfUJ8O6bYwJfRX97YX1vCvrOysjtqy0ZspP24bZLN3HlS4U6PrEJz6BV155Bf/u3/27BGzduXMHv/Irv4K//Jf/MgDgh37oh3Dr1i382q/9Gr7/+78fAPBLv/RL8N7jB3/wB5vp7u3tYW9v7yKL+oy2IDM4vPTbX8fZ1UO8991vgO3jNMhrCKT1Xv1aOXs3W0UD2yfIIT4w4/kvfYDr7yxxSB/D3kGP3oeFPOzSBhPU7/vqRzAi7tYhvLeeojVS3k0vSxiYnUk7A4AIVrK7ly22kG4l+uSXruON/gr+909/DbcPz5Jgb4xNSpmJN0Fa9rHqsVQ+3SeZFSov1l9DBrrEnNlHqy8Ea7Gz4/vVTpFPvsN8PGaJePsP0g4HwxjRFkWSFuuFHEZ6VIuWWUzMlGS0rsNL3/7tqd3uf3AD733xCzmtBBRS7K9ZtSqGl9R3U0rOR2vVuXOkqz8fNdXCd016BKwOuTrtx6W+z+hxIAam/jD0TmothFMJ8TntgyPdgBuDSlJEoN8j4EsZ7BiG0yzsfouB/RGT0pf95fLIu5QD6bIQKbtYfTCClVXaEDE2WXAREWzy49XB2A5d1wcfX53FousDIBZ9fnW2A9lgoTIMcUNEa80EkLqhlygfI0ybB3l3SDcupqhRi8et53lz/F//LsPOAE3SKw1LAR/XyXzspFTsC6uuBAZVqJAOS1pR2n09WRVvelSv/EEJyNkyz+2jqIhrMtyqHVogV1sJbL+fG2ttIKh85hvP4i92oXUTiFA5gucMCJRHt4KfpCyfNLKvaiRhbKH85/Lk5hSZrqpLDdLLIA4CpUpABfocA78j8ad5AgCG+bI/oym1TxVMP2sQCyj9VMlRQz2uJGwL5NL5GiM+KnNfUzq5Mk1P4opvy2HIfrxEtj5bnqE7PcUwDOi7DmaxSGUlIDlclziS57o2KRy1K/CnZfnFzKBPvA76P//3SS8zNgJIov9I/sYA/+mzwH/8jSKNbYw3uFrvKE4yz3l7mT1jjPoUAPR9B2Mo3lgZ2lAfZQTRdM2pNtseukryhNDWQNe9e/fwxS9+Mf1+88038Ru/8Ru4fv06PvrRj+Kv/tW/ir/zd/4OPvnJT+ITn/gEfvZnfxavvfYafuInfgIA8OlPfxp/6k/9Kfylv/SX8E//6T/FMAz4mZ/5GfzUT/3UVjcunou22eV94EXZbQe/kdIFpDGfsh08zOjWhj1/ZhUwVXyPzK+QGmchieo7YdJG69D4STKUgB8CwETo752hO15icTrAOoa1Hbp+EW5jlMUg7pAfOmVyDgShhwBYFn0hU1IQ1JEWyb+h6Ce/RrFOtw+XuLu/xGAFKotiLUtLcNqlJ/G7JZzSKCEv1lVuHaO44yBHF1k5wJdrrA0ZJJ9hzMnhfXCYPxYO8PPRHAVZSX+IA1ZMQb6i37lujbLfTJ+tEPuDAxxevw65yTGBa3E36+TWrdS/LZL1a+cZe54tw/PyiULnqsGtxvwIo2RtsjK2JhlhTgYm9ahdp3X+yEQGr0tRqs1qh7CIrIQnDSBsYxX1AOk85XiQdZjw33posFL+5VF9zLcVZi69Kp4uw8bxVic3JS0t1msRURkOJUyT2FZS5iNfZyRzWyIKjpZHuZiEARcsKIgAus3gr8qNZyjn/AKglyn50KGi+hwBpsRFkZg9kHgpPIOJwAODDME7D2Nd8N3YDTDGwEWgq4u3PnV9D5N2my2Ys1N7IhOs9ozAaoBc7sAK9JmUpwC5ilacgCErR3JqqDa1YQrKedQiAVS/ICuWaTMpgoh5qc1pUJ2eXpeUyEISWo0JKgJtR5z+ab+tcQ2hPMZ2ynY3Ss3B9aMqQHs9b8vo7V6eRC5AHp4JK7/XvV/93XsugFGx4vDs8zhiuVhIK/DFDI5TY04zoWr4r+5IhakW4zG8K/Ng5uAc/jQ/03nRDYBPyzQ2oa0tuB4StbO8GI2wtRave8bQ4Gh4UlpMZdchgTX5FG4Un7sqXo47dfyumUAGzHJJ8vgsN4G0lZF877oAKQgIFZ5FP5IpXcpC9IyFfAZ2VOtXeUE/58onl1hmffRlYNEHA4CPvgI6OoBc6gVro14TLc189BtLBnjledAf+Fgwk45Cf9g0AvjeMfD18lSa9FltpZba+ZXnQZcOwN94Fzg5S+9F/xHn82GNDeXpui5eKBPrk9YJbfkm/VeOn9Rys1Npfo5ta8m1iRr9qGlroOtXf/VX8cf/+B9Pv+VI4Z//838e//yf/3P89b/+13H//n389E//NG7duoUf+ZEfwS/+4i9if38/xflX/+pf4Wd+5mfwJ/7En4AxBj/5kz+Jn//5n7+A6jyjJ5t2XeBaSroi1p8iae6WV2BmHgwDYuDS12/i8tdvxiMie9jb38ce7YNh4FlMgYPwvDAmXvfO8QZE5eeqsdunhWux3gpliN+10CpWSbEpPvfGbXz1hTsxmM1MWOLFRTDBHEF/ApHem2cAJryLlmBdv8hCeUgUQLkzZK4KE1dO8J2D9w7jOEQH+GO0EMsO8IdhiXEYYtoMsA+LEMWFOS3Q2Wy/0TvFEwLBI19Pv3/lKl65ciVZvsVAADOW9+/jm5/9LNzYuvJHFvuSoT98kewiqAVuTUGuaZgWtVa3Nuh1cdSC3xjlkeUZDa7QO5UAX317Rh9OEqGyeKa+T0aUAB/1G1LzRgANFazcRTc5y3cB/FJWeguF5HmAftyAFlkBo2hVYlS5ZXb4iDSxHvNRAWJ4eAc4DIqfRYHaBMe4NgraAnhZa7G/d4S+38s7zcYChkAQP1/RxoyR1zr5RD3j5j7r7y1a/b61OtR5SVkm/ctIyo8AEYUFhM8p59320sF/3swq1+k8JExsblGgCMaa3ZT8QkGuar2C/TLQOum+EZ0PH8uZNo9ZTjSmRgM2382VaH40bCJDTN+tz9ONA8ZhWQRLgIEeG434xSzYtG8YGVCbxGvwM8pfpvwtjHH+NQa+iSQyy6YFRZDiXBt+H2KqQa4m6OU9zs6WBQjKXB4/lN8TnWGjvMTtCYo85IbFGkQDQn9rX1LiQD28C+nt7YU14+DgADLu+n6BrusDqEQy9PKmAEMuX1HcoLKa1sfqZe1p1VfCgwi0vwD9+I8AL14r5b54eUdtPZZ97zLwHZ8APv2JsAElg13a7fe+Av5//n/Kdq37j0vORn/oO4Hv+Dj8v/xfwPffAREl1y/MQQbo+2BhZm0wJtg/2E/GB1maKMvcBp6eybE1bQ10/bE/9seaE1OIiPBzP/dz+Lmf+7nZMNevX8cv/MIvbJv1xVCSZHaJN7MwP0ASgSIJ06wWygKxnStXHvTCGAHAGgPnkZiCXojnpkl3NuLKV97H8soBTp6/tMUqnPOfK6GCXIo3iS1zo+WbyVUiWCXIBZCIUJhkM2fwSAUnxZRL4cNgce8MBx/cx+LOSQRqIsP2ceeEZEdbhN8AQjEinzUEg+CslIImAMAmwTgJQXG8poXMB59a2TdW6EsxjQ0M1gPWgA0F38WRsXOyVpBxE38rgSW6x4rhcs3jz+QHTJS26B0sph/e+bRwWBgTzr6bLhxZtAnck5seM8jnxnATZFhYo7UYRx9i3sM7n8AzJ0cmY305+rUIZVVWd8h3+DHLIdHQZtaYdJSSiNAtFrj2kY+kY0end+/i5PbtYuyEJixH7GNFir9p/TVLq3XQ2M/B7KSc04z420KTbt8AropvAJFcsmAk6XB5G0G77DJuOI/toqzt4KkntBvRfLxomoawhKToScgkW8mYbwigj/O2laKWpXBQVi4g7VVK6vrIk87cKD01ltbF21UJT00zt64xt4oRf6v1a7Imq/RIyiuDt+GnJi4SzFzGPQb4swA6PYJjHpZB32aAg5QJDJFsRsccJWdS/FElJetAtMbFyGA/wrsxgloGw3KElZseiaJz+3AUUpzdyzHJ8tgF8iKCZPNVtF3Zb6UcMC+VaNtP4f/6tWmMh5LHTS4tDIsFmD2WwzJt1CC2ndQr5KUsHih/z3UOCWrfNWGIiMIY25DC4roLe5nypJrJr4hLwC53qxRNvOZ9/UKvTs10WjtJNUi0WW75dX0kWZIXQWbyQj/PxwpZb0hGmTErtXmN81FmKYqRsuHqsyxszQ7mL7+p2ilO5ml/VLKKgAFLAF/i8Ek5HHO09r9XFTHykqJ/OM/jnDyt/J2iqnQ2Vs5p/Ro86/+u0d4rbSmrMTebX6PsdRnrY4JzRwuzpR+nY4A6zRrQaoI91fNWXuvqEwAlcXMivyny/MYNgem7SdZJMbUCEJP1TrdZssKKp0bmytNq5yTniDXXx18DXn8phF/0oKMDIF4Kkeof181wNJCKtIIsHMsVig/Ua9HzV0E/8r1Zd0bQTynpZHGdk3cA6NXngc6CvvfbgY+/Gsp38zbwm7+bbl0U4HERj3bKcdDUPqlU82uhAJe7gF274mNPgkj8RNy6+LBpq4X7IZCWwwqQa4ZKBTd8kQngvMuMKZpWiwLECb1up9udDnju99/D3VevBaBLpOh15Z9RHNPzdqzZKV0mo1uHGs9yvp7FuR+VAldiTjm6kZ0EnWZkINYS9u+c4toX3wVHRT+Ul+B8uDWHTXxmspDO4KzwE8Iuha7JnP6P0MzOBQeFyyUBERAS02BZCJxzoY+NAYwJmEPyJCyJcap3BiAYyfaMy7oTMyQZCSNlQgoXwxLAFIE3i5SOCJR96sBSeATCzY7BIb7snEdQKz5344hhHOKNkGP0ExYAr5HVrYrepYVNt6/zeWfE2rAjxcxpPHWLBa5/9KNpXN78+tdxdvcuEhAKUkNe1xoykkpqCSDtLt6YxJtYTm8zuKE+289AvlZNQlTWLD4eQy2wr9RnLinNJjq/TuNc5HtSeYqA1TAhoCp4HhOK6t9KANGzvvyCelpDA5+1Yv0oQKyWL4m5d9tQS9hJLV8nW+jFF9sGTbWrcZxxLuzKuDPx9AjLa2E15lp9rXaRQ2Slvs6NDS2wg0oFmcvxmefqtKbN1KmqxTHAv64hAp+V4AUBr3lgXyAkgoksP8NKND8HSJfBRWUd8KMqAQHgE0CBWAJw9X2Prgu+vvrFArbr0Pd9cIBvbMqXOVtS1VRzBk5t0OWyTZls/paWssitSR19SRhEo+UzPpFL5j3YOyzPlnDOYRzHZMUgR0pSCuooEMf8jTHxVuTYotESY1TWwl28KIAQlDzjTauCG9EuvCuy5Z3B78kca1DuN66erVw5J69KWa2OsUZxZ4qbU+pZJXumNZVqVqHkE599jHrvkrVfBg/UBpDI0mWus78K5XpSpzCKZ7spTea8otXrfehoJAsRAMAZgN9g8H0uw6ZkSbmxaBDLejE/gDZdw1Yp56vWyHaEuUxaj3j23Sb5rQK5vAI6N3EML8/ESsv5Mt/iaN5M3rWvqpYVWA12STrC37TVlrbc6jo7eS7xJV6Bgcbv1lhYk12wCKAjYSQ/3V71eND+uIrNhOoZvu11mB/5gwUwJuDWFCT08D6AcxlM0+lJON3CDHrxGuhP/KGYfm5r0wQRY5oR+Db/3WdSHPrS10Gf/QKCr0ybni8We8k+QqeX/HtFUTuvbq0xKBsq62l+iu62MLTTq/lv+fZBi97PgK5ntDXt3zrGi//tm7j3yhWcvHD5URenJL2QPxCaX9jPOodf/fg76H0HNhYi6nzi/at47daltSJsLdroH7IYAAGkCdZfgUF3i+BY2BDBegvnPRb74Ril94SIYqLcgeS4yynMHxGhiII/590JES2D9ZlS/FiJOVqbUNc/Bp4si1a2/AnPJFh0SkkdTMc5X1mgIpglwJYWBsQh/nB2P9VNwiFahEHAsOEM3jmM4xLLISovREkhqXv28Lnn0C0WuP3WWzi9e6fql4cPimxOJYSjK5aW76S5Iq46lMAvHy8PEMA0H6sxCfgKftjCguoYcE7vRBsFlMo40XCUFiCmkpEFRV8F+T1RqTZQ+Q/ESkULS5MmUT+krNHwHs63IZ5NdqefFCuvZ3QO2mpdKZV4bjxPz5RiMoXrWunV+cRwI4N/FcBenOwvMPgzpgiVblSDOKrXrEHKoOdqlRMDjBHsCZ6DFO39ACLCOColyAZwy4qzX2NgjMVibw9yI6QRqy+bjzxqXI/TOiQqflAEmFWLKr5GUTNI1lYxMa+UxRIimWj16YteJw2FjaxinfAejnO/JssdysdpvI/Ww1IO4W3pyGdQbsKNmF0Bim1Lu/Kf1RDFygzzOrJDGhtCH9MnIq8001zVBqaxxmcFFSlVjps0DFAGCUqXEgJq+uhOQo9HrvLYleq6bNq/unbV3ePfBPgL8bk8HjmAXbtSUrbnayvrcW1hPGehA0zHcx1Pgx6t96tok7lSW1HpPGsQqfWnAaU5x/CtdGoH87IRW5drLl+h2geXBoa0FZaul/DuxWJRAF8Z9KK4aTGNW4JKut3yJ9J7Kev8DYtb0XNXQD/8PYCNPoRffWHrJOr9rQ1ibJ1Hk168BvrTfxT0u78P/JffxkRuf0YXRs+ArseAVh2V2Xzwr9hV0T84p6aFlW2oP1miP1liebTA6bVDsDXbcIktqU6XC4E4Pgn5px3c1W2WlYwVwURmSBYoWbgm54OZakXOML52/V4siw1OfwFcPdnHi3cO4SnfplOTYVMcECuEJSL1B5AhEGvfHlY5Cw7WTKa36PoO7G1KsBbWxCljurrax8sGOO68p5vDZKSoBVoUIhZgSpU6WfTIB6VmNLE+RkSkVMngHDmLTRlgC3nkMgsQE6y+ItDV2VgvnyzDknWYG8HOgQgYhyFaiI0YvcOijw4gMRWW946OsDg8xMmtW1geHyeAj92GlzJUliEXQ9O0SrWaGuGyeXcRQyl3WuEOR0TjcR3DABl0IJBhkDUpfBgzXIxNgCAmXe1ddCXkFNhBtqwTf0P69jZwm8NNuMOatpYyJGtFxUx01AvbXX5E1Dq6uFG8avZtGXm3BaU1ZC8o3myQLeZmqtYasKtpLTS3LlMVhKsylpN6+qz+6QF8TSW2BPDt+TdZxA2IMM7zLNC5VmtdlQkx4AITjEtCtlBzLluEBv9TQTEK8zj4+2JEC1FjYLsAhnUI/JdsF9cIAZoEXGOAusDHEdedWIYkwMicVpYOZExcv3ziQyUMMW3UqVyRlbikIEqZkP3K6KZKx+kjCFBbyRpjIvCXga4EzjUtAjajXeZr4sZbRg1dr6VHan2EsFXatGLS8mQsVm+LPCswZCZNQPqwCs1KwlAba5DNNTAAr3wWiTuFNArLCqq1NAxHDTQgXEBRNYYuU6O2ktrk2byon8d1OhosYW8gHFNUedXiwHyarRLK23J8A3l+1GBLPbbnACsBl+bmQh1vG5rTteYApToegAkgVfvJ0puwwzAkK85Wuq085bsReapRvtpCTMeTZxmAoghUaeAq/0k4ay329vZKPlqBYkSlo/myTWWJrPqvavN6rrbGxkrqu3DM0RDoyhH4M98KWnQby9lZR8zaBpF+m0pWvZtPraai6krGLejSIei7vg24fx/0W58HxjHe/LhRNaYlKUSaOWHsQenpjzc9A7oeazrHoCRk65uaeJVYtLm2cuUbN3H4/j3c+OTLOLt2uFMxJ3mv0A22SGV9DZqMDWipK7ITzgD27p7i+uffgTkZq3zmC/35V27gq8/fgYefjfEH3r6Ob3nvajN+EJyF6SrQC0hCs+yOf/nFW/j8Szdwd28Ja7vg90MLSyxCHpBAqjQeoiCZAKQg7IWg+QreYGUVP5VwmHQPtik1ESjFOstrWRWCj8S6iUWZEpjTbku0EmKSK8dCPALDAtg/OIAAYuE4Y/gDe5gIgA1nJ1ieneH43l2cnR7j7PSkOKM/R8+98QauvPoqGMB4dob3vvAF+HHEpvPk0dCKehXFzsJQFs5GjM5hGAYMzmP0DGvCDTVyM0wnPgUMcOWVV3Dt1ddg4q7azTffxHByonbspkUyWtmIn1k/GMHJ5qQQidK/FJWTZLARFd6uz1dXC0DLenxX+klSKMjAmkdzfPEZPa10noVsFSCQw8zlwO8A+H9HZksAvt+APlLnwJO0Vi6/BHRGQQ0yxQJnT/shLqbgxGseAVgSTk/vB5cA6jhM3y1gbLzZ0Vj0XQ+yRvksIRB1AFGyhgraVFaemDnd+Cu+tIQfEJlUz6k3oRRQ1J3UXuFoO0DUg30H511qmaSYeZdANPFPQ132q1L2XVYStbIpwHtoyxlr1LW0G886j6hVtuW6lGqlVhJZVe4p9JPcnXIrZOb3dRDPnOQWKUMILhbj2n9SllWACFqo9JOFChBlEKS6Z1lF/o2lGBn4jwzcyW+LMlJ1ZzHntxrcarbwVHwt40m5TlqBHyyts4aetb5W4bW1UA1SrfpsgUr6uJ2mVvjaQuokyjNS5lUAU765sBz3us71Mb1WOc6W+qKQecBFeI+E0bf1EYn1bOlbS6y0ymN7VMnDFFWNxmZAswyIYJc+PtkIzOfgPETh2OAbLwd3GX0P9LbJ2adxkVkVrwOwdqdtRUj61CdAL1wB/39/HfjdL8+HU/8+o+3oGdCV6NEPoHnLril0M/VLMgVQ1JyeUmM20nzoJnWnI+xyhBk3tHBZQYUvrMk3+TVfNtLCavSoLubbrMKUtcyCrcb5p3nnZ2b02LtzCnY+QkDUCF3+vr8YcW9vCMo7TfsJAG7dOcWd/YP4Kx7W8AaHyw5yLKusf7kgjdbj/sGIW0dn+ODSafGOqrACEiXnHGkscPpjb2B8FvgScBCfaXP+DHSFFvdsUvtDCQMUd+VznmJdEPuh6t7sxl+KreqhfgcFwgbhmxmGXXRyH4AuS0GYtXFXyw1LODdiGJaFEtQiIkJ/cJAY5dD36A8P4ePtkG4c4/cVqukaS5BtaG6ktWbz/HjJ419ALk1O+YwYR4+lY/R7Pazp4MgGH2ymA5lwQwwt9kH7BzDWAuyBxR7IOdU/eUddDL+m8nlWUKwfQXB1ABUKWanhDJYFf3U2BmW45RJuGFFcPDHDRuRoZNPvQ/w+t8t8LtP7VjkuaqxU68ksB2282MSyqxlmfkCuT3vXuHPx1Lyb0Qeb0m5KrmX1JUpXbRHQymWD+qRVekXYiQ+lXPiUySTaGcpjSTcZfKksWlI39gjYr+EKLj6K0iaNJjzRijmg54165gEWp/Zk4KKy5Z0LPNmNMNbAuwWstXCdVRs4HYIvsuw/JowDA/E3SWo9SXkz5f4tyigcP1p2UrBgJlZ9IcfpjQmbTGqJYrm5MvqylLXI2GzpUFgJxRbXlmHaoX0u78XM+82J1b/b02RFaQ+Zkp9JNQmT+rZWqPxSHcVTt6Pp/mbVhmrkgVnJT3G9CD+zlbgAjRm41f0X01wycBzucE7DSoZL/Cd5ltXizADgAwC3pWSNyd5gNROaW2YS/+ZmIAZabG5L2jyBbfxybZpOsS6HyFNwKj5vhZFwcoS4jl//FekyYxiGjY8g1pZpwg82yUen5Z0ea1qWKi21YgulPl4sFoWlaOKjE5BLjh9Oj5G2u3BzTiH+urYZd7kfK71trwcuRUMKQ6BXngc+8pKaRmHeJ7aiPlN5JL2oG1IyHFhZC8mgUb/N61XTZH28dABavAS8fB387k3g+AQ0Osjmb12kiT43KVtL0muF2638TyI9A7oAbMTEV+MsD4Qe2jgkqgTBR0stRbh8C7TLqmEqxTRFGoEwCcoSyhqoYEpZ8AlhglBEJGfR5wu/qj+/8MpN/P6Lt6DZ2HP39/FHf+919F48E8pfFt7ZBz8kb12+j//8bW9jaVzyS1I7h6zLIDukacdMAUcToZW1kKiE8vhMN5/zVAga7H3wgcTZmasck2QB06LipHeKBUos0m90O4ELR/MB2jPRegCwNggBe3t76PsFON6MOQwDvBuC1+XNtFL0e3t47dPfEXudceett3Dzq19dGeeiaBN+0GZTa2ImQMTHW0OD/7JhGDF4g5E7XH7lI9i/eg0u+KkOluOG0FuD067Dex/citYWAC5fA115DgcHB7EPolBFARgzE4UPKS6BYHiM1n3TGqTRkYRCOV4r/2QB5saXv4K777yNoBCrdJT+K+RVmjWtOnKQm/DJkBoewTL2VND6dqPNJuhOOQu1hNcNM/2vAH5zJofPMPC9022udn2z5ZaGFKQkGgSoFfkMLjg4xxgZWMqak25xzEf7DIkPysswZoGuX8Aag35vERwcd13iKxTztVFxM4bgPWN0w6QGGhzxqi7JuhME6mwE9ELIfOEGwByufzfiF0ysIcSRM1F0VK4sNwRwVdbY8syLFRrNW+itpV34Dyt+ulOWMxJSDQJr/sks+Gi7zAnE0qMxj7GUppISEmiR2nsKQHiX05oCs3MWOFwck6NvMvz/UcYFsjiWhwuXVQHO5wvrKaLaOkvTynGjP1dnAADJ+bkmOUoooEhy+q6cwGun7YXFWVWGddZoOs/a6kt/tqy+pB7C32RzQDuGrz9r31m1JZwAY9NjvEX1VtBq2SgWel0iqjwqTypBLsktpfbJjwJ/6ofSEz7Ym2V3otYplW+6hCbWskZhmy3/NqGLmhTtzJr/EkB/5HtA3/cp0L/+98DX3z1vxngm7WX68AFdBbjRfNl+wytfb0yb7NZPFgGeGbItOWFNGWcFm13rxggWToZwdjX667oQIvVv+WzV5E27qSvnuAibhOn5Tpp8UDPPzKVb+Hq9C1+7+qppNB5jaroQ+d7+Et+8dh+dN7FewTfVEG8cZAQhu18s8P6lE5z0YxL4yrya6FCuCWshbaaM9e6aArrkC8W0kuNXDv+wMSDvwWzUwm8B2WHjCBZqMTGBaVwugmqHVQWGR3T+G1StVD3DgGeCAYKZtrFBIVHCAKf61OMr56O70/Zders4OsLh9es4u38f7uysCFsOqziez71rLwopV09zntL1JR9pj+JqHQ6PGLCLBQ4Oj9Cjx0g9FkeXYff24QeXBEVPgCMD7xijd0nXF2XPjOH6ZvLZLN5yAMisKKYCblHuNWs6GIQbUjN+EL4YqUoFbMlvTj4OCHuXrwSLLtU6ZVUlLuPk3l24aJk3K3w+JFrts3HzMJOw8jt+bmIVVVtRrgrTTK+mIkgj3lzcRp5z8YpiTtbSqdI8R5mXU1LQU44rLMHmE9pE7FxV+bKCdU0aKkKOOsS/Vk4fIPr3KuO0rFxZhJEXAdqT3CTn2udXWV/SHSMKSVpHwjFAF28SduKvkQjOdzBmhBsHGGPh3KCcuEclL1l/CUAVHTlztrvONVb8QK17lKwCGOzDulDPr4KjzmiMHnntay75ccGtFXfJf2sqtMYtacd4qyxPVwEWTeUz/VSyi+bt8XmyxokzX4AzzxnsSscOWYXxU8ueqsR57twCcFfyRxDcpKzvAXSq3hUplHWaSq8NftGa6qnuc7HmHpbvV3Kngn+so9WZNblVPWe0NVZjzLTAr9qCehXItapv9W+5PVWe17ce6j8NToF5Urbi/Yq61eHqMLW/K6HgJiLfpi5HDAOwRemiD/ldg1s6zfysDXKFMJkV0NwkbbT+1ht8yvKqTnaS+v4C9PpLwOsvAUcHakO+UWj9Qn2KTiKPmWhGl19Vj/a7TdluzdUz0J4FAgKAvUVwqm+tFuLXFivJUVy/bFY0lX02waeQPnxA19NCjTE5HbxbDtymVLaerr35Htxeh7e+72MYD/e2T0AXYeMiT7WuzNjLSZ+sulYyuHbF6+BitFK/J/WnVY6C5vlOk+7tDfiP3/4NyG61CG3DOESz5rAAL/oF0l3yUp54bIPmMuWSAftG9ds3QQl31cc2pHKB6dr8s8wyyw1pF7XegZXCaWFCdry99gtWJBgc0AfFIv8xe3gw4DhYIFkCk4GxPchYBJM2E9to/qKARu1TjY+efx5H16/j3S98AffebezCPPakx03sSSLsXb2Kqx/9KNBfArpDnC2XGN2IwZ8EC70x9N/otK+JMmV7soQYMBBFgCvuPvZ9HwW2vDMpgtqiM+hs5TuCAGtCQmJBERThUtVnchCc+/Krb+DKq6+XwE5UhNIY5ACOvf07/w3D2c0H0sLP6CmgNVLtpkvn6tVmWyr9L+6cw5cBfKUEFeaJg9T4pwC8VFuBtTSW/EOc1KeFQwXxwvO9CzcaamWSHIi6dOtX1yklL/KPYO1l47EdA9svSuupCKSHiy5MkT9HcEEUEGbAubHUoRQvkvSqWgS/lsjKbKsnJmtX1VI7qRqyU7VLvB1pFcC+bqOA1vrFzCCX/BuACRedwUu68dghtF8kn2Sb3NZaOa7KoiEpAvBFBv92uaag+b0ub13X6XGwKe0ocK9K6mHrqhuMuznrp9riaPaoompXQgCB9DsBrcQ6S3/qGwgF6NLWVeuOEQqZqjza4qsFeum6J36g6imWV1r2Kf33Wezt70PAqfqoYn17om6zVeVpPS5ZmgbDyu8xhZl0eTU7iaB0BqM3GKgvPAf6v/6fgEU34bcF2KXy0HpYCkv5hEkm3Rfri3Ju4grgqosTJ7DeWGxu5hX09AJTF03PgK6HTNvsxAOCQmOijNYMpzVZm7I5a2Grnd82lMLzOgF5l1T1wocVbZCBoHQ2fC2TyGRGj6O3b8K44D53eXkfZ88flSXKFU355iLNg2RcfG7YuqqeOf3wnSkAEQG3C4J88hNRMclUPioTZvVPE4yLFS7flmUXtqz7QKdRlIRKWTycjzexv7KH2TxWS0XHxLKYeGSkWLTib2u7CAS6BFyRd/EIXBRIopJDJuz8W9uBnYvWYBsCng1BmQEcXb8O2/e49957cMtlEfQip4Uch5hLW5ez6D3Nd+bkayLYxQLXrl+H3T8AGQsPCq1jLAwI/SL4jiAalbAXEjMqndAvPnUTcdiR9z5YbIx+CFZf1iVrL4rKaN+ZdMRRC4CdsSATbxBK76K3niikmWQJEudDoYkykr8uAshHHz/kcfmll7B/WTkxqokZ9z/4AMPp6XyYC6aLtuyaxE0Qtdbo4+cm8hXXjzfguY2xN2vZtSbP1fHa3JZbC2XddvXuuvAcohnfXKF4Zm41aFaL2kFkgiuT4FzPOlmalDUzd2G2wJzP74JzT3TRSr5IqVII+yUA70owSkpGUQSUYyIdMxaFqkpfNmVMFHj4VQDPB4tcgEHkQExgFxaT0Y3pWPQ4nIHIYDjrg6LYdcHJve1Dv1F2yhwserOvr3Dbb1xLU2Es0q3CqZDlKjGxOBFlTrUXJFwINO2ESoHbaa3Y1LSgRecAu6bFmM6tCX8ioKhlEkV9kk2jvbAqXgg0ujEBWYGiby1IuydtMgS5x+A3fUyqpdDGXtLP35ufL2EMYqNOonpwbxQQsfwqk+L9Ot6qwJhVm5QXSZW1U4vmjim2LKJaAFcNRrl0E2YGnOSvBrr0jYitNOtnczTGdFr1mKuvgPE1uDUFtcobEOXT2i6z8dQuU92osJiM4cIN7CmELl1V1jL9EjPX+ldDzlf5130cnikxHdLmyHO1KIQa84se5rs+CbzyPKi3mS+n4FOeOTcChfdSrBilCnJRT/nOdbFmiVKYfLs4V5/hXYXFxc+JEBT+SWuM+JBs5EsqSlHXHGZOlmrX6QHwhceMPpRA1y7denHiQCzDFgrKyrW1qQBAZM+StHxRvQysZsNVfFVRkkCzTSsLo5ukBl3BFjNqtc46hYsqEMAMDtfefB/dcgABuPv6czi7fpgbEpMskPfSk/ifg1P+bpBN7gkIllbzJZt/xdVfvIUwqvmqDOJUOxe66Ota0JzNjythKe82pCK0ysxcCIpEnBbPtqBZ+hHTC0EAShhyDCXt0qbFs1zA2XuwcxAn9PAjyDswj1lRjb5djA0WAnmlh0q3JU7Ib2mDDPMRES69+CIOr1/H6d27CehqtVBbAN2Mgsk1F923NXAug1+PbVXSbm8fz3384/CecXa2hANhdACZDpaAxcIGcMssw6cLQifF+akFnnEYovIBVeb4Y8jXKMvYkB3FrjPphjUisQILO59iEWatSd+JwtFUaw0Wi0VIKwKkJGNPMpKGZAYbAPGo1NVXXwNNtf1EzIzh9BTD2dmEsW5tvl+lu442Sf+8gNdGxwenEQMV7KUdcetjkq14G+aZXjUkzDoHrsO1slAAV+2gXqkbmR9URW6oQiiOaTcD65qXgn0ZlNR3+UlFGWo5PKsNrZKtKLzMUU/A7+gwpaoxXWKCzyq5ETHrbKIs5GOK2kLB/GEDvAoMI6IlT0zUuWAB5jn61ouZEiW/XjAGfd9jb28fFG+MtTbeGCsgWLxB1iAce6RkcUYAbFYzNHii5tdEaebcZ1Kfoim57PMsM6hWv0DgaWPaMc+5+q0KSwDEklbHy2t9+VtbwDk3hmOK4UH6zMMvzgiJcgfg/+JB2gVnLlHxsYrhldWkOA/m5NVVVPOphhRVt+mqHDYCs3ZdmzaIx3I8NB4PVuXZZM2qbx6sj8POgVFnp6dwyteVBrm0v60a6NK3Ls6BW3N1WCqZTsCoVrwa1Or7PlmgzgFcrd/A9JTFdHq1wcIMrkmcan1LchcVn2Wb13M759kibRkV5H2Km5q6tMgyvAJyJ6vv3gL0I98Lun5lJkzVT8hyeC6LsnSLaTAQrAFZbvTWVoQtoWTdGFZKQ6x3kwXO9GNbB8fMvM6BNjGY2ICtrXv5VNGHEuh6UkmAqLViSTH/Vg1mnuNbW5MZPZ774rtYXt7H7Y89D7YPbxLpnQOi6HOJCJUpXBVH+WZKHCbQwc376D73Fu6/dhVn14+KFiQOSnTJo7Iz+hkdTmLvVsFJX5YC+CSzvIYkh+75Xdx9oRLQSekWlW14adFSequSEWTI4WNeLAtgUZQyEaJwqiQulCw2QtwY9dUz7wkeDoPzEBAwqG0mjQPPQXjIi/9cf8ztpqwmIsJzb7yB5fExbn3ta/DRH8TjSbH+FKwZyFpce+0jsHv7CJ0gx0UBR4hOoikCtQ7hdk1gdFloEZVb2s52fcxLKYJJ2VM+VGISEt95D1D20WWIkgN7Q0g+KcKzbMFlDGGRhMpw1FEc4BNROg5pjQ3hiSCO6r13IPiJgK5/X/vIR3DphRcCoKpacaKcOIebX//6BPB8Rk87TXlGeRhBZkoePUlIn4RpPytJ87ANJOzzEodNG64fqtJg5pchA9NH5s4BpEoWGYhHzUVBiQqI/wKD3gcwZjml3M0nGOZg3fwZANcJkJvzPGHpBgxnpwnAykBXAL66vo/Kbwdx9izHHc3+1XCzbMi03Rdc1p0j4I5GnJnmLDWjRwByrQL318VcRaUSJ6ACYt9HP0kyFiDgF5IS7AsH8Qw4hv9NB74zsy63zLBOEF04KMU6lX3Ttn6clMFNFO+HR6EnfJIptWVP/T3FaYxxfYRw3RFEZsbZctl05i6/9TMBtoR0OVuO4efAWgGrWhZZc9ZaYtElwBOAAsiqQbV5cFDilvWow2y636aBlqACtW6U1qsSV585/rQ8ys1KnGdyuiQDOelVqW5YA/zh7wK99iJw6UASnpS/dVQzlb96V4SRGkS9b9P2uliqV89qvGkVrx6KGwHbz6hFz4CuR0xTBjMbEFqhnI9RKfDbrOnnIOMYR+/dRXc24PZHr58jpVXMvmYKAviEf9ptuZo5kGeQ90XSi/tL7B0vMVzZx/LqQbjStmAyekdCMdf0PDJ7qGDpb6Z+K/pIC9YBaKPScW21YIDVcGna4XMqSalyIQFgWZWoljnd5PGqXk0VFIcaTC3k+qLAKsdUlFymtWoDRcu5iJTFy+Fj/vGoJ+fS1fBMLsn0eFIjWPE4taExOLp+HYuDA9x5++0AiGx4O882lMZW8SzDTC3SQoCAWwnoIgvb9Th6/gWYxQInJ6dIR0cQwEGxH4QxEbCi+KfyiJ9yPLGLN5cxfASH1Q1ZsUxR90kJEDIIlnooXppoSC4VkKOO8cYzAETBgmvo8m6mMQbWELrosLXvO1gy6LrsLywp1uzDX0MIFTq4ejW35Uz7A4AbBtx99921QCd7XwhiF0EbpdfARjY5PjgbZhXWsirurvEk7ky8JihR9+eMhZcOm6y4GmlPLDOZG8cas+WWZKlWHkitSGVSA2Pyql3dlrt4KV+MpZs7mbq00588rHNL0VvjfyYd9d7YyDu8h5d1JFlCMWQnhBF9ab1L4HcBcmp9TgqhKFGhrvwGAVcYcrKNOawHzvkUxywsjFU3lvXBqlcAsKygGnTmAGQ5K6+Kd+Y2UvIYZWVuG3qUYNd5RMOszLaJFVPP/B6A9/BLh8TlOX5Lvrci+KB8bQEMjAz+qgfercYZNRRWKj60SJHK1J5lRSxVfqmzkmoUkFPG15muGw00/Vq3KbV+rOKF51F8N4lb1Vl4wgzYtepTvuvjh+JDaxzH5k2IAnS1QJbCimcF4KFJH4Gsj0jq+tjFYnLMsPatJb9bxxV1+dat0SKr1dZGmQXVMkr5PrRVM+lGXqvmsp5p03abklrdiBA2/9v6Fxlxuk6xnX3w3fdtb4A+8VooVGuzYAYkTG2GVvvEMFLCAhBrFO+BU2slV0yqNedrnlY8k/G0TRmmFU/q9MNbgh4aPQO6ntGHlsgzrn/+bezdPoEdXPkOjKtf+wCX3ruDG9/+CobL++00sFrAv5ByQoMb2aGu52D1opeDJF5GXj4vzJbqW1Jekuyi1bRp+nMpARl8KI9qTAXBLIhK+Li7VjHwejWKGzI6KdgulHgYBNxCWEyjwhfwyGjhFRfR1LBk4tl9rOTyNPnVDmv39vDKpz6Fk9u38cGbbz52KwfJv7Ednv/Yx7B/9SpobzGVs0l824SjPd4HJ80cXsJ2fThCaCPAyIxhGODZ43Q5hBEka3hqci3wNRb9eFHARAmO1h9gDxctyUidyyIQDLksL8RxZSPw1XXRqb2lKKjmchxYB2u4KbTWjl/XHcswXYcXP/nJcIx2hrz3eP+LX3yoPr+e0TlownQ2iIIpSNZM4YGwh1Uwxo4QByHOMQ3XtZX9wE5LACfcgBrCidWWqSwu8tGWAASDg2UmgSDH171YVKqFl37VAL8lVpqykUHo2EZeBeAHGHjVwzsP74BxXIYaULbkkk9/7AHToY/HG/to/SXO77Wia6N1KZnoQ7I6klW2TEUXsTbsmAZjd0UvAxocWbMGMdrgATOAtz38r4y5zHqXQ/4Vnq+egxm4vVtZ6/E+VZ6bX8viIdcNEOU8AyL5vSS0yQGjJ5soyk+To+NVv9dglQBYo/K1pd/VFlySppAAR/U77fi9ts6S8arXbkmnBqjqy3GI4uU5CrhqOYMPbVICW1KOFvBWj5sJKLfxCApjcjKloOd3bfE1B2C149bxW4AhoH3uljlp0M8QwbzyAujH/kgAu6J8xwzg+asqxxmqNx0yWrcyzI6r3oXSJqxa5PMNzm49ow3pKQW6VjOIXYfPAxt2szNQhLYaSuEUSS/f8040Na0KVMMadZyJGDB5Rp7RnwzwNh59Wlj4vsvRWZegkS4zuuUI8iWv8r2F7+20GHm7bYaL5DyojsOMxb0z7N09rZhk+NmdDOjORiyOz8BdXBTP9G1MU3asl4/cc9So8+aUFXcBGMrnRUCucwo7KyVYVQp960tUq2vyLMSepJHQv3afSB2aGxgq6RRT78BAdZ/ElyGAoOgwU1VDiulpcEuDXTmfrCJVC3lR1rbgLE+MMdi7dAneOfT7+3DDcCHHGDmWq27R4jerEFXDyp4WdRa23wvfDWFx6Qh7ly5hdA7Ol8f3hAMl9VG1kTGEznawtoPtLJg9xBzeO4+BlykRPYYpfsltKQpODpRBsCjAURy3LDUJ30kzFA4+e+px5SiUf/SAoXgDp3ZGTQD3jC5acBgyMJZhjYH1iOENTMJIo+Cne4B0bQj94aX5eQrAO4fu8ChcLMHSJkiA3rhcNoGykpe0SCmIadpnvs4pI1WwkvWVI6wx9Um9ax0pntIUGNHxir6vYxbCdpnJqnYI1eZGrEZv1HWcS1jzs7US6woZpFr2Jpwmd5RS/BtJ62UTykpF8cc8UmUSaT9SWQnIvHZNjVZrICjHnSofBwurYvjVil2JKqiVJfJqcMHftFxEtyVc/iitjRl8C8BRVMCLMruUBx0QsCCM/higDr7rYK0Bux7G5ktMjDHgzgafYF3cCGBTDGY9rifjuBlutdxaFHmOGO2xMjPJdH9sRJLECcMP+QH7AE5NLGOYk49SZgZuePA7DtMBV/McabjpOjtPEwEzPNPyTzMRqp5P+2gVyRw9D02jU6r7FDIjtIT9DYs7JdL11V9ajTWVPnT9SwutYMU9OhdualbHEJ3zGMdhCnTJmNE++eripjN8rNhxaY1VWBHq2a4shQJYJRae+WiztvoUgKaL7g6IgguHdPNzAymu/XfNAVmZJZTyFmZ+TajVTdVaHj5JDfHGWEpRufm6sdyUayH0LK4KIJEMQFcvgQ4PQAeHoJeugV5/CbDBaT4lgFylnzJttI9u91gWkSvLuLFc8ohRrisqYL20J9VyUvnWnMxhS1k2plWv8mpDADw/1lH1Cce5T3W/AcU8XjWD5+gi9lweV3rCgS6CuuvrgdIDHwMzI5LTxKxFApmocxpCnIysJwWrv5wSsVdp7ljTmEV/ssQrv/nV9PvWx1/EndfzUUbtGLeejETB19dLn/sm+vvLgg/d+ejzuP2x5yfZMiFwLx985Eb2kf7T6RfffXSazj7+Za7mOQAmHgTDwHO/955c6xY9RJqQFwMcHcEzB19QhmUxK1SP9S27gV6Uv3kweXh2IBA8iRNeI5y8EuTnF7dW1s32apRmrkZex6wF/EbsUi5dzZpbOTIzaGQY9lh0wDj65KwUANgYeDAcGEwWsH1wRt/1MMNZGEM+OrBnl5RDiiuc5JnfSH1W77ntX76M177ru3Dn7bdx86tfXVmvTYiJ4cSzrjqGmZW6ujR6vsczPUQ4vHYZz3/rt6a62W4BkIMxYRzL9daAhQWj90sQTASpGJ4dRj9gsbeHa9euous6dH0Xjhs4D88e7Blny9PgMNqHZ847+Imz2DH4TXPRMsADbIcw30RYjdUyIqSaMN4F+RXBgiFzEqotCC4NtMAneMxChgih1niE44/hdjdjA+BlrUdnPYw16KPwG45CRgCM4g2R4g9MrDvU8E973lFoJCLAMK5/+jMBHPQ+ONOnKPB5h/e/8AXcf//9wF1iF8qOqGeG8wyKgnjmCi7KTPHmUWIYZGCSCRiT5JrHtwY80gdH67nYtoYMqLHWZuBK/qmGHwDWu7wsgtn8TXQyq/IRtXlqHqMDw7CrH04A8ib30vLvVkTwK8Wp8jguUFZdlLx0TC6c0YX3LtxWmhw+S1sSbPwLlhEeXdeDiOA43hDmPWzXoeu67PvGCxidNZiZbltRi+mKVDRaI93gN9NOPELVvJ/TFcL5TXbKbMM7Ox2HySl9o7SJfs0Dv1EHqSL9CAEfJZjxFhgBzPEgjAAQFWNRkMWZfWj3wDP7vke/2EthjO0AouDwXq0lYYqJtBLGOWM/fnKeJ2liUWFBk/ovKnlBX2LVP615VVY3XCDi1G9A84UkaQpfUL/HXxngv+KT1V0Yn1wdOZSMZT4DcNwqWqk4UnsKzquWrZQqLZeUPNBUUxvyiX6k+ELiS0UUqj52YiIAskWQPv6p3+f+qds5h+Xi2SQL/TEhPbtb1lqes7XVOAwBxFK+tbRT+GzJFYAvAdW1RbeM3VRnLl0aTMCrcVClTJ2SgSgKa3S2Ro9gVdej6wOPJCCtn+l4cvThKUCWbLgFLbMBN86MU03hZmm7JpS0dWpkxNmJ3N9lWFWKyTtTWVVRHUW9qIewg08yiwx5iV9vH6fRSUkUQ6lJMrzISQsL83/5YZhveQNmbx9kLTyJBV4ubxrbDSWkrUpwiifHx+W5AFqFVS0h5Fe5XBFAtPzUAWR8KY1OWJnPGk/k1Ll1knAWdQtZG72Lrk0cmL0OGH97SDeW1nNSF+kZPQ9Ytc+u/OfppCca6KqPbW1Cq4S4B0oriznzUiltTLWYXMedipyr67r67UaCRiMQMcMux8QQFndPcXDjHs4u78MtbM6a6njA4u4Z+pNlsKRajkUeIZ37WF7ag9vrYzJcpscT/tWuGzP641N0pyPMWIreyngoVdIMrth1nsIbNP2lVokLG3OxftxauUT2arZBo3ybZLZbEatMHiLD5Sx8JOW+eK0UaCWltEtYDtJ6qdmkVkSEbrHA4ugIB9euYXl8jPGiHJSX660qT35BIOxdOoLpOoCyNcX+5cuwfR8HehDj5vNIHCh/xuYzBHTWouss+q4DmOEpgGVBmd7Lu7sV0CWAmHNdUOQV0OXIg5XQ4VNxWJUZUcEK5fIe2Bstnr9/oI4zBt9sN45OcdaJ1UZ8zpx4KiDpRIswDjyCyMP44HDfGIPB+KDYmiCwBKuweAMkEYwBrLHpuRzzCm1FWYiO5WDTgclnQYko+AnzFvuXrwDOBS9zzuP09h21HigBVAuFAhKEu14nqhCngUL5dz3P1QSeyEstllBbG82lox6X8P/MSrOJsEalqFfmzbl9oBX86X7uPFy92UpaBldp6R1vrh4pMCAdgYlt6dIub/jO0nGEgm8FZTBYUBrV2yJoM4K1oD4GNBWZqzI32r1cDvWxMk0t+aRe5NWzRhJJEeFyXJTDdjpmshVAnV5VW8V6U8/W5XiXAQvIhkehr1B0my9HHa0DGQNvXexDC/fcgPGFMR33tl0XFe8AeBFFlVlZdeQNlTgeWKlptxi4h9juUnjObaXAfn3Um1O6eY5wXeHA6Ip2LlvNT0AIAd/8DQd/L/ugzONLfscsdJ/Uw6ygBvzUki+3kCcK61HhjdKfVIbJpaj4E+lxyK3HIZ01G3TbUuvIXsgny6ir/SQppbcRrKi38CLW/cjlc3C6QMJzPobooi8tfSRRfGxpa626LgK2189a33PdQ5n10UBplHw0LlhZ2mhlqYGuYHneqXTCKpost4xJYEYClWWe8nQ45rm7mtYFaU2RYlamdX19irk8anXbRpTXc1QNIdEt5sLXFtr5T/Hrg73gZH5vPxTUqRtUqdblc521nDOtHk2MCqb9pE85ULygog61qpHKlOVfsWAN0bkIWaxfaiy3p+OaDtpoAFXrYlogdqcLZmnnyEu1qh6fW5TviQa6ntHjT5ffuoWjd27j3e98HccvXloZ9tqX38fRe3fir3IUH717G0fv3cV7n3kN91++ulHeq+bBla/dwKW370zv8N2VhHfK38Mg2XWqnz3NNqgPjLYHzTelo+efx9Fzz+G9L34Rd95994Hk0SQiPPfGR3H43LUkqRGQHGnPjRKlZ0P2mrKySWmck4nATeWzJgQjHBzsg4G4A1w6lBXhN1//nd+dLgcM4xhueON8DMI7F4AA76OlWDhq6TkY5F2/u4f//vOvwXIG7jwB/9unv453rh0jWUKoyyWkz71fFjvIHB26MlxqgHp0GASwz9hgZCLAn9zsFqy/TATDbGojAb3Qe4CCIGpiWcWy6+pHXsdzH3kdxIzh5ATf+I3fhBuGcHFGQNnAZMq+JItwTFn81LnA3mQ3HQA6O9m1LK08RNCn9D23yXSgzI2hYudTC2HqQwToCeAS4/oN+VitHKw73PmwaXqcpvzsOhHDCM47DGMEgzn6jDOiuJUCOjuP0ftws5cxYU5FhIPIghAsLUbnitu+chpln4RXJR+sj9t4dllxnQVJG6AKZEe85DszenhBD1HeBj4L4LO+yDNbAgqQFA5Ijxgh4FUoKIE/A/D3I93k2Ecn1n2/D2tt8vXVdV3092WjXzGOoJG0N8L332Pw78TcOf8JbwSCXxzxD6ZJrL5M4nXFPwkOTRBXPH6YgQtX5Kn7VJzHlzwgpzVRDh9qJzZoh/wnx4PUOGAE/5B5Tu2Q/kyjaF9TNa0EiNTcrS3k1pH2oaVvPCysryNfcj58shcLvvLIoLaUrn1SJT7iPYZhaLbD3G+Jv9hbpBMMafNIAC7xt9XlCyaAnC9X6aV2E7lmMl5lHUQGMzYazOdfg0yGu6s35Yo3BXZWBl+dpwL2TJQXi5tkax4f+blXADun9xHqYiihcrLaN4rVqNFaIGSujeSX9P8mgNZDkB+qtXzLyBdalA8DPQO6nih6iBPxAol8vpHx3stX4LvSlHfv1jH2b5+hPz7LjLSay7LLefD+PdizYO3lO4N7L18GmzrwNL7Q4s4JDm+fYnH3rAlybYRTRX69shceBC/SINYKQOvJHCUXQGm9aze+ADR5iE3DJaxy1SIUFZP1GpoIDQw2BofPPQfTdUEwcA733nvv3LcykjW4/MJL4YhMbcpHQH9wEG6z0TtktMPYiNJeUnhkoZY/E3dE0dKjg7gULmwMORsT4AhjTNwtDkbvzB5kO+z5fETCOY/D0w4fuXUUAa4MfsmRCe8Yl057HHR7ILmkLZb1W25cxQvHB1WdQ6neuXKMG0cnSUirtfCkNii5JIFACBEYnE7ksPMgzxh9PoYmnwG0UFZei9R0MAA6A/TGoLfR70/0C2IXC1x57TV45+Id44RwGUW5eyo3kIVjF+HI4vHNGzi7fxdkQmA2NkwT5vQpx52l+mF0U/EJcGlJWm0g6pDl3KEIkGXxt/gg9ZPn0i5/ziwRZYiUbhWai19rFIn8azJfJkw2W8DpakApgPJZHtMBxjHcQjdGK0fvfQJF+34BY02yihyGIdcoHgWy0VrIR6DC2tDH1nZw3oGdg/iWkS7MoFjVcgyo+6ni+ED0oULRh06jXWMc0gnp95TbP4fR463dxylqGqJ1rzdu3ZN0iwTbXhebG/tc1imVQ7P8AvTINqd4B+DPErxxIGKMdohWX9Eq1GZLk+TYnsJ8tvYAIBNvlI0A2rsAOSp4TjqiIwBZ0DSrVssNwVpUSP0Qwnse40+e/vmwsZCstvS/lQXDpL+gAYUckiah2+vwWmpEmU1nRfLZii4tVvlZzQcEYKrWN53OynLUeTdAK52XDrfueTqOrMoi/CWDoz5ZZdX8KPvIKp3Gp00pzmBYmY6fjBsg37xc16npjw/ZSisdI2w4fM9HEMXySh81jHOqOo5IcmWzGnnykyrepMcp9Ffp8mqjYHUvlzDplNprTgkDNWyNJ+viFDgKgGcxW5u8vlkmxbf1ij1nFRaXBQjEqvMVCcJ8y+swH3kJuHKU2lLfUJxrmecgqe/A9HddaeJpvyXJhVT99adORvNIlL23C3valjSwujZs/Nxahv8Q0zOg66kheigTchciBMuuw/ctTq4dwndy+Dj8c3DjHq6/eWOzdN6+Dbx9GwCwPFzg/gtHYGNLLtWiuAjv3zzG9S+9Bza2vCKeSu5X2/fM7bBtQ+ftnm1LcJ78nigmWggkc7XOi+mcE9EynAi2rTdri1G9CMeSLr34Io5efBEAMJye4vjmTbhtjzJWi7TpOjz3xhvo9w4apShgkN1IgVksyROVKcf3ybeFKkF4HXkT5wNW+rhkaeHC2CcLIN9Y5DzjZXeIP3rjIyAXrBmc88mprQjcznssF+LgNjjEZ+/xqXefz4I+yw5jyPtXP/Y23tu/i/JsQqyPtLEh1QxU+ODy3sONLm1YuiQs+pSPVvm1rNzvA8YSOgrgVGeA/b7D/qKHJRNcERHBLPbw3Mc/nhV9CmCX4wj6qWInJ/uxzP6Ln8fy9EwNm+j8nrIiFHw0ZrFWZMFgX0KRT+ZG4xApAQIJGCGl3ErrJVBEK2VqhLBKWU+2iFTU03Qjeb0Q8nWtkDqAq7BNWiFRto48lY9KJVQ+C4UwDhXvx+BDUCxoAHR9j739fRwcHMDaDsenJxiGAcvhJIBNhOSjS/pV/BJaGwZrAJEBH/25aSfJyYdho26T1ktfxZdlBVTIDsLkmU4ij4f8rFRx1vHadr9Pn+Z0qfFsdWoSNhdUHYqpgY00v2UuMPANAN808Ag+/zziZMNSAT9h/oq1HgEwxmL/cEzKutEWoOqmx2zVlwsjAETJ+Vm9l/GX34ffHvDxBkRlJZYBCy47pWifnJZWsOXXxGqmEX4XYGqi+G4Qr6HXztMMgwm+EHlSnyIeQtswGIaydfMq2dE3NrpqZ+Zri9zYIMiW0D5ZZTnlNiBbUteWgjO3HXJOt+RnU6BLh5mjwjeWMekv+73r8vhX1uLhuKHwclmPte88LdvVvD7/agMneQbx5HFbZpzfD00dUaQ7zWsVKf44s7a0823YLSWkajrA8zhFc76Hl/U8nvIALd0xAsDEMDDf8S0wf+gzoMOjBHKJBZ1PYhdN5nZtLbkKQNZuKCZ9KwXkmGZjjpf7MjFw3RTnVeAaJByzxWXb4R9AIT4E9Azo2pC2WiwfJSWl8lEXZEo0ejz3++9ieWkftz/6PBb3TnH5Gzexd3c3v0V2OeL5z78TLLqYcf+5I9x74WhN1bWKftFMIxuOa3HuYnNopKx3e1sRHiKFMjzcTAMoGfozKOGoGmPaMnKMbZXhVhn+YqeU7Tq88IlPBCsdRffefRcnd+6kMNdefz342AIA8uDKGT0ZG/xtpVK2So5c+hX1bSq4lLMjomBRhQCuhM+sIHnODrVLcUuswFYpq0pQIQLBxJ04hiGg7zvs9QsYG1LzAmb57PxYrL88c3aC76PDex+PYnAQ9EUY/9T9F/HSNy7jc6+8j5sHJ7kUUfkL6WYhkMBwVT0oWtCIBVmOUI0ZNXEZwOkyjNhw7JFhQfB74ajkol+gkzEKgE240U1uaWQAgwvg3jDG26yikG/FcswQ7NXncXnvMCkBzCYV5PT2bdx7791wI5Ju/7rfgNjT+TbSiSIjQrJ4zk/DjWDTeJD+zT8minKBdkxn3FRl4Mm7kBk1QjxAaigieg5MFUGk8SKt6jwnJe/ylSu4cuUKji5dgu06fPDBDRyfnuDe8TEsAdZadGTQUbCODhYUJXg8uugTj5Xlo/IHtymVLczFbvymCwxhqkNts0o8dHGmUHzyKNVKmKw1zJRwrgT2KMspFj6S7rxRipwo5kQYfbS8k5vdjE2KftdnACA52TbBYkXAUVLzLAyvasxJeeK7yEBLXlXwLXWTmZSaYhtInupFafBy8TLA7kpewX02DF8qv0leqIEE9SVhQgywaVgabkgtn1apZAo8q8GocVzmjR9kiyx9FFGOG6Z1M8b1Pm52sFws0Aa5NOXfnMqm+cqcRZaAW704hld/GdAymLPqQpx3MjZNnHNTa7dspS0Wb5ROfzQAn1U6wUad2QhDa97PEsOkTYVtOWUdfgX3VDJJbMXwU4nRLU2mkNg4x9fv0iU6HNYM8oHfMPvEQ2r/sFuBXFNhYPouxg2yS+vO8mm0h7XWlHLPJuG3YyjPILFMTzbQlXa3toiyZqdhjjZxcv5AaE2+84rj40fkPY7evYvueIm7rz2H/v4Sl755CwYGoO12sQDADA6X3r6dJBJnCMfXD8EuLBKuDi+3vsj6sQMlgTHUqBEis6NkMdYwq90y0xS1Lnah3BGioQXNBNqcaMcBr1WCh0eSa7tTi8Wa4j9Fw62g3JnTF0qZaUYpHooAEZ7arsPlaN2VasGM4f59nN27l8JceuEF9Pv7MT0XnJfrGinFaZrp6mpNAcnWTiCis4bSikuO+nnOYJeXpwx1JK0UhlVToN1SGbQVayIioLMG3X6+1ZQdQdxnlcoZJf9GAnSN0WGufIadbQZ7j1fGDi/cvYSvvXwPd7ohKw/iJyWBXbFeCsQBc7qOfDpHE9LTBrsYGMbwaS1gokBojEfXUTwKSaj9qTFC23rPGKP/peUYgTwgA11EIGtgDy5h7+hyuoWK4pIvoNe9D24qizt1+2zq4dwGYeTJXFMV0fpQ3OXX1RUwpiDhV7pZIlBQW4CV1HpeK2DSbqo3ppppynnCAaiOo99Vc76Ux6Eth1pjX6JyMWbLZ9Za7O8f4NKly7h89Qqs7XDv+ASDc+k4a9f16I1FbzoM4xI+gmRSRq3gAlGRJYKLwHrf9blALRao72NPz2K3rZG5WLTLijZ2ilxbD9C0iE2FJXUJTcJMypzG7GaFKjlVqYwJPluz4pS+toDx1bhS6NDoRlmgohWpUUBXD2uyzy9rlQ+iKAcb0uM+WLRCrHQQfd5VoBe8XgV4Wq70U6/qDNlck7AlyDVtsRok2dQia3J8sA60QRwFyW0E8E7GT1LkBUyh3KcVf9HV3OQUwMTibY1VVA10abBruVxiiE7gwUgWovVRxEn6XIJrab2Tuq8sf1muGsyq//Lxww6LxaKIo7/ro4xl+mW+rX6tAcBcV4KBXovKCxAKS7BW3+2CXNK28EQqWhxzrH+sj5Z4bz0HYnEAxYjjWFJe5ykKLCISyLqc2n1mWMhKKy5mJhkzZJFDAslTMWZ4jQK75lpRNhta7/U8LsCuGVWh3mfLa/tOPdgoa5k0p0xVZg3a1vKV1Fi5mJI/+fRkA10fWmqq0k8M9cdLvPRbX4MZaijqfHT0zh0sbt0PyiwY733bSxgOw2K6d/sEL/z++1jIbY6raJMFJf2bBcCEu8ZVYoafno9kFxhISvAzZhZpTUOEzcAZwUZPqUfUoESEq6+9lo43EoVbGx8+VUCDGtOs2ieALhkEEaDLpEgbKpFKWA7KIAfv8krQ4RdvwX/6rRznVz8OfOmlotsMEBx3R79fAkyx7+MnZ4EfALPH7758A28+fxe82MdzpktCsVfXo+cjHy4CaIFv5RvHkPEeltZT9S92J/P3Lh4vtBQs5dzg4JngmUIrkkW85y21pIeAi8DgPQbncTq46HQ8Ao7RXw8zooJB6ONRkN4uIL5NeHGIyx//dpANlgo3v/plDPfvg6LuHG6HTCIsQAyW2zvBgPrOzCA52sYCeIa/kSsvHLVgu9EokV6ee/Zg18JNR/M2PD/J+YZAPrpZ8oxxdFguB5yensEuzmC78Ht0HsZaWNth/+AAh/v7ONzbx927d7BcDjjYD7dZLYcllsslTk7vJf81PoIaTo6xjU51g1gVZSFZccmicoYMbKxkHu/to075q48gQZVeo+3qtgHQvEl4k3beNEydZ1hiw4UORfw01Hz5U1sPJr+fsnGnrK2JgORlIbcHxU0Ex3JTXbiQjBkY4hSk03jMK15mYaKze2MM+kWPvuvDM0OgCCzn47GRH2iFMLEmrUaZsu9p2jq5jVrAw9Mnich41pc51GBRDdQEupi20GuQgNd6TZLn2SeW+NFUwJb402qBzzF86wilVKO2skkbIwAW8XIFDWLV4FZ9/LC0zprJdktQaQKk6vRj3cUerwbnUksUP9WcBjDTOg+UTNFfDQQGmkM1kI0G82sBVPqX+DRrWnRlJCulJO+cbC62RllcC8KFQsG/W2GxxVDtLWOsulmzWQs5y9Ee1+l7lCvlc74lHo0+XRy13JltPH289yLpGdD1mJMcysq/A7EIFjPWJI8zGc/Yv3Oy0Y7XNtSdDTAnS7B3cAQsjpdgQyAG+uMz7N8+Dspb7bw+ETW/TkjzSlnzJ+EzCMU4JxtVzH5ikVjxSI6LlC7mh4pm+22ypLeF8y0UqolCsIll1xrqDw7QHxzMvKVUoKYiOsm1LP225eG0tVdovhHgqspUvSd9dGACRogwU5YxK8nxOQPGMA4WHgdHp8CrN3M+zz8Peq+6xdVZ0OkBRABKE5NiOawcQ8wg2HAFuPPCCHId9ryF+BzxrgK5vEuWYJPbyPRueKpDbboRHxMlx97WWoAIxgB+9GC4DJIl1Hxq3xTwEE6gl+MAYIzRUf+YlB9OzvDHjmGMheuUXxQyMPsH8Vp1AncLeLuEsVH0MuHSBD8Ooa8otWyeO9KHyeFrkGoDOBFv5HJKTZjscFM1RtS3Qmjfjpu1HNy2Jf+2AqF/6VG7USnWBUxrd1GQVBznfAC6zs5gTk5hO4vlcolxGNKmOBCOr3V9H/06OfR7eyAKvrqIRjjvYWESuCLxgDBu0kY+Cbcoj3gkfyatsqdqSnipA0XFstEIlWnWql36eYilKkpTmZvyvCqx5s86bHL6nvhF4GtN8KtRiqw8T2WB8IDSB0FuGZXaihUpJ195AIHcGAGvMa5hAZAjABYM8gYmGq1o8FFKUOiUUiq9YTazebatLDGzJM4Enns8fSGtXwN2Op1ZxXeFTFe8WlfoGYur0qpoCr6E5+209XNtgVWuQbVVcv5k5uTfLfnZUo7nU/rCDteATBrw1qBDApAo/F4sFvGofFxXiJI/wPo2Zg10rWqLdbQOA5vUTcnEUwu0Itga2qC8NPmyUcrTdGScV0AW2uM7c/AyeB2yWQOVxfqSliESt4r8kSfFJeDkDLh1D3hhAXRdWgeoLLH6Ln3TBkOnKlC71HqcabArr091TQouOamyOqvTzG8XSmvCTH/NRmo+3mGcfUjoGdD1WFMpID2jdZRbijzj+d95K8nWRhZ9ygL9qlTWUgV2CduuQQFdqovqx5QdVwz5Q0qx5bFVWygFZJOgInbMKQIPhbbKtBptlKW97cbhVJgXnzJQt4MF8ITgPcEgCBf5GIWfpGVNFmbKyjF6Cs7YAeBo4fE/fPsNHO2NWBglIP/Al8Hf8zVVWwK+eRXuf/kOwNkkiCeBnVKooItHHd5YgrXAQb8AML22veVbKU/9cCzy9PQ0KRY++qBwyhGw/mPvEb2sYX9xEG/IY4w0YDgbcjuQAYwBs08ZFuCiiJhRsSAQDCj6NTNwYzjSKEqZtSMMeXTkkEFeJKf1RAS6+jwWV6+js9nH1/3338PNr34Z1lpYK0eqgsPzoLxQ6nuiLuNzkcsSMwiDDB4kxCDXACIoS5smIGdW8K6121owNe2gD0BQLUnNrEo4DkJ2YNkk4eIYHCOACoSjhcthxPDBDdy6cyeAV8bg9OQUo3MYhiVM12E5DGDPsGRwthwwjg5d18MQ4QSnCSzr+x7GhssdiIC+3wMALJfLJGBz0lBkpz0DJJqYGWwtnGrftsMBAUqFV8rlM4/CLmJ3muOTxYhLYzR1eOhjaaNqyAWDL063V6ZXBHQWaY74eEskxysTQ3AB1gHnRwR+FYDyMOcC2CG8ldW8QrT2KS2wZuo9eRnBTG0NwZzqmlfgFc7aVds9SZTKq8Ai4eUA0qaBBvA5hvdVHPlMVsONo4Tee5ycnKR3Ial5QA2INxdz2IAZZc2FWPYC+ii5lJPSeMhHCbNFlhybNQqgypZZYiUs8YwaVHk1V88mwymvlak+US5P67b8xcWbVPqOPcp1espXJnNziltU4Vcg4DFO25vHgxzRq9ep2bd6kvNcyBCmOFMTTIrjW4riYuLeMCoZrf4wEUA2jiuOfWhSn5n//Dswn30T5v/2Y7Af/0gEZKO8UrXfJhZ/BWiFNmC6rUVgWpuFp12UsrYqQ72JnJ087pLYxZbtKaQnGujKCu7mNPFftHHE3YbTpj4g1pEIx6tcJz0b7oqYYQeXmJUwXVB5k15Nk4U6Jbd5P2aBh8oHuLg+ao39Wo3bdajrNLalrIs/bGg2Sd2rQ4XVOAlV6ztk2oerE8ekHDrqzvxHp6UX4RndnfS7ZknOVwpZn0vfLVFQieVJIBero2wxsPdZeE0VihGZPUCE60cDrhwMOFoM2LOSDsLnYgD6ZSnRXrPAGx8APmp+N4+AewepPCDG0nrcODqNRy6B48WybJlirgZ/DknZTNAMRbwmzvC9vQR0iRCej5SIFZhPN16JgB8UhwB0GRqT1Y0chWrN70Ieyo0erTwMYBguCqnkPLwThZfgAbhk2hMFRZ+HrTViIUIgDoKotz1o/xDUxV17AcYsgb3D6ckJiBjGUrIeIyN2X+H4RQc1JiacNdRMfG2ApUB615UVM4uVT+N9OudZ+qjViNPtYBVkZieXW7lMEkYaww02lAXplkAb2lRuSUS0HnQcrPRAhGGIfua8hxkdiAacnp7ivjE4OzuD9x5nyyUMEc7OzrAcwlFHMh4mOqgmhDGXCtQq5AxlhZ0ByoplAMsqZSWmVfCgahdderhJRXoFKjotV+vFBkvP2niENh+XftQPkMe7WGUJsJlNrGVOM8qWqMpU5KnCaTPttNRx8ReXttz+ApRIElR+pqhJSGrMzKLSlOLJ0fAQhgslMSmLRTqbrz0rLROkGVoXVcwJx5n5rEt2LWnrqOLIononviFroKvlL6sGu/RxxE19dcmn9xJ2Coy1/gLfoeKSg3z0cOoQPgEUJt+AGCyDWxx9tdCr/XAVY4PKdo2VS4OKVfz4spGBnislQ05L5iQMJoO2+Elz47JOeyKFY/PRNUfTfAsuwSpMWl4oIXMalLqGy3gOV1J4fWPzMU7xNt+ISUhtlH2T6pNUK5EDjbLqpXhBQGwzWnoYfwr6xvtAtwB94nWQCRcRrJIJEPOsWxQCcum5N4lJmYfXjImmLcpMiY/pcNIGukgPDgBrTZStQm/8djU9bN3twdMTDXQ9I0UXwU+fMmo2iUbrd+AFO1pbXyjlxTr+12DcH2Za2xbPGqxNUUZOWEiD9HiTzwCNBN9celpR2pUOgFdSEBAELBKhFiLYBuHC+RGGHL77tffx4uUzGCYEP81ZgyqOJ4kA9vwdmJ/4jVQV8799Cvitj+bKMHDr6Bj//tu/AmeilUREMdhpMAWTPETcCUoqp3ouug77e4sMwEXrC49awVHHISP4tVyG8IYYTm5VnOq6CKAURKcO7etTsUDWwhjAmEWQzzqGsSMYFuPoglNqsmAA46gc7mdNN/ULACSf5gZAv8DhGx9HxL8imBXCLO/fwwdv/S7APtzwmHb8M+DVGcLlhdyuFRJN40falaAU+ay4ax0cRVnzOJoe7CzgARVa13GVxLrjwjBHlbDMCjCQXLrOhn7jeGEKjRhdsM44XYbjisn1EwHOOQyDw3C2xJ1bt5LSSBHEunPnDobB4WwJeB7DUSZRqIGJBUpdnvw4WvEoJcF5B8f5vcw9UXZJ9W/RkkRpjsyJKnNq5EVtFm5KUs450hYoRHkkA4GPOB88FmowIcZUaZTjnxEtYGWuQ7MjSnAax3sv9Kg3BFhCmIOGYGwsE5tg/SW3nKHVxrmXkmjEDcusYrxA+SKr0xHQ63FaYM8/fmrASfuiknkyjiPGccRyuUy3Aksc7UtL+9qqwS45DgigCKuPMurytMqlAatgkdWlI4TaKkvXYbFYTOIVPrka6RNROrYPZB5X+F9SzzWRzUBXxpwyaJfqGAFK7WPM2OxQvtg8qIBdQIGSuZCtzlXfVaCqXXej6eqzOYlEtVlcfVyfvQ6f7dW+gz6JP0Y/oJgLpVMvX+Cv4f/h/x08+2DFVfB04UASreQHpusAonBjJ6EcP5Hn07//deD674P+0k+Crh3karEPwkaUD0DRYTxRY+xM5bTIQFGsOKTepTBcyROPjspVY9cUntGm9AzoeiKIMGshM7Mb8eGmuAhjjh2022oz1rHCA4jm/PoVl692Jo6bNFHILhQAeV5VetdRcRHL+qOglbvBBGiTyLSMnqNPmkrbI5iTD2zZixqV7Owzgm8f/ZdELAbgI/TAPqlPSVlWTtKJol2DEkSeO1rixcunMGzRweDAngHeRdP4lozCSWMsBNH3L4G+fh383iHg8+UTDGD/zODb3rkKryUNCjUYDeOrz9/BshPzfeRP1aVZGY2z0HtdqAAExQjGmlB1w/AUj3Z6iv5WHNgTjPEwFQAkIGAGchgyYinln9s1e0oKVlkkn7GTEsggAirJPmo5clK6EFCPCitEF/vcM+BpgcX1lwAOvsCMoXTkkUABHBtH3LlzKwi7JgjNYglAlG+INOkoa5zDBZDAkYeqcpEu5SrYhNUHZ79LaVBM41YxN36nEk1hWX0KqCEP5V1QlMVaKt7kiXhJAYJ1CMVFJPvLCTk557FY9LDWYojHGYfBwTkfAcswPseR4T1gzJj6SdKR9jZxl5x0BpN2ykeRtG7h03ufHBnLP/K9HG9KYeGaj1bKIbffrH64YZDZF1POXiq7kbspCxqxshJrBrXCpMyUoUBMM6dm1JhoMfTU3roEsXlKy6CYbjT/FEunwj9SbH+x4JxmxintluySjw+12qZFdUNPwzfX7rkJ18APaj6QweU1RVtBad1LAAgnMNdaCxPno2cPNzoMQzjKni8FCaSPLspnDVTJ9+VyWfyurciAfBuhflaDVNo3Vu0YvgastP8s7Xhf96sAcRMQLA7aOaCrIM6f4iuzCKvHt0q7SIJLrorqF6Vfsb9a+c8N17ywNMb0uoHUlAZXvlsVOqx4U54jkQ6xj0/RJ2DjJpaEEV5cx2UC3qBXYakv5C7pt+fN8/gh+wdTTDl+aJM8IfIHktwl+VAE1x173ME9fAFfhae4bnmRUwh8MsD9+ufBLz8P8wc+DjaqXqq8pUWgGhyzVpt6oFTjj4tBFX/P9+1cL67jcLsT7Zj4XFvg0Stijxk9A7oeF1o5MKcLwmYC99NHGx0hnJvojGjyTinYOUtTZKnF+Px+21xWLH2bMLALY3LnSeTBLQnbZMvV81nZZmWi6ySjRzQXd850vcJRv42H2dJvAjLIxRxOMnkRaMSnlEc+HhDBGB+PH8ocVnIJA3jp8B6+7yO3QLAwMVfvgq+mQr6pBVHZAZQkv3YF+KVPxukXfdnE90cnFt/35kvIFka5RU56h/eu3MVos7kUo9T5SzkrHk/xqUCpXPp4iBTZGwPvHJgNvPdYLgEPD0s2WUoRBYXXCKBAsU2lNGxiqaQtfbYCi7qPIQG5Qv7MeedcADSk/NoCnyjwyd9L1uezgZzZw9GrHytiSx0k2eH+Xdz42jcB76JyGJStLt4C2XUdrCF0nU2WYCbeFGiMyU6EKzVWH/NKOiiE/XGKo1WGFFfv1KsYsjTUlnwq+Q2mW3HgMqlaGUCs25tA0cdOaKNws56l8BwY4dSdX1pJ9WOwCjEmtOewXGJ0HmdnAdy1cZPce8YwAM4B3g/Jp5MMz2ANqC8pIDVGSuWjVHwBQe5STyTldQoSdbaLoWL/qCDNdiUqLl8p/PK0wtdUlCPOQ2r3KOs4EqaaG1woSHqelLqUVSCETluOj86V3VIcKxKGVHMWCcVxFT8ReRB7D6Zg8pXuQ53JTEBHY7R1TL5AQzddoUJSjN3kHfJMMYuYW0GsxkCrjSmWj8rwWvnVawhFJp7nvVLCGxbAZVkr4unPjNuENiNTHvdjuQRkdFieLXF8fJJ8NG5DAh6enZ1N5NwakJK89bytQazSp1Z2Ct86Mij51dZc+n39LLRzBr5bosQc32RmsFNpqkFWghz5U547tRjpLDP4NiN3F5OpzCBXrcHjEAEbZY2b3hfpsOJpVMgW9UScSpWNOk88IJaexC7jCn6Ufgh72IOUEhD3CRJFd06U5sQ9QcXjXzEv43/qXg9jJL43ZGAhIFcca5Ku+AKM9WQOeb/J38Cb/C4cO4SZ5wJPIgt/MmD89/8V9LFXYb/1DXBvZ0XQGvgOm26NCdoIO0vNYVH3RnWYcsq+NqZ1+mqSEPW6s21es1V/qBrJY03PgK7HgVaNR+HNG85jTURILk9M9K+izamFabnVyWyR4UUl1Ka1IJcIX6yk+Jbk4rlaQygvIXNMtyEUlIuTzlPnqpwmri79mhCBE4qAmf8ma+/F0CqJ/DGjvJTnxVvpBPF5Ds/erx9LiqayUS3UbFfWi2vWWoihmQxK5SMIJfKOUzJhPIn/AxVd5gwFh6RJjAymBICYuoMQvvlgPaL0Xh//YR+EnySUgnB1f4lPvnQX14+G0Dc+OGPOx6IwqVt+lAErunUJ5jc/Dn73CH65hLFBwL90+Qi263C2XMJ5h3F0QKxnOhrhPTp2+K43n8NgHRiE9y+d4Esv3VKKVxQMY1mIAhzHJA6KOTqXF2E7Ko+IPivS5dvRX1KshHdDuJmQpRcZzA4ckInYBrGc0WImOJwObS9Cq6GqX5mxt1hgf98mqwA/nmRlVp7JsdIGW2PENST65hJZP1tzVMJoxYvs4gCXP/otQLTwS1YDFB3eR99exuS/k5s3cHzzJjqrfMEQJefICRCDSUcqZdcZJoAjnsessEWwLliNMYbloH4DgAHYF2BX2QKbMthq4sXxmtuNqlficDz0lY3t4oF4e1oIaawDyc2VlBXbcANguBF0GHP7Hx4sYtBYAGZYGwCvNC4roCYo5QTn1AEYknEe1xmEY0MZRA1zU69F5eApubDME+ecCq/DybwOmXW2g7Ed/DCCvQ/HgQv5JcQgmrR8ZhWN7ktqDKmQKd1gEdVZU7SPxNQOtNPxrQlw2iIusmu9162lv8hYIVRNipKXG2NhbbzVLJIhSuPM+8g3EhhFEEfeWaGf0lS+mF/BtJXXuvDh2LYp2jHxocRzEY/eMihefMFxLWLPac33KC2kOtuBU3+p/IV/q7olhR/lOCZCvOhDzV0FBtsINrnoAF5uRTw7PVXyYLveOf8KTCZC3/fF+NJHDQW80qBVyyoLyFZf2kKr6RdL/W6BXHX4CfgdaqXql14W4ZKYIuO6WmcaLdX8aqg+rSG/Vh1aV3Wj+K4pJ6lUo0Ukx4UhyTwTPl7nJTxFZJby3Sr5b4EefwTfjSMcprJQIw4DOMAeyPdRf5PxaWBMBxGKIqcMY6bvoDfAQFSAtUwElmOhTMi+1/I6ycju6nOtKckHHQGv0Kv4CfqTIBOskuUGbj+MOPGn+D/cr+P0gzug//U/AZ94Ffjub63aLm8SlmOx7PUMaPNKq83QBTFuZQ1YXmqQZeT1pH22bhBadiNFFxTZq9JFhBeBDBjbAeV1+Z5RpmdA16a0qaxbR5sxtdzI7wTLZGpJR8IE1apC6g0Jow4/TFrgZYIjLezpwQVQc5eselebYVeByp8FQ22x+xwn6IKcm6tqNlFq066jbi8t/qzo67CzoYRoFYWKL1MJe90QqgXcad451QpXyzJErlYuwQ5jt2nduwHtOE0ujKR/gDxmSIkKxVGBSjhZtys06c11c6c1vrmtTGxKLIJAVkfLwk36bVazqqhMTychVhXJukbkAUayAqCo4BgOYHqAuyTFeMwlLvbMHmTlpkCPy4sB3/rCHVgCyJvoVFear3XBdvwd+zopJ3cs8NlX4ZfBF1VPPcgQ9g/2ow8SBD843kcsnNItaAyPbmR8/L1LkOM/9kWPN6/7lDEbipq9HPfxubWYAzAVHbqH5z4DXcYgWCVk4CqUP/juYi9HvsSJtQcEFEwCfGy7APGA0m+b24fK/un7Hn2/iOChx0BDtAIL88A5B1I3YEl/6RbPPMfEMsg13bFdpBUUs0k8vlvg8MWX8xCshiIp66Ig3xGWt+7i3vESnbXK95dYfZnwSdEfUQREiTP4Fdod4KgIsosglrEAGI6XCD7lstKXlJrGOGvychkTauKlmSZTUsnWGiSEVtQ4KOyM7IzekIFjhmEGw8BFQ5ukVERrt3ArpwlWhc4lhXax6JLAnEA0Wx6ZEkfZAavO/oQ04CnrixH3KVJuw9EhdQwU+62pJMv84lBHxx6jWK5pYZ5T7VLZOwrWbXA+3lIYgGmvxl9zzKEabrr7VB9IYL3W5eNmGYgTJUlvEgIZNJgDfYVWb6LNqsmQmShr+kQ+KGTLbAWZ6pnmJYVLKKQpxP9B7JdWuepuzL83XU/q+GUfFRZZCoAQ69i8mUBxneEyHCs+JM2hFUcbuTprtTzKAbGvZN3IYFF9jLrtrypbSVkIkG5MCXaRMZUvqbLNdNlrkElba2nfWhrMqh3F62fTts8toPMrwpRBGqILNZ6LjVv4Ptk8rNim8JA059TKvo1MVEpqMRO16ziX1pylWi6JyPZ6TFV10X22VmeKcoH8YsTbpFslDM/2sYfP4FvxPK6B07peAV2kL73IQLYoCF3Xx5s4pehh3CwWe0BsA47pim827324rCb6Cg1lj1Xm3MeSnv4M/D/65rQG180BXrQvorMmrOEx5vL4BDfH2/hV/h2c3LsL/+tfCO34HR8HrAWsXkNoMj90c2d2RK0WiuWrH8RaU3s+NrpjLcn6umokrNtUT5aongGnwa3deO0zmtIzoOtDQWJHIJxPNKFtlpenl7ZuCWk+SERSfw+W6hzSEbKWsIoPKZvM6+8UHibddc/Gf0GNISw3zukxRghAlvyRig4gzQ8TBaZguWNhAXgiBOflBkd7Dj/wsZs4Wgzok8ID2M5AfBGl9EQpK3b8gwNmUADymYDh7BR+CEfBrFlgb7HAtStXcHR0BH/9egB7nEsc0TkP5z2G02O4cUzWA6PzOKQjvPq1a8EKzDv82mtv452j+3BuTGBBAB1svF3Rw5EHy+15cYQZG49ixobjeCNXUPMVKiXtzD46cOW0G5oc/bPi495Hi7owrg2iDyprwH0H9sDh/l4ScEMb2pSXdnDsoqN8Zk7lCw6Ts+NkDQJk2S0PDFaYhegxZAh9v8hdqawuQk3Ep1v2/7V3/SU8f3QlRqB41C5Yf1Hs63zUMzhE/uDLb2I4PQ3KoAH6jmGNCVZgsYR7e30EtYJgbm0fuoQ4HLRlsf7YhWvWhyubQSbIC4GShUL2Hxb+9USwPlitsVEHs6QNrAEog1pWnMxLOpQVLRNBL2NMeiafuc8FAMVEq5C5Pbrgi4gQTMiCD+HQR4YoKjzBWs8qJZxi+Sy6VJ4AxIXy+GhRJ2AgAWAKDvavv3AVfddhWA5wzmG5PIPzHm4cwxEx5wuH3TJDxOomA3iy8x9bMiquSaEyJiqiwYk/fAZTAiBiM8CHbIWUbus6F+lDi3pLsmTIlEKrZ0xIzjsnf3Ua9feHKyGkEW6yddaIMYBZqizOu3DUgIIvrN72GOJFGrJxIiCdwP6GMo+V20UJlI5Li5Irn7LGiIUoQOp7DYzolhfQ04OZ1MYMJWBegC5tSaWBs9oZvH7WstZqgWKSrvw2iX/EEldd3YRXKNcqBy0FynlY5sFRBudI/Q6UvCNsSc45ePYJ0EyAiponkzkX101Zb8qKl42nIK30TkQWELCPffw4fhiXcVSVPydqYXAZlwKIZHoI8C8W0KQtlxH4LRRIG9YCUzQYI1p0dX1a7zkCW4y4fsQ1VjYgiUxaZ62RjaVgEWaNTfMXyd2ASd9BeT2whgDngtsKT9gD49VXvguLsw9w88tfhv/i18H/9/8V5g9/J+g7viW3oJSfqr4QWRB5/ub1dG5UxHcNcHIjvHKOLpJ1MoN/5beB3/sy6L2bF5jwMwKeAV2PB7Wkl53Topk5/6GEPFbSSsuybagZvS2gTspQhDnPQKC0A/Pou/4RgqgJjJm/jCAogmINtD7BDy1gGElArmZTya4fopKqQRtEACYqwAFUoAheGOx1jJevjNjrHJwzSTk31gQBLuHycedSbpxC6QTZwICO98Ene8EiQO3iE4WjIIu9RbKYcT4AXZ7DDWnOOQyW4N2YBMFx9Djwe7g6HGB0IwY/4gvmFm4tlhhGF5wNx9vMwniKShNF4UmsiIgQPa4q1pzBLSq+I32qfdpCXU3vOEhocqORAEcSJhz1C0pe14XjZiCAyCHNT7HqiiCWj2CBc+H5GIEE5yycCw7Ok+WPD2UN4Jc+gock2QcL2ih4y2Cpxk7edY51Z4AWe1gsFkmhMbFSJg4oQ3lsgYIgPZDFEC1cOiZYCn7QhnGISjAiKIk4juRqSeTBzdCFWcONm5ADEjK8JuhUX6L8icB1TFSw5BiJBroozilA+JlyJq+U4aQCmGC1xtlUMhRJACDi6DM4A13pWK8ua3yfLLFcHO8e8IZA3of56w1gBSTKN3Hq4x66WXLTC7MJADkZg/2DA+wvFlj2A5wbYbtwm+g4DvFWUYdhGNKxSI5lry04kvUmT8swsR7QVnQT6xvSTVj+LhsLJWWAraVcUfqXCiuuZK+wMk6OWwattXP9e5dVrRVnbsDPECH1TTpyGEF0YwPfD8Bn6ABRrAXINGoTRFutgZCsNLVlU+CBXSqXBioFLJ/+1nKhni/yGdYkUpZE4eh18JcHDfrS1BJLHzOsga1VANekKQtQrsYFqBm2fia+46ouqsI18p550gzbeJaM+gofEHpulf1V5rSbRKaPp037t/pMawKBqDoCC4LpOxhjE4/wSU7Kc9BEnro/drjiD/E6vYJruJxW+2m7SN4GZPJRQwG5TASx0s25JmwKkhozcpJHLhzhCIhZ0wHkwOzCOwbIBFDWAmBjgM4moMtGsKuLly50NgJdtssynVG8mmSRDn1qEDdYaAQ7B7IdDDrsXbmKvdMB3f4+xtNTuK++DXzmW2RBV21A0qBIDdqU6uO6Wz/XAKQw3fiZAN6pSFL3RJsqWWH6eofx+cFt4GvvbB/vGa2lZ0DXM/pw0gyDWyOirTVDFcHzYQAjYf2n1mpZhNkRNnuCwZ11vSjBqoX1Gc3SVFWK4pzSUg3y7iUQnDIbE32OiGgXFWsi4NL+gEuHh9jrBrgx344Ia4I1Rwyfjls5Fx3/+lQeaw3o+AD9L34//K19mB4YTTg+AuYAXrkR7B1MHxWKeLzSg2G9B3cWlw/2RUYDIMe5wtFA54OT1a980mL/2h2MCfDxGIYBJ6enwdLFuWhh4nDv3v2gdAMIxxXlL/gp80477fepfeoRSYhTvABJKFrThU+Kt/UFP2oeMB4EB4KHNUiAVwAkSHCE0GMEgG2Ro+xCB9AvHueKfE+O0SVrr+gQfYwWYd77+Cxai3G4BZD1QGElCFZMhrRyIX0BAJ6jgQer8ouSRLjy8W9JZTQAOmLceftt3Pr611Mee4vT0B7EWPQ96IqBFcsjxdd34wabc8uCt1KeS7HaQUFCqI41EfKSSweAsGFvAIKBsRl4aSvFYv0SbQKTcqmUd8nbSx7Z6i7/hZBdVLDE+suNPs0RmTMYw3HfMw3dROA1AKsMa00CNVIgxLFtgiWA7Xss9vdx+coVXDo4xDiMCbwM48sloGs5LANgHQGv5C/p7ExZI7rIS1w2akewyKoBrHRzIodjQm50E4U7QY8KlGDVxttTzWWn63AJUdUAF6l3jzcZCmCPHJ8GQjv2XQ9mDn08+nSTqLEm+eSynU2bVeIUXkj4yiJakXrvo2VnDKOBIA1o1M9CYnkDgfLRvNq/nZRhb28fQOCNovwLaCXHEesjiHPWWnMgV330U79r9f46gEy+b+OzdFNaIZauoBaQUb3ekYw1MBHIAbJFl+SXTu8nIYbCuW3kMZpPCzOuv/4aLr34Umq7fPNsBmfCDboWP/yl1/HKnUu4ZA5hoYGpDBaZggdZsDkMZY28nSCX6ijwR4FCHOOLJ9COumhZ24HkyL/zMNbFshIOjg7R2Q62s4C1oEWfyhCli2gviQgwK2thVRZpynTZR+qncPzeI9z66yjcFGz3D/Hipz6D+++/jZtf+9LunboVPRit5kngtx92egZ0PSLKqH+hwSA+LH9XMVdNLVL/thKarmcf4mkq69l0fdqeqoUnJLs+tbqnwsOZ7QYVpzkKZobGLnVaI26sifsYAEdFfzRUBaUYNqM97VSP1xVsRYl9MUZWCEtLhlrIFvP1AHjZZMoQFRZrcPvsEi7xEpf2ToLiyMEyRM8B78MRFweAyWcZCxHoIgt7egCz3Ae6EaARzD5u3gWF2DmHTi6hUGUVU//kY0jKboCTfsDt/WWw3gIDRxZ7e3vofbAY8Z7R9z26vsfoXFK0h8Hh5OQUcrwxNRCXFlwiGOp2ziCOPlIh/aRmlihCqZ2Q2lZ8cGnn97m+uf0V6hHLlpwxgRkwZMGGswIAgvVBoLfxpkBnLbxndAroGm0+Rua9x9K7vJMelUcBU8SqLCtapQNWSjuxoX7FMEtVIJiuL1qKCLD7h+gvXQnWZ8xwy/vwzsETYIy6rVLaM/WT3pOXbGpEpgHUadyhXluApLRIdVrEFfcsVLE07rNVm8kDRo0bnV6OWxayfESM6PMrWmwRRV922c9XOE4TFCrieFOkDSAaQfx+qdFW8YRwPBJ5XvjWGaRozUQBBBMFD4gWMkToYjux79F1AbyyXQfnHfohgGDOO7jRoeu6BLqO45g+tT+nlt/GiYPgxvf62TZgQb3E1/JCZqvls3U5TNbehoBR3xzbHoubrISrSlNODC3nEgJQCgeMw4jRjfDOF0Chizzbex+OMRKSDzIBjQTokmOKOg99pC8fg9qkRiVQOefLJ/GvtH4GMMu5Hn3fowa69A2I6agX8thZN8ZqaoPa1W1xa9LT4/bcpxpm8lmX7KxFEwCkubgpQFEz3nY8edMfXYp+1GI7eA1U52PgAMBuqYoXWnlxdBn9/oEqaQwQBRQC4cpyH5eXe3jRXMe17iBa4WYgM1tm5fU+5GnBpivCZplVwKacX+KTlD122i5aXtkubh5YkHEgEzaiQEDfL2C7LtyIG10epHJEAUVsI036FttRzSuZFXr6lJIHoDeWyRh0e3voDw+xf+Uq/GIvWcS1+zWkSKsEVbRfJYvYyWJdj5E5fSsXatZBvOYTxdcPsX79GNEzoOuJpMZkn5n/BaPh8hlPxOoPITWY6zYtohWRxMc/1PTwj/oVOpxWIhOwUkeoQQSVCOdlcaM8nwJqC6NVG9XaN1q3a4XnRRrGYNF36LsOfd8lyxm50ee33rmEVy4f4498yzsgBHOhEfmGNSA70HbjGJTluLsKDr5YaNGjX/TA3gK+77Ach1A2Q8nqalgug6+s6EsiFiIJmKMbAfZJYCQifPP5e/hP3/Z2qo03jB59GlI+5r9YLOCcw+gcjo9PcHZ2huPj+wFwSmVtC9xAODbGNe9IMiSF43wFiCH2XFT0kljdsPfJZxh7F/4I/3/2/izYkiU7Cwa/5R4Re+8zZObJ6WbmHereqlt1q6RS1a/pFyAQEqKRBPxmIHW3yZoHBjN4Ei88YAZvMjDjAV6ABzDrB0xmjbr7ibafNhDQxq+fXwNCFBpLNd2qunPem3lzPOPeEeGrH9yX+/KI2PvsM+U5J+9ZaSf33hEe7h4+LF/r87WWg4ycmxRKD6iEi+tCm0AFCnZjRDBWyoQP8swAF0G5DGeLswBYAiCEfnPMmEmAaJa+TC5mAj7I79Y1EfzSiph/XgA87kJ1CeeDAEDA5Op1jK9c89ZpTYv7X/8qZltbKCxgC3nPoHgGoEtcMru9tC91BfBFulbvWgLUEECm8ObwhxMwDKVHBOiNcWMWVQvRGXBO2Z1hF8BTBoPJxr4AQj9IPUI6a3QfJRBL/47jkn19pLPYyXhA/HPOg9eOOVhOEprWoW7aWA8yNoDn6TQ5P34cmpBOAxQCuNa1j/E1nU6zz9lshqZp4ljkMG4B9pYO8EBgAsPlnV3WNq5tA7jfDwh+OJoPcmX41ZmXO/oToKkb1E2N3d1d1HWNJhwbKtZa8VTWcBICM2MymaAsS0zGkwiKdd1TpT+KYMElfCe6VWe1SgLxkIVpArMQT4fMngPiWgEDVFWwImsdBInWQBfQB4OGwNFlAdOea+LA5D4OAOskiGioLeal7oIIQ+80D+RKbSK5+NNnCZdffhmj9XWkQ7skgLtf+7R7ODuJSWg6sQhNjI1ooguqDeCTwZfffgFvfHjVr9araqJG3k3DAhhZgFLweA2MZe6tJnd7RQBcTbBilHfw+gmhbhrUdeOt4wGMJ6soisJvCBBQd0W+IE9n3qUdRuTX+tDaIhtKMpPekchbhxlxwQRj9eo1rF5dx6Or17ClJRoRiBYCX0P9vwwtWpyXyeNgQNsFnT5dAF0nTd052RMyB4LY0lBaQdkD06ZOYh6CrBZMZNmNOpvr4IkSy3+cTNJJ874DQ11D3xcki5VIXwbZdA+LkVVH3+uPHQp9yzRwf0miQzJsUauGdhaPm2xLePnROqrGpnnBjFk9Q13PwG2LBi3ev/oUdZlc45J8kXbKcuorkL5/nu/JEozje+8eAXFRwL3U5KdQGIuRh6mBHJUEa2ALi6Isw9BVMAVb2N0C5ddW/Clz7A3dnXHAp++BV6aIwbKNCYqoDdIVwbx1C+bhOiyPgaLwlgKkxqEJJ/9YHScor18aBzZyWS9rEVqjYAK1mypCHYk5f4hzISdkMRL44oNVq7IM+Rhb6TijrBcSeKP3VlXMq8jzNTMIYza8X9rxD39yuqEwPxfaSCNEoQzvIpEEcc8jWyTsUdpAyvSwmygJzCYAF95p0yIHwtj5AwDYObRtEQLfNwHoaiO4wtFyzkXLPA+kSNR7pcJEwCG8nigsxu9IW0O4dPMG6rUVTB99HBWSqGxIPr2fobfnTP1omTPQf1ka6TqgE05EK9tJudDPEkKsE2l9ilNQHQGvo1/pPLj3egIcYHGSeMNb1fmLrSBSod1s3NWXOG2pn1244D/CAQwMGKNGEckeuWpB8sBCURSoyioqjjp+mGMH0wNDEWP76fVAFFMA3srBWjjnUI1GcK1D0zYhBl0bQbGdradwrg2nlwUrMP9Cqa2C3BDjQZHwDWnDJJvpVs3flfMkGa/pJe+Rr1HkNjExd8riGDB/n4X9WJa4fcpgZG6lgAKJXDgMhH0sNrGEKmyRlHxrwomd/XIyYCvOzdQuiaj3K6VIc0isl3unGUZ5O5vMiMCXssAZck2MdR2g/eJy6XfN0pAac3PyXJb2Sx95gn6Frig1lIfajRAL18h2B4f8kHzbuRDy7R5wb4oCq9euJrAKwcbZAYCBqUZAOEwGJAfgyBrvF02JewhUEZzTLoc6CDxRipt1ZW+MF56u4druGiyShR/U+Ehyh4wRDX4ZwIwBBfqmNUsDXjbOCcnLxnkS5BkZT/CnTLdOLKM5BrOXrnTctSFV/RP+16xKf5c1KSwwcZ0Sd0Z/v5M7+b7oDZUuDw3fuyCzUGc7R2fR4RN+ABE0z12CFDsVDrvQWitbXvcp6KOH4Lc/AO4/es41jNOjC6DrWVO+ooZLi09sio/QwLXD0IFm+PNKSRDWgnxGy3Id0faQFm/urrq9ZzC0hi/u00w5YqUxdQVpdKWB55JKZ/B9797A5b0qKIh+FtWzGWYB6JraGg/XdzKgKxINfu2n0ZPvjO6QLkPCZ3qCTCcVkF5Tq08itDCRArjyMaubiuFBJ2s9yFVVFdJMSbmPHqxg/NXbIJeCELuiAd/57+CNR1Fx4aCEutaDLtRY2K9+DvRBEGZHISZLALaCpoGyrHwciiAAOiBanYggaIxFj4gQ41h1mojU99a5IMgmxSxaqSCEzgrWYghCKgPwgeEB3SgCAfSO8FaJOAA5PkB/iGUGEwVtE5UzEY7llMIUxF46TrsUKtjI14GUxYQAF6ouXYE9nYKUJGAGAbaIYySBVvlnGw4C0NfEwib+bv2pmN103hKI1Hv4ExwNvL5grRf+r3/qZTR7u/hw+1EMHO3HuRtcElPsmsRjD7TudljzUJz6oeTaCsuomxEeos69geJ0X1IvQYJH9qlyYndBK3Gtt8hL9ZC+B0QJClhUBL2AAHTBzzs5vTOCv8FFUuakCZY8VVlhPB7DFgXI2Ah8tuJLGwLh58AApRP9As8AvFVcUVUACNWo+9acj8m2xYcfOMxm3l2paRvUYu3V5q4rxngXITBHoH5how5fWIKUpiXfetl0uHHUJEVe8IAXDeR1XLSvaxH8yBNrLlHax5MxiAi7O7uhveto0VXYwsd5DHymCJYqACI/6JIcFCIlLlX3Tko9vmPMNgTxOZMDIjMFwCEAdxqHi0CjtNGqxzAGn1lk/bVfGYso8bnl0w9eX/hUJy13eMtcWXiejNJvi+5VW5W4+uqrsKV3a5fDZ2QTBvCB202wgDLhlEPPrAOAJfwtxoWDWvcUB87WQoObOxv4kXdue54lC5FeK0MQeAGrsgMIABBZwI4UwGWS66t2gSUbT7lNfDhWB0DixYA/yNSIxTVzTOh5NkPOgY6yIqdO6qpIvbmi5z5JhK+Ql3q3TKrk/sZq1qG9S2kzbiF1BkMq+RDb1QseOA7XRH7rLvjf/7pvP3Pg2l3QEnQBdJ0GDTL2IbBLWcYMTvoll3DZVUWKoZHu5eLRJ2maReuFyPyWQT7mUKbB01zFJuuzgVVjUbFpyVEmvkhKj4QfEl1G8LvToZMp+eWH67j9ZA0AYB1h0uQAhcj2up2H9l6iuxINtDmlNBq4UQ9DK9XniQgHOyiB4aMmUfiMO5xBmBcFXOQhGXvS5hQUwaIsUI4qGE69Mq4tvvD+Bi5vVaiKCmAfNJqp9afE/f5nwG/OPP/a2Ib7vrfgQYki+A0amFEJVAVifCkQCudQuhJtUDytTYpvVLaDVQiFQORsbJxPW+MZvn77IR6vTNFGuS1JkLLLT/DVaOomCqAuCMni4iXCK3MSslwI3O2ggENpOxJwK0QcF6Agn90ITm2IjEfKoXQt2EP59+RwVaLJJ9jEW+UonTDGFYvpfMtYSqUnrQ+IAEfq2mh5wyCwsz3xUmoph2sWxoJhEzACJAuuCIaF0y57QJdLhweEtm1r2VH2/W+I4Joapqxw+eVXYeoZXDP1gj0xbFQMcuU4ukhlLY/e+6QnOtQTuBHXhuzZkE6SExAYOoW+o8wIm2K3S19pIX4A5Moq0JUBNH/M48DpOoOB0hqwHIMZb3Ka82oMxB9qbTMMNR/8UQzxJDFmEBwK6y25RtUIk9HEu+AYb3nh3Y46maq3ju0EACQB7/1MWH/hBYxWV1W1hIdr90o/hlZeuOlPdQyujZtbmz5mmYrr1bYNCEA1GmG2vY1H77+n2ju1qW6/PnU6Xj2vnla/A2CVDQb/fkxpvqYBJqNA30vA7nx5Y0hyWUxZv8zJjpnBrQ/uX89qjCdjVFWFS5cuRR493Ztid3cXxhjMZjMfW4goHXbRttEVUL9WKiqMR9Y2sfpNBmRqbW7Jw14WAnpEl8ZOk2TWW/u21pznOlq/tv6aCzDFMge40qI+yfKIiYfv6x8Z4LYAcuD5oIIAKwvlXvW+3W+2rHDlxRdBVp3oq96ViX2ogsKmfILMx+EUZGv9qYnlaAJjLKz1gdj98CFVHvmFSvop9ley7pb816cjfOHD69jYGYOKcZAxk+WXCSeIGlso8Mp2wKuwGJkQL8vI2EOUP+LcV73O8MNX1sV46qLqrrb1btkti0aopArypxXH14msg1LTKrFXs3eKsU9FNk7hGL577THurW5iZ/Mpdts9TG3tNyDYgYyLslKSStQ6qMcliSUaqXudZSaf6JE3MAdZK443gramJcrbKWVB2SfrSgpxj1tc0BmjC6DrtKgrv2DRkpHU0/0MheZTEuo6xeZVmiuQPV+UxMAldgeWpIwno69oUOcz/7VMo/e5sVI5enkf5c34SBZhgyrWgbMwA4P95uYK3vhoY/iZriDYbRz5qQSVfh6HqOvzSqGJJIbUkJwtwoUo6sJdRHACebP6IsToEuHXOMbqrMIbD69hNLVwIai0MX5HkcmA37oTC+GXHsB9313AtN7tzrCPsWULkD463loUwWqkbhu07I+jJwQAJ4BdMY6Pc4DxMYFEYdgpWnzz5mPUNliuAGEHWlwaKMZRYnZo2hYW4l4GBTYhWm85AOQADzyFOEZQAl5oQ3ERjUhGFGLlu3bECfA2he9k0koRlOEEdhEMvJKZ3FMpHQ8eJD2fb4qFJWsGhTbMxGMFSqWkyVVNrrl4qmMCCf2OeVIeIe8t4w4Ao4j91LUCk/hfrEEvwFv9tYyZSa1rjX/3WdvC2BJr118A7+6AP77rreJYdt27PIFjdfrcUCTmAe4bhek+r47fu3NJscxMVRbhnmRceTImr1V6PGmOC1kZJQWRofo+qzLl+ZBSylmUVQcPZnqLPwMOwDjDEUDsrT9l00f+5NQvj+URwjGSAPvTWq2xKAtvBeot7wyIGGQcjATCj+2VgAkO85TZz0dTJPB09eo1rFy9CgFBdMdy+gJmxur1DbRtg9lshr3pFNWTJ76NQow557zFF4MxqirsPHyIJ3fvpnkTKiPtAyADJfN1X/elVvU6HRIvJaU+9rkobaSf4b42iDSelIaO5SnVpw+87C8zeJbbRldRIh9TaDwew1qLnZ2deHJm07SwpkFT+I2EwcMDAo/rSjoCDOl7pAZzF+yKbsGs3LfR2SJTRfQAKXUzuS4utujK3LjmmrWk+12Lrh5AFqwX83qdMOk5NCCbdkeEfk+xxIuyMhFgTKxzr03EIoiBoqpw6YUXYEpRYfUcyKQQNaM8nzHGfxZFBWstRuMRjCk80BVAFH0ACwNwpGKsdYAu4rTpvN6s4nMf34RlA1gKYJqJQef9aZvGu1CHgxQE7JLNsjh+pHG6FHlvWo81F2ld2MTLdh993VtZNxHmERJPBsm6gsRjEqvJ2rIHLjFi+/tngvUtMT66tIVvXn+A3ZWnqGcz1FtNOL7Z5WNGiTz6fdIwoKwczb6GQKrsXoffUXTlxlyQS6Wef7NHvPDnBZ0OXQBdn0QSW9YTXwXPOGXc9GhZKVEqZn3aNKygnY8yq8bih9+6hZVZzqLW96rlajFPcFSCbg52PeeTYbHWO/e3CFEe7Eoui1DfozxFSnIIn2QMTFnAlt79BAAKR/iB797A1a0RVs0YVDGcs16BZAbQggVsYa9M4/EG8O/+5zDA5DqAzXWgKqMwY0yKj4WaQG2yCjLO18daG2UmES5bOQCOAZABx7DtKvqD9gGgNNfJWv9nTPyECO0CIDkHUUM80OXbzUk7AvnOJhMYJiEEMKqC0kvBXTGikEEoj2UECwjnAmDh3X7EtdG7UKR4HxJc27sIBqU+Dod49jqipK2/x/YICmOMP+bdK6DueWrTGNPYgFYmozuH/20NBVCFINZfIqxL/j4vA3aVP2HRtQC3IR5YCHjfAKO1dVy7dR07Dz/G1t33YQsDawiurXsKm7T24gADS9Ac5himk3INTTPQCNhEeWwUEc4PU59iNML11z7trR0C+TGXAJp5ZNR9mQ6ibMVbJDvu3nmFQZhub+PBW28FyzugpQRUSlwY57ylD8Ggtj5AeVM3MGS8NV/rooIWrSTCWBaASsdwG11ax9VPfSoMVUY5maCVwyFAafyDPGiuQKF6FixAQ1mjyrtRjsfjCHQ9fPgA9ayGcy3K1VXc+PwbySIDADuHB9/9DmY7O4foJQzKJnq8p+Gk1VWXPyDPhTiB+qADP4ie8boXNiFkrO3u7mI2m/l+J8Lm5iZmdY3ptEHbBmtNdphOp94quCyxNltDWZT+oAClxJtwUmcPoDpI9TrPcTidjo0UlO51rbBsiP1mrY3A+TyXxEUB5/W9RZZc3XqcisC3gPQ4XYbIWlz/9KdRjsfpWu/d/fg1xoYTEw9BoV9sUcDaAkVRwpgCxhQeiGWE2IMUT2VsqAAoDwZvjIWFwQ+9dxvXdlZA1mLkCly7vhoPLzBy4I30exRAA1BGco3SRheEt0poBf3mCPmkua9xIAJgCgOCiV5wWmwwbIKA4Me6AGIEP9bFLR1AvC5O8tp9V+QnIb12iczywdVNfOvFh9isdlEYQmG8NXBhCI4pboJwl8lJAfGv14HIGeMiBa6v5NF+MQQu6LmjC6DrGZH2Ee7cONKk08qWscWBmH9el+dc0e8Se+GPmJZ69Uz46Czh+v/9aC4Qtt+2wkFoH8FoqSwO+dxR3qBsDMrWL6rjusDNpxOszZYBtvo0b4n0N4f7/Lgs+84mEZBZFAzcn0PcSZKELB04XT4TgM4B7CABvKzFqDEYNxYvbK96835isA3KBJM/SCFIdyzuaExAbYC7o25hvkQrU4dibC4G0LQ2xKHI5y8RZfWS3w7AXtlgt2pVzHfKikyNooSrGOk9SYEeANC7+bla6j/VNZ1MlZmsECi0rk6YhOUexa5OSjADMCHgfozdFeN+SBB5DyYYZjhpp5hLslDxoBjFt4DskBKgRwjCvW67Rfei7HqHBRIHMC+8b2gKVi4ZrMZgaoYCYH8Spj+p04CpTRZ5AGxZYHLlCtxsD3vjMSw7EFwnny4NLdaL1DkRrNU7drKgLHVHYJf3ZVH4UlnxF3MvH10ADcgE5XiMyeVLMEUx8NQCJYAZxHkgXydzMOahFDkV3Nlai6fjcQS6TLDKI1sEMMlb7Lhg7WDLEraqUFQVTFl6iwgbwtYzJ1efMP6b2QzsHEyV3qmYTDC6dCnWPQcX4uxKvICUi3MAiJumiQCpMQaj0SiCadYWaKjx71MUGF++7K3IJPh126IcT+CaVvUJg9s2XFtAvfibeU/JnQ4sMyd9uCeujXo8ntKaJ2CBa/042N7ZBoHCSZgO4uoFAG3TxvhsgD9h0xjjlXYgvFICksRl8chgV2e4DFmOaQArxV8aXjP0+JoHXi174uIwzVkLln36oM/2WGHgRdZmvCWuWHqNFBBZPW7KEuNLl1BNJjFdAnFSSlL93V1Tc5oXpsHXgwxFl2gKG15ggBxCAHtvbehPQCxgYTFpSxj4sWfYoiCD27MNvLC3ClMUIDIwoyK5LBrE8QDoE46zJss2LYSvx9mcRKLOu6p3150XwGxltBtkIJ2HLi3NLbFIVdt4nd8qpla+VIV3YTjjsFc0eLwyxUeXtkHOgQJ+FqUWYiWO9mWanPTvofV2eNzn8TXDe3hk8dnSBah26nQBdD0ntHb9BjZeftkHRl2WGM98Q+/s0OGEvL6wfEHHRZ+/exWv37sCwAsyk9nh2BNl3xb08QG7f57ace5o3osMNFcuDiFYdZFytesIaPF7cDEL1hWiAHzpg5v41IN1jKYmhL3wMXSiOxJzEDw5BL5mcJusu/zIEKkNceczGloFARXGeNii9nEnokVMKMM5dXofEZwpsVc5/B+ffR9PJ1PUBpCdzBREtQNcKOHPu8D5GBhN26JpW7RNC1OVsQxx/xOlnppG5eOlQAFuxP0xC0ov1mHhKSdpVQfGp0KwdWus3/0uLAyAdtr6I76NCdYdFE+KjEeUwwfvToFwCa1rg4VYG4L6NsFKqlFxsxwYLoIZ3mKH0TZ1Z5AloTh30UgDkAFw7QFHY+RkS4pvmYA3JfhS6LMQs0vqIQ0kFnBxl91YrF2/icnlS3j6ztvYefBxHGMnOdMH2Q53v+j1qdvLSnOJA3+4rPWbN3DlxRfz8olCbJsMVcTAsM6rBr+rn8BoOfWxE4RePqOLDFCMx7j1hS9AxnTrQh8FAMpY76Y6qxtYW6AaVXjxxRdx4+ZNlEUJMsaffMjhZE4kkAEM3PvWtzDd3sILb7yBcjxR76jej5QrG+WKd3SHY+9Stb29jd3dHTx9+hR1XWN3dw8bV64AQIwPtbu7i+l0Gk51JFTVyM8BcckyBjc++9no7igje/Ojj/DonXc7PZW70/Rbvn8t/zbEibsKovyd4kpGfjNiPA7B54NF19bmFhhAWZYYT0a4urIa6z3dm6Kua7TB5bGua2+RYy2SZXYOOkXeHvLIpYLlF/4MwJqHBEUWloD0eMqoMb3n9O9F7ohd6qbV7pt+jTob0snkyhVce+21DKTy614CwbXloyZbVbn16gAd9Zwlseq2toinsPoNLw+cG2O8lZe1GI/GMLYEqhVc317Fj775ondLlFdhYOQKmHGKEQpQlI3AAAdMewiGnvsqEYFf8CLpeNcsPzm51BYm45GA4skQC0+fjZebGCbKVyrD+EyIdxgr7Q+sYWhrL8aDlR38xmfeQ121gR+2QNtGC+u2bcBt6/1DrTnFAOydhW6ZpJrOxnS7oCXoAuh6RnTY3aW0fCVkPTf19HeNtShHHYuHTk6ifEq++l63tt1n+9ePwpyGBK0BAYyG0g0IBwO1i6UQkgmw5M/+lKe0s8ZqMc5ruLjf1EIUFqauqNkVOReLrosprqMqx7Tm0LHKr0fLZrmxUTYGGzvJTH1jZ4y16WEsuLhT4XS0sWXCta0JCiZsrU07dRNFR9qS00Y6kCnRBO32MUwnrz5Q+osK+RD1ayHjn3ttpUemf88kfzofBSoIpar08MiiE2wU3yKDlXqEm1vruLQ3wWQ28oBICLLqdXbvO8jMgHVe6RNhLJwE5LdDtcKS9HwEFxPdn7A2BJo3+TzpvLvS27FT1dit2mxaZ/BLttPc4Q65ORJ0P5HOhQmAiTE0BOADh1aLIFAQjRlguGyY+8/gygUpgyN4lVQuyv7BBFdO9oCXB7N8jjG8fThtMT+sIeXhvXIM2ACGrV9XTLIGi/Gy2MMKhUsnSiVgUv6QPYMQM0uEa2L4UzYBWIRYX4Gn+5hu4nYZ2i/E5iIwDHGwKhR3Nwe/tSy940CFgbEjVGurcLMppttP4dpG9XGXOrNc5uFA4v6KRnFNIjVePF/31lLynIx3DkxfFBaJbRUVKpVztboaLBoTjVbXUY4nurL+W9dyRE+C7FXzOe5f16jfaiboF+40ibEGhakgPNe0LsSSEfnFuw2xrVEUJUbjEarJBNUkBKMnAorCA0bq5ENZvkdrayBrUI4nKEYj5Sqk5Ykk98T2pzCWQ+q2dWibBnt7u5ju7fqYMk2DtmkxnU6xs70Da71S2zQe7GVj4mEPGQcgQlFV0UpCWqxaXcX48uW8+Z3DdGsT4iKceKc6/CDwBTFKSB44ib+EWOrIOVdSXkl9j+2QVQS9G6Sv64u9ZUZkqe71vE2MIVhrUJYlGgH7yXdHVZUoyxJVWUb+35bJks8GV7L4HgqodE7NBpJDCbrjXDVL+B17Jj5OaWxAgVxhDRSwQMhIWZTEMM9LnWr9nCvrqui88hSdmUfdeSv1jCMEfYgovajmFV1i9f7leAJbVQP9ONSxVuXnyxhf3kC5up42iEL8PdnoQdzwSXw7rmht49slDjo9d0IZvbHHvf+lPbKWJb/ums688PWyAKVYkjA2xP8sUZoKG3vruL67ikvNpBc7lgFwznZ7NTuoXLhgCglbnp9epmC3UBEn1OaIBoohq/vcyrJqY4nC5fnNw9Up6sJbrj5c3cPWuAEMh9GR5qkLucQ+zo7f5PRi2QYY1Jycs9DOrbSMg1xyylKwfHbS6Hp1e0R4QMxOMdSuMQRJ+sX92iuqM9Ux8HPhqz9jWmSMSh10mg9gYaOf1c8dxPj1AuhakgbX9RMvNAgnUV+SBW1Zs+x8aWPHaJoWDC94khg0dFIfrq6HfUAzFy2UKol5n8yjjD74AgyIoqzK5hjXJh2VjqhU9BfNrNqJS4e4POGENENwoaqO0xuJXnBYq/T+Y74Sjr2w4PzylNdv8LmD0GFH/PL7pVd3xvjxr78CGxrNHLbCDACyY64tEwils/jj33kRj1d38b9/8R3Uxp9J72MwecGHyXoMxYXw3r31lINA4L877oxVRSfLJwjEXdfkfFGlget6Vy8GWSW5LuCDCOcMQw6GWgANLFXevJ+Mkj28a5vh4MrELpSdQBcPTxk4sqByhFef3MCfePga0DJqw0iqqlcy2TmvSBDgA0g4QF61iFXG3NYNPICM39F0TQtnLOBaiN2UJS/kmjBvjWQXABk5uVSr8emzp8aq/1PbGPKBtAtj0RoDlsBcbCCgHloAzoGYYdjBNQ24aQOuxSFBC8AFcEYpccZEKyWmBg5NGPkM0ss5MxBwHWKCcd6CzpS+rWezGYhGGJclgMaP/zbstHPYZLXWx1BSmyMmgFlRTTClj29kKBdKCckdpBzBWouqLIOlW4OmaUPA6QZN22Jvdxetc2gbH0urdcldYm9v6pXcahTz5LpGWzcoJxOUhcWsmQVF2JdPpoYhBwuHFjUILYhqGNQwJEpo46tKjI0Xb4Fv3cDdr/4h9jafdIdWZ+Rp5pDmVjwwJlzXbpUpaeA6HABl5tDPsrEdTo0MFk8IgdhNUYFBqKPLm8RnC6VZi+uvv4HRykrsAv9pZPXPhP104pSKvaaFdlLfw3jyNS3BSDHXSL81wfOCYNyQDhlAZokFAlrnwNymIskDpmwcqGAUlYWtDEzhrXPYAW03eHGsHePKKy+H9xUwP71DtBTVAfjFkowsbCHx3oDd6S72dnfx6MF97O3uwLmU1fbmFrY3t+UAtvhJpgCYIkA6TEmeWbl2A5ONa9ndZjrF3T/8fTTTqUqPKOvJXDBkoTdgDDwAbGARuVsKpBiVTAMDB4bhAEzwchLkvLV8fsgHUt/6CQgeFCjKwoOfpc1AKlmrjAJTy9Jvfknwem99alEUZQS8m9aPJx/sm2DIH3zipAPZg95iLRQtr0IZUdmNFVUAQMc6kGOMsZATGRjDMIY90E4OhBYWLYItKuJGB4e4i0AAKjPoNfSNtG0CIOL/1JcjJZXILllbSrFOFPkwHsS9FkibDiGntRdewqXbtyBzNytFdSmDYOwYIIsYSzHwZ1Mkd0AyFv7wEdnwKIIs4sCtg2uD2zi3mG5vgtlhVAbZ3NXgsB7KEtN2jFGJpTbIb0Cv5X62EFkAFsT+D1wAKAFjAVt6ns2EthgBRQlXTlC1E/yJN1/G6syfyii6mAaMVKP0OwbdnlyOFoEY1EuYKJ7aOPBsWG4gIQGssbAUYt0xAejG0wwbTqLNeMaOKBMRobWM337tI9y/tBv7wMEmQ60Q/N8ZggOjBQMUTsMWK20KZQwpSbHx5oBw2VolwlHeQENjI99wG9D1unkzkDYfGSLc5ZxUKaOSnoHluG13fCzaSB5Kf0Hz6BMHdB12YJyc8or5lRL9CpQE027aA0srQ4xEr14DsMrcRqOF9/anJHLMzWfJDjtI/yyXtsP4qHNZXRvizbJucJ50Mc1rBL3rtW9GA2bfhxn00XLgcDQo5DJw59EaVmrPdtZ3K5TOxB2yo8SnSKXleRD7PUfDuchzkFdblNRPz3wZTWvjPnNNUb4uD7dD3qZzRlZfHp1DFJSog/axLPKizsu63q2zCDD+1+OVKb5bPMH1R2Os7VR5Mg4JtXA/0E6JWwzwKF2ZgBoQewUv1tVrpVEBVxuZ0VWwt6OuTfzmtu1A7BZd6YHf3Rcb7PHBmGq+Pl3xqvNgJ/+Uj4PuuxBcN+QkkAgFfsMhfo5rm6SOhTYmlbWvZrB8MOHEO0e4c38VY64wWr+EsvDuaPcm2/h4ZcfH5mEO7gwO49EouEB6l9XWtWGoMXZ2d70rhhw0wBwsDAlF4YMSUyMB0KVy8p6qlebNKwJAHvhcvXYNxbjCzoMH3uUitNR+nClfHvQvGvidcovfwm51nAqiOAalRZ+UJZ0wXl/HZG0NErOqGI1AtkB3NEXxP1MI5R4hjt849ToamnQy+3by6mOaF5IE0K6iqq6LNDb9/qJwLEg6NPt9tZL224uxpJQZsSIRgET/TsHsE28Vucsa1X6hf4xJ1j66zeZz1DSHqBM3zZYl1m/exGxnB9sPH2bzq5/j/LIWbTN1edtBXN2GSlxmS6uXhnw8Nk0+/hmHKSBWNrKmiqKY5r3ptDkRectdn1m2diRr/qF3QTQUSQOrLxv0XSOR6pp2SAdJjaSYdwTZCOlkPFCSI8IcytY0JGFSXq8YjbGysQFQ4tsEJNdZaWeicFKtbxuJj5bxtdgnhMnlyyjKYBUplmyU8kuuhQSyI8ihE731N6y3OoZlskykYKnpT1omdmAX0oZDaYg1oKgXUr0AIeGCHe7bJQLSO6n+yB/Q91NjWybvsqgLGNKbumNnTl003V/bwaPVaf9GhxUSgNtPVhd7PSwhQ/f1g31q2budJsy9Szt4uDrD9qhGa9LZ0ElRXUaPOILc37O64l5X9OXypZop8a4F1e9KYVmZkacc/v16dVmSjl7i80WfOKDrk0XZfquinIMebApdkCe/wqqN43j5GZScK0hROTgbPTmPKRMTvnD3Gl54urJv2sOU2lXYLugApAV9RYuGs+AJGSashAy1IY4PNrbwdPUufuSbt7C2UymFlXM5K0r3c8AsIApRSp0J8qlSfMIuu8YaaA7IJRBPLzZKqAt1v3cSLZYTtaCnNaojMorscXknLbV3KhUkO8cczfri6VFB+Yr2LpxOqmybBm1wLyLy8XXiEeQEcLC8MoZgycf5ap1D2RC+8OZlbDSruHrrNqqqwmg0wu+8/BF2r38c8xPy8Zek/BDfLShn29vbIbC8izF6ZrMZrLUoQqDy6cwru8YES03ugB7LEBGuvPQi6r097D15gnY2EDB8eGgeiHqjQfomzoWgyFvAWzwaHx9N2Hwof/XadVz/1KcSABYtTbLjA6K1Uhf4Sy4BHqBMimCfC8hpfxSshtIbBDAhjAUBJMRSLHPLEqUZvdEJOfEzvoOsaR05ZX7TL7ijtJoeqKUsFiWmIIMjkOWrkr+D/Inb7ML4TUuSLQtc/dSr2H3yGDuPHh1p0+dUad9m8PxSLIqi+5p6WHNZp1zaWfiVMRFkHCrar0sD64f00xCfz8Cu7KE572BUfgFk1QBKljkFyaTLm3OrMSABevKdOHct01StruLG65/1poWA5+vOpXfoAH5t6yIARZSAViKDoixj/WNcsXjCYLDYysa7gFdlrFdybBPrTyDZ0iQ3RUYbTk0sfFkCcgdX9JYJrm1Bwao5Obz12+BglPo+YnhqfU8ikAB7iieeIL1zbRN/dOfB8M0O//uxb7x0yPAeJ0PfufEE33rhSfh1IXhf0NmkC6DruadMHVQ7psexcHwyKcnfabdJFIouiB/lp3DjUK3dk9l47q3jko+PD4Dy9MqDdbzwZBXre9Wx5y20XL4DQq6SI7UBz3NLQ3gO0LcW9VfDEdQ+gd/NngMiBMEwKi4RuMh+xm+i1nR3LX1HzA96QRFhk2e6FQ+KOxsYmxSpXCFNAm+OGaUBQSm7DhfVOoTWkKj7otkzCflTfxhW/BfR4C4ipU9eBL5lSjsU0BVcHhhgI8CJy4R8z+McnKNoeWGsP4LdBqXFkMFrd9dx+UmFYhdoqY1WW2DGS4/WMa4LfPuFJ3i8Mo0Kr6+PV6B8YHuvmElcHr9u+b5sXYumblDXdTwdbzaboZ7N/Al5weooU7yU8tgfb6ntlgKxjgHsyjPzGcrSLGC9gY+SZ6zF+q07MNUIkMMFbIXR6iqYwiEOhCwe2TCgxbH/Y2xK5bIRn9LAdQS5ZKfchXE8YCkTlOEYjUS1ke4DP+7Iu65EvuLngTWEwhpURYGqsCgLi7rtOYeo1pvXERpOTLJP14ILyIGs7F0Uv4gBvwf+jo0Om9UcIOSZ1uEQz2aWUp3A2hSAEeLkEJ9OiDXptFzAf1cWe0KxjwnBtZogFk0EZRWrFqjsFWiORBGxqe4YINyi6/gcvYxv09v4Nt4JrlkCJGdoihSZZWrKCht37sAYiUeYamAc4XN3N7A6LcEMlNsjrH7nWlyz3rr+BB+v7cT6eIDKA1kMwDIi0GVNEcEqD6obVY9Qz2jBZeK6Emcck3qDZH0awTAjbS2uix5c821voutpXPtcC9c2qKfbqGcEbqce/OK0BWMSqzwcxTWS1F+odxp4nWcWDGpVj5l1+PrtB5gW+5ymOkD31ncW1jkWx8CbLzzGh5eH07/4aA13Hq8O3osiCPqvuEx77hUtvn77AWrrQ72IBPfx+u7+D6tydNkEYHp5gu3bl7F3ZaVrjHlBF3RsdAF0Pe+ULQxdofWCjo0yZV4E6CAKKJDrsM0e1eiIrSlXjHQpJFarWqzAMybOY27derKKz3109dnXY5AGlvuIVSiB5zmcJPMFiVwxhP4V9GF9Kljanc2DbPomVLv0HbDLAXDxaGmlDAcpR6xDev3TUZq1CiK3orpBBMCEjfYU5DtLFIvVSiKp/3Xl1XfBsjIrBK1gdaEUSdZV1VWrHUK646w+opyQUs5oYb5RSQvfDSienORM6HBRHDNhO29LS175LEJsHMsGLz1Yw837Y+xMd9FW3jqMA3h1fXOCa1sT3L+yh6drdQK6BDgzJlramMBAqnASlzVFfPc2nGq5t7eH2WyGRw8foiHvogNCDA6sXeEilNPFZ+e0j1hqDEXETABI6hGd3zDnSMohE8XYMvKAAyLQHpVQGJAtsHrjJsrVNZTlCKYoUJQjNHWNpq5TaTLGVMD9VHKC/eL4iEAXg134TBM8e79kZMXwMYjS0KNszMlJjN35z2jZZSBBPHVNjTFrDApjUBQWhbUorLcQdAvm8FA762TZzOvw9CHAK84J0wfbtRXXvHx6lkYKLNu35sGSBq0E91uSiIb5JuTaEnkNPLrU5tGBnstlz65Fk0rWydCPlwh2hT7gaFUFkCMfa0nyij6AFMEXAblAFNYFBrcuAl/xfRRvFAA3vZuPs2UkHpgxYOdgYXEDV/Ej5ouYYYa38WGMXaiiqIJNsN4MVpJGxVQrizE2XngJtiyz1nRgFI3Blx68jKvTiX+vKYAPUvs8mkzxYHXqwSWCj71kAoilLLH8qYOFj7sZAs1l2HZshMQtohzQ6aI482XtMTbkb+JphsYW/loA14yxYc0ooyuqaxu4psbWkwrgFg3XYbPF9xcJmHZoCTp7LaQW74+73kaS2vzKklJKOStafPvmY2yP6l66A1RLV2Mw0fsbW3PzqBqDW08S0GUG8k3KQr/soTK9mMbYK1t86+Zj7FUNItBF8fiauXXqVL9Hs7Uxnr509QLhuqATpQug6wzT8U19WfiTwJopWhd0JMrkV3Ed6UsEh25xLYR0F6W0O03Z9d4Dz5g2dkb4n965GeNvXdodPbOyl33lGA8kPpP+PwooeTZpkTiTJ8vcOyLPCPASLYP/iUqdpCqBY79252O8s/EE3//WDT8mJMMIztJSw7YLbsm1ADuFrLxCwi7NoAgxBWAtE9OW6XD/8L6JXPgznZEUm5aQl9174QUtoPUxSanyHewf0iAEqcMAAHb+cAAy3omzCEqdsRattbDW+DZkRt020S3NkEFVVTDBhfC1D9bx0v1VrDwhONfCGoINwfMzgZi9m1jbth7AYO9SSQSQM8FqzMWZacJJa04CpwfFsygJRVugDQcZMDwQwXKK3mEmMAFFVeKFN94I4JzD9sOHePLh3aWyk94emm3UTRUumBDzil0b59jazRewduMmHPn3MaMJyBSYrF1CWVUYT1bQ1A2augmB3dkf284eBOTo+unC+tBC3INSnTi4DAoIQ6rCyaUHsBGL6p/ByNkvQE3liHVJHRzAFE9Cjs9l7oTB4YkU/kXJlSgrYLDldWMHVZYQx6xMEnmLbqwnY0wEMLLclfXOIpDrqFStrODWF76A7QcP8fTuXSw7iOdzC1Kfx7iiHVKu8PNynkpNKlEfcEjWWIhxusznXgF+8PPgtoVz7A9ZUsCia5oIkHX70DGj2trD5W9+CDgX3LCRrYGxnCymmudZxlp/3xDWdkp87zcuY6UtARh8Lz6LO7gJioeQpDF3b20Hv/fSx5DF9Yvv38QLT1cBEGhqUH19DZlrJAzI+M2Iy7MJbGEjqEkmnWD4Pz35FN7YSyfRAsCjtSl+95X7HviXvAgAGTj1XvGwk6yNchfG3F3Tz6KqrGCDayMIwdoutLcNgenlQI0QlN6EoOIEb01sCHCtQWMSoNiGwwXADoa8+2IbT3YpTlCuDfL7Eim/eesR3tvY9PUlh71y0WEUJ09v3XgSLayK1uAH334B6103R8o/9wOyHQG/8+o9PFzdRV22ARCG+vR0XJwl+hkxh9hrFzrqBR2dzjfQpRWyZekIAolWhs8LafGGEQTMKJjReXuds0cDwylTJBD6gI+BZTOyAPfdsczq/+ziYQs+xHPEwGhmsb5X4daT1RTA82SKiw/Oe3bebKfer34OefyQTq5DSMt5IqUIzrtNA2LGfPbZVaTCbrkGu5jxZGWKzWqKzfEVVI3FuFE710vbrqeyukBC0tMDt2YCyPUsb3T3MalJlVk/ajFO5T53TmnFP//sWqF1Aa64Y01Y3Abd7KUPxcJhnwEpbkKiMHp3azmpjgDiqDxZUc6YweTBisY1oZuSBVYFi0ld4ur2GLcerWBvNkXDTbTa6fYJwCgbi9GswKxqfQSWAKQa+ID0Esg8g1WU+6EodyCCPxE98FpDWR8ehOtGHcBajC9fhliENLMZbFVJJdA2beaGFysVejnWkLqla6BGwK4EstgiHMZuDKq1NYw3NuDC6bCzFgAZFGWFshpjNJ7AFi2K0gfu98BhE0+yZAESnT/VzLnWg1rkQn+GfoUHwPxxwXqshvpSPlYlJn1cjOAUO9TzJHzynChp3Ysa7IaAWoFvzOmn9GuIGae6d6drVNLUPEvuXiYcdJDfPw5axrLLlCVWrlxBM/Vjrq3rGFx8uTJUM6rxNw9akmd6+cybN0PscZlnD6sRq+ekT4gIsBZYXwFubgCffhHkHMhxOPUvtLNzoLaNekIWYwpAMWtQPt7B5P4eqE0neoqLoQCf0bqvA7Rq67JLxQivmRfA1GKXdrHBl3EF6yCJ/6gQhqrYwrsrqY1eLm7jJboEIMSEexqqDAUwxboDKHRA/pTmam1BjY11YjBKs4vVdgszw2ismidhnSFjA7geuaq3fDMpNlf8jBZswtsI43CiLkl+8mnDKYshH38v8Lew3rLzhzwYAsCmcxKkC2uTeC5IuzOOPb4E58Ny3oEYLbnMNfHB6i7uXtmWh46vPjjc222Na2yOvUVZ2RhsjWcoW4NxU/Tn7RLVra0H7+6v7+Dh6m58Nj1+PH2QRmXqVwY6+4mUfVzQBR2EzjfQdUGHoi4fF/e359FV61lRPNVJfkPppMvq7wcrUIFoSkk45S4czwr8qW++hLW9MlpznR7pXphD1Plbpv2e02ly2N4aeo6A6A4X3UXCdWeA3/rMXVzarfBj33oZo9pG8ORgpS6CMZPQRMEFLQe7fIezKINxp3poIHSU930GCgcFH+xCvKhuuSrbA0Exw7Rvs4nijrzm0Z00xGBzoT7WECz5Ew1diIfTNh5EKbiIp9WJm+HtR6v4wXdvw+6po+0DCOZdY6RwAR8IP/DeC/j8vWv49c99gKeTGVIMJBOsLcSawT/jmEPAet+PYknRtI13YwyBxA0V/jm3TMMsR2vXr2N8+VJoM8a9b30Le5tdFxKNQO7bIcjGERHKlRVc+/RngjJpYKoKDIKLf/4o+NHKCkbjCcar6/AniJoYtL9tA8DVBOArAGDOeQsvdt6iy7FDPZtGF1HupHGu9cBhABx1QHBQmxROiCwRox3FWU4KLpN3JpOsYkyIoQcWa7T0vCE//uRcuAiYKlBwEVgkgMDCXuhYZ8l3ay1sUURgYagcHQvqpILGr127hsmlS3jw9tvYvH9//weyd1Hw4JxGOK0lTCyRNMVN115a3d8qPQDcuQ76v/w58GQU8hgsDfEmUew3BmBmLW78wXsodqagdgDYCGtB11WV40uEPCkVE8E0YxSYalTfeJ51Z7fCX/jWlWgFNalLlBMbeZ+xCRASF+quJZW4J0agC4RZy2gdg8Lzjh029ir82a+v4LsvbOKrrz5SzeyfsaUf60VR+GskcdDkVEQTgKzw2+RtUgZLs9g3JFKX5gq+ucT9mF0IXcChFoaihW/T+sNPWscgklM2DQwcmCnjMsdKgb+J07eOKSj0cHUPv/mZD7xrP3zcqrNKtXX4jdfvYmNnhD/1zZdQtstvOAv9wYsf451rT7FXzfZNS53Pefd7FNt40bp52nrEBZ13ugC6PlGUYnT5xf+06/McUIfDzxUgjyoQs4rrEkGtJEiwKnxAND9UkXRAoOryzgiX9iqs71WY1M+atRwAMBD9WQTpzq1PDMnuHGeXhpKpYb64hTTQK+lFtyExNyDGXtXAwAczXdurcGm7igrBIp0lk5zn1oVjTcVyJSonKiZXitciY52igpGXPQRypTT7CXlZwiG3RxrOa7GiLu8gytecGuh3EQBomfqqm/rwAa8IJWDAOYaZASs71isrAkwYAw4KZDz1T9F4VsC2Bte2JrDO4NHKnnpxDcvl9Ylz1ijXGqldtFRmNdZINcHwG88bSaKUm8KiLCY+rXMYra3HJ7LdaHaop1M0dZ3l2e3xYjxCUVYexAHDEFBOJijGkxjXBmQCsEOAKHhkYG0ZTisrQjwiA6IQzywEpifjLc5scL0UMAsCbLGDsYW3mhDwy2l3xxbsfND/+BncHsEWCK6IPr8WiMAup7YQay5lYpS1sfRjcGUUZiTxkKIFC0SxD88oF2ffuNLXeRdn16BZAGfXsofC3E/WMvNnSFcJ3g98O2haU9jwd9B1tL+m9WgBv1/KkmtuyUP8Z/iC78oEineqleXJ6PcdCgtsrHuwqe0CDv2ZFzdSGKh2pih3a5S7M9hpg6FoaIll0MC6FGa35lOEMBc5WH/500kF9EqxvggWhHFjOuOdvDUaEAPRJ3ArB7nSPXgeGOoSqgAbXL3ZOVQAqqbCtZpwZwpsTWrshjhLBEJRlsENvEj17Jy22LXoksD6yepyEemwGgoQQ1pJU1clwJEioEfxuzxwZJB2cCwL/xLr5nSnJcbD1V3sjBpsjWdwJj5xdomAnarGqLH+kJLBJBSHL4DOCxGmZYPt8Qy65zhLMW/OHpCWtQTQ/P+CLugAdAF0nWVaZh1ZJg9AtlkgCkE6sPcTpdofC/WU+bgQn1Bbci5ieawrufdk7qgnVYd9yDrCD731Am5srsC6Z12Hw08UpUohCa9DYMQRqnemaI4yMldi6UMvlElHc0pRu+EmxOUQtwfnvCvC3qjBr7/xAW4/XsWf/PqL6vCC/WJkzOFbJE+S8g7jKCAR0olwUYkO88VbkSCeQJg3inzvfi5qAA/odV0W9b15rbjvUNPViArH/Ke8AmSSnCg76UEZS3UxSelkoHUM1/qddon75Hf3C8g6UtcNZrMas+ksuvIUtkBL3rKIXQgc79pgGUTRQsM0hB/+1i08Wt3Df/6ed9CUShViH7AZkLhi8MpYHFe+rt4KoI3v37YtghGEUk5FKZT37qmsakTt07dEuPbaqx2Fyz9D7PDxW2/hyYd3h3WHQJdu3caVO7fjKJfDEiL/JgMOLovy2TLDwcCWI9hyBNgCjg0cB3dVYqCw/qNMVopRSdGbI+zdG8EcY685dhHoapvaW33VDVzrT7h0zlvNsasBTsCYxAVzMZi9g1hpsWsjAOY32JJ7WOxp4+tMpgnNS7BFCVuUIFt4wMAYkIPvN5M2exhpbuvhHwGqcEv6IDuVL7a57sMAHCiXNKhn96ODWKT2wa6jrGHPfnk6uh3q0gUlngRE+SYMgYUt1gO4A5+8+u37mDzaAYJbo7bOixsf4boeB6lkk+oSea+P7WYKg6JygK0AU8bNFCOnL0peA9ZaRAZg9vNMSgvrVAoKL+PX10ivzqYcwdoSRVGA4HkhQr5v1FfxxQ9G+B+v38N3rj4J4CGhqkZ+88LKwqfWXs4+MozBhf/attUoshIX0hzUv7P2hTpJUXhziNNlAphmA5Av7cic7dUcigip60hMyyLl6zsRMK1a/Nrn3gdDrJ7PP+07f6WRlsjp4GVf0AU9WzrXQNdhFviT2Q04IToW8DqxNBEO/I+OcHgcRX2iqD/6Fik3WOLevrQAyDq1fQ4GbmxOcGVnjNVpicId3EQ60qFBuv0iEw0UtfCJZXryfNHQZthSqlUuFcZrScAmZK2ZKXDqs+taG0D31jhsjmb4zo3H2Ngd49r2JOQ3p38WxufQ95IAmxXdFcDlh1KalFqVPZ+ssfqtJsHtdWFpuuY5D1TgwAxYQbO92ohV09Dup8To8kGJTXQ/TG2XgC52HgCRYOdiFUHGRMSMAxzlFScfcNj/ThZzSZFLyp4oldYBK7MSr92/jKerM9zf2EPm8hLfJ/9OAeRwErhehqgRUCu5KhGpFjsUi9GKj1h3dEZoQFYnly6p+lJsC13waG01xqOhOEYZ3LahjgZg8q46wbKLDGBsgaIaoSi9RVjjfJrYF51yZQwI3Bqtrpg8iMS+KAHpBJCyRQVmh6IMLpBNA+fEGqwGcwvX+phfbdPAMcff3npMgWDBhZL8gEJ0CYp/Ur4gsOH9yTsuOnkXSuMG8ju8on+11D/S27ENYrK884fU29TfKa8MINOjYt5afADLLvVQr04AMF5fjwcIuNZh6+FDcNOxYFpy3ezzVA3gzH1obj4L19CFmc459TuyzuH2I/gA8Gs3bqBauYTR3SdwBLgQiN6BMbtxCW5c9Z5lIoye7mK8PUO528A4BkOBOgSQuEsroCvejt9Jic6ylhjMKsbbL2xhbavA1QclmErAlor/SRD4BELLXM9BMApzgQDTtS5M+XiXyHAKqK8wqKhAtoS1nrfUdRPB86osURUjVMUIRVX5wz+QrLWiVWXeFfl3hbH5KoZ4jrFB8rU1OQRQeu/8BlJMw8gKIh8CGA4Ohh1AYkXqAKh4aUciQdiG8kr9DQJa46DbJ1X4pOlg7zlvi1BauSszUOceADxameLB2i42x7O5xWdyx3Fvri9o12cGsF/Qc0XnGui6oP3JM6SOgMcdUaKzy3lB+5BaGYasW+YqoL2UhyDZIZf8lNJwLPkfgj59/wpev3flFErWtBi2ye98MhfLpTwNBp9LFlDxGjpCByEIsOpAchFMI/ASnERyFAOPV/bwW5/5AJ//8FoAug43kpMgLVmLO9s+D3JQrqIEPzRzWSbcgnwCpJHx1y74hqDMy3dV/yVfOVPI5yrb+oHkAhKVjmBp5y2j2Cst4Z7oWW2wLmjaFnGzXtwFiQAnwn/I0/h4Lr6gFkTiWqf/BERIgMDKrMAPf/cW3rm+iftX7vbeRU4O1L8F9PAB2FtfBSOWEwFEEgVOKa2HF5SXmzxrN25g9caN1C7IZkTMaTgvin8Sn8vHeDMgSzBFhWq8gtFojHI0BlrAtUFVZA8WxXaKY18C0Qerq3C/LEoFWIQSM2VUspGTGeWQgBqOmwBsMZq6DvF16mj51zYNXNugns3gnAOaWQJyXKoPs4t1b+PcAwTociB/XY3zOPZkkIbo+H1QQiw2AadB+g4xfOwgw8HNkhJQmvLqg1eLrLcO4sa4H63fvIm1MJ7q2Qy7T5/CdYEuXyie33VN+ppQVBWuv/YaxqurKL/xYQBSgzUiAfdXx9gLQFfCfX3brH70FBvvP/Z8DwJYO7AhX4Ryyc4C1wfwq8s94j1jsD1x+MpnP8bL99bwwuYtMFVgU0IArJz3kXpex9/K04ploTEG1th0Iqih9NsovmpLwFiYwFt3p9MwZx3KskRVVRiNR6iqCoGlw1qZA/uAXIMkFm+d3lJ4V/d50jeCS7ZiS5COYyebKC0MHAxaeBtfFvZ+KNJ9GjdH/I0c/CHENOeZNFeI3H6gg1NfET64soXf+dQ97Nf7J0KnpcRc0HNNF0DXJ4qUEhd3xtOdC1qG0iq+Hz/Odz1w6EbOFaThe+mCunLEVXrezqrQzacreOXBOq5vTpT+r5T5U6MDlq0lgYuJkBF1fkTBKeEbCrdRMeNY/8kXRFepCMtSAqQ+Wt/CV175EK88uIzrmytL1lBBSqF+vrhghRQtSOQdKAF+AuoEEEsr9INgF3FKn7KLivWyRNkcOcw8oSSgd+uorvaVjAAEcbDICm4iLBZbAsGouZsCoZvoQhixFPIBiouyQFlWsNbCGOuBAwG9rM12flPw/yGJNkFAvnsoTklRRmL8rwDsROVQu5qRf1exGtsf3OKsvRZAGAtzSXWVdhx+mnRhnTzlsoOfK974jmBNiaKsMJp4oKsaj1GwQeVMBGmZvVOPWABJvzrnwG0Lx+JOGEriBGQ559T1HIzmEL/Of3gXYGP8vCptGecvNLDmWtQKBPP9Be8CGSy9HLtgjeOwN92LwfCr0RhFNYYpShhTwDmAglVV13ILDBUHjNO6Y5Rbl1PWOTFtv28UVJbGuAYPB2gREHZsgeoPsJbOeb1DlDnv8hJ1GUiS3A8H2l6Apu762wHrL9+5g8n6OmxZBjCCMl4FZlx67yFWH2yBGZiNCzx6YR2wwktE1Sc1CRMoKvf0v0QKXYn1DM/GMWdhbQFblICp4MwolmtscuPP3PpjPLrgrhesYjPgy6TnEPITV3Sjgt0zmcg7GYhWmM45WMuZEaVjfxKxU6dJLhw2c7qds2PAu93HvWsAgud+sIzzhpsRfBIwz4TTcwlyqE0Ked8cEgnJZRlS6+8ykvziqyclNh70TRdwqoOVojb0aCBltlaymg770NwkHEWyhc9eiOcXdBi6ALoOSkMz7Rno9F0cIZWdhPtB6nCm5KYykPdx0EBFh8XKA2aHvjA5nGqfJEsVrereR5LChz4Mdx6lXeVjZ9EitVBy7ejXNCgFhz39cJ/Hrm6N8YW71+bX74xSF7yJn3rsEh1oWPkfZ/edu5TiFy2RFgBYO2t1lQNFrOdOsqjSgFdUyNUMYnZ4sLKLByt7WN8Z4ermBPtPm45yqa6ksj2/k5O9Yl07imiM+6Oe6ZUVATpVthHLAN8+Q4qcjtOVLEFUukHQag7plyR0v8R6+q/JaY6kHDIAXFKiqOu2MiT4BwXMGlU0wcDAWqC0PqaSCdYNxCGocgC6BOBKuqzwrH5TpBp34ilpRSgAXcyuoxCaTrtS/nVIYs8adf/1ZVj87+fUfa+5xPIcReVL5oucAAYQKJwGWAWQqxqNUaBAixQvLX6qcezkJEWJpRUtscIJluFkRuY2AL0eYNNvFGcNAaACRN2w0iFV7M/g1tg20fVRetZbfNUx5lvd1HBtCxiLtvUukUU1RlFWMMFChThZ9MUxG62/BAxVq3EGaqVn0islO+z+SJf/coBrnvvivOtSV0lzHCTgTg5mdcZ46IfjXokOawm56DntDhh5oJpArLiNsRbrN25g5coVZTXayY+BlY+exnx3Lk/w6PoaQBw3BiLIJVZVSGthat/kMpjeIz3DKXHkPQJAGVugsCXYVjC2gsQSTCcXymey1jLGZnHh/GmHBD2OdTvGVpF36ABVEexib63omH2MP/I8xbFYUYVTBhcMllhqEntTl/Ew19TDfUh8ZvhnjU6j2t23vV+n5M0FJARSub067ksBJFTzfymcq/fyz47222xe8GA/p7nLW1yE/AaLZpWdz4PVpi+fLUy2T/Muy0bnyWG6IrIRNlhGVx4byOpkJf3T1SMOv1zNf5A7c4cGPSNObn5dAF1LUibAnjLpSTxaXcXGK6+gHI8BJOYta7Fr/ROyrDAHJcUYuBD/w7WtX/CiNvCs3lQJ0EqxGSp9uRolBc//mrMSo/+Wvl2QtV0/1hBFASLJmWnXjYj8rrl6Ny2UHnYa94RxY2AAcF0DzLAmN4snCkc588DDzy0pFZSQBMXQAV3FJu2qekuVaMQTBkIm2HaLGgIrnjkFSXPJaiw09Os8L64aGqQCvOOAWPVQyLNtHdrWwVkX8xXLKBPafrq3G3arU97xJDn1vyj7f3j1Lr678gDf/85NXN4ZxU7LFuBOH4kijTDfMoW/85LRRUsLdI4w4waz2Qy1man0evIO5yXKCxFhujdN1imhfEMGZP04M8agaRq41nXqsuRElfTSL+xdPHzMreDOF3bxAaAoCoxGo+hiQiiiu7Mx/mj5qig8eOR8GxaFAdjHBCJjQaZIiiIBo8bih969jZXag1urdYmyLOOcs9aCGaiqCmwsaDSGtSXYIQaJN+GEQAkobkIQcN2uQ989eNOG+WujBZGMrQTweLAFru++Smrs5A4rwNFDHS8iPdYR+k4Ec3jlLhsHnmNxsH6QwPPMFCztKIFhstAEJkfsVytjfYnM3p2L4pz22i67dCyNWFR5IMphb28XBEJZJqutxtVwaEN7hjkGcTUKbe18jDHHAMOBrZwmR6CCYaoWZRiDY+fgHGO8Oo1WXkVhMaoqUDFC7fwRCQJuOscgIzG91Ex00mKcwAd9P+uBQMYqECFtGBlKIETTNNnzi0CtY7Pg6uYd6m3KEjc/+1nsbW7i47feVuNnuWV+8GCMM0Ecteso26qmvHz7NlauXkUxHoOdy1z5Epgb1hzFQ6qtKW794XsBpLcY7TZBHEytMLfHArMT8ImMTfzcGECV49hbvI4nK1i/fBnXbtwEmzHYjlVW6pRFAVsCI0onJ6qyOxBDVxIF1HoY5BsXxmYMoRje1BqDu9e28dYr9/B4ZQoAsCYcYhGF3ay4+Y2jZMpDiZfCmzoCuLf89AdetNG6NM/fueC6KGZg4CXL9zMkySdqTZA1lKTItKEip1fGlz1HlKx8E8jr4iaeP+BFr7cA8GBtD7/30n0fm+sAJHJB7xogwhjAfuPLWH/4iFjZTz7exAu/V+PpixvYubkOHwzBwHbeJg5SXVDWJ5TSkWw6pkfiQS9xY4Ljkqk3RRO2TL3BneRhLVfq6RremvsyhIBvkqXIaM45gCTWHqL8qvXhCzo6feKArsMOnoPIMPnuy/FyyG5upiyxcuVKWCxTos46ovgDRwBArjm1W3rcNPT2g0wx273qPn+QJTU8ERjpotbvCn2y7pE8r/KL3yMy3VWctbgZ1fZeDoeiDFzg2F5RyNVtJtXQ1T/mbjWOUDUGZXuEYAnHSsPxyea+tuoq6qzSDCyOdy4CU1fRWkTZ4jz8RFbcUvNQVVKQj4UVCm3UW7zz8ufxgOEW5kEhQVtE+ThKPm5P2zYJgOwqNiCwdWDb4v76Hh6sGLz6YAzDEzABtjUY7VbJOlELJPrF408RZDvgVJgbnVmNxjrs2MafDuhadUfKCfmQvHcqX/+1LpxQiKT8csrEvyd3hsE+/d1vdRp8hIiSEBlKjQJ7AHV8PBdfAXGZsUUBawrv1gbAFjaAJi6uFXKS3rgtsNqUuLO1jrVplQA0idUSeREBsIAxYOuBNP/SOc/QPHjeGBTBVAR3Zg7gor8voJ4ItB5wEaDR5Wswdb5Iuwy084lRhwdEuIvkBMWgmAUgK1+JAtilgJl4U7ebniaUWj2yiiBMs3MhDUWwoKkLtE2Dum5AZFCG4NUeCCMQt3FcMzsQMxz50xbhOFjvOa88kkmCvyUQMwxsBKpkMhgrQELrT+4sCg8uILi7hskXwfKsOXOloLsEZs2k2GTaDInN4Z+kNK9PmzwPke/A5PJlgAyKqkLbtBEw35+WlELiuBkQ0oauH5Aib+gJeWqWhi/GWJA1GK2v+fdG6uusfxSP1auUbVqsPJzBn9xpYTsA1T6VjGONFE9zzHFTM1Y1jKOiLFFVI4wnEw90mXGeabZ0ye/ORgfL8R7+3iDWNCBDcHg2yor6HUDYGdW4u7EVwZ1MZtT5LTNMemnmjAkaGC0Ks0B65UyOyCUrnzhuXAXlpjuOiPUz8uSARDgwZlLFOPaFHl/L6H7z5sVx63/LkgArDg57lXdXNzOCZiZd/rZXNLh7Zet4DNekj1Xj+TY1YR33f8VejWLaYOfamnp4cNRDj7MMGEannbUoSDItKM2PrENZ/WVTaDGnYzU+82GlkuRyR4YLKNAxm/+qLhc0RJovLE+fOKDruSRBn4fmx9D1nqaV3TzWqj2vNK+5Pwl0bWuMP/btOxjXdv/EF/TcUrTgCGBC2JzyAXCdj7/jYwIpICEIP8610I6AYGDrxn08ffV9r5jA4H/90h/BhhhEL713E3/h//unEtDl5IODcuDZoN+F9SQG7CZdGH4LYvyPVz/CR5d2sFvVXTk8U3zkQgS+4FDXbYxPBUZmESKB07MSE853OAoKmLHendAHoTHBmoEzIT0qamHH0IT3MEQoqxGq8QRlWcDaAq5tAJY2ZNgQP6ltg9VU6/A/v3MHLzxdwWpbpiPpCRF80W1HSgLMlCqixDyVEk+gYF05zFkZad1KJ9G1caxJvCefos+bgi3FERr+ZEiLuN1riPe64BbpATn3Wa1XdinsBaWT3awFASjIwNgSI+eB0vHYHxDBzICBD/EWLOXacMJiE/uh8S6IcupiBMhCrC64sFmjFAxiP4TBIBTeWqcoYIoCVFhQWwNo1VjSAIAaQOzfltOwPPgaTcja9SzSaHUFd774RWx+/DEevv1uBFoWC//nT2JZvX4dGy+/BFuW+Q2xhEJ64/h2WlOFuinP6U8AcYaIP1xMEkCOECfPGI6gc+Jogc8aAxNic9migC0KOFi0WX8MzVWa0yv9fuxCOIso7GOkg4rURkHiNTmQtHTeC++eF9pvrjwnRMDmpMZ//sI7uP1wFT/45gvHmfU54ybHSFF2OUQLRGsykdE+AePwDNAF0HUUOm9jlJNwG79QJ8EF7UsHYvLP0YpgHOHKzgjXtia4tFfBnELMggs6RdK7sNl/eTyb5C6Wn5YnIEO+Ywu4okEz2UO9to16shusUw2erOzGNOPdEh+8eA+m9XlcebyOle0xZIs6gmiCtu33HuHL1qjGdjXDk/EetkazeD1Z9Q1M3rgr2o0BhmglIkIMdZSdE7MdEgtdUuAWJTcMsbiSPRFjKIIJtiiThRTDH0/P8JY0jkHGYbI7wsrU4lqzhituAtjkKhrLzz7TTqXrvq8yq2FmtJaxuTrF0/F0zg647Lamz/zPdcZbPuaWZ7/798sQKLV8rl0FWwMy3Z3KHMjq5zZHmR9Y1rVF0JBSzdC7+8HSjxEDQ9sYm439CXUEsOFg9GeClYsHt5y1MCHul3UlvPuod9Foahv6KJzEyt4KzLs+mmi14eeQAcO7Pw7OGGXJFtuva9HGyUJjyBIb6sp50jnIWJSTCaqVVYzW12HPODB3WDKFRTmeAFDWEVkfK+BqntLZBYUpxXwSYNSPlQB2hXsJFFerVQ8PUjw+BosPLtjcHVA0+DU6M3G62duX3ue3zkns/HOxXt/Tz3P2hvNgt8V0EP7affJwzzwn4vSJkrSTI8bWaIbdatS7778M9MKCBo5cdJ/Oy/LPZMD0eZi1dHF5+Ur6LOlgmJcSxGIjDGVwMdqBXH5RV3GQtrkAus4lLT8BAn4M6CcOg0Rf0MFJc/XnoMlXZgV+7JsvYTItMBhL8IKeX4rac1idwzrDjqMFF8PvIvv4SCF2CvvYXcaEE/8QgIqgdROA2aUd3P/iNwDrfOwQRlCCk/L/0Qv38f/++X8fq/NT//GP48u/+1lwPAnRV5LbEFNH2Z9rxZ+DxiLi0Nev38M3bj0EW9OX3uRBUaa74JeaAyneSgqoa4jQ6tVZ9CqSU7QON4liHK7Wx1SC0Yt+DnAVZYmyqrwrGLwFFAGwllCNRhiNJyjLEkVRoG1CzL9gFafjjH3/xzfxxt0NWEOgS9IYHYATArLFmsCBMZOg8Uqy00DV02oP/9vn3sOsbOFcupepZCq9/t1GC6IWbZvbXOjVb3FLHyeDXl5903JueqorqIsyrdJIQJmjABxaY+lqHQTAkI9hZQyokPGf7LAAAgxgTOEtJrtWN4K4yTsxo61ryAmPcjKjWOQ1zSx8+hMauW1ROwZci7Fh2Kyx+sCG7sHY63HSHrRhzgdwtLKxgcmVDWx9+CH2Hj480LPn4w2HKc0I7DsHsruyAdGx7BLXaHFxoo4SSjozTjVAALYgMVKNBVkLYws4ZwG3fCsfD/fpxqyS2drnbwmeysGug9PhRtKhnjoqoHsKg/40RP/umpKzTsrSzYFiB38fuB5Kdto/r75MNTffY+7IhQ5OSz6/7NDMLe1DXNXsfRQoGOTtk4r9+EmiC6DrsDQwsI/fLaKfXxdRz9kWd75S71aKrZFPnu5UOs+C0LOkZRjcSSx2xhFefrgOgPHotgPP8yI8SkcycGNzgvU9H8h4XBcY1RYFn5XYXBd0GtQTXDjnJ15wCMFlWx9HxgXQxOu/QbIIMjiTgzON1x0YCkTVSBKjKes4mZxplfAWKhSUdo4XU319bkmol93r67tjzB5dBmDQGsYHV7ZQF/24N/Pmb4wVEawAhLfKaVcpfhBFRYsQTj48LFeIsUx0UN0QEDz2hXdXtCHekQSLb2t/Ap4xBLJFCDbvT/0iW/jd/xDHRuIDMTMKU6CiMvqBsoRBzwCpjjUXCAY+cHhUINn3AjPQwOH9K5t4vLqHPVOjBYNaxHfiTmB4CXgOeHc7BwWKBXe4rtHF8i2cRsbwarh/TupsTfV/Btdl1/uB8BOOSmAQ0xwrLJWdLPGMgdwG0msiinIEq/v+VDYfK4jA/qCOMLEY6BmrDK+BlF4GPjYXigLMDMs+FpcAWsyMovUx4pqmgGtbf2BDcHkkGgjuSym4rwTV1rYl0gOs5mWsbHSf7bbYvi91poiMf7fxpUsoiwKYzsDLxOw6De37AGSrCpPLlzFeW08XB9wRo9KI/V+nH3MsB0vFzTrlmYLGC3+P1VCgfQ4X6b+BOnfo0coeHq7uhecXU/f+UHoT5qsxBOcYO6vb/vAGIny8NlXv2pf9DzXaOX826SSLrGrSGpGudPPtP93npYekebxK60rLPLIkHbptT4CGwC4AqAuHD65s4eP13X7awXWxP+90//TkQwV4DZNsXg1NmTkD5dgGxP6Uj+ZOgSwvdjy9fIbZ8jOgxSjEQQDFLl0AXYehAzQ27cP2932eBvn+8okzKSAoJczqt3qZT/YsOzT13R6GAcqjsMLus4Uz+PK7NwAAv/bCR6jtyXTe6/c28Jl7l08k7ws6P6Rd4bSiO2xp409Sq+sadV2iaZoscLJYe/mMEU9789KQh4FyOUY7/HnRy4BBlA5mALziJ3l2mVn0lpM4PoH3vf5oA68/3oBrgd2iwX/84i6eFk7lo/LQ7ZEaBgDF0ygjyOXEoi09kbsUCth1cGIgxkhy4HByXjjx1amTlQLIVZUlqnDyYk11XI+sLT3IZS1gLIwABia1PgVtxhalB8JCYxJsWtei++hQkHyGCXHKYq4BwKiLFr/z0od4PJn6l2pkCQtWgh2rrvT2ABsPorHTln8KrlpC+z0YP94vw+XQgzBKOsqmhl4DLJO52g3nq9eUAytUCtsJOGn8E5C2ZQc4oNXewIdcxIgINlgVdooHwGD2wFZb16jrGtPpHuq6RtvUILQe9BMOQH6XOwJY4mc8gPRllj+ZD+ewUK3deyO/O+M76us3bqAsSzz57luYbm7NTdexCzyzVK2u4OZnPztfq1EC175vEy24xMWQUr7KjZFjigRu+diGIb3x7twwHCeelqLTLF3ePf3djU383sv389k957HeCNQsIpAJTuLG+DG7vb0d50lRFqgw6uZyZJrH9RZd7/3WLE7kiLjyn8KIHfJjXo69n0vaLRv89qc/xF7hD6ORgz9yhtrtCQUd74NFxTm1gBY3bZbTwpTHQnN2jPIjL/Z7eDGR+lv+qQs6LF0AXcvSgvk1d/JFJPuIk3Pg8bk5yhZwENYi4AwEjIujMtYVOi8m20GI5qza+z51xFIJn75/BRtPR5jM/PT90rs38ejSFG/d3Dy2Ql94soIXH63h2tb42SwuF3QuqHvC6JBgI0BDVZUh0Ln1FkQRhyJAXBSFFGAWDlsPQck5KhAQ10fAW4I0TQTeKBw1L66JumLRXVEpulGRDWkMGVRc4Pvu3sCs8Jr9g7U9vHX9ScoHQOEIb3x0FeO6iAoSsy+fjMFXVz/ER3YWTjssQCAYa1EUBYyxMMaAmQBqQE2Lw5AhgrX+FDFLJgY91lZeCO9nQ9lVWfryyQYgw8GUpQ9AHk5f9B5xrE4m88gHE+DIgI0+2VeBNdqaDwDg4m5/tqcCxvtXtnD30paP2UQtdgrvzibrlK+/POtBLBk32kXVn97EMW8K7RLgNizjsBhp6QVwoRCQ7g/sNQ39pjiyPfDK8ZufK3Iy4dCbREsvzvMEZx8ZKcw1WIAli8Ou05MuiJQBL+mypW6qzGwk9NohHXUfLWRintaDCtaPTdtY75YaUiTQSReMqEAJcJ21T7Be9z8or6xOGLNUgEiWhOLnWQW+iAiXbt1CuzHF4w/uwjXehVt0Vup3x5kjW5S4dPsWqpXVhDYOzKU0ZjwI1TvsYyhzGbjxpx43ajWj/H46mTNsjnBK3SVm4MHKHr7yykdouYDjogdna7q/tgMmHryn36kPcvG8KsT0OfjGvftZWfOzWkhpKmqmwxEEpPBfsrjMwZOhcrn7YwhNOQ4aEN+XeebAj5xSHFsOE74LqAjl86h/M3FnPT+60Nf+79aN+9Z7Qvr4IMxpntA5RNz7km4Noccq4/3grEPx07ghHNbfw+bziaA+4qj3qg5CF0DXEWghwHXsZXka4ptdRpYpnMgZUnbcfXzgAshYmk6zqRgwTHjl4Tpe/HgNu/UuQMDnP1zHu80W3rmx5V2/COqI6uXz1q92fXOC7/3g+rFW/zSJgMwq4IIORvqY9RTHRHGanoQKFEWBoihgJYZJUOVF8QJBjIE8X3IilofMXJsJ7IZNcG0kcNOC2zaCXwQ5Bc712JkHTXwuMUi8yUQ9EICKDT57fyMqGd+98QTvXt8ME8PXauQKfO7+VVzeG3nlhz0gR2RAhvDeS49wf5VQwILJ+dO4rEURgCYyBq4Nwj9NcRjy8bdCkHkyCtiJTR/0RAqAm0Up5dsSjv2JeMYGay4y4U8eTkAXZxmapHtQArqi4i9rC2uXngTfMAMfrm3hq7fuR1fWBE6mPoqjQKz8Qg9nLxhNkFKbyPiMMSkPI0TvRwsE6whgkSo/klYYUtul376iyf3R3xSMJl3ylozybD/AdF6Xfg38F1btksAu/TT1vkr5crmDOYXM+kKpFCrKrz8clLN56nf9DVBYOGfj2M4rQf7dKSiQFFqsH8dhfiNk9/sJSJV1noiIsHbjOtAyNu9/HIGu/fTAs0MEW5a4dPs2itKHSuDOiOwkTx8KgMyxEYpgcT5yRZNPvF/jV9qiS1uAdYGaSExg9mvBk/EUf3jlYziUcB316mD46P6JB1XxgWEbzzidMxiOMjby4tL6nesgWhNJ63WeQweW02z+GKdj7Hb5PH9TfWnqAfanUQOFsM+1KF1qAHbfRVbO5UdvBKqVWBE3Rjv5dFbiBXmmNXzw/txJ35WZD/Ls80f6VYe8AsKdLP1BmucC6DrLRBhGtvZ5pHtF3DiiChHjmgw+cEFnlF77+DJe/fgSrmz2TdBvbE7w419/ycftMMDv37qPj9Z3lgZ2VmYlfuCdmygbH+xrfa8bXPh809peiT/5rRfx0aVN/NGtD0+7OueKZFGR+CSZZdaAmb8oHfWsBgF48uQxdvd2sLO9nfIUYKp12Kkf4u61D2JgecstSIAQiEucgS0M3njzVfzg73wBl+6XuP/0o6AQU7AaMyjKQioXQbVMYSIfCN6fKGcSWGQBwEZADkR44ekKfuIbLynoBbDOYGVWQJinBJ+3tgAZgx/4+A4+8/EG7t+7iqZtUBRVALoqvH1jE2/d3IQtCpTTGTa3d1Afpj+yTwHNAlhgCNaY2C8CNhZFAWMtDCwcO9S1QVFWHogrPBiH1vjcjLeWYvauMMwMsv6ERkhvK3BLQEaJlRXrxyHKk2N8dGkbX73zMZ5Mpou96yV/EPzhj8odksU6QOy2RHTW/YsBGXIOENKlI4Bih1mlu2BXggSBuDirDYjo0quuEfrLeF/4H5IKEthF1E3GSIHydF5d8FEKFxCqI6SSrluKzSPjh5nRBnDTwI8dxw6u9UHq27pG09SogoVlqnSuRscG6QwiQrC+Ui9IQ+2T+SumS+eRTFngxuuvY7q1hYdvvT2oLB1hmJ8IkSFc/dRrGK2uwhaLVZIEaHc3WxY+tEQahGGUjdbE57J1hPK/5Oua/g7YwAcfbv0Ccm6SAK5sIySkSZZsR4VCczBSx8HspxviVjgA2HT8k7LH+obun7UJcwQ6TAt2WHpvrR5sGnUjegHsi3FxnzcfqJYn30lqb21Bmv4hPQlY0zq4C2EnEo+Ja9YFHStdAF0HIFL/L0iw/7VlKY3/ucvHvsUTvKuMZBl94IOgfTGnjkDzl8lc8cDRJOfQZ5d2K9x5tOatITodN5kVWH1UeRcxA7x9+Skej6doSp+uauzCobg6K3H78RrGTYrD8zxR2VrcfryG2h4GWvjkkscuRLlVCiMNCy6anHNo6gZ70z20rkUrrnqECGLVZoqdvcfY2tpMQJdrQeF0NgABmPIxfqoPCC/9gbc03KPdBHQVNpwWOMrqJkGrIxAEANYC4OTlbeQdnbIi8aeMrsxWg9KggAdD2dQ34fQcayxu7K3hSj3C6rZD07QoywrWFijLCtvXGO+Xe2iaCs7xkXhCDESv+UCwYCCTLGHyuGAe5GMmELUe4COTTteTfhZlzSH+bkpgr2JULcHOO00ss55IoBTA2KlqvH9lK9VXKZXqArqDiro/uNtuSb2jLF3+2YsRMvAKC5Wa7uNDZoPdR6Jl1yDsBlFB06/OcQmMYL2Vg02kv3fMNOIsjes8RdAqvVqSZJJuzj0hPrqRsn5BzqxkwgsGgFGBTuq2/pnVNgj74h4rhXEAvaKVZ856kODA8K2jP3sQBNFSDQh9MWTNrok6FT4gaZfh0yIiwuTyZZCxsFWFNpxq2et5P0hOrZ5CZC1sUWBy+RKqtTV/cZlqKf7u5+0c0GtJIEwfgEtq4Gpr1VzD7+a7rxY/ACn1nb/mwVfDRXXv+XD0CeqSbzLz5rtjDbuhze+IjAep1F2wK7VrnykLv51/+DB3vu0HSy1D/X4b5Isq+VG8AE5rhnWXMWcYe2UDblx4v8U6S/dav4/nPLCoEnItyF1icb1sGw2IB2m0yyAayqyn5g6X2BMtFidfnjQPCTtx6cAdT2mdShbun1Sa7544AJIvSRdA13mnQwhVnKTXCzoyyeKYG+aedut++d0beP3uFfzGG3fhDONPfutFVM28oxm9S+Si+xf0SSW1A+UcoGNhcZ5GSOaBIQKzw3R3D7O9KXZ0rBtj0Ez28NEbX8es2sV0ayc+XRFQaEXMFiA2Pp4UMYxieYa8km3UnxiZUbQ+S6cIggjGBtDHILgAAi075d6IBHhR2qETTME4409zM0lYN8bEuFzsAGstmOHdBSnY4mRH3B2hR1iCtes6c7K4a0WQZDRNg7qusTedwhiLlhofaLxtAWNQsj8FD/An1EWhsCMc/tELD/DmlYf4Y9+5jRtPJ2n9cMFJWrkiCqDgAyG7KIxmwnKwGsvBoATcyaEB/t1Smm6MpPTU8o0acVBKQNPwKpqrQEfl6f0y+jnmmA2ni+FNfb3nAWdDuWbaeVJ9xVUxU/Bl3LhgjefA7A85kD6tCChMUpjlOIX4nLoofSKYbgJbCeAAvohFVwRjDcAWriz8CYyuhTEtiFwCkGTSqXGQjQtK7zrfwmQORQvVxKsW7bCfJqg1j4iA0eoqbn/f92H7wQM8fPvt7sA6M7Tx0ktYvX4dRXWAQOnaomuI5mqsR5zDsQ2TzMdhTZG1hZ/ZeJij0QeOpmZG/Oxzja6TYZf2nznzwJEMEBmoY7926n7XBfXEaAG0QzK3z9iEOSTdW9/Bf/zet/Hqu6v4zNv+NFMa6IdlaRmeuihPadkulLlc2Yfsk14R3Lu4cNwtUcX5S4WSo4P85oL8FmNxyrq1z5pzQQenC6DrOGjOzNCOCEcuIAq3B5RYNDfp4ltnUPA5T7TcnsjRqWos1vbKGHx+X2Jv4WVrg6vbYzABl3ZHqNoLIOuCDk4sgTJoQDDpWqso/ZOClZBYZmkLC1tYNK7BtNpBXUzDiYyBWVkDg6DWkwfMjCFYQ7DBukuq0AWY48Y+JeVaK60e5JBPBIuZrmiuPjUaoC5l6oEAYcECRU6VdM6hbVvs2Ra74ymemj00TYu2VdZtx0EdAYmBIEh5QKtuGtBsBmMsGrKxftZaX5eigFHvEF/XJeBgt6ixS4wHK7ug1gOdRUu4tFNmga4ZwNPJDLVtvb4JhkGN7Unt+0RabkAZjS3PuRNfN1EGeEl9Qz/lNlLz2kr/HniCVB07jx5mNRcBNgNm4jcBYigbfXG7e16e8aWDAK3ySr+lPZFfzd6vo3iGGFh5Rbnz8umZWOcO+Jjdi8UpuxEt0mRlSRzAbm55QoIfP77soLIPgAzLrMg9dVZ0XW0Ndm4o1NkSqskY9coKRmtr8RTTdjqNp9+eJtmyRDEaoVpdRTWeAFhybnWs7khfO3aiHm/VcSp1xKlImh31KAfVufcjwVE5PN3NZVku1NUVqPM89f7v1nXeDNKzXfi/xA5kYRcLumX/Hks2m89ESaGTKeW0OEd3hNTWYTpp8XilwIPVApfqMSatGXx2ES2CRYfS9d7/uPCbZSsyl+Y8mETdxZkvYSzSBasyt0WItXR+Rqs+cEU/f77WoOOh+ZZdB6cLoOtc0UFFbT+FNE+IQvQFYnxu6NaTVfyxb9+e7zI0hwpH+GPfvg3QAnejC7qgBaRP8vN6cRcpVyQKfbDYKosC7Hzg87b1AI8/fTFYWrmkcIk1BxGhKguMbIC6yMe/stagqiqMqgpVWcZg5hHQAsPAg2IU3BmTxRVl5QBi4xXeR9zDIui1b6ukdMxo28YLSI4xm81Q1w12d3YxqxsABu9f38ZvvfQRWgu4p8De3h7qWY32kApnso7xroeGTDopkYPLaOMBrp2dHZRliaIoADKYpUhPaFoHW/iTwQT8ipkE0CuChaHf//srH3nFhhnXN8f48a+9hELxFjaE33v1Y3xwZTusPgzLNRycr2coS/dJN5h9XOUGBD4B4iJoImNSAXTHzekOC3DNp35uyW1xifr08aksz/11gCRkxzbvzBGK85QisMwA0LZqnFDqR0pKP6lrkl8+vgAjmmXIW1tpMjNc6/lG0zTgMn9X6uDPx03ncqWcY32ysrGByeUr/qRV53D/m9/E7uMnz75+HVq7cQNXX3lFuVkfnA7eT4frWdkcMURwrCwL9fgHEsh1RkRrzyZoX9DpyIXgoDxyMYh28vSMwLMzQvpNv3vjCd5c+xg/+t2X8OqjKydeXnZd9lDOyPw4NB2x/gxO8isUoPMJGpPPmi6ArgPRwEDsXTp6eMecZLlK+eUCsQkqnhJUJS1BudwEiwluw3cXr4mAKsKjFpm9UDn03rIDvcTejGoIiZ0heeut3XRUeFZQ9nAPJe99kXcXIYSjZYHOb76gLFwnKQGpUeRZ0a7lNLk82KfYCCTh4mim2IaBqjWhGpxk2uiXzspNK5VkiGDcJ2FRVy5IoXEMeaepntrHCf6NJ/ABg02Uu1FJmkP40J8RyfcwCjuloY4Y+0rALwy4jJFgDqnNdIwof42xu/EIzfouQA6WCEQ2WG4ZrwQ7r2wbBCsuyImLDONcjCflOR/BEGCJUbLcI5BTPEYUaw5AHAPEzqdh9u8HUbh9uUDivGJf5ONbyYz372iDVRC7Nlx3YG4xNVN8uLGH+5d2MaUpwL5OcA2ARmapj7PEpIaJIBl6WCpwSGlTyQWN4cMdhfWC5HQ+B6D17mPwgLcUY12JkltYV4NaholTRGlshEyZaykBgzsjwts3HsG0aWQxGE/Hu6jtLNafWCz6jBovAbCCd2FzcIHnBvc3YnjXuXyF4VAGcegBcd+cs+2X1hvuXd+PZOzENSDd6aV1SGeLyaihEMw/I/aQbJZbWGviG5LzQCw7EAwch5M9wWAYOBi44A4r8anyyF0Y/J5VXa1nBIoJCWE+hPEi/1L1CU7JG9127K5B2Y3Abx0E6JIxL7vaYU6xP8CA4OcWKKylJHZseZ/EUzY7YF/s9cDAOPlUxup1d8oJUGspwGHsynoRS2JkALBu2iEJZo7U0qPBtOFiLG6AkacxrtenUGdrIBaUKxtXUFQVmIG2qbH7+NHA+jRvpaBeGy+mfj62qjC5fAmj9TWYwkrl5zzWXV06+YUx0e1DzQ60NC42WCRjiRniXC1yqCEDFzYRpP3EHVEsTWWMuKyGQR70q0gss0+cxp5O0Z0u+RP5PV40gtR4CY1Bst5Bhv68nsul2G62Q5TmuzyT6yrCYXLuqeSybMMi/QnfMfK0rGvxxVIpScz213pTRJt5q2upHpHBxOvx39kQ3Q5Aan72WDDBEWNmW3x0ZQemtPjUbql7Q/Xb/i9OLAeodNac2LUMB4YJfcexqRlM/l69MsL0ygSz1ZFIWOHZFC817880guMSFh7LR4NyWg+MM7edNuFBOW2ak7wjXD5Dhzt8ByJPSn0H0kHxByWDJJFKFt0kRy8hlgxW6QhJju2pA5XwjOfV8wV0DUmvx96iNPh1cfoj1IGcmtFSYPoe7BiQsyavjIg1hgvCc6pHA6IWBO8+Y0BxUrsoblJUovrNKrtEuZARFSRFXVElN0eksLaQKqPLOFX+zDGODDDAUiKXJvUZBOVQNR/Th6IRQL6hqJQNabNeWaG9CQAZABYE69uPCSq0T7Z2H2UMEHkFXMcQYqN7PAjjcTHPj24/d2v1ASnOivDFRGFF5OWwhMap1Bl3AtqqcZLiy6gRzHopVlZB546WYVwpDooxCKd5+vHt28QFqNz5QKDkBRmGjz2QLezWwCphwlGLR596G/XlbViyKGAAA9gQ58owwI5gA/hVkIUBwbQOpnGgpkURYnUVxniQyzAMOZRcA07N/6E/UdSdieksABgO4EQYPRQAbNacgQE2Xj1yPjYXWQNm5+MJwcGSA7czbJXb+G+ffh914WKdPJutATQ+H2f9JxOywRVKI3jAio0I+wAc4FqAOKgC0rTOt7shwBHDGoCoBajxDzFQudAHzqFqLcZYg21bGNjILx3SPPAyYRrpSZUAtic7+G+f2Y58P32m3UqvRBYxL6+os1LMW/8ctUHQTLGb/MqVeHBUTChwPIcY5yK1WGo3KUeFxldCZojnNjDuhzlmN2X+m4nQwAOehgEDB4ILQn5sSL++ko3rrM/GgciBuBUYK6SUpwrUqEKbWDiyaKAOFyEsJ+Z0FZ/QUqJJiNxOTPHPSJeI8kI2KjLSUnGTIQMlU08I8mCMgHaI7iGcnJRBYFilGFgQSmOiBRcH5YCJ/LiAi0BZ9+Wi7ViY87Jhpx2i/G1RavyYi6eykleyuW0hMQUp1EuUc8nDBRffzPJtoOkXd5FW4/ppeyBXlkhWrEWx6vy7XXnxxZjZ3uYWPth8Au65UffbU9cxf6v93ilPM1pbwY3PfiZYci1okd77zUkW1/Egi4Yi2aW+9X3VwlKIyRg6zwVe11IRy2BrfT9S2CgU2YBlwzTFggQj8kpfFxMBsmXl/mVSDbXy4HNJbw6fQV5EOrF1EUi2qDfn1SFXDnR/Z4J+vO7XrDnJOcV4tBTk6Tj5w8YN6XegvHhVj1x/CNxFduyCxXeSCaK0A0QraesPmVGvcp6I4n+p+jFUKBjfuvMY72EHN761jtLZ+Ez/VXtCSbyeYP/+dPUba7LO+81HJoCN/3POr+47GxM8+t47iNop+8VGVn+J8ckSZ1Xx8MFasoz/UCOSk3cDvxExKm4sJsmOKG2EcG9sdcaUMYAcpIK0BuaNr+Si8IYifxjjHRqMOko5Bqjn43EtP4fD9sTofANdIsR0rwF69fE/5f5Rga8o5FHv2tyVZ1+BYB4Fdk7IJ9lgvZK0ywBc6wYnTAqG54JgyiCySIFgddPNr3dkbtyJjUF5c4g3UNeqK8bLIc8Q2Ll80aSUS/JKyUEwYRqZmqN2daIAKKgWs2eb5FQzaqsPgLItnD7rFzcufyKWXEHM3+/Ya7EVCUxxyzqneJpMC3z23hVc3Z4s/YzG+DJDpAPTYcfsadDB5/RRzYS1+HZ+FpQT7NNO1l429YBrYSzYEIyxcG0bx6hjhmsbAD44JwWBc6UaoSrKmEfTOlx7cgk/8Iefw0t3b3reJViVAJEOYJLA6qpKWuLLlJAwQQIDSTwlHcku4m/PiiEAQlpJzgKxBwVjMrP4vveu4+HaHt66vnmw5qfso/djLmtW14UPad4rUG1SihN4m5cljUIQACDfdeR4O5N0w3PC17PKgNA7VUiETQG+WH0XLqqBLBbwKtTChXWOU68diMsunMD9fPpL/f5lZethvNh9bjFHITXe0kW1+HUrtozWmnWEyiAbe9S5r79yr8y5otCh6SA5zks71KbLjpGD88zuE8t0Sde1LHuTea9+KC089WcxGuHqy69EOXHn0SPsPX26f2W7WS2RxhQFLt26hdHqan/sd3hdLqIfZKYdgbI6HdPLL1nh4WT6alcGpX6KAwyD+dXq57v4We7c0ytDX1bXX/JTLhcVlq8F3bKGx/+CN1im2xboPQemZyxGc6ddxVqXu4kCapvJBvOHXI+Wl3uVDtTNYPGFgXxOpjEPtGbtu4xwPyF35+/yNDwW92vM09ZKzp7ueL6BrguaS861fRAq3gvBiCMTMh6IiUBXR4BF56cC1LSeo3XK9DVEH8mUtI7wHMvjAa6THtRl6byICOw88u/UtmdS9JICxS3DGG9B4uOQ6JqG/wk95tSVPMWlJmsTDu5DpEIFE2TTaJh4/r2VWYEvfHDtIoj8maIuRHZ+YK6TpCExRAzbjfVWS9YCLREaQb8d0LRNDNoOB5ADxraCKW3EPRwc1j5exQ//2hdRskVrxMSE0CLs9YW51yqrkhRMOv4XJS6ONxIl/tIx3B/goXE/RcqWvwjOAKO6wBc+uIp3rm3i7Wse6DqYkKMad+hGT77pFjBcmlYbhlxPY6KsGB3oXPFreYwT/8xxLFIStIBcFCyaBNxCyk+vPeovti3DB/yPIGPa0ImCfdY554g0OJgPwIPjMgfU/3oJiebOj/NFy9f67InnJ0tFVQYLL//btW0Cuo6ZbOnLMkUBZW93QIpS5jOl8zfmB+hEQOij0/LwxvnkPqdKrJfe/pqt25P1veME+s4saeECw0NrHnq8DEiL4fk2dwQfBMe7mAYHpgug6zkkIqCsKgDpdKqmaeHjVHjloG1bFALWsBwj7uJxyb1pKluLg7vAQcUYZJCJwUblUgAt2YWnjnJJJsuBMispqDWP4yln7NRx5aGOskCm2EK+HDJJiM8sy+IO0kCbAvDomDd5lXhC1ljvbmUNQEYioeXMLfDSIbjqhacr+MIHVzHE5crWoHCm/9AFXdAzpRzcW249DmB6UWA0HqOwFmVR+KD03GL88MuY7m7j/ivfQUMzNHWN17/xMr70O5+FRDqJ85gYa7sTbG/vojQFysKiKi2KwoDJelcSwJ/w2LTJYpQZxCG+FwFkA18T3xXFv4T/SJyqrrDX4SiIgA574EfmeDJIYiC41d3YnOBPf+MlvH1jE9+9cXRFUnC79BaU8PlOpZO1meBg+wh3vbL2l8BuPVnF5z/YUA9Ja3lJ27GVRoG3qnX46p17uL+2ExtNrLI4NSAQrI5bl+4xJ1cxgODqBtw47wfAHGLzPQ80tK1zgkWdC0oj/MBq78ADentr/4eH0p1F6ODwtH7zJkbr63jy3nuYbm0dS55kDK5+6lOoVlf9hsdR8+v8PTPqjh0ScN/LksoZdmDD4dlSHOrnZl4DwwD/BR2KFgBWfrnNomGpNfdkiDpfkrX8M1rf9qUlhSER+KKeOT8pAckdc6l8L+gk6QLoei6Jwulm/pd3C3Jq41zcaxTAFJQiAKBuoCkAKrRfoqA9KRuJQXuXIZF9aK+4K3iyrl+WMn3JmDSnJ9Phz5zFbojvnFWgw2y72mKuUoZHArs2HvASn39fYs4ExfqrbE3v9MPLOyO89Gi9124XdDJkHWHUWNSxH/oj8YISJZepPthliTEqHarC/7WO9EGKfuYYg7IsMQonJrZtC3YOl3ZX0LS7AJ6gpilqmuFTWy/iS+++gaZu0DYt4BxiuGAitIXnY4ZNiNBDMRwXJPaH8zzJmOBezKm+CRQy6i08tzAK7EovEBkGYmBSknRJyfUyD2WyooBfADCZFXjpYYnNlRp3N3bQunpQuMn2Fxb0iE+rElO6nlV/XhaySTCYanBrE6ERQnGEsqUYwzXxsPS8rg07iSPm+5Ph8N7GY2yN9sCtr8fMIAe5tBuoAF1O3O4TT2YXNjnc0DrwjCnbxNkn6YIkaY1bghvJEDjkqy/L7w4MLJ0YUeaWL9eWrV0/dPLByl787NlppcNQtbKCcjLBzoMHqPf2/EVmuLYbw+sARITxpUsYr6+H7I6/fc7Kmn1W6gEcvi7P7h2yFUJ9DoEOdLYa95yQX+YzRQTR4ECnOQkKrLDXbTEmWkh0Wv06b6ghShadxN00/uGBkZqe4E4Bsts4SMObJkknX7TRckH70QXQ9RwSM3uFMigHzjnM6gZkLYwt4JyDY4a1BYqyBFPh0zYtQJ0A9NFFpDsRdYwtipZjQD6X5bmugKOBIXSZSmTGlKwlOoK8fFpjghLkQngu9oosey2XoU/NUazBsT/5I4QGk3jLvjwJdMtZiRQUXv8XaqgUadnM09d1uJkfeOsFvLC5krVD1VxYbD1LeuHJCv5Pf/gqfv/S2/i99SdqZzjbk83ofKsvx0NDGMzN9Sl+9POPMapKlGWF33v3Cj54PI6ToSxLjMZjXLpyBasrK1hbWwUYKBzhR75xC5c3S9S/9WNgODRti/FOickbI7TOwTlG2zRg59DUtZ/fzp9U6FlHOOeO/ZxtnPOBhqsy8hYYH3iWrYUEoWUygAnBVymdfscSmVyOX1TQWAKEPGDeBh6lNwRyj7vEs9hxsCAFPnP/Ml56sobfvP0u3l57Ep49iLCSwLbBAUnIxrOukdRfeFqsJxSHG6hKd4MCAEa1wY++eQcr0xLMjKoxg+Mj1sC1gR/6YP8Mxvd/9xq+aC4DrsWT8R5+/dPvoKYW4LYHcEHWMgG7XLIOdk0DF8YJO+f79lTkPwVAsgQr70LDidMMbeJ0czszPOdMytN6xMkofVYtlpf1vHn6XP3Up7Dx8ssAgNnODu5961vgo4Bdx0VaJo3yY87tjpu6p75K8bHQMzNJj05naRgnLUPT0baD+6CLXKR+mrPUGIclDayocDPpNz+j8ZvWvax9T23u8Jy/oW6XSvY9hvpphopSG3fzbg+We0HHSRdA13NKuXVBIgrKjmtbuKAcsHFhQzwoGHQw8CUX9HLVKG5yZ2mStVk3Ds3wAtcrRMk8WvkLylznjftGCwnxSq6LQC+rHsmikf4EuWfAn3JDgaETMKotJtPSA2cOuLIzwpXd0dxs96WDLgwX3LNHVWsx2h1hPNGsb2if31+Rk0fj1blj4/mkSdmiGtew1oAMwRqD1rUo3QxXVmpcmjQYVUBVEq6s1NiZWTzZITQtQrw8fzJhURQoqwpr0xIrdYGb7SVcriugvuz5UQCr3YrnRQ7eDZFdizoAXa5tAojAQLDpgguQjXO+foVFtEILlpZkwmlYxoSJHoLS54EDEVE0BURk8bC4a/GFjqCc8mNO4L7EShzXBcZtgY3tMZ7SFFtuhplpUK/uYFbtYUbbsGOD2cSgXrOYrTSwYJAj2O3Kn8wYqzsk9HeZ6nyKR32HF5F4avG9Opx4ZVpgVHuAcFxbXN4ZYWVa9CaDaoEIyJEWqkP/rU593Da0DahtcXWzQk0WcC12yhq7ZQ1uxZIrnLzoFAAGb5Xrg9GLANqtw7OlQaB8bmUEGAs/9SaM4kbz9IF9u3jB/VgkIfQHZet06lI+vcbs0VBLdK8N/da/NGitb3R5QX5Lf6Yy5jXM+UY/iHyQem1BMFpdRTOdoplOD5RXOR6jGI2OxWUxVXDgt4ShOL5SlqZsz6E38Z9hjRYVRQt/LpfVaTTusQtaGdTSvZWW8oH2Or8z2lMutzzLt5nfegtjF58wDZ1OS2rNzRPPb6/BrSrO7/WtWMPvWQ2+/wj0dHuJGl/QUejAQNd/+S//Bf/4H/9jfOUrX8Hdu3fxb/7Nv8Ff+kt/Kd7/a3/tr+GXfumXsmd+6qd+Cr/yK78Sfz98+BB/+2//bfzbf/tvYYzBz/3cz+Gf/tN/irW1tcO/yQVF8nJbOE7VAIa9YkfGW3S1bYvp3h7szjaKpgFMCWagCdYHxob0lICkuHMmv7M4N/6ac22eJtv6yoVGEa4FGIqaF5SI31VEAXAnLwHnWjCYjTezD5YUKX6X+KF7900igikMjLWw1sAYgrUSK8wFiy3JOwW+zhZJSeMYLvjwaBdJMsBLT9bww9+95ZV4Bqr2zGgNF7QUdRZpGr78PNOnb27j8y898UAXEaz1Jyc+3XyCsjAAV1EO+N6XnuCzt7bwv/3RBh5uGezt7aEoLJq2QRvm0fe8dx2vfnwJpgYcCWBDsACYDQwzyBbh+GZOczCAGQQ5nVG+q7OenMNsNlM2mPIZU/vfipcIdwvRC+eYiGMIrY98KsO6IEBZ+Md5nsSEL713A6/hEv4/r7yLp5c3ce+zX8ee28bO1iZWxgZbE4tm4zLWVsawcCh3x7jxO58D1ZXPo6trs7dOjcOTSPFHqbqKVagbByL0ya7j8Pu/8eEGPvfhRhT6ilYjIp1PAcq486eukQtxtVqHS9sFfuIPX4I/TaDBH965jz+48zG4beD8CQP5y0hfkAkui7rlz+PUzIGt7q3ukDz2VSQcDpHALkY6ffgstGYHFDxydhmah0y7jRbqQyDXJ4/KyQS3v+d7sPXgAe5/61sHenbj5Zexdv066JiALor/hubJs+ykJBNHriuLwFkYK7FK1L105hlk2AsZBheeMW74jKHKZ0PKsuvEh4Fy5dcgosh8kGunRtz5S0RDaXg4bS9LILVzT0SS6wT+4AH4//UrQN10Mjnjk/Qc0oGBru3tbXz5y1/G3/gbfwM/+7M/O5jmp3/6p/Gv/tW/ir9Ho9yK5a/8lb+Cu3fv4j/9p/+Euq7x1//6X8ff+lt/C7/8y7980Opc0AD5uRROoqIUO0ZcGnd3drA3nWG3djBFCZBFiIQTgS4Kz4p7YQp4TIlZdf6EklJFKZ9Ofia4CMXnMxQhfGaSZhDEO/UwwWVSXDWdS0pxtFAT83PlZgmok9IYsr09rGmwrpKPyeX/rHp3gnWEW4/XULA/1fHG0xWUjYmg2YWT4vmlHj4wABg8T7RaNbg22sbVVUJVANYwyADWOLRwqKyL7r4AAAIKYlDR4s6VPayNCNO9XZiqgjEGV6YTvPbwCjamY1SugEPrwRlS8znMU2e8u3HUHVj8ipX5eACT4m4++e+mLH1SJCHDQcffSq7MWpQldimFAokQUwigEniHzsHIA6EegWfISYHZ7iH5OHElEfauPsbuxiO4sgG3LVzRwhUMLgBXNHBFAwKjGc2wc+MhTFMAZOGY4JiwvTvFtG7ROoDJoKzGYDDqtgGeFsCjarBvsyFLnQFMnh+OaoubT1ZCIH/CxvYIZWM6T3eALbAS7EQ4DP3WBb2c8xsP7EDOoWwBOIBbwsbTET5VrOHDlU1slU10VeRgtcXsvAsquX5HnQlUQgnxPf6wfP2GHqfe/2pYIu/OLpQzv6rJolWXmSl7dFbFbw3e6poDORTdsfQeQrH2GTuLrXnPwrg7fiIiUFGgmkywdv06Zjs7mO3sLPesMeGUxROq24nlnJNAA7q8uKk5UBFCEicvaD519sGfEfqyiJ7POdwlZuDG5gRX61WMGgs+Kg49IAtrYDXGStZ3Its+hTZnBnHP76dn5ZXFvVQ6tOShX3hQHQgPcmfZib+dA09nIOfAxmQtoZeyPMTBovaizvcLBiR04FXoZ37mZ/AzP/MzC9OMRiPcunVr8N7XvvY1/Mqv/Ap++7d/Gz/0Qz8EAPjn//yf48//+T+Pf/JP/gnu3Llz0Cpd0AC1rVcKjTFx0rRNg8Yxdp5uYlY3cFTAkYGDPzHQ2CJYbSSASsAp0wWrNIgVwJ+qqjwQpK5RJ62kt0FLpgAaWaO5bUoHeNejdC0BZ4a8SxQA74bJ4oKDWI8EsgFEBoZ8nVoGuG3DYksQFKrHqDj9YCYQGRTWwtoCpvAWciALB6CqLX7wOy9gbValIxap60p5OKKuoH5BkT4Z4smzpetrU3z59gOwXQFjFcACs39F1jC+/MpjOOdQ1zM8qUt8d8/i1adX8Kcfv+LnqA3gT7DM8fzBRGGDGWhZ4hyl+Q4ymXUXAAVie9DbViO5HMEusdcCEECuBE5HN21XI4ukH8rOzM4ZwQ1PrnPGjzxK50LSlK4XnxAEGIfHn34Hj67eg9tpgXb+OG6rGR587tuh3gno2tqdYVo3aIM1bDmaeKCrqTF+6zrWHr0ULVMiP+1jfOn11O9LuxX+xLfuoGCjNjEW8x9WAeFj+wTrLWk3iCWX8yAXmjZ8pjhbL3+0ghc/HON/f32KzY0dsBJKo6Ut+ROC073Ur7kL5ikRJeA2XkIOSh063wHFWmgpcCu7T2LQBZIpyTlgpnv/dMVnPXjn1WLeWJUBf/S36GJkPBTc7jmj0fo6br7xBh69887SQNexU1oQFoCSA4ztCCRbKnOLgqyMudr+rOeJQAnnbST2wK5TQ7t6FTm/tACRl6tv3L2K1x9fQ1X5Q3KOc4NIi0PqKtAbn6c5XjluwIn9/XBdtKwpl2SMzh+nvfmvRZKsICXbxOzzVZzjI8u31oWmmNOJbLf86q/+Km4Y9QaGAAEAAElEQVTevImNjQ38mT/zZ/AP/+E/xLVr1wAAv/mbv4krV65EkAsA/uyf/bMwxuC3fuu38Jf/8l8+iSp94sgYb8nlgS7v1gciwAE0reEco+YGDoQ2ADim8G5C7NoETgVAynSku+gypD5j2aK8CtCFHCCL+UVrMK1MieIY7kM9p6y/BPQyZKIll7gKmYCOW2ujBRYFcI2MgSHCaGUdZTVG6Qrvvgjrg1kbQKPwEQiDrycYaOoGzAalKQDr25ogIYDC/kXweBSFPgH0z461PwdL9rOj2M/4RDfcuGzxmWtPsVoEZWZhWywWDpkZ6+MZvnj1MW7yLtzDYPUT/pedMgaUqxSl3XBCsuzyGfr5Y00QUkIGCLIdACeHX4h6QkCypcwBdJBJ85sdYDrvwZzLfxloJYKOP+HWvwf3eFm/xUjpYsoSaSDl0E8G+9hU8d0DryJBKnza6eUtNK+9g+LGFtpL66iqCoYAbmrPL1uHgu7gGq6FNvKPl87i0x9exsb2KBpM9WnAbEgDXCwnUXqrLbQtEugVBEfX+phbbQC4AtDlXc/9OvTyh6tY2TT45vWH2Kn8WuWY0TKDQ7w1f3CBg2PZ6MCZs6boAkXZRfnZrfOS79CFdQ7Cuvq7z/28zy4r7EfcivOO8+tR8csaa+jNjva2iy2+zjdlsVDPCtFpj9A8tme3JodpqqOMn1wZPkBGy9RzwVJ1LEOe83wyXolU9rH1tugRAzmeP7hwgOYMPhr6TiL+Hp3/zStPT9U0Ts8aszzINtHiFSR/MwHKQkPv7oF/6w/BH94PMWZVsrnF0uDXgcIuaICOHej66Z/+afzsz/4sXnvtNXz729/G3//7fx8/8zM/g9/8zd+EtRYffvghbt68mVeiKHD16lV8+OGHg3lOp1NMVSDMp0+fHne1zyfRfJbcdyt03gXIAGQIjh3altE6oGGAyMKC0DY16tl04HkMKnB6Yte1V6LkGSNWW53n9adnsAbd2RsVUGWBMQSKeasN77oIBXQZY2CtTZ8kv71iunENWFkjMLtwn2EMoShCnZG2tX15HiBrmVE3DZgsrGMUCPoxEQpDuewlyvriXryg0yTdX6EfP7FEwErV4ntuP4Vr97C9LSCUBnxV4u7DAPRoZ2asjWq8ePsJLj/dhVN7V2lPjBM+I9YqoVAmfy2u/wSI2XkfGfD3JG55vlUsL2DSy5C+Dg/oc8ym94okO3udoAuEtJkAFldMiu8f/1Rd9x1hQ3xWX+MEs2nASz8/u7SF2eQhyhs74Ah0EbiZhY0BxurmCvAQAKUYX2Vj8Mbdq1jdKyJ4160TqXpIg0VLK+YYNJ7hwsZJE9uOwv1o1dUFuho5YdHhpXuruGHHeHvtMbaNgyPvkN8G93Q2pgNy8RKN+xzRYXUFUTj4cI+fPuUvvkgGAro75MvmPy/PxWDE8wx2aVoE5p9Ymer//vVnW4sEcp1DhnNOqqz1flooeyxJIut19KaIjx8u1zNF+2MghL62lZ49kTbodh3RKYvZ3Pmbl6ZPuo2y0BYL30ctCgzw7hTuv/4B3NNNIMqyC4sdqMWitGcRRDxdOnag6+d//ufj9+/7vu/Dl770JXzmM5/Br/7qr+Inf/InD5XnP/pH/wi/+Iu/eFxVfC7IliWuvvoqyslkjnLuJ5eOXcVkAUrWTZYBJgZqryS44HZThN1yb5WV73vIXmkuzPnlvgrxcbS1l1Qlzbt8AibEn4YFUnWNg18Fq/d1zp/Y1jaNV3qcOgZ7wPrLA3CER0+2YcsRRlUJay0mkwrWGlRVAaJgpRWel1hcxhQeaDMlxuMJVlcZDIMJCnzpw+u4vj3BSlPAkERIUwp8d8vqgs40DSss50RCPAQVxuHLrzzF+mgKaxgyjfZfMucBXgDIePeyeF25HzugGx9KNrwY/sRGCvzJANGyKwkV4mvM2fMwuXjsKVl0RatzUnAbA5YoiIDoIwAJZUP07xIEmwA5+EPihCW0m3r5LC3gLZVOvcw+GcVXENM3MHavPsb9O9+EsRYFF/hTv/GDuP3RNYzD6YoOOlz/ErWJwJ5L3wW8AiO6CjgGwomKrtFAF8O1TXCB9Cax5Bhf/s4NPFzZw/94+R5q06KJsb4cGteicQ4tsz+pM4MUzxPpMTukntCzARfOqIx8cABp3ot0QTLFVwD1vctDLggA1q5fR7Wyko3FZjrFw3feAbftgiePh3RfAafVS+drTDwXFkqnQbJenlGeuAxJ1eXzlYfruPXuNdyoV7w8kml3z75uZ4M6nTtQMS0rDj3SJwGjUg9w0wD/5X+AP7gP7E6XzOeCjoNOLlJkoE9/+tO4fv063nzzTfzkT/4kbt26hXv37mVpmqbBw4cP58b1+nt/7+/h7/ydvxN/P336FC+//PJwgYfYTpsnDh0pgxN+nqzFytWrKAK4lN1T2cqJg84xYDgZNBgDchLfRoL9enMIY7qB4lOuBB+rSiuDUn1rkrVVVyaXo8xZ104j4lCA0CCn8Uokc3RKihYNHNxX2raFc20E7HpDQZRlIridKQCD0agKQNcIRSFAl3dhTMCYxC4rYG2BshyDHVCWE1TjFuyAm09XcPvpqo/9haRP6r7wb3eEwTKw4GpwUMemYV36ETbAniUddiecel/QUwr9L98qBkfsB5/VceQyP+s5RNm3g5Yu6al3zRjGrUt7WB/PsLfXQWc4KYTz69O52tFImBAttHwSGpzqyfZJ7VoF3pFbacnXrgY8FC1FBaBnf03H8AK6XouUxauK81bVOcY1CsIwxbz0S+tqKhfuBbSf4pbtIobfsRk79+R7UuVJX0QzmWLn+kMYa1FygXUHXNutYLsvr63q8tLzd2UNdnGMm9g6AboYcGLV5WJMLv3nnPNAl3MRMLzxaIJiSsAdhoMHtXyPmLDRkSA/ptBX0hakTkZjVeWMMR8YRRkm7SK3T3ZDSSjWQ80AafihATFYxiGkGQKIuptXA/nGQdDPbykgdOCZZVp93pRhmZksFgK6cxlgAsPpB+bDiIPW8WdHFTsJGloN9qNqZQXVyop/LnTMbGcHT+7ehRMLujCXj4PmbYDqNX+hqzjpzwP2p5atYj7L5rHfBsQpkEyLTnseBOg4KJc8CkY0WCt5B+GR3L/naf/277FVjv/FtedcU2gPaRZmxqXdEV55sI7RuBzQ/g/DERb38X5LSvro9hfH+Tdfaj1Emb2UQ8hVAKakzKi7cjZE8qzmrbt+s5BnM2BvCnznfeD9e0DTqCVVy2a5Xp3kvK42CfU7l3h12YeffUehY53xPaOadH35ck4c6Hrvvffw4MED3L59GwDwx//4H8fjx4/xla98BT/4gz8IAPjP//k/wzmHH/mRHxnMYzQa9U5uPDRlZoJLNpQoMueN8UUhwLvktQ5omzbojF4IZGZYa+GVOwMyrmNoMSxkEJAMJTLwSiuElE9FJbQ49X+a7Hlu8+JCxGnOnh2JKmMIYOUyGa1FB/rZtc5bLMymMMbAucaDWwbJEsG1YBdifpGBtSW8RVyBmy/cxmT1EgD2wftDFZvGB0m2JcXmiIGpMW8qL0c9gUTez/GcjM+gsHUCJMuSjGtxm/XKdgsrAjjSyXpghBM6dQvJ+AXOarv1AYeDLetDuWTZ5V/6CRhg5+ePxOIzXeE/uAkmt+e04Dr2ZyA69nPfBmtJZkbTtmiaBtaWKNSR9BLIfHiIs/4I1xTXCX0pooAAH+lVw9hg563IIhZEscBBkIcQNnsTj/KYkIcEPQDjwByZJHK3SWkVju0oQBmp/5l9zKpMUet2eRTCkkuo7svcolTFVgwxC4kM2BL+fz/133D18SX8xf/1T2Pt6Ypqd3HJJmFoflMk7wLICbZN06J1LVzTwnGLup0BrAAs58Ct/3R1A2hLrtZBTlcUzlk3DbZoir26xpS9RVcL9pZdxlsN2qqE1e8f+5BgrG8/xw6ta8MmhrcaND0Akjs8oS9eDlGmCDOrPtS5xFEY17yunibtSPDW1E0ADOVp2bg6LhpS52SIipv/kGvPkFC9DMfsgV1LsbDQmuRzEMtJfUiBrkdXGY4nK0v7h2EMDs7U5A/jIUN+3Y/x/54lHQUSCHM0y2VxbxznFk0xHuP293xPlP2efvghnty9e2z5y/og7tFCIpdpngolB4SnMwNbnwIJ8FmgoWsLY80j8vmQQnWcFXAkGryGDYcYEgDqdQ+HaRyM0lIZx2SvuLi4ymq4YBZoZWIADPD3ZHIDeU653hc3rsJ67eNeJh5mlB5xKljBcVGXrag13YQYpRSux020vEGRpJVuxvn86IklSF2bVyGsYcEAwznpi5TGOYYxYe0LvDnPfLhTtOVVlMeIwhrqw85TpywgX/+ZkU4EDy3g5AykkHG0hOO0HustWrkW3ed/4/eBr30H9GQLMD62KMsBaqJwi6xqrW+b4I0Vx+EnRJ87CTow0LW1tYU333wz/v7ud7+L3/3d38XVq1dx9epV/OIv/iJ+7ud+Drdu3cK3v/1t/N2/+3fx+uuv46d+6qcAAF/4whfw0z/90/ibf/Nv4l/+y3+Juq7xC7/wC/j5n//5A5+4eJBlRac7EN/SC2Yvp/3KnJ/28ILGEs91JHNRkjwY0H8+U/5oXr2VeqiVriEtIFpfBHE+KnYB3WbZi51TdalDpkgiMkzFktQ7ICqbCEqjNhrRlg/CsLyBgVe+nGvFGya6QLZtCxZGSwbWchCs2hiPTNpPmoBFijohhqTjjmjLhXgfn8zTGVPfDo+q7IDerA2HM4vK+2Bew3fmmh4sQwdRXrV2GB+TedJXcwazDg1GxFipWqxWLYzpCIaUH2u86PUETIlxknoStU43/Hy805dDFs8mkY4j3wigESneAcr44WC/ZooMqTtqPnfYHjTfkffoClKdwp5c2sSDyRM0RTP4dknAQsJds8xU3Rbox74u+g2VfkMp7qExvs2ebmyDC4ALH6/QOc1/tdYnzNQLejGOGhkQMcgQDAzYOJAzMNYEq5sAUIhCSN41ESQn5QZnyajQholIBpYtLu9NMLYe6NouamwWs9S8lKAWTi+Z6hfbYWj9C5+cX+iuM9If+h467du5tGDg6rGWrolioMdsLJ1okOfndR24N6cOPHSvbwY97wXU2JjLLJdbBlWaRVxQeAwRUn+yvu8z660BYU1OOvBC6eMYqDuf87KGT2k8jjXbz6s+fxtqj+MjY0y08gKAoqqiHNarYYe3LiKNWSxnSTUnTa/M5RugK8l1qzG4tHIeXuPo1B1PQ2UeIDs9Zw5XoYy0fC+5xunZXS+Hxv4Cftb/Mfw4qWSLm4L6PztrQ/fgrE+CNJ16LnxS3pq9ZWLwan5/P5ltv3ZduKGjmIMHKpfIUCqGVDmWvLL7XTkYGdiesZMM9Q6AV5fdMoDNHeD+48x1IEtGWs4QOSbltww7Efnn+DjPQXM6uzPlwEDXf//v/x0/8RM/EX+LS+Ff/at/Ff/iX/wL/P7v/z5+6Zd+CY8fP8adO3fw5/7cn8M/+Af/ILPI+tf/+l/jF37hF/CTP/mTMMbg537u5/DP/tk/O4bXOUk6OfDiLNXhxN9Q8U9hHvmi1l0Z+49rXmXCQuXmP5KRXhQNeaaSlD6pgmYYFP/FnV+yMMaG0x2TVBnETP99gex/QSdB83pfq5/LiULnh47+HgTgyy89wZ0ruyhLD/Qu/+Sgah/JKesTOQxC77CxY/9HHkA2xqIqjRcMZAstkJ+3A7wh4CG+NiZYp/aBSgG6mdUPX0tfv8LEU2JTEWnnMQkdfSDAkAlWWQEkb1t/wEWwlJWKsGM4cvjVH/0K/uDTb+Jh04BaChvLB+e8eutl4UiQ/CPA5J81xkZ3bO+ubuJva4tMQWd5d5EvQ/D+hOkxbOHbvmyr4LYYTsI1bcCsOLgsMtD4TQQOmwmuCacwSqD5sKPpmDGd1RjD4aff3UDDjLpt8Qe37uN3X7yHJpRTN353VHh66sPzRJnW1b91SrTv+HqmRFjYTjHNYWu8X94XdFqknIcO9XT8dnYG8wUdhM6CCnZBByca6LY5LFofftbVBZPNSfLa0ORlDiS3adnIVrKbbKARMHw6c9hFiRayAZiSesnmuNFyYvxuksdStFbz4RhM0HcNGTByryNtOSjWZFG46jXaBR2GDgx0/fiP//hCpPU//If/sG8eV69exS//8i8ftOhjoYX+/sMP5KlOYaxpKyEiYHz5CsoQELSLxB8P7eO1T/prUHPmIeoDGUW3ILVzTQOPCHJO6gZDgUgdRkUICh3rtJwFhu9WKrN6D+0rpu/eEkAYTnIpiqc6GtNXUAff9ywpCs8ndTdYBhPIbszgyns2aLq1hXpvb+54SXF8MICm6n22rhUBYIoS40uX4uJ9ZTLDpUmD9XGNqvCTZrjcw4AwybVE4jW5to1gklgkeuyEPEAh1j7CSli9q865y4rFggvBHXWQmwioHdpDWepGFcpxDHof8alO8UMtkSwD9XsFsIZdBPYoWOTUVYPppAZvAzhy/Gbq/N/Zax2o8LCTWRo14vqiG1p4KwcLLObkTueTUByPBgAZ44Es8qcjRtcIdv7URWP9Wtx693AuAsAVfQRSjC9TtWB2GMMfPNK0Dq8YoJ6VeH/0BI/tLqZNgza0MUDdcw7UCiOWZUs38KnTYjj5mMuiOYfCnFlSq+uQmVev1Xx6vSZHsPY8vfYZpnIywer16yiOK9zIAtoflsy2SHq3spFCQ+NnqEQstKQ9kmX3YWk/3PeMkqgAcc2Rv0AEKEtb4GQm6RluoGOiyazAtadjXNmpTq0Og7I3DU+XuJ1BeWgBrW8NH16GtKkGxPALUS7LNGZCT1BgpAVhoGJpvIole6bIRmt+E3gLPXgC+uA+8GQz1SP+pVaJsiN3wmeocpNstx/Hu9A4u3TiMbqeHzob2wlkDK5+6lMYra+fdlWORGJuSpxzuq5QPw/TzoRU8vFEWNtJc6726Z1A4S8pqkXfoitZepmoIBNMtDwprEVhCxgysUgBwph66/UZGDnPP/UwR1J/wJnvBGbG0w8/xNMPPzwBoIswWlvD7S9+EWS85c2nru3ge+5s7lOrAVWChi+n237elKW3FGpbh6ZpMJvNglWXgWtdXLxlR8sEECwu5EpgifFUhhCcCHIxmsa7A0bAQwlIOpZKvB+y2KunaLlVaZGlyXAxpB0/ZkbjGlhjYMj4QzHU4Rgt/OmFxnqLsbSzpwE1xbcOM0ZDBb3yleyZcj5G2caIb9P0KTufWghLIqHagSS5n8ZhrHZQRChYe0UAkVL0MBKNhoMQKsiak06MDoihbh7ckk8HH2vrGr2A798C/t3a1/C11Y+wO5uB6xrGWIBNJs4mYI+ypr4gTR4APFcYVxfkOnCnDk24w07CCxJavXYNq9euPdMyM915YLnqpgEii8rTLgSp+sr2/IqckTF0DgAwXvArr+RxRbv95NH1rQn+5DdfxHR3iin2TqkWHYhGs+xMWFd/cg9JHgPgN8L0YsVB2lAW4XG8aEFHFz4o2+YjTJ6IGKxYdGnAO+iH2t0VsCDn0H73LvDvfwPMTXzeW3lpL4F8jMtadhgr/wsapnMNdHXBhGWfEcomWS+hxlDn5bA87YfCDhIPfg0Z5vlFBPvISO78WDyD7yC8iBfEhlJpAMTge1m0I11oRzLp4dqBQbZ1g6cffghTlhhvXPVpxbpDhHaxHqEeHjD8hkFZ7JYMxdistbAmuPcoE1S+WH/PHMkYyPdE+LDT+Oj1cQ6b9+6hmc06N/wAmm5tLaxacvXtvkMHyO1lwmhmMzx6790wZgnTK0dX6rq2mFI3Bx+wvp7V2NzcRPvwIaYffeRd+oyN1TNEIGNQKLfGwlpYMv2SKATHDpZihoK4oQCpwpoMlSL1vP8/n6jSVsYQCDYmHT6FTe3cSa5EsPD19XVT4BIIrWujlczbr9zFe5+5h49vPvFujSTA2lDLciZsZe+hwbEu5bKhF74U2GVtEeU9DzpaPx50m5GyVA3m9rG4iK0Old8BXsMQbVVgC7HKD79CsQzYIGPGuKtp99VAlmMOJ6bCWyUawuub11FtEX69fYwpZjAcE6fmWjDdU2+eNYRHhN1l04c1dc5YinkOl4T5q/dZa5dDkFrT9YnNeYJkzX1BR6MTVdAW9c+cYpeNcdMrRtZaAoQxLZNPh1U+c5rHzWK9zqUCfUwym3SoWArNhUGfPzorhszCiYUXH2T1jRb5PIfPBKv5rHfD5hyMCSExwkFs0Bs7SWiREw4dgkxCHIApgJRcKsBVT94AgR88gfv9b6J9+y5c28JQx85K5KDOK0Re1bVOXoAFDMup4fNIHf78LIbnGug6NAmIJUhxtJBIs4g7aZOyfMqsIpqnBBpUdo8B7Bq+PDcND00qfWyNel5bbIA6SlOy2+w8o7KRuV/XePL++yhXVzHe2BB51acNZUtcGWEcHZ6U6jFI/WgvBII1FtZaFEXZYbZKbQqK2VLW8CdMZ2FxW4qOraJhNydr89QR8V93kToh0ibWzIzNjz7C3uZmN9HB8uz83n8sA81sisfvvRef2H11A8DlpcqTnStfhp6cQ2CZ1xidc6jrGTafPsX04UNsffSRB7RMiNdlfJwoD8DYWMa4qlDaIr6LWHoZ6+PiWetjSxky6V5wJy7LEgBlAkz8HiyIYkDvKEMwrDVpPegKUKz7MG9gE6w+vRszwklGEtMPaLkFMaEF47uvfIDf+JO/790YnQHgEi/sFwkNdul+oF6E307rK2s2Cr8p1jO1jY8zaINVqlimEtggBj+U9xGhLsFPej4lVi/+5GKWzwy0ob2VrVl6F+TCY+TdsYM4WNUmkAJhvBhr8JkH13Flt8RXLn0brgym/wsBnfz3gmY8RdLrzvzaLcS09k04j3jO97MJB86nJRZebTVwQeeXKM2WLkXFsdfPelzM4fuSKjDhbA084xSryur3maeTP0YpV2GWa5WjtN2Z4JdK1nnWNG8l7s/Y5XTrFEmom4df9x3JZNWrZzB2cA4uGEJEy/VOw0T3Wb0hwhwtsDKgS2KQun5gW77/CO5XvwJXN17es34zNYLnujU6/MnzrE69Btpi8QqXS2mfdPpkAl2HocNsCx0jEYD127cxubKBcjw5tXrMnzpdREspxfs0W3yyh3EttoOzowo3Xn/dH8fqCxusjVCG3ovyagggk1VdwRIxF2aKyltRFCiKEmVRwoqbTtCdDXXWlTOAjX5yqb9tcn9tF9+6fR/vt0/AzbNZ/XcePcLmRx/F37Pd3WdS7nFQmkcDYFbvW3qCiFAVJRg+qPjei+9g78ceeaunAEwJ+AIosIMASwC1FvRbnwY9WkW0SLLiOmxgTQDK5IjskFdVVYggT7CyklhhEgzfKnDMC0QEKiwQ64QYSyy5/4XqBTArvbi2S012MbYssL2yh//0I/8V7dhhNKrw8OZTtK6NroHaEv/YWUSsb+666FgDfwqoDO+yuzLDf/ip/4pbd6/jR3/t+wEnParAK8lfWUpGdD9+cizDBDGDZDRpQVKAx8FXCIBdeK5p2lhWwYAF8NWbH+NN+xE2n04BJ33TsWvO8FgVo6u7aXRqFMXxAz5x9FIH98mArOWXgIyeDS2tsOVvRmpe5sJGV14JvOuYqntBJ0sZ7rSUbC4yqdqriY8vAsL6aSNGymnrrFfOeaAzMrljzCK/o5JuqGnKz3BunqMeXEirsxJfevsG1nfLU6qBdGBnrQ2XJw+3ceMP3sPmnQ3sXlfhePQmdJArPNCk5PloqOK/ZzG7BMwKPwToip5PxgTrcg1SBSszx1EuTCyDPFDWigxCINkcNMraMzzHL92C+7/+FNzXv4vmf3wdZFwwTQ8xZJVBh95CTfXNmyrnb1rW7I/UBAAOacGfTDrfQNdhLDIWpV8mr8OOm0NzzrCjbS3Gly5hJcQ+GKwGY/69A9GylV0OkY/iZEe6GFRw4vxfkFaCHluD1WtXfWyetp27QCZVTVWIUxLWrEZv4anhRcH/ReLVeKsSCwre2vKYNq19blbLc0bz2AIB2BnVePvaU2xt7oGfnuwOIodYTbPtbWw/eHB8+Q5d61ykLOURBqLWdBdcTnBPgsWstXDOoWlbuEtP0a49jgqFjcKBPKdyYwfUBEOrwPRKXOgpgGRkDFpDcBSC2DNhVFcwZFEWVQR1xMqrKIIlWOGtwIrCZtZgRAQqvRuythCTskzML3ySAVsfVD4CZ8YrP3tuihlPMZ3U2Fzbxbc+/w5mK02MV2ZcOmEnb82D9dLCtB13RX2qbCYLqt0FgTTayuHN19/D7niG7//K92A8rVC2ZZI5Q/69emRapxwI4JmsEZdQQFnYimu5aJ05J441Cv/5MF6pEs74eF/313bx7ngT0+0G5BijgsGOMJ0X5D+Ck5QunAF/Nep8HvQ5dOZfnmb+uty9I6Ci7oezQ/ME907rqdhxAh9SQCXSmB/OJ4LPZ+m1L2hJmtNpWseWQc8D95bIP7G+DIHp1eJZc5RjWzueFWmALYrfc5Ds+U19MkTZx7mmsrF46dEaqtrO3VA6eVIdqHkrAcVejWJvhumlCaaXV4DS+vU+JGHZEWQetLjMNFAtpKixlKy3oEJ/hJil0To+WYgxuVhW2uCk5PoYfkfbcUouzrGOl9Zgvvcz4MebScYddCcKZUptFfCVe5N1achyXQCwgSIOQEcVh86ikfT5BrqeKZ1e763duIHLL74IW433TXse8ZXuvBJUW+0FzE2ddtN4Top5G8GygxQULUGmqA/Iee5DUUkrihJFUaAsSxgbIX9JmQNqp90Zp13+M6D5r5gkFgKQLFieDe1tbeHBd77Tj8f1zOnoAzHLIYIaNB8II0JZlmBmlGURd9O6i7hzMtsRwRljGBgB+JlvA7WNu70yRRnAbxRP8HW7CzCwur2C/+Xf/hhWtybYC4FWMwFI1wtJFMh4Qoi3J656VsAwawOQZULAeYKxBg9uPMG/+4u/hnbsUBQFrDUh8H6Lpmnx4MHH2OE9TKs6CiRy1LQWsNIhGMc7LpOVm/4zIG19IBKJsbkFGwMf336K/+df+Y/4wtdexZ/6te8HBRfTvNUCZ1VCpOer6pTF2Or6GSCddsS5cAfEsSE1tcZvJpiwm2DAsLbw7uNG/gpMxlP8+Gcf4NFOhd/6zsZCSOR8EqnxcgK5nw3Mbx+isF4fVLVf9sUuUK6zS33bqf3S93kPD1zfn5aZc2dx5FAE9c9azXJiXnKGHkGUGXzsQEDnBR2FSP3r8uRL7z7E6r1NPPz8HcyurCyVn8iTxB0QCQiLWZKDNNglpzm30cIrAWli+dU95bFtQ1oVFzbyBAWqOcdRzqvrGvXuHurtHcDNALQoigJEpA5Ngn+WTMwjbf4uS2dB0Tzb9MkDuob88AfNPyj/PEWyZYlqdRWs0FrlrHz8BYZFZz9r7m6rDe0cCyMaSq8eVA9wLFhvvpHc6+YTlSsVdwnDTiD9+i6guTu//sQ0by1CmNQlJnWB0iV3JorWCosKeIZ0mHqcgsJzlObSYy+erqfutIaxXU2xM6qPUsWliJ1DvbeH2fY2ptvbJ6s9nrBmmuXeAzr6NLjDBgqm4mn+Snw0bYAtgemJHIgYvLEb8nHBzJywSw6b1OJ+8QT37A4YwNrmHu7dfIjVyQRyOiOp8nPeAIi5ut4BZFtEay0yBsaaaPUl1l1ysiJZwoOVJ/jOyjtoxm0AurzVmJyq84SfoG3bGDMqWeHzwJKyzMifk6bTJclWKcyB4J6nrdyY/WEBEWAa6NK6anD/5iNce3AZ9248xvrOKlZ2JwgMLiWMTJpFXoyXRdhMvFTdU5f6xfuX4lA5znZ0vXvBtHKoxy3KlRpXxg22V2qU1ODKZAZm4PJKnYpgRsstHq3uYVbvwRDDjlrMVkcomxJ2dlpuHYvpMPzwMIHAU6sCp8L4T5HOyhJ9QYej+RBOkh69C9KA8tjdAelclxxyVeAIvPqCliLpFu+Eftw0tCuHuWzvyHtQp8ROiYG1aYVLe9XAxv0zrsuCa9I8xbSBrR2qrT1wYf1hPYUFr/kwPQdZ1+LJ5NGKnfvXkACwnPKTGuW2YwY7BgfXQ8kX8PK+xOpi9iEWWudQz2aot3cw294GoQGhxXg8hjEGziU3zOyk66T+qhohxRHXvCwKb4HPnQGs4qzSJw/oeg7oXImihwF8stmexO8+7haYgxPmpO8Ec9CwiM1rs4MJ915Z9G6LBlQAX3j/Kl7/cAPWGZ3snHXS+afMZTReE2XfYGuyh199413Mijrs4p3cotDMZvjwa1/zllynZiJx8gDYwhKYMZ1OI0AhO2sAAKJk4dXB6wmy49ZmE15cB98sp/jV6ilqw6jIx+NqRg7/7v/262DHfqcsVC6z9NQMQsVukA8miwgOhToK48gEH6mjYUx3ZuAdD2yJO7OAYnXtgRZrk9ue7PRJzLCDMEZRsnLr93yvnkCB3ynQN7QdAshVjEo4Bpq2gTE21ouZo1UXyIT3JLz5uffw1msf4id+9Yfxg7/zhazPY104/90bF05jXZQ+u6kp/2ybGs65IJz6wwj8+zLeuvkIf/Tyx3ht4wO8Xn2E99fuYTrdAzlgY9LgJ7/QpHdnhxk3+L9vfgMftVswxBiPKrRXN3D57i1c+84rS/TAMyaa++P4iqBTZE8XdEHHSMvNkISsy8qwSC6cn+ei0s6AshnX0gUnoZ8hUttfc2qrN0lO9n1OUi58llS0Bn/izTvY2BnDtqf/Tj0MJohXSVXy6NPVb90DrJelZpdX8OAHXhs8JIhCplFkIIJjFzYVA6ClLKQ0oGWshSGLlgjknAK10qx3cU+0BRDAq7bF7u5ulJdc26JtGzSNDzjf1DVa5zCbzdA2DfamU9TffhOzN7+N1UmJ0cji8uUrKMsyhNPwMq1j56M9xDoapc8cZbyf/bn/rOgTB3RlGMSQhZCkW+gf+2zIViXGa6uoVheZch7/YNab9JoWI8bz76V85teViUO4lhiyOOzGD2Wvo2plEbbyUoLSpxfHbnakf5Eoi0NWFyk9BSsJkF9QqtamfOmCvTx7SvGHtMtWuguwAWaFQ2Odj6om6Y6hdGbGdGsLzXQKAGhnM7SzGbidFyjoJGn50Xf/4xrfeHMHd25VWF8bXgriXNx37vfRXSMWRUAmkIQvfq6ZJFyk4O/hiQ7QBQLW2eIVN8JHVOMJWogzy85oLwgfSnBJKFUSpjNEXAFZsJDdsmznPnO3FAhd1YnTO8nOnH5PHQcsTyNQ0iFHoLJY7N9TlylPxQCYHVzr0DQNZrNk4UgBgCNjPBgJAqgGCsI7L9zF6HV/omXRWrzyzi1UdREapct5KRziSNEST4+OzNAL4qLeDecchNUACM5GNd595UOsEPBiW2B8bRPXrz3FSjVFZRxGBQNtOAyEGCPTenAvlGHY4RVjYbjAe3YPrmzgygaztR1s33iI0eYKyr3qgJ1wQjQ4JKh3fQkDy+HsBzYFnk8aashMtbqg80IHGquH69ll5NtgVLpQLfBJDnK0xOnRIVnIsZW9fwrK9YDlHjwSPQ9gFwEoW4uyMQshxNMlP/q0vketAzmGcUC5V2Pl/iZgbZJNiDC9soq2KtJGqVjsO4ZzbQo6n7kUuhgz17H/awNAJWnFGr9pWiQrKxc3UNu2xd7eXkzngS4PdrnWoW1bOE5p63qGZnWM+tMvoXz6GHZvz2/cgaNHkDF+XU9VTbLhMMglAmt/jIqFVz/ExAV94oCuw9OzZ36jtTW88Pk3AHWk6fNI4rwUATYs19pHQ7s7RNrpB+qzvxUhQann3H4OlsnzSV0LhQicSBBzEnDiCADDHHp69y4279071jxPmv7wa9v46je28X/+X27MBbq82Hdw/uMtH71LmBy/zHAJ2lEgmL+XyFh9hHOsBgDg026M16Zj/Er5CL9TbGWxF1LZGFjn58Lh6nfiPgnQ1uNExWXQdVeDTvhCUfj2lJMeJZ2LwUwBwCxmFvuxt0VgPATIpew9nGvRtg6z2RRm12CrKGP8CbHoMkWIV2Z9YFhjDH7rc7+P337jqyAC1rZX8Ff/H38RGzuX4rtFL0lDIXh/OtHShFNtkxVFiumVhHCOAqu8OhkLYzx49fTyDv7tX/g/8FIJ/OW9y7jNwB1mPH2yi90dhjUGhQ0Hg5BB02kTy4Qfry/jXlPil8cfQSDo3WuPML32CNe//mmUd2/s0+CnSM9wUeluFDw/1GUMGhG+oHNBJ6S/LTfehyXCforzRaehFp+5dpIlUq/vvfX/go6V/GKNCM5EGd3LDeXODDe++j786dlBjjIG9778CnaurQXrfS9YiLW8B688AOWBrf8/e3/6K0uS5YeBv2PmHnG3t2e+zKysTFZ1VXVlVze7m+yRyBFIaBZghgOIEGY+jAAB8wdKmg+DEUYiQHEEiMMGSXBTs7uqa+uqrKxc3su33i0Wd7MzH8yO2TFz94i4y9uy3sm8LyLcbbdjZ7Njx4LRKv12Hqv1CqtulTyxJMSEdy55ZoXyOOVfr7v0Lhm6JK/ITyILmXwc0X/0Pvy33kP3z/4F7F//Mh19bJom6pGhC54lXlg8Iklq0xR4i4dXhDfa0JWMtheFi1D2pGjJXv4w4y5K85hRplDP1Ffbtrhx/z5mh4fwZJPCoHW+srS67Gyq8cjXmXoK8U4YBuF4ioeoHrKYcjytXFs6NgPEhRr7LN4PyVFCWxkGX6ZBOc/J7bFyA/zwCJEqkxEVueCBZYjDjRmlMT/loVQOgdiD4JO3AdhHg6KBBC33nsASLJvCCJAhtLMZ3l0e4o9+8w7unexlbwlieK8ufVW6c+FIsm0gBpBvgyLk28estVnRr46Iec/wHM6Bv1whhuO8lO3XH/Jll3alsd2UhoLnb94MCcp5361x3i3w65tP8Xx/ifPlKUxL2J838bY+YSQGRDbeSeDhBQ8hnxJzzcP3PU4fPoR3rli/69PTixGjwbLgwasxSpNxX6VSyFXSolKp0wYmRrxF2TM8G/gYEcOD4cmAyQBkY987ENpw2yA4xDiyBGaH8/NzrNcrWNvAGGljxs+iN5RMSMlzS65m1jhijIchX9C7bEEOi8pbTkeWueym+i15SHnoVuMia0pHBBFvJgzli7G7bvQOWnKXj5lNimflYcAR76Jg5GcwHiBPII43SIIBdgD3ACyIXHwmBjgDAwNiA+N7WN/HGBwWxrsgZFEQnHy3AjjEhrDGwxiCYwsDwmw+BxmDdbfOu5rS507Rdpkr2X0EYbU+wf/8/X+OveVcjQbH/ZiQbta1+OO//AEOzvdgOBv7fv2dL/HZRw+Q4m2Z4bHWesxnTQMcrvF30eKeM7CGYCkY0ExjAWPgCXAUxpAhBr6IjSw8jkEI8d/S99j2xTuPwHsLMHuY3uLoy3dBbkQ8Ijk+mnErjhKs8JI4KkyAL9agD7w3tYUUbwp0KJj6Ah8iIngT1qaJvMkwwTDBJj59MSU1jEfOmx5mc2Pqp9AJ/dxgWJ9W/8dpVqYCkl8ogxg7rdh8vQj+Ud4iA1Y3G3NqW/ytO5QECQZYRp4ht2Kxz1FO5TgLRQJiQLBk4JjDemKKHsKU0us+aX4rTZqGiwicF4eybTxK/wb1l8T1tYCB5//okPkgqymszA72Oa6fbGgZk2lBNqYjHocyaZ1mYU1/i/OqNkFRfSa5Gcprt+rGRWB0OjacPCkzK2GTI65T5DnCW1Q5V9eda+qTxyTVUU2lUBSRZELbGMw9vO/A3IHRhwtpmLOOUiy07AWcay3bpOkYJVoWT3cor2UQwXPI4YDIo8O4MTF8rGt0q4+3z8lVhviyFOPjxzdw72wP+53N3JmD0SasDcAYSjdfzzuDH315D08Pl/j1vedg1TFZVzVoXBIdQ8tpgZbHUA1x08uaFp48+hWj7z0MURx3D88uhqHxsX4uypIYW0zAaX+K1dEcT989hGtseC6Gp2jc8i56byVDVwyV4T26vkPf9+E28Hh0MdgSgveWi7K90BJmRtcHQ5lTRx09B12aDQGeo9qo+aYHm/AJa0HWQHbufJyTfCdPHOnYdRIZA3lZQ41vCTL6rBLH+bkUEl2NV43XWTZ6nPZctN7d07/Rhq5LQynh7USMBOkvxB1G5YuRyakemabB7Q8/BM1mUGaloq2myFwzQkopwx1VIYcnwJMHR+ExLKxoABJGGBer3IYmjF4qECMLAdHtUt6NG1Ro8kducGqtWqfZYUr1hevFS4mBG5JrYWOCRLxiGUqREytYUHRCAJmkTEZFiX280l4sKAQYC5AhzOczvLc4wh9/+k7cZchdSx4bcfBEebka7QhtD0Ib4F0ozMbA0sH4aNRuSDb8MKACGb4M2IoFm3NQ8bFx2IojqUojI4R56tZrnK1P8W8OfoXjgyX2Fhb7PEez14Yb3HwOVEvUxHELjNMzkuGBE3Nj+OUKz3/zmxA/6EK9HE87PjVjApwWD1U5PDFSPPKVACJbJAoKpYkxqgBPwe+KyUSEZwA9gtt4JGkmKKZ973C+XADIsev0JQC2aYSAQI4eJoVdvOwkLhSywtZaB2Pi6IpBrKK73nq4ZA0f73dhkqry1+YqvZHACgk1jiVlChDtKI2JrjyQhEybQoOD0dmSCFSAYQNmAnzYYDAEmIRVPUAGBkE45Rh/wsACbOC9gfUdrHfhGQjWOxAMqLHo2YP7FeA7GDhYyzCW4b2BIWBmLTx7dMrQpY9V5uOVefiMiYIYGP/TD7+Mrzl9sowFEQ7P9/HOv57j3uPbMKZJc/gf7vyv+PM/+YsUz6yxFmQEd8zgqCcRYW8+x31u8V+d3sWBD7Et0gUA1oINwRuCJ6Sj70nmBAfFOP0Fjhh4hUt8b3n/a6zufw1mj2Yxx+Gj24AXfpFKVLgk/DW2kw0MGxB8UKIJYVdWCBI444wPxqpcpmCfiMfxinUycAiGLqFThgEb/wI/RwlbyC8XaSg1wQu/LJOHd3EeahlkUMGIbESD71HWUHyKmJGjr3Giv4kGSZNTA3IBJZ4K3VTMAKLwR4WD45FqKJnOA2SRDfmVWkt6vuW4DDSOIpUnTcvlS7t2majLw7hHUlnvdTgFbPJ82t0raoq7lzSnMr3G7AYBa4IBhMCF3FNcgEJhZel3ssLCe5P4CwPJ2yLRDipbq1cAK4QMvFE2Siitses6h5F7tD1lWglxkzP0RV9jNR6W43K4UfGIXIPGuuJdkr3j2JrUtg7erxH4Xh/5SDw6FuX7XFbc2NXtT+0ZgzgvFFeETG7cuJEty0DnOBgn4p63j2Noy16onuaReDFw8Yn57uNb+FuPb6bsMjbMPsgRFHQHa8XQZfFHn9/D53dO8Om9Z0WtUzRfNE5ZV8L3U33RiMXeR/ZpYKkFG0a39Oi74IXdA1jDZW+qGJfT9V3ysgo02kW5yYM//Q361uLBn3yIbr/N3lPewytvq2S0YoZT8g274K3lohEs9C9jUHpm8grunSvmWGKZJoVVxGoKOnccGKQApdaAkrGLghNCof/mm7iD/0W5bsZoq2bjGRcjE2JtfHwLv5uGrtcUyBjc+egjzA4PQc3VpyaqLMjMt1aGK2347aooYIx53Vrs4R/+6mN87+gezJ2swMvYmWRYRH4HGhF+x2Az20y2OgZKxVRcZVN1ZabrkHB3huBVoX+PfU1tVcBA4gtC8+s0U+K8UXPg+hAg8uuvH+Kr4wf4Kf8Ez/YWOJjPcPf2LZiPP0TXrdA0DTogCQBZKVVCLhk8/+ILLI+Pg7eX6+NRPBGPXyaMKQa7pEPCkyjOZUFFvCHBYEMwXikOBMBYkGnBsHAcrkXu+x6rdY+u77Fau6xQGAfxJgwSzxqAEizj96C0x6NtYkBTOGqohyGv5iJ7o4ni8nh+jMfNWVJUpKxGBX/PlxGURxFJ/86Jk4Auig50Gm1AkfqgyWZuB7M++mXyO0jw0WBsImdAHoAhcNxZ9gw4H3YLPQfPRPFEDfMWvHGNtTAmuL8Hw4gBmRDLAsYgmfE90DtG7zws4o2Wcf5tbKs1crSQBVkidrDqUzTaxHQsrvZefnO+fYgZZ+TwP/yD/wWzVQvXZ+P/g/tPcPzsWTFHaZ6R50rGakYG/3t6B+/5Fg/Wp2goBKptmhZt2+Dk5BTL5QLdagXf9+HIKCn6QuJBFTx8Dtng/7y+gycN4ZeyCSHrQ+jHrMPjH/wK85Mj3PzNh0ND16T4/xZeDlyA7o4k3SjqCH5folVv4SVA7b5bb2DQNhkr5hsxkwzTlOWWbwMVpWhA0czhVUgGrw4u2dtiEb7+dPSterQZfPQqMNFTzgBgY0AWsBQ8J7tVh8Viga8fP8ZysYDrenSuw8IvVYD3PvBizjJDcGQAkmHNe7AhtP92Ab4xx7PvvAOW44IhWaEfZQM3sgGIZAUrsywpc5eSGxHTJ2eOnRBBrQnKEmD5fuxZ0aK3cE3w1tB1DZBdaKl+MUgzkjnkNQamaXBw5w7mR0cAMPAYuWiriroHHleZKIQGXGTn6CKtUMu2ruClrOZ6h1DDSAOCSR+ZNJYEab9v8N2nt/CuOQDdFWsIp9Iy79YKnOr6Tn0eJkrHTZJCmj3W8ndOHg2713X9MEqmSe9/IW2ECDDCMLJ+gHL0i/5wJWLJcFM4tuVcj7PTEzx7+hRfzx/i6fwch3tzEDu89+5dELt4FEsKiTuNqj5R3pfHxzj9+mtwXJHakHcZgZYwtDHvWmLtrs9Upk9HLauxSl6FhRYgZTHkeI/oDsEAxsFQYBoEL8fgwt33Lnw6j97lnSQJJSgOcEGgkIYpc5CypGUDluoD9cFMkxQHip/ZKHbmlzhrVrHYuGtvDNqmLY1URCkovklGNfFOy0iTjtIhL13S7yjFV68MYbEewW4ObRHfAOLcx5DByIREjwIxRKdRVJSH8nomQjhOFT0RosErTLhJhq5gsEM8hhuNZ77y1kmkSS0ahQ/SPqhXEkNCdjt9dCXypAxFMY33Hg49fvrdX8F7j27dZ+MZA1hwEoyz8MkD1CdjcEAW9/oD3OUZTlwwpFpj0M5maNsWy+UC63UH5/rokRGOnnlmMBmZUQiDa9ng990+vvLAb+HQw8fj/erIl/FYvPMEvu1x9MX7oJ6AdKtuzbzeiqQvF7j63JZa1iVXT0eKrbwY38LrADVt2p5+XO6pDTK1rK5+18Yz9aU+wir8SR9u/N2DqZ5PCUr1XGwog4VPv7x1ufM8VjLWdcJlijOeYKN3+JWhWnZbdcNkTMopk8d+XBshQHuPs7MznJ2eYb1YYuVWWPSLIDckA1fWFKwJm4LWZNlMaLk9X8De2sf6/RvgRvtPqgvI1Eex+imv3djaICJwlhu1dwKhJBGbB44HT+rNXMhY8fD5Jqh19sE71d63kOGtoes1gTsffYSDO3fQ7u9fX6HR+AGg0K7zbRUhkZx4v6hI8aphjF1qSOYqzgT4Qn0b2gQggQ2dCwo/lVoxep9dXOVd8XusHyPPtxG/4JouaYdGLUPhHPgoxaP6MaVydPmTO6NaUR6DsTN9Xn2fAAmbkNpQfSmV9HFRyQBwABw8uvUKq+UCq8UCK16gIYeuOwJ7ByIPE8/Pyzn++rjWycOHOPnyS6wX5xBPldA9Srh1GY4iBofh8O5i5Bozf2/Lh5AvWRerRlM4wiux68A9Qpwol8wAfRdvnVks0fc9Fus+un9nOw15ERZGDp3EwSoONYi3IZctIhOOsZWFlArM0hKW6Y2AB8enYhzSsVPCMclcljb2WFK+V2lJxzqTF5p6Hms0xsRjd0G8Qty9DAIelJEtN1TMiwbIx8ijgSocyiH4eGRN4opw7A+YwI7h2WPtPDrv47FTCifzKMSjWHUenQccDNi2aPePMGtbWBWlfbDrmQxVYeCTMYoZjbUw1iTDuuccF4O9h6NwdNB5Fw1yweBlmNGoBStBVsWXSozHxTHkKAD6rkfPhNX6DCu/hlO3mDa2gW1sNOJ5zAyBjUXbGHg2WHbByAjKca+Ywxh5A3zQz/Bfr27hx80Z/nVzjESk2KRWrI/O8eCPf4LDh+/ixm8+RMaYIhLbAAvz77Fnb+E6YZsMMIQR+jea5i28cUDZnpnxQq1DosSHBhl3KJwG3+oy3q7v7TC2YjnL6pNpLm7yvEiLvgnwvYe38IMHd3B06duDBYcvOsJUHPOLjt7B4MIcj4wSnPfoXY/FYoGzszOcHp+EI38zXWNYXRLawpoYkzNdcpPny3sf5S8DH0MeTLVcG4i85xCvkXKsRSDLe14pTsno5WPs5zG8pKkbElWfKMTZFJO4PtHy0g/d/A7CW0PXRWHTplAi0zR4NlWOaRvYpsXs8BCzo8MqzzVivzJyDZsRhD+96C8FE1kH4zLoHl2oXmVoVwWN9esKkAxbdZ1BkXQunCtPniomKqoSTDEdk5LN4ujWO+jLkEgSkM5oy2+QEMeYfnAMNf7DSEpz+VIbGDCYqynRbRyGMRg01db5NINJwWKpyqtSD/KmlDxou4lfwvj6ZNRYz3oc2xWe7y3wfL6AIxd2irwHc/iuYxGJiCVY5F2Pfr3G6uwMy9PTfF1x6o9wqctj2XDPZcTsNVa8eNAUUp8yUm+yAhbm3lz/yUmPJ8863LzZBC+uGPCXORgyenh0XQjeue76GMiTU1yfJB7FAUyoOCYzpWfaN62KtzGijHRgnJBLrT/1Hr2DwoC8zlJukhhs4UnwUiMUpcffDcUgtILb6nijNo4B+mguRUErx0NJxjUVBFk+sy4U3jVNMKyIUblQzJT1Onh2eaSApcih1D2oyCPGsnThCAVjWfD+yoHQi/lQPxKtQRl4PIyDCfjB0SgUjXnZ9BpVFZ8doDjceBDpV+wnheUYjMcUvBI1niSBMjznaEyTWHkMoI+GOT2NaXhZWk9pPgC5Zh0AE2aweM/P8Mh3eIdbnKLDqqaa1qO7cY7++ToPVFpglMfr2mEXY8yLgldZ9zRMigdUtrZMVlO7ca7ISEvrrYnrjYRM48s5r+UgGvfKSMxrHDJ32m7MyhThVa0jxXQL+XhL2stAzeDTHIx9yi8l/Kch4u3NkLomdYyrjPZlc05Jq9cDu5bY9gYH6wa3z/dw92w/5a1FQf3JKMsvZ5Imx3O0TUpuSjRVdJTaisNBJpAbC4nihpTWaVTy0jsfhfyWblVXf0VbWeFa6mR5pVxp5FI6cOU9EIxoXC4tLaBv0l/Vhqtu40ANLhtflMu71qXKHuN5v6vw1tD1iuHGu/dx56OPwlXuA3g9hc7XF4QoYJya65SiGIn+kqhOjtAxltV7j+VyicVigfPFIimGwR1JbosKxF3HJmJwjLdTtTcJ6kJwh30ionzMDhRuFYlKX2JmzPAuBEJmNjEoPsfyh+J/rkcJEFrYGzWypCEqmdFYuiHPGmIzlWmYGc5XGi84KbfikCzGgzCBIYYRR6MjWYtfvvcYf3HvC/z79a/x5ZdfoD/x2PMWTUOwYLi+A9iBXQ/2ckwua8qL42N8/bOfgb2EKS3x4dWxDp4kCVwbMCoop1elY8L/9//3BP/6P1j83//Ld3H7tgn95h5Aj+VqgbPOY71ew/UOq1UfAn5W8i2JwDpJrrLhIu+sZ8FXG3bZDxWKz8wa/y/7OAaOZawdo3elgExEsNqFvRiOKaNESNRzB6Rb+BR+ya8KV7VyleX7csexWGJJ2BGhyuLocA9EFl3fo3MOnijddsnxLx8NzO0i28BSG+J0mx4wLWAsTDNP89DCoAWDqUHngMUqGCeb9TrRrDFBUS4ViAOaehuCusoNvoCNlxcYkz3C0pXbjUvCLLMH932RJqxzicnhUgBZ7TVJDFhj0RqLprdoyKbLN+QGpb7rC0EVBHTrNRgNCLNwKyPZcIsqIRoV4wUAbMCw+AN3hB+4ffzT9gn+yp6iXOXS/xxoWk1oOcuTivIVlckCXjTlGSHarwPU7RmShx1MEBnqY+O1QvBWNXidQVFo0rMeg9Sn5bYLNqj8E8s04ceIaFQct45F1aEEXi4ILcJIXzS94pHfV6mzVtkvSkDS4EFuOx2Xca5Gmqj6G3tff78IXXlV8N7xIf7+Lz9A68uN9DFxftT2SWrJXLCzkVsn/UT4uhi6EraZwM9t06BtW8zaFrPZLFyOFk8NpBI5ry0fb8B00dzsKZuvm6aBMeFSGxQeZSWBTxqd3qxGkKUktE46wrjBO0vkt83eW1WeeIrCGIrxyxDGe5NTybW5eL3lZAJvDV1XgQmT7GTMLpXHzlrMD48wPzqCaV/0NCRJvzC+FO/x4gn61Lhcut6kMHPqX6ZBykAxWO/TBKAQYtIfwXqD958d4l2/H66S9Vx6dMU2+OiqG1x281hLnLRCUY4fNPpbPwtHblJZ4mGUDEAI3jfOBc+yeE0uoyamQsyLQayMXuPjRMo4wfJbl6t+FrIel8lUAfHomk4ad3WyDQF5n0gJH4TE7CTINIGxmPd4fvMMz44W6GYO/dyhnzmEiN8M8VJijofCCsOjUnTYw3UdABWMu5iViGsviJFM8dEgjFQv05hW0u2I/Jn7EkuL71drB7uA8oqLAepJVPzg7cTEsJZAPl4yM7pwRxRGru0ACq/ir7pb8rMjxm/NGl+YFc7hwk2LkndkXbOfmpO0UoavKKFdaeZI4xc8j6S9KUVYeLkjxVoaViJGLnHBX63WIGPhordcOvJJBKRji9KuoejtEILXsw/z5qKG4AE4ZjjHWCyXgCGs+g6NMZi5cKMVGXGnp3TTobHBtV48T4lMiTvxC430UxuxwnFChtja9eZuNsfGz2ioRlzTyWBLwAd+hjvcYo4mpIsTZJCPTIrBzkRDVzDwG5DELSP59Ol3VpAJDQxaAN/ycyzh8YVZYkHq5lwQ+r0VFveeoj09RLPcQ446KbR9G7zuqtLkykjvXiUMaHQkdUHpUC0v+AugPU44zjkjBjYWZUr1fJS+voXXArjAggojs9tHJuQDrNH0s4YRIpcy+o2xecaMLzz69OXA2DpOanxibpl+c7JwXBZUXwdl0UTRm6jNxhqmw2nsCANpmEZFpcH3sY7w4P11047N89L2Bu+eHOD+yT72umZL6gr/axmd1HMqX21viTL+KByonQm00FBsy4ooRVS0UoeO0PITAYAxWNw+wPrmXjnq1cmlgReWSlNk01y9lm2qtJJuSrWpIW0imsqji/MpgBp9apwflStrobVI9JaPaXhr6HpFMD+6gfc/+WQCg68JolJSq5WKdqg3VKW6THUqCOCFMl5uDDSjqqvVZqqR16qEEao2yMSY9wZ//5fv4x17C/ReUKicHFMEYGCDopW6FMs1efw9+2qUJW35bMrwJIS+vHExzih79OINQRQVvpyn7PNUnQVCpGvYx/NOtzXc7lbmLcY/CaSUFBYAwfCFfARRAlACFvlQlpQmDCx8N4bx6OYp/vyHX8C5HjNn0FpCawkGHsw9fC+3JvYwjUXbNFieh7FL3Fb4PeVHMqaAZlTDmF4vHkJ9eo2NsbbJ1RQXiqxvCUKfReEw9tYw2AKNDTGPZh4wbOAN0BjZBQNAMfB52sGLAkZsQPC8Qdqh1YJN/mCldMpzk3yrFnD4H9snOI3HFos9y5GO+r6Pr2rlReQ5vQKrNJM7bBN0RPqbsouQNSb2ULEWiTz6/jQYaeDhfR+O8zEBZBGiWJlwDTU49ZwpHFuEBzrHWDuHZANvg+HdA1h3PRbrDouvHwME9K4HwDiyYmgLBi2JMWaMiTukEnOMYKLXFhFhPp+jbdskeCbjWDKK5Z1QjjG+wvIICJDeydynnXsbjA8x/pdRNou/t7yDH/Z7ic6L17OJnmO9c6EPqh1934PZAmjiDqpJXmfGNCDTh3kw4aZKRogj8mfdDfxtHOK/mT/E53YFzQUX955hcfcZ7v7sezj6Yl9x0RJ9XgqQrNkXULR8UWTtpfZtRxjh2iMpAGXxSr+KJJzT6BSvY59/d2Cz9KnpcGFXydq0Kmosll78rYzdo03Q9Y0wVn2bm/bilXa9EhxKw1b1TQ0WFQaJy8v643BdvR7Kq/Va3hm2CEWbdIiLw3WO5vaxPFrN8A9+/iFm/dhpIIwgol4jI2Ocrg/N1HCXGeUoB+mhltMrhLBhmtWELDN67zPDh6yjKJsAkJMsJm5kWUNxA5bgZg2+/v37WB/MQtleYn3mvk+dzMlSdDaGDZ1Syt6ntT5S3tSYpH4B4bK5KDMFWSmcIilGmqTdF1hJr4zYvFnwO2fouojb4SAvKAmZxcKYIKbamkyGcPTufdi2BQDMDg5KDllmLOEFInJpA7l6zJFs7S4ZapVopB3jNbMy3gzPYE+1YqzuTSa4UjHVwo12ow43qAXPh3wMUZ3drgQhTbhC/lKdn6o/SXCUfycXWyW7aG8S9qzcf+VVmWfY7WnfOiIUx8mqjAOvMP2NRSmvRzwqyTm/HO+UNcXJBsZAcFcBK2U5e2Sxc+ioxy/vPcWq6cGe8axd4/zsDN71cK4HfI/WEuazBi4aaRpLwdhlAO9CPC7venjv4NZrHH/1FVanJ/A+mFp8soVoNhdx/Aq0ZDi0u5VZj+mQVHCBv8U7jctAuVNNeY1ZawC2mM0asG1h23k0Wvl0g584+DEC7oV5KdsXjrtlOlgIIXotMBdruXPA2gM/bs7xNXWgBpiliFHKtZzL0WDmFBtKgqAOBkoJLHnMc4LC3b+iH8Nvauyg8LZY9GV5lN3E4LACgWCJAfbR3hrxfVTiKRU0a4Nxiil6PJlgGOu6LsRU63swgjG+j4Hcz4mi4Jl3GI14d8Vg/UZuSpK6CLC2gY2CGojSd/GKLHcq83wQSXQsNXKy9tXYJbogPSXCctlh5Rog4puxeQ16H47P2vhORH0XjyZ69go/fQywD8jNnQGPQh65IVNE81xLuUgXd5/BW4+Dh/fQLPdCjwZ0UCuYE/x9Ei5OT8bE88ukuUg916cYXzdUfFSYScSrpKQI8VL4mHHwde7f7xqMqZVZWZdZpXrdFYSz/Ex4zACMlL59kWZaOBa/SJhqPgL1+sKwfZdv8fhKKTxeti0m0fEZJXsAhgJKMfJXXKVaABuIqTTAnrFfJUwogVeGYXnWEb776BZun89hnbkCzpX5bixn+NHn7+DRjXM8uHV+gXLqAVT6gYgzQDJuSXgXAkXpJK7COL2cXJhiDE/k52mjH/FExiAcjO5d3pTVsiaELcjfrsMnOl3Kr4x7A0O76K2xJWozLhcXxoCrsSIRJif1rx1wf0wFviC8SB+clw2/c4auy0I2gQgRH7ECj9G6uMrIWNz61rcwP6wDzo/kv07YgKwEZGYisvnmLNvruUAfrsOsloHLr0oZ1lCdlhuAHFmcOphGiIpgPHMdPKfGS0zEkNKP0ZT6BkWkVGV/8u5hFNhSekoEl9OtZEopn+rvFiq26XKAje80IkEZbpRWW8bVyYjTNBbWEIB4BIrjcS4fAsiH2GQuBIvvO5ybNf7lR7/A870lvPdorMX8ZAbvHFz03GosYW/WwlkDS8HY5V0HR8FvyLk+eLt4j265wONPfw3fdakLSeghLWgpqeySMMzNg4djNQyeVcLhVt6dOXN+Fr8aCrfdWGuj8QKwmGOP90aNyiGmEvKRNdZ4x3DxNsvwGxmP0244p7Q5L2O5Ypz1Hn89X+K3ZgULg33lGcSgcGwNlG4GlHI4VZa7qjexVTXQVJhZBVXfQMvG5sSYVNz4/FDOKfHTGYD3LmBTDt0Q1yvnAUugBSlKxqemJcA0kCN63jt0XYe+79B3HRyHGFjOV/1HhQIbyUE2LooxVLzCSAxeQGhDnZMIjVVrPgbpzx5hWQjMAe9DmrNujXPXpHKMLY9iMzOsCfEvfDJSBM8w5xwMMwwzghFR4otRqgdREGaP4lZMROE6VxVo+Pm7T3B+9xlmx0ewy3mmaRhZbyzaGy5IKt6aWUZBLiyobRrhJQCRyeLP6JKrFa7CkFWXkZbXN0i6fx2hIGlThHbMYKXfqpg6sZz8S+Vh/VlcrRExhSbmu64/p9VGnKLV17BJ/GbCJllw29OSPhZLklV6rhJNwHbKGedb5pwGb1UbKhx7ZVDpNSA03uAPvriL24v5MM2lyg49vLmc4e98dh9/9a1HFzN0iTFHflY8WozD3nPaKFWWp8HmbvYOj0YtirIdmWKTk4yBjcYjfQkRqy9jp4ySp/muoGTM4vGGLKV+hrSpmOgHSxPHhMxNRq4t7dRjj1eNu68PvDV0vQCYHx3h1re+lR9wFPjn8+lMLwIYiWAUypb8JWWvJOhvrqhdt3y8J9NPSyNNpsikMsUjP6LURSJ8vQRl2MLS8676TG3drSwxjm1swdR72mA8QzQWOFa4hWoIKaOjMnqBGN4ZGALWqyV612O5OAuGqPUqeAx5B+YQFPs/vvsAD+en+OzBM6xN8Oiy1mDWzmJaj9XiFAYOB3stmBsYAI0BFmcnWCAcWXr06ac4f/YMYIbvO2UszOPAQOWNF0VlumZGkrj0OARsHK8xY+8U+xRPJqozhEsWmdMJTkMGZIMxwLIcn0MhzJdGJFN6RSX51ebnLDQnG6UQDWUPaI1/1ZxATF/ON3BM2LeH+BD7YT6BdAGD5xzs1LOUHT49+2zEis/lWKWPceu4ysNgrHuG4zxydbvTKA68yFRdqY8qgZLT9ZgRAvM1BDSWUkZLcp9iwE8qZJfwxftgyHWuDxdQOA8GoXNLrLsOx2fn6Loe686BLIMM0NqAO31XC86qqZX8L7uRoc1xd5RJ6QoM8qzWcmn0D2vbY+2yEIqqL8FRIgqApNQLAv6JX+PfcIv/rLuBW9xAdoqJjKozeqGleGLBM6uFTZ631oSx7V0PZg+QzfxQ5oUIlgz+QX8Tj6jDv2iPsVQ+smlVGY/n3/kMdt0CIDTn+7j1mw8Bnjg+MoCBlWYCWP2h+v47BiO6cQ2Ztglhk8+hUqvIXsQ7Ukk3MLe38FoAA/GUVTZYsTZiRE2X5RRA4W3BKU9t2iiQSwhM9CIJx6mCF6zUI1XVMXh+V01e1wJK5A6/h3TvqlSQgHQCfIoaZ4x5vebyk6/u4N2TAxx0O6jug6ZP8ZKrmkTKEx7pa5Qrvc/ri4AUasBai3D5l0+yZSLFlVdYWLpx7RJAncPdnz/A+miO5995BxyD4ScZs5b9UlfL0wOx9arlrL7rRKIzDWlF1mFSM+sKEo3Qxb4QQ9RljWTfcHhr6NIQd6hHXyELxPIb1TeB9uAAR+++Cx3AeyNcs/xaL7Sg0MXFrzQyfUo55FPB8a7cCFV3hKswjY23VEDPAhffePg45xkrjqvP6jtpZWyQ0QzNDEprFLGszLbFshELGfavIriEIhB3Ctq4ueDJR5OtYiVLjr1mBjvtrTNSnmaKUdIIOnG4eW65XKLrVjg5fo6+W2O1Og8eGezh0aM3Dn/9zmf43B6jP+mC8sqANQZt2yIGO4JzPQiM2awJsSk47OuuFmfhtjfncPLoa5w/eRydL6aPt4rHkXgjGUOwwpmvE2gaJRjljUR1zXqlDUFciQzE06SxCEYAAG0jBo1oKiAGWQJ7gvU+eu6oymtrTlIM9CgKLc0GT6E3azlaxoy1BX49W8NLHwgANWh5hlsMMHzhORaOSYpxKceCCt45XBiwsjEs3PQHFmOYGL1Ce847Ru+lHBSGOBlbMdLpePc6+HpqTzEXsd+UyG7KbykaugwlQ2NW2zjRi/JyB043GoqHY/CIA9Zdh9W6x3KxgHOAi5cGhOODYY56LtuvQRu6CgfGXHWyBeTYbpzy1ktBjGGcZzaNZeqLTl/h7U9ohT0YfHdl4HyLlikJjNn7S+qKfJkMLBnskYW14XintSGOV8KfohqhVUGR/a7bw11q8K+bEyzGbtUgxvLu0zQw8+c3ceOL92B6gHw7HNRrl2brybsO4WGqgRNM8BUof7vXqJWVOucogiomdKGK3sJVYUKn3ArCgqLgkIxc8aU+pDBU6SeY59RDUcAhxi0T6lR6QKJHyJ/XLNJfA7yOiF2v1d3Tj9gSdvstCDGwVyhjB9dPXv3YGU+wnvDBs0N8++mN7Rk2Grmq95mph7qY0DgTbkTcoeuU/imr0HJYkl3BSVYQ726dXdaT+lUUK00lz9h/eAy73MfJt++Am3C7cpLTkizGSe4qhDldBWpjF0bl+oGnGrJeKu8GGoTzgHNhQ1Cluw7YtgbeQoa3hi4FB7dv487HH0++H4tZNCCCBNjm9RhWTiscmn4nhSz+CsyftZv/68emx0CM7NMKf/zNw2dXqxjZKz4xzixAiaBD6bfohhsY+8YGckl4xWqgjA4FIQdGCfVFQBjOuFixKR/BNEYZGiKjqz1hdDMpKPdt06CxBstF8FpZnp9htVpicX4CINz894sPn+LT945xur+CJQeYwEBa28SglYBz4djjbGZhTKsCsHosnj3Dg5//Gr6PXjGrtQp6rxlZaKX2Ws63ygVfADthFH9xMGT8+fnwKVSvOBmdwi8C8Cd/dIg//tFheEvAjaMG3hOCs2IUesAgOFC8SEFQz7PydiFSHo5hUY7tagnGdsT4n+dP8ciEwPFLeMxU18Rrj4vu8jCmCmfFRXsfaQNV+s4ZB0sjVmhVRy0cshu8/HnORizxFvOpHCSDWYgZxfBO1ZMbGd4lA1W8NdWJgTa8d73DzDAaMGz8M5GaZOENaIyBNQ36dQfHPZarFXrnsVp36HoGXDBwxdjtYAd0XWxTZbjSkKaU1LAPAp+Lx5zgwphAWP4YE5ap/CflK5IS4RzAf2+f4l1q8Y9WtzGHiccdw5HRZLzygREYY0DMWPUO1hBsA8xnLaw16LoVwIzZzCJcae5DfxCZiCElmGvFYMxwEvBmfXiGh3/8Vzj4+l3c/PRvoYwXdF2i58vkxzzx+Qph1FioFZNKc+X6WXyeBIZIq9ilNJxJyluN4ZXBZsNHWIn1+iqV4iyvBAMYqTQFvyzi5w2sHul9IFEGkPiEMX0wahW/rixzXS+MGwveeLjCxsGY9jZQ37j6vFxV1w4/eHAb33t4GzeWs90yKJVhxK5TLrMq7Xce3cT94wP8x4++xue3T3erT/ZRlZ1IwhJYCluexhBCeAWGcx5918ObsBs3cGQQvYCygUm8vOSSLO89mtMl3v13v8b5Ozfw7Hv3i/xJqqcsJwIIm6Hel6xDLd+h7Fq1SyvSGGm7Av7x3wD/6i8B43PsUxByROXXBcO+2fB6WGQuCe3+Ptpm85EBdg79ej14bmezdIuTwOzwEPOjo1GkzYb/3RFz7PjX6O7AZv5eNUD/HFd1x+rk5HqJuKgrjScJgSN9ZxZ1K5V3act0Ya/J5V0WdLeGJW9qhhp0Q+j3Z+HIy6o8fjMcEoknY6J9K9/sI66pyeiUFLnpebqoGlHEytFlqEGgDXN5IUhywEQ5Y43XDEbhzGQVFArKcX7EtVlul/TwfY+ucejmDk/3F3hyeB4ZIMNGXLYmBtmW4WYOzwzgVuvgxsIefrlAd3oK54I3jKGoOGPIw5gJRMFbhuJvRqUGKxerEXFZD4v6UuLXhYByEG2SAdOGh2I1xW8GwE3OEbujQnDz3Rbfen8vWzgUo0/CBXz8k7Lj/pymJUD4XaCJNrrm9p6Rxyk5PDRrPDRdkUTvio3izabFQ3po9ZjEWeV8aUT2NkzmVljbwJONxqQRQxeGRx/FM0qnS4YX5LlNhjLv4TkburgLnmVkgvDlDDBrDdomxJNTkWRQY5URAZIoGiODIdgS0FoTd0yzLxVxkEWNpWy6kbGobBpJWB3ZRSg2RXmcx5XOfjy6QaRt/mHKCGWswkDDGMBDdOiJ8TU63OQGN31Y6x7iTZeDzTMA8gzuHdiEthgCvLfwzid6I73QBlIxgBoAt9kCnnFKfRwPTm0q+tH0WN88RbM4RL+/BCgYz+zagnw5a2XWOAuaTaR049pcQWVG1sI4rZ0QwFn1nQOe+YjbgziQxSZFwTkngae/QA+nfktqgJLneWzHOC/J4YZLeUQVLvxF6KJKl48thlUm9FO3a0zOGZc5pN3jz182vKhmlLfM0uS7qTQDog1kgjMyv2NPtQwk8lhOnzVXObbIIbEKmVfOe55Q4RWRB7FgRbzhlSjSxPjMe3gGPGwwhGUsuzRc5IKbsdhG5fvIQ2hqfMu0YzDozehmf5Y9dgHSn4msckX31PofratseHnvh/CCSnrVu5aD1nCZTuoX+WaXTglTHX05fLdtqjVvOly3eOdsf7Sc6SYpgS5+EoI4KHFAiw3CmG6/a7DfNZh3VtU1wY9o2Jo6pWxgiTwvoE8XTQ2wdrrVMmJ67xxmJw79vEV7tkqyjZs38Ea2CSfKVlJtWeeQ7uQg+OOQ+WZABF534OMz0MOnoC8fg+4egI7mFQ/bRY8WWTVlQeGyquS3JGeNrJvLwBh+Xl6l3I771+ntVsMbbeh6/0c/wny+2cK9OjnBg7/+65IpEOGd734Xe7duFWnrWxFeKuwiPRZQaSdjRUYDQPDJEEQKBgAb45eIp0FIP0JzknAQiH6OhbK1+kFbBj0QJgUP8TjZHdkzE6uzJH6mFSnkvjEQgsnHnd1+3uDpn3yM2bLH+z/+KgncibYQkhHLWovDw0PMZzOEI2wmjjGKcfGRaYsMNUUic+DFDT2dGBMbDbV93xfPmqZB13Vwzr0Cr6NScQuGwMw4lCoTP7NhsXcOveswm7Ww5gBn+3shYPy6xYN3F/hfv/8AznrMrAFHz5IQyJth2EWl36BpCGhagEPcrUc//Wt0i/PQFu/RGII1DcC2MBgC0UMEwaiRXY3D/AbjmMc6Gs692Ieo7POWkcFuC2gsjQFg4WOA8bZpYYzNhhnvI56Kx0IwGOIAwP/VAXfq4mcAWuhtTL1GZMXUhl4CYSTu+KgOU8Oft8f4SbPAAm6A9z4OqCi2uuANInr6iK2dTElA4a1WlEEOXqwO1dAzomzBpmoHVWtbzIC6xlhM1QFmBvpoWEhGDwdjADIh3pwBYOU8YyyOAUgMunlr0VqDedvCe0bnAl70Lh8LFe8zH41ta7JINSqDnnhFMQPsc/4kR4nxzmejHYO1g1ehH+g/b7gYUwZ00IxCPyhpRB7Fx+jx3zQP8D23h/9ifbdYc1GtDV9c6XHmPLBY9iD0aEyIh0ZxjEGBfjfWoO/W6PseloBDIvzf1nfxG7PE/3v2GDlq3zQWLt55jNWdM8iAvPOT72L+7AhjjD0pdHpY8qPR36HNOXi/jMs2FXZsNRCCd2IyaFPcZXYezns0TVhF1mT+IpevlJ6T20HjBnsXrouPl7iw8+H2TmPCMXMKXrIc6wRHg64NPNZFb0iKCpohBmzmn9kwIQa70ALhPsbKEWEXx1QuRAjETN/MKe1smiZ5YoocUB9h2WT42h1ekJBfb3i9OF3immA7RjsXZFZjbMBVIvSdQw+XQo9YG25rDfMWVHuKii9M+C1MTHyVxWAecNPF3z0KI4jIM0RYrTs4z5jtHeDg8Ah3770HEKGHg8FVbsO7HCRlmxFiijoHRPnUECGGQgp9FpZ/xSZqEyOgyPoIaHqlv3vv4XoH17u00en6HkSATTuXW1A3CS61YSBzFM8cZWILg3jhTlIWKNGJ0KaAB5YMpuTvwdML04HxxELPjBKykl0Wu9Qh+hzl8mKMWyJC27aRZjkYYzfoKHnc03wpvqu9YH38YinU55wHgcL8RStk363RrVdBXqewCS3HDesR0WNLVD4UeYTSpi9j/8kZ9v7Nr6OsRvj6Dz7A4t6RkseGc0iG4imbaQlT5CA9lqWhPT+z1qZn/rMH6P67/wkzBmZti7ZtYBsbcB0OTdMo3h/wUtOYZKCvW876wZWZzu8MvNGGLtu2sO1IXAwFzd4e9u/cyUpVZPzt/j6a2Y5uoAmuj3ElJqjl4LSQr4jAWlaI5WsiPoSs0EjQ7cn4YgMldFtTKLUnMYwdurebwSuJtUlB0kcydZul1ZxyqToIcDML30+E+laKhTEG89kcbduiaZp0A6PU5iOhF2JlDMVjTR6G8gEygcKjAtNDQ8jlUmxTMCKVymrhpZiUmPGCWddYKfebpjgzWh4vt1KGRmYkPdGoL55CSaEIJwaCYmYYq5kLTFKq9h7L588A59BYkxQlil1nZvi+R79cwK3XQdgTgSHt1uXbUxnyrtIN1FItx6G6BW6ndaHSaJpUJKnK4fycQfCMKEh4kDq+5ZyPipsF7hHodlTm9gA6ArCXhRQAcB3g+vygkCciDpBSCNK7Qm8iLNctlutw0QYT4/joOXrbR2Mvp3QM4GvjcEoMuWqwoHVJUN3qB5g+hkLf2Bxki8L0HIUg8JuqS18TfeUUBFXKyGq19D3Q0eHxPVIdENNTxEcKR0mTiVhbgpDXP6wJRqSIE8YZhGOUKOghM8drvIEZGyjTWhbcZMMj0RLkHUxW5cQ4ZmIoYdU2mW6f0odnvTr+WJSJfHw0o8rI3McHa/I4Ro9fNwvc5QZ3fZvJV7yVj9PvnJdj2zyJY6cLxjz2GNxwG+nLPgz2YIbopHmrIpRsPXrqENy4GJ58mUwXUfBkxZnqpujfcXy0oK0btNF3dkRiFv6eN5sQaaMYckqBvjY8T5D+Ie2abFPdj9y3vu+xWCxiHEWP/XmItyZX08ulFEX7Yr2G9PLMBq/EPznPyfDGTwKMqTY860kpulB8XgwG3OQyhewIL7Ls6wMqaCeVQ09IN72K52zf94nviRHUyRzHQNjOe5ge6OO1qgyE29uAqNyHDSvPPnl5O+fBvgf7YOhijh7MCUcCT1x3Dh7AvgeMbeC8SzfwMlgZKviSOLJlvKpNUm0AzyLaSMXTKD2AIS2u1ixpTB5S0xrPM4fUdLDSEWrZS/GFjdSlNnJVUNLbsfwjeSKbDpZBrl6M17+xYD1fwHifirIrBjBRdVGFKn9YtOCInKDI9F63iADcPd/D6rnD46MF1o1TZVLBw3W9ehMtDBuDTb4J2TmnZKMLAg/HSzZeyDPgXSp57/l54BFgeGuxvHUQr1YWHNS0JvZYyA5lmWEK0kkeSeQ9+ItHoNU6hFH4/AFwdg40LWhvb7BBohpf4sQYWmEL3r9yKISi1xLeaEPXLtDu7+O9Tz551c14JTClMHD1TERdYeZvHChecPGllh3OC0UfFXEhgCjs8B4eHmL/4AAHBwfpph0h7h7huJBzDnITjwjnpgrKnOeDx38Dgw4lwUasOR5wKUg3w4inhQneTXKevaaUzJlpVW8uTFWVqgQw4Lg0Hg26kei7sKV4RIt8pfDntOEWOlFoPYg9XLfG41/8DN1igVn0DDAxQHVg2T5JszH6UuqzKIa6lUOBLaeg/GpUkrgwM7qElhSUdYOuB7rOY4lVECD6Pl3dTBRus6H/lGD+Xlbg2lkL6lRcEQLWffgTVAqCPPJaoHBo0ZAeA5UmGlEfndzDbx++CyLAWYd//wf/Dif7x+hcn9GJ4qgTAIo36EnHqoHzrgdzr16WxzGLfDVep3+qZ9soA/sB6Ruzmde/DQhEwcWfq3zD7OULa5qEicEWlFdNMQ+qXIrGVWMMjA3P2gYIx2rjWKXt3xyzRgxdzouYmYUsEdi4UhT0URLnVGwxZO87PUZJ5ovrWuKWLXuX6GN9JFSMFs5LHp/qLsQnDkeIn7Zr/H9mj/G/Xd/AP1jdysY2VT+ANH56vL0HHDH6vkPfG/R9ByIG2wbBuwsFJOPkqMZQpY0eAHJekaMxsKSncQURAQjH33MsmDx3xCMBtWN53vvgVecQLnpU7TCgEVTVilVex5YMmMK4ex+ilRERmsaGwP0cbqk00fBDmahu9NqYgtBlM1hj9eLy3mOxWODRo0dYnJ9jtVriYH+Oxpo0wULTrLXpr42bTm3TpPcBv1yiVZl4SyPCHOQ+BgRwFEeOM77rdms8exEGjLcwDuGmNgPnPLouGENl/a/WHdZdB9d7ZRBl9L1L8oLQnN4zHDO6mLbve/TOoeuDF3zgp9HQ5Xog0iLxajRNA2MsPILMcfteB8fAqlujQRvkEFMiunjNbIOLHN+pN9oKz5epusbFwe3t0wZx/Xgq+QjRzKaUHHJC+JRsGIucEGQLJet6ADGq4lV0FOGppVemeqe/K93A+ZLqDY7QTbSJ/ZBaFjGnqry6GOfqY351Gsq/R+hTFv3Df4bCRhgTkseqiTIfSA7pZvnqRw/ewe9/fRf/7A8+xaOj89wOcDISaycDANn7OfJ4AuCibNN1Hbr1Om4y8U5Cc+o2XUTGZtz69SPciu1dH+3hiz/7DtjsejPyJaB34H/6L8FfPAr9i7uNxUUVCZvewsuGb7yh67rOfVL5z85Q77MWFuTwYDLtpaESxMY9nlTCC2vpm6re0IcJLikEU4TTTcccAT2niuAmbWesojEILFczWz0GA0YGSoJO27ZooiuqMImgMIq6ogRyE+I6hECEPleh2imK3GjLR7uS03o4aBfeIGRZNPFZdNrfXmQau/pp+Vx+s8pTK/LkUT1Rgg+VXlyiNuXQsXEUrYcxFjYKjd3iHM8+/y0kZhS8g3d9iL8XA0tSdguJvfbKoFcKMrrhpNY1Fy0eWxTafEHFN72MpjGwXH/DWZ+SOMPu9LrvsVytsV6vY9B9Rt/1UalThq5zAp1TMijZZZNQXND9N8+OcPt4BiPon4RMZZwiIJ9WpiKNCKXHZwbHp0sABNf0eHK6xAmviiVFKi+SkFviZl7WDHB+kz0vs6qucpVLd4SWJYzYMDkEB6pmI+8mDxJXEPAu4QBl41XZnLIwIuWxVZQZpLocx6psF7MPQe8lnVLcZSWFrXahSzm3hSwIkRyjtwFxEcM7VxtzGwLYJo8sZpJul70TfsNIHlNznsX3tbcYR6EXhRFM1oW8k51Z7SV21hv8rF/je/0e7vomp1MCuEyidz4azjyMicYcmy8e0HHVJCfJO4TYVTUtGJvTxEuIcX7/MfqDBQ4e3oHprTQlZZEYKQyKeMIghTBal5E1S3rdUByzdAapbJXwxorIFcmScS6CHE1MY+3DWScT8dn74KWykSpuYL2qBYNllZQ/ZnjnsFwucXJ6ivOzU5yfyoZNGBwZh8Qf4nF9awyaeHwkeGXFzR9lwNdjKuEbmsYmRZsQLkLpul4ZdjXHUjP/1sr1wkHj1XrdAQg3yxoysE04su3lIo6uDx4j0ZgvQa/DJplPx7idD0bzPt6WG7zBGC55egbPLjCjsleldRGkkIAb4glLEK8zC6p898vNg82wi84yVU6WBWX0hvyVCGWMxGR4yY0dlC6y+daWqSzDIornxbF9+VO0PonmDHCkjRKTT/dwrK7JNpHIRIUEIZJrkjGo2vQTeiI5qCizrKMYO2NKGZqG+bUEKfIqIzkgKTmec3IAqLyYU2mJh5q4DsKxRe/6yKMZjgjB7TFvWDFQeJ4TA0we3/58H4cHwK/feY7OqBuroWdO8fXIU/NN50EHOjs9w+L8HK7vY5iNmmNNzyPzcJwnQcZQ8PV0AfzLv1ShABXfZCUrVG0BclwuTh7sWiZR4933oOOz4NnluTgbnDaKgIqF7MA/LorgLxhqI2p8eq1lv4j0b7Sha+jGvxu8yKBnk3ARhNVd2rGppfmgIogThRQKQU2LrxOqgqeMYfVZ6N0KRcL4gr/vhBaB6pBoDup5scsS/5V4Ie2sRduGm7ySC6tKaxAMDqLQm8gYJC7AWP8uiseC+076QAAQPJqsbaD3LnZCuYn69fPs8cHTeYQry0+U36teAzBAUviD+CiM0VobYggYg/XZGZ6c/QrELjFoZg92PQwhRcSguCeVgm1qRZRl7YvQJM2gJDSIGlbT8YxhnPC3XnFTdpFiHKovqSz1fCrIb+89lmuPxXKN5XKJrosxw7o+MGEf8c0a0DEBx9JAwfP80xDhb357H/7LeRYoAbXLGH9bm7wWa4FYG6sIIQaaaxwen5zjzC/RzpqcR+YnlTWkw/K7KZR7CvMSpXO9GyrPi1ImflTLu3wHwPgs9OnERdxPDNscZiZfORRwwBc4MSXNZYO4UoQAwV4IdsgIam+qHE8oSk4Rr2WcRJvRRiUAaC0rY6/q45gEo7+aHH8itMOUjUaJ+yGNBROB7azoT0E/eISuREXHxaNr8k6eg4FTZvyFX+M7q0O80+8VsoDzjLUSNIOHhkv8pW0bWG3o4uh9xT6pUazrHPSuGpw4DyRKDTHOvvU1lusGe09vwDgb64pptXLCotyIkU5TFSrXpV43FPDMs8aDaf45Jl8nYxaQjDwEgmOXjX9xzLz38M6BLGVvlYpHsu7X2GiltuXnQYHJl5GAAOejoev4GM+fPQO4V5lCGXKMLfAIkz7F0JW8HmN8Ihk3PZ7WUspjrNzmGRTA9XpdeC1q2lcYEF83TeS1hyQE7jhkSWLCarVG71ycG863t/UOXefQ94K3Obf3QQagRHviPavyWdBPAIgKeqTps7YtPD2lDPYcDV0ii0XeS2GjsSD5ar2heL5dDr44KHlNyysxVhWN0ncuyP6UIFMa0UYMLypdKo40fcq8LN0kDJ++57988kE2xiaqKnq9bcSyd01FDxHXdXxW0wsCYE2dY3N9XCQap8npmaInYlgJuJTLklAGRTmajo+ULbyBnYN3LhzZFyMUGOwNvHNFvaz4R5DJGd/99AD35ha/3H+EVdvFNmcv8fzH6ThxutkwnAsGPOPk5BhnZ6fo+y5eBDV+I3MxgNdBVk/OwH/+lyFmHRDjjFZjOVK9vmyIKxyVNOk3I1xzrclb3CQqjsbrGlJ8sBfBPaZWymWh1kkqmRrTvH/nGgY3fG+D3dO/0YauNwauhAAXXQJh2WyssqStyL5IV4TL9lMR94tWl/kEq/7sDpr5jbxV5YXgp0YpfLqyROxJBH7OTFq4qG7ZmJI/qSWICpIrZSDtmhjbQI5Z2KaBlUCHpKjuKPDwF9cpSq2EVcJh+iicaONYeFLUVrwVIxeCxwVx+PQ2eM49bM7xP+Jf4Gs8lsFQhoAMIobkna/hjGoBZ9jzqDwyRlLEueRNq3EX3M1CuzZc1NOumUihFHqG80GRl11px0hivBw/EiMEC1LK84iOt05u4cOvv42bZzew7vMRUZkHHa/ddwyvrTWSTrqi1g4B8MS4/ZNvoT04w2cffQpnXRZyU15ROEuclkItBe8qbQwjWQOSb8RYJgpvGu3RvPXzAHvUwSZXxFxP7jalDmTjkizveu6rfFDLXQaB82UGefQAwKS4J/WuWZon8kjeYKlwvUstXl267Gj0ZYca++vWj5Ihz2p96AQ08k15tzHBuXUe+7rcNB5caR8EbwzQmEKwFOYlu+S/mHd45oG/390INyUy4EBYwyY88zEelw8B6dDYcASqbdto3BAljkDJY4lBxgJkpwUwPb6JxhNkAn3T4+n3PsXs9BA3f/NBDHxLaV1mOsWRB2tDYFACmU0SslPyhH7RbyQZk/WwDjdgdMOdc0mZMdErqluHgPxn5+fw3oXLLmQ8OIyjMTwq5G6CTUnFE0CMZ6SQwHPwttmbzUKQelE04u2niEpbOH7mAFA0Sii6EvEq0R6IQE1p7o01SSEJ48rY82vUV0+kuVOtfwuXgEsOWztrYXqD1WoN5xyWyzWc93COY/wfH/bAoAN5U8aVpLhW8oO+4IGi92XcrPAcypRLfXScz2xv0B4uspbLjSWRbwtDEQ0lkdA+/X53kHXKsuvlGTDRgO8z36GI48mAy/lCqg0lD9sJABIeQvFEIRBj3F1rJ5R4qRDEaORKGzOkM5Xy/fjQjbY8URRllNCemonXq7aKocanUBhaEAv/ePU9Fp/Klcdp4wFJUYk0PrdH3ulPzQqZgfPzM5yf76X3qR9VXiBs3IDz5WqBRjp00QgFDrF8Ay5TSsMAmILnGkkHOMqd5x5/8B8P8ehogZ+8/whMpZFL4hR3vdqU8EHI8b2D73ssFudYLRfBo8sN5ZA8vsJgSqx5NbA7sUrx6jjPH8mxeH0s9wJ9eZU93wYXlQNeJbw1dO0IXP5zxYIQXHEREF97VdWQRdhN9Y6/29hSrn9yNlBcA/ZqA8m2hR2GtdyN3sTkB8KmGGCEAWypLDFKoFSmUT5LTZBhiXGgdOLMaFC4g4/DxpDBGL/KbsiIBWuITNoND/FGOCktQ9WnbtoQ52gkXcH+GUWK4VBHnJ4wdGXdWwk3MRUVfx6ews1JS9PhL+lv0GEJYq3AoIinACUcULmqBn2ZEtu0ubcW0UQRzVIKLrhOyvnTRq56HEmOk0kL1FQF2UEMXeIFEntP4dMrTx4ZBKPa0K72ce/RfRg2cJ6QdntjLbql4b66HboEgMmDiTF7eAP9vsHpnQ5920HwVeTWTBHGMK40dAFUfkYBesrQ1bYzjW5A3FXL+eqyogJiejSUI1TkI2JKQDEZu2LRaqcu4HRpTKOgVBMpb8J8Q2txpEGNR0EvKyIUljqhOAZdHJOJZXC59hJes1o4Y8CaSqm87Ao81OM7Btl+FflKtXU7MDZWcwkAsGLkmlixzHjYOjwH489WhNY3aJjgyaKhFmLoEi8BHwPhhmD/lLy65OZXBoX4TLG6nqDmVvd8KIBqw2KaX+tx/u4T9PM1jj6/D8MEijd3JvG9WOjyT6mQsX5djeEmCjR4p3ax8w2nwQvFksHZOniKPn/2DMyM27dvI18Hz1kxEwl3wACGrdnYvmgByPiUcULvnlvboLE2beZ4J3GYfPLgEQW56G40gkH0OZY1xLl+iheeiKELwXui2WO0JrcnyybFUL6FFwJjWENxEyO8C3G6uhhjLnh2BbyOybXxirNxObDvuAKr9aNlPoMYd5FDnElxks10ndRClxJqmUPLwFNdu7qsPahSr1ORA2p5j7PcJMaMqWYlgzzVSagsu3pXUslouopzEORW1WZVdhpFGlLZum0XBe3dXPRDqpM0cUx8bKdRkQnHTjakPGLoSrSGRvNJ2uwhNPQyEmMkAKxXK6xXq/ROx7LMn2W5NhA2tRnQS0PSjbMC2dBFKQ1kTGKZH5zN4W+v0d1ZwZnYjjh5xoQNui7WYUDRo4vh1h1c36Nbr9F1XeDD7MenMU55MnQOPq8BKONuNkSOtGOS846XWacc9eja2oVy/DcQjpcMhdSXn/KkCPhawVtD1zcVFF/jESLxOiLnGHOYSAkhfrVbaX6/G2j35NCGUpjNjDzc6Cd/accwpk8GL8o3Ieb3YQbkRqBQcdGK0uOhNiAoQUoesG4rSfwAjt+3ePRVsFtaKr/TFA5pg2lWlUPraEC3STETC1E3AxO0TRu804yRCMFgRK+taNzzZNP86b+6xYMeDPS0LJrJv1NoOKF2T74ZpNxg5NqcL81yqItMuJmSKQXfFe8eFo+OuJPklKHh6xtPcfrJv8e3H3wbHzx6H9FlK81F6gkD3poYxLMS4WucBONvPvwVntx6AjDDG4+uARjBuzDsdsleZVESkiATi3I+CzZ6PaR5JSAfiVAv0MOddWU6UD6WJceJ03rLny13oCh8SZnZg0ryq+cxnfaUK8st/6Te/BkUtzpPyotcN4o2ccqTlTKPvNjEEEfBMJwGKDz10LFGynEd/sgzlDcTcjJ9uyqV/+QJYB7eWAUoWq0VgbLeMT7AhQAaYA2Hf9I+wTu+xT9a30bLIsRyNAoSDFmQQcRAn1EuKh3eAx0z/lnzHA9tF8v16HxJE4r2sf7OIM9xAyv2mcLv9cEZHv7xT3Dw6B5uffqxok9hzlL8KXLB60v1kTnGA4oBbuW2yDHwfvx5KCfzSCJC24Tbqn00HnV9h1//+tf48ssv8eDBA1hr8ad/+qe4c/sObt68mY4Gphs10ynfOP80pID19DHLmskeMj56lvW9j8ZHOzDECaEUW1bAAVmpBsGrZIgrxlhY22Awd6SMd6qktPYMEAy7HjS6+XQR7voWrgt89Nzqexcvx8hyGRButxYc91FAIgIsAY1twKBEjpgZnrJcAmR5j5nhowwiRtAQz82GW61N8Py0BLAxsI1citDAGgvxCZU2bMOWeiNz62btpnIUrzKGYlxZxYMovwtG/7BwCzzfIsaUJxqy51yZN37herVkjUT/lnAUcuOwT+XEEBXJkC0S4MVBcutNQKree++BrscaKzjnkDafXRfbHeX8KPgXBiuvdJHUcdVXVV+9KV79BBAM+sIUz073cH42V2Vx8anz+shv5WKm1HehqSkDpb6w86FNOihd1T4gRv0i/Tvk9xxi2hHCzd+NsSBrQMzoEf4aQ0nGDwMX46KOVElV/S8CZEPl2vJVhkoQgeRYPRmIN9eFPDV3Vyvewgb4nTR0XY6RxH3uSyLd1N7rdjaYCpAM4zBgKBPFaKtOLYgOH10cNjRiuN8VBc3YdiEguxECBhOh22vgweidB68AOLc1Zw0EoFl2sKs+d0BR2kR8ySSvroKBqHRpv0gEHDFOqB02XW9mcaLsSIXVGCQXjZKYSlKlblZGCNo6qTuvBqq+1oqtqrJiWVU7CnVItVNumyPAy01fBqKKZPykVF42VMrNjaJ4Uak5S7nI+vdAEdOtpfw5oltfASpmWD1PjUU9j1lQq3PpP3DW+WRN5U4EWLc91u0x3j9eYDYLOB9Fc7AnrHqblFLOIzuovbcO62aVaj8+OMXzw+fpvYHMHYYDXnVEj3GQZ5XXl5ahCdErSY9U+BIU5vIa7FL49+l7/em8S4au+Dh9pu9GtUHVK4qF9kgp/+I7XScFj8XsRaANXaZqgzJ8gYPyogz0hQENAMWIdSGfSTgQyhhikV7GVHQuv0/KgTa8VWMliJfKi8RpI4/bwHTUNA+y1L8fmg5rMB6bHnMmrFP/gSM0mMs4FAI+sATjjHoweXTk8KXp8MCsRyobMmDWz1nMi5p8h7HkxmN98xSzs0PUpRUehJO0mqvPq4GmPTImnsNth8fHx3j27BmapkHf9yFAd/IwGPeULaBel3W9aS2WtLjws+DcRjnuVWxksdDGineqWqWO4ngY1bPoVVqoNVN1aeOc/G6B6zr4vkczm4Gay6sPwlvGYTO9SJubqTBNa92wXMEDjt8jrmhZIslwaqnl43NKQVUbFwM+oH9z8bERrssrgiFSElIbCx4kBEraG38yoVwnKEWnjSDMQTUiH1yHWqsynuFB5qsh5qp3LsVRFDG4iFuYjFy5r2P93w24+qrm3nt4+HC0O3aQwUC/g6FLByyPBXIqOA8YFUiTnuokoTyXY5U518O5yrd+tMNicANgOG52jRlmlD7BQN4sGCJikhsSGeUBvmbjXlxblOsmSvutMV+WKieBZRwwtodxJdiBi03nJfE23pxOZO+xv11Air901y9AfzbBsLnDlg03vS8HfMGJvogZ53fS0HUZGPOKehNAmLlufdrxB2Eo1r18SKIqc0GUtxGFbq/FV3/0IXpr4LzHwaePcOOXD3ZcbrmOZu1w/y8+izogozwTx+nPxtgu1li1A8bQqeQfOQvPMFkwUwqDzqkNfKyrLnhfzlMwrSikFIwVeaeejBmZY97wa/PT3dbAtEAy9lvYazp1kKRIo6QzJaEhG0PJmBj8P8fFSHhTOK9U8Wwoj+OAdBMVR4rEg8akdZQ9k65LSL0IeIRAoI7DrnbvXfBIcZykbfLByGHJBFy1evwAgPHe/VP84a0vkFV2xmI5w88//RDOlx6LGqSEZ0dP8ZPv/hiC/X2TBTFmoI+CWTLYFGUM8Usf5dO2uUI5HWQrH0iMldFUKvhnzqaU4EITgJJDw78mxqnSOBUkMWVAS+2IwpzMB8pPgOB4EYV+eZeNunUjTPoalQQjgqO+czErZBQvpjDGwCAb541xg3Zm4bs0DGotLhsCKtqcaGQeK10WEdCQLbsk6Yo6iqcIpTLKA8Wb8z+zhP927zmYCZ2nNNb/p/Ud/IE7QLjxtcSXnzQL/C/tMQSHFwQALabU8MRHK3Eg8IUGTCFWlHh2+RjymoWeTZWXehU/4+CF23pNiCOlgqaPgRy928bTvfdYrpbxxsEmxbYTry1R3GazGay1WK/XyctqNpujUQaOUoUboe+cP3P8Gol7g8hH4xqK/Dd5niHEWmIOR9N0eZELxPXOIBsV5GqjI3i/VS0b3BzJUROjFLwe5HI5deqrag9vMJw8eIBnX3yB+9//Pg7v3XupdcsmozEmXUaQV2mY4wIfKR535BDDTeZNtjN8vk5YbS4wgiRi4m3ZlOoKwPHG23BrI8igj15mvXMg42AsFbRYw8DIXPeRxp+HvFvGJ8m00vdg3DeGVAy8VJrKNy0DMo9/5jaJIZxUI0mWsjICxXzCL0Vi9j3YO5ydn2G5WKDvOzjfV/HxOPFnAmHab/VyIO30LkhWQIz5Z0zyjiLfq3FSBixGku3HjjRC6F5il4o+DYz+5bzrYPRDKpTf1SBzLfxAyhaailRW1lPE+KhBbJ/JBkqJTEI90oMYaa6D6zLhZ+18IIiBGGYlrbexfsUaRMiumeVrBlx9Bv6VL0zRBvKLlHnZLr/mw/VS4a2h6yVB8l6Col7hwYBacfEyfFzkQoIxhkixkGnj0dVNXlNW8sm+bytvm3cXEVxr4RqD3hPWR3Oc3z2CPV6AlpORhYbFMGDWPaIaOWgDq+moRykL8DkNQ5hbFLaVkQsQtUeJHJWBT8rJSn9iSyM7M6otkYpuG95dhn9TmmnBaJfyptunNo0UQ1YKbdpxUi2I1Dw5RChDVnhHyTOESBXO0hZWCnMW1rJ/BqVqoLLrujUfnug0QJt3sDaQg8KuEo7WmHB8QgLMimJNKVH6Ey9E7/PqvMEG932LuzBomr7o4WzW4+aNc/h4dkAC3ocUhLPzOdbEOD58juMbz9DNVihnN35SPn4woipOmC5kWqq3KcpnPSAjZYzRC2l/MbhlIdn8k/OnECFJuaZB06K//yCciBG8TGu4Ll5u7Qo7n6B6jMp2ZsNAmGfD8kzFBWMx9uZdVBNscOkzHduKCyShjHwSivpSGyju0qb3VJSTxkxGSrwIQLBUxePQdJTKMa0NXcOnMY+0qRrTNRgh2HQW8j+nFWYUJqMB4Vu+xQoeD8waX9Aap3CxTVz0ZKOgSPqDkAJcK5zhimn38xUWd59hdnqIZrEPzVjCMaKSTxarJCoIiR9FBQv1fOj0ahz1CEo8Ks1XCjsQyY2FOU2dRzVJDYTi16nIcvc7e28pLxMg7OYqIi3KczY0ZbrOCfelopqnZIqmQw8VuJ6elHxEEkhThvRE4WQ95OVgfKOgX6+xPjvD6uwMbr1Ox6BeHkSaZrKHaoCASxIeAlHfluN6EuJA1lZenpMEV1U5kSCiDUF4bDaGld63Y7izudKxjbNy/WyQ/+IRP6IYx9M5GGPixRPhGK6P/eYYk8lEQ7Nnua1Sr9fssZTrLtez926gcAgVk/Ik0H02qgwNXd26Q9d1IVaYMrpoY5GhHeZsC2zNLvSJPcjHY4Acj+wp80v+kp9r2hQ+Rb7M7c6GLt0gLWhoOp2bdbK/wpe3T3HnbA/7nQUGqRVlKpmidArCUQm5fdJ+VmOuc4bm8fAZ6QtnxKjGWbxIDYzyalyTxuRVkepX/LvsWB4Trjp7kWOHZC32b99Gt1xifXZW5K8NgIXITgPU3g1Y5CVFgzILe6MgbSwN2v4ieN1FB3v39G8NXa8xXGaNbYbI4qvF9zp4dV0GAu3OysnZ/Rs4vnuIO3/1OQ6+eL45L08RMcXI85ckFAjz0gWxakM2biEx7F0IcmHjqvKI4HaxvmRX+yGUyuk4jKXZDU+mxbltQl4YSys3Z5EEcTTjeZOmFYQJE/tqMidNDFw9qlqU9kEx8lGmnRpO7CLC7raeN5VjjEHT2hgTJMTLMeQBjrvPAUsBihcSWAPTBO/D3ndR6WN82O/hH6/vgpD30qRfTbvGdz/6PPdZtcc5i5/8zbdxZjr85Af/EX3TQftPle3mEL6Dq3dj45sXT7zNJxgOtkFtWCfQ5gHMMung8RpjzvQ58dQqEgMAgMoLsEo7JijYqCjl/X8pdbCexZBm4MORAIPU4mD74ixcIl/sYCgGX48C5Toeq9AKfDYaiYCWBfd6LPLxHf2qHNgiDTOMOnJBsWARxo0K+K0/RbEtf+c0+l1WLsPYWTKYyW42M/6VOca/NsFr6w43+K/7d/GQOvw/7SM4cLDIytquxp2lvbn1tToCma8QV8oD5MDwYAq/BZUXt59hcfMYd37xXdz6zbfjPIXbBYkBNkOcFh3Fex9umOs9vPXwDYMpBEvWO/caxKu3mJf4OZvN4vDkmwtT/K62jTdSBk8v8foylNW9FKuLM16MG4Yyn5b58BzbTGpOdR+ERlC8ETF68KTxkJsfY6AwbahT1cS+ZQJUXNlAZXqAiwscSOH4FM3/XYLl8TEe/PSnl9T8rg4Bt0yYdxO9lCHzHNZGjH0tORCIpAkGf6KEtz7iiwESn1HSVlEvM9L6LRR0AmxAULRNE9aMbdGYBiJRj3GTbcpzfSyqlh1LubB85/p1MDzFd+v1KhkTRObXwcw5rkNmRtd1qn4uytfx/ep6nesLQ0H2Ws29l+TStrAhE/gSewf2DudnZ1ivV+F4Hofj+ZSO2ec1LLLctWKhqoJF/vc+eM7HuG/GjtSY8CLzs9Dfq7eu3PwBfvXuc/z6nWP8w59+iI+e3lAN1/0QWiyhVXgwd5Ir4AKlNKL3EPuNBI/Un7ZHtdYm3Yg53JYb4lYC1ligYcxmLbqmgdj9NtotNR2vZfYL0uN2bw/v/fCHOH30CA9/9jNVTmnsujKMyH9p00h0mSTnjcCm8XgLV4I32tB1kTOvApcO9Fj+s3t9L8BctRWkibWyVP0o2PErXWGZubPxWLz/FDzrC4JQdsUA9HvoZ0fwNuwWhI2fQCkW947QW4PDB8cw600xuwKpponxUnaUAFH41fG2EiOJ7wtQQ1srl+Ntid8GKMNwTu9ypeagjA0w7vFVPyl+T+v2Iy+rJDxe+pggUpskwodMeils5uHOOyJByZLDgzkRi3KihI6yLUol1a/UnA97mc1foGAyKAJPj/apqPZ6oKpIx4LwHHZhvQg3HFsdpQeJh+GTUBkEfkYwmFljcx9jJemonXpukC8XIOtw/+5zwHSw1sMVXmplWQk3FPPW3annUT/nsTmp0tW7jOkN0Ubv18HySO0zkX5QNS6bgBN+TGO8VKB+x/cSYDcr1ITktchliSZVYcJk+3yMoDiwxnq8Zac2GEXAQI94XIfL2UhjyeOCZLQhBTEtSbjpLXSD5TQaUWiq8WXK4iIBL15lpHsxggDauJa9xcbWvQGhk+5w7hAR4GDw5z1wTA7H7iwrsWZE/FQ8Misy2mMDEV8oCPSeAfLhz8Tr042LYycCbmYoUwJv5i0ezodLTIg6dOs1VqslGAaOLTwxPPnkfRUyIxmueten76GpWV7SRxRF6e26DkSEpmnSkcXlcomzs7N0DJaiQpNufI2KghjFGBTjseRxSkfGWXhqloqSl0dWm5TxLbZNbXRkzGFhgMNJA9J8pQ29+EyMcXKzbVT1Yr2DYgYKbFldxslrUZReI/De4+zrr+HiLWqrs7NigM6ePIHrexy98w5s277w9nAUxgRXgYBjgacROBlGtGeSh3eUaFcuLMt2ysclviT1bzmnKWX84oN1OwbI77Hu1mldJDqJEr/GjEU17tQ36tXppvKy78Ec6IH3HsvlcmAE12seyHTAqeNl2wxd+l3h0ZXoi/bEVKOprNAMBrFPhi4f6UBYr3I8O46D5+CBJsbNa9NVMq2QuU3tlk3tdPGHr3KNw6jsskVHHX1L1fOIosbK5lCZS5NC8XoUA5Ycv5SCRr1zI58km7cu0+xx5nzvGoO/+/zbeHS0wFc3zzJvlZsFTfSujHw9HLwnEDMWJ6dwXQ9rDBwR2Ll4EqGWkaZgIHjsBrJpkQStHaqq01yGvCv9Zedma7EsIdO1IfylQeucbyK80YYuvXwvmu86YUf7xVaYVpwHhxl3KKlcXImOxEVXsKCq0OQZgcykAaQjNhcCRZsGwmAtYwBg43H80efobiwU4ymFUKYWoD8G4144V6/OJzCA0/dvAfeOMH++wGw1NHTViqlWmae6J/QYUFefe+XaXWzBVAZYmlJpqnalJtUCjjzLgymMTe/Gh7RqF58uLoCPyPrTabj4pfJlhqJU2kHKfERH4Zj6QoZy8H8Of/A+69RK+FIqaPw2glwTdZbv42cUeMRUtssoqmHfkGj8MakxqsvR2OO9C54dzsW5lzIpbqbm+BhBMWCQYZCxqRQbY/1QMX8yjvo3wbCLcRQAC8a37z/FjNZojEevmDIPOsfFrOsxGTNWFmPB6UDpxFhtgEl8pw2/ACYLHsTuGWYoRXegVJUqXFOF1fSbATiJ+RWfi0A5tqKExDAI4eiHjx59VJzsTEclYwZGOObIxGAiOLLVEJVzMWxx+E7xBq90k+MgvUkjQbIpzKE91k/NWS1J6oIDvZsmX9NYYNijcX0x6MFYDpwS4X/AcayBk6E8XNxWzq7Ip1p5qz3P0poCoWEKAYDJg4wP684GQ6aJXiiyOZHGJzHjStllBjuG6xk9O8CvsWpXWCyWcJ7Q9QRPPnl0iULLzOj7Pije63X6Lm1OGwdy66F3iYetVisAQNM0aJqmUJSljradw1ibxk7eNU0Dz+FoKNl8VKzQL4jgPdCLIo9Mp8J7mfNs0Od4kyWbiidWnxof9BxZWx5PJxKP38AjGLJJhAKvs5cGZKIKmSjR6xGRZppb8Mi3+jVHvknbEl6nxj+swTk8/fxzdOfno+9PHj7E+ZMn2Lt584KGLhmhWgYbJAGgh52j15ZT8yVxtQgg8b6RW+cA9gyHPt58ZtRmYK07MDIRzZy4pt8EJONYMBaF513XY73usFot0fV9xGll6BoxGI3Gc4rgnBt9PpanxIDovRuNV4vFAkSUjFgiJ9aGrgEvnKirSCN9SMcQSSn2pviUeczlh3zBEBmNXezDujI5NlqYQxdlbbkV0GDQ4JH213VOQqLtCPHfGHGzMMp+JLRsyyVXXH3RvKeucqCYVc8AFJtBEYzaUAhNz3RuKs5XbaAMNNEWR9N1GAKOcXEJpUwtv49whA8f3cOPZ49xdvQg0CplQGpso9KHG1FNUERwdnyCvuvDTepdB9dHiUnbYmWhFQ+qwXqhkMd9TA7T9GgniMa/5MklA7m5+vI3aSlzKD9noXLHNv0Owu+goWtXtXUs3y4LbUjWpknvdqWsyHnBZoeaKYp0YZFJHBekhVceHxgwpBoGhGgH2NRuRiKsAABncOtX30Z3tMDpd74ERy1p//Ed7H99JwgytsHz78zRz3Vg7uC9EhRBADBgjtdOK7qwuHeEs/u30DQO1njs2Tkshfvh2vM1jj5/BnYeXTxyQoZAzoOcQwuDhgxgDTyFY0BGRjgK7I4ZjhgdyY1OBBsVPvG2uSjo3ZoQa0EU37Iw2QEXF3GkFoTPEf5ajr0W7DbM2bYuJCyK8iPnFsjjsi1JoTTx5ruw42eNgTUUnsXYE+IBYKPy6lzwRLJswxEFjdsRWTnuxkm7lD6RzjnWx0+zyuuTAYR8nEd4MFMKakuM7BGycXD0CIimmyd38/Km2E+G9YwQezl6GEaDhnOxUyJgUt7lJjBuc4O/1x3iXd/C+i6NvR6TPD/SHxo2LO3WxrEb67gOuCaUhDNNkWulZXe8gInbfwZwBb5eZ7XwMDFw9dh6EC+m0ValxcIpQU2vy6Ua6pCjMxnX4lHEeihlzPQkqTpk/sfaFuijh2xe6FC+rNud6s2lFN4qnsLFTMh4VzYySWT5I346P7Y2CmqQMrFGwskdpM244dmgr0UbVs1UtVZDULeoaEONF7oVFowWEsqYADsDCPDcwxAwbxjz1uDGXhONLX04/ocwnjm+IgEUAmiT92g5rHXHPYzrsF6dBTxs5+i9R+89GmNhyIN9HxRP38MtFzh99gRnpyc4Oz3O959GupkNXZx2u916jX3foz0AjPFYPfkM7rnFomlCDCJDaIhgidC5cLsd2RYwFmRbHN28hdv33gEZC5CBj7GzWMaZAx4SSfB+A0Rl3SZDncd6tYrXsYdWR1KWJkcMVxwD/SuLQhzDPKnJqEg1v1QelYhHu2JucJYr0tpMvExoNVfyESeSPr6JoonBFH8VowLyepI3I3haAOU2EZlBO/KG4Waiycw4+eorLE9O4KLh8zoh8/5diHeWG4Sb+yhrlUUwBBUK4x8JTQlekcLjuSgV0OMsxRITwARjgh+5JQswg50LBhEy6cIJt15heXaCh198iWY2CzdSMoN8jn1Vxw710VOImNNFIcIJvPfRIBE29pLHvsLHfGTYRL6UaYjExpzbeNS4W6ehstHY3svaiCcF0lFQZH6Tx6P+LcOnYyFGVT7JHWM0WkZe1m1Yw967GHoBUXYJ45bmk2w6EcliQKzEktBzU7SV0xxn3PfMIdwCSc88ghGLUr/DfIV11MxsTBz5ieYHamNEG8m1s3Qaj1hn3gSWZ+Xcq4SK3xA+fnID3356Ax80R9i/2aayqEqvnwU5ldF14Tgog8NRdNuEiwpi7CzkItIGRaq9iH9ISdb7YGnx9397hL+5/xwPb56nlaqj2xqKsfK84GsDhoVHkJ3ZWIRYX3JLZZyTYr0IXuXLv9T+4CVBUxQge+sp2aim7YOxyKERcvw/DuPMgUa0bQPbMMg4hEtTKDPDiVA0Po0g8hSodmQsLZJM9vKqI7UZBkIgxi4WeB3gjTZ0lcxq1yxTKsFF6tw9LW2sr47FMtAolfA2UcqIvJDp7BZvFBork7A5k06pcl9B6Sx2Uj1h/+FdtIsFTj/+KgTdZoPZyREOv3wPngiusTj+dgveo6hYiMKApDwQCGwMvDGAC4TUG4P10T5OP7wD2zgY69FTiwbB0LX3bIGjB8fw7NE7DxZrvPMgz7CQG5linRzi5dhEeBk9h7gpLtJBA4ZhwHCMP3TJcSJSO5XMk4JEsYPDGnMyd0imrzjwNDLnu2N5lVKqUTt5ifSlgMMp6aCk0CaJIxTbylkNRGQmIR57YJHEge3I/ZLaXMuUGcewTzKOBFdMDCvGGpg/Q3Yrw/uwq6t2lNUwczXOw87KYMu8TMUIKBme9JPSdzWPXCoxwY1chGCgBeMmE/6k28OMCYArBCxmSjvdabTiKbmkJKVWUZyc8dhAdfND+VnFSGIEVxJLIndUjl1Ruyh9mniNYdLY8/FHQIh9VS+CLPPJxGo5NwvPRaEpTSkwlr0RnxAquhDmQ8c7gV62qQ2hSeopy5wUWJWFIlKCG6vA8LX2nOaakuIvXgPaa1Zy1GNBlRVJK5Ss0xUlKR9CsXqmT1XJhDF4nAoSPBv9oPg0HBRAT8MjQiKHThZejHCGhsIa65ngmIAmeAj2fYiTdtCEWHo32jZ4xUVxPxhUbDRWxp166bsPhm3DCPPme3TdEqZt0cCh94zexSNARPD9GmCPBj3ceoHVyVOcPX2MZ08fBz4EJKQ2xqZhFc/ZdjZD2zTYnzcwYPSnj9EnhTrgRuMdDHusXbhPkto9wDRgMwP393GwPwNTAyaLniUuUphT7x2sMWgaC2soKd1EhNY2kCNU3bqDUpegNx6ykUvTElkUerIljZ7MmDdpVT7lDfHsIq/hROETrw2oqNfcBCEhXaduxwgKFc/G8FutA2BEdojvRwwLsn8iXdWGQp2mKC16/Jw/fYqzJ09imrpcGuQRw8xofLaEPyUvqxJVD4Z0QuiZ5n/yQjy8knNRyk+JnPioHXNdcPqhBijS00gJC0rNPmy4GUOw0XDm+g7r1RLPnz3FbD7H3sFB8KiNcfUkFhYRwcajXd77KO9kb0klGkWPpibEinJ9gRcUx0wblcL4WkikTgBoomdX38f8RCATYs0axKOX0l8D6IHJU6nXVsEd429Ssl7pHVSCQsaYPUh6iPMf6VKSZSRPmHUyVc0Fb5YqZAS1rJAbzrHPQhc4VRSP2RGiHBi5MzHahkBk4dEkI8/Aq1cZvPRHfjeRh6LHWPo9Xj6I8MGj+/jR6TuBHB7I+3I9JnxNXY5Hfc066QWNtWjbNt3IqZcewUc5SPJLpM8oH8ZUDOD2eo5bT27g6W3GE/IhbiJQ2DkCriGuOx84EFEqN7hRl3LXGGmExqmKTk7uhY1AkokTfumXNZGdOvOBgJOky5D2C2YFl3ZjEQzlhpEuo+JIjFVHRQ/LkkXWS6SvmnzXXZ4egimD82a4uI46wlxeM3jDDV3fdBhd9tX7zciVl58iErK7ldyPqxwv0CV+V5AmzZ7fwO1ffQy7DMFzn33nHSzuHaLbn23ObwmPf/g+2rMV7vzkS3QHMzz5wXvo96bzrW/s4cGffozmy6eY/eqhepN3FcrYAyqFDKNmcmOdepVDm+TmuDMgFK3S2+odhctUk3ENkbkho+AoisXdtbib572Dc744WlOJ3FK42oWqOnpJEMVG1yVCqfa/eVNgD4R/tL6Dd3yDEJlr+mBghQqj8KrZWSlkvFpIO6rpe3pTPRsqEVpJgBJa86Na4dPCfrlGNVbWyoYWQzhqg7Jrqo3mQtvyxRd5bY0r2dOQSQvnQOOVUC6laMVNFLJJL0f9XDw0KkPVptbN13P88Nef4Hy+wC8++vngZsRiZYjsW5sfRpDPRRXTiaGLPGAir43595/cxnu/+D0crNs8CByPFIHSERACg3zwNvIuxK/pvYFxLsYDcui6Lhrz0gG8eLTUoKEGbdNgNp+haVtYa2FjShMCaKU59x7J0NVYi8aGiy4MALmmlJlTPDhrwqaNBWUv5dh2MSg4OHj26DzDxWfMjK7vgkIJUcrynwSb7/sejx8/wcnJKdZribR23ZClovHXrwlxuSIkY8GOys7xgwc4ffgQ68Vip/TeOXz9i19gdnCAd7/3PVDzzVMnBBWMCfgtRiljTNocE8NV73pQZ0CrVTDoVnHwQlox5Pho3NJyJQr6Jh5IWpqxMUaeGI2KOHvRiJAC0tsGNZ6LHSLRWf17DCjzqOz1qMureFRh0AxyM0djRvZIDkZla8Nb9i5sLJJ4Y/p40cQ2an4xCLKn4qHR8BHiSlHkQaHVTdPANg3m8z1Y28A0czVe0fCpB6JYY6XhpnxeGqdQyJRFsuLG2MbqI4vDakd1DdXa8OiicnEyJ6VfXEmPn3xxDx89vol/952v8Gx/swcocxlmJSkDI03KLb0+OXv/1i188Ed/hJOvHuDkwdfXVu4UiM4g39/Cq4M3nDNtN/QMcmxIfgnjZ1HmMP8mD57hi7GNLSGXUzbT/DwbrIapszv/Rtd1sTa/AqgVbPIEu5yjPdvH/PmNtDvZHcywurmPbd4kTIT1jT24xqA/aNEdzrG8dRA8xCZa4BuDfq8Fnp0h3klVtK/eQQmN3gX/Ss+NywKpeRyAXgpcv+IiXSpnk1VjF4vHFBQTGQ1q8XO8iZGFxvFM8c+8h2GDWzjCGRhLnOW2xS81uuZXnH9re56ST+qpI2kvxoxd241c2TuAit9l3t0hlXcFw/MhW9xii2/5Ge74cCRqDMRek2jHhiotCDe5gYHDOV3cVTnFZ1GKfWpHVW+5axZy1+nqGxqzzqCfD/MN65iG6eEYM3LVdY2lCbttyfuvUiYkW1AshrUPDV3ZqX3K0BXwP9+2VNab25Q9F5XAvsHQld+V85j5Ytke3aZNwECM15YLTMY5ZGUQAGbrGchnnsBjEw1gf7WHmye3YPsG+6t9+JGbCzwx1u16YAQL/HycEwel1EfPyNh55T0AAGbdYv7sBqyNAet1uVImK16uN6TAo7xbZl1mWrxNjA0XTmRlOuKSyfMbFHfkOIhx7o0otHGQhWYa4ug1G44Xidor9DKMQ1RomEIsQR+P1HOIKxisYdFPgPXhohD4ue97rFYrdF2fjLCkRmg48ptB75PrdaScSFA8HKH7rztsX0tc0EKuxkKgX62wPDnZXJIyjAPAOgap3+VI5I6NfUFQKu0XysOZRo53M65bZXQylbdMSpmMPbE10dAidC21krWsTpkXqPXM4GCpToXJetQNpXCUOEIRl0lovRoXUmUJCxjGJcy8Jx2/r5mWTpeON2YDhzHBeOP6rgyMzrX9Q1awmoPhsO4InMsHBn3X3oekbpy1toFpGxRe/hUelXLtlLam30F5/k+AVjVMvlU8P+Q62Ua4iAw6yu851yazcmMxw8G6QduP62Os/41yffmuTEUjbwElOlQyzUWwwbYt9tsWi6fPdtTbatidhugU16tSl6P0smHc1vH6c8w33ND1zQaucHoTIRg+DeJMNCEAyB48hUcXuGIlrx6YGfZ8jnf/wycxADlQKANF4uEjbaRx8xYP/vhjsKER+rBDj6M+HhSAcM154dQlyoAIMEk5HanlOmmU5qw88nxDlUnQ5fx78J4v6faqJYmEcxRvV1GCgBqv5PDL4ZiPdx7OBaXnrruB/4f5v+Cv+Gf4p/wvButBlLuNA0uUbw7EEF0ALgSo4oiK+i14UBgjVL93XUEbfAmuBpUhxTDh/9jfxnfdHg74ShJiAbe5wX+1ehe/sAv8k9mzS/ZnfCbyu28+FDusWR/frftaCFZroA7+WxxtoKD0jClsOlB5XVZQlMd7kL6NGLuYB4+GUl9V8Jh3FjTfkjSKhxln8Yef/m0cnR9lHjcxiMSE1rdoz2f4s5/+J4N2MIDlfIm/+MFfYNWuIonasMGg8gdjlyhq0ZATxzPEfFEdK+YgKrpSDzNYYhXGcsmEuFrz+Ryz+Qyz2Qy9J/ReVFsOhi1i2Mai6Vo0TRtiCUXPECId95cSzZPnwtvEyEXxJbFqe3ofqJ1nTsqwHMFwHC5a6HsP5+ONbkSwpgk3rCFcpCExu8CIR+Ac1usO6/Ua3vvgiWYNyPcJG8ZQasOklAM++f7Nh1fOe15ruHifE+ZEg5PXCnrajPPiqxQuamjaYBiJxxBF9iEKxwUBsUUFw04TDSniNNV3XaJfHmH9GQqxfpS0E9LHDVu5JY8AsJkBFG5LBYC2bYPcqm7SM3GdBi9SoL59rzZ0jfEDvXER+Ell6JJ+Dgw+2dDF3sO7Dog3L65if1yMSWYo6CXafHJlg0EkA0mOG/C4vKli4wUb8/kc1jZwKj7TdDPEGDRgrlUjyq8l68y8Jh9nLOO1jxU1BgTdR/Hi3pxHQ/b+C4ZyrUsWzeCyKWm2PeJNOGEtOBdiSorKolUXVvwXVQ008uxlwVhbd4aBovgWXhW80YYu1jr17rnU9+GCTW8m8XJ7/vG8tUA//a4oX6jTRJJEHnjzQtzu0fV6CUDEBLNqEXZYGd1+i/X+DK5tBsQxkuLRHjAR/LwZ793Ibn5BsOOPe6f7uNcdoIlnzDUDF2Pi2JTnlNc3tpUJJtVRxiPhKv0WIX+kecrp48IwuKFHfda3LSGpdzGoY1JgY+wPTzjCAfYwzz3RGqMIYcgKmChehUZZGKfKhVqwotEfSA9FKE3DTYIFl1Q06jGeJi/FY929QRmUP/bZ4IhNUfO2llL1a2A0cAZ+cQCeEzB7NtqN8YLFqKNbUrrC19+Gx1KHO+VTtLrMS2XVVf6C9o+XNl5JoqvTNpx8/E9bp2K/WQKM5s9U3aiRZTw+X2IT4vU00mKWurhco/oIY4qTtXVGt894ih13SUKilS7jDG6c3gCxQfJu4iC8G29wuD7EXreXWrZJLmAwLBNsTJ9fiBhvcOfkLromKIzL2RJne2dV0kqJE8WJA4EgWaRMsM5i7+wQ7dlB4lOZb0s8wHh0UQxbaiMqFB9uy5q1M8xmc8zncxgHGI90gYeFgyWgtYBvWzRtG5TcpJgOsSKRO8rtgdAzQtwg4JyWiwypkGCUsjDxmCQDsJaQrivm0IcQU9GDYBJ+g2MQXhVXjQf1TnPZzP9GQLO5en0CaQMkjD/SbaXfDEgManTutex4oVKrxeWdw+L5c7T7+5gdHGzeINuVCb0IGJNzRpJR/SM9iGsTKLyvxPNnPp+haWMweoQYmjLq6XZDEv5tgkE6GaGCJ5gD0K1WOaZX26KdzZIBWoY+nwanZLxiauGRj0s2bRtu6VNHSk1sgLTfGpPwfSDtJK8ueU+p/elZYehS3HsgPykpkEO8PgeGifkLSbkSTQtSQ1fwuNTWelRTCyTeN9AlhBdv8EqUuH65E6rOSWa0RS5XP9NG+qCoIeXTxjtdVy1LTXF5bbiqvwOIns5KDqu6rcO4KDIeQ5L4ocibHmyZWRofsWuBemhLpWU0/Tbjw5hUe1nQbKm2M2z6fSnHte1UcdTWcbm6Lg8Xqe+NNnS9fJgStnbJ9zLr29wKnly9rw8kN2IAIMLp/Zt48nvvZA6fdgCm1ahil4mn0+WSFLON34wH/s6n9/HR4hb2/1YDqm/LqIeShww0t+Lyvi/ZKJCfZZbMxbMy3yWBN43sDtnjv1mYFoMJF4KjKMK6rRKjq3cdvKuvdRaDRVQSgWR8Gg8OygMGSZyFvZxSjRwVH1lXiMKboXizkQz9dS3Riw43Yai91W3fUMFlm73qWvzisw/xxc3H4JtfbGicrndM+JJ0F9N+Ls/AN5SJiw//lUEJ1oMGxCErbuEBEt6q2Lxh/RBlYUhJIfVRo3x1vaITape/3J3P7zdeloBNtoFSuRiduAnDuM69v9rHH/3yj9H2bcxSleOBGMsdDBQeGFVlSFRyqCHAA5i7PfzRr/52SvDb+7/FTz/+qSQZaTKHMNA+eGCE2wjDzYMMxuzsCO/9+BPcaFpgD5DjTaGNnK4fl1kR2gbPSVFomwaz2Qw3btzA/PAG5jduovNA7wnsOsB7NORhCZjZEEtreXaA2XwGYw1MvHnTKG8TzecQR0WOFGarltJiIo6G17nNxhjM5sH4tjefw/oQp8w6Dx938j0zXO/AbOBM9BJT9Nd7D9cHTy9jTIh51Pfw3mPeEBpDqhE7wphGNWbsqj4vuYP6amFyWMbHrOa5V4FuucSDn/4Uh3fv4r1PPrmmUl8HoBibrhwpCSQvIRnm8z0cHB7i9p07mM3maOfzZCEQ2mqTQSfglaF4vNhaOOeSnLNarfDk9AmaxuLo6Aj7Bwe4ceNG8hTrktcXx3JNNDI36DzBMbBomrBu5nvBOD6bAZDjpVl+IgKsFRVwE75vwJTiOB9GGUHmAFKHh3cOHYC1bRBupMt0T45uD/jQhhbuAkFWzJ7LWSQpT7iEG9tzPCn2ceMh8bAog9SGJClL17jBcD7VH5H0C+9mDh6wFwcueFZ5WLMWOzIPAjL11zYd4ZsDbKn0IMkj9JQj/Xd9XwQfe8Oo7DhUJFYbbi9zKmaq+NHNVEzj0cvfs3l9Z/N3ztBVem2NKV0XKm00X2nt5NF3wzI2VzMlrmQ5VLdlGv2Lc/8K8pGsl7oytkK33+L8nRtY3t7PV7JOrXgZd/UoQZU+EWxSX5QBRh/vNCAYNkhBQ0kziIq6G86WrtSe8prySwENBVOq/tLMFkg2VFw1bIutcS1AunWolo2MohitKAsecqPToAht6agsO/JzBAlqplNjRPitvAqqtNIOHQ9ptE9jujyV/d/q2bUVlJEBw926KsnWUrQH37Ckmr4RPBP2lgf49oOP8PzwGM+Pnm+uhQTXtIAp/wxFYd270RJHHw/p+dD7a9i7yY3aDQtnajdtPF1Na6W1GXen6O7U83GPLN2e4r5VyZXGXBuCTHEuIh9TzGQ2it5cr4iyP2Otr9NOdAYAsL88wL3n90bZ6nw9B62pjPExQbtk93uKtI36Nip6QoQYFy+8v3F+Ax89+DgkI8ajO19j2ZaBdwkxULVHvP6cQN5i/+E97J8dwHiLZJRWhiSOGgFTVm6894mNJE8mCkYqiRkTlFyK+RrAeDQUjn4TcfCsamz2JClopuq9KPKKjMopfzX1EUc5PUxKIwclfjabRWPXHiwTHAjWhaONPtHz4Kkbbivm7C3GSP1eLVfoe4eDg6dYLJdYr1ZqrjWRGlnHlxS0Q8mbVIY3A+rWZ5RW92+Pi3+TMLg1cSqdDjL9DQIJWaFj0Mm6lFhO7azFfD7H4eEB2tkcbRu8z7OhKx9d1AZGYwysMeiphyOCtQ0YK5ydnSXj1f7efvLmlGDkJe1H8KqS2F1MAMXblo2FiXH6xOCQQGh7UsrrucvCQMSAyffK/oNEIoqUY1vIFU4JHVT9qmtl4Goel0nHieWxGhItWyLTI+dcnEObuVmk3YWMQsIvZTtb93hsXYwLilNi5GUpk+5v1l1KvpzLzrUXS1n4KQCw3hAu57OmoBz5m4yE8w7O1xvXF+5QLPzytGbvxg3c+ta3cPbkCbrFYpprDOqoNYZxVVSamS5v0EbVFwgvlvyOM46Xb0y7HLzhhi5l3bhM7kIJlvKoeDfmmjec2HEh6boQTzNHLl+gJLhZICSq02moFS8avnpNZJb10R4e//57WUeIY51aPIoCWUnZ1JF8Uflwh5/jm3yUKHjyiJt40teF2rHOqZpRMNIRKWAnoFTOVKSA1GOlPCiN+iWDEsSiBMCU42TVMcLTPpIwZQbgGb734BRstVT5k+CmPVBEONIJqcyr5Tp5KkaCXLbGnTKvoXArnZka0236Etc/N0xOLKs4GqlRW4CAKc+u3WCk0GItqPFgWRuEo/Ob+MGnN/Grb/3NFkPXsD5ObazweCh5DtsmT+smjwzl0PtLVtC0kDlWax04Ngvk+cVYKwuv0qpwUploUHKJ8VQR9HSkDfrYYeyvqnGIjtmAL+C9GLtKI5eum3faTZ5GurTWiqYoZQnAwfE+fu+X36tWegkO44LymJItpHk0/bA10tDB49vHt3Hr+DYAgjce5wfnWM/WRaZ0aTrJ1fQE27e48+nHmK/mICu3rjGYOBkGhI4Ftq09C+LtmKqdRIS2bdE0FoTAixqS2xotWkJsRw+Kx6lM8oAuV7kxJW5p3kaQPaU4EyauGqHfCAq+iUGorTXY29vD/t4e9g8O4EBwbOCYQswyPVIUtxKisQsKj733WK/W8J7x5OlTMIC+7xAOPG4haeN64+8Y0MQ6231odjVsbSvjOjwZXi4MGDNA0XhtcywnWU8s6yTGzdvf38eNGzcxm83RNLNSlimKzR5LBlEZjoa0EEuL8Oz4BE301Do8PARgYGwD27YwprxQJnvhhpsgfWHoMiBrUzD6LEtJvYAWnkoPoo2jk0XMEfNGllVzTqo+9UUTYnGq+XRhUEqy4+XxSuZLmitzQRXOMwD2paGrbazi1bpQKr5qrynppwY1wqq/48cxa9Eh2ZVqUWLLmKSTDsIDiuS50IjRSSuS14lKp6mNWhirGU7/lIRYnzhx3qF3brPMuwtcUbE+uHMX+7fvolutsF6cQ8tTl2zQ5BuK+sJ1UcOLG5Yu3q+hXaQur5Iox4jDS4Hd63nDDV3XBxmBxkWqYjNkFNm2imKXa9dUDTxMU7dx0JxRJVKALrqCXjjIzTCZZZYENNiX8n+7IT6NfNMPCIs7hzj/5APs/+YRDh6cQliXMSbs7qU2jPyrxl0Yi6S+guiIoQ8RJ9ZEiAyVo/eTMKQdBM6pt5cnVRfImZhj+At9CUq1Zw/n+yBo6HYKTkQl0USjYyghj1Mt7u+2OocEPBwrUzHAIHip9u1ezNKPjUDs33Bcx2xeU0/zO65+b65Yd817gy+/voPz5RzeXwWbt9W629Od6hoI7DfA9IdAiiQUi66D9WuDkVpD6ZghkHANxCD+FMBvR+sf5SsX7FKtPNbet/rIoY6tMviMibxSeky6iU/eVcpIqnc4c6WHsOTTaXUsjzJCn/UNPv7yY8zXwQNif7VfeU9UFG/Sg2uoTIwavmpFgYuPjSDTRZ7w0Rcf4X77XlHWyY0neHz3y1CHZxz95n3Mz27CrBvkzYdywsXLxiP5s6qdYANrgnLKHoVxMvO90C4XI+B7CxihhCzeYeHPwAcDm9yQFj2YU4wfNSzyme9v4axolh2IEYuDx4lpmmAAgwXBxBhFFALWA4qOZm8uUb6tMWAGrLHY29tDE+MK9b2HtYCli1OBcYo5fCN8J6VIcsfLEthfACQjou6zCnQ9KuNerb+r01N8/Ytf4ODuXRzdu3elsl4pKK0+eCICsNPanzEG1ho01mbDMsZ4Dye6S8zwxsSYWRRv+QvemvP5HIRgJO6dw3K9BplwiynHI47WWoDlogeA0MPbGTxZuLjmPYJHJSN7VsYOgCIt2KwTbHsDtVYmEyQpgkRmJYZ3FD085S+mzqQi5n6BwMKfw1ovQl7Er9mzq08Uoti8oryWZGVtqG70x6SRRXQfRrEpkOpO/9aUsVzjpFJoGl9qFBq/4z+VB2Bu7UCxVFk5V1i5hXkXjqxqnLnw/L4qr1ElK9TSxjhfqo7HvlhMfsmwiRO/njzzjTZ0Fa6n21MHoYrMCF2+OBJOG7s2lzf0vNwmUCVNd6Ku+H2sCC3ZDwZqU52vTshjADBhjtgYwJSMhYuEFwOqvw8eBOiO9rDYs5h9fQLrz5NxI7iqj8ztyPZXYtjV+8uSu6xwqAeyADjGO+E8QqkeBi5zXvKqZJmLbxH/RoUXaa8Qz9CfHCPB10mH2BkNCfnWMgwWmj56kEWLoeAgiQo8ix5piMVmxSjuCF4jEysjPFys3CK9J5A3adctCZykUgbEjhWXWr8ExtYyS+8MHj+/icVqPqx7i0F1kxJVzAIRwH6wpHYNLD9ejVHC2RGAHwKkWF+SAsf7UJxq1mhSfDsH8GXZ5vhPVDUKwVLH+wgfJT3XcbFqQ5N4DBV1afwUg0J6JguPYK1Jz8ST0RhTKGhEpceXvKvboQ0vY8/lncjoRh97YEbrW7z/9AMcLg5zR1SQZW2Mqw19Y0c3i0o3wZj8XpSbx1KnCaSU8M7TdwdFfuU8Ht34IhilHGHv4U3sPb8LMgAbodslxgiCMEPZwCh7WKG6oEDnjzSJIcoYg43gKiclLhnIqOiF1JSUH2FrmVpweidegsXYQOoOv6wo+dbCwIBhk2prVMuTssW+aIscy2qsjV5rDQAK/bKAnK2+sEcH5T+td6Sat3hkvglAaSYFNJ5ppXcop8SXW2EXT69+tcLxV1/Bti0O797dmv5lQkbdTUraSL44glMhPwBAjjcaY9MRRS2qDT2lKhlNeWSFmFrzlMd7Rt/36DoLOf4rdTJzvKVQym8Aa8rjwshr1/l8C2y5GXEJDzzFU8pVhVEBTWQm4eMpiW5noRNFns91WVeDUg7RhVcGrCRjxPZFg2LIlTeOAn9X668exuhdp+0/I0xn2E4A4l1lYQL5jjI0sSoQQBF3QqolFM+0vkODdEXOvFa4lkvGWwmEiC3Wk7jrJlknmcV4JBg9KUk6McTNk30BknUpKPWD7e3Iv0t5JLOV2uB14Rap7zTyDFveX22k1B7VRLteD/q+Dd5oQ9dF4OzJEzz77ee49a0PcPTOO6+6OS8YhMhkQZihlAG1O5xoPQ3zvwpga/Dkkw/g9mcgY+BmcmsUjzdrQ1OFGY0q2ZTFcBEUudqd+uSre/iDv76Bu+d7IBvjJMRYCJkoixsvF2UnwZlz87eT8al+jBATLgV3/XzLg51qvCqUfZ0iimH8kvrLwbfBOwffO/R9D+d6aK+9MKcmKs8MmOCZ4xHi2nAx1kqoUoY2yG9pVRL8RppXdCrgBxkD8n4kwdXgyi7dCm58+R5u/cW7mH90Dhz2SUgCT88uK7kyj1fA9c+/vofnpwdYrdtra+MQonCZ1OjrKZPpPwHonTjHLVLU8msEpt8H8K3yGYScfAnifzedd0RsUpo4wFWweYGka4QvJvwoPbr0zmnKW3oHpeKSYSy/y0d2KLVBEGksNphuo3w3xuDu87v4zuffhTYiExOO3GE8sjNshzGmUhKH36eejcWiT/1SA0jVwh87oLkL3eafA+6fM5xj9B54tP41WvM13vn+d2HnbZm/4relwitzEJRnUA+ZL2YkNysdkDqkVQI2x2cmBKs21qAxBoaAxgblyXs/aEgYH5f4oVZhiwlWnfA+eN/W3VMqzvjYxc0MfSGIGoYqLTB2a+DucIF8r4lh5kIwLh4M9jlfVtdenfS4GygKtD2t92GLgvUGOZXvvBiW4logIB5MTEYcWUsSqForw7KR0DQtDg4O8PHHH6cA9UdHN2IweYRLHbyLR4zn1R4Vw1PwAoPQAhPiymoogrEjXE4izwdQb6ZsGqfBl9CwSI6Gz5RRS9OaFLB/TB+5IgKPtVFKrOc2bRgRCjpYf5YFDtuXTP0jfDvRSTaDfADgwPjg2QH+9m/fxdEyXChQWMrUGJZVJ8Eg1B8Z9G4UVBlLSIxQwxWtff2tJ/xvfv0+TvZW+Lffe4BV0+cyUi8Dz+m9HxW2kywx0qLEcV44DcvtvRYqdu2NvQoP/N2Gb5Shy3Vjt7QFWJ+dY3l8jMN79yatlPn5bgg1be3UMG6FLZnUlrr4YiheGBhi+VoJYE05oL6/JGmIycPNOsgus+1bWNfANwb9vMHq1gH6wznk6GK2c1XEZxMtGh/2Ko1mW9kLQhTFm8s57p80mMGCbH6X+MigITJLPMIYr+b7k7szwlTFZSIZdioT0y40u2D0fEU6rwxM8RuJcjbQGss2hyOpPh7Z8WkHc4YGt3CEFZZYowwEHSR5yYtS8U5CUl0vlJcIqZRZyRdloVaGU3mvIZCxsPM9zNaHmD+7ifU9h0UL7LWdiHDQ8zMATdSY0XsL5xucnu/h9Hy/SOqNQ9es0Tc9LoIwExQxPqujzNCgWdOCpQVjr3puAHoXjPcuPmcb0g+P1x0BdEOl0OPYA7hRtFtmIY9BD2CZnmRqcTHxtDCaDN5FPB+dquFYEu0heECb/L5SWoomMqf50a0mMpj1t3Dn5E7MVjWgqnrKu6D23NoUC2i3qR5TTIaQ+rIBxfkUwG8AdgB7xqo9g5s7dIsFDDxa59B5g44MYByYJAYXw8MCxsLujYtjtZdnbQYmANnAySViJZ1HGcN0eaLMpQ5SkQeV8pGdBxT+p3nPGhwrPC5AKXn5lrUatGqZ02PwVD2cJNHZm2SYQDEK+T1Vx+sOmxodp3XAdl9UR7d5VL5CGKqxNWaVtEvEYvFmNEbiucpmwZi/pYD2MI9PxnYqFKswxuDw8DB6cXVo2zbHBZP2xLxh3Yq/ZFUuRVqh15u8VUa2q4KMhepG+p1Yw2BguPiYoqu6bCnv5RuihTgWflsjckjZp9RqIgxxTH5FXBuhX4YJ++sGtxdzvHe8X9ah2ya1DRgCUggTIc0pRtfk4tcZJ4iqyp/GgoG7Z3PMexO8ulIaQLlSZu9iaY/WOXioM2lIqmmFay8SHa6FihUej9cLxV50ePJC6pG6gFew/K4JvlGGrmeff46Thw9H3+lAjL8bEM7gJ4ESWknIO8T5St2sXr5oXO4Olvj6D38Kbx2IgFuffYhbv/0Wnn7vPZy/cwS/10RCSEMBTfcPoipsXuBjDmHpeI/6DzE+zEB5MjGGgpFbF7OCl1MKc8+qemYE+d1lInXVjEXqE6alD7cMPWGmxmaqHS+CWEbGKYwqUWct6XASHsNtiw7e9fDOgZnxPXwb36Z/jH+Bf4d/yz/OLY2T65ljTJjglaGPy6TEqsushDFU+k5qldIZC1yh+qjIy4bpug/u3sW9730ftmnAAP79b27jZ3OHf/j9r3E0rw1S4+UkAZMID5/cwoMn99D3w13HZzee4qff/Wt0ttupxeMK7abfFwPGPcD85xCPLU7/7F2p3E0wSi9QKTT0IYB/LC/S49Lg8zng/7m8UTREe/lUlYgCW21QEJQRSL2bpu1SvhxRBEDvgOl/B6IGiJ5Vnnks21Yl23mG5yW8P57o+0iLriBR6ZumNqSSxMXiN1TjeRSstbEgKTNKCTPasyqkdX2Hhz/9KawB9huHg5ZwtmfQGo+GXCrPgTA7vIH7P/ojABy9pAjeUPBuVceTTPTQYmOqw7DSMAa8A/uQzzsPdh5MBhzLE8MWUXAQk0D0hoz6HvoCoqD3GLnxMhyoZENRgc2cJylsLId1feBSIwYkvQGRsbNUhowhWEtjmnIe94p27wa0Od+bKs2/hQvBLj4u2QNqLORJAFlDNh4BLzWNZO6B3nyQo4RgRtev4ZzDcrmG9x57e3twzsEYE24znc2T92On6EAoXjxqGUyI8f7i6jKUjzfLX6V3i7eVx8hiGFsgAznajI+gGFkmxqw8ASHy1Xadfdr8cnHQvFt0IYlpJvHDpDYdsWToCCG/88VJAr7vCv6c+DrlzyzH5vbcXMzwD37+EfY6G+LQSjX5Q41DOSJJVk11lrJuAawyTcCE2DFSJ6c/Xa9gH7MHksfj5morf+I3Hr45PXkz4Y02dC2eP4ebhaM0BGB9fg63HvH2uAKUtL4mblNp4kK/lBA22ZKq1mGLNnGAMsZCPIYSDV5JYcJGmXJQYdqt2trykkIzefTzNTi6uHZHBss7h+iOZnB7rRJ+kdosJqJknJNPFdAypM3KiD5tEeVvNR7xj0pDH1RZyVMq2mastWisVUQ4GqCoHodcnjAXHSBe+lTk0DtXigkWY8BlWu2GTnrn/YLm97Fk4h1VprmMkS6XR4JgUQLSRYrsQCA458KRxWiEZe/RosEeHWHGs4HCmQc5d90P5qTsnfzLg6cZx6Tw/Fx24NTxMFHT1JzoXas0Dir484WC/sr4RCRKbv4TEp+xBu18FtrNhGUX2v/odA/n6x5gh/3W4dZeX+RLTY1Eq+sbLFZznC/nWK0biCOjNhA647GcLWO/DCBHkUhFhFE7cBqHssdd3V8aWUvqV/opA3MXwDx/pxtIgZ7EiF8gi1SzAy5z9TXi1Hj8rE1gARwOF1rBTm4D9K2AbXExaDFVBOI0PNp4IOVSFjHD+CsPVHW9vfgRpfaTjX+RrpED+A4YhwCapA0xdo/lonGF2WPVEp7cWuNg2WNv1RdjWK+HsTpGj09MGg31uykPttzOel62rs6I3IU5TWhGWuNRmV2vwYbRO4eeDXpjQdSHMY7D7djAzbqUP7Y6XQqQlDFkXic8SHBCxlvmyDOj6zr4ievciXT7M77lDSDpKif+BQoH/ZlIqXQhZTDORYpKVMgR6UhKRN7krSg4rGQQ6W+4qWpHPAClfos8M3YcWHzZBptBoogygyQe3ciYjdPtYT2vElIcNd2MSlEOz65SvhQ7XsiLjsuVA5grOUjosgh+E7sCWWrbMFPFy4yHgpdFnKHwopTVIBHupByR3XKu5M2YXbSS8cpaSrjcti2stWA2Se4lEroNGOF1YHgYhGNwSgdRbTJqg054MwlDUevvYjA+mmNmClKfSTbQ41CXq0Q4Tam0PJbLLtvAaUyRaHKWcTCBH6ptaU5FTh16SJdVqrrz7KvXgpORArGiV/HxnfM9zPuwSXdzOcfRskHj1cZLnKrsqTWOwYorJr6kjXaIZeiBKngpgj5R6xuCy1ncrgUkhXMidoCSXIiRdQuuhnEAGjGHqYp1tSPp3WbgFjm/5CLSSpPS6Dcyp8UYk2735vpyDXV8Vp3z4gt0Sva5PhL9avndrvBGG7q++vGP07WvWrB+tVCT5qsBAZu8SCdrFzAIQilzCMRvKNwQ47yJnjMeUELnmIhYNGa0zi2axICHlQTh9Fu3cPatj1Fc5FYIxIpoRELpXBCs+z4q7GknvlRwklEs1RjOzDvvwxFKIBiqoteC8z7tons5OmcC49rf38Pe3jzcEEXhdkDjc9Be3XYShZ/CzrRBvs1sF7DWFjtOAIrrjoPQZVLaMDQjSkChDAL1ZGwmeCUu57SbMmnpRAtVPhdJgDVIggTAYO9g4zW86/UKy8Ui4YlzPay4HxDUvHLUqwhksw8Xq74Wgu2I/OuVoClN1zgT6uOiTmsbOHYwthRUtxk/tvmZiMKmHhT5kjCnxrUUuIdlMgOrzuBf/epueO0dvnPvDH//954M60/FE07ODvCL336A4BWaDRyaAQMyHuHGqb7z8XfAXeecmpGqgVs1jW3AYFiA/lOA3o9tMjAU1oK/iAcvpX/KGmprXBRKkzEvDli2K5drbWptJUFKJ6D3APpHg2YUaoQIuhQ8DMr2FyIWmKJ3kg1pTQxC3/cdgpkrjI+BAVG4gp7TEZlwGUC47c8PDO9TBqYx47389+TWHp7d2sf3P3uG73xxnN5faJ4UTLUhG5nHFRkufuvxF/weybMD2U6XZyAc9fQcNmHQxNXLYf1aawAOdMckD2IThVsPQvAKYdej84HWW5kXBrquAzUOjQqVJ3TT9T08GK0lOO9wenKK9WodFWMhnyGtuhsuEczwXB9lLIcnLJPg0eVcwBG5nGW9XsP1feDVAUmTh60TfI9DTgAsEYgs2MdbuKKBhgzBNgaztg3HxDyLxjScs6J9EuOloqFx4IRWJkNxNamsiqY0ACNpyiejbXkVUK49TaOzpvRaiMdXAOmic+E2ZvY+3PIpsfx27KAYouojwPm90FhKsQkReaAx4V5TqBApxliQPEem19pQUCuuer6MsQAIe3vzSBMZxhCOjo7y5mq6jVbkqFCetXmDgpjQc/AuE/oChAsdiIC2sZGuZ+9cY0ziaZvxOQkjY5xyOH45B8zIM+mD3GiYDPgUNuiYhzFQPftArsiMtDQs4DE0yJuDwr9MjHNGmfYomdVQoNPW2nDJhjWTUT2n8EfeGUqrcSRPli+IGX/86V18+PSoaEc92KQ/B3y/bFgyCGvDbBoc6bO0LsuUBhHL2KdLDcr6qfzNwVvLs4cmneGCBqDvXJA74pyGUxoe1hqw5xC3a9B8VnVN0/0BHR9PNZJtC77HciPKbWyD4JVXZVKcv7E9hlx/JceIvsJ6Q3FaFt5FSn65UEirrxW80YYurewqOlWnkjcAgOXxMcgYHN69i2Y+vD1sKt94/ePPsxJ4dVTk6vuUCj2FXLJIufil/6KAORAOJ6qo5KmBV1elnG82Pt4E6NtgejcxnOD5Q2DSO7C6TlYEnIvnk8oN536n3V+VIhvClFGsIu6BcJm445uJlOyuyZwLodc7SInJ00Qzq3eJeUjfFVfL7siivASCKrvsWSGhXHDsT4klwmS1IJwkM5W1VnKHbS9A0GGgLEkHU5GpH6KBBNfmwAidc1GwmcLLzJo1yxIlRs9vmgcaFqdTJVyQPzVgeuOTpYMpt8YVFY1No2e6bWjzAI6+1+M13YmN4FkUbsLzRYufPzzCu0cr3Dvq4nuDx8+P0PUWnhmniz2EXWRZ4xTntGyf4KoEpRaFv0K/NHAeDGYDj4/BiLEnKPZbDJ/kAIwHLVUDgSCSHSEdVWRAbuncZvQV2N0zizNtGxiPd1gXE20qM4aLFVJ6GscWIgIZW45PtdZEiGeO9z06ydsAYBijApmboEjp5S+C4NTRzF36KgZixF55Ap7d3MNvw84LyDPuPTpB0417Hb14iNRhx/7tvOouwfb7rsPxVw8wO9jH/s2b+XZBPf4ypmMMF6yUQwJ7j75bw3tXkVxO9HZjt8cRL+aPPAccj9XEC0S8A6JS5SPJULqUYgGRQiq+k3U65bGKKvNkQy9GD4WtDY2aFW27BN6/MthxCAR3xijL3o0buPn++0W/Xd/j7PHjC/Gc1ekpjr/6Cvu3b2O2vz+d8EJ8TLh9yjz2emsJSTJIy6bOSGVZyuqrDVeok0C9I0ksHvdAvq9BKbEUjwfDRDoc8nG8HdFYSuEy9PoocDUis3jv5jhMStSKgmXRrWJMUMxFIT/WoJ/XxoIx9qboP4lMS74QtEZmYPL3JozZBZ1G5RdUVGaQpsAcVd90IJIyHm8ebX2D863FDO89DzcOExNuLmewEpieEa4yFHwa9iTLplJ2/FGPl7bZh9t8M86WOmrt/RxvzC3oeCHQFW0IuKbmVggtOONKNIqx96HcnWlAxauvYLVfnZxgeXyKbrncXOMYPqPEwVEeoeTEbfJ+Nmpt7s94PVN5Lsu3IiZtPda1WzkXg6vWuRneaEPXZeDs8WOcPXmCdm9vi6FrDIbC0EuBK+GAEouT0lqXGY1yU1YYaUPFY6/aNqZ3APrPAFRBhgtjVylgyJ+OWzLa1sRHuWimGLnCn1IBZEt3QkEOgkfYCdKCQzCA5XHLhq6UO0r9XAjwk3oEJH6IByHcoqN3mEmlNUTwMUaDMWH30RClXfZ6LpNbf1GpGhxUXlLJqFYKVRuBdDJOuYmQlDdS76ReAgDPYHZwroPru8AMFSMQo0sSJqk0Tm1r2ib0ljUgSyMx9jg+XhnUGLpnxQpLRq5k7BrWsrmRO8KufH6sv4/PZnhyNsOffvQsGroIji2+ePgOzpczuEJ2FeGHgSIeR15R3gePPNmpE0NvuDVO5eAQL8gx4PAjgO4DJhwFLoQC8gC8UhjqToV/xoTS2kNozAsptIUHv4dCsPIOkfX3Gii/slsYvEq5mJM0jpRpvfdpWxLtrEmeoLVnaH0kSKeZorVj78oyynXw6M4BHt05AAA0ncON4/MXaujatk4KsrEh7eVX7YDZjqRg9MslHv/qb3D0zrvYv3kTQMC/igLnOUqcTK3EZOgy8OzRdWs4l2/AKlOHcse+7gJEwfvLRPrY9yGeIuIRRhf7rQ12mhczxZsxtaevFAzhz5eJaDnWWD2CY0LMWwBCfMfDe/eKZ+uzMyyePp285GkMFs+eYfHsGe7/8IebDV0XhGRXebE6UQF5EzPgi8id4hElso3QwXx0UvPKKJNFPpqMjRRMCdZK6XGjI/HbSAMS/mpzzLgBRDY+k3yqchT9ki8Tm4KDcZh6yHo6uPiQ7wxkIxeyl1GgSTzsyna9/6XBOLvnie9AMhagImmyUaiev3t6gL/3qw9UUVVl1SmIso4xRUzJOvGVIcD7XKvoCvk0RVmC6EypNBLPRy7Uo9qDkhCiN4YC9I2+UrdsXEbvL+8A8HhsuIvAJXDl7MlTPP3Nb65Upa621DBDilJOfMtrXjW84YaumuvRQLAd7gwCYMbzL7/A4vkz3P7wQ9i2Tfnja5V/QjC8UBuvCjQsZkNTarUbiflWhFHcl9TjSYVGKe+1sl54tAix3ti+IzD9PTBuSaWZcEQjS65L9N1o4GKf4nINgiNP1ccVjmA4RkLc9fechZKLfAoCqnfWiSBxdUzQAGBMZOAsAk01LAMPH62uctFu4lC/9rLITVNElUrBTBsCZKyKkaCcRsZfQtuLMl0OZF3CLiBjpJkDR/ST/oRZ8T7E5urXHbrojcBe3cMXz/rn+Yyu6hQMUTo4cs1mRCAdRRkOL5NRh2W8FC6r5ZKKSPJmtSZi1npdyLgOvCB3HMJN0O7t4eb99zA7Cjf/bbPHMIDfPt3HomtiYy36zkLPEhEBPnprGYLRRiT2ODo9wieffgKGD3Ej2MMbjy8+/Byr2TIr2VEJ8DENmGHNX4LoAMY2AN0B04+C95HnKlDtho5sMV5NvdM4lD26hsH2Kf6XvPGqdTdVx4WMYbWRSNGKWm+QYuVINZmoTMXPOk5MEnblEg1kQ6A2dpVHMZGOAnnv0ffhWElB+7b0X3/qo4TbdjfrcurjspvSXilsgaIn8cGGtJevZqywULXQBMLq5ASPfvlLHNy+hf2bNwCUnlelMVLzb1k30ZjcdVgul+i7PioeplA4C62FRuSLsf5ypGlxE0ZoKtijX6/gui4GwadwNDbGfWMyokGBEI7FkLgVpONIkUrLhlvyDJCrRa4CY2r+tU7kNwKuy4g/tmkwSKN5Y354sXoAFWtoS7rYrijw7FxHNgdw3lCTdyTHjk2Slwgxfp2vdJMkf2WiLhu5YnQw0ra4sKReyVfaOmojB4PYRHkkBwUnjqFJ0g09nP/ASGvL+2yiIVTOIpmXEOfx4/iARvqZ3OFZP8vGLqSbtXMa0uNTb7KmYl7Ruq35S823i28EIrUpzYTf/+oObi4klmj4kN963HPxFbIVQkDCaHkoFSVZVp/R0XrA0Muo1kNEHicVgT/OmpaNI5mWFIaAQ9/izz67jyeHC/z0vcdJ+SGkyFZxnq9pA0PgpZPzzZXlvR3aLohfpRWT5IzHHg7zjub7ZsIbbegSWjBqzBoxWmk4e/wEq5MT3HzvPZgU8EIEbF1HiQ1i+NokV2f5sXYFvSxoMhrbuMmglJhqZB2VwjQoOTLHHBSvKpSE0UZlXY2JZtxFe0Yq47gq2eyB6eMgCKcm5wLyWf1sAMvHVJXra1rPNBiHoTFu7JdqbJaGQB6wffgERKBBiqlSS1jCSBiZN1CUFlKzkjGpbsmIcpzkApU2KqgyDwNPCxLCmsvKx8HUs2oXhioGWByMmcDdTUplPmYTP0QJy+w8iW5a8CFD8Ozh+h5930UPgTDnhigGx9RKXp7zJLtlFQ5jy6MQUvXzqq95DIKXV4FaSdCjNN7FmNQyiGSTo7hXIAj1oSUNdtbixvvvwzRDkj7Fax+fzfHkfA8AwYLw3syijfij9Yc07nEewgvG/nIPhw8+TGvSEME1Ds/eeww360LsDQAw8TYjjkoQGES/BpFBY1owfQRPfxhRXO0mbhuPDYalTUaScUNXppO1p56eZ6rmO1c9FB4zH5joDWePF83CMu7KWJR94UivDRCMXdXufZirQNPEyBUCGjO6Luyk6vEZM3YJSFzApmkKQ9fUuOrvmjZNgScCGwI8V2t18zqp6xrm2bLOFJELS3q4aDfyeMX3ZPPlssBp0hnrxQLrxTmatsHBzZsF/0iNkvWokCVxNGbAefi+R7dew7tw02oO8RDHmbnMMyBY1U9FEFiELlkW7NH3XYgR5hw8R1XGiIqjjhOz9NgEHlqPm9zMBVZ/LwbKGX9xCsnLhIuwl1oKGoW4yQe/5Sj5GPggp0HRlQt5NPPkj4o/7VKU8F9cXDEWpT5uZmq5VLy5iCQSVaxPGyqqo0BpHURNNSurY8eJRxo7JmPHNRz4QDZ0yTsGhbPjEGGJy0K0EQoaN+r682+tBUB/15Oi+irlMxANXJmWSZpcJlWf0q4rrtOrZOdybASZiJHiEQLIOkIEwwbffnoD7z87HCsUdVCRrW0ojF26RUr21oY2laY0jPCo7kxACnks0omIvcyIm5q5HEIg9Q1bfP/RLXy5bvDz+48D1SdVNtf1vBjaPi07XK2+avYnoNK3gCSfXQ3qNajeJDmzTj+GV5pGjeW7OJmv4TJHHy9T50XyvNGGrqvCrkzyVcGIKnHBvJkajeXUaUpWVR270mtmbMXu0iwGuDF49IP30B3NU+DjXUGqEP7oIULTeKyRIYMeLzFvQGUzye//lPG3/xy4+5XaOVfGpdGGTUAgdJVCvAXpkgErGbJqIS/89qwuk85cNhnV6gYSBbflcmcsK70itHFUurYrk7lP4kWmkSXF6ElGAnnPELfszHgZru+xXq+wWq+wXq/gfQ8wQznRASx5Ml5PGYBUbek3qedSpgisubxsYpBnBFHXshu3GECC4EvFXIwaN6bWz2sAHsDX6zVmRLjTtqn91hpYk29B89rTIu5Ee+/geweYYAj73i++B98E77vnR8/xN9/+JZwcVYpHP9g5eIo3tdEasB0YNuDgFWjyJk+CMdw1I3RoQP82QJI7LwFXZT2MuLvq1VrStADBUEWgdIlF0wwvuRCvLQExjtWfmgZMHQmV9yUMvbkYjN4SfvK9ezg6XeMHv3qMpjJ67OQZcl0M/JITeXJ6gp/97GdYnZ2XxQEDGlK+VMQg0uNCiVO6AWlBReg7UdzAF+8qDhdyeIbr1ujWKywX5+j7dSglEjrhR9tgnFQppTQ0Jjxlj269Rt8HwxpRE2N4xVxa6ZXSxdOEhZMHQwFF/pg3NcQV5cUSzrQL/0JrebEQfdMhxpjtabf3tpnP8d4nn2Dx7BmefvbZ7m1hxtPf/hanjx7h3ne/i9nBwc55t5Rc68sof1ZK/3gRF5jouNlFegmWGwN6IzQEgOcg36Ygn6oyir42ac1nmSTbLarO7dpWOaLuff4zgSbIwi8McIwQBwqIRwmD7DOgD9pwMypsq/KSwMXpsVCCZHjh6H0qwvxASgMGEww1nFeEi63xyCsnNjKIgb/z6X3cPdtL64mrMSIAt8/3NtQxjpBj7Zwenao8zym0wVA6VnxJbRYSCHZCLUtzp5GVkfAp2bO8B+mg9Aj8wbse7MMfgWGiLmIKfvKy4GoVDnJXrNzEtRY2Ia/qjXwVeBUKx0ufzJ3gG2HoGuPpU1ZFnZYZ6NdrkLWwbasWpkaOTAgC0ytqmWrRSLsuh3A1Ax8zYEzm3RnnhgpMTRxJztQUi3oHIsUAQHCtQT9vsLx9gP5gFsosq98ZWAR3XUYUF4IQMlUwqc+haBReEW6eAN/5FPDrMsGY4A9MK1vJyAXKxp6ca8DbtVIXFJzt+586Zkuuk3JdLPMqulw5iXnO87NwhfaIoLFxpyQLSFoojBmL1Hr0xVmGgHRUyjmJ9ySCuymLUQKnjGPQG6fXI6V/y2ZnHBZFN4+Fnp4c4SY/JYpx5GioWEwqEpzfj/5WIJ6TrGlZQptNAv3FaQ0zY8UOngx6ZlggHsVAFM5F2M+CDcU0jIyHxhGOTo7SLjcTY281x7rpsTZ9iCsnrY8GLzYeII90s9Q1CLRaGRnD2/oYYp2knr9tI6oFxnqnbHLdVOtdviW9IRmsxxSfvH4nPZn01xjg2Np8ZFHn17HNiAjkCM2igW8YtOdG6sE43k8ZxAsbTnjnCTg+msMZwnLeoHGhDY3zsL2fnLutdUnft+i6IwXGtg6NcjlT+a7rOjx9+hToe6S7wGTbe+d1WKXlYPTvVis0TQOytZgWla9kpRf7V1g7zrnkGZvnlZUtTzZScv+Ycz9DOkVlCrordWZ+45nhvIN30YPHRp6i8bsm3pBlrp8L49B/V4NtMyD0DfrzDYSa+wDCE5FZ2yXG01iLvZs34dbr7YkrWJ+fo1+t0C2XME0TQoRcaIgLYbN6PpZ6Qt6TC0qA4bpkLTkNUUCvBQkaD+ErupYqX7IFTJBBUgk0F6ipxuhwFYsSIuSFR4XxKMqQyais6FNRVn42cv3T5rYQlxtTdXmJzGRjSJb7Y5u5bHOqTRUsm69X1duHGy475GFgf92ITTDn42AnfOd0H/dPxJA7pCWXo2I8ilf5HU2PxZjewOrL2BQLH6mS51M+SHxGp9cnbUQQD/GF81FUjpcUSegRjQ/XRnHrhr8IqNCzsLyyfq2wTPjytTaMi2+p6+Piy0RezZt3yfdmwzfC0HVZcOs1Hvz0r7F3dAP3f/j7IDt1iSx22l1+YXCZNZLW34WcxSfZXBYHLjcGT79/H+f3jtC302OcIFJAfSBHm2JKAjkkl1luzcILIcYGUSWIgA+giAOpj9/lIyJTIxmfRcMQm3yziiZ24OhNhcwTPLKQUx87tFGpMpFpFcqcUqBrQ1eh9ADpNmrdr/IIYBm3Z8xTYwr3N3l11EdPC0FGxkfmKT7vujUWi/PoHdDHdxQZqrQd+bli+FwwE+3PVxosBryK9S/Sb9Lv4uAlBUySHVwQ4MgBVBU+AhfxFJooYOT3lGh8kXqyN0nHHl+uljiwFvdm8ySEOjVHhoCD/X1YYzBrGnQdoSMOii5z8O4C4B2wtzrEHz79E3zxwef47UefwtgGjbHp2uqud8nQQsbDkrkWmUCvlzGj1wB3eagoDeZrhyF9GXxCji5LX5wLN+vZGEfLRj5GRMEAEY8fMjOcc7DWYDabhavr45FEeSdl2q8a3Pnv72L1wyVO/g/HBc3QdGTsOGNpeJoYC5XkfK/Fv//Re2kxfvzFMT7+8ngwh0X2qq5r8+yagp2LL9cjc8lbRoFIJQoVPf/yS5w8+Ar3v/99HN65m5JKsOkchSXujhNA1sAzsFousFot0a/XYO9SQ1jqSg0Lv7UNKo2n/Em62Ct9dFmeEjgEoXc9+m6NWTNDM2vhYeAR4u6xKOGR9svV6ykuXNrxCDTWIEQVe9ErqWICbzBM9KFmD0M95yqlbwXvHL7++c8xOzjAe598AtNeQeUo7CHxxy5BunQBIvdBcHzbQASPLq3kC+0NKM1wPl7Iwh5cxZMLwetjqA1k2m10WRCxQodDUPRAy05jxirEAtgnjxrjPUyMpcccPagoczPi0B4DuUVcW3GkpajWRwxdUOATJ9lHpKVIaFKyYkRSv/P4ln1hDNpTZL7CWs3CNiQumq61TJo99fa7Bv/5Tz/A/tqW6TnIB3vdDjrNpZqbJdjdQBZ7/EyKhrJkpOXC5W9S+aOS4oug8oCxecyCl5ZD38UQFfFosyFCv78Kwl9wbUp8QY62p9U3snn2RsCgyZqiZP1L61MvmJG9hS3wDTB0DUkUMM4HxvL0qxXWtsHy+BjNfA/t/j4ArtKHcpnzog9l1lKDCN3DVl75ys4qexG0eCPsyBxYk7SxUnarbcog5mYN+vkmdFPjWpmxgKgHpOA1UerQuw3xS/LGkxsbQYmei7Fi067OJiU1n7WuRqpi1CRtlFSRP6TnSuhQvFcx4KJSELO2V5XEk5SCHgms7KYX8tIITHljjB7RLEZQN3p8zIrYP1UJul1JjmIfAtF3XQhCz1FkrIq+QzfwMT7AIzzBAqtUSKHEFSCHCuV7KQ4MzRvhDUek4ZRHlCJRMvM4vTIDeGzD3uENNIdHI+3Y0q4JsmCJYCf6ZCjEezo6PETbttifz9DFo1IhrppPhqvVcg3nGU1ncXR+hJvPbsNYCzIWiPGpe+/BOITDGqs5sNpvi/q2eWMNuqQMMXUcKu21NHoMTzBFkfXCg280ryznoTaZd8pG1kduSNU5VX0yOkh/JC8Xc5didBGBloTmcZv0P8MG3jOs3HJFwaDdtG00ihmQD4Yuy01qWfuwhXlqYB5aNL9ugmHSZ74oioIxuW8cFVD5VNRN/VunZZB12DtaQQTGxpU36o4ZKEMZXHzWI8xqxzUnUeu9HEapbCO7rKlF27a4ffs21ufnWJ6eSLF1ppFyNoPv+0AHk2Kg61djEy1p2X7F6Lo1+m4db9v0icaG0c18U5CXYj5GFtmJc1/z8XlOHhp5VWRqyt7HuHyZvxlQ3tCJ/4iOGTxiZQEhb/ZA/koeeVmY5IM7ikZvDGwS4EY7up1OCdimwd7Nm8lDa2pNjkG/XgNEQcbe20N7uF/EeZ1u6zCkhrwtl/z2SZRNC87ouhMkmUUbZitjE0fa6KNBSVPtcMOczx7qZAL+Vzffynfpd/oqNEqMAnLEcGTDRm6pFgMHxT7Lp+50lsUqGVqlKJ/l/IVTXBqL3FiqchX9Kd7lduYycsZQtJYex1t6IbhAdmLgztke7qz3cbRssd81sSVTyDNe+GZ027IOmKpVoGTdAd9T0u3Aza7C27H86TVnvgAlsyPLJN6LvB42peUWzcbYZPhiH/QQdvlGbtEHSNpxZajxYxquozrtczk6BalNlY5wRUYjU7Zr2kGLBnmHzELLSFeBy43zZTLtnucbYOi6KAwHZ31+ji//6sc4un8f737/+xOMe6MU8dpCFhjHFPpdy6Di8zKwq+VeK511K4Kilo0LkzsdiULHfnP5KtQznjGTqGGZZEy4/bBQgCeq1n8iwMfb0TgGhjYjHgskjdO/o4CTDVy5fYNRUoYuACBLVcyj6Jnhg39buPSK07tQXRhZU9U3MGKmj7IVyaAQBUN9DFKExWyECLud3juslyssFwu4Pt4UppQ3mcS/S3+AP6Uf4L/z/xS/xGcywCLGql7mJvqqhVrwUAe2UqrsdC1tlCGIWhhM+J9zf7cds3pRYJoW7/7+D2Dne1j77eknIQ5xS4T3ZzNIrJxUT8TdZj7H/v4+vvPd7+LoYB+3b92Edz1c32O5XKCLO3zdeo0HDx5guVrh9PQcHzz7AHcevpPmazZvYawB2QbMBOef4Dfv3cDPPr6NqzPa0quqji8lV8SH3yFN27RDmlCR/GzAQZH/0nbOHTKPcZ2gVPnkwWWsTcau9ssWR//tDaCXdRzppaGMwzUniOvRWpt3IRnwnYf9a4uDnxyld7WCVXt0jXthjfRRCdV7R2f4zp9+CtP00UmjEuyr+azfXQS2ynIXZPNHR0f4O3/6d/Dlbz/Dz3/8VxdrS5z+MUVIzE5iYBRFV0hhOr6fH4T0zuHk+BjnZ2dwrochzkcqVaWiPNdrIxQX47sgz4VUkZUUxUsjpXSux3KxQLt/hJYIBBP5iKLHsb8h5h/SBk96EQqMO+KlIfUtXAauR27du3UL79+8iaeffYZnn322cU2OQb9a4auf/AQHd+/ivT/45MJNKmUUTt8u1bMLZdQbozkTQwxcIr8EYxai8TasCROPEAfPl+ABq2it4LjQ3bFmRS8t51w0JLtAC+IYpDiKZKJXGUNuLCXEu1bjglVbNaqiWM4Fhk81DvniCPnIPTBpzEYGPHa2akZR9HWrW8ovf1Oi9GmY8Gefvo8Pzm5g1vVbS9/2lotfU+9yW4P9n0eKJshx3CyE16VowSX+MyKjDmULp1oQsT8RaknEcH2H9XKBxXk4gSGbfrN2hvVqBdd3YAaMt3DrsBHq+h7wPbJj2Iv22H2JoHVMYWek9Y6xWb5gFVeRNV8KvHz9Z1d4ow1dSv9VCDBm5S6tjINNdAoMYn1+juOvvkoKwcGd22jme4O0utwtLVR1XhxDM0sPv/RSuYzRKRlRdko7kY7KNFMGH3m+urmP1Y099JWnBpCVlEAQaJC/toPrnWBtxOK0QxFyjmkzicWRYncDL7tqv5xEL4/u5koJ/P+z92extmXpWSj4/WOMOedaa3enj8hoMjPSxmmnnRcol6ucoAsIIfsBqa6EH67qAYzEk5W2BOYBgXigEVjwwpPNEzJPLiQkECqDEI1oymDKXFMXt5nOxuns4sTpz957NXPOMcZfD/8/mrnW2vvsc+JERGY6RuaJvfdac4455mj+5vu7yZQQ5Xun4ytKQQGLysvUVrvJiPdRtKrPynw/1ZSSArNHpih9Ix+ASZz/5HxIvqTdfi5QNishqlZ20/7IylR+L7FsJkExhgDvR4zjgEGZZn5lILtFM7OG7jhkl3xKrvdyxvIZydMytUztk6eYq0rKSKENab2235nyVWQIxJT37878XOGobefqmnxH1TpNvqjBBEhVLCrVzSZD2DeG9MiyOZHPTZKb9GxFFeSL1xDQtRHzrsNiscDR0RE4isXOWYth6DGOA1rncOf2bfTDgMXiHKvlBufLDfphgA8ePALRM4wTQc4COFr2eP2dMymJXp1hBtC3Fg+uzfe+0LPAju1QXQA47D2un/Z4etThfNEV8Fy9S/K1XM3/Jes5Dembzv1Fng/7Rr0/tVMBG3ZaALovdLBLC+YId98BPUBRlB/nXAlRtAZz9Vjue/HAG8cRMYiixpYRKU7AKwMDxw4UCBSntK+E2VTDvEDWLiDylNgRCGHd4Ok3boOMJibfAl6IANcEHN9+DLLPFqaeS9ziLQ42EU4v6SmtMURpfbbSf4GC/ozBrp88BoeAxatv6nxERPUSSTRVvEYAguTmWq9X6PsenAp+GOWk+QxMNxnxdM7lZ0Uvk2Jd8Q7NkI86LtN7j81mg4Uf5QxXgBrSc9P7pmIWub/yzkXh/w5ShD6QVmj7XvlzS5S9DLxK9HF2dISjV17B5ulT+L7P96VrLh0NM8b1Gqd375Z+9b7FjRuSwws1ragHiT1/XUATX2Kj/J89T08yGSXZtMhlREZlFQNrGNGInFJkyWKwzeHI1f35bMcIjkG9tWI5i2lEMSoorbNVVTNM4YpAMnhUb7Xn3F3eeO+fnEvwTbtKokWWtbdpDopnT/Y640qC0X45d/L8gXz7Gm0TmguueeX0ALfHIxz0DWx81hO33rya54nOti3GbcEg0y/T++97Fk9+30nSn5aXqOhHVb85yqICviaeinmstX4ntJuZc8jiOI4YhwHD0Oc+CMAwDMJ/rJyDzWaNzWYjlXmFURUDxrbMcMVWn5XUzYVN2c64WWP1+An68/Pnf2DVF1CvQjX5eYtXkR75XL84oapPzlQ13O7z4n26i5PU93/nc9lva6CrbldFOy9jjP3ZKfqzs/z3q5/61BbQtVcLee/b9jl6kZa5cRJaEhl+wR73oQd7ulreOcKTj918bss7UECKmmHkQDJ9l5gsG5zCiAoBrbGVXDln8gr7hL9CeQkQ61yV+2ZflTa5OIFQ8ntdJyr9jNUmLd4VyIxpmyHte8Zkk28rCgygZkz7AJJkmtevE0DD6X/aX0SEheb6wS6guR3mVYe5TAHM6vukKFUIH3OAD6NUW+x79P0mAysmX8MoFixUz6kYwNZb1/ulgF3lTVREmExH/XaYvLGKZVWIEFSITUm+s9L/PpGIqxynNNZtPGJPb2UOdI2S8Oy9KM+5TwBd22Exn+Po8BDXr12T+2OAM4T12qHvZd/cunkTwzji9OwMT548xaPHj/H48VMsVx7DKFm/HLOcL+tw8+kG15+sc3hGGhsAPDqZ4eHJ/Nn5jrbfbA/IRUS4fj7i+3/vCb741k30Jwd6re6X56RVH4SlLXtbBsL8lxZovt5oHhiWs2ssrLXoug5t22I2n6FtW9y+fQsxRpyenmK1WuHs7AybzQbMnPPiJeDGJI8xk4pBbIMh03mKcR/QesnE6HnxfYe7X/h43tM7a0bA7HCNwxunMLbsxW/p/B47Gnmh8buhKBcwUAaevn0X5w8e4rXrd1TJEMNACKF4W8UERHmEocfZ2SnWq6UYCIz6VeW51cTUFTUsnqtlXWu7UX6fifeGBCRKyKOA7H4csVoucTQMkxwtZS3lTY12RVTRdTblQWmOXvLyUs2j97FXuej9P8zvU5sclxfkU4vr17G4fh33Pv/5DHQ9TxtWKzz44pcmzzbG4COLRQa6LmpZNNvGXC74/KW0Sp/Ohp8K2CGVD8nQRPBIXlZS/IPBXPIm1kBXSgWQK9sCQPBZ5omxgNqsXu6UjkYCQriKWmCuvHLkHJn8+5bsWElCWzjHFVs600VOBxKAlU56um730KU6q9v9IYEq1VcTMOfFBru/XXDW37p/gk89voP5vL3E3W373i2Q61J841mHr5rX+r0vVLaqA52nO2+UvE8imxJJcpm+kVWT5FAg6xJjRPAj/Dig32yw6TcY+j4DtRwC+s0G6/USQTfq8vxcPL/6HmEcYUgK0eTHvJtyms9x6+bsHA++9CU8txC506bEs3A2TupfNbx3Ewf1YXtZ7TsG6AIuUjguIgzT+4B0bzk1p3fvYnN6ipPXXoNr261r682+R6rFlHZ868lOW9pvxacvunzv7/v+BtAfzXD+6gk2165aVnoKpdBFScioCKyikyuckXnftgTH5fMKqMjhhIJmTYX66mEEtbgZk0OF1FxSDai6nio6mj/nvBmKh1MdSgRAa9GlML9txZyUcREV5XGX1ycvnKKdEEuOlJS/oVZGzVbp26SQxCiKcqS4F+RK75HAqwnglSxGifGlV2SAoclaK0YbQoT3AcMwSNib96roAEnb4lhLsqK4/SB9L97gO/gf+G2ssCrznP6bvLsmmk0RUCe/VYJiPtFbelY67iVXV3XDnrMxdVp+eYc/h48ScPzqq2gODmGd27tGF7Z0WKpbDAjHzqKhAmowCM4aWNPkHCNpb2WgWb25YghYLpc4Pz/Hei3rMZ/NJJ/X4SG6bobrN27g4cNHODtf4uHDJ+iHEYMfwVAFQvdvEszrtliP+J7fe4THxzPcu3kwGUNq882I195+qiGltZRc1iqFjRz3EYeLA3zXYPHqQ4/Vao1Rc00w0jmRlXtw4wCPr81BW90+b9sBZi5yt0vHg/bvnO73Osx/Zw7vA6KPGN728BtGYw3atsHh0SEOFgc4OjrC4eEhZvMZZrMZnHOYz2eIMeLk5ATr9RrL5RLL5RJ932O5XGIcR/R9nxWsBHQl4CvRj+13yQC5fj8JHQWVyqGTQ4XqMFYSa8VWk7eo7xvc/dJHYUx5/jaAmdrscI1rr927lOc+l1h9hYuvXbuGT37yk3j7nQd48OTp8/QujygkG0AC6Ovvp95cMUruLQOAOSIwA0Es7OvVWj26lGgRAVr1imKqFGt0TfZY/XU8SRxKQAKjmnflYcI7BVwdxwGr1QrD0MP7EaQxKjF75MqYIwAyEuLFqRAKIHmL1Ls+pofGCFxSJOi527ecHPYSWmFt776r2sNjT7ssRP+qnl377nv6jW/gvGkrqASYn5zg4Oaty27chw3vx/CSnPLcRLwQI85nQd/TGBg1KFjrYI2FMVa8ViD7Pc1JKhBijQEqeU7kmyiSkbEA1ODASb6S+8UDxoLIVOPhwpfV26tUXazmSBWjaUXFQnCyhlQLP3vmb1tGT9MzVfmRBWDiejW2VmXCk6fPEXawZ1O/WwY86efd3L4r8E1FjqJnFBBk+6JKVr2g7eJru7pNPYb0UTFYK21WD3nJV6x8vZbPkfTZ9HtloGapqJv2WoxBvbgGzc0qcrs14sEIjuj7HqvVCp7FILNaLrFZr7HpN+JBXskI7zZ1dX79fVt2L53aM2cvvRWPLrpUqX6xNsUr3r97v53btzXQVZPCiyCn5+0vNQKwevQQm7MzHN6+DescElW/GGio+nrGQPjCP/Z98LIk9t12kXFk4s+S0aHdZ14EhIwHHU7fvPHuhlct7kVOvHm0nBIlJwvy/q7SmIs4lS7g3dOvRKoOXTQVc0isSkURTOH8LaSEebpfKwAmySLbylstOIoFMIXyVErkpB+ufgLZRZmlMlvkiBiqXF8GGtZSuDJHlhxA0LxTl3GiNObqmeWdK0+B/OZTwYehSS01hMp7Dx8CrClzPg2FLGv0PfgYXqfb+Bx+Fxv0Or8xJz7OQm01rH2ls/OIJnutnImkaDOpRZQv2Ilp7fccJt7z3D1Tua/Xi68lwsHNm5idXMfINHlsLaRMwdTtMWbYDAbAoXVoSIFRFZhEgAECWJJjR7k+CUMxSrU+P45Yb9ZYrZZYrQTo4hgxn89xdHwMc+hgnUPbdjg4O8c4BixXK/gzj6BW6DTvNcCTRjjrPd58+xRg4P71xY61lIgw7z3efPsMJlZrX009GTnDbduiaRrMFnMcBwt7FvH48SoDPKwAbDrDQ2Px5HiWhZapQXDKgeq/Jnh4JWDUn+8TPKojVFYulo6ab7Y4+O+H6Pse4+gxhggiRjNv4JzD8dExrl27hlu3buH4+BjzxRyz2Uy9C+TMHR4eou836tV1jtVqBWMI6/UawzBkMAUQ5Sx5H/DWFq+FyXJWp4uz37K9S6PLxO3OQxgbPPrGncnERSWc2wr20a0nOHn1AUocaLJoJ6o/peDp12RbYe2/vkZea+r9WrfDw0McLxY4Xw949PQUTKZ6Vjpl6b/bSba3fqs3BRGgeSEjKh6RcjaSrkGMiN5j9CP6foNhHHfmnFF4Amfknsv8VNcRttYWFY+a8Cz5linCBy8hsUrLLSxApij8WnnOEMBRgDbOFcFYqzIWHlbCLGtDxItIFJVquvf26Z7Nusllj7rgu6uMjvN/Lrnmiq+5Hci1/7b9nOTZXOlFGm0LWzvPrGWjtM/OHzyoLiry9eL6DYD2udTsOcMXXLOHDD93E7lrqz9KeeTU81XDFdnIYU1V6wgCihGRAF1AdYZiBs9Y5y5WBShErCAQGZEBTQJ9lQYACDFK+HHcAv9Vpq1D1abUhi9ZK976cJeYFJmq/jhdv50xdQ/YNXV9qa6taC6Kl0z6+8JdS1vvs++6Z2x44mk0xvYwL+qoXENpc0BGG7fGtEPtt7orsvjFY917qCZ/1p7DWR9iBhsjdNhMzYmZb1c/EoGXAkMip4cgsnr6571Xo4YDDIFjwDgO2Gw2GKPkbl2tVtioXJGrqb8g4cn864Kp2HtPdWnO7XwJISjcffsMTPu7qI8L1MiLn5f1m30XXjrQ6Sh3dLWLn8oX7MnJ3S+fOXxg7dsa6Krby2XapacYAu5/6UtqbQHmJ9dw/c03riyISHfPP7Jnds81S9i6R8EYTtekAxEjGFoBJgZYI0w5hJiJGnPK96NdYZq3ZqdCDFViZD54u6N/liUw0dk6UXlNcJPVKuUg2AZBhMkVL6lsMYN6GSQPLhSkvSxLEagjai8BETDSxREAJ88GvS9K/XSQKoWRDdgA3knnBoDxDBN1VpJyov+LMXmPpDEUhTl5V5EqOwFJUTB5rmQ+DGJgjJ7BccQwRLRNKxXV4GXNk0cXV6nZOcBEU9aQALIshnVEAbv2edZxEZImP3XN0nylHFB57TjCkAp9lgCOGIYNzs5P8eD+fWzWK624KO8WwtaaMIM4KOAEAB3+ZPijGDDA+zW+au7iV9xv5blMShRnCxJL3iJrVcCM+YCQlhMrFtMauEgCVCxzxSq6JUXNSKHuqMrcRfLjrs5fyp1jz3UTzw4Sz6ushOm8p6TPRZGuhgyogEP5jJdsF5UYSxANVPdUEsQ95Gj5ECdFBZgJZBy6do7V4LFZ9/CDB0fGW2+9hbZpMAax3vVjjzisNBfUgK4Fbt88xNGBQ0Mjhn7EatUjGaSjgRZ8QH6X9GavPDrD0XoNyvbOBCgQnI8wQZUCsrLnEIuHWAggDjA+4vrJAh/76GtomwaNs1itr2MYRzx98gSbzQaPHj3EODL6HvjY3ad45ckSDMBbg89//Do2swbGCR3wAbBNA+MaDGNQi2lJEix0KhQravTgEMHOZuWDQFVYdBEuYQzcucXxvz0BVixhAqdWQa6AEIDFrMFiPsN3f/d34fj4CK++8kpe16FfYbM8BTPDGIMb16/DOYvOWcAwRow4nhMO2g43jm4jxIDl+TH6vsfjJ0/hnMOsm8M1LYx1+Obb97BarjGMGh5jrOaIswiR4T1gnNE9SaKAjQOsMbBOPB6IDEYve2MM0o9zToEbgxCDKG9EoLy+hbRkJYo5OzAkHc5ag+HsGHf/56dkHjVxP6MA7zCE+fESd976GpiULiq9sE5pPcd8SpIXVdPImgfvK6OCKLSODIxxeOPNN3Hz1k2QMRhHj8997jfh/QDnRBEIMAhsAWY0ZGAJMEkhVss5GAL+kgH++A/Bf/Q13Du5Ad8dAYZgOaDFCAQPxBGmbQFHeHj/Hk4fP8by7ClC8GhmHYgZYw5XNNkj2NTUIimUxsA4CwYjaPl4Ywwa58RQEhmjsVoNV/ihH4OcMWOAOCL0S2zOnmDdOhycXIdzLaKCbpTOBAxIDQcRuoBMAAIQItgPCL5HDAOYPcAmE8T9ORMp/zcZFXbpadaUkbynDaECboXHGOIqX+Nl7YKL9obh7GWgO9dMayunz/QOLiPXHvJcJFpZ6HmqZ1cpUNV9qe+rS6VbSv2FqtuLybkX3bV6+Ahvr9Y4ef11LK5fRzpvyeIQORX0kXyZlozQA5UZ5AFpjqgat/wrhrjd0VMSe3TijYXSb+E4xShpYC1gDSPEHkwC7sY4yr5P/RlhakFFjqgGM2aW3IegbHQkJ3Qv5/4kUhpbCa3MQnuthdV5iL1H9AGRe3CMWG8GWKuRCM5IoccMHkPnM+i7b4cZQvUAockqvGqVV850Co7k6yxCczlTqZsdtxZGZEIwwEiMgQMCAWwJBAcgIvhBdrHSCaPrzYku5tysaadXekCan7SIpAtIqScLYiuChvIcwdcj3nx8hE++cwN34gKECLDKo4k3bx/IZzSTadJ2uyjXWFKEgDjRw3Zfr4ynrAejeFVb58Ro1/dZlrTEIntrbjcBYKHhrrIfxHMr5kqKaa+LAWPEZiVGwX6zRvAjEAPI1XKoB7MHGYZrLIiER0YAIS0NRI9J0nJO9abnIocC6zsyGJmN0RVp10SGJMyuXcOrP/ADOLt7D+f37u2d+XpH1VpZaqUEgMrtif4AolOAgUgwsGgcwRoGWNMtvGTk6DLa+e3XLuIpl7WrnUHgOwjoAopieGm74mbLzI9Z8nYlfdY6+H6AcQ7mQpf63WdcfUn2KMnlPxd2lEOqUNPgqRdRIoLJwmogzDtWnWYrD5W/M7BAyKCXCK7lPRNQwgSExiE2JSfBM13a4+5LJSbP1Tjyb3lxaDIfJTHmnudkJK2es8QcKf/NXM3ZhfJcmejaWiIye0RkQhU9mK1t2bpm8u25ak9+kWoNU06WlAA/PSYSZw+z7KLMAlB4FoXEGqeKRQRQ1jzNH1F6Y5W8drzE0pQlJWQymZP522HkOm9ci+WFk+V/AvQF9egaBAizScDT+5jF80wtn/lJRLAweA0fAWKAxxojRRzQV8Ec1DNN3nnJKzCiME8wAkM9VoIKDgSioD/rPTEVhIsaoSKzrlEW+pIgWgOw2lee0zyFZc/JvpzOYaJl2zRNZLctxSPJc9UaZpWpOreTuy7SU7bGKSCAAlCsoVLgrPgaYxEZGIcRHAVIPD48QjfrsO5XGNTTi714fBAxnCMs5i2sYaxmDQxHjBsIsBkBNurAtE28AMz6EfN+rOZAgBDWHD+RSff9VMQUGhZBEaAItM7g5HCBrhWgazFrMPoRlkesGkK/duhNAAKjHUYcDyNiZAzOYL45BBNgo0VggALg2MKyw8hQaM3qPjGqdiVfQyNnlQmNT7mI0nmWFyUgh6QYw7BLQvOVFnzGiJsIYwhspWCEdYSDxRxHhwe4c/sWjo6OcP3aNbGqrtcI45irYRoiLLoOXdeibRawBDgDGEeIxoC6FkBEYwI2vYUf13CuwWw2Q9N2MLbBwwcWvYEYSfKel/lmkDrlyDlgVYxsJlxASWIun7F637ESpbTskVkB/SrUGahoVxYv8+dCcwhhaLDqryF5PoUEZKWdYAiIBmPfwbgRcClUKOkNFUVTpU0EdQEwmZLBQHgOc0QUtQiLgwXmc/GeG4ce867BSBGzWYdZ26CddeDogOjROoIlgDhA8vEkoIvgo1SLHV57BfETb2BjWmzQ5WNqwQICxREGDgygXy+xXi0xjAPADGebrCCk3JUpL04i7VTNoiwb5TBiCXmhTGCYGZEoK0iypAEgTcfFESGM8MMGY78G4jGIowB5LE8V8Lc605XGlhUdDdGUDZM8K7dlhG0Clt6CdGeUvTHNkzJVXWrRKu+qHcV894mZbu+0K6gfe2S4i/vbIYHIlLy+nHZ+QSLomYdcYPF/HvVi6sF/0Z0TIWvro6tLwr7v4fseB7duFTlrz/31WZ0YVCfXU8XTa5BrujOo4tVJRsocd2e+ZV+K8Q6IHArtiwEcR+X9VOgLF/qWdmfepVGuteT0PpMNv+n38vy0zwU0JwDsGRRk/0ZoyHA6vik9RyV/yV8VuJpF0HovVvLQJCcHT2avFsUnR1UEkzL2JK+S8PgIFlA/nYCMXyXThICYEkmxbRLcGmP9bnntSlElmlyehFTl0pHQDRbXlzO89vQQbeeAJr0jI4NhFa+6Gti1j3ZtjQeYyIvCV9LdW2eMUPpLP7LukT+QSxWUjCEZpQhgW04wF94p4FgEs1TNDiFs6QysBaNGDMMa4zjAj732zSCUgkUmAvPBYnSMUYsNlZlMAFEtTSv9256nilQLfypRFVOBeqId7qEQwr9s22DeXsPm6Wn11XQuJ4/m6cf7V7GSTao3JFKHgRyC+zxU9urtvev5Rdq7Hcnz3n/167+jgK73o60eP8Y3fu3XcO2NN3DykY9c7aYPYjdu84D6q8R4Mu+nyW1XzdWXQbCqDQcd7n3/awjNi28tqkTTIq5WI6zyoxlrdghSGlm+gyoLr94qnlJRlE5AQbJ0jRBdjhGIxfJW57BKc1SEIiM6WVLWGCKwh4joI0yImoPEACgCTO3FkUMOgcxkSiLSQtytdZME0Qm8LC+oAFIAmoZAlHI78ISX1IJTYbTlGhEapwx52nQNthL0C9PS/QXKbv1s0tgY5D0QIrq2w9HRsVh91JKUALFUaSgq001eLsm7C2BViIGmAW6E2/je8XuwXq+wXq/BHLHhHr/Y/H/wxJyhcRYp10Dfj9is1+L1RmZrF9M+DQgJoSxA19bhmsihetW3Che6QEnY2zIRkH2UvAqtNSANNb179y6ICG+88QY2mx6PHz2GtQ7HRydwTQPrHOb2ADNmHB0fZRf39XqNYRxAMHBNixgi1us1AMZ6PWJ5PlZAdj12/TXLJcWKBqTQTdG4836tdd99kkxSMYjQtA6uMbjzyi2M44jjowOsNxucnZ2j7wcM/YD1pscQIv6XL97HCEJISgsBZBxgHb7w3a/g0Y0D7TlmS6kAWhJeZg3BgfCpLz3EYl3CBMdhhDES3tK2LawxWG9W2Jw2+PqTA/AooJzTfyfHx1gsFvjExz+G46Mj3L59W4Dd8zP0mw1WqyU2mw2GYcD5+ZnM9WqF46MjfOITH0fbOLjjY5ydP8V63WN1dgbvx1wR6fq1a3CuQdvOECIQIuPo4ADOOAQW74kQGD4yRp9Coz0ErVQPKWNwcHQkicpXK3lXZjRtC+ssZjMnYnLyhGQBT1trEWPyBuUMWhXFj7JnEYActhOjR4CMFRWfkz2iIIpnPH04w9mvfA9uvH4fr3zXN2GtgyPCMA6IYPHeMgbWErz36GOEHz38MGY8Oxu6GGAf0I9eQpmIAAs0bYNPf/rTMMRYzFvMZy2ODxfqlRrEug4GRQ8Biby+i4DKngm/fe0aHuoeNeoNZa3RZzvhW94j+IAnT57iydOnGIYRzOKVlSq/CV2NcFbyAEX15DAAGjIwIITIGHyq7AYQOUQAgw/wIcCPEWQkHNo6qXwLY8EMjEG9AThgud7Ana9wdOLRuFYK+jBy4Y5i6UFec+SiHpW+Q+Ip+K1DRD9s3xltm8E8+/oU7rQjC1U8iqNUrdXDA+uaIjOGZNhLZmU5B2QAQ1r8IxUBIZsBouxVBdp6YAEd00/nLBiEpm1gQoBt1EtWn+vHUfklq0Fx2l9iiTHLV/ocEh5rqrFIUIEy2BpnwrN0iCLR14n2hS9E0HaOsa07d/WBq7fEQybpMHSeby3n+KHfeQXz4LKsY62Fs5KDDTm/fwVy7QW7uExk4mtVFMXU2L9/khKoGyvDVxJjJqqkfmDy9lD9wLX5OdF7xBhkP2qON2NM5ql+GBE5oh8GxOgRY1+tS9SIEy+e+ZsN/Dhis9loVFDMOozkq5OB3Fov8KOf+wS+fPsUv/bm/Ry2K2G+NIkMePftimBjvc+vBFA+7xi4aK0KqD+Pz+yH7b1t33FA1/Ymft7EmBf1l31MYoTvewzLJTanp2jm82dWi5EbL/luS6Gr/FleYlOquAVqTa5IVvgrHNCJpxeQczkxEfysQbTTSl3bv+8b3c5nVKyHGTSoUH0CMiMveR0uZpL16NO1dU4BNdcU4TvzrD19cgJ0drqdAmMa1piTwBOX0rr1rfsNC/pZCWGkClSa5jHZ7k/BoslXlzPW2npTAzW7eE5i2rufMZXfk8AHVB5NOq9RAURjLdq2xXx+AFQWpAQ0ihAUpkKKggasayBAF2ExjjjYHOA8nmM5noM5oseAT8w+ijOzQtM4LOMSd4cHGPoRAMEHUQC3ZyZDuDtW1ALDmgooSR0k0O9bCuTaaskynmSjxpCEXuUrKnFyAozqmYwRy+UKm/VGcqxpFbi27dC0LYy1olyzeNGRhrcZYxDUuhhmAdZacIxwTYPgR1g3ALzBQAGe0npDwvzEfSSfyR2BV1/GVN4YkRVUBVfYZQI/CkAs1azEctx1rYS2hiCKA0c0zqJ3Em7bjAG8CvCB0Y8RkRLYxYjwOFpuEBuL7Bkaos4bS3gzM6y1aBhYrHrMNhLeEoMAKX1osfEtYtPCWosYDKhv0V0/BHGLWSdgV9M4HB0d4WC+wPHJMQ4XkrcshIC+38AHAV3cQQscWDRWcmssQw/DDisaZDubgN4F9DZgjB7Re5AThctZK95jClpxZMxmnSRedh2YDGIk+CAgz3IpALNPwJ33IBQAm/P8J7pN+QzHfR47FS1O9072MaoaqoJ6Zo+OFOWQr50odeJRN/YW/eoAy6dHmB0McN0o+zRbyCOSp6CsRcgAK7EA3czIqWGKZ6X+NISDgwWcNThYdBnoQvQABxDrz6geXcFnHSlEAVKPh4hw1gMWOHIGZkHpIEroEmk4P4IoztZiNl8geccmoCsED+YIZyWkNCgAK/vRwRiHyCQhLcpbrYbWqmosoBaJDMHQpNrqgSHeraS5iRhePT5lXlLoYaxCyGTdFePSOayzmqnXDU15zWU6ystWX35ftwuwoFG9rOpKvLu37hpAnxtbemmtcIry3wllqK7b/kw/p/J54p117/pNZQyVnFkTP0KlYTklHSVJwmTwIRX9IJQznkIXa9pVqwsJVBLbrwJnxohcpGFp6dCUFBIKOKdQxuTFll+rnEKhlayYTsn5mT24khxc3zkRfeqDS/n+NB4l8OWNdkC2+t2rFcrrUAFWz2pbAgMBsNHg2nqOm+dzHG4aWDIlCzxh6xedqwrkutwpoMhQ4o1UPbtWOy7VkS54QF7z8i47t2QwTxZE9CnxHPZe0gN4PyKEiH4UoCuEPstEaT8HTUKfcmz5qmCU0YIMRr0OAcCxwVHfKGhYjPrIe/mS93rOlmdrMm/lpJfjWs696zp0R0cY1xp6+TLHoS07QHyrKgG/z9p3HND1frXTd97B2f37eOV7vgcHN29+0MO5sGXGwkrwpi49FRHSj3AFgbHWNF/iOc4QQsXbsqu8Pi9bsXTMUglsGiq2DUAlz6R6+DVDJUATLU+l6b3utFuNwRqNo4JMZERiBDA4BP0XYYK6EGfBXaq/1Z5iaTAlDJVgrEH0ESEGqfCDmqkzclAOiRCSylbLazBC4KwXbYMvEjFZvMaSlScp48ZhW2rJK7W/yfpZK/OdKoMBJa9YCNBcawL8NY0kBl/MF7BW8/1kAaHMyeWPZYAixs0G69NTdI8fwzWdAFgE/IWj/x2usWjbBr8+fAH/r/N/CSILHyLOz84wDEMBtIs7gSp0yPOZGHkKv3Gm8i5JJcb1+wT8fjswuhtNi4W1U5lzqyW5mAwhxIj79+5hMZthWK0Q/QgiQtfNMF/M0DQNyBr4MYAMoW0E/HJNI393HebzRfbkGIcB57fv4PzsHKdPT/F4tcJSk1pHLVcdQoQfJF8GF6N52e8mWa+NAlwBIXj44BGjWD1bJ9dbJx58IQSM4whwhG3EU2Y2k6Tzs1mLvu8xm7UYBnHZ3wwjxtHjyek5NsOI0/O1hMGywWbw6AePt37vAegbj9X7kDXPEYk3oeZG7NoO1hqsNwMiA03TwDqDxrX45jt38Pm3X1GAgnDr1k0czBd48399DbPZDAcHCzTOoW0aWGvgyOBoOUM7AuenT9D3PU5PTzGfz3BydAh+4xB8c4aDszOslit87nOfw2lzjsY+EsCdIjaLNUbXoz0NsFG8XIkMrCEE79FvegAWgMG1aydo2w43b39Ez+4Mo/dY9wMeP36C09MzPHn6FOvNGk+ePME4DHh6+hRkDKxzcM7BOqu5sxh9OntKpIyx4kWYFbAiIJMpZxGZ5pYzR2oxZmZwBRol9CmFwKSE0JEZ54/u4PThDbz6PV/Cyavv6PoTNps12DM8GM45LLoO3vvsXQouFc8QGY4sXNcAqvBaKzSh6eZoGoeTk0PMuhZHBzP4YYPgB4wbP6mCm9+rap/42hPwN85BTYfu8BjNp96UfKGSGAiAAwUPA8Li8Aggi6abK0+MmVf0/QYheDhrZcY075gfR/VcMxiGHv0olnpjDA5nncx3jDCuAVkGQ9/fOskfZ8SLJEYFp5jAxmGMjDEymgg0CoqxJsViQvbAG1OxOJTwXfGUTEDXdmroD9sH2c7uvYMnX/s6igf5B9fokr+2ryTKwXHV55cLsJy7vVjeAUo+/hMgGgABAABJREFU3BiEbgWGGI6IkIshRlaQK4G3ChAYK96RZHJlxqkATJe8ndLG9CaaY9O1DWw0aFtR70JVmTEVJQIYhk0G5FGBYvKDMu5UoKxSiTiNixErOS2N9aKSEVvzPQENuXpORee37r5qtMmlTXkByGAxNvhff+d1zHoxukWxYCAwwzLvf48JSFW/y57LJvoWyvJvX7gF3CkseLXXqd5LHlknwGc0KbqGCCF4rNcey5Ukh9/0G5WDPMQjN8nC1Vqp0OW9GEtSVXarRurk9Sb6pfJqGLlG/02A3HfpfHJZu4qz1tGdOzi6dRvvfP7zWD56+PIenuUMjRKp84x92D7Q9m0NdCUrymUH5ypuilc5eIVJFiWcA2P15DFiCFjcuA7jnn86J8Rsexi8xQv0w4vAqPKqe5CBDBTpU/eAW9seXReQeQV3SEEZJcxksL51hOGo20PJ30VLAE2aC6oZiNrEhL4W0EjfiHnf3LII28w7oEb2zKHLGHWaJy4GKFRhh0yTv9P12emnslDXFsDkUVWII2VF3lorzMVaFY5M9lyoXy+7EFNhKjIPKnxka3rtwZXfKv83/c0pPwunYVe7td4/k3dLlp1Y1gwFmEi9JHtnSoJKhpEyyBQLZL10dShgvTpFrDJkYYyDtQ2c6wCIt9esmQs4YBu8Ym/hB93347ftF3Fmz2FtA2umnmT1U8vemAJd8ndKg57mIL0TVb+n4e7YfKbzzXu+vYBPdkdHMEfHsG2759vnb2nM9W7I3+meYZbKixbi0dUPPVbrlYAZo8dsNoNJXpzaaw3+pV6NdXAgWOuUHgmQABCcawQ82WywGqR0tfce6+US4+ixWW8QfIQf/CTXYGQAMSAHcVB5voOVEDESATAyYxwjhlEqxJHuERjJocXR5fU2BnBOwARjCMZZhCBJVbthhLEO/eix3owYvd4TJdm90dBPhuRCdBoCGkPE4ycL9GGO9RgQAQkn04V+fL5ADBZN16BrG9y6+QqOj4/wyit3NCdfBGJEP6wzPW/GHk0gBDsCLqBtHOy8QbjWAB0hhcWF6NHNWlhjMYYRCBEheoxjj+BHxNbr+CHnwIjw78dRgBtrJOeVDzg/O5Wz49ZKLw26rsXJyTGaxmEYB8xmHTbrNR6C1etPAPswBKTwteR9kE5SVi650MdCd5Q25O/1uNYW9kTzrdG/ldZpLjBKFnndkxIyQzh7eIgQPG58ZImmG/PZTQrsODCCl9x/BwdzNM7m+RiHAc42aNsW4zhmKzER0HUturbBfD6THF1No55cHiOg4XxcDjpN6Z7VsZvIaBg4dg5kreTK0rmBsTCOcHh8De1sgUPvi2yknQ3jgBiChmpL/zEEjJuNeF0SYbmUMF2OEdYaXDs5geTsSvkLCerKlmm9UaCLdeEYBm07g2ta2KYFGZurRdZ5K4XapqTpSaqBJhOf/rR5Nva0LWGo6HdbCuaHbU/bpfjP8sRKHtZ7r51gGLz/mm32+hztAuee3Q+pohP6zB22/qJNjxwhJacXecdkayJluhNjlatV0yMkOcJYAbqkoq0Y+LIn12SQu0LArmxK5STl3IEEsiJPieNWRIwAsYVEIiZvWoAiS0hyfnLxOJraxtOccv6SOFHvrEVMx17/RdsfJ6+g2mttV24GKj1u+xF7ZmR3qcs+n+x1ldlslH9jdU/ypCuGlYjdma+8tPbtK56+Myn/SQ+vtmfmNXnrFqGyJmrbh3XyB9UrQchFhQDOhiUfpHLi2fkSfT+gHzYaqqhGcy4eTkmHMEa936wYu5ilEnMd2imRDJTfi8jgZDPDH3hwHb/j1zin8y218N0dxKler9RmS2/YnqxMk4gAQ1hcvw5jLZaPHyKMz+PZVe2srf2Y5f+sa337tquAhi+z7VaNfFa7+vXf1kDX+9+2qSzj6dtv4+z+fbx+8Gm0LwB0Xda2ZLgLR4Gt6561/DXgUBOn9BlPfr8I8pkKMtEZPP6u2xgXL0f5nowXwriztQmJYXD26CKaxt7vBbvS2DnVTCwghSQZToXnKi6/c/g0rC+hE1xCrKTvKdFNoTCm0l4KY2cdY8ndMLGyQRhGiW83WrVMvvMhFJQk9WtIc7hUuVl0/gr0QhW4BoCrXA9ZuChleLNXRV6QNDb5mQS+BBYaBUwDQlFY00RzEqVSnpapB1r0Ekq4DeIljw1KH+TvkrJHABuQaWBch6adZSGqaWYahmXxhn0d/1tzDeQIX7RfhXNd9mzbAbu4zH/t/l2eG/LYEriYqu3lGctSzNY2ot1ftwW0i9jk0e3bsCfX4Bl4mXZ1yv+thU1ZX+8lRMoY8b7Y9Bucnj7FN9/+Jg4WCxweHqKEA0o/zjVIOIRMBcE6B+sa2TPpaZExmy3gxxHXro24ETyGEHIS9dMnTzH0Pc5OT9FveqyXYo0cx1GrHEo+okSRkpXcOQuCRQq+CuOA4BkbH7BeD1guz0F0AGvlnUwk+NZljx8iAbqMkRxec131tusw+oDFQY/z5RoPHj3B6ANGD4A9OAo4TdA9SzllPjgCv3fvBt45vYmey/bY3gQHsxmOjw7w3W99DNevX8fNmzfQ9z3u37uH1XqN5fIc3o/gGHHaNrDWiseXtXjFz4BrM/hXW6Ff44DNeoWx3+BosQARKYg4YBg3iFGsuX42glxE+yiCYAHnpJz4MMB0FqZpEL1H7wPOzpZCW63FbDbH4dEJ5osFjo+OQLdugpnx9OwUy/MlCMByucTp6amum4drGvHycw7pmKT0LKyxOOL1U/ZhqtSX56miEcngxVGKfUjuRvG6CjHR14qzUemHmfHg6zdB3ziB634Lh9fW6JoWIPH6CqMX76sgzz++fQuHhwc4WMwRQsD52TnarsV8scByeY71aoVxHMEQUGzWtTg5OkTjLNrGgtiDwwhAvCxsPvBUebfppsi6L6ExBne6DkPb4HE6qwzANCBLuPnKKwAA56pUCsqfUmVfa7LGheA9htVKeVbEw4cPsTxfgjWX1+3bt0FEGgYr1dtcY8WrMySvO5seIyHKZBGCrFs7P4BxDiHnWksLR5n3JJ9f1ndO+yCyeHbtUy+f1d5n+fzbuu3FDb6F2zPHquzrYq+i52xcSE2m03oeSZV9a1LoYZGfOAC+oFyAynAJFDCVl8sU3Hre1aiuV8+b5N0P9bKxxoBjACUP1PJqyPlOA3KYcwZkqDyhpHDRO6lAB/kz1Pdc8B6Tj1lTG1AG25HkZzOVQ57psMC8I6urdJ1pfD0Eqv7Yxl/qPJBlAgImbfLdBWMiFJl1cs/23EgnlF5DxeRJAfBKLN3fyvqkIAzxthNZOmjo4Xqzxnq9xunZGTabjfApZpA1hcfqHFhrYa1B2zYgY9A0bZbvRdalHLZYBooM8nzk/AgfOT/C6bVTfGPxCIXvJnn/ZdDqrHhd9E31V5l3IsLxq6/i8NYt9L9+fmWga482WW192tk/76X32oft6u07AujaRwSfZ4OVxITvwaa8hAjK1+odVX32rFuf5+G7Xl5bY6CaVlM+sIlBiDfHnpEk4kvA+WvXMRzPEVpXiDg/B5PaP/SdIZMqywTkOHlWCYSrd60Vmu0udz7NljjsMqDK8s9ADreAWrFyzgJKHlsStid5uOQ6iuLdYaG5uYjgrCtWdRUyQMgeXYmZIINhpMlDxeoXK+YlXiKJCQt8RISc+NGQHHFjTSbEElKoc6egBIFAtvKcyNOTxmPKXqlAPbAm4yaGVF6TcaXY/nQ/p7xkaTKrNUnzmuL8p7NOKGW6UpgAF6ain0m4kwEZB9d0aLuQl9S6ThizNbAMtE2HbrbAfHGIYfRIOYjAnN36kQXbshZpDvJIMghYrF/bDO4impI+5T2fXXTtu22iZyY/it3nT55JU9kh7cSksBKA9WqNb3zjG3jlzh3MZzMQ5DtR8gHbWBW89LxoTwSpjggg5zkCGdimhbEOBowZM+bzGYL3mHczjMOA46MjAbpWa6xWawxDj9Wqh/cBwxjgoxQZAFISWNlDpRKO7gcCyKQzLF5eHCX/UoweBKtnR7y9JK9FSpaeIsYMDg9maBqHtmtxvtpgte5xvlxhHEbNKyd6h8wzwxLDdcBbt+/j9vEa94Y/gJEXmguM4b3PoPYrd27j5PgYR4cLOEt4/PA+1qsVHt67r3s9onMW1jRYLGZwrsFiPsN8NFh4g3Hjsfm9J3iMFc4x4PzsVJMRKwhHM5ABurYFs+Qi2/QBHDh7OSU6k3N2xIijk0M0bYcYNXn5GEBkEPwoAM8w5KTKIXg0jcObb76J5XKJR48e4ez8HMvlEt57BGaMfkBSBBMOEhX4B6nyqBOfktim858A5byXE6IaIjgULyQygDW2vI/SG6HXGl5hDaxjHC4WWMw9SMcQQoCBJNVvugata/DKrZs4Pj7OQNdpNxMDQ2NhENBYkpDMGNA0DtYQxnEA2ABsEYKv9GWlY2oMyBB5FpwTH6jPsPzuQ8Dog4Z8E4LutTB6Ad6tyWChsU7pWCWQW4Jpu8xv2m6tyegB5xza+SEARuz7rJTbtoFrDIZhhOHiiUcpDMs2GEYP76USpY8QkBzApHIcJQAYOr5cbk1yv+nnLzVv8Yftme2ZnliX3wy9+dn9XdLaxRxHd17NHc2Oji69vkhJtPN5PSxgytN462cWt6qbRT5XsKQ2YKGSjazN/5Bk51jOWZLfDBlYpwnBVR7LRr4azSDCtfUM33XvpOgGe96lfkcA4DgA0WOz2YCZMT88AKWqtUrHgw/wHPDFVx7jbDbk/KchMCIBhlJOyXoRp4JAHjepvJnBhu2BJZqecg0AqYpr8gzOodt5MYp8Unxikl/StPudLVkTx61rcz8KpBkmfO/bN3BzcwAXSoV4Q3vC63h7p+x5wEUtATtpK+y5eJKJOAleF6hrvPfFtx8pPY5+FI/4tRhe1psNNps11usNNmupiC18ltCQ1fxulGVZ55zkE21aSZNgi5E98y6okVB1kyIg69ox4aMPj4F7r+Lu28DTYYnfvH0fvQ3K1l4ygd+zBy5SP4kIZC2uvfE6emI8feMawv1HwP/vc898zHZEjXwob58cGb4TvLq+U9p3BNC1r71IUvpLAa9nnMfam+iFN/d+yn31cWTOfrWDXt9Cez65yJsrj0MvXd05wvrWkT7r+QlXZTya9L2bU6ESapQhbOcdS8rOjio/EXASsa77Fi8tw4DZqfySBAUuVgiu9guKEG+08qIhhkg78hlBEq+TIa18lbpOObaQvRIygVRhQYQpUzywArIXWAhFWEg5iibglE3E12QGKHJYzPNVX5+BKS7K4ORznb26GmS+X8E9r1aiqLleJOl4ese0FpT/TtfCWFhKsER693RtKgmuXnqVUigABeRz42BdC9fEDG4Y2+TErBKOFtG2M3TdHI1bwVsPqEcgpaQanGQUKoyrLlWNWEa5BWrt+/lCYO9Wk6l4Edqy7yRVsuee56Qzxlv7vIDJwGYz4P69+zhYLBDv3JZ9xoTRe8CQ5CwiaLLsIqqm85fyGwEQT0UQTENwRvL4hDBDjAGz2RxhHLFZLND3PVarNZbLJTabHm27xDB4rPsew+hFYI9RvXhCzhNHBDRWMNNkRM/V/JglfxbLPaKAG4hlXMedADEuIcKucei6DouDAyxWG6zWGwARS0QMvZdwgCTHM2AboG0JbzRPEeIKtPoB9HyCrmsRQsTQ9wLGGoOPvHIbJycnWMzFM/HJk8dYLpd4+uSRgGttm8MbDxZzNE2Dg9kMXU+YtRFxuUI8O8cTfoQHfI71Zg1mxqxboGkaOCeW2nbWABCga/QbRNIKp0z6vuWcM0ccLBZYHBwC0Bx3yzW8D+jHESEEDANJLjYiDbc2eOWVO1iuVvJuTqr+LZcrxFEEcSEHhcakUAprk+APPeNlLCbT21IxNYFYEQEhSO6p5Mkp/YiXl48+C+pS4bJB17VoWsJiPse8k/xwgRmeBex0zgqQOJvhxrVruHZyIkCXD3AgBA7qwTqTqprWIKS9ZAghjAAMwCFX4kSm9UDepKiAqEpJKpq3rkWMed6dGgnKOgHWMhylXIlA6yzI2IoaQHKWNa0o4MbCdTM0oyQZb5oGzWwOZsYYlM9aC9u2cI1FgNFKclAaKZ6azrUI6BHhETXMJXm2WKswQQa7ihKaQ5xTFVUgg10T2pSBgYqIXSCnfIiRXbE9D0BVIQ4X5qHcw2wulSVTU7mnmc1w8tprldHr2XJl4WNXQAKqK3ZAsD1MkhP2wJzBrnR2U5XV4tVuRIZQICjRNGuSd5WTPKRGZbxqI6dXtCAcr1t83zdvToAu3rNO5Y0ZiAM4jthsejCAxeFBpp+5jyBA172bG6wpIkC9VtVYyhpGzVQWOiIBL5zpVTHoKTNNgl1Kd5EANiSDKudxkHqYhRDUwLi9MroQyUOLq/1DSQ7h6TRcRSyqnkNM+PiDY9xZHskTqQ5FLWAOR5GUjYJkmRZfAEbtPC977PHua+aX2yFyk10scmn+Y9JFXQglg6W65N6Pkodrs8EwDlitllivN1r5Wvg1CJpTSt7f2lIYoWkaBboa5aWpqIi8zdSBjqb8K88g8JGnhzg4ZVx7e8SD0ODz1x+it6EytL+89rzdkSEc3bmD9qDD2Q9+FPGLXwV+7QtAjFNjbwqd2LvmnPeDugxU9OCFX+UDbB8M59wXfXX59Ve/9jsW6Ho/W/QBD770ZbQHC9z8+FugGsj4gFolj+S/d3dGEqSL4Lnbz/u56XlC/2tX5noUSRFgIFukLhV4eTofpB/mkDr9+5V3CH/0PzHm98toKClPCioJ8xBBInBUKYgkJMQQjE3wR/IUihLKESOACIomKzFG8zYIkJLCpTSHiv6dACIAqsBHjOOgSuUIjqwKlSp90cDkCo+FeRstjyWKj+TK8WrRSQKLa1x2S079GWNzEmcAWk0rjSHCBz9dLzDCIBXdrGvEo0EtQUmJZbUikb5vXlMU5aZkfShzk78Hw7Dm+bJlniR/akCEQVTgEpAQmDQ+zQqhVlUHhubR4BRCqiCXClsi7OimofSdzq0t48p784WAqKu1+fXruH7nNax9wMa/SNDiC55lVtDBGrAPuZvRezw9X+LsfInz8yWODg/gnMM4Sg4t45yGJRgVnlPepDQUyiBEsQgCYxxLVTgATePgrEXjLOZ+gaOjI2w2Erq4WffwwWMzeAzDiCenp+j7AevNRsGwDcZ+RIgK0AJgA4xjwDgO8KFVcCuAWITDGAM4ltLghiCu/eoJ5INsiMgB1jrMZjN0bYfjw0MgBpy1DZbn5zIHENCjaxscHx3g+PAAbdMgogN//Q2cj8domgYcWSsgBfjgQXHE6vQx4riWfBhgHC06HLzxmgBGamE1RBj6Ncazc4x3N6Ah4P7ao+83WK/WWPo1EAbgukFoCacbqSx4dnaKw6MFrl07xmzWSWjmbI5gGyxvLYHIMGYDcx5hzxneyxzJmhlEFvB9NpshMjDTHCAMzjQi+BEjs9BLBo4OD9G1DW7cuIaHDx9huVrh4cOHGHMJ9BSabRCNAOYhxsneALMmfRY6kQAvp4UsJBSSwCkymhkhjOLNoC5Pxli0TYPDg0McHBzg+OgYhwcLzBcNXvvEU7SLhzg/PUMIUoVy1nU4XCzQdS3atsGiaxDHHo8enMOPI5bn5xjDgI0fNNzDYj5rAGoROWgerx7BANESnAJszlqAreSX0/OQgH1jSLwe1XiRa4IwsHnyBHffvosRBj6B78wYxxGmaXD8+mto2g5knZaH12IonLx/WfOtMEAW0OT2ZFuQ60RPdQ5kGgnLp1R90YjXWAQiW0QIP0qW8Qgj6yKxoyDrYIzBzHVgqIcvkGl/De4ZI7w+BOENCbQo4MWzaFShVfWfH7Zvtba7MkSEGx//ONrFQpRE1xSZdPfqAkbUAHD+9qpQ19WGaWwCtMqTmBkIjIAA8h6jl2IlfhzBMPAxojGdnEEF74zmXqUMfOx/5sHQ4P/61VdxtGmnQMJVXkjBtSzrJ6ApcgHhSCos/+A330Bvg1R61ST1yfAUOeTPNnbEf//YN7FuJNSa8mO0oMc4gkOsUhZAnlNVB49abTgBiYbEiBJDlJyGqSqvVvZN4XPbr55AhKtKPtuznDxXtz1tRPzjPM7AAbxhDKPIEYYIzfZTJxjNFs2p9KxkAM+aDW/dccm6hhoE27lOPsizXIFzo/cIIWKzWeeK2OPoNW2A/Euh7M4JmNV1nXo1aziudQp0GTinnoq6p2KqaUwp2sFU71zyPNdA3fTli4H8Zbd3ffbfuAP6f/5I9uI0TODBg//t/xd4dIa0C/c/W+fkQ4+ub7n2bQ10TbyonnFotpODP+va5zqEzNicnpYqTPvaJd3tgEn78KgXaRMT0BWPP6UcU/VwpvdmUMIZcGNLWNrLasoQeUtozaPIuFwWPXbnncvI9+J7e9p8zXjrywy/YSyV0LH2wpBqgTGmMKak2Jmks2dBIyH8aX9GTSAN5QnJ0ymFdAGoLGTFLZwZk1LHyatBADdfVdMJINXsuHouwCg5pkRM4RjzewQNe0zeWDEaqb5TeWmRmXpNpFkVhTzkSizM5dXjOIiVyBjEWEDfBDAmwC0pdkn5ybpsek5lEKmZJjMnVlv2hFFmm6t01QUDUqrWCthNlsiiP1cAzEVnJW3MC76mrZ/Vfbvk5HmkWPnedR3m165hPFsCfvWMey7sJjeTgNAr3Jqs1pHqeWWMo1fBqgJBQtA9EmFhFLNVoJO36ImuQwYzdR0ic14eMhaGJL+QdREcGjjXwPuAtu0QQsB8FO8WshabzQbNSnIFpj3pfUDKVxEjEKKECiYvISJGCrcFM3wFfopwLgUWIkOS+TIACAjmrAiHsW2xmM+k2uPQS/JvEqBuPutwdDDHydEhuq4DU4eDhzME06BpJKcSs7xTyr3FMcAPPdhIondDDq4rietJAY5h6BGWPcZ3TsGDz3m1hqGHH0ZQDDAH4rnTDyKwe9OjNQZxvgC5RrxxrIxjPTNK5wJay5ijCidEWkuhv865DEyH5P2VriICYsQwDrDWoW07OGcw4xmGYYAxwPn5KQANgdRDKNCOGDGCDwKaJLrILOsYpZIZjHp3Ocmt1lgLGAHKUgJm8caDGCNAaDXcdLGY4/BggeOjQxwdHmC+aHB8dIh20YNSSDhHLGYzHB0cKGgvCej90GO1XMKPIzarFQY/YO03UrWxbeGaDtYI8BMADByBKBXZrBZfSAaEmA8g5XlL/wNoi54wQj9g9egxvLEIVsEoZvR9D9u1aG/ckPfsZpmuRf1FQFqukl8bgAwYCk6pYYOs0+/KGQXEj9VAchExGT2nkoRe9eSpYYk0YT0zQl1hckIQUx9lDjLIlZCLywUo/cnTnx+252vK3qYfpVW5eP73XlOLnhc1EtDZNg3mJyfoDg/13i1B4MKOKG3LPdfvjvJqgvRWJ1lhBUAljxLAOfddDCJLCUgrfK8xWnBF6WQRNVJI1/RZxITOGxxuGnzk6QE6X3lfcn7bi1+xEF2VnSk/g/P9+j6wuLWUueYMdGl4egiaEkNku5XrMbtt4NsCpFD2dCaMa4/opbp4BGNjgxh8U3Jy1N7/ZYjJa2hiqK5kw2Lkrj/Lb/GMJawetLXsRIQ2WMyC04Ix6RbVNZS3jH4EhbL2gZImgMnaFQynlmrKQ+vw+guwqv2vAPEmBqD21e0zJn/vA7p6LeKTqomLgdln3aWOAEkGFymuYmGd0ZBFl43URvW7EDQPKldefcqb6zzFE7k8OSro+vNknt6DRkDlvVBPTTWm6Q2hMYithq8eLkDf/aY6OOgl/Qj8H8egwSMVzCIiYNOD16kwB6pnUT6HH+Jc3xrt2xroqtt7hRB/kO1dEYRK5kuBSzuA0aW3P/uqszdv4Pz1Gwjdy91Giblnxr5nWQkpZC1VDNkFu2qQa/dtiipRX5/kCqGXlBVlVCBXDAGRVPkDctgIMWuxwYjAIixE72ECw4QISZZeKvdZW4SBAiylSnVJICoVGUX4GMUTpVLS5d0imEnDtZKiSlrVR4muChKpH6+eYZRK/xoCswHBZoKdd41a3AmcrX3JNTqFpmW3do4yDzGAowfYKWM0CijIe2VOQNDcZCZ795S11FTiKlAmb5Gk/1l1r25nM1DwAkTYEbAjEMWDwDiXQ8IiEUyMGkZaSnzL2hcPP9L3KWEJWxuFRChKa1fuYlymFOy2y87ZVYXzF2vHzuHEObjK+lpaEVdqV2ynSb69F9fuxhK6thGLoBPPj9F7KapgCLDiLZLBRYRJ4h1OluG8x6XARGObIvjGcogNEdgYEcKchWsaBWGAECNOTq5lT8P1Zo2+H/BI81s9fnQfQz/g/GxAP3osV0ss5h3iYpat5957SZmX1hYSxuUaC2MaEAj94OFjxDBKGNrQb9C0HbqmxdHBgXhZrVcYR8nRRzEgDgNOnzzC+uwJnHUIaPC135vjfDjCbDbDYjHHzRs3cHS0wGzWIQY525IXQ2jiOI5Ynp1jvV5pniuxhp+dnSGuByy+uYGNQKOeNNYYzBoHhsXBuUFcEnrfYAwBm80K89MWB/2Ig6MGs7nF+U0LNAZNJ/Rl3PSSLNxaUeQGCedjpMBd0iRLENpABmBgNhPh9/BIKhmenT5VBWLUUuMWr965CR9OMOsanJ8v8fbdtzH0HuvlOs+795oPTvN5JHuKVZCInFXwzGExX8A6h65p4eOA1eYpjJF5aFwD5xxmMwnxXMwXaDTs1FqLxlgQRcRhg8YAi67FyUfuCHDmHGLwEjq7WWNz3uP8TJLqr1drBD9is9kgICIgYpjP0HYtDsMR2rbFfDFHtATmVhLjBy8TRrLP2RgInjbRRpHyMZKxAkJVxg/xvAjwIaIfNT8js4SnbtZY/+Zv4uTOHRx++tMAOTViaCivaoyknnOWCg8yGvZtDMlZNmLJJ9uqpy/BWJfDdiMzAo9C/4yRnGvDgGEYc/4wYyzarlP2UwBySgc6P10QspRHTcZDWcn6sH1ntutvvonDmzdhu+7dd/YebBVDRgsUZakQQo2T0VEr2gYvXsiUPKgA6/bxVezVuF00+CNffh3Xlx0af8F9qLnypaOGGKzT2a68rRI4qLIXUQMyDGNVngkBYxgRggczMI/AH/vCxxARwEg8sYBPqydPMfY9Ru/xcL7Gf/7E1xBs8bQFEUIVcp5a0zSYzyX0ewpMyRtOxK1sgaypxrNbzqGbu5fx/MA3buO7Tm/hGmZ5ThPQHqLImGk9R+/BMcKx13dWGobtn9NG1X/zu6UxVN9cJCsyWEJG93e8WyOr+noYBt2LAiQfHByAtKCODw5NaJCiOLquVf45F3nYWQ1ftLAuVVOUZpJulCI+qMjswfschppPSqWDprd6+U0XOBnBnrOxNbj/qY9gOOwQLzqvTQP6f/xxwAek1DAAgX7lN4Ff+h/SD5BBd6o8uj5s3xrtuRCKn/mZn8E/+2f/DJ/73Ocwn8/xR/7IH8Hf+3t/D5/85CfzNZvNBn/5L/9l/JN/8k/Q9z1+9Ed/FD/3cz+HV7QiEAB89atfxU/8xE/gP/yH/4DDw0P8+I//OH7mZ35Gy8y/ePugwS4OAf35OVzXoZnNJmOhTKT3HEbe/vMC6nb1kezt94KPLrz/IrArNBZ+0WE4nMFfUGXx+XMSTd+RK4rJmccVZpGNKqpkXWwpKN5DmRhVj6zhrskIiJIql7/giiFnlptvSgKQ/p7GJjfmcdfPr92ZhU7Xgr/eTgnSK2OYem2Vd5muG0/HN2H45fmcwavqHhRgjYzUrUMKkaG0FNVY9T9G805I9flKKCyuUtnpLVlFwZzv336vOlxnMp0JTKq83+RzyvcxqjFQNXCazO5k+nSbTKZMbi10pWbaid5kusOl+3rfZIEo9ftcNKoIeGEc0J+dwQ/+Oe7f3yMggEFTWV6rAZY9q/9J61VbKFPIWNs04slCVCyGlam9dl1P3j+5b+lVFfg0eeWcyPYoGzed4VTNNOWKSJ8RWURmNLGBaxxm8xEcR8xnLQgS6gg+x7yzJcyNa4vx9LnpjKR8dZSKGkC8IEsOFslh0TiH1jndt+o9AwIRI/qAYYyIziGyR4tHmNMGHc0wwwwdPBZmjoVbgJpC66InnD2x8JsBw+mZgGirVQa6eLUBBq95xghMUQFbUnCIwCFKvpdRchC2bDE3LQ7bBeZ2hpYa8TZiBnOLIRL8OMD4lAS+eIXKnKXxqVLFKVS4FNSwmmCcUDxRZSNJknlHFvNZB44BB4s5nB1BMJleGBM15LQoWCmk2rkGLoFWbYv5bC7lzp1DjA26lrPXQNu2cNZhNp+jcRKiaazkIDGU6D+DTETcHGJ04rlobYA5WGEcevSbNfrNBuM4YL1aYhwGjMOgXtwBpIULYvDwAzAOGxAYs3knuU+MAThqXqtCE7nadDrLQKYlZb8X+LymhFOZJ+dtHAaM6w02p2ewbQvbNOJNxZypifcR1iShHFtNzm6sql4qm81g9IQn6hnI9FvpeirgkLyGU+jL5EwrNTCU+E7MPCkpoDXZ/tBZ6z1uaX639kQYR4ybDXzfX3Jr4hnP5m+2beFmHdrFAs18/qKjvbhNEKGrbJry4jz5tPDfvQ9JBkpK4YmmOpM0kSe2UYD54LDonfDRaHC8bnE4NOXa9OREw7c/qweqPJrrDzIPLrwYED5bG+cm4zQQ4wwJ/XUROPFzNeqVAi9J/un8CB8cBj9iDCyFlqx6jKZoAq3QWsurxphCK9JIEr2TP/QxJZdszo/2Io0L7ZiNFofrFnZG6hJVPJSyrKWA1ziOYtiGV/rJRZ5LtHHP9iqAVpFp0ufbMtQFw8UkJ1j9BSBG9elH+bdQ0Wgq7ueZd6bweqMVFa11cE4MGFTl6AIKf8l0Xt+lzFfad9VGr/ZhkhNeNt3Oz66VxC2wa3pELt45xkcYH4Fuf8ohIgJODlCfJYIBFjU4Pz2MZVlfeMd+2F5iey5k6T/9p/+Ez372s/ihH/oheO/x1/7aX8OP/MiP4Ld+67dwcHAAAPhLf+kv4V/+y3+Jf/pP/ylOTk7wkz/5k/gzf+bP4L/8l/8CAAgh4E//6T+NV199Ff/1v/5XvP322/hzf+7PoWka/N2/+3df/hu+j23cbHD3t34LB7du4c4f+APliw9gr0/F4Xdx1Z6vVzcP8Oj7XgeseU9fTZgJFYpVPSy5g6eqaVfqC4WR5rxVFUMGVGGmJMCIB9I2e3XWIarSblhCOVLYDbaYd+rTEME1LjMSHVRSpRHVHdhwBKD5U6oOcnLDpHijjNPUzDK7WEewKpQZfDFQBV1yThgpApZ/T4korTMS1z8ENBzB7HKCaaN5yJxLY3R57pwTSAyq0MbKg0wYXkkIPwWtpI2quKeFNuqZImGeUKxNLKypTHfbdUhWwxCD2B0r0JNIEpsjyU06NxK+GbIAVwrZx2pMtYBYuLjo86z89QKQ67J2mex8SVs9eozH95/A3bwNe3zy/B1cpW0L0NpG74EIzKrKqtZazOdzHJ+c4Pbt2zg9PRXvFg6wSNUwpZKhzD0VIUr7iCjPS4JYyrWWJ9QoiBI1/BFRrIuaIi+CkxFbziIZWFjMFgK+XTs5QgwBw+YNrNcr3Lv7TSm3Hj3a1sHHIEo/StJgUNSEuR7Be+m7szAwcMZK5UZInjfbdGiaFq5pMe82iN6Dg0ccR1j1SumcxTh4DH0PBA9jDD5587fBkCqsxhIcOyx4jgUvcLg4RNu22Gw2OFsb/O5/uY3VkrFZr5EqIFKMsMy45hwMGTSzOQDOuaigVl0AiN7DB8ZyzTC2kTW78yre+sR3Q7BOxrHv4Tce643Fpu/x4NGAoR+w7gc0bYfWOfHosQ48qvCsRQREd1MP20RtWcJWhn4F7z38OFYVnaRk+cG8RddYzFoL7wM2mwE+SJL61VKS5vabXumRh7UGs9kcR0fHODm5hmvXrmM+n6NpWgAE70c4S5h1hWZazWWW9l22yCbZnCiHgKy++SmchQGPHjyCnd3F8Uf/B4Z+hdX5uSa2J4xDD44RjbOwxqBbtIAxMM5gvdmgXy8R/KBeCx2apkHbOIyI8KPQw5pOpSIH6fils5CU1SkHUp6twKs1pPm2lCeC0DQN/HKJb/z6r+Hktddw7fU30Pc9QoxolI4P/SBj77qsfCUvYQlFKaG93nsdCsGzGD+E/os8ZzgpcMIvrbGAFWWRQ0DQ+xOIleMbAU3cDcBpJWJmIHqkQiK2MmR82D64tn76FPe+8AXNNfru2+GtW7jx8Y9NZZdvgZZxqPQzMkKSPaiArwAkd6IVr+K2bdF1M0nXwARnmv0PIH0KR7x1/wif/vptpUMEy4Qih+SL5SftERpqEESPVIxFZslyreYzlW6nfSTcShyrxeglDtiSB1LA65Qvk5Er8Kqcu2haIASpMrtY4PbtM3ibUmaot0+MmTewWq0lx2yvcrymPIjJg3MrQG9Lvk8J2J+3Zf6kuTcZUG89ST8iEi0jsICKMkYxZsCUdcmAXT2f+YeC/olqJ73ClPdMugdt07bcbakqXPc9uaYCAAFotXD5uzPyJuM4TsA7gNS4B8xmUjG6aRopRNK4pPxkkC1WZ70ee8rJxSkvZ47xm6zaZMjS5wd11i9+LoWAW7/9TQyHHd7+Q28iXOTVtbdX2vq76KUFAH/BIX/YXmp7LqDrX//rfz35+x//43+MO3fu4Fd/9Vfxx/7YH8PTp0/xj/7RP8Iv/MIv4E/+yT8JAPj5n/95fN/3fR/+23/7b/jhH/5h/Jt/82/wW7/1W/h3/+7f4ZVXXsEf+kN/CH/7b/9t/JW/8lfwN/7G30Db7vcQepntIm+jGl3fzv21Dz/f23dMVZUqCxeTVDF5Aeq8l9BXo5iIwDvvNfVmKubZ3YEk4spbw6wtF7kZAtsEQF3sRXfRPO9+Lh4P+6mCvsOWNScR44sxrmqGiixQKRLlcSkp/fkh8D8/zTh5G7j+FRXMI8Oq9b9xLjMKIoJhA/mfWBJiCOj9CA/GQFGVEclNEn0AvIFBKdGbcgJ57/NYZ7OZVCtzLjNMfQvxgnDCnMhQVmhrQ0bqUyqqEIIq1Qkgi6EGeCazCc7hhIwQvChHwUuySu5gxL9dchD5lMheAC6xEgnw6XuZNyosTtcqVgsg+ypGn0HF9BIh5W3QRNSucYVhE3Zcg2vlUMI+JUG/pWqfgNULSJJoS5J0GUftAZdkR1PtkaTE1/AcVDjdwcHqjca858v97Ur8UIULglhEEeLkLCe6kIFfKt9kmVgFTdJ3uOg522NLfWcPKugSJoEnAY0xCJire6FeoZqWFhqW/Wm2BD/9VAV16cxkesP6p4wlvc+URkSWcOKcZ4Il0fbNmzfghx7DZg0gan4JEfJDiDlvWYwCGhkYRET40cMYljLy2SqezjLAmnvPWQtnHby1QAgadhtyUmCxBxIaE3QuAigS2A8YNx7r2AN+Ddc0GIYBqzOHcXOI0BPYSwhF9sMjguXkESNl3E1SpoAcEsea7DdGgm0Mum4GYy2GccSmX2McB7AqWZElN5aBgTEOzkVY24CshY8R3ke4pgE0P2HUJMKs4ylLKB5ws67FOnicr1fFmkyAhYTNmgaIwUmuM0OIwSHGiNY5+NGjnw2lEqOxaNpWQhYNYdisEf0I1zQSZmQNEAiBGVAPL2sSgCnzkpT12gupH0cE77FSb62z01OYZoO1X8B2I9xMQ8gjMghjVPllTvnFZE0k3Fk2xXq5hG8bdHMBXRvXiHEmTsOJ9DAJGFyBW5xOTOI5mvsQxsCSRaNKWuQoYcWap8xYAwPAr1ZYPrgvhUeY0d2+DesaqQxsjNJsyoec1dAi7ycfMsu+YqWvxCQhR2WbASyVH40V0DVYqx58UM8+vTQWjy8GC3it9ydQUhQwJyCXotl1MNNEz2SefLbd8ppPKRGmfjuJ1qexYCos5Oe+iHr9fO1CmUn/w/XfSZHekVt3CXuhtbV3+BQr2dfCOGL95Ak2T0/BWpnv3TTbdZhfO8Hs+Ejkid1Bbn1Qr9seuVUYPIpHSdkcvP+WSZvI0hX/yCA4yh6qjZi1XGwUuLDGCPDP6QzHyU7rgsFHHh/AasWdW+czNPkYcZVwibd+ouI3W/K5yvdpvDlvUn47KnyRICyCgajFbEzKwwfhFVlG5KievFOwI/WZ5Cp5toF1DoeY45Ond/B0MeDBySZfa1SeKzqVEU+pmJLe1/IV6WxU8lZe2rJh63XbmZR9LdGB2hMqRkllkQwFlIxzdfh0is1PsnG9T+qDU3k7VcYUyXPlMuiRciMmY3eOTsnvUHQaU6036XunsYUgIZVBc2lKsRh5RtR1tFrlPWjlaaMh56TVj42RlBJT/GlKI6rJK2NJn1Uybl19k6BOBElepewbr45XtUfhs1um3rwnKqc+5Hv0yqs0ExkULtBJmVI07d4+RWee+CWKMbdKCbDzPrWXHHDpXKQtv297Z7qUr93thy6Kcf2WbM871qtf/65iBZ8+fQoAuHHjBgDgV3/1VzGOI/7Un/pT+Zrv/d7vxUc/+lH88i//Mn74h38Yv/zLv4xPf/rTk1DGH/3RH8VP/MRP4Dd/8zfxh//wH955Tt/36CuX6dPT03cz7Pe8ZYUws2eelAl+7v72rOf22agPw/b1SdGvca6SHLAIVwL4VCfrivvospDRmrFcfKA19IUyu6i/yb/tognab+qbOc99Fmy3GGP5nPI9OlDcuwX8v/808Af/G/DHvqIML4hS13Ud5rMZurbNSoc1Fs5YODKImx7Be5yen8JTRGhFoWutRfAjYj8iEmCjy5YRqV44YrVaZQYWY5TcLrYkI02KiLUWrTguwAUn1qa4bdlhtaATbIxobKpohUki+xg9gJi9OZAUZZWGvB+wWp1n8OgwHqrSaLWKS58Vr66T+RF39IiVHxCQupO+GSFhLFk+jxwl6ScZGOeUiUm8vw8eQfM1dSy5dKyGmmUvtUzokxAhngZMjBDH7D4v3m2knmTC7K2VJOmMqBbLmBVYea9k3+TJ/CJfA2TJdN+23tqu78LpfqdR8uII6s2Y9rhRvVA/q5+Z8r6phHrhsLekrmr8ersq9El1jUE8Pvq+lwpKPmDWSrL4NFEGoiSLTF5oYi0c1k+MRcWQ31KhAXXjolgJgIZgdGMxkxZ7KKFyHCO6TpKqWmql+uHBHKvVOZ48eoh+I6FpgAUY8KPkdXPWSJLhMYBYwKkQBhARZrNFBqwIEOVdn5fyOs26TkLZxyWiB8ZhBIHFG8wYCWfTUJCkYHhm+H6DFYCnVMLBNssZ+vUt+MGBYlSPTNnbk5YAnGoJOYaSVzACEQ5kLBYHhwAZnJ6d4/79d/D09Clm8w6ucZgv5rLOxsI2hJYsjG1gjMPoI/pxxLWDI5AxGMaA6ANCGGXPpQqtuqbWWhwfHmLsNzg7fareTQ2sEXCuazsZcXQyF22TFQnvg4SQKKjibCO0whiprLne4PTJAwzDKKGMrsHx8TEaAwTj0amXRbNYwJpWy69KZc0EwkXNNfj06VOsVks8uH8ffd9rSGIEf/kObn2U8cb3PZKdyQxnZWcKiWZwHAEYIMo7NVoRkwh48vgRmrbFTXdLqzHO0Pcb9P1YBF1DQKQpr0RK8J4ARJlSl+igc7BkYchiGAdwCGjVINC2jeZosxjPTtE/fSLhg8bg2q2b6LT4gUlVKnWzSAh70NxmhLaVCqrZKMLIXpXBS8EJUaJlDzsFFoWTcKnklmmOeoSknD1RQ2w1xNeAMOtazLoOi/kMjdPCKNUWrw06aUj7wmNo62fWGCZ0sYAVtfI5UbK/hVotwwHIZyzx4anQljzekXkREYpUesXX832PB1/8klbrfPetOziQaIcrssOJkleBJXWTLVY83afXI39ykcxc8yBQdV0CdlMPeQ+nTSMCdKJJ1jjN90lI2nEtGy96ix/60h10Xitrs56UFK5r9qljKqTXgpN+LvJikmW1YAcbOOv0VeSe+r2Z5KyOoxhMulmnY0E2WKUcVVErH9cyUeKzMbDmZBKji7UO12ODP/HNY/zuK6f45VfvZrDMVp5cKaRdvI0EbBq4nwBhMtXpvZHlX1S6Sr1+k7nat7Gp+jam5wh9igBaLcICQ0iG4mQgco0DswEPaS5Mlt/36TPFs1W+Pzg4UK/ZOmqkXpDJj533A0SmTwWhUhGqfpDfR5W7+r7PBudxFN5ycnICa202drvGwQJoUIoBZF0Q9ZEkfVeqjApSSGhbA0vU2SiYBxaArnFNNvBJUap0PktKgRTavr1YNcic9j4Dk+JUOy2d/XoPvaDMLfkxuRy7PVsqOyCkOdLtSiRnwVp76dOfJ83StuY7/ebF7vz91l4Y6Iox4i/+xb+IP/pH/yh+4Ad+AABw9+5dtG2La9euTa595ZVXcPfu3XxNDXKl79N3+9rP/MzP4G/+zb/5okO9crsKwnqVNiyXePiVr2Bx7RoW168/9/01QHaFi/VaPHvfYw8h3aukX+nJz92uZBHdwbIKqEHVgHn7+md1nZhMwbUyc1URf9JRCV9Ejms3yRuhaTTZ7ghCEBBFCVfTNgAiIolSHgIjei9lnMdi3UpKrPc+e3Slv8kYuBTmY6jsB065D1TZUM+tmDxFqFjapGyzhzOiGG8LMd6HDAQU1/EoinrTwPtRwSNkUC4JPkGrToJZvV48xjExflZPAItkobdWxh+5eDHk/AwE5FzLVha6YQcTTX6v7IFFBaBM88AaKCXBh2KJFGYjZZGtSTmEAkbPEo429AhRymVba+AaC/HOj5Mk5PkXRmUZ4ck+3L93efoBlb+n25W3rt/XanH83Z3KfTWbnnV8VHbJa1vAZGRgtlQuFBAyKwXpfCXrFZV9nIWpMsGFhgm6hXp+aiFsIsCkkI7tKaKKblRP2/gWbz+5heX5Ck8fH2O9Oke/WeG77jzB8bzP+b4iaQLvwIhGPLtEyE2AhELQiUYhWfUtnJNKiqNrMGSh18Ag5R6SERnwzv/qdUnbzBkpAgBrwNU5mLSsKFTW+9SP0k6jtCwy4+x8CRCh7VqpSGgdVus1eA3045hDcpxr0bYWkQV4CZEx+pCvAcSLyqFBUr5yiJo2awiNNWidBThiHHqMvYOBgELGGLQ2eXfoLDABLFUtLZmsOIIiDAjOAF3rsFkTiCP69RIDEcAeDQEdBSyVrjVtq9btad4R2zQSRhgCzs/PsdmsxUMsgVws9AL6LwngUnUs0QQGGRYaEyMsEcgazaGSLNGSpB2N5AoTgMliHBX819UuYilVeznvBKTjIUpgBEiUH2MIDupBSRLOKGNNBVISUBVx+s1voD84xPXXXwfAWK9Xwke8x9Onj7FarjQUtAGpMrg8X+b8Z04F+Hr3yTSkdY9lH3PMdCAfbo5bn8s92Zs8SqXLNG8JBHvZjS74HUT5fL4Xz31/W03dFfTA1d4qhoDTt9/GkIxwSS56XsVpixWm35NSfJX2rDE/u5tLeth5nekHydtf2MzW2+s2iRw1cfkIY6JG5hI4qgc+LL7v/k1cX3ZwIY1YPEYYLPTQjxlUNkpoxJAhZ6fIfeKBlcMBWbyyrLVSvCMBXyCMo5diEG2beReIYCxgo5lyG4LKmhL2L/wleTqlWSlJ5YkimC3IDxDhqfbIpkm/hRlNv89kYeuWixeUdy7ZURcuaUmWFA9vWwzOQTyrPYss3HUd5ou5fKd03FEp+pHBrC09zVRrlGSjrpO0BqTvn0C7eidtg1wZk9czwjouECkAKcbFEAP6flBD40bos3Oa/oOxWCxAJI4iE29iNTKkn0SSSgCQaIrpu5Qonxh5OsdkIAZshlNey1FluUTe9YYEbs18g09/8zYeLdb4/K2Hk1V7l2r3u2p28Lj+5fvYHM1w9urx1rdbNOH+Y/D/+QXw1+7uvWz6Hld7qQ/y3V9+e5GXeW957QsDXZ/97GfxG7/xG/ilX/qllzmeve2v/tW/ip/+6Z/Of5+enuLNN9/ce+02mPJuQavS39X7GddrPP3GN2CMwfzatUzc3pPGO79c3ur5eMaw3hu4a3/bu0yZT6r4nxXlJIo+x/i21jHJ0AzksNLsdFcTLCp5hVJOBuuclpP22RW81dAY11gwE0ZIFZLkWswxIoyjJOZU5gKghBnq+/kQgHHUEr/JQs4K4EwtSclrRZTwkquFgQyeOcNaMLEAXckqFLyvAApRu621WXBLgpFgHFLFscTul90Rgs/rJ8AgwRKyMJGU6wIs6pIowEHVP0CsaOK8o4JNFapI2ZslAXsKuBGyopWshglkE8EowscI9h7eDxpWE2E131jUqpUIaa8kYTRvoHprKLbC9SdTcAz7zta+/fqsPVwjOFQ+ymO8Yqvm/XmEw9wMJAR7y+oadD8zT/OXlBnUsRJt0VINldY9gNpzg+r3rSFBDQTR6xOUkIXlbGmXKymhOypcEwG97/C1x6/h/HyNp4/nWJ6foV+f49WTNQ67HgSGYSBSzMm4OTIiMVL1Op4sxYRYSM4ux+phVEJuCSnEpewpqnooq8ll/HqRNVLdklyxwNYrWPsxlPlBPruSuwwSpqHW1eVyBessFpu5VLq0FptlL2XJ/Yi2bXF8fAJjHbpuhtFLYvjIXJL0sgDKRAbOFeE+ZKu5jCfl/2ucwziOmq9rgCHGrGsAsnBWvRxQeRpH9e4zIjgH9cgyFOEsgWA1t1pEv5HcZTF6OAJGFE82Y6QPQqEbRoE8URYj1usVhmGY8CHOHhehKHOpJgfJc4seJ4CShEkanSvdsWp4EK+bLucLq0OB0r+0n1O/ExrCUG8oBX9YADabgH+9OifYr7QNUoX5/N49jAdL3Hz9dURm9P0Gg3rMn52eYr0SoK9ppOppjBGbzUYT988mOZrkGXmyCtilgCdiCa3OoUmZ8Zbra3qb3i0HflzFOHZJm1LoK7Za8f591Gq6EkPA6TvvYFyvp9dgN2fpTj/7rtlexkuX9fll7v2NMk154aaG0CLfFOKd08eqsccHD0r0L8oFREALg0/cO8b11UxAc6XxQrcjRj+g32ywPD8Xr2BrsjEvPTN58IqcBngFZ5K3j7MO48gIAWiceHSOo4dz4mUmebdskWmtqY4WZ6BLnphAoEour4FsZhgVfEP0pYpy5nUkXtCJ76DuKPG6XaDn8nV4xudTtWZvE3HAFMO1MQAZ8TxjASzJELqmQzfr0LRNph+zRuYjRVAYTTQrIJAMIvN7IkQvYJRzTjxw87ioovtbr8JTj01TAV1pMZIukbzlkkF7GIfyLB1j0wp/W61WoptYlw3Wcp+kKCCCFnGJGegCxBu7hHMCIXoF4TgDfcyy/CknWzLqJnm/zp9MZNBGi++5dwN3D8/xhZuPgMqA/LJO/c68lglOUv3ONXb0OP76I5jbR3uArq3eHp0C//XXigGpbhfK/h+2D7K9END1kz/5k/jFX/xF/Of//J/xxhtv5M9fffVVDMOAJ0+eTLy63nnnHbz66qv5ml/5lV+Z9PfOO+/k7/a1ruvQvYzyw+9zO79/H/35Oa6/8SbmJycvt/MLJLgrOU3RuwMAE8L/vhzmLZArS/9Zp83BZZh8sdV2Py0KYh3bLBjCFNTIylFlAUrJH2PwGEOEVzfuniLYAk3nIKoV4IN4hIzMGkJUCGRSDjORHwYVduwWo4mSH0ir1QgAZ7UstJ+MrxbGjKEMdCUmnLy3gnPZokNEsM5lIcA5BzOfI4URJSaerFyNhr8ws+SmqJ5LySIPVSitrRKSKiCiQlWqXFeqvEDy9GVLEmvYhFjKkmddWpugc+nIIBArYBXE+4ys3iMCTmsNggE4GDSNQ9u1ABhR3fRF6QpF7VRvtgQ81GCXjG0PyPWc7eIde3G/p+/chX/nHmavvAq7WFzpOTXoNDMG1xqH9oo0IINGSOEK2iezgqaaxFpDKvOeTsqs6twJoJJOt8GsLFHL/ynDYJVgUl1PJGFNCXDS/nMeuCRMskmnHAVULUoDIOfzS/fewIPzAd9z56vomiELsek9BZw2BUNCEe6INBTRWMDJaOfdHNEHnFMCcPSMmZTzSABoELRCEmd9X16lAIezbsDHP/1FrJ4e4/5X3hQv0RSmaBh33vo9dAfriaJ69uAmHn/jFSjCBrCBUUQw+IDT01MwIpwzmC06HB4eYvQj+qFHYBGET8/O4ZoeTdtjHAO8j+h7j7btcL5co21bHB0eo2kadLNZWda0mgRJ3m8dulaecXr6FOt1j80GiKFBozmZOi0qQQRA84lZSgUyLBiMYfAABCxsmxZkLE7nI9gbrO5vMA4RZAY0BBxaUuAL+Pitt3F9cY57X/44+tVcwhVDQBiHTO+j9xqWaKtKhAywQeOsgHVKD0w+NkllowxCWdvAWos+jpKfxBogMjarNcBQOUas6xJCXjz8MPnv7tlcrVf4tV/7n/AxAiEgghERsB3SFr3yNqW32TDBQne9Vo6EIUQ/Zi+q8/NTPHn8GE+eCP2/du0anHNo2xbWNug6yaO2EyTHLGHUECUoGTNiKJ6/mYZWIB1BjTCQpPNWFVGrYTYuKaMfqg3vSzu7dw/LBw8AKG2/pMLiB9GmCuvFXPNZPPX5WvKgReaBmTPp1o5cPJuJUo4krUxLWiBFT3lQcFz+Ej/0sd9gvVri/v13MIyDFgIsHlICRDQCWCloMmjhnn7wSmsJzs3hbIeDgwOR38igbTvMZjMJO+QEOElBISiQnydXGZBJGRlMTYdYjIAgSCU/Ac04jFIMJvFbIrxyeog//vmPybwg4v/8yD08OFjlGc1Gz7xOl53v/SuZZLDnaVJYIBnmYvaSk1S3UWVZC9c2aDsBuiRPbcBa0xaI11QD1zYIPiCGgNVyhRAD2qaFcw3miwVsYyU3V0oxkBjizrvWMiQX3AfI8hLFvAFhyYAtYJXOGivGo8Aa7QGDpmvVIG8RY8Bms5GiMN4j5iiQmPU4sACnQPH4ZhYjPZGB98IvV6uV0GoreYLbVnm2sdk7LPiUX1fPhA8YhhHel7zAyeAdI4PNtibJV9gTL9CK2LpHd3051IKq/13Awj9sH1B7LqCLmfFTP/VT+Of//J/jP/7H/4i33npr8v0P/uAPomka/Pt//+/xYz/2YwCAz3/+8/jqV7+Kz3zmMwCAz3zmM/g7f+fv4N69e7hz5w4A4N/+23+L4+NjfOpTn3quwRc32ot31FXC5a4G+jw/3jxuNhg3GxzevIV2sYBx7orPumLbOrFFMdt3sSrsvHvMX+zZibnt++r5CUfuToe3f572Py8JDtseNlXvuIjyJJCMtz4pXICywqlmfOS8I3nsApZwZETLUoHLWhHeQYC1gCbnDTytZrL9JtkrIpVk17Fw9S+9s7FWKsVUYNV2VTtjkteBvoeCXFETZ9fhuunewtBdBrqKBwJg1IqY3j2vjIITSB53KZ+BtWLZU0EQOna5tQ6dTIJWqe7CHOE5bwqQetbVz64WQnKQhRGjH8WbiyWZuJrzKhAmIiWFDqmAhHobZO8xbCnuk5XCTt69i472ZTv5MniWtn6mNq5WWPcj7Mk1UNOAWnfBU/Y3R4SF2a6Yuv/spPNhVJBNglESNEWRViAINBGUcg+TlyTksknpwHMJAtjCu5CA7Cwnpr8Swcj7d0r3Ls6hwWitR2PjBFxdDTMY0yBynZlN35mrM58VAvm+PELPBhnApLC/RO9Zsbmyz1lhUqrmhmm6CkpuYFzE0Y2nMER42o0IgTPASybi8MYZ5kdnk/cPQ4fzBzcxjgQEUu8DAYmC5uAb+h6r9RrdrJXz3jgpKDCKl2jse/nJwDgE+BABGPS95KRquw7WCEglCX1lAOl8WZu8AkjzC7YFZPceI6A5+oC2bWQ+FTDiGLKCYI14OhmS92ALkDOasLwDxYC4dvC9CPGBgNaZTC/bkxWOj5/g6ds9gm8kkS+rl6zOt6MI6yIIFgAJ7aAI4zzalnMFR2OqLZpLuOt2ZPFESh5VaecyFBBWT1qhb1Yqb0E9Uympwvkk7LTgRzx8+ABkHWzbgVlKydf0XbAkDYSdAM7aSRRvnWG9Enkk7XIC/Dhis9lkC/9iPgNRB2O6HAqeQukpHzhShZ9BkRGpVmbilD+keVOQqxzjRG9J973QeKP53t6ttJLZx7vs5zuvpfMqQO+wPMfq8eP9l9ZyZqKO23ln912zb9Z35NbpbqfJGZheXCvnFw3z5YFciafX3Lr69YJXK6H5mOzr6cjK20WNDlhvVuj7XoEu+U86G65pNJy8BQMYxgGj91ivS36r2SygbQJa9VQVuS0xF0nwQGyUZvF0THlSi/xTCzTMNT+t8k0ZI32mdyTCfGwxf9IJWMIRX77+FGfdgMGFDHwXz36aDGE/ALGbbYl5i6agWvsLVDUGcl6xrBFMDG7Kq4wW80i8KopMKREdKU+sRSChb8M4al4sATfnUDnAZepaCzC7A8N0DNPPhecWtLV0RRxhIsMYNTGwGH5bBUSts4AX3hlZIi9CCFv59vSsVXoAMVcyHGv0SsAwjmAGrBOPLteohKZ0PIFjrABXDFFzYBavf95zBp7vxF68S3bn9oJ+mXe/MUBwFvGKVRcvHfFkrX8/thfT/9/Le54L6PrsZz+LX/iFX8C/+Bf/AkdHRzmn1snJCebzOU5OTvAX/sJfwE//9E/jxo0bOD4+xk/91E/hM5/5DH74h38YAPAjP/Ij+NSnPoU/+2f/LP7+3//7uHv3Lv76X//r+OxnP/tt6bV1lfboq7+H07t3ced7vgftFT0w3ou2KwQUwfpltxcBuy7EqS7oP3KpwDbhfFd6tCgiSWifzE22NjEmneWxMZyzmNs5yHnAB4R+EC8iw6DGopnNYMmgMQaBLELbYYwRgTkzhfQvcFFGEoPtuk4rUKnQUjMnkpxV87kkjU5J6UMIcE2DpmnVZZ0Q/QY1eGSqBNY7ylA1d7V7d/Jqqr+3WX4q91NydVDLnzFWPBq0CpAhA9JUPKnSTUoOKkxSLEdIIaKGQGThXAlSnZYjJ7WgRmw2K6xXazx+8gSPHz3E0yeP0ThRmNrGonEO144OMA49lqdP8ZX1l/GV9ZexXp1LGJX23UjMJaxx1XzpPuAXIeHvTWNmPPzdL4OaFne+9wdgutnz3L3n71QZZ39LYbNRQ5PSKgRGDmUzVuYtjAPYJ+CQKjmulkC3BZ4EvNVoz454W+6lLYEmF7MAQKk6jylWRL3zsFvhD3/st/H1+wv8+vKaeAcS8N13voI7R+eYNWP22CECYOScxMhgG1VoFGHZbL1GDRbP5jNJep5HqIKkMZIHjsWDhYgkTLcCDIoSwEWzMxbz41O89X/5jSqhrqyZayUHR6z26Mkrj3B04xxvf+kNPLl7Q8JbmHAwn2OMDFoLcPL44QM0ToAdZwyobRCi5A1cr5aiWDFrgU/C8nwJ5iUeP34MYyxmszlmsw4HB4eYzTq0bYPZbAbXOCwOFiCSnF4gwmKxwPn5uSgJkcGjx3q9hh8lX16qVpiA+KZpYa1B0HmOMWCYAefXGG3n0HaExs9xzTtsNmusVis8efJUQjp8yVsIIpAFPvK9X0IMGh6uM5zonIQJGfzer7+F9dkCzhIOrp3jje/7EozrQbaBobTv5aR4Fgu8saW+rAFgQVIx0BgwUS4QMpgh58BquwbWOlFOQsg5gC4X4hUk0v0nYYwpbBEFuEUEsewHm2Mt9eQwg4cB9z732zi4cQMf+eQntbjIgPmsQ+NsXsM3Xn8Ns9kM8ySzsIRJCuBYMsyloyiW/MT7uUiinMJ9uYBuCgAYI3zYGa0CZqRKWdt2uVrZ72ud4X1oq8eP8fArv4s4js+++N22F2KgNcepP96Sz7bbS0C9krcu0dQLP3sqqmyVZDVjbM7RFVkAfopyVjJ4QHX/BNtYNK0TIMUQukY8zQMXT/+m0dyPahBgxAyQee8xjiPADhwAfzAHkdAc8UJN1a4jolpTJC1FmcdYeeHnf7UMz2lKq+8BkHHVfbm7Ckww+MNffRV/oLmBX/rur+Fs1gMsAL10q1J2IRWXQP1XWK8ryGiBNeVHFB5Oya00lvdIVWWXS6nCa4xGNVgHshYtgH4YsFlv8PDRE/R9j8V8gflijtnBAZwjOOPKPGwNqhZfdlQllnEQAGi6CFK8q25RQbb1Zo0np6c5jcmtWzdxsFhgZi0iIAVk+h7ny3PhGSFivpA8jM7Z6qEJtNKwS4jnXxpqqtw7ejFCNW2XdYS0t4dBChL1m414j40jVqslNv1mkuRf5qA2Y15lvS9WEC+9+wpdj/MW977/NYztFSCRtL+3AfrKYJMMfC/Tr+XD9uLtuYCuf/gP/yEA4E/8iT8x+fznf/7n8ef//J8HAPyDf/APYIzBj/3Yj6Hve/zoj/4ofu7nfi5fa63FL/7iL+InfuIn8JnPfAYHBwf48R//cfytv/W3Xvgl9oEq7y407+oVEa7S/DAghoj+/BxgRrNYvLT+s0q0j5pWeiWla64qOE543IsxnWeBXXXOHqKiuKW8JsAF67iHyNT6777HFpymQmyeuQZTApwJFxWQTDyWADQOFA0aw4AzJXmoXgNrEU0J+8ggEfOk/HKdiyHlaACQK6QAkqOGlaimPEmAhIqke42VEresyr4Q3+KxleYa4BxiEpO1i+t5pwIm5nlI/5lemy2xKVEnpeBNUmsXJx0nr0jKSxC5WI5SmJhVQyFp0mXWhxehKCn2KR9ARAziOTGOI8IongODJTTOoTHAOPQ4Pz/H+focy80SfhzEm0sVYjal1PRej6Cye555ht9TJscMP4xgH9Cfn8OFCMwuB9EJQEMEl0o/U8KeLqEJlb46EdDL1zk5amvb7CWYwKB80U6ZYzmospWKwJMoQElTvx0gWoSdtIsTQJBCevOeZVHC68cbw1iYDY5mBtcONwjrNcy4xEG7wqxZwyQkNj2RCNAiCpGj5imL4GikghVP/6U1lxBbo/u1olfp7FD5E6SeTPX87lgdGcYGWLfO86oUMochlGNFcE0AtRtYF1ALYFZz8TlrJBF7Cj0NKbQgZYlSj5xcbADgqEUtmOG9WP6l2uQowvHYoW1beD+iaRyYA5whdNDQhQQ6pf0HoV0EySko4Z9UhbYk3ia/hQ4ILSE0gHeAsQxDFi1JSKDkJdT7yEi1zsoS7roeDIYNGj5HAjwa9R7iaDA/WoKIYS1hfrTE7LAH2COE2t8qrVEl3CZwVXXvBGDmovQs52QcPNo2FW/QZ6tHVzqHz64Wlc7W/uvKKSKln1M+xsyIwwD2Yx57SpDfOAlLqf85pxUxYxRjBRkJOUzA1YWErvhZy3O3vqv4BmnhFUDBBVPC9t8VGd3u4KIOfx8qJDFE+M0K/fJ8JxfXjifWHh6w0/Zcc7ln1375cP/HvPVz+7ut/l8CyJU7moASCd4tp3Tbm54U5BLjS/E+3/VcA5gEDGu0gAnHIHyDS5oHkTVMfkZ6ZpJDK7gIiTaw5gwLWl1bmmTMSgBUBqgTylN5TyawmjPoUuhTWs08LlN4ppADlhxlyksWYwuKBMNSjmXKvyr9Yu8SX7buW3P5jPUmINOYvI4V/cozWXWUcqU5J6GAxohRROQekVl9CoVn1nRlhVNwVkioGkWGlbZGt2/Ek9Hr74kvqqeWFohJha2CVuOWlCxyT1Q9IYaohamSPCJrW4DOaq8q73Ba7dy6BogBucrtdPaFx6kcnz2YxxFen5sqLyYv3aQj8EUBLnme9nz+rMXeuV5626ZGWcYgwjhvEVwqAPHixEPEjd+HDOVbuD136OKz2mw2w8/+7M/iZ3/2Zy+85mMf+xj+1b/6V8/z6G/7xiHg/he/iHaxwEe+//thNcfRS3yC/PcK57Mol1fu9j1uuyAXFS68I2iknAiZGOt1WcC/AOyqW+o+sYJUUjYR33xdAmyIJGxDASjW6lFkCJYsXNtKRwYIxOgheaL6OEqoH5GUfTYG1tksHNWuvSUPkCQLBaCVc8wkJ1ZSBK21uVR0Ylzp3gRohVQG2gKGy9qncsWAKP/C+AMYKaRv3xwWZl2UJ2XZxGKRB8DJ+kkkCickkXQIhaM1KpyNmqcmhohxTBUoDawVFVE8uwqZSowpu0IzQCxVY9qmQde18q9ts7fW2PdwxgB+xNBv8PTJIzwaHuLJ8ATOapUy9eowmux+EjKzraDpfgnvy9m4vMVxxDu/83m0Rye49b2fyvO90xhoDOEjbVsZBp/9AgzZB/kYVudGZQeMo8dmvUbXtZLYnyMoefmpIFn0Ds73T4O1FLRCAVV3hcE0ipQnBQU0UQBJwih2ZWUmBlXZhW4fn+Iz3/0Q94/fwZNHjzBzXr22qtnJiVUF8KEgIKv1I4xhWBAipIKV4QBbYA24xqFpG5AhcJA+sn0+jVXHlua1CF8aolcrBBOT99QLdRtwrWlYCrnLyhhJrqlZ6zCMmlMjeMQwwI+SjyR6DwQBqSyJEsQqqBKseHMagDli7NcI4wDfb3Cu58c6oT1N06BtHG6eHOVCHpJuT/YImDGMHiEyaNNrbkDxsKs9NyMzgiOc32kQjYROMyQpftO2aNoOR8dHMMbg3v17Mj9tl88yuQZsbK6uBWMz0wgxar4bD44Rtz/xBVFmAE3gLJ5ehliB2Zh3rfoDwxknu0qviSHAwsAYwEPW2lqDGCKWy6V43bYdiKRYhrEjGAQTY964O7SXqr2Sd0k6QymUEHkzJaNMsSoX711RXhpY5zCOgxgYvEfXtjg6OpS8XJ3ws8jiNWKt5K4hNCC4wjOyQoQk4YuiW4G+6aUSYCpTIiCkSWM0NnUCkIEhh8gGPgDNlCW/eHvXqNl3VhvXa9z97d96fzy5Xkq7jF+9D4ub6XEFEpAYD5y1cMZpPkEBuoJ6CDEIPkT4EMXsVwufYMxnc7TW4Ma1a1iv11ivpdJl8sZkIBe5qI2OQqNslsLa1qHrHMiILDcMa7StQYwDrHUamu8hyILVHjS5uk0MSHIKcgRCSEVmrNAq15QzqoYsYx0ItvBsDamPxDDJkIsIa1nprgFQqs1yhc9pD7h4naeSwfM2AfNdBtELMEiKbRRvauscuq7F4dERIkcsZvNJag9AQCYfWOiVdWi7Dm3XwTUNiIxKA2ZrqLXEkz7aBWmTbJCJfpWOJH0mIe8GkQk+MIZR82HFiIhU2EQMPuLdXoyQOYdcCouEGPBCkGqOktpE0g103UzvA4ZxxGbT5yqNqWwIEUGTgIreM/Twg8c4DBj6QYrX1LmIk56S12A6Bbz1O01+qb+7uhD+LOrx4q2sB2UeNoXTPmwfbHvhqovf6m2fW+Gzrn2p+bP2PSdG+GHA+YMHaBcLzI6PX+oznwlyEU1zdNUA0s4veK7z+UKhihe0iXJbCdBTsrZleQFdiejtn26afDkJeaGSnyV7B2wTZWZQqqRoZPSG1IsJQMoF5ZmBmLy1CnAmSkPiZSrMKOMNwU/zZZEwB1HcJTyleIuQutFLzqaSKyIxMikUYsz2XknvXZjWhGinsLL8WVoj1r643E9A7ZoiZbZFaBpH9RpJchIkd40ksmQVrIAYhEWn8dqcHDoleo1ZCJOdkAQsUa5nsxkODw5BiBh6gzAMW+9KGh7TwhnJu+NMygujuXPyuxd5Q+YGW54GBcLZbRd9vs0AL9u3Gc64+AkhCtBw/z7cfAF3cHghXZEQzUset/cB1U9C9o5KI5MqPgOSR+J0vJVVWlAZBQzkbKV9lHeVAjmpsioTV/Ncn1N9BpczTSwvRxU9TwmBhYxwFpiMIbRN+QdUlvpkKWfZ3wL6prxuJOBIJJyurgPUwLoGN449rruQx1iH/kq4Z8zPqF+BJp5uRUiS7xT01+9qBafeg9kmkM57AtGIsDg5RwgWpw+OMA4twEH6ZhFRnSG01qJ1Fn7UkBIWMTklzh/7DXJOKUN5zYq3V4D3GnpoCDEQyAAcPaK3eEqUvYX6YVRDhQi4MnY5z8ES+k4rphogNAxrdf80BDgLMoBlQEqbK720Bk3bwrUjbNOAQ8DgBZyxIHhmKaaqZ1os81J8o8yfCNtRAa/gR7X+i0IogGpACpEFNBRbBVrS/mX6YgZuCDrXZBE4IgYBF733VfEQA0MCoHEmJ8VHA4AoBNkSDv2dsodV5pm152A+g4VGpf8Gjhg2G5zeuwdqGrBzOF+ucHp6CpAUBDk5OUHkKLleKJWIJxiylccHV0eT9EhyPoM6KCQjFilIKXSW8jGmrHwmz2OZ9wnI/sLtkk503Gn+ym/fuY1jxOrxYwznS8TRl3CiiTyodGpXsyy/0iXXXKCQ+qHH2b17aA8O0B0cTB+7jw0+h1iZof/MY16GiqnGtKqn2qBacllty9QiK71ydoiTdYfWixEwVTOUrjmfKzaa5NyNmuex6pskAbixcmaE7gmdbNsWjhktM7q2zYYC5cxgDmD2ygctcpA1RZWbgrKMVEWweN8Ez8oroQnqHbIxiiHl9uyW0UWvMFCQi/XkG0n+bshIHj8iTCnE7rapqde2xLRnma7WmPHgaIXOnOKjmwbzkFTgAtxLvlEtYNS2alQuxZikm5SblDO9Em8vATqh8jsRgy4wPvLet933CVX/av0tFaTSnFwxwjEr71EISYE7aCEnMYLJmifvq6RvKAPMRvfspa5G8aZtwSB4H3KRkGzgAGGS342R57Lk59LxVGs/WbZtUaj6grnir3R1flBzPajOUdMFNoT1jQMMh93Eo35vX7mb6l326L1JJsBzjPM7ob07COBFbr76Pd+xQNe3agvDgAdf+hIObtzA7PiyMqbvT3vZ2N6LAV4q4F5JzOTMZJLnlxByfj6qkodZmIaMwqCUjS8hFQmUEiU8ZsGNY1RgRhOtK0O0ZBBJFKwQAnj0GCLAynAADW8iA1agK+VbAYDgfS7t3rYtmqZRZmuyIFMzZgHKpNJL45qcgyAlDo0xyX91mFVh3ADlsDNjOM9PSphccnXVk6ys2u5n5JnJxYhh9Og1jxkzwznJkxNCKAxEf4bA+l0Ncug1EfChME8RrMQSRQBm7Qw4PkHXtOgah/V6hWGzATT5firFPXMzHJkjGIgwkiytVr258vOYt+gpFUAQL0rct0W8Z11bs+b9m3xcb3D/i1/Ewe07uPFd333pE1+oJYGpHoIeOT+OWK8lpM5Zq+F9lZpeAbFJuC/BiRE0WWXKkgzXn23/1DNAKnQnPVsqjFIu0GBMCp6VZ0H/K8lUG7imFXBk1Bx7Kfkrav1Fy3mz5FIKccT5sMBv3P0YIlpY1+D7cA8nBw+y0mid1QTvFh4RiFGr5EUVfgGqXAJp65f6XG6fjwxk6Qxn8FmF2zJ44MbrD3Dt1Uf40q9+EuPQgjURO6KHI4ZpLOazBgfzGYZ+DY+oVVMZjSX0oyQ8ns0WmM3m6o0qwEwIQqc4BqkEqYqfUTIRrcFABsvlGs45zGczjEMP72NVCZAQDGBMgJ8B62OgaUgqHVpJtGvIwFhgXhVdiCygNxkBrtpuhlmIaGcz9JsNzte9Vgxs0EfGqHNijEE7m6FtHBbzBdq2Qds26NoW1hjcu3sX6/UKq/NRwlDUK0PojIT+FMVOaWMKESFo+ErMSmlgMRM4A8QgCYHHccTQD+i6DmQNrDUAW9QhnckQUPZEqlYr/9IfxBaFJk9QiAnYVULHlWd4j/HpUywfP0Fz/Tqamzfw4OEDfPPttzEMG3Rdh+OTExwdH0mZejCMNXBEmX/lR22BaFx9Vo9JKgQLQOoS79NNnUKy0j42roF4/k0IwXvacj6w99jg+UG3GDwe/u5XMK6lEt77+bb9+TnufeF3cO3119EdvHX1G2vUd6vJWaStv67u3X9ZixyzHzCl80TJU9Zgv0FJIR9j8cm7N/Gxh8fwYy8UJHvSK0gYGSAL6xhN28D7RsMfpSejnuaubUsVbpZK11DPoQR2kNIjayEGRQjI5X0P6wCCBSiocUV5YZT8jmSlcl4MjHEMCF68+sEETQtWLYIYG8EMIpstZwRST18gUhSQixlsIqzjXDFbwPGAusf3oyVvpi/ceYKv2x43vniC+XK2c02SjY0xmHezLUBKvbM1bDFEAfAk+bt69HExVBvDMFNyeaUXZoiJBep1xTvojnwu8r54XZVxNABJ3iwpfgVAK3CGEGCjGORiZIyxVGwHR+XlCewKuZo2kcWs62DIIISqYFPCYskArHl5SdKsRJZE/oE1N3GuvC6hlfVcTACp6YJgBzFSY+hVG2/9VrOTaAiPvuu2AF2o+dYlvTH2E5UsL/4+Q7i+Ddq3N9C1hahexWvrWddtX/9ee3ld3vbZMaYkYVr55kJIvPytwtxF77X3oO98pGO4whztm/ddb7vyLw01IeKorShy886wXmSFyiyqULKnIxazREHu0z8yIlIYyVmDGCShMjPIssS8GIeUgwVECNht6b0Kc+AJmBRCkLLSZNRyFCXxcRpHFpmKNxtlAUy8UayxZZ2QrG8EgsmeS6WMdFpXTN67DkNJ1ppSQZFkDxKykp+T0mfKn9ykJZRSQCoPIPWTwCNM7+PSz5QvUl66xHMk90ApEd21HcLiAM5a9KslwIyT4xNJkjmOOLJHOHYnkjg9BiBXYOMEcyAnTsqeR/X40nzsrus+Hrj92XtDVvYzaQJw4hzanJ9Crt235/fejHJesvdQLI/zIWDT91kZTo4askBRvVR0f2UvDi7ySjVsEcKN/uOyB6iMl7hOYVqEHlk/UgFcATDNJ5RlEJYcFWf9IR4tb+L+owM8fnSMcfMUHAbM5zPxxtLxM0cMw4BxGNE4UUKMa+DjTMMWAhCMCr2iRIiyIV5Mrm0ARIRB8kfFyIoL6znc8nyp6V2yjuf3rKcqgV0VIDKlw9LP03vXsXpyhGHTgYikQENkjBCBNYQIDgExeBgjCekHBbqMsXCG4AyBo8fQb9AyYKyDNRaWLKzpEmFGyvGVQCwJYYvw0ahnwQbJKy55ZpIxCMTYLAKiiwhDzGAReQGdnWtgmdGEoLRNk99CPdCCoPjGWhwcHMJahxUZzLoZ5vM5/LzDUzugcQ5dE/DarYdoTCxhnYakYIYxmC8OQMZis97IXtGTb2DVe5Zg1MOVNXcgYmJV4mGb8nRlqqH8zBDDWYcYGX0/CBhKDoABmXQ2OPM5FuuFngHSvSFrD5PGsRvWXfho8T4T+iYV0iJHDMMGy+UK9+/fw/iV30UPYBUDPIvyNnqPR48fYdNv0PcbHB8f49r163D2EE0KUdf/Zt7ABeoq+7Rs7fQNayhNAvZk35dQejIWxjoJi8phph+2d9uYGWf372E4XyLsC1fcAyhe6Nn1rGsuE86uimzwpX/uSLu73b43GyfTXVZAOiblPQJRQtqSt9tXbp3idD7gE984wHzU4goqvyX5Mr0MR/FsFzpeeXuql3kyNkb12iHWiAP14o85v6kUImq7Bq6xCHFECAQfCAJ+lerX49gDEEDN+4Chl3yKwTOskeT6jWuV4ZfQaoKkC5C8iya/Q5qg5AUkdIzEYKFeT5ECkoHqvVyn7Zbz2ZIWTiKRN6LKkbXhN+WLhREenPLfOpvkeuFLTdMIgBQDrJX5SjxcjKeVt23Wwa7wzpPzU+j4BHTTeTZWDdxJ3jE26x31P9IcwUTqIZi97+VDZpY0KrqPxtED6GFXa5Cxkvc2as5PdQBIGT1THtP6WQkIFhlMxjPaiC+++hhPFj1CSebw0tpFwHayV2cP+W0B/F1swSkdUvBP/7ebm/bD9kG0b2+ga6tNcjt9i7cszOJyoAjYPbx75JHL7686Sl4wk8/3ju7qT3gZ817CFmpmMB177dqQPG1Eb07eWM9DVLaRh+k3KpdPQK4JaGeEgDNFREieLY4BphVCZ+CypSRmbX57jpQhmommr68ocxp8zJ5WtQdXmrOa8WUQKI0vioWlrnQi9xVFIyW9T3siqypqgfHeZ0DCGMreOjEmq1dCNSjnZyhJ9KfgFTMU6GL1npFniaBG+Z2yElTgCZ0TIOVT2P5cLFCyJ1JOs/l8jsZZbA6OQGAcHR6hsQ7Deo3D5hDH7hibfiUJ6YOXNY6hgheSgBGrpxUBLYGxnAG5b02mZgAcO4s27cPnMHEnMJMTqojkyVb6CCFgGAYwC7CaMcIszFc4F3Tf8tTanmW/glth73mBKFZZsalArgSRBQXWMhBrdCcqKhqZcd4v8LUnb+Le4w6PHx9gs3yAGAYsFnNY9QKTxhj6HuMwlvweRoRE1zLIRDCFYv0keT/nLGxjJCl79Ig+BY1EMFIlryIHTWAsLgKyvkoey8VLV4Ea1WfnD6/j4dfvIOh5c9ZA0phF1V3EisshwBLB2ZSrUEIR02cxBowhyvoCaFurieBdMUREmQfvvT5PLMohloqqRnPNhJSYNko+l7O5B1mCGVLIRCqgQej0RMr9yFWyGJKIFyThEGQtFgcHMM7BM2O+OMDh4SF89xrOXIdZ28HMBpzc/E042mDcbGTdQhBlzVjM5gsYY/HEPEaMSvsSTU0JpjWRs0m7RFOzqXoqc8GJnqV9K2XrnYPmVRwRfAeilJdRLmaqPK/yXuCpwpOVFwuCRTrThPQ5qkMku47I6k8DaF7I5XKJr33ta3j69CmePn6CG594C4tbN4EIRB9w+uQpNqs1VqslQoyYHywwn8Ws2O7sN+J8Ni88wpxOQKH39X4FBOiyrhFl3liUZNofthduSjiWDx5g+ejxxazqMoDqWY+4Aii2ff3lkuiuzPRBc9jMBzMrLTlTUw4iObcOIOCrN05x73iJ1+8vsPCpuk7yiEpvJzNXQuHk01yYKBWt0HAxA9ZCQ4AhyZ8loLEHsxhbrCW0rYNzBjGMCB4IHmAEMIdsMB28VEE0wWIYRq2CGxECY9Yu4FyLFHafQema4NWAVX2WsyFGJsvYWGTNRKPkwnpytydbL3k5q55k2gJqTR9jKjk4xggfQ/571HA9a53QfyNgkeRbbGCCVfBIvO5MBriomperH6o9rDyPtNJCMo2UnFkCMInnXzIWqrFGiwYkaMuod+DEcYA5yzHMDD+OIqfZjegxaX8qiJZldJYdPE1hkjy+Etgl/0Yb8flXHmHZjZWi9T413vPrZC9eoYOInTmru5ry3g/bt0r7jgK6vp1af3aGu5/7HA5v3cLRnTsf0CimQMK+9mxXzpc3jh2Qi2hCNHbpx/NCfpc0VcZ3AKUYpUxuUEuH94hW8kgxGKyV71jRoBgimEcMcQQHqWpGYwD5ADTdBLRKgFU9D8kaYK2TBMgdKa8US17UqioAo227nDSdY4QfNaly5cEVQ3qOsl1TvKsoe85MhY1kmRHLEKurspHryRTrTd4/8i9qaXmypT9x5TZwrkUIDO8ZQAG50jXONertMa08KW7b5fKkMAqwJgKjMQbz+RzjOGKzWmcLq3MO1hCOT45hCLh2/TqWzuH87Cn+oP0kPm5fw38Y/xt+13wNMQiYw5GzbCIhm/p+XJhazkvzHdCefYJUIFRQPnm7FSWlAF3QtTPq2ZIekPMOESphSPdKEr0qoUuwzOTPdPG4FHGbfgaClILfVhgAiixJWhNgRzaPN4SA4AcE7wBrBDjRHmMMCNGDor43A5ENKHjJnZTzcBWAxphGEng3DjFYeGM0z68mGdYcLGRMBogzspH+yOhfJRNmN7jpW2Mqs1a0tAhyzIxh0wNEaFqHGAz69ChmLOYdQnRYrc81+bxH0zjMZnMNF2ZY2whooqGYCbgUsiAFOgxBQvKMBZOFozm8DxiHAdYaOGs0PKLsvhCSR9gIH0a40WI2m2nItuQgIY3bI83vJJVZVbGwFm3b4caNmwjMuPnKq3luxnHE5uwcj/wTEEa8880Gh+0Srx98FUbDlg8Wc8zaDieHh5jNZJfHKLmsktAeWUAq8c4ygNGKHczZqzV5zIpCHEFUEjUbY9A6i9F7DMMggCAafOX0LRBGvL74PCSvTgpl53LS6mVXvpjCS1KYcFIgM80SxoA6nxARYfQeX//6N7BcLkHG4v928gfx/YefwHx+hCZ0WK/XMIZw8/wmnhz1+J8H78Bai77vEUN8BtGov9g9v1z9E6+OFHZf+BCReCmksC0i3tvXh+3q7ezePSwfPZLK398CbfnwIYb1Gtc+8hoW165d/UY1Vrw/cmmdh6/IagmIB5CBgVhV75EhxlyldKfl7SzQuKDmiXcZNK7JYHcCCqzRZPfWSmqsMSCyF28t9cAMvkeMAYtFB2MsFvMO1hqEMKIfPELoERUMs04KbgxD8ejabHqcny0RPCMEwBw5lQGpSlavY1f6G2RC9hq60yv+xusPcf9wifUsqgw5lev33VeJDNs9vnAjBaqcdZLEX2XwEKSKudFCUc6JWhxDgB8CIktVQ6tepsYYGKjnljECylMU7y/SCsJaROldiYm1WIAki6hORtBxjRj9iEELOfkgOW9BJHKYglExRgzDqLJ7hLUO1pocBSFefB7j6PPeCyFoXxulxWq8t6WqOgCtsI28D4yR8PZoXZ5vdlH4+AT4gobHXrCue2Sdl9mefuwmNtcW8LP2StfT2Qrh3/134MGTi8ecL34eAO3D9l637zig6yr7b/uajOzXioL+Z6pHXdVWtWdcW3/7cYR/9AjtYnEx+eZ9pD2xgHTJ/ru331HoUKVEXTTASrlKnhf779hiQfvQ8gsesdNTjbfVINfV7oZYktPNdZDPVnlymr4mVV9O35KzAsOc8vOI4hdiQAyA+HFFIHoVaKLq3QEhAkPwApCNIxwTHMQ7QqopqvK6JSBwpTAZIrABrCtATxKoQpgGQqY+kldTHVKq/EfGplsn5YCppnsyz4zaO6CAb9XiVGOuz0/xtEO+R8C1lD/M2lGewWXyrbXCGGMKZSzWy7IH68OYkuPLexhiWOdyXqYE/InsKKChVeCOtN+bfA2v8A38H/zrmIJ9KeStAliT0qj7ghN6o/O5rdrV8uC7b1Tt7e1Wn+dqvIS9n097LZeUBNjT7zn1VdOhqrvUe4xavS+prxqGxPk+PZd5Xrl0njZQWuL6tQBMXZ7q01uJw2kvb70qpQ+T9ZYIYIMxNghRWZ8CJ3XuCIoMqvJqcCYHad9qiEoU7xbDBfCoj4gx4g3lE9C2swg0nQd9VsYotq+vW3V+6vvz3osGMTjESPkSsOSIEuDP5TGl92pdCwsFlFAAiK7rYH2EjwLcAAKgJ5BCvJuSJxIyvTCaxZi1aqr3VCpXGQKxAVuhcyXvYsi/Ny3DATkJbYhSwSuFniTwH7GETbRdJ+E0xmD0kg/LbzboNz02mzWCD3jgDY47oLuxRusiWqtzHxnHh4e5fDwzNEwIJXG6zrJsp0Rfq3CIeltm3mIwRivVr2AxBqD3jM1IQLR4uD6BJY87XaNrRCAEELzS4mlIexqDvLquA4QOZi9fDfXNXpXa5uhAISKcDaA+4sgu8Fb3Ov7v7n+BtQYUCauwBCJwc7yBb/ozfJmfoPMWbh3hNpJDTcI9gcGGaRLfSpZKYcS7Xsflwh25QdcxJ+qvqOm29JLozb7DkowRz+dpPs3Gs0+W5J1fLuvt4mt36NzkuRWde2FlSegia0Xj/vwcy4cP9/S3X4KcpsRADsXbfsTknrSm1bW5n63njusNxvUGhzduXtRd9emUw+67joFC5HaGeDVff2HxSXZKfD8Zeup9qPJTxROK4U9/MgQMYwE/BhcxuAjHtnpeCW+SbaoVt43TMy38JclDAjo5iEFJav4mvhRZeXD0SN7SjXNSTCVIAZIxAiFKqoYmCv33Yy8z7I3kTxwHBA/EmDz0WYCulPYgvV9OFljJ3lsHJtgIbyPuHS/x9sk5vI+SB93Q3nNZc/f8WWKp1Z6anv/qmTvKXS0TlTD1BLIMNmBjPUwAiEuYXS1PBx8Q1LuLAfFUJkwAzOR5nEYVWYpxJOP3Puo3bVtClb5bkqHqy2rPqSyzBKmaG1TnKPlRS5xGyeWr/zLtlDOTdItsfCflfZqSgQFYKmGZxQyZBkzVGUhzrfvWFoNiXvtKAOXJyqf+uOJ3zxExxBf8vqf1x3Osbx2mE73zfRZPdWg8jMAXvwZebqpraGvb79/buwOi/V9lpXR7PBe/P1/w/c7++X3cvs2BLsLzqpV7QeJtXvqsz/Ozr/5x7u+C6y9k3judlkpl9Wfb7J2RwtuMiMqqlGwDIel/5bBUyhMAcZTmXYqbhcgtgWh77BMFofos30lKwGP1ea4NA+KtqiWidSQeK2OL8sQUa1/AOS735AfKRRYMB6FibABu5CvrgYYZXQjwCIgUEUyPgZY4HR6hs0tRchXqAgEwgGvEs8BrWMhquYYhA2sazA8OsJgt0NgTEBqMQw+O+mC1gMQYAJZcOSBohRQGcchWlDh4BD9gGEbEyBJmpMntQxT/itEHrNc9ulknAFJrYdjkZwzjCMuiDBnTToA3mSNRHBP6SBRAFEGWJI9MVl40tXYksTSmBQGAoLenZWPCrLHobItZo+7RqfiyhoBaa7HpgXFkzGatVo5UV30yCIExjDEzkRTuI9a08P9n709/bVuS/DDsF5m51tp7n+HOb66hq6qru7qLNG2aZssUGrQJyqAA64MACRAswP7oD/6nbBgGJMKwZJoUQFOyukWTokiqTXZ3ddf4qt54353OtKe1VmaGP0TksPbe59zh3Vf1XnXnxbl7WkOuHCN+EfELGB7QNRbdvdu4vLjAeNnjYrnCdtvjyeMnCN7DWYdh6LFcLtE6h8ZZXDSMrWmy5mFdBCFKX7BHHEcFMYVbSUUgRBhE7FuC6pl5HVixH65zvYhfzZL8Kr0XZW5UGf1SIgUgifb1tcvrnthfK1b6Kl4rnOdYqnIIOn+cgEM+RGwDY9kHbEbGEAE3W6iHk9Q0hb5JhifxDExAZoxJoSihqgRGA+Fw20tKmOtc1id5SlYKEYbl4nlGADTPOwDCajjFn332LWwGi00PwC7QHjFw/pkOe1EmjDD6gplhGsCRfA6Q96TglSGGRYSJI+B7IVEnCzP2MH7EUdMAw4hNkHSnZC2IlbCfLGAYDIusOWk9I1LbVw9PJAy1XIP5VdNQ+e7i4R08/sW7GLYNjCbKMAYIrYSuDIMX4MoBQwhYDSOak9tCqDtbg8YRPkQY2yDYmaSlR1AONgLzoJlS/cTCDRiEmJQvgBEwxksAQGuVqwWMedeAqcHVPcA7wJKMZR+spEf3Ea6Vbt70Gx2ml5r2Xdc25aVhVfzScB/HAevlFXxQK7dP3mPSRsZYXIRj/Nvxf4Z3bz/Bt+5/As+M9TDgyeUlCIxgCFHHLRkCnAqwkeB5RAiSsZKSMYQMGCZnlBIOe5mNV8MCf/Lk2wgsCUpi4nN7DJCxmJ84GOPwbx5+D5JRlvHOyUd4c/FpJu2dz2YAGfTrLYglYDFGwugJRBImlUJnHaWEAEmpE3CwhcP/Nv5NLEKD/3F7C9Ya3H3rNm41x7jTnGK9WqHvtzBOxlcbe7x9Rvj3Ht9HN+uwWCxweu8Yi+MFjk9O0C8Y//Q7n2DjxMs4kWKn4EUfBIBLYelJESJQDveyGuY+KselhMJ7OAsQRTBGDXWspRwCK7dOGfdpXYAqaepZmcCEes07INdNV2Q6eMzr0hn4movVSmw+sjKoXFfowLtkZFidPcPTn3+AmDi50ha+d8YvsewohtOyn5EtvQZIWHo0BCYD1gRBXHkDprZioBj2yCDqjpBA6TRu0l6aOsVA5o4hC2tk7BIA79N8alQ2iCC24GjBHuBAytFkxNPcyNy3xAgm4J9/5xPcWXX4/Z99DY23mNA6BAZigLELCSkMwmUIFCOgcS3IWUQWfkLhKGxAsBnsMCNg2MAN4v11MpuDOaBfX4Esw1lGHNYIvodbtCADbJZXGMcBq/UW3WyO20cnINPBWEnSYhshOIdxGIJmE3YNgnKRGV1bIpSDMnGdEuNHbz7DT984x6YbAURYG4WcnWRmhrHB0CfvWUnW4ZLcC8oyZuAE9ktzRRUwM5g9GTspIQsBTLDkAJIshOkCIY7Yxi3++W98iNPNDP/Ln7yLbiRIVl0DsINglCTE/MGDeUCMBuMmAG2LZjYDuAdCj2F7CR8CGnsKsh0aiiq5MgwkScBUgjs07ndKXiTE+AMNRRS2X+GhjczwPCIOG6yvzgScNQbwAyg0aiT3iL4HxwHORozjIJEfrZGMxiozsAkajtlm4NRpps+2a5TzS/U0TuHrScgXOZ6ZMPSDRoBImD7NjABxKv8wEaKRpDwheAQmkX9yc6g0p5OUUfT1ZOtJ/G8lGdU0k2J9JUBVGiAbzetQStFxUpOX66V67F43GZwm/NRR9htUdDVEEiVgcsb4ae0I1Xf1Q+Y7Pn9lrqW/l4Yv/oKVrzbQNdENPk+XHhJsrgOybrrP9LfDBobpgPfjiH61hO06yZZx7XWnuG2F1VeHVRPnQCkeCdV1DwFRzylmDGivtgizFrFz+Z6FxyddXhvguiajMt2lGlUWxVRn/V/CHCYnQzaB3c87KuBkXynKjnzUjQQ1os/YLBifvcVYPAO6pSgyIQYMoQf5tNgx2KgCbQhB295zgI8BMXrlF5F0z8bqAgjNNMUC+CRPqRjFGkNqlUdyFScFJhiIcUQIEtrDkRGiV06AYolOdY0xcSLIHYxJ3gcCMUkiOINgrHhjUIIYBMSqArdQ2JUFAIssm1RqS2t1EzYk6dCyBxbyIk9EYEtwbBCNHFYsbLIxOGfALC7V1hoNczw0bMrmlMJ0CBpqpBnNNpsNlsslNpstrq6W8N6DQPDeo99uMSrQtW57bN0A4iDAjhWxxBqaePxNxW5tn4OoeTmlQNI3AVn1GdeVMifKjKkXv0N1fL4lcVc/TIoVIeFIpW2BpDylOURZmYqRMYYAwcAkjCxnXqwmrXgs7i/ZXOlzgLY7dnIdiWQzWQUTmFcLKLtKX63kCtBvsR6PMHgW8IYMjG2QkixMFg6S8Z8IXlN4ChNgTMRxt4KzQlDbmF6TGhgQqzDIkmnKGpp2Gae2JOw/JPL82U13HbzFsOl02drvU0b5frucY7ssGaVkXWUYzQTLJaUgIkf4EEHWwdgW4jelXk3QkD0UPsA6vDs9TPLmSuOBtZ0YKJ6WZBBNRHCqdBoBubxN7UJq1JDnl1DnmEMoQgjq+cnqIWpzhqiUkQwA/Dhgu9lo5tmg9UHmh2Fdz6xRwnwI+TAAjH6Eyq65PXe38IkFuhLIIY8AZmDt5/DRIhqDq2GB1biAZ+mDRFwtazShPWIwDHq/QIwMHwKWwwILd4TAJOkKxxNYAzCNWdiGWs3LEqTet+m3au0FRIm/zcc4iS1uj0doYPEm3UFnWwFoIQp3DB7MEcN2C44BxxtCs2F0a4+FZRwx4cRYzEC4u+5w2RLOm209efKOOt2f0y/iLSBet1adCg6sUdkrIje8ghdT7679dWLnOrvTrKpl/f7V/fV3K3Do+jeXm45kfv5Bu3XnGNFvNhhWK4zrNZInxuR6eAllaLoBPf/Y5xyXfvZ9j365QjOfi2ftzkGprklSSz+IIkzVxXblw1LpBG3VCizqU1F22ASyZENRWtd0TSba997yPsCPHuMwCq0CswBxZMDUgImxmg1ogsl1yJKBTpJEJ5E8pdLvwq2UOEuT0RoQ0MNCPHMjiCKscTAxwqR0GTLRwEp1IRp/AHEU708AYdhiHAaM/UYzJouhj6PKeOSqJlagopJH0g487XbprU0z4mKxzaI3qYxsrHr6UGqJncGSAAgcWBbyFln6kIEMYvDutQ4NRDXULrtB5HFK8sHOvpa/K2MkxrS3izGUORSex5yJUpfnSQ2qsTd5PVzKEKsFJkY9XgmsNB0BwY9qcOJcD/kTDk6NEdSxVjy7kncVUS3zAQlpmnLmSn3yfJjoVDpXGJO/dASzwJa1iW4yH6tbTyXX0qfJcy63QQKurmnV9D5ag3He5npkWcSZSSeJjpnm5+GxlNfQ6v6TPqofhKFGuEk8TK7dS+03Bw89LOFnWfYvSy5fbaCrLi+8Y3+5ytWjR1g9eYL73/lNHN+//1qu+bnG+Au04/zJEouLDc6//SYuv35XT/tlzaxqBS3fPOeM/UUlsig5xFFAn6CbQIz4wXcZf/oe8L/+R8Bf+SMov8yIzXoj2VVaA9uot5QqGt57AVq8R4xCyi3x6SL4+NHDNQNAjBB7yWrik1u4QVCgyzkBeaybqaeTEDkPw4DNdovNZivWbwDdrFE+AQOQBxkvSioTQiRQTFwMCgQFgKN4cjALv4v1Vl3cNW08QzZwJEUKsEQIQe5JxmIcRiyXS6SF35wo94GzQGTEUcEASkIlA6T8PZYkWxBXm4xue13XYTar0hMHUeqicyBD6FqXDUkck/AJ9VZpsLq8wMNPPsH52QUuLi5xdn4ugNfVWpRKMuJNMXohHLeEh/QQH9On6JwAbSeLGdrGYjEXa5YhAxKTLYCAmITHTBD9F6mUxaFOEe2VoyuqJ2DbtpKm2nswG0kcJ+QSKmiomLOL5Og9GJgAYqk8z5ZRh1qnz/oOteAKLiKMMQY2udUnYZkrV3lOgl7F0RIZs26Dv/rOT9C4CGcsutZhHC2cXivVIxHYJxSIIyNSLHV6iTG0vjjGR3/ym4hMewkm6sJ8uG1FjhUhzmShVjj4xtGjcQ2arsUwDOiHAUQWHj4LaQRgGDzAkqQCnK4j9/QhyLW8Au0KPllr8zHLGWN9HHM7R8+ATxxNUqyGOozjiHEYdW2NGFSYX6/XWVhNv6V7gASodpTWBhIgnlF4cEA4nS3x/Xd+DGs8Rh8wRvFE6LoW1hTuEgImY2qnpQ9+xyD86Ok38Gx7KyuG8UBHJyBqHEdYa9E0jSjNIeDjy7fw4cUDBFV+j1Z3cDrb4nfv/wDi7Org2gbWNdV2GLNRJX1OhMQJdUrZtC4uL9E4g/msw9FiAQKw2W6xWm9wdnYG7z2cPc+hpkF5Ks38FrqjU3g/ot20+P0fvoeHpyv8f779wcHW2HVeFS9ATYCgSmNK3pDAmHEc4EMJxSHlYZsY0vLNdoEHeStZvm7qp5v78KtehvUan/7gBwij/1VX5cZy/uGHuHz4EG9973vojk9e+LxDimP9zRQjSKDVy9cvJeNJa0ChVU1KL2O5vAIR8PjhEawT/idYC7IOpyenmHUz5MQ9NQKSgAClxUgk4LKWCSBBmkVFKDQIMWrWRZ3nzokXpY0MZwMsGyFHtwbbfitADEf1ao4gY9HYFm03BzjgarnCMAxCtzGM2Gy2GPwWPgC2OUbTznHr9ptouhZt0yBEwPuo8iJlX3KgZBlUhC19U/WMgNpkCcYEBb+gHnRUAQIFaAIy7vX5fBlQmj0ZAzJoksBGlIQA4pWXwE3lzDVJxlCjapC1bBolo0Ae7XpyvUJl87q2h5pNaEwke7J4YRnmPI4kE3SEH4W7K+1pQAH1Eg2ItSK7BxzY7w7OmwIEA9BQ9gIEpbr5ccQwjMJJOXoEE7J92GpG4RAPXf/1lXHR4uH/5OuINgFjavCqZI7XUUp8VN1df+GUhC9l+UoDXXmyVhtHHlgvML6uG4Q3Dc5DMm9ZgHcAmEPkN7vXYQEythcXAID5rVuwTeqWmxD/3evyNe/1885XE26ofIisQDyp4H4hZtAYxC3n+gpeX52djf4FDBzX30bdSmorzOHjrqnD7nsA0RHGmUF0RfmNkTGOHsYZwDrBloJazSsEPQbhxPBjAEdJSw8WwZshm3uMQ46Xj1EAlxTaFdmBong2FQushw8DYhzAPAIUtL+8On8o0EURYI8QgGFghGAxn82rLIjFkiMkqkYV1URKD7EaqXUmcsQ4eIQQcHW1RAgBTdPCe4/l1QrWOTRNi9lshq5rkTfkLGWqBYdE8JlOzQp4gGyMhiWLnTEpg4xebuJalaxuei299jj0WC9XePLkCZZXKyyXK6xXa/R9j6DhTcm7zVqLJ3SGJ3SGZ+ESIw+gSIjRYmjEQy5Gk6JkkWw84u3ESVL6wtShvaGahJPXumlyNeUOXJfzf5M6Zcen5M4FIeQdRxFmhmGQcA9jMtFoAVgoJ08QFy6eTPukUOwJtDsWqmQZLp/TPNkHuZIyEqLBk+UprrZHeV1Owm5KfoAK6Kqvk71kABAi7h6d43S2gaMBFgxDURV4RuSmgGUooSeiZym4w6yhizcvecyEZ5tTjMonNqyPELybWEv3z6mRgP2DEtQjoIJw/SWh1DkBW9Lpqb4hBAWtgeBHEZhjAlXcZL+cuPRXbRgcMLaAbxiRUMj7NctYOc+oUlOARgmvRgYjS7/s/yUgLz1rAtAIwJ2jSzRWvPiOuxVaJ2EgeSgzC7BSW/YnHh3T/pKxm9pZ/q76IyyHBTZjBx+thDLmtih9UksGIXgQAc61moGXEGEQmMQLjAiDJwy8AE5+F4QrwD+ENkoO3RelLPUzT+73Hr2J+zjBDC2IGE3TgBCx2WzhnMNs1mVOs9F79YBN85GyR11ue71lEwjHfYNvPDvFU3OFz+gxUnB0zoJrLWzTYHbrlp6PnLlLBpoCcrrmSPimhH0459RZoFr387CugWlz81yq+253/XhV4ePLVljm8ubiAv1yhTiOBRCvZa1d0Ofg8p/GKe3+cG1TXXvO3v2rr2NEHEesz84QxhGzW7eLvHLtBpsRoklfTudmvQ7uy+HMyCD9TRt5AqhiWgtUS0/rIXPEZrMBEeHs7AzWWRhj0XQzNF2HxXyB2ET17pfjRXhMtSrzVCgNVbZggDW7a8FLVNch4Q0kXRtJ56gjB6v7iw8RZMRwO/oA5hExDrBGwwcNEDlg2wsAATJCVr5aA9QApkHXdehm8xyKlUuUYOLACnCg7JMAY9lu8fhoiWfNBkM/yjNzMTYTCOMwigwcdwdiMjCoL0/aC7JhcV+XedkyOb1CJabRMUU2EFkh5oMT0DX19ioQnVB3cgboyo1eoFRjMq95gHL3TvdUGYdC+9G2beZScwq2FvmGYFkM3omzMe2LWV7IU2oql1eVmTxC3mWvUXGTLJcAucmzaJ+SMQpyXa8n710XwPb2AqFrpL+SjsFV3Sf1YPhZg9hYREN6PE3H88uUL0rof42Fq7n2l0XKVxroepXy6gMga7xfSLn49FNcPXqEt7//fdjmWL99kRs+Z+bx7jWqRaX6uogFXz2h79W9yZJiRNXnaTpcIsrhJEM/ysZugRJXbmEhQgwxENSNfbPu0bhGCJfnwj0AjIg8IMSNhtwEURajQWRRuhAcGBaRCWARdGIcMI4bhDCA2YOUjJm5l/NYrPbWBjAigh8xDCsAQGsfwDStbpJi1YtRwCsbCJEYBM1ilgRVQ5ngcrm8xHq9xs9//nNstz2Ojo4RI2O72WI+X+Dk5ASL+QxHixnIKk+PuuNEFViIGaDKfZ4gGfAU5M1KZZDQzraDhialTbH0b4xqodRirEHwHuvlEk+fPMb7P3sfo2agWa838D5I9hvtV2MtnLX4GX+KP4z/GtthCe9HRAM4b+AswNygawzaxiiHDOU/AikPjbkR572p7E3JL3XhjHmJrFMLJfLqvceWN1itVlitVrh1egRrLRItTAYhOHlaJCUBWW5NmUH31lkFXZMl9WXkk1qYGYPDjz77JjZjh6RlJCBElBMJFwlRyOjrm8nYkWe1xuPb99/HcbcF2AogCsCzKBWhbSXLkApdbdPANU6Ut+TFxKLcH3Roq545wuAnZ1/HZX8MZka3Bu6++OMfvrT2oKGUAl1CVIZxRNM0mM1mhWiXo3JbJcZHaOa9AKueWl1rUO+pjAqEMmUt9R1wdUfpaHaJb7UUUIo0gYWe7wnRapZHSuBHUb6SF0T2CmMGos/kt+K1F/Hdtz7F6WxZjV4CxxQKJKEVIUiYR22lT2BXpWZMnrcun1w9wAcXbwsn0KR/k/KG8qq/D8MAZsZ8PhcF3BgYBiJFXUqF+zHYO+A3/z2g/wnw5L9EBraquVLWSi4TjBj/C/wOvk+/AU8DVnaJ4+Mj9NstLi8vYa3BfD5D3/fY9r14eISg3sgpGl3qnDx/qdov7qw7/Ls/fQ//A/8A/wY/QNLMMy0aGcxPb+Ot3z2VNZjSNYBx7NXTIIWFMWLwCH6ENeJx5kfJ9hg5Vg1uJgBYev4JiMPIc6zuMTrYc1/9wgCC93jys/cxbrf7nhkHz/jVF2bG2QcfwM1mePuv/FW49qYsaNp/z3226+XCPJd58ql6XyaVrDXyPkbxakzjjCHyy8XFOdbrNYZxzB6Qx6e35O/4BF3XCZ8fcRWyPA2bAuleZIXvMPEkyW+UjxVqCy7k8I1m8Y5ASy0sLHwMCBwkQ2OM2A4DttsVNusrtC2haQyulowYPZbLjfC9Ng22wwbhcoPj0ztYHM1w69ZtHB3dgmsaBR91s2YWQy4ITWMliUXVup8db/CH3/gQw9hjXPbwahxJrWrISKIm9fxNYHoJWq8AQD2JSoe9ctk9ew+HqjC0BHI5axGT7JyOUaArBs5ZeAtwL7KzyIl7d3m5+u4Y3VJFSSoo9XMOXdvh+Pgor82zboa2aUSOj8KxlnitrLMwo81reG3AyQwlFdhVGzRzDQgVWLQDgqJco+zzIRubgRI6CCKY5zgo7BUCzr9xH9v7x3lPgiZjSfv0XhuimupfVPnKyPN/MctXGuhiFDQXUJQ5hSzsSDgvDXBde/j+bClr0fSkEs//YteJMeLy4afYXh3h9M03sxXohcrz8K5pzZAEBto9hqGWlKJE1K8A9he26gL1UjMJNThQmUlf0fS30qmVUnzoUpX1vT6mXEbR7QNZg4qIk3bS9Kzy3Y++S7hcEP7W+8B8EOXTkFEvKVLDXFHgGUISyYYlyx8IxMiEuCEMCjL1SGmp5fE0yxkk3h4gbLchW7KGYcBytUbKqphi5r2miyYVjADxIguRhbCeI9btHE3TwjknmVn8IGBc8MJRAwsfxFW+tvIQMZwjxDCi325wfvYMm80WjbNgFh4c7yzGoUEMI4TIU9otKUZi2pJXSjspCdgWgoSupHTIMYiyA5bsiM41YjXNAF3qMSViT8IfB/ixx9Mnj3Fxfo5xGNS1n+BcAyJxIwckixADYCJR7uMIUmEhUZgGH+AtYfQexjgh/E9jBNJXpMSbr2PjnM6X3fIF7J7ZAsbVKpBuldq0qg9rCIUKNpkbWdE6QvH6ubq8xLOnT3G06GAahxg8qEpfaIzJt5EpqTUgVOvNyzz23qIh31YC3PTZMdFrklIiXHbyF0LI5xchmHK2zlxJjmCWELfsUMMa8lAJqK6R8GJrkkJSBMvywKWcbU7xdHMLABCZ0Psur0fVSXuA30TX379sbi5CBURFCT/hyBLixBJOsDhagImw2fZ6rfJMMcQJJ1YNYkr69kI+TkQIlrA+AsYmVaHsOya7VKSkFAmCKO0IQEPdFHExaewVNGO3r4sXALQdFWzH9Ly8xaSsmCx7MKc6IIUuFo/TNOZTG6fpcrE9wuP1fVxsT9KveX4lYEu7QJUEILFlB+8n4a7JSwMaphSZNVRGsoCZEGAiZ82E1QvCUAHtGBIeSATlwpGGsdaiaRscH5+AY8TFxTlm8xmGccS277HZbNAP4oUxU0+uvu/RtC2OT+aYzxfoZp2mmy+qKWlDRc1KJu2kwCUDfrvBs5+/n73BUvYtbw0CAUPfq1ezx3a7xfJqiYuLcwxDDw5+MqdSFjrnnISW6ZxNMt7UkZ6nWMb+lDj4+tUurOt2/oRJkxw4PJc9nTWtV3T4+LocaLy98+u9JS/fOs/HEecffYTu6AjHb7xRHzC9eJ7vnNfdGx+Ky2wsddl/f6gIsbauByzhYIn7ND2CtRZOeUWZGX2/RTvMMI4DmEPGqVjnR+bj0gvktcYSTJTwRJDKjQrWp1dhByBY3UeEBFyvExmBGU3jYIjhg4exFrfv3EXfz9B1DcZxgxgGNE0DYy0WRydiKHANYpRkM6ent3Fyehvzo2O4boZ+24NMQNMagI0aFaRNDSkVhc5/ZgIHiWwIY4AfhfYjVBxWdQbbXW8fkU80zFJBPdKslNfqEy9cdvYKAoYm4gfvPcXt5QzfeHQ77x3WGA0n1/1GPUZTKL5zDl03QwL1mRnz2Vza1Qj9hm5XO2ja4Xod/K3azOsjGBpwSIBrHDrucOSP4ZzN3l2U62vQOMm05ayV5CxNU7V7ydwJaBIsluRl2ZOvavssFWkYZ57PnLImc76uhIHqfYjxszcv8GS2xOiiGvDji+DVuazvHWG4c4TxqNX1g5ANkgesoJx/q9v5mvZ/3pqW99XnuFWkqf2qHmPXlBfSv+vjwdeOti9jeZlxUE568UO/0kDXRG7VyZgArl3Aa5LyOAlEhzbhneuUk2oQpFxp8mkHTJkAL9d0ymTMcsTVZ5+hmc9xfP++EFvulPy4PP1cP8/OS/4+hRRM6z/VjHKmmslzvMSIyvfmyeuhUsDI3PBanemyzmkjvf52z6lS9UD5QvUr7XSECA8//g7hp98gfP8p4a0ncjNDBrNuDiaxMLN6L5FacyxZMLEQgpLJIFcCurzvFeiSzTzdP9kdxKGAEKO4w0Rm9EOP9XqVLSFN0wKwCL5H1JT10HtEjoghYBjEm2ndzNE2LbpuJvH8XoSOGAK8B4CI4B0IIiABUAVJlM8QPIZhi4vzM6zXG9y+dSogmx/gRyvpqaPw9qRnCVnhT88YIDgBI3l2hSCcFD6MIhSFtDFC3bABaxuk0EQAej3lp1DnjRglbPHpkye4uLjAOAyazli4x4TvQpT5wYsyH0kADR88nDGwzgDBAxDuIWsI4+jhrMkgw4SckirQ41UL3/jxhpNe5b572kvR/26aV7y/bhVrXjpAhLzAjKurS8y6Bu+8/Qa4sZJZTrnUsoKbwUsFzfQ9UapnUQAO1PxQLXfqVwhFczIA7cMi73A+1qhQS0YyMwWR9stzU7luWSoT+KCZFJkRWRSYWnAHCK5xOZQghACuCGXBXGetBwCcb0/ws7P39tp85wlesKgyVm8WqR8gw1j4AaNmlhIlZLFYIDKw7Qck5YArL6wYI6AhZQkcj0mBSZ5VJNBxbBjrk4C4Y/SR5syNixL6ksLRJNtWwqcm1mXmaj+uhYDy3IkrJoe25xW2nJedCCGcioYoC+uZuxdFyT00X5gF9L7sj/Gzs3eREgwk9bmkStjZgtKWx9AwPQFNAVE2fJB1T8aaesGpl60NAUbXQiYNA2UuCidUgcl7MPIWR9bCNQ1OTo6x7TdYrdc4OjrCMIzotz222x7DME76oh8GdLMZTk5OMV/M0XaSrZdMaYwsUek+QJViyGD4foOzD38h8FdOMU/wR0fwhnB2/gzBe/hxwDiO2G63kj136PO10/pARnjXnHOSmECNP/lZd4GQQzrkgfdf2XAPnR90YMHeWzFqUeiaax368SDgdW11eM/Q/CIleI+LTz7G/PYdHD14UO0JctWa9LyWbvN9D4HZqRKc3qW1f++IXOpnFA+udH0J2WYiCRcExFBmxSvYOau8gj3GscfoB2mLigooUUZYU9Z+JgW6NItkzpysmaVLaL16+DNgQpKJNMyRNVQ4RsxcA2MI/XZA6xrcunMHfT9D2zW4OH+C9WqUzMKGFOiCJvkQKq/T09u4dfsO5kfHMLbF5dkSIAtjOhjjJCN2mm9c7UtJVIsAK4VHGAPGwYvXfJCoBQPkkLuYjBi57+KkH/d0qty/rzBXd4YFgTC4iD9/5wxvnR3h649vIxn0jAJdpAZsUn4xQMJFnXHoWoBIwCVmxmw2rzyLdR+jV19XauJzALmf0wZDILimAYhwDOFrc8q3W2QG8YA2RMKx1gSV6Qd47xGCrtksu1QBuigbAVHfX3W1idqqwuLE6SAmsEsMR4EY779xiU+OL2Gz4/VNjiD7ZXv3GFffvJ/Dhj9X2VWkb5Stdu9Xyx43HPYFlUP0EH9Zbi5fbaCrLq+qA77EdV5WzcjnveSJvu/x+Mc/Rnd6itvvfv0FwOHn4My7+/8Nh71cOx7ahL7Ywjvvy6L6Ag9YlchRiNPJKJeBnJ+sEOmPggjR1lg0TSvhiFBrNQEheiF8hJC+OmPRdA5HsyM426BrO7TdDMY1sFEsYk0jQkUMJUNLVqqihOgEL30amSUrzjio8kBCdOkEfCFGJskU7yVV3AmScpoYHIOkgTaAs6SOAOIZxRHwYw9EjzFHLGmWNBW6rCUcHy8wm7X4xje+BoBwcXYuG18MCOOAcdiiMTNJIayZziSsUlJEU9QMZyTf+TAqMfJYWX5EIN32a3g/oLhFJ+uaCFnGCnl/8B7Pnj3F+dkzvP/+zzEMg5AagwDNaGY456cRIYREQbJwcOQky5hmriFmTSwZ4H3I3nMpO1D0QZS2nA3yl7zR5An64uWOc5hZC5dJYg9d9NBzTOdT8twJvihTNfzHAJbLJZw14oHDwGq1UuHLKFeVqYR2vYJ6JxrrKmBtR2Ejql+eW56tbuOjszcKqMYRIRLGsJ/Vtg5RcM6h77cASxY+Q6ZY02lHXK2lTxQgJq8dFMXDSbMDNo1wd4UQD/bCRX+Mn1+8g9WweLGHfOVSxq6sJQZjiAhxxHq9Rjub4fbtO3CuwfnFZQ5dlDOQ+7GpvdTUmivrJGF728G3JAAaUIVo1uu0fGms9L+1RXESpY0mAm0yzhIZ2MZNhMwMjAVVjvResRK0rYkq2Id8TqjWX6Nx0iEE9KPFDx9+CzO7xbfvfQigmCRKS8h+txzm+Omzd7Ae59W9yxMyRCnOnpCoZ5t+GYUbrO8FpJc2jjAhEclHVbgI/TCCvFePrgAmD06U0JrBULJpJXBWs6vFAM9eedhavPPee3BtiydPnqDpOgzeox9H9MOIbS9KdLfZqrLjcPfefXz3t34Ls5NbIEvwYQQCYExKqe6Q14wUSkI0eVrx6JRjvBpc3v/JD3FxeYmHn34Kahxuv/tu9g4Z/ahAtZxjjIBcTevQOOGGTBx8iWMypKQX2Qt4MuSrl9Q7dXk5GeLLUi4ffYbzzQZEkvgmDMPeMYdW+dclMr/uMqxW+OzP/xxHd+/h+M03n3v8dF4V0CUbOQ4I4AccQK4prNtRrNacBLWJp+jx8REWR0d48OANrNdreD/CNY0kFTKmhIJnlFErp9dJ4V1CyxDyskBJrjPVVGLAMOCcyd5dqVpsGYgWTEDgCNu2aGYt2vkcbtZidnKMbjFDv17i8uIcYxixOL6d97a2nWE2P8L8+Bba+UK4ZoetGv9UzgRLkiBrYciCI2FrIv7t1x5h24oMfNVslQNwjsZadE2DRLafAK0YxNNr2gd1+5a/3NoVZcWrF/XKUZCl3H86GMiYnNEcAFIyGmbAKKettQ6typPMQNu0E3Aqqsz7ypMsyRz1KxF2AaIs06p8xRW9RwhejQsWbdNKGKG1CD4gCCKp5gMDsgCMy/smmcqbEFDKBWkqjjoQGUicUGmtznKQeiD/8N4TvL94irN2q+0vhmfvPSJX/MC/4vLc1b9q+ynIVbyJ6///snx5yq8P0KUlW552PbkSil+FCOx6dmVBiGnvu7xH1WLqtR5cE7z75voeImqJEeuzM7nOuzeevnOxnTvuIVfXiTv6ysjEua86VXe9yvbeH7h42s6eZ/ngndekFdUbF+rfkETZsqNl5zHWLa/WqbmcmjOv6CJuyOpm4jKRtFhtCueMWFgcnHXo2hka16B1HUwOoTNgQ7BGgbJ641apLLv9csgLKquAIFZ6qjwbKHtGEJA5aQgMahoRfNIxBFgDRENgQzAab8WafljAtVGfXzkT1IWZwGhbyap4+/YtAceGAUM/YKshJyF4OI46d1LbinkveRdImFtQpVQBQu/zxigdQ/DjkHlbUuOIS3hRjGP08H7A5dU5zi/OcHFxDgJhNpspnwvDQL2GmBApCY3FYkdRyUMrsJQh4Qohu1WTWi8TD4BaTin9duOQvWEkU3l77WE6hj+H5WZmLY6s3duAM0D1HG/JZMVMnlfJ1b30THGrF0+MXsenALTM4i4virjTa0UNWyua58Q6dWiZSofqa4hGhaT9shoWeLy8ixRuAF0fQgzTy2VPIhEEjTEinEK5qQzDMPKzY+IGr3Mz7Se7gBdHWC5jLY3b2ssm6WA+WqzHGR6t7mn7lOsfLvv7SxXlUB1zzfl5ayMFRmT+DUOPcRgwn83gfai8gzgTHidAyqq1t3hascir1iDMDcYZwXvlI/N1Ver6Kk+YKhXpXkmBy0+S29hmzq28LlZ9kc5PQyt5oclwihg9YfAlA2QKSxKvI4fIwh2zGRyeLu9g0awx3n4IQxHWCKcag+BZuKuIGWvf4dH6LmIk5SIsbctABrnSZJK3Vehp2nNU8LdEaJSDLIeSV32e1iZA07VzKN2dlxQF8Kou38YeS17jhI9gjcHJyQm22y1OTk8z51lkqHefnBNZ+rltOhwfn+DuvfuIxiASMreihYYAw1adXCmqlQxisrYes4Hk/LPP8PjxY3z64Yewsw40n8E6K+NLwyPreZD4vVLihHH0Oh6qFS6Birqe131SxtS0/SeN9SXWU6Lul9LBsqZsr64wXlxko8Gk5Oe77qG4aoKdNVi+vOboUnbDEg+13+55k+rsXNIPA/zTp7BNi8Xdu4X788Cx6cscUMzpc70W6j5V9PQsA+YMwLniZWfLL2mN27mnXIDRtgK6npwcA2A1yCV+wnLFSIzBBdhg4IgrZ5KYvTLTnpv2p0l1qMjIxhiwiQiOYaKBDQagmI2PMvV0zyKCdS2c7RDDCAPg8uISIRCc63RNJ8zmC5ye3obp5jBth3EzIPqQQ8YNETxFDBBaB2MjIltsXMDHp0us5oO2K8OyBZyDIcnaHdnpei2dIFn4BMjO3tK7nZY/FgjipaJLnluK7JLkhHQPSs2fB2rZnzKcQUYTCOieaEWdlrURRU5/wbpMCpU3k+mU9hCenpMA1ZQ4hKPqRcohZlAM4LLvlyQttR5hrHria59Q9g47MP6Bqj2KvJH0MY+ArRnx6GiND25fSsbmmCqf5O0XaCAixMaCDT3/2JctN6xZqH+a/H64zlSNpF9GudGz64Aa/uUur1LTFz/n1w7oem45pES94GlfpbK7H0w+6qJ2cF6qEJXAjtodFShKx02T67nfvZbCBaTYs7TtfspSTf6cOT1SG1RC+ES6YOF6apsOJ0en6GZtJqFksC7cBMMSqhPGCPYj4sjw1iO2Ee2M0HQW1jgYtIiWERAyICP8VFwANgZYrRzGELq2QdssMI4eo/dobAdrGzRuJpusuq+HMYlrBrNmrgT4DDIGs/kczAw3WPhxxDiWMKuofFlkyoaVfluvV9is1+IdZgwWsxmYGcuuhR9H4eoaB4RReF0MGbRd8l4xCtp5JJ92H2SB9krGHzL/ChRski4qPF0aIsMGQADYA8zYbldYr5b4+fs/wdXFFVprMZvPcefOXaxXa7GsBuW2YeEuk/2aMz9aYksmQgYsYpD02UM/Ymw9fIho1FsOLM/DckJWqL5qhaczI5dd3a98mzyvCAyfQcS0yKT04LOuxWIxkyxVMWK72aDxDn4xB6HNLv0ijKW5yJJtMxPwshKlX9+yzIRfPHsXjy53qNlVMBUwo57z6fdS5/KV1KdtW/huhuVyhRATYTyLEKhCopC3F4L1Q62VxnQCY1IChLbtJPvVkDij5NyNn+FPHn8HW99d+7yvr6RsXqnqnF9iBC7OLwAyeOdrXxdlxRi1zCYCWQknNlT41sRDStpiuGUx3mqAxsKZROyPHNqRyOfLek051MM6W6zheqxXsuKSNTaIcgFCDszb2Z9EeKYCiOnzMQx+9Pg34awcFxXo0laBtQ6WCMF7xMgY2WE5nuCPPv4+3rn1BN+5/zEEXDL44ZNv4mp7DANGiKSAa1HG5KL1uKB8n4k5R9vU6LjcbrdoI6NxrXJQNbBWPGLrzKBynnjvMHyem4nnUbI4Epy2e+CA/2r1T/Hfjg3+k6O/h7fcPbRtg7v3H+D3/p2/hXHoMfQ9VkvJVtvNI5qmwbe//R0cHx/j7t07ODm9BbgGY/AYhwHLpWThbZsWTdPi+MgJoFfxViaTR+KdtJXXl4TOj2iswax1aFuH6Edcvv8zVeYYt997DydvPBDLf9Q+shZd26JtO8xmM8kUJz2ajU4J4JQmniIqdM0q91UoYRzx2Q9/CD8Mk3HQNQ3alC31VQXcL2FZPnmMzeUF7nz9Gzi6dy8v3buZTqVUAARPgbVaBc/lec2kMqFzQuuQgN2yhomRLnmxdm2D09MTAIzFfJZJ7JkZEREGBsvZiP/2dz/Cu5cn+L2P3qvqYUBkYayDhYLXO+DCrgeJsYQnJwP+5W98ht94chu/++kDDL14m7fzFiEEfPzRB3DWYNtv0LUNZrMW5+fPsF5eod8OAEds+4CmMTg+WgBosF4PsAPD2AFEAoAfHR9Ldl1r8MntC/zR25/JvsCApQVAFms3ggM02yDr+tuAWwdwm42eigDBbQz82MMPVgy/WeROoZvSa6mHD2ItL1to8pJaFjlNSAKnwJP2Tm+ZgeAZkSRzZQpzNzatv0rjoJ7FX8QSU7zUk2FfW0fHWvBBgCxjEVkiOqwx2TCVmzZEsA/KsU+aJKjcI91Gm2hn/qgBj8RozqzAaxSe3+TB+Iu7l/hXdz/AWbhSw7V60RlScI0OUSfvlfX9Y1x+503wbN8j/5dedrb5Q+WXC3ddX359doLPX35tga5dz6LsvUUVj1f5UV7q73e+y4XqBXD6W5Gp9hfJ3XLo2GxX0K9iCBhWK7i2hW2nk/zQxr3vTVXZKbg+85B6i2IprMCu3VIDYLYf0Vxt4ecN2E4tibWgsWfN2+VRq+uwU7/a0jKt617VDn+fHj5tDjRVNHYLIflH5VUfhiysdRK62LRgI8qH2Kes7N8mdZooUXEcwZZBUTb87LGg4Bk0Dp6jhMuJQqbfsT4rCWhFGj7CPCBGwJCT8EUYEIslnqOANLmVnGgdhjjH2scYxesrbVKVYglgooimvxCCKhrp3LQx6vuETFU7QPa4gFGjpy1CaqzQobRH57kJVd7kWtYqz1nKRkTJbiuZubz32KzX2G43qWVzNqPkGZe8TYqQrK/Hc9D8PhA9EAPo0VNgGJV7CcoZlrKvpV2/+vscXlY3lv3l4Iu9z033YEbfWoyNw5FnNKEAkbvnERG6rsV8PgPAE06naVixnFyD0zGyCI5p3KWjKQEEQIhWMybKN6t+gdVwtPMwAOk4Z0iWp30ehemYT9cTJdpVv6c/zs+HBI5PGnGHuD5fu6oTEYyzE06jyISVn2MzzrEcFvDR1dUr9zz0DNMH2mmD8rl4eV2v3NfXHoZBwueMha14xYLWyyTvtHRdYngje6UxBqE1iO1+FqZkUEjebWltqcnsC3gogI2sWcr3NEmFXowU9XkpcUXy6Eqh1xmCYmDrW1AobRpyYgCGCRIWHv0oyTMQEZiwGhZY9gtcbRfKLWKwHI6wHBey9mlfU7X+FcU6t7KORV2/VInO7aOefjFUIfOgEuqbHdf0ed0CNHsbNF4BfolE1hw5ZM+wtGYmnpRzfwEMER93n8EQ4R16A03ToGkc+m0DZy3miwUWR3PYN9ZoFxGLb/U4Om5xct+jm6+BBcB+BHuPsb0QT822A7Ud+NaAOVZ4i0V5YQYuzoFxKPMhRp/bJ7KAmMYKIGeMJkXo+9xmfrPGuF5rKDQD1gHWIhgLaEhwzj7H1Zqv/2ivJ3YXO07b7FTO+BJpCH7oEUYvSvYwoF+vS2ii8ja542PANS9RZ568K6vDAa/6F9gnij/UgYOuOZ/50CWn65Qkz/EYVis08zlgWxxaw8opvNPj1ecarahEkOc/31R63Q2ZTpMzcSB1nYbUukYNQ+k4RiDGxSLgyA84W/SYDw6zwYKyjGPBHIvn8TUyRjCMq9mI8+MeF8cDLvoBF1cDtm4LP464y0egUIyJ6/VW+CER0fcD+sGLkxZZ5dxq4FwHBjCOAZd2xGAYTdPBWIemncPYCNcanM+3OF9ss2zkyAgglhtFFyuSZzZ5rTNFFldAxE4MRlU3pH0PVE3JG8bYS5TcJ/pHN+6t1Tlc3gNpT9X9CMVDqn6S60XEF3gGnqpsRWep66V7CukPpZIiC0Nk/JxsZ7LPVrJN9VwJfMqfce2M07qx6DIpAoKB0UScL3qcL7Y4m2/Rbzw4lAfK8sBz2oItYVx0GI5nGI869Rx+HeWF/Mi+MuVGz66/LAB+nYCuF+3jG4SYFwmf+2WWzeUlPv3jP8atd97BnW98/ZqjXmLK7up8ONQULy7lnXx0hpOHl3j0/XexuXP0/BOeW7399t91ytj9cS9k8fqLTx5LFKmkqOrvTEjhAOrsC4MI14gFebE4wmzegawI6j54hOg17bnUZbvZYhxGLC+XMBCOnuPjLRbzBVxHICtWtxCBMAgQFCtgC7HeWghEDZxxkkmFByAOavG34GgRWIQTViJ3jkLuGccRzkXM5gSwAY+S4jl4n0N+UtYUAQYYAT4rDAkcC2PA0A8Y+wHRWgzbQb05CFa5AZxmHSLNjCZJDg2sBP0DMAIIQgGIQPB2VIWnZPSLCvpZY2GNxenJifDVqCdACskR13zJ0NX3G2y3a/heLFlXlxdYrzfYbLZIlBBpk8/AGRm0//Pfxfzf/W34cURcbxD/r/8vxE+fIngBu0bvMYwe4+hhjQPBgKEpkW1FdP06yy9r932h+SIHffzgCL945xh/9f1zvHG23Tl3KgY9uH8fb7/9FgDJPMUxALA5XNSaGiBMYcMSPhaUK40jAGtAVgS3dIeLzRH+5NPfBLOMvXBN2OLuY9ZLxyGhLU39tusQwxxkrM6PCohAAlMMTLJEHgD6asJ6Sp6IEI+uruuw3WzzPX20+NGjb2M9LhD4JbLrfs6yB3kpMGQtYb1ZwzgRCZy1mM1mAGR9EItwCrsGvB8xuohntwJMIx45rhXLcQKJvR8LoAXKyVW4mjuJOHfST8onlzI7igI4VYKMug8518DGiKYV708YEmUrBhFuiDKAGivlwRgD16RwlLRuqp8YQb33AMSAx8t7OFvdgnEGxhKQDWK1sL6jsE00+cNpBNIIbpxF1GQZfhSiYNfO0LYdmiEgqhclmMXYMvtN4P73gGf/HfD0n+ozRIzDCB88NpsNmqaBdcc58chms8Fms8Hfd/9vvBvfxP9x/h/jmOYAJOSmm83x9jvvYnarBf6jn8K8+wzzxadoZnPYe3cB5+CdQ8rmuP3sEYZhQGg78HyOkwcP8D0CfousKsyM//t/zvjww+JB64cx8+H5YUDwA9rGYTbv4Kx4zLq0tkbG5Sef4OLTT+CaFmRszoQ2n81x5913cf+ttzJwGveA9WkP1WN/2lX7KwId/P5XU84//gRXnz3MwHuQDDLTcqCqr3tr+lWW848+wuWnD3Hvu9+FmwuHoeIoshzU3T2BMVD9wNd06U0NxRhH8RgkEm/dBCIbK+PcaAWIgG7WgswJ3n77LWyHgM0gMglHRlTODEMWj29t8Y9vfYDf+fgu/spH9/I6N5/PMHqL9dqXMax5b4pcTNh0I/7wex9h0waQIXx4f4lP762xWq/gtwP+9g/fw52+hW0aMEdcrdfYDg7bfsA4BDBsDv+9fecNdBp6udmscXFxif/+zsf483tPcHR8grbtcHp6R0FlB3aSvMdEzcwni6fIY5zoKrisfyZXG5KZW2VEBFhLIAOw8hAWt3sAsCCE0qWpE67RWl6sVOclA+jEsoS8v1QuZrr3W9VPYuW9JWtN6r9UDE15Jz9Pyfgsdp5cZXcxchAAm71Zk4cvqbzaaiZIY5z0ASV4DtnwbY2M56h8kIQ6szNP6qJKAyKTktkDzCK/heDxZL7CP/mNX2A1roGt7PeJny1RIEB1I45AuGYKDkczPPlrXwMa98o9/qLlulXguUDfoRP+snzpylcb6HqRNW/XIkB1sm+9TOWZlQTdQ9kay013Lp5Eo10giepjcPDYG0FYloWj5iKZrvzpOjtWpxsueagu9Tm1AvS8YiIDPgjAcc3NXww7f3Fw7TphJRvXX+oalJWuWHll7IyObLGxxslmQcJbJaExRo1YYtVvmgYGBjzX8cYS9gRmcFQgDRYGBs7qfgvNuAMShV/JfCm5zpMBRwOCg7OAs5LePXOIcQqRMpINEhFgQgxA8EpK6UNOUw9Om3FqdlnOxcsLEtefAD8FhhI/mbWS1cVpGIkxwlcTQ4QfR5jIYJc4NUp66HSfQppvhBzfJQ40o8AUizs1lWMT74B4OkAkXE6+d7pls4RR9X2fCaezzJL6lSPOTxgfvxvx8A1CaB0iMSK34G9/DVjMQT/6BYinaY+lZ6na9Q6PlC91SXXXB5t6PFw//wIBvTF4dtIhksE4OAUjDbre4/RiIwcyYz6f4+TkBByj8KxVk1IcbhLQpWDBZExQNR6RvaR8tDjb3MLl9hhjcABXLvZ7zzi1WIIL58nBUnnkGGtgU7hJtihjz1oWYfBsdQf92OLu0eXk3gkA3vVSSrxCdQYjAPBs4aPN7fO8EiywXQB2BJp9vukXKgmYMaRqBEPCTDRjpKSBl/WkcQ2887nuxhB8x4iGMfQRo4nwiLCIiARERFAspO/jOIJZgBzoXC5CdhEhJxx9lbW5ZECUPgo7nFyT9OXM6q1d+iO1f9o/YwhIXss5dTpIvaGmSQISAa+sPQYjO9hAwrtmlMMFlYdwWsdzK9eyAe99R9Wvwt2Y2kKMEa5ltcSXZ4jMmiHUAWYGIley2TLDB8luNgy9gMcakh45CrdXCNjygB5DXgqYGfTgEubeU8Tjn8NffIa4OIMxKzjLcA2Du2NEF8EugAxgEYFZD6YeoYmILcBdD2ssWlUIGwd861vAyQlhHAneR6yXPZyzaNtWxs/AuH/P4urSYtYRLi8Jjx5K2LFVz1wQwF97G3y80BAcCzObge8/wPbtO9g4j1UTxOsrRLRPLkG+cPGlNt6XdHYLV/PjV1/GzRb9aoVhvULwyrn0S0CvXpfnzItd5wUgRZY5EREOCHgJvKrvxdXn5IGsssiNNylVOnQk1ZuTznlr9j1UnbM4WiwAMyJgzJn76vOZgIECni22eP/upciSEbj9hGCjAytHcPa+N8DT4y1WnRgiN41H30TxpmVCQECgiK318M7j4d0NVt2I5XzE3Dt8bXsLjbVoncMn9hmemS0sSWIivr9F0wQ0bsQwDNieBFwdB/Q2IvgNGng0dARnGhjD4gUWXdWecQJiMSKIuHg5T5Y+7ZskD2pG7cRpGaMkPspDYxIxoyNJAZ7PVbiSuysBoYTslX28Xj1qz60E1kwhqAIIJS+rF3eyOfRQU2Auj3KV0aFgVLrfdIfR3/Nzyd5KxghVRJbD5bmSbGIgmduL2quxK7r+CO9XqkfKlg7EIGP64+NLPOwu0VuP0RcC//IMJVqk5js7WAiIzgJW8sp/aUu9xe9+/5flS1G+2kDXK5Qvm9fWq5fXJ/RwkQ0OTthfhoD1QiVVdMd9/FWql9X9KAqakFBjAgak7cJAvJesdbDGIfIIghAoF8LbCBDhaH4EzIHTo1MJxRhDkb3YAFGIe40BnOlySukU5x+CWL+TUmety3w1hgzapkXbShrjYdtLHD5szqoSQpCMKiEg+ohxEIu+gfDVRM2oKOml5Z4mTIXIpHSKN4WDdQ1mswWapsmZrrpui6EfYEgySPoxwI9rSc3TAVDF2BjJEGSUXkaAMYZ1DUyMsKwcPQqYcQT6flSQRISaZKn33k9EY7FSWc2O4xGCx3q1lp5ToUVczOWsEALefzPi7//7EcYZ2N4KkEwM+3f+Bvizp6BffALK4TMVMFOrS1+S6fDSZS+V8vMBZkk5znj/zRPYtwl+TNlFHR48WeJ3LwXoYmbcOj3FGw/u4/HjR9huNzqONKRUAR+JZTCqZCvwa1I2Rqjlu4Qw9qPFnz/8DfS+1e74HOt3kgpR4X6Qr5xrEBv1lJygYwqG6Hzw7PDjx9/ESbfE7fmfwppYni+DJ9CxnzwJZW4mpedVy9gCZw+Ao4vPA3SV50lU/dZINlIOEWH0koEUmtiBJTOqtQK6LG9FbNuAzUrWlRgCYEjBFCHh3W57eO+x7QcRwGedhENaCZcRoVs5CZO3VQaxivdT+i5qWMQ4+qxAZ37BvE4asK4lSeivQyUDcw7BhhoQGs2SRUTyLJrsA0jKDiMlogADFCtli/ZNOHTwA2t78+TZ0iGpjhQjBmawAoRtrLhVyGDQMKQUUpo88cgIX1lkxjj2GIYBm80GzIzFYgEgeTsFDV9CVhbF0s6g3/4I7u/8Efo/+WNcfvIJhmEAnZFY2km8hokl3FY8bOUawnOm1+WY5zOYYS3wt/+2uKOMA9BvI548WaJtWxwtCH4I8J5xfu6wWrb4sz8zeP99wn/5XzgY02Exn6NpGri2xdW//7fgv/FWXuvbtgWaFhezGZ4+XODxkwWCj6De441/uUWz6pOdZQcc2V/v6Jr3v+qyPj/Dk5/+7FddjS9VmQKWqez2bzmWJ98TDn+cnnPoJolnkQHJeEqknqg2hxsKDx2jbRrcuX0LdtUDpkfbdLCmmd5D0DT8/M4FfnZ6BmsNuujwv9q8jZOxAVfeyom64SfvXOFnDy6Kh0+ak5E1IkAMASNF/Mm3nsGSgfcjvrG5g7/16TfRkhDk/+DuGn98/BSNNbDGY7F4CoIYOZyVjKxnjwG6cLi6WoKIcOv2nWrf4mwIkZByr08VtC1DNr4KDkRVw6IgMpQSFQXJyKjrm8hyejyRyMzIpkbsrqEvV7LUjwxu5qyKxWubUv8iJQORQSGAUtofpC6VTQ0AsvHldYSRpWYo9jgGTOGzTfUwVfsKflg7RnAeQwnoIuYShaFyjUsJH0jaJ+h4lhD/oBx1oicFNbowi9wfAiP4iKt2wB9+++e4tD38JiBnyUx7fAa4Cp3Fl8u88PzC2N/3AVz/CF+dR/u1Ll9poKsmoQVUiH8dqCpjL1vj9YVe5KDpxfN5UzlsN4tj3nUPLZo33LJW4vLBeUUu4FDt5UaVEvi8mN+apwvKX5Q/U1mE95aE3KScK1nHiz9vcyAxvevx8YAX1ov2GSSMDwyr7r3pma1u6JkXBJDNwViQdRLaw4BYsJCVO7GOSPY2ycoYwQYwjUVyIyaru5JJWfCqsZuzAbq8KUCvF2OEMb5sSprFkVoJ92tceW5nGzSuFYJ7RLh2hDFCCC3tBh1SyaOLYGyTGhhg4YpJnw2phVH/UKWTJyOKe9PO0C2Oi2mpnSm5u1j36v4wZEGW0DYFsCR9zgRsGdOAGbCuzUTN4AiOgHEW1hm0LOEtD+6/gdY1eLh+CGcd5vMFhnGUkINEoK6eYknRs05CD0wGXQjRa+ic1qdtxbU/eXbIkKUseEzXlRp4Pfj1oRH44qtGBbyWNaH8VjgFy1xM8mQSMlKYarnO7t0ZmWkoe33JuLQaThRUqG7HgK89ucLJsgcYmM+KYipeOIkbLeq9UcZ0CCLkktO2ZF0votZd6pdhJiOhr3VY4E3tlDKU7q8lnEGKtG+kcLByZJlvo/dwVsaaMWV9k/AAoB8b/OLZezidLfHmyTNcbO/gariDru3gXIOjoyM46+CaVkKZlys8eXaMp8+OZW6QQe/dZC2lah2aPla9SQDDDLi6zZitAdfvHQ59zGosJmMAl8/VJyGVNfDeo+97DP0A2zS4e/cu6JxwdXWFbcsIM2AgX0jcjUFjxdszcQD6UDy6EtCXRpOEJ4cyF1mI5glJacI1zy/fG6NrEBTg4Vh5yZUxHWNEGIdy/0rIBkqWrKCAXnrPrB5TpGHOUIUtBnFthIxtCiIfFMxS55y+TqZZrllRRJLBpu6SNE8A8TwL3sOPo4QVdhahl/U/BI8YGxinigvKqsCq+I6jhAj2fV94vjTsL0aGb9cIf/PfIHat3PO9z+DDiPVmjcurS6zXa30maYvNZoP5fIFuJvx7QVPHxxARSUDAFBKenoUjZ066sh6xeMvGAGMIjbPo2gZj6wCOOD1l/P7vG3Rdg1unC/z0p4wPP4qgP/kpzIcPMZ8vINkhGR6ElTEItxcwpzNEw0AtP7Hu8THAWgNHleeNdgQhgawC1hLKWH5Rue46Gedlj0nAo+97XD16hO3V1c65SUaL1TelbdMmxbuDr67FRDyig0flo3dk0T2u2gMnZ3myjpC4Ro6ezJMDe+EeGXiMuHr0CLabIbomr8XG1Asd5bklnuvqFapzc7I1ZxG0tAZnUEHnJyeZNiKOuqfl/ZWQ+O/qtpCqRrRNi9OTDs7K2E7gVo7lowSgyTz2hvHjty7Q3GKc33qmayMymP10vj3Yt0UMkAQxKbNpBCNwxJlb41/c+witc2jbBheLiEV3jMY5WGPQWJsXDzIGZC2OT2/BNa0A5lGEneQlX3QD4UtKMiTDQ/jFRl3HNKkMk2BgehyRyJBMjBDlHEluUryKpntVSfTBCZy6oZR9r/LsTvVM7URpTay9v0VvIUdoGlGLI4fSXzvtvl8PRlozU9SD3G+qjR3Y3nbUu3rcV+CVIUzUOCq7OIMkqgMEkCZMUiMjs8j+OaGLhjcm41sqjSazYKq4ehERKOInd84x0IivfXwEMxJ8ENJ770NuZ9I1sx8GDFYMXTHEHHWS5mX9iOkr+X367Gk/222ZJJ/WfbsnM3CZ1xwrWWciR9eH8+Sc/ZLWgkpfre+b1pIayIPJCXuKM8TOVQ/o2dfJga8CnD7/jOftby97zxfWaH7p5SsNdO0WcUWtpEvUKhOKYpUGWIYbpoqEfrlTdn8on8sY3IFd6sseULx2r52OPzimnzuGDgsU5f7IC2ISAKATsFYgkDaTarIdmmRlsUmVxkQ23FXO5MpTQXT3uiWk5ebHLQrnNUpRff5O1ZOQGzkCIWoa6PI8NfAmzyAZcchYJcN14gkRSYLLVRgSS5RmlmIoabwIMuLN4PJmD5umHedsJLJZ7Dw7EWAsYoiwNGr4kM1tZJQIHwC8Fy4t5xo0TZOBBteNSGmn5ZImXzv1hzEWWapiyYiV2lI4i0j5vwCQbJrWCCE+M+AS0KXZtdDMNFW9ZGLMgBZY2pENTFMEDGNIvldh0LmYgS4wg4MvG421sE0jTmNEeOPBA1hj8NnHn8Fai6OjBXi1wjAMSHt72pRiDABriJpJAIb8Ng4jOKjnhjHCcVOFm2Uhl7Ezr6djb9qB15eDh7zIvpKVmunGn1KJi4WPkgRabfK7l6k21/rdzjKSrNeJ+42Z0fYB3/jwHE5DhGazGe7cuY2mcQpypT+5e1LuhQNJr6sWxHRMCEH7REDgRHhehwCm57/JoysJFTlMMistyGD+tN3S88rxKbudHz0MCNQ0WeHnyDJGwOh9i188exdvnjzBg6MneLo8wceXX4NzDZxzODk+gXUOzjXw3mO93uLJs2M8eXaMaBhMwAIjbGVRfq4Ap2WcAWMHWA+4Yb9vS0mgHrQN6vW3rJIpRLkfRgCEvu+xcAJ0DcOAGCP6FtgeG4xjQPQBKdy6bRoY5SjxIWAcfUleYZ2AaHkfQfbMTNdtmjYTE9fPXAOztXCbgFAWUbI8aW42meeDEnbn+Us16CJ9XStvrGGNVoEOp1xkBgxEgwgCR48YONHmAG0VmkKkskc1QVG2xHrE8s48q/eAJJCH4DGOI5xrYZ1F75XLzgeEGOESukGEOsSHmeH9CGMIfb9F27Zom1aVOwFxQ7dC/L1/Cz4Rj5Sg3GDr9QZXV0tcXFwAANpWvBA3my3atoO1Dh5erfqSNZhNAo/KP05eDVUbZPFAFYG05gshvnAJnZ5E/P7vW5wcN7h3b4F/+A97fPhhD/rTn8BExvzWbQCE9WZTANXf+124v/abCOy1Hkl7gnoZehjTaJIKydibFWEjbR+CB8Hm/cAaczAb2GTNfAFD6EuYMrTvgHGzwflHH03pKlIjVvtLUpzM7vq4e+d6Pdmp3UvVLa0VL6v8HNYtJz/u1mQP5IKsG8tHj4CmQfvW22BQDmk2ppbBUfYafZV4W7u3QU+X1/TBTj4JaFD8OGTpUC/QRB1BZb9hlZ/ado7OzfN8qFcByq8qewLwxPjJ2xcI3uPi9hkS11X6I0zXlwKBpGdR+ooKLAqB8cxu8C/ufYCu6zCfzeCsxZE50TWBgBgmY4WIcHzqcHR0jH67RfABwzhWHrcK0BlIu9iUaGPU8MMB0OQYkihJ9lwBawzYGAW6oiankHVNgK5amEpvDIjSnI75h8OKf1rjD/xUH2WoAn9MHoWpL53yVIr3r/Y37N4Qpvxffe/SB7vlUPRJElF26yzbs46ZLM7VBkD5ORnrksxDxsj+HIRvkiDezulGaU4464C2eESnZ2YAgYLqSALA/uTNc2zsgHcfHcF4yuvqMAyyPxmXE8AM44AhDBqZEorslxWz6bqZnCWSHHhtn+2uYzsNWdaM6V5Yy3h1mxeeTZ687paM0VXzsNaNJ57ourfV9DCMBJBP63ZTeRGnj+cWmrzsjbu/aOXXCuh6bnmRzt6VSn+lRSq8fPoUw2aD07ffwvzWrZwpZGqXx97z0eQr2vms31F6rcXS11D2b/ZSJ2cFIS8Qh+t18/J4fdUS0GE0bAeQBSZmBV1q4CniH/71JX4wEO6efYI3r45x994tUYjbFjNr0MYO6jYkyhcDtpGMSEJKbQGyANdpEfWNtWUNFE0QovhrPUwAkYHrGiReqgRiyL0YcfTgGODHHtZAhHYr4Bw5EsEjKAhVgyS68SYBisiq8GyzMO0D0A8ewyBg07Ad0TgHkBJJBkYYBoS+h20awBh4L5tsItknyGaWNmrZpA3Awh8TA8A+lr7InaqcPkb/KIBYUiQb6+Bawt2792HI4tM7n2K76fHJp0/FFT4GuEZ4bkYfFIxUgnBVBpkjYiLTjCLkNJ3FLAh40zRNZd3X9oJyok368Zdd9kd8M5/h1te+iZPjE9zvOqTKdZ9zw+QKIHER+I0Pz3GyGtFA5hCigMXOScKEruuwmEtGugtDOWSRUgpxVnEhT+m0I18/x7/IIjIPZTDaNY14/ygoJzx8mpXbEMgacCgcQBebE/zpw99CH25lgT0LpflPsx4lzzBc6wD/UmV1AvQz4PgMcAc4qq973jS3CaJcRMjzxhDhKWC5XAJEOG1a+Blh9cCitwF+8ADEUh+Vd1AAZcnSCDI6Z5QYV+/hqjDOuhQ1t/KqqwCpBJil9kzXyNwpCXzkEv6YPMXEC7F4WFG6dlJE9IZyThT+LrV0EzN8UCVBFawcOqPPLYujAJaw+4Iy77zeVIzWUQRjfa4QMQ6DeESYCGcsnBVSXlIjBi9+C9HeBi7+OWj7EdqmAYFxenoK5xxm3UyMGCC0bQcig6OjY8xmDsPgMQwR0Yli7kMUwnfXwgdpt6PjUxwdn8C1HchYaSfIenl8dIKunaFxTkLmfUDQTIqpL41y3gUfQERSLyvgFqkCst1s4KzLHgVpDJAh/LW/ZvH22w3OL9ZYrgJ+8ANC3ze4M5upt1ZE+9FTNI8vcHl1hXHb4+LJFRrb4O7Xv4amncGaBZrGoWlsVv6S3mdICMaD95CQaOnHcRzQ2h3w5AsuwY94+vOfYdxsbtRKfl0Ulpd/DIb3AXEcsf75L+DmCxy/9RaM0kmk4r14+nufEvQESI4ckizZKvPIXwJQph4XAjJpJlCerk/MwoUXIyEoMf04jPCjZGs1zoFmMzAUWFPDyRTunTZCEv0AA1iH+WyuCrQajFIdc3VZxcSUgKhwr0obyGZgjezL8/kCbdOiazu9V1UHTb4SghcwXCk0YB2atoN1EdY5WUNV4WeWezAzulZAL5gIQwym5NEd4QMDoW47Wefieo1xGNU7NYU93zQi6nZ79QmwO53lnlHHxxQUoeRhlvi6Dt32pdaHwyDcfhRPOTytR6nPBS+ZAn2mAr9UkM2yRhgGhBiVs1HBPb2eyCrJW06uy/nqCUA34pXuLIYO+Je/+QgYI7aDREwMw4jvP3sb765O0LgOphlwenKCCIvtZgsP2cco8ZZQ0uzq5yetD+09X9FIp213SIqYfqa9r/dhsL3mPjyyXnbYpTnyGuS7vyyvr3y1ga4a5cgKvE6UHTL5yQTj6bG5VIN6z3KVODmSOykdQsR2UWY9la4XUChpHpPz6usyhrWk2V7cuQ2cnk4Q7en/9XV2FpR0FE2nNNVPqotOun7t3TSt83NW+BcAuYpNKr1iTw543j7yeZaSzLOgJPAZoa+I4JmFM+hHbw9Yhg3OPrnACQG3b59mi7Q1BMsOMXjkFCIE9TYgwEjmwUgk2jLHvOjnNTkpbkmBUa+HhLcZawHTyrmRNfQxXSMJQWIhY25AEKWFjNH787QxE96VvF3yKDDlRxKFilm8uaKGLgYfJG2xhrHFEBF9RPQBpmlBKCEiOWwt37Z4QBCRCJ+aaY9jBDmjlAw7o4MsiCQbjPhWE2AtjCMsjo4wjiOOT04wjhGr1aWQphrA2IqEGiiAJpJS7AVkixpRSoTGGTiCku9b9Y5Kc4vLvGM+OHfr8sVsdYeval2Dk/v3cdJ2OLI2wYvPESBvuAsRRkMIar2SERJx/2KL4/VYtQuyFdNaUcbbpoFvnII9SWgpUkqZ8QVor1xjrn3G112qKajcHFa564Jy5JV6ZYs5ERLMxczY+hbD1X24xqFxBaSpLf+7f+ncw9LzfrnWs6sDfAMsLiFUKSjNWEImpvvPRChGETQFmGYgRvTbHk3bSXhJSxiODPwgnlrOUu5PBpfQbWNySLDMbSteekDOeppvjdLDu56/E68Z5f3KoaO5DdMeRIiUFNcCdhEwAajTPRP4iHx+UXiTgSMpwZINVgRvUmBL1i+jazhXD6EvOxvWdWAX6VqflOs88jOAp7xiwQPWQQBJyTpY+o7BzX2wvQNa/wgYnsC5EQBjPptrVrUmt6e1EoLeNJ2APhwRgnjDiGcKFOhy2m4G3WyGtpvlUPlYebZ07QyNbeCc1ZBIzXroA1LG3vTwrH3Sda0o39Zlz4I0J9I16vLW24T79w2enQHnF4yPPiKsVhaG5kjhqP7iEv6TK6yfncFvt+hDAI4lNKvpOrRNi6axaJzNXj4JjDaU9gExenAMGFU5nIzNQ4LIIf0qvU1A+U6Cg9z/CqzXx4ZhwOrZM4RheK589UtZHa/RDJO0cPOpB455nqZ56Dp7Xhsiawz9BoYkS6GEibk8j50TjwpvS4h0iAK6RDVUFX4/nf/PFVZJwegy52sPlRQqlrNZWwtEI8az/MjlHdf/MSV7HqDrS+MaXY9KJsO8NilfYQoHEzOFXl/X5eylYyyccreKh7qbKCU54yCJHEam6iQiAe0S35TeW4xAQbmoApTyUB9PEw+BKwCr8FVxFDuu17C3lI01ea8VA3Np9/w27dTPkbmeVyZzK3UhgICIwQXM6jZA8VJ9vljy4nUqdUjPW86tNTNUv3Iaa6W3i5NCrf+xeFozSD3sxLvZEAHOVdyhu5E8pUGiEQM/CPCWAWMQG+CTeytJ+DSMGDUj+Td9AIKBnTVwjWSvbtljHDyijRMDV5IZpk9Y5JNyXPlhSllB07ar+q8u+R5cvknns9ajbvbrunait/ej/N0kT+e1IVWvkrF+ReX66v5yZOwvS/lqA1112VkjbzzuVS7/ote/5tzPNdaTULxT99qj66Uea0dZqJ/rZa6TFOB0Ynp/neCQFrpdkOtVSlr4X/l8pPpLG9aAn3AnKFjArMTKPa6WSyyNxWazhvUOrrGact7ApHBEGwXQChLi4zcDfCKHVx4D8aAQy+BkoSbCOI4IMWAYxqxcM6dQERGKu3YmlrrZHM5atMpZAXgQBRgTwbEHRwKpFBVCQPGKsIA1sAre5nCvveYknJycwr8R0LZCQr9e92DeYLW8wnK5xLYfMYwe4xhgO4CspIiPkRFHDXEiBln1bIMIbpv1Rtp1s81C2/HxKRaLBRgkAmBElqKMcXCOU3QliMUDbXF8Cuda/M7v/A4+e/gQPgzw3oswFYJYXxNHBpWJKETKZQi1jUEzczg6WqDzAd2sQ6Mx9ojFqipplxMA8oJAxUuNzOdd6fCcaY3BO52EF01PKYLty5Rnt2b44dduY9uU9UtCLYxaEXeJtUXAIifcZs5aQDlMRJBNxKTyX5JXCSpwqwXxl15UmrHOgblB23VCwD5o1kglzhc+GAPrGkS1ZmcUtwJosvBZtzehhB0b8QiLzODXkUqIbu7aIqxRPj5JiAbCSZgt2pEREPD06VNsbYS9/wb6C4Nu1WK73WC9XmM2a+FSSC8TTCNrinNOwv6sE/CbiyXf7gJ8u/sYlzU4f6ffCyBTPOMiODtVybOJguRHn0nXm6bB0fERQgh5HZAQarluCfcSjkFjDVwUJdAYyspwUmINEZwBhJRL9wxduIkBk9cpXDc9r+s6qVOy1icw1VCuO5OFdYRuMcds1mmmN50vRnnE7v8d0O2/ge7hf4G2f4KunSk4ZhCCJDLpmhlax+jaGbrW4ujIQLnqJVQFHl07w3y2wPHxEay1uHP7Dk5v3cJicQRjDIbRwzrZG0+PTwAgk/3HGJAijLJyqNmIY4hIfEYRAR4+r6eb7Rbb7RaJbnoYZe1mAEQSZn737l3cvg38p//pEZ48afDf/NcLhGAyLwxAuLyUDKhHR0c4vXsX3/2t38JsNkPbtnCJp0w7LWFwJnWiJlwYxwFPnjzGerWC75fgGMpgfElR5eyjj7B6+rQazaUcP3gDd957T35hxpOf/hTbqyuEMcUhH0bW/mKpJtNCJH1rjRCmH9+9h6/99vcyZURUr6agvECjlxBbP47wIaD3aX1IHllRMlHHKHJYAsmz0UYU9HEcAQBt47LSneegrhenJydYzOc5OYfRvU8QqUIVAUAMlayO+5RnymR5bjrhwkuhehMYRL2ihDajeKNzZFxuL7EexVsKQObN7NougxslA2RuWRBZNG0rdal/S3yFRr3sSTPYqudsjAE+LDH6MXvJGiMAvffqsRUCmrbJnqWMiL7fyroUIkL04gmawxKvUUbqRnrlmUA7r+XTs+Mt/snv/AK/s3obv3d1CzWEckj3etFq5L2tAmv2j9m/mADgyPtBkoOTrDx9JJVFdX8athv4ccRmvc79JNyDwn8rY1v5Qc3OnszALx5c4s/eeZbBy6UdYWEQlefXmADrhLbkp79xhUffjuhmCwQw+NKh2bawdoswMXBNqWFeW3mOHnijb1UW4a8fVwQAg0f8B38IfvgU3Pc3rsQp6iOD4r86jOsvS1W+0kDXXghIDbYkT66dWNyXuTawA8ZUA1cEbV0IDxF1HrjiwW8nE01KdmetrPLpCi/nocF5Iu/tGYc+5GtXSgkOI9I5jpgBtxnRrAeMndvNCKwvpQ8OgVtpra62/aq+BNrpgkPPWdZ/nh54zcI69TpitdTvVnxa28LDUIipTWIwTQBKUIG+H+EHj347wI+jhHbAgyEhF8yxZBHL5hnC6Ef4GIQzilGAruBViIuZ8HocegG82plYaojALLwH0vUMjpItyIeQgU1DQlwKJbisR3vpe2kjoy7si6MjraZ4eIXAiIFVUAzigVZ6DDnUh5DPqxpf2igkIIQrhY9KF1bDMXk1JAGk4DcGrmlweusU236Lu3fvYLPZYLPtsdlsxEtlMiBYBTLSTG1SP6dW/6ZxcBBhtlRZxklicyjcdGn+Hxxi9Wg78NWhdYnKlE3dUV5uLAYCdpExVc1eU2FGN0TMhwBTPyyXcTLlYJC/qFbumq9LLkd53uU5VlmXX1vt+TmrvqJApPMvgVHG2JxVCOlpdI5n40B6+ArA4WqsTcfE1KNLR/DnerRs/cxrdLlXqsPEIjn9Zed55FkIAnj1fY+m7+VIY+A0vDr1ZyTJ0iTrYQnLBFC4cbj0bbHKFg+Hmitr8h4l1PBFBWOuxlxqC2OMJvQQkLrwZKTjp96lmfNYXyKLJ1fk5JVK1eq40xe62vGBX3d7+aBInfYtHU6JDy4qJ5xYxkmW68RNWSs89hZgZlgsTkDNttSKCN4Lb1rjNrDWY7YA7txRDryYeKyCGmNiVvbFK694vwTlMGNYGK5IryNnD+QYBDxgFsJn9pKwZRgG9QaJeY1I42XoJVNkWkdSKDlgYCypZ7K0/emprBlvvEnYrA3Wa+H3atsmj2NjRDFvidA1DoujhWSuvAHoMgQMQ4++t3AabpnHTOq0GxTdfQ+C9OHQug+EcUS/WsnHGNGvVhjW6wPHc97Hn7cLHNqD9r86JAXyRGZ7EU+s3aiJvUvWx7yEpvc82TZ5ws1mM3Rdi7bao4PO17brADIKdEWMg4OPES5UQJcXg6P3AoAnaoPCc6VhXgp0EQlfXZJnBDjVWU+EuQJKEgKbQiQNOBoYFhlFsgwSoN6TMRbwPv2U1y9b2jKvOZQ8i8oPmbqKAY4MO1q4YBFJAFrnXFmnIQmW6s9lOHA2MnHqvbSXc+ElgkmZelWfIEKItWyvMienkPAgIZFBri2crgJuJX6z6b65OyCqSu4Oy51zikyW5sJUb6iOnLxPkRveMc6Pepyjx5nf4hYsLDscjtx59fKiOM/BJada82lnrmXvuBix3WwxDj36vs+h/4krkxGLzgFgOR/hKeRLxwicHw04P+rzmIyeQVEyUkYqgBUZwmYewd2Ith0EvF0pfQOoGJT2nizVOr0rr9NjDy1q/PzuuGEZofyqThdEk7Vqf1+We/LTC/CTi71rJ/1MDqsFxufUEYf16tdWrr3/gV3hmmOvDau97sqvVel4vff7SgNdv/7lukX2xWZS1j3T8TcIJumqN983Xbciy2PGnR8/RJg1ePhXv4Y4L+ESr67MUd40D9x9ojTnhzz8IIfrD6j7dYAl5c4xqozFcoHknWFdgxYz3L59B7foFPPFAoyIqAS4AMRLIwasrpbotz0uzs6x3WyxvBR33xgCIglhZ9BNyXsvAowR0nrhQRGhy4eggIwtiodyyaS4fLG2WRzNF5jNZrh9egpngcWiywLEdhgQGfBBlCXXNGjbDq11wjdjqOKcKhby4MU1mcnANi1u3+5grcXx6QmCF9Ct72Vz22y2uLpaYXZyKtxkLITNTjP6ECVQlJHCLy1ZkAPQzbWtCc622jkyfqISMEtmIiOZxli4dMLokV3jDXDr/j3Mj49x7949fPrpQzx69AgPP/sMy+UKAqwxxJfOgAww7zo4azO5+Kxt4LzHfNaJB4qOreKNVEhnEz742tf1F73gVK//Qupy52KLv371ED97+xg/f/sY3/7wDG8828KpUpA4LSIgoSHeI4wD4jhg7HsMfS8Ar5MxbZUDKfG2MfN+Zq8E3lyrWb6+ku4gryLEwRg0TStelT4gOA1hiqwjx5QpossOqeBVQuckHCyNzQS0itenhPYhQImUpdxkUPginrwW5xTjk1dDIAauLi7hmga3nxDG6LIiJ5kVGYQAVq+uJoWogjB6j9GHlBgXXdcpR5s+p97DWEIDixhNTvhgU3pzFMWtaYTYP4PhSABLjYtSFY5RlFS5jigAonAFBdVSFs+0dVT7SHVhzvdMYGKpWwJrSiMaBdRS+6ICvq6Dx6r2T4NJLy5VEKUl+FGWwxjBIWC7WQMAnCYcEaU6wJmAb3/r2zhq3oQxhVg4hQl9+1t/jnv3noDMBsYQhp7Qb8VIMQwD+r7H06fPcHZ2jn4YYK3Fxx9/gtVqja7rJkAtVY8UQyL9FlCLgMx3NiqJdRjHiWLKzNkr8PziHJvNRjzygngUMksodqPh48vLCwxjj37bo20c/sP/0OInP5nhD/+gRds0mGs2SPHk9RjWK5z99KeIb76J4++eZn7AFE5ps0IsGRkb57SthWB5vV6BOOR5cjDjYHqWgyAXcPu993DrnXfqA3O5evQIn/zxH+dzJbT+sBDzqjLUC0iHr3Tdz11eETdgBvp+QHARxycniP2A85/8JNMneA2hfvDd30Z3cgIQ1JslwhmHuZ1VwEq6plQmzdu0dhhj4BqXxwuRJN0AOPP42eQhpfKoIcJ6tQYjef86ydJtEnAq/HviJEgAjPLEFrqIBEq4Rq9tkDMpGqNZva14oQqfqlwHhkAGaFyDEBrAyUScqSeXGE0FxJ7P52jblG2PETgoKCFIfwa1K0DdWafZca0YBIyFiRaGGdYuwNxUoYoBgACKo84nBoTrySJ7mArQJZkriwBTwCnOIFcapy82aMoyMzU2HVITBNvTZDu6F3x4f4mL936B3/v4Pfzms3u6ZxTai5ctSYe4+ZgDv5OmRWDOYbGZQoIAuJLQyo8Dtus1Nps1NpsNVqsVxmGAc7KvzmYzkM4HolIn7yL+xbc/xbPFRuUZaYdgWWRubcNE2WDVezdl7yVENSJY3QNY94BkNDSSuVzHeNoZhSKBVb6WuuyCXun9tM90vr4A1lWasWiSu+fshlJecwGdnjv7/0690r+osrGa114jRPry5RWX2l/L8pUGurIVpurOPU+uA6jk5wmZm8BBE74uufLuMeXY/Vrkdzt1LMcmkflQfW9WBg9t5smd8jB8VI7dqd5zFTETItgXwfD1OdkfuF+Nb+016v6yiNp6rxJ6vmq2oqmCAaouUbxUEqjUdR1adCD1cOCYwieAYRTPrYvLS2w3W1xcXGDoB2zWW1VkGJECmKISzWtq6spSR1AOBE7WbwJRlJqpd1/dB957BApqrYloG4fFfC4kxqr4JeU7xABmAzIBIQpvRfGYoLpBAAh4MY4jBv0zLIqCW1mE4NEPg4BxSIKml5Cu4JGoVjIBuYFuaoyoYQI2E0vbomOqwFHXJSm9lEOHVDVUb4PIEjJDXrxPFsfHODo5xvF6jcXVFWKM6K1sxMYQ5nOgcUA36zDrOvjRg/2I9uPHsE/OYLhwbyWrfiIqllpxHkMHZvnOKHyJdeaGKcPXftg/jiafX30eGmY0nnG6GvDGsw2ONl6yLDLnebU//ViJbUMmBS/Zo6q1SIXKRHN0aFlhBs43p1gNC8nc9BJlugpf3wYEFJ4SFbhEoTDqzaJemzoeSAUeSssE8yQlfeFS2bFUq5JtrFVCWBIr/jWSyC4ocLCwZFx0I2DCzg8vXQoQICHVQQjEA8MSiWeA/pmUU55rF31W7hUBxxXdVhDflP2NucpIRTBG14Gk8GWQiYWGz9jsBcSUhO6UVbTi/sgAmazjzpaY0BSKBAAwBq0DvvZmxOCBh89MXl9S31n16KFMOl+TKSPXD7pOmMn4kTdMUygxKdJ1H9WfkjdC2p1qz+Yo7rPw44hhGLBZC9DVuFYy2+p89PB4ZI4ws3YCdKVwrubR13E5nOBrb36AWbvFMCQesIDtZovVeo3ttsc4eiW2Dri6WsI5h+12i6Zp0bYtShY6uUNUQwEYOfEESPovVSLtMRyLd13igxPjTb0XIY8bq2MugQDDOMBxhDUj7tx2+K3fAn7+c8Jma2G+/jbMg1uID5+Jkabfol8tsXryBN3xEWZHR7qWp3Ux9XkKLUM2xkSO+FxRxZR4Na+5Cgn5/PXlpjl8QID7HOLWdXvGi3h2HbzYzjG71+PJsYcrfnj9K1nNjIIPHCM4lGQSMTK2lxcIo5BlxyAUECCArEGzWKCZzbR+KcsfZQBcgC4BVxPQxUjcnYlXTjjorAJPAOD9KPfebiX8OwYY60A6FynRRTAhcpFhchghJT5N4bLznvISmuZUBrqy4dOp3FjW07HvxQipZPR+HMVAqvx5Qesua5esOT6Kp3+j9BeFb6yMMwaK91jqVV0zSUE7Abqg2bblNUbluY3C+6RbrLQHp2gcymBCHjuTsaFwQZLLrtNfrtsnDxTa+VD2Eann0AQ8Odlgjiu8uTrFLJRIgudcLdf55nLTBJ4oXtXXtfEVCKNQK3g/YhwGrFdLbDYbbDcbbPutJgBpVAeIWLken51uYZ3SDBiDaIFlO6B3Id+bmXKb7LapSaHyalCqDR+yZ0JAYA0Vt9ZkntvUrcyo+n6/XfY1kVcAa9LN8liqdb6btf+9tfDjJ8CTC6AfyncoYOG0jYouWeupL2O//OKMnQe0ldelpn8Fylca6Pr1L9doQpOZnI7bR6iztxHUZTWlJ+bqNJ68KZvP567565tFabHIy0itTOIVVbusAHHhB8iLU/LOKKmljTFYHC2wwAKmcQAMKFLGXlbrNdarFT76+CNs1hssL5di7Y6MVq3TMEJiTIr+GFs2lczfAyFpL9hpsSQZa2FcWbb9RsCltR8xjj04egW7ZpjP53CaLSeqQhOVYJKsg3EBFuqKXsw8qcUxjiPWah1aLpciPDHj4txJm4WAfrsBCBJqOXr4oYclYAhS1/lipvz2hOAHBC/CJzOjbVvhwLJWhEMfVSiKxQqaOF40I6LaVwFAwLrghbAZDD8EuLbF/OQEt/peQkLGEW3XYbPdABAL58O7I2bzNU5PT3F6eoJ+u4G/WgH/338DevhUyFchRJ4ptIWA7Jmi6ucrjLjXUH4FG9NbT9d48+lquiJwUXRTIUImP/VeFI3sFVObwdLuGgE2qnBCCb9FK1Zl2OCnT76Oi80JMlD9mkoGuBKAD+llhlr0rUHQrG4pxXhKnw2qxSZWEIYUuCYIgbCRtuBihRVycFHcLRuEAKC5poLp6s+RRI4ugfny1drAkIbY6PMTEZyxALGC2OIxaaxF52YC8rctgKjtJYqOWP8FTNn2PYZhhLEuk9Iba5BTQLCGtBmGcwpcQYRl6wooECl5URpYWHgknr2ybieC+8QRldKjp1AJVoDKGIO2aeRqxuL2ccT/5m+u8eTC4h/8sxbDGEpiihjRNo2AFJmpOla9zRpSmDLsAjCiHBEDhoEo+mxqVT3z+sGb1hYG8hqX/kRJDQgjY71Zw8eIZ8+e4mizhfUEHxk+VZMZjz65o5tlIeLP4eo/+Tpm3YD/5O/+X/Dm3aeZDB1gXF5e4dnZGZbLJfp+kP7kiEePHmMcPR48eIBbt27h+PgYwzDAK0jDCmwnHh9nHRrnFHQQA0QwAXCNgMah8Kgl5T4p4aby6DOqKLmmQdd1AgwFj81mA2st5rM13nrL4nvfi/hH/xXh088cmr/91+HmDvH//A8xrnoBHZ48wbC8wr1vfhPtfI6UbDNCwVn1cABKOE4C4mQtetHZ9CsqX1VF5QVFzF3AS/4UkFIASOx/eRLg/IMPwMwYB4+g3opM4s19/1vfUi87k8FsUhBMgCSbuQadcwXsRjICRAQ11ETmHJoVfEDwI/rtNgNKZClzt0pG3wZEFgSre00BqKbdyGDNzk05OyjlddIoOGYg8Y0p5JBACAiISM9cQHgfQpaXvB/Rzbqc2MLHAGsMZrNZaXMVb0w2Juj6lL1wWPnNgoQXk8E4qrwMSXIRotEERkapLgBnASID51qpq3rZ6gMUUn7KLVGhI9oVCXF7hZL2uet+TKAjAPz4rXN88PYaf/eHM8yvGjXYXXfV8rp7+R2saue765+jhoUFEJXvY5AM69v1GuM4YrVeoe+3WC2X6Psew9AjRdy4xsCo19xn8xX+6dc/gbEC0gp3oYVtHdIOLXJOGpeMgDIH016OQHAuqEwe8h4swC9krw1RsujqGpv47JJRTHTR/Wff3S33e4qu+f6aBpyAXag658UXdv7v/xjxT34KhBc4VvfhnMGTi2PCl30r+XUvX22gK4OnRSjZ8+TSlwmO+wKj7hDuWxsa6gUtG+4zZ9cLXL/y4tr1YpnWAznicPXsKfzY4/TBAzh1P+adgymjzKkujDpt7KRuCfdK7Zg8LkRT2NsUdj27eOeYpLZOgDRg4lV3yGKY9q+DGTKnl8rgVr4SlzbPOvVNRS+dOK3SyXV8dbZQqGKbLF1prHEIcn8q5262GyxXK6xWKwyaOck6CwOjYRpJwKm5q2J+thiTgibCAWlFCtmvmsky4EJwthE3cijxsBfer74f0LUd4AyMlexSlpV42RWX/MgRHJJXgHJuJSv/dott34OMZN9KRMnOWs3GGDGbdZgv5lgsFrDOildA34OMg3EWzEEsSI1YxMS6U9ozBFYhtSiFyepORCCb2iNlGoqAZrKSZ7DqXKLcQVHBN2a0XYuTkxM457AYFrDG4vT0FJ+ajzD/V/8juu9/B92De+DgQY1DzFZV6VtKFsRUl9RTaYwRdin09kstqD9nWJbjuP6gY/aGBWtPaUgjbBeKevVy6O7JokXMcBp6lsI+pmFOIpynLKfi7UcHL5rWrfwTX3f3ly+77ZDALuK6xUk5gQpJStxZ4+SxqQCxGYBFHhvJjZ+Vh0RSldsMdkkbGbyQ9PS8J5q+TI+YfFkBjaxrOEMs91A+DQOYqN5EDAQfAJf4aQgxBFjNumgVNeDKOmutRdMAxjVlLEAIiCdrbAYLk+CLDAjWnR/USyORRSeheuKVUIOomCoyxhg4Eq6phoDvfn3E/VsBsyYRTjs4lr4gVWRT/5i0mcRQAG51VU1Kb1GcamGAFMTNNSo/Jw/wXdVW7zVVbgArqIzsOb1H4BHDagvHFttuC7F62KwEi1dGWp8UNKL0fBYghz/9+b+DR+ef4Xd/449gaYthHLFcLvHs6TNsN0ISncaJ133g7NkZwBIaJWFbCkqxAAhQADBAPT6TB0mQECZEVi6w5MlcCOrHUcINEycZkYZCB+EMCyHi6OgIzhr0alUXPjAPEONb35IMn4+dwfnYIvz13wZfbWG2SkfAjO3FBc4+/BCnD+6jW8ylvjz9S8q0KG0WpPvAXqHdjzsyUi3/7JSDxr96ueepMvxCFvd8u1qrK6+89/nA43D9YVrXaz27cIO8trcn7T774Y3zuRxdO5fNXt0xcX0i96fwQMWyPhFjff5Mxo1s6rI+dDOcvPkm2Fj1OuJs4KhDFykLynU7yJNbYwArAJllhoNDZCFZB8s+QerJW0jZkQGzJA8akjU1xgSaJFmo9FySQ0NeLynXgylPS/HMHb22NGeuzHEYxIinPEqRI8gY5S1Lc6FeOwjOOJEdNRssV56YrhGP934YkMIWmYN6RBMAC2aDlL0bSJ5sAFHyCEt/teJQ/dUCwYGx+ipFAD0ZFzCsbZb2Q2mzYCJ++sYFzo57fOuzW2jCjofmC6iUeYuaTLR0xu48mIxuqKVXtyExyGyVaP7q6grjOGC1Xokn9TCIVx0YH9y/xNViwOLoCE3jMJt1uDoaEVSOJpB4SOfEuJo8hs0E6Mp8w1FkbpdkuqoN0zqVDCclrLfIf2le1vNH9k6F2HIXV+1BgO09bv/8CcZbCwxvnJQGTT0Uy95fZIu0gGL6WrcsMYgPhy3m037xKfDzT4DPngmvnv5We5jK7VLmSpVldGLXa9mu+L6rV38xXlw3r6WHl9pdueRl6/U6tI0v5n5faaArhU7UIWe7oYugcqx8rNwNd/uRy6a9Nwlo+kGEkumg3x8813dEPYioXsh3bsrVhZdPnmJ9dobF6Sls0+weuic0lcnG1f+HB285UjcTKu10aCLuglx79eeqDQ/Kd9NFr+oo1MBlfrBafqwWlEPX5/2vdoouwtnSUNoqnWetBRjC68ScF3tmRvRBze7JOhGx2WyxWi2xXK8QfUDrWlhj4awTwRkEH8QrisgkNbqg/yBQLF4WIKvCgGTwERJoaY5Ezivp4yWrmSgmEeMgQFc8Uiu1JdicNEcELeG8UqBLSVlDZAyjWEFHdf0fxxFkDbr5DI21MCQZFdMWHb1YCI0+z2ol7iVtN4O1FsEPaNoGXWzQtI14bVipayYgDrLh2ZwiXPonCZnMUEBMgLhk0SO1IBlrwFHI8EMixeeIpm1xcnqCbtYhBMnE9sYbb+CDZ48w/x9+gNm9u2j/py3COALOYSSDCFTZf5CF4UwzrX1FaejlbDgHBuFzyqG58TwvyEO/8s4v5TO9bJVe4sYqnhJAhmENwTmbXdVTeB+hcDskgIKr6k0Uq4weigD2RW2Z16tbRflJYXQp7NemtUJPKN4f6SpTZa9WuBLsmIAu63T+mc8XQH/4ifZ/q+XLYlGVfomqtJAR386SXEvmXggBBAW6SD5b25Q2AhBZPDRBgLVOvbnEoytl4kqhfrXyCEg7RvXG4GjyeEhtl+e0hkgTFQ4dg+J9U8IJkvCJDP4QoHyBwF/51hpv3gkZfHXWgqEhparoWVsMAdJ4EmZDWelg7buJXx+QVgnNlMX6p09a/Z+Gf5JPUgdx4TJTEM1ogpQYGbEfESJhWG1gYbCdbdB0c7i2yc9qNWSx8L+RrpPKk2I6/Mn7fwt3Tx/jt772A8Bu0PcDlldLPHv6FNtePFKScuy9x3bb49mzMxAZtG2Hk5MTzGez3NYBySNuBAcv0K32X51sJIU0p700qJfJoKnqJQydddwJADY2Hs45HB0dYz7rcH5+rpxjYwY/v/1twte+bvAHf2bw02cN+G/8DnCxhvmXP4PRZticn6O/vMTseIF2Mc/1y+MnjyEJpbXWAmE/dGeq2O7Iibk79xWo/c+7b8r7G7Ge5y6KaWE9/PrCp0++KnLz9acdOGYqGt94o9123mv3DAYVgmsgeQOWhAlJ8ZbvQp4HYjRkbM6eYf3sTOtFABnMTk+xuHcP0TIQSNeoMFmrUji72j3LH6lMZQW8cs7pWk/oRxZ+vRhAhgE4Xb/SuNH1N4i1RAyjClpVXksJ7EKSd7PsG1E4ALX1rRgWkBJEDGPhn9V1dhgGkNdwzmq93Op6WoTn4kVmjUuf8t6WohWaVjzsxqEHI2p9pb0lLNiBId5dIYpcYMgiJtl215h+UO/i6i99eUgn2ftq51pVeDTSOOMCZKRnU49dJsZP3jjDcd/ivacncLF44RX1JFHLXH9ztSkVXa42nB0CObjsmVDP8HEY4UeP5fIS222Pi/Nz4RPcrvJ8scaArMEHDy7xwf0rHC1WcM6hmwnHomGjdBEm6xHQzOsxCvUMmcRvGfM6HXV/r8MUd9vb6NgTj/jCK5xkupj4TPK41iiJKiH3bnHbEbfff4z1u3cK0LW7ltbycwJ/sXNofVAy8CVJeTJoKjn6558i/jf/aiLjXdvHBedSWSb1HXAglf1LldcNgr0IwPXrWL7SQNerlAyMveLv6ajrAKMvtvBkuS912S+1ZXD/x6QIpONeTumqQa7aEyr9JQDymkfIdai/YwjKvl+RqZBWBJpkrXu1aVo4dIrSXl+MSLOHkAEjWaQ9IlKYBYMpyu8Zo1NrlRGy4NSqwzAgBg3JMxZdNxPLsfKPMJBDcZK2w7qBGmtyk6TMKsN2izB6DMMW4JTiPSJ65UOIAFwLamdoWLy0jFFieH0NrJm2YsSgvCw10OWcw+LoKBOTWgUBjlRRGIceI0fwyIjqam8UUfN+wOiBzXaNprFouxaLowVms06zWiETgII00511oCCbRFnbZSMu3F1lkxTC6aQcO9jGwPsR/WaT+9grGWpKJ973Wwx9j3EcMPzbH6K/XCEOPWgYwBdXGQgAcebGoDz6ikKahO5qW3yFEfj5C4PROIdvfue7ODo+ySFQX8R9aHfCVi/ZegclHc38DdVv2p7x+pUhX/Lj8zdxsbmF9Tj/Ap5mpyQLpdYxeabZ5HXFyaqu5Kw6NhKIIYpNAmXL2lR7GiQuFlLi1nRPCpBwEPdye0m3lpDFtr++JQ/oigqaSH2sswp0B6Q+Q5D6GwXhhmFAXEhmOzIGKSNf4huDAhjFa0iSRqSYm+TZRiFZ+CMiRdT8H175ZKyNICWDLm0n4TGchGT1bs2Gh/wa845srNP1nHOfRmZ4z/jv/n+E28eEv/HbG2y3AcM4U6FflNVybfFMEoALZZwDysmoYegxhTUWQPMmuaBIDZXgzAKul2uLBytFgmPAg4AE/GaQyGMYetimg1UiYHBaE0VJSTVmljDvYSsZuJxr8Hiw+Pv/5G9jGJY4O3uGu4t/hgdHQuxtjJCz534mwsXlFSJLOPtbb7yJeHorZ1EcBwlHH8dBMkTGQmTtvZBgJ1JwCXlUgEz7drVaYfQj+mHQLrbYbLa4vLwSRa5tMW8NwDGT1o+DhE62XQfvA/oxoO/vw68t+n/8z0GXayybI8yaFovZTIFZwjio8SaHzgQEAEFJ7FPmYEM08bWcGFOfM1WfZ6yYDIbPXXjn9dewVAsZZUEt4T5lcqY1OfgEnLOu3aQ8inKsyByksibBb9Z4/OMfyxpuLG6//TZO7t8XIyKRJLEAsqIvRj1VkiMjQECfZGSTKhoAEdYCfuwxDBGb7QZEFl23EE9S16GSJsBMgHLVJUG0yOfp2YveTJxCFo3uJ6Trh8GsRTGyGIJxGkIIWfMjarBFeGJTBmqOUyOygCAVPyXLqzUu81PGAIAabRdNrJBI5iG/ixenhjzHOnSt6BHCh1mDSNAWqsc5Ay/DoJeAQWDnuqgaF3lvDMELvxszrPcwxiHwiH/2tQ/hYpHFa+/jKVdkBWLhwAxVoMtoeHmNY3BkOE/4/gf3MBsMMI74uDvHH51+hPVaiOa3tIWfj/AnPlNF1HcgIpzfHtG2bTEKKV9W0xSuzaZplHC+zCVGBFWAVIwxG8NrQHWqg0k/J++/JPcV/Up3R+bJvAGxGpZ1DnDyPZXX7FfGhO7ZCvf/5COs376N7YOTXJVEZ5DlA32OuuF3HRgmyzdXby6WiH/4r8G6t/Cjs+kxL6ho5nXm13lN/gqWXwuga6KIpQF+jWdXOr4+NpWD3ly7YO4LIawvMsjL1NszHOZ7pklT/aZC7R7Ytffdbqncm/OxsjDvrM+vVphBPoJCPNBm6ZCqhly193X4FupnqtxH5XZ7m+W0BW54IKo3VrU+6PGxuoZYwmTVTKEXkWJOjS4HJQmk2uCSlY8hZKnqcdQ4B0sGzrZwzqGddUjSjPDOUOUllDhpSvYS8XDwWEbCwFugl7TtTABHcQ3nSOBIgHEg28BwFG+EJCBSIggVAnnvA0bvEYKECAXNYOQa8cIyXrI9EjjH9qdsYDCVFRACXoE0tIQ1E1+wCNELQSUlAFFAgwnfjhWiS9bvOSsVlIW/iWFGwZTUzcaqglf1gwBdI0b1ALjYXmLZr8Rb4ONH8OcrcPAiifV9Hl0k2s50ZO2AXIfKcy2KN5QbT90VClFWBWMt3njwALPFAhGvH+jiLIDs/qD/ZSGS0nJSSgJ0Kktq1WWTkoQjgHC5Ocajq/uv6QGuuVn+vZrvKGT0yYKf6iThcsWzKFvadh5mNySqhFqrolAL8kJDtXd+qQ8OWjubnjFf7VV/78ELOFwJe9k6q5kCqwskA0XN7cKsJPQ0DUfIvFL6TMaksGib1+cERpECYsKJVNbK5LWV6mbYZGCq5rmod/gsuOr3Cfwvz1BWctI1VerC+NknhJMF4/vfXGMcA0I4BQiZH4qgoUQsHlzMkpQhjfM0dmVfqMHN5AWV7l3JIjvzgZGU1WqD0zFSwLYIYqMp3UXYzwezhAxJ+J7cV7gkAaMuTNIelN+HKB7HfvRouw7rNfDxw29gtVrj8eMjfO9rd3D0TVFcyQBdZ2ANZ4657XYrY4IZx0fHaJoWwYvxYOiHDHTFEBC8z4ps8JplWIGuUcmxjTHCrxgD+r6HT157RLAWGMYRm80mcyzFzoI4yrGaRRKwgFnCjx69j+j7ETyMCH/+PvzVBv23vgUzY3SaLY+MyzxF2XChfHMhmFzHND/KGJMxnr3Mufo8nW17M/C6QkQgpxl/X3HTSEPrtStUBzXCFz21tNfzLv9q1a43mKJI57VY0pNm4JchMknk6fHgJAczwjhi9eSxrhUOR7duIYPce/u8rvsqe6aww7zOq2cQURSDiAF8GDEOHqOPILKIEXBNi5kCVFwJ35y4wypxMoW/175Eck/13qo4X9N6n471UcEmzSzurBVOvxiSY4s+w+5+xsphKV9FBfxNWfFBeX9M4f1CT6ErUO6jrPSzhIQm7850jfqoGlyTftV5SqnTXn7QSI3LHphk/QxK7QCnIa2t+t6YCG883j/xk717KtOk18R1tSM7YmdfJ8p6R11ijOgGg298dATAgXnAY3uJH8w/wTIusQorjCSZbJP8a5JsjDJe264tIfim7M8F5HJiQE+gagJFQRnUKlVjXRJ3NrO0N6cxR2lMSLuWuYnSoeWKVV+XY8t6W1Y1ZoZdD2i3I8bjGfo7i1wLo3s0uBaSZJNmjR6gao0lqH4VWYdoqn8ALpfgH/wM2A6504quufcAk74sW3l6jnR+kgiK7Pui5YsJZ9wtr1tb+PKWXwugC6gH1a9zqd3s5fNEidkrlBeoNNXlJU2/aYsdgotetBgfcP9PP0Z/MsPj774JNs/vi+d71x36ksvfq5a8OUcNuZLQq6i8Bsllt14Hg9fwOKMeBiQpZEXcMGiaBk3bCpE1q0DNsggmYl0iB2MaLOYn6GYznN46lbAZZ/KzDl4UgM12k72r5vMOp6e3M1fMRXuOzWaNJ54xDoN4XQUhdA8+qls5AeRgrfjQUAx5Ex+9xzCO6IdRw4LEGth2LQDCHOLCv+23QljprBAJM6MfesQQsNkoF1bb5ixIQ9+LO3sjGYqcNfDBY71aYbW6AsCYLxZo2xa3bt9C07SYuQYMRhw9yFgY59QaG8CsirUhEBtwxWkmQ4HVosSIQXjRjk9Psby8xLbv8fjJYzx7+gwXl5d4ymf4r2f/Gk+GZ/h0+Rnu372Dxlk4SzmrXr5yUmgrYROVRcpYo2rSX8CSlIgE4LCEGgXvJdFACFXIUgnNnS5Z9dzdETpFU3jdlb72lySHGSKwSd6FEl6Y+CqyUKvLjvCVROwKfzW4FWIQoCIGULT5Zkk5EMsja8ZQiNfOzm5MDJw+lcyK9SNMsyw+58knmqUoZ5YZ1hpQmK74KRwlCcDjMMDEBs45zOczHCnnhzHC1xVZiZcVwOFQiJqTokAQh7UcEqJoUVLgxlEsqJEljb1VTzEClPwe8F7Dial43dVtHRMXGpEomWAlSrZwGs5nclzgEqB/CKYH8OE/AKjJfFwSkiPeXJIWRJRhQ+JD4EjGidV6JO6xEAIMWEM/VajVR403OB+Q/idjStO3BwaP4hUhRolKeVSvYj8O2G428COwXArxuvdePIQBeB9S7TEOI4ZhxNNnZ9hsNmi7Lofmbvstzs/P8fTRe/jjH/7vETjCuQH/0d/9A7x59ykwjohR9qA1q4dWYDz+7DG2CkQJ2bDsf9bQJBtd2kClnQCrRhujiQcYBOsiQEazzUtbrtcbxPg0N5CDeGElUBRM+Ff/+gJ/8AefYNSw+6u/903QG0dKsjzkBCoE4M677+LWO28jWovVagVrUgiVAiFBPH/HccAw9PCaSKMoY8/36KoBp+fJocf37mF2fIKzDz/E6unTG4/9y7Jb0ryXT0mJl+YnhDRE9ADxdjd5s87gP4v8lkAiAboYzz76EMsnT9TQ1+H+t7+NZjbTtauSPRXcISIFFQgxtnnMDH6Lsd/g7OwpVqs1Li42YCYsFgvMZnPcun0XzrWwKdthVecEdBlDWD5+hKtPPy2GhmRYgHKuah0MCel7ZGA260DGZGJyNoyTN9/AvW9+XRwASDLaAsjgc/aESUAWSMGrCojTOUqqV4hRQkB/Z50eljyNvO6hDchIOCNHycQcQ/G6y9hj5By6vG8M42vev2LR50xE+kwGHBScDx593ycxB0kYTDJuAS1UgzpgzAMVz69alil7lIaDprGLsvZxiPgHd5/BnDB46LGhHqOXCIuTkxK+l8LAfZA1zihthHNWQlhJOFGNIbStAFxt2wm9hLN5P04GI6GcELJ5qsAxRi27VM9YNycpHzHZnLW0cLUmPtJyXlCaAHBAIIuc4zYbtVJmZZX4DcEw4fiDpzj67KLI5RkgS5MbefA8+86bGI5nuPuDj+E2gy7dMrGuHn6Gq88+y/eMiMDogf6mTLi56Z/zc6WP14DY86/8l+ULLF9poCupppWNZ/IjgfZI6QHsKVIvBfDkDTYt0gcg6xe4Wlkw9o8rykm6dsG4CcC43cI4h6brnq8TqoI2raW2mm56qQESrs/VRRNUNrmknsT5M4DIaFc9ovJeTeo8uQDnvimWmvTcZaOrNABkF7S6e/NtakT9cKtT/VoNmNJ/lMGNcpXaqhAROOBJOMMJCLdxpyD1LOFzwsEjpJ2kpLz5/gRYk+opSmbjLLpONh6yJlsIIwBE8QiLHDF6jzYEGCshJc5abLdbUa6sFY+FUGodYsToQ7FCpJArREQWJWgcPcbRZ7LgRBqdM/oYqwTBIQM+2fsuFhAjg0E5CYO6P5MDUfIIAHwQDpcQA0BCmj+bLwAYtB0hx36CtL4lwE26WPuHSVUOfVpFDeST1N/aBjAOkZGJ+bebDS7CFX60/RnWYaO8MCOC97DkwCooF84LrUfq4nr85LlSlNpDs+uaVam8fxV5LdeFy+X3DynKdjUHOX/evz3tfjG5POVnoOqrZLUi6JjTdO6TTIv1zRjFuxbVmqA3JwJG79D7Fj7aveU6TdVJS+8svXWTvFTz5uuwCofi6p8UAM68bdVD50ZLa0VZ88RVP4F8+muleAE6V9ISxwSKgB2mD0ERaAagGabejFLfMsquf9Y0L6ujdLrFgydpPfW5JdNqhLMSZt007XTf4+KNnDwaIqa8TADAZKQtdpo7r9cqdAcS76N0lNF5X7jDUEC1iaBe2lUvJ+HapZmqtgsw5hkInTxvZDBpdl3lQgSzcMgAmg1UxzlUIczZwTRcKilDeiRDxzczbEwzksCGFfjiMn4qMCX1mCRmqaqMdDgDMYjCGDzGuMU4BqzXa4yj19AlyXDGqmT0/YC+H3B5eYn1ZgPXNDDGomkcxnHEMAy4iDNs+lP4GOBsj8+e3oOzHrOmByDgL2lI6uADmAZcrVY5VMs1DY7bNhsqoirkJdlL8uBQsndrQc7DxAgYp8aXiMhBQ8U8evQZADBxACHqvgRcXAAffhDw4x97+BAQGZh/cgaLBghB9sHg4YN48sIa2FmHSAD7EdBsezKwJEwxjB5+GBG9jAWJCEpCAVVLRL2vl80gjckSvqRyTvYYKTuGcQ26poVtXLpqNa/qGbJbDiiZUwFO70TVa13qupfRWu9rpb5FHgPv7mLT48rld77L4itNPpa2OLx/pvUnva/XOnniCkqcViA/0+7ujHxuaZeJPMgMcITfbhFHj6ZpENse43oFxIDohKPUVvVhl/gC1XOy30oYYwzotxfY9pdYPXuG1WqN1aUAXdxvEOYLtGRgXQPnJCNsNn5oxUjXveXZGZbPnmWQIWXJNrAKvsirAcHrcjLOhUNvHAdZdynCtBaz28fCL2gkzJkJ6PtewLqmkfYhgms7WNeAUJHF67VJ1/0EugkPF1UciwEikIY8brIHq8oEqbmzB+VuH9ZjhlKPFsNaFZJSi1nlCro/XacbEdK4LyMpS34MoOZ803Mi1UfqdXbALlSvebSm+mfdRo4PFLKskbo9UWysnQebCKZBZI+IzH2V1lTJEsyZL9JYgrMOzlnZn/Q4MfAIYbq0OYCUJISL04QxpNFCrNGsqo+kpmZS7juu2lc5JNWwmbiDE0grCb8A11h0XQNA+IaBqOHtgITeKg0CF2MyaVulpGFEhGbwoDHkfk1y5hTokr2vWfVgIrRXW7hNP+n55mKF5nyZrzFuNzkMcrJG5jFf5N2cgYjqKyavxTQ0s2QjKjbVEs90JO6vUcmo8hISbBp3L3POC5WXu97rvvvzbvAyj/uVBrpSuVnQPyQcfP678WQAfzElAU91iRzx6Cc/RTOf4Z3vfQ+uPZyjPsfy65obGEhpXTUoDpkJ0AYwewQaADiAyjVLC5bn5LTh5jqhbCo0FWbyl+l9LSgiiS26YOmFOG8YRcNJV4vEmZQ9/RFh6r2Kuo8rsYjL/YUw0YCjkpBbXWhNBMUAIi/PpBkBl/ES/7fhH+Gv2q/j/4T/AxwsbBV7NHNHQp4bLcBBaXciwCFbtMYhSpY/6mFtg8VCFMAx9Bg1fCPqIjpbNNhsPJ6eP8YQTnF8+xhNd4LuqMNsmCEigBwBIwFOrJGGDHo/4PzqAg/GHuCAwB0CA/0Q0W9HXF6uhQg4BMxmM8walzOm8Cjpojvj0FqDaBq1wrEqUeIZZjli1lhVUEbZdEMo3iB2AY6MwXsMnrEdAWs72MagH1k4VeIF5vM53nTHaJsWbdfp2GSR8HTwJiuMfK7dIxKIIKGypj3KoyzyFpE7GDOHc3N0TY+WOmAUXh0TgdCP2Kw2oMURmsYisHgVwDRgQ2BnlW0iAhYCsulGLLwIukHXOsbOWnDzyvDy60YkhndAcCzjVWnKVNasFAF5VbVK76ZziIxk3Il5Faj+RMNOAh9BlHvPyo0ECV8FCwl5uvqw3eD8PGK9XokVOUomTcMWFC1iICAaECxsVc/SfwRCxOPlbfz0yXsI3E0U/VxBTFf0WkGrW7ToZ4eEi2lJmVMjByAGNM5h1jU4ms/h/YBh3MDZCOcYBhGgCLKybkYSgZ6jF08wEp4XGIORAzgSWiNr9nbYAgS0szmYgCEEBM1+ZYnQ9cDpGYrARyoUayKGRIaewyOqJ6x3oazqMXZ+0fnbNIggbMZevFobq0uc8HUJvxjBjyNW6zUWfoF5M0fTLtB0CyxXKwTvMes6COFwzEJgDB7EQIwCkMleQNiaRgXXxOOlIXlgGCWTHryHqcKmnWuyhT89gbUOkqlvzCBN20qYRtcJ4W6xxu+Mf2ZJDmIcuqZF1zg4MhJOMyrhLnMOpa4VbSZCNAb9OGbOHkOEbjYDLCNQQMMBlj1SWAaDYQJw+1mA9eI9tD0GLu+mJypKBht5tx17GBiYxmbh2uTDI4gZsV8DCHAzi3GzxNiPWF+tsO0HbAYPJoOmnYOMA7kW/ejRD+KxFELAdhhgiHB8dAwiwq2TkxzeiBDQj4T//B//Pu7dPsP/7u/9P3B6PODo9A66WYfZfAF2BpGA9dUV+hjh5kc4PjnF7W9+E1Y9VJL+mniORgXEJHSf4PTPErA8P8N2vcL6g18gbDYYNiOsCWDHmVQbyp9krcGnDxn/2X8WsN4gA+KMiMv/5x8gEmGGgK5xiLRAgMEYN/C8RcQg4g6AcVQl1zmADCII46bHdr1BWAdgC2yDABDWKWE2EWKUfVO87ZQPjkQB5CjJYIx6rYlnoIDEwgWuHGQU0TYGXSNhRdYkr+QUSFn/7ax2BPUOVRkGArJYIliYHGoa1Es7ZXeV8F3OGeWIgLZt1IAQ0+OpJ0bieRMQJCTv9uzhIXVJfIxAkc0Y0GQ6KYmS1llJxyXcOYBjn54oe+/kBD31Ip7ltbotqhCpBJCrp1+CIwnI2Z0RJaMnQsmka5PhLO8dOh4YsBxh2cMxQGPAkz//Y5AhNGpUTPQMBIgXozUwVjzg1+s1+u0Wy+USyyePsXr2BMPg4YPuccYgtC2G2Ry4cxcMgZKQkp/oWlWLshwjWJOCAPVoqKjoWd4HYjAxVhsFebicsV49xqOf/0DqQWUfSXqMtS7f4P43fwOnb76FFGaeZDDSwVPqoByyZDCStr9RiTvtX/q3K5+EKAbXGEYQWDLMkiZIAmApcbBaHQsid4ksKogCVVechI3tangMkU0h/WggoI5l6QFx1mMYS3rdmKdgGoZxl2NA21fW+wpo0Tec7jv9Ib8LuUF2BZgK6NGEYzY/VykWIie0aZs68NipPcZR1jwBNbXFkkhdK24kKle+GNdVithst9IegWC4xaJxCEPEelyjIck6ymGAQ8TRvEFvAhCB+/dPcZKJE2oAAQAASURBVOvWHEDM+3cMAcPYwwfG6FM23pj7ONm7SGUFUyqcGyN5BuaQ2EoJvPuzR1Lt0detAQA4eesBjt+4K2uu9/j0B3+GYbOedlACJjUJmYRAAhTDgb6QfdoCsAxJ9uANKAQYcmigzg972nxqeZ582gsTPXjW3mMdLs859XWXLxLs2r32y0TUfKWBrprwLpXatfIwzIUJup6Ow8673a8OuWzedO/nlT1+gZtKpa8k91pbufHLIVyUwR2MiVE2vqIQVXUvO2apX/opnUPTww+2LQFmDFg8vcI4b9Eft6h23J3V+vpsJXToA+23d3ne6mlqwWhnU07PlTwsSK8ZubYuJQVELRfMAAwiGGve4hlf4kf8CzhYMCsZPQjPzGfY2hWiZZho1BIgG3IWTIlATUR49zHCfIuIB/khGOIBlYicjSqFMUYMQ4/Ly4uc3Q6ApLLWEKsYgwowsuGHGODHAWPfI7YOEeLJFTSsjCDWn0SIWfeLkAj7iaDCKN3IuhkFDV0qli8N1wIpUXEKAwIaV1yTc1avyAg+YLvZSMYXQlYy86ab+yEJzqWehS9BfisZlhLxafEsEutRLEI1yrPJ9YuVhlKmuFRfcPbqSKGj0yFbMwrszAjSsTg5/vCxB9epg9vG9LtDGYCLuH9DuQGkv3Z+I3VB3Q/I4U3jOOrYUWUvE4rHzCN06GZJ4YlsMIameFxUz5iE7BtrmsfH/nPVbcnVv73q6LhP3Bb11eROVI0hqUMW6E1x1c9KQR5n8ltSJhNPXapyNISxBezIsCPyWAUDtUPWXqfwtH7lWROQSNgfSQkklmdNYF/i/BBLpoZF+zBZB7wXst5Gk0qkPmAuI84ohxVzzCnvs0dCyr6p93DOqWeWtrs1VftM9/h9/jNM2pdZwmgT+FZvF7v3z1nUSECAxDmWQi5SaAgjhVGIokrp3gkdAAGG1Qsg303/F7DLqt7kBsZsnXpKn4mAYUZivMlARCX6VhoTU+LjiuAQxVrurPYDK7cMwGRhrBg+YhDwMhH9MwTQmM1mau3n3KcSng5s+xkul6f42cffwZv3r/Cb37hE4xq0TYNgCQEM1zSIkdHN55gv5lgcHcO5BrbpZP1lqIczwSnBr7MOliRNfWMIFoyh6xD8KJmJU7iLMRJaRQwYg0gEH4APPwA+fUhYLYHRl4XDEIGGUXjVWvGEHoYRTdfBHR0hEmGz2Sr3GoODeJn0RpReCwFI+22PcfDwQRStAEiG5bQOsHLH6XyKkjI4j0Vm9UVOng9RQ7YIck9EwJRQ20xDwWXO7pWD877yaAIhhwWn39K4THuaKodFWUzzAapglvpYyzi6fQdN1+lc4jxXUzhyojtI4z+EiO2VUBPkHMWUfcVy5Sc8RfUz7azrWX5Ncz8vVokYW5/TGEnmkZtKDQRpD2cUIH7SZjKZ0vFpPSQwsiuntmdkkU18SOtFuUYcbeZrDcFjeXWFzXaLq8tLjFeX8NutjjUZxwQGe484jgh9L57kRABZCVPOEs9uh1cGDa4lDv2ek8Qac4a86ROTeKV5XZfyflR+D5VH7OrZs6IzABkU2+OkAjA7PYVrWx1qZbzlv3SffC15M2632Fxewiuvnx+9AhbS7uJFSiUzeuQMgs1uH0n4nT5j7Q17qHDe7/7/7P3ZsyVLdt6J/dw9hj2cIac714AqFFBAFQkOAtkkW5Csm92t4aWNZm3Sk/406UGmB5nJZGq1qQfSTN2mJpuUmk0SIIYCURMKVXWHnDPPOXvviPBBD2u5h8c+O/PmvVUYbgGRdnJPMXh4uC9f61trfSvpOK4Lxczzd15MU7mXAnhocZPlebP2OXfzoufNCZslH5vH9InN3Hrziv3MbX7n1/ZCmttTP/v8NoFGLRw1IEdqapsFMK/W5CjVPK33+GkqPIhW7RVrVwVYh6TRaJFpGpl8YJzCTHURY/U8dD2GEtV1DHRlmoilDKTIjPxdfd9SvEZ1BB/wH7zPcHPD4eXLQqmQKTfm6HSxI+ZrZbk0y/G5CHtajouUn9eiVxfP95RmuzzBpwyGv1Dbn1ZbXzW2P337QgNdf/m2z/GgX2mx5v/mZdVQKycUuW/mN5/arnY/8tbv/ZTrdy549K333qiJt41CThi1xweJwItVRMEs9LWxJ9s8C+icWmSTeOyPF8GsU2WPKCnxMD7h/+b/iXwHGCxYeGGf4lzi3++/zjq1pDiSsh9IDVXnHHYbGX/rd3D2kun/+3VsbMtiuyCZdI1W1ILr6xt2u53wsnjPql/RtS1d30t0lvLc5ByfGCP7mxuumxZ3ZknWMgwH/CRkP23b0nWdcvJEArNhHWJkOBzo2pa+74tBCNI34zASvGcah/rhAUb5dhJ9GJXvbMA5R79eScXDUcptJ2NozIoUPM+fPqLve/zZGZvNhn61VgP/yLiIs8cmp1dmj3VMiWGYMICz4McRP01E5Y2axoEQJlxjcMYSTcDl6mKgJNmaXoot5NkpSsSOM1mBvqUufzG3z9DwYmcVzS1WSoMMuRADhyFwOBw4HA64xtE0DZOfcJO8NqGtOJrmP7FVKwX5lOd0bkClutfvZk1iVixn2ba8n+Pf9XOawZp8pZljYr6W2BE5nN4VgNa5Rvn2mhnMMq5UJMwpW41LEsHY9uAPiGksINeL+7B5adi+qASXyXLstjxMR0p+Wvx2uxfEdpyV/kxSTBRw2GnVxOBlvu1udnTjqPNR+udwODAMg3D3OVtIylNKGqFisLbDgFTiA+W/mftgjkpLWn010TTivc771Dxc3vtKCc7jTyqFiRyYOUfGcdS22CLTM3jVNA1N22jb5dkku+RhywCbV7L1GKNUqMo8VM4VECyPC+dcIa9fjh8ZK9l87fbQ7fMYk9+jMzx5H3xDAe5uDc+s+KdE0vQ+P3m6tmO9brk5DMrtGCVNnAHbRFqUQ8dINJW1jpWRSJS3HtwXA957huHAfr+nRPQBu/05/9U//0/59a/9mG99/b+hb1tWbcdkEj5FtpszVn3g4s5dzi8ueHDnDm3X03Y9IaIGt/T/OIyQ1OttJZLLGfk87FrC1NA2jtBYYuskrb/rChfa5AMvryL/+B97njxJxGixNpUxnAAJftA+DZHr6yu6i3M2H3yJCXj65ClJn1v0EmmQ83JMkjWgkPzHhBdYCj/6MsfyGM5QV5hytU+jc9yR04SjjlmLRMAJeZTwuDmDAIZBI+leYQy/6Za5N3OUugCaGZSoKuGqWJmBa3FEeO8Zh1HmXdPywbe+zb3332e9XutcbCUa8HDgZrfnZrcrhN3WWMb9no++8x0BXxWwzEBXSpSICzE6Y8V3pH23FFCz8VgZmYDqKQpQlQqtNdClsoakFVqFlxR9PpmPSLo7Kt4167/JSkEfGUMeksU1CrhHdexV1A0KnTApv9vTp0/Z7/c8f/6cbePYOodtZbYnYypwXPjuXNtinTh2EgYfT7u2FpvqksvvVAbXHUGW8XM/L0GXRKq8ZJn/zhjD4x//GH78Y+YjubX+on399je/yfrOnVtAVv1q5kaU7ebJE558//ulP2OMBWTI4DXVOMkmiHWOd//6r+HONp/WU3JYBkWSVHkNMWIVqE2MR/qGPCublfZUcSSa209mBgxr4GjZD7cAmBNtW35Xf4rVPIbjB5xufV/dxtEJj7WE+jr5vXBuzjp2fbLi3svnS2WQAXB9faVDM5Z52ziHXa90nTa6jspeSYtVjZPnMExlXY+Vs0ciDSVd0xXOr7lf8zqcAa9YVfrMGQszcDaf1wcB47Ld+N6XPmC4vuanv/07YjdolHmox6amZ4aglen9KCmbwZfCKpCDM7OcmUGw2wRAp7YvEpj1xdq+0EDX8QDO39WfP+34V23Hx7/JeT9PhNfCy3XSmAFSBT9VSsEtU+42iJwvUs5zvJm8cyVEj/ctQrIo4lnYzUK4ti9Ngu5m4PJHTzjc3TJcrI9bpMen4r229b2f6rd0/DorKFn+Zptwhu3MyVNBJoWkGNpFiCYr8adRorhSiPB734OrA8mckzatOP2yPaILoGsaUj/xb7sfgPcc9lfq1VDCaRKwoo+O3/R7nFkx+YmWhqZrcTZgTCjGaCyk8WPhk1qv16zXazECWknZqQ1CkhgY3geurq4JMbG1LbZpdQylud0q5Q0IH5EV/olcSUgickKJppFnHEv1tEwijX5fShHHxHDYA5KmQUr4MRD9BMkXr4eErAcSDX6E/U2idZa+bbRzK4Mve1EycT5gmpaULMY5JEJNHr4hSeSbcwIGtq0Yttst7d/+W7RmIB4G2t1Ev/fFUzQH9OV+qZXE+a/oQKlWHurXVw3co+14Qp/YzSz2SPVBGGN49913Wa+3tM1pMf4KaaJv81kr7+XJhqR8QVFkqp/ncQE+UCqitcpd4rXsegizwoDywdXbbux5vH+HZ7uL0/2SL1KU7aXiXJIYKmV/fl0q97JbWtxHyv8pj0Wq3i8Ah8WdZ5JVGQiSJqPvJXNTlLGoxOZG5aWZQZ/c9tq5MM/K+umb+R71/zkeTRkiUt3E44ig/Nyq65THasq8znwvxgYSsRBzAzRNw6rvC7AlFWsplVdjVUnLkR+VgNTTOGKtgJ8kcHMWUbHbrKnuTs8flPPNK0G8sUajZSpwICVyumWO3OQIoCzz1xjGac3vfP/vcL0/E/JmVYRzz9gj4KvuLGOMRBqlKsICZuLyPEYX68o8EgudAHk3g02weQlTC7sulcqHuhAghpTJiadlHua12DhL0za0XUvTWklv1v7yQu9CSIYQkzpuJAXoxfNnZS33XgjuiQpC6DWTTzx+es5/+z/+Tb72wSO++bWPobHCCxMjNslSaWMiTRNJyH+wKLWBKvlSk0VHtQIGMUaIgWk44McBCBg7V+6NKfL970c+/KmsbcMAu50+qyyuTGZHkQjoHIVijBSVGQ4DNzc7aUdEJ6b2HZDJkVKUuStrqI4WU+2nn2VuZMNd5lysBQlGZUEV6VwZhH44sH/ymK41rHrHcHONpIpnubS49GICH8vMU1t5bjDzpquuU4zZIPyXXiP9/HQgBs80TvT9itY1tE0jji5NC25bKQqx2azZbjYchjNubnaM06RyYIW78/cwe+h3iVlBkr86okaGcCx3ZKq2YypQISEpvQvBZmjbhovmS/S2pzcrmotnNNtPuHpyh/3Vmn38fUJ6rueR+aEDcAZSFpJSX7XJJcjKSMv9KCmnjfKokiLTODCOA4f9XlOo1aE2HSBGztdrOqRKodOKrjmlMwfDeC/Fd1xbC8I8OC0nH3du9vFvedi+4ZYdBVkPlvuvI7yqixypA3UTUkpcP37McH09y/MjPX6xnFdL2rjb4ceprGKpAjjmNlYH5WkUI1effMLuWTsDTdUlNvfu06035JW/jgaeFMSYJnFYZEL4uT9mZ4dRWVsqaTZZL0X3m/vJmupe63XshPExH2ZOf148AssCIDlZnr4+d9YN9H9d84sOlG49zuXxWT85bm1uWxIdptht2bNTlrj5Geb7KFxdtu6zZcRW0zS35GV2TrVaPdKpzlSPr1tA11FEV33OHL1XbiTLpBB4+cknxGnizt274vCIsYBdMYaicySNQgsxSmGWKMVYMrda1MI8q5XKzaYpEYm85tEtx81nmMh/SbbX4TRvuv1CAF2zsDoStD/juU+d7/OAY6/b57X7F1BpFla1UNfpejQ1KiPulKBNsyBcVO9dnOLV2a9iFBiKe/D4d71sf3Wguzrw7JeNAl239wNRFN1JgK+60zTfaw4/LnZAVpjsbPuoylfeL684GxrFuDKmEPk6I1E+KSgPj4/wb/4QPnlB+s3fJK23xZDKRh4k2q5liJ5/1f8h19MVz68eYU3CJYMtxk7Peej5xvAltvaSaZqwrqd3Ddb6wg0TYySStArUyOEgHvcMdN29e1ciE5oW55oS8QRopTPDi5cvJae+W9Ot1lpRMacviLGTjbFcirhxko7prCmGpuwzR17k1IVxmmZQSLs4gxnD/kYXMKchyuIlNylHV0AKIzFZLAkfPdN4YN33JCVSXSgCMUhqUKmEaaTUtRPiTYydFdEoZP9N4+i6lr7vaJyluTyj+4/+LlPjCfs93Xd+zOo7Py4Lop+y3TPfU/bUCVA5M6jMq1Zt7p7aTsz/V+1x8jTLL2YCVWnXBx98wOXlPXLh73Tikvm0x95ceaknfzbeb88X9HqLJmZ7UEHCGBKTD0ze03dCeF0iTLyCXSlVYiMbQXAzrPn+w69I9AmIwZPm684odiULswg60dqk91bbNKciuea0GLEUarA+g13V7uW2KUZBVsqRwWNUdBqjYFcihlR2yBLcGlGyZfDmEop12koGwerxZY7u0ZR9atNt/j7fz+y5z7I7VWS+BopX3TSSzpwB6mEYRKFLEtW0Xq817VBllEGjWFBF0koFQ0OJeJUoq1CirvIzXdhDUFKApJ0id733qsyqlznm6Io5+k74jawonRVoldMwaweKNYZh3PA//eFvLZTYlJLUFKn2Fy66VHggxEmgVjBCIp7HZlKwjZQN5MwrUqZJ+X/eR1epCGcvYGwTu3uJ5PL95bXUkI2pJYn23M9t29D1LW3nCClxGD3RQ0wCPkWVHHmgTEjUq7WWpqSIyjN3RfYaCIFPHl3wX/73f4d//zf+J965+H269QrXNhjvccbiUsLGSByE/BeNZjS1sW503VYnSfCjVmn1DIcd0yiRjdYk4fwBQvT8wXcm/sX/ECStUdetWS7LqUvt0zJ+5FlM48ThMHB1dS2peSGPC6k4V+ScprlLHwtX0Qx2piL3cl+X6p0YGetzEMF8/SrysI4wHXd7nvzoR3QNrFZO7ncObqQoOuaEFF5c5NR6I0ZqluDJUFKM5vSdmfA6ZAqCYac8V0HTkXtZO9VJNM97AarFmTHx9OkziTIfJ4xZ09z7Nu6lZXvlq9swZc4s0tdOzIVyV+YVOrKOybZtudO8R+s6WtNxfudPuPuV7/DT6Ws8efmAXfoJIT4VQMkYrG1UL4hkUDz3X21aCoitY8CqWkFiGg4YwHWiP6UUGfd7bm6uefbkMfv9nuEg42SzcXRdx8V2K8RIWi3PWovPekYUOTyNE66ZuXBVK6ux8uWzBW5FFaXlz6e2VxvOuqao/VSDCK+zK+tVlJS4fvjw1EVvHVCDLcf7LlIc632BYzsspciLjz4susBxBojretq12BszMThFn5Vo5FaI3W2m1JgbY4sTal4z5bxducZx1FpJq6u+y/uW6oPHx+kx5fs0fz/vU9ss+tlUz/To0S6yDRb9blSnqfSnk9uSe7levWaVMRWwK39fOw6NpgSLvWAg1ZFYae5TXW+y/bEMWqFkbHTqzC+VHKsU23gEdKW4tFtroKvWf5tWotEBwjQJP+ThwP17d1UdTMWWySmL2TkzjkMZS1ELw+To7xDEJspFBqxTeoqYOd9Ozuq/2l6x/TwArrx9oYGuvNVpBL9IW3E0vHqP13/Oq+bRdtKmfs33x/vkRfLk78UeVSPgVec59iC9oq1ZaSrcGIVPosqdrlo2t1ANE9JJ/SAoj5QxElIegqDxFgnMiElIDmMI4EWY7Q8H1uNQFpzc7kTEOUfbdazWa6YpV4zKWovsHEPiZuf5r//bx/xSu+Z/Fw/Y9UoVdSnRPGm54KCVEyVqq9GKU1J6ffj29+i/keCnP4Wba/wnD+HDc9zvfAWQEN79fi/VGd0n9Ks19x88kL6JkWEa8d6z3Wzpu654W8ZxUIXPqrIehMS4pEUsjYwQhNvFVkaqMQY/jThraRrhXxmHA9lD5mwrMFWYSMlhGifGQkqkMBH9pOWRBUgEfdG/hM73pFVbQlamW0gSSmyQVJ3WOTrn6LuWrpvTZSwJ882vwq98jaZtMJNn+K//KenJc+WLMdgmVzOyArSJ1S4kxCaRjlPs/iy3ZKhduDXQcWvXI2X41r6JSqFazr8MJM+Wi4xTUoKQOUxUEXRoalhLUI6appGy1raRtD7VYBCvoTxQuYRctxtgtYP9FsZerlfAmTxXT4Bci5vJCEG5uazsVd9X4FVR0PR/ifKRyIfgA95HgnL2uDzOtf+NElBZk1NpHc7Ohr4xjjmtScGRBrqup+t60nhDinNE19K4nSNHYE5imOM/4Dgofga5OPqujmBTGac3n4oylySqxcyAjTUGtwt0Hx7Y0jBdXrLdbkUemAxkhQK6yHW0THxC06UsJEmLWXp3j8fa0rhJSdJ7pskrz4cYkUbHhEQJhhLVOlddVK+8a5irWlUGg1l6mHO6hJwjA3BGUrtj1FTL+ckIljPzewWNWnQxK/Hyn/AyUapL1YMtF28p0V4mGwUIYGqT2gHSr8kYMl4qAAWARla1Ftc1rOya8xBohpExXjP6yHSQ4glShcvN8yfl1CxDTLYMurKSWqejy0CKpGDwo3A+Bj+JjFdS/jSMUhnu2TOpIte2ZZFIepbMmyZFS0RGq9DHjwPBe4b9DY8fRf7FPwukJGmpP/lxErA4TmW853SWPGFSDMINaXI0Rl5LEocXL3n0R99lffceq8u7EhCRjAJnmmoYE8nGIh6SdVp1WmS+XCtV9+JVxBwZ2mUu1Ia6OJain3j6ox8y7W8EPCtcZNn4nY3GmZey3OJCimUK3nrel5Rg/Rxi5qjLTsk5UrWunJZCYtiPJYKhe++Se1/5Eslabq6vuLm+wiA8O23bst5sOIzvsh+/yjR9QPSB7tHEZm/40vWWOCXsatLo7tMrUipjTd/H+n7znR4jPbr4W1NSLY2VSrA3z+4wDL/OcH1G03acpd+iT7/BwQwqg5THy0RuzL9hz3cV+BM+MSxl7lsDjTPiGHMOkxI7P+Gnid3VS418kzRFP020xtD0K846o3JB5co0YTSCJEeipCgpwdZIZVrvJ4KfSMGDdaTC63haDX6TrUQYV732agPiGND4nNe0n3KsDuCSOmmq+ZHyKldlVOh2y8itTY7XGClXH3/M/tnzWZYpZGmMYX3nLtv79/F4LTg1E/JDtknswjlSUun8kqrDHL+HsnZUPxbHR/5tAXId/5EBLt3XNifOfQI0q36X02vF6LrvkPXmWNeYp1pW7pfFbk6NDZPPpbqjKQ3I/LwGwiy7TMq6BSqL5gisGCXqfQak5BqNSyRrCUdjwkT1KDLzZ2VS+k81l7W/JII58vzDDzm8fMnu6oro/ZFOnfXFWPrIOUufi2ZlvYfZFvU+y9KZMyxnNFiTjZi/2v48tl8IoAt4Jdj184r0epPorDeJ9vpsUV6JJRNxUT+P94LXfP8mE6zssTB8FydaSsdX/0iJwgBMTJgQSZa5muJxO/U2xYgzi4UsK5jZgKrT9MhGVXWfpmpjUfROXrM2E+1cjl4Vz8SM6qMe0GnScuWLuxcjMSubbdvOHgqzXIhSgnGKfOePrjmsrnj5/o6uXXOuIJ91VgzDQoRsaJqWpvFYKxXChnFkeuea8M0DXH6Mubkh3f0Y3Fuk77yvVfUs/hAlEOrqJeM0cX5+XpRhP00c9nvWfY8xwqdjkoR2O2tpug6j9zVNE9M44jQdrWtnL2QsxPWi4DlNIxRSetGsYwwEP1WesqacW9aRMCu/yoslC2IGKucUh8UylKIsngEwDlxTiPINqIIp7Wqco7GxLNDGAG/fId5/QNN1NOPE/v/zL4lPNf0Jg9SxypEU6EI6QwgzL1Qde7icN+bkt5zYJ0+Xylg+GmV572WKgrm1S60LvolDpEAj6URrKw9bNkZmj6W8aIVrjYawJZU2piQ8cwpyZZ6motDqwh+jJUWHSYZ2Mqz2MHZI4dei5SVVkFJR6BZtrTW60o+1eVh59NIsg3P0XokC0luulTDhsUslHbFEcpUiIGpgZ2ArVzpTMK+8YrQqo5B0O9fgK2NVmibPNxqoYJvyrjxTM6ds1dJP7un4u2XEV06BM5VMZdEf1WbAjBH7bKC7tGw2kjbdFhmw9MLWgFBKYoBbRXXy7zl6IB+TLykeYB1TFb9GCBnoMkq8bnT/QAimgFxNnb5rlmXb58jv/PMcvRCVMFx4RGYlv22biv9n2S81UCf3EPVpmNmITwKOxoSSoJcHRF7iCs6VhUyOKszAf5oPyfcgnEMeO060K+EGcY3FuI5+vSIZi2t3mJgIOhdMBGeTThs5aUwJwhxnSKqmmxo9JXI6JlLwRD8RpmrcAHGStWl/fY2xUhwFY0rqboLiDZd0j5z2mlMQFdQcIk8ew+/+HsRgcU78Cxg5PhcBUASWvNbX6aoyL0zuMPz+wPX0GNetWF3encWc5EgKoGcykK73aYT83sbMqWWL/BfnVyhYeo5OzkBSSZ3RiSryJBKnid2TJ4RpwNl5HhTZi9F26PtKVuUBcDs1rdLu1ECvx3rWH2Cpj4ksyDLYCvAYEyEk3GrN+u5dIjAcDoXvzpBouxXbIbIbLTfDJY1x2GTonk80+8DFMOBDYHK2FE0orcxy1sgYjynLr2qdSnPUmQxGU91jft6auhwyD1Bk2K/Z3fQib1yit1/X6qdS5dbikIj0yBA+xPDHGILOWa9ZDXmRN2RBn6ssRz/hx4HDbidpisNAjkZpncO2rfAHaUsFZJU4Q4ko1YgfObs4CGKSwg8ahSrggkat5sf7OpX9SOXOGonJz/pTt1frxLeu8Sm2wyuvV4ZwKohHzrypI5JqoGe+otFp8Ao75Fab1CWUDIeXV6T08tbvMhgsqzuXmBCY88NlHsxtMMWJg8rgRDpZ4u105OGyfeZoX2Ozk8Qu7j1HOed7B4vVqt41iCWUCRztn4E3ec1cfcu2Llu0iFTN31vL0WGldxdmlsoo6fNUzpd1jTo2Pa93ZRDoT7PuNacJ5t0BYlmfIyXjpk4/TCyLYWU9JtvZcQa/jn8L0RP8xNXjx+yePj16VvVYnG86fyf0C4kY52eWb2qarPBn+kkB+YSwCNQz9ORDuT3Ljpvwl2j7eUZy5e0XBuj6y7Glxf9Z4Tq11KRXvM+bOfE+c0ml153U3P7i5O6qXF18+Iz14yuefuNtDnc3+tObLMZFJlbK0KzI1W0vGU+10K7vyyy/M0A0lmRUGVm0uxwgho+TqCPnLCEGQvBzY6Ao7kZ5rrqup+06JZXPCxoL495Yx6P0gv/j7v/B33bf5h8d/ldYBQlaDNaJhw9jeO+993n+/Dn7/QE/eW5urrm5uaHbDTRKGN/1PeGXruA/+1daycdh/vuvYX54l+vra/ZKLr9er7m8uMSkSC593rWNKHPe8/L5c6y1JUUpez+GYYBRDbyNPMOubRFCyUwEnRDuDQGoUkrsDweMMWzOzhQkDKRJIgKcprYN40i/WnG2PZNItMOhXDuHlmdvYF0dquhKRpIKp7TLA4ToJTLssNtxc31N8F5TmwxEWaAP+z3Pnj7ha88D79549l/7Btd3HvD7v/97xCAExCFGVXJUcdVBGWIUQHQxcE7NsjcV2J82W+V7Ub5ue+o+0xWz0Dj6qig8C0WkPkT6rXESmZS9aSFA27esVy2bszM22zOePX3CfhjYbDas1mv61Zq262marhikGMs09PzkD3+ZYVxzLzhMkIiM7U1kvZM2BQdXdzlh6J3soqP7yjcz/34K5FqYCprmFELQlMtQwK6Si6Y8PvXppViXAK8pJaKJpGQJgjbgtA0iXqTqnxjXGWwRo2i/hqGF8ytDP2Qlbb63RT8UY2JWMtPyJxaHJ1NAmdwX+drOWUKKJZrN0uCsZRwGHj16iFlf0t3ZsFqt6Fc94zgWrdQ5S9v24jvXfjAGmqajaZJWAXSFzF2KbMTibMg9U5R37Zs5ykJTkVvlVEGi64I9NhKUS6fcu3hUx3GSiF1NTer7nlwgQCi3JGXOGiugCqizgqLMy/ezkp0dawZD27Q0MWAJhYg3xCjjyCcIOeVYudpK9Jcatxa8hSD5VmpsZEPEanVcqWRoY8BqpKC1Ftc6ITxP0Pc9MUHXd/g4gQkKwKBp6JLyXdZAEALsIz3CopUGq1DaQu6rKYcWBbSCFDPxw1655xxGQUOjhIy2gDhRopis9remw9/cJP6L/yLw5EnC+ySKSCYzMlJZ0pKKkyk7K/KcyWCtHKFrhhEA1BlH41qapi3FZ3yQyICJqegWKRPoRwV2olRxLIBoSoQIQTsrGbAKHmZMJotMo4ZgipEXf/xDpt0NKQQFPCq5WsbpsfzPsZx1JOapbakPxiyLMkBrzRxBq5mkm77HOcdmsyUGz1VnhWT++gaTAsN+jzOGqW3xXnm8/MRharnav01MB1L6HmdPIt0u8XRMmJgKtyckrRhtSgEESd8zc2VN5fzKRmhxLKSkMkij6ZPci9Q+TnRNT+usRE6pfpm0al+tA4rTTeSAMZJiamPiwv0ma36VaAI+XvPc/+dM/gWDpkiHSVNqtYgNKdFkcnuVC70VegtrJc0rg63y3FMxyhMSjSiFbZRjELRdEXwqRrFVnW/mbXz9Ov4q9fz1mNSrfyzg4mLvN1tw52rXt/c/dkQtIrkqh8fitze4Zt3KT7npxTE3Tx4zXl+V41KKuK7nrW98A9u2yEp6zJlZFKLFpYqulAGcU81D8bFZMGDC8UlO9Fy2V3LJYiqgTD7MrxValc9Up1Lqwctz6LqFmb/LtomE/3K0n1W9Re2XvG/pElPkSwypWi8pILzoPBpVnKJEwydZtwhavT7N9CALALTcy3L9Fa7O2sEwd/7TH/2Iw8uXt38zBim6Ehj3+0KOP5+/6rc0XzrPkVzFOIRQHSdjJFeTnItmSZRnSnaR9fJX25/99gsHdJUUlwXSzK3Pn7a9yX6vQh4/a/TY8XlOH3+8aJSDy8J3S4WqBHG9/8k2L75WTe7k4pP7MwsB2TeRKnlkyg7uMGEPE+3NAd9JOhjWENbdbHQaSMnOTjxTG2e57YnbCiGzgZ6Fst6vwdAcpirUVRaC2DpC647Wx8p7nSDtD6SnL0SBmTzGS1W+oESFcx9V7dC2WK0ENocgz30m/SLPd2TiJ/4T3vFv8Sg+5dyecea22AQpGayNNK5hs9mw3wu5e+gPTGc3THimSSoHNhpBxnbCty9JViK6eHCDedkTh5FkLbuVwTQXnMctpLhYDEPwUklxGrFatanVNLTsvY8hSFRZTvG0UgJeeDv8vPCQZlUhRq1G10AIGhmnRo+RCpEhJjoMtmlIGE1Jygpj5f1TXSMbx7XSFDFMUWKlLZD0OXk/MSnHUHkK2nZ7mLDDFd2zyPoQadcbzORpXIPXBTQbrM7UY23mPppVzjdV0o7GC/V0TNXndPSbfqfPq+tajQp60/TJWTWujassGcwr70ENdDPPj6Jk6RYBY01JU8xV6UIIksrUtKUKoSmKvGEaVgy7NfurM4IXHjUQWdCEOc3BRmi8IWU6DUt5f/pOs8Upf3Uk1ywXK+W1tlDz/kkiDsnvT3m686EkUlLSWpPngChnySw9jtkkIHuKy3iem5UshDYRqwin+Umk6jYWGliRXRTjeParLs5To3P6JyLZVCkEM9dVCF74AcctbZBUHKmEhLLWpRJRVa6YDT9rBahq5ojXXHEtg9ZZntYedfmMpoQqIFUpvSaDTJUMK9FDMZPRm3L+GGU8moikQ4QohPhUinvKY4d5SlcdZytXdwZ5s5JclHmrfZ8kTiommFzSlKWswM9jKGpKo7EJryl3hTib3BQzj5siF2ZwShR3ZrDaSgXQpom4RoDW6MsKWmyoMoer+bGUZqkiFbfsDz2Pn99l3Tyjc6O0TNf4DEWYGMFGLE7W84wCGRmNVoEj8RFoBDUCLD96mHj2LOlIj3MbKjunGBs6Nm3K4/n2q4w/h+vXGJfVXJV4MRENui7IalX6VOeHjRGbJNqv9DUakVP6T3p0Wsnapc2dx1OMDKsG7x1mbzA5CoB5O273mwEM9ZaW07ky6IqhWm7dKLl8y/bsTCpBHs7pug7bNnS9REbFEPHGK0hqGP2aYVhzfbPCRrBhh38RcTeJUOuauv6WORsjOCejw1pIERw4l0q/k+epvppoiCZz8kUyq37UvrdGiKmdguCBVEX0AQUERZ5zCpqL7iFscGFF8hMm9sTpnBg8fprw/oZx3BG8FP7JfKCrTirFOX2uzlqhQDCZGXOWG1nvyWMkFgR0qW7Wcy/qOCvfGzOP/fnBLR/5rBLdOuftLJNPGT6v2l6hEpijT9XqdevXz7RV62A5+0J/XvbKrZlSre86/Y7anwjjSMxFlMhA18i42+G6Nq8G5T6SAde2GoX1qo78lA4+0h2WEfOvP0OpiqlC29Qfy+fZtqjNr8WzqIGx6jU7C/KCoKO3OqwCuip5MkeLmUVbDBlkzxHUdWR1NaAqnWi++UoHUx3pVkch62Pdh3PEvnyKWm19uLnmcHWlGRrM5zMGmHk/T/Q6VNef15NZYZqDLRIllTzNjvi8/xzBbqq+fsX2GTGDv5BbGc+fV+h8hksd6+Wfsv3CAV1AmWS/0NunPeOFAFkaRfU+Rv+ASsS//mLSv5YchpzI4OLpI1NK3P3uJ9xRD/x0vuLh3/gyKRu3qjlm7pJTVz55u2a5MJU9ExACd3/vx3RX+5JmYZLh6kt3efb1twphUzJGlCzl+XDG4H/njxj/m/+h9FfjE9E1HA4HhmEk5dKBdaeptZENQWNdZZhWBkoFOEyT59/5H/F/8v9P/mHz9/kH7m+WalU2BFwjQNf19TUpJcZv/pDhb/2Il5cf0Fxdcv/ePdq2Y7vdctjtpYx7jGAT9t//Afbv/YhW88afjBOHR19l9bv/Mc629F1LCoFxGNhrWP40jvIcSaS+FwGNpAF69XbuFdRYrVd0vQBt+/2OcRwZhkE9HUGi29oOjMNgwbUY45gGaQ/DhHWO9WpN029o+g3JWKZcCYt0YjGa+66IUx0YPkjf21ZJ0KeJwyCVkZSZFmsdbSPe4Ld++IT3/vgJbDc861rW6xXGOlb9itEYybf3SThpGqvcHYKwhJgNpJ/v9mq5vTQmvvLlr3Lv/n2811t7/Vn13CeUA+oe1Xlc5lKlUqrRkNO/Snh9lhvKl+KUT24YJ4ZxotNow6Zpi/c2AjEYfvqHX2d/dU70TeVVzOczRSbZBPeezfN7v4Xri1szfj6+KCDVD7eUleq7GXGqjo2LfWfDpO7B2TCO0RNtJigVA1vSuBxNM0FCSZHlbH7yGt4u4fWZyJ4CduT2VeM91c+LRQeU3evXvHeVTUXKqW9JC1/kc2XASPoghUgyEr162O9JCbYXZ9xpLlh5Q+ssvnFYJaBv25Z+1ZVoJj8JYatFeNk6JfLN0Vheq7YKGO1npdhoKmJOR1QjwzUNxlq893qP89jM0Tx+mrQqksiVrusL4Oq9X1zH6HXaKg174e02plR08t4rkNcWkZ8JabMi3zQNTbI00RKMXJMUiS7y/J6mkxgwmnYiz1i4TAQrEkt4AinYkeS+JO1RjPjMGzl5r5GuUpV38p5h9PgQy+t6s8Y1DRjLfj+y24+UQGRdrzJZvqtVgzznrMR9BY3U8dHz29/9Br//x1/hf/13/wm/8fXfJw9ao+03+SQxCH9fMmVdL3MpG2BGSjAE/RimpGThkJHAsmYDU5SoockL+GImX8AM0jzmAWLUMRKhO7vD+S99A9s4DvvM/WiIyYuKUHcIaFSQPC+JTJBzWwdNC23X0nVtmU+H4cCha3j4rS8TWrcA5DKddfsPvoF7cQ3/1/8Kc30jhqKtpW7V92U+srwpqt9ObIla6VfCfGMwxok0C7OC1/Ur1us1Dx48oLGGdy63sFrB5SW7/Z79YS+gbpLqYT5e8GL4m0TXsNkkVo8n+icTve1xG6vRSsJnmDTVOIUJHxNBH3+jPHfOWZpuxfZMZKQ1tkTCGy13GPVephAIynHjNdqraxxdY1l1wgXnnCVFGFMozzFXfE0apT4cBghCDD+OI5MX2obgJ8bx3yOliCURzO9xMP+YrmlYdw1ds8IZ5eeUgaVXyCSO86PKZn+O2DOIXmmsUX66JGuCET5Yq5GlKSWC97hG6SOMlUjx1xpwqfz/87JwjoGR5XpcoIyjg7Q16hS5fb7bx9y+rdlhedrZf+oOX+eYu9W8Y8uFDLLk9vjDno//4PcXdkedZvj2N7/J6vz8Nnj0itbd2n6GSJ5bIqBWeAu4Uz6WvsyOmHk7bkMFmh0Do4t9Z+dTHp+L72SgL9qanQeZyiQXuBB4CZnjQXgVvffKPWmK7pBbHfXxx+Q0+kvHijGlWMtSZ5MjX3z0ES8/+kizOOJ83oUDIDswlmOvpDgu+ny5j/C0akX6ateyHrEcy9ZKLkhtufwib39R7/AXEuiqt1dFdr1uqyPCTp2r3u9113zd+V4HxNVKS57c896n23/sKXiTAVcvJbdbk24J1vlAWWjMK65TIkCqPzOJomCtIe1G1o+vic6oEZg99sqdYmfhmUgl5SAlKYsdUuJ6K+ziKSXcONFfDYv7NyHS7Efs4FX5kH/9zcD26U0BuoSYFpwK7sYY/JSYNmdFuPqdpOCFKKVkg/fioUT5R1RAxxDIgSDGiAdz2YcUoyWH+0/Jc2MGPuIx300/5m3usWI1C3LdrLXENhBXB8Zw4HCQ6oRiTLe4ZtQ+k0pvppswJtAkMbyG3Z5p+4zrt35I361ZrVZMNwkO54zjWAxBgOA93jomNx2BxmL4YTgRiUF51kEV/YgsSplYX8al+kENGNfQrze0XY9xjfIcacrBYs05rdaVVqWEUa6vECLjKFwa3ntClMgBFxL3nu95ud3zcv2CoX3G8/UzpvWKvm/Zbrf41UT4eoTJYIKFRwY+kdQPMEoYm8rnz7OdUvbm71/1Xj7nanmucfRdT4xTidYoPVLm5CtU4XTqgygSRYG8tYDXqMoJuai8KbkiZ9SUT0kNc0ULSCmxv94y7FeMhxXBt8tW6geTL6ybjZS92imxOoBvJa1RfpnvuDRfFaB5HM3KUC2XiqGc5RSzVz6nRi3SBvRUpm7iQvRqxGK97pjZ+5pt69LiVLdr2c75yxlkTEkUNQ2DXT6TlJYftT25Y+o0zcU4KEryrAwKZiHGqzEGG2UOdaMUDRgwRGuloqyCN7nfM1YnXH1icFM1MbcppaTktdruisMtmVzmfa5cNfN4zCTb5T6TRp5qdEctn5x1JKcp5jWUm476+UiORQXOGq3El9sjMlYcI6REKuTo2iYr7U/GkLnec2qrDPA6oi8rw1nR1jS5JBxfhqjPwyzWQbnXpRfZWkdjHGvX0bY9runp+4l+NeK9kOLn1EVL0nUvny8WMDvHqkw+CNgVAiH1+LHno8dfYtsf+NKDD1n1B03nzuNmHr4pJWxW8M0clZ31ijLUDRgs9+7epWlcFkWL4Wl0Ua3Lxw+Hgeurq3r6YKxhdXaOcTLe+vNzmrZFMZRK1zHaX7nRdZSWApNJUt4ikMLEeNhB12H7XtpoDdP9C/y2J206aGwxwqLyT1oDZrXCeF9ZQsXC1L6oQIWiap3Sqqrt+Ocsy5QmYanZVXMTCu9oCEHSOtuWZr2hv3sX0zQkY7i+WTH5hiE2ELa4q17Syr2nnQwu2oqawch1m0SKUrGQbGjrw7F57KdAClJhWVJLnUbAW4zTtGSVJYXgLuWaoYnoPcEawjRpUZkGYiw8WBjwMZB8YDwcGKeR/W6HiQEbBewOPsjnBJ3bYgBnDI15D2d+DdwzjH2JswZncgZtKuNH6SILkClzKT9ClWsxgMmVPaUfrC4YsZxDXcQp1w3VB5vq529kzV889HQ0XFJ5P0eb/2zbsc4n/x/pEyevU+kTb3Kdaj3+tD3rt6dAp1PfzC0+ff6MKaYwHe2hksAahpcvpWDAiYiufrul6fuTbZkb8Sn3ZpZv6l5f3GdKtcI7n778N39T9Kd0PHZONS+vpa/+vfSivl/armZWY6BUGIxR10rnZP5AtbYveetQ+ZTlVM3DVV712vOYCRxevBSHVMXzO97cEKZJ9jt1Tynp+juvRVTy8VXb8WyA2+OwjKdKvyy80sd69F9tn2v7LFFc9fYLD3Tl7WeN8vq8HfyzXPvW4nL066sE2Bu19MROJksLU0/8pRBIKWnqiJVF2+RJb8prjYLPBqV8FyO43ciD3/1xMbAyp4PNQFcmVlVBFJmrCPkQ8RYOf+NL+G2HD4Hu2RX3f/enughWoGDMn7PRarl4tufixUGisqxwTVlrcSgfjDUE1vi//bekDTHy4R/8AeP1DZP3Erl02BdAJlu8KYWSIiMePKuGgxIV55UriUcDlOsJSXf8Hb7L74cf8Z/xD/nl9GVyKGyOfGiahmAk3Pr6+gZjLF/64AOapqFf9Ux+wlgjfEIhipfUQd92RBc47HcMdz/ho9/8r7m4uODy8pLw3/0d2odfVnAiFYXZq5IZg6QDumJowqARWV2p1rgcnwkYA1gMDkfwgWkaaJxw/gSECNhaR9uvubz3VoniyNUl86JnszF4NA+kK3O1sBz5NRBDYJw81zc7rl++YH8YS/RVf5j4tT/8hI/e+Yjf/+Xf4+N7Az/ajDSNxTnL2dmWrm3Z/s2t8m840n/fEv/folklI8CdwYiL/+e+5Tlz/H7+PBuGp2TCie9OyCyj51kYkixTRBeveR/9Oapnu/5deJBGDocDh+FAUC+4a9sSjZMrxz36k/d49vFbks5aX7ICaWqj9HjrD/J3dQd226OG1AhP/pxUPVqAQfNfBnhiCpAkRdlkjpcof86pAVcZHUVx086R1LUl2b4A0RbXyF+234R+Lw/uo3D3Yuww8xRVSpkpFk6WrcfPazmOivczn6cUHShPViIxsjBTeZlSYhxGmrajbSVN1gCbF5Hz68jhriU0SdtsFgTROcJk1AjRxvVzv5T5nOZxpDyHKReMQGR16xpo5vHug1dwrAJRUaMvSoXcnDqaU60b12B7SxvbEhFWAKsqrV1kSla4kapoITAMo0Z+JeUacgL8qAy3KsuiFbkmZGyJZIV/JGp1wfygcqKfPCNdE6vRnqGcXLl0tnjEQRJ0vNiUCoeRweIsuFWLsY62W4FxYBq8D3gfmCZfPaOkVRcF0spRb9M06Xt5HodxxIeIHacS4/iv/+jv87vf/Vv87//j/wsfvP2TUg008xfm+zJJuZI0uiiRef30kYfSJTjb8q1f/3WGYSURnwmCj+VZaEY8bTsbSD/96Uf823/7e9T2jLOOu1/9ZbrNpuBK4pPQtaJ8WYGQBcGYASgDdD5KZV9geLnjxQ9/SN93rFYrOb5r2f+9X2F6+y7dMGoLbOnrDJBnECYdG4fzyOWzbAut70jcyWnn9HCRa1JwIHMpDYOknV5dXbHqWi5XHavVmnsP3qZpe5q258Mn7/P4+RZSoveG9596XI4MjQJwo2OvUdnnGqfpfBkQSkUeRO9FLsRI9BO7qxcqL10pcuOalsJvpf1VqreqzjlOI35s2F29oOvkWRhj6J0pOsr1sCccDlw/f8L+cOD66gpnoLNG5YqhdxbbtKrDWFprIf0GpG/zMv4TrsM/Fzkco1TnQ/yisx55DHDlvokCGIcow8pZLaIQcRqtFVWWO0MZ3AYZIzHl2fS6py+vtUZUa+ifPfU1i6dl9PxnsVdup0vetndeZT+d+v7TAwjq3z+rXWao0xBfx51kDLz4yZ8AQmB+vD34+te5fO+9eecTW4naPj4xWeyYxXfzLgUGeuU2j4GljeZq7rMaFHvFMyiXrhSvWmVYSJ0EKS0B1ZRMiSLLa2qu0t4kqRwpa/Fc3bT0S5BCXzXYVAPzdYH7cn0kEvLxD77PuNsTU15jq3vidr8epyEunHu3OiN/NPMarLpHTs/Mu5dshRh0N3UmqD0YY6R1bg6f/qvtz3z7hQW6jiO56u9etX2WqK9XXeNnad/rD9BXYzh78IBuuylk3a/dvf4iHX134jdt3On3i0NmIyFvGeQ6FdFVvM4qMLSKvaLdEZIl5cpQZjYEyj75T0GY7U+f0XVOQtpvRpzJVfZcicbIZcSdEg03rlHCXINpG2zj6PuOxjoaJ1FljTUS0TRNZK/+ylim3Q6GkfVqxfX1tRKOmuKRlBDuIBFnmtKTw0lyL4lAtGJ0IABByOk+IRDiwO/b7/OEl/ya+yod4uW0D3a4t36MfVeqyQzDgLMO732pFlaXsa6fvXOWxlkuzs8Zh5Gr62tG3zP5kearH2EvRPG1h4b4B2+TRquRZpNUPFMC6eKN0T6RaovyzL2SuVpraYylsRLXMkxSZSskqc6V+8A6x9lmy2q1xjWtenalrHssS3c2QCpzoBCxp6IQJvWiewUF97sdz56/4MXzZ+wPA5OPJAM79nzv8vs8Wz9jmEZCCsKHhFSGvDkcGIOHxtE2jlXfYb7iaH+rwyDKa/hOwlzXKubn3Wrlg6P3dUh6Wu5jyn/Hp3l1dCVHU/uWdaRvF+BSqv43C4Vs9oSlYmTGGBmniUHTV8EoV5B67a3lcHXB/uUdhpstksKVS2DXhuZ8E7NXLx21SV7bQ2IT5Jto4bDOGlEqfj/RUTJYwO0OquVeSpAiUqFLSUSjVIUsHAuVGZJHYFKDJaHEqEnSWow1pa+WBkrSKNBcqU+1yWNtLj89lR/Ha1Kq+0afRTraod4ntyWXTs93YgyEIA4Ek+e5kpCHGEtxiqZpyFFV0QdWN4lk5T5DK8Te8/AU4zdGSduMYSyOhuzQyM+4litUpOlGle78XmSkn6v2OYuLFVl4la4RY+BwGAofUb6WyOkaIJwrPWXv7Gz4zOeNmmZhtaJmAbcUuAkhCCG7mdP9QspV+moDQMYQ5uhZFSNK5o3FYJzDOkPTdIXIXwAjKQjR9T3dpqPb9LrWWLCNGistQkDekKEHSaGKhEkjd5UvyxlTDHRZj1LhSRSgK3AYJiU6T4TDhAkDH1/9h1yHpwQ/cbl5xq9++fdJSdLFjJZkz+M020/WGna7C16+vC/GEvm5OozpBFwO6kjL1cUsoGDIdrsqa3nC4NWpk/vWWsfF3Ts0rThh2rZls1njFcgb/SQk57nUvTVMJHYahZBBMAM0ONIYuXr8kGm3I+V0eNV7UmgV0E80jdMxJH3pi5BQY6pv4Td/nfTxY/jO9+e01IVsqCCKz4R/GTU+szMtad+WQU3miUkpSeVLEi9evGDabrn31gPC6l2uh29wCDdM7CTS3STc85F2SoRJogqdPhDrDF0Gv6NEJCXti9mRkAPzFZBORsHfHFNpkEqTYqQGn2YgEqWTSEeqqc7d/dUVY9Mw7HfiIGuc6HbGcLi+5nDYM+33pHGkNdBay6ptKkBU9cMkXGyl3Wp4mzhDzzUOWiK2KkMcJCIsPwqDmQuG1AC33nIKgRz2b45+T1G47uZ++Ky6xufRS+Y0ts+znbJfPo89VDvK6+0UUHMroujWVvU5Sx3rNteW9nH9zBbXy6DUUj8BODx/sXCWnNrWl5f0Z9tX/l5djJsnT5gOh6Nrntj1FceX7cSNp+N9qs21LWdvvVUcR/Ndz+Dn8ZF5vczvrYLfwc+R3dRgd3aC5WqmR9HIi/aqjejHgf2jR4uqysZoWr/3+GGcK5dqI+sMkywvSvvL91CnjKTFDc5yc3HjRY+KgKYjl8vMOlZ9C5LlaCv58Sbb0fh/o2P+cmw/S7DRLxTQVXfEKdDqzzN08PghvRGopkrXvLBK9NPle++xOj/Xb05eLZ+gGM9G1SoWwpvyWv/NaTKl8afPXgm7ehE6XpxqoCupVVHbaBHxLJfKPcfHQwkBjZp3ff6jx+V6GOFxyR5855zmh7eFi8U5R6efnXM0qxWua9msexrnNLLL0FqrxOxTiRB49733mIaBJ3/0PYL3vLx6KcaFCmABgkSoZ+4dmyvv5HQZA8YKSa8PAaPpA1GjqVKU9IZ/5f6QM/sn/JJ7j7XpRWC+fUPz7R9g9zvYS+lvYmSaRtomR0PJX4qRaDM5q9H+sKxWPdfX1zx58oRxGOTYX/4xrn8oUTfPt6TvPSCNApblFLS19nEZGzESg2HKpJ4pMmlVM+cczlgilsmHQqJvrdX+lEiwzjq2ZxesVitc0xUDstL7KJxvNVBt8vqZx1Iej2L0HIaRF1dXPH36jCePHzEOe0m/MnBldvze/T9gXE/YwRTvcUzipfH7ATtMJAyrlVTObH7Z4b7hiGEi7hLxRxFepBKlsJgMJ+bH67ZbwIUakp+23ZJhKdtFCpqU+Vgdc9SuAtIc6dGnZVEq5xBlPC7aaUwGuqJEdB0GEkarbbUlCmb34i4Pf/g1aaHNqSZW7TTVAqoCGLfbUrU+JfoddCovQgNDl0iuOua4A44/Fu1GFbIUMMIiIZ5IZyDZAnRZSzFcs9GSo7Jy5ClEqe5pEyZZbKq5vvJ+uo9y28xtOLrVymAUsGt+X4vlAuQdzYny+9G4KvxASfo7KdA1+UiradxW50WIUSu0bQpgFEMgToHNSx2L1rBfJ3bOY10mj88gUZbXgVxpsmkayZczzKBaNh71zxgDYanoJyRtugBdwRIbJTdHIspyZcQQAsM4lIiNnPo4A/XSt1EjfhNz0QVjctU+ecgpCfDjfcC5iLVJnSfzGPXe44DJmJJS6KMAmr5EUNVVmvK6hfZTTrOUyOK2ESDNOcdqvaZtO9abjXLgyXq2Xq2hMeBQMEw4uSIweQrQ1bYdjVa5I8E4DKQkESVOvezFCNdxIZFikf04MfnAYRjlWabEtDvgx4mfvHyL8bFEN3/57e/yN379TwhhB4e9RmApkXjGAIwAUcNwj08++RZZ2yiRAClgjEac6bTIRQNdJ4VRLu/cKevt2fkFb731Dl7X6VJyUM/snGO73XL/3n32hz37Yc/1zTWDpukD4Aw3MTL5qYzHLNdbGvw4cv3RR0T9ffIjU04VDx0mTBiiRjvKDA3uyDxNkNY9/Nbfgu/9CVGBrpRlSSVfF5tR8fAasKPm+5yNS0PKcXaJyqEgrslpmvTPMwH2zl1C9wHP999i9CNDGsD9Cc4+Z/1swI0J30eSs9jGKWCJVNJtG5KfSCHgxwE0LTKnxUoEFZJKqmmsmdagzHdCobzKwELSe0tka3F2MSRjuHn5osieruvo+77oeLuXLzgcDkw3N8QY6Z2lbxo2mY8vzYMkR4qJPa/jMEhkL1keoJw+5SnMRXeyeiLV5GZsypYSdHM0Z16283g31YPL547ZSekqB/bJx3+8os+6SJb1x8DRcTRU/f0CHMhn/gxG5c9iV9XXfhOQqxyXv/9M7XvV3rPsSNV7Y3L3z2Oh1iV2T5+xe/r0+EyL7cHXv8764uLoctWKnNftGLn6+BNunj1btv3k3F/ab/WbRKVE1+15zfNsNxs29+5hnL21n6nHWMotEhuuxmKdlUV9zNWUs85SgVwl2rqqnl7r83X/APjDgac/+lGR5zUYeSuIIt0+fv6Ylt+rAmh4xTi/pXrWulW+nup8tyqvFxeiRJmSSjXqL8r2M+BJb3DuV5/8TxOf+UIDXTWAUm91ZNHx/l+oPNnEyXLyb3SoGl5lwbZGAqVUwRJZZXC5dCxGDRztO2Yv4MK7bu3RhSgRP3nLhoW0Y9no/FtdWthp1EcxSLJX3Sxfk8mAFyX9r2nbsgBZ9bZn47pt20qZr6t+GVzfY9uWvpOUOiFNFBssNA7nLCEKR03bd8T1mv7Xf53h5oZnP/1QCI/7Xj3+OZXG0PcrYpBUw2mKTFOgaxsa5/BBjB+JEJGaU957drsb+tWKrhP+jyGN/JPpX/DW+Yq//1tnrJpHbNnKvWkUX9M0HA57CcXvOqauK/3rnEQbTDEyWEPXtbz11gOapuHFi5e0bcMwDFxe3mGz2YiRuJ3w/8EfYj++Q/s7v0Twwk8zec84SXRXnm8xBiY/4pxcyzWOtmsl9UXz5S2JtnHS/40jdm0J+3XG0DZa2dFJlEVQEul5XGTibCgkK5iyyKHgQgiB4TDwyccP2e9uePn8OTfXN0whYZuOuIZ/81u/w8O3nuIuerqcMlctWnIeT8RwGDwxGazd0TaOrpGiAsZZzP8CzKNE/BcGM1bgw3I6fMpmShrJ7WOOEJkjJefevfs8+OArMuYLT1hSrn0dU9WaX4AsY3CNI6XENPlqH30e2uc+SFSS0zQPZyxTivgQtcqVJSVNS2ycAIQ+YpylbWcepWE4kFLi7OyMcXfBTz76BuP+vAAoM4RzQosvH2vlJe9dKaQFCDLYABcvYGzhehOrw7KsWypWRVnJSkm2NFJimkaGw46r65cy5mOkax3GaARHSnRtC0TGSVKWZMwKj5JrGuUly+fN1oyAHT4EfPSE6AUACoHogvIUWrKypPQ0R0az8kzlFO8cRaaRRbGStcU0M5WynNDKinLTGVe0zuCwhBQhZCOz7vnZIEml7yX12g8TozPEJMnKGBgnqXRqnRh8wzhhTKJplLcry3gFmx2Q2vnx5+sYHYc5/H/UCNEUI03bYKKh7TpZP5xGog4j1ln5Xr3Ai3vJRlW5jhi6Ic4p53ndw0Crqe1GebRiSpJulVyJEIspkYzBJ4nMjcojmTC4foW1UsjC6PWzwTy3SxxYTdtJKroWcHBNI/fh5NVqRUVnHU3byBlMLJFbxsg6R5s5vXIk11Stx8xj1hh55nlOVnMzAa5tME2D6zq5d4CzM1KM3PH3STEQvOer77R86zf+Ginu8dMozp7gCX5UgvKJ/X7DJx99lfX6Dl/72lsc9nuGYeSwP0g0sHL5WeMUpDGM0yARSG0PzhERh4bXKC7XNFLoAmg19W3YHzAG1qsV9+/d42tf+zqBhCfy5JNPuL56ySePPmGaRjDQeY89BIrLXV9a15KaM+59+1vM6bgKphpDbBw/3m45aHXUpBxnMUSpB6PAh1EALSYxDp2zNErUHMtc1GdSGf1zNHvWWwXkKTLMzLym2dGV53yhIQBSCvJ9pZ+5puHeV79Cs3rAv/uT92n7NevtY1Y3hn6XWH/oCS8Thoaub7j/1gNWq56z7ZaubejalrbvsM6SxoHxsOejP/kRfhTQC5uBgVn2ZjkraeTZoSBtcuYYuKgju2e5n2W3yRGQ0eCjJ44HBpWJ0zCQfGDdOFKU+d2kiNF0wrxlri3p9/m65/avs+YdvfbALv0zIldza4zIyyJDgKQpz/J+ntOkpGnSEnWeoMh45ww4h1FdLUeM5mc1r5H1Zm6/M/OkTnMHSj9VlWLrcVT3/cK5cGt7M4Ojjnx6xR6v+W3WeZbnOQJc/ozMtluXKZ36qgaY13yC64ePGK9vTh+adRF9P97sjoCtN7zpW9079+mJEXNri+PE0x/8UEHlI6WjnFu+7LZbLt97Xz6pHkFKah/M40ooXAQQFkehAGN5HJYoLwW9Xj78hN3TZ+S+bpqmOAQLofuR7pcBpyMr/6g7jjWZVNb2N0J0FmCcOMWBylEl95InbF7jRVerHRpfINzhF3D7hQG6jlMUjyOLjj0Yf97b6TDco33K6l4ZwKdXwKPjqv9VwZIIimwoFh92MYRyxasYqxLRxhaxkQ0dp0SvJYohoSlKtvRtneqWt6LU6G8Z0Mj759DzAspVER/C58CsACRKukLbZW91KufNXE+tRnll/oYcmQRg+x7btBIRZQ1tNkQyT48BGyS6qVGVZr09Z/fiBc8/+rh41oVDS4w3UTzb4nX200yKbK1FKl3HBZgXYmAYBjWohKzUJ893zQ+52rT8g2+/Rztcs/p4VaqISD9apnFkahpWZ+elslE2HIWIXbzVTeNYr9eklNhutwStemaMoW1aPB7WEfNrn2BXifY7v4JBjMuhENXn+zDEKJxMTdvQdZ1Uo2o7Jk33VBp6GicgY9s0CBAA4zAWgNVpn4UYicEXwtY82mNePNUIMmqYZaAoIR7qw3Dg+YuX7Hc7rl5eibEVE64Hfx750bc/5PH9Z9jQQHKVR2ZOcwu6KI1eDAPnBkLbkpIETlhrcN8wcN+QfpsyjwhJy8kczdvTk3Kek/Vmjj5oB8wgA5LueXbO+++/z263Z38Y8rCfz6/9x4JDQfqzTtuCpNwhs3gxRoCVlCS9TXikDFJkKtJotE9W6Z2zBEm0KHM4G895HBhjmMaepx89wLmWppnn32z8LG+2GBSLG5sVpEWHZhmaoN+B6eB6VUyjqq+PvH+l45bnS0mqhk1+ZBgOykeWo03QMSNAdUwGH/zCCZAFR5F7RqO49DUmSYOLwUtEV8WLt/Bea3/ENKca5nsp86tEQMbq3uo7yg9WDKss60NQA7gIQgNODOaQi2nkam3a9miSkKk6K84GI+cLKTKGCR8cMUnFM6BwFbZtq/cRVa+0RfHLCrJEZlhckx/Hcs02xpDUQZD5D1OM2Gi1+ZI+Lo6ciLcGEyXiKkfVmrxWVectg03XsqDRKF3UvkqSCtZYp4Z75uGIOtYpwC5BjIOQJGXRpxztYWi6TiKz+u7WmlgbqNZaun5F2zb0qxVt2xawS5xAjc6zZl4/8rPX9ckYi8GCdfIcgyjmIYbCHye3PbcjqjEigJ02S+WIdVIZz5lcEU+Ltqi+AOCM5713rnn7vS9j0kDwEyEciEEA4+A9w2HC2ktC+HW6bsXlxYqrly+5ubkhxYD3lq7rcc7R9yvtJ8tut2MYBqamJRoFDFISDiSM9I+1OOtYdX1JnzHAZrPh8vKSd955GxpHcpbOWV4+X7E/XDMMMsbbccTGqaAW2WhpnBV6g/ffLXOyRCUYCM7yuGnwEf0+SdpbyEBUNYYBRg/eK0id5bHwXpaxmHVUnbGpFLOpzLTjpcXoHFBOuHr/OROAohsYa3Fty/bOW0T7Fj/95A5933Lpr3BXDetrR/ci0t9ANAJoXVxeSn9eXLDqJYLKtE7ScsYDh+trHn30kRQkmaRR1lolJMxzLMvIhIaqsYiSKZ0wL2UZ2IpJjivUODEXgpCKkiEvZCozTUp01mq0aphTFPOzMHptNXht1afOfADmfQBCumbgt5HSG5WhTCCZGYo7NqV1oVT5ptHqUeSezcolIvdQGSUGvSscZfX6Pz/ExUsZLxlAqDdV+6u9X20rHZ3uc25vABqc2G5fM73i99ON+/lbcuY1J309qHVqG66uGa6uP8PVPwfQVR9RouLf/NjkAzePHiORoHHWZ5YNA2A93uXinXfKGJbhUxd/sRL9GzzRGlJslJAxluAEcQZEgvdadCVxePGCl598rOcwGqxg6bqOlDTSrDRpBrnKwK8cWPO8mWemfF/N1Bocrm+w+rSMOKvmDyh1TdbfKKDerTYc6TOLfn/lh6odx7LxTcC5E9vnPOyzXeNP+fzH/fdZcJwvNNBVb39RAKy/CFutUHsfIEYCs+Iwg11SBrzvRAm/bBtct6LdnIln29h5YmWgy2ay06z8UXiihMfFKjdWjgColC1VgASQysp5VpxrMmfZO2WtNU9yM4d+Zy//MAxztS3kJnMqnLO2El9pVrhM0WuLUZmBHFMJMyGRzXWqIFnUO69h+N4vgCxrDcFH1WHmdEKSPAdrWkwz96n3nmkcGQ4HMWxaIRNerRz/yX9wj7futzQNpNTx4P59HobA1dVL3nn7HTabjaSJxcj9e/fo+462bWXxIEcdGPw0MVohyW3bjvfee59Hjx7xySef8PDhQ/a7PV/+ylfo+p79bodfrxl9KLxbXduy6nuaVizR/X4vZboVzEhJIoKS8lo4Y/B+1PcWZxINs9ejacUDncY9Y5wIw05HhmFQcM4YRzIIl1lOAQqBYZoYNe3CVlGEkw/s9geGcWIKiRClytm//l/+Nh9+/SN+en7NEEGSKvICJ/98kGsGTX0phP6Hkf0wafUlSfVZ9x1Na1n/ox6bDI5E/N1E+pczePJGwn52q5axVm9lCdZxcnZ+zje/+U2a1WYB2MyLV7YAzO2z6Zj34wTos0qRmMK87CtnzWql0ZFq0PkgvEt9I0S53isxNElSbfUMVsnbz8/PuHvnDh9//BHjOLLb75j2e4bDQNtmTisFg6xdKO6f3m9pvplK6UjV926Au4/hsIKbsxpAqhQUU2yiqh8jxIkUJ0KYSDHQNAIu9F3Ler2iaRvx5KcoPFPR0LWtjJ0gBqy1diattQ5ikN+sISaJgtwfBm4Oe3b7HWtUVi0iYOUvc1jk0HhDWkQL5AgkAaRO95Y827gYKwnH1MDzC01vtoZc12yaZB6MIVCArjuRs3uJ5p0Ge7fn+cfw1ESNlmoIYYVHKp3OxrSkMBvl5GqbFjF+c8SmQTiYTOEJzwplUSpJWDNX4SOJTDWAbW2RrSEkYjUW27YjBEm3KwnXKZU1JQMPee3KJOzjOBJ84N5Vyyo1Os6Fo23YwP5CFHQB2lJpVwbeMBCtIRgZ4+1qRdM03Llzh77rODvb3kqjzE6fnAbuNPLYLNZPuTVpjlHiXYNJaAEVATyJGtFnoqZ4y71LtLQr/eyVFHwafel/owTB2fkSdYGMJo+Cec6MUfrOYli1I7/67vc5X1/znT/6G6Wi45c++AH37j4khi3j0PBH/+6Xudm1rNaRVb/i7OyMtmnYrNeEaeKwP9A5x3q14u2339Z0tFUZD9fJMCUIUygGUh7411dXApghOkDfC+C1Xq1p25aUItfPXnKzu6Zxhvt3L7k4/7YC7REfPPthzzgODMOBZ8+estvtubk+EMMMAqac2qZRlCZEfuV7D4lOozkR/ObHd9b84P5mNqRiIFztmP7z/xaevcCNI6Z12JALOCTFohNTCLXYL2PCauQ0GEYmYszRzhKJNo4j5PmWnYg6F/Ozu3jvPbYP3pJ78C3DD/8ajBe8HVcC3PzkKU+GwOMx0DQNq+2Wd995h812w1sPHui4TQzjyPXueUkr3fQdxjre/9KX2d9c8/TRQ4nqCgHXKKWD1zmoM1Jv5ZbASkWu1+uYUa4vTR/XeWAqIbcwL7OMtIaULIFcGAcKsJ70iRmjvGbLhuSVxZkVd81/SsLPWqxJ7NK/ZJ/+7e01qzrPXLckS+jstM1Flyy4BpxTR2wuxGSI2cGrDy8tb7TosHUDDBRguuYrzFudZXHKAf1X26dt9tN3Obm9mXbz6mP/LLfT+mi9DddXfPR7v1d016JXaNqtQTMHvNgO/WrFdrOlX63K+h20QvcwjoQojqFJaU7knEdg523YLe/4ue/082w/y5P8q+3Pd/uFAbpgCXYdey/qz6+Kpjq1z/F2amG4NTE/w+JxKursxF6AkAYKGGJnYzgf+5p2zui3CI2ylKsWndPdNqs17WbL6vyyGG6LezsJdKUSzZEJi4WzoEp1qdppF8pYFmL6r1Tx02dW3WU+g0QdKHGukrnnktkllNUUE0flcQIlaJ1BtGwzq6kcE4Wg8FMEqFEtI4ao3BANXddiDQwDBN/RdT3ReUxvSA6STSVKxkxqJVmpNBa8VMSKIbJZrTnbdrz/zop7d10xiPpeuMQAuq5jvVox7HdMkykgU+MsMRqSnzkyAgIOTtOEtY6u6wuR8uFwwBqrlQnFS2G6CHd2mCuLmSSCwDWWvu8BSmWukmKY5JlYP0drCEeHoWlyRICWqg9BwMMUGQ+72ejVsTZOXkP4hZh+8mrYaGTa/jAwjCPjOIqh7Qy7OwemNnB1NjF2Iwe3E06t6Hn4zmM+efcROz1HBjFrsCiTRmdDTm07Jh+xRlRcZzTwxVpS29C/C8ZohM7HiXQH0nWC4bXDZh4/9s0CmY2Vft9ut1xeXhJtw5iHZz1Ebynr9Q+zQS5jN4M8GUOefV25otnMz5uKcm40zSZ7pK2gVhgHbY7sa1vaVlKIUjQcblr83i3nZwVcz9Lotjctf5PnaL6R+nMNYuUJ3Y7gHdgpEYxEJN1OMVWppCCXgLCZR0Lki5DpW9quVYNNZF/KCIehkLdmGWqsU34WswD68ya8V1luhdlg05vOd5MSeJtwLtGkbDRVEVuLzzWIVb+axe8ZFAsNTK2keabc0RYBuqzIgnHSCDRgbBNDE5k6CL0h9BbfG6LL92TxPhIGkcVOOQnRqBxjk4DSLGV7PWgNYDVl0pvqZozI7ew1zefIRlvClAhXQGWlLdfJfSlRHuAybVQ+NiXiBHZMkoo8RWyIuBSx2l8uSZ/ZSea8Ic02T6o4JY20t4xInSdS3c8qufycTi+V5jRKaxzlFOr8KaiUdDBpMYrys89RVRKZUn6XOubcMg+OZITMxYTFYknq1BGQzpTd6xVYXtpmxBqR4+t24Hz1ks5NXF1faHCgYRgv8WEvaYuxZfJvEaKl7V7Sdq0WCWgIU1NkjshXQ9+29F3HqpdIOGcdTTKMCfzkNV1aXlNIjMPAbrcrETO1bpHvcxwP7K6vWG8kYm7V9wp4B2Js6DrHOHVMY0cMkziyksP7TDwsFbRyYYKokXTn+7HMswxQPW8d27NOU1wSzZTg5oB7eo3Zjbj1WsCfKgKAPF4ow72Mrxxdl5NfMplzHts1aF8/p6z+WedwbUfX36Vv35E1i5bh5hLGLeu2kTU2BMYpMHlPv16zWq3Ynp+zXq+xTSPg6DSxPxw47HZS5dMYoYmzlvVmQ4oB51pZU0MocrCW78bM+tOtLS3flPG7kBvMYJWp1uwMciXKvMvH5plQVp380+0WHE0TR8O7NWoFBkb+BMe92w03kBgJXMv6kJ9Ndeay/FkrkaKa2vjZASe52SJB09xfxWGQkPXv5wJsvU4n/ssCln2e+3ylcvbph32ua37O6+m1Zs3sqBm6Re8Zrq/I6yswO38ANHrR+0BsO5gmXIgwTUXfz0DXqEDXdAKYfVXrbq+E+lvWCbMn803vOC3v8VTPvQrg+rMEvn7+kVx/Vi3/i7H9QgFdv+jbnS9/ibMHD9Sb/ulgTO0lt0cLP0lSABKS/rfqe+7du0e72dKdXcweoOJlB9A0Ef2U+XYy6FGXXFcLeQEqwAx0ZZDreMtKwWykzX8xSQRO5jRIaeYO8iRS9moXYV9XRJkVDYOBEIkEQlKlyGmZ58r4TTlVplYgNPc8Kj/RN7/+Nb705S9jES6Zh598xPX1FY01PHzwCc++9gTXdzS9RLslDI2vIou+H5n+6SRcJDHwzV/9Fd5//wHnZx/SulFa3ThILX3fsu47usbhrCHFwDQGXjx/TvCe1XqF95MQMWvor2mkAtcnDx/Rth3b7RaMZbXasD8MHA4DP/3JT0WhdY7mzo7V/+GG5l+/T/PPvipglXNs1usSbdf3kmaS+8l7z26/m39vDH3bcHF5QQxSrerhsyc8f/6CnLL2VAmSJz8TVeenZNXl69WgCBHGaeRmv2d/ODAMA03bMZ5P/Hf/8J/y4t4N+9AKB9I0qgEaiZuJcAjsoicgxqs+SK18FedxKhS5ahhHQkhILl/AIkq9M8ID1Pc9gQhhhF9J8BWI/xjSH7zJYk0xcPPQrKvQlZ2Avuv4jb/xN6TvbWbwrsHharE9uvRyEa4jm1QpSdA0TrjkRikUMARB6kKgGJ8xSXpI2xhaZ1ipZ26OljRcXpxzeXkh6bFEVqsV/rDhJ7/313Ccs17NqU4CbBYcIN+SGPr59lOlcKgxtwC7iiJfyyY91kC3S9y9ibw8j+zWiRzzVPo3UcC3/GdiIIXAYTwwTqNEInVStc2pY8GpAT1NIyElmrbB9T1t25WorFxbz2rFybZVALDrsOMk8zlH0SCGPlYiGHNLI/DyPGE2ibtPoZ20b44NXL3344iuukdKgo0xBAfPHliCqwxkaa2Al06ss9ZEkbUKTu/2e0lhDpHVas12c8bL65clmtV7zzCO5HC5ru8l1dWKsWdX4uUt0bgKPOdn0kxw+SQxdIndRSyVCrMDJWoBhNkRovxgYa64lNerznQiYzXtWKI2I8TE+kmiHavUemuIweFDyzgmQrAkFxhMLIPRGIO7SZztdCxSacZHOFIycHNpmM4M434vwMfVFa5pONuesd1suHPnDuuNAAnOCxjgM1dTJh83FViog3oBFCr4Ya2jNU6MipQkvdFa4SZMiWkKBB8Y4yi8e9bSWiukw+p4aZo5wjqTpE8xSjRfRkIr8Osb73zIu3eeacW4SGN9maT5Fn78ky/x0UfvQQykCONgcA7u3LkjmEGI+HFiHA74cSBMo7TJN/jDnjSNTPsdZ5sN7XrN2eaC5Fom5cyLIelr4ObqBSl6xkH421Z9T0yJm5trtts1IQZ2ux3Pnj3j0eMRUmS96oHEfn9N2zWcnW052264f+eCe5dnxAQ+NsSYGA4HdbJIGuU4DuwPe6ZxZLfby9gfRjHefOTBRxPnH74saYSNE5PQ/PXfwBloW8fHn3zIj/74B8Ts7FMHWKeE6UnlU45aD2EiMZGSpB6DjF3rHG0nTrW+77VaphiQWZ6ev/02b3/jG8RPvsn4B18ra4X1Da5ppMiBczRtW+bn+eUFfd/Tr1aEGPnRj38sgOJ+J9xq+x2b9Yq+bdndvWSzXvPe229J5damIU4jo/fQNDTGaLR0FDD1loBfTqXFWqbjPUfoR+XstNWiUYxfIxOwrDNKdzgz0B6vr2meS5XELFGU9Xnz6NfjN+Y3WZnfOGkVH9K/40X6f936qTgpqrlceDZr525MRGJpA9UxpUtKn82rfETkNcA4jiU9LKeBOWdxzVxo4/Mazn95t88PHn1xQIVjmOtnOM3RvDp9HWY76Hg8qnPqhKgoc+FUJPvn2V73hGr9+vVTZtbG59n8V9tflO0LDXTVAMqrIrlOHXO8b95e9f3x8a87/6cd/9mOy9NMjrGuqSoopXkXZoExn6v6vlwyK8tyzpyul71gjYZR5zQ84RaIar8kXZPn9pvqQse55ZVNOd931SZDXSPu2A9RWb8sz0MG745AsEV0RmXcZa+73qKeW33kab5qEU611KuOjzYyXF4zrq5hQHhjYmT/3p6rBy8hgfcTD28ecs0Vjy8ec312BVuwa4tbNcoxkTA1p9P9RPpaJF4EwrnHbqXi1surnnFKbFcHYvT4acKg6VIhMI5z+NBuJ1ZY/QTyLeQ0hnH0hYfqMBzwMTJ5Dymx2+9ICbZnW2gjduNhlQrBbR0KX6p+rVcLD3eIAWcdzhk2q5a+bVl1rYAok3iCpvEgXJc5QgghQL+52PH87RdyvpS0SpNRQme5s1G9ybvDgWGQiK5p63m8esx1e2BsV6Ikdp4MWykXNrf5i9SYKCsY81zQvWweH3ng6PBNCvwkBBzBARuI70Lan57362HNZr8pYyrzqQlo4rm+utKfZiDr4uKC7XbLarWe5zwKcuk8LGm+JYpj3gcqI+AYBFuIIO2bObtCADDn6FohVrfO0XUNTWNZaWpQMR4wnJ+fcXFxjp8mXr58qedoceYMZzYCCGUev5Pib/ZMm/IMjsDuE/N9CXRlhUllVYykkPnc8iiqFKwMZqeqChapRFvlVJJsFMQoKYsmzSSj1roCaGVy9Ux0JL81mqJpi/Hqc5XVNINaWZlLzCmL2SA8tBAwtJPyqsW8TuR+YTm2Fw83G5bzPsFCsAaSnWWp/mWi+nxOHxKHYeTl1RX3Dwe895KKsN1ydXNFSTMyCh5p+yUVNhUyfWOkYEAzmFKQIuXnbgyNNxgvpNTtQaKoUpTsT2sSTbJEkxhbgwnQDAJSZyJbkHQoY6BVjiQT5nuLMUqY4oCmURnhBcNiksXQYGwiJKdFSaoU+rJu5X6CpG7gsp4ghmYgsUoWF6zeY+LQhPIckpHrGjXcc2W8mSmwWo0KqKXz/Uh9LvdGHfGVyjMlpQImWyTNPqXI4D3GJLq20WqBTqO0bVnPrabnSfMSBsuqHVh3e867G1ZOKuzJOAllwOR2ptjgUwNBirmQZjAsagXLcRgYh4EYAiZFSZ1MkTCOJGvwQGvAkUiuhTboPJGovWQgkGgbS+scnpEYPSkJwOm9VAMeDgcw0PUdw8sd4zTIumAEsIbIODgOOX0z6y12RUzKPZMkYrPvOhpnadsG7z1d1zJNnv3+IJU5p4D3Ce+TptSKwwWTYJWLEhjOtmfcu3ePnEJ+dfVSUmhV17IFiKilocpHexz9vtwMDSv7ZaDFGsuKe3T+K8Db4C7nNOleIq7Pt2fiuGgck0ZUA5LSv9sRQuD65gbvhTYgxAhWxrcPgWEchY9UI+1nD4b2YwUcSSGjfDezNE7VuzzHRIzqokSlgyKRh6bIuiPKkvyb8gEaDb9crC+VPpxfFkukWc7GWcfWj6bH0ev9Lfu/4QF9+oZw3mqhgkhk4CMS42LfOtMiJZXvpjqpqdqdgffq2HlNjKUabUyJcRglAjHEqriPpMAurv1G258uSPN5ALcZTvgMB1RHfuYtzc/hcx38M8Aen/XIz9QvJ44uk6GMtzT/9Cnnv3Wn1bxKx7+fOk16zW/VT4snqOMnR3CaajwtxlbdkBPn/1l67VXb5xxti+2zTI9bc2kp7PJeb3CNn7XVn683P6ss+Cz7f6GBrnqrAaxfnO1oVn6GcRBTjXerEDB1+oiInqhVrIipiuKKpCiAUCn/XcCxGezKSiAxVQuxWVzzuO2pCFOtJFQtITOLQ/bAWSFDjpnMON1SpHLqYq6QlseBMRYTZd9UXUVSM3JE1QxkWCWJzYI9hkgyRvhKMNAHnn3rB0z9gP33EsEH/Oj5k/6P+aj9EO894zDwvcO/43p9xTP7mPV6xSXntE1L3/Xsh1G9bKL7RoCvJtI3PH47MG5ahp/s2V2PfOf752xWLb/61aekKOl6BiGT3+937G5uSsXCp0+f0DYNq1VPBuZQY9g6qZh1GAb8zkvpbS0xHnwgJXj67AXb7cT5xYUAFK6RSDDXSHhx8AKC5lSSVcN2uy4cYzFK2uV6vaLvWt6+c0brJFpolxLjYU8YB8bdrkRv2TSDiz/+6o/4Z/+bf84hc3+ppzMgURyuafFade1mP3I4TFrWKmFcgl1Dapoy5JzNRPd54Jn5NQt/E6VoXVKia83Xy7Yt1pSiDM6K0pqjJCfvMQQBuvL2PwP+9um5ePfje/zKn/xK+ezc7Fl99uwZv/3bv63Aicw/5xxf//ovc+/+/UV10lnd0igMHcslPWQB3C7DvE31n0RwyFyUqB2pFNZa4ds722xYr9ZcXFxwfrHl7HzLer2maRoaZQ3PBpFBorxWq54Pf/ohL3/ykrOzM1arFZd3LrFshLxY523tnCA/ntxGnd9ZcZ8V+dkoWEaIzoCXDPka8BYemxiOo77mfWEm486SaRwn/OQ1Ys0WUAsSQSNbgs8FIZpFxcUMVCWgc0IkblwjFflCZBgFrB0nAZ09WXzOFcGyvI0adff0LNH4yN3HYEJa9Fcs973syhItmJ83YjtFawgIJ5d1rkTF5IigoG03xuAD7A4whhtu9jsuL+9w79597t65w2q14vHTJ5raBY2TqrIihwXIyG2S8dzQDbB9TAEAMtG2VcM9GUMzwJ3BQHL67EUeN21DaA3PHiTsFFk/0giaEDRV0UqhA2MxJijQgZL/V5ExILLFGBwGGotrDI0xtG1HSqmk3pbU+spjswBaK+DUGINPgTF4zuloJlGrgk18splIraVfraSy7mpF00nF33lttfPT03mSU5rq+Z9AC5JIG3wEYysS+SCgSijOHlsinq+vrtnv9zx59AkpJd55+77wz60k4tB2bQFPcrx4wmh/Jb508ZRffvtHkgrvAeVcrGAMJYZXWZnno/woEaPjgB8n/DBw9eI5u+srwjhgYqC1wnk47a6Uh2si7K8Z+hXmcMB2K/rVmqZpWW82yodm2fQd51tN448eSUeUYiu7/Q3Pnj+jcY63336bq6sX7HZ7utapPJdqu7vra3bXVyJfNAq8WV1grNU0fQGF+r7n7GwjNAXOMg4T3ntubm7wPjAME97LfBoOI9MUGAapKum9cloSefDgAfcf3AVkbP6bf/OvefbsOdMgRS+6Tgp/2Myfl2W9MTTKWwdzgZEclQrg7Ib77T+itfdp2pY2daw+WtH3K7q3JUqrySm0zrHdbFVuRa6urri+vuF6d8MwjhyGQaoa50qmTUO36llv1iStwnyzPxBi5PrmRiueOgX3zeLPII7aiCo+WZerxzazfBBZpLqg8rcKJQaUqCidL0bZ5M3ylLqexEofqjdz9F71YV611Wbrq03Ylq9y136ZJhlcskQgpAOP0v+ZyCORI+rdEJjaQFAQN6e9632JLJ65u0pPVc88+lCcjeM4Cviozy0Xzliv1vSrXgtbyFlm8vDPkzb557v97NDRny5498XejvvnzXr6dT1ag8FJP6ej7xcteGMM9g13zEtrVp9qk+DnuM2W7PHfn9N4+9kmyi/U9oUGuo4juk6BXaeitj5PJNeb7PsmC8bnPe6zbKnMZl3IqEK686TX/w1ZeRawwmaDv0SMzKCW3vlCvqRywTTb2SnDWVmiccs4yNFSc3vBEgtIJXb77K2efdZZqz+OYct3NcNlFKBj7phc6UhIZSPRWk3DyM1a5p5jEru3nzJtd6ROqu0M08j+cOD6ZifVQdzMYXG9v2E/7AkpEFIo/Fjj6JS0WIh8BZiQiKgxjNhR7vn7zfd4tHlIiIm2Gfnx7hkpeeXG8oTk+erYcMdbQuPIoIOU9414P4nZpOl3yUhEgbUOCOq1FXAjRIlC+DfxBSke+JXuPtsNXF6uCL/6DB+/zwd/+Bb3Pj6n63v1/KeihKeUiFpVMXQt282GvutwtsGHwNX1C3ZaCXEYJzCWpumI68j3fuMHjCtPAj754BF21dC2BhtacontgFQtsm2LjQGmhtEaJivVKmMegSkJ7kXme8nGVlJjTH+rhh4G4QGr0tfKvkZpeDKnWsbHqggRLXg8j6/X8G4ZZzX1MM8ZU8ZZ36/40pe+XACGbGR3Xa+gSSxzJhIllVBBgjIPdb6nMmeWLTEmk1iTi/DJd0FmVtMKgHl5cUbf99y7e5e+69msN6w3PZuNpOdJuqpctOs6nLW0bcvNeIdPbi65GZ8S/Evizdex6S26do2lpXFaxa/uv4y+qFc+KsE3JIm+iTnqUgGdI3CryLgjD16MM4F0DYyV7462zDmWgpG+jQIcWCshQl7L0hukMid5TGUw3VgBs/R7dBw612iFPEuMFCL63W7PMEwMY6A1RlJibcJ5WB0qIFDlmwVsLuyn/Dx5LAsbHiXCKM8bVO7W60AC4pRoXiSSlVSyGCM2JJqUFkCXdVZkxx6aEVoPzdOJ+MkNeI8bRzZX0Ey2qqJr1LgK2MlgTCoE2pBwQ56LZZYuIqJ0ekEGaJMpBLdSKTLRvUgwSqGMGOYqjNbktS4qOOToujkKMj+TXMmpX/U0TUOvlfqsndP883jI6yZmbmGCeSzpF3kdjVqdMlcrBogWtptEcoa2aWhsS3/oaIKlOcjTTQYOK4cUkdRVMxvy1fqbx0ROiYsxsZ/2XE+apoahq4CgfJ5xnJimkXE4aEStpOi+ePqErm3w2xXrvof1StcyraZnBAxddXveunjBndUL2ihRxaFau2cZI1GwlgRKiRCmkRQi0yiRW34ctGKiPGWTEo3yw7UWGpNwCDeicwYbPXE6EG6uMeOITQHT9Ziuxalc3q46poszrl68YBoTKcl655xl8hNPnz3lzuUF5+dnbDYbJj9pZTspXGCMwoxRqAxcqW5pickwTUMBS/u+o+s71mvh+kLno/CTypiWYWcI2zhHN6bMDapgSgqEKHQF+e/mZoef0Pkdef7iOQ8fPoLgiRFW5tdwXJCylQhYLM40bMyG3qxo+5bWbbm3/oCuORc+TifRuTmSK4XAFAV4MxgO+706BYLwbx0GdpqumXStX637MgEk8jPQOFvWvxgjN7sbwjQJuJxm7stMF5B0DUp5Qp4wBlMyWlhIyKzFCUApztA0Riup6nirQCFz/F2W07n647Hsr/TH4nwtn2q0rBywRNGqr+f9sv3h1IrPlAQdG/4mwVxrRVtDTE6cI8kyxD8m8Eycf2bmfoym3Ik6caWibVLqjhiFFkK48IJE4YX5t5zqWUfkCx/qvM682vb4LMb5n60h/2pNa95DtrR4uf37q7bjA4rl86lt+7QzfZbt81mFP49ncXzlo/58w1ako1PleXt75+OqiPlTql71DEWnqe1BM0dy3Tp/Wrwvd3ISZasykVKVEVG1qn6XI0xNacupe+M1N/7z2d4ssun2Pm+KE/4ibF94oKt+f0pov0ka4esE/pukKp661mcBr14FvM1jc15kbwnbk/c3g1HZI1yM5Tin9mUzPRuIwXtcIfc9an9SkVOUtnqyz9dLKSsdM+HvHBFWbMFq8iclMpyNH2NjtUbNkR1irOfzzc+tNkrI0S4L4GE+xkSDsZBiICVRaMX2t3O7mBsZTeTqg48Y7l6JQTslDvs9V1dXPH7ytHgwDWLoXV9fMw1DUTSCD0zjJAqYqyqsGTBBABs/eE1HHPmD9vcx3ZwumHYzX4cYE4b/7XBGP3ZK/g8xSAWtSdMZjRGFCCDSqHIjCtY4eWIm8U+JMUX+aXzOi9Ty1/t3uNwa3n1wwXT5mOnXfsp/8n//u3z56l26Xipzphh0PEpURnBWuUUiF+fnUsEzTEzDyMNHj9nv9lxfX3MYJoxp6LoVh8uBf/sffofrOzfS0cbQmTVNNtaR9IRcacx2HT4EmmnC4wjAMI2itGupeQcF7HJKgJ/HtyQ/yIO1aiCl/BoDwccSFQGSQpVM0nDo2ejMy26MYoxlwKpsr5IhGGqCaRm78r5bbfjaL3+jnCd77o0xeB8WFfkims5ZpWzlOQK5w+ZvIC/Dy8U+byEmYoDzs4bVquPdd9/h7OyM9999n8ZJumHXOdpOopuAUm1TCKVbNus1zx+9z49fvI87/DusB3/4Ng3v0FfRMTEJQXGRB1HTXLQ5c3RLVGIwlRfp9uuccn1q8b5NbFpHec2PKkdJaAXVJGBHyECXa8BYfIiSzm1Mab9T+WeMEyPMOjWccjl5Q9N02KYBDFOUKoC73Z6rqxv2h5Fh9LQaeWisgFzt09sqfB6BodyvgqHGzrIRKu9olssKiKjhmY3U9oAa8mJQtlHT39QwTYBrxBnQDpI+2A6W9tFAcleYGLHTxPY5rKMASlaJ+6VAiC8AVNc5HTNzhcgMus+fUZm+XO4SKKgjwAkB+oMYceMUSsSCiQmrUU15nnStZdOvSrW6HL2y0kqI67VU5Ov7XqsSzuTlmWdSn3AZK7eWw7Lg6b7OYhrlE9M11hijfJpyj94H/D6QdgLGWmuhscStIzTlxLo0FncNQAFwydX/EtzsdsJRlWTcXd65y2q15qK9KH0xDgeGw57hsGM87DEpQJh48lCArnC+JWw3GL+l73vpq0YK3lgaLpuX/Nr974os9UAF5C2cViRMkucRdX6HcSRqpHP0Hj+OWGNorcEm2b8xkobXmpyqqOl7zpCiJ4wTgw8k1+BSwK5WsF6VlOqzzYrGGh598pD9TuQ52u9+Gnn06CGrdce9/h5n5+dg4HDYAZGu63WwJWLwEKBttFKyc/iYlJdrZLe7oWkcbddydiZ9lbkqjXIWuqalcW2JirbW0jadFpPp5sqXfmQYDwzDnnEaee/9dzX6VCqSHQ4Hvve97/Hi5RVmHPE+seXv0KZfwmtlRgCbHK1t2bJl7Tacb8RRcefOXbquY7Vak4EocbZpddEQChgyDjOQ51UvkIjTSL+WKKDVal0iu1KU1Ou+leI40U+EFHl5dVUApVzFOBTnqKxCoTj63BHgpQIsJWIEH5VfTmUxJoCx9DgB6LGzM0sPz+umvF/OVUzI5YLLmlEq2Kase8rrqzGRvM/yh2Vq1/LCRZM2LefmHwjYJ+5c+UsCpvr4X+B5Us6RHQSGzCU5R3AJyB+Y6ueohZkiWqE6A13KbZgr9M4VXy3G3I5dO20rVd+dBClOfPeG28/i4D/xpD59O/GMXnX2xWHm84FcP4/t81/18x45F5lanK3YfFkL/vm1ypCBpeO9arArVkpOBYCp/Vns4xPD9bi1R9a2/H+kP9XA23JaiJzCVO8XFUSOz13JuJ/z9mZA1emdTh976n4/x/anh+l97u0LDXTB60Gqz7L/p53n53Wdz73lCb388lMPq0GzvGDaKkTaqg5fF7uq32UjMUYhXDFSmgnhnanTGtEFlHmgl1dTwkZL1Epl+Bs7p0Te8mLXJzv53DQarY7ksHNqGDBXBCnq1RzlYbJFWM3uw53nXL/1CTEEIhG/OSzalhWR4APjOBXSzxxKDtC4FpfbUYElchuaAiU3ICmEMRG8Vx6LubKSoeII0tv/Vy7x3V7SRACC8apUqwEZZ+LmZAdAUhymfuLm4kC2JIN6d5/GiekQ+OThQ7z33LlzBz9NDOOBf/Xt7/CDd39CowabnwZNCQr4aWIaRw6HPdM0cnl5KaS2U8QfDlw/fkzwQaPN5LJ91xNXCffOlk3fz/dLBgClQhnGEgUxBeUPcYcDk2nxtiMNB0wIJD9hksFhEc9QEvAqgUlSOMBPEz5FrBUvqc3PShXxxs5VmjIQ5uw8N3J/WYSSq9FS66Yew7dG5jziarBKH/liPMp32difF25ZS7NXWIAujy3KbSKV8VQvTsdSwRgKkf40CV+OIdE2kob67rvvcHFxznvvvstmveHy8hIQsNTa3Dav4zDIHJAfGMeR58+e8dMPE6vH9+kOHesHPU2X8JOkmGZC8RDnKByTcsqlnD/o/chvi04qczV3Xlp24lFvg+8Nhw1MnUQeilywc6p1nsvWaml3mIaI9xFrHI2jcE4ZI+8bZ5kQ73nhxzGWlExJt4kx4jUy0O0HrPNgHJP37PZ7xtGTMEpe79iu1vRYzq4tbWtY3c1yQq6br7+8vaqyXDXyUvU+KmgVQ5xTu9XYMVFO6hR8TClpSouTQh9J5LhKR7q+Y7NZl7TmZ48fsVei9Tz+Q/CM41xFbhhGUorF2G9aAdudsxrp5qTIhXUKFNiSwmhKkQNJS08xlip3McQyVqIWBMnjIVdblHO3rNdnWB17mR8ut2eOQrOlv1LMfesyblN3b3HuLOfxEQgb6jSyvG+ojsnE2rJ+tG0L1rB94RWIT0wd7De6xJLKOmk1FNM0jS5XEb9eEePI82cvOAwHXt5c03c9k59Yr9dcnJ9jLaz6lp1JpDCxv7kiTCMtkZZIEwPGj8TBMoVJIpytPBPXNOzDC4aLFxitgGlWK1zbqnzKAzXfq35WJwo+SGWLEGiMYbPdEoMnTCOEiejHUrWvdYbGSOhirsCYOfQaY4ghMl6/IA47XIo0XUe3WuGalu2m5+xsxTSuOEyTOhakcI0fAi+vrlg/f8b2/Izt2ZYPP/wJ4ziw2w+qP3gBToxwC2Kc3tMMXEtVVVOMsqRRUSF4YsgyLOFsg7MNVueUVSC17xUQbrLeJOOi7zoaJQl3rmN/veL64wfcaf4av/H1/3lxasT9B4SplxRH5dLq2pbVes39+/e5c+eORiNSqAmur68LiBW8xxeAK2j6dSrR3zFFmY+tQygrctpr1rECIUyaym81eshjNcp4N03CtRYD4yRRhI4W45zwrIHwsZmkMtlkhbCSxwnnkL5Rfr6S2msMU0j4JFVRjU24lOVkflamRPrNxZc0wtuZGego62yZyEXAHkEclEhdal20NoSr704sSXkpy06z/BfLOIK1+9v0fIPGrDDGYWMr/aU8aD5XGA8Du/GfMsUnEj1XracxRnHO6fpgNFOhgPX6zxoBCcPJlr7uM5WBX+/y+W2cz28j3dJwPncb3vhyfy7G+8+COHzeY193ozUofHzMseW4fJ+n+vF3rzjFa7dFRH/13cmx9Lm78OhcR46t/LpwJBfA608P3Pqr7fNtX3ig61XbKa8+cFJR/Sypi58lautNoslef1ye/ZVv99hIvv1DmZPHoFH22ueCz1l5X0zeI+U9g0cpCaKeTDaub6cELW7J6AnLLcyRXrlNpW2lDeaWfDDV/SzvMv82R3wt2nLUnrpLF2JIbeh8nugiw/aaq3c/LgqEdW4BVhUDKUYm5UXIfZZT4Ga+s8oIrcCy4sHQvhXOmdlYyPdhc7RImp/3H9s9OGUaS4lAkHS3RkqFJ5twjSjYwUhKQPCe0ESmzVTaEHJVtasAU+DFixe0bcs4jkzTyDCM/OD9n8D7YkgCDMNBFOUgXEZ+GjkMUn1qu93inGMaIY4j4a3narRYmrajcQ1t02CNw7oVfelLSXoxyrdj2xZTAV3JWoZpItiOzifaYPC2Ae+J0wQxYr1GASqYkQC0JHyKCtJkxThXcouq6FuJKoDZS2wMqijOROVGQSVXELCKW6fe0vLD8Uw3uh6WtVPfxCNAVrbZ8xqNIWBLNMtyMuR5LsentJxSxkh4d/AaMWGFdH697rh79y53797l3t17rPoVm82aGCPDMIhKrkC3pE9EjHrUDeCnid3NjudPYfvkjNX+nHinJbXq0Y+GaOsKhzLPbO6DMm9CAV4Mxa94S6F5HcCFHhtaOJwpcAnkMHWT+8nM89hYBT6T9L8taTJNeUjOCjgTQixAkNgtM6F4jGLoBk3bGscJa4VDbvKeSXm5MI6u7WmbxHZzxio13NuJgWY76dc5qk/k7PJWK6CrBhv0DlOicM6FoOT3aiylFJUbbxmh2HWSyjd5r6CSnNM1Dav1ivOLC604adjvD1xf3xSwKCWJQpm0fHgB/CsOGKcRVU3T0HXCCdV1nUYFdpr6lcGnXKhhjqCbplH7N1TzZwYXhYtGri3RWw1tt5a+tDNQUS8uWVaXSEL9axoxEgsyX6bXsRNmbocxqYzd/JeHZV4vM2CdK8hZ6zQi19DvvJ5HgPfDRsZsTk3NRrtU6rR6fomm86EXsuth4DCOEmW5WROj52y7wVpmTioS03Ag+pG+bzVVMGFCAD8SwlQ4KY0RoGuyN0y7Gx2HEo0lt2NngEsNa7LDIgkFgtEUZBOTcgX1TAMcxkEiqr2nsUb/JJLWxIABXDIF4HQpYFLCHybi5NgbaPsVpMDq7IKua1j3HftVy+inwk8aY2AYB0mfv77m3XfeYbVa8fDRJ4yjRFWmGEhxom2cgIgIL5mpn3slJ4wqJAK8ynicpqAk+1GerXEaFadj2ljGocM5BX2tyN+ua2kaIYI3xtK0W8LhEn/9DTbW8JW35xGbOdYOhxHnhLOz73s2mw0XFxfcuXNHeTc9+8Oe4JWrKWq0j1bhy1WrY5AqiH3rdKgmjYA0NMkSrDiGJP0/FudWBo9DDJAj8lIiTloERiOKQghEZ4m536A46+oKyzKJMj+qyjwroFdOb1UOAUJCqmUbWYNiprrI4A5JgFpd37LMd2Z2IMicXExtZmR7hoVUKYTC4XhbBz+lwc/iuso8KHruchNZnWjtL2FxNKwxOExykv4ZIjYEjPcY7yHsCeO/xMdE8MILGaMlJY2YNUnlzZGufWvJXMrB26bIa9bYk9//eRv1tb30mp9/pkukP9vbNLlnP2/jP8dxOYhBr788Sw1yHXfEaZBr8Z0p/y33y8bY65qbl+KFLpSK3QbMNtXC6HvNOW9dI9uk0qiTMWuLRtdgd72dlAqfoSGfvt3GFd78/KchiZ/HBPl5neVPZ/tCA13FLPzcnoEvznZs773RMdovOcqnTEqTBYMad0YN2KzMM4eCnyTnrICqlOZc5hztURbZynOV21OiyayR6DDQ10xCPYejp5QrOyVNwYkzn1j+CxKtEOOcFmUrxdtQVZdkFgmuacC2Wi0Ngg8cLq55/o0f4jsBbhYee2MwESFgnySE3zkrBnHp41iiV4Q7IUhKRBJApaHFNg7rtI9ronGTvcVVK42RqDBTiVajPA1A34p3fxgOyuvUltShrmmxzhHdSoCuRsCRtutK37VtK6CccwJ47fc8efKE737ve0pS7cWrq2S8xfhGwDmvnttxHPDBCzBiLEPosRE2dHRNg+t62q6jaVv1KDpW67W81+gB65ykKgBWU2dCVhCtFVCrG5i6NWz29OOID55xnCB42sM1yQvwlkJQA0ZSLe+byBQj1ynzlYkhl5VCjJGKREYjlVAFI0ZMCljlcXFmyXUXYj07bqOxeb55BRyO52+e03OIdAZrKWBdbTRHY4jGFkAsG/fWajpEFAM9ZLLfJGlpGGiaeaxZa+g6x4MH93nrrQd86Utf4vLigk5TDW9uduTIGfCY5Mt8LwUJGqcpMSOJFY2zXF5ecL4V4EJSYXwZwwVoz2B0meMKMKcMjFAw8uOtAFW3ejEDPvLZ2mzoLBX6Ut5eDaOc6ip92dC2PZeXd6krMRq0uIFTfjkJ31iCGSlhGqn8lxdU13RY5+jXG1JKrDfnXN65jw+B82tLP1o622AxtOcoGbFRcCbL0LkjasAvG4WngC7Qao4aVRN8KNF0pERnZ6MrarRU1wrolMmnp5DJ9p1UWTw74+rqipvra8ZhlOjKRipKSpRWT9+vhMNIUxmttWw2a60U3Op3WtDCWY10qZ/P/Dzzvfb9Cmst09SRNIJLpmuBQQt4mmWT03TRpGtKnt9FPa/WLmdydC6z/NXGLF7LAJzlcnmbezPK+tcpcJfHVUkb1eOsyXxgMA5Sha1xjtV24r1f+QGpiXiX+Mnzd/j45VtF3tiq3blV2/Mz1uc924szpmni5npXQI0QPTe7K7brNReXZ9h4n/NNx3T1nGmwXGx6usax7VupJJgS0UvEog+yvljXMPKS8eVzTQczTPs9Sbm8jKbrWetoFGB0bUfrpOJov3GiY2zWsgYaGKaJq+fPGfc7op/oNyu6tmHdNQJKT0HhskjjRLY1SOr5IUwkPzFcB/ywx0+DVnUMbNcdpAtGHxgnzxQmTcULPH32jJv9jvV6jXWO7fYc6xotYOMgiQOm1bU8hEQMQylQYq1UOxY5YMq4zWBubT2EEPAx0GJoXHZOhLJvMuI4SEThRnSWGAPT2PLxd7/FuG8Ydg8FLHM54tRIEZlxxFhD13Ws12s2G4m+jTHy6NGjUhhmHMdZF9K56DJXl5F2j3HCGLSIA4AVgHwaBaiKsURWTzkKLEyk6PFG+8EYsrPHOiO8ijGKvtA6nQcUeYarqi5m4zWXUHTKjdYkMJEW0QcEX5W1+aBp82hEZEym4nKUZ2DVUWUV8DLG0JhEn3n8FtN5NljzX5Gpeb6HY8M+n6f6/rT1qD8p4CUeNbCV3aKyTiJUE8mOJC/p8jHmFNAckSdjeRP+I1bpMK8HBvb8Ljfp/6eRvLGix5BWlvPEoBxn6gj7S2A3/exbHguvLlPwF2/7WSGH2+N9CXKdUs7MAguU6f0q0Of28dmWPHX5OoUwO5cWDqWf6/aq+VDf2Wc97i8yBPSXY/tCA12wBHP+tIX28TVORYl9lnN9+rHLRTZME9PhQNN1GoHyuuMoixnVq2wZWMqG5rxWm1dO2DfbJPVoaSDUAikbkLdklCo85kiw5Wit8sfyXsr9UQF5xRtv5u/LT/P9GT0+EPHtwNBdcb15SiKAn1NxZoMpFW9lBu2c1rVPUao0tk2DRzxuEvGlkU/eY1uHiUYiiMwcYp8Kd0LmNNMnYUyJpJJmqFmV5pLnoGlWphpTlcfBGitAkRFeFKegVghB9ktJ0jUwTGHAey+pSQqGWU1fCKERb2/jFE/Q9EXlg5g93IlSLcm1YBVQbHpso0CXtdi21ypKAnI1bSNKZUq4VviRRA82wgtjGxpj6RJ402A64aiwwwR+pMMT/cRkIPhJ0klCJBpoo3DwOK2kaYwh652l0lEV+aGzQ55/sjPJssnfV1EgC4Arwyjyn42Wbuqwg0QDlR/LEFwugjWwmsGumJX4BMlYMZSYo0usNXIjatybAogs25fPmY2AzFV0fn7OZrOm73sZixo5k9sSRkeYbAGwXdMQncPRC6/ckDC+Ze061t2KVSMk4CU11EiExAwMpdv3WvUGxpTqWbO3eR7Pr9pquWWBJszdjZE5F/NzVVBpRtVQEEaM3ZQkjRgoEVY53Ubuawa7shOhGBZaMRRNleu6jpTANpFVNBDhbnCsnMXmuLUulaZksKvcdg1+VkBXlklL8K8CsVS2x5CjMWQcdW5Ov8rRHjmiyzYN3gfa4AEtitD3pfCAMYa26+iDAjrO0mhaYNM09Lpv33fK79ZpOtTM1VZ4YnSelYjcWCmvmiaX92/0meTxVFLAmYsslGfvrBqPlSFbAVSnPufvcjSaDr75dTHQjs6RR5+JyhvkFtG8xKgRJHM1YF2Qce2IsYG2bVltD2zv3GCdkHC/POx5eRgKgGsV/hl9N8t3J5xFrnWkKLx5fpIqgAKgRAUzHKu+xwTPZr1iNInGzalpEpeYMFFS1Ai+TJ7kJ/BenAIoR6D3BehKjaS8ESKpFcdUk1rJ/iuArUrN4Al+YlJS+pyi2FiroLNEx4m8CwL2GKPVRRONSRp56YneMA0HxmGPaxucga5tlE+PMk+DRnX54BmnkRAD3WpFIvHSuPJsap1IIiIlPRZdo9umwVrl9Kz5FtMcGRgUoIhB1tRk83g2GgGVCJpOn1IgRIdrLCFMjIfIy+ee6TAR/VDAKadpvdMkwJ0Uv4C2bWkaiTTNPGJe09lKRdxqrM4Swqhcy+JP9BhjDSnke5iBOWNmXlQr4bGif+AK6FqecdZBdI3BzPpbwQuYAeUyswodRpZnSg1gFV/I0YNWorAz8JXPkaMpScK0aoysAcZQ9LamigYp/aLPJusDVT0Ibav+X2zcpHcw72RSdUC1lXWXrIdDiUjJpyx6eZTAsSAA6DTlKrhz6nnUseXSW7ha9wU8j3DcJaSXRA7kEiD1GF3QjFQibZZjv4DG+K1behXw8obbG5cD/DlsP/OlPs8JDFSSYqmsplvf1ZpbIlVdWZ/nDa6aQa5XHZJqOx9cK/av9WG2yVV2HJ/CD+MJY/OVLTl6n47eve64U3t8+pF/vttf5Lb9fLcvPND1l2l79uMf8/Ljj3jn136N/mz72n1z1MdxilNO57BGoj9SjPiUSXgX6sdim43OGUQqv1XHZHHzqYBZdYrytpalVErS8ZYNnVSR7ccMAqW5fG1JYVCljax0GOE4QKLDpm7Px9/4XXy/Jz4/qGCcPTgltSyXi9ZqSl3X0dtc+lquP+z3jMPAi+fPhL9qf+BwOEjfOWhpS1SCtZKul1MXpEJbLMoz+qxSpchhICi4NEBRvqdp4vrqJW3b0XUtw3AgYejONrimYb1elUiDzNlz2O81TXEihsh6tWa73XLn8g4ZKMnGR4nSWK8UCBiVqydJBSoSfd/TuJZt/xYxJPY3O/Eeh0hrOkyzkugO12BbAQBG78Wb3m1wUX1ATk2vXGK8ddgG+n4D/ZYu+FJhaH8YMNOB1ZXFjwOH/Q4/DvhxIHiJLHqSIlMM5KCmvGBKhBEFnDWI4lqifZzFJolLzBFeIUYG9ciHtGS6KOCNfODOy7v8+ve/RRsaBj/mncoYPk6HWoDo+V/luSqRhfnPSvSKkNrOoAExV6xKpdJVCB5joG0dq1XPxcU5d+7c4c6dOwVIUEgFSDgnFRUffnSfRz+8XwHm0s62bQVQiJHO9vzNzYrQBAEXNcIS6rbKxJYouzT3g85LZySqzjpHCnFBuP9qSVLxpFXK/+qQ6Mf5Wby8axm7hFHQuAbd8n33fY9d9az6FSlFdjc7AQmc1bbEonBN0zADMyipu5J4u0b4qEbvMcay3m6FG81HNtew2cl8NStT+jNH8s0A/fwc8lcxA3TzAFuAhEk7SpQ+mefGuAIC5HwdFydA1gEfIsZKdJZrGnqgbVMBc1JKElkZAuv1mq7ruHfvHjEldrtd4W3suo7telOeyma7lgixw0HWIVulKulWomH0+Qr5OTOQBAWQrzm1Fp5cA61ry7xJKWkauSm8R/WW14rFfGIGK4AS4XVMZ/Aq73Her3EOo1GOknKpgIKzxXhPKZFCBhASX/71Dzm7+5IQhbsIE8q0+NKdh7x38WRuuzHcjGt+96ffJERX1gEfRuEgM5az8zNIcK6vzhjaxhGDp+8aWrfll37pKxxurvjpD3+AB5p1j2kb2rbBmURjBdSRtjesnaNXbC6SSEpYnoInGUMYRpICvMZKBVLnGozLJP+mjO8UAruba4b9nrZxrNtzVq0Abn4csEgqpfBfjdA4UrT4KGv2pl+BtQTjmGJkf9gxThPPnj+n35xhbIO1CYxEmg7TxP4w0DQSVTiME5MPvP3OOwyHAw8fPmQcBobdjaTRNk3h7EsmFsCmaRytW2NddjzJGBxHiX66udnjfWAcJqxtxCnTdjjXLMDUOWUulWdqjSUaS9t5vvTX/5Dd80s++s438V7SgTP3aJZzbdfJOI+Bm90N+/1udnqYOX03kYos9tM4V39ULrzGNViTiN5j24a+WxOHgeRnPq9kBVhzLTRNw0ZJ6WOICvxZ/CCcna2TNcgHj0WAuDiJMypmJ4nqSY1rlJMulnmSouhtIWYuWQHrQ0aKMDRtp7qfRiolGSvR52rEkiYr63je1RAJpCTgvVEZUzAwzOzMqNbW7Gyo/6pZL8/k6JsjyXAEdqXybfldRX7wok/kOizD6GVdOV4fTm0p0adv0fJ1nsT/kiH+zlxJWPX7qM9M1t1ZniTVQdE17K+2121fpP75vG2dx+b8enyu29+lxftXpP298mp5Ls3HvdZ2NHD/l36J1eWl2KwZ6Co/z07C4D2f/MF3GA/7N2rPz21Ls8T4iw51/WXZvvhAV/HOUi0rp7dXY67HE/zVlzo97U99++nb7WNfA2mDhI5nvpzq++P9qpPPi22xX6wa+JFqtQdTVehitkNnb9S85Bdnt15ovg9DKp9rcZlLxsuXpS31TiefTl12tjIGq7/6GhRDXw1QvbWoypIp14mE5AkEbrqnjN011+kZ0Y8wCUeI1b4xxuRAI4kuMoZkGnBgO0n7s5rKBYBtMK6lPRyIyWCGUSoDjhN2mESRS0bTvxSwMyDU9LGkYGbDyyvpfwixWLnTmD23U1HKvJ8YBuGySVFTwYyh8V44sQyqZDp8AHIFyxgLyLBa9az6jr5rixfQkXBJvKvWGDp9HgGYUIVJ0xeUCYPOGJIFbw0hV+FMEaLHJIdNUT6j0QQpkvw0K3VRK3Yq31HymbQ8YoLH+oCLHmKknUaYBph24EdsHLBpxOGRJxwwNsp16umlIMFCvzMJa2R8ZEYfa1JRiPPhJfS/ykOYPaWp2DI2WPqhw+aIqzLg80g086J4LFyyYryYFseRPQIEFoXdqrJvchvrqC6d1xEa13C23bBeraQyoirbh90FwVvGccRaqVZ3uD5jGlf58vPcj5qWFCNt29Aa4UxJi05eKvn5C5M1kdztcjNVD98G/hZnXciMIxNEI0JM9WDbqXou+pyCA98kGg/WC1m/NdCZRuab7zAGXFTy6JKmBC4sq8mmmHChwZkGhxi3xqvROUiEkQ2GNhiaJCA3plYIcyXctGwngNGIINJth3JK5ai5Sw2ZQNuYamxlhMw46QL9zZBIxhJAotFsghJ1RHEamBJdYhVERdNNE23T0qgBnlOLSqVRm2M+5nbWZtvcfikIYajSAk0eu0VIyndVqiLGyr0U0O+0aardVXfUUgs1+fGahZyQ1PdXR4vPbZ+PT9LQ+cT6vu0nuvUN+efV2UC78bhS6bGchLaJtJVAMAYijrvbl4SkRQCMJ+DZTef46Ghco8ubkpsbGQshOYxpwBpW23MBptoOHzzX40ggkayhU6LxRMSZwJ3+OZf9tchzjTCJVtf5xEKhlwZaiBMxKD9kjtrLHZUiNkx0FuXlkuq4jszFVOsvUpHOJJX9WTymBEbWD0vmX4ykacC4QEsgmsTagfGJkYBNYANM+xuG3TX23l2atqXteiFOj8KH5PF0bSdrs2Hh4CnpqKmOlkxlvc2AQubvk+qEHuuaeTSmKFQGJMgRNlEK2MSYaNyexq2keqUSG5tcjCHraylrWdIQqS2hc93O0Vk5lh3VJTLQZZFIq5gjDeUwuSdZ8VT/EBDJWIkUNEnkj5G8aKIoMgLcJomKTxF1viT9Tjn/lAA9GYuDUt11oQHr888Vkk3SVP8oBSIkoivLzTz+8jpcWGfnIZRUeGkU4FSt4Et6DYoOVSo3GkMmvrAm84fdJqqvpdr8PssZlavZGZIgJY3aB3WYKrBHKvpOBuyWmRZFyVB5khZfGTqsaWnNB3TmhoYG8Hh+QtRiAak8Y8hAYdHxs8wq45QTmym6+9G35f833+o+++yHvvq4dOKTOfF7rVcsFMDFbvNeetFXODvScufXNemNtldoPX+GW7r9Pt3+vtY9ciZOZY6XGVcS+VPeV2WJytFy7FErjudbs1rRrlY06xWua7Gqg9b6ZH2McY7+8gLTNgzXVxxHM843NkemnvxZ39R69PLH4+9S2X8+5gQAmE6+/QxbrVG9avuzG0NFt3vFPPms26ed57Nc54sNdFVr27y0v0L0Zhl29EM62ve0QTXve/zz532kb37schJFXRbTyUl2dIF8zwkh7sRgTcInL6HSTjhWYkokZxiCx8RIh9WAJuH7kQVahsqCL7sounliU/YRBeL2bZTBGSneRWlvKcZcXsXDrwT6KQrReAykEArpeDZqlfoCEoQcCm6qa+bFS9M5pmlkSiM/ePt/5Gb7FF6IV12iOBrh5GhajGsYQiJisF2DMQ22XUEDzcpIJS/n6LsOZw3dsJNy7tFA85KDn9iPI1f7gd0YaJuWzXZL2zasVrNRFYMvkTA5rWjmIgtM01ieZY7umsPRZ6Ws5uQQAG6HWSXoJf2oaxxET4ieOA3EaaDvhL/j3p0LSWfbrrRktWcTI71WvyIlGA9SOl75T/bGqGIGYZhEMbZ7ea5WlHRvI9bvIQ5CNtw0WCQtsjWW5A/4aadKa5qjZZRAO5RKUVLlKgUBzWxMrFIk+AP7qw9JSTw8NoohMYbAECOtizQ2VXpKrfCkeYyQiHoOhZBKJEkBDXSkRywpNTrqZfBJBc+gRpsMaYsQSOdIG/nB6lFyzsUMTqp2ZmWAWGZESknGNqpmGFF6hfQY5X4zgpkaaWWqos4EmEqs2pYP3nmbexfnbPueGAPjYPjpH3yVw82ayU/kiEOSkUyRwic390FSY2nwkcEflB/FYLTaqHDszaTNy8g1szA0yplV3uRy1rcAhlOAQzqh/WZjKiU217cPOWwNL+/Adgeb6+rwBGBZpW3p8/q16oLy/ekFty3NlftsyCl3eY3KQFGh3j+lkzQs+qi+bqHMNqcNjjnCcBba0UlqaYqJZBNYx6QGZQasZcuE+/qMND06b+vzc72GfI6kErGyn6S4RQZEkloCc19UbdR2y7PKvD86NhqHzehUOcgUomlZD/VeComugGypnuL5jSrX8lHnijk+/fF4W7Z07tv5+7T4bMviJ+DUPIbP3rrig1//QXlWxsqzd/ZYBtRnnreVG/n2V743N81IHdjf/cmWh1cbmnYFCaZw0EgkieyZYgRajIv0Dy7hsMM+fMT1yxd89PhjztY9F0TubDZsugYzTvRu4Nce/C7nfeTcbQgxMU0TpoXJaetquyGPtVxQRb9LaJ+rHN0kWK/zyFUjoLpNjasDJ9HTEYTbyRjGqFHnKtJ6a8Cog2j/ggRcJCm6cr427Aw0gyckT/QjN08+xvgD77z7Dk3bcOfeHaKBh89fEnwkTP9/9v4t5rYlSw8CvxEx51r/be997rfMk1mZWeW64DS2G8uULdwFbpmWaVq0EA9tNTbdEqBSgQS8WCAjgRGU4Ik3eLOlhlJL0EaWSpYbF20KWaaxMBTlrHJVZWZlVmZlnvu+/pe15pwRox/GGBEj5pzr//+9zz6Z59gV5/x7rTVn3C8jxvhixBgJdzcnOOqPcBxH9MVDIAqwNY7m6S6LLaXEwsvogU4koI8A5xHjkHByclK0ZsQLpHhwjjGCxwlpIgy7HXIWW3k07hHShMCi4T1xKvYOBXAVzbm+7EkoV5NzErBYzCnYELTasXaAlpJ6z+075EDAxMgcQYGQ8x6TtjOGgG3cisF5TMjTJFdQeQAYxabl1T4jxoijo7Oi1bgbGCMC+tirCYSAjhOge0UoTh9k/wwwe14ZE8TeGDIjxK3YXew6MAUMk7RHrlkCyATiKJ58odrZuUBfyAgYHY0lVOP3AqDpeiwLyz5IxsQfps9pKlXaLHuiUSXb22UPTOb0IrkFrmVktvWUyro6BKq4hCWwEBqcxH8C2/BPSHn8AFf4y2CcIyEiIapeehQayZPy1ZZLsBYY570skGcFl1dPKwWtW2+6TSBA9wSfW325rMl8355JXuxeuXq1MiFXoWaWaz3gWJR2o3xHTdntMwDqjOmGTNZzfpZEsNWyPp7r8iYBxljK2JCsjEgBHRE6CogU1Cu6xKWkDkqU/CdUMzGydXK5Wl1u1jBw57VX8cJbbymvkE25c1YrJ+tFwis/+mXsLy7wzte+Bp6SDj/XfGupDj3wrTV5O2PZB+ziZDDUcziSxq+3pExGW+/TRY8eiLMiUB98/8MJT0sJflDhMw501Zmu7HBluLzwZHHL90MZ6vblmfEDJ7lW5np2ttKeNu0sHds/rUB+/uEHGHdXOH3lZTGiPQ+2ia8xzHr6XQrnVpgzwYT092Lhu3erlN816qa9up6Ur6D5Lg+y/BvOutZ9/ufVYK0coX8sDCll9Dmjy4yXP3gRR08IH7z0LnJMImgxipASAHAmQE8lKdh9dLWh0UUFu/SUXY24j+Mo9qtSKirj4zAhJTklnsYI8WAnoYJcQlDZrjA6w9hl+FQyY64aRXZ1IehVyuMY0YeALo0IQ0Ac9oic0UcCpYTAjBwIfZTzlhgjTgLhCIw+TZjGEWnYY0ypOAGwTcRsGI3TBHGxmGAuDZkizpPY8RqnSb1JpqLF0vdXapPLrhxRaad5UYOOY1ZwM6tgkfPkTqdTBfzSiGkYAAVWhswYmDHkhCnbZrSYnigrw01Uf6Lr54+/Jma52DjAIAcSJrubOrx+/1XcvbiDGHqdc+UcvroabwRFFKGwCIeu4mV/RqOfpXMnlxNiMzBu2kbeyGcIhOPtBsfHRzjabjFcvIj7T15XW00Bwy6qbbNQ6mgu60vf+O7SU3ar2xoYc12odheq/YWaxRxwIPe1Cp/zd6WvZp/z0I3AyQXQDWgnxwGO9dD5M7n+aRvXNsO0HX1cCoRijPlQcOkPPVs7KZz3fRV0awOFhBc9h3aLLEIBCo2eFb8MZeJ6UNnnYdGW7KR9rSJifS8nsVa/5YjW+lWNYqKw6BffX74/yVVnuc4PhIPzdPmj2wy4++p9nL7wBMW9i9+GZ+Df6pjr2vCQmKV75c4D9HHE4+EtjKmTq7FagO0rmUcRDoLQ2RdeeEGum41X6EnaPU0jBjA2mncI0lfDJNqzBt6R2lAD+X3b1mSdz412t9XdgExrVGFCmoYf6uwan9r1ZFOjs+vmJJoxd8/OMKSEYcriIfjyAuP+ChsSb4VTSjg9PcF+HDGMU9GUnngEqNrBJOhV8OKlU8sNoThbAIm3VnPqsaBL6snSbCuWgz6NN44jOJzjzmvfAZE4bjh/cAe7Jyc6X7ihs2bXhkidqBi/p/xONu3/4oynTnRm0fSB2rKLYz0Q6bpeZddctMBDVPMMUdzqGH/CMJ5RDjSGYSjlmIdVo/HTNIn2dtMnNvwG8Mx4OrOJmAI4pNIPDatMocwtUk12YoF1zOkpZrS37rsCTpXZ6kgdAZhyKk6TSpLZNb8G6GJWO2JU2l1JIRUe1viOupeX6hwOc7Lp8pSVZHpoGQHHOKE/BNCALgRs6AmY75fELVdUOt79PkTl5++eBbSaU421Mg6HeQ3a3cl9p2VONOtDI1drZ2WHynu62i5YgacMz5bqmUuiJb98MK4GLk/c3mSHvQ19X09fyz5QmD9MbOY7yoCSXzhubyYidJsN7r7xBvYXF7h6+PCGReaLvXke3txTqxk/fRoty2+Ts4o8tyKvgS2eWxnX5/OcMnLhsw101eNigGiVIJVns4VSwjXpgNkCmgcHspVH8/pdk+5g2uVxdJPno+9/H93REY5ffMF57jtUz/mWYJ9cCIZkW3bfA/nM6yH/GJNjG7fvXzYG/po+LCDOrKmr4sZsXwbQGDH2gJanu42dIzACEzY5YzMx4nffxHl3hvdP3sW0mRAIwlyB0bGeHlGnWlIBUHX0EKgYUe+6vqSbRjG2u9/vxBuh2tMCQzwEYgTyhNgFTNNQmaRspwCuv5SRbLweXiNwV42uiDsx4CgE8DgiZEa369DnDfoAdMzYcEYXA5K6F48x4pSADRjbcQTvrsAXF9ilCsCVPsyMnMTAPqYJpIZ2QYQEwiPs5XxDDfQmtZtTgBEimHYTA+CsBoCnVGzFsc1PZtg1Sxt8qmgrACAgI9IehhKdc8bl3OaEbYi23nWeZtfX5OpXTsvNxkWuDHoRYgLKmFBhsoEtH+HH3v1xbIctzDa5La1ik6Qw1cbsSnvtRJpZm2MaNdYrBjA7ASFlORObEtRjU16sK2Y5fb9zdoI7pyc4OjrC4++9hifvfglTFm2BftOJEKs1zDmL0Wmqdmnmc24Obi3AsDLKa88M5LJ39Trabfi7Q9fJ7J2v77zu/SB/VpWGaSkfTuKxfGfCeNMH83QLLrvNp2p4LRnBpoxZZwSnzcGlb+unL5/duNl15JK9ThCi2pd2JXANtFyCZ0bubQddp/OtHbqGvFlO5VPyDCvzysqTcuZDbzaMqPTZbA65sfGHQPV124+LNszHfYVjWE/J6I92eONHvw0KSTRQvDBN1HrfPRRWyg3qWfhzL7yPV04/wtfeeQnDdCr7lB4UpCReglMa1G5ehxCA1159FZcnRwh5wLC7xHh1Id76pgnddivl6aHObj+Ih0r1aGd0xQCE2vIKlpYroJUB00H07E+zINyYcGmpMfZFbGoKr/yM5dnFDgzRT4ldj83RMS52e1zs9hjGARfnjP3FJfqux8svvQQiwv0HD3F+uQOwA+eEccwY0oRMXPcDq1nhIyBarszqcIKxYS7a1J7fsP6hQOg3vdBzZy8uhADOGfv9AAoDXnj7XGyG9RvwN38Uw+WZOlkQLab5wUsXxSh9BeG4GDMve4EDq800QmbREM76Pqpdtb7vRStMn3dqj6vyF5pvzhinUR1CMCb12ClmGcTZSYwRozrj2e+HYrJgLTCg3kuVj2PT3EoQU3+i3irX+4ymUFWUVv6PmGXf9Gy+m15Gbw/RaX/FcZqmxVr3NHbOk5WDSdW8K3l6vhi1bTZPrtvL1tqwHipjHHCMu/RPig1XCgC+BuBvoUJrtqJWmOpFqXDxsRLvIEJxbW1vCnRN+sUbT9Lb7dhRpzaOkaX57kWz7UF3nGX5C5ll+Z3J7QszdqLGd/TlGUGG5xmefdQOdHzZ71dydnR8tenKZKzNUgYW8vla3bvtFi//yI/gyYcfCtD1HMMtj8VcgmX82+RwMM4tEq+zNB9vbX5S4ZMAuYDPOtDlg3Hda68wA5F8PLeQngeNuVU+19T1qXLjOUVZz6Mw/yuMv2cojCm6uVor9ffSy4392b4tTANMfbR955lFz0DaiWVSL0HWBmEcaz4CUtQdjYkwpQlIA3779d/Go6OHGGgA5wwKJMwkJuQE0JhBMSPEjDCOoAiEjWhwhU6N+HadGOkFYxoHjPs9xv0e0yju2gMxQgcQCVi12fRi7NsMH4PBIYKLSj2qkFAYqiqY1n8tyEsCsCXgCIxO+yOlATlN2F1SMdJuNjjGYZCrgAo27C4vihHypFppopGW9ZqV1GFixoUCeMJ4C6NrRvlP4x4Evc6U2Q4xZYpQ9ZYE93wBVEKFcuF+S5uraAMgAMHuS1HACMYOcl2iuYXll3vzQK8WaPlgBnIqwifrfE651VAROzYk7s9tvFQTjzhjnMRzUphS0YhiqJFdBhDFL1LpF+sbNuaOEZSTCo2GhP6rwIEZ0hfvYsCkNmPKfLcaK5Pddx1efPFF3L13F0dHRziPQa/I6vpPCQWA1AFiRdyWoEQVBmxezEMxFP8UQYoVI8Ve26tpS1OGoxUrtMsDOAeBL4IKRc57EFf209OnRX2ZmxP+Ncan1GFFe+s6RmlNOxXU1t3TxfLcDZEBal57TvYEFRKVphSbV5bQlXBTaOfAGtVv50EBQ0qdGzHD1UOBLzivTCV625eLHecpNvNmrcz6+zpNOv98bW7ELuGVL3wP27NLNO7p2X+t9hjX8p2HZm+0tUFAFxK+8OK3MWXxbHu+P8P3H74B5oCYIy4udtjvrvDg/hX6PuKLb7+JTRfRU8b5owd4/ADgYY+U5EoT60k4EZBGcawQYwSTXceYNcYIuo3N2jo4NJU8UZ9JkAHqjBcAEStdgNsntBc1nc3BSAEUCSHq1TAKwE7skT346AOM44jXP/82jo+O8NorryDcv4/9/gpXux1SSug3Ypjfe/6strp83euI2EFJoKrJ4+0+gcXmlg6etomw3W6RVfNpd36E937nLRCJOYHh4l49HAJAVB2NkDIKMXQF/DaQyw6DAhGSu4ac1aPuZJ6jEZGTeGo0QLrrOkcTUZ6b/TED1bI6ZwkUEDcC7gkwhGIjlEIo/FsLCuk7ZhlXPSyzPc32RAHkJjBl9NG8jUs9xKGSF+RYWAW98mi02WyrLqfs+oQ0HrTQHMz2Aq5rz9plc9c00c1WpBmGtz5seG0HQjJRiXsorKw6Y55gzFRle+q6JGZs8EUc4R6A3wLwTuEzCOZkZQ5Aerq8VqePLy0dltaeLqz1y5pkxDMK61s234Xa/AnBvfEkypezLJPWx6y8Xcb5dIfDNfUHWIDxKF5ua3OZs+Y0e7Y2N5o5b4XeqtpcPz8hIOWp6vHc8vvBF/lJhk8K5AI+40CXLRgPYpUri7PF4BfRfJGVkxafdpZuHsilqw+vT7NW5rXpFsLlMtZtEeXWPk6bqp4QciFQq8H3Ezc9v6gTaVVvqp2BLGCAqQp2Xl3cg1tNfZmba1rl+xzld/GFqWA1Rj/gvRfew8OT+2IfgvWkUDf9lCeAMiLLu2maENXleQgBXQzoYkRUwCCxeDHKk7hRZ/UKEoLY7uii2N3YdJ14cArNBRoALNcZPL9jG4ZdHQEa5poNRdHQQ4AuM/SY8whQwECEKUaplwJd0zSKvRG9LrgjwK5VGJOY1VaYvyYxMuOhgYs5l6kcQpCT/35E1Hqa/GOMa2FguaZjFVqMkbZEdS5y6SGVKksfVM0WwgTg0nMhq9Oz3XhZ55sZGLanBjSBzPiw/JbTPjUoqw0Sh4IM6FXLlMR+S0y52HgBxEtUZiBQhBnJhcunaGEpVTNj87XWWiVtv/VTzuIJNNtpuOtz04sgAmIXcXbnDo6PT9HFLQihCCyAAHEUcu1jtrVj4zRjGxua0vavzOGweH7TXiZCEgotOnTSvfaciBpvfj7edXn5sktVD0RdO92fl+kzbECmGavtNbkOaXXNQS5w++xaoMuSOSGrtELHRubnUjOvaoG1v+f5zhu83sVL1rVoMhRgqX0vY1npvmlhMbEaKJ/3JYpkXp7P+upQaMCtGWh1CHxazANaTpkQM15440P0xztXyVlgEebXAE2wK4ewiEOu20JgvHL6vthB6np8eJ7w/pPXxctpDJjGEZeXl3jy+CNstz2+8qXPo9t22HYvgfKE4eoCu2lEGuvVvBA7BJowjiyeO0MAkNwinoEHqlFrNL/ptmsA8UbcXJKSukbYwK76W16zdRBsDhowE0LARunufhT7juePHwNEeB2fx2bT4d7dO7i4vEBHQBoH7PcD9hyQo2g5mddP+yvglWubHY4YqFUOTtyebR1QaAYTwOKFkAMjRYDTGR6++4Y4bdFrkV3ntP7cPiHAmhpMD0Fvk0q5tnfmOpEqDVAwzLSlial4Nw0hyCGeGd+HzU/pYtPs8n0BImw2m0ajzAan6adAoEyVdVRwXbY/m9ue/5TPnETDPqYMooziVbZc1yQUr7gKGqHkZLnWfaCdUy1vadcXjb7M16bXBqsmCSq/WnlNgJGAGItH7iY4wKuAp3O0YCWNq3rbU65dDceg14x7vIoTfBkjHmHi9x2N9LzVobKv2RAPwkM+7Xqqtr43p7GUZr/zUGw+8KmckHyfbZXGTjk7/77E9hn5vGf7QPO55N3qg7phrJXZ5nD78PyxgvUM18qxPqxrZS2d27/cZzPDbK+YFziX7Zy8f23FPqVhtaZz2fXWCVd4tNXNdmWmfQq67GlALn9D4bbhMw10PUu4jmR/+sNskT91+jlRcBtzZnFB3ABw60XPH65NuJsFSyfIMgqVLCdks3JN28eDWf50rDBZ0BM1255UkPBAFxHhO298B4/uvIureIWACIKAAZXpAFjtRiUGKCXkiw79ZkLsN8IEBYI4UUqYhhFpkmuJgbIYeKcNNpHRRUIXCGkSZizqrZrApmnmWRYUAlVOQn1fGKhSBsgLF8LA5ooWIavHv/1eNJWGnZ0qeqa03ZIZjD0DO6CCXPouBPMaZOmo3DQzUOf+XjyLIdRrfScU1HsXXJutFfJfCHqNQ8urasm26TN2DOwZ5cRaBGBC4qjGi1cmbemf2k/2NqhAxMrcegE/6An03A6e6m7BNPDKUABILHbBppwRcxaPi1pPtVuMNCVJb0y+McbewCapt5oQCrhFzAgQwJMpgLOZqs91jbQtL2thu+lxfHSEe3fvIl+9gW/9Lz+Bq/NOPSwG1WScgBwQuwiT3DkzkjNoX+U1O40/vNajaiz6uvFsTFf3Kp3jc20tfyJ+I2g1e3/4iiWX37JqZhzwgWe+rpHi6vOSb2HcWjQkpdTkfQjschWRdEgO4D1MgxdtBgHlil+rzdUUw/XTvq9dJ7x9MKGqfVRov2vH/IpgW7HblTanL2tVWT6WsQnXXZud1XUtfYnKVeOm7nEH5ldWL8jz/Gb1nYNrOefSjyGQ2Ndj0Y65u32If/RzX8O7j17Fu49eE29204T7H36IEIDvf/cl3LlzipdeuofTszNgegkfjSMuhgEXV1eIecCYs3hyBWFg0fjMgV2dSqPKT+n2uR2mcKs1ezA0/VrLZiPq5Z3VTWlXyABHsZsYCPfOTpFBuLo6Bzjh/MFH6LdHeOmFu3j04D4iGIETQp4wDmLDMsZYtLkM8Ar62dA0A490vzTQq+zEyqeY7c5xHHH/dz+Pi/uv4OTkRDxm5oxxDDg53pY8zdOgzaOASgNL96jmmb8qx2xX/uS6o0xFiZdUEyurvSwbl5STGHafAmJsNeJh8ZjBQfkMlquKAKPLPWIIOD07FUc2ejA3TRNAhNh1ODk9BY0D+Gos9k8JQfiHnMEIaibBaZBBNI5TlvJjCKAoBtVD7AqNMq3zrHOg7PfGJ9NyD1rTgF0Ex5M2YJf7PKjpq585Z8B5ILXnvh42R2ycbgyl4TUfYRs8X6XG5lmcNxFnnOGPIIZ/BB/RL2Lgd9zymfGgi46Zd5L/fVN9DxHuGwWMA3lVsxeHUvPKc2Of58890OLjtHktAa1lmTNgqxmN9pnv0Xn+lgvhwAHapzL4Ft0wmp6xqIwSysGAHRaU6B9j7/hhhfkE0bb9wOvwGeu2m8Kzan39AwF0NUTLNg8TLq5BOedd5tNel24t7WpZHyedvAEWZFHzYca03wMAYt89FSGQqI0kV0CiQoQ8k+brrpvxgshXiagIqTxb3NQmAHwcAy7sZKwYRaxgTPlEC3SVytkftQuiAcW6BO4TLs7O8fjuY+R9BmVSr2OV6FIBlBQUysA0iXbUOAx6DU2YmBiiGG+fRuQ0gZNeWTM7Xp141iI1oB5Uk8v+sqOK7fUO1rdecX45LguCCi9QiYYOZ3lSPfxUA7WWX3b9OgIYQAUQs3xDIxivMXqMwQzXw5jzgAmMDnbdzsawxKqzg63uXMbAsw8JUjfxTChpGYRJAT1rk6fy7PNl/9tPzzoa0o2ETMpSKeDVAKcgCGvu2BHtJrGPYva/tJ5U3XtnW2sK/GU3P83bTDYPis72EJG6nVfQoQX16ohwmbelg9F3HfpuC+QzTLs7ePLgDGkUZwl2pSSztooNwLM2tzvm/CqcF/q8lteallCNS3WMmzgmqy7T+3wOhUMaXLfR5vKaQLdlEFY1cdD2g4/r43yc0IKajgb6ejhaaGW3gMyagNb+9mN8mz3GAxFWhm+3raH5s7kW1eLA46Zwm6jUfl8TUH07m3G1vpzVda3rLR+hf7XPvWZamWp+D2uyXYk7K9tsI8XY1XWk+fVhj812wMXRCR7vRnRRqMU4itOOJ48fowsEvHQPMXY4OjpC13cIIWLa7zDEEVPO6MgOToT2rnEwrmjIZfBZKHwAY96lbZ8tM677QymglZNm9ajAbwZyAKIYJQ9gxL4HU8Dlfi8mBnZX6LqIvr+DvovoAqEjwhQA03o2LdG5WYc5UG68kec15temcyLsLjqMI2O/n/Dk/hZPPjwB372Lvuv1ymNG11VtacxsRvpyWcE1ClFAo3oKUXmEnEs7CECIESBC3/fLK+5FI202sFR3Rz9u1t9VM4kKGAh1wlNsYJJqwqlJANbhNFN69ZZA7V/Z86jygFqm2L9S8wJuzyVdb8XZy8pcLYFnn/Z9sR9xk5U/WJhr6za8qdbWtO9KUSuTl4GqiecXgZ9bbaUW1beYi8typbNl/nZ4CT1eRo+XkXEOxjlY/TEuO+T6UEfkmv14Frt9M392c9luhtyYei03P3f9M5p9tjU9XNbyOc2ez9Ou8O80r9FzYRE+Zlhv8Rrdrc+WNL68oZW0VHvd36KalypiADdrp7IZh/ej5x3K+i2/brdW5vv2wVS3ye7a/n+6hM+IGT1FCc85/49R4X8ggK5/GMM07PHu3//7OL53D6/92I+uEgkLh6aH0A298lc26DlZ9rm4Tb5EmJFtE2KZ5U7XdUh2A3JVpn4hTKAyGNWT0ArYZXEzNwySZ+jOX/0Aj7/0PQz5En3qkFOHlAhjGkDIyIiFIQskJ2KZBUwRI/N7PHr8WACIIB6uipvsnDHtr5DSiGnYgzgBSOAkNoc2XdRTSmubnnxztQdlIKQxggIMZectrTL+lbF1Rk+DE65QreMYeOSZRlOpjzEgE3CRRUixk97IDPHs2DKasBE35o9Ns0cArk0vV/MkiozrDow9KrhV9i3tBwDg0Y+lwl9kp5y13MIYlrpETErKSpesgAqeMbP+npJUJBRj/ybkJOQETBAbIgAVD1bTOOkVCREwAwk7Q5AT/S5LvuOkVy1Qx4lBGJOIjPK7go9gRgyknq6CCJhBXMULYJgRkCo760AVqYfTMsjtON+9ew/b+Dre+fU/CE5b8DTIiX9KorHGqv1FBEpiqy7EiJREmA7BhK0KvLG7fmraAvL9Ou2f6xlq05iomn11g/NXBJtrMi5t13Xl+9OEBgiamRYLq+7WS0KsaSataQ2YnTuvCVDX8DLtTXUtec3KboJ/N1sSS+DRk+rQkG2zT4SV9tk+0hTYVODpWU/R8Gz7/SbNujYyHX73Aw0rhfuq6UHAswRW+5QxRNmvAisZUftJKeHV4+/htdMPcfngBJcXW5wdn2DYX+Gd738P4+4SL909QRcYJ8fHODk5wTQMeHhxjiu+wuV+B2wz+j4iQWxddUQtqKLtsTnEzI15xGa2LlDUW/QVKj0p19M4l71rbgfQH9YQydpNnEGc0BOASDjuIygQhotzdJ3sVcfbHi/dOQWlEVddwJSGBrw3PiIlp005X+Ma1191tDmcc8bV41N84+9+DrurPa6urkA4AmEo1wZTco4iVMt2MeYkeQ3jgHEURwNHxyfYHh0VLbK5Jq3X/DMNtU69P8aug6ccBJS6r4FrtaMFxIq7HcZxxPnFOTabTfFAue067Pd7pCmVg5xpGkHTiJ4BykAiIMB4B8dh2n5XbKJVPi7njA5CtwJ5rWi5FklBV1OMolGeRSMxcR3HAqRjcSmt7WtPbzzYxZWPMiDU9oByuGSdqaCUHSjN54ovPStT5O3ArdVuTmnnQn+1gmoV1r2UzQNnj3vh/4gR9/GQ/yskPL6mNP/8EDj1LAR2nu42Qiy7f28T8+lrs9aa29Z0fo2xjUvXxmvzlxFc0RP/bIb5gac9xvrMaZ4p+HsDbP0DDrevyXX05Rmz/L3wDOGzDXSZxAyUxVQWkTEhtlk36eYM1zLtIt11wscsfXl8UzpNu5rupsCMtN8jjeMN9VuS6NWos73xYLHGIHiQyuVdQC532nVojEplFCxrGBAnINqfZyLmQq7X8ipXnMA1ncbJMWHa7oGJ0VGHlGQJTEpJ5fSTtcoFSZB3KSFlATBABKaxMJcBMm9ymtQAvQpraneqMI2uvwr4VNrqleK1DjwbFF4ST4IYPe2IDmyOpoVX8yIti5xdlYnNVtXccHLbz009HIdgdRebVVUbiKFQVq45VftULn8Hclm3kxof9vZoJM86r7j0paV1PeS7zvezlisAIgMpAAqq5ey8W6EKd4HNAQIjE8AkWhIJrNcwpKVF248N76vjaobdc6lctWOm3eVHSTuBYKd+5OMfCOXaROmygLx/GSm8gmk4AnIEc1qc6NuY5pwREMDBtMLYLeH63RLVK4W1uvP6tMTleiIzp39rmmP+nf/+NFpcLf1Yk7tdXvO3CwD1+sDwa9vVd1b+7cQGauMqjS3tXasQzT5XXxoV9q8O1UZrQDYj5+bgK2vq9VHVkFBTz0bLrJ2Os+KpNPpmjGQGxMxfH9gv/UHAgQjwW0OTsqyR9bmypkF2ywFfDXW+twc+1p8EIIYJXWR04QiBOsQQEAJhGkbs9ztcXV5iu+mw7cX2khicJ0w54IMnx7ibJrx0NqmmKZWdZD3w7HudG5VWuz7x0VfX9jx74xNqFtYPJY3RGts7FXiLBpQlSRfASNOAPI5AmtDHgLOTY1xenGMaCKCu0FEDq0yDygCJpnwDthSot8ZePj5FTmKo/fLxEcbdBuMeGHZJNL0jCoDG5Yrg0pO2aN1U25AC+iRMKWGcRtAQio0tq1MDQjPEvh3VxcPapeTHx/gCR0/mWmRFQ1QJPpHY+JpSEjumCvRZX9maSikhqPfizCyG+ck0PuuexTDaWK8xgeTqbKKA0GUQJYTQlWG2sS40ReeqHCyuL7FGG6v0s+TRrFVCbXOp6TKv5rvndWfvarlVRrB4DRmcr5m2wPppf8DKTZR23HR0EXCKCMaGvoCJP8SAd5uS1knSOrFqlvHsweGD87WW3byTlplyzVa3IN+NCDST9WalNyLNoWyMpK2U6c9XuE1Vv9PsNy/b8YxbAm7Th4eTtnO+ebU+Ca/NjlB5nDXerea97Kn572vXwPzxAZ6l63sc37uHcXeJabe7ruq3D9eyCjz7fSjiYgU5+WX57lD+B6jczUXeXMPbhZate27h42hyWfhsA10+uM3lucT7VIRbcMG2yV2nQbHk8p0wvPa+hsLsuBoVjasF2HWgfjf2twlKFeRaE1LLZm3aKgeKbbUNZoILywli3/fo+x4gIE4Txv2+aItpy4sGC2le4ziqy+7KECbNOqrGS0dAIMZm0wkApVpOzIw8ZSQHsiwFA/vmNK9sE1CGz6cyzTrmjE0IuGeaJdwSwao0wk0JUI2cKSckAGOy+oltkOi1arTv5qPWfFEhg83rFtcxsGt7Pk35rfkao16uLcwlWg+YuHFlpmIVxk+b+TyYPwOqZlBIuTm5H8dJxxm4FwibQIgBSAB2LABZgnwyi+YfAegCMI0yR9QXgcPvcmWQdG4Zb8G1WfXqBRHEgEnV4CJkAVR5OSbs2tow3qnHk+//YWzjq9i8GMGckcaxALA233LRmNAVyQHmUZO5CntE1n+VKtT1So2g5vnxWXVdaAUqPz6LmLSM69/NtYDmYaH9Wea3E+ysPpavdxM/m5PM6q3ymrJ8GU19ncaGrGNU4OoWoa3tgThLtGC1bvN51JaBIpwerAnVuh8EGAu9mpU9y8rXZxHj+sY29ZmX3fwsj9fnQ81yvcClxvGhcIMwcF1/3RAoMIISjpTlgIVACF0AOCCK8zzRJoHsUTGKw5A8TdhdXuHDDz7A2ckx7pydACBsNluErsfV/hj/v299AW/cu8A//mPfFccrISBCNA38Hj0fxka7jzyi5fdhtONVJr/+bjI0OuqIk0azlTl3e8FgcDZTAQGbLmA37DHljMCihTtcXWDTd8DlBe5uOmxfewW7iyeY9lfouy1YARxrJBMh5QzSZzHGsk8SqTaRel2cUsI0At/7rS/i6vEZCIRpSgDtVFur0vVxEk+XeUqNRlYjHFIFf7zHw5QzLi+vcHW1Q9d1iDHi5OSk7KW2F4i9LjGzIHWV/SXkVHrceBp4m1yuHlZmzhmbvlcj+ITQRaRdBqYRl7sr9H2PDYtnR6MZGYxxmhByKvMn54wI2Vc9XlOaTKbVJbYrh/0eNE7ICIhdL3uS7pXmTRLFAzQBHObkpPCN831yQQca0OcmHrxO2QVN03kjPEJbll8Znt6Z46Gm4tIh88YsylrQG+U1udiDhfJehECneIH+OezxO/go/8J6+hvCPLZbmj+U8HS1f5ZcHcK2ANvqw0+mHp90sPo/fe3nYmABuW7Y3xbrxQ4N2kjPRWY/uncPb9y9iwff+R08/O53PnZ+82B7VAWU3Ts8jzXxtLk8n1KfJnxa5/1nHuhqCOvagrANxAE288GYe2hcS7cWaBa3vriZ2K2mnadbfFnmOO33ePTuu4WYHN27h83JySKeCaZ2yldfXFPJteAFkFWaWMuZC21eG6gtWgkbYbE2G9BnVsySmLQExjMzHRFOYsQYAh4BehUroO97EQK6DkgJKU2FCSOxkipACmckZUjNO6B0qTAPxO6Etzz3DIb9blt+KJABHeDC5HYAuoJlUeP+u3P9bLahpCgzcL42jysjG8E4jgETM3bZAMfZoFA74C0cICXW61g6ZiQA22K+k+XshFIGcq6bHM380VfgT/uVJb8MQsJUM9W8bKZaPJORvLagYUp2RY9ZPGTe6SJCiKAQcdpFbM0mCIANRItryiiGhXMSg68xEI62Gedvvofjy1OcfvQSRLsNZRMvVw/tWgtDtKc8g1s7te1zuw5cG9j0j2kdyBAQrh6+Aowv4M6dU8S4ad2aa39xZmRyGiH6PRvSV9YRAORGk0RZGldtd2JdGHs3DotgzBBKPjZG14Fda4DXGlN1UJBZ5E0HP2VbqbTZKyTVbKw+vl0Wa/GBxS/2iQ8zKD5GeXYAIKD2H6txMz5V+3U9LDQVSpmzsmbjsKx1nQvLPlrGEezDBC+f97ydh2rurztUBn5171sdGy1nZSjm2h72rMFqAHCOePjOazg6u8SdV+6XG+bXj6x7cgOPaoAyl4loGjByXTmEDqyeYF+58xjjHvje7wzYqRbrNI44f/IEyAmB5GoZMwtI0nXYjyN244TdMKDrIrqO9fq07o1geFpf1qzOJ9PmNkC3WXOkdllAdUHN+qEOT6uZVGKx7Tlcdxgt33i6nCcQOjEgzxnI1XbUtN9juLrC1ZPHoBix6erfEMQGYoyx1MgMvguYHvDBxSuY8tYdzuhayhk4H8FXjIvHjHE3IQS5mphSqlfddLxEizxXGlPq7q4yklzTM/oYYkAH0WiapklANE07TRMYjD70qCuAm0O8wP7atFsrnu668v3ewjnj6moHQOZKmTMhyCFk5tJGT2f6zQYhTaB9KjRejKUvjhZKvQQ4FGByShnIhJiTOE0p/IACcQpyNTNJO8wOZ8qtAVo5WF3hKeeHH/Z9QTEbUs51j7A1AD+f236e0535wexqWABz7gutrDeYIyAS4K1wZR0CXsQJ/WMY8S4G/M4ss1uElWiHdlee/b4uLCmBp+c1zpx6LKqzTl6eEQI4vN/Ia+WhUA8n27Rre9ez1eSTCXM+6Xbx1h9XoMt4vNX8nKx9sCdmMjrxii1I2L4wK8TTuY9xsHQ4zBiJ+atD7NxKZ9xmxR3m1m6RdjXps+f3SYbnocll4TMPdFk4LBo8W7xPT6hM+loYri7x4W//dvn96o/+6ALo8tuECQ9FhvBBhf5b12vNp7qr8yHNrOuyvK78RgX7kCDM63H7EPBK32Ovp6VyUhix2WwQ1Y03QzwPZYagD1SBh5xZDPkC6PuNtE+HpbANDAdyAWYTIWdzye4Nph8OjVq7giMAsCXgBFXg1tg+JZir5oUIBqm0tzLXNZ0HGe5CPBqONPO+ieBK8WO+IlgzUOw4BcCkv2CCClUCZvWx9qWUkCY7YW5ZmiJANV439R0YmcaGwWvTVQJfZCX93fdyAj+OqfD1fRfw0skG2+0W2+1ROSkv11SD2KuZUsZud4XLywuMw4A0TWoaZMLDr3wL08OX8MKTl+qVTQoARdUCpAp0ZRFqMnMzHtpZEgdA9Pc3SwMJZsesCCIsfRso4vyDtzFdvInP/eQZ+r4XL1gmIJBcrTWtpMxOEKJcQEeCXekFUqp1tPETwc9oVMvS+n5vZwrDC3sejLWrn/PQMk3tn4XrALKbA61/rsg0XNrHBXDw4JvX/DrEvk0KqltRVd5fICsr+fg15N75uKvF1rW91lcHNd5mtNz/btq9CnLZp9t7UL20HgInRTCf0ZiV/G8ebz83iwS6eKaz0qVa9uHhfq38tIU0dfjgW1/Ayb0nuPPyIwDp1iDXbd6bt9Q8qbc583Kra7KLEZwT8sR4+6UP8UJ/hV/5VeBRFuPs4zDg4f0HSOMA5AldlGuN3WaDxIyLqytcDQPO9ztscoeeMzrIQQDNrsEBQNH+9MghEZBp2TkF8Twghbpo2Qi4I9xWSnB7gCc2AVDto4RIom2FnIA0IU8JoIBBQZTHDzqc3bmLozt3sO0jjvoOE3vaVK/fkGpsZXT47oO38WR/R/cFKXoYRozDgM27A/rHE2JkhLDDZrOR631T0uvyNW8DoHrlTdb4m7K21AtvjALe9X2P8/MLpDTIYVxO6KceDC72CkMQVeTMVfs0qD2riHb9zmlD3Xft4Ey+X1xcYJomnJ2dIXYdur4HgRobqla2gV5HR0fAOILHscQh5UNjmUuVEFIgEMt+G3TvYU7opkn7Te1eablcnOCssChumjUgP1iu6Stvsgp2+TXPs+fz+er4liJ008xEvAO4OC/F9YMHPDfQ6kN0ouCBlVN1YBcQ6WXcwZ/GJf5nDPxd14rDckcpz5DX6+I8Z0F6DjMeoiK3652b39e5RMrvV9FnLp3Nv0tfzvfteUmHnn1Wg9J2gppuMVrHi23gh1S755sfH16zvxc+HeEfGKCrBIcOA7eBFdbT3iZdS9CW+Vy3qlfT3iLdTeHJBx9guLzEvTffRH987LI25sqK4QI2zytmBPrmTYpXv1ZmxWt2AfXkznjWmshsRdgpWwOSrzAfa+E4Rhx3Na0xUzkndHb6rcWaS3fhHQNiF4VRTGGVcJWTWgCsDFYoArrxZgxwUmDFDM3r1UWIZpjv+9r+KuxC238azEtRFWC7EtM04KRNgRRo0LGlUn/WPueF63HLyXw6atGIAE5B2APYsZ0yc6liaWZhiGv9swkjyV8kodp//s/K9SfbPAPY1k48VADxAjMAiNF3E/5rue1aWq6rTo3Qj4N4GDuLhLsnW7z26su4e+cu7t67i77vEUMUOyrMOk8SroYRF+fn6CLh8vwJ9sgIJPbSYiBMZ1d4/yvfwNmjl3Dnw1fFdksISNk0uqIIcsRI2t5QjO8rG1oEvKzAlBjXrep88s9c6/H8w1dw9ehl8PgittttudI3TaK9Id0u/WHGitnxWy1AxbP+pgL4mYHyGt/AyEo7/Lt6uOaBcM/o3Y4xnmsazbUhDmkilRasACYFoFopqwonvKBHlq5oClQEVvoVM7uDPp0XFMiLGAuEZfXZrAVV0BKEYKXOebas2p2ojketowGn69uS9XtLV/zp7drYtOO/Nh5ornAdCnNAoGr9tPt/0eCw8dF10+6/aPp0eT3xwNjcECpYckgQbfvb12D9uf2WA5QYo/aVzKWcshhgz1RsLW23G0yJcHLCOL7MmIZLgOVKmzilyAh9h67Tq29dh4vdDtR1SBD7jWChU4m5rHtvNruORavNXQW+A+HggVndWxmz+Vc3orb/UPmNGAkUxNbWNO4F8Oo7tRtFIM6Y9js8enAfAKOLAcfbDfjuHTy+/whDykL7Y0TsOjy4fBEfXrwsRtARsJu2KBpUrFpMT0b0j/bITwbs9wlHR9sC4teDkoCu67DZ9Oi6Dn2/EdA3y77YaHKpSYTQqAMSEKoQeXx0pBpjU1mHOWdktTNpBxjmZIeI0Jl3ROMLFJApXaxzAzAvw1I06YFP3O+RmdWrdIe+E+2ynBK6rkOIoWh27fY75MzYbjcgzsKLsNqwhLGGlaehss4YIQCBIkJgBErIBLUzFxCjHbDoPgYov4XqxU3nbXHmM5uEBBLbZY73bDS25rwnO15GDzRD0ays40fqaIaIFgCVtH02d9eA4KaeWJVp5jw8o9IngbONzyMkdkCX6GXW3ZYYPb6EM/o/Yce/hj1/+1ZUbr1GuOZpC1St7faNjDDLx+dxc5y1MB+L28qILYNE3JItr1Wq3KnmX3S7tLhDLV6O96czrFPxNZzHDkKM5hV7uAdyvP1807XgQWLjMW6Rz+mLL6LrIh6/9x6Gi4tblLoebuZSfzh5fdpL/WGEzzTQZSrtc8IIt7mUzcFtKEWjZCWdxWX7fQ1Su0g/y+ep0y7SmRA038rmGdT3Vw8fYv/kCU5feglxu0Ul0BJvKfSt1NELjofilKK9kc76ZqF9wAcEJebmcN1ALqZlmTz7zzYp+zsiwl1nCDYHsy2xZLUzq62OUF1Vm80NYTi1Sh6MMgYnJ2FAERTsIvc+18/SK1JX07aRZtexkH7h0gcBjA3kqiIZgz+fioqwiRAV3dxV3k7H2uC9NWHT4tWx1H6EXM3zmlH2pdjcyOzy8yAWgNFprmnlDfjLKZW6AcokKmgo8ZsBXwmEtYjzuVUPiKuG1JpQXYQPkR1wpyPc2fa4d+cOXn75Rbz88ivo1ZPUMOyRsnhdHKcJ3W4HcMI07jHtr5DTKIw8xB5OPtrj8VvvoKOIew9fE8HLrr2CABJQNSEL15Stnq51zfzTdlfpvWHE/Zy6enwPD995C3fvnGFzooIUBPQFEWKsfcCZ3Xozlo0LSF3AWWX0qhfKADNOb2VXoMfq5EfF5j+hzskV1mSF7h5SOW/LrM9uE+agwlw7qq4NLv08B9LK9Zxa+EJQAlCEorYClRl0tVjWs6ylW7RJr1lbvXm+Tg/Q8kMAC0OGIxzo+/n360DFNaDvUF24gCmH460dRtS4hzvrJi3jxfsylO2YLuqzIkRphtfO35vqtQ5yQbccRuyErph25l61YlNO4kQDYpPyaEvYboHNZkIaRVAwkCvnXACYo+Pjoi0UYgSDxBsvdA/TTwLpQUltrAez2464xeQt/eVFH/mrqZVmEMk+rbSpyV1/BBWwxmlCmiaETg4spqBa25yRpoz9MGC72WA4Psa260Anx+APHyJNE7quU/m2w/lwD+88fmsxJmYza5omdJcDNg8GseeZEnLum3lsQh9Q7YT2fQ8iQhqnqg1V2FW7vqfav04sJBKwZ7PZgChgP1BJbyBT2RMU5DJPhuZ1UcAhx+9a9xG16YFijywosJpSKvltNhsB/YiK9nNi2esH1eCKXURkFtuf2WZOhbWMHhZWXUde+DNSnsu06oI74FP6HwicHdhgYBd4dc0WkIup0ucyvZx2m0/Pbs1q/My5zFCfhoxpO0S/Vp/O4nggjNdhEnlNBcC1BVA8UkLMO2QWwMuALqC9/hXodRzjdYx4AMb3XD2rDUpy/bDeEgMsK0/Z1LP2jNbRzfWZHFHBrHn/+fVRc75Vjx7gKW+iTnY0uyZwEqBALfsEK3nM4iwir+wPN9TrYH2fNeHBmtyiHMeLNu28Yb99mnCwWXyL8jTO9s4dbM9OcfXo0ccCum4Kn1Utr89ota8Nn2mgS6n4cpO+ZnPx725kv67L52OG1bm0JiQckvxL5Zdpckr46FvfQlCX1duzM7z8pS9rEVVA4yx3qkzYzyk3qtQEFMPvrPZ6FlhcIfykzIsygUXoCA5smLW1oj7anKVAt6Y5ARbmMjDjla4HQU4fo+Wldc7umtv8qlMXI0IMiLGTk0tlFJIZYtVTRw/gdF2UNuYJKTGS8FYCdmk9c5oqe64AjuWRuBWIU85iayN2OI0RJzEUgGwTzQ6YM44/7xz9nhjF7pIxyWanCzyBOcuVBWOydc2MY9LrAJJVF0vVkBjYgHGRGQO3JRZxmcsSBMB6+k6O1aqiCtRldlRwxuaMaa2J3GJjVR0AsFbIGH777ZlvAiPQoHPEhBBScKcyQGvzwMb2zkkv2myREJDw4KMPcHn+GB+8+32x1UUkRoNzFptcnMV4f9arMDzhqI8IJDZdQlknjN1r9/HO3b+HV975Is4evGr4lNjFgmnViShJ1qF2bbALCLD66ul6dgMCqJME04ARg8FTmrAfBhydHOHO3TuIsZNTZrXHRUTIZH0kXWSiRxGUSBh4gl0jY4QQtW/dKTaL8X1vCF6Wt1w9a6+8wY2HaF0YmbUTv+sYhLXrcv7zENDSgiDLvGTOeYCHG6GGXRpyIDMM3NUGsaX1+5HlrIKa/r9kb5s0luWyPZ6GcPNZal5KFaPTbh2Sy6WR/1oQ3vK3UOy+Yf7K59P21XVtkDpLQuuTZRQ3Zit9U7YLsjbaHGjlkRIHbd/N68ZYAnps5bATU5bbVAUnDk3dFaDL06PrwlxrrbZHxNZhmABA7FBBvf65eZshghhTQOap2DKSOsvekKaE7fYId+/eQegippSArsNp3+H49HsIEaAQsSFgCxTtVjbPrTb3lJ+IReMGhaeIoY6BP0SR9G5FCBMBoIJoDK8pmcvnfK8p6WF7oGi9BdvPc0bfdcgQLTVmAQL3uys8uP8RNpstEAJOT04QJ9FofrS7g299/wt4chnx+OJRWWGbzaaCWChVkqvXmcs8FHop+8Lx0THsgLbrImIISHqdMacJU5pweXlZwMfNZoN+0+Noe1Q0HJk1rhYscbnwccyMKU2YLqbSxwUsI+kD2cMYu92uHPKZppRpG6WU2vQxyl8IOD4+xna7Lfuh9TGFIIb4FfzjnMX+6TTh/PwcHQinMeo6CkickZMcwMi+Wdc5ax4G8Mg1R7EtBwB9SkXDLCCIBmO08ZAxmKZJgDEHQHmgqhxKsPC6dW1XLXMvwNdDcmriWjANXaJQeEgfPIlo9kVcH8ptglrQMg6Ehy18DwvENaaEYZywG0ccZUamCOpC4aNt3drutcUfRcRPKp9yicf815FxroCOrV2JGxj1NoMwvUKDPN/V1Fx5DvbP5HthCxd9MgeiKk9c/11LVwNd8y7MMlhlP3x9/Xta1u+AbtcKyDV/4lv87OEHBVQsyiGAU+XtTDjIqjVsZkeIqDhoqDiuaa7S6rqotP0pG/eJyO/k8HM3ZlSddtif0ZHnU41Poi3PN3i+9tMUngro+vmf/3n8lb/yV/Abv/EbOD4+xh/7Y38M//F//B/jx3/8x0ucn/mZn8Ev//IvN+n+1X/1X8V//p//5+X3d77zHfzsz/4s/ubf/Js4OzvDn/tzfw4///M/X2wKPFOYgVLzBbJYMO75fBH9IK4u3i54AGhNWFgrXML+/BwA1CZERtrvEboeFNs+9oy7bWDtmQuK5LCoQUN0HONqY8EM0/6AK2eekQm/pkJucebCpi8lAOiIcKRAR4adrFaGZC4gFKiIqGhxhUAwj3JWNSNOBcTR9psXo5wr8McE57CAnYvwVkAzum9WZxhq9yhI+hgImxBKmQLqsJ5QHmICdCNBBSOLplYRJBPAGVPx6FTzSInFwKsSbla+zPowAiBj2q0P6/A0WCVQb0FY+7y2StMfXAEpYQj1fa6aBQTTGmAw12tyxm+YhljU8Y9mHBkVhAhWPtvVvlquOSNIqmEWOkIHQhdEG3TY75DGAfurANPCmlJSW21itDkpYBSIEIkQIqnNkzo2INHsujraI330plwmaIT2epmAFJwUpp4Lgw+qmnlljRo6iQrsEnUKBqswlBM61cyYe0LMmcGxetWsNECrTu3gHgKfbL5Zmz2QVWfKUsAvU6GQCj9v14UBzJ4duvbWAmt8MG4LdHmRmeE1UKWrPR2z+aVr1DPehxgxA+nJ1cH31RqQo3UrOa6NB9e1uCCss7VH8wJWthU/HrflWpooT5HGUc3VNLlcrrG9xKJVRnMp7Ph3lV7Z+Mo7aaTXBmSXkx8eW0uu8LVWX9/WTJh2G8TNhNhNs3n/dHmVPI02oNJCmWNB6Z7XrOTSVZs4YNtNoH4A5wSkAZsQ0FFEFxghdNgeHWGDjJdfOsZxOML2SK7oFR0c60NznjGbx0Iv9Q+MRAInlLGAXr82nqL8o/TMeAcFITw9YL/psIqKSwbMRwEAtatl/U5CT91VmmmasN/v1YyB2L8KHLAbIs53R/jg8Sn2+wHDfl95kBAQQ0Sn3v0oBFCxh06oFTctl9YrrGkkpWSAjlw3TFMqV0pDDAip0uk65kp5stF/lDLsoKJ4jDTa4/Z+r4VW6uR4JhPYoO2SbGpHR736WDxAKijWFR6pHrzFEIAYsd/vkYmQZZcs2KYJxTptYYAy23hrG0BChlkPe5i5aNwbbfO0zpzZ2H7f7GE63Rb72nK7KuN9nbaqT9+A13WRV15S091a42MtnpN3qCmDwHqnrq5+4TCIAkLs0HW9zBMApPyPv0rZ8+vo+DUAQMY5uvwKEsRpE/cD+OgKBpLzeQZPNpAoe9xstqLVyjK+rP6077X7ucZr8gJs4rS0XeL4OVGLc7vDNe9cASvP1uIt37YtXfLt81Kuy1XeX1/uIs3TbyXX5tPwQPLEYhws02QYA08rPag5+D4qOc9ALslLrkfHvgc54WV+AOlrZ/26yGv2LfY94maDNE633oL9mLllt6hz1aStV5tdhNsVZoXMKjCfE7fJ7XnNi2vL0M/rDp1vlc8nUNmnQpZ++Zd/GT/3cz+HP/JH/gimacK/8+/8O/hTf+pP4dd//ddxenpa4v3L//K/jL/4F/9i+X3ijKOnlPDP/DP/DN544w387b/9t/HOO+/gz/7ZP4u+7/Ef/Uf/0XNo0u8FoJ38+/NzfP9rfw9nr72OF9/+4oH4VQOqZEDte/lynSTjdi63EVv6dVGuTV7KKcLGjGNVhu7Vvkd/ILdFGhcqkWqJqhmn7zrJVQTMBFZNKAoBfd8hB8I4pMJcRFIT80EZeKaG2SnCkxQCQE5Mc86YWN1+D8AuZXQxIatL9BiEEUmOkZwLcb55/nSkAZ80VmYgBEbiqdjqiD2h23To+23xbjSlhN1uV/K/y4xTBp4wi1/DGYjggRLTiiG1o2VAU+2Htv9BcmXQgMecQxFEAH89UpnVWBududoni4GxjT3AXE5gpQwrR0tWcKiCbMI4F2CPWK5EgAFO4ERIOeiVCciJLzMCT7o8VJsMENtc0PbABDCumz5IPZZ5wc1AZfsDCrjFot1FrKejMrnEO6Mb6AIOseY32yRCiIghQrT6SO2HAGCS9iz8I8yBbsvTxkKAUbHB5QQL62PwiukEPzfb09hSKtf5xDXhIqxpZvl3tw1LhspVabaO7JTeCxaeySaurHkjfNj7piBn86b0GQq9nDNS+q15QGziv711c3zezlkbi8bugT50OaLYRZrRcknO1uAFBlSiFmZ0zT/SzcHmRBGbFlVeOyklGP2uGsIzZwGhZTwbOuoMade36xxt+8g0/dw81I/9xRm+/b/+ftx9/UO88aPfntWVF1m3bVrOp1oB63izHclgysgI1nnqDZjlSjVN+Mk3fxtv3zkHxj3yNGK4ukTfBWz6iCdDwsOHAS+ffQ5370T8kZ+6AibGxf038OjJY9x/8BCXaQLnjE6vc/dHQnfTOOpVQRLNICJM0whAgA6ZI7zox3bJ2eyXz+bqmKWfL84aw/9clOHYh0ov9Y8ZSFMCYwBngGLEsE94fLXB3/32F3C1j7jcPcYwDhiGEV2MiF3E8fYIHQMvPiREBcanfcAQRfO7CHRl/wbSNJV6mPbSoAcnXRSNLLkGKPNws9mi73t0fYcYgmJzLFpS2gdJD/gKQKXzxPb5EKS+Mca6f+o8327EE+80jKIhBpSrh15r1zS37N00TaKp4bwrtnTO1ixhsxWgtO97cMrIw6D1qDsN65x1HKRqYgExCC3qu4ykezBnp6Wu9TONcOh+KnUeQCEihE7KNGVAqjZCvZbX6gGpA8U9ga6gmtH/2bX1efgkpU0ihNiBImGcRgFMdWz6zRHO7r6AV157Da+9/hru3rsHsyE2qROalMSRQUoJ4zghpUmv356hm/4sWK+h4id/HfiT/500JzMe/NeX2P/2hIqiygGxKMfpHIAyx8LgY0o2P0MBI7F2tb82Db7jY1iXQQz8Z8xeX9fvzMVswzyWp7Vd1xXaXvelZap5zervZR3WrzH6EG54/+kK80PK1fezPwte45pcfCLCyYsv4tUvfxmx7+ESfOz19NIXv4i7b76J937jtzBeXd0ukbZxjQf1vMrvhU9XeCqg66//9b/e/P7Lf/kv47XXXsPf/bt/F3/iT/yJ8vzk5ARvvPHGah7/7X/73+LXf/3X8Uu/9Et4/fXX8Qf/4B/Ef/Af/Af483/+z+Pf+/f+PWw2m1vXx6ZVmXIrDPkcmmZg6b3EnQL5vLEStwkuz+bxvOxnDtR8tMEz0yvleEAiM8bdHsPFJXaPH6E7OkLsN5q01cQqRLxoMNS8m42kCL5z5nvZ3/BMwqz+HkCzDceuJxaNLvuPGb2BTsyI9p4dEcXhDbPpHgNi5IeCLXIK3da/Xku06w9BqguTLw3cADktIhO2yG9nmkj7KDODMpCIkSghgQvQZYxfKgb1lYFzQ8Izwdx3v+9lIsJ206PrI46ONs6DYGWs5cRTTrYvLy8xDAP2wwDS9sZcGehaVj21IED7jsqaMQ360iWo8jit/UEM1AbiyhjB5hg7lffaUDFWq8wPQzx86XypebvSCYXBBWkddcgNsLIcpJxcBtvAq6BjymRXj+wKK9e5UOYhl015PL7E5b2H5QprVm9P45SLRy5Dxu4OdxF5U5khIVzNGm0tdsi7ad/j4vEG097AS3dFs2Hoa5r5XCnfdYzXhXyJMe9jzwRKsx3F4Jp2TeuqzqdW28afENHKu6YNB2juIU2u2vYZ3Sj5KORjDZ2ls9/NPnSgDHgmT/MuYpHOkSLmE7lulz7xy70IV9dtEWjfNQLYvMIFUEG7j5Z41MZ36RdZNXkefntTWAzlSlbM80d13Op5em3PbWrix9O6Ys4PsPWHE+gPt4Mw7rcYLk5w+egeNsc79NthsQ58+ZLuMKhb2kKixVW0zjwoyjo/NB8KhKNtQh4nJN4jY0S3GRADIQag5w+Rp2NcPTlBRETkc8QwYNpucTKdYpwy+ssLYNgbtAYDQymIiQI9uSj0u7TB9ZWve+lfv9x831k5jq7YOjE636yb0uc+r0r/CXbhsy2LIQcej6+2GHmLhyPweN/jathgNwIpjdW0g14R3UwBWwT0OSBq1Ronem69m3aUNzSfFYw1DSxWdbBABDnV0euNMRY6XkbYa2EBsAMEUuDH6Haxy2U2rcjmlRwShRC0XbWu5RqRAV2O42MFmbymrP+zNhZtMtT5HPTKYqIAUAYMkPVl6D5nPKBmoPwFgYjV0YJ41CSu2m5rgqbtkmsA1Dod93nN6Tf8VFq8J9Ucrxq7nlOuWfh1cBOrSoC7MbB85zNicNFaZOM/zSyJApVXVzvEbqPrVekY7FYAASTmPChEhNiDc8Y2n6BocPVX4PEngRcegE8fY/oKYbup4K05VDAPmEKfGZyB8Z0EHoznkLKMT6uEvAX+jRfzMKpp+q/0QtlXceD9oR5fPm12c7Vlp/3MdUW0ezJgDrf8YfsS0OL1qjUxnm3P/ORDy8v5Z813nvEbB3NyvJJ/7nm8ENBtt3WPAaod7ZU8bzXiRAh9j85kgYPz5enCGvtZlDwOdMdNNOBQpGUPLOt+GIK4VanPFD5NmlwWPpaNrkePHgEAXnrppeb5f/lf/pf4L/6L/wJvvPEG/tl/9p/Fv/vv/rtFq+t//B//R3z1q1/F66+/XuL/0//0P42f/dmfxa/92q/hD/2hP7QoZ7/fY7/fl9+PHz/+ONX+DIXbCAmHVs/y+cX9j3Bx/z5e/tKXccf1PwBhdDIrw2QaA2p/g5yA7ARCB5EBDsBZl0hQN7Im3TIul01vuZhf6DocARiGfTXVsdIHBfSaB803hGrDKROVKwIhxgomVMgCIKCLERmMHABVbEEMCpCY/ZEYtBtEVRxEoAJSBZBpdAFIWa52MoCRCUMQ5g3MCNmYRl7U3YNHJjBUQa7ty8wJXRfx+uuv4M6dO3j99dew2WzEFonGFdsfYs9iGEacn5/j/fffx/e//z0wC2Nh9rvWVIv1S9WU4An12gAKkwooiOWqLHIRAyqsCaPNOkYG8qEYpLUOCDoPQ8iIJNdYWUEihqjiB2WQCKEIW60GEkCxaid1+gd2Ns4AEIdiRwwQO2MMsWNm7SjzoMwYfzrNYCLcf+u7uP/m9wrQlSCeaKaUkaZJvXcBIQf86Df+IPrzFwGWK5kmKIqwoUstc1kD0u6Mxx/dw+/82pcQQoeu6xC7DjFGAVCB4uo9BDNey3WCW4udvGDXdEOogBlKPt7rlbJ3TqgT22bzE9B5cEx/0ShVJngGZM1BrTUg7KawCkDBSBf7HzemaeLUyAdBLvMLatdEPONWopXotV1kdVoDRVy5i7DWH7S0G7Og1aXclvnjlTgrqZfZmlXkpwxEz8b8SPe6K+QeJDg0PqXM2ud+ZyrC5iEg1fVCs1e6cPHwJVz+6gt4/Svfwcuf/36liXMNsxnw2wry9TOqRzqwaG6JHa5aI1GyyIV8RGJsjo8wjAOuzh+BckLsOhnnnHGHvoYT/k18/euPEDan+NL2fdw5i7hz7y7Ozu7ic59/Gw++821cfPQRhmFAShmxU9Ck68o8zVZ37cNqsNDNGapCPEOqyiYceQ1JtAA9Cl32PESlW+6XDuD8oElTuzkRdK/PTPj6e2/gvScvY9cfYcpAzpcgdkbiIfvlJnZ4+XKDExYtGqCCWKyAmNHClJJcj4E4CKh9oFqHWfp/KrbMQvH02Cn9juX6oNQ9uPTjNAHOYLiZWEgKchDpdUwHjtla2Gw2Ys9xH8t1yU4Pwjo1km/9L3Z2ajuJqvZesR+WM6ZxVLuRqpW23SLGKJ4ZKYJjByZnDzanMvaU655ajwOkrEDCq6VhEpuQ4yjXbp2iBwx4tfU+o7F2aDofg+KMJYvNs0OgmOdNF9fKCAW4XAuLp89VsGNM04gxcTngipsjAKLEdn5xid0w4v2PHqDr+8IXHJ+eitfMzVY/NzjabrHZbHB0fIQYO/HQCRnbvPs8pr/5x5B/5pfAX/6f8Nr/bQTcNdVpHJGmCUNxxpDBOSFdZLz/l/YY3k+i/QkCKJa6GwBb17Zb3862LbPYfALMI3g9sG407Mr69jc3lgd7Ri8qvV8BCwCMdgjpQtlP4PjJpx221dI+q4HboTsca0aTHaznx4dbuO/j9+1aXW5R4d8Ln/nwzEBXzhn/xr/xb+CP//E/jt//+39/ef5n/syfwRe/+EW89dZb+NVf/VX8+T//5/Gbv/mb+Ct/5a8AAN59990G5AJQfr/77rurZf38z/88/v1//99fvjDBltrTbgDXe120OD6feVzb2A60n1y6+vD6NM8SRL5tmbplRW752J30tY+dpoEKtp4RLAznNdVYKUzIF7enHiXDwrgqsaH1TcbibCigj4Q+JwWOjCnWPHj23aUFgN12h0cvP8Ljs0eFkbKNUr7L9YpUNm1LSjUfVz0CYCeP9RCbqg0u5xHIQIq1UYlEOAokmmpUDXWaIV/Z0JcAjasZ/NWlpfAmVy43mx59JyfDOWcMwyBMidkaU6BrGidcXV1hGHbiOTCLwH0MxgTC2DCN/h9/jcj1HBlD4Oy7gAsTEvShsNPZefGStqOkDSBKpa1ZGU4dQifcCpzgdDKKeGMnN6aFJeNUe5LB2DEjQgijtad4fHLCrlw/tZPx2tYqbfl5r5OeMpjk5DTrvJeriBkcMjJlaRsYj1/6ANPpJfquw2ba4t7Dl3Q91bGvLHsLgOVcvYjaFRQDfgUAbNd8yY/8DHU0gTOYI2rzbbzr6f+ahpZ2VcnLwmG175p3wwrRYeHhUD7XlTV/bwz2gpzP4h1qY1PGISCtJtS5sqbxuWxLYcBdHzTxPRjmfkOBD/tu78jHmaeb579Osp4qsGvvM4UZWHjrcjHfO119DtWFqjHceUmL/nXfZ2SvTN9mPyvEQA47bE1anRb1d+BuLY5m71zWRLpnO5pGqF7SRARHp9fgbBMkCgicIQcwCTkxLs6vwMT48P0PMFx1mFLC9ugIRycniF2Pk9NTcXgxTRjGCSEQ+i6KwJuzXpdnsVtIVN3Kz+1XgmrNbB9hx3NwjVPbbXYbfZ/NeAyjOXDbrgPlS/62B4Fw+eQMl4/vYL87Q0aPnIPWm9BlwullQEoB0xSwzQGbPiAQg6mafDBHITEEcOyQKSOGqFc3a1utbm6SAhCzHgIexQoiKWjh+41c3UlBpgLool5LTGbTErS4oV54OzWY3KnWmNi8tLlBpT62bnIS4C4425qmNQY4sI+FjzQzDaXugRC7Xm2cZvCk8zWphpfu+XYNcQ2Uygy1HZqKMXXZ1y1epdelndzOGQOsmgMF16d+7RbtWTjaQct3vp6N+DynQVgJB2QJV9SNIYSATsk4EZr9IqWEzIxhnIQ31bW/Ob9AiGKyw7xp9n2PLgroJQBlj0CELlYP2fS/nIIefQn97/smwr0LxE4dYfQBsdvgaNu5wyNGPs1If3SH4eGEYb+Xq6ZpKnWnVjhwvO2iOxwdkBjz/rERyTtg+E0gTxbL8RWOYHiNRdTHjpag8vGFv2sr1ohGjq5XoM3ND6MBfr9YzIqnEraeT2japY+uLf76ut1q3pJfQz5rRrfZ4Ozll3F89255Xy3N3hwO9aivG4WA01deQX9xicsH9xeOnq7N/6aonn9a4aVuRQeasKQ11xV92zfPE2+/bVbPQ+vrafJ4ZqDr537u5/C1r30Nf+tv/a3m+b/yr/wr5ftXv/pVvPnmm/iTf/JP4pvf/Ca+8pWvPFNZ//a//W/j3/q3/q3y+/Hjx3j77bebOM+BJ/9Uhqq2+3QTwxPc20Q2Ri1zNQje7Am8JghSSe84apdvLgxmGZ/CfaIIfbep5WkIuBsChpEx5cntRH6jWtc8A4CLk3P81o/8BqgjdNQVsAswN+SyEdqpJQNqrNaVUzbYiggEsutzdWtmMrHCNlcAFEqVy55OQE/AXTW0LlkIKe/0hDSEVIG5lX6xMWiYNfc9xKCu5Tfo+w7MGcNetIcuLi6w3+8xjoOePItG2TSJfYZAwpgCjDsgZBAeAo0qvZOhXXC6cLrJB1d/aUtrTFRAwtRcFaairgQQqWNs1Q6wDS8EAW6Eb565Q7f+oRnIBWNAZPyslMzABTM2AO5on5vDguCEFUDtosA8RUl7rU7+koRjkWGCnElfYjvHj6W9Ynz05nfwIBA2XYezJy/g7sMXQBybSSBLqZaVXduLJ60YRXsrM4Bc4oswFBabhWhY6GotIJffXIyJzlB3BWV+Ms8FCi5pjOldm6c1by7x5s+99tbTAF+3DmvkCzqHVuo6T9Ksu3m8A+Cb99i2CmK5OrA7fJmHQ/ueF+jh+u5gsHizdKUetxHYVrKEurK/MY3Pf60vXX1W83IAkNHwsndh1peH8ohx3TKK68OD9Wviu8xnQnEMsbF/NE3TMrkbp7nGV6081wVpVVSwq25wTuMgEPqjI2z2O/UIlwvtDTkjjXLQ8ejhOYa0w3e/87u4eyfi4mqHO3fv4N6LL+K073Hywgu42u8xpYSr/R4xBoRwJMDGNCmgxTg52ujVONOG8IcYKz3H5Ghn7UCjc8qotKCCJfXZ6C87TIAJm1SpdAEz1Gj+5cPX8e633sbuBYCOyvYMAtBPhJMnETkBKRH6fUDXEcJpRo6yX5pRdkDs+RiQaYcN0YBNM9bOZletquROU1LQsC/XCgORM2ZctRIFi5I29LEDR50n2iFmaN4c9MxpkPErBq71XVdotxmOloO3UN5FjhhYeIVi/iBQiedpvwFcWW1pUSk3gHrRQuScwASxHYlcNIOUk9M43MwI4dGEFqVpQu5SAa2MT25ALqLC33Ku/Q64fcXPHu3XQG5vfIat5jnvToeDo0ddFxFBmNKkWsNybGj7fZom7IcR4zhhGLMAhsV7Tqv5ZpqApvXXx4jjo2PR9Do6wuY7Z+g3/yhO/u/fQv8Tj3B8fIyu63BycozYifZe13UCjmk4+ecuxTTGufCdF+dPykFIoVHGT1gdSl1qc0Po0PSwDZMDWcGM6UPGR99KyKOmhbSpDezoS5l5zTMAMydeXrYo3NIC5LIXdadoOAbcPEs+61JtCxhfF6sdT/neHR3h5S9/GbHrVnviut67bc+FGPHi229juLzE1aNH4Lzci1fzd3Sq0Theq8hzC5/1+fDDC88EdP1r/9q/hl/8xV/E//A//A/4/Oc/f23cP/pH/ygA4Bvf+Aa+8pWv4I033sDf+Tt/p4nz3nvvAcBBu17b7Rbb7XbxvDCvRlyIDmpy3UZbay2f+nImlK3Uc9We13WCxU2h7LOt4FjztkfLcj0DWL7rhn/+4YcYrq5w9trr6LZHDYOTZ2BBLUSgiMzrJGdO0Ewwk7vUcmLc1GW9RTcHG3RfDruNBbW/GIyxG/DdN7+Ly9PLAkCVPtLdlbgKgNM0KWAABQpCLZTr9QDrmbLpeSDHQC6iYg+EuZJFE1AIQCLgkqB2Uuq569Sp50EF2+z2BzWbbA0dGMeBXB0AkFw3GJjx4MF9PHnc4eGD+wJoJTHUmnIqJ+6sFWW97hJDdQF8xYwJGQFmV8EqxGUOlpOrZs5z6Rv78wIPaRYEEm0A5vKW3FgTi2F9Mx1nDAmhMrIWuWhsFWYXcJNDhUCpp21SzKKJcATR6JK863UR36Q8B3/Kc64ifZmX2lrXYANzGEG9G7bT2rUEzMB+e4V3fuSbOH3yAu7df23GVLl6cOERCtBlAp4BVsW+BQdh/Itxcog9D6u3GaqH79tQyikgsZuz81PzWicHPq7JtyWOrt3Z+p5fNTMNAebqCfVQ/DlItvZp7V8n6iuPHVhozDh8HS0v7W9rP0H72MornVEp4xyIqeSK2t9UK1apHcoEoDYxTHqYayS07ZrVyf32+6avcTteTlPFNcBki2bnWHbqIv9F3bTevBLJtIJrVrMemNGkQ3ypOQpogg2Yko2yiziACYBzSsBNfalVlcSjD17EsO/x4lvvYXtyeRjIuikwxCahjmuBTHTNk9LvzErJiMSbYNcBFMBEYudIqWnXdYiB8BOf+whTImy7jDQxHj18iN3VDk8en+PNl1/EC6fHODo5AcWI8ZHsl+M4wei60dOsV/OTA7rqDmx7rtDn3FxXRAXwhVS5Bi+7YO2HGWBIYvRRjPLr3BEPzUAC4+r8GA/eewOXj+8isaYjQt9vsUnA3RQQKKO7J3vmlCZ0Ua59HR0dgdQwu2kwGYhlNq/sgCQEMVlQbGFlr/Ek/dN3HaIeTHUKFJh9rRL8PFZ6GUIsWlUF5A258A/J8XR2nczAVaubXZEMFOo1TZqBDkTYbjbVOzpzsQFFVK//bTYbEBGmJCBU3/eIMWK73QofmAPACZyDaHATgXKS2ZOrMxk1GYWgavIhBETOygtx6WsD6wrIx3KV1wzUC2kwutgCW55/NA2ycrhMrU21olHp1nfh6RahbPSOXh0gOuuptQ9ulh/8lgAiTHLnVjXExeZWpIhNCAgUEeOEKe+Qp1x4vnrcp/wCADlcBIa8x0QB434sh2cxRIQIdP/1ywhvMjZ//FcQznaIXVQHQVTm8XbTqyME6eNpHDAMA64uLwtpDcqbm4mEGKg5YAx644KIEHvUfRcoYKb1hWlv0Rlw5/8QgVHpo6673dcY4/fdMPm9A6bRVwEwBpBsBjl+VGMX3jzYejEeSxnAalOs0ed0wR2ELkb1hxEO1eOm+Wv8v363fbHhw9t8SquVcPm10gCNB6s6q5MRwIZOzuJwHYPCJSyH5BMLq1nfsrzbaHPdttSnIEfPLXycA+qPk/apgC5mxr/+r//r+G/+m/8G//1//9/jS1/60o1pfuVXfgUA8OabbwIAfvqnfxr/4X/4H+L999/Ha6+JC9u/8Tf+Bu7evYuf+qmfesrqa72gE5Z5AXCVCa+Tn/07CzPgi3w+pZBrOvkQcHZTuhuDkYE1KawVMObhulKvHj3E7vFjHN17Ed32SOObCn4uJ3ot2OUz1w1cNydPOFqJpPa5b828jlWteD3UM5P2mQe0yjPPuBBj6Ad8/7XvYdpMiGW6V0PPpAKBnexNaVLQD1WLR0+/4aeUMQgzYdW30UipsU7Sx1zfkLAXe5IrjF0kAApw6UkYK9qjlxJKfztOq+QV3UZiX0e1kfDksRxrVdshvh5VxV8YXxQ1ds7COA6c1etiFu+CtqHVxVf7xoCkdsAcs1lGoX5X5tTaVpqoxYhR/Jq+uLpnAb8KkEAoDNH89M5OflFGqgplZtNny16jhUtevrP9lYr5CpF61xngt2rGfG60/dMabq9zdNwM+PD174ED4+7DV2VtEtr8GODUekO0E3ffTiiQ6MFtlHWstn6sDxoa0LZWHtc1WcGq3Dybt1aWjK332kbmebw6Nw9tcGvvboq7CnKVkpc0qFBfN3d8OczONt0sCxmfdq4EozfGSls/lqFfuVrn52xLblw9VurtGM2mbqukljxvWuOVIXdjjQpo+IMDT6UXDBnRerElbvu29Pki7rJ+y7JMEFobz9l+Ou83XuRW6a2tExsjmxMsz2mep6OP5JytXDy8g8vHZzh76eEC6Fpt82xt1BdCBETOMx5E1xYBHIKCKaplzADFKG7aAwGpGnYOBHSxQ+gIX3zlEVLO2A2MlBgX5xe4utwhPjnHveMjnJ0cYXN0BIoRT548QU4J4zTpYQ2JZc+sGiPMFThpaliBLttQmV0b2NE3xnI/aeZquyda+swM2+aIUQDHpO8SA5cXW7z3O29A7uHZ4QOh63p0RLibxM4gTlFsWAXVyDNAx672AXpFzBzKMDtaBwUf9CiEBYTymmDbrYBNogkT0cWugkjNvND+0vnirzlaXGYCIpApg0Io1yqTgk/26eeeaJ7FhXYWoPuJgWJESArugSrvRJC+QKd5aRldjAh6JQ4IyJPub5SALMdKbC6VzR6T0hY5VJMpEgIhsAALTApKZ3cDwfhwXcNew5lcO8ry0XHgMh7OxUJw9MOWtc1BT3PY5YXKV6zecLguHAC06Jp3c6JPJNMYhaeRQ4ZAJABU18sohYDLqwFmv6/hJ61QcjzCJHzDsFaHD+8BZxHh5Y+Alx5AjKxJf242Pfq+x+npCTZ9j03fqyYhYxxH7HdXOq8MJCLVDqXigKFT4Cw4QLVjiWMjVDWjqYBNgQJwBJz872o60WrLGD9gDO/5fZYL/0VAcfQgzZC2J9ffRo+LPrbnaQr/KXFsjgpVuhmmWDiYespp9PzDnL9af17CDIBc0yB3FLH8XuS2kvYQT7CooJf51ytfHzVFHuJQZhV+2mC82sH3c9p+y2E/EKmR2w/QofVunD/8OI0+VKcfbFoLTwV0/dzP/Rx+4Rd+AX/1r/5V3Llzp9jUunfvHo6Pj/HNb34Tv/ALv4A//af/NF5++WX86q/+Kv7Nf/PfxJ/4E38Cf+AP/AEAwJ/6U38KP/VTP4V/8V/8F/Gf/Cf/Cd599138hb/wF/BzP/dzq1pbtw1LVnktEh/eND6V4TatOjwJbjs9ilp3sutruainWzC+Hn4RGeHmXASAtbylBXosZxvCU07eSvdNKwq6OXH59OrHKSR8/fNfx5OTx5iinV664WdhxqnYwxAGz5jPxEAPFAZYNtGgjGrTwJof2XZm/aPCPExzKJdyzZ4UKbAVncc+A60ICuiQaXSFCpf47tNpcuHenZLY/QqxR2YgJbnGMKlh8dgFbPoOIUSYto+5Pg8ETMTYQ6xmZWSAslxU0w2o9IKbnqVvndFbG7EqY3vDk61w6HTn4JvJ2vKAJfNZt9X5ZuEYWh2jooFDThtI63NKJO3z89IB2LbJFiFh1vi6/2uNix05H0+0n8zDUSbRZMhljtTABDUuTYV5ePLifXzn5FflSk4GXvjmj6B/fAYA2F8c4zu/8QXsro50CEK5AkMgPdVXpisQMgfR5qDKpJsjBvM+auCXD8bkrWlZmYBXr3kyWoFpzrwY42jxUIQI1rzXQKk1gKsKeF7AxGqcdfDsMJ2VuJVT8eDSvBjDPoqWZG7rLSWpQKpGmNdD27+1HEd3a6kH6+5EPJjwvwAJ7Pd1fB75FKRt135Q0m8zuO5atkjnDKcTGjW/eRMYKxp3K3GZWrCtxjokOLb9Oo+2ppXY1NvNWVepStcqOSvlEHlbLTUzuVImV938q2Yv0/U2/wQAinq9KNYra0xACjoxA4E5ICMJHQkBse8Rul60bXLGxuoIEiBE9ylioI89OoLseZr+0eNHSNOAt956C0fHp9jv9hj2e1xePEEMoo0UiJDDhCklpCyHOEY/m3m3GBvZP4uSMOq8LGcAZa7NcnGyTdlDHE1lhuy7IIxZNL2GlHF5tcf5xRVAQQCA04h9DAgZ6CZCf8WITMU7YcoJxVak0kqhKUJzN32PELbK6jitNa1TTqloIWV1/sPFWY0ALF3sikZumROqaWgaSoUXYy5XQ03fPHtaGQL62LlOYIwgjDwArOAmie2tjATq1E5XCGJQPCcMV4OCEFGusW02oCjXGc2hCSc94FCQwq421jZm5S8CUg5ma0D4LcuDhW6SNbAZzKqlHTvTzlFvxeMoBtZDLAIys/A5fd8BTOBMTnta11aWiWRArL/WWOyKXUday1pn92iNHn3ygZnB0yjlszjoCVH7A4ycJhnLYcQwTshJ1jgp05mbFeX5J1twVDa3qpOpTq73Z+C/9n8GvfEe8Cf/O3AcwcgYpoQxM8YpFYBLK1u0yW19m154iKT2wKgc1oVgGl26njqJHMnMSoiGWYwBnfLxpg256QQstoPbrutx9scJJ/9o3a1Szhi+z3jyN7PypLp7kV5/JoBCdbZgQGLKbj6xeE+3mwfSLNY9ctaXi89Dg/qMk+FTFiodtL38mvXBjNB1ePlLX8Lm9LQ9RPTRbir0KWX97miL13/8x3H16BEefPe7t063Vpm1gyk/C35w4YdT6qcxPBXQ9Z/9Z/8ZAOBnfuZnmud/6S/9JfxL/9K/hM1mg1/6pV/Cf/qf/qe4uLjA22+/jX/+n//n8Rf+wl8ocWOM+MVf/EX87M/+LH76p38ap6en+HN/7s/hL/7Fv/j0tbeNcCaQNlH0k1yauTrwQvvL8gauVR2mWdz6omHznz3w4ssy1+vm8S0rYOBRAbxMSGezd7CWLRfu0wska11Z0hWZhZsHdopB5QuqwGtMP1XNiLX6e6ZjjCOGOODh2UOcnz4RJtRZUCoCBzv7AM7YuDhBynV6WZtpLkDJ2yIYsXtWWko1jjGnhVN1+RCXjbEAW6zPjMnzUhS17AgDmFz/ZOXRKIjgYId3WfOzU7M+RqSsp13W/UE0ACZiAWVEZQoERlCwLZjA6fZw0j6a2+Qh7Rffe2WFFEmkysO+TfYXoHZFClhQ4940zaV4dwKuYEzO2W4wogchMhcF/rKG3Vouf5YX7KqIVzxvx7aF+PS3NdsNZxXOCsRR4hNkPMbNHulop0AX4fjoNeCqw4iMAVucP7iHKUWtvmp0WT0YDaBkQgpl52HKnYjLhAlljbS9OXtSgERWAUNsd3mtJxNUrG5WJ6DWx/dCpSM3g10t/bl93DYsz1tN0KkzednmSk+MprgpvVJMo1HQMER1nrSgVk1TyVadbeUA4tqVMCfgTv+AhI4XLa0DOSzb4fK9iZ9aksxZfdpnJiweAixvVb9nZPDq/JlX8LpEh2P6ue/bw8xI3YBpswd6M9bNZd+zzMLYgbLR01ZAEsA0IPcJORpIRUBSSbDQEDlmihDgg9RIuVTNzUejXVq8HATYtTTZiXa7PczVa9f32B4dSbrLUMCioF58We1dxqijYX2BOn/q+OoG4jysNcCpzTdDkpsgz+fOF2zPLhpeqN6OpwRcXUXsdoRxHIEQgRAxTsA0MWIagYkwjQzmoJ5rFejSeqeUQMXDrIKNAQvbVUCdjxxjsYPqgXkZkCQCvNNe8e0wWsyujQBEq6nMtQp0EVFxCGB5WTssf/PmyDkjE4GSgRL6LGWM+wEIVK439grsSb9XQ/zyJICi2uwSq/GY9LpmmhKgYwAFDMxMRNmfrG0Nv+RGWnkjRrUDltKE0EUE5zDF2iu2ZvUgyfd1mTaH1/ZtNAkWccjWL/lHEtfouJMtDsoQrsGHKNlivisAY+vG+CVb18xiHkIcEMg6quOon0QoDHmpkqc7bZtABOQe+O4XwOMWeHwXOL4ANldiqk/nEAFyRVcW4rzLyp8p5sUoh5ukdupkLUmsHKViUa/1xk6Ari4GuVasHkNjCEidAJ5Fo5ACwsuE7hUBPhkEyoQcgHA3gDggqNF9kJl8ANK+azzT280IZK62ZNkcKWQ12eJ5d783zGl507WLvvlBBT8Dl+Uu5+cqf3Pg+Y3laqLQdei2Wxzfu4fu6MhlvORhnjkUXrOGECOO7t0VBY/NBnlK4BXbmeuVXz5krnzM9fW4RXa3jHQ7evUUGT6n8KwaWc9Dk8vCU19dvC68/fbb+OVf/uUb8/niF7+Iv/bX/trTFP17AcDTTsjbxvbXmIwJ87YJDpNbIdScnX0mjT8XUuzU8zqh6DrF3io8cvs3A0sYjG+/9S289+J72Hf7WS5e2GYUI1CEcgpJIYjwn8VIsJzcJgSwbrS2RdkJPleGiYBiUIR8taiUHSACCQDBEhSF4kzgUBl54TUYnCenMeHF4Zbhb5UmGJcJuAIJA0+EHAMSAROrAX0APTE2xAgQew6XgUAxYLsRr0hdzkikgAhnbbOcWkHtgXlCHopwFQEOwnTpOBnLblce63Spwl107ZNTtAo2hhARYX7ECQl2HUYvdVIFsoxR9kKl/wSg2nwBZwRsUKxxgWbjZkKibeDMwmDO+OUSp9wpXJvoxj9q+gwqjL75jvIjrPBeZYtsToCRifG9L/4W8lvAfmKM330L/D99FZSi9pfa6NITW9McEDAbYMoqcBSYG5GBHBlBbZ4QcyMkeUAqhGi8YNWC1Gu/YsPFa1it8SmeOW+1aOzrHJy6SbNrDeyyKwt+LqyBJ6wjuPrumn1P+qD2j3HxNUnNs8oluQGr5vlZuvb34bAOBh1K35YpY6N0fHWcarqbQad5mUZsuY3CQiV8Tfwv09pa2A1eCytDw2g16W5XVwmxGB22ueRyncu0Pq2uDWoTAeTH3xNs4N0vfhP05W/pTypYj80ZAuFz3/oJnD16qWj3+DzyKNoI7779LTx56T6GnNBfneDNr/8UQhIDvimJsfSAoIcWQuP7zQZMQMwK1rD0mR0CgETLOTNjYtFEGlNGGhOudoTH5xdgCji9cxf9ZoNxvwcpXQpRPA2OvANyRgidtCvUa4vzcbBPue7orjSDQZSLHO6Gpk1fEV/9NDp5AAEAAElEQVTARH0qF00LwJUZmFLGxfkRvv6/fgm7yw6X+xGgBISIq32PMQbcuz8ijsBlYvVGWAEquW4ltrkM1DItEqNlxY6Rs9ElmiWhjnUR4O1AIjripx8rdLKhRySCdR7rdcms2lWkh1k5c7ErJhpcQYEP0UhLU8IwDkhTKvSbiLAf9sVpDYjQ9R2maUJKCX3fgyhgmkaklLAb5GKbXb3s+77E3e12KJq+ISJ0RzIPmIGcwDlJnbNphqnnTi7kohnvEKPYSxszMkbRrFGNn4gO0jwZp67rwUntsvEMXAyodvV0Qzee8lpZZ510/1CDAIChALCyTWflieTmQhcitn2PGDtM0yVoSkgs790JH+ZrsgG42umJwqMwA++/Avw//wzwE78B/Mm/UZKyzvfYxZJCrhGOJZcCPWg9RPxgEKXSPqONKVQIwYDPspZUE93A4hhDuXLb9z22my2iArZd34sWWL9BfLXDy/+PYxwdHeHk5ASbo61op8aI9AR45/81ID3RvZKhfK3wVHkakVPCNOyRpoRpv9NrzqMyTeZNfMkxGn2q/KLfBz87oQDV7Nto73gZWT8buk6EV778ZRzdvYtus5HHxmQ2yQ2wfv6L8PjeXXzuD/wBPPr+9/Hwd7/3sfO7Tqb9vfCDC8/sdfFTFTyHbpP/WU6C105arouun0tZ4mPUYbWUp9xZFwTgFvVQsKElVl5Y9xuge62v2ismJji1QqklmuuIGMErquIkQMT+4qKAbgFAJsIwDOLWfC/q9CenJzBbDrvNDpf9Jc6Pz3G1uWor6DfrFfzBbOfYqRFzNeSKrNAUxUK41kTlAnLY5g4DSxy2T7Zp1z4u2izMqPc2chmTBsSiAyNCKJpTZUxg6vhBr8IpyEKi8TWBMUG0tibmshmLQd7KXNQWKHNqZblP+N8mNDOVJsF6QOOUemtzTbOqsjPiwqDIMTB9MBWCC6CkIrMKOuz6wM/exV5r/cemPafPncAkTGJdD618VXvGat2WMRslN/gMO/Gx+rs8Z2Wxtp2b0uTN1O8xhowhAmmzL8UIA0hqn8sYebe+yTEmQLmykUNGyKiG6AsjYqDROmhlc1jAclfDGcC4Rg5t7s+ZoTmw5YGrQ3Hmz66/qjhvgaex5IcCc5DD5qmBXDV/L5RaXGo+fZ4ux6Z/loCS5TuvA1Btsq21imZxD78rJa30ExdudK0P53R1pSL+UaGPzVYxK9A9e5YtdC3P1XBz312XYZOOjCZxpSFu7G1NlhyJMG1H4Gjn8mvLIARcnjwGpaBrm/xL5JGRR8bl9gmu+gsMOWFMCY9P7iPkDojAlEakacDQBUQCzncPsc8X6mStXUtyfcjRWa1TYEYm0QyyfXG332Gz6bE9O0Xfd9hsNkjTiDSNYj9HtS041DUCvaq0DnTJXCbo3gM4yjqLvein2t3shqpoELPRO7XbBCBnwnB1hHEgZDZNEzUOzwyaGGFSEElBx3LNkMT2lRwaCGhdaJOufQJV25Geduk42vdFO3QsDHSxsTGa0vBUOj5apbI72OFfTmpsHFOzdAUA6mrdcj0QYL1WCaAYrq9tq3VJKSMELmDWNI5ln/A2vvwhKjPLGolCbcMtBVbjG6wRoYwHkBODkRRYyAAl5TtyMWYOVOB4jScldb1snyUOr9QDxsHewuLSfJ46+cL/9nGvB9hWCXmpnVS+evFEOcCQPpYbA+SAIRQTCwfJOypHVv+tc61ZrFMHPHwB+OBV4Htf0DoAeOVD8PGuSjKFtmtCV26zPc7qZLO7elNFZZfJqIWYUfFaYKS0axwTxjGLvTLV+pLPQUDc44TUTUDHSH3C1PcIXUQ+IqRXMngTEa9OxYxGcLRlGpFzxrjfYdztMOx3ej1ZHScUwN36sxKpllNtONb1wfgUhgXv5r4UmrTC39XYhO7oCN1mg/74uNHkIvf3SQbbP4LaE9ycnOLo7l0Ml5eYhlXrdM+/Ds+a7pmnymdnjn3c8A8G0AU0jOXvhacMDFHjLUK9nFYAt+vSdS2JW0sbiyTMjOHqCu/8+q8jjWNxUZ1SaoCu4+Nj/OE//IfR9TKN33vpXXzjrW8gQRnX64I7aQfsnn+HGDuEICdh5p4beUIAsA1bN8/mEqJ9iIq4CHNOWqN6ms2E6klKONvS3xXhMCbAvOK1AmWAMSylhFqW20NSTmAo0wdGdFc0d8wYiqfNjJzl5D9Npm4tV5to1pcVuJIfBnYFJsjpntUfTV0AZ6umZJkLs2K2iyyoDgIYQEBUj4+VTajafKaJJXpRZoTWyvK2UooQpOVkVs9c7lndqNmdLLr2U3D8WRUx5qxKK62TMjwEO2mtZVETl8snQbyjGZ9vTKVbq7NrAJabnWKakG2aXLDvrMZ3ieSkG6wGN9Q+CQJCRR9dujnDYhpdqRg4NsHCbBDVlrZ5tXk6NtC9OwR2LQTIpk6Hwa5DoJcfQZFXq/bnGiNRwS6S+YCZtgD8ey/EVEcQ3mNlbYLvI993bT2KdmnT9Jvp7dK9+nqoY1B/zzXTfH8dKnvxjqqgWEGv+ptNOLptWIlLFNzhwHK+LuuHWRyevbd2L9vfpHd9VQpz499EjQBCAKktI5+u2gxK+N6bvwV+vQIFBQQBAymAcgB3QL4Chjwh4QoffuHvCLnpSICuNOGoD+gIuHz5I/CHGce/dhdhoAL+VCGY9OoxlO7KtcVNF9H3hCkPyJzw8OFDjOOAF+7dwSZscXJ6isuLc1xdXiBsNghdUM1OLtfjrA+KKMft57wf3SjVh7P+9jIzMwqIj7I+g2gKsQjI2dNttT3GyKUOAoTp1f4AsVzfEutCX6GgGecMyoTECiD4K+NKY1Ox+cQNTbAOEMHcQKTU0BEDaBjmzEaeBTVAH4hVozk2wNI0TAAmDMNQPOD1/UY9IB5BsMdcrvFP04hxlE8BkeSwbbPZFI21PnYgECbly4ZhwJQm7Pd7AdA2GwQi9Aqk2by2v0BqJ5KK7ivKEiMI2MQBxHlBEw2cMW3ilBI4MfKYEOIABtClDhTEm6gAbkCgiECxmVel/wmIiODA4pyBsjppWNlYS21uAXL9gAMDyGkC8gTTbitvdO/PRFDTsGqfQzWnCOpdXNhNc4RTeCcAHvyWq496LXrBgxDw7a8A3/uS0r8M/F/+K+ArX3e249x6vgZh82u7/CbH9OooJHBRiS/27uZpCWDeA3yhNLmlOxTEYH+/3WB7tMVGvYuaN9Ojr97B5slLuPP338Cm26DfbrHpN+i7TrQPM2Mcdrj46CN88M47GPc7DMMeR9sttpu+ac9y5HyLjcjMKviZCPNVsSTszcExGwFn3HvzTdx9441bCZyeW/ykwp3XXsXZK6/gvd/8TTz54INPuLRPvj3/sIfPNNCVmREYMMTcB8/nEqrc3b5ceQdUTolwI7E5SKZnhOppePdblnAwiE2KmsaDWF475eLBRxiHHbZ374KoQ2bxGJSnCeg3AkCYDQrdYBKvEGaa65rIuwoB1BdU+sVsB6BgOlePHmAa9iAKSMMePE1yYpqSAF3TVP5yShj2e7zzzjuILwbgR4DHdx4jR2WkFjcv2fZ8/RSD3Cb42XULuywWkVW1XtToA6i4ARfPTAGZg1wDZCBSLKerwmwbQCVCRBRTr5K2bGYCMBggwFzBKzaARasfmEXjjDzLAYCre2Pr44rFEYIKRaSnepZ/KH2iIBfnsslkVhtcJDVgCs6Qq6VvFbFlHZngLifC7ACdsn8V2b7VUyL1DNaEiMZum4CIqo5froiJhpJd/Ss9pmVw01uVZausEMOk4iIAweatxM9qoNQDYUyExGY7J5fTWTMtLz8VXLJlom1PoFJfsRtTteisFkysNiRSaQ+D5fqh1ouRNY6jELq8SK8uMtS9vJXCWckagVTTT7JXYUpBqwAGBypCk4yh9WUL3hhwRhRAVIXynNvrgDmbVtjyWqkFngkYLThl2lOG2BnT6/PLpS2NNpUXutxsqBPT1dXGzrH3bOACoECnaYYwQuB6LdSBcoDX9FJq2JLDUg9vzcHfuqvCbvNPzcf2vgMboKfKBl63z9vINVvrQx/Z+tDVunQtl+e+PkLTnJBU+sLVy6XxNjFZ7SSKEEauz3Npd+lnX3nAXXtsx35tOzVhzuq3qs/tGrXUvJJgN88rQur7QedezpjU8Hf62lvgjxjpy78F3uyQdP2lYkKAkTi7sTYhX0EO6gXwZBFgpyx0ZTLgZsqYxgnTNGB/NYHyhKtHj8FXCecvXGIbN3jx4T2IIgthYtknolsLQusAkGl3BhAThiEhxgm7fZLrP9sThGFCjpfYZ2AaEyIUONNL7bZPeWps1Cuz0LsMFtOAOjNk+NiNI3nyXrVkDKxz896orJQtczUoUGhX5jjLZps2AeOGkaLsMfvjDqkD4rkcxCQztl5oLwS8srKcAE45KYCkoJc7bBGS1QJdOVVNG1lHtgfUXbJQAce/iWF6u6ZYaYVd16JNpTeitSyHWUACOOqeIlfjY9fBQOaU1AaREr7QhQJ0dV0vV+JJNIYjd0AgjNNUxspsZxkQt9lsqn0zKrratR/E7Z7UJavDHapX9mFjpmMZQ0AMjBgUuGQ92CGoBo/yK6AC4paDRm2TP0Qoa5MZ7kXpdRv3qsWEOiaenhDVye3TN6TJfaNl1DVBv+mHlZqVPSAEgNQABKldMntPoSlQbPUxyLT+9K/EKNPZH/Kx8jHST9KV3ADLAIBEaiSWhLcSN6eu1rX25NT7D2xhi4de+1/ofqXetn0v8tLim73K73dc68c5Y9yP1TxDCNgNE/pHjOGDD9FTj77vqtMI0pqkEVcPH+DRw/sIYHRRLoyT/TFQBZNC4WqY9/Na+2/uoecSboexzSPVxWC8VXvQPIvtEEzb0zLXueX35VIpv1evVbI5VPIzodXZvymIkxfg+IUXACKc3/8QaRybOB4mAOxgl8uhxC1KublGn9wQP2WYcYzX1esWYOUPOnymgS7ZVN2VsEPx8PTvuPzTPFknxmuM73wmPPPgX1f761P5+ph9Aqkag3PCg9/9HcTNBm999augPui9+QFpmIBNBmVhPAFnCNxz3UV+4TnJ1mdOaDAtpyKALpmKR+98D5f37xdbA4Aza65CAiswAwKGYcBv/P2/D/p9QPynIjInkClzuWrab/GYIhJQRkBSLSEiQt8RuhgQwejA6CF9BEDcYwdCmpIyFB1yFoFCNl1CZ3VWw+1yNJaBABEcCEjokdi2PVGzF3mEETMBMKYYQB5RmHRtRqcn7mVysg1B7Xvbr007qitgmrQlAuquWTsm59JOyyXnLNoGdYtGRvXsBVIFcffbGH0C0GEUwUg9RYEhNr1CqB4Zm3lNpe7N5hVRWic2s1O1s1FmmJzUpxxROFmKzTz1LIUIDipaz6bsfMmW66fmiYcdaIOARCoc5DrpggpXZrA0m2tpcwpA7IAutoNVFJPwKpDlEkMZdu0l4fkrA8tE5ToOBcsLCDGg33RgzpjShMQJ4Ky21uTqDsUKnAIQkIsSpomKvToGkCmU+WP2W0hRO9M+kJP2UE7apd9krccYHYO5ZHalKVRtA66Mi3S7rYTKxhjYRSZF84zuzHgJf63QTnZLxwLqXYn1ipIKYZqbgf5WlnkrzerMwey+1f6BeqJs2ylLmAqjZCuh9MwKF8FaizlASKjpl73a9HCzR7bdonTdPWQ4RtQEgEWNjN4cEMAs79B6FSxvdOMu/K5jfAFgUs9sMW4KWJmSgvKswpp5sHTMJRE3ZIbJ9Sm3bbHRrUU7Wlryo/K5YNg1o6B/bUPr95RY1uGYsN8PGMYRw//npzAdfR4X/8KvYHrhA7GBlTPGJN5xE3PRQAqdXKnYHh2LZs1mg822R7/p1AMdA9yVDYBVC3rcZ4y7Ebvzxxj3VxjOHyNPA8bXH+PF7cu49+gVcIjIeQJnsSkTORe7VLUXpLGECKKA/S6D84gnFyOOjrY4OrmLMGXw+SUuhz3SNOJks0EfIwji0RbIiGVPE4nV6F7WfSohIweol0gdkSGAcu3PKujWMSXVqKxuUCpgbFPBNIiELnfI0wBOEYGBYZtx8QKBQgJl4MmdHt1EuHNOoMyOllVD/skZKy5CmvE9OleC2kmMnXg3TFBD8KbFRwA0m03RwHXAmKNjzFy8PNqhT04onulstnVd1O9C/42uMiekKYm3X/Wsi7ABIPa3QgxIucM0ynVEGM+g9kvNkyIRIaB66J1SwqTeJM3Oa+KMjWqPhSgeK/fDXuglpiLYCiuoh0YEcO4a2gbWvZF1HyVGF2Wv2kRATXqhI6APYoycQgBPrOsugyIhivELmBkGo/FFA46rxtzs6KhSP/a/Z8vcNhLy+/ScYj671HpTSmF7OgBR56c/PA3uEFLyiqFDDgSiQeIldrSLi5fESs5mNzzUvi1lx3PONiHZ38T0B2YHWE1eN7TX9v9Csyuy1rIKBjSWcap7VNknHfs8T8+JMaUR035cHkjRQ4QH59h+4wyUBVQ1Mw19FLa2j8B48QT33/kezk6O8fJL9xApQlZjPYq1wtsWzCpWG3W4kz6Fodn9DOQqt0hmXIc7RSszk+cDo8ZfclZtT8/r+L6qvdn22IzPXDy5piEM3HvjDZy+8gp250+QhqHIwHaAKeSr3pqotJbbvG4q6JnCPONnpy/PI/xwS78+fKaBrtWwoJ5G7IyZXc66sraaV54Vfrrw7CkPhBsXyqEarLy5CapntAuVTQD3ApbbzTXkNOHRu+861NsLBxCEHEtBgW0XI2C4vDzYggWTwPO2PN0yW+1SB9gsxDqtp+xFtlmZcL1WjTlXxI754CIkG7G091XUsn/JFWPMlEpvs9bULXTJYDVCrd8OdAMq41rAHcxo8Fyk1mdWN6614LIZ1C4ozF/TbdxUdXGg6lIX7T+e10U+sy9PGQZ/hUz+NUa0MqUpBDUOzwWfLOUaCEQmDteQEDBaGerpSGqT66mxi2+utJkCxikVXQPmasw9c3ZlcOmzBdly9RJhiMH3HiH/zP8X/N3PA7/2Uz4qiASsZSLkMRU7NDkn5ByK8AJdo2UssmhZeA/P1e5F7WNW7RP5Xa/VmVYDN/d0I9p51I7R+jVoHw6t82r83j0SjcBZdv5kXqKRf1nqUd65SWtXx/y8t4nr117DQM/2l9m0vFVot6a1PriG6Zn3py39Gejj41Y+s9K9g3WwvWGlFgu2s1nv7Ql8Sa9fAhEQowi5xQ6Sga0GcKGMe9X+g3p4Azx4ZlcED1QUgAj1VeutVtaXkRVsM+PdKSfkKSENYpg75YRRvw/DqNfChAGe1JZQSuKNjrZXuPcrJ9jceQmBGZenj/Hk5fdUw5PKX5giQhDD4iFG9MOA8/NLMESbJiUB0HJKGMcBnLIaSR6Rpwk87MBpAsYrECf0lHCxeYR3f+QbuPf4Bdx78BIystprsjabFzHTJg6wA4xhP4FzwjDsEDvCEbbouw6nZ6cY7u+w3++AaRSthu0WmeSKdJaBRf0IQFDNfKWdASw3BjMAMtthUnYzd1bnWbvTueUJW7q2UbK2bUoZKQdMExCiHEjkYcTEAJ9ldAOwPZe+mBLPDMzL9C8CjmYezBC9antm5Yu8xmcxit11Sie1cjRvAUrlebbu5tO48rj1aEfyVhtjpS+y3tx0YAYZaBZgh0i2vswWl4Wu70FEOp/toIyqUx9QsfFl68TAQPHGabaj6njKviSHh+WKJqN6uJsNtzXVbE6BxNh/CAE9xBkDBdEnJNeva+u7jg0v6Ekzq27BZj4dJ1rbc7Buh7e85SPbrmqG+sFguH3Y2NxZNossl4S/+SQSz56r9WehYfjf/jDwzueBP/I/A6cXNSc3/tc1U+Ki8BxE5EjBrL/Kx/y38ULCK4IcrzdjEXz3gYEwdYi/+xbo/KSYdzgkRvVHR3jlS19Cl/UaKZZ9OufOFwfVLix4hk8wtBR0vcCb6jNnba7n5YCju3dx+uorOLp758b6yRw41BGei7A6zHgPv5/P6nmwTAgNeeFzn8P+4hyPvvd9ZEcHLY/bDc+hzrsNI/i84jxtePaJdyPW8JzTXRc+40DXkkQf6qO6AbT2dg6lrXFus7PNJBmXcsl+PUP4pKlcI6i1TL3yhKgodt3EbIUz5HTzyXvvYbi60lyk5WYMcm5/Ca4sE9gr8o/S5pY4+X7Q7/Wgqs23CJyHF//88J0ALNRl4Zo6Y67Lb6J2iGw6WOc0AFf76ZlxS2obrRl2pwWBXmsTuXGq1wArmOS4Wdf4ep3HrYHZ2Na2GevsmD9nDLu9GkRSJ5tDjNVNkpsCqOmHRYe6n4VRhkjKRSOKoQw6u7IqQ0WOqycAuSPkUAXm7KShGtfrCaiwi4CJFULkXP0jBhkJx7pUYSuLzkJKSa8A6/UCZeZ9M80hqLVe+q8KMAwPygJ8do78j/3P4H5ogC6Qam2FWLS9RChLCCwgVFQVfDXNU/uiAFVVQ8GYxTp+ZjvIn9hyeZczIYTsevyWkkIhnEYHCOYd0Ma4AYFnNLLR6jpQhmletNcNfXq4OTYD0djFLHTyUJkGwvr8JdRtZn0P8YF8vOviAM0VQC83M9AaQS7vdB3Pwa858GV1uIGBvTloj7k5TrYH6TQp3uhsXQIgCnI1SzVSxAj1TDBlsXPUnCjDXaPQeWO0wY+rCfqejhRaou7lR/U0NyqINU4jxv2A/eUVhnHAOI64urzCOE64vLyUuAYw63VeZoApoNtOuPsbx4inoiVw+eoel9tL8cAbAqCu7s2WV9IrYUPXYRwnDOOI3X4o3vHGccLu6go5JfA4AGAQZ0RkRGZ0mNAFwt3jHlfbc3z04nfRB8JL5y+DmIqGPBEXz5XSr6GuPzCmcQ/mCeOwR78RW1xdF3F8fIyHBAzjAB6BLgQcKcjOrJrCTCDzPmjee1WDOAAK+HPdixyqMd8L5/YjDTmdUxou4+n3WNVuZdEUTBlgUq3tLMbVx2PClhj9Ey4aS1E1os3zoOSZi9arVkSFarlKnRX0mVIFYDebDVhtZ3lAfVXzx+2TDW+j9LhO4ZZDML637r113RGAEAqzUmgXBbluWg8vcjmMMVp/pECd12Aw7d2g2qym7WteIMXjpBuQhmdp/4LxTZB9ZHXbMJ4toPCQZpsyGpuja5ncOi6To2HO61xv1ryjDfXbIdrH1dTCanVnoMzKu48TDpNk39hrAvPCUH7x+F34yTanEAh2T5x8JNS+46//BPC7XwB+/28AJ3vdhzIYLWBwi+rVM+hrt/ZVJrLU0WjLnP9ffLVyUkT3/ddBuw0c9VjJHIjbDc7uvgk+f4J8/8NZveb1XOMIZnFWH9+Ch/qMhM3JKe699dYKD3lT8Py9jaXSlBvYE+HZbX6v8DcWz/GFZ6+9is3lKR6/+y7ggK6nGokDvNundzSXNbsNFPFxgKpPAuQCPvNAF8qJ2s3hlsT+H7KQxhHvf/3r2Jyd4aUvfKEwc4u7xh4YARog5P53voPd48cY93uX8zoZnwNFTbD9ifyVRyNMLo59vwuEfwrAS15wwWHKQQd/yBP10kNehUUqWoplFId0WpQxZuSILZe+MY2FIhBbe8rTmUxfwCIu75ysjaWCitrQAhpQyZh9rzAtsamUaCwx62l5w9RluQ6SiqF6jR3EPtHcqHWpG+uhFxdldy1frBXUK6zaTdn1A5ko04JWTupeMlFadjEyzO1JtDH17ZyonfiQGR0IJzAvUC4WmYBswqltrhkZAdm4LlYhCAyapLB2nkvxxd4OWWODLqPW0LcJfmKgOCxoXAsooowoWdNUCDs6OsLR9gibTY9xv5N6xaCu252VMlvrzqNYqcwEcM6ioUAEDhGsHsegwg2blWergI1RZuGBG4CIl7+tLG5nZjtmtgjg7MU5rbdgNsacPTFmVLeglgejOANgKpp2FJxxXa27Srya0o3/Cm0rp9NloVVGbEHmbgFq3SqUI/kfzL5GvrxbMyR0sxCni53nv3Xim6DMEFtLgBSvpAhEBjoQghpAt6tOUgO4T1aDy6bRKBpYKcm+t9vtME2TXt+asNvvMY0j9sOAcRgxTRPGcUTOCdOUwKw0MqktydyCAsULKdeZbXQ6sdjr+sb/+iaOzi7w6pe/jbyPeOH+F/HRq+/g4cvvyfVFKGgABdMhdKFc+9MyU9IyU9I1aTYlGYmT0tIEJuCKEoh7TMcd7t97B8PRI7z4nddxcv+OGGFv9rcMMZgomttpYphNu93uErEjjOMxQIzt0QYnp8cYhhPsLi8wTCN2+x36ENCHIOszyEUyo3GmmRQAvWImdpwq6Tfqxu6zzq9KCZZkXgii0AFCAAUgRsLx2YQf+QO/jQcfnOE7v/W6W7pK84sdqoB8zHjyuoD2Wa+CRRBevAwIWW1uFluS0qbMLNrtY13rdpUxqv1EUgPg+/0gBtzNQ5xdYTSHE4722Loj1Yoz25YSx67Nc6GlMtdans72RIJeK3NlBgro0CEHoe05sxqnz7IuJlkXDKDve9EuVO91HiDKanzfa/FnNWVgWsHBNjsmIHYIlMQxDHO5Lir3Tyv4V20HUjmEMYcx9bYBIVKUPg9BzDOkrDwLy34eAMqFIpQpU7u5lreYV6uh3RN+GKGwFvrbZs+87jT7Y5/6JpQA85Ya31LnqmzTXHg5AgHjEfDX/zSwGaXML34b+Mf/Nm7Ts6UkW2LXRtI1UZkJGFtOOt/sqrrnPdvWaDvnpGZeDgA35Wa5tKPwe2EZ2t6//Two6Wds5BzUfw6Vu3VcT1vl0dO35x/28EmBXMBnHOhan9CVEfZxWKmWLAZq3i1n9UxDB05UouWzWvRSgKlyz8cYxGdYua3WxeGyOWdcPXpUF6pbtC2o5TW60FCW/fk5Lh89aso07ZNlX6/VyUTHZb81P3iWbgPgRwh04uIvUY0mUCN4tfUlVIZvkYMJ1u5dZYa0Da672urUvj1UNXbCXsnHgEbDU1Dnri+n1sd50eL6zvI0mx8itK8weXCbN+ocyJnb/iW3kc+FeCcDsxfu9KUxDy1zqkKscg+5lG/5uMZg9kxEohboaurvNsTaiFL9gTMmELaueaV/FXCtc9mYeBawJ+SaiBlwdvCaOeCiZHYn2+40yTOpVAQ0D0u6+pEJMG7CkSVRRj9GdF2PrpOrJCmK3bIUY12/Tb5chJPGKGjOooEBEi2TMpdlHvjNHTo1GmP8dfLBJrFoMi4IQtPWBaPA5CZorTOMaS0gZKulJb+xDHNasgLHNFdrXI1KnrP5uTb2TV5t8Y1oXmDHGV1crRmtfG+IwRqRIT9MN4Y5bWnsUz0lN1lpihMceTaYTWj7s+k7cjPECaMFHCCzwafgh85rmbcGBOk1Qr2ONaVJNcMSnjw5xziOGNW779XVFYZhwH6/Lx5/R/U4lzRfA0vh9k+zSVI0lcgAHJ1LDDE+z8Du/S22FxNOXmHQVUT/+BS5B65OrpDUVtc0TSr462kyk2ozeylLV5AnOAXYUHcUujdMEyN10g/7zSXy0SWOtifoY4/AGxTtS1ZiTQRwKHYHDaOYpgHj2COlSYzSdxGbTY+joy32V5dInEW7jhmRSGm1XlMDir0t09UiFmPkYqN6vjcZ4DFbETbBFCxveTRq5U4dk65n3HnlMXZ7AUQCE0KCs+VN5YpljoR0JCAXswJZIPCOnCdb2e+CEnDrp+LIQzUFYxSQ0jyuSjqxyBjYbGdWfqQe/BQGQEH82vZ6Pbvu1wCKFlOrmej61HgFOJpMkAM/BsQ1aCq9be1JKWFS+2TbKGrAYoeRF/YZPd1owaP63PYspgAOamGe7Kq/X/PLfdLZMq97IkM0Ba1sy7+sy1koBS1p0XyPKLW4Bf0rGlyeGbtlaLS/bijKa0qze+rnfAnXyiGFuVhourR7W90LfTes7lM2YDkC3327jvnxrtr9PViX9dDyVrM9knGwv5r51mTUluV2j/YNtV8ZKHRwUVYMiJsNQrydl+PbhfU++QTxgacs6+aKEBFi34OYkd3B1M15Hyq/EsLKliwnQZUlYGyopjqUf+U9/MFk7DdAZqRpbIt36W8L2KzG+gGO5dOEw02av7gdX/isoNa6hu3N4TMNdN0mzCf/U/LoNR/cdgg/20E0utTo94IctItenqAYYkYIjqlZ72e2l9cF19nsCE55zU6AZlND9hoXN4fKgFUumIIYZY171bSxIwJfn7kgXYT3RgabNUf+E96ZgGzel1pepDQJKAx0gDJzoQoFrYhIRcPMgBTLx1+CMHBL7Dk6T05s9jtQhLD6UmQcy0+5YMxZGnZMBgFI6pUuz1xfEsQIuuQr5XgPc1S0Ndj9SWdYXX2pVtUMYDTPle41XH8eCsWhG1yz/aZYe6WUZ54UvfcoHwhmN0Q9xhEBxUy99b/0ZRF4TYAso2OApHwvp1Xad6z95BtIQUC0sOmx2fTYbjaIUezAnJ2eim2doUeaRoyDaKpMk7ifFwcPZt9kK9cZY1Rj6gIS2LWuDhE5Baf96CYM7ITdWtAOiF1DsfqzahQQxZrHKqFd0oH6m2Emp70wVQWblnq3V1Mg5euCtPlvoJ+fwuLx0wCAQhDgAU5WIaFeAfR0tCapbTpANBZtX7Zj/fmhfFqq8UmE9f3RhFpXEzaN0JZpoSaNaiYBiGrvyLS2KkBQ6cQ4jvI5TZimEbvdFZJqoAzDIFpZ+z2maWo+x3HEoOvAbArZumIFZBpmVxpQ15/+Fq/ACZ5uFfqFWtfMapOveI8FgAB6lPHBh2/hzqv38fqPfRsX509weXkhbfWoqmkbi0oCgEl3AFtDUH8rhHLqwAzSv8AKzrE4QUlJrjYSM95985v44MVv4Su/81WcXJ3pKKjnxwxwsn2M0fcECsDjxw+Q8oh7L97FdrtBv4m49+I9nJwcYdjvcHWRnVdZKgJ0BiGx7mlZq6ozIBSAR1o9ufVV5Pf6jz629e7W9WxGEolXZTOy30Wx99bFiNM9YTsAV69EjH0Qe2WpOtYAK22NSvOYMKYJPFZQn4iKdp/Vj/Q+uJlwKFp3Oav3QgW9CBinCQSo0XexN2WAVxHodV7Z9cAilBMVTcKUpjpnrdusPoXXkd92JdicgHhtMgIVTVkQmquZu6udAlsZsYtlbRrobH92nRE6l3LO2I+j9CEFRE0TdfxiiOogJ6tmYkZOpA4o3GZuew8LB2Dg2zROYB0rKB0mBfPaPUGc8njeDCzjJLgutWveJsFnRQpQEBAwuNhoiPEy/uhmLay/q7qT+rsQOJR56OMerB6JdiNmNpduI1A7aUTms09D7vkNoTqVWfIdxGZ2w8yT2D+W97KigtvJXnf68ku498W3cfX+e9jfv39jXT5roQGODgQqn7VjY9/jlR/9MYS+xziOoE5OFp4W+FgHvNZ4pOvSPF3ot1u8+VM/hcsHD/DBN77+8TL7BzTwp5RG/gMEdFXtIftdvhWmZ0aID0z8dYN3S4O8XN7Mq9JwFz+0cB3xKJt+COiPjtAfH1fh0zP3dGjLuJ6YFMG89OUScaj1U0G+bMnUDE4jRPrvriYLkGtlvS1Pd31/SJ/EENyVAXtxMMtbyY1FoFE67LfLWRHathWxlFEAkvk2y+w0BWDCO1A0qFQwLDwB1zTW6yVdUxM9TV6xO8Hln3YdMVBs7TRX7ostYamIgDVc1MdRimYRqvRdYcpWT1wruNWYuGL3MZ921Hyo12vGQATxWdTm0XYHSRtMkDSNKzJvmKG4qTYDuSLE1EnHADKLENqM4eKTy5gbbVswmNz2PQGg00uEz78DOn2hxOPMoC6AVOOCxMJvqbsIMVQANAF5RMMlQBzQc1ZPkWp3ixWcM+0CE4qlPnUwZF21A8IqnECFNhl26TevrFD6AVWQnYdKZ1r6UNquf/69Z9IsvQ9r4HodG01PtkjJjYVLR9X+jH+3zPB6AlJokKcIZW7SeiMW+VJZW+2EOUAI/U8DDq0uh9LdGKpQsQY+trH0uwqypkliWiQi0JtQX9/lnIvW1X6/Q0oKdO39s6RxxGj7NE1izH2SK4xSSb/+Wltw2ojy4YHR7ICu7MZdaKFp1qAAXg1ZzcA4bhCPtjh/cIrhtU4Oj6jpedf/crVc7ECaxpXFdRvWyhymUnc3L4mQNgNyYOzOzkGd7DbMGWmaqpHvq2PEYaN5McZxUptlE5i7CkgC1XNrUzUBu8qeA5SOWJ1VNuUVbPFzkJoopsen8WdLZbEHOG0jCgEhA12GgG7Q8WQHdGn/BpfH0DFSZsRBaJj3EF02/NkV5hDqVTuiXJaSDGku9MTmyYwLMJIDdjQXqA6EyvzLMna+l4zHqZ1Nda5rXpmzeL0GFZAtFG20qPlycbqQcwJlKgedUQEou8roHRuFGOp0nIEL4pWYynwRDTcuhsNrf5bWwPeAlZVyBuVcbL9xzofMuLbzgStPLONR6dXzDteCMPbqKYvl5h8/qVDWRS03F7q1ntP19H1BUa6rK/mv1Hw+c/Ayyay614FcVSttRs+bOSW/2WlFIjD4ziUQM+hi6xLNG15LDrFDf3yMfbciYs/3Zyr/uOfzNiw7+ROYmgfzXlVa4PW4PkEZcyJsTk4QN1v0x8eiyRWj0uk1Kj3by2qpK3XwdFL3xms0BY1eFPMWOh8aeZXX+oDQHx2h29j+t16nm8LB2J/geD5ruA3w/HT5PXsjP07azzTQNRdYfi/cHOabedxs8Nrv+33otlthslQ13RsYXcll5dt8HBY70E37p4va2uiyZwsB1IFb5H7fag2SCeFWLXGn3nW9nCoeBPhq+nmtb9vAVqV/KYhYASXHyt2X574iWdnvrDpUDNbrZq3GFBhqLB2FkDOgVzK0+5zgIyBIQNGoApzEUqPmmSHyBii19prMpsJTVlscLTCBIhQCdr3Rb2alarU7NM10YMyvGxGGXOFhBvZg9AS8qLZDqjwgV01krgQ3bhDVazvF1nlE5gYduQgL7MaSAaQkej5QgTcnE+aTplVbPCRXnuQaDRA1P/j+nRvw/Mpvg37sXfDf/78ifetL2O9FqA/HG4RAosHQRRxtNqKFkhKGcUBKCbv9UE/Gpwm7/YBt3+Fo08kpN2dMk1xfKnZmghsMljVqV2diqB7s6hhnN9dQhfkQSv9YZ/kTYYNj5yKxzR/TNrB+mduMWWqC1U8D2aksCjcvPQlzeZWrJfrdNMuMZpqmRHFhX3Ixxs8qsSbZuDhNpdsopJW3z0WcRdofBid1aAU6xtSuCDdJCBvVBHlw/wF2ux0ePXqEcRyx2+31CuGEQe1mmZbWlTpDCUFsx6ViN8t5uTUmnNp5ZACB/z2nZybkmzaLgVYCCFi6SsvmLZb1HBADFVuQpDYWU8rYPXoZ3/mVF8AvfojwlW9UMMoWjIVACJQRodpSDAfUOa2vUnK13yQ0X9JkABQiYlQa1yd88OPfUm93k/IDk2oYRXzhd/4RvPTR56S/c8JunxG7AcNwhe1RLxrRMQid2fSInXi/M42tDCpOMYLWI9gBQqGhqkipc9ZAQmuL7dnyWdtYhXfjC2QsCugI08/QPIrmEZU44k0zYzfVq4dF+wTmuZORifHwLiOOjHsfMELWbnfrXupgNgNNu8k0wk3YymUedoGK5hcQFOPkSmNLU5X22Miqt0fTrDfnDNZi20PMULvxNqIxXPf9TAnm3dTSkPJF6KTfOjVA3/edXvtNSOOEEcBms8F2uy3tOT8/F63JaQIR4eTkxAifW0+oHj0BgATgJaTiOMVtxmW/Z1ITAMxAMht2jNiPYAJ6U6nWdlII5RppockN/3FLpvGZ3v2gwpwztH9lHHPzaxm/zed27akHzO5KbbMurS4t8CFpn8b4uMtrBkwV2sCzcmmeTm1yOm3FUne0a4yJy60W3o4Yvvp1hAd3sfnffkyM0FK7HImo6e+PPx+eQmD6lIQFDuHWLYWAl7/0JWzv3FGtZsfcm0ByMKz1A7u/efqb+m3G/B2OAdPquzY3bvmFZwo/DNbsH6LwGQe6VNOBbM7edrYcitcK8MAcuHFJPZPcpG4qWL9+HCTuOUP3c7XsoCevIgzUq4hikHkp8BkRJojG0MkLL4BixNXDR8gp6XgQiOr41FTWJCc0EjA3fsZNaey6n0Xt5ksAXiFw1FPLa44X1iCr5onXzNETSftd4jZzYm0jc3HJXzaAXjeownoVoErxWnfN1/WHB8Na21o1qOkkBawYdo5LoKKxZMxHziguz435N3tMxeMgowBi2a4EFtCKi2BatBkcgbd2ztNU+zkSqdjoau8u1rZZVWb717pWHiHO5kzNzo8LFsFcrxMYHZEIG4t8hGkuhpNVUDFgR4QEEbWC23jtRN4ESuulXG5hkHpiM6CrqslXDITKf7URNh+AuSUJioywmUBRGImkDMU4TYhB+skM+cauQ9d1iF0UD4tRhJf9MIgRYtVmEGFDr+ZMExCjGiRmdVEf6jwt841QW6x9ZX3G1Yi8FzSsL+GSeo0ux9IugtE0A5rm4EQVLg+kX0wOGzuXwAFThSaV7i8SY20fKgNUt412t2gBODeOhYa6LrS+sGd141s2rFk3fODx6kbXhpV9rry6If5aojVwv+TkhAfoPAUDj588xpPHT/Due++p/aypgBBew8S0OsCMlNDYSWqBdynA5DIYowqjiZK2fLIKPQ4MmY+rAA2uyaUtbX8YbQQAmG0vMvDJgBkCvv8m8Pe+Cvrid4C7j9qZX/aLOg8JplFEUENRbix0djMD0PYASJkxTgldIGy6IA4nQGJ/EAxOCQisfwSKwNULj/Go67Af9phSwjAxxuMt3jkbcXn3BUwvXcC0SPk7jO6qxzQMSJAr2gRGIgO5WBxcQK/0u7GwK3pG4Wzc2n2ZhC6xt6lTFsuiu2j2F7Srol5XY2T0O7mmue8YHIQ3Cgp0UQgwrSeC2CzMEdifQE+UMroR6Ic6f4BqOD2GgK7r1RB7KHPOtMYCBRWiqcwhAYDCypqH7jvk5iY72Y1KOrseKd535452tNcc/8QgZMotEEB2rVHy22xkX4iTHM6YkX0PHpuXUdPEHIYBIQZ0fe/WQyWrhUegAARuQS7YnlmH1q8shj/84fK+rE/Hb/oD07kWcKELbh+Rx27OlahPydO7dXvw3ex3May+mqTSzcMbo71WjTniAswUhwANHWtp8HpF/Z5o86NecT1UF391lB/cA/63rwJvvgu89v6Byl9bkcNtXqT289hpcmrnFE+Zjr/MyAg5iGOeILSBj/dIb36IeH6M8PjscPGF/Lb8rPxYprpevHua+LfskIPhKefzWrlz8Mh9LaYuUgtwPm2tF6zOSgaHMKwiqmiEZr77vJgP9nPcbnD22msYLs6xO3+yXpcVInV42Fr6I3FnNOlQ2k8gfOz5uNrvzz43n4dW7Wca6JKwtu39XnjWkNmug6jAVgSpyhgYMGTh3uc+h9NhwPf/3tfErgLjIMglRL8yGs3LlVCYEseMcccI/3uAXxOa6a8KHd7vK6NCqIBFI2QFEuPdzg4KWf1mOV832zxLxL7lzBA7P1m1oKwfPLGw+vg+JncijpKm9FE5HKkn5qSgWS4JVMhmkXtDMM2aOdOn8ROrvYr2+oFmZN+E2c5142IG0qx+IpxwaZq1dx7Hbvk170p3aK/OmGl7F1bAxwboWgyYMTw1vwhga4yhctXzqwyeW2WzTQe9VNrwnQZgiQCc2Zl7Iru+I0BkBbuqAMbmUa4RzUrJLShZ+hiOkVMtP71eEvYZMRD6GNHFiC5E9H2H2HWlbUd67ev8/BLjNAHDXtZxzuIIXKuQs4DZYnuFEWNs7LDIFw80+fnB9WpreUfFW6LlMF/HRaAvGgF+nOfXfdDMEQMc1wI5PGAV7CpeQrnSAc5gg0M16/KeZYHZT7PxtBYKyI/ZWnC0c41hq9hWFTAOq+p//PCD2lm9gGWHDiklfPD+B/jggw/wW1//ung6zDL3+r5Te0YRm81G7MepxsmkNrsEpHJ7R1nXufwuABlMYwcOSPNAmaurrTVUmlWMgLt12KzbUp9c8lrOc+kA+vUfB/3Gj4P/hf836O6jVVvZZrbI+iyYcXq1fwTVFJN5STJvs8BhU84YUsbVfkAXCLztQTGKtzoeUQwREhA70dKKIeLxW+/hCd7HfhiQshpR7yI+OtripZdfwutvvCEaEzng5LffwPbqGMN+D86MKWTVegpiF4yiXBVfm+DSoQBnUOCqMVs+213WTLavdCYMvCAT9ks3EWIkdFGN7CfGyZOMDYDzVwCKoXgUtHlh2kCAaFrljnD+IpVrtCdPgDtXXLSsDFDYxA5912F7tC2g02i24aakVwZ7ZD1oCWzaWIzI7OYTu0/pi2Ta96VfqBi1Nw2xsNg3ZR2YTSoDJwEgcZLymJo0MQaAAziK9hYAdZJQ147RIzsszayOFBSA7jcb9JtNzddIs62lEJRP4QJ+Ch2Vb80aDAFEFV3Os7XeUnTlvWxPytwC1jMabe0wzWCUefoU1PAa0OdpQnts+vHzIjBiIHAOiOVA0y8XwmI/aZQIdFw8QDbbi9YA5wY8/N23gN99E/iZXwZebYGum7YymeszQOCW3ePtyHmgsB4iVW2vjIzAQQ8gCXy6w/iT3wJ/7zXEJ2dYEGUDuDCbJYauLFCQm8I1gtEnEp6lvJW2HMpmbV5Zkpk8cLA0bj+fJVQtxMOtZRdvHranZ3j1R38UD7/3uwugq+b/fNbrZyl8mlv8mQa6vMbEHFi5Pl37u6ZZI+azJ0XOXUogM9n8+kKfJnxMIcYv2OsEImMA5LpHUgOgpEwplcVftUtqCDHihc9/DnlKAAHD+QUuPvpI813jZZ3gQUsRU166v0U6E1pWMlemd5HrNd1oG2C5jmUbIpkQLtJMYThX+7HOP39WYIbnK1ewXofMwuCKhpqy75owK6ACs7/Kbr6ZYJ2N0cuw63YFsPQCPVWhrPQl/ImoRDIV4+aaAQGm3cOauGmOLpIFj2fSBSoQ5AEGETzkWs9S442aMfIAlmVowM5NgefftW1JmfI9oN6qal/50orgSChAYEqpoFhdqJoC7AaJUBUtuKwfKnZdZHzYOVJbE5Qh2hbsMiUqTCibwALoGKFqzGleOWdMYDDLtZMYR3SqrUAkWl6np6dIOeM4nYCnQf6sq8mdAqvBYAN45vUt4EE2UKggNG4Q6jMGnFOLFUaD0M43ZhHoy8Ss3FLRRp1zRiakliypzD9rX1Okq4fXBCC5fLpos/VFtQPOZY6Rer70tMODczaxfJRGo9NPPrRAWNtVNX59V8v0Mmb7xrV78eATZrib5ewIFVHRDMkJBQwGpN/EW2IuQqnsXaYl48FPXdMqDMPRuxbkT/ChXN0ymsM2D2oa0d4hd43XM8pzQcw0QzU/ctc4Zu2mwOLptBAJrRFJWV1UBk5Bcw4BMjMDMoux99puQGxMBYCy0idgPyb03YRuP+Coj8iRxMYRZyCLplUMBGbJk5OthaB1iMjMuLi8QuieIPQbbLcbdLHH/q33EI57dL9xgrAPmJRmgM0unxieZ87l6rLZOCSFktn6KzhyR7a/wjYvW0h1/4IrQxOyfs/MCAxEAs7uXuELP/G7uP/eGe6/d4ZxTAiccXIekCPQb5SeB2C3Yew26kmRoTSzruGUM3KWq+mxiwgxYNtvCihrhzE5iSfNnCSfvusq3TYARg+YQghIREVban7tlmA0n8sBXaOxciCUbprt1F4bFRlgavkoA3eNL2j3bCpzmULA0fExur7HZrOBeSaNXVc0usj2jEIzrc71sMPWUauJVSqj10+p8fYMONANVO0MFhp2gAGDkbn5HuB/L3n+uiPRMmtC0Rgq8Z6BlN6k0yHwVUt/5EvVdbQ9w+ytAYQ+90g5YxwnJS9Vm9Dzs0ararY6drke5UoUX4fK/3itrzLmAPDNLwP7DXa//+9hevX9lk8ucoHr38LuuLydLLF2CNqBcRRm/cco3jAb+ci1s4BeWqcE4IoZ8e4TXH3ld3D8/ovYPDqTelp/wfiB2w1y6bvbxD04bQ/P52cJa+VUftjzKrcr9+zlV3Dn5VfQHx21eVoOt5aNufmsyZaHUJ5PWk/rTRislMPLueEDEeH43j28/CNfwpMP3sP+yRLwAm5Ytyt5Py9A+/mH9XrdZuieVSPreWhyWfhMA12ATVjArsodIhvX8elzoVafWsqnTfjZCSsIu5zGpcbbVFGf5hmxcMwmhYA7r78O66+LDz/Exf37lTNdCQcn8tpjo4pkG5SL5IXYOfDyFMFOeqp9ivp8viVR89w1s+yT8s4E6WpUfL2NjmbDWAfLnVmAKdGuQaHDlR9gjVNBqRAkggAdBlKVHBdl24ZTAS2pg8wHx8rpekNoLmfWvMiYrllvUWUYNefSb4DZJpHrM8sTkcrcrzOiuGaO1VZ6kNQ9BTNjmmTOD+qBzBpQtcUsP+mfEAhd7KuNrQQZm04Eoy7WMgoTqP2Wy9M6U4hEg66ySX6TVsbQX0FTbpSKIOKFA5a4IZcrqpZX0uteE4AYJ8QQkLseMUZ0vXgg67peRoiBcX+Jcdcyk74v0pREFa4IPS2zTYDT1jowOMxt/lxnD/k5tobq+Gc2b2aMsMSpY+GnkBcK/RSq3z1tqY+aud/KihWQ4tq2AnjVouHpgZ/z7RxvmThfp7Vr+3W6u7lORovaJsGvx0N72dPsbbeO29JTctN8GTXAbPol1WASed40sVrG1a6BcW73Aa+h6UH9uUZHEdRJ7eOZ97hQgQPTBPFgWkFhrCz5op+13SZoStOqVmAdEu0ERcsJAjIFpEpDdZ/qA7AJemGaCJkCmAljFnohtppq2wE7OAmgINpYQ8rYjxO6KHYGi7aVOqtgCDiWQZWW6JwiCohdjzxNuLraA+ECFCNOT0+x3R4Br14hnvV4+dtfAqWoHvEE0AgK1k05gUOA3hBCtDVgHUOqlWRK1uW92+ubNSZrs1BEZoAERDOQy3anGICTsz02X34P00R4/MEdJGKEzDi5lL2s3+iYEZBOGVedaStx8eYntdE9mAVI7aN4Ijw6PhGaGoPuM1O5zme0KEZhw8ckBwqy10OARuVHOBh9BZbCfJ3jc5DLx2xpd5mSdV/2gIH9JiogRS2PirZW9YQKXae5HJpst9vyZ1qWFKO0l+VArtApV1euo1/WqtkB9e+KRpfZbigtbrWarZ/Noc2MXM+CxjlIy+bPtea21D+mKLDQVLqustR+J9Td0vZAa7MdmBKR8zxK6DoGpUo3ywqrJy2rZVbQynEpZd9ydM8NTZXVXP9+5/PA734Ow5vfxf7V95q21nz9zKBCxy1P/4k52MWMLRGOPNhoNMKela4mcFCeQOkcIahTBFnbl2DQ2Tno7BzxqsfmyWmh/R9z6J8hHJ7Fzz+725Q1jyN06OSFF3HvrbeExz7EC946cPPJPH9+3SgYL7VsS6Wh7Xxt827D0Z072J6dYX/+BLvHj29V++vCcx7NTzQ8RwzqBxI+40CXUFKTdX4v3D5QCHjp7bexOT1FsBNFZT78lY2qul0NqM6J+tqcP753D2/85E+AlMl89L3vY39+fqA2BzSwFpUGwk8T4tsB04sfl2DOszZhtwrrxWaEI6bknpdKeaGtEdCr7RDhAchsu6NqglSmQBhljcu1rCrQcTGyzDDbWCjMgwcnQxGCuW7+TuD3vEhpXcPoSvqCk1hr7SpEdKrfqP0lEkWHdj+hhkHnUgYKo22nwsXwcAETWmigjoTVGco0V02M+UZVNC/KlaE5eMBISeqTCTjuOrx4JAz60dERjo+O1Ih7VwRNzgnjMGB3dYWrywvsrnYYxxFBxzuqopFTBixAnRifFgE1A0CW8TH7QijCuHlAhAqHaoCXxHuXeEME+P/P3p8+S7Ykd2LYzyPOybxbrW/t1ysaDaCBxnAfgpREGTmkZKSZRMpkJvEb/znJpI802RhJo4wmiiPKJBrJGQ6m0QAajUHvjbe/Wu6SeU6E64Mv4XHy5K1b1dXLe0KU3crMs8Ti4eFbeLhDxlUqwKWC5hnTH/2PmP74Gep//W8AP38XxFWMc0k8NOQYiinEYuQrXFWxzwCJgnVycoL756ce1DsqaoZrkVY0r7sWJyteXxq3l4YzDoroAjtX8QCqCEWPvrby+LC9Y+LEQdVrGob78rjAHWMYmhFF1q+N//gxtX5sUaiKbdPiyUgnjwl3h/2+XQD81RVZ8ofelrYOb+XbzEAtSJSQc8Jmk1DmRvctRpe0Q35N3m2G+N6I2ifP6Gm5Hsc12sPtCONq97R+SuRrtecDphUCZpRhliNyQmwsgYLUptqq4xZVAP/o3wS++wegf+//AXrwDDkniYeUMzLPIBSJ+5Qz0rgFpYxKAwoDc2HMtQXNZ65ILN5c24HAZcJ8fYmpAte7GQRCGRISFxBYg6NDPHuqrP+BBiRKmDX4d5rlGOQ8Ey6f73C9+wT37k84PT2Vv7rB+f2HIEp4+umnTtdIs2VyyshC2JBAQBIvLyIgZcX0TKi2SRPmRoAX4q8ZP7RVyOpBpoqox73U6UyU5YQnEjbqITdTRUVBSoMYD0sRgyQBJzfAOGeU2o7nAUC2rITDgO2QcfLGIDG91KDHzBr3UI/UhiD3RAixrdq6dg9Dru55UsEYUlJj73LhEMQaaMaO6N0mxrPkuE7da0sauTQUyEcQsgnIQ8YAMbgaPwcISRMbpJx9igwG281GnlVeVyoANuU3oRIj67yVWv1vrkWyKaqXOgNdX2z1RNoevZviZhUzQRwIuSUMsLGx0aMmz/Rrn3pFwy3cv51aX5ORBDou1yZCHhKoCr7MNGM/qQHJZHtqY3WsXNq8qB2RjYYCa7PzpL2thxxkwl+BIjcDeGKyMcRTdOAB3/zJN3F2feZxTG0TIqXsg3HZqBKenj3Hk/d+AE6y2/zsy+/j+o1PMOaEsYx464ffQC5bb/fzq5K+Hnw+f/wI7/7e7+P00aPX0J/j0FzK8q8D8q8CgV/GA+m3k4J8ccrn3NBlCiTg6o3pHUdx/ZdbCJ3SHzsRn3ndxPoVFtDxs9CMNIggdnL/Prb37rnSCjSG09zFTU4PSmMUzBddtGbzZoOz7cYNR1effIp5t5ObKvD1HYMLdCsH39q43gXomwAmhKBHvap4a+nkvB5GxrijN5c/ZUp6ELDMeLScHordDzfdcKWxsny3iyPc9Ul/zXaKta4QHN7nh+QYlR1TtJn0ZbEsLoyE/lrfbIxkRr9eKTSjhRyTiEcpHChAHiBrsSniS3S0eyZ4m1BpmZ9MOXTBXf+L0HSDGNvusD3GDk+gHdOMAYKXc+b6cQI2RNhsNjg7O8XF+QXOzs6w2YwYhrZ7Pc8Tri8vQVxRy4QyT2CeZZefoRnY2vya3EjqHkCQI0aJIcGeaw04toQTtUo6eBoStba4Sva28uYHKI+AevLHst7KjFwJlDMICXKKrilrxGZgZM3uyJLpMY/YbAZX+HPOvvt7qxFA67Z5NdyJc798Pnpl0OJYwdqxk3ivGQt0fhfPor/tBgXTgQ2ua8Vw22ONBWEebPvofb9kehb9MENeUNrjOJaCfmeUa0tpMSZudORY6WATBhyNjMCibX2Uj7+35HO01okjfGjt8sE0KFJ7XBUSg0dUoJaw8/Xi/Czg0eJ5hDG3o2BCe0ptWQrt+W4KlvTMwSLr9GCawpR3hpplLQx0htSfvQP69AGGf/Mc6WyHjEEUspFAlXzThChhyAMoZ3DeIDOQKiFXMXZB13fmipSAkzGhTHvUaQ9GwVQL9mJ5QGaJDSUmIACFPaQBUkYmMaJJP9XjlwnTXFHngjzuAErIwwYjVwzDBhgTOCWgVjGoayZfAUvCoLyjeviJtjly4Mkb5sJxIBiZgyTjf/G4k81OsjdIg9JTO3aeCCjGw6rEFstzwlAItQq9sVPbQ5aNgw0GjOOIcROCrVeJxyneDJLl1hIcJD3Lbgp4FByaqKU8jOW4ZbDJKN4arA4NP9UrkSyKlcxAFl5erIdjxfiqATgny7hLjgNSpV1r73XrF5KUwOvlnlcICKp7xlmCJMMVgwn7WKlt4qHxEQNUlNni0bk43rYJuOQjjS4s+XKEX+dJdQcp9BisyWSaME67fvfSP+u12fpIDRYpmWEnSXIIpVvstBBOyw7H16/JJkMaKIVfmkfZYellMLrZIl2dgU93QGqZSNdOnKx9v61UADvHjyZunTy9j4tn993QZckaTE4BNJsnA4UJc2mbu0SE6eIa0/kl5kyYpw3mX+wx7DNA40EfVgvHj2NjudsYX0e5vR/6zB1gTomQxxGbszOcPX6Ecbu99fm2of2Cp255JNLDQPaOiB+HOLkuugR5YgU69j0NGXkcMc/TOnz44MsvVaJedfSZo032tPf/X8rn2tBVSvWdGlN2jtmYbrv3RSy37Y48eO89XLz1FpIG7rViZ+dLaQF4U0pIOfkxjaQGjmYPMWNP9KowwtDaf/S1r+HhV74CAjBdX+P9v/xLDVx/yLiWrvJeJbnuE4LCNiHMdkrNoJEo3SokRG8Tq2scR/+bpgm1VoyD7GLX0NdEEqh22u9R5ll3gwib0Y59tR2tyiLsEg0izLBeM+EQQC0VM1dUDVRreC1ZAVkFa0ZBcdh4gNZ6SIQtDo2JnbZL1XvaiJA4DGH3GQ13Usg+aQbLpnTEienFoBlZ56i6EGsZxUwIteM/Fu+E0YLeLz2CYlpwm85+1xlOtbvLDIfd8p712rKQu5MHS8yUhw/u49GjR3j06JHjyPXVFab9Hs8vLzHPE/Y315j3e8zTHokY45DFeGLzwhYkWSGk8UyQB4g/luDUrFloqnkf6Hgadpjdj1FqEeGTCGVfMZfq0I/TMk0Trq+vsGGN3cKCE/uyBw8ZORNm9dLabDbiKVYJoISSqwrAFTdcwHPSoN/i4RWF/xLWsM3Xfr/X2EnFPcBMoC6leNBwIvIg9jXgiig7bTRRQWlz23NpojjfTemy4z4pkXjSKK6ZQcPxCc0YKf0pAJrhW9aheNy1e9Gaae8ywITCRfA1ZhUFw4N8w7KltbE0Q4+ONxiLoyHmgKK9Jua22g/gsL3Y7uJZ/9k9spyrO/ZVJg6brQSwLkUCfkdvlpyTt2b0XBSTxS6Ij499yhii8URlsBnzFkNdfl/eX+BjXT4Qh7X4vfpk6EuaM77y/W9j+4srpJxw+fhTfPC7/xxlnlHmGXk3S2D17QzKA/LmVD7HDYbNFifjBicnJxjGASfjgEyExDP2u2s8O9lid/UcN5fPcXkz4bIWjBpncNSY9tmOVJN4PGUqsLOERBmAHHuukNhTu13FPF9jmoEdA88ud9hMW2zPLrDfXePq8jlonoFacP/8DNs0YjuIZ9B+nuToNwibccCQB7gXWAfnYwp0u5tAyBqQ3zw5jH9JLDP17uOKjIqRAIwZY07YTQAs1qXPSR+vshk0m0ffzc0O19c3rR/U5lv4gmZwDDPPrPcGXd8WQG2BJFyBAglhEL3AUsoqlzUvYKBfz3JQlVxWkOOHAHM5XONri17rqmrgTClpoO6ifKDPbNrNhQIhJ/FgnpVvzPPsvp6smydDzrLsdWOhMjCMI0aN81WZwdPk8oTR8Kry0X6/R+WKrEkEAMjR2GC8ML7gxyFX+nywnpVomBEn0kgHMoCEEJCf1zeBOjiHtpbexh7z704Eoy9mMyVCMLLHxEHCSQaNsTAMg3vQGc+iLLEJSeNgLmUpk7sXLXffLeN2vLfGx+//t/8eyj/9Ezz7j/5TlMefrBq47mRkuYW3xI1aUt4ejVpWuxtKw5BySpp5VYxhWbN16zkAlHHCB9/5C5xfPsD5j75zSz+cM8bR4XCSfxtLNDY12mWfwlMlWPs7v//7uPfggb2lzwQjtMOYD4Zucpiz4hXZzza3l/KFsc3GPldwRg20tHgnjss12M7YBecBsTz8yldw8dZb+Nn3/gzl2VO3RZgOUDUMwK24ud5T3I4Xnxe8+c2Xz7WhK5alrL+kiT3yv2Ib6NFqTcHsGv8ts6zlccSw3WJzdobx5GSRTa8txM67ApEkwBcxs55xV4bXw0Z+RSI0aJYea2N77x7mmxvsr69VN7zl6OKRy77L7oLCutDSqjlktAfPuDGnwWLZAdvd65gk8wLnDCqHuLjOtLUdDvB05b1HKcNjIY4rhieCK/JyDIRaJknrFTcjnxi6UlDyg/GzM3ZRYD5SkymPse7K7WiHG6sCkzPiv3zG6uyOuTG74dL5Iin+LcCn/AttvhrTagaywMTst+5uOvAhxoxpmiRjmI7z+uoa0ywGpDLPKNMeZZ7U8GGZwdpOp/S/NExw7q3r5pDHHy0Ck4bn9hkFjAiLUkWRGNiCOsNh6fPDFUWTThCb8bqCk2QaAtmxRHTZp0xgPC6AtMDgXbe4Cdpm8Fq+K0axdahYLDobpCkd4QnvX+xb9AZjcDeOaCxvGWY5tLHujWg4CP9U6qIKxZrUsvQ2iAZa6wNW+9GErlCZfPQL8sVi0cIgtSyWEdPaj8+vemwt+mPA6nnjMc754hKPkxueR2P4+ogb/Ll98W7Gawc8g4/woZfp/gJO8derSATEhPHmBJtB1tXN+bMQXkCoS2WgTjOoAgV7pGzrXGA06VGyTISagIHUaIDmZcOVATUGZ1OUK1CSbnwQABTPlEgElwEkSxnpUXehn3kqGOqM/TQjlRF53CCXgpQH3QSpKJUxF0mMwSReVmCgJqghqhHJHsODWcDJdu8RY/0ymk7aN/NRkR7LfI3bHc4fXOLq+QDe5TBPkpBH2ugP6y/lCPFsaxtYCiYxurlhsJtZmDeoBE2HOzP3fEyHycHzCc1LtjdsRVxucBJjE/vRtCbHHcLWPM7X5CTSQRzIMPrbTgdYPwE5DkxE4CR9KWDfCIFu7HGoQ/ogeEskhsFkvNNigFlyntBvQDwxqbRYQJ4NeIV2dR5UbrwSWrXcgOUeUN1E8ko/7lqWxq3u3oK/UpyfY+M4VoydqDxLaLhGBPeWXfauIaT+jlUSHcC1BeswEC3rDB6b0HlmBl3eRyojUh3l2hEZ/ag3XITTHfQuBuPy9BKpZJxenYI4HZ09Cv0Wubr1z6aCiTGf3GDiDfb3nqOMK15dPateXF6O61U4xa+3+JJYjicnjKenyGswWK1I31sdcluPa/hmcuBqhSvF9adbumMbIU2mOV4tg5E3G1BK2J6fo5aC+ekTX4+N37y4UPj/WDmqN76w3F3mej3vtXKn9XibbPkayufa0HVMIfq7sl7OHj/Gm7/zO0BMmbwo5n8SlVYzQqyQmE7bXiqQSyXYrg8nJ3j3D/8Qzz/6CB98//t3Xqqx5fXLL14sdEBODpm3xaHqjDt0twW73qYQTofjMvAVIMocwg5Tp9Sio2feLzs6oNK0K392H4TNRo66mAec7C6I95Z56Zgg2rxqxEgyTRNKUQ8yZ2qyi9IMVP2uqGX9YoSjlMFw4EMyIdxgEpgddbDuBcyoaCxhbEqFvS/1thddUPGam8I8DGIOKnNBmXf4+OMP8dlnn+BnKWOaJ4nVEgwnKRE2Q26ZB1VpyinLkQDF9ZLggUxBpPCprpRZiN3lsThQj4MRkyK8QVa/3wGDMU0zbnY7jKUgM6OwGipqRSnkQenlErsRjQhAqRruhVAAzGhKQwzWTQGHYiD6zWaDUooHIa61umJjXmBmBDNFpBNiUkLKwQi1+OyF2t7TUDx8bEzU1evp5EMcOJ9PShatutG0o+vd+mNKsJoSKcyP/lt9m9mzVR3KaBykMeqv+wS9enl5WvvLltfT4qrOtFL/4YZDfLLNydIA1tpZ72uvFK+8tyqE971caU7fbTd9pRvfASSOlClJtaKWijrPnuRB0JUk2PtcUHezGjSyv0w5AylhyPJ3/+IUXGbsry8x728w7yeJ3wVBtZmBqbbhkmZxpWkC1clv5EGy3uVB+Aw0cDwlAtIMqhOeXd0AtMHji4cYRvHO291cYd7dYDftsL/ZY573GFPCxXaDISUgZ8xg1DIDw7hYC9Vn0v6qH5FqB8lsg8eOwJkQw9x78REDb7z7AR689QF+/N1v4pP3HyETPDMiA0CV2D2UMwbKmowlij+9d2uoXhV6iY2WILyUUo9EDDU0BnqfqNGCuqB9tTaDlfFRkx2MFkuMdsN3dO+3kxCp2zxoM44Wj9PqW8RaLKVgyIM8noEyTbi5kViV8zy5p9lmM2rsruxG1apHOnPHO4wmCyNPGtB/GIaQUVXjUZaCUmcAzUOWlX+DgXme1TN/I16bdUYnK0Hkp8TtOH1loyVNVo0bcQYbx8ROvvVZ9CDndy4r9KRV7NPxwhKrWNrlZIOFVp4Ws1RKhMSWLVqgKk3zejIZl0W7nwffD14L7y1DGdSckFMC53xQhxlxZZ7uphivyeuuz4DxF1/7C5zenOFf/It/Cdtp2/fdDHBmhI2Do/ijH9t07wof/It/jvTsG3jro7de2Me/K7+58nKSyXF5DgAoJbz5u9/C7vI5fvw//RPUaf8aevh35XWVz7WhyxhXFAoPOcYaKq8/E2nn0friT3qBLf51WSlfQbk5e/Sos6gzM07v3xeBF7cwCg7MYGHA8ntQAS54dMV2pMsLwT8wDgCemSe22541RSQotG8D6Q0CHi77ewcY0/LnraxYhaC+f30chheVdWUrCpvREJgIB4Jk64lIyimpwuJGoGjo0kHaPa9DsukQegYPFkGm1ALzmEB8hqvHE+nGHo2eEUeAYDggFDcEtOdcMDJYcIAI9/dEFmUfQwU3GwL1Sq9VbUcQo+FDFJomRUa4Lnf+h6wSTK1gAm6KpJknasfvTnJCJsnAlnwQ8kcw4W2hpFp/XTirYDUEQneN2KzIAWmiPEXxj0JyBG20U+6D0jVPE96tH+I+P8DP+U3s0Y4gtOOk7bfhQWWWHXOSXV7z0mCwH+Egj6nSFD4zJFJKsKSTlRm1FAmgrYqK1eFjCPUzM6gWgBpcDKfh4w8KItuRnN7YYUKxw9Zv2n9xDbZnu/qFyIWZCNUwAGL1hOuwrE24NujTxRT6E2CwoJOubkV8cEtHwFwziIUevig+JIX2eHk9vG9eZRzqP0r/Ip1cKvqmNL88C/MaYg/vWk3vVWc8y+hSoFkr7x3yh8WTxwARLVavyPojthEB5w+f4eT8Cnkofn2zO8HDD9/B5ckzXJ8+U/uN/QtB+FF9YTKgsfoATglXxOA6o+x3qErfCKILm+mgdoYu+dPD2Q0IVZXiEmi0Zg1k2qNUws+2P8aD+hD5+YAESU2QhhEjEWoiCcrPDE5KbyAG9mqZDakqbMmYitIKQ2U3bcEzb4eNjrYpID03D1cJgU4StGeoQGLkDGSSGIYZaDxP6SEqgROBNMIXc4sB2TYn3Ie2m0ubYTfqLEqp1Q0wRBQCg1tGgJaUJq5LSi3ofb+5aH81kr1GT4nCej3sz9KTP352/FvrbLyd3SglmZQJOSttDcw70mavN2SJZpV9Sjh54F5sSp9c1iEjhxrIvhTfRIFeJ0VwAh14RbU+rNP7VprHEiIdWVnyPiZ3++nhyhQy/8X+xCkJqHJ046TLxhy/x+ri2OSz5VExj035K2C/dwAOl+Mo4MexMCnrcOw370IpA7Y/+D3kpw8wffNvwGnpEd7XcZey5nEuMgujpIKS5r7ygMfG/zrevhjdIXdk1Fyw31/h+QcfYrq6Dvwf6LFkjQMv770y4/yVljX9JuWMkwcPcXLvXtCB8cq88C5tWiNh+rCKsEEnsbV6Z8jesf8pJ+TNBhdvvond1SWun3x21xZe3IVXtiUcoRl3qm5FPnpNc/nrLp9rQ9ereth80QulhEdf/SpO7t/vFaNjz7vw0iuItstF0UgiD8rHgrsvFcVIdDgoTj3pOSxrygb9ASH9zwm0AzC/Av1c0j4XjKIwqsamsIPpu40mIC5XOvV1v6hPKpersaSlCzf3/BRw2lS75P0NwuYS900A6YQIiVlxsMusnlalFvHqKYeGOSIgt+Qz7dOF56MktAtLtNDh3SCyLFGZcqOV3kvUAs+H5HqxSVGewrxJyUHJ6Z/v+kbAaPEodIDPJSAKgIJSRMk4HTOGpEc9tSICN0MlQb25muhTKQKuosIMQ9qhClem4HW2fnXrIAptVTNjwnY47W2pa5om7Pgaf1T+Cl+pN/jP8CfY8an0oVLzPlClBIBmICNgZlBKEh+FJIi00YFSi7fhsCZRztQhQa5pFjKgBa0vGs/FfkeFqGp2I2YGz7PEC9Npa2syY1nsiIzgVVBAWD23iMFpgcCOBE3oXxpu223GcnGYjiXPmDdecpyIBpalokIg9apMoU+h7q5Xsc32XDfOl+WBL/POq9R/WMkv+b4W6uFx0EowYgVVz/8/5h24Kswtr61Id2ujovA/KKgqvZ670vdjdQFvfe0XuP/Wp4jC/Nmz+zh7fh9/++V/jssvP+tQzowDXU8ZEjmd2nHAaXcplqw6Kw3TQNVmSGfWGE6tPxIOTTJgGu2oDKAQihlZyGLYVfBuD9A1Pr3/3+Ph9Zugn57ifHuKexdnONmcYBwS6n4DLjN4vweYMUMpIAOsdJd4Bh0Q/ka8I+9wxi6UUWi31kmAJgKR59zgVTVeZakY1OttzM04KCc6qxq7khy7JEZxPtq0rJwHDEMv4VDAiSYvHG6dlWkGSDIai5EmHs8Vw1otM5ir029mFs+lYdDlGniEzjXXEJtJeRV7rKIj/HhN1unAHzYHzDiXNAuf0nXznBVZYmh03D154LG2LDB/5UnWawHMe7xUOQ65GeWIUMoZGUBKlhHTElUImqOKR3NKud8YWo7xFoqyNOwJK2i8ooGh0Zi1919Yoo3klyxm2O37E3jF8hoAy+iUNOYUVVkXpbMGLCliQOTbQo6slKXhqbs3jTj/f/4DlLffx2df/Sl4W/y5OC5ZPq/Ol6JB2HhDx28XG0jt28p4ll8ULNdPnuCDv/orjEPGkI/Rri9WyeOIN7/5TQzb7a3z89K627F6DkWzFz5v7d/9ndDbO7w4bEa8+bu/i8tPPsH10ycv18G/K7+y8jk3dJliD4hQsGKH8B15E3Cpe1/KAZs6Knza60L/Dxpbre2XLrcslvH0FPfefrvvRkpCbLRPxxSmY03Vqkpid/RsRdlbamN2vdPDuL8HM3b0loeeDd+Fia0LGMeuacUrnGnxCImwllPCvC4BBqHntq4Fw2AUZkyyVCUZIA2aL9cjSN17ZjmGZXNLY6bhKFm8rXXj4pAzaEwYUvY+SdyUijLPmOeVHbVQgesV9mntLjzd+92WngcefCcLAN7imnBgjbTQeC24rgUatkC/zeC6Er9ChWt2+kEijBDcM8iPNlA75ltzwp4Ie7b4KHCDH+lc5cqOZuIoUEVhrNETR+5XG5kC1o+Bdoz1cJEtj1Icrk1RNPY8SZBgjbcVleGlx2atVb0C5D4p3pVqMdcabbCe+/FQaFawFHd5W6BbooScNfC83rZjrfMsfZznCbXaURGFTDRe1BpA0QiMG6Wp0XbzSiSSrE++m39QIm9gmAfgi7YGiHxyAr0zfxqd/Ujr4gz5hUNlyUdmGTgP2vRhNzBwwI+jymnAFeoVte4JfZ+O/I4Y13XsQCnoHjiA/ZIeHPTSJdIlf10Z2nIc3HtvIdBGPlZv6Ngvw7tlTg43DdaI77FH7N7F409x8cZTbM6v0DaUyPtoeJaoeckwNU8gQCPJH3RADyWpF1WcWTHaqAGG0RJ0AGoESxIkHAZCxXOTv8xARUnXnVZQgefpCn95/3s4Pdni3sUW715/GY+u3kCqRY7xTpKJcQZjTAllkCOCOZPUF5i3rQynEcywDQqnPjoPVfu0BnPDE/PMIhAevvsxxrNrXP7oPfD1CC4JBdXnlGtVlzBymi6bMgmUxQgo8QvNL65v1c1snmHaOsO+MdCOBjZDXRwAUcI4WtZjOf5tR8iN9wHq/cUt+2I0hJlHTu99TOGzz0Bta2cZd7GWYgDokpWklCQpiSbusHpTSqBxlPrUk3CeZ+cV1eaQDFsZ0zxLOyzewrYBeyDzkKGDbPQQEW5ubpATqYdxkx1cjuBeprCxRxppCY5k/o/TFyzqOTQPKX+yubeYchRkXl5Kw4vfa4TDxrAwCK0+b+90t8wjXWNv1ioZPtfE30CplpLJyzgerBkLvZ5nFzj9R/8LTF/6OXZ/9Gcur4SGXlubU97jh1/6GwxVkuM8vHyIt5+8fcgnO7FT14TTvZWN+feA9O8Q8DcAfnHnLob+vfw7r6UcMPk1qnns3vEnj933vyWrX5EZjok3/bz2unvTRRuPO1RkVitdjOOXm5C7v80rP++G46s66RHZ69Y2V+s+emfx65gM+pstn3NDVzi2dWtZkmS9uoYXQYlZ3OlqWX3ieIW/sjJst3j45S93WWWsvKq7Y/Ru6JVqvX/0RaxOhSs2MMEwMBF3jVipC3ABxurp/3rFZUG+jpamjqvgEd5KegxgeYwQ2u+lUte7cK+MgY70ifp3l0cOsDBGIGQcbH2Oc4RmdLEOEnynmwLi2tGIYRwwDANONlsRcCCGhmmasLtBZ+g64A1Bt162EUPn3bYkul14/72A/cp6dMXbrQwaZ4IktpMJ8A4btDocZfSfpJQm5Cx9qElaICJXIKwU/Ztn8YLIEsgKfmqOGaRHL8DAyIx7YV7srwVstXEFY/LBGmq9jzi7FPQ72sRAmQuICXWWYPPsZjVFJ4u1Bcs8BlisKbGdCGbWTKi1DxpfitSTNL4LM6MmhaVOrih72Wm07a6nrB6SLO1OU/bA9FWzvc5FAvzX0CaYUfxQlSECtUxqqcHGDXfJ0ptXMK+5AirsEZWSu1KRvg7tkM8WKZxNIF5OqQV8bhf62rrnF7KDC9nsIrdLgW2n2hHdvx+htFqpvm/PLH+vvRueWRrmnE4uBM3Fq/qD44fyiMP2KNQXr657CZjBabHuuR/N6xTJQnOxiVWF8bZaCMD54yd46+s/d8W71WeVCfGMx9AAO+6mxq+lbOQdlEyDvbFVvE+bkTHwbRLv4wqJm5UWfDchgdjoLiBHs23NMUoFLtM1Pr3/Vzg5ybi42IBuRgzXFxhJfZVmMXRNpWAzqGFrHJDSIOMK1K/j9lx1LVVdD4GOhpXks87t3f6alAdvf4qzR0/x8w/exbTPerSJUKvRCNbkKE2hSnqcPeeshnfpqW20tIOV6D6lbfaLgyYMYDQvrJi5jyD0M6WEYRFfMyVaqbccjJHQGyuM58Y/W1N2z96PXv3mNe18RPt1cnKCRAlZszyLwann7SlnFDNYFTG4mlHNWkgBvkXjhQJtvLYUHF46nqqoME1yJG2/32McMvKQm9zhuES6jCLkKIyZXcZgHasbXZYGpTBHSyXhNvP5UnZcM3L58cZA0/VlJf0Gt2ZkP3gWYcMh8h39tLlPiVBDApZGuxb9pMbtDsYU4HfbvWP6CV2e4fS/+xPQt7+Hm2//WTia2Qa+NHDdxeC1DHsAAFOe8NN3f+L3v/bB1/HW07cRwRdAuOC3q63Ix7sAfRugHR0auhbv/dbYBQ7wIty6SydN6OFDnveyuuiCxRzZLGuz058iWug87a2X7MNyDb3E+0YGXov+fyAR9nfvANtftYGrv/46xvx6y+fa0BXLMXyKluC74Nxdn/uiFtslNWWRK7ejPyvPUiP96884PA8XwMm9e3j329/Gs48+xPOPPmpMPz76ZSD9CaE+6Fs+oITL76HQ4p9dXTbWjivmLrj2elmM2h9d7vihg5ALjCwCsxBDcQ1qsT1YdrlZPVNCe6a7sFZmRhSX7UPXmIG5SoDuNx7fw+npKR4+fKBBWjXIa87YDLKbJQHKC/a7PT744AP84hc/bwxfx1OZD4a9NHTxgstZXw3G8h43RU1uuDCcF0ZG9+jqppolDrgK2skMKrEv5omk73JfmwqsVY8BVn3fcJ/BXFBKE2iyen2pJUjnUjyQesVRYlzMDDzVds2vjgGcgpEsm5dDKIyPm/AevSkrJ4/F0p5bzLuWb/3Tx/id7z/Gg2mDiWfw2PDC1ndTyDQejq7zueixRIixcwL7UZpOESAW1EUDC8OCIoe4bpB5EoFcPOEMC3IeQJRVoZUBzVUMXUV3/Cf9rKWgy2pGi2D41oeAs368htYM900xIACImwXRXVW/HqcGd2MYrnKvGiD6wm4l01fIzKN0e4barpLlz8P3fJRBoVv7HY93MNCM/m3RrzLOY/y04wtacYO4zovSSC935MvupbMARG/yXim/DN/vFuLdRWIiS6BA4Fpx9vAp3vzqz3FycQ1bm5E2CL2Vjj786B2cXF7gg/d+jKt7T6QLbgQgiGvtksYonTKyG3hmrTb3/RgkHhUhgeRYohuVhO4mFq/V6B2k7rL6nZGGjPsXG9lQSMDPH/0Mn118hvd+9g2cXZ0jzTOIGanOGPYJN7liHArGlLHZbuW4mnqMilFEvZcyt3UV5IJmXLK4gu24tCXhcE/aCGISr6Eh/ImRPcAjJ1CSTMUgOaZNJEfy4rFs9yIgdk84593BAMamHKZDmp/kPDmybhR4ApnBPFlTo2s2jkVGY0e0MIbK3DYJjhoNXrwgzMMrQWLUDMOA7XaLYZSjitM0qVeXoUKIDwmJv1WZdVzWqsyv2MoyhrGAIUe+uTCGIcSehR2FZzmJqyjAk8Dh6vIa282AdLJVPkFIqcXuMiNuoxcrRpqFUSYee6P4LDWQcVhjr7Xw4jstPg+eDXxstSIXJmH7iokAJPGGNH8le8ebCPzglxnnMRnbjxd2BotfrWJGRPj40Uf4Z6d/ii//7Zfx+LPHTZi4dUmQyAvkEtId+PNdOcRvf6FEePS1r2F7fnH3TIuvoZis1xt6Foz44J2wqey6yG1tvNo8bc8v8M63v42rTz7B8w8/fKU6/q68vvIFMXTxgXIdCXlv7LoNcY3JhSvBgNFV271Gq7dcYfhlyxFmkIYBaXjNU2hKtu9Y9SpD9yDiDskt5MIMAwtlcdhuMWy32F9f4eqzz9AFd7I2LgD6fQIVAvZLbWJFcbnrzgMFJtvNt8WbWHh0rVTrHkcrqHfQs7ADZMTZ3fRZYn8QWa4bdkOXCRdrGBb09aPDrGro2p6c4OLiHI8fP8ZmsxHlQRWGrC5YpYhxYT+OePp0IwqY91l3bqsJ5wGUnaGLELdz+OALVCBQJqNttx1ktCMT0RbgWbXC/1FhAzzQsU2L4Zthzaos6JYRUQqFTohiFI2IgHolec9NWYpGrr72CriCJDMr908idLgBs1tJHL/oUINCY158UQGGjpkZePTBKb72l/exeTOhnM0Yxz022GBSpdW9Dcw6pAKv1K1B/Cs0nhdcmZDsa/J8SsGTkCHCnrqSRNRsbuNCf2ttGXMlWHHLGEZESFUU6pnIY3gBy0yfMlBOTdHTSz396oxbhwslGsVoYcT1OdagwaaaOk4xBzyltephBgEZXFQ6+nV0IFAFZCVYbMNg7IqfYaF0bvwrPGuNli+Wpiv84P7YYts1DYGvmVsA/BXaS+DDsbXqG1x4uT6P7PjfymbW5rcnkgdP0OLHEf7xos0vey3lAkotG6IrvuHZWnLnJSmbKgyMM04urnH/rU/ReXKFGqLHzWZ/gjwNGN4a2jMMgNSI3tWhs8jB5E7Gf1oH12dQ1zSbISEeJNSnDDcCvpvnptGEcRwBYlRUPNs+xeXmGS7SG2DOyFSQGBgLoVJFrcKPpsyoecAAQuaERECGxWI0j85g7KID6iNjVo+sCsuP28eSrDWhFjn2XsqAhIRMLUA3qS4LmAdXQs4DzNDFqpEf84Q/amRW+mtsoMNWEs+m6OXcPLh6D9Wo8LFmJmx9oAP85bhuD0qQOI7IFgd1aefNazelhLIpoCTZQM0zzQ3YkeeZYTouGKBtPOaM5BsdUfBY9gEdS6UiRxhzkjmVO3bks29nCcvDsQVPZ1MoDkqUe5a85NXL4YkKXWvGcyLhjATbx9I2tRYV+cOG3+7ZZ/X3qxz9sDqJJXZ42Uh7pjMY9p8N55Svlox0fQre7IFh8odX2eyKIXKt3OZtBgDX22vsTnd449M3Ihj7MbhcGRWaQ9MWEQEbAKcE7BhcFg/cCT9eExK99qI4mDLSkHH64CG2FxfdcXd56gX9N7nxJdpcvXNnPbvRnePr+FXrbiVvRpy/8Qbm3Q4wQ9ed6nlxf1q/brl38OXoE3eq76Xeu/sQfm3lc23oMiauv7AO4cgJfgtn4BXLsN3i7d///RcG/nu1wqjcgkcftRIcvAVRjqgZF/26C+Hkz1i59867OHv0GB//6Ie4efJkvW7uv/fqy1pHVkrg226u0LGJwUauJUrdMSwTCFzRs/+iUO99W2gMwVghXkuaKz6cJa969CJpgGrqeogQFN9FAf2fFax9bCcK/4MYw0jYbiWtex4ySi24vrrC1dUlpv0eV9fXmOcJu+sbzPOM3X4PrkU9DXSoHv8ouWBqcLEjK1ABSRj6YhK6dOpN8CbPUtiUzGSp7BV21Q1+rU3YEUFjrEkzUwEwJc+Pyrqgh2YM0b951u+lSKBiLs1YRr1CPuSWLKAyYy4eOtnnxv4M1avZLn2GGGyByPVJXh4jQny+4QLDjsSZYiQKTYIcO1ra+okI+2nC9uY5/u3N/4RP00P8I/4OKhNKZeREahgz/FOQFvG+qgDmmUE1YRwLPCC0wiDrX2fsAkNCvlHnOUHEDtCUktoV+6MEKSVZewlgaDr6WjGOI4rGcqlFsoHKn8VNqZg1JkvKWXb3i2TMZGaklL1vAToAqHPiqu5FyR77DcTgSuJt4cay27xYdW3yLQKSEkenYWvPBZprxixTADqjV4BhZ/ByTadvQ2jXEX6hyi8t+ui/uYmtS2PXap2s6v1KMMf2SuMv7akmjNZjMPR+rDT7G1AOiITEvfX1X+Dhux91jKFBXtbbRz96D5/+4m044wGwOb/Ge9/+PsbNXhXNjor70d+cssaQzPjbN/8G77/5Q+w3OxDIQke5kcT+Oh5lOBW8soB1XGY9mg3IcaYKodcR6MyShKJyFQeySMdKGz9NMy53e4l7mDVmXyJ8/+3vYXxrwHZIuHf1AL/7w+8AyEBK0JD2mK5nEGb1+iEMefCYf1kDoGcdZ9KEGqTEVzIL6zjTAIIkWWnrV+jvxz99Bx//+F2AWejj7lQSjyQCV5KYRfpO1iODw2YEKGEuEtdyv58DbV5A1OYibOg4FTFH7k4JV4pvvFE/K0uay3nWttyA1GQqm+d0ZJ273BGD1KOXf0B2PJE8UHxSVx+h7S1Oo9GAUgpurm9cXjGv8SlPqKVKzK4iCXBKLc2gEnDUvHUrz+JxngjjZkQeshi6AAzDqP0WHrNPk2AKs45b5jgl8TIrteL6+hrDIN5wwzD6sc84bmlfNnRsg8WC/kc6RGFO7B3pcxRSV0F/WBZT9CLa1fupKh+wuTfDcqCfXX/W0IHbg7aV0/DGZNRGlX0jcFFJ44jUXT/Wgfb0Ycfs3uZHX8ej//N/gut/5X/A9b/23690/uXK2tHFeG/5afgZpWqE76syQERmAOnvE9LfI/B/TuCf/Pr50q+6PPzKl3Hx5pvIm+1RnHdP6mA0bgIj37JWOHwu8ar9HRqmIxsymtqxpvhCkGluGehvQKb4u/L6yufe0NXvWN1GzU2pxMEzDcGXilBbHC4Q0vIJHK4gaozhdZTliMbTU4ynp9icnb1WV1EzULUdLO5g3DFZ5kUwelNYeiNX07RaZKIlRcmjeKalEA/pgEmvFOHpd4QyGSMPSoT3ow2kuUsvlcY1liwVH+zlRKXaqaj+xwrniCOhYtt5I+9fy2633MuSR8Wb0WG7KDmLMl/KjP1+h8vLSxdwr6+uMO33uL65wjzP2N/cYJ4L9vsJw5AxjNnrXArRJouzjofCM6tZChbXTNCPsUDcrENA9LykgI+NMQbNg+Cwaf4HCDCJwmGo2/A01qc3TG6UbERCN1oEJvs/Cr9NUHSs4l72tM9iGiZLH5ty1OpanUwEIZOczcv4Q/fjOq2loMwTHtTnmGgE9OhfMsON4c5CajMaUBl+1MQyL9rgTOFxRc3XPzflQOkJO41u8xDHY0IoU5s/91yw44lEKCETKlFx41S/E93qPvDoYhz0pZsr5q5fACRzI7PP1XqcEe7qamDitrajMuDdWXjMxmWyqPrA2LX4XJZo7OqOMB2jmfGebUho8zbWpWGNG+BWBX9ynrugXd5UWEPdL75FOu1bWIdDYNwvYCa9R9wLmlu0nXLB5uwGFi797N41Ti+ufQ4tYLESKTCA9MZnGj2pUad0doXprQ9AnDDenNrIfAjGv1JK4LFgf7bD/uIK0/kV/FihvsOgIKfoXCn+9zGssL6Z3oh+oKYKm4QOP9meZ+5Q11vW9VZZ4+blpORCsro+T1fIBGyHjDoSnmyeYkTGqPyOmLHZnSDXAZnFeFMYyDUhV8kEmYj0WKMZuqDJKRhshi6KSU4k7uD++kRRrOLm+QVurs4avariZWceXYlI91aM0Bm/aeujBWY/FBLduBUMXUtkMzysNa43SUxBakm1bLSWKKiGnZROSTd55QXKW0c3dAIrqgRK1w0nDjGbOhoe1pzzizbz7tkVvXWNjxsuH8LAln3YWKTm0QZEA1w9CDNh/RO5R4P0h7GacbD6UdsGK/MqW/KNIBZ0c9o6LfeiHHgnL5A1grks3NNxHYm+HjY7Ag5EmnxQWRM8FkOy+ab+RuxukPdc7zIKsYJnx1DP3+8EpCaXCd1g0G6LfPMm0tXZMej80mXNs4+IcLO5wfPz59hebpFLzPbcjhzbr3Vg6eeF/m1eirH8RkrsYZRhu2cWv4fNBuPpWVs3QAefV2s99oJXPpd9unt7bOuJm0frrSSy6+G6jnVbyeOIzfk5ym6HOs8v+faRfhyM92V6tQa/V3tv+e5vM4Z/AQxdgC2C25h6b3x5hbbwcuj0qyqUEt783d/FycUFKOcXv/CSxZS5ZebF/qHgqRHImjEo72swelkdlZvhxp6xdqPydzsJWleCVhfaEaPBcVwIXldBoTXhgL3PRxjcLau9Mwat3tVjEUTIwQCknVgwVbbLS9nF7xMBm80IIsJHH30IZqAUlpMctXlO5cF0FT0yUoFkwS6sHx3gKLR/SPwp00piht5QasKRjTFRU4g6RqmwN6+jTo+1Lob6pHITBH0vaaUX8v+gbklZ3ZkEP3U3WIX0qrvQtRYwq5cWwYP6m2IFw1tuCiTH5lkcmZ7WggTChQTCgOtPHbSCYtSmtClO+o4m6Gs4YEJjssxXO9RaMM1nmFFQuKAQAVADkikqYPCoa1TjaRHL95kklkpmFs83wA1ZKWdQrRp8nlvbHIJWQ4/gILvSZskzykKhoVqRUF3oTUQYxo3Amwi1iJfGPM2YZ/kzJdoMp4VqZ5CqmmEuGglJAyab4K6Uz3EtrvkKAImbW/4ta7ztKPYKUrfu4/t3UHSsXoNRNMaZkuPHxNQgsjTYNU/T3pt20Xk1buDArf+wTSkv4om21g6ObXFTbOzBdrS9tdUbKo+X23brmxX48H6jGfKR8pqCuHy4vXL24Apf+3vfx5Cr0OxUu1hv3YaGUrbd3//HePrWzxTbSAwkYHyQK9755B18+2/+sMGLQ2u6di4fPcH73/4B9mWHoQ7OLQ09i67nypotTvm54bPRqwh+CjAw4sOqxtbQF+E37PaeCtnwyv6q+ZaFrLlEqNYfJAAZs7iBoUwzuFZkAJ/wNT548yMMiTBm0icTfu/H/zIeXL8piUZIPKokYYwfRNOpYeQk0Eg6xpws7iZhUA+wPCTsL0/w4z/9A5QpA2DUQpqIsudro2YDLCVjLhVzKajzJHEdKQOUJGtsKXJMbhgwjDInbc22JDeU4poJxioijMOAyuweq3NQjMZhEE+yITfjzHJtY0W+eIHgWi2rIxkcyRmq8QEzEAJNnqvcaKytPfOAKiUh5YIRoyd0IZKjq1QruFSJc0aDe0wRJYWT8BGRU5pnLRFhM25AiUJ2XmCj7dZSUeYCVg/x7fYEw5Cx3Z4AVeas9VUAU0pRA6ICo/M610srWR4bXY+yic9AA/0aU/ev1DflloXjcyW3ufsej7G3ul5g5IoCI2tvSBMAEDe6wNweMYnc+UyDVUO5A0kwDCi8H3vVs5nQ17gWVwDxKyqGIz997yf4+ds/x3f+4o9x//kDI7/9CHV4R1SMrjQ99YtV1uZGMIx/5RO3ogIuftPxpXCkvqOi0SvO3fmbb+L8jTfw8V//9d/F6voNls+5oasJ3sJwbjN2NW+uA1nA9B/qn9er3RW69YlbK/yly/biApuzM4zb7Z1icy0Z7XEjS3zJlLTwLyhUzfuk3QsNHihHvkOnda/1wao4uX8fRITds2fgsSD9DoG/wp0X3Yto57HbvSCgHyvgOPBOivUGJZGOVRD6GQWAg10Ow12rzTQNNwSoymApDNkjpcAsKU0QUNf5aNDxMVJnCUl6XM0MMwBEoNQu2LEYO37mO9ChzqYz82J1AGBVc4gWa4XDY73QFZ87ECb0XUsXvxSdYt9MuZF6mhdWNHCEzh+04i2bTsis2a/QDGoEz9DYK/Hcv7sYk59OUQWlcnvf1kdHXxZAcTnYlKfwgK+xheJKlFAqA7Mcw9jUPb6OX+ApLvBxfbSIb3Uwk4EO9EYHu0eU1DvM7q8vCfHUIve+qgzPTrk0YvjudLjWCRlk2TUTBgyebt5hwwCVZTAMNIVS60vBBa6tt+TjQMQbbnSvQ+O1cS7eXT5HvtYj3QxfNR7YscLLSWajLovFgTZ/hsvW9Frfqb2kFwSpeIEXUVWy+6u99X7aWjmkTZ3wT+i8Ek0PXIfiHUtc76Gdg8eo/7KWwfhAhcsV9x4/wem9S2y2kuGzwbDRBwKwHyZ8cv9T8QwEcHnxBHV7A6eedlwLwPXZFT588wNvkXXDgQBkSjgbBuwunmOiPSrNPq9OEQhqvHaKD6baKWVgdqsY9dMUlHj4MUjGYjopfA/gbRtAzctZNi8AMz8x5Ni01cwB7gxgykWMYlpLAuGj0w9xRTvkRBjmEQ+ePxYvLt0gScEYw3osMRNQzQjMjKQxv8CE6ycPcfP8BE+fTGJ0oTachpxZ9Xk9GqlHogE1DvEMKjMo2fE3eKB481yKxoAI20b3GR4kH0DZ3YC5HUsExNCSU8ZmMypflkkptYD1iJ3FtIybh2ZIqeAuoUPj6aR8qtGNg2Nb9hwi/ewRZU3GNPLmGRm1nmEYQLWioDhcPWA+wcdgXlcevxPNmE8gjUHWjGxdtkvtTtIYauM4Sirl3GcOjoWZQ6zQ5N7O5rEcNz7Mq6/jDTBTkxCxzsvNAdOhQn8dh/c6quo8ZylYwFv2t6jJZV2VUYY4wMnFhkmkuqzbzsEjv21ON+re5OVe6lsIMtYVaNWhe7R4p8Fx+OgtbL/3R5i/8jPUB09flRuszntsP/7VrFmq0xEvHjP4rZaVUx4v7p2/+9tQ1vWsdnE8PcX2/Bzj6cn6s686Sa9cjje4ptcz0Dbj41K7Rb57lWKbumsyxW+6/DJ2yF+n8fl1lM+1oSsqFHcy4nzOy/0vfQn33n77V9qGCbWu2JogsjRo6cMHLt7MC8KiO2gLwagXAoQxPHjvPXAp+NvvfQ/TvSuk/w2Bt1DBODTLr4MQ9fjSCQzRmIWeKC6NAp3gvyhLY5e9L8p+teRVnunPFFGilnnQg85WbsapTlGOn4w2BPky+72sGYeSs+F5niXgrwrWtuu93W4hu6rFd6I7yKlGWl3wq52GtAyUG4CMJmbZZLp7FCyWVhfThxCO3aATGAV2cikqO627DI7w4YB3CxnU+mbXaxVjDFOBZkDHMEp7wyDHbqa5GnKIcMmtmgYr10NBEO+IuRjdCpkXg5xDAQ+W6GW/fZ3ataWiqgLbPM2oEA+B8/QM/xb+FH9N7+H/hQeOh1GTDeqn1s/uMRXjuYgiYIHiNZg2ANbA0x7PCwZPOS4pcbUoXI/RS9v1SCdcyUnN42AYBoiDWPJ7zBJ8eJ5m7Kkdl7J6zHvAlJiUmiI2jCNSarjSKSrcPAuEni0F5vbZaGGvkYjyQa6cANTBulWGfsK7W0ee5V4ZjApRP471el+mePeOWTXXes3HvMi4/7p8ZMl3Xqoc0yyXj7VGCWKsWI6LVp7fnOzx1T/6CcaTHQBN2lHrokWZh6vtc3zvd/4Mcyp2NRj5JGaVlWcPn+EvHvy5G01rEYNG5YoRhLfGEUPKGOYBpcyotfgaEBoq8apA1DY+2I4YyR8zY38TjB+tt/LJhmuR1+hT4mblL1BtxjJL2KD5ECUBBzejPqUka7K0HIamCGRTxJXOTMVoPuOvH/0A0GbPL+/jW+//Sxh5wJAJOROGnDAMGTklsAaRR5IVVgsAlkCMtcyY9gn//H/4Bm6en4LwVNZ+Tsg5tQyuRMhpFKOHeiRtRqVVE2OuM+oMMCWkPCCPI3JO2JClttV1brKpwoFgHrgytlqLHC2vQkevbq7A3DyJh2GQxDGbDU5PTpDVqFZrwfXNtXt9bTYSC+tgc05hWUPWwxjUXqZQJsfoqiTiIY/TZeso0jboXHo7QQaPvN/iXA3DgEQJ2+1WsiymWZ9vz5DyjHEcwVyFl4N6eqa2BTHytfF0BkbFq5wyhizwkwQGYjyrtWLWjZ+48WFtxeORZtyz54q6u1fd+XKZV8GUKB/XQxb07cAL6y7lReSsiUwvTeqJzLgW1ryPj+E7od6G/QsG/oPxxJ70Ri75brJCL+GY/Gd84+Qv/xAnf/VtPPvf/ae4efC9lxzZYVnzEF7Om5wyaLF61+G5Pn9ffE0UOHv0CG/8zu8A+CVY9C9dgmJ55+dX5KgXvvUbG+DflddUPueGLj1iBhIFi+A7mUdL8IShyBnQFix1/zUkJ6wv6p6UI2idL7dAjjHJ5i0hgkSt1YXf5vVjbMqEDo1pY0IlwVlrb5zqDSVSUwLXijLPkIDXzZDBGhPCMhHFcR90/4ChGHNsPDNRI1dEpvebgsMqRWvf9J59NsJlwhZ3Gy29Szk3RVl/y7FMEWJylqw8tRYkIpycbHF1damKhMW7aDBuigCpAF9B3DIpUrKg7dGQkkAs6axBQEVpQyUxHEhcED0wQiqYQu8HGJvHUsS+NnZ21BtdMBXIZ59IAChIVDx7XkqMRBVU9zI3Kco2Ab90nIn1mCFJ/0zhJkTjBRDxUvP5eR9sPAnBc2+h/8KNJxyWVJhrtW65zxs3GDRdmbo6HWdszVd9hvo4cdVQn9TxohJKSSjMmDwkC6nBTT33yHBLjupaMxUERkIlmdOiN+KxCJPpWf+znWqPEEemPLL3v8CUU1+J+PE3nmIagW/+6UM8/OQE19cTyszYjANKIlQkzEUFbhXq5mL4LGyhOIoz5mkGQdYFAOxubkQpzUmPULfAvpklgxqq7XULPaJa5fhR8HiReDmMMs/IwwDk3HbNdTQ5JTCRHhcCQC1Ol9nJiNVTDhlpTDgZNr4bX2Y5HgWiQNcYZZ7CTBfknFGS8Qahm3ZEqQnfQC12pIggZ2Vk7iMts2DNRreJNENcNaWSUawOx3tdI6xHRwmCR3aPSBNEtONC7jVruMNG08zDx561LKJVN+d1DhSHBA9arJtoEHSjJRs1C95ttvZ9HNQeNShRb/hb6HzBSGu0yeDQYJECcM2Y7euCW43dLr1qxmyK2kG7pPXpPQaGLIGqzaumLo1XXIEkR2jj0f5n50/x0cMPYR607tFEjJvNDjRkDNpOVeA5bSi1zbFp8zA6UJ3fFAKecUGqjDwzKhdwrThJwBDU5qUC3TwwGoGlkUwscMi3TRibBjPEB5iW2h15TIG2KplWAxv7cHyTCFU9W5vMQSq0qQlOaJ51rLE2gRuAy80NfvLeD3F+eR8PP3kbqQCJCnJmN1oZPU66Xkjp7ZP338HNs3M8mR6g0Oi4TzODinnkKA3Lk26eZJ+ruTLmlBs0kvCkVIuv+axxocDcMlGiZZmtXOSYXZn1SLzkgWQGEipSztiebLAZR2y2Wwx5EEMoF0/EIfLfjASWBClgoJZufgWUgqNiXZOeMCsdZAhNJQs+3uOMeMLB51FoWZy3ZNwuCr5Ki9hlRgahEgGJUVlmf0hGdxjEFeCCRAMSAWWeUKvFCVWPLF3i0zTDuKy5SOdhQEoJ0yzMuDy/QWVGHrIc80xm5BXhsttEtHVva9ZpX1s3TvFYNn2reQurrAMK2MwMSAJtq6DjYz0hOQB5uNwbVo59typMvvC3ePmAPNPM7OTXDEMpZSFMLl/0cHBaGoyalOKGVjOGOixCexRwxGED9icORkWNbsklBpJ47kF5a6gtvNbeDZK+doOdnkYiJk9WBYvoVW9+8hbuP7+Pzc0GzCILUJ1BPCkuANC6EnEIdaF9deLK4lH7LzD4HQb/Ewaujc4FEDlPjURvcNk7igkGzF6iDa8uUx+2V/pyoJ8S/BzvwojrlRivJgIHHad2rIuAJHJuoYSKhEpCBwoIhUivJYdhLy9Eo3P7W8rxNoSiXrkui6e0WMsRploX2PmV/5lsE3TjpiMscZXbLzZ+V8OfXDNP0eXW5ysXhQEfXDvy8GLe+W4vvlLpJYUjPfolrKK3eWS+qHyuDV2kO5i2wIjD92NcJFjCVoklYtBx7u7ywbOLqmMbWBDqO5Sld1qcyMh07J5lR5OdJB2JPpg0OKvF6yCGuOGmpF5a1VM+xxG4wlZVGLPdK/eMUCXKuYgt+HAMzwXbJQx6lh3vxcc4/lvgcmfkWulDe0YF58oeMyUew7Mx2W7dIPIsbDdxu92Kaz232D+26ylxSWxCACQCFzuSJuPKlFxwb5CxHXeZr9mlEOmtGLlC1kGIsE4AyDMRUhszLfGi4YYR6YxmvCQQEpvAzRghx0SGFFlBBZXq3l9AALMTe27/66Iw9DNDT+QDNhaGBQmOaNA8ACOhbAITIB4TTRkSQYUcBcj+M4OXPmuKZF+SC2Qc+jgXm2OLtswOJ4NvrcrgoYYujY+ViDBYgHSHjQRwL1U9olhWiCgXYhwps66tiLcmYOpfoojz8hCjKeCsKN6GKf3/ydef4adfeYbHPz7Dg09OcX0zYZ4ZQMY0AJwSSlHlbBjASTzNZEd/gHl7ETMS2OPFnJ1KoOwyz5LVLBMSBlU8dBy8QWLxRiHIpBNYdkhRJXA2m1AqnnylFPcS4AB3g73MRcMTogxK2WPFGLyYMnIWbwhb49NuJ95cEG8I1lgytcxN4UIB14TBjuy6wFNNtfJisBAPiwQUBqUMM+PLvOh5V+tzSvDQf9zWahToWfE+UEVfx+YRxhxj5thab7AH+iNDFvPPjl0xi0LoqS1C3DupM7V62ThpXLSLNcUcBOCwgsMzTMFzMdCC/rhK+3RjerU4Qc1Q4JCxdRE7w+23zQMtPSYbaIV+UDO8iqFEFOcyly5GkIBKv1dGnWuLFVQZT06f4m++/ONe0A5NJ8tRyrJBIIkaRMif1dPQ4B4mo8GDJInFsyobE1SaMJ2UhhIXmS1uSjupUQPU41waqE2VCerVvIyNNgaeau9VOA9pcxF+ExxnvTmbp2D4Wc5952URpyyweQCYN3v87Es/xsMP38Hmw7dk7YFAKM4fre6cM4ZBjF2JBvzsb9/Ds4/eEL5GGmdKMwCK8trwMA8ziNiNIt5dNbInonZsVz2maq0YzRtK62l9UpmtVkxlwjRNQpNqVf4sBqsxE85Pt9hutzg9PZN5YcZeadi0n32+CIxx0I2w4Lnqn4EuCq7rbx27LCw52ZeoGSoOFApbj2x0BWoUsYkip2NEKeCT8tACABnMshkypJbxkbiAuKrcA8zThHku2O12ACAeXjqeaSp6bXCcyCmBhgEntYJSwuXVHihFDV1Kc5kcPrIxnER+C8feGyY2/HRPVJMpOG4i6Jg7mUt4BVdda1FWWyns/wUc79Z9/3nQT2Mvvr76h8hk4EVb1h3nNCb3EKtMaUle5LZ79CtNYGZQVokyyVlhS4oQN9FXhtSXhZ6z1H/iWhZwJoAS5GBznC0bn21m9/yC0PiIAKZ2r5PrM6zjAx5/8hBf+uA9fagCXEE8I3FBZTUZmlfhEDN9sjzvgfVVvvvjCnydwX9egasFbHz8JRhmEgiDw0iSQ2hfD9CJAPWsizJtg0749HHiYJ3HEri904xQgc6DycM6I/6c4H7VDUoxcAEF8l2MXBVMumkQj0R7b5d/WDwDMIvhvo8l2Phvb+wKdcWxGJ9uCzDMh8nmi5XYsS6ldSwH7t0xpFts1L+3CuzlzfWH+ZZ7a0/6r+NT/UplbU2/5iZea/lcG7p+NSWu6t98YWacv/EGLt56G6cPHgCQGDXsngdNsDLZ1D2wqCmMKYvnkWWsIa4grj5aOdqjws8KxvZHYhYw6p5/Cfjd6dG7LZ8gR9+5ho6Rrlz3Y1GkKuyBYvbLFYr641E4rBFAXrwMF8o40tfw6buzMDxpu3b2R5oE6bh91gQ+q8Qa16lU1MnKPOJ8mDBRzUCnu4dRAXP89TG1sTXc9iZbYYJH+fX5iv1tL/Hi7eQ7/sYAKcBElT97RR9JKaFwk/WZWLJ7Ecx80IR89+wyoadiVjexTWWPg3u8mGeOrNsosN4VDZmB/W6HT+cR3y3fxPN8D0/HZ3LcJ8uREt8BB1ywr7W6/aroTvY0T2I8SQnkWbXk6EiZZlSuuLm5aceAUtKjTIpzFp9HNHPNarnorxoPzKCZ1KtJBJokgeHZjLk1yBLc8BO6jlMK2VxHMGcMKemxodFxo9ZZsysaLSx+zIohRq0mdCt2JbFciadfhR0fs6mxv0g1ZPUaFjZlak3BPD6fh++seWLZ7/ie2x8W9ONupSfYYk4OG0NGPDrFZWEmjPTuzqyCe5w/8k5Pt5oHalT4DoYS6mOwe8xUNSSZ0CwZ4sL7p3v89bd+AL54hloLbrY3zivivNSg/ClQ3Bvz0Fssfr+VEHflihm74hPb6J/h6eL5RIR7FtOIVImC4kxqOORT5YonGpF+iXJX3I682DwVQWp6jXSfgav7n+Env/9dPPzwXdz/9C19R25GxbmUiqcfvIVnH72F3fOEeX/l/JxDpWaYTEZnVfeqaPqQcw+u4p2b5Mh226ComHjWo3jsvCIRgXPSuQdUakNOpDlBEnJKuDg9xTAMODnZIiXZDJsmOZ643+1Rih5DNGZrcHNPdTIy6Io/uMf8aEQQiwC5MY65olRqx8mN3DnRgLdjAf4d31xhFKAxNwPiXIoEhFfvTDs2mVLCkEWZz5acJHqtMfvak/6VwEP6zRBADJvb7YBSWmzTNeOdb5xoQPvmyVgDkgk9sKzDHa1FX+La9lYCr7Bl4x26rYQ6eOVaYG4HdNdJmuF/pJu3Nqlez951cmO/yDjLSvTYLVfJAko9nyGEtbww9hldsWcMT5d8yumow4Exz1NL0EDUz4O+Xms7nu1wd1qr88et3c1+g9/96bcw1o2fniAi3Lu8h0RZ+kWyjs6vL/DHf/0v4KNHH+Hnb/8MZjBTH1TZU9ffQljdtU//bxKBLRUi8kMECUMbLUNCZvjwZC5NvmzrfIEtbPrLCnDiNeUVt+NjqFtAgM3FGR5+5SsYTk80OZNDNcgCfrbC/4TUMWy7mliNxrzof2DKd2eB8d2XKGtDP+jP6ykPvvQlnD56hE9//GNM19evte6/Ky8uXwxD150F5iOvN95xpHK8UgNR4XjZ92IZT05w8eYbLiA0YSU5CfX/lSBV/dL6YLvMpO6/JrgumeGx8+guRlknHWC+gyuduuMg0QIvUz+BtJW/w62L/vfLuC46Qz2opS/RbdYYkdyIHy9uNwrb6+qGNRi/0vHnsHT/DiyQ4YKBtOm3Fv2J84Xuz96LcgmzCmne7u3jbu8vxuDXCCoFd4/IrhCFvgT2bXMW0JSZumcWDR35HetsArAJ6o73neCreG3PKk7IUaP2jhldjMFHUEWDYlXlqhSL59WOxNrRVJ8LH4IpYP2B0APUPyBTMrZpU3BzUpD2GZ9OI77PD8Bpg7HcYBwHDEN2z71a1LtgsdMNaLZUNQAgtXVi82pCTq3i/VUrY7MZQz3RY0DOd5jxsyMZAd5uEIqGExU63dPJaQ+ZPHZQWhr7DHDS3ceEGjzIpsl25dp4q3rjkRrYfHVG2qdIY3uSFPoc59JWn9PjqLAsF+BtEp4pNXHxxjr0GUcHirjODqMDDyJHnEMI+q40L+7r5ofznTiubt7DYRwbHpTuO1mK/TG+1dZfN7kRoP3XDmxO8uJnP7CmpJH0yXaHDS5i1BXl3GG22aNc3ODJ448x33uix5l62t0MqO1Ym3XKaItvQq0YJV8kbpBaV5iBiRmz7TIo3+9wbFEGIpynFBJ3wL3AzOAVqWvnHVaDd96iz0tjwjH+vJSJlr+XclOvs8lcTdsdpu2HOLk6x/mzh8glgzh1S6fMQCmEZ5+e4OOf31Mv96nj6e6trR7MPv6Axm5005Lc80UQiAN+mlHEPXFV2aU2/ZAjdMnrFM+zjNOzMww5izeqwqFlMqwougEgfXCMl2dhXkbKLwJdiKgvrDgYQoNSzIDOrz3M/s6h8ix3umNG1nZKwie0YYsDOc+zb36YLJmS+DpG45N4SfYB9HsU4G5N+VpNhGHIXT/XPIz6wj5n1s+I+41ncehLM943Yym7jNlg1xZY5Bu8eNbnZ43mB1rerecjPKIzcnlZrrcFKXT+EOReGJk93Exp7TDCNDXcisbU1oSPhRd9Pzo33fMM3Aygqw1wOou81JG4OA/UjmFiMX8gpJI91MF2v8Ubn76J7dyMyzG+qLdBwGbe4q3P3sE0zvjwjQ9h3juUbXFrCB0QEmdsygaJSZN5VqAwUi7gQQyLDWqHchCzGLoOQOJ8Mjy4YGzRm3gpFx6wwI4v9jR3jW3mccTZ40cAUZOPDVBouo4Z9eSkCrp6W5/N88lkJXt23chFtMQVxjHUkTrWbnIHk15e5/A9fHkBL35RISJsL84xnp3hyc9/3nXlruXYUF7pvZdt/DWUl9HVX+e7Vr4Yhi6gl3a/IEWOnrQA4haXy4oLWgQ/Ly+7n9F13gQgCaBNbMJE9O4BuDLmYsd0QrLwA020laWytKCpx8tSAYllC6T/kJAuCNi8qBLrx4saPF7WvLps19G8UtrOIqmickuvVhRYnSX/5lwtcBHvgepLKnbcitfVjAIw+X9pIGLxplGBm42JAKa6QuVu63LoW9fjNj4351jcj0OBqiyPtnA75sG6r1PRdk9J4pkHPTYKSOR9havVbI7azjPrfm5zhHZUJOj3BpjgUQHMZUavuHm3+p4QqXcTuaBocaNk/ViA2ggJqc/CpFQWg4gZrlywtJ1EBipJ5HvyWppCEyHRlaXUakJ4Av67f/BTjE8+Q/qH/yHKk0e4niqAG+z38ADM+/0ewzhiP88SAPnkBEnv2RQzGIUZ+3mW3XdVBnf7CURyVDAK68wV0zSL19gw6JGoCp71+XEEpawGPBX+VcHhWgCubgioZMdNdU4Sh5hbYfdWF0JvMFAlljKy0UUe9blGS+d5ECOHHu1OlES5LOSCrytYRd6rhT0YsmTr0nVhdDMIYqa0xn5xsmOyZoizQZItaPGm8L7qsyHeWOdl4OeCWz1ctS+WmZUVq25V/qB9NwXnmCKChUTMQTNA37coRAba6AYZF2KDN1RtSirHNbzoQizRSHEgrS+ldu0j6YJmVXqXR/H8NwM1zXjy7/xnmL7yE8zbz8Bzca8/BP9Mo7/tiLHx4lZSxyNezMSWvOoum2jLOWZmTET41I4VE+GUCGdLHuhKet8u2ZH8I31YMyosvQtv6/fSyNUUcMDkmbih8+m7P8ezNz7Cl/7m93D+9FFX1/NPH+AXf/U1lP1Gj8q1MUttuhaoBYA3DyxKFUTsMfWiAQBKr5MeE3ejkxrha2U9rg0kTsrDJDaC81utM5FkIxyGAXnYSLxPkIZVYMxV+SlpZsEUkNvWi8fLap7MLrM1wohoNGEFoMmVce7ciB6qiEeD5K80nDYeprQ2Gok5WbutDTd4qWfwYJ6xtUoykVm9ukrt+mVyazH6G66nnJFSxjhKjL1pmiXwPUsg+qjoGH5ZcpJSJIyHZ4A0WkPU4Vv09Dc6RyCwr//AfaMBwuei0UZHYHvnDmu5K5GWrL6rxE5pW9tqaKaIDh4qN4FIeR7UyFpRST3xhjbHFqR9iseurS4yOuxSEAA0nSMcNcOiH5TM2yl1MGMwHvx//l2U7/59PP3f/kOUNz5e0BXb8NXRUTDgMuSoHAv+fOMX38Sbn7wpcWYrYZw30ldW+BBCv1RudVmB8dZn7+Lh9SNwLSgo+MG3vo/n956qDDBgyFt86flX8fc/+teAELcJpaL+QcHTT5/hz/7su5jnAljMzK6wyi0DjmFF52W7nHXfsDNDYTBeG0DQ5syKZC1P4bdtxLbKc0oYchYxROtiSJwsoSkkdBNoGMdV4/lWP0lEXEHuZdd6waFvggORmS9g1P0tS5CD+fhzRgdtzpd8eEVkOFKOztRL13T3ciD9vOb6vzjlc23oMvYZd1d60trfg1+7Q90LHhWZktfzCoLmy7ybcsbm5ATDZnsgLGrtMFEHpoC74qCKtD/Z+uNH1gJBZwqeXAulwtiREE00AEbBac0EvwIDOyLWe2tQRw/oEUD3mnLR13Xs9zGCd9CZrpJj89DtVPY3/Gz+QsRfNNOERofdi3unL9Oi8ibYR1nJFH/ut2UCTvRz7PssHP4QWUIkyiY4R8NewBEToLp+Go7GSw0PuRtU9BwUoagLp8Ptexynrfh+N91gE+c1vhcgyboG7Ehh7Rvj8JyBjlRZEGOdDJohsU3M0GLH8q0t85ZofLsNzuJIVBXIBvcWioocyeQtJY07lbamnj/cA8MOKZ8COAM0sGo0KuyTxBxLOaPUCsoZAw8t1TvMwwaahADu/VBC1rBolACaV5TA1eDEINKjiXQwMV17ZtxxoxbDDT/2rAHdVllHVxaGhe44BbsPhJZRBUQCp6q2JPHUMQOwj0+VTBN+LSW9GUnMyNqmrB2V6GfJvKFan93TaUmEI5xiX1iPAdhrYUXbnPkaCXX2mxSK16sLb21nNEDVUNUMFLHeQLCcexrsjU0B3a5yv54j7+DYXLx0WGzhslOw0F1ePKrjI6VSqzA3vllRuWC6/wn2Dz+QR4slHiCo6O/rxN6LPNK9qsPvAJ1VKB/3gFrzsjle4pzPprwDmABMBGSbD9g9OpjfnrQvOCA3w4c/fwdeu3z/oD4g0FB7RuqdN3vM4x41a2qH0ESdB+wuzxDxNa5DXykMIGy8MJEoYgQQVTRZwPBFr0E9EBbx48SzQ/oraGCfQFWvD8HMZuhmSIzEpDRFNjWLHldU3hl4uTfl3SYX0iigsbOfSE7inFTjysGgzMvnFCsCaaj6IIU5sk3VYZwwbCZYUGbhA4T99anPK1cGJ22bmmd0DcZ764Jt8K4ZUZuM1ctrZsRKyVJ+NNyKsrSta9+IsDWrBCotvJs777VwrccrdqLWDPkG5dZvG6C932T1JY3yhhYXqf/KDZYLigGj8mu/DfZGA4ngMVq9Lgq9i90zXhybs0W1st5Ffmow8N5GITmsb3f6ZSA/vQe62WJ4XzLP18efavzHHset2VQzTm9OAQ7HTyvj4uoeLq7udU4DMk+6IcsNTmFAPsZxHrEpEqS+ouDe1T1QBsZRvDEv0hkezA/xcHqMZugqYK6oFwWJMx48eISiMUJ3NzfY7/YBfOzGr47ediBem+V+3WPlu8d1s3dp+VxrmA+nT9e5fDNZWPgsHP+b9tA+Afbs6UJrm8B8uMnT1qfBPhr2ooxwXAh4UWl1d9detbpby5I/HOtPfNZ49UodB/KYvbGs47Z2Xljdq5flcF+xgdfhyWXlc23o+qKX7b17+NK3v61BmoO3iDNqQe5aqmb7SLKLVStyljxMpkQw4Bm8TPiyQMUAQLVK7Jvasb/WmV5jQtQJuKc8pmOsCraubLEyWlrcWyF7B3Xw8vcL3lhhxmsCUxSE4g5vWfMhxoJkmIAUhegomDnzjn9w7uRGoEB7o5Bq82+Ck3gLLOAeBG6OblomSKKvtzsK598ai1JRza+HR3BojGtlLk3hI4aGz5JdZ8shFkQMby/2pY1dzAEWeNKMXSso1/EpgsXwWBjqTJjXE5ThRNHqZ0Th6AHEJJ5GxqwpPK+2PccjuZi073aEEbhkYAThYRq0n7yQD3VXVD3eXq7080UpdEwHZ14O83wNIsJud4NhGHA2XUhK+7MzZJKEBrYWamFUAoY8oJQZe/XoIs2gA0DiYkkDmpHUFAoGs7jsSzYzODbIbqsGiLeMhXY0xXbQfV6WAdNlQht+s98HmlLGQWASeiYGNAKw3Z6qgULeG8ZZYzUVx7cyi5cAY9LMaUWNH7N6geixHM1wemAI6H4EmkQBr9D8Mhp8uPttpQXit3cikvSCkuOuKl0ctWEnOkG6jQthTeKN7zWrVPvs3ucgv3HHH7rNqYM1qDDihXK1Wpog7AoPFju0K3U4vJWXLjc3uDIKClDk6NWcdtjtJ+ynuRNJm3Go19lik8mMXIs25jK/fmFTy9oRwt4rinEN4KYSLgg4WXu+NqUoreC1FTsCfdcS+9AbXl+uRENUf715ztpzgK8MRO+d5vHVctPZqjCaTsryknq0iCenZfGTNoecMAwZtci1GQCRGVNsOZDyTwInAlWgTBVPnjyTfqq8R9DnvQ8pBAa346+lk/OE57ZxRYN4NHRbSZndSAWDFEUsNhoE9fxqFaQUv7d4po++9D7e+ebPlAdKffurU/zon/4hpn0Wuknq+ZrMkGlrvdUndEI8wITWLvDD1xEhKdzNOL67uRGepOzTJyisvQgb87atCqfo5daa0wzIhgxsG0BistRw7FKP8XMzwK2QoX4D2P7DwRx1ZW3p6csdawNAbEfzoxle6jcRDpB53e/3SEm8r8XTO2noAZWT1EO7lIJpnvx6zrooTK6K3QoyUPPgSj5HFsDe+iQ4FrwSHU46CmZgAs7+b/8B5rc+wpP/+P8KPt0DES8Cfd3utvijv/hjjNMYNqEIqSjOUDuOTibzLnhdU3maHBw5dALh93/yh6BM2G5GbMYRDx7cw+P7j3D+1n3Nxq1H2LmizgXn5w/w6PHbYsCtFX/1V9/Hj374w4CLIiVWzFjSxWN0MvY6+7F02zwOnlG2cWDrPYX3K8BzkDeiMK0NWAIPFzVU/vLkXP5ShYSdb3G6CGLITyzB/RNXtMhpS5g3+WVJ1zuaFkSNDh7HRJYXlEb11u7g6N0XljWB4AtWfpuH9sUzdMXFCawso1tedVpgIs6Lnlci+Qqr6q7vWsDjuMxMYG4pnAEYQ/XYDyZlWNDZUId+ydkyclXJ/KTCOy851rLvMoD23X6GTjZ57HhF5rlh73UKXkfgjlEI7p4XmmsdaYR9+caSWax5yzVYLqnsoguL3T3rzEsteuq/NMiG3wwXECJlj4za9cxgQOy8qMK4PSNhWC8UWJL8iv1BN78uTS1GKqhD/p1IMj2akcGarMGNw4SwNUXXprQxNRPY+aB5q9G8UywAfFTo+7oCKFdQvulIS9FLbpIFqCbd2cZCKTKhmpLOiVVI2j9GIcJN5e54RRSqqE0kJJX5HTFrQcMEb2qX8j7oTKpQSNafm5sbzVJIGBIwkMSRSTlhu9kCAIZxcNhVjjvxDJoLUohrtPwDNLB80mMzPpHNcOX7p76mw5wAEUlg3luxMAdFsTY6E2S29hy1oxhWb1PcUug3IanCWlN1fG64yB6gl3S+zVxs68uOdgDhSAwCCExJ8fW/WBQ2l3Hs3JYk4tpYwKyjxU4LVto3Zc9gFmj0uihI8eVw30ZyuLiap4N1hbzvy/EuW+q1wnbD5hsN6ncqbqTi3gC0LNM7v8Du0fuoZ5cH7focxH6GPqxx+TW4vEyhNTgs2+DmWXVM1rAuzAzslA71JtMAH1rv83Gvs9vLsf51vzl6Jtp66rnT1f3PAGKcP32EXISSjid73Hv7Y+yen2F/deZrRGoQ4wM3pOlg0X0GlBT7uBj7Lbh6pUZbZAOFQGrISZoZO0evL620UtXA2EInCkrDJ2pefwDcIJTsOLl2yHXOuI5DG72hq8cWB7fyJT92FjvK1oelwb1Hg1j/7nqDZ588cOMjEWHebwBOQck2I3ePJ2Y8tGNUlhm7lOLymHv6peQ4IclC2gZIrRwMcfG0wqFXmHSpHdNal1mP4POCkfYybDsWvfr6MSK1uLbcZ1jCTCmWG/28t0T9M0HYMa9kUPPgahkLzTCVXX6xY6WlVsxz8aRWtc4d/7ckHjW2xRzWc6SMK7zK+ha6b3Niv9N+i+HZfZx8/w/AWzF0bc6usD2/chxOlLCdTrCdNshlaBlVdf22zdJmWDNj1xHRo/ULaCdgmDCUAYkJY95gzBts+QSbdIJx3HjWdE+kkCXT6rjZOLzOzs5xcnLqpwvktEHFzDcLg45cN8804x82FnJMWNvEXvBEE5kWuEneX7ugtC1nnD58gJN79xBl/05nCjSA7NUgzzWPrvAXBY9G2PpOBVxoaMVhLXOYx4j2HYXye9bPm/un4O2I86c3yHOEWP8qHbm+QkXC04eLm4hw+vAh8jDg+smTLg7h3Uu/Wtb7cQeigqMi1msrvw2eXFa+eIauL1JhORokXgLJhbSkwgAj+a5AIsl+lkEwDwGGehmQZB6z7DwptwC7ALDf74FpAt/shFkH4rrmmbDSzbsPKXKR8HvJvNfqXepp7feyA+uSRTQSmeu8lRibZenRZe/eOs4omBoHWaU3SxHxsJ6m/DE8IDy6/zqjQT9iE1rb9a5pNNhZBij5n2AR2iTEiKRyPqzl8FevDDBq2EEi3bk2AYL1WEfxmAhSUrL+mHGrCdn2e7nzv5wPgqG+3KjF6jwOgzU7ZTRU2Q7hcvBMCZQHv9Z2rtpD7S1rRDOe+lMVU2V8hoITAPeIQnxO6jrnMDHc4OUauL1UjXslVANKL+yexDKZS8VcKvbzhJwzrq93GDJhzAnjOEosmTyg1C3G7VaHJrH/5moeWBLzJKWEk22SmCoev6wJwOYlaXGmyCclMH8X8GoTQiP9qNxPqME8rnE2wZEl+YUqUbGIIC34b/0jymqsU/i7MF+R86jK1ywZ0fYT3DBUwkpUHBJDWgJSC24OEOYq8dhqxLEoyFnihkgzuhiNBldVIBewa18bzOxqrXxAI6rDudFKQUV5MR4Zg0ObV753AzlC7mTxcY319nO5LHGZLil8E3Kt/6tVvLCs7ZxbnVf/4j/G5b/03/twLGaRtSfKdVR0pacHgpuuA1679ysq0YvrmFHqGsANAw9weBrPio1JvvdHFdfqXraxXmc7InZg9DIizWbskpkXjGlY8OGXf4w8jfjm9/4V5Cuhy6cPnuLL33mKD/75V/HRj06jCUBKIlW+tLYwFbTANj5ATQZgx+K0OgApFw0m3/yUo/HAsgtGDyiLaSOHSJewMe9oeVbihlL3fkqMrNYQWsFf6631NR5hizszpH2LPMzpgNLmtqqjUqeRCRU3PvvgEZ599EbrYwrQVFisGZSJCOM4Cs8m+EbJPM+YphnjZqPwlHG3oP2y8SL1UksiAvEcJjOomHEgFDtuKbyeUcGSTM+OkHaGmKWvrULJ5MZ4zNG97TswNbCbQYXgcnnzOHw1mtBWxqK5sD4bOY5wB8ZxcFlnHAfJYHly4vHjKjOmaXK5a7PZYBgGPH36DPv9HrNmypz2e/X6Mo9oM36ZDCNtpgQM+dAY4AabzmgXvDX1erp8gAf/xX/k7731jZ/i7W/+yGFo2VMN3pw0RpjHfewA5PJFZ+wKRpTOaMjQcHxG+1W2oywxusYtxs0WJydnIWlEW0ciS+gpkVpx//4j3H/wWI3kcr/UGbty2eSOajHqiht+m0zSZC+wnpbo5Ii1ouZ1bkNLgNMnl7u1omFzgre/9XvIm41eZZh8HtsgKB0Ishm5XFd1Q9j+anhr2T02YQ5LHFmTM6J5aW2sh+8BT7/2GLs3LrD9Jz9GniVMRVsb6++sGbAOu2XPHCoWj7/2Ncw3N/jZP/tnKPs9fnXl1yNXfF7KF8LQdZuxZPVpxYG77DquKdOHz9wu5N1e//GdVjNymyxiCpvEcVChJBFyGrA9OcXZ2bk/bLsxlNVgEwImkx2vIfHmev78OW5urnF9s0NFAZc5LPPjC2ZNrUEYz8HYljqS1r90F759jfaErxc8X9xX9j/u+rdUOKIg2Te0IOpLQ8iyXRXUTTD3eB3GIHo+oYyO+hNEZK01ErocrXiQqCGFaH1ugnAm9VJTJAB/3/6iZ1av4Oi3heFJeB+Lrm/9IjE4me++M3IL4GpyRJWA3B2U2eZJ+961dzhA0ZdNWTIhNPalBQ6OMkyDIZoQqnPmxxQWbTGRHl1scJW5NONDiPkCaPB8PTJGGczojsTuvH4RBu5Rgu/dU2Cvd+JfQbgCgM0e9Cf/I+j9t4F/+h2gZI8hZFiViJswWoGCit1+j5IIcyJM8+zJGbb7vR7f0dhiSYLWksLOaEupDCpVg65GMErcrUoafyvsbNVaYbuIrIjqa1N3En1nMAiOMVMSYOu592iw3XUOwqetFVOMisZp6YydkVZQwjBINsmUbQMhu+dBjCXD1g9mVGINXg2QZcDlpqrbtFIbwMp40NZr/G00JtTZ1WGKmLXTraGO+DSsMZgBHjz4QGamQJoiHYlVLsfinSCF//JV9s/Iz03vcRzrgIPQkb6eg7J2+Qj53pzu8OhLH+HZvSf4+OHHKF/+Bbr4uMtqojYPgDoDocnt3PDvtrXM62OIhqCXNZLdSd4BcAPA9oAygK2tA0e5W/jskb41o07jt2vPHPQz4Pey7Y4fgMFDxcfv/hQnlxd49OGXQDUhZ+D+G88wDD8FQKg14bNfvI15PzpeUiP8oS/DQXsNAPF76A+Jfjd7RrWGlkmN7DnZEap6MF6iovjtb7Z2SNZDYfHoz8noEWEYDpb6SjHYk64jM5JF+SUYFIwXtB7IEXKDNgOlwjdLqC1OocUui6RueW3PrnDv7Q8ddM8+eoyb5xf+O+cBcXttnmcUDU6fa0XOdrd5sBOJZ3AJAeVzbsfwEkNDc1TZO4gri7WrQpXBISabe9K0GXbqZDLrygpt8xXlWpMrVh4NM3RwnRZ4GZ87oA+BZiy9I5sxJPZ5Yc6tVePCSWKfucwYckYeRgDwTXfZ8ErYbjd48803XJ4TQ9eEUks3b3ORJDMleHtZmIIutie4HRmN/4dJYDBAlpilfTz/+ALgLwMgpAQ8/vJH2GwnfV+r4haH7baJiPx4yZhts7EqHoEZbLlk/HFSHq8xzpxGUbubbM0DOW+Qhw1giY2YkZE1twx7vyuzhFIw+bk2fG9hOvSZkAQlykn9H1rHwdienuHh2+86nCOY0jAAeWi0gO3VZhxqXoINdk6jA0CNxhFW1kQsq7ya8PydB9idDJj2ez+NlDRI/mazwbgZYSebTMYxLzlJPCHHSKfzbd9WVK5skH3jK52ykRwrUReT59Iw4MF7X8b+8hLPPvxwpZ21cvjMoXzgSNreOdK19SZfTp5Yr4HuOB7rx6u1uSY/3FY+34YuQ8ooEyzkg4Pf4drtBqplBXfozq31vdp7JtgnohA0k2GBty3Tx8nJCe7dv488jJKuerNVA1cwdKlnWDv6KAQTKUsA6mfPMdcdZp6cON617y4Z0eHurv+Oiggvlz96IvMS5UXdbDS2CafGUI4pDOLNFXfZupqk32G+1kjgel9eMEhlPo3WClKbwCx7IaGWIOG6sAnqaXZorjFkfcKNXE2TjHsuyssbY9Q6nLG6Gzj7s8Xrs4825mboqm4MEIGYu/5FcBjcTJ9ejik8hJRaIOBecel3wTudxZ4Jz3Zq9mKeDX5+/FI/JLSCMFSuxYUB63O1sWaZUzP2EYACwl4BSGCc8QrDCLucx8vK/c0e6V//H4Gffwn83W+Diwlg2h9FLj/yCagn1oQC8e4QLwLp0263QU7i5bXdbJBKQkoVQ24GdKgRvRBhmmZfTzYH5kFpgpqtw1qrK09RQGuzpfD13dSqYGpeX8THBLyGEzZm1vmuLPHRSmkeFCkRkrcJzTaV3NExs8SbyXlAmVXQnyfUWnzHNdJCM74lNGOsjWqpqXaGrSZVwoxPiO/od9L3m2BtGNF+uxId6rNml0YEG3doxGu0/+OV1UfXysKOQQtUX/O6sD726E23tsNGKV+KrzRldnN6g7e/+VPMX/oJrr7xl5KoofQjXcJs6fV2wF9uMfTcqXdhrdxFzLitjWNyyk34voHE7TKFex2nX9ym0d9DHFvvT7fBtPKOwcGyWhKAmgo+efdnOHl+gQcfvY1MCZkS7r/5FPfffApmYJ4GPP/4Iea9eF01PhE8PYlAlCErp2Xi62RJWx/OweDwmWvt0E3QtiIRoSy8d0KTSFnhtICFrzFiUK1q6Goe+gxCzXZMsJe9rBaLFdkMjvKMZfy1h5dstae8xqdJs7eKMccNaM4zbb0qbwlrYnt+g7d/56cw2rK/3uDq6Zm3adl7GRoTT+NzCT01uk+BXsn3qnMSDV2DZs6WgPsSEJ9tQ8fprY0LWlf76zYr9JPRjuAdGqZ6ihjA0s/1QjaJ83XwPTy7NHA1Y1tPy5el44GL/gn9lZorV4F3LeLBNe+RU8YwWvpzxjiOyFk8nU+2I87P72EYRjd02XzFuZv2k1+rtaJUuXZ1deXzVWo04MSYdk2u9L1DKorLgO0IX356jstPz0Eg5IFx/40nGDd7m2CRU83rfBFsvu2RNRnYhTbn0QTTG8DcYh93fwRosgnx8LLNW/Z+GNyNXhAS8jBicEOX4SWLl53JZGbo0szUdeHR5fE6ISd0agkJgmrLKlol/bd70nv8Umacbk/x4Ktfa3gTqYGCrAYcO6QVuh65rRVL0hTpuJEEybi9qAg25HDsNxYCnr17H5ePzjBNk3u3WfbrzWaDzWazaui18Vu8tJSSHFnkPpnEYsjLrr1C6WtKw4iHX/4yrj77DM8//Oil6zz+/HJGVp5YvfxqozrehxcLJq9q4HrVdz/fhq4veBEDl+ya2cKtVdKyEsmuQsqS9nfcbHF+cQ8nJ6cYNptwZIuMvjZlOwQ1ZWKUypjmiqubHTDN4ehiL7C3Gm9ZGqa5rN1S88Fyt96MGMeqW8i6B7UeKmS3lKA0rwndcZdVjIgrcbrQhuhC61JbW+0pL34HQZJbvA1mctnQjE1kAlnoazQ+kVZI/qM1wtYYTDGxIM1tt0GcaEiPGsJdpX1XMwge7PVycwUP8Czx6CKZkU7xl83QxQ4DInS7uAtI+6ef5lu5l01ATcH9XG9bQOKUe9f0tR1R98jRI3cmECz7VSExbQw5mQHUFlvK5XtAZB5IOnoGNXg5jNTTR6RNF45ESdfdy4UCfbysM5qUEign1JQ8o5QrKwZFEx4N3oA+x4oPjOdXNxh2clRhu9ng4uwMw5AxDgO22w3GYcBmM8qxP0pISQTccRgwjiPMq7SqkU+8vdpucwUDlJFM0eA+m2El2S1lYoAqWI9FIGnGJBIDZKoWBF93PdF22Pv13CaJ0bJwUlLtKZHjA3SNSBwZgXTKA/Iwog7qdTBkP9YYd2BbsGMN5qramXjAhZTeIgG29epZPTXzpEzmoSGAKKyGhgkRH27DoM47Rj8F7i0uTlTirOnmJULLsHDrbS0uujBL4aYTtaj8tbXfaG6sL2qUvZLSmr59/VCqeOdbv8DJ+Q1qKbh58Bm+93vfxfXpZd8vq35B7wV/egNUx2PIqY/gqdN4DtmwXlyaQe3ly7phbrkmWpkBPI1ByAMtzMy4uEMA+iVe3fbcgTf4Yp7FsNPgRZRUXlHJgoH5bI+f/f5f4t6zx3j7g6/rtAl+D8T40u//BGXOADOunl7gox+/1/cDFjxa46CitU1hnfFizppRwoxH/QOV4QHd5dmFYqXHeJPLHtTWNTWcJhLPUyKAknh55Vodr1Jqhix7P4GRSDIF23ElIoYygdb3jni0/gdJ0KeD2eQG+7Pnq8iYOi8pMENSmmbEol9HpB5bjFnlD4kLZTRUNnhTIokVVeLRH6mrzBLA+/TkBDlbtLmyRg4CnTMYREOD0uUSjjAaP9K+JzcAh3nCi+TcxTrzZbXwobnj8uYwQda/6PXp41yuPZNfk8mMwq+JBuSawWCJ4ZsSJIUQUEvBTMB+D1zfDKAEbHVDHWAkImzGATwM4M1G5ZcmR/rmJlfZSHNjjBnIqhsvxChW5EikJX5RXnh9s0NZ0uIgq4KBv/3BV5CH2WVWS9zkr0VQm3xI2UUtq8fgW7PwqehkYAL3ZpCjnicnW5ycbHH5+DHo9zLe+7JtPkU34J5iAMCX3nsP9+8/wA//5m/w9KkY5GV99HK0eIVmSRqWFbY6mLgxtd2euszgBh6VRczYU4oYCx98+csYtidgrsjDCEpDwCvTLzhimsOPDT5sFKBJHKJrtJi84SB3YOZtc7UJD5E/2cmlADuG6iLLv4XS4/Dl8Le4DEbNhI9/721sn+/w+G8+As0twc9dSuvxixbs4f3N2Tne/oM/wNUnn+DZBx/cqb0Xl7tKEZ/P8qoGsi+coasXxfFK836LrebXXoQ0kAccjQyNXXCSWATjuMH25BSb7VbOyDOLiy2LWzeDXRCvrjgTaoUbu1KpyCuKvfeH7kwDVoszew6/jQ79UjDvjV23VeVC2vL6qrHrsKY13KBjN2KjHbM4AkSFA4dPO14V2cChAXDdQ6AxdlOMw/tds9SxFOHhQbhjE1oiI1p4zOh7lcK+ocn++l/LwLfo522wWyhjPaxF2Ewawy5mErU2zaib7NgDJ9gRw+XOj8XnMGHMBINGE+R5iThgBhD2LI7GzjVpFLxJavjWeUXAcIwX82wwtyb7CVvHnoAli90w34XWMTS/lfa4w9PGqYJMXC9lmjHP4o00zwU5SYamnDIqV5RxBEhiPXDOSLV5b6WcneFUFu8EMwBFY2liAtt5AI543X5HjycRTFKQX+xa2MUOQqs+IqNNgvusc9GaYsdJj/kitianxczwoPtm7wEBicVQxswoSQL58jz7+JhNKVTCF0NrJQIqedttrGZwlhiKgjIRIdp3o9GhS8dxxgXZoBSFT4d5V0Ojkx3JCbp7pCN277BQE3JX5FBT1g/sksvfbI2HLmPZkSPFlHxIP+49eorzR89Fsbr/CT58/H4Xy7HBYr36Jvi3u8dAQBAPE+IYgvmw3qB7dwrsXcureo4B4p1rB6yXrWYI6mbgaJ/6TZnb+7FU0MMdx4FmRAj9caFEPuum4NmbH2GgEfSRGcLk0ZQY99584kBNmfHZ3xbUksDViDU6T4c4erfLuvHXX9E12XhP51etjza+145IeykAEYNTkk+YweoAqAIHIg+sXLkq75MNFVGMm05p46UqXlkEWXYlrGUs15oNzAbe/bZ57R90D41aJWA3t5kS+powT1kNLASu5PWYEUuMlkWPu5UDWm80dLY4j9z6UjUe5DAMSNky+zahlYGuDuNwnWyFQBM6UDSezGBQyk52Dr20OgwVvA58N9Zpj7O+kwLv9viIi3edInN4n9vviJ/sf4v110Qo5/lJcQ8AKAfDrvEqVDCqei3PqCZHaT2WTXnpGQeY7NjWIqF5KpmBa7/fo9biGR7lCOTsMcCq4lUJc18ZehSyGbuuPnvo+NAMXaQ4aLJGAwTpBlqUgyJ+cNaNMA/RAOf5ZujanWyx224xzI9x+VZBmfbOv4xvp0GyOJtdhwHcu7iHi/MLfPD+B7i6vsY8FTDM06jxJm/T+2WyyJJnG841Q5cYGkuTaUsBEuHBm29jPD93L7G62+s8JtURxDDpmBRkKvF2dW6NqKG4x3346xEvnKyIhsNFaTjLrZmlDHi0pUPuTLQQNxLh+vE56nYA//Aj0Epvj5WlCNauxs+1e1KGzQYXb76JOs+4/Phjv15DSJO7lSPr+mXf+zWUX7cnl5UvnKHri1SMOMmOvxwLSiAMSdzq90WI/DQV7KcJu90eadijgJQxMPbqPryfJk1HXbEZNxjGARvN/EF5QBo2GDdbWbjz7IzNd4l+FePDyg5XuHuXFavy6C1t3P77WImMuhm8lhrW8tsdCjcGtEZTLZuLCBdNCDRZzYirMPHGCAjQwM69YFxKNb6on71wLpW2dOa2M8nejjTmRpd+KDoeNYaowl5Tm1kygdx+6xai7Xl7rJCcNFho9QGYgco8XlIykZI8oLcVck+KIFyqkXe2wJ8qqNaws7g0A9iYxdAFV7xIhTgiTeKQCDRkEbDmGfOsglaVGvWkSIcclSXoe0pZUkArs/e4IyyZuGphPOOKXWVskDAyod8VfNnCmKY9aJrECENApoRoeGlCchD7Q9wrCmCqzNjtJQNTrbZTWHB2usV2HHF2dobNZsTD+/fdAMmQJBojpG0TekuReDZVjyvUWlzYNiEtqRJBCe4NwLUCidTzQrtGdjyqGSqjoCd1pBaAmuDGq1oDnoORNXGAaGQMcHHBz+J5iaebJsgWTQ15GEAANtuNjkuUtWma9AjO7DS1FAnuGwOYV417I0c4EywFe0uW0QTLuOkQ1/1t9DCKYdGWpRPbJGk2BSs8HCt2o0ufn68jPkf7ERRPNwjc0meCr0GKA1gb2Eqzx7dtDqvwo7daD1dGVUukGWW9Cwt4M9q7dr03rvbG7IPGX9BNXoD3ly2v6hUGmOINPAUwArj3S9YHBPiET2kLBwPvPNEYYhAAHIZmCFoqDUsP43tvPMfv/mt/jk9++g4+/uk7zmtzzsoDWx+aHMBeFxuj1FJl+0NpVuNTnvXNLV3BMGJ4pDAVNGuxCzupQ9eAJbXIRBoEs2XRztXigQX5JVlsHK2AAGJWTzDxXkoau1Xob1T6A+9XWjEOkoU3Bdogx6qKw5gHi6k1+LHvq88u8Df/5DuaDCVhdz2GI62ElAb5rll/RRxIGAbShEzSv1KaF5AE9jbYCU3abk9AKclRci7uWds8XaLiVIOhj1xGISIklZlrMR+XgGMuG6Q2nRpywAwES5zsi20OcugP6ya0GTi6jzgFje/YRTIpy3BlsWZaVzzLcEoSvH+/3wtaJIJ58WbFiXHcIOWEYZCjYSenJzg/P8fp6RnGtFHjlq0TM2JYf6CZLUg2DLTf5jGfSGPObUeAgbOTjcuevWGTfZN0tu9q+JrmogkLJszBQFYrY9rP6iFWsN/vsdvdwMJ01RLlHxEGHJxhjkEAkxp+VGY0j2JZWwAlVo8rBlDx7KMH+Of/+E2HCHPFMEx47w//CuN2r16VgYYB+Na3fhdf/sp7+LPvfg9XN1fBiAT4sYDFfMoX3TyjxWa/Gb51z3AYTMZtRqKbDz/G7uNP5bcEGMTF22/h3ntfggXBL3VWD7wZEueq+BFUVo+8WmYNY9ISoUnqI/sz+mZyrB7tpHq7wOKLzn72z77I+HGnDZZb795W+bGa4ry9uPbzN97A9t49qbJWfPiDH2B/efmCt/6uvEz5Yhi6VDhxSzkCDjqjOI5wbRckXjMitBSgWnnRLuZdytKjBBBlbDw5waCZzZpL8mGbDKjnVjyDLEH35lJweXmJaZpxvdNw1wScnTG2AIZxXGHw5AzGBHsHTAefu43xxURmDYa8+M4r11++rL293EGO3y2m0GGh7ls7RuMaN+yIxe2tv6CzpnN2ShA7o462J2EdvHzVk5+YUuweWbFOx3+52GRX84xR4YT7sfsvZ9hB3DEhxwVrFYDsPQtiG3CPqAIuNPa7y03JV0UxaovcBJYI5ziGTmCqzRDS6u/hCWYNvj5gGDKyCnoidA8ivA0J87THtN8BNzvMXH1H2xWSFIRju25GMFOGovKkfSkAZjBm1pgsptBxL8z0k7EQh6l9ZWbwsAe9+SHw7B7w7H73ar/CjKAeNxFUZj9qUEpBmQsSWYB9wjzPEr8ra9bXRCIojxtkyi4Eu9DOIvyKEVJd1m056dESjmNSYbkZ4tWjyydRAL6c+yXwGCxuCCka3S1hRAdcuNcNmz5jgiPpJzu9MANQchsmB8VCcU/HGg1WtvtM1OKX9Th9KLg1g4stioZPbU0caNURPQJA2OlWgIb/i9cbgephFIArH4HWkA02GDTAcV5bzU3dC4rfSmEc0vGD3W3H7AXs1JvK8YsBJsbVySVuttfNgNLAcyjCLtijz2dHtxd9XllbC3RrXwN++LvawOs0fL2oMBDoOgDIsTkiOeJoBuREdgQ/8pVFXWFAd7n/ImOle7wEea+zC8dnQ3t5rDgdr3Fy7wonF9fYX2/kWKMaVl0E8v8OGvYbnSPfEmUpXO/e7Str9Bc+6Z3Mabw8MZIbpq1ZdljZEW7bFErVDMUpGCEYXKoewTMZwuhW4zMR9tZDy7LIJpMawhPppkFF1riO4s0iMlIpGfPuwg1f1YP42JCVzrghJnXylR2njrLuPBffDBNDXfZ+uwwQYon6tQh6xzeFBEXEoVtkksUMKj5IdrmAk4G+x/kC4EbQahk2oxxzy/qO3lyrj3ad7ftvhq7OCKreyZZ0ZhxHJI17lHOWzfFxxMnpCU62W2zGEYkP5eOoLhzAixjMhGqZRvUB39T0F3pZxnk49DQKoZt/iwk2TTNqEY+wWlkNX2Kc2e12GMesISm4xQwrh3JuDMlh8on1A1C8t7XoYT2K/jGmfcLlk5NmXGZGHjNunp2g7C37dpNriYDNaUYeMi7unQPEuNxdBj0UgcDcXly27K4d8jGAwdPs/BMsMkmdZvBkRixG3ozIRMizeO0nNXTlarFoGfMsgeFZj/qKN2mGZVlniOBLVCWphe0wRt0rrBc76dDxdJ2L4WbCeLnDFKwX/rwNLsqXaGul27jwZ5fk+hZe80K917wYQz1Lur+oLg0DNpZBtlZszs/BpWC62bl8uFwPKzUd6dqvWUDAoYz121C+GIYu4FZk+ryVYbPBO3/4hxjHQcK11Iqp7kGUxRuiWABWC5WsxvgqHl4Mwn4/4+r6Gt//q7/G5dUVnj5/hs1mg7PzM7zzzrt49OgRTs/OkfKACg0K6G4owDxP2O12IGjKWd0tylkZxdwHXI2wj8qYCStrZd093BSXJXHuBd9GBHtBqevMglAetMXsLtDDMHiddn0YBpyenuLq6gqzxn6g9rLMQUrIKWlsCBM2gWEY21l4E6qMrtvmTDrsvilSdvZehsFIlJzxNi+PKAgzKoq20XatKwtTzXlQz77Z+YvBxgJwj+PgfYnZcKSq1BFcVyxJdv6IyIXJSsF9fTEPy89eoUng1BRW30NlMwC08/Odssk6Bu7rW5tvBIj1xfBePGw2Y8ajR4/w6NFj3L9/HycnWzkOkRK22y0qV+zrhKdPn+CzTz/BJx9/hMvnzzFp/NNxhBt3LIjoXNRjZ0xqCGkwkLEVgNjnhwl4UgtOQHgjawySakJY6HkQLI+OngB64yPwf/x/AX/vj8D/xb/v7b+o2HrsISVxYm52e792fTPhZjfh+fMb5Jzw7Nkzj911fnaG8/MzzA8KTk9PcXFxrkf+yI2OIqxOGMYBOcvOPDF0t5kwDKNnfZqL7dROYAbONhsAErvFFQiFa5kLKovnQgKBRoO7HEWotWLIVreltC9qcGt0rDeYYbFumxFVjFSWjEDmc7MZQbRt9dSK3c21xD2Z265zE97F0y0FLwbvc2UAxeQ5x2vJfEm+tlt/ATsfmdKoc9q0oxS8sngx0Y6m0eAWDNuGIaYgRJreFDF9Hk0JZ9MSanXBtjXaY58ZCG38Ih2a0qZKYm3Z0hDmH+2R1cUhxkvy+ay14nq4xp9+609xs7lRWh1pVqM9bswKxdeiKibRRHOwSWU85LBbB2WNjb3IWHTX8jIbc2tlroxP0ejyRSKcHiiut5db+XRACVdY1upolcmHJuHpKwv1hHE//NKHuP/2x/jZn/8unnzwuCWcyDLnFrvPjCVW2VIHSURAXihnsYNLHIg8Lq6Bg1EGU3NlsHkpc9MXaV40Ywqcrp+UJTOZBW5ORMjMKGBQZeTESEmD4nMKMX6K9yTr5l9l+T6OgyjB2XxgM/a7HXb7vXsE+QiqjFACznOYi6Z4T9Pkz2/GDfJFdu+Rm91O5amd6OTMbuDIFidpe4KUEm5ubgBST/HS6GmDJlZ/S0gDm4a2ei1+U0qHmCcb7NTZISgRUtgAYQrGFG7Bw7vNxJV1eGCYd9l28RuHxgFSGc2MiikvEvKYds/QTIqDe2xttxucnJ5qzM2Ne/qZAUGMm0UdFAP1Vk/xZmZY4LTyp2Qe6kfkQh+/EtlGyxk0mMfd0Cv3HOZRZaQYm8sCke92e0zThMvLK+z3E66urlHmGbvdXo1mk2/gzbOs/Zit0edNwvxhngtKISQq6j01Y553uL56jiG3OL/zDPzon/2OGr/sZENymHz1Oz/AxeMJf/zHf4QnT5/hf/gn/wS1libXvYiU6o5SSoMYfhe0Mhp7TG6wzMAyqQxGxeWnT3D95DlAkln6nW//IbbnF51cJeukeUZO006OnO4noRt1Rk4ZDEJhQqpAyiNSZvA8g1DUKMZ+ugME3wQ1ndNjSZe2Xh7/1fu4N2b8+A/fwXQyYkhK0yg5L7eNcAuLY6c4jMpSapCxZeCeqPpONAy3TcfjReIqsnuouqMITH8SnHcjIzfcRJipN77xDUy7HX7xZ99DVU/LF0z8ix74tZXfnp705Ytj6NLSKcAv+24vx/9ay/biwj248maDPI5IOYG4udOaVBV1rCDrd9crS5B52c0QRk8pYbebcLPb4ebmBtc3OwzDjP1+wjTJ8SuU6rFz7Px8LGseZf5lKfWtlZUJcqa7fPQlV03ftVv64UrbLcK1Mthj4117k7XutXhT3KinK5+mL6uOoJnfzG+kMSnJ5mJB0ZvyajGCg1ymsoNrwO2YVTVhPcCHzNW9ee6R9tXO6BthjgJS8zDsd10rifEz6dHapc4acaXbIdMxRGZCIDBVhw06pf3Q0OVHQ24ltYf3ut0S/UiJJKPgyRbn56c4OzvBZrNRl+2C6+srlFqwm3e4ub7CNO3BLG74ujGDnC1OlzpvE/QoSVNCvEeGG8EgavcqGDOAG27ZYQxnogLPQL/htxgqAUCuwOkNsNnjthIPKr9oCdoqasKUUig7Lh0MT1WPyez3E4gIm82I05OtGmwEKGZkMo8owwYXVEMK+ejdFo80ttgwdpy1LTQX0iNg9BkTAG1kshsZPYU44D7aPZ++HlrcXVsI8okw5CzB9cnimDVPBVt3satm4BKjT/KxC07ZMULWewsNwPvQC1fNMBTvMcz4FMcohv5guuk62O+gHgDCWqE2p6Tt2PTEvrhRiZsXXT+e2+n3wdBvRWTGyb1LbM9vkEeJpTbnCSXPrS93ZEbN+NiuCYkJSqjxiBcKzk1RPmzn7rG6bqvnlylRCY8ecxPLHs6GogL8an0Q/qCMZKm4heci7tFy4fgT4YMAMURKG8MA8FBx8ei5Hzcsc8bVZ/dRa1N4uvkNiLkqD7icAeeFy8095/9r6BAbDaPscKfjI+F3bFpjZoq/MWmQeHm06JH/lBJqYhBVUDHjuvQ4pWwti1yp4TCICPM0ycbQZsCQM7bjiDxkDGVwucD4d0qajMXHvqb0xWOEmkUZhITkJxWqJiApzGqMqGKA0qRNRBK6g5nBM8Ae58voVsAd6r+0n7pOA+iX82PyG7F5ofX3bIytBZWJXO5yQPizhJWN4YWsfKyerAq/9d82POwoasrkMUzJjssbvlRGHjLGYcRmu8E4DtienGDIWTaB7RgsFoXI1xFcjrffHbTah66bzmOHQh2LobdXuLVBKlt5OAurXnmVGnBYHcOFF0tMOALk6G0ilLng9GQrm8D7GfM0YT9N2O/34iG2n1FqxZ6rJEDYz36U1WRTOX5puMdq6Npjt7vCnLNkSNWxTXvpaUpJsFr5NiXg6UenmPaSVGKaN3jzjbdxff0cT58+XaKBAaBHEKVptTIobNJFDOynrgmiDr/c5DAwo4Jx8+wZmBkn9+8H+V9CRFgCkAEqezGBa0EtktwAlCHyiBiCbS4qehplHTXtx/q0xjdyETno7ONL7M832D86d1yKBlz7bptrVo/J/OJpCpx+eont88Vx0tC1QyMsB3or+G8QND0ueiASIN63yXR5XnyGWSJCGgYMzDh//AjT9TV2z56u8M3XwcuPyQ+vV074bShfOEPX57U8eO89XLz11uJqE6IOUW9FYDK1mgml6BGYpJlTKKMWia3z/PmlEIKUkIcBz549x/X1FXY7ieMzqkBhZ7FrrWFnlA7avq10wjjHr7fF5/rVFxP0Dq9HL6a+/70ivKiM+9+di7oSPInRRJ7m2AKYi9AGUNUjH6kRSIvXUUOdfnQR8HYZWMjy2qbGzHDmpU8QyZEyEEFCLLR4OwQRSqPA1Y4QSO1VBV1QE8xsByONo48bgLuBu5EC3O3QGHxkZ+wwLomBOH7GQiSb6L3it7JiKDAvvZCMGdZmwBiGjLPzE9y7d44HD+7j5OQEOWd88sknuNnd4OmTp5jmPXbTtXshlXlCzoRxUOHSFY7qwctpID0aYgYrhQ8x4AH82/8mFEyV8aQUbJBwgubZ438RSJ2E2auEdutuq+7ua9NwNX5WBm52E1KasNvvcXV1jZwSnjx9hu1mg91uh/PzM7z11pvi2aU7eJWB3X7CNJeWJloNOIXlOPY0T2GdirAgsb7IDfPV4rqhCaBGuiw+WVFjQfNoMgN0D7cOj7EwsLF5Wiye7RQ4ET7lOJDthjLGzUaEyS7pQdhk8LgYdsyCPXaXeZ7ZXJlCKYpNT6ficZBlhqLmWNiPGQYHIh+zCaJLg0MUMHvvJ20zYMqB0mLCYliZjr3WhyWtPv7D18TLlje+8j4evfcBNpsRNy//+kEf5PNIR17CcPZbV1aMSNHIBQDXzLhh4FEmbO5c7aHhrnlvLfgrDqk7L7+zxmNU46zpdE2ROfQyZ2a8880PwPgApRTcPD/F3/zj76DuRx9yVJK6dhfLJ3Dow546jeZGsw+H2Aiq9rhTwSh4NIa++EqKshZb8g/WYNoESrM8M1XZ2NkMXrsE/AZOTk4wDAMuTs5dltjvdtjtdhrzqoKLxFS8OD/F6ekJzk5PQWrEt/hLJu0Nw+Dezcv+RZrLll7ZRk4ir9iG7bSXeLNzMW8bIKWKnFul8zRhLkU9ywibnB2PjGbH+gHyGGDNsG2SlPdMPv2oYahniZ/BEGk8hojci9nioUVvXfu+2Wx6OmpGFJAn1Ikbj4bTm80WQ47nubh7Jr4T40LaHJAeNbXnLMkKLeYiFkJeyPX6v4Olh09cyyn0/dhmdzcHZJssy604CqvDeAw7a2GGbgJK/LMTjZ95/96Ftq0eOIUxzWLkurm+kc+bG8yl4GraYb/f49nTp9jtZlxfq+dhFQ/IIQNjJmQCyrzH7uYKz56SHwMl66XGQBOPSkniY3Pzk794CKJHICKcPbjGH/3rFR9+9DN897vfXYDExtp/mnwzT3MIOwPny4JnCzxv1QHdHDSa8tlPf4bx5ARf+nt/D2kYJD4qMyxtMBFjTFvXIWqtqPPsmiIjiWFLuzRbbFeQGrwO6eTSW3npUU+V8dYP3sfNxQne/1fP25gUfwXmhJqqHK8NsoQkAlHZb654868+wPZyB1L9Oal8aG2vfVqA/thPCyFkCTQsnltKCRUzqC4RPMK/1/LzOOKtb30L10+e4Bff/WcuR3bz9XflzuWLZejqBIPlraDsvUyVjV+t3OsXw6uU7b17OHv4EJvz88N6ggBzSOAXvzoBn+Q8fd3g3v37GLdbDBs5NpNywsXFOU5PTjGMo2RM83P5gaCo0rc02hzAgoN3zR3h8DqNXC+tL1h/uR0z6q39dPTP2mvC5HqQfheMFp2zHVIN/+oEqze6cVNEgwAsSnZfCIDJ63GXD2jEkyiDIEGyLdB7jM8A+w6N2YZ2vIjQ43gzdAVPGUCDwTaPrBJgbEJsywCjzMrjK9mYFf42rgVgXRdeu+6XubtmNzpc655vzC/nJNnDlP3ubm7w6SefqAFLjrU+fy7x7na7nQS4xQQLfC7GQU3tbn3hdrzUhcuUUCxTI8iRxX21FvqRCWkVjInlaPLK6YkADFrwzJW1+84HoH/rvwX+5hvAT7+KtSfXmrhtxXZKlpbC8IQApRYkYlS+wX4/Y7P5FDc31yLYj7KLbLG+KIlRaBjY1wyzHTPWtWOGV5bdVNG/DYYSIN8Fe6Oguqsm+GbG5tpioyB4EoEd/80e44JWqgej7ZW1VizLrQmE0UjmYmoSl33xeOBunZRZju6AxEAuyUmCIhj0CDeEu0DXbgp9YMTcqgSjPRTWxWFswXaEc4GYWkkUwmAwNC0Dbbzdu6aBJEuEYR04xtOOl9cm+CXGL978OS7PL1Hyy2Y+6kvnQYJGP42//raVu8oyRtfXb/TlhsUb9Wxh2Dv0fOyD0B8844rqascPmh72Gzz68F2cPr/feDw3L5Y1xX3pAUnEGDZ7vPX1n6OWdmQLAJ588Bg3z0/tSTUIM7plwDg+10oPzHPS3vN141X0wqfxyjD0Xkla8D3Ex5UkVKOT8ToDVFpQ6KIZ6lKewSDMGiqjlordfsbNzQz3MGcgEWM/zdhsJFZWBpBHGPFXelYxF40HVBu846eDipZDIaQEnJ2dtUQyAjBVLBnjKHE0N5uNH80spWDcbJAgfWwbhVWNf/0xxTWZiJ2OLZXdYNzvZESR68y7yo1Zljwg3W7oIhKDYBy7yzDU96EzVkAMKMa/DH/MQGZGgPY74EiQRZe44+vdxIrOIG14R/2rvJhANFyOsljjt7jF0LWiL9Ca3N3OQRgHpzA+40eyX98vDksakJJ5em0w5IRSTnB+cYZaK/YaYuDqwX3sdntcX++w2+8wTROm/bU8sxfj8bTfYRwSmE9R5ooaZFCTScpsAf9zwI9mgKoo+NlfPkahCe996T18+uknePLkCTyZkx/tUyNaSIggRsrUxq4fDkOTY5ayMNpyaOxYvkjcPbgsQUSSIbqDfUWqAwhFQpCA3Wtb1pHWoWFQKDGIU4d7/XfqPAmZdZPfDMzMGPYTHv7oY9Aonof2l1ICcsbTd+9jHlobBHJmIl2zcPnWeKO5bYm0ThkNtqy8XqvqVRzWJHRNmoGxB+0avi8laGA82eLhV76Km+fPcP3pp/3kHJQlr3ldgtFvtrwOeelzbeiK+zJHDSeBefrPpeFmVbjrX4w7E3c26Cys0mvl9MEDPPra147UQG3xcfgI8hArFWn9k3aGccQGwP0HD3A6zTg9v/AxbbdbjOOIcdyACBpsW/782B0bQVn0KAgCBwIrAFoCHIeISs54jgz7JUus/tapsQfNeNfpbf2Osrt7h92B6Fbr7x1tqhfkpG9B0FAFF7WFRiOiRTwSnW+Oacn7cbqAQGHHJhi7hmHrAhAzt6CtYZ6N2Y7j2M2Jxehw2ARjnym4HM5D2k6GxyszphDjfen1yCfsU+1Ai/EdwvYuaHOw89gJiNYueyDSbKm0SRT7m5sb7Pc7PH36qRsd9nt25SIlIA8QI4Xt5qXUYgmV2gwOpGPLIsxUzeBna6XpN0sF0L7I94mBHQNblkxnvPhznYfUWNFVF/DwnQ/E2FUT8LOv+C0TRfuybsxdK7z4Toq3ye8U7KcCwg5AxdXJFillbLdbXFyc+Rwl9ULdmJGICFyBMkvsB66MUY30qloAalAxYVwMXc3oQgw1SrYMl1xLO56d4N52NgJXF1h5Dbe/KBD113tALD1El/ByenCww66GLlXYRKkTz9pOYQuN2TFlCmuykVlZwzk2Y9LjQsE2GMoXaopFWDdeOzcY2eJthrMOEO0VM3wQATHzqRslQ9W/xlKp4mdv/xxP7z95hRTfVoLx/jX27VdRXmajzp/F3eflmhkZwGl8r1sPvYwQZYrmEdO3+EI5jxnDboM3f/p1pLl58cSOR8PuqhCt8zduJ7z1jZ8eGDjm3Qmm67OOPzejk3fjQKY47GzjpdavbtMN6oG58p79bmDyHS9f7/pEa8dAwaEuhmwAFI0pWDWBDRhpko2FaZa1MM+zGLp2s/vDSRZh1phGtpkqm2usWdlqmcGoKL5pQQ43lzO53xRqCiMp/0w4OztTJX7wWI2ltjirANxjahhGlFKwLbPEM6st62IJCZsOZPQoo0UDjhkWkiVXSZJoRY1qPm5VeMdxdI9kN2xR8/AxmcsV+VVj2jp+tk2B/ncpxTdtlrzI5MRELXtflCFt7TVZrXY4A24eUn1nGqFe31Dsx9OhsOHqYsyLwYZ3+GDsXilRSER2ePKik5dN/kRPiwRvEkbKoJOt8iNpvkJiYO734tF4fXONp0+f4urqEp9+ssduJ0cfuTKm/Q3KZgCqzYcNoMWcsvZmPVkhv9uR4f0+4/rPH+Phu4yv/vFT7G6u8cH778Myf6ecOrxKbuSEZH5OfWxC9gWncn2YjOrPyFFFA1jUV1pc2F6/QKiHkJBTRYUdj67eViQ5pAJ0Yhb5glMnr5qqEf+SeooRuTAHEJB3Ex7+8EPRX4eMcRzd0MWbEVdvnKOOqteSHCGM4hu4oZKjGhmNpA7R2AcR5D02+bhfx/JbnEdyzg47xBqXONymyPFy2J7g0de+hqd/+4tg6Lq99N5fLy+FvAa70mspr3ND8HNt6Irl7l5CvwTwAhLe1dh1rGwvLvDgvfewOT+/W7tBIDosGsPGDFMqIOQ04Pz8AqVWnNVGcM2wNW5GgBnX44hpGMRl0446phgAmBetrXUQWNvJWXvUdppsztYMSK+9GJFHYNyV25G8lZKCEOI6GcS4cZc1uIRbqUX8hTTrS2drc/6dnOKakk8kzNefc0EMzgnMUNY4uvzH1Y406ZhydoZqBlJjRrMek4pBFC2FMAJza941PRyK7vq01zkorFFZcRQNgvniHoC0vIFD9GpTJ5XR2kN6fWlMAIBBd762mxFiTMhgDQwOA6ceOduM+s6Q3cAltWsQX4JmHmseQYFNqss3Ai6awN+U4siDE2wHPgxxhQ7YT+7mPwqWbQZiFV/7/e/hy/c/AADM+w3+9P/7v8TV5f2ugSbqvXyxnbh+GgUhrq73EhNDjyheXJxjsxmx3W4w5AEpDwBEmUlZFpx5Zwj+xew+BMxzE9gBEUAIwJBRqxyJTWDUZONpXl1Vj5cyiUJjAowDUGFoGZU47Ahm21FFW+9O31SJtD5zZY0dIu/PXHo4uQcaXNDMkDWbhyEohO14Y2dIaz3Wcck4PM6iCofdfGjfuqDRcVGT4ACTKd4Wn2xlwn38NXDjFdqq/WATdEEAElCrwN/aVaGf7M/mt65V+yvnIC9VOvDQUgj+/JaX9WJnAE9rbbip758QYbtS98EG2tKCtCwEEBPe+MVXcfJcjiLlaQCVGONP6GtSo0ojSmExuIGtvSXjbJ/2/Y2v/i3uvSlKx7Qb8f4//wrKnGEeydD1YrLOocBOvgYaTMg3edwGzM7RWr8dLlpPUOojmA43eromW0kL2cuUS0gMLMwFzy6vnP7OlqXNFFCG8j45wjZPsx5ZZGQ1/nCVY9c31zciewwb72MMyg6YZ3eTscjoD0OzAybJ+Lfd4uLePQDw40KlVD9uV6MHPNdAu1kNXM3Q1dO71GQpqEFBgWJ0Oca5EhoVjFZrhgCyEAm9oWOJ18ewPPaxeb41r/k2x713jOGffQckTptlwGyvmj4TN3NaRYKXfd2RpRgOchBO6JgucCvZWFNyePFplazrJCI/huPyYS1Jfy3ua6jD6UIQSmUmm6zNjCEBebvFdjPi3sUZHtw7x36/x+OHD7Db7XD5/BK2aTrmjHnauWETADbbG/y9P/lHODm7jJDqDEoNzxKALTYnO5w9fI7Tk+f4nW9c4ZNPvo7nzy/wwx/+ELvdrnmt6/FIkBhZzeMLaLjcGXD15IHLHqTG5QhNn3DVE7j66Q2BZZsXE60tvIJtkoueBZEfjLAEOaY3yDZ9oZdrepwQ43n1UBKGty5bqxBNc8HjH7yPkkiOWkNksFqLGL/1+Xy9V2KjEjk32t1AwD6+piMtDaoUcIjbNV1szOqZbxCOArmv1H6t2zScPXyEd/7g23j2wfu4/uwzvLjE9v+ufGEMXV4MSWyt3mmie6LJTEsedKuutxT+XmSJpJwxnp7i4q23OoHkNiGSwWEnrmciSyuwPCEEbbPZNAOY3s26G2BxXsyby5hvZ/w5GEtYhBx96ryXMoaVcUfCZRZ8XnVD/uVLV2eAi/+m9tSBIS8wiD42le13LNT/lfk+2JlWZlqDMBGtGjZfTSGyGyIc5bQwdHUCU8AZ6nGjqKuvXWpxGhIYNTAWoLDtdFoQZngAdmfLKoC2LIetLQuOf2ytRNnOY6FGDy5jUPZM26RefDm8ZiaVfu30wlEfl6KtNSKJeUREqFX+gNqNjaHZqEh2/dzQZfNIgLtAG7x1vL5sNfaJawouaOla4vCsPbIYxe2UJeht8QIDA7f+2d8bb72Pbzx4HwCwuz7FD777L2OatmCIwa/M4jd2N1J4uIrdGBvr0JenuWCaC0qZMI6y+35yskUpp+qtNWAYRgxjwThqjJwqR4ok3lUVg2oiNS629WqCSMoJVMljX7EJtIAibnOBlzUSlR6d1MXzWDzTFIJ+dzjSFGaWsBDEIWkCOoMyEYV4YkEhUgFWEjywv2fxEw+8yfR+BUBBkGyfzUMkGrnMiGjPUreuGs12hdlBs+CdTiEDbOI6Ct97g9mCXoJVgWwwMaG8gheKVBToV8nxC0tNRY4rvsIOaCzMDQZ3Kb9tYuitskzkZTjmXbGoD8BuZUJGYD3RzboF9ZZG5Pr504e4+OSNrp+LlQwzpFW3lPISff0NZbPar/7e2YNnOHvwDACwuzrBJz99FxIE2ixV1GQctDXUGR3IjMYLhQjGMwiEuhh5WE+dphT6uoSOM6DlOAROvZhHnWjJLJtXdbeX3mtsHR2i12nyEYPEeERC67LyVECTjEwTKGXkNDjtWXrKOorVFjO0zZW8k4cB4zji/PwcZgSbZsmS50anIMvKu41Wuud5KcqWezrsRgESb4woK0a5q7XTNijsflVvYQOSvxfB73DmA7xf0yHiJqStHfOoZwDDQJ6d2+BreOibyir7xjletmnXyPCB2kZqR685jmGBX0uGvzpydC+t8ZNj9a3pdQd6U2DhQlrsKG17gPz/lbbZ+mdbkoQ8JKQkHkMnGm5hHDJ2ux02Q9LkCLMkUShFPJe0+mGY8OVvfh8XDz7RwVq7JicF+ZUTKg9+7+JC8PJku8Unn57jpz+ZsccNoFnVwbZBTgAXgBPmSXttnmIksVAlvIYZwhpfNaPeAuCIck/T+9AhD0enCBeVdHPXju4FkVcYpTpfLPEuyjSMDl+bIavnRSZDd6hVGWcfPZd1o2u+MoPLjFosRa0Y410Y4WU3Gy/p6ZTJj3BZbQGuTg5Ybnjw8ovrpOsscDw9xXh6it2zZyuGLj7y/ddbXlfLr9OTy8oXz9D1W16GkxO8/a1veYbFFxVZdLbYohmpCUb9umcVUCRLiAUxL670MJjV9VqJeCL5TrrKnfDBAuxVz7JjApq1+6JysEtrQvKKMe/VyksuigPFr/+MgowZAG1XppQS4L9U8KxEZtE/Ed8gCh5BugszDgOyHpM0Cu9Cxkpb1ufK8p8HSHTGBBAPLghaz+2eu+4H5U6uM3KW/ll6ZaiSa4auSIuS8ljbzFgkdPfxgjSkGJknjr2nHnMqhHg9ITg+gFscBsnh7l5b3scwM81rP4xB0iRPU3FlyNaJpWInym70k/VVZI48VZYYoQnNCzCxBUJmlCrxqiy+SKWkr5Kv186+shgaGXCDJ9ExrG87k63CDQN/csM4rz3lOAuVjNsb/Bv/63+IUgYwEn7+o2/in/6//8GRVtbgf3iNScdX28Di4UACMM1AqTPK/AyXV1d4+uwZhmFEzhnnF5cYxxEX52cYhgGnJ1sMzDLHhZAroyruWgyUcciSGaxUEJlRSIIXgzK4JoDl3pAlc5DIvxUVrPHPZC11qkkYomUGMzyxOYlz4B5dnQGqKbamzLb/W9ZVELUg2pb5THGA1Og9jGPbEe3woe04xmQi0peKoum/rZ/2Fz2O3JiVCBUVCU0pPZTQEFtuyhQMDRnoAn8HPqC3mFli6BApbEUIlyNKIbhsIIQu3LoCGtp4SdbCAH70pR9h/oM/w3w6vdzLq7WFEgx0B+WQjfz2l0inXgRne3bluSvmPug/AwMx7plnwiuUJThv9aI70Mz7mppkFT6WAjgBw3aHr/29v8Tzz+7jb7//jaA0t5pYc93bPycpLo+1+hvIuOnZCJs0UZHTS+ZBEW83YwVUUTxUYAU+Ri/abTtWZ3XNpbjclkiU/apH8xOZXic0Z5pn5ETICWAET6eqiUJqBQfv26jcNXophKFlYBT41SLvXV5eotaK07NzDGr0Es/fjEHjadYFPFLKTuvMw6afzyaQNJyJm2PU5sc/0X4z+xEwMHuipx7ikXw2ubP3Qu5xtm9vsa1sdLabzwbHOL5mtO3x0x5pGx1LXDVPQ5ccA89h91R7cekNTGt9uWuJ1PT4Cj58miFH5CzGZWpAkfs2LrZNRxZjFWRNMBh1mtECBgjSbscRY0oYE6mha/L5qrUFhpeYVQXEZsCOcFjI+VTRDhXCce2tN/8Cjx5mfOntS5SwORVHTZSwn4D/6r8CnnwGUMoeH854adJrfYKChDSMoZ72yfMAlBmUQ7zCKBqpLEK1+lHhJtiaLiPUsbDI3O75ZUcpI35rnxyPgzHOQRLuHROfrQ+8ds9liDWN5fBRVY8PiidAYk0sxOatVoLurHrdUtBfMYC3mH3W/QI4xtwmMASi/3mTK37F5fNt6GprSH/e4h204GndrR7nbnkxvnNorHmRJXLYbrE5O8Pm4sKZ4LG6pZtRe5J+HyC6EWQlzk02My8FBRMvl3r77kf0tFXpgxISy7q4Zo1GYCNkTNlvHIyn8+iK8Ps1LMpISJ04rsxXVPqiR1dUVg48Nvz6YV2xxPft+dZOny3E3rUdyQMPETTBuKWzrT0uACCNBzWrkS4tGUUFzp8/Ri6DBFOE8Kjp7BLTxbPFeHAwVy4rBCNSDJburQVjmP8pLOzTMuOYJ5BlRHRBhRd12vXQF1MMQEF416f6k4thMLpIlF3pJfZn4hzZrpDFPXdhJfwtf5us7muKmlAV4dp9RiEi9qh166A0ps84qcBGAbZlxqMKXNQwR0vYJcaDNz5UCppwfXWB+48/EuHMPP+YcPnsAUoZ9N1DIeuwU014jtQr8uLKjEnji5RSkQfZmQclccMnwmYzIqu3ls0D624pSZeRauoMlS68m7Bjwef1KFWj3xGYwQhEthO+gnPWThR+FuT6YG6MJi/kHTPgcgOT3mIkNrhFBVWE2USQPjK68ZixiEg8LFJSb4aagFTUoNR7oHXKWOwjqwHKZm+hrPhkAk2QC+uJnDG0d3ovoTbkNnRu91R5a8SVnI4fKG/OT16eodxsbnBz/gxjHkHHcPkVSk9ywoJfErPfoGD6KrLMnevG0vtOSqfGhbUwM3c0KvarpyB2McyW0dlbFOiGX9ThSbcGnGa0MawXAlHF9uIS024DBFzvwaeK7GI8cVTte+gf+v6tjcTuMdEq3jNgdiKvv6d7PQI6a4nKf1SwFsTQZL4ArsPC/fTfhlvRGOJylk+X3CxlxjzPKKWIUU6FhJhkh5QP1lr744IGrzCMbt6pv9rCd8h9Yjfno0tJwqG/C5y9SyFrf+W6Hyk7YjDv8B+2oXIo364Zu0wm6fCLATthsDoKRwWB1zGDleHOGmbcaoS+tdBajw5wrHt+caPzxtNn2qwu+hp1BeOHJoTp6wkEhFhtwudtE6pJktGjvvWlfRKaPCno1vpiutxmfI7NCJyecF8BAN8IpYL9Hnj4gFErISUxtKRcmkErJkXQxsuccX3T4gKYYwOlhDSPqKVItvVk9KzB1vWPkIAC3AK9EymcqNFa4kN58Ng66Axci1u2/u5ajpm9liR0DXONrhD192wkHf25S5c4zPcBrhoutXWUxxHj6Qnm3X4RR5T7t0wGeyU2/oq8n7uPX2lZGvJfVD7fhq7PUaGU8Pbv/R425+fiKvlyb0MQHsd4zsGnBFJXhbZWkCp9ieToVUpJM4MwxnHAOEq2ijLtUViypJVSMBf59ECbqQWockLQCU4rnVx02JjKr1u4jwRxKZAsPboAeKBRM0CZoKMPHgjKwax4uAiJ+t0vbu8RNEioXjcBzfpVq6TVRuy/3mNw2FEISro+yrN8liqxpc5ON+qlJpanYdrgf/Zf/yd49NGXMY7Zx/8X3/lv8E//1f8c+/1ePJlUK0l5oadRC6ZvJXcGpl5+tE8RPvtdLGe+ZO/YzoYZcbmbwyica0K+RZwTM/gdBicVNYtbDCity7K6lFncnSULIJrByuthoGqmGxOyoWNhyNELFY6SyeopIYEwhVBd9mfHPg+NiVqrxkBpXjjtifiKzf3vTYzf2+vYwdgY7I8KhH1596s/xP/q//B/QtIslAxg2m3x3/zD/yOefPzWiirWF4YcezHcVhFM8Bnsnl15UNhXxlQYu3kG7eXo7NXNDkNOuLq6wna7wb2LC2w3o8Ro2YwYhoyTky2GnLHZJICaEEo6EXLstqoCUDDPhP1OYmcMQwY0WHILoKz9rAWMDITsRSayujBaWTMwAtTNQu8/4fYNT/LFneLmQl6Q9ppSpxlNzSxA8GDILlyhGeVFVsrgxGAeUIfg9cUM1lhfMY5G+wuZUdVDFACK9pfMkhBHaDhl9NAkQBP4HTaGGAuMqdwd0RV4Lb0LbP3dYoJ6JaXpV1tsXnrFkn2Nfi5Lp5HcrTi/f0GZwfi0Nq/1CyKc9Pr3ai0M1/FeIHpESXzFq9yIPACEhHzttUMVy+aYzYEhvtdVbHX3npOr/bPfjag73zP6EZdRIvIkFdEAf+vG76JflBrtnKtEpLcQF3kYYbSb9aSA9ZYr4P4GRJLlkOBJL0oxOgMMw4DKwKQeXS5TEbVszGFgbUNPx6lBpue5yN80Y8jqNWWGOe2nxRudS0FOEpogjDhAINCxxWwAsukHBPwKb5oRLBrQrNjRxYZDYVzLqhatLj21DFHi794DV8euR/RlI6jHrzWjUnwmk2X8tX6EuZhbO8c2b7trjlZtUS7700b7KmW11Re+tYxDWTXGkx3Hdb3GYKvrCsyYd+Lpm3PWpEMJVb2SJj2uuN/tZd6LrggyZwORHST7J7kX5GHPG4VLxDAZVfS+pv+J/YwXFaRmGCMgnxD+g3/fYtUV2Cplawa93AgGfvxjwn/5XyahapTkdElKyHnAdr/H1fOnGLdbyUKeLFadxm4zXaQUkSPqrLAUWpCJMFgAfVRUYtSSRDZOQ+uPzkGiRXZ4q0znaU2/irA0meG2TY8214arhM7j/ois7M82iAKA4AUB2GwEv3gT39KuG02zsDFNmYp02/SKNk75vP+ld3Hx1lt4/y//EjdPny6H/xsvv61yzRfD0HWL4BWVgZeq0mjGa0SgNAxIt3hy3dofNCXareh2z5XkhmauGJgFXz/FrTwcBUEjCi3jVVCMgnV+oem/sKwy16XQ++taGdFAdOtjPbPr/uTGAcN34krWzOG44xWOsPUwDk2hJcjRU1MgRbg0iat9sP+DM5ow1NY2EcZRjAIPHz7AZrPBZrMBiDHut3jv3lfw6PqryCFd8M/Hh2IMkEBUYHXTShrMuzvO6IxCBOscmY4ryPF3LxxG2HRKcRDUI2425hKAYQxL4dJQtc143MluMFJIRqsT65EMU+ITdUzH5iyrS39bP1A3hWCMcjpiT2iqTQ6jigK9dcHHEmoPFsZEjDcrMJamaFQVoJiAhwU4cTiZN0EToGOG+bWSh4I8XINQkNTVfhgmvPvVH+Lew0/BTLi+usDH77/XZukA9w3uGuAX5tLd7nHrIsIUA2A/Wrvb78HMyClhnkaUecY0jRjHQeocBxBJrEFi1vmyoPKGfxbEXY4WSH+yCvQVsvOqcwMz+pBM9hElQd6zGDCGHzprnUG7p6diMIcbPCjgUAzdFmcogqmiOg5KWxoQX4VqdIJ0U+QSEVI0dIXP9t2OZVYN+L/OXKPRoK0qbYrCvC7GESY4am7eSvQma15wrb0Ih+U3oOeBv84ScTqK3MtjSG0Tghf3fltFxJXS0fQXyANtSfi78hHG7oHb2ysAY4JsEgwsimK3NABHNPI01OSXAYN1q/jQW+NwfjpcfuGUNOUlj3vce+MT3Fye4ObyrB8seqW//33Ydhye3RAPUwLVtollb5r3pifrUAV+0WJjwGFcLdYW+ZgNl42ekWrmROqJx6xKKEPzaQgN0wxyiRh2JNINCvpONGYtjVrHdunZptBoVZXMzka73EMrAND4bc4rMXQ6uNtxaxgBahPik4AFQvRK62q9K7duRacgM5n3zvK6/fbvq9Yjw68lRlH3qNMro98dfrLyQ+7el8cEro5KweDS6qfF79vLXUh2z0/pCDBp/euCQRmVJmW4yXciD8drR4Jlgx+Ce7Vi5lmSS9WKaZ7E04nFa4myxdMUz/+aGODqxhuLI3oEGqrnEeT4otG9Rv9Mzu0GSE2vMuPJyUn8bSgcpOcoAzLw4AHwja/rmqfmFZ5yxXiS8Ob53yJvNiFjaMLTqwtcT1vf6G1yxawyp8inlBlMEgvLDLIeo6sbym1Is4TZOgwPanC60ugL9bd72nG0ZsCMwU4vDZuYNJFOwkYT6sQ5Xhry1zYZ0b3TdJTmqQ+kPIBSwumDB6CUcPP0qWzKHjCQOy6+z1l5Vfnui2HoAo7J479V5dWm6LZl14TCTjdiVS7BGHJyT5+UEoZsRi4A4bS5LmFwOLoTF2cHXt89s1d5Zcdr0U83mGlLFA0Wv9oS+9lKb8Q66CcEhu1Me8tUKG/3s0IkLGmNUEc+a4p+rYx5aimc57k05xEQaukJsrdH679dju2eIT2Hn3F+foYHDx7g61//Oi4uLnDv3j0AjLzf4Dt//kd48Pg9zEWExzLP+PEbjyU9Nhhpbhhmu5iWdUR2ENtOGQEYAxwOPhcwi4atWuIuKIHMyBAB7Ro+d9fFWJDQVCgNLu5HEQEy3EZolyu4VMkYGUpKId5WEuDOc0GtwDQBORE2uY0zAbIOXBiP3TM8y+jNvFHy7NdUv54J0QJCJO39CxPw9qzxv6CeNyDNeScP2o5Vy0FW/SPK9cdKxL9hnPCv/tv/d2XihJ/+9bfx3/7n/3uYe/7BXFkf1NAuMnIRhaUWV17WPHUY4hFWKqNeXuMm32C/u0HOCeMw4OREsh/N0z1sNhucnZ6Ih9d2K3FbNqMOlT2b4VxmlFpxc3MNgLHdbGCxImSeGzw86G+1td+yThl9qFz7rGGmPCxpQBQy1VjJkFgVIrgqHmnQ1rBxuYCIzgcDIj5aqUHZ6z1HfV703mYcQIAHZO49R+XarEpkSsssrLpy3IDQRL2mAmq8OjLlOB7uPRzPEkZxE6GWCpDGl6xBCSarbnmsUYH2GzJ2tRJ2iSNvMdrwG+zZL1eEBtlqvfPm4SvKZjcM7ADcY8aG6BBu0SixBlS+RTCmxtPsyBIpbtOx+lYGYdVvLy7xle/8BT768Xv427/+xpH37DgLHZAIAlazAksjFsuRvU1KJqvomlca+/9j789ibUuO82Dwi1zDPsOd6t6qWzMpzhRJ0ZJl/2bZ8CC3bUJWCzasbhhowFIDfhJsP1h+MAQYhgfIMvxi+EES+kEw/NCCARlw/92225Kl33LbEvXLv2ZRIkWKKhZZ83zvPefsvddaGf2QEZGRudbe55xbRVJFMavO3XuvlStX5BTxRWRkZDKI5YUWMubjxmGhokHGqLZCDtg9RUYILHE1CTrlY2SEJnl05G3gwTzggcTfJ+Hz05TcyhvH5/0CaoRO27LRM59Nv/WkXW2xYRjSgh3meCwr440Y7Zdj74n6azisuAEgtPNrFgh+D5/xxogsG/fkdw/OMGTWeBcqsIuf1MamQrVfzE7Qk/ty/6gCbdvN1PghmG+IgynpS4Xq++dV4n3NsT/VysaSgr/Ac4qFJhLDbHBzUdpSvZ3jFDFx4gurtgNHxmazwXa7xWazFjk52SFFXdeCqLFdBTFGjDTa4U5NaMwjzPBAhTvZf7PYTCXnzW0q81bkoV6fojtpWZ/VfxYMkyyrqo8+Anz3X452z95MALAGhV9NFFjsXMKvPf0+PP/abaz6PusBrLQnGmPbYGoacN/m8B8xguUwCHZ6T92deohQCuZZtlBusZ0M2825bOwqBp4zgGVsVRfhXAqEhmJuSz3V0y0dnqSG1FT2MIx2+IV6xqZYsskDLk6Ti+2VF4PTXGuMDgivuvnud2HcbPDsb/wGxo1zgqgJ+0YC8PVk6KpTRt73+fDbZzU7unkTqytX0HRdfoMZUy4OFncH404ZPGsLIbtWUkwgOyj4lrwsHg6yXyuZCiiZA2pvpiBurEuGIX2n4qnSmFG5O7+9TbtbWC6smF42qbJSu8+S2h12PYe515cK10DJTd9iC0kdVGGzeBKcgQo75lo0n7NClEDJKyFpP75uH4sxYrvd4uTkBJvNGnHD+KVb/1/0zTG2201arRoHfOnKpy2eka44JLCTXmYBSjmPC6VRA7MbFeTJdaLcMe78Gwq3srDQmjPslL250iNtVKzKlavaxZCg3O5pfDNqQTGpsZFcwFikIP0ByRCsBzj47pBuAJlpDQKgJkQmMJPgjRL8zo68lrprjoci4YmR0ESgYeAaAw2pR1/ePGeKSTGH3UohYF4URfPtSAp6SKhR0q/ffAUf+WOfslZmEKaxxRc/+zGsT49tzsQYESk/r6uBtcHE3rUENiJjGNIR8uMoWwa22xS/q2ux3a7Rdx1wNRm+/AmbTWhNiQUngyqYERp/KIfnZdmjS8GxgpbUEJwVM6PVe2vlPsx9K/NXNIcl9mHgtxgTtZzwrvZSbkV/lHLq5yPbMoarV3o2yGlM5iHBEdOUY55NcXKGmtJAVvahq5mh5apDF+ZL0U46btTTjhW4e0BbtoO+ZZdXyK40PPochm/6fYwPv3jhZy6WVAmRvnHBsYuWclP+nZEyb9afpSfB8lNqSEqPlCCBZt4j5ZMbBsbIOFgwiGvzvXnrRayP7oEIaIcVbrzyyFwGe3oLZdFeZR9e5TK6Cw1MsmuMPFdeqWvkeWv5GAtbHFkWdpS+LPvIXTPvN57P4bqiRGV8NG9MygbXxHC9YuuNI8yQgz1UyZaTCOHmGUkxUE90CUYdJ+hph2pE8P1stCg9VVcp7tG21lAGU9R4jvlkQ8ta8E4kCcwuaDeXveIXAarWm7VoVmoVO+wGgW5G5LpWuIWksOKzoqsYXAUxKoedwJxZ65a2DHrZ5Qwtht/2x671nyBIXFcXoHVO5uyH/pvv7Td6ZWSZHp71zYyhup++HMFBxR1tR1Y6Si9ElT3rsw1inDAMW4xDihHHqjdRYztlUj+yLIDlmFVAKSeNv1RElhiylOu7XAMSb9XTNhPG8janXHbpsMDuuqbQeJrqRSpG7fX28PVX0TcbiS2MzOBi9tZqm4CmCei7FlPs8KVXbmE7BozDIDyNxAufrG/V642CXAtpvJHmNS/ehfbg3FLs+tQb12c6KWDOF8obC55SYD1kwWMyQ41SIYVDkfGg46dtu0wDvOdbND18smuT6Vz5E+57wmdN1+H6o49iGkcwGNuTE5y+/rrrsd386Z2Y7tebC3iHG7r8igMggMn6lu0agNLFdscMye2oDLFi1CjZKFdsYDkRrt6+jSsP3iromovC/eUwIIFWq2L8DxN+uh+dbAImrwV5Y0IWAhQmY8bJyOUDsKtwyEYaD3gKwS2Cz96JkknPKiN/b8f6dtkPu1uxpPV8JlAY+XTZpKaXy/7ze8JrIKTB1RP8irZXP0o7e6Xbl5FXc2cwqfipxjJ9R3KnbexUTTAwjRPWZ2sM2y3u3HkTZ2dn+L0HP4vx+oCzszOMEui1bRt0YwuekseTIAxQq8XLlq2QV8a0lcPkVkdIW81LBQ+2szcMwZ3G6Mafa137t+4JNa4lw5MCsnl3ESUjUzLmsr2nce2ehFOS1dOk2yDZTslsxTN9mqJhKwbMa8kb6AgpPpoqDMl21iCHg8/1mxl5qu+PRMKfGoOVMwGIOh+thaSr5BRCpUlPWE0DjkFBgtYCMx63lHxT6ty+cetlfOuf+t8MhDII2+0BXn723dicXUHTBDl1ZrRKtKERD7kA4nzEO5D6PhBshd/ey2lVf4i6vRcYhi26hgCe0LYt+rMWB6sVuq4FI6Jp3WlC3ABwRivxZlJPzcbi28SMXzwwAjDzJBQemoGTu0dU4MFCyYlpS4Ad2OmmsXpHWNdbI2RlzNNtRiyZZF6J1U9/j0iNtyUfacTgl8YlW3tkwMUYxiGB+1pxlbm7i49bFbUuQbCy8VOfE/DKWfZ+zXF+CuCerQs7QW8qeQ5q9dXDE1/CyXf8b0LnHplwAXnhs9YLQundVSt9BXDoWwGD5yZSPkP2G6j7vmrgWRE0+740doyvEnCG5GXVoTwfy7wYwXj9oeetvQ9PruH667dBMQeHNnRgc2lOm287X09v1Js/gxnfDkaXXifjCyxArrBNSCsAk7RxVvzMm1QJcDR4z8fSU5CgFKgc8vgheyggGTqUX8mcTJ6IuTT1eCXDlQE8DfIsindMUzJw8TQkGryiX7EeawNTRnNLeOZoC2BNok89TnXrWIwRetJMLkeed8p/kQoDF7lxUc7byQd8JuuFBSNXOe5TnCIu6pMNg34OpN9LXs0AykMGZspIOfDUkFLayMi1h17n7CFrOlSWFflVDjNATgV2cibhtWBQpjDIeFnE5b1Zk3n6ffXkH4ZfPDKUZ/d3J0KRxXAZbD6U9LHJGz1BT71v1meb5OE1DUlvmtRjKcfMbBr1vEkx7rLc8qccu3ovyQij3OlQpmsxou9H+VfDIED5ji9TWZdOB3lQ+WbRQOxksgwtLlb0WbBePobhsQdewaM3XjEPcXu14Ckwi9GH0LUtNsMBfv/Zj2K97jBOI0ABaNJieXBxv4qdNMa/8vws9CLWOjlToGKSWjQJhkhzM3tdpb4XjCHjwNqKSw+5jDcyDgLBTrHs2tbiIDPcVm/bV+EMb8K/JvXqEqOX4qxpmrDZrG3spMVyRpyApm3xwJNPGj+/8+KLZujK+taOCXIeTCge43l+2lXyZUENFx/nZ18QIBdI72hDV4yTBfHWgV+KC164dpG0qwGXgfnetNMPfmHkVCkyYVAVNjTJ8k1ubzBPaCigaxs0cYtpfQdjyximM0zKrDVg4jDYxFKAoK63w3aLYRjQDGcAxoQmaUJkYBw3GMYWKyQXcWX+tDjQfbBHqVWdyQBUYtsJIEUL7G0chtmYbSone5UpQ4/gfLrE3pZ01005jeBIdlKKHR/s9k4TJes8CfNVYBBDLQAAEoHP4yiQNbvuKs8hbhCggc8FAMZkSFKGSI0aTKII0dRm810NzlupwOEyXji1TSQAiBiHCXfvbjA8fQrdUjOOEmieZYvSNIGY0ZKcsjlFvPtXP44bX3wSgYDhyil+/8/+PMaDM1OiE0CLCEy2RbZBFk5mxBKlJdUtG2H9yoZmYgU3MsgsKL2vvQga/QwYxGAVrFEmMCLleWoB/6X9tBwSjYrBMgbToAqEUrOyoZu4SiQN/p0MTtrfSreOy0hppMfGryylsZ+2ekUxunERVJkpbUe8wYT/ZQBuRQI3hKZt0YaAtluBiXDv9BTjNGE7TsCUtvvpvn3Wo+KDjou89aBpEpnpsAGNA8dIq+CGWPLcWphYCZCxgdG+2eCPPPWzGNaHaa4KD9IUiBCnFp/+n38S9954YNanEuKsuB7tXTmNUzJ+xdMBIUxomgF9N2KILQ4ODnB8PKLtEuBYrZLxpms7EAVMTFhvgDffXKPrehweHeLs5E3EcSveiUArnzyllbaJtP8zOE3G3Yhh2JjC1chqnsaoGcct1AsiGf0iqG3F4BqzZwf5BQYqt+pJuxkzjJyU5SnlCU2ab0F41DSOpgXoiqgqwqPbZqxKNXMARacEIBni0LSizBDQjAhdNMCtY2YcR/OuMG8vh6YJQGsMOgITGSi0TnWgMrcvSWBboAmMtqFUb5E9QWSFHtttz4u3pMr9AuwuiGGCn9ZZaLGbz3Zf5mShcxUFeQ9UmTkWU4nnsJNnV/7Ap7nHEhZ/pcz6jM+1gMdsKPjeyEnNPGeOL3REOHTl1F1BUTUaLu8z504n9wTPe6IYQ6ifcS9T+QbG1QdfQ7vaJpkQA17+4uPYnh5YxrruJT5yBi2ZCzwBkfLhDKVnZ/redp28L2aljDXIdpKReviLyp9xHKTOIXt9WTU9tpDKmUdw3toUGh9iIcm0cRyTZxrDdgqkGZombQRjUuFmHZNlLztPGtPOhU8Nw5hZYIzYrNfo2g6bzRp936NpW8EOue6JJ0qcINdn5tgjnwnPyGdhKFCmON+utJy0EfPYq5/P1c6LVED2xGb3TP7K5TUvD7xly1MiOCN5vekiXD5ljyCHADh6IPgsGA6CjSdHuG2zDxK7NXI0OWPN4MjJGLU0vKlRQXGG7yMAMjZ9vRjMWyFDRlbIXo+uxYq2UBxeLwQk7yuGLuzEmHCwnuo5TCM46vZdBjWcvLfaRvqP0LYNKKjMkEVSkMjRRirPSKvETbq2yPdL6j2nZXm/GxwuL+VLzLK4TXlM64BnmWnki6pGMxm3k+FQMz3O9XH0BXdCteVUrytK7514BIVTfOjxz2KcQtJRJTxFYk/Z4BtCwOnmCF946V1gNGZETOWyGYGICNTBdjCR0h1Udqd4wmk4i/7L0RmfknOH4ifIHJHBksaD4AoGTA9MunXS0UnmDFMLphaT9DOo1UGGCQHM+QAh7U8OLKdVMYLsFPH9EmNEdzhanTVURvKwz/rTFCc07TWsjh9K4zlGvPbM09jcu2tz1/OQ5cUpHU15CapMc4lf8DSCeGfT4jPnI52F93ke4q4zGGHnlul5emcbujgmzK/wwCZgmeoJeKEmr2SIljS33OwBqyGfLHN+cgzGDbPEpFx8GLXuG4CLaEMD4hHT9gzjJmDAiGEYZNUrZqOWMHA9SdFWxsSSTNME4ojQkMR5mDDFUeIb5MnCCrh8c9tqlxuOe4C8gUiOKK0JWnNXduI+1d8s9+6eUEFd/GV6VViqIMyGLjJg4EEOe7qQDX8IqnCp0CYbk+mRAHADXa0hTGYIYn9WtRg9iNhONGyrJiL36b9b0wnWHCmd1xaniHHNODs9KcY2UQqqnr6r9w9APAFTxPXnb+PR3/0AmhCwfuANfPlPfUqAgazyMuVT9czQlYiNYJAIBW1nb+jSEa4nDlo/K8hXQKzHGcsYK4/OZWiMolCMvsx4tXG0xw1EaNvbOKHct5yMFWoWMBJlTDMSsPEKcfoMRYcwM5jStjGV+zaHBNynLSZsQlrfRUgz4woDH5iAltP8b7oWTdPi4OgQRAGbYZuaSYXelCvFrGccZg+ykLQU2FZarZtzN88bIefYKlfPXZCGa8KIJ77pc9b+S2nYdvj93/kI1ieHM3bNAOLUblJwvQABAABJREFUgaMEiq/u6esmFo+77WRG4e0QgXCKgyFiiIS+79F1LcYpGayPj/t0khAIw8g4PdviWneAvj/C+uRO2opAjh8AaUXWgfQEnlQhSFRN42ggpEVj80rBsx7nnRYJJiTVLxgvYmYxCsIMN3C1J890hD+YyyEnUBdk/CeQU3JECmT8YKI8ojN/kndbS+tYhm1LDqEBue2KFGT1kbbp5EqMKLYpifE6QMGyyqyk2NQr2dnIhNQ2KQhRMuQF3SrNjt+l95RG/qzs7DJy5VXyCO4GcOtjne1O7P78NauGq5OOC3195huqcPm+vNDrF5Py7FT8HPfM8y/nXfIq2FvuTLFeRKM7yzZj16ztlhok/x4WrtLiOxgxTEnWmJwvbpfYRempEzlaNedie+SP1fEpVsen4BgQxxavP3sbAx2gGIhVEaXXsssmRjl2sNPLac1vp0KrV4UZivJ8NAO63ptSwSqXwZBdD6Vioq/J41zlraNW5TDLYhnEM1eMjUEEW5r+hOiPWa0aMapkFNnsPY30cJIQQtrKvh0wDgOGYUDbtpUyU85UL1OL/neyK//MAGlxbliJVaoMW7vmZN3bpM8ahs41KOip36W4VL7Pc7EtwGhqGkO8slVLicj4RRfCtOhQ1cV71ZgB1m8/dsOIiobOr0rdyzZ2dvGk0kiu/6aFYQ3ForTqeDVTgee5GRAVDZwMbXnLWPLaSgfWjNNoDgJdqzHfpPVI42mSeSN5bsiKX/22TlLDV63v6IP1mPWLUqzQ09VlVoBrhawz2hhycilNqbJfZJkK5ShMdzy/KcODwGo7r06iReV+jBOIJty+8bJAn3Tg0DCM9ozSHELA63QVw/YGIsvCoPCBTAoB1GCagvA2v13Uyy/5M8NvMq6hEf80mXpmRwhpgDKi6MHIO3Vknk0Qb3OIVyNC6ldqwGgQBeMp3ZGbtDCuvEb7osYvFaBpALT+wCBWL3eJsSqxvaZpQttfwerqLUzjiHEYcPflVzGcbaAnPBo+E/yY55zn+/pZ9n99vxwCyrvkb1cRlRCu5YcaZsuHlkiSU9SXePCO9I42dP1BT1dv38a1Rx5Bd3Dw9hToJhsB4vLIiJsUW2k7DDg9O0PbtthuNuaCq0qHenR5Y45ap/1vAE4I2M/9w8qjsa9CKmi91HPuSyFFuRI0OamAW07CfMVCkVeVKvDPcIHWWVYu82EAymibkOKrqYGrCUAIjCbMe8CdJix1EEQqKIAYdhoKNanMBD6R30kQd2FPLptAefqpX8Czf+RX0QQCdxOGwzPXZlq3RFv2eBu1lo6hG2yGuj4nOTjZigYF53ZvQFq8NuxxLkC5GruWei5CzTUMsAP0riVj5IIB1556+0ZYAUt0m0Iog6+oQPfebdmtf19sGuCQgU9ugJtI40Dn6uqgxcHhIQ4OkqcAhWziS95DAd5kBUAUkJQX0iZ6vLYqQq1u4fNxTwDsGvn3m9p2xB/7jv+Mcdst3v/0L/0ZPPuFDxpI9i1Uykq5J3N5GEbcuXMH6/UGm80mKT9tg1W/Qtd1WK/XaZtj36PvOhweHmIYEqClJiC0jSlTAGw7QpBtoAoN85aE5DHQtI14zjLGKaJhAgeYGzrAGMcA3cKgq4cjlwHhLS5FdVCHGUUNq6c4DfrOEDOQ9x6pAArllkEINMlcZDA7RcXNz2yWly3vQWOyCC8RLTdEAijFnsjbNrLiwAmRoZlSwOJJ9qSmFUg9btavIAs98tc0LRoAXduibRrjiTLlRT4x/KqzLVics9g3PvYc7v6f/gvi1Tvzm/chV3bNEhufXy/pqyfi96YtA28w45AIhxVNm4NTPP3hX8fV12/h9jPv+arSpWP4paefwJ2Xb2JzejjLk/k/z57bZQAulXYUeUcxtJuHl2yd0aDI/h26uDmOY1IULmbnrSqQsWFS9pLCqrxTFwibphHZkjmLLqxqHsUQk8RN1MVRT3cUPgKJzZNOuhtxtl4jNA3avhPlj4swE4bbGHnrW2qIhToJ/6x+kzOizJ6t+sY+3b2ldygv1baybVGUvVm4esY4vDeGVYaxQAGltEwoIBu6CIEi2MVDMiPRzHjlq5uNpD5vqutu3FwWsqy0pnAe2ZM526Cc/NP3Sru1TVd1g/Qdl7LP2oRTrCfF6Wr8G4YBcZJPPZTGjb22aUsjGpXvcxSYOpHf71Gm9lPylJuNPm/F9mXG+5mcl0muXwCbNzWFmSyqfsPyN43uVCmT4XNmwzf6yczoug4HB4dZF3X45caVLZ760GeSI3fMuELLG8cRd8+O8Ftf+gAYHbquQ9s2CTc0jXjWzw8RUq9R5RVNOwrWaytdj1ystnQlYjJ9WdtMFzI1zilJxaPrv9A0aIPGNsxtYiO9MDrNm1KmIRpKvKFtQnHf6xmvP/tlnL74Iq4dHOD4odtl28YoziuyUOl2c6R8k+VRjwLTiYQ3K93KAQyQkVy1Bi8NYktsop4LjhUW7VDmC2WeC6Q/NIauWQOWd6vfOdP+5/RpFUZlprZf4eDK1XMIw6y3uZYGy9lyboZ5FXCMGJoGw7BNro1qfJBPz6SzgPCCmsv3F8/sFt7aQDUgu3Tl367k6TLa9FZW2i6SiLJwL4Uci0FIvTzYIxJ7Nj+y3JYCy0qwAUoxi0JRhdlz9sn6svyZtrr6d2Ql1eoFVEY8XZ1JtTq78QbObrwhdORg+WpsKr2pFejJp94sLHJ2JmDKmQIMQL0+jFkqUCBp12KsZAGhQMugRcVYc218/+vffAQU82N2N7e6wRgrVG7L3n8QivGW/zwwnr9Ty7oK4DqA2xG4KhJD65dOT22SYUqBma8KlfWVhgATkkeTAlUnwNXAQFAD4W7wOhuBhRKRM80Emw1YxvWbr+x8w40HX8LdNx50ikPOOawPsDk7Njr8wQRqZNH6te2IpgmYpgnd0Jnyp2CqbVtshy36IW3LDiFgGkuwnBWB4PrN9We9uskKyBQkzP/K7OU9z2MKXurGChXP5K2/RDX4Ea8qF8/Lr6LrNJsPvzwDtaGXFG2EgIaTka+kW2liUIggpG3iDBaDcHRz116hPVpcT0qW8t+sM5mibRXIdF1kASSu1hgffQ5ozrGIqQZzXiKV/+zak92/bmqoobG4e3/pfhZ79snm+t7F5PhXPzGAEWlr98gSbUHlfBOxvnIPq7MjANIvO6pRoADacw/ntHX17HZ9gLO7xxd7Vu77tr5Iv5qhJHoDkzdSlIYLVcqKsg087E7k/jWM4WRpXUbCCSFvySkyI/EAd9rdnAeql0R5T2umhq9xTPFEdbEiG9AU2BhBu40LS6nCyBnSkWCVZdygeEDlUmlGWHjHDl5VGMwW0nkzssSc1RiuSso2FnI81huyFEtwMY52FOho8PNKShHMqM+pYUu9ompDl5eJng/radi6cJiw1jIhXqZqHlXyp3HCFCczFEc5QTxAPCQp705YWjkpsebuOVR66Sx7CdbjUavr+5Ey0Jf7JY6sNILF4plp59AveZDnI2X58+d3vZeRu07jROfP9L4AIhcjVa7HOKHvGA80p4ZjaswzDAOACYfdPURu0YQUGiagQcMBgSW+IcNOTgcAjR6j8Q+30xHG2ErdCGTHQJJhDNMZ4Ob6QgtovfUQHWlYcBDcVqFnLp7VOTebpcULMluT/DFiGraG03i7BW82aJsGTVglwx44xwOLrcWZSx5hEc2kcyB5NSaPX6FdTmrXmGssp4XD5lSe016lqs67qtopY6Dimh62ovW2Fs0oaleM9X3pHW3ourip4p2adACphwUVTDOdkpVcNic5xnkctum2agX1pHRNZif8OYU1ckwxfuQ3ywwvVh+Vsnq87VEK6nKIKmLOSSYAF5TF855TYSol1JRBlZPZ5HLKrh2d6+pSvIcI0M1zpEKjepNjCsyZNhZCtU2IsjAPQYJ0h4js2A/jkOk7CWjSfsz1bYRfBX2BxNywNnE8VFf+kpNTuWVDh5PSPEHwi6lreXsUEOddG5LJKdr7XKwG2cnIO5xRyaBy9paL0mHRei2IQ2tmg9lgk7dBSm9njyfHp4Vy12ElHf5nen32/pkZMLxB0AtKP3TsxER3jRNT/rNb4HEmHIWkFHjh2jYNVqsV+n4FZrZtayT9y0ixn1LH5+N3QmhwsOptPI/DgHGQlRvW7XMCLrPsOl9J23v38ukjf/wX8OE/+ktKdvGG3/utb8Ov//x3zN/N2RAYtylwOpDGmno4rNdrdG2K4bU6WOHs+BjbYYOzs1Ncu7JC2/TYamzCKaJB8orUv7RTMEnz5B0HW81LY2sysJFsGZlf52OjE1CIMa8sLxm7ivZlRrQAsEnRaziXN02jOzVR2b6+J30qX+EJmUerQhOdJ5VL+fARt5qvWxlli26QeBbzFXgx+HAEjY2tGpqSocBKXfA1aDXrVlSlmey49GqqWr+bIZxI2dvFEtU/z1Uh99yhQjEpVmst09c7XvnqpzMG1sy4FkiiiPqkBv3Ll3u/2LJYPT+Hb9aGg4sYFReN4NW7x3FM80YMPz6wc4GfsiAq6ULGJCb0qwxqlIiytTB5RASLH9k1DcDpwBENSB+nSrlRNiR7+ne1l24n07p6g1bXddhutxZTycfySXV86/KpVMZ8O5gWLxlr7wzXlosFK5rJvz2Pm9sT9o8PRvbcShgy8Wa/DXE21gwLhrJTivfung95ocGTWTPWqhWEDubotsaH4g3FWKjaUw8IMJp0PIqs0ud1YUXn4zAM2G63VrbJXiQw3ohXTvIGCkU9UvB5Lua33Ysqs+c9XRqrLp6IUowvmkk9KobcW3mHluffuasOmveC9uHq+YQfSo8uQD2xPU8yvcXmsTdR6CJS+hzHEYdHwJ+//gWJ5BCd59ecBh3HaZFYMHDs8H/83kdw7+wYQ9tAA+EbHrK5Ld78xn/Jxp2F/1BP+xhBgRFYd08A47AFY7QG1ZiJeoiXGpmBbOQ3jdTwXMn7tYrbkxO8+JnPpF0GAKJiX2oACnBhi2dtCJsDetiPeH1N+eAhO5xhlHBIY/KAHKdkFPPYtpzmtI+lFNfJeEyWTYlMVSr9wmbKMl48RNc729AF3B8gmU+CWQ7UvWPMpeQ51VPpZtv1WF25gu7woIa67lHyDy6WV97UQV4aRACYhboeOaXAmRNOVbmFVJYX2QSTQUxmPFimEguK2hIF5Y2s4FEkrN64hjC22Fy/hxSvateDi0XtnFw2WXg5Zpt/rjDsWVuWNdAmIyLnveRLLJMvoVrkgQpRiCJdCAL33mXABdXzoIJQb8zbgsrxQ/b69D7OcXAWNmHmd9U0OENMBLITlx/m5NtAQJ1rh9II5F/nXyjvcR5O6Zpsa9C9+eD03fNesmGcBNJMMrMzdJFjtj5HUWX55BlP8SuXSqfXL9i1kUIZZuDBCFyPwA1OWxeVT6ixgWWAZ8FYcUBmf9CVjV1G2l52sFolMBcCNkjtE6cxCTxrLNluQoTIZZ3LV+U7PPsyT7PQDjsEYNdvQLSdvQNI3l6PSQwwTdPY4ZXnH8c0dfZMjO45iV2z2WzklEc2V20AGMcJXXMVq77DOOrJN8nLMEYxzvqxY7QqX8hgRYW9Grz9/dxuda2Xvb3mgoFNWcmgQgC9PlvLJAOQCXgUL2cG6m0ytviR5yk4H8SRptf8cAi/6mjKhpQQmgZMKe4WUbDtkDEyKMr2gDi6eqT6TbKVRPuj4A2L44zLcbiQh7sthie+jPGx52xAvrUFs1JRKBYzsIAkiGRld2clLpxqhWd3vh0YhGjx+0VT1u/nz361bHraxlupY4u8gAeofN2FtOtL8/ZQnpj97/bjue3ZAdb3DjCs+1m77zJo1dcvupDXHWxweOUsjSkQTt48wrhtC4+J2oNrtjDj6oa63XztrK/z74R9sqwo/wALpikYhmXApkOFsleO994xHAiyWKC63VKVVa1XCAGhyYYJLdcwHGQ7m+NNnr9pnqXrxT3fEjNc7fJzntVqCLT5r3g6N+LOd1zIauGsG5pb27Lcvom0EONkh4ZIVQqzHNOyc6nemDQncXl8lxeXya99OcoxX8lC1zepXR1wqvC6zlfdihinaN/VA9DqJeNWD6TyRuF6Lubm9ny7lMdL87o0LLu61eNtgZkv8a6L8fxd2sf982Vv7KrLyWOhxiu7ZFzNT2pZVJdRDPdibLRgdK0aZPJhaTUm9zy2CbI4HAKayLh19U0crTYITcIogbyhS2kgjFPAK3evIMZQ8A1dTFEDbNOkCF1M3qGgHN9WMx3DggnSV8edFD8q/tLrDHCM2Ny9i829e5icARdIRm51WLA+MHpU/2BAFyqFd6guHtxJ5Bb+qGmTI8zYiRdYPvVWQ3lM44RS3iR6zSDOmU/BYXSb1zVjLmSIGyBmsLhYemcbuipg/RVPF2zbg2vX8PCHPvQ2oD0ZpMYv0m9lroAXvKXaUXsg5cGnQKd6TaUZpHmlJzeyu7+vTllJUdp25uS5PGdm0BRw83PvwXDlDC9+26cxteNyAVrTBXC4SCXnSVcQUGhG2YshX6sDueZtSUJA+lAwpQYxntNBRPC2+kB6KmJNVvYASnEntM/3NkXdMMajlYEww8J4AXYid3ovcdppAH92phTl/ooLC4kB6KF93pjH7nMRxlHVHVWpTu1IANaV5U1zZvNlO6TNyoyTM8apMaiineGYsykFOYMfLuTu1Z9eTuv00bKzcEfRjgTgW0bgW4alLatafiogX8/EaRwn72XfNMFW0Pq+x/Ub18WlucHJyQlOT06w3aStz9M45hYWIKCGsxkNVbt9tdLj7/k8Hvum3yv67vTuNfzMT/4NnN67XgxNM0yNk5yCmpSA9bqxbYx37tzBarUCx4dx5fhITo9S5YDQNIyx2m4LeDCmBytQfufEQOdX1Q2uZVATk79hBnDKW+rZp/fgulqZgY5PRo72h6REMuxK8vpTzz5/oqaQ4waa37LCRBZThNUQinTCkiqqqQxyipPj+wSAg3kWNAacRAnhiFFWCfVTPb2YGdthQIyM7XbEMI42Zw08gtwkYgOI+wwF05V7uPN//n8jXrmHueXVN3nJ389LVmWvvGtRqNilR+3fSG9LOuXk2XUjZBlLHtXfZ/ILe7uMXD7deekmnvvck7gIKt1laLyowevqrTfx+Ie+IIp6gy/86gdw55Vr8B4nqrwzp63ac4P65RQGE2uCL4IehBHadGCFYiXNLEKPGZhEkHRdm2WtbqfhrDABwEhZiZrE0BXEINE2DUIT0B+ssFqtxLu5R9d3ZrQw5Ux4JVFYrGXGNF4QCx8z7OvqTFQYUtV4ZUYu1sN3slRgLdMZwnb1beHdskAPADuQqk5R3LizbqAHo+RtoMHFH0r/UmHousgY35eKcVwcck2ChRggjQ+6VF/2hVmZ2u6FfFcF3f3pmFHj6HazzQduiddJI/in67pk7JBA88HFOtWy0oJYLN9qWC97xyS+79vW4QF5QA9PY7lhsldzFyCfYaf/ubJKceTHJixPfa9Mns/M717UyP5WnvNGw9JwnPFKylfhCZT167pkvtBFzTI+ac3nXBkxgmPyCu2aiI+9+wuZFlDaVq19qDIEwL31Ef77pz+CYWxtJwlAyQMqpJM3Y9OgCQFo0smXeoq3GbnLVst1BoAoO01imVMN1XWKwxYvf/7zGNfrlK/GcNH1S2bc+afTIXT86fx3Z1ymfwW7ATmeoo+Jp/Nlc3aWtkPGWMzHdNDDZN+Zk6euNyQrn/LwUS/kzaSC+QhY2k68K72zDV3ATOm+yOplnZYxba2xLj24I4sMbPWkWH5UmbsnviqPPHutaebZHc8wNBDefsaXPZy85dW7EHrrOMMpeBdgbEttzqak72vX88Hp4mpp/czi++VZzsChzOXdn5XeDBaz11X6NJDg41C5fuRcrOXXsotbaqFggMWjK/+VAsA/p4pf3RY1f0tseV5f/31Xk5fiohrTjoGaB9hc3i/ri1R+9V1IVRm74LiOS40pz7q9DHosNmaeW8WYZl/DbEjzRq2ZEUtSWLhet/usuu6G7SoE8FAEnpyAh6NtgJ39gbNQ11VzZjhhEt38yu8kAG3Xou879F2KZdCE5L6dDGHkDK4JqAcG4sJW0ssofXW6AEfN+XbycQnW7m73B2f4wMd/BdvNgZVPBDz/xffgtZcfsXzTlDyDFPjq33a7xauvdjg9PUXTprZZ9T3arsUUGV3boW3Z2krJ0+C1TdMCyNvIgbwNWCutYCd9yGcICFxug/CtQOT6G/Uo9RcV2OlB2ekeUTnWiSl5ViGPoQzi7YHc1rJl2HtdpHkhn0VeKoxfuRp+QzJBAw+nE/GSNZdj2sISY0SYGlEWU3BrYBKwGEqewIBuWaQQcf32q2j7QZRnWVnU9zMjUsRLN1/E+vrr4NUmT17fsJdMy4pC9duR/LVIF1FALuLZta+cSy3AfAVTRDJ2Xd0yPvIacOXePTxAT0Nb/zU8hDWO9xVxX4lA2J4d4O7Lt3D6xjWEXaeqVan2tPKLk4DOz8Tvrt1+Fd3BBnDz++javXQ4qWyhv/rQK2gPTvHmiw9hGkovFd2+7Q1gcx5eYsrsTQz7ZPliHqUmJ52hQZ5lNRLECMR0MlgkAjVpK3OcosTWijlOkjvZ1eQAEULToO97NE2Dvu/QdT2Oj49xeHyEg8MDdH0nHhmU6XN0L1gJtJGLOs5aQ+jwXjuL3jtAabTw9yoDlTdk7mM/hnn0+VmG8rqiF/WK1R0BJc3ZEzy/xO0OmXlnLrSbEqbYc6Et7PuCepO6gjLAddSnZ0rvQF9I4u9+S1U+NT7FJK4UbM7KdNu0oEDFFkUKHu9n/ceU+MU54vFjbowyZhYX+Yvn6/Gg3/PDDit63lzTUrZ7+V4Zi4u8ueove7XHjvuZuhqq5Fehcyy9K++I8XSJVlLh6Hpu6dRd0mV1LHn+Wcz9hfpwnMCRijLyA9pfhGoko2+2eM/Dz2OcQtYpOPGmEAI64U+r1SofBiIegi/deRB31leyvk9utw3TbM5oV5IqNWWL4OTVV7E9OUUctnLfxUglpT7hLT+Gd0px1587kLcZXoMcPGCn+zo7QkMN8umXWTdhOdFUcR0zF9uBFYsbMdIAbN8BFPOREXdWZp7e0YauOSi7aM2X4eeyLCzzZkPQucXlTikm0jzPRcrzzMgbP/z9fIoWsLRP2Zdjr6rLy9LVKUk8q4K6ke+i2Vvj63ekdq4FwOXTHHxnRpqJzf1WKH0LeZOyVtUHOUaX1kGVWS3CyyMiwQo7hqafqEtjzYxpjBTAWU6krQ4HzLoedAw5IrLonoFUlS8kWy3JC9gKlCiWrVPp6k7zunpS6u++tgtyeyaXCK7FKtqcgIz+B1CMXa+U52cZ1SNzSFPy2OXqVRjGf1XZTtV4IDdWNM/jTPgzo7xH99TX9DgQmzwPA4jSySmT7JdnTgY0Aw0CcPu+T6vffW8rl62sPgU56ZMgnkEs0eAmTvHBZm2QBeqsPXa0V3FvNh7y6OUdD9dGDj93VgcbfOxP/HzxGAEYhk/itZcfNvqnOIEAJHmaCmiajXiuTehXPQ4PD9F1LY6Pj9F3HaYp4mClpyJ2sCO/OXnBEQj+7Ei/kqX5lCDrM7mUT1l0230wN+R5wK18PuoJjpZXvCG0LKmhnagbYwbTrpUY7nhsx+dTCak8ryzYZ6wGO4Ag3lvsTkH0c4IIFouFkFYpAyfDVhPbvPLHEVOMGMQdX4+81zLSF878N0y49eRzOLx2In3AxaECzIwpjHjum38Fp1f0lMXlwXtZiVQoco6f1NLN2nXfxHgb02VW2L3ifrkV/f3K0Fc9MeOUgWsb4I99ibGKb4LwppwaCqxxiDUf7X5cPpd8sbJE5YXrhO3JIV74vXcDTGiaGlfy4uec/DmeURlx8/EXceWBO/rS9CF9FsXb8sajz+PKrR6nr98EYm9GLjV0+S1ZM/w2a4XiVVZ/IonFKd4piABCxnd6EnjKM5nrNDNjnCYgBFDXgWMycg2ynUyVn0JuAyKbUh1WBys5pe0Afb/C1WvXcHh4gMOjo+Sd405+VeJ3bRd1jb5Q63mfREiEEDHKL+Iib+hakmEp02y+mdy7YGLPaOxZhyxZfu+cy47OUPLBaq2jekJ/eIrdVkJ3RbMteYqlBZwUVzSabFP5lvtLx6+vsyrIzGxx2fRTwxLkhspfdQ50fScLLWUMrqznlPhxf8f4+VweLODHcJH/Eh29u//OL2Q+3OlC9y7O0+tnCJWd3lKByypj3VI7ZS+fJVp4lk/zqgF3hhVQ/uZIEi/Q6wl1mdq3+c19u8WHH//S7Jm0HTig7ToxxPcIzmMwhAbrbYM3TlZGn3omJX0z78oyXcE8IIWPep2LGXeffx6nb7xZtVumm4iAprN36QxjUZwMoXnlVdqq7I+Kf5J6Vy3LsnZ1YO1n7aSnO3KO92WYlBNl6/Ua6/Xa6FOZYQbn6L8Lxr7EXHpHG7q+Eol5iREAyENj2TgFoF2tcOOJJ9AfHZWP3TcxWUCUAns+CfWBvMKwqx6ATqgscOvTvpA/K0ZEaiFeYMKqpO5jULksKu6Uq2T7G20/GHdK1o77yVAVslJoVqD0rCmcYihq5IQ7Dfas4KRMuV9qr6cMRNK2R13NYnE1l7nuDDBkRe7Eo0XyEkbGqDDLFNQZsyZN47yyvhR5uMjLYr1jIqmJVwh0Xmi9s6NpKobgt50zuBg+GVyUBC71sgqYKDEKo7jnRjkJxAO1JQMr63v8d1fbi43AlE8xIvuL8mECa2EueKF2k4FvGwm3IqMhRgxl25AzXmtxBv6leS3Id5KH9m5mYJwmhMiIXYdp2OLk5B7UY/Ps9Azb7SatrHBeEYs0ubZaVgTmszjXVWWnGUPKTLsb9S2muqnf882/iVsPP1+89e4bN/E7v/wU4pSUIvXyunvvFO16jbP1Bm3b4OR0jb7rcHiwwtHREQ4PD3HlyhX0fYembQFOLtyhaUAg27ZjRi6pevbWCnZyqc4BVTaJgMOr9/DQu19K2yraJgn2ifDCFx7B9mxldUrzUAOHwl1PXrwUAhrvUaL0yKAIDeVpqXKMGWrUkss6baFGRfKD28rOBmaCep9FFN5XECO9DIr8XYqgAFCKmUFNNny1zGiaFl0/Yb0ZpV9aA0pXbr6Gqw++mo71boD+cF1xo/tM1Xi/aFm1cnkRPnJZBfcbaX/qI/Cnnmc8dAq0Cw37KJ7BTXp5sc1f44fwGm4DcJir7n1K/Nj/Hjc9Xv7iE9icHKJQRvxjtOwFVCePa67cfBPXH3lJX4PV0elO3KkKBRGhaUY88v4vYn3vGK888wSYM08iyic0ZgUz478dVC20g8gvcJLreoJivaKTpKTgKnk/gHEYMYwDhmFIW5KnWBjlADVMNGKc6NG2HY6ODtG2HQ5WK7Rti6OjI3RdmzwnKDhZn5iMepledJJZNmdU0UXexHUTspk0XhjKeT5bfN6LUyE0OsQqfbjEe843QLteUozEk93Lr/QGpOzJ5etxHs9TXLxrC6UVOMOXeat+oABqSIzQUWRH1e4i07zHeoyMKNsSI4sXlxvT6lXs66kLsxrTLRkZIJibzVB8vl5R3/ccXHG70s0WLyrndp5z5/GC1BB787wT0nlVyDoPsDRRPVYuPY992bWuUusTZbkB6fRxvaW6g+peXkfNapHMVbtV9iUlAIQIYNhsQCFgHAczqt48+BxWDz7rxmUj/DrFBEs4Rj3XnTejQzUEwm//DuOZLzK2p6dQoFYYCw2/pMMM/P7hOZJX5dIvtFZx5So9Xf/J8V5V90u0jHYKVtknCI2cfonZKbwA0LY9Dg6OzPDNEuA+xfyKgtNlK7HwgTDsD2vk0zva0CWi7C2UsDwLdxm7PNBYAh2hbXHloYeSInTeKz3Y3wGsdMDVLu2advNKPue+Pr98vHGmQ1c1SqKXiz1fNShXPHbTxSGAmwBGB5jxRDRC3ux+sKBliY50fV5nN2lJ88kdIjTBbfGK+jyhzCnliPDj4pu6YGYGbNd3GBJmxZ6LQCqGVFzyq31qfFCQtRviFCsdjowMdebvZZuVhNlpkErLTBiVRq26Tby8MkMXq1CD/I5VGfmTq9/+c2lVgF21jPJSvwEAMzQt2XHUq6ZYMZXUUZBTMIEbE+GjMTH/SBEB862WKjcIVMWQkzFowSCFLhfaIUbGBHUdHrGR/fzMjO12k2IjmZEwewMBEgdNytk1Pm1cyHNeAbCA/A5YzhqzbrtzkZHLvlCMf81Djz6Hhx59zp5jAK88/zg+/5vfhmlMfljT1CDGBpvtFtsBGOTkru0wopcTvabIaQtj1wNE6IRDTgK+Mz0ZpMwNXem+GbkAhCbxhRAn9Edr3HhUDF0SCHQaA1597gGM29aVoTwmmuEsvSMdxBAiZHuisEswwBFRDKaMTIONHzsHOl9LXcGmQHrZpKDG2lWUwRRLMC+i+F5J40je50Et6bjTE6YaUzpCaDBNE7quQ9e3aHtgYgamCQdX7+HGoy9bUFnSCMsLKYaIKUyLY7helKjTLk6/lDPXy8mPhfLKt9vT55R/sXQ5j6z5c+cZY3y6SNavpq7WRuBDrwMPrisaAICAa3gdwOuLhG2pxxt8034Hib0XEawTSVbZYxTZBmAcerz54oOYhq5ajHTvv4CRS/MBaSvu6vgENx55eWH8ONzJ9bMAhYhrD72KbrXFK888lmhF9h4tjFwM6OKeGd5nLVdivtkVqr3JZQaQyn/JJsqULr5M45S3kjOnhUQi8zxr22TA6vseq4MDdF2XvG3bFn3fo21brORgldA0QGG8kz4QvrIkVzKmqLCGAwjK13wbR06nE5/rieWVxcooZr93KBpFP3jMrPeVZl+Of1b4O3vgQ3kckJZrdPnxtCTwq/L1e3VvSbwXUoD0tfLeQCkuUSSoZ7J50EVdBOYizECK2ZaUX+/l5T0OkwGhKT4LDy6trr7LxRqy9tgxXffqLR7fsy5ko3qvw2+ztlxqt4sw0IvzbKWvfP3bJXt2l7e/3ebP1EYtb/TxzefLLWVf7otZIi1D5gQJb6S8+0gzGr6VskhenMnLfcvMQJwwqiF8GqEeVcftGkctDKvouFR+1zSt6JiN5ckGL43zGvCFGLF+Pe0r6NpEVIzAMNSG2mQssg0IVTskLMggDoURUdtZXRmq5jTc6HXgXD7bvPXvsQYnF0esbD00bYeO2WLBTtNkhi4fcy/JDAl4T8NC5y6nd7Shy6e8NvI1TF+R1yeGSZS9ZArZSOVv1tOpdjFqAECOgwCGraZEExjNwjP6Or/iVAO6lHsfqDsPiMcm4LVvfhTD1Raxfzf02NMYRjCPYPofAJ4uytltsFt+vyrzgXKAyzyFyaG5xGi6rsUUe3R9DwYwDEOqJ0xyFxo2W2l6md0bisZaMBftqoVnua6Y6mota9SQsyRMMitLzChK0O0EksTdVZRgRkAEISB59EVnvNIWnETHI7QOLJRg1wMwljGXju7NoEXpzeCzbA/z1HL5fN6LKGCap7ZD2U91KdarTrCpKAhLLIdS4Vp/BfeaGgB/biA8JApID1Xtl+oKFKqFrASNw4izs7UZ+NTjcJqmJExCGp0AMOpolMDf9+7dsWJ1hdRMBI2u9LYuSHDq133ctR6D9r0yyF000Z6X7WFtIkizQled0owYgRu3Xsaf+6v/FspHP/Mr/wue/szHrNRhmDAMEzabIcVdEO+uw8MDrNdrHByscHhwiNAkj7q+XyHGiK7rLNizurLPBrHNRQaFCY9/+Bn0R2fYDls07agIORHMjBAmPPbBLyCO4n2qjSMKV4oxkmJbDesOz33mfYhjL0dzc8GWmCcQ59HrGybJiyCKvM539fKNIDQJ+BAALgP21kDTe4+orGDpm4JPKa+QZgoy33xPt22X/roeh1cmfNMf+V0M4ynGcUTTbdxgEXqLUZLTM49+ES/feBmnhye7Rs59pgroVZP3DwAiefvT3gn4zk0P4Tlcw2v2OxBhgyN8gb8Zo8JkqfcrX3wS9167AQDgGMBTtxfz+JRX6ucpxoiDKyd49AO/j/ZgM+eDntGSjnnnoeMU+EkPeJhyzEAfjP5SBlEqvzL8Vvep2LLkZTGFxGsoRjACOBB4ihglfl7TNOj6tMXyYLVCI8Yr3f7TdR1WfY9ePLiyUpi861NsxNQOWTcVbBeaTAPP5yGlhgLIKbNqkDRMRwhL7VQZx/YZLBabszJ0ZHtDhe2UPkdXgcX1S3HgieL6qo+lDI4R0ehlBHaG3AKr5eS9dlnkpsmR2tog7y/aUx7ORsR5m9RxRtkZn+p7rRy+kLeAOfpr4lnmAyRmMXKoAJVzi6kANUoPqrkj7VJ25w6jDoFQejrvTexn0lczvVXmnvF7fW0ppXncFUbLJd6ULsXqXkmrb1vVl4MD+HnY63bqMvaVcKt5iGjOqox5pFN+Qgk0XXWmaxFI4gfGmN4xjulz64xZFIKMkexhFUJA1/Vm+PrwhwLe9aTy+2TAfeUV4Of+KzDFYAt/IMLAqul7LCL/Rm1v1QInR66L5kx+XlGecwGVniNZYmO6Xe4337fyqXqgMGcKZF6eqd+SrGpbR6fMVy0j6eEXS18Xhq635tV1/8l7YrWrFdrV6uKUeK3wsm/1Rh7hyFm5xC5Oa6+rxBIyVBDufg5NSZcnU+qtmEsx5jkVY98gHvTYXDvEeLwC6Kp76QjGCNADAF4D0MnvU+w7faGQeezksmMmIOffwMkdnximqIUQxKurcTED0nNFXUi/Z2VRb3sLeO1DsNTchT4h9GoZe30QvPJZ4hz3Qq/s5rzM3siVVUcm/Z48uZJOV6qVJNeYIcYwsjA6Hn+oy6vm1ZhQGYzmerK1o08+eGUetZaHq7Yr3o0Z0PDzIT9TMvilFbgg/TBL+qytkASswDiU3WwtgIcj4bYbsnUpWr9ScCvgTZ5EwzCgaROYT2ChQduIRHbHhwueM4FvAR9tyMqYcg0Wgnj+gMExn3Cp4HVGOGVQWxugnTbg5sv56SKA8MIs1HVy12/x4COynTEANx58GVdvvCYCNtE/TQ1O7lxF8paabAW/a9u0sjRF8bwKokC6IM8V7bndMjFNv0Hbb3F47R5Wx2dot8loY6e5ugl8cHxqDaJ8V0F/27YIYuDc9j26w1PwOKHrNMgnEIYBzThic9aCo1iV9DU6I4VAO0zW8UnjNnKv5j1LCw71OGABhYWIUKVN3+WkuPKe7mBEaCYcnG4whjUOpxN044ms7qWVTG0ba23HG4ZmwLbZ4u7RXdy12FxLw+Ot4IeSai2v5j9a5/zY1waz+LTkxVVfm23H+gNA91tKtVIunz026JFdwQgBLQYc4BQT0mETm/EA6+EI63vHOLtztShnX7tcps2adsLh9XugsAPTGENJn342eqU/hIjuYI1x22HcdjMFkoicJ6cvfFclchZFD+b9a4qLGLmbHMPKsZR0X/IREaht0UmQ/NXBAdq2xcHhQfrdp3hc+udjjKUtPmpIF0VJJZkqoFTO63P7wINDZ/xazLfj2QI/LOWr8+wlZ85HoTQtPbvfyrJYfvrUI7IBHVQmto2X1uoyFXXJ2IvL4an0u0FQjlfMDFmTxPLxhq7aU0+3uKqRtybE4+6izjr2fM8WGJln8k7zFEo6w9EDo2vngrsz9mnb1el+PXF3o5/zec7yED3vuWU6S4PG+fnPe+eSQSvjfn1uqaycv/QKI7s/N1jmZ9K31Pl+LOdyljmD1Fx0mVo/4xQZQkPfFOVlPQFQQ1JQFmaxodUYdngQcHSkWx81djTh2tXksBKaRk7FBl6/C2yHc9p/aaowJ3BstXJ8x+Yz5eHs208WCMh4gfzr54vT0dge1XlBhgmzysDw4Xk8lr5o+rowdH2tU2hb3P7gB9EfHYGai524c5FEBHcqSAbS0bnEMpfHHTNHZPf2pYFA0ICA6m2iQzoVK0wFymyy4kUVjy6BBC7C0/am1997G2e3rwKrbn5TJyT9UXDzzeDmDMAbQPwZAOt5/h1J8UxiIgoO9B6D9CRX0voSmrZFx+l4bj0dyHDBTkjkFD1TgCQRgQIv25t44c8anVxp1buEY2RBLE8ooEEugqykYEyKkbeqZaOcemQkxpeApRqo5kHKJwYQCQ2nMesNUTUOUxo1xpat/hHALEYWj5bNGEPVGEx1nOD2a1ddos4iiwJGj/8t4pwhgz2U47xIyvSXynVEfnAiPLXNw6WPEsjX2kSVBLZT9nJbVZVlYH12hmkcEKcRoZETAtsWBwdytHacLAhmKwEx0/Ha6TQ6pU+VlSj3WFzy2ibIIQgBmKJ5BaT+dF55BZ2weaE20OBBqNT9K5mYgTHqyk/y1tOdK/N+Spc+9K3/E+/9yK+BQz4B8PWXHsZ//w/fg2nsMcWIs/Uam80W6/UabRNwcJA8DPq+R993uHJ0F1euHOP4+BgHqwO5pycg+rmbtj8//N4v4+qDr2J1lBpF+zw5gSlYZJs/Rv7MSqvGekK3GvCuj/0OQkjeEHp/u91i2EY8/evvxemdq0k2+IlLITF+da1yoJKMqbN4CjOY1CNWDVfKaHJgff/JDAycAGLTeDd5pzTNmGD6e+ibnsHVB1/D0csv47XXXsGz/8eYwanx5/oxNg+EF269gKcf+wKG5uIrf29rojlQfqenXdLu6y0xM1Z0hg/jV6BK/adf/AQ+8/SfwDTuxng+zpSWA5RbmGvl3SvxOrcWFe49tHpPlUABR1c3eN8f+yzefPEWnv/d99iWaM2v3xNv39Gr9QRbeO8UgUhpdT0EwjAMiDGFnlBveZYDJrbDmLyDQzAD1uHhAbo+HQKi2xGb0KB3J5aZ0VXeG6PEegq6uCBeRkFPxaWi3Y3DVHXx2+z9vaXmTltqpK9qJZmyl57R6oxmet3LXGvfhRSnaXZt7xDYUY5/jxkl9R2C7eOY+j642FaM0ogY3UKyeQ9KLEYP6EysAGbE8otdGQ3CjFr6mcZN8kL080HHbXBjIVCWq4UxDFzSCrKYXUE8n6dpEk/DnMdW8ozG9DvvQGDDQMDc40hjUmZjV5R4vnW/7FmgXkw7ort/TdOusZYxYWnn3c/AmGHGzfS7QOkl1nf4vzZ2ZbxdAk41wMWYDZSEmD0190/FitbZCM+VgOjeZbEO/2nc1nphP+fOC+tlzOXNei0ySDy/qPzsAuEv/oUAogZBDphiBPz0zzT40rPCP2XewD0LN4/yR7rua6pzm6cxq7xFK8MAdaB6bqglIr8rndpY6kiFPCxewGYcrMfItHha+XL6ujB0FczpnAHLF8hzzssWU2hbhK7dm+f8oqtBsvDuIg8DehzqvgUBv9KM+nl9kSg2OqhMCZYYCtlQ4VbkKMWvmmLpUrq0QqzXvY6l94bDHtOVQwzHPaa+ne3jNVIZSJu9BLrQBOAxMN4E8yuWcfeqRKqZd4n27tW7ntOrrWwRa+R4bI6TxcBoFJBJ5shsbqQaOBMQbzFvRYHpdYVBqO59i3mhnTUzNLD8TwLESnBoZUoeY6pWVA6e6ceSRr7iKL5c0odx4ln5k1jKyO2XrOuVSVXAiGJM+DyzNtD4PyjHh3rg+WqS+8wLBZSfFIJCoJyhSntHQw107Wt+6hDAQxNwewIOGVbfGNMOeF+GGZVR8qhiq4uNWXeyH6XjsokCmpCAXhPFrT8Q2rYxY16MbnsXu/YLKbZTLMZ/misUKG1vEBojJ0NJFCPfPr5TKlAs/aEA1eep+MS+Ii+SlM1VBS3pF12/RdttU1zAhM4xbN/Ao9/0+4hTMrjfe+MWTu/exDiNiDFZzpohnRY2DukEscgprsBwMMipO0DbMQ6uvZECcArvaLsGq+MzdKsRzKGod71anK/lOI1eWfXVI2I0/ZACm7b59MWOBiBEHN+4i6Yd0XStjfdxs8L29NjmfzZsSSPK/C1PyK2MnJlQAaBlP3pjbQYyAHnOwQzdvkwEdIdr9Idn6I/O0HRbtP0WbTfmt+k4CiqHcjEAMHQDXj++g7vHd7CRLY71MM2jkuc3Z2kfUF8GZ/oxP+ny7UxeucgybJd3wC7vLC8DL/re9FxRWlX2BUrZzzwuRMO56TL1ooqhcUSHjfGs6eprOHn8GbQvP4zm3tXFImpPAa+078JIABCaiKPr93B07Z6JI3Jb+ut36P1UWPpOIt9BAEJEt5rQdFOB3WqatM6Ui1puWX1G3+cfQDKGqFdOIAIHDUvAYJ7SVhkCmtCg7Xu0XYe+6yT+Vo9Vv0LTNui7dCpw07ZIHguunbyhqFZs7Zq/bpMj0VRVaWlkLIiNvUoDA6jxo9HntxQuPa/lOq3dL25kQmme15VpNS1uuS2PlYHNxqGTwdlepYsUNGsI45kieyJHhydKqhXzKTZNuEeDvov31jjmE9gE/9QnEauBS3dV6FbUevFRDVJFvVyW2jvMti5W17XtZmVaO/m8pSd8bttaH2PcfPgFXL3xKtrWLbqcw/92jpuvWKpA9CVenxfHl8qjHb/d2xZfVNOQsaNiDf/dz/klnpcNXbvo18eX99xkD0VyVzPPSEYiJ5PLF1RtkPJzUUJZB6NLJpP6G6Y5Hc3wBRD6nkA0WZB7IODBW43gVV0AIZycBrz6KolOEGybY+bnGsNVK+DmW31iZl0/Fi/h82TJnpTe6/hapZ/7uRvo4obgrwtD17J0Wsqk6e1lHn6l4u0tF2KIqABqzeSriNq7QKt5ei1g8tmLkQb/OE0Yh1FOhgh56xPSaktoGozrtcQHKlfggN1gNsZoIObk0eu4875H0uk9cMyoqkcJFAOIrmKiPwvwMwB+puriHW3Auv1rAo0At10CbrqiVb9PBSMYfd8BYExxwma9wXq7xUSpHkeHh2hCwHabmNcUI0jaxyt4mT4RpDWBAu40tnJkN1qFc3D+khVjdhlUIEDz6uNe8kM8+MoVsRIrZApZjm72ivgyIE55i3eVrzWmX4/qEqyVQHo+Z6nI4k909xjYVlIds1TXYA9SC/oyiXalHsZ+xitbrst6aGJ81xoIYiBSz524YBheGq7kFAp2igQAM6ASpYCWatgy2jgZvUgNJBKhfpoaM5IxcwpYiZA8dfS5mD24mhAs6r5/DpSUl8yjRNi7emjsvyVFIAMRKsYfFsq5aCL7Z/n5XWVSQD4VlAjXbr2BP/3d/y8AaU3113/+O/CZX3kK0xQxIa06p1dx9ux64030XYcrV45xsFrh+vWruPrAgI98y++jP2D0bYembdA2Lbq+kUDrowEwTcJyzOisHqQhhBSwuZMjoyWosB61rH8TT+BBT2BL7qltCzzygWcSH9O4ORTw2nOP4IXPvRcyIwAE10eZphxzy6gEW49ro2s93Mmy1qTZOJfxsPJ4UWrECEsEXH/4FTz8nmdBpiyXb1UFQ8Gbtpteu3f1Ln7j3b+OqLEol7t9x2CguULpeI1PhWxbeInxuq+qsrLA096SQakqe+edC4Gwt5D/8ukypWcxk3mofQq4Xn/4t/HG45/Ftf/wV3H42x9bLEe9RlJRnt/NvX586g82eNdHv4B2lbcx7zXCOlzoeb/SkL2VaHbNjwfzPKkM1PBzPUKUIfmEegDBjo2fphQoeBinxHs4YUeWU7IAoGkbdKsVjq8/YDG3VqsVujYFndcTZ9UrTRcOl9prl5d1jjMr+QRPhapfDYPUxt+lQkk9ddgUsdmcqpTfEELFQzy2cPhHGX6VZ06CU7J3zecZpqCd7eRRoRp05pgkK8g1djQc4k/YLYxw+jNjhmG7xRSz99Y0TZUxi9CqfHP0k4w1OxU65nlRj/NZk0S2Q3HUg8wvHCWvxMkwtF+s1vuKYZYWyP0JwywYb5ryYiQRITTAx5/6/+GRd30BRHNvvftNl+W2X8m3VsN4z7Mlvlia2zX2rq/l9k6/87uXCSgN/KWuvsuTzNPmDW1L+gLJnGzEQJzYKVc0LfPXHa0J306JbKeRzTwFgXGcX/vYx7LRi5C2fH/2M4T/8jRJ8Pukn+qBHjqeTa/R8a1GMaHYImwYRZpkp0ouwDRSr1taO9R6Qb5hv0kMcUttdZkx/fVh6AKgGpdZU98iuMzlXCBvjLj70kvoj49x5cEH3UrOsrJ/KTqqR2kH6C7uv+UkQ1MU4fpUEkEfu4VooeTMQcHUNTh95DpCl5TEzfWj3NBS4UUYXF1I5S6ctuWU1rpWBkSIzCinShy5nMzZgKHPKuBpmsaOvvZtZUE7FZy5Ktk2BOzHKksV1fhYCZR4r7hshMkGJEMdAFM6pcyKnSunvhwNoqj8mfOvbADjzNiWqpBKnwoD28Ignj8s+uV8fBPcwvX8X0ovCG5POaBdL7lCdpUlJ6yyvPCwzzejUzQczWw/S/BMDHxgAo5FyD0QGSRebtHa1Ztz2MrOfZq2c9rpx5yP5Pa8jZDHmP4ORBZuIzIQOCsnLCsukDgBhBQYk2UbQhKm4tHJ5XywY7OdUYGZwOmIyJ0CJ+teOqnZ/ypSaWTePTkMIO25t/jcjofI8xrPt5q8Wn37iS+mvrYpzBjHHnffvA0KSWFTb8+DgxX6rkM4PkLsI15/8w30ZwGr1Sr99T0i0tZHVU51iwQ4AfNpytseG28o5xyAs/RqKNssr8rbJIZ5Zdn0jzi8eg8PPvkc1JX97ssPYtgc2LNLXiiFDFiYCUnNDPYtBXZ1E6fqBvK8QIYIEUBhrnSZEYKz8dTek01gCVRRabj/aqW90tcBtq8UWW+3keut4qhSKdmfZyb3Lkn6EIBff5Bw+5TxkdeB9gLPl6KG8LnrwGsHJdtPtwhfvsZAE7F9/+eAozMcfOYjCCdX9pdPc+VI0/HNNywGX9ONaLsU2D2yw3HnDBaPKwrvMXlodXSKW08+j/WdG9icXLN8fh7vijuT66DoI//p6VoJD4UUNL5PJyVSkJ0AYhDQeIargxW6fmXeW3qyog80b5gMWbZpnQqaLoRz3YJK0Wglb6nv1yXXnj7FvYXfxhlnNJdyxuOBvNiTry3RsDQprCd1EaMwnDkMs2Mcef6ZsvtdGzD5ECjHDtK66SmOavgapxEcyy2ESv8UJ1uU99g7hBKLu4cSLVJUNtaWcrP25jLZhYWF/ao9l/ijeZ077JtEdQARJ2MAT0JTkqtEsNPgpnrrKTOIJlCYHFi/WKr507l5qqTj6SIyZ7bjZ2eJy7jjIpTt4vWe0WWZYQjU6Uz52r7k5U6JZ8pXE3Ls29orrZYBWnfPM3JoGOXXbO3tD/aZ06z+XPvrUw7PgrsUZS09TzzJ5TRp40S4fp3wLd9CaMKY5lxoME2Ez32OcLYBdLEzGZeTkUt3jOQthxpPzDdQ5tN6ArvyMaPO+Fv5HPsmMLGn5eWy6zSbZ3vS14+hC1jWoPQW71OEdou5ixi8eIp448vPor9yjKObN8V7IoPwr1XarYKec7+QNSlGT4wxbV/TgUcE3Sa3rHRmpSR9ZmE+rlq8/r7bCAfpJMMQmmQtVn0YO7uxoH6J7tlzix2XJrGuImX3eM7AAwyNXlYoeyGga+VUumnCNI15a6KsfIL0VCJdBdQJ771bNC87BEn2p2pbri1pCYlG1WEL/ONXN9LvaXL9bFrlnDEaKza8kD2Q5qAL84Z2wokxVQJa/ql4s7W6MGPfF7PetWfLsNV6s/Eriy5/Vhg8YCYzcMzqhdw6AmGKKqi3IWtfSSek0cL4+BZ4WLd1FiC2rCsWlAvtz7oPC4GPDDSJXBwsA6VO4FqMBxlTnEBaAowBhJgCegcyutKnbKmjBDKTMiVGDs3LesR6FG81zFIZO9DVUgWgNzzq2MxW26Is37dUX6v7umjRi6f5uErp8fd+Ho+/9/OSJ907O7uKp7/wbWDuivgmrayQNV2LqWnw0sspqPLR0RGOj45wfHyMCEbf91it+gzuhT96j70QUnlAXo0exwRQ1IvPVzVPkTyIbKuG1ipb8HF0/S6u3LgnwfYDNifHGDYrBw5LxaJ07y/5iPKrdCVKS0keA3wLwJ2RFG0Zf94bPc8891cbuwxIKh2LfrJ/aNI+pfzrK83rNzTApx4FHjkBPvgmo51QaAoXGRW/8SDhd26WZRtLlbm6+dhvYfjg76J//gmE0ytCDbn89fPV/BFqrj30Mm4+9pLhxORlQnZy7K6ti7BpmBV5n4/Btq3x4NpdPHLtLl7+wnuxOZlvtzQFcsdwKQxuyDNc4+p0bVr0Ozw8QN+16Pu0lTvhosR71AB25cpVtF2P/uBAFgvTdfXkWjJ2FO1aKJmeF+1I5DiSOyzEKu5+L86Xai6pzFo0NjnDiZe8xbuIZvXTbe8pFEb29F6s1i7Lryg3FnvH8X2VK358ZCXS0QUVvYp3M2YJukW8gXnaZSNV8haJQ6J9HEdM04RpnOydHpdkA5qEXAgZt5iBiRkM56kcueBrbdMKRnZjgFHkqxdAtN6z+eL0knKpLbedPU0aOiCFLMmYm83AlTy6sqeal0jLRjX9QovX/RPE5c1dzxblyNjYp1P5Wi8rURV+U1lbXNufagPXboPXxcq9yMKJYuTa2JUiWGk5LLhe8pxbE/ceT6HrsHQ9x6vV32Xh7D73yOo9ytcuvKpXYpzsnua4+QDw1J/IhmUQ4ewM+N3PMO7dSUWHkHg6USOGLlmEUG/b4LxuHfZNPKgtO6c22jtFSA8pyvRVA1x/VeNb5900/iE7dfGiab+xy3Jh78D7OknF8NuBpdQVN8bJjDmEBhRk65RT4H3ygtAABmUdtnSdn291JC5YSHoeJejZy+i8caK67g0Ealjx1n+GY0pijFBbQqDkxt00DbquA3PEdgMwp2O8owhnAkyAl9M8C5zMIHVVas76lJ4Y9apbvWI1QgAS/suAin/lVHjcOMWzaFnVXW0Nyxm8diQ/TRzDIgLkZG+7nD6XmVjm1SxHzLK1k1CyIFFm3P8+Z+yyYcRauhrfHszeioSPDRLMXw03DBxPEVMs+92PxjzWpR4yptK7kt9XhA29c3B8CaBtewYBjRit/JYWgCSGSrAYcjEyOKb3T0JHRAZvCJy8tkTAkhweQNBVX9maGdi2MirRXgzXvbZrjhYAdl+SweVBDXAOmNxT1II3+OxZ/73v13j08d+FnkV95+5t3Lt7y1adx3EAEWG9WaNtW5yt1zg9PcXJyQkOj46w6ntcu34tnTrWpriEerpjjGNWBhp1P88gHVW/p8TF55LipjylqI9cJDBuPfksrt9+GUQB27NDvPqlx5c7rwCiGRib16AZsACwup6XgMaAp/JEIhxevYdbT7yIw2sn2ZDlZEkhJ+R9gWBlbLsNnnnsi7i7OrnYGPpG+rpMb/bAT72L8OQ9xh99OV2rR8OdDvjUo4TRrQUAwPPHOQ8Vcs3zGgDdhJM/9T/QvnwbR5/6k6Dt6sL0HT/wBq4//AqOb9yBk7h5fJ8HQXU+mozm4nNpcfXa7VdxcGWLV7/0CNb3ji5Ma04lUdkDl81AP4nRBgBC04qyRDg+PpTA84do+x79waEFGDdPrqY0ci16Ip7HyE1mZqNFMvrdR3X3JTMM5QWE3SySjemyyugQchzaEICYQwxoWyquKMrbYWTT56Y4+nUModXh8ZmFRHmnx7u6QDWXMWrMyWQwpjHHC7VTEwUvqBLcNo1913I8UDADlCNvqZp55wEX64TqQWYmJc71KmWGm2twIROWjGNOnDJz2qOgoo1d6Admk9E+uH4a340Svjye8dXQNpfwMhbHQqZoV1L8K7+Yi+sXrclXcg1Gebb/zMYu/cy+a6RGTnILgvt0y9ogaTim5ANqNCNnmLocJtk3MtjdX85DyO1sRje5k48eI4AJfQf8yT8JbNaKg0cAk8z9IGE2CL/8K4STk7ytnIodUeL12fUAZSNa7oeC6QjlsguHZNbVuHKh5ZTvuB8XSpcydP3Yj/0YfuzHfgxPP/00AOCjH/0o/uE//If4zu/8TgDAer3G3/t7fw//9t/+W2w2G3zyk5/Ej/7oj+Lhhx+2Mp555hl8//d/P/7rf/2vuHLlCr7v+74PP/zDPyzbwC6X/DrFZTyn6vaZT7yFQaZt66RmYs5qzYQJq5pGADlw6H2kt/DovCz7loZ+sbKxkD8FGeXs0dVcvK11EhRMvtC05it0jgUVqz9L3HFRqdW+ID9RPD35U08FmokCz79JQrfrxA3BthN1XYdpHDFNZNs79aXB1csELGUGqPUXqWx/5rkljDltY2Do5mdvgJGFN0Rn6CrahYsDZXKlir7eBZzc3ZJHlV+0na292QyDhWJgz1Rejq7A1MQlZQXvm33lhYzuFu0SwZn1N5ypSTw09Va0Ntb2Kj+vTcBHtjmuFdsnl9tFoWOtbq9MFYUANrd8drSo0NwN/hS+pvbOZZtR30CuAHMN9ioGLSJGJNiWAm/ESqupMYkjMz5rsNgo7wgpyD2zxESae3d5EFDTnuitOtdnrOvs8ZkZovMDvg19QR7u1onnmRaeK2lu2wEPPPCCGZ232x5371zHNCWvjFGe3W6BpgkYhsH+tsNgMWn6vsfBYfJw6MSTI3J0fIpc0E3x6ETJ+9QQpqc2Ft4FBciWtql+piIjrtx8zco6u3MNbzz3MDg2aR5xAMclvs8moAgiHzl7CIAAxJD5u+N/Nk6RgnGvjk7xwGMvwUIQhGAr0jZv7LXKU3N/D82IFx58AeuwBbZY6uo/NGmXYvWHIZ11hN94EJgI+LaXlxdB1i3wOw8AG4GdkYDoT2NzGMIJuyzLQsT0/s+Cbr6C9pe/DRgaRHYHRQjTDsRI+9eVhzMOr57g5mMvWZkzBYgUWy5jrbpvyzmORWZ7eO0ujq+f4s7LN83QNVe8SrlVF1boKt4ox7oYGiT2ajLktG0KIJ4CznfoVyu0XYdV34MaDTAunlyVIaT2xrlwMrkvuG2Hoj9/zsndKplcrfLUSm5dnuEJdrxviaepsctjKRPgy1VcSsnYxCbvzWNaApgGCott6o07tWLqbWssewjzoUWM7WawLUTZgJVSQFpIVqOmxRCN6gE15nFUAHUZ9+yorWSab3TvueavmbFrAW/OZGMtE6s8tqgXAphRGLo03tc0ZWNf9k4cEZoBlFYIF/uNifJ2U9MbynpbHxFMl8yO/jnPsmpWcRGqrlqbLBHnlaElHcM9tBc/lTwkG6LfatrNm0pcmD89V1fupgYw7ee9b/TGU+YZHzAjl3tG7++ifznxjhyeNy/xbKUz3bf6uTJT7kRl2xA++IF8R/X9bMRqsN0SfvM3GHcnghqyKEpMMk6GLhChZQaFJp/wWHnpmk3AyddzRwL7vqodNy6WLmVdeuKJJ/DP//k/xwc+8AEwM/7Nv/k3+Ct/5a/gV3/1V/HRj34Uf/fv/l38x//4H/GTP/mTuH79Ov723/7b+Gt/7a/h53/+5wGk7Rff9V3fhUceeQS/8Au/gOeffx7f+73fi67r8M/+2T+7DCmzpKrrufl2y49zyl8ekjff9S4cXL8OIB2bGZrdR09/9dN5Qr4GM7UYJFPuI6e/IMYWBW27jE2zgc3OIJBuuHyVBw/b2wtKi1UpT6mUkZmZ42oor9VMarFVlHEJ+GIwKKYTJtUdtGkCQuiToStGDNutrMRVo4QTU1fmF5lTAFiUbEoNV8zAxDnymIbWiSS+PmKAgeYHkmeXK4x98zhyZrC2lK1VG1SPV21LcnAAqPwkAtowyjXs/KzeVlOGdAqbthFbfd2X4vlYWYPZ/WNglzJzVyPJHx8YT7gtLlHGaQIyOsYdDVJuz8C2ODLeXpiKl7oqw4cydtIVEZ0b8jkRJiDFJtITCBR0avuGAAiI0lXw0OTj7IOcruhjFeZTJSFCKQWMpKgCXjwPAxDEIBEnrXtMGuCUwV4ILIqNeCI60BtjsPHJzCkYsY0xckC6nIeu5TLI1Ualsrvvg3Wf+4z203lic6kc5Q83H3wR127cwcsvvQ8nJzdsoKSVdsZ6s8UwjDg9PUPb3kXTBLzxxhvouw43btzAarXC1WvXLF5N4i9kY4+Rx6UHj3oalY0V8gA950srboxxEvBjoI5kS7qOkdTm/dEJnvz4bwvvCnj1S4/izZdu7WgZAcEOvhZAnYPLSWkno1nDA/qjNR7/0NNYHW4cU8rtq96KwcmVXemtA+dvpD8M6cYG+L9+nk1Z/PWHCL/2kM+xf5y1kfHJLzIevPcG2o/8JF567d34pc//BXhDNFHEIx982uJwabntaluUpQqqKfDnJK/0XnTAk/23eHOxHCr+SizViLfKOA6I44iwSfcPVyu0TYvVQY+jwwP0XYej4yPbqqifpGEjVGkquFploKCSbr/NTE/KXaqvl51an3PTgjFrZ9aFa2akcrQyu/ituq1Ng0Arf5OA0Oo1VRt5WD8Np7CVr3VrmhZtU9XXyVOPrQsvJipP89Xascmw7LXlvbeYGTwl7yoSQ5Z5qhEZNtHTEhUX2A4RaQvDjr69l7B5RbtfRK8/Dbcv4HH7GvPCcWqq/AxXfRjjZLIo1X8yg1/TJLQe45ROXh5Gw2Tv//gv48kPfBrXb748r895ydOgdWHIwUG0Wym9z7RsXM4mBkcYMjBbuj8vufysy74PWr1eU6iCXu/M7+SC1nlBBR5aMuJdhCB9Xt/kjA0BJb68TNEXT1z9iig9pYzYhW9e1/MuRDrGge/4DiDtFsz61Kd/C/it38r15LNTFN5eGsieXBw++UxbIAGN/9WEptQnVS6ojoSSV8SLH7p4OUPXd3/3dxe/f+iHfgg/9mM/hl/8xV/EE088gR//8R/HT/zET+DP//k/DwD41//6X+Obv/mb8Yu/+Iv4xCc+gZ/+6Z/Gb//2b+NnfuZn8PDDD+Nbv/Vb8U//6T/F3//7fx//6B/9I/R9fxly9ibP8M7PC8lbXJXPPBHalacvdcTqyhUcXrtWFVg8+jVOVI7/CyAdxVte5rC3pMAZAPa088ybKxe2/OZ9/HJRyZkAPgP4zAwLfjVLn/P0aL8tv8KD1Gy4IfeMCkEPTpqmwegtQ4yS2UnZC2GMXLV9oPlsEAwMMVxkQW6GLnl4V7lvJXkhkX9D+iELkmLlmVItnN5dPKt9tBSfSqqSwQyxGfnsNyqDkn/Ol2d4Lj1zzBIzQ40BGc7gwRF4eLSCs6HLGQtsyLo2Z6SQ+zU1pDLAUKavfDbupvGTGkS3LlLU8ZmVffITESieL//EqCUv1yfU0JYpTQ7DkewwRQBphSVtmSTAPIPSSSuBY9kOni+EvAUge4LJHFJXwwqULRpWq94sM/GOvEoHyxicj9v56Fie+wyAFva4LEEz/015Qd+vsVptcffgFMNwiGHooSdKJtts2tYzxohhGtO20WlCLzFqhmFAEA+vvu8ldk1Iq/BqcHc8IMZkdMxtr/QsgyhdbCjq6+iv+XRoRhxeuwP1KLv32jV0B8dFHo6EcdsX8nPBBl1cbNsRTTfZuA6BsDpc4+j6HTRtOrHxvD6oExOw6TbY9JvC4/obqUwXwUJ/0NNFqrA4/vWefPYRePwkX3/+OBm/0jtEIlP1vB2dTugn4LET4PbZFrj6ZcSxw9XD1yV2D2NAD27SdtzDqyfLxACFIl5smXL35osCPNPZdnlAaRnT2GKcVmkxYint0jlVq9CyjIdnnuR5Yorv0ooHV49V32O1WolhJ5+wp3xFMVmqWO6lus47x65TJpfyZw/fPc9XVa+bofSWK/PbHZW5Qg+7vPqcwhkCNB6FKX1Ka1p4iBbQ2ZRl/fSxxpQWVaaJkkJdG/Z4j/lCsFxQT295p+FQw0Fq3IrmOcbMCAJScp/meeMXJ/L4FCzr2pHclyzjXHvPjG9lvxi11W9vGEIuwTrOG7l88uUtGdK8MRAur7aLb5/ja2/goce+nLMvJW3vWoByOWq1Hha7T+Geyn6LdTmrUE7umdpDbDeNNZ5yINcDwr2SWue41iXrU3lhVueBtmnJtUvjFhXToniT01FSXiBjHGNmWtDMyLXXo3L+ssWaWzlWgx2LDK5+FzJ+2WSZPb5YLs++EVQvMgawYCAgPylFp7v9kJTkhtnzzzGuXMn6SpQtkRa7y+J5eQNXNnSNE+HsjNBMDbhtknZCXs/RvCInxEmAsWBb2JPuO0bXNE34yZ/8SZycnOCpp57CL//yL2MYBvyFv/AXLM+HP/xhvOtd78KnPvUpfOITn8CnPvUpfMu3fEuxlfGTn/wkvv/7vx+f/vSn8W3f9m2L79psNthsNvb7zp0790v2fafu6BCPfPjDM4+tpuu+6rR8ZZOCPH8Sitxxlu4kJKITipgp8kWp7ITmOa9Xe7LubzYDibwD0IDY90D8MwBO3T3sZD7plgIryrOVKAcnlN8MlolZ8rbIEeM0oW1b9F2H1SrF5ojiaeNXu2wVT9ozGaWS4GYutxUqS0mn5Ynxijk5QzgAIpczrXMela7ZsX1xdluTBn4P1Q1yjMY/TNZ+nhEhgzxn6NJydr3bG0v8pV1jw2R4HoKWVEiW4JPBEVgx8Oc3jBtR75Vv6EbGmrloUzPqaNmMqmz57uS7wXVtO2P0btVWxp7GI9FVP0qyHqCYh3DI/eAVjUZWSBvZQtuIAlH2WRboOoenKZnl9LwEEMCNCHYJLB/IxfVSA0pMQkYNf3a0dtr4KKBVVmvlpDy/tYGZ3cqpb8SojVX3tNFXA799oFTHx6LBvSx9dl/7wEOBXXnq5OOZAMBDtz+PGw88gy9+8WPYbI5cgVlxGeWwgmk4wxmtcXa2Qde1OHjlVRwcHODg4ADHx8fo+xWuXDmybT/JAyDxmGnYgmOb4oB0eZzs87BlZlOUgIxRvaFM7sC2ZDAjEuPm48/ixqMvFOWe3T3Gl37rgwA32Dl7GQAma4ebjz+HW0++YDwxnezDCMGdEKSZnazwK4HWGVLX2ER89n2/jTtHdzG1o73uG+kbaa9QcelbXwW++Q0/k2WeiEyzspyicDTmom9f/xK+69v/tV14mj+EV/Ewmm68OK1eZ0TibfvUozplD6j5vdeefQRvPPcYpqHLsrsOdr/YVnnBzxcdGSCOtlJ/dHSMo6NDXH/gBlarHgerPgWo71NsLj2xCyBwrJXQWq/MGKOgxLCHtA+zPLvM88p0caVoV1IDzRKG1YVRO3Fd80rllP9GCTo/xYgYAiZyB5hUZZk8U+MZs5ySjMTHKcnlpJNyivcYGouLa15XUn8CbPtgoMZkhmIHjhETczpkSbyT1LhVtjGhEcWza/tUVrBOKXCCnZToFHTz4iqAvW/n+jOXmW9QMV6daU4vKKnL/ejKLW/CZGLh9RbcwreJoBRjyC+QJ6+uEdPUYJrqdjsnLebdM/+VVuUTF3mVay/VScwQeAFaF8flBV57EZoun1Q3XVKCdrfb4usUACp+rnnPksKyVAbS3K/5EklYihmZMpbzq3XMObLObZ8dGawOc4WRZdSAJ/iJpLqUxpj2ryhaWX5/y8eAD30w64qD7BiAGRtj1g91zmprBsIzzwA//VNIhksLbI8c8L5JJz42jR4e1xj/GMev4KmLv/mbv4mnnnoK6/UaV65cwb//9/8eH/nIR/Brv/Zr6PseN27cKPI//PDDeOGFBJBfeOGFwsil9/XervTDP/zD+Mf/+B/Pb0ibemPx+cObqu85NV2H/sgH6sz3u8NDtKtVDjBYAZJ0qXq7V8bve6WZ3t5gmgtAJhuw9C+1ZDnQa4FQenSlkna88pyZSpTpmPdMZgT5YgTwMoBXANwDYbA5VHt0ZbZHTkBV313+9EYu8isZXuBqnVJA1cZizM0s+cy5frk6ZfvAw+eqqb0gV2ZTMZ26T/P75zA5keKAJGVDV15BBtRgUzxn97zQJ9f2+f0ELupZNeW8EaDGy1wdtvGYh6X/8+UxA0cM3IwufwR6ZlwZCYfswVB+MEbGGDG77mlYFoy5nXSuKJBMbeH2pvtPaywpw5i/vM/KTJ92aovXtVIjw2e9aMr4JAMVHYGk72cRPDofCTkgvV6TFWDWYly/qKdYY3nYjF+xaFAfVLYck1bpJevSQo/s4v01H4DVtM5XllmeneDmwU4ml/4JYYu2m3B09Dradg0QMI0rbDZXYBNFGkrpGMcxnb4VGdOYtj7EKaJfbcEc0fcdjiKjaZt04iuz5bcgqs7YXDSRjLHscal8KNGiRq5adSs8yMCgZkDbOqWdgH5scOWBNxFjeaDIvHEbG+cHx/fQ9RuYd62cTptiv1VNuiQ3dC5xii13enSCzeEaZwdn2PZbo+0PW6rbquDdVd9cSvn6A5t284VVZDx8D3joTPLtkEM+rSZgtega7TyWjFfWbwQCDTjqB5uDfPAK1p1Iutjg6N617DlhvHxuaLqMYWtvkmKGTYfNyRHW944xWsB8oUsVdAMZua1K2VLSRIDIgcSfQwjJGN/3ODw8RN93WPVd8kptW9vCpt6tmYm69iiEnH8zFVlrOpzkWpbTJm64eKbMU82dpWK8kasydNUeIDoGkjylrLzWBhYpJ8oChGKEQu4tzGsGFuWaYijvvZINlFVwdntQcLwEdI9i3Cq2J3I5XurPWvqalzFlTJ+hkiy6mMVIQd5cxSjq7HC19mcxn3Ixxbt9h3u+t48Hzngp5mNGdQg2wFa209GVe3jkyVdwfPWOtYx6Mc2Na8u0XMgD1+sHl0hL7VPQMtOf5LbiDGfkSlN3+f0Z6rlYdmr8BWyxuDTo6PjScUF1aRUOq9tpH2ZMFNfv0q+7Wty85i7wJpgG6a7sgrJGEWZtag8ulL4/efCnMqbuaK2s62FPY8UmkmhIvILsN9CvCOLrASJgio5+xWpaEJd9AGI8cAN48sm8/qr6pZ702jR591Ta7i5biEHYfiUNXR/60Ifwa7/2a3jzzTfx7/7dv8P3fd/34b/9t/922WIulX7wB38QP/ADP2C/79y5gyeffPI+S9ulEgGHN27g9gc+sOO5uZfS10UyIQDMxKYTtlxcy9djdEEWad5GlwfVDDUqRcpH9GaaAKIRgX8BHF/G4sa9pX5yDFUNNOohEcwFST9ScHlfB/Vgi9OEYbtNnhyrlZy40iNO0eIcjONYrQjJH6vzdga41dQvjTxAOuVOnlpcuZx91/4JszwkQDpbzTW2E6BKcNl0+X1p6x9bOcufLLx1TlVRWjHmMliIMQNusRuYoUmNqjNDl9wfEfHwSPiLWwLYxZhigCJjy+VI0eftlTNqq9/1jQDzzALy4QMU0kmM5rKvRlUVKuT+fLl1k9UYTmIzKdAtEvvR40eUtk++V7yG5CoR/JYx4jwHQ5NOaGzUECMAKU7qtRitn6J5eKby+l5PEUygeRwj4E7mUuig404DWspsy2BLhaS22Q7vPK6yLaWZIlnj/up6cWlPuUpJqtuIRx79DIDkDXf37sN49tmPW94oMdja0ICYMQ4DRh5xdrbFSThN2/lWPdq2xZUrx1itVhbH68qVKwhNQNs0tsVF69W4k7sSLTlmYFaQQgmeKq8OW+VVPow8p/O6XMrTH57gyW/5jLVXgZusGQnpDFD5JUPRFJcoYCyy8SBFUbqCz268KICSG3jmsS/i5QdfwkTfcOP6RkrpgTXwf/k9xoENia8CbiswEPDyY8/g9x56BmBGvz7CBz79x9AOZWiOYt5dhkZCDkiN5a3Hmk5eu4Fnf+d9CE2bF7TU2HABbLZTOXNePqEJODo6wtWrV3HjxgPo+gZd1+a4LEEOtLBtdwuFeljuxZld20Er2z9FHsUKlkmV5l1l1YYjj30VtwnwiBd43uS/edanZ9RLyjCiXiPCJMYui0W4aMyS14m3re1EULnMesq5bvcpG8u266m8hgRQHydpM2fgQi6r/tOkp7GHpjE6o8h4w0GuDJ/MQwtll/hshq900ayqTZ28MZGojD9ZQKPq0WJMGtbkLNTkRGmlOUjsofS9DAsQQsAT7/19/Lnv/u9A+NrKpV1GEfPirtThy3JKP00vYn6h9HKYQWe3Ov42pgoT700OfLsr+QefXwylAyfYDWTDsCjbYWmLcmrLUue9r7WpQGJIDFmRcnjQfxph+jXWL+TcEE7VKHRLInSd41nOVuDnpVQdAPD4I8D3/LV0kMM0RSufaAIh73oxT1nHR85OI/4f/+ZiTXFpQ1ff93j/+98PAPj2b/92/M//+T/xr/7Vv8Jf/+t/HdvtFm+88Ubh1fXiiy/ikUceAQA88sgj+KVf+qWivBdffNHu7Uqr1cq2iPl07ZFH0LROofd9Nk04efVVRDkRZNH2EQKOH3xQtiMyDq5etc4516a1MEF3ena95fSV5ARexefiSrH9SIS8gSRh/vuoLIFU/t5sR1x99nXwA1eAxw8A6CpPskZ4JVc9oohfBvHzID4F8RnAp5gZuVQQoza26O25wFbjTynnVDj6MvJE1Xg60zSZQG3aZOQahqF6N+9QvrX8mqGQM0wA4F2iylOlJannhoayT0EQCZzr6gKhLxljyJXm3yKzIr9MKPUKLilBlI2TOiOyUcsZqyAMT79HHTM+v/8jPDIxHprInsmGLsbtyOCJBJzCGWAWsM2CvMp9VHr8+U/LEQihyY1G+rwZDD3A0+u5/OqFQlKNvsgqGZnLgOnsKkV5nsSYa5oezxVVgenrKbUVgUgmvDTeQ3R9T5SCW8aYA7YGEaIcgcjJWGmGKujWN8IEAhpCJELUgPu+Pcop6IgU+n37BVmdViMN5zWr1DT55JyMVUs0V47l8vl9aZchXy+HEIo2DwE4ODjDrQe/jLPTazg9vWY0T2PugUCE0JIpKBwZ4zji7PQMwzAASLJ3s9mkrUFykpl6kqYTHPO2JE9rMfIc/ayTxMYLmc00dT8brYGCsSzlj2lY67bE3TIz8w41dFHBYlifL3gdyymPOQac5i1+EyOG2iXzG6n2wvDpokaOd0JaUgJOW+DXHwRunwLvuwPsHRjnAr1zkhuXViQApggZvhi7LV65/WU0U5qrhydXceXuAzuKcwqOMMXaS7wkv/S81OeGTYe7L9/C6ZtX0yKG89Yq35MXP9jNyYU3uX/LfGnlPXm1JwN9g7ZrgWqxUA/ryd4wWhS739kYPsPXe8bsLkXKoVmfub4i241KbyktT3kOHN+pB52S698WnHKmFQxNCrjcIhuEyoUHNo5cnMS3r/+ReWy9lV6p8QtO5rnFLIcrKeFu7BlWnMsTbRf7VCCXQVNuYzOe5fqNO7dE6qNz/GX3kWWALcqYMZIFLvh6zAPW1+1XDo35XPJvNrzfpO36RGTtqqcuAgAFRtNOdnr30pg7z3qxyLsvqAtmL83q97zARSBsJ4y+Ff64UD+V9WbQUSiwPK0AcHWt5rRL1/IumjJJH7pnKyhsP5ZrzaXK6Q1ZPg8je755ssmxNT9fXAX1FGkSZpy3PvtiqHpG7xQkpDlm/ev5fdZN/Dwq0qwBVHlAYQTz3sAMRpi1zwLPcGUSERpKjhRN3lqE3D8K4KPTfYScS8SouO8YXZpijNhsNvj2b/92dF2Hn/3Zn8X3fM/3AAA++9nP4plnnsFTTz0FAHjqqafwQz/0Q3jppZdw+/ZtAMB/+S//BdeuXcNHPvKRS7/71nveg65zVXDyYNxscPbmm2boWkqhaXDzySfRHR5c+t0Aco+9Raz0lU67VkvcVWhl8nTIwkGFsQpvNQKNtGxo0ufs+coFut2MuPm5F7F9YsTdxx8sAZi+mbNQSenLoPi/g+IZiAcAVYBXqcWyS3f5e7YyRUv5KLcH5XIjM9abtPVm2/do2ka2L3YIFLDdbBBDqPiGMusKhCiAIZ4xhfyko+fcPawEIACUYz+l8H4ZqKRVRpITj1JAWM1bfDKBLYqYYzo1VerlZXeSNw8XDC5/qjEr6m/FeVFP9vTtBTNYRcn37g3wR7dluRGMUagabfzAqfB7Wkz61gs821ZVGUW1DS1ftY+9MJRVebWdZ5LVg0e9nB6GbclQMKf5KwOyysyEscpac2SL96X5loCk9Zd6CijGVnAHIHA6UIEDW9B+nacpCGtApIhofEHmTAwIFBFoQuSQjGFyqmV+l/a5C7arDN33jwo5BbZZ9EtZXDTRDCxS+WntspRnMfFiBqro9Lzr6PgER8e/ixdffA/unVyFbj0cxuSl18rWnrZtrZw4TZiGEeOQjmBfr9eiSCavruvXr6Hve7RtihHZdZ0B8KYJBW1+2/wSf/a0qpKphk41dEWKErtN81AGbkvWBmtKz7cYhZHLt73zTtObOkaWtgvlup0/x7+Rvv5SwWtti0u6cqcn/OyThI++ynjfnYwn6oe9wsFAYVh4K5AuA/L0bWi3eO5dnxeFhfDQ8+/C8d0bpTpFmA1kU8nOMUzmhYVMwHC2wvOfezfiVHp5LpX/VpLWIAWgTwZ45UFTHMFiSGFmTDEmD3pjF05O8QKvruldINc/UvK0snyRpFZIrXSRKPe1BxYv5J0ZuUQ+Rmcs01i+huqErzdIXk5RDCS6WDrbVif8zreJb52CAhnDukOhpk0x+DRNGMcxnQw4bu0aEaHvXOw2gmwTCsW1ghe7v3oYGfYRumJkEE+mfI+jojW3YLEHm/hP76lXj2k9ATq1T/k5azQS2WRKsxsXnPOkD6Up02GxggA7RVK99WyRnALAU6Zzn2FrwaCnRuE67Z23503pojnKzLrgWbzRj8tZWfXzZb6d+T3PXSIxT7SF1/CO744Owzio+k1wxSLVS7/8m3ghB+XSCgWiUtVsjFUyR419iThX0YyRlPzi7a79HHIvHgen077jQm3VU8qg8ML8hY0D1Qu4oNEvlFj7RACIZZ3geJhnFabvpsqp96+vUTnPlSeKPoQU5uOi6VKGrh/8wR/Ed37nd+Jd73oX7t69i5/4iZ/Az/3cz+GnfuqncP36dfzNv/k38QM/8AO4efMmrl27hr/zd/4OnnrqKXziE58AAPylv/SX8JGPfAR/42/8DfyLf/Ev8MILL+Af/IN/gL/1t/7WosfWW0mhbXHz3e82d+mUypWx0DRfh8Hk31pyOogJ+WzsAnSVB5Q9gjwYOP8Fuf37O2e49TvP2xGk0zRhohFvPPEspoMtQA2AAKIG4JcMLKRiylXBTH35jvIe5TyMUgCZwl+yf2/o0ODM282AEAJWwxY9elCXaAkVONCUPSc8faUAsfbOuexqMk4FJLs3F89m/kpIIfVDFpAEtEju7YmveC8u7UuYQcW2JgoRTm3PDTJjip6W1CGTbatwzEoNXALippgYVmTgsYnw4UGBlAesienJ7jgwGA9PwOTADpD4676QvybrTMEhq58GQMyZ1SvOe2KRa48sNCl4AViBrlycjNv8u/YgtNbzoNaGq0B06RMVCEGO7E5zp9yS6MU5Cf2MLFSpFpwUdKRZYyVZyQgMAT/JgFlcF8mlPCKtaBJi1C2LSgMkaH4og9q7E4osgH2MgPUJGy1aF68QEqVgvGnYZSnqpvNiIuvDXM7lPFzyLN1lVKu9kLLRM805BELTSBfLStY0TZkP2YmVKU3jZCc6TdOEs7MzHBwcoO97DMMWq9UKMcZ0SEbf2wlnCXRlPp2hGZc0cikbIf2rfRJCAKKrr7CivCpYKilFe7P9g2LkOSVDlQ4dn3Djh91Cif69cv0VvPzAS7h7/GbZM7xfn/hG+sOTnjsG/tO7gQ++zni/Hya1orXAMHYpYecl5gT4P/Qi49Zd4NcfBe6syvt3r7+GL78vbflVWdCOHR768rvRjO1MxhZzsxLJ3nuUmRHHFq9+6QlsTo7EI3IHjXvSrnp7pVEKAgVCYycttmJwT7fV06URTNR1XaI1GgdyZfs4TNnrwCfv0VzzmcK7h1gOQIF0JEOVT49VC+O5jgkzVFRywbfZgmG/5qPRhRoAYAY0X3ZoGlAIpqMYNtqzOK9Vqt+LGDExkieh8Es1oumn3wquB9l0XVqgbdumfIOTjXX19ToRIcqWx8hshuLo3kWAHJaTcXH28kqBsEsvvDkKnnlksZQs4mTJUGjjSZVm8MKIOj/Z/LQYvLk++q5pmjAMA7bbDWJMbTuOI8ZxgD10qXdK+/qtp374YR5T876Ta+p9bTR7G88p2Nu6dRvsAGkXN3ItN6uP67UwTYXOywXQ39/WNfLekYWXLrgbS+1zAcp2UiWYPbi6sioRlHUz1QWsFnJxtqVUGlMxeOaNri6E8qR1P55m9dMswnfZvy7jfsOD0Hdm+ptw8V68lKHrpZdewvd+7/fi+eefx/Xr1/Hxj38cP/VTP4W/+Bf/IgDgX/7Lf4kQAr7ne74Hm80Gn/zkJ/GjP/qj9nzTNPgP/+E/4Pu///vx1FNP4fj4GN/3fd+Hf/JP/sllyMhpzhOt70NocPWh205xU20E1QNOUdELCxOkwheLs3qWZ0bsPHcNr7jIkdn0hWYmzb7M3s1W8tJ9HWBkhgUw20qJKmxqeHH6eyp1pr9nbxClynR3MLqzLVZffi2tjoRk6BqbAXdvfw5Tfwo1dKVgxrzU5O7dxq29DlXUq6LM6EsXOJ+i5yukLUIq3CgJsaHBMAxJgY9NcrsMSHuVyE/SDMB8mXN6kI0bJRFiKPBGLv3z5Yihi8TQpc8hraCSvDu4ky20bCvHgIYHtQwfx2dG9UwQEYIGJGS1viN5FjFAsrWNpnSDGHhgZHxkIyf3xTxGWfolbz1MVEzubfpZR2orWplK4ECUQWcyFhH8bLN2ce2UUnDtlU4ezNK0kmaOOWeDWcm0Z275ZoBUGqr7cMf0Bj2FxPORLCA8GcaXbFzqXNI6Z0OIl0skAog5bT9MICIYyLH2jwm4ZmGlBgmNZ5HbiFiBaEinNI4jAN3a4PmF/stFW9gciVmQGrBd4JP5nh+7ro2WcApr+2OeKiav89Z7BeZicqbUpYwQoix8EcQOZc8kJTmvwfnxMk0RFCOmacQwDDg9PcPh4RarVY8QAoZhMK+K5NmVTuVUQ25A9ihUfCENtMAriwZMeVgjCyqAzCjJ2STnjxOKm2pu9WA996EjQeaVbv2olfO7x3fw3O1nJTbMHsmgLMz9LAnc/WhRzD7L6SXTZUD2OyddoH3cQDvPGH3xtLs1Xz8AXj8gXNkC776T5ZeeEVoWU3rMGj/0efcpHz4zMx67Azx0D/jdW6Whi4iwPrqH9fFJYfToNwd44IVHQVPN84PF41raZsVI8jFOCSGNQ4M3XngQw/oAeYHtYqngu5UQoeqiVVfkWDKctLKliy1eYxQjua3YR9lSU9HljVz5he6VouDshLhFYchrgvYxbwe7sqC0V8Tl7yrvd2nRUhdv/KHagKZ4EmxB2c27g5Pnm1UxAwLhY2VtPH5NMbfKOGDeawzIOzIaiS/ahCQjzAuYIXG+eNYungebwcpkvVvyk1Mlg9Cv94IoCE3TIEaNd8VF+Yo5lJjayFXoL4ziXpHPGbvsHi3E6/L1m1+SMUeg0BqOD4IZdQvXFCPGMXnL6cLbNE2Ypihx8fYzOh32M0My3O/isuIeq3RBe57H9ylplubDwkLApdLifGFYbNiCXO3DvSTuvoelFndlkkOAu7qG8zPFS6t+MKli4HmJsIIRFV+5fq4Y5zUNXNBsrNHw6sIcUUTObuxbVdS0WWJAlnrO7qhsNM9+D/wqUmuZMet/4S8OQ7J/WC7OZoPMEUbeGn6RdClD14//+I/vvX9wcIAf+ZEfwY/8yI/szPPud78b/+k//afLvHZPatJfsR2iHpxwSBx5QPrtFJBrhfZSFjMPeZ6FVvo838Y+m1O0cEMsAzoEWzQwowwWQL9oQ6S06OCQgcMxpu8zzqCDSSqsq2DUAqEHT5MoqgGRA9ZnWwRqcPVKYvRtIMRA4JC2jk2ICHFMJ/AgGMVAxMQTGgI4EAIlNwZd9dput+j6Hm0QxaxNcQwSKJJWl0CXgUh73AXhVOAg7+MIntLe5IayJpnaLoL1EGeekocCRylEtvgFiW9FlFw/mTFGwjgFoOmB0CNSi83AiHfOAOrT0aeUAB64AXODOAFEAQ0FRJIVLNb+nUAAWooIgZEO8kxCP2CSLYVi9ABLQE+NlZRq4yFnvibGF9fDDUVr7/ynXnmZ+Vt/sYx128KmHnuZYSq4LgCODK8jBv7MpsMh5xVK9eJJf+LtY0CYccTAPfXa4mVg6k9nKQCvpMbqmIFkzpe+BPksXOJVGSAu8pbl5znl72fjeQkAAZY2Ztsi6g1eOie7tjEDzUgMjiOmQDLsYzL6JbcxNA0hEAMYEWhEQyOa0CIEbTBPg/+Z6heUNziDUdXClSDUcmNaIdd5JO/LnlmMSIyICAppNb2RPNylk/Qm89qKdriCnRYYAI6E0IY0piIVXl92GgtIjqiXGFbSdSFSCsSr3dPouIR5AlnwezkRMwTvyegH2BKPLNuo/l2WwZan2rwLIOKB68/iytFrePHF9+Dk3gPgsH9lkYt/bJIm/tcQ7q3PcLJZ42SzRtt2eO3OXaxWK1y7dk3ieKUT0Nq2tW2RbQjq4JAlnvImqIdGsDoklTTKan0GNH48ZxykhtoSZEVrE5J5RoiY8oTX+QH1VEyKcWQGxQiNDReQvFMbEBr1XGUCRZV+BtUwYBK5l7u2gmWLiWyrb5ogHBnUEBoKmIRmsYvnuDPnlPkHPb11I94lnt/ZAfOLqb92x6faSY1h6lTCbzxEePp6GtOrifHJZxg3NnOyAFTHPyEbyT0NeyZtxmHJwN82yXNTnzOPceVLMq82dIYvfuA3QTGIDEwvefj5d+PGaw/PsaLpRYzXnn0Eb754M91kwjSsZkp+bpuMAwICaBZ0uFQ4dD7bPZ3uTZJLExgTGByQ4uUpTiFC2zYi/1J7BiJZt2wKLJvpJPsrF4L0pU79c895T5/aSwyU5nCcYq53aAqMsC8tLZ5Iy9jiToyTsDIXG4hEAphxS7flZJauRqK6/OT5VnspCTWs3lqJM6dg6ynPOE4pVItcCESghtC3vfRjcP3pdB1OXknaJnqwTowZv6FqB4/9ouGudD1aNwYgECbmRJd6qpF4fUFwRA7glQxv2vcVdsxjgquxnegjmXOQsXU+t/dPa8eKLiAGQQ06H6lDnBjb7QbDZsBms0mGrWnEyem95NG1mdC0DVaHB6C2ByMYGl/eMJflafosw1toFefsz1/Ii0f5tpO/wgvtCfJzZd4Sxp8cjUst6OeOLlTVhdrio9YxW62Xq7KvmtWFNDx2M2KejZGylL2LY6jH1nmJi8/SQ1Go4Tk9nrfo95kVgXMPKz/OOoh1gMkR9xAaT/0OeaCLOpZt9t5ybM08i+H4NOv6M2fsNa9xSYfiTl928d6lntLnF49JXkxvOUbX1zZlwag8bZE5cH0BIrFrRrik7PhiFPzk/FrCjNn4UknzOuWHlgjV93iowfkKaynlQPErAaQX67IKoJDqnieavkMHYhLSzDqIyVYowHlQBvtLJejmOv3N8MGshfEVE4VM0BMRYj8i9gOoQQHUtIXsBBdXHgRc6HfW+jOq/lVQQTAzmStf3TDVWJjNR6nXGAKQ5G9iBg8TxjFiioy0IEZWRhYuOmUpCztpQ5AoTXoQGss2QzAaASWBTPaagmpvMhDl2ylTrvcyHboloBz32mZm8OLcf7NrnMZHZEYbgZXKN2GMh5Hw4BY4ljwAOa+M3KcxQsZYupejNiwk7XDktkDFnHM7UfGXc6A4dUrLYq+sEqrpWI4/nUOqyJNj2AUmlzmRgFIyLAbpTAIQxaOsFQ2IoR5T2esrCxwZl+Tej4i0XZFlrlUgylfC15nc6ZAehEjSe7qKw8pcVHDJuAazGKwgc0zKCak9vTdEoYQQIHseE/0EgMVoRQTiAA4RmGDb1vJcRqlIGF9bEoTpvgbyzPHHAJstNgVyxxWjxeZW2Y618pG9I+0FSpZL6Xrfn6Hv1jhY3cawPcQ4rMBcr0q5eVkg1JyivFwNeVOMaJoBIMJWDsoYxjF5ejCji8kw3YSA0FSyw6hz/aTtzJl3Kz0zsVrxEl8DKtq3ymBgiMsxrhTp+0mnv0jYMGGz2mBsx7LHuHoXVUCLsEDpInXy+gqkn/vQhW6+zWmH1yHyON2nDCwZkC5kVJq5Phs57v1GoV5xN1E10+531rN7H3l+mxVRftGbB8CbB+neakyeXlpMNzGOdN97Mbfd9if3mYdExXNndKYrxwPhygCcdaIEyHvYv48ZkSacXHkTSrX227U3buFodc1tsZc66qEfMeIsDDiJDDo9BsZ2bx/OF3lKynfOZvJYN8uDVJeMMR3CTHIvpFIzHyXxCBDMWStaajSpZLdPedGsXvjlohz3yqI+wW2jq9tqNueFHWWPfP8a278NrzBqP+W23FGXhcUVNZKCKHn3ujGiiz/ps4ztRSRxHWM26GkIgNBkj7o8R2Qbo8a1WmCO2RC3oKQ7Q5cXr7qoxFI9raH3LqznSpYjJX4r5kh+8cLXUu6q2Cye3CG/9e2K+5WGHIIk7dCIkTBGxnZkbLYjTs82GMcB0zji7CwZvThG8bZvQEmJcXNmmcvN+IabRCw4iWvZttAcvi08n9A2mT1D8xJTP+WTUTO+y63pvRLnBVBRLoPNGzWPkXlLzKBYNWuWUs03Lpuodoip5JT/d0GCeUqEnvq3v65zZT6HypIW3qD8BzK2kfuzHN9e+ML6oebtu4xdqYgSexYYqLq/eE35VqFHlO/35e+jwxvZdiOYi6d3uKGL8x/VrG3XJJgLxfOGsuaYBfn1TBOMGbgU5t60jZ2Gogw/Z8krMqWgTGnUODcANMi4KuyGN9V44ASyesxoWcltOMfX0ueSd46sTInSNE1bE2RdlzkXMzBFPVmBQKFB07ZoZBVJYwc1TQP1pAiUvL1UcBnIEANA0zSpfZqAN97/LM4efB0cRrTUAswpSHPXWbwHW2mhHBuMUQpI6zMNbrcwqQgoAvJZPgFPeiMQoW1aEAU5/XODVvbgD8MW6806uYEfHqIJIf01GVDUgfiL/lWJTNKnnDx3kkt5cHxDwJmMNE3BjdudLF/3MVP2fFHxqiTpgpoGfGcAkwTYVOOGrd65Y5bfNwKf2ErIDU4KODEQhjXOjDIWRl31wQLBTYCNEyFZO8HarViJdWU0bg5lj5J5yoI6UQenxOjUyCslTqgDbutjytuaDHfz1vcXEagJyffE+lPpT33MzBinEVFWvhs5qrrmBTnQvLxR51vltWi066m8Nuflt3nrKODl2T1tmiTs1ISvfMUrGYzGDhFQEJ7zjKOeeEtyGiFsLBlfkrEROMf1CgLupjDZvLcaMmOa/FjKWzHAKfabSvomBDCRbX3VNson8aZ+SN4NNkKsPc4DWjnNFZbyWlnSww9/AbdufRlfeubjWK+P97xlOZVtksfI6ekpNpsNNpsNuq7DarXC0dER+r7H0dERurbF4Sp5oHZtl8ZPE9CIATrGiCjHzRsPohRbJwdN1qop+pJxRwTSrSHOI6qufp4rbm+Ra9O07YZBFNE0bZ7P4un1xvU38VuP/ya2YSjKkxKEoLcDGn0jfcXSZfWTXVrifaRNA/yv7yU0Mn3e/ybwnU+/jeNF+BlHRmDCn/lCxJuHhP/8QcJpV77H5sieur302Bfx6iNfFj7vsJiGk+CI8UO/gmnbov3//FWEZ75pmawKm+pcfjua1cpQBl8pRElmK58qFeQgMlBlahCPeu+5k3FKadzx9+xdpjFnpSlQQNtfTNXxcpeIUmwmytsBp2lKMiRGxMlhO0KBfycxOiGk0BEZt2ZJk55VzzDXPyIj45Tln8aznKYRkaPF8WJWj39C23Xo+t5h4Sx7ydUNyHIYASBOuyuyHiE6SszGNVTPa3eDKy8Njw9iBIfE54uFa5X9ShfrP9VJlQuJ7Z/iClQPNLnIgI61bDhj00v8uGnbBoFCkjeyYurjnE1TxOt37mIYRpydnWGzWePs9BTjJIH9t2vEGNG1DYC0Tzk0AV3fSx+mWGQ2JhWSe9woV+w6qU6Z65mbROeGNnmp0y5MwQulXbuSClx5+UL3qdUpy9vE2/8gp4tImF1jPlR67E5PNT+vKqOVfi56wlb5/O+lcpau1TQsPVssGL0Nad8iXp3e2YYuYsy3IC4l7/znpXtCGaVb6S7pn/fR73qb2tpMWScUXjg2wEz5L8iYAXSGbN8QdVOFuMnyTJroHWzFOVUeBEIEWTBOLNJBgPkTwRTA5O6sSqp4D7gBr8I9gxVRHpUCMR6YTUexDpEFTNaB32w7dOsDjIdbxJDfsbjy5iZsIcQXBr/2W31UrhmhNC4OUQrgStoWuX19XUmMEdPEGIcR2+0WfdcBcnS0ATVlLDvGptjVrCsVmBTGSGnEWq3Wa/bd4ccaZtq2M3sxzKDHUO8ZzoYuZkzS1/rwgxPQsW5HTMatWyNwOGZ8a+X58bWQyAZC/s3QIJ+FVmyDhpA/veFG8+Xxpm70y8yUXH7NxQUw1LL8O8pV5gRY83G4CuS13z1gzzHRguUJAqZCCEkhiqVnBqutxgjOA0W3Ve2aF7lWUs9AVhczEkoeEzqavW57lmfAcgpn8jhkIjf/hLbI0OO0SMBkCKoEEEBRAGQpbNN4ShxKx0IIWn6Oiba4kADAVjydGCj6jijFSWE3LpkLnqRem/r+GVBUxq7tVgF311HuGxfXHHFo20GMQlnoLxrjd4F9Lj0hVBnxJ3jp6Vr6HQC6tgVxRNs24Mho2hYdafDrzKuYkYyNynvY17umBTPZFaVdg1yvnaep+Ce3bW6HtGXewJF7XwwR636dPIUXPYsuDn6+HtM+8FcvtiwB1/PL086cp6X+8Cd++ulQ8OcdJBeryUbPvLCa/D1QACDCiTt/6JUD4OlrLNiI7CHP649G4PZ6mcZdNCuqfLMDXuuBLYDR8dBQTIZiBhTlTe2ASGOJCSD9InM99mvwAYEf+zJiDGhefAwYdx+yVCjGSQDm5vFU7BoWwiQLY7anPDNWYYOJxxufEMNMfqo0zLgXWSGKS7Jxa9c4z/1W0Ftfs7eX5fhx6Y08xVwRjE+BZrtnClxKrpYVJsoL3tmjSmXcNE3gmIPK66fm8XXxC79N07jTHgnk1+Vn+NkaIPWlpx/JgBolYOoST7Hxp+03U6YjWHi4SdmZ/C4NTnsVYM1IZSzOGW5C3iVSj5H0Sw1vXr/IDgC2SDcMEmR+xDhOODk5xTCMWK/XGLZbbDabZITkmLaRcgRzQNuvcfuJZ3DtgVddvZSAcs4vph1GBMUl5cTKzbKIiZaL3WlY8voIO96wiImKinD5U++6+uroX8bll5fZc/x1fn77jrlsyB5eZL+5kmdL7aqtNe+fMs+SEfEicteMtLyEOedpn15Ql7/PYLVE32UMVPuMXEvGLo9pl+q6hJP/8Bi6bMIvIhqXx10zgM0L9/eliDiWKxvl6k8eZFmwpvLTiowXmI7pL1Dgp6T6GqiuZQp19QSrUuGrKu9nea+Pq2TZCPAnogQEBA7mKt+2LdqmATNh4ohhGFL8lL4HySpI0+Qz77IhiAAXgBMFXSkIZtM0aLsOaum4/vQTiM+NeP7jv4Xh6CQBIjVuyONKvwn/3NCz5E/cND1LypykTxoJKK9WDlIiA6poV5xPvKMUR2mzYQRaYxxHNBRSPBzn8szQoJ4VXewBTsnQkrt/ZZGHY3yOInJVN+hIOQdTIRINLKqxYZKgsHFKMXrUW4s5eRCp4atl4I9vgIcjldVhYMtLY7ikFYB5QwVtZyJPquQJDhzKYLdCyjlV/kYG3lWb1MnuyaeusKpBSLccpjy753kgQuMMcwY8i/p5w1ymxupJBKYIjtlbL06MOOate7bFj2DvbBp/6iL5Js+YQ+sTgrWDGrX8b12NttXmAjjq1jW2shWMKz+BxG8ikpMYGQiSJ4RGxlIC7ZN8+gDjk6xWI4qxiSLQZK825gAKenqUrqBHiR8CUEj9HqPN3Ny/KfgdggpReT4awOb8HmGYpRAuDZA25tKTko9m9/34LDtnXtZbTdqHpiCxtn0aI3oy4+HhIfquw+bKMbquS7/7DgcHB2iCnoiZT/vyZ+c0MtZmwT+9sibVJGI75VFjt2h1c1uSG4NWWIrlxTr2JxmvoVD67F3fSG8p3f/Kaj22L5/u2zvgPt50Hr770lXg337QyzUq/iUCPvgG8Ne+cMlaMzAG4KffFfDcFWAiCKAgrAAc7jAW7qK2aHWHHe03McY/97Ogu9cQfuL/Drz+wKJiVKzu4/w67RoiXnYoCYrL1Dud01HLidy00oASzc2xsx+TUU9mdosju3Qbw8UOW9Sy+SKpaB9mbLdbAMlDR2VkaAJaao0nDeNQYDrlv21oCpEQY8SEqTJaqYwlqXPEvXv3ZtiwjBmVsYaeZuw9pqsaVR/OEKUGocoAlWKOJVy41DZKZzI46bPRPo1Xa0gOUEmXbrtlMRA5UOmV3Ho3hG+TnCoQ6esI1yCUQo+kXRfpdbWXneo3wzDg7PQUm+0WZ2drDMOIN+6c5YDzMX3qImZkDUUScOPBl/BnvvtncOVqAPPBgnmj7Blyn/66jg2tW642VznnTbJslDo/+aAnHmZbeZmcWUWWTTl12o3H7ydd1NBxf3JuV1k1DYDXRdSwq9/J2m9Ow0Xo1/lwWcNeSfPcuOTL24UF6vz1tX00n0fHrjy7jGG75NhF0zva0JWgcd7WokYsVUSQflqynZ8VyNjVZOSfZ//bsygvHOXtRkd6KHoGLYqmWSj31pCgXaTQxvpXZcOCIqa0AOy8mIJTaMXrpElbKpu2TUacpgFRC6Le6hBEwW67FNA4KbjuCGRn6KhhZTkpWPGYKe9EemR0epKY0qlDrD4W1UCvjFwKKDwA1BWppASXCpUGBg8huP4QI4QaH0I6uVCVXm1HT4M30kxTxLBNXl0EBsk2SwVeYM5jYmFyFu2l9LhPFdaKKWvhmLfQs+JoJ65c7CtRSqO5o+dguO/ZAgfMtoVR8Y/uAgsAjmKyQRidSn8xv1LK2+NSPexTaCsMP86YVRi/ckXK0ovLeXJ6I5cHzIXRQh4JxftKo1TtOm/kEUE9t5TOJt+0/g72m+RdZESXIoIRKIBlq0PbNmlLbDNC48ky562soQno24DVKh0J3rQO4MrgoAW3PnK0eM+uRAGX17RuyimFCItfKi6hyTCU+KkaewJSUHrRZ6yNGECMhCkGUJwwxYAQU1w7UwwCwBzSvA2EFLcr83ESHkrIHq6EaGA2jefJlCjrO50l+ltPi1mIYanzjKQ87fjsT+vb1Xsk6FiyUqzxM+/wM1bzR1y//hIODk7x5psPofAgrWmr+MY+sFGDA/XmApBOiaW0eDGOE/q+wzCM6LsubUFvvDKVQVs6QSsIsLfCzbjla13UlmDjRPmJ8qyg2xtdw9a1SkbJES888Dxe7l/Flx56Bq82r5p82Kmp726eP3Bpp3LAe+5d9h0LcmfXGLpfMH3RZL1c8aFlYuyhmeisV+Dn330BuxMTMBEVcr4u7dUD4Jdvo3RkK04iLsdxoo8wBcKdHpiC8oMsk9cLpPWlE/kCsXvqQwCaCByeIX7Lb4Bevg367IckuH2p0BQLnTteRpjfSKxeZ7f2n/45fMYy52MyZJAxAt9OM+Qzw1p+US4rkIrJ0jszXMryet5sbnGXVCYuZ/Y4kwHzvs4LcDBDSpT65UVXtlYxmio5HMUglBZ/JvnTnQWyIGPPZmyiJywrHYwSv/gmzf2b21jLLTzK2OV1slQx/q6UDXoxv8KEAc/z6GnVnl9XOF4xhxnfNL/+WapQVFw4GCk1fh7DgmuaENC0TSZZxtcYB0xTxHbYYjskb62zszW2m/R9GCdstmMai7JQl/skxaFruy3e++FP45EnX0fbDSBqRUdS7C5zhqvqIM8n5XPKFXN1L8uTa0+5Xaxjt6A07ipYqDBAqESvLGozCU41IlpOu3jQ3sQQOi5TVm7Zgpe79sls3Osivhb7CPUDtyJEYupaTteepqtXMkibt5TJtKc/4cryC7Hs7gl+d123bITzXUtFvn22LuXT8ss9n8fkeRAj13vxbpHvounrxtBFxfXlAZ/0wF3o2Cey/P5KDisiAkyZukP7O9teBKsKvNrLw8opyghgtMnwwKrYqTfEvHwv8DQQuF1XxkwBoUneVJ0oOH3fi7LdousOsFodQydLFDfqcRxASKtr0xQxTpO9T08nTB5hZSP4VS65AAta6JiJCdl0/nQSvKSgQgHFJHEakstw5JhOadHWU9ChrcfZQ0W91kKTAENyWWDzirHTvpo2MXYgHZNsdHvjWgYX05jo3WzWYDlN0cfPMQnPmcH4Hi/7UBiTbBX17IJR9rmBKa9pVmUyMwYZCwWIiWroAtoIfPQUuB0FaOygjkBQfw9vi1MMG+weoW2amaHJY1wqCqgY50UkYyFAMhbQ5ksGzWzYNWALuBMQM4D0nlcFcKRMdy6H7J067uZ1LT/rpGAuyPFtRC1i7NB1Q4rBEUczOnZdAlNt26LvWqz6Fv2qR9/3dpKeza8aZ/j60JwebxgrDX7ZkFN7JdarLbrNMMa0HYdJTnh0ZUTmZNyaCEFPX5wmA9M6X2KMQAw2IDikWH+NfMaQvMImirZVz06f4hQHI4S8dcP6UJSsvMXarxJLY6g3I5S167bOvNWUqnKrXtUnXfsDbEf+KepjaTfG7dtPY7O5gnv3bmIcdxu6Zsop7V/h8/2sWxiHYUj1H0e0bYuzszPx9Dowr6+DgwM0bYNett2mUz+zsCFqBIQ4ZSlXydS8YpeSy8fMNi896MoqiR5MkPnUNmzxe4/8Hp4dnsNnXvodbNYb8DjTFqqmv6xi8LVPXyuK367V7rmZErt5OO3IvytdBLItvWaPQnCZ9NIR4T+/q4LvXBHleL5fNADmpA+c/jxpAUAbnLlbiTeAlL/vqxKvNpj+7M8hPPskmt97P7BdjtdybirGRSU37F/Ov9VAJCcKp7ivU8JYgn2Sp2cAoAHTK9pZsW3ixMoDSpK8olfzW3L5cko7Kibrk+TBkxetMgFq/IhmkOq6rjQkkQsIP6kcKnc0+NHtZapQn+I2gYUvbzEMA8ZxTF5CRDg6OrIFtxBC8rhtfJxWxcVlXzJye2XDW66bPevad97++aRDbWHfvtk4FW0HQMHQGS7Ya0Q6STDmkhhgEvzud2VI27CuhlRKf6YB0FmSjE4LcXALI6ELjdK2aFrVp5BibMUJ6/Ua2+2Aeycn2Gw2Futyux2w3Q6CnxsUczwEWxwCBxxdOcO3/en/gQcePEVobiByxDiNhi09OsjYPet81naah+btf9HkZTRQ6hz72f0O3iC8Rz3XCm8buUc7Ci9n6Dzteu4iicg5LBQFnpNqgqxT9ggs+ZzloPqHFMbqzcUyXJewoWl2lbHLkWb80POqOe9MeX1ZNg0WCNby9mHOsp8vhxO8Elfi7Fy/emSUs6OyoeaS71Oev6MNXSnui7jMQoahgnDNYnnPBwk574K2TUCDpjxwiCoLd11a3VGO6eWVo3QhbdvIpZAwljFmWlTQpxPcgrhTa/DzYAo+EaHrezNohRDQNm363TYiOJt0TZRoCskNmqgRhSbRM41JGGzOzvIKFkR5JfUOS8LMVqWKhiYYS/dGL9fEBgGIQLHF9WeexPb4BHff9QIolCPeFGw/i3dMwtpbRwEZM4M0AP+UhDAzgBhl+1VS78dpSsq0AK6z9Rqb7UbeL14JqUhstgPiFJOyzy6AZzUm1DCQmki8ZxxoZm1buGD72lauYRmprbU+UjXLop9bxRxgPBiBjw1lUcTAFe0HynCs6EK4e1QCxMJbyPLCGYhyeXU3lVHG7GJ+hlDeK8ormWSOhSWGS9uOq7RT+VuviZdKGh8LBuiiLpKL0vvJcWOv3Fg7WQFlvbXabSNbG7gBURpTfddiODxQtIOuTXO0aRs0RGgaSltk207qqDoXyTZG5TFp3Og8CQvGLh1bSq8/jUp5USotgIndWK0SqWemlpvqGN32CALy8fJ6qAbHBPxD2nrIHGy7io5lzzMS2wtoAmOKE5ompCPVOXl0+cHPSogHB9KHLPVlhsUQ8oDCamiGuAQck7LG4hFqg9EBER2brmlccKoMXTNw6botHnnk8zg7u4bXXnu8eL42bp2X6q2Fvu00wPwp0lbEFLC+xXq9xuHhIVarHsMwpMDzh2k7Y9c2Nr8hio3OF/VUzLNXt9hmQ6kqGYx6zDHSKn8yfK1Xazz76JcRJUK4eiFP04SRR2y6DTCcW/0/hMmrTZdPXxEj154ilUcCywreclrAVciA18dSqb283g4jV/lqx//2tV11y8/jQiF3KQJYRymXgZYYXaVY+acUnxktC2XqfCwU0wUy9ZNr2g1eZe8AN5NnYjjzGZHtIgfmhraEuczjgLKiV8dwzFjAUcnaTIqfOZdNSlrFc4T/MXE+VIad57KrMwUCyVZ4275nbZHlvS6UNdxYnqChJ2QBTQPWj2MKIq+n801xEjyajGld19nuBO9VnhfkslwGIx9GALdjIE8u19Z7ku8/1UcsKH3eUVEvrNiiO4sBSysi9wAV4Avj0trP402PrRbIJIDZLVaKZ/aIPOb0Ndr2TdskncjFLIvMGIYJwzhiihHrszMM44h7J6cYtlucnp5iGEdst4MdPkAhpMjF1M7GYCp4wvs//r/j5u3n0a5OdMgLHgsORy0YMapuKOBDqfZcMvl37ZIRNYY+p0SHjcj9Vt4TijmUv1P99l262oUpEXpcjDUjrM7jLYfnppqC3RTpO33L1oZhzplhyLjCizvL3XF/bvCa3ysWFV3s7F3vWirP81/vebYr//60b5zV0u3twSNL6Z1t6IIyevnl/BHNI4HKobekrPmBO/+izF7+UO2XJlXXHVM3A4yjlP2kSJ/R9qojB0R3NEUmjHrCISExXSIgiPLbtWhC8sTS016U0R8fH6f4Wm2HEBqsxPDVdq3kkz9yXi0hBYuexrxCMo2J6Y/jBIwjpnFIBiJWQ7WCEDHwLDB0IriAVyYKchORGssAcMDxSw+iOz7EyRMvZmZVTUzveZOMjaXg0E9lwD6vgkQSZRxRQVI6oU1PkRvEG2KMSclbb9YYhm16ltJJf6qQj0PyfGvbBFbSyWHyXs50s6MlbfjKgNUr29pcMXLJDpwSn4OVZoXc419mYJLmZgBHE/DhLeV+s/ZHPikNMsZdO6rRJnsH5bgG/iRC616MJuBseOSbLpEZAmremZ/L92pQ5IpJxl7AAGY+HloNWZSNPiEbvlxTWH/l9df8mkyLU+71KOZqjOXV6t3ChIhsq5i2U6C0rWwSb0mS30FO80zgk9G2rZ1s6mn0hqooK+uZHprRUNadzNvNbrBBNKgxf14Ph2kBqDtP4h21C31u12TwlTpxBtIhsBm7ii0JzHYaewgMmoAYZJyKAT6nNAmi8GQ/BgDYFkYm3Z7LQjYZMJVS3GSCnNWxHD+g1DV1HJTCm0jnd77WNANu3nwed+4MeP31R+0e83J/+Xcupbkhs1SsNzHR3oQt2rY1UD8MKwCEvh9lYaQBobeTGSdRUBv4U3NhvAGi8KQ5pOM6zdMM9bJiFpE88BiMTbfBc7efxdROBcNQj73x3pD5g04Wr2xofS8FbN+5aR/gXUoXybcEdndk3FvebM27zsr+a4XDloCu9vUFkjd+vaVUA4nLPr6gHFwkbRjwK6md7HNipWVPecvvI4AY1ExAg3TEbQxAJMMiO8ubfcnfc4/kEtTokhcx531rzwkYZs74AVBeVXrn6CEupAuEwj5zXdnaxl7LOrZKGkyOeSXODDWZTpVzZkSRcvzJ5V6e+gUGv7AKkrhcccJmu5ET+rbWTk1I4Qq6JoUi6LoOhOSF6+e4YoNcvXLRmKUNSE/mnDf/7nnnplcuD9bONW5QGVa0f/WC8l41iRxALRar4XmQJ36uq+nhWICePOnuh5BicckifjJ0JTk0DQOGccRmu8UoBq7tdsDde/ew3Q5Yr89M5ti7JNwJBefRhQmgESFEhHbC4+/9DG4/8TTargWj19c5DFW2RM1e9F6d56LsJzdhKmXOJnJppQGsfN7rJlXm4loxsxQLeX7ijD4ZEknb1ToyLl7POi0afBZwwf2mXfLpony9aOrdzlOlHnsBOXyeIWzJSLVk2LoofljGuwttX+GS2jjmn7usbHyr6R1u6HLpgrPFVkCKa+cXFxkYYiwy7+wqUgGaJr+6Amflt0DtAAGhS9uQ2ka9q1qEpkPoj8QolbyymqZB13cITYO+X4lHVpf2n8uWMV1F9wq/P6odZihInksWc3ISoKErJMxgCkBI1uEYggUpBpJQaZoGTRPAHDCNEV4wiu3I/gqBJEp7IDJjJOcWqVuo6JckQ9wKFwAQ2Ylw9tsdy2oedGIcopg8cliEedoCJcqvbM8c5PjgKaY+3GzW2Gy32G42GIfR6ggGRgbilLbaBAEDactTY5XXLYT6IBeGqlT7EEoxyOp55rCD5jbgpx8GWNJnB+BPD4TrYnw4ZEKS187ryP5qLw1l9LkndPiWz+eeIQWcWh8f3NwCPeXqaf+bgqzKss4JNVDotlN9h0PcSofGD6Lak4vyMwR/HWUZqpaHmjuokUTqK5+pLrlNLJ9uL/DGFSrzNRpQlshAeRMCqEvbE9M4cCvekK3BMtg8sPbeOgXVVAJ6/ZwFFHfl1EaRpAgoUCvLWgJB2m/WxaRqg25rpDTnJG8qa5KTacXDipPxM8YEipghwLOkrWkCAuRE2BjRyAmWk2yJTE2l3r7i4m7x/GScsYQEQwrybzxP6+nqykAyiIPBIXkj+RZXaHdB7DBLR0dv4pu+6desJV966ZtwcnJz7zO7AEu9laPgyeYxoXxuwjhNODtb42y9Rts2ODo8RNt2ODo6TFtm++RxkGI0pniO1KWV7iJGorYFV9iOyi9MwNOP/z7evPYGKATEZsJIySPP85MQGhBIDjxpbIFmtnUSuJhc/kaydLlV2a91KlSmS6S3NhJ2KQrnPePz71pg0Hu7qB0ARGf0OgSjKRiOUyKqZ70xAe/9feBP/kJyP0cD/NyfA5593J67WK125PJYxF6brxR4gUgP5YWDOxkk+oIkBUqhNkgPOIrqfe/i2wjWqo0KdUoexyw4TIzsyVXXeFhe6IMZAodhMMMXQkgnLYs8T9g14T41aOnLx2mU8B7ZS6ttGvTHxxlnUPkHaT+2BXDl3+U6cbonXnHiIa2xblMTqkFv37xxeMzjUuTf5XBTz+Bl44cWkNpF4zHm9tRksGvPfMrjqIQZWRynLyE0aWw0re0sCaIDsWCmzdk6YfkxbVE8PT3FervFOIw4OT3FOI5Yb7aylTK1Wyh0pboGwGPv/Rw++Ec+JYYwxrWbz5v3eqZXntFBr4DD4fhZo+y/9NVPtdK2lBQ3KsZ1z9ZjaGcRF8z3FUsXfPl8VvjryFOqxt1gmcBlW+5yuNll7Ko9rZbSkrxZMnLto2OpzPtJXnbWiz/1wszS77czfV0YuupTrWnhWnFvVsBSnqxMax5d/V9+zCnfTOZ9MNeoxXuJAEI+3VBPUmvFhbltOzRtj/bgqgQ8bNC1aujq0TQBXb9CCCmQteZRI8Q4JQMJmfdKKIwEpszZCoB+UlkXfTY0oKCKo4VWhFqxsgHNtUg16Za6xBQw7OgbzVeBGOsWdqdSVM+Yd5SeeKnbCacpnRTHwDSm2A3jmE7DidBVuGguzupZMo4jJjl1Rb3IzObBGvaLxTF/iSmWqy06nLIRqzSIah+lOAT5IV/PwMAhlzJUUw/gMQTcAsEC55gBBjYOy3hWjkHNe8Hqa8Yjp5imS2zD3v7gmsLmhb4vg2BvSPKGqiBAzk40hCtLDUzOS8s/q0PUw67g2qGivnTB1ns2D7wg0krAXdNA9+ROmSyD24OSkUYbIhlQOF1XsCbgGwrmmcEaE8+RVxum6rQkSOtr3its5z1n7JoL8SKLY3OlUVAxk+kyIRu2InJ/sU6kAGis24hya3juT0r55HqU2F0BwMTuxBuvCJWdng9zgPM48FWqDX9K42x6uzEBv6hRtGglwHPZbTvgypU3oK88OHgIm80Rpqm3EyWLt+0AMzUoqsGTnY4FPUp9AjNhaiTmYdMgToyua8FgdG2LaVqVRsbQIDQxbZ+XNjVqGO4EYJ1xwEQTxnZM44wYd67cwevXXs9zHCHFjHPG40AEDnoKbeVJ8TVHx29TOkePKLLqVCX/OwNH/3leOi/f3pXX+pLnSdnku5i3UKnre1Q9O5tfu1LNt/ZkvWRiZnRMOJ5UIs/5QiJP+UcyVJx1wNjsbsP5vKzqAMLofkfkQ0EUnWY5SBU9BDQTcPUO8ODL4Hd/UfhtAzo8K2jW8oDzppNiA+FwGodJn2f3B+dlxChp1bo6Zlu/1xa8KMvzAEpyQLfQizFH+UCpUGnZmg/ZkGQyjBHVk9i3xQIm8HQn+RTBIZhxw04VnvKJiuM0YhwnMc4TiNJn2zbmeV01Corg7q5fvOHHmtvJmIzZMt1+nimWq4dh7bHC/k/4er3wVWLYWmJ6XFjO5fPGlq+vUrEwxYQOfYegAA1V4U6kVM+szWaLcZyw2Q44W5/h5PQU280Wwzji7GyNaZqwlQNbkuGKXDkiywNjdXhPwqgA12+9hIef/KKN0Tjt3lefMZATWJXsWmyboq6alhmvx+RzVnNxIWk9Zd06HwNF8kOyYj/QMefKc9PSzf1049Ism/VjtzzZm2r5R+WXXZ5h9ZyZXXdzVcuo9gjsIGd3P9W4fR/m93Jll+Fop8zZY2i6CK5YKndJ59h177x31sayy6R3tKHLlCZUMmMmosp78yeoeh478pAD8fM8SXgF8xLSp7pVn2LsaEysrpMth8lluW1bdH2Ptm3Qr1YpPkrXARQwUZ8FftAVLjIG75mnxYAE0LSdxItK92PBXbP3CkBom1yVQEATNIAnAxIEfooTaAgYhsHAQUT2DkhykWBGL8DAjn5PoCP1GtF8IOeteHE+CfWTXbDMWnHVPPL8OKRjn8dpMk6sQffbkIAHi5v4dtiawSltXYxi5GJAwmvrCZQpAKUo0rJdUHeKtW2KtxSnyY0qlvqJ8KYMmtT7xEIj2GDyIMcZw7QXpesfAPCXB2CF7AGUmR1w3K8Q4F3ryxlTsZI8QopAhe50owUJXYNu3b7pt8QqPXnC6qpoENdwp+AmBJFPB6VcDrlnTShrG5PzSvOGLLZ/ClCgn96IFTytDkQCmBuvzhNclJ/3Rl83O1AfAaBlRgG9KcZHAtEUkjcYUwRBT9PyXDALWPPqMSUmWHtbi1XgWUPGmoDmPFe94jB71mqVxxYBaJSxsCoTsHk7xRTsXAWX90LSY8n1GiF5N4yj8ho3HkNInlrThOg8OFtmTMLDvLea8Smo8T+PJa5qwk6oFoY95f/C3kiBHbmtyUuCaTbblozJKd2+/fu4efNZfOlLH8XZ2ZUduaTUBR7oV9H8X1xQvsdpBEbIybHASXOKpgk4uLdC13bo+x7Hx0c4PDxA36/QNA2Ojg7RNMnbSwMmm3FPeExIUahBDLxy8xV8/j2fs4WdsR/g/fnNMIc8X3RlPRl+qzk9S5cHP++k9HYab97SammlpP1hSE/eZXzXM4yQmdiCyqlYJMn0n30S+Myty3mD7UwMnLBF7UQDwrFakIp8Mu9ACA++Cvzf/p/gboAaDTJvv5RGuPOqyi8SGlk84UlOGFNbTqQcI1KNFBp0nImdXMyLU34bfhEmQcZf8ljKxq6ZV0VtgDG8FR0vF57DUpaeyuvk3NHREWyRM04JJ4phSzGyL1Pr0XUdDg+PitihKheTt5E8G8sdFESEru+kz2Shy8KaiEeV1ENLjHb4TvpTue+383M1XOr28skMgc5T3MtQqyUx1KMg53M6Bumi44IXucKWanh5OW3tWZXDUGyVx4jK5c0wYJwmnJ6cYRgG3Ll7F8Mw4Oxsg+0wYDtsMU1pUWeaRCchF9dLvMS1T6fIODy8g6e+89/h6Mo9hBDQ9ZuETy1umsQBk0UZrwP5mWKAoW6HXNPi8v1yDW/0vI+nq+9seIZdPTLa0353jwkr5IXfpQ6Q799PZe/H4FG8921KO41cPo9hdSHhEoYj/V7i2Pki90zPcPj1rcigtyy/3uZ0P8aud7ahi5BPeAKQlXc30WedpDOwntBYmAB5tiYjV7DLnvkSBduORI0GQQwmuPtVLyd0tMkzq2vFE6uzLRlt1yE0AV3XIzTJzTmFJG+Fceq7ssCc1c3xUlLvruj5iip48kuf9+CAANmjY6BI2zJPMN3mA2PqFMhiP1gb1f21MDiVKe8cuEU5C8/rn9SdAQtOPYmX1jiOsBVAJGPXFJMnQ5QGGqcp1xMloyICGgZuMWFNhHXXYQoBYQwmlOOU8rdtm55WLzJpqLp6XhH19boVgRXnrhX8g3qM6klyNwA8QIQeALzibkpnqMYJLXzTN9HCdRk3rh8I/gtZH+g1W4X1Biov1KRNCRks2GmIKBl2KmcOFrOxy7UeuWc9zQ6QKUjWe94oqHTkujpDF+kn5bhvVfP5LnbTwLWPqAam0OsUIne/LiwHYZfq2zi25+Hoc8WUwvYiaMKvPbG/XFxbnMeOeg/t9AIBpXs7BXDDADRgJowPqEHYC7QUrD6B9xj1LVlx0JNUNQCnPQc9GEKN4w5waetRBmrlvNT6K1JTEIP8XXmuf07yM/I8XWrrXYkoeXiFMOHw8A5CSMb4aeqw2Ryj7sclwOM/fT5HnhtmZO3DAFg8E7ZbUQpE4ZmmCavVJPIroG2nxBubBtAt0UTpdGKk+k/NiHvHd/Dm0Zs468/SgSlF/DwdU9rEuS42hoq+0LafbySwOftWYzT9AUtvxch13krx7neWALnsl4ogh5Hs0q4+uEhdjHcqI75YA+yEEOexPSsAuLUGjodSIXnsFLi+EbPs3s7I/OHRU8Jpn949BsaLR4SpYCkXXZ3ORpeoOIA4eXvJo+ofnE32BDQj+NqbUJKZxLvpoZeBs0Pg2VvA0GCe5o2lvNK/Q+Wvka+AkLNRRq0rHAmRMu70CnB+q4sB6eV4PfcLuggzJlCVV9eIQMXBKQaT/Nh1C0QaL2scB0wx2m8vY8pFLDXSN47PVbKZM5aeNwbnRmWejTcqc6ZrCm+SYHKLMznXMrLbnerxWRqg3K6DwsDncI+rt/Jway/XN2UqkYNiRDswSE7LjA6JMmAGwylGbLYb8dY6w3a7xdnZGYZhxHqzwTimbfq6UJ4ocAfwgHB45S6u3njDwozEOOHg8B6u3Hgdh0enO0M/OCZY4kWvR5gRsBj4C23g8zi+Oxv/xSgu9ITdPG8/vyGbENrvrjw31wxD+JJtPmRaNE5pxh5anmCxy7F4VwuZo4vDyKN3LLTx/FqNwHcVXT86m74eTBZPlNfm7berw/J4qOW15ykZZu7II2Xl0rJn7D46L8MzACzynnwTi/e0LZbxSFn//Ozl6HpHG7qSiA+oPbj8OnmlhrtUDoDltXU/MAigRrxPkvU/NA36LnlirQ4O0TQNDg5WaJoWbddLUMQUUysZtHRbYgOIgSwVzhb7KgsDfX+wIcFF3ciUKDIvL/U9IovXpQoIoMAhG8vUCDPJNkeOk2zLm9IpMbraFCdstyPGYUwxC9oGTQympKd3JQ8MQmbwqhDqqpStRDnmSQuMzrxhNB5CZVwg92UOhhIoGccRw1YD6actM22ThnsydCUQQQIAh2GQd+ZjnVWgBwKOAfzlIeAN9PhfrzXYSoB+BQAas6ttW2u3tOqXDWhw3njpJckoBw1cz8AnRuCbpswEUxsHNK3CWQdoOW05bPssqGvpw/BG3+JjmVWovF7Im0HM8qf2XfLESHT7LYf2As6eJsF91qufgcjeO2PyNcn6nAJk106+YrleuYIJnKKgR+sCqJcXScw1ymNWS1YDigOFi43KIqDFCNq0jSj+jT2vK736TJAYHF2bDDgTx8JTzjxhdL4svF/BtwfjWj/LuyD4d7lp70pe0JKng9RgqZlSrDgw0ISkGEXXdt64AqQYXdM0IQRyW0RED4B6KwQEOVHLvCWlnHFKvCmOssLNIii17/VQCBsTNa/ReDAC2Ni1jDy2aOTKt+8rEUU89thnbf7evXsLzzzzMSuxXtWzOeVO7dI805QC9waaK7fK86zPYkScItbrLYgGrGmNk5MThCbg6PAIXdfh+vUt+r7HlSvH6LoOq77PcbQ4nQDM9P9n70+fZVuy+zDst3JXnXPvm3sCGo1GA91NDAZIAAJJB0gaoiRTthSWwwrpgxyyP/hvs6XwF9m0HJSs0GAOYUkO0yRokAABogmwQQz9CPT03r3nnKraO5c/rDFz566qc+593X1B5o1zq2rvHFZmrlxTrlxJeHl7j1/9yt/Hsl9QagFp+/1RehnKwAEC5FikjbH1V7ngCjNN6fWe/Kv0pyeNBPBPJv3P/pDxM99KMhjJdmNQhMuJQPhLHwK//C+kyHdugf/kp4EXe3mf+URsDF6PswsDHycZ6jmxeHQnuoBEi/QhQBX4q38LePEO8H/8j4BvfurqNnvwmhnh8CCyTQWAVTIHlqntZym7WMVaiW2K9V7g3h8MV32Cr+XnbWKIAY5E9izF6zSZwfvB7B79tVZ8dPeR8A6ln1AY7WRAsU1tg13rdGMKh6Lf98fG0UJImCA8L7Mxt8iU+qlSSRoXm4+QQ4xOphHoNB6Rb0HtPORU9Vbk1rCXxg0QgzazeO8Cfls49EZdSjLpGMU7uc5DPYQ8ZhdsFb3mfFHeXxfWi1ROOByPOBwOeHknBq6XL1/idJpxd3/vBkrTlQCR83fuuEDaX+BHvvyb+KV//b+VPI5TDKIjIti/jJdcOCUGNpeWGI4Lsum2Pp1ybbpWdsjLfG18elLTw+R6XboBM9pZGy4yZkL1kBUOcDJ2PSbxum+bdQwR73Xyk44/uSyS1/m58x/jpPsE+T+YATkyWV6jBd3xZ1p9aX63cn5gXFYL+FpEVFk8qTsdjDEsKw3JcWOroaQ/PkGyfqMNXZUJzEJMmQLZmgUgVNdxxSaiNf6EsciuB863GHow+P2t70gXFer3egxxf3sjxxH3e2V+GiiRcj165TCmFkF1sQNwYmow7ZJi0ijgrtAnI0fkDMKTCII8y+7MythrMHjiBcSLMzXmqky7Nrs8yzxjnooor7oSssqSgHZCYwqMMXWG3Woj4770AkBw/xWzEOMZo1K6IXJZwrBVK75yYjxnAmMHAmHiCdNC2B2FgYvQA4AJlSfFDe3FEqICEeMZCG/pmP8Cy72Ci7k4g7HouJRa8HFl/AYJTlYbG0q7iER4zowfn4UgLpVgsWk+WwjPmvUrFoJsLMq7qs0n1ioBta9Dl28ecfOeUlZDrWJ4RvacfGqzMAMAZapOtMJISVqPdUnKlGRwcEOX5UFJZbI3kMuEAXkJOMjz5HFJgnAyZMQQC4yTGbUo4Irujbh0GjqfjvWA56nKsYu8npy7Kd73m0Kg1U/PoVzE4k7FDmI7FtFOGEWAVgHzMU50VRQB7V8jhFNrZ3DQU9+Toc2KMez2ResL+zM38CsDLHps02qImxnt+nfptIrvUrYQgILJjVBB8xgQY7T3b3KgmjVEZmy1cSelheQKBfvYmEdC8JV8xTPlMfYxaEetGSMCgOq4c3t7h09/+g9h6+rFiw/w8PDcy+WyV7msb71reKlAaNetH4rcHjZNO+z38n2/3+H29hY3+xvs9zvc3NwAe8J3PvMdvHjrBU50kv4yqXLA2q/k0al4YApmrRVgGT8zghY7uk+kxkZ2njLtdgBL8OgcMNn0/T4xUgwRG6vBuNVlscB7iRudS8PGrnm0mVZGBsevR1TSlb82TzMeWR4GVoMx8gJd1XuNcKqLg8FBw/q2uC8wfrc1/8MhIOD33pWjdj/1HcbzWWloZohbifJXwsTiTfrb7xP++C3gNHAEaedh1Id2HW7lO1k+U05IjMTPsveJ8jNMFXj+gMPP/jrqi7fSNuqoP0a/Y3MnvAgqME+4+SdfBdXblpeZ7Ig0zmkSKteo22DT/GwGqZpkgVHqhJyoZ52HAJB5+oL82J9tKhkd8WOI6TjiZDed6+19YcToPVNpDYPhscm9GewsC5/pWvD4Lm/CB9mbWECUbwZsIsoNmrG3Kkvk0AHJyLY2Ljbc0eUio7kGlnmgO99M5X2jPekiUV9Rfq8GKa2fWU5dAIy5Cv8/Hk44zSfc39/jcDji4XDAw8ODGr5OyrOML5tepRvGyqf3twd88Su/jWkvPOqHvvh7mHZqFEujJv1TOd4EkzwNGQ9sOfp4xqg5jiScSNPhY0XD0d+mESKXhXzWyF7tCHflR3U7pF35eD5O65Mr0U7vIYghfCPe1Oh+jSB9nos6tJ2FrZe+h0llDKtnCz6y9ROETmVWlTcT+xgNX6s18/Cd0I/gg0P+7cuyrJ8P2hcvUMU1Tt60HR5yPNgWWjLJS3YHL8/tu3Y+U19zYPWOn1pdebO+PMJz/402dDEXME+KlPAbWJi7wURCPA5EJCJMRY4GmuFqt9thv5dbpm5vn+mtUzfY7fZ4/vY7uruQb4Kya2zD48aS37IXc+2XL5hQ74SQSOtVYX7aya5DugHE/5zBtjdeZYPW8XhSI5KNRTJo9UwtlSXMmPTaXqvL4xGoNwnAOM2zqNx1wX63U6+XLIxlM1Wsk9wPQOLDTNMe5g3B5hUGY5JwbzBOCoy5K4NjV2ee1eMMwJ6Bv7Ds8CNc5NpmY1wzwDNjR7FrKLCUmDNmVNSwQEM9rkrB2wD+WlWhiSTfUisqJjAq6qninzPhn5QiMYKQjt6lEXqPCX/1COwYqCiY1NCKXSNGADmmUovRzccwLh1Zr1rhpGtBx6D7bX+FwsjgPEb9YIp56uQYYJCrzDsB3YTCUkp4b2WION2y6HOyFnbLqpPjF9lrqemfE8rorAlkYpRTOHvDgTG0vC2RhBJhaDLOUS4x1wzeRL5LQhBc7uFr+iLcGgQN0M2iEHS5wFyRGYFq7m02g51i19FfGV0wIcImA9lziBPsaYytudTOVAzqyJPHhQjgWlBRURhxiQMRaCoamyS8/9xLlQhyM2O1U9ZusJp0fGqF0skKogmV9YZXpRd21EFlZ+z2WnfTV4U239YIuJGr9rQUMd6tsNnjko4jOmF3kLJweHv7El/4wm+58P8Hf/A/weHwVowvWvyxsit85PR91R5aqDi8TgGg1geUUnA6zZh2E16+fKm88hbPnz/Hs2fP8PbbbwME/Pbnfxv3b937BoDtgAvZtnkV3jFNO/WcYMzzgtPpKIrmNOkYw/ms7ZSjMljp9LPdMwDA/cODbNggLnNwdE7jT+kzJxvrSQ1spgCLskleF9tYmQx9vczVDfhG2S2BFuO53krt/P8Ap9VE2Ac7bXlKCoXKBvlcTYRf/SHgNz4tRw/fmgNpsqLR/B7Br03NBPwPnwf+4J32/UpZWhkDoqJzBj1LJwaOaoC3bDdEuE3NCi/XjdZnJ9z91b+DuVYAFVlf6ElD0HYz+FvfK+j+GT74o/896LsfxIhkRWc01MxiPCaLK2WbJOr9VRfnXbbp7DQ/KV1jA0z7y40GZMcVdVuCZAOyeqymRWlPir2lZZ/dPnM+edbbTAkBxQsDNMb1UlJaYEcrW1kj+hg8VuiffCUNl9LKOCP08S1c+50C6Scufwbo6L9tCC5Lkildxo+YmVbOZC0QUHhy/un16RjvdjtvptaKZV48wPxcxej18uVLPDw84KOPP8LDwwH39w+Yl9kvn3IpVueMLI5Z6sKzt+7xr/3K/xPP3n6h/aZG5jYe0npOa75OTrBYsyAxH2c88iaNliWjQjZaxhyHbLmVuMGNVtbOMlbT4ZRy2ACbm/Opr9NbhhkAe/tT+32NUMxpSh7JpzJ+NyVTO3mteP1ZVzi3MLOucA6KdBMYgdTL0crH9757683nAR9Ia3Zo9s/8SGlzYxhDlM8DxsRu4JIuxPcMW0PfBnS3aWcFepJ0KzfPVuVH/H/Y3cj/GHx5ow1d8wzYJobgbuwGEOKc/M6MUX6b4SQ3RxWNiWV5ppIMWJq3iPGLSgGmNl4WiFBRwEwaoyk5DHOowmEYEA8vuwLXFSA3AOiRSPUYA0JZcQOeIk2tFZXn+J52ozKiByxhABQevFbO5P2CZTm6gaEuC7iKNijGHgrBiEzhqx6fq1XqlKHZ7hc0GPw0+XjLUT/ZkfrSZz/Eu89fyu7+zYIjClguRcThCBwPjI/uZjw8nPDixVGYcwpgX5nAVeZoIsKndzvsoUwTsTDCw+KMBJ0Uo02ZNhlRTPkEAe8z4V8/AaeZcDqF14LqSygEvMXABA3aylY04OkZ6xqIZDhTQjViRIUQAiJCoPQZWhmX0jtmEZ4KiSHOiDWph1dJsbVyoztvDC2htzVgRxVyPvliwrSJ1i4YNTBHU0mGasbISlAqVNqX0ZbiQhZSbTX37GIr9S23gkM7L6Z8b9a1ejfiAueTt6X/lVLaOVcDZr7JshKcRkSLacc7G8cbnCVn0qTtMXWsOZVpuVjgozpXasXFbzG1EZDY5gK70DxCXSRPJfMIEPjkivOKwoSFGIVZbu3SvtVSUJYFtQhsmXYauIZ7zDUu/rAB1cUXwlPxgMcxdDZWqo5Y3fp6yrHrvMh6bke7s8zA++9/iNvbl/jWt76I4/H5qlwum6cgyMxadLL3sbumMKsEyxDD10mDM9elapDfGcfTCfcPD/jd938X92/f46OPvot6qOL1rEf4d7spjjgWiW1ZTUguRTYgVNGxo1CLHhOfZ7nJzI6uUiEXoKrO624qWKrs+udlcr1IdCF1NOu12JBaWdnrHxs/rN3rA533XmqPMX41nl2P6esW6KM6rqh3sCxeawoFjTAXxv/wI8DbM7UZ0PL+NZnWNaKwVpJji+eQ5JMyQi4AXrrRifG8FNwCeGDGzHFUXIDQbA1gPaD5hyo9uyPu/tJ/D14+wIsvfQn0ztt49rnP4uZ3vozbr31VaQg15F42LHbO21vjkNJvsGxao+qNs2pkUx6WxM+Q4xByjhsZGGCumNVQHycYasitus6ISC6GolZWNF3CQk40G0Po4ty4PN0P5plEzYf2wgpHRZz6ZwU6qWgsz2Z2ZLKYfdf31goDvrkUfNd4DznNgcsDKl9SRvHMb4KXWh3eC39WQHYhAWkYB+jRz4UxVwuZIpvY87Lg5d0DTvOMw8MBp/mEu/t7zCe5IT2MNop7vm4NUMaP//Sv4zOfF8/o/e0D9reH8RJVWYXQbtSy3UClsop7/5ssjBijpqrVGPVIEmPdDNIjkzQbXpNSZ992bi/pBz4vPMg/bE3LcSrbt9XiQfMM7JcSkW9+DXDIavOdpQ66vkzPMIzAO6Hf6Ne57g6mY8Sj3dgFqEdwErwGbWQa4tRwMPwjw9gIluFmucpzKy8utMauUVrRuUcmAsnt6GaX6Pp2tSzyClLcG23oqkyocss5KuxYgxiriApuNDbWzf7GPbaeP3+Om5tb7HY7TKVgf3MrBq+dBIgvk8bh0rP3dka8AjhWTusnsyPS3WW4QSkzLCeSJMcZixrQpt3O6zdvhWm3U8+uSXeTF2fMclsIY17EW8viaM3zLLsduivFzLjZ79HfnJfknvTZEiGLRyDwmsBgx4MiVpYxAEANbzQmUoac4vBG2E+EaUfY7cR7bZoIM1csdcEPvf8tfOHT33Kj5A1uwIt4Tx1OwMOx4rsPC+7vZ7y4nz0wqICmAhHtPDaAjanvCgZgDR6FAULpIJT4ZIXfmF424g0MFgTCOwz8wkyYZ8K8EKhKvRZE26bFdLGebAfmMCzaz4p59IJ3SeUTTK2fYTIauPJMKqyY0TUH3U1u+r2hS7+bh5bt6AAATTngbFC11jPRhFQkBhJeSr2ARV2/8mhw/jEo3wxbny/hLOmcmmdoszGzmc4JE4N5wzVK5hlpNXek01WavnISmHy+4r3cdtl6dBWyuB8xHqxHc2OXtAOjwcNozwS1JEJ1XbFVZm2beCj1cHoGIldyiGUniiC3+i1gPw5nR1O4yhxSNUGJfS07vajVPbwqM+q87mMETu2CRktFYZCltOvb1WGxxmhZmueddnBVag0VwLvvfgtvv/0dfPzx5zDPz/xds+JXFoJeOLrUqP6nxNHqm+cZRIR5XjDNkygi8wnT6QH/dPdP8dHtd3Hz4ga7wx5vvfWWbGhwRa177Ha6sCagTq0Xomw2Ce97eHjAojv0tS4eq606zRfvYh97U0TA6oH2NMHsBymNDTzbNGRkKAVaHF7h8yNSQ2e6KkaC8EqAf3S6Bs5Wocr8/ClpKYR/9JmxznPJy+6yYtgmn4eny/DDVAHcJU/hHTNumXEAcGQ0h8auGyaR5TKYPM14+Ll/CL65wd2X/gjTO+/g7nOfAZ0m3PzOTwieEclNPpZKwbTXI6lccvUh9diGSmqLQBKzr+E7ycjViLrsxw/NU2vRC4lGx/JMPswhRowvLolurzzxBspf9nwYGYv0Qep0K8cNlclOuZf133LQXkEew8XDPHHcKP1OymjvnWxhA9h5Qj82cbxvhFumH0l9QsftNl6byKq0/ng64Xg84niUz9M849vf+QinU2x6HNX71/h3Dv9ifSjEquQzfuTHfwdf/tl/GB1sIV/zZZKjjxRQp9yh96j47J00mSPAoAbPTfZtDZQJV4a8+9xqTVjE5/Oa7OJtYZt3jFLWHbNumWHJbYSNacU05JnrLx3OcP9E8qhGsJqqXH1SPQZGrg4OH7orCPE1w9TkITRT3LeJ9fodvrOq3fg3AKTXC61MNrxZWdKx3AwPIHnI5oBy+QTuxng4XoHb/rWkosP/dVpVr3zgMYa3N9rQ9f4Hn8Fbb0tw3JubWw0Mv5NbodSwZTGyzH1ZvLwmvyWxuQ5Wx81k5MWu8CVRnJZi8bIoFOZ0DXL20MrMoZSpccMuft5fkGleKo6nHBcL+llRaxhzwmpuv2Mspkl2xzHprrsqB472hkuUlk1CLqt2oglU9rH7tcwSy2aZRelYTl5Ubr0sfmyLSHZ43AOk6jGhZcGf+fzX8am3P/K5ubm99UCey8KoC+Odm5caAFnG7v7+HnbU6GjBJl++xOFwcCNfL6Rk45b37WoCnhhQNz5BXFtPFWmLYMFB5RgapecpZfqaBA8ZtzjOZ4ZTAKDJLixo60k8JHPShmgQgF2iIfYuDE3CvCXIOtyIGfnDkBUxF6JJIjOCtYauqhzfBT0X1NZGq6YfGpPLBQrPG0JROzVhUAvlN3DddnvJK+yZBuvxiTy+sqPsu7O5tUcYJlo7RoZ/W8kcyjbDfNQwjCyEpubka1k/W1eonyp0OYZTjJetJxMmh55H+p9PN4eModUPy7hCZHTDGGQlROBTFs9PhhrWNSaeGucWvfSh1ipHit24zACq1+MGr9IGDK68yDFI7mmr0OFemHejL2IpM5PffpU9JrIhJj0URe8CTl3CuVIYP/Ijv41lkUjX9/fv4sMPv4JzePaU1G9gZJ40zzMIwO++/w1883N/gsPxgOWbC3a7HXa7Hd5++20JAXB7g9ubG+xvbnB7K7z69vYGu2nCs3nW37eYdjvs9xIzcZpmzIvUlRVQUn5qnhvLMsOuiSfu3Ln+FCVy+n09LQIU7xtD6ePKNwD4d1w9zKYQPin1wvG/So9ODwzMSjdfS1LeIHRV5Qn13D/+7G9g+fwf+mbYbpqSHklgKnj2j38Ob/3/fsnlEU5MYstgah5YOe6h8Sr30tLjh6fTSWXrGW4OI5PXyvDTjS0IeudyJLewdMDJhxm5mK9SwrZngjNTaRtByAkuy9hcrODLhqsNo1aG0yrm7SUXOoqcIjHnglBqu7GAyWTqraXjLPrQZNKWnkxhnOYjal3w8HDA6XTC3cMDjocDDocDjscj5nnBi7t7zIvFVwueHpvd1BxP+/QP/yH+3C//bVAR6N7/zJ9sjvxWynJo/9z0vVUoCFXIfW4y3R3ZKDo5c8y+Q1jbWsq9jmjrK2T3jcDwjyHoZ8slgRs2JwazxXPLZURvCgFyo19da+dIWWPoSygvovMAu4fj0XUpA3ExPXUsBzUNDJFbNdN4Ys/Vvl3btQrJxRZaHaTHlEelrEw8ArQ32tD11ltv4+133sHN/ga3t89wc3OL/V5ibFkQeWdggCrOsvDsJrVQPgGQ7O6jYbpw1c8O2VhdIKinQRiv3CDggbXJGUEW0gHoLkTEwIpYWKaAVdR6WjEnNwCYl4Pf9iL/MduOXWKOShlogLiM7Llk560lfgP7bvqMqsHerS3x4gJudzN2E0fMpkkEkYoKLifQdMR7z7+DT7/zbfGkmzRov8WMqHLGn5lxPLbwscZQOB5POJ3kz+IJyFAEg8lHYhovi2Q8tPGTWY8R6B5sLED2+bcggzYWTtYplBGDz+YaZoFJc2C4FMfI2rZbq3gSHHI/HIB2F4UgnnQZNssThrgwsLmHVYIhDMJhpIp+RswtY56cBs+OO+Xd7liHWPUV6VkWLHpDF6UfNpwBl44hWX+SFyLlkZFRtTzhj4kVATUhoeUhIwzJcKY+01b+aGzMT9p3jlcdnz5n6BqlbOxrzbarrsAENYEjAoqe8yiJsYpxZqSdoQxzmhHDbT/mp8UtLlnR44E1wQOYUYnVcCXvSgFqJRTdKazMoGrvlN5z0IhSGBbvqZ2L9W5li4/k/XVjFwPkFzxmftIKITxCNuDs2I7yvPXWx+l51SDxO8zz4IZF/8/a7iS4LE0aA+zh0L9KFafpYFiKb998G9946xvYLTuUh6DHRHIUcZ5nLPOCm1m8lHe7CczVQwNUZvFyNu/mSWJw9nTdwPNLLlxQrg1teCPSYIhtjkYkodlQewVB+pIRdKjUmdzRMUpf0xbn42zF516tX/LqSw/Tucpfj6LR1NiN2zXeEFcZ+Jp19/rTMlbvusZzMl7C7ZyTqu0cMlA8l1Q/+C7q+98WT/FC4NIaQhYQpm99Gss7H8Fkcrp/Dlo0XAe28SjzHzOmLNq7bOjyv6X6Tekii4ehpdkUNT5H4/Z8pEYGorSI2Uw3HLx1bOTt5Nz8uyPFLp+nAe9hFaPfCL7YlDhn7Gr6OSAtvaHc9BNmu508sCTOIwRsKLIJAZPLKC4asQuvzEA5zzPu7x9wPJ1wd3+Hw+GI4+GA40nClRw0/rBJiqb3EAi3zw7Y7SWYvNk63vvUN/H5L/0OSsn8N/A7jSKuS2s+bHKkjEFbj2+u5VbydCe5tN9Me0rqaVEvv7bGr9weXH5ap05OSM+2aV/vcdWt3QGiXWOnkTyqmY+a7tRlb53yszUdPyuPeZ2P4SmjMRu9z2kAdP6e2+f1OmMgbgXPZTua0kDXD/hGH42WcdfuKp/Vx/HbTndt3bB5diRG7TE/ai7eaEPXj3zhx/D87bflGKAJws3NbSlYu1ognEhXjufIAy2GKRhzpIhjs5gxywhr9wcgEKrKrTtgxjwf4wjLRv6EFarkF1X8IEY2NlUcgAWZr0vAzi3rLaWg9AvNFE1Vvsyo5/EMwOA6o+quyrJUHA8PWOYZ9/f38myWO36oyA11u4nw01/5XXzu/Y/CGELFDVSn0wnzacZU7/Hd784hXEw7G27MJ4nBYsH58wJx6BOyUyE8e3arylAYM81rzgiWG7nyyJjynJV9zZ+9WRrDUlfWAGR7xun2OLagy+td94YBBnVCIQn2Pu0mn39j5KTB/7mvR3HQx8mZPRqcvklB390O0uAhkoGtZUzyLgxZQmcFkjjuGO17O0xN/1oFvRmShsARoRm3DK8xzWY9x/DDXHhyHX1g+ZFy6MZQe6zy05iIbqsK416N8/b86vpEjYAb85qVkNQIMPbEVmmCmeV4nwkNNczjDHa8MOG0reJ8B/JRSfNEzcfqoroGA6T1KjGtPI8JZiQdKgRUPfO/LJBA9jpnfhyxMiolTz9mkE6u5aUqhjEG46aIB5HE+mMsy6weqSbQh1AYN0LlSxhsfdhmhrRr63h9eYC0EfUl7wG04529p/p3fXrrrY/w5S//PXz721/Ahx/+xDrDqugWTm8rYmb4vnvrJX79K7+OpSwAM467IxgSKJj09lsiwvF48otebm7kopdnz57JbY3PbrHTkAK3z27xzrvveFD7m5sb3NzssdRnOBwOuL29xTzPOB4ipoocVYx1TE9fXD+QKXdH9MXY1DGv7cemoTfmE5WqVT2dkaLfzf1epj9lqPAJpSsHqCcTBB9cSq+GcaRSObl4Yo/lF38TH//01yXPaY/3/u//PqYPP99UD7S8zejjfDphqRXH41EDlc8OYjas7/YSnsQ6kA0sJqe6GK70I282Q+uT0uH9uzU8xjmdWvLaiNTonmwcLzTzvvpGPegE0tUGl4v57IUaoxbH2vcbD422QHh2dYNNmx+Aj4uFMxFPaj16nmOuanmLSTztd/5d6mHnEyeNu3h/f4/T6YQXL+/Ek+vuJU7zgsPhqKFZZt/gLmWPstu18q+2+mf/0v8LX/zKP/ExYgC73QlycCfx1HaYryNPKjeJQR+uZ5oonuVh1xuzMRGJlicYzAmhMVxeBGrDyDPsnYPeGb1WGs4rpFzXufoI5M4UgF+XNZQHzyeTJ9s1Fbj/mHSNl/Pr9JC/Opmsbj/PZk06sj57Jb7eG0xT+70Rqs/nRrent341XNekN9rQNe3kNkTy3QIKBU//27IgqvbmxDcTy2zEQvqEWdydCoUiJ58Ig1P6Xqt4RoHkiI63lYxTGTEFUVLQQ+8Rt14R1hU16ORVYEqrlTVjkRj5MsOS2F+xI3bCMh/xfH+H5zcHnPiIZZpxgwNqXTR+lyiUcqQNeL77Lm7KCz0CJ88rMyZeQNOMiSVQpF1BTGSB2QXmZdEbb5idIfRUn3TMzZg2lUl5g85RiZ2ULGoTIQICquQV+bJLb76tQiQQM3lFrQEWqZRiTM6EFmszpmbbyGPVuWdUKQ6Lw27ef5TnPPXDuWzG4VAuJmrb7Y1cADVGq7Y8u8Gi94rK6wSpDWYxIo5viuUGmHZXkhvY8nj1Ah2ll1bcvNNAqY/J8EqpfJOcGquxh+zYnq1t4PrAnFuJmvFpmj9Ls7M4lJ42YwiMDFybIkwymkQe+dYzylhD62NwrtAqsVuzRPJyI4FqOBV5mDnnW2cuELNVoYKqQnVrUMvKgykQJcFDKCU8uCbdWAApXeYC1iOPJpiPR7TvV4u77j22KkftXDRj1T4bpS2jF9GCm5sFz569wNtvf9eN+ABQueBwfNeNcW0fuq70KK/0+u75HebdjEKEl89f4OH5vRq6WlrH1gdmAEujQNrx13neuWeXwFfF2J/GUoLSR1+NZudheV1GmteTNoj8xqNzu+E2Cd+L7vX4NMIvx8lO1vDkrHND6Gp4wmM7NVZNXw99fnq6xmh4jYH6+5KuBKedq95fZ12d0WxKzykTFAL42QPq8wMAoJxuQHuh4SE/h+Ep8yFALkiyG7f9ufLA9e3OoUhnmcV4UojOIRcPUzIY5RzU5+H4NN7arJs0dBYDNBu6oh7jYfa3JTf1YOaN3eAvDhcCH20d915EZr7pN1jyCYmtFHWJTmaxQDNdMV4wL4sGmZ9xd3+P4/GEu7s7nOYZ9w8H3Sif/YZkl4BNbyPg5tk93vv0t4wa4P3P/Ane/uA7aazW8A3lInvmsmA3rpBxJ5MRWX8RVEeIf7C8FI4VhLbehtWqAmEYEjCeX6BjGWpbbghjl32u5Y6nGJxa+a6jFZ3sE7pW29a43Zau5y7F91E/t2myrcMhBmclzuexl2vOCuy5xVSvscZGaNkW/rnL1z9vJ3FY3vFoMGjc/U5grtvaKp/pYA/vhiwx7J89SjpMX2/+nUteOxPAG27oWgAsrDvzZgii9aKymwLtillxqRZC3AQsl+wAYhCzEYt14ZKf/w2iH55icfTQJmq3kxsGgwkmJt7lddghlu8y1RUemdLeKrcEP9TDwOl0aI9B2s2MaqyqdfGreJd5cXjm+YT5dMSf/dLX8eUf/hBQY1uti2E4LGy0jzkvuL9nlCm80aCK8+IKTvRBhkFh03P+u5sbf997OOQ5zTG5AOB4PK4WkguW+v80iL1gXh89raD0H0GPQlG8W4nbxHobnIyMxI1p8TAE3WBvZtAzb67dNGG3m9SDK8p4DLnoUDDTzJwo4MzvJj/oBTdmuYdUOrIIryLBrQYEq17g0lEwAamTuXJ9CZhugLUXLlR0TDbVudq1LPE7C9LA1OTNa7pZK03/tE0WnLX+2jvpr8D3fdnNATDGunhzjRa8Ury693EUoRWRfXxrv3i3KkoPzTCrAxw7eKNkApFW3uULG6sgBqshilQ4LMxiOOccs8tuUoyg84sb9qXCWpMgWuQO1EmPkhNZIPkFtRIWpX+hIkibIQ7FugLM8Ao3KvWx/IXkr+OdtULn+POa9N57f4x3341YJMyM4+kZfvfrv4T59GxcaBvVwAAqKr72Y1/Dt9//lnv7cYmjr1mwykZT40Nya+KMw6HgcDjITYx7Ocr+7Nkdbm5v8fDwgOdvPcfz58/x3nvv4/b2FpUrTqfw2lgqwzwSiORGWBvTf7nS977DsRm0kXocGmR9dSPXlaX+pcOHp6Qziz7n6qcsy7KJZqspwGtu5trk40VPN0waW5V3uNGQI3bL6mmePVTFrCEzBA7yeH373Q77SS91suOROuk5luRUih6TTl5bHKc6nP5SyApTmRLYndI3UkQ7Y1LmFPaaEDywIEx/vXdVGuD+4UYKGaWVW9ZqoT3Pc8aqNEdu42NJLuj6FcZC/VNjo4WLgclf6djq6TTr0cMjDocjXty9xOl4EkPX3R2Op5NcQFIr5nkJIUQNWx5vFJPTlc9+4Q/xV/7dvw7SWAGlZA/XLO9GX0fUx6Ty0VOtSfpEBEZBJfaQH0BJt0+Sn4IwD7l2LripV4ECkE6RuD5xlXi37sugzNrWEPGyemPXtW20da7LZmNUb8gayTSNw8jFlGUmqXfL7nOt/GRFafBMvl/PUNbksl1djdHKM6U+dc/6+pzWbRmT0MqSK6PRmdTTu2b9XzCWGUzDjbJR/q7cJ5XeaEOXEFsLQl4aYti6zLcELyuIVZUlXkxrid3iPLkMYCG9w64xjHTImRFTmSbb7lPHyFwgGM0vR1SwrAjacUNmgysb1+zoH+M0n/yq4Ge7I37ovW+B/RYaOSYoBq7qLsHmebYsM957/jEmmmG7pVysXxazIck6VY0EzpRC4SMi1BJ3/1msBNbxraWi0ISpTKvFMbII2xFQH/9eiecg3KUzGvUpE/jseRKsyOqOxZ2fmCDnTAkQw1cDUiLexsCc8cm7UsRTbSqT4C/FUaepBFN3uPX/NMxudMq5iESgyvmzgGLKeBvDrh3L5tiidaTxkJN23cOHgGLXig/pVsdObH3m4abmo8MHcoE0j0UhE0ZMWPWB0VbtyYDge3uJKeju8qYiQCl/hoR64NteS3U6fqPqUz8EFPUrbHCY03zZPMS7tn/WgOF2FhBUtNJHcd06vC9ECi71HQnBLYxUW8nGpn/CSTdQAZzZ8bZPGS6hdwRoXC1wcUHfd7UrwDqN9sxiUMh4mheYmex1KAthQooHVQlUNYhqNghyhe3DyujGbnizg9gJkcbTqZRmXnsjka1VK59/92V8XL0dDtqtY7rbnfDBBx964Pp+cF+8+AxOp9uhLP7xOx/h4+cf4+HZPepU12jQf09rylceZ2+u2Y/ATJNsjCx1ARUxKp5OM0qZ0vHHQyNwMQsvNG8B6+P307ixEkZxhWC5makX5IN39H/fs+S0oWvT5joFrlwZs1pW+skB+AOcfmA9uwZpDSGlNc3NM7+UxrzSlZrKRduUNpqq3jouaocZv3FifOeLv4bd7kPsf/ur4OPkxvFSCvZE2E07x6syxWYnqWDSbm52x8ABCVzuPICbMque9jLNaiTieegI3Xe09We6TdAj9R3Pto8sW/tzamXbqBeIC1uwzRtShX2PRIcY8JEkf0e71lbylqeIh2wbs4Dep7TI8epaKx4eDnJM8eGAw/GAl3d3mE+y+fFwkHcn3XRPArXD8sNf/Dreef87qOaRTMCnP/chpv0R5HS0Z17UPKIzdIiaFx1htnA2xukV77IBR4xcBnZwPkJAFNL4RsoyIfET+Vn2kAp5o8nR/JZG2/kd5QN8lAZ15vp6mVDyr9swXLLnQyFiIGT040I+VpSe5fdZHuvrbIqNxJ9xOjM3Q6MY86qH/fu++mYEqMMdWnsnmtE6G6m22jiHWr3to09XyTYZnq7OVX2ULCkbxrSmlNo5rk1vuKGrgMqEaTd5kPNJ42hJcvUljFdgxE46xDjUKDBJgOSMsASUVHfHxOyTCMgxgQjAMs9qUEuMX8sYYYQvQIU7KwqUrkrWHS+ujHk5eYwCc+de6hxHJbX/z979Dr76md8AYdGrgat4OyxmIFu8z9LepLsVFJeXUBEjDqJfyt399jLtRjAn6w1l5S+eVw1CWaigZKWzE+C3hHrb3csGsd7IZfl6JbJ/t3Lz9Pc694lIDRe+zVcpoFKbOTa+HZpCLFIzPpUy6U4laXMCv8eI4LblNeNaWRHUBhWxE2ze3NspCRGt4UhglHFJ5YE0D5Y/lzWcPhdrqAt6ChrCDup+Opzpe/OupDKUO5J61PyXOhVfjODamkTtZ9tgb3G572sDfJ9ckEmfqY7ekMuBQF37I+GgT5HHGHz2tkEy/NjtgtE23DCNzljTwLLBChvvpPym4cz5C6vRaDR/1PQ01q0eR2Ttg10oQhVExT2pwhAiN4/VWkVd0T5XVQQMNlGi2I9h5wDHy7IEv0hjKQrQ2thl8GY4BL8mnw/faOAQbg3XTanLdT3FwLHbzfiRz39t+I6Z8M/+2S+KoWswPx9+9kP8/ud/HwB7/N4Gjww2/0w8MVMV1pt46wIiwjyLZ+nxdMTuuMfxdNLYXDeoteL58+fY7Xc4HA7NJSQNP7A1k/j2D0q6RiA8Z6BrdFXubz39Xne0ne/He2Y9NV0rVv+r9LrT1hwHbaO4CGg3+TFk8hvLkwzJQJl22N/eevzW0+GI0+mE7/zc30D5/Af44Nf+D5ju3nWZ3v6yh5VUleQ5lo1qzvQyGV4ktuzc0uuVphz9yjSr3TCX3xV1xfpW9fZKK4cnURiwQs7vjVypo1GewqCPVIXwkNLQvrV6en79jIywW5s1WX4s034lS1pzy7JgXhYcDnKD4osXL3E6nfDyTo4p3t/fY1kWLHXBvNQUIgAaoiQ8woiAn/yFX8WXfvI3sLh3dDbKmEdPjGDrTYhWzhoNQiN2pAJJp6E2ezNWHuYjx8UFWRSqs+Ig5SaZNR7ptry/rmH7GXnlOGOgGnHx61Jf3zYvO+c19jppfFtX1n/s9znx6fXztdD3VqM8MG6tftu42eSlDmQdKBu5VgHmnw75Kl2reVh56uTkvi7P93QwL6Y32tD17Nkz7G9vZcCJMOu570ahTczPPHaAxJjsWB0zXIJPZYKYisuqG79UzrTpc6Rl/WWKjX5VWql5rTxrkVByLPaAeG5VVIjXld3OCF7wpc/+AZ7vH+QmRK4aONkUMTVaJUPX85sD5uM9VBv0xROLRZVAhGAi66mVstnH1AwNabGRKR8JYUnHwoUA+EsLPG87W0TUjgFaRtt/P7cr2htXeiGEG4IBZy4BdqdoK4ytfcbgYfc+8ZheI/g46FRvtDOPLgnUWhLRUkOX5x8LZ+eS3YQ5Gr9+XMN4AoB7DzDpBFcTtGTgiuOCETXx6GrHMASlynVz7mwnNaS+BJvDjlbosM/S1tkLqNle3QxcEhxDb9b5dGQO2tEwQepjHXV9ufC8N7CO5qXZvbWeUXzGDlXuZNNiw0trOq7RCswj75A42mc3H2ZcyvkAbuBaiwvhhbYql3pXgCaOocCWS9haC+bOZqkiwoIq+EcEopqODwALWVD5qgpQdQVhyZsdulZLAZjkiGQphGUJAV88YS3GV01wirGugMC8Nu43ikQ/itQjq/U/jGGX8GpsrE9jSYP3Og+f+czvN8cdDRQG4w/f+Q70RPrKVtz3pzd8O+auBGI5Po4aFwgwM06nEw6HA4gIDw8PuLm98WNMtS7NJkaqLAD+fhhFOnJjkPTP+ne5eO7BOcmPU1/PeqV0v59iHH1MYrCGdVAZqRuMrQ2I66Zrm9mtu7UlTl+fPkmh+7zC971Pj1LsEm0nlQEnveF8UoOXEInwZjHWzHqc/OHhwU8hlFJwc3OD/X4P2k2Y/r1fxf7DL+CtX/slEMctfQDck6tJ3NJHkSmreyjFRlF7drynIdlwNlonw7XD8W5lWMradFLyRh4W2cuHrahDxSpyt/wwy4OyrqpFGRn2y+pvYWz7YX3JcgUpDwv+oy0avVNYTY9irlgq603pRw0sf4/j6YSXLyX+lmxaVJw646PF2X3+zgv89C/+Pez2S8M0PvjsNwSGdELEdbU07I2wjhhLCzGS+94f2GzHJ9XhOhncocAMW7upKJ4Xlw9CdoXcOKmVu6e6yQpZp2j+fzUutpYlZDXGcG7XbnKMoPCYh2+TL1eosO5JyJD5M3O/MYtqDZpIa7WFpZctN2DrZdgLAz32adrIs5WVW1wDMDZGjWgP2lnMRvM+kdZr+V5b0slqHEOQZiPpMCP40eXzd5RwfsMY9jrSG23o2t8+82C1NRl6zFACACC4W7VZ3QFlIYk56kO5nUNWgrhZp/hOdaGGhvbITcmQYgwLKgg0868cyduvjFpnYRJ6nJCreF3Ny9HjCSy1otAJn3n+dXzw9seoFmOrioeBG7mc4wUh0Au+bJ37ojM9zPpsz8JukHfJXRyA3wqpAq2dxNIBaJC1QVy2Y0Kp/2g91nrFP+8Y5d8Aml3+fpHlhX52J8/mj9KDbP2wOR/I6T2RdY83irHtYcpeG5bMyNUHpJ80yPr2Dv45BgHETZgKXYpbZQajaA1udnABojO6UGkbyvWQ4kmpLT4BcpmhCXU94xDQjAFlaJBw0nYMQ7Dx+R4NdJ/SPDVLkddsbGwsWJc9w+0d5kvv+p1Sw+9hfm5/Z6EzvOwy7OP1EJ/wsmOmGG0GPeveA8ix5xrDaQ+B0sPoOxqGmTrnjfUGudxuHrupqDBuxwFV0WIdIzNuh3GxOtOuzCiwgOrtHxCxvPI6ZD2eKzSLmrEEu93Nu5PHxIXbDtd7I2juox3Z7pXkawyqXqcTukF+MN5//18kGt6+f34TdKF/34iX3fzDbqjqiGcYFGU8zWtuqUvcoEyE4/GI22fiATKf5Dj+NKWLB6Qyq3Q4Fm9yyvoykJWQdVD+NiUFboA363Yu0E/Jlf7fajUDu66/8e7r8XHQl469bvS3E557Fn9N1wbp3Jh80kbDH9RESBucFPKOKP1FeReDfLMyz6Ec/z6eDg2vM48werug/MpvYfc7M55/7S+DZ3K50IxiLpMkPMretr5ZykmORMRM3NooJVAc3R8ZrjaS582aKBA36SX5YiSDCseO0wLGDy/LekkuJ6g+0avS4zRaxexzSj5nAkt/2iHLDsG7bSNebkhcNN7WAcfjAR+/eInj8Yi7u3sPQO9wksiUITNPePudO/z0L/597G8PrR5hY0kDg2c3Zq28FCNqpVZy/Op51h0igHnVo5jzPLu8zpOUKiUC7xOCd5vO6eOqR7zFYNHPWCeJD0lQh7tn6Fs7Tr08uM5vuNXn35LBpEwvc56LyWqyErvMFHLrGHtD1m0g3YRvm0f4Kov8nfB50WC1qrXNv6IbzuKexi9GhnEATfD2LQRo9JxBXtrgYc1sNnrw2Mi1Wku9Hp7q3ML25t01vDXpCNekN9rQdXd354NjDDZ23IMZAxAGhghInPT51jCh0ycGs0W/y3QWqPt0ZgaraVaSWAGGGJwW1ZoshlZNsbEkOHzFV37o9/CZd77jxxyZ1TONwiC01AqgYuKPcH93SsaPLOjrEUk1kJBaoJqF1uocLZHQ3Rh2L6OCNt5BIsCmbOSg+l5hWgL+G0BDnEhiSKng0gshjUu0ppExLH82M5EFiq4ehimzHCv2ESmKZOJJIK6+0xMaLlyAAiE2F/V57rvdFmTCzzTyXmhEIQ7iN8hTpkntQMkDSifwsS66Jvjk3360kQhmXJg6QZSBcF+tGtfIBoHy3HUaTx4//5pw6pHEzo5U5iIVSN6PLSJsKjNka+tpGlRv5LLPHvctj68twxenV1nYaI0xI+NKNpjk9Wj40AsseSc3P8/DEMJKXovFBb1B7612L2e3DvmOPC4vx0ZOcYG8YA/5XplRagEz/EIPi9NiPMBiRNUqBrKFY8PEgh9b/2xuZGx3qngJnziddGe6hhFf1iWBaBoYp+BGGsd8ouGc2xjGhR7h+fk60rU0QMYp5tRolk2i0RbNnEvKIvMxLF6fbcp4H7kCNeIwLsuCMhU8e/YMzCyeIMzthR2J59gcVb4Gg96MNBby/e1wjfXr8vueVPZ6Kr38V+kHLCntkrATZoBgp+GN8uKKs17yUQqe7Z/J6kxGoFqrywiz36oox+blNkY4TQZautXTykbWczkdbpBy2t8rtRT12qdtpK5i/yL3ez1EZDwtGT2ati4NcSfad2/DyIXot0ZFa/JdlQhxq7bVQCafRxzJGGehrxI2RcKPzBpo/ng8utfWw8MBh8MBd/f34pE7V6cD5u/3lZ/7Nfz4T/+6y1QMYH9zRNnJBj9gckXaAGzof2tc6O06iTttjslAc1j9XpZFNmOWBfNcMc8Vu13FVAi7iQC71Mx0mYRHJemLIGqP/mf5qmmWmpvLh/3roB+y381eEmgQAyyrcCFHdvrco1OWNw2XWjiGpZKMm/mgeMqHB/gltmK8cMgTn6D7fa9TlnNi2Fq5K3S71EHr9CPT2SHROh0jEp1zeLY78mhYXld6ow1d8zxjmWexqqNdDK1QZYpHKDsib7e7F57bsnM+SidT68K9Z1ePCj8SpIJ7Dc+qiY4gWsR4VRlQIxotC1Dl763dH+P9Z3+SYglUIdQllM2aGM2yBBcMZakzQthbUqWrtdVKf6wPPlKxU84NEVUFvBlVjjKJK+cA13nVOM3UFmXOWuGh91boPYqMsdsRrOa2nWYOg7CGYQeJGyCO8XSySrApqdOr5tQ/gz3hgRkT4klPWLn9lhql/EeU5nRkUIlxByjBlSpULln0HCqlcc8T4VjBgUvG0sgMMGls2/4lAgsCCtQ9nKId66hWGkaWEERtLNcDRk22Rgjtx8QMQa0JJMbQqzbG2s6Tk+6WHzewZAEwt3RV6gVJbON6U7/Cng9eZMNLrrPJkxpqRoSaHIPv8psgtEeEidx24L7VanMdnyP6O2rP+tniV+/NFGs52u7XmiU5Yik0j23XUOWEakoBhRBXq9DNKQkFBIhHLSJfMzJ6UYHR26mosYxkg8J6zKkPfUpkyFpMypnAQhyXj+Qjp6zKmuejMHKGYDpKHY5DaIYpHVHSxsgyjb1Qm7ULap+bEtaOXMprND0VZbscBkrjF+AU75ZFjrJMCQ/GvTQAxsFf22KMYabNlAemYzud0oW+2jMEY0ButiGgNHZnUi/g53W0Jp/rNbYC4lEELwEBCD9qYEhZut63VK2lI2NlbnsCt4xrPRiP7dqrGu1W42D0c4BDHeFun+MC6vakt0ubrxpynfiu/eYaEl82OGujgU3cyDoEiTfIibZB63DFv8xY3v4Y5eEZ6HjrfMVk9wYWYGxwGvBpY/u2aZDLuQeQd1G++OmQ7KKbe3lu8FV2Go/MOL/1Jw1Z6meuR/9vBMlViY12up/pZnF7L3J5Cbz0eWTUCj1lUnGcK5ZacTqeMM8Wj2vG4ShGruPhCKaPMO0PoJ3UHXGUCZ/+oQ/xhS//rkIbdG1Fs03mQcg5AZVJwt0c2tcsAHVjs+IFkM2YvAHDLDf91spYFunvUhmlAoUMJ+PIp7NxbnWPBh7OLY5nasuoFXreORq01u2GKclxPLKsdVBGnhEd1//PoPioVAth7+mF1UCEt5jp42mKHdRMg/JzbA7byvDthtZumWVYxo+HuNZzuRUYnCSWjTH0x4lGOH2z30ZHVoXTiIQwNgS5p1tIYx4DEr+3xsH5Qwej1RmgDUqveGRrwbhaZMMbbui6JcIeAHQ3yBIBjpnh6mwLJJQfIsi5cA4re4tjYkCToMELUO+V2VZ1YZWjFhIYftbjhYseRYwYWT/3xX+Kz733bSeINXtAKULd7o+YT7ET7ThQoX1jFO1Tcob2Hq+I2lAKNinR/rPjhxbIm1CKxLCxOvxaZz3yVsNiImPFQDXzV7lAVLXOlaGAk5t7qsBu71nJMGRH+qAGS27qibx5fPKYEfyspc9BjW65wcF2yFphjFXhIh0vk9csuDWBUahCgveLcbACmCZl1AunKlnfyh/RpOPQemyU0u/WjWXfPhHVJ+kn0F6bscugmXwkYzyLCoruyYYQAlnHmYsKlH5hTivUARbjYCuWTMZtgGrmXPYHmRf9a2/AQRIkIYIMIEcssrANpFB9JlikT8qQXEdq+/E3eHpvPYORImMD96rewXNjRr77qg+NHoWhcwDfyJhZJkwlYDZvGjdYnpHQVocwsoFgCEEryIXdZ9RP7j7b5i0ALANyKywzqhq+XFAnoBaAmVC4oAJYFgJXxqmQe3bVym74CrjE4DJNhB0RDI2cH8yL73gHbS2YShzLW6DKYrrtkhS/zBNzsiHWC0hsZ3k5Lh7TxI/luxdvO54xyqyexlYpRzbKl0jI8woGVOAv0DHNi1BzjVOsR+hG1DLCl+Li/2Ydx8Ms8JUsrow2AKCLu6Igtl9oA02bZDrSJDc3z1X53q6ACTjVWWprDLFtFVsjcVVqZf3UHW7WPw2eNdVsCfENrFk83irfr8kkkDxGwkxt1i5O0tjoPgJqnW9lR0d4Gzvk60xXNPNUbvmKKU8Jt3yx2bT0LA2S6FtqnyUDlb9TnmAxF8f9TYConLPCKxKZiggi99klOokfW5FihGPagUHiUds3mUIqzD/6h/jO/+7/hGe/9gt467//Fe9rLjOoYdUVlxC49bEpVMGomJPBS27LJpdPHVfd89xuYY6NYB/bpFhyZdSlOh0xEdM3Knz40saWA6x0dwlZFKlugt7WiPDoyqNQILKetGUGGNtQJucXZHqN1UuEsisRM8jFIfOOrnrk9IR5nnE8HjEvM5Z5wUcvH3A4yrNlWfDw8KBeTxorhSr+4r/1t/HDP/bPZLQIjpsE4Pb5vWJKu7aL9xgIkcViYZ5gGzRUxOvMsN+MXa28H3+M6h5W4dVn7ReUacJud6PHLk8ydwzcneCOBqQwVgIWEhmXqWKaGNO0oPAp5nVRfCkFhLL2RlYY4nSO9rcQJrMMAivcNnxZr4yQIeLdNu3LnIUIwG4a5gtZsrrokGmQ3Q7P+ryhXwYUQmL3emt13SuLJFbcHEv6TWAQ+Vg2vfHbzFuZPmAGSg1P1GvTOU5yXnrZyrEmVjZf+UIFdGtjBIHTI/8vyV4UOoG3SoknmJHKcUmdeuzyD5tn5iTfZKxrYRvSZeg8mu5gZZNMverVxtwYLmWcuia90YYuAru3yarLOpqSJ/+O12qlSYxUd62NmSAxE17AixydqLXidnePm/2DKh4VC4mL86JxsuwqeoDxfPcd3E7flTaYwSW5G7vVuD3THEJaLFjKv4fjkVJTV5svCzgjpYiy5TTDqYKAW3SzoER4NPJ1PRyWH8hXYzm9V3zbl12N3H1rWwyPoYEyxZHHXKqDiXbtmTDSEW83jAXNTv3rCHp6FvDn/G3do96sesmDHwNaar1bKQ6cJoBTgW5GOdfdyC3nWMPGu4x3IcIqXA6gN+d/HW1wAaOfjNxObu8MiNdjepvX4brCgPVYz4FYommuVLA7ox+v2mmN0cnLrHs+5uGUhLDu+RbcUakEcr/Q7dbTa7NG7XTbvAjShKoXSbCKzQDApM9VwGIVFiqRGk9ChhK5yoxNhjoTKqpuGJALfr4SOQmBRsz6cUkGWRvLQgS5iHXyI5eAbwUACG+oLE6080oBR7eGTKDpvQTTXWEDZXc0/h09SeO/Sjrpw9eJxpjC5nw+4/eqzLr5/HsMw/h3Px4uINI2vb02nSvOOYMgTQejAbB9bOMS3djyNLz8fsw1Dawon7LH0/7BOA2yrLAksRrzzLZA+MM5vUBQmPo21h6Mr+rF9ToTYRDrkvJ6WfPtLEHETESfeilpzbXanGv6fh3sIxnNiu4IoJsZ+PS3gR/6F+Af/X3g2x+AX77V5eTRR98QfFZVjrel43YFRstHyPL2MpPQ6Uxv26Qzwik/qGnIeEFPYzdTpwO4nrLVZ5/32ETPDZnM2pyS8Jch9xr9Yb0V/TQvYsQ6HDGfTjgcxWtrWRbc3T/geJIji7VWHI4n3Ny+wPuf+qZuvjDe/8yf4N1PfQfuNZcgp8T42w3EbFyN72a2oDw8zqXIDVE+Fh09l3ns5UfZ1KYyYZp2mHY7AEeNOyZ8dakURymhTt15bNOf//ZpMR2UY1OL7WRKVcg4xCnvq3F4e9iu642l0I1NM9zDNeej4wJSX4bX3/rdo25M80uLzBu94UGvOuDsEa+9sjPOeDFHEHI1QQ8yWUVNHWMT4TpRl2mdPyaBu99NP7DmYdmYtx6RVu5oC11HaLultn5G0VojOQ3GrOM0w3Eb0kz7OrTRhCDVlBzq8O3IPFb8eqMNXcZE/Ax0GSFSJvjsxMgIjdycJWevW0NVTa7SjLrMOB4+gsUW+qkvfB1f/eE/SEdLzNKdPCk07QpDbqQ3RrWepn4Hz34XWiN14Ac1z64esvZJs+AyEWmMW1Z4oDEXGiP+1ekVNIfh+eXWYujvhmK7vi+uxkbGEBAtZpYQgVJkty4Lls64lir5K4OrnExdFvEiseOtFmpimow5Riw0u32xOcI2MIqM5nEwOrjmDPsw2RjYmupl3g2mZPi01WTuR69MyXpcNvPnZ21Z8iOaPahWb7M283yliytW69KYLKcAjJSEqSvHdeuI4rl+bvV7C9YRTWkE2mxgeUTyAMODsd1qU7+4YLhdN7Wf9qKcpyeZjtpfeOtuw1RKxBtpLiyBippKJLJ3FHOB7PbDY0LwyCtK25kmW8tyPGealobPAIxFbwYpu11DR7xPGicsVYyJhOaUfZHA7LME9I2xqO58UKlVaPyKdhg/ITcOcA0xJ267ldkgilhx4uX7FJ+lpxCf72NyFmB8w3id8cZtUavdCFhVOW5uJIh2D7JiIwJ8y38/qdRuwoXHy5/+9P3pY+ZpvSH/nGHyHO/oaWx+bjzx0XD6f2tlarQGOGXqxNaUhzEBeA/hPY6f+U3wn/lt4P/x74B/7c9tTstgS6V5x5XdCEpEfmmTn6xQ2l+I9ZZ0GijGG5QsWxUahZjBejGWiKitnBFGn9yCvMt8qskx0lz7GjiHOJGnsSFLKGXSS7aEp8sxPfFA7us6zTPmecaLl3c4nk548fHHHmR+WcTQ9XCsmGt7a/wXv/pP8T/9a/+Fexrvb+KmXOGbT1FVI9nNnj5EaowCL15tQZK1QBqGwS4saNfFfr/HNO1wc/NMbg/d7XF4OAI44DjP0j8kT6ckG+c4xmWK20d9g1UINszTrC61xT0zvBE8kL0Jl/n2ecKGTAh4jFN/luQpWW+xJs+PfGvyGK4rsvGl1YKQUxI8KDfimUYPtm8QXIOnZk4eLbl2hWadLYzL3ebFFWh4LZaOevyYlOn9uU3cczrA41K2RVDzbBvGV2P/zQw9he8kuZ+wluHPpTfa0PWjn/kQb731bKU4GoF3a3m1QeXmnSnW2dAVNxeyBhc2prGgPr/zwX7n9rsAH/3IZInzTsMUtqLrlD/5LrDGd4CdYcc7a7TZvXgSQpqm1wDsn14lURwVNaL6CiuAUj3xkNZ5ujYZ0EDiuQvXw2GW9EwUXSlON7t4HhVQPEh+MaMHwZww8y1C065ityugIjtDu2lCKSTx1UiOMt7sd7i9vcF+v8NuN2Gaih8TbTrfTcsqgGNDtF+PoL5paFspZ4qjdsNawpUtQXtLcO8NviNYVp+U8nZGk4a1Dgxd16SRQSaMIdvwj8puPdvKs/U+t3cNU+yNXpdSMN2N9pPROytMW0YnW+OhtLe41QhnZySfXH+Ga4RP54xeto5dmEQ6+kB2S5ccibDg6EQaiwsVzGLMJo9LZ9CLQCvrU4/BaPlaw7BqvAZM6eKQziWbW+HAjwRQGO2YSNz/05jIDjKHkatWj2Ppx3mTANgrvOzwZ8FxNBm25nrpsf91tSibqn5FqcraP1fNJbAIjhWglvfmOhu2dM7IxSNR/8pEzcdrSSNalYXtnK95twE5JytGFO/lsifC2rWZvbfsOw89DM/Xk+tbbXT1ZTd40+tM59o4R7evgedVNz3aZLRo3e4OwI4IJ66oaW34hhNhRXNuCNjpC6FLANMC7BfgS18XG/s//XJ4dplYmixu5wxetovR8H/7p0Yo8ZHNi7uja82iRyIEMg4h8yDqt/f9vCodb+lDVj7TfHMYD/JmYoKshdZ4qnq30GS3Aeqt3soLkAwufkELQ4/rV9w/POB0OuHFi5c4nk54+fIlTvOM4+HoRqO5Emg64Ud/4mvY3RwAZnzuR38fN7ezy0hr3FzLFvLA6Evfs774eqaD/46yczMFsaksf7e3tyhlh91uB6JptZE9SmaPIkoyjG+GDGDQhZANgmHokr4TARUU9IyrG7LMw5yopG4adw0txvq72jxUoLl/1tUkFfh/KyZlZUfjbSpI72261d4KljUix7skb4JsHSRCPRAaXb/j1lEBWbahtp9naYhDldvdgH2kgGwkm68t/jvKfymPNL3VuHqXOvnewgp798iU12e2I3T419A50wEs38gom2XUR0L2Rhu6fv7Hfxtvv72PBywT6Ds25qWlQeHB0J2IqrcqVizL3BIeP98OGDNXOzJ21BpVOueTTWX8WsvjWAE+N52JJXR4+pr0hBUE4c3yVBXmFdI1ndrIs+KpSB464BSfBolpUeRlDsNWUs5NWHKPsEnGaL/fC+7d7mCBLW9vblDKhMri9TVNE3b7PW5vb3Bzc4Ob/U14UHESdBIxuqi49ZrVE1PjEXKlUJ+J00UdslOkRs/z702jG5TxbEoYQUzZPq80dDUGmM4IQaW9JS+X6RnRlmFr1M9z+R+r+OT8eZc4w3hZ4dl4T2LsNoOEe2/19eV+5X64cJh+9xm3INowco2MYC0oUrEZuLKxi7TZCXJEUAReu9mnuJGq1gpapI2FGKgalJ6tBkmTjtw0QfmMxPsS704xmJ0W8crKQrfhsh0wlP8DVxdeBO6pOL+qOgeG30CsQaoSk2RxuoWQ0nWszUCd57pRpF6JyL9C4acysVcA2BWPpr5VA8BqxOCbPT3Eox48qlfUfET/XieTR6sgbb97fe29tvQDCtYPfHoF3HEDjvxq3t2C8BYxPmLgADMyZCPRmve8RSTKCNutzKnCn/9V8M/+Q+A//Y8BP8KYgbnwu7byvMv1Izkgr39fZgSPXZPrFwGy4zdGA0KnMN1jmDqFuIfJyjeB+/vuZt6JkNkm896axMgVhk6gWqxH8zBiue1ynhc8HA44Ho948fKlfL54idNpxsPDA5YqxxjdQa3s8ez2Hr/4V/5bvPupbztft3irn0SqNeJeZiNTM5bCDGO+F3F6KFSw24lR6+bmBtM0qaFrgm1sMROmQjCbkv31NgxSw5PFphXjWGn5j+mUduNz9ujqjEEuk6gsIZBL3VXlzcZUkPrbk8DYlOhlyO1xJUBjV6ExnNmQNn0f8HUGPBTEajNykDcvswazhzBSwOH1ai2c+tUbjBoz4CO8x65Nr5n3nOO/ryO11XBj7JK2X32EfHZ6nSAZuzYAcpnG5Xl0eN0UvX5M3mhD1+HwgN3u5IzBjhsuyTsrK2GE2K2QPHGNvDG4sMqrouE0ZW1DbJWBscLVe1JcMho0Sm7DhO05mt9tWYOL0++e0MVuUMjLQXJaQtITlu5ZQsYtw1ejCPhDZeID5X67d1pXx0SGKTH+7OmTFYXR3Nn3bOSy3YPsAeHvVf7J3mDZMr/b77C/2fsg7G9uUNRVHCReY9NuEtfpMsltRCoYNoF7jU7k0ewGSEiUMXvbURGoz2HcFj4a7pC1f4aptpfAUKNHn2ujF+gueTSdTZ2SmXebt2oyvLX+NO2nd9koY88ey5C2x/lyn1+X90BPh6717LJr4QHEziLgRi5nSJ2Q7teBXw/geaVg9KJbEowWP1s6kLwyqQBFhMtCBVNRIY3lqAnphocEmecIBF8KiDRAexWPBQsezJw8BgDfODTvMNLvsslSsJxivOoivCsUhaAxcW8GB/wWvFnrludWXxoY43+GQ3phiAcmtjaIoEHAOrrK0q9mhPs5uAI/n7ieH1XO876iULhSnOPIxDkD+SsFox+kVc9H9Ow10QZLW0bjeHaxBq2nl1eeBE2ai7aiJi6XyufU4eE1u/NPhuwM7XwKve6N96ONoL7NLGtcw3dynnNK6HVpW8Mzw/wtRMEoJJ4q9xwBja39GwB7YHXLV8iyUiPKAv7z/1/gJ39LXnz7U8Cv/iJQi8tMPuO5LlY63Mi0oSiH74nSzV4GWPWr7basiZJoBMspA8rRDeN/F47sL8t2nqXpfBiyOhnWZC2D1W8gd9lP2hJWpjyqhlFLLtESfehwOOI0zzgcjri7v8fheMTd3R3mecbhePLNmc/88B/hi3/m14O/lj12Nwuev3NQg9qGHpB0sGaMXcB8XHJ5MTF6UqMHdAzaumVjeZoKbm72mHaTfE4if8tmtugFVeegkFxo1EoxYUAZAAXmGhtnZpy0+476Ne7yOvuAmdFRMqXLYbi4gY+cX2vHE1yGg24sMGgDcUyTXOmSOcShzyKZJoF2mgb0psVNHo9RB4WtgZan5R55g9ok2S80QlaAe5nupzzXYd4FCpl4D9tAdfEidbVu0umtzfGetm99z2UiQ8J+Sg8RsoyI3OSXgEUdPJri8ymPa6cLuEWN1/ooQ/SKlfRm+sBrSG+0oes0P+BwKK4otEYsBtsxRASqxjnt6kQJ0CMdVDBNYtUPJY19kRsT7dM5I9eWt8corTw5tmWJVKb9nYnB2igmSks+9rZqs0PWYWLx5Mg72D0D4y5/86xj5DRAaO47lvLndEkZyIaueE4eTNHJfmdwcEIDYxhBuLMhjImb65ntrD4Vwr7ucXNz44r1brf3uqydojhntyz2Oz3a8fVYoO1nLwRlF/wRmW6Z0gYpb4yKCYt6xtSVb773+IU1Xp3z6BqlnilkohwCbvS9H72mjWzEGvQhex81/WlbW/VjBPOlvm3lWfe3g/URRqtrYO3bYubmqHIvdNsYjXbIM8QXx+Aq+FR4TApHZpCUPg3ermcoKKhUdfdR1q7H5FJhRILL62et6uVlN1pZnqIeVUXjokB5j9HD5OE4ZUOXHGeclkWOjNS4kc6N5ZPdvqpjW2Mzp0Tke+mP31Qahi43oNl8pAViu8YRfyvhtioK5sXcGM2a0e6fb86Wfnk1gWU0nyvB6DH1OfL2oLVKsj0xPcXG+XuRkg6nD5SPnqPZ19S7IcPk91mGyWXcKxB53M7Rvb6da+C7Lt8qUf8zyTR9wPoryv9pSFtGMn379IoJGBm4Rd4WmnMDk3GABcADx4aIpRsAzwwUCg8DdtnMcH4Bfu4fRdmv/wTwD/8scNrFRaBdXxM38brYnyTa3HSj4R5NfakJa1D5XvVn7PlZlXD7nutvWxs8diOF6R6rDTHjE4kWTBoaI/gwlGco/XLdhzHPc+PF9fLlSxyPJ9w/PODl3R0eHg7uwSW3gcvG7Aef+xA/+xf/P/BjhmWPMMgkk1AnByTgB7JTL6W149+H6fApUGShNrPaPtrnRKReXHvsb/bY7Sbs9zuUIh5eYL2NubIbJWLzmrv5sd+ZA2X+q/hXqxq7jHcELI2O50aXiBkHg8HWmdVT9BIap83rMbZwLm2ewBPH+S70gFys08tPWsZ1nI6eeObW6Cqy1BX0JelOnvrfq/UMuJ6aHlqXzPY13uJvDTjbMOb+tBi74std/YnzNLAB5/WgppZXlJfM7nG+/qQ3OY05xy8An12L8TrI5vJmrjwaafArr+Whzt/ZBp4q873Rhq6XH3+EOsfxoXz+2Z65UkayY09gTEUmijmCvRciDy6YhTmrB0CK9dWm3itlZJ29Rhnd3Lm7cjyuWxsd03Ch0tAvEHSkXGw1kcf60enJkm2XrjJyAQBvXjlPaMebDLz02YDKkQ9E2E0StHIqcbSoaIyEqkdonY05njHAi9TCFeAKotrUvwIyG94oP2+Z1MDK01az8e4x6VU9jq411ACZeef1pvQwMvnn8LYPJIa/8a4x6AwUy16wHu2q9+u/f35N/7berWAejGFv2BrBeM6I5gK14yq1OJLrIgKVgunCXPrGQ56bzkjL8XUzkQpX+gtAv8GwFpAtX60WOyt5RFDROFcaPFgvF7GjgVZvZUaZjM9If+QovMbvYjkiUTkIDJksVwwuOdbxvDwTZeMkx+lPpxMsqDyzHGPY6Y0VBKEpvZecjYMJKdnIJfNQm2cw5Sf1SWK5UBOXkACPr2NlBrOAyyLHa6Drr5g6WelRyY2Fzdi+XvguAwEV3I30vyZ+ea7JgbELaGczxvUaPHhs+59QF7dA/f6jaZP6cX9Vxed1Jye/ZohH0Jiq9I9UJqSJUEB4T2NDhVfXWgHZmgahR0lo+9yHwH/wnwH/5CfBf+/PN7w4f2YabL9d0TfCzLKyzMNB8meDLq/rBWAGCNbFaYq31hZ0P5dzK559Boy9fuG/Eo0XGi08JCYhqlnswhSWUwFm6FrqgmVecDydMJ9mPBwOmJcFp9MJp9MJH794gXmW38fjCfMsmzA3z+/x5//q38Jb79xhKgXP3/kI0xQbO6Iv86Zxwrug4ykGM3Ja2s7wdTg+ecgI+e2hYVgulTK+WcqE/X5CIcI0Fez2E3a7CWVSvl+rHOkH6XhOogNa3Ewi6KnD80llpNAesqJPGsfTkMl6S7F+zOigntlmOJV7nuHlGAzW+L7WIswz24bQGIUZFbiXi9gNQusTIuRO3elhgGmguD7EBhiI1t77ZjdJUuhg7LbWfDJNU6xN1mpIVSXJylFZowzklnPb3P3+5FNvAxg5wuTn+fdrhgTreRAHGIHz6bJS38Jj9Dowr+Ntv8b0Rhu6jqcDdru4gaO1UipCgfy69WzhdYam67PAebb+xQp96qLISuTTEPZ1nSm2xZWeNAKAidCMZhEMFPy22u+z8JUFBk29UaI3dnm5/Nnn7d6ZLNSMgymJuXyqo0AEESbWnbaCeT41x2jtzzFMmRynPOckP7ONE42eI0l0TSf7aoZpNLMheK0Vn967qjecbOF/ZsKvajAbJjWsDOc/JNn29whnclnj4BgI1k3WNdPa8pSwdI5WjN71Rr/cVg/LyNC11Y5/kgiBGbcZ8KMm3K89Sp6e6V3Talp/dvxRcD0JKo9OMifZ8Nm+s+rlyvOYN7ihywRbMcap0FmgcitBQ8UmRt6PZ/WjnVJnC4FWBdYVutuVUBQQt7NWVumaKG5QTEdHz+22rZd7hx/Wb3vGHLSqcCpDOl69MpITD56N0rX5rk893bVWnlRXP2YVuH0AqJrCKH/HPePUSUznevV95o6vnC4Zu1r20sVVGvR+W5rYGKlgOMPXq6erdUH+kb27zlpTNuu6Pr2O3fhreeFj6fm1POBsfVJZfBdA5EO/+8anwyDeWwBhSeLJqt70uYKT07Nnd8BXvgZ8/A7w1ku43H9/C15S7MxeFjEv28zGqTdyZby+wOcZYeDihFzWSJ8aI1dYD1b8uhmJUJT9yLkeXW/Ud45YXswRYH6pVTy3Tic5ong64e7+Xo8lyu+XL+8AOqBM95j2FTRV7Ah4/vZL/MhPfB3vvPeRbN5CeGFu2/rv4/xI/ArRccRfurxtgdD1GGL4KGK4kguhCvY789qaMO0KdhP5sNYq/I8LA8SiJ1Ivma+0ohVklMtR95ayTmLvE6Z7UwTZ4AaqGR22xsNwDtSEjqM1RiDjkONy34GU1Q1h2iXzjgPa51ZzTDUne1Mn+HAPU07bcr9qN8GHgPDW6pehdmpoPMrfdOzOo6jJUWktD0Bv5Mweh0eXhaHVd84ZuzYh25D3R/na4+DXSUm9apz5u/w2OjiujwDfwA6j6lp2WLWbGz2Xpwf0yvRmG7oOB+x3UzABtazbDYj2P6VfltwY4AuR4Ts0HIoAmFXnIBSK4TrnWfH60lpxebVkSJqeOHNOC8fHct2fhuH3RpNPwlBxKT1RaBsZL7cIz3bTkS/iI8S7fEyWSlxr7QyjlLUgBg7BnLYJw1WpYarfu2TCdK8k9fjRPx+Ne59nuy4ZV49HtDWHWSDHmng6gTY8GCh6o7pzsPe+z49ZF5e8oSxtjUOfP8N0Ca8zHY3fJW74g+6ecr7CPIyUHpRVvRqXeW7bTN9rNw89HEKD/Ik+P//b6GXejY/xkVXnhi1mTBbQnSV2DAMgjbnHJDcrujAMjcUCYdwMNYBURikVpSziIQZGrQVFr5WHj5PUWxlgSAwPURwIhB12kwjhEbRejuHXZQaIUKvQl6AzawG2G2IQRZy0aZoEFr1JuFbjbWFYL5PsftvV8z5udj36UDV9Gv39QU2VGe9+DPw7/3nBWy9l178yYamM//evAL/1c5LvdVLVPmjzcE34l67lVzRaPDolvt+PwYhEuu7zmsG4rr5e0TtT36AzPwheVI8xZI3KnOObbiR4YgosSDwuKVcBRyj6l7du1++tHr8hN9P9n/7HwBd/T37OBfgb/yvgD77gRi6tYViv8xjnkUh8Qz6Xah6x4Rkb/U3y9Kot4281PReYQ77o8E7lvsY7Rnlwo+NQMiqzbI7WyjjNM5Ykc57mE5ZaxUNLPbUeDg84Ho+4uwtDV62MZV7wEz/zG/hzf/nvpHbkxvC337kDQJjrQH/oVrjw3967Jx+RSjGonpAYrJtAZgYx2VvO60zTDhMV7G/2mIrG4yoFu51tM2n8LFL5myR2V8Zmm8H8t5VM3piIMJWif5Mik22MpVpagbNpV+BhTNBYveaolmSItopklaDi9RXroNY8Zhlx6qnpDMsGnWyKqRyGqK+ROgjpduTAg+ZwWtJ3RlrXaHwzRnGXN0AloAwMVsxdhZkpdZ/D9Lo41YqhxLcrjF1NyQF9H+lMK51IcmzWuW5yvb4fk8w4SIg4dzb/o0qdUhp9189NWecV0htt6JIzHgTojjT5IgNWE6x8j6glZgDgBgXz4iI0dRD659elSwruZcXzch3b7T2VmZCP0cgQMdrh7dtnoL2Basso+EQIx5UlQqK/n7JgLHZDqnidx/pPfY7APeaIVcFcgVqaKek9z1YtXmEFvyYZ8Rmmc8S1z3ohT2/4NALWEHO0ASrXhgor0z5rPYxMGOxmiS4YKh9JvVfL3QT4NG8Zzr6v5xSMV6cL5xlk773lHoIb+Xuj3MpIl5QYAGHw6mHt+0ptzAdOdXQAtz/P9j6akmIhDgXcaPpxbgX1Xg7FjFipLrX16NFDBuUQWUXrZ91hnyYQSdBYZnhsLVFGxJsM1Y76BKyyAz2txj+OZUScFdjtTtiaf+9dp0jpWDGDqOp8hFhqBj8TTjKevsOEH1qA7xTg2PDH10rFV+ls7R1eXp7trRbyGIqgf7xh7E7mzSXHVJeprT9w8PHctm318oZWK7unfm8UfIzg/JjEXd0jQ35DC/u2nzwfMoYAAQAASURBVNjuFshG97cTn52cLbq8JeN8L41fm15E3fs8B4/xBnv1RN3/qd0Es+ueHVhrMMnzR9l2g2Y1FrcP8gfIAv38NyRu1598GmxhTXy1cfBxfdM0za2RSog4AN0MMENXXvdDjA72d1bsyP034xChu8QlGbkynfANmqWiaqzheZ4x14pFDV6H4wHzvOBwOOB0mnE6nvSZGL0qH/Hup74BItmQ+uBzH+K9T38btmkF5zG1W/fdXGMt54Scxy2Z0vHPvDoq6RTdzRT6WCkFhSa95XHCVOT0xG6a3PBk4WhszHxDjij1NYLRI/XTdSGsjS7BB6Q8UfTbN6NGVhtuTT5ESTc1uAa83VCUOoJGue1edl4Ncoxfj+2quLVP889mrtB4cAUtSu1650JuXPGDBHLb3aDbI97HsNjIuVb93tWT3w5q3EzZIN1BvVmmE0nO5Fsbu3K7o/wZpv77qG7TldbwyIRe5m+jvvdtjeoOvmzGrh4HjSeYTrjuM61+rVfD9enNNnQZEXJilJBepHiYJ4IL74UAdfv1anoG7M9J140snthR2vZUucalcPR9K2+qWetvf/dQZ+NBjzsBdzDstg9xjj4r9KmCFqsH/XcLvubN5TfXzFMFs2Z81sz2XL15R+6KZrDuSMsQGGJ0tfP1EmunovICruJlKEy5NSagr7ZjDNsAXQE3zuCYclZnuOfoDGNAaEZ1jnLIODlBawyJvbCU4SVf30CeWzVqd/hptPRVFJGGOV+Tv1vL/dpfG+OeiOddGjHIXinaUpKysas3aJm3UIOfmXOznKPvDWk9XJam5AnmhpqkAGfvRq/D2ooP9O7SFl/R1nCMASA0zGhZaaZSyreMPARwuZyE9VZUl+0oxrEwmr4TMyZIrC+eJDC9xS8RBURvU2QOD60KD3R/WsTDqqjharebRHmpFfO8k13508m9vLhWLAAKF6jTHAxrRyqCC9t5GlWqNjywWF2hzIWXXg5W//Mn4Gdnwn95C/zzaSS9/2Cl0Y7npWS49/FbwH/x70sgYeZk6NqFvBHtXBZqPW/3hbSC3qMrAPpBG9vwdge26dslQ/ybkL7fsD8Kb59g3JL6X61/ppyDjHcrL1nBnry8AFxWUiRXTZsEAXOm85kOQW5m/Gv/Dfi77wP/6f8W+O57Xk4Oa4jf7kqhhoaMQBy5ZD2zbl74taa4PhwbDX0K/il1m8yTSWXkKf6Zy+/3e5g20yvudrP86TRLzK3jEcuyYJ5nLAAWZjw83EvcrY9f4Hiy2xMXzKc5A4q33v0Yv/Lv/ed4/u7HADPKjjFNu1CohOWn4/wM45nCG9R7KCrNs9H06ZKs8KikWvKu7DCVCfv9LXbTDjs9pljUC50A9W4KeZyZgWJGsSJxRacJzMCysMbj0uOPRNgVAibCqW6TY9dB0xrwzMmo5TfzuaFJ+C583ZjXdpKBdez9E4k2uIhGyciV4aKVjgTAL+bIspmpM22UJM1X2ZiVz7Cv+yZn0jnyC51/7jNi8P1anQxyjDdH2/L5ebRxZp3G+kQrSz0mDWw9CZ52fbwu3pPdfvpBGa+918nvbJM72WRGqUOKrBuu6EgD4eNgfaMNXbbA23O7Cds75HEy3NIJtKtSArNRetwsbkf26z6BdrFcUoab/q3qyYuvFzIzbJF3ZJvqF10ohsnQFZW6koqk3BoETX+14hFqb6F7CP80fp7r6PMwN8HGH2PoavKhYz4OQ6qP4ndV5uSMQHcXOP22cs50jfjbn4NHqY4oHcRbDuFHn7rxWX9pHpXcIDj9H3kH6JReQtfW+NDByFBmFzzk0U0LVHlfHA2EGb8GTLmfQxsnA5mbNznfuisbXWvbXcG+DUsD14AxnRPmthTxs7vXqexIkTxn5BrtAo1olf3OBkfRK9qjzIUojFZp/BiBK1aPP2MNUoyGSsdvDjxY9Xn1vetDzpEIXLNVwOEdFb3TtW1am5YtGjgeRZ5ZX5kljhYQMbcmu+mK9IhjFRy1YMwSZFh2kiuRB/KtGii+Q2QJnluKgrNDKWE8r3p8RDZddO00tKFfQ+3itqbMc41K0eOLZYU3eWOnEOGGCF9agFsmfH0CTtTWPUpG3V45nVuX1xc/nzgo5Gkfj2ua876+s8qPZaQOT5WXeHzivIZTpdcIu1vdeoqh77oURuYtWvKYneqnplH/Hlv/yOh/bbtPbfOauvt1uLkxttH3Ed0f53OS8ajkNSjxCh4a3ii9so9L7SR5ypR6NgNUkjs9cxICGulmf5KYXT/zm8Affxb43Z+AbEBaHRHXyTZKwpAQAY/68Qy5lxt5gVpBQvpfCgi17S9DL5jLxwJFPrSxg+oYZlTz4bPxYAkHUGvF4eGIeZ7xcHgQT67TjOOyYK4Vx9MRyzzj7v4eyzJjnhe8/f4f41Of+/2YBCLcPr/H7Vt32O2P3ifnzgyA09qmOJLmGyir+QxDeDM+WONhX+7aRABosgDzk/+VSeRsN3Q5PbLBR4y79rUyg/QWY4Zt9tk8hjgg60QMq7ZmbAgces7zJFE4Ob0gv5EyreUzQqpjmPMK1TF6mfLM+LbeZSkvSPGRm0952cmjaU26vkWKzEgbhYo2oUNGmwazGRFDdnPJP41VDEz6Ci+wQjtKOoyM9RY25XFvx8vobdtgS9o7WWtde1NXKx/k+tfwjDast2T7/vsohSHUxia8ULfgX+sMtpGQ1xGwFZtr3b+O9qfxCbpm9FjaCaP5GQ93G8+8AK9Ib7Shq8B2VXThNiYCSUFwB0p0n4KDww5ZZaNJoYLAofaIyejTaxsos1cJVgMBZ3unNCNka7DqhfIsg7Qwx05U06YW5g0i0hiWskFElSl7doauX5VWdZjy3cFxbmw5lWvrVmYC83BIc0yGP53QThAl1nCPgjFYXCNShpxjdG13npvPLJw1AsbKVJXmOv0gELLvos2MMKxoShiOdwx9hRd35zmVAzxwtte3JaQnfNm6HTE3QVqf4+NK+U2S4VZKsFjwUereXYuX1yg5I8Z1idlcm7aMa6N3vSJq3/Pz/k/qQbN+yyReR1QivpXPsZWpFSCLfRFwVWYUEwQTPYlddF7hy2qdJlpDo/nKeDjCvY1xKSQGKHKjla5fIRjaVxs7i9cS60z6V11RWXScl4XApaJUzeNKDKPMMiYWNNgNSwB2UwFD4n3UavVWzPOCWrkxQgEhvPuI5DWdhAuD12gaILdMeTxBmxfDEch6LqWggPDnZ+AlAf9ZAb57NQEfUf8f0LQmra7k+OMz/TaZwWWHsl5XxW5M04oOh8Nq3a6MX7mNTEeukSNeV3J9aEzHtoxewONp26je151eyavkE05PHa+tjZMtw82TE2dMSHKHG0E6odNgIFcZo66eRNs/9bKtegNuyOPyS6WiBIV+Pn8J/Nv/NfB7XwJ+74vAvNP2a9dv9vYiVqHWrflqHRna2i6aMQJQI5ePQ6IZCPnRjC2+CVqKl2dAb98Nb1JmYJllHMyD6+7uHif11jqdZhyPJ9wdHnBUQ1hr1AN++Eu/g7/wb/7XTvOz4c7G0XTI3lBKZXLDkZfJ859wzBT7mKtWnoj19lQcJOz3GmB+2oln1hRHFs3QlfUCS6WIIYvIYF0UPonx5UZHklsaLZ/d0hxRsPrEkBMdrHpSDZnYd0i44bkgqOGqOi4ZS3BcCVRv9JOLilTm9Ul/8d9dvsaYhfBsNNmvya5rWMYpGe8gHlaU++gwyDgWw7EODm+i/xzpOflXkt19uK+RM3I5ttr6I8m9qHhedv8k0kjnesqasX61ev8637q/T+lrljVH+ol9Gn1ih621QWzXb/TrMdC90YYuGHNgAHped6guqybPsAlOSlxIb029no/J5/taHNtSMvvfI4GwLb/dYJRVODFC3r5dQ5IsMLRtOrM/v+o7OFNrfV8VVhdUBn3Z6uW6O2l2N1YspbxX1dlAYMSUXCBbGT+y0MOh1PiMdXcR53gLfhSo6wsD7lHSCBlWL1EIGh08veKf+0/eNS1jc0zUfM/v8rj1QkxO2UPBPdl6AcnqS7jEA5zKo78yXiW4riW9VEp348gAN5Mif5WxK+UxfLb7jc/ttm8peiOj1zVMtA96fy3jG+0ejT57oZQH9LGBWR7kjsVaaKwr1AjLzdznubLv6Vk/Kj7+XV0OW16TanTbgjfvfhUK47R7nqmQZnjOIKDIhod7gWodxeKsUD/3BCI5cmI3Ndq/wgAtdozQZOUkaBbB+v1uh8oVpUyoy4J5WVL9VdsQCltMYEhHIMJw5YStWVtlmuQYB9KFAxqIuS7ym2sFEWFHwL9GhD8phN/YRzyz1ZgihOggU91a69bpaE6HKbfZK9UJh+2YqOogXR0IdVnJVK3czC2iyqb87YHwZ3+VPDyQBPGf8M9+EvijLyY8tHWXcGXRDQ8V9ZJiuu6f88wNunT17m7f9UcK7I4/PsbWH/U4RoFtD45oGtv4deBk+rLChCQwR5XUvMy9UDFvUP5sz9JHy2Eu0eaR8eh1KUKX6rk0r5c2VV5b0nXFEFyoy4IDVyxc3aP1ea2YQCiTxCk1vynq1m1P7wvgt86iRpwo0ok2GZYzLAoQA8D73wb/638b+Oc/iuW3frIFGhm9fAvQ6XKt/SGuwNOgZWrU4uCTXKvKMBVAVX4aXv1mCDOjCkB6rJ2bTxuWWiuWyjgdT5jnWQxcs9ySOM8zDoeDXl5ScaoLFiV0N8/u8dU/9/exvzkADHz6h7/R8kHKMVOVV/iArGkrN2sj81Pu6pWnK/k0jTkh42/yfOqSjFdsDphscrOfPAB98RhcSPIu+62U8pwAYmjUGtgRVjPU1LoIz1YaVd1zKo6nrteVyuxsxxzDwFmXFPC+71MaJxH5LRRHJ0ZBDEPNVNiPzLr1v6wHcOInKzl6kLzewi4D5Y23mo11SYsjSlc+piZGdDCPW9O2wu4GJ13Dhi1bYJuM2Cc5aZBftZ51zABs7XHHTXoWPGo3CxINw0nroJf1cTke1pYtoMe7/P3cZrbBsRJ5GjA6XrqCcZt3jLpqa3+jhOcxw5bPOViN0KUbOutn/n4VU1+lPxWGLk/JKNUMdyO/CGOKF3myYjLMNZN7ZL5K1R5AuqFc5vdrZXgt/K3XC208vwYpBMmsrZDsObAR/XIYt5ONWbmMKZ1ZWB9UcBbC+LFmwK+SqPvmv/tLYxDMgJtnaPrdEEGF0Y0H2I7FYrPQGCFgjFB+NwFKc9kNY4WnAQ61vcgcs3tsylhPUKN7gibYxo2s8J3b3c9i11bq6egI5NTwppDhwPfP+7Ec1JcNKSH4rpl639+seOR5HnlXRZPbec7t9Izq6uvsf2897x46nmdD5tbubu3wWQTW9e5uUx5haNnEqdRWGAzkeXNjYDKa5bn1tZratL7Y/OTd28qtsJINdnIzIgdOlPURQK6iSFWq5l0PZmrWvHguqKFFPbaqrgjp0gTmCbsJmE8nAOg8wVhteiQxSEgvv3Djm81DjLmNQL7Vy+euVkC9A0T5ipiOExH+LBd8OAH/ZE84pXG01G/WuIjc41tIPM1crI6p+5f1uuXunQyBBBceXpowSC2+c9Mhhytl2R+An/9VwnvfFZljN03Y7W4wf5rxza90mQExbum8LlVv1ewFa2q/NJsFKxgH/OaRqd1Vv6Ie7gaFWOO3ELgobnVko8G7TsbJBmSvMzeHwKGsW/R5ox8tzd+mIMPOhQxE1NS1RSNzP/L3LV59tvXEI8611bd3Tf7Ru36j86nJ4dbPZVmwgHHgigIxf+5tQyjJPyLbrCoL+ARIUJIvfBORctkeh5O30bvfBX75fwTf/ALwW18JGm3emUz9Uo8+pXqsiUb2o/AEUoYCu5kRbKq6KnBEftFI8QtHdLOExWNonhc8PDxgqRYMSviDxWd8eDjgeDzio49f6K2JGnfLbzZmYFKDFQH7Z/f4qV/8u3j+zgvtAnmdPS8wwcrmZxszQsLP+BPrpMX7tcTcj6PJNWvSYm2Yl9Y0Te6ttd/HzcNGI0UeY+TbGEXesLkCiBilwDdwbBzMm88MJHWBkgEK2SLTrkzmOOStUqTdZVlQCmGy8c6KUYgiGgQfKndE3UYXYRJxpxOIzNCOc+gZYhzuTtrH2GYDWEdMzbBo/D/6nGmTHsMUJm0D73X3Royeb69JEblMHUPa6h3ZgOatcbdwKTunGAw28L0ew7CNmdSoQZNBW48dtybf1q6QAWphz3mvcYQZ5YkN0Fa+3Kqrq0Hf5/709a/5Qoz9qqlB+30bY56U8UPkT2uX0ryt570f08dwrz9dhq5WbenytSkPdFMUsgys3GBdPir1SGkEaeRZ8bSmlClyj8RbY3FlSsR1M0v/eUbYOtvUBRjO5Xl1Ue1pKcPju2OJQDnjURru/ODMEGW86PFjW1g9n64ycg1+528XmzF5KTEz4zntQCGUocS0Vng0qP+ansbXLQ0SIezqd9v9IqO+W+OcBIk4tjeAQh9mBXul3A0Y21PWzjmj1yXD1Yj2DA1pG8w0C0pbSrIdg2uMtwNDR29Y9HW0YYxKHQ1Dl3pu5d0spDZW5a3+JLzmdkxc5sQN+uVreUqJwMGkdVYVHArJ8ZtlId8p9psY1TgF0lZ04bB6cYEJpB4CtcoRh8rAze0Nbm5vJQBxrTgdT6h1wWkWT6F5ZpRSXbEqGg8GMHzPoxoKYu5dIQJ2OxRmTJMe7UnecZUZ7y2Mv/YS+Oc74B/sw6MsaJ+MZOWlwQlfaw0Ury/JGCz+HYDTYUkRHFeWKXvss3PJDILTNKF+QPgf/4Md9nOK5wbCH38WMM8W8d5SY6QdjWI4r5hEQ4ng02oQsHUDKF7rbwUV9uF09vuUNsjlkP5Y6nlkz+dGtGSLfl5j3HnSDrDRlQH/PUdHn7rb/DrSuTHv0+uAVUiImOLNA0qMuBXPADwjYFJ+b3dXCD0dw9ivv7YrQUusdVNic8yYnq654vXV3wX9R389PWbg/hn4v/s3gRdvweOAJbrcy+21hvfTKBFIQzYoDdT9Fiomb0jf50W9YNiOv0tg+XlZMKtR63A8iofWSW5HPB6POByOOM0nPbpYsSitp2JXADN+8hf/Hj7/4/8MAGHan3Dz/AA51o6AK4Zlsy+PS3leXqGWxKOdf6iXR3sskZQPAYAdNYzrcLMMKeOvQemNpyJ9ZhoLjTlaoRtOyu80CfXtpGlq6YHNp8gjQPVQKECBel2r51zIKfD5cR5lcmaOkZb6R7yeN8EzCt56YX333JdAsgbZbmOWlTqViHfW6xIMduNzGE2TIJWteshzk+XxNWykOVjXvN0hxDFkAJOs11xHp/L6bJOsvTBUmkdX7pfBbZuj7fjA4Nkc19im52Zc01i8wnp7DL1+DC94GgyPXe+Gx/Jd5AaTAUae0DJz2fjWGr8eT2/eaEOXLu1WdWcfVvm/pewqaMoXzqskVdIqcbZqkncAWiGt9+AYpS0L7SUDxmXkMqRA25+oYfDsQuoUWX88Unr7z0F/gu5xk9cV0HOLcjQ+Xt02POfKZ1jG79YVjYjXCu5UrjFSKQMyt/pROocPw7bOPF+NS/O7b/88AemXz/o9OzPpF1FL5PNz8qcN/lBMVyvnrpnluC8byTQyEyCSAcSYV+OllPLYOqCu7Ei8W3nyXGBOW8rTY+jIuXzXKGeX8IfbqbMKmnnYrMOMfUhCx8gAtbXGacNLNOWq6iJFKy+KDpF83tYIxh1dYs2XjVwuGyteO59pFkiimypsEooYuCACqsSbUXzT2Ft5PgoxqipKhSHfOcaiQK9UL+ohoAomZoAo4sn47Y61qrfNBIIYUVYSoW+WxBEeg4eIpNFFcjk3YsZtZfz4wjiCcFsYcylYKMplYb5J3IrMK2jO8JDREetV3s643KboWxaeLLd4HLZrwAzddvyolALeFfzBn4nf4vVmHnZxHHFRg1flUJpyjC4znBHp7Z2KN7arnvuTSfRm7zbW+rl0Db1Z06h2Cvrx6mWi3qC+1dY1/GxL7urp3VP77vhwJa291tj1WGXlXDuPrXu4ifEqKcml2dOAWY6I3TBjIvNLCbrrv6mHo/Xak3iI+XebL8aam3e5v6Ys0QcfgT713ZSDgRdvA3/3LwCVxIXnNIEPu7TWsrELrjeMvPLDk5HkFxHKFB78tm6FDtj6tmPSVYLJL+LlOS8LDocj5nnB4XDA4XCUz+MR87K4AR0glLLg9uagMDI++yN/iC9+9bfRCl/J06XRiYCUKXcmPi6iScxum84VzLIFr2SQfCu5GbosaL97pTktrYB65jDYwQljUcvrvZkk7zEjeQpy2Ijsy5a87ry+7RsrPvZcVkILpOFqhq2nX3m9pDV/iZzRxvc+GQ9xuSe8amsKxzGiN1syrnu894yhA6d3HQlU5NHTeEUiC9lbbiv18VRJJohMvEr9IBtklUUCT9jRKE9QYrpneUorR/Y/XtdGyDldcWWLoP59TwNyvW2ejMXc4Ew7V9v8vIV51K7R8jEcwSfC6MVY355+Ob3Rhq51SozFf9HgXZJsh+NlAkE76D3Sjoxdo5QDB1+Tf51aZOvfBX3ZYjznkgkE7e/riiYOsqE0/6lMiRHFo5YRmXGLGkJw/eLMQumWQWKUVsS0ngnaF9TLP03AN+UuqSfp/57U2RcxNpSecNlnfm5CcGqbuvyW75VTFp7yn7ZbOcd0IG9zBU8ekyfge29g6gWJpzDCXggZKX2PgTPXEbiXjEi5/+mZFmjrstfdM2o54LpPXdk1RYscK3w8M4SNHOjKbMbstVu684AkoPZ5YEIsAAvbvyuyy8yu4Ex6zHERj50q3hBiFLHjAsUNJHJ0EaiLMnj1GpI5kV363W7CVGXHtdaK/WmHWqt7dtUax4nsKAIQsLZDz/H/YOLsSKgb0pKx6ksnxn+4AH9/X/Ebe6ub9AiXqbnjieHu++vgIG6McuVb69fOtWwrrQ+n6+SxYaYyCa6XULzNe+XhYdb65XinO6Ukmm1K2p72qgDbxQHkgvnpdNowaoWmPzK0D2N7/QCkkYxzaVNv9D7eLZs2p1G5172jPdrIfN2yziUj2TXp3Bi+/rSWE40+MYDsdEJkXjVF6X8LM2Aycsi5boTQ9SXrNq/l6nn1SYIr1nYDX27z+UvU/83/BVgKmCv4N38K+Jt/NfUu9IVWbrB4WxNyUHkgjtmVMonBgwBoYPJFPWWWRQzi8zz70cOHwwNOpxMeDkfMpxkvXt5hWWYcTyfMpxmn08k9Q32DoxA++4U/wp//t/4r2AbH83dfgsqEPskwbCiTq9w506UMr5JaT47dboepFEy7Kca0FxxgOH5F3bWiUtx1WC02JlfUKnTbxBrxJpRNJgbBY64pNzc50ZAty7NC40cKfFIwSfkfRww4UuJPBFBVXqByREEBE+tla48Y0SfSD+PkvcfWlqGrlw+3NlWfTnvG/WjkNwKqeUuakcuNbnDcdb6ZCjKjOdrZ1xsGlhaac73pIR7lfR1LabTBs2qnMXK9Ov3vae5jUy9vZnrUbjj2BrR2U+NVeOQbbeiSXZ9QUCy5XkJj4TnToLXJwl7Rms4/QRJ/zMSMBDZugV0JfNnIZTs9/ZKKG6OoKZdytAJDp+inN5f7kGAflRG9UOvfyNMA2XW4791qOnqlOykLqzQaTH+3BVRWNkYjNB67zXqTpr4lsNOZOrn9z8tF9YMjdg0Vj8+e4JTcz4QT3stsCbZ6kRQUq1ffmTcP5TnKnCUbf/qONnOzxptzy3K0008G04bRaWsNtJaP7bSlFD1GEemNVqM687NzXgC5rkueE+1nGEY2OFZurFlT1H16O7iAR33mFeEd9BMp1s8gEdr1upUz3VrvJVfwWkYAOS4k3GqW9mNJlT5WoZVZAiuXoscpAMDieukONcsnmCPmV5Ugq3Gagh2HzdPIDGRiQJNgyCtvCw34ubUp0uCQT0usFxPSM/7cMuO2Ap+tjM9Vkps1CfgOKpYOdy6xzxVEZ+j3ag7PrI81DbS4h7b+dW0gjFBOFxpyye6JYd5a7MeQAk7zTLC5mVRBjTg4pHgR3l953XEPdNZMHymDfLIbUI+r+9wu9Lky1xiZrpG1nqwMdkrdU4xe19D6x6SM4+c2UD+R+RdBrlkno2ZIeULm655PaS3r4lkdjWLzsMkbOPZuC7COeiudy7IIMwNUwZ/6ptZVwZ/7APzD3xBYNQ/VAnzrM8C8c5pnxq5s5JJNsgiMXkpBZb3BtkpdyyLG8dNp9mOJ8jfj/uEBp/mEh4cjTvPssbrmeZaYZ1zx1rvfxf7ZvdORUgo++NyHeP8zfwIzdEEDtI/makh96cLqvYrWPBZvyS8KokQjSykoU2m8ZnMTgRttfNBefgPMo4rlezVd0Oh0dXprwd4lzmBqg43rr7s5Ho4tSQcJ2RvTqco8YzyuXENWGTWY1o/2WGEOGahZ8834vWLa4OMjQ5f9ZiSZLxlhGpltA7y1NIn1k6RCNIVWQOaKRw0GjRGjoxpa3Go2KtJtjubmKBpVSfrJ/Ket97zhJ8aYAm/PoCZzP2cjmekauFsZfaAaJp5l4zziW/0Eyui9irHrzTZ0pT974CoowXdYi+EpPU6g6BWexxN1LTlQdK8RPqLFVgFtYGR0iMLoYXW32Wul5GuF6WyoAMarqYPZq055t2WW9s1wBoiuAnVF2J5IcAitwowOpjEtPONVdaGti1D2GVwjk/8aXWmjaPYi6HFsLUhEGZv7q3DajFwZjmTkeuoYNbDChBqnqm0fNt75jUgX1uQ5o1KjpG7g1jVrfrS78To8FLYYYp67c7BfqFw+0m8zqmADN2y+h61x/srNJ9Ctv8wANkAnM160D1tSmct29UkWE3daPCUQqtJWdlnI+gzFeZJjiETyV6vGlxAjltzCJ7cbVq6olcIby72ybL4k3zJXQGNvTTvZxZ92O3Bl7OwYjHoNLPobkBumALjBKxSKPBsZ9+S3zF/cTGk3TNqxj1orfn4Bfm5hMCruAfzfbhnfnQjTLm6vWs/NYNp6vvKEdK64rflpN7kHRlEPLptdm4tlWbDU6oqqKd/WhiUJOj2FYWu3k3amghDuIpYRV8asty8u+QZNH4JeAVh35hO1X11IYhi0v7Vy82p1t+XFi+Uy7R09e0pgeFPCttLrUFZWTSr/eQoNbg1B3xtjl827GXbsz43GZpAwJImSSX0Jo1KOYZf7AeRb3+BkhBKNtQ2ZbISPf9aWiUSstNcMH7qev/I14Me+nuoH8PIt0P/5PwZ9+1PSohq4JDD6hKns0jFy67+UnueK02nBssiFHke9NfHh4QGnecbhcJTYW8cjHh7uMc8nObK4VByORwDU0JJf+Ct/Fz/x07/ReKKUUuV8O5lx/gyuP2X+rxJAtzON1hCpImbr0vBmp7TYjnHbZoOntCYmjbc12gQ2HLK4kAvMU1D+iPQYObOMFyeRuWlSjXDkJ/fPjkDeLCHI8V0CYaLkwdvLISp/sFrj2MrrDcrTNKWsPBzPnEYykh3pNA+yPl/bD4qLuDjJXiN6dMa4LWWii7m7CYgw0GVdcMXvtvREwxFbsNxn8FL+2GQVzrXnBR9fTJWm9LwZt9S/0Qrox0V9+p5sqIl6W3n9LM+4Vo+/2GZrZ+jfbZTCFcTjTNm+fulrrTlM0/XpzTZ02S0n0Dk1BO6UGAn0mxfCpkYEJAL7upTLc7uYI8NCC6UJ1meIDhTuoeZ2PcKxLwyW4Wp2BRKZGghVjeLKvPrUAi7YEMb1n4Wvf9AZuZq2BnXmX43Bpc8/mK9GVOvniLnN5b/zPlSg17pe/X/FHFL/+BLdivm3HbM890GvHbklHwUEK+t6FlJt7kYw9EYkXK8M9IJ5D2ffVlNrY8VL+Q0vBkYWXyGpLA36uWorP2NZXyPD18hQlY1oQ4PP4NmWx8CrGL1GxrNrdkl6o+bZMiO4H2nsMhXF4j5cwqVzMDUCc0csXBgkmBjiAmUIlvqNYNw+EUqpu6RXq5v0kiBVQBo4C+DCmFhjZhH8ZkbSeO8EOx5YZVfaPLtUMSuZPgfhFpDMkDNNDpeMTUU1o5oeZRTDlwmso4EajXfksVuaSinYM2PHgWdfXoBvMeMPC0tg3ivXWPTpTLKOjfJyHNvs4c4eBGa8EwMUQBSGRVaFeKlLExw+e6/k74UiblooAeT1mDJvRq5aKxZObSmPb+nb+SEweC6l12GYMSOr8U0KdFM4YnyR3vcKS0PXus8+Ob+htFbTc61Q1k+SkaLJHM8ntdTwjb7F4CGjdM1YXrWJOaCF554/FZYLUOApykiSGNIaEMwwRT9vLHEVGvtgfFMnjBHHb6e65stIv53vuYgmUMzMmL0XJkcxbjvZMIA3HDA0UOQpFbg9IOvOAAE/9TXgxTsgKqCPPkD5wy8NDHtSYFk0YDkzDscTDkfx0KqL3Kg4z+K9Nauh6zSfNOD8UeNzVUy7B3zxS1/DNC0an0q8xN7/zJ9gd3uAbUh6b3XhFSrIS+AcCac0BoOJbd+dReU+U/t7PQPsT32DsVBsmrDe9ofAKTtCnoOtEyrIrzJUgweTqS5gk80YgAWR5wq3eSsemiEjcfN1D3lrhayfEkhuGlUcKs3RVmgQ+W59r+rJOkPiO0kmcZlma/lS/rpuL/Q18vGKckFnfZwGlbe0vgWkZc2j8u1mUSuXBqQNbH0dtk4Z6BySnE7IWgn6YX2KOdUKyEZKzVGZqQVk9jYrEZvrI5MQgmCheXSd4w+jjYotHaHP+/gNktWT9LyXnaiZ1/Smexa0IHuKhei8nuvgfVtwkpd9qu7zhhu6OmUzfyEbXEbldodgMFf6GW9e9w7YKPXKWa+oxfe0WIe6JSfCk5EVze+rupR0ptRAqmkM/ybsveCCJMB29T86bXUqCQNbsAOf/BwHsxi195i2r81L6280eusA+XOGHLexuTRB1Y7gNIYkK8NiKMv5gScI4G48eHrqjWW9kaXP2zSf4bimLf2vx/eRkatp5wyzGtXTP9vC136XZwjzALYRs9wyyNla6w3bmvliX1fwICk2Ov9ZSXaxw9rbEDcb+DvG2UivA2GoL2fCjGS3eBrBoMnwlFqB1daP8Zt+CmKcCgokNgin8WQuHsB8qRVLXSQovd70VSmNvT5bVOiK4zESA0bWMUBTDpQ+pbhS9zBlrNH3acuzcTSPSbghEeCrnRHRjxtm/MoR+BeF8X+dFlSCHPGhZDD/hOgvM6vSGakUhIfEtGtomuQXr6rTPLuXmq8ZANl4lb0Q5FmKzaNr1W7tmufw2qrVPPa2eVJ+dml4vhcyyqpNqIc8Aj7C2aWmiZXGn2VInjd7apBZ2GBVpF1s01USC+l5fwPDFbyUcudwmZ9tbUo8NWXFZUTTL/2+to1XNZRlI5co9GHEEBIZY7Ew8N1lUY+koLm2Tt4DYxrwJvu+ZQg8gfCi4w4FwE1TTzumgSyjMRBMJgB4fgL+l/+dGlgKyj/6edDf+DJK2blXl+FprYz5NKPWBfO84O5wwL0Gkp/nGS9fvsRpPuH+7h7zMuN0lLhbmR4AwFvvfYxf/rf/Kzx76z7opW4mVP3L419AoDLJZSxL3eST38uUN3daQ4ubCjBNE3Y7UT+Nz7JdrALbOCiYUFB2E3bTzr29wDPCgK1hV5g88JJsLpiHoMUxlFsPd7uSoNFPyr8ENUZymL9PGYmD9hXSvyJroaiRy2Jt9QZGhq1dQhe4DgxgqUuSadvNv8bgdRbIlDLptfVPfd6gwTYWq2p8vLKssKoIcKNaD1Crp5pc1cuo25jMAIt3vMtvaZxyudhICuPnSvp3+pD0HOU5vUaVDc2j1E+H/S4gMXYN6O5I9u55yqjMWQPYCJirUz9X1mb+fYnOrPEhq+sx19fCtG73kodjTm+2oQvVLaU52YQEDpg1t2OUK8ksn//uXiGGOCsD1+6o9hba/vum4JGUNyMYK0XKmfio75bHvzW/103ytjw4gM8VVuByzK2tdG4ML62EjvBwKtMLvK0Skc6zXwHiaOkHo2pzJb25ETyYQjDqCeg5GGwnq7XktrB4TuJuPEX99Va6V6xMgxH4ZZMat4NtELlk3GpfZw0aK3xybxlbY86oGC1GZZi1B8qcXV5N4HBLSddMAJD4SP4gea5lcJPBbBP7VkLcNvNpd73boxhjw/Y4XXo/okWP2QXpFReiOELnxih0M0SdKJvpnACQgYEbbCDjTF25EDjahppWOmYZ3h52BJcbnNial6YOwzG2D/lSch1NWwaKjpO3W3tCE4pzqkeELvP0YV238LW2UOxaO13VfDY3ixq+qq5dDTXicb1MwQsDDWG/38OCp/dCoHl5yc535iH2fSyccJ6/ootT5+A9MP7iccGHBfjavjbwjJRXH6v1RMlHWpubvMHXWvBKZrjbO1H1fDauMQbyWSgMWiAKpdOUeFWwpA8LlqWCaIl69NKBHH/L5jrjzwr09KXZQBjIG4ZD/r0ZrsfTikvJdLIEjo+HrduVSJXK5p67rSHlphT3jlO+Le64VgxkzlvZ5sI4jPoZha9OW/LdVp5L7y7RrXPtbOVd8aWrS3d1RaXD4WUGKhgnlVn9Yg2IJLLa2AFwz+x0biLC87Q2R/2YmXEAMHM7Vc9IlZokFwpqcJJ3pPfkogXFelMCXAyfyX4XYCdHFAE92rxI/xY9Hv7wIEat4/GIu4cj7o9H99Z6eHjAvIgnV60VyzLr8DG+9FP/GB989o9BhXD7/A43zxaUKY792xhlOgujQxSxGZvJGKHGim/2rzOPHRB5bDzKfMK+9cr7oJVaa6InrU5VilyyYp5cPdyt0SjGJGTLTIkcEzDP5v/HPueGPzm+WS69SSOab9pm4hFFvbdzzK2RzLi1iJZlaccH5B5uRSPgb9JHaj4CxDSWZhSyPC6XrOBrK8mPxrpsV4KAdRyoaFVkQYGt30hdc8tcDztPIsMDApx7EFr+qPQobxzbmrJPx8N+ncXiASWotvhdb4Ts+9enkc7gcHfv+2dbclReGufTWq6LNZFrzPlpVaaHabxJ039nVQu2Vprhj/H1AvePozrMP0pvtKHLCFbDADQlPI28hqtOBFpqIPisysUogPuQSF0nND5FiW1Qi9vPhsCm76aThvDZ1nidfPs4Ic9FzGxo8CbbxXfNs8e0u1pIq0xjxSKOJqXRy7iyhrApG1WPdn6oyxef3qbhnNOMIIy9jOEMKvP2TR0vbquRj+rfVmPN7CYwXiOY5ws89wFYzVd+FTADPTdYHw1rwMkNNBW3zQnO58NlTpgThc4Ki8O3oRie7UvzMgQWCyxt9Z1TSnKsmJ5B9eVH769J5xSia2jUyNDlHkq6tkVn2KK5aYePt7xts9FIy/XtI71wtOTVs2FfOyNX0/8GrYaiSYOjLfJmoNqnItBKEHjZVV5x//hk1uOLLEHbVcGzI4xEegkEESqJ8lJyP5hBVAX3lqpGrto1U5Kgkg1LBft962G06FE6mAAIBmoIHu3abMci5jfRCQKmlO/dWvFLxwW/tWN8bUKKyT82CPdcd82Ft1POW/yWRPYA/mYotMEKVDKDFMJOqfxz2k0o6r1ha9hi+yxL3JCZjWT52RaqnqMxxrt7wbtXGm3+mjG4kmZs7QavYdmWIcZCsNXl31bl7X3Pb+Pq80wXxws+Kx8mKMdxJkkyH6uiHewN1AHjYO4a+jZ4J7Bsex9d3NTcqLMvf026rLC+YkrGF6e3KgsxSfuHyjiC1WMpe2i1cDIz7tPDG2Y3dK36pDR0AXCHNWbcAthrI7UZg348TKaKOXWjthkViGBB54WwTeCJ9OgxY1nk83g44HSa8fLlHU6nE+7v73F/OOHucMQ8i5fXaT6It67diAs7ogd88au/iZ/4mX/sXriCwuk4XwYaQWf7TRO9WuPCvK2/ruTeK9GM+oyJPm0ZuuK38a3g+f2mTGw0KFjMAOkR/yS7By0QHi9eTwGlzZ/Q5Ao2k+tCIYuQbUBGkCqKWgd9735pxtbwrzDXtlBrkFD61gjX0oclefr5uGh/LJ5XKeP5dr7dydhm2GvEoRCOO55Oq/qSAOX6TV7/8oWarH2fm/qcgKSwEUNj1zpJP1R2sXG3/IREaDhDB7jRi43US7s2f0h8t9g4tLJ6jEY3/n3X0zibzDyized4Rd/mKPWbImve1f5mjlw9r77MZmI8TKTdgqeHvecBrbq5ze/CIC2jKWvs+vibb7ihS5LKgS68xuINohopL2T2JwS41bVVcEbKzutJIwRo3q9a5u5znEvqK8M6e8SULFci+AZWXzM62zs82Fyc59q0tCIAVwp0rzKjsUhd1Bu34cQnlTEl+hyK9bQzEcLYiblA+JLyudnXpOxlA0V+v0HFWjC3cMIX5jjPqM6sAZUOZ/q5FV4m+Y0pNqnVptbtNQbIxIjQTkEDubXjQjC8jvzZf8/96JWiLQVzi1kMd3CoFRD6vKGkb7cVQmZytae1qOH0shu3rtJ8RWCb8rxoG+eYvX+qEWuE0Qw+vyYaaSPDKc8KpZ1jmD+Xtqs0kkOq7vqqV4IDcsxE4VxR6X5tEUBMbsCSvslV6DsicClY9Fp0KuKFVdXAgroAKCgFmCYx0piNzZSf2gUMY664ubkBI4KiL8si3glm9FrhZAgV7fyMeUvwXH1fgGkq+DEw/tcz8JsT8LWpm9e0LrbW+qOS4rAZnPJx0pB9WW4pS+0yA7fP9ipAhRAvgePn1diYgZGZXfkF0rxTjFK/qZYl4pubG0AFfDcWpD/zAG02Shy4i1LpVemxRvXvXTonf4WwLYmaz1Jsrvp10JYf1ctNfefTazciGRQD/rG1U35NXa8fTlMgW4/FB2acuIImAGktuSE7ieCmVMqRZyFeC4CP2PhjeJ+WInKTG3i0DhDwDHJcccIomdeA5PWYSSXxPdg8rnmQ0dLl81/D/O/+Jzj9/Z/B/I++iuNxTp5cC+7u7jGfTjgcDjjMFcdZLrKYdgf8uV/+m3j7ve+G7EQhw33m838ECyTfyhowaVE2Noh8E8T6JIYbpT2lbPQ/Tdfo8Rkx6Ukp03OYHKE00D51s4AgvHfa7eRzSnGtnESmo8oVoF2Sb/3/JFsRIQI3GaYsqHXxS12Q8IHVECufdvMxupqTAdu7Gd5bIT3IeJoMYXAXDXyf+ZvUrZvNmYZJgGS0HiuGhwVErHtlBl0nF7sxS/AkG7dSrsQXs2D0ND5wSR+5OvU6UZb3GjqfYKXWgcO0GsGFAjQbJ9Dbq+u6q0ZzSGOhcRi9ot4NeC+k7zV3zcN4XTKZ5vz7q2vb0Gv61OtE16SnlHnjDV1Npyn9tv84EB9oRZjEb81OKGQnMaHe4n5xx6SDbWuyV55IVwsi6/qcKHc7mmt44nMbB9deX03Q464wdZ8JmESXWsQcGl/6Z51SOAS3NwIk2FZtj8qPqzvL9MeGjBDkonxr5JJnQmUNx3oZfk3Q0/MNHjTcPU71Zk+wrdTyvyvxO+UT4ZX98zHKKmk+XysjXNmoz7uZjFwX15DV23H+zOZ9qPNcJ3jZ4Yo1nuHN3lmbnitnmMDIgDVKfd29IrRlEBu1N4Ix/ciNykdur//9ClJzX7Ixcm2k/O4xRmCRKUP4XsPdSl357aoFXWZV62KGe76ZIasvY3zGai4g1FLUg4tVRtdr6qH0Xb1UKrMH163mCWOCWtV29ZijGX3MMAYAtRQ/qrjQAlIFgAG9AS2NLqPbOQ7vmd741dM1guw6vw/C+xX4VmH8AYADxCvjkqHmqbi0tW6ClISSErADO70t0RVc9dpaanhvCdiuasO6MTRsD+iw7RrbDnJu0wyO/ZFHU86yOfeakXm9to0VBscbFw0uzedT290quJZXruT2AOLYUjufa555lj5utTDCB2zLeqONz5zvnJFrC57MAz5JY2bG0xNXnLjippj5P8GJsEFs8SWG0AeGxaUSr9OJJrXxpPHT6ncUcbnWsEXrhFj7ZYqb/5rGETwlvLcWLM+/ieOXv4GH33wXx5c/IrckzjMeHo6YZzmeyHxA5RdSujAKMXY39/jhH/sa3v/sN/0WVgken7y1kDbYei9GNd4QkcTi8rccyrnxi5WHDw+/jgfqwvsrMmU5zMa60cvITELtcTHz3jJDV950smYdf3mwPqXy+O1yv65rZ+VqFLTLUdQYpAwbJrevjSDjteytOzqqARIWDqSrqMH94P2gPk8boy7ACBjXepzx6vb0QOPpk8ReC/IdtHCbzsYr5fuZxze05ToC367J0NnSY5fNmkS5jVYvyK/MOFpUdzQZiEjkpZ6urgGUupp3q2WpE0AdDPmL6ybnpdLH2Am23q02ijGajVZmyc9G/OcxxioboFxkq/w5/vkY3eja9EYbuhoiShE4u+GByhgdSxMjS0OGKNEqH4GeDML6+NEnmV6lhRGyrBF7/Tt2X1o40gimFy2hGaWVwEaPMRVeTuaeLjSYN2F5vbN1zlpN3lreScmKSm+QGBofsL2gre2abpSy3f4tI9q1aa0zDATkXujHQAXqccPqaamg4wNB1m/liJPnBpiMM7T2uJJxzFeQb3Sc0grWerNRamiAReCYG/M0TdPadXbt9bE2OI0MS2tQW6XosgKZca5tW3bDr3fzze0GNiNRwpQn5a02n9fQxsywE9wNI7tKRIhUqIB2rWdMTla37+jntrIBD6Q3kiJ4QYd0GeddyUh1MxhMBK418hr+GFwqZ0v/AaqULoTQuUPxGHbMLBuUVBvBtaoSMC92mXqMmBzhszlhnE4Hf17KhN00uWGlHCV+zGleNDBwForsCLTx1zD05rHkhCSsQuDt7a3j4S9yxU/OjL85Lfg6qUEtjYct0F5xeUxijuDy1ldRpiaUEsHoKXl92XHE4+GwMlrl3XkA4bnl62wgjyt9kbYLyqSKXJk0kHVxL43T6dQatXQ+srHLBkVnwHnKJ2i7uJiC3Wbp4JOXi65NgZ/52IN8bh2JtPf4Hst6PZ+4ZoNktMlyrv7X34+kLCL1wWUdKM6K57PzIENnI35eRxiS3YBTw/t0miatb6C+nUE9C2Jul1GIsSngIZAb0+xm1Krf7+/usSwVp9MsxxLv7nH/4Yd4+MY33JNrWapfJvIjP/41/MJf+W+AsgOXndLAirff+9iPPwdto4Zgutd1Xk+dQi4xppJuA0Q8q0u04BzKv4ZE3afB3vNbAjDt9tjtdz4WLnvZvCPWAghyOyMsTuLAU9yGq5DTSGmbIEativ1+h0LPND5aVVmScTyeAIjhx/VDThtGaGUQ7yeRegVmnAzeUFmD0RfCRAWy6TM574lYT4zWqCKf044aviD1prY7fA8xtbruATAklMHl9W9rxIwVjQG1yQcdYfL5KZ1ov5VWeoLNcy8bjQFs2u9rGvXH6EXh4OOlFBOatJ/VPw3GnqaGfJPiezoDDLx+SnoKbb7KAIXrl/tVc3fBsPbY9Bhj2qumN9rQZUiclbHudfrGVsAVtF5oBwaLKKj2kMECY0Q9Z3ldwTkQaNZ9iHXV1kfr99hA8pHx6+xSyHBws7hHxCBRYTdUrMY4MbuAYZ38WacQX5N6RkuDNs/VloepX8shbLYjvLXobb+CtqjOAHn7XR5TtrPRdYxSIe1lY+01KSuW5sVouoFNe8rYjAs3ZdIOTWPkCty0ysKrIrkHc1uug9CWcIvjI0Yx+N3jwRCHE3zytR1oN1hkBXQrbzI4taC8fqY2Sps4uUFvroUrj/+6XOBmJ/qFEIm0jkQODaNZU19S8H0IFAE218CWINQ+X3W1X5+XpATDw2ZdrKsMnLenvM7uZDV8j/2PJLCznNrRUoUALiGEsijuhUk8vkjV9CSLsX4vlIzhDp8oItNuAi0aWJ8IcogoC9CcJp9CD+t5nxZi2LyFoe0dAG9Vxg+BcQfCt6litrq9LZbA+snoZcc7qMGh9Xg7hWxoOK3+jCD3RmEzLjVT5t+5HYthOwJJ0SDKZEr2VPwmMSrkx6YYaIxa/r2OaYzN2bVpLSmQI19TsxL5Hp0v7EMnOarliaPlE14MqYGRJLBqclibfvT0JuWlVe7oH0ENwJzkqgaDulIdjjsPW/ej4ZfDMjQo3+a7Rikd7cA/Jq2x3Gtzw1HDgXui1Sn/hOj4drmuXiWi9g+ItZgJp+mTqruCoDROeUdJdMlkGfu0G1FtI7yogdkVrcrgCswaQ2tZzHhVca/GrOPxhNPphLu7ezxMf4LDe7+H3c0Rz5bqBhEw8O5nvoF3P/MvQNMONO1l88dooQKf5cER/mQO6zidxiKzkqzMkwzGurqNse9x9Bopg1pmLHWw4eMID0O2sFAPBIB0Ttpc6HA68UVKhpVGCIx3BodraokeC8kXujtRbBIzgGlnBg/F+wrpI2VDV0sZ2i72CN29ouhD8eOylne8/qxwyAN+yNFxKdNR9jloY98mDHIcauURexJlxGNO1x0TuLOgGssnHw1bkWthKOC3xnqOom+dsa6qaMYiE5MtOW8T9/NYFB0zVg8vDs9469JAqonPvIgRIxDt9GMWjjVDfSDR/J5nr0bskj6Q5OettW7ZmDO8LdyXmnE736PSmpdGfTz8/jrSG23oWhm5GuGTBsgK2O5SCPqlWzBjwkNdXVs7cFseFU1tZxTL/MzceU0ANgW7L8Yd8cho2+Qb9CwzIiealWMdO0xBoMfMGWi3lNo+jnYg2pzbYlfz/Mxi8F30fnztMzPRBHsoNhvCNKjBEeY4yjMc49UitfGLuhocSELXaIjMQ2GTWjWQ5haF1LUEeFRF7EoZPMwsMZZsCDf6aw8zZFyXpu42T6uY9IauUriZr7XaEeMW6yvGIq+fnnC6cBAPVeAqvrbOiB2i/Ke1vSzLCv6mzwmGkWdXs7a7NCrX17/VTs53zpOrXZudwbFZrEl5SUIbuvGM+ajNOhjROccBFS4Kx612tvOelZ9u4sbfe3K0yYR5RW3qYG1lxatPznk0GKoIa0A+jCJ2IdMEkmDR0FX40USQeqWRGpuYceQTqKqYS8BU5HjkpHUxMyaN3VXA4ALUIktX/izGjcRyof3kxhWDcSqEqUzY7yaI14AEqj8eT1hqlYDKSxz5AMkOrseyIqOHRslbDyg+2W2OhEJ7TDvCvwHgDoy/flPxTTDm5aRrYcGyCLyTGoechJSEmxuTS0rx5AZKo7kSptlI2lLl5i3z4qocfDorBz1HGMpeymxLIRnHaYdSCvY7+SyTKHNVx6PaeCZj1uF47LxzuyZWTMaE7VCE1pxzzREa7pyEYavTYtENq+uqJYUral1vq2QhnXKO1Vq+JC2PgNkqx8OvPVxAGtdG/pPP02JY3I7TliJvyY5eNR56HW1uDVmG0/K951mP3SQdvc80ta03qaDOc6OvTpQGYp7zC1n+2E07TEW8T6ciXixiiKrJcyoZswBdpwwwo/LidErySmwdKnKkm1liExlW7YjwHgS/KlcU9Vqd1GvKj8ARqcy/c6TNCqXRudO84HA84OFwxOF4xPF4wjzP+PjFC5zmEx4ejvp5wPLlv4X6hb+Dv3Qk/OhCHjCdAVBZcJwmFAIKlhDEfHiVF4BiNyJmHKvBtjHX/2nwdNsCc3llecuZzZ4rRGawkkziOWt8zbyyCIXgNJ8ht1Vmr1ZpM+F66qNTNDZZXuh37HwU/Vka3DZDek9mrN7KFQtXlGkvI6nw3uyfwYyts3ru0Y6AHWMhlo2YtMNSGZgr4wbieV10TBgFhILdtHO+bwYOKuw8oqi8LfyAQ6/r1Ke6ZH1F+Vnmgekz05YmxmqeYwDceQlnmZRIYqSFoGcls6eh4Ury9uKMen2bLS/1P8dZBvHSlA0j3rXY2/dysMWfuqP7gZ6r2A05xoKTXsEKW3NgpGurpOfGkXteR7AQFK4FJZATgaBwqOmjDq/4fK/f9r2+wlhkMqmvHeVBy7JIb5LeHsHfL9cbYLX803AHSQ+M/MH/4jTBWq4J/fk6OIA33NDVCjUMUdDlZ5o3TRkJNhDjTDvM7bCGYPz4AKGjcmNlcHtX9zHpWmHJLMvcP2s+gVY4szb6OkdwbNGubglvwTtqJE/4QFFvxpU6YR/dXHTKgANFLeyNUSop+5w72RjVsOq4t9vDkUeCI+/FMdnAH99pswo3mIiDDWhg7DVBpcHvUHOiItt3ysaQ6GcaRyCU1q6NJIKvjDcjEudwG3zaB07l+vwZBh7M26hc4EorJPTp3Jrr6cU1ysrIaJfLjj0/1vWO+tPDdI4mNc+2F/TVgsqIdo4Uw2g7ng09GpqP6+j7NfS1bytvOLiS2kp8jRDRChRRp9GMXnjKbdk15aGo9XHYquI+R7wuX0EFRBW1ishtNtWI27Vub5rkc7dj0CKC3kIVtNRu3YmSCc7HIwd01+lY/NhBbkdzkU7zy9EOjjWG9F8lIHnggGLs06ijFXSd8jX0gH28BkdDKL6vMIPSJRkl2iqlYKdeCmSeW2mOFg2qbbddVuah19YWKo4xOc/dmL5ph2A3GXJfbKPR7jb4RgHONHqgUjSZyL2k1jLDq6e+I5fTCl0G5a/xqBrDsl7jTUsDGbFv6zHtXkPfr08b8s8wJ2JNI6NPlrUi34rfJWXdjzxVwdG4IVUPYSeDXK2MQhL7aw9bhwS5LLFoUHMxdO2EiCnJnECYXNGc5xmVGaeTBpM/HHA6nfBwEEPX8XQSI/8y4/7+HvO84HA6YV4kuPx7WPDujvEeCDdMbnCRsWAwFyNDMRz9vDS8o324xbt6muYTMJJbVqXbFNlHgvsIr/ryWYJSudL+YHwrb6D1Y9AquomzN20myuEPra4yMnSZJ5L+36x3JrAcgHTckBbjCD1Pshkx7Sbsdjvs9zMYi510c5iZWxmESFszI6AiP6mFxTbGOukLtOr1cPi1jVZ2OCc3DenAQK5q6ZFdqNLqCMZjDVr5Hcwx15CGetR0+2NAbNZ62zYmZ3miQ61Bse16tuVdqYhVgYoLmwMjvYTZH4yOJvmw4X2uCAXGS3GzMdSolSJeXTPGlEqmcepF83NJSIbBldfyFv48hi8ZDOS4cj5UwBrmAUkbtXQ1TG+0ocuIDWDIOhKkNkREz+uYl4hYS2ytwDKo7ZKCeE4R3SqfUw5+O6rjWgV3K8+aARujAmKBroXUx8pTtvBHNpuGt16hdHo5bPT1GuBS/1tj12BMM4NIRC4zy6h222ji1Wn5Rpkbgdi1fy71zMbasIDTrLD1Qdhzqo1yed08jODP3h3NeKEV9ntWZkYvM+w5znMIUuuOa94qSrh5Z8mrxEgQ89fKlgnHjVklmrKFYzJGXYy0bq33eESpD1t5+vRYQ/oo37UKkeNKR8PO3dg4YorXKlsjIS3DMcpjz7MX3NOVu/Npa8x7mt3T+y2Bs/eum+cZ3HnzmeHK0jSJl9U0TciCiMWgkph2etyuEkplVCqoGseLiwZz1rx1rh4Hj9m8Cdvx200TaikgkoD1O/VCWuZFg0Mzlrl2noiyq21eyESx+6yBw2CKK6uMvECuUK/UjqN9zrPedOhjU+UmJDd2DbxjtTdhyPPCQQPSOLf1jz9l8oRUlGIeK0WOeqqiNZUJk1wzB2b4UcT5dJK4Z8uMZdFbLnuU6vjqI1jglXua691Tli3trpJkcL1qSZGK5eQMZ1yMHi8wfF8T5csCH5ViTW3LZiNjV277Bz/FOhZ2224E972OjToGSsQpknfyvhQzcumaTEeIbXe/1hk7Iry932Mi9SwqBKKdx73b6ad5UgIAoYAw4TSfsMwL7h/EsPXixQscTye8fHmnhq4HHI4nnGbx6qm1Yl6q0zwziv/4DPzsidz7tpcJ04d+v4Y/vuK8k5knetzyb1dX1chvUZPWt9ZDxKNNPQcpjFvCBxD8wIwlvPZgB86TCEr1l8m+J0NXOhJoPjHt5hcHDKkh6c/S9IuZcXt7C0B40DQxlmPFol7SUHQ2b2lpwjyW27phJwa0bRvWlaHCjTNuTYGRoC1ZcUse7Dcvt8r2shVXdi8yN1CW7MGX6XhrWBF9Jn6sWIv96Jkt2vYy/JfWRCsDRv4sHyToPM+5cet1hEZf2VhCjT5H2diVbQy5PtN5gwZCZbrw7CaUaecnTpr6Df7HMeur0zl5eq1brMtsyy/ntF2TfWyuQovlWBKprcf1+Y02dBnzjMGRxyvBd6joAbZY4/0ZZkAE1NjRHiq/HSI+RuE7V86IUmuAi76Nnlu5/nvssGyMTTKEbL9aC87rPhk8TsEfl4y452cDgBolM/09RrD2JZWMHec62Fj0jVhZPXkuO9hGyYxK50kAEkMc5MqC1qiNPE4XxmUonPeUpn+fy2eG08FmfT0HQx6HjPc+RxvlGzzW+eufmeEKRBpsfL1WQihHM4crYTX1bVRHvyYfY3zu67zGyPUq9Y/e9fTiXPvnBIdz9OhcmyPhzp7nd9lN/9w4X2NY3IJn6/dj2+j7bEJ6UxbtMcoQ4FpcnojEIGjKIDMmiNFI7mAXJaMyS5wNZhRmzFXWELPsHYpBKMMIV5qmojBqnKmpTBK7hivA4hUhtxIa5HYcUGAOp34xqmSdiwHswPj5GfgmAb+xA5Y0h7KEpyTMJk3anzB8ZzSt+UaJMBrSdFDLdhXG1JCPeyvwSx5KihtA4MqY64KF4xiPGReXZdH3obgXF3IpwWLgrUMTfCLJ5wzNMPiNeAOlZUAB2yoHrL6lwXBT2veii09Oiv9bSmJOW4bws9Vv0lN65bm/ZpPj9aaQf5DWWYNejYAAN66bmGXrpNbqBnxOBgRTO/f7PfbThNv9DhMVDzKfFVpmSPD4WTcCqnnrkMfZevHyJY7HoxxLPJ1wf/+AeZlxPJ0wz4tc6lHNwAU8r8CXZ6jhoeCHWWgjKGAzWcLEXaI1jve0v33XjtEVQ77x8wpd5kLFIxoUvC3lprjow48RuvEp0/K+c53Oov+FmEnrPzQkswWZQhYnX7vtGgaJB2AxIp7GiGt4Y9tlIUSEm5s9pqngeJqxezhiWSrmWS4uATNubwpu9hP2NxJYPx8PjjFKY2D4Dm4iHpgBtdGr5HzwVbOYdbktHDuHe5ZcPu8fUtb3Mq9qgIBPDrNPqkUWJqC7LNMEAjOk2fcexgx3AqsHUwdTaMq5NcBnxzREgAwpNS+99sfQ/k49yQ8qVyx18RuXJQ+Bugj/ZNCvps/WlH0/q75eTCHzS335c92/zLN63DdYQqsLNXY8R3n+xiprvHsMa3uzDV0wvXktYfULxojgaOFcIwy0BJ6azzbf02632Sp3SWgawdMLaFs7i8O88mNIMEwwaeGDv9Nv+nsg9aLN24xp09K6ga1RWBm6rF/nGhsARJYnr66smA/a7dvuPT2GTW3UJ/ykU6xTX2gDrlUfrknnOMZwcpIwm+Ec9HHIFFwI5Ab+puU8Zqot9gbetWqaYLI2kuFjZWxK+TiNV2/k6g0yjSdOxq9uzK9Zb+cUkZGhpcenx+zi9ekcXFtpZKy6hp6MyvZwjMZitNOY322Vu9TWuefnxna0yXAu7+iz35QYCaZmjOFaGyQngh+R82UHwfOliLGLwaAqkjNZjBtmcCFQNa9INYbNDCnBACo8JK8K3pTX7STHPFhhraWilOpKIJYFKRwf1sJQ8hBKwNvbHYBfmIE/LoTf3uuaTArSNIXCNZqHoArU0m4buKx4W7kEm8FzTjnJ1957vVlYNkWlLljmtaFLjieGjx6RCbEi4APAkoxgW2mlU/jDS/IBbee5Qhh2dcOUSEIYw5KR4yLvoTbfVWXaXl8G9jUmMmvFID3W8PXJG5u+D8l4H+mfmY51/XO10AVItEVoGC81ZApd0xb83W9LZancL3Ugws3NLW6mCbc3e0zpeLDVY+UrM07HI5Za1TNL4h0d9IjiRx9/jMPxiI8/foF5PuFwOEgswqXKjafWD+3aLRN+9liwpwIqk4BeWpkoCSJpzWwN3bb+gGxZXr8580Lo3aYcfbHGVkFe4zHHRzJCkN4qGMcIJ/8NpD4OeLptYAb57ulwS3e2N7LYx51gxiyT+ULvM48rKmZYUX6S5DuDbbfbYZ5vcXNzg9M8Y7q7x7wsOJ2O4m1YF+x3O+ymCTf7G+x2ezXytXGMCGoMVNjaUxMSK2ok6wKQgJw+3Ou5Cl0re9DRRW/3bXqU+FqjIiQ+XOOZSREEcrnby7JD5wYaAtTYldsnW0qpPz2c7fN2DHK/ut50i5PzsG3JfL3O1TAqbj68fJIzhsnkWv3eziQH7arhJU9EKOAmjIzLiG2v0PL4rq+vkHpj10gONjvBJRa3VltbOPP73pbQ1ZTgub4vb7yhywjg5Tz9s/XisYlt81o+BlAwYlIj5Wyk1FzyJsiEvK+/hbntTN9O/67P049Bm2xXnpDP7q4RtRWgg1HJwpPfQSXWxCt/56YupKf5sycoToy0gVgfVwiWA0NOMMt1PT10vUEtBLm1Bw51ZexZY1w8l3oGv9G/LbJgbT9V4L5OKTlXQSyqc3N67piuEfl8rM2TzVta6KTP/fuZtGYTLQO0NkkXgTH13k19tNavMVS3XWnXx2PrGdGZxypf32/FbCs4/8iAf2nTYfQ5en+O7p5LjSF2IMzn+ke0wds03CLbA7V3paVDDV2RHXQmlqOKhVAqganAxFAqQstNedztJ4k3UuVIY63m9VBD6O76SNDjemQ7fYL/daqYi3p2ebypUDqBxRWPEW+zXn3AwP/iyPj9wvgH+/C0FGPX5H2244Ax5u1xRGicMA++b9oE0mcSokyBcIUc6ZhNpzwYb2OWo1SVq3qzcRNvK2ThzF8yHQ5w/Drzyn2JK5LCvyFk96vhMXVnWJNO4PXkEXUa2PCnQaXc5flBTyu5kIe/L8l1P2jp6bAmKYDIwoP7K1vz1Qz15vFEBJg3pGYX8q44z7FuxIt0p+tFgpdPajghKph2O3Ap+JgJewLeBuSWWTCWeca8VHz74QEP84wHja11PB5wPM64fzjidJIA8/cP95jnGYfDMW45lY6Bih4/BnAL4JdPhE8x4WbK3kCiAJv01lJkoyvfY5zoDfgOUZc6RdtKcPznRr7ekC50sLi3lhiN1Nt36uNl2RZJtOu4Z3RFf5gO50YtZC9aO5rYBZxnRsTjovCk6/s9IE9SNtrJeayN3U68iW9vb1Brxc3bbwlfWRbhLbVCURt7vYBELk+xtUEwfTHGMxmgGigNr5S6MiT4PYfDwZh02pps9axWV2t1tKBb8SzPrx0rJq+v14FyiB/5LV7jEZMXqgsKyW+1h4YPEtDHqnpMmqbSwZ9lupxzJNFcmRrw1rCuN9AiK8FiMHdl9H8z8C91UU8uXsscpJtmqQkOsyGoO2PfyjyP7OvVyeoPQ1itNtejy6+4gWs0ZGu7y6W2H5febEPXSnhuzBSvUjGMeDRCebdLkZWXemZX9hrFccvItVW2V/pyOqfQnavTBI5MLNaE08qP210buwKBtyz0ST9Y1xmVr/L4cusNHLnyLp2bCcKZ8e7hsWep3ZGBs8/r9bhSq+8Ghrc8Wrmtc2mUYyXYnDO4brxr2VU8G+d0GSSOB2bFP8PQPbdnm3h9bo0Nxm2FF305yzOCI7eb29GC59bRFh6cS/3678tfUlJGbZ7zaLoGtmsVo0vG+GvTJW+oHqZL/T1n7BoZnJ6qCD52nHKbQEsfMjoaX8hCZkJBX5emJKBogGfYnxi9KkQEKXozWiUGVQKhgqA7y7WCkceg3TwgFWIrsyoCavBSgY3tuI8aKmuVuqm5Rp4AaufsloGvLALvbzBjZrnpyo6Q2ID4ushjyZ2qyaNjFtyNaR77ECh7IbPfHFA90G9M9DhptT3KT/kLjWlPgwcbxqqVeN5UbN8EC0blG35r+D/I15RRhOpYdQBEonhZHrZ2+vWuckDSbVeVBZb16Wlr8HWmbA6QPsYP7zPGdHRFCwa0oa+vaex1pmbIOxq4PQFdGnH/9pF5eFSuouAxoYKT2mNyAFTfV1O8rVeWMW89gyYJLm+GkyIXajywKFa3avCoteI0z5jnBR89PODudMLdyzsxZh0PeHg44uXdg8QZXBa55XRZMM+Lg5bXvt3utwfhCwx8wBT0T4ku9/1C5lVFO9nR+n4MuRtXsrEe5G2a2pJpBlANaMao2kubQkDwGNu46A1Q7V/QJuuq6wb2kXh7X9aMikN63BKVMMoM+kX6pV2ja3z2dlOAe2b2jRaq+5A/ncdJ6ABrx6JoFu076XwKfod+KMcW1ZEg3SocBqLgW8zhcJY3W3JfVoYwNrrUkp6RiNLLGnKBqPG92AyyjaVcF3mdLc81417fPghrvCb/r3+Y4DIcyv0MXPFOd+lJslwvJKySHXNNOsqGvpKNXSOdQgxdixvbA8dTTDSQh7LIhi6D0eYZbnTa7NiZd2doQzeHqzltcIIw6GnzuTZEBhMKnDW6YG3SoOxoVLfTG23o6gVRSy2uClGLhVcT0c2fFxvDNLi2tVecRkrxSIF93WmkXI88Y7bKtH/AWjm4KA29Euw5QGWsgV5QaJPs+qxEqatS0MvEbLtnW+WYedhWHv9RHh/DLs8nKdY389YLM5bHPkvZEmkfnRom0L5o2u6ZhY1f/qt68xsDoozbu1xtV3djQDiXjIZowEfUumJcVpe549t14iOD9Nb6u8ZIlT/te66vlNJ4tPWCYl++h+Up6RINOVfuqYYj2zRYrScaG7sAueb8ksI56su5zYnHwH7JwJfpa35mQnWuh0pxBbG4sUc8iSzwfJb1qRRMRktY4nRZW/loI4NxUyYwEDFolvDqWqoaqzQv1ziOZHSqKGxFvcbE4CXGnqUuqMuC0zxLUFuPUzU7joYymYRoGQ18cQH+wwfGr+2Af7iD8gQJeA42H7Vu/vR3rSb4BAXLQnE7R/E8qITRZh1DFs+UqgK+6De1U3K1DjLvZ1ZDHvwTBhUHrplh7LErw2SYPmVjl6onQRMUDOtH1Yavkol10m1+iIBas3cOQYwC1PS3BS7a++QkiE8gcR0PNtp+9FkYSJcNXKFcUOyBfwJiYSCNfrpO3Smuj6x0LTsYT16tb3bFJR8JlL6GMl38Ygd5lgN46wpEPS1Os14y45unGfMyYz7NOJzEY+vF/T2Opxn3d3dYlkW9uBYcT7MaqCsWo8NF4BSjSlGLgvJLyDxy+s3M6Z6QoCWNgcuV+dYztxu+8WLoB/UTTNds/FjKxp9pihhWOQi9yWOJkjYp0wyRtyJwu/ykti6tb2XoAgA9PkrqZbw2hgl/MtitjQaYdjRgmyaL8tFeDnu23+sPKPKKsYNMd2Eko1cc9auL8MSQdxsO5WvF1oERSwIDHHzT1q5NkfF10SEqauNx/cR1vSqWeWnQeIZcHiE8DUnOSJ1Elj+NBll1r47g1NSTdfxs/DGc3taytt447MMxGciVONerjEsarmARo/vxdHJ5br/fY9rtMKlXXTXem3SohqZ0jX5SumQpsnER8kuKm2rf0pjHMzT5to1c9n10om6rzsfxyzfe0BUEwlKL2PkKTVuYJrhGPetBWyssY0UmE5aRkrNljGsg7gjDufpGCuRTlMreyOVwXKmQr5WJJlfzroVP5iaP+UoBHDecau6eZaa0DfgYyjN1XDuavZEjGxiGWNQr8EATGH3NhvWZa7dX9LdvE0E0DVZ/5g1xMyZnKU6Gp68H3Lzv28jPsqHLDBwh5BoY5LjJijgGJ+V6+7XZfY7erZ4TrZmWtWPCnCmQA8PKpTU7WqdbBvFRvZfybuHiVpuj1Pejp0fXGs9GxsJrYdhKo76cMya+rk2FrTHs+3jNGJ0zrgGtspCHKJSFppDHvitEYgSuFZWyUbACRXghF935KxBNrgBwfy9G1U8xmLWbD7ltv9y0FBAxiht6GLUWECqYZVe8LhVmLYu+d3wawA2AzzLwVuILADb4gSmUIWS1PH171TevcqRsbnFJDF75eFUrNMR8KRyioazHy8g2rsNHG5Xzguval6vBGTJ8lGd2wKEwX3dahJuPGF/VtgT3E4/39nvuudXYJyWWv/5Emz/WD1qBf1smG0kjhkWPTbnEUMq5pD1slBy/WgnKvhYoxc0SpVsMv6HMsxsrSA1B1uv2plZyfKssBnk5nrio99aCpS44Ho6YZwkifzgecJpnPNw/+GetC+aTHK2eK/tNjswt7LLJ1Y7+uxV4l23dJCQfjEsrO14pm53TjDfeUZPhfAshe/dV84rOjRoyQ5F9JyK92VLmyJ7FfHW0lbkFL9Fr3/RwOSraMFwpWlk2gLlhrEQd67+RjJRGK323380QOJ/KY0lJBkyUzpDULkNT3TKfiiCqMOMGN0YSWxMd/fB1kQdzY6a1OtY2GVfyly05OTGeVn4cQWDrWb77WGwmM2RwtEn2PGXJXxyXbNIYDb/uQOr55koG4PXKCZa2LaedW8dm5Mp19fqTczqTCYHGSJjpUTYgi6XrnASQvxOYbLOz6/RW+Q0a0b5fG5+2N3PX7a2NXZfhirzGB3jw7kzxQXqjDV3byXaRYjRksvKzvPB6Y1mbnE+fSavrzLEmuCsoB7PVBxK0enuDVK9I9e9yMMgtw9m53ZxYq2vlrTd2jdKKxiQFZ438mQH09Wy0fWFsL6UmwPggba2jrHxttUz9+0vIdWnVmoHH6rxKcN2oBwijUe4LEfSg9ZPH1NoAWlxlf66po7D2RmLdqAsvRywsZINC13dfBwkExxX10rJ6zKiY8+SjVs27QRvNzuGq1YEAQeQeWPa5Zcy+ZLgavTuX+rZ6fN8SiJ5iNH9KOtdGT0uzIGsw2ufopqPHwrH1rB/DS3kN9vx7vQsWqY3/FPWtjg+zbdIkwccEeuaIVWFtqmemeSYF/wAOdkviAlCR9VCIwIWxVOnnspgnViibsKZt6SIUEmYGF0YphFplZ5mZsexEMT08HKwj0jDLbmUmoJQUHQlmnNcmNdK46EfkfQreaJ8E5ks40dIeDRzktx45t2Lul3mikdQauWCeZdv8FG231yprVsoGTV9KpkAUspvPjMXoeKng2B+3HLaT3xv51WOn7vBUGSDGVAoYEVi4FfEJZ0SFP1Wp3yB4FC1tRdZHpIb7Dd71KmAvb51V5cQctZGFSkGZJuz2e9zc7HF7c4tChKmYL1aCr0pMGSqTr1cxIKRA2rrm53nGaZ5xOh4xL4sHll+WBQ8HMWrd3z/gdDrheDzidDrKzYnHk96ON8MMOlQmlN0EqMeV99jQMhkcWA0Wf/lI+PGFcNt0PNF6Mrmi9ZJj9WzJXj3f39TSI/dQNTql74seDRX6GwHlxcAURq2eFwcd3E5mgMqxGrMnVjammTEre2L5eOs7P1mTLirIm0RRbozjtpWZdZw8RjFuqVfqQVX1xkUwq8GPsCsShL6Q7P7UujgulLLTTSGN51iNl1aHxGLWNUf+CdiXFoR+TEffcxrRnfPyJjucRiqoXzDsObWNqLevK/63L0kHTD9tftcdQPt89XubWGZZ3h0saNWN7XQteWzaABJSNZ92WsbksqVWlc3g8sRUJvHm0hMjvLQx3RRr44mtC+e2sXmw6U36hFTs4g23qZg+FTGVLZ0zsj1Fpcjq3quoJH8KDF39mWVgzdhN2IN/P1fHSMFhMzZ0hqVVywOic62g03s25Wf53ZbBaqQkj7xBLsHXMoC0sAZpm5lngc+/nX22rntMlLMhIgSV8+lqmYM5keNxeccJe27jb++J1qPWrdZcvqHf5wwQBlNWhh8jTeVF0D/v26LzwgsMlkzkBjAbYW8WXzdeDsagDq/XyiUGMhJwhG+osGTvN8ZIFDY5ztDUGxka2KxPBJtjgfic59LISLJlNOnr6Ne1GXaupT1bBppL7Y/eb9GcUd+34B/BNdoc6NsfCdeX+tDXt9WPUR+fajgblT8H6+pmKqyVY1OcOB0nFKWj+HqQj5aaCI4CUK8qMIsDV1Uxs5QQtn15Gm6RvhODCFjaMt20X/EEoEKVlGIB5EVYr5Ww7KbIz6Zmd8f3En34dGV8dSH8ERgfpwtR/H9K3iAmkDPkCW8YcAYCGKu07fkzTjtdSUJ4M4edcpTIjBuFtlhbljVStWRSOElhJoAqhjRx1aUMmcnARHY6S8YbEpFNmmk9uxzmM/V6u2lQBYPiNjE1S/qYNeO3gj5T7aYH+v/rFNc/mXRO3nsMnUpa3+OBuKiUtbJwm3ofpHMjvn5H/a9Eq3veLLH5CqZpN5B1hQ4ti9yceDgccTwdcTgccdLYWg+HA5ZlxsPhKJ8PB8zzgtMsBrClLnp7Y1q/SpPYAaHcZLStn59h4FMV+BQKnlEnAzdyseF2t+jPjI4/vWqK1/W1Il83V9RmivWsNDcRpdYLVNanxNsSo1aZit82K4av4vnI5J7RWGz0tTgtknhUo7he2RMQMOVajVHerlSY+abo+jEPDRQMoXPcPvfeb/J79jqtTTuCnUc9x1k3+CyshtMA7RdXAliNEAxUppgXauUpZUs+d/Z89NnqRIBvALkxqcOj1Ccff+81+7nr7G0Z1QST6A1dNl9baUvfc49PAENq3yhHl5PPl7c7kH/7drj73K4ZhhtWx4i29/RPGbBsMtV24zE8WWX9mWyTPdcaXXMFT5c6vLlm7PoutChDTT4TjdgJ6sjp5nKbj5nUVzFwWXqjDV2CLCPmbMJ6OiNsRBPApUF2C7BOosRGgQtzkUdr21AKR8rguTxbxGyrjnNpS+naqm9dfyZcTxC+sM3Qe6IXjHtdeL1Ts8HUXgUoG+81gJudcNzKxpe+Ka8ijfuZ92ztbcDjxO5Mm5dSbmu4E5HafUwLPPgmP1mEqyRoNQxgAz7JOl43Jhhlt/ZcphGeOhj7/rLdFGVlNuCyvESq1JG57ffdXdMFg6dXgB6bTMAb0YqRceVV2sp1nTNybRmzRjDl8ufgGnlb9sJD3/Y5hfISbNc8O0ebL6Ut/jBNk9c1qk+8qhb3dLRUyhR4yunYntJRlatACI8rQIPGq2dPpSoOnKn9qcj3iWVXuZB4IpqHlwln4RkEPzJRCOCJQFw0poMGqq9V3jH7zYQWfNVva5TeqkEO+OoJ+OpM+C9vGB9HHPuGJbniBRE9szIn45YtRJmPts9CYOvoA0w564zlHOPlt0BCvNnKpEc1O2+p3G7GBPs+6UkF0nhXLKOhsDDYurJCz1BKciLAFcyAX3brC4uiVSg8xQ0+/0sjtsJKxbNQyGwthzcewW5kW/f1X4bU099RehWa/AOVDGmQcEWsGX7ErCRleioTdrsbX6O2jiwo8/FwxPF4wscvX2gg+Qccjyec5gUvXr7A6XRyz655nhtczXJFKTtvu7LEXgLWvMyTWlR+din4pVk9jJz29CrmWn7h/BzfC2+u8/jjxg6Xu7oMFPCWUiTofxGvpGmaWmNXb6zmVVXDJDQtjFhTNpxRtE2AtJd5PHXyk312cl0rW28YSuwdQTeIg6dn/SLqWhtrgSUZoEIW7/vu/MjGVmOaobY8w3lgignL0BBwqrOaZxdiia3G13Ga2rHA9rS3MnRJfWRGNdreyzkuvo/ln4ZFKrNiNm62AqsF6BNMV8u/Z7N0XNuWA5F7guf28qelCrlAwy/t0XLTbu/rzOV7xRUzcBkE7Mx3ABZs47DbeH+FAc5GrTU9Gw/YDypb+1Ng6Mqsrk1ZAWqNRvaem99dadiOgX2fqBWG+7q3lKL+2MpIaduC/9z7nKeve+udpU2Fzfo7aCsQ38h8O37Zqp+bDgJo72KlSp3brvG5Es9isNP2Ml49TwxNqgjDy1qYD2NIw8zIPAaSYDdQ5rfabow8/TvAvbS2bipctZMEu63UGBu65yvPmfTphDyX6WHJY9coiK2i1AijOVPfbt+vgTEnM2pTQEeGpH5ETLhw+HtGkupu+t0L8Q3Q6/UU3RsbX4jiGOOoXJ/33LOt+nP7uc1LbYy+m0Bk7fVGrkwD+/kb7TqeM3L1RoZrxrQ3ePWB3c/195o8/WbDtUa1UTu9QSvzh1Hf+z+vN4iYrkE2pLYKjArbT/1F2KkxZiExhNg1D0EOJS5V1Trkk1woZ4hnswnhDV1igCmteQamQig3+2Qc0qNJywKuFbMFw+c4tmHpz5wIn66yRu8K4zd3wJz642J0R8Mzj/Zx7oaoTaEE2xEDGz2vyyxAXjfnEQazBZmPsYxxh56aSnFpGhVAFWMKbuOBaEluyFwrLLLzO1LuCDIXVqUpSya1yrwJHG6nIPaQIF13m1GST+4foBa4EikXFagUsaLFXdmz6RPWgl5D6mnU1sbDufzx7Ao56JNKKtKFVHc+s63vRenCPC/6N4OnSZV3NXxOanQCgUGYZ/G8Wqrkr0vF8XTEPC+4u7vD8XjERx9/jMPxgPsHuS1xXipOpyMWbYs1dlfwfz3uY31R+ORuPE1ZXsi94fYHcelQr5VeGuW/EapMjnDKcXYUx3N9zeh39TQPY8OgP1rk3ltJZiLIht1+t/NnRY/kmYGy7SKhedgAY4TP+qf1p/bkSGReGyH/EyHoIwXt6GUzMZQF7fV+K0FrPFo6+HVAunHJukTWaRgUV0WIQc4AddzTt1WMRJZKKVKnn+U2ul88piaV4vpEYXavbZs7Pt07P1nLATobeS4HMulQrgCnXISgO+RB5kMmaGWD/JkTJd7lvJEaVSq/alpv67g+XROOYySrOT+PJ8P6Y4x7SNPSL7SmA3l0TRauwl/NoC9wFex2uzBy2Rx74bxRr40YHwcS9zecCeM28+XwPNuJk66vTzr6EnLOVYx8QOtGc31dXVbfY9DljTZ0Qc+4OlFqhAujRVm58oLy/2pcG7HdibARFCPQWRjfUnrOKSqjv54g5XoupV6o6g1pj6tvbCSQemzMCBHcP4SA1TW3Vl+i9fZM6lXmVhJDYF+6ze9hMoZxoUdbyedxk3APfuexvlA/pfz5O0bPmYcGLk9GALs53TR22eBmOFMZx9tL45t/9q9TnlYU1Da2+tLDk8qcNQKbsGRCWOPC3hm7sJ4fX4sbcLgg3L0bGSeQcL83AF0yNPdGqGtTHpcGljP5r8nXw5bb6tscpS0D0JbhbEs5PPesN6r1dHXUl1G/zuU5178M+9b8jcawbzPDuywSy+OioauL20gAkGJvZRj1h+Qrtr4UD4iw07yFCAtUyG+KmqGL3dBViDDPImg5zSeb9xC4erlHZHvCdCM3VnGtmNVDjEiONbIaeXjOAr2U/0kUUCUAjD8pwNcmMXRxom3N2uzma3N80pg0QqkC7TK5ChcN3XD60pZjAMuyxkU7OjhNemtZF5eNWb3P2kEDqodMlL8G/gs0Q2Vio4FZyQihXdUdx0kCVUZNc1m77ihYK0bAYPBinoUETABRgZy9zPC2wnHsd21oQZdSr8BcU+RRDaw6emWFOp4DOuA0YMSHhlVdme9Muo7H9LJAz9G7N5q3ssSbmdXD6nSaRWGfCna7CUDBVCDrqhRwZRxPsxu55FbEGfcPEm/r448/xuFwwEcffYSHgxi6zKu1THpjWUJMkQPsZtpYU2E00Lwp2H3caeuaALIxnAH3VB2mrEcojq/k+VrBvLRjeGYazm+6b0DC7VuyCozu9fxR6XF/U2EpBTu9STE/G/H+EJV0rDudyfNQGKfMa6g5ntiKXKlt+Fx63tQekXmGrUYw0Wgk4nJm2JPs2h6TtmN7BEZ1EkaAxwVLlTjjM74U/RZXXdtUAABSb4kJyj97/qQftc44nh6c92RPsJiLtZ7Xy8Jj2QqrOuQ7QLSLviS4VpsbOiac+m71Unrez9OaFgUinJNTR7LUFl0byVL6IvVBufZGm46HCcZxexQCQP+8gQm+IWDwlAl6wYN4U9ZlQa0L7P7KKenEvYzW1B1UTA1qY5kn+pZ1CIyAT+/q4NklQ9eAZyTcyJ+Wl7s+aqmzsD+Gm7/Rhi45j5+Iq6axoedKZh/icgj1EAaxcEaQdjGNvp+D55JS1BvGNiG+SojZTn35fEVtEMpMxAwxM6zA9UJqHqurANwoDWeG/fOQQ5JyokxIdYCrlP8VDPrZWMo35pFyuR72UceDO6wS9/D21KKvLxP2V8CPs2OU4DUBw/JPU+tVk41qJsSY+3keN794ITXT7D52fyZUZDzgUd85LmhgrC982Oqzw9owBoNvveatrHlsubCTxuGcgeuc8cbKPMZ4lcv1uzvn6MZWQPWR0T5/9m30nmtZ6DgHf+PGzXJ8D4AEGEZLT8/1a6uP1xq5+v6O5uecce/SHEldehHCSiCUz2mysTDlGcgKxdaYmjhOqtwQRRwaZsYC9ehaYpdX5D4CsRw3JBAqyV/BTm5AsyOHi7RXmR0e0RXtOKIa6Bioy+xQFQJoKiiYUFkMP5UZ825CXarG45FA+BVVAlgXwjsM/M8PBX84Af/gJhRUH8vu18iLOsbGxn/ENdq5bMeUs3SAPhHFn9EtMXARdhpkdrIjOummN9nlZcyq0Ncqd2+RK+CcbhyLiwZ6EHy+jS4q3yatw1FH58k4la/jiTBBA1azXfoUx0uZN2R6H09ps+rxDG5i8SD6kEZ8k7trQzQY61Cyf/BSjE8oUWwGvxBMPC8R0kUz6Xa2fnovKYHUjmuu//9P3r8F3bZkZ2HgN3LO9e99ThUSUlGqEqgodxcgXGrJgPClHN2EaQJoIBR0B/1EBOgJCAVP8EIQAYSNA0PwBE/CD35wBPBitx3uph3m4gZ1dAOGboNFgwODAIOjJWhuVdI5tfe/1szRD+OaY+aca/37HF2OnOf8e601Z87MkSNHjvGNMfNi6Nd4Sbk8ynv8lbpI8tu8gsE58fYwti7LCrfthtZk2d/SGp4uFyxLw7pctc8Yt+uGD7/+VvbU2jbZbP52xYdf/zqutxs+/PBDXK83vH3zFlvfhLa2YIHMgJAGxeg3G82DJJEGJJJPmxrQk+xb+gI3fOcV+CyPsrXXGtb8Iqv6VPjSBzZ8etXulJfmZ8G2XB/HS6CKbSu+yn9D8CnZ/KMg11ky3TL4OPLFg/32B/tU3WOy6c8Rxcb4GeNb/3H3OFbYQ/bf7u+VMVPEAOawgyli8lZPGg8MfWExXAEOO8dtLXwfLyeFbXyPmLkOb6KGV69fw150dd28XJb7dg3kahusaNX1lCckkiIBCn4afZ0BbLZthzxjE5RyW4R35A0KiD3KmUB8xnw7ISnljHHDCM74HuEDDS8JJjpxd2WSJwew5gHm+kzEAgyLjrjTMGHBpIqPbAb7dZMDthpiLEpfyIz2DgYaoRkucRnpQZHpJ8OiSBLgY6KMl577KedJ1mpgwDhpwIJQnIT4OCj1uM7YlcCcxvNxuS9QS54+0YGuI6drHkiyZ/bljMqSykAOdULcpt34SCT6LLA1BAMwOk8zJ7LWd3ZvRs9sGdPgPCo9daZBwkaq1ADhVx+um1AOwGjyOyo/du4PGuE0T0ormPIg2MU85nuwTgCxEfQRPS8ECafJ6H6ArqPnHUg/YBjOTdGYJ6qYKctMIjnvzeASAlRZHnt+y4EoYABmA19TOfnahAAZU9pvvqF7CrztjOhR+aXds0CZ/Vk9NXB8TzZ2s0+SXphdP0pn+mQWxJrdn7XrrLwaHKh6bfY5ozsHuob9LNL9dxlnR+2rba3fZ0GvWRtnunyWR5/U30AdVTJctH2FTTwY/z3o0JphZ4L5zC4mcCMP8PQOYIFueE8xC4Js5hZpwEwWHTUmWfLIjA1d7veRD/IuXN8+G4jTGUu2fxMaxJamsUFE2Ein9XfZQ8wCJ+iMJyJ86SZvwv97AIwFjAVX3JSW7Kjv+yV4MwImcxTtsb2NsplKjAi87BMR4H446ZJNIixr8xkTzQNdujcKZBOgWyNfFkq2rEEpyDNLQh4emOWTnDko7X49+XFkxCfWeZ9wzOoKUF2KrvUaICYNVGp5jQi0tB3/SGUtB2oGj9Ru+liZjNsMTFIRMx6dwvEDPHEKTUrVA39ypp0jG5Tu8YttSBzl3evv3INjeeOsZ5GdwLUm9Gaez19u5Q/ydnHveH77FksjPD8/+Ql6zIx1WbA1cQ63bcPz8xU/9mMf+hIeCXTd8OGbr/vMrm3r2G6b6zmhXfevIwmc8EReeCTQcQaXfPBrotMuIHymA9/eLShwxNu4MpUfAZaOIw7YN0+KpWmgkXeBK7g9UN77ibhjfTUIUYNcS5nBZfn8t4/BPe0D3Ep1eBn1d8Z86fnW7JrN5LIMivvIVtGMdt50kfUtqc3a0znpOQqJcNsMtr3mo4yEYzI79gPRhS39kge4PGMex+hfVlExvjUslwtQ8A+pjRT7uH+hw/5Pav/Qr8FkZvbDQzhYmGgobcw/k+2ucjvFJEMGw8OpjiKvO6x0gMNekgafu3zL+ls6j13/5P7atg0W1MsYYVaPz7DqXZd4s4+7ZVk8GA/kYJQJW375mEuPoNMu0AUdS6Wt+yDWyIGqrgYdZPDhnXg+8s/M+Rx720tfealbaZBrpxr0NH2iA13xtjsr1MzImaLbXSnfeeiQzOQlOV9HqQawZp/1+9m9KVhPzsG7OHv15LahnKI8I4gWQpsNlXwug3OqpRaa59dP0wTACpYwZyw5KPkxf3w0aFQboNfijepI7ClfD/rvxf2R2jDQXI65DyM1PjsH1ikLEr8Q4CDX9ZI0KFEt02ZKNfEa/c09Q3g78F8BzzBrKPOb9aj61Pekbz6szNx+G6xEddvLA/pTXRxa3L8PAZ8kZ0P5qc9yIAsYeZoDM/neSwJWZ4GZs6DUUfmPBNkyD2Y6pgazjnTZUYBu1o5ahu+nVmipdVT+BxAZdeS9ts8chXsBuXovBwFndc36ZQZIBp1f9AMQ490Ai2z6bfIcZYc69hGPhuZOIhHQWJYnMktAnAnDyYVdcfGyynKR3mVs3jadfdlt+wB5eykBLgZzkw3v2QrRoaqU2IwxsyHrsqDziqfLitsmwPD5epNZ2440O771Rvjff0hg/gXo/J34y6//G/zD9R+6LjQa7uu2el9+x3L2gf1D9sU22W7JWVwgf9pBi54wZst2bMnioupO2NqDF41wWRuYG9aFhQdbB/iqR5EbGh1nQFS5sH4limWTnpMFeCPlG59OsgVZtGC0MSenxhhD4XRWdjMDfVPXjuxlS5zkZTR2kP93ZMjyHFpOOv8oZRv1Ljbup0YyLGoWe9bjeoXZD0yKZ+HP7vVm7MXzrtwxW97Vgbttm45bBkgOZ3j79i3eMuPrX/86rtcbPvixH8Obt2/x1a9+ANA4q6rrrIXdbOsWm5T3maAd6vTHMNhnGPjlz8Cn+bH8ku6hLrl9EA47KE+/cfk9fIdvfs1VMflYZA8QteRUx7LpVpbfsRHrTbLXFZzGa24XEGwn3y9Lymi6r5DZJA9yK45znYiQRdEF5PbAP2tdGH8/nFI5LnMHesS50g3zabCBHuhNcg08qT9muCWL70Em+x3dGnvFLa2huQm0U5j7YHNdHjjP8DJMGzbappg1lr5tyyJ4XDHAlk8gd9JH/EQEGLioEENmSDFam+Fd3sm3BHjmWmgX3DR80ff7edZn7vljNXj8iEgREV69enJ9W/GeBbGkX7rPWpVZYM3HYYyFIivVhs4uzuiCjeI9zo04xh7fEs0w6bzdZ8lwwT1aRzkfkUvFvjE83QP28uVSTLB5JH2iA13ViTGFab9zyjGT846rTpxce3Qg3HP6HknViZs5RI84cNkJfLR+c97Pad47uce0ZJB1UFpRfgcZxgKSQp8NsUHZp2uBBYsyr99rewoN2QDEIy+wwNWBrQYq054VscmG/WQe255lJdfB4wy2XO9AlrXPNE0uGgf9nACDv6Ob4yNYYGtXjpVR5bWOqdLvlocrP2tSHtYxwZnvR89iwjcEVhqrOTIq4/g9y5/v2Wd13I7G3dCuUs8j8pnLvxdkfzTN6Mk01++ZjqP8+fdLAogv4cFL0qyPz/RypWWqq2OQ74UzORf1OnjS31z1H/uyChofVWAPcIMEqdRxpdbQyDZS1aDSZsCO0VgCWwQFKmgg7mDfkBfhXKdhD8hMDUp8adwCyKZN3l8x41s2oPN76PxZfGb7DH6s/agsD+ANX6Wv+cb2M16b4zIwxr9xvRRsdXrTZs1LWv7TAFrY+RkOX8xWIL1HCN5r6wEAC2mgkWJD/NbMwfcGOR1MvBcN93ut/3MgOAoiz5UFI8kjSJwWnzqjDlJ62jQucd3Jo5Cj/zAXGRz4azO7GMSpr0pZpDzY2S+1H2ZfUO9HRYn2dHmXdzK2phaiZnq57jhK+yDXPDHnGY1jn5P3HYb7/mk6gMr1HTEjJfF9tOfMjE03imfdc+aDD2SDedl/64oPP/wwncioDt9wgrG+qAjXLegacMfuy8H14z65MPDZDlz8yiN9HLJJtQ4Xx8BAYZ/2dexNRLGTVDBitnVJh1Jx/EwvtWaBLuV1OvHQFf3Q0pCBzH2ryDCglWFBK5OBZthPZUqCVhKwseBVowhsDxjH/vNns95FouVx7DHat3iZn/GmjwNP+/HBNvWpFo4oS2R2zOYBMrPXw9PW9vCBbO9jIoB63rJAn7XDUnT2dfcXTd1xvuncznKiY9/Eho8v5eD2WOgcmz9AkJkO5dpSpT/xZeaDy6MnegZz/JUDXS/BZ1O8WrHxISXWP3HXt1fhLZme0UeXF4AxE89ezlBL4y//yVOJvrm/Uak1Wc7h6DyeBq1fTCL5EtQ6+y7aMFwt+CDKGmf2PZJGf59gOi/8qdCXo6wUIX1B+kQHuuDGJFTZceIH8pw/3blOCz8iay/4u/KKE/qSdOYgVsf5EaWQjae8BbC9dcYlRPLZB0E1g6q1v6gdH0tSxf4wDzPvJteG67maVN8QSJrVe3T9JIUfwyOQdxLnAP2eehkCFyhK/Y5sDOVWkFMc6WyAHLPSXgH7flezwIblWRZRoKUMa+9REOQR1Vfp2ABw7wFXc7te0IdHe3HlOmf64KVBo5ze9bmaZoGi0YDt8z5S3qP0nfHnXt5Z3cw8men78pmvNSB6Rs+9cjJ9cg3IoMLbldBnXkZI6eQ9GxHexjaW7S9CUp3xdNfgCKPpSXt2mrAhctZAy9Ll2d6bHJPuIM/swLisYvN9RPLS94a+tLTfk+Z1uoxHAENmaHdmrNqGbeu43mS5xvP1JqxRHQkA//rbX4rvfv4l2LaOf0H/Ev/n1/8Fbrged8a0G3n6lShmb5E6io3ize1qJ5W1BqCDqbtjZbxPMT51Is15Ip/pppMfZLNtklkX1635Ei5wODRmf8yZ3IJcL7alPzIgafdR6Rlh/jiHg7Rf4Lqww3SwPNfVGZM33PBg1s5OMbDd5E7G+HlPUBujPHGS7kKL7LwavS9wiCYFPlDpx51mdYYzbPdHRyE9PcCOsaxqZ0b/KktFcXBmPGCgs2yqfFlXXJ5WPL1+hfWygpnx/PyM5+dnvPm6bDD/Yz/6o7heb/j6h88AGLTkvaFiVmRulQVyGMBWnNKxAYXsaZcR8p5Lk7svuv7jm2QDdPkWDbMlil03uGcdZLG0D7JEnXUGkC+XJqzrbMVFDA9ONUutjNzzGfcNtpTgG8M33RjKA1bum4WdytsN6OOePE++T1n2E4cS/D7mIoYKKP1JATwECubIWr+lDb4ToIU2OHCqjiXrB9JZvYKV00b8KG3zgEM4+ACDt8AJ8WmNl39sRhc47Lz1nAVZbtsN7Pt7xaxeq4u1jUSEdVn1OjtNTpe9eEpGp46R6Gvy+/YSI/R8c/VsmGCWKi6tuPro+xDsUb232yIl2YnH8aroK6G3D/Jt20N07rjerrrx/M2fXJbFT58FMDnUALCtzXh2UevPbXSdXugfdWmsUNPmDvwace1Z++OFnZPmJtfs0hFGPh6rezrCbsUzUf6IpU/ILemTHeiaNHRk/iwddeZe0WVGEx5zwOrve4Gnev/MqTpL957LQnJKgwWOEIZqfC4UYHbqI8+uZi3jTDDfDZDOzJNVZPeGNzipLVTKqdbUcWDuu3xdn/F9r0zxHLRmCtCkgvTVVNNxGuqf0HWUvL8m9U7rqYEBikAXDgIHWemawzfcS5+ZD7NgwtBPSf5c3hD9y9aeu4ZqLC8DOG9jkZWZbETSkTIxrNV41uD0IwGuvWLfy8pR8GxuyM7repd7Z/ep9Nss7xEvztp6LzB2Fgw74/kR4Jn1w+xlwxCwmnyOOjPESsaNFRZvZOOZcYwPb9qTQ6HUeQ4H0VkpWRtVj8usHZv5YQRJ9kYNzEBvEjhsJLMsxOGC0yZOizRITkmU09V8r0eQA/LNa5E9vlgdjTFQLd/XZXEaNiK0rYfTQf8SxH8fT/wtAH8aGzM+zTd88fpFvMFbcGd8tX0V/3z5F1PbnXozmp2YHEsObSYbOQ/MYVuWcNwYJMvwgoXeB94X2jJKfM60sCpNaoSFZbmg0VHpfkDVxQNsdOSH9i/tFE5qf+w5BdgOGoC5VLIEjtAogmnuPE3KH79I4IxYl7oA01mGNGygc9JwHVQZMu9chKqrBqeg3HpId/LwMa3j4VIofcu21zKRBzPHOinGX8qfMQztZnQknnqhB0H9ynKCT+EbglSdZSP5t2/x5s0bvHnzBtfnK67Xq5+0StTQ1vHEv9za3F9chH02Drz/Mt4Y6I3AzSxR+Zyl+toxU5GX1Y7PWAMm8rHLmAtglx95POPPKMv6OYJK5LNIm+4D6Ce8Yo/VBqxVy8LIb/LlhDlQZf0XMkApbw7k5MDV+Jn1WX6RiuH5/CmkFgHfRQdK/t1QCsF3yRj4sy/MX7xme0qR27vKvigWJqSNGwtB0cadEGihLWcHQANu8PlTWYiZhpfJzIwVOkmDtiHQ5bg5t5yVK1k9KCDJWSm1PWXyySDM1j7Txyq9SUEZPrFTULMv+VIfOD+Ty8g+6jRNAl7TbLAuNYxodYYQ22E9dpo2kIK7S5OTX/XhKm1ZFStBXs/eZNGujfcSFfne4/GKIyXf/lrSfpTdrpmOPaJLMIOVb7JiAbNMz8wnfJf0yQ50IQbh4BScjpEsGPtBbtfzd/u3p5kfOVWnPzs3DoQPiKrXZ87SmTA/Kui1vtPgG+BTy6vBySn2hTCH54zO436pduAlqQZj8mcGQ1Tzc4IvNf8k5SAUazm+bDAJXVX8AyArCu6ndCKbqTCCEWSgk7Jz5ms6JcT43dKzQ7oX3JsBNI5ZfBPc8WDzYozVWYved6luHh/eCbO3U2e95H3wsh44SzODPBuvRwGeWf5q/GsZj/5+JJ0BirPrVT+elXMviDVrxyO8n92vLwdq0KrWeS/gtm/nid5ToXaVliC6vYSwMRWPsINtQsKUAxKXz+alGdAL8BYjKU6BGwN98kBnxtYJvRM2YrQuk5SWNoLOvsmMn947tiZAcOkk15JdsPe6Mqeh4dVllda2K263DX1jbNTB24aGHwLT3wPzr0bvPx9g4NP8afyKD3+FnHQE4K+9+mv4y8tfKrrhBBwo7RbEaq1hXVcstr+NnxSrPULRtx0E1u1NjINEwkF33oaejN9Clf6yvWlYIj8L6QEAiXI7Aay+B889t7tORof2qZ5oN7JjvztP8C4BbxVMZgZI9Fynpss1Ys8uK75y3O6TYTeYIxby5zMCiJSHk4Y5QXss8y4vCz+W9K71sv3jA36aymgHoPvrDEvSsi1D6AAEb2JWR67InI8oe05q9HFrC5a2AAzcbrLZ/IcffIAPP/gAb9++lU3lta5Xry8yhpZl36FZ56sS83H2wGFLSvkBxc6A4Yp93rd0+Vk6uH7yyOTJwwc8AFkBs/wW3Z9sTwv7drlcZDYXjQEpf/yIXjKbIoolB6tyHXKIhsxeaXpqrGB+0zFjndUPGk5QNLqVhHzPyZoMhfl3U668yzPlcf4+HW4vxT6jFFVJIzJeneNUSjZf4ietyHvMmp0/3wabtNhTi3zLL4pttpd9suL229aTnKSKnF1V/tX+2YFkdtI2S06b0bzzteyTAZvBOLzInmDCM+xXMaN9t5O/80noL03ODY7N6O3ExFz39RozuSzPuq5YlgW9regY/akSScQ4eyvSEdY98w2Gcmdt8mftucOsp0nMr/H1qL4cRBOZsaBWle+9DqhjYKz70fSJDnRV4c6Y51ygx06u14/SFEQWcHEUZa2/HwFi2Zl6ZNZEfeYs/1Ea1JgBUcq8TubFlNgDdOb0YixoBlE9w6mxsDxH7fZs5lhg/8Z2BhRReKv12Hekcg6bpYI5qIIaiKj1ZtqYkxM4tsNpyPVNGEwlHxcHoZZFuC8rwzM5EJi151mfIRk3ey49646WydU7OBH1zWXdVHQI/mh91XmqZXmwzZf4BpjLbZolM4A1iHJE8+z5Q5rulPGuwaOzVEHJkQF+JFWDfcTHI91ar9elGmdlVJ090+HvorPP+JdvBU4gjEioOoQIMJuycnpLF3NajC/2y0eU8JZkM3oH+8lhGaMxmS/yc9RbUlbG+xkqMxTwEgGNQGiyAX7Tfb4AdJYNcjtL8Evo0iWUjYBFTixksC6dMMfv76G1HwURg/tr9P4lEFagMz5/+zx+Cb4bAqU7/s7l7+DD9mMDfbV3mjpxy9LwjfhG/MLbL8RKiyw9yA+Q8pNMb7ADdiL4XjXiwNm+NLkvgEY/BKKvASB8QMB/v8jsNwkeyYw32w9sAIocBZnc2CWTDc9foln2tr+TzQICbKZQqmEIdo2MivJCPysNeqy9qWpG+jRSBmpSiSxOj5DHbjfEZ4ogmJ3U+VJkfgjBZ2M6YQT58sC4f1dPIZeh/xLy/lpADNCgZ0AN3ucOyDB41Sw8TA1C3CTPa49IkeS3h6Tl2ZI5ZnHsPvzwQwDAdtvw/PYtrrrMeAiUNAlw+cEKyTkaZpnUNulYy5hrpKlioD2/MocB2ZvrX70BP4vl7NPHNj4Yyxiulirr3lcDuah2X/pjtJsVm43L+vJyQOPVZV2w5OVRD1Dum8ZD2Zh0h65GHDeIbzGzNQfw84s+pN8e/AJiuZbSazqx5nfasn3M1A8YLizg/DWyyf0co+cxZvqdauXDA/aPZ4QF510HOH1hDC04LPqRY2jRgew53B1lhUc2BFFGC+KkXMlD2qfBHWZGU/waAS/5vW03q9H5NujBJKOjDtLg6DCjL622sJJYxzJK4CrjEB/rBYcVOJTb4/3Adc8poC5Odd2WUkhRei77gM7PxFe9nrdvyAE1OVnRXpCNQeeRs1ao7k+ZaHP+Fb/lHrYc2zI8GXb4AZVnMYCcxmrHmWBz+aw01OeNJgvQj+WNPM/64XGb+6JA1/d///fj+7//+/EP/sE/AAB8x3d8B37f7/t9+DW/5tcAAP6df+ffwQ/8wA8Mz/y23/bb8Mf+2B/z3//wH/5DfN/3fR/+/J//8/j0pz+N7/3e78Uf/IN/EOv6LjG3bLBHpkR6NwCyAxknpWWnpkaS3zWKnNPMCcvJ6qo0HeU/p2kcfFwUx7FTbMtxXt5Wxl45BfspRo9+d6VVaaG5qZvSzYwHxvk0AMUY+zwy85iXUoDH2lGDYlwMCapaGe8NbUz9OCr9UJAjcEjf74DGoc6De9Ngmd2259U5ceehBmTsz94sWVXpc3jiTDsng7DLxQlopLIzSPMgmAXncqBlF+Qa9y/IY30WdJoFxPK9R4NdR4HtdwkqHcnGrL6jlANSjwR3ZmXO9NNLnt+B6gfaNSvz0UDbrNzZG8V7gUOiUR+ZcMpHGp/JHzJbH8AsySeHk2ROi5dJ8sVGB9vQbZWXiS7CTlaZDOQmx8AHkvh3tucUIIeEsenBBlAnUFv0VKYgfYMBRgl09WgSVl3X1lqT06KIxDFmBtH/gEZ/B2iETj8TW/8ier8AYPyc28/Bz7n9HADADc/4keWH8SH9WLR11zlxkvOyNHxz/yb8289fwYUuaFsLByA9TMoEAgMt9ElT3vkSyHRdnuhY16+h0dcBEH6EgH+wdOguRtp4WTopwS4g9kNmQGeXmz4LXRYzvpJ2dVp98+gEqC3IlB2kgrdTkkWaksde+tgsPgALxYlUGPs492lQ5cWGzbI2NUBmjKRAl9Y5Qt6TdKQXaehNuXTwzCOa9e7LrrspO1UW7FKi7uj2QY/YheGZI9vybtRmHbv1DuYbPvjgQzAzttsN223DdrOZDzKbhCCOX0fak4fZnd+xAv1HlVGjWU8/jjNnOV8x8EtvwDdOHDlLU7LuFF7xy71yTV/nz12gi+COsi2Xtn0C3TEkwnq5YF2Wsa6CWwbSJ1i+pRliuz/TRTajy+hK5VUb7OO12JNGNYCf6bBnZxzT3wX3gmQjfPNDctuHseV4LTE3/bYAXL5Iwphiz3OeFOQaIjHyPU4Nln8ssJVntEaQJ8pn0wG1zl0ixwS2pYDhDwJ89pEFp40PEvCKGV29bwMdGdPId91YPc3alZlcnOTR+tHqgT9vLGGwHzhicu1BMPuu/CJKGFnzj8mUZEcDBa/tLuc5ymrrynYAMw4faU/na8LhtlzRlyySnGbZ0imLQIMFv0uIEFMByDAjY8ZEw0telke+KHzOAuUyATydYTb6+ZRpH1vl18d66hiX+kS+svxYO8fyfUY6s39/JL0ouvRt3/Zt+EN/6A/h5//8nw9mxn/8H//H+PW//tfjr/21v4bv+I7vAAD8lt/yW/D7f//v92fef/99/75tG37dr/t1+PznP4+/+Bf/In74h38Yv/k3/2ZcLhf8B//Bf/ASUlIaler4GXn824OOj3V2TjO2HpWXFYQJ+0ud0Xt1nNVrwa8zJ3JabhoIo+MXn8f0PEZnfTwPvoEMBWwEeFAlFJ4+aKAuf06SY8b0+eORpoGmAoI5Mk9/ezriczXylYZSlgONnGcHhiflHAVs7O+g9h2Q07qms2TsuGT7y+NmAsSs/+c1YxfAq329k50HUgWLObg1S7NAloD+Yz3wSFkVQN4Lcn0cAfZ7U77PgkFHdDwS6JuVcaa7Mo+P8lS6d0Gch8EC7649GnzL9dryrDxGVNkBaTp/oTwpMTJCIQDEtgoHHEjYPwyAJOCCBCyHAP6A78ueJJAAii0xk5lYHQTbe0djZk2DW6rTY08naVE4N/a2VwMgnSEzuDYpTwMlGfD5DAAbh53lpEMYPz/EZf1/YOsNPCzsk+DMv3X7Gt5sn8K2fTeIfhSt/XcetLF2vyYJci3c8CkmNNib73A+SfP6qYukTuASb7NbE8fLl0ISobX/L9b2t9wpafRVEK1oy4rPA/h1vGETPwLX3nDdNnzttuDtbcOHz6Q0RLd3ABvLksErGP/ta8KHuvl0I6kb3IegmP016wMTPcTyyA4LhxowH1OGqipW/gkGaCGA9bRIczFYNhW3F2e2ZJVT+TtJZx72EG8a9GoL7RzSj6bpfgqnNP5219P3urzYnLtZGvSe5z9OM3PvKogZG294vj5roGvTmXl62h/F6am9i46hxaSwuEhiwDMgArME05zuB23avVznCOpeeoRr9X7qCxsHpoP1iIejmVwW4JIN5tdhg/khSDWxj/dsaz20JV+re3Ll30ac6P3Q6UMwOvthGbuAkkylPJljw+9iW3e/LVV7DQwBff03UT88n/UjEv8I8GXrbrdAA7GcSp7pMafA+z3srtc9HJhA6FiCjzQGkcaxHu2TNnP4Hule9rP8RURqC7UFy2p2P+yvzRb3l9EUyx4bB5aI5ee792cl7W+GXEnAI14khx9LND4fm9iPfMu/I/g2zjR8Scp2zvYU9ACXLlXs6seQLldseiCE0cnUASwR5JqOyUrbsf6ev1hOEwWIoNuvOs48q2vPF3J5nAe8rIwYv0SEbTvH8ccpdELWXb3Xvkzjko7Oet6nFwW6vud7vmf4/Qf+wB/A93//9+Mv/+W/7IGu999/H5///Oenz/+ZP/Nn8Lf+1t/Cn/tzfw6f+9zn8It+0S/Cv//v//v4Xb/rd+Hf/Xf/XTw9Pb2EHOQB/5Jg17Hez8/sn6fh9/00c0RfGux6lyCXfZ85ajUivQs8jP+k8va81VIP6H6YbBig2V8WFJ4DGGN0P/I8ErhwcFYIPFIDQ/5KVypjZthEMe5n+mVapmWepFAr2LWVcxkHQS5K9BIfzMiqwbf0vQbtctlnzTiT+Uz38NYx8yzJ7Az318BTzlOdqGFftZLqM0aHB7fKmLoX5Mhj7V4ga1burJ6899e9ANe9IPwsz0t11VmeR/lzNgtsFtw6a99ZUC3TW8fkvYDdGZ1H92Z5x0BcyidenoBKpOVLyDJssJQ9JuZ3zEnyNhhQ0Xfumjkwjy0HjiVBERzi+FACsj31WWP6mzjvFyYXHFgn4NK0ZQna+5KqRtAlajID1HSd8YAo9N8A3weF8Ixl+SGAGBvHrBGpG/hXOgP8Dbjdvgiif4Zl+UF3ZIyi9y4NC7WYHYBnMDZlyYL8uovQ5HRDXdKzLLFEYdG9ttbW0Yghqy+/isv6Q85H0jKXywUXAN9xlbBbZ+CZgSsDX+sNb3vDBxth68FTANhA2LTb34Lwd0DYiPC66WlrjcB6siOUj75vS3LKwuGRz2eSpaQXjjz2TLNfRbSzwwQRq8H56yRt8hkHqXuqjTV6hpiH3hARk4BXdp69T2Z2Md/3G+UO7V+g7EbvTD+8g+M0S2eadofjUNsojJotyQmdsefTtDkntNSmcqKtdz0oovc4uEH3i/IArWE00xO1TFYKdClLtbltn9m02zwNorrvXZrklVu8vwbslyciCeheWCb0hCNqgS7TpTnIlZtJoIGfy7pgaWlGV5oa+xI7VO8dnVJc8cvgaA75kfLl0wW9ovG5E18rXTrs3d31QVf4jofYdzLpWBnLqbYlf0ZQnfwZ9kwVXxSyLLBlNx3jpk/IOCU5mcNr7hhnsAL7/pDLetf8Dox9brOvZ7Od0vxZECV8wvGiywNdihnyuHcZ7uW3cemoHwuWz352Nuq2R9ORnzFR46mMKNOu50Bs1Ifajcj+JLs8RcY8k2u6ZNH8Fc3HjQXrZN55kHOvt50MTPLwONZHn5jzwz4ez8xU4PF8zVhwPFlmj8PnlmN8fJ4n48vqH8xp5dM21fTOe3Rt24b/5D/5T/DBBx/gK1/5il//E3/iT+CP//E/js9//vP4nu/5Hvze3/t7fVbXX/pLfwnf+Z3fic997nOe/1f/6l+N7/u+78Pf/Jt/E7/4F//iaV1v377F27dv/ffXvvY1AMcM3we53i0NjshhnvuVmBP10mjyPSf5kfrPgl0vTY84po8nKt/PoB5Cmb9rdSUg9kCNoXJd4UVZropTucxxDLGBNCJxXuhR+mu+AhCm7Uq0cbUAZrhSfz3SdtYyMo5jZsA2Wz8CVfrvYNzt2Ts0DNfc+R55ZvXmNg/tPuJTatdDfZD6tYIKa/8wI8dv0+77AA4nhmOs+uhtzVjO7N4jQadHZ1BlY/xoIKrStj/O/J7UHadc3iw4+NJUj7Q+a+e9ANuZLnwxjT5sjP/7cuRrLrdHdMCJMrA5gvahR4h8naHoqxYgltPy3BjNqRIBf41kJhM3QmcC94atb2B928kM0GobletMsPAS0FnBGfeyX1LwWoJgsdzF7s4ck175sEsfYF3/KwBXEPXheSJgXRqWddU9xf45Gv6v3t5t+yVg/l/6/jTrasscZYmCnHYmrvfSGlp7g1dPfwGNPpSAGL1Ba+vgnBPJke5mZ5hlRhxI6Vkbrjd1JJFAYzGfTwB+9W0BsODTr15jpQVPywKmDUwbtutNNqC/de1bClkDYPt0XUH4r5+AtwT8imfCK4YGJw1wN1Ccez+RCrjTmedO/OMG/PkL4wZb+iBLVMlkbCLCNbG236pnYiBthg0kh/1kf76friktKMZu1M50GwG2afSL6uGooTUJCi/LIjMsiYZAwjCDoTV0Ztw2OXvVgsKA6tDs7xE8oGC44CHbrbWOOXn33Gwh1LtbkzNSpFTbrJvV7tTZdtln8ZlTtl+gLqW2QJdsCk+BdShm1UiVPJQ5r2ecpVVnbwHH+215HarrxA7EXmE2Y6vqiJgTtffNwtcqdKZntHXwQ1IGezHpPQoLaC99ctajGY9WdsZJ/pkFVItkDvn04vlEnjK+RM7cB53cwX4KrW7FBgtANS2nom8CQEvzMSPxtFgsx2Z/7doQfO3o281JDN6prKxSR8PFWWn1f/3N19G3HoEWfT73I3O8SPMXiySznS2oEqVm/o/eggVWZeaXDbHQErmvbSZXPtzkkTTkSx1pyxMN45i/ZziANCBttMcfVFZGeVJuYKaFR+ne7981BrkiuOtl2UnGvsSv+ikRoDY644C5uZ+ReTNj5Sxo9rJUgM1A87uW+Q6Brr/xN/4GvvKVr+DNmzf49Kc/jf/8P//P8eUvfxkA8Bt/42/EF7/4Rfzsn/2z8YM/+IP4Xb/rd+Fv/+2/jf/sP/vPAAA/8iM/MgS5APjvH/mRHzms8w/+wT+If+/f+/f2N2jP9H0nVO4czB46fCYLfMzUmT+fjECu8U6A6Ky8I+dq9vwjDmzN/8hzBmxqPnk+g4oMrPaDYd8GA2WEfT9l0FPozddKnpekeZBG0rBUMvWbO8TQ1hI5WNcM4SxaGUDIjRm5PTH7Np5cH5yCg2CXcdXbaZ+Dkh3L8PqYi6LdK74h0JLozaBrSClAaLwbni/jx/gcRU9m9Fm5haenBq0E3cqDsfzRgm2zOilmV33UmU9H6RGjfPT2I9M1C4i9NFB975mZMaz03Pt+pD8rAK966Ky8Gd+nYONAhl6if2d1HNG1y+Pgk3f0eTYf55wu5gKsgvgcxj+n5yjaZ8ueuEt+2yDeADiP2maoL9tb4oautPWWADY1We6wA+ZBLlkZGGdu2EsCuw8H3uzO1FBqttHMw2mwQucG4J8OlY86RoNVDSC6otE/BXn7/zmYP6OBrgWtfRNa61iWD1KgS6CmBbqW5Z+htQ+w6HU/rQzWFj2pFUBrgU2W1rC1WBpZWS+XEqAH8LNAuKDhG2jF2ha8Xi/o2wbGDbemJ18q6PaZXs4aaeUzCJ9h4C2AzzHhNQMxCw+yLM2cvEES3M0YnCe38QR8Mwg3nUHYIbP5epf92b5GLPu08VhelBCtNR51vWBmVe65R5H6NLW1lDkwofD5JRr7nXG90TPpY/n4CCVzPC9Bo4RjhkCP/ft4bZmPricTzCDrmEmpA37S59Orw0gBnKZ6IyiZ3d1fp/KdzHlEOIoZu+xQbQp23A8PcowDnuj0pD/zbI0h+GTBrRTo8j1/ZjxRfh3ZyXy9BrjOAl2z58sNrd4aMZJUSRwfi9kmlHgw4l2fQ5VKyDbU9GbgXuNPLvM0FSwwYE0zm8Sj2TUbA/Nh4EEvo8naaP7TlBPMRnSx6yY/WefxyAH3J0j/J/9+XO5ex46JyieG8j0obTLIsUeXE6zBG2+y2xj2gyd6l2OKRznLdQa/55D9fKYSMGIG+W1BHbsf+jE9kGxN8f16R+eOvm1qSzkFpvdBrpyiLaMc0dhka3l6PgWzmAZ6apArcSZ68ZBJMRszaKkSUYLEqbyKY5lrXQW/fgzpXV9uvzjQ9e3f/u3463/9r+OrX/0q/tP/9D/F937v9+IHfuAH8OUvfxm/9bf+Vs/3nd/5nfjWb/1W/Ipf8SvwQz/0Q/jSl770TgQCwO/+3b8bv/N3/k7//bWvfQ1f+MIX4GrQlcn9dC+gY4ot+bkhoGmvAHcSJg7gmYGZBZny59FzR+04qtuUxxkdUwcYx6BtnAUR0eBRkRw8fJJm/UfjzT2/9PYwU+is8r01PR2BBBzuC5YVnNXvEfECatxJS7Q7SJlou6GP/Nao3Dg9O3PaLZl7drdLBodb2zN5rl6btQsAqB/TdC/INKUp1et9kZwptrqY403+QR2nvKjtsP5Ps9jMea7jztqapzBXOZgdGhFVPzbLapbvKECUn5vpg3elo9Z79HlG90sN1kxnMU8ciKQXZ7o555uDkbk+r3Xndh4FteQNWZ/2lzybgDmQHNMcOPd/cgVz/T98pXFsaupdZlO0JcBlI30DvHCSYwPtOgPINhhPjoM4SPFpAO5GhM52rLcA3p6OSu/JaWkgMAHLQmgMUAvX/LbxsNxCgOR4yEvaX1c4lyMlO2tmv/dWTngldKxr8/23lhYOE/PfAvPf1jo/DeDXo7UP8Orpv0Zbui9dlP2xZNbFulzR2oq12cyHmPFgGt5sxtJsXyugtQXLwlIOWW8mDzw3wZ4heav86tUTni4XvPf6FXjb0Lcb3r4h3FrD7foM3jZs6fGQkYYnBn7lVXTsk9x0t4VhOnCs176aYzBL39IJ/8e3WpZ2ke3N9mME/Bdrx1dJHAnZGJ+HcmvqiQbrHwB6WAHrqZf7MftTOeXZWKdA7B1Snlk1OqQvTxn3NQrHrrMEU/1EPjtFC2lGYCOsy8VpQSFj6O8HyHsI35w9/OOUWAXdTpgU7Jz0OsW4I93Y3XSp7b8lyxQjyJVthlqJoRGtyWyvnDLuyE657SM0bmp/PmaqLyHjrgQtT3sjclnP7WH5GOQK1yCXPJspHi+gM/aLNiU9x4aj2XEj57IoB7lE84m+SeEDW1d9yKvxt/ULNR0Hvu8Rw0+GSRvDSyHkvb2Zwts2Ka8EKOVUYEptGusnNZSuoxVrZKyy0Ir2tPqznOixZzq6z5o2bQUAr1+/J/xyOe/KA/a9vWyZ39bl87bdsLSWNvrPsqcvZApGy3IyYtqYOZUDRFbm3se8g4O9Phpk4+3zW9Vz3WnIs7qh4y3T3ZqeMj2UfFz/2Iej3p4dElMDzP76QpzYhFNtDIQfknnYD6fDJ5/0rotts0CF9zJD7Hhy0T5ljV5xdXURH1fgLw50PT094ef9vJ8HAPju7/5u/NW/+lfxR//oH8V/+B/+h7u8/+a/+W8CAP7u3/27+NKXvoTPf/7z+Ct/5a8Mef7xP/7HAHC4rxcAvHr1Cq9evdpdF+Vlv4RBIhCmaPZogZPwpJK8vPz84CwNTtpIQ30DINdt4MI/7zmE47UkrCVvrafem5c3Omz3nnNdOwmkjMIGFWTjv+XhVA4lnnopANKyA81QMXTeXHzHN+NDMowg2g2TbPxyXcdGqnQw4CekYAIEos3JudTxam/rpiCCCiyYyMWgmnMf4MhlG9ts/DlS8Wd4uubzNuZyJzKUT1Walmu8N2ASNw4oOQC0SV6O5HqQmZPyZ2NyN5YAn5VCJc9RIOcs2HI+/ua01iV3lf6zZ3Pedwk0nX2f6bKjwNaZjppdPwLfR4EnqyO3M3+vgD0HpHe6hDxkZE+kjwwoUtsYfiqgyXgqVf5lxrhhupUhYGP3Yi1pRgL5rALXN6lsszXxnwF7LYXSeMq85fhgxDLDnsaZNz4BU9EFDQ7lWgN12TwcTTY39wb1DlmnNr6xbKRBNJumAwaavjhoDGLGZWnoG4G6LHPMM51s/xCYvi1YX8Z/H3pBlkxKN60LSZCrNaxNZ2YRdCaWPk83EG4J0P1PaO0NVvoADYwF5E6+7fO1YNFPKUPKHZcqSDAQWNcFvQM3MJalY2N1cHXGF1u1CB+L1CEgyIywpTGWhbAsyv8FWKiBXl2wLYQrdWwb4XrNyyrM8ZFZd+8rX3uTmlg3HA7oJPeHPYuU2Y1sRm/MCmQAjYH3k2vEEL53vfdFBj5g2RuMmcEd+KcN+Jfal9V+ZfsHLYsQKt6WYIh8uoH2np/741oqA+Fi3knFJtdvL0rv/NiZzZrM0+LJj4O6dZRnFx+j9MaLYcDGify5BKiutH73GEHCi0ZKJWOw2yNYSG0/QkDRhzWXalnk3uNpToxbds2qm5Jg+l31mm7gjcQnajJeFjtcIb00aBooH0+ISyMqgVsyPZxam8xT2ox6fEFgVmP65//kMTaWK/ox24DQSWJk6ox8a8IwchMTrZ6K6xV3Wz62nmIgBdr2C1Rdaw7l+8/RQKQAU3qeRX6JxSYL/uNShuiYPUa1pYc0UDdbog+1KdYmgGTPLo5ejyfSmFCZYu6woEZCxW7jY5Dy2IdZaih0Y+BWfYZCL0qT2dsOpECG+z5L6F3IPnKixxvaIrZ9UcyQl2hGQanVqa+8GhbMYPY+uBv+Oue2Gc2wF3JdXoqrjTBWGp8oM4ll6XFPZcrJ0TrLcllBbfENUGWcs8cSRBfu2zaqs9TeWb7k885tkvVxaq+pG45ypJ+THcx+CtLEjEYu+8nB3dHNgzXIenqcEUnUDQ5HvkTLIEOJJbO4wwtdFwAfYY8uS733Yf+snP76X//rAIBv/dZvBQB85StfwR/4A38A/+Sf/BN8y7d8CwDgz/7ZP4tv+IZv8OWPHy1Zp+Xf2jmJ+VX5jf5SVbhI0dURVOS6ZsGno7/x+f2sgpzPaBh/05A3T/20WQS1PGB8C1BpyBwLuvpuFpcdURtCV+nPtI3XRqd45Jed6AUub/EBn6Wzc3ZrUCNft2cPnOjBsD2SVH6ICIr/w6CYNiakt5lU2usZ45rnRRVCzR5KyPuhtHeHuVxR2YyEUTamTSM6UJ4l3+RvmCGjn7ebrfNPcm+0mqJOyhdEvvfWqOjlGdvglk/2XVnXdcfvytdZoKNlGSp5ZwGh3Es9zfDMn/fkqpeZoTmdzQLKQZtZgOkooJbbU5+f8aTWe0TrrN7BeT6gK18/CwLOdOburfJBnqPA44xuOzLddXvyI0bMS8nY51mPCYR0/dsEpRJkfw2b+WDAg9GxoSdZZ3cCU4nDd/8kgCh2PGlk4z4H5qIh0cfAs/W7jici8uV9dmbjxnJM98Z6UprjHNP9Wb81gOQkIvmfsbQVEsyRTSJ40dlc2w28beDtBt5uABuP2ANK8bKecCGxBQt3bGDQ0wLabvjgtkmQq0kf2CQulo28xs7j7qeC9S57oNgsLYDRNyHj1dOC168WfOppwWVpCvqkPfZ805kXoleeQfTn5TdLIGuB6UXCwqSfG1rXDe6pwWa5JLHCrd/QaMF777/Gbev4+tsrmFYwNSxPF7Tbhg2y1+NyEV5um6DYtQE3hTTr0nFZO15dGOvS0XCVoNeFsLx+DTDw9s2C2+2KDz9g9G3D7WZv2c1paL7xsunzzXR7lw3w2d/aRl85HoDZAka34+jVi6q2miHBuE8z8L/boAG1cET+743x3y6QPkrDdzc2U7K9viwHtR52tpnOaO7QVc1k7gZh2927l0ZU+fL00pcPhwRYMrOGrBNq6tqR+ZCFKI9Aslwm4xmrKwEQmQxAaG1xUjbbc6hZTSoLfZSDvXnY47zB6Rvucbqa8djIjBoEUXKL01Q17ZB7qGJ4IpPgT3QwyQwYNsWeYEZrEuCSWZ+x71YOeJHN5iQA6LJ3X8GQjZrO+oy9EQmGLeHlRICr4AbewNCZeSDYARvULBhGA46uUGn10whRcFv2sxIb8/eEO3mog8zI6R6z2hbX2pti3LBJsV+TYQ+zebLhIZkQmgIfXBYVBPtEnk2kWdh0h3R203aTC0CVwhL42gXRclI0bTpKszfewCkAYOVl9sjyWwDp9HLnobfNCE3BQvs3gYo9Zgu9nlPFjMyM67Zf7eR/tr/YckFjxvL0Csxij7fbM25vvz76BsbPVLc1A+yvXLCYbA5stM4dcUB4sTrbDF0DVYsXsN02ayBIx6PJwbPayY6mB88sMotrWdDakvA0gKYy2GIUyKy2xKPUD4mxVSEpfhxXYxy9KA6x5ySRB1hc5VbeOcb9tZysOutrIMmZ/mM9MXsN78NqbrGdzmDBsR0c7z1uL18U6Prdv/t349f8ml+Dn/tzfy5+9Ed/FH/yT/5J/IW/8Bfwp//0n8YP/dAP4U/+yT+JX/trfy0+85nP4Ad/8AfxO37H78Av+2W/DN/1Xd8FAPhVv+pX4ctf/jJ+02/6TfjDf/gP40d+5Efwe37P78Fv/+2/fTpj6+NPdbZXVeBjJHcY5Apod8705POekzZzoI+SG6uJxjkKnp1de8Qpj2v6hsAdnZqv0rM/USzKCTqm/NULfjdHrvV7noJNlt+VxlhgfhY5zwHt+wcLaW5k2UGy569yYqAwf8fBYM8GNoRzCPh4oIso3gZp3mrYPNClvBn4AHNCEhUZvB4lo213+XzPuUEOU9uSKfK+4cqHdN+DUam/XT1Ogj+ZhoGu/NxZe1P7UoH15ukzZ4Gqd0lHvH7J8zkAdK+sI/1Wv9+r8+xandmWaRTA/25HQs9oPqLB6x5OPPK7h+NCdFAEZ0OrsWJWk2EON1Pr7X1zIBQF7scgFf65v9RiSZADX4w8NLDvs3X0d7eKbG1i4nEfnh35I/tWtV2fsiDWWH5A4QQ0IhBLcKR3RieJQ3X9495lqQMz/Bi+4YQ2aVejBm7sS/mWRU6k6jDbJD3g4Nx5XZSzOwyhh0hpWpaGdVl0yWHTt8WxAb47oblvE2bQFRius7RToI3I/kRykOTq61evAGpY2uJLVATgUixdItnLirsso+kdaEuqRvvKZoMsjZweZva9XYhk/6/33nstga7rDbet47ZtKhLhplnQyOtYCOBWTu8iZMcQSX6ImuMXY792K5J1F/4pk5hZgrBo+CIzlo3BvbkM/xgBf7sxtsElOk6DvHZjrOoZm+lypCfK73fXvu+ejjXQg88+/Lh3zHmWU11c9wAzQmgs96Cc3RXKBNFx3ozF0u+9y7i7OARF7ccMl4LHeWxD3EsGmV5QuSTEMiMfA3nWli15knFvQSgiOb3Vq+FxnMTm2pGndwZj83rsBFwPmKW/lr5HuXZSHJy24ZmZr6RtM/1Yx/6M1/WS43gtdIoBrbyOsmxLdPsemlbchaGO7D8EhoxHzZxkPajEju3gDmbjUba/qe7I7LScpQissQf+AjeOuK2eknlWZvWZjgb5GZa/h10fwbfRnjyL/gKCLvUD6/5deZax/VaepzxiXwIv+ou+1ET3d9IhENQIxBY86t7vYc+Tz6YnyXbdeH5YMqoB5uyTDDp0gpnvYdLAjY+lOo6rvjC5yfVQ0sf7iSp7mma/afJt/wwPnzSRvRwPmL+MnpL24vSiQNc/+Sf/BL/5N/9m/PAP/zC+8Ru/Ed/1Xd+FP/2n/zR+5a/8lfhH/+gf4c/9uT+HP/JH/gg++OADfOELX8Bv+A2/Ab/n9/wef35ZFvypP/Wn8H3f9334yle+gk996lP43u/9Xvz+3//735F8Y9Kso444NA8Cyafdj+cjqym0vdDeC3bldCZYNd9ZObN6rNxWorKzZ04qLvlFmczaEEJqyveo7JGXkccu8GB8ZPlD9CwDguyJhv2RSOn1TY5zkKi2KSq3i8f9cCJOBh7HKZslq9MXAa9dQYkup6MESVxN2AwfbWvOu69z7H/OeevncTMBLYdznYk2DzraMxTcyCAslxeGtrIkQM1sbBLFW0lzoge+Teo6bOMs+HL2zAnPKgg4mx316Cyne+nec48YrVmw66jcqlvO6rhHy73nsv46C3LVmXT27CNBuQz8/DfMCR89nQx8wlHKrhEXUByJGjRulnQiK2jSmS7iWDwgp0OdkmwGGhW6DJj5bFzO7QK6ziywcZ33jTMeDAFHZYQvoUv3PV9roN6939zGLAsaQ2eGdTmRkQidaAh0SbBsk5lw9jY06dfWmuzjBWBZb+IIsp5OiHBYrL9HbsWSO3ddgh2y2mCR0xbXdcXSFt1rS/q/EdwhlfzxIsELgS0bdCL8+az+M41ENlOB8OrplZxmi4a2kfal4A0LwFl9fZNAl8XxkmTqyY6E1TauVmDJLIuozGlsS8OnLu+h947r9YbrTf+uN2xbh0xGzKCW3EkEp5ctBlARs1DFGTGe6F5DSwMzcL3lncEKtrJ+1LHJRPgSd3xpIwArwCKrP0yMH1o2398LqcRUXCR3ltIlk/nOwz6c+XEuxWC4u09Zprhk+Ziw+rulSUO4cIyGjI/pdnku+j8VpHJZ9O6RnkPOe79uqt8GgDHqwl3esxQgYAxWZNx4ZN/Z/yn3ZHT6jFuKANewtw+NM4TasritmL388f26kj3Zese6yiwTozs/M3xO/JXIMz5jNsD6SLBY8MZmsaLYBFiAofQAlT4KHiYsnHjdte2tNcW/wmvLItumjPKzgwy0/7qT9uST74JcqV+tL3o3HT42J+u0faKSJ8oe/+R6S305lDLBOTXlwEnFPEdpVt4RhpsHJebPH/nJAMBN9sSUl3+KB3rIvgWZ3I5xd71PZPtkjeOr4kKzfxbUotbQAN9rKxowrnhifcZoYGZdpqgvlFLe1OIoLv2qq66OeHkWCDvKdxzsosm1sayZX/Bo39bnZ7/vlZOxdbCo5rGya1mP26oXBbr+o//oPzq894UvfAE/8AM/cLeML37xi/gv/8v/8iXVfqzpSDeYU6O/9NqomPKbjUeDXfnamRA8orxmec8CWkfpVBgT8CMKyMdqzGePBhbIsHuv9DOPM3kDsFCDVp1R+3TlUR1YJMWSHM8wZDwYeHMU3gWFHq2SlsLhdeSAl907473RPjjdXGozILB7mEdZqNph4oyfJS+LxLHpRVF6MGDynIGS0/oekHN73oBUQjdeVyLqofK8+qGSPU+PjEEuwGb0HAVcztLwpo3qmxga8uRr9ftZOgM3j+ibR/TWS3XaLjh5QMcRH3OfVB7Wco70YqWhM6eZkiobthxvlhijnundHgJsOSLLG8pFtZLvXUQYlicOYDsaOa83E5DbpP/YW8dtuzlIlNwWNNLKOZWSAgFphEcwxwAkyZR9mb4PDVDpUzqjC8wyIysd5b0Q4UIE5obeGetC6H1B3xZw3+RUwM7gTWd9WcCLhWpX0wwwES7rBevlAt5kzeGA6YjkbW0HZO7anI+c9L4tIbpcVjw9XbCsS4BYimWtS4vZSWFHxj4h6n5xCLeZ/mRG035pMjVP2sjdjw73zeQhG/i/fXvFtnUsRArOdQaaHh3eb8IgAnwZ02VdsS4L1iabA/d+g4bVsLQLbG8yGx+tNSzrissqgP5627B1xvVqR6mPYy74F1aXyF50NTSVKTdBuqyGlFDrz5GJZaYugFgiKdQ3Aj4Dxq/cZDllVxm05T1XAv7KCnyQzYLJODPY9kbTfqQW8m02gGAvb2ygFh1ANPGOx/reAVL8+KY7RO3N3+goPZ6m2myS5ycvEYBfcgM+twHvIyBFDq4MyYHiLHEIWM5l9ogicLQsDUS2aTXpxvEpoJTK3B96hSEP96RnKPbzsg2xZ/4BqWy34XfKk/SbBw08j/IuYKyOFa0fEZDKL30q1zJdTOTtrP0z8F6fsfJFb7HeshldWcCrDIZP4jkM1wz1qI447OtjLBI68J5sZ18qrplOfQTC3sNtMzx6dj+Xew+7ngVaZnvH3sNngAV1ZRsF5jHAxToW8nXHNQMtALMsm+OtOzYf2gcC0aL31GDqxv6sOfI2L3JCsc107o4JIwAsNinzpKsdyi9gjoJQQ1B4wrNZsO4szfuNhr6ZlTELiGY6Hk336DummYrqrdgq88949+KqPvoeXT/V05xh9/LuFUoo+f2SmnvK50xo7zlm9xzVl6a7jqkq/ajDBkCOmYxKJuet10fBPRDidIKJAYQhsJGCPRWzCWiujpoZrXEg9+HZ5O1RvcRDYY/2SwSZdrdOy/KqC8052FUqPxZiq6fmB3bmv/6udGZAQIUO56tkHp4nmiyZ1HxDXe4J7ekbyE/1h39EuzxnGvBsjM6e9beShbYZn2ZvRc5kphqTo4BaBayze0fpni56F/1xZihn9QzA9sRwztp3Vn99O5V5+FLjXPs5aNrlTv/alwj8sztE7DrLAJW58KYCBzXh6vY+b2vwRNqarglFDgY79/I8YjAZuJ6NOnesYkaq/R7K8bHBoC4bmUP35vLZZiQAkhloJPvWcCN0YnAnbOrwdA0U2ea09hYWkNMYwbKp+rI2LOuCW3JATROZLppudDbwVVlAADWbzbVgWdfYCJpso+imgSV1BFvwhSj3UQehDXWS9SHFvlO9S7mdSLY3s9MouQMkTvDlsgphaLhcVlzWJZZFarmtyd5VXbcVIUpLHVuTNrWGTtA9lpQ1WoqB3wXigDdmbL63yBVtkyDS1ju67hWTg6JZjowmd2A1Ehby6Oa9SmMQn/rQi3a8oDikNXyKGV/WffB6jwMTmIGvA/hbK+OqBSQRBSB7mbFjDQ3/Gt5QJzqwT6YxD1gaB9IwRmfo5Niu/Xim3WzzStok3XcgDvT3AKBoOnvLZ39xlLPX1TOa6TTLDs8Bwwz0uMVoTLgA+Fc24As9YRuT49qdrt/PdPMEm0EKNV0iga5lOJ2t+XLFsQgGdoEu20w+MJi8NCGQb1Yv43+cCe3YLOty111jsCu/BK73gOiGbLvsz54bsFIVpow7Mr7PWdJnxoihanh4NGx/7YeJnJ7hggMwvBtD6pTXNNrioH504HEgS6a/MsIc8eS+KeP4uftS9pDeKG/2wvUsPYpHZy90B2zogQ6bzSf2kJoGttQmNZ3JZXaUmdE321UUzsPw3WLLiCz3ShUw3U1KKGKWzee3bRP7Z9vGDH9l3ywE9jJ67LrL/EE6igfcS/f7YC8nZzTsfKoHg13VRwp67L7J2P7Z0Cu5nlHnDFredUDgv0fST/tA17ukynxX+vXagw6apaMo7pmSAHgncNWBrFFiYH8620xop/USQU7v2Oe7Z1TYHSty4QbCGB2zSsDjoMDVShDg0X6nD8mcaPAjB1cyn7MDbHsXyOyDE9y3wy7hOD0SXY9idB8fjMsczyTGwIn3F3Psf1OM2YwKd7u4br+aTGjm7Z02VMBxpyMF4Cn9RsOUX4+Om6O2JuPjb3mw5+1U5pMM+duhlK/y94xHR2N6ls8+H9EZR+O9Bs0fLac+OzNqZ2k2nmbPHumYGYiqOvSszHcJBj7SjlQQRCmcgxItxT9lvGq5vaNvunO26kK2GUGLBH+WRljaAoBl8+CkT7nUUXoofe26Z8kYpsqHGFADGkewyRyZzYJxqcwIqBsrxFklagrdyYNmeRm1s87piiCb6TGU8SaqXmYQMMlsUSZ5CdF7l2O4eQxgAJDYFRPWZcXlcsGtM2TXqlQ3IOVZ/47Ngk41gsUiQeIcXi5S5uVywZJOQpueiOZ2xJwvgm14nHuDqnZljqO2SfuldxA13Egc3+VJ9vx4dVkhp1YteP10we15xdNK2Fbg9lZhemB8rE1meD0tDRcNzDleyQ65dT0z+nYL3jY5HXJZpZ+Wyyqz7y4ym+z5etW9wVgDX+IEdE5HkhNAJJvui60g9E1k5eanXQZXmOCypZ3jwuQOEfbOIRGwLovusyX7hXXu6J3xPgO/+tpx9QBFsocA/p8X4H9avDuATfqDDHtkXWQBA+OkEb5TDVWvTTP9FE1G608czYKHfjzqyk7sPP1rN+DbN8I3pyxDfAI0yh6AbbuVUjjVRl7t6LxDZoauEdBaNYi+6DJkIpv1Hvo4v5wlp2dsnbrTIDRQg26KHQGuyg2jzXVwphex3Qi1MsOrFpJaT/qFCa7r80FS+xc0Ix3Z8c74MtOVeUlBdPCADcaevUA7MecUmqcGYcC5Tst+PMM76hddQYl5REEvYPqy4hsrw549PnRphpUsVYxZXwgelfNokGtW9xm+O/q986spjVq7podaZAuBND7AMXOduSx3tKCY8Z3VPqnQEOvJzwibDsMdfdMA14Zti5n6Mm5tnCVfM9kaf7FY167DaBjx7RG/X/LS9iUxiFlwsyXf+sw/eDTtnzuXrRjH71Tdw+mnSaDr8U4Z+4F212v0d69kz1NWvEeK59FACVKQ68jxq3Uflf94nedNNf6EaiKYIq/Km3mvSOW68TaBhkmlFrwyY8eTIMuOtxid2UHZJ8KS63WY2EHNO7zpyLZPP2lSq3NR2zbH0gfKbOasl/ZmRRggZVLXI0ETwN+WOhia5DGDLY7KpNzy7PAG9o7yT4I1zZuvnEH4XR/MjDKfLFJlM3L7t2nngWsc5hnA1uTemVG7V/fs2UfAzeFYOgWY72Ykz1KmdaYPjwDgQ+N2Z+ArrziBFy6fXpEHu9ijEBbgtpOs8glSegoZQs4m0HVXkzsZ7iBl8C9ljUBbwgt2Wm7nzduSZ67mwJA3uemSztZcFw5yYHqUYraXXbfxKQGN4FmMSfmW+601Arg5ONXmoOl36uSzIuwlSpRUe4WdR6GCo93kZBLa0uSvNVDTZXhpvLXyGY4JnIbqtKUFcMUUlJ42oO5HwLE4nU3quawLLpcVr19d/HREcyaJZNnQukhA7ulywWVdJRgnVKn0RRosdzHj5oiuIPTGuvmuSmmXIBelk5ipd9lbzYupzlvC99l5LPTsORQviKxYt8VmV2yMcge4yRVmfEsXfJH3bwNkrH2GgR9L7/8YwI2AD1vO6d2Sfwk9lG/sAf3+28vTx6U5M3ZJF4dKzPkmiiVgud1HWPlemiODIMH73G36SVk7gz5ix7GAGHNA6P4nBt5nwmc74fO9PnHcW4ZfRlsXOs/rSzrBg+G6ybxvWu2HXDR4fCyxwF5qJ49/x5aMk2V5dT6pMTms9TnXsSOOMFw9vWb1UyqPqJTPA3aqnPRRne3rjK5UvtuTYs+Hl2D2WQNUHiiaUTG2AYlXNcjlutAfjxk8R8lkYH8993HQPS8j+oNRddDIi+pj1vRyX/OxNAQpH8R5pzSkMc3DxQgYkv1LjIxD7JO5C1bR2VfEDZ1sL6/AAS6rpe/hbbL97jYPmslLuXHPOvOrznSHMuvO7f1MN7s+y3svHeHzo5fTR/7GTLbuvcyeBa0zNhqRh2dMn4/Kaejdl6SfJoGuj5ZcpyWDkD/P0iNBpW3bQETYNtnzIs+22m3gW8pobVz/TDRuIFzz1+DaGV2zCDt25Vi9o1HUElTRyPfumwTaG5eYRh0D6z5fj5zYfD8b2BkPdhFzC+5wBionNBSXiUDT8eVwhAof82eB88PzWdgmyoJzHmtTagfXcjIvKGZyeP01yHUAUuTNSAFOBoQKjcNzflnbU2gdnq+8OCgz1+XBzrQZ/mFwDKMKpXLtSL3yAU9q6XkGzUwPvEvApwZ06mc+aviRQNXHlc6CeXl8VxD2EkCUy8ttrfdy248O3rhXZ+WtBYJengQ49U32m7pen9H75mO5L9qOLo4PWvMghgfEVH8ifYy06qd7qF0OJ9wjYfloiNOAUjuZAbrF3lW2isv2lHA7o+V2BYEE+GEQcXpRqhYWzhvfxgMAdZb1deGdaJtlJmUz8KpBLpkNKrq2Q/ak6tSlHLBszr6uvp+GwU3baFaqiDBg0DgCONaLNqNLTlwkrOvipzA2Ata0bKipM9N0GaMwVA+w1M84NEN5QkFn/pQ+kdlPRlfvG0AdxIy2MLAs+NR7r/C0LuBv+1a8fb7ixz74Oq7XG96+fYt1XbCuC56U/k996n2sq8wCM163pQFtVf6w9/WyPoG7zcwCuG+y5Ixktt2ChtfLKzAz3rOgI0idgA3Pz1fctg1v37zBtm2ynxcYvV9FIkikYmmEhRaXsyy2zMaRhHuQ9bL9mzX4iNEWXXbJeqCN7OXP6C1hAYis/69vwL+VhhsD+Hsr8H97EjkjlUUiOUDBHH9A+zXJkIu42TrK1uQnRid/XOkRTPZTIr3cvwEAfGkj/G+uwNNRmcj2e8SQ7vBqvcNBO2anFhnz67K63RqC50Roy+I6xOrxl2mqE42Gy2VVs9LlwAQwaBG7ITPDNNifAsN929B0Y/uasl22QypMh8UG9c3FeGc7Mx6vX5gHafcxMhOoGW2JxkxrvfbS5Bg01VLFx20/oHuGsWeQNoT+RlmqluXkoGkTeiKNplv0Wj6llhB7Pg20Hmybk/ewqn7QLNXAyizvGQ6dfT6aqo+atvQNfqhtIMJgH+Q5AJDtBkRmGfnlHTOLr907brebnC58u/mm8rItAUzY3de5Xq/oveN22xz3tGWNJcFmr6Ui2OssqM1pNgM+4aah4xPPM44/Svf893xt5gvM9uaa9d0jL7uPaNvJ0LwlAEZ/Zf58Lv+MouzBPZY+0YEu06ezfnp07LkTMTA+RZO9HHYv/qXO5Usd0kcdxCPF9GgdB3eS8Q3ezoKAR0UwHyu/wyZNggseeCvOM/L1g3Zl2GkKRwBvLHXcKZIHAergyKVAl92j9BosB7sO257a86JU2j+0J9No32dBLkqBA7sG+HfnY67L2xTf2fsjFJCrI4pg10vaVlOmz34/WmaWmxx4M7D5MtJoGBd1rM7AWn3+6K1IfaYCwBromdV/1P5q8GbB8bPnjgzmrP2z8vL13J78bL43e+aIxpeArhnvM2+jXODQaaWYc8J5yrz+QUEzd8kleyUxwA3UDcCNsud1Z8EmAimokv2vjoIAcokcwO11NijN9krjIfqwDgUOs2f5nYDQruOYtxlrBjyNkVlnGv9grxCgHhL87R9re1hONBTyNQiz5KXcVq7O00qOIxJ/2dhCQQQpj2wzZ9vjqjXC6jMl5GniyD+UA3KgLQ6jfaojSc05EZ9JVlN5BAPsDFmeKnv4rOuCT73/nmyWvyy43W54fvuEZRFeXC5yWuTrV6/QlibBOWYNbqmjpnugMHWXrzhUgAeZsv6QWUzkvBURYPSmwL4RuF+wbTJ/TGacbbtxEzbSHDg4DeOifiU1PR+9iyRR+Wok4z/b2GSANSjcCHhPN+ns7NKBb+6ML265ELn+j1fGMyde6IsVkwPvPzZeYYIN53QeXuP8zDum8vjpzK6a02TvwTTHS5P6DlPCEVPCJrbTs1K9UEnAayZ8rgOf68CntGMHSed4STvI7MzeATAcaoGIphvn5eCRB5HyqYW0fwFghEYdo652HaoXFg2exR5fNq61HcBBHaN984DX7pq1L+M6U/6jXAyanOA48SjA5TZgYndzeae4KWPYcql+4gRrZ//AHnKNkp6xQBftC4cN+iPclZs6Ou9hfGJG4uxF/rwdRwGmTMcZljtKZwGUWuZZsKLS+VDdgOsdTkv+AmNT7qwYovpTpd7tFfRFBRjo1LA4zYIjtr6BuIOwOZ0WAOtb95f7jWiYiRnA56BtRR3lz8BAGHj36EvgR/LO+t3h5IFf8UgQdBYAPcL6Huxinsr/7FnHo6j5ZnQpbnYfYUr+NH2iA10vTUeMieDWgZJN6Z7DNZa5v/+yIBk7XS+Nur5I2dQ2cR44GD6l7PysnFBxRF8GhfdI2kWES5DLC3wwaNLqc0PZeCdMaVNZ82/9Mnwf7k2qrzcOg1QIuZlx+F5A5TQZL5Oxz0rZAdSdcpyVrA7R5AQWq+td08zw5rbnE1MOCjjm4UsISXUevZWZ9cnR99lz937Pgkz3AE6dFZrTuwTuzwJUR4Cs0lzLqOXPUtWhNrvVPl/KW/usxz/HW/byHDIojv3hti5vDnvf5ERAdRI6CGDCxnJaISkKIwDrup4CVG+PgW4DdATdYoLLmHJ3ZyDYXDt566jhOa9Xiuldx67eG+mQv0aIPFzr1Dxpmr/d7Tm/8s3AKHhRuqqBIbQudN1Y2roQsHbG0+UyjndngwZydin0RQTiJDWdxSV73SxS9iIzkaIFDPQt+NCsL4LPcnJnzNBeUvDMA1tanl1xoG20RCbAjjOnhrY2fPPP/AbhJYvMb7fN5XRV59f6eLs+635x1ne234ksrQXLMsRtM50sZZnoOK7XvgiKzd4T1kX67dXTBbfbhrdv3+J2u+Ht87PscbLFkhGb6zfaOCnLcqRuimAYJJ4RtcPHZUi1PSP9saxLsJAZt01nbLAuo2XWfdzk2W9j4FufMxHAGwD/p9eMr7fAGbvAgB4OYEGMsAsv16dDQ35S0hEYeilRH7UR7wDITur9TAd+3VvgUoJ8o34vetf7Lhw2Dwz58sOYHUWNsOo+XEMQigAmjj2wKLduH6yR72NQzJZMtdZ8jC/LgpwsxHWIv+3PdZfp54ZxKXbC6iehx1xuptm+12R40rDXDis9WE6t3bc9MZop3zt4LEegUqZGYiS5sdu2fOhIaO6g7cwPjPuFahrLK084iQPXX+DHvUt6lwDKLNX+O8N3YwXQmHVeCmgvVfRTCoXZTsvVOdwK8n4XXNAWkpnRuqR3XcWiSEDrGdvtrQe4rjrbS2ZyQV6mrRfBZ4oz+qYviFq8mjkecZNmfgTfR5r/eAzAPm2FVb6fsdlZORlnV9/h7IW87dPtQcpJO+zTdKuPr3J4UjR35l/xi8bGT4tA13l76SBPVqpzB22fey84NT0S/cy/zwIUZkxfGuQ6qi/nnwlsXIuwB7ljcuZEWrlVkIP3Vk7Nj7jsX91dO+IPoG9tJzzI163+KdXnyoeS4s0gvdI0DW5VAzcEw44qzGWO11zpWKCmBPqq3GaF54GrKnv66XtuHQW1Mg9Lx+24p1ZnN+/ErdFIX02ZVkr9OeQxmcUeng+Bl5Lf6Ob8CcQBBWMlU/q8fAejL5t+fDYej/Ic6YeZnjl+w3hc/rumU5lLgSzLcy8oVumcBfCqAZ6ls7eNs+9n/AhAw0nQsn4ZgboFo2xGCQF+RHvQHE66L0HfySV7OeNShQB6ErA6o19mmNF4ac8HSFDB7QxnuOmN8/1gui6l6TxuBG9BNzlBMfS3upMW30pBH307Z/QM413GpAVKbPN+JmBZWB3KDHkRpRpfsnZioyH3P/Q0RQt0SXBLlhwRFgNTgMx6QgqycByBKNfilLTRkQrUQBM+eFZruue24Gn32Ue2Oa9rftsmgAHYEic/jUqXzlrBHOWKntfZXiajjbBSWprhAXzAloLYLCyrw4DqZW3CtwbcbouciHm94bbJpr69p+q1Rg3JuRz4fbI6LaiqYpF5TXUsJXanL8Z9O7HOT/UCgfTFXNd2NF16anU/gfHlG/BPG/A/LPDlkAyxk9QItJGfeNda1r0nuunwDpzmj5wmmEouz+bOpfs7iFCt61hWrmtWbj150cf9R2xk4Dz9mGz8fGHgF2zAZzuwIHSBBRE4j4EACvYlaE76d7Egly4PtH4nstmbsYRR9IDiGMcKIxY1R5DMhlDSB7DZpYvP4lpmS/RN5lIAjFIlrhPTQRo+TAZpDBvuOnkctP7dW6GqzoPQFJ85ZVyZDyeKwx6C10jP116tL16Md/HsGEQayEgKJmMkr5NDXqdjhHi4E0GYmC00S+OYynWStyEIpEGv1Vf5Z7juDBcdBUju4aN5e3j33T4NP8xw3lF9kc8pGGCA4ZwkySp6hgwUazKB0dETTzPCIZLDgADBDzds4K3pDHzjH2QWph4YsfjLI1ueuN8uJmnCidxIn86WD37c6ZE4RL5+L2hW71ff4p6PcVRmfM/XaFf+cYBr+PUiX+anRaDrXVMNcp06P+aAp2fPot0zp/NIudR11/asGdKjOo7qO3OWs6BPHT+Y8wFYdFzwO+0EMYJidt9KiN+jcebh+YFGq6h8r203Z+KuiJc+RemrYVZCKiwHqijM+MDb4e10fTalcFsTrws9uY3OpVmeI0PmzZ3LrLzJpgBF+gxnXitdrsSTbGeQVmnKQQ14HZjv7ZXHSy4r02TP7VH3vmnALjj3SACkOvM1YHqU9oAs+rsGo4+C3XXWkH3eC26dBmOKzpiVX8vIsjwLKM3SGVjKeWpfZN06a1el+Wzfs0cCXRY8mgXbzj5Ly2CB7iPWZ3lojWT2DERsmwFxxDVYgCv5DhZAyW0NZ8McJilLZpaRlk+78eG6ZgC/KQDjraoNIg8qzBrrfedKUYM+hkStMXbKERjMW8ovf0zGC3XYjCLVG8h6nSRM2NS+LEv0Q+8sS/UWW7ojPB36AxYosX0GWfWWztDwvEBbGi6r7tGlSwGXpWEhALAlqelEJedxlkEDwEXHK3kGzP3TiLDs7rtbcEFORbxdr7jeZDmFLYUCpX1/oNc66zJEneVlJ8WR1smj7OU2yOSTJpvXU9PpXJJ166xHuu/3f3Hn/iIO9uVpxbZteHWT/buu1xuen5+xbR1XfVNu9TL5yl6vCwQwhw1ilpmANnYsj9mYsQ/I+zZ+C5+X1rS80dEVBymCHp11Xy4AKwjffQP+GTH+/iLXOTpTDvuksOu2pMLlrw0t+8lJJkr38iDn4/L52PM5qLUryvr9xCU8SyMUmuDsGhJg4BUD/8YV+Bk98kxfmJijnOsb6o5TEhfdXD7P2grdHmOakg4zXR22Jtpi2NjtBFFWG2gkwSvZh6/M/E3RAPMfqDUf/7kyo0VOi5WZlT5z1O1SgnUCrBInZnbfM85trGVK+IyZNcCdMVR9aTymAScO9Y+8suqirPsSNuA5UzpImENZIH7C2H+hXwYI+0AyGx6+kn2afnK+5oa9Q6p478cr2GW/K+6ysma4r1ChujU6waBFxghjEYLOur4FivHNQ47sQ8dSYoD7DRvJoTdymrA8KXvqLb4PHrV0MI4Slvv7TEuavrqHV3fcmPDqzLc4esZk6yw2cS/Yles7ws1Vr86G3oy8pAK8vEMdH4pgaNtL0v9sA12ZwQFOjmcYgBIgfSGXZ85srvv4uWMlVcvP9cyc6Jlzm+mIex28hRGe8SW1QJ/bXzcFfmR0gkZ969poND53Um3PLLgwBBB5BDv2SaNWTYAszI0Zw3bn5JWzdCQDQx4jY5A72hn6e/WYYjYQlwNHBJwGd6qBnRnccBwQRgCjshrqGawD7z8pzU5JAQpXpoh+DigQdXq7lc4jSf243I4dIJsY/xqcJRqX182CTB93yuXWYHqm7V7APn+v+tGez0DHyp3pmjNaz+o6SnUz+iH4mto4+5wTcrfKMVAiO5dLUElPz+tosLlMBq70vMXQiwTwlvie9ZPSyG6bgIY8IyPAXx4j3BlMPLxFHOSsBDuO2mxlDicN9ZGvu3GH2OvCizU9tJg+JrAv/dGNdzNXWYLytg9SM72rS4EWUJrRZTy2Bkh5NhPL+W8gOOkl68Om+Rffm0s2oM87ctgSQgPS3KVMIopgWleNZHZGA5jdaQkmk/JJHE+Vg84J5Ek527bJcgmjVYN1W980qGozSRKAt+CVysWyNJlhxxv6JjP8jGs+Y2qxwJbM/DAwz9DlmA3aHzTIib9T1wCs8O+Cy+WCp8sFW+948+atLmuUgNfz9eb8N6fX2sf2JSUfRRx8cHMtBsa5avRYP1toUdGLv9hhxwskfQugky47VVNrlu8b0PDLr4ybyvI/WBh/d5XSiRkyhYDhcS2SmT9o4/Kyn7SUDeVJFrzIWc8PvlOVD+V5uMKUGgO/6AZ8SwdeZ1l1TKSOsc3k8AWyZdaV2WgglgyuC5YmgSdbvjiUj4wdhaGZp9lZJyCN97hnQbFFA1sEGYu32y2C2418CaU582QDo5WZGPYPxThwu3HC2yN02NRu7eyo4bsJzqOK7VLw69wOJ9t4FwMTokWPS9YjQR0PvR/4P3L5ZfjNglpyaJfZcduIXvNg3+QZJjrCSUcvW3ctKDipbscxDRAXbHsU7MovG+vY8mdn7YT5QcbZrDFijEWQUnjpXVX4IDgkDtrZtjgpWLaTEN6vl9UDzKIyrL35sKKMWOIV1kg/xxivGCfRNeuHR/rykWQ4s/oX92R+toVHDXYd5XFZfAjv+7eUnf26YZlYfhl8tnHzkvQ/i0BXMDKW5u2jxPv+IXIIBos4HwWsHg1GHQnymQBmp/HR9GjenQLicQaGAenzsitv6qAdlVQOcuUSkACGdcbwBivR7GWbES9GtyrY7IQ4krfyXUGqIc+qiUbjPjTnHZLLQfkNTMyl0ZzyZeegFDythyf3YziUdh6kamJ2wapSZ3bqKvDZfc8KvvRdlodZkGtKO6dQ5T2FawA48+H8iWnKwdYZGJjlz889AkKO7t2rpwae6rOP6InZG6UMZmagaEbDGf27N0OTts10aA0cnunZfH3PvyxD4yXKI4CtHPktAYVF9uZaGtrWxONifVI3gLdNyd0pAfxkoNruoNWcshb1w4BxBhxCYW92pPa8nxyYTbqc6r+Jr41IffoS1E5lHQFi8+dIT1VU1IgWr/cx2A93bOB63QJCQMy48v1lvL/DuZQZXayzhjJU5ihXq5bli2k/LYpnfAs0xQyzgCRgOiT30KgLGaMNs2WnrLNCzPHetm2we5x44KEcm7XB8vxCy6i/yN5MSxCvk5Gvpy5m3ewvl1SgtBzra+MlDxEg+b4N8iUYQfi4gNfVA563myyjvF433G5bCgZYr6uz57wa8RrBZlrFoDQQD4LLV+ds86IWC0hQymsOFhrJSZkk47QhQQNqeA3gy5vqFTDeEuEfMGODwUGpJW+F0uhMp46AR+ix/pjo84pHX2CdnAOmr1yCagrdNm4GPcn5LsZxV6WPkD0NlPPAnd3z8iVDA3AB8L/YgJ+z7W77jMw6ht0RpdGWWCB7SXtj+Z/PrtRxOuxRG7THywj98+ZS4oDOMrU6m8wwNVpND/TeNbglus9mmtm+iVY1JRqO2Os2MLObyj0qD/uv0X4OjDa8Wsp33GaYLtGRS+FJWaAxcDLSNtJnj71LOhofIz6rvBGqzw5x2OMQtURstjyYH5MKJGfWabOyakBpTvP9dOTTzq7NcC6RvJixuiuNs2WN3p/EPg5MDl21EpxPY99njKcvaCxg4vY6bKjpb2ZdMaCbzvdEv+A4DTC3JmO6B4aRSQ77ZaqDBJMjNLPW8AMh616vBZvPPmf8fEl6VAZqvrPfR/ELlwXMJ4NEM6r+348di9FUnRpjB3r/rFVj+mka6Nora/teHYrYLDIb/FSSXack+DyPVAPjxm2W7FqOhFqaKaU8CGaOak2zcrdt29G5C2oVOnJ5x4NvVDxxLRTPcYpZCNJGa6+UMXuyDgNWWim1zZDEYMhzuwFXWF5ebo5hQhJn0ACHEdC7OJAbbzDHFrkMJIWXyt0Zz7HBnnrq64HfCZT1ohRn5Qx8C4Ef68/PPIAMdqDEnITk9NbgRCP4bK6p0U1AKB/b7n1UgVh9dnA0hZamS1SMBruey3D6q4YsfMiAbAbEzJgtS9vpk6Nxei8A9qixeeT6DBw9EjSbPW/3Z8Yu66a8Se5s9piBDLtWwU/lzTzwM9dJVnamtc70OmuvtyUDfpRn2RxopUs3LSJCOB4AiBm9N2y3mxtsrdR1X/CJwGjKF6dORFxp2rYbepeZtrJJ6gqGbCove3AlHrsetj4oPHS6MV5zfZnGZNKdQhUHAmWOkyaLvSMr05hmV5nRN50d1bsEeayfDKzK4NcyyY/2ZtoEmGJB77L5+tPlgtevn/Dh16/Yto62QpyGfnMgRJCjxGnRJrKTj9aA108Nr55WPF1WvH71hFevnsC3m5wcqMsWofucLcsC0zCjQ8JyKiQ1sM4qA9LSPgXhYLEhPutN+QAA23Zzlg12euhd2U9oMXZan/CWQLRc7bxJ69tN9XQK0mV5tL4h041JLIiwMEkQh1mPuk8YIRlmp6NHG5al4b3Xr8Cd8frVK2xbx9u3b7FtHbdbx/P1itttw/V6Q2fZj8xlhWSWnc4hAbDpxsNp9oqOR9kDjF0+hXXN8UXXvcjCQmdsKHLXiMCLjH8bshqfk+WTyrVv34DPd+C/uQD/cJnbp9vWsfV4S91aojvxvVoBmSVG9eI5nHpBigDnTB9OcnPWVRMiZo34CNR91PSvPTO+dAO+OWGliPUxfD+uZFdEv4msSjBrTSewigzJssHRHrgTq0EnLKOuZbDPEDWbETqRvPxG6fREhF9Rrw34RF98sM0O16A/dFYqUZM8GHHQjt/Zx8Fol2pvD789MDPyMLE7bIQ9YmUne3KIOyu2S7VV3GFtMUiYP5Htd+q/6EOkQ5NGbDPgFh2EMx8rfMXRVxt1zLSRnj9mdDF6N7tS+Jl5ke0DjX5i9k0zPUcvDl+SZpir+ozVD7DvdTPzgccEXy4PmI0meJCrIXy9AY2wj4FlWbUgsX097b1nh9Z0ZnkZ2Rm3m2wLAJLZk4vbcrEZ2xZbSoAawHZYT+XfRF8Dk3x67YD9tX8qfs48n4+BQtWBjzB75iV56/UZRt+6rOuvcpKxsM2gM/6F3ov2yl+eXRhB/0TAlMZZ+kQHukYbUJULDd/tXlYOY8qWOxRWCNdHQxz3lMyghIsw2f13Lf8o8j8nxP+ZOJZ2b6wrqs4BxVp/rmAsFxTLcigeSjRR/NYOZ/0e+DF2OEFVpqlmjoZ4ICYIxdjNGfhXp9H1NI3f030B4AHKsxnMknZqiI6CIwk87NqYAIXLTy4y502ykfmSaTziY5UEV0igfdml7mkbaOCgFZqMjszg4CIPeUbD7o0S9l3KVk6pB0XeUfj4Emw/Czzlz7vj8E5Z9frMGB6VU8t4xKgdBcwe0U9Vn83qfBSMzcb17OXDDlCdJA9yAYao7zwQsq5EuYPCGvDj1sW56kBI4H4cmXMegY5ClzudEnCh3iNjHS8D3TM+ltFQeE1Q/tYnJo6Sgxfe67WhL30AabigA9wEOLYWbSRuieLQRzno09SZW5cFl8uKp8sFb99uuKXonfUlOQ3ClrpUTk5bbOHkNtlU/SaKqwAzrd94Q7OxR4MeCpugBYDAlHjGrEGU7AjUMpOWVeKbuV6kb6u9lywnW0xMAyfJbqa+GTCTlzHaYCLdOJ7MVlh7eA8ymQHq6rhJCUuz5bcNSxP5vW0blrZ5+cwdsnf+JLANkwGTTfh3O6nLZu6N/A7++X78vLdYoeb1pZuxWpoi/GaW9jPwMxj4NBN+Vmd8VenoAD4gmQXHsOcD7witHMFRmP0a2WddPI5nfOwprHOu4p7eSKqFEAG5vbF+hAClYv+8b/U11b+FQZr3iYH3mPHZDny+65gtAYd9W0QX5ZcistG86QHZdJ5IThcdxSacrSyfKM5dXgnhj+sAynXaQRsAhpc1c8KNBBPS6Idm+klnzjJnORtQ2hCQskAO5fKtbfrt+N4kVVzl7Y4A707aDrCAVTtutXFPxrQ9aWxbK6y/zabx7pnIWxNVJuAYy1h51abXbHI9+GxdGgHTnHc+sWKG+2YHmB3Til2+WXrkheHsZe4ZHdMXjlD5UhzGwRT5yJKQTFsUdYxl40WTBMMbjS9DTRZH6ZOyfQndQPJOY8foqn19SNlIY/6sKfffGa4d/YX58/eCXu8kJ17+vs/H6zbecvCKwRwvqCq+elR+j9InOtA1plHoqqKze60toLyh63iWNqpRsGvy1vn4lLXZIM/38uc952sMLL0s5ahwre/sc6BpcHDjc3yTAITR5/TYTOnbvcxf5eudRp6KdaF7F1RJwQmvtTUsqa/I9jVgUVLcGR0d1POMMFLQs3484DNr5oMgiNHubdP2+nc8RgolL3pnmGAOTLIYdt3GxkQuWI1BdtoY8DdkbdnDklqHG69l2QEhy+Pu3+BAjvmMhi3dH55JhmsnS+457eH+LlXeU1bgc4P+aPBmlh4J+MzAwjhG75dxVHfWHTOANcv7KO1Tp3ZiZI/qnLUj/53N5qo8OwwuAy4wFbxkVcYANttzadVN0plxu8pyxu36DAbrCT9qR0CjXkpgNY5YLm+1II7Q7e3bYTNkZcCoHw74RuYATEAY8mUdUz3/RsjUzJFxfYBxhmpuy/hWXGxH1yUPOolLaNZ2d95AXU4RZBAu6wXt9YL16UlnAcnsq95vuG52ip5jZPQN6DfI5ucAlgVYCHj9Cnh6avjU++/hvVdPuCwyC6LfbljAsqSP7FSwrLdGEEeA5wM1UFvQuesM4K5BJ0rt7bCN3cGM2N8+d4rp1Nwz9bvm7JtvyKs1aD8Zz5OZKc82+OZbgm7cmQg9t5hj0QiNG2yWG7PMdPLetf7uLMt2Nxl/Rprsa0Z49eoJT8zorxivb3Iq4/PzFbc02+v6/Iyts/at8oEKi4h8XyxeCMtCzodN+etvlpGcI86zxtJ40DKzbK+rntfHMXPR9Na/fSP86zfJ+S+J8X95BXy99g0LybI0UvgFaMAr6yD/qEHrXXfv0uiSfRzA5CcqZQz4kqdM1tll/Esb8G9fgadhL5ex+IUIrV32OByKc3Q54rrIRtRrOnXNdV6XZbeiBnQMkM0oyfqNAhugB360Gb87OyU6RO4Z7lLCVSfmsetjmqJ9NsmKmUF2GquOkTwTTdqu48P2KfJTIeZ9Ua+e9tiB3XdMZ/w3XXNW1mkKZZD9EyDPhskYIPEg+QSGQb1IpHE0jMvZy7URg5054u/om0/TLFA0w5kzXPhIsOClPqql2YyuSlN9lojA1JJ+9n8QF8j9A/m1b+PtdvP8WQ5E/3Z07nowyobn52cQeho/aSCBUV9n2y+fcV7SI10rkyHyxJtIs1MZZ/vd/kSkj+Kv7PBDDLc0zKLfY9zGMt4x/7l8vzT9NAp05XQE+ON3nGg4zkIKf9yYr8rBBtEdXr+0M6qT9kj+o/rOAmpnwa1ZAGuWIj5DLryZnNlb08cSYdB1ucJJaVk1nVmRfKqZPEi7/PH2hGHBrmoMpo6j6WCMb0idQMDffNqSSC/zQcU1ApzRoo8SPZaZecPl3nD/TqpvOuQjOX45yFX7gWPm1fRtUMo340d1qKk48zmI6XRpntFh2Pe5l/eScZfqzjTmz/p99vsonYGUs6DQjs7Mn5SvTh+/R8NZ2bM6HgU2luejgK1H+XEE7GayOvz0f+w3pxvpFomTwRBZ903WmXUPFaD3BbZsLZ5lDy44QBj0UPbuyZ0Yhm3OGZtzKwMGPoRdCwCRWURIY+LMnvhv29+rMMbypHwwRxDzZLQ5sNFveTz7LFmOebDmBC5EoKXh6emC9957jU+9/z4A4M2bG26bLEtgBnzFGmSZXSPgaW1YFsLrpwVPTxe8//o1Xr16wmVdddmPbgitHZu0H6xQTrwb+E2S11942QmIif/Dy7DkX81eQOxB/z6/yA+XrDYDkLHbsDUEBjaTY3A4dUpNpYYM+CQAZD0YfmLik87sio3LGNA+sAMWAHhgYNk2yMyuDeAO2jbgxiDS5Z4wMbVG2swxuO21fc9abhvkfi+sHCckxfjy5lEca89smIgcH77PwlsZq4QvdMa/IOD/l5qMKEqet6BFDz6O81Q45B7RrqEzOPLm3zOD/lM38JWILkGG+MHjz/yYapxXDHy2A9+yAZ/qoX8iiJXLCRwyBJrss8Wszrxth+kkt/2q662bRCellnEsozN97RvMp+VIMzpAQNMZDb7RfVO/w3RrfR6he2x4uJ9iPHAajdBiK0DelprksczPSXfl/BNbm5OPygNcX7HtvD41upNco14MmvzTAiYZF8x8pDQOheiKXwJWml6vwSdv8xQP7Vs2ljVv/az8WXrXwMhHCSQc1XtEy+jPkPL5eDZgGLnUN4ZICpTxmdeQpet9E9uybZseBBMzbLMYZdeGcoGGa5K9cWqKLPsM4qEgIMtn1HccJP0oQa4cOKrl1e8vK3OfakAuHzYR+nAW5BtjCLNmjjTvYPqL0k/DQNdcodtvi/hHoCsnMSh5p39xVuoa4fREcvDOBOilCioEaNy3aVbO0QCZRfXrvf2nCV8dKKNyL5SnZ9VVId4J5qDbcIcnR8aw1Jr3/fFeG07KSvmt74mGDURNvfqnazyphJcRhAaN2F+b0rlDay9LtR9f8ug71joG9Ua+nAYKiHRmRYBLA4x2P9fBqZ9zP3Iq19mcny3tyl1BebYL4CdtUc4zGR+nfDoAYdO2TPg0BpP3138y0pl+AO4bxLvAlnlXZr4340N+MzjTU0e8PeLvkV6e6lJXIOo02aX8OA0/ELMM9EqTANdKGuQiQt823bNLZvroWW94Wpbh9K7eZdaPzB7JbdQZBGwzS/abomYeGdD3WUnpekOyY6T75usm7OZsc+KbOWz2VpvNmUxm1fJwnxE18ttn2w060ZzUERBZUE/aojMdFMR+6r3XWOib8PrVa7x5+xb/8l9+FW/evMU/++c/in5lbLeo/mkFLivwMz79Ck+XCz79/vt4errg0596H6+eVrx69aS6QTYkJwtyJUAtNkX2U8syYO2yPUC2201m3t1sj0wpq9W+SCwaT7oSRBc2KbNyfFb25klv0rnaXAt67Q3XAObVqNMOmGs9ABgkpxOqfDSyeq3/YZKj9JN3LRvt3GM/Id1X5XKRjevXdcG2bXizLrjdbrg+X30/s+vWfUakBBFt+a4GJdIpeI0XMHOaVag4gRnI4ybxhJWpDroB3eCYwLoMrFMZEyxLJr+RGb/2mfD3G+NPPUk8K+9aZxNmvN4mNbYGfwFmcjF9afZIehCH/NRKo2TPr4/JlroAEuT6njcM2Votz4S1UoKXpjuXZZH9/Z6esKwrLhfZfLqpIx39KrNFAWBtyzB+GqV9+FqSIZcLoxVJbzWfIZZba0Eqn52rumRxHFTxaFpulfZ+C/I4jUXyf5Hy+AsLkkXQRweJH+IcK89LK/etomKgPoKPmgt/QWmU+KPIj8j3dWKWIGT0F2mW0rLREOzIEZ1h+41WzPQy9B0Bj1LEO6Z7mLNiqXt47qV1nt23xGi+uwMXXVk0dFxJoCywotxvbdF+leu3281ncvkYHQbFuBB38Ecq3dWfxUnvZh8SwCw4m3lVZ3FleuZxgXdLH7V/76UaZGaWoGJPM00ztqCD8ZUDvh8HyZ/4QNc9P3EWMZxF5t1ImJMzMFdEOvygkfNHkez8V6/N8s3KOKvj7kyFgzIeV0YxwyuUeB1oo1M5lgPYW+Us/Pm31IK5YSzBLgfmJXHJd9RPto7AHMZhM+eJfOynfR+8USl6uJaTrgwBndHBGN8IZWMUvkfqyx0NvMvjpJmg76jZl7svtszYSrz2QIC1YbKxqrWFaARFO+Oizx+Og+QgWp2Z9tlYs3ooDfThfqmLjr6PymPgg90/eztTy8mBnDNDdi8QNRvHs3qPAm617Npf2ambteWRwH7VbZWWDLbM4NdA1Sx4ddS+HPiueXK7hnuSIf1Icr8ryIgfZYQZ2FJgBgyZvaLAi0g2Oe20gTeb7SPOclNZbIvMIKHWnA8W9JL6ZEZS5m9N2bZFY+AIkm2XJxL9JvvVYQD5kT83m+9jdn1mHGPwpYB5uwALdpmDGvGHYKzcIy+4dzkMhCH7aT09XfAzGuH161doRHjz5g1ut47b1nHbSJzCRnj9asVlbfjU+69xWRe8fvWEdV3w+ukJyypLlmzWBNmBJLnl2qbOlb9ZAEYdqSFB5XlGD8L3ua1gCcYMLJUnmz5DGG0poaVxerLfXv7mutIrj/q078d368YbSu2XDfV757Q3Wf2UryQGxPtPAlQhZAT2zecvlxWL7sUmQV/Gcrth611PKWXcZFMvDXAA1Lvu4xPYIpxYaYcFM0SMwzZMGJSCdnHD7BcbXmR9e80y4+YzBPySLksUOwP/YwP+eatlhtzYkkam0G+NCsYg7Deoh45bHcPvFEE4Nvc/SYn3P2nwZ9EY+NIGfErV0Dd1YGHoDIK+G5AeVLL999JyxGWNZYku0yqngheWwK0JH7as1zDCh2wnow8n+IeQ5JRcVgkkG28nzDnHfRq8aRHKkk9OQiby0dFBTPD/KowhwvBK0L4a/shdYyorqS5yXowFUyrD+TP8CD5NMVht/4QPsxRVih4XWJn6Kjt8jgejUWaTch9Zsu3fMilSn+owL3aGPWZNqPl4l9d5iRPfA3P8V4NZuwDTCf7Mz9VyX5qOaE4luxqbscbbH8Cs0KQvsKn5wS/M0EN8Om63q84UlnxLa6DGe1OV7LfzZqCCd3KR89lMpgksSF/2fTHrg5qO7p33SRq475CO8P1pnbT/QdWmYa4/495LiHw86yc60DWflRUp69EaB4jglueeOnZxdCzJm/g7Az6D/DZx3GdO6rkyGNHMowpo5vTP6soOrdUGA4VJ+XL5nSg4rN/o39MxPjs4ZWFB9u2bKOv6m+v3WpaW0e2YdoSBy8AnX9NWKEg+mN2FdG9gRDQ1wI6BJ33D1BqQHPSZUriXQowraEwGYgBMpfxaD5Efv1uDXLNELVB9vHEPXrY6ywoBDr2fchBkRhP2fZ5BYW4Tj5kclHG6lgod8g1AawK6Zlx4NMiV23APbOzaeEc+zgJC98qXNy9t1wab7l3TvXrOgnBHfKqb8dZ8Z8E1uz6j1Z6dBfNycCcC5tMeLhWK02sy3iFgB53dSSYC2rIC6HIy120D3wjoNnNAnFsLtw9jxPjOFugyp+jgFfyOIXBBZd2dnDHqr9YaOrGcOmQukw2kjDxV7+2WTE14RBS89T3+COKYUUNrC5Yl28XJxrn6b9gFPTlpu+kYFed1ff2E99t7IGp479UrvHnzBsy6bxXkFLV1XfH61StcLhe8fvWky5O0bwDQEPYI4CyXOO4MS+XCJg+YIekwIgW/2rTOVb+b3s1jpSUbYvREjXXc+h5CTsf+FFi7R957YYMPbctgKtg38mcE5rKgWp65HTNQgLyDvQVw+nazBoNo3P9xWWwJ2QW9rwNf37y94rZtuF5llheuuvfKZvsmkdZnZWsQFeyLfC1Q6L1tMs3Rz94fxrgkG7bShbUeZpZlkiyHCnyOGZ/rEuy+9Y4/cwH+RagWrVvNsHGWDWrpygEaHQMyHrqo0Pg9jdHo3ZCrdwqC/XgnGj4wI1LG0vhIA+EX34CfvUUekcm+xw7J3hMRLpcLXr16NQm0FxxEuvcbi/6oY4mc/cdowJxvQGaK2dLFHFjOn04T2X5diZ40VqXWalsTCcOMEeFfjw3i9nSQHDSBVWZAco3kaDmEoZLEr/gS+xnWmwNjdnxy3lY8UsoZuM2cNXSi2dovnzKGMuZIL8DMxyiYKPsAe/r74ENWtyQfwjG2M9bQj30bLcs+aLRnfCl3zw+YBbKO8py9lK24LWO2e+XP6nssQFb4s3Ouoo9zcb3LASdtabo9gepj7rheJcB1fX7rpzgTyenY0ScxxursyYzJd1KYrottfUTV1skzc4w86+csk2f8fNdg5FF6vP/8ieK3hU7atyuuUxjcu/TE9/tjIqdPdKArjMGMSaHwRMi55M2dYYoXw72qmEgdjiFAMhHS7ETNTsDI+WeOYC7L6BuW6E2Uz5EimjnSNd8ueFCA/Pg5PH2nzrbj4TylciZtyrX4CWCPKv5ilXIwLPy2CpL2Aa8h32inSks4AKrVcUKqc7oaX/v8GJXXbAQckZf73Zy4mjecKP2sx+Ia/VlhnrXL6jCHRfPTpA8tjcZIkhnAASipQ4jcrvQcFf573ZXEPdW7NDMQR2PwKNj1LumjGLqsu2rfV9ru1WN5s+6bvUSo9Vm+I7B5j0dnwbfMZ/sbNkd3IJtGB9kYmdCi/5jTYFdtyZRZpubTpRqoyYbozAx0Qt9uehS2bJzte8UsTWdBLaDe0Vr0wdIWddBnVI0Ejjo7jz+SpVnGZ/tu3jx49Jl6Hl8E1GXpWWaU32gk+oAcxiID+wAqlBwS0zWqa0XtQI6aEMeMmvAGXfZ1gm5UvzTC69dP+NxnP6vBhEVPUVuw6gyOxSecmnMce52Znu82U4k3/VTdl48XF4UdS+QhfbPqjBEJ6siLlK3vZ5vs+ymbM+FvDailHkyBEnswy3rOIU+J3CP4CsA2wGYf93vT4z+8YimrkW5MDwJaT/2UbIyrU4rlewpomTkC0sXpWxrpflshB0SEjRnb7YKtdzypE3O76kwvPUkL0BlmMNuU5JEiuGELMLcumfIBEE4S98FeDHZCL9gdmbEWs6wIDd/FjG/bZMnchwD+6gq8TXw1kbAu9DFhLCfW34IniEiuZWzhpnQvX9/QgV98owHgdwA/uDL+2UczMx85xQmome7ahvj97Tfg2zrjGzbt00FPK58Ua0rgSGZtmWO7rhc8XS6af2/TTfarDRRZT9gv2Y5qX5otn3XHTfuuxQynjsAZOfBkM3534CrR1RSTYpChoKGzLBFqRG6DNNOUu64nbGwe8j+jpD1a3IlS4qHd53TdrxkPy/Va+76vaMTwln8OJ1Fb7vSkMiwoPnUPtYhYegXM9hwqENWvVef8OGXsor8nGNLsS34puSvpxN4cBa4+apoF5B7CjQM+GC7H/SyKahfklmFFuM29bTds2002n79t6F0i460tMj4aoXMEQr0a8w+qH1D4Gy9G2feb9HYmjJk4Y9k/VqxfaZuV+UgXH9Exe+k9C4zuKmwPvojdU4K9ljIaH8t3lj7RgS541Nt+G8QRZRQgz+EXYoPWIyM7meIrV31AzQJaNeW3RzMHr6aZY5Zpq2XMFNYjzuFRZDgCEQVIe92ZFn9qeN6LIONN/J7TV9qT788MdMqz42ZFjrm+5OA6rdpWExl/k66iEnshBL+GZQSZVFPVeZdbFrA6XD9KMwuZvg99fF7SPpBwlhcYDP9ReZxmyewBRnT63hlIvJs8O9SphiaXQaksJnI6TFZqkCvEMmaJiYMwCVhloFOMT/Ej5u1O5ef08rcg+3QGEHL59XtNR2/rztIs+H6oKw6er595Gd4sT66ntmcWaBv3NDrRZel37mN7adB7j2BXeFDm6cIdX702Hyfioex0pt2hcCps77im8tu3m+zZZXzpDeu6RhAKALXm+4pke9J176fdmOOgw3g+2kioA1WC+R740gwMQA4j1H1ccl9lIJqQqAf1sNOdrmuczco371cCYMtWOfb74jjFEaTBLu0L7vCARmsLlrbi6Rt+hvbGEqdTktW9OSBmPRnRajbHE1v3mduWF2w6JzGQoy29M5ZVnV1tbzd5s2WqMwyQfo63lIfKtTC9xf5S/pGXz8BBu2+Oy9o/buZDxsyhtu4ERkDv9tSe8/uMpkthrW5DYNKb2jcmTg0ekGIPLCsdzWTRTsE2nhHoacHKwLbIWFlak7f1bcH1dgNtN515qn284+cCIvayFRnCl5caOxPWs8CGtTt3TeoiMMueSiLj0moC8HNZ/rZNTmb8/wB+CqX1ZAdiKWRiNVkfku7lBfgJekbCkoixmWlZPH8GA/+rG3BJ1Hcw/lEjfJUiGNijmJ/AxKFiEfgJzNou44lc/8IG/Ku6556/SEhQCxQzp5ZV9t1a19X3xlqXFcuyxDgOMuADAIE5YCJPwNIWpae7Hatj2QJMtjSytaYrBroHsQxfui0j8lkoJvsxNuFttMCy66eRY7BAe+YFKQOLFUzfDeeOsj8z62bNMoIyKdyJTbX9fjnltXsnGCLjwPFGvFSY+7rFRtExVuGkRL1varBrmj94FT4OZTU5UnRwIExp1sH3PSEVy9xv3/G9R/K8NN0Lbk3bhMJTwPUr9Hs8O9q7BHiw9Y7b9Yrr7Yrr8/OANw2HORYo+INDYGC+xQynOjnFPt4LYtVg0T2eeF2ZvnItP/9owPPITziq+zgucT9lHR7tmNXj36Z5RvKSHnrAn7H0CQ90nSUFiS4E9fc+zQJC7qTYd97nP3NK8+c9xZKdvGzU8rMvVUBHgbhat3+ynYj+SD2VX/JMa6Eo8veRT/Z8WRp3j9ZS85QvzHtlxOG8MNsbtRZAgRUwJvArSjfepGVQMactDGYOmlmqsz2y2h7Qbqb9XdOknFmJnB18b0fIjTmpxt9WZN0DRkl22xLBAwbA2+Yb9A5jgsZglveT5clvB1KQSzBamv2V2jfrnQF4FWWd5cm66yVvXs4MeTUMZ0GpnMf5PilrNp7PynuJMZg9tyzLcL0C/Zm+a5O3Onvn4GVvfu71RdWdM106AwgOhkxnRGt2dQRASmUYiNWlecQWhBOn6Na3CBCQyPR6uYCxAk2W4z0/P6MzY9s6qG+gLk4TtQZS58lmCF23W7RxRqkKctW5xj87bcidKJ0BEfmr/GdQPwYL57ZItJo4htLmzfYjgm2yL3XIG9aQL+kPDTDZ/omUZlX0Dbe+oT8/ezDDAnSLLUdqC8AE9A1d3+CGfpP2yD4dBNCi+q9722+9o/cNfdv8xCbTfxKolJk1YDitW++gDtjyFSJgWcYNii1vllX7tLOB3TE8kL/MYeNH9PsBAHRdKjLoAcSZU6YXQ8eb7YuXWDN7sdPA+mEBLjP1Tbdc2zyLOivWJyB/KNtFk4PLugBY8HRZZbz0jtvthttNNhu2z80PAzCbq5qdkyPLDAtKGb/dFhENByt49klym+NtbqCF5ZAHlqWd38jA99w6boDODJTy/t8r8PfWqAOpHrFxupk96WwgyAyhz26EX3YjLFpt52ibwlW8Au3AfQPwlavM9GLI0sofeAJu86b9BKUYm59i4Jc/A68yr5nxM40neoq2nYjZdBwvS/MZG+t6QWsNa5rRxSxL8I03jutUZyxLcx3Nrr9ECDfenD7HQHlT+aR7lnWRoFSTvRSP7L35Eu6AlxEkh26Myxpbo5QvMJfPOEUK1ptt8PoRdKRxLLfH2Yxjn4z9kIxBwd8xqz87/VHnHtdTOkDCa5xgpQEfk9muQHp1XJ65R0f6F0Q+axKEmDk5Pm2UP+KmeJLg+iDQd/LPc7qtSC+9JP+ekOlLlQfTDK/O6Rxx6NGWEUdl+29m3xzepaps3O7f7DAKDdAubRWR7B3bJssVr7dnXK83f4nl+/Ipju19K0Eu4yP8mtAZOOleMj0Aw00WKecY2zLp4eUzuawvZ7GJo99xfcTFj8rEUfn3gpiV7nuy/rKU++Llkwl+GgS6qsM1uq45yGWflUlhCOw5JEXiuQYFO+aZC8IhxSlfVrrHnbd3KmuqiueIjiPHfDAsU17muvbX9nyh4XOkx4TW+iOMpBvnw5Zm+iZGC7mn93m8RQogegqgTN5R7XnKDjNqs+WnGsn85okp51darNyjPr1nTeu9WUBl1objEuXZk/KGepkP1ZjLNjAEqOyzBp52z1c6k2yafMom2uyg7l67hmDahPeuIQYnf6JQT/qktnE2zo2WdzF4M3pq+e8a2DpLOSiVZ0PN0kuC+9Vo3jPGj+SpfJ+BwiOdsSvL6s13J7rPoP4gz1q0LdsanZsGAgOrnNDYdIYRup3HKJsvW/6hHt3TL+a97NtshI7xjpghRihyMti/VBe75UmZom3+exhOOaCj7jlHERZcJGqqGvKSfNPRY62539g2JdcMBD1lSRsgVatu6LIDVwTpoZ86s4ds5oXRrTSrLbaTebNO5JkNMNrKGBxlD9Nkdef2mizdsxHBqwDZ3i1j5ydnIT3vAbbkvB0o0zDNPJBDVRZ8VjOPJsx4Ru4DDHre+pkoAolJKet93QqBGhrLzEhxYmx5iuxrR3qAQ++su75npu37Ls9Ss+BDt0YLoxHO19hgm8c18jbpm97xBOBnd5HRzibnwP/IjH/KTpbz1VRM6AxIIF476Bs78K03woq0LDX1U3yOOoCZ8Bk3osBrAr6BgavW+QbA88dvPnaJwXjFOaAlsvINzPjWDXgvLiduxwtJ22TPglyy0bwEuyLAlVZUdMbGPMqB40+zA4lXFDIRY7ryNAKju72/CADswIVoS9QdASkLrnhACEizG3WfrzZiaJsZxtDdC5P+H7GVVbfvVHNE9y8ws/ZNdBt9eUAPZUUet9Hldw167ejS+27nvZv2OO/lMEee5vQrNQC+FbPS5S+rc/vk7mCXbfyFP1Nq5dxOpWEHKfdKN5mFeWtOsNBHCXTZ87PvQuvetuXrs3KOymMbkzwXM7821J/0JEU5vW/618WG6xi2JcVVut36+I3xRd5Zkr6Z8HeGjfQB0xlC916u7vXXLGD1CNY/i03MfLJ7Zd31j4byAbwguDdlqevcYsRfmD7hga4KPh5hwEwx7J0C+czXzHhM3lik586Etwa1jiLizLF/zIyuPZ3nEf4ZDTP6Uq6D67X+8V4+zr7y8GwwOfZ6ZMCZ0VPafUZGIsqo7yXIklthAMOXQTUxbD6NPKPw+vCZmDH82PCsyAmhoQ98CSV/0o9FrvxeAuJEZW8GrScr+Vze7rcpT2vepB8G40aEZk6r3p8dvjApZPybJG+rH01VZv3pJ1seqXzXPnfuS/3e/zxxZK1+A2n2TAaQGA3uvokZBO1ncrxrMOrMyHxcAa5pECiVXWdiTQOYB7KTnz0KQN0LkB0Bu1rXLNhlv7dtG571+3Yt/RsjIknSbEylJ8DqWLEGT5BO1kIspb1cnoALoy2rT7sXeelyEIQurSRm8LJg2zZsXc5NpKYAG2lGkBIVx96Tz5RxvrYdynY91XvoVguisI+JOKGWWWZc2f0YCJLXNkHu6kB2FqePqKHzprTbDLNxOWvE00QHE8Wswud+BXPH7foswb62YCVxaiWm0XG9vsXSFjytr9EaZFmZDlZbYnTR8rZtA28d1+uz954dUjIGQc2mDJAb9rK+cQOYcbteQweS9nUa87uA3rAprkndXLbGIBLClrBbT2QZNZnL/QwAtKTxlccuZPaTBLGttNSvmnfrHdzngWSvxmV+1JG5ztZIYxYSdFzWxQM7UjOBdW+6fu1u2xjh/C9oOmOHsa4X9K3j6elJ9u+6bbjdbnjzNmb/2aw65gjWNbf1wjtryrII8Tok5NS1IchH3lvFDXY+SPsWbW8TGqxNzPg3mPGLnqMPzuZEZJO/ggFssnMdjY73S9I3MfB/eBvN+X+twH/34+4RiLz+ghvwr18TzSyHHrw+edKWIdssjXVdsSxN9+AbT1L0caCzNS9P64AZ8zJEe2Yh0jIXrBdhxNu3bxWPU6rDZloBWWayXVh0CaP50jn4T0Sqv9o4fpTsZbGxEHap2kof23l8oRd9U/dMzXjEZJmy4dp31S5ZO5K/Y5i76BNObci8mUHrHe5MZWQsFmU6y1MJ9miZgVqTgbczELd7pL643xd33zk4Lju3wX72szakNMNs9d55vR891b2oZxh1+t3NH4OJ0bvytpcXh7kuVa5mq23j+dvtCgC+V+aIORMO17+eg5lgzHY1cjEBp7GD8QVPTu/A0nuY+13LOwpsnT1j34/qn2HrXZwDoWMOarPSTuuKOiute5rvpU90oCsAIzCCEGCMku8dqpQTs4j6jvea5VGlM5ZVlfB9Jy4b4KOyqvE7E5h7UX5/NhmJWtzMqFRhHp3W6KMYEGEMKvC34EOubNaifW/tCIy8WTkZaCgOt99Lf410mcrE+NfrszxO/CT/QGU2uvo7AxttRDyd+7rI1dCH+jk8U+s9+O3fJgoz8yvvcUTIgS62Tp0+h+z0ZTqBQX6SAI1AqjwDQGa6zPhi5WYeWxsVoNl+EUfjIwMso3GOn84V9lmQ+eMOVJ2lWV2PAqJq6GZ5q56d6adqKO25Iz11xp979/Lf2ZsoH4r627NQyONcvrLznJ1pjiCTLrFjGx+I2V5tWVz3bduGbRNHmBJfDLR5QM5ldt8IE/URmAegy2mQyaHcsR27vPm+82hSDhiyL6a0e6CDI5Y99BfkhUPQ6vOWQKTLOqnp0iOlS3m5LIvO2JKZtUnLuB7pukF8326+TBFU6FBeZqfZadc+MD6LDuyjSuVUL0YZ9ZkpQyqgdAih0Oxj5Ld9USxDBjZNXs6S8sXHRdaz6RtzzHLL7bLeCT0JwGc1y8URcWFu5xJcyxbLZuXYfZspCGgggSKge7lcNBCygahh6+yb1fum8zxubUDe+fZb20vGx72ZHjkT5Pthk8C4cbxV14FO8pLovd49sMPQU47H4ndYjBKPGNInMuMnP0XT7zbDyMpcIHt5WWGf7Yxv20I/NQaoEVYSsWp5TE7MxdcJstG9FvHNDLw/MyvM+OwGfLpE9qqcjuyLgJ7M3mppNpfoA1uWDVTcN+5x5fsc+v6FgTEG3U26DQNL4DN0sAapEJ1TZTr+LIswhTm9DPZP0i6Y2FUVumy3pmNGGbaHdaG7Rl4mQRorHD5215Nzus8yaowjOyuknthsIThwPnMcmuFhiiG3js/Rxpin4GPIys0YoGKSCVmZV9ano08nYys39QyGzZo+2hm51k7493FizblffD9VWRx9v3mQa3cts1w73DCY9b+pKHtRSPr7tt3Qdfm6HQxDlIPIWigX3DPRs06PKAGv2LC+2eysK0YrlYm9z7czvnhxBzh6Vs7sWsW8R/W9q89gz47YJr5FsT6SPYdh5RoDGOtEem7UJy8U1U96oMtA9COtng3m3XByg7QDnszDjJka1cxl7yKc+rvua5I7ri4FskBRNkoxyysZrxOFV+k5G0xHgYeXpwSKD8B8pntQiDMkeVpLwsbJCZ05aZbHprI6mNEZXIs6m41aqiPPJJo25YQ+3gFdJWJnXPNm6Q6QalsNnGPS7zNDZcqx1o2RZ/n62AB1tpF4TYQ8a6sR+ewNApyHMkMi6hS+at3DSXfxdpuZ/dQiv31n3f/gaGu7PBhgp4ZYvtTOOrMoy7yBXecfkS8Tc3Cq3/sdQ1RpzYGcdwls1X4/G/8vDRbV5+q4qc+fBbrufZ89k+9vuh9VdhhmNM6en+nYqm8qIMtiR7RXfxUQe3s0szlN+RPq5MumyOnNoufpYL6hEfD61SswM5Z1kb2GtpvvyWVjbllWNOrAOs6i4gzhWHWOLm209lALvbbpW9BZH8x4zKl99f49oCXfHTFaTUaqUJ/HWbMglzitXHhrsyoufoIacNs2bD1Orfz0p94Hd8b1zU2rktlWrAEPgP0QgO1208DizWeJWJKTBVlniu5n7TDkhEDWKgAJnlUHaMZjYnmbvGm7lsP96kbHpxQmVGz5oBAD4xJ0a36IwIgbpkmfQ5F/k+XAKdFfDqKTt2IvdczSsNJPgC8xje1vyO0DeTnxlt1OAWUQGode2LzNdlLpogEPsUEMmXl2vd4AIp/h9Yyb7tVEHkTxQANKfxl/nQ8Hfkwy8ZInwn7szlnm/Th7zpwrqfuGNLQHenzLMDa6B1In6eX25cs34Bfe5FmTb2rAqkGeOJTCnMcx/b2F8F89hT76pVfg528lkzqSzX8cNiA5OqYHZYxeLvb55PvvWBGmK27bzXVHowXrcvGgmOGUQb9o8Hvrm+pUWVXx6ulpsCHZ+bKvds9PUmzNPLc0u1bam/WjvUwN25QOWTHbAgwnjWeZDcw7788ZLjH/xvYQZCagKw+GThq/Mz+GH3b1u46A68eP7mPMUrYv8ZJ9zHL8wmsMCFae5qD8bPLBzNd5AeW6JHvEOvdXpjySXvLMjC9n5eb8jwRhHrpvdkYVLjnvY4UTabD1zZuvi/2+3WC2wGZ4Wv7b9ep7+xHJC5EOxIsTJftoxpYF4wznbX1UaJR1QfpSZUiKPcZYQ5kTnH+WKlaztCxh92fBrrPv9/C65R/xjr0sqPSNKn68bxjxpel84k5Nn+hAV6QAEaNizveDocluTGxsnRnmkruz7EfR0Xy9CkIuNwv0bFnP4CDVFj8o/PeU5F5hwZnymF2bwr/j3F6m9AePzNaPfcUDBk2d6/yZKIamgMN63vansTw5cJNBgynSmA8wuJN+fdq+Amyz/AxNTe3yaegUbwaj4Tzkz89lKiwgwwCgyzkMaFiZQ9kTRzWGy0h7y9eNn0T+mekVh7QNwTnO9Zd2udPO7Ptu1VMSuTyTeeUgCsr7xJgaMPRWcvR/59hs2irLfBhpFlkIIBAgfAC/TnMQ06iBd4Ao6Y20SbSByqHfhtJTCQ8Ck2jSvIzZ59lzNe/MMI+n3syfz0bT/mY678i41pRPZDwKBGb9YAH5npxzIHom12eiLj9Z+4yB3mFvmn0pVC6NEdO3ABCajh9GB+HGqpdaAy3AegFupCcyguR0QS2TllXGCLMGghngWL5tDgUI4L6BW9MliWyiD7g7fpLUITLpsyViluzUvG3T2VF908KznlSadcYJNXEKBLzK2EiqL5XNsEk7syCr0W9jv2k+CZRJ/W0hHUubz+bpyife5LjGroOddInRQLnPjHKiXFYGzu3s2d5uhnaINjcirEsE44/AXoYwVQ+Y859n2eR+9RkrpqPcxmXHbW+957Jhui6/CNKADUM399fxAXHcbKPs7v00DKCxdGphoxMGkYq5XJJyAAEAAElEQVQYm8qwzskLDMesY8sCyZKfmLEQ4/WrC7atYVsXrIuc1vh8u6H3CKCO+s6+E5hDz/uQ5sw3CvvG4Vz7QSkIYXCJt1lVmpeT4N148cBL77Fpv1U98CvZOTm9L3IJ/8YAZG4aJVlnG7Mkdr4l+W5az6JtozRjqE8iXd/EwHf1KPObujwbLDXZb0giq3Ro32q77KTBprO3GjW0ZdFr5Laet46tj9i1gbC2VWSPNEgmYAHdDgcx3aI8Jj0EwTe4b1av7ZEVwYiBoamPPNClFZB3v46NMAAuE6ONmthSZ13Wg5T0lfGMVEd1hByYdMbYdV2gcsxgcGPHeOz+D3vRcsElOkhlVn2+D5Jl7EwBarQsnSXD+eVJlfAYh66v9Hd3DRWBR5ej1F7nO6W83naz7WNdDEz1kx2AME+5/0xnBB/3Lg6lz1xuth8ZX82c+lwnmzLx/s3t2z2b+4IolTfWde9FltPAooBCFxa6zsr1bipWUHGU2QzS8QSGHBLjeplkRryPpTboVDXwMjZAukdi0V00SMxIB6wZ1ha7X8Z0pV0fDPuSx+SYKnaeYeI5DgKy/Trz8R+5XmMVZ7Qe+h3ZH8s2KUoYMJ/54Mwch6rk+gCXp6iLVR8cjcd9+sQHumpn9J4ZxenzkSh1Vn657Ax0uDyzV0L5d55hMAuuxBHotBPmeIP0WMBqdu2eMNvnUOfBC+ZZ1VmYQ11gMgjmTo3ZYpvpM3ViZxWrkm7LeGqXfdbZQZ5HP/Mb/CMlcpTceEfLpuUMQVIET3Itwj4agnBG5ywICIop3Wx1FPka2prrm9xD+vTy8memNdHvbx1TfpMj7xPmqQwi9VO9nmkYbyUjk4x0lrMwluSO1ZEydF51jOe+Wzm054UFP3NQDCCdeZCJlX/cGVMDbKmz6YT8Rj+VaZsx0yzwicAXR8YGcx7O7h29Dcp5qyHmSb/WwH0uu+q3IyNqZdrYPKtn9hwQswpnZVc6w6ns2Lyvxv621Ihs9aGV6HtEAHB5C0PhFA/9m2dEbpCA8LWrA9eAtq5Y6QK0K7bthu12A3NHA6ORnDQEAMQdHZucvLfDnhaQYfRNN3vXDZzZUd1k6Umi3PU62XgatRN3mc3Ztw0dugGs65pky1oEnYSPgyrzPrHfbPt7mZ1sc7myQIVM+gkbKkFHwrKK/MgMttiTZ9dof5lUZSZsPusMPJOVIVdm2ND32aHMpQpabwTVkxZwmXTGQA12smWHEuRkMu1jx+gwh6G87DHaB32EvUMjARqTXXIdZo5YAwLLmBT4UkE9AYts/7LattCzscdZtAfEaPonp3F2c6M0yNVHJ0tpX1vD5fUFnVf0zrjdbti2jq+/fYtt2/D27bNc38ZZoOIoLVqMvT4SgvIMHe9pjtCgvRTz0cUjn0vD0yXCDQs6M65X0UfWxiNNbuIguqlijdkDCZ/ppTrhCs76yBt4ZzA+yIEKIsJnO+F/q/tuddZxk/C4dGtDa3HUpMlQ5837johAC2FpK54uT1jX1ffjkqpFxjedzcka0JVZXnrq4pICshyzxnmT/iZCmsWv+o1iWaQF2JYWL51rUMpFRnkmNiBUgelQ0h/VRu5sexCcwzwH8kPGQkl6mIkHFhJGAnXV/zHW7L4Fu2C8TTyzTx/nrlPi/qJHqQ6UkZWUdCEgNkfr5c7oG2D7nQ2K0n6mUrIvNn5aDZgEuchxHCVaOFWXnWdl/dQumtbcY4uoL5dnvmS2F6Y7Qy4ofaa2+CqlbgWNGEgKUwwjNsX/43gZYfSM7fRKijwZ3X2QvzPDNHgyPZRZ1qQyyHvIz6wc1ZGtyHkeLx6U7V2Xooudb21BQ2A+44nLqG2kqTzYGLLHJJIEKVH5fMzckiz72VbNAtKDj2X6TV9ynmHyGUbOqwQsj9VteY5wu9N9krLPlsutzz7qFwPDaNg/l/RP7VuQHC6T6z4P4L0kzPUJD3QZsLIUewaJEbJ1unlTRnsTXfuAHSXZb1YlbG9CEFOIJ+lIqMwAG72zzxy1zcKXg25HQauZMBw5kvbMjF6v02Yp7Nq3L3tU3EiAfeYwh0Jz++t6LYBtpdpBZG5fBgonbazBGje9ide1Lsm3t3aHw4rK/TujLwemdnXTOIPAaC5V7U09jdS5sk6CnnnBSLIzUWiD0SA6lvs8kAYAdDAnYKf4Rl7Y863yYtZWGzu9+5HeQ9EgsbGIN8XCY6WjY1i2Opy+meUxjbHgoYJDVdz57U6eXTF16AjhXdTONXyGUP77oOl9AzS7PgtE1TTTJUdGcJbnSAc98mymsea7Z2hn9djvo+DdIzTM7msrHqLtXjkBeBF93YAFC2z5mQCsBuiUeTv8gShsi4gNl4MnwikJoEzgZfEhZ2N1aDtMjjHq5GanFWrSgEm1YaG3QpYIuqQSLDPn0kZG05cEGRDpWPCxgyB5NwvaID+z+nw2882Q70H/EO02l7VWWMx5uFftsDYmL/Q2O5c4mPombCYgAc4Z/sjf4/boSM1syVGg9yxofDR27NPom9lMC/5zZ3QSfWyeBCGWzUbwM5UxM3AY5YG2HnKQ62fT7QSb0xiOOIDGuiRSAlTruqItDGoNW++4XC64bRuuz7GEdbNgAY19uMOL9u/QJ+yYdMbvGYYTX2y06BKAYZGLQZ7D5LYmz7UWwZmQ5yhb6twHUsVxrNey3E0MWHpWDg9YhqXaAA8b/g/BZdJgAeWZT/GSaMWqeTQvNZ8l2Psmwb9N2rguCxbdjF7kbvP67C/bEQtcBfYk5WGaze9ts43mjcZ8oiLUl1Bd2tlP1KZhTMPLsIvDzJSKX3cyjV2eIzsTKoYcG3G5T1auntib9Z5hYSR+gRmcxn/ey4wA/wSgr2rmacDRCScCguFlpmfXmYLlpZ7ZxpFTEB1kp+aW67ovYD60Y8A9pjNTFM0CKPm02JGxRv6M/6PutLGZx1rIy0hL9Z3G4jmN29GOOyYf2LrnkhM0+ezAvj+V8BqQ4lqGtXfAGiUvAstnX2DqI5PMwASzL+cmwOXUV+Uwo28bNg1wD0ttd0x8HC963xkfDtqUX2bMkvtv2eeCbu9iL38O7LKNsYylKr3178zHn9FfMe6jz1U6qj2b0iuZ79Z3FjM5bd+DfkFOn+hAlxkswJRMCLo5AvFn/LG3k7kvcuflGtSgcb8zdPZ05bRbHlfyZIEZBTnrqL3wz4JVs7yPOoyh1PyKXt/na3UWCwxUHZaegMZ4ZwgsVFrOCR6+D8UWPrshVQJsfwShLNo9BCqG8oamDDiwOmt7bVnKqNbQm7BjdGpOAT4TsnbpACyZezjbAWsAQZZXQXE1grlsM8TyGUZoB2BOaDzq8SPFmQHhzEjkwKUDboaA0wZQJ5+BYM7JMEacFeTERT9EsMt++3VbNpLlKTPLiE/X835u7uxnGaY9HzI9j1ybOanVITv6nOmrWV0zPTWrz+4d6bVdcDED8QfadpS30jVz8M/05CMAIOc9pJ8wBG+S5QIIWJqcvMV+QpiCXpu9YGCTzVkkD3QxWDa9dgcU2Ew/tnBNHPQ7TVKOy7UBdwALyxK5vOGzAVEG0HgZgLm338aetdfGn6vZNEuSgIbmeRo3cV6Y/ZnhjWCLMZd5zumz68mGu/7x8ZUCjf6cOQC7Lp30MeA4AdlmZ8fX+GG0R4+LjDTYgThHtjt/j88gcgZk81g6wgb1pVsF0jt6ELot9yE65JTEzruTPT2Qw2YP4g39jKa9UQvrkOnTIvd8CYZB9h3T8bHIDLi2LOhdZo7ebhsaPeN6vQKwmT/d+yj6s2KhsC35t4+JolvPdJHJPpQvzV/A2Oxf4HYTbGWHN7QmwbtlXZwnwyl/Wq4EnpTSQxJegm4lLSlgIvXoaaUa6OpFFwh7Gqh1+IbsLehe2hJtV5Ls2a4N37ZN8zafvSV9vOB2u0ne6XJUYFlllnn2C3yWVtEppLNfZ5g967+uQZpq43P5VikhriOXWfiaMU3FbzVxvZexFKf5Tdle2/UBW0SAjIiGvVEtUDhzPAnwFzBCT9JVdyi2wKQtCW1DW3M9tC9BaR7v0g5H+WW1lzuazMah9OFBOg92mf6uEI1THpOdsDvZZ61cC90BhL6ZqUeVN5P7YdyNn9n2R7Arllsaht/Zi4LZsrwM+VKr/Xq2P4X02Yxkuz7AZZ3JJS8kNp/5ncfKDB9Pk43rlJ8Sfdl+GE2cfntdKZ/fJ/Ky3DcZ+njCq1zPBA+f2fYzXDy7/2iQq2L0M4w7q++ROupzjwTjzmg5S5/oQJelDD6CP5TA25D7bjnBRHsTpsDjDoOPOmcAIiXf2ebJWWnWPFWojgDVPXpfMgAkHxCKuirr4zT4Uh5ANOChtOTMgTDndBjNd9rn+axy/25VGZhKS0M5ns+f+0blsg/JeCxpmx2c5HZEg0a6PmKVOWB0N5/KW5/w2+joUDm0vZlsqkJRYp5M9oDYn2useMg3SxXM7QIJTmMBMwUxuNNlDktyOn2M8Ah8HYzvMQrMYa7XBhqRaKREcxpTPovGaR31QE2PBmmO9MIjQZucd3+M86iL6nP7pV8FyJbnatmV/qMA1ywwd2a0nd9JR1d9egYczozvXPZhG+t4eb7Rt9mb1oB11aWV4oB3XUK3bV0cPiKs65MDQ+aObbuhswBDcyKWtrh+kep5B+8jyEOi23ymkWzoDcgGpxEg0o2gy8zq3bhpC4bEabzxXp53wUHwML7cRrZwUn28iRIyT39Xx/75UZ8aYGUN1vckh3nsG9i38jyYnrShqL4GZlvytndTzIaGPcygV1ovmx3PdAd2wH7HOx6fncnojO9VzuM5c9SkX3pxiuVNe+IZUh9NLM2gd00uYpuhqDHRZLP2e+9qM1IwJ3pFaO66+17CLYA4Uqvu+bSQfL+sK246q+t2g8xQ4wgwhRtEQ99b2da7eZaTBZsHa+AqP9MF513ug7VddAmvvcip/Sib88d+iPDZEKY7rV+GJa2+lxOhiOTdxMyuD+yAgL7lRZDRhjzTTJYejth1aYtuIC2HdljAa3B6lCtv3771tgAAXZ+Fi2ovbaP5qrPjVMrgSSu0Wb+4PUsnNbYW+3RlezzgZ4QsND1MY5jFpZ2zG2tHPA6SptfBef4oBoyUr3nAq9ad2u7jC4ZnKDC41ZWwc9Y77MGRsq3DkOattDGS643ueEd0q0xxiGYHnFBwawhTWBMFzBk1oU849e1Bu8Instk52aa1lG/S/xmD8liH7BEIZLsRL1Tb8DtrPjsEw+zJGNTK8hEf1uViNpPOT5jc+sl8NZJM8xM0k+yFpppkwyhPFU/61hJ6cEzv3ZchL8mve0dpGejItObrjzxrfLLAcLYP5ssDGPpiV84EY9dU8fNuJcqkzKM9b981aDRLFQ8/Wmbex3e3KucOL16SPuGBLh4EyD4pKczsK++DQGOeXekOXA2MjXXl9FKns9Jsn3U5xqy+IwF9xJE9cvD8u2p2c3AwBA8t/8uCXIUCBKj3UkfHVAg9LCEbnpmhj3aEca6d7PC69kGf1EvFONbbXoe3xkrPle3bmOlWmgkYDEc2ArkdFSjN+DB8n8mn1uVAY1IOFce/0jzQ0cf1/YMzUNJgPI0GwJea0CQvZnKvhnboR4K8adWNaHdvXRkxqyT5nuas5qDY6awDxnQc+nOcvtc0YK0iP+oghh9iN3h8EMfj7+j6zGHOzzxioKpDPHOMj+rMTtoZjY8Y/aNnz3QjVVk5addR+bP890DDLnAA02MnoCA5q721tOn2Ld5opr1jiEM+DHQ5jb5HF4eeQbZu8G9+PdkA08nm+JHJZmtorMtJCKMu8bYWXqotruMiHJI9b0tGvzfo2sNhRr7EyMu24VV1mLd/Xn+YlhzsmOMLKy3Lh9ic4Ho4SeP3/Dx2DqQpn2O7tLPrwDD2at57+CXsLQGcDnKYLfVhhOOLAwB+4kLsxm6hgYjkYAMmO2MBPJ2fbDKhONGEVkoBQYMRrYEXqwNoegqfbLje9TCImV0NOWINuDBzwhBmYFLaObgZx2R7Le0cTgr0k0jlEAgLWHVm4Bb7PhqNs31Ps2MUc34eSQULZ53ek1wNcGu0D3bgAGD7iskpaUtrsTcW7fertfD8LW0xENiNYzw67m9DnigvAlczx2rUCaaP4mbGu+Lsd6ShPOpiouC/yUmy67tAVxkju14ZMI9k8N5TrGv7X+VsFUe7HeRxZtdRmuFP4xGXe+c2cI9hh8bcSV6iPWt+ygnlXs0gkxN6ANFUzr+5dZzWMjTraMnVHlfMAl3z8ql0YbI7jpRN16baBv2SX0aMGueQ92LQxktWW8IPcNxROHWA+aZVYbTF2bezGe05wLXz9bKdqnQc1Wn9lPyVI1y4K4/Zt26AyXsaex601fv2YXrqJRj7Hu/u5TmWyXk5+fORvPfyV6w/a5ct26zY+tE6Hkmf6ECXGfrjDhoZ1TsPxupd6rt3b1Z2jbqeTW23T9sTwMo8CnY9QtssTwWxoyBmvlkezz1VzjKIbT06D8/W56fK1RSDKY1MRSrIZ1xkkHLAG07E57XTAND1tLBZsNHIdMfLiyl0j7hZP45lKyvXyU1RmqnIQ/BTQdJZYh4NlO/pc5zfaAXUCOkzjCJDtRynK0xw5dmZMvVlNPUZy2/9ldpv13sGHAVM+nfbtwesG1Iq4EUTsA72+7kfe9p0l8GwLaBdNgjDM2dOnD+HJCs0vzb8jhaflj1LVb/Mgk21n/L4md2zz3yYxuFYunNtVsdRume4Z0GymW6d0TCr6yjfjG+PBhGcr3ahy95Vvrmzinh+al0WcJOjs2/PwFX3qOidsd02dNLNVBWot7aALm0/e6FvfuKbOebYBVJMZwTgd77qeFuXmUMqoDN8EQMy7GKbwQ1zOq476Vj787e7aD42q751PtvYs9MSkynyAAFizBt/98XNAiZGm5TXhrGRuJZkL2Swg1mca7kmhFW5OR5jNiMMwcvswKe+mclo3sf0aIwKNhpnZln9edaLOLfKZ9WXrceMIdHF8KBj5w4QkLfMdz1ZjFAOcgK6ZM8DKCpXmocXyAsRaqDeQb27brdCyeuDOm2I5XUML9PSssiMo85PYGasi5zmZ7MIttutOFxauvGJjG5I0M2vqwPaky8UkGLAILG8ToIki84yW5YVl8sK2y+KmXGz2Q19w3JtuLYNnaV9NtuKOg8y0FqL9tgMrBO1G6Y2d1bYBHdaKF6GHto+ZvB2w7KueO/9T2FtC5Z1kf229PAahhyewdxx2zaXb5PB916/NqPveaN4o8ECMamPiyyvy+p8qTTbxv52OIi310omazvQsAwsHHThaMYDDzmFextyih8Ua8SLN0MDqp+Lr7PTB0nvZv3ESdfO8PaOjB1ZeRCTv4A5LKO0NfAODe06lEtmMJ/JrgWcrfyWBXl4bFS5tmSfXI8wW/DrgJaixNQ0luZGkNV+x/WRompL1nX17zM/LNMe4xKwWWT2jC0VlnaNs9Vy4wIPBO3Zd9i13OSsYqGK9U7kye5bMN8OsrIZXM/Pz6KvVG4J0FMWE9EvTJzozlptCKJVeTE9nmWJUtC3tjEA1o7GI+y6D4LamNjb9iM7ntP8kJ3j5ystHzU4doSZ7XvWU4Yfjngwq6vObjtLn/BA1/0x5OZgMubCBo5GvApHjjAfdf1RBx0FqQ6pTUA/PXH32SMH8izNaR6d/Mjr33Z0mSLeC/b4TMIcqX0GYnOJpe6xsBFk2aaEVUHz0awFrYcDmFsb7iYrzEHMiGZ2isHKdrD0+DTRQ2UYGcbrpgSOSM8O2Oz5s2cfoHdK40iA0+H0WP4kGBGcIgW0YYA8yJX61mrMRmEg3G1vCipjnue4PbFvkdAq1w5nU6T88jEC0WmgS0G0X58VnWiftvfk+o4HxSE/ksthrOW+KwaoGq6z8o4CaLXOqgcfDYbNUq7z0TGY88/o/ij07AnEECTw+oMQGSLc0JbFQTBYT6LjOh7gDszgQBGGzeDllgF7++5FDzYyB5/G/pn3lxClDqjXp+N3sI/exNTqytvygsX5VVVZcjKJPCCjd2KsDcxNxYrCOZFjtZG7vj+yy9bk/cwuuR8zgbKdrPXler1fjvTP4EzR7rfUe/9N+7xMocmCh+JHhl4YwWc4jBEgGARv1Htato2BIbg54LaMJ1QuSYJwuTVFnN1R4nTfsAMBYLKTtwjr0uRkTACd5EVZJ8JGBPL9p+AyODqM5HbC2Wt9nGWzjL9Flyi2FoGuZVllCXMJgsQSH+NFw20TXstywtAljnMo+sqc2JxslFQdYJ+yDMrwmDcr7CLSNe0gyv0FRmuLz+BatI0SZGGdhS2BYakzHBrXZ15HnpFVnXYLKCd7SJDN+4fN5YsdBnTJ4WwMRTtd7lyGvbkY9JR3sAxY1wEJY9egV6UndYwEFG2mOgzLkV+XPKFf743t6jNMcx/YOJ7dz/gs6fVaVua7Yz9OL2RzWf5s8CUCKLV80x6mUwE5oTVjCKRaqDxuT+/vRlv2fkbk5JKX0l80p7I0aKrX4+ADb8+RzRpSO+o2WNvF7owPhh2mcn1i70xeij3f07aXqqwf4mvCDqrDfD8u01nQ4A1NLF969l5y/ItRhHJgjgp9g39p9KbP+ryNd6jtiBZUsumh3y/FrUHpWEZOZ0GuWf763NHvWnbGPUf+yaNtOwvsnaVPdKBrn5IRGkB3FemDp3dIugD3E+ft7DMe3zt4VQjqMaNhxPed+0jQ6+jezthPjL4AhrnAM8fb5bPj0bNyH50iqS3+nTzrVAQNlT+bEYMEc0yJKV97JiKBpxrXnL1pM0BTVesOqBy2ItLUYEzaHMAp8r5cyb08zUbJDg4kHg75mM1LBJLzYqBlplS9X6mMM1OGmp9tbxGEkcn5GpG/Fa4zEwbFaCdCYT4OBY/OjREjjVFquzy7Z6oznWRtF9TK+U7SR5GAWRDqKHCV752VB8QbYvs+zBbAXBfWgEjVi7M9BY6erW2rdR3R/YgRryDjkTZUWu+myYDLQMzBlMkeZCNoXJ5wvV6xbTfcnp91XzzZj+ayrmg2U0IGkc9mcdqEQJd5GxXmE2PMiXVdQBQzQ3Zjx8obmlX6nqABOdaqbZ+gcBAGc7vjT9zsqhfcWdL6GyUNyuIcDjLvXmMqmHXhG5st6/vxkhgzA53W3qA/a/KaRufoeKgZb6oDdZB7Ip/3QOtL09D3DDC3FFxhbDQDodLeOMAm07mntWt5Yjc6ZCVgHgNqM5ptZk3eJ1lmmBk31tNIGwBa/DrD9BVjs/7tIbWvLq/ARN6u221x3XbzfWO0zTrLq3cJ5Kzr6k20Uwg3Tn2o6p+acoalDa9fv8ayLFgvq2y6viy+XOd228BbvPWWYPeCZXnyOq7XZ2zbhjdvn7H1Dbeb7NXXb6aPQ+aWJodLbA8YlZmDHScO6kzJJrig5X7SWZ9LmoW/NJnF1ZamG78HxgIBLKfEiFz12JNQsOhVNqFfV9+M3uiymWo2SAzfLssifc1dT7MUrNCSvGW7r3BkkCvBKHodeiIkypiqKpADaxAk4E5E8lKCNFCMd1iebyqh4gqrXOWdmbHYyhFgp4mOnFw4H87pysGHHISK+0YOB1O93FFnWzOIdU88jHw1HW+6u3Mf2z3Lq3rFsL9dJ93fD1Rxj+bjYG/+nOlpeV7uZX/N2n/AOew7cdIUklnZ8zLz72w786xhDLTJ/Rwk2MsAUU941Pgh/Zd9qwHD2x5LS9mHc2zMMC7rZ8Y4Xcfxm7dvsd1uuN1uaHrCagTFk9w+6BfNhovLpn1njvuc9jzL16099qn0g8fgci4HMNNSkNWDY3+GdysmrQGkeSzhsXT2TK7zLMCVv8/orfVlrJXzHvkmL/WHP/GBLlOc8j06uQaLWiPkl40hq3vwlXKNeU6cmX2dj+W5F/w4ckzvpbM8WbAqHaJ+s1LnQqMoaQFXArxqoCuDBgP/Iw/GfouajunNn174jDfjgzuHxvNU+w4DMxTOU/q9r788e9SQnSPr3tL4aUUWWdiZRDfcx1UOz0/KSzeHcvNbjmmAIv0+MnzOXPMLk5HgUUjCwCFkUjM6PTsjk9tl48nATZKFnWObnst97WSn/Lm/82yQnVHxRh6kYl0tf5apIeA1y59+51TH98z4HOmVqaM+MWCz4M7sOWA87Sob2xpYmhnmWdCk1nXUrlmd2fGd0XoEDh4xso+mM97X9sR1W9YmuhXjcBBwmtoojhsAW1KlAUZxDPPMnxChrJMNHBs9dbxlXS2gqfkbVc3h9EklnO4dYNDRjKS8vL9R9kbyN/r2b1KMg97W3DbTQWa8Jf02BbiusPYkUxA+ykXYyYaGNN1kYDgl2p3oPLS97Sy3OBcidPUMxLna5ErvHmMcAdA6bvL3aflZZhKvDF/lbRkyK00OXT5K31e+UrpnVmmnM0ln+BCARmCO2WMi/4yFN7UTTok7Sgy2RbG5S5RYtmLBJIHerqf0tr5JgIzkcBa6bXL4g5bT0yndzOK8+/J3igAMlReNy7oMywxba+78t9bBaDK2Sbnfu5y94H0gAvj0dEHvMnPKDq4IvJY7s/Zvmnk8DmWpL80+ZDDSCk23pzIbSmhf1sVnbRFp4Ev/g+LG6/WqzykeVL4vS9MDarrXaTpOgqmLbxC/6MbvtCwwh1MOzbBAl+gBmzG3TBxAD4QQBlnx/bzS5vQZByX2wPSB84gjkE+wPa0kr5zkTmB0v3doa7S/q34iMm0SKJFa85N5dzoiYceA92fLpkesmZ/xKyT1xxi258rg9/KKbrIsqtschSVzQER+EJA9NGAvG/P55Goj06uSjulGjjBcbULonB1WdV2JaYoxMV53ez2x83Oc4Tkq2xC2nMvvncmdJOM9Axh1bP3NTL5tyKy5Zj/t/qGPmRhCEyL9kAa9b9vQdJYl2dumQXpbgq1Yxw7l6PryYTYO6z51mR7Kn8aZ0g9ejjR4aLvRrppq50vVsZT9qT1J+/F5hOmPZea04w/teMXntbwj2z/j01E6ynPv2XttemmAy9InOtAVHelXipIeUXVr49R6e27O3P1GnlWjHDlvs+/1z66bAZ/TMb5VnkUyjxynWTpzFl3YpVYdmLzLY0bIgUfviadUBs2s3bn98M9kOu+n/GBqV37WFVVqV1w3ap3qMKgOZmg41WuHCdNzh+mlY7K0K+p5WVFhx3chOC1+/0bNrmdezZLtOSJAwk7ZQgCC7J1nurN8Gl2GKnN7kzN31LamxnE27hgqlzyu37Y8eemC79FRaK9LC2rwq6ZdMK1wkM2ZKrSEaJ0r94+a6rg/MlhHgaWcjozmkY7K+ulITx7ptBlN1nf5Wtah5lTZX3XmZ3XM6ssz1e4Z3yPazwIRA0pNoE9okOU7nGYo2P6SHcBCopvWywruDQ2E3jdcn58h+9t00Kan/+iJYTbTQuo3HeAUDbz0TAhd4TN5Bl6lRhVx4fLlkIPh3TgNRDrDLAVL7BqpsbBxWXmd7b7laSTBF52AEodXqK6xIBKm5UU7Z3IyOESZB4S53FlExQ3S7EWBfJmNraHOXbvn43MW2Kopn3ZVZ1QeYY+xXp0p0ZO+o9yg+wCWUr8MzHAnOITJAybQ/bHINrOl/BgA25My24j0R4Bv45NmnN10tiGRnVoqGTsDzHIS6u22yN4x7aob6sreUrLvnJTVDStp0KM1CWg9PT35LAWbgWEnfPrG7E0dWgbQFnT0kCtmdN5cT1EKjq3rKoG47YbbbcP1esX1dsNtO5gJs+uM+sUtvv5idzZz0Mh0yrLo/mKXC9ZlxeUpzVDrHbfnqwbgbj7GTf4ul4vwaJG96TLGtFlbzB2tbWDuMjvschG+JVrsdNjWFrcPxlebrQWMPsCoE0VmPNAFSjO5Jswa7JTt66lS5rgqBYJYgn42O9zw1LmtMX2SdVIyIybj6eTJqs+jbXpvYq8GH2XyjC+PjPCdj12XWRvLXs4E29p3ho9vzjTrPemHcbPqGohSNg+iS5TtiXz3xYDqyyDZld3QSGWfpcLGoXnmK2W6zwIW+3J2PTCUPZYxjtP987kM+Qz8ZbLfcNbg0XQlOzRpvKj/vYxlrGPBK2bRKc/Pz7jdbnh+fhb9oi8E7BOAb1C/nM0iy3RkmS31G01ZrndtfsC3zuVknpjc1SIqHr5vXx8LcmUajgJWFZPb52z8V3pndT/iN8zunem6e5j7JZgc+IQHuiJRGujlTuLHXjEcA8R9DaWwybOPMP9MKPaAdL9JbK07/65OXRXYCrzz/SFYpHXLpQxUq5CTgoZcbtRrb9zseyjTMlAA32MKXv8Is4zGRuIAttb2Sin/PusLgkbkKUAz6XcqMwP8Y/w9TW4X54PdYTSJw3jk0JtxcKDAaZaF8WYCRLRwBSFjXV6u5cl0YDZyktLMz5nhmDhdQGzUfGQ0rN3+l+/xOFOBUn777Uenl+c23sBdNrf2TYytb8tpSH66U6NYzmh/FtSisR+Z2felMYfI3ioOM6/0OXPInUcpny1f2MlLFt8fx+DXmaGqeYxfNf8MvM3K59SnBlyOyqq66CjlIFTVibmPa0DvkYDaLM+MnkeN+1F9ecxl20LqQHSwv50X4WH/0KNNdMPkBXQhMItzs20btv7swLFxAzMBuoFr01kd47R2Gvk04addD5ArVzpnHVT1+wi8c7DYT0St/ThzGEqQOfTBHMj5iNJ/hhxJL422TmZg1D5ybDHgCF16qY2333lJc5U9q9DGfpWfIyxQ7+fPimVm43T2ObIj6cS2X5pqQYKjgFmUKXy0/s+O14AjPL/xwGbBWN+qqKvz1VrTUwxV0Ozk2WSXyWxSEQU73MH0utHdt+hvAL60UXgh+9vwTWZSyWGiYUOb0s0aQO69y8wplplTz9cb3jw/O+5hbfLSO0BymMR6uUig63KJQBfDnTtAZ2slPrcmY31BjHOpcxP6+obWFtcJbYEGjBYPMt22BdfrVWdGGa6cLBOfAQLHIvqUnjq2rqsH70jHf5Yp6DhhdGwqq09PT9j6hmVbYsmh9o8sFSUALcmB9NF7r18DgOe37u6969LqcTsOu0dkfBgDciarPlOrNQ/ceAAO5O0KeU4zcAyb7cbwoBi9zKrv8olj95zYoYsSvIoxh5i5WssyzFTxvuZpk3xUKsr6f0Zh1Bl5B22abAMnGmpp9SVGpjNoZwz6A4CF3hTIyzNIulZlMfPB/ZUdGab9rSWxH9wuz6C7IlgqQ2Yf5Ig22TOjTqxw/TBl7On0xESE7BNnGmXmW+JNqGrtQ73EeZbdnqAcfKw4IUgaX55n3O++Ccdszb5t7t/ZuPXDKgo+KazYpRnGYoSP4tf0+3D6uzGr2HGy0xat7OQ7gKtsIR2CdiYHow9Sg1s1b7D2GMeb3a4BrPrso/rmLD0a9zjC0o+W8VGe+UQHuvZMqxZ6Llyh0+cAWsqeVGgK0X/On68gcBgoE8frzGlizjPQop6ZkNd6do5KGSSH5aCCWQDgwwFT6TKwGM7UfK2wGSowBUg1GpNS2znVgK8Nf+eU6cb4acGKNgOBli83xUiu6taK48yvUnfmSTYsVTEYP5zmfXtyvrgcIH0n0hXUlNRIpnp3k6lUHrHsTQIi2Jrg0ZiWYNdORvaBvsFkp/Y0ouFkl9wma5e95eGeZkhqP9UAiIBade4xGhkpTwNe2XMykETky0fs+YG5aiVnBuTR4MgO6H00O7Qvf2IgZgb0yEjmZ2YG7EjHVfBdHfxHjO6sPrtW5SrXdy8YdVRmpelMjz9Ku9c53pzSk4eQiUTXvYR8D5x1AXPDbdsky5Xgh20QAUweQIOXefyyx3VC+vOlc4lMHkRfQWL2hmYes17KLxd2vJuwMQe7dnp70j9sjnD4OAFqqz00O3SQaGgPok90Qxcvs4DHR+y7XTvLexSomo2Xma2f/bZ8dSaXL6srbYlg1xFdefwHv1wEFUNY3XZdltQZztnjCpE9myHFyDLlASjCTlcDapZYT3BkYOtd9nvsfdCvcTJpYJXrtgEpWCFtih8M0hcfTVYKsG7nAOC63UC0DDKxdfbZVpfLBU+vXsmMrnVVPrGc7OjBua4BPnl+WRcdk835zSVgRyCwzgQD6WmlLPuGtUagq9jJG8ueYWxNmumtmSpj4QcBMoOMCOsq+22tq55kGANc+Ql1ZIXfvgdZb7jh5jLUu/C79+hrkUGxhiDg1asntNY8INjTXpCAzlxtsRG3jSvhe8z0jf5U8XH5l/rA0p+BHQYmeH85TzDqnXMWzsf/ka0a0F4pcDf27W9it4b8OiAzJTnQtauKaBh5R1bO6Z/mUX1ygFMtj9QRM+hr+fotxoDpTjLbJkHjoDe9JM6BJBX+rIvAmadKy8gWmE4L1lQbGs0zvXcGC8b7JluJRY6fZw87N6Z82uONJEesfCYaOtVf8h7Zj4J1Tn3SCdlEEeTKNqbrkkU71TYHulrKF0FLyizIhA6BKCp5vXdTR5nMtiK7pr/NHzPW5We50FXLdzl0eTjuq6N+y/lmaedHTfDCmU440kn30hmNU0z2gja8lJZ76RMd6PIjrZHBFBCKsA6zzDA6+DxOVYhng/uITi/jAQEer/GunqNAQT46OAPYIyGyMgJs5OCRmgnPH+DDwAHRAoB9k9k4xnw/nd1AS7xlHVqMzP/oRk7elA4WXSqXFclRmvWsfbc3dbM0Cxq68WVMX4I+ksyx8zXqxejXtlhQ7yMlircUuzSxwg5mssOU6FsMvKtC7cBO5nLwqAKqmezWPEj88SOMi4GNR1mBdOgCk0MfA8t+qdtLlKfN3HKZKKDAg1sJoFXHPcvPuxiRj5oeCfRYinH8GA2zsmuw6ajO3K8V/Bzp16rD6qEaR3TfC0gZPVkfHk2PfzSAdlRPpmcAOIAO1qx3CUDszeMBAN0Q+qbOLjNAreHp9esYnzounq83gBkr5RkOXWaE0RioIXca9jbHHRbVHdwn7Tf+qTMyLhdJfEg6uIJ1AcQyvjwoU05Sm+mCDDir3pmlUQ3l54P/oSalfyzoZ7ztvcuyihNwNwO0Ne/Rs7M81qZHMUg9LfMIlB7VYW/vDSMEjePv82RlmQzZc4xtk8+ojyCnh4nM2dK/veOkEtlUVlJooJO+qOnWZx2kr6/YxhjZc5p02fDTZQVT9JctQaxBCCICrSItnSXo/Pq916C2wJxo9vYJwbKR/MXHWdfA29PTRevq6dSxG3pn3Larjltdprc0tEU2ZOdue3BJ0PB6vSrOaMpzuB6zzfWv15vwYNb3WfVMEgPgbUMnYL2sIBAuiyxPbAuVR9n+B3eZ1fUmzTSQANQC5lXlYXyB2QigZXVnVzaV11kVl1X3AFs1yBX6yXBnIz2ljZKs1Nb42DbDbnZ9xB2mn2eehaW4P0eXQSGczzIzVJ5i4pgZ+kIIQNrX04BZ1pnZziLkeITkBzbbyC7YtebRynAfwcbLVv2i3VH0ZJZTW9KvusODNiCf/WnL3MYmcaJf/jG7ZLN5bKZTagRcT0gpiZTRDtGQJ9uNQ3YeJwZw8szORpzkzXZ2FtDKsj1zFszn2gVgKfpuDKiFvffgSsITji99D8EIchERVp3FRUS+rDGfvtiIgJMDix5NRnvGmjYOLCDnPLD2Z5uM0Z8gAEwxO9LKMN8IqD72PuVgVMWJOR1h9NyfeUsks+GzZ2Y0WHqJH3KGh898hJ+I9IkOdB2NbgcxmoShZrAAM/4B2qEG4l7Z5zMcpKw5wLVnHo2e5gDeQEEakDWAtXMk6Jzelwnxvm7jYQ0w2Iyukcb8eewc2Z2sWGdvEwawYZ03a6Pe3915oOluPE151DdNHPkG4ndoPD69P4b7UerO6TkgdTDaIzkzYY7fxlNTwhjBFxdeDXUYWsx0p77w/j7oC1ieGV3p+yA3k76rQbjpSE3K3ctSQJQdlnqCohu9GSTORgjxaRtm52s7ehJ4mgZcMljLLTKcFV+m6V4QZ5Z31rbM+2FjaYzA5SUBnhowmd171Amv9d7Txx81nfF1CFCdtPGBSkYg6U00uYKOJ3WhBr0fM7wkW8OypLeQt5u/JWXdR0j29CJIxL7vlrx5G3h0Cnb3jayhKVy+c4BelFmSs5TVi+2RSArWiRC2e+QzO7F7Ogb6kmME8E7WMs32j6s0vcQp2JMD+rVl0+BWtRlB2HB9oH/SlDpWj0BxHV+PLG+sMn8s22mG36CHj7HGWFbWKWEKcv863TurBLWnSTYo35WN6rmRbGTt+o3Vbo3lpCYBYAnYmMOgYyd4Ng6JsIENy9KwgnSJfXMebXpgj7wYsn3QTNbk3qL7G4FN73Ydp139ekajDWgNDeEIdiK0pssZu85GSjJOFPtBkQa/XprMxhu2Zk7jjfKMwGT92EeZLuGRZ3vf0l5ZsRcZ4JPDHd+QOo7kgczxRVZriwbtTZag90QmFj2lTbrLxkuW1BQES50auaTlNSCQR1kSPUeIA0wqeeVaBot5rIf9Jy3PdJAp4yi76GQUPTCzQ9X+pmeiDYkc/3Lf3u9sNUYspJyM31z0V7Ezro935WaUpIxJAsqAb24/ITI1LJXt/kfmepKGgyFTbVH4RJjqtHnKEzMyf5yAwW7ubMSBTQkMPSMc2vxxpk/1KZ34WZCrPFODpx48K/ntN6tezUvjLY+/YLR82S4Zpj/q41SHNmTX9MgS42XmV/qYKLjX8FqmKz+b/RcAcZrnC7HzvkmP6W5KfLN0Vu8RbngkXnEvFpLpsetV7ma0f5zpEx3oWpbVN520Kd2D4NlbQNJ9CzwQg/QGLDN/oqzNsEO36StKIf+uYDEDxhqYyvlzygPdwM4+wPQYkLRIeL1en6k05UjwOFsrTw1Ppl0dEJseHnzYA+l9/WayxgGZ/2ZL56wvlwRGUQb2WWIHXqMxznw5cqJnjosROH+PF+UOxiAbElWqZiBOCPevxpfAm2OQYqC3POs0BHHyXLpnIGMoy5w8/d10HyGGgPlU1JAv0wKiYU+2XWtP0IH1P4pcNWpgYt83J/LWspGcgNgzp46T4VndYDlPpwbk7TimOoMH0GHOeoPsC3bTTXiHPX0gtHfdgckDdF3HsToHpu92PMVeH+3Zup/WXANcg3OZZnFk5+LIePp4LUtZ66zSnM502oz2vY4/NpaVxjqrJd+3N4Z1jyIAu/ZUumpbct574MKCJBkseXnpiwd51OmyZQfizGmdw76FKoFEoG1D2zoY5C9CNw1+kc5ay+32fiRxklvaoDbPFAYAXsSWdlsSlnWj8cB8EW2rtD3PzCUsa+zluJsR7M7d2GeDDJgzQqKjrD97qtNdV7YATbHRVsWg2nXZVdKhVQa9zC3OwLPgo+uCIgZZkmYSMrg8hBToofC77uCJrA9Mhuvs8myvb7eb57FldkNfM2NV3WfOye12Q2f2ZYF5/7zW8ml7GXyPs/EbkS7hs3bIP73flH/ZQdJu9mVqTZecKN+3rvryVjgcGMNwXsVxzIyuMtFdt+teVI3QObBGZ3O3R52p4Rmf4bcsF0D3gxS+ydizoJTjTgDbdnN6LuuCVzrDi1lmYG2943a9oW83bNtNxoUGemyjdamDVaelPto6tr6hbzdw37wfeBeO2CeHSmS8NGwtwbl1keA6kfYbM8B5hrUEqtb1YoWA2U6DvOJ2Ez63pkshNRAoz8eBN68ul6TDk04MKJrwan0hG7prUbnMTmkOmwCy95jQ6YDBcY49M/gLGT8lfJHTGAyZwZu932D+S35+aHMuD+TBC++4WoNtN6EPGt4cbFvFCAdlTRqILEupW0qgVPBaW6Ndhuv8Gc3sODT5EvJjDIB4Pk194OFIDwo/h27QsvLMVSJCW5eRRwDsJMPj/nwsuStRZ8f6ukn7GH8fJbOZ54P64DnXY4EnepKHwcZk7JNmCxFibzwGfA+8prbDTlR8fn6O5uh97/8sgwmjMvO4qucdmG4Hd+zaY7Skuutp4qL3C8/Sd8c8Jd9s9MzqBzDY2+xvHOHfXF5ONiuuzsKuNNR7g5+a6jqaIWb3avnVB815rG1n+P0IO8983HvpEx3oAtQIFz4R2fVqIMa8lZkGfqOT5fdPVjJwfxTkmgHbj1ZfVqSZd+Z8hIEfnQ4vwZ8xAMecB1Ntmz1zP0CVjZSB5qxgBgWVnvMBNSnLHCQGOxA9Cm5ZwWyheb80/CiGdd4fXBhx1mtH92aOsbX/TEYmBQFJ4bgzZ8+W5z1olsuuwMqcyJIvO2cVPOXfA9A7MAYPJ0NYqdyhPFslkPrdlThJH3Z05091Dqf15U/Ay5kF3h4JiFh5s+DOkfHKzttZ+v+T9/ew1izNWTB8Vc/M2vs+jzHISNiJITUWvAIiOwULB85wiMBCRJZBFiawLBHwb0QCAbaEECJDlkgBCQwCIYERlkkQSKQmwHYE5nnOvfeama43qJ+urumZtfZ5zPfp+O1z9r3Wmunpru6urrqqprv6zMnVy8zzuTGaJ2dBSkf9NirzmfE+m6cjBZrpfUaGjvr3TCk/Q+epQgfUWH6u3eEhuNEoFTQjLP5LBaUA0zyLgVubMybmttRoUMrombGIIC/IepUtnYSzLE1Ju7qRsVGHl52MRscti6MxGRmW/aqt/pnOoAwNsfHIej/OvfZs1AU2t63fmniL6w/6jvDCD1dHUWp6nZnaOuDjR/x6dT+XF2W96V+rhwZ5yXnh2I5osJpOyBhtvMNDDNw4PPYO/lRGMcQpJlHlUQrnoe2S8yIzmNtqXS9Myy7KqyByhx5RUadfA6XMMHcYAHM0E+TUPTHIhSQGdPtx7icxdqITugZHqmy1lP5qbQY3LmkH97QTBxufAU9McadHhtWUKucM2odHUG4GKpGdsmbB/G28QmZqMoXRtgKZQ74ZOomzDH9RM64jprWVYaWQh4+Atl83JXsfxv4xLBRx7aB3tOVh+zk1WXg2H81Z0n4HGNXV1W+hDoJ0REyv4/zLGG95xeHaECuNa3pwuy9XMB1c3vu1LAMAi5nu9DaRovmj4W+0Gt2KuXp/Txhz54uDdOoqC6+fMxRGHIM4ji1fkOuDbhrN9Q6zjbp+MO2OWcZY8yp/q9Dka9uK103NK+yb8sUxj8+508OEfJiL9vugLaONMtCXlk4PwRqlEfYL9tBpu0K9j7AwQv9FeT5qS1f+AIc/m1oZ7feVLZDvjeq8cqjFZzrbDX1bz2yWR/U9yvtM+lo7ukTh2ylSDaA3p4x1zJFhjKdtCbn067lwN3b9SEcfHWnH7yNASdS8sPHN1MiDmRk0n5j0DI2H3w7YbcL1E683FOPbpXPF2+5Lv8f+Rquu/2n1BYAQg+YCOU6bwt6g/AC4QPWghkkYRjAkH4EYHrzdmc49yZVrUzSjHojK2DrjxDPdAdJHDotBPQ951YR6WKXVKdzrp4f0asEdWHuUOqACALYqILWha432TXwzI+WwA15vQTCaRkKWiDDRBBAw6cpPO0UKgLwJDwHubY7kbViXACU2gAd5glLq5rrWY+2KK8+uVkrlFRz9KXup6jC38hzPv88UZqTZ8kRaz5xdI5qu+DYbspFmA1C5jDPQkB0eo/Y/8+apl4djR9voWeO50elweiHQCRjTyIqHCQwLgl39lDaCxrUhMehspcw0z6i14u2bv9nkGBWUaZI3qSo7eydE2wqU6Y8rd6TvCKCiRrfGrmJhdDOuz/q+OZyi4QPfuuj9Z3PEV9ZUX/GI1j1uhyted10/Tk0n5WQnZpltMZZl7Hn9NFaOjksO43c0gp7F5GPSr2V0Pz5HZ+GVLADaGMc5azppBI4Na+kVI3JwSqr9HbFFKy++RY+B8DUWHemoFFlN5M5QfftdasMHS5lhxjQQVn1pXJht31TfECwi36b822ho+NIcLsvthjJNWJabxqea8f5+x+f3d407U7GtdzAg84wKplniSs3T1NQAQ+mRlQ7v93fse8W+6Ra/UjAvC5ZS8IIbaq24v6+yMmzbsa1bNxZinJJv67tNk/adtKUQ4f39Lg5KRjitMmPRA3t4aoHbIacdbzssGHwL7C51brp9eltXTNOE5fai8mnqVk6x98MOMKNorJ55mjCFFaf9X8YFRl+/wsQcnqQ63h3rodk83FYtfVSpHRJgl/tuC3Nd6Yg4Mhu28r23769Sk2Myb5rx2DtgYp3ZKHfJbjQG+SH+V2qVIXPDx1NCWv1X/XOZf1mSSWAZ7GmeXQYBtno2rXJhNH9VpGnA1H0+dYgnpmpy60hT23UT7Z82zo9T1PPhe45/GTDi6LPLN7JlvLag1DIZMXvA4K4vTpg2rvoymqi047w6ebttw3EYkdC3K9gEz06cUR3pRNuOkojZmMG6swrcj2dT460MSs/HT1v1fuYQGuHFjCuvnFXDdqpcynw1KjemZ2OKX+10iNczHo5+jEzLR9JH8n+tHV1AFHb6tsiBU+zEcWe2PpZZ3/i5gZq+nGPd2XAbeW1zvSNaGk1jIHpmKNj3s9gbZ+WfJQJ0GerI+KRDnzble1Gm91GIgeKTEF0ftyEZKGwVnlnIRQFciPoYKvKljUfYnmOJ3agL7eB2rwGhZpCdmRgP+5eOXnzmsIaAj0tjo9Mp90/m8NP6OzRESR23PF/FwQWge0PKeiphZ/QjGENmLNlYRQWGxAtX9ETh/xVRmZrSYA1CGg3qAxg44pieT4BLOgy4xBaxWdLox87eRvpvNew6ciKoCHKjA3wpX19eX/7IYZN/jxTumaNq9PlRZTYqd1TnM8/E35mOzjCiZtzHzzOlH/tl9FxOntcG+KxPiPSNNiEvu3DDNQD8rr/JLQltoDizltvSbcFh6KoS13Vtm6LRuu/7wanqY0ltQtgKKiVd8fbZCxJ1INTq8vRgxCr97vjKY4mw4qb2str0lS1m6WKchLpb/lhu6xskXo+gF931rtsSfxF60mW1kNSbVwqcWSBWXbw/WCeW+zD1/UMjSa9lx/gI51wBb+lfaV+jwV4qxjaPZEQbDyKSsaUQCL8q32sQ75EctM95tm0fI1AveGLC3MtNAMSy0srbY21GC3BuPGRb60Cy5fPl5YZt3bFPO+7r7kZrpQreVu8LcWLZlh3hkUqEve4g7I5pXA/ayZRsjqYCzADpacPWtOaU4/DnLZYyyQzzltPqeTaRKHnYC2cpoUJWjrVDPEhxGQL2MlnjslYP1qi1rQYk6LbWznmm4TTIVn0q3cYvUmF3iiBpA4vF+Qovj8ENw3ZzIfACbMyZwSg+6/LMsT7sTIjWWSmD8nizkIPcSeXbfODkbEjY6KCjAo7qbBUioNbuha/JulHbR8nK7OoyTN9da5gZ1Mo03OXOLgol64DJC77QAaEsskFn9q3LpDpI9IkV2fBVp676HkZ8YZ+dbxy6pqU2mL2uj7Iafv/Ye0DsjaY34+6KsxGIjNQx0bEu6j7aE4HvOynAohNdgnQ2UaKHQsdGGyXonELtxGaTlUMHSRychGfySfOx19KAinPK8hsfx+cDJs78S+F7piu2LfKi0UNx7sQ52uWK1Y1x4hVe5BPan8XCsbxHz+QXmVH/nznNznwXmcYzX8jzfoSPt/lr7+gCImhqoMpWQvkd7gGWC0q038x9edFDf9atj5xZMd9Zuhq0EdN0QF3T1QlhH0kGcrUmu5ropG6uS5+fl2dOrqgEImOftT9PIopv9FL5XRkaN6o3RNifMwFphiKBuhMrO8Vr8isLKjPOEOM7nAurDoQkQdkJx66O85SF8uW0fwK8mgEXFV8+cjqWF0vM2wSqziEOgqnLEwEYcIzBdtIGMzbs+c7oBBTTXAEEa04bJ/8exrx7E5vKsnnnDgYe80auKyqrg6Lo9O1xBQtI4nvVxNNXKdd1ZexelXFVZrw+modn36+uPZNGjhNLz+7bHynikTPno+Xksc33fQUqZ0OhfbgB5hfsS8tffTVzfPum8jFv6VH5XFAwffoE1reqDjyZAUjMOJnzOo+5xVWwlRWHtgejOgbsBnTOo21DjLRFZ5/JYSvTxwJtHrjjK/YVN4ekkuDONnNG1OB078apVjfWzPBuN1t53TOshkDMk++fJjOKjuI+O5FEv2YHWMMnh2KvaiU6rITJ9z+SH9yvdJJLR3lgn02FtPhwAyoDLdQ9Y7wXZe2OHWCgoqJw60hzINnzEtNwktVR++7xxGzbX+S1yOtgYJKJ2AIfQ3WVn7QpQdVRLfZdQa2MeVnwxcsN67Jh23YQvWPbK97vq6wkWOXFTikTlmXBTDMWi5E3EfZdHClb2RCxqMTVsrnT8G2Mo1htdeO+y3NcwVWcZ2Kssc4lmZv1afmbcCAAex0nTryqp0PK2E1Te2lQ9I98FTyBeQfz5GMkczzqFXY+mHSVmGFbkSFo5XbyofFNhPd2Z8jXLkuaDJLqha/iSzDHR1yPGIObhB726sE30QwRSs9QyEgGdxwrJEM6i5wwd5D6RMQHd2V4j8fVJiP6H6WICa1vrwxqCl+GWUwmWFFKMwHwrexCLal8Z9gL43YNT+DB0IRe1T6cH1r+Cf75aDo4zHqVP6z7+PlsXVGFmbzu8URXdVZGA9zTSwmbqwVUJfJsd7oi4DG7Hjk4cr00oidmybSn5zNOyTRb4liXYebwQvTUOcPibHNH2zW5A/1vxYyvPddfX50PY91n/Gw6J2PmjAnOcP+Hxvy3IH2tHV39lgj7FKAr/diUMdAAzlg4MGx6NCHQq59WVj+QX3XQotI9d/a0791bmUG6Ap+Z1nMFRC5o81JuUxxnIJzoiGR78BI/E9iPF3Gcpk6vtdHyhb5jCGCpUCBXip++QkjbtxzTjI33WK4YgMUBledRJd05NlKsr9TkoxB2egarAwf90PWRA7oAQOPznROoCd2mxzttd6TbeNO+a5n+JvBE+bkzKzlZbAw8LzNqKBd0nAdniiQnC0Zvzi4Hv0Td+HTgN3cuN0Mmrg6xrTPWeYWacdGKjYBbDXrjMY7bb5JR2M2Hniaj2/LYgRCjdMW/MU8EUxmYPZIdo+/52UfHJ4/oGZWTg96fPT96Ll4bLcMetWV0L8v4cxl9fOaMxk5GV9uGBSA6dZDmdTQKQjnxGigGig8r74C2FZiAZb7BVobs+w6GbC+N6zHi2oJYp63sikHrAXvpsuuqEj20AQhOAtL2taDkemA5KMaxASBn5cncsSD2pPdbzBt28cMacqxXM01HGR8dxkhP4+v7F+5MzvzMVtFJYmbU3QKgUzdmR7YhNANN7jf6rI29njWnkfzOJsURS4wcVldGWOT/0Vyw32ZMHprjeRq9kdLWttAmBF7n4o5Lfy7MacvHXGErN6ycWhlFjam26qeAGerkqhqgXYg1Y0VWgigtewURUOuOyoxNVygtS0GZCm432544+dzatuqB+K3N27piV4cas8WVmjBNMyQAux6SoAccbNvmup+KOLlKkWD0hV5cH+26amv3VYg6xlNxPgdI27zrfG3b191RGOL0DUwQmXom99LIdfhCZUspspVTDi6QnL6qnkhPhBRn9zxP0rdbcxa73CbS1W3FpIV8Vyxaufp2yM7hTRreQ5RvMFhjqxr+sL/cvnalCRLj4KaFxzHlmhA3zHy25muQmAezOfyi/pPy7/RIxIyZVsdvbK8D0Fb3jgA9riSepJqeC2Lau5OIWlx1iiMAbb/hHnMo9uVl3N2jJquLmqJwQakEBDlPYc4/aly8PRadUWZGGqnTa/3LqAHXUXthE22vUo4EXohwH9te3ms/UKPX8hp97dmeViD1QSCCgg3m7Yp1a+GGweLCAw9OfxIQPtc97nrq8gz5Nc8RNzaDnRVkRmyPzYkOR+GIkTl8H9kl8blse39Vp+gVDx3q53Y/8ka8lml7xpl2Xt+17XB17VEZGcd9pP++1o4uO6HJUm53dLK0vouMGhVbK6OPO9UD0JyeHdhRGgHSY9ljw+nK2fWRdACz3bfOeoAAqbPyKQDxI60iRFt5Y5CPJrBGijwJHOu7WDHzMYjiqY7qhPxxOehTxgI14OWGatceBAfMoeoAzOggtJ222C+BNkKoK4GZLoUyRqN3BZ5yPSZwzOxz4RMFUDj9rVOOuf/sWhLAzyYDcvajczim+nyMAkgW5dz318EZweFNrz5/pggcUFu9hrO6edC2SNqKwL5B6AcgtAfAQ3AQ88bvkYbs7Iopy5cjCDvWEZ0CozkU813RPQICz8i56OR6pr5s1J/N7dh3GZw8q3QzDbF/fevcSG54wf6PleD15RcRtiUHgcZYXwFhWmYFcGJWFI48H+vUL24/6IlD1BxcgBpKXLFb3A0RCrIKg5oejUZAmql9ldpEN9hctPdOn/4T4bNJ1xHfynWAKwFFHAPyAoxa3VnHivLq5HIus9Y+jlPTa63sxkMAdFtOEr1hTI/4pHd2oeOZzMcxjuUZtshy4Cx2Rtd3SCskYhPJVLHS2VcIDqvhAhIA0FZUk3ZKrL0E+o0XYowVQJ1d4HZssOb1rYVeZ5jrRZ1nlXWLKwOw+F3x9EiJx7UsC5Zl8bLf31fs+473+x1VTxG00xRte52sRCpYtI9tVcO27XLyaa247zuIgOV28/ZCV3n5iabbhp136UMGLBB+b7jYybgWJ89ksjjJamWNT+bau+eJ4YjH+23FDDwukfCZxdqSrU+s481Co8a9nOdZT5xsTjY3vmyFmvGvHR5A5PUB0wHj2zwznWrXujzWpwjzZdA+gsnFhHsjlkk4QwejlaB2hYnC0+TzI6wWC/e6F3EDDBavP6imb6+VYThCHbcPV4sH/Nldjlf7D29DkK7pWb3j/ZtlC3mnU3quV1Fxd0WUmlmGKp8F4jkTfZJO5SH1Nkyv5wCLKWjNMdl4zGtyuP2eplynzr6kB+NcbkMYhHJ4NqasP9H3/iGdjaNTl3UM4Cfx2vZuwydRph9tKleGXs6jZPbNVf5Yy5nN05UTbAHv6YwNnIDjb473BkSdYcmzdJXnI88/s+sh4v6zcrJtYekZJ9mVM2uUMgb/qL34tXZ0CaCjA4+1t/jkgkjymw42YcF+vYHRJrx6AH09yR/RORqUeFT7mPnGDPRRh0CmIX/P+fq6Iw1NicfHmiFyjONjRpH1e3wu9rsJmCgcTCj25oLdlrwTteftmov4YPTFxLAjuMNxpzHwY1ZEBB8nq9uvRyOG2glh2iNeoYBcVr3eYlbFduWeB/PwFJFW/xG0Wfut70u+FwyELPgolOn5uDkUT435pMTEkBsrAs8X6uBUTtfOyLNK3wj0edwWA44RfOSZa+NJLd7GSMBeOpOg/PCMFiZ0qxXcGDVeCQM/7GOto5BtkemPCx45nbzqwb2POssfKeRzh8LHnZffTnrGyT9q20f7IT6X+TAr/7O+JjOCOc4bCnMwyE31/ESH3rzMul0oyDDINLPDOKrzk8S5IQLe76vMn1IwLzdMyw1131D3im1bfTUIETD7wQwFdd9l1Rbrli0hyB1dnaHEkC1TdVPju7gjJQMokwH56Oqsox45ZHMaHXcdHgarY6I5n62/ayq7GRFXvGJDlmX5wcEen7HP0nIds6WXFEF+N8qafsrOrmPT5Yl4UIR9mrPpKsjsVAqKqSTlNTOnCghMBTRZhqY/jeDOeejtIgNerj/YDEhvadNPk67Ubs4uc+oAVGXlDwcdMJVJtII6I/dtw86M/b65/i3ThOV2w+unL0BUsO4tYDIV0tVRGypLMHMiwjzPmKZJTjRVWt7e3/H582ds2+66TfLKirBlmbEsM5h1K0+tvgJM5lfkO4BItu1NU/FnamVdjSn9Z6u95KWfzHPZ7gdd8WWrKhjbtqLWovVo4zO4Svw3vKmDPk8TlmXG6+uL632pa/eg/1wrdjC2TcqZ58nlkscpUwws/GV8bPSp3NOt1eLjM5mWtkZ3uDTwzaFZEcTGmZT5c7DNqSuQ+m96s5rcPjggOiIgeLraw1oOQT2+rS7tizN9k2nxoWX2Ie6MGv3dyStKjqILfcqDb49TPxIc/qXk+O+eCp1AAHwZLyIm1PkeZCPczmvYhZpQGcpkmbNsBdgHCCV0h0vdjr4rbHTsg+dxUV9+xM6E6EgzumznUilNnzKPsFh8EXauL/2phMG7T7eVGn113xU3VN+uGPV6fgn4VVPk1adKG9hUrbBez545uvriqGfcES2GDwbz9wpXxDpGmCdj7CtbYJQ/piuHVbYbD07N0Ffx2llduc2xH0Zljdrw/xlHl6SmDGLndHoMuSMBMyKsDOC4rM/KlNx67QmGHP0+E4JxK0hMUTA7GD8p+9j261g5I4dX7IlAxWVbR6l3bh1Xx8RaDJh0gmrUv9SrJAeQaVIhT45oOCbDqhfyfZ0U/0vK0fM7GoADkEhldKA0YcnBGnXTZqzdcd4vnZFtZWmfHARFLjsI7a491l/BAKm1+jaPUT9FOiOoepTOuKrp65CDudsXb0o1K83KtRGCExCD4JjAcS5dv886EpplRCO5rdTKq8GcV6JcSMbGUFa4OZnGf5D/SkHE+8+CjFPlflHHM+n/hiPsGUfWlQK+UvZW3uj6I3ry/AVw2A7dgUVWB0CQGyZDCsywKyo/24sdoDfbYDKsSCDwuosTayoTqBCmQtgBECSGEdACkVqgdyqlbX8051ttRqzJ3tRyoDKYKuKWw1G/RP026tczfr0am4Mz2PpVaWO2exxk4jW4uuIbMYbOHZ+H56j/Go2YlrUpmdwHzNxtG8oOwhGdI10c+/3s2fhbdgb2J90ijL+IMwP+rT1C79m25obFjJYSZHzjLdUvpaDYqbLeLsA438bWQ1uobmYwCjN2Io0rVX3+TUQo04zl9iKOJXXqbnoCIENXNO6ypTHGnIzxo7Z9lxNRuQVfBhEK7dqeuevnouUTV90u2Va+MTOmyRxXrY6q+SpDXtBpbB1mAqE2bKFjYavjRf/1MccOfqxm0dmk8a89W2gdGi9rsm2Gxk/Kukarfae80jDEGus+XTY2bOd9jqMulWfPdUlDWwG0eRtDHzA83EWUacc5cVaHpILusOeQTjCUDobJ2EgreTt7Wto1GhbdydQ4jw541/BPwHFEhz44tmR0L+iwYRob9rFuZdw2zt5mir1yqIuUSd02IAJxa49hR3s8lu906FwX+hqP5BO2c3sbf+R83I0RRVpDnTF/MmFS+fF345P2TJOVccV3J0bR5+2wSc5yJKT/tNvppYrJPovJxcwHOzc6TjrKM6EjHsyY9wN5R+lga0X91pGSdG6uQ/nObKHoJIvPxc+rFDHNCINkfd3jU+GNbwdjP2MrPHJMxZTbk+9d4cD4/Edth98Gjq6oqaVzYiwuZtLgmBHEjQ2foyJp94EG4EZGS0z52lmQ4zhYowE2mT9KZ0xif7HOPElyXc8yzFiYt+0U2cFVa7+iqz2bmbwHzUaXbUukkyD7jBBTyf4yhVEwh76tlfXUpgC40IAXUXtLZJVV7oOQd0K7MrKWyE6nXcGzAQs7OnzCOd4cttviX6jxGc9JM8PT3nbno5iVMHeKGXA2A8LoOMSqsTni3RpBR6CXEj8Zr4/aofeNfqMJiTetvz6aGmBjJ5CZu2DdUUCTA6w2P81plY1044+DQ3M3iw0dD7nTVHlMsjT+ujKEW0e3ORUN07hy4zAf4lz6NlKOvTVS1u7A0bpG8boeGdXPKMwsJ2MZ27Z1ZZ8BgWfSgTcGKccAs3x2/Wz1XZQ5QyFPtv2X9X92XqtcsenKKxBQqAV2lmfhcxzdv+QxuCYijaFVUCaZc9NegV3fXLOsFJG6NkyTrCyxANyrr+CyFZ/Kiz4nGPu+AdBVPhfjHft6xB9nYOscMEawF+Ve65se5Pe81DnH5OLhXqZnKoQyLQca+spjuzFM0WjP7Wv9IOVt+45t3w9yIPfzSB705R15fDQHiQi8F+yFghyqTk/DWJa/BY02x0/fP7Hfe6OOXI8Q6r63lxQmQ1UvOL9RnkekKx9vqg+BypsfvsCAb6mbpsm3JS63G+Z5xqtuxbNDG/Z90xVYO97f3iWWlyyZxLwsmKcJt9sNX3zxBb7xjW/g7e0N9/sdX375Gdu24X5/BxHhvt4x6Ta+Mk2YSsHy6RMA4H27Y98r1nWVOrmiVgnyPk3NQTbptkbb/nq/37Gum49bjAMmL1JnTHr65LZKTLBCJFs9RyldHs0uIj3hWuXEel/9mo3dNE+YuHjw5+LX55CXwrhCYogRAYV1pVbBrKdSuhSL/H2wvweYd9iKjLhacXKHwQkLHMSM8v2oJCrKm+F0VaGrt1WONv2z25gGaoPoIO58Hj+hUw0nupyLcifhZ31q8PMot0jj5sVxa7L0oq1WXnYmcUO8LURJpoW6r702tNylz2twjPng7CQ9aOEZw78noxzHyVOPns1ubWWzz6W2IivyIXueaCsebS4ry9H7oe6GwM9IDTwQdLSNYORZc3Bt24Z1XWNn+BZiZllZa47vj6P73+KUxrXZM9LmrIMpd3rKn+dLm4bt+UdOnVF6xgkUSQGuyz/DBjlPpj3fN7vjWUdUxhoRw/Cgv0fPfgTL/zZwdAFRaSV7HhbQtTtBkYAY7HWoNC7SyMl0le/M2DoD/c+krBCzwXCW/8zZZfRE4R6VRwYSHSTohGz/+VxjnEiYsyoqXS9s0M/RkHyghg/3GG1szoxjArmheSA7CjK7H3AMp//GbQ8GXrrubX7QmR0owTkP5HTZPw94+rrg/J6sr4+7rMecmbcbqD0CrwMPD97QtR+moNA1XtbO0PHTlV4yUtX50M0/cJ/fcEOYLsNeGaLkUE+4ZnMzOwUORSbF9RGF4NWdyJacZ+RwOhvTR/U8qsuuP1Lc8ZkzhflMGc/0cy4r5/+ITE+Ft+8qrIw3s9PAtr51xp/LjQZqmbkLEM8mo5RdqRAKF/A0QU5ssy1huxi18nq8M6Ao/TVyQ14c+yf34aj/PuLk6vgoiU6ni7rbjVqNoRjLNhlzPnOyTMjAjlLePsQC0TlfGEDNho3Q1bAMWVyrAaiM/fcMmLVn4vfRXKoszvxjeY9XLsS+EezV8sS25mdEt1eI66AV2o19wlpx3ltgeBvTFiAeamhNcgIYyemL275j1hVFIHMgziAqKLX4brbKsn2Qa0UleWFUpuA8mxcsS3O8R3DkqyYLANZ4VP6CoIVIaNBIV2yZ81A83DDHlwXbN8dT6zsbP30qvMg7B70D40IvG9+avGFmXR23+4vJUsi3TSE48stELn+ik6unReSGES4OGKE767M8rzNmaPjx2C7r2SazqLvelz/AImz/NPnqz3iVA+dYSA3GjHTL8Amt3+RJ/O05pOZcwCMMkPFU+G0E5ZPkWs1j26bD0NTfEwckdc9GOv2es1B41ur0obB+7vnCfmQ8F3McHWXcyjZYnbDeR9PxWdNp4crQfhtggCA35cIRi0a7Vn5b7oZvGwF9XVdohZQHIp84D3B7aW7B5x9hpsqywhahjJyvq/+CtkfJn72wp5qYyPOZ/Lkmj1sHkz0TbLC+vFTPRb80Mp/H0B9NI0z7DO5+Nj3r4Iq0PFPmtzMHv9aOrr7zj0on5pP9zMbDTTA2kDUCWC2/lfNVO/sSmF+kR57WzKCPGDIbbyOjoiTaIvCOCqUp29EEiYoc3XOjtueRG4j63BAA4dSXBEYoXYv3wOwn+nQruOwvKkLmzonRlYPW7mrBWe3Ny6BP4ilPBz7QTjqM99V4Dtre3+ZOIGfarY96UKK0xu2CCAGBKcATGhiiyiMxT6Qn0u139I2OG09BSWZAPuL3U3M0dqMrdwNLvdLvwBDj4Jwc1VFjXAP/6B1eJK+Fu/5sjk1tIys9HYgepLQFzIylrsl8dIScpTMHziidyaHstHgk156p75GT7owOa/dlPLkBjWd1XMnUkePgkTMtO2N2rojS5jCW7cnOoKnMqOvq294L0BxYnRxsgNL4YVlubtLttWJjhlnuEgtowswTuFZs64pt27Ctmxg4PHle0vLj6poG81JgY+6dY7k/PqJTsyGVT9kEAJQiq7g51mn4QAyBWhlEqrtqM5ri/KR2OfGCGhIw/WByqoS6rkV3TqZHMxY58qrlB2S1QO3K6PohfB+tyLxy4EYZEnXdnlb6xvIafVEmRHrpkD+UMMBfbK5dHUvdllegeoiCHtfTOqk5cutecV8/t/J1vry8vKKUCfOyKF9C+XzFl19+xq4ypJSC+bZgmWe8vr76Cqy7nqz45WdZrbVvG7Z9R31/xzzPWJYFpchJjbPG79o2WRF2v9/bigdb6VRWWdl9W1BmCbgucbja1p/dV+pC+X7y+Uq3G+Z50dMlJc5l3avG0gOM9wka50qdcYXb+HwY1erkqHoS5KryaFInn9EncSWl7mmawAB2NMzRY81GZ1+XXg/YLOOVj6UmE/qDp55L0WjujP3+JkI2/93mrzl7H+3kkLbLfYKdi9ueQ1fuV+2RvoHkjouGVeDbAZskNdyeX7QIb7iTMl73KqIzurUUXg4dOKHJmBZbNdy9apD+23BfTN4ezs80vrNNADJlbRwQxuWkZhrJtZ7nz51c8qJJQhiY7TLi/f5liG0tz/g7UYE4D/rP8ydg/J54wVZt7roCdtO4g0A4CEKf77BAM7JbH1xS8fEU56v9PqvDrweaIv/SgL7GP8kRdpFG8/6ZdIYxv0pZ9vwIy3Y24cjOS+mrYLmrNKo7p4+c8P61dnQBZ4bLEWQ24NbePI4UkOWVz+fqy+nMcBo5u64Z58jEI6brjP5kCFzRd2UMtrxAD0Lbd1PI/WdTjnKSUVs5N6LBnvE3NYM3AVGVZEHSKV0DTjRwdAX04H2o1ll+49TqTRo40Z4JPBNeDtCoH6eDwooC357VdpiDLpacx7GBrcEEyM/E78mp5XWGz2cEmCvCIRiyJgaBavwaxsaFbngu19/1rzPj88LenGOdcyk0gsF+OEHM49tbqa2scTIKucOqozHhoGa06XwOdDgIG2liav2Q2+mrAwYKq2tz5peBLMsy5UxWTCfbiUdljO6dOeji99GYnynlUX1ncjIH7T6jNV/PsvcRyDiTxQZYDeRdgy69z/a9AcM477lWj8WT6xRZrEZRAJpsfKhlu3OHJjARJgsgywxwxbptmFROWnB7QqNL5gy3ea+6I7bvjK+udNVIr43Gr5URlsB3OLof61x2q7N9LyFP1rPdHPfiTddFDBGB/LGOmIIoTO3KvJzLHX+33yOddHU9pzPHmPVdKccx6enhUE7/bGtPT69jAjRe0hwuhwvJ9n9z9Abu6xzFMFxA1H77PcUr04SJGfCtf7Ilz5xN0zzL6YJKrMlAOwil1optFYdWNPKJ2nZDIvKTF/N2j33fNbaVlV8ajypN27Z7nTt2zRrHQFaS1VLBof64YsmNYOCgnz6aDHNZ+2bd4jx5YPmwrbkUGZ84l8P4RicWkTgmW3f0LzAIvSP6IEd0IpkDGRznT5uwwVQPrTKZG509rZ+B8Ai1n139fS+dznej6Ti3Go39fam4/W7yQFb7BcdbwHAd9Sf4kEPfxebxabu0XqT+t3lGNk4+4fteobYb5CBzvF+TswwBTz+ZPGdp5V3nbtgs1tmaID3TZHW8J+kJGNrV2XTS4NnIywj8og+QgF+ntwDdqfMHKHmGOYj6uMeXJI/x266rudzJFbCWp/gCJfH9EIfFZzMvI/Anc4eBDm0b0B3vR5vSy831PirHsgP9+MCG8THfjnB6xscx75UP4UpnP6IhPj8q52DHnsqIa5x8ZTePsN9Xceh97R1d4yTOFUumEGyfcwRlecqYAXAsMQj+ATj+MIVh8IaOEaeNDwzV2nRkevt8FJPnq9DfP9IcWCac22fbQy/XaKzMrK1F7lsATxp4av3JMOmjQDoshc/PxXYTYdg7breEvh3K3d5gsu9EdFzZZc+UHuyMDH43QBNJDiSCFhwBK8vX8WdWatQcV95XWREBfT8+ECwROgLQ1RKNJqZmVOXT0Cjwth1FnJ2YB9pGNCqdHxGE7uAMBnCFxTjrV5WVcBpU0TdmW91ACCdSpvEdOWWyceyrunQe+Cqw3GCdV1nYW59aOvRv6KMzJ9NTfZUUWnZ0ZRq6tg7SmTPs0dhFPoq0RRqznBydwOeroXTsPHD0g7pzuVHWjuT4EOhZO7Zx25tcO/KKXcsnGOY+KVMJcX2Ed5gZdate4MERqHNhKgXAhLnIaYvLPOPz5y9xf3/HbZnFgJ0mf8vNvLcVJMx+OlopExhi3F4N66h/zgCUXR/FvWz9L0YyfIyaCDPHgK3mQhDx0YiW36OyJceQb32uj3nbnj1LUYe2R/vy5J78brFIB2N5Mr+sPWdz9Oo5e9YM7WbgnWOq6JiLMbuO4x3bJ+229s0l5ieVhVqv8bmt6ILMk8oAqmzVNYdP0Zh00Lr2oKfKpPFA1UH69v4uK7A+f/Y2LMuCl5cXvLy8+NbEqUzidNp3bPuG9+3dt/HZqq5J43cBwO128xUPtsrL4oa9r3ehJayKWhbps23X4Pl4x74z9m1X+bFimmZM84yip0HaVsYybZ38k8D1DHB/uvGZs+uRGqVA6+12C44udXIVe/GoOqNMABGqmn5muBM1/NZ0acAeyhc09TKB4ifgLzmNoWyrFXe8PkBXzN5+l7AjfO1frI4mPEbGac4eOzmr4HNjss2Ndj863/rMRGGFqfVD+u2fI1wSUmfzhGc6xGkDiH5MHFOeYI2mq5WMQI9TMnjUXwQO0ukrI70sTnHqrg3tKOgLyyD/zWIoxTBdr1dyM1P3XiTvXX+GCOquDNF3MzaIGJ+SQ5N6hxWF58we6K6FfLEh+blRQ+1XNUf8uip+5iHGiv0cV3PGOffRlPnzmOHI+4epA3Tbcs8oyUH3r2jO8uKjTi6b751NNNDXB5svURDlykdpuIr/m/FXpm/kkBvh4NyOES2j9BGH19fc0dWDqh5AjZf1Nv3Zv3mN/Wlvv7tBA/wkIHse4bvVexYQNufNnsquVYPfVx7dWN9ZvbH+1v4jo/iKqKCIAAPVbXvF+aSKwJaGtB7b2JyLRcGmZkojjHbdAhiqZnBj067F503hBvB0Ceh17Nvbz/CGKvW3tFwVI8Pf7sY81g9TaSC7m+Ct2n5crI7Yh6YJrfzUl7aNqXMGBiF3AGveZm4AxS8FB6tet/Jq7j+nuf/ZGe8KWmPNeb6UUlogfH3eHArdWBqNtZ2CdQaqhKwGkGw8dt47jRbHbZomGc/wds/HRvFHfNOY54SVLW1xIgBSJ4XxjNGm953O+EzoS1s6b6dwOe3RoAmGIFFxI1Rwfm8s94n7YRzIE3tu33dvd/yM+WKeLJuyYhzRkxVqduiMFOdI4Wb6Yh7jrW3bHirOEa3M7AHwz/JfAQbgCDCN9wG4XLGMw/7WOeXAkeTtrhxaoaDZ5JnF2Yo0KB0TCioRPOYJE0ATUAi3l0+YphtqlX56v0ubJwuoD+HHiqqrTRg7M4C28qvJEfJdfkQAiBHXgIqftz3baQCCOjKqzpUmgz3oMQNUZZsUTa2NjMb7zAXALkZ33cHVTplNAgxZV4TfNp6Wb9/C9d5w8vFDTFEeQ1fJ2coXwBwS+aATEQns/7aObFifjN4oS0L/BQsmlNrYUMoJ8xYQiUWABXGOxVaW1XNE1k4ZY6KCgn7e9tgi6pXYooYjFHk03iFC1TJqJWxqdLb5oXmnBS+32YmyOVNZHGHbuvpca7GjCkoBPt1u4FoxE6FWCaxcasX2/gaqu25jlG2GSyHMNGOZCrapSDB5ruC64/7+JnTuK4o6x4iA2zJjngiVZ+y7zMW53lC5om4b9srY1rvzDJUJM4DpdpM4YrpybNs2oK7Y1w0wh58GwL4tssWrVo2tVhnLvogMKAzeK4odVkzmfKKOpwiEHcUjpIl0YJgf4HZb8KJ/sm1RXwpNLZYYBb4GgClwMPlfwldGgyxPka9sjjF53rZESjwwBqH2TKnlsMpAK7mT844z+tnQuqAhUMsXNInnMWeqz6aHMfja8x1W4lZXfLHVaAmJtQy7TMXHzLEjWZvbQ03SHoRKXzRshUzA4aV3qkjfNknm8jrM7dZg+x3q5padvKxYXsDejo16/dtaZRcpdIvxVeoHFTitqNi3batilBmtXyAHNwUsbndjv7q5YfosjYHZFybh8gD0jrvWdxnLtnYlQd8lbSt7053apkPlih1kFfFL1AP+4jqs3Kr77gdWAZDDboiazZzsnMhujuO8w3LL0c2BK5yWW23lWT2xveMCgp2R8o+eyivIHOWl6zXYhUapY/QEDJozqQYSehmQREhoZhjgIFOjLW91RDJLaXxkdAEctr8Hyn3+HhcFmY7PL2Lj/SvfSKuDDp/Zd/H/oa2LBjzbIEZH1xU/Z8EgA3w8oji+BTr6gft82RNqA5oNs2ecXVf1xM9c35n3fFTO0LiELYHHYWJY/vb2tqQnx7QewXRSBIgT78JRl/MERTMyxk3JHpwjJpwPR9C3PBLrom9TodLlcSHlrRQw2QRqc2oUjStgxx1HBxFbZyQBHwVtdIi1uscCMK+g6pIpnn5wh8I8KqCufKPbHAWhfnfKhN4jYMhrB963NoU6EL7ntykdf1Fz/ByUIfV8Fd9KyO3gdApK3YqOTk9AhXUwnByIhbeFViabpeakkK8Ms36y64479Lvdiyt7bEyKOk0BuHO1Oe+1FAfK9imxW5Bo6uqIlBpYSSuWxkbrsX+j0rPPkUMsfh8BmZGT/5FTCkBHo7dqIAfMKTcEdgMFm+tgbm8vc9kWM+yqrmZ46LMYtzGC/7xidyg32Rw77ooRAxdV/lPjF1Y/R1Da/kMhzMuEZQHe3j7rapQ7CMAyTShFVoGxrnDYWFZ2oTIKMRadG8L7UwNdZgCElke5RGpeo+uh5gAHw0+OlPJ0zHiS3rJ5rv+Jo0b71lZDMXwVJ3O47vMp6tHMl05oL/dzCvO6H6KMGZr+ZtYg6ia/OfExetNodM9B7xj9dzw40tEN8Brw1/s+FE0+S/gsqa8UgjgvZQWFnD6XDacI8psWNakY7eB1B6oFYg+6vBoJzNDIT8oPwm9LmXB7eUVgNjAz7uuKWnesuvpAMI/GlFpkC95yI6BWFDD2veBdV3zWteJeZcXWbdFVTPMssp8mTCRG8v1+x4aKVVdpMe+Y5xlTkZco8zwBELmw66EPNxTse8Ubf0bd7+6IA2QlWNHTIRmMlYB1ZaBC4oPtsk6qcAFNE4iKxCBj6Ompwk9LncFUXQ5QbTjJYgExEBwc8imnWwKFCYWq6/d5md3ZJas4ZXVcKQU2lYquLAXJuphiwxv1HXod5PxgulXxkawAV0wFffFq+bO8DDYBhzX8EW+OZ3bUF/1zsRrDPdnJZXW2LUvXukrme6K/O2UvhJboympzwTGuP6P9lvrWYSdC/1gPxhigRKk7Gw507GFtPoHrrZdiHeFW55Dqc3ubBp9MgxeUbG00HYa+b1rm1sYBnQ339M/trAb/qZ0mdTcpSod7tgKQu+tNP3UEjlLS8Ucs1WUd3jNtf8R7ct1ycdA9duq9L4JgORrEHGIWQxBqo/gihERjvNbZr/bnmBjD+2c2y6HxV9e8UPI8HK5RLhdnMiKUn+yjXL78zpi78Wrktdb2i10Lp22I8wCKeY68PHoJPLK5R7tDYtVyK3BzwscRQ+eyzuzBM2dXxuKP/Bs5fa0dXa2dvbPrKmXPZrsOhCkVlKRsKX5UdF6ZcmYsNdrPnV4h18HIGjFSvB/j9YzSpTe8Y3grV+iw+Gasmk1WivTBsJuh3d6c93VGYJ3lSQ88YgYHMbl/bNITdasZRn1twsD7cGAwm2BoTij9MAUVrjNxUmb6fBR69t3lkdBwCAyMJ1MSdh5ba5hV8lhNdJLPaVfauj36qtBiXS5odLUOmN2x5nVy72A447gGHLnbwkhAz+9xMoZngBCfylV4+945spgx2q9qTicziL0vEg+Iva/OZH1bzZV9fJui09+FUFBQuHg5w8DZaOX782jfo5PL81EDd14Wh7oTeuTKzQk3SGZwZqdbVoBZPo2cVlH22PbGKAPP5E8sKzqGvH3o+yw71/LnKI22EfbG/ricLJ8jHfE45Fh2XLWV57tdz30Syz+j5wyU5PYMn4UEwG+GWjM0DjrLCwHA+kabGfOyYJonTCvpaWsb6s7Yq7zFNYcfg11GMGQlIpGspCGqIE5x0rzeKC8BrvsAeBLcrFGnc42nuQEaaJu7P5FL4ZoG0patY+qw7F7eNGPTau77OBqGSM/26Yyv7PnI4zFvPm47jnM83KTvn67mwxWkeTjGHqNGODoSeRPmOqPvawCOD0i3sM3zbNWfYjXhhzBPCZhvNzCVFph925pBQM34NmOauekn0uDr0zR78HZxwjCmacK+i8Or1h37vmFd7yAifMfLC6YiNOfYWluVz/f67iuQSymYZqljXiQg/b7vWLdVg89X1L3iy299Kf2hDjLJv+icmVCKrFRalgW324J1bVsct33Dtq3apwXzvGCeF9dd6yb9c3+/y9woK6AxzCxQ/DxN4GnGXCbsZcdOjP4VWjI0idx4aluNCPM8YZkn3JYFy7JIUPyO+/SlMYljj4hkNRADxZzrnZABYohxg+NN9bctiB2tijn9NEjPXwKfJZkZMEbcrpQKbu2Pv1M/Ga3MuRe9WUOac0GGY63cKBvjLgvHranw+Gsoa2AvS8+cHC05TgkNJLT5GLFOte65dJz0bX0W8Nr4SX8N5FhXrIOhHle6jGoOrEZbx21J1vefxvvNCfixMBlPpSeKGsnqEVbJaSTfT7EYNDal4rcpxECE2gQZk2Vd1Dl+Ml+PVuLk+RnHEYllrvp8MJ9zy3tt3p473aUSny1Hx7e9UCOiLjaatUU+BnJE6zzTvUXDL/RcekwHKl1OtBffZzr+iofPMPvomYZLTfeXQ96zus7mUsZE2ck10gdn6Wvt6AIiaBpL0H5sTdBdObv636yALoPDUXpkgGRDZvQ5es4+R0ZRzgeMT2Mb5RsaU/6YOA/lGfttDqz+fssvn/Y713ekwVBJWNbaAawQFNP6R4VgR7fmN4OtprJyH1Zunu7TFPVgYi0Gy8FiUcQoGPCAl6FP/Y1NJ+NCG2LeOD44cjSFdsY+QHouks3aP7GvDgohXIs0usKJfZkMM6eDL+BOUHZnyccvKb3Y9tjWPK7R4dV9jnAStzJbuWlME7ENeKqjq1ghOvaBT2wuibKCA8QzZSPF9GOaeSaCzOb/SvPZaKD025o0MKi7NvjPazT6yMkFHE/uzON1aD+leRPG9YqG/PwZ0MvOqExLrv+sbfneqD9y3zzjTDhzPozoGvXfWXntfgNAMuC2cgvHvunmWpNhk8VC4lkN/011QtU3ubqixuQ0c5tXEmkbDKBo8Hzbplcir7KRml5KuGDTbVYwZ49GUFHZYW2Kjkb5Xt0hA370VpBANMYUsX/z41dj/Mz4j4DhiGdFD4SXLQOA33XmM1bUkeJInDXCnZGZXtP/LXaYbVtloBTMB3lz5GP/00DmIALNM5j67fj2Wag5V4WWhtWYbfs0gai6471ME4gZs/7e9x28736yIQGoy6y83JxSNgaVJdB7DCY/TROokDi7SgGSg4zZHF47ICQ5jdM8tzlDAJH8brsLGPf7LiehsvD8bDGwdAs7g7sVFswAV4kpJHPDVkGZY1Cdwq5OdP653mx8ZS8AhZWaLJOA85PGBisyX7jJFG2M7gAotoCnbVtuAw9z9nQzpEGj7keTgc6c6B4bzpuTuTfAPX7dSjcj40RWNOyBNE+O+cKvQZVtda9hSG/DATv0pcf+7hxTXltzco1e0EYaYqHxxcNRN6qcpcAfuc3dZ5/vOI7Hp+Vekl+kJRoG6uRP+9JkU3y+78OOv4J9mPOe2Wt9HeM2DL8+sCUzHutKHGCJM9x0hQ0yVnLeczyqZceV+KQO54jhRhiIejvFnz3BQZbX51CaP97DD/rt9G5sk/ULy0v6aLcMHTvpe66DT/L21R/vWFuv8GonUw4FnMgtk1ee7Tz+1UfujX7ntp1978k+vjRm5sML7vzMmSPsmfS1d3Rdpb6fr0HmKI368axzY2DiLGgyY9j3ETP1zNEbhiNmjOVFUG/AbFR3fPZoAMa6ei9q7BeinmHNMGjVSFlnhufDFIF7BC5hEh8EjAECa28CxdFJU8rUlHjSgVIPgUswUAnd1jRGPyZFg9zGgOW538/GIlTd99eJoPClwWeGUwQktbZVWmeCR4hq3wNN7jQN2zw5PTNsS8dTrX18Uk9Ht77JgG6LzDBiBBfNeI0rl8xRVDV2R3a8eOVnhRs/KJ+IAUatjtrqGLn4nA8iX3XjG66j7y8Hphqfxw85QK8gYl0NjKR2oG3FrVwbvWzg4gh+v0rKsmKo3IOcinlGTqhcrqUzh1QGezl/riPK1VxezHMlw5ox3a/uOstvRnF8fhQYPG5Fz/TEz0fOk9w3HF6ClbClFbBVsdflsZY1LwvmecY8T9i2Dev9Heu2436/Y1rk1LWXlxcpbdt7/cUWvwvY667zqzmR3bY5tuLQTx6rCdz1V2Xq9CGz8T77XA2SLPFRrM+cD21SxbZIHbvLiMu+SzwZxzDzvn23VVAjnnXe4TDdg2gxA7nV3fTAcFvEsQMa7aFHDs9RC4wfX7J6+7iAK3BfNzQni6wSmKIRZYVZ3+p1iXlF3ZbfYqf8zYuvjDLDQPqF/YCJve7Y77uuhmpOq3me/STFbduwrivWVU5Z/Na3voVCsrLKAq773zxj17hdtVZsFoj+/o55ltVcZhzOWv58W1D36uXb6jRpG2vg+Vfpk3nCXNpKqW3bMJUi9WybzJ9t01WM1R1J8zS748nikFW2VYu70roJv7IZ0kc5JV0cjL/KYGLwpHrZsQ98zslWTACo7nyEnbaoc6fuPf93vEb2T6AnzEOioL8Dszf937eh2C5XAW5AdJSd4KGRxI47JIjaqrKMSQ4pGZv9LZOD4WKYgyYLXD53K5EpF+bP233Hq1a/EpvtiOFrSYY/X2iAl/qsrjvYPJWnUP9hjz1MHMZdLZVjXw7rf1T3I73X64gr4//5NKD9I0+fOBke4YFscw5pT1jJQ1fYYVHhc9juPLftcr4W5ggN8ngbz9pixeAB6zlZCTOargl24dU4ep9AY1KmOqPdNtoCSUAXfzrWmbEfqPkS9m1rz1y1Dw2fme0baRvxhuOlFF4p2iojHjnHt0bJMe9TffsAO0d6ysXJ7zl97R1djWc7COYdPuYN6/i+nNy/nTDD44n0yOuYwe1zQvJ6AmYA/Ey6FIYcV4Qd31g/okHaIwXFNl73nhoJZ/2hQqPrr9GAjZqT+iU/QSCP22K/Afg1X2XzbStpPryRcOEehP1IIEUlYII2MnY0IK1fujKRRI8DHRwEoteZQWDs67N+p76XDorFxi/TY7/zuFpbYnsTDzhojdqO2vyKK7o6Ba//5beCPt6jORI1q/1mtDqAg9PozBETy3MjOdp7Ch77OTQiicZIoMMTxxV4eRA6OaVzgvC8ghs5dJ9xwly1baQgRw6ur5JG8nIEFJ8FsVcO7VGZMY3eZJ058yLtj3hjQKWV7kYgBWdOZIim8wJvGpuzxWEiTJgFjE2Tnx5HlQE7/Qt9nzJDAhg7uJQCLU81WUxnwL3XST7lU5+LYysBydzH0rndyym/F+ei/+j1mF33VZuZ0geA7Vj+MZ99Dsc645JoGBx4Tu6cGUj+XPrW+ix+slWC7hGO+Rr28rGtDHmHoQwVwK2VJQazyH3ZSkIeX8oaUqZJHEK2FVE/TbdYXczsh0xUZj218Bgs11aETcrDBKCuElx527ZhWIqpTODJ5uAOVty07xVE8gyF5woRMBXMaCu9/GVZrRrzpqKwjTOcTtve2GE9XVVReQezrKaKzjVpMzz+V5wD/ZYPnZCuXhs2jnzFzjvyF+dLxCUcHUpnqCnKtYFhFFmqsWngp0a5Y6b+qSbbDg61D6ZuS5bhUKMttSenkUw/syViWXT2h9QWw0vhOaC9iOvkbsIlhoHsXiYmY5RxMrCFhqUo8o3/c5lic87riT/tFQX3ty+qkjqS7iCTReMhjPPQ8Fh7ts1TGYaoIK/SIAMhhHDyWQTrW6MlPfKgmt5mGiXXnYEvvcpONjca2D4jptT8Z62N87Wrv1eyPe3PtDG14+zeh8o60c0u47L9Euyn0TWEa7meUTqUNcqbJoz3r9lfPvaZhOML3VhHvn/lOI39FJ+LIukME48w9SnGuUgfsQG+1o4uF+xp8DJoj6n1bzbgjtfjtWQXDsqVzIf4S9QHmM33RoZkD0KPdV0xoN2/+p6ZOV6rXB+cqCZvD8f3I0gbLe09A/4GegIQOM7SXnBbf3PvgY6n9skqlus0dvN4S9ubKtcKcABVoQ5BDsA5wDtztPjqFS8XPdiL9wJPPDONs9KhLCiIDuVweFa/dPmfTprXg40HPmiY7HF5LqitLZmmXCezr/qiEyPzkLiNdaSpm68UVuR1e/F7R5GtQnFnWg1xmCgoicEINnDf6OrJjNuRRs14prHj1Dm5rvJFxx0DRNdO9OzYibLwTFZdOZCMD0YrnezZDMDs80ymRnoeOZa+SvqIcj6Ax9RvucxR/1450Ub9mvM3IzDRnbC6yyqyE2OrO7AKEZbbDWXSY9tJYoDtLPG57qusRLlZm93QbuO75wNBkiyP83AEQu1kQAfben+P/YW+7K6x4b7RZDqMOhnWDG3pf6DWvXvG4xY+SMc2HPkz98Ww/a3AI5CGPYtuiJ9yQjO8vFgsA+oksVVEUTFKDhsC0+kes41ZeYcsJwACowUutmqjTmMGdhQwFd3iJ6uspOyp9VHpj7I3p5XF4FrXFe/3O/Z9x/3+DqKC2+2GSQO8T6Vgut1wWxYwV3zrN3fs24b73YLJM6Z58oDw8zTjZXoBAKwaQ0tifVW8vW3e57Yi7OX1FVOZ8PLy4vx/X+9+ciJXccSJU28POkRiHX7jiy/AzNh0Ndj72xu2bZPA+rvU+/r6imme8XK76ZwgrNsG8LuuOtvBewX7gSQSO8/Q7UE/qCyoVVZpaTQ8EBh1J+xT8TGnAj1oRweRjHkC/rRfYjXqxR7/IHpKyHjK5EGSdbqKkMlkiJ7aTYJRnT8Nr/qDre7RLIgzybY21ThHrbLRs0EGAaO51sv0vkHU8XVH68AAyXmKbis/YAzFrH56K8tfHu/80sxXlWPgFLOPB9u7c7vPfj6f2orcSMdlzQOZL/xuXTdyL2ju81udrJN85zZOKtXpio7PvpxU14DKjnToePq8E1ndHDNRynbmjNPi93VelNhvOgdMptpLpP7Z1MrQNuNRf+F0gSetTLcDBhhn8IDYA3H+HWTLgcCu/NivB9s26GKC9K3NdbJ2pbaDe9x8ZX9HJ6KXYfZrJ1OeSCYPwmNn2NLuRToi7rjCCUdHVmjL4d4Rp0c6RhhnhG1jmj/gvfpaO7pKwQEIy2fMlQfqOYYZ6qGkCCTf4/JGzH723Jmhcua8GpVt388YZeTAOhpRIqIelalPwxSHlDFs2slzwEe03oH2EyOXrfRIjNFP5Ma8OaOEiqTo7V5qjymNEoJN2Klio2ebw+yinVmYqeDr+IHIY2a5ArHx4qMLxIVyFvgDoUpGA44AajScGTRav0rxVfVl4uUwNrlOzzKqK4O+k+T8Se23lMnd/eiE6hxUOv5XjhTJSt1hBNGgtmvt7Wv7Hp0Mka5D+UQNSEaFgbaS55AS4Lk0ZBMei/ScOUmuFGXMl2m+eubMKRW3m8XyRgr4qs6rMXzUlmeTGdWjEyWBxl8xbqLR/wh8PAILV+0YPQtkXqQ09pHHjc97MOyOCgYqGJuuGKEyYV5uAOkWs1qxatyj2DcO6BDeynOikYyCsPok9peCUwHSQiCDJeaXbX30xnvDPa9v0aRjH7nxkYZS6B+Nl5w0x7W2I+dxnIPPOIotWXDzeGJn13+xr/K818YSDWSR6aCRfOD+y5Da0yb0fdOKbqthiHQlFpEAN9h2R1nNZEXEKmx10LK8gIo4mQqFrb/aFmboNkVGmbgz0GxFlPXPVooEs2dgXe/YN/ndHGUyJ8xBta0tthZvDOxy4ludqm+BFKefnD7atiW2l1zMjHVdhY6gDyZ1aMgYo+23w3HFlLVp0rAFrPQREdZ185eTXGUVGmnfsTqppjKBZtUrLLH2pN7qI35lf4pcZogEqABRcyrB+JB1y47QAXVMWfy8ovFLS1xxZM+3QQ8CR35YHfI9EKWWnJy/KF03luRaKFF/P+OiQTLOLioX/CXJUAc3nGYrB5vM13EjzafjkLEQZRqVD5gIxOQYEKHvojw8NDm17mDD8LX+Mxkb0WWHiTnJxY5/Bi/7KH5Y2XrtGTVsq0F7d9fp84/Gts/Dx/b4rxEuak97K5KeYAZGk6o5ELUXyIZxPAGvgkuYrDDdlX/n3mrktPnU9NtgToQyXS4F2XTSMfLV+P+RUcjHXrY50aX4+wQ/dXo3ltVVF8ZL+6qprZb7bG5QG7Cmn0/aaL0abVOLUXrWfxyePaOD07VjG615R31/ZiPk61d+h9EL42ds/yvb4YqWK9oepa+1o6u9tbHfH3p6cO1slAYKyOv8ijGo0IPreK3/3bfranCjEZhPeIvG4YjpjZa6x33XURD28Vzk00C9fJfn4rWW5zJFcPNE2876wAVJMpQBM9zgnSnA7XhMcSy/hoA2cay61VvlSM9hSTXS25GTxDgaMp33e9RWVTpRiPqgKfOMlMyVM+LpaRToGs6mbGxnoRhAmxjRY3ripz8XaTDgqIScOZbse27hoS9Sgwg6xzVb5epHbF/1VnPQpd+xbjNqaqDBHxvMU3OeprKzw8D5xmjUzwID6jg4Zw+0cZvTI6fM6C1MHnNTiCMnTzbgo4F/yZ8fE/SpLc2RcOacuno2pxxLK7YlP9+cKEdZfKb8R3X3TqHjc1dOwF5eOfMAnOIwhhyR14hkBWXlXXh2l9Un0zThZZnxik94f3/Huq745rf+D4gZxVfgtD6qyss9cG50NWBosjS1M8bKUYOeiEQ2kE3g3rFNIWZQNze8zZx4r9dvZmC1cZyU/oKK/TDGeZyecVzGfrK5cP3siC/tWkVyI/i3kozXVvaguCdSgcRLO8wTFZulEOZJ4KasBmhb/YLdBULxUxptK96nL76Bebkd5pg5lfZ9c94tu4zzVGU74zJJzCyL41VrxefPn7GuK97e3pz/LLaW5X399Aqu7HnrumK/Sz3rXZxWL68vmOcZLy8vLk9sZde2bR5TK8q2eZNTS42epdiJi8C9sse/sRheNiC+vTJus9x37Lcb3t/f8a4nLe77jv2+SneqY5FAuM3yfSoSP+82L9jWisqbG9hMYlBnE9YWAhEzSE8uLZATHCcq7sRx/cM6XWuFBcEnKnJQT6cL1UkYeOXAPMgyzqgjE05iqJ7kj87wLg0wVWDDLp9hExvHU8xP7UWkOwwcs5ZO1hTN1+8AOeo237Kr8tHlscu1JO+JBB9kDKTyrvljyPtl2JaEi8+TDfZ1Ou/n5ux6VqvH/F9lhTudfIfSc7x6vaL9OvHJ90ADAbIymfucT1XJaCyS9Za0Jb64ic3wl13Brst0sj4kGLW2VUZdGVety+SOcz18dmQHDHDQYZrHsqMxbXZDLDNcG5JwQn90esXU6ex4jcNp9jaPg26zfI7BvgLeleeMrMehEiLOPNjOA7v74PhMdXpbO3qu2/GcP2SkEx6nr7eja6AYcvsPNuypocRopwjGN7qhkwcBXPP3R+lKYD4qZ+SgyveuDJ+zMuKqAwPy4WlEgyE+ZwCpGRaxTut7OozJMHFSWYnmKBQQHB3u2PuoMBgZgQYYzJmABGhcWQQnQjCkYnmygkvye0DyzqgLbYzCIt4PeQrRQP32n7FtrM9SKMOUll0/CKJU56mzIX6n8EbuI2AgjSmVgvJEfQ5DzJi06wpo41iM3iZGmdEJUTN6GbK1JPRq5Wb8+vPG8gzZtqU2px1z3wURD+De347ysX+jg/QAzgldu9pcgGLN5CxLddtRpAeDOdRx5lgxoNc5XQcG/ZliGynKWEZ8PgacznmvZNyo3q6dg7ZHp1OkY0SnPTNyUF3RMzKKRv2UaXnUtuwkHNE9qrNAAzOHf+O6gsbnzX4xwKw/mmxRcKy2VYqjNOPl9RPAVQ1ecqeU5QlEiFhCA+YV7CtBDn3QGhVbKPqbZM2JObyIw1xsyBG++rKbVwBN7RARZuvnRhefWSB0nBN5fLrsJ2P1DJawPIVIVpFVNZqRaGPTZfkYbm1HB8TPjDDXtCDXd2gnIsa5o7rFnB0RFjBr3CxYfxh+0ENcijhMbNWXrawCSYyubd9RzKER5l4pBfOy+DZSrvK31U22Apa2DdDGwQKn79uGvVYJ7L7vuKv8mUrB7dacs8uyACQvAc1xxcy43+/YNqlnmiSfzZVpmlGmyeNlRSc7r7LNVZxdM5ZlBkicWFwKJmZ1yu3Yt923N9qYE5qDfZ5m8MIoVDToPOPOq46vjZzweKHjnw2bs3WbXPLDP1hxisyjylUD/u/a95PQRXrSZqFQc8QG1F4SWV4VIDKskRMDznO+MUwT7jrYJOS52c0m5uMqCuOl0Oo4L/IctpVdBzlmOsaxFQBUUAiFYHrbjFhm9jHwuq0sbtslW7vb/CJdTdGebytko5Mr//X9pvkjLrH6XHagT/4oBZ6xfGcIddDP3EY6whREm24kkpoQR7RVRiqTU8de6eoeux4LY9QDbLes2RHbvejucJ5dbzrWx7OB70B/oG9AdnzR0TBOk9GxzqNZYTxy/G16r7LN+fAXCDL6Xd8htrVvRF59lOdNtv8IuV/7e4BD2pZ/8IyLNCufOTb6IB9Gtk+z6SL/Hq/1zetlk4+1OQqDDMgO6xFdsf9cJub+6fT5eLz77I13HmFUKyPKw7G9IPfzIR5ndY/qOKN5hN+fTV9rR9dXSQai9BeACOTZvx8ET1A8ozLjp6Wv/hbAyj2v48zJdcVUZ0ZXZtgYa+nMSG1g1QCw/TXF8wRmt9IODY+POrgN4Nrux7e8UYCZ4I33MojJ1ZrhHwFJJjOCAXeyGQ0cynHayYODjpSAq+1oMKQ8IyejC2Q8SLEv7bn4GfIJvX3duazT1CnBBBy13JGyOwCxi/K7T4pv9dAZVXaxvfWNVSqo83Jw7Fvk1S2xn/ryvK5BWw5OtA4kKiDlVP4gdc6yMCdjucyMWqqDq/wc41oxnCsuY5We77MCu3JynV1/VnHlPh0pzxHvjOo4q++RrL5qx1X+R46L7KR65BR55MzK9eZtoMIsvexwEJxFI7f5FW1IhunIpicFWKlDmArKRHh5fQXXHfz25k4uL2sE3K103T4iKz7bXdJno2pmRXQi0swRRWAqbXUX2zZza3e/EcR+90Auz4nsLDqm7IQ846kz3R2vZVCZ65G/ggJG1RhFBUeR3azRcf2H3wGf20BFLDSVtPUM0n/yjkxPtfQlQNYG4RgJBt8MFAL5yXzTNHuAedtGaHmY4SucDjK2FEywuV6x8Qau0K18OzYCZt1aHON3AXKiJe07qpbN+45tXZ3maZpkBZSuwNr2DfM24/39Hdtu8btIHV2yWky2MU++TdFSPmVxt2FhSOyvYi/EzAFVUeuEO9/bCi873ZUIyyJOMo8xpqcziuPOtk6qfjHoBEKBbO+1VY3d3C8IxmxzKDXdK3/M0DhjVXYA7OL0mnQlngTijxOcm17SWH5tDJueGu3aOsMj0ZnT1XMQLKR+mObkGuVqYia6/UMpeW7nPEP9oKvdqJ2gCMBXb5hzuKqsIfQyp+URCqNhbCtYa5jfouN7emWOtPrNydj1Y8QlfNyqeJoyyHsijUTiMzrQqySnFAg4LsPZVEMi+EjQoybEvu3oQZbz3D6DDunujXS8/et9ygdyI4/2TeDR5ZTn/F4wm7oy5cVBdb6LtgrSmHXOrkQXiB6+BL+6y9YAK+cBpuradlL2kNe0Xd3cA46yYcAzZ/jTPu1u1TqiL4EBf8mfn4lOcW+Pg67hZMpUHPN4Vj79zPglY5Jor44cXbGcUZ2j9CxmfqasnL7mjq4PSNiPljyYT9lh9OyAPJPyIEcgEK/n/KN7kdbMvLHsIR3HksJnEw6Nx46gvafzuvRI70hvHgCJgoPDZA/CdzgBgnDyunKFCga7N/0UwUYDWId2xrwqXXPeh7hgAMQMnNj2hmO92vZHBjeCoantN4PjYPB/QID4c1purDPTd4CgCupxxo9PghBp1zGKQWs7dfk6vxUlx1fXpgDwvTG9khwaoThrTyjDnF3Wdur5xcqJfOj3BuWbQW90ndU76kwrz7bqcprTJTlqHzkm7XpJy7GtjJHsOnOUxfpivpGzYFTOWZln+R8BltHnwTAJ6Szw/SidlXFVd6y/W0UYnuvpSzI18GPmQbvv7EPtNLsyiVE+TXoEdt2xbWKQFzWsXl6/ALhi1VhMjVbArFoqBajsAaUBWS0it2N7+hcczTBgILWJ0zdm7lYrF9ZVRGQrS4JDTFeiiNMuz/GDNoIJeze9skH8CODzeGvvGUCM+fQ8Dth2Uuvbag6nDECD/KppdfrQiNMtaRReDJbg6BJ9Jy0vhQEuzmAGy2XoSOmyVSfNqWMnJ95usv1vsgizzrfA+10cOERRH07iwJpkJdQ0TwBPIGrbPcVBtOGuAcRdLunn7XYDM2NZZtlqqH/Msr2RiPDy8qLOpBvmWbY1llKwaVB7c0LZlsVpEtrEETXJYQ2l+MqueZ5bAHrWUyE/ywodWlpeorhaS/piL4S6bQDkubpX1LLJqZNlwnR7AYMxTwuqxurath3v9xX3VQLer9bO+x37uvX6IOqJdDEchgpAHHfrfcXnz5/BdQPvK+ZJ2r2oY9D1foevemzrK9VVB+a5HLhXjESYVIBjHoIaf9zn9xeWg/KeSZ2BGwz9Z8oji86vlDS+bwQSdOVpZed3b4tMLqE/dEhpndho4V5nC8nhdwVqqSgoIlszfuCmJ+Tnb71dFZ09vWwbydTRc/b7FOoe0iP5e3AQZafHCR06I/R75oqGL6MjgLo8CHo3XTin9vy3zRuX78p3ETNS/4hNSjYGouLYoOr26apB57Pt1FERYmhGqqKTyLfzXgxcJi+naF+4LZFtPxvvgBM+wsmc2voor/WHT+mB7s72lz3ruCzXH/JZqroi3tp66uyz8iJe6XhgjH9HmHKEy7P/48z+id+t/Gew8qicWNfI+fZs+lo7uvLEM37XX+fPcQOo/bXc+QpiP9Ch304aMdzIWMz5cxo5uTKDPOeoy8inObjkeSD381fwkcAB8SNqmA8CcWhQRGeNFRwmJjN3e6LTO8xIFsxhlY3/7rP3QvgzoQIEaXhoVzepYdBIUjwGfdAh5wENU/nWb5SuWznycS600o0BHj4Z+Jg3lReVwNmzcSzzG5asOPpn7aONkTuDqM0JO1Dgq8xxd4A6rjg6uRgM4ubU6vEJyalF1POLOx1GfHaBCCQQdx+U9JCS4nOHWrzGdMxzNnYnsiTft/6Kv88U65UTzfLk5x7lO6sv1vlMmXbf/k77eVDH2f1cxhndIwdbpP+pN1zRKCKAuDlULx7pvncqlgqACmZZXbDXZpyVaQZxxT5PkABArI4yi1DRADlF5W0gslZUIt1sKWA8x4Mhc3YhNoFTtgDqGaikjhD9lHawyoWw2qL7HPVMlKo0nAvPjM0jfotAL9fuhjwBXE1PBeOeu8wnNI5xs5WfnXB+M/WDy5KOnVSb5eU6REpPaYHmJ1sJpY4BPc22sp3OqY7KypBsVgZjClsgAYD9pEdpYIy3GeNcidPW8IesYNh0iyJRXP3FGnRenXFEsrVw31GrbBU0A7GUXcpSxxbS6aE2ppbf8EgpUletVYLOa0wuTOLUE+ZtKzQrS8ycReNfTZOdujd14ShYt2fu2y4HROgpkbWGU0JtwDh82IEG3Gch6Nw05x4BExh1nkBgFILTb4VR4D9zcvnUsx8XyfNFciN+SExsWu1pR1fEFgE7crreGfDA4aCfA98jTkF9HRexoBfE/lMynMSuCnNs5JjKssZ1rWEQPq7Wyjo6l9n3k37YdkWKaLWvc5RaXSZTQu8Mnjs6uvhw+maqwe2So8w8rspyGSE/LsoNfYljH7ZR5tZHbm+k1cCqNpr2UBwIJOwVdC2f00f+T7hG6QvzUceTFdyvxnLZpJ8HW8pIuhivjNXPks/RJ/o+alvub7a52jsBehpcdx35Z4jjBvZJ55yy8dWfpXt0jCef0fXezoTzjJao0v258LzRFm2vjKkf2f/P4Or8mbHCGU4f4dvszMplPUPzVfp6O7oMuQKQyfpQX7pg6wL/cRRKTWCRCnETrAZ6rhj3KWPjIuWyDYzFsi1PfINvwmmkGEYGUWQiKycKNXumVva+sv4YMSqRnaLU7zfvx2Q8OKQANQqQSENHT5zIoU2d1ziWHfsCTYgD6hgIcY1keTvDnVteZ6+oCsIb+NSm45ueJAhSGxtY7ye15S16EpM7q2Lf0Il3PwlGu+tbUils+2P2IMIO5jKt+ozTdSUEwd6n9rb2kTPOhHusx9phdD0ET4YcTu7HFSsdX2G8EsyeYf2vwzHM7dPK4B58xra5I9WQfbiXkYDRGU/0DDe9PgCNd31YY+FQu6iqMdcb8OaQi1tMqEjflBq3Axt2OM632F9ZqeU8Nuey7LJrJudyPTFlGX0lh68U7UjpDo35lM7kLhF1svfMuZHleDwNLsqlkUzLDsIYtD+ChCjPR05FNzIIshiKmsxyXhjIX5s7ZZoA1qX3e8W2vat8AuZlwXLTOEXM+Pz2BgJjmWbAtjlhB0PWd7FUKgZvIVnZpfHxmCu2fQczMJHQP4dT6qRNHXndOJ3xTrtvn6Xr62b8Z3nTT8ReTLEEuudyGOOYJ9NxlhfoY1zEZ+IWvGjMAwAXNZuqynVzKPJxTu7FeEfaahioa3ExOVi0vdI/vT5MxkM3KDbHxWFze13AlbEb32p+Nn6qDJ6axjL+eH39JE7UfUOtrCuidqzr5icl2smn86Sxq5YZ0yzb+rZtxa4rmcTxswOwZ6g9T7KaqtaK93fZMrhtUtf7+x3TVLqtgl988Q3pSw2Gv64r1nWVrY3qKHt/v2OeJ3z69EkC3t9uEsj+dsOm2xmFLon5RUQS5N3+lL4vPn2SebFXXU11l35YV3U6VUxl8i2JO0FWUuw7tvs73u+rn864bTve3zasaz3VmTYAnIdUVVhRvnp/e8O+3vH5m7Jt8+VlxqfXV3z69Am32w3zPGN+nTFNEksNRODS86NjoDgX2P9pPCYKdkDyUVcUmx+ivLB/BVye8edhTgNPb6WyFaIibxhExUpIOZsj0HFchwl1ADjOcflussH1SO3pJyJf0dUcmkdd+pxnsNH7kdTbV9E1cKx0JDMBOfjUaz9g59anI+M+OraivpXPvtzYunG8/UQzN6xotqnpQs+pJJoD9lHvWYvOquxpDW0Nc4IUxOUdCj4SzBJ3T6/u0Rmu802wYn8YSPwzO8XbG9qc23lmV/R444jRvDxb4aRzu+uWq3l+Nk+V5i6rP9Lss4zRYv9B7SgAEmfS+iTYLxnXUbgeY3dtsW5uPEREEsQ+2X0dHeEztuEMS3bj13UVHfBlriNjzziP+kM2+nJH+Nr61rDNGcY/w/SP0tfa0QUAbbyzUhzzdQR2/fV4IYPUiONo+Dkq65mB6Bw0eSIM7p0Z/NFYGjmiRobjiBYGuqD7UUyN6jZ5c06b9fVBZDt4jkrlKR1rQmZkTDzq89Snx6J5+L0vol8Fc9a37iAJys3ob3ngAi8r19iWrm+SQqCYV/tgPBIXitWURlAeuX6vK14Lzwvwa+CpE7ipXB+D0H6YAMeRDzJvjIR219D0sDm0GHzMHwrPzigrr1uZxWk7GLKgz4A4IQsc+cwB7GCARs5Ud+xxyBPAa5QFI2feKEUajHejsnxGhnRtulBSZ3k6etI8PZuP384zUa5mWftM3lG9BhKepdmev9ItnXwY6Ib8OaKTufGSzcywu6aNf2yzeUzjDQdgcCDcTlcjfYpR6wZSJmIF21RKY/NK4pxhNgKCyCmQAMDCvW40pD7t5JGJQPR9Mx4DmzwVGt0KEm/STZvDGOTfJi7tLIrR5B3x0ZUeb2UfAaX99lhVaIewjOaRusFUP5fEM/ZnQHXAq9Q70tTP4LrXdTBRFOSaXwPKE4FIVmsty4LKjLJXXzFAVMCQOFfCBvZMaTQQobC1M4DvfYfEsmpjXRSLePDvYquyAiBXZ6Y4CoDI4oUkvtSyLNhD8Hnb+tqMAtIthgAwo5Q23+1Ajfh9nld9dvJ+scMEpiLOD/NLMEuwejCDp4KJNLg9FdAk8bVYt2Na3C55pgIFzRm4bljXDdu6ueHqK7mCbh6gOu/70R0K37kyKiqYpcyNGPewgq3WillPXSUb3xL4yjBFZ5zZC5g4BzQQfMjb2HSkk46yLP7MeDpjma6OUV8FnOLXE347znMKj9o8GWHqJGvDtYM86uyd9ILJfGmD5/KKpA6DXOQblZXLiZ9nyfXERbYzR9ewPLRV8wdcYeX1pae6jnWbWPPsnW5oMrErio3uILfPaLf5TuxzoyM40C+3x9tLmTPP9HzhfRcnbqrGaK7Mfmp9KFz6I/A8YzAu2tbnEM/jNJrrdp04bvPN7Ugp21XZzsnZ/TFq+kjLcf0Znu9Y4ASzZYfQcA6lvjvaEWiy0uwtjPnj/3Y6kwG/ldVfteUjTi7gt4Gj61FqHWKfFc2PY4I0P9NvZ2o+hAZ+DUz5Unm9Z8ZljoExYsLRtkTLa3EaYspv/KMiMBBjby1vGhvinCF7IRWdMLa1xACr1B1XarV+Imo0T9NR6FgV3TJ5f7Z/Mx5P+QgZG31B0Nq9yfp/2MpYDGGiZknVvR0Hn5VC5dopEutH78+A9g7GJdoKnuZqj3n50PcN3LeYVSb0dpYYHdCVFLHOrn/suz47glAcjRP0/AzA+9Lzt2Y2QHrsWL/ewO3e9Ys7saLS+EAioL1NGioIU4r2MymInTutbhTEbaEU4s4Y3fL2/ziXvV3BGHYHB9dkaDYa7e2rffpKGjqCNFeG3SD0bXD5ofdtK4wFPu6caVMERmGVmodYGI9KrbVr5zMpz4mzWF3xMwL5KFNHhv5ZnVnOjvLGsrKzKAKQ0aooXx2XglpbivWPwPnorRkgK7uyo8vq2vf9UEZJhuRZ+yw+mJfNYaWg5e/o0TZo2TtXgGUORHAF2HwGCreg2wzZuggIf07TAnDFur1Lf5UJ8zS39tWKbb3L1qodkO2D+lYPwCYlOn0SewpgnWN2ctzRGYUwjw+t7PLKKmSTV9yNRRuPtoKq9ZuudGYxVEYxvZpT5Dg+mUdGcyviCMtn/LDvOwjiZBOaCyiNbaHigcGLrobze8wdvZ0BlZYvxHu6A1W2oNYQVJeaxiGNv/U6L5jnBa+fPmGaJjkdkSHjrquQ7uuKvVZ8+eVnKUvn1bIsuN1uWJZFHVZFTktkBt9usqpp21CrxqqyuDJV+0W3Jt6WBfOyYF5mvNykndu2+ra7uldsq8X/slMDCd/4ju8AAKzrim3bZOXSvvtJi6UUvL6+anyxG4hmvLy84NOnT9j3ivf3t7C6a8U3v7lhmia8vb3Lyq5lwbLIyYy3T58AAHftz01PgVzvd+/T15cXzNOM15dXiYU1zdj2Hbfl5jS9reJMW9cN67rjyy+/hff7is/at7U2nXZbSBzI96AX4vQY6TDNJNOLIdsUCRMVjTHP2NcVn7cNb19+llV104zv2iteXl5kxdwy4za/NrlrWytV3k2lrZoz3pNx3j2mnp98CZNtpQv2bs4F13OKEzkZ8WYkO+aitKosJDd00XCUw7tg8EbjGEAnQ3JqcqKrpT03KsecZdZ2Dm3Wx6/CnTxMTxqqJg850N/j27PCSCEqA9Q8ca0PxjbZgUjrKmYwt5ANIMNPDYdlG8JMCYt9l1wVZ5CruyPDU5QvzG4w2qvzoMW09Jc4XYfF/mz4gcpR3/j3Yvyd+JQDT+iz2RY1nJvtQpsntVZZIRqIKsG+yvG6nPAB1kHsw8Nc6HHX8JC3awYAA7qdu+3y6Q6QCs+7bRSfzyuOyF4LHWl2kYiErwwPjfgs0mFyB22ldtfG3Kc5RRsvtN/lTbjnQSEi9n+AnfO9bLtlP0HkH7svvNboeTbkUsQ/EU9f0fxRJxfwNXd0mX6KKQvMcAcAdQL4+L3Pe6zvCABHhoblfeSRHA14b+iioyOXeXAmoDcUR3Q/9JIW8iPoG+DvcgX6reykoEM7+jZZnvZcLKdXN4k2YLgFzgHB6KHYV/Y7gotzjfY4WdEULzUj7+F7DdO2FPs5GFix0+O4Z6FofQt0J5t4/hOB01F31n+xeQNh6/REgOnZx3vmKdzP5VB4znnhTKhxc9o90InDMe7mBNqKJwMRlfNpdYnmwKwOMiP6BXoeyMAk1OsgLTfR7htQMgP0gzzb+nTshHFHWwDRBpwEiASgNJjfWZbFckf3rmRQLjuW9VuRHsnlnJcGvH2lfPPn6P6Vc2NUzpnDbtSmo5PmaAilghSoB5FGUb6gzeOB3rQ8BvadnkYdbHsi1FB1A64UlGkCU4vJBCKXY67HzOmnq1jY7hGBpsmNDa/P6NYJ2eiVp/s+bYbLoYNcP5zImKwDLthqBB5HDtyDATIAfL3zVYgsxKBiGKdhB5NnMIPO7KVSVB3GlZ+pPej5wnWmfrDrbd3SSqb7rG64c6hMcwuyTXoK3ExYAJS9Yt8rqNZuO5+1s0wLqDCIWuiIMk2YAdRK4EmdsWBv7664bNdT5twoUEBNegpnZXkx4I1TiLDvu88j2ZL3gm3ffeuu9L3UsepJjW3e2Vbsvn+tPeKsZD2lsaBOs2wbLxPAGt+KGZgmdczISYpgYKW7GKs6ac2ZbYHna62431eJx7WKw8yw1aRLDyuNt5XYuAJoKz3tYpoapOPo+A3214y4qs7Y+/s7wCyO7tsCTOL0lnEA8sti1pc1wsISow+6Qs/G3wSB8Z/1vfdzJDljKWfsgF00f3Pqwsd5iH0irok4zvLR4LlIRxSwAm49y0GHBHzWvxzTcXKkkWRyuIPQtvzb9T6l33GyexsCHdbeBmU7OTm2r6LQZNhhIi3roSWDxK3bQABqqJz6fChh7h11V+ti05NA44i+JKH6uDq+79cx5dR9PmEfmDwm9PUlfdDrBb1doS9fgk4h+EuhqGOiMyy/HBW2bDzMYb7kLbsHnHyCg0a2QvdcaGOkI9sBcU4ZbSOs1v0OTDrs/Sg3Qp6GHMa05LZF+lyOpMlhNg5CvoawcrHHcg+ySOuJMvBgR4a6r36PsOvomWO+8zJyXZ2sHpT1KD2L4S19vR1dsLeY0XCLzPSoQ8ZvHiJfmoAUB1IvIJyOkVGRa0qC4MqQa17S3k8xMhhzXaM4Yh9JhQowlcMR4n29mrf0q77GqZUTY30d/9obFm9XEkgmeB1QhO9acE9kKA+sy3KbthMFEnTjs5NnNFm7LgjKqTOQI50RHFFbHXjmNOiMnnTPtw99ILkS4+RUSoougqyzlJ1wDoZMQA7GO2STR4natibrVxzHpOONPF5R0B6R+WWy1SKxDjH+QpsMhFLjHYeYDtLbKsFTB0/ilVHqnGBWF/UgK97LiYJRS0Qt9lEwBk/rQmtX5dq/EcxjeDK2XXsH6ZHDJ+aLK5OecZI9SpH2s1W1j561unJeozW/fDirP9PdgZRQXkwj58jZeHR0MvoxzqBZy49xEGMg3SzJPBsSP3HftqnMLvtdRpcCAmOCxPSisnuAa2iQ7TLNKEVW4EBjC5lpM5WCRU+yQymIXcxsKxH7/gLEAdTeqraXONFJAbSXMqwrmaX7BkZOExpe15kTq+n1OvxtdESevOJnDsZJVSJbP+i8AWOiSVZkF3Z9J32HzsnVYShqcsDuMcv2OhdjKrPtVMKiAch3XWG17TvWdcfn+x3TNOF1+8LjZs3zIrGoZsVSpchKprc3MLOspNp3lFLw8vpJA8ALRihlwlyKB2i31Qhc5bl937Gvq8aetNV/BdNc9FRDWS2E2w3M4lSLcWn2vWJ7l1WItqrs9fXVHXC2ysviXd3vq7O2rUQrZcLtNuGmMevMCWVxvO73QJfG43r54hvSn0rrPE2Npm3Dtq7Y7neUUnBbFj9tse477m9veH+XuF3yKc7DqnNxmSbl9w3blni3SwR3VgZsdMhF4mwjsu8FtsrLOAe6Uuvzl1/ifr/j/n7H8nLDuq94fXnF6+srbrcbpnnCVOWFyrqusvJsf/dVeaXI9k3jQTvpVfj1qI8aJou6Eg33UXPEu5Ec8pzOuSi3oz7qLbzxs8du7vo79mvn3IhYyb/3n62RTV7H4Oau8yGNdFwT5LdhFlDiizPxo91rDmOzwczmajLOCuntMtEHtlqot92eNWFl9IOuMltN65TuarJ+zMx0GD6hmTp5OBzVYJ9I3mBXwPo11tTV2gL6h/sU2gIbo2ifnNhGcTzbjgGdmxq3sIQ5YWO06w6gTVcK2zOjRIOOMjuC97xj58KO8f46yUfeYG1b6LuIqQY4yp+JWDH31wltsb4jdpAU4w6zKFB/5jRpX5WTfn2UsgMw2k8XIlpihQW5Gdsz8h3kOq+cVRGLf9TpFOvIZT3yW3T29Afq/Xo7ugyAMrmAOnN4WbLjwxuLPNdZUQBkoyQbPCMmGA3glVHYnh9dGwPps3rO6sjPNAeStLj/jAA3lnn8nelo/UH+fHZydQ+fGGBRWHeKP7fZlV6a1EHgadN6h8CJyDgY8VpAHPdYjhuUwVjo2ofU5wP6kXiDk0DNlJoC6YARIAFpRwqnEeL54u/UAYc6/Xmr94QHLwVXzBevpXGP5buSTIK625L1AX2SxzQfPEAgoCgcLYEPWN+MB7B4NPh5SEtB6a4fASsafyHF47JPNsDetsz6dQSwnHjSnFxtbl3H75KYMn3g+Pw9K83opOmalRX1hcy8klVnCjbOx9GLiFzO1f1R/pHjMjumnlHYGeSN9MkVbSPnyOgz1uV1Hhw1FX03MhC2wwjPSByrbv4rsE8iW2qgdt3kLKOtQIi6lMqkAJ/ApCu2qpjL7b0So5JtPWKA5Q2+OWGqt81bgIp+y19LvWEj/RW34JeY87QfU491c+qs/7OTK+exFLc3XIJRBJtAMgfDUow+aw0XBtW21YKDPPC/VlIbzyjSrH+YgjWgo1cmTPOEeV50dQCjbBt2DehORNjrDt6sH1hOWix2quHczd3NYlQBGucK4nQshLlU34IjeMBe0IW+81WousWXK7DrCjgNhl6mApAESTenym6rota765p4MIA4ymaUUjz+Vt3bqghxNL27g8ZeXs1zi9tnWyxtbN1Z+eWXKGXCsswe+J40SP7KskJqW1cAhF23T87TjPfPb3h/f8fb27sE6b+vAQ8UD8wOai9gmsw6469HMlGfq5BJrTqqKJ4jkLxYBGPfdnnRslds+wbmivXlHff3d3V2LZgniePVwicEOpUaU6edYwvUhTXwQNWxWeZk1+DQ4MeOi7PeGDrU8hwlQtd/p7pm/JJWYpgZdjzScHxE7Z/Kfa6BiZNfzEVAadggv0xzSnVcex0yNojlBY3oFh+SKGOYgODo6ZwSTtZoNHrs36uuDjGCfQs2ex/lz/6Fhy1qMF3civV+6LBwlJWcMLDlGrTB7I3BcDlvRjwf+yTZfl3zpQVOQAyx4FhDy9jySq5BgHe3s1qDzrG5PZd44UyPxZ7xLYDekFZ/10UDu+jwPdAZoHJH90PJltsY9HqZps4Gie3pykhtocG1PLdtx9Khrx7h01yejsXIXzDyG1zhxytnV/x8No1wcmdHX9Qd8fEjR11OX2tHV0xnbc7X21wR1hvpqbM0MrKyk6uv6zgRn/KWh/y19uXHQc5LTWNcmWfaMvzdXTamHD1/pDVe53RMblbwx/J7RYfQvy7w9QmPy2ITekTcQJjkPKPJ1Shs/WHxHz5izOYJ/LT3nLkLdGjPWj+c8lrL7ArNheuo7rP+GYA2Sr+hZdtkOrQt0o4AToeUx6KPOTh/moDLgu7AY/bc9eQeGqUZ1BjgDo4uZu6Ogs5zPa62IjXGrmg9gEsFnNHJFeUP4fg2pGtT6grbihnbdwC9Slukp6TVMjGNZGFMhy0pfHwhED+d1iDXnpFljxTes4r0UZm5r7t4C0/SExX01bNXssnAaWfw0dHgOIyLffiJw/p2tZtlFIUJzDB0Y9HLiYAJiAzH3AA3Ay7PGBofmeST3AgHQMXjOFbYqXjKe8zYSYJoM1XxYZDFh2myMbZKbTZNx5c1fqfrvz42Suy39rKi+whp7Owdgc2u7PTdnn0GVxCN9Ev/Wfc0R+VJbHvtDOXcniYbTJ60dSQgyMmOxj8kK7nKNGOeFx8XW90Flrgv5gCrlbFXYJoqlqXF07K/bdtAduqXxxzUU5lItiqWqWCaCjBNKGgx6+T0RAK4QVs3uHd1Dk/w1Wces6ZMmJgxTbp1su7dPItjOs9StskpWYVUwWtzdjEz5nl2I1N8LLJSft931L3oqWZ6GikDdd3E8ccvwCIr3kqZMBWgbhsYEmDeAuPb9r+3tze8v73j7e1NTolcZcmWOBIh23spjB3pyriRIW4/A284I+gvsnzO01B9B58/fkADazxUXT1C24ptW3F7v+F+e8e+rdheXvDp0xeYpxnzMjeMkbCGUes4NzjDfP6bMwtGk2KhMJViq4ey+gyjGy2BPjaD4iBYjuUMdZC5okPW7qVdmLdWRSbPfwc6fHUWD+yHkd7vvo76BKBwWIc5vMxRlOki0m3FLHKq6YiAPbgfCxxk45iOA7jpEoehiMzcaJCdKK0c+y5OU3mMB0Pa2hbLyzq22ZT+GWyJ2M5kRI3xNPfaOdZ15jyyMTI7afLYwlK2x0LOp+oxy/wxWW+N6Ho30JXpcBtyjIsPdIYuGUiidj3ZE6Pr2Q4clXeNEnt6O1wRZB9nTBvql0zn/XVGR+6Dw8tOe24kZ2K7o7yk40quKwfRCD/m+7Ec+z7Oc1rMIf8I51z9/qhjzdLX2tEl8RXOBsc89vJ9mMMEHNFhcB7ZV9mplLcbnHlNR86Pc+NLQUQibsSwV4bRR5LVR9Q+o6GgtY1koD9PjoSuaWl9pNujorMn9mFXNTmIBhACQCbDwQRA6GN/oxGvRxpV0kg+drBgjgPPW9DfQwNVo2SAgFE75TEyTCPN3hd2LQqyB8nzZN7pKxw+22Fd7h1sDVNRC+aalOVQwSRBX5BAGLU33j7+J3QS4FtYmRm22urYwOdSoYKKdux2no/xz/iAiDwwKINRaulA5Cg1U/GDc9QwFMIbjfA90zt07DC6uA2x3ExfVzXzoY5Du8JYZDqsjPgZ6RrRfpUe3R86rU+UeBzXM+X9iMbYP0On6UB2x5UdZ23+iEJ/5OBqZUkspwapYh39aqDYNmEeCXPqEvlgi7Tnun/jtGT2BSDsTuMWQ2lSI7mW0kA4GDRNco/QtjdqeUzmxIUDdIYc4nGOAVjFaYtnJb/HOsuMMnegxX5lm5etd0bpCiBKPCfu+HH0/OE7tXAKrHRE88GM0Fh31by1Sgwsc/hYJzCio1nk6jzN7oQq0wyUgvW+Yq+7x7Latgpg02fEuTPPC6YZWF5ewJUl/hZXd1q5I0m3IZKvfpq9TwBg26vGIrMVXhtqJexb2/Jvq6zE+VWw6JZBdkfZ7tsH67oCJA6nMk3t2TJpDC4AhVrA+rrjXQPDM8u2T6vTx68y9mXHvm8es8u2QRK1l2VlKrK1kYq3f90kKP7nz2+o+4b1riuTuGKeZj2cQba+VD1w6F3jXjFLsPZ921E3cSjZCxnfugJbFbe781Be3BT4aSQ9t2tqMzkapYDsjLAVdaTuJM+nc052ypLEBguCoK4b3jfZbnl/e8M8z/jGd3wHluWGb3zxDVkZuMwgPUxBveJKS9JSDF855kZpBDCqr01fOnawORHl70jPJfyYEzXhcQk9Gn4arxi9umZi2eTzyG4Yy/QxHYWKrLDz+FjcPZYxTMQU7jw0WVbrOe4lcfDWKqeKSviERGLWc4/0HjNGgf0P2U6eBRhcC5j0oBCGYMck+x2zh3afINuGe91eaePgLyufTMzNDjp0xQUmdmqUT3MYFDtNsar+3HS1ba1ik7SDjdqKOe+NwZyIjiAEe6xlOTpUItanUP7IJsntzM4ur/fQC8f6bI4+NQo2nwfJ5KjTl8q0ehrmbnLFZVNqi/d1sK8iQot1H+h5gMtHOPB0TE6evcIiV3kepW5ufQDrftX6vt6OrtoPXGv/aHmq/D4ONqVn+7KcVzEe2AxOzwYtPjsyCGMZjzyYV17Zbydlg88cgPJGZvQWpKMq0Gf5Rivm2hS2ewZ8u0KTwOsmVwQXI6OOT8AAUTxx+aQT7COMBQ3G3JwdAQGeORGisyFYXofxdqgSBOQpmQ/4rav3SNKh7IeixvodR9DHQeHwAxZ0IR6FXGSSKJRHdQPdEt8Dzx9+Rks70sHd/QiGg83e2pqRPsS57SfB2YqXVM9xjPvPM7ojjZ6FG2hy/o5Aivs6I98+JRvUKIhzINaXy3j0ezQ3v10ZlevLyvLM+XfmjIvXR06pnHd075GD7+yZq7n7jHwf6QwHoENQo6ydwWRnIPWxSXq5HoF8u3U0dJJR2KG2NvOUQbUdcrfoLSYx6qsFqC8FBVNzcJszhusB+DL6U4KPfGk6jQ88lM2SDiSO+pfhjq5CxzHL4zCaCxlDPAKf3q0dTwahlRxdWU8yszpgtP/V2RTviapiFDaDqWCaZkzLIoHlGaA6gfnu5VZ1Zk2QOFplUkdImeSFlJ6wyLyFuvZ2+AC3Uy/tEwRg3YQmfUZOEIxxzmzVFaMUc3hNSlPc4mun3gpG2ABMaKfvglp8tAULainY6+5xCm1VbIy1YkYlF/aVIlav4BpdXaVOm2me3EnmJ/oSsNPuMUrrvmOHuA2xyOliXJuhum8b7u/vIYB04LOAJQuRrwIQQ7et4hDa0c3NONtdGrBP8m6Wy6qt8BKI0ZxcsD/F30l5cq0eL7Vuu67CK9hvG5ZpwrwvIMiKNEC2+lMxfdQndz6jP70tzqXsyIkYwrFFwBgd1mgF4jSF/A1X0eGZjAFSQxpxdikYH/K1b32tnaTyvj8nM73AReubzpETi6WA1czJFZ1d3F669c2JY2Hd27DV0O3AmfseJxp8k1imx2LY6OJw39oHgryBOY5Zfol9kOdBxsvnCR5rF7r2tr7oX3QfIMBBb+eWo5v/ZmtEuSmrSXd3cmXsYvRFm2RUp12z56NM5ExnbIjOu0sbNz4/+N5lTX3ZJQqjFr53OjnP0SgHEHhf87veyVXptQ5jBto580iqB0DX597eqLsbUZ6fQzkUrp91yai+3Nbc7jNn11fB81flj3DzM/6SZ9LX2tElQU8BwADG6A3u2BCQa+ju9ek4+TooeWL4xPJjYOJRPgckgxg4UTieGUQZKP9WpDPjNRojZ+q0p1N66zifeyFuQNXBKg1hgGWWt5FBkNg2ASWy0X1s2FmpD1MrXwFeWDofmqRfkzESVTGFY5AxGLcryWSAEv0YNQOt/Y55r4zpr5TaBOuF+wX9WRFbOS7kgkB3JYCE/UaKweoHHcBZny+gb4QxoTZfzWgdEc6QbYoev0tBW5mK190BoeYB0KYmgPsVWdHoGDm7PE8aA6vbDqnICpcH8iXSKTz0gK6UIcq/fO3KgROdVZdAaPBslqW5rLPyzpxgV3XZ93zi7oimmM4cXR9pr+WPb2xH9WRnl7VvstU7CIZO/zQC1PKvzQjqZmVP16j9PiaBFnC//dzYrchpeFQKwBV33aJV3XZQw50IKJPoAQu2rG+m985Ykkk/BmSR50QHAYSt7v6oyw2r23hYD3awrXCVK4gYdWDwxdV7IywQxzJedypPwKg73roxkVR0BQ3pigWjnaGrbwHMeoKhGZ0WM8rFIFl8PlnlRNMEFMI0L5iWRZ1XFctyEwNqE+fVtlVs+wrCqlvnCiaNv1WmGWWSgO1GsunvdV2xqTyaJon1JUHrJ7y+voBA+mKzerD7fW8Os7pv4NpkXZQ9ZZpB2o5aOcTWkthf93VD2eWUwqLbGZe5oEwFL7cXWWFWZEvlukmQ/Pu64l0D1tuKsGVesCw3vL5+0qD4G97e3nzVFpHokGWegcq6iqxgur2AF8Yyzdi3HW+fP2NfN3zr85uvzjIH1dvnz9jU0WUOtVJsNZweEKTzqEziYDQn167B4avxzqmYibqsn+n2fdKVcMskWyuJw4quxv3Ky3rIDCxmUBE69qp0bfjW//kmPpeCL7/1LTnc4PaC28sNLy8veH19xXK7YZ4XX31o/ghzsBp/i39JHLM2t4S3z0+a7Fp+Iru//dT3zFnq5IP/82TKgzVIRWMdduYRA7xf6NjwX+ccCjqw7zfu6DA8YQ4o5qh7gq55upnXcUVDxcOidV2x0x535zR92uwdAiSkmNGukNVxalaNeLJJWlBHZod9Kf1+LnGtunLXS4G9VNh9hWs7CTb2geU/kIoDMuiuS3PyS6Mj5onfR/XEfvitsFxGmKTWKjgh2DF6sw2ufha1RxxVXNEV7dCEdxt2CDE6ze5RGqhjrvZCJjgqOnp9ug9so9zmIS1hPOKLo6F9GeyzjGNiHb9V6ar8ryKjv9aOLsDGmDsB1HsKhR3ifbnX8mYNEXgNydy+oCOvLjtfmpe9mSPmsrpHTBXTmTF15fy6ZCK5cHLfGMzK8RLD71z2GFA15RDeJMWHNNNIVxnAA3AwNsf9GJ49kiJ5TRnHN1HW3ujQonDPL7Pf799kNUPyo0uYtQAXYgcnV+yj2M6UNyqOKCDzwHwcbpykro9CO1IWZN43oT5Q7FcC3UctTlPuxycSE1fqZYcRCBJ3a/BcfPM5TKEDRyDs4OTKWZ7sfKdZwV4+Ejze6+ofKK/YVyO+948LJ8xIaT7rXB3Jx6tnHzn8z64/qxDPZPWovKz8r+h59vdVP58p+mfGxr5HwCNOpiATOvSakTunCXnkOTEMBCiaDml8RAATyIJW69xk0GDean7YaZuTxiy2oPmhDgAgcYrx6Vjk9jcBJXntJVlrZ6QpxuE7oH1/kAIYvn5D2dP2cf58LmPSE2cWiiZbFWN9USY5Sc23zakTxZwmZKvsoE4sXVlS1ZECFlMSzECtsmKM7CWkOaQbAXELrzkuWpDkomFjWpwrAiA+rSmsamo0AG2VlmG8Vm8z0L0+ZnCVw0UKM6hKPnPGFmrbFBmMlVcQE/Zam05mRtVtlLaFknnCPM3YsaMWC5IPd7ZFOUJEmMsELq0d67r6CEFptdMe88sZop6ffPgzT5AVF3BXZCv3ILUC2ozpZUYrOmIOydvlsTni9yQ+mMecYQarEc5cNdB/C9jf5LKsFKSJtKLiPNvkjvWHIQMj4TgHoyMg4oqDrjw+GBo/npMmTigQJcZ909kdgWdloPUrorxE3C1hmOWisDT/Df90uj4/nvrS+8VFXi9LGz+PSWlik7q+IJWf6Gjiy252R4rR1jr7gNc7UjqVxqEdiVYniboHyehqjBU+Thodfhzmhcso9voaPSf6l/LXvnMMX9tDMsVa0Hm2eK2Oe11JKj1xh0agmdvLlTNO67BRbmsowz79Zdco76P0Qb05tA1p0IPB7so2h/NdzJ7LDG20Z85SV160g+x5x+pyr+f5IJsPthEd6Uy4dYR3naZssw2w1TFZPx+xZ6z/9OkBhsv0PrLvz9LX3tEFRJ5sIEY6oaJtuYsAx65LHleWAwM1pg4POCjrT1GKk6qBrXMmiUyVB9IAX/aiNtB2XDFh9Bgw6+in81UIfT4r8zrf2EPcWURNEXfl9s8REVCigXROiIv+cGoI0L+RaCuuelrZ6mQJ5DqaKHTUIkfHRWfshDaZ8tRnmsBvYxMnrK346+jInR5A+mWKPAT4nnnbDtG3ES48G27qBfiotii8oyKLBoM9exD+o7Jw6MavlJgZe7XjkclBvQFwA1OP+tAMgdHqrJEToZvXuUEY8M1vUcrOrlEHxu0FsV3NAAjtyoZPoJ08cCs8v827KHOyLCQiX0UGHJVcllcxjZw3zziUcr7Ri4Qr54PNs2eUeizPjFYzcs/yZ0dZfBse5UGO3TWUUycyYeSY89+QFSWEfkwv25lAW6gplNq+kV9prwmAonaz6FqwrNIiQFZrgUEUZYfw7rK8YFkY63pHrTvWu62opJ4vmcHbqnJA+m60lcIwQOyRrj1Mx2banAlygSzIssY3khiFO5i3Y/9lo3kAImN61inGzBY3OBgnYZVcKE9WbMW518qouvUTaLGxXl5fZcXONIOZsVWJNbVtG7b6BiprW8W0LJiJALxoTCqJ/+IygSUmk/G1xfqa59n/AN0GHpw7XCvW+x3bumLRUxHjKWLTNGFelkOd6/0OEOF+v2OeZ7y8vPpcsdhhtn2HSAPCb7alsvXRtjEKwdt5e7lhWRa81Bfc73es24r7m2wf3LYNu5a7LBIPzObzp0+fAEC2QO4V2yp8er/fJUaY9qFhs7rJyYr393d8/vJbvgUSiq2ivCxUQDO1mFyFdIeDGeO2yol0lRsgWn7Htbl6nUjHx1cBQtZsFYFx5vroHQ5g+PyvpGG3Gq8aNdu7HFzw/vaOty9nzMuX+NbrDfOy4Hf8ju/Estww3xZM84zb7QVlmjAtk+MkwyBVV65t+9YMzjAnRm2C9hXSd8dLXyFx0M0CDR6jHcFmvWS1r81BPDD41LaB14OnhtgdlW5UwzFFvJex0beVIrZ2LBq2RLqOGjVA7jNw2Gr2bHKXDVuc39bO+Oe0Og+f0XTWzOxuyLzWQsQAcDkeUd6xTurLyW3TmJVNPYaVOFqOHxZhU9D1RKSt2RNedihz9Nue6ey4hBlrcNSXacI8TR8fwzg+xj+DOWrYxeyVp2sRh4Kuim7PTxlHhjaOkslHn7WK8bpnQ95YVoe7jAY6n4G5fVdcOnJ6XaUr3HxVfi7jI86pR899pKjfFo4ul0fecmNGIK/26pMKTDNMif25VvaJoZ4N3XB95HkcDVY2fnI5AljOlwvG+tozx7L7MseJWyeoYj/WIZ/He8dJMDIiG8AeJe+H+IB9PSmV0ISqlXHoz2wcWzl0PraHB1LlpjDcyYAjsMgrfxjttBO/luOS5WpzuwaOgkym5cfF7+aAwyFez5Aa5u5+hMhZ0DfHSipJ6e8Uj07MrwpWnkmRdxstgDslne2jYj+fN7b6qXOIaFnxDbkbxWft+gq4+QBeAyCNzq9uvkZ6g/ExvJ6YwEBoPeE7a5sZqTGAdM4b83dtunDMZCdXzjtS1CPH2UhGj65nOnKdIxluec4cZF9FsT/l2E70PGpLeEhOlEKWGeF7y6y8kVfdXkAtXREZY/tGCWPzxTiW0AzAxs7y3YJd29bHMk1izJFwL/k81j4Ljkbpwx4D5D6xPN6mPG+pOcuPndUC+Dbn77ncjeM0cuTG74/0eCSDwliaXHYzqYZA3ax9oMeKWV6vSvVhPgGxMuvBIeY8qOBdKi/MYcWX9pc+T3aggDTo4Ay3+TL7tkbbvmkrrNo8tlP7WLcVAqIvCsnqrsYjcYtoiP0JffmlvGONbjwzqTHWtqbXugor721VkfHCPM9CBwtt+757mXutwLqqU674KZDzNMuqLsCdct0WIgDr+4pt3bDeV2x6kqOswrAVFnGOtPEPHKH8ECae4xy5N+mKMaGPAyA6SeFFMdDP6wgCbIpEw9gwS6SRmcHmdNVGGNYhAFMpYABVeXbfd9zvK/a9Yp4/Y9t23GrFvIijcmKJcUZ2qAIQ+N30c1iFNpCTGWt11/3HwJBOmNWM2oiXjpXRkIZDNrYXiW2Mon0zlC3Ko1GfOy4ZiG9brWqB2ZuTBU0wI2CiIB/7LjjS4vyS8FLEJW5oBAzSy8dxP3Fgn6s0cvYZ/fEe50yPSuURtgnwKe8KGKSr20dn1/nzPvYn5cRPe87HOth8VkjOG3VKV0/idX8pZ/k7QEHtM+q7VM5Z8roHetDmbrRpcjrYKJGmnCfl7Z7BCZ5L9suj9nRyY5Tv4n4e90fpyuYfO4/GOOWZZ4+o8hx752sZ54wwUOeMx1Ni1NO35ej6W3/rb+FnfuZn8JM/+ZP4u3/37wIA3t7e8Bf/4l/EL/zCL+D9/R0//MM/jJ//+Z/Hd3/3d/tzv/qrv4of//Efx7/5N/8G3/Ed34Ef+7Efw8/+7M8OVyFdpfYG/REIZ3C3dSLcceeNDFJ2lvkcVYFtj+eVXJL3qCxdANBYORm4jPcbcB47uez76OjrHsRTl/8sZeWi2CDngr15OBqCHORCQD9dGq0iIC/3bEp1ICSVzJCApc9OfgLcI94ZLx+YMBZ8HGjHQB+M31igspy8LalAnNT2mVegpfbG0h1MpXbF5w7X9V73HI+3hUayLV98pirNNcSVMZpO+WygjLu3FxfK+tnksSe6Nih4qsERQdzFuRL6jEzqj/ZGalOQBXZv1OYz53Ug7DFKeyZdlNM5udBWuTKC0Ybk7ApKxGi3LSSj9kTlM1rJZCfUjJ49S1lmPXqhkB2ZZ1uZR6tf4/eRoo1/Z2Ma6Tw4VMP1WH4OAjui68wpeLVVO18b3RP5xWAO237is60yNJh7aQm3J40fw6fLvdCG+JzIYvlpcX7MDWMn8U3TrCsZxBnRTl3Ufqxi6BYCJsxwBSaIU0WYvfCybXOkjoL42Y+TOQjyHKMCxFVRgAWGHsuOK963MX3W+Rp/+4quqBM48m5w/FhvU2jXoA5zVE3zjGleJEZJ4NttY2x1ky2MJCtoip6aaHjs6ACsvuoqrsAqRU4gnKYJt9sCTMA8S+yvbdv0hM2KTVfrSd9LQPdpmrHMCwCZ25PSb/n2yiCt17AUqOElZpa4XSDMs66wDGOw3e/gWnHfd1CRmFLzNGGZF9xuNxARbssNdd/x/h5Wdu071vvdg8+/vLyA5hkvLy9SxzTj/f1d8q2ry8haK96/+bm7bvfiSI2xUlyx1xxHsoKqeB855th3iZdWCaD9seJlw2GJX2zOd9eMRllJzY4T9GHdtuk0FXU2kjDzVCZxdGkcHTkhTlZ5ibNrxuunV8y3G7a9YrktuNUq/KryAhBHmR0iUIznz7CTzfvW3EOK93wuxjkZ8IxhIR8R4yulweVLLuOQRJD2MqHJ7CyvhIeDrfIoBTwj/XPEO43WsRHa20zxMrn8zfiCwj3DpYYAzcbo9MqoW2I933Ya9bPeibZRWgjRsgddNtAXOTWbsv1rDmAGo5Z26q1XpLzjTyQ5cMa7rlcsXylJxzderbHf01w5moN9uX6SK9DkjH4OG39W7pOJjIYnx98c3o5m8nOpPYffVu/ouYgbMRiLCxvBxpXTdb+fMF/GqaP0bJ+e+Q6AsX/jqoyvmp7BO1nOPUNXTl/Z0fXLv/zL+Pt//+/j//l//p/u+l/4C38B/+yf/TP8k3/yT/A7f+fvxJ/7c38Of+JP/An8+3//7wGI8fMjP/Ij+J7v+R78h//wH/A//+f/xJ/+038ay7Lgb/7Nv/khGkqBg9bzZIOov05AHgAXsBH8dsZAOuUxG0mZYbKRNmLSM29l1UC8jwyZM2MzM8qzjNHeSsX6gNaPrf90VWcQ/DYhm3Eh/cfox2EkotMENaMngpAAEEwBeZuTYZrfTJjgLVYOtzeLl6DAX/JaI1uhjHgsbwADobi40qYDVZlnYvuCwugmt3dNRpdRZXqmHpQNUjauOt6236muuC00vsUxuqPyJAMxzlPnPc1RYYx4NShNCtesjeVSBvTjd6Ai2Kgc5tyZk8WAZO63DhQmkJjrzL/PXb2Hhviz3TMcPr2pqc4Lh43Tka6LfD3fjmflxjrscxyodlxOloHPOAmelXFX9T8EDYMxfiTDr8o6c46e6RVLtrpjFDQ064OzdsW6e6dalyt9mnHXXcpZ5IcIbPScRz73w0eYI/qnswRhXt3XFbK6y1Z4TQDLKi85Jp1d7guAJ5RpAu8VdVvVyZbawlYne90i08IYNguwa57Lcp1jeRzz4TPP8ELM93FQqfxkq6U6Wk03az0hOLc4ixZx6Oiqolortl0dWOpcvN2q98k0zxIfaWZMuzgcmRn3+woi4E7k2x2nqV9ZZ99fXl66mFrMrKubdjBsy6ltuS+gqQBTWwFlL4r2bRPdzS3wvPzpSxhmFNXt27apUUiyCovIwxZQKZjKjAmQExC5esB7WhZwbau1bMshuG1nBMRwnOe5rRyjgp2Kr/R6e3/DtMpK11J6LbVtG+73u7Rvr9jfV3CtesJki/8lfdiD/NaHFawHMkFxa1FnUcMLyhTQLb26dXTKi187iBNNtnBfL8nW0RnzPGEqBMIenFzweeS4x/hxkAcMXf1HXZWlEAgFEyYwie1QuYIJmLYN2y4OruW2YF4WCY6vjtMyTQBBx1q3anFYVe+CiPqDMZzQsXHaYR3rK+YWI9DGp3V8J2BNjMpn0OCDrs5AXGR+P6f6Z3o86/Ikw8UOy3c3tA0BX1D7jGU12RUeP5TXMJ28XGyOZpHbhyYEv8GA/wKdfi/qu4S7n3b4DerpZXHGUenpOIiBRwaPttoCPgxKUT50RRgHGyg7VNyWOBLu+eI23mC2dPaU427lrcxXB/JNj9szIc/hJR8wOOE54BSzER7sbOH24IGuKxvE80W7I7S3o+vEBsrpsKosY8Fk46Rp067l58K1QibLW4iLDluGcR9BMpNMpC9bIua7wpkRU+bnopP6YA89iaEfpWfsg1jeR5xdX8nR9c1vfhN/8k/+SfyDf/AP8Nf/+l/36//7f/9v/MN/+A/xj//xP8Yf/aN/FADwj/7RP8Lv//2/H//xP/5H/MAP/AD+5b/8l/hv/+2/4V/9q3+F7/7u78Yf+kN/CH/tr/01/PRP/zT+8l/+y7jdbk/T0QyjeDWDTBOEoxJGBsfIcDHW2TXP0Xk1OjlplK83zoS+M6NE8ugSc/QDm2mMyu8R452lJjRyv1D3vRPs/hmdW/kzTeoBYI/155qlD9CWpocJaXGAaq0ao6CBf6+rFBRAjzqXcdq33VeqGI2HlVgIJltDJ55KKahcBZTnVULD9pyvHkD4PnJ0xTczw34yXkrX+94f8TuPPxFXx7CXXZk97tfB4DdCtFJX1KGuM8Hcz9bwUARSWn4EzqRVejyoOG58BHsZDGZ2jRQOnaY2RsHZlXtdQHMA8iG/1dXmmsmWsVP7OaCWngkyx95hcT3S/oxvbQSqzxxb+TN+fySbogy1mFf2bHSA5Wce0f6sE+gsWbyLYZl6zeTKdTnHfont6trHRyd1duJf65Vzh1ujo6pctRXRSbhZ/vBd+GmULTiHTf92doI5ultAeVIDqvg80Yf09EOuchJfrTsWNaaXeQagWwR5Q6Wa+kGCgNeyY903x7RV35Q3ucFo2+ibju/60mluL37cuc0NS4e1Uh2A7u9d8Ztt7erH+jrZ3NB4o9q+1OU684OMJdkiWMqEl5cbamXQtmHdNj05cZfA6QzfhjzPk5x4VyaUZULZga2yO2gkfproiWmaJI7V7YZ5bjLZHDXzPGHfZDXXpqc07vuGfZcYVoXayjDbOmnOoV3jd1Vd5WVB201uTJPJF41zx1D61jYK6gjDLA7RWbcX2mrgtlWwArSg1uLXLIaX3AMmnry8aZqcb2qRLdx2OmJdm5Eya/9EJ9/9fsfnz59R9x1l7/mHCgUnXnHc1cVtrQF3qRPTZO0O6Mu8xqO2omOeZ0w7n3BmRA2BnvDdTsac5kni1tj2yqjIdY73QiOs4KfAq8HBAsV6xU5gVSff+31F3TQOXyl4u9/dqXV7ecFyu+GLL76Q2GyfXvVUS3V0Aaio8hmdBnHOX+Bwu9egb/o9wGcjFN3hsWHn9/3e2EExKve7OLqVykEKHPFcsh2C88q/c8QM4V5or9MVW+eyP7TAaWwXKbww89PngOAMMdviaDP4cz50ka5mk5jMbk7W1h4C2hkL4bCF9MXbmaBjGwzKEj32pX3ataZr/B51j7T+sziViqGN8kNPUC6vtxEiT7pzt3s8guomc9o8aM3Njqo2xjoQjKYj0frfME1N9JsMYgCTVRI/Q/usPOMnsyfivTgmIGrbMUN90f6I12O9Z86TPIe7+0GOxNkRx9VpZO7a0tGYZJE53klDghyw3Un7nB79jD4J029As+sOfJPsuow/8/3cJ1/V7xDTqIwRvs122aP0lRxdP/ETP4Ef+ZEfwQ/90A91jq5f+ZVfwbqu+KEf+iG/9n3f9334vb/39+KXfumX8AM/8AP4pV/6JfzBP/gHu62MP/zDP4wf//Efx3/9r/8Vf/gP/+FDfe/v73h/f/ffv/mbvwkgG1MjPdUcCwDUiJKVUvF+FiVyhHUU1MJcUzHG8JzBuSP3xBPa+E1eQmpAUcRVSLF8M14aHfM8pTpivbFd5G8yW/sD2O6Mo6jfW1vY32RKAFY4Y/XlWl6j18p3qvQZU8Y2KSxexcExQgj9z5gClBKBaBO/wD0aWp8FaL1vm/dBkGj+ncGQd/3aXn27IceRVwc4zSlhfdW2fEQHARUFtm3wwuAkb74aX0X7cNt3NzDBBrgkr4A6coEuAEC2ZiKMYazWxlMCwEY+iE6BozCg+A/BFUh8hitr/xg/tCGQPqpjBW5XWALEO/CgNJbeZewgt/henJCSpleudMM1K7GD8KNWRuxv48cOLAQesGcIfX8KcDg50IHaFpG28q1tebbnOqeHtmC0DZbB3YpC4T8lj+1qkBtsUDcCveKltXaG+sf4QhVjW91qabwNrdEdty3FrYtnKW/bzn0QldrIcZbpiPXnz6z4TfmbvCKEwPq+RVnfooPgjppoGKms8OjqIT5HMyDitYYPGyAssqU2yGQgbVPUOTR5+yQPQ2UHmcEttbgMs34x/tYXST3fG5+HgVF+pVqhay2QYJVNRi/NjOrI0wxGXTcFXjL/TR5SON0xgkA5WW12oAcAOxj7bnK9ALQA8wwqMhlsS+a6S7D9+fXVt8hhb+Mv8ZIWpaUFrbcg2vbbVn40fuAoAMNkMaANQOcwaywrn3PonWz2WBSXptqYY26VU5rhKOsIsgU1gH2nqg99MJUZoAllWnQ1zisAYJp3zLr6aN02XU3E2LYdX35+k22Fm2wjneYZrPw3L7LKa1rkjbw7ruodb/cNZS24LQuKOnf85c0yYZoLljpLDK2wooxZgocXlhU80HkylRkTsfBTVb3CoqO2+4p93UAa42ueJObXMs2Ypwm3ZZHTIsNz4lzbse+b6PPSVoVNcwGhoNYFpU6gaRI+Wjfsdce67dj3NxAVLMuMQgWTOstKKaioqLTjZXnBRBO29Y7KjLdvfZbVWup8e39/x3pfZXUaczMcnb9kPFmNxaq6WHiEUUFgKrZUSYe/yTYQQMywjXx2UiZIVj9/WgjgCa8vE9at4r6yTmfGPFksL3mJvG/QxTmM2wQsM/DyQri9EDCxxHhSR6PE/1MO1iX/nSxmoO6N9xXyNNxiEoQZtW4av17nqOZHrbLNmSt4I1Qi3N/fsBLh/psL5mkSh9ey4NOnT5hvNyyfXv2kR9Y+65CCYRH0Uo4NB0SZ38/81j7TB0QoXAOa7Z+wzXouPvWqjp7KnohJDNKqrlG7ApC2m55hoJ3oyH2djakaboxio6BEYrr8+RIRUKwaOtbArhPYVZ+X5AqpgHlXnZGda62/o5hlZm1f1P2t0PavNs4mjDW2Azvha7APnXLvb33O8FloRqcNOdJAIA+R0fJ0fXDAXTqftbOIGVS3dgCy2YHGo4plptJW/ex7bdudXVeZvUIGy1VfNnuFA4E9/GavG1Z/Gm1hUXnhz2yrMAPNtdft1lbr42yvZF5qL9BC12WMb/0fDdyY1/IHvI885h0mb53S6DaMMzg8yYtsMgzMfV6bxxamwPk74FG1Ta3dxV4UhV00Oc5zR4O1T8td13XcV6HdMWXMPHpJnLH48Xkf7cOzo7ry90zb6MXuV3GsfdjR9Qu/8Av4z//5P+OXf/mXD/d+7dd+DbfbDb/rd/2u7vp3f/d349d+7dc8T3Ry2X27N0o/+7M/i7/yV/7K4Xoe88TnmhJDU+T7/l50mvkk1+9EhAmtjD5fX2lfR8vnGJf7t7jRwdAYoy8ze1IjA43aYWVGL64wSdh+pgqg0ScmTb+VI5fbGPrIoMXbZfTGv5yazUDBMI/349u20OcmrDUGh5RdHCqATTgDxEG4BeVlfw7AuzHt+5BTH0/ByPa8odxe4EDezBJJYFsnpQckbNs7owBAE9Ru9Fp/mOEV+jJyjeeJ/ZnrNjzQyAjfmtCycg8efgUTvSJ3V1Hr52pBi4XI9pawKW+rMr9RbCX23zt+cTmQHI3xS5LLzlvWro4/xVmb8/uc0s94slsEw63sRmuFGODR0I0dx2B3WHhLAi9afx1GsZNVcRTVMRZIzPezAonyyBwlIgfGzqOcRm+CYt9FOfKMAsz8lj9H988cYFZefKYFyGYUDczsJ4kdlGmsn0K/NFkY3yLLw2jqIfMfjGePb56jnOr6Cwp6tMyq25vsDeDUvd0H9iAiDOjmU4OA5mTtVu4xgGqGlJ3UqKf2RrYvAaQSH3gMALju8tICEwoxSml9ZHxucFjaKbKiYAaohnGKp1Sag1Q7sorDZOMNExFo0lGyuIhsjq4igc9tbIPc7CC1y12N8cTsAchxiAsKl8tMkL9exLYy3XgK8yVglPgsVK8hzU1RE8I17Pn6OSx39kYBFf+jMvlWT/tdSgWjALRhW22r4K7O7gm1MhYQaGLQRCiT1FUmO8mZQxyuih1i9ExgTPPUHJzKYxPLC8FtBfa9ObMFyFdQJewqlyeaPYYTFwbt5DGxZHwAquqoohYcv2gweFuRhb0ZhDK8Vfh3YkyQFVryPABMEjZBV0kxA7xafDIA2HXOMcpcXNbaCrQ67QBP2FcCanWn1vvbmzu6WF/WeSD+0sbSxt8xQMea3I05Z2ygc8r42UK0g9nn8VQKlpnwskwACNu2+1ycCzAVgIhh/n7jrKkAtxmYZ8I0i0F/AB+gtmpK9Xv34s0xg8T8LIqR/GkGdj8YoAFpk3NsbQmHP2zaB9ubOGdLrXIiKNQt8vLS6fqMcjL+MXncfilGcP0cxsK2+VgsD23D5CcgjlLDLobVstEN71pqCsN0c+stlQEQJ95RpbYWJCxg8oIZwTll3d2wdF8QxQ8fx9aqwML6Qleu9wJR6isAVaQiYLq1f8mWAFOXDMtr97vKNh7Ui03pxqoadkulghm+IZxDKI5AUcjaitQqqVA7eCHkP+CSoKU7muJLDB2/WvstzbKC1eRZOpV1sm278QVy458DjGMAFOOkIfVZxlNGFwF7mx7NKdSea/1GrX86UdfCnKQKehKH2Czr2HYtOroolBnxo123axz45mBbp+6KeXxumA0YyjJKuy3NUMylZXTxNLUzhxg4tzXRaJ8x1EW+f+YkOnM6PeMY0ycAPI5pG+2peO+sntG9/2uOrv/xP/4HfvInfxK/+Iu/iNfX1488+m2ln/mZn8FP/dRP+e/f/M3fxPd+7/f67+yQ6QVhc85EvjgORAMJvlIlKG7PFQHGoPNHRuDI2XPmPY3PnKWDQT3IG9+SWj2Wl9MENgPHV6MEwHyd+n5y5cej/o0qIuZrRUXjJzqt5Aj05jTJE9gNqmww6rXKtdv33k79oTjIwcA/TnY3JIlk6XxoFQAHm+ZxJ6jAMwBPzTFDfUcBaMZqpCWCqrhPOwrsrrzcuSFf1mpRCQx5thQxis/KHgkk+5ePfckBNqYHDrziwM71PqGxw3iroBuhoS3RsdIAT2gD4HvuKeQ544MarhP68Yr86nXKDTds47VRG2L7urpD0RzmdHz2zPmU7+dTz1p39I6onK7Kz2WMZFp2cp3VHe/Fz9F4xLIPPDRQ6h0/JsAkBnPrm/gywACk/UU5mtt31h+nChyMgtLyom/7WTuZua0CLOQ8E/ko19WVG4CsH9ZQB/HpooFCaPNMrzlNDKCgA/ZmvE7zdJgvngckTn6T85vOFbBvCct93Ok9nUuMpt/q9o5vfetbmOcJ823BS3kBgbDr1rd1XVFItkKabLG2bu+bz9c2RgCoGRHNAdz6ofDkuIJIY9sxgc7GAW3FpOndGgyDJvy0rTmoNwjMe7etzlKhSft91thTagRxxfv7HfdV4xtNE5bl5p/LTbYzvr29+bY6roz39zeUMkm/zRI7y04eXOYFU5kwvRZdJTXrARYVq26LvOsWs0+fPul2Mt0yqLxUSnsZt+22pVGCpHNloLSXAERy6iGzOB73bce277rtUlZqlUKYtrWdAKnOLwteL7GeZNUaV8ZWV4mptW1y8AGR0EQtBtg8zdjmGfM0+5baum/gnQB9kTPpisFpnnF/e8d6v+Ob3/ymOLbe3mWln26NJBInocsaIjlp8DBD+nQmF85kTL4W5doyL/jd3/VdWLcNb2/vuN/vWNcV21ZRN3GUW3XTBLzegNfbjJeXBbd5woT2erEAbbsys3C4Opmbs0D+OnReK2rG0KM2EKnhTt1KiSgTbC5sOr7TNOHt7Q0vX3yBT+sqji89GMC2xgLiVLNVf61gkSvz3HZfOK5Be6GpGWUcuY1fN1dP9FaDHFknJkwaeyTj/aRHs8lpz+SrRl/PH0eM/ig95thUKqdP83yFXxemz6hEee5gh7W+HeVjBrr99czdiawH/Mq93j8z5LNNlmMd9TT2ttmBPj72rutEfTaf4AogOPobfu9wz4AWoO9R02XyTNtd5LQd8hRkGST90MaqLaCQZ6uu5utYwNoWbaEBnY+5Dl27CWGeWcwyoz3YSNEuinXTYCWXpar2HizWWMKWrS96eRDHSOFTh88PMT9jux/gcQI8Vmbk5Su/whW+Hn0fPZNjpo9sCqMlxpuNOztiHTFPlpPP7Bix9CFH16/8yq/gN37jN/BH/sgf8Wv7vuPf/bt/h7/39/4e/sW/+Be43+/4X//rf3Wrun79138d3/M93wMA+J7v+R78p//0n7pyf/3Xf93vjdLLywteXl4uaWuCG2gd3ZxcQJs/Q+ZrJYUy27U47T4y8DHPR/I+e/2svLPv+fdBMMm3Qz8OKPL+yaQdhV0/Hu1erKMr2YFGI3rQLnUKBKrHZcXU1U/t0oVRbVM3CiqmVHJQPl11zCEYeyaO+u9REJ6AGcvbK6UmLAF0wd87GDNSdiFvpIkSDYpRO4fQGY1xzjmNo7E5AQnhof7ZMz4jv5Af7fr0bAaNHGF5qA4jSwP6E7+aAd85uRjNuM/PqSbrV7m0+XCmiEZz/UxeXMmFs+vZQZTzRPA3cmQ9Q8uj+s/SiIfy9ytla/dtk9/IUTZyjtnvkZMt037WHyYTzEkTnSCR3kO5STZ2juBcT+y6xIcdv+W2oh/zzqHVTdHGu/lY9eyAOpvf0fjhait7qoO93G+jsjqDQmMuccyrK6Ni3zOzrkKzOcd+Sl9r1wBWM+t8DH3MoRFhTDr5a/OabX635xx4s4H/qNNieyOQ1NiV1HCOt1eDszPLrtp932SrIIujZdUtc0UDs5epxYGaZ9n+585djQW2beKUJZYtNoWLB3YvhbwsYJex5122NWqf7tsOnli35AOE0r1kA4CpFu9te1FHKkslDpeCdwg4roXFwcCyskueITC2ULbIfntRVaYi2990bKtu05fdx7saPtytyJA2TphnhoS2AHgPMU9Ml5Jt5VyxrvIn8cxaMPvIzz6u1Ea7Z7XnZd+z19wIJ8LLbREHHYCJtK94x44K3ln7j3T1F+F2W3BbxLlpW38bR+pYQTFINy8Ac3JleZjlql5stPoc9gYMsZY5AJjZHQBglpMfbzeN77a7rPB+N3CTywv/WhZ3PHHLlLGGvnbo9KG1MzXSZcjQyeX/hFtEKVegKeansPooy2wafQaFgPCy6oCfw7j5rUFnZD508rhr2FG6DrACD4c7VDPCF307rOwjdG3z1itJNgArvQ0iH3HOlX2WMUT+HOKm/KlzIDuvRD7LSlgO+aJ+dM00sG1az3T/+OdFsw7my2gc+n4xumK7QxNHBVvinglM5pxLR/S8avmj7XPxDKffsd6z8rNciu2hMH5tiqrj1NqT8RECrz1q6yCN/A1nfHvmjI102v0znCuf1zwT6Rg9n3XDGU0fTR9ydP2xP/bH8F/+y3/prv2ZP/Nn8H3f93346Z/+aXzv934vlmXBv/7X/xo/+qM/CgD47//9v+NXf/VX8YM/+IMAgB/8wR/E3/gbfwO/8Ru/gd/ze34PAOAXf/EX8Z3f+Z34/u///q/UCAOAvTeRO1lhnduCesa8o/LipxXZAHAc7EdMMkrP5DU6R4M/qn9U7jVTHoW0bVO6Sk1BWl/EZ3qFHas/GorNQGn60UDNAJzF/NQbUSVsr4pGT3fPkFbEXmHim+MnzlYCWvyOGPheU2mdEQCelBEVTa9yBikLzTBGWTB6rKEglCmUYycAgYPX3O6lunKi0B4vL9OGs5nTN9FWcTBxCwTcKccM9OX5M8fB4f1Wj/YGzqhUzmAe+ViHMT/rHQfbg7hSOUVjefTWMzonnMbEl6P8X0XonzlqvF5NNb21isrtSsaMlOeZQryi7Yyus/vZEZLvZRkZgzgfngE6x4jN9UhffP7shNuzNh7ldRtvp4cu+iM6Q/XT5Fp0cg3nSNB/Xbk610wumnMpt7srLs6h1OyRQ65YjKmLNhGRnHiHil1Puqu7xU0b6IFBinqhYAG9vkIM3oqN5c2f7AwrmJcW52zfGTs2GPw0p8ykMRN7PhqvnPRZ7jFnjNZsKJLzWHMotvBu9pDAGXPM2YqSflsq9DmJ30SNp1AwLwumedaDfaTk+7pi2za83+/Y911W7xDhritdlmXB7faCeZ7xxRdfgJnx+vqKbdvw+e2zr/BCFUNrWmWr337bJI7X7aaOoBvmSRxH7+/vUlet2LcdX37rWxrEfPbVNfOsn7rFULY+7li31eN37bZSSldXLfMivKUB7stUULbSnq877mt1nT3Ps5waqTRONDlf1loBdfox71hX4ZVlknGoFgtn0gMRXl5wWxZwrbhb++4rNnWi2GmLn7/8jPv7O7788ktx8OncMgfR0CEFXCGE0/SMnB3pVCLgdZnB84JvvLxg/fSKbd/w+cvPsrJrvQMsjs9lnvDFpxcfK1PZQaq1T4VQhVWmhoN6SJ24hBYCAGgr1s9o93sHGdZWRZp8q8y6ulC20q614r7vWHRefHp9xbwseP30CdMsvOvGaHJstQM0eizm+TXuIEOC3V/Ky5PECW9292JZoe8Oz47wT1eO4ZEOLQ5+n107LzkQqJ/jtrTsJ7ZP69yQp5ef+dnGMpG/GXmFkXxvzxyGJGOai97MzqlDOx6krIsjf9BJ30VcQiS7SjgekhHmwRRjkYb63LYBek7wjvHaeloOTRqNX9xmmcfoGBqBRlg2VxQN+JQvwKDhSPHgurXX7vn4JVttlM4cmjE/BxnW6XO03VJeFoeXUlpO1z844oRnZ2SrWp7oDi8J7Tg4RAd8OCrz4JQN189OWu/1zgO7aUDPozIfpQ85un7H7/gd+AN/4A90177xjW/gd//u3+3X/+yf/bP4qZ/6KXzXd30XvvM7vxN//s//efzgD/4gfuAHfgAA8Mf/+B/H93//9+NP/ak/hb/9t/82fu3Xfg1/6S/9JfzET/zEw1Vb50nYoOmLMUhv6fkOOsgA9B196pE3ygJD52tXCvBcyPQpC8so9K4MzjMmMoUofTkSaEC0tojatbj1JzwhpWajDkcQ0PWjObGikRQNB/1uebqJhP57Rw8HJaYMczYO3YQ6GHHkwsgVO7OfMsIhj9dl1wf1VmaLMNrljwLTwFVJ9BgAIw5vpvRaJ4iHrUwpgK5Ydhb0FOgBB+eav7FDG8fwHxji+MKRN6PzpxszCvdx/G6rTxwaXRgRQhP68UxtPj4c3loTaRyBa0eX0TUkRG4ejHghZQx+HAieKIGzZ0fyKJZ7VsYjh8fZc2fpkXJ7lDcryihTP6Lwcn2tDDmXK5Z95iCMBw5kGs764SiHBwbCk8nnCYXvHA47yLIzxc4a0mUisX1RQNaT2qjnA/ryFwmZ3gs9dGndc+rPDp3jUL+vopoKlttNjF09UVC2wEmPTEWPPTGZYfITLW7N0cmlL2N6INB0AOCr0Zz8g1gJfEVOcRobaYP0r/Vb08tOD8mqLaokoXAs9j0RPHaXt6Ngdr2qJxjeV+Vr6Co2yb/vFbfbDWJUFQAS0N14pJKtaGFwhcfzIhTMs27Bh9DmK8O0/+XQmxZX0/grnipopyfKahzrx3ZymPG4BZEH6YusGShVVnpRDTGYWE7pw7ZhKwVTrSANzlyKORLntnKtimPDYuFIfElp0zS1OF6sNglXxraKU25bN2zbim3dcH9/lwD9lVV1B5lxZHO1dJpGeCRPEfnuxDi4MsLdKV6rBtInlHmWkyhfKrZpwjZPAOQggnma8HK7YbIXfnpYT1eDNoQBVJbJSmgYQKlwPux4PwNtyxDxvNPeeMMwSNS1ZjxasbZdudaKadsAZswaqHmaZ1nlpQ5RIltlSENI4LWYTqjwE0Bh8rJz0nD6HKXWN4ZRvLxh9nDf8JfJEjShc+SziLvs8eYkpxQD1GRR3/CzJvhri/Apcs7lXdbzIA9W3/B9ovlQLw2/93CuVyrm/OrzczdUXTXOk3JDHo/Y80hJYGiEzj2UedCpSfTH5+LLTdMzUa7ZdeOZiEk62+rQ7/AdKU4hPTfQDROF8ppKOth5R+dEJqmtarS2R5o4VTQc/UGeoTMmtaXJiB5bPmOfP0wnczDfd5oNg8ROfObZwTVzfudiPtKezjYN4TrivZGdET8f4fKD0/CBHX71/VH6SqcuXqW/83f+Dkop+NEf/VG8v7/jh3/4h/HzP//zfn+aJvzTf/pP8eM//uP4wR/8QXzjG9/Aj/3Yj+Gv/tW/+pXrNKdMe6t5nHCWct+MbdwT5dQp0H4CW12jCTICHDnvyMPaz4UjkLHf5kmNHlUDmbnuvGpjROczhmejGbiYzgM6owLSuL4QJVxQHLQcnABhONxtMmifCP80GRxDkcS/BDVQMmIAFTw+HmkFj5+CQWlFCbOv6GIEYW+3A40I+a4S6b5vq2sKx4fHOrz8CD4/Iti6H+zP5lM+fEYkhZTr6t7gdkWz3z9zTo6S933IF43y/CZhpAy61YMXYNLuc3juMAcc1PZ0nDcA7Ujr+Ews0hx20bESZUAhEPp9+2eO7qhorudvuzeSDV9F2X9VgPDISIv0DsfkotxDv8ayAZ3jx5V6uT9tHsYVno+ch6M2NlXlwqk9r/eGDssKj8nVnWAKc0CEysJLVmYe82eHxcMqxANKkr9Yj/GrFEOH8rpqDqA15A3fm8w9viGMTj0AvjU4v/yYpgXLy4T393d83r/0U/Z4mjCVCbM6U1AY8PhWUqhsv2u0dPSGKWkOMaNdxGRNvAAJ459kjTvTQl87dlGekN+2moSAwiAqsjJJVzgxoPGeCR60H8BeGVTl0/TFcrthAXB7fUWtFW+f332V1rpu2Pd3vL9LLK1vfOMbWJY+ltG+71hvG9Z9xVZ3dxy8rxuICNuy4+V2A+FVVlBNE15uL2BmzPOMbdvw9vamsa12bOsKIsLtJjHCXl5eNBZWW221FzkZ8b7ese27xNYHsJZV44otuiJswrIIlJ1WWdn1fl+72DU7kcbvKl7nrA68ZUa3AqjWirrtPl6liCNtoiJB+DX+GvTUyLfPn7Gtm58O/v725nwiTqQJs8Wp0/H2+KndfD1OniyLRunMKHv00oLB4HpHmWbMy4KyLChE+GKZ/TACIUtPKPXdEHpoh+kLLw9gNr2puEqst0isijcLWA/vqxMfRtcelwk2F4m6/KbjC5qOrbXi/e3NZcvb58/Cc19+KSu8Pn3Ccrvh9fVVeGpZUCx+XywnGKRasJyKGfueayI92hEnArjTA9TQr4k7w6gZ63b4Ceo0yrgmPROcXdanPY7nwzMPk9NhzpMo2KNtBuQ+8BoDhnxOrT+HF9vujnb69EN4Yp3pGJXCtUhfxoT2rPdyw/gm4znM40xHet52KLktgh6PgG0Fs/CCO7m6Mrn/TP0zTkLIEX+M8RNz7xSOJoOxbeOxQVUxc05Bdx7sDjTeybaW29g4dnPMM7IX7Ftnr43oy/LgIpG2IaY8Q53W1MbO+TXoo9FY2kusK9x7ljLePbOzR76IHPz+6Og82iQ2Vo9ozHT8/9TR9W//7b/tfr++vuLnfu7n8HM/93Onz/y+3/f78M//+T//dqsOqTlQHhl18WRAf9r7N7JeE/hRl16V31GUhMTZ27X4ecZYwudHprLPM2P3Ix5Td9qw0estPtDc1wNYvzWjZNwnfZ0B8KuCPrQ9GFZNuNsthr1lje1j1jgk3BS6B21G6HPmFmcrjw3QCS9WZ5NN4WajhpUKJ44HdGX1JUclWEMOJN5AGteq9FhgcgNa/mwQ3geBGeo25Wu0mlPL2uf9FMoYbWw9OBI4cA31+foOTCkAtZHzwI1d6Pgz+Rv+nC+391iXlQMHDE6ntvswZ4fPc3NgnVSXnQDR0GiVRoDY8h3bcFTdIyeXJXsbE7fztiYcFUcGwL9VKRtdmY4z+Qb0AZQ/YvhZG2KfjJz52RYbydZnnGxX/TUGiFL7gV8Jst0nx3EL4jg68EfjLs78ASGEPs8JnRz+6zOEOqNjze0BOi3bXmJYOd337gVI226eaW5ksM8Zd5qrXGFmcfaUgpfXT5imWR0sejLbvrf4QnEbOEfBFfs09YE6EHscEfrrYMA0Y6MzALRxEUi7PjDdxwBY+oOKrEaz1SfGtNO2o1Zx0hjN276D7yumWjFP1bf9lTKhlAmfPknw+GmesK2bHkUuzrK3t89Y1wnbJnGuZnWuvb6+YNon7FXKq7uslLG2bfuO9/d3WTkzTZh0++VUJtBMwIs4SPZt9/hf9/vdZdNUzGElmGCeJ0yTxeMij58mn/12jHmWoPM2N283cV4R4DpStkLKtb0IbpBTOCd1ShHmMqESNV3Izcis+44NEgB63zZ88/98E/f7O96+/OxOMtY6HVNRlBUynhZXB4ZnBkZge7FjT8Y51c9Kw06s/JvlQFd0mL+AnnjIFdDDOLgUUK0osQyjFU4uqBqfB0Pa2sOGE3oMC8gKHvZyyOdvN9/Rt8FlBfuPLp/gMy0/0GoVG68VPUETiqHu9zuKjuW8LHh/e8PL6ytutxe8vIqTt0yTEi9jVLSf3bnF6EBRQVh1k+2JgGvb74DXYHI+yFDqeaD/DOUThZq7rm8XON8LNk6X164PZFnKJqQqd1JbV9braXIbZqTrG++O9GfKKw8MGjhWdgEKKy1QWgh6Bh46h0jG0l40HejLdmSmR1ixt5HkudZHiVU72ksJRCudeRsakY194JOEBw7YINuFkeY4z7w8a89x3CK9kkYLKSjYe0csdKAt2T0EdDGRvRy7F7BqY212fRqfGzlKRs4uL8bq6BsuH9GGPElxTGKbOnwd9D+l52A05/Z9IEXcmq+dOY5iEHjrt7Nxi89lOyPP+fxM5ImPOONiWc+k3/IVXf//SH0ntQ60yZUdKI8dQHF6KB+SgoLBZD0btNFAnNFw7uh6jgHOnF25rsywuc4hUB84H8wAiKTZMeN9uT2AybTYW8Iy6BdfOcDivLI3eabgCf2KqoMiUGWS4z9E5ZDrBMXtk33f7jk2V6169PhAAFj/e7uOipFDXsTxCvdzmVXrhAK8TqEB4XSuo2DPNLKg7tZf9t3GhujICrEMKcifbau/THEY0B7wlWZjatusyhRWqHAbYwFU5IDenjc+iEojLt32ju/GIcxRo+VCLjxSLO6AuM7UmRt2imhspzSp8XvnFIy0nNR1BmryfUtx+52Xn2TblSPpUfmj6yOZN6r7TLaeObqyM+qR0hyVQYnvgBbbAOhBwqPVZCN9cKTL5gOF6WKgBs4HfcHt80NOSIbz0VAmDOoavafMTio2w9abEeUoOt7t6Le5G+5H4C6n0KXKz/geaRu0FrvtVVZvvUj8qVor3j+/6cqdDZUIyzTLli2ylwZthYqcVhhX3sRTb8mNW7L+DX0Jn9taVrzNbRtKtMKa1JTvlW0LnZRn26XNybXcbqJbiTDN4jiiEH9LgsDfxTE1z7jdCDMV3LTN1ifzMuOuK7ne39+wris+f5bVVuu6Yp4XfPHFFxKE/HbDVGdxdJVJHUnkcdX2bQPriYvTNOG2yFa3eZ7lcxLn2UoSoL3uO9ZtAwBUPQWS+dbiamlw+8rVV/jt6qyqFe74krG/YZrayV7TVLBtsk1wU7o8/95itU7ThEUH0hyfhQk89RiOII6uuu14f3/D/X7HN//P/8F6v+Pz589uGLhDRfVne7Gqat4D/LdynRei8eNGejBwKPJV47MOVwzEXpNDgUf1eTktkVG3VYL778bjwISAT2AvTUK5kem1TJv2DY5n3UqoBFS0WKrxJacR2kIh6KXqwuLQPpND7Fu30XS+YZOa4g/WitX4AUDRFYJffPENfPq0AWBZ3XW76XhG152uGLMxqKx4shmllfeDi8ZFoo2Xj1uwTdqgNZnquDw7MCyrhrMIL/348OWYrC0K+OKg+YMjPdAKoMCd2ckVtq06BDu+GAb1sjumONS9yurto7PW2VZMmx9NDyPQZ3UNyjnRbQ7NGGjhXdIcC46uWBB1Yz6oMqjKGMsvOvn98AvAV/daGw42QbANrNxDS0Me1+uHLI3nrA0RYqfc4d55PFu3Ny8SAUMnl9/rZGZoz0GedhWP59vgu/UXWbmJfufC1M+xT6MC4Jg3zAEr69iV3MWBjjSPefbYo1d24CiNfAnPpIzRH/kiPkrHyAZ4Nv02cXTFz2OgQF8CSlHQxImbvZW9cjbP+rMdnA2pbPiceVNHg3h0Lo3rKqU4yLLfmemO7ezr6QwX74NjPiCu4BlPCCLbltgCN5sClO9maMdxQTOC8neIsvGT7NAL5c5wQuozDZxlx92LoVKaIIyNVCHZOaBi29QQsxr8aFn7HTzhsbzYq9GJNlQ84R7UCKuq6MzBBsCVmvUtEfnWSRtrO4J1xHOxTV5nmDtW/zm4lLZ1Qb65xTTp+tueQ6M33rOxdKdYyG/OLh97Un4N40+dcdFB8McpjVFupynU0dub6/c5gYghqHlOgbRipP35yN38/Splx3a+Pqy3m9fXMmT0eyR7ct2jZ7NzKOaLzpFYTnTcnbV9RN++12Z0pvtnc+ewXTZ9H6WuDfqvOYOdPkU8MYhzbsPIUeR5BvPNnWlEwzkWCHoIPmM9bNZtoC3OaZ+3QHcqo81dM2DboRmNXnMie59edS21z6aTSKx1koDl8+0Fpe7Y1+JyvRpmAIFIYw+5fGkvb9xBxRKoHhVyTF2QHUav4ZDQpQ34HuYA6Y4YAnmg8oIF5PQxoPcKGIS9MrDtcnJhmUDTjHkGplmdV7c76l6x7Zvrl22vYJZ4ZYUK5nmS7plmvLzq1sbbItsZ39+x71XnhWw5tFMEadK+nGdM84R5mWVb4331VU3bKnGq2JxXtUoQ+HnCPM0SWL6UtgqqWgDxDe/v7AHn2yo0wjItIJKXTXQvsjJs33Ff7/J3v2Oaim6BlJVh01RAWLyudV31oIMNdQfqvomDQ7daWn1EhGVewMwtoL46EXcN6L9tK7781pfeXh1QWSk4Tc4DhpGM6wHRVVOUT08D92h29Xi1FPLT7cfRKUhVeXREAEXjXXGtujNU8VowzmpthqvpV5dT3rQgjzmQxwgrII+4x/FrlM3UtgN2cjzKuWAcIpQVHXM2xwnARISJZJsXmVzaq/MdiLDd79jXDW9ffikHJ8wzXj+9ijP0dnMHcykyBxw7NmsZJsEcs/jlLFObwDrKN/L2NSeLSNtdwaw75RFo4MwXg5SMZVCT1rENGJGcE3OLK2c4MX6OWmtjNMIRT5AfmvCBFPW3Od6aXeQvaHUr6uOGP05xzvfOGJmHR4d2/9zBLAF8Vequji7DOxErnR64Q2GUL/Bbtw33gg9Md0Xb7ZiPDu3IJJFtA78Y1Ec2EqffkQfz9l5fJNC1UIiPcwLh+knjLtMJ5D9Nse6MGey6t80vUds+3lVu8yvVkfr4zKHF3B+2dJY/4mnLbzvrPmKXxDKyv+IsnMqVHTJKvy0cXTmNvLxtwmUPf5TPR4Ol+wxC8BmDZvQ7MsczDrAz43FUtjm7cj32+8pAjfd7hyAQRYk5uqoGbT1zcsm93utvwlF+60oufbNqRlN8Q9+10Y2I4MiM+QjN6EpYMBvch36OY9WIb8LwYgxGQpjDs1HMUqiK0I8JdXlTeVCHmipiH5XkBPBlo0Fo16AUSQX/mSMoO4jpBLTEPogOh66fvGvJQV9soBuxOoZuFCfD3IiMTi7Ld3ByRBBubRsBZr3HaZwj6Z26tz5hPijOA62xLgctfb9GQ6CN/1H29PRq//AJkDlJPu5nvJ/y5jacOZpi/nhtNFfOHFyPUpZLuZ7Md9mxf9a2IX3Kg1f9EssetauTTamvjuOVuIwC/cbjthXkKEwa/6DR4u/Xnf+NZ6K8osPzHX1xDqLN0/iMXc9OrvjZlc/aPwPn3KEvT8objotnzv1jL2DEUWQB0qd5BtUigdH11CqwyNZJg4Szeqp62WFf24oAsZkcOCCuDsip9W14CRFa4a1RGT5NM6CnLVarH+R1V2Zg38GQrXFT0SDps768UccOabyqWnU1QK3gDSCSrV4eE8tfRAHzNGsAdovDxS1uVa1YbjeAxDFUqGCeZtRpBzGwAhL8v7JspVQgPmn5M8sKLdKTwyYNCl/rjnUVh9fGm4dQsJVh84s4rZhnkNKBXbagyuquqs60olstGcusTkMNbUAk2ybBrKcgykugotsN53kGlgU0z7KqayJwhTiAtg3vb28hptmKfVPnntZvPEq6zVOcd0CLsyZpvHL9iCHO0xFxRBjDfCbb272mi9qLMd63Nu+5X7HKtTmMarHDcNKqyyijuf0GoTm4I5RIWDrjVTkaBF4mIZzSSG31w8h4sx7yXiJxcplo1ckt7a4htp2ulllXGeNpnrBtK+Z5xuunT1gWWUW5LEqzO7tC/WjyIAA1gLJ86A3X6Ozq5Lji8PZ+NwBcy2vAMrwEPsjGQTrq+yNvPYIZTZ80WSifvR6JpI90ZStjXGcYerty0a5YYc5Lh+8te8B4lw2Pel1KiAd3NXEfFwLQga7mLIq0R5rjnBJ+NVnX6upfCFqe2BkHeZDb9gFMltOIXqtCxP7x5WJnJhjuAQ50RhxP/uzjXRZeMB/xXJuS7GXbdQ7PdSnkHUCwQ95uJgV7bZis7JCvowUX/TLAma3Yhl2yfB3h6Hw975SK37Mvo5fd4/IepUzfGe7/iP0Q028LRxeZMkiMUQbBPY/satdyedb58JNyomLqnj4xaEbOpvj5OH2cYaKH/8zo62oIzNSYFrA+Mr1V68ihcdZW9nLselth5k+kz1acC2puitzHFGGrYGqWjJMd98z9KViD6h4lM0hc8AyEbJ6UddDXGdSe8kQSioym5Kyu+OnbHzJgYcau92zJsymSQ2D9KLRCkHu9eFAM9j23cqio0FZ3ROckCB6TI45l5Qpf2YIQp4e0TntbEAxmo9MASoRq/nZrsPLG2tAtA6dxLKtReshGnMYrANiYp31l51spP6IfJ/oxXaNxPVGUTlu6NwJPo2dzOnNI2WecJ0NnXnAEjOg7c3SNaMhtGvVDTJWFD+Lq00x7pjs7AIkIeZXXqO/bPbnWrb69Uk1JdckpcdoP4GEZTiPai4TOURy+57E5AtQEHJWniSyGVHOqMhSUG1/rHHBaRrwc9O6o76QLeDg3+rlFQJFYUvf17vrstswo04yXF3EArfc7uO6yQirqTI3bxLqypcngaHzYT3NcccIGURKRUy5tIB0PPXwlnMwnK59mTPOCMlkcLjlOvlbGfd2w7xX1vqLMFWWvuN3EQSWxtAjL8qLbLjdsm2zVtJMBV43jZbGxJj1RT+JhzZjnBbeXm8QwepdVTLaq6f39Hbdtx7zMsi1Rt3sVmnC7vXj8r01XTokzqeLt7Q2lFGyrOLGmefK6y6vwxjzd/XQ8rhX37Q1mBL7wqzgp9aXY7bZg32Wl17qu7ojjveL9/R3bJmVM04RlXmQVTym4LQtqKSjan+t6B7hi022U+7pKsH8irEVWon3zm9/C+/0d3/rmt3wFWmSAiQraCW6sq4QaXnAWVd6adFtufMHD+/kBQRnkZEPRroXqHiYzsEUB7t6WBpGiDuIuRj45/+9JNh0NnUg+Q2P4aymRWOb2AqmEOWRnaZjRZ3jIDOPQIP9tTtUYYw2Kbby/db6DpW3LPDseYGaJWXdfAQI+a+D610+yfffTp0+43V5kBeSyYJpnzMushw70dkIcVRPdwRd1krIMN5khX4ucphQM9QvdnIz5Q9K+GeH58c9BSQwg0ETmYMjyOJE28if0MvM8HfTQV07N+UnQwwasP/SGtUNo1blHSMS3OdkwO8BxK6l/N0wrznyigU2gBe0Bv+66qwOWN2LdSEvg9YMeHeD2rs5D99vzR/niNohuZz7isfZCyFaEtjzaE7rTairXIVJysrlN5bjq6Cqdcoz1i/OuPTDY2nq20ol7B6MtKCDrhI8m5l6G4QJ7jyeT2+wjTBsPr8vzKYfmyH6EkY8j5hnZFFe/x80f4/tY52jV2Vn6Wju6TPiYwJIUDZreWz7ygI69j80p42WZ0DjQcDQKR0xy9j0+cyXAzwb87N6obWeMM34WANqKtzMvbWf3pPaN/7qn+6/NjnBlkR0E5igxw0mMBPJ78fuOvSlgNfRiWa7QgnDz1tl16gMaJoZyoHAmBLp8+j0qIC87GuK9RnlaCcT2dDRmulMycILUVqOLQzszeDo1SrWg0Zwb+Zp9vEdlDhVpoD+0Nb6Nu3qG0307PeVqfpzNzY6nzBCITuor/NZwQSsrsli0FC5SlAXZyXXmYDprKyWezs/l34fxTeVn+TZyIOVrOV+m94y+h6DgQRrReJVG7XqU3z7tjWdJcSzimJ+WmedEksMHmaRytLum5WdHlxTf5p6v3kqkZLlr/8U5YOXbHIj383y3+g7XEMYV1Fa6YZw3PmPAOog4QA3SUopsBGJ1QnEcHzGzqQDE/Vt064p44hLDHIkx2+BtLkGNKDNoo+ywP7nuwbNRAKoAVdBevd7KDFR9oVOCi7xMmMBqSAhvxXhzBnDbNbm+LHaiqJxOycygldyRBAhA3rcdexGja9LVWUSkMbaajuiCx1fpjRiHUVaFqT7XcmxVjYybfJZtQwX7SdJTmbp2MDMqpA45KZDVoSfB+0l5xFZ41Umd0ntpK3r2HbvySyHCziuqOs58FZfS1mEBtrnS9Mc5OEezKImckU7QGwbFPJCzkZO8Zr8XMbLnI+FcP5OOw5ce+gLtUqKvKbis/+yJNld0vENlQaq3/IM53fBjw0kMBjUQ1eQM6TxSDBsRpFFHoVyLCVZDuVxZ4s5VxjqJU1T4Rk/ztJWAeJXTTfWACCoSkj7iqtS8rPbzACUHS7h6ptb6xwf3HVgHmTW4f7je/8jcJz6Qk2eFZHfcjIiWaRD1XgRLRz5u5LYeNJ44QFCVbZxozGU5Du/wuJfutPhawUDeCJ2bDOzxibaTlJ44vzREAVFse5Mltoqrsw9Nf2S+GXzv5lK2JyisphrKCH9MdWjuTwZz20qb5ZPQLM/LtjbTx+oIS3j3UXL5ysFmi9+fwX3RzooyiNtq0GhHHXg+YM041lGmxXKGFMWywzgSQh8Gm8RxZqYn8sCg768w6ZVP4bcyXZUZaRy9WB1h/LEv4Tp9rR1dlgQvjpbRRfnewEC7PxKC9pv8L79BinXkUzDsb3TCwVXKxtJHvJ59++TT3zymlD23uT1SBmBKyBdXDSaNB+ikftVWC1pqwNlOQ4rlSx1aUtemCMrBbfWPG3AwAQM3wMjQDIUJoUf8RNolmHuIcWDCw422QJFe64IBRvqujHG9530MDJWB1V0oqtSmLKuWlb3XndLrb4gRpANnxkEPokL2YwnjZALdvnth1I0/mOUkLm7tFABhCoCcR6wdfioSSseTMd4Sox1I4M5Najy877vQEWjL8QrsjWscN6vbwK4DiNA+G38fA+WDeFLcsb8a3W7Xc9jScNBYVrQjLLhjNhkUV7IhO8xtbPKxv96vob9Gb0iyTO3j7YXmJvkHNEPX2040/IxlnKURgIo05thcoz64SnbwQla2sd8m3wZ1/kYpy4Hcb/F5MdiT7HXjV0Eut9WtXh4BNKUVdwyUORxEYY6XC/CTn8+gvaOrCi3RKWcSiwp1ches+XWlCpfm8nGnlxDZ+gel3W+d0c0fux+dcKNUmbHuMqenefHr276Ddln1QURYXl7BdUetC7ZVVvV48NxJainc3qpzbU4YsG1NU3FAQlkvGqnddyMi4BQNtk5F50utqAAqVi2LNBi2tKMwAyTbEss0gUGoIEjIrgpaV41vxbATCOfZHFCir3eJ4o511218+45tKyjljtt+wzLPeHmRLVq3283jVq3r6qun7HRHkyulFFnZVQo+vb5imyVu1+fPn7GuK+7vd5gTq5SCtayygmye9ECA0sXHMuxiDrbP/297Xx+z21Ld9Vuz9/O851xuL5fyTSmIEUWkEARLbtCYCCk2xNSPmKbBhKhJ00pjq42x/mHxH4VoNLGmoX4k0kQjWhPUNlIlpb1NldJyCyktBqmiYIUSrcC995z3fZ69Z/nHzFqz1tqzn/c958I9fU/3ujn3ed5nz55Zs2bN+pqZNbdvgRLh7OwGxmHEcKPsQNvvd5imHebJ5tAq/6bjrRKE4HoDZA3epUQYbwzlGOaQzLsZ83HCsV5KcPvJW6WuedbcOODAi/XIG0TOt4HXsR9E1tZ/xdnzO7g6PsrCRgoqN5S185xCOcbaRElEGMcmlzIbx5qLA1vqqfJuMGU7um8Z5Gr4tUmgNbiSxTYKQWw1u8qXsQY4NbipOrj0cREIg3Gsa5giAborQ9p2eVYlZ2yVR8e58Pp0PGA6HnD71i2kNIBSwo0bN7AbR3zdQw9hv9/jwQcfxDiOGIcBM1rwQoJxwiWrmkh0htUrbKhp+Eryn9rchgnmAiHzXhZbNea7qXLsJHT9I/s8Q3YnyQvqvEP0EEzA6KmB9dd8UKe01nlDy8sOF/EXbYyFiHQBBGzsy+p7ZMlZyMW3cSc3jL7mypPynZI/JSA2Y2LU1FR1blHSi5mAottL/sKseXaBZe5la5/IwogExsj4Hras9VFa+y3H15KOxe6MdkMfZGzSoqykuxGQRRLJeaxBo7Wa5XmVu9bW13nVFO2VgcP37tvGloxg5SYgvh6XG1uv0n4dK5k3LsBp7dkwnpfW2xmnaHPLb/Zyqmj32veuaoefwqcXM4nv2oU1wN/muOr7noBrHegiIyhOBbn8O83JK59Z50Yb8LSoj1GUpP0tfrdtrOG03hfvYPWEyilH8CrPe7jad4kIp3RabKMkkgck35YYVv3IazOcPJ6V0SE3TS0nQEb2ipKxKDPwsNp/5/QxMPPclB2ghkEg1mlChH702haBpzUZKaq/rQgQN0ZBmEg11plWQRHHuA3MEkd1TMVALd+VF2zCftN2x2bKVgAAiydJREFUtLqb42vYxwRq2Bm4S0M49tcKRPlbeEPLUnhH8FqZO6LMbb9VwIa2I06OT0w7vXds3zSggzgmjUZKNGrvL4xCHaa+gRFpd2qe9yDKlzVeXAscxXkQA172nVMy8RS+8VlPYZ/qn6VLT2HafIL2nVPQU/4xwBV/t2XHoQb/qTkCccdq10Gov6tcg69bnSsj97Td4A+LzHdBMYbmxEtoeWiI1/RseW+ux5nUkOnxsjYfnFmQlxfAIsjl2jM0sP0SOaFP3DjUsbbzmRIooRxZS8ncPFva1qlajbCBCDPajiPnKNVdYFyNdWbW/GCSvFpv9iNCSkOR/6iJhquDNE0zgGMJpKWEYWCkoQTsrDE411PXuRr/NE36vATzRsVtGBIYA8Z5BwlQSZ4yRnECyy2KdadVanOjBMzaggnNs4q/aZoxDFzzbRV8S5ANusNrHkflL0nuP81yVB0YeNAgcmlr0CBBSgkHPkIdP2YMx3LcksZC23L8suLHjEyMPM1gcxSSUwaNAA2pHrNN4JSQU651H3E8HDHNE/I84+LiAJ6zmV2FF1KSnc3KjI5/YeSS6ktlT67FT8lweVcZ1P3uQPxV8djZT++2W4LC+1zneK9KLy9k7lv95KqyJiMbOWf6pM67lmODe0SAwaZJsotTlVclmKO7N1a8UyKhjpFC1k43eNpfm3RogSNHPc7gmculDXXOHfZ7JKKSw44ZGIeaH87aQEIs1vYbXZZWkciRimTlNTIsYXd6lOdRFyw+l2TybRoeVVXl7L2GOVAXjqVvFU2LqwQuVROI7gg+gIX2OPJtpA8Qbz1szxgii2MX9F2YOWDtdNF3HTtMeeqErbIeqonVtSCXtU1ETroFf1c/6lgHW83w8Zr9YZ/1pk17b2lT9j47mJl3bLulNTtezKwX1di2CVWnRdykhQX/wI+d/U3nRx96/WDABdEuA6snF/jA2GUw9nFut8CqTydjb/wYlcVEoJyLr9LZ9NCDmIal5xfFenp2+2Ug5XOWXeT9uIj9W3jc8lMs1/u9tZW7iy1rcF8FugA7mMtyQIsayjb0stUdNb9EvU1oGEDGaNUbudJyAC2TRycnBr/ib6eYzed6WWdAN1lWGP6yAJcLmMAGp5rc6FUtBnRciQXIjEu1aziaC61+2QYOLA0toK1iDDQ0+sxLZ4q4H1GmRCAuxv2cZ2TOetOS7ZzDsDeW8ptJ+t4zINRwohb80f5XBSv0YWagnsGXvrYjK2Z82ET0xeEwPCKr4ujg6wSY0DU6rKZM5rITbTB4Wlq4/gZDSvrgFfBiSBa8rAY1mhDMNVm0rWdtR5HgFK9XBtoOjiTOmGkDKbntznYFQR3T+lxWbmRldJFnrOJoaZYoKX/qrqPK4zQYmcWSJwrK07GPmbPuXIvn6NfgVCAmGld25VDKXAWEj2XM7IqN4Op3dkZZHYKpHVnXC47Z90Vp9uRr7+YWIPCSkZ89+RNpRoFnouzt4Sy0kZ1uN85KsCNhuUtqMYeqDM31+EzzBKGrxPM0ayLvZsyWdyQBd5EtZHLKEDLVMZtY5xwRgQcGhhrsAoEGb5Rr/ZpLhBdzIc79U/NXeF/HIPPqXLBt2IDePM0ALfVAGeLBoSM7OcotfeVWv9u3bmGeJszHahegBDfGMYGSrNAeaqCo1p0ISMWxlWNwKocIGFK5xW8ca06r1HYvMYDhILmwjpjmGcfpgMNxQkoHTHPGuNvhxo2kMr78G3GcMvI0Y67J5o/TsTjbux3GGlzS3UzjiFSDPLkazDnnkrur8qXNdzUMg+b8GuruKzAwjjtMNV9XyXN2xFyDP9K3YheUvF3Fniq70C7OL5qBOk+l//VmxrOzMwxDvQ0SA8bdTo8VPn77CRymIw4X5yAi5HnCfrfHzRs3S9AwJez3O3Aecaz9m1COGt6+dQtDKoExrjtwbpzdrDFJ1psUz2/fxq1bT9YcX3MJ6oI0n5hdRFJZ19NhwspWL1L8zfNlsZdkuhjDy3tLxtbwNofot2zKFHs1qS1i7UoJoBAAHpoOm/XSAskFJDsIRP9lbUNy8jU7INhPRECVM3B0aceASYIJxsFlZg2ciB0kc0VsdqTlTXOWvs3Zl3xoSsKlnJbyJIt4ULsSqDvy5BnM+DPj4vw2cs544onHMY4jzm/dws2bN/HMZz4T+wcewP6Bm2086xzJVBZ8SWS05SkZV+fAsfkgsCz68tKa1otqpLOGJiddQsdnMkYlkM+dYm3HGandbu0e0WPRJlZbii63XZpZuhqicH/1bBzptZ9vTS+K3WVrXLMx1DdK5ui9ee5t7JY/09WnU7sGuAazkxWEaa7HZA9VJs/tVI6zQTv2jNj70daJ/FALu76Kj1IeLXPUig8qNknRrS0Q2pNr7fe2g05kXSwju4LtfJBb5q2/oj5LCBKpvwXray37KfrEObfMbRdkpxPLObZMTRQX0MEmCGnsYIuDBK/0lEmVKWw+pby1+TklRA93YSvXz6JLlzvEeoEusZ+lLWCZq8v6B9Z/Fd+hjGPbpRdt4Gjja6oDg4PtUw9PeZZzXj211oNrHugSJQHYiefLAGWwha/b1swyCHL7H7n6Gu+2I1kiMNaE9Fpgyzp9UUE7gwh+gMvcTqsDvk4PH6QRiJM01inPG+7t97KSafvn2yt1BeFDHU8ngKIg9Dbn1aMj3ATYkta6Dhdo5dbqdCzN+yfo2pugER/9rESJn74+c3zTUKYp3/LPrZK5vni87fstWOT5zrUPsZdCvwKuCR4nZzTFPoU+LL7rwJ74W2niHfv2ld27MXgQFZrFS/FGUZ5qWJqcB+JwWvzXnBbLX7LrRZwZDRJb69rQQZx2DeCRK7A4vuUcG2Ok92i9Jh/kedz+fhn0AksCUY7Yd+J111bpuT518D0lm061ewouaweAOoXWKIiyJ9YV+7GQR0HJW1qYgkt8O4H++qDxRTbHeDt4WoM6UQISStBKnas+raJ8bMGY5S7BNVko7YtTsOjfyhiKc6nOh4r600EuRzfntZx+xznFZv7vdjsMKeGIapTOc5HJXAJWiRJ2u3017soOI9lpwtUZTcPgjh9JEGLOGTTNGErMqCYmJ11YKz78ANCkYj/nGdMROKQBqQafZMf5MCTsiDDP1BbtGLoza05VfwzV7jHybrffa8J2WWgSR9nylRx/TMkspoCQd8UAn3gCEWqgbFLnzqqucdzVXFkNzxIoKgtPDEaaEnJuR4NBBEoJAxH2+z3SkMrlAVyOER1xLHUPI1IaMNQdc7txLPJ1FplfFik5Z0yHkncrT8WgPk5HHA4HnNcjliX/Vk0Yz9TnPUY/oAuR8WFOtNcc37kXzV9tDvVlIQsO7WErb5wj/bvqbHF4Vb5pfUbH1Hd0IY+a41iCemXXYeaMYRjr5SmWNCzxmGIfpjqOVlaA2g1jIiPRh8yMxH7lX2gQ9bU12nu2mOjfcotpPUJlaQcGKLnwDAN646SEBlPl7XIktVxYkbkcTTxcXOguyd35bexu3dDjv/uzs7qbs9FCj6WDnD1tg0fyDFVuN35k1QkiM5lZd6KIT6R6g5109CC2CLOhCytZLEjQQz65viO8TxB+NZSUspqInRf1+oAWdb8qrvGnpVlqXm45ojwfdqtqZpnRt/ah0HLBc9R2HHIiJPbHT+0lUDLPqT4TuaM7bJX+TRa47gV7ZNUiEv62Y78230wZL/MsP7Xxl1aFBGV3TayZFp/NfWm4ZW47NaXFFjRc2h6947m2X2u0sjKkZwNyLW9xi3wiY2aBze+xbOQxtu8YedbjfsGHQhDw0liAKRdt2V4AqWfLWf2vuJ/wMa7iL/Rsf9t2TD9iv5+q/ypwvQNdVYWJcSa/AkIY6PMil1QUax1+td4oiDbt23b1PK8qizXHD1gOrGU23bliyvnBZfdehB7TnIJF8CMIEec8OKFAelSxPZfJYxW2KO11X8PSVurX3TFoW70XIpn8qxJUWAtM2Pd0MjLVHQpYCCwnbFYcO1A7zx5vN1l7VwhhbwFVY7NO8LhdNdbTC8wtnptyiQg5KnbzfCGcgjAyiLaMIs4wbA5Jj3Z3HOwCjOHXH0OtG+FIFrNu5yUpGoQ94IM9Qm85kuNYq8NLxej1u8Vc3qsa3LLOUVOY0GABw+98cUERs8NLdrO4YAa4u1ISoceTa8rtsr/vpA3lveDk208vq5dlurS/RO6twVqQKwagQGJknTYQgGWei95Y9GgnZaxC16CTsolpo2dom37JrjAJEC07Wj+s0b2Y2ia4hGUA1O7eajLGzF/pAxv+p/bZ03+27eWPng49mvag13/RHs3d6uPCEFlAdTfUHjxWeSG3+aEGuqiuwI/FbDoey86uw+FQbtpj1ptbm1wVOudyW2I+YmTGiKb3hmEs4qvm36KUMM1zCSrMskX/ogTQiDAMQEplpxTVTbx5JkxVF+d5xlRlfh5LcMLGHFMiDKkchZQdhnmeNeF6kZNF7rRk8yNoSBgGAlHWfG0iy+Y5Y55KAKoExajuCCv5u4ASRCw5vo44HA/guQT/5hrIyKmkFEh115rw49nZGcY8ApXvj8cJec6YjhN2u125WfFsX29mrDfo1UAXD1lX0Q+HI4AjLiofSN6xi/PzspNtNjsLQn4qlQXZ6h3DSIE91bgXJlvhU2ApI+ofXX411anus46SlV0kMnrF8QFVnWvlkLEDxT6RG5yZy26vnBmgthNaRCdrd4pzBvLB7kLHtqBD1OSGdEwdWKOz14Jh5L4syzjZJbYmc7VbsyVktZ2EFq2uMv8bjTO1wHQaSqBP7IqL83Mca+B02O8x7Hd48MEHcXbjhp4WGVPZaTmZhQqqMiMNY5E1spOHANLbbFveqMYENcguuafag/bBxZeJ+r8H3AagsoG39xtd7UusHyR1wO56UsZqvy3wsNZXVFPBjhHdEHFn7yu1mtomB1u74LsAXs5SDjSF0NrwCQMtQIy6W5hkUZM1uGVPCADehmy74bP6F0oFS3Tu06A8Wtrv9rMnsmICd/GXPYh/zJDNFxL06vnM7k1qvy3Qq+9Tzj5zYbRXW0Ul8MNFd1jbvxQh9JiWqNyCqnLJI6fzW/tl+SD4PT0cIw1t/VY223pZ2sPCNHN91pNHtp5e+WB3ZuNnnLKle3X37PRe7MC2WRa5fdnFIsUJ3FNKXfs6lrtqXyxc60BXkPr6vRFn6TTJ7yRGufnunTE2OaiKsJzn5UDL550Q/dJerdS3Fsw5xQx3CpwzJp5N38r12Y2JjXHTWkRTIOz+biIE5m/4Z3ECqcpm71hxKEOot95Agx8FN1JHUXYWSACiTZLs25X+1u/2s2d8NruQumPRc8zEYJNrg60GFv6b6w4CEYjtuJsZ82AEk9RljN5TwmANN/mUfkk9zAyffJMjA9iKENMm2MBWDHK1Oi/nWzFYu8JOVrFlK7DBXejZ6/eqEx5wKcGn7J4ndPrTcXh6fSz5aUzgw9Kmvqe7djqOv5SR+nrBGQsx+f9lRx97gay1MlEp9QJdp8Z1ra1I/3jsrRdIkh1lvfbWjs3lzHJDugPpm+1D/C3CmozuQzUSqTkZEuS0uaY0gAQoz7h+hzLihOuOQxGcZORktUvlu8hJV2d9R+qUoKDrgfxu2tHN9Svs03feA99a2dFR804niDA2z9f3LFpdBc3RUuZFa7cETcoNhOWYYtmFdMgSbAZACTQQdvszZBBmqsfIUtLLRSQX1lR3f4EZPNUgVgZSyvXYZE04X48lTvOMaSr/Zi63CFLdkToMA3Y7rjvHhtKmuJmcIDcPTtMRc57LMdVB8oKVsR3qkTUJKLHJkSXHC6e57rYahpIIv/JISgk7qtfGp1SDT4eSBH6adDD2Z2cu4bAEvoah4DNPc8mJVYNdzAw+XmCYB4zjruCcUjl6OSQgA3OeMaSjJp6fjhOm4wQwYx5nnO3PAAC7cSz0r4n3j4cjLg4FR5gdPRI0dgY2y6KUn8vln8jS5rDI0V4ko/vuAtactC6IzrfvGlzrj+UjtmHKOFUtgZTMbi6J7dENqVP8bgLiUV8tvqkVtShVaO0dLdkB2frtBELHW+T2QeVLsefK3qJs0IiBEJEwKRHApMcKAZSjhakKC2ooFV6aME/lGGIG44nHH8ftW7dxfvs2xnHEzZs3MY67ksh+GDGMgwa8puOxHluSo50JTBlZjjrW+VYNM4lJLalYH9jFU6HpAipd2rMez3ReMyZxRy0YyEXIMkoG9kZF00rkAayUaz+xbZtO1yG4tmlB5u/+hG3zQ2zsDlbWfpffxA5BuW5Bdh9p+hUTtIh2W7w8SXsTA2pic7m5sA5XF0mXB0MbL5D+LbcutletUhbT3Nty5Xezyz3II4dV9T9kB1S6qoy0CPN6QMkVD2WcpLG2YO9ZbDPUi8ob4lfZugTHVViR1+p2GN1xmQ8lnz071voTl9XVq7dne6/VdWpxOOqpGFS7U7jWga5T/Y0TUlY2gLZK0YhHuttmGcBZ7pzoOTxXcejWcV1juvbcth3hKg5Y790151JuR5KIPWB3xS3lK1UDR4Jc/WDXch43BbUCdpysEqvVq5BEc+CYuW6pb05i3JmgeNpmViZaczBtT1p5o2m90LFQy5BpXwIntBJwcGr7EoFolaVQvSusrGCR+g3+UkbwlDwuvTYjxvZpCwza8nTKGroUenXahktQ1Fk+jS5allXZ1ErX52tQLOqkmuds+FCCWIoLm/dMH8RhAKDBrsy57LpxzsVy9d1yRQwyedT7z5RHQuAm4mlxle9XbSPWEb9f9t6akgSgAbo1nE5BT0l6Q/NqdVwlABjrX8NBZanllyz5f0xSdaISiKMq48QgJSwCUiA0HlvIW5FTfoeKPNN/Rue1ObQe6NJ6DA7lR/nT0LyD19oza9y4epcvujJEXs4Xz4j9qiuLnKx/FutTV5VTDSClustqnto170PlgWFIIJS8Uu29movO6M4MAuoCBnMGcnUKaCqJ2MdRd4IBCcMA0DSh3JLIINllRaQJ2TXpPCXjkEuQtx1BRM6YAQy55iCtwSPmFhgGM5CS5miSQEV5n9olMRA9RnUXWrGpiKjkNcNseDeXmyG57ZotgTlC3bzd9DTV/EucwVMux2yJMKA4hSXRfMI4MlJOQC56Tm5FZC6BQABld1fIB5hzSWR/cX5ujih6u0A9F1WV5mY+54y2+SA86oA8v5c6VEmdhuDQXkkonQKG0ldwjfJLdj4yCN0jZdWScj+r8dDwRv+nEICRoHg4+hVlPlqwx8pPNvTRdyra8p6rx5o9Otmb1adkIFNOkJbxrf9LoCYrUBYjyKXBKHUX+T0D8wzUXYJEBxyPB4zjiDxn3LhxA2f7PdI41BsaUQPfx5qKoVHC2TN1XjoZyW0PVfm72Q4yemK3NFoaP8iVL88KnzQ5akjUlcGWjB69E7bVQoc6TgnF12wFYR9rU7SdXRFhqvnRjGIy9qOpdNGutw+cXd7tS9Vd1jcgv5ur6U17g2gn+Xz0CSuu3WBXzxYMnwjzCYC/vdD4eaG32o8lrI+PPPeoWX9lcD5LbSTUw7pDDoC/lRR+PGwdrpZAp7gDawXxE71bPlMO7viEEd/VeEHn77WxK7LJb8bw89y0ucKjvb+fSgyjocrduqxPcRVb+tTzO/EBrnWgyztiorhs5E/KtXeoGsJiKN6J42QH8yqDdJXAUu8MrBipV61fcLnTiGfX+UOhV1N0TZnEpMvtStJBjdU23b1S6clvZkNTYzxqGQmORMNKnjHKai5QdiOoHGOnvO2m2CI0M8ZhaCuEpnobGV8TUlaY9ARdVNlitNptnKrU6tEYaVf5gdtqhwj6CM1kK9/tqkcM8nTVUx1kNZYMH6TqmGhd8hn50rQhgTZJAttots6Pyk+8NFRjOQJVA7PtYtGriWW8BVdDA8FX+dWsquW6mm+DX0IvGTcLzahb9ikGuNTZrOXF6UiUkNFW73hmsZO1DnHgBOxOpZ7ssc+AtoPLzvEYOFiTE7aey64LXmvfvnuqzRjIsuVinTb/l+2TfeeqAbWId57LADwVxWv7s/bpcfU4SwCqzLP6aW8/RNvNqIF8wOfC4qVekPas0+udG2j7NshlQQIYFlepJ1rT4qzZoNkqr101CBBBdLvQof6tya97yt8YoPKrbuKqtMpT0WH7cVeOFe5HpJo4/Xg4YM5TuZyGCHsqR/l2uz0wDNhrctUm3wlld/TIu+rMzCrPD4cJwISpJmTf7fcYUsK422G322MYijM9TTMO9fbAeZpKbqzjEcM4YhhG7HYj0jBgN44AAWNOyPOMw+FQj0uWhOtEwDS0ZPElifseQ02KXPKT1ZsS6/tEhDwzjpAA2+iCSPv9HnnMSEPCeDwijUM5AlnxLP+m4uTnXBMwJ+zO9jgjwn7eI+eMi/PzujPsWHax6WJbSTSvO8OIcPPsBuZdxm7c4Xgoxw/zNOM4MxLaRQvH4xHnt89xfn6Oi/NzXJxf4Hg8QoITcgFBsrZDPTKeEqvjZANckk/GsCBAaDcFUrupr7BVsQaY/RGOLktbA4LDpAqsb51dayI1p6c51mofA8jJVsumUT+NrY2jAVEQygZ6hmyBXcpzO/Xq8VmjkwjQ28WkDwvZsCIzuzTrUshWVY5emm5WGVHfJvM+N9uxiSWudpmxGWrAe56rjq07PHfDWPLhYSy8k2dkLgHu+XjEMSVMhwNu7fY4v30LN27cKDu7JI9XvYghG/qwmAaiG3PNMyr413G1FJTvXIe32THBWlV+446crDVJGW3PvG9+0d3AvTERPZAIREnpz66qqzutjS8b2k3XFYRPq2nBdWlx+nnbdKSNnTW8w9vW9q4/9S41krKcc71tt+Xmiv4E2OxECu9fGa5YtvUdl9DPgiyYtIvCSh0df8U9M/ZNB1LV4bkN8NLfrac3YuBLy8PMBds/6SQ6HG18HWlT/iZAdz73KSFflsSzPoj4UYs5p18NH3HN7Wnqsf/kIhJbXvx0kdk9PE6BPe2xFsBaAxdL6PgHsR0Zy+jv9No+1dZlcK0DXYAIO79La72cL7P26aeH/btf/yJK3xmcHgP0Iqr+XTGS1ge759RcxUCwbTpnEcE4opWjYljv7x3wX6srODwt8OC/i5GqDr0cAZMbTjg4X7aN4Djb4EbPUOjjeVk/Oope6dQMSKtQFR94XvROsDiOHRw64x6V5mo/2qQoH1XL6XM7cbDk2V4/iv1I64TkNt69QFdvB4geuSLfTzFuTDVeWUk5YEFPhxL7IIdVhqYx9+5i5Z5b8MEFpdB2Gzr6mD5mlzPEGNwOb9bt3msyJEI/wLL+TpzTdhfVZe3EQFz8jHj0fl/DO7ZxWT9s+csVYnQCTuNxJziv4wUMQ5Pvyt+xnipQ3Nxe4yVj9Es5kZd3A6cliIE1b5NhrpdfzvNLq7d2fSi8kBEwMkfkeddQsn83usmOLmdkqn6ot+BS/eeyiRSDG2lAGneQW+UyUHe5lRVyGgaknJEJwFx2POV6fF6MvJQSaBwhwZGW/L0GGiUQx3XhQ3d3VTyHkvB9qLu7fM6LdrRE5p4koi8GMzSgIW3GYzbFsZ9dgELeGSveLqeg3uKXgWnCcTpixKgpIdKQMFIJgE01BYHcPNbyF2XMU1J8E6WSKywlYLcDz5LHrNBzOk5qqB+PRxwPB0zHEpyMvNDwpKac65hGvdb+W4J1qOwnF2IDJ+Rgr7KlXeX1GCRAE3UWm3kgha0uFlkgMqVTM5vvUrCNdcut5SxjY38sY1a80Mc93Xun0FvQWLNTpf0S7PL2FVDmfjS7u7JY3oO3Mwht522pkjCrrmp9nDmDD5J8nOvtrGWO7Ha7EniV1AtOprL5vyBL6O3AiyN6mrIrdrLaXJUDapO0UqHQRHhN54NNMK+daj+YuJT+1mcFb9faT4tD5IH2rFdnqH3h18jCaaPHpbBiK7TbJknL2QCK/dtXF4JcdzBPGuuw/+zg23Y3NYnQLgcQOxPudzLjeTUbK0LpmbYiutf6YjLXVvptZY/v1p3Lk6WkXf7dq9VxtPEnHS6xX/W9k7vKOnjEtqKPyGashXdVFdzh+LiYwIq/0YsF9OTy2njE+Wo3HKzK8hUcL4NrH+gCYoct8YGmqMuqC7ljbGv12ffFwLuzQNIpxjjlPImBJwZqMnlT5DMGbK4KfSXgiZCG1PJeqeIWQQRY4SbQcB06NG3boMUQ8oFFAvNsi5u2wzEao32JTGJvtABDqYLab7Y9rsqQfSS8KyxLJ9t38/fdwmLHCsSBmPUa7dHkNAGgO6h6V8qqAuxAx52LFXTLSnmuR14WVxlbhSsCygoqEMaBVhqV9lgNeuu0i3COQQzmdkNRygk55Xo8qF5xzgzm2SsrY1RHhQBmNURdvyItjYUn9cB89gS9HvOx/6rskKCsxcfSwl2ve8KyWgscyWdM6AjESzeuriAkWfVaANb13bQrjnss81ThVD0LuocxXu+3JBBvv8Qksb16erRwtdp5zOzGmDkj5wSitvMuda72LoW94yU8Flfe5Hl5haVrRQZ2bkCkRD5mI80x6/zVIFJNai/tyOUhzie27Uen+ynAVQNuOhbGcF97M/psXD26YdwBYEz12B+h7m6lcnPabrevNxTWZogwZ8YwJozjvtwomDJ4IhAyEgBOAxIPdcxzSbo+l+NNnHPZZYSSu3Gs+bnGmr9nHNq/nDMuDkfMuQR05mnC4XhAzjPGYQDAGIZUbiIkwn63QyLCnBImsxOMa5+GYShGcV1dltsid/s9RmakoQTKpqnI1mmey1FKmpGHmm9rrHprt8MwjtifnZW2pgkXh7JL63BxgcyM2+fnGMcB87zDfr/HbleCV+M44uzGGfI8glI5nimJ/vOcgdzGNqWEGzdulB0wu73q8vOaUP72rdsa9Doejrh96xZk9/du3BXbxsjbPGdMeW4OaT12mqMcCfwCVEfFOgSmTJuv6LwZZXf5xS52dG1EG8ASG4iLDTTzrLaQDfyemn8SlOg9KXglpXmzoZud6mxirc/kqrF6Xvgs0OyUPbqm4+Jva8EuD83rszlbm73Z7I9iZhI41xMDhveoBr0JQEK7LU4WopSgdW7LBRISmDyen+PAjCe/8hXs9nvszvZ46Osewo2bN/HgM55RjvmO7fbRuCNWdq/IvkLWneEIsi8SCn1PXWlji3m7jvLSB2n4CVnNDmOpUfi0057yJpk5ww39U+ZC0zG1Lhk7WB5orGb9ltbf/pxWmz9+Au60BOy7giy1/guNhrpwIPIkz21Hrw1yOboFTKUN7cEd2G93BHdpohFBcz7mvLQFG7oR7wHM7fQCo+XWpMHMAfJSLK35bkFeA/4G+X6UIPQFTVIwvHyh2oZr0+BmZWEE7ry3xuQLGWgmRbO/6o62cAIIpu/RL+5BLyaxZtP2ZGt8P96cGO3e3rtSryyqR1/Fvu98pzvwKa55oKta8Qpx0KgKO7kxsO1UsuB5kPQ9gA0vst62197rHyGKz3pM0wuE2WdemPfftXCnEVj7zJXXvvfLD+Y4m9BHhFvhz9gfO4FcbVqnKCbbjgsI2DqrFJJJLNugF32hZhimweTxkglp3nG9tIJiRaHJrR9OIIZOdpWWeR/hfXnueEr4wAoeTyiHN0JdpZ9L46dvRNf2jADWIFcQSLFdqxRU6IOWrFDbdjs8Il6BDyy+DEZGy2clAaRg/5dPasHBKLjn3G7ikiMxl4EbY4sfN8PQ4h77F/sWoWfUR/nS7Kl1B2D5DnfLncIjOgxWllzmbKzhFL/36jrVj8vKxDbsvzXauvrI85s6kR1DYK3/sX8R31g2wuJ3JxyWPOVfPv23zLvm2J3YYbJg9CZLrWy2v7PZXbBa71VAh0Nkc5g3a9YqeTytk9V7nY1j6uVwKZHrfCVwueAiJRANSCSyUdwkQmaAMteE6rUe4W9KADHKVq52sYvSikivpc85Y8YEHADe1SP2467l7yKqeapmEBjHIyNPZWfIDMZ0PIDzUBJX1/ZLHjFoMCvnrLpLgtiaKBneiSh5uMrhzjafUOlTbnvD7HneJp0vN03O2q7kAJvnkrSewSWgZubKMIp9URL4l+8yTiUQlOe56JDEKsdLcOyI4+GolzmU4F6uFwOILVHHI/KP6uMS/MlmPrt5Z/mP/GfcBeSnc7SDespRUOEu37v5C1rIKQmUqV40OBXSGRzQFtpavbKgo9aZkYtGNiq+Xve2mg3aVI8fVduA0I6sWFppleJUrsiPnr19abDLyi/9rVKj9mFpLxOQlhegBANFgxr2qdhNZP5JUMP+4zwjTxOOh0OhS7Wvx/1O55JciDFIfrvabqp2mibUd8bHUo/obrY1208FoDJhqy6UtfKSC/HUhhdWIZiCi5pMLdWGaoiUR0SBN06pPkMDzwPLFx0JeFGB+1vbd8/D9zDHXWBS5g6hXvBg7ZKs+FnTfk29qV9SOyB8UD7Ilz9hq9wtNNtTaEOg1Zs3Wp6vZget1uz6BeOv2DlFtAzKc0VMAzzmn8KKHRaBal1MVPSj82UMK6/YuG484Oe7s01Dm+7vFRwH4y+6sV0ZZ6HHqfgDBEfzaX/v2e9rvsRVfIyenX4nQauuXL8DuOaBLg+5Gp9NacmKVNuSX3hPyrV320T2dUrZ7sMVOBWIWmMqG/n0EVDjYHScpsjMpyZ0z8HrBYiAdjWplC85PUgTywLQHBxTvYa9FzSwSqiDUbcfqiySDfCgSZtquBBIkzRbeoqRqMb+2HZJifiap6NeC23fdZ+yKmE6QlQDKFYwu95gKfBUEJfa5H0JnHLAw7Yt2znJHiPpUFNwXDjc4+jLnAAGVMiroIbnkRhwUyVklJQNPkXQIFfHbmQuq9PibFnDXHmRSs41gjh/UNysMlIj0yhOoNBzmmfNIXPjxg3dwcimLU+YlmvEziFtPxueMX1bBCbUbmKHt+NxtN/VcQLrCro8W7xr/o47ByNEpyCCrV/miFVKPVm0Fuixz6086dV1Shmekpu2/l5bpwJ2SofO7Fh7P/av11ZvXJzBIx4Km3qp8QyJA2DIaOeA7miM5RasW/Gaa364wTtubvdHZ97qLo04/vA8YHcm6r9LJY42om1dCoEm/bpE/pKO64pJqE9kjwFqvqY5c7kuCsCAchxQbi4ElZ1OXBPM58yaP6vIHABI5RY+XRSZyw4xYtCQkBKDUI46Ai3oNM8zcDhgOIxlp9NZxjiOGHc7jKkc2ZNg0TldlEDPPCPPE+bjESkNODs7q++WWw8xlp3W81xuZMy5BbpEd8/zjDHPdYfVzthLjHFsNsnxONWdXQXvueqncax4jiP21UbY7UbkPOOw3+luK+aM4zThOJecYbtdyb91tt+XXWj7PfI4Iw2EYRpKQOyYyxHFXIJr03EAckkQfjwccXFxgVtP3sLhcMDh4qLyn9hUuepae+lLdGEaf8hNdbnHMWTfXVbFgObW63IbtUXETk2lTTbzyM5NhLlZbaBoN9rnGXlVflqdw2Cz45PMRQpSzpTNTQYRUd1t1yeJ3H+seUZT2yEG+F0fa/TytOvrql6QywbT7OKtgGrWSm/bhm9r79+rPGjL21vgcg28JiKMstvC3KKrtiNRybqYGee3buHi/BxPPP44Ukq4+cADSMOAcTdiHMvux/3ZGcaai49Ss2ky5XbUFy1Aq+Mg+kF63eEFKcud7+U1o9uqbeWeK+1dy0uo9WSWW5/7xU5CM6dXmrA7vBYmOiBzRqzoKzvOp8tJG0U9GD5KYtPkKmen2n6/jjCFl+Vqh06qwVMEuqQTxP1F6FMgTTW/OsqaJkfimBeffW5zaeVyLt/eevCoy/9Bjqx2Qvw08kEueX/NP7BlroQzm80Bth7xn0y/CMX3Fn1dfCR/2iAG3BIRuObglBbuNEDU24F1CgQHe1txzw5f1UPm76sE5qKfcxncR4EuG0VuxxRt4lRn2Fwy7vZ58+GrcrFHjO6QgaJztlZHYdK+02h/i8ZAxCseH+o5yRGnkiCRVXDBGFTeWTTKXhWXEUBOAAqO7bPJIH/EZ7GsYRxA+U0VSG67Ntboufa7BkeM4nGT0nbCv1g+GnrtUa9sFZ6hS0Y4tKT4kqBSYJbtnBUXPtGfXl+VNtKnjrPenH20PovA7fBLD6LTS261l/R3JZJT6O2oKVPbpdVz9sXJ1j6aepJlLulHoI39hQwTamDRKCNXl/atPLNBGflPgquRJnZ13tI/maT9XeOT/NFGoqtdnnGZodBrb+0dmzByLdC1FgC6rM2egyIKLAbhorzrBceiQ7cWzLP9ae/llufvkvfbUR5vRJyaj/Y7EZU99WaO6HM7L8Kcql9ARBjScMLSXdEz4LIbsn7X9qp8XTjUjDIfba4VbrjIO6VB/7uUlWcNMbT6yD9fBLpOzA2Lh+2vDSb491ZcA/K42MsjoHMttYAWtUUgVJsipbJrpeSHIhAlDFFeihFLVa8TodRaju7J8Y2y8ymXo09cAhAtuX/b1l92Tg3Y73aY5qnOmYx5ZhyPpY1hSEjDgCENeitjCT5JOgYALAGsIxhcc1kV43oYx2I41ws/UhrKDhIi3T0kgSEJiDMzeBycnJJd4Lv9DrkG8zKXgNvxWBacSjtlUar0O2EYSsAscwZTCcoB5bbFPBecLy4ucLg4aKL5aZKktqR1AmV8ykUDCwZoOc6Er0i/Gmep1hidrGBTcdd5tg6e2A5LneB0StUrNtDs5pupTueyspqXzc5uq/Nbjh7r7q+a57bpqrYHSkIbpQp2+q+5NQ4lfc+pcON03qnd3FtAsL+v6k+xZQKSZgQXw2XbsCcYZH5CaNQcDvcuUeMTqscdx5qsO1t9hWK/5hoEB1DK375dgurHEbtxh+l4xDRPGHc7nJ2d1SPDo9NBKRHKfSpGKlY8rB2n/Gp5WIs336gXHC0VVXoRaj5Xe/OkKRZobFVCqRuKj7Tp3wlQbUZ5t+0m6i2CmddoOb5WH0ac60uhEo9YS7wfykHs01afBCIkANpz9mPT2i/TGeeLGJ4T2/5S6NnEZg5rGyLnsCzuoSwmtO9NPnSa6NRn7GB7KZizq8UmCn4P/JCkwHsLTR/m6LIr7OoOiDo6OXvQljH+guKsctxUJWVMfeprmf4rTtEG7vVlRfYXWX/aBo6/9b7Huk/b+IAd27V3rup/yLPe8zvRIdc60GUVfNGhQhAfHSY1MGGUFfQ9Py2WgrH+7P80CnYtELU2QNGg6UUmbaBrrW5bV8Sp116vjhgI6+PEYG63vvl6/Fb0Vld79zIotxQlZ9iJxFJHH6yOqO1Pb/eKVWQEAmVDLw261Hc6GIqgOgXWeOg+gzFmVEDVPhnhloiAGrEH1yTDNtdRwCkKToN0UQb1e+yPKAr51w1y2j6IkVbLLI5AmvekjGuPuRkmHYyjg0xy3T3MnBWnW4wcNZ79+Me5ZpX/YiyNwdwL2KyOvfCW5KMTgjE0N4r0S/CWT2Z2R7uE2HbHYkbWPGSEthIoK2xzvW0pzrWeA9ALAp1SYpYHoqwQR3UtyLUk02mFZn+PQS6LK58Yp3bba+rWZfvU4/M1fCJvSFuLVTODU8S31+++PCYRIr6MEUy9HU5MrLfKleJB5tf31DmWnbkiR1OTjczcbjHtjamVV2j1yvu6+muEqMx713+EwLe0FZp0/VV7z9cvNFrc1sTWSLR1l0lK4YHODe/ygjOAKvsEjRJsaTKtHU1Kmp+HM3CYjiVANKDs2nIyrMhPqnq9aLyCgx71M45Qud2x4DQNE0DF6d6NO8jNZbthAO1H4JAxgXE8yq4eBvNcdmDzDjTW/FNDwq7e/kg06YKW7iJnRkolGJRz1ryRqeatAghjHW/KNXfGNGsQSXaGMe8wjANS7fc4jqCUsGfGNB2BI5CPc91dNiv1U0rYo/SPKGHcJTAP5eY6s3PF7kK7OL/AxcUFzs8vyu4vw3fjMCDRsOgnqq8wJJFrPo8ecy7Brjo/fcDZ8OWShSvvUleHWCfWOW9Rdsh/Rh5pkItDOTPvK7b6jrWfNMclJTPPov4zHZS+u7BVOSrH+ndzAGFfk+fUnFAGQDVgekrWn4K1IMHpwEENcp1wDqXTzB6HovsKb8z1wgNtT+nkd9eIvpynCZxzzQXbD5i1vE0ZlvTTdCxzr96EutvtykUOu13ZeTmOONuXgFcam25W+9H2X3FkPb4oMtUXFdo2g8uPh+EztmXbTq7IDX4asDGBGSDxMXpH0pY2iBA5+lvRfnC4wrcv5X2Z+rt2QpBWo7O2vdT/oQGvdgx+snghwS7Xrwi2nfr/xTzxDXTfVx8k4nnSdis6bekN9P4OT3nFb17xre14kepFrWyRI9EGjx02ROXm5AXdoO9YX0V8LzZtWXwu851t+iKdsx3/wtbiaiAyMwxuvGIA2r3WwU3bW7X9va3TXvFzJvoLp3ZKnYo7xO+9906BnuTp1NGLU9wJXO9Al2rmMqiShyslOarW1K4IcublboFOzfpetMl7js2p+oj88R/7TjbCzzKQd+KWgtE6Yba+iNdlzNUNgJUHVTFL/+WzGqo6gWDoLAGKXjtWzpK+44ITLNuvjaNEzRGxxgUztxXJWo6KlNZAiDh6GjABNHeH4m52q0jSdw1O1V7anVgqjO4UmnQv+OYMFhpTC14Uo2d2u7oIKDlijHC2+cEskbk+s4Mg/KCKQ4w146wrH1lhX43SXm8drxlFIrTuXhBwBbpRIhD7ALXi0+R2aUNpWnhELkJQOokjYemPZojKESC5lEDHOQh5mQ+ihMTpLU37IIK+QGZuGnvKrSASaVJcx/O1nDhhFpGlrX51GXQq4BTL9YJd8Z0ob3pyJ7Z7lWCcyEVmDrtxl+/FdqID1ev3miGjwclOvUT9BP+2jrW+Lgw6rRtgpibTwI5HnMNKcEnjHd+ZNmIfCGWHJIMX+OvqMlgXAsqRGKDuH3U4EVML1orTYZ3vq4hFW87M5VNwtQAl4G/rkCDcojL/iWZwuuCb3OJcxQ6Yq0wTHVCc1xI0KFAC1VzlB4NoAHMqNyCiGfMlV1bBe67yk+qOXTlCneU4IjPmaUKu9sMwDMi7rMcKqb6TuR3VkmBZnmccDod6rLIkmk8pYbfbgWtdcz2KCKAd56Z29Evq3e1qcK0e/R/ldsnqEOY843icC57ThDnPSMdU8oMRqSs7jmNN7F/4bZoGTNMBzIzD4aC20jiW45MlaDiUgBdlHC4u9AhkSZlwrMc9i+7e7eTWS8Y0z9W26gSh6//k2OWQvB4cMOCIuegVvXTB6hzv3Db2svJajB5SvdQYTKrxOnkcRqcjSv11bsddkKZxArndwW5OcUtyL0Hp1le/IKT/ah+l74OhQUpl92uTMR6ZZo2Xo4txpjGXI5prOsTuIHZ0uESOR1gE8Iw9KM+tbJcyvUWNVgccn1h7VGSI2IiDc9wz5qn03Y5vKkJE35fjwLJbl3PG4XDA8XjE4XBAGgZcXFxgHEfcvHkT427E2dkNnSclc4u3/xZ0EZQcLcV+kCdx4aP81uNNMn0H2nFV1UhkxoqaEef0l0PQWt9LxMnMK+mq4H5135fD5xLEKhCpn8BqB4pNKPhauWCDIMQMm4Q+m+er9rDhfeZW58LWMvY7xfdTWlR7NRAfytJ3LYAV3iTSMWhda7aO9gfNBxf9kSgVvWlsJsntaGVB9AnYtdJs9YhutAurQG6/r9h24kuIT2V9ATfmrXO+XV9ZkQ0heXw8Haa2LEzAyfKUqU9wDJ1tnwXhk7LzTux2MjzX8xtgcD7l710lSBX9ith2odVvm6OLnti6+mgy9wP+JggJjhXeLYK3Cck2qSkK3BWD+5RjaH+XGwXse/FfVMTlM3UFTQya9Rgjlr8KgwmIIdTq8U4o0HKfyW00vj2hZaFjb7K0/lZhISRHc+Zsn+DGZoUe9SPBJ6kXQ09oNZhcNVbAqHDDiv8mgrYgVr5L34xAEugax8waobdjLuUyN8d0MImLLQ7RbLa4svkjCvmuMGc277IKd2bW5IwySeRt6zjbm03cuEXEjTUSx9YFJoUm1nDvGPFWWVYLszWF5tBEYSm705zB0oHFPK74u7kHg7+aR70dMl62uHHnimcWY9O0S9BbxxD6bj/XglS2L2uBqV65ngxz7dacIJGv3PvB6FZDwX5WY9IGuWyg61RgqYef7eeaQpe/Le8L3eN8FGOkt7PLtxlwKRN8UdbhzDL0/bnggrtWfhpnwfWN2lzRcnUiyI2OC3nQXBLHw1qmw9+CO8B1ZxV1fQZ5R98j/7vD2b7H7FVvcLKKjG46gbkdr3ROgBlj83L7Km6M0FZoIHpDxpA9/8gOp7ZbhY1+ycic6nHDEvBqeXmKocuzJHivtx0mAqoeHYYBQz22iBqsAQAcj5BbbWV3yDCUQJrosnEYMKPdYiVH/QjAWGkymB0gNM8aCKJ5LjfRSqBOEtQPI0qQq5RLw6C7u2S+qkyXhTuWvF1twVFugbR6BkDJLcZzy5fJXGlS8pGVIA6BU81jNs24qAEvuUGyjEldGGBCpgxMEwA59tkx9qUt1JxBks+12jEkC4yWP6MsNJ/VkgwGAzXVpCOh4l77qz5JrSNzk60L+Wv5Xuho531HRzhw8sTavh15Euacvs9tp7fP68+qH+OGyyYOWQNLsohr1YT2mUjL2/4sZbpZjKZ+32PQq5WvuyurDVqmGi/wsYRzznb2Tm6xYcsIlCBWqjKh6UvYgEn9l8WukPep6UTRhfM0gaoOKnlygd28K3Jdc4z63WUL3YvGqz3NVMhJ3vbV/4mcb5LYml4eSF+zWoMB2HhtN9DlRLWZNdzeFXSaidHGrK9yu711T6jzYpEn0A7KPBb+dLXF99kEuYxN08WOGx8t57vHfuFPVBtd8RV0GwO339CnhAUbZPN07duVpW4S1oAnjbFVTE8WgbuAFTO73c2926UdLdDjQRQZ0gp35QdXfbOgq9iGdsGfAi9LjzrjGn9RednxJRxO8s/gpDZAHOfwqXyktGkzXWyU9mwJS5np/452dy/YZXXIqWBXbNP2wT8TGb+0ze8ErnWgS2giAZeiuAohrGDpDeyoZ9xbIlghbLnlpO0sie/bbchrQa6GYxtIGxywTBHz7jCXiPbawDI3JhAHTZhBjN52vKc9I72+vq6s6UqWrbz8L6vTDaWRd2iLoaArvUQ1vwfXVb/Wf/mt4DdovXJ1uRjC4lj1HDiPYqNPTK4sfbDOR7yulJJ3htm2ZQRdWplU9l053iekm43hr0aLyTmkSXFJkuMbgwlAGkZQ8oNSHH5gIT0X4r0ZqGKni3klPEvmqmNUhULmjLwI4MwMyrnEWcyz7pyiNrYgQs4HpavcAAZqhkjJJTOX76iBBrkoIFEbD0NHsAhTv/pSTkRxSRBbb1Ki2lg5FgqA00KZKuW4fB/qijhTUh6UY1/Z7MgUx4tSm1viLGbO4DljzkDK/ngdCEhDaVVWbOd5qvlyJjXqJZ+O7IaQPo40eJ51c7Hxgb3MomfsO6UoPFx/Ux6JMk1IpXzTjsIA7arjUgbI9Xa1VHP8WAUM2RmT4AwHKYfM2NWjTlbRW1qqg236dpkCPBUcK8Svx2rkNj2SnRip7HSq/S6BMQKj4sPQ4IALxiCVC/cWcgk61rLz0X4qntVOUZlVgzADD8qfCX73g1tIqbtXM8fVysozSdyRJr3kKJnolLZDusnzhSzmVidgeRNqyI1jS+gcg3oiG2wgjqszLLsaJW+fzr/q8MlNfiUwUHagSCCneptlKO2x+4Xcki4VasxzRkY7cqWyejC0JWAGXMJySgk3h3ZUdJ6OmBmYq24caxLpRAkYCOABTOU2pRklB9dwNoLyDAwj0nSs8qHcEHs8HnE8HnC4OMduN+LmzRvgPAKyS2ockNIZ8pxxOFxgqju6jscjzum8JajPN5CGhCENGIaEMxoxDIRxSDgcD5o/i+cZEzGYJ6TEwFBuneQ8AlVGJQJoN2JOBILcfFjyZ+WcMR+qnYAqz86qmmHGjsaSY4xKzrBpnjRQholxOB5wwAEAcOvxJ3A8lF0teS7J7GUyqZOVy7jJkOzGHSKQOPGGh6PrwvWik5GoOHf+TqBiQw1NR0odRISBCHNm8GyP0xv7oOoUmSdiAwxD1SN1p4PYELKjTtL5SZ+LnPLBIsBcjlJlhezkAurN01Ry+1GSEC8XOUWox5cTOFHND5frjsPC5yIHZG6J+zQHm42A8lvFrdlwbYFDnENve5Kx55pzXORYDSDXPicj76yMVrkJNjqZMQ4l35vudhSaEMT6MDZ14dGyQ440QLVwLkHl1k/b1lz0wMRlp7j4JCROLZrTWk5IZ7VVQCg3jjKAXHLWDYAGyYV3US/ReaLugHxiHLHblYT1Z894BnZ1h1cLxjQ5S9Qcf3ekHSVQHANPPoAiHFNuvhbbbaQEQkK5/IEAZUFyfStzVGR/vUyIBtOafG0TjmV+1zme6sSdeRb1aNlHx852QmtfuoAOhCd9JVD7vppuCz+BjO2Daue0I9LNvxD+t2jEPqjdq7ubTKBGeP4yR1/GXYzt3nPX8Yoz1wVr3RotOtzjHBelTDXaO2bTLxkXNNlR7Hjhg1ZI+u+O9dbvyaQoiX2RS6K6/Vt0n3Q+ifzuHdXTcQ5BptnIr5PtdH6TAJ7iUeuN9qiOsVxAVsdy4Rf12uEWYE3JBNKMvxAXCHTWi32rPjKqH1nlbkrN7hW0cpXNc9sAA7Q4RGkvQy4KBGDs+NJu2ZHdt+PtQoPIemtvXhWudaAL6DgtsMRZm+tiwNsVHUANkFIKsurVJjAv6um1uYaL/B2d1LXop/19rX7Bz77vo5/+91KX9NXjqA6CCi1y5WxbEiS0bXjaRUMGpnxrX50iMjs7onQN+NfXwYIL/O8RHH2NwlpGwFuRGHmP9UXHqTdOcUSb4vfmtdQhBlUveMosJlmoVYyRKmQM56uhCNN1sm3beYIOWOFo8QyfEZcmQVmNHIeVEcZAMyZ816wBVJyCaGQ4SquQRU2gbcaEqmHq5II594+lIcsVdwns2KbWQHiX0HYBNdJYBW3Kc8vbsBqI6bXTkQe9VZX4fK2+td/EQHF1Np3lbhhqcqN1U3c5qMGHBT2Jyxy2Oye688nItbX+3yks5HN7gGYMSL3NIBMDjQgmD8YCI9idrkWuNWOwORb9vqhxWJvWPFcVgZ7ekL8l55vvXxs4wWsxttDpZvptp3TkKVO7e8T9fmF5BMY8bGiuAXk+EJyYucx71UWXm0HCnwuZamSC0nihYnwvtIjKDE/TzJKHUDoBDebqDZySE3HISDV4B5Rj1XQ8lqOMeUZKJUhORKCc9Pj1UN9PKSGZ9iWvFQAMwxGJB9DYaDikBBqBnIvjyVOuuiMjE5DzBKIBlAFQKg4nl0CAJLnPw4CygJHAuTiiegSfGZwHTOnYFuCq/VWOrZR8ZTPNOM5H5Dlrvq2cM249eRvHw6El7Gcb+ITY6I0BLW/o+FRZT4vRXvp+tUIyoyxzUYMFRO6Yu0qIOsV0/sLrbGvbyK+yiyyzmYOIUJeE3PMV/e1kLOudF5aPm83XbDYn5jryqZl3zWlvNpvB1PC8PuO64Lhi63rkfV0yR+RkhtXXgk8zNBiBAPWXsjixsHlUzi1tGXnH2oPa7rIZCCNKnyU9hPCjyBI7xkryYBf7ttjweg2kzyVn5zxNyNMEnudywzYlYLcz6R9qtSmVgEydA4YChvIEq2Lg5hA1iU5m4cPIW2sqlyEJ+ktNhMZXZOrw+ATc2BK7Qz8EIPOc298L23HNrxJ667j7x1b3SjlXv/ERuvYV4C7Bis/ArOPVUFrKrsjP9jl3yvSAw6eaCdwhT2NYiwTI8cRlQKAFtqfB9cHOC0ROkSJtni3kva94BcNKAjPOOr4r49Ztw8jKbrkVWWjfd2071M3JiRN90fJG93huafPR6jv7TNsLv9m6Cz62bxYt75dI8FzfdsPr7TqP753dBilwrQNdQxr0u9w6pKtoJEfrCEAyRGfHvBLwGseSU4NZcsO0QBHVlddLBcaKg9nbthqdtZ5DJ+/24DKnrpeke60OmxMp51l3sNRSBieAmRztKvZ1/suxD3GkxPFenkOW9+0Ory4t5L+OkQZGyweVZAUp9NEamWYMJ8l9YmkgfVLlHN4tX1QAitCzQTGNdgvNUgKb/CnCR1ZwiaIURWbH7G6cd32PUVbnM2MmG9ytZYIilX7Gv08FY4HK30TgaVJz0xk5tR6uSTnZ0G2ouWPGYSi7CS474+14w9NqWVQM7nDbjbXtyfNXDIhpQ+z/ZmbnjEWDxl+E4eehJFO2twtGWsmORaXdmkImfyWz0DO+44LZps41esfyQsM8y+1QpLSL5WU3RW9sNJBt8AehXUJQb5k7mv6v0bLHq6cSacZnUeZasEHDnuyOMiwGGK/Cl3pMSpaLBziHuhSu/MCztlF2/SXlw1JJv882sCTy0eJuZcJqAPtEH2w9a7xV5L8ZO4OsCzSx+a3H+9XWKTsKym9D3Skl7+S6A2POZhdmwM/WvdaX2Nc4H2KZeSo5rtIwIA2S16pIQ6VHvXFQcgRKTq7DhTn+ZygDUC1TVtvL7YgHAISL8wPyrjj/41B2QErAa9zvQPMAUFKZmmu+n2makNJQbm+rya5TxYUSYcwjDhclqDTnGTwxLvJFsYmGhN0+Yxx3QL0RcRiKrbTb7cpRymHAdJwwTxMONThVdqMdcXF+UXaf7Ha4cXaGcbfTmxWPhwOm4xGHenvirVu3FN+p7uTKOm+W+jkMWHNQ5Scp35nLcawBtOBjrYRgd2M3pyHaIgDMjhpvf7ihFWeSTBoAsxtc56aTBYFPdYGIHF2YuSRoRuMnZgYk8FjpoEE7LOWdUZFdyL25E+pSvODnYRqGZgcxqwujfQzzU2CxM78jczyd26580dWyEOXkHi1tG5FTdidnBJGnsrM35o0F+sGHtdiB7ZvtPwNtl4/sCKs2VDa5jC6mGRgexwMPPIDdbocbN2r+rt1YL8YoNGk6o3Fn2clbfJ1U+VfodZya7hH9MQqPz8aRBbeUIcp9pBfrKC3rcbA4F7v0DdC45cpRFedxX6bbxP6Pcl4uzZD5aG0uCeiKrJ2mtjvV+hPWf5C/qTXsg56CA7WdR9bXUNs25wUlmgxrR6DNQ/UznIy0fGfwixD5WXCXW4ajTrWyRI65ux2rMg+tPWV3yNVnREtu6OW3EvnRgjLLfsQAUTJtaLuBbpHu2jfhKSvvqCxOWT3VHVtTb7fO0kn9PXfaQqjP1cl1VnbyVC4jpo1Q1qfpEVBvJ6dmvyVK9aKjdbtXIPoccpKkRw/rW9l5d6d+8bUOdPkOFyJbHpDRLH9bRljWY53DJSH7ircHPeM5GsrRqY24yOcp57b3Gb/bIMVVcC5/rLfX+25tsFKPp7OXsexorHUAQOdWulIAbVJRZ1XM/k0tkbKdyOqMi3GKNhaKaP3U8bF0DHRSg8HUcdVpd5mCF+OTsBzLTuGiuEzdFlc25SJfWgUb20fAUZRGj1d7wRRXj8UnCHHpozXm7XguDNlWmSoPRyMZV27OfWxbCdVeUsfF8UnsI8HzVJUpEV9555QgtkpkzbG2n/G7vLcGd/Ksl/zX0YoY9lYyW484DLpSRK1OG4Rxba7YqG0ekRMcPadmgaOB3sUeV6FnxEVoEoNjvfHqydyebF6TszZAb4M8p/BUup8AKUPmrFYTdf3gz1WgK8PN92jIiE7uzgtqdZY/mwHlG23z0s2dREic9F02iy49esS/I09YnlnIzDDPL6vfoS91AeqceiaoTiYxstojqdxcCAKqYznPZXFCbvLCPAMgJNEDtZ5haHnjNNjFJUl7yhlpSBi5HeuX9A+ASc1ggjlznusu1ZKziyD5OZscKO0OJQfZMLjxR5WhnEuy+DlnDHNGOQQKTDUYVo4/+u9s5aX2UY4ONydQbze2NEUTTdb5sc/v1HD2K+NLO0vslTj+EjhQhyLIzUXQR+wQ8rlm9Bkaz0Xd78pZmSQ0if3tzRf05a+bG6dJ5frv9YCf4eQLL5ztpd1p7DTuS0LhFXAJjosMOWXPNhzQbE/zm7MrwgKCrccv51wBqpBk+ONpLcBETZBae4bbolhmADnj4uJCdz+mYcBu3mEcR+z3e2PjlqOAciTW5bTVsS38SYFnVPcHOgDNFii4EUhyOAqdAJmM9pCiEE7pTGhF9UcDPTs1QpzRQeKull34JvB8uJAXwbZ19mbg89686evgwJdNiXqciLo7w9ReXrGT5D39bvFbe8e0u8hpFhPgWxtO3gF0l6OtQ/WueVeCRV0ca7+kHvl+GTQuXdqPp962fkY3N63RQTKHbZ8dTUy5OO6R5mpnrbUHeBoh8krrAKH5MdbGEr9HfRz2bVvCNV1T5ULk0ROUjDaV/BZtdFvW0ucq9twpuNaBLjkDz9VolPEFLBGX78XE6VIX0BLXA5Hx+hO/53BFA/nU0aS1AZR/a07x2mesNzp+EeeFA40+7ZbGoKcTc7uxhjmFPprcBDlGZkPnozYiqAJeFQgSpOBl2UgPgRKBxkLgqHEU+madO+UVbokS7TSPBqdN2IvwDIA7TtE7WiG0dSAGrLRnacOsK36q0NTQ9n12VaLRLrYZDdXe+2qo1z64CyHMrTMivIlakCuO7ZoQ0+d2sutDNKcBHaMDgQ+qsBbHpGvEaH/iPGs5S7jygZ3nPQFu56R1qnu82pMrd+KQXaZE15x5+8lsbh1juNs07e4GMWwJJfAw7opaOR6P6lg0w9TToiFU+YFT4yFqDm2UmWvJXeMctX21/Yq0kLHzl5gs84Ct0b8nhyPOcSwWhhB6PzTaynNtC+vBLjVinBAXvJa4x7715F6PZ+SdmDC2lak9DXOs/OoNKYuP5B+zueCkzVxzvBCR7uq28z13xtjW3QtWSXnpR++Wzd57DueUUCNT5j02dnDBazLPAGC/22Goieg5FZ04kwRhSrmB6m7rXHL0zMeyU2qaM6ZhRkoJ+/2+3FI4lqTv4zDW2wlnXBwPyDWBO1B01ziWW/7Krq56nHAYgN0O8zCAjoQ5z2UH6iQ7UGsuzl0uu0epBhvrjrIEAGOjpewkYTQHPueM4+FYA36FLhfn55imCbdu3Sq7v2rC+XmegcxON2n+I7Pyb/UdYJyTqifVYTDjteD5NtCL8WWwHkdvfNZyYC14gytPYt3Was01+8nyE4Xn1maQ/ttchraMdbKdvWUb7tgarm2hkclDapBeDRqICae41N/jcX61Q9oEaf0w9FLH2OCmYyttdRYkoLwXbBnJ+Sc3olrdvtYp1/VOIZFtaLItR544VZ+hg7s1L9AkqR2dddfQXHeK8jAAacDxeGy6cyi7N2/cvIEHH3yw5Orb1ST2JDKYQIPYtLnljKz9GoL+zW68vD0FZnCSsc+ofxieKv9j07cOKd1noJabx18roE77ylOGHjJvdSfXim3i9KmvVNuzfwONt21Z56tUvpG50qOX80U8QlUn0yX0vho4PelQNrur6sKEytAw922u4CH182pqOyKbpC93iWt44L9bGpnxZsf/Hi6jocixU36O5SmY8mLbSNtEJYcgDE/UL2autTFInLyss+2lrIK78WnrnwbDgJZLVnxutLmhnbQ0CXZhtB+FH3qxCnnm9MZdwLUOdDVmAQBCO7JoBREANTa8a1EI6AkrRm5LnmadtL5jZT/XfluD6Ax3AxC0xPGUY3WqXWc8BDyFoYYFUzW6teZ6TGt4XSai0p175Fv03z9c+7nj4HEzaKIRq6tM5h0Nkhq6rAmpSGM58ue25MPQXZSZMbI5Z38MQcrH8RZ62ucdo9KudNg2naEL6FgunNMVPiMqR7Fmc3yVa3vqrHR4rks3i58YCGKoU1vZYWZzGYQhRaBHZKBWvpk+a7xh8T01P/qrFKUOzwdLZbHmPMdnlj9tACG+08OzN8evKmfWwM9Vv12YzcUIUf64QBexP85IMqfIzT3ntMHQm1o/dDUv/LPvx8Dv2vG7y+TjZY6IpU2UuZfRvfeOfGfw4mYy7V8wMPR7Ij3iCRh5ZqaB/kbtXR/wWtdhiluHB3t97wULlnwOgNuNdsrvVSZHXBUfCvSVKU6GrtTePTXua8+u4oRaOCnrRC+gye7SXt+QLf/KAbOcctUfciy43hpd816BJTMFIaWasHoUW7wkc+XMONJUF5Ls7dMDxpEwc9axtfP8eDzqfJJjz0CZT7vdDsNcjmXNmGtbkwaVBlN2GIbWUy5HUsZhLIGvQpAWuMkZh7k4hfNxwpwzDnUXyvFwLEcmczvazpRLzkXJ7zW0myN7ulHHKupbOxod3lU+gTkGaOYYw+spCcJGnWF5u9XpeTnyu7UrxFGJuNuyFhYOtMrWxpdl/i3rW+NopRX5YFhsS+eSrdce5TdlE6CX3Nh3Lc5Sd5Strp0VmyniL7QseLQOq1zs0dKOHeriDdqYqnw2Ok10nMr1jp2+pisULUMny4exfxIcsI6vHGsueaO5JLUHAUyYmXHBGTmXo9X7szPsdjvs9jukNGC33+nFOsxAQtnl5XSX8QdYAk1yWyvKuLreydjXRNaCNxGKzqt9iGBcCz+nlBhKoZ4auxxsm12hYfC3P1dbrz2uN6NXuz6motCqgnzpo2T8DqFLUZp6aYKWYS651jpyz84PinXZeRDatl2P2qpZ1Qa/E/1wNrrFJ9o+VjZwCHDUd60v5drgFuwZTGCs16/e/NHfnW3RgnELn9byfpSzQU7bQJP2RdoyPC90ZkOPU/aK7Yt9z7bl+qtlaTGwMdDV6Awn33paNeq1Pm8v+yHtSWymt/GnZ2sCS7ve4XOJ/W3h2ge6SnDG7hBKZuxZjUEJuCyP4fQNnuLoC+GTifCvE3ztc618qZsW0cqe47D2uVbvZe3G3+2zlAb42+1OCzj5LDi1pISSN60FDt2baGKZ3S0wi74Zw0Mgjpf8J4aJ7AhoVQSaD8mtzjoaqLLpG1gaKOoErxzKQhtRgKIs1wRjcOYdpS5TmOa73dEg167P83ypbSC8mGrOIbcKisYFVok7A7fi7lama1kbmRelIgJuNoovGr8s9LEGhGmz1MWNRgbRSEfp45WDXeS/r9FszflY+7sXwCFav5U1tnWq7ljefp4qF4Mb8V+UUxpoAPT4mAQzHP3FS++NCQPs76ev9fWC7e39tRslASxkaa9cb3XIKtlIL2f0rziZvfnZe0fLMgOJ0LpvdIa1x+vuAxsksuVdWbSdX7LjKcpTZ+t3cF8zKHr82/tuodE5KT5dOlWDzAbm1Ohie+wKEAfT9jU6r7bttpN4yTPW+FrrS6TPah+sXGE2NzIG/UkluG8do1GPDLYco2koieHzzIYnSOV5GgYcjxPyNKPe2wgGSg6wGiRLwwAaCEMi7LBzNJGAzfF41DxaJc/WUHaG1byJuR5jPALGqTuCa64xofU4jG7XEIGwG0fwMGBIg9JlmqZyg+LFBQ6HA87rTq7D4aD9tONCqd76y/YmaX/TsXWc7NjFUbK6F+T5UfS1yoGeg8NtF5fyEi15Qo7Ox7ksfGplp/CX6MbIU7B9M/JIgo2keAVdARgaJkcz2y/te+2/a9t8Srl2o1dalqk4yZgg4DUbfN042vfX8LB4o41XLO/6RnXHg9UtgQqnbPfFIk2QSw0fvxgiDnLq2AzRXhKwdDplm1gbVXmy/p7nIgtSKsFNRsmpeTxknJ+f44lEGuh68MEHsT/bY7f7OhCNdXEJyLlSyG4AMHMk5xJYm7mcUii3Cy/tC8657ODJQh+AaYZIB0cM+cPIDumj6XnrN9qYqDNv3nOLKKbssk5TLdkmoj4vOahg5uNc7RDJuyhHw8V3WMgWrYqWOChq7J6zkTPWbujxR2++qp1hP023qTbC5u+Fbgt/L30zE+DiQGfBKVn/GaoDgaKvrD8R25O+M6CXm8juzcHID+t/OBywEMENZ1vOyC07vwlhl7/5nagtIkQ5ZWWr0ifagXXudn07J18EeVrQUT45vON0UuXtUz4k2/9sPfB1yBHwXjtx8Sba1Ks86rrt3/GblsqztdMcp+BaB7pKwllJZCbEbM9lV5YTwE6hMQCzyswlMCbXrMv7RSGXK7gtrNe7Dpc9vyygYes55cBeVo9lPDuRZSW4nLazwS7fRutvq6/UIxcAeLlX2jJH/czuu3m2KyFNcVlF6J6b/jnmr2OdKCFT9jSgVreOdc7uOJ0p2j6tYdyQUQEWnWAV1ub3lFJLAuvo4Q0J2PqNAqF6BCSCExhoAjURyTraoozFU5VEOKJohU0PVEl2gODnAgNFoHcS7UodorzEKLfGnH5a+ksbZhySFcgWUWMs9JB2DjjBf9aO9oIKOTNynrrzvucMrznLvQDT2jt3A1d5by3IVX7LbeeC0EYNUd+OtCW7AZWGtazMzziXLR7MdYXa4N6Tc1F29VZ+olyMCrcHUSFfFuSK7171GQOawNX9Ts1BtuaYW00zQTEXwMcSz/jbPEtIxPdjLVi3Bj1atqPrfpwSDW4MXRCAWjkXG6rzljNrsn4iv7Miz9nlg1vrR+TrGFiw78Rgc+xzD7TunHV+ULGEWwfReEKS0Qse81yPBvKsASYi6C4pTkW6F0doAFB+pzRgGspODTk6k1LC+cUFhnHEHk2f2yAR54xjfUectLlezmLzdElC/XEczbsXyPOEeZrLleI5l50h44hxHLEbx5qQvxxr5Fx2Lk7ThPPbtzXv1vn5uSaol8T34KZzqeIJasFgG1DJaI6PNXztzX7qvAn9rV6ubZjBaV/teIc5F7/H5wQqjr/VHeJkENxCgLShgR8r50T/E7UjSsbJU/1Zn9ldNVK9S9xrHTnb3yh/hO/NPJEyltYx5YClm+IgeIV5lOsCYQb8QmHF81IwTmRsT8fazvc6FjEQknN2AXKOi7FGBqvcCZ+Wds0IA1K1dWHG9JSdaeVmFr4PesiB8HD9p7xD7WgvGCVQrMccGRfMemx43O1wuDhg3I24cfNmkUt1HpcLFQqvyphLcFzGv9C7+EbZ8ouhnx0v/YnaH71A5kmo9qoGF8HtNuIO6NF3xgK3OI/tXPQ2CtfAYdU7NT9iFtlpTyOY+bpAvfa/p0cUkw5vW/ssmaNq9pnY/dYPaCQjW1mHSlpwYY9QeG77oe+Yvvdqj7wr+Fl5FSkifKbJ9o1ckvdyoIV91u3nCn62b4t3DR6lWNMhCxs/1sfsxzzMD47vADqXOaUFnSyeKjvCgozgXgJy7NsMCoLQFs6bDcPN/5EyK76/fLcLlUlSSQRZ110YOfFd6zbv9ObnVeFaB7oaMa3KaM/UOPRvuUGwR93K31z/ZWf0FuY77eicIv5lg7MwGkTQnnA+TrWfjCEdn1lDPzJfMWgJzG1n1mVtCd1bm0Cjs7RZylkHadFfM8GsMqy16fcYwLLOE3PN4RLbYKDk22yGRzbGn+9JMz66SskIlAhdpzglza1gy2lZK6wk2aFph6xxvtKeVbQMVOUThITpVzJ4ZlMHUQt8rd3KKEYlgL7iqHTNFXerqNQgNU6LKjFqW1t7c6U3P/QT2l1Nvt1zVqNxqnMgCHdpj9FWdm3Qq1x3PuMUxKCJQAzK2F0nvb7eTZCrF7Cx/Y7QM8SB0m3JrbIWyClOV3Mi4o1ltvxVFJSdX72+R+XX62vMsdSTc7a9WGfv+xquizlo+3Hib0s3izuDkZHdMzBaEMzUt6YnHP+YxQPq+JJrYxL7Ln1dld/dulZudVQnCE7oCu+I0SWGlJuTucn7iJ+oCQq4WFqd4sFeuTU9YMsXR3LWsomGZeEqv0X+yu7WaToWxymXPDsEYByHajRyuXAtJRBnUK23GKDFRcg5g5jV+QKVxNRypBBoutnmPpmJ1M6RgJfcwAhmDXAN5qjg4aLk+BI9dcwZKc1q1EuuMTl+zKk5B3KLoiSbl79znlU3aP5Uo5ttMETGVea4JuWXZ+JQGLZS8tcxgHlm9RAvCnfkBPpHgPT3wbzPYe6JQ2B5ySCa5BKAqv/0ZkPbl96OVWsb2Dkh/9CcS3dzV+yfvG/43+kOq6tXoBeQofCcURYyBuZuTlJT2NUT25G+E9COdJn3hEeSyI9oU2a/ULBw6ETXM9yLp4Ke6kueoJP+Gvja9Yu5jfWK7LFyWGWs+b3gYezdnMutyVRuBUxDyYO33+/BDOx2O5ydldx+iZLuVtHTFjkbe14CusU2sk7oKhTDtPSNiuyyzB13N6/V1Gw+E+xac8jZ2yRaJra1gn/xO0gVp8qcmj9wsVO4VGabUNkoY7NOn9aDtbJqQ9v6e/V0bQ2vdi+DLq5BDi8eS91BdsWS0XaJclj1qmkntqc76FqlDkeLk8P7sr5Gey62E+wBlbuRXnZu9+gmPBfL189Ey8BcT4fZMtYfKvt0gs1l9JJdMFWnM9DDLmq7xVZrW2EZbI7jK74W0PJu2bIiw+xYX+YDXcWXELjWga4CXPNSZMxzCXBYJ8cqAnGi/ZWVctTRXONZBXr5x00m3wFhLURjaeEkUj8IdpmTdao9ybdhV2Gkb7ZNoYvFxUJ5z87hMlOsTCGy77bnra9kyto26jOpS8ol8o+vQBuryDRwkfxE6Tlo7pnUt2KcsQ2KVsWniSkFn7pzaSHYS0Ul3hZwdwIr/GbLdYjgyqjRaz7nnJ1wl2MMdsyljzaxqe4i6whbZi55OGL/ah/lc9bbxRovSJ4uTTxJ5Jww26bdzi8C3jooDOj1u6W/gAtGCc/X5NWpbufX4Kir/87mWIQYHIn07QUFoiyydd1JgCW21cNDdlldVc7YOaFjJ84C9xwaKBNIW+7aYJDWYWeHW2U3feOaMyjiZ2WZLW+TyXPkuWDE9mi69ltPNl4lYBIvJoh45ZyRqYZw7M11VWaNVTXLUSm3Mo1O+yzGLN01L/eCZlE/rdGwZ6CUT16OrTpzTUbbAIItEw0ma2gVPuFFf1lkj4Eo99d0gejLU7zSHf+mAsqtgjwVvCRvHaUWsAnzexzHuutihpi9VI+Qp1Tk+ARCZpEXJSfXMIwYxz2IUkmEfDiAOdcd0hMA1mDXOI5lt9g4tvxbNbA1TxOmaitk5rIj7HgsQYK6sytRwm7c44EHgLPdvgSomDFPU5n6c8acZj2KkqdyHDLPM26fn+NwOOArX/4y8px1B5cE1hKR2SFS5wezBnxIbnBk1pvfbKBL9Z3MNWoLOejM0cVRmg5w5pa0vM5LSsXp15QH1fCP89rKwua0t90nRU9D35W/h2FQ3bdwcCoeuhhi51sp4PqqPk1nTi1oEuwdZ0vAzAEqO7QkiCO3/WmbRg6zrVdttLy0s9ZsoICj7Y84uGvyCkT1NtJansoeSBvkYBthwZIXZPFxcQmQxY/qmx0es0dLBY84rsKrQid5R+jqxkRoIDqffB7LQY771xtR89ySo4MZYxow7PaQC3iP04RpnnF+fo40jLh9fo79boezGzdw84GbODu7gbOzM03xAUAv/rB05rnJd8s3BNSgsym7pKRCtJjXdRijjV44Lmr0lPgD9qSHvh6BjN6qbBHbn+YZMPax3cW18EUMj8bTGK7WMHcENd3JWhc6aoE+/awjZutiHyhoTZpFADvHDf53A4q7sf/js4gzB9yFx8X+i7JKbTF594T9pe9I3caOkx2O6kvIbmeRveaIpOtXnWfiy8nvs4x1R7crTwT62DpkN2Qsa/UhzG9St/4kvBHoWlOA+iAvo9nxZKstvyWkgEvfvop2vMyxdMmY2Lrjwr7d5BDjFVGPRRpcBtc+0FX4z6/C9q6Eb+WtAQ0IW512Xnxk+apwlYGwg9YTTldxeHvtWUM+9i06ib4OQEROX5bw4jcf5FrWaUq6eqDOzbIPMhlP0rwqJNtPu2q6oKWUDbhrH+RvETClMxXdJkzIPF8dYaNETsEpHnF8CyPQgnFoyzuFT7JDxPMDxfo780NzEtj6XfeWhqgKWvkx7KqBlLFOiKH3nUDkCp1HsoIJ7yTL3wsH3QpyO6CMlj8qNMw9fhUDdCXo1MP1soDJVXjjMvlwmQyy8qGHdxzz1ZFSO7KzmggqTiNofT7fmWhVvKU+m9DU4qt4X4EO8T37+1rdp3Baa7vhBZQVbjRZBnLBH+TCh5Qv35XXEPF/9oyVUxADPad4pIePx81vnVf+4M777PXzspE+rtI118cgnHvzMQa7eu2eGvde2aYuuAY2RB6YcuF9DUZnWVSrutTo1DIXE4gYqDmgJNn8UHMqpjQgl0Q7ALwdpMdabJtEZQOSGJXMoLnsCpOj5CNz2dGVCCmV3R5DpfScsyYeB5egY55nTDWRvCSYv6iBrsPhUHfCmmPsQHUGW25V2aHm9G+A+CuZf93xsnrPDsha/caWUMeXgHau2iMR9YyPaLQ5aINcyu8w5ZnN10Yj6XOciwu8TR+tLbAa5BIa1AUosRk0YCRtBrrFsVnM257c7NinVwZmR1I2v6/ZQw6caJBd2svgge338t3ajtAptFl4Bks82fgP9V3l1xN2QqzL9bVLS6o81vCx/kUSJ13+nzOmaUbKjMP5eZn3wjO54DqMI8bd6IL0liTCoSR0tfiJLIt2RDGuyveq/6zj7OsOEOZctHnXbKs2lzpcIgOpn952Z3AJ6HFeOOJ2LNzc5HrBR5hHa13Sd7s6xdPFEMB910WAQJ9a0fIdGZee/b1mTxqcl+iw67/WY/E4YfOuSTUrd1SGEzk90n0v6Hl53+oJ5xdVOuR6AifbEy12DK1vZfrLod5F/6J/JL9JnT06EOkCQRcu8SFand4G0+qb8VTmIZm/AedP2Xdk3p6CNZvaPhca9uIVvXdP2ocn4FoHupqB6hOUxdX0Uoa1nEuyzULIpQErN5EIrAXQrqqwTzlicbAj/ndTdy8Bb2Qa2X4rMA4DdrtxQROr/81cB9B25PjjQkslYLBTursAgdYvQtG8D3OMLPYdrQ52hnld3dJVRhat0hSx1hEmZukIgJaA1QkqM3Yq/NAX9jIO1rixfGnfs8qTiNpNXrK6QNSOMspgOFr0DeIY5JJ+EMxNitXZ4coTa21EGkUBvjCuTb/jHJVcLpKbS3c5GdqIUknBCWD5O8wfLMpIPSudoKUwLWPa3hH+s6uX4zg62sr3NYh9Fzhl7Nr3IkR5carNyG+99mOyed2FZOjYrjz2c8gGuGxbi/lL5ugZWBWpG4NAz1PBBRljXQVfoWVPgV5FtvYCIVdRtJEWFgd3PJeh11ZxYohTncjnHgOXRKBuThvnoMRFAi8EpwDwuvFOoBfEi3X3fmeewbrpcv14iYw/o+zAZGbd6WYtU0ajka3KLXjAJ8GOc3PV4ejJyyvOx3Jb8dCOs+S6IJTz4riZzXkDlCNDKQ1IIL1YByj51HLNpdXuXTSKGARQwjDuACq7OZizOqxl50G7FUx2tGryeCIM+x3yOGA37zAcDpiOEw7HA3LOuLi4qO+WY4zjOGI/7jAMZxiHETnPOKQBcnvjfDzieHGhMvzi/KImmi8Br2ma2ljVIdW8nobOQ0r19rekc0LHzcoq9o4uUb2RMY5VcOhO8n7Vg8LrgxxBtbZCzcElvKkJ6jO7cdVFN5GV7OuJc0EujOnd3nYSRD6FfhMar6purrvZ7MUEyuf2iLHRtdYRphpUFVxl54W1Y3QsJEdYfTd36qsveb1+oquLuRdpI7Y71d0ZNk/ZKT0JYzuZduS3Hmhtd+gHGON5+Tu3/Ff+UesXAPAwFHtNdjwAJWcUT9iNOyQinO32ZddlTbEwT5NaMAlAGkYtMx1L3r2LiwvcvnUbwzDgxs2b2I0jHnjwGRjHETfOznSHaCahQBPOdpFZ6dFMeQ2GtV/kI+4OKb9YGgvHFPnf7G1rY1s6Obv65GCEIUDbrdIWQBmHw0Wpy7Yj/bQpYLicokDA4xQIj7mjakYO+cKnbZq1sq1//fbXyq9CoH83yHUCyPSV5B0Z106fVW6L7OCy09fhEHFDsM07vwHQHXQ56Gn1WWDmndE5C3wDr1nddJImXIKUvbEUXaq4iI3D60dYFWfJXwpZyLKXiy35XBekV/hA5rM9Di11CSJU5YKcxrB9ElkV/YyeXdk73hjL9S6VWoNrH+iywa7yGYkDABlEqRjdvMz/0+PDMgDybF1oWWFzStE5pjf4Xa1vdyKqPfNclTmkXE7940GqzJQuRR15h8C+Q8a+l3fX8TXF6lfSSWrNIqfwwpg3RzkIM9EkDHXW125eU6FkmCIam1m2xQP1ZpkTEXeYscdSyEq79jYRS5OTykz715RsNCJbEW/s5Zz1+KD0mepKhhWmQgerZHoKJRrZ8TmskpIywqfST0C3Dbt65Lk5FsGx7c47LjBlAjM9+p+CGOSKDssp6AVmXN0nnOme3LlKYCsG/eznGj/FgEwMdNkj0LrryNCyjXmbuzLfejJPAhwauGC/osuh/BrtIs5WFkc6xQDcZUGbSMM7lcO9tm2wy20YrHpGjjY5w194gY1jao2UFXbwBgh5moc+Rkf1FFw1yNf+XrnMoOIm+Giw1PDNInhp+ktp7UglQa7jOBX47EGcK1fR15GvJHjDVU7Y5yq7jGyVXIaVHACagTsdj3V3Vamn3NBYd3aRLMRRdUBHMNdE35LnKc9gbo6gHmFObWdyolRvZxzAAyNNSW9Xkh1YEkjONCANSd8bUnG4iRnzXAJe01RucjzUpNfzVOwuNait44K+XWCN6t4RdgQ+lQCOpSFUXmmlXT3E9h1gbTo5G0ILcuuHDWAvZC8CP6nX1Rp3/GFxrp+EMD+lH7Vel7Ij0EHQFz3u8uY5vKg5bMKjjgZmvlUHTfCyOMv4ys2KXO2LNbL29He0ZTjwAZv+a78tvqb9bqAr2Cmi1lW969gFuEQ+WtsRFU/EMTF9ivJBxkNsnmgHaHnzXSBZPhOb0yNXgkhm7iUYXZ9Z8+YREeaxLBqPux3AJeC9240gSjUvWgrkMHxff1f5bu31K9pPPXD2eLCTFjbTQp+3epqn0n4pCyiBH7htGnA2OrC4dc/yjo6hVr/C20S6g9WWz72gmu17B9S2wYqdy+xlHXm/tIurrcMR0MsV4W87n68CJ83ptb5SOUbtcK7t9ubY8vXlDkB3icCKHdh8TK+DeKVsz86wum+BfweuYnfa9i3e4kNLoeg3F14Jz7HkHbW5vJPukBfrvcd30Y7v+SJxY4677bJzhPwyO9XC9Q50IRJ0obsAMOaZYdaTghHihXDfGDYGaQ+PSwgejeZepDKWleMI3RwBnfqjwjwej4u+2puXbNti/JZklYQ8lLxnXi5bp88a9dRlWvt7E2N9hb1GGy1jJxnDCSfJWyI36IgTmGiZPFtpSWUV1jrypkEXkIo4yuq1vCG50Hq3vomyk3PLKfS19YH9mX/42+TsGFlc9J/UVYVv4haoLPbdsk0beJNkwwPRIgcKEfmcJsaw1TEPhp0b4/pOvCbWbTtOqZwImWdNLBwq6xrvtkXNw8X2Ji1TgFB2iBheVac6zEdxxuU/CcbYOu28tccV4zy0n/G7vBP5v/fPll2ShxfvRnxsvqzYfvwuMkJ2Tch4yU4VG0im5GkJtNxc0zQp3V1sg8uNeT2lRqkdCbE5YCK9UzAwZZ7YnYhrwew4DpcFM+L43k3AazEHM7tVQuHmzLkcU4Q/jjHnWYMOKsPJ19/xanx/GW5V7xS/MvvLSrr1wfPMWrl5mpucSacDuzag7No3XokGrYPBZnVFQkced/6OIPVE/urxjS0PLkElyYE4juWAX646Sm4WbrjWIBGhBLO48ENCWVmepxIkurgoR4r2+13ZbX3zAXWw5swtEXsasBuqOcclMAW6wDT5XIDTVMZc8u0kKjtqkRLG3QhKVHal1d1gnBnzsdzImKcZ2DHyMKvOKP1kHAAcj0c8+eSTdSfYUXODyLGnwYznUh8td7kKjnma/HwtzFHoIPPROCgSMIjvdKbHpaDjDm5JuYU/SXYskdoUQAsmWjnZdjd5Wdh8DMZkb28zdLDFRSZD+d3keRJ9bGSU1GYdf8GHQz2Lvtfybq5bXVR3FUk9JVCS9aKFcRhcAFKDr6ov+os5tYEWC6y4LXZC13LSL8FB+mPtOFuPlM/ynu2zoVtv4XABoe6eLqHaVs8BtzJeArrJ0ExwXdiV8kjGhLnML83VhZJ4Pi5qVMoJr8qxqP1up3bmnGccp4zD4QAiwq1btzCOI57xjGdgv9/j5gM3sdvtSp6/cQfoBRnQcViAsU0yo9qEYtGJr0Faz0JKGx+ATBnL38w+ELWogsxuksB3i/bM7+WIp5dBeutoxSWOP1/GOx06EbXdQznXnXjSZrAT3TsdW6arj4N9CCJ/u3Xo+yng8KkB7dqW2/nW7X74XcZF8BacTuDSu9TJ4bViq+nt7rLzORyBtMFLyfeYqj8e+cvKGvd766iTs2s2fG9xX+qR0zzaVpQ5DRn93fn5iTX8EW11rYfhglwn/QUzFy3OFnU7NvG4b4+H7QKR9UmtjRrz4vXEzBpc60CXwNJQKruJyu/m187kLz/1mG8pPCzDRWPYKqzo2IpREZXggmHN81MBrmh8x6RuFBg+9tkqWFvOGkBr9bT6fODCyu22yiMrzqzP/KTgZri5ZyKIAbti6jvS+puorEDbcZjzXIIewcEWY5NgHXR7xKpULdtFY/8ZwDiOKkjttuUljs2AYWbdnppKpa1++K2aYsA5npLfmVGX98vup1je7Iha9Nv0QYwj/d7pg+2bUxwGJ6uI3bu0zGEBU97xTs6Y0Ryy6GS23QltR1dM7EyhMeVlWaXTTqA5IGhnzeM6kDcs0W4VoWZsLZJIGv6182stqCJ/9+Z/rNP2ybbRq9O2G4+qXXajZWyDjZO8wEto4QxIuFUjDa5wKSt1DWN1YucWfNZ6GWDiriyyffRH0JcLBlEO2/kU+70G0o5VuHHrdc+5WcNVlDpQbvgtJDL4SGDVQuVXpkJzhg/ad4Pspj5fTzkn2XXIjMyxz07xZ49P5ffyW3Vo6qs55yar0aFbkNeVQA4XmdcafEA5YmbHVg1DU5ftZ+SBXt97sGaoGiSLbObl2MbScU4VGSpzpPw91OTxskvsOB0NLcrNjEUW23bqnBwGjIDqOqAZnQTCMCSAdxqcIxS5ut+NyMNQgtFoc3KeMyY+IqdZd5rMNbn8+fltHC4OJS/XNNVAdpn3aRyhCwoEd/mCBnQ7jpGzgYh0oXEgcjaD7tAmWlBbbaRSoeqMQiVj5dVxE91cFmIa37RdKU1fSN5Ba/xH6Npm7P92dqPRp1Tbc6qN2sITtL6qk6vud2W5cYYNqMgxUnd00dDCc1NrS8rNOS92oBNQbg21c8nMO0cLoX1nztkxAk44gaL/YeaTzKlqQ/SO0MhcaOMaemtkUWXZgo/2hUXAODtOvkdbEtwWFY2RXG1X0qCanhTo9HNNltl2ZXHZ6l+Z0wu919Ez1v5U3uO2o/Pi4gLT8YiLiwvsxhHDOOKBZzxYA16jBjejDHR46NxtxLU0WxO/zpaq823NjnF2qak7FPQXYAC6+Nr0TjtpIfxtZQeA9rwef7OdIMsbgOl7/Vu+rPh6RKalMD/t3yID1mxtraVHGy1afhM5aumgtn59V9+xuCLoVcFJxtV2SvCP+g9Y8Ixtw46L9EXbBfSiK+ub9GxwZgaqXSs2vMVL+B9oPslQn0kyeouLyBpZ4IjBVAvW/9bfOn3Xsmhj4mRITy8EfmuPCEgAcdkIsJAfldgaBjc6qme/9HyY0idAb7swz9ZtpgZrMZJYxv5+ma1m4VoHuhhNENvjEc1RlufWWYqDXAhbVhfEGfQra/bqXvub7OaxE1wi/5c5XjKga6vmTvBYbFfKRmdlbfdW6Z8/aifvDLpCl02ukHWHyCun/k6KGLBjtgzahGB3BYBFiLWcSXbFX43lxEgsN2ckdYBc8At2PJtzxsYB1bJVsesYmL6mlLDf79v7FmdeBjjEsARaYESDU7bdheAhNRac82be0RXgKoT1NijdiUXNULNVS/06JtEIXBpXovQ1aBeN3BCckt9haGNH3dJJlImsyAjfan/E2DIrL3ITl648kD/TLf1frjqw3pwlz8XxUydG6d34zAZ1lCczd/Hs0c8K8d5Ooxg4sPSxv/WUjH0mTl/MRWhzsvTGG4BbRZFnU93dYekA1B2RnACuMmwwu4+EL6nRW0DaP9uXfB/HupsFQJmznNVQj3KmN7fi97hzMMrGWN7KyB59oyPYw8nuJos0tXrBOYCFiHUQxShuxxF1tqid62/QnOe53IhFy9tTdcwpad3yzOq5Hh0WjnelQeRZ4RV5vrYwQwTQkHQelt1C2e2CBYA5t11fpdukQSzbL6UD+51KsrvGrupaeq/xCELZpb7iRZn4XIIikGA4+4U3kWmmtUI3rg5wSkimdK5zJ4Gw3+2rzCv4H2S+MGO/v4FxNxr6G5uDCMMwYkjlxsU8z8i57BCTOTrUYNYwjhiHsTqjCWf7s0ovaI6vaZqRpwkXXHYZnN+6hXmecZym8llvWLQ7j4WW4zCqrVaO7FLbXSvujATsqI2VjkUN7MhcHIwjobu57dhQCxLZMczcHETrIChfBd3FaPniIj/0+CLmFQHa7q5eQMzOIQDeFqmfGuSpOKtdZ/qbuQUjRM8oPpVOlgaUW94XjjTp6CHhUdvuXHOxqd6vZSwwM9gEb6IzrXPatGvbZrRdGmrntEJNFqPNQ+U5Y9MWG8zsKoD/9NDcxygfmxyRcfK6RukldDK1xsU7W1ZbrcFDRvM1CCWPqSHqYjFTdtCRkYG2jYHI5+I1tpH2UWwrqytlB+OcMWfGeaXvNE2QnITPfu5zcfOBB3Dj5k2Mw1ACXUC7iKgMrutrIqgtSfDzjknG2hABUJugjA4bR7zRSWxme1mA99qCHpHTGHVsJZehvdWz3ESbm8wxoOlGAl8mw5swfCA4OruljmmEMv9N3mLpX+uIk3cI/Gb9kujbyKkNMnVlZq+TjQzO7OeJ9UFatw3tF1QP9gkZv6C+p8/qZ9UK3uYDWlCQGai31FqcrKyz/hmF38WfYObCs9EeqJ+z8U1SSrhx44aTNZZu8cZmSweHu+mrIdCCBgJDzAUsc6cjD3sgv4ssFJt8bRGu4Lv+zNZZ8EGz9TtlejGMBe+s4RFsd+trLWX3OlzrQNfTCkSQnUo9J9Z+nho4+85Vyt3tez0m6DlnVwpyAIuyrS7AGgZ3A1QsbGjAIQYYxCBW6Xf3bd0RXlgKbOdgYwUPEeRWoXD/2OvlSJA0fDdv3zWIAib79wpYw1wEsb6zokDkPeHnBV9XI8IpbFOfKs66kkahvlK+ORYxcKRB0tC+fsLnhtM2yQh3+3unT2sQeeaUgurNw1jHWvtxlaSnHNxOwiDTLptj6iyIESoKNHsHUZ2vOrctbV3/EpBy0kWhy+Rsj173GqJspcivK/K2GIBogVdq8lCNCBmTp1cUfG3AWv9i896dhDzdTIcnevOq99udQJkDGcgiI1DGrdcnEUvBObBOdvu/OAa5qpW2A6H4p4y5OqTaEhEIqZ4GYRClknszpzIvdVdXxZwzcp5LsFDep1QcykSYUZzLzIz5cMQ8TbioNyqKwT93jt0pbawMQm8O+2B4QaHmDBNn5SqD0IG4G3NxY55xvHLHYbxTkPkvgVedr0611aBfXZSLO2YtLy50WniuPERen7kgSnwWkbY0ke/B2bRlIh4LJ1yqrd2WMczMLqhxR3Q1bUjQS4NfHYeKpG0T+L4X4PRox8FzTqCUM326w8bUXtJxa425z1SFkLjeKo6JMKDq4IrOMJQgmiwwWN564vHHcfv2OW4+cBPjuMMDD9wsO7t2ZqeoBHSr2TTbgBuSw9WNLZrNAJhgVzPrIgFO/k0kFy+Z55yRQUaG5RYEYPixk0rqb/UOme4R2GsJlldX7D8CWioTIw+0ClziK8DIhUvQkfrJ/+iDfE8zuAtDaqBrqDg2v+NyOjwd4AN+p+1H1QpmYC4Ldp2Cnn0V/YyeTfy1gi3QdUUoE7zjnK2Vf4qGs0DPKT4VxIrv9ZxYaxTZ8sUQkrLln5ssWpevpzy/iuhaAyp1MvQ4gHniAhcMbsfI7hJOYRkFVK8Zt8Jg/ra+mypE+7lS39cKnlJbvBRz7u/Qn2j0LhRUB69ekEsNVMApXavcZPXIGuSowSdfxgvTtWc2eBqDXHYXl3uHvLHfDwIvhX2v7KkA+VUDXbF/1uGJ5U/huGhD6uWg+AzNtHyWHYzmJq74nsUBJoAtIIuY0aHr9D3KtN8K0JOzApbfxfgoD/pyXXjxqVpMT8VgecrQM5po+encb3Ew4u9XBCuT3O8hWPBVBfbyo/xWJJkNdoluVRlWfsQyGmJ8XQ0+eOO/GNys804DbFWftoW5+l7OGOcZmeaa/65gV4IBVNAl0p05Oj9rPIFzSY4/HY/llkVzQcVlgXEGa/dscFz7J2VE3oquJ8IsCNzxmLAuhDhaG/1Nlr6GrncLPgDUdpg3nFD9a0YmOcLsE9jD8GkvWG7bEgfcBqB6OEniduuQOTvGBLZg6ODo0ZFPrr5OObGnos10x2D7JQGdnDVwtkajFqi424bvHmy/Zfem1WF2J7GUfyqNyTiu0dryV6OXK6C6NzGAVOhsdxEyyW618uL57XOALpDnGeNuB+Zcbmetfw/jiIEA6JGvlntTjqD7foRgi3av2RK0ohJVXEo3efk8JfI8LoG1nPUkj0uJgGZrUJhr3LHvI90pPLsTuNO3TtncV32fs9+JbGnl8Orp0CAf1vwopaHa30Gu1GexP/r9Htl6whtF7/rbZiMsfJh7AK7thTBY2la6qHrXNie5oTllY/Vs968lrbZA11WBoMdEgP7g9CKWRORW7L7maEYjpmMo9XIg2bIt0AX9vQl/Rs4Jw2AZtRjU89w/vnK3uIux6HbmBLyeFlgLNlz6WlWCkofsDvD1I2DavnIFXwVlIIaGVUimH6rw5Ay5CeSoA4GggIOA05VjY/hJW3rks3O81JYhIozjqIGX3m4hF/yxwVOtq3wv63vkkLZBLn2X4d5f+1wnbd/gXQtQybN4LKG3c0jq7AWye7sDbH22XTe/1Iq0nYA6bUjQANeaEaB0E9qS+c3O70SL/sR/V6Xz0w1rQZRegDKOrQ+S1Pqqw+/6f5cu0T0NeFWIc9MGjr9mbYbxOJXT7O6hMLbcLsgQUWecIzvvJCplAi8mUlDL1olRvxY5SfqMGZhzuzim5qCuOdGK0ZnkX0oAlxQP0wScn98uwQ1KLeFuGpAoYRxHtXXmOePi4gKHwwEX5xc4Hg6YpwmHw8EdaZWAB4mNFA1eCrxfL7Ww/ExqKBekJSX33dpP1iG1DqrVRTaYI3roqcgUF+iidows2i0ypzPnKje9XUamPqsT9J/k6ZI2JcGyOcYp+Z9mlS1LnWiPs6kY5rYjyDrz8aiM6n5D055txMY57B3bvypIUGsSGlbc0jAo/w0h4CDHgO9prF+CKQYvy89PhSbahvzHLVhhc7nB6BprqxG395pdRyXtRSXlmAZ9j+uRV/k31BsY8zzhMM+4OJwX3ksDdvs99mdneMYznoHd2R43bt7AMAzY7XbIOeM4TQC4oSf8xjZA2ZzuJivubqFC0s3owkANnGVmPXYt9ovK6IqHvUiDZX6UP9o8ue5g+g54eanHHYMNLlOL6/vRR1iADLbVeyvgfAbT3r2EaZ6d36Fg5Lbyg6XD02ynOl0LY3uuDou3x54KP6/ZwGsLN0/H3LmWgS4hzO3bfkUMQBWyzbwsW8PXc3SJQCtHy8Wwijm6ar3w/NobsN7OjlOGmqxs9PoX64nfe23GOoZxaXwRsRo5zO1GP6KMYUgYkgjvVr/kAJFyLUcZQTZAt2R8DR9JuCxoS53Sl2GQIxnrfVfhIas67MvlnDHJKhF5R9AGX/Jcbywb2sQXoyCllpRQtjGr4k/sjMphQFdw2TK2L213SxN6tl+r/VYHwec6G4fyfJmjywYCGMmgqP2rg8AGl0VeIwlUhP5xfBdiTNUE8mbcTyoxywzS96AQmlMPt8pkbyQSg1HHxDZRHcQefQnLPmubcTWDCr+X8WgGUJErM1JqQSUbiOoFjaw88OQwtxzW8r1g0VrwqHdD3FqQS496duRO66fJ3WHq6ilKzXVGLRA3T9Ni+K3BXZyvkudjnlpOH6U9ke6etfRQOVr5vRfssvSw/bbl4m9xZT0CddqKwcJTytrSz16sEPMDunqDMa+Osc1LVXmml3MKMAszOt0YOU8Or0iHSDda4ZVh8PxsczO5frMg0MrmnJEGH9jWVX4yQShqAQKL5ziWv+c8Ky12Y8FzzuZ22jW6JD83ym8+oeyasdbrYxnLGVzzjFlnUvruRIrk9iGTR0YLNHdYnlKHfxqOTZ7U+BbSkPSZBLrE7pmOM47HGY8/UXJ9lV1HEhgpOWt2g+RyA+aZcXFxxOHigPPzQ7mBcZpwmIruCReqNtGOcqQSAHZjXEjjNs6I8qzJE6H/PJublYkwjlllWXnGxY4I8YKSKN/bH0TizHuECWhBm6Ane8FpO93FnhI7sfBd6V2e5H1vr5TcLrPaYQCQhqUj2dqutBNbNFn7UuSuHEmt+Ji8iS3g5o+yu8VJimv8EhjhyiOsNGq70HKXXoq10SGZgUQzxtHYxZGYhv6i++Wp5Ek6zk2XlVsG202P8l6jmdh1DZ/4bwnNwmhmidCy8SzV+m0XlBesrhfbttUKoNCipAeqOxfdQnHjU8fXSkvjn6gOgsunlMiPNYveTMXGlzakviZXSvtC+XFg/W2eGYdj6/uwY1BiPcbV5C9hf2PGbp8xzSP2Z4wpjxgSkMZyw/bFcTK6hbx9GYalBbmuLpsjDAMwJNNGHQu59VzyhYpclHYBYH+2DHS53LLOvlz6XLEvtp41W9md5rY2jv5Eq8+s3exkqbE7bB1ep7TAkrPNa1splDEd83PLod+nwUk/IYKRT6tvGXzVfxAZpPwu9oPk6MKiL/KXHM9PiT1NTL+OxwlpKLcTMxhDaosYWvRSdhWZt9Qvpvsa18iMxbjYLih5bZCr/LDWtOfvlRxekaeJqFun+EmCQ86WZrnLD5exQpTbt271L+/oAfFVSv0Wg//1v/4XvvEbv/Feo7HBBhtssMEGG2ywwQYbbLDBBhtssMHTBJ/73Ofw4he/+GSZaxnoyjnjU5/6FF75ylfic5/7HB566KF7jdIGGzwl+MpXvoJv/MZv3Ph5g/sGNp7e4H6CjZ83uJ9g4+cN7jfYeHqD+wk2fl4HZsbjjz+OF73oRZce/76WRxdTSviGb/gGAMBDDz20McAG9w1s/LzB/QYbT29wP8HGzxvcT7Dx8wb3G2w8vcH9BBs/9+GZz3zmlco99SyIG2ywwQYbbLDBBhtssMEGG2ywwQYbbPBbALZA1wYbbLDBBhtssMEGG2ywwQYbbLDBBvcFXNtA19nZGd75znfi7OzsXqOywQZPGTZ+3uB+g42nN7ifYOPnDe4n2Ph5g/sNNp7e4H6CjZ+/OnAtk9FvsMEGG2ywwQYbbLDBBhtssMEGG2ywQYRru6Nrgw022GCDDTbYYIMNNthggw022GCDDSxsga4NNthggw022GCDDTbYYIMNNthggw3uC9gCXRtssMEGG2ywwQYbbLDBBhtssMEGG9wXsAW6Nthggw022GCDDTbYYIMNNthggw02uC/gWga6fviHfxi/43f8Dty4cQNveMMb8Au/8Av3GqUNNujCz/7sz+KP/bE/hhe96EUgIvybf/Nv3HNmxg/+4A/ihS98IW7evIk3v/nN+PSnP+3K/OZv/ibe9ra34aGHHsLDDz+MP//n/zyeeOKJp7EXG2xQ4F3vehf+wB/4A/i6r/s6PO95z8Mf/+N/HJ/61KdcmfPzc7zjHe/As5/9bDz44IP4U3/qT+E3fuM3XJnPfvazeOtb34oHHngAz3ve8/BX/spfwTRNT2dXNtgA73nPe/DqV78aDz30EB566CE88sgj+MAHPqDPN17e4DrDu9/9bhARvu/7vk9/23h6g+sEf+Nv/A0Qkfv3ile8Qp9v/LzBdYNf//Vfx5/5M38Gz372s3Hz5k180zd9Ez760Y/q880v/OrCtQt0/ct/+S/xl//yX8Y73/lO/NIv/RJe85rX4C1veQu++MUv3mvUNthgAU8++SRe85rX4Id/+Ie7z//23/7b+KEf+iH8yI/8CD7ykY/gGc94Bt7ylrfg/Pxcy7ztbW/Dr/7qr+KDH/wgfuInfgI/+7M/i+/8zu98urqwwQYKjz76KN7xjnfg53/+5/HBD34Qx+MR3/It34Inn3xSy/ylv/SX8OM//uP4sR/7MTz66KP43//7f+NP/sk/qc/necZb3/pWHA4H/Of//J/xoz/6o3jve9+LH/zBH7wXXdrgtzG8+MUvxrvf/W489thj+OhHP4o/8kf+CL7t274Nv/qrvwpg4+UNri/84i/+Iv7hP/yHePWrX+1+33h6g+sGv+/3/T58/vOf138/93M/p882ft7gOsH/+3//D2984xux2+3wgQ98AJ/85Cfxd//u38WznvUsLbP5hV9l4GsG3/zN38zveMc79O95nvlFL3oRv+td77qHWG2wweUAgN///vfr3zlnfsELXsB/5+/8Hf3tS1/6Ep+dnfG/+Bf/gpmZP/nJTzIA/sVf/EUt84EPfICJiH/913/9acN9gw168MUvfpEB8KOPPsrMhX93ux3/2I/9mJb5L//lvzAA/vCHP8zMzP/+3/97TinxF77wBS3znve8hx966CG+uLh4ejuwwQYBnvWsZ/E/+Sf/ZOPlDa4tPP744/zyl7+cP/jBD/If/sN/mL/3e7+XmTf5vMH1g3e+8538mte8pvts4+cNrhv81b/6V/kP/sE/uPp88wu/+nCtdnQdDgc89thjePOb36y/pZTw5je/GR/+8IfvIWYbbHDn8JnPfAZf+MIXHD8/85nPxBve8Abl5w9/+MN4+OGH8frXv17LvPnNb0ZKCR/5yEeedpw32MDCl7/8ZQDA13/91wMAHnvsMRyPR8fTr3jFK/CSl7zE8fQ3fdM34fnPf76Wectb3oKvfOUrupNmgw2ebpjnGe973/vw5JNP4pFHHtl4eYNrC+94xzvw1re+1fEusMnnDa4nfPrTn8aLXvQi/M7f+Tvxtre9DZ/97GcBbPy8wfWDf/fv/h1e//rX40//6T+N5z3veXjta1+Lf/yP/7E+3/zCrz5cq0DX//k//wfzPDuBBQDPf/7z8YUvfOEeYbXBBncHwrOn+PkLX/gCnve857nn4zji67/+6zee3+CeQs4Z3/d934c3vvGNeNWrXgWg8Ot+v8fDDz/sykae7vG8PNtgg6cTPvGJT+DBBx/E2dkZvuu7vgvvf//78cpXvnLj5Q2uJbzvfe/DL/3SL+Fd73rX4tnG0xtcN3jDG96A9773vfjJn/xJvOc978FnPvMZ/KE/9Ifw+OOPb/y8wbWD//7f/zve85734OUvfzn+w3/4D/ju7/5u/MW/+Bfxoz/6owA2v/BrAeO9RmCDDTbYYIPrB+94xzvwK7/yKy5fxgYbXDf4Pb/n9+DjH/84vvzlL+Nf/+t/jbe//e149NFH7zVaG2xwx/C5z30O3/u934sPfvCDuHHjxr1GZ4MNnjJ867d+q35/9atfjTe84Q146Utfin/1r/4Vbt68eQ8x22CDO4ecM17/+tfjb/2tvwUAeO1rX4tf+ZVfwY/8yI/g7W9/+z3G7v6Ea7Wj6znPeQ6GYVjcqPEbv/EbeMELXnCPsNpgg7sD4dlT/PyCF7xgcdHCNE34zd/8zY3nN7hn8D3f8z34iZ/4Cfz0T/80XvziF+vvL3jBC3A4HPClL33JlY883eN5ebbBBk8n7Pd7/K7f9bvwute9Du9617vwmte8Bn//7//9jZc3uHbw2GOP4Ytf/CJ+/+///RjHEeM44tFHH8UP/dAPYRxHPP/5z994eoNrDQ8//DB+9+/+3fi1X/u1TUZvcO3ghS98IV75yle6337v7/29ehx38wu/+nCtAl37/R6ve93r8FM/9VP6W84ZP/VTP4VHHnnkHmK2wQZ3Di972cvwghe8wPHzV77yFXzkIx9Rfn7kkUfwpS99CY899piW+dCHPoScM97whjc87Thv8NsbmBnf8z3fg/e///340Ic+hJe97GXu+ete9zrsdjvH05/61Kfw2c9+1vH0Jz7xCaeoP/jBD+Khhx5aGAAbbPB0Q84ZFxcXGy9vcO3gTW96Ez7xiU/g4x//uP57/etfj7e97W36fePpDa4zPPHEE/hv/+2/4YUvfOEmoze4dvDGN74Rn/rUp9xv//W//le89KUvBbD5hV8TuNfZ8O8U3ve+9/HZ2Rm/973v5U9+8pP8nd/5nfzwww+7GzU22OC3Cjz++OP8sY99jD/2sY8xAP57f+/v8cc+9jH+n//zfzIz87vf/W5++OGH+d/+23/Lv/zLv8zf9m3fxi972cv49u3bWscf/aN/lF/72tfyRz7yEf65n/s5fvnLX87f8R3fca+6tMFvY/ju7/5ufuYzn8k/8zM/w5///Of1361bt7TMd33Xd/FLXvIS/tCHPsQf/ehH+ZFHHuFHHnlEn0/TxK961av4W77lW/jjH/84/+RP/iQ/97nP5b/21/7avejSBr+N4Qd+4Af40Ucf5c985jP8y7/8y/wDP/ADTET8H//jf2TmjZc3uP5gb11k3nh6g+sF3//9388/8zM/w5/5zGf4P/2n/8RvfvOb+TnPeQ5/8YtfZOaNnze4XvALv/ALPI4j/82/+Tf505/+NP/zf/7P+YEHHuB/9s/+mZbZ/MKvLly7QBcz8z/4B/+AX/KSl/B+v+dv/uZv5p//+Z+/1yhtsEEXfvqnf5oBLP69/e1vZ+Zylexf/+t/nZ///Ofz2dkZv+lNb+JPfepTro7/+3//L3/Hd3wHP/jgg/zQQw/xn/2zf5Yff/zxe9CbDX67Q4+XAfA//af/VMvcvn2b/8Jf+Av8rGc9ix944AH+E3/iT/DnP/95V8//+B//g7/1W7+Vb968yc95znP4+7//+/l4PD7Nvdngtzv8uT/35/ilL30p7/d7fu5zn8tvetObNMjFvPHyBtcfYqBr4+kNrhN8+7d/O7/whS/k/X7P3/AN38Df/u3fzr/2a7+mzzd+3uC6wY//+I/zq171Kj47O+NXvOIV/I/+0T9yzze/8KsLxMx8b/aSbbDBBhtssMEGG2ywwQYbbLDBBhtssMFXD65Vjq4NNthggw022GCDDTbYYIMNNthggw02WIMt0LXBBhtssMEGG2ywwQYbbLDBBhtssMF9AVuga4MNNthggw022GCDDTbYYIMNNthgg/sCtkDXBhtssMEGG2ywwQYbbLDBBhtssMEG9wVsga4NNthggw022GCDDTbYYIMNNthggw3uC9gCXRtssMEGG2ywwQYbbLDBBhtssMEGG9wXsAW6Nthggw022GCDDTbYYIMNNthggw02uC9gC3RtsMEGG2ywwQYbbLDBBhtssMEGG2xwX8AW6Npggw022GCDDTbYYIMNNthggw022OC+gC3QtcEGG2ywwQYbbLDBBhtssMEGG2ywwX0BW6Brgw022GCDDTbYYIMNNthggw022GCD+wK2QNcGG2ywwQYbbLDBBhtssMEGG2ywwQb3Bfx/RdBuqNdea0UAAAAASUVORK5CYII=",
+ "text/plain": [
+ ""
+ ]
+ },
+ "metadata": {},
+ "output_type": "display_data"
+ }
+ ],
+ "source": [
+ "import matplotlib.pyplot as plt\n",
+ "\n",
+ "color_seg = np.zeros((pred_seg.shape[0], pred_seg.shape[1], 3), dtype=np.uint8)\n",
+ "palette = np.array(ade_palette())\n",
+ "\n",
+ "for label, color in enumerate(palette):\n",
+ " color_seg[pred_seg == label, :] = color\n",
+ "color_seg = color_seg[..., ::-1] # convert to BGR\n",
+ "\n",
+ "img = np.array(image) * 0.5 + color_seg * 0.5 # plot the image with the segmentation map\n",
+ "img = img.astype(np.uint8)\n",
+ "\n",
+ "plt.figure(figsize=(15, 10))\n",
+ "plt.imshow(img)\n",
+ "plt.show()"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "q1aGuHYFLP7i"
+ },
+ "source": [
+ "The results are definitely not as expected and as mentioned above, this example is not meant to provide a state-of-the-art model. It exists to familiarize you with the end-to-end workflow. \n",
+ "\n",
+ "On the other hand, if you perform full fine-tuning on the same setup (same model variant, same dataset, same training schedule, etc.), the results would not have been any different. This is a crucial aspect of parameter-efficient fine-tuning -- to be able to match up to the results of the full fine-tuning but with a fraction of total trainable parameters. \n",
+ "\n",
+ "Here are some things that you can try to get better results:\n",
+ "\n",
+ "* Increase the number of training samples. \n",
+ "* Try a larger SegFormer model variant (know about the available model variants [here](https://huggingface.co/models?search=segformer)). \n",
+ "* Try different values for the arguments available in `LoraConfig`. \n",
+ "* Tune the learning rate and batch size. "
+ ]
+ }
+ ],
+ "metadata": {
+ "accelerator": "GPU",
+ "colab": {
+ "machine_shape": "hm",
+ "provenance": []
+ },
+ "gpuClass": "premium",
+ "kernelspec": {
+ "display_name": "Python 3",
+ "language": "python",
+ "name": "python3"
+ },
+ "language_info": {
+ "codemirror_mode": {
+ "name": "ipython",
+ "version": 3
+ },
+ "file_extension": ".py",
+ "mimetype": "text/x-python",
+ "name": "python",
+ "nbconvert_exporter": "python",
+ "pygments_lexer": "ipython3",
+ "version": "3.11.13"
+ },
+ "widgets": {
+ "application/vnd.jupyter.widget-state+json": {
+ "0dcc5a2866a349e0843673bef499dc66": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_24fde588dc1a49a397e379cda320ed71",
+ "placeholder": "",
+ "style": "IPY_MODEL_9746875e74b845daab06619393b4d46b",
+ "value": "\nPro Tip: If you don't already have one, you can create a dedicated\n'notebooks' token with 'write' access, that you can then easily reuse for all\nnotebooks. "
+ }
+ },
+ "14ac809ba0bc4cd5bcd51f83105947b0": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "21bf954f54db41e6ba78f76195721614": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "24fde588dc1a49a397e379cda320ed71": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "3f69c7b15e5e48039777e4b6b1a51f53": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "42a7b8268d8945b5bbe9d3f20bc8840c": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "554b55f29a5e4d5a81608d912d3635e8": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "5bcfe3da0ffb41ccbb9404ac35ae8945": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "6c6d19cd893e4d82bae9972fa10c6d74": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "PasswordModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "PasswordModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "PasswordView",
+ "continuous_update": true,
+ "description": "Token:",
+ "description_tooltip": null,
+ "disabled": false,
+ "layout": "IPY_MODEL_42a7b8268d8945b5bbe9d3f20bc8840c",
+ "placeholder": "",
+ "style": "IPY_MODEL_554b55f29a5e4d5a81608d912d3635e8",
+ "value": ""
+ }
+ },
+ "6c88a55a635b4c9f946a1aa838d69f20": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_14ac809ba0bc4cd5bcd51f83105947b0",
+ "placeholder": "",
+ "style": "IPY_MODEL_e7393e78f41b496495982490b72ef2a3",
+ "value": "
Copy a token from your Hugging Face\ntokens page and paste it below.
Immediately click login after copying\nyour token or it might be stored in plain text in this notebook file. "
+ }
+ },
+ "9746875e74b845daab06619393b4d46b": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "b7431f99d93b4e9b8c8177ac4a7b4070": {
+ "model_module": "@jupyter-widgets/base",
+ "model_module_version": "1.2.0",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": "center",
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": "flex",
+ "flex": null,
+ "flex_flow": "column",
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": "50%"
+ }
+ },
+ "cb4053f102fc4207a1c9513f81ad6415": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ButtonModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ButtonModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "ButtonView",
+ "button_style": "",
+ "description": "Login",
+ "disabled": false,
+ "icon": "",
+ "layout": "IPY_MODEL_21bf954f54db41e6ba78f76195721614",
+ "style": "IPY_MODEL_f83dd354396e4aa3acd214a6fd98efb2",
+ "tooltip": ""
+ }
+ },
+ "e7393e78f41b496495982490b72ef2a3": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "f2a722f371904cce80dc1c087b153ad6": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "VBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "VBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "VBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_6c88a55a635b4c9f946a1aa838d69f20",
+ "IPY_MODEL_6c6d19cd893e4d82bae9972fa10c6d74",
+ "IPY_MODEL_fc48ee28c2e44f1daa03149c8004c314",
+ "IPY_MODEL_cb4053f102fc4207a1c9513f81ad6415",
+ "IPY_MODEL_0dcc5a2866a349e0843673bef499dc66"
+ ],
+ "layout": "IPY_MODEL_b7431f99d93b4e9b8c8177ac4a7b4070"
+ }
+ },
+ "f83dd354396e4aa3acd214a6fd98efb2": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "ButtonStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ButtonStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "button_color": null,
+ "font_weight": ""
+ }
+ },
+ "fc48ee28c2e44f1daa03149c8004c314": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_module_version": "1.5.0",
+ "model_name": "CheckboxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "CheckboxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "CheckboxView",
+ "description": "Add token as git credential?",
+ "description_tooltip": null,
+ "disabled": false,
+ "indent": true,
+ "layout": "IPY_MODEL_3f69c7b15e5e48039777e4b6b1a51f53",
+ "style": "IPY_MODEL_5bcfe3da0ffb41ccbb9404ac35ae8945",
+ "value": true
+ }
+ }
+ }
+ }
+ },
+ "nbformat": 4,
+ "nbformat_minor": 1
+}
diff --git a/peft/examples/sequence_classification/C3A.ipynb b/peft/examples/sequence_classification/C3A.ipynb
new file mode 100644
index 0000000000000000000000000000000000000000..dbd8282a76cb3e4655d63b2e4411c4c0bd3dd3dc
--- /dev/null
+++ b/peft/examples/sequence_classification/C3A.ipynb
@@ -0,0 +1,512 @@
+{
+ "cells": [
+ {
+ "cell_type": "markdown",
+ "id": "d36e1e93-ae93-4a4e-93c6-68fd868d2882",
+ "metadata": {},
+ "source": [
+ "# Using C3A for sequence classification"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "ddfc0610-55f6-4343-a950-125ccf0f45ac",
+ "metadata": {},
+ "source": [
+ "In this example, we fine-tune Roberta (base) on a sequence classification task using C3A."
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "45addd81-d4f3-4dfd-960d-3920d347f0a6",
+ "metadata": {},
+ "source": [
+ "## Imports"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "id": "a9935ae2",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "# To run this notebook, please run `pip install evaluate` to install additional dependencies not covered by PEFT.\n",
+ "import torch\n",
+ "from torch.optim import AdamW\n",
+ "from torch.utils.data import DataLoader\n",
+ "from peft import (\n",
+ " get_peft_model,\n",
+ " C3AConfig,\n",
+ " PeftType,\n",
+ ")\n",
+ "from peft.utils import infer_device\n",
+ "\n",
+ "import evaluate\n",
+ "from datasets import load_dataset\n",
+ "from transformers import AutoModelForSequenceClassification, AutoTokenizer, get_linear_schedule_with_warmup, set_seed, AutoConfig\n",
+ "from tqdm import tqdm"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "62c959bf-7cc2-49e0-b97e-4c10ec3b9bf3",
+ "metadata": {},
+ "source": [
+ "## Parameters"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "id": "e3b13308",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "batch_size = 32\n",
+ "model_name_or_path = \"roberta-base\"\n",
+ "task = \"mrpc\"\n",
+ "peft_type = PeftType.C3A\n",
+ "device = infer_device()\n",
+ "num_epochs = 5 # for better results, increase this number\n",
+ "block_size = 768 # for better results, increase this number\n",
+ "max_length = 512\n",
+ "torch.manual_seed(0)"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "id": "0526f571",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "peft_config = C3AConfig(\n",
+ " task_type=\"SEQ_CLS\", \n",
+ " block_size=block_size,\n",
+ " target_modules=[\"query\", \"value\"],\n",
+ ")\n",
+ "head_lr = 4e-6 # the learning rate for the classification head for NLU tasks\n",
+ "ft_lr = 3e-1 # the learning rate for C3A parameters, a much larger LR than that is usually used, at least 1e-1"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "c075c5d2-a457-4f37-a7f1-94fd0d277972",
+ "metadata": {},
+ "source": [
+ "## Loading data"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 4,
+ "id": "7bb52cb4-d1c3-4b04-8bf0-f39ca88af139",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "if any(k in model_name_or_path for k in (\"gpt\", \"opt\", \"bloom\")):\n",
+ " padding_side = \"left\"\n",
+ "else:\n",
+ " padding_side = \"right\"\n",
+ "\n",
+ "tokenizer = AutoTokenizer.from_pretrained(model_name_or_path, padding_side=padding_side)\n",
+ "if getattr(tokenizer, \"pad_token_id\") is None:\n",
+ " tokenizer.pad_token_id = tokenizer.eos_token_id"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 5,
+ "id": "e69c5e1f-d27b-4264-a41e-fc9b99d025e6",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "datasets = load_dataset(\"glue\", task)\n",
+ "metric = evaluate.load(\"glue\", task)"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 6,
+ "id": "0209f778-c93b-40eb-a4e0-24c25db03980",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "def tokenize_function(examples):\n",
+ " # max_length=None => use the model max length (it's actually the default)\n",
+ " outputs = tokenizer(examples[\"sentence1\"], examples[\"sentence2\"], truncation=True, max_length=max_length)\n",
+ " return outputs\n",
+ "\n",
+ "\n",
+ "tokenized_datasets = datasets.map(\n",
+ " tokenize_function,\n",
+ " batched=True,\n",
+ " remove_columns=[\"idx\", \"sentence1\", \"sentence2\"],\n",
+ ")\n",
+ "\n",
+ "# We also rename the 'label' column to 'labels' which is the expected name for labels by the models of the\n",
+ "# transformers library\n",
+ "tokenized_datasets = tokenized_datasets.rename_column(\"label\", \"labels\")"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 7,
+ "id": "7453954e-982c-46f0-b09c-589776e6d6cb",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "def collate_fn(examples):\n",
+ " return tokenizer.pad(examples, padding=\"longest\", return_tensors=\"pt\")\n",
+ "\n",
+ "\n",
+ "# Instantiate dataloaders.\n",
+ "train_dataloader = DataLoader(tokenized_datasets[\"train\"], shuffle=True, collate_fn=collate_fn, batch_size=batch_size)\n",
+ "eval_dataloader = DataLoader(\n",
+ " tokenized_datasets[\"validation\"], shuffle=False, collate_fn=collate_fn, batch_size=batch_size\n",
+ ")"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "f3b9b2e8-f415-4d0f-9fb4-436f1a3585ea",
+ "metadata": {},
+ "source": [
+ "## Preparing the C3A model"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 8,
+ "id": "2ed5ac74",
+ "metadata": {},
+ "outputs": [
+ {
+ "name": "stderr",
+ "output_type": "stream",
+ "text": [
+ "Some weights of RobertaForSequenceClassification were not initialized from the model checkpoint at roberta-base and are newly initialized: ['classifier.dense.bias', 'classifier.dense.weight', 'classifier.out_proj.bias', 'classifier.out_proj.weight']\n",
+ "You should probably TRAIN this model on a down-stream task to be able to use it for predictions and inference.\n"
+ ]
+ },
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "trainable params: 610,562 || all params: 125,257,732 || trainable%: 0.4874\n"
+ ]
+ }
+ ],
+ "source": [
+ "model = AutoModelForSequenceClassification.from_pretrained(model_name_or_path, return_dict=True, max_length=None)\n",
+ "model = get_peft_model(model, peft_config)\n",
+ "model.print_trainable_parameters()"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 9,
+ "id": "0d2d0381",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "head_param = list(map(id, model.classifier.parameters()))\n",
+ "\n",
+ "others_param = filter(lambda p: id(p) not in head_param, model.parameters()) \n",
+ "\n",
+ "optimizer = AdamW([\n",
+ " {\"params\": model.classifier.parameters(), \"lr\": head_lr},\n",
+ " {\"params\": others_param, \"lr\": ft_lr}\n",
+ "],weight_decay=0.)\n",
+ "\n",
+ "\n",
+ "# Instantiate scheduler\n",
+ "lr_scheduler = get_linear_schedule_with_warmup(\n",
+ " optimizer=optimizer,\n",
+ " num_warmup_steps=0.06 * (len(train_dataloader) * num_epochs),\n",
+ " num_training_steps=(len(train_dataloader) * num_epochs),\n",
+ ")"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "c0dd5aa8-977b-4ac0-8b96-884b17bcdd00",
+ "metadata": {},
+ "source": [
+ "## Training"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 10,
+ "id": "fa0e73be",
+ "metadata": {},
+ "outputs": [
+ {
+ "name": "stderr",
+ "output_type": "stream",
+ "text": [
+ " 0%| | 0/115 [00:00"
+ ]
+ },
+ "execution_count": 2,
+ "metadata": {},
+ "output_type": "execute_result"
+ }
+ ],
+ "source": [
+ "batch_size = 32\n",
+ "model_name_or_path = \"roberta-base\"\n",
+ "task = \"mrpc\"\n",
+ "peft_type = PeftType.FOURIERFT\n",
+ "device = torch.accelerator.current_accelerator().type if hasattr(torch, \"accelerator\") else \"cuda\"\n",
+ "num_epochs = 5 # for better results, increase this number\n",
+ "n_frequency = 1000 # for better results, increase this number\n",
+ "scaling = 150.0\n",
+ "max_length = 512\n",
+ "torch.manual_seed(0)"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 3,
+ "id": "0526f571",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "peft_config = FourierFTConfig(\n",
+ " task_type=\"SEQ_CLS\", \n",
+ " n_frequency=n_frequency,\n",
+ " target_modules=[\"query\", \"value\"],\n",
+ " scaling = scaling,\n",
+ ")\n",
+ "head_lr = 6e-3 # the learning rate for the classification head for NLU tasks\n",
+ "fft_lr = 6e-2 # the learning rate for the parameters other than the classification head (q,v in this case)"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "c075c5d2-a457-4f37-a7f1-94fd0d277972",
+ "metadata": {},
+ "source": [
+ "## Loading data"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 4,
+ "id": "7bb52cb4-d1c3-4b04-8bf0-f39ca88af139",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "if any(k in model_name_or_path for k in (\"gpt\", \"opt\", \"bloom\")):\n",
+ " padding_side = \"left\"\n",
+ "else:\n",
+ " padding_side = \"right\"\n",
+ "\n",
+ "tokenizer = AutoTokenizer.from_pretrained(model_name_or_path, padding_side=padding_side)\n",
+ "if getattr(tokenizer, \"pad_token_id\") is None:\n",
+ " tokenizer.pad_token_id = tokenizer.eos_token_id"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 5,
+ "id": "e69c5e1f-d27b-4264-a41e-fc9b99d025e6",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "datasets = load_dataset(\"glue\", task)\n",
+ "metric = evaluate.load(\"glue\", task)"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 6,
+ "id": "0209f778-c93b-40eb-a4e0-24c25db03980",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "def tokenize_function(examples):\n",
+ " # max_length=None => use the model max length (it's actually the default)\n",
+ " outputs = tokenizer(examples[\"sentence1\"], examples[\"sentence2\"], truncation=True, max_length=max_length)\n",
+ " return outputs\n",
+ "\n",
+ "\n",
+ "tokenized_datasets = datasets.map(\n",
+ " tokenize_function,\n",
+ " batched=True,\n",
+ " remove_columns=[\"idx\", \"sentence1\", \"sentence2\"],\n",
+ ")\n",
+ "\n",
+ "# We also rename the 'label' column to 'labels' which is the expected name for labels by the models of the\n",
+ "# transformers library\n",
+ "tokenized_datasets = tokenized_datasets.rename_column(\"label\", \"labels\")"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 7,
+ "id": "7453954e-982c-46f0-b09c-589776e6d6cb",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "def collate_fn(examples):\n",
+ " return tokenizer.pad(examples, padding=\"longest\", return_tensors=\"pt\")\n",
+ "\n",
+ "\n",
+ "# Instantiate dataloaders.\n",
+ "train_dataloader = DataLoader(tokenized_datasets[\"train\"], shuffle=True, collate_fn=collate_fn, batch_size=batch_size)\n",
+ "eval_dataloader = DataLoader(\n",
+ " tokenized_datasets[\"validation\"], shuffle=False, collate_fn=collate_fn, batch_size=batch_size\n",
+ ")"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "f3b9b2e8-f415-4d0f-9fb4-436f1a3585ea",
+ "metadata": {},
+ "source": [
+ "## Preparing the FourierFT model"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 8,
+ "id": "2ed5ac74",
+ "metadata": {},
+ "outputs": [
+ {
+ "name": "stderr",
+ "output_type": "stream",
+ "text": [
+ "Some weights of RobertaForSequenceClassification were not initialized from the model checkpoint at roberta-base and are newly initialized: ['classifier.dense.bias', 'classifier.dense.weight', 'classifier.out_proj.bias', 'classifier.out_proj.weight']\n",
+ "You should probably TRAIN this model on a down-stream task to be able to use it for predictions and inference.\n"
+ ]
+ },
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "trainable params: 616,130 || all params: 125,263,300 || trainable%: 0.4919\n"
+ ]
+ }
+ ],
+ "source": [
+ "model = AutoModelForSequenceClassification.from_pretrained(model_name_or_path, return_dict=True, max_length=None)\n",
+ "model = get_peft_model(model, peft_config)\n",
+ "model.print_trainable_parameters()"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 9,
+ "id": "0d2d0381",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "head_param = list(map(id, model.classifier.parameters()))\n",
+ "\n",
+ "others_param = filter(lambda p: id(p) not in head_param, model.parameters()) \n",
+ "\n",
+ "optimizer = AdamW([\n",
+ " {\"params\": model.classifier.parameters(), \"lr\": head_lr},\n",
+ " {\"params\": others_param, \"lr\": fft_lr}\n",
+ "],weight_decay=0.)\n",
+ "\n",
+ "\n",
+ "# Instantiate scheduler\n",
+ "lr_scheduler = get_linear_schedule_with_warmup(\n",
+ " optimizer=optimizer,\n",
+ " num_warmup_steps=0.06 * (len(train_dataloader) * num_epochs),\n",
+ " num_training_steps=(len(train_dataloader) * num_epochs),\n",
+ ")"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "c0dd5aa8-977b-4ac0-8b96-884b17bcdd00",
+ "metadata": {},
+ "source": [
+ "## Training"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 10,
+ "id": "fa0e73be",
+ "metadata": {},
+ "outputs": [
+ {
+ "name": "stderr",
+ "output_type": "stream",
+ "text": [
+ " 0%| | 0/115 [00:00 use the model max length (it's actually the default)\n",
+ " outputs = tokenizer(examples[\"sentence1\"], examples[\"sentence2\"], truncation=True, max_length=None)\n",
+ " return outputs\n",
+ "\n",
+ "\n",
+ "tokenized_datasets = datasets.map(\n",
+ " tokenize_function,\n",
+ " batched=True,\n",
+ " remove_columns=[\"idx\", \"sentence1\", \"sentence2\"],\n",
+ ")\n",
+ "\n",
+ "# We also rename the 'label' column to 'labels' which is the expected name for labels by the models of the\n",
+ "# transformers library\n",
+ "tokenized_datasets = tokenized_datasets.rename_column(\"label\", \"labels\")\n",
+ "\n",
+ "\n",
+ "def collate_fn(examples):\n",
+ " return tokenizer.pad(examples, padding=\"longest\", return_tensors=\"pt\")\n",
+ "\n",
+ "\n",
+ "# Instantiate dataloaders.\n",
+ "train_dataloader = DataLoader(tokenized_datasets[\"train\"], shuffle=True, collate_fn=collate_fn, batch_size=batch_size)\n",
+ "eval_dataloader = DataLoader(\n",
+ " tokenized_datasets[\"validation\"], shuffle=False, collate_fn=collate_fn, batch_size=batch_size\n",
+ ")\n",
+ "test_dataloader = DataLoader(tokenized_datasets[\"test\"], shuffle=False, collate_fn=collate_fn, batch_size=batch_size)"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 6,
+ "id": "2ed5ac74",
+ "metadata": {
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 1000,
+ "referenced_widgets": [
+ "0cecb897c86c4892b94a1990ab08a926",
+ "b8af0294819e4280ad41fa1c11006adf",
+ "c7530d63b2f745e799713284abacbd2c",
+ "12a1e302a69543c5bc0e0a66be008ca0",
+ "9c372e9e9b20433faed8530ca0f4424c",
+ "b07f26a21325493cac19113f1aa1ee96",
+ "fbdf6c544fb54294903524a69384e773",
+ "6c6f2223243b4a7485aef7fbbfe07668",
+ "a93509d61ac94628a74bc0f98c0eec06",
+ "3a8de0eb7db44647a734590b6b351b44",
+ "64d8affd2e854a1c9043fec7ca8a2796"
+ ]
+ },
+ "id": "2ed5ac74",
+ "outputId": "18ea15ac-ed8d-4d80-b166-706681ee49ab"
+ },
+ "outputs": [
+ {
+ "data": {
+ "application/vnd.jupyter.widget-view+json": {
+ "model_id": "0cecb897c86c4892b94a1990ab08a926",
+ "version_major": 2,
+ "version_minor": 0
+ },
+ "text/plain": [
+ "Downloading model.safetensors: 0%| | 0.00/1.42G [00:00 use the model max length (it's actually the default)\n",
+ " outputs = tokenizer(examples[\"sentence1\"], examples[\"sentence2\"], truncation=True, max_length=None)\n",
+ " return outputs"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 5,
+ "id": "cf5ef289-f42f-4582-bd5e-9852ad8beff2",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "tokenized_datasets = datasets.map(\n",
+ " tokenize_function,\n",
+ " batched=True,\n",
+ " remove_columns=[\"idx\", \"sentence1\", \"sentence2\"],\n",
+ ")\n",
+ "\n",
+ "# We also rename the 'label' column to 'labels' which is the expected name for labels by the models of the\n",
+ "# transformers library\n",
+ "tokenized_datasets = tokenized_datasets.rename_column(\"label\", \"labels\")"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 6,
+ "id": "739b3655-9db0-48bc-8542-308c6d5e0b8b",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "def collate_fn(examples):\n",
+ " return tokenizer.pad(examples, padding=\"longest\", return_tensors=\"pt\")"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 7,
+ "id": "0288f311-8475-4a0e-99af-e4b909d10e01",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "# Instantiate dataloaders.\n",
+ "train_dataloader = DataLoader(\n",
+ " tokenized_datasets[\"train\"],\n",
+ " shuffle=True,\n",
+ " collate_fn=collate_fn,\n",
+ " batch_size=batch_size,\n",
+ ")\n",
+ "eval_dataloader = DataLoader(\n",
+ " tokenized_datasets[\"validation\"],\n",
+ " shuffle=False,\n",
+ " collate_fn=collate_fn,\n",
+ " batch_size=batch_size,\n",
+ ")"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "fcaf6f9e-c9d1-445a-9f08-18ef462f67ce",
+ "metadata": {},
+ "source": [
+ "## Model"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 8,
+ "id": "e5dfff56-ea80-4561-aeaf-43216bbb9af7",
+ "metadata": {
+ "scrolled": true
+ },
+ "outputs": [
+ {
+ "data": {
+ "application/vnd.jupyter.widget-view+json": {
+ "model_id": "2ac42f98e60d412496fe77ed7eb5c6df",
+ "version_major": 2,
+ "version_minor": 0
+ },
+ "text/plain": [
+ "Loading checkpoint shards: 0%| | 0/3 [00:00, weight=AffineQuantizedTensor(shape=torch.Size([2048, 2304]), block_size=(1, 2304), device=cuda:0, layout_type=PlainLayoutType(), layout_tensor_dtype=torch.int8, quant_min=None, quant_max=None)))\n",
+ " (lora_dropout): ModuleDict(\n",
+ " (default): Dropout(p=0.1, inplace=False)\n",
+ " )\n",
+ " (lora_A): ModuleDict(\n",
+ " (default): Linear(in_features=2304, out_features=16, bias=False)\n",
+ " )\n",
+ " (lora_B): ModuleDict(\n",
+ " (default): Linear(in_features=16, out_features=2048, bias=False)\n",
+ " )\n",
+ " (lora_embedding_A): ParameterDict()\n",
+ " (lora_embedding_B): ParameterDict()\n",
+ " (lora_magnitude_vector): ModuleDict()\n",
+ " )\n",
+ " (k_proj): Linear(in_features=2304, out_features=1024, weight=LinearActivationQuantizedTensor(activation=, weight=AffineQuantizedTensor(shape=torch.Size([1024, 2304]), block_size=(1, 2304), device=cuda:0, layout_type=PlainLayoutType(), layout_tensor_dtype=torch.int8, quant_min=None, quant_max=None)))\n",
+ " (v_proj): lora.TorchaoLoraLinear(\n",
+ " (base_layer): Linear(in_features=2304, out_features=1024, weight=LinearActivationQuantizedTensor(activation=, weight=AffineQuantizedTensor(shape=torch.Size([1024, 2304]), block_size=(1, 2304), device=cuda:0, layout_type=PlainLayoutType(), layout_tensor_dtype=torch.int8, quant_min=None, quant_max=None)))\n",
+ " (lora_dropout): ModuleDict(\n",
+ " (default): Dropout(p=0.1, inplace=False)\n",
+ " )\n",
+ " (lora_A): ModuleDict(\n",
+ " (default): Linear(in_features=2304, out_features=16, bias=False)\n",
+ " )\n",
+ " (lora_B): ModuleDict(\n",
+ " (default): Linear(in_features=16, out_features=1024, bias=False)\n",
+ " )\n",
+ " (lora_embedding_A): ParameterDict()\n",
+ " (lora_embedding_B): ParameterDict()\n",
+ " (lora_magnitude_vector): ModuleDict()\n",
+ " )\n",
+ " (o_proj): Linear(in_features=2048, out_features=2304, weight=LinearActivationQuantizedTensor(activation=, weight=AffineQuantizedTensor(shape=torch.Size([2304, 2048]), block_size=(1, 2048), device=cuda:0, layout_type=PlainLayoutType(), layout_tensor_dtype=torch.int8, quant_min=None, quant_max=None)))\n",
+ " (rotary_emb): Gemma2RotaryEmbedding()\n",
+ " )\n",
+ " (mlp): Gemma2MLP(\n",
+ " (gate_proj): Linear(in_features=2304, out_features=9216, weight=LinearActivationQuantizedTensor(activation=, weight=AffineQuantizedTensor(shape=torch.Size([9216, 2304]), block_size=(1, 2304), device=cuda:0, layout_type=PlainLayoutType(), layout_tensor_dtype=torch.int8, quant_min=None, quant_max=None)))\n",
+ " (up_proj): Linear(in_features=2304, out_features=9216, weight=LinearActivationQuantizedTensor(activation=, weight=AffineQuantizedTensor(shape=torch.Size([9216, 2304]), block_size=(1, 2304), device=cuda:0, layout_type=PlainLayoutType(), layout_tensor_dtype=torch.int8, quant_min=None, quant_max=None)))\n",
+ " (down_proj): Linear(in_features=9216, out_features=2304, weight=LinearActivationQuantizedTensor(activation=, weight=AffineQuantizedTensor(shape=torch.Size([2304, 9216]), block_size=(1, 9216), device=cuda:0, layout_type=PlainLayoutType(), layout_tensor_dtype=torch.int8, quant_min=None, quant_max=None)))\n",
+ " (act_fn): PytorchGELUTanh()\n",
+ " )\n",
+ " (input_layernorm): Gemma2RMSNorm((2304,), eps=1e-06)\n",
+ " (post_attention_layernorm): Gemma2RMSNorm((2304,), eps=1e-06)\n",
+ " (pre_feedforward_layernorm): Gemma2RMSNorm((2304,), eps=1e-06)\n",
+ " (post_feedforward_layernorm): Gemma2RMSNorm((2304,), eps=1e-06)\n",
+ " )\n",
+ " )\n",
+ " (norm): Gemma2RMSNorm((2304,), eps=1e-06)\n",
+ " )\n",
+ " (score): ModulesToSaveWrapper(\n",
+ " (original_module): Linear(in_features=2304, out_features=2, bias=False)\n",
+ " (modules_to_save): ModuleDict(\n",
+ " (default): Linear(in_features=2304, out_features=2, bias=False)\n",
+ " )\n",
+ " )\n",
+ " )\n",
+ " )\n",
+ ")"
+ ]
+ },
+ "execution_count": 12,
+ "metadata": {},
+ "output_type": "execute_result"
+ }
+ ],
+ "source": [
+ "model.config.use_cache = False\n",
+ "model.to(device)"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 13,
+ "id": "fa0e73be",
+ "metadata": {},
+ "outputs": [
+ {
+ "name": "stderr",
+ "output_type": "stream",
+ "text": [
+ " 0%| | 0/230 [00:00 use the model max length (it's actually the default)\n",
+ " outputs = tokenizer(examples[\"sentence1\"], examples[\"sentence2\"], truncation=True, max_length=None)\n",
+ " return outputs"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 5,
+ "id": "cf5ef289-f42f-4582-bd5e-9852ad8beff2",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "tokenized_datasets = datasets.map(\n",
+ " tokenize_function,\n",
+ " batched=True,\n",
+ " remove_columns=[\"idx\", \"sentence1\", \"sentence2\"],\n",
+ ")\n",
+ "\n",
+ "# We also rename the 'label' column to 'labels' which is the expected name for labels by the models of the\n",
+ "# transformers library\n",
+ "tokenized_datasets = tokenized_datasets.rename_column(\"label\", \"labels\")"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 6,
+ "id": "739b3655-9db0-48bc-8542-308c6d5e0b8b",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "def collate_fn(examples):\n",
+ " return tokenizer.pad(examples, padding=\"longest\", return_tensors=\"pt\")"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 7,
+ "id": "0288f311-8475-4a0e-99af-e4b909d10e01",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "# Instantiate dataloaders.\n",
+ "train_dataloader = DataLoader(\n",
+ " tokenized_datasets[\"train\"],\n",
+ " shuffle=True,\n",
+ " collate_fn=collate_fn,\n",
+ " batch_size=batch_size,\n",
+ ")\n",
+ "eval_dataloader = DataLoader(\n",
+ " tokenized_datasets[\"validation\"],\n",
+ " shuffle=False,\n",
+ " collate_fn=collate_fn,\n",
+ " batch_size=batch_size,\n",
+ ")"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "fcaf6f9e-c9d1-445a-9f08-18ef462f67ce",
+ "metadata": {},
+ "source": [
+ "## Model"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 8,
+ "id": "e5dfff56-ea80-4561-aeaf-43216bbb9af7",
+ "metadata": {
+ "scrolled": true
+ },
+ "outputs": [
+ {
+ "data": {
+ "application/vnd.jupyter.widget-view+json": {
+ "model_id": "512d9dc10a4d4ecc88b9440575b0973a",
+ "version_major": 2,
+ "version_minor": 0
+ },
+ "text/plain": [
+ "Loading checkpoint shards: 0%| | 0/3 [00:00 use the model max length (it's actually the default)\n",
+ " outputs = tokenizer(examples[\"sentence1\"], examples[\"sentence2\"], truncation=True, max_length=None)\n",
+ " return outputs\n",
+ "\n",
+ "\n",
+ "tokenized_datasets = datasets.map(\n",
+ " tokenize_function,\n",
+ " batched=True,\n",
+ " remove_columns=[\"idx\", \"sentence1\", \"sentence2\"],\n",
+ ")\n",
+ "\n",
+ "# We also rename the 'label' column to 'labels' which is the expected name for labels by the models of the\n",
+ "# transformers library\n",
+ "tokenized_datasets = tokenized_datasets.rename_column(\"label\", \"labels\")\n",
+ "\n",
+ "\n",
+ "def collate_fn(examples):\n",
+ " return tokenizer.pad(examples, padding=\"longest\", return_tensors=\"pt\")\n",
+ "\n",
+ "\n",
+ "# Instantiate dataloaders.\n",
+ "train_dataloader = DataLoader(tokenized_datasets[\"train\"], shuffle=True, collate_fn=collate_fn, batch_size=batch_size)\n",
+ "eval_dataloader = DataLoader(\n",
+ " tokenized_datasets[\"validation\"], shuffle=False, collate_fn=collate_fn, batch_size=batch_size\n",
+ ")"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "id": "2ed5ac74",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "model = AutoModelForSequenceClassification.from_pretrained(model_name_or_path, return_dict=True)\n",
+ "model = get_peft_model(model, peft_config)\n",
+ "model.print_trainable_parameters()\n",
+ "model"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 6,
+ "id": "0d2d0381",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "optimizer = AdamW(params=model.parameters(), lr=lr)\n",
+ "\n",
+ "# Instantiate scheduler\n",
+ "lr_scheduler = get_linear_schedule_with_warmup(\n",
+ " optimizer=optimizer,\n",
+ " num_warmup_steps=0.06 * (len(train_dataloader) * num_epochs),\n",
+ " num_training_steps=(len(train_dataloader) * num_epochs),\n",
+ ")"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 7,
+ "id": "fa0e73be",
+ "metadata": {},
+ "outputs": [
+ {
+ "name": "stderr",
+ "output_type": "stream",
+ "text": [
+ " 0%| | 0/115 [00:00 use the model max length (it's actually the default)\n",
+ " outputs = tokenizer(examples[\"sentence1\"], examples[\"sentence2\"], truncation=True, max_length=None)\n",
+ " return outputs\n",
+ "\n",
+ "\n",
+ "tokenized_datasets = datasets.map(\n",
+ " tokenize_function,\n",
+ " batched=True,\n",
+ " remove_columns=[\"idx\", \"sentence1\", \"sentence2\"],\n",
+ ")\n",
+ "\n",
+ "# We also rename the 'label' column to 'labels' which is the expected name for labels by the models of the\n",
+ "# transformers library\n",
+ "tokenized_datasets = tokenized_datasets.rename_column(\"label\", \"labels\")\n",
+ "\n",
+ "\n",
+ "def collate_fn(examples):\n",
+ " return tokenizer.pad(examples, padding=\"longest\", return_tensors=\"pt\")\n",
+ "\n",
+ "\n",
+ "# Instantiate dataloaders.\n",
+ "train_dataloader = DataLoader(tokenized_datasets[\"train\"], shuffle=True, collate_fn=collate_fn, batch_size=batch_size)\n",
+ "eval_dataloader = DataLoader(\n",
+ " tokenized_datasets[\"validation\"], shuffle=False, collate_fn=collate_fn, batch_size=batch_size\n",
+ ")"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "id": "f6bc8144",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "model = AutoModelForSequenceClassification.from_pretrained(model_name_or_path, return_dict=True)\n",
+ "model = get_peft_model(model, peft_config)\n",
+ "model.print_trainable_parameters()\n",
+ "model"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 6,
+ "id": "af41c571",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "optimizer = AdamW(params=model.parameters(), lr=lr)\n",
+ "\n",
+ "# Instantiate scheduler\n",
+ "lr_scheduler = get_linear_schedule_with_warmup(\n",
+ " optimizer=optimizer,\n",
+ " num_warmup_steps=0, # 0.06*(len(train_dataloader) * num_epochs),\n",
+ " num_training_steps=(len(train_dataloader) * num_epochs),\n",
+ ")"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 7,
+ "id": "90993c93",
+ "metadata": {},
+ "outputs": [
+ {
+ "name": "stderr",
+ "output_type": "stream",
+ "text": [
+ " 0%| | 0/115 [00:00 use the model max length (it's actually the default)\n",
+ " outputs = tokenizer(examples[\"sentence1\"], examples[\"sentence2\"], truncation=True, max_length=None)\n",
+ " return outputs\n",
+ "\n",
+ "\n",
+ "tokenized_datasets = datasets.map(\n",
+ " tokenize_function,\n",
+ " batched=True,\n",
+ " remove_columns=[\"idx\", \"sentence1\", \"sentence2\"],\n",
+ ")\n",
+ "\n",
+ "# We also rename the 'label' column to 'labels' which is the expected name for labels by the models of the\n",
+ "# transformers library\n",
+ "tokenized_datasets = tokenized_datasets.rename_column(\"label\", \"labels\")\n",
+ "\n",
+ "\n",
+ "def collate_fn(examples):\n",
+ " return tokenizer.pad(examples, padding=\"longest\", return_tensors=\"pt\")\n",
+ "\n",
+ "\n",
+ "# Instantiate dataloaders.\n",
+ "train_dataloader = DataLoader(tokenized_datasets[\"train\"], shuffle=True, collate_fn=collate_fn, batch_size=batch_size)\n",
+ "eval_dataloader = DataLoader(\n",
+ " tokenized_datasets[\"validation\"], shuffle=False, collate_fn=collate_fn, batch_size=batch_size\n",
+ ")"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "id": "a3c15af0",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "model = AutoModelForSequenceClassification.from_pretrained(model_name_or_path, return_dict=True)\n",
+ "model = get_peft_model(model, peft_config)\n",
+ "model.print_trainable_parameters()\n",
+ "model"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 6,
+ "id": "6d3c5edb",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "optimizer = AdamW(params=model.parameters(), lr=lr)\n",
+ "\n",
+ "# Instantiate scheduler\n",
+ "lr_scheduler = get_linear_schedule_with_warmup(\n",
+ " optimizer=optimizer,\n",
+ " num_warmup_steps=0.06 * (len(train_dataloader) * num_epochs),\n",
+ " num_training_steps=(len(train_dataloader) * num_epochs),\n",
+ ")"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 7,
+ "id": "4d279225",
+ "metadata": {},
+ "outputs": [
+ {
+ "name": "stderr",
+ "output_type": "stream",
+ "text": [
+ " 0%| | 0/115 [00:00"
+ ]
+ },
+ "execution_count": 2,
+ "metadata": {},
+ "output_type": "execute_result"
+ }
+ ],
+ "source": [
+ "batch_size = 32\n",
+ "model_name_or_path = \"roberta-large\"\n",
+ "task = \"mrpc\"\n",
+ "peft_type = PeftType.VBLORA\n",
+ "device = torch.accelerator.current_accelerator().type if hasattr(torch, \"accelerator\") else \"cuda\"\n",
+ "num_epochs = 20\n",
+ "rank = 4\n",
+ "max_length = 128\n",
+ "num_vectors = 90\n",
+ "vector_length = 256\n",
+ "torch.manual_seed(0)"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 3,
+ "id": "0526f571",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "peft_config = VBLoRAConfig(\n",
+ " task_type=\"SEQ_CLS\", \n",
+ " r=rank,\n",
+ " topk=2,\n",
+ " target_modules=['key', 'value', 'query', 'output.dense', 'intermediate.dense'],\n",
+ " num_vectors=num_vectors,\n",
+ " vector_length=vector_length,\n",
+ " save_only_topk_weights=True, # Set to True to reduce storage space. Note that the saved parameters cannot be used to resume training from checkpoints.\n",
+ " vblora_dropout=0.,\n",
+ ")\n",
+ "head_lr = 4e-3\n",
+ "vector_bank_lr = 1e-3\n",
+ "logits_lr = 1e-2"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "c075c5d2-a457-4f37-a7f1-94fd0d277972",
+ "metadata": {},
+ "source": [
+ "## Loading data"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 4,
+ "id": "7bb52cb4-d1c3-4b04-8bf0-f39ca88af139",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "if any(k in model_name_or_path for k in (\"gpt\", \"opt\", \"bloom\")):\n",
+ " padding_side = \"left\"\n",
+ "else:\n",
+ " padding_side = \"right\"\n",
+ "\n",
+ "tokenizer = AutoTokenizer.from_pretrained(model_name_or_path, padding_side=padding_side)\n",
+ "if getattr(tokenizer, \"pad_token_id\") is None:\n",
+ " tokenizer.pad_token_id = tokenizer.eos_token_id"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 5,
+ "id": "e69c5e1f-d27b-4264-a41e-fc9b99d025e6",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "datasets = load_dataset(\"glue\", task)\n",
+ "metric = evaluate.load(\"glue\", task)"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 6,
+ "id": "0209f778-c93b-40eb-a4e0-24c25db03980",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "def tokenize_function(examples):\n",
+ " # max_length=None => use the model max length (it's actually the default)\n",
+ " outputs = tokenizer(examples[\"sentence1\"], examples[\"sentence2\"], truncation=True, max_length=max_length)\n",
+ " return outputs\n",
+ "\n",
+ "\n",
+ "tokenized_datasets = datasets.map(\n",
+ " tokenize_function,\n",
+ " batched=True,\n",
+ " remove_columns=[\"idx\", \"sentence1\", \"sentence2\"],\n",
+ ")\n",
+ "\n",
+ "# We also rename the 'label' column to 'labels' which is the expected name for labels by the models of the\n",
+ "# transformers library\n",
+ "tokenized_datasets = tokenized_datasets.rename_column(\"label\", \"labels\")"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 7,
+ "id": "7453954e-982c-46f0-b09c-589776e6d6cb",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "def collate_fn(examples):\n",
+ " return tokenizer.pad(examples, padding=\"longest\", return_tensors=\"pt\")\n",
+ "\n",
+ "\n",
+ "# Instantiate dataloaders.\n",
+ "train_dataloader = DataLoader(tokenized_datasets[\"train\"], shuffle=True, collate_fn=collate_fn, batch_size=batch_size)\n",
+ "eval_dataloader = DataLoader(\n",
+ " tokenized_datasets[\"validation\"], shuffle=False, collate_fn=collate_fn, batch_size=batch_size\n",
+ ")"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "f3b9b2e8-f415-4d0f-9fb4-436f1a3585ea",
+ "metadata": {},
+ "source": [
+ "## Preparing the VB-LoRA model"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 8,
+ "id": "2ed5ac74",
+ "metadata": {},
+ "outputs": [
+ {
+ "name": "stderr",
+ "output_type": "stream",
+ "text": [
+ "Some weights of RobertaForSequenceClassification were not initialized from the model checkpoint at roberta-large and are newly initialized: ['classifier.dense.bias', 'classifier.dense.weight', 'classifier.out_proj.bias', 'classifier.out_proj.weight']\n",
+ "You should probably TRAIN this model on a down-stream task to be able to use it for predictions and inference.\n"
+ ]
+ },
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "trainable params: 1,696,770 || all params: 357,058,564 || trainable%: 0.4752\n",
+ "VB-LoRA params to-be-saved (float32-equivalent): 33,408 || total params to-be-saved: 1,085,058\n"
+ ]
+ }
+ ],
+ "source": [
+ "model = AutoModelForSequenceClassification.from_pretrained(model_name_or_path, return_dict=True, max_length=None)\n",
+ "model = get_peft_model(model, peft_config)\n",
+ "model.print_trainable_parameters()\n",
+ "model.print_savable_parameters()"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 9,
+ "id": "0d2d0381",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "\n",
+ "from transformers.pytorch_utils import ALL_LAYERNORM_LAYERS\n",
+ "from transformers.trainer_pt_utils import get_parameter_names\n",
+ "\n",
+ "decay_parameters = get_parameter_names(model, ALL_LAYERNORM_LAYERS)\n",
+ "decay_parameters = [name for name in decay_parameters if \"bias\" not in name]\n",
+ "vector_bank_parameters = [name for name, _ in model.named_parameters() if \"vector_bank\" in name]\n",
+ "logits_parameters = [name for name, _ in model.named_parameters() if \"logits\" in name ]\n",
+ "\n",
+ "optimizer_grouped_parameters = [\n",
+ " {\n",
+ " \"params\": [p for n, p in model.named_parameters() if n in decay_parameters and \\\n",
+ " n not in logits_parameters and n not in vector_bank_parameters],\n",
+ " \"weight_decay\": 0.1,\n",
+ " \"lr\": head_lr,\n",
+ " },\n",
+ " {\n",
+ " \"params\": [p for n, p in model.named_parameters() if n not in decay_parameters and \\\n",
+ " n not in logits_parameters and n not in vector_bank_parameters],\n",
+ " \"weight_decay\": 0.0,\n",
+ " \"lr\": head_lr,\n",
+ " },\n",
+ " {\n",
+ " \"params\": [p for n, p in model.named_parameters() if n in vector_bank_parameters],\n",
+ " \"lr\": vector_bank_lr,\n",
+ " \"weight_decay\": 0.0,\n",
+ " },\n",
+ " {\n",
+ " \"params\": [p for n, p in model.named_parameters() if n in logits_parameters],\n",
+ " \"lr\": logits_lr,\n",
+ " \"weight_decay\": 0.0,\n",
+ " },\n",
+ "]\n",
+ "\n",
+ "optimizer = AdamW(optimizer_grouped_parameters)\n",
+ "lr_scheduler = get_linear_schedule_with_warmup(\n",
+ " optimizer=optimizer,\n",
+ " num_warmup_steps=0.06 * (len(train_dataloader) * num_epochs),\n",
+ " num_training_steps=(len(train_dataloader) * num_epochs),\n",
+ ")"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "c0dd5aa8-977b-4ac0-8b96-884b17bcdd00",
+ "metadata": {},
+ "source": [
+ "## Training"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 10,
+ "id": "fa0e73be",
+ "metadata": {},
+ "outputs": [
+ {
+ "name": "stderr",
+ "output_type": "stream",
+ "text": [
+ " 0%| | 0/115 [00:00"
+ ]
+ },
+ "execution_count": 2,
+ "metadata": {},
+ "output_type": "execute_result"
+ }
+ ],
+ "source": [
+ "batch_size = 128\n",
+ "model_name_or_path = \"roberta-base\"\n",
+ "task = \"mrpc\"\n",
+ "peft_type = PeftType.VERA\n",
+ "device = torch.accelerator.current_accelerator().type if hasattr(torch, \"accelerator\") else \"cuda\"\n",
+ "num_epochs = 5 # for best results, increase this number\n",
+ "rank = 8 # for best results, increase this number\n",
+ "max_length = 128\n",
+ "torch.manual_seed(0)"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 3,
+ "id": "0526f571",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "peft_config = VeraConfig(\n",
+ " task_type=\"SEQ_CLS\", \n",
+ " r=rank,\n",
+ " d_initial=0.1,\n",
+ " target_modules=[\"query\", \"value\", \"intermediate.dense\"],\n",
+ " save_projection=True,\n",
+ ")\n",
+ "head_lr = 1e-2\n",
+ "vera_lr = 2e-2"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "c075c5d2-a457-4f37-a7f1-94fd0d277972",
+ "metadata": {},
+ "source": [
+ "## Loading data"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 4,
+ "id": "7bb52cb4-d1c3-4b04-8bf0-f39ca88af139",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "if any(k in model_name_or_path for k in (\"gpt\", \"opt\", \"bloom\")):\n",
+ " padding_side = \"left\"\n",
+ "else:\n",
+ " padding_side = \"right\"\n",
+ "\n",
+ "tokenizer = AutoTokenizer.from_pretrained(model_name_or_path, padding_side=padding_side)\n",
+ "if getattr(tokenizer, \"pad_token_id\") is None:\n",
+ " tokenizer.pad_token_id = tokenizer.eos_token_id"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 5,
+ "id": "e69c5e1f-d27b-4264-a41e-fc9b99d025e6",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "datasets = load_dataset(\"glue\", task)\n",
+ "metric = evaluate.load(\"glue\", task)"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 6,
+ "id": "0209f778-c93b-40eb-a4e0-24c25db03980",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "def tokenize_function(examples):\n",
+ " # max_length=None => use the model max length (it's actually the default)\n",
+ " outputs = tokenizer(examples[\"sentence1\"], examples[\"sentence2\"], truncation=True, max_length=max_length)\n",
+ " return outputs\n",
+ "\n",
+ "\n",
+ "tokenized_datasets = datasets.map(\n",
+ " tokenize_function,\n",
+ " batched=True,\n",
+ " remove_columns=[\"idx\", \"sentence1\", \"sentence2\"],\n",
+ ")\n",
+ "\n",
+ "# We also rename the 'label' column to 'labels' which is the expected name for labels by the models of the\n",
+ "# transformers library\n",
+ "tokenized_datasets = tokenized_datasets.rename_column(\"label\", \"labels\")"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 7,
+ "id": "7453954e-982c-46f0-b09c-589776e6d6cb",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "def collate_fn(examples):\n",
+ " return tokenizer.pad(examples, padding=\"longest\", return_tensors=\"pt\")\n",
+ "\n",
+ "\n",
+ "# Instantiate dataloaders.\n",
+ "train_dataloader = DataLoader(tokenized_datasets[\"train\"], shuffle=True, collate_fn=collate_fn, batch_size=batch_size)\n",
+ "eval_dataloader = DataLoader(\n",
+ " tokenized_datasets[\"validation\"], shuffle=False, collate_fn=collate_fn, batch_size=batch_size\n",
+ ")"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "f3b9b2e8-f415-4d0f-9fb4-436f1a3585ea",
+ "metadata": {},
+ "source": [
+ "## Preparing the VeRA model"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 8,
+ "id": "2ed5ac74",
+ "metadata": {},
+ "outputs": [
+ {
+ "name": "stderr",
+ "output_type": "stream",
+ "text": [
+ "Some weights of RobertaForSequenceClassification were not initialized from the model checkpoint at roberta-base and are newly initialized: ['classifier.dense.bias', 'classifier.dense.weight', 'classifier.out_proj.bias', 'classifier.out_proj.weight']\n",
+ "You should probably TRAIN this model on a down-stream task to be able to use it for predictions and inference.\n"
+ ]
+ },
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "trainable params: 647,714 || all params: 125,294,884 || trainable%: 0.5170\n"
+ ]
+ }
+ ],
+ "source": [
+ "model = AutoModelForSequenceClassification.from_pretrained(model_name_or_path, return_dict=True, max_length=None)\n",
+ "model = get_peft_model(model, peft_config)\n",
+ "model.print_trainable_parameters()"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 9,
+ "id": "0d2d0381",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "optimizer = AdamW(\n",
+ " [\n",
+ " {\"params\": [p for n, p in model.named_parameters() if \"vera_lambda_\" in n], \"lr\": vera_lr},\n",
+ " {\"params\": [p for n, p in model.named_parameters() if \"classifier\" in n], \"lr\": head_lr},\n",
+ " ]\n",
+ ")\n",
+ "\n",
+ "# Instantiate scheduler\n",
+ "lr_scheduler = get_linear_schedule_with_warmup(\n",
+ " optimizer=optimizer,\n",
+ " num_warmup_steps=0.06 * (len(train_dataloader) * num_epochs),\n",
+ " num_training_steps=(len(train_dataloader) * num_epochs),\n",
+ ")"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "id": "c0dd5aa8-977b-4ac0-8b96-884b17bcdd00",
+ "metadata": {},
+ "source": [
+ "## Training"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 10,
+ "id": "fa0e73be",
+ "metadata": {},
+ "outputs": [
+ {
+ "name": "stderr",
+ "output_type": "stream",
+ "text": [
+ " 0%| | 0/29 [00:00 use the model max length (it's actually the default)
+ outputs = tokenizer(examples["sentence1"], examples["sentence2"], truncation=True, max_length=None)
+ return outputs
+
+ def collate_fn(examples):
+ return tokenizer.pad(examples, padding="longest", return_tensors="pt")
+
+ with accelerator.main_process_first():
+ tokenized_datasets = datasets.map(
+ tokenize_function,
+ batched=True,
+ remove_columns=["idx", "sentence1", "sentence2"],
+ )
+
+ # We also rename the 'label' column to 'labels' which is the expected name for labels by the models of the
+ # transformers library
+ tokenized_datasets = tokenized_datasets.rename_column("label", "labels")
+
+ # Instantiate dataloaders.
+ train_dataloader = DataLoader(
+ tokenized_datasets["train"], shuffle=True, collate_fn=collate_fn, batch_size=args.per_device_train_batch_size
+ )
+ eval_dataloader = DataLoader(
+ tokenized_datasets["validation"],
+ shuffle=False,
+ collate_fn=collate_fn,
+ batch_size=args.per_device_eval_batch_size,
+ )
+
+ model = AutoModelForSequenceClassification.from_pretrained(args.model_name_or_path)
+ model = get_peft_model(model, peft_config)
+ model.print_trainable_parameters()
+
+ if getattr(accelerator.state, "fsdp_plugin", None) is not None:
+ accelerator.state.fsdp_plugin.auto_wrap_policy = fsdp_auto_wrap_policy(model)
+ model = accelerator.prepare(model)
+
+ optimizer = AdamW(params=model.parameters(), lr=args.learning_rate)
+
+ # Instantiate scheduler
+ lr_scheduler = get_linear_schedule_with_warmup(
+ optimizer=optimizer,
+ num_warmup_steps=args.num_warmup_steps,
+ num_training_steps=(len(train_dataloader) * args.num_train_epochs),
+ )
+
+ if getattr(accelerator.state, "fsdp_plugin", None) is not None:
+ train_dataloader, eval_dataloader, optimizer, lr_scheduler = accelerator.prepare(
+ train_dataloader, eval_dataloader, optimizer, lr_scheduler
+ )
+ else:
+ model, train_dataloader, eval_dataloader, optimizer, lr_scheduler = accelerator.prepare(
+ model, train_dataloader, eval_dataloader, optimizer, lr_scheduler
+ )
+
+ for epoch in range(args.num_train_epochs):
+ model.train()
+ for step, batch in enumerate(tqdm(train_dataloader)):
+ outputs = model(**batch)
+ loss = outputs.loss
+ accelerator.backward(loss)
+ optimizer.step()
+ lr_scheduler.step()
+ optimizer.zero_grad()
+
+ model.eval()
+ samples_seen = 0
+ for step, batch in enumerate(tqdm(eval_dataloader)):
+ with torch.no_grad():
+ outputs = model(**batch)
+ predictions = outputs.logits.argmax(dim=-1)
+ predictions, references = accelerator.gather((predictions, batch["labels"]))
+ # If we are in a multiprocess environment, the last batch has duplicates
+ if accelerator.num_processes > 1:
+ if step == len(eval_dataloader) - 1:
+ predictions = predictions[: len(eval_dataloader.dataset) - samples_seen]
+ references = references[: len(eval_dataloader.dataset) - samples_seen]
+ else:
+ samples_seen += references.shape[0]
+ metric.add_batch(
+ predictions=predictions,
+ references=references,
+ )
+ eval_metric = metric.compute()
+ accelerator.print(f"epoch {epoch}:", eval_metric)
+
+ accelerator.wait_for_everyone()
+ unwrapped_model = accelerator.unwrap_model(model)
+ unwrapped_model.save_pretrained(args.output_dir, state_dict=accelerator.get_state_dict(model))
+ if accelerator.is_main_process:
+ tokenizer.save_pretrained(args.output_dir)
+
+
+if __name__ == "__main__":
+ main()
diff --git a/peft/examples/sequence_classification/prefix_tuning.ipynb b/peft/examples/sequence_classification/prefix_tuning.ipynb
new file mode 100644
index 0000000000000000000000000000000000000000..bd2fc1fa1b29a795e93662124cfd3412b1c51d66
--- /dev/null
+++ b/peft/examples/sequence_classification/prefix_tuning.ipynb
@@ -0,0 +1,710 @@
+{
+ "cells": [
+ {
+ "cell_type": "code",
+ "execution_count": 1,
+ "id": "a825ba6b",
+ "metadata": {},
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "\n",
+ "===================================BUG REPORT===================================\n",
+ "Welcome to bitsandbytes. For bug reports, please submit your error trace to: https://github.com/TimDettmers/bitsandbytes/issues\n",
+ "For effortless bug reporting copy-paste your error into this form: https://docs.google.com/forms/d/e/1FAIpQLScPB8emS3Thkp66nvqwmjTEgxp8Y9ufuWTzFyr9kJ5AoI47dQ/viewform?usp=sf_link\n",
+ "================================================================================\n",
+ "CUDA SETUP: CUDA runtime path found: /home/sourab/miniconda3/envs/ml/lib/libcudart.so\n",
+ "CUDA SETUP: Highest compute capability among GPUs detected: 7.5\n",
+ "CUDA SETUP: Detected CUDA version 117\n",
+ "CUDA SETUP: Loading binary /home/sourab/miniconda3/envs/ml/lib/python3.10/site-packages/bitsandbytes/libbitsandbytes_cuda117.so...\n"
+ ]
+ }
+ ],
+ "source": [
+ "import argparse\n",
+ "import os\n",
+ "\n",
+ "import torch\n",
+ "from torch.optim import AdamW\n",
+ "from torch.utils.data import DataLoader\n",
+ "from peft import (\n",
+ " get_peft_config,\n",
+ " get_peft_model,\n",
+ " get_peft_model_state_dict,\n",
+ " set_peft_model_state_dict,\n",
+ " PeftType,\n",
+ " PrefixTuningConfig,\n",
+ " PromptEncoderConfig,\n",
+ ")\n",
+ "\n",
+ "import evaluate\n",
+ "from datasets import load_dataset\n",
+ "from transformers import AutoModelForSequenceClassification, AutoTokenizer, get_linear_schedule_with_warmup, set_seed\n",
+ "from tqdm import tqdm"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "id": "2bd7cbb2",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "batch_size = 32\n",
+ "model_name_or_path = \"roberta-large\"\n",
+ "task = \"mrpc\"\n",
+ "peft_type = PeftType.PREFIX_TUNING\n",
+ "device = torch.accelerator.current_accelerator().type if hasattr(torch, \"accelerator\") else \"cuda\"\n",
+ "num_epochs = 20"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 3,
+ "id": "33d9b62e",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "peft_config = PrefixTuningConfig(task_type=\"SEQ_CLS\", num_virtual_tokens=20)\n",
+ "lr = 1e-2"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 4,
+ "id": "152b6177",
+ "metadata": {},
+ "outputs": [
+ {
+ "name": "stderr",
+ "output_type": "stream",
+ "text": [
+ "Found cached dataset glue (/home/sourab/.cache/huggingface/datasets/glue/mrpc/1.0.0/dacbe3125aa31d7f70367a07a8a9e72a5a0bfeb5fc42e75c9db75b96da6053ad)\n"
+ ]
+ },
+ {
+ "data": {
+ "application/vnd.jupyter.widget-view+json": {
+ "model_id": "be1eddbb9a7d4e6dae32fd026e167f96",
+ "version_major": 2,
+ "version_minor": 0
+ },
+ "text/plain": [
+ " 0%| | 0/3 [00:00 use the model max length (it's actually the default)\n",
+ " outputs = tokenizer(examples[\"sentence1\"], examples[\"sentence2\"], truncation=True, max_length=None)\n",
+ " return outputs\n",
+ "\n",
+ "\n",
+ "tokenized_datasets = datasets.map(\n",
+ " tokenize_function,\n",
+ " batched=True,\n",
+ " remove_columns=[\"idx\", \"sentence1\", \"sentence2\"],\n",
+ ")\n",
+ "\n",
+ "# We also rename the 'label' column to 'labels' which is the expected name for labels by the models of the\n",
+ "# transformers library\n",
+ "tokenized_datasets = tokenized_datasets.rename_column(\"label\", \"labels\")\n",
+ "\n",
+ "\n",
+ "def collate_fn(examples):\n",
+ " return tokenizer.pad(examples, padding=\"longest\", return_tensors=\"pt\")\n",
+ "\n",
+ "\n",
+ "# Instantiate dataloaders.\n",
+ "train_dataloader = DataLoader(tokenized_datasets[\"train\"], shuffle=True, collate_fn=collate_fn, batch_size=batch_size)\n",
+ "eval_dataloader = DataLoader(\n",
+ " tokenized_datasets[\"validation\"], shuffle=False, collate_fn=collate_fn, batch_size=batch_size\n",
+ ")"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "id": "f6bc8144",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "model = AutoModelForSequenceClassification.from_pretrained(model_name_or_path, return_dict=True)\n",
+ "model = get_peft_model(model, peft_config)\n",
+ "model.print_trainable_parameters()\n",
+ "model"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 6,
+ "id": "af41c571",
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "optimizer = AdamW(params=model.parameters(), lr=lr)\n",
+ "\n",
+ "# Instantiate scheduler\n",
+ "lr_scheduler = get_linear_schedule_with_warmup(\n",
+ " optimizer=optimizer,\n",
+ " num_warmup_steps=0.06 * (len(train_dataloader) * num_epochs),\n",
+ " num_training_steps=(len(train_dataloader) * num_epochs),\n",
+ ")"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 7,
+ "id": "90993c93",
+ "metadata": {},
+ "outputs": [
+ {
+ "name": "stderr",
+ "output_type": "stream",
+ "text": [
+ " 0%| | 0/115 [00:00
+  +
+Optimization in Unsloth to speed up QLoRA finetuning while reducing GPU memory usage
+
+## Multi-GPU SFT with QLoRA
+To speed up QLoRA finetuning when you have access to multiple GPUs, look at the launch command at [run_peft_multigpu.sh](https://github.com/huggingface/peft/blob/main/examples/sft/run_peft_multigpu.sh). This example to performs DDP on 8 GPUs.
+
+Note:
+1. At present, `use_reentrant` needs to be `False` when using gradient checkpointing with Multi-GPU QLoRA else it will lead to errors. However, this leads to huge GPU memory consumption.
+
+## Multi-GPU SFT with LoRA and DeepSpeed
+When you have access to multiple GPUs, it would be better to use normal LoRA with DeepSpeed/FSDP. To use LoRA with DeepSpeed, refer to the docs at [PEFT with DeepSpeed](https://huggingface.co/docs/peft/accelerate/deepspeed).
+
+
+## Multi-GPU SFT with LoRA and FSDP
+When you have access to multiple GPUs, it would be better to use normal LoRA with DeepSpeed/FSDP. To use LoRA with FSDP, refer to the docs at [PEFT with FSDP](https://huggingface.co/docs/peft/accelerate/fsdp).
+
+
+## Multi-GPU SFT with LoRA and FSDP for GPTQModel:
+As in [Multi-GPU SFT with LoRA and FSDP](https://github.com/huggingface/peft/blob/main/examples/sft/README.md#multi-gpu-sft-with-lora-and-fsdp), we also support other quantization methods like GPTQModel. You may need to install [GPTQModel](https://github.com/ModelCloud/GPTQModel) > v3.0.0 or from source. Here is the launch command for reference: [run_peft_fsdp_gptq.sh]. For the `--model_name_or_path` argument, it is important to pass a model that is already quantized with GPTQModel, like `"hugging-quants/Meta-Llama-3.1-8B-Instruct-GPTQ-INT4"`.
+
+Note: there is a bug in transformers v4.53.0 for this case, please skip this transformers version.
+
+## Tip
+
+Generally try to upgrade to the latest package versions for best results, especially when it comes to `bitsandbytes`, `accelerate`, `transformers`, `trl`, and `peft`.
diff --git a/peft/examples/sft/configs/deepspeed_config.yaml b/peft/examples/sft/configs/deepspeed_config.yaml
new file mode 100644
index 0000000000000000000000000000000000000000..56eef6e48b75727ede1d522b595b5ecde3a205a1
--- /dev/null
+++ b/peft/examples/sft/configs/deepspeed_config.yaml
@@ -0,0 +1,23 @@
+compute_environment: LOCAL_MACHINE
+debug: false
+deepspeed_config:
+ deepspeed_multinode_launcher: standard
+ gradient_accumulation_steps: 4
+ offload_optimizer_device: none
+ offload_param_device: none
+ zero3_init_flag: true
+ zero3_save_16bit_model: true
+ zero_stage: 3
+distributed_type: DEEPSPEED
+downcast_bf16: 'no'
+machine_rank: 0
+main_training_function: main
+mixed_precision: bf16
+num_machines: 1
+num_processes: 8
+rdzv_backend: static
+same_network: true
+tpu_env: []
+tpu_use_cluster: false
+tpu_use_sudo: false
+use_cpu: false
\ No newline at end of file
diff --git a/peft/examples/sft/configs/deepspeed_config_z3_qlora.yaml b/peft/examples/sft/configs/deepspeed_config_z3_qlora.yaml
new file mode 100644
index 0000000000000000000000000000000000000000..07dddcef7853b963ea64d20d39078893c4e21c33
--- /dev/null
+++ b/peft/examples/sft/configs/deepspeed_config_z3_qlora.yaml
@@ -0,0 +1,22 @@
+compute_environment: LOCAL_MACHINE
+debug: false
+deepspeed_config:
+ deepspeed_multinode_launcher: standard
+ offload_optimizer_device: none
+ offload_param_device: none
+ zero3_init_flag: true
+ zero3_save_16bit_model: true
+ zero_stage: 3
+distributed_type: DEEPSPEED
+downcast_bf16: 'no'
+machine_rank: 0
+main_training_function: main
+mixed_precision: bf16
+num_machines: 1
+num_processes: 2
+rdzv_backend: static
+same_network: true
+tpu_env: []
+tpu_use_cluster: false
+tpu_use_sudo: false
+use_cpu: false
\ No newline at end of file
diff --git a/peft/examples/sft/configs/fsdp_config.yaml b/peft/examples/sft/configs/fsdp_config.yaml
new file mode 100644
index 0000000000000000000000000000000000000000..7cccb74ca0dfa1a916b5057ceee561271c301ec5
--- /dev/null
+++ b/peft/examples/sft/configs/fsdp_config.yaml
@@ -0,0 +1,25 @@
+compute_environment: LOCAL_MACHINE
+debug: false
+distributed_type: FSDP
+downcast_bf16: 'no'
+fsdp_config:
+ fsdp_auto_wrap_policy: TRANSFORMER_BASED_WRAP
+ fsdp_backward_prefetch: BACKWARD_PRE
+ fsdp_cpu_ram_efficient_loading: true
+ fsdp_forward_prefetch: false
+ fsdp_offload_params: false
+ fsdp_sharding_strategy: FULL_SHARD
+ fsdp_state_dict_type: SHARDED_STATE_DICT
+ fsdp_sync_module_states: true
+ fsdp_use_orig_params: false
+machine_rank: 0
+main_training_function: main
+mixed_precision: bf16
+num_machines: 1
+num_processes: 8
+rdzv_backend: static
+same_network: true
+tpu_env: []
+tpu_use_cluster: false
+tpu_use_sudo: false
+use_cpu: false
\ No newline at end of file
diff --git a/peft/examples/sft/configs/fsdp_config_qlora.yaml b/peft/examples/sft/configs/fsdp_config_qlora.yaml
new file mode 100644
index 0000000000000000000000000000000000000000..f28a0f1046a735579045655dcdb9d3bf7c6ffdcc
--- /dev/null
+++ b/peft/examples/sft/configs/fsdp_config_qlora.yaml
@@ -0,0 +1,25 @@
+compute_environment: LOCAL_MACHINE
+debug: false
+distributed_type: FSDP
+downcast_bf16: 'no'
+fsdp_config:
+ fsdp_auto_wrap_policy: TRANSFORMER_BASED_WRAP
+ fsdp_backward_prefetch: BACKWARD_PRE
+ fsdp_cpu_ram_efficient_loading: true
+ fsdp_forward_prefetch: false
+ fsdp_offload_params: true
+ fsdp_sharding_strategy: FULL_SHARD
+ fsdp_state_dict_type: SHARDED_STATE_DICT
+ fsdp_sync_module_states: true
+ fsdp_use_orig_params: false
+machine_rank: 0
+main_training_function: main
+mixed_precision: 'no'
+num_machines: 1
+num_processes: 2
+rdzv_backend: static
+same_network: true
+tpu_env: []
+tpu_use_cluster: false
+tpu_use_sudo: false
+use_cpu: false
\ No newline at end of file
diff --git a/peft/examples/sft/requirements.txt b/peft/examples/sft/requirements.txt
new file mode 100644
index 0000000000000000000000000000000000000000..752b6976e62f4acff6193804c5422807bc5e8806
--- /dev/null
+++ b/peft/examples/sft/requirements.txt
@@ -0,0 +1,25 @@
+git+https://github.com/huggingface/transformers
+git+https://github.com/huggingface/accelerate
+git+https://github.com/huggingface/peft
+git+https://github.com/huggingface/trl
+git+https://github.com/huggingface/datatrove.git
+unsloth[conda]@git+https://github.com/unslothai/unsloth.git
+deepspeed
+PyGithub
+flash-attn
+huggingface-hub
+evaluate
+datasets
+bitsandbytes
+einops
+wandb
+tensorboard
+tiktoken
+pandas
+numpy
+scipy
+matplotlib
+sentencepiece
+nltk
+xformers
+hf_transfer
\ No newline at end of file
diff --git a/peft/examples/sft/requirements_colab.txt b/peft/examples/sft/requirements_colab.txt
new file mode 100644
index 0000000000000000000000000000000000000000..b8c375dc44bf85305fa53964537f4877210b10bd
--- /dev/null
+++ b/peft/examples/sft/requirements_colab.txt
@@ -0,0 +1,25 @@
+git+https://github.com/huggingface/transformers
+git+https://github.com/huggingface/accelerate
+git+https://github.com/huggingface/peft
+git+https://github.com/huggingface/trl
+unsloth[colab_ampere] @ git+https://github.com/unslothai/unsloth.git
+datasets
+deepspeed
+PyGithub
+flash-attn
+huggingface-hub
+evaluate
+bitsandbytes
+einops
+wandb
+tensorboard
+tiktoken
+pandas
+numpy
+scipy
+matplotlib
+sentencepiece
+nltk
+xformers
+git+https://github.com/huggingface/datatrove.git
+hf_transfer
\ No newline at end of file
diff --git a/peft/examples/sft/requirements_xpu.txt b/peft/examples/sft/requirements_xpu.txt
new file mode 100644
index 0000000000000000000000000000000000000000..9e5918b95180acbdc5789115ba0af71c8adf3aa5
--- /dev/null
+++ b/peft/examples/sft/requirements_xpu.txt
@@ -0,0 +1,22 @@
+git+https://github.com/huggingface/transformers
+git+https://github.com/huggingface/accelerate
+git+https://github.com/huggingface/peft
+git+https://github.com/huggingface/trl
+git+https://github.com/huggingface/datatrove.git
+deepspeed
+PyGithub
+huggingface-hub
+evaluate
+datasets
+bitsandbytes
+einops
+wandb
+tensorboard
+tiktoken
+pandas
+numpy
+scipy
+matplotlib
+sentencepiece
+nltk
+hf_transfer
\ No newline at end of file
diff --git a/peft/examples/sft/run_peft.sh b/peft/examples/sft/run_peft.sh
new file mode 100644
index 0000000000000000000000000000000000000000..8aa48648d34636eb07cd25c0abd91b943c00b49f
--- /dev/null
+++ b/peft/examples/sft/run_peft.sh
@@ -0,0 +1,41 @@
+python train.py \
+--seed 100 \
+--model_name_or_path "mistralai/Mistral-7B-v0.1" \
+--dataset_name "smangrul/ultrachat-10k-chatml" \
+--chat_template_format "chatml" \
+--add_special_tokens False \
+--append_concat_token False \
+--splits "train,test" \
+--max_seq_len 2048 \
+--num_train_epochs 1 \
+--logging_steps 5 \
+--log_level "info" \
+--logging_strategy "steps" \
+--eval_strategy "epoch" \
+--save_strategy "epoch" \
+--push_to_hub \
+--hub_private_repo True \
+--hub_strategy "every_save" \
+--bf16 True \
+--packing True \
+--learning_rate 1e-4 \
+--lr_scheduler_type "cosine" \
+--weight_decay 1e-4 \
+--warmup_ratio 0.0 \
+--max_grad_norm 1.0 \
+--output_dir "mistral-sft-lora" \
+--per_device_train_batch_size 8 \
+--per_device_eval_batch_size 8 \
+--gradient_accumulation_steps 8 \
+--gradient_checkpointing True \
+--use_reentrant True \
+--dataset_text_field "content" \
+--use_peft_lora True \
+--lora_r 8 \
+--lora_alpha 16 \
+--lora_dropout 0.1 \
+--lora_target_modules "all-linear" \
+--use_4bit_quantization True \
+--use_nested_quant True \
+--bnb_4bit_compute_dtype "bfloat16" \
+--use_flash_attn True
diff --git a/peft/examples/sft/run_peft_deepspeed.sh b/peft/examples/sft/run_peft_deepspeed.sh
new file mode 100644
index 0000000000000000000000000000000000000000..95dbf08892db530b6b5fac89c9bba5995cb6ea0b
--- /dev/null
+++ b/peft/examples/sft/run_peft_deepspeed.sh
@@ -0,0 +1,39 @@
+accelerate launch --config_file "configs/deepspeed_config.yaml" train.py \
+--seed 100 \
+--model_name_or_path "meta-llama/Llama-2-70b-hf" \
+--dataset_name "smangrul/ultrachat-10k-chatml" \
+--chat_template_format "chatml" \
+--add_special_tokens False \
+--append_concat_token False \
+--splits "train,test" \
+--max_seq_len 2048 \
+--num_train_epochs 1 \
+--logging_steps 5 \
+--log_level "info" \
+--logging_strategy "steps" \
+--eval_strategy "epoch" \
+--save_strategy "epoch" \
+--push_to_hub \
+--hub_private_repo True \
+--hub_strategy "every_save" \
+--bf16 True \
+--packing True \
+--learning_rate 1e-4 \
+--lr_scheduler_type "cosine" \
+--weight_decay 1e-4 \
+--warmup_ratio 0.0 \
+--max_grad_norm 1.0 \
+--output_dir "mistral-sft-lora-deepspeed" \
+--per_device_train_batch_size 8 \
+--per_device_eval_batch_size 8 \
+--gradient_accumulation_steps 4 \
+--gradient_checkpointing True \
+--use_reentrant False \
+--dataset_text_field "content" \
+--use_flash_attn True \
+--use_peft_lora True \
+--lora_r 8 \
+--lora_alpha 16 \
+--lora_dropout 0.1 \
+--lora_target_modules "all-linear" \
+--use_4bit_quantization False
\ No newline at end of file
diff --git a/peft/examples/sft/run_peft_fsdp.sh b/peft/examples/sft/run_peft_fsdp.sh
new file mode 100644
index 0000000000000000000000000000000000000000..63dd475f44ad062f6241ebee9c4fa9047bcace2b
--- /dev/null
+++ b/peft/examples/sft/run_peft_fsdp.sh
@@ -0,0 +1,39 @@
+accelerate launch --config_file "configs/fsdp_config.yaml" train.py \
+--seed 100 \
+--model_name_or_path "meta-llama/Llama-2-70b-hf" \
+--dataset_name "smangrul/ultrachat-10k-chatml" \
+--chat_template_format "chatml" \
+--add_special_tokens False \
+--append_concat_token False \
+--splits "train,test" \
+--max_seq_len 2048 \
+--num_train_epochs 1 \
+--logging_steps 5 \
+--log_level "info" \
+--logging_strategy "steps" \
+--eval_strategy "epoch" \
+--save_strategy "epoch" \
+--push_to_hub \
+--hub_private_repo True \
+--hub_strategy "every_save" \
+--bf16 True \
+--packing True \
+--learning_rate 1e-4 \
+--lr_scheduler_type "cosine" \
+--weight_decay 1e-4 \
+--warmup_ratio 0.0 \
+--max_grad_norm 1.0 \
+--output_dir "mistral-sft-lora-fsdp" \
+--per_device_train_batch_size 8 \
+--per_device_eval_batch_size 8 \
+--gradient_accumulation_steps 4 \
+--gradient_checkpointing True \
+--use_reentrant False \
+--dataset_text_field "content" \
+--use_flash_attn True \
+--use_peft_lora True \
+--lora_r 8 \
+--lora_alpha 16 \
+--lora_dropout 0.1 \
+--lora_target_modules "all-linear" \
+--use_4bit_quantization False
\ No newline at end of file
diff --git a/peft/examples/sft/run_peft_fsdp_gptq.sh b/peft/examples/sft/run_peft_fsdp_gptq.sh
new file mode 100644
index 0000000000000000000000000000000000000000..479a7eac834aea664f02c6b6ae6de359290ed3dd
--- /dev/null
+++ b/peft/examples/sft/run_peft_fsdp_gptq.sh
@@ -0,0 +1,36 @@
+accelerate launch --config_file "configs/fsdp_config.yaml" train.py \
+--seed 100 \
+--model_name_or_path "hugging-quants/Meta-Llama-3.1-8B-Instruct-GPTQ-INT4" \
+--dataset_name "smangrul/ultrachat-10k-chatml" \
+--chat_template_format "chatml" \
+--add_special_tokens False \
+--append_concat_token False \
+--splits "train,test" \
+--max_seq_len 2048 \
+--num_train_epochs 1 \
+--logging_steps 5 \
+--log_level "info" \
+--logging_strategy "steps" \
+--eval_strategy "epoch" \
+--save_strategy "epoch" \
+--bf16 True \
+--packing True \
+--learning_rate 1e-4 \
+--lr_scheduler_type "cosine" \
+--weight_decay 1e-4 \
+--warmup_ratio 0.0 \
+--max_grad_norm 1.0 \
+--output_dir "llama3-8B-gptq-sft-lora-fsdp" \
+--per_device_train_batch_size 8 \
+--per_device_eval_batch_size 8 \
+--gradient_accumulation_steps 4 \
+--gradient_checkpointing True \
+--use_reentrant False \
+--dataset_text_field "content" \
+--use_flash_attn True \
+--use_peft_lora True \
+--lora_r 8 \
+--lora_alpha 16 \
+--lora_dropout 0.1 \
+--lora_target_modules "q_proj,k_proj,v_proj,o_proj,up_proj,gate_proj" \
+--use_4bit_quantization False
\ No newline at end of file
diff --git a/peft/examples/sft/run_peft_multigpu.sh b/peft/examples/sft/run_peft_multigpu.sh
new file mode 100644
index 0000000000000000000000000000000000000000..dbd108d0e055c4fad1076068d15ee1560faa96ad
--- /dev/null
+++ b/peft/examples/sft/run_peft_multigpu.sh
@@ -0,0 +1,41 @@
+torchrun --nproc_per_node 8 --nnodes 1 train.py \
+--seed 100 \
+--model_name_or_path "mistralai/Mistral-7B-v0.1" \
+--dataset_name "smangrul/ultrachat-10k-chatml" \
+--chat_template_format "chatml" \
+--add_special_tokens False \
+--append_concat_token False \
+--splits "train,test" \
+--max_seq_len 2048 \
+--num_train_epochs 1 \
+--logging_steps 5 \
+--log_level "info" \
+--logging_strategy "steps" \
+--eval_strategy "epoch" \
+--save_strategy "epoch" \
+--push_to_hub \
+--hub_private_repo True \
+--hub_strategy "every_save" \
+--bf16 True \
+--packing True \
+--learning_rate 1e-4 \
+--lr_scheduler_type "cosine" \
+--weight_decay 1e-4 \
+--warmup_ratio 0.0 \
+--max_grad_norm 1.0 \
+--output_dir "mistral-sft-lora-multigpu" \
+--per_device_train_batch_size 8 \
+--per_device_eval_batch_size 8 \
+--gradient_accumulation_steps 8 \
+--gradient_checkpointing True \
+--use_reentrant False \
+--dataset_text_field "content" \
+--use_peft_lora True \
+--lora_r 8 \
+--lora_alpha 16 \
+--lora_dropout 0.1 \
+--lora_target_modules "all-linear" \
+--use_4bit_quantization True \
+--use_nested_quant True \
+--bnb_4bit_compute_dtype "bfloat16" \
+--use_flash_attn True
diff --git a/peft/examples/sft/run_peft_qlora_deepspeed_stage3.sh b/peft/examples/sft/run_peft_qlora_deepspeed_stage3.sh
new file mode 100644
index 0000000000000000000000000000000000000000..4bbc1bbcc4bd06351add38d7d5142da02787d5d4
--- /dev/null
+++ b/peft/examples/sft/run_peft_qlora_deepspeed_stage3.sh
@@ -0,0 +1,42 @@
+accelerate launch --config_file "configs/deepspeed_config_z3_qlora.yaml" train.py \
+--seed 100 \
+--model_name_or_path "meta-llama/Llama-2-70b-hf" \
+--dataset_name "smangrul/ultrachat-10k-chatml" \
+--chat_template_format "chatml" \
+--add_special_tokens False \
+--append_concat_token False \
+--splits "train,test" \
+--max_seq_len 2048 \
+--num_train_epochs 1 \
+--logging_steps 5 \
+--log_level "info" \
+--logging_strategy "steps" \
+--eval_strategy "epoch" \
+--save_strategy "epoch" \
+--push_to_hub \
+--hub_private_repo True \
+--hub_strategy "every_save" \
+--bf16 True \
+--packing True \
+--learning_rate 1e-4 \
+--lr_scheduler_type "cosine" \
+--weight_decay 1e-4 \
+--warmup_ratio 0.0 \
+--max_grad_norm 1.0 \
+--output_dir "llama-sft-qlora-dsz3" \
+--per_device_train_batch_size 2 \
+--per_device_eval_batch_size 2 \
+--gradient_accumulation_steps 2 \
+--gradient_checkpointing True \
+--use_reentrant True \
+--dataset_text_field "content" \
+--use_flash_attn True \
+--use_peft_lora True \
+--lora_r 8 \
+--lora_alpha 16 \
+--lora_dropout 0.1 \
+--lora_target_modules "all-linear" \
+--use_4bit_quantization True \
+--use_nested_quant True \
+--bnb_4bit_compute_dtype "bfloat16" \
+--bnb_4bit_quant_storage_dtype "bfloat16"
\ No newline at end of file
diff --git a/peft/examples/sft/run_peft_qlora_fsdp.sh b/peft/examples/sft/run_peft_qlora_fsdp.sh
new file mode 100644
index 0000000000000000000000000000000000000000..4ed3218c8277fd0ab8f66c2b3ea3f2fe41e7fe04
--- /dev/null
+++ b/peft/examples/sft/run_peft_qlora_fsdp.sh
@@ -0,0 +1,42 @@
+accelerate launch --config_file "configs/fsdp_config_qlora.yaml" train.py \
+--seed 100 \
+--model_name_or_path "meta-llama/Llama-2-70b-hf" \
+--dataset_name "smangrul/ultrachat-10k-chatml" \
+--chat_template_format "chatml" \
+--add_special_tokens False \
+--append_concat_token False \
+--splits "train,test" \
+--max_seq_len 2048 \
+--num_train_epochs 1 \
+--logging_steps 5 \
+--log_level "info" \
+--logging_strategy "steps" \
+--eval_strategy "epoch" \
+--save_strategy "epoch" \
+--push_to_hub \
+--hub_private_repo True \
+--hub_strategy "every_save" \
+--bf16 True \
+--packing True \
+--learning_rate 1e-4 \
+--lr_scheduler_type "cosine" \
+--weight_decay 1e-4 \
+--warmup_ratio 0.0 \
+--max_grad_norm 1.0 \
+--output_dir "llama-sft-qlora-fsdp" \
+--per_device_train_batch_size 2 \
+--per_device_eval_batch_size 2 \
+--gradient_accumulation_steps 2 \
+--gradient_checkpointing True \
+--use_reentrant True \
+--dataset_text_field "content" \
+--use_flash_attn True \
+--use_peft_lora True \
+--lora_r 8 \
+--lora_alpha 16 \
+--lora_dropout 0.1 \
+--lora_target_modules "all-linear" \
+--use_4bit_quantization True \
+--use_nested_quant True \
+--bnb_4bit_compute_dtype "bfloat16" \
+--bnb_4bit_quant_storage_dtype "bfloat16"
\ No newline at end of file
diff --git a/peft/examples/sft/run_unsloth_peft.sh b/peft/examples/sft/run_unsloth_peft.sh
new file mode 100644
index 0000000000000000000000000000000000000000..97a4a6b520e1112a85cd25387f3cb46deb465f9e
--- /dev/null
+++ b/peft/examples/sft/run_unsloth_peft.sh
@@ -0,0 +1,42 @@
+python train.py \
+--seed 100 \
+--model_name_or_path "mistralai/Mistral-7B-v0.1" \
+--dataset_name "smangrul/ultrachat-10k-chatml" \
+--chat_template_format "chatml" \
+--add_special_tokens False \
+--append_concat_token False \
+--splits "train,test" \
+--max_seq_len 2048 \
+--num_train_epochs 1 \
+--logging_steps 5 \
+--log_level "info" \
+--logging_strategy "steps" \
+--eval_strategy "epoch" \
+--save_strategy "epoch" \
+--push_to_hub \
+--hub_private_repo True \
+--hub_strategy "every_save" \
+--bf16 True \
+--packing True \
+--learning_rate 1e-4 \
+--lr_scheduler_type "cosine" \
+--weight_decay 1e-4 \
+--warmup_ratio 0.0 \
+--max_grad_norm 1.0 \
+--output_dir "mistral-sft-lora-unsloth" \
+--per_device_train_batch_size 8 \
+--per_device_eval_batch_size 8 \
+--gradient_accumulation_steps 8 \
+--gradient_checkpointing True \
+--use_reentrant True \
+--dataset_text_field "content" \
+--use_peft_lora True \
+--use_unsloth True \
+--lora_r 8 \
+--lora_alpha 16 \
+--lora_dropout 0.1 \
+--lora_target_modules "q_proj,k_proj,v_proj,o_proj,down_proj,up_proj,gate_proj" \
+--use_4bit_quantization True \
+--use_nested_quant True \
+--bnb_4bit_compute_dtype "bfloat16" \
+--use_flash_attn True
diff --git a/peft/examples/sft/train.py b/peft/examples/sft/train.py
new file mode 100644
index 0000000000000000000000000000000000000000..5a34f69357b0505e84b16436e894a2ab924ce1a7
--- /dev/null
+++ b/peft/examples/sft/train.py
@@ -0,0 +1,159 @@
+import os
+import sys
+from dataclasses import dataclass, field
+from typing import Optional
+
+from transformers import HfArgumentParser, set_seed
+from trl import SFTConfig, SFTTrainer
+from utils import create_and_prepare_model, create_datasets
+
+
+# Define and parse arguments.
+@dataclass
+class ModelArguments:
+ """
+ Arguments pertaining to which model/config/tokenizer we are going to fine-tune from.
+ """
+
+ model_name_or_path: str = field(
+ metadata={"help": "Path to pretrained model or model identifier from huggingface.co/models"}
+ )
+ max_seq_length: Optional[int] = field(
+ default=512,
+ metadata={"help": "The maximum total input sequence length after tokenization."},
+ )
+ chat_template_format: Optional[str] = field(
+ default="none",
+ metadata={
+ "help": "chatml|zephyr|none. Pass `none` if the dataset is already formatted with the chat template."
+ },
+ )
+ lora_alpha: Optional[int] = field(default=16)
+ lora_dropout: Optional[float] = field(default=0.1)
+ lora_r: Optional[int] = field(default=64)
+ lora_target_modules: Optional[str] = field(
+ default="q_proj,k_proj,v_proj,o_proj,down_proj,up_proj,gate_proj",
+ metadata={"help": "comma separated list of target modules to apply LoRA layers to"},
+ )
+ use_nested_quant: Optional[bool] = field(
+ default=False,
+ metadata={"help": "Activate nested quantization for 4bit base models"},
+ )
+ bnb_4bit_compute_dtype: Optional[str] = field(
+ default="float16",
+ metadata={"help": "Compute dtype for 4bit base models"},
+ )
+ bnb_4bit_quant_storage_dtype: Optional[str] = field(
+ default="uint8",
+ metadata={"help": "Quantization storage dtype for 4bit base models"},
+ )
+ bnb_4bit_quant_type: Optional[str] = field(
+ default="nf4",
+ metadata={"help": "Quantization type fp4 or nf4"},
+ )
+ use_flash_attn: Optional[bool] = field(
+ default=False,
+ metadata={"help": "Enables Flash attention for training."},
+ )
+ use_peft_lora: Optional[bool] = field(
+ default=False,
+ metadata={"help": "Enables PEFT LoRA for training."},
+ )
+ use_8bit_quantization: Optional[bool] = field(
+ default=False,
+ metadata={"help": "Enables loading model in 8bit."},
+ )
+ use_4bit_quantization: Optional[bool] = field(
+ default=False,
+ metadata={"help": "Enables loading model in 4bit."},
+ )
+ use_reentrant: Optional[bool] = field(
+ default=False,
+ metadata={"help": "Gradient Checkpointing param. Refer the related docs"},
+ )
+ use_unsloth: Optional[bool] = field(
+ default=False,
+ metadata={"help": "Enables UnSloth for training."},
+ )
+
+
+@dataclass
+class DataTrainingArguments:
+ dataset_name: Optional[str] = field(
+ default="timdettmers/openassistant-guanaco",
+ metadata={"help": "The preference dataset to use."},
+ )
+ append_concat_token: Optional[bool] = field(
+ default=False,
+ metadata={"help": "If True, appends `eos_token_id` at the end of each sample being packed."},
+ )
+ add_special_tokens: Optional[bool] = field(
+ default=False,
+ metadata={"help": "If True, tokenizers adds special tokens to each sample being packed."},
+ )
+ splits: Optional[str] = field(
+ default="train,test",
+ metadata={"help": "Comma separate list of the splits to use from the dataset."},
+ )
+
+
+def main(model_args, data_args, training_args):
+ # Set seed for reproducibility
+ set_seed(training_args.seed)
+
+ # model
+ model, peft_config, tokenizer = create_and_prepare_model(model_args, data_args, training_args)
+
+ # gradient ckpt
+ model.config.use_cache = not training_args.gradient_checkpointing
+ training_args.gradient_checkpointing = training_args.gradient_checkpointing and not model_args.use_unsloth
+ if training_args.gradient_checkpointing:
+ training_args.gradient_checkpointing_kwargs = {"use_reentrant": model_args.use_reentrant}
+
+ training_args.dataset_kwargs = {
+ "append_concat_token": data_args.append_concat_token,
+ "add_special_tokens": data_args.add_special_tokens,
+ }
+
+ # datasets
+ train_dataset, eval_dataset = create_datasets(
+ tokenizer,
+ data_args,
+ training_args,
+ apply_chat_template=model_args.chat_template_format != "none",
+ )
+
+ # trainer
+ trainer = SFTTrainer(
+ model=model,
+ processing_class=tokenizer,
+ args=training_args,
+ train_dataset=train_dataset,
+ eval_dataset=eval_dataset,
+ peft_config=peft_config,
+ )
+ trainer.accelerator.print(f"{trainer.model}")
+ if hasattr(trainer.model, "print_trainable_parameters"):
+ trainer.model.print_trainable_parameters()
+
+ # train
+ checkpoint = None
+ if training_args.resume_from_checkpoint is not None:
+ checkpoint = training_args.resume_from_checkpoint
+ trainer.train(resume_from_checkpoint=checkpoint)
+
+ # saving final model
+ if trainer.is_fsdp_enabled:
+ trainer.accelerator.state.fsdp_plugin.set_state_dict_type("FULL_STATE_DICT")
+ trainer.save_model()
+
+
+if __name__ == "__main__":
+ parser = HfArgumentParser((ModelArguments, DataTrainingArguments, SFTConfig))
+ if len(sys.argv) == 2 and sys.argv[1].endswith(".json"):
+ # If we pass only one argument to the script and it's the path to a json file,
+ # let's parse it to get our arguments.
+ model_args, data_args, training_args = parser.parse_json_file(json_file=os.path.abspath(sys.argv[1]))
+ else:
+ model_args, data_args, training_args = parser.parse_args_into_dataclasses()
+ main(model_args, data_args, training_args)
diff --git a/peft/examples/sft/utils.py b/peft/examples/sft/utils.py
new file mode 100644
index 0000000000000000000000000000000000000000..ea0d36bb647628561a3d447c0fdd9360caa03ba9
--- /dev/null
+++ b/peft/examples/sft/utils.py
@@ -0,0 +1,219 @@
+import os
+from enum import Enum
+
+import packaging.version
+import torch
+import transformers
+from datasets import DatasetDict, load_dataset, load_from_disk
+from datasets.builder import DatasetGenerationError
+from transformers import (
+ AutoModelForCausalLM,
+ AutoTokenizer,
+ BitsAndBytesConfig,
+)
+
+from peft import LoraConfig
+
+
+DEFAULT_CHATML_CHAT_TEMPLATE = "{% for message in messages %}\n{{'<|im_start|>' + message['role'] + '\n' + message['content'] + '<|im_end|>' + '\n'}}{% if loop.last and add_generation_prompt %}{{'<|im_start|>assistant\n' }}{% endif %}{% endfor %}"
+DEFAULT_ZEPHYR_CHAT_TEMPLATE = "{% for message in messages %}\n{% if message['role'] == 'user' %}\n{{ '<|user|>\n' + message['content'] + eos_token }}\n{% elif message['role'] == 'system' %}\n{{ '<|system|>\n' + message['content'] + eos_token }}\n{% elif message['role'] == 'assistant' %}\n{{ '<|assistant|>\n' + message['content'] + eos_token }}\n{% endif %}\n{% if loop.last and add_generation_prompt %}\n{{ '<|assistant|>' }}\n{% endif %}\n{% endfor %}"
+
+
+class ZephyrSpecialTokens(str, Enum):
+ user = "<|user|>"
+ assistant = "<|assistant|>"
+ system = "<|system|>"
+ eos_token = ""
+ bos_token = "
+
+Optimization in Unsloth to speed up QLoRA finetuning while reducing GPU memory usage
+
+## Multi-GPU SFT with QLoRA
+To speed up QLoRA finetuning when you have access to multiple GPUs, look at the launch command at [run_peft_multigpu.sh](https://github.com/huggingface/peft/blob/main/examples/sft/run_peft_multigpu.sh). This example to performs DDP on 8 GPUs.
+
+Note:
+1. At present, `use_reentrant` needs to be `False` when using gradient checkpointing with Multi-GPU QLoRA else it will lead to errors. However, this leads to huge GPU memory consumption.
+
+## Multi-GPU SFT with LoRA and DeepSpeed
+When you have access to multiple GPUs, it would be better to use normal LoRA with DeepSpeed/FSDP. To use LoRA with DeepSpeed, refer to the docs at [PEFT with DeepSpeed](https://huggingface.co/docs/peft/accelerate/deepspeed).
+
+
+## Multi-GPU SFT with LoRA and FSDP
+When you have access to multiple GPUs, it would be better to use normal LoRA with DeepSpeed/FSDP. To use LoRA with FSDP, refer to the docs at [PEFT with FSDP](https://huggingface.co/docs/peft/accelerate/fsdp).
+
+
+## Multi-GPU SFT with LoRA and FSDP for GPTQModel:
+As in [Multi-GPU SFT with LoRA and FSDP](https://github.com/huggingface/peft/blob/main/examples/sft/README.md#multi-gpu-sft-with-lora-and-fsdp), we also support other quantization methods like GPTQModel. You may need to install [GPTQModel](https://github.com/ModelCloud/GPTQModel) > v3.0.0 or from source. Here is the launch command for reference: [run_peft_fsdp_gptq.sh]. For the `--model_name_or_path` argument, it is important to pass a model that is already quantized with GPTQModel, like `"hugging-quants/Meta-Llama-3.1-8B-Instruct-GPTQ-INT4"`.
+
+Note: there is a bug in transformers v4.53.0 for this case, please skip this transformers version.
+
+## Tip
+
+Generally try to upgrade to the latest package versions for best results, especially when it comes to `bitsandbytes`, `accelerate`, `transformers`, `trl`, and `peft`.
diff --git a/peft/examples/sft/configs/deepspeed_config.yaml b/peft/examples/sft/configs/deepspeed_config.yaml
new file mode 100644
index 0000000000000000000000000000000000000000..56eef6e48b75727ede1d522b595b5ecde3a205a1
--- /dev/null
+++ b/peft/examples/sft/configs/deepspeed_config.yaml
@@ -0,0 +1,23 @@
+compute_environment: LOCAL_MACHINE
+debug: false
+deepspeed_config:
+ deepspeed_multinode_launcher: standard
+ gradient_accumulation_steps: 4
+ offload_optimizer_device: none
+ offload_param_device: none
+ zero3_init_flag: true
+ zero3_save_16bit_model: true
+ zero_stage: 3
+distributed_type: DEEPSPEED
+downcast_bf16: 'no'
+machine_rank: 0
+main_training_function: main
+mixed_precision: bf16
+num_machines: 1
+num_processes: 8
+rdzv_backend: static
+same_network: true
+tpu_env: []
+tpu_use_cluster: false
+tpu_use_sudo: false
+use_cpu: false
\ No newline at end of file
diff --git a/peft/examples/sft/configs/deepspeed_config_z3_qlora.yaml b/peft/examples/sft/configs/deepspeed_config_z3_qlora.yaml
new file mode 100644
index 0000000000000000000000000000000000000000..07dddcef7853b963ea64d20d39078893c4e21c33
--- /dev/null
+++ b/peft/examples/sft/configs/deepspeed_config_z3_qlora.yaml
@@ -0,0 +1,22 @@
+compute_environment: LOCAL_MACHINE
+debug: false
+deepspeed_config:
+ deepspeed_multinode_launcher: standard
+ offload_optimizer_device: none
+ offload_param_device: none
+ zero3_init_flag: true
+ zero3_save_16bit_model: true
+ zero_stage: 3
+distributed_type: DEEPSPEED
+downcast_bf16: 'no'
+machine_rank: 0
+main_training_function: main
+mixed_precision: bf16
+num_machines: 1
+num_processes: 2
+rdzv_backend: static
+same_network: true
+tpu_env: []
+tpu_use_cluster: false
+tpu_use_sudo: false
+use_cpu: false
\ No newline at end of file
diff --git a/peft/examples/sft/configs/fsdp_config.yaml b/peft/examples/sft/configs/fsdp_config.yaml
new file mode 100644
index 0000000000000000000000000000000000000000..7cccb74ca0dfa1a916b5057ceee561271c301ec5
--- /dev/null
+++ b/peft/examples/sft/configs/fsdp_config.yaml
@@ -0,0 +1,25 @@
+compute_environment: LOCAL_MACHINE
+debug: false
+distributed_type: FSDP
+downcast_bf16: 'no'
+fsdp_config:
+ fsdp_auto_wrap_policy: TRANSFORMER_BASED_WRAP
+ fsdp_backward_prefetch: BACKWARD_PRE
+ fsdp_cpu_ram_efficient_loading: true
+ fsdp_forward_prefetch: false
+ fsdp_offload_params: false
+ fsdp_sharding_strategy: FULL_SHARD
+ fsdp_state_dict_type: SHARDED_STATE_DICT
+ fsdp_sync_module_states: true
+ fsdp_use_orig_params: false
+machine_rank: 0
+main_training_function: main
+mixed_precision: bf16
+num_machines: 1
+num_processes: 8
+rdzv_backend: static
+same_network: true
+tpu_env: []
+tpu_use_cluster: false
+tpu_use_sudo: false
+use_cpu: false
\ No newline at end of file
diff --git a/peft/examples/sft/configs/fsdp_config_qlora.yaml b/peft/examples/sft/configs/fsdp_config_qlora.yaml
new file mode 100644
index 0000000000000000000000000000000000000000..f28a0f1046a735579045655dcdb9d3bf7c6ffdcc
--- /dev/null
+++ b/peft/examples/sft/configs/fsdp_config_qlora.yaml
@@ -0,0 +1,25 @@
+compute_environment: LOCAL_MACHINE
+debug: false
+distributed_type: FSDP
+downcast_bf16: 'no'
+fsdp_config:
+ fsdp_auto_wrap_policy: TRANSFORMER_BASED_WRAP
+ fsdp_backward_prefetch: BACKWARD_PRE
+ fsdp_cpu_ram_efficient_loading: true
+ fsdp_forward_prefetch: false
+ fsdp_offload_params: true
+ fsdp_sharding_strategy: FULL_SHARD
+ fsdp_state_dict_type: SHARDED_STATE_DICT
+ fsdp_sync_module_states: true
+ fsdp_use_orig_params: false
+machine_rank: 0
+main_training_function: main
+mixed_precision: 'no'
+num_machines: 1
+num_processes: 2
+rdzv_backend: static
+same_network: true
+tpu_env: []
+tpu_use_cluster: false
+tpu_use_sudo: false
+use_cpu: false
\ No newline at end of file
diff --git a/peft/examples/sft/requirements.txt b/peft/examples/sft/requirements.txt
new file mode 100644
index 0000000000000000000000000000000000000000..752b6976e62f4acff6193804c5422807bc5e8806
--- /dev/null
+++ b/peft/examples/sft/requirements.txt
@@ -0,0 +1,25 @@
+git+https://github.com/huggingface/transformers
+git+https://github.com/huggingface/accelerate
+git+https://github.com/huggingface/peft
+git+https://github.com/huggingface/trl
+git+https://github.com/huggingface/datatrove.git
+unsloth[conda]@git+https://github.com/unslothai/unsloth.git
+deepspeed
+PyGithub
+flash-attn
+huggingface-hub
+evaluate
+datasets
+bitsandbytes
+einops
+wandb
+tensorboard
+tiktoken
+pandas
+numpy
+scipy
+matplotlib
+sentencepiece
+nltk
+xformers
+hf_transfer
\ No newline at end of file
diff --git a/peft/examples/sft/requirements_colab.txt b/peft/examples/sft/requirements_colab.txt
new file mode 100644
index 0000000000000000000000000000000000000000..b8c375dc44bf85305fa53964537f4877210b10bd
--- /dev/null
+++ b/peft/examples/sft/requirements_colab.txt
@@ -0,0 +1,25 @@
+git+https://github.com/huggingface/transformers
+git+https://github.com/huggingface/accelerate
+git+https://github.com/huggingface/peft
+git+https://github.com/huggingface/trl
+unsloth[colab_ampere] @ git+https://github.com/unslothai/unsloth.git
+datasets
+deepspeed
+PyGithub
+flash-attn
+huggingface-hub
+evaluate
+bitsandbytes
+einops
+wandb
+tensorboard
+tiktoken
+pandas
+numpy
+scipy
+matplotlib
+sentencepiece
+nltk
+xformers
+git+https://github.com/huggingface/datatrove.git
+hf_transfer
\ No newline at end of file
diff --git a/peft/examples/sft/requirements_xpu.txt b/peft/examples/sft/requirements_xpu.txt
new file mode 100644
index 0000000000000000000000000000000000000000..9e5918b95180acbdc5789115ba0af71c8adf3aa5
--- /dev/null
+++ b/peft/examples/sft/requirements_xpu.txt
@@ -0,0 +1,22 @@
+git+https://github.com/huggingface/transformers
+git+https://github.com/huggingface/accelerate
+git+https://github.com/huggingface/peft
+git+https://github.com/huggingface/trl
+git+https://github.com/huggingface/datatrove.git
+deepspeed
+PyGithub
+huggingface-hub
+evaluate
+datasets
+bitsandbytes
+einops
+wandb
+tensorboard
+tiktoken
+pandas
+numpy
+scipy
+matplotlib
+sentencepiece
+nltk
+hf_transfer
\ No newline at end of file
diff --git a/peft/examples/sft/run_peft.sh b/peft/examples/sft/run_peft.sh
new file mode 100644
index 0000000000000000000000000000000000000000..8aa48648d34636eb07cd25c0abd91b943c00b49f
--- /dev/null
+++ b/peft/examples/sft/run_peft.sh
@@ -0,0 +1,41 @@
+python train.py \
+--seed 100 \
+--model_name_or_path "mistralai/Mistral-7B-v0.1" \
+--dataset_name "smangrul/ultrachat-10k-chatml" \
+--chat_template_format "chatml" \
+--add_special_tokens False \
+--append_concat_token False \
+--splits "train,test" \
+--max_seq_len 2048 \
+--num_train_epochs 1 \
+--logging_steps 5 \
+--log_level "info" \
+--logging_strategy "steps" \
+--eval_strategy "epoch" \
+--save_strategy "epoch" \
+--push_to_hub \
+--hub_private_repo True \
+--hub_strategy "every_save" \
+--bf16 True \
+--packing True \
+--learning_rate 1e-4 \
+--lr_scheduler_type "cosine" \
+--weight_decay 1e-4 \
+--warmup_ratio 0.0 \
+--max_grad_norm 1.0 \
+--output_dir "mistral-sft-lora" \
+--per_device_train_batch_size 8 \
+--per_device_eval_batch_size 8 \
+--gradient_accumulation_steps 8 \
+--gradient_checkpointing True \
+--use_reentrant True \
+--dataset_text_field "content" \
+--use_peft_lora True \
+--lora_r 8 \
+--lora_alpha 16 \
+--lora_dropout 0.1 \
+--lora_target_modules "all-linear" \
+--use_4bit_quantization True \
+--use_nested_quant True \
+--bnb_4bit_compute_dtype "bfloat16" \
+--use_flash_attn True
diff --git a/peft/examples/sft/run_peft_deepspeed.sh b/peft/examples/sft/run_peft_deepspeed.sh
new file mode 100644
index 0000000000000000000000000000000000000000..95dbf08892db530b6b5fac89c9bba5995cb6ea0b
--- /dev/null
+++ b/peft/examples/sft/run_peft_deepspeed.sh
@@ -0,0 +1,39 @@
+accelerate launch --config_file "configs/deepspeed_config.yaml" train.py \
+--seed 100 \
+--model_name_or_path "meta-llama/Llama-2-70b-hf" \
+--dataset_name "smangrul/ultrachat-10k-chatml" \
+--chat_template_format "chatml" \
+--add_special_tokens False \
+--append_concat_token False \
+--splits "train,test" \
+--max_seq_len 2048 \
+--num_train_epochs 1 \
+--logging_steps 5 \
+--log_level "info" \
+--logging_strategy "steps" \
+--eval_strategy "epoch" \
+--save_strategy "epoch" \
+--push_to_hub \
+--hub_private_repo True \
+--hub_strategy "every_save" \
+--bf16 True \
+--packing True \
+--learning_rate 1e-4 \
+--lr_scheduler_type "cosine" \
+--weight_decay 1e-4 \
+--warmup_ratio 0.0 \
+--max_grad_norm 1.0 \
+--output_dir "mistral-sft-lora-deepspeed" \
+--per_device_train_batch_size 8 \
+--per_device_eval_batch_size 8 \
+--gradient_accumulation_steps 4 \
+--gradient_checkpointing True \
+--use_reentrant False \
+--dataset_text_field "content" \
+--use_flash_attn True \
+--use_peft_lora True \
+--lora_r 8 \
+--lora_alpha 16 \
+--lora_dropout 0.1 \
+--lora_target_modules "all-linear" \
+--use_4bit_quantization False
\ No newline at end of file
diff --git a/peft/examples/sft/run_peft_fsdp.sh b/peft/examples/sft/run_peft_fsdp.sh
new file mode 100644
index 0000000000000000000000000000000000000000..63dd475f44ad062f6241ebee9c4fa9047bcace2b
--- /dev/null
+++ b/peft/examples/sft/run_peft_fsdp.sh
@@ -0,0 +1,39 @@
+accelerate launch --config_file "configs/fsdp_config.yaml" train.py \
+--seed 100 \
+--model_name_or_path "meta-llama/Llama-2-70b-hf" \
+--dataset_name "smangrul/ultrachat-10k-chatml" \
+--chat_template_format "chatml" \
+--add_special_tokens False \
+--append_concat_token False \
+--splits "train,test" \
+--max_seq_len 2048 \
+--num_train_epochs 1 \
+--logging_steps 5 \
+--log_level "info" \
+--logging_strategy "steps" \
+--eval_strategy "epoch" \
+--save_strategy "epoch" \
+--push_to_hub \
+--hub_private_repo True \
+--hub_strategy "every_save" \
+--bf16 True \
+--packing True \
+--learning_rate 1e-4 \
+--lr_scheduler_type "cosine" \
+--weight_decay 1e-4 \
+--warmup_ratio 0.0 \
+--max_grad_norm 1.0 \
+--output_dir "mistral-sft-lora-fsdp" \
+--per_device_train_batch_size 8 \
+--per_device_eval_batch_size 8 \
+--gradient_accumulation_steps 4 \
+--gradient_checkpointing True \
+--use_reentrant False \
+--dataset_text_field "content" \
+--use_flash_attn True \
+--use_peft_lora True \
+--lora_r 8 \
+--lora_alpha 16 \
+--lora_dropout 0.1 \
+--lora_target_modules "all-linear" \
+--use_4bit_quantization False
\ No newline at end of file
diff --git a/peft/examples/sft/run_peft_fsdp_gptq.sh b/peft/examples/sft/run_peft_fsdp_gptq.sh
new file mode 100644
index 0000000000000000000000000000000000000000..479a7eac834aea664f02c6b6ae6de359290ed3dd
--- /dev/null
+++ b/peft/examples/sft/run_peft_fsdp_gptq.sh
@@ -0,0 +1,36 @@
+accelerate launch --config_file "configs/fsdp_config.yaml" train.py \
+--seed 100 \
+--model_name_or_path "hugging-quants/Meta-Llama-3.1-8B-Instruct-GPTQ-INT4" \
+--dataset_name "smangrul/ultrachat-10k-chatml" \
+--chat_template_format "chatml" \
+--add_special_tokens False \
+--append_concat_token False \
+--splits "train,test" \
+--max_seq_len 2048 \
+--num_train_epochs 1 \
+--logging_steps 5 \
+--log_level "info" \
+--logging_strategy "steps" \
+--eval_strategy "epoch" \
+--save_strategy "epoch" \
+--bf16 True \
+--packing True \
+--learning_rate 1e-4 \
+--lr_scheduler_type "cosine" \
+--weight_decay 1e-4 \
+--warmup_ratio 0.0 \
+--max_grad_norm 1.0 \
+--output_dir "llama3-8B-gptq-sft-lora-fsdp" \
+--per_device_train_batch_size 8 \
+--per_device_eval_batch_size 8 \
+--gradient_accumulation_steps 4 \
+--gradient_checkpointing True \
+--use_reentrant False \
+--dataset_text_field "content" \
+--use_flash_attn True \
+--use_peft_lora True \
+--lora_r 8 \
+--lora_alpha 16 \
+--lora_dropout 0.1 \
+--lora_target_modules "q_proj,k_proj,v_proj,o_proj,up_proj,gate_proj" \
+--use_4bit_quantization False
\ No newline at end of file
diff --git a/peft/examples/sft/run_peft_multigpu.sh b/peft/examples/sft/run_peft_multigpu.sh
new file mode 100644
index 0000000000000000000000000000000000000000..dbd108d0e055c4fad1076068d15ee1560faa96ad
--- /dev/null
+++ b/peft/examples/sft/run_peft_multigpu.sh
@@ -0,0 +1,41 @@
+torchrun --nproc_per_node 8 --nnodes 1 train.py \
+--seed 100 \
+--model_name_or_path "mistralai/Mistral-7B-v0.1" \
+--dataset_name "smangrul/ultrachat-10k-chatml" \
+--chat_template_format "chatml" \
+--add_special_tokens False \
+--append_concat_token False \
+--splits "train,test" \
+--max_seq_len 2048 \
+--num_train_epochs 1 \
+--logging_steps 5 \
+--log_level "info" \
+--logging_strategy "steps" \
+--eval_strategy "epoch" \
+--save_strategy "epoch" \
+--push_to_hub \
+--hub_private_repo True \
+--hub_strategy "every_save" \
+--bf16 True \
+--packing True \
+--learning_rate 1e-4 \
+--lr_scheduler_type "cosine" \
+--weight_decay 1e-4 \
+--warmup_ratio 0.0 \
+--max_grad_norm 1.0 \
+--output_dir "mistral-sft-lora-multigpu" \
+--per_device_train_batch_size 8 \
+--per_device_eval_batch_size 8 \
+--gradient_accumulation_steps 8 \
+--gradient_checkpointing True \
+--use_reentrant False \
+--dataset_text_field "content" \
+--use_peft_lora True \
+--lora_r 8 \
+--lora_alpha 16 \
+--lora_dropout 0.1 \
+--lora_target_modules "all-linear" \
+--use_4bit_quantization True \
+--use_nested_quant True \
+--bnb_4bit_compute_dtype "bfloat16" \
+--use_flash_attn True
diff --git a/peft/examples/sft/run_peft_qlora_deepspeed_stage3.sh b/peft/examples/sft/run_peft_qlora_deepspeed_stage3.sh
new file mode 100644
index 0000000000000000000000000000000000000000..4bbc1bbcc4bd06351add38d7d5142da02787d5d4
--- /dev/null
+++ b/peft/examples/sft/run_peft_qlora_deepspeed_stage3.sh
@@ -0,0 +1,42 @@
+accelerate launch --config_file "configs/deepspeed_config_z3_qlora.yaml" train.py \
+--seed 100 \
+--model_name_or_path "meta-llama/Llama-2-70b-hf" \
+--dataset_name "smangrul/ultrachat-10k-chatml" \
+--chat_template_format "chatml" \
+--add_special_tokens False \
+--append_concat_token False \
+--splits "train,test" \
+--max_seq_len 2048 \
+--num_train_epochs 1 \
+--logging_steps 5 \
+--log_level "info" \
+--logging_strategy "steps" \
+--eval_strategy "epoch" \
+--save_strategy "epoch" \
+--push_to_hub \
+--hub_private_repo True \
+--hub_strategy "every_save" \
+--bf16 True \
+--packing True \
+--learning_rate 1e-4 \
+--lr_scheduler_type "cosine" \
+--weight_decay 1e-4 \
+--warmup_ratio 0.0 \
+--max_grad_norm 1.0 \
+--output_dir "llama-sft-qlora-dsz3" \
+--per_device_train_batch_size 2 \
+--per_device_eval_batch_size 2 \
+--gradient_accumulation_steps 2 \
+--gradient_checkpointing True \
+--use_reentrant True \
+--dataset_text_field "content" \
+--use_flash_attn True \
+--use_peft_lora True \
+--lora_r 8 \
+--lora_alpha 16 \
+--lora_dropout 0.1 \
+--lora_target_modules "all-linear" \
+--use_4bit_quantization True \
+--use_nested_quant True \
+--bnb_4bit_compute_dtype "bfloat16" \
+--bnb_4bit_quant_storage_dtype "bfloat16"
\ No newline at end of file
diff --git a/peft/examples/sft/run_peft_qlora_fsdp.sh b/peft/examples/sft/run_peft_qlora_fsdp.sh
new file mode 100644
index 0000000000000000000000000000000000000000..4ed3218c8277fd0ab8f66c2b3ea3f2fe41e7fe04
--- /dev/null
+++ b/peft/examples/sft/run_peft_qlora_fsdp.sh
@@ -0,0 +1,42 @@
+accelerate launch --config_file "configs/fsdp_config_qlora.yaml" train.py \
+--seed 100 \
+--model_name_or_path "meta-llama/Llama-2-70b-hf" \
+--dataset_name "smangrul/ultrachat-10k-chatml" \
+--chat_template_format "chatml" \
+--add_special_tokens False \
+--append_concat_token False \
+--splits "train,test" \
+--max_seq_len 2048 \
+--num_train_epochs 1 \
+--logging_steps 5 \
+--log_level "info" \
+--logging_strategy "steps" \
+--eval_strategy "epoch" \
+--save_strategy "epoch" \
+--push_to_hub \
+--hub_private_repo True \
+--hub_strategy "every_save" \
+--bf16 True \
+--packing True \
+--learning_rate 1e-4 \
+--lr_scheduler_type "cosine" \
+--weight_decay 1e-4 \
+--warmup_ratio 0.0 \
+--max_grad_norm 1.0 \
+--output_dir "llama-sft-qlora-fsdp" \
+--per_device_train_batch_size 2 \
+--per_device_eval_batch_size 2 \
+--gradient_accumulation_steps 2 \
+--gradient_checkpointing True \
+--use_reentrant True \
+--dataset_text_field "content" \
+--use_flash_attn True \
+--use_peft_lora True \
+--lora_r 8 \
+--lora_alpha 16 \
+--lora_dropout 0.1 \
+--lora_target_modules "all-linear" \
+--use_4bit_quantization True \
+--use_nested_quant True \
+--bnb_4bit_compute_dtype "bfloat16" \
+--bnb_4bit_quant_storage_dtype "bfloat16"
\ No newline at end of file
diff --git a/peft/examples/sft/run_unsloth_peft.sh b/peft/examples/sft/run_unsloth_peft.sh
new file mode 100644
index 0000000000000000000000000000000000000000..97a4a6b520e1112a85cd25387f3cb46deb465f9e
--- /dev/null
+++ b/peft/examples/sft/run_unsloth_peft.sh
@@ -0,0 +1,42 @@
+python train.py \
+--seed 100 \
+--model_name_or_path "mistralai/Mistral-7B-v0.1" \
+--dataset_name "smangrul/ultrachat-10k-chatml" \
+--chat_template_format "chatml" \
+--add_special_tokens False \
+--append_concat_token False \
+--splits "train,test" \
+--max_seq_len 2048 \
+--num_train_epochs 1 \
+--logging_steps 5 \
+--log_level "info" \
+--logging_strategy "steps" \
+--eval_strategy "epoch" \
+--save_strategy "epoch" \
+--push_to_hub \
+--hub_private_repo True \
+--hub_strategy "every_save" \
+--bf16 True \
+--packing True \
+--learning_rate 1e-4 \
+--lr_scheduler_type "cosine" \
+--weight_decay 1e-4 \
+--warmup_ratio 0.0 \
+--max_grad_norm 1.0 \
+--output_dir "mistral-sft-lora-unsloth" \
+--per_device_train_batch_size 8 \
+--per_device_eval_batch_size 8 \
+--gradient_accumulation_steps 8 \
+--gradient_checkpointing True \
+--use_reentrant True \
+--dataset_text_field "content" \
+--use_peft_lora True \
+--use_unsloth True \
+--lora_r 8 \
+--lora_alpha 16 \
+--lora_dropout 0.1 \
+--lora_target_modules "q_proj,k_proj,v_proj,o_proj,down_proj,up_proj,gate_proj" \
+--use_4bit_quantization True \
+--use_nested_quant True \
+--bnb_4bit_compute_dtype "bfloat16" \
+--use_flash_attn True
diff --git a/peft/examples/sft/train.py b/peft/examples/sft/train.py
new file mode 100644
index 0000000000000000000000000000000000000000..5a34f69357b0505e84b16436e894a2ab924ce1a7
--- /dev/null
+++ b/peft/examples/sft/train.py
@@ -0,0 +1,159 @@
+import os
+import sys
+from dataclasses import dataclass, field
+from typing import Optional
+
+from transformers import HfArgumentParser, set_seed
+from trl import SFTConfig, SFTTrainer
+from utils import create_and_prepare_model, create_datasets
+
+
+# Define and parse arguments.
+@dataclass
+class ModelArguments:
+ """
+ Arguments pertaining to which model/config/tokenizer we are going to fine-tune from.
+ """
+
+ model_name_or_path: str = field(
+ metadata={"help": "Path to pretrained model or model identifier from huggingface.co/models"}
+ )
+ max_seq_length: Optional[int] = field(
+ default=512,
+ metadata={"help": "The maximum total input sequence length after tokenization."},
+ )
+ chat_template_format: Optional[str] = field(
+ default="none",
+ metadata={
+ "help": "chatml|zephyr|none. Pass `none` if the dataset is already formatted with the chat template."
+ },
+ )
+ lora_alpha: Optional[int] = field(default=16)
+ lora_dropout: Optional[float] = field(default=0.1)
+ lora_r: Optional[int] = field(default=64)
+ lora_target_modules: Optional[str] = field(
+ default="q_proj,k_proj,v_proj,o_proj,down_proj,up_proj,gate_proj",
+ metadata={"help": "comma separated list of target modules to apply LoRA layers to"},
+ )
+ use_nested_quant: Optional[bool] = field(
+ default=False,
+ metadata={"help": "Activate nested quantization for 4bit base models"},
+ )
+ bnb_4bit_compute_dtype: Optional[str] = field(
+ default="float16",
+ metadata={"help": "Compute dtype for 4bit base models"},
+ )
+ bnb_4bit_quant_storage_dtype: Optional[str] = field(
+ default="uint8",
+ metadata={"help": "Quantization storage dtype for 4bit base models"},
+ )
+ bnb_4bit_quant_type: Optional[str] = field(
+ default="nf4",
+ metadata={"help": "Quantization type fp4 or nf4"},
+ )
+ use_flash_attn: Optional[bool] = field(
+ default=False,
+ metadata={"help": "Enables Flash attention for training."},
+ )
+ use_peft_lora: Optional[bool] = field(
+ default=False,
+ metadata={"help": "Enables PEFT LoRA for training."},
+ )
+ use_8bit_quantization: Optional[bool] = field(
+ default=False,
+ metadata={"help": "Enables loading model in 8bit."},
+ )
+ use_4bit_quantization: Optional[bool] = field(
+ default=False,
+ metadata={"help": "Enables loading model in 4bit."},
+ )
+ use_reentrant: Optional[bool] = field(
+ default=False,
+ metadata={"help": "Gradient Checkpointing param. Refer the related docs"},
+ )
+ use_unsloth: Optional[bool] = field(
+ default=False,
+ metadata={"help": "Enables UnSloth for training."},
+ )
+
+
+@dataclass
+class DataTrainingArguments:
+ dataset_name: Optional[str] = field(
+ default="timdettmers/openassistant-guanaco",
+ metadata={"help": "The preference dataset to use."},
+ )
+ append_concat_token: Optional[bool] = field(
+ default=False,
+ metadata={"help": "If True, appends `eos_token_id` at the end of each sample being packed."},
+ )
+ add_special_tokens: Optional[bool] = field(
+ default=False,
+ metadata={"help": "If True, tokenizers adds special tokens to each sample being packed."},
+ )
+ splits: Optional[str] = field(
+ default="train,test",
+ metadata={"help": "Comma separate list of the splits to use from the dataset."},
+ )
+
+
+def main(model_args, data_args, training_args):
+ # Set seed for reproducibility
+ set_seed(training_args.seed)
+
+ # model
+ model, peft_config, tokenizer = create_and_prepare_model(model_args, data_args, training_args)
+
+ # gradient ckpt
+ model.config.use_cache = not training_args.gradient_checkpointing
+ training_args.gradient_checkpointing = training_args.gradient_checkpointing and not model_args.use_unsloth
+ if training_args.gradient_checkpointing:
+ training_args.gradient_checkpointing_kwargs = {"use_reentrant": model_args.use_reentrant}
+
+ training_args.dataset_kwargs = {
+ "append_concat_token": data_args.append_concat_token,
+ "add_special_tokens": data_args.add_special_tokens,
+ }
+
+ # datasets
+ train_dataset, eval_dataset = create_datasets(
+ tokenizer,
+ data_args,
+ training_args,
+ apply_chat_template=model_args.chat_template_format != "none",
+ )
+
+ # trainer
+ trainer = SFTTrainer(
+ model=model,
+ processing_class=tokenizer,
+ args=training_args,
+ train_dataset=train_dataset,
+ eval_dataset=eval_dataset,
+ peft_config=peft_config,
+ )
+ trainer.accelerator.print(f"{trainer.model}")
+ if hasattr(trainer.model, "print_trainable_parameters"):
+ trainer.model.print_trainable_parameters()
+
+ # train
+ checkpoint = None
+ if training_args.resume_from_checkpoint is not None:
+ checkpoint = training_args.resume_from_checkpoint
+ trainer.train(resume_from_checkpoint=checkpoint)
+
+ # saving final model
+ if trainer.is_fsdp_enabled:
+ trainer.accelerator.state.fsdp_plugin.set_state_dict_type("FULL_STATE_DICT")
+ trainer.save_model()
+
+
+if __name__ == "__main__":
+ parser = HfArgumentParser((ModelArguments, DataTrainingArguments, SFTConfig))
+ if len(sys.argv) == 2 and sys.argv[1].endswith(".json"):
+ # If we pass only one argument to the script and it's the path to a json file,
+ # let's parse it to get our arguments.
+ model_args, data_args, training_args = parser.parse_json_file(json_file=os.path.abspath(sys.argv[1]))
+ else:
+ model_args, data_args, training_args = parser.parse_args_into_dataclasses()
+ main(model_args, data_args, training_args)
diff --git a/peft/examples/sft/utils.py b/peft/examples/sft/utils.py
new file mode 100644
index 0000000000000000000000000000000000000000..ea0d36bb647628561a3d447c0fdd9360caa03ba9
--- /dev/null
+++ b/peft/examples/sft/utils.py
@@ -0,0 +1,219 @@
+import os
+from enum import Enum
+
+import packaging.version
+import torch
+import transformers
+from datasets import DatasetDict, load_dataset, load_from_disk
+from datasets.builder import DatasetGenerationError
+from transformers import (
+ AutoModelForCausalLM,
+ AutoTokenizer,
+ BitsAndBytesConfig,
+)
+
+from peft import LoraConfig
+
+
+DEFAULT_CHATML_CHAT_TEMPLATE = "{% for message in messages %}\n{{'<|im_start|>' + message['role'] + '\n' + message['content'] + '<|im_end|>' + '\n'}}{% if loop.last and add_generation_prompt %}{{'<|im_start|>assistant\n' }}{% endif %}{% endfor %}"
+DEFAULT_ZEPHYR_CHAT_TEMPLATE = "{% for message in messages %}\n{% if message['role'] == 'user' %}\n{{ '<|user|>\n' + message['content'] + eos_token }}\n{% elif message['role'] == 'system' %}\n{{ '<|system|>\n' + message['content'] + eos_token }}\n{% elif message['role'] == 'assistant' %}\n{{ '<|assistant|>\n' + message['content'] + eos_token }}\n{% endif %}\n{% if loop.last and add_generation_prompt %}\n{{ '<|assistant|>' }}\n{% endif %}\n{% endfor %}"
+
+
+class ZephyrSpecialTokens(str, Enum):
+ user = "<|user|>"
+ assistant = "<|assistant|>"
+ system = "<|system|>"
+ eos_token = ""
+ bos_token = ""
+ pad_token = ""
+
+ @classmethod
+ def list(cls):
+ return [c.value for c in cls]
+
+
+class ChatmlSpecialTokens(str, Enum):
+ user = "<|im_start|>user"
+ assistant = "<|im_start|>assistant"
+ system = "<|im_start|>system"
+ eos_token = "<|im_end|>"
+ bos_token = ""
+ pad_token = ""
+
+ @classmethod
+ def list(cls):
+ return [c.value for c in cls]
+
+
+def create_datasets(tokenizer, data_args, training_args, apply_chat_template=False):
+ def preprocess(samples):
+ batch = []
+ for conversation in samples["messages"]:
+ batch.append(tokenizer.apply_chat_template(conversation, tokenize=False))
+ return {"content": batch}
+
+ raw_datasets = DatasetDict()
+ for split in data_args.splits.split(","):
+ try:
+ # Try first if dataset on a Hub repo
+ dataset = load_dataset(data_args.dataset_name, split=split)
+ except DatasetGenerationError:
+ # If not, check local dataset
+ dataset = load_from_disk(os.path.join(data_args.dataset_name, split))
+
+ if "train" in split:
+ raw_datasets["train"] = dataset
+ elif "test" in split:
+ raw_datasets["test"] = dataset
+ else:
+ raise ValueError(f"Split type {split} not recognized as one of test or train.")
+
+ if apply_chat_template:
+ raw_datasets = raw_datasets.map(
+ preprocess,
+ batched=True,
+ remove_columns=raw_datasets["train"].column_names,
+ )
+
+ train_data = raw_datasets["train"]
+ valid_data = raw_datasets["test"]
+ print(f"Size of the train set: {len(train_data)}. Size of the validation set: {len(valid_data)}")
+ print(f"A sample of train dataset: {train_data[0]}")
+
+ return train_data, valid_data
+
+
+def create_and_prepare_model(args, data_args, training_args):
+ if args.use_unsloth:
+ from unsloth import FastLanguageModel
+ bnb_config = None
+ quant_storage_dtype = None
+
+ if (
+ torch.distributed.is_available()
+ and torch.distributed.is_initialized()
+ and torch.distributed.get_world_size() > 1
+ and args.use_unsloth
+ ):
+ raise NotImplementedError("Unsloth is not supported in distributed training")
+
+ if args.use_4bit_quantization:
+ compute_dtype = getattr(torch, args.bnb_4bit_compute_dtype)
+ quant_storage_dtype = getattr(torch, args.bnb_4bit_quant_storage_dtype)
+
+ bnb_config = BitsAndBytesConfig(
+ load_in_4bit=args.use_4bit_quantization,
+ bnb_4bit_quant_type=args.bnb_4bit_quant_type,
+ bnb_4bit_compute_dtype=compute_dtype,
+ bnb_4bit_use_double_quant=args.use_nested_quant,
+ bnb_4bit_quant_storage=quant_storage_dtype,
+ )
+
+ if compute_dtype == torch.float16 and args.use_4bit_quantization:
+ major, _ = torch.cuda.get_device_capability()
+ if major >= 8:
+ print("=" * 80)
+ print("Your GPU supports bfloat16, you can accelerate training with the argument --bf16")
+ print("=" * 80)
+ elif args.use_8bit_quantization:
+ bnb_config = BitsAndBytesConfig(load_in_8bit=args.use_8bit_quantization)
+
+ if args.use_unsloth:
+ if torch.xpu.is_available():
+ raise NotImplementedError("XPU hasn't supported unsloth yet")
+ # Load model
+ model, _ = FastLanguageModel.from_pretrained(
+ model_name=args.model_name_or_path,
+ max_seq_length=training_args.max_seq_length,
+ dtype=None,
+ load_in_4bit=args.use_4bit_quantization,
+ )
+ else:
+ torch_dtype = (
+ quant_storage_dtype if quant_storage_dtype and quant_storage_dtype.is_floating_point else torch.float32
+ )
+
+ # Prepare model loading arguments
+ model_kwargs = {
+ "trust_remote_code": True,
+ "torch_dtype": torch_dtype,
+ }
+ if args.use_flash_attn:
+ if torch.xpu.is_available():
+ print("XPU hasn't supported flash_attn yet, use eager implementation instead.")
+ model_kwargs["attn_implementation"] = "eager"
+ else:
+ model_kwargs["attn_implementation"] = "flash_attention_2"
+
+ # Only add quantization_config if bnb_config is not None
+ if bnb_config is not None:
+ model_kwargs["quantization_config"] = bnb_config
+
+ model = AutoModelForCausalLM.from_pretrained(args.model_name_or_path, **model_kwargs)
+
+ peft_config = None
+ chat_template = None
+ if args.use_peft_lora and not args.use_unsloth:
+ peft_config = LoraConfig(
+ lora_alpha=args.lora_alpha,
+ lora_dropout=args.lora_dropout,
+ r=args.lora_r,
+ bias="none",
+ task_type="CAUSAL_LM",
+ target_modules=args.lora_target_modules.split(",")
+ if args.lora_target_modules != "all-linear"
+ else args.lora_target_modules,
+ )
+
+ special_tokens = None
+ chat_template = None
+ if args.chat_template_format == "chatml":
+ special_tokens = ChatmlSpecialTokens
+ chat_template = DEFAULT_CHATML_CHAT_TEMPLATE
+ elif args.chat_template_format == "zephyr":
+ special_tokens = ZephyrSpecialTokens
+ chat_template = DEFAULT_ZEPHYR_CHAT_TEMPLATE
+
+ if special_tokens is not None:
+ tokenizer = AutoTokenizer.from_pretrained(
+ args.model_name_or_path,
+ pad_token=special_tokens.pad_token.value,
+ bos_token=special_tokens.bos_token.value,
+ eos_token=special_tokens.eos_token.value,
+ additional_special_tokens=special_tokens.list(),
+ trust_remote_code=True,
+ )
+ tokenizer.chat_template = chat_template
+
+ # make embedding resizing configurable?
+ # Transformers 4.46.0+ defaults uses mean_resizing by default, which fails with QLoRA + FSDP because the
+ # embedding could be on meta device, therefore, we set mean_resizing=False in that case (i.e. the status quo
+ # ante). See https://github.com/huggingface/accelerate/issues/1620.
+ uses_transformers_4_46 = packaging.version.parse(transformers.__version__) >= packaging.version.parse("4.46.0")
+ uses_fsdp = os.environ.get("ACCELERATE_USE_FSDP", "false").lower() == "true"
+ # Check if the model is quantized
+ is_quantized = (bnb_config is not None) or (getattr(model, "hf_quantizer", None) is not None)
+ if is_quantized and uses_fsdp and uses_transformers_4_46:
+ model.resize_token_embeddings(len(tokenizer), pad_to_multiple_of=8, mean_resizing=False)
+ else:
+ model.resize_token_embeddings(len(tokenizer), pad_to_multiple_of=8)
+ else:
+ tokenizer = AutoTokenizer.from_pretrained(args.model_name_or_path, trust_remote_code=True)
+ tokenizer.pad_token = tokenizer.eos_token
+
+ if args.use_unsloth:
+ # Do model patching and add fast LoRA weights
+ model = FastLanguageModel.get_peft_model(
+ model,
+ lora_alpha=args.lora_alpha,
+ lora_dropout=args.lora_dropout,
+ r=args.lora_r,
+ target_modules=args.lora_target_modules.split(",")
+ if args.lora_target_modules != "all-linear"
+ else args.lora_target_modules,
+ use_gradient_checkpointing=training_args.gradient_checkpointing,
+ random_state=training_args.seed,
+ max_seq_length=training_args.max_seq_length,
+ )
+
+ return model, peft_config, tokenizer
diff --git a/peft/examples/shira_finetuning/README.md b/peft/examples/shira_finetuning/README.md
new file mode 100644
index 0000000000000000000000000000000000000000..81bbf66374be4e4d4d0355a7e730992e20734982
--- /dev/null
+++ b/peft/examples/shira_finetuning/README.md
@@ -0,0 +1,73 @@
+# Sparse High Rank Adapters
+
+## Introduction
+Sparse High Rank Adapters or [SHiRA](https://arxiv.org/abs/2406.13175) is an alternate type of adapter and has been found to have significant advantages over the low rank adapters. Specifically, SHiRA achieves better accuracy than LoRA for a variety of vision and language tasks. It also offers simpler and higher quality multi-adapter fusion by significantly reducing concept loss, a common problem faced by low rank adapters. SHiRA directly finetunes a small number of the base model's parameters to finetune the model on any adaptation task.
+
+## Quick start
+```python
+import torch
+from peft import ShiraConfig, get_peft_model
+from transformers import AutoTokenizer, AutoModelForCausalLM
+from trl import SFTConfig, SFTTrainer
+from datasets import load_dataset
+
+model = AutoModelForCausalLM.from_pretrained("facebook/opt-350m", torch_dtype=torch.bfloat16, device_map="auto")
+tokenizer = AutoTokenizer.from_pretrained("facebook/opt-350m")
+dataset = load_dataset("imdb", split="train[:1%]")
+shira_config = ShiraConfig(
+ r=32,
+)
+peft_model = get_peft_model(model, shira_config)
+training_args = SFTConfig(dataset_text_field="text", max_seq_length=128)
+trainer = SFTTrainer(
+ model=peft_model,
+ train_dataset=dataset,
+ processing_class=tokenizer,
+)
+trainer.train()
+peft_model.save_pretrained("shira-opt-350m")
+```
+
+For more options and a more detailed example code, you can refer to shira finetuning script.
+Run the script simply by running:
+```bash
+python3 examples/shira_finetuning/shira_finetuning.py --base_model facebook/opt-350m
+```
+
+If you want to run DDP by [accelerate](https://huggingface.co/docs/accelerate/en/index), please run `accelerate config` to set your ddp config, and run:
+```bash
+accelerate launch examples/shira_finetuning/shira_finetuning.py --base_model facebook/opt-350m
+```
+please add `--device_map cpu` if you want to run finetune on CPU.
+
+If you want to train SHiRA with a custom sparse mask function which requires custom keyword arguments, please see the definition of `custom_random_mask_function_with_custom_kwargs` function provided in the `shira_fintuning.py` script. You can run this code using the `--use_custom_random_mask_function_with_custom_kwargs` argument. Without this argument, SHiRA defaults to a random sparse mask. Please run the code as follows. :
+```bash
+python3 examples/shira_finetuning/shira_finetuning.py --base_model facebook/opt-350m --use_custom_random_mask_function_with_custom_kwargs
+
+```
+
+
+## Use the model
+You can load and use the model as any other 🤗 PEFT model
+```python
+from peft import PeftModel
+from transformers import AutoTokenizer, AutoModelForCausalLM
+model = AutoModelForCausalLM.from_pretrained("facebook/opt-350m")
+tokenizer = AutoTokenizer.from_pretrained("facebook/opt-350m")
+shira_model = PeftModel.from_pretrained(model, "shira-opt-350m")
+```
+
+## Citation
+```
+@inproceedings{NEURIPS2024_18c0102c,
+ author = {Bhardwaj, Kartikeya and Pandey, Nilesh Prasad and Priyadarshi, Sweta and Ganapathy, Viswanath and Kadambi, Shreya and Esteves, Rafael and Borse, Shubhankar and Whatmough, Paul and Garrepalli, Risheek and Van Baalen, Mart and Teague, Harris and Nagel, Markus},
+ booktitle = {Advances in Neural Information Processing Systems},
+ editor = {A. Globerson and L. Mackey and D. Belgrave and A. Fan and U. Paquet and J. Tomczak and C. Zhang},
+ pages = {13685--13715},
+ publisher = {Curran Associates, Inc.},
+ title = {Sparse High Rank Adapters},
+ url = {https://proceedings.neurips.cc/paper_files/paper/2024/file/18c0102cb7f1a02c14f0929089b2e576-Paper-Conference.pdf},
+ volume = {37},
+ year = {2024}
+}
+```
diff --git a/peft/examples/shira_finetuning/shira_finetuning.py b/peft/examples/shira_finetuning/shira_finetuning.py
new file mode 100644
index 0000000000000000000000000000000000000000..b1f32d7cb62412fb79dbeebdfd6a7cc6998eb386
--- /dev/null
+++ b/peft/examples/shira_finetuning/shira_finetuning.py
@@ -0,0 +1,217 @@
+# Copyright 2025-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+
+import os
+from typing import Optional
+
+import torch
+import transformers
+from datasets import load_dataset
+from transformers import AutoModelForCausalLM, AutoTokenizer, set_seed
+
+from peft import (
+ PeftModel,
+ ShiraConfig,
+ get_peft_model,
+)
+
+
+def train(
+ base_model: str = "path/to/model",
+ data_path: str = "yahma/alpaca-cleaned",
+ output_dir: str = "shira",
+ batch_size: int = 16,
+ num_epochs: int = 1,
+ learning_rate: float = 3e-4,
+ cutoff_len: int = 256,
+ val_set_size: int = 16,
+ eval_step: int = 100,
+ save_step: int = 100,
+ device_map: str = "auto",
+ shira_r: int = 32,
+ shira_target_modules: list[str] = None,
+ torch_dtype: str = "float16",
+ seed: Optional[int] = None,
+ use_custom_random_mask_function_with_custom_kwargs: Optional[bool] = False,
+):
+ # Set device_map to the right place when enabling DDP.
+ world_size = int(os.environ.get("WORLD_SIZE", 0)) or int(os.environ.get("PMI_SIZE", 0))
+ if world_size > 1 and device_map != "cpu":
+ from accelerate import Accelerator
+
+ device_map = {"": Accelerator().process_index}
+ # Set seed
+ if seed is not None:
+ set_seed(seed)
+ model_kwargs = {"torch_dtype": getattr(torch, torch_dtype), "device_map": device_map}
+ model = AutoModelForCausalLM.from_pretrained(base_model, **model_kwargs)
+
+ tokenizer = AutoTokenizer.from_pretrained(base_model, trust_remote_code=True)
+ # For some tokenizer with no pad token like llama
+ if tokenizer.pad_token is None:
+ tokenizer.pad_token = tokenizer.eos_token
+
+ def tokenize(prompt, add_eos_token=True):
+ result = tokenizer(
+ prompt,
+ truncation=True,
+ max_length=cutoff_len,
+ padding=False,
+ return_tensors=None,
+ )
+ if (
+ result["input_ids"][-1] != tokenizer.eos_token_id
+ and len(result["input_ids"]) < cutoff_len
+ and add_eos_token
+ ):
+ result["input_ids"].append(tokenizer.eos_token_id)
+ result["attention_mask"].append(1)
+
+ result["labels"] = result["input_ids"].copy()
+
+ return result
+
+ def generate_and_tokenize_prompt(example):
+ full_prompt = generate_prompt(example)
+ tokenized_full_prompt = tokenize(full_prompt)
+ return tokenized_full_prompt
+
+ def custom_random_mask_function_with_custom_kwargs(custom_arg):
+ def mask_fn(base_layer, r):
+ """
+ This mask function is similar to the random_mask provided in src/peft/tuners/shira/mask_functions.py except the seed is derived from custom_kwargs.
+ Please use this as an example to create your own custom sparse masks that may use custom_kwargs. Remember, for a pretrained weight with shape m, n,
+ mask_fn must return only one mask (shape: m, n) which must be binary 0 or 1 with num_shira_parameters = r(m+n) for linear layers. Device and dtype
+ of mask must be same as base layer's weight's device and dtype.
+ """
+ new_seed = custom_arg
+ shape = base_layer.weight.shape
+ num_shira_weights = r * (shape[0] + shape[1])
+ random_generator = torch.Generator()
+ random_generator.manual_seed(new_seed)
+
+ idx = (torch.randperm(base_layer.weight.numel(), generator=random_generator)[:num_shira_weights]).to(
+ base_layer.weight.device
+ )
+ val = torch.ones_like(idx.type(base_layer.weight.dtype))
+ mask = torch.zeros_like(base_layer.weight.view(1, -1))
+ mask = mask.scatter_(1, idx.unsqueeze(0), val.unsqueeze(0)).view(shape)
+
+ return mask
+
+ return mask_fn
+
+ mask_type = "random" if not use_custom_random_mask_function_with_custom_kwargs else "custom"
+ config = ShiraConfig(
+ r=shira_r,
+ mask_type=mask_type,
+ target_modules=shira_target_modules,
+ task_type="CAUSAL_LM",
+ )
+ if use_custom_random_mask_function_with_custom_kwargs:
+ custom_arg = 120
+ custom_mask_fn = custom_random_mask_function_with_custom_kwargs(custom_arg)
+ config.mask_fn = custom_mask_fn
+
+ model = get_peft_model(model, config)
+
+ data = load_dataset(data_path)
+
+ train_val = data["train"].train_test_split(test_size=val_set_size, shuffle=True, seed=42)
+ train_data = train_val["train"].shuffle().map(generate_and_tokenize_prompt)
+ val_data = train_val["test"].shuffle().map(generate_and_tokenize_prompt)
+
+ trainer = transformers.Trainer(
+ model=model,
+ train_dataset=train_data,
+ eval_dataset=val_data,
+ args=transformers.TrainingArguments(
+ per_device_train_batch_size=batch_size,
+ warmup_steps=100,
+ num_train_epochs=num_epochs,
+ learning_rate=learning_rate,
+ logging_steps=100,
+ optim="adamw_torch",
+ eval_strategy="steps",
+ save_strategy="steps",
+ eval_steps=eval_step,
+ save_steps=save_step,
+ output_dir=output_dir,
+ save_total_limit=3,
+ load_best_model_at_end=True,
+ ddp_find_unused_parameters=False if world_size > 1 else None,
+ ),
+ data_collator=transformers.DataCollatorForSeq2Seq(
+ tokenizer, pad_to_multiple_of=8, return_tensors="pt", padding=True
+ ),
+ )
+ trainer.train()
+ model.save_pretrained(output_dir)
+
+ # Delete the model and load it again from the checkpoint.
+ del model
+ model = AutoModelForCausalLM.from_pretrained(base_model, **model_kwargs)
+ model = PeftModel.from_pretrained(model, output_dir)
+
+
+def generate_prompt(example):
+ return f"""Below is an instruction that describes a task. Write a response that appropriately completes the request.
+ ### Instruction:
+ {example["instruction"]}
+ ### Response:
+ {example["output"]}"""
+
+
+if __name__ == "__main__":
+ import argparse
+
+ parser = argparse.ArgumentParser()
+ parser.add_argument("--base_model", type=str, default="path/to/model")
+ parser.add_argument("--data_path", type=str, default="yahma/alpaca-cleaned")
+ parser.add_argument("--output_dir", type=str, default="shira")
+ parser.add_argument("--batch_size", type=int, default=16)
+ parser.add_argument("--num_epochs", type=int, default=1)
+ parser.add_argument("--learning_rate", type=float, default=3e-4)
+ parser.add_argument("--cutoff_len", type=int, default=256)
+ parser.add_argument("--val_set_size", type=int, default=16)
+ parser.add_argument("--eval_step", type=int, default=100)
+ parser.add_argument("--save_step", type=int, default=100)
+ parser.add_argument("--device_map", type=str, default="auto")
+ parser.add_argument("--shira_r", type=int, default=32)
+ parser.add_argument("--shira_target_modules", type=str, default=None)
+ parser.add_argument("--torch_dtype", type=str, default="float16")
+ parser.add_argument("--seed", type=int, default=None)
+ parser.add_argument("--use_custom_random_mask_function_with_custom_kwargs", action="store_true")
+
+ args = parser.parse_args()
+
+ train(
+ base_model=args.base_model,
+ data_path=args.data_path,
+ output_dir=args.output_dir,
+ batch_size=args.batch_size,
+ num_epochs=args.num_epochs,
+ learning_rate=args.learning_rate,
+ cutoff_len=args.cutoff_len,
+ val_set_size=args.val_set_size,
+ eval_step=args.eval_step,
+ save_step=args.save_step,
+ device_map=args.device_map,
+ shira_r=args.shira_r,
+ shira_target_modules=args.shira_target_modules,
+ torch_dtype=args.torch_dtype,
+ seed=args.seed,
+ use_custom_random_mask_function_with_custom_kwargs=args.use_custom_random_mask_function_with_custom_kwargs,
+ )
diff --git a/peft/examples/stable_diffusion/convert_sd_adapter_to_peft.py b/peft/examples/stable_diffusion/convert_sd_adapter_to_peft.py
new file mode 100644
index 0000000000000000000000000000000000000000..61712b1eea860347da08d6f30c7c51954f6e4194
--- /dev/null
+++ b/peft/examples/stable_diffusion/convert_sd_adapter_to_peft.py
@@ -0,0 +1,514 @@
+import argparse
+import json
+import logging
+import os
+from collections import Counter
+from dataclasses import dataclass
+from operator import attrgetter
+from typing import Optional, Union
+
+import safetensors
+import torch
+import torch.nn as nn
+from diffusers import UNet2DConditionModel
+from transformers import CLIPTextModel
+
+from peft import LoHaConfig, LoKrConfig, LoraConfig, PeftType, get_peft_model, set_peft_model_state_dict
+from peft.tuners.lokr.layer import factorization
+
+
+# Default kohya_ss LoRA replacement modules
+# https://github.com/kohya-ss/sd-scripts/blob/c924c47f374ac1b6e33e71f82948eb1853e2243f/networks/lora.py#L661
+UNET_TARGET_REPLACE_MODULE = ["Transformer2DModel", "Attention"]
+UNET_TARGET_REPLACE_MODULE_CONV2D_3X3 = ["ResnetBlock2D", "Downsample2D", "Upsample2D"]
+TEXT_ENCODER_TARGET_REPLACE_MODULE = ["CLIPAttention", "CLIPMLP"]
+PREFIX_UNET = "lora_unet"
+PREFIX_TEXT_ENCODER = "lora_te"
+
+
+@dataclass
+class LoRAInfo:
+ kohya_key: str
+ peft_key: str
+ alpha: Optional[float] = None
+ rank: Optional[int] = None
+ lora_A: Optional[torch.Tensor] = None
+ lora_B: Optional[torch.Tensor] = None
+
+ def peft_state_dict(self) -> dict[str, torch.Tensor]:
+ if self.lora_A is None or self.lora_B is None:
+ raise ValueError("At least one of lora_A or lora_B is None, they must both be provided")
+ return {
+ f"base_model.model.{self.peft_key}.lora_A.weight": self.lora_A,
+ f"base_model.model.{self.peft_key}.lora_B.weight": self.lora_B,
+ }
+
+
+@dataclass
+class LoHaInfo:
+ kohya_key: str
+ peft_key: str
+ alpha: Optional[float] = None
+ rank: Optional[int] = None
+ hada_w1_a: Optional[torch.Tensor] = None
+ hada_w1_b: Optional[torch.Tensor] = None
+ hada_w2_a: Optional[torch.Tensor] = None
+ hada_w2_b: Optional[torch.Tensor] = None
+ hada_t1: Optional[torch.Tensor] = None
+ hada_t2: Optional[torch.Tensor] = None
+
+ def peft_state_dict(self) -> dict[str, torch.Tensor]:
+ if self.hada_w1_a is None or self.hada_w1_b is None or self.hada_w2_a is None or self.hada_w2_b is None:
+ raise ValueError(
+ "At least one of hada_w1_a, hada_w1_b, hada_w2_a, hada_w2_b is missing, they all must be provided"
+ )
+ state_dict = {
+ f"base_model.model.{self.peft_key}.hada_w1_a": self.hada_w1_a,
+ f"base_model.model.{self.peft_key}.hada_w1_b": self.hada_w1_b,
+ f"base_model.model.{self.peft_key}.hada_w2_a": self.hada_w2_a,
+ f"base_model.model.{self.peft_key}.hada_w2_b": self.hada_w2_b,
+ }
+ if not (
+ (self.hada_t1 is None and self.hada_t2 is None) or (self.hada_t1 is not None and self.hada_t2 is not None)
+ ):
+ raise ValueError("hada_t1 and hada_t2 must be either both present or not present at the same time")
+ if self.hada_t1 is not None and self.hada_t2 is not None:
+ state_dict[f"base_model.model.{self.peft_key}.hada_t1"] = self.hada_t1
+ state_dict[f"base_model.model.{self.peft_key}.hada_t2"] = self.hada_t2
+ return state_dict
+
+
+@dataclass
+class LoKrInfo:
+ kohya_key: str
+ peft_key: str
+ alpha: Optional[float] = None
+ rank: Optional[int] = None
+ lokr_w1: Optional[torch.Tensor] = None
+ lokr_w1_a: Optional[torch.Tensor] = None
+ lokr_w1_b: Optional[torch.Tensor] = None
+ lokr_w2: Optional[torch.Tensor] = None
+ lokr_w2_a: Optional[torch.Tensor] = None
+ lokr_w2_b: Optional[torch.Tensor] = None
+ lokr_t2: Optional[torch.Tensor] = None
+
+ def peft_state_dict(self) -> dict[str, torch.Tensor]:
+ if (self.lokr_w1 is None) and ((self.lokr_w1_a is None) or (self.lokr_w1_b is None)):
+ raise ValueError("Either lokr_w1 or both lokr_w1_a and lokr_w1_b should be provided")
+
+ if (self.lokr_w2 is None) and ((self.lokr_w2_a is None) or (self.lokr_w2_b is None)):
+ raise ValueError("Either lokr_w2 or both lokr_w2_a and lokr_w2_b should be provided")
+
+ state_dict = {}
+
+ if self.lokr_w1 is not None:
+ state_dict[f"base_model.model.{self.peft_key}.lokr_w1"] = self.lokr_w1
+ elif self.lokr_w1_a is not None:
+ state_dict[f"base_model.model.{self.peft_key}.lokr_w1_a"] = self.lokr_w1_a
+ state_dict[f"base_model.model.{self.peft_key}.lokr_w1_b"] = self.lokr_w1_b
+
+ if self.lokr_w2 is not None:
+ state_dict[f"base_model.model.{self.peft_key}.lokr_w2"] = self.lokr_w2
+ elif self.lokr_w2_a is not None:
+ state_dict[f"base_model.model.{self.peft_key}.lokr_w2_a"] = self.lokr_w2_a
+ state_dict[f"base_model.model.{self.peft_key}.lokr_w2_b"] = self.lokr_w2_b
+
+ if self.lokr_t2 is not None:
+ state_dict[f"base_model.model.{self.peft_key}.lokr_t2"] = self.lokr_t2
+
+ return state_dict
+
+
+def construct_peft_loraconfig(info: dict[str, LoRAInfo], **kwargs) -> LoraConfig:
+ """Constructs LoraConfig from data extracted from adapter checkpoint
+
+ Args:
+ info (Dict[str, LoRAInfo]): Information extracted from adapter checkpoint
+
+ Returns:
+ LoraConfig: config for constructing LoRA
+ """
+
+ # Unpack all ranks and alphas
+ ranks = {key: val.rank for key, val in info.items()}
+ alphas = {x[0]: x[1].alpha or x[1].rank for x in info.items()}
+
+ # Determine which modules needs to be transformed
+ target_modules = sorted(info.keys())
+
+ # Determine most common rank and alpha
+ r = int(Counter(ranks.values()).most_common(1)[0][0])
+ lora_alpha = Counter(alphas.values()).most_common(1)[0][0]
+
+ # Determine which modules have different rank and alpha
+ rank_pattern = dict(sorted(filter(lambda x: x[1] != r, ranks.items()), key=lambda x: x[0]))
+ alpha_pattern = dict(sorted(filter(lambda x: x[1] != lora_alpha, alphas.items()), key=lambda x: x[0]))
+
+ config = LoraConfig(
+ r=r,
+ lora_alpha=lora_alpha,
+ target_modules=target_modules,
+ lora_dropout=0.0,
+ bias="none",
+ init_lora_weights=False,
+ rank_pattern=rank_pattern,
+ alpha_pattern=alpha_pattern,
+ )
+
+ return config
+
+
+def construct_peft_lohaconfig(info: dict[str, LoHaInfo], **kwargs) -> LoHaConfig:
+ """Constructs LoHaConfig from data extracted from adapter checkpoint
+
+ Args:
+ info (Dict[str, LoHaInfo]): Information extracted from adapter checkpoint
+
+ Returns:
+ LoHaConfig: config for constructing LoHA
+ """
+
+ # Unpack all ranks and alphas
+ ranks = {x[0]: x[1].rank for x in info.items()}
+ alphas = {x[0]: x[1].alpha or x[1].rank for x in info.items()}
+
+ # Determine which modules needs to be transformed
+ target_modules = sorted(info.keys())
+
+ # Determine most common rank and alpha
+ r = int(Counter(ranks.values()).most_common(1)[0][0])
+ alpha = Counter(alphas.values()).most_common(1)[0][0]
+
+ # Determine which modules have different rank and alpha
+ rank_pattern = dict(sorted(filter(lambda x: x[1] != r, ranks.items()), key=lambda x: x[0]))
+ alpha_pattern = dict(sorted(filter(lambda x: x[1] != alpha, alphas.items()), key=lambda x: x[0]))
+
+ # Determine whether any of modules have effective conv2d decomposition
+ use_effective_conv2d = any((val.hada_t1 is not None) or (val.hada_t2 is not None) for val in info.values())
+
+ config = LoHaConfig(
+ r=r,
+ alpha=alpha,
+ target_modules=target_modules,
+ rank_dropout=0.0,
+ module_dropout=0.0,
+ init_weights=False,
+ rank_pattern=rank_pattern,
+ alpha_pattern=alpha_pattern,
+ use_effective_conv2d=use_effective_conv2d,
+ )
+
+ return config
+
+
+def construct_peft_lokrconfig(info: dict[str, LoKrInfo], decompose_factor: int = -1, **kwargs) -> LoKrConfig:
+ """Constructs LoKrConfig from data extracted from adapter checkpoint
+
+ Args:
+ info (Dict[str, LoKrInfo]): Information extracted from adapter checkpoint
+
+ Returns:
+ LoKrConfig: config for constructing LoKr
+ """
+
+ # Unpack all ranks and alphas
+ ranks = {x[0]: x[1].rank for x in info.items()}
+ alphas = {x[0]: x[1].alpha or x[1].rank for x in info.items()}
+
+ # Determine which modules needs to be transformed
+ target_modules = sorted(info.keys())
+
+ # Determine most common rank and alpha
+ r = int(Counter(ranks.values()).most_common(1)[0][0])
+ alpha = Counter(alphas.values()).most_common(1)[0][0]
+
+ # Determine which modules have different rank and alpha
+ rank_pattern = dict(sorted(filter(lambda x: x[1] != r, ranks.items()), key=lambda x: x[0]))
+ alpha_pattern = dict(sorted(filter(lambda x: x[1] != alpha, alphas.items()), key=lambda x: x[0]))
+
+ # Determine whether any of modules have effective conv2d decomposition
+ use_effective_conv2d = any((val.lokr_t2 is not None) for val in info.values())
+
+ # decompose_both should be enabled if any w1 matrix in any layer is decomposed into 2
+ decompose_both = any((val.lokr_w1_a is not None and val.lokr_w1_b is not None) for val in info.values())
+
+ # Determining decompose factor is a bit tricky (but it is most often -1)
+ # Check that decompose_factor is equal to provided
+ for val in info.values():
+ # Determine shape of first matrix
+ if val.lokr_w1 is not None:
+ w1_shape = tuple(val.lokr_w1.shape)
+ else:
+ w1_shape = (val.lokr_w1_a.shape[0], val.lokr_w1_b.shape[1])
+
+ # Determine shape of second matrix
+ if val.lokr_w2 is not None:
+ w2_shape = tuple(val.lokr_w2.shape[:2])
+ elif val.lokr_t2 is not None:
+ w2_shape = (val.lokr_w2_a.shape[1], val.lokr_w2_b.shape[1])
+ else:
+ # We may iterate over Conv2d layer, for which second item in shape is multiplied by ksize^2
+ w2_shape = (val.lokr_w2_a.shape[0], val.lokr_w2_b.shape[1])
+
+ # We need to check, whether decompose_factor is really -1 or not
+ shape = (w1_shape[0], w2_shape[0])
+ if factorization(shape[0] * shape[1], factor=-1) != shape:
+ raise ValueError("Cannot infer decompose_factor, probably it is not equal to -1")
+
+ config = LoKrConfig(
+ r=r,
+ alpha=alpha,
+ target_modules=target_modules,
+ rank_dropout=0.0,
+ module_dropout=0.0,
+ init_weights=False,
+ rank_pattern=rank_pattern,
+ alpha_pattern=alpha_pattern,
+ use_effective_conv2d=use_effective_conv2d,
+ decompose_both=decompose_both,
+ decompose_factor=decompose_factor,
+ )
+
+ return config
+
+
+def combine_peft_state_dict(info: dict[str, Union[LoRAInfo, LoHaInfo]]) -> dict[str, torch.Tensor]:
+ result = {}
+ for key_info in info.values():
+ result.update(key_info.peft_state_dict())
+ return result
+
+
+def detect_adapter_type(keys: list[str]) -> PeftType:
+ # Detect type of adapter by keys
+ # Inspired by this:
+ # https://github.com/bmaltais/kohya_ss/blob/ed4e3b0239a40506de9a17e550e6cf2d0b867a4f/tools/lycoris_utils.py#L312
+ for key in keys:
+ if "alpha" in key:
+ continue
+ elif any(x in key for x in ["lora_down", "lora_up"]):
+ # LoRA
+ return PeftType.LORA
+ elif any(x in key for x in ["hada_w1", "hada_w2", "hada_t1", "hada_t2"]):
+ # LoHa may have the following keys:
+ # hada_w1_a, hada_w1_b, hada_w2_a, hada_w2_b, hada_t1, hada_t2
+ return PeftType.LOHA
+ elif any(x in key for x in ["lokr_w1", "lokr_w2", "lokr_t1", "lokr_t2"]):
+ # LoKr may have the following keys:
+ # lokr_w1, lokr_w2, lokr_w1_a, lokr_w1_b, lokr_w2_a, lokr_w2_b, lokr_t1, lokr_t2
+ return PeftType.LOKR
+ elif "diff" in key:
+ raise ValueError("Currently full diff adapters are not implemented")
+ else:
+ raise ValueError("Unknown adapter type, probably not implemented")
+
+
+if __name__ == "__main__":
+ parser = argparse.ArgumentParser()
+
+ parser.add_argument("--sd_checkpoint", default=None, type=str, required=True, help="SD checkpoint to use")
+
+ parser.add_argument(
+ "--adapter_path",
+ default=None,
+ type=str,
+ required=True,
+ help="Path to downloaded adapter to convert",
+ )
+
+ parser.add_argument("--dump_path", default=None, type=str, required=True, help="Path to the output peft adapter.")
+
+ parser.add_argument("--half", action="store_true", help="Save weights in half precision.")
+ parser.add_argument(
+ "--loha_conv2d_weights_fix",
+ action="store_true",
+ help="""LoHa checkpoints trained with lycoris-lora<=1.9.0 contain a bug described in this PR https://github.com/KohakuBlueleaf/LyCORIS/pull/115.
+ This option fixes this bug during weight conversion (replaces hada_t2 with hada_t1 for Conv2d 3x3 layers).
+ The output results may differ from webui, but in general, they should be better in terms of quality.
+ This option should be set to True in case the provided checkpoint has been trained with lycoris-lora version for which the mentioned PR wasn't merged.
+ This option should be set to False in case the provided checkpoint has been trained with lycoris-lora version for which the mentioned PR is merged or full compatibility with webui outputs is required.""",
+ )
+ args = parser.parse_args()
+
+ # Load all models that we need to add adapter to
+ text_encoder = CLIPTextModel.from_pretrained(args.sd_checkpoint, subfolder="text_encoder")
+ unet = UNet2DConditionModel.from_pretrained(args.sd_checkpoint, subfolder="unet")
+
+ # Construct possible mapping from kohya keys to peft keys
+ models_keys = {}
+ for model, model_key, model_name in [
+ (text_encoder, PREFIX_TEXT_ENCODER, "text_encoder"),
+ (unet, PREFIX_UNET, "unet"),
+ ]:
+ models_keys.update(
+ {
+ f"{model_key}.{peft_key}".replace(".", "_"): peft_key
+ for peft_key in (x[0] for x in model.named_modules())
+ }
+ )
+
+ # Store conversion info (model_type -> peft_key -> LoRAInfo | LoHaInfo | LoKrInfo)
+ adapter_info: dict[str, dict[str, Union[LoRAInfo, LoHaInfo, LoKrInfo]]] = {
+ "text_encoder": {},
+ "unet": {},
+ }
+
+ # Store decompose_factor for LoKr
+ decompose_factor = -1
+
+ # Open adapter checkpoint
+ with safetensors.safe_open(args.adapter_path, framework="pt", device="cpu") as f:
+ # Extract information about adapter structure
+ metadata = f.metadata()
+
+ # It may be difficult to determine rank for LoKr adapters
+ # If checkpoint was trained with large rank it may not be utilized during weights creation at all
+ # So we need to get it from checkpoint metadata (along with decompose_factor)
+ rank, conv_rank = None, None
+ if metadata is not None:
+ rank = metadata.get("ss_network_dim", None)
+ rank = int(rank) if rank else None
+ if "ss_network_args" in metadata:
+ network_args = json.loads(metadata["ss_network_args"])
+ conv_rank = network_args.get("conv_dim", None)
+ conv_rank = int(conv_rank) if conv_rank else rank
+ decompose_factor = network_args.get("factor", -1)
+ decompose_factor = int(decompose_factor)
+
+ # Detect adapter type based on keys
+ adapter_type = detect_adapter_type(f.keys())
+ adapter_info_cls = {
+ PeftType.LORA: LoRAInfo,
+ PeftType.LOHA: LoHaInfo,
+ PeftType.LOKR: LoKrInfo,
+ }[adapter_type]
+
+ # Iterate through available info and unpack all the values
+ for key in f.keys():
+ kohya_key, kohya_type = key.split(".")[:2]
+
+ # Find which model this key belongs to
+ if kohya_key.startswith(PREFIX_TEXT_ENCODER):
+ model_type, model = "text_encoder", text_encoder
+ elif kohya_key.startswith(PREFIX_UNET):
+ model_type, model = "unet", unet
+ else:
+ raise ValueError(f"Cannot determine model for key: {key}")
+
+ # Find corresponding peft key
+ if kohya_key not in models_keys:
+ raise ValueError(f"Cannot find corresponding key for diffusers/transformers model: {kohya_key}")
+ peft_key = models_keys[kohya_key]
+
+ # Retrieve corresponding layer of model
+ layer = attrgetter(peft_key)(model)
+
+ # Create a corresponding adapter info
+ if peft_key not in adapter_info[model_type]:
+ adapter_info[model_type][peft_key] = adapter_info_cls(kohya_key=kohya_key, peft_key=peft_key)
+
+ tensor = f.get_tensor(key)
+ if kohya_type == "alpha":
+ adapter_info[model_type][peft_key].alpha = tensor.item()
+ elif kohya_type == "lora_down":
+ adapter_info[model_type][peft_key].lora_A = tensor
+ adapter_info[model_type][peft_key].rank = tensor.shape[0]
+ elif kohya_type == "lora_up":
+ adapter_info[model_type][peft_key].lora_B = tensor
+ adapter_info[model_type][peft_key].rank = tensor.shape[1]
+ elif kohya_type == "hada_w1_a":
+ adapter_info[model_type][peft_key].hada_w1_a = tensor
+ elif kohya_type == "hada_w1_b":
+ adapter_info[model_type][peft_key].hada_w1_b = tensor
+ adapter_info[model_type][peft_key].rank = tensor.shape[0]
+ elif kohya_type == "hada_w2_a":
+ adapter_info[model_type][peft_key].hada_w2_a = tensor
+ elif kohya_type == "hada_w2_b":
+ adapter_info[model_type][peft_key].hada_w2_b = tensor
+ adapter_info[model_type][peft_key].rank = tensor.shape[0]
+ elif kohya_type in {"hada_t1", "hada_t2"}:
+ if args.loha_conv2d_weights_fix:
+ if kohya_type == "hada_t1":
+ # This code block fixes a bug that exists for some LoHa checkpoints
+ # that resulted in accidentally using hada_t1 weight instead of hada_t2, see
+ # https://github.com/KohakuBlueleaf/LyCORIS/pull/115
+ adapter_info[model_type][peft_key].hada_t1 = tensor
+ adapter_info[model_type][peft_key].hada_t2 = tensor
+ adapter_info[model_type][peft_key].rank = tensor.shape[0]
+ else:
+ if kohya_type == "hada_t1":
+ adapter_info[model_type][peft_key].hada_t1 = tensor
+ adapter_info[model_type][peft_key].rank = tensor.shape[0]
+ elif kohya_type == "hada_t2":
+ adapter_info[model_type][peft_key].hada_t2 = tensor
+ adapter_info[model_type][peft_key].rank = tensor.shape[0]
+ elif kohya_type == "lokr_t2":
+ adapter_info[model_type][peft_key].lokr_t2 = tensor
+ adapter_info[model_type][peft_key].rank = tensor.shape[0]
+ elif kohya_type == "lokr_w1":
+ adapter_info[model_type][peft_key].lokr_w1 = tensor
+ if isinstance(layer, nn.Linear) or (
+ isinstance(layer, nn.Conv2d) and tuple(layer.weight.shape[2:]) == (1, 1)
+ ):
+ adapter_info[model_type][peft_key].rank = rank
+ elif isinstance(layer, nn.Conv2d):
+ adapter_info[model_type][peft_key].rank = conv_rank
+ elif kohya_type == "lokr_w2":
+ adapter_info[model_type][peft_key].lokr_w2 = tensor
+ if isinstance(layer, nn.Linear) or (
+ isinstance(layer, nn.Conv2d) and tuple(layer.weight.shape[2:]) == (1, 1)
+ ):
+ adapter_info[model_type][peft_key].rank = rank
+ elif isinstance(layer, nn.Conv2d):
+ adapter_info[model_type][peft_key].rank = conv_rank
+ elif kohya_type == "lokr_w1_a":
+ adapter_info[model_type][peft_key].lokr_w1_a = tensor
+ adapter_info[model_type][peft_key].rank = tensor.shape[1]
+ elif kohya_type == "lokr_w1_b":
+ adapter_info[model_type][peft_key].lokr_w1_b = tensor
+ adapter_info[model_type][peft_key].rank = tensor.shape[0]
+ elif kohya_type == "lokr_w2_a":
+ adapter_info[model_type][peft_key].lokr_w2_a = tensor
+ elif kohya_type == "lokr_w2_b":
+ adapter_info[model_type][peft_key].lokr_w2_b = tensor
+ else:
+ raise ValueError(f"Unknown weight name in key: {key} - {kohya_type}")
+
+ # Get function which will create adapter config based on extracted info
+ construct_config_fn = {
+ PeftType.LORA: construct_peft_loraconfig,
+ PeftType.LOHA: construct_peft_lohaconfig,
+ PeftType.LOKR: construct_peft_lokrconfig,
+ }[adapter_type]
+
+ # Process each model sequentially
+ for model, model_name in [(text_encoder, "text_encoder"), (unet, "unet")]:
+ # Skip model if no data was provided
+ if len(adapter_info[model_name]) == 0:
+ continue
+
+ config = construct_config_fn(adapter_info[model_name], decompose_factor=decompose_factor)
+
+ # Output warning for LoHa with use_effective_conv2d
+ if (
+ isinstance(config, LoHaConfig)
+ and getattr(config, "use_effective_conv2d", False)
+ and args.loha_conv2d_weights_fix is False
+ ):
+ logging.warning(
+ 'lycoris-lora<=1.9.0 LoHa implementation contains a bug, which can be fixed with "--loha_conv2d_weights_fix".\n'
+ "For more info, please refer to https://github.com/huggingface/peft/pull/1021 and https://github.com/KohakuBlueleaf/LyCORIS/pull/115"
+ )
+
+ model = get_peft_model(model, config)
+ missing_keys, unexpected_keys = set_peft_model_state_dict(
+ model, combine_peft_state_dict(adapter_info[model_name])
+ )
+ if len(unexpected_keys) > 0:
+ raise ValueError(f"Unexpected keys {unexpected_keys} found during conversion")
+
+ if args.half:
+ model.to(torch.float16)
+
+ # Save model to disk
+ model.save_pretrained(os.path.join(args.dump_path, model_name))
diff --git a/peft/examples/stable_diffusion/inc_flux_lora_hpu.py b/peft/examples/stable_diffusion/inc_flux_lora_hpu.py
new file mode 100644
index 0000000000000000000000000000000000000000..5c0b24928100c3756a3c7148a740dfeb48cbe9f2
--- /dev/null
+++ b/peft/examples/stable_diffusion/inc_flux_lora_hpu.py
@@ -0,0 +1,67 @@
+"""
+This exampe demonstrates loading of LoRA adapter (via PEFT) into an FP8 INC-quantized FLUX model.
+
+More info on Intel Neural Compressor (INC) FP8 quantization is available at:
+https://github.com/intel/neural-compressor/tree/master/examples/helloworld/fp8_example
+
+Requirements:
+pip install optimum-habana sentencepiece neural-compressor[pt] peft
+"""
+
+import importlib
+
+import torch
+from neural_compressor.torch.quantization import FP8Config, convert, finalize_calibration, prepare
+
+
+# Checks if HPU device is available
+# Adapted from https://github.com/huggingface/accelerate/blob/b451956fd69a135efc283aadaa478f0d33fcbe6a/src/accelerate/utils/imports.py#L435
+def is_hpu_available():
+ if (
+ importlib.util.find_spec("habana_frameworks") is None
+ or importlib.util.find_spec("habana_frameworks.torch") is None
+ ):
+ return False
+
+ import habana_frameworks.torch # noqa: F401
+
+ return hasattr(torch, "hpu") and torch.hpu.is_available()
+
+
+# Ensure HPU device is available before proceeding
+if is_hpu_available():
+ from optimum.habana.diffusers import GaudiFluxPipeline
+else:
+ raise RuntimeError("HPU device not found. This code requires Intel Gaudi device to run.")
+
+# Example: FLUX model inference on HPU via optimum-habana pipeline
+hpu_configs = {
+ "use_habana": True,
+ "use_hpu_graphs": True,
+ "sdp_on_bf16": True,
+ "gaudi_config": "Habana/stable-diffusion",
+}
+pipe = GaudiFluxPipeline.from_pretrained("black-forest-labs/FLUX.1-dev", torch_dtype=torch.bfloat16, **hpu_configs)
+prompt = "A picture of sks dog in a bucket"
+
+# Quantize FLUX transformer to FP8 using INC (Intel Neural Compressor)
+quant_configs = {
+ "mode": "AUTO",
+ "observer": "maxabs",
+ "scale_method": "maxabs_hw",
+ "allowlist": {"types": [], "names": []},
+ "blocklist": {"types": [], "names": []},
+ "dump_stats_path": "/tmp/hqt_output/measure",
+}
+config = FP8Config(**quant_configs)
+pipe.transformer = prepare(pipe.transformer, config)
+pipe(prompt)
+finalize_calibration(pipe.transformer)
+pipe.transformer = convert(pipe.transformer)
+
+# Load LoRA weights with PEFT
+pipe.load_lora_weights("dsocek/lora-flux-dog", adapter_name="user_lora")
+
+# Run inference
+image = pipe(prompt).images[0]
+image.save("dog.png")
diff --git a/peft/examples/stable_diffusion/train_dreambooth.py b/peft/examples/stable_diffusion/train_dreambooth.py
new file mode 100644
index 0000000000000000000000000000000000000000..9af5fee335d0ce210bd85ae45c2185cd6cffa471
--- /dev/null
+++ b/peft/examples/stable_diffusion/train_dreambooth.py
@@ -0,0 +1,1275 @@
+import argparse
+import gc
+import hashlib
+import itertools
+import logging
+import math
+import os
+import threading
+import warnings
+from pathlib import Path
+from typing import Union
+
+import datasets
+import diffusers
+import numpy as np
+import psutil
+import torch
+import torch.nn.functional as F
+import torch.utils.checkpoint
+import transformers
+from accelerate import Accelerator
+from accelerate.logging import get_logger
+from accelerate.utils import set_seed
+from diffusers import (
+ AutoencoderKL,
+ DDPMScheduler,
+ DiffusionPipeline,
+ DPMSolverMultistepScheduler,
+ UNet2DConditionModel,
+)
+from diffusers.optimization import get_scheduler
+from diffusers.utils import check_min_version
+from diffusers.utils.import_utils import is_xformers_available
+from huggingface_hub import HfApi
+from PIL import Image
+from torch.utils.data import Dataset
+from torchvision import transforms
+from tqdm.auto import tqdm
+from transformers import AutoTokenizer, PretrainedConfig
+
+from peft import LoHaConfig, LoKrConfig, LoraConfig, get_peft_model
+
+
+# Will error if the minimal version of diffusers is not installed. Remove at your own risks.
+check_min_version("0.10.0.dev0")
+
+logger = get_logger(__name__)
+
+UNET_TARGET_MODULES = [
+ "to_q",
+ "to_k",
+ "to_v",
+ "proj",
+ "proj_in",
+ "proj_out",
+ "conv",
+ "conv1",
+ "conv2",
+ "conv_shortcut",
+ "to_out.0",
+ "time_emb_proj",
+ "ff.net.2",
+]
+
+TEXT_ENCODER_TARGET_MODULES = ["fc1", "fc2", "q_proj", "k_proj", "v_proj", "out_proj"]
+
+
+def import_model_class_from_model_name_or_path(pretrained_model_name_or_path: str, revision: str):
+ text_encoder_config = PretrainedConfig.from_pretrained(
+ pretrained_model_name_or_path,
+ subfolder="text_encoder",
+ revision=revision,
+ )
+ model_class = text_encoder_config.architectures[0]
+
+ if model_class == "CLIPTextModel":
+ from transformers import CLIPTextModel
+
+ return CLIPTextModel
+ elif model_class == "RobertaSeriesModelWithTransformation":
+ from diffusers.pipelines.alt_diffusion.modeling_roberta_series import RobertaSeriesModelWithTransformation
+
+ return RobertaSeriesModelWithTransformation
+ else:
+ raise ValueError(f"{model_class} is not supported.")
+
+
+def create_unet_adapter_config(args: argparse.Namespace) -> Union[LoraConfig, LoHaConfig, LoKrConfig]:
+ if args.adapter == "full":
+ raise ValueError("Cannot create unet adapter config for full parameter")
+
+ if args.adapter == "lora":
+ config = LoraConfig(
+ r=args.unet_r,
+ lora_alpha=args.unet_alpha,
+ target_modules=UNET_TARGET_MODULES,
+ lora_dropout=args.unet_dropout,
+ bias=args.unet_bias,
+ init_lora_weights=True,
+ )
+ elif args.adapter == "loha":
+ config = LoHaConfig(
+ r=args.unet_r,
+ alpha=args.unet_alpha,
+ target_modules=UNET_TARGET_MODULES,
+ rank_dropout=args.unet_rank_dropout,
+ module_dropout=args.unet_module_dropout,
+ use_effective_conv2d=args.unet_use_effective_conv2d,
+ init_weights=True,
+ )
+ elif args.adapter == "lokr":
+ config = LoKrConfig(
+ r=args.unet_r,
+ alpha=args.unet_alpha,
+ target_modules=UNET_TARGET_MODULES,
+ rank_dropout=args.unet_rank_dropout,
+ module_dropout=args.unet_module_dropout,
+ use_effective_conv2d=args.unet_use_effective_conv2d,
+ decompose_both=args.unet_decompose_both,
+ decompose_factor=args.unet_decompose_factor,
+ init_weights=True,
+ )
+ else:
+ raise ValueError(f"Unknown adapter type {args.adapter}")
+
+ return config
+
+
+def create_text_encoder_adapter_config(args: argparse.Namespace) -> Union[LoraConfig, LoHaConfig, LoKrConfig]:
+ if args.adapter == "full":
+ raise ValueError("Cannot create text_encoder adapter config for full parameter")
+
+ if args.adapter == "lora":
+ config = LoraConfig(
+ r=args.te_r,
+ lora_alpha=args.te_alpha,
+ target_modules=TEXT_ENCODER_TARGET_MODULES,
+ lora_dropout=args.te_dropout,
+ bias=args.te_bias,
+ init_lora_weights=True,
+ )
+ elif args.adapter == "loha":
+ config = LoHaConfig(
+ r=args.te_r,
+ alpha=args.te_alpha,
+ target_modules=TEXT_ENCODER_TARGET_MODULES,
+ rank_dropout=args.te_rank_dropout,
+ module_dropout=args.te_module_dropout,
+ init_weights=True,
+ )
+ elif args.adapter == "lokr":
+ config = LoKrConfig(
+ r=args.te_r,
+ alpha=args.te_alpha,
+ target_modules=TEXT_ENCODER_TARGET_MODULES,
+ rank_dropout=args.te_rank_dropout,
+ module_dropout=args.te_module_dropout,
+ decompose_both=args.te_decompose_both,
+ decompose_factor=args.te_decompose_factor,
+ init_weights=True,
+ )
+ else:
+ raise ValueError(f"Unknown adapter type {args.adapter}")
+
+ return config
+
+
+def parse_args(input_args=None):
+ parser = argparse.ArgumentParser(description="Simple example of a training script.")
+ parser.add_argument(
+ "--pretrained_model_name_or_path",
+ type=str,
+ default=None,
+ required=True,
+ help="Path to pretrained model or model identifier from huggingface.co/models.",
+ )
+ parser.add_argument(
+ "--revision",
+ type=str,
+ default=None,
+ required=False,
+ help="Revision of pretrained model identifier from huggingface.co/models.",
+ )
+ parser.add_argument(
+ "--tokenizer_name",
+ type=str,
+ default=None,
+ help="Pretrained tokenizer name or path if not the same as model_name",
+ )
+ parser.add_argument(
+ "--instance_data_dir",
+ type=str,
+ default=None,
+ required=True,
+ help="A folder containing the training data of instance images.",
+ )
+ parser.add_argument(
+ "--class_data_dir",
+ type=str,
+ default=None,
+ required=False,
+ help="A folder containing the training data of class images.",
+ )
+ parser.add_argument(
+ "--instance_prompt",
+ type=str,
+ default=None,
+ required=True,
+ help="The prompt with identifier specifying the instance",
+ )
+ parser.add_argument(
+ "--class_prompt",
+ type=str,
+ default=None,
+ help="The prompt to specify images in the same class as provided instance images.",
+ )
+ parser.add_argument(
+ "--with_prior_preservation",
+ default=False,
+ action="store_true",
+ help="Flag to add prior preservation loss.",
+ )
+ parser.add_argument("--prior_loss_weight", type=float, default=1.0, help="The weight of prior preservation loss.")
+ parser.add_argument(
+ "--num_class_images",
+ type=int,
+ default=100,
+ help=(
+ "Minimal class images for prior preservation loss. If there are not enough images already present in"
+ " class_data_dir, additional images will be sampled with class_prompt."
+ ),
+ )
+ parser.add_argument(
+ "--validation_prompt",
+ type=str,
+ default=None,
+ help="A prompt that is used during validation to verify that the model is learning.",
+ )
+ parser.add_argument(
+ "--num_validation_images",
+ type=int,
+ default=4,
+ help="Number of images that should be generated during validation with `validation_prompt`.",
+ )
+ parser.add_argument(
+ "--validation_steps",
+ type=int,
+ default=100,
+ help=(
+ "Run dreambooth validation every X steps. Dreambooth validation consists of running the prompt"
+ " `args.validation_prompt` multiple times: `args.num_validation_images`."
+ ),
+ )
+ parser.add_argument(
+ "--output_dir",
+ type=str,
+ default="text-inversion-model",
+ help="The output directory where the model predictions and checkpoints will be written.",
+ )
+ parser.add_argument("--seed", type=int, default=None, help="A seed for reproducible training.")
+ parser.add_argument(
+ "--resolution",
+ type=int,
+ default=512,
+ help=(
+ "The resolution for input images, all the images in the train/validation dataset will be resized to this"
+ " resolution"
+ ),
+ )
+ parser.add_argument(
+ "--center_crop", action="store_true", help="Whether to center crop images before resizing to resolution"
+ )
+ parser.add_argument("--train_text_encoder", action="store_true", help="Whether to train the text encoder")
+
+ parser.add_argument(
+ "--train_batch_size", type=int, default=4, help="Batch size (per device) for the training dataloader."
+ )
+ parser.add_argument(
+ "--sample_batch_size", type=int, default=4, help="Batch size (per device) for sampling images."
+ )
+ parser.add_argument("--num_train_epochs", type=int, default=1)
+ parser.add_argument(
+ "--max_train_steps",
+ type=int,
+ default=None,
+ help="Total number of training steps to perform. If provided, overrides num_train_epochs.",
+ )
+ parser.add_argument(
+ "--checkpointing_steps",
+ type=int,
+ default=500,
+ help=(
+ "Save a checkpoint of the training state every X updates. These checkpoints can be used both as final"
+ " checkpoints in case they are better than the last checkpoint, and are also suitable for resuming"
+ " training using `--resume_from_checkpoint`."
+ ),
+ )
+ parser.add_argument(
+ "--resume_from_checkpoint",
+ type=str,
+ default=None,
+ help=(
+ "Whether training should be resumed from a previous checkpoint. Use a path saved by"
+ ' `--checkpointing_steps`, or `"latest"` to automatically select the last available checkpoint.'
+ ),
+ )
+ parser.add_argument(
+ "--gradient_accumulation_steps",
+ type=int,
+ default=1,
+ help="Number of updates steps to accumulate before performing a backward/update pass.",
+ )
+ parser.add_argument(
+ "--gradient_checkpointing",
+ action="store_true",
+ help="Whether or not to use gradient checkpointing to save memory at the expense of slower backward pass.",
+ )
+ parser.add_argument(
+ "--learning_rate",
+ type=float,
+ default=5e-6,
+ help="Initial learning rate (after the potential warmup period) to use.",
+ )
+ parser.add_argument(
+ "--scale_lr",
+ action="store_true",
+ default=False,
+ help="Scale the learning rate by the number of accelerators, gradient accumulation steps, and batch size.",
+ )
+ parser.add_argument(
+ "--lr_scheduler",
+ type=str,
+ default="constant",
+ help=(
+ 'The scheduler type to use. Choose between ["linear", "cosine", "cosine_with_restarts", "polynomial",'
+ ' "constant", "constant_with_warmup"]'
+ ),
+ )
+ parser.add_argument(
+ "--lr_warmup_steps", type=int, default=500, help="Number of steps for the warmup in the lr scheduler."
+ )
+ parser.add_argument(
+ "--lr_num_cycles",
+ type=int,
+ default=1,
+ help="Number of hard resets of the lr in cosine_with_restarts scheduler.",
+ )
+ parser.add_argument("--lr_power", type=float, default=1.0, help="Power factor of the polynomial scheduler.")
+ parser.add_argument(
+ "--use_8bit_adam", action="store_true", help="Whether or not to use 8-bit Adam from bitsandbytes."
+ )
+ parser.add_argument("--adam_beta1", type=float, default=0.9, help="The beta1 parameter for the Adam optimizer.")
+ parser.add_argument("--adam_beta2", type=float, default=0.999, help="The beta2 parameter for the Adam optimizer.")
+ parser.add_argument("--adam_weight_decay", type=float, default=1e-2, help="Weight decay to use.")
+ parser.add_argument("--adam_epsilon", type=float, default=1e-08, help="Epsilon value for the Adam optimizer")
+ parser.add_argument("--max_grad_norm", default=1.0, type=float, help="Max gradient norm.")
+ parser.add_argument("--push_to_hub", action="store_true", help="Whether or not to push the model to the Hub.")
+ parser.add_argument("--hub_token", type=str, default=None, help="The token to use to push to the Model Hub.")
+ parser.add_argument(
+ "--hub_model_id",
+ type=str,
+ default=None,
+ help="The name of the repository to keep in sync with the local `output_dir`.",
+ )
+ parser.add_argument(
+ "--logging_dir",
+ type=str,
+ default="logs",
+ help=(
+ "[TensorBoard](https://www.tensorflow.org/tensorboard) log directory. Will default to"
+ " *output_dir/runs/**CURRENT_DATETIME_HOSTNAME***."
+ ),
+ )
+ parser.add_argument(
+ "--allow_tf32",
+ action="store_true",
+ help=(
+ "Whether or not to allow TF32 on Ampere GPUs. Can be used to speed up training. For more information, see"
+ " https://pytorch.org/docs/stable/notes/cuda.html#tensorfloat-32-tf32-on-ampere-devices"
+ ),
+ )
+ parser.add_argument(
+ "--report_to",
+ type=str,
+ default="tensorboard",
+ help=(
+ 'The integration to report the results and logs to. Supported platforms are `"tensorboard"`'
+ ' (default), `"wandb"` and `"comet_ml"`. Use `"all"` to report to all integrations.'
+ ),
+ )
+ parser.add_argument(
+ "--wandb_key",
+ type=str,
+ default=None,
+ help=("If report to option is set to wandb, api-key for wandb used for login to wandb "),
+ )
+ parser.add_argument(
+ "--wandb_project_name",
+ type=str,
+ default=None,
+ help=("If report to option is set to wandb, project name in wandb for log tracking "),
+ )
+ parser.add_argument(
+ "--mixed_precision",
+ type=str,
+ default=None,
+ choices=["no", "fp16", "bf16"],
+ help=(
+ "Whether to use mixed precision. Choose between fp16 and bf16 (bfloat16). Bf16 requires PyTorch >="
+ " 1.10. and an Nvidia Ampere GPU or Intel XPU. Default to the value of accelerate config of the current system or the"
+ " flag passed with the `accelerate.launch` command. Use this argument to override the accelerate config."
+ ),
+ )
+ parser.add_argument(
+ "--prior_generation_precision",
+ type=str,
+ default=None,
+ choices=["no", "fp32", "fp16", "bf16"],
+ help=(
+ "Choose prior generation precision between fp32, fp16 and bf16 (bfloat16). Bf16 requires PyTorch >="
+ " 1.10. and an Nvidia Ampere GPU or Intel XPU. Default to fp16 if an accelerator is available else fp32."
+ ),
+ )
+ parser.add_argument("--local_rank", type=int, default=-1, help="For distributed training: local_rank")
+ parser.add_argument(
+ "--enable_xformers_memory_efficient_attention", action="store_true", help="Whether or not to use xformers."
+ )
+
+ # Adapter arguments
+ subparsers = parser.add_subparsers(dest="adapter")
+
+ # Dummy subparser to train whole model
+ subparsers.add_parser("full", help="Train full model without adapters")
+
+ # LoRA adapter
+ lora = subparsers.add_parser("lora", help="Use LoRA adapter")
+ lora.add_argument("--unet_r", type=int, default=8, help="LoRA rank for unet")
+ lora.add_argument("--unet_alpha", type=int, default=8, help="LoRA alpha for unet")
+ lora.add_argument("--unet_dropout", type=float, default=0.0, help="LoRA dropout probability for unet")
+ lora.add_argument(
+ "--unet_bias",
+ type=str,
+ default="none",
+ help="Bias type for LoRA. Can be 'none', 'all' or 'lora_only'",
+ )
+ lora.add_argument(
+ "--te_r", type=int, default=8, help="LoRA rank for text_encoder, only used if `train_text_encoder` is True"
+ )
+ lora.add_argument(
+ "--te_alpha",
+ type=int,
+ default=8,
+ help="LoRA alpha for text_encoder, only used if `train_text_encoder` is True",
+ )
+ lora.add_argument(
+ "--te_dropout",
+ type=float,
+ default=0.0,
+ help="LoRA dropout probability for text_encoder, only used if `train_text_encoder` is True",
+ )
+ lora.add_argument(
+ "--te_bias",
+ type=str,
+ default="none",
+ help="Bias type for LoRA. Can be 'none', 'all' or 'lora_only', only used if `train_text_encoder` is True",
+ )
+
+ # LoHa adapter
+ loha = subparsers.add_parser("loha", help="Use LoHa adapter")
+ loha.add_argument("--unet_r", type=int, default=8, help="LoHa rank for unet")
+ loha.add_argument("--unet_alpha", type=int, default=8, help="LoHa alpha for unet")
+ loha.add_argument("--unet_rank_dropout", type=float, default=0.0, help="LoHa rank_dropout probability for unet")
+ loha.add_argument(
+ "--unet_module_dropout", type=float, default=0.0, help="LoHa module_dropout probability for unet"
+ )
+ loha.add_argument(
+ "--unet_use_effective_conv2d",
+ action="store_true",
+ help="Use parameter effective decomposition in unet for Conv2d 3x3 with ksize > 1",
+ )
+ loha.add_argument(
+ "--te_r", type=int, default=8, help="LoHa rank for text_encoder, only used if `train_text_encoder` is True"
+ )
+ loha.add_argument(
+ "--te_alpha",
+ type=int,
+ default=8,
+ help="LoHa alpha for text_encoder, only used if `train_text_encoder` is True",
+ )
+ loha.add_argument(
+ "--te_rank_dropout",
+ type=float,
+ default=0.0,
+ help="LoHa rank_dropout probability for text_encoder, only used if `train_text_encoder` is True",
+ )
+ loha.add_argument(
+ "--te_module_dropout",
+ type=float,
+ default=0.0,
+ help="LoHa module_dropout probability for text_encoder, only used if `train_text_encoder` is True",
+ )
+
+ # LoKr adapter
+ lokr = subparsers.add_parser("lokr", help="Use LoKr adapter")
+ lokr.add_argument("--unet_r", type=int, default=8, help="LoKr rank for unet")
+ lokr.add_argument("--unet_alpha", type=int, default=8, help="LoKr alpha for unet")
+ lokr.add_argument("--unet_rank_dropout", type=float, default=0.0, help="LoKr rank_dropout probability for unet")
+ lokr.add_argument(
+ "--unet_module_dropout", type=float, default=0.0, help="LoKr module_dropout probability for unet"
+ )
+ lokr.add_argument(
+ "--unet_use_effective_conv2d",
+ action="store_true",
+ help="Use parameter effective decomposition in unet for Conv2d 3x3 with ksize > 1",
+ )
+ lokr.add_argument(
+ "--unet_decompose_both", action="store_true", help="Decompose left matrix in kronecker product for unet"
+ )
+ lokr.add_argument(
+ "--unet_decompose_factor", type=int, default=-1, help="Decompose factor in kronecker product for unet"
+ )
+ lokr.add_argument(
+ "--te_r", type=int, default=8, help="LoKr rank for text_encoder, only used if `train_text_encoder` is True"
+ )
+ lokr.add_argument(
+ "--te_alpha",
+ type=int,
+ default=8,
+ help="LoKr alpha for text_encoder, only used if `train_text_encoder` is True",
+ )
+ lokr.add_argument(
+ "--te_rank_dropout",
+ type=float,
+ default=0.0,
+ help="LoKr rank_dropout probability for text_encoder, only used if `train_text_encoder` is True",
+ )
+ lokr.add_argument(
+ "--te_module_dropout",
+ type=float,
+ default=0.0,
+ help="LoKr module_dropout probability for text_encoder, only used if `train_text_encoder` is True",
+ )
+ lokr.add_argument(
+ "--te_decompose_both",
+ action="store_true",
+ help="Decompose left matrix in kronecker product for text_encoder, only used if `train_text_encoder` is True",
+ )
+ lokr.add_argument(
+ "--te_decompose_factor",
+ type=int,
+ default=-1,
+ help="Decompose factor in kronecker product for text_encoder, only used if `train_text_encoder` is True",
+ )
+
+ if input_args is not None:
+ args = parser.parse_args(input_args)
+ else:
+ args = parser.parse_args()
+
+ env_local_rank = int(os.environ.get("LOCAL_RANK", -1))
+ if env_local_rank != -1 and env_local_rank != args.local_rank:
+ args.local_rank = env_local_rank
+
+ if args.with_prior_preservation:
+ if args.class_data_dir is None:
+ raise ValueError("You must specify a data directory for class images.")
+ if args.class_prompt is None:
+ raise ValueError("You must specify prompt for class images.")
+ else:
+ # logger is not available yet
+ if args.class_data_dir is not None:
+ warnings.warn("You need not use --class_data_dir without --with_prior_preservation.")
+ if args.class_prompt is not None:
+ warnings.warn("You need not use --class_prompt without --with_prior_preservation.")
+
+ return args
+
+
+# Converting Bytes to Megabytes
+def b2mb(x):
+ return int(x / 2**20)
+
+
+# This context manager is used to track the peak memory usage of the process
+class TorchTracemalloc:
+ def __enter__(self):
+ gc.collect()
+ self.device_type = torch.accelerator.current_accelerator().type if hasattr(torch, "accelerator") else "cuda"
+ self.device_module = getattr(torch, self.device_type, torch.cuda)
+ self.device_module.empty_cache()
+ self.device_module.reset_peak_memory_stats() # reset the peak gauge to zero
+ self.begin = self.device_module.memory_allocated()
+ self.process = psutil.Process()
+
+ self.cpu_begin = self.cpu_mem_used()
+ self.peak_monitoring = True
+ peak_monitor_thread = threading.Thread(target=self.peak_monitor_func)
+ peak_monitor_thread.daemon = True
+ peak_monitor_thread.start()
+ return self
+
+ def cpu_mem_used(self):
+ """get resident set size memory for the current process"""
+ return self.process.memory_info().rss
+
+ def peak_monitor_func(self):
+ self.cpu_peak = -1
+
+ while True:
+ self.cpu_peak = max(self.cpu_mem_used(), self.cpu_peak)
+
+ # can't sleep or will not catch the peak right (this comment is here on purpose)
+ # time.sleep(0.001) # 1msec
+
+ if not self.peak_monitoring:
+ break
+
+ def __exit__(self, *exc):
+ self.peak_monitoring = False
+
+ gc.collect()
+ self.device_module.empty_cache()
+ self.end = self.device_module.memory_allocated()
+ self.peak = self.device_module.max_memory_allocated()
+ self.used = b2mb(self.end - self.begin)
+ self.peaked = b2mb(self.peak - self.begin)
+
+ self.cpu_end = self.cpu_mem_used()
+ self.cpu_used = b2mb(self.cpu_end - self.cpu_begin)
+ self.cpu_peaked = b2mb(self.cpu_peak - self.cpu_begin)
+ # print(f"delta used/peak {self.used:4d}/{self.peaked:4d}")
+
+
+class DreamBoothDataset(Dataset):
+ """
+ A dataset to prepare the instance and class images with the prompts for fine-tuning the model.
+ It pre-processes the images and the tokenizes prompts.
+ """
+
+ def __init__(
+ self,
+ instance_data_root,
+ instance_prompt,
+ tokenizer,
+ class_data_root=None,
+ class_prompt=None,
+ size=512,
+ center_crop=False,
+ ):
+ self.size = size
+ self.center_crop = center_crop
+ self.tokenizer = tokenizer
+
+ self.instance_data_root = Path(instance_data_root)
+ if not self.instance_data_root.exists():
+ raise ValueError("Instance images root doesn't exists.")
+
+ self.instance_images_path = list(Path(instance_data_root).iterdir())
+ self.num_instance_images = len(self.instance_images_path)
+ self.instance_prompt = instance_prompt
+ self._length = self.num_instance_images
+
+ if class_data_root is not None:
+ self.class_data_root = Path(class_data_root)
+ self.class_data_root.mkdir(parents=True, exist_ok=True)
+ self.class_images_path = list(self.class_data_root.iterdir())
+ self.num_class_images = len(self.class_images_path)
+ self._length = max(self.num_class_images, self.num_instance_images)
+ self.class_prompt = class_prompt
+ else:
+ self.class_data_root = None
+
+ self.image_transforms = transforms.Compose(
+ [
+ transforms.Resize(size, interpolation=transforms.InterpolationMode.BILINEAR),
+ transforms.CenterCrop(size) if center_crop else transforms.RandomCrop(size),
+ transforms.ToTensor(),
+ transforms.Normalize([0.5], [0.5]),
+ ]
+ )
+
+ def __len__(self):
+ return self._length
+
+ def __getitem__(self, index):
+ example = {}
+ instance_image = Image.open(self.instance_images_path[index % self.num_instance_images])
+ if not instance_image.mode == "RGB":
+ instance_image = instance_image.convert("RGB")
+ example["instance_images"] = self.image_transforms(instance_image)
+ example["instance_prompt_ids"] = self.tokenizer(
+ self.instance_prompt,
+ truncation=True,
+ padding="max_length",
+ max_length=self.tokenizer.model_max_length,
+ return_tensors="pt",
+ ).input_ids
+
+ if self.class_data_root:
+ class_image = Image.open(self.class_images_path[index % self.num_class_images])
+ if not class_image.mode == "RGB":
+ class_image = class_image.convert("RGB")
+ example["class_images"] = self.image_transforms(class_image)
+ example["class_prompt_ids"] = self.tokenizer(
+ self.class_prompt,
+ truncation=True,
+ padding="max_length",
+ max_length=self.tokenizer.model_max_length,
+ return_tensors="pt",
+ ).input_ids
+
+ return example
+
+
+def collate_fn(examples, with_prior_preservation=False):
+ input_ids = [example["instance_prompt_ids"] for example in examples]
+ pixel_values = [example["instance_images"] for example in examples]
+
+ # Concat class and instance examples for prior preservation.
+ # We do this to avoid doing two forward passes.
+ if with_prior_preservation:
+ input_ids += [example["class_prompt_ids"] for example in examples]
+ pixel_values += [example["class_images"] for example in examples]
+
+ pixel_values = torch.stack(pixel_values)
+ pixel_values = pixel_values.to(memory_format=torch.contiguous_format).float()
+
+ input_ids = torch.cat(input_ids, dim=0)
+
+ batch = {
+ "input_ids": input_ids,
+ "pixel_values": pixel_values,
+ }
+ return batch
+
+
+class PromptDataset(Dataset):
+ "A simple dataset to prepare the prompts to generate class images on multiple accelerators."
+
+ def __init__(self, prompt, num_samples):
+ self.prompt = prompt
+ self.num_samples = num_samples
+
+ def __len__(self):
+ return self.num_samples
+
+ def __getitem__(self, index):
+ example = {}
+ example["prompt"] = self.prompt
+ example["index"] = index
+ return example
+
+
+def main(args):
+ logging_dir = Path(args.output_dir, args.logging_dir)
+
+ accelerator = Accelerator(
+ gradient_accumulation_steps=args.gradient_accumulation_steps,
+ mixed_precision=args.mixed_precision,
+ log_with=args.report_to,
+ project_dir=logging_dir,
+ )
+ if args.report_to == "wandb":
+ import wandb
+
+ wandb.login(key=args.wandb_key)
+ wandb.init(project=args.wandb_project_name)
+ # Currently, it's not possible to do gradient accumulation when training two models with accelerate.accumulate
+ # This will be enabled soon in accelerate. For now, we don't allow gradient accumulation when training two models.
+ # TODO (patil-suraj): Remove this check when gradient accumulation with two models is enabled in accelerate.
+ if args.train_text_encoder and args.gradient_accumulation_steps > 1 and accelerator.num_processes > 1:
+ raise ValueError(
+ "Gradient accumulation is not supported when training the text encoder in distributed training. "
+ "Please set gradient_accumulation_steps to 1. This feature will be supported in the future."
+ )
+
+ # Make one log on every process with the configuration for debugging.
+ logging.basicConfig(
+ format="%(asctime)s - %(levelname)s - %(name)s - %(message)s",
+ datefmt="%m/%d/%Y %H:%M:%S",
+ level=logging.INFO,
+ )
+ logger.info(accelerator.state, main_process_only=False)
+ if accelerator.is_local_main_process:
+ datasets.utils.logging.set_verbosity_warning()
+ transformers.utils.logging.set_verbosity_warning()
+ diffusers.utils.logging.set_verbosity_info()
+ else:
+ datasets.utils.logging.set_verbosity_error()
+ transformers.utils.logging.set_verbosity_error()
+ diffusers.utils.logging.set_verbosity_error()
+
+ # If passed along, set the training seed now.
+ if args.seed is not None:
+ set_seed(args.seed)
+
+ # Generate class images if prior preservation is enabled.
+ if args.with_prior_preservation:
+ class_images_dir = Path(args.class_data_dir)
+ if not class_images_dir.exists():
+ class_images_dir.mkdir(parents=True)
+ cur_class_images = len(list(class_images_dir.iterdir()))
+
+ if cur_class_images < args.num_class_images:
+ torch_dtype = torch.float16 if accelerator.device.type in ["cuda", "xpu"] else torch.float32
+ if args.prior_generation_precision == "fp32":
+ torch_dtype = torch.float32
+ elif args.prior_generation_precision == "fp16":
+ torch_dtype = torch.float16
+ elif args.prior_generation_precision == "bf16":
+ torch_dtype = torch.bfloat16
+ pipeline = DiffusionPipeline.from_pretrained(
+ args.pretrained_model_name_or_path,
+ torch_dtype=torch_dtype,
+ safety_checker=None,
+ revision=args.revision,
+ )
+ pipeline.set_progress_bar_config(disable=True)
+
+ num_new_images = args.num_class_images - cur_class_images
+ logger.info(f"Number of class images to sample: {num_new_images}.")
+
+ sample_dataset = PromptDataset(args.class_prompt, num_new_images)
+ sample_dataloader = torch.utils.data.DataLoader(sample_dataset, batch_size=args.sample_batch_size)
+
+ sample_dataloader = accelerator.prepare(sample_dataloader)
+ pipeline.to(accelerator.device)
+
+ for example in tqdm(
+ sample_dataloader, desc="Generating class images", disable=not accelerator.is_local_main_process
+ ):
+ images = pipeline(example["prompt"]).images
+
+ for i, image in enumerate(images):
+ hash_image = hashlib.sha1(image.tobytes()).hexdigest()
+ image_filename = class_images_dir / f"{example['index'][i] + cur_class_images}-{hash_image}.jpg"
+ image.save(image_filename)
+
+ del pipeline
+
+ if torch.cuda.is_available():
+ torch.cuda.empty_cache()
+ elif torch.xpu.is_available():
+ torch.xpu.empty_cache()
+
+ # Handle the repository creation
+ if accelerator.is_main_process:
+ if args.push_to_hub:
+ api = HfApi(token=args.hub_token)
+
+ # Create repo (repo_name from args or inferred)
+ repo_name = args.hub_model_id
+ if repo_name is None:
+ repo_name = Path(args.output_dir).absolute().name
+ repo_id = api.create_repo(repo_name, exist_ok=True).repo_id
+
+ with open(os.path.join(args.output_dir, ".gitignore"), "w+") as gitignore:
+ if "step_*" not in gitignore:
+ gitignore.write("step_*\n")
+ if "epoch_*" not in gitignore:
+ gitignore.write("epoch_*\n")
+ elif args.output_dir is not None:
+ os.makedirs(args.output_dir, exist_ok=True)
+
+ # Load the tokenizer
+ if args.tokenizer_name:
+ tokenizer = AutoTokenizer.from_pretrained(args.tokenizer_name, revision=args.revision, use_fast=False)
+ elif args.pretrained_model_name_or_path:
+ tokenizer = AutoTokenizer.from_pretrained(
+ args.pretrained_model_name_or_path,
+ subfolder="tokenizer",
+ revision=args.revision,
+ use_fast=False,
+ )
+
+ # import correct text encoder class
+ text_encoder_cls = import_model_class_from_model_name_or_path(args.pretrained_model_name_or_path, args.revision)
+
+ # Load scheduler and models
+ noise_scheduler = DDPMScheduler(
+ beta_start=0.00085,
+ beta_end=0.012,
+ beta_schedule="scaled_linear",
+ num_train_timesteps=1000,
+ ) # DDPMScheduler.from_pretrained(args.pretrained_model_name_or_path, subfolder="scheduler")
+ text_encoder = text_encoder_cls.from_pretrained(
+ args.pretrained_model_name_or_path, subfolder="text_encoder", revision=args.revision
+ )
+ vae = AutoencoderKL.from_pretrained(args.pretrained_model_name_or_path, subfolder="vae", revision=args.revision)
+ unet = UNet2DConditionModel.from_pretrained(
+ args.pretrained_model_name_or_path, subfolder="unet", revision=args.revision
+ )
+
+ if args.adapter != "full":
+ config = create_unet_adapter_config(args)
+ unet = get_peft_model(unet, config)
+ unet.print_trainable_parameters()
+ print(unet)
+
+ vae.requires_grad_(False)
+ if not args.train_text_encoder:
+ text_encoder.requires_grad_(False)
+ elif args.train_text_encoder and args.adapter != "full":
+ config = create_text_encoder_adapter_config(args)
+ text_encoder = get_peft_model(text_encoder, config)
+ text_encoder.print_trainable_parameters()
+ print(text_encoder)
+
+ if args.enable_xformers_memory_efficient_attention:
+ if accelerator.device.type == "xpu":
+ logger.warn("XPU hasn't support xformers yet, ignore it.")
+ elif is_xformers_available():
+ unet.enable_xformers_memory_efficient_attention()
+ else:
+ raise ValueError("xformers is not available. Make sure it is installed correctly")
+
+ if args.gradient_checkpointing:
+ unet.enable_gradient_checkpointing()
+ if args.train_text_encoder and not args.adapter != "full":
+ text_encoder.gradient_checkpointing_enable()
+
+ # Enable TF32 for faster training on Ampere GPUs,
+ # cf https://pytorch.org/docs/stable/notes/cuda.html#tensorfloat-32-tf32-on-ampere-devices
+ if args.allow_tf32 and torch.cuda.is_available():
+ torch.backends.cuda.matmul.allow_tf32 = True
+
+ if args.scale_lr:
+ args.learning_rate = (
+ args.learning_rate * args.gradient_accumulation_steps * args.train_batch_size * accelerator.num_processes
+ )
+
+ # Use 8-bit Adam for lower memory usage or to fine-tune the model in 16GB accelerators
+ if args.use_8bit_adam:
+ try:
+ import bitsandbytes as bnb
+ except ImportError:
+ raise ImportError(
+ "To use 8-bit Adam, please install the bitsandbytes library: `pip install bitsandbytes`."
+ )
+
+ optimizer_class = bnb.optim.AdamW8bit
+ else:
+ optimizer_class = torch.optim.AdamW
+
+ # Optimizer creation
+ params_to_optimize = (
+ itertools.chain(unet.parameters(), text_encoder.parameters()) if args.train_text_encoder else unet.parameters()
+ )
+ optimizer = optimizer_class(
+ params_to_optimize,
+ lr=args.learning_rate,
+ betas=(args.adam_beta1, args.adam_beta2),
+ weight_decay=args.adam_weight_decay,
+ eps=args.adam_epsilon,
+ )
+
+ # Dataset and DataLoaders creation:
+ train_dataset = DreamBoothDataset(
+ instance_data_root=args.instance_data_dir,
+ instance_prompt=args.instance_prompt,
+ class_data_root=args.class_data_dir if args.with_prior_preservation else None,
+ class_prompt=args.class_prompt,
+ tokenizer=tokenizer,
+ size=args.resolution,
+ center_crop=args.center_crop,
+ )
+
+ train_dataloader = torch.utils.data.DataLoader(
+ train_dataset,
+ batch_size=args.train_batch_size,
+ shuffle=True,
+ collate_fn=lambda examples: collate_fn(examples, args.with_prior_preservation),
+ num_workers=1,
+ )
+
+ # Scheduler and math around the number of training steps.
+ overrode_max_train_steps = False
+ num_update_steps_per_epoch = math.ceil(len(train_dataloader) / args.gradient_accumulation_steps)
+ if args.max_train_steps is None:
+ args.max_train_steps = args.num_train_epochs * num_update_steps_per_epoch
+ overrode_max_train_steps = True
+
+ lr_scheduler = get_scheduler(
+ args.lr_scheduler,
+ optimizer=optimizer,
+ num_warmup_steps=args.lr_warmup_steps * args.gradient_accumulation_steps,
+ num_training_steps=args.max_train_steps * args.gradient_accumulation_steps,
+ num_cycles=args.lr_num_cycles,
+ power=args.lr_power,
+ )
+
+ # Prepare everything with our `accelerator`.
+ if args.train_text_encoder:
+ unet, text_encoder, optimizer, train_dataloader, lr_scheduler = accelerator.prepare(
+ unet, text_encoder, optimizer, train_dataloader, lr_scheduler
+ )
+ else:
+ unet, optimizer, train_dataloader, lr_scheduler = accelerator.prepare(
+ unet, optimizer, train_dataloader, lr_scheduler
+ )
+
+ # For mixed precision training we cast the text_encoder and vae weights to half-precision
+ # as these models are only used for inference, keeping weights in full precision is not required.
+ weight_dtype = torch.float32
+ if accelerator.mixed_precision == "fp16":
+ weight_dtype = torch.float16
+ elif accelerator.mixed_precision == "bf16":
+ weight_dtype = torch.bfloat16
+
+ # Move vae and text_encoder to device and cast to weight_dtype
+ vae.to(accelerator.device, dtype=weight_dtype)
+ if not args.train_text_encoder:
+ text_encoder.to(accelerator.device, dtype=weight_dtype)
+
+ # We need to recalculate our total training steps as the size of the training dataloader may have changed.
+ num_update_steps_per_epoch = math.ceil(len(train_dataloader) / args.gradient_accumulation_steps)
+ if overrode_max_train_steps:
+ args.max_train_steps = args.num_train_epochs * num_update_steps_per_epoch
+ # Afterwards we recalculate our number of training epochs
+ args.num_train_epochs = math.ceil(args.max_train_steps / num_update_steps_per_epoch)
+
+ # We need to initialize the trackers we use, and also store our configuration.
+ # The trackers initializes automatically on the main process.
+ if accelerator.is_main_process:
+ accelerator.init_trackers("dreambooth", config=vars(args))
+
+ # Train!
+ total_batch_size = args.train_batch_size * accelerator.num_processes * args.gradient_accumulation_steps
+
+ logger.info("***** Running training *****")
+ logger.info(f" Num examples = {len(train_dataset)}")
+ logger.info(f" Num batches each epoch = {len(train_dataloader)}")
+ logger.info(f" Num Epochs = {args.num_train_epochs}")
+ logger.info(f" Instantaneous batch size per device = {args.train_batch_size}")
+ logger.info(f" Total train batch size (w. parallel, distributed & accumulation) = {total_batch_size}")
+ logger.info(f" Gradient Accumulation steps = {args.gradient_accumulation_steps}")
+ logger.info(f" Total optimization steps = {args.max_train_steps}")
+ global_step = 0
+ first_epoch = 0
+
+ # Potentially load in the weights and states from a previous save
+ if args.resume_from_checkpoint:
+ if args.resume_from_checkpoint != "latest":
+ path = os.path.basename(args.resume_from_checkpoint)
+ else:
+ # Get the mos recent checkpoint
+ dirs = os.listdir(args.output_dir)
+ dirs = [d for d in dirs if d.startswith("checkpoint")]
+ dirs = sorted(dirs, key=lambda x: int(x.split("-")[1]))
+ path = dirs[-1]
+ accelerator.print(f"Resuming from checkpoint {path}")
+ accelerator.load_state(os.path.join(args.output_dir, path))
+ global_step = int(path.split("-")[1])
+
+ resume_global_step = global_step * args.gradient_accumulation_steps
+ first_epoch = resume_global_step // num_update_steps_per_epoch
+ resume_step = resume_global_step % num_update_steps_per_epoch
+
+ # Only show the progress bar once on each machine.
+ progress_bar = tqdm(range(global_step, args.max_train_steps), disable=not accelerator.is_local_main_process)
+ progress_bar.set_description("Steps")
+
+ for epoch in range(first_epoch, args.num_train_epochs):
+ unet.train()
+ if args.train_text_encoder:
+ text_encoder.train()
+ with TorchTracemalloc() as tracemalloc:
+ for step, batch in enumerate(train_dataloader):
+ # Skip steps until we reach the resumed step
+ if args.resume_from_checkpoint and epoch == first_epoch and step < resume_step:
+ if step % args.gradient_accumulation_steps == 0:
+ progress_bar.update(1)
+ if args.report_to == "wandb":
+ accelerator.print(progress_bar)
+ continue
+
+ with accelerator.accumulate(unet):
+ # Convert images to latent space
+ latents = vae.encode(batch["pixel_values"].to(dtype=weight_dtype)).latent_dist.sample()
+ latents = latents * 0.18215
+
+ # Sample noise that we'll add to the latents
+ noise = torch.randn_like(latents)
+ bsz = latents.shape[0]
+ # Sample a random timestep for each image
+ timesteps = torch.randint(
+ 0, noise_scheduler.config.num_train_timesteps, (bsz,), device=latents.device
+ )
+ timesteps = timesteps.long()
+
+ # Add noise to the latents according to the noise magnitude at each timestep
+ # (this is the forward diffusion process)
+ noisy_latents = noise_scheduler.add_noise(latents, noise, timesteps)
+
+ # Get the text embedding for conditioning
+ encoder_hidden_states = text_encoder(batch["input_ids"])[0]
+
+ # Predict the noise residual
+ model_pred = unet(noisy_latents, timesteps, encoder_hidden_states).sample
+
+ # Get the target for loss depending on the prediction type
+ if noise_scheduler.config.prediction_type == "epsilon":
+ target = noise
+ elif noise_scheduler.config.prediction_type == "v_prediction":
+ target = noise_scheduler.get_velocity(latents, noise, timesteps)
+ else:
+ raise ValueError(f"Unknown prediction type {noise_scheduler.config.prediction_type}")
+
+ if args.with_prior_preservation:
+ # Chunk the noise and model_pred into two parts and compute the loss on each part separately.
+ model_pred, model_pred_prior = torch.chunk(model_pred, 2, dim=0)
+ target, target_prior = torch.chunk(target, 2, dim=0)
+
+ # Compute instance loss
+ loss = F.mse_loss(model_pred.float(), target.float(), reduction="mean")
+
+ # Compute prior loss
+ prior_loss = F.mse_loss(model_pred_prior.float(), target_prior.float(), reduction="mean")
+
+ # Add the prior loss to the instance loss.
+ loss = loss + args.prior_loss_weight * prior_loss
+ else:
+ loss = F.mse_loss(model_pred.float(), target.float(), reduction="mean")
+
+ accelerator.backward(loss)
+ if accelerator.sync_gradients:
+ params_to_clip = (
+ itertools.chain(unet.parameters(), text_encoder.parameters())
+ if args.train_text_encoder
+ else unet.parameters()
+ )
+ accelerator.clip_grad_norm_(params_to_clip, args.max_grad_norm)
+ optimizer.step()
+ lr_scheduler.step()
+ optimizer.zero_grad()
+
+ # Checks if the accelerator has performed an optimization step behind the scenes
+ if accelerator.sync_gradients:
+ progress_bar.update(1)
+ if args.report_to == "wandb":
+ accelerator.print(progress_bar)
+ global_step += 1
+
+ # if global_step % args.checkpointing_steps == 0:
+ # if accelerator.is_main_process:
+ # save_path = os.path.join(args.output_dir, f"checkpoint-{global_step}")
+ # accelerator.save_state(save_path)
+ # logger.info(f"Saved state to {save_path}")
+
+ logs = {"loss": loss.detach().item(), "lr": lr_scheduler.get_last_lr()[0]}
+ progress_bar.set_postfix(**logs)
+ accelerator.log(logs, step=global_step)
+
+ if (
+ args.validation_prompt is not None
+ and (step + num_update_steps_per_epoch * epoch) % args.validation_steps == 0
+ ):
+ logger.info(
+ f"Running validation... \n Generating {args.num_validation_images} images with prompt:"
+ f" {args.validation_prompt}."
+ )
+ # create pipeline
+ pipeline = DiffusionPipeline.from_pretrained(
+ args.pretrained_model_name_or_path,
+ safety_checker=None,
+ revision=args.revision,
+ )
+ # set `keep_fp32_wrapper` to True because we do not want to remove
+ # mixed precision hooks while we are still training
+ pipeline.unet = accelerator.unwrap_model(unet, keep_fp32_wrapper=True)
+ pipeline.text_encoder = accelerator.unwrap_model(text_encoder, keep_fp32_wrapper=True)
+ pipeline.scheduler = DPMSolverMultistepScheduler.from_config(pipeline.scheduler.config)
+ pipeline = pipeline.to(accelerator.device)
+ pipeline.set_progress_bar_config(disable=True)
+
+ # Set evaliation mode
+ pipeline.unet.eval()
+ pipeline.text_encoder.eval()
+
+ # run inference
+ if args.seed is not None:
+ generator = torch.Generator(device=accelerator.device).manual_seed(args.seed)
+ else:
+ generator = None
+ images = []
+ for _ in range(args.num_validation_images):
+ image = pipeline(args.validation_prompt, num_inference_steps=25, generator=generator).images[0]
+ images.append(image)
+
+ for tracker in accelerator.trackers:
+ if tracker.name == "tensorboard":
+ np_images = np.stack([np.asarray(img) for img in images])
+ tracker.writer.add_images("validation", np_images, epoch, dataformats="NHWC")
+ if tracker.name == "wandb":
+ import wandb
+
+ tracker.log(
+ {
+ "validation": [
+ wandb.Image(image, caption=f"{i}: {args.validation_prompt}")
+ for i, image in enumerate(images)
+ ]
+ }
+ )
+
+ # Set evaliation mode
+ pipeline.unet.train()
+ pipeline.text_encoder.train()
+
+ del pipeline
+ if torch.cuda.is_available():
+ torch.cuda.empty_cache()
+ elif torch.xpu.is_available():
+ torch.xpu.empty_cache()
+
+ if global_step >= args.max_train_steps:
+ break
+ # Printing the accelerator memory usage details such as allocated memory, peak memory, and total memory usage
+ accelerator.print(
+ f"{accelerator.device.type.upper()} Memory before entering the train : {b2mb(tracemalloc.begin)}"
+ )
+ accelerator.print(
+ f"{accelerator.device.type.upper()} Memory consumed at the end of the train (end-begin): {tracemalloc.used}"
+ )
+ accelerator.print(
+ f"{accelerator.device.type.upper()} Peak Memory consumed during the train (max-begin): {tracemalloc.peaked}"
+ )
+ accelerator.print(
+ f"{accelerator.device.type.upper()} Total Peak Memory consumed during the train (max): {tracemalloc.peaked + b2mb(tracemalloc.begin)}"
+ )
+
+ accelerator.print(f"CPU Memory before entering the train : {b2mb(tracemalloc.cpu_begin)}")
+ accelerator.print(f"CPU Memory consumed at the end of the train (end-begin): {tracemalloc.cpu_used}")
+ accelerator.print(f"CPU Peak Memory consumed during the train (max-begin): {tracemalloc.cpu_peaked}")
+ accelerator.print(
+ f"CPU Total Peak Memory consumed during the train (max): {tracemalloc.cpu_peaked + b2mb(tracemalloc.cpu_begin)}"
+ )
+
+ # Create the pipeline using using the trained modules and save it.
+ accelerator.wait_for_everyone()
+ if accelerator.is_main_process:
+ if args.adapter != "full":
+ unwarpped_unet = accelerator.unwrap_model(unet)
+ unwarpped_unet.save_pretrained(
+ os.path.join(args.output_dir, "unet"), state_dict=accelerator.get_state_dict(unet)
+ )
+ if args.train_text_encoder:
+ unwarpped_text_encoder = accelerator.unwrap_model(text_encoder)
+ unwarpped_text_encoder.save_pretrained(
+ os.path.join(args.output_dir, "text_encoder"),
+ state_dict=accelerator.get_state_dict(text_encoder),
+ )
+ else:
+ pipeline = DiffusionPipeline.from_pretrained(
+ args.pretrained_model_name_or_path,
+ unet=accelerator.unwrap_model(unet),
+ text_encoder=accelerator.unwrap_model(text_encoder),
+ revision=args.revision,
+ )
+ pipeline.save_pretrained(args.output_dir)
+
+ if args.push_to_hub:
+ api.upload_folder(
+ repo_id=repo_id,
+ folder_path=args.output_dir,
+ commit_message="End of training",
+ run_as_future=True,
+ )
+
+ accelerator.end_training()
+
+
+if __name__ == "__main__":
+ args = parse_args()
+ main(args)
diff --git a/peft/examples/token_classification/peft_lora_ner.ipynb b/peft/examples/token_classification/peft_lora_ner.ipynb
new file mode 100644
index 0000000000000000000000000000000000000000..e2a6c048daef2200a4c08f55d1c33ba2732a5ee2
--- /dev/null
+++ b/peft/examples/token_classification/peft_lora_ner.ipynb
@@ -0,0 +1,554 @@
+{
+ "cells": [
+ {
+ "cell_type": "markdown",
+ "metadata": {},
+ "source": [
+ "## Named Entity Recognition with Peft Model 🤗\n",
+ "\n",
+ "##### In this notebook, we will learn how to perform Named Entity Recognition(NER) on the CoNLL-2003 dataset using the Trainer class\n",
+ "\n",
+ "##### This notebook has been adapted from the main NLP course here - https://huggingface.co/learn/nlp-course/chapter7/2?fw=pt#fine-tuning-the-model"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "#install the required libraries\n",
+ "!pip install -q datasets evaluate transformers seqeval"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "# Import required libraries\n",
+ "from datasets import load_dataset\n",
+ "from transformers import AutoTokenizer, AutoModelForTokenClassification, DataCollatorForTokenClassification, TrainingArguments, Trainer, pipeline\n",
+ "from peft import get_peft_model, LoraConfig, TaskType\n",
+ "import evaluate\n",
+ "import numpy as np\n",
+ "from huggingface_hub import notebook_login"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 2,
+ "metadata": {},
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "DatasetDict({\n",
+ " train: Dataset({\n",
+ " features: ['id', 'tokens', 'pos_tags', 'chunk_tags', 'ner_tags'],\n",
+ " num_rows: 14041\n",
+ " })\n",
+ " validation: Dataset({\n",
+ " features: ['id', 'tokens', 'pos_tags', 'chunk_tags', 'ner_tags'],\n",
+ " num_rows: 3250\n",
+ " })\n",
+ " test: Dataset({\n",
+ " features: ['id', 'tokens', 'pos_tags', 'chunk_tags', 'ner_tags'],\n",
+ " num_rows: 3453\n",
+ " })\n",
+ "})\n"
+ ]
+ }
+ ],
+ "source": [
+ "raw_datasets = load_dataset(\"conll2003\")\n",
+ "print(raw_datasets)"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 3,
+ "metadata": {},
+ "outputs": [
+ {
+ "data": {
+ "text/plain": [
+ "['EU', 'rejects', 'German', 'call', 'to', 'boycott', 'British', 'lamb', '.']"
+ ]
+ },
+ "execution_count": 3,
+ "metadata": {},
+ "output_type": "execute_result"
+ }
+ ],
+ "source": [
+ "# Look at the tokens of the first training example\n",
+ "raw_datasets[\"train\"][0][\"tokens\"]"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 4,
+ "metadata": {},
+ "outputs": [
+ {
+ "data": {
+ "text/plain": [
+ "[3, 0, 7, 0, 0, 0, 7, 0, 0]"
+ ]
+ },
+ "execution_count": 4,
+ "metadata": {},
+ "output_type": "execute_result"
+ }
+ ],
+ "source": [
+ "# Look at the NER tags of the first training example\n",
+ "raw_datasets[\"train\"][0][\"ner_tags\"]"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 5,
+ "metadata": {},
+ "outputs": [
+ {
+ "data": {
+ "text/plain": [
+ "['O', 'B-PER', 'I-PER', 'B-ORG', 'I-ORG', 'B-LOC', 'I-LOC', 'B-MISC', 'I-MISC']"
+ ]
+ },
+ "execution_count": 5,
+ "metadata": {},
+ "output_type": "execute_result"
+ }
+ ],
+ "source": [
+ "# Get the label names for the NER tags\n",
+ "ner_feature = raw_datasets[\"train\"].features[\"ner_tags\"]\n",
+ "label_names = ner_feature.feature.names\n",
+ "label_names"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 6,
+ "metadata": {},
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "EU rejects German call to boycott British lamb . \n",
+ "B-ORG O B-MISC O O O B-MISC O O \n"
+ ]
+ }
+ ],
+ "source": [
+ "words = raw_datasets[\"train\"][0][\"tokens\"]\n",
+ "labels = raw_datasets[\"train\"][0][\"ner_tags\"]\n",
+ "line1 = \"\"\n",
+ "line2 = \"\"\n",
+ "for word, label in zip(words, labels):\n",
+ " full_label = label_names[label]\n",
+ " max_length = max(len(word), len(full_label))\n",
+ " line1 += word + \" \" * (max_length - len(word) + 1)\n",
+ " line2 += full_label + \" \" * (max_length - len(full_label) + 1)\n",
+ "\n",
+ "print(line1)\n",
+ "print(line2)"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 7,
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "# Load the tokenizer\n",
+ "model_checkpoint = \"bert-base-cased\"\n",
+ "tokenizer = AutoTokenizer.from_pretrained(model_checkpoint)"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 8,
+ "metadata": {},
+ "outputs": [
+ {
+ "data": {
+ "text/plain": [
+ "['[CLS]',\n",
+ " 'EU',\n",
+ " 'rejects',\n",
+ " 'German',\n",
+ " 'call',\n",
+ " 'to',\n",
+ " 'boycott',\n",
+ " 'British',\n",
+ " 'la',\n",
+ " '##mb',\n",
+ " '.',\n",
+ " '[SEP]']"
+ ]
+ },
+ "execution_count": 8,
+ "metadata": {},
+ "output_type": "execute_result"
+ }
+ ],
+ "source": [
+ "# Tokenize the first training example\n",
+ "inputs = tokenizer(raw_datasets[\"train\"][0][\"tokens\"], is_split_into_words=True)\n",
+ "inputs.tokens()"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 9,
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "def align_labels_with_tokens(labels, word_ids):\n",
+ " new_labels = []\n",
+ " current_word = None\n",
+ " for word_id in word_ids:\n",
+ " if word_id != current_word:\n",
+ " # Start of a new word!\n",
+ " current_word = word_id\n",
+ " label = -100 if word_id is None else labels[word_id]\n",
+ " new_labels.append(label)\n",
+ " elif word_id is None:\n",
+ " # Special token\n",
+ " new_labels.append(-100)\n",
+ " else:\n",
+ " # Same word as previous token\n",
+ " label = labels[word_id]\n",
+ " # If the label is B-XXX we change it to I-XXX\n",
+ " if label % 2 == 1:\n",
+ " label += 1\n",
+ " new_labels.append(label)\n",
+ "\n",
+ " return new_labels"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 10,
+ "metadata": {},
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "[3, 0, 7, 0, 0, 0, 7, 0, 0]\n",
+ "[-100, 3, 0, 7, 0, 0, 0, 7, 0, 0, 0, -100]\n"
+ ]
+ }
+ ],
+ "source": [
+ "labels = raw_datasets[\"train\"][0][\"ner_tags\"]\n",
+ "word_ids = inputs.word_ids()\n",
+ "print(labels)\n",
+ "print(align_labels_with_tokens(labels, word_ids))"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 11,
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "def tokenize_and_align_labels(examples):\n",
+ " tokenized_inputs = tokenizer(\n",
+ " examples[\"tokens\"], truncation=True, is_split_into_words=True\n",
+ " )\n",
+ " all_labels = examples[\"ner_tags\"]\n",
+ " new_labels = []\n",
+ " for i, labels in enumerate(all_labels):\n",
+ " word_ids = tokenized_inputs.word_ids(i)\n",
+ " new_labels.append(align_labels_with_tokens(labels, word_ids))\n",
+ "\n",
+ " tokenized_inputs[\"labels\"] = new_labels\n",
+ " return tokenized_inputs"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 12,
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "tokenized_datasets = raw_datasets.map(\n",
+ " tokenize_and_align_labels,\n",
+ " batched=True,\n",
+ " remove_columns=raw_datasets[\"train\"].column_names,\n",
+ ")"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 13,
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "data_collator = DataCollatorForTokenClassification(tokenizer=tokenizer)"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 14,
+ "metadata": {},
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "[-100, 3, 0, 7, 0, 0, 0, 7, 0, 0, 0, -100]\n",
+ "[-100, 1, 2, -100]\n"
+ ]
+ }
+ ],
+ "source": [
+ "for i in range(2):\n",
+ " print(tokenized_datasets[\"train\"][i][\"labels\"])"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 15,
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "metric = evaluate.load(\"seqeval\")"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 16,
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "# Create label mappings\n",
+ "id2label = {i: label for i, label in enumerate(label_names)}\n",
+ "label2id = {v: k for k, v in id2label.items()}"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "# Load the pre-trained model\n",
+ "model = AutoModelForTokenClassification.from_pretrained(\n",
+ " model_checkpoint,\n",
+ " id2label=id2label,\n",
+ " label2id=label2id,\n",
+ ")"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 18,
+ "metadata": {},
+ "outputs": [
+ {
+ "data": {
+ "text/plain": [
+ "9"
+ ]
+ },
+ "execution_count": 18,
+ "metadata": {},
+ "output_type": "execute_result"
+ }
+ ],
+ "source": [
+ "model.config.num_labels"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "model"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "# Configure LoRA (Low-Rank Adaptation) for fine-tuning\n",
+ "peft_config = LoraConfig(target_modules = [\"query\", \"key\"], task_type = TaskType.TOKEN_CLS)\n",
+ "\n",
+ "model = get_peft_model(model, peft_config)\n",
+ "model.print_trainable_parameters()"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 21,
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "def compute_metrics(eval_preds):\n",
+ " logits, labels = eval_preds\n",
+ " predictions = np.argmax(logits, axis=-1)\n",
+ "\n",
+ " # Remove ignored index (special tokens) and convert to labels\n",
+ " true_labels = [[label_names[l] for l in label if l != -100] for label in labels]\n",
+ " true_predictions = [\n",
+ " [label_names[p] for (p, l) in zip(prediction, label) if l != -100]\n",
+ " for prediction, label in zip(predictions, labels)\n",
+ " ]\n",
+ " all_metrics = metric.compute(predictions=true_predictions, references=true_labels)\n",
+ " return {\n",
+ " \"precision\": all_metrics[\"overall_precision\"],\n",
+ " \"recall\": all_metrics[\"overall_recall\"],\n",
+ " \"f1\": all_metrics[\"overall_f1\"],\n",
+ " \"accuracy\": all_metrics[\"overall_accuracy\"],\n",
+ " }"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "notebook_login()"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "args = TrainingArguments(\n",
+ " \"bert-finetuned-ner-lora\",\n",
+ " eval_strategy=\"epoch\",\n",
+ " per_device_train_batch_size=32, # decrease this for OOM error\n",
+ " per_device_eval_batch_size=64,\n",
+ " save_strategy=\"epoch\",\n",
+ " learning_rate=2e-3,\n",
+ " num_train_epochs=5,\n",
+ " weight_decay=0.01,\n",
+ " load_best_model_at_end=True,\n",
+ " do_eval=True,\n",
+ " do_predict=True,\n",
+ " metric_for_best_model=\"accuracy\",\n",
+ " label_names=[\"labels\"],\n",
+ " push_to_hub=True,\n",
+ ")"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "trainer = Trainer(\n",
+ " model=model,\n",
+ " args=args,\n",
+ " train_dataset=tokenized_datasets[\"train\"],\n",
+ " eval_dataset=tokenized_datasets[\"validation\"],\n",
+ " data_collator=data_collator,\n",
+ " processing_class=tokenizer,\n",
+ " compute_metrics=compute_metrics\n",
+ ")\n",
+ "trainer.train()"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 31,
+ "metadata": {},
+ "outputs": [
+ {
+ "name": "stderr",
+ "output_type": "stream",
+ "text": [
+ "Some weights of BertForTokenClassification were not initialized from the model checkpoint at bert-base-cased and are newly initialized: ['classifier.bias', 'classifier.weight']\n",
+ "You should probably TRAIN this model on a down-stream task to be able to use it for predictions and inference.\n",
+ "Device set to use xpu:0\n"
+ ]
+ },
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "entity_idx: 0, id2label: {0: 'O', 1: 'B-PER', 2: 'I-PER', 3: 'B-ORG', 4: 'I-ORG', 5: 'B-LOC', 6: 'I-LOC', 7: 'B-MISC', 8: 'I-MISC'}\n",
+ "entity_idx: 0, id2label: {0: 'O', 1: 'B-PER', 2: 'I-PER', 3: 'B-ORG', 4: 'I-ORG', 5: 'B-LOC', 6: 'I-LOC', 7: 'B-MISC', 8: 'I-MISC'}\n",
+ "entity_idx: 0, id2label: {0: 'O', 1: 'B-PER', 2: 'I-PER', 3: 'B-ORG', 4: 'I-ORG', 5: 'B-LOC', 6: 'I-LOC', 7: 'B-MISC', 8: 'I-MISC'}\n",
+ "entity_idx: 1, id2label: {0: 'O', 1: 'B-PER', 2: 'I-PER', 3: 'B-ORG', 4: 'I-ORG', 5: 'B-LOC', 6: 'I-LOC', 7: 'B-MISC', 8: 'I-MISC'}\n",
+ "entity_idx: 2, id2label: {0: 'O', 1: 'B-PER', 2: 'I-PER', 3: 'B-ORG', 4: 'I-ORG', 5: 'B-LOC', 6: 'I-LOC', 7: 'B-MISC', 8: 'I-MISC'}\n",
+ "entity_idx: 0, id2label: {0: 'O', 1: 'B-PER', 2: 'I-PER', 3: 'B-ORG', 4: 'I-ORG', 5: 'B-LOC', 6: 'I-LOC', 7: 'B-MISC', 8: 'I-MISC'}\n"
+ ]
+ },
+ {
+ "data": {
+ "text/plain": [
+ "[{'entity_group': 'PER',\n",
+ " 'score': 0.9702984,\n",
+ " 'word': 'Jino',\n",
+ " 'start': 11,\n",
+ " 'end': 15}]"
+ ]
+ },
+ "execution_count": 31,
+ "metadata": {},
+ "output_type": "execute_result"
+ }
+ ],
+ "source": [
+ "from peft import PeftModel\n",
+ "\n",
+ "# Replace this with your own checkpoint\n",
+ "lora_checkpoint = \"./bert-finetuned-ner-lora\"\n",
+ "\n",
+ "tokenizer = AutoTokenizer.from_pretrained(model_checkpoint)\n",
+ "base_model = AutoModelForTokenClassification.from_pretrained(\n",
+ " model_checkpoint,\n",
+ " id2label=id2label,\n",
+ " label2id=label2id,\n",
+ ")\n",
+ "lora_model = PeftModel.from_pretrained(base_model, lora_checkpoint)\n",
+ "token_classifier = pipeline(\n",
+ " \"token-classification\", model=lora_model, tokenizer=tokenizer, aggregation_strategy=\"simple\"\n",
+ ")\n",
+ "\n",
+ "token_classifier(\"My name is Jino.\")"
+ ]
+ }
+ ],
+ "metadata": {
+ "kernelspec": {
+ "display_name": "Python 3",
+ "language": "python",
+ "name": "python3"
+ },
+ "language_info": {
+ "codemirror_mode": {
+ "name": "ipython",
+ "version": 3
+ },
+ "file_extension": ".py",
+ "mimetype": "text/x-python",
+ "name": "python",
+ "nbconvert_exporter": "python",
+ "pygments_lexer": "ipython3",
+ "version": "3.11.13"
+ }
+ },
+ "nbformat": 4,
+ "nbformat_minor": 2
+}
diff --git a/peft/examples/token_classification/peft_lora_token_cls.ipynb b/peft/examples/token_classification/peft_lora_token_cls.ipynb
new file mode 100644
index 0000000000000000000000000000000000000000..0c6c686ae5b40f04fa4edb8aa5a31ac4ef253942
--- /dev/null
+++ b/peft/examples/token_classification/peft_lora_token_cls.ipynb
@@ -0,0 +1,1430 @@
+{
+ "cells": [
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "colab_type": "text",
+ "id": "view-in-github"
+ },
+ "source": [
+ " "
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "ngqdEv0rP01q"
+ },
+ "source": [
+ "## Introduction\n",
+ "\n",
+ "In this notebook, we are going to fine-tune the LayoutLM model by Microsoft Research on the [FUNSD](https://guillaumejaume.github.io/FUNSD/) dataset, which is a collection of annotated form documents. The goal of our model is to learn the annotations of a number of labels (\"question\", \"answer\", \"header\" and \"other\") on those forms, such that it can be used to annotate unseen forms in the future.\n",
+ "\n",
+ "* Original LayoutLM paper: https://huggingface.co/papers/1912.13318\n",
+ "\n",
+ "* Original FUNSD paper: https://huggingface.co/papers/1905.13538\n"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "6K4S2s33ebY0"
+ },
+ "source": [
+ "## Install libraries\n",
+ "\n",
+ "Currently you have to first install the `unilm` package, and then the `transformers` package (which updates the outdated `transformers` package that is included in the `unilm` package). The reason we also install the `unilm` package is because we need its preprocessing files. I've forked it, and removed some statements which introduced some issues."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 1000
+ },
+ "id": "5cngOTr6SqEf",
+ "outputId": "6c7a2f76-682b-4f93-a3db-59ab010e5ffe"
+ },
+ "outputs": [],
+ "source": [
+ "! rm -r unilm\n",
+ "! git clone https://github.com/microsoft/unilm.git"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "RGMkEG5aRB0D"
+ },
+ "source": [
+ "## Getting the data\n",
+ "\n",
+ "Here we download the data of the [FUNSD dataset](https://guillaumejaume.github.io/FUNSD/) from the web. This results in a directory called \"data\" being created, which has 2 subdirectories, one for training and one for testing. Each of those has 2 subdirectories in turn, one containing the images as png files and one containing the annotations in json format."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "colab": {
+ "base_uri": "https://localhost:8080/"
+ },
+ "id": "DTFnEZagQm4v",
+ "outputId": "97ce03ba-a6bb-4444-8eba-77eceece44e0"
+ },
+ "outputs": [],
+ "source": [
+ "! wget https://guillaumejaume.github.io/FUNSD/dataset.zip\n",
+ "! unzip dataset.zip && mv dataset data && rm -rf dataset.zip __MACOSX"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "UrNMR64LsJXm"
+ },
+ "source": [
+ "Let's take a look at a training example. For this, we are going to use PIL (Python Image Library)."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 5,
+ "metadata": {
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 1000
+ },
+ "id": "eG-eGcj3sNPs",
+ "outputId": "69ead0ea-15d6-4d5e-af61-a99a7533d31b"
+ },
+ "outputs": [
+ {
+ "data": {
+ "image/jpeg": "/9j/4AAQSkZJRgABAQAAAQABAAD/2wBDAAgGBgcGBQgHBwcJCQgKDBQNDAsLDBkSEw8UHRofHh0aHBwgJC4nICIsIxwcKDcpLDAxNDQ0Hyc5PTgyPC4zNDL/2wBDAQkJCQwLDBgNDRgyIRwhMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjL/wAARCAPoAvoDASIAAhEBAxEB/8QAHwAAAQUBAQEBAQEAAAAAAAAAAAECAwQFBgcICQoL/8QAtRAAAgEDAwIEAwUFBAQAAAF9AQIDAAQRBRIhMUEGE1FhByJxFDKBkaEII0KxwRVS0fAkM2JyggkKFhcYGRolJicoKSo0NTY3ODk6Q0RFRkdISUpTVFVWV1hZWmNkZWZnaGlqc3R1dnd4eXqDhIWGh4iJipKTlJWWl5iZmqKjpKWmp6ipqrKztLW2t7i5usLDxMXGx8jJytLT1NXW19jZ2uHi4+Tl5ufo6erx8vP09fb3+Pn6/8QAHwEAAwEBAQEBAQEBAQAAAAAAAAECAwQFBgcICQoL/8QAtREAAgECBAQDBAcFBAQAAQJ3AAECAxEEBSExBhJBUQdhcRMiMoEIFEKRobHBCSMzUvAVYnLRChYkNOEl8RcYGRomJygpKjU2Nzg5OkNERUZHSElKU1RVVldYWVpjZGVmZ2hpanN0dXZ3eHl6goOEhYaHiImKkpOUlZaXmJmaoqOkpaanqKmqsrO0tba3uLm6wsPExcbHyMnK0tPU1dbX2Nna4uPk5ebn6Onq8vP09fb3+Pn6/9oADAMBAAIRAxEAPwDa/wCGb/DH/QX1f/vqL/4ij/hm/wAMf9BfV/8AvqL/AOIr2WigDxr/AIZv8Mf9BfV/++ov/iKP+Gb/AAx/0F9X/wC+ov8A4ivZaKAPGv8Ahm/wx/0F9X/76i/+Io/4Zv8ADH/QX1f/AL6i/wDiK9looA8a/wCGb/DH/QX1f/vqL/4ij/hm/wAMf9BfV/8AvqL/AOIr2WigDxr/AIZv8Mf9BfV/++ov/iKP+Gb/AAx/0F9X/wC+ov8A4ivZaKAPGv8Ahm/wx/0F9X/76i/+Io/4Zv8ADH/QX1f/AL6i/wDiK9looA8a/wCGb/DH/QX1f/vqL/4ij/hm/wAMf9BfV/8AvqL/AOIr2WigDxr/AIZv8Mf9BfV/++ov/iKP+Gb/AAx/0F9X/wC+ov8A4ivZaKAPE2/Zs0HexXXdSClgVBRCQuOQTjk578Y9D1qrJ+zRYkjy/E1wo5zutFPfj+Idsf54r3aigDw+H9mvSFiUT+IL55Nx3MkKKCOwAOcHrzn8Knh/Zt8PLHifW9Ud8nmMRoMduCp/nXtNFAHisf7Nvh8TSmTW9TaIkeUqiMMoxzuODu59APxqvP8As1aWzubfxHeRqfuiS3VyOe5BGeMen9K9yooA8JX9miyAXf4muCd2Ti0UZX0+919/0ph/ZntcnHiibH/XkP8A4uveaKAPBv8Ahme2/wChpm/8Ah/8XR/wzPbf9DTN/wCAQ/8Ai695ooA8G/4Zntv+hpm/8Ah/8XR/wzPbf9DTN/4BD/4uveaKAPBv+GZ7b/oaZv8AwCH/AMXR/wAMz23/AENM3/gEP/i695ooA8G/4Zntv+hpm/8AAIf/ABdH/DM9t/0NM3/gEP8A4uveaKAPBv8Ahme2/wChpm/8Ah/8XR/wzPbf9DTN/wCAQ/8Ai695ooA8G/4Zntv+hpm/8Ah/8XR/wzPbf9DTN/4BD/4uveaKAPBv+GZ7b/oaZv8AwCH/AMXR/wAMz23/AENM3/gEP/i695ooA8G/4Zntv+hpm/8AAIf/ABdH/DM9t/0NM3/gEP8A4uveaKAPBv8Ahme2/wChpm/8Ah/8XR/wzPbf9DTN/wCAQ/8Ai695ooA8G/4Zntv+hpm/8Ah/8XR/wzPbf9DTN/4BD/4uveaKAPBv+GZ7b/oaZv8AwCH/AMXR/wAMz23/AENM3/gEP/i695ooA8G/4Zntv+hpm/8AAIf/ABdH/DM9t/0NM3/gEP8A4uveaKAPBv8Ahme2/wChpm/8Ah/8XR/wzPbf9DTN/wCAQ/8Ai695ooA8G/4Zntv+hpm/8Ah/8XR/wzPbf9DTN/4BD/4uveaKAPBv+GZ7b/oaZv8AwCH/AMXR/wAMz23/AENM3/gEP/i695ooA8G/4Zntv+hpm/8AAIf/ABdH/DM9t/0NM3/gEP8A4uveaKAPBv8Ahme2/wChpm/8Ah/8XR/wzPbf9DTN/wCAQ/8Ai695ooA8G/4Zntv+hpm/8Ah/8XR/wzPbf9DTN/4BD/4uveaKAPBv+GZ7b/oaZv8AwCH/AMXR/wAMz23/AENM3/gEP/i695ooA8G/4Zntv+hpm/8AAIf/ABdH/DM9t/0NM3/gEP8A4uveaKAPBv8Ahme2/wChpm/8Ah/8XR/wzPbf9DTN/wCAQ/8Ai695ooA8G/4Zntv+hpm/8Ah/8XR/wzPbf9DTN/4BD/4uveaKAPBv+GZ7b/oaZv8AwCH/AMXR/wAMz23/AENM3/gEP/i695ooA8G/4Zntv+hpm/8AAIf/ABdH/DM9t/0NM3/gEP8A4uveaKAPBv8Ahme2/wChpm/8Ah/8XR/wzPbf9DTN/wCAQ/8Ai695ooA8G/4Zntv+hpm/8Ah/8XR/wzPbf9DTN/4BD/4uveaKAPBv+GZ7b/oaZv8AwCH/AMXR/wAMz23/AENM3/gEP/i695ooA8G/4Zntv+hpm/8AAIf/ABdH/DM9t/0NM3/gEP8A4uveaKAPBv8Ahme2/wChpm/8Ah/8XR/wzPbf9DTN/wCAQ/8Ai695ooA8G/4Zntv+hpm/8Ah/8XR/wzPbf9DTN/4BD/4uveaKAPBv+GZ7b/oaZv8AwCH/AMXVe7/ZoYQj7H4mDS7uRNabRj8GPNfQNFAHzj/wzVqv/QxWf/fhv8aP+GatV/6GKz/78N/jX0dRQB83Tfs36pDBJKfENmQilsCBucDPrXpHwJ/5JRp//Xaf/wBGNXoN/wD8g65/65P/ACNeffAn/klGn/8AXaf/ANGNQB6TRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAV7/wD5B1z/ANcn/ka8++BP/JKNP/67T/8Aoxq9Bv8A/kHXP/XJ/wCRrz74E/8AJKNP/wCu0/8A6MagD0miiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAr3/APyDrn/rk/8AI1598Cf+SUaf/wBdp/8A0Y1eg3//ACDrn/rk/wDI1598Cf8AklGn/wDXaf8A9GNQB6TRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAZ+vXaaf4d1O9kVmS3tJZWVepCoTgflXDfAn/klGn/8AXaf/ANGNXbeI4hceGNWhMDTiSzmQxK20yZQjaD2J6ZrifgT/AMko0/8A67T/APoxqAPSaKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigCpqsMdxo97DMgeKS3kR1PQgqQRXA/An/klGn/9dp//AEY1eg3/APyDrn/rk/8AI1598Cf+SUaf/wBdp/8A0Y1AHpNFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRXP65410Lw/ObW6uzNflcpY2qGa4fjPCLk9O5wKAOgoriYvE3jDVlH9l+D/ALBHkAz6zdCPHPOI0DMRjnJI/Gs3VNW8cWdyBN4i8D2AcZSKd5MkdCQSRnmgD0iivO7HUPiFNA11b6l4O1WM/KiW7yqGbP8AeBI49KtyfEK70hwPE/hbUtLhXiS9hIurZOTg7k5wQM8qMd6AO5oqlpWsabrlkLzS76C8tyceZC4YZ9Djoau0AFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAVNVmS30e9mlbbHHbyOxxnACkmuB+BP/ACSjT/8ArtP/AOjGruddhjuPD2pwzOEiktJUdycbQUIJzxiuG+BP/JKNP/67T/8AoxqAPSaKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKRmVFLMQFAySTwBS1wfiqQ+LNZk8KR3Bg0e1jE+uXaSbSF6rb7s8FgMt6Lj1oAr3viDUfF8NxJpN6+ieFYELza82FknAzuEIb7q/8ATQjtwK8s1T4uaP4WmurPwHo8LSsPLk1q8y81we7HPzHnkbjj27Vz3xR+JL+Lb5dM0dpLXw9Zr5UMCnas2P42UduBgHoBnqa84AycCgDrI9d8deN9TWxh1LVtSuZCWEEcrbRngnaCFVfyArrtN/Z58X3tuk11Pp1iW6xSyszjjP8ACpHt1rduDqXwX0fQrGxm0y31HU4bi41C6u4Wkw6qpWJSvOP4fQk5q943+K3imx8P+GZrOe00++1Gza7uooohK8Yz+7Yh8hUYHPr19KAPPNe+D3jXwtFJf/ZUuYLb94bixm3FAMHdjhuPp2NVfDvxb8Y+HrlXXVZb+3ACtbXzGVCo7DJyv4EV7XqXi/xHqfxA0rR/Dmvab5Fxo7zu3krPbyXCNIG+YYYDK4yDx1wa8g+IOnR6ro1n40trCGzkubqWy1KG2O6H7Qh/1iEZG1x+oPXOaAPQ/CWv+H/Fl1DL4UuP+ES8TJ8zWEY/0O+I5AdQAG6kZ4YZ74Fep+FvFT61Jc6bqlkNM12zwbixaTf8h6SIf4kPqOnQ18TxyPDKksTskiEMrqcFSOhB7GvoTwN4ln+I2kIxnhg8c6EvmWV0QB9rjxjZJ6qclW9Mhh3oA95orK8Oa5D4i0K31KKN4mfKSwyDDRSKSrow9QwIrVoAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigCjrUvkaFqEweNPLtpG3ynCLhScsfT1rhPgT/ySjT/+u0//AKMau08T2xvPCes2obYZrGePcQTjMbDOByetcX8Cf+SUaf8A9dp//RjUAek0UUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQBT1XUrfRtIu9Su3CW9rE0sh9gM189+ONVuPDnwlt7G4kk/tjxZctqd5nI2I207efby1x7GvW/i1JOnw01ZLZC8s5htwgXcWEkqIQB6kMa8L/aAu/M+IEFgkflwWNjFFGgPy4OWyB26gfgKAOC8LeGdQ8XeIbbRtNVTPMSS7cLGg5Zj7Af4V9M+FPgd4V0CCJ9Qtxq98p3NLcD93njpHnGOO+etZH7O+gQ2nhC61tocXV7cNGsjKQfKTAwD3G7d07j2q/8AEb4i6z4e8WWuhaJHbm7Nstykc6bxdlnZfKGCCrfLkY65xxxkA63xH4G0zxRrmkalqDOy6csy/Z9oMcyyLtIbI9q8y8ZeE/AngyOyi1HUvElzcGB4Vt7a6VpGtF+Yo/AxEOfQ8nrji94P/aA0/VLyPT/Edj/Zlyx2CeMlot3+0D8yc8d/c1wvjS+k1XXdZ1W+ilkt7mOeGxu9vlSWkiRMDaSKcjoScdSSCDywoA9Ps/hD4S1W0stQ0zWtZNkbdo7c296NhgdmYxg7c7TuYEZ7nPNdrF4N8PR+GYPDraXbzaVAMRwTLvAPPzZPO75j83XmvDPg/wDFC08MeEtWstcuWa3ststlEoy7Fs7kX8cHJ4Gatn41eI/FEl4+nJaaDpFlH5t1ePiaVVzwq7sKXY8KuOvfHNAGh8QvgNYtpsuo+D4ZIryLLvYmQssq9TszyG9s4OMcHr4d4a1u58KeKrHVo0YS2U4Z42GCR0ZT6ZGRX2P4K12TxN4P03WZYxG91GW2ZzgBiBk9zgDPA59K+a/jp4et9C+IkklpGkcOoQi7KKScOWYMfbJBOPegD3DQLmDTPiNILMudK8VWS6nbFjgCdQN+AR/EjIccnivQ68I8JXy6j4T+GupWaFZtM1ZtNmcn7okRgwAPUMNv0r3egAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAKOtXAtNB1G5MbyCG1kk2RjLNhScAetcJ8Cf+SUaf/wBdp/8A0Y1d7qwLaNfKJjCTbyDzRjKfKfm544681wXwJ/5JRp//AF2n/wDRjUAek0UUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQBx/xPmktfAd3eRwmY2txa3LIDjKx3EbnntwprwP9oG1kg+JhmfbsubOKSPB7DK8/ipr6b1/SYte8P6hpM3Ed3bvCT6ZGAfwPNfO/xM08eIvh1ofimOF1v9KxpOpxgcIyZGcZPAfOPZxQB6n8DLmKf4UaZHG2WgkmjkGDw3mM2PyYfnVL41WWpR6Zput6VFpxktJWjna9t4HUI2NpLSjAww/Nq4L9nzxrFp2oXPhe/nCQ3jebZl2wBL0KD3YYx7r719FXdrBfWc1pcxrLBOhjkRujKRgigD5U8ReFtT8S6bca3NHYf8JDFhrm3sby2lF5GAS0qpExIcYG4Yweo5yKpeFPED3sUkN8ftDi1ltpUlCv5yeS4hbB/jibGG67WxkAYPc+LfhXpngq9TWNL0rxHdW8LrMk9hfxBrdw3HyGItwcc5PvXP6NLa6p4huta8KWjpJe209jf6SygyR+ZEVEybQBtLBcgAbWOOjCgDjvCFpJe2usWiLABeQR2gmn4SEmVZC5PYBInJPoD6jPQ3A1CSa08LeFLjSm05ZljQiWGR72Ynb57qdzd+Bj5V/Gp9Gk06HQZfBVppWs6lfXMqvqU2kTxhZWBJWLcUfKL6jALA9QAT7H8OvhRo3haVNaksblNTdPkiu7hJzbZ64Koo3dj1x2PJoA77R7H+zNFsbHj/R4EiJAAyQoB6AD8gK+ev2k7sv4n0Wz2KBFZtLuHU73Iwfps/U19HXFxDaW0lxcSpFDEpeSRzhVUckk9hXxr4p1a8+JXxKkks0Be+uFtbNDwFTO1M/zJ9zQB6r4RtG0/wAG/DXT4Chm1DWGv5UQcuqByWP+6u3Ne815zoFhHc+PrSxt/Lew8IaYtmr7MlrmVQGwcAZCIM+7+9ejUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFNCnzC287SAAuBgHnn/PpQA6iiigAooooAKKKKACiiigAooooAKKKKACiiigDD8Z/wDIi+If+wZc/wDopq5L4E/8ko0//rtP/wCjGruddgS58Palbyqzxy2sqMqjkgoQQK4b4E/8ko0//rtP/wCjGoA9JooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigArzjxBpttomv3kGowxN4U8UsIb0ltv2a7KkB89AHCqM9mAP19HqpqWmWWsafNYahbRXNrMu14pVDA/n37g9qAPjLxh4V1P4f+LGspXfdC4mtLtFKiRc5Vl9wevoRXvHwz+NVjr1mmm+JrqG01dSESZsJHc5OAeOFbPUcDuPQO8T6TbaXpseheNorrVfDnzC010jfcWTkcCUjnA7Pgg8ZHFePeIvhH4g0qE6jpKrrmiuokivbEhtynuUBJ/LIoA+pPFd99j8Ozuiyu8pWKMQXaW8hLHA2O5A3eg79MGvnn4mw3Vtplhqlw/iO1v8Af5AmvbO2h3oyYZTLDhnOBj5s5Gema8+tfGGv2dmtidQkuLFCpFneKLiEbTkfu5AVHPoKo6prF7rF1JPdyj523eVGNkanp8qDhfwFAHvvhZv+Ef0nSZNKj8StpI23CSXP2Swtip+YvK4+Z1I7MSQOK9pvdSstO0+S/vLuGC0jTe0zuAoXrnNfEmleKdT0eNktzby9PLa6tknMBHQxlwdh+noKi1fxJrevlTquqXd2qnKJLISif7q9F6dgKAPTfi78Xl8UI+gaA7DR8gzzlSGuSDkAA8hQQPckenV/w+8OP4K0pfF+q2wbWrwfZ/D+nSqQ0szgBXPTg7h17ZPpXjVekeGfibG2nQeH/GdkNW0dMrFdNzdWYIwDG5544x0I9ccUAfSvgvw5/wAI14dit5xG+pTk3GoTqOZp25ck9+Tgew7V0VeS6L4t1DwrpNpdyX58T+D2JDayhLXNkDjCzLyWAyMnqO44APqVhf2mqWEF9YzpcWs6B4pUOQwNAFiiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAp6sYl0e+NwUEIt5DIZMbdu05znjGK4L4E/8ko0//rtP/wCjGrr/ABgpfwRr6AgFtOuACxAH+rbqT0rkPgT/AMko0/8A67T/APoxqAPSaKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAGyRpNE8UqK8bgqyMMhgeoI71xVz8Pm065e+8IavcaJcMdxtQPNs39QYjwuT3XHU129FAHkuo6H4gljdPEvw/wBA8QqQzNd6dKIZWzxkq4B3nrkHjPHIrEbwH4XvbZRP8LvEdhMr5xaXSSBhjuWl/p+Ne60UAeK6b4QWK4judI+EdrbTbtpk1bU96x9CG2ZfIB9BntUPijRobq3h0r4gaDpmlCb93p2uaKjeRbOf4Zc4wCfXg5PTBNe4VXvrG01Oxmsr63juLWZSkkUi5Vh7igD4r8Y+CNZ8EamtnqkSMki74biElopBz0OOvHTrWt4I+HkviG0l17WLldM8M2jZubyQ4MgHVYxjk5wM+p7niva9f8N3nhjS7nTJdIm8TeC533ixQlruwPJ/dnOWTPTnIz9c6OheELvxJNaah4m0+Ox0mxYNpGgoAFgUcbpgB8zcKQM4HcUAUPDvh1/F2jxWENpPovgWIJ5FpkLc6kRyWlYEkIfTqcdq9Vt7eG0t47e3iSKGJQiRouFVR0AHYVJRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFAFHWrWO+0HUbSbPlT2skT4ODtZSD/ADrhPgT/AMko0/8A67T/APoxq9Bv/wDkHXP/AFyf+Rrz74E/8ko0/wD67T/+jGoA9JooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAKWsLM2iX627hJzbSCNiMgNtOD+dcH8Cf+SUaf/12n/8ARjV3OvSGLw7qciy+SyWkrCTj5MIeeQenXoa4b4E/8ko0/wD67T/+jGoA9JooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKwdU8X6Vo2qNp979pjkWD7S8gt2MaxBgrOWAxhSwz6ZyeKs/8JBYnxCNEQXEt55QmcxwO0candt3uBtXO1sZPOKANWisCPxjpMmqtpxNzHIt0bIyyQMIvPADbN+MZIYEeueK2Ly8t9PsZ727lEVtbxtLLIeiqoyT+QoAnorjW+JOlppV/qD6fqaR2lul2sbRIHuLd2wJYhvwV7nJBGRkcircfjixDa4Luxv7FdFhWa5e5RACrAsNu1zkkDvjtQB09FcbrvxBh0rRNC1az0u41C21iWKKIxyIuxpACgbk8nkcccHmrnjDxXP4Vhs5o9Hkvo7mdbfetwkQSRyAgO49z36CgDpqK871L4mahpl3LbS+EbtniD79t3H95IFmkC/3sK3UdSMCpLX4lXU2vxaHN4ZuLfUpJolFu11GWMTqzGYeqKF5I78daAPQKKZKZBE5iVWkCnYGOAT2yecCvOG+IXiODQNe1e68PafHFotybedF1BmZypG4r+79GGM4z7UAelUV5lefFpW0TxHrOj2EF7YaPJbxiRrgqZjJgNjCkDaSB155/Ft38Ur61sbSdrPRF825urd5pNUKwBoVDfLJ5fzbuQOBzgUAen0VxVx401W6toW0LRI7u5XTYtRuoLi5MLRrKCURPlO5ztfrgDA55rOu/iRfoLiS002zmRo7SbT0a4cSXcdw21CAEO0g5BHPSgD0aiuITxjqk/i278O29npz3ltMoZDcSA+SVRmk+5jI3gbc5ODXOaP8UNZ8SzabpOkx6WmtOl016LiKUwp5TYQLhgRuHPfAoA9aoryDS/ih4g1DwnqmtRxaRcPZ20MphiilQpJI6gRtub5sgt8w4BXvW1ZeNPEOvaxc22iR6YLaKOGWQ3MUnm2wZZg8cihx86yQhT0+90oA9FormvA+s6vr/h2HU9XgtYjcpHNB9mDBWjeJG5DEnIYsPwFdLQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFAGX4lnjtfCur3E0KzxRWUzvE3R1CElT9elcV8Cf+SUaf/wBdp/8A0Y1dxr8ltF4c1SS8UNapaStMCuQUCHdx34zXD/An/klGn/8AXaf/ANGNQB6TRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRSMdqk4JwM4HU0AedeOvDOreIPFVm1pYytbJp0sQuftCpCJWkRwkqbtzxkRlWG1h84444zdf8J+M9U1abVrBRZXVwiKNmqNH5UQjCvbkKhDAtvZXBBUtng1o23xB1q90TWNVh0vT1is7Ka4WE3LG4hkQjEU8RUFGK5PGRx15FOh8Y+JYLQX17b6TLb3NjZSWscIkRhPcuI1DkkjYGySQM4x1oAgHhLxJfalNa3NvbWemy64mrG6jvWkmCxoirGF2jkmMZYnueDXe65paa3oGo6U8hiS9tpLcyKMlQ6lc49s1yP/AAlPieKJNMmtdGOsz6h9hguIpma2OImkZ2QEuuAjDaTknuBzWX4l8f694e0bSbqa40UvObtbqWG3kuEJiyyeWFkGNygfePBPJAFAEFr4d1rWr/U9D8QobS5XQk061vLeNpIrhN2WlLYAVtyr8hweT161auvA3ibW9MvG1O6sIr/UL20e7WCRwhgg9CBncx5xjAqbXfF/ifSIdPhml0GxuJrEzvdXkU32WWbPEauGAj4xy55LACq/iHUfiJF4htrbTL7TIxeLIbO3MIZJfKijckuTkBmZwOmAB60AV/8AhXHia20C10W0vtMa00/Wl1KxNw8jMI1ZmEbEL6kdPU1qa54Y8ba7pEUM9/pAul1RL5SDKEiSMJsRMLn7wckn1q2154jh+Ic1lLrMR0yOx/tD7Mtmu7G4qY9+c9s7qwrfxp4lm0ez1iS5tlt9bsbua1ijgVjYyRIzoCc/vAVU5yBgjtnFAHR6xo3iu/1rw7qdvJoySacrtcJIZcO7qUcLgfdxyM8561Jc+F9Sm+J9r4njmsEs4bFrRk2N5zgtk5PTjsffpXP/AA78Za14i8QTWmqXOz7LpkUt1bNAq7ZmPDK46oUww/3/AGFNuvE/iS806XX9Lmk/s271NILaGOFHl+xxhg8sSNy7O2TjJO0DAPNAHqD7tjbCA2OCRkZrz9/AGsTaL4j06TW7ADWrg3LSJpzAxuWUkH978w2rgdMdfamWGta1rr6Hptnr8YlmtLq7uL6K0CmXy5VRE8tx8hBYbhjsQOoNM0XU9a1XX/Ck1zrMqx3umz3F1bWwjMEkkTRrlSVJ2t5hJwewxigCfW/h7qOq6brmm2+sWVjZ6mkMaRW+nbRCqHcw4cZ3En8z1rS1rwQuvNoi3tzbtBYiQXUC2g2XW9NrADPydzxkjjB4rnNY1PWYLjxS0OvXYjtNQ077L5YjwsU7IHT7pyP3hwevA/GbTbPxfD46TTrrxRNOsUC3s0LJH5bxtPKm0ERhgQgQ/wC8D2oA0rr4e3VxarGnie/glNkdPnmjijLXEA+6HJB+YZYb+vzH3zpN4G0san4evYWmh/sOEwQRo3yyJtAUP64IBHvXJyX+taNF45uzqd7cS6ICLBLiTeipJEsm5lGN5BORu6Diqviu/wBT03Ttb0vTfEN1LItpY3ttePcfOs01wYyAw/5ZsADs5HJxxxQB0z+AL5tcuNTXxXfxm4vUvJI44IlyUCqqbgM7dqKpGfmA5zVe2+GUlkulm28S3sM2nrOizJbwhnWXqD8vbtnOKPhpqM2qXXiOea41FmjvEhe2vZmf7NIsYMiJkn5d5bBGOMccCovie95BdeH3sLjUTPPcyQmzs9Ra1+0KIXfGR33KvbPbvQAsPwtdNHk0qXxLfSWpshZxIIY02AMjKx2gb2XywAWzgE+tb8Xguwt7jV7q1ury2vNWiiju7mBkVmMYI3gbcBmycnH5GuO1iS506XU7K+8SanaSaPpS3GmymdlN053lmkH/AC3KlUXac5zzknNZSTtB8Ubu4a6e1jW/tvtF094xRFktgXgaLOArOfvHhTjkcUAereHtDh8N6Jb6TbXNzPb267ImuXDMq9lyAOAOBWpXgWl6jeWninSrOS/tx4Wh8T3Edqy3bNIW/eCNH5JKgqCCTg7xnPb32gAooooAKKKKACiiigAooooAKKKKACiiigAooooAKrXVxNBLbLFZy3CyybJHRlHkrgnedxGRkAcZPPSrNFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFAGfr0c0vh3U47ckTPaSrGQcYYocc4OOfY1w3wJ/wCSUaf/ANdp/wD0Y1d9qsKXGj3sMgJjkt5EYAkZBUg8jkVwPwJ/5JRp/wD12n/9GNQB6TRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABSMu5GXJGRjI6ilooA4jTfh6YplfWdXfVRHYPp6M0AjkeJ8bvNbJ808cZ4GScE81PB4BjXQptLu9av7rMdvHbzsscb2wgbdFt2KASrc5bOe9dhRQBxkHw8ht7ObZq94NTlv/wC0f7RWGFZFm27CQoTbgqSCCCOSe5qOP4cRWdno8Gma1d2L6YZ3WWKCAmV5vvsyshXoSAAMAfQV29FAHFXXw8F7B5Fx4i1Z45bQWd4rNGwuowzsc7lO1iXPK4OBWxd+FrW61DSbxLu8tm0pClskLrtAI2kHcpLZAA5Pb15rdooA52fwhBceJxr7apqa3QQReUkqiIxg58srt5XJPXn3qpB8OtEtobiCGW+WB7eW2gi+0EraRyf6wQgj5c++fautooA4a98ANZ6TNF4evpYdQuLWLT5Lu6fe32dXJPQffCsVB7AD0zW/feE9G1DTdOsJ7VhBpzI9p5UrxNCyDapVkIIwK2qKAOam8A+HZtNgsGtJxFBJJIjpeTLKWk/1haQNvbdnnJOeKZd/Dzw1eLp6vZzxjToDbWvkXk0XlRnqBscde5PJ711FFAHNx+A/DkWoWN9HYMs9lFDFDieTbtiBEe5d2HK54LAn3q3H4V0mLxPL4jSGYapKgjeX7TJtZQMAFN23A+nXnrWzRQBzGm/D3wzpWr3Gq21hIb25R45pJ7mWbzFb7wYOxBzip4/A3heLSptMTQ7JbKd1klhEfDsvQn6dq6CigCpY6XY6Z5n2K1jg83bv2DG7aoRc/RVUfhUGqaBpOtS2kupWEF1JaP5lu0i5MbcHI/IflWlRQBQ1HQ9K1eW2l1HTrW7ktn3wtNEHMZ9Rn/PApr6Bo0s888mk2DzXClZ5GtkLSg9QxxyOB19K0aKAMlPC/h+MKE0LTFCuHULaRjDDoRx1961qKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAr3/wDyDrn/AK5P/I1598Cf+SUaf/12n/8ARjV6Df8A/IOuf+uT/wAjXn3wJ/5JRp//AF2n/wDRjUAek0UUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFAFXUlD6XdoSQGhcEqSD909COlcB8Cf+SUaf/12n/8ARjV3etXH2TQtRuSjP5VtJJsXGWwpOBmuE+BP/JKNP/67T/8AoxqAPSaKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooJABJOAOpNNR1kQOjBlPIIOQaAHUUUUAFFFFABRRRQAUVTv9X03SzGNQ1C0tDJnZ9omWPdjrjJ5q0jrIiujBkYAqynII9RQA6ik3LvCbhuIzjPOKWgAooooAKKKKACisfXfEdtoPkJJbXd3PMGZLe0QPJsXG58Ej5RkZ+oq4dUsxo51YTq9j5H2kSpyDHt3bh68UAXKK5xvGNpHfafbSafqca3vkhZ5bbZHG8oYqjFiPm+UggA4JAPJrW1PVINKhhkmDuZp47eOOPBZ3dgBgEjOMkn2BPagC7RXP2Pi/T795NkN1HAFneO4dBsnWF9shTBJ4PqAT2qbQvEtrr8k6QWt5btFHFMBcxbPMjkBKOvJ4O08HBGOQKANqiiigAooooAKKKKACiiigAooooAKKKKACiiigCvf/8AIOuf+uT/AMjXn3wJ/wCSUaf/ANdp/wD0Y1eg3/8AyDrn/rk/8jXn3wJ/5JRp/wD12n/9GNQB6TRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFUNS1rT9HezXULgQfbJxbwFlYhpDnCkgYGcHrgVfrjPiRo0uvaRpllHb3Msf9pRSTNbffiQBsuPcEg0AdBoviHS/EMVxJplw0y28phlLQvHtcdR8wGfwrTrx7VNP8bR+H7XT7jTZ7meW/uZ7+bTpNqzYQrH8okRtrsQ5wwwV6dqyn0LXruzsZtQ0LxPJfR2dtHceReGMSSIxV+koGDGF5AGT7kmgD3as/VtZtdGS0a53lru6itIUQZLO5wPwAyx9ApNeProfjy91LSJ7xNWDQ29mItjqoV4wvnCVvOGNzBjkq5YHoK9BsQfEvjefUZIlbTdEJtrJzj57ogiZx7KMIM991AFJ/izonlXjRWGrSPbeepU2u3e8IzIikkAsq5YjrgGu1sruO+sYLuMEJNGsig9QGGRn868m0LwNeS2fi25vtM1GPU5Lq/fTY5rhRD+/VlDKofG7BIJPYjFOg8Aa1aWd1aaNp0OlWt5oEMNxEtwBvvI5csCykn54yyl/Rh6YoA9ZjuYJoFnimjeFhlZFcFSPUHpUD6rp0dil8+oWq2b4C3BmURtnphs4NeU6j8PNQutDj+z+HbW3Q67b3y6QJ0KwQJGEkXd935yuSB6880av8P8AxJd3VxFaQQRaRbajcS2tgrw7XSZAN43xuowxfKsvAc7TwAQD2LqMiuV1DxsLDxLLow0W/nMXkF7iN4QgExIUgM4Y8q3ABPynitbw5Y3GmeHNOsLvb59tAsTbZjL90YHzlVJ4A5wK4zxH4P12/wDHcmv2dlp0wjjtxZvNqEsRikj3nc0axlX5k6E/w9Rk0Ad3Hq2mzOiRahau7yNEqrMpLOoyyjnkgckdqoab4v0HVtRl06z1O3e+ikkia334fMZw2B3A9RXO23hXWbXxzJr0dppJt5ruQNB5rARxlUH2hRsx57bSG7EBRnqTqeHdJ1/R7qaznfTpdM+1z3C3GXNxIsrM4UjopVmxnJyB0FAHTTTR28Ek0zqkUal3djgKAMkmmWd5b6hZw3dpMk9vMgeOVDlXU9CDVezOqNbXX25LMTedILcQsxUxZ/d78j72MZxx6U/SlvE0q1XUI7aO7WJRMlrnylbHITPO30oAt1wvjH4lWnhGXU7aW0M13bWkdzboGIE+5ipXO35SoG49fl54wa7qvM/HFje6pfazZvoV/ew3FmkNpcW1qr+RJtlVmO+VN3yzMBgcZ70AejWjyyWcD3ARZmjUyCMkqGxzjPOM0XZnFpMbXy/tAQmMS52bscZxziuMj8Va6l7aE+FtdNnHblJ4hawBnl+XDKfPOFwG49xyauyeML5onVPBviNWIIBMNuQD9POGaAM7w54/m1u70dZBYLDd6TJqFz5Mpd4GRlGwjtw69eeG4q1cfE7w/bac15ImogefHCsJs3WV/M3eW4UgHa21sE4zjFchY6dqtrb6ZbLpPiSMWWlz6WssNjbxuVk24k3faTtZSinp2NVB4K8U2139qh0iZrh5rWeSSNraIM8LSckb2yWWTBJP9MAHoNj8RNE1PSrnULKLUZ0geJPKSzcySeZ9xkXHKnnn2p0/j/TIDYp9i1SSW+tnuYYo7QliqHDg+jL3B/mQK8303wL4mtIYorzR9Ru44hAoi+2WixOIkZEEiHIcAEYz0IzzW3pujeJtMm0mSHw/qbf2ZDNbwqdQs1DRykEqdqjGCq4xjGKAN+9+KOjWhYpY6rcRJaR3zzRW3yLbOMiXJI49uvB44NduDkAjvXjr+GfFH2OW0Hh/Up4bnTV0q5M2qWgYwKXKsCE++N5HPBHXJ5retLj4mi70+WTR7ERRwmGeGbU0xI3aRisOQRg8Lwc9OKAPRCCQQDg+vpXl/gTxP4i1nWrGKbUZtQt9l0uoh9PEMcDJIViKSAAMWxyBuxz+HT/bfHf/AEA9A/8ABrL/APGKx/DeleNPDOl/YLbTNJni3vJmfVXyCzFj922Hdu+aAPQq47x5rt3oV14blga+aCfUhDcW9lEskky+W7AAEZxlRnGOM1Dpkfj3TYJY2sNKuzJM82+51iViu452r+44UdAKW/0bxF4hn02bVbDTLd9OuhdW/wBn1CRhvAOCcwjPcY9zQBTXxjP4f8IwahPHdX811eXKoNSnjtnjCyOAjfLwcKAAFPJxxkVo6j4w1I3OlW+h6RDfHVrFry0lluvKX5dhIYFcgYkUg9T0wKpXPgvU5I1aE2gulecrNNe3LfLM26RCEKEqSAQM8ED8a8Hg3xPbS6fJDNoSNp8Xk2uHvv3UZxlQPP5HyqMHsAOgoAv2/jy9l1+/01tB/d2GowWNxNHdbivnfckC7B8uSuecjPel0vx+2q+Jl0q3012hlkuIkuF8zEbRFl/eEoFAYo2NrEjjI5rFh8AeJ08RXutzXehXFxdXUV35ckVyIo5Y12qwQSAEjr82cHpitGy8FavFqS38zaGs/wBpafCR3TIjN950jabar5zyAOp9TQBq+Ftc1/XZZJbux063s7eWa0maOd2kaaJyjFAVA2ZHGTnjpXVZzXFaf4Iv9EE/9h6vbWD3DbpmNrNPubOScSzsASSckdc81FpHgzxNodrLbWPi+BYZJ5Lgq+lBtrO25sZl4GSTj3oAteP47n7Pok9q14WXVIY5YrW8MBljfKsp+ZQ3O36Yz61p+EtP1LS9D+z6rcPLL58rxiW4ad44mYlEaRuWIBxnn61z2s+BNd8QxQR6r4lsrlLeUTRBtJ27XHQ8SiptQ8G+ItVtIrW+8T2U9vFIkqRtpAwGQ5U8S84I6GgDuK8V1qx15PFlpEJg3hmbxMkrDzmDrKWCmLGeVJy+OmfTv2914b8a3KgL48W3x3h0ePJ/76c1hQ/CK5kkmOo+KWuUluftbhNJtULTc/Ocq2W5649fWgC7a+NdTufHEOlmeyOmX091b2sqQMrAxLncHZsSfMCpAQAEYDHFP8IXviPXbC+vrrxHbSwQNdWUaW9sm5njcqs7Hs2BnaPlxg96tf8ACv5/tRuv+EnvvtJJYzfYLLfk9Tu8jPNOtPANzYOz2Xim/tmYYLQWNkhI9DiAUAc/4duL3UPhTczXXjCK+lfSEd45Y4na2+TLCQ5y2RlSX579abbeIbg+C/BH9h63YWAvHh0+4it4UdUZ4ycgNyrKV6d93OeK6Bfh/OkU8SeJ75YpzmZBYWQWU+rDyPm/Gp7DwFHZnEmsXMyK4kRPsdpGEkH8Y2wj5uOtAHPah4x1cmz0q11W2S7WG9WW8PkxiSeGTy1Qh/lXqHZRzg8YFS614rvYtbtLVPE9tYNJbwXVzH5CNHbxdHALDdI7sQEUYwASe1dcnhhYs+Vq2oR7pDK/l+Su9z1ZsR/MT7+1Un8DRySM7eJPEuWJPGpMAM+gA4oA6qioraH7NawwCSSQRoE3ytudsDGWPcnualoAKKKKAOQ8d3EdrN4auJlkMMGrCaUxxNIVQQTAnCgnqwH4iuF1bVNW07whY21vFqdmXF5eWXlJNGoXzmMERESFtwQghG2p0DZ7e00UAeVawltd+I9A8Q3zeIPs9zpDxj7CLiKR598TBDHHym4buDhTgc8CrMNxrUnxHukv5dUhMV3GbKKGOZoJbUqoOcER8EncXyQenQCvTKKAMm1Np/wk+oLGl4Lv7PCZWff5JXL7dmfl3dc7fbNa1FFACEgdSB9aqXOrabZE/atQtIMEA+bMq4JGR1NRavoOk6/BHBq+n297FG29EnQMFbGMjPsayP8AhW/gr/oV9K/8BloAzPGGpaLdww3djqkT6nHHLbwyWl/bpsWUAMHMhI25CkkAsNvHoc68vNAksfDvguLxFYC0tYYZb1/tCESQwbQqbsgZZwvvhW4rqrXwF4RspfNt/Delo+NufsqHj8RU0fg3wxDPLNH4e0sSS43t9lTnHTtQByPjDWtP1bVNNjsJLf7VZ3Ec1tqv9p24gt8nEhMZk3P8m4Y2nr1FaEHiLQtZ8aSX02sWC2ejqbe1El1GBJO6gySKM9ApCA/7T49+k/4Rfw9/0AtM/wDASP8Awo/4Rfw//wBALTP/AAEj/wAKAON0e40XT/Ect7Bf2dvp1nBcRW1tLqcUhlkkkDl4xvKop28ZOTv5wBy/wZ4ms3vdRvtaW20/Ur0hpp5NSt3jZVLCONAsrEbVPJwMkk966/8A4Rfw9/0AtM/8BI/8KP8AhF/D3/QC0z/wEj/woAcPEmhMMrrWnEeouk/xqzY6pYamJjYXkF0IX8uQwyBwrYBwSO+CD+NPtrCys4BBa2kEEQJIjijCqM9eAKnChRhQAPYUALRRRQAUUUUAFFFFABRRRQAUUUUAFFFFAFe//wCQdc/9cn/ka8++BP8AySjT/wDrtP8A+jGr0DUWVNMu2YhVELkknAA2mvP/AIE/8ko0/wD67T/+jGoA9JooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKZFDHAmyKNI1yW2ooAyTkn6kkn8afRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQBW1ABtNulYAgwuCD34Nef/AAJ/5JRp/wD12n/9GNXoN/8A8g65/wCuT/yNeffAn/klGn/9dp//AEY1AHpNFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUU2SRIYnlldUjRSzMxwFA6kmgB1FUdK1nTdcs/telX1veW4YoZIHDKGHUZHfkVeoAKKKKACiiqFhrNhqd5f2lnOZJrCUQ3K+WwCORnGSMHgjpnrQBfoopCQOpxQAtFIWVVLFgFHJJPArmF+IXhw6bcXr3jxrBZrevHJCyv5LHCsoIw2TwME8ketAHUUVHFKJYo3wyF1DBHGGGR0I9aeHUnAYE/WgBaKjS4gklliSaNpIseYqsCUyMjI7cVXh1bTri3kuINQtZYIlLSSJMrKgGckkHAHB/I0AXKKpPrGmxw2szX9sIruQR27+aCsrHOAp7ng9PSq6eJdEk0xdSTVbRrFpfIFwJQUMmdu0H1zxQBq0UUUAFFcyfFU6/ERPCh0vCNZG9F59oH3Adv3Mf3uOvvXTUAFFZXiLW4/D2jvqEkXmKJEj5fYil2Chnb+FQTy3OBTtC1K61Wwe5urKK2/essRiuVnSaMdJFYAcH0IzQBp0UVwN7431a1uvFdsLbTRcaQA1pA8kgkuh5fm9MY+4GHGfmU545oA76iudtNeu5vE9to00MEcv9nC7uhiQFXJUYQldrLknvmpoPF2i3OsJpUN1K148ssKL9mlCs8X+sAfbt+XvzQBuUVyzeP9FVNQcx6gFsrYXb7rKRS8JOC6AgEgEHPAxg9qd/wnujAXPmLeRSQ+Tsilt2V5xMxWIxg9dxU4zjGOcUAdPRXMeENf1HXLnxBFqNqtsbDUmtoY9m1/K2KyluSCSGzkcdK6egAooooAKKKKACiiigAooooAKKKKACisLxmzJ4N1aRZZ4mjt2kD28xicFeeHBGOnqK4S01jUofDetWMMl+t5caqmnWFnd3pe4tyUViJJskgMA7BlZsBhg+gB6xRXlb6va+IJvDmmW17q1qtrqMum34+3ukm8W0rMjOr7mKsi4c9exPNdb4B1i91vwyLq9PmFbiWGC527ftMKsQkvb7w7jg9RQB09FeV67ravqXi5Nb1K+05rEQx2SWVyUdISM+eqb13ks2D16AYznPQW2v6rceO7rSDq2ixWkHlSC3dCbpw6sTHgSYDDbnODwelAHaUV5voXj7VNamtlCWSXF4L1TYIpaaxMOQrSfN8wLKBjC8uMH1rah8TZZbK7uNHv8AT3kh0Aan5D27MwlDYdGIcY9NvUck0Aeo0Vx+j+IbnVf7fhOqWhtbSCJ4NVgiAjUujMxOWKnZgE89+a6fTpRNplpKt2t2HhRhcqABNlR84A4GevHrQBZooooAjSeGSRo0ljZ1+8oYEj8KRLq3kuZbZJ4muIgrSRK4LIDnBI6jODj6VwsGqeG/Dni/xRdRrA1zsgaaKxtA0287ywIQZYkkMSfXnpUujTCx8d+KwGknluBA1sZYgpdwsm6MOFGVXCjknGetAHdUV5fpep+JZNG1e9tNW1C+1ddMDPpt3prRLb3fcRuUVWA5AUFskZyap3V/rw8E6lewa9rDrHdW/wBkdLZ2uMFtsqtutk3LgkjC8bRz2IB65RXm97P4ijtdV0uwv78yWepW5iuriF3aeBoVdlLRxkgbtw3KpI4BxnNRu3iPUfDugR3b6tZMftBu5AJDMJFI8osIhu2kbiAQAcDcD0IB6ZRXmmtR+K7vULGOa5uIIo9PV4bq0SRd95n5vNjjkxjgEK5KcnJ9PRIbhXgjeRlR2UFlJAIOOR1P8zQBPRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAV7/8A5B1z/wBcn/ka8++BP/JKNP8A+u0//oxq9Bv/APkHXP8A1yf+Rrz74E/8ko0//rtP/wCjGoA9JooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACsDxtbwXng7Ura6tb66gmjEckViMzbSwBKjvjqRg5AIwelb9FAHk2jvrtjaxap9kv/sVprG6Y29g9tcahA0OwySWygbir7OQOQpIHAzj3Mk9zDoiaz/wlccTahfwT20QnEs8R8yaFlVfmbAMYz22kHpXuNZ9/oWl6pfWV7fWUc9zYsXtpHzmJjjJH5D8qAPI9btfHZt9AVlvjjTVEckKyySQ3QZipkVHVd+zYMyZTIbPXNb9/4ekvfiBG+oWGvz6fcWcKTyW108UH2nkF2VZQQAu37mRnPXk16bRQB53a+DL2x8Y2trCJpNBhuG1ETzXcjOjbNgt+Wyw3ASfMSMDFXNJlnS88QWUfhvWrOG9eSVJ3MYUkRKhwfMYqSV+XjHI6V3FFAHk2k+GvFg0PVrTy5QkkdqImuZBBLOIpD5kZCSOFLrkeYCCdw47ifW/B2qahoGsQjSHlWfU4LnTrKS5TfaqmzzG37vk3BXACk43e5x6lRQBwmqWsLWlj4R0exOltqcjT30SMFaG1DDzWLIT8z8ICD/ETnisvxD4Ek1XxJq12dCWa3t9Mhh0rbcoitKiyDaVzwB5gIzxmMV6dgZzgZ6ZpaAPMtQ8LeKdT8UQeIFtdPtpBc2sphacFxDGAWjZ/LbDbiw+QqpB5zmn6d4AvdKvUu7Cy023nXX5L8SpKdwtXQqY87M9/u5x716VRQB5KnhbX/D9rq2pXNpZeQdEuoJ4tPb5pJWYuGSNY14HIG4kjJ5Peno/hVb7wxqHh/TXsjqbJa3VxeW7ZgkaPYBCSqAKrCPOPmOSSRk17NRQB5qfA2sw+A59Gt4dOeebUorzyJrmRo0RZEdlLlPmyUxwij5jx69bc2epJ4fsodO07SIruOSJ3tpMm3iwwL7CFByOSpwOea3aKACkPQ9fwpaKAPLdMuNYg8Xt4g1Tw94gvLiOx/s+Ax2cEZMe/eWf9+QXJ9ABgdBnFbtl4t1uOW7N74U16aN5i1ssdtApjjwMKx875jnPPHWu1ooA4XWtf1bVtONnZeHfEunzu6ETm1tpFwGBKspm5UjgjI4NO0ay1XRfDdxp9hp+oRXcsskv2lorYRpIx5KQibATjhc+9dxRQBg3Gsa1DaKbfwzeXNwMAh7i3iDepz5hx9K4bXPDuoeINfXWb3wPfC6WOOMCHWYY1IRiecHncCUOf4emOter0UAecTr4sl8Upr6eG7+GZbf7N5K6haGMx7gxByM5JHXNUNJ0jxfba3LqH/CPLHc3l7JNO9xewNHFE5wyRlBvU7VXkdWyTnNerUUAeaweAry1guo47Tc11ZyWErm+RSYH3Zztg+ZhuJDHk4GSaW58MeI57nzf7G0x3SCC3jmbWJFcCBi0UnFvgOCzcjjkjBFek0UAef6PpfjHRLrULmDS9Mnm1CUTXDXOtSvlwu3IAtwBwAOOwHpWv9t8d/wDQD0D/AMGsv/xiupooA5Ca7+IjPGYNI8NoozvD6hM5bjjBEQxz9c+3Wqtu/wAUnlC3EfhGKPuyG4c/lx/Ou5ooA5XyvH//AD9+Gf8AwFn/APjlHleP/wDn78M/+As//wAcrqqKAOMu7L4jXGzydZ8PWu3OfLspW3f99OaS00f4gszfbPFmloMfL5Ol7s/XLiu0ooA5T+xfGX/Q42v/AIJ1/wDjldFp8N3BYQxX10t3cqMSTrF5Yc+u3Jx+dWaKACiiigCtqGn2eq2Mtlf20VzaygCSKVdysAc8j6gVWn8PaNdWTWc+l2clu8SwtG0KkGNfuqeOgwMDtWlRQBlReGNBgt0t49F05YU+6gtkwOMenpWmiJHGscaqqKAFVRgADsBTqKAK02n2VxdRXU9nby3EP+rleJWdPoSMimf2Tpv2/wC3/wBn2n2zOftHkr5mcYzuxnpxVyigCGO0tobiW4it4kmmx5sioAz44G49Tj3qrqmjWWr6Re6Zcx7be8jaOby/lYhhgnPr71oUUAQw26xWi27s0yhdrNIAS/1wAP0qSONIYkiiRUjRQqoowFA6ADsKdRQAVzl74G0HUL2a7uIb0zTNvcpqVygz7KsgA+gFdHRQByw+HfhtSSINQBPXGq3X/wAco/4V54cxjydQx/2Frr/47XU0UAYsXhPRYUCLZlgMAb5pHPAA6lie39epqT/hGdHzn7EufXe3+Na1FAHO3PgLwpey+bd6BY3EmNu+aLe2PTJqH/hW/gv/AKFfS/8AwHWuoooAwrLwX4X04OLTw/psQfBbFsnOPqKtf8I5of8A0BtO/wDAVP8ACtOigBFVUUKqhVUYAAwAKWiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAr3/8AyDrn/rk/8jXn3wJ/5JRp/wD12n/9GNXoN/8A8g65/wCuT/yNeffAn/klGn/9dp//AEY1AHpNFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFQ3V5bWMPnXdxFbxbgu+Vwi5JwBk9yeKAJqKKiubq3sraS5up4oIIxueWVwqqPUk8CgCWikLAYyRz0oJAIBIyegoAWiiqs+o2dtfWtlNcIlzdlhBET80m0bmx9BzQBaooooAKKKKACiiigAooooAKKKKACiiigAooooAr3/APyDrn/rk/8AI1598Cf+SUaf/wBdp/8A0Y1eg3//ACDrn/rk/wDI1598Cf8AklGn/wDXaf8A9GNQB6TRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFBIAJJwB1NFZ3iCOGXw3qkdyZRA9pKshhGXClDnaPXHSgCey1Kw1FXaxvba6CHDmCVX2n3weKtV4/4VdtP0nUrjRDm3026sjLeafYGL+0bdVxIhifOGVSSSmCcDv1nuPFHiIafq1xBPqTxnWoV09DaCOa5tHUErDuTDDOTuwSFUnjrQB6zRXkGqeItdfQtC06x1a51DVZ5bmK++yIUlikQAgtiPKrGWQEbRuBHrgrq+o+KbiSxm0rU9SurVbJRbXdpbM6zXiyMsoljCAAcbQHKqOuQc0AevU1XRmZVZSyHDAHkHGefwrzi/1DXW+IMMMcOtzW/2i3Xy0gkgghXbmRhIMxyJ1yHw2eFPHN/Q7CbTPG2t/aLDWZDdXyywXIuHa3EJgUDdl8HDK4xgkbl7YwAdfZ6pZahNdw2lyk0lnN5Fwq/8s3wDtP4EVbrg7KHVIdN8VafptnqUDTGSXTZLl2zloVBxIzMQfM3EZ6fSsKfSNaGg6i2n2GvwQJNZSWdrNeM1wZFfNwwbzOFKEjBONwJGOKAPWaK89tNLlstL8WaVPourXulvIktlbG6ctNG0Ue6NZGfcpEgYnJGM8Z6V38P+oj+Ur8o+UnJHHTNAD6KKKAOe0bxppGt3jWcLXFvc+ZLGsV1A0RkMTbX2k8Ng8EA54PFX9K1u01lr8WolxZXT2kjSJtBdcbtp7jnGa4vw/oGvvrFqNS0sWNrZare6ok32hJPOMxkCxhVORgSkkn+771Fo2k+Io9A8S6Nc+FYoLfUJLmaBRqEaqVlIHlfICVOC3zAY4FAHpDzRRxPK8iLGgJZ2YAKB1JPaoJdTsIbFb6W+to7RwCs7SqIyD0w2cc159Y+BtWh8P3dkbbTVH2u2mjtZdu26jhA+SZkjCjJAIYITgLnvVmXwfqLWGnvHomiI1peT3DaSbl3tZTIuN+4x8MCWIATHPGKAO1udY0uzdkutSs4GVQxWWdVIBzg8nocH8qr3HiXRbTU00+41O0iuXhMwV5lGFBUZOT33DHrzXGWXgHU7K80gyJpl2lrpt5aSyys27MrZjRQVYmNAAgy2drH6G9pfhfXtOj0K736fLqNnpP8AZlws0jshwVIkDbcsfkGQQOvXigDpRrtu3iOXRkUNJDai5mlEseIstgKy7twJ65xjHenDxFohhllXWLBo4o2lkZblCFQdWOD0HrWcdG1VPHTa5E9kbSSzjs3ibd5mFcvuB6Z+YjH05rGh8AXI06zsZbi2WCO9vpZkhDKHhuVlBQehXzeO3yigDrv7b0vMw/tC2zBbrcy/vB8kRyQ59FODz7U/TdW0/WLb7Rp15BdQg4LROGAPofSuRbwPq93po0++1yEwixSy8yG2ZJD5bhkckP3wAwH4EZzW54Y8PyaHHeSXEkEl1eyiadofNIL7QucyO7HgDuPpQBp3+p2WlxJJe3McCyNsTeeWbBOAO5wCfwqhfeLdB06G1ludTgEd0oeFkzJuQ/xnaDhPVzhR3NO1bRHv9S07Ura6W3vLDzBGZIvMRlkUBgVBU9lIIPbvmsDUvAV3f25RNaigefTG0u8ZLBQskRYkbFDARkbmHfqPSgDob/xNpGm39vY3V3tuLjbsVY3cAMcKWZQQgJ4BYgHnHSse08Rav/ws+68NXkNl9i/s37fbSw7vMx5uzD54z7D0684GbrPw2utQ+yxWfiOa2tLNLZLWGWAyiLydpGAHVTkopJKk8HBAOK15vDOry+MLTXhr0SpBb/ZjbixHzxkozjdv4JZBg4496AOmlkEMLylXYIpYhFLMcegHJPtXL6X8Q9C1a0nvIftkdnb27Tz3M1q6xRbSdyM2Mbxjp/XiuqYMUIU7WI4OM4NcbpHga5tfCV74Z1TWvt2nXEDwp5VqIHjDlixzubJy3HHGKAJ7/wAfWNp4Vv8AXI7DUJDZOsctm9u0UyuxXaCG7EMpzyMH14p174+0zTNEi1PULPUrNZZzBHb3FtsmZgu4kKTyMA8+1Oi8FW48O6ho1zfTzw3gHziGGExkAYZRGignIB5B5HpxTNR8ELq1haR32sXVxe2ru0d7Nb27vtcAMm0xlMcL/DnjrQBDJ8StG3QfZ7XU7uOeyN9HLbWpZGhABZs5/hyAR1BOOtLN44lfxBb6dpmg32owzWKXyzwvEgaNyArAO6nHXPGc9qll8CWzPaNFqV7B5FnPZMI1iAljmOWyNmBhgCNoGMelPi8FQ26aYbbVtQgmsrNbFp4igeeBeitlcDB7rg+9AD7TUNVuPH19aSGW30y1s0ZYZYEIndmb94kgYnA24KkD171TtfiHaXcUk0elX4heKaWxkbywL9Yid3l/PxwNw3bcjkZrXbw+7eIW1f8Ate/DEKn2cGPyvLHJTG3JBPOScjkAgHFVLTwNpFkoSF7vyo45o7WJpty2qyjD+UCOOOBnOBwMDNADvD3i+DX7mKAWF1ZvPZR39uLjYfNhY43Daxxg44OD8w98aGvazHoGkvfywSTKronlxsqklmC9WIHfPXoKr6b4XsNKurG4t3nL2VgNPj3uCDCCCAeOSMDmpdS0/TPEtqLeScv9nnWVXtp9rxSKeCCp4PUUAYUPxBS/s9Km0zSLi7bVJLiG2AmjVd8RcNubJ+UhCQwzwRx2qvqHxMt7Pw5p+rxaa8n2uOWVoZLmOMxJGcPyTyeDgDrjkit208HaHYm3NtbTIba5e7iP2qUlJXBDnJbo2TkdDk8c1lXvhjwNazQaVdmC2mvIWtY7ZtQkje4jZyxTG8FxuY4HOMnFAFnV7i7tvHfhpYb24W2vhcJPbEgxtsi3KcYyDn0NNPjC6TW10V9Nt/7SN4kX2dbwk/Z2Qt9oGUGVG1hj1GM9K0Z/Cmk3NxYTypdtLYAC1b7bMDHxt7PySOCTnPfNZun3ekaj44luJNb0m51K3he1t7K2lRpYV3ZkLfxbjtUEYwu0+poAkg8ZhtV1G0uLBrdbMXBXzJMSzCLacqhUAqwbIKsenOKzNH+Ic+saXqd7baPNN5Fst1apGsieaGztjJkRRv6fdLA54J77+meDtB0e6kubOxKyOHH72aSVVDnLbVdiFyeu0DNFr4N8PWVtdW0GlwiC6UJLE5Z12A5CKGJCrnnauBntQBD4N8QXPiHS5pr1bWO6im2PDb+YCg2ggMsiqynJPbBABBINM8T+Ir3TNT0rSNLt7eS/1Ayssl4zJAiRpubcygnPTAx61tafpOn6UJvsNpFAZ38yUovMjYxlj1JwB1pmsaXpWsWQtNYtLa6ti6kR3Chl3dB178/rQBxMPj3WtVe1fSLDTVgm0htTJvJ2UjaxRlBAxjIGGPbn2rvbC6F9p1tdhdgniSULnONwBxn8ayNW0/wzbT2E2pWVoJSPsFoTDuIDgr5agDgEEj0xWzaWlvY2kNpawpDbwoI440GFRQMAAelAHIWVnbaf8XL37ODH9r0lZ5lMjENIZiN2CcA4AHFQaHeTWHiXxxJcSreXVsIZwkTOu9fJyqhCzY6YyByc+wHXNoulvetevp1o10zBzO0Kl9wAAO7GcjA/Klt9I0y0uTc22nWkM5yDLHAqsc9eQM0Acdc+L9RtvBuq6zbalo2q3ENrFNBDaK37pmOG3gvkqMggnaeDnFUpfGuuNodlctNYWLyaxHZPPKI5EMLqfmIjlZVIP+32Hriu9sbPSkSeSwtrNUnZhM0EagSMCQ27HUg7gc9805tJ057JLJ9PtWtIyCkBhUxqR0wuMCgDzvVfE3iKy0cWsOs2M97a6jNBdzw+Stw0KjKlI5GWPf8AMoYZHsDUV9421p7LRFttQhtZptJ/tBp7qGOFLl8gbGV2+Qd22En5hivRbmXSNFiM1ybSzS4nALMFQSSucDPqxpt9q9laCx3Brj7ZMsMIgUP1/i9lHc9qAON1jxVq6eIEit7qGzgiS0fypjGsd0JGzIVZvnYAfKNg+91r0SopZreMgyyRIQQAXYDk9Pzps17aW8ixz3MMTsMhXkCk/gaAPPdN8T6prOt3VhaazvlkS68o29ujxwD/AJYmRWUSRsMEEOCrEHBHFc94z8RazrHh24t7Y3jmbRI7mS1+xENBeJPDwCF+9jeSuTjbmvacAZOAKx9C8SWniD+0JLRR9ms7hrfzxNG6SlQCSNjHA574PtQBwV5rGuKPstpqeqT6empWkYvhCDKQ8UhkjJCcqGEfzY434zxxn/8ACQarqPw71x7281BtQEEE1sn2Z1k+0PCC8YXbyglDYGOMcnGK9X0zW9K1pJH0rUrS+SJtsjW0yyBD6HaTik1TXdI0QRHVdUs7ESkiM3M6x78dcbiM4yPzoA5Dxnc21/beHdYhuNQ+x2mqAXD2iS/IvlyAsUVSThtoBwfvccGs7xJDavqfhTVHPiVtLW1uYvMtmuBNuPlmLeF+cF8MOevGenHc3finQbHSY9VudXs0sJGKxz+aCrkEghSOpGDnHTB9Ko61488P6Dc6dDe3bEaghlhkhjMieWFzvJXPyngAjPLDtzQBzE+peI2+IcqvFqMNqJbd7QRRSsktuwXzVZf9WCGzlmII3cdOY1tdUTxxo99f22t3d7bancxylUc2i28iyCJ15CKArICR83BzXpsUqTwpLGco6hlOMZB5FPoAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAK9//wAg65/65P8AyNeffAn/AJJRp/8A12n/APRjV6Df/wDIOuf+uT/yNeffAn/klGn/APXaf/0Y1AHpNFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFZmtaBp+vwRRX8TkwyebDLDK0UkTYxlXUhl4JHB5FadFAHOSeBtEktoIQt7G8O/FxFfTJO4Y5YPKG3sCQDgk9B6VsaZplno+mwafYQLBawLtjjXsP6knJJPUnNW6KACiiigAooooAKKKKACiiigDm7Dxrp2o3n2eO2voy9xPaQvNEEWaaLO9Fycg4VsbgAdp9KZB40gms7nUH0nUrfTbSKd7m6njVRGYidy7d25vutyoI461keE/Bl9Z67qd/rM9wyR6vdXmm2wlRoUWXP7wADcGwzggnHzZxnmt2y8JxwWGpWF7ql/qVpqAkWSG5MYVRIWL7diKRncepPtQBGfGlmIrsGxvlu4PJC2jIvmSmbPlbSGK4YgjJIAIOcYrP8LeK9Rvb28s9Ys5opzqslnCm1MwqLdJgHKMQerYIJ7ZxWivgnS/sN3bSS30rXSwq9w9y3nKIeY9rjBG08/Uk9zVW38GaBd2VzHb395O73oupLuO/ZpknVNmQ4OVO35TjHBxQAlt48W/tIPsGjXlzqEnns9irxh4kikaJmZi23l1wACSc+gJFjVtd16DWbCy0nRrS6E9q9zKtze+Q6YKjAAVum8fX8KYvw90KGzitrb7da+TJI8UsF5IkqLIdzoHzu2FuSuevPWrd94O0e/tLC1dLmKGyVkiWC6kjJRgNyMQcspwM5PagDf7VyVl4zmuvF91okumLaxQ+b5cs9yFlmCBcuse3BQ5IDBj05Arq40WKNY0UKigKoHYCsKDw74bsNXMiwQi+uPNZY5p2fO8kyFEZiBnnO0DjI6UAYlj8QLq/tb+ZNEVGt7ZLmNXuTh1LlcbwhQ4UbsoXHOM06XxxqkFtLJNodskkd3DamP7cT/rLh7cNny/7ybseh9eKuXvhDwbpemXE19aw2tksRilllupEVUZgcFi3AyBj06Dg4qvrXw+0680q6TRo4bW8uZ4p3lnMkySbJhNhl3cgkHoR1NAGT4q1K61z4deJZpzcaZqehyypvsLx1VpERXDAjaSpDj5WH8ga6DxP4l1DSLmzs9LsY7u6khe5ZJDJ8yJtBVdisQxLD5iMDvWp/wjejyaYLC40yze3ZvMkiEQ8tnIwSQeuffNOuPDeiXcFvDcaVaTR24YQrJEG8sN94DPQHv60Acx4i8b6hp8MFxY21nHbNZxXUsl2zvsMjAKjiMExjBPzt8pxx0Nd0WUMFJG49Bnk1mT+G9EuruO7n0mykuI0WNJHhUkKpyq9OgPIHarcmn2c1/DfyWsL3cCskU7IC6K33gD1ANAFmkJwCQM0B1LMoYFl6gHkUjuI42chiFBJCgk/gByaAPLb64vbz4a6Zq0V/LZatquqWkk0yysPJkeZUKYz91B8pX/AGTkZzT9P8UTafaPv3aSbrWms7qbUZmmjsmW3VmALNjazgheQPnBx2rqtBk8Pa3pV9qFrA8trLdySTwXkJ/dTKNrjy2HyngkgDkknqTWvZyadrmjxXEdustndqJNk0G3cOMblYdRgdR2oA4G48W6lcxeDb+51eDS7O+kuRcTrCRBKygiIkvjarAFgCR25OKdrXxHu9M1K2gtEgvbZrSG5juRJGi3YZyrbVLbzjAwI1dsnp0z6NPZ21zb/Z57eGWHj93IgZeOnB4oktLaaWKWW3ieSHmJ2QEp/unt+FAGc1+n/CSWcH9qogntGdNPaIB5MEfvMnkYHGPetemeVH5wl2J5oXaHx82OuM+lCyxtK8SyIZEALoGGVz0yO2cGgDE8arqD+C9XXShMb9rZhCIM793+zjnP0rkZdV0ix0q7ufBFp9jtxPZx3t9Z2PyLGZCJCFK/M6LncSpxkZ5HHo8dxBK8qxzRu0R2yBWBKHrg+hplrfWd8rNaXcFwFOGMMgfH1xQB5xfa5rT+CybS81W5D6g8dvfpbiGSW2Vd2WIjfGeVV1TLELwM1VuNburzwR4Qv9Ytb+TUl1SKW4I0+VpESKQ7iQqcfLt7Dd2HWvWaKAIra4ju7WK5h3eXKgddyFTg+oOCD7GvJFtvL8VXt/JDdzafZ+IDdyLBpkqyozRhRIHZcvGCrhlQE9DkgjPoGr+LbXSLq6ia0ubiOxtxdXs0GwrbRknBYFgScKzYAJwp9s2D4o0Yas+lm+jF4sccnltkZEmdnPqcfyoA5XQovEreKJJtTmvITLc3Ec9ukMjwNDg+UyyFgiYAH3RuJPzc9KGnaFqWleG9YttFg1uHxB5d0IpLq6kkhH74lShc7NzKQQQCRzuOeT2Gg+LbPWJJ7WZ7e11CG6mtja+eHZjE20leASO/TpWj/bulZulF/blrVd06q4JjGSMkDnqCPwoA4BLTVU8LTbP+EjcpeWk0Uf72OZcsvnLuZ3dhtLEg/LkfL7WJdJvbyy1LT30rU7u1s9fhuLZJrlkeSEFCzI7MMqrbyoz0A7nNdppXiDS9bJ/s27FwBEkpKowAVs45Ixng5HUdwKg8S6+PD1raTtDE6XF0ls0k03lRQ7gxDu+DgZAXp1YUAY+t2d9dWehPZaTqSGz1BJXh+0IW8pG535lw2eCOWPHaqPiPS/El9e6jc2MV8s9xb240x0u1iSykViXMq7sNyQTgPkDbnpWg/jyIWXhqUWBjl18kQC5nWJIyF3AM3JO7+HC85HTIp2oeJ9Ws7vxHD9isI006GOa0kuLhkFzuVmYH5eMBH6Z5H1wAY99outJqd/dWdhqbXCaray20329Sht/3XnhUMnyg7ZPlI5yOnb0aoLWWWSxglnRVlaNWkWMlgGxkgcZI/CsCPxjYaqz2WkXDJfSxyC1lu7KZYXkXO5eQuSuMlQQcUAc9b+GtUTw3q2i2GhW2lXgjmSHU45EH2jMm5QNuXAZeCTjHYHtEnh/xC3hHVLJ7C7QXdzE8dsk9vG0CqQWCIoMZT5V+Vj84Zt2DnOt4e+IdtqHhWPUtRtrqK6jsEvJ0is5Asi4G5oc/fVSRkgnGa0ovHGjS2t1dA3K21tbQ3LzNAQpWVQ0YU92IYcDpQBzsnhHUdS8EWlpd6PpwuYNVS++xOFVHjEmSrY3IHZSQdvy8kDitS+0e5aw0VrLwrpkVzZXfmJGkyKLWMPk+WwTguAMgADsSeps6/wCK5rDwdqOs2NhcCa13qY7mAjyyv3nZdwJUDJ4PPatHVPEVrpL20MkN3czzxPMkdpbtIdiAFmIHQcgepJAGTQBx/ijwRd67f65cR6VYZ1HR44oZJWXfBdoXOfu+jqN4OflFc54lmhk+IEl1qek2d4bK4ssWZKG4eQxHcI8oWljG/dgYBaMnjHPoWtePtH0S2tbi4S6eK5tvtYZYwu2HjLEMQcjcPlGW56VJJqGow/EW0083avpt3ps04g8oAo8bxLnf1ORIePagDpa4nRtB1mzg8Sxtp2lwR6rcyzxxC5cqpMSxgMFQcNs3Eg5G49TzXbUUAcp4K8N6j4cS7ivLiB7ZxEttDGd5iCqQQZCqsw6BQc4A6kk1P4v8P3WvLo5tBZb7HUortjdAn5EzkLgHk9K6SigDgrfwTqtvql1fLdac7C9upbWGeFpIxFcFS+4ZGHG3AxxgsD97Is2fgi80u38Nf2fq0az6LbzW5M1tuSdZAuflDArgqpGD0GK7SigCO3WZLaJbiRZZggEjqm0M2OSBk4Htk1JRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAV7//AJB1z/1yf+Rrz74E/wDJKNP/AOu0/wD6MavQb/8A5B1z/wBcn/ka8++BP/JKNP8A+u0//oxqAPSaKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooA85sfF+uDxiNPvLjT5YG1aXTfs0FuwkVFh84TZ3k4+ZVIxgZzmovC3ju+126nguNRsbd7q2mkhR44xJYSIfuyIJSzADJJYR/c967TR/Dtpot7qd3DLLNNqNy1zK8wUlSQBtUhQdoCrgHPStAWdoHmYW0O6UYlIQZcf7Xr+NAHnXhrX9Q1nwPfa5f8AjTTkElqIvkgiVbKXJG5yWOWbjg4HIwKqaW0Oh+B7CbRNctyt7dQRahqtrb25+xJ5ecMsabSd2Fy4JHmZOcCvTlsLFYXhS0txExy6CNdpPuKfbwW1vGVtoookJyRGoUE/hQB5pf8AirWD4d8NX7a9HYve6jLZTTpaDypYdzqs4VxlThFI52/Pk7hVDxH4i1rRvENxp6+Mbtkt7SF0As4GaaVkmbHEf+xF04+evWZry1t2jWa5hjaUlYw8gBcgZIGevFRHVtNW2guW1C0EFwwWGUzLtkJ6BTnBP0oA84tPGmsahq1gpujb+aLOSOBYSwuoWRGmdUEZY/MzrncAuzJ71JPc6q/jPQ7jUotSmlt9auUMEVnmKC3aKRInDqnKkMhJLHGTxxgd9Jr+jQ3DW8urWCTq21omuUDA+hGc5qdtTsEuZLZ722WeNS7xGVQyqBkkjOQMc5oAyPHlvNd/D/xBb28LzTSafMsccalmZihwAByTWEg1TXdL1W0sNV1e2EEFvLa3l1B9nImwxZPupuTAQNkcEn046q28S6He3FxBa6vZTy28XnSrFOrFE/vHB6VjxeK/B3i7R7grq9vNZxRGa5X7QYikfIJcAghT6HrnpQBN4Ilvr7RpdYvmmU6nMbqG2llMn2aIgBUB6EcFsjj5sdqo+Lkvn1iBrVta8uK3SRo7BnVZP38YYHHG7Zv7g4/Cuk0bV9K1mx8/Rry2urWNvK3W7BlUgD5eOmARxT9S1jTtISJtQvIbYStsj8xsFzgkgDvwCaAPOM+NZvD6GcaquoDTQll5Qxi7EjAmYcAgr5WC3y4355qzrNt4jn8Z6dcm1v50t5bVXSOWSKEd5HQodjJk/MJF3fLgcHjrNW8a+HdEtrW4v9TRIrqLzoWjR5d0eAd+EBIXkfMeOetbkUqTRJLE4eN1DKynIIPQigDz2x0M6T8R9Tujo+sXP2y6jnt7mG6b7NGpiVX8wNIASGDkDaeNoHYD0KaQwwSSiN5CiltiDLNgdB71lHxTow1ltJ+2f6YpKlRE5XcBnZvxtL45253e1U9M8feGtX2Gy1BmR1lZXktpY0IiAMnzMoHygjNAHP8AhxpptE8T22qeGNX8m5u7i7FvLGimeORshFw/3sdRkfU1Q03Std1D4f8Ah+wu9FvXTT7gJqGnXUyxtdRbWA2tu+ZVLKcMQG2YrodP8fWl5q2oMWQaJb6Ympx3vkyoxiJYMSrKMj5SQVzke9dRYahb6lAZrbztgbb+9heI9AejAHGCOelAHnGseFNSu9E0eCDQ7j7FapPH/ZTXMMklu7MCkgkZtvygMBgkqCPeqmueBdSvZZjJokuoSnQPs0dxLeRswvVyI3JJXLBSPmC9frmvRda8R6foMlpDdGZ7m9dktbeCIu8zAZIGOBgc8kVm3HjVE1PQ7S00jULsarby3IZUCNEiAZ3K5BzllGDjr36UAcpJ4X1+88aaXqkmkTrtaza5luLqGSNRGmWK4/eKwYsMAlWPJzni3oHg7W9O8VXV7cgyyNdXMi6kbhBujlBCAoELuVwo2swUcbc12GoeJrPTdRtLG4huRJcvHGriMbFaQkKpOeTwcgZx1OMisDw14unFxNp2tvPNO+r3Gn214tuqxOUyyodp4O0HqOcdaAKXh/wTqGiWV2iWtubmTTWtGkF35aXEnOGIjiUjJ53ElhuIHrWv4G8Mz+G0v1lt7aGOdo/LWMR7wFXGGZEQMB0BILHkk84Euj6tqus6h4msHcWUtlOILctbqWjDJuVziRg+QQRwvuKj8M6trEvhrVJLpn1S/sr66tUMcccbTCOQqvGVUHA9R9aAOms3uZLOJ7yGOG5K5kjjkLqp9AxAz+QqeuDXxdqNl8MdN16KJ9XvrtoUQSqluWaWQIMhSQMFgOD9T1Nbep+Kf7G+wNqOmz28V27xmZpY/LhcKWUOd3G7bgEZGeuKAKmreHNVfUNaudJubVDq9pHbStcA5gKBl3KACG+VzwccgdRxSy6DrVj4ll1LRrjT/JuLS2tZVvEcsgiZzldpGSRIeuORWx4d1SfW/D1jqlxZNZSXUQl+zs+8op+7k4HUYPTvWF4j8exeH/ENrpRsfPEjwLLILhQ0Ylk8tSE5JAPUnaORgknFAFODwdrMV/ZSibTxFBr0+qvy5ZklDjYOBggSHnvgU/wx4L1Pw5NK63lrP9ms3tbBnaZiwLbh5gLlVwQMhAM+2MVYk8aX9vqcMNz4eeKyfUxpz3f2tG2u2PLYIBkgkgHpgnuOag0zxBf6x4x0e6hYxaLfWF08Ufm7vN2SRhJCu0FSQx4yeCOhFAG34T03VNI0OKw1RtPLQAJF9ijZV245Lbj94nJOKf4j0a81hLD7HfQ2j2l0tzmWAyh8AgKQHXj5j1z271pXxulsJzYrC10EPlCZiqFscbiASB9BXE6T4h1G08AeE7u1iju5dQMMLtqN8Q4MgJB37SXOcds47UAEvw6uTo62EOsQBpLae2unlsA6uJJDIDEN4MW1mOACRwvoKhn+FUV7ptjZXusTTLaWvkArGUEjBztdgGwTseVGz97zWPHFTz+NdbFhBFbaVZy6ot3Pa3uJZHhgMQB3AKpkYMGTkKQu75iKhfxzrZW0mit9I+zz6KdWDvPIAQmzeudvA+f5Tg9OQKAPQgAoAAwBwBXF6L4Ymk1O7ursXdtHbandXNjC/llA8gZfNBBLEEM52tjG88cDCXvjPUYvEM1pa6fbvZWstrHcyTzLEVWYZLAsQMAEY4O4hh1FXrPxLdXmrMqrYx2I1CWwKyzFJwyA/MAeCSw4Uc7SGz2oArweGo/C1lpV7bG+1B9GsXskt4kQyTxuyHpwNw2L3GcGlsfCU0nhGfT5bya0nvbhrqUiOOTy1ZsrCVcMhVUCpjGPl4pPCup3lze6lBeeILK5kW+u4ktfJ2SxFH+UDLfMoXB6fxDmsuw8Vy6b4D1TUWuIbi9g1OeGVpJXdYgboxCRlLEqirhtoIGBxgUAa8ngVG8GXHhuPV7qGO6aQ3E8cMKtIHzvXaE2qDn+ECri+Fi/9mz3Gs38mo2CSxpeoI0Z0cjKsgTYR8q/w/wg1zl346vraKOOO502XGsW+ni+CkwXCSg/cw3DpkFhkj5e2eOn8L63NrEGoxXRiN1p19LZytEMB9uCG25JXII4yaAKfiDwTpOuJI9/d3cYe0FpJIJVyY85+8ynaSTyVxu6HOBV+48OJcaza6r/AGlfR3NtbtboUMeNjFS2QUPJKLn6cYrlPiT5U+ueGNPutXs7ezurmUTWl3EkkT4hkIkdWI3BW2gA8bip6gVDr3iu80PV49P03ULFGt0tUtNKW1LNqAkOGZCPuhRnG0kDB3cYoA9Lorg4NeuZviXeaAfFNqqQmKeKyFuhlkBVy8O70AVWz975vSu4uJPJtpZc42IWztLdB6Dk/QUASUhIVSzEAAZJPavK9M8U+LLjS9a+z/aNQ1G1s0aPEMYg3seXU7FbeFO7yWXPAGSTSy3+oXPhjxNBc6jq02jiJP7P1MwbbmeR0O+LyxHkruIH3OASM8ZAB6Np2taVrAkOmanZ3wiIEhtp1l2Z6Z2k46Gr1eZXllG/gazutF1LWZobfUoJrubyDDM8KyL5gZBGjMqrkgBc8d673RXik0mGSC4vJ4nyyyXiMkjAkkZDKpx6ZHTFAGhRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAV7/AP5B1z/1yf8Aka8++BP/ACSjT/8ArtP/AOjGr0G//wCQdc/9cn/ka8++BP8AySjT/wDrtP8A+jGoA9JooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigDyS38LeJ4fEcF0NOuxCt7LIX+3J8iG7EiHbv8AmxCCm0jvWjofhLxHpF5NdRLB9vMdwtxNJOBDeuwJiZgFLkA4zkqUGQpYV1U/jLS4dfbRlS8nuY3WOVre1eRInZdyqzKOCRz6etV9L8eaXqd39nNtqFkG83ypb23MSS+USJApJ6rgkg46UAc5Y+EfEcVnrFvLBbJFqFlDbAQ3nlSI6M4d9yxnJKtkFtx+UAn0v6Z4T1TT9Pylrpa3Nvqsd5bovyhoxEsTbiqACQrvGQuOme9aum+OdP1iC6awtL15o7Y3UEM0XlNdxdA8ZYgFSccnHUetNPjI2nhI6/qukXVlGIYX8vzI5NzSYGFYNjAJHzNt6+1AHJS/D/XJ9EtYW0/RIbqHxCdT2QzMIxATlowSmcn7pGACBWj4r8C3+sXVnLYQ2S2osHs3sHlEUVsWYMZIyImJPUHG08DBGTXX+HPEFv4l0kahbQyxR+Y0RWQqcspw21lJVhnIyDg4qh4w1O+0/wDsWOynltlu9Tht5Z44kkwrH7pDHgN03DJHpQBxurfDbWL3UL26jTTJpJ/MHnTSOHcNZpBydhIIkQsOT1z1rVs/h7dWvitdSN60toL5r8pNdSt87IVI2DAyOBuJOV4K8c62ueNJtDutRSTw/qE1tp8CXM11G8ZTyTnLgbs8FXyMZwpPpnqkkSSJZFOUZQwPtQBxOgeB7rRv+Ed/fWgGlyXjSrEhUSCckjHuOBz6UWnhDWbfwbd+GpbjSLizWIQWglt5CWj3ZPmkOMnHGVxg8itvQfEo1/E9tYyrp8hlEF2XUrL5b7M4HIB5Iz2BrH0fxJLZeG/EusaiL64bTr258y33JI0apg7YyAuVxg89OeuM0AafgzQL/wAPaTcW+pagL24nuWnLjcQgKqoXLEscbepOeaj8W+GLnxG1kIL8WyQ+YsineNwdcZBR1YEY6ZwcnNULPx7Ld+GrzVRpKq8MyW8Mf2xSlxI23AR8cgBxnAJyGABI5mufGF7F4bsdVh023eS4vxYvD9pYAMZjCpVig4LYJyBgE8HpQBU1L4eTaloOn6a+rRxzWVmtpHex27pKAuBnKyjOQBlW3KSM4rtoIjDbxRGR5CiBS7nLNgdT71xOveO73wzLaWF7paXWpSWkt1Itn5zphWwqrtjY5b1YADHXmo9T8R+JpfG1jp2j/wBnQ20+kG9MWoh153oOWVfvDONoJ7k9qALtt4Ags9ekvre8At3vft/kyQCSRZj97EjE4U8/w5GThhUNt4BuINL03TW1iN7eze5D/wChgPLDNndHu3/KRuPzDrxxxQda8Sn4galp0U+kLpVtHZuVuWZXAkLhthA5YlSACcfd9TUOgePb/VvET21xpS22lSNOsNzITGyNEWBV93BYhS2B90DnNAFy38BtbSCRdfvmYacumjdDAwMKnK5BTBPJHTBB6Vs+HvD0Hh23ngt5pHilkDiLAWOLgDCIoAUcZOOpJNYng/xffa9qLWeow2tvMbX7SIIdzELvKgiQEpIhGMMp654xzWt4u8RReGNBe/keNHaRYYvMUspdj049s9SB6kdaAH+IfDy+IEgSS8eGOLfuj8mKVJNwxysisMjsRg8nsazJvAcH2TQo7LV9RsrnRoWgt7uNkeRkZQrBg6lTnaD04wMYrl5PiHqcvhW0v7fVdFiuk1g6bctOoMbqZNqyfLIQgC/N1YEDrjmrfifxd4k0KPS7azuNLvbmaBrg3TrHBBdDdhUQyTqF4IyQXPIIFAGrqnw4t9T1M6gdc1OG5PkuZE8pmEkX3XVmQlfdVIUknircHgqxs9WbU5tRvJIY7yXUUtpHVYYpnBDPwATgMQMkgV0dnObmygnYANJGrkA5AJGeK4iV7p/HmpWOpeJWSwkNusWlT2kTR3McgYFAWBZgSCDjp344ABtaR4a+x65f61Fr17crqEnmyRHyfKOF2KAVQHCrgDn+EZzzT7LwjBp9rqFvb6rqiJfSPLKROoZZHILOhC/KT7ccnjNef+DPEGo6Fo3h+1S6gvLe7sb0QWKxhCk8JDJEGBJ3MHIIPoMAd7X/AAkfi5dIn+yX0upzJYw6jJNFYqjwOJFEtqU24yULEKf3g2nPUUAdfbeAtHt/C0/hyR72602XG1Li4LmLGCuw/wAOCARjvWfqfh+Nkt/C0dza3Ftev9ou31O8ae7kCld3lowI5UAbsgL6ZNZuseN500fW7vSdTmuAtxafZGFqCwjlZFZYsqA5zuCk5GcgnioXt9UuPFHhg3WsXA1CJ7xbueKGCSS3V9hjhk2KUUle5HXODigD1ADAwOlc7qvgXw7rWoSX1/YyPcSlDI0d1LGHKY2llRgCRgYJGeB6Vxl1eahrFv4Q1K7vtds4ke7gvZre3Mb7tjKkjRhDtLYyPl43djXptjcx3dhBcRed5ciBl86NkcjH8SsAQfYgUAZNz4N0K7klea0kYy3iXzYuZVHnp91wA2B9BwepFSx+FNDi1n+1109PtwYskrOzeWSMHYCcJnvtAz3zXNwxpZfFDVZLw6sn277L9jMKztBJtQh9xUFAAcfex1pujX2uP4utbYnVH2y3Y1VbmEiCNMkwGNuFJxtA2E8E7sEUAdfrN/pthYZ1WVY7Wd1t8sCQzOdoXj1JxVZfCegJaRWq6VbC3ilSaKPb8sbpnayjsRk4x61mfEzTr7Vvh5q1npkU0t6yxvCkP3yyyK3HI5+X6+mTxWFqY8UPpuoDT01CXTBeWwVZ/MW6aEqRPswVkwCVI5BOHAOMUAddP4Q8PXMzSz6PaSSNI8rOyZJdwA5z6sAAfUCq174N0+/8R2Gp3EdvJa2Vm9rHYvbI0Y3Mp3DPTG0DAFSeDU1GLQjDqT3UjRzyLBJdR7HaHPyZBZm4HGXO44yRXOfEePWHvrJtMttXugLWdBBZ71iaRtoQs6SIUYc4Y7gOeKAO3m0nTbm5W5n0+0lnTG2V4VZhg5GCRnjtWTe6loNr4ojt5NOafVtiSGaCwaVolYlFZnVTtBwwznoD2rn/ABba+JDbaxZaXp+pXEl9HBNa3FvfKgilTaHQ7nXYMKDxw2T3zlYfC8T/ABPvNdufDM/lPDbeRdebGQs6ly7kCTOACg6fwnA9QDeTVNCbxRcWcGmyS6iGEFzdRWDMqlkDbXlC4Hy7epxyParOjwaFcJePpumW8KLK9pMRZiISbThhyBuXPGeQcGuW8K+Gl0vxlr99L4VlgW7uXe2u2liceWY1DDbvJG5lY9P4ucVBpuleI38Ma5odtos2iI87T2LvdIQYi6kw5jkZkLAONwwACMc0AdpqcOi6VoUk15Y2w06wUziMW4ZY9uTlUA69enPNWbN7AWf9oW8cUEV0qzu5QRltwGC3TnGOvNcgNFdvBetWSeD/ACo7kGSDTpbqOYtIw2k4Y+XHggMAGI6ng1mXXhfX9c8N+E7e5sXto9KIivdOnlhcXAWIIJBw6HBzgN654IFAHot1HYFlmvEti0PKvMFymSOQT05A/IVDca1pVnqMdhc31vDdvE0qRu4B2KQCfb7wrhpvAE1xrOgyXdjb3unWeky2NxFcursx/wCWeflAOPXsT+NTN4X1T7ZoOqTaHpl7cWelmymtppR/rQ8ZV/MKHIGwkfLkFvfgA9BAT7w2+uarxalYTyLHDe20kjdFSVST+ANWV+6MgA46DpXmtt4B1BNV0q6itNNsPsgjaWaE/vGYC5QkELycTI/PcY7ZoA9FiuracyCGeKQxnEgRwdp98dOlMGo2LW0tyt5bmCEFpJRKpVABkknOBxXEaR4J1bTNPmij/s2O7bS/sQuGkknDsDnJjYBQpySRhuT3HFQReCNbij8QRBNJaDUmtnihlnmbZ5W0YLKqkcDII6EAYxQB3MWtaXMsDRajaOJ5PKiKzKfMfG7aOeTjnHpSPrmkxqjPqdoqu7xqxmUBmQkOo56qQcjtiuWfwnrb6fHKbuzbUbTVTqFmkuXjC7Cmx5Aqu3DMdxBPAHQVnHwd4rXSLS0SbRHmttZbVVZzKFJZmk2EYP8AHIRn0A7ngA7hNe0l4rWQajbBbvP2fdIFMmDg4B5PJA/GpZtV0+3vo7Ga+t47uTGyFpAHbOcYHXnB/KuP8W+BL3xHqkGoxXcCSyWYsruGSWdYiu4tuAjdd4ySNjcEY5GOZ28Har/wmMutx6tDCkptw/lRMrskYG5GXdsfcd2GYFlDcGgDtaKKKACiiigAooooAKKKKACiiigAooooAKKKKAK9/wD8g65/65P/ACNeffAn/klGn/8AXaf/ANGNXoN//wAg65/65P8AyNeffAn/AJJRp/8A12n/APRjUAek0UUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQByU/gCxuvFsfiKbUb97iK4E8ce6MKuFxsDBd+zoSu7GRVTw/4Snmvbu78QQy4S5uhaWZmjeBI5mO5lCqGG5WIIYnvjGaLzU7vT/iDexXuumz05rS1a3ikiBV3aWRWVM9T9zJHI3DNQWXi3WpvEunWjRRv9qvLqC7sVjw9jFHny5GbqQwCnJAB3gCgDc0PwVpmhXP2iKW7uZEthZwG6l3/AGe3ByIk46e5yeBzwKenhK1jsJLNNR1cRMI1XF8/7tU6KvoOx/vDrmtHW9RGkaHfaiY5ZBbQtJtij8xuB2XIz9Mj615jpPxB1G68O+IFOrQm7tUgktry4gyq+ZgMG8pNoCtwDg4zyWxQB6VoWgWHh2xe009GWOSZ55C7ZLOxyT7duBgcVB4i8MWXiZLVL24vohay+dH9luWhw46MdvUjHB7VxEfifVZfBdrcwa3c+fNqZi+13FsnzQryyq8cTJzg4YoO68EZq/Z61q6aZpd5eXeuGHULGeLK6cjSQzh8xyMqJwWXIGRtOBwM0AdTceFtLuzcG6S4nNzZLYz+ZcyfvIRng4bqcnJ6nJ9TWtDClvBHDGCEjUIoLEnAGByeT+NeZXN9qOqap4e+0an4ksrK+01hefZbN49lwjKFz+7JjyfMJPGQB2IzeebxEfH4gFzdQJHOqonlTSW01rtGS2E2CQkn5t4Ix0x1AOvt/DulWt4LqGzVZVkaVPmYrG7Z3Mik7UJyclQM5OaydS8EWMuga3p+lyTWU2rI4mmaeWUM7DBYhm7gYJGCRXRXhuFsbg2iq1yI2MQboXxxn8cVyPhiPUEgP9qS6/JcSWAF7HOP3aTD7xiZeQTkgCM4wo6HFAEmgaVDraXF7fX9jqmnMUht7WBWaCBoWYFl3sfn3EjIxwq/Wtn/AIRXQPsa2n9j2f2ZZfOWLyhtEn94D175rhLea+0P4Of2attfWmpxFYYoWUxvM0k5xGjkj5mU4LA5XOeoqDztTu/DlrosS6pNeQXwOrBZ7gvbRsGaNP4JJFKYXKsvzKCT1oA9IvvD2j6nHbpfaZa3K2yMkIliDeWpABAz0BAAPqKS/wDDmiaqlsmoaTZXS2oxAJoFcRDj7uRx0H5V5yum6vc6J4Qj1iy8Rie2kmg1E207BmiCsBvKSZILFMHlsBufXd1rQ9Ra7xYWurPaw6bFHYyW96BJFMrknPmygFsBMl1bPr1BAOon0rQrvXYrmeysJtWt4w0cjxq00aZIBBPIGc/rUkGmaQuq3d/BZ2Y1B8R3E6Rr5h+UEBm6/dI/AiuWuNDvLbx7fa2NDk1AXVtaJDNHdJH5TIzb9wLDjBVuAQdvTNR6V4eudN8Z6pdy+HvtH2rUjdW+pC5TbEjQhDlC27IIYcL/AB9cUAdfp2jaXpAcabp1raBzlvIhVN31wKtT28N1C0NxDHNE33kkUMp+oNefeA/DWu6RrIudVS7WQ2Ziu5TdI8N1MGGJQoJZmwCNzbcDAx6aXxSt4p/A8rS26TiG8tZBG7hQ379ARk8DKlhzxzQBoajL4f0zUtJ0e40mE/2lK62+21QxK6puOfQkL+OPato6fYtHBGbS3KQENCpjXEZHQqMcfhXnZ8L6vPNozS6MVsf7ce9l04zRFLOAwmPaRnDfMzPtXj5mGDVS+8PytothZXS2tn4ka4uLW2iQRyMbOWRlyVGPlSM7gexQZ6kUAeove2kflb7qFfOz5e6QDfjk49fwqD+04zrg0tYZHkFuZ3lUrsT5gAp5zk5JHGMA81wPirwBfX13ax6TY6cbW2s4reP7VsZCVckhozGdowScxshY8HgAjpbmz1iDxpHqFjpOnPaSW629xctdGOYjcCTtEZ3bRnALd+1AHQrdWz3L2yTxNcIAzxBwWUHoSOoqGa+Vra7On+Te3VuCPs6TKCXxwrHnaT71yujeGNS03xM1zJp+kOqSTt/aoZhdTpJ8211AAJDY5LEYXgCqfg7wn4h0HVrrUbpdLD3NoIpYoW2h5lYkSDbGoAbPIIYj1NAGzp8lt8QPCcFzf2U9i/2iTCJPiW3likaMlZFxg5U8jsSKTULnSfh34cuLoMJJZGyDeXirLdy44BlkPJwOMngDirPhLSdS0PTpLG9+yMhnnnWSCRicyyvJggqOm/Gc84o8a6NqHiHwteaRpz2kcl2hieS6DEIhBBKhf4ulAFq/8UaJpDJHq2q2WnzNEJfKubhEYKTjPXkZ4yKjvfFui6fqFvZXF5iSe3NyjKhZDGMc7gMc54HU1lS+HdavNd0TV7w6RJPaWlxbXUfluUIkKlTHnkHCAHPZmp1l4c1+0tdDaLVbGG5sLJ7KZFtS8LKdu1lG4MCPLXvg5PAoA2pvEejW+tR6PNqMCahJjbAzYJJ5A9NxGSB1IBIHBqGLxboM2uS6LHqUTajESrQYbJIxkA4wxGRkAkjPNZh8Er/wk1zqv2i3eK4vIr1oprdnZJERV+Vt4UfdBBKkjn1rA0GxvrLxxeXTW95Jd3F9MfJuLWQxWls7/M0c27y/mCIxABOcDA5NAHXaf4z0HVpZYdOvHupYo2eRIraVim04Kt8vDZ/hPzdOOao2/jP7P4Fl8TatAhSNnHlafvlLYfYFAdVO7cMHIAHrWloWkX2kW15BJe204muJriIpa+XsaR2chvnO4AtjPB461k6d4Ini8I3vh3U9WF3bXG9kkitvJaJ2kaQsPmbPzsCAfTnOaANlvEumRfYRcPcWz303kQJPayoWkxnbyvB+vBwcZxVzTdTtNXsUvbJ3e3ckKzRsmcHB4YA9Qa5bxLpWq3WkyaSLi8vr29YNa3ohjjj090Aw5ZcMpzkgjJzkDA4rpBpbW+l2thp93JZpbeWFZVVyyLjKncD1AwT154NAGhQenFFFAHnFvr/jye+1K0mGh28lhFFNcKsEjGNJEkbAPmYZlKAdADkntitTw/4+sbnw7b3Oqme2u49Jj1G4M0JjV0K4Z0PQjd29x61ei8JSJretai+tXjjVYPIkgMcQWMAEIVIXOVDMBknOec8Vnx/DeyNtDa3mpXt1bppJ0ho3CLvhyCDlVBBGAPw5zzQBv6L4j0/XpLuKzdvNtComRsEruGV5BIORnv2qDxJ4mXw59gB0y+v3vZ/s8S2gj4cgkA72UcgH8qm0Lw9aeH4XitJJmRsfK21VXHoiKqgnqTjJ7ms/xnol9rg0SKzkEKW2pR3M0yzeXIiqrD5MqQT83Q/1oASfxosVrp08Oh6pdfbXkhEcIiLQzJuzG+XAByjDIJGR1qGfx5HZKy3mjagk1rZpeaksWx1sUb++xYbiAGOFycKfYVPdeB7GfT9PtItR1S0FlK86y21ztkllfO53ODuY7mOf9o1Nq3g3S9auY57t7sP5QhuBDOYxdxjoswXG4Z+nUjoSKAKbePIE1K4tn0q9WC2vIbSe6Zo9imbb5TABiSrb17ZG7kdaWx8bpfazbQLps6aXeTy2tpqLOAJpowxZdn3gvyPhu+2o7Xwhu8a6zqd/BHJY3EltNaqLl8b4owo3RfcOCMgnPb0Fa1t4T0a01dtTitnFyZXnAad2jSR+GdYydqseeQAeT6nIBz2lfEy31G61dJdMe0g062mum8y4Tz9sZIO+D76EgZGQeCPWn2HxItrrR9QvZdOnjktFg/doSySNMwRFV2VQTvOCRkDggkVrad4G8P6XdSXEFpLJJJA1sftV1LOBE2NyASMQAcAYHYVPaeEdFs7K4tFtZJoJwA63NxJNwDlQC7EqAeQBjB5FAFDwjqOo3eq+JrXUpw8lpqCrHEHDiFGhjcKCFUkZZsZGfriuqrM0jw/pmh+c2n23lyT7fOld2kkl2jClnYksQO5NadABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAV7/wD5B1z/ANcn/ka8++BP/JKNP/67T/8Aoxq9Bv8A/kHXP/XJ/wCRrz74E/8AJKNP/wCu0/8A6MagD0miiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAEJAOCRmjIzjIz6V5r4t8PeIL7x5ZatZ6Nb3kNrLbNFOZY1KRoxZ1+ckgknqoHAGSeg1rXQruHxqL6Xw9bTSLcTSrrL3p3iKQY2BMEkgbVCn5QBkEE0AdPba1pd5cyW1tqNrLPEzI8aSqWUrjcMZzxkZ9M1X0LxBba9ps1/DFLBbxzSRB5ioDhDjeCCflPvWB4a0K/0TWb2E6DpgtftFxMupIyLLKkrF1jVAvGCdpyQOARnPGfH4M1i48E6voTRWeni8vXu4o4pd0ex5fMMDgIMDHykr/LqAdx/bOl/Zorn+0rPyJSRHL567XxnODnBxg5+lWLe4gu4Entpo5oXGVkjYMrfQjg157c+BL+5ghlaw0kbdbi1AaaHPkQxJH5ZVW2cs2A5+UDP5113hzTJ9Kt7+CW3tbeJ76aa3S2YkeWzZBI2jaxJJIGR7mgC+2p2CzzQNfWwmgTzJYzKu6NcZ3MM5AwRyaq/27atr1vpMTJLJPam6DpMhwgIAO3duIOeCARwea5vxV4J1bWNcbUdH10aWJbYRTxrAG85xuUMx7jZJIMdM7TzitS80K+PifRtRtGtRbadbS2+yUtvcSbMngY4EYx657UAWbPXZ5/FuoaFPYCEW1tFcxXAm3ecjll5XA2kFG7ml0LXJ9VvtXsrqyS1n025WBtk/mrIGjWQMDtXHDjjFQx6RqMfji41rfam1ms4rTy8tvARnfd0xkl8Y9BTdD0fU9O1/XL66ktHg1K4EyiLcGjCxpGoOeD8qZJ9T0oA0ddi0ubRrldZgjnsAu6RJIy446EAAnOcYxznpWPouq+HdF8K6Vcg2WmWt+qNEqy7xI7KMAOQC7EAcnk4rpZ1leCRYXRJSpCs6FgD6kAjP5iuUs/Bt7Z6FoGlrq8JXRp0kjc2Z/eqiFArDzOvzE5Htx6gGrceLdCtdLg1KXUE+zTkrFsRndyDhgEUFiR3GOMHOMVHf+M9A02SCO5vjuuLf7TB5UEkoljz1QopDHvgZOOcY5rPPg68TVItRttWhingubmSFDZboxHOVZ0YbwWOVB3AjqeKnufDGoS6pod9Fq8IfSrd4gstluErOoVmO11AGAMKOlAFuXxfoUF/a2U16Y57pUaIPDIB8/3AzFcIx7KxB9ql/wCEn0j+3RopumF+XMYQwuFLBN+0PjaTt5xnOKwdT+HVpqPi9tf+0QxvKYnlVrNJJBJHwrRyNnZwFBGD0yMHmobn4dS3HjGLxH/bZS4gu/tEOLNDIEIIaJnJJK4JC4xtz3PNAHQweLNFuZbhIrpytvHJLJKYJBEFjYq5EhXacEEcHsfSl0TxHYeIhPHDDcwywhGe3vIDE+xs7H2nqp2nB9jWRafD2zivr+6vNQurz+0LSS0u0ZI4hcBzy7+Wq7nA+UN2BPqTWl4d8MR+HjKUvZLgOqphreCIAL0z5aKSevXPU0AM8cX+qaT4O1LU9Jnt4bmzge4PnwmRWVVJKgBhgn15+lTa34jsvD9jBe30M8hkBA8iLcVAXcxJ6KOO55OByam8SaIPEeg3WkPeT2kV0hjlkgClih4ZfmBHI46ZrI1DwLBq0OlLqOq3t1Jp4lXzJI4T5yycEMuzbkAAAgAgd+TQBk/8J8bLxDfXE7XV5oD6Xa6jDJBajFrHIXBZ+dxHyqe568YBrobnxda2+ttpws7uWOKaK3uLyNVMUEsgHlo3O4k7l6AgbhnGaqxfD/TIrNLVby/8r+z4tNlAlA86CMttViFyPvsMrg4rRufDFjc6ibwyXMe+WKaWGOTbHLJERsZhjORhehGdoznFAFO08XSXviC60eHQNS8yzuBDczExCOJWAZHzvyQynOACR3Apuj+N7TWdan0uKyuIp0hknj3vGfMVJAh4ViVOSCAwGQc1fsPDlvp2q6jqEd3eSSag++4jlkDIxwFGOMgBQAAD0qrpHgrS9FurG4tZbwvYwPa24knLKsLEHy8dwCARnngc8CgCvb+L7i38Kw6zrGky2/mRRMiW7rL5skpAREAOckso5x1pmpeORp+mXl0NIuJJ7C8itbu081FkQSFQjrzhgd645HfkYqyngPQf7PnsJobq5tJVVPJuLyV1jRWDKqAt8oBAII596sSeD9DmsprR7WQxTzrczn7TIHlkXBVncNubG1cZPGB6UAQ3nimTR7W0n1rTWsVuHkjMhnV4omALJvYdN4HXBAPHpnX0m7ub7SbW7u7QWk80Yd7cSCTyye24AZrO1rRp9UtbfSPLifSmKm6ead2lIRlZVHXOccsWyPfPG7QByGoeN5NP1nVLaTSs2OmPapPci4+c+eQFKx7eQCRnLCp7XxDq194g1HT4dMto7fSrhY7qd7hmMiNGJB5ahPvAMMg4HPBPZi+CoJfHV94hvSsySrAbeMSSL5bxgjLKG2P2IyDgitG28J6Naa/NrkFvMmoTuXlk+1SlXYrtyULbenA447UAYo+IUcFrBd3umvFDdadNqVssUvmStFGAxDpgbGKsp6kZyM8VnXfiXWNCk1bVriC1m3RWM/2RNQeRUheR0ZkyoAP3c4GD1z2rsrTw9o9jcTz2umWsUtwhjlZYxllJJK/TJJx05qK38J+H7RHSDRrJFeH7Ow8kHMWc7Of4c846UAYY8b3Et3e2EFlELtNXOmW7ySYiOIxJucjkcbgBj5jgDqSHah4g1yOHw4kX9nQ3l7qDWd4iuZ40KxythWGO8Y68jOK2IvCHhyCxnsotDsEtbiNY5olgULIqklQwxzgkkfWpm8N6I+i/2M2k2Z0zj/RfJXy+Dn7vrmgDIv5mu9S8MXTalaPam6ZWa2mdRJJ5UmMEPgrlcYIPWs7WPEXiWy1+50WA6f8AabqWBtKdrWRleJmYTB8PyUADEjAAI9eOsk0HR5Y4o5NKsXSFdkStboQi+g44FXDbwmSOQwx74gVjbaMoD1APboPyoA5TTbmyt/iNrUV1qdi9/PBb+REkhWQJmT5CpcgsMA5ABwRkVV8N6rrWp2mpQNrunnVIrq7jjtpbcb0CTMqFlDg7doHYcEcnv1Y0bS1vvto02zF3u3+eIF8zd67sZzS3OmxypdNasLK8uUCteQRp5ox0OWBBx2yDQBz3hHX9V1x7y7vhBBYWsaQOhhaOQXKqPPDEsQFVsrxkdfmOK1tbjsNY8L3bNcI1q0BmjuYpB8hUblkVxwCpAIPtVrTdJttM0xbGPdKh3NK8vzNM7El2b1LEkntz6Ul3oum3uknSp7OI6eQqm2UbEKgghcDHHHToehoAr+Fbu71Dwhot5fkm8uLGGWcldpLsgLcduSa16RVCqFUAKBgAdBS0AFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQBXv8A/kHXP/XJ/wCRrz74E/8AJKNP/wCu0/8A6MavQb//AJB1z/1yf+Rrz74E/wDJKNP/AOu0/wD6MagD0miiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAr3//ACDrn/rk/wDI1598Cf8AklGn/wDXaf8A9GNXoN//AMg65/65P/I1598Cf+SUaf8A9dp//RjUAek0UUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFAFe//wCQdc/9cn/ka8++BP8AySjT/wDrtP8A+jGr0G//AOQdc/8AXJ/5GvPvgT/ySjT/APrtP/6MagD0miiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiuc/wCEzsD4kbREtb95EnFtJdLB+4SXy/M2l88Hbjt3rYj1TT5Xt0jvrZ3uVLwKsykyqOpXn5gPagC3RWfba9o95JNHa6tYzvApeVYrhGMajqWAPAHvUcPiTQriGaWDWtNlihUNK6XSMIwTgFiDwM8c0AalFU5NX0yGyjvZdRtEtJDtSdp1CMfQNnB6H8qzdW8aeHdENj/aGq28SXyl4JN4KuoGdwI7dOfcUAb1FZc3iXRLe+tbGfVLWK7u1DQQySBXcHpwfXtnrVS78V2UPiGy0a3khuLiW4MFwolw0B8ppBxg5JC9MjAOaAN+io55fIt5JdjPsUttQZLYGcD3rlPDHjWXW9NutT1GwttO0+GBJxcJfLOvIJZHwo2OuBlT/eoA6+iuS1fxe8nhLUNY8Mi3vLixRpJ7a6WSORFVSxUx4DhiBwCBnOatWnjHTWg0SO+l8m/1Wx+2RQJE7ggRh3wQD0B6dTQB0dFc2/jXT2l0f7JbX17b6pFJNHPbWzuI1TGS4xuHLAYxkHrRP4jlHjXTdGjjMUFxbyyu9xA6eYwCkLGx4JAJLD09waAOkormv+E40k60dNWO9fEjwC6W2byGmUEmJX7v8p4HcYzniotE+IGka9qVrZW1vqMTXccjwSXFq0ccjR8SIGPVlPB7ccE0AdVRXJaP4tFz4Y1LxXdmQaQHkktYo4CZBBGSm49yWKsw9AR6E1I2t6h4i8LT3/h3da3sDhkS5VJEn2gMUDKxUqwO3cp4OfQ0AdTRWT/bTzeH7TVbGwmvftKROsELpuCvjnJIHGcnnsa1qACiivOdL13xDBrVxcXepR3mnf25LpbW8sccRhTG5HVgAWIPBBzxz2JoA9GorktH8XxeKcWcNpqNkt5atLBdom4BegO/BVWIIYZzkflUdvrx8N+BjeX013qUsF3LaRtNxLM32ho4wxwAO3OOgoA7GiuBvvHOqv4Tvby10pbLU7e9gsyLvcYCZZEQSI21S6/P6L0P43/EPjd/DclhZ3en+bqF75pjjtvNmjAQA4LJEWycjgLx345oA6+iqOjamus6NaaikE0AuIxJ5Uy7XQnqCPUVzeo+LNUXxNd6bpljZSW+mPb/AG97i6EchSXndGDhcKOcseegHHIB2VFcMnju5/4SIQPa2x0xtVOjgI7NcrOFJDsoGBGcfUAgnjNQaL44m8QeKJNEnjgGn3sFy1pPatKrlY3CElmC8kEkFOmOvegD0CiuP+HKJbaJqNlFNJJDa6teQxCSUyMqLK2Bkkk1c8barqWh6Iup6fc2EQgmjEyXoIWVWYLtDg/IeeuG+lAHSUV5x4l8VeI/DsdjYPe6ZLfXonmS+NuIrZQiriL55gCxY/e3Dj+E03WPEWtHVfDMo1/T9Ct77TpJZVuokngaYbPl8wSAE4YlcHopPOeAD0mivNZfHutSfEFdGtrW1XT4XhR2laNWuUcf66PMgYrzwFV845Izwui+K9bm1m4l1LV9L+x2+ty6S1qkYjO0BtshJYkOSowOhGepxgA9JpqSJICUdWAJUlTnBHUV574H1HUZry9i1jxRcS3ourqH+z7i3iQqEb5ZRhQwXZtPPy/Mfas7w/rLaN8OtVXSZ7a51C31C4DSQom4RfaNhuWReoCfNnBBwO1AHqtFeRXXjDXo7Q+Xrn+hW+r21nFqptYyuoQzAb8DbtDRncdy8HbgjrXbeCdTvtRstUhv7wXsthqc9mtz5aoZVXBBIUAZG4rx/doA3r7UbLTLf7Rf3cFrDnbvmkCLn0yfoamiljniWWGRZI3GVdDkEeoNeffEGKZ/GfguZZLyK3gnuGnlt4fMEQMWAx+VgMk459aml+0z/EE2EOs6rbaRNZRTCKGILH5wYYRX2fICgyQCM5PI6UAd9RXnFpqusnxdcQX9xq6zG8uImthaEWiWQV2jlWQLjecJzuLZJGKoeGNZ1lfEuhQTXGuyQ3EK/akvYGKIWt92CQvB8wHOTxkDjpQB6sTgZNULrWdOs7+xsri7RLm/LC2j5JkIG44x7c81Q8a2V5qPgrWLSwVnu5bVxEiOyFzj7oKkHnp75rh2tra60/w0LOw8SW1nDqkXni4Nw0kIa3mjwjElwqsQpYYHIOcc0AerUV5PNb+KJdDtLa8i1dba0vb2FmiaZ7iRQ2bd/kdGZdu5eSckKT149D8NHUz4csP7YLnUBEBMZEVGY+pVWYAkYJAJ/pQA8a7YnxCNDzML0wNcANA4RkUqDhyNpILL0Pepl1S0fWJNKDt9sjgFwybDjYSQDuxjOR0zmuU1u/urL4kabdromrXVrBp81u89tb70DyyRFecjgCNs+nFQ6Y8+n/FDXPJ0HVFs9QigX7UIx5JmTzC75LcAhkGR1K9KAO9qOCeG5hWaCVJYm+66MCD9CK888H6BrdvrN3JqtjOYrq2nL3F3IvmB3dcI6xzMjkqB8yqmAgAq18MvDknhvS/sdz4dOn3kcSxzXvnJIt0QTyoViQO/IHUcUAd7WX4g1618OaZ9uu0mlDSxwRxQgF5JHYKqrkgZye5FVfF+nS6poggSyN/EsyST2SzCI3CA52hiQM5wcEgHbgkZrhrzwvrP/CE6bYy+GzfvHrC3kVk9xFIbO2WUP5JeRgDlAVwCRzjOKAPTNNvTqOnxXZtbi1Mgz5NwFDrz32kj8ialmu7a3dEnuIomf7qu4Ut9M9ag0kbdJtgNO/s0BMfY/k/c/wCz8hK/ka4jxV4L1DW/FX9oQ2lpIitb7GudkiFUYM3Vd8eOf9WwDcZHXIB2w1rS21CWwGoW32uIqHhMoDLu+7x74NTm9tFeVDdQh4hukUyDKD1PpXPRaXqFn4uv7mLS7G4s76SKU3LyhHhKoFYbQhLH5QQSe+OABXMaZ4P8SQa//aF7ZaXKgkvjNGsyqlyJ8EHaIs/wgEOzfhigD0eG+tLksILqCUoMtskDbR74rOsfE2n3+rajp8bFWsI45ZJi6GNkcsFIYMf7jZBx2rgIfh3rX/COaTpiR2dlKmi3On3UkMpx5jPG6McKCwbyyG6HDnr31R4N1xpdVbydDt4b2zs7UW0AYx4hclhhkIAZXcDg4+XrzQB2kmuaRFawXUmqWSW9xIIoZWnULI5zhVOcE8HgelU7/wAVaTaeH31iG+s7m3Kv5DJdRqkzKDlVcnbn5TnnjB9K56Xwlq8vhe70mSLTZjPqS3QE9zIw8oSB9pYIDu+ULn0J/HR1zRdbupLK60uLR4547aa3mhug7Iok2klGUA5+XByBnNAG9o+pxazotjqkCOkV5bpcIr/eAdQwB9+au1leGNLn0TwtpWlXMkcs1laR27PGCFbYoXIzz2rVoAKKKKACiiigAooooAKKKKACiiigAooooAr3/wDyDrn/AK5P/I1598Cf+SUaf/12n/8ARjV6Df8A/IOuf+uT/wAjXn3wJ/5JRp//AF2n/wDRjUAek0UUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQB563hvXJviZ/akenWlnp4mLXF5FdFWvYfK2iOSEDDEMQdzdl+lVYPB2vabrOkXkkelSaZokl55SwbhcSW8ofagGwBSgIULuweuRivTKKAPnvwtJINJ122htrfU5LrR3gaW18xWs0ThIpAIl+YeYd2Gdjt57Vp+HfDd94l8O6vpsRtheNPb3p1SFZIYp5kIxCQYo2QAIpygON2ck17gFVc7QBk5OB1NLQB55D8Pb1NBhsTPaxSpfSXu9JpzKjupyVnLbt+4nLYAIJG3JzWhD4R1a0svDLQ6naS3+ixSxM8tuVjmDpt+6pGMYX68+tdnRQBwt98P573X7rU5b+3k+3JAbqOSKXYJYfuOiCUKR32tuwRn1Buz+F9ZbWDNba1bW9h9u+3hBZbpS5XayFi2CpGecZGfQV1tFAEc8bTW8sSyNGzoVDr1UkdRXExfDnMur3Fzq7G61G3giMtrbiELJE25ZmXJDvuwST7joa7qigDlIvCF1FZa4Tq4fU9Zws92bUBUQJsULGG7Ankk89fSq6+BrldM0NBrhXU9EDR2l8tomfKZNhRkJIPy98jkA4OK7OigDjrbwReWGk2NpZeJb2KeyaVIrpokZjBIQTGy42kjaCGxwR0xxVnUvCl9f6/pOqJ4guIhpqFY4jbxvvZgFdmOByy5HTAJyPSuoooA5mLwTZRa4uofbr1rZLp72PTmZPs8c7A5cDbuzks2N2AxJxmo9N8C22mXWlzRanfuumzXEsEb+XjE3LqcJkgEkjnPvXVUUAcnZ+DzbaNqPh5LiS10eSbzbR7OUpNGHcvJGflxt3EgdcqxB6c2E8K/2Z4d1LTtCuzaXN9IZHupFDFXYKrMFXaAdq8YwAea6SigDLutDjuNCh0mC8vbKOFY1jmtZtkoCEYG7uCBg+oJrUoooAKxbPwpo9leG7jtneczvcbpZ3kHmvwzhWJUNjjIGccVtV5jL4wvJfiX/ZMepXcdi909o8YjjIhPkkKQBGzcychmYdPu4oA7iw8NaTpjs1nbPDlWVQJpCsYY5IQFsIOf4cdvSqNx4e8M6RoGoRXqiLSZgWuhd3kjR/M2SxLsdpLHORg5rhvDHirVI7nRbzUdcv9RN4t7Bd232dMLLDgxoiqgwxBJz3yPQVb8AeKL681LUP7SubufTDYLeie5VnXeGIcK3lIowNuUUMAc4PWgDs9P0Lw1e+HHtbK2trrSb6PDMHMonXsS5JLY7HORU6+FNAS3SAaRabEl85cxgkSbQu/J53bQBnriuH0KC7l+GthHZXN/Zavoyee9qzNbLJ85by5Ny4IYKR7ZpL+41238GWGoC+1QT6jf8A28wLFNP5UDKWW2Z4gXRQNvzAdc9jQB6TZWNrptnHZ2NtFbW0QwkUSBVUdeAKp3nhrQ9Q1Bb+90ixuLsBQJpYFZ8A5HJHavLdabxnfaL4eQLqdnE9huMriaWaO83fKZPJwSduCN67OTuAPTQ8UDWb7xJYbE1rfHBbHyUimjQyA73KSRMY9xHysJRtG3g80AekLoulpq7auunWo1Jk8trsRL5pXpjd1xwKq2PhTw9pl19qsdE0+2uPm/exW6q3zDDcgZ571rOgkjZGztYEHBIOD7jpXj/gnT9XksjNpV3qw1CM6jbzzXty80JKsyQL8zFN4YIcqDwrZ6igD07SfDeiaC8r6TpNlYtKAJDbQLGWA6ZwOetP1ttJh0qa61tbY2NsPOdrhAypt/iwQef1rgtC0fWrfRNae7t9V819NWM2ryMd10u4lo2aZyxJI5G1TgY74qS+GZp/gvqlra6Jqf8Abt3axxXQu23XFzMmPmLFjlQS2OegxjtQB3+lT6Vr2kBYtMkjs1PywXdiYl9iqsoBHcEetaU1hZ3McUc9pBKkX+rV4wwT6AjiuEl0KfVtI8PCXRL46ZbCRbzSp5lR5WKDY5Bk2sFYHhm7g44FZ8vgvUpYPCZ1fSZdWktop4dSCXSljCcmKN2Zl83aSuexK5oA9PNvA1wtwYYzOqlVkKjcAeoB64pqWtvGWKQRKWfzG2oBl/7x9/evFvE/gDXZtZ1GXQ/DzxRGbdbSR3cSDYLYRrwXBB8wBhkcYyOtbun+FPEa/EQavewXDxC+kuo5/tEARIXTb5bYXzSVB2hc7MqDkUAeiyanbxazb6Y6yCe4heaNtnyEIVDDPr8w496tsyxozsQqqMlicACvOPCvhrXtF1ewW40Wyc2Znin1drvMt3HKwYPjBYsNoyrEAfwnFdh4r0mfXfC9/pttIiTTxgL5h+R8EHY2P4WxtPsTQBopfWckEc6XUDQynEciyAq554B79D+Rp9vcwXcKzW00c0TdHjYMp/EV5jP4B1Se0u7j+xtFglm1GzuYtMik/cRJCfnO7YPmkHynCDjGc113hLQ7jQJtatza2sFjcX7XVoLdsBUZVBUoAAuCvbOc0ASeI/E8vh/UNHgOlyXFvqN5HZm5WVVETuSBlep6H07c1Pe+JLa08VaZoCiOS5vUkkb9+itEqqSDsJ3NkgjgdjmqPjbTdY1O20xNHtbSd7a/hvH+03BiH7pgwAwjdeRnt71T1vS/Ed74r8Oara6bpRSwV2nMl0yvukQoyqRGcquc/wC1gdKAOk/tzSf7XGkf2laf2kV3C085fNx67c57VB/wlXh//Tf+J3p/+g/8fX+kL+45x8/PHPHNYWk+EdT0rxFez+fp1zp1zqMmorJcQu11E7qFKqc7QAMgH0PSsvwx8MX0KW5aae3ncQTW8FxvnaR1kySXVnKKScE7V5IzxQB2Nn4p0DULa5ubPWbCeC2TzJ5Y51ZY15+ZjngfK3PsaeviTRZNOmv49TtXtYXEckqSBgrEAheO53LgdTketcnbeBNRS3sIZ5dNmji0IaTPG8TsjlXUhsZGRgHPIOT2qxZ+Br6LRp7SbVwZWu47mBSsk0cOzjG538xsj1fg9OByAdBceKtDtdKi1OTUoTZyuY45I8yb2BIIAUEkjBzxxg5xg1p21xBeW0VzbSpNBMgeOSNgyupGQQR1BFcjJ4EIsrSK2urS2lgupp3EdowilEikMCvmbs9Du3ckc9a6XRtMi0bR7bToRGI4E2gRR+WvrwvYe1AEN34j0my1FbCe7xdFo1KJGz7DI21N5UEJuJwN2M1Hc+JdMigiZLoeZcXL2VuGjfD3ClgUPHHKnnoccVm6t4TvdT8QjUE1hba33wOY4rbbL+7JOPNDDcG44dWAGQOpplx4I87VftMeqzxW39pLqn2cRK2ZwoU5Y87cDoMc55oAi8PfEHTdR8NWeoalKbe5ks2u5o0tptqqhAk2kr820nBxnGCela1v4t0m/F2ljLNPcW8cjmH7NIrsUxuVQVBYjcvAyfmHrWNafDuG1sobU6tdPHbW1zBany0BhM5y79PmPJAB456Z5q3p3gv+y9RnvrbVJTPK8z5khRghlEe7bxnrGp60ARReNWi+Gr+Lrq0EuyFpmt7Xf2YrjLKCMY5JHHPpWhqvic6Zptldf2VfSyXd5HaJbhAJBuPLYyRgAE/h2qgngSI+C7rwrcancS2E8ZjVgoSSPLFycjryeh4xwc1ZufCtzfaGlje+IL+a7iuUuYL7y4kkidCCuFVApHUEEHOTmgB2qeNtI0VITqRmtpJI3mMLoN6RqcF2APT6ZJ7DrVDxX44TS9Jnk0hknuolt5Hd4i0MUcrqqlzuXBIJIGc8cjFM1b4c22tfYpr/AFW6nvreN4pLuWCB2mjdtxXayFFwehUAj1qfVvh5puqxtCb2/t4JreO2u0hkH+krHgxsxIOGUj7wwe3SgDrR0HOaWo7eH7PbRQeZJJ5aBN8jZZsDGSe5qSgAopkU0UylopEkAOCUYGn0AFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQBXv8A/kHXP/XJ/wCRrz74E/8AJKNP/wCu0/8A6MavQb//AJB1z/1yf+Rrz74E/wDJKNP/AOu0/wD6MagD0miiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAqmmrabJfGxTULRrwEg26zKZAR1+XOeKuV5VpehpqXxH8RCxsLGC3tdWt7tr3aVnjcRLuVFKYKuyurHcPvMcdKAPR4da0q4nSCDU7OWaQsqRpOrMxXqAAeSO9Pi1XTp0uHhv7WRbbPnskykRYzndg/L0PX0rjND8HXth4g12WXStIt7fULmWW3v7WQ/arcMgRQoMYCngtw3Vj1qC3+HM76Fe6bINMsDJYpYLLZQkmdVcN5ko+XlgMFcn7zfMc0AaMur+H/ABrfX2g3vmCC0liAYXirFe7wxCrsf5xhTlT+XFdE+vaNBp9xeNqdmlnauYppfOXZGw6qTnAI9K5WLwbqrajf6kx0i0mkWyFtBbwsyRm2diCScfeVivA4BA5xzJb+C9Ttr2bUEu7FrhtWOqLC0B8rc0PlMh7ggchxySTleaAN2+8XaFp0WnzXOoxLBqAZreZTuRlVC5bcOAAB1rWtrmC9tYbq2lSWCZBJHIhyrqRkEH0IrkpfCF/b2GitpU2l2t7pU00scQtGW2bzVZWG1X3DAcnOeT1611tqtwtrGt08TzhfnaJCik+wJJA/GgDPuPE2iWupDTp9UtY7wyJF5LSDdvf7i/U9h3qlY6t4S0f7XY6fcabZrA0stxFbhUCsmPMYheMjK7vTjNV5fB0j+KJtZh1BbczXEM0iRROC4jUDa37zYc4xuKbgDgHgGsr/AIV5qLTy3M/iJLi5mguIJJZrNmDLL/0z83ywQPRRnvmgDeHjnw01td3C6rE0VpE007KjHYikZPT/AGlPHUMD0INRP4qj1fQNRu/C0tvd3tmPmhu0kh2nG75lKhhleRxg+tcxqXw/1Wx8Oa8tpqaX8t3p8sS2/wBk2M8jW8UXytvwM+Sh5Bxk/Wt7S/DupNpl/fPqRi1fVLeGJ5ZbIAQIgIC+UHOW+d8nd1I7CgC5b+MNPi8IaRr2qObZdQghkWOON5WLum7aqoCx79ugqa88YaJZWtrcSXTyLdQPcwLBBJKzxoAWbaqkgDIznHJxXOTfDFb3wzpOl6jqUN5caOdtjcS2QMax7Amx4t2H4Gc5Bzg9uXat8NBfaNpulWuqxW1tYrMF3afEzK0jbt8ZXb5bLyAR65OTQB3cUizQpKudrqGGfQ0+swaZdRTaULfVbhLayQpPFIqyG7GzapdyMhgQGyOvOa06AGysUid1QuyqSFHU+1eeeHvH97Jo2qa1r5tVtrSFJZLG1t5FurMlmBWRXOWAXad4AB+Y9BXoUsfmwvGWKh1K5U4Iz6VwWr/D+dvD+uNHqN5q2sXeltp9vJeNGm1OoT5FUctgknJ460Aap8d2UVlqct5ZXdnc6fJHG9pcGNXcynERVt2zDH1bjBzjFMX4gWM2lQXNtYXlzez3bWSWEPltIZlXew3hvLwEG7cGxjvnipLXwZBcaXONWmuJtRvPIe4uPNUujxHdHsKooG05wdoJ71Y1LStKtLCGXU9Vlha2uDcQ31xcqjxOQQdpI2gbSV24xgnigDN1bxReXOgaBfafHe6b/aWoQ28pntkaSEM+0q6Mwxk8ZGcdcVqa34st9E1e00+S0nla42EyK8aqgaQRj7zAscnOFBOAadqHhqzutMtbe61C+WKzmW6Ez3ALGRDuVmZgehGccD2xVa48F6Rq14NQnu76cywJFMY7xkS5VCShfZjJBYkEYoAct5exfEddON5JJZTaW9z5DqmI3WVFG0gA9GPUmujkLLGxRQzgEqpOMn0z2rCPhGyPiWDXftmpfaoIhAqfa28soMfKR3BIBOTyRk1vMAylTnBGODg0AcfB40v49FvdZ1Xw89jp1nDI0ji7SV3dGKlUUDlcg4YlfpUqeNd1vc/8S1zdR3UNtCiyHypml+6RIVGAOd3BxjjPGZIdM8KWmhavpqzLLpsSsl/BJeSTiLOWYEFiVJ3E8YJz9KpRW3geDwXPqIkL6HdYd7iWeeViVbClWYmRSrZxjGDk8daAJdN8bTXuqW2nzaUsM0uoXVg5W53hHhj37h8gyGH0I96zpvilDHpunXA0t2uLy2nuPIVpJMCN9m0GOJiST3IUDuau6H4G0VvDstpLJ/aGmXl6dStTukRo94BXD7y547kgkEg1YXw14NW8i0CPT4I5oFa9jtow6BUchWIIwNpIAK5we4oAr6z4+Ol6vbWS6eAktuk7S3UjRKpdgAhZUYIw5zv2g8AE1Lbal4mm8d6jZK+kNpVv5GYmkcTIrBjuHy4LHgYJx8vB61sSeF9CluRcPpNoZQiJkRgfKhyq46EA9B2p134a0S/1aHVbvSrSfUINvlXMkQLptORg+xJNAGDo3jK81HxlPpFxbWlvakz/AGUl5PNmWNgu9Ts8tgeThWyMc11t19o+yyfZWiW42nyzKCUz2zjnFZun+FNA0rUX1Cw0eytryTduniiAc7jk8+9O8T3Wk2fhu+n12IS6Wkf+koYjICuR1UA5FAHD6GZ/CXhCDW5Egl1TU2hjkdruYwCSVv8AWylicDJ6gcdPejVfHniDTvCl3fIulT3um6pHY3DormC5VtnMZ3ZUjeAc7sFSOa7PTPC/hux0+eHTdHsYbS+QeckcICzKRxuHcYP60l5pXh/SPD5STSLb+zbIGZbeK08wKQCMqgBycE9s80AaGmLfpYRjU57ae7yd720RjQ88AAsx4GB159q5XX/EuqWviSawttQ0bS7a2hilLaqrA3W5jv8ALYMMBVGM4PzHGB1rq1lsdPtraPMFpFIyxQRnEYLHoijjnrxVbUn0NL+z/tMWP2v5mtjcKpcbeWKk8jHHP0oA5nUvF+oWniOe1hn090S/tbWKw8tzcSxyhC8oOei7yeFIwjZPpS0/x61z45+yz6nbrpk91NY28LIi5aMfezuL53KwywVSCMZJye/aGzN9HO0cH2zyyqSFR5mzIJAPXGcVl6v4m0rRdU0ywustcajci2jEahtjkErv5yAcdcGgDm/Ak2k2Xi3xhpGnS2EEK38TwWduoTH+jpvKgcEZU5AHBBz1r0CmhFByFAPriovttoEkf7VDsibbI3mDCH0PoaAJ6Kht7u2uwxtriKYLwTG4bH5VNQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAV7//AJB1z/1yf+Rrz74E/wDJKNP/AOu0/wD6MavQb/8A5B1z/wBcn/ka8++BP/JKNP8A+u0//oxqAPSaKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACucfxLqA8RSaQnhnUJNjIxuRNCI/KZivmcvnqp+XG7jpXR1kP4egbxGNbF7qC3GxUMS3LCFlAOAY+h+8T9TQBh6J8SdK17xTJodpDKSDIsdwJI2WQoeflDFlHBwSB+oo0bxnqFz4cvtd1XSI7bT7SO5kMkFxvdvJkdSuwgYOEPOetall4O0nT9XbUbb7WjGRplt/tcnkJIwIZxHnaCcntjmm2/gjQre6vJhbSOl2JVe3kmdoVEn+sCx52ru6nA70AYkHxKEnhy51htDu2WF4AkcDhxMszbUKOcKWBIDLng9yMEx+IvG+uaZ4Wur1NItrTU7fUYbQ289x5qMsmwghlHUhwOeAc9cDO/8A8IP4fOlT6Y1nK1nPs82NruZtwT7oyXzgemcVPceE9Eul1Bbmy85dR2falkldg5QAK2CflYADkYPHWgDA8XX3iEeGdNmeMaVcyarbQz/Y73eUieVU4Yxjdnd0wMcHJxirHijxnd6HqFxBY6bHdR6fZf2hqDyziLbCSyqsfBy5KMecDC4zkitG68E+Hr3SrfTLiwL2dvJ5safaJAQ/94sGyx9yTUreD9AeGzil02OVbMFYfNZnIU5+VixJYZOcNkZwewoA5XVviFrGmvPff2NaNokFxbJ5/wBpYyzRzY2lU2jaw3BiG9cepr0Q52nbjOOM1nXfh7R783Ju9MtZ/tRQz+ZGG8wrjaTnrjAx9Kspf2X9oNpqXMP2xIhKbcON6xk4DbeuM8ZoA4vS/EfiTT/D+r654gbTLqztUu5o47QuspMTsNmGAG0BSMnnpmmW3jPX20HWbqXT7B7q2hhlsSjvHHcmXICfvNpzkcEcMWAFdguhaSl3PdrptoLicESyeSu5weuTjv39aItC0mC1ktYtMs0t5eZIhAu1uc8jHPJNAHDXfjDV77wpNcRXltY3cetw6e1zHayFYVLR5MiSbSPvYPJHIweci34tuLqTSdIkm1SxuETXLeK5Fr5kYYNMq7crLwV3ZIbIOBkCuklGg6OLDQ/sdvDFfOY4LaO2/dsUXcc4G0YCjr6cVdOj6Y0CwHTrQwqxZYzAu0E9SBjrQByHizxVrWj3erSafcaS9tp2nJqHkSKzTSruYMvDAAfL97B7DBqJvFms6r4pg03S7mzt0MVtcSRyWxmKwyIWZmfeoU5AUDBJyDjFdt/ZWnYx9gtceX5X+pX7n93p09q43WfCnh6/8QHSLuW7J1LFw1tHCuxEiVQFEuzdGvyDChhyDjqaAO5ndo7eR0XcyqSF9TjpXmWleOtXu9AvtVj1PS769bSnvI9IiiYS2kyZyjDqV6Z3YORxwa9QAAAA6Coo7W3hnlnigiSWXHmSKgDPjpk96APN7HxbqbW+qTjXU1LTdPazuX1K3tF2lHbM0RAB4CYbIBIHU5p994k0LW/Cnio6nqdhqMFrM7WbTW4URh4h5O0EcndvAccnBNelIixqFRQqjoAMCloA888TeKbDU7ewSLV/I8O3sc0c9/DbLcLJICqiAhkYLuDNyRyVAHXB2PhojxfDjQ4ZYpopIrYRvHNE0bKykg5VgCOldXRQB53q+oavL8RLOK1utRbT47mKKSG2RolTgli4aMiVDxllcbRxgnqaJA9l8SNZivNR8QlpbwSWkDJI9rJGYE5LhNoCtuABYfdHB7+iUUAed+A9Ws7KfxJbyJqhaTUbi9SS4sJwZIdic7igyeCAv3jjoa0PDfibTBompO0Gpxx29zPM6y6dOCUkmcqUUplgQw4AyO4FdpRQBheD72O78MWEaRXMT21vFBIs9u8JDqi5ADgZHuOKy/Gemx32paa9wuteRHb3Q36S8iOHPl7QxjOcHacZ4yBmuxooA8nubDxpejTIdSbUYbqLT7eSK4six/0lTmZJNkqxknC4L5XGcHOc+roSyKWUqSMlT29qWigDzWKy1u88W3FuINYS3uHuvMubl2iWCN1KrsKyFJADgqAqsAc561TOkeMJNDg0qexv5nGgXlhdTSXcbJPcOAIm5kyejfMRn5ufb1aigDzSPR9fiiuRFpmpJZLHp6LaG+HmSMjsZ2U+b8oKFV+8M46d6x9N8N+KIvBviKxvdEvp76/06CGMS3cUu66Ebo825pDjnyznrwPSvY6KAOJ1yy1DU9G0O7/4RtLqewuUafT7sQtI6GMq2xi+zILA8nnb9Kz9a0K9vtS0HWH8GWd7DFZS2s+lSPCTbsxUoct8hUbSDjONxwDXo1FAHl+peEvEFx4ta+js4/KeO2ktWhnhjFi8ewNHvMZkKZBOFwGGQQM5JqPgvXbnxTaXZ0zSrk2+tjUF1Z5ylx9n3EiErsJIUHaPmIwo4FeoUUAVdTs31DSbyyjuHtnuIHiWdBloyykbh7jOa8wg+HOqN4d1Owm07SoGbSlsFjt5PkvplYMtzJ8o2twOu48nmvWaKAOP8MaDf6V4o1S+fT7GysL20tVSC2lz5MkakMgUKFK8nDYHTp6dhRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAV7/wD5B1z/ANcn/ka8++BP/JKNP/67T/8Aoxq9Bv8A/kHXP/XJ/wCRrz74E/8AJKNP/wCu0/8A6MagD0miiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigArznxD43fSfGYifU2t7C0ngt57YwofNMi7mYYDOwCspyNoBz97t6NRQB5RpPi7WYdUurrU9Ymnt7fxC2lfZFtUCeS+fLkLBdwIJx1x8uCM16RrdzeWeg6jc6dB9ovYbaSS3hxnzJApKrgdcnAq/RQB5jpGua7eeG9UvLrWb3zFto5YfsmnmaSGYZV05hQOS2PkxlcHJA5p9p4h8SSaGZL0anHd/2vtvhb2IJtLYkgCHKHzkyFywBYBie1el0UAee6xNrkuiaZHb6nqskb3Myz3iWht5NuSYtwWNmCj5VyFG7HOATWPf6h4gXUbC3vdR1dr99EmdIrKBkVrtZFRHZFXgHOTv8Al55wOK9aqjNo9hPrFvq0kGb62jaKKYOwKo3VcA4IPvQBxc9lfR+MYdY1Sz1V2OiQxv8A2e8m37QJGZ0wjY9OvFT20epQfFjUrtbfUf7MudNjgSV1doxOHJ4z91QG+nJru6KAPNdPg8VNpqpdSat9uTT7n+0mdjtkuAf3XkbcAc5I2ADbgHmr3hG31bT9btUuY9TNveaTDLdtcs8ii9yd/LE7OOwwvSu8ooA5nxvZteaVaAWF7exRXaSTQ2MpjmKBWBKsGU5GR0Iz071w2qad4un8M2FpDZamEkuLs28f2hmmt4zxAsxEi5wCTuZzt4yDivX6KAPK9R0nxTq+g+H7n+zb9tStNP2T29xdKqSTDCkkrKjI5wSJBuwGIxk1v6hpeo/8LE0bXLfSbkrHayQX8sVzHsbcBsUKzAsFbJzgfQ12tFAHnNl4f1v/AIWd/bEmjolss0rNeXMySPsKFFEbK24Lgg7GTAy3PSu7tbm6muruOexe3iicLDK0isJxjJYAHK4PGDirdFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQBXv/APkHXP8A1yf+Rrz74E/8ko0//rtP/wCjGr0G/wD+Qdc/9cn/AJGvPvgT/wAko0//AK7T/wDoxqAPSaKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigCvf8A/IOuf+uT/wAjXn3wJ/5JRp//AF2n/wDRjV6Df/8AIOuf+uT/AMjXn3wJ/wCSUaf/ANdp/wD0Y1AHpNFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABUe6X7Rt8tPJ2537/m3Z6Yx0x3z+FSUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAV7/8A5B1z/wBcn/ka8++BP/JKNP8A+u0//oxq9Bv/APkHXP8A1yf+Rrz74E/8ko0//rtP/wCjGoA9JooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKy7jxFpFrqNxp899Gl5b2pvJISDuEI6uOOQMds1a03UrPWNOg1CwmE9pOu+KQAgMPXnmgC1RRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFAFe//wCQdc/9cn/ka8++BP8AySjT/wDrtP8A+jGr0G//AOQdc/8AXJ/5GvPvgT/ySjT/APrtP/6MagD0miiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAMXUPFekaXqcmnXcs6XMdo94yraysPJT7zBgpBx6A5yR61oadqFtq2m22oWbs9tcxiWJmRkLKRkHDAEfjXE+MdH1PVPFsX2az1D7K+i3Vq11ayoirJIVZVYlt2P3fYdWX3xymu+HPF17aaIthpt9b3FnpFtChjmjCiVCDIGPmDYw2DaVDZ3EEgUAe10mQSQCMjqK4KXwTeS+KYriJlh0K5livrm2eZhLDPGrAKm042sWUsM4+Rv71N0Lwrqll4sGoX0LyTJc3DtepNEiTxuTsDKE3sVDYCscDaSDzigDv2ZUXczBR6k4pvnRZI8xMqMkbhwKp61babe6NdWusCA6fKmyYTsAmD6k9OcYPrivN9I8HX2teEZL10tWvru8t5EMwMQubKAqsaOU3Y3ou48dW6YxgA9UEsbbcSKd3IwetOVldQykEHoQa4aPwffWdzYahZWmmxTWuo3F0tkJmESxzRFGVX2Eg5+fAUDJPpWx4G0fUNA8J2ulaktqJ7dnANrIzIVLFh1VSPvYxjtQBs3Wo2NlJDHd3lvBJO2yJZZVUyN6KCeT7CkbUrBb/AOwNe2wvNnmfZzKvmbf723Oce9cZ4i8GX+peJL++istFvre9toIwdRMge1kjckFNgyV5zgMpJHXFQ3ngLUrvxD5xmsltW1WPVWvVLC6UqqgwqNuNny9d3Q4xQB2lrrukXzlLTVbG4YR+aRFcI5Cf3uD096z9G8a+G9fW4bTNXt5xbKzzHJXy1UkFjuxgcHnpjmueh8H6tHqGi3SWWi2z2GrXFzI1vK4LW0gYbcCMAt8/Q8fIvPJxeGgeKP7J1HSItQ0u1tZEmW2mjgZ5dzvu3OCdvRmUjBz1yM4oA24vFOgzaNNrEerWjadAxWW5Eg2IRxgn15H5iq19410Gw07Tr9r5ZrbUZlhtWgG/zWZscAdh39MGuXtvhxqQhuDdanaS3CXtvf2TtHLJtliXaFlLuWkTaOmRgkkY6V0E2gazLoixJqFjBqEd6LyHyrQi3X5slCm7cwOWJO7O4546UAX5vFmg29nbXcupwLBcxtLE/OGRSAzdOAMjJPrVLxV4ztPDUSqqLd3m+HNsGKlY5JNm8kKQBnOM4zjGaxde+Hd34jls7zUdVglvkt5La4Jt3WJo3bd8qpIpyvQbiwI6ip9X+Hs1+t1HZa19iiu4LaO4T7KJNzQEFGUlht6AY5oA7hmCIzHOAMnAzXPWnjjQL1rIQ3co+2GcRGS2kQAw/wCt3blGzbjndit9A0cKq7mR1UAtgAscdcDjmuN0bQU1XVdd1W4sZ7Ow1GLyIbWdSkgJBE0u3/lmX+Uep2AnqKANEePPDv2Oa6N5KsUQjZt9rKpKO+xHAK5KFuNw496sXvi3SNPh1KWeWbbpkiR3e2Bz5RYBgTx93BByOKx7T4dWvl3C6tqE2oM9kunQuEEPk26NuUYXhmDAHcfQcdcvm8Ard2usRXmu6hK2sJGt4wSFQSihcqNny5AGetAHSaZqSapbNPHbXcChygF1C0TMB0YA84Pb+lcf44+Ir+DL24tn05rovY+faFAcNNlso5HQbVLZ44Vh6V3FtFJDbpHLO87r1lcKC34KAP0rG1bwtDrL6j9pvZ/KvrT7K0YSMiNcMNyEqSG+d+ST96gCC58ZWemRWA1CK5MlxFA0ssMDeTEZWCLlj2LHGBkjqfWkt/HGnTX8tpJaX9v5N4tjLLPCFRJm+4pOc/MCuCBj5lzjNULn4a2N4yG51fU5QI4UIYxctFjY4Pl5VvlXO0gHHIq/L4Js5r28uXvr4/atSt9SaPcm1ZYdu0D5c7TsXIJ/hGCKALFv4u0248QPopE0V2FldRIoG9Y2CscAlgMngsAG5xmqcXj/AEh9IudXljuoNOt7RLtriRVw0bkhMAMWy2DgEA+uKbb+AtP0yaO80uaaK/t4pUtnlYMoMnJ34AZxuAPJzxwRWDoHgnUXsl0nVLCC20R4JIb62e5WZ7tztKyAqgK/NubJYtk9O9AG8njgTeG7jV7fR7m4a1b/AEm2hngdo02lt+4OUbgA4BLc4xWlHr7Q6Bd6vq+m3GlxWwZ2juHjZigGd3yMQM9ME5yKgbwdYSaXeWMl3qbi8RI5pjeP5hROAobPAxkHHXJzmmXPhaSf+xrM39xNpthObqYXMpkmnkU5iVnPVQSSc8/KvvQBzmqav4r03TrS5v5ZNMtGgmvL26ihW7a1kLEpAyKCfLVeDIATkdVFampeOzpNvq3maXPcPpVvbXEjrIiiaKXcPMXnjGxsggHjitLXfBmleINQW+upL2G4+zm1drW6eHzYiclH2nkZJ/OpNU8G+H9Zl8y/05ZWMKwNiV1DxrnarBSAwGTjOcZoAyh45mTWJLWfRZEtItTTS5LlbhWKzOEaM7MD5SHGSDkHseSF0jxzLq2sy2CaNPHHIspsrklzHKUJGJG2YiJ2kjluPQ4BdpXgS0sfFmo61cpDcedMk1pkyboCsax8gsVY/KCGxuGTzWra+E9EstSl1C3sdlzKWYsZXIUtncVUnCE5P3QOpoA5vSPGHi3VtAfWoPC1nJbeQWjhGoYlldWKuF+QjBxxnB496TV/GGoal4O8U3+hx2ywWVmz2uoJcEiQ+XvbC7eGRSPUbjjPBx1Og+GtJ8M20lvpFqbeGRtzIZncZ9txOPwp8vhzRptFm0dtNt106bdvt402IdxyT8uOSTnNAGDf+JbvT/BmjX2mxG8ku7eN/Oug7lU8veZHSMF2J4B2qcFsnArNn8farLbWEenWWnSXr6KNZuTNcMsZj6bI8AkknPJ4HGetdSnhHw8lraWw0i0MVoCLcMm4xZAU4J5GQoB9cVNceG9Eu7S2tLjSLKW3tVCwRPApWIDoFGOB7UAcw/i3Xr7xRZ6Zo9rpZtr3TY9SilvJHR0jJAKlRnLc8Y4HerZtL3/hY6GHULzasX2i4Esh8kwMCiQxxj5dwdS5fG4cDJB437nQNIvNSi1G5021lvYgojuHiBdADkAHqMHmrQsrVb974W8Qu3jETT7BvKAkhc9cZJOPegCeiiigAooooAKKK5u88G295eTXLa14giMrlzHDqkqIueyqDgD2FAHSVDd2lvfWslrdQpNBKu143GQwrmx4FtgQf7e8SnBzzq83+NdVQB5Npl7b2Gl+JNR0O6t9V1nRrX7DZpCM4t1+ZWKqPmbJIJHUpx15taV4w1zUPCeo3Md7BLcJcRJazxxvKCrY3AyLCEzww3bCE43CvT6KAMXwrqUuq6DFczi48ze6l51UFwGOGUqqhlx0baMgZxW1RRQAUUUUAFIzKi7mYKPUnFLVTUdMsdXsms9Ss4Lu2cgtDOgdSQcjg+9AE/2iD/ntH/30KckiSZ2OrY64Oa5z/hXngz/oVtH/APANP8K1NJ0DSNBSVNJ0y0sVlIMgtoVjDEdM469aAOM8V6JqN/4/iubG3mSYaUUtb4Rboo5Q7Fo5D2V0JX/gQPUCspfDfi6HRoLB4L3EOhWtvYfYr4RC0u0UBzJ843fMByAw2gjvz6zRQAgztGeveloooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigCvf/APIOuf8Ark/8jXn3wJ/5JRp//Xaf/wBGNXoN/wD8g65/65P/ACNeffAn/klGn/8AXaf/ANGNQB6TRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUANdFkUq6hlPUEZFOAwMCiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAK9/8A8g65/wCuT/yNeffAn/klGn/9dp//AEY1eg3/APyDrn/rk/8AI1598Cf+SUaf/wBdp/8A0Y1AHpNFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFU7jVtPtL+GxuLyGK6njeSOJ2wWVOWI9h3pdN1Oz1iwjvrCcT2sufLlUEBwCRkZ6jI69DQBbooooAKKMjOM81G08SRPK0qLGmSzlgAuOuT2oAkoqNJ4pXdI5UdkxuVWBK56Z9Kz9a1610SKLzY7i4uJiVhtbWPzJpccnavoByT0H4igDUorI0fxJp2s6PZ6nG7W0V47Rwx3YEUhdWZSu0nr8rce1WJNc0iK4NvJqlkk4cR+U1wgbcSAFxnOckDHvQBforNg8RaJc3gs7fWdPluixUQR3SM5I6jaDnIwfyqU6zpai6J1KzAtOLkmdf3P8Av8/L+NAF2ism68T6JaadfXzanayQ2MZkuPKmVyg56gHqSCB6nipLfxBo9zpi6lHqdp9jO3MzTKqqWxgNk8HkcHnmgDSoqlNrGmwaaNRkvrcWRZVFwJAYyWYKPmHH3iBV2gAoorhrX4jJd6lp+lR6cF1O41GexnhechYPKDNv3bcsGC/LwAeeflNAHc0VjDxVojNdKt+jG1R3k2qxyqHDlcD5wp4O3ODwagtPG3h29ivJIdRUJaQrPKZI3T903R13AblP94ZFAHQUVhN4x0RdFbVmupBbLMIGU28glEpIAQxbd+45GBtzgg9KhXxzoLadFfCe58qUyBENnMJGEYy7CMru2jucYzx1oA6OiuW1Lx7pWm39jafZdSu3v7b7TaPZ2plSdf7qkd8EHnAGRkjNdNDL50Ecux496htkgwy5HQjsaAH0UhOFJwTjsK5XRvHWn+Ip4LO2t9RspbyGZ7Wa5gCq5jba4Xk5ZTzg+lAHV0VwvhvxRPY+Ftdv/EmpfaRpeo3Ft9oeJIWdUICjaMLuJOB65FXoPHllJ4cvNWezuEazmEE1sskUjKx24O9XKbfmHzFgBg56UAdZRXJXPj21t/DljqwsZXa8keJIfPhVVZCwfMxcRADYcHdz2zUGo/EnTdOjsw9rM91NZrfSWwliDxQsQAclsOeThVJJAPtkA7SiiubtvFrXWsLaxaPfNYNcy2o1FdrRB4wdxIBJC7gy7iMZBoA6SiuNb4gRrFDMdIuhDdWk95auZE/exxYLcZypKkMOxHeq9349uW8O6vcw6YbW+t9H/ta2SeQOrRENtLbejZU/L9OeeADuqKwJ9cvbDQkvb62s1uJWiSGJLptrl8dygPGScAMcCs+DxwLxNKtrSyDapqS3DR28sjJGBCxVyXKZ5I4+XPPIFAHX0Vymo67rSeKNC0+ytbRUvLKe5niuJyCGTyxtDKrDgydRkHn2rqUbdGrHbkjPynI/A0AOorhv+Ey1VvG66QbWytrM3DQRm4Mm+cBSdyOoMecgjYTuG1sjinaJ43utTfw8s9rbR/2nZXNxKEkJMbxMo2gHsd3U+lAHb0V5x4e+IGsal4Z1nX76wsorO0skurcxtJhiULlWJHO0YBKjrnFPl8Y+ID4de9SCzD3WpR2VjMsLAeWxwZpEd125wQqkrzjJ5oA9EorznWvG+r2nhrTbqA2ENzNPMs8u6KbEUeQXSMTDcSdmVDkqCc9KffeJLufUfDV1b+JbTT9OvdMlnea4tgIJpP3e3l2VgfmJC8HCmgD0OivOpPHmqyeOjpNtZwrYxTQxh5ZYlNxG4y0qZkDEcjbsVgcHJ54s6XrV/f8AxB1bRx4ntDb2M6SLbCKIyyqyktFkHhUwcnG7JGTxggHeUVV1O7+waVeXmx3+zwPLsRdzNtUnAHc8dK8n0zxt4hvNI1f7Xrlra3VpZW1/5ojhkWJnZg8XykgoMJ33jdycmgD2KmRTRTxiSGRJEPAZGBH5ivNv+Ep1eyvr3R5dZF4lre2vn6qsEatBbSxs5JUApwUUbyMYlGema2/hmqR+FJYolkEaajd+WzRbA6NM7oy8AFSrKQVGOeKAOpvb+z023+0X13Baw5C+ZPIEXJ4AyamjkSaNZInV0YZVlOQR9a4TxtcW0PjHwwLvVbm0gb7QCiRo6bimFOGVvmJJABB74xzkvtZ1q21zU7S2aeP7NPapp1mlniK6jYIXLSbDjkuCQRt2gkeoB3tFcPaC5n8e6pbTa7rSW8M8MtvbmNVhkbYS6htnMY4GMjkHkmsPw3qnii61LT7DU7bV4RpsU8k93khb1oxsZSCpBJcqycj5aAPVKK8i0fxTq13NrMN6dea1/skXKSLbSrJ9oUncqMYowpwVG0KVPr1zq2t5cjwXDqVrc6/dzm4txq0kkUsc4RQDJ5UTKMDkA+WBkZwSRQB31hqVjqkDT6feQXUSuY2eCQOAw6gkdx6Vari/hxDNBYa15ttfxRzarNcQPfRlHljcKVbnn8wD6812lABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFAFe/wD+Qdc/9cn/AJGvPvgT/wAko0//AK7T/wDoxq9Bv/8AkHXP/XJ/5GvPvgT/AMko0/8A67T/APoxqAPSaKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooA8+8Z+F5vEPjbS5Tb3i20FhMgvbcj9zIzpkEbgTujWROOm8fUcje6L4pm8D6RosegarE9npskaGGZRsud2ELATIMAAEN8xG4/LXrmua/pvh2xF3qdwYo2cRoqoXeRj2VVBLHvwOgNZt74+8O2Fhp97LdyvDfxNPb+TbSSMY1GWYqqkqADyTjFAHCy+HNal1zWNTutG1afdaWVzYol5jbcgIJRt8wLu9c/Kdp/Gy2keKLv4m22uDTtQtrZLxfNBuF8s2xj2j/lqecnLKFABBwW79Te/ErwzYai9jPc3XmoyqWSymeP5k8wHeFK42ZbOegJ7U6P4i+HZdYGlJLeG6M5txixm2bw6ofn27cBmUE5wNw9aAPNvCwa68Y3c7TXMV7fzahFpdykibAzGVlkkUylyVUEBTGAB7810OleDNUs9E1mzm0ON0utOEL28l1Ey3FyCcSbQgGTnJdyW4Xjit+z8R+CItdujZW1uupr55aWGwIknMZ/ehGC5kIPUKSTg9cVcs/H2iajZzXFmbt9li9/GklpJEZoV6sm5RuGcDj1HrQA3wFoX9ieH4kuNFg03USiR3TxyLK1yyDHmM45JJLHnJGad4i0W8/4SDTfE2l2yXd7YxS27WjzeUJY5MchiCAVIzyOQT7Ulr44tJPC0eu3en39rE0UDCNocl2lwFVD0bkgZ4HIJwK29J1RNXsBdx29xbgsVMdwgVwR14BI/I0AcVrPgzXtYD3F9/Y+o3U+mtZslzvSO3cys4kTAJOFZV42k7AcjPEHiPwLrOqNfpaWuj7p2JjvJZmWUfuUTccRnDBk3de/rXV6z4jm0nXtI0yPSp7v+0PN/eRSIu0om7ADMMn6kD69KjuvGdhZ31xay215/oiRPezBF8u08zG0O27rggnbuwOelAHMf8IRrkmoWl59j0O3khvFumeCV95/0oylQfLHWNtv146VNp/w/wBRtbW5tp7ixuD9juLSO4mVpGlEvzbnThQd4BOd+ccEZNeiV51e+M9fvdH8VG10eWwXTPtccWpLPC4RoY9y5RskliPQgBvagC/D4NvxZeQktjYebof9mSraRk7XG7aykgAqNzcEfxHpVvVtA1rW9Ijs72608bLiKXECSx5CAnIcNuVt+1gR0245zVW38ffZdCur3W9Ku7E2tnFdL5rxk3CudoI2sQpLYGDjG4Vp+EPF9r4vsLi4t7We3e3l8qVJMMucZG1hwwwfwNAE1lpmq2Ph1LQXdpcX6ymTzZoPkIMm7BCkEsF43dSfmOelblcnrl9qV54utPDlhqR0tXsnvXuo0R5X2uECKrqVxzknBPTp3w9G+JN5cW0ltNpLzXlvpM1/5nnKi3HlTNC3bCk7S3tQB6RXIHwQx1PTdSF7AL2yu5J/NFqcyo3m4jPz/wAPnyYPuOOuWa348XStZsLGKxW4SdrcTyCcZiE0gRcKAe7A/NtBHQk8VZiL23xQmhF1dNHd6T53kNIWjVklClgCflOHHAwOuc8YAMqw+Gz2GsvqSa0zyPZT2j74Cxk8zne2XwGyFJ2hQcdBmrF14EvruZ7h/ELRXL6WummWC1CHCyB933j1xtI9CcEZrS0M6kdb8S/a7gM4njFtD5peOJPKUggEAgkkkiub8P6/451LwYNXVtBurhoTNHCFkV2AZgQQDjOBge/WgCrqXgXWdM0aa3s9QlvTfatBeTPbWkcTWuxR+8RdwzykY4YEDJHNS2ngG48R6TZDX1jgk0yWWGxWWyiffbtt3GSNi67iVypByOCckkHqvDOuX/iC5v71UtToW5Bp08e7zJxtBZmB4ABJXscg56VS8WXDz+JtA0O4u57XSr9bhrhoWaMytGqlIvNXBTOWbggnZjvQBbPg+JLjSJrbU7y3OlW7W9sqJEQFYAHIKeiqOMAY6Vp3VpqMuvafcwXpisIY5RcwcHzmIATtkY+Y5yPTBzxwp8Tz6Ho62ehX1rc2ljpsl8b7WHctcgSMAiHIJxtbLHPVP72akuPiFqkMGsytb6fB9m+wTWa3DFDLFcY3Bvm+8vI4x0zigD0iuB8EeDLrTk+06010Lu0luUsk+0K8UUcrli6BVGCc4+YsRjjAOKmg8VazJqF+WOlrZ2etJprIVcSGNtvz53YzlwMYwcE8dKTw54o1LWdat2bUdGa0uDOj6em4XVs0bEDv82QATlVAyMZyKALNr8PrCCw1Sz1DVNQ1Kz1GQzzxXZiAWXIPmKURSGyo7446VaufCWka7aQvc3t5fqtwl1DM10XUOgIUqv3Mcntz3rI8Fajo91aeJ7K5u9OnWDU7l7lWkVg0fy5kdSxAXIPPC8U/4Y6vpX/CvLVYb+0YWSStOkUqsYV8xyNwH3RgZHtQBrxeDLGCyFpHfaksYkmk/wCPknPm/fBBGCpOTjHBORikj8C6FbSWb2cNxaPawfZVa2uZIy8OSdjEHLDJJ9Qehrcsb621OxgvrOZZradBJFIvRlPQirFADIokhhSKMEIihVBJOAOByax4vCWiwaj9uitpUn+0G6wtzKE809W2btuT9K26KAMBPBXh6N3ddOALwyW4HnSYSOQ5dUG7CAn+7ipV8J6IoA+xllFmbEq80jBoOf3bAt8w+Y4znHatqigDml8AeGUsWsxp8nkmRZebqYsGUEAht+4cEjAOOaWPwF4Zi0kaWmmlbRZjOqi4l3I5GCVfduXI6gHBrpKKAMa78JaDfWdjaT6XAbexObVEBQRcYwNuOCOCOh7g1rQwx28KQwxrHFGoVEQYCgcAAdhT6KAMqLw1ocGqtqkWkWSX7OZDcrAokLEEFt2M5IJ596hufCWiTm5mj061tr2cu32yGFVmSRlKmRWxkNgnmtuigDz2z+Flta6ffWq3dtF9psBZbrPT0gzyCXkwf3hJUZB4wWH8RrZ8LeCLLw5BfK4tLh73YJlhsY7eIqudo8teCfmOSc9vSupooApyaTps0EUEmn2jwxZ8uNoVKpnrgY4qWaytbiFIZraGWKMgojxhlUjoQD0xU9FAEZt4WuFuDDGZ1UqshUbgD1APXFQx6bYxXTXUdlbJcsSTMsShznrzjPNWqKACjFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAV7//AJB1z/1yf+Rrz74E/wDJKNP/AOu0/wD6MavQb/8A5B1z/wBcn/ka8++BP/JKNP8A+u0//oxqAPSaKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAwPEfh2TWbnTL+zvPsepaZMZbeVk3oQw2urrkZBX3BBxVC88G3txNbXkPiGe31JLZrS4uVtYiJ4i27GwjCkEnBH45rrqKAPO7r4VJJIy2msvb2ojjjiha2WTYEtmthyTydjnr3xT7X4ZTWlzFcReIZY3jlkkAjs41X53ikKgc4AaFTx646V6DRQBxWmfDXTNJ1qXULSZYvnleBY7K3V4zIGDAyBNzAb/lGeMAHIqXSPAUemrpyT6rcXcdnpcml7GjRA8Tsp7DIICqOvb657CigDmk8HKmmJp41zVTbRpDFEhaLaiR9Fx5eGBGA24HIFaPh/QLLw3pn2CwUrCZHlIwqjcxycKoCqPZQB+Oa1KKAMnWtAg1prSVrm5tLq0cvBc2rhZEyMMPmBGCODx9MVRm8DaPcSSvMbt/tCRR3INwxFyIjlPN/v+hz1HByK6SigArnZfBWky3N/KWvVjv/ADftNul3IsMhkTY5KA4yR+R5HNdFRQBzreCdGkXbOlzOP7P/ALN/fXDsfJ3bu5+9kD5uvA54rQ0jQrPRVk+zPdSyShRJNdXMk8j4zjLOSeMmtKigDL1rw/Ya9FGt2sqTQ58m5t5Wimiz97bIpDAEDBGcHvWTa+BtOn0eysdctrS+ayRoIZI4jCDESPlYBsNnaNw6EjOBXVUUActN8OPCNwUMmixHYqKAJHUYThcgNyQAACeeB6Vcl8HaDNrqa3JYBtRjKlJ/NfK7cYAG7GOBxjFbtFAGDYeDPD+may+r2eniK/csWm81yTuznILY7ntxSS+GoLFbq58N2umaZqlwfnums9+4E5YEKynk89cZ5wcmt+igDP0PSINB0W10y3Z3jgXG9/vOxJLMfcsSfxqbUNMsNWtGtNSsre8tmIJiuIhIhI6HB4q1RQBTn0nTrqG3huLC1mityGhSSFWERHQqCOMe1SzWVrcSCSa2hkcDaGeMEgemT25qeigCs2n2T799pbtvIL5jB3EdCeOcVKlvDHM8yQxrLJje4UBmx0ye9SUUAV49PsoQ4itIE3rtfbGBuHoeORSw2drbo6Q20MaP95UQAN9cdanooAbHGkUaxxoqIowqqMAD2FOoooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigCvf/wDIOuf+uT/yNeffAn/klGn/APXaf/0Y1eg3/wDyDrn/AK5P/I1598Cf+SUaf/12n/8ARjUAek0UUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFNeRI0Lu6qqjJJOABQA6iqD65pEUjRyarYo6kqytcICCOoIzTf+Eg0X/oL2H/gSn+NAGjRWd/wkGi/9Bew/8CU/xo/t/Rv+gvYf+BKf40AaNFZ39v6N/wBBaw/8CU/xo/t/Rv8AoLWH/gSn+NAGjRWPd+LPDljGJLrXdNhQ93ukHp7+4oXxXoLorpq1qysMhlfII9QaANiisj/hKND/AOgpbf8AfdH/AAlGh/8AQUtv++6ANeisC68a+HbMAy6irZBP7qJ5ehA/hU+o/X0NU/8AhZHhb/n+uf8AwX3H/wAboA6uiuU/4WR4W/5/rn/wX3H/AMbrUi8S6fNGJI01BkPQjTbj6f3KANeiufvfF1pZlAuma5c7s8waVO2365UVV/4Tu2/6AHib/wAE83+FAHVUVyv/AAndt/0APE3/AIJ5v8K0IfERnhSVNF1cK4yA9sEb8VZgR+IoA2qK5+78S3duEMHhjWrrOciNYV2/XfIP0qr/AMJdqf8A0JHiD87X/wCPUAdVRXK/8Jdqf/QkeIfztf8A49WmuraiyBv+EdvhkZwZoMj/AMiUAa9FZP8Aauo/9C/ef9/4P/i6P7V1H/oX7z/v/B/8XQBrUVk/2pqP/Qv3v/f6D/4uqFtrHiqa6WOXwnDbxEn97JqiED6hUJoA6WisaG98QyJufRbKI5xtbUST9eIjUn2nXv8AoFWH/gwf/wCNUAatFZX2nXv+gVYf+DB//jVRXFz4l8h/s2l6X52Pl83UH2598Q5oA2qK5X7R4+/6Bnhv/wAGE/8A8Zo+0ePv+gZ4b/8ABhP/APGaAOqorn7STxhJv+22uhwYxt8m4llz65yi4/WrP/FRf9Qv/wAiUAa9Fc1cQ+N3nZra/wDD8UR+6klnM7D6sJRn8hUX2fx9/wBBPw3/AOC+f/49QB1VFc1b2/jfz0+06poHk/xeVp8278MzYrQ+za9/0FbD/wAF7/8Ax2gDVorBvdO8S3MSrB4htbRg2S8em7iR6fNIRVL+wfF//Q6p/wCCmP8A+KoA6uiuWj0LxYHBk8Zhk7hdKiBP45Naf9laj/0MF5/34g/+IoA1qKyf7K1H/oYLz/vxB/8AEUf2VqP/AEMF5/34g/8AiKANaishtJ1FlI/4SG9GRjIhgyP/ACHVS08MXtu7NP4r1u6UjAWRoFAPr8kQNAHRUVjroMqjB1vVWOScmVPXpwnbpS/2G/8A0GdU/wC/q/8AxNAGvRWR/Yb/APQZ1T/v6v8A8TR/Yb/9BnVP+/q//E0Aa9Fc7d+EY751ebXNeUqMDydQeIfiEwD+NV/+EEtv+g/4m/8ABxN/jQB1VFc5beDbW28zOra/NvXb+91ac7fcYYc1f/4R+y/57aj/AODK4/8Ai6ANSiuZufAPh28uHuLm2u5Zn+87ahcEnjH/AD0qL/hW/hb/AJ8bn/wYXH/xygDq6K5T/hW/hb/nxuf/AAYXH/xyprbwB4ZtJ1mj0+RnXOBLdzSLz/ss5B/KgDpaKzrbQNJs7hLi2sIIpkztdVwRxitGgAooooAKKKKACiiigAooooAKKKKACiiigCvf/wDIOuf+uT/yNeffAn/klGn/APXaf/0Y1eg3/wDyDrn/AK5P/I1598Cf+SUaf/12n/8ARjUAek0UUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQBl6z4d0fxCkKavp8F4sJLRiUZ2k9cVk/wDCtfBn/QuWP/fH/wBeuqooA5dPhx4NjkV18O2IZSGB8vPIrSXwt4fSMRjQ9N2+htUP9K1qKAMY+EPDLEk+HdJJPJJso+f/AB2k/wCEP8Mf9C5pH/gDH/8AE1tUUAYv/CH+GP8AoXNI/wDAGP8A+JrQg0ywtYEgt7G2hhQYWOOJVVR7ADirVFAEP2S2/wCfeL/vgUfZLb/n3i/74FTUUARC1tx0giH/AAAVKAAAAMAUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQBXv/wDkHXP/AFyf+Rrz74E/8ko0/wD67T/+jGr0G/8A+Qdc/wDXJ/5GvPvgT/ySjT/+u0//AKMagD0miiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACisvWdP1K/SEadrc2lshJdo7eOXzB2B3g4x7Vk/8ACOeJ/wDoebz/AMF9t/8AEUAdVRXMQ+H/ABGk6NN41vZIwcsgsbZdw9M7OK0/7KvP+hg1L/vi3/8AjVAGpRWX/ZV5/wBDBqX/AHxb/wDxqo5tEu54jGfEWqoCQcoLdTwc9RFQBsUVzEXg6SOTe/inxFKMg7XukA6g9kHpj6H1wa0P+Efh/wCghqn/AIGyf40Aa9FZH/CPxf8AQQ1T/wADZP8AGg+HoSCDqGqc/wDT9J/jQBr0VzMvgXS55DJJe65uOB8usXKjgY6B8Uz/AIQDSP8An913/wAHV1/8coA6miuat/A2k286yi51mQr/AAy6vcup+oMmDV1PDGmIgXF4cd2vpifz30AbFFczc/D7wteztPdaUs8zYzJLNIzHHA5LVF/wrTwd/wBAOD/vt/8A4qgDq6bJIkSb5HVFGBuY4HPArmIvhx4QhlSVNDt9yMGGWYjI9icGtN/C3h+Rdr6FprL6NaIR/KgC5JqenxPskvrZGGDtaVQeeR3pn9r6Z/0EbT/v+v8AjVB/BnhaRtz+GtHZvVrGIn/0Gk/4Qnwn/wBCxov/AIARf/E0AaH9saZ/0EbT/v8Ar/jR/bOl/wDQSs/+/wCv+NVrTwv4fsJTLZ6FpltIV2l4bSNCR6ZA6Vd/s2x/58rf/v0v+FAEf9s6X/0ErP8A7/r/AI0f2xpf/QSs/wDv+v8AjUn9m2P/AD5W/wD36X/Cj+zbH/nyt/8Av0v+FAGa3jHwyswhPiHS/NIUhPtabjkZHGe/apf+Eo0H/oMWP/f9f8a0Es7WI5jtoUOc5VAKmoAyf+Eo0H/oMWP/AH/X/Gj/AISjQf8AoMWP/f8AX/GtaigDn7nxv4atbZbiXV4DGx2jywztn/dUEjp6VT/4WV4R/wCgsf8AwFm/+IrrKKAOT/4WV4R/6Cx/8BZv/iKP+Fl+Ef8AoLH/AMBZv/iK6yigDFh8V6Tcb/Ja8k2NtbbYTnBwDg/J6EH8ar3njPT7SRU+wa3PkZ3QaTcOB7EhOtdFRQByv/Ce6f8A9AjxH/4Jbn/4ij/hPdP/AOgR4j/8Etz/APEV1VFAHO2njC2vWKw6TrgI/wCeumSxD83Aq3/bw/6BWqf+Ax/xrXooA52fxVPFDG6eGNemZiQY0gjDJ7ndIB+RNV/+ExvP+hM8S/8Afq3/APj1dVRQBz9n4kvb1nA8Ka3BtAOZ/s6A/T97Vv8AtW+/6F/UP+/tv/8AHa1aKAMr+1b7/oX9Q/7+2/8A8do/tW+/6F/UP+/tv/8AHa1aKAOfuda15Z40tPClxLGwO6Sa9gj2n6BmzVr7Zrv/AEB7T/wPP/xutaigDJ+2a7/0CLT/AMDz/wDG6Ptmu/8AQItP/A8//G61qKAMaS88Q+U/laPYmTB2h79gM9s4j6Vn/bfHf/QD0D/way//ABiupooA5b7b47/6Aegf+DWX/wCMUfbfHf8A0A9A/wDBrL/8YrqaKAOdiufGLeV5umaKmc+Ztv5W289v3Qzxz29PerMreJjE4ij0lZCp2s8kjAHsSMDI9sitmigDlnj8el2KXXhtUz8oa2nJA9zvGaTyvH//AD9+Gf8AwFn/APjldVRQBz1lD4xMjfb77QlTHy+RZzMc++ZRV3yNe/6CWm/+C9//AI9WpRQBl+Rr3/QS03/wXv8A/HqPI17/AKCWm/8Agvf/AOPVqUUAZT22vsjBdU05SRgMNPfj3/11U7bSPEabPtXigS43bvK0+OPPTbjJbGOc9c5HTHPQ0UAZ1tY6hDcJJNrE08YzmNoI1DceoGa0aKKACiiigAooooAKKKKACiiigAooooAKKKKAK9//AMg65/65P/I1598Cf+SUaf8A9dp//RjV6Df/APIOuf8Ark/8jXn3wJ/5JRp//Xaf/wBGNQB6TRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRUcs8UABllSMHgF2AzQBJRVf7fZ/8AP3B/38H+NJ/aVj/z+2//AH9X/GgCzRVb+0rH/n9t/wDv6v8AjTW1TT0Rna+tlVRkkzKAB69aALdFZF14r8O2Uoiu9f0qCQqGCS3kanB6HBPSof8AhNvCf/Qz6L/4Hxf/ABVAG7RWF/wm3hP/AKGfRf8AwPi/+KqWLxZ4cmTfFr+lyLnG5LyNhn8DQBsUVi3Pi7w7aW7zy63YeWgyds6sfyGSazv+Fl+Dv+g5B/3w/wD8TQB1dFcp/wALL8Hf9ByD/vh//iat2fjfw9qAJsr9rkL18m3lfHT0X3H50AdBRWIfFmkh5EDXjNGgdgtjOTg5wPudeOlU5fHekxSvGbTW2Kkjcmj3TKfoRHyKAOnorlv+E/0j/ny13/wS3X/xupofGunXCO8djrRCFQ27SbhepwMAoM/h070AdHRWOviKBwSNP1Xgkc2Mg5Bx6Uv/AAkEX/QP1T/wCk/woA16KyP+Egi/6B+qf+AUn+FQXficW0PmRaJrV02ceXDZkN9fnKj9aAN6iuY/4TGYzGNfCfiNhkgP9mjCn35kFaKaxeSRq48PaoAwBwzW4I+o83igDWorL/tW8/6F/Uv++7f/AOO0f2ref9C/qX/fdv8A/HaANSiuVPiLxNnjwNeY/wCwhbf/ABdH/CR+J/8AoRrz/wAGFt/8XQB1VFcr/wAJH4n/AOhGvP8AwYW3/wAXWmL7WyAf7EiHsb0cf+O0Aa9FYNzf+Jgh+yaDZO+BgTaiUHX2jPaqf9peOP8AoWtG/wDBw/8A8YoA6qiucs7/AMXyXkKXmgaVDbFwJZI9Ud2Ve5CmEZPtkV0dABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFAFe//wCQdc/9cn/ka8++BP8AySjT/wDrtP8A+jGr0G//AOQdc/8AXJ/5GvPvgT/ySjT/APrtP/6MagD0miiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAK9292kQNnBBNJu5WaYxgD1yFbn2xVPz9e/6Bum/+DB//AIzWpRQBy8svjvzn8mz8OCLcdge7nLY7ZxH1pvm+P/8An08M/wDgVP8A/G66qigDlfN8f/8APp4Z/wDAqf8A+N1JA/jhnIuIPDsa44Mc07nP0KiumooAxJI/E7J+7utIjbaRzbyMAccH744H6+1UPsXjv/oOaB/4Kpf/AI/XVUUAct9i8d/9BzQP/BVL/wDH6BZeOsjOuaDj20qX/wCP11NFAGOln4g2DfrFlvxztsDj/wBGVnz6F4plneRPGTQoxyI00yEqvsM5P5k11FFAHKf8I94r/wCh4l/8FkH+FH/CPeLP+h4l/wDBZBXV0UAZI0q/wM+IdQJxyfKt/wD41S/2Vff9DBqH/fq3/wDjVatFAGV/ZV9/0MGof9+rf/41VOTwzdzXouJPFOubQRmFHhSNsdsCIHn2IroaKAMj+wR/0FNU/wDAk/4Uf2CP+gpqn/gSf8K16KAMj+wR/wBBTVP/AAJP+FZ83geynmeV9W8Qb3OTs1e4QfgFYAfgK6eigDlf+EC0/wD6C/iP/wAHVz/8XT4vAunxSpJ/aniB9rA7X1m5Kn2I38iunooAyT4c08ggtfYP/UQn/wDi6yf+Fa+Ef+gSf/Aqb/4uusooA5P/AIVr4R/6BJ/8Cpv/AIuj/hWvhH/oEn/wKm/+LrrKKAMCz8FeG7GMpDpFuQf+euZD+bE+tWf+EX0H/oD2P/fhf8K1qKAMn/hF9B/6A9j/AN+F/wAKin8HeGbpQtx4f0yZQcgS2qMAfxFbdFAHO/8ACA+D/wDoVdF/8AIv/ia1f7G0v/oG2f8A34X/AAq7RQBS/sbS/wDoG2f/AH4X/Cj+x9L/AOgbZ/8Afhf8Ku0UAUv7H0z/AKB1p/34X/Cj+yNM/wCgdaf9+F/wq7RQBS/sjTP+gdaf9+F/wqzBbwW0fl28McSZztjUKM/QVJRQAUUUUAFFFFAEUFutv5u1pG8yQyHfIWwT2GTwPYcVLRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQBXv/APkHXP8A1yf+Rrz74E/8ko0//rtP/wCjGr0G/wD+Qdc/9cn/AJGvPvgT/wAko0//AK7T/wDoxqAPSaKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKoatrFjodn9r1CSSODcE3JC8mCenCAn8aw/wDhZHhb/n+uf/Bfcf8AxugDq6K5+x8a6HqRcWUt7OY8FtmnXBxnp/yzovfF1pZlAuma5c7s8waVO2365UUAdBRXK/8ACd23/QA8Tf8Agnm/wo/4Tu2/6AHib/wTzf4UAdVRXNW/jOG6lEceheIQx7yaZJGPzbAq9/bj/wDQG1T/AL9L/wDFUAa9FcxN4r1GOZ0Twbr0qKcCRfswDD1AMwP5imf8Jdqf/QkeIPztf/j1AHVUVyv/AAl2p/8AQkeIPztf/j1X7fW9SuIFlPhnUod2fklltww+oEhoA26Kyf7V1H/oX7z/AL/wf/F0f2rqP/Qv3n/f+D/4ugDWorJ/tTUf+hfvf+/0H/xdU7XVfE9xcOkvhiC2jAJWSXU1O7ngYVCQf85oA6Kisr7Tr3/QKsP/AAYP/wDGqPtOvf8AQKsP/Bg//wAaoA1aKxLq58T+Qfsml6V52RjztQk2+/SHNUPtHj7/AKBnhv8A8GE//wAZoA6qiuV+0ePv+gZ4b/8ABhP/APGau2r+K3hzdw6NDLk/LFLLIMfUqv8AKgDdorBu08WyRqLO40WF88tLDLKCPTAZcfXNU/s/j7/oJ+G//BfP/wDHqAOqorlfs/j7/oJ+G/8AwXz/APx6pYLfxt5h+06poHl7TjytPmznt1m6UAdLRWSLbX8DOq6fnvjT3/8AjtL9m17/AKCth/4L3/8AjtAGrRWS1rr5UgatYAkcEae3H/kWssaF4tCYPjMFsjn+yosY5yMZ+lAHVUVk/wBlaj/0MF5/34g/+Io/srUf+hgvP+/EH/xFAGtRWT/ZWo/9DBef9+IP/iKo3HhnU7iQuPGGtQ5OdsSWwA4AxzEfT9TQB0lFcr/wiOp/9Dv4g/K1/wDjNH/CI6n/ANDv4g/K1/8AjNAHVUVyv/CI6n/0O/iD8rX/AOM1ctfDlzBEUm8SazdNnO+R4lIHp8sYH6UAb1FYdz4a+1wGGTW9ZVSQcxXfltx/tKAf1qj/AMIJbf8AQf8AE3/g4m/xoA6qiuV/4QS2/wCg/wCJv/BxN/jWlD4as4Y9hutVk5J3SancE8nOPv8AbpQBsUVz174J0LUnR7yK8nZBhS+o3BwP+/lVf+Fb+Fv+fG5/8GFx/wDHKAOrorlP+Fb+Fv8Anxuf/Bhcf/HKvW3g3w/axlI9NQgkH967SHgAdWJPb+vUmgDdorI/4RfQ/wDoF23/AHxR/wAIvof/AEC7b/vigDWJCjJIA9TTDcQDrNH/AN9CsqTwl4fmQxy6RaOh6q8YIP4GqyeAfCEcqyr4Y0kSK24N9kTIPXPSgDcN1bjrcRf99ij7Xbf8/EX/AH2KoQeGNAtYzHBomnRoWLELbIBk9T0qT+wNG/6BNh/4DJ/hQBb+123/AD8Rf99ij7Xbf8/EX/fYqp/YGjf9Amw/8Bk/wo/sDRv+gTYf+Ayf4UAMufE2gWc7QXWuabBMuMxy3casM8jgmof+Ew8Mf9DHpH/gdH/8VVn/AIR/Rf8AoEWH/gMn+FH/AAj+i/8AQIsP/AZP8KAIF8W+G3OE8Q6Sx9Bexn+tOfxRoEcbO2t6cFUEn/SkPA/GrMGj6ZbOXg060icjBaOBVOM57D1A/KrmB6CgDlv+FleDP+hjsf8Avs/4Uf8ACyvBn/Qx2P8A33/9auqooA5ZfiP4Oc4TxDZMcE4DE8AZJ6elaKeKdGljWSO6Z0YBlZYJCCD0IO2tiigDJHiXSi6Ks0pZ2CAC2k6k4H8PTnr2rWoooAKKKKACiiigAooooAKKKKACiiigAooooAr3/wDyDrn/AK5P/I1598Cf+SUaf/12n/8ARjV6Df8A/IOuf+uT/wAjXn3wJ/5JRp//AF2n/wDRjUAek0UUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFAFe/8A+Qdc/wDXJ/5GvPvgT/ySjT/+u0//AKMavQb/AP5B1z/1yf8Aka8++BP/ACSjT/8ArtP/AOjGoA9JooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAK9/wD8g65/65P/ACNeffAn/klGn/8AXaf/ANGNXoN//wAg65/65P8AyNeffAn/AJJRp/8A12n/APRjUAek0UUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUVT1bUodH0e91O4DGG0gedwoySFBJx+Vc1oev+I9cgnEmnadaGbTory0Zbp3wZd20P8AIOgXnHce/AB2NFeYaRr2uaV8L/Dc1gsN5f3l4tnLLqE8jhS8jrvJ6kZA4yMA12HhjXp9X0+7/tCKGC8sLp7O5MLEws64+ZGPYgjjqDkHpQBv0VwHi/4gN4P16W11C4s4LSazElm7QSOxlyQd+CBsBAzjn5xgcVUufGXi3TYvtd7DoTWyRWczxJ5qyus7bCFySAVOeue30oA9KooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAK9/8A8g65/wCuT/yNeffAn/klGn/9dp//AEY1eg3/APyDrn/rk/8AI1598Cf+SUaf/wBdp/8A0Y1AHpNFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAIQGUqwBBGCD3rjLDwHDp/ifU5oY7WPQL+xFvJZI0gJcMTuOTgDBYDbjHYd67SigDh9X+G+nvoKaXoMdtYRfbYruVJ1kmjl8s5Cld4OCcZ5FdPNoOlT6PJpMlhb/YJeXt0TajHO48D35rRooAp3mk6dqIUXthbXIVGjUTRK+FbGQMjodq8ew9KyT4Ut5/GU+v3v2a7zBHFbRTWqM9sylslJDyAdxyK6KigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiimsxBUBCwJwSMfLx1P8AL8aAHUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFAFe/8A+Qdc/wDXJ/5GvPvgT/ySjT/+u0//AKMavQb/AP5B1z/1yf8Aka8++BP/ACSjT/8ArtP/AOjGoA9JooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAK9/wD8g65/65P/ACNeffAn/klGn/8AXaf/ANGNXoN//wAg65/65P8AyNeffAn/AJJRp/8A12n/APRjUAek0UUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFAFe/wD+Qdc/9cn/AJGvPvgT/wAko0//AK7T/wDoxq9Bv/8AkHXP/XJ/5GvPvgT/AMko0/8A67T/APoxqAPSaKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigCvf/8AIOuf+uT/AMjXn3wJ/wCSUaf/ANdp/wD0Y1eg3/8AyDrn/rk/8jXn3wJ/5JRp/wD12n/9GNQB6TRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRXIn4n+C0uJ7eXxBaQzQSSRyJKSpDISG6jnkHHr2pZPiV4XTQbfWUvzLbXNwba2VIyHnkBxtVTjv3OByOaAOtorDg8U2T+II9Cuobmx1KWEzww3Cr+9QdSrIzKcemc8Zxism6+Knguzs7a6n1uJY7iZ4VARi6spw25QMqB6kAcigDsqKxv+Es0A2l9dpq9nJb2Eay3MscoZY1YEqSRxyBxjrWfa/ELw7dTaTGtxPH/AGuSLB5raRFnx6EjHcdfUUAdTRWPrHijSdCvLKyvZ2+2XzlLa2hjaSSQjqQqgnA9TxTNH8XaJrmm3d/Y3oaCyZ1uvNRo2hK53B1YAjGD1oA26K4yD4s+Bp7IXS+IrVU2s2x9yvwMn5SM59PXtV2H4g+F5tMk1AarFHClp9tKygpJ5JLAMEOGOSvHHOV/vDIB01Fc3pXj7wzrVlZ3djqkbx3lz9khDKys0uCdu0jI4HXp0rI1H4u+FNNvbiBpb2eG1k8q6vLa0eSC3fsHcdycgYzQB3dFY2q+KtE0Xw8uvX9/HFprqjJNgneG5XaBySRzgVjaN8U/B+vapDptjqv+lzjMSTQSReZ6BSwAJP60AdlRRRQAUUUUAFFFFABRRRQBXv8A/kHXP/XJ/wCRrz74E/8AJKNP/wCu0/8A6MavQb//AJB1z/1yf+Rrz74E/wDJKNP/AOu0/wD6MagD0miiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKRmCqWYgKBkkngClqOeFLi3kgkzskUo2PQjBoA8sstGu/BHw/vLzTB4f16C2aa7MjQlWkXJZhvBYMw6duBjtVK507S/i74L0fWbNotD1mGZ/sEUkg8syKwLDaPvA4ByBke/e1/wrHxfpvhy48MaJ4ut4NDkLhFltP3wR8lkLDtyeRz9OlX7P4M6KfBmlaLqM873mns8sd9bN5bpI5yduc8ZxgH0oA4j4l3Pja18beCHv59MW4+0gWkdi8mwyb4wxcsAcNuAwO2R3ruda0P4f+AtDiN/omn3tzcTMtuLuGJprmViWwZGACjnqcADH46emfDtIvE8PiLXdau9c1K1Ux2jXEaRpAueMKgALDJ575zgcUfEP4eQ+PV0kyXfkHT7jzCjLlZUYrvU4IIOF4IoA898Y6Lqvhj4b6/qv9i6dZnVrm2WbTbRR5VnAmcElcB2LY3cY+bvirfxItpZvgT4ZvIbTzXtIrKZpEX5oV8oAkccDOB1HavX9X0ix13SLjStRh86zuE2SR7iuR16jkcgVwUnws1K8tdP0fUvFtzd+HbGRGSxNsEaRFPyxvIrAkAYGfbp0oA5TSryfUP2oJZbhHVRZ/uElTBRDArAfXLH9aVkH/C6fiBo0L2tnb6horB5JDsjR2ijG9j0HMhJPvXoHib4fRav4msPFGl3i6drtnkCdofNSVdpUBlyOQCcH+fGKNj8MpJ9P8RnxDq323VdeVYri7ghEflxrwqoOR2GfoPTNAGPEt98O/h9HqGp6F4d1Sy022jSOWylbzJQ7qN5LoRg5BODyfatS30XwV4qsIPiBq1tC1o9ggEV0wMNqi53DHTIJYfh0zWRcfDTxtP4K/wCERfxPpjaUI1iXdZt5m1WDL8271A/Cuvk8B2zfC/8A4QtLgxR/ZBB56qPv53Fse7cn60AeYaXpOjeOLmfVfBfhwaRZ6MbiSO+RxHLdztEdiKP4QG2tkngdMEnFj4LQQ3Xwd8TrcRJKslxcBxIobd+4Q85616d8PvCb+C/B1tok08VxLE8jvLGm0OWYnofYgfhXNar8MdVt2u7fwd4iOiabqLO99aGJZFLNwTHxlPl4wCOgoA8ps9Ov/E3wS0LTbN5rjVU1qVLC2BGHUIWYZPAC5JySB1p8nj3WL/VdI8M+NNMtrO8ttTt3bUHg8qW3RXBAAAxjBIyOMH8a9nv/AIfNaeGdH0/wrf8A9l3ukOWtbmVTKPnBEu5ScEtuJzjjtisXxD8OfE/jS70tPEutaXJp1nOsskNpaNG8mAA3zEkjIz7c+wwAep0UAYGBRQAUUUUAFFFFABRRRQBXv/8AkHXP/XJ/5GvPvgT/AMko0/8A67T/APoxq9DvEaSynRBlmjYAepxXF/CHRdR8P/Dqy07VbV7W7jllLROQSAXJHT2oA7qiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAP/2Q==",
+ "image/png": "iVBORw0KGgoAAAANSUhEUgAAAvoAAAPoCAIAAAAgFM2mAAEAAElEQVR4AezdeaB91fw+cA2SIWODsRBCipSkJJmJQgNFmTIlVMgQZShziQyJZMxchkSGMoRKRBoQSUSSKaGMvxfvb8v+nXPv+dx7P+feu++9z/nj3nXWXnvttZ61z34/63m/19pXu1o+QSAIBIEgEASCQBAYKwKf+9zn/t2nz4pj7V0qCwJBIAgEgSAQBIJA7xAI3endkKRBQSAIBIEgEASCwHgRWPl73/veeGtMbdNFYKWVVtp7773vf//777DDDu94xztWXXXV9ddf/8c//vE73/nOpz3taZ///OcvueSSFVf8HzG98sort9hiixe96EUf+9jH/va3v62yyiprr732+eeff9xxxz31qU/dZJNNZLY2qNzpe+2117rrrnvQQQf9/e9/r0PXuMY1jj32WH+PPPLILbfc8upXv/qJJ57oax1Vw1ZbbSX9la98hRi5yy67fOtb3/rpT3+qtlZzEkEgCASBILAIEPj+97/fTMMi6M5kXViBMZvsWPKDQBAIAkEgCASBRYwADmDSe9lll3Un1TPur5nzueee+5a3vEUNYnce+MAHzriqsZ+48thrTIVBIAgEgSAQBILAgkBghRVW2H333cfY1C9/+ctFd8ZY51iq+p+LZCzVpZIgEASCQBAIAkEgCPQNgdCdvo1I2hMEgkAQCAJBIAiMGYHQnTEDmuqCQBAIAkEgCASBviEQutO3EUl7gkAQCAJBIAgEgTEjELozZkBTXRAIAkEgCASBINA3BEJ3+jYiaU8QCAJBIAgEgSAwZgRCd8YMaKoLAkEgCASBIBAE+oZA6E7fRiTtCQJBIAgEgSAQBMaMQOjOmAFNdUEgCASBIBAEgkDfEAjd6duIpD1BIAgEgSAQBILAmBEI3RkzoKkuCASBIBAEgkAQ6BsCoTt9G5G0JwgEgSAQBIJAEBgzAqE7YwY01QWBIBAEgkAQCAJ9QyB0p28jkvYEgSAQBIJAEAgCY0YgdGfMgKa6IBAEgkAQCAJBoG8IhO70bUTSniAQBIJAEAgCQWDMCITujBnQVBcEgkAQCAJBIAj0DYHQnb6NSNoTBIJAEAgCQSAIjBmB0J0xA5rqgkAQCAJBIAgEgb4hELrTtxFJe4JAEAgCQSAIBIExIxC6M2ZAU10QCAJBIAgEgSDQNwRCd/o2ImlPEAgCQSAIBIEgMGYEQnfGDGiqCwJBIAgEgSAQBPqGQOhO30Yk7QkCQSAIBIEgEATGjEDozpgBTXVBIAgEgSAQBIJA3xAI3enbiKQ9QSAIBIEgEASCwJgRCN0ZM6CpLggEgSAQBIJAEOgbAqE7fRuRtCcIBIEgEASCQBAYMwKhO2MGNNUFgSAQBIJAEAgCfUMgdKdvI5L2BIEgEASCQBAIAmNGIHRnzICmuiAQBIJAEAgCQaBvCITu9G1E0p4gEASCQBAIAkFgzAiE7owZ0FQXBIJAEAgCQSAI9A2B0J2+jUjaEwSCQBAIAkEgCIwZgdCdMQOa6oJAEAgCQSAIBIG+IRC607cRSXuCQBAIAkEgCASBMSMQujNmQFNdEAgCQSAIBIEg0DcEQnf6NiJpTxAIAkEgCASBIDBmBEJ3xgxoqgsCQSAIBIEgEAT6hkDoTt9GJO0JAkEgCASBIBAExoxA6M6YAU11QSAIBIEgEASCQN8QCN3p24ikPUEgCASBIBAEgsCYEQjdGTOgqS4IBIEgEASCQBDoGwKhO30bkbQnCASBIBAEgkAQGDMCoTtjBjTVBYEgEASCQBAIAn1DIHSnbyOS9gSBIBAEgkAQCAJjRiB0Z8yAprogEASCQBAIAksWgTPPPLOffQ/d6ee4pFVBIAgEgSAQBBYeAoceemg/Gx26089xSauCQBAIAkEgCASBsSEQujM2KFNREAgCQSAIBIEg0E8EQnf6OS5pVRAIAkEgCASBIDA2BEJ3xgZlKgoCQSAIBIEgEAT6iUDoTj/HJa0KAkEgCASBILDwENhtt9362ejQnX6OS1oVBIJAEAgCQWDhIXDve9+7n40O3ennuKRVQSAIBIEgEAQWHgKHHXZYPxsdutPPcUmrgkAQCAJBIAgsPATOOOOMfjY6dKef45JWBYEgEASCQBBYeAjst99+/Wx06E4/xyWtCgJBIAgEgSCw8BBYd911+9no0J1+jktaFQSCQBAIAkFg4SGw995797PRoTv9HJe0KggEgSAQBILAwkNg22237WejQ3f6OS5pVRAIAkEgCASBhYfA1ltv3c9Gh+70c1zSqiAQBIJAEAgCQWBsCITujA3KVBQEgkAQCAJBIAj0E4HQnX6OS1oVBIJAEAgCQSAIjA2B0J2xQZmKgkAQCAJBIAgEgX4iELrTz3FJq4JAEAgCQSAIBIGxIRC6MzYoU1EQCAJBIAgEgSDQTwRCd/o5LmlVEAgCQSAIBIEgMDYEQnfGBmUqCgJBIAgEgSAQBPqJQOhOP8clrQoCQSAIBIEgEATGhkDoztigTEVBIAgEgSAQBIJAPxEI3ennuKRVQSAIBIEgEASCwNgQCN0ZG5SpKAgEgSAQBIJAEOgnAqE7/RyXtCoIBIEgEASCQBAYGwKhO2ODMhUFgSAQBIJAEAgC/UQgdKef45JWBYEgEASCQBAIAmNDIHRnbFCmoiAQBIJAEAgCQaCfCITu9HNc0qogEASCQBAIAkFgbAiE7owNylQUBIJAEAgCQSAI9BOB0J1+jktaFQSCQBAIAkEgCIwNgdCdsUGZioJAEAgCQSAILHEE3vjGN/YTgdCdfo5LWhUEgkAQCAJBYOEhcJ3rXKefjQ7d6ee4pFVBIAgEgSAQBBYeApdffnk/Gx26089xSauCQBAIAkEgCCw8BL73ve/1s9Er97NZaVUQCALLj8BZZ531l7/8ZYUVVhiu6t///vfVr371u9zlLhMeHS6fnCAQBILAVBB4zGMec+CBB06l5ByXCd2ZY8BzuSAwKwj885//XGmllfCbN73pTdKuseKKK37sYx/7wx/+MNn1Vl111Uc96lHXvva1MZ4Xv/jFa621VqjPZFglPwgEgSkiYCo1xZJzXGyF3rZsjoHI5YLAgkPgH//4x5e+9CV/EZ399tvvRz/6kfTf//73zTffXI7uXPOa10R6JuuX3/4VV1xx+umnX3bZZUjP9a9//de//vXXu971VLLlllv6OtmJyQ8CQSAITIbAl7/85a233trRz33ucw984AMnKzb3+VF35h7zXDEILC8CGMmpp55KMf7iF78ojdysvPLKu+2220Me8hD8Zptttim6M5XLnHTSSRSgc889V21qwJachTDtueee22+//SqrrDKVSlImCASBINBzBKLu9HyA0rwg8P8hwF2F6HzkIx/5/Oc/L/hml112IdI8+MEP5pbiw0J6/r/SU/7yr3/9S9nTTjvtrW9967Wuda1jjjnmN7/5zR3ucIfnPve5t7zlLe9zn/tMuaYUDAJBYEkj0Ft1J3RnSd+X6fwCQuBvf/vb3nvv/clPfvKXv/zl2muvfeihh970pjfdeOONh4WcP/3pT7/61a/IPKJz3vnOdx5//PHXuMY1Wk85sJ7ylKc86EEPuvLKK1Elh9TWjlbiBz/4wdve9rYPfOADv/3tb294wxve8573VM8aa6wxUCxfg0AQCAIDCBCJ3/e+98nsmzMrdGdgpPI1CPQRgc9+9rNvectbPvOZz2icsOJXvOIVw62k93zta1+zxxf559hjjx0uMGHO6quvzm9Fwnnc4x43UOCiiy56wAMecM4558jfdNNNtQH1GSiTr0EgCASBLgI87Pe///3lhO50YUk6CASBUQj89a9//e53v7vvvvvayuImN7nJK1/5yo022oioQ7ZxGu/V97///Ze//OXKyLn44ot///vfj6pu8mOCmtdZZx0V3uAGNxCwfNe73lXwsuLqFMj8xz/+caeddhLWI5PMI5B58ppyJAgEgSWNQG+dWTP09C/pwUzng8BcIbD//vsjH672pCc9Cc/oXlYQz2tf+9oPfehDFVzcPTSDNF7FgVUn3ute93roQx/6jGc8g8Prxv/9yOcRE8Fj8Zf4ZSLT3e52txlcJacEgSCw6BGw11c/+zjpItV+NjetCgJLBAGCzR577MGBtd1225199tkiaarjP/nJT7AN3nGEg4N8LFxnGNLjjjvOdak4HGR1CWHLLn344Yff/OY35+E6+uijL7300uETkxMEgsASR+ATn/hEPxFI7E4/xyWtWtII2E2HiMKFdOSRRz7xiU8sLIQVH3DAAR/+8IdJLFNEx0It0TZOFJVs9dYll1yCRfk6Yu/BgZrFQd/73vd23ebAEge94447nnDCCRxee+2116677jpwSr4GgSCwlBGwEuId73gHBBK7s5Rvg/Q9CCwbAYF+ts+xmw7xxnbs7YRnPvOZb37zm9vX0YnrXve6om1ufetbv+AFLyh5BnFBdCzX+vGPf8wLZrX5pz/96QsuuGB0PXVUODPG8+hHP1pCDvL0yEc+stxbVor19gXIU+laygSBIDBeBMyF+MHV2Te6czVPwHyCQBDoCQK2z8EedthhBzHI9sKpViEWXm41lT11RBwTXU488cQzzjhjmT0SrGOjnfvd735TfNjd9ra35cOqai1Q/9SnPmULZszMC5CXea0UCAJBYIkgIKCwHinoTq+6HLrTq+FIY5Y0AmiKnQMf8YhHkHYaEF/4whcoMVNkJEJ82olTTFh4JTZ5ivVvtdVWNuNpNVOJnGifeJHOLTOJIBAEljICt7rVrfpJdxKqPMXnfIoFgdlFQFCw8Bpc54Mf/GDtHCjUxjxJEM9UVjoIJcZ1nva0p023lauttprA5CnuqfOVr3xFsI4dDusqT3/6023rTCJ6+MMfLqZnupdO+SAQBILAnCEQujNnUOdCQWBSBE4++WTxv2Ji7KxTOyCLU0Z0dt55Z+rLpKd1DnitxAiuI3zHZsrqb2dIy6mwHoyHr93r06cShcPFZnPniiJSntiz++6789YL4mmVJxEEgkAQ6BsCoTt9G5G0ZykiICoZrXnve9+77rrrVv+tbsCBpojFs571rNvc5jYf/ehHP/7fD+rjjVd1LlFd7DPdyBvO73SnO9XmOt5HseGGG9pREMdCUxAd8TdeYkzmkTmVi4qbfsMb3lAl7XOo/qc+9anf+MY3pnJuygSBIBAE5gGBpexiTN+DQB8QeM5znuOX/653vas1hlgiCniKjwOe8vPPP9+2y93yQptRKBWW44l37EY3upECL3nJS2SSduoFWEKFavfke9zjHkiPQ5xT3XpGpC3yetOb3lRtxtWEPGuzLYIqJ3+DQBBYmggkdmfEYzOHgsDSRcD6poMPPpiW84QnPKFQEMRjiz/OrCmCYus/zxfRzVXeNjnWZ9lfxy7MfFVrrrmmfF4nUcbDFT75yU+mA3nP6De/+U3vzMJaNGYqS8BUxatFVbKCTJo7zIZAJCK+reGrJCcIBIGlg8B973vffnY2zqx+jktatSQQ8I6ql770pRxYz3/+86vDlm5yMImqmWL/H//4x+M3rbCAZWvFa2dCr9ZCXKxs9x4I5OmYY46RI7i4FZZAWXAjPix7NP/5z3/25lGFheZ0y4xOe59XBSnbz/CQQw4Re2Qn6NGn5GgQCAKLGIHubmG96mboTq+GI41ZWgiIm7FBzute9zr7AVbPxcRMMTZZeZoKd9Iqq6zSUDv33HO9XYtfjItKMM0KK6xgL0F75FQBC9q9Z5TTCstpp0igOJiKxE9/+lN/11577e7R0Wn8zNbPVYbYs/nmmx9xxBEzflPp6GvlaBAIAv1HwBOmn40M3ennuKRVix8B/ibbCZJbuK70FgV59rOfbcvj5ey5JeV2weHD4r3yGlHqDpfWne985zve8Y5CfG55y1t6FdfXv/71Wv9V17rwwgtL9VlvvfXk8HBtsMEGU2+GUOWvfe1rVV788plnnmkDoamfnpJBIAgsJgQ222yzfnYndKef45JWLX4EDjvsMJGML3vZy8T86i1/Fqlm6t2m3FSU8cAp3Fv8Sj//+c+PPfZYAT21+PxVr3rVfvvth1H97Gc/4zvjXK98Dfjd737n/eeIkUDj5z73uWrDhKzP4ghziYHKJ/xKy/FOie985zuObrTRRvbgsX7+y1/+8oSFkxkEgsDiRsBbhPvZwdCdfo5LWrXIEbAgnJupiI6u0lcsIZ9iny0pJwvtv//+1JrhnXJsVEhiQXRwDn6lqtMWPpxclT7llFNEJSM6vnJ7cV1VuLHAnbYK3UvXhTDTgXAXq7eW2TBvRz/vvPMUU3jTTTelJ1kXtsyzUiAIBIEgMGcIhO7MGdS5UBD4HwL2yMEnROrUgnBvxaq4mf+VmChlcx0lcRGni3EWZdwEGJJMrajyF7nhyVp11VW/9a1veQcFN5Y3hpKC6ElEF7vvCOIRtiyOx9WF/jzjGc+wNw+e1K6JRSFV9hLkhrdSzEbPt7jFLUbzHtJUbVooUHH99ddHpC6++OJWYRJBIAgEgXlGwCQvnyAQBOYSAS+FsEsN/nHqqae6LiVGhM3oBwGqQZ4RiTyinZaCv/GNb6wC/FaWffn46q+vPnWovv7n2FWfdmhE5Q615WMTNhXNoldVDQQkZWrjn9F15mgQCAKLDIGTTjqpHhF9e0Vo1J0JH93JDAKziMBFF11ETfEucX4flxHbO3otg1hmuwi+/e1vv/3tbz+iWTvttJO1UVWA6sNTVs4yfwktxCRsyVFf29H/lPjv1xHVtkMCgJ73vOe1rwMJpI3vDHOST0zCz7zDy/bNA8XyNQgEgcWNwC9+8Yt+djB0p5/jklYtZgS85EH3LGiqTopWprNM1mFvs+JLsqFOvTd0smIj8kXVeGn5Nttsg2CNKLbMQ0iSV6DXHtATFqbufPWrX3VIa+udEnImLJnMIBAEFisCwgr72bXQnX6OS1q1aBEQ1fue97zHVjckEJ0UWzPi5ZqCdWwPKEZnxnCQW4Qbe7eD615wwQXCdEZQq6lc5fWvf/0LXvCCyUo2+ed2t7udMlT6yUomPwgEgSAwlwiE7swl2rlWELjaJz7xiR/96Ef2thEsDA5xPCNA2WuvvZaH61i6JSrIXj6uVarMW9/61sZIRlx39CFereY1GyjJZVYOLBv5WA/f3FsDxfI1CASBxYqAV+L0s2uhO/0cl7RqqSAgWnmyrnpqEGMmOzqVfPspiwrCPwTotPL247H7Tvs6s4Q3iVq6NXyumpGhyud9O+200xK+M4xScoLAIkYg2wwu4sFN14LANBAQ0mtNVr3WChXwIs8JT/bWz2m9u2q4Ensrv/jFL0aYrDyXbsvCubS8V2u4/EDOH/7wB2vjvUhrIL++3v3ud3/AAx4w4aHawBDB8g52S9NtYzhhsWQGgSCwKBHo7U/+f3O+RYl7OhUEeoWASBrBOrw8XuYwumH2yJlsHRaGZNOdinceUYnNBm2Zg7XYwNCuOe09D0550Yte9P73v3+yc+2PLEDHRsne5GWDn8mK2Vmn+3bSgWLojkq46g444ICBQ/kaBILAIkagNmfvYQdDd3o4KGnSokUA+RCY3F7q6VUPE/p66jUOwygQS+yAbJtBTOIJT3iCNzagRIiLpez0m275YjlyPvCBDxx44IF2F3zsYx/bLTCw9P3yyy9Xs1AbexI+7GEPE99j84xHP/rRlCHUqntiS9OolnOpV6sqiSAQBBYNApaa9rMvoTv9HJe0akkggLX88Y9/HO6ql1h5tfhw/iWXXLLhhhtusskm++yzD+HES0Z/+MMf7rrrrt4A6r0QXf1GYA3usvrqq6vEdn/ilLvhOzK//e1vO7cuQQRChtRs9bi9eX75y1/Kt57LayW8raJeMVElB/62PZ27+SeccEJ7B3s3P+kgEASWAgK05H52M3Snn+OSVgWBiRHAMETkePmDV2J1S/A62VxHPE05zh/84Afzmnk7epVBQQbkH1uBeW+Xo5/61KdsYziwGJ4nS4XUHaHHI94d4SUYwx43vjCbKKrZYntbLS/nuvduH5MOAkEgCMwYgdCdGUOXE4PADBHwyqrRZ44oUIKK8J3yOnXrQWhQnPvf//7cW1ZF2dTY/oS27VlzzTV5wQbojhN/9atfiZj2ueKKK7r1qOFDH/qQV1LYyrmbP5zmdGuOue7Rgw8+2NeNN97YuzIGKu8WSzoIBIEgMGcIhO7MGdS5UBD4DwLUjmIDk8Hh1Z6vec1rJjta+YJ1rK7yhiwqzkBJ4srhhx/u7Z48WVjLPe95TzHFmI0gnpvf/Obdwvvttx932IDjic9r9913R5i4tywi65ZPOggEgSCwTAS+/vWvL7PMvBQI3ZkX2HPRJY0AUWR0/ycrcLOb3cyOxrZaXm+99X7/+9+LyLFBMzFmoDaPmz322IN/ijvpHve4hzXtXqflJecDoTarrbbawG6BNCH7ECrs5Q+2RRanfJe73GX0toSj3xs60LB8DQJBYNEjcOSRR/azjyv3s1lpVRAIAhMicNBBB62zzjqIiFhmr2jAYGzTbC3ViSee2C0vascuhUKh73Of+wg6Fkyz9tprb7HFFtaCtWKCnR//+Me/4x3v+MY3vlGZ0gKfaUt3u9vdvL5U/cSe9ddfv50ynBiO3VFGqPVwyeQEgSAQBOYRgdCdeQQ/lw4CM0GAACOC2PIHu/jY0+91r3vd0572tAG6o16MxwsorEIX2mzF+FlnnTX6JaOI1G677SY8ubtGfd11191zzz2n28rtt9/eKVaKfe5znxMbNN3TUz4IBIEgMHYE4swaO6SpMAgsAwE0ZRklRh62VMq2OtaHe/Gn92F5K5ZwH0HKw5v+2W5nq622outYh6XKAWcWl5kXmNf6LA6vHXfcUbxOl+s4BVWyv86I5ggJmuzoZZdd5tDAAvjJCic/CASBIDCrCITuzCq8qTwIDCJAYhFzM5g7ne+HHHJIt7iNCh/xiEf86U9/Ov7449daa63uIYvSqTXCfRw955xzBtQdtEmosjKCgU4++WT79Aht7p4+lXStOe+WtGH0hK/T6pZJOggEgSAwxwiE7swx4LlcELha21qQo2d4zbmImcneVFXYeQeFjwge/izvpZImwIjUsXOgxVYD+F500UVewC7i2DKugQhomhAaJGDZNoOEH74nL04nBfmoXP6hhx5qJflAhcv8akMgIdXLLJYCQSAIBIG5RCCxO3OJdq611BHAS4QYX3jhhQWE3ZDlCBnu4iIcZ99997VlTjezmxY7bFMc5OYGN7iBWOPa+YaDzMeycxLOwHvUrULnqxre7s8mgVZdeRkFdmUpFqdY21EQMfJOLvsWDqxd7zZjmemvfOUrylgatsySKRAEgkAQmG0EQndmG+HUHwT+hwAascsuu3hDp+CbER4fuwL+75yJUgQYL3w4//zz3/ve99q5mCCkFJ5017ve9ZWvfCX+hDBVpnz+JgqQJVcVwdPq05jb3va23m2+7bbbevl5y68EuWjCVVfdYnjSZLsI2rPn3e9+9/Wudz397Z6SdBAIAkFgXhAI3ZkX2HPRpYsAdmLLHPE3L3/5y2eMgk1xhCF7ZcTAjl6nnnoqWUg4jmVZba2WjQTf/va3Wy215ZZbtivSe0Qx86ZRm4a5DppilVYrPFnCGjGesu5RvjlL37s5SQeBIBAE+oBAYnf6MAppwxJC4CY3uYnecjz5y/Fkpfdw522lY83UcH43R+COtVTdnErTjfineLu8RnT4aMvxViyXfvWrX33KKae0zEqQgmxRaJOegfzhr9bDD2SKlW7hPtQmlE6E0ECZfA0CQWARI+D9Nv3sXehOP8clrVq0CGyzzTYbbbRRvcEK3eHYGu6qOBvCyXD+QM5LXvISzixbDgo0FsHTPrZa9jJz74Kwq3KdUsvF20J0C87tQOhFEy984Qu1oZ1IeaLrHHvssYSfgWsNf+VKe8tb3jKQr4bK8YZRC9GL2w2UydcgMGcIEDsn87fOWRuW2oWszexplzn48wkCQWAuEaiN+2yZUxd90IMeNPx0sDDqjDPOmEqruMa4q4TRdD8ynXvSSSdVzfYbtE/P1ltv7St/k2geRy0Qu/zyy9tZ0s669NJLp3JRZax+H26296s7hMx5tYXYIM61KdaWYkFgNhD4zW9+Y/IwGzWnzskQMNWpJ4NdRicrMy/5id0ZfmInJwjMLgLPfvazKSsibMqTxet0wgkn+P13r2qJuDLefN7NnDAt5Bl9ee1rX8tthGFUPf6Kd7ZJ4Gc+8xl7Lnt3hG11HFUDL5XwZAIPokPaqTpFFluWZSkWTWjCqwxk2qdneMcdZSyM9xe1su2hLX+8iWLgxHwNAnOJgBflzuXlci0I9Bbz0J3cn0FgrhHACSxBp45QX6yNsikOqmG3wIF2eNPe05/+9I033nggf/ir/ZSt+rZ0fCBw2IsjxDJ7E1YJSAiQ2rCr6173ugPsig/L6VOPMn7f+96HkA20BKMS+CyzoqS93WKgQL4GgSCw6BGwj1c/+5jYnX6OS1q1mBGwX451UjYA/NKXvqSfa6yxxt577z1hh0X2DLOK4ZIiZgTrIE9WYJWEU2UsubrXve5l0z+Xo+XQdYQy2G+wy3UEF3ur+emnn26dV4u8Gb5EN4cbDt3p5kgTmWrNuZCdww8/XKd40AbK5GsQCAKLHoHl2axrdsHx4MsnCASBOUaAM4jvyZs7iTou/b3vfW/g/Q/tZy/gRlTN1Jv38Y9/3Hoo68xbDVxmwoBsmmypVFe/wU6QJH6uqVeupD0SJ9yPx74+VY+Nf1z6sMMOm1a1KRwEgsDiQKCFDPYtdudqiwPf9CIILDgEHvrQh6IFl1xySbV8xD43FdkzrQ6KOLZyyvscbGrsJZ3eimUXZuHDrigI2lpxX+1GOK06q/Amm2zSiFRLoG6ecQrYyZDMYwnYMcccM4PKc0oQCAILHQEzn3oyhO4s9KFM+4PAeBCoDW8sCK/qfvjDHzb2MJDgkJr6JUX8PPzhD/da0FqQIl6nLUevahGgqs2lt9tuO+8rnXrlfGHtRRPdRqJuVYm18fLf9ra3Tb3OlAwCQWAxIdBbdSexO92HdtJBYO4QsDyK+iKO2BItV7VR8lFHHTUhmRBuzNVlG+WpNK4kHFHDFBef61znOr/+9a+7J1ocLt+FvP/civH2vtJumQnT9vh5zGMegz8NHBV27XIyL774Yl3YY489rAUbKJOvQSAIBIH5RSArs+YX/1x9SSPgDZ2bbbYZMcYbOq2N8r5Pi8+5mQZAodPwee2www48RJSegaMDX+22bJ/A73znO4JsuLFsIfjd735XyLPpo5JPfvKTd9ppJ24sdZJ5CD/oi9ggrGignoGvRx99tLdo1WbQA4e8kdR2gjZzoxVxZvU3UHGg3fkaBILAUkJghXoILqUup69BoEcI2JzGCx8oIrVD8QUXXGCF1HnnnTdhE4Xd2Een++qrgWJOVxvlxmosbzhvR1ElIcwieLo1H3/88T/5yU+sXbcw/qUvfWkrPJywDmuy0KLnPve5teDciy8srV9nnXUsB2vbNw9XlZwgEAQWNwJ06NrRVOyOrbz609moO/0Zi7RkKSLA+0No8ZdG4l0z9l+n9AgHprgMw2FROikIcbHRzvBROV5i9YY3vMGegVxUL3vZy+SYz1iabvmVNOmFB82KdCIN4Yf8o0KRxa961asmrE2mkGftsf3PhAX4torrqLDeeiEeKFxnQqySGQSCwPwiELozv/jn6ksdAZvTIAprrrmmEOODDz4YHOuttx5hxtcJoRHo46iXgIr18T7zgTLedSWA5txzz/3Yxz6G9DhK6TnnnHMsdJfmbzrttNMoSSKBHKUVIT2Wo0/2Zis79AgtOvvssweuUl+tv+Aak7armNhk2yjztU34ZokJT09mEAgCQWBOEVhMAeHpSxBYoAgceOCBfvZ77bVXLafCRZ761KeOfhAQUQ466CDeqG6XDz30UDvuWLhOtmn5xx13XLeqH/zgB3WIG+tb3/qWt4faZHlg3bjtmLGi7lkDaWE6rX7NdpRKNK39gdrpSQSBILCYEGivjunbQvSoOwOP8XwNAvOAgCVa4mOQFdHKFjp5lRXJRxDxu971rsla4/m43377UV+EHu+///6KXfva18ZyfvWrX/GX83nRbCy8slGygJ5uJd6CjpooTJXBeG5605vSZrw3FNOy5+Ef/vCHAw44APvx2tHuWQNp5VtO7ePsXGqTyrU//qwGThJBYKkh4LWsPe3yYiKV6UsQWLgICH+xUMtjglhSvcA/rKjyUq3Rzw4OKfSFU8zKKfHCvGAWXqmttsCZ7FwuM/sQupC3oHuNuXnYNttsoxJKz2SndPMRMlHJ1nypweV8ajNl7Iqvjdds4Q5EWh4EgsDyINC2dO+bupOVWd1neNJBYD4RsKaJMGPxFLWmAo21xguqvGuiu6JqdBMF63hTBMXFvoUjti5UideFWjROzvF60dF1TnbU6XSgDTbYwEY+ynh5BWVIQjzQu9/9bi2Z7MTkB4EgsFgRuPWtb+1Rpnd9W5kVurNYb7n0a0EiQHERxyO42AJ1b0qvFVi8UTYPxHv62aWHPexh9hXEyTTPO0o54AREP/KRj7RFkMxlqlP97FRaFQSCwMwQCN2ZGW45KwgsRQQsJt9nn30wHsu8a9c+ETkcVfxcQmR6iIjNDBEdgUfaJujHxhvieLwaff3117dRELdXD9ucJgWBIDAbCPSW7uQlErMx3KkzCCwXAvQSL73ykgc78ZSnSdyxzW8++tGPPvjBD16uqmfnZCSMwLPnnntSp2xauP3222sqD5dF7Bp80UUXzc5lU2sQCAK9Q8Dkp3dt+m+DQnf6OS5p1ZJGwPbHtv57z3veI+ZXNI+P12ZZnb7tttvaNJnSc8ghhxBOeoXRlVdeaWNoLfziF79oJ0N7Q9vVkEZlEyBNxYREXveqwWlMEAgCs4GA3Udno9ox1Lk8Adg5NwgEgVlF4MQTT7SkvH7nr3nNa7rXsp3g4YcfvsYaa1iZNYYHwdWuZvV4RRwvf202DWpNfeYzn1kV1nu7Wn4SQSAILEoEersyK/vuLP+zPTUEgdlCwKtntthiC5vZeHHE85//fKuoNtxwQ8LJDW94QzsjW3lue+XXvva13//+960h96pzWwhOtylWntszkPTiLaH2RLbfj20JPYWnW08rb7vn1VdfvX2tBK+cpg5k5msQCAJBYM4QyMqsOYM6FwoCM0fAsiyhPLWVjn38vGDL7oJeot6t0Z6B1nDxf3ltp7+115+/NsWpjb9simNTwTrFxjxOFwptzx6vRu/WY/dCGw/aj6ebOfU0FWrfffdVHmd6znOeI+wa1xGw7HVgU68kJYNAEFigCPQ2VDl0Z4HeUWn2UkTAFoJCYd7//vf/+te/tsAb6RElw1M+eumTUyybsjEgQaiIyDKx82auBz3oQV4xscyS3QJ3uMMdnvSkJ6E4Mr/61a/a8VlTZXqdlje0d0smHQSCwGJFwHOpXhicfXcW6xCnX0FgjhDwenP05b3vfW+955yn3CsdvD8L6eGQEuY8xXZYRYXWOPeDH/zgRz7yETsTCjcmID32sY9VwyWXXMLJdcopp0yxNrSGhFNue4+5HXbYwXIt0UVWmQkwmmIlKRYEgsBCR8A+FLzwehG6s9CHMu0PAr1A4MILL7QTz+mnn+5lW61BNunZcccdK/LGSi7kw9oofisFRDRjMFhRhTY7KkZn4HVainF4HX300SqR5gKzjPzb3/52q3+yBI5Fwil31Ze+9CU8ieykYcWcJjsr+UEgCCw+BEJ3Ft+YpkdBYP4REJdDofG6BgE3uAuygp1ceuml1TIOLHpPayXe4x2ivgro8dbi1VZbTZqb6dWvfrVQZbtl0HK8+uqMM86wdPzYY49de+211e/96qKhxUFPGL/srCOOOMJGOy7kunjSN7/5TSXtrdzf9agNkSSCQBAYNwKhO+NGNPUFgSAwEQLYBi8V3uMg2tHd7QbLQYDkE3hskFNvMh+ogwIkstjOyHe6050++9nPtj2dhQoRbAYKq1A4US25smqM3+rkk0/217tOt9xyy4HC+RoEgsBSQKC3dCcL0ZfC7Zc+LiEELLMaWGk1rc6Ls7Gjj7Vdb3zjG21viPHQeOzpLLjnsMMO44xvtWFURx11VLmr6Dr4E6blJV9eHxGu01BKIggEgZ4gMJ4NynrSmTQjCASB5USAYIPHHHzwwZZXeFMp+mLXH14wL/v89Kc/7U0RVb8yfFjFdcQjb7755riOl3yhR21fxOVsSU4PAkEgCIwRgdCdMYKZqoLAIkGAz+vNb37zoYceat2WyB6vJtUxFMd+PMV46Drlw7I9j5ddnHfeebiOGOdx7cu8SHBMN4JAEOgNAqE7vRmKNCQI9AyBZz/72daWC+XhxsJ4KgzIzoRnnXVWhSG/4hWvcFSoEAcWAkQZ6lkP0pwgEASCwP8hELqTWyEIBIFJEbCXz/HHH7/eeusJ5bGVjnd4WYFl3RZmYw3X/vvvLxpapoDl6DqTgpgDQSAI9ACBhCr3YBDShCDQYwSK8ey999421LG5jkgda9dPOukk0o51W95l0bd3s/cYyzQtCASBeUMgdGfeoM+Fg8BCQcBLcD75yU/ax1m8zq677lrNRnoIPxtssMFC6UXaGQSCwFJGIM6spTz66XsQmAYCu+2224c//OH73Oc+PFk777yzRVjhOtOAL0WDQBCYVwSi7swr/Ll4EFhQCAjfud/97nf22WdvttlmtWPhgmp+GhsEgsDSRSB0Z+mOfXoeBGaAwPWvf/0ttthiBifmlCAQBILAPCIQZ9Y8gp9LB4EgEASCQBAIAnOBQOjOXKCcawSBIBAEgkAQWAoIvPOd7+xnN0N3+jkuaVUQCAJBIAgEgYWHwPC7hHvSh9CdngxEmhEEgkAQCAJBYMEjsNZaa/WzD6E7/RyXtCoIBIEgEASCwMJDYNttt+1no0N3+jkuaVUQCAJBIAgEgYWHgPcK97PRoTv9HJe0KggEgSAQBIJAEBgbAqE7Y4MyFQWBIBAEgkAQCAL9RCB0p5/jklYFgSAQBIJAEFh4CPz973/vZ6NDd/o5LmlVEAgCQSAIBIGFh8CznvWsfjY6dKef45JWBYEgEASCQBBYeAg8/OEP72ejQ3f6OS5pVRAIAkEgCASBhYfAFVdc0c9Gh+70c1zSqiAQBIJAEAgCCw+BTTbZpJ+NDt3p57ikVUEgCASBIBAEFh4C3/nOd/rZ6NCdfo5LWhUEgkAQCAJBYOEhcNppp/Wz0aE7/RyXtCoIBIEgEASCwMJD4Ne//nU/Gx26089xSauCQBAIAkEgCCw8BA499NB+Njp0p5/jklYFgSAQBIJAEFh4COSdWQtvzNLiIBAEgkAQCAJBYHEgEHVncYxjehEEgkAQCAJBYP4ReNnLXjb/jZioBaE7E6GSvCAQBIJAEAgCQWD6CPzsZz+b/klzcUbozlygnGsEgSAQBIJAEAgC84hA6M48gp9LB4EgEASCQBAIAnOBQOjOXKCcawSBIBAEgkAQCALziEDozjyCn0sHgSAQBIJAEFhUCDz3uc/tZ39Cd/o5LmlVEAgC40Hg3//+93gqSi1BIAhMAYE73vGOUyg1D0VWnodr5pJBIAj0CYFf/epXF1100Yor/mfy869//esmN7nJX/7ylz/84Q/Xv/71b3vb28r88Y9//Pvf/37DDTf87W9/+8tf/rKVvOlNb3qjG93orLPOWmGFFerc9dZbb7XVVpNGMuT/7W9/k1511VXXX399Lw6U+c9//vOvf/2r8te85jWvfvWrq+Hcc891yhVXXPH3v//dBmXXvva1L7300kc/+tG77rrra17zGqdLf+tb33KuelZZZRVtU8mVV155yCGH3O1ud9t+++39ffvb3/7Zz3527733vsENbvC85z3v+c9/vl6o02edddbR5i9+8YsOqS2fIBAEliYCoTtLc9zT67lDAIFwMQbeR6J9bapDOyTHp8iEkl/60peOOeYYR+9whzs84xnPqBYr8IpXvAJBQReYfJ8nPelJn/jEJy677LKVV17ZuXLqkDQ+sdJKKz384Q8/+uijXZfIfJvb3Kbq6f5929veps6Wo9i3v/3tk046aauttvryl78sf8899zzhhBN+9KMfvfe97z3wwANbyRe/+MW77bbbJpts0nKe+tSnHn744b7+4x//eMADHnDxxRdLu+h555137LHHOtfMT4P14k1vetOFF17oKl//+tdf+tKX7rzzzpttthl+I/Ob3/zmmmuu+f73v/8pT3nKuuuuizbd6la3euQjH/nOd77zjDPO2H333e90pzshSW95y1u+8pWvAOeII45AiR784Aefeuqpr371q3Ey/MzR888//+lPfzoO9OQnP1l7WiOTCAJBYCki8J/naz5BYGkjQHj41Kc+RR74yEc+cuKJJ3bBYPiRCWa1MikQn/nMZ44//viPfexj8n/yk590Cw+njzvuOHIF/rHvvvs6+rvf/e7mN785MYNdRyboDdLK1InYAIpQ6T//+c9bbLFFPZLufe97t5q/8IUvOJEo4tDtbnc7ZT7+8Y/TPDbeeGOZ17ve9eqsO9/5zre+9a2Vka9H8l0Ib2j1dBP0Eh2k0yjzuc99zlefPfbYw+naRheRKI7yxz/+8cY3vjGVxdYamM1ee+2lnsc85jGbbropZF73utehKXJoKjvttJMa/vSnP334wx9GvF772tfKR1nuf//716VpRViU9OWXX64j3/3udwlIro57yXz84x/vol/96lc/8IEPSNTpmJD01772NZnve9/7KDpKIjoysaKf//znBksaF3zc4x7n0kiPr5jW0572tAsuuKCum79BIAjMKgKHHXaY352Pn/OsXmi6lf9Hc84nCCxxBBj7cqMceeSRG2ywwXve854C5PTTT0cC/G6xhwYRoYW9f/e7381LojA3UDvUTeArlA9iBmUFj6GyEBsUwBsQIMwDC9l88815fy655BL5XiN8y1veEjtplfz0pz91CVf/0Ic+1DIr8exnPxvtKBNem3ox7c961rPuda978R8RhPQIObjFLW5xz3vek4JCX6HTDFQy8JW+8qAHPahlvvCFL3RpT66HPexhEsVsHEXXsDe9e85znlOZeA9hxiGFi+5QWZyCdlRtsEJHUL1TTjll7bXX1veTTz4ZIK961asUwEv0GmtR5hvf+EadUnTnvve9b0lHRXcoWIbpHve4BxcbjadK0q4wPORJe84880zXhSf+Ss1CdHz19/vf/z5SVeXzNwgEgVlFgBbrd+fTN7rzH299PkFgiSOAJXCUeAQ88YlPxC1oA2QbmOAQfEO0CrynQcTcXuMa1xBZgm3gK7vssks71E2gHapCC9CI/fbbjwTCsaIA005EEcuy9dZbYyEYyRprrCH/05/+tArpE8hW1YP9YA/StJPKaX95qfiJTjvtNDnI02Mf+9gb3vCGIlp0wSHtV6eaMS3E4j73uc/tb397fWynT5jgC+Ouwrq6RxEaAk83p1xvSNvBBx/sWg5hP3gMhemZz3wmj1K3cKXREXj+5je/ufvd707CIaF973vfW2uttUTYKOC6cMYa1dPO5XsiVv3gBz+gM+lgeQDrKPBdt/ouR0mkkOTmPcxvfOMbsSg4bLTRRtpZ5RXg/FJJqzyJIBAEliACoTtLcNDT5QkQYESZSYIKTYKEwAYrtOWWWyINBx10EF3BV3oJu9vsqBw2nmjhxAlq/K8l3n///euQCjGnCYvJxI0IGDgEDxQ/F5I0WcnK5zkSiktT8ZX+xLPDL8auoztyjjrqKBEtEnxY+iWTWNJtdlUy8Fdf6E+EkMrXWpwMV+OBQptaRNETnvAEscY77rgjdYquo7CS6AXvlbTAYX8RFx8qS1WlRxLVNqKRqBqKFArYmoRQAuoFL3iBfuE9CqsTN/rgBz+IutFy5FdV8oUZiS7Cw37xi1/IVImO05zkEOeqWP4GgSAwXwi0h958NWCy64buTIZM8pcWAlQBphTbeMQjHkGDLS/SS17yEnaUfeVVET8r86Mf/Sgy1KDh1cIPqDgtp5tgicuf0s2cMP2ud72LssJ+YxKCcEUFTVhMzFCtdSJvoGWUmwmLtUy+NlG67evoBB2FM+t+97tfFUPsUBZESpTSXe9610ZNRCujUEJwqFPcTworeZ3rXEdk8UMf+lBRMnJcF0/icZM+55xzdMfiKd43X3n3hBLjdhiSr+3j6gQwIAOcDqSDKA66KeZJgj/OVT7/+c9jliBCubgXMVGxRBpJEoPG61//epU36imoWSyR+qlQfFvtQkkEgSAwqwhM8aE3q22YsPLQnQlhSeaSQ4CZJG+cffbZGI+/+k9yoGqw2TQDvhhUgN/qUY96FMPc0GGDpcsb1TJbAoWiT7SvlSDz8ENROLr5pXwgEAw86oBhdI9Wmr8GmSiVpchHXb2VdIjU1G1eO7TMhO4jGdgDN1NFBCMQNC21oReiguheP/zhDxEyoTZaK8jGSnXVUlaoOMKH+ZKsveJ94xCkEpGXLLkCph5ZWC7UhtSk/DbbbMOtBur6aoU5EonDKaCweSGiY0ma+GukU5gUpcpwUJIE8bzoRS9SAzeikuopEJQ3OuUX0wbMDBtTodcyC2BCs9SGSjoxnyAQBOYAgeGH3hxcdCqX+I9in08QCAJMOCJCHqAcWEqN1qAdMhlO9hsP2GeffcTDAoqBL7iwFuu5cBTLqYYBtGkNeiQQR+yL2BT8gLNGMcusbnazm6FQCISQ3gMOOABrsdTI1Vl0XidRKfIJS2oWvOIUtry2t6E/KSbCV6CP/He84x2WTdlmRrNFQ+MEGAndhY9JlLQC5A2KiIRFTMgBt5T08MdqL/RLVfjZXe5yFz3Fb6yoUhLHIp9UJVaEoUS0GfkuWplCgO1qQ+YhejkdX6FO6Sx/EwRQIiQMBxJdVNfVfvWLpNFmOQJ0hBg7F6pwwF18iEPWk2Ng4pddjmyjZhRHzBM25iwldQdn0jbeLkpPRVDpu09daDKFrI7mbxAIArOEAGX3la985SxVvjzVrlDTyuWpIucGgUWAANrBxHJLieoVb4vr8BzhHNwobDyrzOISaTEMv2RMRQFMiA1WrK1EGMDBj0t4MqohH5VRlbOk1UMrIp/wHBGQGG92nYiCpghkttkMk08x4lbDQjADEosyeINlTVY5KYA/yac/YRtvfvObnSXuR6tkigXmVCpqRd6wpY3auLTwAPxjoIX1FaXAS5zrqzZrJP5RkTdCghALopFDmuSK1B1pBUqekSYCIStipaXzCQLTRcD9g6k/8IEPRF6ne27K9xABfmr7SmgYgdaw9qeFoTv9GYu0ZN4QQFxs/YIoePJahEWNsMZHhCz+wU1jwZS4YIxHOIhFUhQUVp/24IPEOHFEuwUd26CPFkKesSKpNq1RnoOm6M6Ic3MoCCwFBES/0U1FyNm1cin0d9H3UWReOZdDdxb9WKeDCxIBfqJSOrlI6CjUFF8pOmPpDMJkNTglhsBjudNY6kwlQWBxIOCHZv5AIOSsXBw9WuK9sMUXRzwQ+kZ3EruzxO/MdP//EBDf2sUC4+l+Xc60HXRoPNxV4TrLiWROX3wI8JbGjbX4hrWHPQrd6eGgpEmLEIF61+Yi7FhvumQhmNkk20moE28uBquFOYuCEt4kBMqi9Ote97q1Qr43DU9DgsCiQsCb/vrZn9Cdfo5LWhUExoAA95n3Kggw4qGbrDpRz9ZVYQkK4Ae2ybF4imdB/LUtcMQnWWYlx+Y3iimsKp4+MdpWmzvLhzNCjp2LnWUtusVTVpWLbraird5BgX9YbiZq29Kwl7/85S5kOx+7AtYuzAKrRT2LibbpjgsNtFNsuLBrUdKioFzFJSy5srG1dgq+dmlB05/85CfJZl6wZXmaNlPmbI9koZldkSxhEyZlKRy6AwoLx2yhFLozAHK+BoExIlBxymOscGxVeV7kEwSCQBcBNlXwshx22sfXOsr2+8rwdwtXpvw6hUn+zzmdTztdgZZdmbbsq5dL4AeWjlvWrmZr1C2rRg5k2qqYwa7L2VTQV8XwDDnePCVtyRWW4F2bEkUyum2r96hjHupUWOS1ZdsCCauMl3H6KtTauZXZ3e/HArQqplqPG5vl2I+nXPKq2nbbbQeeQXbKsTTMzjfoi0OYjXeeW4OmEovSLb+3laJtoKtai9VREMVwlEMOOUSMFApSlxv4i6N4pbmSlphZlWaDAIgpoy8PechDrHoT4uq9Y9qGAOE3CJa1Y7iaRlZVmJm3WEjTeNSDvQ1cIl+DQBAYIwIiFP3QfKitY6x2+avKK0KXH8PUsLAREFVjzRRL743oesIAYxu2n7FNsIVUVmV7R2btrWe5lt+wXXbE4qE1Ctu/jhkmeDC0TpFj9ZZABKuyqQ5CLx1ijyufgRchJFMBNp7Jt0Scz0WdVpiTNxSuHQjL82XXYCTDSnWn89QQMCxfZ8gRFFvdoDtOca6Hi217qCzyMRuF62PzPaoJeiFmyOZ7mkTzcCE771UBvETviDHFJ1Qiv14iAYrG0vADegklxlE4qNM2YqiSq1u+LiyJZKKqer25MrUnEKzqKoQcjaxe2G+QL6neAF9vwNAkfBEsFJoqP/y3Jot2OPTOc5XrL04Domqh9XT6bi9BJ9qxkLtKAlA2/6iqkCENqO0NJUJ3hhFOThAYIwK9pTvjjMf0KMknCCwsBAgG1AIih51v6AEaTzthm1EEvIQ7hj9IJieLd4haXcmoc47QKmxFKJ+Yge540QHXDFsux27C3htqKbstfBwlLbDK8r03ijFmrW2Qo3I5lB5CUTli0AXCCfkHn9hjjz28cZM5Z7NtnMNs22zQ9hVqxkIwLRey1zD2Q95QDwOvjAtpbREgmT6UDzSCCkIW8hYFpG2HHXawS1ARLNsZoxFYgjXANmvGwFzaWauvvrq/uFFblcZzpEfaJh89ko/9oG4cTKiPr9bYQ6CVr5IK10e1WKMW+gpSaFiGc9XB/wCoNsgPnNUKSGAz/qrBNkVe8A58NEtOXdFmQqgYMOXoBSYETByo67HCI0GXV0mAKJ8gsGQRGPSUL1kg0vEliIBIFDGtDCQSQ5WRZoxZd1Cw5fw1PnQU+/hx0/D4oB2kAtxIPmLBU/PWt77VXy82dwphBo9hcX3FY+xViPQQjSxBt8UOboEtCTfxEUzDeFudbsNAtAZ1cCJfD5JB/FCVhEyyRw2KmrGusu7kGeyBROEQhclXYTG2Q6xNAqu8vyrnn7Lfj6qwBH4c+zsjKzxTPGgK8P6QgihS0mQhTKhoma/L/Ij55VarDcRMCjXemyI4jOpEQpeE/NH1iMXxulBsT1W2dcZRRpfXayBMWK09r4sSAQT3UgyH84bRqtCFbCBpo2ojawgmrGH0pXM0CASBRYBA1J1FMIjpwgwRIH5wOQmGZfsZfmG2VBx8BedgOKtSJMOnbCSRQCaygmFQg1h9XytTgtNKhRLsvc0JbS1KYyBdyLFLIX6D3BAnBKMgQPLpMQQYdtq1MBtKiZZgSMoPfOrqaFbl4zHe7YCsICgq3G677dTDCcU11k4UEawx9cJOmXxP3Gfcc6QRek8r1hLIWetyyxydaB2vYtVTaZoTHatxNR0kvYBiuDZAaSd/FrUGyMMFKqe6j3R63XpVC08ss15z4VwErhrjQt5WQQCjwKGA7XTI8KnxQqKh3m8/2YWSHwSCwCJGIOrOIh7cdG0ZCAiOYRopNMwzZsAh5QRcxxKkCaUOlpvpZaF5XrxAirKivEw2GNdhSjl9xIj4utZaa5ErhNeUqVbMjrHEleJVOBavVoX9OrTMj0sog6wgJRLIFtZCtkFQXJR0gSfJb4TDdalK3nuFUcm3DTTnl8tRqpAerjphQwNkxXushOAoPPARZ+Oi1YCBQ1P8ipAB09u7RBFxpeGIWI6YJ6FFquWwo8SggCNqQ0Md5Rzcb7/9qhiHIJ9jhUKTvrwzSyXCm37961/rOGHMaLpi8Ug7ZYvNsik2yiWHf9ArCzDOEVfMoSAQBBYfAv+ZeuYTBJYmArww6IigWoRAgAvvDCPK90E5GF4RXRApbwkSy81glyDBZsskUch0omIoCH+WF3my6N52KcAWAeIv47URqiIi2CUEzUwdc8xGe1Rbp4gUtppaWrWYhKO1ZXurUOgP6lOvzZLJZydyCDlg7ElBXgHG3gvlIVPx3wlVxnWQhuqyfjlFa71M44gjjiApuS7py9ouTMJ6MVxQtFNdC/+A2M9+9jOXqBxIiuORAw1rwi3NsECdKuM1n1gIBEhcGKFgRrwHR1R/vZpUX6qG4b+ooUyxON39PLxLFYzedKZVlmsJOXJp4U0EHsFMGuzNo8qLQ8eEKEC6wyOpy7yHrbXD10pOEAgCixYBT+p8gsDSRKDYCWlB9y38IfaI9pUW8sJGSuAHCAFWRA7xCGDdZXKLUICQAOaWxoNVyCSfoB0SPrQHMk+lLXpyljXSTmebZfJzUVZIKVVA3K5oHj4swUNEI5kMNjYgApc2gx/UmiYN48HZddddmXZtY9rZbAFGMrWW74Z0VIvJtYqgUk2tS6AyzLwGFEnCV3TcIWygyTZIAHIms2JoGtsToiQURg0kmXoIEpmqWpwGqSr/HaZYmWQnxRQuzxpqKF9sDW+a151SoYpiAoSoJodyo4C4JcFGVcPwX+0UGK6wXnePGh0BSdWXbn7SQSAIzCMCvV2ZlYXo83hX5NLzjEDRHZIAlw2BBF+phdz8Jqw1UoINUEGqlVZmtUwvCiUqyGduMYNyDAkHllOrposHFBXAbAgqFpDf8Y53lI9U0UiwHIVxJnvSYDCuIhhIRI5MdGrHHXckw/gIN3HU7n9Mu0YiEyiLSyhmnRFPEHaCA/lqPZdte5AJa9eF64qqltk+lkdZz8WZ5S/yUfnqVLNPN5Prx9fK9xcgipFeWo50nd4ylXdWZXZPl4+6tTYkEQSCwFJAoLd05z86fE3a8jcILDUEGGxrmPEVSoOFRXwrdBGMBA5+sUUL6DQCcQoZPiDmXFphykplckvVEm7ncqk4S3SISrAEBfy+LPy2nosygS3hKHQUsSZ17tj/8t3gQBw91KaxV54Kg0AQCALLREBAZAUm9u0VoaE7yxy7FFjMCBQp8ZeQM2Jx0EKBgAKEtInFoQktlDannUEgCCwmBHpLd7IyazHdZunLtBEoLaf+Tvvk/p1AduIRq60C+9e6tCgIBIEgMG8IhO7MG/S5cBAYOwLdXZXHXnkqDAJBIAgsXASyEH3hjl1aHgSCQBAIAkEgCEwJgdCdKcGUQkEgCASBIBAEgsDCRSB0Z+GOXVoeBIJAEAgCQSAITAmB0J0pwZRCQSAIBIEgEASCwMJFIHRn4Y5dWh4EgkAQCAJBIAhMCYHQnSnBlEJBIAgEgSAQBILAwkUgdGfhjl1aHgSCQBAIAkEgCEwJgdCdKcGUQkEgCASBIBAEgsDCRSB0Z+GOXVoeBIJAEAgCQSAITAmB0J0pwZRCQSAIBIEgEASCwMJFIHRn4Y5dWh4EgkAQCAJBoF8IHHXUUf1q0FWtCd25Con8DwJBIAgEgSAQBJYPgcc85jHLV8FsnR26M1vIpt4gEASCQBAIAksNgVVWWaWfXQ7d6ee4pFVBIAgEgSAQBILA2BAI3RkblKkoCASBIBAEgkAQ6CcCoTv9HJe0KggEgSAQBIJAEBgbAqE7Y4MyFQWBIBAEgkAQCAL9RCB0p5/jklYFgSAQBIJAEAgCY0MgdGdsUKaiIBAEgkAQCAJBoJ8IhO70c1zSqiAQBIJAEAgCQWBsCITujA3KVBQEgkAQCAJBIAj0E4HQnX6OS1oVBIJAEAgCQWDhIXDmmWf2s9GhO/0cl7QqCASBIBAEgsDCQ+DQQw/tZ6NDd/o5LmlVEAgCQSAIBIGFh8DWW2/dz0aH7vRzXNKqIBAEgkAQCAILD4GVVlqpn40O3ennuKRVQSAIBIEgEAQWHgI77bRTPxsdutPPcUmrgkAQCAJBIAgsPARWXnnlfjY6dKef45JWBYEgEASCQBAIAmNDIHRnbFCmoiAQBIJAEAgCQaCfCITu9HNc0qogEASCQBAIAkFgbAiE7owNylQUBIJAEAgCQSAI9BOB0J1+jktaFQSCQBAIAkEgCIwNgdCdsUGZioJAEAgCQSAIBIF+IhC6089xSauCQBAIAkEgCASBsSEQujM2KFNREAgCQSAIBIEg0E8EQnf6OS5pVRAIAkEgCASBIDA2BEJ3xgZlKgoCQSAIBIEgEAT6iUDoTj/HJa0KAkEgCASBIBAExoZA6M7YoExFQSAIBIEgMBkCf/rTnx760Ieus84622+//V//+tfhYuecc86zn/3sK6+8skre737322STTT7/+c8Pl7zsssvucpe7nH766Q49/OEPf9CDHvSQhzzkPe95T5X8wx/+8KEPfei+973vBhts8JGPfGT49OQsTQRCd5bmuKfXQSAILCQE/v3vf+MBWvz3/34WUtOvauuRRx652mqrPe1pT5Px/ve//6rs//1/2cte9olPfAITevvb3/7FL37xwAMPvPDCC3/5y1/+r8RVqb/85S+rrLLKLW95yy9/+cvf//73X/Oa17zlLW9529ve9uc//1mR1772tU95ylPe8IY3YEsu949//OOq8/J/SSMQurOkhz+dDwJLEIELLrjghBNOmNCO9hYNhn/33Xe/3e1uRxq5//3vjxCMbupvfvObr371q//6179GF5uzo7/97W8POOCAvfba64UvfOEee+zxohe96PLLL+9eHYPx+dznPnf9619fT3/84x9vttlmT3jCE9773vf+85//7JZ04pOe9KRtt9129dVX/8IXvnDta1/7zne+861udavb3OY2Z5xxhpIEpEc96lEbbrjhK17xio022uhvf/tb9/SklywCoTtLdujT8SAwiwhQI/gUGLA//vGPl156qWn3hP6LyVpwxRVX7LbbbuWtUOYDH/jAdttt97WvfW2y8hPmM/auO2Dyf/e732EM3B+f/exnJzyrn5lMOGfNJZdc8pjHPObDH/4w6YK/pjWV8IMENFqgy/icPgIf7AaiHQKskgNjcd5552EVrbbZSNCkeKBWWGEFlfuL/QyILo997GNvfOMb3+EOd1AA47n5zW/+1re+lU7z5Cc/eaWVVuo2ycB95Stfee5zn9vNlNY1PZV46lOf+o53vEPixBNP/Na3vkUHks4nCITu5B4IAgsPge985zsV0/DTn/70qKOOqkltr7rBpD396U/nvCBF7LPPPte5znU23XRTEsUUG7nyyiuzwTvssIPyQjrYwi996UtTPLcVo+KsscYaP/nJT1qOxA1veEMaw4tf/OInPvGJ3fyFksYS1lprLfzPp9xbCNy97nUvUL/pTW+qXhx99NF6h9Moea1rXesBD3gAquHQZz7zmXve855KUol+9KMftS5/7GMfe9zjHjerd5EbQCTNySef7KKnnHLKiiuu2K4u8b3vfe/Tn/70lltu2TJ/8YtfICu+fvvb326ZEnjbM5/5zMMOO2zVVVf1la6DSH3wgx+UqbybrRXGfp71rGep073UMpNY0giYhOUTBILAXCLw85///N73vrdQykc84hH3uc99iA1cD1NvAKfAjW50o2222cYpD3vYwzy/GO+pnz5nJUkLd7rTnYg0rmhGbsrOSk396my2rr3rXe869dRTJQSu1rnsPVtYH2mZxx9/PFNKDOABYc7vcY97nHTSSfK5Qpy48cYbs3n+cu7INPX39SUveYm0D5lhiy22qFAPZQyH0alDtKVHPvKR3CKgJlPJFPdq1LhakAkXeuUrX1kl5+YvS3+9611P1IvLnX/++bp21llnSWseqQMDZvvf+c53VmPEwVA1PvnJT37qU59CHGVy3t3gBjcgC+mXSJeXv/zlVdJfzAATIo20nNlIGDLIP/7xj3f3EnIwsHYVI7Xuuusai5YjQaP65je/ufnmm+tLyz/44IP5p37/+9+3HOE7H/3oRw2NO0SMc8t/1ateBatp/bLauUksDwJ+fW5OH67J5aln7OeG9ta45G8fEeC88Fg375xK40zlPd3MZX3EJ7773e+++OKLb33rW++0005TOX0uy4g28LymOjBFVHdz0zXXXJO1nmIbLEJhAKq80E7W9wUveMEyzz3zzDPxBq6BESWZT46DcigoRozBNoRQbL311m984xtpCQ984AOJNCNq6B667nWvyyVh8i2TY0WvB/xK3cLD6RIAaBg/+9nPukdZ9Ap3lWmU3R4Em9ve9rZ77rknh5dGolnsuqM3u9nN/BXSoQCpQ3t8XW+99fAesS+PfvSj73jHO5r63/Wud33f+96nGJ7E74Y7qlZJbiNcTf24KTZAavrhD3/oNhNF+4xnPINQwXIrNu8fxAUbM76/+tWvmpS1/vrr6xrYmytH0AxYrnGNa7gNfvCDH7jlWstluqna11lKGA7UxLAed9xxxpTIVBfScgqlcGPD1L00gdC9J9Nt2fJRN9MD1LnlbLXVVtLHHnssbtQ669Ghv/jTQJ3trCSWIgJjJ1CpcIoImOuwBMOF/UTpt0z18KGx53jqffeqDymbU3/sl5hWhYwQA8MyOcsEGnFhwKZYgye+ibjfsJmrU8zCpenbUzx9ZsUMYk2dp3u6UE2ChLNM2e9+97uzqVOvwYjp2te//vU6BVAiVKRNZJmNW9ziFkieGbwcRoUJR19e97rXWcbC/iFYJCWiCwaz6667YgkMedVDq+AT4fi4/e1vX9MyTgdygvIGBXExIz/iiCOq8BT/MqIYEpaw7777snam4FM8UTGhKiyWvnBbMI0aXOfuvPPO0BPFgshSCyqz1A5f/XyaPGNoAHXuuecOXBShkd9tDIj2339/xVRL/pEQy6K/1JGzzz4b3SHzyMQn/GQM+k1ucpPDDz98oNrZ/jqs7ugazcYAIV6AuulNb+pXXM3gn/LzQf5aq9BivabunHbaabgaF1g7NGcJMhK/lQVTxxxzTLuogeD3bF8lfv3rXxOrODFNYMQjG4I6SiN06w4INu4u3ZGPmlcxBVBYtzeepB7j1a086dlGoLfqztVmu+epf0IEPIj9IFmpN7/5zSIJnvOc55ib2nMC0fHw8lRqYvuEp48r0xTQtdrHlGhEzYSEroY8ouSMD3k6e0Z7UqvBxE7DpkUmyOPECUGaTi+Xf3vSebhDWORjtc2TEeweslZ2HHLIIXvvvXejegIgGDz6gUmwwqyaCABpZZT3sPYUlnje857HGKMsLB+txXO8ap7i30Z3+F/El1hpMsUTFdMGyKA1uqBTfDHFm0kOKIUGW7RSICiMzZglI4Jmz5QkOZrtdLeZND+IJS0SKAIfATPDPYSgkDpk+oAF2xiwRnVoKn9NxF2LpIRLEU6mckorY90y80ZVssRG9I/7oQ4ZSl9f+tKXAp/vqTK7zp1Ww2R0x9jZtaUVkximOwgiqoccWN1jRbRIqSoPIpbVmufu6XOT7tIdig4vD7UMtuSNaoBO6Vqli+4YTQ12M3NUcfkZC+RYASTJzYMaVmEkD6Ttx1KZY/9LfSGYaYMx7VYu4OYb3/hGN8fvVLH6VIPrqHhtzqxuSWk3sLmNp1PL9/B0rtu+avAbaYeSmAMEQnfmAOSxXcLUlijKQaBGTuXyNLfn3Vgu42FKQPb8qimXOD6zcD/Ogw46qEIW9ttvv7FcaHQl9QS0eIGgwtU9wtWqgKkzEcLslhY92s1PnVZmuuZNU7UELMxbeRMAMha6w7V/9atfnT4huEHgC75iHqxyD0omDdugjZe+ggYR24Vl0EJITZqE6yhJXWD5PFWRG/2idshUktkjYCAE3UCE0ZjXUQxJDWau+stuTQurojta7kSuJVbfjaRaZFTvzO9ZMkS2LoQJubus4mmtYlpcumQzRgLaDvHvYIoIt2p5nZj/Ko/ugK4pQK2SKSbcLdMSrrrVojsf//jHtZ9zisUqugMobIxdZzuNwoC6U7EsrZLJ6E6pO11MGt1Rv3AoNOL1r3+9GwNXUBvSgHg5RN0BLPXLRIVfpnGLdsVZTRh3dxouzuobrArTwc6luWw8piTck+hsNYNQpzyNyk2CyrhJ+OPccpx67mQdbK3F59wSZggtZzYSfiPcozhW3a51Cfcq+jhwOU8baCvpbxOoTEuAb2gGCrvtSw9u+YTeOr1qKO2zHZ0soRKjPN0f8mS1LeX83tKdxO74mQ9+6C5WLtDSqeWmj5aEeNQ2r/Bg6el/97tCazy2PJvQGo8tT1tGiAmU78fpScTM+GGXsbnmNa9ZF/HoZ5DYVx/n2k+CqMBeeg6qRyYFokpqvKc597yJVNfPPdBYj0g5ggSZeTM8Zp4qICiEj5/bQoKdoz8Jd+BAof14slAOrOmwDqItAxmo01dkTjCEEIfyKA0XmCzH44kJ118ImNVp1WQlJ8s3TBrmseX53sp4/EHGbh/66NEvrlNPSegAZzKRIVzWEiflmU/BIqI6rBMRpSGH8VAhLcFz2Y1hJgpwSglnh3zzZk4EoLVrTTHBggKZ5sHBpM4aiCmeW8WMLCYhTRliEoBmsPgpDj30UBXWitxlVoj0CHqoYowQc2LQ8Rs5brZKTFiJoy6KSE14tGUC2W3cvraE0/0KGOMRPyv1+y3Ah3l2q2ue040LTkyLMl4IB6tGeOMNdMM4yiK690zrYeur3wgGgCpV1I5BxO3cvbWE2yDylWD5fB+IkdXdhliP3Lc26sVu3fmoj8p1wU/AhMRdzbGCRvB8qUSi9WgOEtBArzXmbne7mxtGI11U71BwRlpnYQWlyneIgkhdQ9pKMJbjVmeKICAf75FTH7+OtddeG8W/KmNK/93DfllNRDGUhtt96AdimLS2HarqtNC4a6ET9UJ5aV4to6M93fukBq7OUsYhXbOdILpJp1RJt30OKeDTMov2ta8OqaR9RUSg596TaJmuCEPj61nqJmn5SSwmBEJ3JhhNDwhPNzNLDz4TOJae46AC4pRmVC666CKPBg87QaZ+ujL9sH08oLn52T85JATRFX5FSg5Yfc9KNMXaWsW6Pzlf62N6zZiJQVG5p61nhyap3Ck0ao88nAAJI4HwMihMe1CMHG2ib3mCJzJfPl5CrfEEb0rJVdUP/vegZ+TYclVpP5cHtuTqbCczo19OEOQBAZfmLpEz8MQZqJHJ4WEZ6PVAmQm/6gXkCfWmpLojEmXCYiMyNYzPXt+RM1hVSRTHQJDrmCgPR5ke03R1XFYal8VXqptGzUyX7RQQQDZvF0KPpIW24Bae45VfglwrM62Ey7H3MLcaaFontsKicIruyGE53KVuD83G1I2gjUlayQkTAJHvPgGUBLkL62UVDByNhBFVFRVE+A5I/RAwUXy60TKGDX1EOLjAJqyfjfELYsw0DO02KKS1VtINxgvDT1RCS8tvCQPkZ4LNaAbMkW+HBNCoEDvh/PUVN9U2to2JUhIable8n/ZjLqGAX6J7G6fRGPEiZcYIWmB3rt+g6QQc/AbV7Mbwc/O3UPWzdWkVKmawyCf+mmwg+jJ9zExGcLXWkTEm3G/Dt5xW1XL94Qv5wfoM5AuB8hnI5EE2QAOZy/xqksAZCv9WEs7a46tEy+wmtMctBHA4m05gro4Od8rpAzUYaPePgfOr6VYoXU/gbqbb2Keb002rym/fTWIQu/la7qHnGdjNTHoxIRC6M/FoFgshp/NlmDzVVzNmvxOeGssdzYNxDr4DSyFqmuJXZFojn4Wg2ZINKOFqJ8ULeOw+YjjOCfKmaO3arKzfPDODVch0OQ8Rxh7L8ZYZBsnjGLNRD4JFrfGUEYS7yy67MMwa4Jn+4Ac/GBER4Ox0goRZO4vC5rFnNOrJbGo9m8wCyTasvnN1gXlwCWTOQ1BoSz3TUSi12cajJsqt5RMmFCt7M+HR0ZnVd7aQHS3YR5cfOOoUM3tTzJq8MmaehuwBKkDUwQXLe6jjzJghc7pYEH/N9thXBhjzEwyL69TwVf2MvYT5JZKBAUPG18qU8GxVSa008RBXOcdZ1wxUJd2/5qkMqkc/oQKZbofcA/ynwGdNW+ZAwv0jB+f2FxEx0O4lio67BQVBdwSy8EnB0OjTDuWbtlK8UIG6wZzI5+Wo7iDWvuI6ZtjMOY4ouhPj3HHHHfXF/Y8JuSUQDgJkozvuELNhSthkdAcIBAN+H8igHSW3uFB9DJB7koB3VcZ/jBbywQKxZzVq7m1jJIpIpqsbWd3Ud82u+1YxCeUdQsSrKmbScPgB1lc8tX56LdPpdQ8oUKdTdBB0X3EmXAotluaG00gdx/+A46dH7HGT1KWrcvePscPq6utS+2s4eMO793kDpyW6mBgaD5n2APH7QoWV9Oir3063cNJBYOwIhO5MDKnJpTklwRyN8MSvp6enm583zcMv3E/ds54sTCjGgVgpM12CBF6iRj4Oj1cnkmRI6ExauwyGZL0MGtFyJEwpTFzYpzIAnvuqYqE96D1ziTSqtdaGoeVnYQN4GZgHDw6TTnTHelqPfubh+c9/vocINUiBMjCsRTNR3StWuviEaFmXQHQoRtQdz3SWz1QeZZnj+atWwU2nxNuyN75WCyVgYu6FRGKf1fjhv1W4+1cIkWmrYWK5eT0knEWfA53hQyU9bWHrilgpq+ao6yKazCc2w1obQZmYpfGl6yAZpCMcwj2AFVkSAi4FZJKIiFIOYSqIcteWK9D9oMvoIx6gsLFTeTuKdxroZo9bfjeBzTDJjIeFOZilmw270nj+O54par9D7gdI+svAaKocsPja6iF1DMh+nDs+bjk3T5kr9xiDVHqYE3WQN1CUj7tCGZZe90WVOqVV2024dV1FB+GGphe5bAXAjoRVpoahGnh5eamqTLVWs33KplYvWg3jSvjp+ZlP2AvNQxO1BBR4z8AVIdxdzj1wdNF/RaPhNuNuunXN+mZ8ek4MAtNFIHRnUsQ84F796lfzg5gHi7FQrkgPY8auePLWI1g+28BfbsbP2rENxBhGwjPatFslNNhmoVk4AbCoDEvQvbDYQ7a8m9PS7Irpo9mty9W0vkxRK9BNaJWHiBzqjgkrEibHLFxjJjyrdjRhX0n9SlrRwAOFImAVpvJUHwyMVmR2bjaPD5n9o2tsuUBR5t+FzK35BShP2GFrCecCKqDYsEzdykyY0GYMAKXTDAbStNtXNlhhO9RpD/dTA3O4BlHeoqDMwjFCOjmq568uOFdEix6hERxSzBs/BXUBVhrPfUYKYsi5sfj+cBFmTNAG0AyTvwI7ioSRTFBDJtCJOAclQD2uogDpi0SHa2IbeBXWQgoaMPCtwW4SJFgZ0ogy1JQ6VAYeC5HfMttZEgYR/cJg9IJ5VoNMyMvEQgwQUoiFSNRZA+NeX8sdgNrSgQy6zCqscl91R2dRPRTQuEvXUX91WQv9CurOVwCP4Tib8NZqdUq0S7SqJJzVzVczWMzyh+UivB9Kbumint1Klj+tyygLZXT5q0oNQSAI9BmB0J1JR8eDnoRjn65SPjADcxHPYvEfDHCtYnCyRzZOY76LJbAf0vRzxVgFhIAdxQ94HNgnRohowZp2p0QMc2uBJ28ZPM99Co34we7ckVUTN+CJrx4uMza7nWiWzBFjZs9FwmCw7kqyRibfbLB6hHC2wt1ErQ9qcyztd1RgBLcdlqbx2Ab2RvAwTVc/EuAvDQkfqnq0mVCBEXarZf4JD0xvN3Mqac4mSNIqFNY2DprmfNEjsJRZctEJayNHkTqMiA+5BX2RUFg+NEhoKCm+IsRYvsm6IePCVxWz7ai9YVyiW7N7gFWuQTGyqiq5S9ooIDcIFpcNS4zFNnnAKUa8W89wuiiCZkx4aML8Kin6QZvBa9TaFbuVCLvpfh1O645e6NowG5PJj6ZaI0gucicPn56cIBAEgsBCROD/e7gvxA7MRptNmvksiCJmzAIbuXWYN84OHi6G3+wZZXFdkRAsPac+44RnEBLIJAwGCYTZ5g1hCNkVIRqiRlhHZYSGiCMRUNyaTcOQdi49QyAFo4ujsM3Ks6A0gAqn1QBmjI2kGCmDcxQnMNF3CaKRSqwj4wvwUZLaRNXQQoyhOcvbRVtCABDb1kwvJckhvXY5woYG4Ell4OVjfiqX6OorCARvmga3OiX4wghg2FI3c5lpvfARhySaBLGAKhC0pMiNRuo4vQ3Cy6yqW0ANFIvaXYYsQcXpHl2eNN4AE/Vje+isGwOF0mz5nJUGGjUZryChcqNpaLDkWQ13EJe2PMjk3CAQBIJA3xD4//TkvjVuvtrDqFuuyb4KyxCwaRKP61A+EJEKRGXPfNhdXIHtqVkyrsAw+/BMmRYLE+HxoRZgHuy0vlBNKta1oj2qd3QFGoMaKEm8KvPV5T5cFxHBHeFZ9GtcTUJHjN103WrjunrqCQJBIAgsKQS4Nbb+7+o/jpHmOugDAqE7czQK4h74sATHCESYo0vmMkEgCASBIBAE5haBWuLqmn2jO/9bqTG3gCy5qxEtOJ56+LrKJTcS6XAQCAJBIAjMGgIj1gLP2jWnVHFid6YE0/IXEu8i7Gb560kNQSAIBIEgEAR6i0B3Q9FeNTLqTq+GI40JAkEgCASBIBAExo9A6M74MU2NQSAIBIEgEASCQK8QCN3p1XCkMUEgCASBIBAEgsD4EQjdGT+mqTEIBIEgEASCQBDoFQKhO70ajjQmCASBIBAEgkAQGD8CoTvjxzQ1BoEgEASCQBAIAr1CIHSnV8ORxgSBIBAEgkAQCALjRyB0Z/yYpsYgEASCQBAIAkGgVwiE7vRqONKYIBAEgkAQCAJBYPwIhO6MH9PUGASCQBAIAkEgCPQKgdCdXg1HGhMEgkAQCAJBIAiMH4HQnfFjmhqDQBAIAkEgCASBXiEQutOr4UhjgkAQCAJBIAgEgfEjELozfkxTYxAIAkEgCASBINArBEJ3ejUcaUwQCAJBIAgEgSAwfgRCd8aPaWoMAkEgCASBIBAEeoVA6E6vhiONCQJBIAgEgSAQBMaPQOjO+DFNjUEgCASBIBAEgkCvEAjd6dVwpDFBIAgEgSAQBILA+BEI3Rk/pqkxCASBIBAEgkAQ6BUCoTu9Go40JggEgSAQBIJAEBg/AqE748c0NQaBIBAEFgQC//znP7/61a+eeOKJX/rSl04++eSBNr/lLW+5853v/POf/3wgP1+DwEJEYOWF2Oi0OQgEgSAwMwT++te//utf/6pzr3Wta62wwgqtnr/85S///ve/W6aS2MDf//73a1zjGte85jW7JdspLfG3v/3tj3/8o9OvfvWrr7rqqsq3Q31OXHHFFQ9/+MN///vfa+TrXve6e97znq21l19++Sc+8Yk//elPl112WcucpQT0fOC28sr/M0mVueKKKxqRWbpuql1SCPzv3lpS3U5ng0AQWJoIPPjBDyZj4C6rrLLKIYccst122934xjcGxfe///373ve+DP8nP/nJhzzkIXK23nrrc845Z5NNNvnGN77xmc98xtHJEPvzn/+88847s8prrLHGWWed9bvf/e573/veZIV7la/NxJuf/OQnRxxxxHOf+9xu277+9a8/4AEPWHfddddff/1u/tlnn3366ac78WEPexiC4hBKBDTUcPPNN7/tbW+LQh177LEQRv7+8d/P7W53uy222EJJzOnTn/70lVdeudJKK8m8xz3uIROt3HHHHSG81157veENb6hrydxhhx2OP/74a1/72p/97Ge33HLLys/fIDBzBNyR+QSBILBwEfjNb35z4YUXmgov3C7MZcvf8573POpRj+K+YZIpB5/61Kfq6i94wQuOPPLIE0444ZRTTqmc9773vR6sZ5xxxsc+9jFW/KSTTpqsnewx83/JJZco8Na3vhV/kjj//PPRCNTHxwD97Gc/a6f7eu6556JWlfPTn/4UYZLGDX7xi18YUFX98Ic/lPZXSfUQmaowbnHve98bFaivY/n7xCc+cY899hioiuqj+xtttFE3f999973VrW5V2tXzn/98hzTsSU96kpzrXOc6d7jDHV75yldqIdqH7oCXXPTABz4QMapKHv/4x2OZH//4x9EXRLMyH/OYxzz72c/+7ne/+8hHPvJ5z3teZWJFT37yk/Gqj370o7vuumtl5u+CQMAvpRjJ5z73uV41OLE7NS75GwSWF4EPf/jDr3/96w866CAPbobqwAMPJB6YNFe9X/jCF/bff3/Wa3kvM3T+LrvssvbaazOKQ0eSMQECd7zjHekKlJsHPehBHE8ex60QDG9961vf/e53r5wNN9xQ4oY3vOH222+/33773ec+9/na177WCrfEd77znUc84hGGm42X6aynPOUpEjxB22yzzVZbbeVEA+RmkPnLX/7y5S9/OSbh60Mf+tDyIrkx3v/+9zt68cUX3/zmN6c/kYgY/nXWWefNb34z1vXYxz6Wp0kBH7pIdaG+juXvTW5yE9RkoCp0UFPxsJb/ox/9SObBBx9MEEJ6EEGH3vnOd9Jg+AGxHEoYHon3oGs0IXwIYn4XulkBQE6h6DgKlp122qlqRgc1QMm73OUuuvmVr3yFqOauhsa3v/1tVO9973tfs6CtMUkEgekiEGfWdBFL+QWAwEte8hIzck9wz1aP42m12IP1Fa94xY1udCNmjJ177WtfO8XT6fkf/OAHWcdb3OIWu+22G3eGNmy66aZl/Dy4UR/tWW+99aZY4RSLdQ32FE9ZysXQhV//+tf0FZaVMmG8Cg02+F3vetf1r399zIa3ReRKlwHc7GY3g7MhHvaqEIS4bzCnqofXphw3e++9N3b79v9+jDsipQChAiFg9Zl2BegZ7jeGX3scdZU999yTeIONaRv/Dva82mqr4VJHHXXUC1/4QmXoKCKI61rj+qtV73jHO4ZrK4dUy0dE/vCHP+B2cr785S9DSQJK8CTwKEzQuutd71rlffWRFvn0rW99S5f9Lt72trf5afhN6RR6RKMi9kBe2FN1WQ6JiMzmKEVt44035tXCfjC/qjZ/g8CMEVhxxmfmxAWNwJve9CZy8UAXzDg90AcyF9xX8QH8/SaUnpJ3u9vdptV+8Qoe3K9+9asZKc/xH/zgB1M/3VkKM2Ye6BLsh8f9q171KmlhDawd02Xi3q2QB6psBi+GMnXIfFoUxQEHHFARtSbHBksx3panP/3pnC9V7LzzzhPrwDZLdOtMejQCvE54ZwknNJUKzsUkLrjgAn4o6sW73/3uww47zMAp2aq66U1ver3rXa+NUcsfSNAhDIrP5z//eYfEAHGc4bsbbLCBe1IOlxa+ReyRZv65sSSYfFJQVU7dmVBDUmxuPiQcqkzdliOuqAu3uc1tFNDsNddcE0Fxw1vkdeihhw6f5YfgVpev+yQ0rAjbe+Mb31iaDeqD4ZkYoEomDD/+8Y/9Bm9/+9ufeuqpqA/FyE/AiAxXm5wgMD0EeuVa61tjGB5TN455Suzct83jgyw8S35rDxFu+Be96EXiDEzU9M6Dxq3DzM9lT2keQkRd0RPwuOOOM8etqwPcVzr2jBvDwOgOp9K0ahAowBDWWb/97W/NO6d+uke5K97vfvdzCp5EomfPzjzzTF9f9rKXMWOCGLq13ete91KYR2P11VdHy5hbR4VKyBcVaxKP8aBufC7sLnuA2ey+++4sh8pdixKAP1100UUCL1yXmNStPOnJEBAOgk0y56Q72EJYSWaVR0nCjWc4bnnLWypg7ABb96RfijSeNFwtP46xeOpTn+oQ8YMDiGJ06aWX+krSGPj9imJBo90bjopNMfoSKLLKWXe3HFZ0pzvdSWYRptNOO01aJVooUR/3J6Hlqm/L+99Nrl/QcEVsD49xv3n0aTyuhuf5JfpduNPwb0TEQ0kHcZTXvOY1ro3HPOEJT5B53etel6yFMsqkRekRGueuRuUdpWPJf8YznvG4xz1Ox7n5UEwVyhQsBQeZ4odc1KVlQpKmpQHkLvf28jwK1JbPXCJQLNYN0LfYnavNJQoL7lrUZmPmY8VBLVKdyy6Y07NtHkDTvaj5loc4fZge7iNBbO9WYhLmgW6FhYeL3m277baKmV2x9K0YMd9zUNSk2mR6EKvTpzLrkSSf1KzkPvvsY67WzqWsUDjYEhNl+VWYASDaM/kmglXSPI/PSEk2plw8hx9+eB0iemsYp1Krc7qJmdEdV8E2KDGev1wJ07qox7pnuhmqXjsdYt3wT6QEZelWyEbyShgaoj2DUYf4v775zW9KUx2YlsoUFFKGlp0DCxcJqup0FkiBolkChqpw/o5GgGNF7Iu70XorQgvDrDynCfFMwu3NbAP56KOPRjUk+DRpMNgncjlZzSJslBSjQ3sTlSJsRUkqxVprrWXsOGjIPEiqTPIhEuD2oPP5daP7Mv1e3HUmHoJ2UQ1iibb5kaoTyxHF4nT74tTV0Qts2OjX1+X/65az/Jt2Jcr4Qx/60Ec+8hG6r2q/+MUvAkFYMQ3MLV103I9dAR8EyG+/rs7xRIBRWJcrR0IZNTskR7W67xGKRLrhfTxwdMRRjxT50pUvXZn+IoU+fkcVu/2roY9AqKq/Lpq/PUGgt3QnsTseKRN//MKtiiQyM3uEFr9zj7xuUdNEDyOzMebHk8vkDDMoY1nFPMVKLWDj5bD6vkqIhaQY+xlXcIBnrh+/+T3zX795VtMvuTReMky7qOmmiyrsciZYJmQS7JwnuHmSerAHnnU8RrykYAITI88X8y3W0VSs1SP4kYrgoe9EmR7x97///V2xwgvkWKmrzbQHDyPzMLNh0gKa4pAnL1MBDdf1lVBPe1fSUQ0we5OJJopexJ+oEQDBAGjXuI4eeZTTpQFlMmeNq4mdQ2ZyZrQWo5oiO91HS3AFFqi+zuVf82ZD70n9nOc8x+ND96d4dd03WGwknQwFYQAQoBHnClaAM0DY1zbKGIzxMjpuKphMdjoASUdm3pMVSP5kCFgExMvpJ2agySrQhj8BA1nhjhRoYsUQeI0dwuGmpXf6xTn0rGc9a7I63fZIjJkJk69mt66SajBNUqEfdTtxs80280N75jOfiWGw5UWtBAxRWD1n3EJ+R2iEfPzGV5zDD9lX9VQlvjq9tJ9W7VQSKJSOdze2cZYHiN6JPpYma7miex7n8BOoXXBAoWuu7mcOLo8sNfjoHc+dwk6U6dmoKpBqthwFnO6o34IGi7x+9KMfrXKHpvJxUUzRA0FiRHkPN4873HFEmRwKAv9DwB2ZzzACnlCm1ywK0+6pVO4e1hcp8chQni2khWADMk3LiBPl6WfaPSwUOOaYY0zyzJkcZTvl0DDQEdCTiz2/8BUfOR4NDL8LldubffW8M6FEUDxEhAG25vGpU2VQBBNNps6UyCG8gV30lPEcV63W4lUccB5eHqMIFkWR7WyVcJFoQ622RdE8qmgzcmjLntqeIEriNx4iaBA+ZO8NOUWMPKz1zooJa1twJvnQMKN1UW3Ti7qKhSceVficakt10B5pOj/i5UEGpSpZZTwl6+ty/vUIVmFVMjN1B40joXvIqsROKgSqaTUJWXHPYHX6qL9oXzudVOPmaV8lymKZBGNIpeobLDdSuaVwYo9yE1ol1QY6iVJ3UElTbR3Ewt1UJAHXGu/K5G47F1naPe9uhPlAv8xAEA70gvkfODQvX90eCIR21vNk+dvg+YC11GOn+9cjyLPCp5s5YdrTzA8fq+OSMw+UmOLHI0JUwNQ/Bqg0zuXvdWqYewSi7nggL6SP54JFxX7VngLmUjVds1qS1SdF6AlDaErkecQ+oS90Fz9mhoo7xoOApTQppDlz5ViBjDGY65sp4jQ0FfMe1osPuxDhsrFIBGNAERg/E0QF0BrMgPnEXRpwqImvntcmTDiKv4QcNk/gi3WhCBAKIgSBfKJ5LCh1ihVsp0uwl7iXFShtta0fA4JFo9KkigJRjNij4+a7pmUaLIf8oFP0KgzMx0SNXi1fnKzAFEDhT9ojx8d0EMsxIUZrqO5yXMVfpytjVW0FOf6n6Fg/hkZfYGhEGC2E1VO7XYEfAe1rfWz53YRJLbpjWHFQ8juO0o76DRtinoVan9zyuwlDoIMvfelLFdMSY1FHVesOcfPIx02FYmBF7itHSXoGRc2uZbAQa9v2W4TMJ4K9uRkMtMYUPWVvBJGIY+AKMY48XCJLIFycu9uSeU+7/fwW+BrctAONMTSODmQOfFUGDpSSgfzl/0p0nLASLkWfCQ/NS6YnAD3pAx/4gEnIWBpmNlUTquXvTm3Js/z1pIYgMJcIxJk1KdoIAbc9174YGpMYBomVMkMqy82iO5O+YuMsTIUGw2vjQ/Jlbnl8TM7MvE2GCAZK4ijojgT5BNFpXEcOl5PZj/L0IcE0VbP84Q8FhbMfmxGOw6LjDaUPc52gO56JBCc2cvjElsMrj6BUSypTdxAazMZXaVdHcdAXQYJUBHaUBt5O7yZwMmRLVXQs/WWh+fhBgWFolbmyeAgLwkkdzrrBDW6AB6ifKkauBylkXJS1dlRhZ+FA6qxLwNDyFkJUc291Lz1Z2jxVJJARKRXEOibMrBXGV7SHm0wMTcscSDidTmbtOoEHzyjfXJUxNJilu2IE3VESX9Flupobpvou0zpkwhgOTbdzz4jnQGQRZWUIhHqtZlwHIUOy0SA5htKJ2C2Bx0xXVWK6tcqd46/bAAfiSQQpcqYkAuF2lZjiR2OQ7FpKg5syq3LauRop7W9V3vKnntAwg6upw6eYNuiOAsOHWg6gADIbdKddoucJP+dxsZOe9zTNCwJzg0DozqQ4swTiKhhIgSl88GbqfNVKdx/Tw5PUZn4kOFZ4iCRMcGvzlbpY1dBKogLMP8cHcYgxK5NfR/31qYsyPKb4uII1PtgAOmKtrAeitiElDtkult2qR6RZNXpBG+AQwWDK6rM9eoEk0XKqJdQgCf1CVtAappqB1192jrpDHBJjqHl64XKsKevLhtGo8AmCMzkKa0EBpcVAQEPzVOVCWAXdok5RjFahKgZM8+xcohlFsEgpGsAf5y81BQOohqFNzDxvWn2d+l86HOcORghww9cGyBCIlSFr4Totc7haS0iwNwV8Sksr/JVUs55CpvirHPxAICee2mWo0rqPdMJfok6X2eUNMkXtYMPGvUoKycJm6HkOOdHV5WONcOa3IrZhRRDGlYfbvJw5QlWGa6joddct3jNcYCo5A72uU8g2SAy/51RqSJkgEASCwLgQWKE9zcdV4+Koh9sFq2CVzcv5IMSyUCDMt5hnFp3VZJ8YJ14qEoj1NRw6nAsEAKdQRwjRPBoy/VUPBoCaMOrEFQK1WEVTczpHGftCTCgfkcY8vr7aiUt0MItbkoAZv01x1Ca8gOsKe2AL+cuIIgwhIcRZJJ+nPe1pTBQb6VykxBTZ1QUP1V55WBFCgxjVJfwlhPBJcfpwPInWtDSDVUabWH3VKoAYMb3qET4CEzk4BIvFbSSfR4btl2YUlXQvuZYuEHvEHLB29CosyiXoUsoL+vFXgJFPtQGtEZpQVMAlwFL5eBWyiGk1gaTyR//VGNt1oHrOUq1rtfLaBkn1y2+ZEybwDPqNAGqCHDJX/ZqwpNGh6mmnxIQFJsusxhhBwFYZOeKx4Anb7lnK+GA5LgHMLmfqFht7mjoFvWmBP/Y2pMIgEAQWIgKsjLmllgsbrWU6PelF6M6kA4GXEAkYSPYP2zARV5S2ISyGbsFTw91ACTC0zLklSCblbBWRBi9REikReYphsJ0V3SL8WQRPE1oYMJ6gZuCRKta67hKnm+uTRjAGhlC1loCJOaiFFZiWNVld18OkfegcEDtiHs9/QWLpZI8/afmGyBJN5bJB70Q4iUrpeoXGf8mragQUtyPutTy0wHALORIIDOdaeXdV9fkfBIJAEAgCy0AgdGcZAPXwMLOHoDCcCAcHU+MlZuScFL7iKywrIQS/QYY4HWgSJSFUd8yPaQlKln9qfvsoQkhoiNAiDZ7tlnC74Gp6TXCiBtUy19m+aOoPAkEgCASBeUcgdGfeh2C2GsDFQwwQh2Eljrjm7lKg2brkjOrFPHwEOM/o7JwUBIJAEAgCQWDZCPSW7iRUedmDN7qE0Ao+KW4UcTy95Tq6YA2zz+i+5GgQCAJBIAgEgUWJQOjO8g6rqNvuhsXLW13ODwJBIAgEgSAQBMaNwPRWlIz76qkvCASBIBAEgkAQCAKzjkDozqxDnAsEgSAQBIJAEAgC84tA6M784p+rB4EgEASCQBAIArOOQOjOrEOcCwSBIBAEgkAQCALzi0Dozvzin6sHgSAQBIJAEAgCs45A6M6sQ5wLBIEgEASCQBAIAvOLQOjO/OKfqweBIBAEgkAQCAKzjkDozqxDnAsEgSAQBIJAEAgC84tA6M784p+rB4EgEASCQBAIArOOQOjOrEOcCwSBIBAEgkAQCALzi0Dozvzin6sHgSAQBIJAEAgCs45A6M6sQ5wLBIEgEASCQBAIAvOLQOjO/OKfqweBIBAEgkAQCAKzjkDozqxDnAsEgSAQBIJAEAgC84tA6M784p+rB4EgEASCQBAIArOOQOjOrEOcCwSBIBAEgkAQCALzi0Dozvzin6sHgSAQBIJAEAgCs45A6M6sQ5wLBIEgEASCQBAIAvOLQOjO/OKfqweBIBAEgkAQCAKzjkDozqxDnAsEgSAQBJYUAv/85z//9a9/9aTLX/7yl1/72tf2pDFpxjwiELozj+Dn0kEgCASBRYjA17/+9Vve8pZvfOMbp963N73pTTe72c0uv/zy7im/+c1vfvWrX3VzpC+55JKLL754IHOyr3/5y1/23Xffd77znZMVSP7SQSB0Z+mMdXoaBILA/CPw9re/fdttt91pp50+8IEPdFvz73//+6Uvfenhhx/ezVyg6Xvd617Xv/718ZKpt3/11Vd/5Stfueqqq7ZT/vGPf+y2225f+MIX5Fx55ZWV//e//33XXXf97Gc/C66//vWv3cJ//vOf29dKqOFa17rWDjvs8Le//W3gUL4uQQRCd5bgoKfLQWBhI/D973//He94x/vf//6vfvWrC64nTK/P8ccfTwLpNl6nDjvssEMOOWRYz+gWWyjplVde+ayzzvroRz+K1elvNRt3ec973vO5z30OWZH/iU98Qv7vf/97mWefffZ5553nrCpJ5nnIQx6i5De+8Y0PfehD97nPfU455RSHnve8533+859/8pOfvOKKK2688cZV+Mwzz3zWs5615pprHnHEEb/97W8r83vf+94zn/nMFVZY4fnPf/51rnOdyszfpYxA6M5SHv30fZ4R8ND/5S9/2Z2kznODJrk8E/KABzzg8Y9//GWXXTZJkTnNvva1r/2HP/zBLJ8eMKcXHsfF2GBW/G53u1tTLNTKO7PWWmvd4x73oP3c5CY3addxb/zoRz/6yU9+wq1TmWJi8CHM4Pzzz6deyFTPy172Ml+/+c1vbrrppk972tNIIFX46KOP3myzze5+97vvscceLfNd73qXq2+xxRbnnHNOuxCiQJJ58IMfzPXTMidMKPmoRz3qSU96khq+9d+PE9/73vcq7O/mm2/uqDSd5lOf+tQb3vAGnGaTTTZRUOaLXvQiJ2rn9ttvf+qppz7lKU/54x//iOKQgtCX173udX/605/qorqmI2jKNa5xDX+f+9znrrbaag45/epXv7qvmNPb3va2KuwquilG54c//KE6ZZ577rnYko7LfOITn9j/n1h1JH9nFwEP3HyCQBCYewSYjZe//OWe3c94xjPm/uqTXdFUm4UYOPqLX/zCY4i9oaYMHJrHrwzbPe95zxk3gDH+yEc+0j395z//Of7kg3NgFd1D3bRDCij2ile84mc/+5lDOOtrXvOagw8++NWvfvVBBx105JFHdstPmL73ve/NDLdDKMgGG2xw05ve9DnPeU7LlNh5550f+chHIhZ3utOdKv/jH/+4sXjc4x6HZLioTNRHoIxMDrI999wTe3jrW98qvyjIjjvuqE6Z2izzwgsvRD722WcfBGjDDTf8wQ9+IPOnP/3pXe5yF9rSxz72sfXWW0+FMif8IFUuRDhxdLvttqPQSGg50UUC8ZJ5vetdTxrvURJXk37Qgx709Kc/XeIOd7gD3BAdoovCuvDUpz5Vvs8JJ5yw0kor4dP11V/xzqqi4bUcCaQN+6H3tEzyjwuBQvsRpvvf//4OfeUrX5GJpksbl3XWWaeVT2K2ETjppJOA71My3mxfbur1R92pccnfxYaAed53v/vdNqPtYfeue93rCtTQQka3qf3L306miDGbWcd5EBAacZ2s1BlnnEFU0B7z74suuogJR4O23HLL1kKWTxmfSy+9VCbjxKfgRBEb/A7SpT208gMJlZ922mlKcnl4YJmOs4IcOqeffvpd73rX17/+9b/+9a/rFCyEwaZ5cGB1K2Ey21fl2U42++STT9YGMommVvuPO+445pYqgDeUoKLBHsS4JhtJiiisNJvkwF7qvtpGLCxC/g488EBsVXvQDjoTjviSl7yEdHHMMce4hGs14aG1cHSCUsVI3OY2t+nG6tIwoOr2QHHud7/7VQ3ve9/70JQXvOAFAn0+85nPaLaz7njHOyrwwQ9+kMnHZqpH5enDgZ797GeTWB796EerYf/991977bWRD9oJrva1r31NJrqDTiEKaAHqNuBl67Z8lVVWuf3tb889ZNxRHJqKoxheuZAc1ZHuvVdjRBfUbCV9rZyq85rXvKYrduufcfqAAw4QpuN3xKulEtT8Rje6UQ0iyUqXATXjynPiIkFg6swoJYPAMAKeYiaUnvVXXHHFwFH2wCOVbRjIH/vXD3/4w8N1snx+onNw9eFLTz2Habzhfz8SI85CCCgZjBlNnukiKpT24Ovee+/94he/uJ1rXl724xGPeATRiPGuQ2Ij1GAmbQ4tx+TY0DBXxk4N6qx5MC2h+1yjQFThyvzOd77TLoTNNJ8LV4J8fEgxAadbbbXVQx/6UDN1PpdWfiDBtcEgsdAuXXP6T37ykw984APVwOiq8Ha3ux12UmexxNtss42m8o90Z/+601V30IWa2TsLv9GXOt16H0uEpCGAl0jouNujjooaPuqoo6Rf+MIXunqlv/SlLzGcVWDgL6upbUJJKh+32GuvvaRJNQWXNAEDHRk4ceDrgLpTR3WnqR1ykJJhDMtVVCNy4xvfGEFUsttfoS0CgGSim6SdVhL7lwkibJLggbFhdVimzK233pp7y9fKNFWQOeLz7ne/m45FMSrpxV3nKlUVfQjtcG6pOyUUud9IMjLRsle96lWl7nhiuEsF99SFRqs7CLc7RElc6gY3uIF+SWOrn/70p/m/7nznOxPGCFcItFHm53IUkvirvljzpXnor5J1rfydVQSi7tSPLn/HgICftF+7OfcY6lruKkyg3/zmN3voMACe4N36mGdkaIy6RbfyljZDFaDQvrbEfvvtR9Bm6lrOcMJjt57U2AML1+Z/OqVHBIDuPHX4dDmEBBN6H4ykFfDc51xgivCDlikSExExnbVOxIO+5U8lQUXgmMAn2GYJDdNaxsy6FX1kJ5AMXglVMedEEZdGX0RIVHAGwYCvRANwFAZGmIgyhAE2DwLIhJGiUjhdjvk6g0r/uOCCC/BImdwTTtSjrlrDi6EXjBA1Ba/1gKMiMPPUCO2Enm4iKJP1jvsDHWGZRFc4Bc66JjxIy1k1BIIBa3fOwx/+cM1TABsoeWbCat1+BDOhJ6yaQBCSQxUTzkKNcCuiUxX/gTax/WussQYBgPZTygTZgzJB8jFGhCtOxgmvQmoy6JMdrVPICRow4enTynRDUowGTrGyGhTA12x+HF0eKNC+svTGAkGkVxl0zw2HoC2kF8v0A6GHlXOKYIMuIL4ySxWb7M7XtV122UV5v/cnPOEJ5S+DKvkEzTJ2SLZfk5sNi3W5L37xi8cee6zIYrKTr5gQhMuD5oahKrm3hSU5URmnuLcf9rCHkY4UhiEShkcaJl4wspNM4hBuR2jUcb3TL0Rq9913F86FwqocQcTnlKR+/e53vzMZIFa5c1AfJeXns2QR+L8w+CXb/9EdZ0rN+TxZcGFzVk/h0eXHftQz2m/bc7lbsxmVKRR92JS3mz/FtL6wGd0Fn1M8ccJi9HZ2xTSLy59Z8ij0XPN4YnKI/B6It7rVrepE17VS1NOWJsGiePCxGTJZNZaGQT300ENve9vblp2wbkX8gbR5uRpYbo8t1sjT2eOMGeDd8LAWjsDW/vjHPxb+yRirVktchdrkMaphyrg6oy7fUc9lj1Rtc7pLO1rtZ+8f+9jHYi3YgIcvYD1V+Qhc3WS0hKLh7msMw4NzeNS6N7QZdXBpE1btgbAHujq5HtACrgQzfvSLfuD5e9/73leFrqIYQIYr7+ZABpgUGlfBSHAFR1kXPg7ylVhOF9IpmcwDyURPeUBaDUwIVmRoIMNYEofe8pa3aImWIyscEMxPLfcl2GiP7hhBn6pBjiuaK7d2uhb9QD1spA8YjSC3CNZlxr/uuus6USVlSlszugl2WiVwoBNoQDukLxrfvkpgTpqnKg12CQW6RwfSfq0QgAx468ZzV/AYso7uJfcDAQCGMv2mDK470G/BoKsH76FYIIJMtZLKEMAG6veVpYdwQXHiiSe6bzEA+YbSKW4qCffk6Ha6511XJUAwKPhHDZ9zixy4kdQAczcSO+1Xo2YtJ8OIuXH3GjtAGSOOM1c3RkaZH4eSgdx8+9vf1kHNc6IoYPxD9A9dR0lER4UYrcFCx1FSzMb94Mfl9+sGQARdVMkJPyZaWuhewoZph1xIigmyhp57CXp+aJqKY2Ebbk499YMi19XV3TN+vBqDJ7muu0XbkBInYiq+4uukwcZ0FbPm3CWQGwRawu/X9IafzqRCg11apl4g5TL9yopmyUSdISCRTxD4PwTcmvlMhoDnGphMCv1y/AgnKzZL+R4ZJqzdoDwX8lxg/NiAgYuyBMIFmu9GSITHn0cJbsTwd90QvPiqLefFQCUz+Eo5YDNIBc6tlaIsiuc+f4EwQ/PFVieD7RHsIethiuvQhBzypPMgM/fyLPPIrmhK0gJjaZaJTFhrit/wfWgzY4CUqMeImM85nc0w/aWa6I5ipnq67Oq+mm6yXnV1D31GwlAye+w9a+T56BBpnRgg4cnr0hV3ia6VJwKAThHQWpUM/8VjypHEbnnOmpIqw9hbJiOhnZDBAqU1iT1jEpgifUc+ZNbHReXoyFUZE/9nZvS6e4xR1zwWkZHj9aiYWQXcqCX1V2FdY00hTE1h5B7zmMewQw6V06Gu23XuwLkbQtuuiPa1Zrszda3Bqw3qVxKwhrhO6Tp3WiWVMBz4mQ9YimbV/YzJGcoqowuMGQz1sRpc/S1nXJUxpje/+c1RyfpafyHslBaDbCzwHvc8/YDjqfxu+u5ecg9gqLgaHulcxFdtDmEValBPt9pumjHmaFPGB6R64ajafK3uu3WlS8PonlhpdwJNy3TFp2Jo5PidIi5ELB3HPModo7z+mvAYU/W3m0Sz8R6/dydWnaibMviZr35ffk1+huZpfhQ+dBG/0yrpB+Isj5FupkM65eczkFmndP8aO9WiaO4BVXUPJR0ECoHeOrOulhEagQBby4wpIPbThEaCUanHqx88P4gpDvMp38NCmu+AH4TYUI8hmXRvqq85Cg28POKmL+Yx5ojmKO1pxep7prsWDaniLRCImg9RcWn+noCqdaHacKJrz2R6Snqm4w2iCjymXYIgYVbHoiBqJFxTcM1T0gdRYKvQo/q6nH+7dMe80FO+2V1uEc/oVr9WmXgVP2DjCdEOmRx7TBeGrFFlsjeIZj3cN9poI6TEE9YDWuV0Gmdx5TBXKpRmdG9961tLDHxkNnvsUCkNFRXL8pk6yzS+sK0T2Rsfac1Yf/31tZwkjpw1G1/Fun9pUWar3Rzpdl3No1uU/SZjsIv0CfIDEExD21ld2tEyhxNGHFDdfIaQYqFfgEIQmbc66mZQ0pTaiNegk15IZTiZ2wwhJl0oSRkCgnuYASPCAbnMdk39VUjkcKKSOAcriAJiBip0J8vktzIcuu/RRgYzIjJ9xXFN36XdZsYO2ZIe/iBYjrpW3aLuWx2BP5LK6vtxETBk+kFB7Ba3uAVGVVN5PwdtcDnyBo5lgPxkSETtEq5uBbKeVo65gSaJj8Ipxaa0YgKiURYAVpiLfL8vfJQa5/boDlA7pZsAL85BeGgXQm7kkBMUU7lDjWF0T5T2WIDtQGa+BoFFg0DozoIcSl5/Szzwkmq9J6lHvKewr8yGJ6+vHpG+4ijS/NYyPZ09u2WiNZ7Inte4iEl/8RgFBPExJKaSptpVM8PJlrA3Hr5tbu2Zrk6Ts5pOMUsKe1aK2sEk8Ko6119zShNrCfaGmE/bUJjQXWIJ/qEeXKSVH2Ni6nSHuWUjES/dN8mmt2tGN8SytQrXYczqK7ah8SxugT9GumNuWja7ZuHEjxLSOG5M9OvqQBthmRSjheiXQSF+mGE7i6BlKMkV5U4yfZdpfGkzyBa2pzvIK+VfPsWCycc+ucBM1uuiw3+xDSqRD08B94FbQhlWH89QW/liqFx1IppFG5PvU3yFIa+FynLcHqWrETz+U+JqV2OYMQYJKqAadEcMja/usWoSBNxggmlcAkcBWl2Ik8gNT0soG4+zivwgNbH6Cqif2IDOVuHhv+pBuUohwIqKbLlvcZ3hTLeZX4FKqqS/copLya9DjmIhiD6VaPhyyQkCQWBuEAjdmRucx3wVEQZkGPN10/3aasIEUbouw8KxCqXDlx4g32y1zcLZJ55ymQySuakEIsI7zkKwVSXeiB+Ub+7OdJlusq/iVOT4kATUX3Plyqm/7AHS0CagrLUrslKOImFOKSZhRlvLTOaM7nDqs4tkmGonWsOWt5YLS+RuZ3opCtwrNatmEYU+mMRrs0/1nYIlXFFhaLCyTDV7VtuUlZOCGdbNMqU8EQbIUUyIVGO2jXwYOBTTtN5MveoszxT7qj0yna5+NIKqAT1MFA1FSggMXHLsvQHVMAmxlq0LwwkihFFDzjSyfCKGA7XFFXBlXKdMMkrhRlKhSxCNaBiiJQDFqeEmkeP0AV9V91qa5ES+MzcJuagxMCPLTanj/tYN4Cy8wWod0HGutUzgK+NTVEkxpFkBOcpoCUHCzVkXRRp8beMo05CVqAOxVmcV7slfrfJ7ccMbUNJUT1qVZgSBJYhA6M4CHnRPf7aQrao+8LgzqNK1bqViO0y7WTg+LyVbtA0hnVllCz2C+SycUi/mxX4YbAbPBBfvqWqFlYgaYc/aAtqiO2V1StqpkrzmHC7cZPWVCMS+4gq+8lOwoLQQaXTHehyJojsVWeIrtsRb1E6XszyfCpUAjkAKfWcm1cb24AE4me4LI6ABsPq8gb7qHZGAZ6G0EP0iccmvD3okx+Se66dyiCXIkDqREjnFNblCpJWplhsIwY86BXAXgg8mik4hMRAuXiUYWWYxEtqbBbclQqiB2oEtSSAlzZYbC1Sg6s/f/iNA0yJtdr1a/W/z/LawJLTxtsFTbiCUarz1V21a3n0ezsYlUufyIBC6szzozdu5bG0xG5SFh6Xa0fR80QmMbjmzah0yFkLDb821QkcB7oMWWUylMDsnQpR3n9Jjam7ebO4uZpZcwWzLNBdXiVgfO0xYY8Kbhh8oKVPEhsAX7g9ra12rQgesJBKpQzRyuXJAqEooD6cGbcOMXD4fXFWLrvnqjlTb8n/wCb4b3hBiRouDwajoIoKW+KqEbfpQDhA7/IPugpMJimyRDRIQoEv5O5xZ6oh2VnhKkT8wClVpaoSjGF4rufydSg1BYHEjYMmn58B4fzImWh4sZnSzDZ1nIO22eTBn+3Kpf7oI9JburKAn7tF8JkSAtTaNEOrLSIvSKDmHQsDGi3IlkPAa8F55dpAHqDu8MMI/RdUIYhD0w0nBBYYEWHOEl6iHoiMYhdUXiczVIkH8YMKpI+y9WQt+gxs5t9ojoFgIsweTYRKAKTDT/Ilpt6Dar12MKk+KTA4vjwBeDIqO1UzCeLWnQlI8FzyGuJnoFtiYBa6iRsgbusajNGGvkxkE+oOAm1xUkPag+CP2TfHboepVs/1YlFR+jnvhuiKrzHz8rgmu47q67ltz7kc9gwoRmgqxEpTdPd0MhPjqwdXdBaBbYLpp00KqtqZ6WHnctdPbAq4RI2LFhsesUwCoHp01VasajL6Hrcke7dajVabVDGZ0tGpPMIVdrisPt+smMY8I8FRYOagBQgj46OexJYOXdoflMxkCXB5ibjASq126AQGcRH5+fttkDIIEb4v4VjQFpeD5QoyswaGv0GxkKuZH6ycqdrgu5KtfuHPbdZVRj08301EP8UxiGkpJLFwEOFtxfQvERsdCDXdQVHs9s1pI3HAZORg8ftP27GnB5hMWXv5MSqRpz4A64jlgTiIOffnrbzXolzo9MVrO1BM4hAeXxw6PM/AFqznXE8ZXHt5yf1dtZlAVRChKzM493WUQ5leeXYKi/GXGJry65x6BGR3x3Os+JwWQ0apr+DigJzxXpqkjNoYkUaMF/JmhVUmNMa8Te24/Ho7yyizvOTmZW1yEnynoZNUmf74Q6K268x9Cnc9yImBVlJ+0hS3iQAktIkg8o62KEojjq9AZkZ74kFDT5bxQTu8VAowQw8Ag8dPNbzABOaECtymOFQ2mYayvr13zM1/omYsLJ2d3TdMFrk2rGbyWNE6GjZ939Il4hhhwPt9iSEK1Wnk/wxajXZlYF5NJnQUXHtCmGUr6tZp+VDHo8QWbddBsOJfLd+yQn7wNBVyLfFs1K+NEOd3NF2T6+QstZ/hrXExpnOKeMUAC/oTey2ntHEigUxY0EGDsFOBjzWZtvmC6BRBURrXtFHFLtF7L+Hnb680MvL3kXrKQBQSc3SWHmI+hIOqkmtS5iA4qaaGoS9CVsRaydM2ykAnisY9K9Neyu3a5bkIXbBSElygGwHaIw53KBV4eru5wtAKVoD070ek0ac3znKzAPrKNQTcztKOEB2wtPoUJoajFRw5Ula99QCB0pw+jMIttsJtZTWL8xXIqSsbq4pYpdMaDbxZbkKrnHAF2q8bXHJRoP+fX/78Lsg0iuNkJ32uPXZqieC9OTA2rWfuEbWPjxVHxok54dFyZeBibp0kqZK1rf8iqnOmyz83AhTwrxbkPxInjEJzFAyUHvlp13zQApr2F/AsUs1aAZiAmvZa7Uym6fjGr/yomjEE1LTGmtV+f1hIeKBZQUjmrT9OtixbO2ulDsZeJ7zLqPERYSGsYQoxn2PDX6drAJ4481WvCaMZ2JWDRBec1dtVObAmuKFtrajb+URTEJl5W+dU2S1wGNb6YjWaX+oJYWOVQNbg3tL/S0Ea/Kk04qc0w6yvu5fRaw2hzBMym7mfytjYrw/Neu1JV+Qn/Dq8ktQcH0LRneJQHauiOr4GGKnKpSe3m5Igv8EN3BqDr4dfQnR4Oyjib5ElkpmgK6OFO6K6qabzDmeO86iKqy3PNYih2ZQH1yaCbuGMVdPj5ojvcEJwdpRyArtbby2F9mfC2eI29ZLdIGs1+aDAxgEVBAoRzmZ2zxGpgoT2tfG111oiImSAbzGDdDQeWvS6rEs2oGjAJTn27UpnTW4rfVArMAJjoETWo65DqmsOqavivKDemHQfFWpzOVFcZUfPaQKchFdAbZFIglCEFkRP8Zqvj/Ds0BhoJCQdVss5LSQVso0WvlZZpNUDVaUeDVn/l1N8uzZJjb0beGRZa2iaiOBb8Iaydtc+nqxsCYk+3km6aSEz86OYIziP5WFeo/c7le3KUBGJCpX4CjKA98NYpXbrTrWSA7miVqsq9JQqw0R2/RzwDi0Lj5HdrGE4P0x182koO0z+CjQUNRn/4rMrpji+6Y42IQRHIWARO71Ri3avCwEShED4JSNqPY4Q8Ntnlkj+rCPSW7vx/8Wvu+HxmhgAFWBSwSbbZIVm4KvHgHs6cWf2L/izWiC/AfJdKMd3O2s7RGnJneZ6OPhcJUMbHr72VFPDI9pdNkqlMhVIpJt9RHw9cXz1eBTFoap1r0E3ZXd25rTYJJT2vrcz3uG/5ysi0E494dqe0/OVJaKodmzz6LferekzfhbCIhDBHF4reYlmYPVdHd8RYoJUKs4jMW62mMa0nElS/hKQgH7ZH0lOEqTUPCSgVpOXMIMGOMpxOtLrQBgpaxZ4hGU0HtVsB1sIHZz0jsz2tS+g15Nl7iwMILZYLOB0tIF0QVlEWXic0hR3l3EFi0Cm23G+24kscZUeRPOfy9eiv040vbkGPkUaArDNAlaTdPy0qxdf28ZPXnfbVtfjvhJ7IEcXMMKPI7iKjgOq1YiMSziXUVQGDK6FtJlTUHdoJqgoomYgO/YyOosEUKfAO1KnBwGmZqnLztK+VaDkKV1pfqCyUNnwRaxwoP/C1TvFL0U13O1HN3W4QjaZtpRC77o+ue66SuBTfq/Wq8v2sqEFGyv5YfkREHSTY6LjVHQWIdbLqNHy8b1CdrNruJZIOAv9BwL2STxCYPQTID7UubMQlzHSZZ/NUNyS6wx7Uw9EpLLRVbAhHnW4yJ9zBo7AkNE/Y2g6ADWBXWKARKgsPY7150ROzfCueyxbzi+Hw3CTX1048Is1FMPA1oAserMIaSCYi1n3levDVhWq6X03qzoblsGcW61mWrx5GqNwKLkRKwS14BGrjxDp3Of/qLALRnXbDigNLp9BuGJbnSAGZjIrL0SdaDFl39+pqiU2kLIrRX1KQIBtdaC3UBePSvk490VV3jGPFGHVVB3pP83BpuRAf03p3QpOmXKs7+5/s0mx8xfdQbpRnp5UsZompsJcQQOkMkHw0CyZNBZHDfKI7LC4moUmkWZloAX5W8bA4k1aVEEW00MhyQrHoLabH+KKzTqyPmCpxMHXUvgwmQtgSENxs5QJbprpjx2pcgfl3c9qVStsoMUJ6/ViQVDDWGMHK6k6/DhNrDcNoqwGu4g5xG4sTMrL66+p+j7x+qAy2JK2P+qtr/H0SNTXnrVMD5icf28OivIxzhGO0wmvcdYaS9802V7gySkfuUpWfWHsL2P9B0/mHW/PK6YiHgGw8lSRWTjTjhQq7ZyTaGUZQO82OnIhdtfwkeoJAb9Wd0J2e3CELtRnmr2bkAifFUdpO0MNUT4RSMvlmZjwgtRCxAhWRDIW9/0hmcQuFPXA9iGkSWAjWwoQLomymjqfD87q22GF1FHCIWbJAw7nkE0bOg9IhT1irSEqkGUYT6yqe4afoeYowKeOJqXKNl/ZQrvhHa1j4KfhENMnDlFTA8nFaee6X08F0UwQoplVXGaA7jJDeedYzcjiTObFiOkUkEJGgweJ2W9+rhhn/nZDuaDYDpg3In78qN0s2Yy77rXmkhbqiJhmm7tVrp6gaDiYZyKrqFphBGt2hphRVwmUxTnKLkBQerhosaNfu2+4EPguMjcKEk3HJ1eXIEkaHEoNeTGbelDHE+Cha5m5hnokBTicDsNPojl2kxczqbw0iHNxL7CjCgYniEOgRxLATppTKKPAZpXY5aNROlcbdPVBvzMDCcY665zWsOBzXFTec28ydr8HFL91s7k86B7JLwNAkshkejGsaF+KEZnTDaIYRRrVdFzKIvkEEGrLlKjJBV93xyyKB8DbK1NpumKAGC/fxMbh+nmqQ9mNRG5z9fFQo0y/CunQQQU8mZqPvWJG4bz8uNzlk6gWCwy2UA0a1GdkJjyZzSSEQurOkhnsJddaz2xPWo5YhtwcGy1E2DGnAJIRtil7ykHWUvfFkZ9J8RVlQATB5kgqzqLci1I8ESzBp8zRngRRgV9TvyevpjPogKDJNwRWWqI/rTsUq282Z3TX/tqS26nE6s+cVS+VZ0DY5wjXqVVNMFNYyTHfUgAqMoDvMG8tHR+E/kqhGssfoDgMJhK44VEdn9ncyusN6mQ0jFiJj1EyzgSHEtJk6xTzX5Yya/Nq+UswKZmCw+MVqIi6gB0kqWqm8Q5rd9uaeeoPVg3XRHuDm0kQO58rk9xGGwiOjDWyqTFKEvRtQZJ6mcgmVBMLQKlMfPTIow1dn9asA0uwWcluy/XQRJZlw5MNwEB7clu1cF6LEyHQ/VCabzaIbdx6xWmFEbaJVGEc3GAEDWS/iDkncC8gInBu7bj9EAdlyr8p0yIirVkmaipySguQoIy2zCksbx9aq4QSmqMyAtOarUW63vYTf3UDmcFXTyik1qxDDzDDIFv09rXpSeKkhELqz1EZ8qfTXI5ucYEauw3R+Jqdmlh79rGk5DgoLz3c2TMSGr0yskkwC+ZrYUwUq1NGJZtXsU2XWK0LVYzbcJJ86VH9dmu+pmzNhmjEwt9ZCNYtoqbdI4jo4ASKFb/F6mPI6F92hn0twiMyA7pgWcwrU0rzSCVTl0hpZmWQDTo3WSADyhpRxbZlTT3BSEGlaeaoJlolMyOHvYPIlcE2eKSoFi0VXMFOv8pqK/xEk8AkLiNAR+RgqL4+IEHICQNjpKkwzMGSkmvo6rb+MMbaB32CcTQDQa1RDXKpmFEVWp3AiA8rTxL/pb7mBZFaOm8EN05rUbQPb7yhvjk8xA+Ab326ZpKeLADLqZubqJcUJW+6KRtOtKuWXDgKhO0tnrJdWTyejO1CgZDC0DY5husPG+xD5ecQUK7rDmGE8LGtFvYgbQJJcxbZGMkuKMJWXTxmqygkGDJuwBpm140i7aEswrggHdxW+xZtTThw+DubWfF2MAi4lzoDy77EuBIQkgATwX+BD1BFqkKuz2Y46XdfUzFtBB+JA0UKRH0WhcDjSFI3EvmqkiMpk0Z1u7YxiIkm7GgP9wKFa+dxaO60EZ1y9uA2rwH54T1y6fBxtATB5QFPhU3Sz1a9h+kh2ahyCOMGVQ94or00riUaUT6flJLEUEHBToY/+LoXOpo9jQSB0ZywwppLeIYCIEAzIBgwnD4K4TgxGK5Eb/gsm07y8ljSjPtYQ8VbIYfjLy+N0meQW9rXWmGAeTrc8R2yE9boYA89R0QvSgugKl7AEFxfhXik4+MW4XXgu+EoqPGIYJoxKVRiPBbEISsUYKSb6oVYaC1zQAMKSuSxRhGNLp/g1eMrwofKVYBW8ORaqFI3DIdAvObgUTUi4T10XAoI5HCIwVA7tAX/SYCgVt2stRC/kC6RtOdNNWFRMYFP/dE9M+SAQBILA2BHoLd1ZQVdNLvMJAjNDgOHnmhEl6nRrl4gH5BDxCoJ4kIPKFAsi8lRaNChXBS3EXSeGV0mZuIJl5DItJMZ7hEr4i7XUohL+DrwBKxLnoTBFh4rD/6J+X+tDDRImSXXnsrkqb8z/ebu0FulxlTFXvdzVAQfRFFchgnu5K0sFfUGAoCL6R2tEI/lpzLhZfmt8hQixn9h0KxFTbxogMJ+oyd053dNTfmkiYELbz3dmhe4szRtybL1Gd/j1KTH0DI/UWkLsSU2uEJPrUdsyx3bJ+aio6I4re/ojZPPRhFxzgSGAhXvu+wlYVk2SNOXlMbRMzKrsqfREeRsu2/UA5yBJTuWUCcvYtoc46gY2SZiwwIhMSx3FtFEfrRsgtY4omUNBoCHQW7rzn/2v8gkCy4kAOccctLiOqkxGF9nDkftMHIxZcu3Lt5xw5fTlR4DyIZCZP1EENMI9YYW8ioKjMW9BVwKzJiwzg0wMRsC7iBYypNteeBa6rx4ym8VrvIr8quQQQdncrPKtEkd3BIphMOLMKKBTuSg1kWjHl+pCUyk/WRlMxVL2KaqSugDYJuRov4WTos0mqzz5QWAhIeCnm08QmDECnsWW6Xoot6jYGVeVE6eLAPAtoiY4DZ/IstZC6OFDiyPn9a9/veesbQLQAnyidUqEO9dqfcXChUaJ96o3LbQyy5lQLUJQS/SFebn/VYgKU27kW83nonUJUWK18L6+eoWFGK8RV3eiNfltpb0F6sTReic5kaZO5PlFqmyN46u/yFZtoOCrOH2hb3JoOb7igsLd+JrtPuBWqdP9pdYoI/DcX67kyhd55l4SpI8YuaNacJtlcXCuXSFaDUkEgREIePgUB6qNJEaUnONDV5vj6+VyQaDnCAisFjnUNQ+9bTD7ZNG4J4vtcbuNtEuKzNrMppu/aNL8RNbHYTbcpgiEjZhrQyBUwNJ68WHCyYV8Fe1g7/EDuwoNhLHbF0CUdwvxRjKoKYLZmXbL3UXQD5TvoudorVMT/95eLW7BHbGnu1rbQjwB++1EUtOEGxdpm+uKbxOgprUElWIz6A5nlk2hiIu4VC1FtHGDwUVKVItLUZiswJe2w7JK+BGcXvTOPewr7qJ822jKGgLLBm1/7JB1A+qh6Djdmj6XEF1nLwMcq20FFLrThi+JKSLQW7oz8wg4P6F8gsC4ELCdoGXS9vkQDDSuOieshxLACFlsVXGgw2VsNGdNloDo4UNzlmN/oHq9wOgrWr5uqRcfoo0ZuyWtNSMk1Ma73fzlTBMwCBvdSvhlmMlujrSHnRVtta1AHeJ1MrKWx++777728hkoP4OvRAsUQUyM8Fv7A6nfRz0Mv/gY9xLCR/OoHQ3EkImap5HQWigx2IySSIm3b9qCiL+GMClH8BkYUQT3ho2LMA9LAidrG67jLhJbY98BXatiqIybCg/jPpODitkUwFgAzUpDA2oxv8YM14l2GC+R5lYFWhtolwScQ0s4hf1VidbasAC79dUhcfoS6sGQ+Mjq7Ztm0riXwCDdL5era/lquWL3ingMz5olkw5hdXaBqjhosaVYI33I2xts3dQ9JekgsEgQmCJfS7EgMHsImGebLgsR8LfWnM/etdgnGr45scXhE16FyfTbbrPhCcuMMVN7arm+raJVa/JNojDFF/xBn2C62r58k13U1kF2RGxH8QxTdvP+7uJ2a8rspsN+8+w0hdlmRSyfTKEt2IMaXBRJskcAp4z1OHZD1h75Nv1jtplhDMPOwnUt8oB9rtlau0hLVyaySIowlCijllQmtsGWs8G0inplR+XP+C8bjyK0072EwXsVfIWYset2XKaWo1kSXDyO1suYdLN2PyJ+eFtF2w/TAjdcrdU8WQIlIupgTtCo8uB1rtHUGJV7fTc+hLujpBgGAmETZ+RssvtKA4xaeeVqu068hzfKibUtZFdlUS3eZshcvXnunAt2QUUih+yc2VpOvurezzZHMLLl7WplJDTb21LLTUajirrTBSfpaSEQdccvLp8gcDUKARRMfMvAFCJm5Cas7L0HvelmZYoe6Jbxe/O1JrX+SqvKR6I+NHmfBjE2w/YwBq5VmSbZ7ATvjzBqtbWSAwnL6eUw85747XQvEGDs8SSHbMqnkSUJDJzrK0No6Za3E5ipe4kY/0XJSBppbyG8xNJ6XpI60SElUROMgfYgUyPtB8iOmtPjBzY/9I6C4auMyAEOpwYKxaPRirkuFw8Dz4uhSZXvRZKYDZGD4dQ7QGEqICJC6Cnqg8R4lZLCmoSveNcSumNzRTkGS/Cv3QSwQ/aVsa86tZZnzVGigi5UpjdDwYTnCO8BQmWO8S9ZYsSA6lcFzvNzuWiVNLJ0JjRII41C3VeOkspasydroQqpO1iUau3bRHThAHUrWsSkJcbdfaiAkaWvEI3cBhL2yaQYOWvCao27DZn8dVRV/o5YN441YlH15paSoIiRkAe7iCIvIFOVGrTTXed3JK2DVTn+pO80OZ4+dzi2Z8QRRGOkhUaHjOTSMqsGhSX8HCS6vy+Z+QSBhYVAnFkLa7z62FpKOy8AGZxs0G0fY+lhSjCvTA9xFEFQs+kmTmCKyfixPU7EAMyVbRXIIJliKs/em6rSYEw3TXPlWGVDcqgNAPkvHGLCvfFAPfWx8aDXKdTEQnu23HJL74JAF5olVhVjY85tnj2hT6HbePae2bOkhQ2TTwDQnYqJsaCXSZhsObEWmojjAUgDYgSTqsEbK5lVtEloBXIjRFS14jBYKSBYbOwtGXLYS+qO5nmlg8k9aUeF3YYtM80rIfKDwMDUVWFt0BhCEUaFvng/tnxyiOEAOP7HfGI8gmCQEsJSaWwMqvdOMJkKi2Bltq0/ohKV70aQh/pVSxnCLEWoKKbN8Hch/WJf22IouHE24ZEs8TKRrzZP/S+bzROkC1M/RUkkAPkwNCgCVaaowBRr4P1xilHGKuDpfsA5DKu7EdT4BHVEVbxpblp3KT+aktrp3naTT3gV7cc+qTV+MggTJHEp8piGEeHaKaSpSguv8TtqzNW1jJ1FanXn1I9IHwUp83A5xV3k1jIKAnRoPxrmh8B97LdjWGl+AoOwYYNeA4ccO4uz0ut+jZrAIHqSjtTV8zcILEgEPGrzCQIzRkB0p8e91TFMoycpV4UnqdpM+ukBnr84Cmsnx+yQcVWMwODh7qhHqnxHnU7dIdoT5D1tZZIWKA3l1vG8ZlA9u9kSRMfPzBTWWQywHF9Fcngiqw25sdOg09m/Wjgjk2FgmIVxECG8CLOuyOqoU3r40xX/9YUhN6lVjMLBZkiYzQv2xAOGz5Wj48icBJNvAr3ppptSUMqNUk4W9E6bkTBldEHvqDuImvUyVaGGaV6BVjmj/w44s6owccXbISqtKiC010RUJmTYOWYS7wGjGCB81CFUrPkTjdcRRxwhEycjF7G+xhf1kVOqD5MpbcgAhcyhWQwntGX6S3IAnY/R1CmXEHfCojvaPgKECQnt6xQT1BRjQUZyXb4k1NZVnFtuIBIFHmCPbHRTPpqFubp/DATkiSJKaglOgJWS0PCeOh0ddA/TxlTofSOTNYYshDpY/V7b4VSosu5z7WEPBDBck7TD3aZ5sK2wYjwG2Z2sTvluTg1GKZCMKkYPM0CosK+GAD3FL+sQHmxMkc76qncGFAtXvpVxiJvYWYbYPdB+XHVK/gaBWUKgt86s/8xC8gkCM0aAaGGJLDPjcSxUk8TCzqmNOTEvZB3NR0VamOibAXv6M8MlFTAPNQlmbExkPZTZnmoGw8w+iRexJoWRIFfQORgSoSQe8YiCAIUqKVMCXTB7xplQEHUS3mn1GI/ZqmAOfAV7QDXYyIGwzapkxF/2XnRLTf0FNzAeFYjKho3wNYyo0CFsDwWsOjEMNttUHtcBCyWsgkxbDdVsBrjlTCXBFuos4lKFywyD17SeUcQ8YEKvYvjZS+MCNPgjXqgDhAkeKIgmGVMURz3EDP47VJU8UJGt6KnREdLLA4LyqgfPQ2X46chUlAbUh1DERYIMMfN21ibsyTTc3S5gBnik63Yzl5lGN9EC1eqp+w23qJ1v1Iam4M0uqtfycSwSnWbrOwEGkyvHFjJKCNEqMUYWb+u1izqkee5MmAy0s9skFeq+G8DwqaQAIeoIRmY/ZLrfHJWWCXbKmdNxKTndegbSmo2vG5SW370ZgF+bhlMZIY/TYF1exlKFtd+AthNbAsX3aV+TCAJLGoFZ4nepdukgwFozD/pr6w6/JWaPBeJsIqTbFkVQiGl020qkqzo0iPAk0/H2FStSTwW6MlTWv2AzdfQOd7gD69hK1iobjiEciE8N9/Kp9Tgsq2p5HFhiMoOIEySDXORc01z1i6hgFFtVLVHqDqMiR7QKa9GK4QFO1KNWeDjhdRZqZjJ5uxhXIoToXV+5CZgrTbVACSDiijjpEAIWTu94iDRPO6tCBph+oBg1C9vQo+ELyRF6QjkAtYgTCZeWieRhadqJCzL/JRXgo1xUTC+LrmEQVlJ3nEVF4+NjOykcihkgOciidewSOBBgWXe0z1ftqVBfp2NU+kJE4W1pMgOs8FQXNXwkB8V8QMo8y3RuaUiV768V4+3eaJlLMIGDgpcyhJaN7j5OSUIziKOL5WgQmC8Eou54/OazJBAwx+VeoV54KAuD1WfKgcgAQR5T7D/jbW7NA8JXQp/nRjFddm699twkWFV8YXJM5f0VqWOazmq6NB1IggaD2VAa6BbkfcabkSBsmO6zuBU3wyrjUsMb8pZsQ8wgUdAPSgaolgsnIlGYW9fXCf8y7drjEkQpjxuePlzHhbjA7IyHVWAnxCFsxulcRSWQ6CBFqsWx6j5lRQEYIk8TXkgmTxlpwStaXQhZ4T2RKfKjzkU6cRTSl0y8R8MU64pSulOvPm31W9hMDillwl/usDpUrqtWrBIkFrRsIJPaMYwPpuUzULK+ooMT5i+1TG5foWzQQ+hH9x2hN6wj7orRp+doEFi6CMwXAcx1Fw0CdBTWGplg5wQ91GQdv2GGGXW8hF0UFKm/NBi/NPae66Fia/AANp6wIZqHJkF7IHsoabJLRKFGYE4lWshEbmgPZsAidUr7EaXB0UN7oDHgJVxgXEUMNoZBSuGnED1KRGlxNoQKAgYaxAkyEMui/vrQJJAAC4YF1iAu3cgS1ARF6OZcddL//mt5Ld7+X1ZSQWDhIOAmNzv3C5r7JtNiPQE8MXju0PS5b0CuOBYEeqvu/MfBvHS5Xno+DgTE7mAVljJ5VCEirUoyjGAXVAMHwkK4OQTiVKAD4YEaz1kjE1siBYly8IT1V4iDmW6rpCcJcdY6Qu/RwRY51JO2pRmzjYCHJNXQben+nO1rTbH+apKfDD/yFE+ZSjGOaeogYU+0Fv+y+KepnDWuMsRXDwqh5dA2BTKNUbN1lGY+tXv4uC6UemYVAZEAtG2XIGMLuJzVa02r8oQqTwuuFJ4AAetHzMYsuC0q00oM3OgUIAvO29FKyBTgMpDZw68ir2lCXELhOj0cneVpkkcz/Y/3s8LeJ6yKo7AUSpHXExaY1UwL+7XNIoDuVeiUIq/FTg3vat0tNq209YPmLULURUATWRGOaZ0+rcIc035QQuY55pxoEwR6qmgwAfs8ekiPuZDYO1MpsWgEV5KwYuK4ebqndaEUDgINgRVbKokgMAMEeHYsc8VahFjO4PSFcoo1zMKWrTBfKA2e7XYS6jgQzbyHL2T5vRBywh7twVHePQFPnJKWbfN4dstzZYrUFottT5pu/lym7WJgIyLOzREXxeMtUJ9V8z/i6gLSSafi2UEq0FtJCHOYigarpfXtXBHoIrR4kyuHHmkPZaMg1F0sOcmklRxOWOlGuXSKsbC03t8SWa1tFF9lMmOwyhVg6PF+3moh/3jJaL4FW25l0fromo2v6rpIFcFGnaY6NfSuJVqfE4TX2y2hciXB7kenSdieLpMKpru70nA3k7OUEYi6s5RHfwx9F4UjwMUjqVZWj6HGVDFNBBgMNpsDQqjT3ET+ckGKxba+uvYTGmivpfX8IHYSEnsrVJxa4K+GidaiSXQLWxpmZZYVfF0nkZV9TDtnSrfk7KVtoGcnpBE+fZIDFw8LXevAtURhah+0kQ+x5xI0iWoh6i84jD6hy5YlEj5FkjHSvLcKW2Mo8kxJPxnTA+bcr8bpiGOdLhMvMZRkD1FiMmuBoemEcHsL95h8a84JIbbMdmkMsqkdiE5xRyvgHBJ1juVY7YVV4GqaoRL5AxJsXddfETNEHVe3rYAy5BZfBdPwbXFMiGZTwIAaLNH9VhRiMHxPWl7yTKunmzCUIoF0CpupfagdtUbPR6aoOwE6PhqMNrk37Edga1AV1nAgVTazALuLes7oCGS69ScdBKaHgBsrnyAQBBY0AuiFnz2LMpZemK/bMGmZVU24vSGjziSX72+gBqFduEXLRIN86D0m7i3TCjsR7uwcQ2vpnCVmdh5ieu1xgFIrL1ad9ZVup3QTBAwUig0W/y6M3SHMyfo1GxbbH4hDSvS6CHT5NA/G1SonZht02EC3nm5aUDy6oIy2VT4Kwu66BFJi6Zx4fLqLQ8gEq1xr+5XHTuw4JYerl4HH/yzT4zirkpb0a4lMp+ujTGsJcRT8AC8UkVOZuKwNdbANXbOZgmL1qSV1tdOPHMW0p3bRtIwOU4GVfMoQPkTjkbb3ld0Q6vQJ/yJqmo12tKPaj474yp2EnaBTdcjyRoxnmSH5EHC6rRxwJoKf0dRsRBBLq3rK322s66sRqV7XV3/dHuhdbQLZMpPoOQK9DVWOM8sPPJ8gMIiAaS47N5g739895pg9xr7bEKbIon1WVqLlE2D4GQdKtqPdhP11WEEREpVJmyEksGecCzwLtdWQQx5hCIQZdm0uIIeGIfDFajuZyESdzpyXWTVlr5zJ/mJF5vSCZmo3gSrmcmwb4y1gxYeB5KBRIQIkQWhRwFmTzfKZf3yIGMC+0j84Ynh2UBw7F2AkouDFixAMXEvL2XUag+77CtjJ2kmPoabQnxqYNjWwDJD5t98x+61t9WIp+ChG8RJ0wu+J6ADHukLUyoaB9pBEF2pTKJ4ju2ISS8TfyKH9uDrk0QtCkW0IbMFQ0SpCdKkp+JavxbombCeWCXn3gKMifDFR73yQRjFpSyXA4D0AnPD0yTLhrEmO4hxoWUNAwq4H1cLJzpWPgfFGgYWIhR7ZMQvjBFd5OUecOOGh4Tt/wmLJDAKTIRC6MxkyyV9CCHAEcEMwqNVnptHEnRk2KTfnrn16HDLzttyM3SI8jDCQSirAmPl0ORN7ZqLPbIhjqNn5ZBDbz4axpHNwo9R12SqOCdaC8SAMiNuQz/azcCQKfMUM3rxZJq5gcs8ZhIXssMMOk11Cvshx1WI2KlRYTIbM8rb4K66Ct8IhmSpXWLwFo8VUV52MFpvtRJVw3NTmjSwcQYV97XKvKj/w16Y+LDQXCVPdDlGVpHmXyBIvfelL1UbwADiTT3vQWWoKKtPKDyQUsJURyaR2vFSzbRKtp+MiwQh91Fl7CIER03I6nG11M10DbOfoUia4aSw8rD2l8CedAprKuYRq96OBFvrK9uNJro5+oTXoDv2DLdfNGkE7MuBJbckVsjXFoDFkTv2YrvFCCqU5HLuOwuHGdHPq9G4OumPc3cNIoR9Ic5WqFv2tF1Y0DtQ9sdJeSaab9qeoHaGIW9xkTtQ1PMyd4yYBmmpxRMyPrGUsQNpCwv0MQWr03Ql77LFHvZ52+ELJCQJTQqDnsliat3AR8FhneoeFaM4Ljy1PutY1T0wrQUzEHZL2cSILpABjwGwId5XmLCDs4x/MPJHcrn1VA7JiQk8DwEXkeDQzzFz+eIAgWQGYyIF8FdItzMvNzmkPcuwiqJgdBT1q/VpUUheqp61Hc5kK1kth4ZMexCQNJT2s9U7mhB9PbWX22WcfJ+IoVYZ/R6aaGXKJ7t7QA5Xw+BADvOSIYbY+RYItrPcJsNYKYzPm3BLspapswyitC7ojwcXAStFOpEf4aByFj9NZWchYAiOgRCZvgky6iHT7qFMcBpvEetU7pxxqzixQMGCYWSuPlomubV8rMeDMqkyWTOBRK0mecXX8suVUgmkU0UwdQeMGDnW/aqTT8Q+iggS26qgONjcfbDE2mcalrksD4/yiJHXrGUi7G90JdXfVIbTMTgp1ixpKApJ8pNOCI4niDW5LaYMoaKaCiI1RZZLNuORoQvxZ7rrCih6DqPkhuL1xqdZmN7Y2o85uftG+6vTbERWkg67ovkI+ZNp40IXc7W4VVFWOnaXwJy0nYvnqt6AA5Ul6+EPuQq8VNr4YG7qmDI2zvYPCKrA6C56GG010m2Fm9ZMZrlCOwCzsU+90Vvv9rquYe4wc6FfJw1U5ukM1NGqu6xD3ZasQe6OQVXxVy0yizwhgtG5On3oK9aep/5kO5hMEZowAA0MLYfCQA89Wzz5zOCGZ3Pb4AdPuSY1bsNAu4bmsvKcwRcGDklvBE5PAztaaOyrpb8UZsIKkFFEXXCqemCboHnlskqo8Z031ah5cdTrKvnpYm8TzBbAZZTlYTZv5mlyKaTBJ9dj1zGWz2XKRp56q4jZQE01lk1gdFIod8tg1t65lL76ia4yEC3kEuwRTpP1Mu5ZPBhooyDNqY7y1gVHUWkoDo2jyylZZ+TKwpqZVhdtRWZTxYR5ci6rBu8E8WxlUPAzPqPJoELvLlrTTJRAylA4tEOta5btHu2kIUJvQKY3xSOoum2K2gd8KQx5RoJQU/2v5s5QwoUdqCWCsoI6AGoMh2BBFRi+hYqcBgsa5IbXNLeRE4oSBQAJIVoYPyWDF3WnuT1E46IWRxYD1sRSRgU4Rq+h88HF1cpRVQiiyelB2j3Uyj9ATw4Ti0Lfcpdi2m4quhhOoSuMNvdds+YpXUcJk4ql+Ne5t94a7xb0nE79BZzFypyDWBr1aojbUmahmZCvTFd2l2qwvyK5bhXxCO1Q5guuGNxNwrvIu5I7SeF/la7MrVrUDf91USJIWorZoZd3zfragK5rSVkXx4vnN1p1QTR2oqn0l2/i4OmFGj1q+X7ffY/sqYXR8ujktrReWd7WvSQSBmSPgXswnCMwYAcTFzXfggQd6fuEcLE3FIZqlsdAMSS1bJci7hMmc5z7Sg0OgRB6aMk1PRQYw6kyUGWrFKnKOlACDP6nQbjfVQo9jl2MIW4OZahditEw60RFTbbZHGVoFccW5jIH6MSo8TLQBPkQnEBLhWioR5MvIVW1MlwdrpQdUB5lMnZI2XnO6zrapapXv/mWfTMSLHJgct0Om5ria5z5nFlhafjdRs3aWiTKBf1AUIKMAYBnFKsl+A1xalAZuV5l6x1JKgwK8WB1myblTprrKDPzF/you1SwcRAZCAegxzGpj5h3FBVlQpk6XHWXLdYHplcYe8EXW1MtTAY5KymTanUjIscO14a5Ve7WSyzBBQ211M7hzjKbraiRAUJM6HWVxCcMEauzQXSHfR/1YbKUn+4u+oCPchT7cXiyokoaD8TayhBxEGWtERuVjvaJhNAnIoMaBJqyWMKO/4pQ1QALFUczoYD+UEmE3zvXRU+NiOos6Q75V5RQ3m3ueTtkykwgCixiBqDueh/ksQgSEVrBY5tCe6e5ysrm0GSHzQHUobd8UkN6AvrCCZr1eocWIMgk1gzStRFNQEyq62SS9AUxUmZqgIwdmrk3PGECQFMSDYxtWS2/QGpZSNEmd2EoywKypdrJtaIS/crTN3LqVGZ3wYNIFbWah9cu1WD7Ta5nDJ9qehJdEN9VPPmH1q4wTec3IRayvdrJ/w+fKYaEpBIiI2b+gTsoWM0x4gBUwUS4Gm00FNe7lKqb4Yln0GsWxokom02v2j8yZx5sZs/oTXkgmm/2c5zxH3AllAqEpKimYBpeSWfGtBsVry/jOlNRyFMdw08bQVpVzzRgdPIZ+VmE3Wliewde97nXMPw3PLcFHCQqaAeTRL3QKK9VI41IuIUSkdrUhg+kyCoLRYjzdMB39qhZO1h350PAZKIAr+1SmQWxHyVdTiQXRBR6idlYl3OQtB7WtNI7YMluCTKX7BrEknJafRBAIAnOMQJxZcwz4Yr4cWR7/wFfMsE3WaQ+MmZm96TtrTadhJFg1i4D4AmqrGHBQxYlAqIPwXuEFnBdMr0yeKdIFYmEvOxyCujCMHf7EMUQpwSRYSqGRam7OHe1xImagAYJgVG6qzV8gTIFFxxtYUwKGyAwzb3qAixIkmGQWHeFA0fyl4ghxFbOCo9D5sQHyCYuu8uH2yNF98g9mgJ2o0KXpClYJVZddhYklIwlGmfB0mcqjblrIu1fxwjKxCvhgCWQz7ESzsUYkA79BdDC8cpPTRWBOIVMDlsbElhtxwmtRm6BBn9AXDWvW2hDghUZE3yl2zsV+tNlVAA4ElTsFg3E56PGhYJx1CQXIUc5VALMsn6PKy73SbcYIBGpdfRUmrvi4W8hCtKVuDQsijb9yw40YhQXRizQyCCwCBFbwTFwE3UgX5gsBfIJVEwlhnw+yBEuPu/DIiG5BQZAVhtM0neU2O6fi4EDMKlbEVCMQwm4svhAMwR5wBwhG5goxn+aL4SixA5v4HgEKSAOOgmfIQU1M1jmbCCe1FNbaY1IBBFRO1RAiQ9LAURhm8RnCOZUU4oAGIUYMp/bQD5RUM17CqKtWkIHYC5YJB2KzNUPgpF8H1UrkAeNNq9AG9lt5EkLxgAlhd5ZIF1wNx5qwQDKnjgBOxodlgNCjEpCmfm5KBoEgMPcIeE7WnNMcbOBVQnPfmO4VQ3e6aCQ9bQRILwImOD6IIiJnqTike74PngIRIRQaISxkEjIAyaciOvEGAgYCQZbAWqg+EhXPS9eR45B2WKiFrziRRkIiKicUgoJw8H0oYI10lTT7pzfIcQk1ECFqeRGmolWkBdyFKlO+M7Em6izVYdq9zQlzjoB7w5ARBY3anF98Hi5ItyOPodQ4d4sWF+WGiNPMfJD7clCaHrjPu261CZsLQObH/T+ZR3jCs5IZBGaMQG/pztXMRPMJAkEgCPQWAewW352X5hEXCUvciHNzdcROkBlXKecpFyEHqOsi/WRC5L7ELYKlTDMH+iLqs8yGCQxnt1pI+zLLDxQQRCVEbG7irDEzsV+G2xSommF6U0NvDgMHkyL5Zi+EXgmOVJ5xcnIVNtFyOmdxfe1mkpM5bbv5Sc8eAglVnjFTzIlBIAgsAAQIbHQ+chobLAZ5LC1m+SypE2DEn2VHvrHUOa1KRHFZ8cflyic7rRNnVpjBthMPlmMTgTLz6mHU+XZJPkLXZRI7ZbJV/AVk1GVeSFC89YnDfkCxZQRUIedVA2e0ACwaKsANInetvltzwP8r4k17uJgNh6htstPARZESAemUJ6KUs9wJ1FNB7k5BPpyuPOW19hSQJkpZv6a8Ym6VikDHqJyC1Ylk5/XmjBb/h2vyettGS4y58DXgWKyH4vCScDrLxG/g45ZzIW3DC2m6QumxRhdCjATIS4vJI5W1dQMD7c/XpYLA7FG81BwEgsDSQYAyISLKc7N28RlLx83yrRJnhhm/4QrZsAnzh0tavsejWtrA8NHRORVnPVyG3mD1HIs7fGggB6uw/RI+QSnBJBx1Iuoggb7wSbHK0ngViw5ANhuzqY0SLOyqja0tvhNeVkvouYNtfiNODmVp1+JKttROJBynFVGq8q1/NCiIhXi1bkmEwHo6TjGqjxM1BhuotX5VHsVUnmcNvUCwbPyD5RCWJpR5QGGjBJyjlsUhprzMljGqQbC8Xaz4tdVv5WC1QTHrFi3jF2bnPVmV6XSR+NJC6NA4CYjhQzi0NOggg35VYeoXBLS8vmqA00V3oT5A4Lkj5zgEDW5QaYSscqp8/s4qAr1VdyZeXeLGyicILHEE7L9n1fQSB2F099ldC/KrjCVprDirU2+AGn1i96gnb/erdD2LJYRbmd+b7pMNfK2/VZjdZfPsrUf2QHpcuvKH/wrtMo7aKXbeejex6lXGxjliy3zwjOGzWo5oMLtlEga6JQXTMNiICDaAUrTCwwklWXoag22NeKkQCLbZPgs2F1CYp0klxRKwOiZcJq5jeV3FuZNbKuZGpq2qrNRTwHYAot+YcCJHuyIZhopDBlOJYrX7FJYDGfwDoWklLfUXhm9ZADcQKkZS0kd8Bb2gtShvj00kTHmUyJoDDUZ3kEsqC5Gm1dMSyI0eQVjNVgZgLSXzWLKg+6QaEFF0irI4C4OhltmaAUWu8DuZNBjijYWWTsGQ5CBDAraGbw+HNAktay/tQmQBq9luFSAYFBdVTJw7nyCiZhsFPZWTz5JGYFZZXioPAnOAAPHcxI61sDZ7XJfzaLaazDSxTSjHVfNAPWwtT4EudPPN6Sn8M1MjuvUMpIkl9ADr2Cufm8MUnKOEJZNg/Ep74Bfw1S58o8MdLHZDccy/GR5Wud7pYd011w96AT29YJLrWuiCIHQr7CoehW2GLfvkqMVxThfeKM1MskyUDHaarWXUZVI18B6WuDSJkjRs+cNI25aJfkAUGXjrRV20/oLR8hAkQE/1S8yvfHqDeT+La8EgG0lR6J7STeuIHYYYbN1xIX8dtUMBBUIEiWYDwcrE7indtHuSgSE5yASRXaElvAOrQnCkbXyMD9UpBkJhywzra/1lyGVidd1MaQKMt1ZVJlUDvNxGvmI2btruzeP9D1YMVEk0CPIEG++msOTQisgauFrkX+oRatJEl1rzqGF1+mR/cUElBd+gOxqjwXDGe+wV6X4zZPQtqzidTg9DYa3idPtpVbuQX5wxJfm4fyx9qLdtGJp6OcmAuqPxXGOtMTpLmrJdAp1M342Rv5QzTBHBdT+burhbeL7aKUnMHgK9VXey744fZj7zjIAfnumaRzDVfQZN8VxjyUz1ymE/gxqGT2GYTVW1pybZrYB2Slf8RGVqvKctosAkV74y5rXSnrZskjk9s62wfARCYU1lQeX4atNCj3i7SJvmMvbsjYgH0Qnssa2GZKpfJhOlTmKGar0aQp11dWaebMByIxau0vYcqqPdv+QEO+WIscBIVOUQK8gMqBmxcDnUgZ1jFWwBwIproYX9pvWTbe5HFWCnSQIUheq+Op3OPvGSOJH6gveQDWyyR4Dh5NJO1t2+hZDB8Bgnp9hWwOVQB2mmEZNAhoCgvLm+TCXpGSrEbMgkdB2Z5ARqjXHHVHwd8YEYOgV8akErphKeDpsJwRxoXluh8na0mwCLUUC5BIVA2EaRusMvI0evSUes+whtCc2qxYnqN/S4kcqZ87qRpPVUhd0rTjGt5TYoquAbLaFeIKDiVwyBm9bRCesxBJQVJNte2IYP/4PkcMl2ulCedtTtit36tJxuQo/cM0gzRgtzyo22uRlARKxy67rPUSs3PMoFScVQH3cRLuUQYN1v2Il7GymsXS7dG9Q4QTyokmuR2XRZF1Arw2EnLZfwcTnsUwLCrqvNLme4AUsxci7Gow1u9W6Dk15qCKy41Dqc/vYQAfZPhES9DsmksLWQ8RvtKaiSnrCYgcdibZRHw1BhyRjm0Cx6t85WeUuwtV5ASNuviXvle4ERLUGrWjEJdZqYehkW6qC8pSIybSFIWBIDwf5VYVfHJCzRp6trm8o9bR1ihDzQOUFY2bJwpv7lNTB5rQ+7pSTbz94wopVZPAmrYCc8u9l+fEgx83hGFEehnaAOrlUNGP4rysH+hMJBUEN2UduUQX3wCdeCnr5wIjAk1A6+AI4eWwfpCGsxXFvleH+T8BGmxY7YJJnaNtD8Xm34mUx2t6ymGb9LkzSYK0yI1sKDQxNqJh96DFW7EKGCDwJLqKhYdAfmRUeULL2hFZ5ZQsPK+KEy1nJ3rz5QIQ9Oa2c7ZKwJNnQIAgbGQFpohwYSQne5Ztw54KKgYKUKoFAwwRSl3QCGACeQJuH4O/CpTIWVBG8dRU/pH7iC8UJ5+Zjc6uKc7HTFw8XthfdUSayCjoIEKOkOQVYMEEj5nowv6cgPpF2xfiluTlwfpZOv+zbkdD8ghW6Mkppa+ZYAkSHWWee6b93naCiU/ATcSAKnXEs9hhVi5Ew8BvXBpFFtIh8ugntpqkp4SB0tXoj7qkFnzSUEJPkduXvJgVx7lDaKUf0GNcPe1r6WJgRM8JqrOEVMND7HXUgJA3trcBJLEYHZU7RS89JBwNOTNbVtIDvq2coMe8qY3NOcWcSSowsN9pvd8nRDFyqHJWB4zM88ktgPn8onj3uieY6bhY+OSCVv+Ol6xNeJpoweux6sjJDnpkPkijo0/FfLPXDpBBwBzLCZepVhMzyLNbWdooOqMgdl2skzelriPBtAbvEU1t/m/WEeFC4XRtWAoHjs1uuiqFDt/dL0D7QAC2kXkpAp+AD1aZlsA1LFaQIfFkvsrUNaaxJMKWEwRGIO+zva6apyLpPAnDhdY+oQU4RStGISQODgQEfYBpN1bKZ7dCBtSt3Gqw6J3aGUSLuiLuiINLPH0VAFqr/SzCfGg8BJo6rl3HHnGEc95bqiQNQpbgMXqrRZOw5aaSat3EDF4Vi+yh/+S0tgNY0OUYfJVMBdp3fuRg4O/XW54bMqB4dmayvW2Fgbd/neiGJ8SREoiOYZgslOZ2WVdCP5IbgtXVFJvdZyNx5aACUjAhZEgePMVwzDfYsbKYkBGGKZsHLb2DdcJn5Dr3IToqcqp2rI9FGJrxrpx9UWzyNzrlsl2w9B+4XvWPQkjKbuPT9bpxtuKCEc8ptrGAfCG5Qf4THkPPKT0Qb9Xabn67+NzZ9Fi0BvnVlXW7SQp2NziABGwpbXhJJNNZOrhyz/Oibh+VuMx7SP8WAeqND1UNZGE2uPV6+39Ng1za2HL+vCbe/hbqJmUljWfUSHWL5mckzc2VrmpJ7XwhXZACrRhKeba4oUqUPiCZjbVkzj0bX2tWyJvx7o2mY6W4fMNQk8/EQ6Xo2XbybNxpiLt9NL/GjzS2TOIeXxOZ92YpV3FRauS3f4gJAATILmZAluvT+1CpuFm69TRBizgXra1ZlVxpXMAG3mE8upQ8N0R8PU1k7kH+n2ouVXAgsxmtIm/SiLBI7Y6A4TW5EZtQCYOVcAdHQOidI2DDH02HsGnmkvhY98pZ3K1IcqRg9jTWlUYlexw3qfaI0Ikg0TQ0zYuOqMwf/MP7qjjA/CV4cJGL6iMhxkRUMHT/vvd8YeWzJ8WugOaWVQRoMis8vm29GWqGAU95Lda9w5LV/CV15FPaVHup3wDGqNv2g0PkSPUaZlGgU5CshUXsLf+rRBd+fLaV/rWr5eVfCvyH1l5m8QmD0EQndmD9vUPM8IcC6YaLKRZBUSQgVjmiyaztaTl5QtXEArBbKw4kyjtPIUaU9zaSaBS77bDQ4as3/T7poEm0N3jw6nWaNGdxz13MeoqphJP1m7yw/a6eb6QikJEpXDGJTYUF8H6I5MxIslxoFYyirD50UYYKdJ9xwuzdIM0x0ddC12F1ymzk6pGrh4oMdtBzdT5AKE1CET54OVE/1VAC1TLUXH04SSxPbjWBQsPjgdwWbQoKpz+K/YIOQDB+VHwMMwJzIJG69HqIaaUdVStvBLdeqUDx7gEsAcrrByeNCQPFCjIyU8AA2epcYZESJEySHEBu4tJbW2VDHtx1qwXkIXTEgaCBDHIjajg+p3V6jBq0bxJFzHO7NkYsYYGGSqAfQGHhyfOlqZE/7FpJ2o5qIRymAYauOKGtHBCatKZhAIAiMQ8Cv778ziaiX4jSg5x4ei7swx4IvzcsJTBLW4xck8NYVluiyuqdkkusPQ6rm9zkgLBYFMqkbN+Lt0h+1p5gdHIUjQD0oPGIHdAN1Rkr+srCYqoGHW4Ex4Oo+J0EiTbEcxAIa/nB2+0qVYa7ytnSiqtDSMlkPJIKvQSMzdERTUhC1nVrEHQSEMebkklCfVqI2WgN+oRwRPVYLJCYuupwOUinO4aL2Ti5tPSV1QWFgu9JQkKqAFcnjQgIyyYBiAYrmrzuG/uAUdy4JkTaK1+MjBujjmnChTRwR21IlYCGqicINiuMKWY7CQvK4QRa5oKoKjTaeR2ehgO30ggf1oZ2UKG+LB4RUdKJOvQSAI9BmB0J0+j07atlwIcCKYhaMmQl8ZYxP9qo5VFtKLyogtKOFBRAuhRfgLeqRki+fg7MdpKB8YBvJBdeCnwB6szVGnsB5WeUQTcSyKhVAM/KnqJCEQMwgPxBJxLWSk5sIYrkertNmltYq+Uv4Cl67oY5WjBc4SPaPNuqlHVBbOO4qLyFPEjrQgU5ikhCsKByHeUCAQCDa7rsjwYzZOqcyujKT7qIxPN1MlcirUo7WZfqaFfBOVg2QQY2g/U+ElrZI+JzA2dwJW5yOoOVynz4M1S21zhwt667qVZ+lCqXaWEOgt3VlBhz3E8wkCM0aA50XUCB6DGXArCOlFHdSGLtReapYiC4HkNJFJ3rTaAkUQ5ik2meeirosoUCwoImiEuE4F6C6IjvtTGU4QushkLcSTEAWMh2JBnhFsq6SfHHfYZKfMIN/CKLIHsuJci5hIMlwwPD4zqCqnjEAA4xFHrICQHX7DESWXwqGSx/RUgvcNp5cQiOaXZfnbokSgnhtCpsa4r8SiBKq3nfIkr2evp309jXvS1NCdngzEAm4GD4V4CHSHsCEU18IZrEXwja1dERHPaDpNozX6ad7mFErMwuqziFQ0jtMHrxKmylnG+dX2v1lYfUlrp4UAfxy9kKjG1zZizfm06pxiYa493k8/Ky5LYdrUQUqkcDRR//S/KVaysIrx5Ipys8yQKLuwWp7WFgK9pTsTbxiVYQsCU0eA7iL0daC82SdqL4TFwqWB3Ws8tX0Gyvf/qxXXgm/ISJrK7UXKwvD63+wRLcREmXDB4yPKLPMQKsD6FsddZuFuAdbaiip3AjYsnNmucd2jw2l3FH5pkzqGf/jorObg8byxIqjEPDW6Q3cU/sxniv7O0tX5VS27E+DPMcoravdFW0SaRZgwoN0zvqhBV3Pdvf4aO3/NWIij+mIgeEgFb9lewdZHxlc4mvmJGYuS5T/1kycyEVBJtgLyaE7VGCsoxewboNr6sjJ5gfm7MTbhfQLCZHJXab9iKjGgtcWOfDsfCtiXKb3Qf1zV9/ztFwKz5L1LtUscAUtmeKC4q4SbLHEo+tl9dsWac5pzrZOacSNr4+MZbLViVRcGiWwxlhWLPboNFpx7dGLPo4vhcMoscynf6EqGj1rD1cKw6igTrj3C0ocLjysHL/GeB7FZSE8t+OfzJXvgPQiHHRYsDBQ738Jc7LzAw8VZLNO5EzYDX6kNI3iKtZ8Qa5tBJYXLoB3ojrV1ZaIqur9C1qw6VJJ/WbX2iVbA9kj2uUaALMWvCyEr6JE1gIRbG0NUJq6mMLIoGMtCS4MuX/S9qHyh647aIKDC821FIS0YDhlyyohNpKrm/O0tAr2N3cnKrN7eM2lYHxGwlMzWwG3l0ew1kTeQ5R6of8LMgTJT/MrGkArYlRHruaZSle0ZyQBTKTlhGfvXacNoukNcIW/YWte2Nw15QdzGgnXk3/Epk0+KIEuokMwg0JuEIMd16U8uZBE+ytJ4ACLOvqIRaJ9YMbodkmSNm1B6UVlUHLEjItNlCrq38g5LIDxUL4SlW5FHsZDJxVmL8IlVIs8QDnvkCJO3uSJVf8JeTzez7W9UJ9aOl6Lvbf2nsxWe76KEFmE9ouZdvRGOgWsB04hb8kYlQimQtsZXBOBjnwLzzVWEqVF0OKOpLHiMu8VRIq6QGmAiNJiWmkVZYTzWFmBgWqK8TNRQJvyl4YknGSCkSn41BnR0MhSqonOMrHx16pcEeqeq0J3CaiH+7S3diTPLLyufIDBVBARS2IvWk3q2Q/BM621749NtGSNh0fuM3U8enSb3ZvBsGJ+FvQBqn1yXqHzmHD8gt2BaMgkAthUQpVSBVi5tdm6dHTPPlivAnLOLAtW7jZQmMDBa9kyi37RDdtDBMNi/2hWw8uu9H63MhAm0psI47JT9iEc8opxHmoG7iGXmM3UWjkLtsDKfcRU/rjvMtr2ISsPgQ+ELs1sg+2rVfQX5YjlCzu33g0wIhbEjok2VBKQjN5xr8LfHsYEGmrAtOWhu87CgNcgT/46VgxCrfEv67S/FzPPQaYN80E3Yo+XM1Dt7GXDtqccQ4GoS+muhgHGBj+5MdgmyEHmGA1HvoGq/AxILSmcfbSQJCBSa9nKxyhc/pDbgYIT8dzB084BFJsEGVUWGXBFBrDsBg5RZr8uw4yjobD6Jjxp6qyC13KCQcPi2dAT+hJ/h1rrxErszDEtylgeBFZfn5JwbBJYUAqQFPiAOoAGu81994ZwBKAgAPB21ksuh9hVjMPsxCxcqIZ9hUIwZwDxaDXbr8bhnZRVjzgkSDqELJArqhTk9m+GtETK5oqx6sz2PTCEXrYaBBE8QoyIC1FQeRWC0FLACDjngs8B7CAOuiFiwWFaAkysE59qLmY2vzYuRAwEZ1A4lnch6qUH8DcXFrL17OT4OJbWcfsAA1yE98pImqoleuGK3/DLTmo0nmfqLOGmF+XekqQh6zaDWGyf0kRTB5GMetjrEXZShE4AIy9FyPapNEORjdWgZx4o0gYQ5l1AGSaJSqF+mnKIyRZt8bZ9GfcSv1FGMAXrGlxXn3WPIW+E5SGiP+xMOOmvjhtbN0ZfWcjdS3TnIrgHt9hQZcofUrlQiiKHto0KZfggSbhj3HgqFUBodt40YIH4xOhBuqoDpgbvF/UANsjsDfilTgL9ldzbTwlmdVXcyBkk6cofYkVKZ8hVK5BMExobAQtTK0ua+IUDf5p73LJtxw1gI5r9cD60SmSy9T3NheCL7auLYMiXo806hvZtlVkl/0QK2lgDAwvE4lLRutsorIYcm0a4yYUJ5+z77sHlVv2K++uFRXLqn4DqsrDdPiVowOfbsdpTJ5y9QmE2td1ngNEQRH6pA/Xo5aJT0xFeGcGIuyzFUNfNEMCHWf3nBgkP6Jd/VnS6000dwBucFDYb8oIU0Bg4Cc2jGo2oY+GsDGxdFBeSbzXNjwbZsT2UiN2y/o4aAguJa0gw2QyXBeDudKZLGbxjUNiJoDZMmvz7onaiOci3Z+7G2LHIIJeKJc6Itmljiq4r/2+lqHu3MqsJGkyUuKORojBNbzJDbr4bJVag4rX4JvhslaT9ws0k0p0wdFVvGeG+33XbWOjHSlcnwI3/d0yuNbJG4uvlQciNVjkvDs9KqNZRokzuzlYdqu4ta5tQT3IW4lJvfx1n6gu/WWAuP45KTifPpZt1C0gDBHia7BEaIcIAU98VKq5i7Vw1a7lxCTmXiqTL9ajAY+ZVZ8g8Obd8HlVQmByLKRdAiL9GcKpP84/TahMKNUTgbbsqffG8U0Ze6FppIdVMDJ532tzd2VT35u4AQ6K0zK7E7C+gu6mlTuS0qnpHhZM88qsz8tJXNY+24fsgD3Uf/cDfYzpLBu5sBslKV6bEoPKLOInjwFLDxMj1t8R4TTfNyRwUQkCXq2c1zwaJ77GIh3rdAj6lHv+YRZjzQPaZbJMFweygxzAkdQj2e1PhElWFgTEmd3j2FU0BsLLNtlbKOl9ljgeCgGLtCY6jyJZOI7YWMJz6yUjRRQgG0RqcQMmkleayaBa3T9b37ri6ZbD+qRMlAVmgSTm/mv05pf13OUY2UU2KMc1kamRW74xAHh/Yo4E0g5t9m8/Bsr8uw4qbm67pm+t7a5sQu3aEr+NR19av4q/HFn4xmDSgZqQr463RtGCPdccupkA9F5eWqA6lFQEQyOSJ+YFVXZ7yB7IbBsyvHXyTSDVZaUcuUcA9wXZHQ2iFQA584hGu6WxDTKk/E0gAj2D0dPTV2vE7dzCmmrQFUoY8BwgkwntrBHLsVplPMoyAlsWBguDKcEf0RBIuvjXLjZ+V+5gGslpgh+OpyeAle2Jqn8X5i7oo26M61b5a7BTtsxRylGqL7dRdVvl+owfVxqEhw5cNZTrekfF1TsjHpVnMSCwuB3tKdxO7UkyR/Z46AObfnvvP9pUl4ZtVkTqCoJ6kpIx2btlFmYMLLCElhY2jdEpwOeIZiqA+d3C/HM7H9fsz/vIqLT4fFNb9nQswCMSrlTX+LWkl7XrPNdBQXRXfk+DCEDLzJKBpk50OGgUpfGkwVaH/Voy+MgZXnLsTM1CHWUQdRt1ZSQmc96Jl21TID0GDjNV5fxGAiQMSDKs8o+ogyYTh9ZDqFOKQkzwtixJRiGN3Kp5LWJFeHiakzQJZ5ikcntA2TDhojX+sU/ZIpDTE+MpxSNAb7J4eVpZpw8ZCXeBn0iK0SwKGn7BMWiDw5HVwUHcaYoTXXR2XEl/DTcUVhhMYXPr7qLPNJWVFtOTKwEKNsZRB8Jmw/1xJ9RfOwVcQOmShfEkeJXbMZSPIV0+sq1A71Y97aiYgjrMKDDDftDU91zxDn2u6F2LD7xIiAjgRIzUKIDT3uorNksCKRLgFeQgXOhAXaB08jdRapKo1NAQSiWm4sKG0DQVc4BHGo2jxhB0dkciMSnNxXRkprVYJJY3KIDoaNbJEJSyypH86IqloL9ZcKpYPdwkW4uzmV9hP26eZrg3ve3Wsdfsv3QyhXV8uRmOyGdAf6dEtKq7aixAby8zUIjAeBhUUb09p+ItB1dlQLuTw8+2pyz6a6WW2+PFnjGSqeFA9xBIVhqGIEfGd5IstnSiuTkiHTX06WNk334GYIFWCSPZer5ICzQ6bAAhYat7Dk1UTWWpIqOfwX5RKwOZwvh+FkYruHWiRKOYAcYvIp/96fxSQIzyxKIZ/VF8paen7VwFhSoUzEfWXveVvMhqXZMN3EEdEI2klJBegam0dI42hj/rktwILrsIV4lck3Mzzw0om6ir9IiXOF35qp0zPQPpklhNS6Kq11RTa+TlHeWKBi9bXGl+1HHxkwMa01shXz60Qflk93lNeSIojIBKce869TpAhlUCg5xgs7kWkUUA1wgcjATfbKCKwItj5KOpeG4SqiTMgYQqGF5vCgYTmYSrXWX+zEWU0n0AYMzBWbwICIGwv9UsZR8SLl1AOpHB1RuPqotsr0VcmW2a41kMDwBDsPZPbqq9vMWOB8XVlrWi0sSanuommdmMJLAYE2Oy1JtT9dvlp/mpKWLFwEhulON9ah6M6AvN86a4osjMA8FW/AJGgDdci830yaDeOJQFBkssFy2GD2nn+K8FAlGWacgD3z60JHzOnlF90xuS8bLEcjneKomBWV+FqnD/9lD6gsbDkXGFLFfVNhSQIzXZeZlM8HVLbTUQ41YoZ4oIoQ0hg5yITgG66u4liuQr9hZsgM2sZay2FZzcsxPLactIAfWOEiX83EBod4JWSWA0VHhFBoGIUDJqKGlbTCxekCYmgPZAA5E34IMAJ+qWVqwzlQK8W0RD2kGmmeMjWU98dX/UX48DNpH3FRdnyx6hgD4wsj7VQ+SiHTWXQy4g02UPm8NvABV33112jCp/lNWv58JXSHwAZD0kjdTojg8jQGDbKXjEVJnJUjvEjLc4lxnesNa8YLw5sx3TG+Br2xyXE1LPUsDgR6S3fizGKA8hkPAh5/KqITsNxIAHWHSiHt6c/QIiUTXoYJRGJM+j1/WVmWmNLD2SG0Qhgp3sC3Ui4PeoxQCdIL2RxrYY+rQm4p+SyxfL80j3J2uoJz2XJsgP6hKpbeKfwpzhJnKlPOhE2iInB8CF9AxXTK6qQ6C51Cd8gk8pk3r83i3OH7oLV4TskkvXi3KLpD3ihjL+SF2lFb5JEikBiSDwechmFC3AGNYWiJzlZ7WOKKOVVtyyT+13IbmWT/Kokpcg91cybsERHI5QgPrtsKdN2LBAkfh/QLjIZADDUyVIX1seSZdm4lcC+fgUxfhUYNZIrm9hnInMevumO88FFjQYHD/GqMZtwkI4KsQ4/4ZFhnXM8cnMgN57M8Fxoe3+WpLecGgblBYAUPyrm5Uq6yuBFgO8kzPB0cK4In+Dv4aKgyrKyVF6a8JYAPg0A54GQheLCyWIKvYnvRERZIDTIZD0qJ4FkSBTOMbcjBpYRH1PbzGAmpBqlinrElhkeCW8e1cAVKiWJluVWOObnnRVcMhw4Mt22ZObid/dNQFmE9TB0246+1P8s8cY4LUIaYKBy0NqYbcXUjxe1obxVqB11qRMlFcMi9wQEqIGY46GQR9G5EFzhJaaX4+ogyORQEZoaAdXmmhc41PyRFz6yS2TgrdGc2UE2dSwUBRId6JBiWJwjf8iHAVBhy3yCw3Aztm0zQaq1lCDl36kUBLTOJQoAyh8620PXlhEVVYquFUhHPRlfFbIiGNgFocfejyy/zKG8s2ZVZmlCcW+bpKRAERiDQW7rzf+L5iKbnUBAIApMhINBYJARvGtGIRmU1UD+5jvaLjlom11EMJQrXmXC4sROC4hg3SsZ1BGjXxjYTXrFlYidurVo31zKxUgpN+zqthJ2BxImTYCvqblrnpnAQWKAIhO4s0IFLs/uCgKm5yCETGqvfOdr60qwptIP9FuQkplgIy4jiPIDWQInDtYHNiGKL/hAcKDET7lywzL6L3LeCbKCYmHcLDIWfV771XwLYLdzz1V9ERCS4ND6NVYtFE0/WahAsTOkR/c1pK9raOjL7ThlNoe4kqDq94uvbKQMJeyUoKd6IJDlwKF+DwKJEIHRnUQ5rOhUElo0AtYB/ZIstthCaPYLKiLnm4WJZ/V12pdMsIR5chNY0TxpzcdFmXgslwn10vdag2RWmQMAk7M2DLjjFid2IKEqMLQ9sgSOMrCp0FE8S3CaS3SEF5Av5Ep6PaLa3hlEHLfXHPyxws9BPtJn3KriExYkiIUStdZsnPky0vmhr1fJzYTxWPoq5tpRPvJqdGpzubwtp757b0jbaAX7oTgMkiUWOgLDNfIJAHxCwOLxtXT977TEbtgjZbLhdwta0zAzTYlVXyyTY8OlYV2y9WMucLCEQ2OlTKTlZDfOVzyTXai/awIg2lMsDULwnRIhuSYuZhZnXPtrySSDYQ9VmkbxDbTU7kyzUSU7beUi1duuxlMkptnNsmwY5EZjoheB0dVKhLKMTBu4qFsEJo2bpXRfPqFMoH2LPEYJuw1pak/A5Q2mtGQWuNiC2GHDnnXe2Ug9dsD2BlYO1EB23s1DfvgB2s2yvm3BnyhTojRpa0qVm+x0wDLXy39ZQuAUaJF/LXUiovijvtlECpqgwZlMr+QVHK0mekS+ApraM0kfyj1PsKaDXlvrXSjolReLbWIgfTbp9dFydLtdyJFAoOpyEVY22PdTx7tHhtHX4+JB7YPhQcoLAjBHo7UL07Lsz4zHNieNEwGbHFmHZdGeZz+jlvGrtCmiFfKuH0a3dCwde08MusihiJlrJyRLmx6bj5TuYrMy48hm/tr1N1cleWmE0kGni7m2gNIZlXlcIs24O0B07yKEIIksYWjUU3bELMwrIQjPMVS1SIm7J6RaZ155DZYYFwJIuKowJdVC4xldYt0xbAtbpzC3ugsF4IwF9RUCufEv3LeIjhGAnrijHVgUohaAiK/IwDCW5DnECmz6TPRRAHYSKt9c7VOXtr00srUrDSLiKlKSm1GueECYLCe3jDNIqjEXZncie2r7iUhYDYiSislRem1KC2j6HjgLE3gTVEWvZIMAtxfdka++6tbC39v4NDVBgwpeWqK07cIWzRtpcgMzTutCu23ImpDsG0YV009iRfFrhyRKhO5Mhk/zlQSB0Z3nQy7mLCgFz9HpPU7dXzIkg0LI03fyxp03rzdpNprs141jMcNvqpg6RMWxXY8bcLTmcrqgdTgSkp45yEDBXbCqqxGjhE+0s5tOyZ+azZAnXZX3pASw92YA5Fz2qMPGJnGAFEPnBfkK1HRyrKYCGw4IZtla/VAF6mEuwmjK5Wlhcp7O41CahIcw8mapdfcLEMN1hp1lNaoeabQ8NhwoiQVaYUlsiITfVpMc97nEYqtbaxZi+oiTjrbDGoBe0B9IOQch1FbCxjYTttkFdpNbfYg+tYQy2+CduHTmApXAUi/LVWvEB/UbfqTKg49MZGLtWYSW8NNSGQ5VGkmwfIK21tk3SsFZ4wPwbF6wLTdGkEm+6tAM4NB7n2pYay5Ew3G4Y1bYKKzF1uuPdHaATwiygp+BqVdk4qsunJ6Q7CttayeiQiJqE1moYTgz0d7hAcoLADBDoLd1J7I4Hez5jQMAUmUkw52YIW3UyyfIy2YDK9Mhm0b1w0WyYRSfvyyfvs1g8SgMbgYhaEI9JTlCJYmiKcxm2ehXiQDRDuyhxnrBBGDDH1SRtoPDb/U8BlpiVst2fCXQrv5wJddIhRE6Y0FdV+stcyTRZRw4k6BMOWQvDhhEzWF8bC7FtwpwJMGQt6oW9p83ItVlJ3hlGS3QIhgElwaoydURJ5dVjOQ/mIRMmuCOCYm9Dp2M8oj0YaV9JL2qQqNMVnuIHo/I2CWqKFrKaqGGFgNBg8A8Vlu3XO9zF3tM0En3EzAy9wBHSDtKjO7ZARHo0yXWV0XiZxnTEumsEyLmUIaegvxQUXahme+xWVa0XuA5iJBqGvjJwqJUZTmhha4A6uzvu2Paat0vvnEVkEs+EgEKDY6hevGAIcDjgKACTit3RYOTD/t28XWogjMkHhXgdo6OkK6pHDiQFS8n3cwCsu5qbzDtS4Fw/EFSYRlX3qtGsxpsekNCokn4LopXLNWYgaEvkNz4+rit+xiosAFnD+OkMX+X4q8F8c1rYciQ0G7Z+Kd33XnULJB0EFhkC2VV5kQ3o/HTHo5Mhr4BNT2TTXO3wcDf7Z5XNjwUlkElkKiM8gnVkpJvVqcIEHrNSNqP6oKTTTcrVY19js3CTbPMGb3VAd0RR+Gs9bXeb4DqRzeChwIo4YhgnhIOCUmuw5SMBvmoD81zll/Mv04LfMORsZ1XlilrFOLFtuJd+oTv2saVdsZo6RfNgrspC4z10FOSG9arTqUTkB0aXxdX31jzdVy3CV+Sj8tXGKkOSaMGh5hDDydmEiFBHmGfGdVr7xBAwkCd22juVXLFdvSW4e2yQjZdgMAhNt4WtzECCwWaVhUzBHN0pg60MAsRVRNEpfQvzUKd8VpzVF1TkzhG1M1Bb96sXXamWSFPbmnUPddMuBHNWX7OxseIT3FW+UjhAbZdI96Q7B7zoNa2OfoYKYJbqwY+92wspoWARwwyiMngzoADuJsRKwYW1a7Y3l1HUUBy3AZbjdP0ylBgwiuP2dqsYETeDiCUdx5KFNHH5ufkVdnMaU8pcA9+vSTupO6AuKqaYmv1ANA/p1J3uPEEHaXvKjP4QpWiQbpLRxXI0CCweBGYgVeWUIDCAgAe9Bbp24/XxWK+jNBVmQxgvQtAyGWB8SLzqQA2+YiQiTirf/Ngju8IzBaaonHFyiHdGbVUG3RmItql8f822sQ1KEuOBV9GBvMmhjqqZbRt4gRdzMmNnlmoZIcapIkLqKibTCEelmWT2TLp7XZbPRasAEkPvqbS/8pEhAhhDTv0SQlTuMBoGE2VdD33FA8iEXmHWDmNA7EgvMklN6A77iu3hoNxMCrRg4XaJlkCt2Hsnent5hdD66yvmZOBKxuD+K30I/0BexfbycBkUlTD8dk1VP8bGypY7j/6kBiYfy9FNxQwEQobxGBe3hKO6UG0QDMR9Y7AYbK8HkYk3c/a5echa5Ac5LgofQ4lSoALNvVU14AFoZaUn+1ucCSy20m4OUwxGjr4YF9SkzkUpUBaY85EZ1pbJpUhyc2n3Yb3XzCHI4yLoJqyMfnUf4GiE02V22+NE+YVbN39caZzbMAEWD1tmnUpa3N5+FMssnwJBYOoI9NaZFXXHszef5UWAFTE99QxlZc1rqzrMhlCPRpjQtwswBma6ZbBb5nBC+IKFPCV4qJANLn8QE25CXOXtm0eKGD5XDtvJRtYWKTw7PGUDSv6EZ80404PAufVXQiNxEdpAVaiRuux9n0w+AsHECsFhk4RZCNRlO0lQHHlVA7VAsUMOOQSr4wkiA4AUHxJMjTMRP0gjuIXC1AiHaAnq59Ap34c0qQODoXbgjpiKsBLUgT5Rjfl/7d15oHXl+P9xzYMmpXlQJA3mIlMlIukbmSNTKRRKQsoYDeZMISoiZEgqkoqilMwkaUBRaVBK8/x76fJd3/3b+5x99tnPfp6z9z6f/cc+a9/rXve67/e9zro+67qutVbbt+fBcKUoFDmyIc66Jx2Hw4Bt1gj/DQcAtcHBRn75mFa23LTaSuiN/RZZs19eN5krXCBEwJ577kk3VKyE20lMiruIXOAOMbMCRvZVPSFG6ULCgumtEnUAJB24ZDSokOvL6KAgVX2abas+j8v73ve+Wp7smwTEsLLUmzqiTj7Nz1ogWyHtLJzQe6RjPlUZtFqg2n3aWvCTvOgsHGAJBU8pcryRa1M2W27Ocj5NWTkVQmA8CETujMc8zvAo2EImlk1iDtnv6g0bw/KVOuGTqDQOtopBVYcdlUCjjhN047dvhsE8cxK4U4bZ86ptZl6gwVrShwOjqhE0jW+/2bBZYGK1z55xAvEKMOdWueAmGlhT/hJX2wSTll0WW1YokYKhcluQvAcuFj4D32pyAOjtZC+QshW1IaLhETKEHXVFH5Av3vNFBHBp2CP/B3+PFGag3v72t3PeCMbROrpEx+iDsZBHJIJUGGEvDjBSj14hVogJe1dTnoou1S0/QnI8DRwewj06CSNFRR/oqpo6w98jRxgumk+Oi8IJP5JtmWH8aTWVjdGyUfDHmC+tsaC+2UUpRxO24LVoreUidBM+Jpja8KmalHHrJhw2rT8t60PrG810rNQVIehTlaXCcKtQseaL8W5roe0nqaSmQ5TSals1Nj/l98gccgD3ksYEqc/YjD0DCYFeCMzXXJL2Ujt1QmBCAmJV5IicRxfQJA6r7NEjoh6CHS6L+QNcsjOiPBY2t0pchpFTwY05PEBusXGBLheB9JHeIfVS0EpAgX5yNU89iJHJlrCt/AbqgenlP7A75pm7aMITt9thjjzySJmbLnZVEC6xOe+F3QleaJaQsiPKQ4c5OaqQdFDIZmhW1EOhzvvQIoI1E449hTNCQOKLo8VhQJBJJ+reB6EoulAcrXENdq+ftSEQAn0TcMYubyg3cF4R2jfGbDikBGSbSoklnUUfKAkWyI1R+ur2K8ELl+YCN2xSxSa4IuRSSOwgd2RpuF637N5pF/0cLQQHvwKdYXPOG6rF5gIWpWkIIzLFMkXCzWPBqiGFkm7NTQIOM/FNGrTTNTg3d5u2QyAEpiAQuTMFoKwOgRAIgRAIgRAYdQJDK3cSvh31Qyv9D4EQCIEQCIEQmIJA5M4UgLI6BEIgBEIgBEJg1AlE7oz6DKb/IRACIRACIRACUxCI3JkCUFaHQAiEQAiEQAiMOoHInVGfwfQ/BEIgBEIgBEJgCgKRO1MAyuoQCIEQCIEQCIFRJxC5M+ozmP6HQAiEQAiEQAhMQSByZwpAWR0CIRACIRACITDqBCJ3Rn0G0/8QCIEQCIEQCIEpCETuTAEoq0MgBEIgBEIgBEadQOTOqM9g+h8CIRACIRACITAFgcidKQBldQiEQAiEQAiEwKgTiNwZ9RlM/0MgBEIgBEIgBKYgELkzBaCsDoEQCIEQCIEQGHUCkTujPoPpfwiEQAiEQAiEwBQEInemAJTVIRACIRACIRACo04gcmfUZzD9D4EQCIEQCIEQmIJA5M4UgLI6BEIgBEIgBEJg1AlE7oz6DKb/IRACIRACIRACUxCI3JkCUFaHQAiEQAiEQAiMOoHInVGfwfQ/BEIgBEIgBEJgCgKRO1MAyuoQCIEQCIEQCIFRJxC5M+ozmP6HQAiEQAiEQAhMQSByZwpAWR0CIRACIRACITDqBCJ3Rn0G0/8QCIEQCIEQCIEpCETuTAEoq0MgBEIgBEIgBEadQOTOqM9g+h8CIRACIRACITAFgcidKQBldQiEQAiEQAiEwKgTiNwZ9RlM/0MgBEIgBEIgBKYgELkzBaCsDoEQCIEQCIEQGHUCkTujPoPpfwiEQAiEQAiEwBQEInemAJTVIRACIRACIRACo04gcmfUZzD9D4EQCIEQCIEQmIJA5M4UgLI6BEIgBEIgBEJg1AlE7oz6DKb/IRACIRACIRACUxCI3JkCUFaHQAiEQAiEQAiMOoHInVGfwfQ/BEIgBEIgBEJgCgKRO1MAyuoQCIEQCIF77rnn7ns/FmaExu23337zzTfrQn97t/lb3vKWs846q7/Ns9UYEIjcGYNJzBBCIATGnMAZZ5xx4okn3nrrrW3j/NOf/kQEtBUO/OeNN9747Gc/e4kllrjvfe/7kpe85Lbbbhv4LqZs8Ec/+tELX/jCBzzgAVdfffWUlTsrfP/73//e9773nOc854Ybbuhcm5LZQCByZzbMcsYYAiHwHwIu8S+//PKrrrqqbyfBdDna0Tve8Y7/+Z//ufDCC6e7bdW/9tprX/e61z33uc/daqutrrnmmtZG/vKXv2y66ab77rtva+GEy3fcccecaJTTTz/9+OOP/9znPnfkkUduueWW0xVYP/nJT374wx9O2LHeC5/xjGe8613vuvTSS++6665mK/qv+cntdN111/373/+21rflxhF1/fXXP/nJTz7ooINMfVO/aSQLs4TAgrNknBlmCITACBG48847v/rVrz7lKU9ZbbXVBtVtxm+XXXZhBZlMxu9Vr3rVOuusM6jGW9shUC6++OJHP/rRCv/4xz+ec845/Apvf/vbH/zgB7dW63F5mWWWOfDAA7fbbjvKpnOTLbbY4v73v39neVvJfvvtt8oqq7zmNa9pK+/xJ72iJs8K784jHvGIBRZYYLINL7nkEoNdaKGF0N54441VPvPMM7/whS8cddRRH/rQh+aff37lL3vZy5Zaaqm//vWv/FUm2hRzupiUY489VvtKqFKi5KlPfer6669vRxdddNHJJ59spxaa/ZKPRNi3vvWthz70ocb1oAc96J///OfKK6+stXe/+91vfetbKZ5//OMfyy677HnnnYfeE57whK985SuLLrpo00IWZh0BB18+IRACs4EA38AHP/hBwYhbbrllyMfrOt65WPBigP1kArV59tlnc/B8+9vfZpgH2HjTFCfKtttu++pXv5pHAXDeHR4F+5U1ctNNNzHqTU0Ll112GROuP62FEy7/6le/0kjr5ocffjgxYV/UVesm/CiPetSj1CdxBKGs+uxnP2tbYuWxj32sVV/+8pdb67ctP+95z3vkIx+p2g9+8INa9bWvfY3k0gIB9/CHP/wb3/hG2ybNzyuvvJImu9/97rfCCiuoz+1k1S9/+UvixjLJwkXk4/AjaDbYYINVV131hBNOIDrtgv+J+8pWD3zgA+36Ix/5yJprrokhROutt57lk046SaEKRIxmP/OZz1A2hklFfexjH1OizZ/+9KdrrbXWC17wArG/U089lWaibmmmL33pSyp86lOforf+9a9/Wc5n7hFA3jT5kLNzby99tBzvTs1LvkOgfwIuMX/96187+e666679tzL3t5R+wQzYzyabbPLa1752UDss++oyur8GXdMLSbzoRS9q3dwl+5ve9Kadd965tXCyZSc+q+abb77JKlT5+eefb4HzgA+AO8HCAQccsNhii+2xxx4UyUc/+lFm9RWveIU6HAOMqGo1od/5znfML9vJ28QnQZ3YZMkll+zcnTrUpPpWnXLKKcsvv/xOO+1EtLGyLC5PzwUXXEB18UbY7+9+97unP/3pdu3IIQXWXXfdzga7lFAAlIF9tUapuGHe8IY3PP/5z+cQ0gHJuVpQc8EFF+T/IGLsV38ma5akOPfccx0nxisAx1wZMteIwSJ22mmnSd/pEge0u4UXXpj80j7twqFiYcMNN/zkJz+5yCKLcEQ1+yVNNMjNQ+vsvvvuNJ8efv3rXyeV6BhYuKz23HNPMwu1w4OLyHQsvfTSTQs02Te/+U0Ont///vePecxjlHMp2aMe8qI98YlPrJoSfbRmR36a3zpUmkayMLsI9CGRskkITIvA3/72tzl0J7h6636h8J73vMdJTRLitDrWpfLPf/5zV8Ms0IorruhKnWmcrDJX+eMe97jllluO0ZqsTmu5K+Df/OY3rSXzbFmqB4vLBn/iE5/ostMrrriCKwIBF9w2YWmaDptKP12vN0BcnbNkfAy//e1vbeVyvFoWzVHTxTcFoIRbwloG3q7ZXZGIqsYEil8IMTDJK620kkaU23CNNdbgSLBJVfPNqFMSOs9m64aS9773vUwgySKrg+Nh7bXXbppttmoWGEVT6eS+9dZb77DDDkSG0bGOHA/6wzY/5CEPoRXUL7cB0+gAkHajRLfNLwHEIcFIcx68+MUvblpuXTBYwoVEsDtbAQWgIIv9SnzRvSOOOIIs4/Wx1W677carYVlCDHfIH/7wh9am2pY7vTsq8FRpubwdfmrKEauT1IMU5r///e+kSbWD7ac//em2Njt/Uhj6rxxt7VBOVafiU+Ur6tyqKXFsP+lJT/KPYF4+8IEPVPaMpsTRyLKmmgXd819TbjDHz/vf/36FVKaIVXmVarxakLTkIKlta7z2opwme9vb3kaWbbTRRq3Hs4OExGn2hT+5VgchXQ5+vDsNnLm0MLTenfvMpQGn2Rkk4BznVN69A8yVOvXpUtPtDC6MXIzK8utSrcsqvmjXoKLpXep0X+Uk64TIB9Cl2o9//GPXds985jMbM9ylci+rnDEf9rCHMR6slGYR6L6Vq3bpIM7srdVqIupUW+WVMskeGJTlpr4FZ3AZoK2bT7YM5stf/nJXzE0F1shZXjIKy9oU1ty99KUvbbNzIggf//jHm2qdC1pmRF1tMzw0hGWbqEYGkSB++nz+85+vDV1k31vw3y9nOuUMLXqKTFzFEUiTqqGF973vfeIL6qgpo0U5ycK5wkCW5bZKHeW0VO3FtwGKsxjLXnvtpRGmnTqhkxgw/RTZUZ/9a+p3LjCQ6tBSraue9rSnaa2JB5kXbfI3qGOChGb+/Oc/Oxgk/SgRHiJiyBRGvbWR1mU9pC1aSyqYJc6i0IGqD3ZXhf65zKahKTRTrVu1Lfcid2xCZjm6tOafDsP6d3CpoOSQQw5pa7PzJ/cM706VkyOvf/3ra7lHuSNQReE5fhwehOk73/nO2tzQeG4sc+qUIDZkiraOAXLTYWCtfwFuMMet5RqvQ06bOr/99ts7WZW3T0BWTYdQdRVDrqzakZFSWkcffXTFyxRqgYTiqeLOrGCZ/+iqnO+5RCByZy6BTbMTEDj00EN5dFvD/G2VXB65ruV25qNmyfxsq1A/nfqdlVw8Od10Ob832zrKOy+vXWiyKHvvvXdTbVoL+vCsZz1LXKNtK6f1No8R4+cisi7Qm8qGVpGmpqT3BVfw3Abqf/e730Wg8gO4H7jQXZT7rhN30+COO+4oOaP56Vz8xje+0YbaYQOqnGosmDxGbECJA74T+kMJn3yXxAgtsOuyKNghBpUUYzIV6p5lHgVz6jq4Lm0lptB/ckU333zzxz/+8eVOqD5MKXdoL11ijRxFhlm22ba6V2bJjPCmlC/NYWan3DD2K8pD2/HrsLWkCaFDx1irJjun0NhdbYtN6HDNVJn/1u5VJ827/rOy9dO3YJmMVwuGph3i0rJ0ZodxYXeQMIEKJ/tMKHe0Y+KaTdr2y/zz3vEH8AkZmuFMKXdYet1jkps2W+WO4Iu1IlyECH8SW+4QNXw2vrv/sovcKXeI3eGsweOOO07j4C+++OKlp/Wf+CDZ1fTvoKmmb20LPFuOGV4Q/7D6edhhh6lAyu+zzz5Eg4PzmGOO4SBs26r5iaTThSCaHXEOldK11lGkNX4aR6lwIciycMyvA8xBpZA4dtaiKVUTirIJt41lvjTXDDbku6Xm/T/KX+ZyI33MiP8sJN0p5mDTc4UcOSqoTwM1pwIHidjWZpttZkf8SY7ApsNZmBsEInfmBtV51yZr5F/FxcE222wjA2De7fjePTkh1nmnx/26jvRf3aWfzixOha6B+JBZiyZT0lmSe6DNinM7O+80csdJ39nZ1ZXOsGGWy2HOhjl9yxMkRMQatKMmW+gky643V8+2clZywnWSYgidGZXYxInMZbRL/DohNn1wfW/v9tKMncqhDOzIGJ1ea++11iWgM11T04JcBJs7UbYW9rjcyB31ncTLQUX/OXVy+FuQA2GM1Rq74lTbqsCcjg2QeTP88kCoaSD6w8a39oELQWtKVHZpXkxaKzTLbLPKsNNSzH/lnDZX4TpDDNVFPIAHH3ywmfVtj60qakq5U7tj6VtzWisfhS2kKmgdbTKKanaaYZrAWpaMmOYiwqGEEf3kCrsaN9GmxjKbpPL+++9f5c13m+xgpFUr81lyR0hL5Vavg+zmSs5oGmlb6EXucLDJGvGfrs8gk2iSdRQy9v6tGGkOBr4fOb9tjTc/uTMdnD7MKp8WD4cYjc5TpepU7hTzbNlMcSzRcDKEBLMcJ00jbQv+VY1XIw4A+lU3VDCn5VojZagBRp2zxJEmBkdnw67zJXdUlqVrLnwkx7T5t9r25ZxgR7wstRdr3/zmNytxvPHVWWh8Nm0b+kmjmCMBO4Nq9cw5D+iew6nRr041jigl5KOTCU1pc6LZhQTFZplEs0nbf0rnHlMyhASGVu4s6PDNpzsBAWMnuLJtzjt13dN9kwGudXJ3+pAk6LB22uXAcK7UvuUvfvGLzkGsbLM7F4hUjkIW0YmvKW9bIBEkTFAGyp0TnQSrAlFFnay++uqOVx7mtq3qpxtKqQonX6c2GTNsm6tJKhAlZ1tb0VKkj2RY7Ut3UOjE5+Tb9JOHQ7Ymg0FySVB17Wt0XAK2ZbmlUhqvjArxeHtkXFma1p6QHQb+s5/9zBnTtR3xRLFVBT7tsrVNfY4lZ96yc01hHwusBRXCeJgObeozbcHekEFkgQadtSvdsho3Ec7sjDrlZ6bMnUtkNqlz14J0TD7r4kRvIgyHfe2sViWG7KLZZTE3Bm+KrdpqCsRIv6AC2QyQaRElbXV6/2kem8rVjqCAa2tjb9s1odbMLzFkLf3qUDF3bsNmz6gfByQ52DRYC3WU1qU8hpxnlSzcVs1+HU4GRVLjbK2Ldd/MIWKEiElxBCLTtmHzkwoxBX6We0PIw/+RI83xaZhEISVnNh1+Js7uKhPZUaqmqTdkBpg9duARVRKbRGfa0qtrX/5DxYD8K9lWGJQiMXZXC9Q5hecgB6o6T7U77P2vweIeaeK46W3bgiPc/6mcX8eS3vrHUUGh1nhH/LPjTKIRuyr47/btWDKW5l+D44TotxXgpVradtH8dDw73VX7VejfqmKL9bM5XTSbNAtOCz7Nz2aBwnbx0Py0oMOt/5WVg+zf36eqGUvbJq2bZzkE+iEwhNpw2LrkZIqsk6yOOdc7qzrxOb1W8h23v3/R5srMdSpHvf95Z0/ntRqLmzCr0FnPglObchkANIEzJgtd1RgzzxNz+a41NoNlVc5w2rszl9Ou685KYaEPnEZFNFwxa7PcM5466iTyyle+0gWWM5ozaTXb+c3XQn+4J4JwEdt2KlfHcNzX6mwu9O56scIWtS2p51Rbyxwb+lNRAzEal5s0R61ikKrP9bO+NW5fBlU/7Y494PDn53DiFmdxUW4VsBwbwCp0yWsUVV8h+1fL9c0JpOe8327ZcJ3K2jVrjYspqivFprDvhVbvDlvlqpeRM3YzAgJDS0wYTtM+kdEEs6xlkySU6KGt/KxE1PLu8O3bipEzFm4YbB0tqjmWzB3j2uqyatq34KijUxndMpCVoekQYhtoJoeog6QuyoE1NfyCDkh9Jrxszi5yOcjYdYHOzPOgtDbeuky+cAM4jHk4yK9aJYYl0KC3jj2HLrefcvNr3plAhay4xBqFbvM2fHPBpLGU3BsKKRU9+fCHP2xZ9xwSdDAFKfAhAOEo4jarcJWWDcq+bC5LqdwJhmwWHHgqkwhQo0Sg8ItwPxB/FvRE4xN+zBSwnCs0B0eL41w1JZryj0NImYtmQ5Ol3KciwnSYOv7LlJhKbi3/gBVJbDZpW/Df10QwrSK2ao9t1fIzBMaPgH8T/+k+TpVDNbr7DFVvhrMzLJaZk7PJLUGR6KTznZKKGshMtFzmnwlhql0bkTIK69TvxMc2cy+7zUEhI8qqVQvMnvOpwnpABTeJZVefTD4JJcRTQFz2Oem3whGZZo2UOC/bpCwcn0ejulyiMVStm7Qts7u6xw/kao9RtJYpdfa34DxOk7lYbDbRGmNWPyWT2mONVwld0mStWp7QTvMY0WS1OXNr8+YmFD4AQKySHIBS1Wkdr4taV6h6W6vqW2yRY4n1Zd1Lq1W5vrlibq05J8s6JuKmBXpXN3wDRRGaXxPNmOlzY8PMqUvtUsDVJaaXLCOSfExf5XoTZ7pNCphxuHhByJ1KsxXoIQU4FbgWWjVc6xA4mdAjAR0exK7MWTXpgMYxoELVp3XU9BH7oJUrWFZ+kSr3Xb1tbb9ZJnaJD7EYSoKTpiknFAzfx81ETaG8k3IJiD40hWqK0VCETYlZI1wqCgl5rAAAoTtJREFUTEmctapSxBzz9c+lvp8VhTE6C1Ra04hVPs3PLIRACAwbgcidYZuRafTH2VaEyDUlj6tAT90ryw3e5M86ibuNVou/+MUvXGe7NmULmZM617OICuXwcgspdKWoJoFimYFktCw0V6UMCWPG/0EiNK6CVvNvW+aN1iEC3E/LjHEM1I74z0mlGlh3ucMsOSLVdGFt74wxS2OnTYYQJ7zISzXlu1Xu+Ekn1XiRcZXvErxqknqCApZZssaYMU7sd+PdsZarn58fB5Xd31vOA/YV20rxsWtDLuMnZKCHjdzBti7izQi3ELnWavxA88SR6kx9G6ZZ637DTmv9ZtmsmR1yh9dBZ4CqVXrLo2C+rBJ+qjuhCD4/KUKSkcOsKtMWfBhUsr0L6DTZSwINwig1QYZjmD6GYxI5eCr003SjbYH5V5NYdBDWzdhVAR/qFvNGJ1krpVShVXpS/hXSQR079W1VpdS07aJ+OsZqaBOuTWEIhEAITEYgcmcyMiNQzjyUOBBIYno5e3SaT9uy4AsT4jq47iZQztrRK5wBFEMTLOCZF3WSvcjwl4gRiLG51BZX9p55WjERHgJXvS6mXbVbW0/Z0iZzq1kL7KI0CCbNdTMJ5YKYN4Ul04i1FBhniQWmTuCAARb18LPzwy8l20bP+ULsqK7U5dxYJpiqsJSTPTKWohIElvJy4It2cRhIBahkFEOrcAPnRD3QXbjEkO2Xz1+XNKsOz1PtiNBpHnvfPNijYi6gMeTo2aQ4s9Y8GRUB0SALbVwwiq/xqwn9NP4kJrzxrzRD5u/RWjmQmsJeFvjkStf2Ujl1QmBICPiHbf4jZrBLTk1kvROg/sxgN7LrGSEwtHJnQXYln+4ExOwpCSLDJW9Ts1Ishfz9PwtzcNKQBS7lJUuKT1UKjut1Xg0WWuSeBGHa+UIU+hbIoFG4EGgaCxwAUgo4AGQn8BmUGqBsanfklNgH3wmhQGBJhiA1XLtTPGQTqcThoSZjL1IgUCK9g8uHDCKtmg63Luink5FOUgNu9SQyrOUr4jZwr4RVomyVEG1oVAVfjk3IPsm5tuJEcc+zgB0/BwXD/2F3WjAWyUNcR24Kla+jRAVkNEX9cB1VhMVAJI3iqUKlKFoQ7NMOmPI6JY7AaHTK+W90xiqhLr4Ta+WFKBcGakvCpavsSwzO2uajRBpsTVZT2MuC21t8eqmZOiEwJAT843iojAwq/y+9dEnCE8vkn84/JuduL5v0WIefW+aiixwxTf/CPW6VaiEwdwnMiPobrZ1W7o5pYGKZW//J+u/CRRIGO8pnIzpjgatGuX9ygoOp9s0ei2s4BxEBFAnTziniQySpyZGjhCuIPpAIqYRwEbshIJR4vkUTa+CG4ViS4EwJNR4j2osOaG7stLlPKRWJtPVzbL4lMkvTaSI1E44L1c5E6QlrpnC2EeDwoOzlIVHMPKNtw/cf5/bytsJR/MnZ6TRV6d699F/itpi4Rz+0Bi75mF0COZO0tiA6L4DLZ9Na2H3Z9Ynktu51snYsCcS7M3dF21xtnYeAN4VkqRfd0St2x4PipnSnUUKHDJKL48Th1l/eFy6WuldTRMm5g89G8EgL1Uk+GGkTwjF8PGJDNm/unhUDEqPpHIuWSau2clpKnkpbob51FrbVGcWfnFviZV3ugDUoSEdxaEPeZ9KZP1I0cG77uuRNuzdKGpm7AgfORIKXRDFOVsPhZ21t3zWGMKvU+9bCEV2WK6bngr899l8emGx02fdS6JpNXFO51pJX7oynKacpq6rQkzbd8gkm57RNBHxdcTmDySBsnEPuRXBidCLiFNdC02wWQmDGCSSYNfUU8N9UXktb1VbrW//Ykm1dWr373e/mmHG7Cpki38W5w4Mr6iky/MZSSdyxXE2p0NZmfk5IgKAcOVZO98KRjAH73eQqTTi64Sx0xe9AFTPlUOR9FB+ZUIsPqvMQeeKAO/jmhtzxryoE7DqEP4O1bu0zN4ZM87YJ8n8qNu1ixqVOE4txO54AsescsV0tmF8NOjJdoHN7MPCuZOqcoKacM5tzBiusk4P6TgIUCbcH7ViF+mPUMvfdvufsobXWvjXLzieSBeXMadC8uK/TlZLoLaevs5NVrqY8WYdr2SZmTQodGWdo7rV0naCaPHqb6BLHsz5U7qD4Mte1aa0Eu9qdE5dRSNdzQWX4VWiPuqfn/g01wnXtLkUJhZSisdcDCBwhxihszTlEJKmDTDOELITAzBMYS2faTA1KMEX+Cm+Ns5Jbb6SwVE+kvHCkc+26p4lTfaa6l/3OSwLO+/Xv3fcLNOZlbzv3VY/TrMgI8996B1xn5c4Sm7CLPhZa14rMdjZViXEiTSK/rZXblvkSJMA1j2B2Y6BLC4KM/0kmGd9qpdK3bdX8VJ9dpw+aEu4N+SWmST5ZUyiDTcCLTlXuLoEK6/DIelaeEkFVHhFD4PGq+VVT4j/5Uv/aEuzk9YsQ6Sr5Ul0SAfd8SJc9NIGaxJDduVWTV8ljtzhLyAiO4aYPbQs25FaRO89BJU+OzJKWJ39OXpqavGIcw3LvLNMZnpZkQea++yc4WqhVm6jj6RWy9MgUFZqzkNedcou27k78XQ/rVr6mnITynIvmpwXPTSCGuF09EoKEqoOccw6xqubJYXRVE5Fv3TbL400gwaw6M4z5t1Ond+XUudJZtRmtc4pP8zMLs4EAz790LqnTLn/7Hq9gKMPDXLXmZTNyCllZxnJCXwiTJq+c0SrBIW+sCdYI5cgTd7aVNOYKXsfcvsd2uhaXDSaFhfeCwVaBe8NaN8a7shfv4P9g+JlthzcLKiWWMRPeZdeJBrZQiaeKecivi3uuFNbdvwA/AfUgvZ0ngNrg7ERDiWoivGy8ZU8k0iBlINJUN+hNiEs/NeJRRgbOzyFPhSmlxnheWVYOFUPT23rryIQtuA4hawiXZi2DTUJxbxBhTaF7EmXzGL57DmhWMLlz3C8pKu2WBbrBExBEedxhgKrOe3yACtSPdHvV9BNJlze6WtJKy5woQBFbFnTYtRDPCteO2wwdIa6OAHQthEnTjdYFk2VbekgfKDwHA3TUISeNmx85jCkYeG3CB1MD9OgsPiR+HTk3HqLhSEDYh2xyVaadxnPTuiPLDo+Seq3lNqzjoSlUoj9cQdDh4NOsahb0s9xdTUkWQmAGCUzsO53BDo36rp0FnH1atc6oj2g299+pnI2nLcqWWGCtuSJcHDOEJEUDhz7w+AA31jGHVcicsD1iHFYpYW8YOeEGwQuGmYaw4KJZm9YKOljFH6CQh6NaoB5crLtrph5MoFB0TMzC/f8eHqjc3XxVs+2bEbLWtqIMavp4ZKU6PA3umHNjHTkibERqKHR7jleRu/uP3dU4H4lj2DBZRGtLOdUtfp6NpFnxCy5M1pe1VsGTongRdEnevWc3u+i3U/LFjiTjS6WXTKZNNWkd/ScIuDlZdy4ZhYi5GdCzGGSHuIOvizTUuF0TNDakb2gLhpwD1aBsSxe6Y0A2iTa7fHhoTERTgVwTSOIZavZrpJ56QPxRMG6rJBcEsxQSr0QA3wxnDKkBDlvOp0JTVrjK8yGx0jIyMuv5UYhU/VFZoW0Zfj23dzqJF6QKCSNZwHQYCMRc07G2BQMnjwgR/XHhBKMKjitjr5q8TaVRhLpMXxXaV+UFcrA11UyNY2xCdVJ1HAy6Wse5g7O25a+i3euQcDuFSBnZhADpRnxzbjmeqR/Hs2Pb1PjH0Q1X+UJp1Wy+Q2DGCUTuzPgUpANDSsAZ3+33dWFNDeili2nnfX4OSehcC6IJlZJlmZeFX4FtkLZZT45uG5Wzv4tswQhuCa4I1/quy+s1T+wEg6E+WaORUiHu4LU7V+qcDXwebtZTgd2lDKxi6uiJVp9E6+4ER/RNCV8C88a2cUv4SU+INRBk9kLGMZ8KZcEzzBYkmRFkQh6W+XjoAAvq881UnrKtxCx8qCJqidBRwUMmeYlUZvk4h3hKeFD4kygGAqW1hx67QMApJ4lsWObZiKT5o6qEy6QxzH62feQPEXAKmXCOpXqQQVudgf80LpKIbnAwGK/h4ElkkDhd9oWDTchWIkaMSU3zBakDgCbjKmt8HoQpBw/PkEEREJO1iaRnOpBQjhPi0iGhpgQdezFr1CTHWPlsiE761cMa9JaQknHMK8PlzGOnA3bnBkaPyqROlLjZ01acWBQMP1mpGQ/mNthS6gSfuJt90WdaNq36Sa3aL1VkFvSBnhOs564ziZSu49OR4E0j3EvCZDXLk40r5SEwLwkkVXle0s6+RokAjw5TxCeh0+IXvokbmSJMMgvNEhA95ZthSJziK3xAW4iPCEx0DtV1vw9j7+K4zIAHc3P/uMR3ocxXZENPOZIQalt3EjE/KpdzqHQDX4LcEc4VptG9MDRT516qpBwMTLW+udpmrvRZz2kszgwig3Gqt2Cqb6RSWetRSZM1qFxPiBULbB5/A2dPVVZePozWbQ3QrltLDIE2EgtjLPknqikOEuiIJAtUI+Oqk40aaN2cUedi4UYiONjmyqRRgWPDLNiXPRqInyi1btgsW6umvRME6nDb0Hy8EVKV7ZFfhISC19zxfhXbitYBaLD8OhSb+UK+YtO20pT+8/qYQWyl1/hQOeQv0WAqSUMdUJ9wpDYoSxq0YnZGbSC+9YSq5nVrutq2YLqJEqrI4ccFiGG1CQLZ4SilRO0OVS4igtX80qPUBiy8jNQPjW4reots0n8QEDBxtIumHIF2UcckZc+HpNBEOKTNi2WyhlTlrLIJdVv3YdHQxqKEymkSurkSaSnHg/iaDfMJgeEhELkzPHORngwXAfaYbXDuJh2c7nWO8XDVyzbQOn460VePeW5cXpMU6jfxi8kGwwy4j4aNFA6rxxMwFcwVGyl1wxU5K8LMMEjkiPwPNph/pTQQ0+XmF4mrjDQfEmNTdwl17ku4rSlkCAkFP7XJQkv+cBcxH1IT9Whqdl8Q7eKx0B+6gWaq+4Bsok2OIj6DiuEK2dBzZAcmbKoPd4hCWode5Aawd+NlgIWiuB8EyKhAVp9zSw+pCg6kzp5QDPiUyuFA4lFQxy5swu0hsmZ2OK60I15GkHW2YFUZcl4KasBYTBb9xOWmMoFChTD/plvurYwcLYvEEQ3WgkYgkjucK/QQ0aOQtCX7yjXFzMsgNlhzJ6EHEPE1Sc1K1KSixBNx8yEsaCOFxqIOFWhHJdcUTvihmYgh20LdOjQ+PN4dMqWUim1F0ttakBgkm6oKJVRZqOxsC3VUt9U3L52PvVDHcevTWhlGscjWklouZ2FneUpCYIYJOGXnEwIh0EmA9XXNLYrEBFbOqTqMLvtXlVk+bgDLnDSsphCVh1DTKGIHTWsEEN9A89MCo+hy3L+9e2eq3FZSHPgJuAe4E1hi5QIibKrsB+W8PuyKQs4eYRSJPrwgtILgDvFRjbR910OxJbUw26InLs1V0D65JuVF0IpN4mxQyOSLUzDALKUISLUjDaXSO1zcu9znT1LOKovFsJ2EGn8GFaXQqIk/2xJD/Ap0mJzligBqgYGkRey03pDKbDP82pTkUT3n0SE79JCek+TrQ3xUHzq/qZmqYy/VH/rDACUJoUpj+Un3VMc6NydBbK6+b26SqiDPuhoRWJxsw86mUhICITAZgaG9M2s+PZ5hwZXdh8BQEmCbXU+z3CwoGykWQADxx1Ab3C2iG3wMrrYteEQeR4u8Ct4L/1DCFtJrjImjgu1n7IkhoQFuA5faymXkaFwab4WT5K6Wm8cqYQJ3ArvsFo8Qz+KV4aepi3uawE+uCyXsPf+KK/4SJZ38+FpIEEqLlCHLWtNg3dZELbl1qDojiGNHBiJIJKRFylRrzlnlyyFE+EWaXRA9lls9Q4bMu1DnvnsdDfOpUIWtC00LWQiBEBhjAi6rODsN0FVWXdoNyWATzBqSiUg3ho4AuSCtmNDh0SFZiANxBELEzUH8MborVVOMRjU3rYjs8NZI/PQtTiRgQVKIU9icG0OIikApecFb47lwPCJN6ow7ZWSKlFzg0eH/0LjohmwVsRIuB9EHckQhmaWyEgG1pnBCcLqhXLOVBN1aR/JH60/BC5Ga1pJadsKqc1bbqlahU6sqktIIndZCy7W2rZH8DIFOAgKgLi18WyVJvP5fOqulJAT6IxDvTn/cslUITJsA9SOTQxBKLEnohLdm2k30vIGkVLcyiViJ1PS8USrOOgKCiSKV/IUyq2jrSiqaKQo6w5la6f9uHOM9nameZL9zQiDenTmhl21DYBwICDCJc/GO1N3Ic3VIcnJ5lconNFd3NK6Nc4/xe034FMdxGrKYpsww4piHksIQ6JzB0XHnyMT3byJ+ytk5gz3JrseSQIJZYzmtGdQwEnDPjvtoRMSkyMzt/g0kECBqJrIgrDa3e9vZPmsn9ViekAWpza23I3VW7r3Ejd+8a9KwPJposq3EHz0OgO13W5wH0kxWbRjK5VmTzm5Sq7vD+uiShK3jjjtOzrs08KYRzMkOak9MttqsuZBYJtNLINUdgpPNiGNGHRFMjcgbq4itTRRKR1NSsVrNcnbqv+x7dxdKX+NYspWDTba+tR5G1cdwskkIdCGQxwx2gZNVITBgAm7DngdaZ847zTi53JdA7d6uOW+tjxbkcUtOEtqQNVXPXeyjkbZNJJ7zZEi3qmfJtK1tfnpkM1XkBjQ1m8JhWBCdrCcBVmckhHn8oMR5T1SSFC8ttMpFprxw1NMKCLvKK5+w85LraT7zKyHdDYZu0Ktn50gy85Qp2D1xqiKhduHORI/ctCOPgjQv9YDKCZsVqLVtTVw9/kA1D8zUgrR9t+m5R89tdAo9DUg8V7zV0488j6CtNXc7tpXkZwjMKQEaPJ8QCIG5R8BN3R6077Erk900Pvd23XfL7JknKbNbPBwuyvtup78N4eJXcD8ak+whPV7U1bTD3jPzfA9NiVvesCVNOgvroX/8DVXZ84UpBoqn2daCSeHIkUqlMn9Ds4pikITe/JxwwQs4Rbs8XMeNeFgx3nqupnCMZxO7Ha/1kQR2LfXbg3w0+7a3vU232X4PBVCfk8MDC2Sm117cpe9OOlpEmrlEFoUOIeLAXEivcW+/CJRCaoYjhLPEnXfcLdqszb1LS7lCHj6vnqjCzm/PLfR8Rc8D1CWcwVEHQ54eSTPepMHZ41FSCj0agEZhaVT2NjG0eWs6G1TCReRhPJo1IrfkCI0pdPxwC8n6t0zFascjoyx79pLXi5JZxKUnHimpj3x/dURj/7cgf0eMwNDeiP6f+0XzCYEQmHsEXHk7fUujcdk93b0IplRAZ7obDqS+QIncamGFKVtjvOkGN6w1z7OZcpMuFSgDxDxuUR0OBo/2scA0suj16GcOGP6naoFFV9mH58zdcFXIkVCFvr21uwqZVT+FFOtnffNYKCQ7fJcZrvJe5I579CCyoQcGEj08JbYVC+MIISD4MPSTh0OhUVA5bjvSQ2vpGIUkBU1pwaeeZ2iBqXDX3r1l93ghSW2uTVKDv0053SP8VBWAqsL6Wd86U0854u+ZTJc09cX16J7mp+Hw39TPkh1UoJ/lOqLAmpoTLpBHstPaVpkpjqIqLEcdOeioJnE4gdzeaKd8Uc1WrfttCrMwQgSGVu4kmOVklU8IzEUC3PuMmUvztiQYjgqBg2bHLoI994/rokqc3Tw1x10zPAeMjYc7kxRN5bYFFsJ1s8f/eGaPc03dyuu6uQo1a19Eg+tprXliIbtLOpQO8wImF9+8FNIsmGF3xzSNCzToRvPTgk34DDgPPHhXDEKJCBEj58UCkjA8H1mSR2v9/pZ1hmvBLffekCDwxChqx7gqasNksqCeDqBQb6VD8SVw4XiVQT0OmAhgX6kc2ovzo56BpDJrTTPh3NorHaZs+Gnq3Rqtq6Zc9lQCjz7ihbIjD4qsx0zzM3nWAK3DY+TpzOBrh9zxRGMPbBQwIstIQ4Wtt+g3y56z7KmJ8ma4tegn8khNm3iDhClzCBksFVV940yqhdZvk6gFc+rg4W5pXTW3lx0GXmRRt1bZF4+R3CB9dox5/rWSkjukP0oeWMX7RRc6bIhFFwOt3Uswq5VGlgdCIKnKA8GYRsaQgGcGkgUuQ5lSYsVlNFeHQpLCad1zQXgL5Fdy3TNOTGxdUrNqzCfrRQ14wg17zOIyAJz83oolSYI18sRkjciQUI0V96wdgsa7FTnw5XKyDXWJzABohO1k5yy4Cmc+O0GzrNrUSY8xZNFVYMLV92BlxlJnPOyYp8QLB+TieHejngtYGAhLzO5SQnZEWBAZOiyMwnlQe2EyW+UO54d22CHZG/qvz5wiHpno9RfecE6dtOm5zq72WEJGEGp8ABwAsoZJPR4Rz7YW/ZECQpYBKDiiNRNEzdBD3vjBcFb7TKxYmNiQ2aHw6h0RtYqKaktn4Qu58MILKUtNeaxRjz1squFjyiq7tgrNKWHKJWZHnj1NtVR5a50q4bCxoAWbmIiSs44xs+xYclTwzYhMqWOMKoNslVkWfaucKtE3ecrmFxMHAC0lVEcgem6kqBNtJ7mn8X7VTpvveiyC/cLlaLEvmzt+HJDEotQl0tbLPRz5NtG4b3UcyXprd007rQsOVIcT75T5kssMrG5wpznwvBhE9I388l7S+l/QiN7S9x5cDoIpIIC0Zr8OJOFUUtItWuU/a91LlkOgTwKOs3xCIATaCPCXOGX7p+Lb50hgPisPgyFxClYuN4Ke4CnhaWAtmIqq6SxfKQsEgWr8Da5367qfCnHBzaLYF/tR73mgSJhGWzFpDB5zblmhOpwZFexgkJgZ5rOtk/WznP8sDf+Ni2bmqsrZEg4GLh/mkI1RKEuaE4Kx1DEN8sdombfAT5ZJBQaVEWICqwU6g21rglmcPWry7jDwLtCb1JZ6biFzLoTU5RUQ1WYv34SdXqnJdtJnUkks40kK6LZlqhF/C1SRntipWaAsq+dUo/lim1Vo+0iJpW+aQspSt9FGnlllj5tVZGIzwKawc4HYpUgcAM0qshUiLeNPalQcR7avDtPHZIo0neY9JISdJ1Y3j3kkZbRTr+Ii1KgNRw4alTojp4cSNQtETO1OkMuMwOJb+yCIClWJeXQg6V7TsbaF0hbmtzbXkwq20h/kiEb0UyzVVhx4JLLImkOXcHFEtTXV+tPmRudDrJTmq7XGSMQL/9VPB7P58jI12ULlELJ3U+ZjwSwrtMoB0Np4lkeCgFOQ48fHFdFQdfg/1xb5hEAIdBIQVvAfW3kSDJWrz6pDOjCxrUkqLIcXXVVKL5NZiQie2yYvwenbVmSHppzcGWZmtdqpRzM7oUvFJX3KVPMxiETUciN3OvvWVuI6nokVzSnfjLWshZt7vceKP4Pngw9AIY+Oml3kjjdUaGcyuePpLEYhd4SVpTNKQgmciVM4wZ100kkeKdQ8HtruyC+fyVRa2xBaf1J+BA0V4uE3XjsvBmQtuaN9nacaCSzOKoXkmgVeGaYR9sr2ZSwNXHCKUFDI9eW5ZypTA0Qh5wctxe5SnPxbjD0BQbLweHkfmaZ0WC4wk08zMfk1m63da5a9e4s85dszfWQN5laZ5XpkNvJcO56gXfWpBBKknD3qV6FIHOAGKNpFida+pMt4lQedhyodpqa4JMtx/PHHC7qhjXltzrEHiw9tJE6kkAfOoJSob9RNzarf+s19YiuzVptzPTZrwTEFpbkV6kM13lTIQgh0ITC0cifBLCfwfEJgAgKc8Aye/2rrJE/ssMMOLCjzpoSznRluthHQYfOoCiUuzSuqwtIIsrQ+ptaGLrjlW7jRhtFlvdSnnJg6gRumiy1k+cTFiCSmsWnfQnXDtXhrYS27StasPAlt0iJMqTiFMJN27MuNPLw7LtBVJlCMiAizTK+w9JqtlllHXiuhB+JAl1RwfzKRZy23lht/jN21vruN9FYwy1ofV/z0B63g2l3LhAI+1Ss2UoqJ/VInrRBqbfdveNl+H9V4pGgCC7SO9t2aZLAocZ8oVFPqDNkhpRc0zjOF0PGsEHZ8OVAQeZxkyplwdWQaeR29ctKQ+4RHynypUJ4VGghko+DSE07y07zbdsIPMcQrBqNq+qa+amKCJE5nffKXDlMOGrdHVeAdNH21XM4zy+7wojursL51z6e1pJa5psxIa7me+7SWTLbMG+Qz4VqeHp9mlQHWq9SbkiyEwEgS+M/ZLp8QCIEOAkwjAyZwwBnAfDY3+LgEd0XOJePDltvOhTJ7wJvC9gtp1S1FkhXcnCyaoJBacnYQH+E4oRXYZg4StyXTN3w8XBTiNbwUBAS3BAdJXVizeTInhFSYOoWHHHJIRx//U8BjJO7GPAs0uHGp4heyWyQYyW8VgKBjpGLII+HAsEw9+LY7twpTQkSAvlFFeq4+HaBNAQWV7Z1k0QG+q/ITcKKIa5B0PAdcL2r6NnY1dZJrpPEMWSWnR5ukgOVpfQDhWuPkINea6Bg/hH76xryL02JaO5r3lalSMGFxO/e833v2GALzgMDQenfmM/iRlGnpdAjMZQLstDwPwSb7YdHrphIRKz4bYYvaOc+HG68su8oXwiBldt99d5fvtVbAS64P34+LeM4JcoQ3QjuSS7gQRGR4SrRfLyEnDiRyuuDmdajNfYu/cD+w7lqgUZryAS6IYhBG+l+5SgNsebBNSX/hRtJJ0RzP4R1s42ltZgnwjfkHmdk+ZO+DIuBayLWc1viMh+qN6JE7g5ritDNuBMgd6ReyTYU8OC2EiozQ5QHvgrNzLbtThqenRu4WKnEWJfWzvm3IS9R5V05rnZldLrnDvSTnw61YM9uZLnvn6ZEjxdnGjVRxwy6Vs2pKAuZdTK0im1NWVkF0kuLkp6z0o1426bEOoe+xyyKtQ2Uae+x8qnUSGFq5E0HdOVkpCYH/EBA8onici911VVpHIa+MG8t5fXy4eRqtY5WkjTato5AAGmato4cG4nYhidhNEonCIfwIqxFkHFE9ah1RucqVmdtjcZBw0dld7YjA5eEjkT1ooNm1HCbOPIUyiprCzgVBTDfbS5TuXDXYEtLcs6DknkuN77FlXkaR1vJxNptwdrorrflZC24VdItfW2GXn9AZuIcudqmTVSEw5wT+k5OYTwiEQCcBCbZuEqZ1xJJka3ZWGI8Sib11n/x4DMco3Mck4CVfWHJV3WbfOjSBSDnXQieebjdZrm5r/SmXxSsJFE8fqCfE2KlUdMFBGsjT82pzqVoUhhwvCeldFA8xLV1MC1PudA4rkOZ77bWXrG39lEvUS2vSvzg73f3XWlng1VMJJKs1hbK+ZE9jK3HNeFUouU8VuXKQQW/XTWX61d1zyDQlky3Q4kQ5D5MOiCyTmDLbuFqV0JdmU/aY/LbJNk95CPyHwDxIXMouQiAExpsAI+dGqtab82dwvASNLB9W1u1Fnd1gg91o5tRXOd2dFbqUuNVLJlZbBfJFgyROazkZ0dxt3pSLH/GpND8nW5D7JaPZLeV0W5OUzQUitasKxVIn21Y5KWAiJMiTerwmNpROblu+LmvdA+hW+dqcz5ILSlflTcsSU2geVfaTh8YDEdx6Jr1MuVvTCRd6Qgp5bUtnEHk0jTqy4Ckn21rl1jmijRNOPjslLf6oUHRDoMq9/R69421iTQsez2OaqCjT0fn2iarmWwqIVHo6ybWH29ZAoH7cC2lHImtUlG3d18aF1myShRkkMLSpypE7M3hUZNchMAUBEQQGqW4In6LqPFnNoriTq21XTLKIGItVj8dtWzuDP92Vxth3dsAdcPwBngfYuaopcXc6/wf4NShBHK+XMkZPz3OPntvulKhsrVvV2OBmw2ZB6jqnTvPTgs7UQyZbCzuXm3dE6GQ9MEkdD5C0dx+ORo8b6NyqKZE7z/zvt99+MrE8DYguqQSdkneSn7Rf4sas8cR4iID7+NRxQ5zHE1AqWqAk6Bu37zWSUcqavXvyZLMjC9qn84yLxioRRk1qwRMNqhrXiwXuQ/c2WqhR0F6W3UtYTyykzLQ8mdxxdNGI9YBvW3nWIteRBY/bpjIt+LgJgPqx6/qZ75klMLRyJ7k7/zmD5BMCM06A+eTYb+sG8yMgUvdgt63q+6eMDWmh/W3uRnSX8p5kY3N+gkrZ9ixBxpWFY8CaZr0OjKljgdi2ptBZWKTGvfe+uQ3cZN6salvQMivISUNkMHi1Vn2v8pAgJQ/GJb5CD3V0wxpza9nbLQRc2tpp/cnWeiaNpGyba79LgFLfDJOwk1DiIT0akR9dLzgzF9wJxqVEOfcGf089qah1X9rneOjvDjIqx9szUCWtPBrAc4rFxYgVzh7agopqeypP634tWyuhmFtFV8V9DJOSaOpoUNJ3TQrxSknwTlE8nl3EGyS7yDONPONRH5AXeyq2NvdcJRqoaceC+BTZJDvNCy6ateUZao4EZCghTzIkjPTc46HrQUpEGK1jW+2YEQ9EaHuXWbMjTimP+qyaTaEFmXNN0rQjTbMDCU227iLLY0YgcmfMJjTDmRkCnpvMGcDIsc2+m04w8M7svpuSWlBHeVOTt99TdCVHW+vc7WauqsaRYIHxq5/1zRAyxixfUygHQiFPgMto1rEpb1sQxXAdzJYLKLigl56sD1WHu8JLr/gehC2qxFMQVWbzGCqBqhoCj4irfFf/njooPMFiqSzE41l8Mlca0+j+fG4DnZTcqlq9i1RNL7rSoJo8ItwJnlRU+2r7FsrRGe+4kKhB0Mj8VYG+EbAgqigehrneBsrQCnDYr4/n9JQGamut+cmxwax6sDIFwww3Kqqp0CwYoMcOEaDkppEql5MuR8eCpxaJ/njIYWWpS3zxbMPOdF0zK6mlNU+laXzKBQ4V08Gce5GZykQJgUWhcvLJEKIyaYsujajDfWVGLEirV7OLsGttR7OEhfmldVrLJ1vm6eFnquc2GW8dIbZFox4CqdDH5r4dD1SUgfB4wQK+uSvZ7Ugmf9u0VLNT6lZ0j9b0+AaF9lLdExoTLPPPolBTDvt6DHqzYRZCoJ2AoyefEAiBTgLMp7O2ZxO7FPbwfmfbek0EH4yfzB6fbbMV6eBfyxN0PIuZaHA2t4ovhIJhRbhDyBElHBskgkRaddRnVhW6/HXh66ezNiMqRdpzCJXTQFz0yllxP+ujHVkRnAqsqVCLwjL8NmQmXSi75GU8/rf6//dXz1nxCmFY8CwfcseHrKE/6BJhCA+2UWIzL2RggQRrPBOPaakRyf/1JEMZIUy+9I6KiZQ91nnRkNqf+31YKXIHMa/CMIR645gdMeTqeFSjzFMb/n/9+98f5QwnkhSQRDSKBR4C7RiCZfrPMJlAy1wglYzCDSD+oqT5gEwG1U9WWY4I1PVTHEQ0pKnZtqBlySImTnZLM8v1bjJHRVtls4BbWyEzbO9thTrTWdhWx0916AMLRkSpOGY4RcyvBR3DXGoOUdK5oRIbyhAyTDeZO7oQczCYOwdSjZcyVlhRNrJDtNRWJVnIBZnUDgNq0kFI3tFbUoBrR/WoaJKxdb+yeQg+q8hTj2ywSsu4ccsp5ONxYCssD5nZJ14dVB6ErdArLBzDUrPrVrsux61BmWXdVlkkruadu0uJfvovK0nKt9fatyzPFIH6/zU7kq5mqg8T7vc/YjmfEAiBTgK8C/5jmRkRAc4A5lw0QTUO/8qvJALqjVoKncHV5HtgxV2zusBly3kjPHiQnRb4EO5RjV2pq1iGmQ5gGFzaKqce2B7naypKlkNjpMv/0cgd1khnhEic8UkiV7csPQMjK9aO5Ip6Moo+d7GpnWZYaqpNNGIVE1JXzLokxiGCwCbpm/uKywBzzFA/1rZ9eEFUbuSOtfSfDS2UWSr/EAllQUxK6EH0pK2R5ie3gS65YacpsQAj21/5tvwuaJfp5abi8FCBtCph1GyFQ0PSTJk1ppHtV2juBKqamq0L1tqLcJWTNe+U4E6tLbkjgdcwqY0arNaoCprA3gmR2p1pEn4yRnJZUm1TaCv3+qlmwRHSutPWZYcNaSLh2nstHHi0o257trX3ljgSCBSxKhPdukmzbJgOD04+qpTmIIV1wFqCifIgC8hZz7pULtQly5heUciTRPuaYlqcBFGTW4gipIl9mw4RVWPEHDfZM6VENWuV+qbef4eDpLqhZajNoMHqvEL9J3SIFd5KTJrjhBfKP4sb5XyArc0n/LYJ56X/ryZBx6T7X/NBngbVjuNqwm1TOI8JRO7MY+DZXQjMKYHyPXgOimCNtgSYfNMrjA1vjUK2360lZcwEGkRVWnfp8poZELuRS1HhGNKEDSN3XOZWTW9dKFNtc+aheU9F0w67rryRO5XcU84bOokF4k9SmZbiCrLAQqvfRe4wP0bUtG+h5A5PjEe9GRHvSzlyrNpnn33YNgKI36gKDYQhZPhbW7DcRe4QUlSdplTj1sKE/4Ddamuh9WedLmWZKBRco0tkhIAgOYOXiOiUcUL21SY0okxhDRoX28yRQEmYFAuUmYBOczuVyQKH3ip/GMcAN1Xrfmu5MmNoBbqTGqieW0XE8IFpwYfXR2qRQmmz9xb894stV8jh0VpIQyisfGHCl3NOP/lgFE74kUnDWWIuCG6yqYSmAJ+Yjmky0Qx8FXZuThbwstAW5IsoZCOq1HfsUZAq8P0YeFFqColdrWnZx0itrQXflnWDbLKhZY3YqnatWf8X9Wm61BRWm601m0Ors+cpGRsCQyt3Fmz9t8xyCIRAQ4Bhtsy6Uw8WWEffLjFlvLIHzIZzN6eO61rlE35cmqtvlUQKjXDXsxbuMfEazqrPXeEcZ5kh8V2On1rV5Zt7wFoKwJUuG181q7ddtqpVghqskW7Yl5iF0VVihxI2kn+IM0YFkoIm4FvyknA/622mWiB3VHAdz48iZ4We4LBhOxljA9EllPiZ9FCWj2t6V+3WEh/Emc2lejCBXpbJZUJmsfp1E3JbtzWrfcqM+0HwTp+pOh4IXSI+ODBoRL2trcgXQROy0r3QdiRF109ah0OCG0PYi8EWWSMy6B4JUsQTuUmEkbOUXNuu/SRxnK+NWmv8K+5Oqjo8FvrPZeWnqax3evCxsf0Yqu94qEKpUcSu2cdEZFCE0SYcNkQDnWSmtNz6itlqv/nmV2uWmwUTUZkuTcmEC4ZMoVpVvsmmjunmhml+EqC13Hb0TvYIR46ZZtvWZc3W/0Wz1kLvha1bZTkE5jaB+epsO7d3k/ZDYEQJuJ4WNCnnvCHwIsg7YVw5ZoQk2DBPH7FWEq4rcmaSI4Srn1nldWDLXWS7TKdLKAm3DrEuSsgC0Sibu2VGUoIbhaRNsLJMsoxOykOCAgPPiyN/wjPc7I5h1iadZO+8BRohF9hXWUSkEtFDuHDMuPKudgQU6ubwTuzCTISOPgvZWOZ1MEDpIH4KozDGbDx1opAzSbCAoBFo03lmTGticBSMZf3Uf0ETAS8uB2ZPf2gIASCuF9X8ZHTpQo1Us9KEWXqt4WBo7pPSzwk1hx1xn9BbDDO3k9HVQGSk2hHIneNqLSEyqI3WkiyHQAjMGwLOBsP5zqz7kDv5hEAITEiAJ8BtIPIVSI1KkOS3dyM3C81JIzDhwp0Pw7asuOALK67QJb4btRSy1uJNFIw0Dq9DV8IZwFRTFaI/9Ap9Y7myX20iKCNe486jymuWJuwnOaJcykXlNWvE2YRvgFCgJPwkdygD2ohGIUE06yf/k1UTfgzBrch0Q2V1VB0b6kZr9EE5v0iJqgnbmW6hPXIM6KQN7drYSa4a6XSbSv0QCIGhJTC0wax4d+aN3s1eRo8AD4GYCBeFD6eF/M0mdYNY4Q7hPmlefm54xAd9w3VB94zeaOd+j4VyOKWk3ELkZngaTnJJBXrm/s6zhxAIgXlEYGi9O5E78+gIyG5CIAQ4daT1uCoV2xKfSrwph0QIjB+BoZU7CW+P38GWEYXAkBIQBPQZ0s6lWyEQAmNNoKenZ441gQwuBEKgVwKCUO456rX2JPXczO/hjZOsTHEIhEAIzBUCkTtzBWsaDYFhICCLWY5RPa1nzvvj4XUesSgJek6acgub+8vcoD4njWTbEAiBEJgugcid6RJL/RAYGQKe0eee8LZHsPTde7e4u1NMBnffLUj6dvu9G909J7DvRrJhCIRACPRBIHKnD2jZJASGjoCnAHtHaVu33K/utnnPAWorn/CnhwN5J4D7pyZcq9CNVB6n4cH/Xt7kXlOP12tqemqfJyZLUWx8P/KRPUzInWsezecW9KrpIdHurhfJIpuabS24P98zijy7zwOXW8uzHAIhEAKDIpBU5UGRTDvjSYDZ9kwdT9VrHkQrQuTGIo+oMWD3FnW/vci2bkfysFqbe/auZR4OPz2hxyqNK9e4Qj89/EZrHk5jbT3Tz9tJPcbQY3u8h1KJOl4T4eUG6vCyeI5wPc6L+JBV4z1KHjNoWy8xeOlLX0q7eNmFb0/oqfu97U63vXHCcwI9U8cTDptnDHp2H7Fy7rnn8rt4i0I9annCGa2H9lpFynjool7VIxbt0Qu/vL3LcxGt9eRlNXXeE5n1wVOLFNqpJxi5Xd+7J5vHInvYsXY8sNHo3OE/4U5TGAIhEAJzSCDenTkEmM3HmUC92tDT9z0t0HsSDJWw8DYDjxj2NgCag8PD2wMmQ+CdhZ477LUG3tpYL22mVDx10EOTbeL9i16PUG+EIBG8UcHLkrxuQvvlOPEySEKHRqFjFJJZNIT3anGQeAiQmt6OSaNoimrxngSSyHMRPbnYc40VelGDtyVYqDoWvHtBNe/E9moFusRjoHllPLKZuDGuM8880y48BtBTjFWe7MO1w4VDmQFiX6rZyhsbPNPZS6l0tTZUx3vCvQ7Ceyfstwq9kMHTqCk88q5p3+ae5eiNY7w7NFNTnoUQCIEQGCCByJ0BwkxT40aAy4QvhEPF+6G8CcHweF8Y8i9/+ctcGt7RTZeUDOocOSvuBQt0iUiN7BneC2krHB5eAeHN0nwbPD3eUOGZe7aVTUyseK+CNzY0TanAAUPc0B+El5iUn14u4d0LXimlZY9v5hpRn2+GU4fTiGggreiGKmzevVBtUmYeqUx+ET3yhT0A2h5tS8/Z3DOOywXFB9P0oXPBtmqSejQK0aMCP5O4lYcrGpp2ahOvpzBqr6+iqyiqqmkVqUfnceQ0LROCEHnphLfE009G3azKQgiEQAgMikDkzqBIpp0xJPDc5z7XK7Xd3MQ/UdEl1po+IAvIBX4a2kKoaMKRkzteJ0mjeGk2ZwaHkNc3quntE2I3FADdwMwrEYHi16lXUfLT+FkvzuR0oXI4TqTLcIpQORPuaLqF2q9NqBbKY1qbUzY1XkC8otyIZPzom1dheHOFhyZ7NRiNqE2pPKuvvjqBRcFwU3mHRu3IWyO8mKKJAHpLvHjcj3/8Yx4pKczqnHXWWVXTi73e9773Na6pKsx3CIRACPRHILk7/XHLVuNPgAeCe4b/RgYMu175trwXJA4jXeOXCuM91V4COiEOLXiDt3ddUTaCVqSAh+zxncgp5mKR6UJLeT+oNrlhyAJpLrSUF4iqL5mXVqAqZLpo3N5pAgtUlxYk2dhK35qXZdJGl1xyiVxgjiLvDOf14SbRlE1U430hobx4i/fIKtKKjKA86mXvRJXKXoIhJ8ljdYyOy0rlzkHZCwly2GGHqSP6xjFDvblB3WvSxeMqRMWD5QVeYl7uNucYsxe5RHV3GJ2nGrFoXOJWNkTYy7NwUAgXpxcRWfslpEok0YudPUlJCIRACEyLQOTOtHCl8iwiIGnmjDPOIEpoFDcTCWDRBGI00n4FmCTV1m1KknA5NrwBqg0N34k4zkEHHUQSseWerSfRRw6QaBQHifgUUUIucB3J55U6Q4LwGK2xxhqUBH8JuePGb3rFLVcSgLhVKt1YCMkLvDRF3BBSu+yyS+2XhCJ03AblJ2XDhaNjF198MfeSgXhxOgcMoSZH2FurvvGNb2hQPI6XhQ5zAxdxozKxxUNjF3wzE8qdZz3rWeJTek51SQyidezOgpaNl2LTpkLq8D3veQ+XlV2r6VOdFK7y8VN5s6r0XFVo/Uaje1ittXKWQyAEQqA7gbwzqzufrJ29BKgKeoXlFpaSdEyyCCeRL9wS7mxitkkfrg7ZxzREZQe3wZIo4zXj4lYHHnggoUMTsPEcJ/SEdBmCQ8t8KqUV+H64YThI/JTcU02RSiJiVAiNUiX2xZWiWdqrLTWnbe/5GQIhEALzngDPcd0xyrk7VI+WiNyZ9wdD9hgC/ROQ0ssbxD3Dy9J/K9kyBEIgBOYOgaGVO0lVnjsTnlZDYO4QcHe3fJdjjz12zt9dNXc6mFZDIARCYBgJJHdnGGclfQqByQg8897PZGtTHgIhEAIhMCGBeHcmxJLCEAiBEAiBEAiB8SEQuTM+c5mRhEAIhEAIhEAITEggcmdCLCkMgRAIgRAIgRAYHwKRO+MzlxlJCIRACIRACITAhAQidybEksIQCIEQCIEQCIHxIRC5Mz5zmZGEQAiEQAiEQAhMSCByZ0IsKQyBEAiBEAiBEBgfApE74zOXGUkIhEAIhEAIhMCEBCJ3JsSSwhAIgRAIgRAIgfEhELkzPnOZkYRACIRACIRACExIIHJnQiwpDIEQCIEQCIEQGB8CkTvjM5cZSQiEQAiEQAiEwIQEIncmxJLCEAiBEAiBEAiB8SEQuTM+c5mRhEAIhEAIhEAITEggcmdCLCkMgRAIgRAIgRAYHwKRO+MzlxlJCIRACIRACITAhAQidybEksIQCIEQCIEQCIHxIRC5Mz5zmZGEQAiEQAiEQAhMSCByZ0IsKQyBEAiBEAiBEBgfApE74zOXGUkIhEAIhEAIhMCEBCJ3JsSSwhAIgRAIgRAIgfEhELkzPnOZkYRACIRACIRACExIIHJnQiwpDIEQCIEQCIEQGB8CkTvjM5cZSQiEQAiEQAiEwIQEIncmxJLCEAiBEAiBEAiB8SEQuTM+c5mRhEAIhEB3Ah/+8IePOOKI7nWyNgTGksCCYzmqDCoEQiAEQqCTwGtf+9r5589VbieYlIw/gcid8Z/jjDAEQiAEisASSywRFCEwOwlE5s/Oec+oQyAEQiAEQmAWEYjcmUWTnaGGQAiEQAiEwOwkELkzO+c9ow6BEAiBEAiBWUQgcmcWTXaGGgIhEAIhEAKzk0Dkzuyc94w6BEIgBEIgBGYRgcidWTTZGWoIhEAIhEAIzE4CkTuzc94z6hAIgRAIgRCYRQQid2bRZGeoIRACIRACITA7CUTuzM55z6hDIARCIARCYBYRiNyZRZOdoYZACIRACITA7CQQuTM75z2jDoEQCIEQCIFZRCByZxZNdoYaAiEQAiEQArOTQOTO7Jz3jDoEQiAEQiAEZhGByJ1ZNNkZagiEQAiEQAjMTgKRO7Nz3jPqEAiBEAiBEJhFBCJ3ZtFkZ6ghEAIhEAIhMDsJRO7MznnPqEMgBEIgBEJgFhGI3JlFk52hhkAIhEAIhMDsJBC5MzvnPaMOgRAIgRAIgVlEIHJnFk12hhoCIRACIRACs5NA5M7snPeMOgRCIARCIARmEYHInVk02RlqCIRACIRACMxOApE7s3PeM+oQCIEQCIEQmEUEIndm0WRnqCEQAiEw7wn89Kc/ffrTn/7Zz362dv2a17xmm222+dCHPjTve5I9zmYCkTuzefYz9hAIgRCY6wQWWWSRX/7yl7vsssuvfvUrO/vXv/713e9+d67vNTsIgf+fQOTO/88jv0IgBIaGwF133fWXv/zlsssuG5oe9d+RAw888GlPe9omm2zy85///Nxzz33KU56y1VZbXXLJJf23ODpbbrTRRo9//OP196CDDvL92te+dr755tt5551rBH//+99///vfX3TRRTfeeOPojCk9HT0CkTujN2fpcQi0Evje9753++23t5bMyPJtt932wQ9+8OMf//gA93744Yc/6EEPevjDH843MMBmZ6Spvffem5lfbLHFHvvYx26wwQZ33333iiuu+IAHPKA6c8+9n7aOKVPNd1v5KP68+eabxbBuueWWX/ziFwsvvLAhzD///Ao/8IEPPOtZz/rqV7/60Ic+VIVRHFr6PCoEIndGZabSzxCYmMCnPvUp1sI6rgLKwIdllS0xce25VsqSveMd7/j6178+qD0ce+yxb3/7288777zPfe5zW2655ZVXXjmolmeqnec973m0y0c/+tHvf//7N9xwwwEHHFA9OfLII6W2POMZzyDvmr4dccQRW2yxBReINBderqZ8dBfomz322IO4caAueO/nd7/73dve9rb3vve973//+2X2fOMb34BldAeYng85gQWHvH/p3uwk4KLWx/nRZwYJ/OY3v6EkmKWFFlqIoXr3u99900037bfffq7RZ7BXrbs+++yzr7322le+8pWXX345u/g///M/q6222oknnrj55pu3VrOMpwiCj4H4WGBEGZ2m2r3I7/azKbzzzjuPPvpoZlj9ffbZ581vfvNKK60EhW3VgaIWbOJ6/bDDDrvjjjv233//pkEL//73v9/61rcqX3TRRd/1rnfxZyiUurHXXnuRRy9+8Yuf+cxn2ovGr776aobwwgsvxPxRj3qUrdZZZx2GcN111+W7Mkbeo9aWR3TZ4bT11ls/4hGP+Pa3v73KKqsYxTHHHLPvvvty0QFL9AD78pe/HHYkjzvuOMM/9dRT8R/R8bZ220Q/6UlPIsc/9rGPGabx+ldSYdVVV/VN0T7ucY8bBj9la5+zPE4EZtKWjBPHjGWwBFzmOhsONjLSRw+dmk8//XS22bYuQN/3vvex93NV6/zwhz88/vjjm5P+T37yE5aP/19yg4WTTjqp1fIRHLQIFaJ722677TnnnPO6171u1113lRO6/PLL//nPf7YJRwJZ8+tf//oNb3jDIYcccvHFFxNtLql9Ex8qXHfddUVmzz33xFx4xb6qRHBhu+2223HHHZ/znOd85jOfkXfyxje+cfXVV3/IQx5CwZgj5nmttdYiuWTYMNi2IoBqW99kDUHzxz/+8U9/+tOnP/1pPxWSYjYha84///znP//5+sPySexwZf+iF72I7ZfJ8Y9//EPN9dZbT/Tnb3/720tf+lJaao011mhaHt0F8/LsZz/7mmuuacJYUnmkrSBA5BlsuTee+tSnCng5/KT4LL744hCN7pCbnpeP6jvf+c7SSy9N+pDXBmjtb3/7W98O1z/84Q/jMdJmyFkYLgLOnvlMScDFpavPf/7znwyMf1pnK8u33nrrlBuOTQXmzaidofobkTsyXvjCF/ZOjAFYeeWVBUcm3B01gL+PXvEfCHPom3lRmQ/gqquu4upwPvVTTRMnBdLy9ddfr2b1wfKXvvQlIoANZtG/+MUvTrgjhfQEiXPyySezvv51v/CFLyi0Ly3svvvuvCmkg5If/ehHT3jCE1hlooF5Fk5SWB+FSjhgXMT/b9k9QhUKhSoIAptUbzXOti2wwAKSYKrmE5/4RDtdYYUVHvjAB1ogFGqYtfYjH/kI79dpp53mp4gPFwtNQ77omxI6o/wH4PzgBz+wOZlCZOiwZbEDHaNOXvKSl6hMkXA5CEUJtbDElJNC7VQHTAQrpRGFZB/BR5FYfuc732krCz5IslUVr6kSuo1TB39zBLKwlHKGXPvGa+64owiaqsznoVdmpH7Wtzbl7nzyk59sLRz1Zcftq1/96mYU5TPj7HGz0je/+U24HMOO20svvVQ474QTTnjYwx528MEHN/VHdMH/0TLLLEOL6z8Rv9xyyzkqLJPUlsl03h0oRnR06XYrAf5I/8s+rm1ay2d8+T4z3oOR6MBXvvIVF77mb7fddnP1ee9U3ufzn//8SHR+IJ3k2EDgwx/+MNvD4dG0yRvB6LoqbUrcR6OOj4UqdP3q/M6K25zD5mc/+5lyyunLX/6ynz5HHXVU1WTL5TFwPDg58iKwpk2zrQvNv9OPf/xjjd///vdntiUEqOPsSTHIBn3LW96i5JRTTjFZVIVVJAtBINPFMrXhepoC8/2KV7zCViWJWvdSy+RIXYM+5jGPqZCNcqZIs+SOnlv41re+5QqVq8My+60pMRouFjVdrOvMmWeeSWYttdRS7JlCvg01ScArrrjiZS97GQ2t0OGksDRB5TEoZPmsJSn4dRBr1YtU3ZOf/GRHo2r1ER5iMOgD7SCj8IwzzrBc0gRnuk1hpfXY3LK5E/yyQJ+Rbl/72tfcRGMTJlahzwte8AI3ENVy8y299FWvepXOI9NMPWmCDynTVLNAwJVg4nySl0riLLnkkmxb1TFHj3zkI2vZWLiRWre1zCIaex0wbatG9Ke5cIsWZeyUUsqV0KFZHYE8bbAL4Tl+KGDeLP8gPnJ4S2SP6JCr25/4xCccSyVoDNyxWuWEryOcyHP8tEr5kR7sLO98c36O3BnVI8FFrYvXska87q62uXymOxib8N532Yo9cJPqBRdcoKazgGV7FFywiQs+zl7Jfby+zgv1s2w8q+BynPnp0jLzJkNi/fXXdzdsY6KIFSXyA7g67I7t5MNgdZyVNt54Y6cndl2bruw54VlBbgY2Wzu1IwaSKHFxJlPECUshR4Lw/H3v/fDDVzXyhdZZc801uQfY/ve85z3KiSGtuWwF1pm9YOrA/e53P1kL4iPM8GTeHV4HV70kjm9N6X9ZSn6LzTbbDCVGhQairqxlv81X9YQxZuBrWXRmiSWWaFBUYec3f4lOGrsMHs4VThR1nKNdeTPDnCKAlHPIXKhG96hQqRiQWqY8qKvSTCV31LRrnac8dthhh9qpxAWbi++QhtSeU0aVkzhNnSqpb1PGAVa7UOK4YjAsyH0RpaLzLMOozZI7wkmdcocGkjmhJizUm6gZ+aiF5jzlGDDLKrR+7Gjttdd25NArTXmn3KEFCUEqhyHXDaxUNlnGzv3GC0UzGWm1QFQ5ahzqBGLTpgUHGwXcWjLSyybX/4sD3hyZwRoLTeP/i/PDfdqlXwUH/W8CyCtGFs/4kB1m/IJkevePE5eZnfHepgMzS2Bo5c44hISdSefBx/ndxWvFFJyt/PMzzPbrlERqML0suiQPLgSX8oQRp70rV0l5pAmbYVmkgGtBiIEFdQ0niDBht53fmVJJmu5iEBpwGWSBuGGeCR0dkDPh/CgUwtXEWjsBMf9iAex62ZXOZtkw/SE1dEOypKRR14su/V1nyw/VWxf3YiIsIqtjCBwVb3rTm5gZW/HlyDZgiqgH/naVm/ZduGuK20NWB03jZK0+HcPkEwQkCPXGJ0TfuGzVSc361OYGiJhC/5ksnEes0hPuxNlwww0RUAde/oxmX60LFIZ+Pve5z3VlbEHIRnanCgyqrSQ9WCZ3BFNcJVs7YTv2y+6Sa60tdy6z1uJQWnCRXbpHHYkm5IV5V84SmP3ODZV4uhoZYTYpBoGbkq3KHT/wbr/99maWH6h1WxAe/OAHa1kWy6abbjpZpjY5wt/G5cOVVZvTDYQLCWWKSVX8lVfHzBplSXkQow5OvbLKjrAy6Q5OP21FjDKxjjQ/6TDBBWJXdEkj5sVcN12VeyHRxMEm8qWyjyPTse1QJ2JUJivZdfqJijWbEKkDuG/S2XFC1dF8qhmIQsew/wvVZCjrgBRdx5tyx5J+1vHg5xh8HEIyqAwEjeaw9L/s0zo6wtpHCaXeWj5Ty04CDrBe9u5cYYp7qZk6ITCPCfyf6ZrHOx653TnpOxEzD9wYbJggSA3BJRrd4CzGsrq4oRgYide//vXMJPeGqzRea3ZLVEJNQQpXdcIc9O+EcoeYEFBgyJ36GWN7IReYDVpHpgWNwvRSXSyN8yOJw0WsGxwhLBxhNBlVCsa1I7PH1DEkrvLVVGhQAhOWCQUqSrcNjS+BslHIN0AxSKNx6cl82l2r1uFMohXEg0RP2H6G1sAZLd4d0tDmDHZTX3mbsKB1WF96BRniz0W/Tab1AYqniocDYU6dtm21zzdmFjTOZps73KiHv/71r201p/xp7MioZqE2N4+YQMelQagZnbX1DZf4i2X78iEyDJx0IOmYeVfqZgoWOpg4Vm6izzrrLBMt/Mei0IjUISFLoJCSdACdoY65EwEhQB0VLCWTqQMUWNN5bjnACQhrOYSoSasoUULWkWPZvGBFctWhSyrVnJpxa/nnyLLK5qEgDz30UIXcQuSU/BtK3fHTyB2HjdAbIVITrabeCld5Og4lZEEnFfq/oHd1HgeOnLpUkD/kn6W8pJSo2JaaHB6ONAdnHcPNYeOfRU1+QXVm/MPRwmeGRveeGDLBWmHEzprN0DB0iHZWGM4SB4//JvPYvXsEnEuR7nWyNgRmikDkTq/knZ6YB7Ekp3LODHa0tmTvXac60TtlVyyGy8TlqUscJscJ3cmdVaN1XMjy/5MvPEPKJ9uxPFB2kbtCZIGdJiPUdA517U7rWHb35nSvd5lAzfrYXDimLiuNyM/61DLL9L8F//krNuTy3bZVaPgWfNucdGAmxWhUcKHvYp25IuAoOSGeqq/NnXbaSW9ZWaE0F4j8GfI0RcqIQi0wbzQWxw9QZSBpOC2owPpyGBBDlBlnWDXY9o0k1PizxLWKUNPn8io5NdOUrDU5ghslwW9k1jghKANagVoiC+gYco2Xpa1xPzGXXMwxRsgaBZcVPhIv6CcC1JCJTsLU7jjw1a9vFfjkLBudFrg6CCCJzCogpgUKmDigOfRBnEsPzYhuaMddVLI4SSJ9Lm3hoDLXWMFOsaEHlGCTo8sR1dpnjXCtmRo7NSMkV60lSlqrWebg8U2460CzymQJbPk0JRaoJfKotaRZJmt8mp9UC8VpipsSC40Yai20zMy3CjUly977aavmJ3HQhw7ubGcgJRwt/KONXpmsTVNgNJOtHdFy10jOXSPa+XQ7BP5LgDHLpxcCLtNZJq4IlZsUS54eQQpqprJYXANVUy5J8WVEKYxK1uGYYZVZfZKI0XIV232ndfMzC10ptC79nXHoJFu5xCQLLFAYPN6sKStegSqhhAmbZR2Zf7dFcMlINGGJeW5czTP8VvEcyCxhv20r8cUoFDpr1+08HEjKGWYtiNxZa2i8QZwQFhh+F99lA2hB4QxAGGlCR2Fzh5FVoksECksgKZVAZPiNguFn+QCsZEymmmbisyFiIFXOtE84oiqkD/hOinCV6LkeMr2VQ1OFJVzQM3w3Z5kFH3FAy0RVk1JdlZtvBLRsLYFCanDk8HZowbZW+bY58g6Jmk1jV1JJSAqrWtNa64LJarJehPMYkgmzc1o3aV1+9KMfTdW1lkxrueQOKaOH09owlUMgBEJgSgJDm7vznxByPr0QoBJol0rdlWHARNmKk58KqUt2DhvZM8whW+hT4Q/36bCCaipn5rmFXLsLZEiY4Dbosl/WmiihcqqO/VIk1A9/Rt2nU+XaZLc8FoUPWU+4TyZrkwJQwTfBwTFQmcVCEi616RgjEn+xLecEmUKZMeSUB78C46qcFRczshfOBpKCkaZ4SEA+Eum3wiiWCQI1mXyqSIYQv5SfzYezSmUCpSmxwB9AeLWWTGtZei/Xy7Q2GYbK+HBaSGPic+KSEbJxVPTeMTeLgd97/baaYoj8UiZoyjTttg3zMwRCIASmJDC0cmc+XXeNnk93Ai7u5ceQCKpx73OrCFII5ZAvMipIGY59IQzXzTJ/uT0II4pHBTGpJkJPB1AV3P4CE5w38lWbVZ17d7+SduppLrXWVnwGekIG8TM1hSIy9lUpBdbSNK1RqqZlHg7VfNucl6XKzb4SyyQO0WOBOPOxUAEUm2itqa/9pma1MCPfxB+BJeVFf4itCcc7Ix3rfafidKWV3YbGxdXlSOhs05FgFjrLUxICIRACM05AoFw2gm7I3+Chn/H+NB2I3GlQdFsgC2TnlGLg7eDGEEJyge663HW2oAC3h3tbREbqqSfd2uptnRQWmc5110xvW8yiWjxP8kZNCq0zZeroLOKSoYZACITATBOI3JnpGRiR/TPk7oqS2uImL8Ggum9lRPqeboZACIRACMx2AkMrd+ISH65DU6TJgyv4LYS6onWGa27SmxAIgRAIgZElELkzXFMnh6O5hXi4epbehEAIhEAIhMDIEvhPdmo+IRACIRACIRACITDGBCJ3xnhyM7QQCIEQCIEQCIH/EIjcyXEQAiEQAiEQAiEw5gQid8Z8gjO8EAiBEAiBEAiByJ0cAyEQAiEQAiEQAmNOIHJnzCc4wwuBEAiBEAiBEIjcyTEQAiEQAiEQAiEw5gQid8Z8gjO8EAiBEAiBEAiByJ0cAyEQAiEQAiEQAmNOIHJnzCc4wwuBEAiBEAiBEIjcyTEQAiEQAiEQAiEw5gQid8Z8gjO8EAiBEAiBEAiByJ0cAyEQAiEQAiEQAmNOIHJnzCc4wwuBEAiBEAiBEIjcyTEQAiEQAiEQAiEw5gQid8Z8gjO8EAiBEAiBEAiByJ0cAyEQAiEQAiEQAmNOIHJnzCc4wwuBEAiBEAiBEIjcyTEQAiEQAiEQAiEw5gQid8Z8gjO8EAiBEAiBEAiBBYMgBEIgBEJgXAnccMMNCy200KKLLjojA7z66qsXXHDBhRde+L73ve+MdCA7DYGGQLw7DYoshEAIhMBoEPje9773uc997rrrruvS3VtvvfXLX/7yuuuu+5znPOezn/3seeed16XyXFr1jne8Y9lll33Na14zl9pPsyHQO4F4d3pnlZohEAIhMBQEDjnkkOOPP/6JT3ziMsssM1mH6JtvfvObX//612+66aZbbrllHvhX+HLuuuuulVZaqenSpz/96Ysuuuhf//pXU5KFEJgpApE7M0U++w2BEBhJAj/84Q8f9ahHcVrMYO8/9rGPkTvdO/CWt7xl1VVXfdKTntRW7e6771Yy//z/de3//ve//9rXvrbllls+7GEP++AHP7jBBhu87GUv+/CHPywCtfvuu19xxRUHH3zwfPPN98IXvvChD32oDX/yk5/Y9fOf//yNN96YijrooINuvPHGrbfe+oILLrD5WmutdcIJJ6h2xBFH/PnPf15iiSWuvPLKBz7wgW19yM8QmPcEEsya98yzxxCYmMBHP/pRV8YPetCD9thjj4lrDHGpy/pf/OIX//73v/vu4xe+8IWf//znfW8+hxteeumlP/3pT//5z3+2tvP3v//9Z/d+/vKXv1T5d77zHab9la985VlnnXX66ac3fotLLrnklFNO0f977rmnam6++ebrrbfexRdfrHz11Vf/yle+0tpy6zK5QEOIOj3ykY+0N6ve//73L7fcch/4wAce8YhHOCT23HPP0ijiUy996Utf/OIX77XXXq0ttC3feeedb3rTm/7whz8Y0c477/yKV7ziqquuUufcc8/dbrvtqJltt932bW97mxKzZl8OvG222Ua1b33rWwalcJ999ll88cWNbrHFFjOn73vf+3hufvOb32y00Ub777//yiuvLD5luq39n//5n1//+tdPfvKTv/3tb3MmcTtp9qtf/eq73vWu5z73uauttpqdSt9p62F+hsAMEPDPmU8IjBwBJ3Sf6jZLcMcddzgp33777SM3kNYOM5avfvWrnQWe97zntZYP5zLs7GLTt3/84x967rr/tttuk1Piu1apJlv25ptvbmpaqDqthddee+3jH/94MoLDwObdp1Lmyvbbb7/jjjvutNNOv/rVrzR4wAEHHH300RYEbojFKvRTTfrgta99rcqsshIfNVnr3XbbDe29995bCZVDaug/s33kkUfeW+seEuHhD3+4Qh+7q8IDDzzQT9Lkve9972Me8xjOD+V/+9vf6BK64XGPe9yhhx5aNembTTfd1KCkCdvq8MMPr/LO7x/96Efa5CbRggXuFv3fYYcdOGCU0A0KSQ0bcrEQKxb++te/KiRoOltrSggRCqb5WfGs173udUrMyGabbUaI1FqeGP0kbuqnf6UFFliAVPrIRz5C/ZgL9GqV+TVrxkuUP/OZz6xC3aDtiLb66dt4dbt+EmfPeMYzmlVZGHsCp556qoPT58QTTxyqwUZ017zke8QIuGZ1wX3ccccttdRSchQ22WQTJ1zeew72ERtJS3eZT59rrrmGRWkpvg9jfNpppwkTbLjhhq3l7Ld4AQu9/PLLVzkLzUoJPcDylKc8pQpFE2y+yCKLsL5dQjB0CT/E9ddfL4pxv/vdT2WbEzQ/+MEPFLpA52bAmcEjNF3WC15o9q1vfSsbr6Yre99yNcoistbVAW4GNQ3qjW98I9dCtUkT6DwTbvMXvehFCiXe8pc4OQqgGP4uu+zyhCc8QXnnx6RLgF1llVVoXEJhq6220uH3vOc92udOOOaYY+gGxvvRj340z4qYCyHC9cKW00Za05m3v/3t3Bj0CocEb41CqohOYsW5T97whjfw38iJsYry+NOf/rT00ktrtnry+te/HqUPfehD4lm6irO9PPWpT7U7mTQ8IhwbRMmSSy75kpe85KSTTjJB/CLyZkxKtTDZt4gPztYal9ae/exnr7/++m9+85uV6BV9dvbZZ5sLoSUlQE3WTlOuG2eeeWbz04KJe/rTn25BjMkuqL0zzjjDT4P1j9OkATlUQCN0LrzwQuJPeKsOsApsHXvssQ5I4ypxZvNf/vKXjoEmN0hv4XrVq15lVT4hMEQEhkp8jVZnnB9br26HqvP65mzr1Oak6UQ5j/vmNhChgbm6U85//0VMrL2QPpaZtGaP7CWb0fx0/nWF6uqW4fHdlDv7O3GzMU2JBT8VMs++XQTXKsaSVbO5ppRYeNaznuXqmdUUfWBcZS20NtJ9GRzbCigw/4IIlEHTW6vWWGMNjbe2wG4ZIANvpESJVfrjgltmhvLGFWRoWmNW68ZjJkdNR8LTnva0l7/85QQKYdHabNvyJz/5Sa3ZBWvn2h1DFcRTKDBNcW9omdRg7EvfiHcY/oMf/GD2T01dUkFeS2uzXD52ChpKNEStoksoD8vMJDlSheUcYtFbN59weYstthBMIXZN38knn3zZZZepJsiiWQtIsuVHHXWUZdbaiASk7M5W1ZqdlkfHiBp0XDvVAgUAVF2VfvGLX9SUDfGnI2uO+F202Xp4cywpIbl4cThFDLM5bGBv9lt7n/AbBC2QrTxAFso1hbnAUNUXS1pnnXUsE17lfKrgWndcdq0DzR4dHnpIjVUJ3XbYYYfVsvyetrOEvegJPg95yEMs1Hj9X/Oc2eTHP/6xQsdVbS6nh0Y0y/5r6vjUsgpm4Xe/+52oHIywV+V8jz2BofXuJHfHf2VPH9aUPXDpXLVd+bFJrpt72njeVmLhmFLRAZdrTFFlDs6zLpACLq9lG/SyR0EN5/TLL7+8l8qtdVybOoe6vFZYFqhZyx67ytcB1+UKOQCEM2Qq0H8uUp3WiVTlrvK5BO5///s7WbtUrc3dRaJlhWr6FltRrh2OCsmhMjCcwZUQBKzsd7/7XYYKagkKzaVttdP9m9WxR1fqpSGEEprjir1sS3Rw/V0ai7Zj3hhdjXOrMMmcE06dTGB5g9h7k87e0HacJSII7G6ZW7v4/ve/LwKi/mR9427Zd999bVjuGRf3aop3MPbGyP6tvfbarBdPBrVBV8nhYA7B7HKHs76x4m6H5kqp9BGCCckaI2eV+4Ym689k5d/4xjf861EnVN0f//hH452sZpXbu7nGoX6aKaEWUSqsPv7xj1eh49C1gRQWh66gTLlARKyEdSghUmbFFVfEvCq3fTtglNC79AQFpvHu94e3be4n9UBJMBIO6WYtRKXptcnvZbBWge8/WtJMeWVIlqZ+24L/KdN9/vnnUx6f+MQniHhHHQi09ac+9SlONYec6bOVM5uPgJSpd4pzzCikchzktKyb2JuWleBD1AqEKaQ1HYTSnG1rQ+07MFwkWEWLc7VS8zrs4DFftmrayUIIzAiBBWdkr6O409/+9reC/f6BuazlVPp/dsrw7z2QsThROuE2zmRtOhc7cTB+a665pm8lZIQzl2vlFVZYwRmf29xy595ZPmcoHgLxAmtZFJkKVY294exxpctIs0N0BinAVDsVOs8yh1z6ToJO+s5NdXplOF0O8mZrwYWda3Tn/c985jMG7gSnBakALuh1hkX50pe+5BoUFlfV2rcjg3LtSyWw0+hxzjuZOpPut99+dfpjWrjr6RWn2s6xdCmhAFhcFXganLWZ6qpMghA0TALDzGidc845UOgzP4RcCgrAWgEdZ21jYXrZSw5/16nqC0A4ffNSMCcMjBE5ZeuwrVz0My0speEw/2rCxRC6n4WrgFXo0tXOVa53zRFVwcdDSHEOcSSUCXEMYFuCzIbCK6QbVjrgMMDZ1FNvOixIpEsOBhf6LI3KJJ1qJJqxkCZm2RAMBH/lhM4DHvCAyayOwxuNEi4aBwc382jh3e9+t8YdopjX5pqqY7JzaK0lZt/hYSym3rjKYVC6sFFdBihw5mipDUsS2ZdBURsT7sXhhzkjqn1TT5USsgJtRIZoixbskRilVOrmI8cYGy8M5zKgUaUmkW/M5HLa+RcTnHJ4S0aBFzHT4VhF2JANgdCheGpbOkkmECvO9uu5w09Mx9HF12UrhOmwUuH6RhAYl6boWhG0Vjity/ZOkwntORT1CigSygUVQez/wgEgpuY/1H+rf0ZHuPa5oPRKKK21ndZl/1MOAC4i/6ekWP0766GmcOO9448p7Iam3MzW/FZNo/A/q31gYalglgWarKj6xtnNXNSYnvhpTjXSnMRIZ/UhEhdr7ViWQ2DGCDhG8+mFgLNPTZLzhetay5///OebDaUsODk6ayhhbJhwIsCpiu33sUnVdDpjQX2c0aqEcdUaA8Zwui5kTSkMq1wN1+6aDMeKIHBa1NWk01ATAamm6psht2FnbEU7wvPO1AwhwUFLuaa08M53vpNuIIMYOV11OiNZnJr55Jlkp3V71LLhMBj0kMtQ7hDddiovK0v8lXumnPAqS7xgb3TPibWc2zZ0GiXF2CRWuRI81fTT6bt6Pq1vVo0d4jx3hjU0365QtcBmgA+jkeJQTnjpDrSFtbYyZDKo9kU+qkkAOVlbpZBtIA4sGIKLYAuCLK6zywZokNUxduU+VI4oQy1P95t1ZCpqq7agQ2tqp+tmO+UgqZpgsi7mjtIiRwhTNolaqmPG3Okb5gbFzEhwIeZsXlEk2wrryCaZsKtW6Q9VxL+lTZPOhqnJZtfm7kzWVB1XjhafakfGiQPYsl0znJSHHFVyBBkSSpsOKhExmUB0CRPoqKBX9J+KcpgBSzTbnK31L8C+qkPHOyaNtHbR9l1+GplMLjwIWb43FWgayVs1WP9NFlh6WsqCY8PHQkXQyufXFDb/R5ygRk30UO21R4eNnw5XbrMKm1Y5kvQ6udAEhpQ7PzhmyO6q4xsr908ZI7VXadTNqs4FWBAgIKyq/+vWb4U19bWhalWzs52UhMCME3Ai8u/mU0HhGe9P04H7NEtZ6E7A2dP8sYXO5i59LFMzNmEmXR2645QfxQWfi34uaCdTV04uBF3ZuDCqEyhNoJABYJ/UdHq1ecXgXYdVZl+ZQNrCtqLd3NE2LxNlRwyz/ZJWtnLl7QzY2efJ5A6VQ5DVHl2DEiuWeQJ8C9C4PKXVnPq1WYUEmTM4Scf9o47RMQbO5gIoLuDqng51GC1rfTRedsulOZ0kzFfl9W0sWuCKoCFolNZV/S2jQdDYlkCBF5aSO36yxNJIeaTMQpvcUZ9brtQDI81w2oo33uYld1A1Zewi1KUhKqeEEiUyCFntU1TV5wnlDrvrAKAzqs5k36ygw4bzqeIp2leT1HBzFt1J2vIwVeyJHtUl2tSHS4OeEK3jXsKTGKp0Ud4LmzPA0nu1QF6YbsJUIdFD4XEw6DlnUmm4CXtFJLnop29UIyZKzTvSRCJAc6XOzWByyQWOKE4pql07/BYwOuos051cMo5hZPRBCVVnmT7W28c+9rGUOrelcp1Rbo4c6lwsSnyge8ELXqC3zpKWq7Dzm4iB19jJKSqtqWCC8CSgeXEEcZTLYi7lbZZdcugnDWH2ecV0w/+jqSTo1W8ayUIIhMAcEhhauZNgFkvX08fllEtPasZ1qss1Z1VXn7bk4pbdSSIwM8y8cyjbwH/AEc3tUU5pplRNjgFGzgnaZRyHuRaaHbt0ds8nYaF9hYwEjwKBxR0i0qS+QrpHB1wWO4M3G3YuuES2o+qbtXbkylL7dAy1oYQlc8FdbXZuPlmJIZAO7L0uGRpbpSafTYVgLOteSTfGXiypchVBsyMhGCkaLBxDxVi6KOc5cF1e+6IqXOLX9fdke+8sr9iKbZkuY1SB1cTK5TjpRvGYI5pMN8hTRo7xZu2IMKa0YmoSd0SpXIKXD4CvyLKOsaPkLFxVYlzcLaSAieOy4sBgpEGgQsxgBb/EXDgzSFjdYGgdIWbBqs5uNyUqC6NQBlqjGu3CKvFKXarbgCUIGxpo/HxoUz8qECKOLqwoYD4Y39rhhABZZygPQlZWB2eVgVQis45R0hQtGaHBpgOdC1wyPm3ljhaz2VqoHY03JTrfLFNdPs1PCzSlT2tJLetJZ2f8K4kldVZuK3HJ0VZSP4UIfWqZh9ICTSNHykRTihKG6C3/Vo4Nssx/onO6ucbZ8TlhgykMgRAYJwKRO9OYTRqCcfLcCyfTRk84k4qpUwMCNNrqYrZV41NxXd4pNZgQl8WuzstEseIu03nRGXWeBtesTs1dWm4dAz+TE7oL39qEneO9IHec6F3gqkmOiP2TLJbZV/qMyWRNORvIDtZawge7zhKIVZVCUpPMIrYYP33j1tIZAoLZk0PAYFB1lJBQHctK6gl/uLBmUaTLCGHwKDAw5Aj3gAYt0B/VZwaJ9RK/EIGqkh6/kbQt1wWNYix8DxQJ/xMFZl++eWVoDr3FwcDt0ailXlEYxuVyn+/KtuQXsaK3hILwEPeVsZTPgLIhQEUxxCyUc1+RpBwtSJJxrDXV6DAQPNJCE+2yuSmDpftAHANUl45xLQBblTl1SEaN+6nbjRl2yLW1pqZPW6FgpU9boZ9m1rHUWT72Jdx+VK+IEh1s0gsjB5KLCge5Y0N81mEz9hwywBAIgf8QcFbNpxcCfCRkQROIkU/KWNpQxoDTKGcAu8UTIJ1CoWt0bKkBy5IQpSJaEMPiB7IgymCtC3fL5RFxVV2OE/pDoWtcwQjGW2sEFkGgfaaR9aWWOFToA9Um+zClomOuZflRmHyCTE1ahNqQFaFlisS5nm+AFtGaEIkFTn5qRif5BjgMGGMfaRZCV8yD0bm7h2GmSygAUkObhsCuUx7EhD7TVRXkEroiEQzcN0ujJkVirRIWqDXQQysAK0l2srHMy/JywvHE1k6JG26eZsZ77AmlSHPwGHWvLwhIJIkT8cp0r5m1IRACITBCBIY2mDUfiP9RPflMRcDVPBFAQ8ic4AIR8hd0kGbLlyCdpdmaQ17OJgEhNYcngJeF24Dx4/bgV5DzqCZJIYmHP4CZF9EgMggpfgKX9UI8SlyJEgGCWRwJknj4FWzFQ8PjoiYB4TkZnbGApg8WNEUtSYDgwxfbqlUKeVY4LTTC1paTyX4dAwpJFl3y07e1BJatLFAkfDm65CeRpEv0UDWojvq2rZ+j/g0IdUhWir+4R4lTyh28XG7TGhcgiNVdPF02dHgI8IFpgkjYLjWzKgRCIARGiIDr/LpvQEDfGXV4eh6509NcsOu8IyURXPFLihTvIALc0szYywhpFIA6JBE9xE/DF0LxuF9JqgdvkJiCmBFzKBZGcJAOIjsyQ8UsXOuztbSIRBOpJ3WDaE89S6WBEjCV5s5cmEcyUYItRTLQPaSxEAiBEBhnApE74zy7czI2t+RIInHbLReLHB1yWEilXClz0my2HScCEowEQIUm5Z2M07gylhAIgfEjMLRyJ1euM3ywuaVL0IpHh6+I48edRNE6vU8JD5kblNx23gTset92ujXdFi7OyI3ndn2p5dPdvMf6HIEeG+MOI5ngtYlQqYQnwS9J5ZE7PWJMtRAIgRBoIxC50wZkXv8U5HIH+7ze6yD2R5xJ9xHLE/fpuz0t1I1IYkbTDRt5aIp8JtnQnvzbekeSUKObsGREeRZc0zHOMzua7i6azd3J5e4tcS4l0r3rVRLN2gEuyPsha5r7vLQswdzHU4DdpjfAHaWpEAiBEJhVBP6bczqrxpzBDoSA58HIOurlQSmT7U5Ot/vC3Nvlw6VB+kxWc8Jyt9y7EV0CuGcBt1agaeoJja2FHg/Tqn5aV0257MZ76VbunqOZ3EvFATPlJj1W0E93q9E3TX1PzXEfu8T2piQLIRACIRACc04g3p05ZzjvWmBu3Q7WdyKzbblkpFf312O3WAu6cZzU5h7v61b8vm2/vGwPzXOTmjRtgTxv+JIMTv2UD4MAshd3lsnpblwd9uW2bcOv+55E/dz1ZrlV7rhhXtSJw6luZ6uuulXe0/kEoYgJjXhMgDa9VsLTfkkZmTGeziIuRg+55a0NDmgeGez+uFe84hVW6W25o9R3c5zUZg0KpbmTzlMDPO9HTQ9K5rHTpuf+2S/tQtjJW0ceQw9NxtBWHtvjGUjutnPDv6bqrRcUpC65Qc/DAtp6kp8hEAIhEAJ9E4h3p290M7Chl1SX0e1v3541JyzS37YiRB4eKGHW7dkeIySbxHMRKQ9W39snvDGgXtFcjXtOjxTsJvtkwj3qDEtPDbhTkWn34GAvJaASiAO30NuEgOBK8VaH2lzyiocEegwjDSHiU4XEAe1S73moEo+PIzvcRt6IJOWkBv2kt5455D0JxIR26CoyyFoSygLR07zdsJqqb7rEKs8gqJ+eIuixipaVGCBPDMVmILrnWUdy9OpF4vYl8mU41JiheXiBcXnJhnu+KnaJj6dTuOldfjoN5Pa9at8DDnSSKq2f+Q6BEAiBEBgIgXh3po2R84BnwrNSZIfUxp65x2JxUbjKd7e55+J40E5za7qb2BWK1Mj/aH1EDQ+EEIlqlIT3M6jmWX8e7OvOrMre0CDrKDRjR/VoFm+l8ER/D/ezSjl/AMPvRUu77rorr4aH/Xh9gc+EQxJ78lxBPfeoQ1txddRjEj1zlt0lAjwjkVui6XZbIzrPqOu/h+/ZnF/k5S9/OQ3hznlignTQmhyaet2Bxwvpnqa83ku0S2Fba34aGungIYq1ijrxoEVW371ptSEp4+0Q2lHBQ43106OTeUHII3wa+Hw83CFeu1HtSFsWHiIyyJQq8S2zR3Ixz029UKzK+ZZE0Op5ifwu9mtQzSZtC028iRCxid4arwfnuKXOh2TxDEayj2Ayj7a1O2+Vkphl2XD8rCdPwuVxi9V4OaUQIIAMtm2P+RkCIRACITBAAvHuTA8mu+uxOp6m4xH+HiFoY7afv0EIQxKJC33v6PGyCD/ZzvpY9pYrr5jwbof/LfvPX5W5RlhlMqXe8cQq01ICH7JiVWAI5abYkZc32RGlwmHAM2HBQ33oG4V2p6YNWW6JIBwVCif8MLQ8B5QHnwTDXK+W5GLhqiGA5N7yozRPw+xswRNoZMsKNukh2085qUPDuTtaH4ghFTyAWCEfBtHmeULkBUT8QJ2tdZZoiiYAipITs0MGBAGpUi2EkWW6oe39TZ3tVEk9h3qytVVO4ngWFvKkqhCVt2R0qe+FGLUWOs+V1kkTyg3TbEIG0Vj8Uo3MEoaTXdRUqAXCtwQcVVSvFVNO5jqu2mpO9lMorRSVCqSkuBi9O1nllIdACIRACBSByJ1pHAm8Fy7ZGXgBHcasohI//elPGXXvkeCh4SPhafCiULZf1EloQ+vyOagB9ptDQkTDK6AVMm8MrULZG1rgDqk3+0jsYPXr7eskhRAJj4tbkdXk4CEgOAx4MrxEoiI+CldZZRUuDa+A8BJvC13Gw0j7qEA3+FhgLzVVbgaRoyYvp0sjratoFBEuJbwdyHByWOYmccO28I07pxQaZusmzTJ1iE+9ErUptGD4zHn1k7SqYJb4FG8KgUJytVbusiwC1bqWL80sVNxKCKlWmTVagQuq8mZa6zfL3GAEnJHqrewiN4KZAl4cW5GJps+Tlz05qdRS+ZxMsTcxqVyOHHBqv8YlymZEyJQSkntkHpt7vuyUGLUVxcxT2LywU/hMaM/x4AZ1arsJ3nkqt72j3fQ2CyEQAiEQAhMSSDBrQiwTF4oHuTqvmAWXjCRW9bxxWpClrtRV8NptGa8u9GVveMWVCuyl8BbVIhLETFYhO8ee0RysuG8KhkEVl2HmXb6LK9mw3vzMxvN2TNyhe+swrlJqJA6rQ77UVpPVb8o5pSg2faDGuCsEUygq/WwqdC7oW+WUcCzps0iWEltVTf2XwUMB0HmehUP0cGNIbRbx8RzqztaEpdxGLjTGY8ShpRtKVINCeEjmsiwchp8eIum0LJ+Xc8v7v9QRvINds77pD/nCcpJIPW8plzojYkVSEAFe8aFOxbm8C0LHJAl5sLUwljxl7ZgayUOWW4OMnV0lB01BPRadMNIZdTiiOLF4ffi6+MYqKYqfD0kvBRPgQ4A+rr6ZULqKJMXN6FTgjdMZIgZSSc2Oh9qvI4fiIc7EBxuHE0kka7sKObrqPbLq6xgF3AQEO3uekhAIgRAIgSIQuTONI6HyS7gcWFYmp6wOo84MC2FMln7BKLJznCisbNvOmDp+C8aM/6aSW4WTWLUu+qZakBvkWp/lIyx4EeT0kE0sMbvb5Ul0fE4MsBd80iicE5Jt6ST2kn01tD322IOFbuth60816Qz6gMKQp8ynZcg0igCZngiWcdioz5DrjwYJNeGzyl9pbaeWcfN6VHqF5DJeuqGcTCgp5BwCx47IFzXFsAAUPwKHsCA66RgeMg42PREuJJgIOC0Ti2SoLnGf8KlUofIXv/jFVKmRykrWYPWBRJOQ5OXz9bPLt5Rkj9vRT3KkqcazxX1lj4bQFPLtNcv6Zln8kVarQt47n1r2ChGaqalcCyVb2wrlaLeV1M97M7UmTtWasH4KQyAEQmD2EnAGz6dHAiIXrJ2gj2wPMRrCgr3kb+B+YHF5KaTRvOc972H/5OVIyKAnWP16qbgsGcaJhXNB72jjBHJBz67LwnHpL0JBGbjcZ8h1pjJFWHR7rPANl5JyDg974UFhMjUleMR3Yu/MIZHBbcDSdx+LF1LaO8PPm8LHwGcgXqZL3DCcHJW3O1kLxkWFCLSpqWOqGTshQnPgoEFRudpW0rFyEZnJmmrKCS/6gy8HQHnK8pebVXN1gUtGSMgouLjkHs3VfaXxEAiBEJg9BJocUNfPQzXqvCJ0ekqXd4QocbEu0EDu0Ci2ZzXdmGNBOVcNtwf7LdDDi+BbxgZHhQURE9ZdvMMj79SsAAq3gQ25LkgoUTAixk9pQG5UFpYikgRfKsOmvEeaEubQckW+VNa+EkeVCmIlSrp86uDTGZ8u1eb9KnFA+cKkYZc0mgH2SjqOHYnH8avVPVMDbDxNhUAIhMCsJSDNMW9EH5PZl20q8CRBeEzGMxzD4GsRoZPrzSs2D3pENfKNUZxJfJkHtLOLEAiB2UNgaOVOcnemfRB23l087SayQQcBKT6TZfl01B1AAfdY97vYBrCPNBECIRACITA0BKaIfQxNP9OREAiBEAiBEAiBEOiTQOROn+CyWQiEQAiEQAiEwKgQiNwZlZlKP0MgBEIgBEIgBPokELnTJ7hsFgIhEAIhEAIhMCoEIndGZabSzxAIgRAIgRAIgT4JRO70CS6bhUAIhEAIhEAIjAqByJ1Rman0MwRCIARCIARCoE8CkTt9gstmIRACIRACIRACo0IgcmdUZir9DIEQCIEQCIEQ6JNA5E6f4LJZCIRACIRACITAqBCI3BmVmUo/QyAEQiAEQiAE+iQQudMnuGwWAiEQAiEQAiEwKgQid0ZlptLPEAiBEAiBEAiBPglE7vQJLpuFQAiEQAiEQAiMCoHInVGZqfQzBEIgBEIgBEKgTwKRO32Cy2YhEAIhEAIhEAKjQiByZ1RmKv0MgRAIgRAIgRDok0DkTp/gslkIhEAIhEAIhMCoEFhwVDqafoZACIRACIwugbvv/ej//PPPb3HCgVj1r3/966Mf/eiEa/sunG+++bQ84eZ77rnn0ksvPeGqFI4ZgcidMZvQDCcEQmDMCVx11VXnn3/+AgssUOO86667br311mbMiyyyyG233db8nBsLiy666KGHHnrCCSfYV4/t6+Saa665wQYb3HHHHeedd95DH/rQe+65p3NbukTnzznnnM5VfZfceeedD3jAAw444AB96GxkscUW6yxMyVgSiNwZy2nNoEJgbAkwk0xm38OjDCZzLbS2ueCCC/7tb3/bf//9LbSWd1/WN1JAnblnRBdaaKHf//73J598ctOT9ddff9ddd7399tuVGNrXv/717bffvpcxNi30sfDoRz96ww037H1DU7bRRhttttlmNMepp566xRZb9L5taobAQAhM4z95IPtLIyEQAmNJ4Oyzz7744ounJQ5aORAKvfgkuDSuvvrqt73tba3b9r7M1m611VYrrrjihBf6re2Um+HKK6+00FrefdkQnv70p+vkC17wgsb70n2T6a4FiuIhpyzY1jcXS2s45tWvfvWSSy453WbnWX1YonXmGe3sqJVA5E4rjSyHwDQISDJwzTotc1itlyllGvvYtpf+LbzwwgceeOAf/vAHdrHqS1xYffXVWRp9VuLnUkstVfaylwanrEPl/PjHP/7zn//cn9zhilhmmWU++MEP6mH3XpEpyy233Je+9KUpuzRhBZuztcsuu+yEa8ejcJi1zngQzihGlEDkzohOXLo9BQE+gCOPPHJOrrDZ4C6ml11nni+99NIp+jHJ6sc+9rGbbLLJnARlJmn4P8VU1C233LLGGmuUnDKQJZZY4r3vfS9DePzxxyvkD2D1e/GmdNlL2yptzgltvWrEWVvL+RkCIRACc04gcmfOGY5tCzIiGTD+fM4Al8Us6KCGyrbJH9xtt92e//znH3PMMTfccEMZ5h7bZ7/ZclrBt+XOrXT4+uuvP/PMMy10ru2lRIbHLrvs8rSnPa2LJvja177WX/tgStvkbumlJ4OtI8jSNDj38kuaXWQhBEIgBIaEQOTOvJgIpr1209hm1p09PuOMMzbddFNxh2kZ+8l6zPTOyeV1W7O8FyeeeOLiiy9+2mmnWUVY7LTTToP1RnAw/Pvf/958883bdj3lT93Yeuutb7zxRt8N27atIB0gjbbG8zMEQiAEQmC0CETuTGO+dthhB66I6V4Tu5R3S4JvAmLllVe2ULtks7lPjj76aDkW0+jEJFU5IQRH3vjGN3bxRkyy6aTF2223XSVCUmlGvdpqq01adeZW9JcsMnP9zZ5DIARCIARmgEDkzjSgv+hFL3L75XTtK1mzzTbbcELYcK211prG/lI1BEIgBEIgBEJgEAQid6ZB8Rn3fqaxQaqGQAiEQAiEQAgMAYE+EzmHoOfpQgiEQAiEQAiEQAj0RCBypydMqRQCIRACIRACITC6BCJ3Rnfu0vMQCIEQCIEQCIGeCETu9IQplUIgBEIgBEIgBEaXQOTO6M5deh4CIRACIRACIdATgcidnjClUgiEQAiEQAiEwOgSiNwZ3blLz0MgBEIgBEIgBHoiELnTE6ZUCoEQCIEQCIEQGF0CkTujO3fpeQiEQAiEQAiEQE8EInd6wpRKIRACIRACIRACo0sgcmd05y49D4EQCIEQCIEQ6IlA5E5PmFIpBEIgBEIgBEJgdAlE7ozu3KXnIRACIRACIRACPRGI3OkJUyqFQAiEQAiEQAiMLoHIndGdu/Q8BEIgBEIgBEKgJwIL9lQrlUIgBEIgBEJgzgjcc889c9bA1FvPN998p5122o9+9KOFF15YbT/t1PdkW77hDW9YaqmlJlub8nEiELkzTrOZsYRACIw5gbvuuuucc865++67BzVOUuDmm2+ef/75F1100dtuu81P322NW3vjjTfuvvvuL3vZy4488sg77rijrcKUP3V79dVXf8hDHmJhyspzUmGBBRb461//evHFF995552bbrrpDjvssPPOO++77752PWG3F1lkkTnZXbYdIQKROyM0WelqCMx2AuUeqIt1y/WzRyis+FyytUzmUUcddeqppy600ELlVJhLRtTAb7311kMOOWRCy90jh85qr3nNa6666qpjjjlmiy22IH223XbbCUHtuOOOgBMQnS1MWaLDG2+88dOe9rQpaw68wp///OeBt5kGR5FA5M4ozlr6HALDQuD000+//vrrXf3PYYfYUZfjnBaT+S1Y+uuuu+6EE05Q4QUveIEAxBe/+MXvfve7PQoLjW+yySYcDBMa8jnsvOFfccUV1157LaO+5ZZb+vmiF72Im2EOm51wcxz22muvEnwTVphuIfIrrLCCnl9zzTX3u9/94F166aWn20jqh8DwE4jcGf45Sg9HmIBr5cUXX/yGG25gZVncGokL9IGYK5b+lFNOYfg32mgj5ord2nvvvRndORcf1U8NLrfccrr6r3/9a+WVV+6cBjv69re/ffXVV8+haWdiV1xxxSc+8YkPfOADN9hgA2Pp3JcSPXnWs55l4ZZ7P9tssw0/xIQ1OwvBf+pTn7raaqt1rkoJApxS973vfYMiBMaYQOTOGE/u7Bral7/85Yc97GEspW/L/Q1+MkPbX2tEwBFHHLH99tsfcMABl19++YMf/GB2XeFWW201kB0x/+y+bz4P0kQnNTtAoyX685KXvESH8Xzve99rR50cPvCBDwxEXWlkwQUX9D2HyqmzhykJgRAIAQT+k7UeECFQBG6//fbyRlx66aUT2rZeQN10002MuotFh1bjz2jdkD3bZ599LrnkEuattbz3ZVmHHBtth+5JJ53EN2CPvi333lrVLB/+Rz7yEekXbS1Pt6nW+jigKglUIQeJvbDoHBitdbIcAiEQAmNDwJ1xm2++ueGceOKJYrvDM64+7c3wDGD4e8J2zrn5ZCMPPvjgdddd94ILLrjsssuaK2Dl5TCYcw7a1PL5559vL5/+9Kf7bnDXXXddfvnlzz77bG6G9dZbb0LFQ5GstdZa/e0CTLkLdtGWhEFYKKHSfFvur/FsFQIhEAIhMJYEInemMa2vfvWrjz322MUWW6z3bWgR2Q8bbrhhm23uvYWqSdb87ne/k0goi4L7pFwvDP9OO+102GGHffCDH1xppZXmcBd2ZC88LgQKyTLdHjb111lnHQ4S/dTUkksu2ZQPfKHTOVQljRYc+B7TYAiEQAiEwIgSiNyZxsRtvfXWD3rQg9jy3rep2Mrzn//83jeZbs0999xzupvMg/qU2TzYS3YRAiEQAiEQAr0QiNzphdJ/6zz73s80NkjVEAiBEAiBEAiBISAwp0/LGIIhpAshEAIhEAIhEAIh0I1A5E43OlkXAiEQAiEQAiEwBgQid8ZgEjOEEAiBEAiBEAiBbgQid7rRyboQCIEQCIEQCIExIBC5MwaTmCGEQAiEQAiEQAh0IxC5041O1oVACIRACIRACIwBgcidMZjEDCEEQiAEQiAEQqAbgcidbnSyLgRCIARCIARCYAwIRO6MwSRmCCEQAiEQAiEQAt0IRO50o5N1IRACIRACIRACY0AgcmcMJjFDCIEQCIEQCIEQ6EYgcqcbnawLgRAIgRAIgRAYAwKRO2MwiRlCCIRACIRACIRANwKRO93oZF0IhEAIhEAIhMAYEFhwDMaQIYRACIRACMxmArfccsv8889/9913X3fddfPNN1+PKO65555FFllk2WWX7bF+qo00gcidkZ6+dD4EQiAEhpfA4Ycffu211xIic9hFusRnskYWXnjhs88+2/ett9561FFHTVZtwvItttji5JNPnnBVCseMQOTOmE1ohhMCITADBK644gpOAhbXvi+77LJVV131oosuYn179zQ0nb755pt5Ke573/vefu9n0UUXve2225q1c76w0EILvfOd77zgggsIiFe96lXf/e53r7nmmlIk9rvccsstsMACd91113rrred7TnZn7GeddZbh9AGhdb8w6PDDH/5wC63lrcuPetSjDMeO3vSmN3URRq2bWDbeZZZZpq0wP8eVQOTOuM5sxhUCs44AO9fFIsLB0n/84x//y1/+suCCfZ76tGAvbZvTByeccMLGG29cYZHjjz/+mc985qGHHkpG9DEHr33ta1dbbbX9999/yy23fMITnvC1r31t6623tt8+mppsk8c85jEbbbSRtXBxbzTV7rjjjoc97GH2ZeHFL34xNdCs6m9hzv06/e03W4VAJ4H5ehfCnRunJARCYPwIXHrppeeddx4TPtnQnDT4Lebw1CFngiFndNddd92f/OQnBx10kJLJ9thLOdtMbWy66aZdjDTre+GFF9500019+xu23357Po9tttmm8bjw6JxzzjmXX345iSODRFcNxNrFF1+8D2OPKq2jzUsuuYSjZYkllvjnP/9poe8O94IudUJggAROO+20zTffXIMnnngiyT7AluewqcidOQSYzceWAIt155139j08dquMX1sLZITAx7ve9a4+bGFbU/XTjgQ+fDONE1aYVqEr+1//+tenn376ZPbVjhZbbLH99tvPt+VpNd5WGQrSRCNQdFFXbVtN9pMKWWmllbbddtvJKsylcvs10QOBP5d6mGZDYF4SGFq506dHd16yy75CYDICp5566t///veylAwnD/xkNadb7gJdMML/bX9BBCZcC9ttt53N2zQBGaGfjW9guh3rrK+pTTbZRJt217l2uiV6y7Wg823dbm3HEJZaaqnJ9FBrzdmwfMABB9CvBx988GwYbMYYAqNLIHJndOfuPjfeeCNryjJdeeWVrN2cmx+KgT/DpzMcYC+f+9znTjnlFAt9I2NBV1999XJF9N1Is6H8CXJEEIHckYLwyEc+cu+99+6eutFs28vCHnvs8Za3vKWXmp11SjQ85SlPmXOnRWfjKRkqAlTm8ssvP1RdSmdCIAQ6CUTudDKZoxKyw3Vef3dkdNlx56W2S3DiQ5j/IQ95iOtLd3t22bzHVSussMLaa6/9wAc+cJVVVmm7KYOWMii3P8yJqAJnt912k6thoccuda9GezV6QsfmpG/dd5S1ITAZgQc/+MGTrUp5CITA8BCI3JnGXNxwww3ucuzuR6ESPAGie51p7PLeWyWpEJlfZM25557Lh7HWWmvZCwH0+Mc/nhvG8g9+8IM5TwTRoORKt2UuvfTSFqbVyelWnhMX0XT3lfohEAIhEAIhELkzjWNgySWXFNCZcoP4GKZElAohEAIhEAIhMC8JRO5Mj3akzPR4pXYIhEAIhEAIDAGBOX229xAMIV0IgRAIgRAIgRAIgW4EIne60cm6EAiBEAiBEAiBMSAQuTMGk5ghhEAIhEAIhEAIdCMQudONTtaFQAiEQAiEQAiMAYHInTGYxAwhBEIgBEIgBEKgG4HInW50si4EQiAEQiAEQmAMCETujMEkZgghEAIhEAIhEALdCETudKOTdSEQAiEQAiEQAmNAIHJnDCYxQwiBEAiBEAiBEOhGIHKnG52sC4EQCIEQCIEQGAMCkTtjMIkZQgiEQAiEQAiEQDcCkTvd6GRdCIRACIRACITAGBCI3BmDScwQQiAEQiAEQiAEuhGI3OlGJ+tCIARCIARCIATGgEDkzhhMYoYQAiEQAiEwbQL33HPPTTfdNO3NssFoElhwNLudXodACIRACIwVgR/+8IfnnnvuQgstNCejuvvuu+eff3465q677pqynTvuuOOrX/3qUUcdtfbaa09ZORVGnUDkzqjPYPofAiEwiwj84x//YM4Z9RtvvHG++eZrHfnNN9+84IILLrLIIrfeeuvtt9/etra15pwsL7DAAnvvvfcll1xiX9NqR5/XX3/96667bplllllsscUoktbNNfub3/zm73//u4XW8mkt28XOO+/8uc99bt11133Pe94DwpSbH3jggYsvvviU1VJhDAhM73gdgwFnCCEQAiFQPoA777xzQhQM+emnn37cccctvPDCE1bopbBEyZwY78696M+XvvQlWuGWW2658MIL2yq86lWv+utf//qjH/3oGc94xuMe97hejH1bCz3+3GCDDQiXHis31dDec889zznnHJuvssoqnd4X2EFr6ve9sN9++/W9bTYcYwKRO2M8uRlaCMxFArfddtuvfvUrUYCLLrpoLu2GA4DHYrLG2X4dcHXOnzFZnQnL2VRX/+edd95mm22mkTY3g01UuOKKKzgw+ra+NnzlK1/5xS9+8aCDDlp66aWpqwl7Mt1CXd12221rqzbnilVrrbUWXJdffvlqq63GgzLdxudN/VVXXbV2NFghOG86n72MNIHInZGevnR+JgkwMGL/A+mBC1/qgel1yTuHplEjZ5xxxuGHH14iQESDM6BEAxu81FJLDaTDmrr++uu/8IUvbLHFFqeccspA2uxshFB417ve1SUooxvvfOc7OzfsXmKrpzzlKbwgO+2006KLLtq98pysfeMb3zgnm/exreEsu+yyfWyYTUJg7AlE7oz9FM/qAV555ZWnnXZa23Vw70SIj8kEjTYvvvhixrjvxptu0DrrrbfeJptscvbZZ6+xxhrLLbfcnCge4uCGG264+uqrGXWCjNZ54QtfeNhhh/m58sorv+lNb5qTxps+W7CjD3zgA1TadJ0rrY10X9ZnNLrX6XttH+GYvveVDUMgBGacQOTOjE/BXO+Aq3A2qcslcu89cNMmC9p7/R5rspdHH330N7/5zTKcvNy88XPeYe1ceumlJ598cn+KROqDBIjdd98dvc6B0Cirr7662zo6V023RFPrrLPOox71KLelcPXPjTDEy172sun2KvVDIARCYJwIRO7M69l02X3kkUcOKm5dV+pdJIjQxic+8YkLLrhgzsdJNOy4446dt1TMecuUjdTLNddc04IRCbjsu+++7kftMq4ed4rznPgeeBf6k0o9dq+tmhTOtpL8DIEQCIEQGAiByJ1pYOTb2H777d0Q0YtYYap5y+973/u22mzmk6/lzDPPtDCNHU9SVcuu2vkenvOc50zogajtDj300F46PMlO/q9YnzfaaKN5af7/b99ZCoEQCIEQCIE5IBC5Mw14tMtee+317W9/m8tkys1EKF7/+teLd1horcyBMRDx0dpmlkMgBEIgBEIgBLoQiNzpAmeCVY+/9zPBismL4g6ZnE3WhEAIhEAIhMC8IDCAkMq86Gb2EQIhEAIhEAIhEAL9Eojc6ZdctguBEAiBEAiBEBgRApE7IzJR6WYIhEAIhEAIhEC/BCJ3+iWX7UIgBEIgBEIgBEaEQOTOiExUuhkCIRACIRACIdAvgcidfslluxAIgRAIgRAIgREhELkzIhOVboZACIRACIRACPRLIHKnX3LZLgRCIARCIARCYEQIRO6MyESlmyEQAiEQAiEQAv0SiNzpl1y2C4EQCIEQCIEQGBECkTsjMlHpZgiEQAiEQAiEQL8EInf6JZftQiAEQiAEQiAERoRA5M6ITFS6GQIhEAIhEAIh0C+ByJ1+yWW7EAiBEAiBEAiBESEQuTMiE5VuhkAIhEAIhEAI9EsgcqdfctkuBEIgBEIgBEJgRAhE7ozIRKWbIRACIRACIRAC/RKI3OmXXLYLgRAIgRAIgRAYEQKROyMyUelmCIRACIRACIRAvwQid/oll+1CIARCIARCIARGhEDkzohMVLoZAiEQAiEQAiHQL4HInX7JZbsQCIEQCIEQCIERIRC5MyITlW6GQAiEQAiEQAj0SyByp19y2S4EQiAEQiAEQmBECETujMhEpZshEAIhEAIhEAL9Eojc6ZdctguBEAiBEAiBEBgRApE7IzJR6WYIhEAIhEAIhEC/BCJ3+iWX7UIgBEIgBEIgBEaEQOTOiExUuhkCIRACIRACIdAvgcidfslluxAIgRAIgRAIgREhELkzIhOVboZACIRACIRACPRLIHKnX3LZLgRCIARCIARCYEQIRO6MyESlmyEQAiEQAiEQAv0SiNzpl1y2C4EQCIEQCIEQGBECkTsjMlHpZgiEQAiEQAiEQL8EInf6JZftQiAEQiAEQiAERoRA5M6ITFS6GQIhEAIhEAIh0C+ByJ1+yWW7EAiBEAiBEAiBESEQuTMiE5VuhkAIhEAIhEAI9EsgcqdfcpNs96c//emPf/zjJCtTHAIhEAIhEAIhMAMEFpyBfY7vLi+88MLNNttsoYUWOu2009Zee+3xHWhGFgIhEAIhEAKjRCDenUHO1l133TXffPPtvPPOD3rQgwbZbtoKgRAIgRAIgRCYAwLx7vQJ79///vfBBx/83Oc+99hjj33lK1+5wgorXHvttfvuu+8999yz6KKLEj3V7ic/+cnjjjtO4e23377ffvttuummE+5v7733/tWvfqXaxz72sZtuummfffaZf/75l1lmGXvR1K233nrnnXdyF336059ebLHFJmwhhSEQAiEQAiEQApMRiHdnMjLdyn/xi1+svvrqxxxzzIYbbrjXXnu9733vU/uss85afPHFF1xwQWtr49///ve77bbbKaec4ucCCyyw5ZZb/vSnP52w3a222urkk09+6lOfusEGGzz2sY999KMffcUVV+y+++6iYxpZZ5111ltvvW9+85sf+tCHJtw8hSEQAiEQAiEQAl0IxLvTBc6kqz7zmc8sv/zyBMpll1321re+dZdddlF163s/L3zhC2+55Zba8uEPf/jznve8884777vf/e7dd99tlQ2f+MQndrb7pCc9ydptttnmzW9+89JLL73ttttKAFKTovrIRz5yyCGH2ORnP/vZbbfd1rltSkIgBEIgBEIgBLoTiHenO58J1p5//vlf+MIXVl55Zbpk/fXXX2mllVZbbbUJ6t1bpNpSSy0lvMXx8/SnP/0rX/kKb01nZaGrZZdd9pnPfCZhdPTRRz/nOc8R2FJtjTXWWHjhhTvrpyQEQiAEQiAEQqB3ApE7vbP6b80lllji/ve/v6zkXrYUnJJ5c91116l81FFHvfSlL+XyqQ3POeecc889t2lk3XXX/dvf/kbl/OEPf7jqqqsEsKwig/75z3+efvrpomDXX3+9n039LIRACIRACIRACPRIIOazR1D/V23VVVf9wQ9+cOONNwo/+UgxrnVSkv2UwaNECvMRRxyhfMUVV/zd734npLXHHnvQPa973euahuQ1S9a5+OKLq8QqjqL9999/1113pXWkPyvnFiJ0JDiLdr343k9VzncIhEAIhEAIhEDvBCJ3emf1fzWlEh9++OF8Nm6Y+stf/kK4WLf55pu7bWqjjTaSc+OOqjvuuEMhx4wsHOnMbrb64Q9/+LjHPa5pZeONN37DG96w5pprVokcZ48ofPazn/3hD3+4SXY+44wzSCJ5P277cmOX2FmzeRZCIARCIARCIAR6JJBU5R5BtVcja0466SSl/C7CTBaWXHLJ8ui0ViV6RK/U4adpC0W95S1vaa1pWTJQlTT5OuJfPttttx0Z1FY5P0MgBEIgBEIgBHokEO9Oj6AmruaJgoJNso+vueaazhpk0G9+85tf/vKXolSeptNZYcoSYSzun1//+tc9pgpN2WAqhEAIhEAIhMAsJBDvTv+TToK8/vWvF7dy7xXXTmdDnrXjSTmLLLKIBXdmdVaYskS6DsXj/qwpa6ZCCIRACIRACITAZAQidyYjM3U5EfOIRzzi61//+mRV3cP1+Mc/frK1vZTbRbROL6BSJwRCIARCIAS6EEgwqwucrAqBEAiBEAiBEBgHApE74zCLGUMIhEAIhEAIhEAXApE7XeBkVQiEQAiEQAiEwDgQiNwZh1nMGEIgBEIgBEIgBLoQiNzpAierQiAEQiAEQiAExoFA5M44zGLGEAIhEAIhEAIh0IVA5E4XOFkVAiEwKwjcdttts2KcGWQIzGICkTuzePIz9BAIgXsJfOUrX7nnnnsCIwRCYIwJ5DGDYzy5GVoIhEBPBHbcccee6qVSCITAyBKId2dkpy4dD4EQCIEQCIEQ6I1A5E5vnFIrBEIgBEIgBEJgZAlE7ozs1KXjIRACIRACIRACvRGI3OmNU2qFQAiEQAiEQAiMLIHInZGdunQ8BEIgBEIgBEKgNwKRO71xSq0QCIEQCIEQCIGRJRC5M7JTl46HQAiEQAiEQAj0RiBypzdOqRUCIRACIRACITCyBCJ3Rnbq0vEQCIEQCIEQCIHeCETu9MYptUIgBEIgBEIgBEaWQOTOyE5dOh4CIRACIRACIdAbgcid3jilVgiEQAiEQAiEwMgSiNwZ2alLx0MgBEIgBEIgBHojELnTG6fUCoEQCIEQCIEQGFkCkTsjO3XpeAiEQAiEQAiEQG8EInd645RaIRACIRACIRACI0sgcmdkpy4dD4EQCIEQCIEQ6I1A5E5vnFIrBEIgBEIgBEJgZAlE7ozs1KXjIRACIRACIRACvRGI3OmNU2qFQAiEQAiEQAiMLIHInZGdunQ8BEIgBEIgBEKgNwKRO71xSq0QCIEQCIEQCIGRJRC5M7JTl46HQAiEQAiEQAj0RiBypzdOqRUCIRACIRACITCyBCJ3Rnbq0vEQCIEQCIEQCIHeCETu9MYptUIgBEIgBEIgBEaWQOTOyE5dOh4CIRACIRACIdAbgcid3jilVgiEQAiEQAiEwMgSiNwZ2alLx0MgBEIgBEIgBHojELnTG6fUCoEQCIEQCIEQGFkCkTsjO3XpeAiEQAiEQAiEQG8EInd645RaIRACIRACIRACI0sgcmdkpy4dD4EQCIEQCIEQ6I1A5E5vnFIrBEIgBEIgBEJgZAlE7ozs1KXjIRACIRACIRACvRGI3OmNU2qFQAiEQAiEQAiMLIHInZGdunQ8BEIgBEIgBEKgNwKRO71xSq0QCIEQCIEQCIGRJRC5M7JTl46HQAiEQAiEQAj0RiBypzdOqRUCIRACIRACITCyBCJ3Rnbq0vEQCIEQCIEQCIHeCETu9MYptUIgBEIgBEIgBEaWQOTOyE5dOh4CIRACIRACIdAbgcid3jilVgiEQAiEQAiEwMgSiNwZ2alLx0MgBEIgBEIgBHojELnTG6fUCoEQCIEQCIEQGFkCkTsjO3XpeAiEQAiEQAiEQG8EInd645RaIRACIRACIRACI0sgcmdkpy4dD4EQCIEQCIEQ6I1A5E5vnFIrBEIgBEIgBEJgZAlE7ozs1KXjIRACIRACIRACvRGI3OmNU2qFQAiEQAiEQAiMLIHInZGdunQ8BEIgBEIgBEKgNwKRO71xSq0QCIEQCIEQCIGRJRC5M7JTl46HQAiEQAiEQAj0RiBypzdOqRUCIRACIRACITCyBCJ3Rnbq0vEQCIEQCIEQCIHeCETu9MYptUIgBEIgBEIgBEaWQOTOyE5dOh4CIRACIRACIdAbgcid3jilVgiEQAiEQAiEwMgSiNwZ2alLx0MgBEIgBEIgBHojELnTG6fUCoEQCIEQCIEQGFkCC45sz9PxEAiBEAiBeUrg9ttvv+CCCx784AcvssgirTu++uqrL7/88tVXX33ZZZdV/u9///vMM8/8+Mc/vsoqq/h52WWXbbfddk94whNUWGyxxZT8/e9/v+eee9ZYYw3Lt95660UXXVQ/l156aSVtn+uuu+7SSy+94447brvttvnmm2/xxRdfaKGFHvKQh1hurXnnnXfq21133XXzzTers+CCC66zzjoLLLBAU+emm27685//rIerrbZaU2hB49dee+2iiy6qvq6uuuqqCrWjtbvvvlvHmvEa44orrlht2osNf/7zn3/oQx/Sk/e+973rrrvummuuufDCC7c2fuWVV1511VXzz/9fz4LWEHjQgx7UWifL84gA+vmEQAiEQAiEwJQE/vKXv7BMO+200zve8Y699trrAx/4AFmz9957b7rppso/85nPaIEo2Xrrrf3cd999q8Hzzz//AQ94gBLioEpe8pKXrLzyyn/961/9fOc732mVzwte8AIiQ8mPfvSjj3zkI1WTiHnOc55j7SabbPL+97//3e9+933ve1/y4utf/3pVaL4POeQQ1e5///vvv//+NI06u+66q103FU499VQV1ltvvbe97W0nnnii+vvss8/vfvc7MkU57UXcvPKVr6z6//rXv+xIuU8zkBe+8IVf+MIXqsKee+5Za1u/DzzwwGZ3FqiojTfeuLWC5RVWWAE97bfWHKfl4mykIA/VuO4zVL1JZ0IgBEIgBIaWwAknnNBqvDktllhiiaak5M6rXvWqKuHwaAbypje9SeFmm21WJVSFnw9/+MMpj6rsW2u8QbZaZpllHvnIR1bN173udVXh85//vBI+npVWWknJM57xDLqq6vg++OCDy4Ny3HHH+fntb3+7tmpkk8LHPvaxVei7XEQWllxyySq04aGHHmqZ68UwKZsq982TdPbZZ3/iE5+wvOOOO2qqlv182tOeRrh88YtfLHfX+uuvf80116hQn2c+85nVCIcQuca/1XikuLv+t9a4/Y3cGbcZzXhCIARCYLYRePKTn8x+c4cceeSR/ByHH344iWDB53Of+xzfzx//+EfhnrLxrXKHk4bzhiL5zne+A1rJHfEmOoDy4Eepj0hQhYoe9ahHFdtnP/vZWltrrbUa1I03qPHE2HvJCE6m66+/Xk0SZPPNN7ehPX7pS1+qbTWihOj52te+dthhh6lgw+o/LSUed8455yy//PLVefEyCqaJTDUy5TWveY1Q3SMe8YiqVsPRPhRVApHwnBJWv7QgDUR+iQOKf+G23377qXm/+92v8XVV98bme2jlTnJ36hDNdwiEQAiEQE8EvvKVrzz60Y+esOqxxx4rW6VzFf0hRCVa9KIXvUgGDPVACpxyyikPe9jD6IDW+twtBMFXv/pVhRdeeOG5557LEfK3v/3NtuW/oaJ++9vfHn/88WeccUZtyPVCK1gmLJZaaikL/EPf+ta31l57bfulKl72spcprDpa8/HTN6VlofkIkBE9HEs23G233W655RbpPgpl5AjYyeyRhUMAkVlCYLayzGFTm++www7nnXeePJ6f/OQnp5122pZbbvmHP/zhxhtvtNZ+n/SkJ9FPPttvv70SiD75yU/KDXrMYx5Tm+d7HhD4b/7UPNhTdhECIRACITAGBHgvJhvFE5/4RPpAAo0KfCd/+tOfLLD3NIooj2URKJKCL+d5z3uevBaCgzRp/XDPHHHEERKHVZYjTFf985//lNPjZ/NpnC5KSKJjjjmmWdUsaLlcMqU5lOsGf1JpHT/btI4S2oWy4b/55je/Kfb09Kc/XdrQUUcdJWdIDjXFo46u0kAWOj/VZ7KMr8jaJsxHBj3lKU/ZYostyLvaivwi3doG1dlgSgZLIN6dwfJMayEQAiEw5gR4aHbffXfxKeMkIMp78fjHP95PQkfWi7Rf2coykbfaaispvbwvgjgNlF122YWnx1ZNSbPA4SEPxoaV0/PmN7/5G9/4hrXiUOXaaWo2C1TUhP6kpoIGJQBttNFGWtBnXXrFK17BcyNXmkumqWZBlEoghuJpLWyW3U1GIdFtMpCawi4LnECf/vSnf/GLX6jD0+Pzq1/96l3vehdVJLZFNjURsS6NZNUACUTuDBBmmgqBEAiBcSYgQYcmoFSkoUhtOeigg77//e8roXKkwkiIqczfxz3ucUcffXRlGX/0ox8VxBFm4uQoiVPfTTZM8ZKD/MY3vpEOuOKKK97ylrcccMABqvGsdNIU3vrpT3+qnJPphhtumEwGtW5Ye5Ry5CZwsTOBJLvTSbe4f/azn9U9ST9um+/UMSrzHvHrSEsiwj71qU9plv+mtfEuy4JiJXeqjt1VyrafnD2RO13QzY1VkTtzg2raDIEQCIExJCC61DoqckTgiRtDvEkASMjmta99bVWQsUuXNJWJGA/dKYeQnOWmvFl4wxve4M5wCoDQKafLZKpigw02EDIjpzz2hnDZZpttmka6L7TdVqbyD3/4Q42Qbrr63Oc+lwRpa4Gea+4d4yXiFmqr0P2nm967V8jaeUkguTvzknb2FQIhEAJjRUAMi46Z1pCEk1rr8/pwDp1++unCPT/+8Y+bABO3zQc/+MHWms3yoGTEU5/61Eoz0rJ7ypr2a8HzexqtI4bVaJ0Pf/jDbTUn/EkeCV25OZ9Tx+YynVuryeOR1t1akuW5TSByZ24TTvshEAIhMA4EKJLnP//5Un15RJrxyBqWvlM/Kz5Fo8jwde9Sq3um7s1WTf228JMIkfwbakOgRwpz07IFD9eRc9NaUsvUg1ucVN522205nOr2eKvabvJqNlSTtpAc7ZlAfDlNeeuCJ/S0/uTX8TDAKpGK9NKXvrRZu9xyyzXLEy5UzrJnDHq4IneXNGc3z7tda8MNN7Sq7rS3YcXUJmwhhXODQOTO3KCaNkMgBEJg3Ah4A4MQkhuv3DzVjE1ib711QYnMGOEhT1v2NBq3c7sru6km6bhuRJIHU09Yblb97Gc/q+WzzjpLBnFTbsHDkSd838LJJ5/sbiwP+JESREDUY5HV9/Cb1lyZaurVr361atKlJQYJvTW3r7fuqHNZ/aaQqKpn9lSJR+Y89KEPbda2LUhpmtApJTOaXuTpaeJ97pDvco9bW7P5OecEInfmnGFaCIEQCIFZRKBuKTdgmcIekOOGoxq8m8w5WppYlVyc3/zmN9J6PLD4pJNOUkdqjhdQTEaKuGk8H00dz/0jaKQJf+xjH6vXZtE6bv7ipGkeCfj617++kVCVHsTN41E9lt0N7iaypjWSq3keYFNYCxO+FKJWEUytlXl3vve975Ev9iLg5WE8niQEAi3FcaUndkq3SRWi/7yES4Xa3E9iqB69o2TC8bbuKMuDJfBfJ+RgG01rIRACIRACY0bAk445VNz1LbKzxx57MO1uxfIk4homEaACvSJn2auj/vGPfxAWrU8j9ETBH/zgB80zlzvhkA6dz8IR8aGQPLXPHrmObMUJxL0kfYerqRqRvExOeZ8DiUNzcMx4VZZbrqyVcMO107ovjwJyE1YT9nJbWa1tq9a6Seey8JbQm6CeR+xorangcYJcOH66F0x2jic4ex3pAx/4QJXdfs8j5Q6vpv6E422aysLgCZiVfEIgBEIgBEJgSgICTzRN5aa0WSM5Pa2bC9NIxyF93Iy98847W+bnaK3QLBMxlJDWvvzlLzeFbQv2yzNE1ni/Jl3iI32nrc7vf/97DykWXOM14USRSCSth/ioapxMwnDNG7LaOs8jxfHT2iDBpOdVTQ5166rW5bo1varpm362rpXqVKt0RjisVczpKg9Qa+WxWR7al0jMB3HbxOdnCIRACIRACExGgC4RoGkNPMlKdkeVpJbJNpmynDPGw2/omO413bpF93hG32TVOJ9Evi666CIRN89HblNmnEByqD1op3VzMTJ6S1p0a6FlEk3QyjC5iCZLT5bPJCVIgxrR/7b3n+tDRbi0JtKnWqVpi7Jx+bj1vW2P4/FTUna9sMwb0bnlhmdQkTvDMxfpSQiEQAiEQAiMNoGhlTvJ3RntAyu9D4EQCIEQCIHhIcBF5yWyAkf8cMPTKz2Jd2eopiOdCYEQCIEQCIEQGDyB3Ig+eKZpMQRCIARCIARCYKgIRO4M1XSkMyEQAiEQAiEQAoMnELkzeKZpMQRCIARCIARCYKgIRO4M1XSkMyEQAiEQAiEQAoMnELkzeKZpMQRCIARCIARCYKgIRO4M1XSkMyEQAiEQAiEQAoMnELkzeKZpMQRCIARCIARCYKgIRO4M1XSkMyEQAiEQAiEQAoMnELkzeKZpMQRCIARCIARCYKgIRO4M1XSkMyEQAiEQAiEQAoMnELkzeKZpMQRCIARCIARCYKgIRO4M1XSkMyEQAiEQAiEQAoMnELkzeKZpMQRCIARCIARCYKgIRO4M1XSkMyEQAiEQAiEQAoMnELkzeKZpMQRCIARCIARCYKgIRO4M1XSkMyEQAiEQAiEQAoMnELkzeKZpMQRCIARCIARCYKgIRO4M1XSkMyEQAiEQAiEQAoMnELkzeKZpMQRCIARCIARCYKgIRO4M1XSkMyEQAiEQAiEQAoMnELkzeKZpMQRCIARCIARCYKgIRO4M1XSkMyEQAiEQAiEQAoMnELkzeKZpMQRCIARCIARCYKgIRO4M1XSkMyEQAiEQAiEQAoMnELkzeKZpMQRCIARCIARCYKgIRO4M1XSkMyEQAiEQAiEQAoMnELkzeKZpMQRCIARCIARCYKgIRO4M1XSkMyEQAiEQAiEQAoMnELkzeKZpMQRCIARCIARCYKgIRO4M1XSkMyEQAiEQAiEQAoMnELkzeKZpMQRCIARCIARCYKgIRO4M1XSkMyEQAiEQAiEQAoMnELkzeKZpMQRCIARCIARCYKgIRO4M1XSkMyEQAiEQAiEQAoMnELkzeKZpMQRCIARCIARCYKgIRO4M1XSkMyEQAiEQAiEQAoMnELkzeKZpMQRCIARCIARCYKgIRO4M1XSkMyEQAiEQAiEQAoMnELkzeKZpMQRCIARCIARCYKgIRO4M1XSkMyEQAiEQAiEQAoMnELkzeKZpMQRCIARCIARCYKgIRO4M1XSkMyEQAiEQAiEQAoMnELkzeKZpMQRCIARCIARCYKgIRO4M1XSkMyEQAiEQAiEQAoMnELkzeKZpMQRCIARCIARCYKgIRO4M1XSkMyEQAiEQAiEQAoMnELkzeKZpMQRCIARCIARCYKgIRO4M1XSkMyEQAiEQAiEQAoMnELkzeKZpMQRCIARCIARCYKgIRO4M1XSkMyEQAiEQAiEQAoMnELkzeKZpMQRCIARCIARCYKgIRO4M1XSkMyEQAiEQAiEQAoMnELkzeKZpMQRCIARCIARCYKgIRO4M1XSkMyEQAiEQAiEQAoMnELkzeKZpMQRCIARCIARCYKgIRO4M1XSkMyEQAiEQAiEQAoMnELkzeKZpMQRCIARCIARCYKgIRO4M1XSkMyEQAiEQAiEQAoMnELkzeKZpMQRCIARCIARCYKgIRO4M1XSkMyEQAiEQAiEQAoMnELkzeKZpMQRCIARCIARCYKgIRO4M1XSkMyEQAiEQAiEQAoMnELkzeKZpMQRCIARCIARCYKgIRO4M1XSkMyEQAiEQAiEQAoMnELkzeKZpMQRCIARCIARCYKgIRO4M1XSkMyEQAiEQAiEQAoMnELkzeKZpMQRCIARCIARCYKgIRO4M1XSkMyEQAiEQAiEQAoMnELkzeKZpMQRCIARCIARCYKgIRO4M1XSkMyEQAiEQAiEQAoMnELkzeKZpMQRCIARCIARCYKgIRO4M1XSkMyEQAiEQAiEQAoMn8P8AZJA4DPH5A3EAAAAASUVORK5CYII=",
+ "text/plain": [
+ ""
+ ]
+ },
+ "execution_count": 5,
+ "metadata": {},
+ "output_type": "execute_result"
+ }
+ ],
+ "source": [
+ "from PIL import Image, ImageDraw, ImageFont\n",
+ "import os\n",
+ "\n",
+ "base_path = \"./data\"\n",
+ "\n",
+ "image = Image.open(os.path.join(base_path, \"training_data/images/0000971160.png\"))\n",
+ "image = image.convert(\"RGB\")\n",
+ "image"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "uAVffmnZyUvw"
+ },
+ "source": [
+ "Now let's plot its corresponding annotations. Basically, if you type `data['form']`, you get a list of all general annotations. Each general annotation has a label, a bounding box, and one or more words, which in also have their own bounding box. The bounding boxes are in [xleft, ytop, xright, ybottom] format.\n",
+ " "
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 6,
+ "metadata": {
+ "colab": {
+ "base_uri": "https://localhost:8080/"
+ },
+ "id": "JPKkuJQ4sdZc",
+ "outputId": "c95bf306-98bb-4480-cc6b-ebb3aea548b3"
+ },
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "{'box': [292, 91, 376, 175], 'text': 'R&D', 'label': 'other', 'words': [{'box': [292, 91, 376, 175], 'text': 'R&D'}], 'linking': [], 'id': 0}\n",
+ "{'box': [219, 316, 225, 327], 'text': ':', 'label': 'question', 'words': [{'box': [219, 316, 225, 327], 'text': ':'}], 'linking': [], 'id': 1}\n",
+ "{'box': [95, 355, 169, 370], 'text': 'Suggestion:', 'label': 'question', 'words': [{'box': [95, 355, 169, 370], 'text': 'Suggestion:'}], 'linking': [[2, 16]], 'id': 2}\n",
+ "{'box': [482, 268, 518, 282], 'text': 'Date:', 'label': 'question', 'words': [{'box': [482, 268, 518, 282], 'text': 'Date:'}], 'linking': [[3, 12]], 'id': 3}\n",
+ "{'box': [511, 309, 570, 323], 'text': 'Licensee', 'label': 'answer', 'words': [{'box': [511, 309, 570, 323], 'text': 'Licensee'}], 'linking': [[13, 4]], 'id': 4}\n",
+ "{'box': [211, 651, 217, 662], 'text': '', 'label': 'question', 'words': [{'box': [211, 651, 217, 662], 'text': ''}], 'linking': [], 'id': 5}\n",
+ "{'box': [461, 605, 483, 619], 'text': 'Yes', 'label': 'question', 'words': [{'box': [461, 605, 483, 619], 'text': 'Yes'}], 'linking': [[19, 6]], 'id': 6}\n",
+ "{'box': [545, 603, 563, 617], 'text': 'No', 'label': 'question', 'words': [{'box': [545, 603, 563, 617], 'text': 'No'}], 'linking': [[19, 7]], 'id': 7}\n",
+ "{'box': [525, 904, 641, 926], 'text': '597005708', 'label': 'other', 'words': [{'box': [525, 904, 641, 926], 'text': '597005708'}], 'linking': [], 'id': 8}\n",
+ "{'text': 'R&D QUALITY IMPROVEMENT SUGGESTION/ SOLUTION FORM', 'box': [256, 201, 423, 230], 'linking': [], 'label': 'header', 'words': [{'text': 'R&D', 'box': [257, 203, 279, 214]}, {'text': 'QUALITY', 'box': [285, 203, 334, 216]}, {'text': 'IMPROVEMENT', 'box': [341, 201, 418, 211]}, {'text': 'SUGGESTION/', 'box': [256, 215, 324, 229]}, {'text': '', 'box': [324, 216, 332, 230]}, {'text': 'SOLUTION', 'box': [331, 214, 387, 228]}, {'text': 'FORM', 'box': [395, 215, 423, 228]}], 'id': 9}\n",
+ "{'text': 'Name / Phone Ext. :', 'box': [89, 272, 204, 289], 'linking': [[10, 11]], 'label': 'question', 'words': [{'text': 'Name', 'box': [89, 274, 118, 289]}, {'text': '/', 'box': [117, 274, 127, 288]}, {'text': 'Phone', 'box': [128, 274, 163, 289]}, {'text': 'Ext.', 'box': [169, 272, 196, 287]}, {'text': ':', 'box': [196, 274, 204, 288]}], 'id': 10}\n",
+ "{'text': 'M. Hamann P. Harper, P. Martinez', 'box': [215, 271, 451, 287], 'linking': [[10, 11]], 'label': 'answer', 'words': [{'text': 'M.', 'box': [215, 272, 230, 287]}, {'text': 'Hamann', 'box': [237, 272, 287, 286]}, {'text': 'P.', 'box': [293, 272, 307, 286]}, {'text': 'Harper,', 'box': [314, 274, 363, 285]}, {'text': 'P.', 'box': [370, 272, 384, 285]}, {'text': 'Martinez', 'box': [390, 271, 451, 282]}], 'id': 11}\n",
+ "{'text': '9/ 3/ 92', 'box': [543, 264, 590, 279], 'linking': [[3, 12]], 'label': 'answer', 'words': [{'text': '9/', 'box': [543, 265, 560, 279]}, {'text': '3/', 'box': [560, 264, 575, 279]}, {'text': '92', 'box': [575, 264, 590, 279]}], 'id': 12}\n",
+ "{'text': 'R&D Group:', 'box': [420, 310, 491, 323], 'linking': [[13, 4]], 'label': 'question', 'words': [{'text': 'R&D', 'box': [420, 310, 442, 323]}, {'text': 'Group:', 'box': [448, 310, 491, 323]}], 'id': 13}\n",
+ "{'text': 'J. S. Wigand', 'box': [236, 313, 327, 327], 'linking': [[15, 14]], 'label': 'answer', 'words': [{'text': 'J.', 'box': [236, 313, 251, 327]}, {'text': 'S.', 'box': [256, 313, 273, 326]}, {'text': 'Wigand', 'box': [278, 313, 327, 327]}], 'id': 14}\n",
+ "{'text': 'Supervisor / Manager', 'box': [91, 316, 218, 331], 'linking': [[15, 14]], 'label': 'question', 'words': [{'text': 'Supervisor', 'box': [91, 316, 161, 330]}, {'text': '/', 'box': [163, 318, 169, 331]}, {'text': 'Manager', 'box': [169, 317, 218, 327]}], 'id': 15}\n",
+ "{'text': 'Discontinue coal retention analyses on licensee submitted product samples (Note : Coal Retention testing is not performed by most licensees. Other B&W physical measurements as ends stability and inspection for soft spots in ciparettes are thought to be sufficient measures to assure cigarette physical integrity. The proposed action will increase laboratory productivity . )', 'box': [190, 346, 594, 447], 'linking': [[2, 16]], 'label': 'answer', 'words': [{'text': 'Discontinue', 'box': [190, 355, 268, 366]}, {'text': 'coal', 'box': [274, 353, 303, 366]}, {'text': 'retention', 'box': [309, 352, 375, 365]}, {'text': 'analyses', 'box': [381, 351, 435, 365]}, {'text': 'on', 'box': [443, 352, 458, 363]}, {'text': 'licensee', 'box': [464, 348, 520, 362]}, {'text': 'submitted', 'box': [527, 346, 594, 361]}, {'text': 'product', 'box': [190, 369, 240, 383]}, {'text': 'samples', 'box': [247, 367, 301, 380]}, {'text': '(Note', 'box': [318, 365, 352, 379]}, {'text': ':', 'box': [352, 367, 359, 380]}, {'text': 'Coal', 'box': [373, 366, 402, 376]}, {'text': 'Retention', 'box': [408, 366, 472, 376]}, {'text': 'testing', 'box': [479, 365, 529, 376]}, {'text': 'is', 'box': [536, 363, 549, 374]}, {'text': 'not', 'box': [554, 363, 578, 374]}, {'text': 'performed', 'box': [190, 383, 256, 394]}, {'text': 'by', 'box': [261, 381, 275, 394]}, {'text': 'most', 'box': [282, 383, 311, 393]}, {'text': 'licensees.', 'box': [318, 380, 386, 391]}, {'text': 'Other', 'box': [401, 378, 437, 389]}, {'text': 'B&W', 'box': [443, 378, 465, 389]}, {'text': 'physical', 'box': [471, 377, 528, 391]}, {'text': 'measurements', 'box': [191, 398, 275, 406]}, {'text': 'as', 'box': [282, 397, 297, 405]}, {'text': 'ends', 'box': [304, 394, 332, 405]}, {'text': 'stability', 'box': [339, 394, 402, 405]}, {'text': 'and', 'box': [409, 392, 430, 402]}, {'text': 'inspection', 'box': [437, 392, 508, 403]}, {'text': 'for', 'box': [515, 391, 535, 402]}, {'text': 'soft', 'box': [542, 391, 571, 401]}, {'text': 'spots', 'box': [193, 411, 228, 422]}, {'text': 'in', 'box': [235, 409, 250, 420]}, {'text': 'ciparettes', 'box': [256, 409, 327, 419]}, {'text': 'are', 'box': [332, 408, 352, 418]}, {'text': 'thought', 'box': [360, 406, 410, 419]}, {'text': 'to', 'box': [415, 406, 430, 416]}, {'text': 'be', 'box': [436, 404, 453, 417]}, {'text': 'sufficient', 'box': [458, 405, 529, 415]}, {'text': 'measures', 'box': [535, 405, 592, 415]}, {'text': 'to', 'box': [193, 425, 208, 433]}, {'text': 'assure', 'box': [214, 423, 255, 431]}, {'text': 'cigarette', 'box': [261, 420, 325, 434]}, {'text': 'physical', 'box': [331, 419, 390, 432]}, {'text': 'integrity.', 'box': [395, 418, 463, 431]}, {'text': 'The', 'box': [478, 416, 500, 429]}, {'text': 'proposed', 'box': [506, 418, 566, 431]}, {'text': 'action', 'box': [193, 436, 236, 447]}, {'text': 'will', 'box': [240, 436, 269, 447]}, {'text': 'increase', 'box': [277, 434, 333, 445]}, {'text': 'laboratory', 'box': [339, 433, 410, 446]}, {'text': 'productivity', 'box': [418, 430, 502, 445]}, {'text': '.', 'box': [503, 433, 507, 444]}, {'text': ')', 'box': [508, 430, 514, 444]}], 'id': 16}\n",
+ "{'text': 'Suggested Solutions (s) :', 'box': [95, 486, 250, 504], 'linking': [[17, 18]], 'label': 'question', 'words': [{'text': 'Suggested', 'box': [95, 489, 159, 504]}, {'text': 'Solutions', 'box': [165, 487, 222, 501]}, {'text': '(s)', 'box': [223, 486, 241, 503]}, {'text': ':', 'box': [243, 489, 250, 503]}], 'id': 17}\n",
+ "{'text': 'Delete coal retention from the list of standard analyses performed on licensee submitted product samples. Special requests for coal retention testing could still be submitted on an exception basis.', 'box': [263, 483, 593, 553], 'linking': [[17, 18]], 'label': 'answer', 'words': [{'text': 'Delete', 'box': [263, 486, 306, 500]}, {'text': 'coal', 'box': [313, 486, 341, 499]}, {'text': 'retention', 'box': [348, 486, 412, 497]}, {'text': 'from', 'box': [416, 485, 447, 498]}, {'text': 'the', 'box': [453, 485, 475, 498]}, {'text': 'list', 'box': [480, 483, 508, 496]}, {'text': 'of', 'box': [515, 483, 532, 494]}, {'text': 'standard', 'box': [536, 483, 593, 494]}, {'text': 'analyses', 'box': [264, 501, 320, 514]}, {'text': 'performed', 'box': [324, 501, 392, 512]}, {'text': 'on', 'box': [397, 501, 412, 511]}, {'text': 'licensee', 'box': [419, 499, 475, 512]}, {'text': 'submitted', 'box': [482, 499, 546, 510]}, {'text': 'product', 'box': [264, 517, 314, 528]}, {'text': 'samples.', 'box': [320, 514, 374, 528]}, {'text': 'Special', 'box': [390, 513, 439, 526]}, {'text': 'requests', 'box': [446, 513, 502, 524]}, {'text': 'for', 'box': [508, 511, 530, 522]}, {'text': 'coal', 'box': [538, 510, 566, 523]}, {'text': 'retention', 'box': [263, 529, 330, 540]}, {'text': 'testing', 'box': [335, 527, 387, 540]}, {'text': 'could', 'box': [390, 527, 428, 538]}, {'text': 'still', 'box': [433, 525, 468, 536]}, {'text': 'be', 'box': [473, 525, 488, 535]}, {'text': 'submitted', 'box': [496, 524, 560, 537]}, {'text': 'on', 'box': [566, 524, 584, 537]}, {'text': 'an', 'box': [264, 543, 281, 553]}, {'text': 'exception', 'box': [286, 539, 350, 553]}, {'text': 'basis.', 'box': [355, 541, 397, 551]}], 'id': 18}\n",
+ "{'text': 'Have you contacted your Manager/ Supervisor?', 'box': [96, 608, 398, 624], 'linking': [[19, 6], [19, 7]], 'label': 'header', 'words': [{'text': 'Have', 'box': [96, 612, 127, 623]}, {'text': 'you', 'box': [131, 613, 156, 624]}, {'text': 'contacted', 'box': [161, 612, 225, 623]}, {'text': 'your', 'box': [229, 610, 260, 623]}, {'text': 'Manager/', 'box': [264, 609, 314, 622]}, {'text': '', 'box': [314, 608, 322, 622]}, {'text': 'Supervisor?', 'box': [323, 608, 398, 621]}], 'id': 19}\n",
+ "{'text': 'Manager Comments:', 'box': [98, 651, 211, 665], 'linking': [[20, 21], [20, 22]], 'label': 'question', 'words': [{'text': 'Manager', 'box': [98, 654, 150, 665]}, {'text': 'Comments:', 'box': [154, 651, 211, 664]}], 'id': 20}\n",
+ "{'text': 'Manager, please contact suggester and forward', 'box': [232, 644, 547, 662], 'linking': [[20, 21]], 'label': 'answer', 'words': [{'text': 'Manager,', 'box': [232, 648, 288, 662]}, {'text': 'please', 'box': [296, 649, 338, 662]}, {'text': 'contact', 'box': [344, 648, 394, 662]}, {'text': 'suggester', 'box': [401, 648, 464, 661]}, {'text': 'and', 'box': [469, 647, 491, 658]}, {'text': 'forward', 'box': [497, 644, 547, 657]}], 'id': 21}\n",
+ "{'text': 'comments to the Quality Council.', 'box': [99, 662, 323, 677], 'linking': [[20, 22]], 'label': 'answer', 'words': [{'text': 'comments', 'box': [99, 666, 155, 677]}, {'text': 'to', 'box': [162, 665, 177, 676]}, {'text': 'the', 'box': [183, 665, 205, 675]}, {'text': 'Quality', 'box': [211, 663, 261, 676]}, {'text': 'Council.', 'box': [267, 662, 323, 676]}], 'id': 22}\n",
+ "{'text': 'qip . wp', 'box': [102, 823, 145, 838], 'linking': [], 'label': 'other', 'words': [{'text': 'qip', 'box': [102, 824, 123, 837]}, {'text': '.', 'box': [124, 824, 130, 838]}, {'text': 'wp', 'box': [130, 823, 145, 837]}], 'id': 23}\n"
+ ]
+ }
+ ],
+ "source": [
+ "import json\n",
+ "\n",
+ "with open(os.path.join(base_path, \"training_data/annotations/0000971160.json\")) as f:\n",
+ " data = json.load(f)\n",
+ "\n",
+ "for annotation in data[\"form\"]:\n",
+ " print(annotation)"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "Hs4L3S5a2Gfb"
+ },
+ "source": [
+ "The PIL library has a handy ImageDraw module, which -you guessed it- allows to draw things (such as rectangles) on an image:"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 7,
+ "metadata": {
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 1000
+ },
+ "id": "gWaHFM_LtKPP",
+ "outputId": "c498e560-035f-4170-b0b9-85ba3956711c"
+ },
+ "outputs": [
+ {
+ "data": {
+ "image/jpeg": "/9j/4AAQSkZJRgABAQAAAQABAAD/2wBDAAgGBgcGBQgHBwcJCQgKDBQNDAsLDBkSEw8UHRofHh0aHBwgJC4nICIsIxwcKDcpLDAxNDQ0Hyc5PTgyPC4zNDL/2wBDAQkJCQwLDBgNDRgyIRwhMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjL/wAARCAPoAvoDASIAAhEBAxEB/8QAHwAAAQUBAQEBAQEAAAAAAAAAAAECAwQFBgcICQoL/8QAtRAAAgEDAwIEAwUFBAQAAAF9AQIDAAQRBRIhMUEGE1FhByJxFDKBkaEII0KxwRVS0fAkM2JyggkKFhcYGRolJicoKSo0NTY3ODk6Q0RFRkdISUpTVFVWV1hZWmNkZWZnaGlqc3R1dnd4eXqDhIWGh4iJipKTlJWWl5iZmqKjpKWmp6ipqrKztLW2t7i5usLDxMXGx8jJytLT1NXW19jZ2uHi4+Tl5ufo6erx8vP09fb3+Pn6/8QAHwEAAwEBAQEBAQEBAQAAAAAAAAECAwQFBgcICQoL/8QAtREAAgECBAQDBAcFBAQAAQJ3AAECAxEEBSExBhJBUQdhcRMiMoEIFEKRobHBCSMzUvAVYnLRChYkNOEl8RcYGRomJygpKjU2Nzg5OkNERUZHSElKU1RVVldYWVpjZGVmZ2hpanN0dXZ3eHl6goOEhYaHiImKkpOUlZaXmJmaoqOkpaanqKmqsrO0tba3uLm6wsPExcbHyMnK0tPU1dbX2Nna4uPk5ebn6Onq8vP09fb3+Pn6/9oADAMBAAIRAxEAPwDa/wCGb/DH/QX1f/vqL/4ij/hm/wAMf9BfV/8AvqL/AOIr2WigDxr/AIZv8Mf9BfV/++ov/iKP+Gb/AAx/0F9X/wC+ov8A4ivZaKAPGv8Ahm/wx/0F9X/76i/+Io/4Zv8ADH/QX1f/AL6i/wDiK9looA8a/wCGb/DH/QX1f/vqL/4ij/hm/wAMf9BfV/8AvqL/AOIr2WigDxr/AIZv8Mf9BfV/++ov/iKP+Gb/AAx/0F9X/wC+ov8A4ivZaKAPGv8Ahm/wx/0F9X/76i/+Io/4Zv8ADH/QX1f/AL6i/wDiK9looA8a/wCGb/DH/QX1f/vqL/4ij/hm/wAMf9BfV/8AvqL/AOIr2WigDxr/AIZv8Mf9BfV/++ov/iKP+Gb/AAx/0F9X/wC+ov8A4ivZaKAPE2/Zs0HexXXdSClgVBRCQuOQTjk578Y9D1qrJ+zRYkjy/E1wo5zutFPfj+Idsf54r3aigDw+H9mvSFiUT+IL55Nx3MkKKCOwAOcHrzn8Knh/Zt8PLHifW9Ud8nmMRoMduCp/nXtNFAHisf7Nvh8TSmTW9TaIkeUqiMMoxzuODu59APxqvP8As1aWzubfxHeRqfuiS3VyOe5BGeMen9K9yooA8JX9miyAXf4muCd2Ti0UZX0+919/0ph/ZntcnHiibH/XkP8A4uveaKAPBv8Ahme2/wChpm/8Ah/8XR/wzPbf9DTN/wCAQ/8Ai695ooA8G/4Zntv+hpm/8Ah/8XR/wzPbf9DTN/4BD/4uveaKAPBv+GZ7b/oaZv8AwCH/AMXR/wAMz23/AENM3/gEP/i695ooA8G/4Zntv+hpm/8AAIf/ABdH/DM9t/0NM3/gEP8A4uveaKAPBv8Ahme2/wChpm/8Ah/8XR/wzPbf9DTN/wCAQ/8Ai695ooA8G/4Zntv+hpm/8Ah/8XR/wzPbf9DTN/4BD/4uveaKAPBv+GZ7b/oaZv8AwCH/AMXR/wAMz23/AENM3/gEP/i695ooA8G/4Zntv+hpm/8AAIf/ABdH/DM9t/0NM3/gEP8A4uveaKAPBv8Ahme2/wChpm/8Ah/8XR/wzPbf9DTN/wCAQ/8Ai695ooA8G/4Zntv+hpm/8Ah/8XR/wzPbf9DTN/4BD/4uveaKAPBv+GZ7b/oaZv8AwCH/AMXR/wAMz23/AENM3/gEP/i695ooA8G/4Zntv+hpm/8AAIf/ABdH/DM9t/0NM3/gEP8A4uveaKAPBv8Ahme2/wChpm/8Ah/8XR/wzPbf9DTN/wCAQ/8Ai695ooA8G/4Zntv+hpm/8Ah/8XR/wzPbf9DTN/4BD/4uveaKAPBv+GZ7b/oaZv8AwCH/AMXR/wAMz23/AENM3/gEP/i695ooA8G/4Zntv+hpm/8AAIf/ABdH/DM9t/0NM3/gEP8A4uveaKAPBv8Ahme2/wChpm/8Ah/8XR/wzPbf9DTN/wCAQ/8Ai695ooA8G/4Zntv+hpm/8Ah/8XR/wzPbf9DTN/4BD/4uveaKAPBv+GZ7b/oaZv8AwCH/AMXR/wAMz23/AENM3/gEP/i695ooA8G/4Zntv+hpm/8AAIf/ABdH/DM9t/0NM3/gEP8A4uveaKAPBv8Ahme2/wChpm/8Ah/8XR/wzPbf9DTN/wCAQ/8Ai695ooA8G/4Zntv+hpm/8Ah/8XR/wzPbf9DTN/4BD/4uveaKAPBv+GZ7b/oaZv8AwCH/AMXR/wAMz23/AENM3/gEP/i695ooA8G/4Zntv+hpm/8AAIf/ABdH/DM9t/0NM3/gEP8A4uveaKAPBv8Ahme2/wChpm/8Ah/8XR/wzPbf9DTN/wCAQ/8Ai695ooA8G/4Zntv+hpm/8Ah/8XR/wzPbf9DTN/4BD/4uveaKAPBv+GZ7b/oaZv8AwCH/AMXR/wAMz23/AENM3/gEP/i695ooA8G/4Zntv+hpm/8AAIf/ABdH/DM9t/0NM3/gEP8A4uveaKAPBv8Ahme2/wChpm/8Ah/8XR/wzPbf9DTN/wCAQ/8Ai695ooA8G/4Zntv+hpm/8Ah/8XR/wzPbf9DTN/4BD/4uveaKAPBv+GZ7b/oaZv8AwCH/AMXVe7/ZoYQj7H4mDS7uRNabRj8GPNfQNFAHzj/wzVqv/QxWf/fhv8aP+GatV/6GKz/78N/jX0dRQB83Tfs36pDBJKfENmQilsCBucDPrXpHwJ/5JRp//Xaf/wBGNXoN/wD8g65/65P/ACNeffAn/klGn/8AXaf/ANGNQB6TRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAV7/wD5B1z/ANcn/ka8++BP/JKNP/67T/8Aoxq9Bv8A/kHXP/XJ/wCRrz74E/8AJKNP/wCu0/8A6MagD0miiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAr3/APyDrn/rk/8AI1598Cf+SUaf/wBdp/8A0Y1eg3//ACDrn/rk/wDI1598Cf8AklGn/wDXaf8A9GNQB6TRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAZ+vXaaf4d1O9kVmS3tJZWVepCoTgflXDfAn/klGn/8AXaf/ANGNXbeI4hceGNWhMDTiSzmQxK20yZQjaD2J6ZrifgT/AMko0/8A67T/APoxqAPSaKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigCpqsMdxo97DMgeKS3kR1PQgqQRXA/An/klGn/9dp//AEY1eg3/APyDrn/rk/8AI1598Cf+SUaf/wBdp/8A0Y1AHpNFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFMmlWGIyNkgYGB1JJwB+dUdRu7uG7tLazEBeffzMDgbQD2/GoZotcniMbf2cAcEEb8gg5B/OtI09m2bRpXs20kya41NoxII4WDJDI7b8fKygEA4PT5h09RUr6lFGD5qPGw24V9oznOOc4/hPX0rLfTtZcPuksizq6u2WywYAHt/sj8qw/EPipdEvTFdXti+plVMdlZpJNcHAYjEYBPIY9eMVryQ7o19nTstV952Ud9HM0IjV280MQRjA2kA559T2zVquJ0PV/EmqMkzeH7mxWNWQPfhE3biCTtEhbt6AelXb/WLmxlVbzXdDs2cZVJZwmR6jdzUSpro0ZypR6NfedTRXN2moancwfaLPUNK1CM/Kvkyhgxz2IwM/jWDqXj7V9EuWXV/D93ZWinDXzW/mwKOxJidiBx6cd8VPs/NE+y/vL7z0Kiue0rWLzXLIXml32jXluTjzIXdhn0OOhq7/xPv+ob/wCP0ez80Hsv7y+81KKx55tct7eSZxpxWNC5A35wBmtKzma4soJnADSRq5A6ZIzSlBpXuKVNxV7k1FFFQZhRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQBU1WZLfR72aVtscdvI7HGcAKSa4H4E/8AJKNP/wCu0/8A6Mau512GO48PanDM4SKS0lR3JxtBQgnPGK4b4E/8ko0//rtP/wCjGoA9JooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigDLvv+Q9pP/bb/wBBFabMqKWYgKBkkngCsy+/5D2k/wDbb/0EVy/iqQ+LNZk8KR3Bg0e1jE+uXaSbSF6rb7s8FgMt6Lj1rSfwx9P1ZrU+GHp+rK974g1HxfDcSaTevonhWBC82vNhZJwM7hCG+6v/AE0I7cCvLNU+Lmj+Fprqz8B6PC0rDy5NavMvNcHuxz8x55G449u1c98UfiS/i2+XTNHaS18PWa+VDAp2rNj+NlHbgYB6AZ6mvOAMnArMyOsj13x1431NbGHUtW1K5kJYQRyttGeCdoIVV/ICuu039nnxfe26TXU+nWJbrFLKzOOM/wAKke3Wt24OpfBfR9CsbGbTLfUdThuLjULq7haTDqqlYlK84/h9CTmr3jf4reKbHw/4Zms57TT77UbNru6iiiErxjP7tiHyFRgc+vX0oA88174PeNfC0Ul/9lS5gtv3huLGbcUAwd2OG4+nY1V8O/Fvxj4euVddVlv7cAK1tfMZUKjsMnK/gRXtepeL/Eep/EDStH8Oa9pvkXGjvO7eSs9vJcI0gb5hhgMrjIPHXBryD4g6dHqujWfjS2sIbOS5upbLUobY7oftCH/WIRkbXH6g9c5oA9D8Ja/4f8WXUMvhS4/4RLxMnzNYRj/Q74jkB1AAbqRnhhnvgV6n4W8VPrUlzpuqWQ0zXbPBuLFpN/yHpIh/iQ+o6dDXxPHI8MqSxOySIQyupwVI6EHsa+hPA3iWf4jaQjGeGDxzoS+ZZXRAH2uPGNknqpyVb0yGHegD2/U/+QVef9cH/wDQTRpn/IKs/wDrgn/oIrK07XIfEXg2TUoo3iZ4JUlhkGGikXKujD1DAitXTP8AkFWf/XBP/QRWn/Lv5mv/AC6+ZaooorMyCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigCjrUvkaFqEweNPLtpG3ynCLhScsfT1rhPgT/wAko0//AK7T/wDoxq7TxPbG88J6zahthmsZ49xBOMxsM4HJ61xfwJ/5JRp//Xaf/wBGNQB6TRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFAHP8AiTUrfRp7TUrtwlvaxXEsh9gma8P8carceHPhLb2NxJJ/bHiy5bU7zORsRtp28+3lrj2NekfGZ518IMlsheWb9wEC5LCSSNCAPUhjXj37QF35nxAgsEj8uCxsYoo0B+XBy2QO3UD8BWk/hj6fqzWp8MPT9WcF4W8M6h4u8Q22jaaqmeYkl24WNByzH2A/wr6Z8KfA7wroEET6hbjV75TuaW4H7vPHSPOMcd89ayP2d9AhtPCF1rbQ4ur24aNZGUg+UmBgHuN27p3HtV/4jfEXWfD3iy10LRI7c3ZtluUjnTeLss7L5QwQVb5cjHXOOOM5mR1viPwNpnijXNI1LUGdl05Zl+z7QY5lkXaQ2R7V5l4y8J+BPBkdlFqOpeJLm4MDwrb210rSNaL8xR+BiIc+h5PXHF7wf+0Bp+qXken+I7H+zLljsE8ZLRbv9oH5k547+5rhfGl9Jquu6zqt9FLJb3Mc8Njd7fKktJEiYG0kU5HQk46kkEHlhQB6fZ/CHwlqtpZahpmtaybI27R25t70bDA7MxjB252ncwIz3Oea7WLwb4ej8MweHW0u3m0qAYjgmXeAefmyed3zH5uvNeGfB/4oWnhjwlq1lrlyzW9ltlsolGXYtnci/jg5PAzVs/GrxH4okvH05LTQdIso/Nurx8TSqueFXdhS7HhVx1745oA0PiF8BrFtNl1HwfDJFeRZd7EyFllXqdmeQ3tnBxjg9fDvDWt3PhTxVY6tGjCWynDPGwwSOjKfTIyK+x/BWuyeJvB+m6zLGI3uoy2zOcAMQMnucAZ4HPpXzX8dPD1voXxEkktI0jh1CEXZRSThyzBj7ZIJx70AezWdzBpnjHUBZlzpXirSzqdsWOAJ1X58Aj+JGQ45PFeh6Z/yCrP/AK4J/wCgivCNEvl1H4feAdSs0KzaZfy6bM5P3RJGwYAHqGG36V7vpn/IKs/+uCf+gitP+XfzNf8Al18y1RRRWZkFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFAFHWrgWmg6jcmN5BDaySbIxlmwpOAPWuE+BP/ACSjT/8ArtP/AOjGrvdWBbRr5RMYSbeQeaMZT5T83PHHXmuC+BP/ACSjT/8ArtP/AOjGoA9JooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigDz34uTva+H7a7jhMxtZ47goDjKxzROee3CmvFf2gbWSD4mGZ9uy5s4pI8HsMrz+KmvofxbpMWvJDpM3Ed3b3MJPpmPAP4HmvC/iZp48RfDrQ/FMcLrf6VjSdTjA4RkyM4yeA+cezitJ/DH0/VmtT4Yen6s9T+BlzFP8KNMjjbLQSTRyDB4bzGbH5MPzql8arLUo9M03W9Ki04yWkrRzte28DqEbG0lpRgYYfm1cF+z541i07ULnwvfzhIbxvNsy7YAl6FB7sMY9196+iru1gvrOa0uY1lgnQxyI3RlIwRWZkfKniLwtqfiXTbjW5o7D/hIYsNc29jeW0ovIwCWlVImJDjA3DGD1HORVLwp4ge9ikhvj9ocWsttKkoV/OTyXELYP8AHE2MN12tjIAwe58W/CvTPBV6msaXpXiO6t4XWZJ7C/iDW7huPkMRbg45yfeuf0aW11TxDda14UtHSS9tp7G/0llBkj8yIqJk2gDaWC5AA2scdGFAHHeELSS9tdYtEWAC8gjtBNPwkJMqyFyewCROSfQH1GehuBqEk1p4W8KXGlNpyzLGhEsMj3sxO3z3U7m78DHyr+NT6NJp0Ogy+CrTStZ1K+uZVfUptInjCysCSsW4o+UX1GAWB6gAn2P4dfCjRvC0qa1JY3Kam6fJFd3CTm2z1wVRRu7HrjseTQB32j2P9maLY2PH+jwJESABkhQD0AH5AV89ftJ3ZfxPotnsUCKzaXcOp3uRg/TZ+pr6OuLiG0tpLi4lSKGJS8kjnCqo5JJ7CvjXxTq158SviVJJZoC99cLa2aHgKmdqZ/mT7mgD0vRLRtP+HHgHT4Chm1DUpb+VEHLqiOSx/wB1dua950z/AJBVn/1wT/0EV5zZ2Edz4pNjb+W9h4Q0Y2avsyWuZYwGwcAZCIM+7+9ejaZ/yCrP/rgn/oIrT/l38zX/AJdfMtUUUVmZBRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFNCnzC287SAAuBgHnn/AD6UAOooooAKKKKACiiigAooooAKKKKACiiigAooooAw/Gf/ACIviH/sGXP/AKKauS+BP/JKNP8A+u0//oxq7nXYEufD2pW8qs8ctrKjKo5IKEECuG+BP/JKNP8A+u0//oxqAPSaKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAy77/kPaT/ANtv/QRXGeINNttE1+8g1GGJvCnilhDektt+zXZUgPnoA4VRnswB+vZ33/Ie0n/tt/6CKs6lpllrGnzWGoW0VzazLteKVQwP59+4PatJ/DH0/VmtT4Yen6s+MvGHhXU/h/4sayld90Lia0u0UqJFzlWX3B6+hFe8fDP41WOvWaab4muobTV1IRJmwkdzk4B44Vs9RwO49A7xPpNtpemx6F42iutV8OfMLTXSN9xZORwJSOcDs+CDxkcV494i+EfiDSoTqOkquuaK6iSK9sSG3Ke5QEn8siszI+pPFd99j8Ozuiyu8pWKMQXaW8hLHA2O5A3eg79MGvnn4mw3Vtplhqlw/iO1v9/kCa9s7aHejJhlMsOGc4GPmzkZ6Zrz618Ya/Z2a2J1CS4sUKkWd4ouIRtOR+7kBUc+gqjqmsXusXUk93KPnbd5UY2RqenyoOF/AUAe++Fm/wCEf0nSZNKj8StpI23CSXP2Swtip+YvK4+Z1I7MSQOK9pvdSstO0+S/vLuGC0jTe0zuAoXrnNfEmleKdT0eNktzby9PLa6tknMBHQxlwdh+noKi1fxJrevlTquqXd2qnKJLISif7q9F6dgKAPTfi78Xl8UI+gaA7DR8gzzlSGuSDkAA8hQQPckenV/w+8OP4K0pfF+q2wbWrwfZ/D+nSqQ0szgBXPTg7h17ZPpXjVekeGfibG2nQeH/ABnZDVtHTKxXTc3VmCMAxueeOMdCPXHFAH0X4d8Of8I14Imt5xG+pTwyXGoTqOZp2BLknvycD2Haui0z/kFWf/XBP/QRXl2k6/rGkaLbRQXh8VeGLvMEerI2bi0Z/lVJlzyAWGT1Geegz6fpMiS6RaNG6uBEqkqc8gYI/AgitP8Al38zX/l18y5RRRWZkFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFAFPVjEuj3xuCghFvIZDJjbt2nOc8YxXBfAn/klGn/8AXaf/ANGNXX+MFL+CNfQEAtp1wAWIA/1bdSelch8Cf+SUaf8A9dp//RjUAek0UUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQBl33/Ie0n/ALbf+gitSsbV7mK01bTJ532Rr5uWwTjKgdql/wCEi0r/AJ+v/Ibf4Vu4SlGLir6fqzolTnKEXFN6fqzSkjSaJ4pUV43BVkYZDA9QR3rirn4fNp1y994Q1e40S4Y7jagebZv6gxHhcnuuOpro/wDhItK/5+v/ACG3+FH/AAkWlf8AP1/5Db/Co9jU/lf3Eewq/wAr+4851HQ/EEsbp4l+H+geIVIZmu9OlEMrZ4yVcA7z1yDxnjkViN4D8L3tson+F3iOwmV84tLpJAwx3LS/0/GvYf8AhItK/wCfr/yG3+FH/CRaV/z9f+Q2/wAKPY1P5X9wewq/yv7jynTfCCxXEdzpHwjtbabdtMmranvWPoQ2zL5APoM9qh8UaNDdW8OlfEDQdM0oTfu9O1zRUbyLZz/DLnGAT68HJ6YJr1z/AISLSv8An6/8ht/hVe+1Tw/qdjNZXzR3FrMpSSKSFirD3GKPY1P5X9wewq/yv7j4/wDGPgjWfBGprZ6pEjJIu+G4hJaKQc9Djrx061reCPh5L4htJde1i5XTPDNo2bm8kODIB1WMY5OcDPqe54r2HUNOTSrebQksx4m8I3Tl0sXk8u5sDyf3buVBXPT5gRn65t6Rptvrt5b3fimKCy0vTnH9k6DCu6OEDjdKVUhzwpABIFHsan8r+4PYVf5X9w3QdKu9c0NP7Ot59B8HWKLNZ2/AudQdPm3ynnCZA46nFeo6YANKs8AD9yn8hWdfa9pk2n3MUdzl3iZVHlsMkg47VpaZ/wAgqz/64J/6CKqUZRp+8ralShKNL3lbUtUUUViYBRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQBR1q1jvtB1G0mz5U9rJE+Dg7WUg/wA64T4E/wDJKNP/AOu0/wD6MavQb/8A5B1z/wBcn/ka8++BP/JKNP8A+u0//oxqAPSaKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigClrCzNol+tu4Sc20gjYjIDbTg/nXB/An/klGn/9dp//AEY1dzr0hi8O6nIsvkslpKwk4+TCHnkHp16GuG+BP/JKNP8A+u0//oxqAPSaKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACs66nuILq6kjZTHFbLIVYE55fpzxnHX6VxLa7FbSpDe6zqUEhgNy7CCR40iD7GcuDjAJGfTOTxzWiyLJ4hOiDWb+a8eBZJSltI8aId20O4O0Z2tgE88148sVia9OM6dF2eqfNHqtOvmdyo0acnGU122ff0OkOoSiR2aNVhVpFy2BjaDz1yenTb3pIr64lkMJ8pJFLZZlOMBVPTPB+f17Vxcuo2cd9dQnV75Z45ntGlktnWNplUN5ZkzjJBXGeueM1u6vpVppdgJpNSuILZGaSWSRtyxqsbMWwMdlrH22OV7welvtLW+nT+kaezw/SX4Pp/XzNOzv7hobcbNyhYldmIyxZVOcls9/Q5xV+0lkmSR5NmBI6KFHZWI5/KvMj4itItMvNSafWEWxto7qNDbqHntmO1ZYv3vKeuSCARkcir0OrhDrq3N7q9gmjRCe6aeNQpDAsNu2U5JwTzjrWlCpjoW5qTf/AG9H/MipHDy2ml8mej0V5drviK60rRNC1azudR1C21iWKKIxyBdjSAFA3znk8jjjg81d8YXmr+FYbOaOW+vo7mdbfes6xBJHICA7n7nv0FdX1rFf8+H/AOBR/wAzL2NH/n4vuf8AkeiUV45qXi3X9Mu5baXTtUZ4g+/bdL95IFmkC/N82FbqOpGBU9h4r1ObxJDod/HqFnfSSxqIXugWaNkZvMXBOV+ULnsWANJ4zExV3Qdv8Uf8wVCk3ZVF9zPXKKwrvS5ofJWDUb9nkdlAe5IGdjMOQOOQOxrz5vE/iODQNe1e6smji0W5NvOi6wzM5UjcV/dejDGcZ9q0WIrttKnt5oh0qat7/wCB69RXj158QFbRPEes6PJd3tho8lvGJG1AqZjJgNjCEDaSB155/Fl343vrWxtJ2ntl825urd5pNcKwBoVDfLJ5XzbuQOBzgVXtsR/z7/FC5Kf8/wCB7JRXmtxrOq3VtC2hW99d3K6bFqN1BcagYWjWUEoifIdzna/XAGBzzWdd+Lb9BcSWjTTI0dpNp6NfuJLuO4bahAEZ2kHII56Ue2xH/Pv8UHJT/n/A9borzRNW1Sfxbd+Hbe4L3ltMoZDfyA+SVRmk/wBXjI3gbc5ODXOaP411nxLNpuk6TfqmtOl016Lh5TCnlNhAuCCNw574FHtsR/z7/FByU/5/wPbqK8M0vxr4g1DwnqmtR38dw9nbQymGJpUKSSOoEbbm+bILfMOAV71s2Ws+Ide1i5ttEvwLaKOGWQ3LSebbBlmDxyKGHzrJCFPT73Sj22I/59/ig5Kf8/4HrVFee6Dd6jqXgeLW7q/uRcyRQyhYpWCASKrYwSTwH9a9Cow+JdWcoSjZq3W/Vr9GFWkoRUk73/4D/UKKKK6zEKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAMvxLPHa+FdXuJoVniispneJujqEJKn69K4r4E/8ko0/wD67T/+jGruNfktovDmqSXihrVLSVpgVyCgQ7uO/Ga4f4E/8ko0/wD67T/+jGoA9JooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAoopGO1ScE4GcDqaAPF/EFlNqup6bHFDL5UOnTxGfztsIlaVXVJUBzJGQm1hhh84444j8QW2u6pq02rWFwLK6uERRs1CSPyohGFe3IWMhgW3srggqWzwa6iHxRq+m6Nq5tLXTbm30yxluEKXRaVZVwwjljwCu4MxBBOQB0zRD4x8SwWgvr230mW3ubGyktY4RIjCe5cRqHJJGwNkkgZxjrXl4KGJ+rU+Wcbcq+y+3+I7MRKj7aV4vd9V39Dnri01HULi8tJRZ21jLrK6qJ1uJJJCI40VY9pQcsYxli3QnrXoniVNP13SJNLbUYI47tJYHkWRSUDwyLu6/7VYn/CU+J4ok0ya10Y6zPqH2GC4imZrY4iaRnZAS64CMNpOSe4HNY/irxvrGjaHpE96+hSmZrsXLpayXMZMQLIY1WTjco/iPBbkgZrZ0MQ7tyTen2Wtnf+ZmaqUlZJPr17/JFO10691q81PRvENzBaTroaaba31ufMhnXdkyluArblX5CQeT1HNWbrwzq+t6ZeNqesaPFf6he2j3awXRCGCD0IGdzHnGMCptd1zV9Ih0+Ga38MWNxNYmd7q8tZPsss2eI1cECPjHLnksAKr+IV8aReIba20z+w4xeLIbO3NmjJL5UUbklzyAzM4HTAA9av/a/7v4k/ufP8Cv8A8IVq9toFrotprmhtaafrS6lYm4uXZhGrMwjYgepHT1NaeuaX4m13SIoZ9d8Pi6XVEvlIncJEkYTYiYGfvBySfWrjQapD8Q5rKW7sTpkdj/aH2ZdOj3Y3FTHv69s7qwbfxDqs2j2esSR6atvrdjdzWsUdmjGxkiRnQE5/eAqpzkDBHbOKP9r/ALv4h+58/wADqNSsvEOr674e1CxvNAabTUd7iPzZGDM67H24GdoBGCe/Wota0K7PxOs/EPm2otoLVLdo0gkaZg0oIyQNvVTjn1GO9ZHw612XxHrFzb6rBAstpp0ElxA1qiBJXJJYEDlWUI49NxFUrnxBqt3J/a+j2iR2U18BbCG2R5Ws1O0yRxn7zlkZh32njOMVhWq13HkaV2+W+vVdv+Ca04U+bmTeiv8AceoXVys3ktCZ0kifeN9nKwPylccAf3q5WXwrFNpWt6e13OsesXDXNwy2D7g5KnCnb0G0AZzVew1rWtdfQ9Ns9fjEs1pdXdxfRWgUy+XKqInluPkILDcMdiB1Bpmi6nrWq6/4UmudZlWO902e4ura2EZgkkiaNcqSpO1vMJOD2GMV0OhNtvm39V/7cZKpFK1vy/yLOqeEoNT0vVdNF1PaWmopHG8dppzRBFRt2FwvGSTnOc5PSp9Z8MWmvHT1vpGaGzEgMK6Y4SUOm1gwx6d12kHkGsXWNT1mC48UtDr12I7TUNO+y+WI8LFOyB0+6cj94cHrwPxm02z8Xw+Ok0668UTTrFAt7NCyR+W8bTyptBEYYEIEP+8D2pfV5/zf+lf/ACQe1j2/L/Is3Pg5riARr4j1mBmsP7PmljsfnnhGcByUOWGSAwweTzyasnwnYDUNAvIpriJ9EhMFskdjKFdNoAVx/FjAI6c1iyX+taNF45uzqd7cS6ICLBLiTeipJEsm5lGN5BORu6Diqviu/wBT03Ttb0vTfEN1LItpY3ttePcfOs01wYyAw/5ZsADs5HJxxxR9Xn/N/wClf/JB7WPb8v8AI6CPwXPdazdX8XirU4p5buO9ljFqkQJUBVXJQNsKxhSM8hec1XT4fQ6W2nBPFtxaz2KTLDJ5UCuyy/eDZXkdcelT/DTU5NUn8Ryyy3xkivUieG8kLtbyCNfMjUkn5BIXx0GD0qj8TJr2HW9FFhNfmaWTyjaWd+1qbhfLmfGR1IZFx35wPvVCi3Fa6ttby6X6X8u5Tau9NLJ9PLyCPwDYJpDaW3jKd7T7ILNU/crtUMjK3ygbmGwAFs4BPrWpH4asLe41e6tPEMNreatFFHdXEIRXYxgjePmwGbJycfQA1haxJc6dLqdlfeJNTtJNH0pbjTZTOym6c7yzSD/luVKou05znnJOayknaD4o3dw109rGt/bfaLp7xiiLJbAvA0WcBWc/ePCnHI4q/q8/5v8A0r/5In2se35f5HaWum2Ph3wQ+jW2qreiPaIy8il9oKgLwecAY+grtq+fbW71aPWrbT4Lu3fw3Frt6lsEujJKcRy7UbJJKgLkEn+Ide30FWeHg4YmcX/LH8592y6sualF+b/KIUUUV3nMFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFVrq4mgltlis5bhZZNkjoyjyVwTvO4jIyAOMnnpVmigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigDP16OaXw7qcduSJntJVjIOMMUOOcHHPsa4b4E/wDJKNP/AOu0/wD6Mau+1WFLjR72GQExyW8iMASMgqQeRyK4H4E/8ko0/wD67T/+jGoA9JooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigApGXcjLkjIxkdRS0UAecW3h9ZdQku9WtL2dDZy2SQQ2WzEcn3g75zJ3IBAC5PBPNOg8NxroU2l3c3iG6zHbx287W0cb2wgbdFt2AAlW5y2c969ForhpYWtShGnGpolbZdDonWpzk5OGr8zzeDwvDb2c2yTXhqct/wD2j/aK2UKyLNt2EhQu3BUkEEEck9zUcfhOKzs9Hg0ybXbF9MM7rLFYQEyvN99mVlK9CQABgD6CvTKKv2OI/wCfn4Innp/yfiebXXhcXsHkXF94oeOW0FneK0MbC6jDOxzuB2sS55XBwK2LuxtbrUNJvEt9etm0pClskMS7QCNpB3AlsgAcnt6812NFHscR/wA/PwQc9P8Ak/E4mfS4LjxONfY+JVuggi8pFURGMHPllccrknrz71Tg8KaJbQ3EENh4hWB7eW2gi5K2kcn+sEIP3c++favQqKPY4j/n5+CDnp/yfieY3vhyez02WDw7HqsF3cWcdhNd3cW9/JV88ED7wRnUHsNvpmtDU9Hsb59Pi/sG/a00+OMWqKZIGhdMhWVk54Bx+Nd9RWM8FWn/AMvet9luaRrwj9jpbdnnc2gaZNpsFg3hjUBFBJJIjpeXCylpP9YWkHztuzzknPFMu/Dek3i6er+FtQjGnQG2tfIvbiLyoz1A2Y69yeT3r0ein9VxX/P9/wDgMf8AIPbUf+fa+9/5nnsehaXFqFjfR+E7tZ7KKGKHFxNt2xAiPcuMOVzwWBPvVqO0gi8Ty+I08O6gNUlQRvL9qm2soGACn3cD6deetdxRR9VxX/P9/wDgMf8AIPbUf+fa+9/5nnOm+HNI0rV7jVbbwnem9uUeOaSe6nm8xW+8GD5Bzip49F0aLSptMTwNGtlO6ySwiM4dl6E/L27V39FH1XFf8/3/AOAx/wAg9tR/59r73/mcvpMsemz3Lw6BdWqzLECkMRbJRdoJzj+EIPotVdYt7PV9TgvLzwzNetbhTAbiIgxOGJyuAfb8q7Kil9Tr8qXtno73sut/l1D29O9+T8WcjqLw6vLbS6j4RF3JbPvhaaLeYz6jKf5wKR/s0s888ngyF5rhSs8jW4LSg9Qx2cjgdfSuvop/VcV/z/f/AIDH/IPbUf8An2vvf+Zws9lam1aKz8Hw2cmQyyw2oUoehIwg5IyPoa7qiitcPhp0pynUnzN2WyW1+3qZ1asZxUYxslf8bd/QKKKK6zEKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAK9//AMg65/65P/I1598Cf+SUaf8A9dp//RjV6Df/APIOuf8Ark/8jXn3wJ/5JRp//Xaf/wBGNQB6TRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAVdSUPpd2hJAaFwSpIP3T0I6VwHwJ/5JRp/wD12n/9GNXd61cfZNC1G5KM/lW0kmxcZbCk4Ga4T4E/8ko0/wD67T/+jGoA9JooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAori/GmuXelpqXlap/Zxt9MNzafu0b7TN8+V+cHO3anAx9/J4FSaj4klsr6/snvUjuv7XsobWEqu428htw5AxypLTDd2PGRgV2QwNWcYyXX18vLzX4k8yOworzm28R65PZTzS6nZwObdZJkLhjZyGVAUb9ziLguPnL4IB6AksttXuZtQa7/ALSmlaVNNRI5o4sMDfyROwABB+XA3qcHeCMZXG39mVVe7Wjt18vLzFzo9Jorzv8A4SLWJbS3Fvqmbq4Fv9rXyYz/AGfK91DGYsY7rJIMNk/u855rrNCuLp59WtLm5e5NleCGOWRVVmUwxSfNtAGQZCOAOAKwq4OdKLk2tPXy8vP+kNSubFFFFchQUUUUAFFFFABRRRQAUUyWWOCF5ppEjijUs7ucKoHJJJ6Csz/hKvDv/Qe0v/wMj/xpOSW7JcordmtRXmd54utXutZ8jXETNjehB9ryBIpURFDnbkjcQE59ST0san4g0u1uZoIPEoa1CQSbhfNJvc+cHG5G3qOIz8ucHbxgmsPrETn+tQ/pnolFeYN4sVE3x63HmAZVJL1GMhnQYDEHB8tyc46D0FXtM8SWMeuIk/ie2ZY5pVdWnyjQgERkuZNhJ+Q/Ku7Oc9zQsRFuwLFQbseg0VyvhzxJokPhzTxdeIbNrlreNpjcXys+8qNwO5sjntWp/wAJV4d/6D2l/wDgZH/jWqqRavc2jVg0ndGtRWT/AMJV4d/6D2l/+Bkf+NH/AAlXh3/oPaX/AOBkf+NPnj3H7SHdGtRWT/wlXh3/AKD2l/8AgZH/AI0f8JV4d/6D2l/+Bkf+NHPHuHtId0a1FZP/AAlXh3/oPaX/AOBkf+NH/CVeHf8AoPaX/wCBkf8AjRzx7h7SHdGtRWT/AMJV4d/6D2l/+Bkf+NH/AAlXh3/oPaX/AOBkf+NHPHuHtId0a1FZP/CVeHf+g9pf/gZH/jR/wlXh3/oPaX/4GR/40c8e4e0h3RrUVk/8JV4d/wCg9pf/AIGR/wCNH/CVeHf+g9pf/gZH/jRzx7h7SHdGtRWT/wAJV4d/6D2l/wDgZH/jR/wlXh3/AKD2l/8AgZH/AI0c8e4e0h3RrUVk/wDCVeHf+g9pf/gZH/jR/wAJV4d/6D2l/wDgZH/jRzx7h7SHdGtRWT/wlXh3/oPaX/4GR/40f8JV4d/6D2l/+Bkf+NHPHuHtId0a1FZP/CVeHf8AoPaX/wCBkf8AjR/wlXh3/oPaX/4GR/40c8e4e0h3RrUVk/8ACVeHf+g9pf8A4GR/40f8JV4d/wCg9pf/AIGR/wCNHPHuHtId0a1FVLHVdO1PzPsF/a3fl43+RMsm3OcZweM4P5Vbppp6opNNXQUUUUxhVO/1Wz0wR/apHBkzsWOJpGIAyTtUE4Hc9BXD678TLzS/FOpaJaaDa3P2Hyt01xrEVru3xhxhZBzjnoT07Zqtf6x8Qb66s9RsPA0cM0UUkau2rwSo8cmwnAGOcohBz+BzXpUstqNr2jik1fWcE9VdaN3V9OhDmuh3KeItKexlvVus28VkmoO/ltxA4Yq+MZ5CNx146dKJvEOl280sc10Y/KDlpGjcR/IpZwHxtJABJAORg+hryma0+IX9jnSrbwjHD52jxaXOz6lA7OkauodRuG3/AFjZBz1HTrVkWnjZL65uI/h7aIJXnlV/ttq0weUNndIwO5QXbC4HGASQMHs/sqhr+9j5e/Dy8+9/kT7R9vwO+uPGemwz+Won2i1uLmSSS3lQRCHYWDgpleHz09P7y5u3HibSLV7lZrooLZJHlcxPtxGu5wGxhmUZJUEng8cV5Ncy+LLJ7Gy1vw6mn22qvNo6yrepKkAuhGo8uMMWAUxbsE4OWHy5GPRdQ8HPqFpdWTaiEs5DdSQp5GWjlnSRWYtu+ZR5shC4HUc8VniMFhaHJzy0d9U0+vdJr5f02pSZuafq9lqbSpayOzxBWZZInjO1s7WAYDKnBwRwcH0q9VGLTvK1u61Lzc+fbQ2/l7fu+W0rZznnPm9Mcbffiv4q/wCRQ1r/AK8J/wD0W1ePWcItuG1v01/Epu0W2a1cVeeIr1LrWVt7wHyLG9lRGVMwyQlQp24zg5J+YndwcAcVzy+HvBun+HNEuLzQbu/vr2zSZorSSRpGARTJJt3gBQWGcf3hgVunwN4DGjnVhpyvY+R9pEqXMxBj27tw+bniuWXtZpNJL5v/ACOaXt6kU4pL5v8AyLep6hqOnXM1q2q/KiQSmaRY42+fzgyqxXYOY1I3e4zkiqjeI9UjTeJGkWAbpA8IQyeegMAx/Dhztxn65rntO0TwYlvodvf+Hr9576C2D3oaRYPNlQkAtvHJKn7oIGVHGRWh4w8HeDvD/hi9vRpbLceWY7fZcSFvMIwpAL4IH3j14UnBxWbVa3Mvzf8AkZtV+XmVrb7v/I6DTNS1STXEtbi7hbbNLFLAWG/YoO2TYIwV3YU5LY+bAHTGt4cmubnw5p91d3DTz3FvHM7lVXllBwAoAxzXDWOhfD+/eTZoV1HAFneO4eaTZOsL7ZCmJCeD6gE9qyZbTwuL/Q7jRNHvLC5XVrElrnf+9hl3MjKCzDB2exGMECrvVgry/N/5F3rU1zSSa9X5eR7HRRRXSdgUUUUAFFFFABRRRQAUUUUAFFFFABRRRQBXv/8AkHXP/XJ/5GvPvgT/AMko0/8A67T/APoxq9Bv/wDkHXP/AFyf+Rrz74E/8ko0/wD67T/+jGoA9JooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACvArfwV4U13Wde1DxDqV/ZzT+JrrT7cQEBHbO5QSUbBOTySB0r32vFF0aXXtI1yyjt7mWP8A4TeeSZrb78SADLj3BINergMTVw9CtUoys/d1+ZE0m0mP0X4ReAfEMVxJpmsa3MtvKYZSxWPa46j5oRn8K0/+FA+Ff+ghrP8A3+i/+N1T1TT/ABtH4ftdPuNNnuZ5b+5nv5tOk2rNhCsfyiRG2uxDnDDBXp2rKfQteu7Oxm1DQvE8l9HZ20dx5F4YxJIjFX6SgYMYXkAZPuSaP7czH/n6xeyh2G+LvhB4f0D+wvst5qb/ANoaxb2EvmyxnbHJuyVwg+bgYzke1O8bfCnwh4R8L3Opm+1l7jBjtozJGweUglcgIDtGCTg9AaztcsfGI1Pwnc6zHej9/p1vbCRwAs6riQMQ5w5cEhipyD1GMHvPE4PiWPxRqMkStpuiabdW1k5x890YnEzj2UYQZ77q9GOb47loP2j95u/nqifZx10PLNK0PwBe+Ho72Q+KZLpLZnlWFIljkljQNMkbMmCVGWxnO0Zr0Ky+BfhG+sYLuO/1oJNGsigzRZAYZGf3fvWJ8NvA11L4C1K5u9Pv/wC0JIrh9LWS4AgYTw7Q6LuxuIOCWHQitmDwBrVpZ3Vpo2nQ6Va3mgQw3ES3AG+8jlywLKSfnjLKX9GHpiuTEZ1mEa04qq7Jv8ylThbYkj+BXg6aBZ4tW1V4WGVkW5hKkeoPl4qF/gt4EjsUvn1+/WzfAW4N5AI2z0w2zBpuo/DzULrQ4/s/h21t0Ou298ukCdCsECRhJF3fd+crkgevPNGr/D/xJd3VxFaQQRaRbajcS2tgrw7XSZAN43xuowxfKsvAc7TwAcf7czH/AJ+sPZQ7FnR/hB4Rt/Empadc29zqEMdnazxtcXDKys7zq2DHtBGI165rA07QPBQ1K70u48GX91LBfSRNdR3u1BG11LFFgGYM2BGRgKT8hPPU+keErG40zWJrC72+fbaLp8TbZjL92S6A+cqpPAHOBXmzWyL4tv8AVG1Dw2k9vfzi2S91s28kEiXdywZ4gpDZ83gHsBgjca6amPx9SMnCpJv3Nm+sXfYShBdDtY/hp8MpnRIrK1d3kaJVXUZSWdRllH7zkgckdqoab4N+EurajLp1na2730UkkTW/26YPmM4bA38geoqG2u9NtfHMmvR634QNvNdyBoP7TUCOMqg+0KMY89tpDdiAoz1J1PDuv2mj3U1nP4p8Ky6Z9rnuFuP7QU3EiyszhSM4UqzYzk5A6Cub61mv89T75D5YdkZGvfCXwadesLSOK40y0Njd3U8kFyST5bQAZMm4AASP0xTPAnhvR/DXxUEOhXk15Y3fh43STSyK+7dOo4KqBjCium0zWxrPjK38rUNHvZorLUBGLC581ViM1t5XmYzhiBz24OKqaUt4nxhtV1CO2ju18KKJktc+UrfaeQmedvpXbHG4udKVGtNtcjbT9X31J5Y3uu513ir/AJFDWv8Arwn/APRbV5je+JvC/hjw3HHd+GdPur+HR7W8i3W6n7SzjDAtsOGGNx65HPrXp3ir/kUNa/68J/8A0W1eKar4n0i80Z9MuYZrkPo9va28sFsGNtMsUkbk75U3HErgYGPrXys3BVPftt1M6kqaq/vGtuvqeo6p4e0ddCs5n0PSorh7myEnk2yY+aeMMAduSpBI56g0a/4c0mGbShZaJpKzPdOoV7VAj4tpmAfAyV3AH8Ae1cPqPxXgvWsIo7S/W0hMLzxtbxBnkjmjfKnzjgYRwB6kZPcXdS+LukXs+nyw6Xq0ZtZ2mPmRwnIMMkYwBLycyA8kcA85xUSnRvuunbuZyqYe+66du5Y8Oaroet3ejrJ4f8OLDd6TJqFz5MCO8DIyjYRjjh1688NxVq48S/D2205ryTw8gHnxwrCdHCyv5m7y3ClQdrbWwTjOMVwll4r0u0ttMt1l1uNbLSp9LEsNlAkhWTbiTd9oOGUop4HY+tZI1iC2u/tUJma4ea1nkkjgjiDPC0nJGWyWWTBJP9Mac9DuvwNfaYbvH8D1ex1rwHqelXOoWXhxJ0geJPKTRwZJPM+4yLt5U88+1On1XwVAbFP+EU8yW+tnuYYo9IQsVQ4cHjhl7g/zIFeQ6bqdtaQxRXg1G7jiECiLfEsTiJGRBIhUhwARjPQjPNbem+NLXTJtJkht9Tb+zIZreFTPAoaOUglTtiGMFVxjGMUc9DuvwD2mG7x/A7a98UeBbQsU8JG4iS0jvnmi0qPYts4yJcnHHt14PHBro/EfhvQYfCurzw6Lp0ciWUzo6WqBlIQkEEDg140/ie3+xy2gt9SnhudNXSrkzXcQYwKXKsCIvvjeRzwR1yea0rv4la5f2K28v2VYJLGW0uIjcFjIWXAkOIBhhzwCAcjp1qZzo8rs1+BM6mH5XZx/A9T1bw1oSahoqR6LpyCW9ZHC2kYDD7PMcEY5GQDj1Arg/Aif2zrVjFNY2GoW+y6XUQ+hxQxwMkhWIpIEAYtjkDdjn8Jb34nXVzdafKY9EBtrgyjZdXJGTFInzZtxgfP2BOccYyRS8N+OJPDOl/YLaXSZ4t7yZnvLjILMWP3bQd275ojOjd6r8AjUw93rH8OyPRYPDehHxTfwnRdNMS2VsyobVNoJecEgY6naPyHpXF+Lbax0zWYTHpwNq+spYm2sNMt3k2G1WXKgxkk7zzkkYzxWdo/j680rUb64a4067e5C5e6vrlgoDysFU/Zs4HmYxgAADBJJxSv/ABvBfaslzfWSSNBqCahC9lcNsWRYkjH30UsMJ3A+8euATDnRsrtbv9TJ1MPZXa3f69jVu4NN0rwxb6p9jZnurq4jSG7gsbcpsdwA2+BmDEKBgA/MccZFWdR05Tc6Vb6HpsN8dWsWvLSWWGyiX5dhIYG1yBiRSD1PTArnLnxhYyRq0Nnci6V5ys01xK3yzNukQhJEJUkAgZ4IH41oPGUttLp8kMFsjafF5Nrhbr91GcZUD7VyPlUYPYAdBRz4buP2mE7r8TpreKCXX7/TW0f93YajBY3E0cNkxXzvuSBfso+XJXPORnvS6Wum6r4mXSreydoZZLiJLhdPtsRtEWX94TaBQGKNjaxI4yOa46HxLMniK91uYW1xcXV1Fd+XJbSiKOWNdqsEFwASOvzZwemK0rLxfaxakt/NaW6z/aWnwltMyIzfedI2utqvnPIA6n1NHPhu4e0wndfidX4W8NXeuyyS3dvp1vZ28s1pM0dtatI00TlGKA2wGzI4yc8dK6fTPC+kQa7f2M9jZXsUdtBMhnsbcFWZpg33I14+Retebaf4t03RBP8A2Hd3dg9w26ZjYNPubOScS3bAEknJHXPNN8L65FpdzqBt/GDaek5D5utHMm9i8jsqqsjbQC5PXnf045OfD3Vmg9pheZWa/pHReKfDGmPdGW30iJvI8Q28JhtmWDfC9vFuTqoI3NnHbJPrXS+E/A1hpeifZ9V0nTpZfPkePzY1neOJmJRGkZcsQDjPP1ry/WtatNSu54r/AF038Qu0uo5o9HAV3EaKGwZkK42hcYIO3PfFWNQ8ZnVbSK1vtbnnt4pElSNtDiwGQ5U8XHOCOhpxq0Fu0ONfDJWbXX8zvodA0Y+BdCuDpFgZ5f7O8yT7Mm590sQbJxk5BIPrk1wuseF7mDxjaeXZWP8Awjs3iJNxUbZEYkIYOOTGeX2/d7cd7UGuLcaJp1pN8Q0tI4I4SLVdEZ/LZNrKpfPzbWUcjGcVDDB4TkkmOo+MYblJbn7W4TQQhabn5zlGy3PXHr60ozpK22y7ChUoK22y6r/M27W7sLnxxDpZ0jw8dMvp7q3tZU0xVYGJc7g7HEnzAqQEABGAxxTvCGhNrthfX1zLoUsEDXVlGlvpUG5njcqs7HHDYGdo+XGD3pv9reEftRuv+Evl+0kljN/ZMe/J6nd5GeaW01nwnYOz2XjGe2ZhgtBpUaEj0OIBV+1o+X4f5l+3w/l98f8AMoeF9FsLj4YTXz6vpN1djSkm+axtmktGCbjvbG4k4xlue/Wlzp1/4V8G3WnSaBBPqEsVjd7bCGbEjxk5+cZDqV6Hru5zxV1dW8IpFPEni+ZYpzmZBpMYWU+rDyPm/GiHU/BUQVf+ErnVEkEqCLSok2v/AHh/o/X360e1o+X4f5h7fD+X3x/zKOoXFqTZ6Va22hJdrDerLeG0tYxJPDJ5aoQ42r1Dso5weMCptaOlRa3aWqXGhWDSW8F1cx/2bA0dvF0cAsm6R3YgIoxgAk9q0k8Q+EYt3leNdVj3SGV/LtVXe56s2Lf5ifeqb6h4Okdnb4g+KMkk8XEwA+gEfH4Ue1o+X4f5h7fD+X3x/wAzqPC1rb2Xjrxdb2lvFbwJ9j2xxIEVcxMTgDjqSa7OvPvh7c2t34k8TTWWoT6hbFbNUubgYkkCxsPm+VckYxkjJxnnrXoNXQacLru/zZphmnTutrv82FFFFbHQeL6ncR2vxZ1i4mWQwwatps0pjiaQqgspwThQT1YD8RSatqmrad4Qsba3i1OzLi8vLLykmjUL5zGCIiJC24IQQjbU6Bs9u41P4d2mo6/fazDr+v6dc33l+eun3ghRtihV4C5PA7k9TUH/AArX/qdvGX/g1/8Asa9Sv9WryjN1Le7FW5X0ik/yIXMtLGFrCW134j0DxDfN4g+z3OkPGPsIuIpHn3xMEMcfKbhu4OFOBzwKsw3GtSfEe6S/l1SExXcZsooY5mgltSqg5wRHwSdxfJB6dAK1P+Fa/wDU7eMv/Br/APY0f8K1/wCp28Zf+DX/AOxrH2GF/wCf3/krHeXYyfiAbT/hJ9AWNLwXf9vaYZWff5JXM23Zn5d3XO32zXp1cPH8MbT7fY3V14l8TX32K5juooby/EsfmIcgkFPqOMHBNdxRip0vZU6dOXNy36W3YRvdtiEgdSB9awPF2o2MPhbWIZby3SVrOZFRpVDFjGcADPU9hV/V9B0nX4I4NX0+3vYo23ok6BgrYxkZ9jWR/wAK38Ff9CvpX/gMtcEldNBJcyaOEv8Axb4b/wCEV0byLy9/tq0sBZq1ouwx741Vw5kUrtyqklQT8ox7z3fiTwvJoPh3w1FrZGmWnki9k+zykyRwhdsf3QfmYLk46KemRXdWvgLwjZS+bb+G9LR8bc/ZUPH4ipo/BvhiGeWaPw9pYklxvb7KnOOnaslGola6+7/gmUYVkrcy+5/5nlWo+M9GudP8M2MEd0moaYlsY9Tz+5tWCqsuUzl8LuGNpzng961fEPjLw9rl/qUr3x8q006aDTkaJ8TTyxkNIPl+XAwgLY+8/Y5Po3/CL+Hv+gFpn/gJH/hR/wAIv4f/AOgFpn/gJH/hRyVOXluvu/4IvZ1eXl5l9z/zPNtH8WeFtP8AEct7Bcz2+nWcFxFbW0gkkMskkgcvGMFUU7eNxB+fnaBzh2njGy1vUrC5vLOez1SbWbW5u55pF8kQxs4RF+c4CK4ycDJLHvXsv/CL+Hv+gFpn/gJH/hR/wi/h7/oBaZ/4CR/4UShUkrNr7v8AghKnVmuVyX3f8EcPEmhMMrrWnEeouk/xqzY6pYamJjYXkF0IX8uQwyBwrYBwSO+CD+NPtrCys4BBa2kEEQJIjijCqM9eAKnChRhQAPYVsdAtFFFABRRRQAUUUUAFFFFABRRRQAUUUUAV7/8A5B1z/wBcn/ka8++BP/JKNP8A+u0//oxq9A1FlTTLtmIVRC5JJwANprz/AOBP/JKNP/67T/8AoxqAPSaKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigArjr34V+C9Rv7i+utG8y5uZWmlf7VMNzsSScB8DknpXY0VtRxNag26M3G/ZtfkJpPc4f/hT3gP8A6AX/AJNz/wDxdH/CnvAf/QC/8m5//i67iiuj+1Md/wA/p/8AgT/zFyR7HD/8Ke8B/wDQC/8AJuf/AOLo/wCFPeA/+gF/5Nz/APxddxRR/amO/wCf0/8AwJ/5hyR7HD/8Ke8B/wDQC/8AJuf/AOLo/wCFPeA/+gF/5Nz/APxddxRR/amO/wCf0/8AwJ/5hyR7HD/8Ke8B/wDQC/8AJuf/AOLo/wCFPeA/+gF/5Nz/APxddxRR/amO/wCf0/8AwJ/5hyR7HD/8Ke8B/wDQC/8AJuf/AOLo/wCFPeA/+gF/5Nz/APxddxRR/amO/wCf0/8AwJ/5hyR7HD/8Ke8B/wDQC/8AJuf/AOLo/wCFPeA/+gF/5Nz/APxddxRR/amO/wCf0/8AwJ/5hyR7HD/8Ke8B/wDQC/8AJuf/AOLrV8P+A/DXhe/e+0bTfs1zJEYWfz5HyhIJGGYjqo/KujoqKmYYupFwnVk0+jk7fmChFbIKKKK5CgooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiori5htYxJPII0LpGCe7OwVR+LED8aejiRNyhgMkfMpU8exp2drgOooopAFFFFABRRRQAUUVWbULJXnRry3D2675lMq5jXGctzwMdzRewm0tyzRVL+19M8h5/7RtPJRtjyeeu1W9Cc8H2qVb6zcoFu4CXLBcSD5tv3seuO/pS5kHMu5YoqtFqFlPP5EN5byTFQ/lpKpbaeQcA9ORz70+2ure8hE1rcRTxHo8ThlP4ii6C6ZNRRRTGFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQBW1ABtNulYAgwuCD34Nef/An/klGn/8AXaf/ANGNXoN//wAg65/65P8AyNeffAn/AJJRp/8A12n/APRjUAek0UUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRXF+JPGup6R4nGh6X4dXVJV0/wC3ySNfpbCOPeUOd644wO/fpxW1DD1K8uWn66tJW9W0hNpbnV31/badAJbl2VWYIoRGdmY9AqqCSfYDsar2OuadqRgFpcFzOszRgxspIicRydQMYZgOevbNedf8Jh4t8V2Vrf6H4PtpTZ3PmRTx63BNGHCMjKwGM/LIe46g1Xtj8SLNbWS38HILuE3m+Z9SgKutxMJWwuRgghcHJHB4549KGVxdP3pxUv8AHDs/Pvbr1enUhz12/A9Jh8SaTcC2MVyzpcrG0cghfZ+8AKBmxhSwIwGIPI45FVf+Ev0yW4sIbTz7g3s4hRhBIAMxu6vyvKHYcMOOpzhTjzbTtL8a6e9kR4AtZfIW23yyX1s0zPDGiAo5zsU+Wpxgkc4IzmprGL4h2d1az/8ACFxkW9yk6xJqUKR8Ryxt8ucKzCUklcLlR8vXPQ8rw6vapF6ae/Df7xc77fgelWvibSrr7IEuctdRxuhWNyn7xdyAuVAUkdA2CcjjmpNL8RaXrJjFhcPJ5sPnxl4XjEicAspZRuAJAOOmRmvMdPtvH+n2trZDwUHs4zayTJ/akAaSWBI1Vg2flU+VGSuD0PPNHhzxB4s+12dpZ+CTcTeHbI6Vcr/akSAuwhOckY6RA4GfvdeOc6mV0knyTjfp+8h2fn3svx9BTfb8GexUVw//AAlHjz/onP8A5W4P8KQ+KfHY6/DrH/ccg/wrh/s6t3h/4Mh/8kXzr+kzuaK8pl+LHiKKeSEfD28meIMZBb3hmCbZHjO4pEQPnikHPXaSOOaqQfG3ULmxuL2LwevkW9uLmRm1VFPllym4AoC3zgrwCc/UVrPKMVBc01FLznD/AOSF7SLPYaK4RPFnjl1Vh8OSNwyA2tQg/kVyKUeK/HJOB8OwT/2HIP8ACsv7Ord4f+DIf/JD51/SZ3VFcEnjDxrJLLEnw/jaSLHmKuvW5KZGRkY44qCHx94quLeS4g8E2ssESlpJE8Q2zKgGckkDAHB/I0f2dW7w/wDBkP8A5IOdf0meiUV5y/xA8Uxw2szeCLYRXcgjt3/4SC3Kysc4CnHJ4PT0rDtPjjeX19NZ2/hWBpYThy2sxqn3wnDlArZZgBgnOeK0hlWJmnKPK0t/fhp6+8L2kUes31/badAJbl2VWYIoRGdmY9AqqCSfYDsar2OuadqRgFpcFzOszRgxspIicRydQMYZgOevbNYmiajJ478KaRr8CLp1ys7zwo/79VKmSEhvu7gVLemMj0rmdS0XVf7S8NaSdSuNPu7m61VnurdtrMjTecPut0YBTjPGRnkVz1qVOhBqp8alytX9V2eidtU/lsyalRxjzJX2/FpHaXPiqwNhHNYzmV7hImgf7PKyfvMFAxC4UkMMKxUnI6ZzXPQeP5b+60SzsjAZ9Re4iZzbSMqlCfLcAN9xgrZIJA55+U1xZ8Cxn4mWnheee8eAaat1Jd+aoZ1QCMbBg7QGCqFOcAda37D4ayQ641kPEmoILBYrmB4fkMaymVZFX5jtYiMfMPU5Brnn7NT91O1u/X7jnnKu5L3dPX5/kbTeOpwsUzi1ijeCGUI0bsDvjEhXzAcB8bwEYAng5OcUQePnvPMW0iSRtxkizE6b4GdEjcbiATuk55x8p6ZzXI3fgu0sfDOneIp9W1AwzW9r5sXmBdrsECkyniONTs5KttCj2rV8N/D59Ssoru+1XU7dkhez3W1+kqXEQK7WjcD5Yjhv3ZB7c8c86UnG63fn/wAD+vMmLxLV7fidhHrGqSfZYGit4riTUDauXUH5BC0udqyNtbjGNx9e/HR15fF4QWDQ4riLXtdjMOqm2jRLzCoDdmAsBt4bYTyO5PY4rEvY9WtbrxXbDxFqwuNIAa0gfVZBJdDy/N6bMfcDDjPzKc8c1MJz7fiaU6lTrH8T2uivMLTQrubxPbaNN4l8Qxy/2cLu6H2+QFXJUYQmPay5J75qaCy0W51hNKh8aeLWvHllhRftEoVni/1gD+Xt+XvzV80/5fxNeep/L+J6TRXlLSaKqag58T+OAtlbC7fdJIpeEnBdAUBIBBzwMYPanbtGAufM8UeNIpIfJ2RS3DK84mYrEYwV53FTjOMY5xRzT/l/EOep/L+J6pRXiDLrMfh7xZfza54hguNI1EW1vDLesMxny8FwCckiTOQQOle304Tbbi1YcKjlJxkrWt+N/wDIKKKK0NQooooAKKKKACiiigAooooAw/EXjDQfCf2b+27/AOy/ad3k/uXfdtxu+6px94dfWuP8Q/FbwXe6JNBba15jl42aL7NMvmorqzx5KY+ZQy88c1V+LbMniHwxIss8TR2+pSB7eYxOCsCnhwRjp6im2msalD4b1qxhkv1vLjVU06ws7u9L3FuSisRJNkkBgHYMrNgMMH09SKwuHhSqTjKUmubSSS0lJbcr7dyPed0jGsviR4RspzeW7NBDHrZvI7KOBg3lGy8gkcbAd5JxkcA47Zz5PHPh27jZrrUrhWla4aKOGEf6NI91NJvLPGxXKvGd0fzDb0ziutfV7XxBN4c0y2vdWtVtdRl02/H290k3i2lZkZ1fcxVkXDnr2J5rY+FepXGr6Xrl5czfaHbVnRZ9u3zo0hhRH/4Eiq2Rwc5HFd1PMsM1KXsndJfbXR2/k8733IcJdzgL7xz4Pnvr5tyzwvdx3DGa2Zml23UchCnaNwMYfiQAr90Eg06fx74XZL1WvfOlnNyLKXyJP9Bke6mkE3K5GVeJvly3yYIqxpGtq/ha9TW9SvtOax0uwjsksrko6QmFT56pvXeSzYPXoBjOc97ba/qtx47utIOraLFaQeVILd0JunDqxMeBJgMNuc4PB6UVczw9OTp+yk+V/wA66afyeQKDetzi9O8e+CbK+sb1NQSO6OsXs11MLWXcbeQ3BQE7OVJaE7ex5xwa7D/hcPgP/oO/+Sk//wARWfoXj7VNamtlCWSXF4L1TYIpaaxMOQrSfN8wLKBjC8uMH1rah8TZZbK7uNHv9PeSHQBqfkPbszCUNh0Yhxj029RyTXDWxeErS5p05f8Aga7t/wAnmWoyXX+vvNn/AIXD4D/6Dv8A5KT/APxFbnh3xhoPiz7T/Yl/9q+zbfO/cum3dnb95Rn7p6elZej+IbnVf7fhOqWhtbSCJ4NVgiAjUujMxOWKnZgE89+azfA0om+IHjKVbtbsPDpjC5UACbNufnAHAz149alQwtWlUlTjJOKT1kmviituVd+4XkmrnoVV9QvY9O026vpldoraF5nCDLEKCTjPfirFZPir/kUNa/68J/8A0W1eXJ2i2ObtFtGDb/Ee1u1Vrbw74imDKGBjsg2R68N0rlJ/EN1fahq9uPD+tNK9ldwiNbU7k89lMZaMfcGEIJ5LHnntZ8Hap4b8OfbrqNYGuf7NsWmisbQNNvMZLAhBlmJIYk+vPStzRphY+O/FYDSTy3Aga2MsQUu4WTdGHCjKrhRyTjPWsfZynFNy/A5nSnUim5fgZepa9cT6g9za+EvEIURQJEps2jZCnnAkEZA4lA5BBG4EdDWfJf37I+PDuvhwqCEpppQIXQJOQAeMjLKB39KvaXqfiWTRtXvbTVtQvtXXTAz6bd6a0S2933EblFVgOQFBbJGcmqd1f68PBOpXsGvaw6x3Vv8AZHS2drjBbbKrbrZNy4JIwvG0c9inh2/tA8LJ7y/Au2Oty2mqpMfCniUwRXEs8bfZpSfn3YUR7ti43kZ54HTnNami+LX03QtPsZPCviUyW9vHE5TT/lLKoBI+b1zVK9n8RR2uq6XYX9+ZLPUrcxXVxC7tPA0Kuylo4yQN24blUkcA4zmo3bxHqPh3QI7t9WsmP2g3cgEhmEikeUWEQ3bSNxAIAOBuB6Go0pR2l+BUaEo7S/BG/wD8J3/1Knij/wAF3/2Va/h/xBb+I7Oe4t7e6t/IuGt5I7pAjq6gEggE464/OuK1qPxXd6hYxzXNxBFHp6vDdWiSLvvM/N5sccmMcAhXJTk5PpsfD+cNB4heUhHbW7lirYBBIX3P8zT9+M0m73H78ZpN3Tv0OzooorY6AooooAKKKKACiiigAooooAKKKKACiiigAooooAr3/wDyDrn/AK5P/I1598Cf+SUaf/12n/8ARjV6Df8A/IOuf+uT/wAjXn3wJ/5JRp//AF2n/wDRjUAek0UUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABXk/ja3gvPiLqVtdWt9dQTeFhHJFYjM203YBKjvjqRg5AIwelesVx3iDwdq2o+LE8Q6N4l/si5FiLJh9hS43J5hc/ebA5I7duvNduBlTUpxqS5bxau72v8k3+BMr9Dl9HfXbG1i1T7Jf/AGK01jdMbewe2uNQgaHYZJLZQNxV9nIHIUkDgZx7mSe5h0RNZ/4SuOJtQv4J7aITiWeI+ZNCyqvzNgGMZ7bSD0ruf+EX8ef9FG/8okH+NZ1/8OvFGqX1le33jqOe5sWL20j6HDmJjjJHzew/Kn9Uo/8AP+H3T/8AkA5n2/I5zW7Xx2bfQFZb4401RHJCsskkN0GYqZFR1Xfs2DMmUyGz1zW/f+HpL34gRvqFhr8+n3FnCk8ltdPFB9p5BdlWUEALt+5kZz15Nav/AAi/jz/oo3/lEg/xo/4Rfx5/0Ub/AMokH+NH1Sj/AM/4fdP/AOQDmfb8ina+DL2x8Y2trCJpNBhuG1ETzXcjOjbNgt+Wyw3ASfMSMDFXNJlnS88QWUfhvWrOG9eSVJ3MYUkRKhwfMYqSV+XjHI6Uf8Iv48/6KN/5RIP8aP8AhF/Hn/RRv/KJB/jR9Uo/8/4fdP8A+QDmfb8jntJ8NeLBoerWnlyhJI7URNcyCCWcRSHzIyEkcKXXI8wEE7hx3E+t+DtU1DQNYhGkPKs+pwXOnWUlym+1VNnmNv3fJuCuAFJxu9zja/4Rfx5/0Ub/AMokH+NH/CL+PP8Aoo3/AJRIP8aPqlH/AJ/w+6f/AMgHM+35HHaTbvcaxd+GtOt3s/7UJa72ttMNrFf3olG5SfmIKRjB/iznisg6XocmreITff2XGbQXMOmwy6pDCfNW5ucKyMwIH71SN3HyA+ldzY/D7xZp11Pc2nj7y5p8+Y39jRHdmSSU9W4+eWQ8f3sdAAJ7TwX40sYWhtviHsjaWSYj+xYT87uXY8t3Zifxr0K8cJVnNutGza/nWya/kZC5lbT+vvOW1C7Gp+KIPEC654WtpBc2sphbVoS4hjALRs+1sNuLD5CqkHnOafp1poWlXqXdhrPhS3nXX5L8Spqce4WroVMecZ7/AHc49667/hF/Hn/RRv8AyiQf40f8Iv48/wCijf8AlEg/xrm+rYL/AJ+r75//ACofNLt/X3nBQ3FtocGqX82s+GnjfRbm2lg03UIi8szMWUxxqi5HYBiWGTye8dlb6Cvhi98Pxa5oNvqkqW11LeC8RYJmi2ARZCqApEfQbjkkkZPPoP8Awi/jz/oo3/lEg/xo/wCEX8ef9FG/8okH+NH1bBf8/V98/wD5UHNLt/X3nImLTofAc+jW/iDwq882pRXnkTauGjRFkR2UuR82SmOEUfMePXgfDniK30D4ha1qDnR4VkkkEe9ZJ7Zf9IRj5RjXJwqko2AOB0r2z/hF/Hn/AEUb/wAokH+Navg3wxP4XsL+G61P+0bm+vpL2WfyBDl3Cg/KCR1UnjHXpXXQrYPCUKsVLn50lZNp793TS/MTUpNf1+plfB7/AJJXo3/bf/0fJSeNNTs9H8Y+FL+/m8m2i+2b5ApbGY1A4AJ6kV3NFeHjajxNWdVac0ubvbW/kE6blDlT7fg7nhemfEPT4PFzeIdUh1a8uI7EafAY7WGMmPfvLP8AvyC5PoAMDoM4rR034t2lvr2q6hfWOpTQ3KxR2qRQwq8UaFzh8y4JzJ1B/AY59jorlcaj6r7v+CS4Vnb3l9z/AMzxZ/idYN4RstFgj1izureGCJrmO3gljbYFDAq0oLI2CCODg/hUuj+PtF0Tw3cadYz38V5LJJL9pNjH5aOxySkIkwq+i5r2SihRqJWuvu/4IRhWStzL7n/meNP8StOj8Oi0S2up7oaj9rJZVRWX7UZ/U4JGB7E+1YGueK9A8Qa+us3vh6+F0sccYEOoeWpCMTzhedwJQ5/h6Y619CUUKFRdV93/AARRp1Y7SX3P/M8Ln+JaS+KU19LK/hmW3+zeSs8RjMe4MQcx5ySOuaoaT42+za3LqH2VY7m8vZJp3uJA0cUTnDJGUj3qdqryOrZJzmvoOinar3X3f8ErlrfzL7n/AJnhEGoeG7WC6jjvNzXVnJYSuZWUmB92c7bX5mG4kMeTgZJpbnxNZT3Pm7dMd0ggt45mv7lXAgYtFJxa4Dgs3I45IwRXu1FFqvdfd/wQ5a38y+5/5nz3qHiMNo2t2ySWksmrSxzXD/briVy6lcFVa3RRwoB5HAHoBXrf23x3/wBAPQP/AAay/wDxiupopwhJScpP+tfN9xwhJScpO97dLbX833OQmu/iIzxmDSPDaKM7w+oTOW44wREMc/XPt1qrbv8AFJ5QtxH4Rij7shuHP5cfzruaK0NTlfK8f/8AP34Z/wDAWf8A+OUeV4//AOfvwz/4Cz//AByuqooA4y7sviNcbPJ1nw9a7c58uylbd/305pLTR/iCzN9s8WaWgx8vk6Xuz9cuK7SigDlP7F8Zf9Dja/8AgnX/AOOV0Wnw3cFhDFfXS3dyoxJOsXlhz67cnH51ZooAKKKKAOM8eeA38aT6ZNHqcVk1iJhiWyW5WQSBQcqxA4C9wevbFY8/w28R3Vk1nP4ys5Ld4lhaNvD1sQY1+6p56DAwO1el0V2Qx9aEI0/daW14xfVvdpvdslxV7nmMXww12C3S3j8WacsKfdQeGrXA4x/Krtp4I8ZWL3DW3xAWI3EgkkC6JDgsEVBgbsD5UUYGBxXoNFWsyrrZR/8AAIf/ACIci/ps83g+Hfie3iso4/G9ufsMSw2zPoFu7xIoAADMSew70/8A4QHxV9v+3/8ACbWn2zOftH/CO23mZxjO7OenFei0UPMq7d2o/wDgEP8A5EORf02cDH4M8Zw3EtxF4+iSabHmyLoNuGfHA3HOTj3qC/8AAPi3U9NutPu/Hqva3aMk6LokKbw3XlWB59c5r0Wil/aNbtD/AMFw/wDkQ5F/TZwY8JeOBF5X/CxAY8bSp0OA5Hvk81f8H+D7vw1qGrX19rK6lcaisCsy2a24QRKyqAqkjG0gcAdK62ipnj604Sp+6k97Riuqe6Se6QKKvcK5bWPAOi6v9tmYXcd3cq370Xs5RXIwD5fmBSB/dxg11NFcTV1ZjaTVmeUL8GrpOE8X3yDphFkUAegAl4FL/wAKcvcY/wCEy1DH/bX/AOPV6tRWfsY+f3v/ADMlh4Lv97/zPOIvhpqsKBF8WFgMAb7BXPAA6lye39epqT/hXOsZz/wla59f7MT/AOKr0Oij2UfP73/mHsI9397/AMzzC5+Ect7L5t3rNjcSY275tFhdsemSah/4UvF/0ENL/wDBDB/jXqtFHso+f3v/ADD2Ee7+9/5nmtl8K7jTg4tNY02IPgtjQLfnH1roPDvgaw0izuIr+Oy1Oee4aczPZIm3cB8oXkAZBOBgc9K6qimqUU7/AKscaMYvm1+9v82IqqihVUKqjAAGABS0UVoahRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQBXv/wDkHXP/AFyf+Rrz74E/8ko0/wD67T/+jGr0G/8A+Qdc/wDXJ/5GvPvgT/ySjT/+u0//AKMagD0miiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiisVfEtu+qW9ktpdlLi5ktY7ravlGSNXZx97dx5bDOOo/GrhTlO/KthXNqisCTxhpkOnWN9MJo4b2y+2xFwowuYlCsc4DEzIOuOuSKgi8cabOIRBBczSSSvGY4TG5UoELchyrcSKcIWJ544ONlhK7V1H+luHMjpqK5a28YqU3XtnNAzSXaRxKqsZDDcJAoBD9WaRRgjrnkDBNk+LITdx2UemahLet5u+2RY90Zj8skMS4XkSoRgkEH14oeDrJ2t3/Df7hcyOgoqvY3kOo6fbX1sxaC5iWaMkYJVgCOPoasVztNOzKCiiikAUUVzvjrU7zRvBt/f2E3k3UXl7H2hsZkUHggjoTUykoxcn0JnNQi5PodFXNL4rd4bpksVeSJ7cRqs+RIJpTGp3bcZBBPGR7+lf/hH/ABh/0PH/AJSYf8azIPh9rlsrLF4wYKfJ4Onq2BE2+MDLcBW6AcdulYynUfwxf4f5nPOpVfwwf4f5m9N4luLd3jl0+NXinMMz/aCIlO1HGHK9SJBjdtGQRnplq+K90ixfYf3hiHHm8CfzRGYs47Eg59O1Ytz4C167klkm8YsWmYtKV05F35VVIOG5UhEBXocdKUeBNeEwlHi8bxcm7B/suP8A1pGC33vTt0zzjNTzVr7P8P8AMjnxF/hf/kv+ZsR+LTLYXV6unTeRHZSXkLEOokVQCFJZAASCMbSw6/j0MDSvCjTRrHIR8yK24D8cDNcIPAOurFcRf8JgTHPE0LqdOQgRt95V+b5AfRcdvStL/hH/ABh/0PH/AJSYf8aqE6i+KL/D/MuFSqvii/w/zOtorkv+Ef8AGH/Q8f8AlJh/xo/4R/xh/wBDx/5SYf8AGr9pL+V/h/mae1l/I/w/zOtorkv+Ef8AGH/Q8f8AlJh/xo/4R/xh/wBDx/5SYf8AGj2kv5X+H+Ye1l/I/wAP8zraK5L/AIR/xh/0PH/lJh/xo/4R/wAYf9Dx/wCUmH/Gj2kv5X+H+Ye1l/I/w/zOtorkv+Ef8Yf9Dx/5SYf8aP8AhH/GH/Q8f+UmH/Gj2kv5X+H+Ye1l/I/w/wAzraK5L/hH/GH/AEPH/lJh/wAaP+Ef8Yf9Dx/5SYf8aPaS/lf4f5h7WX8j/D/M62iuS/4R/wAYf9Dx/wCUmH/Gj/hH/GH/AEPH/lJh/wAaPaS/lf4f5h7WX8j/AA/zOtorkv8AhH/GH/Q8f+UmH/Gj/hH/ABh/0PH/AJSYf8aPaS/lf4f5h7WX8j/D/M62iuS/4R/xh/0PH/lJh/xo/wCEf8Yf9Dx/5SYf8aPaS/lf4f5h7WX8j/D/ADOtorkv+Ef8Yf8AQ8f+UmH/ABqve6f4j06ETX3xDt7WJm2h59OgRSeuMluvB/Kh1Gt4v8P8xOtJauD/AA/zO1orzz7Vff8ARVtL/wDAW2/+Ko+1X3/RVtL/APAW2/8Aiqn2/l+K/wAyfrK/lf3x/wAz0OivPPtV9/0VbS//AAFtv/iqPtV9/wBFW0v/AMBbb/4qj2/l+K/zD6yv5X98f8z0OivPPtV9/wBFW0v/AMBbb/4qj7Vff9FW0v8A8Bbb/wCKo9v5fiv8w+sr+V/fH/M9Dorh7G01/U/M+wfEe1u/Lxv8jT4JNuc4zhuM4P5Vb/4R/wAYf9Dx/wCUmH/GqVRvVRf4f5lKtJq6g/w/zOtorkv+Ef8AGH/Q8f8AlJh/xo/4R/xh/wBDx/5SYf8AGj2kv5X+H+Y/ay/kf4f5nW0V5np9p8TdR021vofEWmrFcwpMgeJQwDAEZxF15qz/AGP8Uf8AoZNL/wC/a/8AxmpVdvXkf4f5maxLauoS/D/M9Dorzz+x/ij/ANDJpf8A37X/AOM0f2P8Uf8AoZNL/wC/a/8Axmj2z/kf4f5j+sP+SX4f5nodFeef2P8AFH/oZNL/AO/a/wDxmj+x/ij/ANDJpf8A37X/AOM0e2f8j/D/ADD6w/5Jfh/meh0V55/Y/wAUf+hk0v8A79r/APGaPK8Yf8Ih/b3/AAmH/Lh9t8j+zIf+ee/bu/TOPwo9u/5X+H+YfWH/ACP8P8z0OiuS/wCEf8Yf9Dx/5SYf8ahutL8TWMPnXfxAit4twXfLpkCLknAGSepPFV7SX8r/AA/zL9rL+R/h/mdnRXJf8I/4w/6Hj/ykw/41Fc6T4osraS5uvH8UEEY3PLLpkKqo9SScCj2kv5X+H+Ye1l/I/wAP8zsqK5E6D4uGM+ORz0/4lUP+NB0DxcCAfHIyeg/sqH/Gj2kv5X+H+Ye1l/I/w/zOuorkv+Ef8Yf9Dx/5SYf8aqz2HiS2vrWym+ICJc3ZYQRHSot0m0bmxz2HNHtJfyv8P8w9rL+R/h/mdvRXMeCL/Ur2z1WPVL37ZPZ6nNaLN5Sx7lQL/Cox1JPfrXT1cJc0bouE1OKkgoooqiwooooAKKKKACiiigAooooAKKKKAK9//wAg65/65P8AyNeffAn/AJJRp/8A12n/APRjV6Df/wDIOuf+uT/yNeffAn/klGn/APXaf/0Y1AHpNFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAVm+IdQl0nw1qupQKjTWlnNPGsgJUsiFgDgg4yPWtKsPxp/wAiJ4h/7Blz/wCimrbDxUq0IvZtfmJ7HI6JrvxE8Q6bBfafceCpEliSRow9wXi3DIVwCdreo9qrJ4a+JkepwXi3fhgJBdSXcdtun8pZJFdXP3d3PmMevU8elZPgS5uIPCs9/pkRhFi+nyXU9jaEG+iCDzYmV8gsgZsumC2Ae/OhceKPEQ0/VriCfUnjOtQrp6G0Ec1zaOoJWHcmGGcndgkKpPHWvQqZg6NScIU42u1t8iFC6V2RJ4J+I6CBWvvDkiW1t9mtUZ58W6B43XbhQcq0SYJz05zU954U+J1/Zm2udS8OyLIzGZmec+bu29Rt2rgKMFApHOCCTmvqniLXX0LQtOsdWudQ1WeW5ivvsiFJYpEAILYjyqxlkBG0bgR64K6vqPim4ksZtK1PUrq1WyUW13aWzOs14sjLKJYwgAHG0ByqjrkHNP8AtmtdPkjp/dD2aJn8I/EaRiWuPC5w1w8fzXA8ppZknJX5eokjDLnOMnORjE9hoXxJtNT+3LdeE7i8QSrM8jTkuZPKJLBQACFhjAxgY7HrVi/1DXW+IMMMcOtzW/2i3Xy0gkgghXbmRhIMxyJ1yHw2eFPHN/Q7CbTPG2t/aLDWZDdXyywXIuHa3EJgUDdl8HDK4xgkbl7YxLzeq1Zwj16d9/vH7NGXoEvxCjsBpOm3fgy4XSQljJk3JZGRFwG4AzjHTitb/i6n/Um/+TVR2UOqQ6b4q0/TbPUoGmMkumyXLtnLQqDiRmYg+ZuIz0+lYU+ka0NB1FtPsNfggSayks7Wa8ZrgyK+bhg3mcKUJGCcbgSMcVjLHuTbdON35ByeZ0H/ABdT/qTf/JqtbwH4gu/FHgvT9Zvo4Y7m58zesCkINsjKMAknoo71gWmly2Wl+LNKn0XVr3S3kSWytjdOWmjaKPdGsjPuUiQMTkjGeM9KtfB7/klejf8Abf8A9HyVpOca2EnNwSalFaK2jU7/AJIErSsdxXJfE3/knmqf9sv/AEaldbXJfE3/AJJ5qn/bL/0alePW/hS9GRiP4M/R/kVdG8WXWt3jWcOrWdvc+ZLGsV1o00RkMTbX2kz4bB4IBzweKv6Vqer6y1+LXU7DFldPaSNJpciguuN20+fyOcZrivD8movrFqNS0TU7G1stVvdUSb7FNJ5xmMgWMKqZGBKSSf7vvUejX2qR6B4l0a58HX8FvqElzNAoimVSspA8r5IiVOC3zAY4FHud/wAQvT/m/H/gno7rrscTyvrGkLGgJZ209wFA6knz+Kglu9ShsVvpfEWhR2jgFZ2s2EZB6Yb7RjmvP7HSbiHw/d2R09lH2u2mjtZdKn23UcIHyTMluFGSAQwQnAXPerMtk7WGnvH4dgRrS8nuG0k2d69rKZFxv3G34YEsQAmOeMUe53/EL0/5vx/4J2lzqF9ZuyXXibw/AyqGKy2jKQDnB5uOhwfyqC4124tNTTT7jxPoEVy8JmCvZsMKCoyc3HfcMevNcXZaJLZXmkGS1N2lrpt5aSyy6ZebsytmNFBhYmNAAgy2drH6G/pcWoadHoV35ckuo2ek/wBmXCzadeMhwVIkDeVlj8gyCB168Ue53/EL0/5vx/4J0o1XWW8Ry6MmpaU0kNqLmaUWfEWWwFZftO4E9c4xjvThrUxhllXxZ4caOKNpZGW2JCoOrHFx0HrWVPqD2vjSbxEfMj0/7CltMsumXasqI5cvu8vAxubg+g5FcnDfeGBp1nYy6/bLBHe30syQ2s6h4blZQUHycFfN47fKKTlSW8vx/wCCS50VvL8f+Cei/wBp3uZh/wAJJoWYLdbmX/Qn+SI5Ic/v+FODz7UaLr0uo6rBCmq6ZqVrNbzSeZZwMhRkaIYOZG6iTPQdBXnraro93po0++8ZwmEWKWXmQ6bOkh8twyOSPXADAfgRnNafhHVvD9p4l+1f23YtLPbzyXUp86JfMYwADdO5LEhD0PQdKl1KfSX4kurS+zPX1/4J1E7aaNS1efV9Ru4FW+SCBU1CaJf+PeJ9qqjgE5LHp61HfXXhPTobWW51q+Ed0oeFk1W6k3If4ztc4T1c4UdzXP33iDw5H4pudQ/4SCC3vLa8Z7dxA9zDJFJbQowOzjqnZuCp9ay9S1Dw1f25RPGMUDz6Y2l3jJo8gWSIsSNijAjI3MO/UelCnR6tdewo1KGvM1e77dzuL9vDWm39vY3Wp6otxcbdirqN44AY4UsyuQgJ4BYgHnHSuW1S5v7LxZr2iSSTpBBoMup2U8OqXZkBVio3hpMZz2wRx74GPrMnhnUPssVn46mtrSzS2S1hl0+eUReTtIwAVU5KKSSpPBwQDirmt6na6/qs13pfiv7Rdtpk1jFYQ6NKzTKyhnG7sSyA5x8o/OiU6NnZr8AnUw7i7NX+R6F4nhtp5dGjvLZbm3+2uzwtF5gfFtOfu4OTkcD1rndL1rwBq1pPeQ6Dbx2dvbtPPczaUFii2k7kZtuN4x0/rxXU69HdmTTLi0tZblra6aR0iKBgphlTI3soPLrxmuIsdH1HSfBt54e1uDVLzS7pBaRmKC1heNpXI6idsktIMZGBVvlTbkvwNHyJtyX4eRcv9U8H2nhW/wBcj8JRyGydY5bN9LWKZXYrtBDL0IZTnkYPrxT73VPBemaJFqeoeFVs1lnMEdvcaXGkzMF3EhT1GAefanRaDMPDuoaNc6Vrc8N4B84WwhMZAGGURuoJyAeQeR6cUzUdAvNWsLSO+s9euL21d2jvZo9Nd9rgBk2klMcL/DnjrR7nb8B2p/y/h/wCCTxB4E3QfZ/C4u457I30cttpKMjQgAs2cfw5AI6gnHWnTX+hP4gt9O0zwHDqMM1il8s8NtbIGjcgKwDspx1zxnPapJfDkrPaNFp3iGDyLOeyYRtYgSxzHLZG/AwwBG0DGPSnxaDcW6aYbax8SQTWVmti08UtkHngXorZkwMHuuD70e52/ALU/wCX8P8AgElpotlcePr60k0Kwt9MtbNGWGXTICJ3Zm/eJICTgbcFSB696pWus+E7uKSaPwZEIXimlsZGs7cC/WInd5fPHA3DdtyORmmx+JdMuNbXXF1DUV8xEC2zX2nogj67Cpk3cnnn5hyMjkVetPDttZKEh8Pa/wCVHHNHaxNdWzLarKMP5QMvHHAznA4GBmknSey/AmMqMtlf5GdJd+GtY8PakIfC0Gn3D6K+o2jy2sIZ4mVsOpTO0g7euDyMd8dN401ZNDj0bUZIJJli1DHlxlQTuglUcsQP4s9elc5q9pDpGkIkWg68LhtLfRbQEwTblKFlDKjljgJnIHQGrninV9N16309La21q8S0v1mmWwspklTbHIFIYqoBDFe+etS5QTdtNvzJcoJu2m35luH4gpf2elTaZpFxdtqklxDbATRqu+IuG3Nk/KQhIYZ4I47VX1D4mW9n4c0/V4tNeT7XHLK0MlzHGYkjOH5J5PBwB1xyRWfaXOh2JtzbeC/FyG2uXu4j5MpKSuCHOTJ0bJyOhyeOay7zUvA9rNDpd34W8Q2015C1rHbNvie4iZyxQL5oLjcxwOcZOKv20O5p9Yp9ztdXuLu28d+Glhvbhba+Fwk9sSDG2yLcpxjIOfQ00+MLpNbXRX023/tI3iRfZ1vCT9nZC32gZQZUbWGPUYz0rPthputy2t1H4Z8SNLpTiGHzbvyXhbYP4WnBJKsMkg5B5zWBpfxJ0bVvGTXws7+8vooHt7S0tLaOSSNN2XYkPuJOFBGMLtPqaftYdx+3prqdlB4zDarqNpcWDW62YuCvmSYlmEW05VCoBVg2QVY9OcVmaP8AEOfWNL1O9ttHmm8i2W6tUjWRPNDZ2xkyIo39Pulgc8E96OmXWg6PdSXNn4G8UrI4cfvbWSVVDnLbVeQhcnrtAzRa3Ph6ytrq2g8AeIhBdKElifT2ddgOQihnIVc87VwM9qXtodxfWKfc0/A2u3niDWNWur6O2iuI7e2iaOASDZhpjhhIqsG+b0xjBGQaoeLLxP8AhP7fSotI0y/vr2xjaF9TTMMKRmdny20kE/LjA5wc9Kt+Hb/T7LWdTuofD+saZBcxQArJpkpaWRTLuY7A3ZkGSe3tSeIU03WLqWS4jMltPHDE0GoeHrqddyNIVK/dwT5hHeo5otL1f6mfPBxXXV/r3MCHU7fVXtX0jwl4ZWCbSG1Mm8jCkbWKMoITGMgYY9ufau38H/ZjDqb2drFa28l1HKkEShVTdawNgAADqa52/ew+0Wct+dPWZYzZ2pl8L3anaylTEmX7gkbR2rZ8P3NlodrPD5d4RLKrqltod1DHGqxpGqqpVuAIx3701KF1bT7hqVPmTSS+4wfBNnbaf4tsvs4Mf2vw1bTzKZGIaQuBuwTgHAA4q/od5NYeJfHElxKt5dWwhnCRM6718nKqELNjpjIHJz7ARW+kaLamJorjXRJEECSNoIZxsUKvzG1JyAoGc9q0E0awsNKk8RWmqXYjFq1150FnaJI8e3fx+4ByR2OPenGaUbdvT/MqFRKKVtl5f5lK58X6jbeDdV1m21LRtVuIbWKaCG0Vv3TMcNvBfJUZBBO08HOKpS+NdcbQ7K5aawsXk1iOyeeURyIYXU/MRHKyqQf9vsPXFaFjZzok8lhba4qTswmaCPSgJGBIbdjqQdwOe+ac2k3T2SWT6frzWkZBSAw6UY1I6YXGBT9r5Mftv7r+4yNV8TeIrLRxaw6zYz3trqM0F3PD5K3DQqMqUjkZY9/zKGGR7A1FfeNtaey0RbbUIbWabSf7Qae6hjhS5fIGxldvkHdthJ+YYrYuZZdFiM1ydds0uJwCzDSkEkrnAz6sadcanewfZBJL4mf7VII4PLTTZNxPf5QcD/aPA9aPa+TD2391/cVtY8VauniBIre6hs4IktH8qYxrHdCRsyFWb52AHyjYPvda1/8AmkP/AHAf/aFRSzapGQZZPEaEEAF20scnp+dTG+gstGi0K50PUPs/2UWuya6tVd49uztMOo7jFS5c3R7MmUufo1o+hhab4n1TWdburC01nfLIl15Rt7dHjgH/ACxMisokjYYIIcFWIOCOK57xn4i1nWPDtxb2xvHM2iR3Mlr9iIaC8SeHgEL97G8lcnG3NekaZpWnalZfakOsQfvJI2jl1W43KyOyMDtlI6qehNcl4SN74s02e9i1JreOFxG5a5unG7aGYZW8OMZx8wB9hVc8tLIp1J6WV7+f/AILzWNcUfZbTU9Un09NStIxfCEGUh4pDJGSE5UMI/mxxvxnjjP/AOEg1XUfh3rj3t5qDagIIJrZPszrJ9oeEF4wu3lBKGwMcY5OMV0unC1vb+xFr4kh1W2muWt5vsOoXWYz5Ukg+YXLgfc6Ed6TUTaWOo3qXXiaDSbeK4EEIv8AULrdJ+6jkYhjcoDzJ0A9KPaS7fiL2s/5fx+Y/wAZ3Ntf23h3WIbjUPsdpqgFw9okvyL5cgLFFUk4baAcH73HBrO8SQ2r6n4U1Rz4lbS1tbmLzLZrgTbj5Zi3hfnBfDDnrxnpxcu1tLHSY9VufGdmlhIxWOf7TeFXIJBCkXfJGDnHTB9Ko61qFnoNzp0N74mYjUEMsMkP26RPLC53krdn5TwARnlh25o5p/y/iPnqfy/iTT6l4jb4hyq8Wow2olt3tBFFKyS27BfNVl/1YIbOWYgjdx05jW11RPHGj31/ba3d3ttqdzHKVRzaLbyLIInXkIoCsgJHzcHNdHoWlx3y3y3V5ezNb3CxpLBf3cSurRRyA7WmYg/vCOvatf8A4Ryx/wCe+qf+DW5/+OVSlJq9v6+4qMptXt+P/AMjwJ/zMv8A2Hrr/wBlrra4/wCH8aww+IolLlU1y5UF3LNgbepOST7nmuwqaPwInD/w0FFFFamwUUUUAFFFFABRRRQAUUUUAFFFFAFe/wD+Qdc/9cn/AJGvPvgT/wAko0//AK7T/wDoxq9Bv/8AkHXP/XJ/5GvPvgT/AMko0/8A67T/APoxqAPSaKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAqpqmnxatpN5ps7OsN3A8EjRkBgrqVJGQRnB9Kt0U4ycWpLdAcHB8L4raCOCDxj4vihiUJHHHqYVUUDAAATAAHao7j4T2l3LBLc+LPFk0lu2+FpNRDGNsYypKcHBIyK9AorueZ4p6uf4L/ACJ5Inni/CKwS5NwnijxSs5BBlGoKGIJBIzszyQCfoKktPhTa6fapa2Xi3xZbW6Z2RQ6iERcnJwAmBySfxrv6KX9pYr+b8F/kHJE4f8A4Vr/ANTt4y/8Gv8A9jR/wrX/AKnbxl/4Nf8A7Gu4oo/tLFfzfgv8g5InD/8ACtf+p28Zf+DX/wCxo/4Vr/1O3jL/AMGv/wBjXcUUf2liv5vwX+QckTh/+Fa/9Tt4y/8ABr/9jXR+G/D9p4X0C10axkmktrbfsadgXO5ixyQAOrHtWrRWdbG160OSpK636b/0wUUtUFcl8Tf+Seap/wBsv/RqV1tcl8Tf+Seap/2y/wDRqVwVv4UvRmeI/gz9H+RRsNS0HUbz7PGviKMvcT2kLzahcIs00Wd6LmXIOFbG4AHafSmwajpc1nc6g9h4mt9NtIp3ubqfUZ1EZiJ3Lt87c33W5UEcdax/Cdrpdnrup3+s+JbNkj1e6vNNthqMDQosuf3gAO4NhnBBOPmzjPNb1kvhmCw1KwvfGUWpWmoCRZIbm9twqiQsX27ApGdx6k+1H7ryD9z5fgRnUNFEV2DB4iW7g8kLaNqU/mSmbPlbSJiuGIIySACDnGKzvC1w97e3lnrEWtRTnVZLOFP7TmzCot0mAcpMQerYIJ7ZxWktl4J+w3dtJ4khla6WFXuH1VfOUQ8x7XDAjaefqSe5qL+y/A/2SeE+JkMs12L1rr+2B5yyhNm5X3ZX5fl46jij915B+58vwIbbWNPv7SD7BpviC51CTz2exXWJQ8SRSNEzMxm28uuAASTn0BIn1aHUINZsLLSdNuboT2r3Mq3PiG6gdMFRgAM3TePr+FNXR/AENnFbW2vQ2vkySPFLBrGyVFkO50D792wtyVz1561bvoPA1/aWFq+t2kUNkrJEsGreWSjAbkYh8spwM5Paj915B+58vwLcssk/wneaaR5JZNDLO7nLMTBkkk9TTLLxnNdeL7rRJdMW1ih83y5Z7kLLMEC5dY9uChyQGDHpyBVS11jRrr4cQaX/AG5pcN1LpC2+2a7RdjmHbhucjB68VQtZtDtL6S9ij8LGeQyEmXxE8ijzDl9qtGVXdk5wBwcdKmNSK1b6IzhVgrNvoi7Y/EC6v7W/mTRFRre2S5jV7k4dS5XG8IUOFG7KFxzjNOl8capBbSyTaHbJJHdw2pj+3E/6y4e3DZ8v+8m7HofXisPW7DStA0WK7n8NaVJZXY+zq8WuyKpRgZPvuiqF+Tjn2HBxVXVvDutXunXKaX4Gjs7m5ninknl1VbhZCkwmwyFhkFgehHU4q/ax8/uf+Ro68PP7n/kanirUrrXPh14lmnNxpmp6HLKm+wvHVWkRFcMCNpKkOPlYfyBroPE/iXUNIubOz0uxju7qSF7lkkMnzIm0FV2KxDEsPmIwO9ZlhBdajBcaLd+CdJt1iVLiW3nvQUkMm9d2EjcHOxhyc9KXUX01DFYanpvhFWtARHDc6rhogwyQA0OQCCPrR7WNr/ox+2ha/wCjF8ReN9Q0+GC4sbazjtms4rqWS7Z32GRgFRxGCYxgn52+U446Guk1gj+1fD65GftznH/btPXKz32iXV3Hdz2fgqS4jRY0kfV1JCqcqv8AqegPIHarD6vp1/r+lajeXnhiB7F3Pnxasssuxo3UoMxrwWZSef4amVWD0TIlWg1ZPt+Z3NZHiU40qIgZ/wBPs/8A0pipf+Eq8O/9B7S//AyP/Gq/jF54/DjPahDcrdWpiEgYrv8AtEeMheSM46c+lVOScHYuck4Ss76HE31xe3nw10zVor+Wy1bVdUtJJpllYeTI8yoUxn7qD5Sv+ycjOafp/iibT7R9+7STda01ndTajM00dky26swBZsbWcELyB84OO1M0GTxHrelX2oWsHhqW1lu5JJ4LyG5/dTKNrjy2HyngkgDkknqTWvZyeMtc0eK4jt/CstndqJNk0Fwu4cY3Kw6jA6jtS9r5MXtv7r+4zrjxbqVzF4Nv7nV4NLs76S5FxOsJEErKCIiS+NqsAWAJHbk4p2tfEe70zUraC0SC9tmtIbmO5EkaLdhnKttUtvOMDAjV2yenTOzPZ+Orm3+zz2/hGWHj93Ik7Lx04PFElp46mlillt/CTyQ8xOyTkp/unt+FHtfJh7b+6/uKE12sfgm2tG1WNDL4Ydl08xjdJiEZkDdeOmOnNehVx/8AY+u/8IsNG/s/SPNGnfYBdfbX3Y2bc48np3xmtdb7XWleJdP0gyIAXQam+Vz0yPI4zg0oO2/ZdCacrbp7LozE+Ji6g/h63XShMb9ppRCIM7932af7uOc/SseXVdIsdKu7nwRafY7cT2cd7fWdj8ixmQiQhSvzOi53EqcZGeRx1Fyb7V0e3utG8P3qQPl45dQaQRvjuDAcHB/Ws610yzvlZrTwv4QuApwxhug+Pri3p8zTdl+f+Q+dpuy39f8AIxb7XNafwWTaXmq3IfUHjt79LcQyS2yruyxEb4zyquqZYheBmqtxrd1eeCPCF/rFrfyakuqRS3BGnytIiRSHcSFTj5dvYbuw612WlaLo16b2K78MaNbz2lwIWWKFJVbMaOCCY1PRwOnatH/hFfDv/QB0v/wDj/wqlKTV0v6+4tSk1dL8f+AQ+HriO7utauYd3ly3kbruQqcG1g6g4IPsa8l8KWpiSyvpYbufT7LUYruRbfTJBKjNAiiQOVzJGCrhlQE9DkgjPWQ6rDpKamtrPqNvb2ctxPerplvZpDaRLM8algybidkeeNxIU+wqU6N4SGrPpZ1OMXixxyeW2n2QyJM7Ofs/U4/lWactGl/TMoueklHv+Oo/QovEreKJJtTmvITLc3Ec9ukMjwNDg+UyyFgiYAH3RuJPzc9KGnaFqWleG9YttFg1uHxB5d0IpLq6kkhH74lShc7NzKQQQCRzuOeS/QdK8P6xJPazXFva6hDdTWxtfs9i7MYm2kr/AKOCR36dK0f+Eb8L5ulGq25a1XdOq2ViTGMkZIEGeoI/Cq5p/wAv4l89T+X8TNS01VPC02z/AISNyl5aTRR/vY5lyy+cu5nd2G0sSD8uR8vtYl0m9vLLUtPfStTu7Wz1+G4tkmuWR5IQULMjswyqtvKjPQDuc0mn2Hhi61XSl06a21KK4lAljl022CbGhldeVhUhsxjjOR3HNReLLLStL1lUSwsLa1ItYywtraOKNpWny8jvC+B+6RR7sPWj2ku34i9rP+X8fmbet2d9dWehPZaTqSGz1BJXh+0IW8pG535lw2eCOWPHaqPiPS/El9e6jc2MV8s9xb240x0u1iSykViXMq7sNyQTgPkDbnpWE8WjCy8NSi2McuvkiAXNtYRJGQu4Bm+zknd/DhecjpkU7UNFazu/EcP2ewjTToY5rSS4t7RBc7lZmB/0bjAR+meR9cHNP+X8R89T+X8TVvtF1pNTv7qzsNTa4TVbWW2m+3qUNv8AuvPCoZPlB2yfKRzkdO2z/wA0h/7gP/tCsiDRdOm+Gmo3d1pOmm/it71TMlpECGRpFUgqi8jaOQB0zTo5PDOq2z6NpFxqKSSwSRWq3ct8ts5UENHguoO0DlARxU3lPZdPz+RDc6my6d+/y8iK38NaonhvVtFsNCttKvBHMkOpxyIPtGZNygbcuAy8EnGOwPaJPD/iFvCOqWT2F2gu7mJ47ZJ7eNoFUgsERQYynyr8rH5wzbsHOcjw9a+BtQ8Kx6lqPh+6iuo7BLydIkugsi4G5oct86qSMkE4zWlFpfw3ltbq6Gk3K21tbQ3LzM04UrKoaMKd3LEMOB0qr1ey+/8A4BfNW/lX3v8AyLcnhHUdS8EWlpd6PpwuYNVS++xOFVHjEmSrY3IHZSQdvy8kDitS+0e5aw0VrLwrpkVzZXfmJGkyKLWMPk+WwTguAMgADsSep5vX/D3hWw8HajrNj4ZuBNa71Mdy0w8sr952XzASoGTwee1aOqeFPAukvbQyaFd3M88TzJHaGeQ7EALMQH4HIHqSQBk0Xq9l9/8AwA5q38q+9/5DPFHgi712/wBcuI9KsM6jo8cUMkrLvgu0LnP3fR1G8HPyiuc8SzQyfECS61PSbO8NlcWWLMlDcPIYjuEeULSxjfuwMAtGTxjnV1qx+HGiW1rcXGi3TxXNt9rDLLKu2HjLENIDkbh8oy3PSpJPAWgQ/EW0082avpt3ps04g8yQFJI3iXO7fk5Eh49qL1ey+/8A4Ac1b+Vfe/8AI7vw5/yC5v8Ar/vf/SmWvPfB0eoaN4d1WxuNIaI3+XEZs7s7W8hIsOEh/iKFiQ2RuPXqfQPCMUcPg7RVijRFNlCxCjAyUBJ+pJJPua2aIpuKa7BCLcYtdjzLwlpl7p+qWFu/2h7ZLpGijNlMot41tpkOZpIk3DcyhQckDHJJNT+J7CW71VlW1bfb67b6gHk0+4mVokgiUhGjRhklSOvY16NRT5XvcfI9763/AEseWW+mT2+qXV8ru7C9upbWGfRLySMRXBUvuGwYcbcDHGCwP3sizZ6Wul2/hr+z7/UFn0W3mtyZtBumSdZAuflCgrgqpGD0GK9KoqrS7/195Vp9193/AATB8MmaT+1J5xMTLdowkltnt/MxbwqWCOMgblb8u9b1FFOKshxVlY5LwJ/zMv8A2Hrr/wBlrra5LwJ/zMv/AGHrr/2WutrOj8CM8P8Aw0FFFFamwUUUUAFFFFABRRRQAUUUUAFFFFAFe/8A+Qdc/wDXJ/5GvPvgT/ySjT/+u0//AKMavQb/AP5B1z/1yf8Aka8++BP/ACSjT/8ArtP/AOjGoA9JooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACuS+Jv/JPNU/7Zf+jUrra5L4m/8k81T/tl/wCjUrKt/Cl6MxxH8Gfo/wAjGsfF+uDxiNPvLjT5YG1aXTfs0FuwkVFh84TZ3k4+ZVIxgZzmovC3ju+126nguNRsbd7q2mkhR44xJYSIfuyIJSzADJJYR/c96v2Nlp+m3V5dWmp+Jo57yYzTyf2OWZ3IA6m2OBhV4GBx0qwPsgeZhqniLdKMSkaGMuP9r/Refxo9qv6t/mHt4/01/mY/hrX9Q1nwPfa5f+NNOQSWoi+SCJVspckbnJY5ZuODgcjAqppbQ6H4HsJtE1y3K3t1BFqGq2tvbn7Enl5wyxptJ3YXLgkeZk5wK6FUsVheFNS8QCJjl0GhLtJ9x9lp9vLbW8ZW21jxHEhOSI9ECgn8LWj2q/q3+Ye3j/TX+Zg3/irWD4d8NX7a9HYve6jLZTTpaDypYdzqs4VxlThFI52/Pk7hVDxH4i1rRvENxp6+Mbtkt7SF0As4GaaVkmbHEf8AsRdOPnrrJtYtbdo1m8TeIo2lJWMPpQBcgZIGbbnioj4i01baC5bxbroguGCwynTF2yE9Ap+zYJ+lHtV/Vv8AMPbx/pr/ADMW08aaxqGrWCm6Nv5os5I4FhLC6hZEaZ1QRlj8zOudwC7MnvUk9zqr+M9DuNSi1KaW31q5QwRWeYoLdopEicOqcqQyEkscZPHGBoyeKtGhuGt5fGespOrbWibT0DA+hH2bOanbXrBLmS2fxVr6zxqXeI6WoZVAySR9myBjnNHtV/Vv8w9vH+mv8zI8VW8138JNFt7eF5ppNPZY441LMzHT5sAAck1oINU13S9VtLDVdXthBBby2t5dQfZyJsMWT7qbkwEDZHBJ9OEh8S+Er2ysdN07Xb4SaPGsqvbWjySIixmPc4MTDG1jk4H4VnSeKPCniLTbmNvG+r3FrEhkuRDbphE5BLlIOFOe5x61MJqKt/l2IhNQVv1Xb1NbwBPf3+p6rqt+ZVOpW9vdwW0knmfZomecKgbuPlLccfPxWfqyXz+K9Za1bWvLinikaOwZ1WT5bUMDjjds39wcfhW94N1TQdYmvbrRtcm1VkjhhkZ4lRYlUuUVQsaD+J/XtVPXNT0TT9VvHuLXVlke4WKSS31L7Oksvko2FTz0yRHtyQvanfRNd3+va47+6mu7/Xtcw8+NZvD6GcaquoDTQll5Qxi7EjAmYcAgr5WC3y4355qzrNt4jn8Z6dcm1v50t5bVXSOWSKEd5HQodjJk/MJF3fLgcHhNW8U+HdEtrW4v7XxKkV1F50LR6s8u6PAO/CXJIXkfMeOetdRpFhpes6ZHfQSaxHG7Ou2TVbgkFXKn7spB5U9CapTbdrfn/kWqkm7W/P8AyOI1zQzpOs+Lbk6PrFyLyJ57e5iun+zRKbfa/mBpACQwcgbTxgDsB33i+5jsvDxu5c+XBd2kj4IHC3EZPUgdu9cNpdpo2sWtnY3njLxG95d2qGaAXTmIs0YZo9xQqWwT8mS2O1bemeJtI1fYbLxpqzI6ysryWUcaERAGT5mtwPlBGahOUk3bdGac5pvl3Xl5mB4c8WaJNonie21S2fybm7uLsW8txCpnjkbIRcSfex1GR9TWfpuqxah8P/D9hdyQOmn3ATUNOutShja6i2sBtbf8yqWU4YgNsxXQ6f4me81bUGPibURolvpianHe/ZYkYxEsGJVrcZHykgrnI966PSL6WXXLaOPVNQvLWa1ndlvbZISGRodpGI0OMSH1H5VXNPr/AF+JfNNb/l/wTz7WF0+70TR4IGs/sVqk8f8AZTaraySW7swKSCRn2/KAwGCSoI96qa5p+n3ssxkew1CU6B9mjuJdYt2YXq5Ebkl1ywUj5gvX65rv/EXiFNP8Trp02q6hbvNbRG0tbG3jkeeQtLv+/G2MKinkgcGqVxr12mp6HaWl54kuxqtvLchlgtUaJEAzuV4gc5ZRg469+lHNPp/X4hzTe35f8E5SRkvPGml6pJPZLtaza5luNWtZI1EaZYrhvMVgxYYBKseTnPFzQIINO8VXV7c67pksjXVzIupHVIBujlBCAoAXcrhRtZgo425rr9Qvm03UbSxuNe10SXLxxq4t7XYrSEhVJ8rk8HIGcdTjIrH0PXdSmvZLHV9d1VJW1WfTre5gtLcQyNGCQD+7YqxAPXjii8+39feHNU7f195meH7PTtEsrtE1TQzcyaa1o0g1eONLiTnDERopGTzuJLDcQPWtbwM+i+G0v1l1bQoY52j8tY7u33gKuMMyKgYDoCQWPJJ5wLWhv4g1bVPEVlL4h1C2k0+5WGBZLO2yFK7lZioO8EEHjYR3GaTRZvEN9oeq3MutahdXllfXNrHFawWqeaI3KggOmMkDPLAfSi8+39feHNU7f195s+Er06iNYuy1sWkvVLfZZ/OjyLeEEK+Bu5HoK6OvM59d1uH4c6f4jttW1K+u7xoESHyrWAbpZAgyDG2OSB94/UVq6nqN9o32BtR1LW7eK7d4zM32Ly4XCllDny+N23AIyM9cU4tpbfl/mOLkla35f5mRNoniXT7rxD/ZmlSudXMsbzPJBiIedKVdAZPmykvRgMEdxxV2WDxRY+JZdS0bQ5PJuLS2tZVvDCWQRM5yu2cZJEh645Fa/gLWNQ1vRJ7vUVnSQzKY45yhdI2hjcAlEQH75PTvjtXI3OvaDpmrCzvPDVhfzT6lKtxcSCIyKJbySNDtILMAQMlto6AEnipV9FF/l0+RC5tFF/l0+TJYNG8TxX9lKNCkEUGvT6q/72EsyShxsH70YIEh574FP8MaF4h8OTSuuj3U/wBms3tbBnmRiwLbh5gNwVXBAyEAz7YxVmS70y31OGG58AadFZPqY057vEDbXbHlsEC5IJIB6YJ7jmsec2t34l8Palp2lWNnpl5teDyY0DPsvLdVkICAoSrtxuPB5xQ+dK/9fkOXtEr3/r7jo/DFl4jig0Sx1XSEtksLln82Dy1TZ5EiZIErEsWcdBjvU3irSNZu/EEV1p0EhjjFtKHWOOQM8ZnyrK00fGJQe/4EVpeMLZryPSoEtrS5drx9kN2MxMwtpyN3B4yB2NcfpNtp9p4A8J3dr4c0e8l1EwwyNqLIHzICQd+wlznHbOO1HK7u3f8AT0Dlld27/p6BL4S1c6OthDaXoaS2ntrp5bS1dXEkhkBiH2kGLazHABI4X0FQz+Arm902xsr2z1qZbS18gFfsyCRg52uwFxgnY8qNn73mseOKmnu4RYQRW3gzw/Lqi3c9re4g3wwGIA7gFjMjBgychSF3fMRUL6hAVtJovDHhT7PPop1YO8WAQmzeudnA+f5Tg9OQKdp9/wCvuHy1O/8AX3HX3NvPbfDrW0uLdreR4b+XymKkqrtK6g7SRnDDoTXPaK+iSand3V3r1tbR22p3VzYwveQFA8gZfNBDFiCGc7WxjeeOBgvbnT4vEM1pa+EdDeytZbWO5kniiiKrMMlgWwMAEY4O4hh1FXrOLR7zVmVfD/h2OxGoS2BWWFEnDID8wBGCSw4Uc7SGz2pKM1tYSjUj8NtitBJ4a8LWWlXttr8OoPo1i9klvFcwGSeN2Q9NwG4bF7jODS2MehyeEZ9Pl8V2NpPe3DXUpFxbyeWrNlYSrlkKqgVMYx8vFHhXSNJub3UoLxvD1zIt9dxJa/2bGksRR/lAyfmULg9P4hzWXYNoem+A9T1FtJ0a4vbfU54JGkgDrEDdGISMrElUVcNtBAwOMCn+98h/vvL8TWk07w03gy48Nx+NbWGO6aQ3E8c1qrSB8712gbVBz/CBV1T4ff8As2e48bxSajYJLGl6l3bozo5GVZANhHyr/D/CDXOXeo6XbRRxx6V4ZlxrFvp4vhYoYLhJQfuYPDpkFhkj5e2eNvwlNaS+KHihsLC1urIX1ncNZwLEJdkluVYqORw3Qk9/Whuot7Cbqre34jtd0/wX4h3/AGzxPArSWgs5GS/hLNGCT1bJUnJyVxnoc4FXLibw1caza6r/AMJhDHdW1u1uhS8t8bGKlsgqeSUXP04xXMfELyZ/iJo+n3WpWltaXUcYmgvI0kikAS6IdlYgMFbbgHjLKeoFXde8V3mh6vHp+m6hYo1ulqlppS2pZtQEhwzIR90KM42kgYO7jFNcz6/195UXNq9193/BOh8N+JNCg8LaRDNrWmxyx2UKuj3SBlIQAggng10l1dW9lbvcXdxFbwJjdJK4RVycDJPHUgV5n4j165m1zxNoB8U2qpDYtPFZC3QyyAwyF4d3oAqtn73zeldv4rk8nQxLnGy8tGztLdLiPsOT9BSTcU12Qk5Qi0+iJf8AhKvDv/Qe0v8A8DI/8aP+Eq8O/wDQe0v/AMDI/wDGuA0zxT4suNL1r7P9o1DUbWzRo8QxiDex5dTsVt4U7vJZc8AZJNLLf6hc+GPE0FzqOrTaOIk/s/UzBtuZ5HQ74vLEeSu4gfc4BIzxkXaXf+vvLtPuvu/4J33/AAlXh3/oPaX/AOBkf+NW7HVdO1PzPsF/a3fl43+RMsm3OcZweM4P5V57eWUb+BrO60XUtZmht9Sgmu5vIMMzwrIvmBkEaMyquSAFzx3rp/DjxSazdyQXF5PE9hbMsl4jJIwMtyRkMqnHpkdMUryTVxXkmr/1+J01FFFWaHJeBP8AmZf+w9df+y11tcl4E/5mX/sPXX/stdbWVH4EY4f+GgooorU2CiiigAooooAKKKKACiiigAooooAr3/8AyDrn/rk/8jXn3wJ/5JRp/wD12n/9GNXoN/8A8g65/wCuT/yNeffAn/klGn/9dp//AEY1AHpNFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAVyXxN/5J5qn/bL/wBGpXW1yXxN/wCSeap/2y/9GpWVb+FL0ZjiP4M/R/ked28Wsw+I4LoaPr4hW9lkL+TP8iG7EiHbj5sQgptI71oaHa6rpF5NdRWt79vMdwtxNJY3IhvXYExMwEJcgHGclSgyFLCuij8b3V1rlxpkF1H5sV3LbMsejzTrCQ7BA7rKBkqobOMc0ul+M73U7v7ObyOyDeb5Ut7oskSS+USJApNx1XBJBx0oUpvVf1+IlKo1dfl/wTm7G11WKz1i3lsbtItQsobYCG2uopEdGcO+5bc5JVsgtuPygE+mhpltNp+n5TTttzb6rHeW6LpVyoaMRLE24rAAJCu8ZC46Z71qab4x1LWILprC5geaO2N1BDNpDxNdxdA8Za4AKk45OOo9aQ+KvEVp4SOv6qlrZRiGGTy/sPmbmkwMKwucYBI+ZtvX2ovPt/X3j5qnb+vvORl0K+n0S1hbSIIbqHxCdT2Q2F4IxATlowTBnJ+6RgAgVpeK9IOsXVnLYWU62osHs3sH0+4iitizBjJGRbMSeoONp4GCMmur8J+KL3Xri3aVoGt54rg/JbeWVeJ40OGEsiuuXYZH92svxtNeHxVY2sV9qNrBLNYws9rOyhfMknDAqHX721RuwSMUc0+n9fiLmn03/p9zldW8M3V7qF7dR2pmkn8wedNp94HcNZpByfJJBEiFhyeuetatnoEdr4rXUjNq0toL5r8pNaXzfOyFSNgjAyOBuJOV4K8c6+uajb6HdaikmjeJJrbT4EuZrqPWJSnknOXA87PBV8jGcKT6Z6bw9tSTV4o555beK8URGeZ5Sqm3hbG5yTjLE9e9F6l9bDvVTSdjjdA0uPRv+Ed4uQNLkvGlWLSLtRIJySMfu+o4HPpSWlpd2/g278NSlLizWIQWgl0K+JaPdk+aQBk44yuMHkVoeDCniDR7Ce4t9aVZIWBu21efEkkZCOdqyfLltxHsDwKq6XJBbeG/EesalL4guG0y7uVe3XVJWZFjwdqFWXIwc5bnrycZpJ1Gr6Ci6zV9PxLXw50i+0y+1l765ubprhYGE01tNEAQZRsBmG5sDacnP3sVD4o8O6xqWrXJt7W8Nu900m+F0AdGt4o8gieNwysh4zg55zUNnrVtd+GrzVRYakrwzJbwx/8ACQzlLiRtuAj7+QA4zgE5DAAkczXN4IvDdjqsNpePJcX4sXh/t67ADGYwqVYkcFsE5AwCeD0p8s7f1/kHJOy/r9CnqXhTVNS0HT9Nex1COays1tI72OOFJQFwM5W7GcgDKtuUkZxXc+GLS5sdCSG7SVJvPnkImZWfDTOwLFSRkhgTg1w+vawPDMtpYXtlqN1qUlpLdSLZ6rfumFbCqu0Mct6sABjrzUWp/wBsS+NrHTtHneG2n0g3pi1HVL1ed6Dllb7wzjaCe5PahKd7/wBfkNRmnd/n/wAAPD3g280R7NhpOobYpY7p49lrIwuAoDlZGm4U4P8ACCAeCOlWLbwzq0Gl6bprWeoPb2b3If8A0e1DywzZ3R7vtHykbj8w68ccUhttXPxA1LTor5F0q2js3K3OrXiuBIXDbCH5YlSACcfd9TUOga02reIntrix1K20qRp1huZNWu42RoiwKvukwWIUtgfdA5zQozStf+vuEoVErJ/j/wAAu2/hrULaQSLF4iZhpy6aNy6ewMKnK5BfBPJHTBB6Vp+F9Am0rW0kjsb62tFgmG24aARxsxhwsaROQoxGxPA5PvXMafqs2oabqwuJLqzvYdKlvYo4dTu3KYLBWD+YY5E4GGB5IPGK3/iHqWm6Vd6fc6lb2k6/ZrhIUu4PNTzDJbgcdM43dSB2yM5pPm6+X5+gnzbPy/P0JvFGgXep+IHnFtezWjWkce23S1kRmDS53LOeoDggj1PPUVSm8Nz/AGTQo7Ky8S2Vzo0LQW93HNZvIyMoVgweQqc7QenGBjFctJrVhL4VtL+3tvCMV0msHTblp7GIxupk2rJ8rkIAvzdWBA645q54nkbQo9LtrPSfC97czQNcG6ext4ILobsKiGSZQvBGSC55BAp8s+n9fgVyzW35/wDANTVPCE2p6mdQNv4nhuT5LmRJLBmEkX3XVmclfdVIUkniqNnd6ZFqA1k6T4yuLT7XJqcMLWaeQksgOZAVIJG1jjJI5zXofhX/AJFDRf8Arwg/9FrXA+Gnunvbex1LxKyWEljYLFpU9pE0dzHJFgoCwLMCQQcdO/HAXvO1nuT78rWluvLyJNI1b7Hrl/rUVl41uV1CTzZIjp0PlHC7FAKgHCrgDn+EZzzT7K9g0+11C3t9J8eIl9I8spFqoZZHILOhH3Sfbjk8ZrM8GeINR0LRvD9ql1BeW93Y3ogsVjCFJ4SGSIMCTuYOQQfQYA72v+Ej8XLpE/2S+l1OZLGHUZJorFUeBxIoltSm3GShYhT+8G056inyz/m/ArkqfzfgOtl0e38LT+HJPDHjW602XG1Li2LmLGCuw7vlwQCMd6oalrUbRQeF4/D2uz214/2i7bU4mnu5ApXd5aMSPugDdkBfTmtrWPG86aPrd3pOpzXAW4tPsjC1BYRysissWVAc53BScjOQTxUL2+qXHijwwbrWLgahE94t3PFDBJJbq+wxwybFKKSvcjrnBxRyz/m/AOSp/N+B0eh6/EJtVuLjTNZtBc3Ykjil0yYttEMSZOxWHVD3rAvPAfhTWW1XWpNS1qBI5nnvEG6AI4/fZMZjDHG4EEgnGMHgVWurzUNYt/CGpXd9rtnEj3cF7Nb25jfdsZUkaMIdpbGR8vG7sa6CS5ju/CvjK4i87y5Edl86Nkcj7FF95WAIPsQKmScVq+/+ZEouC1d9/Lz7mTc+GdCu5JXm1HxYxlvEvmxp8qjz0+64At8D6Dg9SKenhzw1/b9tqlxd68919rieN7rTmSNZN67QCYAIwzYB2lc55q3DGll8UNVkvDqyfbvsv2MwrO0Em1CH3FQUABx97HWsa6vtcfW9OtidUfbqijVVuYSII0+1IYDG3Ck/dA2E8E7sEU5QaTd/z/zHKDUW7/n/AJnQ+P8AUHtpNIt43sY2eV5A98ZPKPAhCEICcsbgYOQBis5fCfiRLSK1XSvBwt4pUmij23G2N0ztZR2IycY9af8AFTTr7VtLls9MimlvW06d4Uh++WW4tG45HPy/X0yeKh1MeKH03UBp6ahLpgvLYKs/mLdNCVIn2YKyYBKkcgnDgHGKfJeTd3/SH7PmlJ3a/wCGQk3hrVW1WzXVdL8KYvbqX99FbzSuJGiZnYgsv3hHtPPp1pL/AEK+v/Ey3H2O3vxpMRsVhTS4fsy7ljk4WS5DZAKDIwOorU0RNRitdAh1J7qRo9WmWCS6j2O0P2efZkFmbgcZc7jjJFcf481Z7HxPqMcV1d+YXl22sU5iR3a3twjMyyoUIIbDEMBzxUNW0be/fyIcbaOT37+R100GvXNytzP4ftJZ0xtlfS7dmGDkYJvM8dqzbvXb+38SLDLook1cIkvmRaEsrorEorM63R2g4YZJHAPaqXi3X3NtrFlpd8txJfRwTWtxb61EgilTaHQ7pF2DCg8cNk985IW8Mv8AE+8125gsvKeG28i6/tG3IWdS5dyBLnABQdP4TgertH+b8R8sP5395dj1/UH8RXNvDou/U1cQXE0Wgq2CyBtryi62j5dvVvT2qbSZtRnjun0zw/bRoJHtZyuiwxbypwy83Y3LnjIyDzWX4Vl8N6X4y1++ls7CBbu5d7a7bUbZx5ZjUMNvmkjcysen8XOKr6bqjP4Y1zQ7aSx0RHnaexd9WgIMRdSYcxysyFgHG4YABGOaLR/m/EOWH87+839QuNV0zRGkvdEtY9NsVM+z+yYWWLGTlUF4eeT0Geas6XcX63sevT6PL5Ulu5Bgtbe2L+aY23uWuWJOI1HIB5rGF/oDeC9ask03S4o7kGSDTpdWt5i0jDaThn8uPBAYAMR1PBrLumTXPDfhO3udQ062j0oiK906fUbVxcBYggkHLocHOA3rnggUWj/N+IcsP5/xOy1WNrjUzqkmmaxZzLCkZYNp7AKrMVP7xmKnLHoRnA9KrXGtTWeox2FzfeIIbt4mlSN30sHYpAJ9vvCudm0nQ7jWdBku9R0O906z0mWxuIrm+hdmP/LPPQHHr2J/GpmNj9s0HVJm8MXtxZ6WbKa2m1GL/Wh4yr+YQcgbCR8uQW9+C0f5vxDlh/P+J1E0Iv8Awrf311rGtC0ENwlzA0dp5hVN6SLlY8Z+VsEN+NWLnXLfWIfsMmj30wdlYJDe2yvuVgwIKzhgQVB49KriWOf4a65LE6PG66kyNG25WBlmIIPce9cfbaXpqarpV1Fqfhmw+yCNpZobyPzGYC5QkEDk4mR+e4x2zSjbq90v61FHltq90vn9510S205kEOleI5DGcSBNcB2n3xdcdKYJrFraW5XT/EBghBaSUa8pVABkkn7VgcVz2kWdnpmnzRR694Zju20v7ELhtQ88OwOcmNsKFOSSMNye44qGKxhij8QRDW/CrQak1s8UMups2zytowWXaRwMgjoQBjFPlp9/yHy0v5l+H+R0UV9pcywNFaa64nk8qIrr6nzHxu2j/SuTjnHpU9prumaTI9xHp2oB7kmEy3GpwSljEWygL3B+6S+QOhzmsV0gfT45T4q8PtqNpqp1CzSW8R4wuwpseQBXbhmO4gngDoKzjBdLpFpaJ4k8IPNbay2qqz3pCkszSbCOf45CM+gHc8CUFqn+Q1GmndS/L/I7hPG1u8VrINMuwt3n7PuuLVTJg4OAZsnkgfjUs3i1be+jsZtJvI7uTGyFrm0DtnOMDzs84P5Vx3i3TdK8R6pBqMXinRElksxZXcMmousRXcW3ARyLvGSRsbgjHIxzO1vZ/wDCYy63H400WFJTbh/KnVXZIwNyMu/Y+47sMwLKG4NVdfzfkVzR/n/I1/hrex6jpuuX0KusVzrE8yBxhgGCEZx35rta88+Df/IoXf8A1/v/AOi469DpYd3pJk4R3oxbCiiitjoCiiigAooooAKKKKACiiigAooooAr3/wDyDrn/AK5P/I1598Cf+SUaf/12n/8ARjV6Df8A/IOuf+uT/wAjXn3wJ/5JRp//AF2n/wDRjUAek0UUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABXJfE3/knmqf9sv8A0aldbXJfE3/knmqf9sv/AEalZVv4UvRmOI/gz9H+Rztr4Z0uPxO+tahLr4vYNTuLiOGLT5GjA8x9oDrEWKMCrFd5BPNL4ftYJr27u/EFlrOEuboWlmbCZ4EjmY7mULCGG5WIIYnvjGaqwSTSeMtSGreJL+0sGcm2jN1Kiu/2ueIom1xnASMYHTI4HWn2V1eTeJdOtGbUH+1Xl1Bd2K6jdB7GKPPlyM3mZIYBTkgA7wBSj7SytYmHteVWtY1tNg8LeFS+oTS60yRWws4pb+yuSttb5GIlJjAAzjk5J4GeBVFNf8Cx2ElmninVxEwjVcS3P7tU6Kvy8Dsf7w65rW1bU3s/hRYatO8kskMFhcuxUyO5EkTE4yCxOPUZ9a5fTviNevomtW82tW6ajGsLWNxdxdS+N6ny02naeMgNjOTuAzS55X3S+X/BF7SbfxJaJ6r/AIJreHNY8GadrdvFpGqRR2ywXcs8lyzRZlkkgPVwoydp4HQLSeKodF1/WkuxrumNCkUOwR68bRkljaRg3yK2cbxg8YOfWs8eOZz4XgSPxRt1FtS2PJdRxiTyFALAGOMqAR91mQddvB5qW08ewx6fp1xe+JbrZe2M8LgQQtLbzq+Y5HVFypK5HI2nA4GaXrJf18xes1f+l3L9xc6Xdm4N1P4fnNzZLYz+Z4nk/eQjPBxH1OTk9Tk+prY0DWtHsEvTda1osRnnV0jh1JZgqLDHGAWbaSf3eeneuKufGNpquqeH/P8AFmp2Vle6awvfsq+WUuEZQu75CY8kyEnjIA7EZg8T+KJrjVdWtYfEMKgRSRRRJK8tvcWxi74XZ5pYkZ3gggfKR1G7a8ydgcmlzOadjqP+Ea1LwyukQaW2kXNw0/kwG6t5lWNvKdmkGJWCswQ52qMljmqU3gnxY+matYQf2HbJqoYXbxXV2zOW4Y/OWAJAwTjpXZeJDcLNpBtFVrkXcpiDdC/2WfGfxxWP4Yj1BID/AGpLr8lxJYAXsc4/dpMPvGJl5BOSAIzjCjocVSp6tJvQpUrtpNq3n5GLZab4m12NryC48L6jp52wx27yTyQRPCzDcgP3XycE5/hGPe1/wiviT7Gtp/Y/gv7MsvnLF5U+0Sf3gPXvmqNvNfaH8HP7NW2vrTU4isMULKY3maSc4jRyR8zKcFgcrnPUVB52p3fhy10WJdUmvIL4HVgs9wXto2DNGn8EkilMLlWX5lBJ60/ZebK9j/ef3m3feHvFepx26X2meDblbZGSESxTt5akAEDPQEAA+opL/wAOeKNVS2TUNJ8FXS2oxAJoJnEQ4+7kcdB+VYy6bq9zonhCPWLLxGJ7aSaDUTbTsGaIKwG8pJkgsUweWwG59d3WtD1FrvFha6s9rDpsUdjJb3oEkUyuSc+bKAWwEyXVs+vUE9l5sPY/3n95FPpXia712K5nsvBE2rW8YaOR45WmjTJAIJ5Azn9akg0zxYuq3d/BZ+CxqD4juJ0jm8w/KCAzdfukfgRUlxod5bePb7WxocmoC6trRIZo7pI/KZGbfuBYcYKtwCDt6ZqPSvD1zpvjPVLuXw99o+1akbq31IXKbYkaEIcoW3ZBDDhf4+uKPZebD2P95/eVl0TX7JBpDWfhfTrXVzJaSS6daybxmJ2JwSoPCHv1I4Na+v6VqGv+IzbWupQ2KWdkpO+yW480TSNkEOcYBt0I4z1rlPDXhvXNH8WaDc6sl2spZ4rqU3KPDczCGXEoUEsW2gjc23AwMemh8SreKe21dpbdJxCmlSCN3Chv9LlBGTwMqWHPHNTyK9m+v6XM/Zq/K29+/lf8yHUdEv8ATNS0nR7jxFCf7Sldbfb4ftzErqm4554JC/jj2raPg/xE0cEZ8WW5SAhoVOiwYjI6FRnj8KyD4X1eebRml0YrY/2497LpxmiKWcBhMe0jOG+ZmfavHzMMGql94flbRbCyultbPxI1xcWttEgjkY2csjLkqMfKkZ3A9igz1IqvZR8/vf8Amaewj3f3v/M7Kyt9T0rTrCxTX9HESQrFAZLJt0iooGR+/GTgc4qCwXWtPurTw7b6hZSC1slPnnTiQirhFVv9IB3Ec9McGsDxV4Avr67tY9JsdONrbWcVvH9q2MhKuSQ0ZjO0YJOY2QseDwAR0tzZ6xB40j1Cx0nTntJLdbe4uWujHMRuBJ2iM7tozgFu/aq9nFf8OylSiv8Ah2W1bWXuXtk1vRmuEAZ4hYOWUHoSPPyKgmm8QNbXZ0/VNFvbq3BH2dLNgS+OFY+edpPvWZo3hjUtN8TNcyafpDqkk7f2qGYXU6SfNtdQACQ2OSxGF4Aqn4O8J+IdB1a61G6XSw9zaCKWKFtoeZWJEg2xqAGzyCGI9TT5F/TY/Zrz+9lc3OseMPBVrf3z2Vq7X6QCJLaRZbaUXHkF1kWbggknjqMjvWfrP9qeCYb9YPFNvbvHBFNmWGPzL6Z2lADSTyMSwWL+9jAwAMc9Fa6TqWh+G1sb37IyHVop1kgkYnMt8smCCo6b8ZzziqnjuMX02taQupaVYSX+m28XmajLsATfcBig7sMj6ZrKaXNZvT1fmYziuazbt6vz8xL+41TSGSPVvibZafM0Ql8q5sbdGCk4z97kZ4yKXzLXTLmXT9X8YXVxPqcbXjtDYwiGSLYkfIMbg5AAAB59O5ZLcW95ruiavea/4UkntLS4trqP7QChEhUqY8tkHCAHPZmpbKdLS10NovGfh2G5sLJ7KZFZHhZTt2so3hgR5a98HJ4FHLT7/i/8wUKP83/kz/zJJtB8J2+tR6PNq8CahJjbA1jZAknkD/UY3EZIHUgEgcGmWth4SHiJtLtdbVdWtnyETT7RWV1wflb7PgsMjODkcVn3d/4RtPF13fSeILKVJbyG9eM2cs+yREUDZIjbP4VOcEqc/hj6L4q0fTfElzrb6k0r3d/MBBPbyMLS3d/mZGDYG4IjEbSc4GByan9wuq+8n/Zk/iX3/wDBOpEmieKLsfZvGGv3F1aRSEmzj8to1yA6N5cIO7Kr8h+bgcVk29v9n8Cy+JtW8SeJSkbOPK0/UHlLYfYFAeNTu3DByAB61paF428PaRbXkEniS2nE1xNcRFNMmj2NI7OQ3XcAWxng8daydO1bwtF4RvfDup+LRd21xvZJItNlhaJ2kaQsPvZ+dgQD6c5zQ3Qera+8G8M3dyX3/wDBNyPTdMsrvS7ifxR4pjnnuDFZrfbm/fFCMbZIiAdrMAT74PFaNxcXE3hS+1vTPEuqSpDbzSxGW2gQMyA9Q0IOMiuS8R+MtHvtDuNNTxBcX13csrW159j8pdPdcYfhQ2c5OVDHOegrQ1zxj4Wk8FXGj6TrskDJamKJVtnJkAUjYSyYG7oTwec5FJyoqL5ZL7xOeHjF8sl9/wDwT02sXxTFHPoqQyxpJHJe2aujgFWBuYwQQeoNSf8ACR2P/PDVP/BVc/8AxusvxBrsM+lAW1jq88sdzbzeUmmXAZgkyO2CyAZwp6kVrOceV6m1SpBwav0OLt7TWp77UrSbQPB9vJYRRTXCrpu4xpIkjYB3YZlKAdADkntitTw/qvhC58O29zquhWVtdx6THqNwZtNSNXQrhnQ4wRu7e49arxX0ia3rWovp3jRxqsHkSQHSogsYAIQqRzlQzAZJznnPFZ8dlZG2htbzR/Gt1bppJ0ho305F3w5BByuCCMAfhznmp56P9Ij2lDy+46rQL7w9d+M44tEs7e1lgsZxcpDCiHloCmSnB4J78c1Hr/iG903VJ187W5Vk1FLG2g02O1IDGCOQAmZc5JZ+/btVPw1NY6Zr9q0ema9YWvkPbhr+x8qPzJJIQgURrtUkqcsQMkjJPFUfGmoWces/ZJ9TSyaLX4byR0ZvNSNbWJcqFRupbvgHBHPOFzQ3vZX9OhPPTWt7K/p0NifXLyK106eGfxRdfbXkhEcMViWhmTdmN8oADlGGQSMjrUE/iS6slZby68SJNa2aXmpLFHZOtijf32MY3EAMcLk4U+wpEHgrVtJsYbTxZcWSWE7yrIt6LeWWVhlpH8wAsTubnGMsfwv6tb+CtauY57vxDbB/KENwIdTSMXcY6LMFI3DP06kdCRVp03s/xNE6T1Uvx/4JSbxJOmpXFs9/4hWC2vIbSe6ZbHYpm2+UwAjJKtvXtkbuR1p1j4gu77WbaBdR1tNLvJ5bW01FhaATTRhiy7PJ3BfkfDd9tRWsPh5vGus6nf6vo8ljcSW01qo1UY3xRhRuizsOCMgnPb0Fa1svgW01dtTi1XThcmV5wG1INGkj8M6xl9qseeQAeT6nJ7nf8R3p/wA34/8ABOf0rxpNqN1q6S6jq9pBp1tNdN5kln5+2MkHfB5O9CQMjIPBHrT7DxjLdaPqF7LqWtxyWiwfu0S3ZJGmYIiq7W6gnecEjIHBBIrV06w+Hul3UlxBqdhJJJA1sftWqmcCJsbkAkcgA4AwOwqe0j8B2dlcWi6rp80E4AdbnVPO4ByoBdyVAPIAxg8ij3O/4hen/N+P/BM3StR1wXmsLd6xOZdP1i0tfs4MMitHL5Gdx8pTz5jYxt6e2T6JXCuPCVhaLBol7YPd3V/Y+YUvBNNPsuI8FiWLMQM8nPFd1Tg1d2Y4Ncz5Xfbz7hRRRWhqcl4E/wCZl/7D11/7LXW1yXgT/mZf+w9df+y11tZUfgRjh/4aCiiitTYKKKKACiiigAooooAKKKKACiiigCvf/wDIOuf+uT/yNeffAn/klGn/APXaf/0Y1eg3/wDyDrn/AK5P/I1598Cf+SUaf/12n/8ARjUAek0UUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABXJfE3/knmqf9sv/AEaldbXJfE3/AJJ5qn/bL/0alZVv4UvRmOI/gz9H+RDBYXF69zPZaeI4Wu7hQP8AhILuHcyyurNsRSq5YE4HrUv9i6nnH2MZ9P8AhJ73/wCIryTU/EVs/i221GKK3uUt9R86GYoQUh+0yyEZZSVLbwflA4wDk8Dp7Xxh4ah8ai+ltbaaRbiaVdZeSbeIpBjYE2EkgbVCn5QBkEE1jGVJpNyX4HPGdBpNzX/kp3Gl6zOEXTNOh0FvsgMAgTWHZkEYAI/1Ofl4B/Wm6H4o1jXtOmv4NGsYbaOV4w8+pMA4Q8uMRH5T2Jx9K4nw14w8PaJrN7CYNMFr9ouJl1JIHWWVJWLrGqCLjBO05IHAIznjPj1rR7jwTq+hNqVnp4vL17uKOKOZo9jy+YYHAiGBj5SV/l109pT/AJ/xRqqtJf8ALxfej07/AISG++zRXO3w/wCRKSI5f7Zba+M5wfJwcYOfpVnTtaurvULe3mt7Hybm3knins70zq2xkUjmNR/y0HIJ6GvJrnUvD9zBDK1xpI263FqA00QTeRDEkfllVbyeWbAc/KBn863dC8YeHNM1wyPeWsFmHvjELaGYgLLJC6ZBjGGO1yQMgY680nVgvt/ihOvTWqqL70ddY+KL6/tY547fRELW63LRSasweKNlDZceTxwR7UDxLqr63b6VFp2kyzz2xulZNXyBGCADjytxBzwQCODyK8yu73S7u306aw8ZDSJV0uC2u4FsHfzJUQplm2nICSSDHTIU84rpbzxf4ePifRtRtNatRbadbS2+yW3n3uJNmTxHjgRjHrntRGrBpXn+Qo16bim6i+9G1e6hrer+If7FGnQ2V7p6Jfx3EWogqyuJIhjdA3+2CCo7VV07VNcuvEEulXV9eweTeCzkkS4t5PnNuZwVH2UZXaMckHJ6VTj8baBH44uNa/tq1NrNZxWnl/Z594CM77vuYyS+MegrNtPFej23i6XUptYtJba61P7W3lW84aJVtWhUEFOf4c47npiplOnvz/iiZVKW6qduqOp8WaeI7K0g1XW724065nMdws1tbyYURSSAqBDnduRcYBPpziquirpei+FdKuR4ln0y1v1RolU2ziR2UYAcwAuxAHJ5OKg8RfEfw8406ewvmnlt7ppGVbZyQDDKgOG2A8uvG4Vyln4z0qz0LQNLW6viujTpJG505P3qohQKw8/r8xOR7cep7akm7y/EPb0E3ef4s9BuNWsLXS4NSl8aaj9mnJWLZBA7uQcMAiwFiR3GOMHOMUy/1vTtNkgjufGWq7ri3+0weVaRSiWPPVCluQx74GTjnGOa4I+M9JTVItRtrq+ingubmSFDpsbRiOcqzow84FjlQdwI6nip7nx9p0uqaHfRXd8H0q3eILLpsbCVnUKzHbMoAwBhR0p+2o/zfix/WMP/AD/izuJdYsIL+1spvGOqxz3So0Qe1hA+f7gZjb4Rj2ViD7VL9vtv7dGinxdqwvy5jCG1hClgm/aH8jaTt5xnOK8z1PX/AAlqPi9tf8q+jeUxPKradBJIJI+FaORnOzgKCMHpkYPNRXOv6FceMYvEf27VUuILv7RDjToDIEIIaJnMhJXBIXGNue55o9tR/m/Fh9Yw/wDP+LPSFu9N1G63f8JXq7nT/NuRMbWJYk2bonYSeQEbGXGMnv6ZqhaTaXr+t6e07XV5OZ/Jmt9Y063WTyWhmkRh+6DbSyHBBxw3FchaeI/CMV9f3V4+vXn9oWklpdo1vbxC4Dnl38srucD5Q3YE+pNWtC8V+G9P1XTmW71FYop98klzZW8aqoglQf6hdzHLjrnqelTKrQf2vxJlXw72l1XVmn4/8MadFb69e2Gn2EEmm6XDdInksqH5pywxGyfMdi8nOMdK0Nb8L+BPD+nQXd7odw4lB4gkmbGFLEk78KMDufQVT13xR4U8QS6xZy+IJ7SzvrGC2aaC2YswDTb0w0Zxw68478GodQ1LwTq0OlLqPiy9upNPEq+ZJZA+csnBDL5O3IAABABA78mhPDve34BF4V6vl69u5k/YPCFl4hvrifSrq80B9LtdRhkgEuLWOQuCz/PuI+VT3PXjANdDc6B4Ft9bbTh4cu5Y4pore4vI55DFBLIB5aN+83EncvQEDcM4zVWK9+HsVmlqviO/8r+z4tNlAjkHnQRltqsRHkffYZXBxWjc+JvANzqJvDrdzHvlimlhjimWOWSIjYzDZnIwvQjO0Zziq/2b+7+BX+x/3fwKdpoHhS98QXWjw+CdS8yzuBDczG6xHErAMj587JDKc4AJHcCm6PpPgTWdan0uLw3cRTpDJPHvvCfMVJAh4WUlTkggMBkHNX7DxV4H07VdR1CPxFeSSag++4jlikZGOAox+7yAFAAAPSqukax8PNFurG4tdcvC9jA9rbiRZ2VYWIPl42cgEAjPPA54FH+zf3fwD/Y/7v4EVlo3hyw8N22v6l4Wns5SkMkP2W+kdnlkZRGseHyCSy8nGK0dS1ax0/TLy6Gn65JPYXkVrd2n9tTLIgkKhHX97hgd645HfkYqimo/DH+z57CbUbq5tJVVPJuHu3WNFYMqoCPlAIBBHPvViTXfhpNZTWj3shinnW5nP+lB5ZFwVZ3A3NjauMnjA9Kalh1s1+BSlhVs4/gaF5Na6Pa2k+tWmrWK3DyRmQ65O8UTAFk3sJON4HXBAPHpnV8Fz3M9lfm6ingcXKEW8121yYQ1vC+3zG5PLE/ia5rWvGnhbVLW30j+04n0pipunmW5aUhGVlUfIc5xyxbI988XNN+IfhW3v9Xkl1TalxdrJEfs8p3KIIkz93j5lYc+lDqUU1Zr8AdWgmnGS+9dh7+KpNF8R+JUk08SWNvd2jz3Anw6+dHHEu1NvzYKgn5hwfatO18Q6tfeINR0+HTLaO30q4WO6ne4ZjIjRiQeWoT7wDDIOBzwT286k8U+FU+Iuq67dR3l9BJ9ma0NuHUBo05LKzqG56blOCuQav23jjwJaa/NrkGla0moTuXlk80lXYrtyUM23pwOOO1KOIpLRy7iji6CVnJbv8zqh8Qo4LWC7vdNeKG606bUrZYpfMlaKMBiHTA2MVZT1IzkZ4rOu/EusaFJq2rXEFrNuisZ/siag8ipC8jozJlQAfu5wMHrntWdafEPwLY3E89roF1FLcIY5WW2iyykklfv9MknHTmobfxz8PbRHSDwzOivD9nYfZIjmLOdnL/dzzjpVfWaP8xX1yh/MjqB43uJbu9sILKIXaaudMt3kkxEcRiTc5HI43ADHzHAHUkO1DxBrkcPhxIv7OhvL3UGs7xFczxoVjlbCsMd4x15GcVycXjX4dQWM9lF4XlS1uI1jmiWzhCyKpJUMN/OCSR9amb4geAn0X+xm8O3B0zj/RfskXl8HP3d/XNH1mj/ADB9cofzI62/ma71LwxdNqVo9qbplZraZ1EknlSYwQ+CuVxgg9aztY8ReJbLX7nRYDp/2m6lgbSna1kZXiZmEwfD8lAAxIwACPXjHk+I/gaWOKOTw7M6QrsiVrKAhF9B83Aq4fi54XMkch03UN8QKxt5EWUB6gHfx0H5UfWaP8wfXKH8yNnTbmyt/iNrUV1qdi9/PBb+REkhWQJmT5CpcgsMA5ABwRkVV8N6rrWp2mpQNrunnVIrq7jjtpbcb0CTMqFlDg7doHYcEcnvjj4l+CVvvto0C4F3u3+eLOHzN3ru3ZzRc/FPwzKl01ra6nZXlygVryC2g80Y6HLMQcdsg0fWaP8AMH1yh/MiLV/EWt6z4I1u+lKW1vaC1iUJC0cy3iyRmbndwEf5RjPP8RxVzULPT7rxVdWyX08unHw891FO1883lP5wIljd2baRsQ5Bx8orn9W8a+Hr3wXN4dsE1CKS4dC11eIpDOZVd5JCrEkk7icKfYUt34g8P3usm5nGjHTzp62JsFkukQqJRIDkW444xtxg9/SsJ1qbqXv2/U5p4ik6vMpLp+t/0O7+Ht3d6hok15fkm8uDbSzkrtJdrO3LcduSa66vPdF+IPhu1bUJrzUreJ7q5EqxW8c8iooijjAyYl/uE9O9av8Aws3wf/0F/wDyWm/+IreFanb4l950wxFG3xLr1Xc62iuS/wCFm+D/APoL/wDktN/8RR/ws3wf/wBBf/yWm/8AiKr21L+ZfeX9Yo/zr70dbRXJf8LN8H/9Bf8A8lpv/iKP+Fm+D/8AoL/+S03/AMRR7al/MvvD6xR/nX3o62iuS/4Wb4P/AOgv/wCS03/xFH/CzfB//QX/APJab/4ij21L+ZfeH1ij/OvvR1tFcl/ws3wf/wBBf/yWm/8AiKP+Fm+D/wDoL/8AktN/8RR7al/MvvD6xR/nX3oPAn/My/8AYeuv/Za62uM+HV1De2ev3du++CfWriSNsEblYIQcHnoa7Oij/DQYd3pIKKKK1NgooooAKKKKACiiigAooooAKKKKAK9//wAg65/65P8AyNeffAn/AJJRp/8A12n/APRjV6Df/wDIOuf+uT/yNeffAn/klGn/APXaf/0Y1AHpNFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQBXv/8AkHXP/XJ/5GvPvgT/AMko0/8A67T/APoxq9Bv/wDkHXP/AFyf+Rrz74E/8ko0/wD67T/+jGoA9JooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACioLe8gus+Q/mAM6FlU7QyMUYZ6ZDAjHsanptNOzAKKKKQBRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUVjXHiWztZr6KWG4DWlvLctwvzpHjdtGc9xjIAOeMimy+JreAlJbO7jn3RhYXCBmDhypyW2jPluOSDkYxkjMe0j3I9pDubdFYn/CUWKtEskdxEXMwIkQAp5a7juGeMryP1xS2fijT73UY7FN6zOzIAzJkOoJZSoYsCMNyRjjr0ye0j3F7WG1zaoqnpeoJqumwX0cM0MU6CRFmADFSMg8E+tXKpO6ui001dBRRRTGFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQBXv/8AkHXP/XJ/5GvPvgT/AMko0/8A67T/APoxq9Bv/wDkHXP/AFyf+Rrz74E/8ko0/wD67T/+jGoA9JooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACoL28g06wuL66k8u2tommlfBO1FBJOByeAelT1h+NP8AkRPEP/YMuf8A0U1aUYKdSMH1aQnojD/4XD4D/wCg7/5KT/8AxFcXF8RfB6+J7C6kud0sOp3FxNqX2eT54XimEa427jt3xrjHG3jjJrV8I3mgXNhomlbPErTG2t4ZbmG/u0to5jbrLsyJQF+UjgDHIArsI9G8PSvbpHq+oO9ypeBV8QXRMqjqV/ffMB7V7arZbhpTpqM3ut4+a7f8AztN2eh5SfiJoU2m6VYi+lt/7O0k2ckoiY+cwktiyoNp4dIXA3DHOGA7k/jnwktlGbe5nlZZppIILiAbYtwjA3IiIqZKMd0RLLknncRXqNtY+FbySaO11+7neBS8qxeI7ljGo6lgJuAPeo4bfwhcQzSweI7iWKFQ0rp4kuGEYJwCxE3AzxzW6zXL1a1OfV7rr8hck+55qfHHhOMFLa7SKNZL9pFS2dRcJJeQSqnC/wAcKMnOMYwcDGbdl438B3OuQzX08aaUq3Zis5bSRlt9/wBmCqVCleTHM/GQM9jivRpNK8Nw2Ud7LrV8lpIdqTt4hugjH0Dedg9D+VZurXHgzRDY/wBoa9qMSXyl4JP7duyrqBncCJenTn3FS8zwDXwz6/aXXfoHJLyKHh74teDrXw1pVvf66wvIrOFJ91tMx8wIA2SEOec81pf8Lh8B/wDQd/8AJSf/AOIqea38J299a2M+u38V3dqGghk167V3B6cGXv2z1rA8ZXekaRaXlppuoanJqKQ3CsRr13utpFt3lQ7S5DH5B8pxxz7Vyp5ZWq25Z3k+8ev/AG6V76XQ2P8AhcPgP/oO/wDkpP8A/EUf8Lh8B/8AQd/8lJ//AIitjxLL5Go+HJdjPs1CRtqDJbFncnA96oeGPGsut6bdanqNhbadp8MCTi4S+WdeQSyPhRsdcDKn+9XPN4GKi/Zz1V/jXdr+TyH73f8Ar7yt/wALh8B/9B3/AMlJ/wD4ij/hcPgP/oO/+Sk//wARVvV/F7yeEtQ1jwyLe8uLFGkntrpZI5EVVLFTHgOGIHAIGc5q1aeMdNaDRI76Xyb/AFWx+2RQJE7ggRh3wQD0B6dTWftMD/z7n/4Gv/lY7S7/ANfeZX/C4fAf/Qd/8lJ//iKP+Fw+A/8AoO/+Sk//AMRWo/jXT2l0f7JbX17b6pFJNHPbWzuI1TGS4xuHLAYxkHrRP4jlHjXTdGjjMUFxbyyu9xA6eYwCkLGx4JAJLD09waPaYH/n3P8A8DX/AMrC0u/9feZf/C4fAf8A0Hf/ACUn/wDiKP8AhcPgP/oO/wDkpP8A/EVp/wDCcaSdaOmrHeviR4BdLbN5DTKCTEr93+U8DuMZzxXA/Eb4gaRr3w9v7K2t9Ria7jR4JLi1aOORo54xIgY9WU8HtxwTW+Fhga9eFHkmuZpX511dv5CZcyTd/wCvvOr/AOFw+A/+g7/5KT//ABFH/C4fAf8A0Hf/ACUn/wDiKt6P4tFz4Y1LxXdmQaQHkktYo4CZBBGSm49yWKsw9AR6E1I2t6h4i8LT3/h3da3sDhkS5VJEn2gMUDKxUqwO3cp4OfQ1h7TA/wDPuf8A4Gv/AJWVaXf+vvKH/C4fAf8A0Hf/ACUn/wDiK6Pw/wCJNJ8UWD32jXf2m2jlMLP5bphwASMMAejD86888OXP9tR3l9HBq11Cw8+G0sdRkt9vnX97uY7JFU4AXJOeF4rc+F8K28HiuFC5SPxHdopkcuxACDlmJJPuSSa7MXhMJCnU9kpKULbtNa+kUyYyldXOu1q9k07QtRvoVRpba2kmQOMqSqkjOO3FcJa+K/Gd3ZwXKW+lhJo1kUf2ZqDcEZ6qhB+oJHoTXZ+Kv+RQ1r/rwn/9FtXnXgPXvEEWmadc3Wox3emG+GmG2kSOIwR+UrI6MACxHQg5457E189NSlOydtDKopSqcqlbQikh8VSPeFjabbqG4hZP7Lv8IJyGcj9znOVGMk46dKtXtz4wvbiacmyieWOOJtml35UqnmYBVoSDnzGzkHoOhFdTo/i+LxTizhtNRslvLVpYLtE3AL0B34KqxBDDOcj8qjt9ePhvwMby+mu9Slgu5bSNpuJZm+0NHGGOAB25x0FT9X/vEfVH/N/X3nHG18SGKWPyrPbIsKn/AIluonAjAXqYv4lAVvUelX4L3xjb3hnQ2fl+Y8q2/wDZmoeWrvncf9Vk5JJwSRknitW+8c6q/hO9vLXSlstTt72CzIu9xgJlkRBIjbVLr8/ovQ/jf8Q+N38NyWFnd6f5uoXvmmOO282aMBADgskRbJyOAvHfjmhYe20gWEa2l/X3mdoM/jZtLjtLB/DzRWKrakXEN1FICqKRuDKpztKnpjmmHxJ4z3yIi6NJ5cjRs0WnahIu5WKsAyoQcEEcHtW/4P1NdZi1TUUgmgFxdxyeVMu10JtoMgj1Fc3pnizVF1PUdN0yxspLfTNSk+3vcXQjkKS3Mh3Rg4XCjnLHnoBxyKm9EpPr+ARpy0Sk+v4OxL/wkfjX/nhpf/gq1H/43R/wkfjX/nhpf/gq1H/43VpPHdz/AMJEIHtbY6Y2qnRwEdmuVnCkh2UDAjOPqAQTxmoNF8cTeIPFEmiTxwDT72C5a0ntWlVysbhCSzBeSCSCnTHXvVeyl/MX7Cf87/r5iQeIPGs93DbBdDjlnYrH59jfRKxCliNzoBnCk9e1TX+r+ONOmhhn/wCEeaWZWZEgtryZiF2hjhFOANy9fWqfhFEtoLGyimkkhtfEt9DEJJTIyosdxgZJJNXvHurX+h3+m6lYT2MTwwTeYt7kJIjTWylQwPynkHOD06VPJKz957/5E+zlZ+891+hV/wCEj8a/88NL/wDBVqP/AMbo/wCEj8a/88NL/wDBVqP/AMbqPxL4q8R+HY7Gwe90yW+vRPMl8bcRWyhFXEXzzAFix+9uHH8JpuseItaOq+GZRr+n6Fb32nSSyrdRJPA0w2fL5gkAJwxK4PRSec8V7KX8xXsJ/wA7/r5k3/CR+Nf+eGl/+CrUf/jdH/CR+Nf+eGl/+CrUf/jdQS+Pdak+IK6NbWtqunwvCjtK0atco4/10eZAxXngKr5xyRnhdF8V63NrNxLqWr6X9jt9bl0lrVIxGdoDbZCSxIclRgdCM9TjB7KX8wewn/O/6+ZN/wAJH41/54aX/wCCrUf/AI3TU8T+MpASkeksASpK6XqJwR1H+rpfA+o6jNeXsWseKLiW9F1dQ/2fcW8SFQjfLKMKGC7Np5+X5j7VneH9ZbRvh1qq6TPbXOoW+oXAaSFE3CL7RsNyyL1AT5s4IOB2o9lL+YPYT/nf9fM0v+Ej8a/88NL/APBVqP8A8bqWz1vxte3gtIhoKTmNpAs9new7lUgEguoBwWXp61gXXjDXo7Q+Xrn+hW+r21nFqptYyuoQzAb8DbtDRncdy8HbgjrXQeEdTvtR8RPDf3gvZbCTUbNbny1QyqslsQSFAGRuK8f3aTpyX2hOlNa8zMqTxl4+h0uDUp9J0SCynVXjmmnWNWDDI+9MO3OKuRa78TZ4llh8P6TJG4yrpMpBHqD51ZerxTPJ8MZlkvIreC3LTy28PmCIG3UBj8rAZJxz61uS/aZ/iCbCHWdVttImsophFDEFj84MMIr7PkBQZIBGcnkdKI0m0nzv8P8AIUKEnFPnl+H+RF/bHxR/6FvS/wDv4v8A8eqG68Q/Euys57u48PaWkEEbSSNvB2qoyTgTZ6CnWmq6yfF1xBf3GrrMby4ia2FoRaJZBXaOVZAuN5wnO4tkkYrmW1nWVtVgmuNdkhuNKl+1JewMUQtaFsEheD5gOcnjIHHSiVJpN87/AA/yCdCSi3zy/D/I7LU9T+IWmrbAWvh65kuZfJjjgMoJOxnJy7KAMIe9ZF14x+IFnf2NlcaNpCXN+WFtH5gJkIG44xL6c81vfE2yvNR8OwWlgrPdyyyiJEdkLn7LP8oKkHnp75xXOtbW11p/hoWdh4ktrOHVIvPFwbhpIQ1vNHhGJLhVYhSwwOQc45o9k237zH7Fyb99/wBfI0/7Y+KP/Qt6X/38X/49Uun6r8RL28uLSWw0GzngjjkKzmQ7lcuAQUdh1RuuKxZrfxRLodpbXkWrrbWl7ews0TTPcSKGzbv8jozLt3LyTkhSevHW+EjqZvH/ALYLnUBpdoJjIiozHzLjkqrMASMEgE/0o9k017z/AK+QOi0177/r5GFp/irxjqWoWtjCNAS5urIX0aywXSqYztz82NpI3rkAnGavrqnjh9Yk0oP4Z+2RwC4ZNlzjYSQDuxjOR0zmsqwv7qy1nwndromrXVrBoAt3ntrfegeXyCvORwBG2fTitHTHn0/4oa55Og6otnqEUC/ahGPJMyeYXfJbgEMgyOpXpVRp3indlQpXim5P7zQ/4uH/ANSv/wCTFU01TxzNeW1vC/haX7RDJNHJGZ2QqjIp5z1y4/I1R8H6BrdvrN3JqtjOYrq2nL3F3IvmB3dcI6xzMjkqB8yqmAgAqt8OfD0vhvVLCxudBbTruPTZ0mufOSRbwrJD8yhWJAGe4B+aiVOy3YSpWXxPp1NtL3x++pT2IXwz5sMMczEifaQ5cDHv+7P6VT8Qa9458OaZ9uu08OyhpY4I4oRMXkkdgqquSBnJ7kVJ41idr+7WTS77ULWSC0Mltbwyn7SqSTlk3qpAILI2GIB6Z5rj7uK7PgrTrCXwpqt+8esLeRWT2ckhs7ZZQ/kl5FAbKArwSOcZxUqK6yf3kqMftTf3nW2GtfEC9azRrPQbWa6gknWK4WYMioyKQ21iMnepGCRjvUtrrHja5sLK7M/hSFbyJJokmeZWIYAgYz15HStDQ7tL/VNKkt9GvNLig0+4R7aazaFYCzw7UBwFJwrH5SelefXei3F7Ppkr6VcmS2trKIi50uaZMxhS45i3x4Ib/VthuM98qyv8Tt6+hKS5tZu3r6HYjWvF7ahLYDUPB32uIqHhMswZd33ePfBqc3vjhXlQ3XhEPEN0imSfKD1PpVSK/az8XX9zFok1xZ30kUpuX0+4R4SqBWG0QEsflBBJ744AFcxpllq0Gv8A9oXul+agkvjNGthcKlyJ8EHaLbP8IBDs34YqrR/m/Evlh/O/vOxhvvHFyWEF14QlKDLbJJm2j3xWdZeJvGd/q2o6fG3hhWsI45ZJi8pjZXLAEMGP9xs5x2rl4fD15/wjmk6YlpcWUqaLc6fdSQ2F1jzGeN0Y4hBYN5ZDdDhz176gsL9pdVb7Fb28N7Z2dqLaDSrsx4hclhhoCAGV3A4OPl680Wj/ADfiHLD+d/eb0mueLYrWC6k1TwUlvcSCKGVp5gsjnOFU5wTweB6VVu/FPiq10P8AtddQ8Gz2bBvKeK4kxKVzlVZmCkja3fsapy2t1L4Xu9Jks2mM+pLdAT2d8w8oSB9pYQA7vlC59Cfx0Ncub26ksrrS7OOOeO2mt5obrSrxkUSbSSjLEDn5cHIGc0Wj/N+IcsP539503g/WbjxB4VstUu0iSeffuWIEKNrsoxkk9AO9blcl8Mv+SeaX/wBtf/Rr11tXSbdOLfZGlBuVKLfZBRRRWhqFFFFABRRRQAUUUUAFFFFABRRRQBXv/wDkHXP/AFyf+Rrz74E/8ko0/wD67T/+jGr0G/8A+Qdc/wDXJ/5GvPvgT/ySjT/+u0//AKMagD0miiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKw/Gn/ACIniH/sGXP/AKKatyo54IrmCSCeJJYZVKSRyKGV1IwQQeCCO1aUZ+zqRm+jTE9UeGeE7m2j1jQrx9Q8Padaw2kAu7gauiSXcYtgvkywA4LK56tzhcegq/bvaadrWkXb+IfCMum6JJd+UtvfoLiS3lD7Y1GAAUDBQucHrkYr0z/hC/Cv/Qs6N/4ARf8AxNH/AAhfhX/oWdG/8AIv/ia7ak8FObm+bV36EpSSPCdC1zT9N0nV7a4udLuZNQ0doUljnaJreMcRxuPLXc37w7trOx2d+Kt6PJpusaBq2kza7odvfvNb3/8AaQufs0dxKhAERVo42RcRqcoDgnOSeK9r/wCEL8K/9Czo3/gBF/8AE0f8IX4V/wChZ0b/AMAIv/iaj/Yf7/4D9487hstCTQYbE+LfDkUqX0l7vTVWMqO6nJWcybt+4nLYAIJG3JzWhDNpdpZeGWh8c+G5b/RYpYmeWaNY5g6bfuq4xjC/Xn1rtP8AhC/Cv/Qs6N/4ARf/ABNH/CF+Ff8AoWdG/wDACL/4mj/Yf7/4B7xwl9Z+HL3X7rU5fGvh6T7ckBuo5Lr5BLD9x0QTBSO+1t2CM+oNbxjPY3Oka59h8c6ALSQT3qW0ZjeeSQwshi3eZgggkA7d2SPQCvRP+EL8K/8AQs6N/wCAEX/xNH/CF+Ff+hZ0b/wAi/8AiaunPBU5qa5tHfoJ8zOe8VeK9CmGlT2Ot6dctbXbySLbalbLIqtbzR7l3yKOGkXvXFRXmjGXV7i51BjdajbwRGW1vNNhCyRNuWZl+1kO+7BJPuOhr1b/AIQvwr/0LOjf+AEX/wATR/whfhX/AKFnRv8AwAi/+JrRVsByqMoydv8AO/RruK0jziLxHYRWWuE6gH1PWcLPdm600KiBNihYxd9gTySeevpVddZsF0zQ0GqldT0QNHaXy3Ol58pk2FGQ3RB+XvkcgHBxXp//AAhfhX/oWdG/8AIv/iaP+EL8K/8AQs6N/wCAEX/xNHtsu/59v+vmFp9zzK21uysNJsbSy169insmlSK6a/0tmMEhBMbL9p2kjaCGxwR0xxVnUvE9pf6/pOqJrNxENNQrHEbzSn3swCuzH7QOWXI6YBOR6V6J/wAIX4V/6FnRv/ACL/4mj/hC/Cv/AELOjf8AgBF/8TR7bLv+fb/r5hafc88i1zw1Fri6h5961sl097Hpzatpn2eOdgcuB5+7OSzY3YDEnGa5XxgNFvfB32OwvrtpLF5p7dJ9T01lxI4eRSI5S7YwSoAJzgc17b/whfhX/oWdG/8AACL/AOJo/wCEL8K/9Czo3/gBF/8AE1rQxeAo1Y1Y03eLT+7XuDjNq1zk7OTwtbaNqPh5PF2k2ujyTebaPZ6pGk0Ydy8kZ7bdxIHXKsQenNhLrwrpnh3UtO0Lxjo9pc30hke6kvImKuwVWYKrKAdq8YwAea6T/hC/Cv8A0LOjf+AEX/xNH/CF+Ff+hZ0b/wAAIv8A4muP/Yf7/wCBXvHnPhq88NqdV04+KYdNt1VVguIdRSJyEv71wAxPIKshPqrj1FdN8L54rmDxXPBKksMviO7eOSNgyupCEEEcEEd66D/hC/Cv/Qs6N/4ARf8AxNaOn6Xp+kwNBptjbWcLNvaO2hWNS2AM4UAZwBz7V0YrGYepGp7NO87b2toTGLVrlTxV/wAihrX/AF4T/wDotq8/8LWWpafpWnXNn4Ea5xGJ455NZXa7ugBkEbZCkrx0yBxXoHir/kUNa/68J/8A0W1eYeGvGF5LrmiaTHqV3HYvFHaPGI4yIT9lAUgCNm5k5DMw6fdxXhSi3U0dtDKcXKto7aeXfzTOisIdZ0x2az+Hzw5VlUDXFKxhjkhAThBz/Djt6VRuBdaRoGoRXvgURaTMC10LvxCGj+ZsliXJ2ksc5GDmqfhjxVqkdzot5qOuX+om8W9gu7b7OmFlhwY0RVQYYgk575HoKt+APFF9ealqH9pXN3PphsFvRPcqzrvDEOFbykUYG3KKGAOcHrVezl/M/wAP8i/ZS/nf4f5E2nvdXvhx7Wy+H1tdaTfR4ZhrMUonXsS5yWx2Ocip1tNRS3SAfDC02JL5y51GEkSbQu/JGd20AZ64qpoUF3L8NbCOyub+y1fRk897Vma2WT5y3lyblwQwUj2zSX9xrtv4MsNQF9qgn1G/+3mBYpp/KgZSy2zPEC6KBt+YDrnsaPZy/mf4f5B7KX87/D/I3/DQ1DRre9jPg+eyjmuBLFbWc9s0caiKNMZLryShPTvWVJ4eu3vpLpvC9tPKZ5JUlutNtpZVDSNIAW+1jOCxxwKwNabxnfaL4eQLqdnE9huMriaWaO83fKZPJwSduCN67OTuAPTQ8UDWb7xJYbE1rfHBbHyUimjQyA73KSRMY9xHysJRtG3g80ey82Hsf7z/AK+RsL9qbUtP1qzstOudU1KzM6TxaSqzCICPhme5X++gwCagsdDv9MuvtVj4U0+2uPm/exaTbq3zDDci8zz3rW0FBJH4VRs7W0CQHBIOP9F7jpXGeCdP1eSyM2lXerDUIzqNvPNe3LzQkqzJAvzMU3hghyoPCtnqKmEeZXu/6REIOavd/f5I3tI0C40nU7a6t/C0VqkMplddPsLa3aU+W6AFvtTcDzCelX/FUmmXdh/aHiLwzqYtbBGk81rqFBGDgk/LOM8qvryOKxtC0fWrfRNae7t9V819NWM2ryMd10u4lo2aZyxJI5G1TgY74qS+GZp/gvqlra6Jqf8Abt3axxXQu23XFzMmPmLFjlQS2OegxjtV+z0tctUVa13+H+Rrafb6RrWmCODwr4oayXG2K4unhX1BVZJxke4FXptEs7mOKOfwv4hlSL/Vq+qhgn0BueKoy6FPq2keHhLol8dMthIt5pU8yo8rFBscgybWCsDwzdwccCs+XwXqUsHhM6vpMurSW0U8OpBLpSxhOTFG7My+btJXPYlc0vZL+rf5B7CP9Jf5HRHTIGuFuD4d8SGdVKrIdXG4A9QD9qzimppNvGWKeG/Ealn8xturAZf+8f8ASevvXB+J/AGuzazqMuh+HniiM262kju4kGwWwjXguCD5gDDI4xkda3dP8KeI1+Ig1e9guHiF9JdRz/aIAiQum3y2wvmkqDtC52ZUHIo9kv6t/kHsI/0l/kbcklrFqUGnvo3ikXU8byRr/azYZUIDfN9pxxuHGc81YlXSo9K03UIo9dmXUAphjTVZlYAxtJ8xaYKMKpzzWL4V8Na9our2C3Gi2TmzM8U+rtd5lu45WDB8YLFhtGVYgD+E4pviOzW/+Gfhe1a7t7USRwjzLl9kR/0SQ7HPZW+6fZjUyio/0vIicIx/4Zd15GsjWckEc6ab4haGU4jkXXQVc88A/aueh/I1c0GbTpdXheGz1JJpLaUwz3V+LpGQPGHCkTSAHJTsOlefT6VYz2l3ced4Rglm1GzuYtMi1CPyIkhPzndtHzSD5ThBxjOa6PwZb21l40vbexm0uSxk+13VuthcK4jRzbDayKMJyhx65PpRaC2f5BaCaaa/ApeIbzxB4Y13RtC0nWbtdNkNpZiWW3gkMJkaRE/hUkYi/wATV29k8T2nirTNAXxtHJc3qSSN/oFsrRKqkg7C25skEcDsc1Y8W6brGp+Jgmj2tpO9t/Z14/2m4MQ/dTTsAMI3XkZ7e9W9b0vxHe+K/Dmq2um6UUsFdpzJdMr7pEKMqkRnKrnP+1gdKcaUWuv3v/McaMWt316v/MrbNa/tcaR/wsq0/tIruFp/Z8Hm49du7PaqV39qvbPVLW4+KGnvBBG0V8v2OAeUp+UhyGyvXHatbSfCOp6V4ivZ/P0650651GTUVkuIXa6id1ClVOdoAGQD6HpWX4Y+GL6FLctNPbzuIJreC43ztI6yZJLqzlFJOCdq8kZ4p+xj5/e/8ynh4Pv97/zLs183iK1+1WXjjRETTW+1Pc2loGEQKOmWLTMu3BfqO3tUKyarJp01/H8S7V7WFxHJKmmwsFYgELwep3LgdTketLbeBNRS3sIZ5dNmji0IaTPG8TsjlXUhsZGRgHPIOT2qxZ+Br6LRp7SbVwZWu47mBSsk0cOzjG538xsj1fg9OBy3Si9dfvf+Y3Ri3fX73/mUri61O10qLU5PiVCbOVzHHJHpMcm9gSCAFySRg544wc4wa2fCqXa61fy3etJrHn2NpLDdRwpEpjLT4ACkgjqc+9QSeBCLK0itrq0tpYLqadxHaMIpRIpDAr5m7PQ7t3JHPWr3h7TItG1i406ERiODTbRQIo/LX/WXB4XsPap9moyTV/vfYn2UYyi1f72+j7s5+7TRE8Q32mraeHbVoLiGFI30Np2/eJHtZ2RgFDO5UZA+6eeDSz2elwxQsB4WLXF09lAp8PON86lgUz5nHKkZPHHGaZqekzyeNNSu5b2+tLc3dtKq2ulTyu4jjQ5E0fykE/KVYMBtPA3GpLjS7GbVftMd9rcVt/aS6p9nGiztmcKFOWMeduB0GOc81KjT6kKFHXm8+vmY+i6jo+p6DbaldW3huzkltGu5IT4clfYqECTa24b9pODtHHPYVtaVd2qS3j6HNoiXkEUm+ODw9NDI4TaWQfvAWIJTKjJyRx0qraeHtLtbKG1N/rzx21tcwWp/sacGEznLv/qvmPJAB456Z5pI5dA8Mai99Nrl/az3LzvGbvSpFAMgj37Mxg9Y1PU9adqK1v8AiPloR1ul8yz/AMJdr6fDiTxfJNprIkDSm2gsJmPDFcZaRSOnJKjHPpV3Vdf8RaZptldYhlku7yO0S3GluJBuPLY88jAAJ/DtXNJqXgs+C7rwrceKriWwnjMasLSRJI8sXJyE55PQ8Y4Oas3PiPwxfaGlje+N7+a7iuUuYL77FskidCCuFWIKR1BBBzk5o9pR/m/H/gh7Wh/Ov/Av+CbOqeLbvRUhOparY20kkbzGF9KfekanBdgLjp9Mk9h1qvr/AIy1PSLKaa2v9PvmhSCSXy9OkVIklcKpdzN8uQS2MZwO2c1mXOmeHPFkNneHWtX1G6tVkt5b5dIM/mqxDFCpgKIRkYKgEA1c1PRfDetCa3W68QwxNBHaX0VvYXBM/lhWjLkxEh14IIwcH0qr039r8SlKk9pfj/wTtNGu7y4fUYL6S3kltLkQiSCIxqymKN87Szc/OR17VqVyei6pb6fLqSyQ6wySXCNFJJptyzSKtvEm4ny+u5G6+lav/CR2P/PDVP8AwVXP/wAbpxnG2rKhUjbVmvRWLF4q0qZkCNeAPIsQd7CdU3sQqgsUAGSQOT3raq1JPZlqSlswoooplHJfDL/knml/9tf/AEa9dbXJfDL/AJJ5pf8A21/9GvXW1lR/hR9EY4f+DD0X5BRRRWpsFFFFABRRRQAUUUUAFFFFABRRRQBXv/8AkHXP/XJ/5GvPvgT/AMko0/8A67T/APoxq9Bv/wDkHXP/AFyf+Rrz74E/8ko0/wD67T/+jGoA9JooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAyfFX/ACKGtf8AXhP/AOi2ri/DurTSaVpljb6hrDXAtYwtvBNphIAQfdVjvwB/e5x1rtPFX/Ioa1/14T/+i2ryrwFoi6nrNx9isbGGC2nsLt77aVuEcW0ZZUBTBV2Vwx3D7zHHSsJR5qm/Q5pw5q29tP1Owh1qe4nSCDU9clmkLKkaT6UzMV6gAHkjvT4tVu50uHhv9ekW2z57JNpREWM53YPy9D19Kh0Pwde2HiDXZZdK0i3t9QuZZbe/tZD9qtwyBFCgxgKeC3DdWPWoLf4czvoV7psg0ywMlilgstlCSZ1Vw3mSj5eWAwVyfvN8xzVey82X7H+8/vM+7vrPxY8+j3V74huY43jDRR3VgiSlwSqkqQsgIB+XLDjkVrPrzwafcXjanriWdq5iml87StkbDqpOcAj0p8Xg3VW1G/1JjpFpNItkLaC3hZkjNs7EEk4+8rFeBwCBzjmS38F6nbXs2oJd2LXDasdUWFoD5W5ofKZD3BA5DjkknK80ey82Hsf7z+8o3nixdPhsZ7nU/EKQ3ys9tKP7NZJFVdzHcAQAF5ycVuaHJNr1pJc2+vazGiOq4kSzbcGRZFYFI2BBV1PWq8vhC/t7DRW0qbS7W90qaaWOIWjLbN5qsrDar7hgOTnPJ69a1vDy3C3WtrdPE84vk3tEhRSfs0HQEkgfjRyWa1YvZ8rWr+85Cwj8P3ukaHY6p4kVroW1vHFazQ2knlPJGpVF3wkgkAYBOSB3qY6N4NSa5gOt2vmWwkaZfsdidgjxvz+4/hyM+mak8N+DpHt9K1mHUFtzNBZTSJFE4LiOJBtb95sOcY3FNwBwDwDSS+Ab2I3F/e+JopJGt7mOe4ubVtuyUckp5ojXaO4UZ75pRpQcU2KFGm4ptdCmLfwM1td3C63E0VpE007LplodiKRk/wDHt/tKeOoYHoQaifSNH1fQNRu/C11b3d7Zj5oLvTbaHacbsMptgwyvI4wfWs/UtIs7Hw5ry2njHSL+W70+WJbfMaM8jW8UXyt5uBnyUPIOMn61u6Xcae2mX98/jHTItX1S3hieWURAQIgIC+UJDlvnfJ3dSOwpclH+mL2dDy+8q2+neHI/COka9qlwbZdQghkWOPS7WVt7pu2qq25Y9+3QVNead4QsrW1uJNQeRbqB7mBYNItpWeNACzbVtiQBkZzjk4qnN4b8N3vhnSdL1Hxhot5caOdtjcSrEY1j2BNjxeZh+BnOQc4PbldW8O+Hb7RtN0q18Z6NbW1iswXdHbsytI27fGVZfLZeQCPXJyaOSj/TD2dDy+82rzwjpllZ2t9EI5le5tUMc2n2e1kkmRCDthB6MehFdL/wivh3/oA6X/4Bx/4VzGvalphtNESz8X2pgsbq2E8BuIpWukEsfzO2dwK43kj0Ofbp/wDhKvDv/Qe0v/wMj/xoSpqT2FFUVJrT+rmN4p8M6Cmhny9DsVZrq2Q+TbrG5Vp41IDKARkEjj1rj/DGrxJoOo6rrMtxDY2FvG7adZXd6lxY/Mw2OjS8gKFIYAAgNgYFdr4l1vSLvw1PPDqltNBb3No9xJbSiQxL9oQ5+XJ6A4+leeave+Fm8P640fii81bWLvS20+3kvICm1OoT5I1HLYJJyeOtJuipa228vMG6EZ+9ZaLt5nWHWNEistTlvIdfs7nT5I43tLjVpldzKcRFW87Zhj6txg5xio113Q5tKguba38QXN7PdtZJYQ6rM0hmVd7DeJvLwEG7cGxjvnis211rwRcaXONW124m1G88h7i48uQujxHdHsKxKBtOcHaCe9aMvijwNPbwLL4ivHuLe4NzDdtHL5sbkEHb+72gbSV24xgninz0O6/AftMN3j+BmeI9K0jW9G8P6oun6pbyahfQWjyX0kkssCtIVKMskuQCcjIzjOcc1c1vw94I0TV7TT5PDk8rXGwmRbxlVA0gjH3pQWOTnCgnANSXviXwPf2FnaTeJdQK2s63KyFZWdpFO5WJaM9CM4GB7Yo87wR4i1Vp01PWL65a3SO5itkuR56ITtaRY0HKluCMckUv9nb+z+BP+ySf2fwMbXvBWh6Z4i1K3gt3MA0C5voo3lYiKVGUKVOckcnhia7PxR4X0JdExDoenq73VtH+6gWJiGnjUgMoyMgkZHrXKa49hqt3fX9lpXjOa6FpNp8LrHJ9nYAFMMCdxG4AkHnI5GeK7LXbvVr/AEsw2vhvUDMs8EyiS4t0U+XKjkbhKSMhSM4NRal73KunRepFqLUuSPTovXyOJg0fw/Hot7rOq+B3sdOs4ZGkcao8ru6MVKooblcg4YlfpUqaP4Qa3uf+KWc3Ud1DbQot7N5UzS/dIkJGAOd3BxjjPGZIb2W00LV9NXwasumxKyX8EniITiLOWYEEkqTuJ4wTn6VSi1e3g8Fz6iPBZfQ7rDvcS66ZWJVsKVZsyKVbOMYwcnjrVWo/yf8Akr/yKth/5P8AyV/5Eum6R4WvdUttPm8JrDNLqF1YOV1KZwjwx79w6ZDD6Ee9Q2+teGtI02xuNP0O9trjULaa4eC11C85ET7AuYgxYkk4LBQPXmpfDOj3dzpzaNe+HIJLG/nk1iyefVXUqvyDiRA7kgOvJIyGP0p8LWst7/YNj8PrVzaPNPHHBqYjXHmeVIVyq/IWTBU8HAyKF7FaqP8A5K/8hr6utVD/AMlf+RoazrVlper21ktvqYSW3SdpbrWbuJVLsAELKWCMOc79oPABNTW2naxN471GyW6RtKt/IzE2s3gmRWDHcPmwWPAwTj5eD1pZLfUpbkXD/DG0MoREyNShHyocquMYIB6DtWhHp7eIZdP8Ry+FNDlu2hjmt557xjLGuNy8+QcEZ/OrTpvS34P/ACLUqTduX/yV/wCRzaa7MPFIsQZraL7dGloX1S8d50W5jjZgGzE6sC3AYkDrXeal9o/4SWy+ytEtx/Z135ZlBKZ8y3xnHOK5mx8NreWlrrGleFdBsZ7poLwTrdMJCvmJMVOIep24PPfvUnjaO9OjzalrFraQWVtBJHP5N2Zg0TshYMjWr5GUU5A45pXW8Vpp0E2t4rTTp5mfoZn8JeEINbkSCXVNTaGOR2u5jAJJW/1spYnAyeoHHT3o1Xx54g07wpd3yLpU97puqR2Nw6K5guVbZzGd2VI3gHO7BUjmptM8EXljp88Om29jDaXyDzkjngCzKRxuH2LkYP60l54b1DSPD5SS3tv7NsgZlt4nhkCkAjKoLE5OCe2ear2vky/bf3X9x1HhVb5ZNaGpT28139vHmSW0ZSM/6PDjAJJ4GB15xnjpXM3mv6nY+M9fs7XVdD063imguG/tMNun3RRhghDADaqZ6Nyw6VsaXFqfh212G30wC9uFKm41Hyi0hRVVFVbZQDhBwBnrWVqdvrdrr7Tyx+EI57ub7RbrfvJLJGUjRWKNsXA+RTnAwT16VPNZLR7/AOZHNZJ2e76epa1LxfqFp4jntYZ9PdEv7W1isPLc3EscoQvKDnou8nhSMI2T6UtP8etc+Ofss+p266ZPdTWNvCyIuWjH3s7i+dysMsFUgjGScnSaHxub6Odo/CH2zyyqSFZvM2ZBIB64zisvV/E3i7RdU0ywuv8AhGGuNRuRbRiNZm2OQSu/nIBx1war2vky/bf3X9xR0ebSbLWvFWkadLYQQrr2nPBZ26hMc2+8qBwRlTkAcEHPWvV64i5l1u+8MaZqck2mOLiaxnFulq8R3NNEQvmeY2BkjJ2njtWz/a2rhJH+y6LsibbI39qvhD6H9zwaFNOV/T9RRqJyvZ7L9exvUVh2+p6zdhjbWejTBeCY9VdsflBWjpV9/aej2V/5fl/areObZuzt3KDjPfGatSTdjVTTdjnfhl/yTzS/+2v/AKNeutrkvhl/yTzS/wDtr/6NeutqKP8ACj6Izw/8GHovyCiiitTYKKKKACiiigAooooAKKKKACiiigCvf/8AIOuf+uT/AMjXn3wJ/wCSUaf/ANdp/wD0Y1eg3/8AyDrn/rk/8jXn3wJ/5JRp/wD12n/9GNQB6TRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQBk+Kv+RQ1r/rwn/wDRbV5poeg6LeLp9nL4F1CeeS1t5pbsXyrGUkGDLjzQRyG+XGeOlel+Kv8AkUNa/wCvCf8A9FtXAaFdQQjS9UGraZHcR2MEJhfxG0aFVTAV4fKIB5Jxzgk81zVOT2nvroclX2ftV7RX07X6lTRI/h1r3imTQ7TQpSQZFjuBesyyFDz8okLKODgkD9RRo2i+H7nw5fa7qvhGO20+0juZDJBqMru3kyOpXYSMHCHnPWtSyOk6fq7ajbXWhIxkaZbf/hKJPISRgQziPy9oJye2OaJtF8ixutS03TdIni1CTyFB1aa5tV8+VY5NsQRVAYsd2D6/QlqHSK+4VsNbSK+7/gGFAng6Tw5c6w3gu7ZYXgCRwXkjiZZm2oUcsFLAkBlzwe5GCY/EWk6Zpnha6vU8IW1pqdvqMNobefUZpUZZNhBDKepDgc8A564Gd/8A4QfxGdKn0xrPw41nPs82Nru+bcE+6Ml84HpnFT3HhPxRdLqC3Nl4XmXUdn2pZJbtg5QAK2CflYADkYPHWjlpf8+/wDlo/wDPr8EYvibwRaWvh3TrgaFFpl3Lqltb3At9RefZE8qocF1wxO70GODk4IOjrn2Dwld3Nloek3H2awtP7S1HGsT26iMllAQB/mc7GPIxhQM8jD7rwT4ivdKt9MuLDww9nbyebGn2i8BD/wB4sGyx9yTUreD/ABI8NnFLpvhOVbMFYfNa6chTn5WLElhk5w2RnB7ChKmtofgNKktVT/A5XVrTSNNee+/4Q+0bRILi2Tz/AO0pzLNHNjaVTjaw3BiG9ceprr5vC+hWPh/xhHBpVr/ovm+Q8kYkeP8A0SN+HbLD5iT14zUl34e8V35uTd6Z4Nn+1FDP5kc7eYVxtJz1xgY+lPSx126h1zR7jV9Aj1O/iaWSzhikciNolhDZLgqDsxna2Dzz0EyhF/DD8CJQg/gp2+SXQx9LgbT/AA/q+ueIND8MXVnapdzRx2loFlJidhswyAbQFIyeemabbXStoOs3UvhHw491bQwy2JS2EcdyZcgJ+8VTnI4I4YsAK2V0Lxal3PdrpvgwXE4Ilk8mbc4PXJx37+tRPYeJNIswk2keEDYTXEMU0EEUq+ZvlCjqCOr9SDj0PStOaC3j+Bq5QWrh+Bg3c1pfeFJriLTdCsbuPW4dPa5j0nKwqWjyZEkCkfeweSORg85F7xRoemJpmkT+ToEgTW4ILn7Ha+SGVpQmzKPkFQ3IbIOOQKv32vTaDqFp4Vg8G6fL9pjVo7e1ugIT97AO6JQDiI9fQVZNxrjQLAfhtaGFWLLGb+32gnqQNvWjmp9vwf8AkHPR/l/8lf8AkZPieaPQNR1O50nTfC4j0uwj1NIzZr574ZgQCCNo+XIYZxxwavt4s1nVfFMGm6Xc2duhitriSOS2MxWGRCzMz71CnICgYJOQcYqz9r17GP8AhXFrjy/K/wCQhB9z+793p7Vx+r2N7qGuPpV34Pud+o7bg2iX8G0JGqqFWUR5iX5B8oZec46mmqkFsn9z/wAilVprZP8A8Bf+R2/iJ2j1TUHRdzKukkL6n7ZJxXP6V461e70C+1WPU9Lvr1tKe8j0iKJhLaTJnKMOpXpndg5HHBrY265qNzey6j4bv7ISx2qxGzvLaVlaGV5A2XYDqy8YPQ1NbwXUOqQpJJr1jLfyGP7Q8WnfOyoz4YorMeEbtUxnZ3s9f82RCpZ3s9fLzfcxLHxbqbW+qTjXU1LTdPazuX1K3tF2lHbM0RAB4CYbIBIHU5p994k0LW/Cnio6nqdhqMFrM7WbTW4URh4h5O0EcndvAccnBNdmmi3kahU8RamqjoBFagf+iaX+x77/AKGTVP8Av3bf/Ga25n2/I35n/K/w/wAzk/E3imw1O3sEi1fyPDt7HNHPfw2y3CySAqogIZGC7gzckclQB1wXfDxHi0fwjDLFNFJFo91G8c0TRsrLLADlWAI6V1f9j33/AEMmqf8Afu2/+M0610d4NSS+n1O9vJY4XhQTiIKocqW+4i8/IvWk23pYTblpb8jzu2vdZbxlBBbXWoPYR6vNG8NqrRqgNxKzFw0ZEqnjLK429MZ66miQPZfEjWYrzUfEJaW8ElpAySPayRmBOS4TaArbgAWH3Rwe/YS+G9CnmeabRdNklkYs7vaoWYnkkkjk03/hFfDv/QB0v/wDj/woXMla39fcEVOKSsvv/wCAcj4D1azsp/ElvImqFpNRuL1JLiwnBkh2JzuKDJ4IC/eOOhrQ8N+JtMGiak7QanHHb3M8zrLp04JSSZypRSmWBDDgDI7gVvf8Ir4d/wCgDpf/AIBx/wCFH/CK+Hf+gDpf/gHH/hTvLt/X3DvPsvv/AOAYPhi9ju7jw/GkVzE9tpE0Eiz27wkOv2XIAcDI9xxXN61e6EZ7aLUtUu4PIn1UMun3hilR2uMoH2MGwQCRnjIGeK9KstF0rTpjNY6ZZWsrLtLwQKjEdcZA6cD8qvVPLK9/66EqEr839dPTseIXOtanejTIdS8QJDdRafbyRXFleqf9JU5mSTZMsZJwuC+VxnBznPrPhX/kUNF/68IP/Ra1rUVSTvdlKLvds8g8J2OtXR0+2WLVxbT2j+Zd3DvEkMbw7V2FZCsgBwVG1WAIOetWTpHjCTQ4NKnsb+ZxoF5YXU0l3GyT3DgCJuZMno3zEZ+bn272LwvpsEKQwvqUcUahURNTuQqgcAACTgU//hHLH/nvqn/g1uf/AI5Ux5kkrf19xMedRSsvv/4BxUej6/FFciLTNSSyWPT0W0N8PMkZHYzsp835QUKr94Zx071j6b4b8UReDfEVje6JfT31/p0EMYlu4pd10I3R5tzSHHPlnPXgelem/wDCOWP/AD31T/wa3P8A8co/4Ryx/wCe+qf+DW5/+OVV5dv6+4q8+y+//gHP65ZahqejaHd/8I2l1PYXKNPp92IWkdDGVbYxfZkFgeTzt+lZ+taFe32paDrD+DLO9hispbWfSpHhJt2YqUOW+QqNpBxnG44BrsP+Ecsf+e+qf+DW5/8AjlH/AAjlj/z31T/wa3P/AMcovLt/X3BefZff/wAA4XUvCXiC48WtfR2cflPHbSWrQzwxixePYGj3mMyFMgnC4DDIIGck1HwXrtz4ptLs6ZpVybfWxqC6s85S4+z7iRCV2EkKDtHzEYUcCu6/4Ryx/wCe+qf+DW5/+OUf8I5Y/wDPfVP/AAa3P/xyi8u39fcF59l9/wDwDnry0fUPhPpVlHcPbvcQafEsyDLRlpIgGHuM5rnYPhzqjeHdTsJtO0qBm0pbBY7eT5L6ZWDLcyfKNrcDruPJ5r0uTR7GTSItLMTiziWNY0SV1ZRGQUwwO4EFRznPFV/+Ecsf+e+qf+DW5/8AjlSoyj9yJjGUduy/rYxfDGg3+leKNUvn0+xsrC9tLVUgtpc+TJGpDIFChSvJw2B06em14V/5FDRf+vCD/wBFrR/wjlj/AM99U/8ABrc//HK0LW1hsrOC0t02QQRrHGuSdqqMAZPPQU0ne7KSk5XZzHwy/wCSeaX/ANtf/Rr11tcl8Mv+SeaX/wBtf/Rr11tTR/hR9ERh/wCDD0X5BRRRWpsFFFFABRRRQAUUUUAFFFFABRRRQBXv/wDkHXP/AFyf+Rrz74E/8ko0/wD67T/+jGr0G/8A+Qdc/wDXJ/5GvPvgT/ySjT/+u0//AKMagD0miiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigDJ8Vf8ihrX/XhP8A+i2rzm38bvpMmiRPqbW9haW9jbz2xhQ+aZIlZmGAzsArKcjaAc/e7erXVrDe2c9pcJvgnjaORckblYYIyOehrmP+FZeD/wDoEf8AkzN/8XWUlPn5o/1+DMZxmp80Unp3t+jOV0nxdrMOqXV1qesTT29v4hbSvsi2qBPJfPlyFgu4EE464+XBGa3NauLuz+HWo3Onwefew6rJJbw4z5kg1AlVwOuTgVe/4Vl4P/6BH/kzN/8AF0f8Ky8H/wDQI/8AJmb/AOLqZKq+i+//AIBE1Wl0Wz6v/I57SNc1288N6peXWs3vmLbRyw/ZNPM0kMwyrpzCgclsfJjK4OSBzT7TxD4kk0MyXo1OO7/tfbfC3sQTaWxJAEOUPnJkLlgCwDE9q3v+FZeD/wDoEf8AkzN/8XR/wrLwf/0CP/Jmb/4uqvV7L7/+AXzVv5V97/yMrWJtcl0TTI7fU9Vkje5mWe8S0NvJtyTFuCxswUfKuQo3Y5wCax7/AFDxAuo2Fve6jq7X76JM6RWUDIrXayKiOyKvAOcnf8vPOBxXW/8ACsvB/wD0CP8AyZm/+Lo/4Vl4P/6BH/kzN/8AF0Xq9l9//ADmrfyr73/kZU9lfR+MYdY1Sz1V2OiQxv8A2e8m37QJGZ0wjY9OvFT20epQfFjUrtbfUf7MudNjgSV1doxOHJ4z91QG+nJq9/wrLwf/ANAj/wAmZv8A4uj/AIVl4P8A+gR/5Mzf/F0Xq9l9/wDwA5q38q+9/wCRhafB4qbTVS6k1b7cmn3P9pM7HbJcA/uvI24A5yRsAG3APNV7S31bT7jT0uY9TNveQabLdtcs8ii9+1R7+WJ2cdhheldL/wAKy8H/APQI/wDJmb/4uj/hWXg//oEf+TM3/wAXSl7Vpqy+/wD4BMvbSTXKvvf+RiePLmxg1pxfl3iEdnI0MF2LeZ0VroMUbepyNy9COuO9clqms3k/hmwtIdRASS4uzbx/2orTW8Z4gWYiZc4BJ3M528ZBxXpH/CsvB/8A0CP/ACZm/wDi6P8AhWXg/wD6BH/kzN/8XUr2y2S+9/5Er6wtkvvf+RwWo6pPq+g+H7n7bE2pWmn7J7e41WFUkmGFJJWdGRzgkSDdgMRjJre1DVtP/wCFiaNrlvcWhWO1kgv5YtUt9jbgNihWkBYK2TnA+hrf/wCFZeD/APoEf+TM3/xdH/CsvB//AECP/Jmb/wCLp3r9l+P+Q74ntH73/kcfZXUH/Czv7Ykm0hLZZpWa8udSgkfYUKKI2V9wXBB2MmBlueldcfEdprHiPTLWCW2byNQYxNFdxSmZPss2XCoxKgE45xTv+FZeD/8AoEf+TM3/AMXR/wAKy8H/APQI/wDJmb/4uk/bPdL73/kJ/WHuo/e/8jraK5L/AIVl4P8A+gR/5Mzf/F0f8Ky8H/8AQI/8mZv/AIurvV7L7/8AgGnNW/lX3v8AyOtorkv+FZeD/wDoEf8AkzN/8XR/wrLwf/0CP/Jmb/4ui9Xsvv8A+AHNW/lX3v8AyOtorkv+FZeD/wDoEf8AkzN/8XR/wrLwf/0CP/Jmb/4ui9Xsvv8A+AHNW/lX3v8AyOtorkv+FZeD/wDoEf8AkzN/8XR/wrLwf/0CP/Jmb/4ui9Xsvv8A+AHNW/lX3v8AyOtorkv+FZeD/wDoEf8AkzN/8XR/wrLwf/0CP/Jmb/4ui9Xsvv8A+AHNW/lX3v8AyOtorkv+FZeD/wDoEf8AkzN/8XR/wrLwf/0CP/Jmb/4ui9Xsvv8A+AHNW/lX3v8AyOtorkv+FZeD/wDoEf8AkzN/8XR/wrLwf/0CP/Jmb/4ui9Xsvv8A+AHNW/lX3v8AyOtorkv+FZeD/wDoEf8AkzN/8XR/wrLwf/0CP/Jmb/4ui9Xsvv8A+AHNW/lX3v8AyOtorkv+FZeD/wDoEf8AkzN/8XR/wrLwf/0CP/Jmb/4ui9Xsvv8A+AHNW/lX3v8AyOtorkv+FZeD/wDoEf8AkzN/8XR/wrLwf/0CP/Jmb/4ui9Xsvv8A+AHNW/lX3v8AyOtorkv+FZeD/wDoEf8AkzN/8XR/wrLwf/0CP/Jmb/4ui9Xsvv8A+AHNW/lX3v8AyOtorkv+FZeD/wDoEf8AkzN/8XR/wrLwf/0CP/Jmb/4ui9Xsvv8A+AHNW/lX3v8AyD4Zf8k80v8A7a/+jXrraqaZplno2nRWFhD5NrFnYm4tjJJPJJPUmrdVTi4wUX0RVKDhTjF9EgoooqzQKKKKACiiigAooooAKKKKACiiigCvf/8AIOuf+uT/AMjXn3wJ/wCSUaf/ANdp/wD0Y1eg3/8AyDrn/rk/8jXn3wJ/5JRp/wD12n/9GNQB6TRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAV7//AJB1z/1yf+Rrz74E/wDJKNP/AOu0/wD6MavQb/8A5B1z/wBcn/ka8++BP/JKNP8A+u0//oxqAPSaKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACo90v2jb5aeTtzv3/Nuz0xjpjvn8KkooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAr3/APyDrn/rk/8AI1598Cf+SUaf/wBdp/8A0Y1eg3//ACDrn/rk/wDI1598Cf8AklGn/wDXaf8A9GNQB6TRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRWXeNLHdXk0UpQxWqPgAHcQZDg57cVlWq+zSbV/+Gb/QuEOd2NSisk3twtxLudQEMmYx8zBVBwduO+B1OOabDfSuSsl0FjDsPOG05O1CBnGP4m/KsPr1O9rP+vmafV5mxRWHZXNwI7SIOiqEhUITy6lRk425PfnI6Vp2TySRyPJIW/eyKBgDaA5AH6VVDFRrWSTFUouG7LNFFFdRiFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFYfinxTaeE7C2urq0vbr7TcraxQ2cYeRpGDEAAkZ+6RxzkitKVKdWahBXbE3bVm4TgZPSqMGtaVdK7W+p2cwRkVjHOrbS7bUBweCzcD1PAridV8enUtHvrAeDvGcRubeSESDSuU3KRn7/AGzXNyeKdXupr66l8DeIYJpEsPJih05yha2maXDHggNkAEA4Hrjn06OUVZxbno9Oq7rz7X9LeZDqLoeu3Gq6daJI9zf2sKxyCJzJMqhXKhgpyeDtIOPQg1X1HxDpOlwXMl1f26tbQG4kiEqmTYBnIXOTnt65Fec+HLq98X65rNx/Z1zY39rcb5bK7nltNqTQRKh3J8xI+znggAh8/TfuvBeoNa3FlaPZQ28tk1uW3udzfZfJU7GDbSDj51bJUbSD1pSwNGjNU60rOyb28n59Nu9/UOZtXR1R1zS0haeXULSKEOIxI9wgViVDjBz3VgQDzg56EVIdX00XosjqFoLsttEBmXfnAbG3Oc4IP0Irn20DVU1i51aNLCSaeRz9mllbywrwW6E7tnJDQEdOVbtnFMsvCE9lpk1qs0MkjX1hOszZDNHbrbht3H3j5MmByPmHIycYeww9k3Povv0v92/n0Kuzr6KKK4CgooooAKxda8S2+iLcl7S7uvstsbq4+zKp8qP5sE7mHXa2AM/dNcBF4/8AFWpa94gsNOufC0A0q4uAYr1bgTGGJseZ8hII9cc57dKjuNM+IHjLTWv7PUfC6Wmo2Zt3ktTcKJ4ctjO9SRgs+CMfePUV61HL4QqWxE4r5/10/Ezc9NEeky69aw/a90cx+y3sFi+AOXl8raRz9398ue/B4PGcpPH+iypM8TPIscYkQo8TeYpdUzw/ycuv39vBz2OOb8Mwavrni3xHp3iK4ghm0+6sLx4tLJEMsu0OrEyAseIowQMDg9+a7GHwxDb2xt4tR1BIkjEVuokUC3QMGCqNuGHygfPu4GOhOVUoYbDvkqav3Xo9LNJ9vP7vMabeqKg8WO2oyQvp9zBAqWbB5FUtunnaHaQH6ZAIYZGAx5G3c+TxpYx2y3DWd95cqxvbYRSblHlSMMg3dN0iH5sHDDinW/g2wtlVY7i6CjyCy5QBjFcG4Q4C8fOzDC4G04AGBhyeELFFhRrm7eO2MQtkZlxAiSpKEXC/dLRoDnJwoGRUN4K/ldd9rL8b/h5h7xpabqaaktwBBNbzW03kzQzbdyNtVxypIOVdTwT1q9VW1sIrO5vp42cteTieQMRgMI0jwPbEY9ec1argqcvN7u39X/EtBRRRUAFFFFABRRRQAUUUUAFFFFABRRRQBXv/APkHXP8A1yf+Rrz74E/8ko0//rtP/wCjGr0G/wD+Qdc/9cn/AJGvPvgT/wAko0//AK7T/wDoxqAPSaKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooA85h1TRLXFpe2pa6W0lvGJFx80KE7mGxCvHTAOenc1vadYWGrabbahZ6dA9tcxiWJmuZkLKRkHDICPxri9StZ77U7KONblIG0W8tXuLe5ijCySSBlVssGxhOw/iX3xja7p+v3tpoi2EUtvcWekW0KGO7iCiVCDIGPmjYw2DaVDZ3EEgV4OEwuDlh6bly3sukO3oelXrV1Vkle131f+Z6t/YEP/QLtv8AwMk/+JqOfR7aCCWVtMtiIkLsFvJM4Az/AHa5qXw4kvimK4iv7SHQrmWK+ubZ7vEsM8asAqbWxtYspYZx8jf3qqWeizWus3V9dzxTXCvdsbuO7hVbhJA2wMqr5jFQ20KTgbcg8gVrVwuCjBtct7dof5EQrV3JJ3++X+Z2k+k6TDM0Q02WQqquzLLgAEkD7zj0NM/s3S8kf2RNlRkj7QvA/wC/lSX40bVzf2OoS2k9lc2yRujyKVbl8/iMg+3Fef6d4bk1LwxcT3U2npqc99A225cQma0t2VUjk2kld6Jk8dW5HHDjhsFO7fKtX0h39BOriI6a/fL/ADO9GmaY23GkTndyMTrz/wCRKdBpOkzTLEdNljLIXVmlyCAQD91z6iuZj0JbO5sNQsn0SKa11G4ulshdkRLHNEUZVfaSDn58BQMk+laHgqB9A0bTtN1K600S20c67rW43xkNIrDkhcHkjHtRLDYKFmuV6rpDv6AquIlpr97/AMy3NbaPBJGs0FhAZpmhhW41Bo2lYMVwARyeOgzStZaUt/8AYGg00XmzzPs51F/M2/3tuM4965jVPDh1DXdRvUHh29gvUVF/tKZg9s8czsGTaMlSGDYDLkgc4p954Va78Q+cdT0lbVtVj1Vr1ZsXSlVUGFRjGz5eu7ocYpU8LgpQUny3a7Q/yHOtiFJpX++X+Zv2qaFfOUtDpFwwj80iLVGchP73A6e9UNG1bwrr63DaY+nTi2VnmP22VfLVSQWO5RgcHnpjmqMOhTx6hot0h8OWz2GrXFzI1vdsC1tIGG3AQAt8/Q8fIvPJxeFnrP8AZOo6RFrug2trIky200al5dzvu3OC23ozKRg565GcVf1PA/3fuh/kT7fEef3y/wAyeK68NzaNNrEbaW2nQMVluRqD7EI4wTt68j8xVa+1bw1Yadp1+0NnNbajMsNq0F5I/mszY4AXoO/pg1mW3gtxDcG68Q6XLcJe29/ZOxeTbLEu0LKXkLSJtHTIwSSMdK6CayuZdEWJNe0iDUI70XkPlRAW6/NkoU3bmByxJ3Z3HPHSj6ngf7v3Q/yD2+I8/vl/mQzXvhu3s7a7lGnrBcxtLE/2yXDIpAZvucAZGSfWodf1HQvDvyXenxSz/uz5EFzI7BXfYrH5QAM55JHTjJ4qnr3g6PxHLZ3mo+I9Olvkt5La4JUrE0btu+VUlU5XoNxYEdRU+r+ELa/W6jsvFFtZRXcFtHcJ5SSbmgIKMpLDb0AxzR9TwP8Ad+6H+Qe3xHn98v8AM3ZNG0+WC3b7O1uWneOTypGc4UP0z15UdqxbS68IXrWQh1G+H2wziIyQOgBh/wBbu3INm3HO7FdDb3ttFDZrJexSPHdSs7F1BIxJ8xHQZyPbmuf0a003VdV13VbjbZ2GoxeRDazyBJASCJpduf3Zf5R6nYCeorGhhcBUjecY307Lou1uppUrYmLtFv8ApsjF94O+xzXR1K+WKIRs2+B1JR32I4BjyULcbhx71ZvR4Z0+HUpZ7u/26ZIkd3tjJ8osAwJ+X7uCDkcVFaeDdG8u4XVteTUGeyXToXDpD5NujblGFOGYMAdx9Bx1zJN4U067tdYivPFc8rawka3jBrdQSihcqNny5AGetbfUct/lj9//AATP6xi+7Lukabpl9OrLa36xMsgC3sbRM20phgMA4Ibv+QNcn4q8Taf4SQRzaK13JNpiXNqyPIA8/wA2UfBwBtUvnjhWHpXoUV5bRXdqJdTiuCkMoaZ3QEksmM7cAdP0rnLi10bU7K4ivdWnVbvT0s5IhApEQCsNyEoTu+d+cn71YRpZdTqtSUEtd7do9/maOeKlC6cr/PzFub/w9pkVgNQ0+5MlxFA0ssKSeTEZWCLli3QscYGSOp9aS31XwxNfy2kmlX9v5N4tjLLOrKiTN9xSd2fmBXBAx8y5xmqFz4Y8N3jIbnxDqcoEcKEMictFjY4PlZVvlXO0gHHIq/Lpnh2a9vLl9Zvj9q1K31Jo9vyrLDt2gfJnadi5BP8ACMEVv/wlf9O//JTP/bf734lm3u/C9x4gfRTZzRXYWV1EjEb1jYKxwGLAZPBYANzjNU4tc8JPpFzq8tjdQadb2iXbXEjcNG5ITADlstg4BAPrimW+i+GdMmjvNL1CaK/t4pUtnlVmUGTk78KGcbgDyc8cEVhaBpkb2S6TqkcFtojwSQ31s8pme7c7SsgKxgr825sli2T070f8JX/Tv/yUP9t/vfibqarpE3hu41e38O3Nw1q3+k20N5G7RptLb9wkKNwAcAlucYrQt49Li0PUNX1bS5tPjtiztBNNl40CA8lWIyeuM/xY9qjax8NSaXeWMmram4vESOaY3E3mFE4ChscDGQcdcnOaqNbafJNp9q+rzyaZZ3n2uT7Q0ks1w6qnlBmI5UNuJzz8q9qzn/ZfNG3s9/7vZlR+uWd+b8e6Ocv01W1gWbURJplvHE9zezQw/afsjEBo4mC5JTBYFwCfkHIzW5qWsaXpNvq3maBPcPpVvbXEjrcbRNFLuHmL83GNjZBAPHFWdV0zSPEOrXN3c3N6IinkobW9+zeYjKu9XBZSynav5GrmqaV4W1mXzL/TFlYwrA2LxFDxrnarBZQGAycZzjNZ4ZZfyPmjF6y+zfTmdum1rW8i6rxPNo3suvkr/iZY1bT01iS1n8NyJaRammlyXK3m4rM4RozsyPlIcZIOQex5IXSNW07VtZlsE8OTxxyLKbK5MsxjlKEjEjbcRE7SRy3HocArpWg6XY+LNR1q5ihuPOmSa0zcrugKxrHyDKVY/KCGxuGTzWta2Phuy1KXULfT9lzKWYsbxCFLZ3FVMuEJyfugdTXRbLf5I/8AgP8AwDK+L/mf3/8ABOb0i91fVtAfWoPBdnJbeQWjhGqOJZXVirhflIwccZwePel1PUI77wl4n1PQbC1ENhaGS01AXTusjeXvbCFfvIMcHI3HB6Gun0GDQPDNtJb6RZm3hkbcyG9Rxn23SnH4U6WLw7Nos2jtpduunTbt9vHJCiHcck/K45JOc0Wy3+SP/gP/AAAvi/5n9/8AwTD1KW2s/CGkajp2n/a5r2COQy3BkO1DHvLtHFlmzwMIvBbPAFZc+t+bbWEenaRp0l6+ijWbkzXkixmPpsjxkkk55PA4z1rqU07wqlraWw0W0MVoCLcNJCxiyApwS+RkKAfXFT3EPhu7tLa0uNGspbe1ULBE/wBnKxAdAo38D2otlv8AJH/wH/gBfF/zP7/+Ccu91c33iiz0zR9L0s217psepRS3lxKjpGSAVKgnLc8Y4HetSa1j03xjBYxLM6tJHcb3ICxqzBVjUdWwUdiSeNwHOeNa5Xw/ealFqNzpVrLexBRHcO8BdADkAHfkYPNMvpdPu9UsrqK1iW8a4ijafdEzlASQuVYnGWJ9OawxKwHs37OMVLS3u26+hpSeJ5/ebt6/8E6miiivdPOCiiigAoorm7zwbb3l5NctrXiCIyuXMcOqSoi57KoOAPYUAdJXBfFKCK6tvCtvPGJIZfEdokiN0ZSHBB/CtMeBbYEH+3vEpwc86vN/jU/jLwxP4osLCG11P+zrmxvo72KfyBNh0DAfKSB1YHnPTpXXgKkKeIjKbsu/y8iZK60OJ0y9t7DS/Emo6HdW+q6zo1r9hs0hGcW6/MrFVHzNkkEjqU4682tK8Ya5qHhPUbmO9gluEuIktZ443lBVsbgZFhCZ4YbthCcbhWt/wi/jv/oo3/lEg/xpf+EX8ef9FG/8okH+NX9Uo/8AP+H3T/8AkA5n2/IyPhhfS6l4z8aXc7TNJIbLLShckCNwCCqqCuAMHAyMHHNen1yvhPwnf6Bqusanqeuf2teap5HmSfZFg2+UrKOFJHQjsOnfNdVU4+cJ1v3crpRir69IpPdJ7rsEU7ahRRRXGUFIzKi7mYKPUnFLVTUdMsdXsms9Ss4Lu2cgtDOgdSQcjg+9AE/2iD/ntH/30KckiSZ2OrY64Oa5z/hXngz/AKFbR/8AwDT/AArU0nQNI0FJU0nTLSxWUgyC2hWMMR0zjr1oA8U0DRNRv/H/AIqubG3mSYajepa3wi3RRyhwWjkPZXQlf+BA9QK6NfDfi6HRoLB4L3EOhWtvYfYr4RC0u0UBzJ843fMByAw2gjvz1F78K/Beo39xfXWjeZc3MrTSv9qmG52JJOA+ByT0qD/hT3gP/oBf+Tc//wAXXqYieCr1HUc5K9tORPp/jX5ELmStb+vuE8LZ/wCFpePc9f8AiXZ/78Gu5rD8O+D9B8J/af7EsPsv2nb537533bc7fvMcfePT1rcrmxtWFWrzU72SitdH7sUtrvt3HFNLUKKKK5CgooooAKKKKACiiigAooooAKKKKACiiigAooooAr3/APyDrn/rk/8AI1598Cf+SUaf/wBdp/8A0Y1eg3//ACDrn/rk/wDI1598Cf8AklGn/wDXaf8A9GNQB6TRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFAFX+zLD/nxtv+/S/wCFH9mWH/Pjbf8Afpf8KtUVl9Xpfyr7kX7SfdlX+zLD/nxtv+/S/wCFH9mWH/Pjbf8Afpf8KtUUfV6X8q+5B7SfdlX+zLD/AJ8bb/v0v+FH9mWH/Pjbf9+l/wAKtUUfV6X8q+5B7SfdlX+zLD/nxtv+/S/4Uf2ZYf8APjbf9+l/wq1RR9Xpfyr7kHtJ92Vf7MsP+fG2/wC/S/4Uf2ZYf8+Nt/36X/CrVFH1el/KvuQe0n3ZV/syw/58bb/v0v8AhR/Zlh/z423/AH6X/CrVFH1el/KvuQe0n3ZV/syw/wCfG2/79L/hR/Zlh/z423/fpf8ACrVFH1el/KvuQe0n3ZV/syw/58bb/v0v+FH9mWH/AD423/fpf8KtUUfV6X8q+5B7SfdlX+zLD/nxtv8Av0v+FH9mWH/Pjbf9+l/wq1RR9Xpfyr7kHtJ92Vf7MsP+fG2/79L/AIUf2ZYf8+Nt/wB+l/wpG1O0XUFsDKftDcBdjYzgtjdjGcAnGc45qpD4m0meATx3LmNkEiEwSDzFJCjYCvzcsowMnJA71PsqH8q+5EvENfa/Euf2ZYf8+Nt/36X/AAo/syw/58bb/v0v+FV49f0yQIVucb51twGjZT5jDIXBHH9CCOopU1zTpJERJ2bewQMIn2hicAFsYBJ6ZPORjqKPZUP5V9yD6w/5vxJ/7MsP+fG2/wC/S/4Uf2ZYf8+Nt/36X/Cls7+2v/O+zOziGRonJRlAdSVYAkc4IPSrNNUKL2ivuRSqzeql+JV/syw/58bb/v0v+FH9mWH/AD423/fpf8KtUU/q9L+Vfcg9pPuyr/Zlh/z423/fpf8ACj+zLD/nxtv+/S/4Vaoo+r0v5V9yD2k+7Kv9mWH/AD423/fpf8KP7MsP+fG2/wC/S/4Vaoo+r0v5V9yD2k+7Kv8AZlh/z423/fpf8KP7MsP+fG2/79L/AIVaoo+r0v5V9yD2k+7Kv9mWH/Pjbf8Afpf8KP7MsP8Anxtv+/S/4Vaoo+r0v5V9yD2k+7Kv9mWH/Pjbf9+l/wAKP7MsP+fG2/79L/hVqij6vS/lX3IPaT7sq/2ZYf8APjbf9+l/wpV06yR1dLO3VlOQREoIP5VZoo9hSX2V9we0n3YUUUVqQFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAV7/AP5B1z/1yf8Aka8++BP/ACSjT/8ArtP/AOjGr0G//wCQdc/9cn/ka8++BP8AySjT/wDrtP8A+jGoA9JooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigArP1HVU0+aCBba4uriZXdYbcKW2Ljc3zEDA3KOucsMA15z4h+IviCy8eap4f059FjW0WNolurW7mlkUxK7keSG4XPOQOCOvNZUviLxvr6WmpWVxpICo6w3VlpOpsHjfG5QTCwIJVTkc5UYIr2KGUVW4ym1Zq/XqrrZehm6i6Hpsfi2wk0q41FYrnyYNLi1VgVXcYpFkYAc/exG2R05HNQzeONHhvri1Z3ZoPODFGRiWiVmdQgbfkBG5KgEjryM+Uz2vjWbSxpyS2sEB06PTZfK0jUszQoGC7iYDyNzcjGdxzxxV0XXj1ZpmSW0jhkaWRYI9K1VFjeTO91Ih3ZyzHkkAnIHSu3+x6Ku7/i/Ly73+XmT7RnoFz40MRWRdNuUtRYXV48rCN8CHyz8u2TDgh+oPUgZ4bF288X2NjHdTTW939mgE4E6quyV4VZpET5s7gEfqADtPNeSNa+NHiuI2eyLXEVzDO40XUVLrOqK/AtwoP7tCMAcgk5ycuvpPF93bXouJdOWykFwxiGk6mI4HlVlkkU+RkHDv94kDceKt5RRdtV1vv8A5f0vMXtGe0adrCahcz2xtbm1nhSOUx3AUEo+4Kw2sepRhg4IxyK0a8dt/EvjY65LdrJ4fS4uVtrNhLpupJGp3v5eS0YClmmIyTjpVu/8W/EWwkuoDD4YnuoLn7MtrbxXMkszeUkpKKDyoWQZJxjn2z5tbK5Rd1KKVur9L7ruy1M9XorzDR/EnxE1nR7PU438H20V47Rwx3YuYpC6syldpPX5W49qnk1zx9FcG3k1T4fpOHEflNcThtxIAXGc5yQMe9c/1H/p5D7yubyPSKK80g8ReObm8Fnb6z8PZbosVEEd1OzkjqNoOcjB/KpTrPxAUXROpeAQLTi5Jnn/AHP+/wA/L+NH1H/p5D7w5vI9GorzC68T+OrTTr6+bU/AUkNjGZLjyprhyg56gHqSCB6nipLfxB49udMXUo9T8BfYztzM01wqqWxgNk8HkcHnmj6j/wBPIfeHN5HpdU9R1GPTo4S0Us8s8oihhhA3SNgtgbiBwqseSOAa8li+I/jKXxJe6N9p8HIbOJJXvGac27BjGqhXDEk5lUdOua7bwpfT+OvA+k6xfsLS+MskySWY2+WyvJHlQ+4crkHOfvGtauXTw8VUqtOOmzv8Sbj8nYSmnojY0zxFa6pLbRRwXMUk63LBZlUFPIlWJw2CedzDHXjPSuKs/ivd6gqG28PQOzypCsZ1WNXZ2IAAUqG6kc4xXUWHhRoLOFZdQuYrqCa82zwOpZ4p5zIVbcp5ICEkAEEcGvLvCg8P3Efh2x+wreajeXkkVzFLsWNditIHYlGfBXACghWKsD0auKuqHtuWEnb3tvJ6bp9PxMKrqucYxdtH28vJ9zcj8ReIdS17T9Vg8OLJHNPutla8UksbeQeWH4CgBXcqQCCMHkioLfXdbu9G0z7P4bjkhtbSGwEkl1GySNN9nePcpHG4KnGcjzByCBW3baF4FimlYXKztYHzWDW8bAxxbkZQBHiRQXIYjc24LlsqMQ6Zp/w9mVpYblXh023hmnS4t1USoFwsxLRhmDY5KHax6g5OcpYajraT+9fP7Hp8zL6vU/m381/8iZNnfeI9SWzkt9AkklvLBp7V3vlGdkgZJRu5wnmqoUnJBHPGa04bPxPb3kUsfgm3KIYWJkvIHlzGqqNrn7oOxc8E9cEZq9b2vgKz0W01ZreOS2sk/s9lmsMyySsYwPMi8veZflGPlBw7HGGqwt/8P206K+GkWnlSmQIh0dhIwjGXYRmPdtHc4xnjrXPUw8b+43b1Xd/3ew1hZ9/xX/yIunan4vsLZ4f+EL37p5ps/wBqQj/WSM+Onbdj8Kt/8JB4w/6Ef/yrQ/4Vm6lqngnTb+xtP+EXW7e/tvtNo9npKypOv91SB1wQecAZGSM10sPhrw9NBHL/AMI7p0e9Q2ySyjDLkdCMcGkqdRK3N+X/AMiaKlVSspP8P/kTM/4SDxh/0I//AJVof8KP+Eg8Yf8AQj/+VaH/AArW8LnHg7RTgnFhBwP+ua1xfhbVNK1+006wkl8QwX93ZuyXUt9Osc0keEkKYlwSGycYHHbFFpu1pPX0/wAg5ajtaT19P/kTe/4SDxh/0I//AJVof8KP+Eg8Yf8AQj/+VaH/AArnPDcsFj4W12/8SazqlyNL1G4tvtD6hNCzqhAUbRIF3EnA9cir0Gs6JJ4cvNWeLXEazmEE1susSyMrHbg71mKbfmHzFgBg56U+Sp/N+X/yI/Z1f5n+H/yJq/8ACQeMP+hH/wDKtD/hR/wkHjD/AKEf/wAq0P8AhWRc61o9v4csdWEGsu15I8SQ/wBuSKqshYPmYziIAbDg7ue2ah1HxL4f06OzDprT3U1mt9JbDWpQ8ULEAHJmw55OFUkkA+2Tkqfzfl/8iHs6v8z/AA/+RN3/AISDxh/0I/8A5Vof8KP+Eg8Yf9CP/wCVaH/CtTQYzBc6zbCa4kigvVWPz53lZQYIWI3OScZYnr3rivCc+iahp+jxN4LSW2kQW76o1pC6GVIwXLYywG4Mu4jqDmlab2k/w/yJ5ajslJ9e3T/t06H/AISDxh/0I/8A5Vof8KP+Eg8Yf9CP/wCVaH/CsNtW8NLFDMfBVqIbq0nvLVzbwfvY4sFuOqkqQw7Ed6r3ep6O3h3V7mHwdplrfW+j/wBrWyT28Tq0RDbS20cNlT8v0554fJU/m/L/AORK9nV/mf4f/InSf8JB4w/6Ef8A8q0P+FH/AAkHjD/oR/8AyrQ/4VWnstKsNCS9vvDHh9biVokhiRV2uXx3MYPGScAMcCqEF/4cvE0q2tPCelNqmpLcNHby26pGBCxVyXMeeSOPlzzyBRyVP5vy/wDkQ9nV/mf4f/Imx/wkHjD/AKEf/wAq0P8AhR/wkHjD/oR//KtD/hWVqNnbp4o0LT7LwvoCpeWU9zPFcRICGTyxtDKjDgydRkHn2rpPDdtb2lxrcNrBBBCt8pWOBQqLm2gJwAAOpJo5Z3V5P8P8g5KiaTk9fT/5Eof8JB4w/wChH/8AKtD/AIUf8JB4w/6Ef/yrQ/4VyVhdxTeMZdMu9B0NoZdTukE97auZbgeZI2Uk2FCQfl2k7sITjAq7ol9pGpv4eWfwtoUf9p2VzcShLdCY3iZRtAK9Du6n0pKNRq/N+X/yIowqtX5n+H/yJ0H/AAkHjD/oR/8AyrQ/4Uf8JB4w/wChH/8AKtD/AIVx/h7V7XUvDOs6/feEfD0VnaWSXVuY7XhiULlWJTnaMAlR1ziny3APh171PDPh8PdalHZWMy6aoHlscGaRHK7c4IVSV5xk80+Sp/N+X/yI/Z1f5n+H/wAidb/wkHjD/oR//KtD/hR/wkHjD/oR/wDyrQ/4VyGtXtpaeGtNuoNC8OQ3M08yzy/ZbabEUeQXSMSjcSdmVDkqCc9KffQ6TPqPhq6t59A0/Tr3TJZ3muNKiEE0n7vby+1gfmJC8HCmjkqfzfl/8iHs6v8AM/w/+ROs/wCEg8Yf9CP/AOVaH/Cj/hIPGH/Qj/8AlWh/wrkJNSs5PHR0m28KaKtjFNDGHlgtlNxG4y0qZYMRyNuxWBwcnni1pdhpt/8AEHVtHFzoBt7GdJFthp1uZZVZSWiyBwqYOTjdkjJ4wTkqfzfl/wDIh7Or/M/w/wDkTdvfF/iPToRNfeEre1iZtoefWoEUnrjJHXg/lVH/AIWTff8AQF0v/wAKK2q4bv7B4O8I3mx3+zwCXYi7mbbYzHAHc8dK5TTPG3iG80jV/teuWtrdWllbX/miOGRYmdmDxfKSCgwnfeN3JyamMZy1U3+H+RMYVJ6qbXyXb0N//hZN9/0BdL/8KK2q3Y+Ndf1PzPsHha1u/Lxv8jXIJNuc4zjpnB/Ksv8A4SnV7K+vdHl1kXiWt7a+fqqwRq0FtLGzklQCnBRRvIxiUZ6ZqX4VqkcmrxRLII0Y+WzRbA6NdXboy8AFSrKQVGOeKfJUTV5v7l/kP2dVNXqP7l/kXJPHOuwWTXk/hWCC2WVoTLPrMMah1coVywH8QI9+1XI/EniyaNZIvBSujDKsurwkEfXFc1qdxbQ694eF3qtzaQNf6oCiRo6bjNIFOGVvmJJABB74xznXvtZ1q21zU7S2aeP7NPapp1mlniK6jYIXLSbDjkuCQRt2gketRhJpPmf4f5FQhNxT53+H+Rof8JB4w/6Ef/yrQ/4Uf8JB4w/6Ef8A8q0P+FVLQXM/j3VLabXdaS3hnhlt7cxqsMjbCXUNs5jHAxkcg8k1h+G9U8UXWpafYanbavCNNinknu8kLetGNjKQVIJLlWTkfLT9nL+Z/h/kV7KX87/D/I6f/hIPGH/Qj/8AlWh/wo/4SDxh/wBCP/5Vof8ACuP0fxTq13NrMN6dea1/skXKSLbSrJ9oUncqMYowpwVG0KVPr1zq2t5cjwXDqVrc6/dzm4txq0kkUsc4RQDJ5UTKMDkA+WBkZwSRR7OX8z/D/IPZS/nf4f5G/wCEPGDeKZ9RhexitmsjGGMV2twrFt3G5Rjjbg8nnjjFdTXmnwujMeveLSVuwslzHKn2tSspR2lZSwIBGVIPPPPPNel06Tbjq+r/ADHRbcPed9X+DaCiiitDUKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigCvf8A/IOuf+uT/wAjXn3wJ/5JRp//AF2n/wDRjV6Df/8AIOuf+uT/AMjXn3wJ/wCSUaf/ANdp/wD0Y1AHpNFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAfPniiDTj8cNbn1We4tLcQRpFdwDcYpDDDkEA5wyb046b88YyMu/8SC88F6LoKQ3Ea2mnyRuRI2EnydnCyAH7q4b5sB24yMHs/iBonhaf4gSNr8tzbW89glwxtizSTTh/KUKuGJ+Reij+HPrWfe+BfhhYWGn3supay8N/E09v5KtIxjUZZiqxkqADyTjFdFSpSxT5qk3FpKOkE/hilu6ke3Y4W68uaMbWu/63MWTUdGmfUri5N3NdmytDZyLLINtwscav/EOh3Hnj5WxyRll34iVfHK+INPkuEzftO6SMT+62kAA7j1ycrgAAcFq1b3wh8K7DUXsZ9Q17zUZVLJC7x/MnmA7xEVxsy2c9AT2p0fgz4Xy6wNKS88QG6M5txiF9m8OqH5/K24DMoJzgbh61j9Wwv8Az9l/4Lj/APLTP2Nfy+7/AIJztpf2UGs3EjSXKKr3EcEscSvGyEvseQOxJP3MDaBj0PNXNIvNAtbS9W5tA/maXLCIJiHSS5Zhh8CMYOCcs2ThQP4Rnbj8C/DCa/nsotR1mS4iE2FXJ80xf6wR/u/nK+i5PB9KbZ+BfhtqNnNcWdxr77LF7+NJEaIzQr1ZN0Y3DOBx6j1oWGwq/wCXkv8AwXH/AOWjjRrra33f8Et6H4k8L2Xgy0tvJgsdVF3YNdtGju1wIZ4naVn2DJwHOCSe3elvPE+h23jK78V2N2lzdR3LLHauskYuIXtrdCwbYdpV424I5GfbNK1+H/geTwtHrt3beI7WJooGEbFSXaXAVUO3DckDPA5BOBWx4W+GfgvUL+9jk0rUJIUt4ZFS/maORGZ5lYfuyAR8i+v1rqjOgoez9pKzv/y7Xk/+fv8AdNb4i6vb7v8AgmfrOtabrAe4vtX0fUbqfTWs2S5trhI7dzKziRMRknCsq8bSdgORniDxHqekao1+lpe6PunYmO8lS4WUfuUTccQHDBk3de/rWnL4S8Jad4r/ALGHg576O4u3iidLogxqttFKVG6QbjlmPJHB4Jxir914a+HFnfXFrL4Xn/0RInvZg7eXaeZjaHbzOuCCdu7A56VxuMW3yz0/w/8A2408S9nH8f8AM53+1tLk1C0vPteh28kN4t0zwR3G8/6UZSoPkDrG2368dKm0+90C1tbm2n1+xuD9juLSO4mtLiRpRL82502BQd4BOd+ccEZNbM3w18IjwjrGpDR1F3bfbjE4nlwvlSSKny7sHAVeo5xzmsC98N6Ne6P4qa18EfYF0z7XHFqK3gkCNDHuXKM5J3EehADe1Nqm0uSo9tbwt/7e7/gJSxMtnH7n/makOt+HhZeQmuWNh5uh/wBmSraWUx2uN21lJQAqNzcEfxHpVvVvF2la3pEdne+IdPGy4ilxBZ3UeQgJyHHzK2/awI6bcc5rPt9F8D2uh3V7rfguaxa1s4rpfNucm4VztBG2QhSWwMHGNwpdE8PeAvFa2DWnhp7UHUDbXSPM5DD7PLINrq+CMqpyCDxj6pRSa5p6f4f/ALcbeJW7j+P+ZymmeIm8OfEHV9ZSUaolxAscVwtsMMd8THKMyHICMu7qWAYg5Nd38N/Gvh7QPAGmaZqeoeReQeb5kfkyNt3Suw5VSOhHerNv4fi0Dx23hrwvdnQra805b2Z4yJpXdJGTC+dvGCHyeP4RjGTU2jfEm8uLaS2m0l5ry30ma/8AM85UW48qZoW7YUnaW9q68Vj61en7JNcq5Vflab5E4q652urvYdOFbfmXXo+/qbf/AAs3wf8A9Bf/AMlpv/iK8q0TxHothb6DNOtzHqOlzO7SRWiuJUPmhUJMq9POkOcdSOOOfUNb8eLpWs2FjFYrcJO1uJ5BOMxCaQIuFAPdgfm2gjoSeKsxF7b4oTQi6umju9J87yGkLRqyShSwBPynDjgYHXOeMea6dRtS5l93/BHKlWclLmSt5d7efkeT2Gt6DYay+pJfas8j2U9o++zRjJ5nO9sz4DZCk7QoOOgzU914q0y7me4fVNWiuX0tdNMsFhEhwsgfd/rj1xtI9CcEZr1bQzqR1vxL9ruAzieMW0Pml44k8pSCAQCCSSSK5vw/r/jnUvBg1dW0G6uGhM0cIWRXYBmBBAOM4GB79aOSt/P+H/BD2df+dfd/wTz1tdsotNubK31G/JvNShvpZvsEUX2cxqOY1WQ5YlIx1XAyc56ySa3oWq2dlBrQnlbTHeOyePToHV4HC7hJHI5XfleGHTgktzn0yw1y/wDEGu6feqlqdC/tHGnTx7vMnH2SYszA8AAkr2OQc9Kp+JZ3n+KVjok95Pa6Zf6erXLQs0ZlaNpikfmrgoDl2yCCdmO5qbVr25vw8vUi1e9udb9vK/c50+NPDKXGkTW0/iC3OlW7W9sqW9sQFYAHIPsqjjAGOlaV18WdOl17T7mA6rFYQxyi5t/KiPnMQAn8WRj5jnI7DBzxaPiefQ9HWz0K+tbm0sdNkvjfaw7lrkCRgEQ5BONrZY56p/ezUlx8QtUhg1mVrfT4Ps32CazW4YoZYrjG4N833l5HGOmcVXJW/n/D/gl+zr/zr7v+CVdF+LGhadoWnWM1pqTS21tHC5SNCpKqAcZfpxXJeCfE+i6FbW8msf2vcXlp56WgieNoYElYlig+Uhjnndu6cHnA9Hg8VazJqF+WOlrZ2etJprIVcSGNtvz53YzlwMYwcE8dKTw54o1LWdat2bUdGa0uDOj6em4XVs0bEDv82QATlVAyMZyKSpVVb3/w/wCCSqNZW9/by/4Jwtn4i8IRWOp2N/N4k1O01GQzTRXcdvgSkg+YpTaQ2VHfHHSrt/4x8GapFGmoR+I7porhLmN5XRtjqCFwu/Zjk8bec811PgrUdHurTxPZXN3p06wancvcq0isGj+XMjqWIC5B54Xin/DHV9K/4V5arDf2jCySVp0ilVjCvmORuA+6MDI9qfJW/n/D/glezr/zr7v+Cc7pmuaBeWTWml2PjC5jiklkk8hRLjzs7gwDEbSckAjrkircZ0K2ks3s/B3jC0e1g+yq1tbyRl4ck7GIfLDJJ9Qehrc8I31tqfjTxVfWcyzW06WMkUi9GUwnBFdrSpqpJXcu/TsxU1VlG7l1fTs7HA6X4qbT5tQP/CK+JvKnuFkiAsCSqiGOPBy3XKH14xWRoL6VpFnp5Pg3xULy3CSOYoJfKMwQKzhPMC88/wAP4V6rRVKnNfa/ApUpp35vw7nmaTeHo3d18CeJwXhktwPskmEjkOXVB5mEBP8AdxUq32iKAP8AhCPFLKLM2JV7WRg0HP7tgZPmHzHGc47V6PRT5Z/zfgVyVP5vwPLVj8MpYtZjwJ4s8kyLLzDMWDKCAQ3m7hwSMA45pY18MxaSNLTwF4pW0WYzqotpdyORglX8zcuR1AODXqNFHLP+b8A5Kn834HnN3faDfWdjaT+APEJt7E5tUTTSgi4xgbWHBHBHQ9wasaX4p/s6bUNnhLxGkE86vDHHp2AiLDHGBjOByh4HbFd9RQ4Tf2vwE6dR/a/A8z0m/wBMsbuXUZfAettqb3U8/wBrXSgZMPI5X5ic5CMF/TpUlzfaJObmaPwHr1tezl2+2Q6QqzJIylTIrZyGwTzXpFFChNK3N+AKnUSspfgeIWejW1rp99aroGvxfabAWW6z8PpBnkEvJh/3hJUZB4wWH8RrZ8LPZeHIL5X8J67cPe7BMsOgR28RVc7R5anBPzHJOe3pXq1FHLP+b8B8lT+b8DhpPEumzQRQSeBNdeGLPlxtpClUz1wM8VLN4utbiFIZvBfiKWKMgoj6WGVSOhALcYrtKKOWf834ByVP5vwOOPjOFrhbg+DvEhnVSqyHTBuAPUA7s4qGPxTYxXTXUfgfxAlyxJMy6Soc5685zzXb0Ucs/wCb8A5Kn834Hm1vrj/2DotlLoHi23utNjjxNa6ep+dYjGcb8gghm6j0qX/hI73/AJ9/Hn/gqtv/AI3XolFT7GX8xCoTX2jzv/hI77/nh48/8FVt/wDG6m0/xKbK8uLuXQ/GV5PPHHGWn02MbVQuQAECjq7dc131FCpSvfmBUZp35zzw6vp++R08L+N4/MkaRli+0RruZizEKsoAySTwO9H9sWP/AELfjz/v5c//AB6vQ6KPYvv+CD2D7r7keef2xY/9C348/wC/lz/8eo/tix/6Fvx5/wB/Ln/49XodFHsX3/BB7B919yPPP7Ysf+hb8ef9/Ln/AOPUf2xY/wDQt+PP+/lz/wDHq9Doo9i+/wCCD2D7r7kcP4GilbxD4jvf7P1Sztbj7N5I1JX8xtqMG+ZySefc4BFdxRRWlOHJGxrSp+zjy/1q7hRRRVmgUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFAFe/wD+Qdc/9cn/AJGvPvgT/wAko0//AK7T/wDoxq9Bv/8AkHXP/XJ/5GvPvgT/AMko0/8A67T/APoxqAPSaKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooA818caB4lufG+na74fs/NksrdBG5mjVd+59ysrEFgUcjjHJBzxis6803x7cTW15DpM9vqSWzWlxcreWpE8RbdjYVwpBJwR+Oa9borL2bu2pNfd/kY+xabcZNX9P8AI8OuvBXiySRltNAe3tRHHHFC17BJsCWzWw5PU7HPXvin2vhLxraXMVxFpEsbxyySAR3Vsq/O8UhUDBwA0Knj1x0r26ij2cv5n+H+Qeyl/O/w/wAjx3TPCuu6TrUuoWng1YvnleBY7myV4zIGDAyCLcwG/wCUZ4wAcipdI0LxZpq6ck/hy4u47PS5NL2NqVugeJ2U9lyCAqjr2+ufXaKPZy/mf4f5B7KX87/D/I8tTTvFyaYmnjQ9VNtGkMUSHWLTaiR9Fx5WGBGA24HIFS+G7LxF4XlufsHgkiGdEBj/ALTgUKweRiQFUKoPmY2qoAx3JNem0Uezf8z/AA/yE6Mn9t/h/keY31l4o1C7lu28KXNvdfa/tME9rq8CSQ5hSJlyysCGCc8d+MYzTJtG1e4klebwRdv9oSKO5B15CLkRHKebx8/oc9RwcivUaKFTa+0/w/yBUZLab/D/ACPPHl8YP4e1DSf+EPx9s+1fvf7Th+TzndunfG/HXnHaudl0Lx3Lc38p8OwLHf8Am/abdL9lhkMibHJQT4yR+R5HNey0VPsH/M/w/wAifq7/AJ3+H+R402g+OJF2z+GLScf2f/Zv769LHyd27vP97IHzdeBzxVzR9P8AHOmXtrPN4bW5EMvmuz6mXllIjkRQXklfgCU9uwr1mij2D/nf4f5B9Wf88vw/yPM9WsvEGtanLfXfgmVZTBHDDLb6zHDNBtaQsVkXDAMHwR0O3nPatBo2uTaRZWOs+ALbUDZRtDFImoRwZiJHysqnDZ2jPYkZwK9VoqlTa+0/w/yKVGS2m/w/yPKZvDBuChk+FsR2KigDWlUYThcgHkgAAE88D0q5Lp2oza6mtyfDgNqMZUpP/ba5XbjAA6Y4HGMV6VRR7OX8z/D/ACH7KX87/D/I80sNM1DTNZfV7P4biK/csWm/ttSTuznIPHc9uKV4fE1j9pufD3w/03S9SuD+8ujcQybgTkghSh5PPXGecHJr0qij2cv5n+H+Qeyl/O/w/wAjzfT4vFOmafo1lb+DnMemStLufVIS0zNHIrE8DBLSFv0xU15/wkOp3l1JqXw/t722uIYYjbXGoQOgMbSMG5BB/wBZ6cY969Copeye/M/w/wAifYO9+d/h/kcNPda9dQ28Nx8OLWaK3IaFJNQgYREdCoK8Y9qlm1PxLcSCSb4fQyOBtDPqUBIHpkjpzXaUU/Zy/mf4f5Feyl/O/wAP8jiW1DxG+/f8PLdt5BfOowHcR0J+XnFSprHimOZ5k8BRrLJje41SEM2OmTjmuxoo9nL+Z/h/kHspfzv8P8jio9Q8RwhxF8PIE3rtfbqMA3D0Py8ilh1TxNbo6Q/D6GNH+8qalAA31wOa7Sij2cv5n+H+Qeyl/O/w/wAjkPCFhqsWva9qWo6SumJei2EMCzpKAI0ZTgr+HYda6+iirhHlVi6cOSNr3/4OoUUUVRYUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAV7//AJB1z/1yf+Rrz74E/wDJKNP/AOu0/wD6MavQb/8A5B1z/wBcn/ka8++BP/JKNP8A+u0//oxqAPSaKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiimvIkaF3dVVRkknAAoAdRVB9c0iKRo5NVsUdSVZWuEBBHUEZpv/CQaL/0F7D/wJT/GgDRorO/4SDRf+gvYf+BKf40f2/o3/QXsP/AlP8aANGis7+39G/6C1h/4Ep/jR/b+jf8AQWsP/AlP8aANGise78WeHLGMSXWu6bCh7vdIPT39xQvivQXRXTVrVlYZDK+QR6g0AbFFZH/CUaH/ANBS2/77o/4SjQ/+gpbf990Aa9FYF1418O2YBl1FWyCf3UTy9CB/Cp9R+voap/8ACyPC3/P9c/8AgvuP/jdAHV0Vyn/CyPC3/P8AXP8A4L7j/wCN1qReJdPmjEkaagyHoRptx9P7lAGvRXP3vi60sygXTNcud2eYNKnbb9cqKq/8J3bf9ADxN/4J5v8ACgDqqK5X/hO7b/oAeJv/AATzf4VoQ+IjPCkqaLq4VxkB7YI34qzAj8RQBtUVz934lu7cIYPDGtXWc5Eawrt+u+QfpVX/AIS7U/8AoSPEH52v/wAeoA6qiuV/4S7U/wDoSPEP52v/AMerTXVtRZA3/CO3wyM4M0GR/wCRKANeisn+1dR/6F+8/wC/8H/xdH9q6j/0L95/3/g/+LoA1qKyf7U1H/oX73/v9B/8XVC21jxVNdLHL4Tht4iT+9k1RCB9QqE0AdLRWNDe+IZE3PotlEc42tqJJ+vERqT7Tr3/AECrD/wYP/8AGqANWisr7Tr3/QKsP/Bg/wD8aqK4ufEvkP8AZtL0vzsfL5uoPtz74hzQBtUVyv2jx9/0DPDf/gwn/wDjNH2jx9/0DPDf/gwn/wDjNAHVUVz9pJ4wk3/bbXQ4MY2+TcSy59c5RcfrVn/iov8AqF/+RKANeiuauIfG7zs1tf8Ah+KI/dSSzmdh9WEoz+QqL7P4+/6Cfhv/AMF8/wD8eoA6qiuat7fxv56fadU0Dyf4vK0+bd+GZsVofZte/wCgrYf+C9//AI7QBq0Vg3uneJbmJVg8Q2towbJePTdxI9PmkIql/YPi/wD6HVP/AAUx/wDxVAHV0Vy0eheLA4MnjMMncLpUQJ/HJrT/ALK1H/oYLz/vxB/8RQBrUVk/2VqP/QwXn/fiD/4ij+ytR/6GC8/78Qf/ABFAGtRWQ2k6iykf8JDejIxkQwZH/kOqlp4Yvbd2afxXrd0pGAsjQKAfX5IgaAOiorHXQZVGDreqsck5MqevThO3Sl/sN/8AoM6p/wB/V/8AiaANeisj+w3/AOgzqn/f1f8A4mj+w3/6DOqf9/V/+JoA16K5278Ix3zq82ua8pUYHk6g8Q/EJgH8ar/8IJbf9B/xN/4OJv8AGgDqqK5y28G2tt5mdW1+beu397q052+4ww5q/wD8I/Zf89tR/wDBlcf/ABdAGpRXM3PgHw7eXD3FzbXcsz/edtQuCTxj/npUX/Ct/C3/AD43P/gwuP8A45QB1dFcp/wrfwt/z43P/gwuP/jlTW3gDwzaTrNHp8jOucCW7mkXn/ZZyD+VAHS0VnW2gaTZ3CXFtYQRTJna6rgjjFaNABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFAFe//wCQdc/9cn/ka8++BP8AySjT/wDrtP8A+jGr0G//AOQdc/8AXJ/5GvPvgT/ySjT/APrtP/6MagD0miiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAMvWfDuj+IUhTV9PgvFhJaMSjO0nrisn/AIVr4M/6Fyx/74/+vXVUUAcunw48GxyK6+HbEMpDA+XnkVpL4W8PpGIxoem7fQ2qH+la1FAGMfCHhliSfDukknkk2UfP/jtJ/wAIf4Y/6FzSP/AGP/4mtqigDF/4Q/wx/wBC5pH/AIAx/wDxNaEGmWFrAkFvY20MKDCxxxKqqPYAcVaooAh+yW3/AD7xf98Cj7Jbf8+8X/fAqaigCIWtuOkEQ/4AKlAAAAGAKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAr3/8AyDrn/rk/8jXn3wJ/5JRp/wD12n/9GNXoN/8A8g65/wCuT/yNeffAn/klGn/9dp//AEY1AHpNFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFZes6fqV+kI07W5tLZCS7R28cvmDsDvBxj2rJ/4RzxP/ANDzef8Agvtv/iKAOqormIfD/iNJ0abxreyRg5ZBY2y7h6Z2cVp/2Vef9DBqX/fFv/8AGqANSisv+yrz/oYNS/74t/8A41Uc2iXc8RjPiLVUBIOUFup4OeoioA2KK5iLwdJHJvfxT4ilGQdr3SAdQeyD0x9D64NaH/CPw/8AQQ1T/wADZP8AGgDXorI/4R+L/oIap/4Gyf40Hw9CQQdQ1Tn/AKfpP8aANeiuZl8C6XPIZJL3XNxwPl1i5UcDHQPimf8ACAaR/wA/uu/+Dq6/+OUAdTRXNW/gbSbedZRc6zIV/hl1e5dT9QZMGrqeGNMRAuLw47tfTE/nvoA2KK5m5+H3ha9nae60pZ5mxmSWaRmOOByWqL/hWng7/oBwf99v/wDFUAdXTZJEiTfI6oowNzHA54FcxF8OPCEMqSpodvuRgwyzEZHsTg1pv4W8PyLtfQtNZfRrRCP5UAXJNT0+J9kl9bIwwdrSqDzyO9M/tfTP+gjaf9/1/wAaoP4M8LSNufw1o7N6tYxE/wDoNJ/whPhP/oWNF/8AACL/AOJoA0P7Y0z/AKCNp/3/AF/xo/tnS/8AoJWf/f8AX/Gq1p4X8P2Epls9C0y2kK7S8NpGhI9MgdKu/wBm2P8Az5W//fpf8KAI/wC2dL/6CVn/AN/1/wAaP7Y0v/oJWf8A3/X/ABqT+zbH/nyt/wDv0v8AhR/Ztj/z5W//AH6X/CgDNbxj4ZWYQnxDpfmkKQn2tNxyMjjPftUv/CUaD/0GLH/v+v8AjWglnaxHMdtChznKoBU1AGT/AMJRoP8A0GLH/v8Ar/jR/wAJRoP/AEGLH/v+v+Na1FAHP3Pjfw1a2y3EurwGNjtHlhnbP+6oJHT0qn/wsrwj/wBBY/8AgLN/8RXWUUAcn/wsrwj/ANBY/wDgLN/8RR/wsvwj/wBBY/8AgLN/8RXWUUAYsPivSbjf5LXkmxtrbbCc4OAcH5PQg/jVe88Z6faSKn2DW58jO6DSbhwPYkJ1roqKAOV/4T3T/wDoEeI//BLc/wDxFH/Ce6f/ANAjxH/4Jbn/AOIrqqKAOdtPGFtesVh0nXAR/wA9dMliH5uBVv8At4f9ArVP/AY/41r0UAc7P4qnihjdPDGvTMxIMaQRhk9zukA/Imq//CY3n/QmeJf+/Vv/APHq6qigDn7PxJe3rOB4U1uDaAcz/Z0B+n72rf8Aat9/0L+of9/bf/47WrRQBlf2rff9C/qH/f23/wDjtH9q33/Qv6h/39t//jtatFAHP3Ota8s8aWnhS4ljYHdJNewR7T9AzZq19s13/oD2n/gef/jda1FAGT9s13/oEWn/AIHn/wCN0fbNd/6BFp/4Hn/43WtRQBjSXniHyn8rR7EyYO0PfsBntnEfSs/7b47/AOgHoH/g1l/+MV1NFAHLfbfHf/QD0D/way//ABij7b47/wCgHoH/AINZf/jFdTRQBzsVz4xbyvN0zRUznzNt/K23nt+6GeOe3p71ZlbxMYnEUekrIVO1nkkYA9iRgZHtkVs0UAcs8fj0uxS68NqmflDW05IHud4zSeV4/wD+fvwz/wCAs/8A8crqqKAOesofGJkb7ffaEqY+XyLOZjn3zKKu+Rr3/QS03/wXv/8AHq1KKAMvyNe/6CWm/wDgvf8A+PUeRr3/AEEtN/8ABe//AMerUooAynttfZGC6ppykjAYae/Hv/rqp22keI02favFAlxu3eVp8ceem3GS2Mc565yOmOehooAzrax1CG4SSbWJp4xnMbQRqG49QM1o0UUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAV7//AJB1z/1yf+Rrz74E/wDJKNP/AOu0/wD6MavQb/8A5B1z/wBcn/ka8++BP/JKNP8A+u0//oxqAPSaKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKjlnigAMsqRg8AuwGaAJKKr/b7P/n7g/wC/g/xpP7Ssf+f23/7+r/jQBZoqt/aVj/z+2/8A39X/ABprapp6IztfWyqoySZlAA9etAFuisi68V+HbKURXev6VBIVDBJbyNTg9DgnpUP/AAm3hP8A6GfRf/A+L/4qgDdorC/4Tbwn/wBDPov/AIHxf/FVLF4s8OTJvi1/S5Fzjcl5Gwz+BoA2KKxbnxd4dtLd55dbsPLQZO2dWP5DJNZ3/Cy/B3/Qcg/74f8A+JoA6uiuU/4WX4O/6DkH/fD/APxNW7Pxv4e1AE2V+1yF6+Tbyvjp6L7j86AOgorEPizSQ8iBrxmjQOwWxnJwc4H3OvHSqcvjvSYpXjNprbFSRuTR7plP0Ij5FAHT0Vy3/Cf6R/z5a7/4Jbr/AON1ND41064R3jsdaIQqG3aTcL1OBgFBn8OnegDo6Kx18RQOCRp+q8EjmxkHIOPSl/4SCL/oH6p/4BSf4UAa9FZH/CQRf9A/VP8AwCk/wqC78Ti2h8yLRNaumzjy4bMhvr85UfrQBvUVzH/CYzGYxr4T8RsMkB/s0YU+/MgrRTWLySNXHh7VAGAOGa3BH1Hm8UAa1FZf9q3n/Qv6l/33b/8Ax2j+1bz/AKF/Uv8Avu3/APjtAGpRXKnxF4mzx4GvMf8AYQtv/i6P+Ej8T/8AQjXn/gwtv/i6AOqorlf+Ej8T/wDQjXn/AIMLb/4utMX2tkA/2JEPY3o4/wDHaANeisG5v/EwQ/ZNBsnfAwJtRKDr7RntVP8AtLxx/wBC1o3/AIOH/wDjFAHVUVzlnf8Ai+S8hS80DSobYuBLJHqjuyr3IUwjJ9siujoAKKKKACiiigAooooAKKKKACiiigAooooAr3//ACDrn/rk/wDI1598Cf8AklGn/wDXaf8A9GNXoN//AMg65/65P/I1598Cf+SUaf8A9dp//RjUAek0UUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQBXu3u0iBs4IJpN3KzTGMAeuQrc+2Kp+fr3/QN03/wYP/8AGa1KKAOXll8d+c/k2fhwRbjsD3c5bHbOI+tN83x//wA+nhn/AMCp/wD43XVUUAcr5vj/AP59PDP/AIFT/wDxupIH8cM5FxB4djXHBjmnc5+hUV01FAGJJH4nZP3d1pEbbSObeRgDjg/fHA/X2qh9i8d/9BzQP/BVL/8AH66qigDlvsXjv/oOaB/4Kpf/AI/QLLx1kZ1zQce2lS//AB+upooAx0s/EGwb9Yst+Odtgcf+jKz59C8UyzvInjJoUY5EaaZCVX2Gcn8ya6iigDlP+Ee8V/8AQ8S/+CyD/Cj/AIR7xZ/0PEv/AILIK6uigDJGlX+BnxDqBOOT5Vv/APGqX+yr7/oYNQ/79W//AMarVooAyv7Kvv8AoYNQ/wC/Vv8A/GqpyeGbua9FxJ4p1zaCMwo8KRtjtgRA8+xFdDRQBkf2CP8AoKap/wCBJ/wo/sEf9BTVP/Ak/wCFa9FAGR/YI/6Cmqf+BJ/wrPm8D2U8zyvq3iDe5ydmr3CD8ArAD8BXT0UAcr/wgWn/APQX8R/+Dq5/+Lp8XgXT4pUk/tTxA+1gdr6zclT7Eb+RXT0UAZJ8OaeQQWvsH/qIT/8AxdZP/CtfCP8A0CT/AOBU3/xddZRQByf/AArXwj/0CT/4FTf/ABdH/CtfCP8A0CT/AOBU3/xddZRQBgWfgrw3YxlIdItyD/z1zIfzYn1qz/wi+g/9Aex/78L/AIVrUUAZP/CL6D/0B7H/AL8L/hUU/g7wzdKFuPD+mTKDkCW1RgD+IrbooA53/hAfB/8A0Kui/wDgBF/8TWr/AGNpf/QNs/8Avwv+FXaKAKX9jaX/ANA2z/78L/hR/Y+l/wDQNs/+/C/4VdooApf2Ppn/AEDrT/vwv+FH9kaZ/wBA60/78L/hV2igCl/ZGmf9A60/78L/AIVZgt4LaPy7eGOJM52xqFGfoKkooAKKKKACiiigCKC3W383a0jeZIZDvkLYJ7DJ4HsOKloooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAr3/wDyDrn/AK5P/I1598Cf+SUaf/12n/8ARjV6Df8A/IOuf+uT/wAjXn3wJ/5JRp//AF2n/wDRjUAek0UUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUVQ1bWLHQ7P7XqEkkcG4JuSF5ME9OEBP41h/wDCyPC3/P8AXP8A4L7j/wCN0AdXRXP2PjXQ9SLiylvZzHgts064OM9P+WdF74utLMoF0zXLndnmDSp22/XKigDoKK5X/hO7b/oAeJv/AATzf4Uf8J3bf9ADxN/4J5v8KAOqormrfxnDdSiOPQvEIY95NMkjH5tgVe/tx/8AoDap/wB+l/8AiqANeiuYm8V6jHM6J4N16VFOBIv2YBh6gGYH8xTP+Eu1P/oSPEH52v8A8eoA6qiuV/4S7U/+hI8Qfna//Hqv2+t6lcQLKfDOpQ7s/JLLbhh9QJDQBt0Vk/2rqP8A0L95/wB/4P8A4uj+1dR/6F+8/wC/8H/xdAGtRWT/AGpqP/Qv3v8A3+g/+Lqna6r4nuLh0l8MQW0YBKyS6mp3c8DCoSD/AJzQB0VFZX2nXv8AoFWH/gwf/wCNUfade/6BVh/4MH/+NUAatFYl1c+J/IP2TS9K87Ix52oSbffpDmqH2jx9/wBAzw3/AODCf/4zQB1VFcr9o8ff9Azw3/4MJ/8A4zV21fxW8ObuHRoZcn5YpZZBj6lV/lQBu0Vg3aeLZI1FncaLC+eWlhllBHpgMuPrmqf2fx9/0E/Df/gvn/8Aj1AHVUVyv2fx9/0E/Df/AIL5/wD49UsFv428w/adU0Dy9px5WnzZz26zdKAOlorJFtr+BnVdPz3xp7//AB2l+za9/wBBWw/8F7//AB2gDVorJa118qQNWsASOCNPbj/yLWWNC8WhMHxmC2Rz/ZUWMc5GM/SgDqqKyf7K1H/oYLz/AL8Qf/EUf2VqP/QwXn/fiD/4igDWorJ/srUf+hgvP+/EH/xFUbjwzqdxIXHjDWocnO2JLYAcAY5iPp+poA6SiuV/4RHU/wDod/EH5Wv/AMZo/wCER1P/AKHfxB+Vr/8AGaAOqorlf+ER1P8A6HfxB+Vr/wDGauWvhy5giKTeJNZumznfI8SkD0+WMD9KAN6isO58Nfa4DDJresqpIOYrvy24/wBpQD+tUf8AhBLb/oP+Jv8AwcTf40AdVRXK/wDCCW3/AEH/ABN/4OJv8a0ofDVnDHsN1qsnJO6TU7gnk5x9/t0oA2KK5698E6FqTo95FeTsgwpfUbg4H/fyqv8Awrfwt/z43P8A4MLj/wCOUAdXRXKf8K38Lf8APjc/+DC4/wDjlXrbwb4ftYykemoQSD+9dpDwAOrEnt/XqTQBu0Vkf8Ivof8A0C7b/vij/hF9D/6Bdt/3xQBrEhRkkAepphuIB1mj/wC+hWVJ4S8PzIY5dItHQ9VeMEH8DVZPAPhCOVZV8MaSJFbcG+yJkHrnpQBuG6tx1uIv++xR9rtv+fiL/vsVQg8MaBaxmODRNOjQsWIW2QDJ6npUn9gaN/0CbD/wGT/CgC39rtv+fiL/AL7FH2u2/wCfiL/vsVU/sDRv+gTYf+Ayf4Uf2Bo3/QJsP/AZP8KAGXPibQLOdoLrXNNgmXGY5buNWGeRwTUP/CYeGP8AoY9I/wDA6P8A+Kqz/wAI/ov/AECLD/wGT/Cj/hH9F/6BFh/4DJ/hQBAvi3w25wniHSWPoL2M/wBac/ijQI42dtb04KoJP+lIeB+NWYNH0y2cvBp1pE5GC0cCqcZz2HqB+VXMD0FAHLf8LK8Gf9DHY/8AfZ/wo/4WV4M/6GOx/wC+/wD61dVRQByy/Efwc5wniGyY4JwGJ4AyT09K0U8U6NLGskd0zowDKywSEEHoQdtbFFAGSPEulF0VZpSzsEAFtJ1JwP4enPXtWtRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQBXv/wDkHXP/AFyf+Rrz74E/8ko0/wD67T/+jGr0G/8A+Qdc/wDXJ/5GvPvgT/ySjT/+u0//AKMagD0miiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAr3/wDyDrn/AK5P/I1598Cf+SUaf/12n/8ARjV6Df8A/IOuf+uT/wAjXn3wJ/5JRp//AF2n/wDRjUAek0UUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFISAMkgduaFZXGVYEZIyD3HBoAWiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAK9//wAg65/65P8AyNeffAn/AJJRp/8A12n/APRjV6Df/wDIOuf+uT/yNeffAn/klGn/APXaf/0Y1AHpNFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUANkljhjMkrqiDqzHAH41X/tOw/wCf22/7+r/jVXxF/wAgG5/4D/6EK5jQ7zVNcgnEmg6LaGbTory0ZZC+DLu2h/kHQLzjuPfjRRjy80jVRgoKUr7v9P8AM13v7eSKMPeZI2NODMfvB1+7z0xu6e1SfbYYot8F7H5rzT/KZhtAO8rxnA528+/vXEaXfX+m/DHw5cWVjY3uo3l4tnLNqLNIAWkdd5P3iMgcZGAa3fDF/Hq+qXceoWFlBcWIktblYVzA0qOPmTI6EMPcHI7VupwkmtTojUpyTWumptLqEDQSAaipDPEB85Uj5xuxlienXt+tao1KwAA+3W/HrMv+Ned+KvGOn+EvEV7Z30WnQWsluHtWktGkbzcAHOCAIx8ucfMS/FRXOv69psX2u90zwy1skVnM8SROsrrO2whckgFTnrnt9Kzm6b7mdSVN9/w7I9SjljmjEkTq6HoynIP406svw7/yAbb/AIF/6Ea1KynHlk49jGpHlm49mFFFFSQFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAV7/8A5B1z/wBcn/ka8++BP/JKNP8A+u0//oxq9Bv/APkHXP8A1yf+Rrz74E/8ko0//rtP/wCjGoA9JooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigDO16KSbRbiOJGdztwqjJPzDtXEWHh2HT/E+pzQ6RcR6Bf2It5LJIZAS4YncctgDBYDbjHYd69IorRTXLytXNY1Fy8slf+v8AgHmer+EdPfQU0vQdIuLCL7bFdypPbSTRy+WchSvmA4JxnkVtTWGnTtJayeHrj+y5bfyntktdoZvM3k4B9ea7KimqkVtEqNWC2j+JzMwsL2Sc3/h6e5VyQglsw+1CqArz2JQcewrPOnW8/jKfX73TLm7zBHFbRTaajPbMpbJSQnIB3HIrtqKHOL+z+InUg/s/iZ2gxSQ6LbxyoyON2VYYI+Y9q0aKKiUuaTl3M5y5pOXcKKKKkkKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKazEFQELAnBIx8vHU/y/GgB1FFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQBXv/wDkHXP/AFyf+Rrz74E/8ko0/wD67T/+jGr0G/8A+Qdc/wDXJ/5GvPvgT/ySjT/+u0//AKMagD0miiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAr3/wDyDrn/AK5P/I1598Cf+SUaf/12n/8ARjV6Df8A/IOuf+uT/wAjXn3wJ/5JRp//AF2n/wDRjUAek0UUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFAFe/8A+Qdc/wDXJ/5GvPvgT/ySjT/+u0//AKMavQb/AP5B1z/1yf8Aka8++BP/ACSjT/8ArtP/AOjGoA9JooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAK9/wD8g65/65P/ACNeffAn/klGn/8AXaf/ANGNXoN//wAg65/65P8AyNeffAn/AJJRp/8A12n/APRjUAek0UUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRWTr8aTRWMUgyj3kasM9Qc5qoR5pWLpx5pKJpXDvHbSvGu51QlV9TjgVmeez3dsBdmSESr+8G0Ako+VPHsP++vpXKHxb8NkuJ7eXVrSGaCSSORJZZFIZCQ3XryDj17UsnijwEmg2+spKZba5uDbWyp5geeQHG1VJHfucDkc1rF00t39y/wAzWLoxW7+5f5nTQz3FtYWgWTeHtg2GAATBQZ6dgx656VYjnuJFgXzwQ9wU3phsqEJ67QDyOoFYUE/h1/EEehXWnXNjqUsJnhhuG/1qDqVZHZTj0znjOMVk3XjL4bWdnbXU+oxLHcTPCoBlLqynDblHKgepAHIqnOk/+GX+ZbnRff7l/mejUVyX2rwWbS+u0vbOS3sI1luZY7kssasCVJIOOQOMdaz7XxB4IuptJjVZ4/7XJFg80UyLPj0J47jr6isrU+7+7/gmNqXd/d/wTvaK5PWJvCmhXllZXqN9svnKW1tD5kkkhHUhVycD1PFM0e88H65pt3f2LhoLJnW680yRtCVzuDq2CMYPWi1Pu/u/4IWpd393/BOvorziDxt8MZ7IXS6xaqm1m2PJIr8DJ+U859PXtV2HX/AU2mSagLuKOFLT7aVleRJPJJYBghIY5K8cc5X+8Mlqfd/d/wAELUu7+7/gndUVw+la54E1qys7uxuo3jvLn7JCGaRWaXBO3aeRwOvTpWRqPjv4f6be3EDRXs8NrJ5V1eW0EskFu/YO4PUnIGM0Wp9393/BC1Lu/u/4J6fRXJarceD9F8PLr1/JHFprqjJNvc7w3K7QDkkjnArG0bxj8Ote1SHTbG7/ANLnGYkmSaLzPQKWwCT+tFqfd/d/wQtS7v7v+CejUVl+Hf8AkA23/Av/AEI1qVM48snHsTOPJJx7BRRRUkBRRRQAUUUUAV7/AP5B1z/1yf8Aka8++BP/ACSjT/8ArtP/AOjGr0G//wCQdc/9cn/ka8++BP8AySjT/wDrtP8A+jGoA9JooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACsrXGCrp7MQFF7GSSeAOa1ax/EUBuLKBPJlmT7QpkWJcttwc1pS+NGtH+IjgLLRrvwR8P7y80weH9egtmmuzI0JVpFyWYbwWDMOnbgY7VSudO0v4u+C9H1mzaLQ9Zhmf7BFJIPLMisCw2j7wOAcgZHv3q/8IX4v03w5ceGNE1u5g0OQuEWXTP3wR8lkLA9OTyOfp0q/Z/DPRT4M0rRdRs9Ye809nljvraLy3SRzk7ck8ZxgH0o9lPsHsZ9jnPiXc+NrXxt4Ie/n0xbj7SBaR2LybDJvjDFywBw24DA7ZHeu51rQ/h/4C0OI3+iafe3NxMy24u4YmmuZWJbBkYAKOepwAMfimmeFUi8Tw+Itdn13XNStVMdo1xaJGkC54wqYBYZPPfOcDij4h+F4fHq6SZLfUoDp9x5hRrXKyoxXepwwIOF4Io9lPsHsZ9jkfGOi6r4Y+G+v6r/YunWZ1a5tlm020UeVZwJnBJXAdi2N3GPm74q38SLaWb4E+GbyG0817SKymaRF+aFfKAJHHAzgdR2r0vV3sdd0i40rUdG1KazuE2SR+UVyOvUHI5ArgpPA+pXlrp+j6lrWtXfh2xkRksTp4RpEU/LG8iuCQBgZ9unSj2U+wexn2MjSryfUP2oJZbhHVRZ/uElTBRDArAfXLH9aVkH/AAun4gaNC9rZ2+oaKweSQ7I0dooxvY9BzIST711nibwxFq/iaw8UaXBqGna7Z5Anay81JV2lQGXcOQCcH+fGKNj4Mkn0/wARnxC+pXuq68qxXF3BYiPy414VUGSOwz9B6Zo9lPsHsZ9iOJb74d/D6PUNT0Lw7qllpttGkctlK3mSh3UbyXQjByCcHk+1alvovgrxVYQfEDVraFrR7BAIrpgYbVFzuGOmQSw/DpmuUuPB3jafwV/wiL6oG0oRrEu7TG8zarBl+bd6gfhXXyeHrZvhf/whaWmpxR/ZBB562o+/ncWxnu3J+tHsp9g9jPscJpek6N44uZ9V8F+HBpFnoxuJI75HEct3O0R2Io/hAba2SeB0wScWPgtBDdfB3xOtxEkqyXFwHEiht37hDznrXdfD7TX8F+DrbRJrO9uJYnkd5Y7XaHLMT0J9CB+Fc1qvgvVbdru38HX+p6Jpuos731obJZFLNwTH3T5eMAjoKPZT7B7GfY89s9Ov/E3wS0LTbN5rjVU1qVLC2BGHUIWYZPAC5JySB1p8nj3WL/VdI8M+NNMtrO8ttTt3bUHg8qW3RXBAAAxjBIyOMH8a9Tv/AAw1p4Z0fT/Cseo6Xe6Q5a1uZbYyj5wRLuUnBLbic447YrF8Q+E/E/jS70tPEs6yadZzrLJDaaa0byYADfMWJGRn259hg9lPsHsZ9j1Pw7/yAbb/AIF/6Ea1KztBikh0W3jlRkcbsqwwR8x7Vo0Vf4kvVhX1qy9WFFFFZmQUUUUAFFFFAFe//wCQdc/9cn/ka8++BP8AySjT/wDrtP8A+jGr0O8RpLKdEGWaNgB6nFcX8IdF1Hw/8OrLTtVtXtbuOWUtE5BIBckdPagDuqKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooA//Z",
+ "image/png": "iVBORw0KGgoAAAANSUhEUgAAAvoAAAPoCAIAAAAgFM2mAAEAAElEQVR4AezdB5wkRfUH8D44kmSJShABRSUHyUklJ0GC5KigBBHJIJKUJAKSM0gSFAlKzjmLZFAySJQ/OR3p/t+5d9cMM7N7s7uze7O7r+GzV11d8Vc99X713qvqosgrEUgEEoFEIBFIBBKBliJwxRVXDG+na6yW9i4LSwQSgUQgEUgEEoFEoO0QSLrTdkOSDUoEEoFEIBFIBBKB1iIw9P77729tiVlaVxEYe+yxd9hhh2WXXXattdY66aSTxh9//Nlnn/2JJ544+eSTf/azn1111VWvvvrqWGN9TkyHDRu22GKL7bHHHueff/5HH3007rjjzjjjjE899dQll1yy1VZbLbDAAiLLNihc9l/+8pezzDLL7373u48//jgejTfeeBdeeKG/p5xyyhJLLDHOOONcd911buOpEpZaainhG2+8kTJy/fXXv/vuu59++mmllSVnIBFIBBKBRGAAIPDggw+WomEAdKejLgwhzDp6lvGJQCKQCCQCiUAiMIARwAEset9+++3qRXW3+2vl/Oijjx5zzDFK4Luz/PLLd7uolmcc2vISs8BEIBFIBBKBRCAR6BcIDBky5Cc/+UkLm3rDDTcE3WlhmS0p6nMTSUuKy0ISgUQgEUgEEoFEIBFoNwSS7rTbiGR7EoFEIBFIBBKBRKDFCCTdaTGgWVwikAgkAolAIpAItBsCSXfabUSyPYlAIpAIJAKJQCLQYgSS7rQY0CwuEUgEEoFEIBFIBNoNgaQ77TYi2Z5EIBFIBBKBRCARaDECSXdaDGgWlwgkAolAIpAIJALthkDSnXYbkWxPIpAIJAKJQCKQCLQYgaQ7LQY0i0sEEoFEIBFIBBKBdkMg6U67jUi2JxFIBBKBRCARSARajEDSnRYDmsUlAolAIpAIJAKJQLshkHSn3UYk25MIJAKJQCKQCCQCLUYg6U6LAc3iEoFEIBFIBBKBRKDdEEi6024jku1JBBKBRCARSAQSgRYjkHSnxYBmcYlAIpAIJAKJQCLQbggk3Wm3Ecn2JAKJQCKQCCQCiUCLEUi602JAs7hEIBFIBBKBRCARaDcEku6024hkexKBRCARSAQSgUSgxQgk3WkxoFlcIpAIJAKJQCKQCLQbAkl32m1Esj2JQCKQCCQCiUAi0GIEku60GNAsLhFIBBKBRCARSATaDYGkO+02ItmeRCARSAQSgUQgEWgxAkl3WgxoFpcIJAKJQCKQCCQC7YZA0p12G5FsTyKQCCQCiUAikAi0GIGkOy0GNItLBBKBRCARSAQSgXZDIOlOu41IticRSAQSgUQgEUgEWoxA0p0WA5rFJQKJQCKQCCQCiUC7IZB0p91GJNuTCCQCiUAikAgkAi1GIOlOiwHN4hKBRCARSAQSgUSg3RBIutNuI5LtSQQSgUQgEUgEEoEWI5B0p8WAZnGJQCKQCCQCiUAi0G4IJN1ptxHJ9iQCiUAikAgkAolAixFIutNiQLO4RCARSAQSgUQgEWg3BJLutNuIZHsSgUQgEUgEEoFEoMUIJN1pMaBZXCKQCCQCiUAikAi0GwJJd9ptRLI9iUAikAgkAolAItBiBJLutBjQLC4RSAQSgUQgEUgE2g2BpDvtNiLZnkQgEUgEEoFEIBFoMQJJd1oMaBaXCCQCiUAikAgkAu2GQNKddhuRbE8ikAgkAolAIpAItBiBpDstBjSLSwQSgUQgEUgEEoF2QyDpTruNSLYnEUgEEoFEIBFIBFqMQNKdFgOaxSUCiUAikAgkAolAuyGQdKfdRiTbkwgkAolAIpAIJAItRiDpTosBzeISgUQgEUgEEoFEoN0QSLrTbiOS7UkEEoFEIBFIBBKBFiOQdKfFgGZxiUAikAgkAonAoEXggQceaM++J91pz3HJViUCiUAikAgkAv0PgSOOOKI9G510pz3HJVuVCCQCiUAikAgkAi1DIOlOy6DMghKBRCARSAQSgUSgPRFIutOe45KtSgQSgUQgEUgEEoGWIZB0p2VQZkGJQCKQCCQCiUAi0J4IJN1pz3HJViUCiUAikAgkAv0PgY033rg9G510pz3HJVuVCCQCiUAikAj0PwSWXnrp9mx00p32HJdsVSKQCCQCiUAi0P8QOOqoo9qz0Ul32nNcslWJQCKQCCQCiUD/Q+Bf//pXezY66U57jku2KhFIBBKBRCAR6H8I7Lnnnu3Z6KQ77Tku2apEIBFIBBKBRKD/ITDLLLO0Z6OT7rTnuGSrEoFEIBFIBBKB/ofADjvs0J6NTrrTnuOSrUoEEoFEIBFIBPofAquttlp7NjrpTnuOS7YqEUgEEoFEIBHofwh873vfa89GJ91pz3HJViUCiUAikAgkAolAyxBIutMyKLOgRCARSAQSgUQgEWhPBJLutOe4ZKsSgUQgEUgEEoFEoGUIJN1pGZRZUCKQCCQCiUAikAi0JwJJd9pzXLJViUAikAgkAolAItAyBJLutAzKLCgRSAQSgUQgEUgE2hOBpDvtOS7ZqkQgEUgEEoFEIBFoGQJJd1oGZRaUCCQCiUAikAgkAu2JQNKd9hyXbFUikAgkAolAIpAItAyBpDstgzILSgQSgUQgEUgEEoH2RCDpTnuOS7YqEUgEEoFEIBFIBFqGQNKdlkGZBSUCiUAikAgkAolAeyKQdKc9xyVblQgkAolAIpAIJAItQyDpTsugzIISgUQgEUgEEoFEoD0RSLrTnuOSrUoEEoFEIBFIBBKBliGQdKdlUGZBiUAikAgkAolAItCeCCTdac9xyVYlAsWHt34YKLx5yJsJRyKQCCQCiUBPEEi60xP0Mm8i0IsIlHSnF+vIohOBRCARGBwIDB0c3cxeJgLtjsBn7372/j/eH/7R8CHjDvnSql8a9s9hwu+e/e5EG0yk6R9c/8Enz30y/MPhEyw1wTjfGkfg/Svel6X4tJhg2QmGfrXyQ6YE8mjotEPHW3C8du9tti8RSAQSgb5FIOlO3+KdtSUCHSDwwdUfjDv7uOPONe5HD3z0wTUfTLj6hMPuHBZcB6cZ8qUhE28y8af/9+m7Z7076bcmlWC87443dLqhn7312bvnvTvJlpNUSv20UMI4s4zTQQ0ZnQgkAolAryPwxz/+sdfr6FYFSXe6BVtmSgRajcAnz34y4WoTKhVl+eC6D6qLHz58+HhzVxQ2Y08x9vBhwwU+fvLjT1//NNIM/3h4IW5I5f9xZk6uU41chhOBRKCvEZhooopCug2vpDttOCjZpEGJQIXGNL6GjD1kyPjoTNX1WTHR+hMNGToE0fnk+U8qXMfFE++LqaoyZDARSAQSgb5A4N133+2LarpeR7oqdx2zzJEI9AICQ2ca+tEjHynY36FfG7EOQYCCA9WRmKEzDP34sY8l/viJjz+8ZeQGrl5oVBaZCCQCiUDXELj//vu7lqGvUqd2p6+QznoSgU4RmGCZCbgqD7t32JBxhnxptS9JO3TGofxyJlq3gWZ4guUmeP+S97kz0+hMuErFBNbweuihh95///0hQ+roEh41fPg444wzzzzzNHzasLSMTAQSgURgtAhssMEGv/3tb0ebrO8TJN3pe8yzxkGKwBv7v9Fkz986/K0yZeSqzlsdluyto2sTl3mnK6Yrww0Db17yZsP43oicfK/Je6PYLDMRSATaCgFLqbZqT9mYNGaVUGQgEUgEEoFEIBFIBHqEwDLLLNOj/L2WObU7vQZtFpwINEKgJUqOTz755M4776Qxvuaaa4THHnvsoUOHbrzxxiuttNJYY4218sori2lUeYO466+//s0333z00UeVpqiPP664BC266KLbbrvtmmuuOe644zbI08WoGnVUF3Nn8kQgEUgEWoBA0p0WgJhFJAJ9hgB3HETnL3/5y1VXXcX5hpmc6njFFVf88Y9//OmnnyI9XW3J9773PVl++MMf7rbbbnfdddexxx77pS996YILLlh//fW//e1v77TTTjPNNNP3v//9rhab6ROBRCARaCsEujw5tlXrszGJwOBB4KOPPtphhx0uvvjiF198ccYZZ7zwwgu/+tWvzj///KUip+Q677zzzksvvUTNM/7445988smXXXbZeON9fs7yhx9+uOWWW66wwgrDhg2rnOgz3nhKkxiSC4+4BH75y18ed9xxZ5999hZbbPHlL3958cUXV85UU001eNDOniYCiUD3EDj11FO7l7G3cw1pW6+i3u55lp8I9DECYdPpnjHr8ssvP+aYYy699FJt/vWvf73//vvXN56+5+abb3bGF/UPMlSfoGHMlFNOyW5FhbPJJpvUJHjhhReWW265Rx55RPyCCy6oDahPTZpmbnvS8WbKzzSJQCLQPgiwsC+77LLac8UVVyy//PLt07DU7rTPWGRLEoFaBD744IP77rtvl112cZTFV77ylfPPP3/eeeel1Il0rFcPPvjgfvvtJw1Fzssvv/zGG81u/ipreu211/bZZ58JJpjgoIMOUuDkk09+6KGHzjfffBNOOOF000137bXXvv3222+99dY666wz11xziaTmWWKJJcrsGUgEEoFEoBqBUs1cHdkO4aQ77TAK2YZEoDECv/nNb5APzxiV8IzqRJx4DjnkkHPPPTeci6sfdSOMVz322GORcckll1xllVW22WYbBq9pR1ziWcR48PznP//hv0zJ9N3vfrcbtWSWRCARGPAIOOurPfuYG9Hbc1yyVYMdAQqbrbfemgGLE/HDDz/MkyYQefLJJ7ENm7AQjjPPPLMlXKce60suuUS9tDgMZFEFt2VVH3/88dNPPz0L1znnnEMtVJ8xYxKBRGCQI3DRRRe1JwKp3WnPcclWDWoEmJAoUZiQTjnllM033zyw4Ga39957n3feeVQsTaJDq8zbRkZeyXZvvfrqq1iUWzvPR1sCz+hbbrnFzvall15avaiPHVtbbbWVHVtrr722HWEMXjyaN9poo9EWlQkSgUQgERjjCCTdGeNDkA1IBL6AAEc/JMMROGeddRZWUT77xS9+cfTRR5e3nQcmmWQS3jYzzzyz7eWhnrGBC9GxA+uJJ55gBcNd/vGPfzzzzDOdl8ObB/fiOYTxrLvuuvyaJ554YrvDfvSjHzFvnX766WussUbbfgC5867l00QgEegNBCzVTjrppN4ouadlmgHzSgQSgT5A4PX9Xvd/5xU5Pgd7WGuttfggf/bZZ5EYsfBxq2YcAHkcU7pcd911//rXvzqvyFPOOg7aaf4I1G984xtsWFHs//3f//3973+fdNJJMTMfQO68rmY63nkJ+TQRSAT6CwIcCoOX2JnVVm1O352e8sXMnwi0CgEHHDvfzx5O88Ucc8wRH++k7MF+GKHoe0Zb0WGHHfbPf/7TyYHo0WgTzzbbbByA1Mg3ebSJJXj88cdPOOEEjEeYjWzVVVfdc889UTGLOWf5NFNCpkkEEoEBj8Duu+/enn1MutOe45KtGnQIcArmXsM29Oc//zlODuRqg/cgE83sdOBKzJ35Zz/7WVeBY5zimNzkmTo33ngjZ50jjjgiavn5z3/OlYeKaPXVV3e2YVerzvSJQCKQCPQZAkl3+gzqrCgR6BABTsH8fzkUH3DAAXECMj9lRGe99dZz7E2H2aoe+KxEJ1yH+w4FjPLLHMJiwq0H47Hn3KE+zXjhMLE53Dm8iKR38vJPfvKTK6+8kkNPWXgGEoFEIBFoNwSS7rTbiGR7BiMCtpSjNWecccYss8wS/fedBxyoSSx4Mc8666x//etf/zbiQn3+97//RV62c+YweqPJJpuMgSwO17HrypmBThTEsdAURIf/DRMYNY/IZirdbrvtDj/88EjpnEPl27R12223NZM30yQCiUAiMAYQaCtPomxMIjCAEejIY3fHHXf0y/ehmbLvlCW8gJucDr7+9a8/9dRTNk9Vp+e7g0IpMAxPrGNTTDGFBHvttZdIqp34AJaPjDooWfwiiyyC9HjEOFVdTidhm7yOPPLIaDOuxuVZmx0RFDHVfzvqeHWaDCcCicDAQMCMFPNGuip3Mn/mo0Rg0CFgf9Mf/vAHupzNNtssOs+JxxF/jFlNYuHoP/NL6cjsmBz7s7g2O4WZrWrqqadWDqvTUkstVV/gT3/6U3og3xm9/fbbfTMLa9GYZraAKYpVi1bJDjJh5jAHAlERsW3V15IxiUAiMHgQ+MEPftCenU1jVnuOS7ZqUCDgVBvfq2LA2nXXXaPD1kMMTM1vdNp0003xmxIsDst2TsXJhD6thbjY2e47EMiTHVhiOBeXiQVQFtyIDcsWrffee8+XRyXmmlOdpvOw73mFk7K9WvaF8T1yEnTnWfJpIpAIDGAEqk8La6tuJt1pq+HIxgwuBPjNOCDn97//vfMAo+d8Ypr0TZaeToU5adxxxy1Re/TRR31di12MiYozja3szhJ0Rk4kcLRgfGcUyymzCKA4mIrA008/7e+MM85Y/bTzMH7m6OdIQ9mz6KKLnnjiid34UmnnteTTRCAR6C8IMIu3Z1OT7rTnuGSrBj4C7E0O1KFuYbrSWxRk++23d+RxD3tuS7nvfbJhsV75jCjtDpPW3HPP/Z3vfIeLz0wzzeRTXLfeemvs/4q6nnvuudD6OIlHDAvXnHPO2XwzuCrffPPNkZ7/8gMPPOCcw+azZ8pEIBEYSAgsvPDC7dmdpDvtOS7ZqoGPwFFHHcUzcd999+Xzq7fsWVQ1zXeb5ia8jGuyMG+xKz3//PMXXnghh57YfH7ggQc6EhCjevbZZ9nOGNcjXgNef/113z9HjDga77TTTkrDhOzPYgiLcw5ryq+/pcvxTYl7773Xo3nnndcZPPbP33DDDfUpMyYRSAQGPAK+ItyefUy6057jkq0a4AjYEM7MFERHV+lXbCFvss+2lFML/eY3v6GtqT8px0GFVCyIDs7BrhRlOsKHkSvCd9xxB69kRMctsxfTVbgbc9wpd6H76DoXZnog3MXurdE2zNfRnbksmcQLLrggfZJ9YaPNlQkSgUQgEegzBJLu9BnUWVEi8DkCzsjBJ3jqxIZwn2IIv5nPUzQKOVxHSlxEdj7OvIxLBQyVTOyo8he5Yckaf/zx77777quvvpoZyxdDqYLokyhdnL7DiYfbMj8etXP92WabbZzNgyeVdWJRSJWzBJnh7RRz0PMMM8zQOe+hmopDCzkqzj777IjUyy+/XBaYgUQgEUgExiwC+UX0MYt/1j4YEeBbc9NNN+EfcciN/VmjNf2gGhtvvDFj07e+9a2GkGEYNoFjGL7ZKYHPb4X+hgKJ8iZYUfx1Qo9API2i3LoaFuvAntj55XPoPq5+8MEHN0wm0qckHBfELkZdxHmZ/R6F2nDDDTtKn/GJQCKQCPQlAqnd6Uu0s65EoILACy+8gArgJew+bvn2dr6XgS8zjuLznB1xnYB1nXXWsTcqwugLouNy6y8aRJlk31bclk9HJBmrI64TRZV/OQDtvPPO5W1NgPmM7Sz2fFEm4We+4eX45ppkeZsIJAIDG4H//ve/7dnBpDvtOS7ZqoGMgI886J4NTdFJ3soUPB112Nes2JIcqBPfDe0oWSfxvGqWX375lVdeORQ/naTs/BFWdMghh8QZ0A1T8kaitfJIa+ObEmIapszIRCARGKgIcCtsz64l3WnPcclWDVgEePX+6U9/ctQNFYhO8q3p5OOanHUcD8hHp9twULdwN/ZtB/U+88wz3HQ6oVbN1HLooYeyanWUslT/fPOb35Sm2mTWUZaMTwQSgUSgDxBIutMHIGcVicDnCFx00UX/+c9/nG3DWVjs+++///mzutAvf/nLnnAdW7ecu+MsH3WFVubYY48tGUldbc1GsGqVVrOaPExmYcBykI/98KV5qyZZ3iYCicBARcAncdqza0l32nNcslWDBYE777yzo66aNShjOnraTLzzlHkF4R/hxBNZnMfj9J1msneShpO1rVv1CZSMDEU86xv/5XTfqUcpYxKBAYxAHjM4gAc3u5YIdAEBLr32ZMVnrVABH/JsmNlXP7v07ar6Quz/+vWvf40w2XkuXG4LZ9LyXa369DUxb775pr3xPqRVEx+3Cy200HLLLdfwURxgiGD5Brut6Y4xbJgsIxOBRGBAItC2P/nU7gzI9y071b4IcNZh5fExh86b6IycjvZhYUgO3Ql/504KcdigI3OwFgcYOjWn/M6DLHvsscdZZ53VUV7nI3PQcVCyL3k54KejZE7Wqf46aU0ydEchTHV77713zaO8TQQSgQGMQBzO3oYdTLrThoOSTRrICHBMLj/q6VMPDW098RmHehQoSxyi45hBTGKzzTbzxQaUCHGxlZ3+pjp9sBwxDuP57W9/61yfmiNwara+v/vuu0rmauNMwlVXXZV/j5N7nLVDM4RaVZdchumoerjVqywqA4lAIjBgELDVtD37knSnPcclWzUoEMBa3nrrrfquOqzPp8Xr41999dW55pprgQUW+NWvfkVx4iOj//73vzfaaCNfAPVdiGr9Dcca3GXKKadUiO858FOudt8R+c9//lPeqIISCBlSst3jzuZ58cUXxdvP5bMSvlYRn5iIlDV/Gx7Y47DB8hvsNenzNhFIBAY8AnTJ7dnHpDvtOS7ZqkSgMQIYBo8cH3/wSazqFKxODtfhTxOG8xVXXJHVzNfRIw0KUqP+cRSY73Z5+ve//90xhjWb4VmyFEi7w/W4k29H+AhGvcWNLcwhikq22d4XLXq47726jxlOBBKBRKDbCCTd6TZ0mTER6CYCPlnVec5OEoRChftOWJ2qy0FoUJxll12WecuuKIcaO5/QsT1TTz01K1gN3ZHxpZde4jHt+vDDD6vLUcK555573nnnOcq5Or4+zOhWGuaqn/7hD39wO//88y+zzDI1hVcny3AikAgkAn2GQNKdPoM6K0oEKgjQdgQb6AgOn/bs5NNUkYuzjt1Vf/zjH2lxasqhXDn++ON93ZMlC2tZfPHF+RRjNpx4pp9++urEe+65J3NYjeGJzesnP/kJwsS8ZRNZdfoMJwKJQCIwWgRuvfXW0aYZIwmS7owR2LPSQY0ApUjn/e8owXTTTedEY0ctzzbbbG+88QaPHAc0U8bUlGa62XrrrdmnmJMWWWQRe9p9TstHzmtcbSaeeOKa0wLphJxDKLGPPzgWmZ/yPPPM0/mxhLvuumtN7XmbCCQCgxkBXwhuz+7nF9Hbc1yyVYlAYwR+97vffe1rX0NE+DL7RAMG45hme6muu+666gy8dpxSyBX6+9//PqdjzjQ+VL7YYovZC1Ym4+y86aabnnTSSbfddltECnN8plv67ne/6/Olyqfs8a31Mkt9oN53Rxqu1vUpMyYRSAQSgTGIQNKdMQh+Vp0IdAcBChgexLY/+B6WM/1+//vf/+xnP6uhO8rFeHyAwi50rs12jD/00EOdf2QUkdp44425J1fvUZ9lllm23XbbrrZyzTXXlMVOsSuuuIJvUFezZ/pEIBFIBFqOQBqzWg5pFpgIjAYBNGU0KTp9bKuUY3XsD/fhT9/D8lUs7j6clOsP/XPczlJLLUWvYx+WImuMWUxmPmAe+7MYvNZee23+OtVcRxZUyfk6nTSHS1BHT99++22PajbAd5Q44xOBRCAR6FUEku70KrxZeCJQiwAVC5+b2tiu3B922GHVyR1UuMYaa7zzzjuXXXbZNNNMU/3IpnTaGu4+nj7yyCM12h20iauyNJyBbrnlFuf0cG2uzt5MOPacV6d0YHTDz2lVp8lwIpAIJAJ9jEDSnT4GPKtLBIryaEGGnvo95zxmOvpSVWDnGxQuHjzsWb5LJUwBw1PHyYE2W9Xg+8ILL/gAO49j27hqPKDphNAgDsuOGaT4YXvy4XSqIJfCxR9xxBF2ktcUONpbBwJxqR5tskyQCCQCiUBfIpC+O32JdtaVCBRcjJ977rkAwmnImAqX4WpcuOPssssujsypjqwO8x12KA5yM/nkk/M1jpNvGMhctp1T4dR8R90udLaq+uP+HBJo15WPUWBXtmIxipUnCiJGvsnl3MKavevVzRht+MYbb5TG1rDihdGmzQSJQCKQCPQuAkl3ehffLD0RqEFg/fXX94VOzjedWHycCliTq+aWAsYHH5566qkzzjjDycUUQhLgSfPNN98BBxyAPyFMESmevYkGyJar8OApi8JpvvGNb/i2+Wqrrebj52V8BKiLGu66qk6GJ3V0iqAze04//fRJJ51Ufz/4/QfVuTKcCCQCiUDfI5B0p+8xzxoHNQLYiSNz+N/st99+3QbCoTjckH0youZErzvvvJNaiDuObVnlXi0HCZ5wwgl2Sy2xxBJljfQ9vJhZ02ib6rkOmmKXVpm4o4A9Yixl1U/Z5mx9r47JcCKQCCQC7YBA+u60wyhkGwYRAl/5ylf0luHJX4YnO73rO+8oHXum6uOrYzju2EtVHRNheiP2KdYunxGtf1rG+CqWqg866KA77rijjIwAVZAjCh3SUxNff2s/fE0kX+nS3Ye2CaXjIVSTJm8TgURgACPg+zbt2bukO+05LtmqAYvAyiuvPO+888YXrNAdhq36rvKzoTipj6+J2WuvvRizHDnI0ZgHT3k5atnHzH0LwqnKkSW2i5cb0W04dwKhD03svvvu2lBmpHmi17nwwgspfmrqqr9lSjvmmGNq4pUQMb4waiN6cLuaNHmbCPQZApSdHdlb+6wNg60iezPbs8tJd9pzXLJVAxkBihPGrCeffFInHYi8wgor1PfWrnK7xOvjq2N4FvPIsaPqtddeYyArLy41++6777e//e3S39lxf44ZDC7C3sTBWTnMVe+++65tYpGRCex///ufVi255JLVtXQU3mmnneofxefACJjTTjuNb5AdXvVpMiYR6DMEfGIFm++z6rIiCNQfANYmsKTvTpsMRDZjECGw/fbb06ygF2HJYnW68sorS8/iAMIWcWl8+Xy0uHB55ox8yCGHMBthGFGOv/ydHRJ46aWXOnPZtyMcq+Op0pAt7skUPFgR1U6Uz7MYebIVi05otDVK4Jye+hN3xNsY768jEB176MgfX6JoprRMkwj0EgI+lNtLJWexHSHQtpgn3eloyDI+EegtBHACW9CdDXj99dfbG+VQHFTDaYE19fnS3s9//vP555+/Jr7+1nLKrm9bx2sch2l0+DL7ElYokBAgpWFXk0wySQ27YsOSvXkv4zPPPBMhq2kJRsXxWWR4Sfu6RU2CvE0EEoEBj4BzvNqzj2nMas9xyVYNZAScl2OflAMAr732Wv2caqqpdthhh4Yd5tlTzyrqU7JScdZBnuzAChVOpLHlimXKoX+qo8uh12Hect5gNdfhXOyr5vfcc499XqXnTX0V1TG+XIHuVMcIUzLZcy7AZef444/XKV/sqkmTt4lAIjDgEejJYV29Ck5qd3oV3iw8EWiMAD2KA3Ic7rfFFltQ7SAKTql55ZVXalJbJ/3whz+UrPMPV0UuZyI7LIcm2be0uM7E9nLUxBfRfQmLmw7T0oorrlhuUFcp/x5+PF2antjF+BuFq3V1a0VGI/kvP/PMM0cddVQYtqrTZDgRSAQGPAK5M2vAD3F2MBHoAgIULTZs80e2b1y2ueaai99Mw/x0NjWH6zRMVkbaYW7H1t13323nlO85ONQY77FlnYfyKqusguv4OoSqHcrMMYhzT5e4jlqUH18VLWsU4DYUXz6nsuJFZAtYfkeiGp8MJwKDB4FTTz21PTubxqz2HJds1cBHANXQSTvJo6v1n7sqIfjd735XhkcbMNfwCrLP3K6oc845x/k9U089NR0Prx3uw7LbuC7g/GV73Sl+Gm6w6qgW3xC9//7765/iT7EdgzUNgVOyNtQny5hEIBEY8AjEyqcNu5l0pw0HJZs0KBCwPYr2hR+xLVo67KBkFiiGrfrO0+7wsHGMcv2j+hg7b0XyGqZxcU000UQ1NjInL4tXEe7CJlV+r7S+qJoYzGyDDTao/8AFt2vVSfzyyy/rwtZbb20vWE3evE0EEoFEYMwikL47Yxb/rH1QI+ALnQsvvDAVC+8ce6O40dh8zsxUA4pTB1999dW11lrrggsuGO2hOE5bdk7gvffe60OkY401lkNHnN/D5Tnck3/605+us846PqqlTHYu5xCiL9x6sKKaSmtuKYo4BsVh0DWPfJHUcYLO2uFm5LNcXbWO1ZSWt4lAIpAI9AYCSXd6A9UsMxFoCgHHKzP6+OADOhInFPMptkPq8ccfr8/v01ecb5yjU/3pq5pkfISVRnPDdcYXzuOpXeg2Xv3tb3+bddZZQw0T8TyHHCpo7zqf4n322aemqOpb+7A6+oQWWxgKJbGTDO+66y4WtN122606b4YTgUQgEWgHBJLutMMoZBsGLwKsPxQt/tKR2NHg/HWangUWWIDGpR4Um9KpghCXjs4t9RGrww8/3JmBTFQOVlYCpY6t6bZTCVO9sKDZkU5JQ/FD/aNAG8gPPPDA+roixnnN2uP4n4YJ2LbicB0Fxlcv+AyVn6pomCUjE4FEIBEYIwgk3RkjsGelicBIBBxOgyjwJnaoYHyBYbbZZqOYcdsQI44+nvoIKF+fepdA37riQPPoo4/SEiE9SqDpeeSRR8K/mL2JAoZvDU8gT23RQnpsR+/oy1ZO6OFaZFt7w5b4fkXodeyWP+6447g/s7Wlh3JDrDIyEUgExjwCFn95JQKJQB8g8Pp+r/u/YUW//e1vzQW//OUvaXokwEW22mqrzmcHShQ7tlijqgs84ogjvv71r/skBbVNGX/JJZdUF2UbeTxixrJf3ddDHbKMqZTpBRzHjBVV56oJc9Mp02u2p7RENFJlZHWgk45XJ8twIpAIDAAEyk/HMHC3VXdSu1MzjedtIjAGELBFi38MssJb2UYnn7Ki8uFE3MkJFuYRe9dpX7ge/+Y3v9Fop/xhOS+99JIjfNi86GxsvHJQMoee6i75CjpqIjGtDMbjcEK6GafyYFo+ZGEb+d577439cBWqzlUTlr6MiXOc5aVtUrj2pz2rBCcDicBgQ8CXhtu0y21FvrIxicAARqBzJQf3Fxu1TBOUJQEC/sGF2Ue1Op87GKTQF0YxO6cuuugiVjAbr5TmsMFOMjKZOYdQRT6H/ve//906bOWVV1YITU8nucpHCBmvZHu+lKA6l0OiPcWu2NpYzarHsfOOV6fMcCKQCPR3BCiYY6JoN+3OEMiWU1gGEoFEoPcQeGP/NxQ++V6Td1SF448pZmzLoq0JR2MpnRC40korNdyr1bAczjq+UEHj8u8RV8M0EengQZvGqXN8XrSTZJ08kp0eaM4553SQj2T77bcfzZBAfBNDSyLvaDveSRX5KBFIBPoXAjPPPHN8wQbd6eiw+DHSozRmjRHYs9JEoAECVkUmCH48nG98RtSX0u3Asnuc1cnhgXhPgzx1UUxgstdFN4hwwE/9GT8N0nUcZasXO72vZTlXECfD0jhBM8A5pIeCxxFBIkerneq4+HySCCQCiUDLEMhTlVsGZRaUCPQcAQsjdIE9yDfSfZABn1Cm3em+BcGbx5mBPa+i5SXYqW5Dlk+cKpmHteN87Au75pprWOXE2xvf8hqzwEQgEUgEuopA0p2uIpbpE4FeR4C+xGF9PvLgJJ6wNPE7dvjNX//6V5807/Xqu14BP2UKnm233ZY/kEML11xzTU1l4bKJvT0b3PUuZo5EIBFoCoH2XJVpetKdpsYvEyUCfYkAA5aj//70pz8xCTF+u3w2y+701VZbzaHJ9l4ddthhs88+e182abR1DRs2zMHQWkiv4yRDZ0NTTf3qV79yCFDk5Xk92kIyQSKQCPR3BJw+2p5dSLrTnuOSrUoECt9t4IVDO8J3Z/HFF0dxgOJsQB+6Yuq69tprjz/++KmmmsrOrJaAZfd4eBz3pDTqHG5GO+64o0KoeRycuN1220WBsVu+J4Vn3kQgEWh/BJwR356NTFfl9hyXbFUiUEHge9/73mKLLeYwGx+O2HXXXe2immuuuShOvvzlL3MKtvPc8cqHHHLIgw8+aA+5T507QrCrwNl57sxAqhdfCeVqw0PIsYQ92bDpuOcpp5yyvhmaWh+ZMYlAIpAI9A0CuRG9b3DOWhKBoif7sW3L4soTR+k4x88Htpwu6CPq1bA6M9CJguxfPtvpb5z1569DceLgL4fiOFQwsjiYR3ZfvHJmj0+jV5fj9EIHDzqPpzqy+fDBBx+8yy67SI8zUfP4hpdzd9x2sgO/+cIzZSKQCLQ5Am27ET3pTpu/Odm8gYNAT+hOoOAIQa4wZ5111iuvvGKDN9LDS4al3Il/ncAki01eDgakEAoi0knieOTLXL6j7hMTo01ZneDb3/72FltsEZYsW8mc+KypIm9d71bJku5UY5XhRGCgImBeoiTWu3Y7dyfpzkB95bJfbYdAz+lOdMnnzdGXM844I75z7rQen3Tw/Sykh0GKm3OTPbeLCq2R989//vNf/vIXJxNyN6ZA2nDDDZXw6quvMnLdcccdTZaG1lx66aVxoKppbq211rJdi3eRXWZDj68YzZPuNIlkJksE+jUCN9xwAyu8LrQb3UnfnX79XmXjByMCM8wwg6MI45MR99xzj49tQcFHsvx1zPHaa68dnjd2ciEf9kaxW3nEoxmDwYrCtdlTPjo1n9OSjIcN3qMQH2n3cQmO0s0cRYhjOW7H+UBK4EON61A7aVgwpzeKbtrFlJZXIpAIJAItQSC1Oy2BMQtJBEaPQKu0O9U18cuhofG5Bg43uAvvHOzktddeizQMWPQ9ZXq8xzdE3XLocRqyTV7C00033UEHHcRV2WkZdDk+ffWvf/3LLvcLL7xwxhlnVL7dYbyh+UE39F+W68QTT3TQjorUiyfdfvvtUjossdyP2hsdLzuVgUQgEWgrBFK701bDkY1JBAYIAkxRLp05+eSTo0vYBisV3uMW7ag+7QbLQYDEU/A4ICe+ZB654i/D00ILLeRsw3vvvdcXQy+//HLqItu1Fl54Ya5CFDbViYUVyFy1ySabCNs1JuUtt9yiEN86XWKJJWoS520ikAgkAmMQgTRmjUHws+pEoPUI2GZVs9OqS3U4yOfll1+2t+uPf/yj4w0xHjoeZzpz7jnqqKMY48vSMCoHbIS5il4Hf8K0fORr8803T65TopSBRCARaBMEWnNAWZt0JpuRCCQCPUSAwgaPcTyg7RWPPPII+uLUH1YwH/v0bSxfiojypWHDCq5DwbPoooviOuuuuy56FF5EPWxGZk8EEoFEoLUIJN1pLZ5ZWiIwEBBg8zr66KOPOOIIljKePT72qVcojvN4gvHQ68SxgY7n8bGLxx9/HNfxIfSen8s8EODLPiQCiUD7IZB0p/3GJFuUCLQHAttvv7295Vx5mLEwnnADcjLhQw89FG7I+++/v6dchRiwECCaofZoeLYiEUgEEoFaBJLu1CKS94lAIlAi4CwfO8xnm202rjy2l1933XV2YNm3hdnYw+UzWLyhRTr/MPU6JWgZSAQSgTZEIF2V23BQskmJQBshEIwnPkp69dVX89Sxd/3666+n2rFvy7cs2u3b7G2EXTYlEUgE2gaBpDttMxTZkESgXRHwEZyLL77YOc78dTbaaKNoJtJD8TPnnHO2a6uzXYlAIpAIfI5A0p3PschQItAHCMSZe31QUcurWLVY9bV9Rh5gOLLwi4o3LsoTk1uOdBaYCCQCrUcgfXdaj2mWmAgkAolAIpAIJAJthUBqd9pqOLIxAxmB/EbmQB7d7FsikAi0NwKp3Wnv8cnWJQKJQCKQCCQCiUCPEUi602MIs4BEIBFIBBKBRCARGIFA+f2+dsMj6U67jUi2JxFIBBKBRCAR6K8I1H9LuE16knSnTQYim5EIJAKJQCKQCPR7BKaZZpr27EPSnfYcl2xVIpAIJAKJQCLQ/xBYbbXV2rPRSXfac1yyVYlAIpAIJAKJQP9DwHeF27PRSXfac1yyVYlAIpAIJAKJQCLQMgSS7rQMyiwoEUgEEoFEIBFIBNoTgaQ77Tku2apEIBFIBBKBRKD/IfDxxx+3Z6OT7rTnuGSrEoFEIBFIBBKB/ofAL37xi/ZsdNKd9hyXbFUikAgkAolAItD/EFh99dXbs9FJd9pzXLJViUAikAgkAolA/0Pgww8/bM9GJ91pz3HJViUCiUAikAgkAv0PgQUWWKA9G510pz3HJVuVCCQCiUAikAj0PwTuvffe9mx00p32HJdsVSKQCCQCiUAi0P8QuOuuu9qz0Ul32nNcslWJQCKQCCQCiUD/Q+CVV15pz0Yn3WnPcclWtQ0Cf52sR03pYfYe1Z2ZE4FEIBHoawSOOOKIvq6yufqS7jSHU6ZKBBKBRCARSAQSgdEh0LbfzBo6upbn80Rg0CNw/57F/24pPnq9mHO/YoY1io/eKO7Zrvjw5eKzj4p5Dy2mWLB46+Hirq2Kj94sZtmi+NYOxYevFHf+tJJs4llGYlefxQOKH6VNPm8xW5ueyjXoBz4BSAQSgYGDQNKdgTOW2ZNeQeCzYcV4UxbL3Fi885/i2mUqBOVfOxezbVdMsVDx3nPFTasVK95X/OfoYu4Di8lmLy6do0J37t2p+NqPi5k2KP57UfHMuZVW1WcRqeSvrVt8ZfleaXYWmggkAonAmEBg3333HRPVjr7OpDujxyhTDGoEhg8vZt6sgsDE3yw+fqsSeOnK4p0nKgHXJ+8Vwz8t5jmkePbc4sVLio/frkS+ekOx8MmVwHSrFGONXQnUZxkyduH/aZetPM0rEUgEEoGBgsCzzz7bnl1JutOe45KtahsExh63GHeyUa0ZUgl89knxvSuKsccvhn9WMXJhLbesXcywZvHN7YrHjxuR4KOR6SXAlhpmETlkaDEknedGQpX/JAKJQCLQqwjkbNur8GbhAwCBut/IVIsV/72w0rGXLi8ePrASeP2e4mvrFJ9+WHw6rHI75aLFfy+uBJ6XbATdqc9SeZxXIpAIJAKJQB8hkNqdPgI6qxk4CMx/eHHnlsXjx1fUMwudVOnXN7Yurlq0mGzuih6IR858hxV3bFJx6MF7xhqvkqA+SyU2r0QgEUgEEoE+QmDI8FC291F1WU0i0GYInDPCPtVmjcrm9DoC64/QuvV6NVlBIjDoEDj22GO32WYb3b7iiiuWX76NtmLUKeoH3dBkhxOBRCARSAQSgUSgNQh85zvfaU1BrS4ljVmtRjTLG5wI1GgL2lNpVNNII6Wd6w9/6aWXXnjhhbHGqix+Pvvss6985Svvv//+m2++Odlkk33jG98Q+cQTT7zxxhtzzTXX//3f/7344otlyq9+9atTTDHFQw89NGRIRUkm72yzzTbxxBMLUxuL/+ijitf2+OOPP/vss/twoMhPP/30gw8+kH6CCSYYZ5xxlPDoo4/K8uGHH3788ccOKJtwwglfe+21ddddd6ONNjr44INlF7777rvlVc64446rbQoZNmzYYYcd9t3vfnfNNdf094QTTrj88st32GGHySeffOedd9511131Qpmur33ta/9Y75I3VnzdI6VVupxXIpAIDD4Eku4MvjHPHtcjUM8D6tN0EtNQgo4qEwmQlYB3CZS3pR25fCTGFWRCymuvvfaCCy7w9Nvf/nYoh0VKsP/++yMo6AKR79piiy0uuuiit99+e+jQofKKiUfC+MTYY4+9+uqrn3POOccufhzWMuussyqk5jruuOOUWUbutNNO//znP6+//vqlllrqhhtuEL/tttteeeWV//nPf84444zf/va3Zcpf//rXG2+88QILLFDGbLXVVscff7zbTz75ZLnllnv55ZeFVfr4449feOGF8lr5abBeHHnkkc8995xabr311n322We99dZbeOGF8RuRt99++9RTT33WWWdtueWWs8wyC9r09a9//Uc/+tHJJ5/8r3/96yc/+ckcc8yBJB1zzDE33ngjcE488USUaMUVV7zzzjsPOuggnExPPX3qqad+/vOf40BFcYn2lI3MQCKQCAxGBCrza16JwKBF4Oxi+NkFxcPf//536oG//OUv1113XTUYBD8yQaxGJA3EpZdeetlll51//vnin3zyyUq8QmquUTGXXHIJdQX+scsuu0jy+uuvTz/99JQZ5DoyQd8gLE3kxgZQhAi/9957iy22WExJSy+9dFn81VdfLSOliEff/OY3pfnb3/5G5zH//POLnHTSSSPX3HPPPfPMM0sjXo/EayTeUJYzMjCinfQlOkhPozHM7W5dW2+9tezads011wgER3nrrbemnXZaWhZHa2A2v/zlL5WzwQYbLLjggpD5/e9/j6aIoVNZZ511lPDOO++cd955iNchhxwiHmVZdtllo2q6IixK+N1339WR++67jwJJ7biXyE033VSlN91009lnny0Q2TEh4ZtvvlnkmWeeSaMjJaIjEit6/vnnDZYwLrjJJpuoGulxi2np+zPPPBP1VgZr1OiMjMl/EoFEoHUIHHXUUX53Lj/n1pXagpLSdyfGJf8OagSIRlJzrbXWEth+++3pMAIO4hP/oB35xS9GfueBBgXXIbYJaSk9YtxpiB3GQOhiOSeddNKee+75hz/84emnn8Zv+O5R8Ky88sp77703zQSOgiso4dVXX6W9oJmI0ph1qDcYYtz+7Gc/K6tYZpllaFzWXntttOOqq6665ZZbKFfYjLAK7cdy6EsohOhOJJthhhkwLbdTTTWVEliUynKqA9IsueSSeooqaZ5bF4YkjTb/8Y9/FMCE/J1kkkkgoMApp5xyookmikIEEBrxaFDE3H///YjjXnvt5RHec+qpp6Im2Aw0/v3vfz/88MM0Ov5ON9100pvGFE4royPKr+6s41kPP/zwKNNfxjWwKIQ2CD+j+xGJWmk2TunDhLRZYii0DI0YJZd5NbgMZyARSAR6DwFW5t4rvCclJ93pCXqZd4AgQNijGqTj5ptvfu6556Ip1Db6Rj3ANkSg3nPPPWVXF1lkkfHGG49nCYXBoosuuv7665ePqgMoiKIoaZhp0B0qEIYVCahbSHfM43vf+x4rD0YSXOQf//iHAhGsP/3pT1HOTDPNRFkiHHyounBynZ3orrvuEkmub7jhhl/+8pd5tOiCR9qvTCWzYeFD3//+97/1rW9VZ28YxleYq1555ZXqp/Q3FDzVMbiOi7IHgQt6gRvdcccdNEzbbbcdi1J14gijI/D83//+t9BCCyE9mBA+NM000/CwkUC9cOY8pJwyL9sTIvjYY49hjToYFsB4Cnz1Rt/FSIkUUrmhO5gZrgOHeeedVyMjfZixFFIWnoFEIBEYhAgk3RmEg55dboAAIUpMUmYwhVAhkMESLbHEEkjD7373O54xbhlTyN1Sjooh49mnGhQ3Ioqg/c1vfhNPFYg5dZQSN2KvwSFYoNi5kKSOUkY8yxFXXM4ubhmhWHbojVQX+ozTTjuN3sgjGhr9Ehm2oc7L1BfOLg8++GAk01qcDFejykKb6G8ifrPNNuNrTL3ERsaeJVJK9IIWR5jjsL8V7dAEE9BXRRY9Eoi27b777rxq2MJQwBJJhBJQu+22m37hPRIrEzf685//jLpxlxYfRYnnZsS7CA/773//K1IhOs5EKOaUU06JZPk3EUgExhQC5aQ3phrQUb1JdzpCJuMHFwK0AkQptrHGGmswOYcViTmGHCVff/CDH/CfFfnXv/4VGSqhYb4p+UEZWQZIYo4j5W0nAeYemhXyG5PghMsrqGFidrTY60S9gZbR3DRMVkbOOeecP/3pT8vbzgP0KCussAJjWSRD7FAWRIqX0nzzzVdSE5Y+FIoLDu0UjxmJpWS0YnpbZZVVwhSlXjyJRcnTRx55RHdsnmJ9c8tVmcEOt8OQoqL4q3YKMCADnB5IB1EcdJPpSoCFTi2MdygpiFAuZjtMlC+RRlKJQePQQw9VuARRIKdmvkTCtFDVFWU4EUgEehWBJie9Xm1Dw8KT7jSEJSMHHQLEJPUGhxKMx1/9p3Kg1SCz6QzYYlABdqsf//jHBHOJDhlchusDKBT9RE08NQ87FA1HdXxoPhAIAh51wDCqn0aYvQaZCC1LkI+a2j2iaqpuXn0hHcXoPpKBPTAzhUcwAkGnpTT0gusSvRe3G4SMe5PW3nbbbXaqK41mhRaH+zBbkr1XrG8MgrRE1EscdICpRzaW204VzkCclpgOQR23dpgjkTicBBJbFyI6tqTxv0Y67UejqTIcNEk8e/bYYw81MiNKqZwAQXqjE3YxbcDMsDEF8vvh34NmKa2jXmd8IpAItByB+kmv5VV0r8A8Vbl7uGWugYJA7CFffzj5ak81KxL/DyKWOgHt4GTjp0vfw2H2V7/6FXdaYpV6g/hHLIh5kps24rqfXO/0mi8gMuI8G0oIjjj2fPFN4avLWMM0Y+mD1qAFXGq4xXBYRqGUYxM1AW+LNRMVPRPDlmRcodELlqM43iZ8aw488EBt4Ndii5Yd2o6ZodWwq4t+BSPhTsTGpC/aQ73BJ0kuypirNr26tpFSNNxC/4WeDJSbcoBGjfhA6Vj2IxFoLwTYqQ844ABtMqG11anKFQeFvBKBROCBBx6gqKCfsEEJuaGTYDlCRGh3KHW4zfIgwVfQDr9kWhDKCSoEaoaKv8jtMzcEkImKpmHVVVf1lHIi/FqUg0vRFTlqneXIU5u87EhafPHF6VcoVHgo01hQkLDX8GvmY0s7glqJDEdgihaOO9yc6Z+QHtoX5YuMRvIFLjeL8XHWC+qTiknr46sbNHIECWBdoqoJZ16aGzyPwU6N0nMJokQJ/yTuz2pEv8RLEOoZYW0GHV/pBuVnVCIwOgS8P7R3sSVwdGnzeT9AwJzTnq1M7U57jku2qq8QGLHW/2itYY5+QRTMvDZhUb3Q8eAl1CTMNDZMoRfIBHcQBIIGhdRn/XEhMTLG2cRfaPEI7Y4Y6iIH9FHA4El2JMWhNeIZaFiLSkeZL+TtpZtRTeql4vtNsandabOh4v3mECYeck6tbLOmZXO6gwDPvDAut5t2J+lOd4Yz8wwcBEL49bw/pa0kivoit0CYmK5oceh1Ojr8pudNaFxCqzrYuPSWxtZg2NKyPy8s6c7nWLRFiELR+oGCMM52aos2ZSN6gIATvxjiFdBudCeNWT0Y1cyaCJQI1LOKqpiZiuKp345Iev8cxf1lnl4INGQMEak9DZ/2Qiu6U2QVXF/I3lH8FxLlTT9GgLXU9rp+3IFsej9BIOlOPxmobGavItByHjCmhHTDehtG9iqerS28udGxEcxqkuzk6M1J3MmKfJLsTrc/jrM5Lyi7zGxK32uWkSchtbaNWVoikAgEAr70155QJN1pz3HJVvVzBJqT0C3uJFrzxXqZzyb6+8SVWr4YX12vXWOOz8ESROIHjsmxVZ5lwZ4vm874J9lzLsbhN5JJbA+5DfB8tDlTy+VijBBjT5lcfL1tZbernHezHem+nsMXG/9wCLJDpZ1YuN9++6nIcT5OBYxTmJ3Ww+v5if0qe9pVVN22CHN74iXNC0ot0jjFx8HW2hmf3+I0ffHFFzMR+sCW7WnabEO+45F86supSM6q5iblaxXoDm90G933Oru+hoxJBBKBliHg+3ctK6ulBaXvTkvhzML6HQKh+fgiGyDjSVY7oeJMP+oBl56FuCVNq6VyRHpK8MtC9pdHAAcYZXbxnlZHkvocmW3L8khdPnqFHNjP5agYDEAk12nHzCAEctFe+BIWEe6LUbgIKc4l0M4vrMInM1GKE5c+6Y0VX7eXKqrw1zc4j160csDPqR+e4hAaJgNOEpgB12mRPl3u4w9O9rOhnV+2SLvxtSGy24DmBGRhu7rsZrdV3kZ3G+m5H9nlbieXDfaRMv7K68wbzAPPsMEes/FlU1vJ7CBTMgdwuXy6fLXVVlOsDWXctB2gjKN4JMEnZ3zamJOdM+RX9+xgr5xe27PmM67A1xJHEPkm6A9/+EM7yNz6cipupwH23jtCmuurvXXxOQ4sjae5Ixk1CRvzfdDK9cURjy7k30QgEeg5Am3ru1M52T2vRGDwIjDi+9j2TDnZjyiFAwFs5/k888xDiNpIZVc2ChJn68XHMu1U93vGciR2pA0xTOGBhcgixu4trMKubFoHrpce2XIS8XQM2IlICXxFz+nJ6FF8zWrGGWdEUySOEwiRD5OOU4ORDEcdyo7roCm2ryM69oLZau7z5sFs8A90p6JlObugU5E4Lofv4UzxAXA8QJPoPFTk5L1IgEXpHWXMDjvsoDqFiI9DokFBjxLJaHcwPJoYt3BQprOIfLdc7UgPCkJloqj4vLk0FCpKg1VkR+ncRi/sqMftkCGP4gsYmoRcgqXDr5SfXcRi0QmH+I3C9ZfSCETRQvvp9B1BVKYt98xVAoByrHM0YLbZZtOAON5QIACJR/k3EUgEWo6AX6gfmotxueWF96TAsaJZ+TcRGMwIUFr4InoczcdGQzY7zAYvoTihM4AMjQINh92VhDq1Cr0F1Yh4x/iiOz50wDRDlotxmrCD/mxl931QTxl9SGXxvhtFGJPWzg+Mk3LoY+hvwhCDLtjLQMGDT2y99daULsQ5mU0lQ2zThTiVRMlYCKalIgchYj8rrbSSkgl4aVQkXK3acbAhGiHSde+99yJtNDeOxAiC5ThjNAJLoAihKcHA4kCd+HI4bhQKLXlZjvRI24TRI/HYD+rGwIT6uGVsgkCZPlJWah1xKRZr1EJ3IIUGDdPIZyMAVFogX0bWBLAZMUqgEHI6EfDRLDFRo8+ko2LAFKMXmBAwcaD4hIVIFx4JOiDEbf5NBBKBQYhAA0v5IEQhuzw4EeCJMuuInnNipZXh30oYk+7iyHJmFxc9ytFHH+0QPzYdtIOqADcSj1g4H9lRgf6y18hCMYPHkLhu8Rh2HKSH0sgWdEfs4BbYEncTl9N6CG+707fccku0BnWQkQ0LyaD8UJSASGqPEa2rlIx1hXSnnsEeaFw8omFyyy3Gt71qvvitcKYuRiJHK0vJV5dlB1nhVeNEZjG+FEEVRCMlTF2ECQUtczvaC1w+CBrnpVpsaTzLkc+eR0aKLgHxnZfDF4dVC9tTFFPUiUt3nrzQayA0LNapj0GJAIJ7SYbD+cJolKgix2E7tNrIjjgOpEKM8koEEoHBhkBqdwbbiGd/P0egVH6Q/QQ/xw5aHHwF5yA4Ix2S4QopS0kgElnBMGiDSH23ESnAaBUFkvcOJ/QJTDoGqguP+I7gN8gN5QSHWQRIPH0MBQw5rS7MhqbkpJNOwpCkr7midjQr4vEY389CVhAUBfJfUU7Nl0p5BGtMfLBTLrYn5jPmOaqR+Ix5TRXIWdnlmkcd3ZYdjwTRU2E6J3qskqvpINULKOrLAZR2smeFtqY+QcRE95FOx1JHsfDEMs877zwJ5EXgojEq2nDDDSnAaOBQwDI7oyGbGiskGtpRLRmfCCQCAxuB1O4M7PHN3nWGAOeYeEw8YwYMUm5xHc6tDVUdJDfRS0Kz13DvpVmRXiQZjOsQpYw+fETcTjPNNEwq3GtCVEvmxFjKleBV3HpYteIkLo9Ge6lCGmQlPiKBbGEtNEAIikqpLvCk6kLUS6vkw14VC9cdlSdcfVVHU4X0MNVxG6ohK74IxgWnupAI87NRaTSg/mkzMQgZMHkQ831mSsMRsRw+T1yLFMtgRxODAnZSFBrqKeOgb/FEMgZBNkeO20gP1ZevbSiEe9Mrr7yi4xRjRlONwSO5e/PNcig2ytVVStdJq/JRIpAI9C8EUrvTv8YrW9tKBMKHRom+C2HnDusMIcr2QYhW772qrhJ9sQWJ5CawaX08IrNFUlGIlFEMCsKe5UOeJPqcc87JwRYB4vTDasObh0ewKjjNVBfbeRiz0Z5SM8FT+Ac/+IEsisUkPI0j28tCuP7QtfjCVxnDcwg5IOypgnyZyyeKuPJQU7HfcVXGdZCG6LJ+yaW1NkzZSEWlpF6qL58GwyRsJscFN9hggygZ/4DYs88+yywYMZDkxyMGGvaE81W0QZ1Wxvk3WAgEqLgwQs6MeA+OqHw7uQLJsrU1AdRQDF+c6vM8bL8Cow+sapVPm3E5UjX3JgoezkwavOOOO0pv4xsmRAOkOyySulxTeN4mAonAYEHATJ1XIjA4EcBOyn06Nv5Q9vBNBgWXFzJSAD9ACLAi6hAzAukuklmEBggJIG7peLAKkXyH0Q4BF90DNU+EbXqSyyExspPNItm5aFaoUiIBv13ePGxYnIcojUQS2NgAD1y6Gfwg9jRpGAuOTelEu7YR7RgGByORWst2Q3UUm5u0ikIlmlqpYsTWsxDzQZLwlUrHhw/HBkq1DRci5EwkpZSmlmyPixJXGGSISibmREqmSrHDh+M0SFXY7zDFiKR2kkxi9iMB1FA83xrWtGOOOYYWCphiAMLtSUxlZ/jw4fyWovHCtdfZhXZyDJdYr6ufGh0OSdGX6vjRhEcAMpo0+TgRSAS6i0Db7szKjejdHdLM1/8RKOkOkw0FCb4SG7nZTUhrpAQboAWJjtqZVUb6UCilgnjiFjMIwxB3YDGxazp4QFABzIZCxQby73znO+KRKjoSLEdinGmnnXbCYNTCGYhHjkh0au2116aGcXE38dTpf0S7RiITKIsqJLPPiCUIO8GB3NrPhTEgE/auc9flVS2yco2Q7rZH2c/FmOUv8hFPlKlkV3Uk04/biPcXIJJRI5UxwpG9jJReroiszi4edYv40f/VzoZXR/ENEzcTmXSnGZQyTSLQXQTalu5U9PCxaMu/icBgQ4DAHvu8ivva0I3HtrGIbYVeBCMR4xcbtICehiNOIMMGRJwLS0yzEpHMUrGFW14mFbnsHlcIliCB35eN3/Zz0UxgSzgKPQpfk8jb4r/nDLlyiitwIIYe2qaRhTc6R7HF9bakuLojoT9vf2uPBOwvgLQE1SwkEehzBOwVCMfE/ERon2OfFSYCHSBQuozQtVDklLeSN/QjtqOqvqSwEJXxNljZpl7eloE47K7iO9ybF3URzRPGU1tJyPja2H5y368b308wzmYmAgMegdyZNeCHODs4egSG/qXiaDIArlXeXnWV7fkwr1ucs27/607Smv43ZtniRKDfIFDR2+eVCCQCiUAikAgkAonAAEYgtTsDeHCza00g0Fq/kCYqzCSJQCKQCCQCfY9Aanf6HvOsMRFIBBKBRCARSAT6FIGkO30Kd1aWCCQCiUAikAgkAn2PQNKdvsc8a0wEEoFEIBFIBBKBPkUg6U6fwp2VJQKJQCKQCCQCiUDfI5B0p+8xzxoTgUQgEUgEEoFEoE8RSLrTp3BnZYlAIpAIJAKJQCLQ9wgk3el7zLPGRCARSAQSgUQgEehTBJLu9CncWVkikAgkAolAIpAI9D0CSXf6HvOsMRFIBBKBRCARSAT6FIGkO30Kd1aWCCQCiUAikAgMYAROO+209uxd0p32HJdsVSKQCCQCiUAi0P8Q2GCDDdqz0Ul32nNcslWJQCKQCCQCiUD/Q2Dcccdtz0Yn3WnPcclWJQKJQCKQCCQCiUDLEEi60zIos6BEIBFIBBKBRCARaE8Eku6057hkqxKBRCARSAQSgUSgZQgk3WkZlFlQIpAIJAKJQCKQCLQnAkl32nNcslWJQCKQCCQCiUAi0DIEku60DMosKBFIBBKBRCARSATaE4GkO+05LtmqRCARSAQSgUQgEWgZAkl3WgZlFpQIJAKJQCKQCCQC7YlA0p32HJdsVSKQCCQCiUAi0P8QeOCBB9qz0Ul32nNcslWJQCKQCCQCiUD/Q+CII45oz0Yn3WnPcclWJQKJQCKQCCQC/Q+B733ve+3Z6KQ77Tku2apEIBFIBBKBRKD/ITD22GO3Z6OT7rTnuGSrEoFEIBFIBBKB/ofAOuus056NTrrTnuOSrUoEEoFEIBFIBPofAkOHDm3PRifdac9xyVYlAolAIjCQEXj4fw8vfuricxw7x+F3HB79nOygyfa8bs+lTl9q7uPnvvCxC0UedddR854w73wnzHfVk1fNdvRsz771rMjlz1p++yu2F7jhmRvW+9t6b3z4xoYXbLjMGcssedqSd71wV1nUZhdvduSdR8Zt/k0EINCmLCzHJhFIBBKBRGAAI3D0XUcfuMyBs081O8azw8I76OlHn3405ZemvHHTG59646mlT196jW+tsf+N+z+5/ZMvvP3CATcfsMKsK9z07E0bzLnBZ8M/u+/l+6R3u+KsK+581c7bLbTdQtMt9Nxbz63259Xu+1nl0bBPh607x7rLz7K8cF6JQCCQ2p18ExKBRCARSASKgw6qgPDww8Vxx/UFGocse8hjrz128K0Hvz3s7agPj9lsns2EZ5585reGvSWw0jdW2vjCjZ9/+/kz1jgj6M5Drz4077Tzjj90/Hc+egfdWX7W5a988spdr94VPZLyvY/f+3T4pzKOPWTsZWdeNorNv4lAIJB0J9+ERCARSAQSgZF0Z/bZi5//vC/QWPsva6tmuwW3G2vISDE07tjjTjb+ZFH3kGKIwOmrn07xc9zdx7FMLT3T0ne/cPdtz9+2+IyLLzz9wixZVDjTTDjNJ599csWGV9yw6Q3XbXLdKaudgujIOHSsoWWxUWD+TQSS7uQ7kAgkAolAP0bglVeK1VYrllii2HTTYrLJRnakDLiP8BtvFBtuWCyzTLHkksVdI1xcjjqqmHfeYr75iquuKvbeu3j33WK55SrZI/3LLxcrrVRJ7K9wxO+5Z7HUUsXccxcXVlxrenTd8+I968y+zoeffIi1REE1BIWChx/PIjMscuaPzrzs8csmGDrBtBNNe8GjFyw242IYz2G3H7bU15aScbEZFgtHn8ufuPzAWw7sUZsy84BGIOnOgB7e7FwikAgMdAR22qn48Y+Lm28uVl+9+PDDDnu7887FdtsV11xTnHVWseWWlWT771/cdFNxzjmVmH33LSaaqMJ7ymvHHYv11qsk8FcVro8+KqacsrjxxgrX2b7iK9yja+vvbr3oKYv+5vrf0OiUjKe6xEnHm3SVb66y8MkL82jea8m9PGLPeuGdF6aYYAranZufvdmtyMNXOPyM+89AjBCgY1Y6prqEDCcC1QgMGT58ePV9hnsbAQby3XarGMjNI32jNO7tHmX5iUAiMAYRmGGG4oknivHGKz75pJh00uK99yptoaF5882RjZpkkuLttwvJZpllZMwLLxSPPVZssUXx1lvF1lsXy47wcimzRGC66YqnnqoUO2xYMfPMhSzjj19R84TuR0Xydn4N2bdikGqfa/jeKez6YjRuuOGGOFj5iiuuWH75NvIWT+1OXwx/dR3hD9hnBvLqqvtpODes9tOBy2b3DQKULnF99llRrl6F40J6IgEydMUVxQ03FNddV5xySuHk29NPL3bYoeKYvNlmIxNX/1MWVUaOO+5IriNmSHsxmbKNGUgEOkQgN6J3CE3NAwbyn/60YP+2QrroopErp3I9JHGEJaAxtgYyxRx6aLHgggUD+amnVmYHROfWW0cayCmNI72Um29eiaRJlmzaaSvx22xT3HJLpYp99inWWKOmIYPuNjesDrohzw53BYFFFy0uvrhwki0bU8lRaF+okC2rzj57JDVZbLFKApapyy8vjj664n/D44dta/75K8obF4bk/7FGLYF9+Oj884sNNqj8XXrpSoLyUeWm6atLOhUKoebTN5+43fRMTYOXCVuJwKhXu5VlDsyy+qmBfAAMRm5YHQCDmF3oPQQOO6xCX/gU/+tfFdtTXEceWSFAKMtzz42MPPzw4owzKo7G0h9zTMXstcoqxcILF4svXuxVcYypODsjQOX1+99XfHoU66+VW16JQH9HILU7zY4gJfDJJ1cSmyMafgEttMdXXlmxo8fFiP7pp5V9DRtvXDGQm2vqL8VS6rjMTXx6XMoJ3bIl12it45UMA/2yYXXN76xpw6r9qNHXhhtWHcJxxB1HnPPgOceufOzu1+weG1YnGGeCmg2rTuxwvMctz92SG1YH+oszcPrXpOWIt7KrOvEjj1SsVzWRbksnnsozu8G3q/wfl+yhIvrqVyt6oOqrdAYSWR2uTpPhRKBtEUjtTrNDkwbyZpFqdbrcsNpqRLO8RGAMIPDOO++sssoqX/va19Zcc80PPvigvgWPYGcORB42LFIus8wyCyywwFXVu8VG5Xn77bfnmWeeuFt99dVXWGGFlVZa6U9/+lPEvPnmm+eee+4PfvCDOeec8y9/+cuoTPnvYEcg6U6zb0AYyKWuN5CLrDGQi7EwOvDAinqG9niRRYozzywuu6xSVxjIK6ERVxjIBXtoIB9Z3ED8JzesDsRRzT51GYEPPxxG7/LRRx/7X6A3/u9ym7qS4ZRTTpl44ol/9rOfyXQWC1ndta/d8EWBCZ1wwgnXXHPNb3/72+eee+7FF1+sS1i8//7743Kc9tmsG2548MEHDz744GOOOea44457b8S2tEMOOWTLLbc8/PDDsSXVfcJJO69EgOIzN6I3+Ro8/XSxySaVtHjP8ceP1OWiPr/+dTH11BWX5BNOqEQ+/3zlTIv33y98FPakkyo+gEzg555bYTm2fW67bbHyyhVt8yWXjHRV9lsW70c64YQVq9ZXvjIyPlpV7QrdZDv7Y7J0JOyPo5ZtrkGgeR/bmoyjvQ371IYbbnTnnXd+61vfottYb731ttpqq04y/u9//3v00UcXX3zxsbriYBwVhTGrk8KbfBS/64Dl//7v/2aeeWaqmoUWWujaa69dd911n3766Yls0Bh1YTA//vGPL1ngEumpZ959993pp59+1113vfvuu6+++uqxqxwIPJJykUUW2evTvfb4aI9//OMfDzzwgGI23HBD5EaXsaV77rnnpJNO+u9//7vJJptIMOHvJ5Sg9wZoVCfy3woCOGh7bkRP353PX9D4qX9+30GoVQZyxdfUyFgeV3V8dbiDFvWD6FZNoP2gq9nERKB3EGCs+fKXv7z//vsvvfTSSy211KSTToo0RFUMQB9//PEEE0wQtOCzzz678soraTheeOGF8ccf31NqlXj04Ycf0nYIS1w28/HHH7/99ts35mPYa5fmYWlDRkxn/mI/NUoXZGVaG1NHXJONuI499lh6mnPOOaea63h++eWX33jjjX/729/2OniEi/WoNusanuQOEQwueN1112FLoQcalSr/HcQI0O7kFQhg//l/LyHQ+TtW7FP4v/M05dOGKRtGllnGVKC+VfUxHbWt85T//Oc/yTN5n3rqqVNPPfXee+/tqJwxEh+NJ4ypFr773e9utNFGptg55pjj2WefrWlPfTcjhnRceOGF+XlI/7Ad1QX154Q33XRTTfbOb5988klC/T//+U9NsjPOOOPXv/41TlAT3+1bba7vSLdLq88Yv8pPP/0UxWEGkoD2gh8MAS+MOixIvVzYcnVY5D3zzDPHGWccMfHXELz++useXXLJJfPbd14UFCf//ve/I7G/BxxwgEhvUVRUxvcwUA0LdxyeNH/4wx+U+bvf/Q6DeeONN8ry77vvvqFDh1acb0bNA88//zwXH63acccdy2QCSNI000zjnReW+LzzzqPuQom23XbbySefPACJ9Ixi4OLTEynLkuNp/u09BK6//noD53LMYO/V0o2SU7sT4zIo/taoWCy0amJ6iMLAUET1EIRmstOxYwBm/EkmmeStt94yTR9//PFTOp9/dFet1e/2URmeK4q/jwr3+b8d2QjYFB566KFvf/vbxNj666/P/vL3v/+dWGqmgYTfL37xC7lOO+202Z0eU3CAW2QJW6ULux0/fTm+4VQ4p2paMFrus3r8/Oc/X2655TbddFMJyG8qEM4fZJ56v/SlL7GVcOZQAnsHl1hPQ9OAB6y22mqq0E5MgoDUWmxARTilcjAG1pO//vWvmJO/OvX1r38dVcKiiNLdd9+9me60PA01D+7yxBNPaDmtzJJLLukV2myzzbxRW2yxBU0JHoxVaLBu6pp37KWXXvLW/eY3v9EFRjFEYa/YgF4Uv/rVr+aee27Gppa3syyQ3cowGQuuNqxLU001VbXO5o9//CNqi8AVR43MYQg0XjvRnf3220+z44GUX/3qV9cYdRzZOuusg/2w3EHgsccew5LHG7UX/4gjjuDQ01an+pZoZGCMIJB0pxb23mAAHZUZ/KCjp7Ut69l933CR+r70pN6bb77ZrM363kzXn3nmGeKKYHMRaaeffjqhaAY3ITaTvS/TUFRY2tI9EP88DP785z9PPfXUVPfNtAG3uOuuuzhA0JTMOOOM5O5PfvKTo446SpmdZ+ffQHj81FmZHV/YCSFEOkYSjqKW0bQsLPHEDJsI4RGKhLKMWgZWPigKopfQIoHE2TujhVpb9Xw0wXA6Ofvss/W0OunJJ59sfCPGKHs9yP5vfOMbiNQPf/hDjQwGKcF0voNQFLPOOqsEeI/2uJ1tttloiYh8yqfvfOc7eNV8881HHSIZRvXaa69R/ChWyg022ACTUD5udOmll6611lo0Il4zXrTbbLPNLbfcglpJNsYvbACZM74IjZcq2oMG6RrYS1MOZob0YANeA8zAK1e2XCTqVt72UsBw8OowrIiaMWVfi4q0HKnlbmyYqqtG1Lx7Ir2WZTy7G60PY1cZw64nfOGFF7LHlZ01degvvVdNmWWuDAxCBJLujLFBZ1Y3IddXb7lpSjU1WLXUP21tjOmb+jfKpBskM0YrNVvbgJrSTjzxxFtvvZUo4nBgkWo36bLLLtsk3QGXadGa1ZJOsagPj0jG+5oqWntrEMlRkrJLxZI6K6+8sjUuGmGyRumIq+ZLiPUrFRG6Q3iQCi7ZiWqCxDqYQsL+W2YLfIVQ59Cw+eabg0UW6hCihcywvMZF7rjjDovgEHUHHngg5TPk5RKJ2RCfAt///vcRMkiyI8heQ3c6b7bmeZ8pQuzKkfIrXPGbvhAXEsuA2ptDNNLZRFZ+G3vssccvf/lL/EaxXg/k79BDD73gggsgoAvADPWMRxQ8++yzD3tHWe0OO+ygSeLZyNAdHOjII4/EYIBgZxA9Qeg8ECC0iQHOX6VBAN3BLNdee22DTrjSpnhFy2LHSAA3NUb6QimFw+E3nZB7b4U3DaqLLbYYXY6+932bcV9zDpyNYFm7GJq5XXbZpYx59dVXgexVZF/zihrxeGRwsczSVhKR3i6j5rVH+oPueA28HlRZwMGrqoldWUUGBiECYw3CPrdDl2mhqdCjJebfnXbaabvttvMT9fM2pRJUIbN7u6nWSY6viGveeef9l2NZO74uvvji8ATsOElPn1gun3/++VbSCmJxILeIsSYLZWugKSEAgnxwcpTxm9/8ZmSnTYHw722TG3ER+WDfeuutyTk2Dsr82MLqoUmT8sD8S4niFvfafvvthaWR3krUhhcBs7Mpe8UVV6RFt7wmRaLkrv61P4UQIqiazxjkBo/RBZ0iLWKWJ9dpJvbcc09C2rpWgfiQGEt5rh56ZKfuqquuSvbjhdbHXFjgE9YlTIjtwHXZZZcxK0QkGkHqsEEgwXwpCI/OlUP1XTAofIwMouruv/9+XKE+TUcx2BVsga+R6kUrI6WfBo5OGWYgwjelLEEHreaD65SR9QGD5Z3vvDGvvPKKGg0NFuUAmNAnYXuoKpUJ4RrOsPWF900MNr/ooovSVO29997Ym/eZXodc58VS3QA/B9TB0CNtP/rRjzxiS+LKQ+vppZUxEqMLbEbGujpvy8OIC4KIaSEipTVKLX62YqqrY0+kckPIWOXMkyUzMwoMdjVmX8MBBJzPoygEfzWRgsgPQTkHxXcKqyvI8KBEoAuT7ODBxwTtN0a8We9aFrM4mFXJBpqGVoFw0UUXhQOmAi2gGbb58VHGmrDMwtaOXVL7d7tVxL9Frc0L5gXNKEV+fYEEDDdDDbPgxtXs9rSgrE8WMaZUGgKK6CmmmKKjNA3jkQmLeBMxbwmTY8M03YhEoXiBUP9ojz7axYoE0BlwwiAecAWLTlM/EwaxgXQSJMQ//keTgXWZPcVrFd2JuVXvFEKyUl0QvZQ03hPMo3QaaKaFEiuHioULJ3ZLk99Mruo09rkgYTgBqawlHpnxSQIcBb/x9oYJgDsLskK66HVkx3g0OF4wNILkFo91AZ+rChCUiSeVdRmRilNFty7uI95tSrtu5a4cr4JZIsE4XJSAxrEx4SLwx0U0uxslA59vLL1RiUlZCCS9GDSdOKUXw2vjJwkBe6FV7T1BfdwyclE54OXBqsvsvRowoIgaMw00vJ+IuEaaNxgcvdjCViMGEXU2jlYyYAc+omk0/aCo6yiozGZ+uRgPpl4aeqTk5gzYhvrmHnbqC+bOb1R8urd/Y/vt993+82IXK66+6uriqpERI9PvM/L2VAd07HvqyJvNih3f2XHHfXcceWtz675Dik2Kp4unr73v2uK+UdFjj/Acr2w9qVxH+6+JyxTH1kb1VVrZmsiUSfoTAkl3GoyWBYEFpRUGzTBNPpsIyR0L6Aapux5FPhEDVoe+axMXb4nbbruNjlc8UWo1bHoikPzFtCyRI5nZ1mIXQXGZlz/66CM/UXO3dbMZUCShGyk1niXITM3lotrOPbK+Uf8EHZllllnMmFaBSAyqZ91sCWsGFDChH3300RaRxIN5lo4EEaQ9plRAAkYVU/svFsUWQHHiYNPaZ53ekyiohv5CANHUqk6TN3homDSMQoI8KB+TmqHL0UcMhi5NT5l7AE5uUWk4DiQEJ1dWziIUJ0gMk6IS0DsFUpygQV4MlBfg2An6K95y00IZaGVdTQZQCiATS4STMrvKC9ViZMPMZ8VMCgLNYCFAaKsCm9TDcXZBYaPNpDiHD4MeKhMvW43upLprnqqUNK2OrA8DuSFxl92vgLWiPksZo3y/BfiwN3nVNc8j44KdUzUZL8KJ2YInShizPCWzvXsEP2zd+o1Qb9BUhdeOQZxrrrm8vX4anhpECgDMj26DdQ/7McR65L11UC+dnzcfNVS4LvgJ8OzxVlulYJA4okIElNNnV5BsjUFWvDAaqWq9YyLEfXUWVlCKeI9oH5EelLpUpXjVWYIgIL5aR+LXgRLNNNNMcjV/eYf9sqAdWfz0DLf30A/EMGltMVK12nyRvZsycMBloefdEyjrgx4Mja+51EtSxmdgICGQdKfBaJogzG7OdTDx7bzzziT9DDPMEA5xUhMqtL6mBpMdi77fvEi/eZcJmldjbHCgFeCGUhQ/ra/AXImm0NN2RBgsxwkzmgOFm23NHZqkcFkoKqxrcQIkzEKcmlpiyxHJLOgt9aw+zcgWxHgJU7cZXLL6NlTHmOgJObJcUdpPt4wtqZ3sJGb0S2JuPRBQNaciMcRVdQk1YSLHIqmrXEchegF5ehRWA92hU6kpebS3GkYxru/IGawiPYpjOtttt92IKCJBpGnaWhaXFcZl8ZXoplGjI0G2WIhos8rq0CNhthXcojKPj7jIvzJBVwOqI+9hTrXT1byR3jK99GoiabylXg/NxtSNYOnu0FHhAPHIewIoAbtdsF7C0sDRIhCiiqIDo2MDqR8CJopPl7SMYKN3QTg6Kp9U9gtiCdIwtNugsGKUib1gFEuOkCljagIGyM8Em9EMmId+iDlGgWF5kR431TaEhoiSEhpeV7yfoSosTX6J3m2cRmMcsBtijGIV7PL6DVpOwIHYU7IXw8/N30DVD1zVCpTMYFGE+GuxgeiLdFmZtHAJVNP9hrfet/pXTqvobBqm94N11TziLuaqieTdX2NOqknQ8NYigQsa/MuncNYetwJlZHVAe7xCnspFAYy5ekrtZObpKEtkN0ZYlFx+NdUFdiPsnfHb95IYxOrsWm7S05LqyAwPJASS7jQezSD+HCHthrV4ilsrZr8T6mIGCOtgnIPNmMncrEdO+BX5QYonIfySqQ2o3IPuWFFVTzG05X7hlmhl3aSsiYyYwSpEqs4Pm7DHctgRCCTTMWbDewbBoq0xy3AdpWknmDXAnE41jYjEBl0KCat2EoXMI8/sp+1IpsbcZBVIbUPqq1oXiAdVIHMmQTr8mNNRKKWxB8VCuWx5w4Bk3fZsiL6ThWxJAXvDKjqKlMXK3hIzFq+EGRlGHqAClDq4INcoeXWcGDNkwuHBYLVHvhLAmJ/tsrjOiOEbWQ9hL8T8hGRgwJBxG5ECRl8hoQOnE1I495FqMTCylKp/+MEQqKZ+igpkunziHeCCUFEbjFvG1Qa8P6LC0wIRMdDeJRodbwsKgu6w8jBYwNDo28ck3rKVxgsViBdMdn5anuoOYu0W17HiJ85xRH4PGCejqr54/zEhrwTCQQFZ0h1viNUwTVgxcW3z4h4IFAb8hCCDdoS6pUxqgLyTFHh7nbRXRBom5CMkEEzcereNEU8skWo3srqp75od763BFSD/PELEoxxS03D4AcYtnho/vTJS9ngHJIjsNDoIulucCZdCi4UZBDVSx/E/4PjpUfZ4SaLqKNz7Y+ywurjt7b8jiERvV9KF8g0HT6/q97wEpwxUF2doTDLlBOL3hQpLaepL+1E1UBnuJQSS7jQG1uLSmpLCHI0w48fsaXbz86bz8Av3UzfXUwtTkOJApJSVLoUEXqJENg7Tq4yx28D0XVaDIdksgEaUMQKWFFac5BMB4Na8rygS2kRvzqWkUSxvU4KWnYUMYGUgD0wcFp3oDlc+Uz/x4PQRkwhtkAQhYEiLUkRV1xjh4BN8cVSB6NAY0e6Y00k+S3mUpY/Xr1oFN52y7YW8cRstFICJtRcSGS1v+DcSV//lbWPZaphIblYPARnp50Bn+FBJsy1s1ciXk1TzVL2IJvGJzZDWlGoiMUvjS6+DZFAd4RDeAazIPhFwSSCSiohSyiPrfkQ5htKj+gtdRh/xAImNncLLNHinga7I45fLuNoANkMkEx58dTFLLxt2pfHsdyxT/FE88j5A0l8CRlPFgMVtWRZVR43aj3HH5ZXz8oS48o4RSKEPk1EHWQPtAPJWSEPS636xYsVnqCy2DADBq6sWHYQbmh7kskwAdiTMrewahmrg5ZVfyibFjKfOWCb7Ag5//zy670I3F4X/XT9sUOfdxd1f8E1pkGTARqHRpsdud8+ra9XX7eyZMRHoKgJJdzpEzFzPpZ8dxDqYj4V0QXrM4+QK+VEua8gG9nIrftKObKCMISRIF8vuothZxnL/LQnHwRCVIQmqK7YXhiyvjinD5Irlo9Wt6mJZH6KoTFAd0CqTiBjaHQtWJEyMVfgIBlBRMtdccaIJ+UrVL6UtuCxQKAJWYSlP64OB0RVZnVvN40NW/+gaWc6rmvhXmrU1uwDNE3ZYFs64gApIVq97L9M0DGgzBoDSaQYBadntlgyW2IYp7QnzU8O8Ivkd84KyCscI6clRPX91QV4eLXqERjBIYZbsFLQLsNJ45jOqIIKc3GX7w0UQBU4bQDNM/nLsCBJGZYIaEtsy4hw0AcpRiwRUX1R0uCa2gVdhLVRBmkRTUtNaMV4SfiTS0GAprUwTdAQLEV9c2CCvougOMRi9wEuUIAbyOBkWYoCQQixEICrV+Oq3JW7DHIDa0gMZdJGRWEq3uqOzqB4KaNyF46m/uqyFfgXx5ksQdj1uTGWakYENioiM2ssqqpN5VIkflVLJYLHKn/fieauTCeP9UIozdWoe9fxWl9naaEZ7UlRvM55RQ9STNmbeRGCwI5B0p8M3wERPhWMnTmg+MANrEXKI/wcBbCUak7i/iJH1LpZAfgjTn0tGKiAEU01VKZ/FgXwihCgtSNOOlkRm3hB45n0aGv6DJuKyfaQavwGCTTlMZmR2+cgqmSHGyp6JhMAg3aUkjSy+yWDlcOEsE1cH+Oq6LddY2u/WllRmO54WSAC2gb1ReFimKx8J8JcOqdSyaDNFRc0OduKf4oHora6rmTBjEyRjI7G2MdCUxhc9AkuIJZXWlyaSOoqqw4i4qFvQF4GIhwYVGkqKr3AxFs9IYciY8BVFbHtqb7kqqkv2DpDKMShGVlGh7hI2CsgNgsVkQxJjsfhH5JXFiFfC+xS1ZsRRMaPnAaNSVrdHgfQ62gxeo1bWWJ0m9pBXx9SEdUcvdK1G3SKZSHY0xRpB6iJvck3e+luSPnRm1Y8aRlYnKMPNpyyzZCARSAQSgW4g8IXJvRv5B2QWi2Y2C0oRK2aOjcw6xBtjBwsXwW/1jLLoOE8Ikp5Rn+zEMygSqEkIDCoQYps1hCDkFCslD2LSURquIfxI3NbgJi99BkcKQhdHIZulJ0HpAEKfoQHEGBlJYyQNzhGcwEKf6KI0UqB9ZGwBLilpm2g1tBBjKI3lNZW65QBEtpWilyZJpF6rjmJDA/CkEPDiMT+FC5TKKmEEgjVNg4XLiy2MAiy8Z8rI0Qb0wsUPiTcJYgFVIGiJsLwaqeOVIzR+UdRUVyl5h0aRI6pUAo2FPecKpJagxRkR3YI/eANMlI/tobNeDBRKLeIZKw30Wg+tBYfqmqY/efqamOqn1eGGKUXe+D1nrt1YLFpc9c5V1em7Fq68lY2vPS/dc+SDZ4ri2sZpmontbYVHM23INIlAIpAIlAiM0CeXd4M7EJ6A9MaEOudi8pVbBodNi3hch+YDEQlHVPLMhdngCmhBrJJxBYLZxTJlWWzJy+Kz6aabADV00bQm4esa3h7io8Zzzz1PCTRJrCq9NwLqqlGJ18f0sPaGBUYfa6quqShFYw0gedsfEejo22H9sS/Z5kSg2wgwa8T+AIaR0nTQ7dJamDHpzudgNiOYP0/dXKgsk98DGxbnGI4IZdbyaRnTewF11XCOqL21NdZUofBm+ph0p7WjkKWNEQSS7owR2LPSdkMgtrhqVbvRnTRm1b4qvUECRpQ5c1H821HpXzwtvVJ7b9RY26sR931QUfeqSDnRcLwyMhFIBBKBfodAJ3uBx2xfxhqz1WftiUAikAgkAolAIjBgEKg+ULStOpXanc+Ho94Q8/mzDCUCiUAikAgkAolAv0UgtTv9duiy4YlAIpAIJAKJQCLQHAJJd5rDKVMlAolAIpAIJAKJQL9FIOlOvx26bHgikAgkAolAIpAINIdA0p3mcMpUiUAikAgkAolAItBvEUi602+HLhueCCQCiUAikAgkAs0hkHSnOZwyVSKQCCQCiUAikAj0WwSS7vTbocuGJwKJQCKQCCQCiUBzCCTdaQ6nTJUIJAKJQCKQCCQC/RaBpDv9duiy4YlAIpAIJAKJQCLQHAJJd5rDKVMlAolAIpAIJAKJQL9FIOlOvx26bHgikAgkAolAIpAINIdA0p3mcMpUiUAikAg0gcBBB1USPfxwcdxxTaTOJIlAItBXCCTd6Suks55EIBEYBAgE3Zl99uLnP+/fvX34fw8vfuricxw7x+F3HB49meygyfa8bs+lTl9q7uPnvvCxC0UedddR854w73wnzHfVk1fNdvRsz771rMjlz1p++yu2F7jhmRvW+9t6b3z4xoYXbLjMGcssedqSd71wV1nUZhdvduSdR8Zt/k0E+gCBpDt9AHJWkQgkAu2OwCuvFKutViyxRLHppsVkk41sbRlwH+E33ig23LBYZpliySWLu0bI7qOOKuadt5hvvuKqq4q99y7efbdYbrlK9kj/8svFSitVEvsrHPF77lkstVQx99zFhRXO0KbX0XcdfeAyB9602U2/v/X30cSPPv1oyi9NeeOmN1744wu3v7xCaPa/cX8JzlnznLMeOGuFWVe46dmbPhv+mf/ve/k+T92uOOuKO1+183YLbXfNxtec9aOztvzHllHUsE+HrTvHur9Y6Bdxm38TgT5AIOlOH4CcVSQCiUC7I7DTTsWPf1zcfHOx+urFhx922Nqddy6226645prirLOKLUfI7v33L266qTjnnErMvvsWE01U4T3lteOOxXrrVRL4qwrXRx8VU05Z3HhjhetsX+EMbXodsuwhj7322MG3Hvz2sLejiXjMZvNsJjzz5DO/NewtgZW+sdLGF278/NvPn7HGGUF3Hnr1oXmnnXf8oeO/89E76M7ysy5/5ZNX7nr1rkufvrSU73383qfDP5Vx7CFjLzvzslFs/k0E+gaBoX1TTdaSCCQCiUA7I3DDDcXJJ1cauMoqxdhjN2jpZ59VIq+8snjiiZFP33uv+PTTitpm442LrbcuzjijQS7FnnpqJX6ddYrddqsElLNZhTMUM89cvFXhDG16rf2Xtdf8zprbLbjdcXeP9EIad+xxJxt/smjukGKIwOmrn47THHHHEec8eM6xKx+7+zW73/b8bYvPuPgE40zAkkWFM82E03zy2SdXbHgFAoQt3fLcLYiOjEPHGjrWkFxsB5b5t48QyBeuj4DOasYUAumCMKaQ71/1UrrEhY4MH/55OEJvvlnRyrg++aS44ooCibnuuuKUUyrE6PTTix12qDgmB4kZmXPUP2VRoyKKccf93Fg2pMIZ2vS658V71pl9nQ8/+RBriSbWEBQKHn48i8ywyJk/OvOyxy+bYOgE00407QWPXrDYjIthPIfdfthSX1tKxsVmWCwcfS5/4vIDbzmwTXubzRoECCTdGTODnNs3+gz3hi4I999ecUE4ZL4Ltzg/XRD6bCjauqJFFy0uvrjSQjamkqNMOmllj5Xr7LOLoCaLLTbS4ebyy4sDD6yoZ3jhLLJIceaZxWWXVVJiS6EHqtwUxfe+V5x/fiXg79JLVwJj9ZNJd+vvbr3oKYv+5vrf0OiUjKfSgVHXpONNuso3V1n45IV5NO+15F6i2bNeeOeFKSaYYuHpF7752Zvdijx8hcPPuP8MxAgBOmalY0blzn8Tgb5GYMjw8pfd11UP6vq4MVov5tUHCPAhOPehc594/Ylj7jrm3T3eVeP4vx1/vKNefuuVyYQnPWjSt3Z7a9OLNrVUNb/zJ7AGtUKlw+d9ef8r95+/zvlrnLvG2WuevcCJC8wy+SzRYHP6Y9s+Ri0/0QETvb372zWr3kiTf/sXAk8/XWyySaXJeM/xx4/8eaI+v/51MfXUxYILFiecUIl8/vmKy8777xdDhxYnnVQxSP3+98W551YozhZbFNtuW6y8coUYXXJJRYUj/YsvVuKZvSacsGLV+spXRsYHOGN2Hhiybxsrlzp4e4bvPUrz1kGCjB7jCNxwww3fQ/MLetArll9++THenrIB6btTQtFUwPaNn/60sDtjllmKiy4aOSdWz1kRloA/o40YFOCHHlqZK23fMNmZB+l1br115PYNLo2RXsrNN69E8nOUbNppK/HbbFPcckulin32KdZYo6nmDfhE3cD/4x+vvfkia0708HYffHCc7TPwH/7puO/932S2z8D/nbcrM/5BC5+++vY3rXfzEeMX59yy27F3v7D7wmvftspSi//7+QnmOuuGCZZJF4SB8Gb59TVz8VZ2VSd+5JGK9aom0q1JoPryk/d/XJG9uhDxX/3qF55Wpxz5oFv/5Iq1W7BlpsGHAO1OXs0jsOGGw886q5L8wguHjzfeyHyTTjoy4J8Ib7HF8DvuqEQ+++zwueeuBKaaavjbbw9/9NHhG21UuS2zRGD99YefcUYl3t8NNqgEJphg+GGHVQJPPjl8hhkqgbwg0A38h+4xxZsfvvnlWR8fd/9xA/9JD5y0xH/I7pN6OvWuS572p4/e/ejdSfafGv7Ln7n8WJsuu/8fXnOayELHLT3J6nuqes3z1uSPKXDJfy5Z4awVYjgUFYH82/4IFAXFwAD8v9vIF/sU/r/xxhuvvfbaa6655uabb64p6uijj55rrrmee+65mvgxchutHSNVZ6VdQuD6668PJkW706WMvZ04tTtdY7gWebl9o2uQtTR1N/CfZMqtFz150UlXn/u9YZM99eywM84Yb7KDvtAmLggfPrDKkV9f+I+nfrbv9/f6/XHFztuucNWdJ227+RRjf2nhe169efx/7y8DFwSnhhx/z/E2lZy06klfKCJv+g8C77//wWejnGu+9KUvDanSwLz//vsm3DLygw8++PTTTz/++OPxxhtvggkmkFLaGlVKGfPRRx+99dZbso8zzjjjjz++9H0ASVXbu1/b6quv/gZ1dMEq9/vFF1+8LOjdd9+96KKL3nnnnbfffruM7KUA9FxwG8pGOOqKyLHGGsuIjIrLfxOB7iOQvjtdw26aaYrnnivGG69ipWJvYsJ3TTJJERMCwxM7lEM7WOi5Aow/fsWizyDlkDGXszeOOKLg/HjaaZ/b78OYRcstvWKHDat4A7zwwudlyhhpKkUM+qsh/v3RBaG3RzJdHOoRDnKw1FJL33LLLZjLuOOOe9hhh/3whz+c1o+2KB588MEf/OAHBP/FF1+8ks3lRbHwwgs/8sgjCyywwG233XbppZd6WpKbsvCIee+999Zbbz1SeaqppnrooYdef/31+++/v0zTe4HoUQ0Da766+OG8u9O7Tz755IknnkiXU533yiuvfOCBB2aZZZYf/ehH1fEPP/zwPffco7OrrroqguIRSgQ01HDRRRf9xje+8eGHH1544YUQRv4+GXF985vfXIyPd2GefPsf//jHsGHDxh57bJGL8PEuCrRy7bXXhvAvf/nLww8/POoSudZaa1122WUTTjjh5ZdfvsQSS0Rr88UOfNr5b/rutPPodKFtsX3DERr12zccG1+zfcPBYrZvmEMcn+rAVkeTzT9/hc240CD/l3s0YvvGBhv0v+0bXcCuFUkb4t+KgrOMwYLA5ptvjt9stdVWlDFrrrnmV7/6VWJb588555yDDjpo+umnZ+kMLLbZZpuNN94YJcIGfv7znyMERbF0Q5iYgdiDnnnmGXTnuOOO22+//SR7+umnyfvJJ59cmKZEeMYZZ4zszz//PIakGZNZyhSFjFNPPTUCgTG8/PLLlEkSI14kvWR0UZiZvKH5UJQGTznllH/961+jtB7+Vcsf//jHIC7VRR1//PG0O/POO2813dl1113Vq5HoiDDE8JkddtgBehjMDDPMsNFGG2233Xbbb7/9a6+9hvEgQMrX/r///e8KFy/ln//85yOOOOLLX/6y8kX+9Kc/nXXWWe+77z647bLLLocccohIeE433XR4FRhPOukkdEdkXolATxD4XHPYk1IGT97DDqts38BgyF3KmLiOPLJyhlhs34hISxTbN+zviO0b5k9nly28cIXi7FXZsFk5qx4Bsn0jLps7bN+w9SO2b4yMzX/qEGiIf6Ra+obhzWyfuW/1IRaI5fYZS0a3Xdo+E1nKppW35513HjFm5bryyiuTRqeffjoBNtFEE2054vDdq6++mlDcYIMNZptttjJvSwLLLbecwqkTuFkoMBbBLSl5QBbyne9854knnrBzhBKC4QmxKLv56KOPLrnkkkRvxASepPI888yDZHz/+9+3TikTl4F77713jTXWOOCAA3AdkXLFiJPlGJIq8ACynKQn41988cWTTz6ZLmT++eenOqLqwId+85vfsCLJhUbgW/RJRL7EFB5bb721V8hyGcXZfffdla80XQieVLahh4GvfOUryF9NITQ0+++//1nOih51/ec//xH5hz/8AUrf/e53//Wvf3miO3Qw7IDC2OF1112nna+++uqcc86pzWBR8iqrrOKngQzJQqPj6VJLLfXtb387CqYMk9ivA86g8POB5Prrr7/00kv/85//RPvOPPPMzRoeajSqYflvItAMAkl3alEK/XBtbN19v9u+UdeD/hRRiqSvf71iE4wLm6y+wj3u4IMrcSeeuNczz5zP6m9unXnmylm5zv73v2vIvpW/l15a+VtejIn0cHHxs9tgg/2XXXaKWWa51+qf4GGjbOYiwyxbSUfTunkf/zj//PMXXHDBEH4mbsJPe1pOd6oFdjPtHORp0IVXXnmF+y1XFX45xisAIYNPPfVUNGLPPffEWfEb70+JFU1DRzgz+gRzisSsNmG4ofP497//fcKIa8R7OLMElB8IAalPtEtAceJ9W2eddbTHU7Vsu+22xDw2pm3ozu9+97uJJ574t7/97WmnnRZ0h1fQMce0+PQaraJBKTtbBsIgVd5yan7zzTdxOzEYGJQEoATPLbbYQuKnnnpqPrsfR1xuXYKUVXfffbcu+11Qfflp+E3pFBMYcxXFD+RRouiyGDTolFNO8ZRdDCmkRsILv/a1rxU3RcH5NxHoJgJJd7oJXGZrWwT4B9CfWxSahX/xi190qZ233nqrifvcc8+1xF9ooYUee+yx5rNT7KM7hNncjJeFQ1lO+tvf/nago+gKnxr4dOaZZya6VlxxxeoCOWMSouQBiwDZQBJ7yn6x995764K/ZAmlkY4wvrglFZSwGsVgUTz++OPEnmQC1WVmuHMEqNzwTpdkDCvhnItJsCgde+yxBC3OwRBD0cKAVRbF5sXIVacBKZ+PDNBD4LVueP/QuvmLHwTfjRTPPvusUQ6rFvFPWSKeyKcKMsQe0e7Qc+DZI0vs83+ocIDAruS17KRyXQj+591miZPFbcTU5/Jue9XF6z4VGqvcJptswoLmZXYuC+qD4VkYYDZ+L/iQ3+Chhx565513Ui/5Cfhl9Y3rd33LM2YgITDWQOpMC/tCneD/9957/8orr7r88iuef/6/EdOXf0866eSJJpp4o4027mGlYFFCw2uPPfacdtqv3HDDjRL8+c/n0n2ccMKJPayuS9n/+c97H3zwIVmeeurp6hYC/JJLLn3yyaeqI2vCHSldJplkkt12280ULD0tek2uzm9feuklrhIEnkW/2dYk3nn6+qc7jfgOpGW9qZ/oCgMHorPjjjvWOFvQ59PbW85Kw8Xhv//9r9IsjslItg+6ByLHGpdRjDBeYYUVCAmsyD4ahVMGWA3rI/8SLrT1zciYjhCgtjFGNBMoxRlnnAFhKWnm8B78Bu3Yeeed8UhWmDDQhIri7LPPrjf3RBUcbL0wPJTdYqJTTDEF0kMt4RYnQGUiWfxlh/JiRJnINCOOeAYv5kg8iVmHgOe2IlIaTCIINwpSvWXphRdeuKlUclaX3q3w//73P6Vhe9qg+8suuyyfZVV7CXUK+aZkoqdkhvvJT36ig9iJPvqVeUVVKBJrEUkxxshFmSXSS8v1G2XBb/RO460ExHMSlx7/+7//+z9vNUYoEps56qijRBoX6i7MUuQdd9yhWI5WhkMkX2aReSUCPUKgQsjzqkIgTuaICNrmAJc0MvdVpeqL4JFHHmnKs/7ramWmKhoOszN9uEuPKNsrnGfUZXabaaaZxNAw66ApTDKrKxrjUUmGkwqUzKZCpYk0PSnTFZEmwUhpQSblr371K2u1Mi/NiiUaCW3WEx+JrZgp7S3myoWgdZ55U0p2/REmHqRs5P+U3hpm6o+YsuSGgWKfyvEhNY9CkOAQNfE1KWtuJTZl08TgSWb5mrxxW5OlvMVFzMv4il7LDjGOF2UJJm5L2PJWgIwkVg0NpT3XhHhErtx+++3CpK81bkTiQ7QRwkGJ0B0enbITeyJJFFgRTpFYe8omRUz+HYnMiLeLYQXn8Dbab0WbwkjkKXaCIgt4vQlyeFL83HXXXQJcc3jL0i7grN7GmitiYk8T5x4OuVjs7LPPLhkPoWmmmcbYYbQoLOIikvoQAfJ6kOV+3SiOSL8Xbx3PZa5dlE9YrLYFoWHZ4cUiOw4UVVOTILhG320zv47I1fBvvCpeOXSE7grDo9f8y1/+wqNIeifxAIGGkvuOVxofEunHLoELd/fbj2JRRjpIiXU5YgSkUbJHYhSr+6ZQLNML7zLh6IinphTxwhEvHJH+In8uvyOzkHGJ1lqQlBcGFuVHpfm3TRDIc3fMG/3s8gu3K9Jyh9hjmPA7r1Go2jVgMmJNIH7MXJQBmEEIy+iqWcykgEPEQdqkfqzvWUks1/yMwznAnOvHz/WP+I/fPKnplxw6Xn6LJXD2hapUYtVRP1ieCpBzZnA6CeVgDyzrdoryl7So4gcwwr5+DAfAoji4LMei1oaLZ54pFCXSVGJJp0ZiPtJYhGnzMsssYzKigbDq4tAQqg4zL1EBDfVKbE1G9y6lpxpA2SASTeS9iD9ZyQEEA+CpgOvokancSg5QtmPY42oN5xGF/xxzzPHvf0fllb9agiuQQOHZ/fmD3g9xUDD0Zmr6GNOH7jdZp+4bLDLSQhYFIQAQoE7yUs/AGSDkaznKGAyTitHxUsGko+wAZAqJdXBHaTK+IQJchvmC+IkZaJZHaMP/kksuQVaoGVhwbE0Hr7FDOLy01BV+Jh4xjO65Z8MiHYC+DRJjZULkK9mrK50SLJMU6EddZrO53Q/N3iUMgywPakUvwhXGPOMV8jtCI8TjN25xDj9kt6Vpya3sVzkRvIsXCqXj1VqiKMA0xftYmH+9Gr3zOIefQJyCAwpdU7ufObhMWUpw6R0llsQyijQ3motAGqopCWT31G9Bg2mJ1l13XYU32WSVYoo0OgKfZ5mmEqTyLGNMbqa7rmpwy+wZGHQIeCPzqkYgFkxmKMtrEoVoNyuZjKQhfZESU4YwWYjHYAMiLcsoJyzLvD1Eu8lCggsuuMAiz5rJU7JTDB0GOiINFbf5C19xiTE1EPwqshfDU/LVfGdBefDBB5tE+G3IG5edn7QyKIKFJlFnSSQebyAXzTLmccVqLV7lpAqTl2l0BMEaTnaWC1MuIGpRiBgUzVRFNyOGbtmsbQZRJn5jEkGDECkKZzEC0pis9Y5bgzMzcCbx0LCiVam26YUYF4OLqQqfkyW0DtojbKqiljCRQSlSRhqzpNtAPv7G0zKyvG0YiGWfR6ZgBUaa7ml30DhuoSZZhThJhYKqvkbVVUdW3yIr3hmsTh/1F+0rU1LVeHnKW4GQWBbBGBK2KsZgeZH4OAvjxKZyC1lhpYFOILQ7qKSltg5i4V4qKgF1USFI4CrRiNv8WyIQr5Z33tsI8zI+AlYgCAd6gdzUPCpvlVBz1cfUJOj2rdcDgdDOmE8alhM9avioPtL8gLXEtBN/41UxBZkrXNWPGobNZn74WJ0tV9aBAk1epggO3c1fBih0nNW9yBe7Go12Dqd2x4Tcny7zAsOzX7VZwFoqlmu2a5L6VBF6QhBaEpmPyCf0hd7Fj5mgisMqSEqLQjpnphwWcYzBWt9KEaehSLfuIb046wUiTDas4BgDikD4WSBKgNZgBsQn7lICh5q4NV9bMOEo/lLkkHk2RHz9619HgFAQihzqE80jQWmnSEHZTVJRCHmJe9mBQppGjJ8NgkVHpUkMLhFJ2aPj1ruWZRoskvpBpywEMTCXhRp9tXh+svvuuy+g8CftieyWg1iOBTFaQ+suUi3+yi7NhhtuWO71jfSt+mto9AWGRoTQQljN2mXh7AgjaF8Z0SBgUYvuGFYclPodRykT+Q0bYpaFMqY+YAh0cJ999pFMS0Yo1SqpFOsN8fKIx01thMGKvFceUekZFCWry2Ah1jyd+SuwiWBvXgYDrTHghSF5s8ceezgGhinEOLJwceKBcHDu+vaMwRivn98CW4OXtqYZhsbTmsiaW2ngQFNSE9/z24UWWrCDQr5RFP4fzTVis9EX0tTHfOFx92+Wte/d2QqtuqymYkFVFhhnFvzfdpVlSZPXW8Vba9y/RjF/8Y/7/tFklu4nu7L7WTNnIlCPwND6qIwJBBACZnumfT40FjEEEillhRSSm0SXjH5l0003xVToYFhtXFS+xC2Lj8WZlTeeQWEgJY6C7ghQnyA6JdcRw+Rk9SM9/RBnmihZfP1Fg8LYj83wyyHR8YbQDzOdoDtcQCicyMj6jGUMqzyCEi2JSN1BaEacKVIhJWpHcdCXH//4x7QI5CgdeJm9OoCTIVuKosfSXxKajR8UGIZWWSvzh9hrr72oOuRyuAgeoHxaMep6kEJGpbH/VuIRvORz2w0MeYCOUERtVV1p52HrVJ5ARiS0IDxPMbMyC76iPcU+ZUSDgOz0ZI4SoeDBM8I2F+kMDWZZ0sQGmUdE4Su6TK/mhYm+i7YPmWIMh6a3887w50BkEWVpKAghqWRcByFDstEgMYZSRuyWgsdKV1F8P7XKm+Ov1wAHYkkEKXImJQLhdR3RhMqf6nAZWR3QGCSbvYYIxE254oopE2iksL9ReBnffEDDDK6m1mexbNAdCeoflTGAAkhv0J2yigwkAonAoEIg6U6Hw00S8KsgIDmmsMFbqbNVS109TdcvUkvxI8CwwkIkYIFLMpU1RQllSlSA+Gf4oBwizIi6qIWkkcZV3lri4wr2+2AD6IhNm2SVtiElHv3pT38it2IBZ1WNXtANjDgkY9KomuzRCySJLidiaIME9AtZQWuIagJef8k52h3KIT6GmqcXqiNBSV8yjI4Kn6Bwpo7CWlBAYT4Q0NA8RamI8w29RWSRjK5CUQSY5jkgVTOCYFGlaAB73Ij2fC7/0CZivuKf2MWLHo5xJzZ6GL5ygAwBXxlqrc2f27yMjLKrbx3phr2JcYUuLfCXUsl6WuEBD1QOyRWDH3DkFPjZz34WRfmLL+o+0gl/gcguspo3iOS1gw0b90jJJQuboc/zSEa1i8ca4cxuRdmGFUF4hCdWWVUHgX0q8bEzqIMUX4jmqvKF+xE34b2u3uA99QmaianpdWShtkFi2D2bKaG1aTrlV62tqn+UNnzvz39x/aPF2cpEoAcIJN1pDB6zC3sBqRz+KxLhFlQFDE/oAqlJPokkWalArLPRC8oDCgCCn3aE0YFmgpWHeQU7wQCIRkKdcoUYQ6E8oucIYa8cq3/WKxKR/j8aZOXNO5jEZQex0rXid5i9Vf6vf/1rpivsAXXQPInVSBHCDkXlQ0XkERkpL4EXGYuiwmlcIokZjCRu/SW2HYkWDjQYhmU3woR4oRrkqwQaSfQqh/uIz9uKQYP0jmwWzyKDFOojoYhyEdUclei3YMLngLSjr8KiUDGt4tCjYXJxMHJFG5hjEKCgAtNPH3GVvxRpNEYjDpz9PHK0Id351re+ZSwoD8ClrjKLthkCI1VsVVRbuIodvng7wsOUozcHago5ZA41lLcspxKYsXIWvn+NDq0exT4t1xcSjO5GgboGSShFWjHeDXhiA9W5MR4XlqMu2qZqzlSdrDo8/ckVHEFdHdnVMO0U9ErtVFezZ/pEIBFIBNoNgYr+oN3aNGbbE5Z4qNiIQUlAQCIo2IaFuIbRbXCLobdAJpgbaAJoRHix2IJkUU5W4QoErZRICc9TJIDsDO8W7s88eMK8Yt1PgLEEVQTwiItjB2lNAxG3+ATVCMZggBRrC5iNTrGxAtOyJ6va9BBZOvqrR7rj70wzfR2LwpMiZcR3lKvb8bZvYIqaymRDhPNw4pVSbRXqqORAvuHTzl/S/GxCPWi5cK/HJGMSgUSgDxAgE0OQWSHHruQ+qLSZKpLu1KIUQpd8xXIQFOtphIOBqeQlVB3Iilt8hVaD+QO/QYYYHdh6RqoQRpRqfWxXhZRhn6qtqa/ug9b4O88881K9aHDU3Am96KumNVtP0p1mkRqVLunOKCTy30QgEehTBNqW7qQxq8P3AE0pmUF1omrvV9oXZi9KILYDPhD8mku3GFnwoYYlVJfWl2FHx9a0p3Ma0ZdtU1dJNLtab4r2riKW6ROBRCARGGwIJN3p6YhzrWCTYm+y2/wLTiE9Lbj1+W3man2hWWIikAgkAolAItD2CCTdaTxEXTH08Lo9WCmHH964qHaIje7Ud6o+ph1am21IBBKBRCARSARai8BYrS0uS0sEEoFEIBFIBBKBRKDdEEjtTu2ItJU7S23j8j4RSAQSgUQgEUgEuo5Aane6jlnmSAQSgUQgEUgEEoF+hUDSnX41XNnYRCARSAQSgUQgEeg6Akl3uo5Z5kgEEoFEIBFIBBKBfoVA0p1+NVzZ2EQgEUgEEoFEIBHoOgJJd7qOWeZIBBKBRCARSAQSgX6FQNKdfjVc2dhEIBFIBBKBRCAR6DoCSXe6jlnmSAQSgUQgEUgEEoF+hUDSnX41XP2nsQ//7+HFT118jmPnOPyOkadNT3bQZHtet+dSpy819/FzX/jYhbpy1F1HzXvCvPOdMN9VT14129GzPfvWsyKXP2v57a/YXuCGZ25Y72/rvfHhGxtesOEyZyyz5GlL3vXCXQGAoja7eLMj7zwybvNvIpAIJAKJQCLQOQJ5zGDn+OTTbiJw9F1HH7jMgbNPNTvGs8PCOyjlo08/mvJLU9646Y1PvfHU0qcvvca31tj/xv2f3P7JF95+4YCbD1hh1hVuevamDebc4LPhn9338n3Su11x1hV3vmrn7RbabqHpFnruredW+/Nq9/2s8mjYp8PWnWPd5WdZXjivRCARSAQSgURgtAgk3RktRJmgOwgcsuwh5z507iX/ueTtYW9Hfjxms3k2E5558pnfGvaWwErfWGnjCzfe+rtbn7HGGZc/cfkFj14w9zRzzzvtvPe/cv87H72D7my1wFYUQk+8/kSU8N7H7306/NOxh4zt/2VnXjYi828ikAgkAolAIjBaBJLujBaiTNAdBNb+y9prfmfN7Rbc7ri7j4v844497mTjTxbhIcUQgdNXPx2nOeKOI8558JxjVz5292t2v+352xafcfEJxpmAJYsKZ5oJp/nks0+u2PCK8YeOjy3d8twtiI6MQ8caOtaQtMMGlvk3EUgEEoFEYPQIpMwYPUaZohsI3PPiPevMvs6Hn3yItUT2GoJCwcOPZ5EZFjnzR2de9vhlEwydYNqJpqXgWWzGxTCew24/bKmvLSXjYjMsFo4+1D8H3nJgN1qSWRKBRCARSAQSgdTu5DvQKwgwUS16yqKMUzQ6GM94Y49XU82k4026yjdXWfjkhalt9lpyL0+575x070lTTDDFwtMvfPOzN+//vf1FHr7C4Vv+Y8vj7zmeRuekVU+qKSRvE4FEIBFIBBKBZhAYMjy/AN4MTpmmDoEh+1YMUnklAolAItDvEBi+9/B+1+b+0uAbbrjhe9/7ntZeccUVyy/fRhtK0pg15l+hgw6qtOHhh4vjRnq5jPkmZQsSgUQgEUgEEoGBhEAas8b8aKI7u+1WzD575f9+d+Uiqd8NWTZ4DCLQj3Si9T9tja+PHINgdq/qfjQE3etg5uoIgaQ7HSEz+vhXXil++tPijTeKWWYpLrqoePPNSpbJJhsZKMMSbLdd8fLLxUcfFYceWiy4YHHUUcWppxZDhhSIzq23Fu++Wyy3XHHVVSPzSrn55pXIiSaqJJt22kr8NtsUt9xSKXmffYo11qhUlFcikAj0RwT6BWNITtAfX61sc+cIpDGrc3w6e7rTTsWPf1zcfHOx+urFhx92mHLnnSt055prirPOKrbcspJs//2Lm24qzjmnErPvvhVag+uU1447FuutV0ngrypceNKUUxY33lhceGGxfeXA4bwSgUQgEWhfBD799NPPPvusTdrHleSQQw5pk8ZkM8YgAqnd6T74N9xQnHxyJfsqqxRjV46Dqb3i937llcUTI8/JK957r/j002KllYqNNy623ro444zaLO4VS6njWmedipHLpZzNNqsEZp65eOutSiCvRKBfI9AvlAf9Qg3Tnq/BrbfeuuGGG+64447bN70+O/LIIw8++OB///vfE1n/jbr+97//ffLJJ1/5yldGRVT+ffXVV3Gpaem9m7jef//9XXbZ5c033/S3ieSZZCAjkHSn+6NL6RIXOlLubyuXNAxPkeCTTzioF+OPX2EtDFKI0emnV5Q3RxxRUfCcdlptA8qiygfjjluxZ8XFBJbX4EGgX9CCZoajnjrUxzRTTp+l6Qj5juI7alh9N0844YRLL710/PHH/+EPf7jBBhuUGW2S3XfffUnxn/3sZ2VkPw0sueSSk002GV7SfPunnHLKAw44ACxlFkRn4403Xm+99fwdNmzYeONVDrP4+OOPN9poo3XXXXfTTTf98MMPJ5hggkgvsTQTTjhhmV1A5Je+9KW11lrr2GOPrY7P8OBEIOlO98d90UWLiy+u6GDYmEqOMumklT1WnI7PPrvineNabLFKApapyy8vjj66mHvuYrXVKrat+eevaGtcaJD/xxplV7SD7/zzC9Ogv0svXUlQPqrc5NUGCHRV5jXf5HrpWB/TfGltkrLlcD344IN33HEHUTfjjDOSrH3czeZHpGHHPxpxXXfddQR8Nd3RqaOOOmqKKaZAg2r0GX3cwZZUN3To0Iceeuivf/2r7q699trjWrQVxdVXX/3iiy9OM8009iefc8452Mnqq6/+xhtv/P3vf//Pf/4zZMgQuaL2d99990c/+pH0X/va1+SFzB/+8IeFF1545513vuqqq6699trNN9/829/+9iOPPCL9Aw88cPzxx//pT386/PDD11xzTRiKvP/++0W6hGfvj9tAAoj820IELCny6h4CTz01fIklKv/vuuvwSScdWcYFFwz/zneGL7308F12GRn53HPDV1hh+JJLDv/+94c/+WQl2SGHDJ9vvuHzzDP8qKMqtyutNHzllSuBKOSFFyrpFevviy9+Hl8JjUoT4TH7t9in8P+YbcOYqr1VHaeTf+GFF+jboyP1xdbHjJEuv/baa8suu+wmm2zy1ltvdaMB9b2oj+lSsU8++WR4Y5CaXcrYfOKOWthRfMOS6xOXMUsvvTSBXeZ66aWXXn755ZVXXhkNKiMFvBvsO0888QRNScRzi8EYkAMgUHWIpOTYZ5993N52223f/e53t9pqKwwjEp999tkLLbTQggsu+POf/7yMPOWUUxZYYIFFF1304YcfjmT+0jktscQSK6ywAj7htmxnmaCMlHKdddbReCXcNeKSEdWQwN9FFlnEU2EBcspfypU555xTQpHqHXvssX/zm9+sscYa22233VRTTcXM9Pbbb1900UW//vWv0RphyVw40N/+9jeGrV/84hf/+Mc/LrjgAuRJPGYzzjjj7LrrrpgQp5wRaYfT9KhaFb/61a+QJJFo0Fe/+tXTTjtNGk2deeaZI6W/utawd2WCDPQQgeuvvz4oinN3elhUa7OndifGpfHfJi1HvJVd1YktObjg1ES6tYer+uLC7P+4Int1IeK/+tUvPK1OOfJBz/4plVLdLqbh+rXbpbVtxuYX9M134aSTTiLh9t9//y233PJoer/2uIgfy+KlllqqujkEKuky8cQTb7HFFmRb9aMxEia9SGUkIBb33WsDIapfFA9l9v/+979nnnmm21APlPE1AVOwsfu///s/zIOdhYYJWZGRZgL/EMkgRcTW5Or89vLLL6eZUCY7VxzRFukBzkbzyiuvIJrUPyIxAwoM1PPpp59Gj7ikPP/886effjrGg2cgN/QZc889N36jSZqng1r4xz/+cZ555vGmSXzcccdRiek7O9Ff/vKX2Wab7ZlnnhGpLlqlPffcU7KOWqtSdMobMtdcc1HMPP744+uvv753BheRhY0JL7mSu2JlPqwot7GQb3zjGyuuuCLmgYq99957Xvgf/OAH/mqAchAXDabQoqs78MADy3rZwpSPG+Fqq/COHHXR6LBqzTvvvMsss0zE3X777bovHlXS/kCJ0w9SuNpqq335y1/+5z//SRs0qoD8d/AikHRn8I59S3reGzygJQ2zJv7ggw8osa0Fe1hgL1G6SSaZhIgiIImcww47LLT9PWyq7EQIGcPrsxsdZ0G46aabGCCIDZJJC2eZZRaClgqKSoC8nG+++coWPvXUUx65nWGGGdhliHnaAr4XBJVHfCa+853vlLaJMlcZoI0g3em3rOAN02OPPUZcyUW6E7eEKBcNVg/pSegjjjiC7WO//fb7qbMfRl0hUOPu0EMPZRBRAuI49dRTYwOqJgW1/5JLLhE53XTTURj8+c9/Jiwpq+655x6lIS7nn3/+WWedBSvqEzSC/J588slJ2eJzp5pR9Y36Fyv67W9/K43Gk6MXXnihkvfaay/twTMoSIKjIByjcoz+X50lm2kmDEGZeqeddoKq10ODD4rTSIsCiUE1dtttNxzL+0OxMeuss4LaX70ba6yxdM1LpRBD6W9wIBQqeCrNCvajbX4ddD8333wzuoPEzDHHHBR477zzDpbA0bhsQ03AW/qtb30LR+Fng3GG0e13v/sdEialpzqCGZe5Yow08ic/+QkHGrcREwlQHLaqMnFPAnvvvfcxxxzjBaANUg5qjrMaIGFkS/OMrxejJ1Vk3v6OQNKd0Y9gz1Ugo6+jz1PUqJG6XT9Rceedd5IQFoXhS1gWZQV877330lGTNGVkbwTIA3N6TckWmvfddx/J1Nu119Tb/O2Pf/xjKn0Cg0jrPBcaYd8KiWW9S87hFtAmNqyP99hjDw4Q1spRAoWHhfKzzz5rvU6ZP9NMMxGZHp1xxhlkmCwE6nLLLXfeeedR8hMJZB5JTyqQgtbBeAaRKb1h9XfppZeml6aRBqZbo+lvXNbQDEkkrltqiV/+8pc4FjGvbbiLkqkrgN/J9hkLdKoIiXERdAHPIA4pBghdOgnKBqt25gzlr7TSSoQimwhJpiUKH9mIqn90k6GEDF588cVFo1zeSVxHmOcvFYi81BL66y1lCCOS//Wvf3kKLlKfPMaoWEMoIYRZlH5w8w+qiv9CkF6BxiIUBjQW/IshYCMSkhdqfJzvueee+0Ke0d0gZ6V4LtOyZNHK4FVonyoiXvsZdCgz3II3pLgRZBjCdUSicaFroTXBR0N9JaVxxMYwVywTNQQFihZweX/QLLzQG4U3VOxQz0RttX/9mh599FFjzYHGTxuhpGnTGFwN+8GEajN0fI9rYreQ7DjJ50+QMDROLaK8sV4MPx/jiOd5S/WLOsebQ1168sknw98YeWEMvVfimmuuwercXnbZZdXbvj4vPUODA4HKzyOv/oWASdkUFgvrMd5ya3Tiil3g+9//vnmnuj0Ep5Uoj4HqyJaHiXbr/vpiEYIbb7yxc66DqJGy8sYyneSIcnRKj4iHWCXXF17GcKGgvXeFgIl48gDPIGCq+QHKQmZbzpp2CZWyhGYCiCO+Qr9iuhfQMLI29q3oI4qAZNCOKApvYPhQNZGGLoSthyQ79dRTNYCYRLCIBGkYTfh+QsCy3khRh8ge3qAECXUCwoQViUQIZNQjNZatRRH0guy85ZZbTjzxRGIe4yRaUDfthJ5ubrvttmX6+gBLCnaF8cgCZ13Dw7T84osvRp4IsPLNQfI0TwKyme6nvqiI8fpRR2E2VBQEP5VDxLOG0EZ4FfGzoErEISqMH2AYZDyspET4aCZwBWOEuHRUi3iD3rnmjDohmEcnhTTzyAuJztakxIFAAXzN5qyjyzUJylsKTmNB4YEBGHTzhkfQpuSwP9wPhEkreoqmIMc77LCDSEog739ZSE1A1yjepPd732yzzbyNEkCVxggBMnbbbLONX5OXraIhK+zJuIb2i06Or7Fb/AbC3lVcxwtDq+TdxlRklEYW7/aqq64aTBSG2CSzoGHCqDAeJaDs9GfIuo7rnX5hMFRHSD/to8JR8NBBUn29/vrrOBmi782hukuuA8DBfKV2Z/SjH75vvBnMwqNP3dIU5mi/bfNydalW3jTw1qAs99XxTYZNNCNkxvhNpu88mVU1ucJ0QiVOLJkKY3cJkcOib0L8+te/HiWol33EbGtZSaKY+MgMkaQaSUOgWl5b6oWcsA6z1he2ulUCyW3aIo3MzqYzYsCRHiZrXpNkLZUGt0fCWLFaohbLVtOohsW2HUJdvKfmZVOqtsmuak+j/eS91TnWgg2YfAFrVmUdUHu1P0ENFBpD8FBFmGq9G9qMOqiaMUh7yFQTujKZHtACagmKGfSL/sD8y31BaWqRDCA1JdfcQgaYltRqwUg4fkpAuljj0qBY7qtIp0QSD9a1ekrjVRZChGBFhgYyhKWlPLW/lmg5ssIAQfyEAYKqSXt0h4BxRQli1BiqkYhRF+ubcshIFxiNoAU01kVLEToVhYQoLZtRE1AIHKgHqq14+qLx1SkxJ81TlAarQoLqpzXh3XffHQKQAW+8eN4KSg7S0bvkfaB0gaFIvymD6w30WzDoysF7GIwQQaJaymLdmrI/v4VwDBklkPcWA/DMUCrWSyXgney8nd559SoECAYF/4jhkzfIgRdJCTD3IpHTfjVK1nIavq233trba+wAZYxo1NRujIwyDRYtIHLDW0UHNU9Gii78Y7HFFqP8kBLRUSBGa7DQcZQU1/Q++HH5/XoBEEGVft7bL4YstLTQu4QN//73v6cK8pzyCXreJej5oWkqjoVteDn11A+Kaipq98748WoMnqReb4u2ISUyYipu8XWeOiXTlYyaUBXIDQIt4PdrecNOZ1GhwWHu1AukXKRfWdAsKVFnCAjklQgEAkl3Rv8mkBD8IcxlppvRp25dCjOgRTlhYG4qSzVZECdkQA3XMddQMFgYhT6DgCcgLZdNDWbV+eefn+0gCqHHJj6L4vqyzJ4HgEN1Qa7YKWq+M8Oa14ioan2PGRCbMRVa1luWUURbCGoktQFCYG6yOCOBrPgtW8lvSzT2CNOrmZRYMi1a59m4S5kEEESQlEWnCDCaBgYFUyRpYcbEadzqplZF14hA8zj+ROxZ6+OLRAJahtBEGgWSOiHDqDTIPyyH1gTXJF06wkcyzbP+ttS2LzqKwpyIIgKJ+s1yWUdIa73D2HAOi1HCWHyUqV9kRrU/Skd1eQkpJ0qLhmQ6CxM9JRe/+c1vxrxfn12r4Gx1C3lCEYBj3INBs7WTJEbdyDaCkJai2h01emEoYYhQEpzEKkIGKzB6qyMBwUboWvSjXBHjPUdzrfVpKSKGwgmjghu4gkmLlwyzUSkzmddASwyZn4xx8dPAFQxZZG/4F68lVhXoqTcnRD7y4TdoFPxC/RIxs46Oz6FsQ5jCGkXtZFz0y0tOQ8Yw5FXxK9AeaSCDvmg8KPxMsAQ1eicji1cLRw+NBRpkoEMZqQ1+7JZnXk7sQRbp0QUEVNgUIdLrpNdlpHgsHO0wNBG50b4biay/rLK8QvK6VB0gSIYQu+rT18RofMQEJy6fWiyV4eqAn21Dp2+/fVd1Sg5k1bv6qx9lOBEIBJLujP5NsGwivQgqSQlXU4/p1XxhniWuCA8znYnGrUiyx+RixjEXiDQdm/XMEeYjT4klAt4Mi4VYEJt6YrYyAZnXTLJUF+Z9KgdTqpmXeLbusUYhic2q5ghKDlzB+qxaPCjfygZLMDNS5nuqUlUTDOJNr6Ywk3t4BZpYrapH3+2upyBNZdJ9cgibMePH/BsliTefWn9jQlgRiiDe+s+0RRUBQ6QEtiL5gfIeYG1B9ZAeK3XLUCwEqtadk046qT4SBoQEXqVrquN3ErX4G7dRVESScyBFd6xoVaQcQtEoCBsOaSQmDLRQmBIF2kCDmPSqi0Lq/0pmuMXrOJYTCRQSkQKEQXSTKDW+xCExZllfCglZInF94fUxXrbqSOXrF3mJ4GLG3q54asXvTWCNQuDEGHQvAyGKGmqwZDooXhtILO8zESsxsugWdLLLqAQvHszRKZxDLn8prqy2pZl++unFU1YZX0SKZY2aTZmyxGqeakHbZCGDqwciWhi0gxkRV1Catvl9ceIxLjqFrMCKcQSn95vywnjh/S4ULoElh+U+a4te4NPgpWnQtTDGKR89QmK8HlGX4fPWEZlS0h/EisUP5O6778aE/Ij4OBsUiaGEnWu/nyqF7pLXfUGaRmnx10Dor3bCkDFOF8RTMKg3fgJ+hlQaUKrOVYaNuGUMp5MyRoCobiit/YRd1SmF6ZNCpVTG0+u44hZ6ZTxsy3AEtNmcE9NO9SOdAm91TMPw2PtXOptXItAfEUi6M/pRI8ksQ6UzhREeKAujOIJiYqVQxR4oWizIeOpZRqMmJKV1vAnFCtJSni0cUyEezKeErsMqKC2szMhsEj18Qk2a1jHymqrCCySmTitakdITRTGTUjuboC30zfUEVbQeN6J+pyRAFEzEtA5WqHgYokBiEWmaTa4H3SHpXSOWpqPvewtTaD+iQzejR9adsTgDgt6hHSoigaI6CCCUYePA+axTyapqitCSVpGsxB7djLM6LC6NBX24ktERsgSXEqbVqyEZ1VVLT9IbUwLPG8I8R+SINByEN25BdhpHWfBRg0VddO655xpK+BP5FuvG19uFNBi4UkVRXUWECXtGE2EkEvMI+qLNynQZbvYFHamYYIoCYgRtGEBRai9eqApCTYVTBjPQZj2lb8MevEu8fKzviXAvpC7geShppGSJwwM0z3seCi0UxIViclhmrWO7QRH01zDJwqUUgJgEouMH0tGi3zugCwo0sliRv8xPNH8K8T54yf18RCIlwFG40hCFSInh+cm4FakXJWJ4G3LALuOliki2G1eZoAxQ8IQfdBljLeEqb4vrPg/Wh+BTQzj0xRUpFV6fpYwZ94Bxy3D/CrTtNswuwdhLGy271IZMPEYQSLozetgpVAgS+hg2F7MwqSCPCZcUMemTmm4pzC3vKAwsWAmk8BtgZKG8NV9T20hGLlpooh2Wnpab1PISmItJIHYc3nk4EPlU2RYx4gp+QyyZ1iPGX9KXdMRgCCGiTgzuZeo3xQtb5lqC0+tQiqix2iuiLKH3AhwPSdlotlpIdHK6rI56jGzTRw0j6f3VSCp6vsaEInkmJX5AykJPYqCRZAiENMoMn2KJWaP4ispufzLtDpooIxFLD08NQEYimm4lYJBiMkD7lCmLZLBCRASULIyFkO7GBaPisiAXaYqLGAXOExQMqAlCJn3DCyWS16JcjbRoiIVk/C3QAi+M9tjuG0ttfxlK4qgYvcaGNQnVMFjeB4SAba4iLEeOfG1thltpSIC2GX0YWrUjr8gWNYwY5YRxRE62PJY1LYdA7JQhxRlKEHRPwRUrfgTFKyeNjJoEzHhpQe21hDPrQJi96CEousRjUV7ykknoaXVDNQ8vKWNwJld5Wx/w2ykjsZYIe2ewxghXR4YhRnwZWQbi14EkUQEaZa9Qqekpy29toCfycmAwhno8m8ekGoHmc9XXWBNTXWzNo7xNBEYiYL7LqyMEWGb8T6lDJFjMRTIy0pQqTHECRD4iwhxWCDB6Aimt4COldbYEWBGBwblYpNW5GFLfPlt6GkwINYnE7FbYEm8SC9yICZMTHb7bkF4RzwnGntsQ+WLIPPKMOkeYlEV9SFBhi286cwGiS6Uh29wyVYxQ6Ve61pOr2KdyOCknGIUDh/JA34Nn4C7ME6Gu4GBI6UUkMzpIqXf0EEQafZja9atah0/dIoZoxxoldmEJFA9ShvEOWRHGGzySJtpvIPAnnQK4iuCD6PClRUcgLCAZJYpIFhBhygyCmQ4mslM4USwJ03NoeUQaC+IzwroZgfJvfUz5qCeB+mLrY3pS/pjKW9+L+pgetg2Zozu06uhhOWX2lrewLLlNAn5lLWxJwGWWswzrpNgaVGtuO8lY/UjLq+dDj7pUjsRdSl9ddYabQcDiqjJ3Fz4WeUUz6fssTWp3Ylw6+0txTQHDjSASMXDQ8VibskSICUcEC3peFHQDZGq5qA2vYaoLZCikNV0FlkMFokAsio6HvYn+xq5OHIjjIaqE9+BAVBrqtZLGEmy+YGXwDlFssI7R2GsDTQY9EJOQvBbxyqHgIaQRKf4KrAwaw9MFBQkbFnLAmKJY5INUcFpKZ31u+hnHTG2g0EJ0mO1CjW8+0gCtog9D11woCObBgxIv0RGEI7wHoMf6FmYLL73+Bp56B2S2DP4EsY7XZrXEUp5g07VyxU/bwbrnNlJSb3ArqekB39IyhhqjdGUVCZB4VPpRuqXGKNOP2UALV8BjtiM1tfdKv54pNt1305qK+u9tr0DUCjgaqlKs9/ioWdHFaqQV9TQuw8TLnmterVZ7N06asYlAFQJJd6rA6CCIiFDmc1+I58xPJDdxTr/CWoSg4DokMTlN2HNMYXEgTXERySKSAsbmZAIe16FgoHWgnkFKBFg0sAE6CUoIAp6856GJlKiLk5DjKGxLQVyQmDBd4Q3qYvugvZfRKkdKWhxURjKHh/IoEuMppQUCoWTOpxpJb8GpyCPkiSFjxDEr7np67fHRHsX3RxZyV3HXifueOPJm0S+UPMVRU4y8v6ry757H7/mFx/3wpm9EUUO5EmhpQCdPW4VoD2spUSoDrWpYTd9bXr529kaZnXS/pkeRUqTfO0Mh6t9J3o4e+fnbL4nQxyqiTGZlQvlqGumGvbsjWOh3ab5dZS0C5qtQI5n9OnKD42gf85j5iuJcZ+0/iEIYnc2ilMF0t0FuLIRMhjTW3MklVl21eri66gwnAjUIJN2pAaTBLZ0BY014K3vMM8APmOuoH15o4awzcAjUhFMOSsEH08UyIiwy9DcYCR8gdIebCCbkh2oCCjcFFIe9RpkKN6lFZLTDthc2l+pFTBw+UdNKPhbhu1PG0x65ytvSNiRGma5W0Z2Gc3RZb5sEOpqgm29ez0sYbV1ti2TDvjff2kjJMsijyOuNxPtFjBaNMgEDZezbpx+1Eoj4hk0a53fj+Kmi9dLwqbKWKAtpecCOQgsbmtdQKEb55gH1Wl3E4XtdqrRhj5TAH46ikSt6N3iJKcX2BXspTCl4Q6iBkSeGXVzBRFSWaQ+dxZsZg3rGaYTWb7G40gAO3fTQPLesoKiK5arvl0ciHSFBIW3qkzjSUEKbOcOBj8onTPn12cONTGPouR0vKT3tr2QaYys+S729C1aJcWameIZ7zbBcNMF2RKHqa8mYRKDWKSHkd/4NBMJ3Z7Ro2JniTaLU8UNl3DFB24nKRsMRx62FCDdb7qgsO6Mtqs8SNNm1TtrTj0zgvWSqJ0LsiDY1Mz7WOBN0glvDR91oYXUWoh3/VjKhFd5gGkY8uGX6bFhjk5HVtZRZGkaWT6sDkZLfGPGJB5C7dKXVCUYb5qbtRANHNoR7e6Svb4AYjJ93ORnp1+f3yKxcFu5n6LdZ3go47ZfIpKMFF5rCoS2eSunXihPELfRYsfEGEpdvu60GEe8nTzari0SPkqWRUQx2Emn8Fenn79xCjvAxLiS0LN4ZA8TG7QgGMVLW9ygiyXs8wBYEF9s3FyXx1k4Ase5SrNu4WHuRGOsuJmO6ZJHc2DnwoZis55z62WqtsnAX7urKpDWJjPgNKskPXRVWYhZXXNcxGE95xWEwLoXoL1u8yPqm6oJI+y0kA2AU6y/7PrICXkQnhqMmb9wiczLKzoVO88yT4dhHbWPQ6X4Yuw0ozJVJX0VRVPpHRl01xZYNaBiQuEvpGxaSkZ0gkL47Xtf+ejWhRf5pUVSfFbf9qK5uWfVNugdENlHUqKz95N+OVqVjsPnNKx562Eh7xyxGFcJbiIemvz0ssHvZbfsi6sKIQIJSOtKCEBJkBsbDkIpnNCyZUEfNSc1wMmuYpueRKAWVpMaQqZzoqx07mF81FQGqroXvGoUEURcHY9og5iJ3CcLqZPVhLlkcyPi3udh2Y+u+ZGy+FBu0Ptzn+XwQ23bGOZCXkI5N8gaRSxwqZsXC+02DJWMx0Vo+YTYJMtOgts5t4l0XXAqtQXDj6GqMxGY3sz+xDU+3ZdvIZoXjVf5y4+XXz06NrDA06zXnNtpf66JSa1VmLAOc97mvaRisROIiLFDYgwaDRb+MOK0MHuYFAJ26kIPYJYDrOAJDYrooeZWg77gLAqf9IIpaZDc6eAn1DP8bnjFUMoiRuhA4WzFwIGyJZrojs1F40UmAnZQtF6DApjdiYbfrsGaUq5MZC+Y2Y8fEL95A4LiYuh2CWo7coE3QK7U71XkznAg0j0Aas5rHKlM2QKBV3AJdIC1Y+u3balBN01F9Sb9M4hbu1tzW6003sMUJiRNyy6FBxJiimRLCuYEEZTOyHA+bJtlsEY/fELFBbvAhAtKpOYwCFtbYgF1v1v3kHE81opFXWTi5R4tDSCMiIUqb74bDFelOwlUfI4zt+pgE53HxOAevf2wGIVAmyac7WuhloKvokkGKcPX+YDlkOWFpXKKRtkbSuPBnt4fAfntswE5JrnJ257HU8BRBC5iD8Rh8yDETvN9IX09Znzm+aAZx7rUk+8PFRLGOU6pxeFc7JsfCBcASHGwjdmWyeWmSM4FQZPyD8OYCyKbs/XHkQRxhWuaqDlB7YDxoiivi5UV0aJtkRwuYCA0xbQ0rIZD1GjlreGBgtd2tugrhMJcrRBhvK5+q3SvEpxACVERlfJMBACJA3G4wGEQQOE1mpBXzqrDy+z6Ml8FL4oWBcGRnLOPRCBbJjDVdVJPFZrJBjsDIF2iQo9BR9/3wB/b/HXW87+NZDYgT8+NoF/H1bXNaLk8p8bECrk9QxhBX0riq53TyiZi0EI9IadACM6xk4j11IQduLfGJQ02NAgkJwkzt8pZVCEjJ3YTUIc7LeGlEOomHGlCWMr4nAU3FbzCYkpcQALwZCAarfyKcLI/yLd/VzoLDLYMCQySzCB8IxxYIOwIKGYp+cZJgIiFm9JRepGwe/QFGUh1TPmo+QGYHW7Jwp3bSKgoJMtW5QVEIbxiSDDMgwjGD5kuWUq8hTzzTUqAUsfmO6xuzEYsSccvqhN/QbZDcGAM/G+qEIHmye4oyMjnJS/Drr0jjS1sTBxXaD0gtxFgj3qsSBz4JV18kse6UMeoi6YNnoD5eKkYib5FRQFbKZJ0E5HXiVyQwuALahrQhOmgiLVHQWSoQBJfBSINtmABvTZkaDJwyUlEldSsjyxiJI6wvTHj8rmi26g93LjNGILL4peimtx2H87YbRKNJp4Wfxe+rJpdbKXFcyhsKHrd+Vli4kaL68iPClvBUo+NV9xQg+KsyDR/rG1Q7Kra+oowZ5Agk3RnkL0Cvdz+02eHM2FFlFACkCFcnM5cZFr2w6o3EhCKJVfIJbhz8EsyGoZ83a2MPpjxaAQtQrhsdVSGeJKPGIBiQAOoQMeiIKdU8bkolAp0SIZK/uctMallpu7tFJFO0GdYtxwhV4xbkdEcVEWZ0/hQkXBbYOASiIsoMrIKQ46AQJ1V2VELz8WiZFTODS5kFgCSuYwucjgjDELSoDw6hp8ShUwPiqCRY0d9QUNFkkBy0Fyw7RKYwj1TMhpqkevc+0cXsEgamsrquBowjU5FcRCMNhHU53ZIhLrURRB2NDtpB3xMmkuarYI7xCuFPnDz8JRHlRenQHYOum8aCLiRMe94BfIjOoCwfdC4KEiKWX4vLI8m8FWG0wiNhQu6KBzKgwi0aIYgjHMUz21U3G6RoUzzVAP4x9hzJq3cEfFl1JwE6JC8MXRdCT0GF6OBt/vqNeJnBGKc1GinvsFEzoPiQjkSZbpEJ9kqo6rj+GgLWJW8y9sb8JCxxUDQbGvAz2f2s9E4J3h/0BVn0eniZtaSTpnq19Nc75lVBVrBPLkoYtl+oSUCX422sL8HPEDJehgDKb8RvDWmzfczpnRDTZW1gaIu8hgYCNHaWDWxtBre+zIxJBOoRSGNWPSYZ0wUEzP5mRnMiukA2sAiQCsQ5IUFombOICjO7SdBZOEwhdoVQU2MeVsxcBNRkwjUdkxymXVMtgWcTHPMQb0RPCQmaBmSIxUFR3FE5ARCQTBKmbCzKtg4JzLDmaFWv9dBaDVtvwkWJrDs1zBRMWkim8dgMwwRLjdmZLkekRaRplyuopT95wMDBH4IygBqAhCB+qEnMs5iQLPV1cctVF96gMdQMbDe6r20gMo9rvHJCZNbnbUkMTJhjuJ5QS/D6VKYY/UUshKlPYtuLMCFXQ0NxNSAQq4aDWsJA3PDfG6R0VUvxiGn+L6msAQYXMhqAeBllkfQNRKC3JeScN4E9yLYmeiZVQyyqkFJ7JPZXuCPxRmWCGZOdxpSApIjywuABBlE5ukOWY8beHIOoATpLarKiOkSb/xOpTCliyIxdbHUmVvmseGekUUJ47YTWB2XRIxLXO8+e4v1hecE84rwJL63Cnfnpp4FhMIdhkBqGd/qZcLTSCxYiaShOwMIdpyMwvd5ojRIwOe2RHWKoA65Gj8Xipmp5ORVhsX5TXj92ujiNQjwqzBcn1gasnAZR1YDVZZo2eGLMYvy4EBRho++dgQMqrOOGRq8p5PxG9E7Jfr8dNZVe0BtebumSzOKko8TV8XhqtZ1Lp8qnKFq9KtTYddWiWhaYgcGMQNKdwTz6Leg7WU7ZTtvMRGKWJ13MxVQjZlLTsVnYtE5+WFOaSckhT4klrMU0je4QSKZRag9KeCtykzupRtxKRsZY5JFVdC1EAkFijqaxMO9bsocsJMOITxM6jhIr1OKhxp0i7NXL5VOxlpLBAxRFsWTRbx0pEP4lHF01WAI6EgKgvjg0qHP1DDFGSBBvSJKpWQkYntU5j0skyWcrmEuC6tUX3pIYDSCxll566bA9QUYMxYb1NxlcGqSgB398TpfJKl9zC7sYwQlzh3pXdozvPrJFjBFYJuZH+napkZC0cMc1Kb2wECY2EpHDCh7gfUD+UOFgEqiDptJG0EWR0FQp3i4CW/PQApVqsNpFNmwAaiLem4Mco00YDFpjI7f3ykvITuqd1H6RklEV4DReWiQbL/SmifQikbUuVBXfwi0wM9QBK5KMesPLhtx4S12srl6P4OjGV3aVqkUMEqkj0R7S2pvvrUY1dFAy7yo9ihFRC19jb4Wnex+2t0cNLz3CSLATv4JI4E3WZhza2xWvvRgbr8RUR0ZiTa0uVqU1h1Z4ikJhVGUy3RRmL6OhVKnfIyVKdKpMUx/Y5OlNiqfro0cT05fOdqNpSj4e8Aj4ceaVCHQDgWKfyn5OS0ATKNuQEvh8+L1QOwvbBIsDmSLLkq3gTc1EphgyQ0qLeOtdn16KNPHRDBlJF5qbiOQtIaVyCGBCoiytDKjazpHyVpPKcBkQiW9xDtBCJZM6hJmnaBa5S+RjUcSSlatIGnuuJALW7piB5T4xGcY1ehHx+AryRAIJu0hfoohIi1tOMCFl3aJWIf9UrZFEr0jCBt+KxP4CsOKk0qjZZZqGgchiYw7JVybgWqsxqJsY8p7tSQDxolViFMApqUY0ONJrKolubY2OkM36JZ6mjfDmEYILVpbyoxpmZW8g+HBIU0ZGOZ38jZRkMJ5HI8ImwrQU6fUaoUQ7NMPoRCQia0ARFIoBf6lSxIuMGC+DF6bi3TWqVWXVYjxl+3BhEuKBb3zLBG0eqO+RBjeM7MuOWIp4ma1eUD1EOX7aY7xVPURA+/t7F3qIQG9nz43opsq8BhEC1OMU0ThBJ30mBS3WcQvGndLxU6RFPMW7PSb0DXxlkCTLX1yHucFXyaz18QbeM55ad1Kz4y5UFxboAsXkjSskZREd2n4rV/qD4FusWsS/R4xrCA01DycSMpJqXTK3FA/+WvQzRiiXEiLccaglWLKQIeJfdm3GlnRB86guEAuaFW2TMVbSOI1iKSqoClAfUqRspTbQfFSm4G5dfHSQG+oo1jezGGsRoyGdBG0/hoFXKRWelD2MOJ5qAI1CVIXT4BaUcxgSDhR7u3i/Ukphb1pFMbDevutFYjotjIfRsKvNHLl8n6IodisOKA444MyKT8zIS+umLxa8bMHislExNf/eUHM/4va2RpFFsdT1S418cF1Vgiurwv0wOIaVH1STFZXN08XPij0/3nPP0/bshxBmkxOBkQikMStfhZ4iQKNOjU9PgDGQsqGxZ6pAYrAKtMC+DO69tOIcJ51owqJEZUIqy0LxQAZTMKAyCIGmsBMpjTmDBzGVgzTYA7sYAkQHQAZjP3TvZDPdQDQdtUIvsI2KwF6lcXcUQkmDJNFFEedhjaJ6URrKwqDDkkUdwmWBIwUjBd0DlRI9ATGvX5RAyqVHkZcdSkfcKpMRQb8wNsa1sDUgeVgORqU63qPhZMCFk10AaROJEpXcTiEMRrx35/zbnI3b3UQsNw7GOKYfpqia77eXh50YlNgBXlMexuOqjsT/uChVx0RYFa76+M5jhu89vPMErXraZxW1qsHV5QSnGcPMprpBnYb7NdSd9iwfDnAEhlgRDvAuZvd6B4GYnd/d6V0qBORGJdwy2KowA0odrgDs/RFJ/IevjD0s1AkYhrcOmwkOgVjwaxGJGJHK3H38pQLhU0zrgNPgTLQj4X3Jj4FLAXpU7WrA/sX1hNaddNeq+um4YWSXUAnGw5illi5lbDJxN1pYZgEO9uZT86GeabLGJpOVtVSnbxhZnaBXw2rv1fJrCq95nVpSe32ZNTHaQGWIHwsg934aNa1q/tZvzToBy/cTaz5XpOT6jf1bTrBkhSvSmB36rra/YfoYwXrAGybOyG4gwPQcHmPmcCrtbpTQS1lSu9NLwA6iYk3KbEC0C6ZU+1P0PFQmPF5NtWWkeEqR0ItUo0Mn4aqOEeZl4orI0vjilkmrJqVbChUqk/r4lscwVJn9EbKWl9y9AqtF7y+O+UX3CumPufpMVlUjXALVZO1YuHnfT4DVlZKPQwOvI7+UpW9YuiyqkwBXJJo/hkicg495Jyk7f8QBi10YX7dI6Dxl/VNqThlpHzldBd2pT5MxiUB/QSDpTn8ZqbZuJ3WONWhwHQ21GI2tLu3T6IZyq2vN26eSfKMnN9po3426lrGfp24IXcPInnS0SQ5RVoFkc2Qmj3lAc6gq46sDtmiR04yq3JhsXKp+1JMwBsMPjKGTGtJrz2MsdulTs9l6xmrJeksdwqkrPujLswrdYSLEeCrcvTnqQvdJaefkaxX1pLX2uDEBN6mV1AXAlsxG+1F8x0n0pAGZNxFoEwSS7rTJQPTXZlDecLux68pitPQUabfONC9KuyTFmy+2lwAZtvsw+/l529QrnOgVuNqwBvZS1a0ttkuwR9XcsJxqwwksPMrjEAGP3NrcHocMse7hH76u4MDu1tId5/7Z3I702NTGc4sTN5ZgLxtqwmJLJaMlfOrtvUe2om383/mrIRDfvfQLzlLVSGIbdKLc5NmFea2x2PpxcRu34U6P2CslZiBQhaeScTPnJYaRVLzdi8L3JXjxG3SdpRzlKOaMH5vtbQjQvPAtk8yZAja4hU2Z81koXGlnQWd3ntOJ+N1To/ppS5xXIjBgEEi6M2CGcsx0xBwaW5THTPW9UOszmz5DZ0DzX4qHhpV0Q0I3LKcnkbgO32Re0ty9HXpUFsVryikA9pHxlS4jB1KAXoemxMkFtvfbpk662+BGqKMCzr8m4zmDc1gh8nFB4p8fDMZD5McOu4DCdjx769CIsKVSBTEbOZHZCU9cx3jH2xXYEDTKS/okLMRTmh7MQ4Cax7lQtv7xcEdWIqNmxLGEcaslkkW45i+DF7d9aiEnDCEoVEHYjDQ4B8bGXw2Rkt12P4cxOt6atkYC/vsc/PVaSo72Tua0l5DpSi59l95fMbYHKgEbk4ybHfrFy14tuJSNeGxVtFMK8UO2jR+wSvD+JN2pGaO87e8INP7t9fdeZfv7DIF2kPo1ne1qk2qUNE5KtK2ddAzxUFN457ddrbrz0qqf1jQyHtnmZksaSelc6erEto85vC4+ulkd38MwAkHSE6JlOTzTfedIXWWMAHnpKCMKp/L72ES+jxhgGzQKjgIKLUV1lq6GbabzjQgdl9EwKd8lTMXIPwb1Ic7xA44y6A7aiv+hsHiMYwbtwuNc7wgZpIE1SlMpM+hRqDfAKBd+wBuMa3yoiBq2DTNAGpwS7uyo8lgBJxrrI30J3Qmig2PZNAccpl70hV4Hmejoo+KS4StOuHGIgAKpc+KwA+1RCD7nnRSPhXikj241zA4ABzHw7FEvvoLw6aDuV44mGvF1LbeVU52qLiyNZQ0gVF/ayV4WftB8S/n7gwiw1UNclTWDiUA/R8DqJK9EoBsIFPu07LQuGngrbC4C/lpZdqMxzWeJDxSQc1T9culFdV63RKbfNLpTHV8frskYCRpG1uetjtEeZg62J7xBPLOgfWrkMecPW9KILi4gDYstI53U50TEskw6D0t/PiLMKGWkPWV23ZPfxDC5GPEUAySfSK4thJxIlSJJbC68N+zHsatCe8Q79A+FolrAMCgVIrs2s4OQtSiXcEQii77GZSjpFbQkIkO4+hwpK0+cDxTx5d+yL2VMJwGJsQdHBpRp7LHHPNzGcUrVHRep5XRgArxujSyTjbBuOrBbgO85xkAlI+xCxZwtFGF/6xsWMSiRTzpwi4FGpAevvEZTYxTOd56tjcIGJcUwEAiaGGzPe9WwTA0warx8VBrHdTpsE0WTMY6FpMTSeDVKoFhfMjFkaqetidbKC3b2NSoiHC4i/eVLVP0+O33RyIKiTBABzWYEpElyRBMVlDZHfHW9YuobX1NO+9/qwgDoRTvjbMHjlXOVU02btHasaFb+TQT6BgEaAhVZ+IaAiUotRi2vyXsTfZzLJ943iarT+MG4tdj1yF9hRbkE4uL34IoC/cVmyB7CQF0RaZFNTjgymBu10sqUNYGwRBDzZvwyuzP6CPvKMYZFQT1QNrImr1uCkGKDmcBKnYGJq6yVt3iNZB/BS2ytZyuJjB5JiZpgDLHu10g2EVLNmh4/4ELBUFVfSycxwGHiQaFoC8pk6nUEAAHvBCBNinjmDMyGkoPg1DtAYSogooTQU9QHifEpJYk1iTLA16zQHc4iYgwWlYPTBLBD8pWwjzK1ln3EU+cV6UJE+lIVTCgk8B4gRGQL/1LGdDKg+hWO82F1ipRG1pYlNEgjjUK8V5rE3b5sdkctVCDtDhalWF+c8DEKdjGvIi2Rlhh376EERpZiidLIayDguCkaI7kaFmvcOc3466mi/MWNGqYUiTViUTQ9BitUUGxVkAc71x9qIUVJpp3eOr8jYR2MwvEnfXcYNxuoNxzbUwiCaIy00OgwlqlaZJQgsYCfg0D170tkXolA/0Ig6U7/Gq92bC27ACsANTguX90+wtJkSmEekSZxzhB2mlhu4gSWmIQf2SMjBmCt7LhCAskSU3ry3lKVDsZy0zJXDNcKKgemEF6i7BceEeG+eKCcuDiNOgYwFhbaw1GXDym6UEpiRRE21tzW2Z375aiOvCf2eICSYW4pAHSHoUGYWw+RINDw0kILYjwAaUCMYBIl+FISsYo2cSxFbsLE4AMapBQQeI34SoYCyUvaHc3jNGpxT7WjwIYVdRTJKmGBTsFA1EUabdAYiiKMCn3h3SKeOsRwABz/Iz4xHl/PQEoolkLHRqAyCRGZEjNLEds8PGiJwnbDW1b5iqUZwizjE2DaDH8V6Rf5ig9FA+DG2IRHksSjRT6yNP+XzGYJCu/g5nMhAciHoUERaGWCCjSZnfVHFqOMVcDT+4BzGFZvI6jxiXDQ8aJ6ab2lPIil1E7vdnxDrb4i7cc+aWv8ZBAmSOJS1GMaFsdvRhaqqQhwrPE7KpmruoydTWrx5sSPSB9Z3Fi4ZPEWebWMAgMf3Y+G+SHwNPLbMax0fk60woYNegwcciwXYyX/MKPGMZw+SUei9vybCPRLBEy1eSUC3UCg2KeiE2b7N93bNEs0mkmZKsykSrPopw8w/+IopJ0Yq0PCVTIKBpO7p6ZU8Z7KTrtDaU8hb7YVSbVA0xBmHfM1gWruJkvCn8YSVi4CWIxfHU8OM7LSkBu7w2Qn/6QREEkwEMwOQaGE4MQaNZI6yhTWBX/Ly2218l9fCHKLWgloOMgMAat5h0TXZIwSROo4MueWyLeAtj2HBiXMKGFkQe+0GQmTRhf0jnYHUeMxGoVomOYFaGWxEaj+WzagxpgVaShX+ClHWFFAoEKrzg4Zco6YxHvAWH64ChUr7YnGi+uuXDgZdRHpa3xRHzGh9SEyhQ0ZoJA5NIvghLZIf6kcQOcymjqlCn4nJLqn5cVZuKJI+OIolE8bBiSmTTEW1EjqZUtCbdUicZiBqCjwAKdFo5vi0SzM1ftjICBPKSKlluAEWCkVGt4T2dFB7zDdmAK5/UpW3zAx1EKoA2/lOA4HU5dS95n2sAcKMFyTaoe5TfNgy0olAR6D7HZUpngvpwajFPFdOTH0YQYIFRY2BOgpfinswoONKdIZt3pnQLFw6cs0HjETy2WIvQPljyuydO9vPSDdK2cM5tKFAdCLMQjgaKtuW2NWuiqbAPPqPgKUFnbDEjOmY66aVCzknOKIE+tC0tF6lKeFhb4VsNmfGA5VAfEQi2DCxkLWpEz2RDsIZvKJv8jiiy9OSFBX0HMQJFxJTPGIAgeFSClSAF2wesaZqCKUSfFOV4/xWK1y5sBXsAdUg4xUe2Rs8i95z7sllv6cGwgPjqiKIsO+fd63myykJhm2hwJGmTReZLalPK4DFpow0rc6fTS7OqaZMFmos4hLJA4xDF7LekIR84AJfRXBT14aF6DBH/FCHSBM4YGCaJIxRXGUQ5nBfoeqUg+EZyt6anR8rosFBOVVDp6HyrDTUVPRNKA+FEVMJMgQMe9kbYo9kYa7uguYAR5ZHdNMGN1ECxSrp9433AJ1k1FpaArerFK9Fo9jUdFptr5TwGByYdhCRilCtIqPkQ/U67XsHmmeNxMmNe2sbpUCdZ/Fx/ApJACh1LHBmyQQ6X3zVFgk2GnOZMelxFSXUxPWbHzdoJTx1S8D8OOgB1pGyOM0WJc99pFY+w1ombEMoPiu8jYDicBgRiDpzmAe/Rb0nZihwydUlGVy9xcnsJ620KTbsKyk1GGN8jd8YoiBEA/BdaIFkbGmNZGMAHO2LOlVPo348rY+EELFphWSzErd3hwNYPxCMgSs6ZWgQJoJDhb12SOGRydNErJlqU1HFZGU/wgTN5fYutwwL57BEofNMFdJT/iJIXqZCbbeemuKH6Y0YtU6XjKyDcuxY5whgwYItVKm6hBEgpn+QDuRhmLphlUVKB1dEWcabAOP8aExhiq6LgF+S+gmca6P6CBRyomYE4la9Cv4IndabFVTIUbk46b3339/eGlogNpdYghv9EICQ0a68+CJ1mBpCCW6w0kI7wzRi7t4GSgbcBH6laARYlBYUKChNZ/oorqAxtbHbd24hx3EjtwBN92Ix5MWpz112sb7bvx52q+NDJ517lmVUAXU4rgnjqv8M2Plz/777l/5xzVb5c8RBxxR+cf1pRH/jwgeccgRI/5t8GeCgydoENuzKKQNs2QXBp1B6aQwgKOV0MZ7OkmWjxKBRKAGgaQ7NYDkbU8RsMZlXiFE2TW4wSqO5oBnACePJovmLmptzQKCkaBNzCgkrrycGNhHSG5FsYWJsZT3l6cOuc4somp6IAE6GIYwmgYSmnofLSAhEALLfdqm8JuhPbLor28SQiaSMoOKgswONUAk405ERWFtXZ+rjGEL0x5VUEqhESx9tAUqYgJzMJ0VOeJFOcQaIgtTUShIdBAVKP1YdZ9mRQIY4igd7W9nKUPd8DkVMcewnsjC8yPykqD4E64jEmvUMMmid2JcusMXJ8LxF0dETUIz4W95bE+YrqpTCgcHqonEh+rxwQ47Iohd9UxSXcM9+TXN6L3bXqodx+XKBr3qk4Ea9gIZMqzeioZPMzIRSAQ6QqCice3oWcYnAp0gEDLY7M+YRRWB01BdkJGsDBQ5bAdUCKHVpwGi/+cpzHfYThbynpDm/CgBXQJJTA9kUSuZ6Z46ARUgqimN6IQ4eLKwhHctzoQxSIME0ExwkqA+4WDrltqGHQ0HIjOoT4RJBToPugQ10h+EmMeW1KgEDWMdkF4vqgWY24/2+CjUM4w+fIwUXrrBWn+rkR1BTE3GAErkB7t+oPE0SZ1A19VHHdXV1XLaOX31KLRzO3ujbca3N4rtyzLrh6/3OlVfV5d6Gg3rYSFdqnGwJaZ3tNjTa+u6/EToYBv9gd9fuhwqDcoALsPRWxYfDhAMW/xpOH5yWGGXoQ/ARSRACGiABPAGlhfZ2bNoQfwNJwyLXeSmBjieDa7qSJyp+lYYuYkY9KvmkVvuz676+OoY9he+pdUxwoiXjlA44V4l+6lJE7da7mr4qLWROV/X4Nlz+VoPac/LrGlkm9w27KlIBkraQWsD3lrcvRlhm2lwRyjV19J5aZSvJgqLJTpaCwYOUtKbMUwm9g9G3o7q6rzkfJoIQCCNWfka9BQB+0doSmy4rfGqqeH1FCo2nNdUJpJmqCayDW95XjONUUSVXtIdNTKn446Q6YP4rspXTbISpRpk/ZziqIp5sf5SJu0jpk6xx/O6PkFvx9jYzzWKwrK6Ig5hPK933nlnNtDq+GbCHb2i/LqoVLmocwzi+9VaDWVNwxim/aC4zIe/Gh2tAxh1iisb5SvSw8fO1geaY/5hVL9Uwkqo9uOuKTBvE4HRIpB0Z7QQZYLOEKhMncTEL4qx9x+7s3T951lHwqCYpdKHg/Y9qJOudEPc1pTWUe0dxddk7+i2vmE9LLCjivosvr5H3auaZzd37/C176gEPN4G9V4V/x1VLd5ZiBx6fIUj/NZpH9EvNlneYNQe1RntfHTgAm6kteLpI+3sE+bLhb7wDOtcMUk1Kwvzsa31HNs5qivE3kZe9liIM4o41VH88N9nU6b7UZq/XNyq21ATZobWWqsa29OEwxsMqeKQp0m+ccHqbbFEIeo8J/sDDATVjrDqwM4vXpP0SNeYkumcasrP20SgeQSS7jSPVaZsgACpYz5yMUiZ1Bqk6FdRrRKiPel0V9tAPpHZ5JA9zw09fztiNl2tqOwUuUsa2UJP11W/u40LFynoJCF+VMQYAcYjm5B2EhLjo+1pZTk23nO5dRQeE2QYMT2yod2xAp0Lto56VJbcfECT0J1OXBipHJh4SOjYB65kiWn7oG2vGd9zAWwgarQV0aEM9BN85H2tneJT99EC1luJ7THkcCYlyy8xT5z71che7lYTyeHMUFJ7cCSX0tZ9Sg6/LO72PM84Q0CSIsRuOFU7+AcFiaq5ojP1OjXAXkKPeJ2jPky31K4Yj2YoRLxKI339X0odtcdXtKhb3DpKkW2LHwaX9nCMM1hokN2C+BDbk5ZX1DNf8Hf/vGBDyRNfp7wG3pPwxOf65hJp1yQ/epcGU+fYlcZSzL1PgTEclKl2F4JdpV4PHYHM56VnKBHoKgJerLwSgW4gUOyTp3V1A7bRZIHqaFI0eoxe+OGTKI0eNjgrT7JOKmIfsSm9YVHVkQ2PNyTUieSw/VUnFuYwjluUkYwmLtvlrP7LSDvsbDQj5whaW+eoJegniF4O7Ci19A4CqHhBNkJJJMWAQ4PIYJLVYYOKxZzsX7PP3/5tBilnEzjaUTxHMcKVPzuxDTpsoKMyKRVCWaJt0U4UhNxVBVLCk51nPR81j5AJUpnjV/iHYSf284uhvSDg8T/b9BjOIqXjALREpOz6KNJeQhwFP8AL+b1FJC7rQB1sQ9ecOCBZXLGlLk76ESOZ9sQpmrbRYSqwEk8zhA/Rmgg7+4qeRqCjnsYhjWiHNHFpPzoizJyEnaBTEW97I8ZDwxS3HRUIAdkd/IMzcf83mpqNCGJpkTHs3cY6bo1I9Dpu/fV6oHdxCGRENqyrTN9MQAk9L6SZigZtmjxm0JSSVyLQbxCwzKVsL1ftTba7q1qHrupXTKD2i1krV6/RiSI+1GStQNlOChgSPTbBlZENA0790VnL69jbTGdDkUAGMygQsTbkx9mMpjBb+nEOKW3OVxQdBscXpz7y40ZQrPVFEufx7QgMo/M91VgR1xNZEJHSqQtZIdsIbw4rakdQyFQFUlQQ9hQtEuAx1xfXN+wL8Y/cOBCS1oT+yekDVBoojpMLMEIH/THTUBjospaT66SpYkceoNywxKKgj6FNQRr0PZIoNk4x4E1PbcPvBwIeaRhfex4wxohCC9EBDhAYcRwYSJXl8EwdQRTsXnQqJu0X/xssSiGyQx698MohK6R+eKtw0aVNwbfcRky0oeYvlgn5cLHn4esMZd98UDKKSbcU/jG6AMCajJ3fYnWaJA3O4ZUoERBw6kEn7YliMTDWKIocREqvOT9h5F4Vb2bn9TZ86n3w5jd8lJGJQDMIpDGrGZQyTYcIdFXAd1hQez64prNmNSQrEUkcktMyExIlZyLPCF2SgxQn8GY5c4Q3UKManOlHZhM21CR8I6z4qVticwrbB78HRMFSmOynn6ASoGOwgrduVhiugKCQpjQE1tMNd6hFnUgGTYBDkAljlgJKCOQmrC3+ciEPZxGJFS7xn/70Jy3R8qA7hJZaZORMynBDKmskCUehogHV3KtRFwtuHDQrrG9EdZlACWgW61KYcsQrEFFAKYhM4lxPqQqOvPjIMkt1QAI8Q6vCgVfJugZAhWA/UqJodvqgO6hJ0DukBCPpqgAGGmwVSADbeIhOGXH8yUFNQftopOhCOJ1UNy/CqJjDFVmjFKJeDEwyslw3w9LnLG88qcyIbLEPBu0oIxsGOP9SnBg14+WtkIbHTMMzPDvKXhPvDTTu+CjtFzudpkYCxQb9RaTqj1kqC4G510/2+OAo5RaaLiNk8DBWKi8J0IwOjmjoaYCwdmQR4fb+K4f+zHvi1eI4xRRYNqCsIgOJQPMIJN1pHqtM2QCBhiI/0lkCmuZMcCRKdU7Ld/GmeII/4iktHMRHDFiJRmJphM3U4klxUopcsQrnJkm0kAe09JT8ziZWgjP9iH+Sw4oWG3DAj30fRJ2MSmMrIVeo8ZVveW0hLobTCTU7ocgTk/WEwYKanYsAQasie+PNtlpuupeLaGSFsUjlwKFT5miT9Qs/faG6U9VhApWQcDKQJjkm0YTuqRMXtdzWHrM5NoM6FGNVZ/o8TBASEuZ92R1SjIUwedgSrKkapgRhSgIZ9NR6nbqCfcdSXnqRWsg1hHKFpYDQ/bzcuhBiBA1MBRR6RC8iSWgCiNs4tDAygZFLhyFDd8rRVBF/DqIIVqpTmsQwx0jKka2r8/MIKa34/f08alTIiIwKVv61KWmttdbCJCg5+Kb42EVxcfXzz8Pkve7gHzhHfHTMM+0sHVwEvGwivWAGV8A7pjqD8nkpTYQMn/56H2SPt1cmIy6GjY8bDZUS2iEyXiHcyJB5gRFKWTTSniNUlblHFsMnL+JoQPEzY+pFNXzeZyUAnJXK6ITDEB2Jd5vrrkcIdHxzzWBhb5gBrRjSYFsTPQr1pLdO87zV6qLoQjXCYiVv/aVV2uZttxUc33WiJtiRlSA0fmKYqFzeNA3TKlouL4Au1BcVMRiMlwERRNCpsvy+xGPt3ljkyeuqQC+eSMPhi2bURX5u4itDPOKCHr8u/NVsoDERmX8Tge4h0GCu6V5BmWtwIsAbkeOCSQo5ILqIDWs46zCTIFU/UkKkcUWkn4ePRaH0vifA9o+ymPVMZyZ3U7/pT0p/w8+AECVZTfEmROt1C3QCxlSuKPOs5WApJpXpKX0JocXPkSoFOTAd+4sGOczXZE1a4B8+cm7OtY7EG8gY8zjtAj8JTaXkMBeT+mQJCUHY2/Zi/nVrIiYnNB51UAWFivbzXf1j8ceORhwUCI3S2Fa0wfSttUQUEUiRgC1ZpCo89A31haB00rjIaXWRTw5Z5g5igRsboePIIhmpBEiUii9L1YUa0r5w9aUg6XzjNARwKbRAYwhFlp2yGHwx2E/EQB7hI4SIwzJN7wWIbY4sCChXXx3xkmAw3HcoRXwkq5N6sRyAEO1eSMm8QjLisgYCjSDCDR+Gx3jnTfN+8sLBCYwsyV1s3bhgyqqwdqmdwQjno5ZQDisY9oBJcz0xTJiWb3B6S6mOvFRkM+2aEjXe0Dtm0y2noiBezGp+Nd5t74a3JXgAgoLOUmzIgnOXH+1SGjJEqWZkI1KN3lJt1hdMwquC7qA+CqeG8cLbOaVq6VWEaQXDE6/Namzcz6Kgz9NCWknal3jn/WxB5z1UAsIRGTnx+M3GmxBN7ahAqjuXvLRWelQm8+v2eyxvBYyOqzqmDOtFnDJaxmQgEegmAt7FvBKBbiBQ7FPx+ENcvHlWYOYvnIOkCT9EygASmiAhvFnrKeRVYd1p3kdQcAiUyKQp0pqVMoBQJ6KsUMNX0UITs/EUf1IgZUy00HSsOoIwbv0lqlVEaLEFoCPUIWSPNDQc1qnyEgbKx6jwMMtHfIiGwBJTXbKzLnFGidKILhNrhM3ItjtFOP4SdVLSrMhemaw78JaVmHyieQpywE+zLMTaHVcz71NXgKWjEjSeZOLcin/4YgZklABYQjGKIr8BLsxLA6uLSL0jKYVBAV6sDrNk3CGqO6oI/6N5kuXee+8FkYEQhh7BrDRi3lNckAQl6nTZU7JcF4heYewBXyRNw+6ASook2mW0ZKefMNxGgbCk50D7DBM0lBYvgzfHaKpXIwGCmkR2lEUVhgnU2KG3QrxL+VhshDvqEfqCjjAguugVSFDpDQfhbWTpFBFlrBEZFY/1UhdpEpArVK+DAaVH0V8qDQ0QQHHkNTrYjz1T3G7kdempceGQhDpDXpq4ZPGyeedpd0bFjeF/O+ppt5vVUYHie+P/brczMkaTelhIZu8EAb8Rk5jLz6GTZH3/KLU7MS75t5sIcBEgsayhzenechYfYStC4oHWgZLAO20JSN+AvpCCVr0sNYQokRArSLoKNAU1cYaY1SR9g6bQysQCHTmwci31GTWtpApi46B7Z0xBa0hKeu/IWKYkgElT7STb0Ah/xWhbaObLZJ0EogvaTELrl7pIvo6UAaxveJJuKp/6hNSPkmVkyKAuIn21k/wrOlCU0BAgIlb/aCLNFlUE5QqsgIlyEdgmEVDjXmqxxOfLotcoDtucSKLX6h+Zs463Mib1i8cad47MZg1kYqOZQGiCSjJP4FIiw6plUNjjOI5IqeUojuGmG0NbFc5qY3TwGPozahXVaCH3WwHnxBD/dHheCdZDUNAZQB79QqewUo00Lk5e0U5EJE61oQbTZRQEo8V4dK1sun5FC8uY+sAGj2/gCKjyeql4aaRv2e7FGcUZZ/z+jGKLysNd3t9ll313qYR+Xvmz/O3LV/7p4NKF8qzwMomXvAyjthHGEcvIMkBNpfsGMVQ4ZXwbBlrrhzd874rRMK9EoH0QSLrTPmPR71tCLY9/4Cvh5EH3QJhZ2Vu+k9b0NIQEqcazlS0gjorRZ1pxSiCUiI2fuwDjBdErkmWK6gKx4AqDQ1QUKnUX/sQwRFOCSZCUzENKLo072iMjZqABvBkUbqnNXmBXDomON5CmFBicMKy86QNUSiFBJJPoCAeK5i/lhH1PXGVxFHp+bID6hER/tag4T9Rfuk/9gxlgJwpUNb0Cd5zosloYFKiROGrsf9z+9dnFSI+6aSHrHvuCekViFfDBEqjNsBPNxhqRDPwG0cHwYiFFLwJzGjIlYGlEbMWMOHKtVVsbbRM06CcApWGltDYEeKER0XcaO9mwH21WC8CBoHBZMBjVQY8NBeOM0iWgjpJXAswybI4KD/NKdQsgUH1bHY599RFDueLytlAL0S1VJ6sJ95J87SkJmKGi4Vj1n6sW/6xpb3vd9hJ67dXJbM3gRiDpzuAe/x73HpshVlEZIhCnoWtBHSgGUAQUhP8KwUkZQHJjIc4CwYGwE6xIzQgNtxubLzhDkMrMASEdPWLqIk1pFPj3uCVBKVfwDIt+twpnbKI4YZyiRGE+cIqJeIVzVgjvBJ4ZSmNq4fNBo8A6hjfQFZHl1Aa8Q7AfkpsGBWNQOJFMIyIx4UpmoyzK1zVaK2oJwpvWAU9SJhJApzLT6TOpsf6SgGjHpXA1HKtM0LwySRbcrobeITquKA1pK4ul1ynDZQDaZbiTACVKw6egcFU/wv9ip4/IktkE5hXtUdVF5QPSqoieBlkh2bB4oDOZjXbnc08r+2L+7hGd5A1fRDHvEoF2QWCICb1d2pLt6FcIhDA4efqTOUzgN5QiPGcxHqp7tg+OrjxCEBouLNQk1ABUPuHRycZBgYFAUEtgLaiSAI6CKNDriPEIEq+88go6IiMdCVIVRii+mZKxfUhA3EZKBAXZEqMKJVBCUG+4xVS0iuTmTUIro20iESBlKkS4J5fu1wu2rgrInpfQZBf6rKIm29PzZPU96nmZNSU0HOKaNDW3NVm6+j7UlNa2tzXg98du1nShbaHujw2zLAwVO5VzzZcTx2x3ku6MWfz7ce39cY5rLdyDecZs29GvHpSuNrI6r1dF9lNnPJVqEGunpGzm5ZGlupCa29GWwDLI4Iv989EORzHb61B8tWP8Im3+orb0qSyaTocb8StiCO68WEpTllC6Rr78nads+JQPmf2VNoJZS0SC+k7VxzQsarSRljFWOCqyjImdXBYnVHpUhlSqwLGAsfixmBFjGWNlRVVsZQUKhcMNVjSRlkZlXRGpQOkteDQ1HlUPU5k4Ay1BoG3pTk/XuC1BJwvpvwjkrNF/x66HLa8Zego2ej7qNLKHD3IPC4/s5B9jFgcj9qyddtpptGWWwqxMWdPIMr4+UJ9XGrITS2BybZLu1BfbpRjy25cluHlhOWEmlp2Yt8+OPZeVUCR5L5JW3gK6mbMHOcXbnxiO5NWN4VtGgcrlPCIZmpkpEQWAG0TmWn235wCfYDzVHtTKcNR7bUd2pt5w9pLLm0B7ysldFp5qYXtFYuJMAenxFQZo6SXzqoQHOiO4LFS2PNntXWCwtlmPEZODGnrH3Iy0AQfn4/xHbcDxTiTXePh45VSkbczHKBHredheqXVZooX55GFF5b6BaHP+HWwIJN0ZbCOe/R10CDQU5M2j0CRj4PLMVdzhAo4GaBXdIdr5SjN0hrGyps08wOxiq/ZrrklQ3tqzRktBTAZXKONHG0B0uHmxltanpG8gbhXIT6v+aXWM7JQWOAQrqsRkPJRwC4ZX/SKwBbhA2bvHe0xG0loaBMtROuQ6P3GRWoJJYAyO+6P4Qf7oKkjx0k+LURhPcv6yuniqxaY2m++UybGdhTfKUZSUjuTmwq9JfMDjPEa+YuJt/leI9Fro0CZ+9/RJ+sgMrTFOBurIfcrmQQjzwMOWtE1KzAPd4TDHnM2pzjmfWktRpAESGFYkhqcdz/qgOz4VYo8bDy1HIuF2ktnWoIXhiofeCcBcPC9+CXBrmz2jPeLxOfs3bVzwiOcfJzwWdp3C2OjDII+ryZvXYEYg6c5gHv2B0PeuyvIa4d3V7P0Fsppu1tw234vO8eGGRZzwzVIg0UjgEV3xBajmqyDJLPSr04dDoUgS3frecj/knL/hrSUxZYDtcpgEGWmPOm2ETXDVhZRhaRikSEFqACc9UjPEtxocnEPDIRn7kVrK9DUBXISQtsVP1WVKbMBBlDbusbmoncyuyVXeSsntneRGX/AtpiUe4s5ZsD/fmYGOIOJsLgHygQA5wU8MLQ5XM2kUQt1CisslEiWyU0+k4wB4vzEwIUPlGQ3UMAaCLsrWd8lsysM2eOWHNQqXKptEE+NTVnQnOAf0qJRU7WAnRAqdcgSzkj2V3hEDTtSk2nHOoc6WJdQHtBbNxZa8BnzqeesjZ06J1H0dd+oEjU7sM5AXUwG+JrFVlQNKB0N5g68oIb6hYbDQlHgZamrE3sBYci9MCEVzDBKEpTdM9EOy/D97dwKo21T+D3zfa56ViFBRpFQyVIZMRaSSkikUiYZ/kjTJj0ilVJQ0UzKlASkhyZyiUZISZY6UeZ7O//Oe51q2d7rvOec9577n3Gd3e6299hq/a539fNfzPGttew+xKDsPHNyF9sXZCk1F5e1shIDJkVciMAoEqv0bO2xHkbG/WbTBEtmuZq9se7O7F97a4NaYKMGr2bqZ1CHOu5c5xqfkE3GiC/VySCy8wUu8Htl7uKlT5dbynYC3jz2KYuagJ2AosewW4AViMe0Ru4Bbp/A1iEuHIRbvPF+SiR6C4CGVSTh5nexHD4FeQE8v+FJEXewInNAxEsoDMWQzbDEGYZv2ZWfvF0ZobMfDAMhpspZQF+lkXryHxojaQ6QuiHTkDyKCbZDrzBxaK7KptXELRv6SmISe6pd1v5T86FEQEhdZQafoMJryltJ0hKcIga07KvLrEdnPkMSBRrOBQCEh0tVUiFtzkjihZfEURE6FFqCDoXJoZBgaouFgZ4mwgZDYiURxG78EuUh0rR4pzMbno60RicmBl9nILTWGSVufPHgMFUukpKeBPIUNHoD20cfEwMUm/ziAETWh/on0GqN2DYtbv019jBjuTVJylKHF0RhZ4Iz3IEDmmyFzziTKKDGVGHJJLWf6aVWpyF+cMUVZzB+8RFhiQ4NvCQRVKn+MGo+ZiY9LZ+2vpL5ivZLGGPll+MMFqYLMZxoss4UiTePj3+NZ87/9RwB3NwFc6Hj/Sx9DiandiXHJ39Ej0F0BMPpy2+Vsq6XwXiPJLPXKZul2WUcWRzCHO0J9M7kiLCv9khalOH993raIApEc8dJY1wp725JJDukhtiMvAiGxppKgYtw6tNArnvXBMpewJ28syi1SyWOqeJHKF0lEKZNBQbGsDHGUnxKIeachk9yIhVpiQ0RpWz3A3GBvP6UCRqIoj0hBYkDJOITqUAdyjlRwVjIproVsEFVDxdD+ohUgp/l8cKyJ7ksnO/lED0EfQPuC91AbOGSPK4bVv3aS7s4thAyGRzjJYuWtOtRBmGjEJJAhIEhvrS9SSvoMBWI2XDHodURSJzjpwLg3mErXC2LolEGhLSgJFeIEBIcJwRxoLFbVjuXhkwJgMQooF6cQCDsoUndYx8ToNdUR6U6D8qQ8tRs0KzYnaryhx408JM5jIgnrqQJrOXoNajlDXjjfaAlHHASU/4ohMGk9bVtQ6JmQbGYjw4f/hRqpKXHJzjhVHpmu2G25bQrokTmDNGO0MKe50TaTAUS0X6aueY5amfAoFyQlQ33MIlzKI8Cab9iJuY0UhibG3GBuo2pClVRHzabLuoBaGQ5nSajCpTrsUwDC6tVm1RluwNIYyYvxaIOp3tTmvJ2tEOg4d2crFLKzY0SgLQvpvUyLVG8urzCOihaF5eAWws+bsVgKOvEqb1jMwEswDsqjw/BZABLO0pAwJq6oH0qZra0ia9XiRakEq8YwrHA+cIaQpX89vUUqNbuU1rKySOyEPUcI4jTereFnKj1xTmYTOd7OXsr6ZTlr8S2G+UAjLT0xDwtfS392ClksXoPukFtuyX7yhhDVGHSHICFpsArCkkQh+zWAct46nhClHHKEMRoBh050xxkBzieUBZNQr5MbCRLURzvJDz431spYIwSMBW9QLadUUGP10ToATwqzxYDXeUJOVyoPrO+NBX6mzRb3ITWt+FVNpaEvFnx0LQo3KEXk2zcE1VIIrPQUS2CGEInuqEJPhaWEJyJVEo8uoGEh/MDO9kHcdiqHiwl4m57iOhQ2JDejCcmthU0Jyi2bjjmDV8FKRRQq6jUnObVQYtFJmACGGyegnqTCKRlLICJlZ9mBTJhp0FP6D1POFFUgCktdZCwcy2mGaDAADaVCsAp6FCRASlXQGhog6igWK3TTHwtOUE6v9tcnixhcH+P3WRLdN0/YnnAIlimkuTSsHjCUhthRkPKat4gLGmoa8JL2tTV5MRhWLX8vZgXvItPP7NUY0FHyqQj30lSFmBueBi80P3UKjTNpHcGFxGB1lFj+nFEcGiNFRTNY5dyaaag2MJks/e3IAmpKHfPHEFiQ1Nuc4dkOAS+gvBKBUSBQdMIC3lmkqTc4Oerd6kVm5wWZhBDwSwh1dFRBrpNbGIwvfkcMDuF97eXF/YIe2xXxJDrbgdeWVTjdgEgVxaP6r0jqDX+3/BMj3pKRjPFiJUu8Nz2irohHrSWIodugJ/AOJYat1CMlqexdrKmlLh1UlDUoawv1TJz17ClyQN3iLay/SEmkJx4kDhNGxFDYWEbH56JooWhWIp7+w3Ic1YjbEkmqoT4l0rKYrCKl4GOFjYp5pLUWwTQlBAa/3WLvaOqmW0XJSyQQJ7KHi4MSiCKUotQiAAQGDryTnCA4m4oqKSPekrqMVzyyR4amRFiNuqB3wsgBQ0MkiP4KY2YYD9YobAUfxh0zxzjqKdMVDURkMQ1UFGECz47iCJNtYQaCHvwbku/JM6TcYiTkrtGh1LHQl92s0zuzkSzU34Zv9ZPzShMx6CkxSZQiHMbauHvESdb4UkUgK5pnCKJJTYW4Dc5hIvlDMC3VKKVea7mJhxZAyYiABVFgOHOLYZi3rEtSYgCGWCSsTBvEVGR87cskRE81g1ZDpEshbjXSH5czuCMSx1JvpCx/CNrPfcemJ240Mff82cqOl0CJS5b4YhrGgfAG6dtaDNWimxh8WC70t275ijYMzq+mxr/BadLUa8nAGrPayI+ph372aDwQKG8NAYyELI9NqmQq9Ua8ZOkMMAnv32A8ln2EB/FAlxMvZQ2zrPd6tbzz2rXMjZcv6UI34+VuoWYzS0h3FbV2JCJJviJyLNzJWuIk3tfcFcmA+GpjawliLLKjWP4ExG2pQuPRtXIbssSvF7q2Wc7GI64nFDy0NToejRdvJU3GUHWU7PHNBBxCY1zInEfS43OukjHSq4WEq9MdyhskAJPgv2ItTlyVkhlWrNet+wmzKKepm26JVcI1VFPEJ5YT2VvpjoYprRQub70X9XhhLMRoCliRoywCOGKhO0RseGbEBmDiXALQUQsJYA9wMMTQI+8JeKI9PnhOfWVWSBMXrZilOWlKR0XDgR2ybngUI4Jkw0RRjQ+ZPXmGlFviH91p4F5VCF8US4HhFpVhIENDS+IZtT5Odwh7bMnwaaEZUp6ijAZFZJ3NNxXilt4IIzSXfODMzCnZBdyyKuopFYvphGfQ1vhlfMGH6GOkKZFGQYwEIqUX8BtXmTxmvphyG3W5fTxh4+jziBzLb1MfFdUaM5byxzWvpsa/ca1lNi98YOlOGrMab8C8xogAe5BXPzU1SYzHsL4z7vBHsXy0hsZFKGAkIC2swvlbEL2kFBLj8xHkDQFGuyOlhXu0hFC04CZI6CQopYmK7i0kL0sC6ZWmAQoXSRYyytRtJSVlOAQUCkImkSgaUxLUA4QilQzZTM3OWMAI4qkluEYSnLxeSKZ6+qawXBTyzF50CcicsAS6rEwin5iHA7FErSKgC+SfSCt4Rgc7bjAGcpcpB49kzaHs4RRiCa49TAYICl1IcQlqqtot/RlVEM7H6kGU0paBiCJHOUaEGkx7qK+Y3qhh6FcYyORCZarnN9xxWguMGMKemsSgW9AHn9B+XITPDRsZBoxx0vfQgiCO+IE24CjaIDviK6VpQPNBbYC06Xjsyo7mUVZhSzi0QhBlpFAHdZP81h0lGBEGF05LwkgMplX9QbDNhQiCjhsHYBuKnOFL4xEpMYiy3zbZhqPoVMzb1qfMUq7W+KaYVU9ZtXrujLgfXfqjqmEsql1uz6jdTtpgJ0PzpO1QNnwKIvCEkJiCncsuTRQCFN3UG0gMNQ+Wg+6QSZQTRYpEgJwm9SXTLuKWbKMVIP7rzbQwcktXwWDvslBg5uCmyqm2nqx7WHUEJBLGgmDJq0y/rVlIUJFID3FLBmMtaBnvBH4/4lEoS3Pr/obUH74QGit1Mjhu/TKccYCgnWI7IPi5fzpThJym/MdX3FKlNNxgq0qYHYRaC+PhGISgBKXgyate5EwaVIZaiNRn/aHLQRfIdYSApgdocCCzVYc4IklkPzUJQglwDaaBoF5SSNuLiguktCOQwTyksVeZdoHdRDkxWLQvqAnPWaYx7hqomL58/+vfL4PYWjI/CXzUQCN/wThZQ3Q80AZIQZ7fBoTdKjbKUa/tV9yz4lbvBOCgUqMmbIYwPJlLZkiZJBQ/kT5+6fDqt63hNmL4vJZUZ7bE9Cli6OONyTy6q03LR17QWBrQe20TU0vv7emesi/Adq8inw4mAkl3BnNcJlmreBRakRPhxCfhx5mAhYi3AecVChv6A4t+XUIUOLgQ/4QfpQVFQogxItZpH3QMXF5QB47GiBGdAUcZa3EuruR6F0SIeRyFVFYXKkDhwfBBF0IHQwVCcnNsZF9jEGlbCHcQVh6SWy10D8wlknGQJGuRFW1AcfgV6SO9CC0INoNz8OChdcBdKAloZeg2WHaYGOhC0CPZAeIWd4lKCW9dY01gLwOC6iKekgNVolVyi+LQrwgogeaDLgQnoMCIlKgA24dIWUIjha6hLGpXS1C0SNn6qxx8qylep1xNkW6xEFdrfNsYsBcGEwn01BVhT0uYda9tCfVIjJA2jn1QJG5kaJjh6glGFB67GJ61onGM7Z+1jR/RSNUT0/5agVgMdFEr1tNnOBHoEYGkOz0Clcm6IUAMIxNUO2QbNUMkxXKCYYQCQ6QECA3egFXQBhVZy1uWSYgyhuEAYcKNiHDsQWmsJIwglCJdquceRGNBmtJeoFlSusVFYpsSU5qrS3atcjUlwLGaYrSE8iN2IfFKYZDSSEY3V1NKDqeupkiCH01pioxb3Xc1PWotQYKmA3wpVDDFpoxtbyeL5ENP6auohfSCpck4jrTlI03fFq6xRHZvwEgZDD1Z2GEFqM0wSwFGSfyeEXOk7ezetpGWNr7pz36i+JGC9kTODCUCNQSS7tTAyOBoEcBsiHO2HlqH8L/hy0IY2yzjHU21EJYOxRNgTDasJ2FIKhWyStQNEzQ9rvK0e4DPTWuCTluyW1P2KgMWrarXNT4bOaOE/avVf7p69dPW8gYr5okGj7ZdnUroFD/aelryXexYoZbImUWMh2hEOJxch93yS+t9Wra2dBSIUR9i3v6sMF16R7Y/Swh/Vmy1o6A7mjQe+LT2dCwx9oiFDjUOjxgFaGOpPfNOYQSS7kzhwZ24rrHCNFVm9cmixM+UYaI4IEcab21XU/qx3I7lhdj09h9LUWPpQh/zNvVIya0xUR0mSoRzDBpL7agA6WuIw3e796J4brFbmQnYMBtWWPFkNwT1BpdbM4pty1E3TSqu3mscdUo8nmnVJnYO44XusLXZSEjP14uRbnRVM4by4MZ4qBL5WTszif8Tpyv20HAIG12xBl3J1iey+zV2fplTKUf1xUDYDvm+973P8QqOPjK+TEvWJ0xLUjJVe8p4SsnEr84yxseqijXT5gPH7RggPnCx9V0V3OFtmsPYnD7FMUuMXevaL5lCDGgcsSOevZV7vshomN+8EoF+IuCPNq9EYBQIVPs3tnTKGL9NJXD+ZYFiruLM2/Ro1LdtKxp1aW0zTkAVbevtV2Rr+1tjoi5yxZ5zOjDCbCy1x8HHozhqhf8Tpyhki7DEJEobmhpcbrlse/FhzyVl2wAOJ43jcNo+HXUkvyuEo569se+9anxJox7ZPVz60j1ZPJUYL7H5izs/0sOdS7xz/LiO4T0IB/dzPu/2/5fTExhwqXwYi0XK21qdGHwlDowInyokNT4Rys0O7UB3iq7UFzbUiKzoJhuulLbFKZbBUYztezYQIEB816LByAp6xHGe4pb5OCJxNYmRRW5wHPUMuniebVS8/Ng85fTGHU2koyiE7bNDhmTRzSihtRcRP+pfBfa9zFE3ZkpmHNiN6G0OMpmSA5Cd6jsC5a0RgYn57Xsvmgqc6XvQ9iUnDvfl/JKmqptuWQNJ7l4i62la298aE+nJmNgQ7jMC9RJGGnY8IzXASHOV9LawkW3d6Q7lCvWGc4RtCC/IO6/PWJCO7DuuEPlUEdQSCqRm4PFKhSBGXfRPKuL9irIQ2FE7Ik6+ohFon0OA+KEjSdyzOKfzlKfF4UnmfCOR/N8dhYAlUDxEXica2+lGYyGS61ic/kdZZTMdwuGMHO7zttdxRys9Feg0FvU0JVxPzI8t6E48jRMv7b23I1Jn4whHlVK0cOuxnVDtDX+14dVIKVBADDCNuG0EtEQoBdJW+Ipdgdin0w2sVXjK0+g4r4jiB48xW+JQZjsAgInQYFoK5GWF8di9iIFpSZwdihqKhL8E8MSTDBBSJT4aAzp6MhQKwnIZWfHK1C8B9E5k0p3AajL+DizdSWOWv6y8xoRA3fQwioJYK3rPNaLEvRQ70sZzpOBL603t0Jpeyh91Gst658q46iUQEg4GHLX5yavT4t4Kngxjs3CcD8EmUhURT5zjB9QtmJZICgA7vxyBHY5WqrY6t+2OmCfLJSDOyUWn2tQbKUzBQGhxxqK/KY9slMMwyD+0oER2ct8uCQTQmnDjcFK2s5TCeKQZuAtXMDZTaXAU2g4+ZISr3Xy6Q2zbvR86DDYUtjBO9OSrPfzh9YLl+CoC13hkgiuMbYN2uTuiCblhXIM/b3EDDR9+9GLQXLhFw9Ca2Dpk3x/EIt7+PlsOiXkWOm0QD7p6R/oV1jsu6kx7CjQEcWCj/trSaFzgozuNupZsUyG1EPUMA6LeQdVXTahYUDr7A5AkINDQxLEIMke887SEgYMRst/B0OSJaUNhg6oiQ2pEEGMmYGYi4zwkOyJB50gkfNTQ26mg5QaFCodtS0fgT/HT2lATLwa99VHGJAKjQyDpzuhwy1z9RGCknKNfdY+UPFEtsAExADVxHYtXTSpCIppHAUBDQzA0jr+rqnJrExb5TSqL5w9BMFgxW3NbEIe6RWKnF3rdEwbWwbQRpCb5hC5QURAzG2ywgW3wlr+KYooi76k0rLbJ/qi69ZclKNbuquB7QTQ60cf5fprBZkFrgp1gP6Q4RmXJziSheaojSjEAsh85oMghyEkvIpM/qTD/G3k5YZSWq5qNgwOHrnHgINsCKz1y9AAfLys/4s0BQq2N7BTDcRVPomgJe1YkY9+xnw5ouqM6NhfIKJkqQgMwj1IaoJwGBD30Cxdx5EHQHawOLUNo5KUgCU95ChIkyWZA4EQJQWWCNpUyBQr1KW74GAN5bzIYONa90DPVs4xrWHvMT/YmXjimB5vUAp+buYecfvn8CAw1Htk1oPWeIkNmiH2XxteIQ9ulFyL9IQiYySaS+YBQmi20XHgnu5iBxk0lsDygRnJ4EqpkXPBLU8KtbXfOfcCqUUkNcIyCuecPgV6NJk9GaqcwhAnnlQj0BYGkO32BcbYuZKSkoS25sRQmJEig+ttWpAu4ImNNT6TRsbu8YSMSUfCid+tdL57iQUpFef/G8TZemhJ4EaMj3tG+s+217s3b/WgZQouEVnXwDOULMx84I6dJ44LHEN6qUJ0mEbSEbpzK4+WuR3bd00k4xUcChXjRe6cLeK0T5A4rsuQljB1DjFKEXwXRokbiPPxFoqki9Y7awGJad7iC6ohN/gp0MCDh2ljuN2pocymKRwsqYKXulyynleGaqgQtR0RwJl3WTmxAmbQ40rBQgBENIpCcjKzZamdAgbB+qYYdh0RkHClV+hCENpNb6A4OgczFI/KSAMZ1nIoUhwyVLDMNgAKjgmpoFCJ9eMcjPcQngao7JoCUOmX062Xiiy4TiSoLDmw38VQyFh/6GHudyNqINJ2kKVynXk5TGAihAxNv4hl6vIeGiZ8Kpogz2cZVskgZM7nEjCggr75H942XPsrOekXPp8EG0a0G+DVephDm0fhoybM6VmIi+aqdeWWSm5ZxeKMs5io1DAaDEfo1vkaQNogtD4nBBUPj4o+CexAAMWPU2QxUEzDjc57mAw4d3RfAHSGjC9x9THgpqXyAzOvLIQ5mI6xEItOoD+hwa5Q62FLHDuSDRGAUCMRfUf4mAiNFgB9AOAf4DX9Gby7LaK8qrEJp3ptehUw/3qHkTZQfWep1iSGoQg1evmckgZdmsZJ47UYWL0RKBStyU91an8LcQtPL2lMOBM7uI/mEWS7IVwKJ/sPbnD6GABaveZQN3tqO5+FJ0LYxkmEwhCgKohxv6vCNEG8/iyWp7MLlYhTAJPhMeL/rOBngEacQOAgwLtCORGI4aLa3PGRIESKQGwTpKCABU5GnzAfCUpJkUVTk9avvxEMkjki8B+1AsGyTDpnRqUdBOzRSxkbHq0peslkAziI9IsO0R9hBydbf2BU8nfgsxkWDEhJI10i+0jYZreAjjV88zxW3mhpy2vhidUYzBpTiqqSXXRs0r8Q0daHcstSQ6JodKYMyFhdpMBL8HplyCiRQhcNUB1JsCZ8Tw+MHVlGCLEA2YbCHiPGLQ5hgdCQlJgLmAAKH6pVHqgY+Ac+eZbagcZESd9QAI1gvATlonM/U4kxTT9MULokxAwW6DBAaitwwA7nFDLjphE4xIMV1nMqIdsAZ6SwllJJLDNqKp/qzMp9ZACMBxuxWdXiJY7FKLo33JxbHZ0ekvOiv2UItVJKZEkxdmHHMooj3F2pwXR6Z9iUxnMXUU3qka1KaLSWZQGlzPXIsYQX2vcyxtGfq5U3fncafa15TFYFY6/u1vPbOCvU+R1FvUt4A7Cw2sIQYaIsAAwoZQzEgwLUCz5AM9bG+9JfjnVj+fiw6mXIsXklcAo8IsRsFo5KeNj6olbD3NdnMu0KloVMRSRAS8KQmGkSB0Tiu992i21zK0RfCgI5dRcRMJCIddRB1q+fRWS96ol2xxACRTMZrvL7wwUSA4qxFWQhFF20/wekSIwudipSOYEaMiNJy2nK9iu5hTVI7TGhNtrxsy+6JPfV6hbZh0kFj5Day6JdIYYixkeGUvDHIPzGkLMMcR1RaAVYGPSKr2On0lHzCArEQ2cFFQ0AYYx6chVEZCie6K6YojND4wsetzhKfzCKKJR2Vj4UYZTuD4BONafqlxeHHqnnYKmKHTFBySEMNQ7NFQNJVEL1qsRlQ+Zi3drLQIazcgww38xyeas5QzhWrHzZsnhiRBnRbbsmPBCE29LiLztILBolUBXj5qeBMWGBY4nQWqSK2gS8BAhFtdssE2aQCxCH4P237t22b+tXLLZ0fBZt5ZaS0VscxaUwO0cGwkS1qwrDExR/OE2We9ESwHtJC/Y3vmdTjg3DXYyLsT9hVj9cGc97sLbvNPfWHEKauesoGyWt3mYGupieKDS+xpvi8TQT6gkAas/oC4+xeCOpgaUjOlZe+dTAigu54TWMYeAYKQpy0RQrFYTehgCFEeVdEGoKW0KJvtzQPZwvxIi0rndVBpxJ+oG94wxtiKe9dyYlSuF4Fv8tyG3t5cC9CmlKdF+2OV+9YntYDxCq5S56JjG239adNYevgkH8UGDrrKXUOIeRW+4klgiGycOFUr9qbSiCh6ahwC/qbkFtuyVGGM96dbAG+I0F86qBI1gey01KbFMdLRFIzCKAOfGWqdZrKfuJW23yXCrxoB0JADhHtHuNYyIcxinAoYBRI+Bm1AIGgRRfIfsyMrEV3gq5pDAdeGamsSD4tseVHJHqh2ciEZsuLtlJF6AsKBRZciu3JfKAU1H4MCRNlD1Js209GYFo0NLYuwxkCSlOjAaLGcIuMErR4jwvP8EgfcSOcJlKKwQO0EAkjoaPluBF1IH8gRjHIUHFh5FKigHgA/mSYsFsxLnogzTYoWlvYoUqL3iWSxa/Jo2v1GGGwuLY9YDR0p3UGmvyuqIIhKWxJTTV2uUXOsHAzE0MtVL5L+tZHMDS3gym2Ps2YRGAwEUi6M5jjMulb5aVPMIT4j84UOdHaN8Ym6S2p6TZImkhAvtojQzY7kMOSmraAmLS5BjlQFBlJuxDLdO60Vv9IRhAmuoQZlp1h/xhiONaRzBZKU6zs7BeNw80a3pZtLtkRNTKSLgGNYKzB3mgmNAMhQ19YCmjm+TF479vXQxCSprxAqGqsuYl5yQghliAuO/iBBmBpmBnrA25nsU7KklgUCRqjg7JQkDAzkdmICLZB2cDNiFEJ6YmNx7LzreFdyx9CRVRQdC3UFQrk7gAc3OIX1S/a9Gf40+u0X0iY/cAol0Iko31BJcO2pdm0F6qL7BQ2dABF3uMWTnwRQ0BSzyghRhZlxEJ0Xy+I/5CdGi+xEqz1lalAPUJDbd5B+MLnJmrppE6Ip+XXrMApy20EoEdsl8iwYZVbBKWEBbSQDsxVIil+6N542iJM+sWlCUXzFKR+saKSskTWY1rDCjGNDbeqjXhrglHEjNQrrscq9BT7LCy8x1z1ZHizv6DYnVePz3AiMMgIJN0Z5NGZZG0LpsLllhaHhwdpR74KW1VbZzMtdeoPGsF3mFzn28uoQRjTNxAbBDxBRXyGyYMGiKsE6U6yEldFc0MlED6S4pm9bCTBeFg3VEdhYAmOXigKpZAF0pir3wAA4alJREFUaxGPN4js1B5ciuGDiCWkdYoCI3KxZRBpJL14q39KF9IRZUG2yHuR1BU4CnpE8BOlIrm80MTEliLkAIkhZui9NIzAJlbDv0RKjdHZaBIWxXNTpKtE4kz8iCUQSc0QKZEq/KPEHHjAgRHf9EvSq45pSb3lUd28iFm6PNIvMBoCO72RoUisjwRkyVgCiIir3JZAfLms3ApwNHbVYyYy3J43fLh61QWPq2HWr875zznvOeA9Y2rVcGEfe+hjH/vMxzqV074lnVKPOT6qG/r4DHtllLfk1xs6sMb1y/hP47cpzRMP2oVax7ddqoxLBAYLgSd0s4PVrmzNwCNQ3qQC3pVkJ62DdbxFM1uJMzyoQOgtSFl7UCk/wqcyEtc7F+XUYyYy3PSWb21e98bgdvQlKAtFCKKAzfi15bt7rvF72tr+iKHDIKJwUGqq7rUbKWt3ZkEOqvRn3ROPx9OmLrgdj1pmVZlN820CmlHHc5KC2V/QAoT+ljkB4ziJqnAWlGWhBlsfUpAPTstTuzM4YzG5W0JZ0qQvITLtgplpryb1e4fSiMeMv21WG0osXCcUMDPt9UQmmCHkdq6OqY455oBjZl71m6o/V38+9pBjZ55y/FP0ZXpAoC/l0MwZ4tH5u7RCpSi+1WyslGetT+sxxAbLHTssTWc9fqThAAEaf9riT9SuxFIo5/qFz0jbk+kTgYlEIOnORKI9ZeuaIVCnbP86dsx2d+4aTD9cfe2gsWus7q7UMdsEPugk5gd5yMbStk79HTvk2AnvKO7YPJPGXpoScB07nmySogTtXiCnNBvNuEvXk/HI5prduhmqnibCrXhyO7O3gAqWsZX+tTVLxiQCUw+BpDtTb0wnukfjJ2AmuifD9bXKhp6asWF13oXnVRf2lHZcE3Vqf+swPbzPwxyxyW8O1HbOd2qVPVO2asd2J/7OnZINQnynvvelbXCgiZmpNbBtXZzNOfYWb7NIw7edarB4U3ED5+HOg55FGAfi681ti8MTPo1V80XjT1YK557vlq+3DX3cy/AeJmMeWjym0Rd+xLLjZ+FzJlcZ/QKREacx4hrP160Um4FEYAojkHRnCg9udm3ECBSp0GNOwmOkWXosub/JipCrF2s3HPtIbEFnYu9EZfhc2zVm67jfeva+hPmDk+Xsnn0pbXSF8DbjZk7Vseaaa3YpwQnCToUJEPjUU7fQzXA2Rxf42tszGHlpYrhzMXhRxtiqLRJDwpNsm3d2ACLCAEq5Io29+qhMMQHbXme3HQ7ExmQfoovvlGONnBfg5EbO+/Vd+vzDeOtrti30rKhOrOY554AG7vNinDzJLZ3vuaMNuvQIW7K3X/YuafJRIjBlEEi6M2WGcpZ1pK0oneDWFM4xfo0pVbR2zaZ0h8qQ3GRV69OBjeEy4rw+B/HFHuxO7cRF7Ml37B5lg+3udo3Fbu1ITyfhEGq7/WMTO00DPRA5jTwJ0IjYxB47vNAmSgvbvjxqnAJQVTbc2fWGFjhcgDM1tQRpLV5GG/Sk5F7NB5zGgiqC5sPxSzas2XPOBKNYvvC2tctip5sEtuy17UJsGORcZRcbnYdtdzadOXTHh9y1HGVBHVAEXizoDuIiRl+c9KNAHEiZkslFWaIlUZpmc9LSJF/zwBftPLfXT6+1HJhO7nE8AYKI08gen0GlhnEqFbjiKCORGhBnMdtnp2RHPoLXgUDSOB8ZU7HLD51yoDMf8zi4vHSQWc1uRMnKoTsaj0XxlmNONSHV5WjEkr5toOzva/s0IxOBqYZAY6trXonAyBGo9n/iIxIjz92cg8wg3hxUSEA2P5vZvZaUJPVwiawHLIL9DdshXyJZc+KLkqRmiRRwML+UFvHCnYqNeOtja3Er/nr2cQoTt0RjvXBKGuKtKdLC3ceh0JRI2dr+EkOW6ybxXy/TAYMEPMH/29/+VjyIpHEEnyPvuLj66GYkdnZAqBzYXEh6kc5ylBJ1cLIAYiSMzYiP8XUogMg4OUmkU/5wKdv4HUrk5BsOuSJRGZv4SHekRI1inIHkgGMMieznICUl/QfigkBwEpeAZQebcV5i6ZTIciEQ4lEu37+UEs/QGE8pWpiN0CaQRmL6EkcKUbG4pbNBelAWnEzhDkEQCWpURgAg7ETREXvZdJNZimUQk4up5TDu8v2NRgOqyvlGUUv9V2n1gQucNdLhAsxMJWWpt8QEzr4rXmIEDKKKdNPYMVTFI32vw1K/hT/Gg1nWE9QLnJLhOgJTsoOzvFPlEPz4i57l7SkNmO7PI69EYCIR8KZmF2iqkUhwgDL5MdNdKk0ZR3pLSlnN1+0CzuMhRIlhQqVemjMMOUP4U6lHtoYd1me/DAYQR/pKQFxZZJO+JDcHi/jCc2Qk8xhEyFRn7okhaAlI0pQAdp6yvsfWG1oQJ/NqEocP7w7LfYk5Z1jlM2o4rA+ZiIZRMDhpmm5DJK9VBxBLSfFA2tGm+Fy5rfJRde+/1FQ0DTgHwak9yFyc/aMuspxIpvOIJnG2pZXxXSR8RYOlBC+pz5SjDVx6HYCEzagaaXCQEimuYUwwoSOhDKOEoClxWLNTehnU6FSwHB7fzDfaoO8OVKTCoQjBdXBK2hQpHahN6+McZFCDzhnBOEecbd3aTYRGJMxpj6iLoGrIxJD0uLXmKTlyqZ12h7HJLRMbNQnSg8UqPyIjmV9zBtmKk/oUYhDZpBxiCbHwsHH6Yv377SVj94C24VjONaCYqR9oFKQEG+ueXTPYsLRcS/wpdU+cTxOB2Q2BpDuz24iPV38JMG4N1twWzaUOkWSkyJCO4gkPwpJ+3mrYJwWC9xDSRKCzjMOWUbLzWiBuqRMUIhJNkZc5Iz6FGEcDl8QlYLVKsUExYI2rSdrAbYJdQAKS2KLZcX/EZEk/xoAySWhWIQv6KEp/fUFaJGaAnQjQT3hkLwwRSL7y82D7YLnAbyhgqLVoL0h3VECbpeSXSl/C0kEdAiUeHiJ1RErpleNDDSSryDDEUCQ421B2XIoMphpxS/WiBIHILnGPF8Mc0xVtihYiXow4YfXAaTAGBUIV2dI7dIqBiY5EH/nhGnrEiJwO0ww7C51KfAVJGo3XR2Oq151agjrIi8xJgNMgT7oQidUYRZW8zq7k74IA4TpNj0qa1oAWlgYos76zCblE2sI7B1XFfjAhaOBk3GIUZQgoVIAjDJOgOxqMwbMJIqNKoBgTDwr+OkZHSjUqRwwkOUuJ9+cAWLMamWMIg3P8gfD1wZJjrhrNaDyyhZ3TSvpbwKUonMQbCISG+s1RT3gkZ/NIjPhqGFeeMBdGpF8MUgvLrYBmw9ZfSv27V/UEGU4EphgC6bszxQZ01nTHq5Mgj00r3sgMQNrh5f62t72NVKbSoIEIPwZpaB1IR94SRepEYvYC/gdkRvRBStntW1EOBYD1rtW25T7FCbpDFeSXs0LZ2FJ6TmZY0GNFDDGEE8LBfmE5LoF4JMCtNjRtkynZRxogWvAbgjzULbKrUasIJ7IN99IvdIfHBisJqalTdB7EVUhovMeBfshNWY7TkVDJELokrr6X9ui+YhG+IB8RrzRSGZKUDZQfHhGcVE2ICIsP8Uy4juicGCou5ImcptxSY6m9BKhJHJCNl2AwCE29hSVNU4DAJpUpe2CO7oTAlgYBovVhgqGaovfGPJQpnhQn9emHzJziydtUZtzS9CiWLxGrVtsEJRLmaIpmY2PBJ2hu3DLogJquyJw0c8CLXvtwmG+SoAKYpRLwY3vTkBIKPLY/gygN3gwogJuEWCm4sHbNpmTiVYPimAahN9IvQ4kBozimt6liREwGLtI6jiVT5zD5haO0yWlM6b0K+P6atJN6CdRBxTRJyf5ANA/p1J36OkEHV1pppdLxTgEKM8o2k6RTgoxPBKYYAkl3ptiAzprusLN4azuNV/WkVDSCCkeArQETinWwW5KApp3xyIo5kvn1gqbdwQCK7BSgReCPSWtiWUysEgkkCnU9uU7DIRelBZ5RCqkHyEhEh2ygR8E2SI6Qo4RE72qAeoEjDas6/HlJULITg1ECPhSR9FhYDi5SJ3ylilAGkH8UVHikbpJ2ntrMLAshTUqBkfRVDrqAHJCFcEawqJrUyGeWhFYFfBibiowsVZSAkmVx65fIJ85ZFSneMCd6JkIaOyTFQ1VAh8GupHYin5mP5YXajB2K8cuHMuxIim+T0S0xu1BdSE8BIy9ao6fUWgYOreFp5EOthLSeap5h9WVveg6EgK7IbGFs0il2JeoHIJDoatEvE4x4xn3jhO7ohZZoVelRp4DSTEgDYT+ULJKZcoiICYZJcyFCd0QiEAxeWqid+EqURmVi1mGuaAQrFeZqRuGyGI9vlmkM3DAzPVUyzRwfal1DWQIQhbDTGSBDRmUFNzE6GIW3/jZ5JSNertZk2qAvJR6Smm2SaAwfuBIfgSZag39T9vBOK31sSp+3icDUQyDpztQb01nQI6914plgplPxoo8WkM0U9V7uFvSlTUQXIYrKlJi2AU4hXF5C4aFAEjfsQcS/BXFkISObvG1KURa7tEq+QS2G8CDYmjT5JWVfAqHXKdodjWRcoBuIwjVSl8M1h4KBiCUySUpuFqQsJx7MDHGRWAm0BZgBNkBpxBJEDQBSSh3O1Agf0kY1QhskMfHsEV2C8hl0wvYhjFHRWNB28FYm4xFEpKRTN0nHkLvEsIxw1jzCEhdBaxSCaJKUWCOSQY/iMqyoQMhslIiIZVlTL60bYU+iY2A8bxDWsJUgCuEvhQdQhxhZBqOgfVpFyUcRhZAhTNFIaQCIlyBJwUuovvQOFEizq+SN9KS7bVCdOljiYRhe6iWG1clVbiOAQ7T6AIlsqz3SMFdkLAyDHjFUiU0lc6lpiunvLd6GKVK80TDNtORQc4byaaaJM0EiMDUQSLozNcZxFveCLCRiySTiMJxwNYhVheQLdmLpH24cZBWBKg05yoFGGi9o4qSpA5QTNAGUBMQebRAxb3EvDeoT2ghhhKaL3oKIVT55xuZFf0Ccy2IFjDSQpvQT1CQIk5KpQIRFUjAQVBbrlunUHpbvfqXsrjyQC9tg0aDkQOywK/wAfbFfGglgxFEjSwrnCYt+QFFU0GMxxuE6moTHaIO+oEcoAvUG5QGDIKqHryAryASspOSnokmx5YfSxU4ohg9KBY0EI0aFH0RTNYYhz5Et4ML5qFh2PGBHJbRedk2HTy6mJTG1kLHQCy5WxktpJKhfcpFupjW7mKYTgSnPNLg1JbbhinjMuJ6A7aZ+K6wNRS/iVsOCXSGCrkhM58eKh8Uar3BGbiqk6VZKUxTTaoqfMrf8e3gOmcC96C9B6poyfc+OJAK9IJB0pxeUMs1MEGDMwics+ikqUBwS3VdCxbCnWBbTB1iyE6I0FuxWNPOsVIScr4raiEsDJLsFOi7CvwfF4XrJoIA34E+8IrAHVgwaEY1gcKEeQKHoDyQgnsO7orV9kjm5hFWLpqe83DEbztE8WykJrPXRDlQDZ8JImG9EEorEPLqjSTZMkdwaL7K1/BJD3FpYl1sBHMJVYqg9ShgHKuEItMaIRwrDEaqemP4AC4kYBC4CwQLrySKMCbla45tiUE9Xl8i2ioqm9LPklvIPUTYNELJeGoCShgqtl8STMQ2W04XoNJ1H1XQ7GfubbU4ERopA0p2RIpbp2yDAOMUlloaA7MQVwlMS1RCDdlia0+5wcY2c9t3wFBbjQilEIhxoEJdVdISuAuEQiSpZi3MlkZ3BIvLSYdD3oC8UAAopPCae1n/pJGKDT2wMjkdqiSN26ilJ9NZITKgeue8B+9az1MMpOepoTFiYjYxKzIC2qgbbtmG/x/bb7/j92j6a8pFdTsic8n3PDiYCBYFpBFK5yUAi0DsCKeZ7xypTJgKJwEAhkBRw/IaDPj583ej7OemPX0UjLTnNtyNFLNMnAolAIpAIJAKJwCRDII1Zk2zABqe5uTwanLHIliQCiUAikAh0RyC1O93xyaeJQCKQCCQCiUAiMOkRSLoz6YcwO5AIJAKJQCKQCCQC3RFIutMdn3yaCCQCiUAikAgkApMegaQ7k34IswOJQCKQCCQCiUAi0B2BpDvd8cmniUAikAgkAolAIjDpEUi6M+mHMDuQCCQCiUAikAgkAt0RSLrTHZ98mggkAolAIpAIJAKTHoGkO5N+CLMDiUAikAgkAolAItAdgaQ73fHJp4lAIpAIJAKJQCIw6RFIujPphzA7kAgkAolAIpAIJALdEUi60x2ffJoIJAKJQCKQCCQCkx6BpDuTfgizA4lAIpAIJAKJQCLQHYGkO93xyaeJQCKQCCQCiUAiMOkRSLoz6YcwO5AIJAKJQCKQCCQC3RFIutMdn3yaCCQCiUAikAgkApMegaQ7k34IswOJQCKQCCQCiUAi0B2BpDvd8cmniUAikAgkAolAIjDpEUi6M+mHMDuQCCQCiUAikAgkAt0RSLrTHZ98mggkAolAIpAIJAKTHoGkO5N+CLMDiUAikAgkAolAItAdgaQ73fHJp4lAIpAIJAKJQCIw6RFIujPphzA7kAgkAolAIpAIJALdEUi60x2ffJoIJAKJQCKQCCQCkx6BpDuTfgizA4lAIpAIJAKJQCLQHYGkO93xyaeJQCKQCCQCiUAiMOkRSLoz6YcwO5AIJAKJQCKQCCQC3RFIutMdn3yaCCQCiUAikAgkApMegaQ7k34IswOJQCKQCCQCiUAi0B2BpDvd8cmniUAzApffevkrvv2KF371hYf+5tB4tuhnFt3n7H3WP2r9Vb6+ysl/O1nkly/58qrfWHW1b6x25tVnPu/w511757UiNzl2kz3O2EPg3GvO3e7E7W5/4PYdTtpho6M3Wu87611y4yWlqJ1P2fmwiw+L2/xNBBKBRCAR6AsCSXf6AuOYCvnMZxrZL7+8+trXxlROZp4YBA6/5PCDNjro/J3P/9yvPhc1PvToQ0+b/2nn7XTeyducvMfpDUJz4HkHSnD8lscf++djN33upudfe/5jQ4/596eb/+Sp29c89zUfOvNDu79897Peetaxbzp2t5/uFkU9+OiD275w2/e9/H1xm7+JQCKQCCQCfUFgzr6UkoWMBQF056MfrVZeufEvr8FH4OCNDz7hLyeceuWpdz14V7QWj9n5JTsLL/+U5e988E6BzVbY7K0nv/U9L33P0W88+vSrTj/pipNWefoqqy656qW3XHr3Q3ejO+9c450UQlfddlWUcO/D9z469Ogc0+bwb+PlN47I/E0EEoFEIBHoFwKp3Rk9krfcUm2+ebXuutVOO1WLLjqjnBJwH+Hbb6922KHaaKNqvfWqS4ZNFl/+crXqqtVqq1Vnnll9/OPVPfdUr351I3ukv/nmarPNGon9Ckf8PvtU669frbJKdXLDVJLXrERgqx9spfrdX7b79Gkz/nzmnmPuReddNNo0rZomcNQWR+255p5f++3XWKY2ePYGv73xtxddf9ErnvmKNZdZkyWLCufpCzz9kcceOWOHM87d6dyz33b2kZsfiejIOOf0OUuxUWD+JgKJQCKQCIwdgaQ7o8fwgx+sttmmuuCCaostqgce6FjOhz5U7b57ddZZ1bHHVrsNmywOPLA6//zq+OMbMQccUC24YIP3lGuvvarttmsk8KsK10MPVU97WnXeeQ2us0fDVJLXrETgdzf9buuVt37gkQewlmhHE0Gh4OHHs9ayax3zpmNO+8dp880535ILLknBs84z18F4Dvn1Ies/a30Z11l2nXD0of456MKDZmWXsu5EIBFIBKY6AmnMGv0In3tudcQRjeyve101R2Nl3nw99lgj5uc/r66aYbKo7r23evTRhtrmrW+t3vOe6uijm7O4V+y3v92I33rrhpHLpZydG6aSavnlqzsbppK8ZiUCTFRrH7k24xSNDsYzzxzzNLVmkXkWed2Kr1vziDUZufZdb19Pue986w/fWmy+xWh3Lrj2ggM3PFDkoZseymXn67/7Oo3Ot17/raZC8jYRSAQSgUSgjwhMGxoa6mNxs1VRT396dd111TzzNLQv7FD33dfo/cILV3fd1QjccUe15JINrc9SS1X/+lc177wN1nLhhQ0rlYvy5otfrBZZpPrOdxp5JXZF4BnPaKRX7IMPNvjNjTc+UWZJ00id17ghMO2AhkEqr0QgEZiSCAx9PKXeOA7sueeeu+GGG6rgjDPO2GSTTcaxphEWncasEQJWS7722tUppzTu2ZgKacRg7LFyHXdcNW1YaK6zzgyHm9NPrw46qKGe4YWz1lrVMcdUp53WSIkGhR6ocVNV5smPftQI+N1gg0Zgeo5SA4a8EoFEIBFIBBKBUSKQxqxRAifbIYdUb3tbdfjhFd5DGRPXYYc1jFBLLFG97GUzIg89tOGy8/WvV3POWX3rWw2NDuPXmms2KM6+DUNHw9mZy/Opp84o4XOfq3bZpfrGN6oFFphh1ZrxIP8zsQjkEnBi8R6X2sZbUdc0SfpSXb1MBcbthRdeeM8992ywwQbzUhTXrr/97W/PfOYz559//lrcTIKlzHq6tpElgarf8pa3nHXWWawBW2yxxVFHHTXPPPPUs9TDJVd/A1QFhx9++KWXXvqHP/xh8cUXH2nhp5xyyt57733FNleMNGOmnzIIJN3pNpShnumWYvgZb2VXPfFf/9pwwWmKdPuc5zQiy8WF2b+4Inu9EPEMW/WnreEZj/M/PSNQ9HAzzeENPtM045egLvOilnFqz4RVNH5YtZZc71Q9/NBDD/33v/+dc845n/a0p00fs9a07YjUq9Owxx57bL/99vvTn/506KGHrrDCCq1NbYppLfO2227bd999f/jDH95666033HDD0ksvXbL885//XG+99XbeeefPfvazJbJt4OGHH9YSHKXt05lGXnDBBT/96U+POeaY+eab7+67777vvvtGVNT555+vAa961atmWlGXBJtuuulTn/rUl7/85Y/yf3z8euCBB+aaa6455phDBCp25513GtaFF174rrvu0t9FFllk2vArVfwGG2xgCDb9zaaPZ83/znYIJN2Z7YY8O9wjAk1yq8dcfUnWKvOi2L43acIqGiksjzzyyPHHH//KV75ymWWWGWnejp0aGnr3u999xx13IA2E3y677LLiiiuOtPBe0iMo11xzzWqOmqiqv/71r5dddtnPfvazffbZpxe601r+oosuetBBB2277baYTevTjTbaCHVrjW+K+eQnP/mMZzzjne98Z1N8j7f4ipTPetazFlhggVVWWSXoRdu81157rc6iIMgHaiLxRRdd9J3vfOeEE0743Oc+h4uI33HHHTGSf/3rXxQ2BtoQv/GNbzQoFDDKF4OV4jTo0Qte8AK1XHXVVb/4xS9UKlAq/cc//oGE/ehHP3rhC1+oX895znMQ2aWWWkppH//4xz/84Q9jPP/+978xpCuuuAJ6a6+99nE8DPYqBWRgtkMg6c7Mh7x3fcDMy5rVKSx1Jkt3hldlo2ltpz5GgbN6BGZl/cTwkUceSdPgt8kmMiub1a7uAw888BOf+MTWW2/9/e9/v93z0cR99KMf/fa3v33xxRcvu+yyv/nNb8YJAaIakVpiiSVId5J75ZVXPuKII9xSM1CK3H777XX1zE033XT//fczRZHTnboU6go8oCkBDvGlL31pueWWe8c73lF/dPbZZ3/wgx9U6emnn/7+979fxm984xvARFZ0n5alekM9eXP4zW9+89VXX621n/nMZ149fCAYpvJ1xviqUpoe/d///d9WWzWOnmq9/vOf/7z1rW9F79Ad4QMOOADdoQc66aSTGJJWWmklyhi55p57bs14/etfj3p+61vfUuyDDz6oXjxJm5dffvmvfe1rf/nLX1772tcyXbGjbb755lD65je/KVwq/eUvf/mpT30KQ9LfU089dY899sAL0bIddthBIT/+8Y9VIYZeR8mGHsdCjN773/eWEjIwuyGQdGfmIz6pxeRkITczH4YRppjIUbPE5E9gWfkepwsM8PWGN7yBC4gGrrvuuu9617v61VKCZ9VVV7WMHl2BJBYpuI0zrGoXyfSBD3xg1113rcV1DFIYeBZmi46Jqurvf/+7pwQ2bkGdIPDpT3+adWbPPfckmw855JDnP//5b+OOV9lceReyIlkMKNlpfOkbaJvoJHAUWRZaaKG2dfFxkd4jni5cTHARpA1lOfroo2l6rrzySooH2gj1kuX4hKrNHNoLbKBtgZ0in/3sZ2MG6sIVShryfvfddyfgKYQ04ENO/aoqKdnv6D8Mk3r/WP2xpG8KnHnmmZdffrl5or+ve93raF90mWpEZyFmx82CCy7ISNSUq9yqDpXBqsW85jWvoVARWH311b/85S8jPRRRJSVSqEAUhIINU6G20ULU9ilPeQquAxYqq7322svIgtr0oCIyHIxTpYSXvOQlDHwUPH/+859f+tKXisex1KiFtGjr2CEyfLEAKk1F7oxvdUFE5+/siEDu+Zn5qHuXTtJ/M+/bhKS4/vrrY1U36tqsYn/u/KLOl3WkHY/1xZ+0TaPWOXf7J4SE9+OSSy5JONXdBZpS8xX9whe+YOlJwDQ9antLvNGvtH003pEhccngxhK/60X58dvf/hYhIN1//etflwYbSre///3vCyBW0lbh9BmEt1yIQhTMqCElqRnS8cYbb/SUZCL5nvvc5xarxMYbb7z99tvvtNNOtBTkmUJkl5F+grS2+i/NJCClpCZhJNIM8TRADDRg32yzzdZYYw1CrhRbcpUAlYMGuEVx3v72t5OCwtQJ+++/v/ZoAN6APYikyaCSOfHEEw8++GBOM2LEf/WrXyWJCebTTjuN4qGLVQiPRBH09OSTT/7KV77CIgNtIKAaNC5UJmgcXYVi6VpM7P/9738i119/fTxDZO+Xvb6UFkH1IheeoWFoHxUL61VoWTzyp4E94ECf//zngdalCnTHAGkPfQkiErxN+qCSSJtAF0sWjugvnfLMuGhesBADR7XTpEszr4zvRz7yEQ2+7rrrMJVOrTIJETVzoyTQDDobjUSUGfjYqsojgRe96EUYUonR2ptvvrkLRSspMzDlEUi6MwWH2BvQO6J7x4graeLqktLyzqvTG/yLjgka1WUpvMEGG3g3jSp3I9O9997rtVhfwrYW5d16zjnn0BAUMdyaZqQx3AtkIR54Ffy///f/OmW3KCeeXaSmN3s9WQxE/VWLDWgkNb5OCZf0At7gIQXrJbQNk9CUEHaplKdkMCpAkUB2lsgYO+tay+WIRCkQOOvvuows6euBtdZay0KZmcDKWMBC39NbbrlFwC1uwZIS6T/2sY8ZGnLRalsu/EY8xPRRSlfDYWJYtHvKtEHk4xb0B9KI594BCs6873vf+0ippzvMqqrIS3odjIHpx21cHHJVhNdqkmYQ7eaVBHxiZHzve9+L6zDSPZ68+b+k4Jr2Q1aV9HgGzked8Ktf/UoDmHs0Em2l9NIYpW255ZY0MRpAWcIdmPCmocHAtttuO+ATvcG3musYvudTIq/qXvziF1NswDwmAAplhuDQwEca8K3DDjvMwMUvEjyWv5FoCQXbD37wAxNJRSig/VNRtaUCkd+FppSOYBI669YkodGZ6TwpGSNwySWXeFH4a2U7Q60sA6Io/C/+fjG/IMQSeDOgVgxtlFvcn6XUWjXW/16QJ+OOGDFReVmZPJJ997vf9QtncxuJNKWNmhiXnnoPGDUZg9MzFFICmW/ctjQpkuXv7IlA0p0pOO7e5lai1tOd+ubdalXkLe/96P3rtm1KLxF7MSyevJIsdtumqUfSdbcur4lwi7Mi1+vpewlrA+sAtsF+X09v5VrXGOkOkwolBKV3PZmuafkf/9hRe19P3BRmTwEOucuiAQELcQmoH5iueDP4LZoM8VQLdADeyKUQMs863rLVm5o6JOINDZQU65FORWs1m0aBjcMS36u5lNAasPg2st7pAjQHRUVB7U+ehUsmh00ZrZghxnRiGhjEsC+0FtgpBmLEHqlPdyJvAIjBuAgkJaNQoUujBmCkwPY0hgAzEPQ6OkI3QJnEadSvlPQQoTtBjJg8iDTre7XjLn4t8ZEMCNCluSX/3IKuLm6xNyyH0DIciIi2YSfwlOwVr3gFoQjSn/zkJ5161CmeUMTeoFoSYMzRKnwXGTJ1ESN4ajM2UJJ1CmiPsaDnaJsgStBTf3rPe97zsCjdIfUpycyTtllmGgmNSANn4FNEmYdombEL9q8X6B0matp0/0M2RlRfaC4WSxmGTCgZscALdR85M3xN2pR68yi0LI3wD3vj6eGKaza2geUbMrur8Fp/1IggP2IpX/ayl3EqMnCoKiWQWiRQZuiTDDfd4Zve9CazS8lYJm2ZvzvvLjySBsufp7/x3/3ud/6C9BrD492MvO62226hzEOgzX+0WLO7L5nqHcnw1ETACyWvTgiwhwxvbxwi6ixQWKO97nkAdEo/TvFW1d4FvRfu3eRsjGFPheZM0R2LJIseLz4LSss4UirSeV8QllaH9WxWvaY+iRKRXqBUCKwMbkkCYW8oYeTD69s7yMuXbFCOlFbwJJn3OJFZyiRgiH8KdmLSuk28LN6DHCT5T8CZ6kIbAnxvWLWrpWTHn7zLVKSPXs1Rezyl4fBmjD7Gr/e77EwtEkSBpZwugWr/yj9Lea2KZCQiyS2Me3EL4GkhQFbpYyTwJuXioG1x69drWgf5Fui+dzeOIlJHtOe8884ryQRQBKUJSEzSw0Tt9QQRFkmfITHYGT7IS+9xjygt6DYENIZvJmYmDEB8yMj6VaNFfxTil6us+Ry3nSryFCmJ8iNl2DUITqwi9hzhlx4FkzPQkcwva5EauVBQDyAKcLB2F08EkliRzEAbGmELcYn5nEZ8+SW58QbGpohBLiXDnNyS6MIksbAEkkksTEVEfArUO1UPE7oyopjSlAukZlG55U3M7uMvXZuBTPyjZSKpRvxZUVeQr0xahLQs9cKjBDH4pcnpohaiw2AOC1qMF0oTvlMEv7CRogGiJ8N4kAPzpLXMqMKfajAPraXI1AwpjSmNmh6hMviZjWzYgJmGPXD+BbvGm5ZSuugCjYWrQew6zK5IGUomtCxqEUmtpRbzLTaf61GkrJcTYYzKGNG+6JS/3Ejm1/TQPNOpDKhXjRklxvrBywQXkQxp/t73vmfHuzCCIkvTX0opcNQB7aw3e9TlZMYuCFCwmTAuS5QuySb+0ZzRrPztgoCtHF5wIdu8dyxBuiTu+yMvd68PKgGTw2s31txqEbaU8Q4iZUulpheWI5JEjOVReVQPoAiWR8PMoOGX4CUYT5Eq7IQpwXylkqlnKWGKDazCy9erzQqSbLMywwKh5G0rFy6F+lh5K98aV6QXn5dvaafTL6xuCQyUy5rP4kzvbNyVl+TmSqm/w4akw1RKuDYp4dEOHbd088ZkvkGeMLZonuVsyNrSWq4h3rwh50rkKAKkBRZCeBgOZWozbkHeoEHhDeqtTbNVkDQQ3uyEOuZnpIwdRUvoDJpq539A5JMuXvSy606oPZqSxa0us4kQ8Jaw1ruhKqin5CFB00N+kxlAxkWafCbqiWcaruvPohz6FRtz9L2pakStjC8y5CmmaKoYO3o48gz7MSFbrXUxS8MEBkOKrnAWbmqbek0nnUKpQ4NIgSQNcQgxRMSgmIGQacpYbrEQQ+AWcwILgxTOYaaZn7qJFGJyRtP0M3CqC09ks1RKQ6/LBDB5bOIhVaw2nbaM+QvFPv0pycuihJHou9UCdo7hmeSAisZj7aa9vzWwUEggx6W1TQEz3N8pjYi5pLX+cCQQqTT+Mf7Y4YyiIbsS+Ov2ay7pS/nToCZB+uUC+Lyfmbep/Lh9YgP//pWT3ve6e6+9Dtir8WjBBkW4zf+GrwMZeA84MML13yeyRyxSekn9+XD46qr67ZMjxbReM5ShVWXEZojO1kQZkwiMEIGJZ1iTqMbQB3iZAtVLVsu9671Vvfi8Xq1OxNDzE9KxMnNrncqZAxvw9vRei85yOIhIbz0BrzbxdLY4AXlPQkcywoyBw/JdaWQGySqe4FS7N5fXrnUn6SgSP/Aapfm3YlZmqGeooL31OEZYYFmHeZNqf9MVMXQt+AdzA+JC8e5VLpnucK3wNqdat17k4lDyonpetXFLsaE9xK1bOmTLTZwjHhFI0eaSUUDh6tKpiFQdeWD3KT2HFzd/DotyjwBLsQFYkZa8ehHgiyT/Im/8UgJpeTgkWqmTduWpfhFF0ce2fW+NLHnrgVgC1rU7ZJVVLyGn70YECAQtqak7JSOSQUsft56SSUwtWiiXW/6tHoV2h8VKmJDTF2oY2JotkplLxq6Ldsesw1MJ3RCQ3D6UYwrFFlxT1CSJRTlgDQ29oAmpzYiXlOQilQP1vgU6MU8p0nalKxJ9oQYwjWk40C95XWxYzBNaa+6ZutR+Io2vcSdcRZLi/DZE2nis+8YC0eT8RL0hElPREv4TwppnSuDBGCS9FwuFWURthpt6qmSdUpfsXMdCnaDLRsHEkxhFADW5jqDQi1A/IH8CWiJ7vVMlbKQAS7mCc1C0mOdSilGUPxxEyliIictgiXeF1goPk8ZfmRhDSa3lDxDlLYU/nu+Jqv31+eso8chW1FhiOgWaymy67ZRrRPHjUeaIGjALE+v77Nz9iUHen4m/dJdX5cTU2GMtqd2Jcen2GwtQq1VchD4DpfDuI/DsdJAtFnyhr/ZytOZjpoE+UUTeSIABWFDKTjBgEoSoV7YSJCD2vPdJdDKb1Pf2t8qU2OJS3mGDTmNXhWUfimAlWlpp7ahY0p004mJCMUALQpGgcAJDMktq8qCkbwqQZMSqjSdoB40xSUBUqJqkJHetI4VjwR0ZqcdjZexWdaU0ko8biiwRQyVDM1SeRsBCXwe1M26tO4kNvaaCEmNnKc8AAaJLq4htYY1xK+CyPNU70jrSi9E8A4EYaaEFOsyHEzZ+yE5i+MkbNcrD0QSMo2woC3MbLQ4cMEJuFuQrJkHVhwGEdy21BEFoVpDQGk+WG3EMCQdSAj8e1IFiBkSyIHBi0AijoCO6IxluxMMUM24s/ddo31qFq8KpJyAlUGkRUGS6Lto1NcpDC6U0AXyXSNY2tg9cmegVaYaoQgAFcYV9ym3r5T1llpp7phNKYZSlQbVpPjRAmFIh6IvxZd+hZsClzAQz0FN7jKm+zGcahbB8iWSyYeKUWNgpwCg16i9M6WWG+xPAmfxxiUF0IGPo9Q6Y8QdIvcQ1JCaGSiVz2T4WAb9GpIRbA6BwNcVjTk0xcWuk6vH4d9xik/X4LmFTxVUS+Pt1ldsRBZq1JiPKnIkTgUTgcQTmfDyQ/+2IgNc9C5GXNa5D7loI8i9BPqz55KEl5nPHCC2MN5AoYqybsRlKkYi0kiaEsBN0h8+mt6dyPBIOUhJFEVqsZuzuFD/CRIg0rRf9h+WpjGQkAU/GBK9Cpyx/W9O3xiAQXtyEsY4QaQQ5WYuRoFASk0MoBUnTmlEMlZIVfGjyiShrYgLb0twj/IMHK6DC3SeEGflkaVvkE58GQlrLMS1LbeIqJDGRxuShKKRHYpQoamefstAvLTEQ5DqFlnglhydEeWqAgFxuBYh8mBgR6evxvYSpW5AD4hmx0C+bjORCEbANAwp/KqhgD+x3SCrzB5qIwlJIEOHYpJ0jHqHFEI7D5Uh0Jh7xZohIE4C2RnqKDTFGELVCGRf94qJtW8jUSMEDdqOD/wW5VKbhMPfgFu2RF11QILpmvKCKQYqUnpMEqMVDj2qw+lPbeqpPzfWpauPqV4/9qmHI+Fu17QFPGEyrpwxnuara4YAdnsi8QFX5d2X1lgPe8kTkEtVXf/rV6qdPRFRzVAceemDtPoMzQWDo4w3CnVcikAiMHYGkOzPHkP4foaH35qRieU0/IY/1rjU6NTulPVVNOA0gRgw3lqoWpsz2sfxFR1AK60grV2qbEEihk+C5udhii1kWB02hIaCuoPlglWDcYfIvOycJQpX6JcMISGtoWhkyWEViyFpraGKPcFUCYaypFBK0iW27xw0T4yG/6SckIJu1jVultTh1C22/dbkyo0bCHrsiTclaWyGQIaoFK2kUR0WsHqQm1ZTsxLYmqRcnwMDIdQoPpIqqQBoynsKD+QyB8IiaRPmORAvNARiVxorHtKf7MI+WA5OtkI6BS4oYpIGaBGKQV4Vdr7H09wjHMkYUVPE9+ciOckE4aFzE9P4LnGhkPYvW1jUK8QgUrnoyYWwVd2mKdEvXEtjWHzHP1W87hQ1x25Soj6ueq65mK4/MluCg9ZSt4SkmYidYOzLB1TUNn1cE1lv+KJqeTtitZRg+7aKTC43dhFWdFSUCnRBIutMJmSfiaRrociypeQ+U2Hih0PRYZ3PusYYmpFEZvAeVocuhhODb4Re3oN6g9SHamVpE+qUYoFBhzifFBazykQyaCbwHEeGjoyLajqjO0p+Ng06IEshKnRkCL2ENYfqxXzdMUVKSr+xfeAM+hGOFfS1KaPrVTqRNI9E4dgfMTAJbebksUFN5REWBNonUNftayXhZ8AkWCrnwHlSJCgq9O/bYY0l61UmsL15twcPQPjESQEZRNDQMcKGF0hGmMXhKUI5JpdNSDjCRPBQKjMP6iMZ+EI3xiLMOxYan/EJk9E5vcsLFpdTFYdPTcomhcxrd27+V65RiZ1Vg1orSWdXrsdRbqNs4QTdOxTZ1eWJqaaq0v7dlIPpbbJaWCPSOQEOt3Xvq2S3ltGmNHl900a/DkEHEIhP8sEhxtgybh9EdVIBoZ8VgvIiDyGhWLKNpICxuuDvIQszTMVjxiFQg0kDNQ6izWLGAyEgq87GgMqEOwQNURAdAsUG6Sy8XBQktjnhZsBmRYdJSeJAVMS6EjHcFGiSvW+1vGt7WmOF8g/gT4Ef76XKwJZSReqNTW6mgEClqpOhja0/rBXYqJOIHQbqkeOg+RiN66i03/RPTP3jPBy0YOAb5a61nt3XA351zseuRsyps7rUOfdvI1hZaq9CwUoUOe/q3Pm+OsZhhzmYa9kbygorHdMw0tTDxCioZLNKoXa1kYi96ie8S8MfoZRWe8j22v0tp/XoUf9qtCPer/CwHAlwIiDMBYotlY3Aw6Sg8BqeJs7wluAhtCr0FP1NalngL4ByMHQgNzQEWwoaC4tj6S/tCxRJSmTHLXhs6GwdsKCE6QgfDSwbdoeOxuUP2snuWK2W4+zR1Wcn8W5si6TbCV7oer22tkfUEwiH1myIH/BbsGE8XrqP9IB3wXoyoefFe7iVLeXf3nqWXYmd5mtIvLRlp1+p5ZQ9bMCUrP2ukud41ylEmVH7Z9chJGmYH13LG3x7bzxMOs6HFLFxHRtplLuFOZvLGU5TXVIlkO0Z3gIlOycLMTfPqDWbhVxyxmaG9GL2IKMWV0GNLMlkiMAEIJN2ZOci8a/nEtKarS9/4w+YwYWnlYBgGLPt30BRHa3h38JPluawExhpewBx1ozQJWosd15gmZc+41jX2wgszQyhnAVYfH5Pi0+ueOZIw4O0U1smxA9JaQhMPaBLzrel7j7GLykRlM6VWtFJnT2zLxXsvsHtKXue0pEy6YRht6pe8vXetNW/8qXIsU0tQn9IYplte800D5O+UbdpixlKneD7xLWMgts4JbzPja2FjZlIdUbUS8FYyUZGUThyQnXZWZLwcpPcSwEiYZW3aikjt4QLohB4ubt4eSisNawpQXtrooEDjYie8lRLrLeWxtxPVlNUUf/w4+sio2T6JxukabzbrBMkcEyCLJlH9agMjuPJpTLmXGVZFleq8uPTCIQIWVLof8WrUPC33Z6gQSmWqaH54mKK+xwEEZog+MluzjyNJ0qTpoKCagYFAwIzMqxMC3rH5b4oh0Gms6/HV/n04nKNsKHMuZb3w/oY1tRRYD5fIUQfiOE30XQnEP5YwoqJkIRddAvWMTLqtRYVjHN8sFt5I3NSXuKVL4ABXjmBm5LW0QMiYWniS0a2S6LI35S0FSk+u4welPdQbrJ9exPhcieTBZnchniqeURhp8IhGNvbW2dJII6ILseVeGilZbdAXnnBSspfZXchIpKnoSzSJe7vN7ZY9OIGUyJCUTvCiVWIkoixBIyiGRXZqPLUKMxMFFTqIZjGms7DzS5PF7kiKYb53wngGX34BW/CY7ShasFVZpLFXgOEbTZEgmiqZbYbUogLlcgySFsZRSSUShXLeQbkVsM0CGaJ2tR0ShYpJzpQGsUhm8wReZeHntm2n6qVNWFhLBqcxE9brCa5oYM/dme7PNa9EIBHoOwI0/+wmhJzl76gLZwy1dm8qgZBjHRfvbL22JYcTGM2B85qlRAhKMk2y4mfTIQ4j0sFRYqzyreCpHq3gcRTinHpDAgc4iSeJSW6CX6V6RDlBKIYvPLmOByiQ4OSI5pYSwr53Yo/KgVc7AcwRRFHYBrlOIuIWZLNbkbiFZPQEYhTSxTVEOyXzJrWtD+eQmOccNoYkkbh6SgVLUxKdavvLaqxq9Ks8JbBRKN1BwkqkfXMc8HVfZzUPmB6plFXalgX7Cu1DhIkdBjYN0P04OIoG1wmH3O2ljEMgufE5VCLOVBQJXsggW6gGbJ1BINIA8WzgXI8ZQMP5DiI7XfIaBfwMw6N3oTvR8VDSGLXYrigvHYzhE7AFT7/odaijbAsVaQRdEI4juzpVZBtBUL16AhljPpRIMdpDFaQKpM1VHpWAdtZV4CU+A4nALEEg6U432C1L8t8UQ6DbeLc8IwXJeHI9ZLMA5kEVYXFMeRPHC0Um6ye79G2ss4yOGKKU7GHj8EgMeUPIMTcQyTgHeSlg0RykAeHwiD5AJA1HlMDRD1fYYIMNlBwxrGNsFg4O4Akonukn4pt+CSFP5WVlkNI1fCpBRdPAYISCkNMcVMlyGXEmh/7Z/UfuKpyOhCTTzTjBiLDXTboEKR20rVj2C1vwSF/SWiShTougSTbZOU3Kol+lNAoqQkE4znMmU6aUDLvajzf4/CRVAZWMSIhxsPV9Ry4jdvA1ETsJyqVwVaNfMuIHuAWGwT6lU/Lihc5z4k1S0rcNYGbBBuIpbzyGJJqhUq+e4ijIBIuVbZVkOUIjMo48oJuhjKGJAQ5ZTqdCERLmKlQviBFknCJBj0Knoj0SqwuBIPi1XO14Es4XkfYWOHcKDwMCMte2zRHJ8ISIaA9aGXs2zSt9j6coVHAUpi7DF5HqCr/AwvAkMzTmWFt2ErlMBk2NeW5yRl76Kh+EiSkRhzyhTRBAMZFvyq3gxOazuW1o/OFoBm7KlBbF5m8iMMsRSLozy4cgGzCgCHjj237vkCECDBvQSotp731+HpzQaelZE8IlS5iDjsOKyAZum+XQoHrHvP0tshkjHADIt8Nan94lPvNklUxgSIzWKCRYCF8N1bGhUDYw39gUIwG5ixl4RNThE3WdRL0uSpTYS0ipQLyRbXEkNz5B6YKQqQWNi5OyecGHuwwVBULG5KEoKgE8QEB6Rw/QEwjLxWbhwoqwJURHpJOo+HlITPLRfHAEoUGh3cEYEJR6Cx27gMCJR4lkDPGsR9z8oSqGY2wRzG6bLqdbIXAiiXBWkjjIoClN32/1CyXCG0wG/dUdeCIZKE6XuuAgC9qKxNBaSWm8QsuCk3ENLjoPxJSCh11Mp7potpRgNygKZZ4gl3FuEwcdtRg1bJKuK3Q2SCf+6rAGrUWkeBzTytj7ycSmAaqjEnOcN3YihtZNrjgLnp4s2IyDuXU2mDrCF589wc+UbFi1E1tVL1ZkFLQBn7OxyynbBhHTNT/NBOetUy8xk7Uqirrglo8SgXFFIF2VxxXeLHwSI0CjQxTRSegD+4Vf5IZhiEgmoUkCpCd0MwSJV3yYD3AL9pG2hgm0yUXYcyMNMeDTH9Q/lvgWypQoMjrliDlJXTZLEz8Sh3IoeANdAjsO5QrRaC8MzlR9tz3CoWAgqrXNapu40mYtx7EoM5AMwolCIjLrKVdW/Kl9WY/Hagmy4o7Mo2ih7Ikn4kOH8XjCxn91UNX1GF3AjbjFEJb0E1EUBQnokCQBrJFw1cjCBurZCXUqFmokhINsDk8aCWgsjIK61Kgjbuu56mFPpVQ7QgBJahucjzaCq7Ia6UVQKPAaO9qvBrZVBUABAOosvQ7GZrwgT8XiqVyK0n5aHyMIW+41LiwH/UUaDCVqKKX0iCO2gVnioLE9W691xK+WYNW0bvXWNoWREqzI9KMChGGUCQS0wyzFRFUHVSoihNX44qPYBlhoGbEfHF0uhBtt0n4gQMDA4S6KMgPNqJiTmD0dkkgDYUobF2G0BlWlrJIFu419WDi0vojBcnRBMhdVIi5lPrCvRUz+JgIDgkDSnQEZiGzGwCFAHpMN3t2og9e99hEeVr1kA67j1os+Gk1zY3mNUkhf7Bed+kMM8FYhI5nDBCQjKogrMtKBBVbkpAgxQyChI85QJoPpV4IDEV02v/B4JaTpkAibTrUwt5VHBCGi4FaZJDTnD7uI6ZCK1aOk7B5g7aKx0B68AWeKfUCyKJOiiM6AF7BbJht8Du2ACZnqog4Rievgi9QAatdfApgpivqBgQwLJPUpt7QQq6BAam0JxgCfYDkUSDQK0qhCFmoPljWjQ3GlnOrFrbkbMR6FIKelwAb0xWDhT1RuniIoWAjxb7j53vqEiJJZ4pAGT4GGIKI7lCv4ENIjErVF+0I1RczzINZZY3fooYcChH2NU7MYKbEo9kS4uRAL3EikvkiDBaoo6JrITpdZJy+occ2Shg6PdgdNCaYinh9PeRoBm7lslYowvyuB8M4WiFkdj8qvcWk99sJT89ZVkgmAkS2yHhPhUBa2xmdMIjCLEfDKzisRSATqCFT7N7ZvkL7W3KxIRGDZzkPokn+RmOSjBhCmpCE1maic24ajsB2U0hAguoFyK0AoWo77s+csHPFycXGgJ6AeoE4gicUziJCpvB/E0/qQKyIpe5hROPrQguAKDeNOh51ZcSg2pxZim/XE0lx25aNrXF4YrcgkygaRRD47BQFMUrKAiHFxQwn3Dot7y336JJGkMlsM2Ymo0WdgUSL1GvmTFxmiV8DDnNcXFkAlEJC4iEoxAImpOgh+ZXLyQJvE0OigHVqIz3HydSEf4uv9KrfYTKRRi0jtwT90kJMQVHEstw2PohomksUlEgWRXXq/1CQRz/k3CmFYjB49nmPW/LdT42dNa/pUa9tO9anskRWjJYPTmJE1ffKk9tYKWhOvncFpeJ6qHOOSv4nAEwjEwS3vuvld1tMkNwlKRrIFIED0MdgGdQvrBh2D1baAb4RRtPCroL3wt81swb1GcRQVZD9hjwwxDVAbWGqL55FD8HPjDXMS39VQ83jETGDTk2U3ewR7Fq0MPY3ELB04gVuuvmLIe/oVkSv/cOVyII1mlzBdCwqCaaEyaFndDdbOKWzJ1qFoDCOOinSEkYhJC5UJILyzQpeDiDRUJo9fSIZgXTOky7QL8VIbVjRMkyAi64HHC+jpv/W+yNB0272ItonbRnYvZ5Y8bdtOkbOkMQNSaZnVY29PINnHAsfepKlXgmUVZad+oTuxtBuQPqYxa0AGIpsxcAigC9yKER0aHZQFOWBHQERsDqKP0Vyummw0ktm0wrJDW8Px0y87EYMFSsFOITs1BhMVghL0grbGDmcakeI6Y6cMB5GgCzQ69B8KZ93grcJWQuXA+oCOiESzJBbDtFEi2wIX+8wVG07Q9TScP+q3jBcsNfWYCHthxTur6VGd6MSjsKQUolOPFI6nTYWM4nZ2Fvn9Fc99QbJtk5TcNr7H4WYAtbQI7ytO4vH30pfW9tiATDa1EUjtztQe3+zdaBCIN+xYXtxta8V+eHIwQrElMZ3Q1rRNNqLIuoCZYoKhv/hPInD62/HW6VSfM4yJLJX0hTyrcOtwKmrN0hRTL6H+qFN8PU2XsMZQpob7v41jtKcSj7HMpuqUJma8EW6qdHa7Te3O7Dbi2d9EoBkBBiZ2LtqR2I3c/HjM9/WXOMsUrRKdUNEhjbn4CSogBJLKSmCCKu5aTR3bSDh+zet7ya2NL31l0+QZZscWDSWGwdBZHk18gDqHJ74/E/ZTys6Jb0DWOLURSGPW1B7f7N3oEei71Gk0ZdfGzxeqL3zhgC80Qv24xqWd/WhYKaOLuC1p6gHpXVyP+QkJcG2ub0eqpxxp2MZv2jVuWI4m6pSX/dFxAGS/bXGO1JOsE8Ij7VenGkcdz88adbZJLXaHtS2nU+MjMVr8k5/8hM87N/BSCMzRDlZONtlIFmPBsYynF0Nq24oikqVVGhZMhfAbC7Yti0juaGLCVisxZaf28753oiP3NYoludhweet76jCqLrXko0RgNAiYlHklAolAHYFJtH1jnLaZcDCyv8yRic6kqSMzivBIWxjpnYYX7kpeavFlqFFU3ZSFfLV9jHbNNvimR/VbWjE0y9egbIKL+LZdaBtZL6fvYWcicAgrxfoOVxwKxVneFvrYZ+dpHFXATR5pa/jBtOxTixj+Z/zAMAx5bZjngB8l8z/jUy/ewQq2sIm02x8X4VXmvOkZ5yu2lBl5lYx+FTmk2IjnU8+M69hMvvAOn3Q+kPg4OZM3PTuaL6RGSr8aoAR7+iKmtf0l5SgCSutvgaNow5TPMrA7s6aXqZmBRCARGA8EnDrjeBUOzjZnjUf541GmtbXtWnZmsXE4i288quhSJrgceGMrvv1uDukJ39VIr2Hcw+unCnkKW5SoNZKGxoXlRF575nlNUdggPaV2g+JEHBodKW3EE49mEfYUG8RSSdY24Pg+Z884jMAmO57jZLmWS2lvP/TsSYFeyUgG8Bzn9o4xOFhIs53rGOcF2CHvOKJyNKVtetxoHMfs/BvuLEowhZyvY4OekwJ8QEMvRPJ/j8+H0e4wQvF/j7qQGCcz0WNxdfexjohs/XVStiMPqM20mY01PvMOQ1XT92g5xkkTJqMDBRRIQ+NEBiwwPkjSWmDEaAyKTG2j+6EuMn/i62aIDmrl1IY4vtnhRj52hu44ZKE+xFGOR52qyPhEYHQIpDFrdLhlrqmPQHcrwKzq/8QYUOxdJ7Pt4SLwkIA4AblLl4kr5ABpIOGcutslZS+PrP5xFN+UsPcNk3C4olwELUMJZiOGyPe9MExIvFMZYxs/xmDjaxzvyzgSmo/IGIdiY284hGMAcanSDGcH8NV1FhHu4uTGOCmxPO0eYO2yb1/hDgykwAAanQSlC62YPX1OIdpwww2dL4yj8Ex3UpFI4DjxyEkEtB3YT/jKKAfbiC+5cvOMr5Oq2vEBOiI7hYetf7gCVxu8J/RezEDO9Ub+RNbbqRxYoRFONHDe8S6f3aX+tIS1WZNwHSQmDm/0iE6IcgvzE8bMUCLshE99jKl+zTjR4KRSTHOAf7FixRqLeIYnOaoqPk4SXyPBJs0WVTtsUyN9caI0oBQXKcttBhKBsSOQdGfsGGYJUxOBfhEL+oM4/t9xdnXHYWtcnhPliFueDY7Lc7avkwkBSh5Q/p944olMEpbgLqJrrk89caJuHXTi0O53gorFgXy1y500xVeIVZEUFUSs8nEFZhoyhoB0MhAnCaLOB5gc4SMZMuGAYyaG0ki51F6viDh0sQdJSbWABiFDxJuuqZQ4J73GTneAgDbRUlA24BN262gD7QhlD5WGzyY4upAw9hUtyg/iny6BdGSCoQ6xk1k8rkPkS8MJV0+D7vDXAZRvbdZ7xCuFJYVmBasAUf3RTMNOJcByUD0lhMeJLPgHU6BjD1EcCgw2JiXDx4nG8eU1tCwcU0j9UkUJIwGmAb8ZE0CyMB7JYgp99KMfdWSAEymDOshLp1VKKAFHDyiBLRLzC9+j8mgCAqiqrVWBBt6GqnLHMcdQTJ9wj+/BoWtQYoMz2fTLJNcjw13cerQTzWK8m4AGZxWzDwJJd2afsc6ejgwB636yEz/AA6y/qfdxCJEh0Z0Lwl7Ap4HqnnAiYuPgYFKN8CO96PBpR8hjL3ECgNXDV7EYPkgjZhqFkMGSkeI4iqWwbyv6xAFfTrKBcYG0I+wVQnaScwK+mtS2AySrMjWSvA8PXCJceoYSrh4aQ5ZQgfjgAC2IlbSWc03VEZIYy8G6VIRDIBkabPnOlhEVcU3VjFIp5YdyyCEUTfu1mVIEo/L5C0YT4opgK4nHEkAjqHDs0KHPwLeIPd9qxcywHNoXbAyAqJUqDBA2gw8hXuWTGkgkhseUY3S46cQ3IqI9WJQBrbeNXuEf//gHXYiiHGtUf9RLGD6GrHAdWYwpgoupqAgRDBWU+HqaKDk+NKYEWQxE2DrNMSTJXDIr6EVQBIn1UWIge2SUaV+cly2eDozxyPjCxATAb2yz4tnNlHbssceyB7EfVc+M2pp/5VWXesFltqhLdvPHhEQWnZ2N1/q4h5kvp8L9SmMma21zWbV7Ci3E13gh6IDVDOo0E4/9jqaQQ7TvksbfgjZrLf6K9ADBECBASlKvicTAh0rGt1NqxWcwERgDAuZZXolAIlBHoNq/4c/ole0Pi0mFkoD4jE9DECTxCma5wCe4HdhyQloQFZHSW56FQmkIgez0Dda78XkpLITdhETxlPwIvw2MhGiUi0gj8Ihz4fBI9VFPSguJCSRipiGnW1xExYRrJ0rEN8WimbiSxUWWUDA48Zk4JGPEcC6hGwhThQJZQ5RMNaKdJJMEBCohRAQ28g8N4Rlkm+YN3w1R9khptzABb4HufMWIj3MLiXNHSMcnICI+flvbXH/aGpYesdMqj1Ax/Ix9RBiexLNmC2ON8BfAirREpUYBs4yWY43Gi2yWoOnyiS78pkRilpoNbcjzsSWPyyM0sXSwbRciEtnFSEyAkhFtBZGS4U+ThDp4xBFYg/FjNIX2rnyHBLFzYnU55hGVkTg+xYWoYRtmDjSwH8j78gYmahSQmKiO9VA8WPwqHwicbCLGOJpImtfa+IgJbmF8I7uWYL2KxT/QEYVoJ+WQGAo8FJkly9RFXMyo1jKjPeJl1zsXshKcLx7pIxJPvxi3JrPx4pPEsToUQmo3ZC4BoyzSo4aXT8ucjxJG96u0/hY4umZM7VxeQeaPy4pooHqa2p0Yl/xNBJoRIK64YlAq0J3gAcES7GG2wqbJIFOL1YaUIqLIYzoG0s6bWlnUElxPCAw6BmYpph82IKqREEjksTA1PnlD548Vce0keGhKSIImTUB3rQldi3W8XTP20dBzxFcgqHyIE/HMKNbxuqBJ5GVDfnS+NNXrqdPzOOWWWkUtdE7RTa3VeGoeVIN4ZuQqNohO6qhO5Zd4HxVn0wE1cYiQUZ7FI22j8qG9EE8XJZKBjySmDyC8iXbylZqKgoFbDPsUBQ88aX2wTCnRGqIUs6E5IMLxA8AyYFEaARwBpe5ibcFWZdRNGLIiBSstbasHYKtqOCOUtDgIMSIICuoKTkJ4mBHnEiRLHGwjGSWNZpQy8TaR6JqiULfwkZLdJEFMjSk9nFlB12KyQVizfclE76IZfHeCVTOomQbaYPSRWvXCymjKvuuBu9bbXMLmMOOaRkopO24XPlL4pRHEoc1eJF56pXEhis+Lzsj+p1JMc0B2jsnNsTjG/vvXI0170ylmVMTjZxGIZggDs54lw4nAGBFIujNGADP7lEWAEh4pCfFP7BFgfFziW6HEJElTes6gQySHrMJ7wqpChKAFRE5JpigLbv4WPsBJZodUIG+IOlKccCWuSCB2MWvc8vaP7NGMUlQ9QNwqFmdSJuFKlOI3hK5y1IWxEajEpCx0PHpEjAkTruSoYqNk6zBaK6YHxEiTJODYSxvhKSlOAuk76ubjX1pLsnrqsuLHAqk3rN2VjPoUV1+sgkNxo949643tKQxewt4lNeHNO0eA0FW+fUM6CyXqE5FS2q+E5/maGNDQGpGgQ1XJV7ocUDDbhd8r/Zk09lfzXhLPbIef0UgZr3D90VmkhyTWCyo95iS3xn3vr++t2NaL/oNWDIySaZv00uBhZZNUPYvt1pQWYoCGlsUj2kHDF+FQnglzDUaOIzJ+Nc9Vj4kwlmZE6vFa7qrHtA23ccNv6ImefP3uybcNvPNKBCYxAkl3JvHgZdPHGwEilrcBZYBPUHF9DUHCZoTKhJeob2khGQiB9TdyYGlLqUAAa1iwB5KV+iEOI5GAPKbzIMx40rA04TfU+wQqzQQdCc0EbQFJTForgdkFh+Csqjq/obZp7TJ5qWQaEcKPvYxWicCWniaDv5ESMBI6DFt+qBYIWpYXbaPDQAtoUKJYy3cpdZAeSxXKoS9By1AWLIcTjy5oLcZAQtO4qCXW62S8dT8bjWbzfUE7ooU4E5sL299vqt9ETO+/yCXtjl7gEOANRU7QMgY+ti0xhiYKRIBcTYWjQfreFEmf4WqKpPFyRaQag7OCpSlZ29vghR7VSW3blCXSdDJ/cEHjHlbR8mjCAv3ywW/b4DZEqm26jEwEJhyB/GbWhEOeFQ48AvHKvv8j9yMcYf0h0WNTCd5AZxN2HP1AdOIQFKt8HprUHrbhWL5HF20JJu/pflAE4pnfAzGsHIYwkpXLC02J8oNwMLuQhSwsM/b6DhfBG4P6Ad1RAumoYU2yqjVmpOhyoGYo0f7wVRpp9pmmH2kLO6Xn/kKNpJFOvYtDYmZadb8StG2SyH6Vn+XUEWid4fWnvYebyomMMWptH/VecqbsjkB+M6s7Pvk0ERhEBChCGICYPLhNRPus/pEYWge39A38eCIeTXH8GjtLiRHPsBVGlrovDp9QV+SKfTcRZnKKQP2XjYzzUD1mnMJMYDxXaHHGqfyxF8uPxEDQGIUj7dgL7FRCWx7TNrJTCb3H1+XuSKuo5y01KqRtfElQAmguVV9YNktklwCNFMZJ8UbJ1yXZKB4h+pzb/KFxX2sLQo89qlfdtpx6ggzPhgikMWs2HPTsck8IfOMb3+CT4V1ctDWy0crUTwepFxQ2l3qMMALkaoocqFsaLKYoTi3FiWSWN6+jrFqzOuMHZ8yS5nWRuCYJWkxvxxqobZixY43sLGPE9BWFaC0fJnZMKjTb94rTbms3//ve/2K9WDIn5e7dbM3bPX3TU57mDsJxsoDTGp2t3PS07S0tI2OlhTun75KAsrNYAEskN2d7c2zjKjHdA8yg3Ld1Gd3pnjKfJgJjQSDpzljQy7xTGQEOGTYJUyqwJXFHnQJdnYmMvG68ujiTeh+vtguleDzJeP23XrXW1m9nWiV7JX7DFyo8tJyqzOcJs2GmLHTHjnEMgxMYh/RCd1pLRh34Qimh9VF/Y1BzTma8trWzR7rDO82pRXWuo0kMr/ZPOY2pNI/HGO9pG/S4temvBKHaxAitHHjQ11cFFIpc2SBTsncK4OJIOQ2TBrAso5gc4KhXxeCXLMXOByob1joVkvGzOQJJd2bzCZDd74jAu25+V/WCxtOvf/LrHRMNwIMeycQsbGkv7KHei17Sd+kOSmFfFU9wrlQ8gptSEvC8rPhicw+Pzx3Uq25K3HRrk5fDY2hf6vEct+1cw4wjkhO6y0Y5JyGVZCiFi8rHmQUlsjWAWzubAEXgxUWEu5AGv1LSD2EG+JBb/WrNW2IoS6htkAB8nTHUZm+3vNTxDM7pztqmiBKmRuJ25lZT6fbYMVmpwMIvTV4khpLGWQmHH364LWMczhxEhMpw87JXTl3WADrIYZ8vuVMfNY+jPRzs4Yew5YFjGzll22Nv57ytarbWcz+3n44XWhznqAQO7w6AnulawmZ7pxTqviwAsVNP+zWeTghi7MX4Fj5kq+CAa1LLGGVgliCQdGeWwJ6VJgKjRKB32RwV1KmDvPXbUbSAIGT+8G3Lel6eTAQwwRbfBKg/miVholojVW3LGzFM0tebwcvKxjdKArKzHt8Utrk9jit0HoEPHfA3J5tdTs/DDGgXkJLYkuY8QCK/yaOISzWlBT0NZ5dSso1v9ZNmSnxTgFdNuI1jNnQYqJsECId9fwLIQWzca8pVbm3gRyzoV7TWcX9+bT3TnaB3uILjBuCD3MQhCCiUA/2UzwccfaGpkotpiQ0XdBghysjbzJ44bKac26QZ9r7ZWu/oIP5qFC2Bs7PC4wMR8NEk2he/DqNSDvOZ8vXCJ1od8wNVkY5j4PRm731pf2vA9kYKM4ctecTfX3cYy2jOXBiYSCY2g4W6GdzW7BmTCAQCSXdyJiQC7REYIzNoX2jnWPKG2LDtq57EUth7nGDAJOrxPYbbciNH3hEYIY16LKckIxeJKEttx/A4K8hhMESyRbwVvIV1COZIfN1113FykoZctCs+IglFp+4GBYmVOs+hUng9gEKRskQvAcZOpBBPg1H5sgTNBOdWItM5yMS5MvnNUEWoLg7pqRdVwsQwiUvDoTTlR5nlaT1gx5xu4gEK5G0Dfz3VI2kQBRmJZzFuKRswIZSonl1Y+fjE6HaQgVQfWZqcSqBqJElPkRXinKnLOcs4UOgdmyqNW0/tzHeOgMnjwECtpZFCd+KpAgFFe6R5BgIgdDOANfEonziDAxCD4RJuN75cPNgiI4QBUq+RfcrOQeNeJ5S4C7VQmQkYFWpIPeOKA5DiICUbGJ3OHP49ThYwoJRM9cLrYWdJtzrMabAuRDIsXLHJdeqgZbgVgYaaNK9EIBEYIwJMJ5whCDlS3G8pLdwL/JaYCEhj4VtSWp5a9YZo8e5mXIhkDvsRIPzq2dELwth6t0TygRDp80lkIdlf4lsDFsdkOQsFIecrRbH4lgyDcSYN8VOsP5bdEpN5PoNAYRBdsExn72BHQHc4lja+J1BVTvOjR+G5wowSNdqfz4FDI63jJSO2I95RxQqUkhuvPUEO+4n4pl+ST2N844IOBqEhGiVgkWFVoZmgVCCYHVMkkqBlzlCvy8lD0jQVVb8lwolVJhjaAmK4i3ZHB51HjIA6jFFPFUIrw0dHABtgrGGUCT0NExUfZIK/XpGwkaVkqvupNCXockuVYjiIc+YhyZASXi82LjldCfPDwMInulMJ0jDrGBGBYAldiF29EMUiFsYX36rHdwrjUo61dBSTBPobM0ReaMQhkCJd8dR8wKJ0hBsTWIBv7HTKUzOZGqyJS9UrpWfCNfF+kWqJ5lGnYa7+WEQqyrSn06rnynAi0IRAT9O6KU/eJgKzAwJO5+NIQW1OiHqtkwQh1SyF3ZL0OErBwZKajPdeJquwhHjL07RblJOL6AXPA4kd4OutbUOvNJbF4d5BVDuVmFRTgjc41067YCTm8WBdXqqIgHIswekYHOsc31pyXK/PIHAoIU4ch+hpF8ZDVHM4VQXGYBVOxhA8eIkjmEkdoogzafAAvhfkK6mPAGlPCDP0hSVLv5AAvQjHVVKZGKuLfKceK40Qkhe/oWmIQ/+IYXvviSWeHDxP694t9W7qI1qD0PB0QYniMGIcCPIsR4gaSw2pjOGBkTcJAIlqwHY5uA9xQQq1xBhhlpxaYozq9ZYwXRoo+L6gj1hLiZ9VAeC7MAbU0+AiQ11aQtVkaHxmyyjzKJIeW9XfYAZIobxN3CIiJeDt6xejMjlFmgklJbWNNsSnVKJ2B3BLb27wv6EvNFvEY2nGwmGVIqHngx5gZAhzWKVJgi57inD7ZZKL72bQXbHfmZCd5q05oOOUVY6B0IA4CdPUUo4+mo3iuRyZ/9Gw/E0E2iMw/HeUP4lAIvAEAtX+je8I0i74m0FWuGhQBhDerAkS4RNeskiD9SUOFNmcpCwlIU2KW7OS/egLbQSnFmp8hg/mHikthUN+sCWRAV76aIF4LMSS1+YXygNigPyOYkP/gW/FLSdcjWEisdjloYkbcWggmJ2aoyLvfXJOmylpIr1eRKDcEmblaURiSLIoxCPkLFbMHtlAROahF9pGwCAHIilmGHciY/2X3JKY026JpDqS0a0ylR/6IX6sAlgL0wNDSUksUJoqEF/d4vtSTwBGWgrURyS9C7Rpa4SxH+JZwKZoyhuBculpQdJIGTXGOCJcpLHjnhIpS9XlVi12FfmwBnqHukU8dqgjpLhuIlvRWaVRBdkWpHaWnajOMPFx0UdKDi60JVIu/EMygQY7bBmdqMi0YaEjv7E9Ew/v1GycAME1E9CLhj/Qk/NGRr/iTQ88AyvFLFFGDRCP/XDQRlJ5BXFVFo8x+wgGviISR0EmDDESj95JSS3EUwfZ9Ws4eMnoI8zhhtlQ10WNHklv6P11mCQRqWRQw0pnNV6k9tPSscTRVsKkzBP01x8LJuQCrJSt/YoYWSgv/X0Zl6jFoPtbc0EeM1OOeRWP2pYTj5TWWkXJlYG+IGCJaPRdg/aJ0Ce9DfvS1SwkEZjsCMQ7EV/REYoTxhoBBia/+AphwwtBJNnPqTOEmaUtq0q9485wIwboNih+whyDmpBh6A6dRKS0RSVEdayMCYN6CcLkurdGoTuhIqL59whPIoGcyCyMS1E1CXi/SF8ITdOb3S3xo0dSlivoDgUPbxg9ojkgwuOpEw7JNgSIyioidYQgJPhL9gh0oTuIFFanKCk5w8KEeYvcaiqhNFUgXpe8TKSxiMdLqBaAwDmDAgzp5HGC9kUJOCJPGgXqF9nMUIVJGBQBzIxBx0hxr5HYYAEH3wpDGK2DrT3iS9VRoFsXroB3YgPRco+QGDa4xrOq4ptMzSCSnmk4YsYPWS6ShaseiUOIjAP9EF96OO2kz2itVzIXpR1bnrFAuNGmIJqUW/RShslAE/BNeSOjX/E+w45boC80IqCIRwox9zBIvIEzjY4HSiUS2ZVSyS499TQCfoU1A22SUVghcpVi/V3EFe0ULxAxUWY9ZZlaEdn629qv1pjWXK0xnXKJ7/SotZCMGR0CA0t35qz/WWY4EUgECgIEszDpjj0IkI5+LTF5vJIHxIZ3N6WOda34tpelufQecaRQCM9K0sK+nvg+uXjqCi8UAYLEbzEcCHe5qAc8xQCsdMn4SBmt7ZIrHoURRzPUxXygd+HYIYaMpB+ijCGuUAqcgG6Jl7Hb8o1rdEcC63h6FD4r+ASFDdlJGOuIJkGJnkkLmS2s6a3aPUU+kDMNYAQkAlnfqEzQLFKfkqy1zYpVPmZG/cBipc1YHQ2EJiEf9DQ4otZGRvSFYyxaybdXRcxVbnEdCglqDG5PBDYfcCQD72HGQp7QTSQMncXkWmsX432t10qjX7GrPNLQWGg/lZVbQxmGMzo2sh+G0psPEcl2iewafZjwjuKKKwuFDdKAJxkpJdc/MRvl+53hWj6tqpabEff1w75enlYrNoJHnHtEde4Tca0hDFVk6CbLU8Ndt8ohoPGoafbGJ8NKrhKgmGkbVmz8XZSnAr1H1nNlOBEYbwSS7ow3wln+lELAop+HAeFKMcMkQYYxfBCE3CcJMytvihCqfmKV1oH8ox5gWaAJwCQoY8gGNg5fyyLyZWcLYFxwy35BJNPNkJqYhw9zEvC0OOEeS0ITzMrEk2z05RPNEoQu8LNhpECVlOPTFpoR0ossp9hvu+mJlHUxfkms5UxOtA7UCbJTfmiGEshpRIE1BD9gLEBoqHzIMANplxAagcHgExQVVCwiuWlTO0lD9YVDMACJ1yndRw4IeOYeMt6K36+N3GgQNw5dUxrDRyvngBKnZqDhWwQztRNapiI4ANNTIJdZ5ZPvyFa5jQAaqgFNkexBLHSupvjW2w3P2/CJyPOfCD4pdNKT7mbctE3cNrIl+9DHG8Q3r0QgERgnBKbF4nKcSs9iE4HJiEAssokf7jWEPe1CHG7mF7dAC/AJQprwtmLGUQhjYp7+hmuzMCaBDTB8MFE5nI0vBTMWOY2mIBAeIRNYC+mLdijHhizmGGWG9cGvxJQZqAYionYEiIoCf2LKgScXZqSBmYbiQVFUBfQ0GkCtojSWJmGVakbTQTtxqwuoEl6F9/DGiAHCReiK0BRcpwyZejkJYWk9btUpGdsGaMX4gtAb8f+gG0OtkCRmJj2VvjS1BNoWMh6RE1/jePQiytSX8St8Ykpuon2j7lFTOXV82j6amN7NDrVY9W24YWPB4N04UB8GSbozO0y/7OPIEIg37MP7PIyaUFG4EAj+m8V1g6sKdQj1CXeKUjQRThvB45jTSYmctQEdqb/Zm24nuG20XxxKkDwQ2VOD4SF2YejRktK2AH+C21ZHaYKrzuomEoGYXTnc44p50p1xhTcLTwT6iUBf3omzRGz3EwVnnPTbvMLdlVsPjTLFGDVYXZMErr5X1180srQpgEBf/rSnAA7j2oWBpTtPKK7Htf9ZeCIw6RCYAnwF5nUOMdIejTT9pBvibHAikAjMPggk3Zl9xjp7OjIE6kRhZDmHU+MKYyxhFJV2zzKi9jS1fwKoT/cqRtT47jjk00QgEZgNEUi6MxsOenZ5dkGAV7LjavgshzvwGLu9zRXb8D10pBs/6FEXZcuVQ2V47ZSPMfVSVHcm1EsJmSYRSARmcwSS7szmEyC73xGBUYjYQdNAOKOPe7Ut5fFho45d7e2BTfU+LVk+s9Vbpiel4vRt+73DbPh9P+lB3iQCiUAiMM4IJN0ZZ4Cz+EmLwEi5yyjoUR+xcSCQ03rio5KlWFvNff+8fKGzxLcN2IjuTD/H2Dgeum0CKhkn3Dj435mBtqpJ6aygSGkXvaMXOSCLjOPs+CPTA/lUlhOQ7ZB3YKCUDon2OSqb5x30V6/CYX1OlLbdXTIfi6g/ynAikAgkAn1BIOlOX2DMQqYsAsS2g20cslcOomUhItedDqzP9hbVtxe1oiCv7UgOq5Xd2bvCNBxunebnkcLFK1ykW+fcKM0Jtp7GsX60KR/84AedTOicHjHSMCf5uIE0tCzOEY7zLZwCbGu3D2Y54F9eHzHYYYcdnD3oYxd+HeUX+71Vp9m+OOGcQAf5OLzHGYO+PGVTvbP77KdwCg524qsXcdRya3fExKG9Ajbh+3SDVoV9So0++OUkoe9+97ueOnlZSo13IrM2OL9HpEodlmi7PlpWjkV2FpFyHNiod3b4S5ZXIpAIJAJ9R2B630vMAhOBKYNAfNqQusJRe3F0L2LBD+YDH/iAw4JxDgoP5/V16q+jjX3S3GcNOLv4EKNkmIrvWlPDCDtzzxGC8UUIFMEXFRwq6HMTyvddAgl8DBLRwVHwGJFoFg5BC0JBwhgkpa9j4ihSYi0ULSiRc4d9Zty5xiJ9qCGUKJFGjG8vSObD4D6tgJfwoaGVcUI0cqNfvtauCpobpxhL3On61a9+Fd9UAkh80lwuRy07VdkBjPGNUnml8a1yn4Pw3Qn1RmnORXQaNYaH3pXyZafXoVLyZQacqcRnIBFIBBKBPiKQdKePYGZRUw0BKhO6EAoV34dyxrHu0b4Q5L6BQKXB7IKXtH7BoKDAaQYvYanxASPaC24rFB4+GOksY7oNmh5ffHTmnvTOF0ZWfFfBIc4luwQUMMgN/oF4sUm59XEJ317wSSkl+0IT1Yj0dDOUOpRGSANqhTdEZHx7oRSImTk9Gf1CenyPwlcg1CgvPic7j+ZQQdHBlCytAXmlRPVwFOooCeiZ/vjHPzpcUdeUE1l8nkKvfb4Kr8KoIqVHqB6eR5FTSkYEQeQAa1+Jx5/0ujzKQCKQCCQC/UIg6U6/kMxypiACPkrlWw1sPfQTYV0irfEDtABdoKfBLZiKOvXcF6NwFB/NpsygEOKzIqVPhLLdYAB4AzEvhgWKXic+RUlP4zY+nEnpguVQnHCXoRTBcjpVNKJ45Ud6rAXzGFFezCb6CxB7vvSIx4+2+SKET1w5NNmnwXBEZfr4uW9uIFgYDDWVj2lERdyDfMKiWAB9XoM9zmcxaKS4MEvjc2CR0pcxDjzwwKKaisj8TQQSgURgdAik787ocMtcUx8BGgjqGfobHjDkui+D6jPtBYpDSEf/ucIcd9xx733ve9vCoQRf8PaBTMyG0QoV8E0ruhMfz6Ji4emCS/mSpTKpYdACbi64lO+KS7/CCivgClgFTxeFqx0nEMC6lMDJRi5tKx/LxI18LYsvMEWRb4bT+lCTKEoWyWhfUCifI6U98gi1QiMwj/jYO1IlsY9g8EnyKW+966SyUgsKcuSRR0rD+kYxg735wpfPpLPHhYmKBsvHTdm8fA6dYkwtfIniA914nmTIon6xW8kIYd8qh4NIcFF6IZEBJiIVJAlfjJj8TQQSgURg1Agk3Rk1dJlxiiPAaebCCy9ESnCUs88+mwELJ2Cj4fbLwMSpllqC3oUTLsWGL0C1wsGO44vlKBFZbis4Rx8+QKxRFCTsU0gJukB1xJ+X6wwKQmNkExMmQV+C7tj4ja/YcsUBiFol3I2ZkOyKUhRyg0j59HfUi0IhOieddJJbzIYKR8N8j5N6SUd8u5QCBlHjI+yrVT/4wQ8UyB5Hy4KH2cCFCUmMbNHQqIJuprU7YjbffHP2KS3HujgG4ToiBZRMV4SxKVMkdujD41RWqpbSFaUxV7ncii+Pgs+1VgeN7ma11iwZkwgkAolAJwTyE6GdkMn42ReB2FL+4N4P4iskN19aTscoC3MS+kItYWcTsY36UHXwPsYh2GLkqu9dd3vfh++zGZvd6qCDDkJ0cAIynuIEn+Aug3AomU4luALdDzUMBYnb8qFyVIlFDAvBUWI81EWVoljcq8k1p78D1tqd/pY/0tLq2I40b6ZPBAKB+NPOuTSu84HmOHaMUu7mF9HHFeosPBEYKwLxThxrKZk/EUgEBhKBpDvjOiwDS3fSVXlcxz0LTwQSgUQgEUgEEoFZj0D67sz6McgWDBoCufgbtBHJ9iQCiUAiMEYEUrszRgAzeyKQCCQCiUAikAgMOgJJdwZ9hLJ9iUAikAgkAolAIjBGBJLujBHAzJ4IJAKJQCKQCCQCg45A0p1BH6FsXyKQCCQCiUAikAiMEYGkO2MEMLMnAolAIpAIJAKJwKAjkHRn0Eco25cIJAKJQCKQCCQCY0Qg6c4YAczsiUAikAgkAolAIjDoCCTdGfQRyvYlAolAIpAIJAKJwBgRSLozRgAzeyKQCCQCiUAikAgMOgJJdwZ9hLJ9iUAikAgkAolAIjBGBJLujBHAzJ4IJAKJQCKQCCQCg45A0p1BH6FsXyKQCCQCiUAikAiMEYGkO2MEMLMnAolAIpAIJAKJwKAjkHRn0Eco25cIJAKJQCKQCCQCY0Qg6c4YAczsiUAikAgkAolAIjDoCCTdGfQRyvYlAolAIpAIJAKJwBgRSLozRgAzeyKQCCQCiUAikAgMOgJJdwZ9hLJ9iUAikAgkAolAIjBGBJLujBHAzJ4IJAKJQCKQCCQCg45A0p1BH6FsXyKQCCQCiUAikAiMEYGkO2MEMLMnAolAIpAIJAKJwKAjkHRn0Eco25cIJAKJQCKQCCQCY0Qg6c4YAczsiUAikAgkAolAIjDoCCTdGfQRyvYlAolAIpAIJAKJwBgRSLozRgAzeyKQCCQCiUAikAgMOgJJdwZ9hLJ9iUAikAj0C4HPf/7z3/3ud/tVWpaTCEwiBOacRG3NpiYCiUAikAiMBYF3vetd06fnKncsEGbeyYpA0p3JOnLZ7kQgEUgERorAggsuONIsmT4RmBoIJM2fGuOYvUgEEoFEIBFIBBKBjggk3ekITT5IBBKBRCARSAQSgamBQNKdqTGO2YtEIBFIBBKBRCAR6IhA0p2O0OSDRCARSAQSgUQgEZgaCCTdmRrjmL1IBBKBRCARSAQSgY4IJN3pCE0+SAQSgUQgEUgEEoGpgUDSnakxjtmLRCARSAQSgUQgEeiIQNKdjtDkg0QgEUgEEoFEIBGYGggk3Zka45i9SAQSgUQgEUgEEoGOCCTd6QhNPkgEEoFEIBFIBBKBqYFA0p2pMY7Zi0QgEUgEEoFEIBHoiEDSnY7Q5INEIBFIBBKBRCARmBoIJN2ZGuOYvUgEEoFEYPZF4DOfafT98surr31t9gUhe94dgaQ73fHJp4lAIpAIJAKDjkDQnZVXrt797kFvarZvViGQdGdWIZ/1JgKJQCLQTwQmo4bjlluqzTev1l232mmnatFFZ6BRAu4jfPvt1Q47VBttVK23XnXJJY1kX/5yteqq1WqrVWeeWX3849U991SvfnUjPtLffHO12WaNxH6FI36ffar1169WWaU6+eRGTF6zGwJJd2a3Ec/+JgKJwNREYDJqOD74wWqbbaoLLqi22KJ64IGO4/KhD1W7716ddVZ17LHVbrs1kh14YHX++dXxxzdiDjigWnDBBu8p1157Vdtt10jgVxWuhx6qnva06rzzGlxnjz1KwgzMRggk3ZmNBju7mggkAgOIwOys4Tj33OrNb26MyeteV80xR5vBeeyxRuTPf1595CPVBhtUb31rde+91aOPNtQ2wtdfXx19dJtcit1660a833POaQSUs/POjcDyy1d33tkI5DW7IZB0Z8wj/sNFx1TEGLOPqe7MnAgkArMegdlZw0HpEhc6MjT0RDhCd9zR0Mq4HnmkOuOMCok5++zqyCMbxOioo6o992w4JgeJmZHz8f+Uoh6PqOae+wlj2bRpJToDsxECSXdmo8HOriYCicAAIjA7azjWXrs65ZTGmLAxFY6yyCKNPVau446rgpqss84Mh5vTT68OOqihnuGFs9Za1THHVKed1kiJLYUeqHFTVRtuWP3oR42A3w02aASmp6xrwDBbX3PO1r3vV+cv3ae69cLqoduqF32iWvaN1UO3V7/bvXrg5uqxh6pVP18t9rLqzsurS95ZPXRH9ZxdqpX2rB64pbp410ayhZ4zowmtWTyg+FHaU1atnve+frU0y0kEEoFBQ2BEGo55523I9QsvnKHh4J7yxS82XFi+853mbhX2UB4MoIbjkEOqt72tOvzwCu+ZZ54ZLT3ssIYRaoklqpe9bEbkoYc2XHa+/vVqzjmrb32rwocYv9ZcswHFvvs2cnF25vJ86qkzSvjc56pddqm+8Y1qgQWqb397RmT+Z3ZHYCivMSJwwrxDVxzSKOOuvw+dvGwj8Jtdhv77m0bgnmuHTlulEbjkXUO3nD/04P+GTlqqcfurHYb+dWwjcP3JQ9+bpxFozSJSyTed0XiaVyKQCExdBLbYYuj7329074QThuadd0Y/l1lm6C9/aYQPP3xG5JZbDh1/fCPm1FOHNt106I47htZbb+ihh4buuWdoiSUa8QstNPToo43AIos0ft/ylqFjh18zfoVdEd8IPTkcMeP0W1VsVKP5N07tyWLHG4FzwluqYn8cLPmV2p0x811rqOV3bpSy0IrVw3c2Av/+eXX3VY2A65F7q6FHq5ccXF17QnXTqdXDdzUi/3NuteYRjcDSr6umz9EItGaZNkfl35IbN57mlQgkAlMXgdRwTN2xzZ4NEAJJd8Y8GHPMXc296OOlTGsEHnuk2vCMao55q6HHGkYurOXCraplt6xW3L36x/CRn4xccUkQGufWLBJMm7OalgbnGVDlfxKByYtAj76x9mO76on/+teGf25EelXwXKlftmf7V66f/WxGkIev6xnPaE4f8ZGoHo6Ycf1ttax1qa6OQJdk+SgRGBECKU1HBFfbxC0YLr5OdcPJjaT/Pr26/KBG4LbfVc/aunr0gerRBxu3T1u7uuGURuB6yah5q6o1SyM2r0QgEUgEpgICr371q7/O9Wb4euc73/n617/+c/xr8koEJhCB1O6MA9irH1pdvFv1j6831DMv/1ajghXeU525drXoKg090GMPVqsdUv3mbdWVhzd4z/Rh97zWLOPQriwyEUgEZiECI9Jw1Ns5BbQdv/vd737xi1+89KUvXX311W+//fZTTz11PWce55UITCAC03gtTWB1k7Cq44ftU5Ow4dnkRGCqIfCWyfqyCr6y0UYbP/DAA1/4whcWWGCB3XfffZ555qHweNaznjXTYYrsk/RVHY3fbLPXnnbaadtvv/2xxx579tlnb7TRRrfddtuiw198uP766xGg+eeff8kll1zQ6ciPm/MmaX9nOppTPsG55567oZMAhl2VN9lkk8Hpb4shZnCali1JBBKBRGAKIfCud71rvvnme9nLXrbyyis/9thjT3/60wvXic0yTX0VKdnUWJHed999bFj333//b3/727ltiG8chDNd5Gc/+9nNN9/8+OOPf+ELXyhBEwJ5mwj0EYE0ZvUG5qRdVvbWvcmTaryVbWWgVVTCgwNPu1a95jWvOX3HM7Tx2nWu4RIh8NrXvvZ1r3vdOo5mm8DrjjvuWGKJJdZYY42LLrqoL9Wecsopu+666/nnn3/55Zdv+eCb+1LmrC1kyy23pM455JBDnv/85999992f/vSnoz0UHt/97neJ/2222ebtb397RIo5+uijn/3sZ9/iGxPVqbO25X2pXQf33HNP5Obzn//8nMPXpZde+tGPfvQnP/mJebvSSisZbvgstNBCfakuC0kEmhBIutMESN4OBAIWtS7vR1dzg8aPhbRwqT/+8Y/WncTSXHPNZZH98Y9//N577/3kJz9pjd7cqll0f/HFFzMKROVkBpazzDLLOO4ilMn1RsFz2vAVigTBRx99lNApaYYhf8xtiXzkkUdOPPHETZ3xMjT0sY997IMf/CBzAyjklQYUEZDFev3II498+OGHP/WpT5UCBe66664Pf/jD4uedd9799tuPPkMky8VHPvIRC/3ttttus802U4vCb731VoLwH//4B8xXXXVVuVZcccVPfOITpOBDjuH7S73USRw2nZDRVVZZ5aSTTnqGrVON04RPPuCAA372s58Blj8vYN/61reCHZJ4gO47xaRsuZrEPW98COKRV7ziFS9+8Yu/+MUv6qb++lPSo6WXXtovq8eaa67ZGOu8EoHxQeCJl934lD9VSm0RhH3r2PgJ79LE8Wt8qaLfARznSTRnAlBq1wWv5ne/+91ksxX5Zz7zmQMPPPDggw8eV67zy1/+kobfqz8U/nQbeMAzn/lMfh6owJY28g0NIRnRWIQDF/nmN79ZPby1mMsuu+z0008nPJZbbrnFF1/86quv/tOf/sQlghC1jEZHXvSiF0n/7W9/mwcJ/vGVr3xF3le96lXhQrHXXnuRQ2SwQnRcgYwLEr/pTW/CqNjjqVuIajKY68nf/vY3j77//e//61//OuGEE1RKYMtS2iaM1uywww7UGHgVlQ9vFXQHFdt2220RGo1/85vf/Ne//pUCY6211pLyuOOO48c6xxxzIFWyU4G4rrvuOo/+/FERU+EyLm94wxt+//vfFzPWJZdcctVVV0EASigguPTToDB4GQX84CAfTZgSlw7qx49//GO8HPVBr3WQQ49Zutpqq5muf/nLX9CgKdHX7MRAIhBLvfztiMBx1dBxldc9qfPf//7XO9of7f/+9z9hMqNjrh4fKLxcwxWpqz//SrEC9Vrq8SMJW6DrtTfUSDI9kdb7feutt+4dMQJgqaWW+r//+79GEfX2D4ctAeHv0ir6A9p+bTMu0j744IP/+c9/brrpJu9Tt1IauHucOzs0dOedd0oZbRBmKfjDH/5AJJO+Rx11lAStFYnDD0hfm0qIXn/B3/nOd0SqSwl77LEHbQptvBjel2uvvTZKgTQQz3vvvbfIuESK2WmnnSziH48bYqoQSXtPwyFLtFbh2Al5j1RFyjBIMRIt7zvOuM5xvgU9fG7u8GNOr7RfiEij5cc1VCwoBaOStnmOSYT+ADg/90Xpqnre857397//XYOFWQ00DDt5y/CBu+gLlQP6gtiRxJiTEpQTDTAQpJRCRKJ9CN+///1v4X333VcuARckySr2mrj1+9Of/hSpgr8xAvIVV1whkiBXvv4aO2KPO0ukR6S0yoiU7ALKfM5znvPlL385Olh/NLnCcaxwtNm83W233Ur7Q2dG2WOz0g9/+ENwmcPm7Q033IBfYgNIaj17yThZAtF4f0dY9Xve8x7NRuIXW2wxs0IYpRb+f//v/6H4oIhOTer+TpZxGb92DuypyjVxO369n9QlDwsS606qV6/j973vffYRCLi+9a1vjbVnLYJ8rAVG/nqxYppuR1UHxQYEGN3JngsuuKCUQRtB6FqCl5gbb7xRGpdARFq/er+T4rJ/6Utf+s1vfiMeczrmmGPcuqgHIiVZzo+BzcjLcdlllyVNG/H19g+Hy5/Teeedp/CnPe1pxPa1114rrbcnxsAb9EMf+pCYs846y0hhFR6hLAjB4c7kH2qwDetpDMzv2972NrkalKilIinRkVB12EMbJhuRRJFi0R0tF/jRj35khUqJIkx+K4qNhlpISot1jaHbQLMWXnhh8kwkPY2UKODNN9+844474tAiTSeRwQlwkR/84AciST5PUYozzzyzwTVrLcTqNthgA7NRskb8cRXdAIGBHygHMqIv9Gklxz8NUxM4420if/WrX4mUXdjYMX4J4Geo2/e+9z3ON54SsSJdW221Fd+gCJdf7qW77LKLxkOmDD1qAh9UpiQTQOCCMG2xxRa0VigOzwyyLdIYo5e85CUR1hduK/W8wiSivjcmzHAHm55Ootsiv40FbQ1m7JUSzBXRwVnNQAYssDPhmT8YMJWePxAXH96SfRJ1uTQ1Gn/YYYeZS0FodNxcjQSIrxmO5Jk/hcpP6v6Wjs+2gfJ+HrSPSCTdmdmcfPw9a1Fr8RrSiEeh1TaVz8wyNz+X5Zprrnkitia9QpKRBxwzr7zySim9BYTV+Oc//1kWCz7KXlYJWl/vhbgNGU8qWI4TPzNKrhcraviWeOMh8YIXvGDjjTcuIgpZEcM/gKpDdWQnHQap46308pe/3OuJXFeAlT0lPClIzUBmKycqIiCREoszniJeWCIpEqjfGTtcr3zlKyMZ+oLrsFlQD5D9+++/v3hkSGnsKYD1Zg8wNeApT3kKrwUuKcRwJ+0OrYNVL4rjV1HaH5KS3mL99deHEqGCA2FXnpLfxitaQhgT8BH+2te+ZtdrgaIRWcft8TB9iUbqOw8eRiLWHwm9o628iWFKEYCEcshYSIb3SBCuGCAVxjywq+BMQXekVLXGYx4777yzNC6OC7Kz76CG2J5XxnD0EJ5U0tRbaMgowKKKRvxxDeORLHxf2IzwPGEwKjPozle/+tVWuoMDsUNJCRbsza4Z9FEJ5T1lDhhlCeqXip773OeaOfhKiW+lO7ggIojlEOSaASuJDZa+U7/RQuFMeholIFXmjKmOIJYyBUw2DDg6WI+fXOEivw2uvxcT3hgZwegFTuPvi/Lj0EMPDf76z3/+098mAGnF0OKSfVb12jSjF0TTu19eXEa2qZGjaPwosjRVmrezEIGBpTtpKPUe7unyfrd4DZuCt5U/foJZTq8kVIPoJdE5eVAhWMojRpT2Vq6cIVATMkOYpYBqgYmBBLWGY0RoW7H3O1HKSdMuBqYByyAB5IZ4RnQ0gM+E9yNTCFUTae0FRPyzBZDrIVdaiyXDtAfV0AzOkpxGLbst/a2z+YdqrcU9mwiJSOroAkXFBz7wAWJGLroc3gZEEfZA3y5xKd/CXVHUHuuuuy5O42UtPR5D5CMEKAj2RieE31i2aqRiXZFdByEm0p8lCeeIVXxin3324b0BAWnAS59R6qoHMAzt5FNiZSzAZMO7UwICVS5OD8LoDmOKVbKnbctRL7mLrtVLbg2T1uxQSrDIDt4jDdUL2mrcxZMERr81oxgON2iE0cQYGG6Ctoo3f8DrDBIjSw9UzwuEFVZYQck8WJ3D1sZTezg1OkLfRuVDlVWyo0oolCFGVeEvPhpm1DBLzAMZNTm1yiMVwcqgm5xu5UJGiVgzzS0exriA7LIuKcS4GOvS1EUWWYTzjcnG8iWxy8w0t011JEZitJJcx5+wWKMJImkA7hd1Nk80FeeTTEdEmsP+LiTjoawB4R4k3lzSzsZ8aAzpVLhMoW/4TvcwGmVa+lt21buHWLvEYOr1+FkV9hJATHup3bvCELem7PAn0powYxKB8ULgCdE1XjVMlXK99L2IiQdqDDKMESR6ZomGN3iLkawWNxgDIfHe976XmKTesEqjtSa3WCWkZKSwqmPmwH/b0h1kgkGBIPfqJ4zVgi4QG7gOTwschejFukga70cUh4pYMyhCSDjEqBPYGIy1I7FH1CEuVvlSitQphglhRAGL0mxdo0vAbETSDWAM3GgsPYlP1dW5DmUSrsAexHpC9hO0Ok5o0e6ghrIT2CW9+CZigeuQvvgKZJA/i35ZRnQBiqaKhgPClDpNeZVPN2YUFE5mGzu4YQ9ca5tSzvRW3yEjmUBkN44wAR2VBqKmd57GL7jYX4TV5UIydBx1QOmIeSt1IwUWPBg5Fm+gf/3rXxto5j8SBUfEDhFZBAWVxAPwDGmMHQvIjxseyQ3eQGRqwLCZoxETF7KCQHhKIYRNisREEVkzR9i4wArliqmLKsWYGnFP6efQsvDmwSCPOOIIkdRC6BT/G0zd/Cl0x7RhekNEYqCl1FrmKifnYkICpq5Ifxf4rsbDgSInlgr8h/yxhJYUE41dxxQeZprJGXO4TBt/LFLSC1YnfVqBs/aiaKEzg0b3ZugywhpmxNaUpWswNEVbEwxmjMnjr8k4dm8eAmcp0j1NPk0EZhUCSXd6Rd7riXhgS/Iqp8wgRyMneW+d6kXvlR22GCoTy1NLHCLHC93LnVTDdSxk6f/RF5oh8Z0q5gdKLlJXsCyQ02iElN6hjA64jrDdm6H/6FRCazwRqFiXR8wxsazUo5IywiRTiRFgG7J8lzcidV/Ar+yoAzHJRiOBhb7FOnGFwGFyTDyRXpnveMc7tJaUZUqzQKTP4KfJUoYUKoF4w7EofgAVAhKHU4IEpC+FATKEme2+WJTX/AtJUMOfJI5niJo2h1bJqxmnJK3REbhhEvRGRo0SgsEOV8CW0AI8Bl2jZWkufRhzzsUUY4isXlBZwYfjBf6EgOoy0omYqo4CX/b4lYBOTljvjBpVBwLEkVkCiCkBA0YOcA5tYOfSQiOiGcqxJYoXJ0qkzcEtTCpjDSuwD+tdTlEOY5PZZUY1tVnXDI1KjQjKFU+RkqZkFDxiEHcNKI8MFsOWq8QIYEvoUT2mhNEaV7nFWjBOQ1xiBAoZqkcKE/NNRO2pw1dTMrfIwSh4cGs5fYmhaKEfLXylU5mGQG/aPq39wbV9PriR1kjeXaNr3+Pvj9HlzlyJQP8QIMzy6obAsFeEBJbpJBNVhHBxsaTpYaTAZsKLxRooirIkNUSEKIYRzjoUM6QyqY8SEflWsY2UjzuINIeHhiz9lUBCx64iS39vHDxJSktMtEAAw6DxJk1J8TBUMSW0FqUW0pH4ty2CSoajCUlMc2M1T/B7RHPAs4T8lpfji16I9NaO7TwUSOIJZiWw3HmqYbRBlBACBL/Fd8gAXJA5AyCENKIjsuww8oh1CUEhCTbYYAMEkeDXC4Kf5AMgfNRCVONMdDZIDEjFE+1dUMIP6E7q7lBaroVEb/jQKNOlWMQFerpvc5ZRcLEDCiNVxaW6qSIIKNlTBAXVoMih7VCCvB75lR3ypkSMpr6LCSckkZEsGtD0a7CK1wtzHkHyhHdOU9Km2+EJY9cuVvekJ4/P0idFdrgJuoPKaGGHJIMXPZIODl7rLRj68G8A+5VNSgRaERhY352GYjyvbgg8/p7FEnCXcN3lYUBEyUXJj4XEkp3ChvcMcUgWusL8YZ8OKSileGKeWsjanSGDwwS1QZN8rTeDtEZKsJyIVC9Ggv3QZ8Q+nYhXJrn1xje+kQ5ZS6hPGvHDQjESlFsMQAK/CAfFQHgWM0lYauMxesT+IjHlBJqCmRHkmAe9AuEqnhRnM1ILZQNKQUhjPCggHQn3W3YrYYRASiIfK+IhRC/ltlyUVRIjKCVGgD4A8arHtAnXu1MPD7v3Ur20yTK6qHrh9fDoSuucCz6UFtyY6Jx4OzHZmBWdk9eeDLfKZjHg12KHR7znBrMh0ksZoCe5aT+puMG70bueOzh4rc8WJQKzEQIDS3emGQRr9Lw6IjB8Rt9Db36QfwyKIBn1PrUKIwVTDvrCowKVodhnwrBu5vlL7YEYYTwSsEkVCz0egFVQ+zNMUN7wV53j+3M+8aUCFdUO07NfSTlxmku0TS46A2oGNIieqUSyyKgrXAo8xWmmfW96vahquGQaDsn8yk7LEtmNvhhhFAfpEUDOXAJhQJGFmaOkV35JGSVMxG8dmeEw8odgcXnRHmQrLHF9aElLRX0os0MR7HTBlW1Do+Iqk6RD8sejh1toJhiFx6OG/yt+drhqfyCzQ3ezj4nAZESAoZw3gpbz36ChH5wuPPmlOTjtGrCWkPe2Fgdj4OrhpBYOpBbo1uWYLKMAtYe9LSwjceqJ5mMPLBT1fkiMANVjuoSZe2y/wqVKGhLOhc2UGAEx4fUSkThK/Wk9HJQF16lHIgpNWcjdInoVXk8s3JS46emE3VJQ8bPG1frJdVpbP54c4k1V9aY3DFd5zndaa+4Wc/y05lGJ1FObCoznWHRDO58lAonAVEEgtTszG8l8z84MoXyeCEwQAlOb0k0QiFlNIjC+CAysdqdhv8grEUgEEoFEIBFIBBKBKYxAe734FO7wiLuWC8oRQ5YZEoFEIBFIBBKBwUIgtTuDNR7ZmkQgEUgEEoFEIBHoOwJJd/oOaRaYCCQCiUAikAgkAoOFQNKdwRqPbE0ikAgkAolAIpAI9B2BpDt9hzQLTAQSgUQgEUgEEoHBQiDpzmCNR7YmEUgEEoFEIBFIBPqOQNKdvkOaBSYCiUAikAgkAonAYCGQdGewxiNbkwgkAolAIpAIJAJ9RyDpTt8hzQITgUQgEUgEEoFEYLAQSLozWOORrUkEEoFEIBFIBBKBviOQdKfvkGaBiUAikAgkAolAIjBYCCTdGazxyNYkAolAIpAIJAKJQN8RSLrTd0izwEQgEUgEEoFEIBEYLASS7gzWeGRr+oLA5bde/opvv+KFX33hob85NApc9DOL7nP2Pusftf4qX1/l5L+dLPLLl3x51W+suto3Vjvz6jOfd/jzrr3zWpGbHLvJHmfsIXDuNedud+J2tz9w+w4n7bDR0Rut9531LrnxklLUzqfsfNjFh8Vt/iYCiUAikAgMPgL5RfTBH6Ns4YgROPySww/a6KCVF18Z49lzzT3lf+jRh542/9PO2+m8f97+zw2O2uCNK73xwPMOvHqPq2+868ZPX/DpTZ+76fnXnr/9i7Z/bOixP938J+ndvua5r/nQmR/a/eW7v3zpl19353Wbf2/zP72r8ejBRx/c9oXbbvKcTYTzSgQSgUQgEZgUCCTdmRTDlI0cGQIHb3zwCX854dQrT73rwbsiJx6z80t2Fl7+Kcvf+eCdAputsNlbT37re176nqPfePTpV51+0hUnrfL0VVZdctVLb7n07ofuRnfeucY7KYSuuu2qKOHeh+99dOjROabN4d/Gy28ckfmbCCQCiUAiMCkQSLozKYYpGzkyBLb6wVZbvmDL3V+2+9d++7XIOfcccy8676IRnlZNEzhqi6Nwmi/+5ovHX3b8V1/71b3P2vui6y96xTNfMd9c87FkUeE8fYGnP/LYI2fscMa8c86LLV143YWIjoxzTp9z+rS0AgeW+ZsIJAKJwORAIN/ak2OcspUjQuB3N/1u65W3fuCRB7CWyNhEUCh4+PGstexax7zpmNP+cdp8c8635IJLUvCs88x1MJ5Dfn3I+s9aX8Z1ll0nHH2ofw668KARtSETJwKJQCKQCAwOAkl3Bmcsqs98ptGYyy+vvjZDJTFAbZtcTWGiWvvItfc7Z7+5H1sU4wHpQw89qQeLzLPI61Z83ZpHrMmjed/19vWM+86Nd9+42HyLrbnMmhdce4FbkYdueujRlx6NGCFAX9nsK08qIm8SgUQgEUgEJg8C04aGhiZPa6d4SxddtLrjjinex351b9oBDYNUXolAIjBZEBj6eMqayTJWY2rnueeeu+GGGyrijDPO2GSTAdrSkdqdMY1rZL7llmrzzat116122qlCWeIqAbcRvv32aocdqo02qtZbr7pkeFPzl79crbpqtdpq1ZlnVh//eHXPPdWrX93IHelvvrnabLNGYr/CEb/PPtX661errFKdfHIjZqpeM4V0qnY8+5UIJAKJQCIwLgjQ7uQ1RgR22GHo2GMbZZx88tA888wobJFFZgT8J8K77DL0m980Iq+9dmiVVRqBxRcfuuuuoSuuGNpxx8ZtyRKBt7xl6OijG/F+t9++EZhvvqFDDmkErr56aNllG4Gpes0U0mr/yr+EdKpOgOzXqBHwd1HPe9ddd91///31mIkM/+c//7ntttvir3Ui6826ZiEC55xzTpAV2p1Z2IzWqtOY1QcSueyy1VVXVfPMUz3ySLXIItW99zbKpKEplqmFF67uuquS7DnPmVHdjTdWf/sbaV3deWf1nvdUGw/vay5ZIrD00tU//9ko9sEHq+WXr2SZd96Gmid0PyqSd6peM4U0jFnLHDGUkE7VOTA79KsvNtkmI5EyI+aBBx744Q9/+NGPfvTFL37xG97whvXXX//5z3/+BKP6zne+85vf/GaD7lRVUzsnuCVZ3YQhMLDGrNyI3oc5UNxgH3vMumpGgcJxIT2RABk644wGZfHowgurOeaojjqqOv/86otfrI4/vvrOd5pbUooqD+aeewbXETNtSvuuzBTSwOSGd0y7oaBji/gnq2q5xv2PL6oq/1x7VtMOqAV2q+Yd9gdvRO02/Gjv6ilfGk7g5wOPJ348oi//nRRv+b7I3b7A1VRIK3oD29Smlne6bepR022nXE3xm2+++U9/+tO//OUvL/zRC5seldsrrrgC3fn+979/7733UvAssMAC5dE4BW699dZHH310ySWXLOV/9atfveqqq86uzi4xGUgEZhUCSXf6gPzaa1ennFJtvXXDn6ZwFNoXG4JWXrk67rgZ1GSddRoJttuuOv306vDDG/43PH7OOqtaffWG8saFBvk3ffqMJnH2+tGPqu23b/xusEEjsjyakWLq/memkEbXt7xsaMstG5D+7GcNSE84YQak2BJIOQDRq6GbcAuFGTA5Qvk1KKed1vgtGjUF1sP9graTbO4U3696Z1pOq5RtjZlpIeOdoBNKs7apv/zlL1ddddWnPvWpo+h+px6NtKgvfvGL6E73XB/60IeWXnrpV7ziFU3JHhteik1//G3y5z//+Xvf+x6X0he96EUHH3zwyiuvvOOOO37+85+fe+6599hjj5tvvvkrX/nKtGnTtt566xe+sEGtzj//fFW/+c1vfvnLX45FHXrooffcc89rX/vaK6+8UvblllvuNH9aVfXd73736quvXnDBBW/xd5hXIjAICLTatzJmpAj8859D667b+PeRjzzhf3PSSUMveMHQBhsMffjDMyKvu25o002H1ltv6JWvbDjfuA4+eGi11YZe8pKhL3+5cbvZZkOvfW0jEL47N97YSK9Yvzfd9ER8I/R4mghPvd+ZQtpQj+9fDT6kGtl2dNrGf+ELX3j605++/PLLv//972+bq1+RrbW3xoy0rkceeeSSSy658847R5qxpP/2t7998cUXl1uBtq1qG1nPNbrw9ddff+GFF9JP1LNfd911vx6+SO6IP/nkk+eZZ57Xv/71F110EcHPMSXir7nmml/84hfaj0xEzAYbbLDSSiv961//Er/MMsscO+zf19T4uL377rvPO++85z3veaussoraZD/ooIPQqc985jPsUKbEBz7wAVoT8ejF9ttvv+2222IbxAftTlOB0oh5+OGH99xzTxmf85znvOMd73jrW9+Kc3gk/TbbbPOWt7xF+z/ibTU0ZNS22247zAYvQVnMPelln3POORmh9O6OO+543/vep66zzz77D3/4w+qrr/7qV7/aRNVUw62ESy+9FFWS/nWve91ll10GMZHHHXfcM5/5zD/+8Y8CDTG3f+Of+LxmBwQG1ncnp2BP04/dOf9NAAJtB6N4cNef1l+gBIwXNJfMhx56qJ5mEMKd3vJt48mP3XbbjXTYcsstx7XxrbW3xsy0AWAPGRwp//3vf2u5df+DDz5IRvqNeMmI8/vuu69eYKSpR5Ksa6211k477USiyx5D2bZVIn/2s5+R+m9/+9vJ5t///vdK/vSnP33iiScKMNyQ9BHpVsoddtjhXe96l8SkdbRBSj4lpDi09957b5H//e9/X/KSl2g/jhK8RCQ3W2xDpEt1kRcRcYvHfOITn3jpS19K+SGejCf+sZM111zziCOOiJQk/XrrradT8847r1zInPimHsUtJqFMahIlCFC3aP/OO+9MASNmv/32E4k6yE7FQvUigEWJ7ER3JHDhH29729uGg40fwLJn/b//9/+EjQhXnssvvzye0sRo5+233x63/pTmmGOOX/3qV2jNBRdcYCygF4+Mr1HTX0RqM+uz4UszbDym44lbv/qr2XGLTulmU8dLygxMPQQGlu6kMctLI6/JioD38sILL8xHYd111/XCpb2nYJ+snakq4tP1v//9j0Sp94Iw5v3HTGBtXY8nv2kdSOjFF1884kloUorpASyvfOUrI9LKXnY6CdK3iwkGLznrrLOoZ6z1n/KUp0gsO0Lz85//XKTlO58MOBN4VALzzTcf44ViP/zhD5PxUnIT8ctXIyQiaR0NoJmQUqeorKglokycQOOJcNnpG0TSJYRigwFF99/97nevzaLZ4eJ++4xnPAPHRRRe85rXaPD++++v/De96U20L3gD4b3aaqvRuNCCICLXXnstWY4bKU9j9tlnnx/96Ef4ykknnfTjH/9YJFaEJ5Hi3Ht33313eo5FF13UI8zjb3/72yKLLKLYaMt73/teKH3uc59jz9JUOKvlVa96lerWWWed+eef//jjj0dKFlpoIUqUM8880wDRGOEZBiVK6PRLswJnT/VLaZyLX/CCF3zwgx8Uo1X4GdWRsWBaEkNGdiqnxGsGFVS5FTBwdDMCdDmqwPYotNzqrD8cv8IuUwVoiM4//vEP5I95KyZYGLZOOeUUE1K/gpxJ/7vf/c4cKL5BWguuXWzEyCsRGCgEph61HI8ehWKjqWTvx/rqtunpLLkdfg02atY2b1uvNi9NL8oJbszXv/71G264oUulRVFU0rRFuDxtDcR6kYj1aNddd/U3RaSVZOQlmVFuvX+tUK1uCR6/Jd7b34u7yf7iViTx7NciOBITlqSa7IoSI8BX1OqZ1PzNb35DuPJaKMXWA20XtcARv8UWWxD/zAqYQWmtR6wACq8XQm7pIAGvp0iJR9pjwc0zQ3xRBema0ojVueaai0aByJHSTNh4442ZMxAUxCKKbW2VmC87BqqqVEHaWbvDUOLPfvazGJiiqDeU/JOf/ISwD37zsY99TPdXWGEF8k9KTZKAX0tUEb9UPioFGpRwiIjESzAPYWISHSkp1d6jMWuppZb65z//afjYiW5k9B0aWmONNRQrAEmy/IQTThAmrZXJSqW6jTbaKCpSaWh09KhAR7UTJWAAgIoNtEcddZSiZIQ/HhljRO+izPr0plgSg3LBnFJEN8u0AXupN2pvQj5uwzKFttIAKSpUUzD/xje+EbkOPPDAFVdcURjxCuWT7ksJrqYCpSkxqtaAKMGv6aGF2FjE4G1HHnlkhPn3NL0l1KJ8+DCxCUR//V3TnMnC9CbSvIrsfHpwRKPsrybmp5IlMApMXYsttpgmlVZFlvydwggMrHZnukmZV48IWJ7V/y2wwPxzzDG9HjOrwk3tJ+GIUtYByzWiKDwHm9KM3y0qYHm911579VIFo4Z3+k033dRL4tY0ltciQwKVp+SxVb4GWJeLpABgzqAPwP8sUr3WkVTxVvlUAk972tO8rC1VI7tdJFa9IqX0y7YiXjkUFZxDl112WW9wMQgBKXvqqacSVKDmmVGWtlFO919SRwIr9eAQTAlUMpGFvKRHqWe3/g6OhdsRb4Sup9QqRDLlhJcmERjaIPLeoJM3uB1lyaabbkruhrhVxemnn84CIn298HqYuuWAAw6QMdQzFveesncQ9vpI/j33uc8lvWgysA286lOf+hRxCEzatXo59bC2bbDBBscccwxVCsbgEcIEyegjZZV9Q/X0PYbRQewEq/vrX/+qv91zqd1YwyGSGSmmFlYqWH3pS1+KSPPQ2uCQQw4xdRllQgXCYkV9iAmhMvxgYN62IhNGPL6LT2BgCmeMa5uyUyT2gEkQEthVSQMivkFulUnvpbPCwPcX/dvf/ja0MihLSd8U8DdluP/+979jHocddhgSb9YBAbc+/PDDKdVMOcMnl3WCi0HK0KO85oxILMckx2Xf+MY3lpLFwAepZQgTiWuahNyc5ZVR+SaGRYJHuDhVKzavwSZPKSEDicAsROBJL9ZZ2I5JUvU0f8D+vL/zne/4e/bKsPbtS8u9KL1wizJZmd7FXhyE37Of/Wy/YtAIby5r5SWWWOIHP/gBtbmweByrfpF83lA0BOwF4kkUngqRgLyh7LHSJaTJITwDFSCqvQq9Z4lDKn0vQS/90BDIRXBaDtJmC1vYWaN773/ta1/zXvOCUwJXAAt6jSFRjj76aGtQsFhVK19FOmXtiyWQ01wlKOe9TIfXi5+KJhEt1PXDfOWbETOiX69dmgZvbaI6MqIgCA2RQDATWnwnQaHN9BB8KTAATxl0vLX1heglLyn8rVOlZ4Dw+qalIE4IGD3yytZguSz6iRaSUneIfynBRRBy0qQqIBVG1OzGereqsAf6IUSKcogiIUSIOQDbIGTSMK+gboZDA0wDOBt67E2DGYk0yWSw0A/+hNJJhqLpi8KNsi7oCPzFIzrPetazFNWpqdAI4qJw4MDNOAp83IHfVWWKYl2RXVExJzsVFfFG3/TQF0OvX6EwCF5YWJcOMpyZLZElKJG6dArb6FQ+zAlR5Rt6rBSRZWhDMlhblKBGZBRTic1H5hgZzwxnGVBYqUGkGzO4lHb+xBinTG/OKOCFmOEwVyGsy7qA6GA8kRdP4glEipP9Wm76semYXXRdckEYDwsWrm0IgS4oCq9lQevUHbXjZEx7pqJWAQqFYkpDiFEQE4BNzV+ov1Z/jGa48qmgtIopbbWfNMhW6+VvygSgIvJ3iooFW9JCRcGN9o4+JmDXNfFGNsY3UuqFv1nlAxYsYcwSwMkCVb9wtpkLG9MSt8ZUIeUlhjpLDyJ2sSMPaCh78koEZjEC5mheM0XgceNLY7C8L6xrBb71rW+VjPsetu8z9n3G0p9a2rckCRsifIFPLrDZ5zdbdr9lF99v8UPPOFTKwy4+bIUvrLDEfkts9dGtlvzUktfccY3IV377lWt9Yi0C7KVbvXSVT6yy76f33e5H273qu6961v7PqpZuVEe/vchBi+z0452evc2z3VJaxGrSayi068WApTRhglyyVtuKcpjnvakJQoQDl4rNIPvuu6+VOhpEyGEqXmcoi1cznTza5LWuRiXjNAQGPmQZSh2CE3iVh5RF/kI9E0p4iTlekDea58Uaym0ZvUZRMTKJVH4czyG3Xt/R8npHxHS/qv0b6nHKc29YXfNrhSoLmQF8pERP4RBKeO4ONBaekoX6jgZF4eijlAiQl7VHIskG5EBAFyyCBZhjrLNDBiiQ1NF38S4sh5Uhwp1+NbLtI/FERTxqMjpw7USw4lHDF3XYfzZugUm6GDtMCx1BTMkkbAkrlcDYaRvMdYqY+b//+z9kTvawIsnLrMObRMrWVkV7sCL6LWUadDJMSjI7stuZrKiYV2aLy1MXjxN/DgKqJjgxDz6q6Ahk/vSnP+ljrAp4AuElRKBZgS5rPxZlmgEWaZadrMUdyVdp8HhzUk9b2ymlSBdPJr4yiCzdm0ichvOWeK311yRA0uNSAuaGSyAsaKHzK5Hl74gSVK+RHqxdgS7Txq3pSm0WZtOIh+QnP/lJdKEYhsRjJ+YM2h1p/MLK7id9xPbCjVpkU4/KLVgggEBIE3/X9V+RMfQCLskipXApYfhJ46c1pjyaVQFNGsBWzSo0pny9XkT+3FxhFB6c/qZ2J8al11+y0EouzENGUTZKl5e97GV3rnvnEjcvcc1vr/lk9ck11l3DjoZqn+pPf/jT4lcvfv091x8494Hv3+T9B5xzwMNfeHjJFZY894Xn3vaX2w5f9vDP7vDZBx9+8Nf/+vXSDyz96LKPXnripdetet3pbz393r/f+96vvXfFvVb8+Rt/rvD7d79/2xdue/CXD9530X2VzBuUOPS+62WFXTpGBDIByE7FTTCgBaQsScnKwKBAohMY3uyWqlxEvc3pQoh2vSN+iDpCi1WC4oE0xSHwG9kpkCgAwuJjKcwrAhXz1rbIVqCr1E4sWRZbRpOFVCbx7XdPrS/Jp5JspAF6Gop6FcVYyE7Jr0nkHAYQQq5epkUqGRl+DwDxZ4nxWFKTuJEMsDrFfwW2ZH9EkrssFCJxOPYF+gDSul5sPUyFQOYR7TM9wZZqAZuxZGd9U75C2NRCq+cRMBVCr4aP0ruEXQOXpeChWZQSK8XbkEXaCIwN52PbIlyZijSeAoneThuQHqJaOYQxbYEO4rX1BpcwmgUNDNIQs2FRrlA4UTwQ9txOjSk1AxnPPoKkqsKUINFNITBqlWSosBgaNXMAt7Csx1rUThHiQoxo3ZSAiYLUwKFHXohmuDZIgBNQw+AQbEy8SbpM77BhKSS6KTvVi4pwU3+hKBTQ4EO7oNcQkJIK0xQVUDutmGmvkZy4kWNTxRTi8uwqaAi8x3nn7S7zCs5NT4IC1iPN8/pt93Djr+Xxv5cI1H/lVWkBJPQrXQrs1+k+XarIR4nApEPgCYE06Zo+8Q229GTCsE61XPPG9+rUBu9ZgvDN27/5S2d96avVV6tHfCt0XXLo59XPj//w8eu/fH3Lvu3+vJ2Umyy/yaXvu3SF21dY/O7Fv/X3b/3+f7//y3/+svJTV/7VI7864KADNj1q06XuW6paufrILz6Cizz20sfmunOuLx32Ja/p6dX0jZffePq06RpA0HqDd+m7JTKaEm2TjCwkRfAVq0OGDzGWxQSVd32XQlofUX5gORRXNDSkZphv6GzCBCM9JhE0gmAm1QhOkTiZishCjIriBAuxtkY4quoJbw/CZlh30tHI0tqYEiMv0aWPYlAEWFmO46NkjzEiszUDwbJQporDz4g38jVsahx3yH7iOXQAbBbCVBooCE0+uCJGv/AA3IhqBN0hoVEHIBCo5kAYv8ghygwCWzOwATPEKHhU2tk2gDZRfiiN8aKxWXeYOmtSbAPmIKxrQCOYoc2+JgHjF65D8lHS0MH4VSklBJA1hsWEMQXhIw51JByZNQxZ4XJEraXAti2JSCoZV1MCs8Vo1iOVo/ASEyaquEVWXOWRAMWPqx4TYS1pbYw/Jbak1sStMW2pJOrjisS4jgDuiBcaaIpMLBCvwiHMDdQQX0GRjTWczc/WKiYspu/UZOjjjWXYQF197+NA9S4bM1kQSLozgpHCIQgn5154mRY+4U1qgf7N+765xH+XqC6upq37uNh+tFporoWidC7OAlvPvfWVf7rykmdeMn2e6dU11T8f+OdF11+0xhJrfPOGb77kjS+Ze8O593vHfodOO/SMHc5Y+7C111p7rc233Xy1xVbb9R27vvTEl0YJvbSVJPBCZ0fwNicXyTnORuiOFz0znBLQEbZ/lEWY8oaehsgkTale0A7SmsMHuU4SsFUFQ5ISzUK2CD8Mgz+BkhEIYo8PAYFBqYMJUZOQrKgehY2FMolCRURFwSpEwKAj1AMKFCgdIZAsxymQquqDJbL3gIU7jqIv1vEYCWMEBqYuvxb6OIfWwkHHMR695nqFYegXyxcaKi/6haxoLaLAPEQxoy+YjVyYDQUJnQF9g3i6AboxGgtIonGkNdZoGtCFKGGYsTUaLjvFBlhm2gusS8NogwAbiTmCoIwKd6sBRQybck2lSelqimSsdDVFujWywwbE1idTPIZZCutlUcKDDXrAuNVWW1m0mOTmhpWJaTMLURhAajIL0ciqE4HxRcBbNa+ZIhC+JmgBVX8kZtYhLIUZhrxGF/vsYv++7d9Pfe5T59h/DpHW6NVHK2xAmBPivAfMe8cDdyy8x8K77LbLPQ/ds9AnGjTo+Z96/sZHb/z7K35fPad65n7P3PV7u9IZvO6Y1x1/2fHWuEutv9Sz/+/ZnDMQrOkfm07ZQDSSvpxkKVTwg2iG37rLS4St9XkpWsvSoxD5CJlkuAi2wSuC7w5G4l1PN4CLKI3XpwBbFTbDNkE3QGFAGLu4WfA9JB5IZbt7CGbKfwwATVEm3QO5zokHmdBmvCoOLmOIQRF03C9JIyVG4qkYEmjYoaTRbP9wBconxpq4lbLHazy8AWiwjAvTTLQBuaHmKSPeY8MwRZyDxijSd3JZEI8kMS/SyvRYch+TtbaqNaaP1Y26qLatahs56iomOOOkbvyosdLr2bPjo0ZsUmccWN+daWAdXz41JUp/fDvLNByCpwUVCB9eRgeeE+EzUW1oA0ZV3VxNe860uw64a5sttzntxaetcvoqtCzUBte95bpdbt3l1hVv/ck/f0LRs9ztyz3vzuddv/T1Q6sN/Wyzny230nK40fTvTn/smsee9pynrfbx1R549IHb/3v78pcvv+jQolxePvHQJ+746B00NDQuKBcCwbOh2AK0rYxhCdMQUHVwx6HDZ9uKQRBJs0JpoRCyNuxZ9BPmgEiUhYrCrV9PESy5BDASupzwSkaS6DaK64A00ss70kF+HM/mfKUjzQ9a7lM93gJJRiQCA41AqrIGenj61zjrfFoA5THoW2/3r+CxlpR0pycEG+J5f//PKxFIBBKBRGA0CCTdGQ1qkzDPwNKd9N2ZhLMpm5wItEMgxUk7VDIuEUgEEoEGAkl3RjgP9k/b3wgR65R8/2ljF8+MazYo+XpRMdh1qq3HeDayplaVGBv47aViyHNSi91JPRY40mT8txwbY4cRT/DIa3s5hydnH3Cx6rRxKU17I8U50ycCicDshkDSndljxEdqiWtidSPN3hbUpjKH03AYio1IXIJcbfN1irRdnz8Tb2gn/9Z3JDmFzyYsbtdODyp5+SepaKRVlOx2ctm9xWdLDHfv+JREedrHAE8pe+XKPi8lczB3OQXYWcN9rCiLSgQSgURgtkJgZAJmtoKm3lkutNMOGI7oi+CvFz0O4Sb9hBo0vjWyU80NfcaTdVhtszvPxpku2EacGdOptIhvW6ZzeG1Zj1NzcAj7tupivnuBnsYZeg61cx6gbfAlPU5ja1i5jYDjYeIIlqb4Xm5tvHc4nt+3ve1tNvlTwPSSq5c02um7Ddzeff4z0js1xz52W+J7yZ5pEoFEIBFIBHpEIOlOj0DNSNY7aRhZub2lpqKwHax8YKhtpi52DXltpHIScduMM420xdoJfhQnkdLnAmzFH4vsd2iefe8+JmDnl7OMbZW3Kz50GHFujZ1lNpEVDqQu27Z1P75eZLOYXW/C5fhjDbNhntXJhjLH5JQe2SrvdD5GKGRCIY4JUKbPSvgaBhLj6B2ns7CL1bVBJa+As4ztj8N1hLU21FHS2xzn3EIFMqXZTu/UAOf9SOlQ4EsuuUSZzv1Tr7OIEDt7+CEPQ4caw1Aux/Y4A8luOxv+FRVfvXDWjiY5hNphAfU2ZDgRSAQSgURgLAhMH0vmzDvBCPhIdQjd0dXrrDlmkdHlZSGiifGVAGcG+rAAbxIfGcA8SH3fF/SpVEyilOycHl9FKN4nJb4pQNJjA3YqEu0ODnboPpaAHNhCLyUC4VgaX4SIXJxXHBLopGAcgsUnIpED3MWJgqVkx8ehHVQmhSR5hGrgT1rrzCEfR0QmlINXxRccUSgBpKd83bCUFgGPHEQUYacIOlZRWIwO0sRgbDqiec46siUhPiSuLpYv3cHGdM3hBfrlUxU2/4uUHT5Op3CWEu0UDlQ+6k7To5FYaVSXv4lAIpAIJAJ9QSC1OyOGkfLA6TWO++MdEpmduUdiUVFY5TvB1rk4TpmrH04jkpMK/4/6ETU0EE5nlgyT8H0GZ9g4648Vw2F34b2hQNKRaUZFqlOXj3E60d/hfh6Jpw8g+H3T0cd9aDW4svp8Qaf++BaBcwW13Ccv5KLqiGMSnTlL7iIBvpZALVGa3VSOxhPq2u/wPdnpRd761rfiEExayATqoDQ+NPG5A59P0jxF+bwX71qRTaXFLergEMUIYycMUqS+oxoiIyrDzqUcCRxqrJ2OTqYFQY/gU8Cn46EO8T3qKIfbMqMYkkF9EjF+efZwLnZYUXw/NeLpljgFx3mJ9C7q1anqxJLpSQE1xj0iIovW6q8vY/gmlAtlcQYj2ocwxXlFqvOpc2dRyqU7bhsnT1YVuBy3GEWFUgoCCJDORmT+JgKJQCKQCIwHAqndGRmq5K6TBn1JwBH+jhCUmeynb2DC8HUCC30OIr4p4ZbsjEvYV658YZHbx+Nxjf9KTDVCKqMpHrF9kMq4FMMHr1gJCEIfSVCRjzepCFOhMKCZEPDxB/xGpOqklJHk5ghCUSGy7UXQ0hxgHnQSBLNPgUpG30NVgwDxvaVHKadhtpaw+uqr85ZlbNJCsh9zkgaHc3CzNiBDEjiAWCQdBtLmS9roBYjogVpLa41RFE4AKEyOzQ4yQGCQCtaCGAnjDU3fb2otJ2J8mCJoR6cE4lEcZ2FBHlVloury1U+JyychQedcaY00oNQwpXw0CMeilyo0ixmu9dNOiG8QOM2Lz4opAc01r0pR3QNMaaVrqCS7GL7bPUs+TQQSgUQgEUi6M7I5YMlOwDPoEGZhlfjVr35FqPuOBA0NHQlNwxvf+Eayn9WJaUPp/DmwAfKbQoJF45e//KVI4o2gFcl7QwnUIfFlH44dpP7JJ58sDUrBRELjYiuylBQ8CASFAU2Gj0iExUckL1cqjQ022MBnsQVk7HQR0i5P8QaXAHmpqFAzsBwVv5xOJTTF4ygsXCJpOyBDySFMTWLDNvONnVMidbMpV7mFD7NXuY2A7hPn0U7UKoxZ7FO0KQgKytWUvtMtC1T9EV2aUQi7FRNSPDJquAIVVPjN1NPXwwicnmot7yKu2YaAFkcuNNHw+bK3z28FWwqdkyH2JSaJQ5EDnKhXv1jZ9AgywYT4HhnHsudLpcioXBgzTWH5YCfzGdOe+WCDOrZdjHc+vqF2aNdbm+FEIBFIBBKBVgTSmNWKSbcYq/OwWVDJ8PyV1O4kRpZYqTMY+ew2j1cLfd4bPnElAbMR8xbWwhJETEYkOUee4RykuF8MhkBllyHmLd/ZlWSkovBLxtN2CLS9pCFcudRwHJag07ksrXkppTA2bcDGqCsYUzAq7WxNWWK0LXxKKJa0mSVLjFyRQPt58GAAeJ6zcJAeagyuzSw+vjxVCqkHONAwjdEYUWhpRnwWAxTMQzyXeeEQ/PgQSqdk/ryUW77/pQTGO7ArNraG8Rfmk4Tq+Uo51xkWK5QCCfCJD2nCzmVrlYZxEvIxVGYsfsrKMTSch4TrRsZ6CyOMDhqCOBYdMdIY8RRRlFi0PnRddGPhFEXPB0kfBWPggwDrXrTNgOJVKCnc9E4C2jiNQWJASrFnPkRdZg7Gg5yxDxaFE0rEazsiKbriU+fSaxgG3DAI/ipy528ikAgkAolAewSS7rTHpVMs/xIqB5KVyAmpQ6gTw0wYndwvCEVyjhKFlG0qlqijtyDM6G/CuZU5iVTrwm+iBL5B1vokH2JBi8CnB20iiRvnwby4qZInbumcCGAf+MRRKCc42+JJ5CX5SgOx5557ktBPpG4JSYln4Ac0HPyU6bR0GUdhINMSxjLmPJkIcu1RIKLGfBb+Ky2FNSJ8/RtfQbn0F28IJROURFIOAUdF6AuE2bAAyH4EHMQC6cRjaMgo2LSEuRBhQuCUiSyioZpEfUKnEpHi7ZbHSvWUV3KYk0SiaByS1l57beHuF5dkW+W1Ex0pKWm2qK/UqAslkm6vhLVNmP0RV4tI2jtXhH0cHmcqiSMQtLUpko92U0zcctVytX2UkYlAIpAIJAJ1BJLu1NGYeZi023///X0nnOCnEiCPaRRIaI44T3nKUziv8AIhkslRj9hlSH0ajnCeJWUFQriSnTQQtAs4ChuQhT4dhoxUGmIokDSFqQUZorDBpeg5KCfoTgh4tIDqAvGi12HdQAWkVDjdzHHHHXfSISd16obsimIPIvjRC9odtIC9jCKBIKfkYCjplFc8Yxnfap5DCAdyJoZ/Lkqh47RW1DN+ReIZYc/So9CIiGx7ARBJot1hZmKUUSxFhVbxWCrpy6E+rWYvHCuUNCWxAGbpqsdEmFpFO+39jlv2IKopQ+BT7cNfaG/N8aQYQxO9e1JsVcWG+abIvE0EEoFEIBEYNASS7oxsRGgdUBOCmaFhq622QjIsrxlNCH4FsVNQ1VB7kMRUKaQp5QcnEjYOxggKCXoIrjZcjy33w4DCTdVWLKoLDrOsYFb8ysF4qCsYqtZdd10WLvohdYnHTjQAO1FvWL74Kdv/HHyFroVQ794fdhNmHZLeFSk5jnTPEk/bHOdz9uP5/lhVpz0e/sXjgfjv+U++bblDB5n/ROs+xPBIfW9J1f8IXi8qQla43Sy//PL9ryBLTAQSgUQgERgkBPKL6L2ORht532vWTJcITAQCs/YMzInoYdaRCCQCA4+AXR2h16fmd27I4LR3JsqAwWlotiQRSAQSgUQgEUgEEoHRIZDGrF5xy6Vzr0hlukQgEUgEEoFEYMAQSO3OgA1INicRSAQSgUQgEUgE+o1A0p1+I5rlJQKJQCKQCCQCicCAIZB0Z8AGJJuTCCQCiUAikAgkAv1GIOlOvxHN8hKBRCARSAQSgURgwBBIujNgA5LNSQQSgUQgEUgEEoF+I5B0p9+IZnmJQCKQCCQCiUAiMGAIJN0ZsAHJ5iQCiUAikAgkAolAvxFIutNvRLO8RCARSAQSgUQgERgwBJLuDNiAZHMSgUQgEUgEEoFEoN8IJN3pN6JZXiKQCCQCiUAikAgMGAJJdwZsQLI5iUAikAgkAolAItBvBJLu9BvRLC8RSAQSgUQgEUgEBgyBpDsDNiDZnEQgEUgEEoFEIBHoNwJJd/qNaJaXCCQCiUAikAgkAgOGQNKdARuQbE4ikAgkAolAIpAI9BuBpDv9RjTLSwQSgUQgEUgEEoEBQyDpzoANSDYnEUgEEoFEIBFIBPqNwJz9LjDLSwQSgUQgEUgEmhF4bPgSO336dMHmx8P3Ht1+++2HHHJI26ejjpw2bZqS22bfa6+9FllkkbaPMnKKIZB0Z4oNaHYnEUgEpjgC//nPf/7+97/PMccc0c9HH330gQceKH2eZ555HnzwwXI7HoF55533iCOOOO2009TVY/ka+exnP3vllVd++OGHr7jiihe+8IVDQ0OtefESjb/ssstaH4065pFHHnnWs5716U9/WhtaC5lvvvlaIzNmSiKQdGdKDmt2KhGYsggQk0TmqLuHGXRSLdTLnHPOOa+77rpPfepTAvX47mFtQwWkGT8hOtdcc/35z3/+xS9+UVryghe84D3vec9DDz0kRte+//3vb7/99r30sZQwisBqq622+uqr957RkK2xxhrrr78+znHOOedstNFGvefNlIlAXxAYwV9yX+rLQhKBRGBKInDxxRdfc801IyIHdRwQhV50ElQat95660c/+tF63t7DZO1rXvOapz/96W0X+vVyQs1wyy23CNTju4d14dWvfrVGbrXVVkX70j3LSJ8CCuNBpwTk9UvFUjfH7LbbbgsttNBIi52w9GBJrjNhaGdFdQSS7tTRyHAiMAIEOBlYs45IHEbpIUqJxlHk7aV9c88990EHHfSXv/yFXIz0HBeWXXZZkkabxbhdeOGFQ172UuBM02A555133tVXXz06ukMVseiiix588MFa2L1VaMpiiy129NFHz7RJbRPITtY+9alPbft0akQOMteZGghnLyYpAkl3JunAZbNnggAdwLHHHjuWFTYZ3EX0kuvE8w033DCTdnR4/LKXvWzdddcdi1GmQ8GNaCzq/vvvf+Yznxl0SkcWXHDBT3ziEwThT3/6U5H0AaR+L9qULrU0PVLmWNDWqkLOmkrO20QgEUgExo5A0p2xYzhlS+ARSYDR51MGWBaToP3qKtnGf/B973vfm9/85pNPPvnuu+8Owdxj+eQ3WY4r+BVuzaXBd95550UXXSTQ+rSXGB4e7373uzfeeOMunOB73/ve6MoHJrdN6pZeWtLfNIwspcDx8y8pVWQgEUgEEoEBQSDpzkQMBNEe1RTZTLqTxxdeeOF6663H7jAiYd+pxUTvWJbXTcXSXpxxxhnzzz//ueee6xFi8Y53vKO/2ggKhrvuumvDDTdsqnqmt5rx2te+9p577vFbsG3KBdI+otFUeN4mAolAIpAITC4Eku6MYLx23nlnqoiRrokt5W1J8ItALLXUUgJRJZlNfXLiiSfysRhBIzokpYRgHHn/+9/fRRvRIWvH6G233TYcIbE0vV5mmWU6Jp11D0bnLDLr2ps1JwKJQCKQCMwCBJLujAD0bbbZxvbLkcpXtOb1r389JYSMyy233Ajqy6SJQCKQCCQCiUAi0A8Eku6MAMVNh68RZMikiUAikAgkAolAIjAACIzSkXMAWp5NSAQSgUQgEUgEEoFEoCcEku70BFMmSgQSgUQgEUgEEoHJi0DSnck7dtnyRCARSAQSgUQgEegJgaQ7PcGUiRKBRCARSAQSgURg8iKQdGfyjl22PBFIBBKBRCARSAR6QiDpTk8wZaJEIBFIBBKBRCARmLwIJN2ZvGOXLU8EEoFEIBFIBBKBnhBIutMTTJkoEUgEEoFEIBFIBCYvAkl3Ju/YZcsTgUQgEUgEEoFEoCcEku70BFMmSgQSgUQgEUgEEoHJi0DSnck7dtnyRCARSAQSgUQgEegJgaQ7PcGUiRKBRCARSAQSgURg8iKQdGfyjl22PBFIBBKBRCARSAR6QiDpTk8wZaJEIBFIBBKBRCARmLwIJN2ZvGOXLU8EEoFEIBFIBBKBnhCYs6dUmSgRSAQSgUQgERgbAkNDQ2MrYOa5p02bdu6555599tlzzz231G5V6rdTzt13333hhRfu9DTjpxICSXem0mhmXxKBRGCKI/Doo49edtlljz32WL/6iQrcd99906dPn3feeR988EG3fpsK9/See+7ZY489dtxxx2OPPfbhhx9uSjDTW81edtlln/e85wnMNPFYEswxxxz/+te/rrnmmkceeWS99dbbeeedd9111wMOOEDVbZs9zzzzjKW6zDuJEEi6M4kGK5uaCMzuCIR6IBbrwnHbIyik+DjJWiLzhBNOOOecc+aaa65QKoyTENXxBx544Bvf+EZbyd0jDq3J3vnOd/7nP/85+eSTN9poI9Rniy22aAvU29/+doAjEK0lzDRGg1/+8pdvvPHGM03Z9wRXX31138vMAicjAkl3JuOoZZsTgUFB4IILLrjzzjut/sfYIHLUcpzSopPegqS/4447TjvtNAm22morBoijjjrq1FNP7ZFYKHzdddelYGgryMfYeN2/+eabb7vtNkJ9k002cbvNNttQM4yx2LbZ4fCRj3wkCF/bBCONhPwSSyyh5f/73/+e8pSngHeRRRYZaSGZPhEYfASS7gz+GGULJzEC1srzzz//3XffTcqSuNETC/S+iCuS/qyzziL411hjDeKK3Np7770J3bGTj2inAhdbbDFNvf3225daaqnWYVDRSSeddOutt45RtBOxT3/609dZZ53ll19+5ZVX1pfWusRoyeabby5w//D1+te/nh6ibcrWSOC/6lWvWmaZZVofZQwEKKUWWGCBhCIRmMIIJN2ZwoM7e3XtmGOOedGLXkRS+hUeXec7CdrRlYYEfPe7391+++0//elP33TTTSussAK5LvI1r3lNXyoi/sl9v3QeqIlGKraPQov15y1veYsGw/MTn/iEilpx+OxnP9sXdqWQOeec0+8YmVNrCzMmEUgEEgEINLzWE4hEIBB46KGHQhtxww03tJVtvQB17733EuoWi6ZW0WfUM5JnH/vYx6699lrirR7fe5jXIcVG09Q988wz6QbU6Fe499IiZejwv/CFL3C/aCp5pEXV08MBqpxARVKQqIVEp8Cop8lwIpAIJAJTBgE74zbccEPdOeOMM9h2B6dfo5Q3g9OBwW8J2Tl28UlGfuUrX1lppZWuvPLKG2+8sayAxYfCYOw4KFPJf//739Xy1a9+ddQFvuc971l88cUvvvhiaobnP//5bRkPRrLccsuNrgpg8l1QRZMTBmIhBkvzKzy6wjNXIpAIJAKJwJREIOnOCIZ1t912O+WUU+abb77e8+AivB9WX331JtncewmREq259NJLORLyoqA+CdULwf+Od7zjyCOPPPjgg5dccskxVqEitdC4ICgoy0hbWNKvuOKKFCTaqaiFFlqoxPc90KocipjCBfteYxaYCCQCiUAiMEkRSLozgoF77Wtf+5znPIcs7z1P2Fbe/OY3955lpCn32muvkWaZgPSY2QTUklUkAolAIpAIJAK9IJB0pxeUZqR5w/A1ggyZNBFIBBKBRCARSAQGAIGxnpYxAF3IJiQCiUAikAgkAolAItANgaQ73dDJZ4lAIpAIJAKJQCIwBRBIujMFBjG7kAgkAolAIpAIJALdEEi60w2dfJYIJAKJQCKQCCQCUwCBpDtTYBCzC4lAIpAIJAKJQCLQDYGkO93QyWeJQCKQCCQCiUAiMAUQSLozBQYxu5AIJAKJQCKQCCQC3RBIutMNnXyWCCQCiUAikAgkAlMAgaQ7U2AQswuJQCKQCCQCiUAi0A2BpDvd0MlniUAikAgkAolAIjAFEEi6MwUGMbuQCCQCiUAikAgkAt0QSLrTDZ18lggkAolAIpAIJAJTAIGkO1NgELMLiUAikAgkAolAItANgaQ73dDJZ4lAIpAIJAKJQCIwBRCYcwr0IbuQCCQCiUAiMDsjcP/990+fPv2xxx674447pk2b1iMUQ0ND88wzz1Of+tQe02eySY1A0p1JPXzZ+EQgEUgEBheBb3/727fddhsiMsYm4iWuToXMPffcF198sd8HHnjghBNO6JSsbfxGG230i1/8ou2jjJxiCCTdmWIDmt1JBBKBWYDAzTffTElA4qr7xhtvXHrppa+66irSt3dNQ2n0fffdR0uxwAILPDR8zTvvvA8++GB5OvbAXHPNte+++1555ZUIxC677HLqqaf+73//C0ai3sUWW2yOOeZ49NFHn//85/sdS3X6/utf/1p3RgFCvV4waPCLX/xigXp8Pbzqqqvqjoo+8IEPdCFG9SzC+rvooos2RebtVEUg6c5UHdnsVyIw2yFAznWRiOAg6b/0pS/985//nHPOUb76lKCWpuz4wWmnnfbyl788zCI//elPN9tssyOOOAKNGMUYvOtd71pmmWU+9alPbbLJJmuvvfb3vve91772teodRVGdsrz0pS9dY401PAUX9UZJ9vDDD7/oRS9Sl8B2222HDZRHowuMXa8zunozVyLQisC03olwa+aMSQQSgamHwA033HDFFVcQ4Z265qVBbzHGVwefCYKc0F1ppZXOP//8Qw89VEynGnuJJ5uxjfXWW6+LkCZ9//GPf9x7772j1jdsv/32dB6vf/3ri8aFRueyyy676aabUBweJJqqI57OP//8oxD2UMV1lHnttddStCy44IL//e9/BUbd4F6gyzSJQB8ROPfcczfccEMFnnHGGSh7H0seY1FJd8YIYGafsgiQWI888siou0duhfBrKgGNYPjYb7/9RiELm4qKWxUxfPglGtsmGFGklf0f/vCHCy64oJN8VdF88833yU9+0q/wiApvSgwK1EQhoOjCrppydbrFQpZccsktttiiU4Jxilevge4L+OPUwiw2EZhIBAaW7oxSozuR2GVdiUAnBM4555zrr78+JCXBSQPfKeVI4y3QGSP83Y7OiECEK2HbbbeVvYkToBHaWXQDI21Ya3pFrbvuuspUXevTkcZoLdWCxjc1u16OLiy88MKd+FA95ewQ/vSnP42/fuUrX5kdOpt9TAQmLwJJdybv2FX33HMPaUoy3XLLLaTd2MUPxkCf4Wo1B6jlm9/85llnnSUwashI0GWXXTZUEaMupGTkP4GOMCKgO1wQXvKSl+y9997dXTdK3l4Ce+6554c+9KFeUramCdLwyle+cuxKi9bCM2agEMAyF1988YFqUjYmEUgEWhFIutOKyZhi0A7rvNHtyOhScetS2xIc+WDmf97znmd9abdnl+w9PlpiiSWe+9znLr/88s94xjOaNmXgUjpl+8NYSBVw3ve+9/HVEOixSd2T4V6FT2jYWNrWvaJ8mgh0QmCFFVbo9CjjE4FEYHAQSLozgrG4++677XLsrkfBEpwA0T3NCKoc3iqJhfD8Qmsuv/xyOozllltOLQjQWmutRQ0j/POf/3zsjiAK5FxpW+YiiywiMKJGjjTxWFREI60r0ycCiUAikAgkAkl3RjAHFlpoIQadmWZIHcNMIcoEiUAikAgkAonARCKQdGdkaCeVGRlemToRSAQSgUQgERgABMZ6tvcAdCGbkAgkAolAIpAIJAKJQDcEku50QyefJQKJQCKQCCQCicAUQCDpzhQYxOxCIpAIJAKJQCKQCHRDIOlON3TyWSKQCCQCiUAikAhMAQSS7kyBQcwuJAKJQCKQCCQCiUA3BJLudEMnnyUCiUAikAgkAonAFEAg6c4UGMTsQiKQCCQCiUAikAh0QyDpTjd08lkikAgkAolAIpAITAEEku5MgUHMLiQCiUAikAgkAolANwSS7nRDJ58lAolAIpAIJAKJwBRAIOnOFBjE7EIikAgkAolAIpAIdEMg6U43dPJZIpAIJAKJQCKQCEwBBJLuTIFBzC4kAolAIpAIJAKJQDcEku50QyefJQKJQCKQCCQCicAUQCDpzhQYxOxCIpAIJAKJwIgRGBoauvfee0ecLTNMTgTmnJzNzlYnAolAIpAITCkEfvnLX15++eVzzTXXWHr12GOPTZ8+HY959NFHZ1rOww8/fPzxx59wwgnPfe5zZ5o4E0x2BJLuTPYRzPYnAonAbITAv//9b+KcUL/nnnumTZtW7/l9990355xzzjPPPA888MBDDz3U9LSecizhOeaYY++997722mvVNaJytPkFL3jBHXfcseiii84333wYST27Yv/4xz9ef/31AvX4EYVVseuuu37zm99caaWV9t9/fyDMNPtBBx00//zzzzRZJpgCCIxsvk6BDmcXEoFEIBEIHcAjjzzSFgqC/IILLvjJT34y99xzt03QS2SQkrEI79ZatOfoo4/GFe6///5//OMfTQl22WWXf/3rX2efffamm2665ppr9iLsm0ro8XbllVdGXHpMXJJBe6+99rrssstkf8YzntGqfQE70Er6UQc++clPjjpvZpzCCCTdmcKDm11LBMYRgQcffPD3v/89K8BVV101TtVQANBYdCqc7NcAq3P6jE5p2saTqVb/V1xxxfrrr6+QJjWDLBLcfPPNFBijlr4y7rTTTkcdddShhx66yCKLYFdtWzLSSE3dYostIleTcsWj5ZZbDlw33XTTMsssQ4My0sInJv3SSy8dFfWXCE5M47OWSY1A0p1JPXzZ+FmJAAHD9t+XFlj4Yg9EryXvGEWjQi688MJvf/vbQQJYNCgDgjSQwQsvvHBfGqyoO++88zvf+c5GG2101lln9aXM1kIQhf3226+LUUYz9t1339aM3WPkeuUrX0kL8o53vGPeeeftnngsT9///vePJfso8urOU5/61FFkzCyJwJRHIOnOlB/i2bqDt9xyy7nnntu0Du4dEeSjE6FR5jXXXEMYj7rw0gxc5/nPf/6666578cUXP/OZz1xsscXGwniQg7vvvvvWW28l1BEyXGfrrbc+8sgj3S611FIf+MAHxlJ4abOAij772c9iaSNVrtQL6R7WZmh0TzPqp6Mwx4y6rsyYCCQCsxyBpDuzfAjGvQFW4WRSlyVy7y2waZME7T19jynJyxNPPPGHP/xhCE5abtr4sTdYOTfccMMvfvGL0TESrg8cIPbYYw/otXYER1l22WVt62h9NNIYRa244oqrrrqqbSlU/eNhhthxxx1H2qpMnwgkAonAVEIg6c5Ej6Zl97HHHtsvu3Ws1LtQEKaNww477Morrxx7P5GGt7/97a1bKsZeMmbD9fLZz362gB4xuBxwwAH2o3bpV4+VwnksugfahdFRpR6b15SMC2dTTN4mAolAIpAI9AWBpDsjgJFuY/vtt7choheyQlTTli+wwAJ1mU180rVcdNFFAiOouENSJVu10z288Y1vbKuBiHxHHHFELw3uUMkT0dq8xhprTKT4f6LuDCUCiUAikAgkAmNAIOnOCMDDXT7ykY+cdNJJVCYzzcZC8d73vpe9Q6CemAKjL+SjXmaGE4FEIBFIBBKBRKALAkl3uoDT5tFaw1ebB52jUh3SGZt8kggkAolAIpAITAQCfTCpTEQzs45EIBFIBBKBRCARSARGi0DSndEil/kSgUQgEUgEEoFEYJIgkHRnkgxUNjMRSAQSgUQgEUgERotA0p3RIpf5EoFEIBFIBBKBRGCSIJB0Z5IMVDYzEUgEEoFEIBFIBEaLQNKd0SKX+RKBRCARSAQSgURgkiCQdGeSDFQ2MxFIBBKBRCARSARGi0DSndEil/kSgUQgEUgEEoFEYJIgkHRnkgxUNjMRSAQSgUQgEUgERotA0p3RIpf5EoFEIBFIBBKBRGCSIJB0Z5IMVDYzEUgEEoFEIBFIBEaLQNKd0SKX+RKBRCARSAQSgURgkiCQdGeSDFQ2MxFIBBKBRCARSARGi0DSndEil/kSgUQgEUgEEoFEYJIgkHRnkgxUNjMRSAQSgUQgEUgERotA0p3RIpf5EoFEIBFIBBKBRGCSIJB0Z5IMVDYzEUgEEoFEIBFIBEaLQNKd0SKX+RKBRCARSAQSgURgkiCQdGeSDFQ2MxFIBBKBRCARSARGi0DSndEil/kSgUQgEUgEEoFEYJIgkHRnkgxUNjMRSAQSgUQgEUgERotA0p3RIpf5EoFEIBFIBBKBRGCSIJB0Z5IMVDYzEUgEEoFEIBFIBEaLQNKd0SKX+RKBRCARSAQSgURgkiCQdGeSDFQ2MxFIBBKBRCARSARGi0DSndEil/kSgUQgEUgEEoFEYJIgkHRnkgxUNjMRSAQSgUQgEUgERotA0p3RIpf5EoFEIBFIBBKBRGCSIJB0Z5IMVDYzEUgEEoFEIBFIBEaLQNKd/9/enUDZURR6GJ9L7sxkJhsBgbAkRBIhEA3KElAQRCAoEAigmAcoiIKyi4IoR/RAwIVF0QiIC8qReEBEJESNJCxKIiAGJGxRAmIQRSQbDjOZ/X1DYVvcmZsMndm6893DmVe3u6q7+teek/+rqu6bVs52CiiggAIKKJARAeNOr9+oNQvXhHOsunRVr5/MEyiggAIKKKBAJwHjTieSnt6QxJ2ePrDHU0ABBRRQQIFuCRS7VctK3RZoq2urv72+vam9UFWonVrbuKiRct2suqHHDuUYDXc3tCxraV/TXrNvTeWESgr1c+tpUtFaUXNgTXGrjtvBIBC7iqOK1ZOru31aKyqggAIKKKBAWQHjTlmadDsa5jVUTayqmlTVtLipYX7DkGlDGh9oDFmHTFOoLQw7fljr8ta6G+pGTBhBherdq4tbF9tWt9XdVDf85OEdJ22t4AiV4yrTdcBWCiiggAIKKFAiYNwpAVnfry1/axly2BCOQmRpuKshPlx7e3v1zh0DNoM2HdTe2E6h+enm1hWtoU57c3sF2wod/1VuZ9aJ5SwroIACCiiwXgLGnfXi66JxR4zp+lMYVCgMJs5En7aKoccMLRQLBJ2W51o6sg4f1lO9vlbUwKICCiiggAIKvGEBlyq/YbK1NyiOLTY90UQd/ha3fTVNEoBCBuoUYoqji81LmqncvLR5zYLXHuBa+/Hdq4ACCiiggAJvVMDRnTcqto76NQfUsFS58aHGQmWh9rBaahfHFFmXM3R6x1Llkk/NlJr6OfUsZ2ZEZ8ihHVNgfhRQQAEFFFCgxwUKLCjp8YPm+4ArZ6zs9wscecHIfu+DHVBAAQUUUKBE4J577tlvv/3YOHfu3IMOOqhkbz9+dTKrH/E9tQIKKKCAAgr0hYCTWSmVuxxfeeqpp/bee+/Kykri7fjx47s8dBgcKmnOxpItXbZl40AYWyrXN7croIACCigwMAUc3enJ+9La2looFE466aRx48b15HE9lgIKKKCAAgqsh4CjOynxXn755auuuurII4+87bbbTjjhhM0333zFihUXXngha6EGDx5M6AnHnTlz5uzZs9nY1NR08cUX77PPPuXON2XKFKpdeeWVr7zyyvnnn7/RRhttvPHGnIVDrVmzpqWlheGiq6++ulxztyuggAIKKKBAOQFHd8rJrGP76NGjb7311l133fW8886bMWMGte+7777a2tpisfjggw+GxosXLz7zzDPnz5/P10GDBrFoa+HCheWOO2/evP3333/ixImTJ0/eZZddXnjhhbPOOovZMQ6y/fbb77jjjjfffPNll11WrrnbFVBAAQUUUKCcgKM75WTWsX2zzTYjoDz//POf/exnTznlFGof8urn6KOPbmh47WXKkyZNOuqoo5588sk5c+a0tbWx65prrpm5w8wuD83eqVOnnnPOOSNGjJg2bRoLgPbaay8S1RVXXHHttdfS5P77729sbKwY3GVrNyqggAIKKKBAWQFHd8rSrH3HlltuSS7ZaaedRo0atc0225SrTLXhw4czvcXAD9NVs2bNKldzk002OfjggwlGt9xyyxFHHBFeEDBmzJiqqqpyTdyugAIKKKCAAt0RMO50R6mLOqxK7mJrp01MTrHyZtWqVey58cYbjzvuuKTKo48++vjjjydfJ0yYsGzZMlLOY4899uKLLzKBxS5W8Lz00kv33nsvs2CrV6/ma1LfggIKKKCAAgp0U8B/PrsJVVqtrq6O6Sc+ixYtCvtYksxXVvCwhSXM119/Pdu32GKLRx55hCmts88+m9xz2mmnJQdiXTOLdZ599tmwhV0MFF1yySWnnnoqWYflz2xnWIigwwJnnm//v1c/obJ/FVBAAQUUUKD7Asad7lu9ruZ1113HmA0PTD3zzDMEF/bxHsmamprddtuNNTc8UdXc3MxGBmZYhcNyZh62uvPOO/fcc8/kKHvssccZZ5wxduzYsIU1zkuWLDn88MMvv/zyZLHzggULiESs++GxLx7sYu4saW5BAQUUUEABBbop4FLlbkKVViPW3HHHHWxl3IVpJgrDhg0LIzpxVUIPC5apwzhNyVTUueeeG9ekzGKgsCVZr8P8F5/p06cTg0oq+1UBBRRQQAEFuing6E43obquxhsFmWziWfHly5d3rkEMevjhh//4xz8yS8XbdDpXWOcWprEY/nnooYe6uVRonQe0ggIKKKCAAhuggKM76W86EeT0009n3opnrxja6Xwg3rXDm3Kqq6sp8GRW5wrr3MJyHRIPz2ets6YVFFBAAQUUUKCcgL+IXk6m7PaB8KtV3fyBrbLX4A4FFFBAAQV6QcBfRO8FVA+pgAIKKKCAAgp0Q8DJrG4gvb6KIyuv9/CbAgoooIACA13ApcoD/Q7ZPwUUUEABBRRYTwHjznoC2lwBBRRQQAEFBrqAcWeg3yH7p4ACCiiggALrKWDcWU9AmyuggAIKKKDAQBcw7gz0O2T/FFCgtwUaGxt7+xQeXwEF+lfAuNO//p5dAQX6X2DWrFnt7e393w97oIACvSbgg+i9RuuBFVAgIwInnnhiRnpqNxVQIKWAozsp4WymgAIKKKCAAlkRMO5k5U7ZTwUUUEABBRRIKWDcSQlnMwUUUEABBRTIioBxJyt3yn4qoIACCiigQEoB405KOJspoIACCiigQFYEjDtZuVP2UwEFFFBAAQVSChh3UsLZTAEFFFBAAQWyImDcycqdsp8KKKCAAgookFLAuJMSzmYKKKCAAgookBUB405W7pT9VEABBRRQQIGUAsadlHA2U0ABBRRQQIGsCBh3snKn7KcCCiiggAIKpBQw7qSEs5kCCiiggAIKZEXAuJOVO2U/FVBAAQUUUCClgHEnJZzNFFBAAQUUUCArAsadrNwp+6mAAgoooIACKQWMOynhbKaAAgoooIACWREw7mTlTtlPBRRQQAEFFEgpYNxJCWczBRRQQAEFFMiKgHEnK3fKfiqggAIKKKBASgHjTko4mymggAIKKKBAVgSMO1m5U/ZTAQUUUEABBVIKGHdSwtlMAQUUUEABBbIiYNzJyp2ynwoooIACCiiQUsC4kxLOZgoooIACCiiQFQHjTlbulP1UQAEFFFBAgZQCxp2UcDZTQAEFFFBAgawIGHeycqfspwIKKKCAAgqkFDDupISzmQIKKKCAAgpkRcC4k5U7ZT8VUEABBRRQIKWAcSclnM0UUEABBRRQICsCxp2s3Cn7qYACCiiggAIpBYw7KeFspoACCiiggAJZETDuZOVO2U8FFFBAAQUUSClg3EkJZzMFFFBAAQUUyIqAcScrd8p+KqCAAgoooEBKAeNOSjibKaCAAgoooEBWBIw7WblT9lMBBRRQQAEFUgoYd1LC2UwBBRRQQAEFsiJg3MnKnbKfCiiggAIKKJBSwLiTEs5mCiiggAIKKJAVAeNOVu6U/VRAAQUUUECBlALGnZRwNlNAAQUUUECBrAgYd7Jyp+ynAgoooIACCqQUMO6khLOZAgoooIACCmRFwLiTlTtlPxVQQAEFFFAgpYBxJyWczRRQQAEFFFAgKwLGnazcKfupgAIKKKCAAikFjDsp4WymgAIKKKCAAlkRMO5k5U7ZTwUUUCAbAmsWrgkdXXXpqmz02F5uAALGnQ3gJnuJCiigQB8KJHGnD8/pqRRYh0BxHfvdrYACCiigQHmBtrq2+tvr25vaC1WF2qm1jYsaKdfNqht67FAaNdzd0LKspX1Ne82+NZUTKinUz62nSUVrRc2BNcWtOv4NYhCIXcVRxerJ1eXP4x4F1kvAuLNefDZWQAEFNnCBhnkNVROrqiZVNS1uapjfMGTakMYHGkPWIdMUagvDjh/Wury17oa6ERNGUKF69+ri1sW21W11N9UNP3l4h15rBUeoHFe5gUt6+b0qYNzpVV4ProACCuRcoOVvLUMOG8JFElka7mqIr7a9vb16544Bm0GbDmpvbKfQ/HRz64rWUKe9ub2CbYWO/yq3M+vEcpZ7XsC40/OmHlEBBRTYgAQ6YkzXn8KgQmEwcSb6tFUMPWZooVgg6LQ819KRdfiwiPT1taIGFhXoGQGXKveMo0dRQAEFNkyB4thi0xNNXDt/i9u++v9CE4BCBuoUYoqji81LmqncvLR5zYLXHuDaMN286j4WcHSnj8E9nQIKKJArgZoDaliq3PhQY6GyUHtYLddWHFNkXc7Q6R1LlUs+NVNq6ufUs5yZEZ0hh3ZMgflRoG8ECsyt9s2ZPIsCCiigQBYFVs5YmcVuZ6XPIy8YmZWudqef99xzz3777UfNuXPnHnTQQd1p0jd1nMzqG2fPooACCiiggAL9JuBkVr/Re2IFFFAgQwI5G4QYCPIOm/XlXXB0py+1PZcCCiiggAIK9IOAcacf0D2lAgoooIACCvSlgJNZfantuRRQQIEMCzQ1Nf3lL395y1veUl39ul97+Pe///2Pf/xj9OjRm2yyCZf38ssv//73v//mN7+51VZb8fX555+fPn36u971LirU1NSw5bnnnuMpmTFjxlBes2bN0qVLw9cRI0awpeSzatWqv//9783NzY2NjYVCoba2trKycocddqAc12xpaaFvra2t9fX11CkWi9tvv/2gQYOSOq+88srTTz9ND7fZZptkIwUOvmLFisGDB1Ofrm699dZs5Dgcra2tjY4l18s1brHFFuGYnIWGf/jDHy677DJ6ctFFF02YMGHs2LFVVVXxwf/1r3+9+OKLG2302sgCR0Ng3LhxcR3LfSSAvh8FFFBAAQXKCay4aAX/sfeZZ57hX6aPf/zjX/jCF84777yvfe1rxJrPf/7z++yzD9uvueYa6hBKDjnkEL5eeOGF4YB//vOft912W7YQDsKWY445Zsstt/zrX//K1wsuuIBdfD74wQ8SMthy1113XXHFFaEmIeaII45g77vf/e6vfvWrX/rSl4YMGUK8uOmmm0KF5O+1115LtTe96U2XXHIJmYY6p556KqdOKtx9991U2HHHHT/3uc/x0BD1zz///EceeYSYwnayF+HmhBNOCPVXrlzJidjOJ7mQo48++oc//GGo8JnPfCbsjf9+5StfSU5HgRS1xx57xBUob7755uhx/I4K/4WNW2W9HJy5UpAH1LVUDKje2BkFFFBAgYEmkPyr/Ktf/Sr+x5tBi6FD//dynRB3Pvaxj4U6DHgkF/LpT3+ajfvuu2/YQqrg66RJk0geoTJ/ORqjQbTaeOON3/72t4eap512Wqjwve99jy2M8YwaNYot73vf+8hVoQ5/r7rqqjCCMnv2bL7+/Oc/D62S2MTGyZMnh438DUNEFIYNGxY20vD73/8+ZYZeuEySTdjOX0aSHnjggW9961uUTzzxRA4Vynw98MADCS4/+tGPwnDXTjvttHz5ciqEz8EHHxwOwoAQcY3xrWREiuEu6iSw/22Rh/87YOOOk1nhf43+VUABBRRYh8Cll15KDYZDGJ8gefCPMyMiYXKHrwcccMCTTz45Z86czkehIRNYt9xyy2233Xb44YeHCk888cTjjz9O8khCwEsvvcRQCmM8yRYmjKj85je/mSElCkxRnXTSSTNmzGDk4BOf+ARjLWwkbZx++ul0hkEmEhVbeO8LH/7dPffcczfbbLMPf/jDbGTGjb+EnrPPPpupqBtuuOEjH/kI56L/jCG9853vfOGFF6jMhBcxhfkyEgzHZP6OIaI999yTMs3Z/p///OcHP/gBZT6kMcLZ8ccfjwNJiCs66qij6Bttef3M7373O+qQgS6++OJDDz2Us5DDnn32WfR+85vfPPjgg+Mrxr96GP/0hUCxL07iORRQQAEF8iIwa9asXXbZpcurIc2wWqXzLoZAmKIiE3zoQx9iBQxphmGh+fPnv+1tbyNPxPUZbiEc/OQnP2HjU089RR5iIGTZsmW0DeM3DP/86U9/uv322xcsWBAaMvQSsgjBYvjw4WwkgvzsZz8bP34852UGLcSdUIej8aEOf0la4QjhLxNkRCIGlmh45plnNjQ0sNyHjazIYcKOlT2swmFpDkNTTIHRhDIDNqHtRz/6UaIe63iIOAQdXq/32GOP1dXVsZfz7r333uQkPsceeyxbIJo5cyZrg4w7Qa9v/m7UN6fxLAoooIAC+RBgcXG5C9lrr73IByygoQJDL0uWLKHAv/dkFGZ5KDMDRaRgWQyjIKxrIXAQTeLP6tWrr7/+ehYOU5k1wuQqhnwYg+Fr8omXAxOJbr311mRXUkgGjULmYDvdYHAoZB2+lmQdtpBdSDYMGt18883MPU2ZMoVlQzfeeCNrhlhDTeKhDl0lA1Ho/Al9JpYx78beZJqPGPTe976XoS/iXWhF/CK6lVxU5wO6pWcFHN3pWU+PpoACCuRcgBGas846i6kZrpMAEUYvmAziK0GHVS8s+2W1MiuR3//+97Okl9EXZo4SlFNOOYWRHlolW5ICAx7MTNEwrOk555xzfvrTn7KXyawwtJPUTAqkqC7Hk5IKHJApp912240j0Ge6xNwTIzeslWZIJqlGgQfKmP8i8cQbkzKTcSQkcluYL0u2lyswCHT11VczY0UFRnr4LFq06Itf/CKpiCktYtPOO+9c8bdyrd3e8wLGnZ439YgKKKBALgW++93vkglIKqx9YXnKN77xjV//+tdsIeWwVoYVLWHlLytdWKYTVhl//etfZxKHaSYGOULECX+T1TkBiqU/n/rUp8gBLKBhwc2Xv/xlqjGy0pmR6a2FCxeynUEmltGUi0Fxw3BGlhzxEDhzZ0wkcTo6ySPu3/nOd+gei354bL5zjqEyo0eM6/BIGiHs29/+Nodl/CY++FrKTIqFuBPqcLqwZJuvDPYQd1bOXrmW5u7qWQHjTs96ejQFFFAgtwLMLsXXRhxh4olhDOabmABiyuaTn/xkqPCe97yHXJJUJsTw0p0wIMQD58n2pHDGGWfwZDgJgKATBl3KpYqJEycyZUacYhUzwWXq1KnJQdZeKHmsjMp33nknByG60dUjjzySCFJyBPJc8uwYo0QMC5VUWPtXHnpfewX39qWAa3f6UttzKaCAArkSYA6LHPOGLonppLg+oz4MDt17771M9/z2t79NJpgYtgkPgsWVQ7mnYsT+++8flhlxWB6qKjkR7+9Jsg5zWEnWufzyy0tqdvmVeMTUFQ/nM6hDc1Y6x9VYx8Oy7niL5d4WMO70trDHV0ABBfIgQCL5wAc+wFLf8HB4uCRWDbN8J5TD/BQZhRW+PLsUD88w8RRmlKhfMv3EDBHrb0gbTPQkb/YLB+TlOqy56WxHeuARJypPmzaNASdGkkKdkoe8kobUJFuwOJp3AjGWk2yPC7yhJ/7KuA6Pi4ctLEU67rjjkr2bbrppUu6yENYs845BXq7IcBfLnHmVIo9r7brrruwKz+3TkKGpLpu7sZcEjDu9BOthFVBAgVwJ8EIappB48IqHp5ILY2Fv+NUFtrAyhukh3rb8i1/8gse5eSo7qcai4/AgEutgwhuWk133339/KN93332sIE62U+DlyF3+3sK8efN4Govfc2BJEAEivBaZ+tddd128ViYc6uSTT6Yay6VZGMTUW/L4enyizmXqJxsJVayVTr6OHDnyrW99a/K1pMCSpi4HpVgZTV5kpCeZ7+MJ+ZK2fu1VAeNOr/J6cAUUUCBvAuGRcq6KlcK8IIcHjsIV8pA5Ay3JXBVrcR5++GGW9fDC4jvuuIM6LM0JbwvsUoRwk4x8JBV47x+BhmXCV155JeuLOQVZh4e/GKRhV6jGOwaTCBWWBzHMw6t6KPM0OA+RJUcjchGJkq9xocsfhQgVCExxTUZ3fvnLXxJfOAsTXryMhzcJgUCWYuCKnnBSchtLhch//AgXFUJzvhKGwqt32ML1xoe13NsCLlXubWGPr4ACCuRB4B3veAcDKjz1zcwOLybmn3YexXr00UfDtRECqEBeYc0yPx31z3/+k2ARv42QNwryKmGOUM6C6ND5XTjM+JCQeGsfZ2ToiLYMAjG8xPIdhprCoVi8TJzi9xyIOGQOBmZ4DzKPXLGXBTcM7cRn5FVAPISVTHvxWFnYW1ItbtK5zPQWU29M6vGKHY6WVOB1ggzh8JWZO1bn8AZnfo50u+22ozKP3zMixRNeSX2ut+KZpKmF3hfgrvhRQAEFFFCgnEDy005MPJFpwtqUkn+dWNMTN2exDstxiD48jM3PPlBmnCOukJQJMSQhjvbjH/842VhS4LyMDBFr+H1Ncgkflu+U1Fm8ePHuu+/O5BqjJgyisJCIZT2Ej1CNQSam4ZJfyCrpPCNSDPzEByQw0fNQjTXU8a64HB5ND9XoG/2M97LUKeyiM0yHxWGOrjIClMDGrbJeHrC/mVVAtuTG+1UBBRRQQIFEYOWMjtfDjLxgZNhCLmGCJp54YlUyT1SxqCVp8kYLDMbw8htyzNob8ugWuYd39JWrxuATM19Lly5lxo33I5ckMwaBWEPNi3bi5syRkbdYFh1vpExEY9KKy2SIqNzyZNYzsSSIA3IQ+l/y++f0IcxwcTSm4agWlmkzy8aQD4++l8CWdCCjX1mUzUuY6Dy/Hcaw3MC5CuPOwLkX9kQBBRQYiALhX+WB2LNc9CnJkbm4mooBG3dcu5OP/4F5FQoooIACCvS/AEN0/IgsE0eMw/V/b6IeOLoTYVhUQAEFFFBAgTwK+CB6Hu+q16SAAgoooIACkYBxJ8KwqIACCiiggAJ5FDDu5PGuek0KKKCAAgooEAkYdyIMiwoooIACCiiQRwHjTh7vqtekgAIKKKCAApGAcSfCsKiAAgoooIACeRQw7uTxrnpNCiiggAIKKBAJGHciDIsKKKCAAgookEcB404e76rXpIACCiiggAKRgHEnwrCogAIKKKCAAnkUMO7k8a56TQoooIACCigQCRh3IgyLCiiggAIKKJBHAeNOHu+q16SAAgoooIACkYBxJ8KwqIACCiiggAJ5FDDu5PGuek0KKKCAAgooEAkYdyIMiwoooIACCiiQRwHjTh7vqtekgAIKKKCAApGAcSfCsKiAAgoooIACeRQw7uTxrnpNCiiggAIKKBAJGHciDIsKKKCAAgookEcB404e76rXpIACCiiggAKRgHEnwrCogAIKKKCAAnkUMO7k8a56TQoooIACCigQCRh3IgyLCiiggAIKKJBHAeNOHu+q16SAAgoooIACkYBxJ8KwqIACCiiggAJ5FDDu5PGuek0KKKCAAgooEAkYdyIMiwoooIACCiiQRwHjTh7vqtekgAIKKKCAApGAcSfCsKiAAgoooIACeRQw7uTxrnpNCiiggAIKKBAJGHciDIsKKKCAAgookEcB404e76rXpIACCiiggAKRgHEnwrCogAIKKKCAAnkUMO7k8a56TQoooIACCigQCRh3IgyLCiiggAIKKJBHAeNOHu+q16SAAgoooIACkYBxJ8KwqIACCiiggAJ5FDDu5PGuek0KKKCAAgooEAkYdyIMiwoooIACCiiQRwHjTh7vqtekgAIKKKCAApGAcSfCsKiAAgoooIACeRQw7uTxrnpNCiiggAIKKBAJGHciDIsKKKCAAgookEcB404e76rXpIACCiiggAKRgHEnwrCogAIKKKCAAnkUMO7k8a56TQoooIACCigQCRh3IgyLCiiggAIKKJBHAeNOHu+q16SAAgoooIACkYBxJ8KwqIACCiiggAJ5FDDu5PGuek0KKKCAAgooEAkYdyIMiwoooIACCiiQRwHjTh7vqtekgAIKKKCAApGAcSfCsKiAAgoooIACeRQw7uTxrnpNCiiggAIKKBAJGHciDIsKKKCAAgookEcB404e76rXpIACCiiggAKRgHEnwrCogAIKKKCAAnkUMO7k8a56TQoooIACCigQCRh3IgyLCiiggAIKKJBHAeNOHu+q16SAAgoooIACkYBxJ8KwqIACCiiggAJ5FDDu5PGuek0KKKCAAgooEAkYdyIMiwoooIACCiiQRwHjTh7vqtekgAIKKKCAApGAcSfCsKiAAgoooIACeRQw7uTxrnpNCiiggAIKKBAJGHciDIsKKKCAAgookEcB404e76rXpIACCiiggAKRgHEnwrCogAIKKKCAAnkUMO7k8a56TQoooIACCigQCRh3IgyLCiiggAIKKJBHgf8H+0r8wwOE6jAAAAAASUVORK5CYII=",
+ "text/plain": [
+ ""
+ ]
+ },
+ "execution_count": 7,
+ "metadata": {},
+ "output_type": "execute_result"
+ }
+ ],
+ "source": [
+ "draw = ImageDraw.Draw(image, \"RGBA\")\n",
+ "\n",
+ "font = ImageFont.load_default()\n",
+ "\n",
+ "label2color = {\"question\": \"blue\", \"answer\": \"green\", \"header\": \"orange\", \"other\": \"violet\"}\n",
+ "\n",
+ "for annotation in data[\"form\"]:\n",
+ " label = annotation[\"label\"]\n",
+ " general_box = annotation[\"box\"]\n",
+ " draw.rectangle(general_box, outline=label2color[label], width=2)\n",
+ " draw.text((general_box[0] + 10, general_box[1] - 10), label, fill=label2color[label], font=font)\n",
+ " words = annotation[\"words\"]\n",
+ " for word in words:\n",
+ " box = word[\"box\"]\n",
+ " draw.rectangle(box, outline=label2color[label], width=1)\n",
+ "\n",
+ "image"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "uyWQNLSCRJN7"
+ },
+ "source": [
+ "## Preprocessing the data\n",
+ "\n",
+ "Next, we need to turn the document images into individual tokens and corresponding labels (BIOES format, see further). We do this both for the training and test datasets. Make sure to run this from the `/content` directory:"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "colab": {
+ "base_uri": "https://localhost:8080/"
+ },
+ "id": "4DWRyOR9RuY6",
+ "outputId": "4215a24b-8049-4b1a-a23f-5aaa48e14083"
+ },
+ "outputs": [],
+ "source": [
+ "! python unilm/layoutlm/deprecated/examples/seq_labeling/preprocess.py --data_dir data/training_data/annotations \\\n",
+ " --data_split train \\\n",
+ " --output_dir data \\\n",
+ " --model_name_or_path microsoft/layoutlm-base-uncased \\\n",
+ " --max_len 510\n",
+ "\n",
+ "! python unilm/layoutlm/deprecated/examples/seq_labeling/preprocess.py --data_dir data/testing_data/annotations \\\n",
+ " --data_split test \\\n",
+ " --output_dir data \\\n",
+ " --model_name_or_path microsoft/layoutlm-base-uncased \\\n",
+ " --max_len 510"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "gc4Cu0ZyO5M_"
+ },
+ "source": [
+ "Next, we create a labels.txt file that contains the unique labels of the FUNSD dataset:"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "id": "8iGOU0s3UR2u"
+ },
+ "outputs": [],
+ "source": [
+ "! cat data/train.txt | cut -d$'\\t' -f 2 | grep -v \"^$\"| sort | uniq > data/labels.txt"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "mC9FhkG9U8yg"
+ },
+ "source": [
+ "## Define a PyTorch dataset\n",
+ "\n",
+ "First, we create a list containing the unique labels based on `data/labels.txt` (run this from the content directory):"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 19,
+ "metadata": {
+ "id": "675rRa0QXnMp"
+ },
+ "outputs": [],
+ "source": [
+ "from torch.nn import CrossEntropyLoss\n",
+ "\n",
+ "\n",
+ "def get_labels(path):\n",
+ " with open(path, \"r\") as f:\n",
+ " labels = f.read().splitlines()\n",
+ " if \"O\" not in labels:\n",
+ " labels = [\"O\"] + labels\n",
+ " return labels\n",
+ "\n",
+ "\n",
+ "labels = get_labels(\"data/labels.txt\")\n",
+ "num_labels = len(labels)\n",
+ "label_map = {i: label for i, label in enumerate(labels)}\n",
+ "# Use cross entropy ignore index as padding label id so that only real label ids contribute to the loss later\n",
+ "pad_token_label_id = CrossEntropyLoss().ignore_index"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "kZ2LGEsez2u2"
+ },
+ "source": [
+ "We can see that the dataset uses the so-called BIOES annotation scheme to annotate the tokens. This means that a given token can be either at the beginning (B), inside (I), outside (O), at the end (E) or start (S) of a given entity. Entities include ANSWER, QUESTION, HEADER and OTHER: "
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 20,
+ "metadata": {
+ "colab": {
+ "base_uri": "https://localhost:8080/"
+ },
+ "id": "_-qXLkP9Yq_L",
+ "outputId": "32ab46a4-4cf0-400c-816b-570f950035ec"
+ },
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "['B-ANSWER', 'B-HEADER', 'B-QUESTION', 'E-ANSWER', 'E-HEADER', 'E-QUESTION', 'I-ANSWER', 'I-HEADER', 'I-QUESTION', 'O', 'S-ANSWER', 'S-HEADER', 'S-QUESTION']\n"
+ ]
+ }
+ ],
+ "source": [
+ "print(labels)"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "9_ck0ZFfZInR"
+ },
+ "source": [
+ "Next, we can create a PyTorch dataset and corresponding dataloader (both for training and evaluation):"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 21,
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "import logging\n",
+ "import os\n",
+ "\n",
+ "import torch\n",
+ "from torch.utils.data import Dataset\n",
+ "\n",
+ "logger = logging.getLogger(__name__)\n",
+ "\n",
+ "\n",
+ "class FunsdDataset(Dataset):\n",
+ " def __init__(self, args, tokenizer, labels, pad_token_label_id, mode):\n",
+ " if args.local_rank not in [-1, 0] and mode == \"train\":\n",
+ " torch.distributed.barrier() # Make sure only the first process in distributed training process the dataset, and the others will use the cache\n",
+ "\n",
+ " # Load data features from cache or dataset file\n",
+ " cached_features_file = os.path.join(\n",
+ " args.data_dir,\n",
+ " \"cached_{}_{}_{}\".format(\n",
+ " mode,\n",
+ " list(filter(None, args.model_name_or_path.split(\"/\"))).pop(),\n",
+ " str(args.max_seq_length),\n",
+ " ),\n",
+ " )\n",
+ " if os.path.exists(cached_features_file) and not args.overwrite_cache:\n",
+ " logger.info(\"Loading features from cached file %s\", cached_features_file)\n",
+ " features = torch.load(cached_features_file)\n",
+ " else:\n",
+ " logger.info(\"Creating features from dataset file at %s\", args.data_dir)\n",
+ " examples = read_examples_from_file(args.data_dir, mode)\n",
+ " features = convert_examples_to_features(\n",
+ " examples,\n",
+ " labels,\n",
+ " args.max_seq_length,\n",
+ " tokenizer,\n",
+ " cls_token_at_end=bool(args.model_type in [\"xlnet\"]),\n",
+ " # xlnet has a cls token at the end\n",
+ " cls_token=tokenizer.cls_token,\n",
+ " cls_token_segment_id=2 if args.model_type in [\"xlnet\"] else 0,\n",
+ " sep_token=tokenizer.sep_token,\n",
+ " sep_token_extra=bool(args.model_type in [\"roberta\"]),\n",
+ " # roberta uses an extra separator b/w pairs of sentences, cf. github.com/pytorch/fairseq/commit/1684e166e3da03f5b600dbb7855cb98ddfcd0805\n",
+ " pad_on_left=bool(args.model_type in [\"xlnet\"]),\n",
+ " # pad on the left for xlnet\n",
+ " pad_token=tokenizer.convert_tokens_to_ids([tokenizer.pad_token])[0],\n",
+ " pad_token_segment_id=4 if args.model_type in [\"xlnet\"] else 0,\n",
+ " pad_token_label_id=pad_token_label_id,\n",
+ " )\n",
+ " # if args.local_rank in [-1, 0]:\n",
+ " # logger.info(\"Saving features into cached file %s\", cached_features_file)\n",
+ " # torch.save(features, cached_features_file)\n",
+ "\n",
+ " if args.local_rank == 0 and mode == \"train\":\n",
+ " torch.distributed.barrier() # Make sure only the first process in distributed training process the dataset, and the others will use the cache\n",
+ "\n",
+ " self.features = features\n",
+ " # Convert to Tensors and build dataset\n",
+ " self.all_input_ids = torch.tensor([f.input_ids for f in features], dtype=torch.long)\n",
+ " self.all_input_mask = torch.tensor([f.input_mask for f in features], dtype=torch.long)\n",
+ " self.all_segment_ids = torch.tensor([f.segment_ids for f in features], dtype=torch.long)\n",
+ " self.all_label_ids = torch.tensor([f.label_ids for f in features], dtype=torch.long)\n",
+ " self.all_bboxes = torch.tensor([f.boxes for f in features], dtype=torch.long)\n",
+ "\n",
+ " def __len__(self):\n",
+ " return len(self.features)\n",
+ "\n",
+ " def __getitem__(self, index):\n",
+ " return (\n",
+ " self.all_input_ids[index],\n",
+ " self.all_input_mask[index],\n",
+ " self.all_segment_ids[index],\n",
+ " self.all_label_ids[index],\n",
+ " self.all_bboxes[index],\n",
+ " )\n",
+ "\n",
+ "\n",
+ "class InputExample(object):\n",
+ " \"\"\"A single training/test example for token classification.\"\"\"\n",
+ "\n",
+ " def __init__(self, guid, words, labels, boxes, actual_bboxes, file_name, page_size):\n",
+ " \"\"\"Constructs a InputExample.\n",
+ "\n",
+ " Args:\n",
+ " guid: Unique id for the example.\n",
+ " words: list. The words of the sequence.\n",
+ " labels: (Optional) list. The labels for each word of the sequence. This should be\n",
+ " specified for train and dev examples, but not for test examples.\n",
+ " \"\"\"\n",
+ " self.guid = guid\n",
+ " self.words = words\n",
+ " self.labels = labels\n",
+ " self.boxes = boxes\n",
+ " self.actual_bboxes = actual_bboxes\n",
+ " self.file_name = file_name\n",
+ " self.page_size = page_size\n",
+ "\n",
+ "\n",
+ "class InputFeatures(object):\n",
+ " \"\"\"A single set of features of data.\"\"\"\n",
+ "\n",
+ " def __init__(\n",
+ " self,\n",
+ " input_ids,\n",
+ " input_mask,\n",
+ " segment_ids,\n",
+ " label_ids,\n",
+ " boxes,\n",
+ " actual_bboxes,\n",
+ " file_name,\n",
+ " page_size,\n",
+ " ):\n",
+ " assert (\n",
+ " 0 <= all(boxes) <= 1000\n",
+ " ), \"Error with input bbox ({}): the coordinate value is not between 0 and 1000\".format(boxes)\n",
+ " self.input_ids = input_ids\n",
+ " self.input_mask = input_mask\n",
+ " self.segment_ids = segment_ids\n",
+ " self.label_ids = label_ids\n",
+ " self.boxes = boxes\n",
+ " self.actual_bboxes = actual_bboxes\n",
+ " self.file_name = file_name\n",
+ " self.page_size = page_size\n",
+ "\n",
+ "\n",
+ "def read_examples_from_file(data_dir, mode):\n",
+ " file_path = os.path.join(data_dir, \"{}.txt\".format(mode))\n",
+ " box_file_path = os.path.join(data_dir, \"{}_box.txt\".format(mode))\n",
+ " image_file_path = os.path.join(data_dir, \"{}_image.txt\".format(mode))\n",
+ " guid_index = 1\n",
+ " examples = []\n",
+ " with open(file_path, encoding=\"utf-8\") as f, open(box_file_path, encoding=\"utf-8\") as fb, open(\n",
+ " image_file_path, encoding=\"utf-8\"\n",
+ " ) as fi:\n",
+ " words = []\n",
+ " boxes = []\n",
+ " actual_bboxes = []\n",
+ " file_name = None\n",
+ " page_size = None\n",
+ " labels = []\n",
+ " for line, bline, iline in zip(f, fb, fi):\n",
+ " if line.startswith(\"-DOCSTART-\") or line == \"\" or line == \"\\n\":\n",
+ " if words:\n",
+ " examples.append(\n",
+ " InputExample(\n",
+ " guid=\"{}-{}\".format(mode, guid_index),\n",
+ " words=words,\n",
+ " labels=labels,\n",
+ " boxes=boxes,\n",
+ " actual_bboxes=actual_bboxes,\n",
+ " file_name=file_name,\n",
+ " page_size=page_size,\n",
+ " )\n",
+ " )\n",
+ " guid_index += 1\n",
+ " words = []\n",
+ " boxes = []\n",
+ " actual_bboxes = []\n",
+ " file_name = None\n",
+ " page_size = None\n",
+ " labels = []\n",
+ " else:\n",
+ " splits = line.split(\"\\t\")\n",
+ " bsplits = bline.split(\"\\t\")\n",
+ " isplits = iline.split(\"\\t\")\n",
+ " assert len(splits) == 2\n",
+ " assert len(bsplits) == 2\n",
+ " assert len(isplits) == 4\n",
+ " assert splits[0] == bsplits[0]\n",
+ " words.append(splits[0])\n",
+ " if len(splits) > 1:\n",
+ " labels.append(splits[-1].replace(\"\\n\", \"\"))\n",
+ " box = bsplits[-1].replace(\"\\n\", \"\")\n",
+ " box = [int(b) for b in box.split()]\n",
+ " boxes.append(box)\n",
+ " actual_bbox = [int(b) for b in isplits[1].split()]\n",
+ " actual_bboxes.append(actual_bbox)\n",
+ " page_size = [int(i) for i in isplits[2].split()]\n",
+ " file_name = isplits[3].strip()\n",
+ " else:\n",
+ " # Examples could have no label for mode = \"test\"\n",
+ " labels.append(\"O\")\n",
+ " if words:\n",
+ " examples.append(\n",
+ " InputExample(\n",
+ " guid=\"%s-%d\".format(mode, guid_index),\n",
+ " words=words,\n",
+ " labels=labels,\n",
+ " boxes=boxes,\n",
+ " actual_bboxes=actual_bboxes,\n",
+ " file_name=file_name,\n",
+ " page_size=page_size,\n",
+ " )\n",
+ " )\n",
+ " return examples\n",
+ "\n",
+ "\n",
+ "def convert_examples_to_features(\n",
+ " examples,\n",
+ " label_list,\n",
+ " max_seq_length,\n",
+ " tokenizer,\n",
+ " cls_token_at_end=False,\n",
+ " cls_token=\"[CLS]\",\n",
+ " cls_token_segment_id=1,\n",
+ " sep_token=\"[SEP]\",\n",
+ " sep_token_extra=False,\n",
+ " pad_on_left=False,\n",
+ " pad_token=0,\n",
+ " cls_token_box=[0, 0, 0, 0],\n",
+ " sep_token_box=[1000, 1000, 1000, 1000],\n",
+ " pad_token_box=[0, 0, 0, 0],\n",
+ " pad_token_segment_id=0,\n",
+ " pad_token_label_id=-1,\n",
+ " sequence_a_segment_id=0,\n",
+ " mask_padding_with_zero=True,\n",
+ "):\n",
+ " \"\"\"Loads a data file into a list of `InputBatch`s\n",
+ " `cls_token_at_end` define the location of the CLS token:\n",
+ " - False (Default, BERT/XLM pattern): [CLS] + A + [SEP] + B + [SEP]\n",
+ " - True (XLNet/GPT pattern): A + [SEP] + B + [SEP] + [CLS]\n",
+ " `cls_token_segment_id` define the segment id associated to the CLS token (0 for BERT, 2 for XLNet)\n",
+ " \"\"\"\n",
+ "\n",
+ " label_map = {label: i for i, label in enumerate(label_list)}\n",
+ "\n",
+ " features = []\n",
+ " for ex_index, example in enumerate(examples):\n",
+ " file_name = example.file_name\n",
+ " page_size = example.page_size\n",
+ " width, height = page_size\n",
+ " if ex_index % 10000 == 0:\n",
+ " logger.info(\"Writing example %d of %d\", ex_index, len(examples))\n",
+ "\n",
+ " tokens = []\n",
+ " token_boxes = []\n",
+ " actual_bboxes = []\n",
+ " label_ids = []\n",
+ " for word, label, box, actual_bbox in zip(example.words, example.labels, example.boxes, example.actual_bboxes):\n",
+ " word_tokens = tokenizer.tokenize(word)\n",
+ " tokens.extend(word_tokens)\n",
+ " token_boxes.extend([box] * len(word_tokens))\n",
+ " actual_bboxes.extend([actual_bbox] * len(word_tokens))\n",
+ " # Use the real label id for the first token of the word, and padding ids for the remaining tokens\n",
+ " label_ids.extend([label_map[label]] + [pad_token_label_id] * (len(word_tokens) - 1))\n",
+ "\n",
+ " # Account for [CLS] and [SEP] with \"- 2\" and with \"- 3\" for RoBERTa.\n",
+ " special_tokens_count = 3 if sep_token_extra else 2\n",
+ " if len(tokens) > max_seq_length - special_tokens_count:\n",
+ " tokens = tokens[: (max_seq_length - special_tokens_count)]\n",
+ " token_boxes = token_boxes[: (max_seq_length - special_tokens_count)]\n",
+ " actual_bboxes = actual_bboxes[: (max_seq_length - special_tokens_count)]\n",
+ " label_ids = label_ids[: (max_seq_length - special_tokens_count)]\n",
+ "\n",
+ " # The convention in BERT is:\n",
+ " # (a) For sequence pairs:\n",
+ " # tokens: [CLS] is this jack ##son ##ville ? [SEP] no it is not . [SEP]\n",
+ " # type_ids: 0 0 0 0 0 0 0 0 1 1 1 1 1 1\n",
+ " # (b) For single sequences:\n",
+ " # tokens: [CLS] the dog is hairy . [SEP]\n",
+ " # type_ids: 0 0 0 0 0 0 0\n",
+ " #\n",
+ " # Where \"type_ids\" are used to indicate whether this is the first\n",
+ " # sequence or the second sequence. The embedding vectors for `type=0` and\n",
+ " # `type=1` were learned during pre-training and are added to the wordpiece\n",
+ " # embedding vector (and position vector). This is not *strictly* necessary\n",
+ " # since the [SEP] token unambiguously separates the sequences, but it makes\n",
+ " # it easier for the model to learn the concept of sequences.\n",
+ " #\n",
+ " # For classification tasks, the first vector (corresponding to [CLS]) is\n",
+ " # used as as the \"sentence vector\". Note that this only makes sense because\n",
+ " # the entire model is fine-tuned.\n",
+ " tokens += [sep_token]\n",
+ " token_boxes += [sep_token_box]\n",
+ " actual_bboxes += [[0, 0, width, height]]\n",
+ " label_ids += [pad_token_label_id]\n",
+ " if sep_token_extra:\n",
+ " # roberta uses an extra separator b/w pairs of sentences\n",
+ " tokens += [sep_token]\n",
+ " token_boxes += [sep_token_box]\n",
+ " actual_bboxes += [[0, 0, width, height]]\n",
+ " label_ids += [pad_token_label_id]\n",
+ " segment_ids = [sequence_a_segment_id] * len(tokens)\n",
+ "\n",
+ " if cls_token_at_end:\n",
+ " tokens += [cls_token]\n",
+ " token_boxes += [cls_token_box]\n",
+ " actual_bboxes += [[0, 0, width, height]]\n",
+ " label_ids += [pad_token_label_id]\n",
+ " segment_ids += [cls_token_segment_id]\n",
+ " else:\n",
+ " tokens = [cls_token] + tokens\n",
+ " token_boxes = [cls_token_box] + token_boxes\n",
+ " actual_bboxes = [[0, 0, width, height]] + actual_bboxes\n",
+ " label_ids = [pad_token_label_id] + label_ids\n",
+ " segment_ids = [cls_token_segment_id] + segment_ids\n",
+ "\n",
+ " input_ids = tokenizer.convert_tokens_to_ids(tokens)\n",
+ "\n",
+ " # The mask has 1 for real tokens and 0 for padding tokens. Only real\n",
+ " # tokens are attended to.\n",
+ " input_mask = [1 if mask_padding_with_zero else 0] * len(input_ids)\n",
+ "\n",
+ " # Zero-pad up to the sequence length.\n",
+ " padding_length = max_seq_length - len(input_ids)\n",
+ " if pad_on_left:\n",
+ " input_ids = ([pad_token] * padding_length) + input_ids\n",
+ " input_mask = ([0 if mask_padding_with_zero else 1] * padding_length) + input_mask\n",
+ " segment_ids = ([pad_token_segment_id] * padding_length) + segment_ids\n",
+ " label_ids = ([pad_token_label_id] * padding_length) + label_ids\n",
+ " token_boxes = ([pad_token_box] * padding_length) + token_boxes\n",
+ " else:\n",
+ " input_ids += [pad_token] * padding_length\n",
+ " input_mask += [0 if mask_padding_with_zero else 1] * padding_length\n",
+ " segment_ids += [pad_token_segment_id] * padding_length\n",
+ " label_ids += [pad_token_label_id] * padding_length\n",
+ " token_boxes += [pad_token_box] * padding_length\n",
+ "\n",
+ " assert len(input_ids) == max_seq_length\n",
+ " assert len(input_mask) == max_seq_length\n",
+ " assert len(segment_ids) == max_seq_length\n",
+ " assert len(label_ids) == max_seq_length\n",
+ " assert len(token_boxes) == max_seq_length\n",
+ "\n",
+ " if ex_index < 5:\n",
+ " logger.info(\"*** Example ***\")\n",
+ " logger.info(\"guid: %s\", example.guid)\n",
+ " logger.info(\"tokens: %s\", \" \".join([str(x) for x in tokens]))\n",
+ " logger.info(\"input_ids: %s\", \" \".join([str(x) for x in input_ids]))\n",
+ " logger.info(\"input_mask: %s\", \" \".join([str(x) for x in input_mask]))\n",
+ " logger.info(\"segment_ids: %s\", \" \".join([str(x) for x in segment_ids]))\n",
+ " logger.info(\"label_ids: %s\", \" \".join([str(x) for x in label_ids]))\n",
+ " logger.info(\"boxes: %s\", \" \".join([str(x) for x in token_boxes]))\n",
+ " logger.info(\"actual_bboxes: %s\", \" \".join([str(x) for x in actual_bboxes]))\n",
+ "\n",
+ " features.append(\n",
+ " InputFeatures(\n",
+ " input_ids=input_ids,\n",
+ " input_mask=input_mask,\n",
+ " segment_ids=segment_ids,\n",
+ " label_ids=label_ids,\n",
+ " boxes=token_boxes,\n",
+ " actual_bboxes=actual_bboxes,\n",
+ " file_name=file_name,\n",
+ " page_size=page_size,\n",
+ " )\n",
+ " )\n",
+ " return features"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 23,
+ "metadata": {
+ "id": "HUJftzeBWh2S"
+ },
+ "outputs": [],
+ "source": [
+ "from transformers import LayoutLMTokenizer\n",
+ "\n",
+ "# from .unilm.layoutlm.data.funsd import FunsdDataset, InputFeatures\n",
+ "from torch.utils.data import DataLoader, RandomSampler, SequentialSampler\n",
+ "\n",
+ "batch_size = 16\n",
+ "args = {\n",
+ " \"local_rank\": -1,\n",
+ " \"overwrite_cache\": True,\n",
+ " \"data_dir\": \"data/\",\n",
+ " \"model_name_or_path\": \"microsoft/layoutlm-base-uncased\",\n",
+ " \"max_seq_length\": 512,\n",
+ " \"model_type\": \"layoutlm\",\n",
+ "}\n",
+ "\n",
+ "\n",
+ "# class to turn the keys of a dict into attributes (thanks Stackoverflow)\n",
+ "class AttrDict(dict):\n",
+ " def __init__(self, *args, **kwargs):\n",
+ " super(AttrDict, self).__init__(*args, **kwargs)\n",
+ " self.__dict__ = self\n",
+ "\n",
+ "\n",
+ "args = AttrDict(args)\n",
+ "\n",
+ "tokenizer = LayoutLMTokenizer.from_pretrained(\"microsoft/layoutlm-base-uncased\")\n",
+ "\n",
+ "# the LayoutLM authors already defined a specific FunsdDataset, so we are going to use this here\n",
+ "train_dataset = FunsdDataset(args, tokenizer, labels, pad_token_label_id, mode=\"train\")\n",
+ "train_sampler = RandomSampler(train_dataset)\n",
+ "train_dataloader = DataLoader(train_dataset, sampler=train_sampler, batch_size=batch_size)\n",
+ "\n",
+ "eval_dataset = FunsdDataset(args, tokenizer, labels, pad_token_label_id, mode=\"test\")\n",
+ "eval_sampler = SequentialSampler(eval_dataset)\n",
+ "eval_dataloader = DataLoader(eval_dataset, sampler=eval_sampler, batch_size=batch_size)"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 24,
+ "metadata": {
+ "colab": {
+ "base_uri": "https://localhost:8080/"
+ },
+ "id": "18NMUBzgOdqu",
+ "outputId": "eef47b70-3a9a-4b19-be6b-95900c58337b"
+ },
+ "outputs": [
+ {
+ "data": {
+ "text/plain": [
+ "10"
+ ]
+ },
+ "execution_count": 24,
+ "metadata": {},
+ "output_type": "execute_result"
+ }
+ ],
+ "source": [
+ "len(train_dataloader)"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 25,
+ "metadata": {
+ "colab": {
+ "base_uri": "https://localhost:8080/"
+ },
+ "id": "toFjxtn71B1U",
+ "outputId": "f4651896-cafc-449a-98b4-c81f41177e6d"
+ },
+ "outputs": [
+ {
+ "data": {
+ "text/plain": [
+ "4"
+ ]
+ },
+ "execution_count": 25,
+ "metadata": {},
+ "output_type": "execute_result"
+ }
+ ],
+ "source": [
+ "len(eval_dataloader)"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 26,
+ "metadata": {
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 137
+ },
+ "id": "RhINSBw9I24G",
+ "outputId": "28738ce2-617c-47d3-b8c9-f949d3066d60"
+ },
+ "outputs": [
+ {
+ "data": {
+ "text/plain": [
+ "'[CLS] account agency ss : date 1 / 31 / 88 insert signed 91581919 4th new albany tribune advertisements. bookkeeper mar 08 reco affidavit of performance from newspaper new albany tribune harley davidson cigarettes lorillard media service state of county of indiana ) floyd ) before me a notary public, personally appeared holly inzer who being duly sworn, says that ( he ) ( she ) is of the abovementioned newspaper and that display ads for the above account were made through the aforesaid newspaper during the month of january, 1988 as follows : column inches exclusive advertising for harley davidson cigarettes we hereby certify charges shown above on dates per attached bill are true and correct as billed to the account in upper right hand corner of the affidavit and are exclusive sworn to and subscribed before me this day of march, 1988 in testimony whereof i have set my hand and seal the day and year aforesaid. my commission expires : 2 - 9 - 90 betty j. murphy ( notary public ) [SEP] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD]'"
+ ]
+ },
+ "execution_count": 26,
+ "metadata": {},
+ "output_type": "execute_result"
+ }
+ ],
+ "source": [
+ "batch = next(iter(train_dataloader))\n",
+ "input_ids = batch[0][0]\n",
+ "tokenizer.decode(input_ids)"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "66cEmLDoUFcm"
+ },
+ "source": [
+ "## Define and fine-tune the model\n",
+ "\n",
+ "As this is a sequence labeling task, we are going to load `LayoutLMForTokenClassification` (the base sized model) from the hub. We are going to fine-tune it on a downstream task, namely FUNSD."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 27,
+ "metadata": {},
+ "outputs": [
+ {
+ "data": {
+ "text/plain": [
+ "LoraConfig(task_type=, peft_type=, auto_mapping=None, base_model_name_or_path=None, revision=None, inference_mode=False, r=16, target_modules=None, exclude_modules=None, lora_alpha=16, lora_dropout=0.1, fan_in_fan_out=False, bias='all', use_rslora=False, modules_to_save=None, init_lora_weights=True, layers_to_transform=None, layers_pattern=None, rank_pattern={}, alpha_pattern={}, megatron_config=None, megatron_core='megatron.core', trainable_token_indices=None, loftq_config={}, eva_config=None, corda_config=None, use_dora=False, use_qalora=False, qalora_group_size=16, layer_replication=None, runtime_config=LoraRuntimeConfig(ephemeral_gpu_offload=False), lora_bias=False, target_parameters=None)"
+ ]
+ },
+ "execution_count": 27,
+ "metadata": {},
+ "output_type": "execute_result"
+ }
+ ],
+ "source": [
+ "from peft import get_peft_config, PeftModel, get_peft_model, LoraConfig, TaskType\n",
+ "\n",
+ "peft_config = LoraConfig(\n",
+ " task_type=TaskType.TOKEN_CLS, inference_mode=False, r=16, lora_alpha=16, lora_dropout=0.1, bias=\"all\"\n",
+ ")\n",
+ "peft_config"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 1000,
+ "referenced_widgets": [
+ "da1094982d044ab28eb0effebbfcbb78",
+ "513e00b619924f5693259cd919a927ab",
+ "63e819a04f6e4829838c0e30e65516ed",
+ "d1c3e1a66db04227a74ef8d6481d6daf",
+ "c75f0da13a1e4dbe94800711d55390a6",
+ "31642aacae2a44879960da09f938ecc4",
+ "138a6b922e454ebbaeb315ecd5f476b8",
+ "a8126ba98376402888e9ba344cf1c538"
+ ]
+ },
+ "id": "xIdOsFBiTsuw",
+ "outputId": "95e8811c-025a-41a0-9d03-4285a17f2a9b"
+ },
+ "outputs": [],
+ "source": [
+ "from transformers import LayoutLMForTokenClassification\n",
+ "import torch\n",
+ "from transformers import set_seed\n",
+ "\n",
+ "seed = 100\n",
+ "set_seed(seed)\n",
+ "device = torch.accelerator.current_accelerator().type if hasattr(torch, \"accelerator\") else \"cuda\"\n",
+ "\n",
+ "model = LayoutLMForTokenClassification.from_pretrained(\"microsoft/layoutlm-base-uncased\", num_labels=num_labels)\n",
+ "model = get_peft_model(model, peft_config)\n",
+ "model.to(device)"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "print(model.model.layoutlm.encoder.layer[0].attention.self.query.weight)\n",
+ "print(model.model.layoutlm.encoder.layer[0].attention.self.query.lora_A.default.weight)\n",
+ "print(model.model.classifier.weight)"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "3weFr_pz1mla"
+ },
+ "source": [
+ "Now we can start training:"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "colab": {
+ "base_uri": "https://localhost:8080/"
+ },
+ "id": "Yu0qePs2cRKo",
+ "outputId": "cdbb9a03-eb9b-4740-bbe3-da06b9192bae"
+ },
+ "outputs": [],
+ "source": [
+ "from transformers import get_linear_schedule_with_warmup\n",
+ "from tqdm import tqdm\n",
+ "\n",
+ "num_train_epochs = 100\n",
+ "\n",
+ "optimizer = torch.optim.AdamW(model.parameters(), lr=3e-3)\n",
+ "lr_scheduler = get_linear_schedule_with_warmup(\n",
+ " optimizer=optimizer,\n",
+ " num_warmup_steps=0.06 * (len(train_dataloader) * num_train_epochs),\n",
+ " num_training_steps=(len(train_dataloader) * num_train_epochs),\n",
+ ")\n",
+ "\n",
+ "\n",
+ "global_step = 0\n",
+ "\n",
+ "t_total = len(train_dataloader) * num_train_epochs # total number of training steps\n",
+ "\n",
+ "# put the model in training mode\n",
+ "model.train()\n",
+ "for epoch in range(num_train_epochs):\n",
+ " for batch in tqdm(train_dataloader, desc=\"Training\"):\n",
+ " input_ids = batch[0].to(device)\n",
+ " bbox = batch[4].to(device)\n",
+ " attention_mask = batch[1].to(device)\n",
+ " token_type_ids = batch[2].to(device)\n",
+ " labels = batch[3].to(device)\n",
+ "\n",
+ " # forward pass\n",
+ " outputs = model(\n",
+ " input_ids=input_ids, bbox=bbox, attention_mask=attention_mask, token_type_ids=token_type_ids, labels=labels\n",
+ " )\n",
+ " loss = outputs.loss\n",
+ "\n",
+ " # print loss every 100 steps\n",
+ " if global_step % 10 == 0:\n",
+ " print(f\"Loss after {global_step} steps: {loss.item()}\")\n",
+ "\n",
+ " # backward pass to get the gradients\n",
+ " loss.backward()\n",
+ "\n",
+ " # print(\"Gradients on classification head:\")\n",
+ " # print(model.classifier.weight.grad[6,:].sum())\n",
+ "\n",
+ " # update\n",
+ " optimizer.step()\n",
+ " lr_scheduler.step()\n",
+ " optimizer.zero_grad()\n",
+ " global_step += 1"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 35,
+ "metadata": {
+ "colab": {
+ "base_uri": "https://localhost:8080/"
+ },
+ "id": "u1rNslap5Y3N",
+ "outputId": "877183d4-1d29-4d09-bd3a-0e5f88611dc8"
+ },
+ "outputs": [
+ {
+ "name": "stderr",
+ "output_type": "stream",
+ "text": [
+ "Evaluating: 100%|██████████| 4/4 [00:00<00:00, 10.90it/s]\n"
+ ]
+ },
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "{'loss': 1.467050313949585, 'precision': 0.7295341474445952, 'recall': 0.806903451725863, 'f1': 0.7662707838479811}\n"
+ ]
+ }
+ ],
+ "source": [
+ "import numpy as np\n",
+ "from seqeval.metrics import (\n",
+ " classification_report,\n",
+ " f1_score,\n",
+ " precision_score,\n",
+ " recall_score,\n",
+ ")\n",
+ "\n",
+ "eval_loss = 0.0\n",
+ "nb_eval_steps = 0\n",
+ "preds = None\n",
+ "out_label_ids = None\n",
+ "\n",
+ "# put model in evaluation mode\n",
+ "model.eval()\n",
+ "for batch in tqdm(eval_dataloader, desc=\"Evaluating\"):\n",
+ " with torch.no_grad():\n",
+ " input_ids = batch[0].to(device)\n",
+ " bbox = batch[4].to(device)\n",
+ " attention_mask = batch[1].to(device)\n",
+ " token_type_ids = batch[2].to(device)\n",
+ " labels = batch[3].to(device)\n",
+ "\n",
+ " # forward pass\n",
+ " outputs = model(\n",
+ " input_ids=input_ids, bbox=bbox, attention_mask=attention_mask, token_type_ids=token_type_ids, labels=labels\n",
+ " )\n",
+ " # get the loss and logits\n",
+ " tmp_eval_loss = outputs.loss\n",
+ " logits = outputs.logits\n",
+ "\n",
+ " eval_loss += tmp_eval_loss.item()\n",
+ " nb_eval_steps += 1\n",
+ "\n",
+ " # compute the predictions\n",
+ " if preds is None:\n",
+ " preds = logits.detach().cpu().numpy()\n",
+ " out_label_ids = labels.detach().cpu().numpy()\n",
+ " else:\n",
+ " preds = np.append(preds, logits.detach().cpu().numpy(), axis=0)\n",
+ " out_label_ids = np.append(out_label_ids, labels.detach().cpu().numpy(), axis=0)\n",
+ "\n",
+ "# compute average evaluation loss\n",
+ "eval_loss = eval_loss / nb_eval_steps\n",
+ "preds = np.argmax(preds, axis=2)\n",
+ "\n",
+ "out_label_list = [[] for _ in range(out_label_ids.shape[0])]\n",
+ "preds_list = [[] for _ in range(out_label_ids.shape[0])]\n",
+ "\n",
+ "for i in range(out_label_ids.shape[0]):\n",
+ " for j in range(out_label_ids.shape[1]):\n",
+ " if out_label_ids[i, j] != pad_token_label_id:\n",
+ " out_label_list[i].append(label_map[out_label_ids[i][j]])\n",
+ " preds_list[i].append(label_map[preds[i][j]])\n",
+ "\n",
+ "results = {\n",
+ " \"loss\": eval_loss,\n",
+ " \"precision\": precision_score(out_label_list, preds_list),\n",
+ " \"recall\": recall_score(out_label_list, preds_list),\n",
+ " \"f1\": f1_score(out_label_list, preds_list),\n",
+ "}\n",
+ "print(results)"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 36,
+ "metadata": {},
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "trainable params: 702,733 || all params: 113,237,786 || trainable%: 0.6206\n"
+ ]
+ }
+ ],
+ "source": [
+ "model.print_trainable_parameters()"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 37,
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "model.save_pretrained(\"peft_layoutlm\")"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 40,
+ "metadata": {},
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "2.8M\t./peft_layoutlm/adapter_model.safetensors\n"
+ ]
+ }
+ ],
+ "source": [
+ "!du -h ./peft_layoutlm/adapter_model.safetensors"
+ ]
+ }
+ ],
+ "metadata": {
+ "accelerator": "GPU",
+ "colab": {
+ "collapsed_sections": [],
+ "include_colab_link": true,
+ "name": "Fine-tuning LayoutLMForTokenClassification on FUNSD.ipynb",
+ "provenance": [],
+ "toc_visible": true
+ },
+ "kernelspec": {
+ "display_name": "Python 3",
+ "language": "python",
+ "name": "python3"
+ },
+ "language_info": {
+ "codemirror_mode": {
+ "name": "ipython",
+ "version": 3
+ },
+ "file_extension": ".py",
+ "mimetype": "text/x-python",
+ "name": "python",
+ "nbconvert_exporter": "python",
+ "pygments_lexer": "ipython3",
+ "version": "3.11.13"
+ },
+ "vscode": {
+ "interpreter": {
+ "hash": "aee8b7b246df8f9039afb4144a1f6fd8d2ca17a180786b69acc140d282b71a49"
+ }
+ },
+ "widgets": {
+ "application/vnd.jupyter.widget-state+json": {
+ "138a6b922e454ebbaeb315ecd5f476b8": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "31642aacae2a44879960da09f938ecc4": {
+ "model_module": "@jupyter-widgets/base",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "513e00b619924f5693259cd919a927ab": {
+ "model_module": "@jupyter-widgets/base",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "63e819a04f6e4829838c0e30e65516ed": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_name": "FloatProgressModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "FloatProgressModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "ProgressView",
+ "bar_style": "success",
+ "description": "Downloading: 100%",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_31642aacae2a44879960da09f938ecc4",
+ "max": 453093832,
+ "min": 0,
+ "orientation": "horizontal",
+ "style": "IPY_MODEL_c75f0da13a1e4dbe94800711d55390a6",
+ "value": 453093832
+ }
+ },
+ "a8126ba98376402888e9ba344cf1c538": {
+ "model_module": "@jupyter-widgets/base",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "c75f0da13a1e4dbe94800711d55390a6": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": "initial"
+ }
+ },
+ "d1c3e1a66db04227a74ef8d6481d6daf": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_a8126ba98376402888e9ba344cf1c538",
+ "placeholder": "",
+ "style": "IPY_MODEL_138a6b922e454ebbaeb315ecd5f476b8",
+ "value": " 453M/453M [00:15<00:00, 30.0MB/s]"
+ }
+ },
+ "da1094982d044ab28eb0effebbfcbb78": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_63e819a04f6e4829838c0e30e65516ed",
+ "IPY_MODEL_d1c3e1a66db04227a74ef8d6481d6daf"
+ ],
+ "layout": "IPY_MODEL_513e00b619924f5693259cd919a927ab"
+ }
+ }
+ }
+ }
+ },
+ "nbformat": 4,
+ "nbformat_minor": 1
+}
diff --git a/peft/examples/token_classification/requirements.txt b/peft/examples/token_classification/requirements.txt
new file mode 100644
index 0000000000000000000000000000000000000000..2cde65e15268b67b28864f3fd7e6932fb7949802
--- /dev/null
+++ b/peft/examples/token_classification/requirements.txt
@@ -0,0 +1,7 @@
+transformers
+accelerate
+evaluate
+tqdm
+datasets
+Pillow
+torchvision
\ No newline at end of file
diff --git a/peft/examples/waveft_finetuning/README.md b/peft/examples/waveft_finetuning/README.md
new file mode 100644
index 0000000000000000000000000000000000000000..ad2d231698ad24381e289f18a0fe81029d11930f
--- /dev/null
+++ b/peft/examples/waveft_finetuning/README.md
@@ -0,0 +1,64 @@
+
+
+# WaveFT: Wavelet Fine-Tuning
+
+## Introduction
+[WaveFT](https://arxiv.org/abs/2505.12532) is a novel parameter-efficient fine-tuning (PEFT) method that introduces sparse updates in the **wavelet domain** of residual matrices. Unlike LoRA, which is constrained by discrete low-rank choices, WaveFT enables fine-grained control over the number of trainable parameters by directly learning a sparse set of coefficients in the transformed space. These coefficients are then mapped back to the weight domain via the Inverse Discrete Wavelet Transform (IDWT), producing high-rank updates without incurring inference overhead.
+
+## Quick start
+```python
+import torch
+from peft import WaveFTConfig, get_peft_model
+from transformers import AutoTokenizer, AutoModelForCausalLM
+from trl import SFTConfig, SFTTrainer
+from datasets import load_dataset
+
+model = AutoModelForCausalLM.from_pretrained("facebook/opt-350m", dtype=torch.bfloat16, device_map="auto")
+tokenizer = AutoTokenizer.from_pretrained("facebook/opt-350m")
+dataset = load_dataset("imdb", split="train[:1%]")
+waveft_config = WaveFTConfig(
+ n_frequency=2592,
+)
+peft_model = get_peft_model(model, waveft_config)
+training_args = SFTConfig(dataset_text_field="text", max_seq_length=128)
+trainer = SFTTrainer(
+ model=peft_model,
+ train_dataset=dataset,
+ processing_class=tokenizer,
+)
+trainer.train()
+peft_model.save_pretrained("waveft-opt-350m")
+```
+
+For more options and a more detailed example code, you can refer to waveft finetuning script.
+Run the script simply by running:
+```bash
+python3 examples/waveft_finetuning/waveft_finetuning.py --base_model facebook/opt-350m
+```
+
+If you want to run DDP by [accelerate](https://huggingface.co/docs/accelerate/en/index), please run `accelerate config` to set your ddp config, and run:
+```bash
+accelerate launch examples/waveft_finetuning/waveft_finetuning.py --base_model facebook/opt-350m
+```
+please add `--device_map cpu` if you want to run finetune on CPU.
+
+## Use the model
+You can load and use the model as any other 🤗 PEFT model
+```python
+from peft import PeftModel
+from transformers import AutoTokenizer, AutoModelForCausalLM
+model = AutoModelForCausalLM.from_pretrained("facebook/opt-350m")
+tokenizer = AutoTokenizer.from_pretrained("facebook/opt-350m")
+waveft_model = PeftModel.from_pretrained(model, "waveft-opt-350m")
+```
+
+## Citation
+@misc{bilican2025exploringsparsityparameterefficient,
+ title={Exploring Sparsity for Parameter Efficient Fine Tuning Using Wavelets},
+ author={Ahmet Bilican and M. Akın Yılmaz and A. Murat Tekalp and R. Gökberk Cinbiş},
+ year={2025},
+ eprint={2505.12532},
+ archivePrefix={arXiv},
+ primaryClass={cs.CV},
+ url={https://arxiv.org/abs/2505.12532},
+}
\ No newline at end of file
diff --git a/peft/examples/waveft_finetuning/waveft_finetuning.py b/peft/examples/waveft_finetuning/waveft_finetuning.py
new file mode 100644
index 0000000000000000000000000000000000000000..1855f86a26132da9d914e5d5ac504bdef42d54b1
--- /dev/null
+++ b/peft/examples/waveft_finetuning/waveft_finetuning.py
@@ -0,0 +1,189 @@
+# Copyright 2025-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+
+import os
+from typing import Optional
+
+import torch
+import transformers
+from datasets import load_dataset
+from transformers import AutoModelForCausalLM, AutoTokenizer, set_seed
+
+from peft import (
+ WaveFTConfig,
+ get_peft_model,
+)
+
+
+def train(
+ base_model: str,
+ data_path: str = "yahma/alpaca-cleaned",
+ output_dir: str = "waveft",
+ batch_size: int = 16,
+ num_epochs: int = 1,
+ learning_rate: float = 3e-4,
+ cutoff_len: int = 256,
+ val_set_size: int = 16,
+ eval_step: int = 100,
+ save_step: int = 100,
+ device_map: str = "auto",
+ waveft_n_frequency: int = 2592,
+ waveft_target_modules: list[str] = None,
+ waveft_scaling: float = 25.0,
+ waveft_wavelet_family: str = "db1",
+ waveft_use_idwt: bool = True,
+ torch_dtype: str = "float16",
+ seed: Optional[int] = None,
+):
+ # Set device_map to the right place when enabling DDP.
+ world_size = int(os.environ.get("WORLD_SIZE", 0)) or int(os.environ.get("PMI_SIZE", 0))
+ if world_size > 1 and device_map != "cpu":
+ from accelerate import Accelerator
+
+ device_map = {"": Accelerator().process_index}
+ # Set seed
+ if seed is not None:
+ set_seed(seed)
+ model_kwargs = {"dtype": getattr(torch, torch_dtype), "device_map": device_map}
+ model = AutoModelForCausalLM.from_pretrained(base_model, **model_kwargs)
+
+ tokenizer = AutoTokenizer.from_pretrained(base_model, trust_remote_code=True)
+ # For some tokenizer with no pad token like llama
+ if tokenizer.pad_token is None:
+ tokenizer.pad_token = tokenizer.eos_token
+
+ def tokenize(prompt, add_eos_token=True):
+ result = tokenizer(
+ prompt,
+ truncation=True,
+ max_length=cutoff_len,
+ padding=False,
+ return_tensors=None,
+ )
+ if (
+ result["input_ids"][-1] != tokenizer.eos_token_id
+ and len(result["input_ids"]) < cutoff_len
+ and add_eos_token
+ ):
+ result["input_ids"].append(tokenizer.eos_token_id)
+ result["attention_mask"].append(1)
+
+ result["labels"] = result["input_ids"].copy()
+
+ return result
+
+ def generate_and_tokenize_prompt(example):
+ full_prompt = generate_prompt(example)
+ tokenized_full_prompt = tokenize(full_prompt)
+ return tokenized_full_prompt
+
+ config = WaveFTConfig(
+ n_frequency=waveft_n_frequency,
+ scaling=waveft_scaling,
+ wavelet_family=waveft_wavelet_family,
+ use_idwt=waveft_use_idwt,
+ target_modules=waveft_target_modules,
+ task_type="CAUSAL_LM",
+ )
+
+ model = get_peft_model(model, config)
+
+ data = load_dataset(data_path)
+
+ train_val = data["train"].train_test_split(test_size=val_set_size, shuffle=True, seed=42)
+ train_data = train_val["train"].shuffle().map(generate_and_tokenize_prompt)
+ val_data = train_val["test"].shuffle().map(generate_and_tokenize_prompt)
+
+ trainer = transformers.Trainer(
+ model=model,
+ train_dataset=train_data,
+ eval_dataset=val_data,
+ args=transformers.TrainingArguments(
+ per_device_train_batch_size=batch_size,
+ warmup_steps=100,
+ num_train_epochs=num_epochs,
+ learning_rate=learning_rate,
+ logging_steps=100,
+ optim="adamw_torch",
+ eval_strategy="steps",
+ save_strategy="steps",
+ eval_steps=eval_step,
+ save_steps=save_step,
+ output_dir=output_dir,
+ save_total_limit=3,
+ load_best_model_at_end=True,
+ ddp_find_unused_parameters=False if world_size > 1 else None,
+ ),
+ data_collator=transformers.DataCollatorForSeq2Seq(
+ tokenizer, pad_to_multiple_of=8, return_tensors="pt", padding=True
+ ),
+ )
+ trainer.train()
+ model.save_pretrained(output_dir)
+
+
+def generate_prompt(example):
+ return f"""Below is an instruction that describes a task. Write a response that appropriately completes the request.
+ ### Instruction:
+ {example["instruction"]}
+ ### Response:
+ {example["output"]}"""
+
+
+if __name__ == "__main__":
+ import argparse
+
+ parser = argparse.ArgumentParser()
+ parser.add_argument("--base_model", type=str)
+ parser.add_argument("--data_path", type=str, default="yahma/alpaca-cleaned")
+ parser.add_argument("--output_dir", type=str, default="waveft")
+ parser.add_argument("--batch_size", type=int, default=16)
+ parser.add_argument("--num_epochs", type=int, default=1)
+ parser.add_argument("--learning_rate", type=float, default=3e-4)
+ parser.add_argument("--cutoff_len", type=int, default=256)
+ parser.add_argument("--val_set_size", type=int, default=16)
+ parser.add_argument("--eval_step", type=int, default=100)
+ parser.add_argument("--save_step", type=int, default=100)
+ parser.add_argument("--device_map", type=str, default="auto")
+ parser.add_argument("--waveft_n_frequency", type=int, default=2592)
+ parser.add_argument("--waveft_target_modules", type=str, default=None)
+ parser.add_argument("--waveft_scaling", type=float, default=25.0)
+ parser.add_argument("--waveft_wavelet_family", type=str, default="db1")
+ parser.add_argument("--waveft_use_idwt", action="store_true", default=True)
+ parser.add_argument("--torch_dtype", type=str, default="float16")
+ parser.add_argument("--seed", type=int, default=None)
+
+ args = parser.parse_args()
+
+ train(
+ base_model=args.base_model,
+ data_path=args.data_path,
+ output_dir=args.output_dir,
+ batch_size=args.batch_size,
+ num_epochs=args.num_epochs,
+ learning_rate=args.learning_rate,
+ cutoff_len=args.cutoff_len,
+ val_set_size=args.val_set_size,
+ eval_step=args.eval_step,
+ save_step=args.save_step,
+ device_map=args.device_map,
+ waveft_n_frequency=args.waveft_n_frequency,
+ waveft_target_modules=args.waveft_target_modules,
+ waveft_scaling=args.waveft_scaling,
+ waveft_wavelet_family=args.waveft_wavelet_family,
+ waveft_use_idwt=args.waveft_use_idwt,
+ torch_dtype=args.torch_dtype,
+ seed=args.seed,
+ )
diff --git a/peft/examples/xlora/README.md b/peft/examples/xlora/README.md
new file mode 100644
index 0000000000000000000000000000000000000000..ae81cfcd45e5940262504a95dc4805d45bdf280d
--- /dev/null
+++ b/peft/examples/xlora/README.md
@@ -0,0 +1,15 @@
+# X-LoRA examples
+
+## `xlora_inference_mistralrs.py`
+
+Perform inference of an X-LoRA model using the inference engine mistral.rs.
+
+Mistral.rs supports many base models besides Mistral, and can load models directly from saved LoRA checkpoints. Check out [adapter model docs](https://github.com/EricLBuehler/mistral.rs/blob/master/docs/ADAPTER_MODELS.md) and the [models support matrix](https://github.com/EricLBuehler/mistral.rs?tab=readme-ov-file#support-matrix).
+
+Mistral.rs features X-LoRA support and incorporates techniques such as a dual-KV cache, continuous batching, Paged Attention, and optional non granular scalings, will allow vastly improved throughput.
+
+Links:
+
+- Installation: https://github.com/EricLBuehler/mistral.rs/blob/master/mistralrs-pyo3/README.md
+- Runnable example: https://github.com/EricLBuehler/mistral.rs/blob/master/examples/python/xlora_zephyr.py
+- Adapter model docs and making the ordering file: https://github.com/EricLBuehler/mistral.rs/blob/master/docs/ADAPTER_MODELS.md
\ No newline at end of file
diff --git a/peft/examples/xlora/xlora_inference_mistralrs.py b/peft/examples/xlora/xlora_inference_mistralrs.py
new file mode 100644
index 0000000000000000000000000000000000000000..8a3f4de4261ea5613aa3acbfc12930bc89f1344b
--- /dev/null
+++ b/peft/examples/xlora/xlora_inference_mistralrs.py
@@ -0,0 +1,25 @@
+from mistralrs import ChatCompletionRequest, Runner, Which
+
+
+runner = Runner(
+ which=Which.XLora(
+ tok_model_id=None, # Automatically determine from ordering file
+ model_id=..., # Model ID of the base model (local path of HF model ID)
+ xlora_model_id=..., # X-LoRA Model ID of the base model (local path of HF model ID)
+ order=..., # Ordering file to ensure compatability with PEFT
+ tgt_non_granular_index=3, # Only generate scalings for the first 3 decoding tokens, and then use the last generated one
+ )
+)
+
+res = runner.send_chat_completion_request(
+ ChatCompletionRequest(
+ model="mistral",
+ messages=[{"role": "user", "content": "Tell me a story about 2 low rank matrices."}],
+ max_tokens=256,
+ presence_penalty=1.0,
+ top_p=0.1,
+ temperature=0.5,
+ )
+)
+print(res.choices[0].message.content)
+print(res.usage)
diff --git a/peft/method_comparison/MetaMathQA/Makefile b/peft/method_comparison/MetaMathQA/Makefile
new file mode 100644
index 0000000000000000000000000000000000000000..47ce7ab90d5c75e52b57d73a34b35a9056229d83
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/Makefile
@@ -0,0 +1,90 @@
+# Makefile for running MetaMathQA experiments.
+
+# --- Configuration ---
+PYTHON := python
+RUN_SCRIPT := run.py
+EXPERIMENTS_DIR := experiments
+RESULTS_DIR := results
+
+# --- Automatic Experiment and Result Discovery ---
+
+# 1. Find all experiment directories by looking for adapter_config.json files.
+# This gives us a list like: experiments/lora/llama-3.2-3B-rank32 ...
+EXPERIMENT_PATHS := $(shell find $(EXPERIMENTS_DIR) \
+ -name "adapter_config.json" -or \
+ -name "training_params.json" | xargs dirname | sort -u)
+
+# 2. Define a function to replace all occurrences of a character in a string.
+# This is needed to replicate the result naming logic from run.py (e.g., "lora/foo" -> "lora-foo").
+# Usage: $(call replace-all, string, char_to_replace, replacement_char)
+replace-all = $(if $(findstring $(2),$(1)),$(call replace-all,$(subst $(2),$(3),$(1)),$(2),$(3)),$(1))
+
+# 3. Define a function to convert an experiment path to its flat result file path.
+# e.g., "experiments/lora/llama-3.2-3B-rank32" -> "results/lora-llama-3.2-3B-rank32.json"
+exp_to_res = $(RESULTS_DIR)/$(call replace-all,$(patsubst $(EXPERIMENTS_DIR)/%,%,$(1)),/,--).json
+
+# 4. Generate the list of all target result files we want to build.
+RESULT_FILES := $(foreach exp,$(EXPERIMENT_PATHS),$(call exp_to_res,$(exp)))
+
+
+# --- Main Rules ---
+
+# The default 'all' target depends on all possible result files.
+# Running `make` or `make all` will check and run any outdated or missing experiments.
+all: $(RESULT_FILES)
+
+
+# --- Dynamic Rule Generation ---
+
+# This is the core logic. We dynamically generate a specific Makefile rule for each experiment found.
+# This avoids a complex pattern rule and makes the logic clearer.
+define EXPERIMENT_template
+# Input $1: The full experiment path (e.g., experiments/lora/llama-3.2-3B-rank32)
+
+# Define the rule:
+# The target is the result file (e.g., results/lora-llama-3.2-3B-rank32.json).
+# The dependencies are its config files, code changes need to be audited manually since they can
+# vary in degree of importance. Note that we explicitly ignore when the script fails to run
+# so that the other experiments still have a chance to run.
+$(call exp_to_res,$(1)): $(wildcard $(1)/adapter_config.json) $(wildcard $(1)/training_params.json)
+ @echo "---"
+ @echo "Running experiment: $(1)"
+ -$(PYTHON) $(RUN_SCRIPT) -v $(1)
+ @echo "Finished: $$@"
+ @echo "---"
+
+endef
+
+# This command iterates through every found experiment path and evaluates the template,
+# effectively stamping out a unique, explicit rule for each one.
+$(foreach exp_path,$(EXPERIMENT_PATHS),$(eval $(call EXPERIMENT_template,$(exp_path))))
+
+
+# --- Utility Rules ---
+
+.PHONY: all clean list dump_rules
+
+# The 'clean' rule removes all generated results.
+clean:
+ @echo "Cleaning results directory..."
+ @([ -n "$(wildcard $(RESULTS_DIR)/*.json)" ] && rm $(RESULTS_DIR)/*.json) || exit 0
+
+# The 'list' rule is for debugging. It shows the discovered experiments
+# and the result files the Makefile expects to create for them.
+list:
+ @echo "Discovered experiment configurations:"
+ @$(foreach exp,$(EXPERIMENT_PATHS),echo " - $(exp)/adapter_config.json";)
+ @echo "\nTarget result files:"
+ @$(foreach res,$(RESULT_FILES),echo " - $(res)";)
+
+# The 'dump_rules' rule is for debugging. It dumps all dynamically defined rules.
+define newline
+
+
+endef
+define DUMPED_RULES
+ $(foreach exp_path,$(EXPERIMENT_PATHS),$(call EXPERIMENT_template,$(exp_path)))
+endef
+
+dump_rules:
+ @echo -e "$(subst $(newline),\n,${DUMPED_RULES})"
diff --git a/peft/method_comparison/MetaMathQA/README.md b/peft/method_comparison/MetaMathQA/README.md
new file mode 100644
index 0000000000000000000000000000000000000000..4c762406619c56be43fdc0e93c6b6e4dbef02e58
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/README.md
@@ -0,0 +1,241 @@
+# PEFT method comparison on the MetaMathQA and GSM8K datasets
+
+## Goal
+
+This goal is to provide a benchmarking framework for the different PEFT methods that are implemented. It is important that evaluating different PEFT methods is reproducible, idempotent, and version-controlled. Results for more PEFT methods can be added over time.
+
+## Dataset
+
+This task trains on the [MetaMathQA]((https://huggingface.co/datasets/meta-math/MetaMathQA)) dataset and validates/tests on the [GSM8K](https://huggingface.co/datasets/openai/gsm8k) dataset ("main").
+
+For the model to attain good accuracy, it needs to learn to adhere to the output format and it must express basic chain of thought reasoning capabilities to get to the correct result in the first place. The task is challenging for models in the sub 7B parameter range.
+
+The train set uses the whole of MetaMathQA. The validation set is a random sample from the train set of GSM8K. The test set is the whole of the GSM8K test set.
+
+## Running
+
+Create an experiment in the `experiment/` folder of your choice and give it a name (the name itself does not matter but helps identify the experiment). An example would be `experiments/lora/llama-3.2-3B-rank32/`. Inside that directory, create 2 files:
+
+- `adapter_config.json`
+- Optional: `training_parameters.json`
+
+Once you created these two files, you can either
+
+- run the whole suite using by simply calling `make` (takes >24h)
+- run one specific experiment by calling `make results/-.json`,
+ for example `results/vblora-llama-3.2-3B-default.json`
+
+You can get a list of all runnable experiments by running `make list`, e.g.:
+```
+% make list (git)-[method-comparison-results] ⛓ peft
+Discovered experiment configurations:
+ - experiments/ptuning/llama-3.2-3B-default/adapter_config.json
+ [...]
+ - experiments/vblora/llama-3.2-3B-default/adapter_config.json
+
+Target result files:
+ - results/ptuning-llama-3.2-3B-default.json
+ [...]
+ - results/vblora-llama-3.2-3B-default.json
+```
+
+In case you want to force the execution of an experiment, you can simply `touch` the respective adapter config
+without modifying it. For example:
+
+ touch experiments/vblora/llama-3.2-3B-default/adapter_config.json
+ make
+
+to run the VBLoRA default experiment again.
+
+### `adapter_config.json`
+
+This must be a valid PEFT configuration. It is easiest to create it programmatically, e.g.:
+
+```python
+from peft import LoraConfig
+
+config = LoraConfig(...)
+config.save_pretrained()
+```
+
+### `training_parameters.json`
+
+There is a default file for the non-PEFT parameters: `default_training_params.json`. This contains all the other parameters that are relevant for training, e.g. the base model id, number of steps, batch size, learning rate, etc. If parameters that differ from the defaults are needed for a specific experiment, place a `training_parameters.json` into the experiment directory and adjust the parameters that need changing. The other parametes are taken from the aforementioned default config.
+
+For an overview of all possible arguments, you can also check the `TrainConfig` `dataclass` in `utils.py`.
+
+### Runtime performance
+
+Several factors should be considered to achieve a fast runtime performance. Besides the obvious factors like `max_steps` or the base model size, we found the following factors to have a significant impact:
+
+#### Eval batch size
+
+Regarding the `batch_size_eval` parameter, it is quite critical since evaluation takes up a significant portion of the training time and batching helps with reducing that. It should be possible to choose a value that is multiple times higher than the batch size used for training (`batch_size`). You should also pay attention to the size of the validation set -- e.g. if it's 50, don't choose a `batch_size_eval` of 40, as that results in a large batch of 30 and a small batch of 10. 25 might be a better choice. Also, ensure via a quick train run that the batch size does not lead to out of memory errors -- getting this error at the very end on evaluating the test set would be quite a loss of time.
+
+#### Generation length
+
+During testing, we discovered that the validation time is greatly inflated by just a few very long generations. Those can inflate the validation time by a factor of 3 or more. At the same time, we discovered that these long generations do not help with accuracy -- in fact, if they exceed the maximum configured length, they're just cut off mid sentence and would thus produce an accuracy of 0 anyway.
+
+To remedy this, we now set both `max_length` and `max_new_tokens` for the generation kwargs in the default training parameters. Normally, this is not possible when using transformers, as the latter argument overrides the former. However, we have added special logic inside of `get_generation_config` which takes both and chooses the smaller of the two. This way, we can get rid of these excessively long generations, thus considerably reducing eval times, while still guaranteeing a maximum total generation length to guard against OOM errors. Testing showed that this does not hamper test accuracy. It is therefore recommended not to change these settings.
+
+#### Bucketing
+
+The length of the sequences in the training data can vary a lot. Therefore, if samples are taken randomly from the training dataset, we will end up with batches containing very short and very long sequences. This is bad because the batch will be padded to the longest sequence, slowing down training. The obvious solution would be to sort the whole dataset by sequence length, but this is also bad because it introduces an order bias (e.g. first training on only short and then on only long answers).
+
+The solution is to find a trade off between the two factors. This is achieved by the `BucketIterator`. It first creates buckets that contain multiple batches, e.g. 20x the batch size. The bucket is then sorted by sequence length and then batches are yielded from the bucket. Therefore, we have a small order bias within a bucket but not between buckets, stricking a good balance between training speed and training loss.
+
+From practical experiments, for a batch size of 4, a bucket size of 80 provides a good balance with only slightly lower training loss but cutting training time by 25%. For eval, we don't use the iterator since there, the batch size is relatively big and thus there is little upside.
+
+### Start a run
+
+Once everything is set up properly, start a run by using the `run.py` script. Pass `-v` for verbose output to the console (recommended if observing the progress is desired). As an example, for `experiments/lora/llama-3.2-3B-rank32/` the invocation would be:
+
+```sh
+python run.py -v experiments/lora/llama-3.2-3B-rank32/
+```
+
+By default, the adapter will be saved in a temporary file for further inspection if needed. The prevent this, add the `--clean` flag to the call.
+
+### Run status
+
+The run can be categorized 3 different states:
+
+1. Main run: You are on the `main` branch and the run ended successfully. The results are stored in the `results` folder and are used for further analysis.
+2. Test run: You are not on the `main` branch and the run ended successfully. The results are stored in the `temporary_results` folder and are not used for further analysis.
+3. The run was cancelled (`ctrl + c`). The results are stored in the `cancelled_results` folder and are not used for further analysis.
+
+## Outputs
+
+Results are stored in one of the result directories. An example output could look like so:
+
+```js
+{
+ "run_info": {
+ "created_at": "2025-03-05T13:50:05+00:00",
+ "total_time": 2711.0915009640157,
+ "experiment_name": "ia3/lr_0.001",
+ "peft_branch": "ben-method-comparison",
+ "train_config": {
+ "model_id": "meta-llama/Llama-3.2-3B",
+ "dtype": "bfloat16",
+ "max_seq_length": 768,
+ "batch_size": 4,
+ "batch_size_eval": 51,
+ "max_steps": 5000,
+ "eval_steps": 250,
+ "compile": false,
+ "query_template": "Question: {query} Think step by step.\nAnswer:",
+ "seed": 0,
+ "grad_norm_clip": 1.0,
+ "optimizer_kwargs": {
+ "lr": 0.001
+ },
+ "lr_scheduler": "cosine",
+ "use_amp": false,
+ "generation_kwargs": {
+ "max_length": 800
+ },
+ "attn_implementation": null
+ },
+ "peft_config": {
+ "task_type": null,
+ "peft_type": "IA3",
+ "auto_mapping": null,
+ "base_model_name_or_path": "meta-llama/Llama-3.2-3B",
+ "revision": null,
+ "inference_mode": false,
+ "target_modules": [
+ "v_proj",
+ "k_proj",
+ "down_proj"
+ ],
+ "exclude_modules": null,
+ "feedforward_modules": [
+ "down_proj"
+ ],
+ "fan_in_fan_out": false,
+ "modules_to_save": null,
+ "init_ia3_weights": true
+ }
+ },
+ "train_info": {
+ "accelerator_memory_reserved_avg": 14229219940,
+ "accelerator_memory_max": 24847056896,
+ "accelerator_memory_reserved_99th": 19115624366,
+ "train_time": 2238.65277833899,
+ "file_size": 1157064,
+ "status": "success",
+ "metrics": [
+ {
+ "step": 250,
+ "valid accuracy": 0.0784313725490196,
+ "train loss": 1.1336498007774354,
+ "train samples": 1000
+ },
+ [...]
+ {
+ "step": 5000,
+ "valid accuracy": 0.21568627450980393,
+ "train loss": 0.6345920492410659,
+ "train samples": 20000
+ },
+ {
+ "step": 5000,
+ "test accuracy": 0.35129740518962077,
+ "train loss": 0.6345920492410659,
+ "train samples": 20000,
+ "train total tokens": 4197579
+ }
+ ]
+ },
+ "meta_info": {
+ "model_sha": "13afe5124825b4f3751f836b40dafda64c1ed062",
+ "model_created_at": "2024-09-18T15:23:48+00:00",
+ "dataset_sha": "aa4f34d3d2d3231299b5b03d9b3e5a20da45aa18",
+ "dataset_created_at": "2023-09-21T17:22:46+00:00",
+ "package_info": {
+ "transformers-version": "4.50.0.dev0",
+ "transformers-commit-hash": "752ef3fd4e70869626ec70657a770a85c0ad9219",
+ "peft-version": "0.14.1.dev0",
+ "peft-commit-hash": "a447a4e5ecd87b7d57733f4df9616a328cf130f4",
+ "datasets-version": "3.3.2",
+ "datasets-commit-hash": null,
+ "bitsandbytes-version": "0.45.2",
+ "bitsandbytes-commit-hash": null,
+ "torch-version": "2.6.0+cu124",
+ "torch-commit-hash": null
+ },
+ "system_info": {
+ "system": "Linux",
+ "release": "6.11.0-17-generic",
+ "version": "#17~24.04.2-Ubuntu SMP PREEMPT_DYNAMIC Mon Jan 20 22:48:29 UTC 2",
+ "machine": "x86_64",
+ "processor": "x86_64",
+ "accelerator": "NVIDIA GeForce RTX 4090"
+ },
+ "pytorch_info": "PyTorch built with: [...]"
+ }
+}
+```
+
+## Dependencies
+
+Apart from the normal PEFT dependencies, ensure that the packages in the `requirements.txt` are installed, e.g. via:
+
+```sh
+python -m pip install -r requirements.txt
+```
+
+Python 3.12+ is required.
+
+## Open tasks
+
+- consider using `DataLoader`
+- consider adding https://github.com/huggingface/Math-Verify
+- consider adding `weight` argument to cross entropy calculation to downweight the EOS token, but it would require calculating the loss manually instead of relying on transformers (see https://github.com/huggingface/transformers/blob/6a876462c308bd7cd7d3ca8e93abaa7d5b02e90e/src/transformers/loss/loss_utils.py#L24-L48)
+- do a sanity check against/comparison with transformers Trainer
+- consider using vLLM to potentially speed up generations, at least for the test set
+- using `torch.compile` leads to a huge slowdown, investigate (maybe recompiles), although it does save memory
+- AMP does not appear to help, investigate
+- packing of sequences (but this probably requires adjusting the attention matrix)
+- clean up what gets printed and where (stdout, stderr)
diff --git a/peft/method_comparison/MetaMathQA/cancelled_results/.gitkeep b/peft/method_comparison/MetaMathQA/cancelled_results/.gitkeep
new file mode 100644
index 0000000000000000000000000000000000000000..e69de29bb2d1d6434b8b29ae775ad8c2e48c5391
diff --git a/peft/method_comparison/MetaMathQA/data.py b/peft/method_comparison/MetaMathQA/data.py
new file mode 100644
index 0000000000000000000000000000000000000000..be3ace83cfa83c211f5f41086fee9f36660363f7
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/data.py
@@ -0,0 +1,109 @@
+# Copyright 2025-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""
+All utilities related to data handling.
+"""
+
+from functools import partial
+from typing import Callable
+
+import datasets
+import numpy as np
+from datasets import Dataset, load_dataset
+
+
+# with a token limit of 768 for query + response, we have to exclude all texts with length > 1304; this leaves 93.8% of
+# the dataset
+CHAR_LIMIT = 1300
+# train/valid/test split -- note that evaluation takes quite long, so don't choose too large sizes for the valid set,
+# since it's run multiple times during training; test is only run once at the end and thus can be larger
+VALID_SIZE = 50
+
+
+def get_filtered_dataset(*, ds: datasets.Dataset, print_fn: Callable[..., None]) -> Dataset:
+ """Return the filtered dataset, with long queries removed.
+
+ We determined that 99% of queries have 529 or fewer characters. Characters roughly correspond to tokens, so this is
+ a good proxy. We cannot use tokens directly, as that depends on the tokenizer, which can be different for each
+ model, but we want the same filter for each model.
+
+ """
+ char_lengths = [len(f"{q} {r}") for q, r in zip(ds["query"], ds["response"])]
+ idx_filtered = [i for i, length in enumerate(char_lengths) if length <= CHAR_LIMIT]
+ print_fn(f"Filtered dataset: {100 * len(idx_filtered) / len(ds):.1f}% of the original dataset")
+ return ds.select(idx_filtered)
+
+
+def get_train_valid_test_datasets(
+ *, tokenizer, query_template: str, print_fn: Callable[..., None]
+) -> tuple[Dataset, Dataset, Dataset]:
+ """
+ Return the indices of the train, valid, and test splits of the dataset.
+
+ We cannot use ds.train_test_split(..., stratify_by_column="type") as it gives:
+
+ > ValueError: Stratifying by column is only supported for ClassLabel column, and column type is Value.
+
+ even after calling ds_filtered.class_encode_column("type"). Thus, using sklearn's StratifiedKFold instead.
+ """
+ metamath = load_dataset("meta-math/MetaMathQA")["train"]
+ metamath = get_filtered_dataset(ds=metamath, print_fn=print_fn)
+
+ # gsmk8k does not need to be filtered as query and response are short enough
+ gsm8k = load_dataset("openai/gsm8k", "main")
+ gsm8k = gsm8k.rename_columns({"question": "query", "answer": "response"})
+ gsm8k_train = gsm8k["train"]
+ gsm8k_test = gsm8k["test"]
+
+ np.random.seed(0)
+ indices = np.arange(len(gsm8k_train))
+ np.random.shuffle(indices)
+ idx_valid = indices[:VALID_SIZE]
+
+ ds_train = metamath
+ ds_valid = gsm8k_train.select(idx_valid)
+ ds_test = gsm8k_test
+
+ print_fn(f"Train size: {len(ds_train)}")
+ print_fn(f"Valid size: {len(ds_valid)}")
+ print_fn(f"Test size: {len(ds_test)}")
+
+ tokenize_with_answer_ = partial(tokenize_with_answer, tokenizer=tokenizer, template=query_template)
+ tokenize_wo_answer_ = partial(tokenize_wo_answer, tokenizer=tokenizer, template=query_template)
+ ds_train = ds_train.map(tokenize_with_answer_, batched=True).remove_columns(["type", "query", "original_question"])
+ ds_valid = ds_valid.map(tokenize_wo_answer_, batched=True).remove_columns(["query"])
+ ds_test = ds_test.map(tokenize_wo_answer_, batched=True).remove_columns(["query"])
+
+ return ds_train, ds_valid, ds_test
+
+
+def tokenize_with_answer(samples, tokenizer, template):
+ queries = [template.format(query=sample) + answer for sample, answer in zip(samples["query"], samples["response"])]
+ tokenized = tokenizer(queries)
+ tokenized["input_ids"] = [input_ids[: tokenizer.model_max_length] for input_ids in tokenized["input_ids"]]
+ tokenized["attention_mask"] = [
+ input_ids[: tokenizer.model_max_length] for input_ids in tokenized["attention_mask"]
+ ]
+ return tokenized
+
+
+def tokenize_wo_answer(samples, tokenizer, template):
+ queries = [template.format(query=sample) for sample in samples["query"]]
+ tokenized = tokenizer(queries)
+ tokenized["input_ids"] = [input_ids[: tokenizer.model_max_length] for input_ids in tokenized["input_ids"]]
+ tokenized["attention_mask"] = [
+ input_ids[: tokenizer.model_max_length] for input_ids in tokenized["attention_mask"]
+ ]
+ return tokenized
diff --git a/peft/method_comparison/MetaMathQA/default_training_params.json b/peft/method_comparison/MetaMathQA/default_training_params.json
new file mode 100644
index 0000000000000000000000000000000000000000..a200a41ed96409033011b7e4fc33e05fe9c61162
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/default_training_params.json
@@ -0,0 +1,26 @@
+{
+ "model_id": "meta-llama/Llama-3.2-3B",
+ "dtype": "bfloat16",
+ "max_seq_length": 768,
+ "batch_size": 4,
+ "batch_size_eval": 50,
+ "max_steps": 5000,
+ "eval_steps": 250,
+ "compile": false,
+ "seed": 0,
+ "grad_norm_clip": 1.0,
+ "optimizer_type": "AdamW",
+ "optimizer_kwargs": {
+ "lr": 1e-4,
+ "weight_decay": 0.1
+ },
+ "lr_scheduler": "cosine",
+ "use_amp": false,
+ "autocast_adapter_dtype": true,
+ "attn_implementation": null,
+ "generation_kwargs": {
+ "max_length": 800,
+ "max_new_tokens": 300
+ },
+ "query_template": "Question: {query} Think step by step.\nAnswer:"
+}
diff --git a/peft/method_comparison/MetaMathQA/experiments/adalora/llama-3.2-3B-rank32/adapter_config.json b/peft/method_comparison/MetaMathQA/experiments/adalora/llama-3.2-3B-rank32/adapter_config.json
new file mode 100644
index 0000000000000000000000000000000000000000..d20357b52d92ad65b3af6e932c9dd8d16b47bcb4
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/experiments/adalora/llama-3.2-3B-rank32/adapter_config.json
@@ -0,0 +1,39 @@
+{
+ "alpha_pattern": {},
+ "auto_mapping": null,
+ "base_model_name_or_path": null,
+ "beta1": 0.85,
+ "beta2": 0.85,
+ "bias": "none",
+ "corda_config": null,
+ "deltaT": 1,
+ "eva_config": null,
+ "exclude_modules": null,
+ "fan_in_fan_out": false,
+ "inference_mode": false,
+ "init_lora_weights": true,
+ "init_r": 64,
+ "layer_replication": null,
+ "layers_pattern": null,
+ "layers_to_transform": null,
+ "loftq_config": {},
+ "lora_alpha": 8,
+ "lora_bias": false,
+ "lora_dropout": 0.0,
+ "megatron_config": null,
+ "megatron_core": "megatron.core",
+ "modules_to_save": null,
+ "orth_reg_weight": 0.5,
+ "peft_type": "ADALORA",
+ "r": 8,
+ "rank_pattern": null,
+ "revision": null,
+ "target_modules": null,
+ "target_r": 32,
+ "task_type": null,
+ "tfinal": 500,
+ "tinit": 200,
+ "total_step": 5000,
+ "use_dora": false,
+ "use_rslora": false
+}
\ No newline at end of file
diff --git a/peft/method_comparison/MetaMathQA/experiments/adaptionprompt/llama-3.2-3B-lr_0.0005/adapter_config.json b/peft/method_comparison/MetaMathQA/experiments/adaptionprompt/llama-3.2-3B-lr_0.0005/adapter_config.json
new file mode 100644
index 0000000000000000000000000000000000000000..367bea4cf187d10c96a4d8b53f355bfd269a1e6a
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/experiments/adaptionprompt/llama-3.2-3B-lr_0.0005/adapter_config.json
@@ -0,0 +1,11 @@
+{
+ "adapter_layers": 28,
+ "adapter_len": 100,
+ "auto_mapping": null,
+ "base_model_name_or_path": null,
+ "inference_mode": false,
+ "peft_type": "ADAPTION_PROMPT",
+ "revision": null,
+ "target_modules": null,
+ "task_type": "CAUSAL_LM"
+}
\ No newline at end of file
diff --git a/peft/method_comparison/MetaMathQA/experiments/adaptionprompt/llama-3.2-3B-lr_0.0005/training_params.json b/peft/method_comparison/MetaMathQA/experiments/adaptionprompt/llama-3.2-3B-lr_0.0005/training_params.json
new file mode 100644
index 0000000000000000000000000000000000000000..e8106a88d0de4099e2cbd2648abbe43bdebe6091
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/experiments/adaptionprompt/llama-3.2-3B-lr_0.0005/training_params.json
@@ -0,0 +1,6 @@
+{
+ "optimizer_kwargs": {
+ "lr": 5e-4
+ }
+}
+
diff --git a/peft/method_comparison/MetaMathQA/experiments/boft/llama-3.2-3B-default/adapter_config.json b/peft/method_comparison/MetaMathQA/experiments/boft/llama-3.2-3B-default/adapter_config.json
new file mode 100644
index 0000000000000000000000000000000000000000..44d50893ff7f19c1851a2150e879c444ec134fe1
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/experiments/boft/llama-3.2-3B-default/adapter_config.json
@@ -0,0 +1,20 @@
+{
+ "auto_mapping": null,
+ "base_model_name_or_path": null,
+ "bias": "none",
+ "boft_block_num": 0,
+ "boft_block_size": 4,
+ "boft_dropout": 0.0,
+ "boft_n_butterfly_factor": 1,
+ "exclude_modules": null,
+ "fan_in_fan_out": false,
+ "inference_mode": false,
+ "init_weights": true,
+ "layers_pattern": null,
+ "layers_to_transform": null,
+ "modules_to_save": null,
+ "peft_type": "BOFT",
+ "revision": null,
+ "target_modules": null,
+ "task_type": null
+}
\ No newline at end of file
diff --git a/peft/method_comparison/MetaMathQA/experiments/bone/llama-3.2-3B-bat/adapter_config.json b/peft/method_comparison/MetaMathQA/experiments/bone/llama-3.2-3B-bat/adapter_config.json
new file mode 100644
index 0000000000000000000000000000000000000000..cd69e4389edfe1738ceec6c42be177dd17d924c6
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/experiments/bone/llama-3.2-3B-bat/adapter_config.json
@@ -0,0 +1,19 @@
+{
+ "auto_mapping": null,
+ "base_model_name_or_path": null,
+ "bias": "none",
+ "exclude_modules": null,
+ "inference_mode": false,
+ "init_weights": "bat",
+ "layers_pattern": null,
+ "layers_to_transform": null,
+ "modules_to_save": null,
+ "peft_type": "BONE",
+ "r": 64,
+ "revision": null,
+ "target_modules": [
+ "v_proj",
+ "q_proj"
+ ],
+ "task_type": null
+}
\ No newline at end of file
diff --git a/peft/method_comparison/MetaMathQA/experiments/bone/llama-3.2-3B-default/adapter_config.json b/peft/method_comparison/MetaMathQA/experiments/bone/llama-3.2-3B-default/adapter_config.json
new file mode 100644
index 0000000000000000000000000000000000000000..abc68802718821c659614b5fdeabb45db2df824b
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/experiments/bone/llama-3.2-3B-default/adapter_config.json
@@ -0,0 +1,19 @@
+{
+ "auto_mapping": null,
+ "base_model_name_or_path": null,
+ "bias": "none",
+ "exclude_modules": null,
+ "inference_mode": false,
+ "init_weights": true,
+ "layers_pattern": null,
+ "layers_to_transform": null,
+ "modules_to_save": null,
+ "peft_type": "BONE",
+ "r": 64,
+ "revision": null,
+ "target_modules": [
+ "v_proj",
+ "q_proj"
+ ],
+ "task_type": null
+}
\ No newline at end of file
diff --git a/peft/method_comparison/MetaMathQA/experiments/c3a/llama-3.2-3B-default/adapter_config.json b/peft/method_comparison/MetaMathQA/experiments/c3a/llama-3.2-3B-default/adapter_config.json
new file mode 100644
index 0000000000000000000000000000000000000000..170c4bb33e558339b07da8044fb3cb2093d2e4eb
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/experiments/c3a/llama-3.2-3B-default/adapter_config.json
@@ -0,0 +1,21 @@
+{
+ "auto_mapping": null,
+ "base_model_name_or_path": null,
+ "bias": "none",
+ "exclude_modules": null,
+ "fan_in_fan_out": false,
+ "inference_mode": false,
+ "init_weights": false,
+ "layers_pattern": null,
+ "layers_to_transform": null,
+ "modules_to_save": null,
+ "block_size": 64,
+ "block_size_pattern": {},
+ "peft_type": "C3A",
+ "revision": null,
+ "target_modules": [
+ "v_proj",
+ "q_proj"
+ ],
+ "task_type": null
+}
diff --git a/peft/method_comparison/MetaMathQA/experiments/c3a/llama-3.2-3B-default/training_params.json b/peft/method_comparison/MetaMathQA/experiments/c3a/llama-3.2-3B-default/training_params.json
new file mode 100644
index 0000000000000000000000000000000000000000..a39b9dc8a825e9b79ace91032d0755835548eb44
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/experiments/c3a/llama-3.2-3B-default/training_params.json
@@ -0,0 +1,6 @@
+{
+ "optimizer_kwargs": {
+ "lr": 3e-1,
+ "weight_decay": 1e-5
+ }
+}
diff --git a/peft/method_comparison/MetaMathQA/experiments/fourierft/llama-3.2-3B-default/adapter_config.json b/peft/method_comparison/MetaMathQA/experiments/fourierft/llama-3.2-3B-default/adapter_config.json
new file mode 100644
index 0000000000000000000000000000000000000000..a2a379f07427f4c68eeaf06756004ddaa377f96b
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/experiments/fourierft/llama-3.2-3B-default/adapter_config.json
@@ -0,0 +1,23 @@
+{
+ "auto_mapping": null,
+ "base_model_name_or_path": null,
+ "bias": "none",
+ "exclude_modules": null,
+ "fan_in_fan_out": false,
+ "inference_mode": false,
+ "init_weights": false,
+ "layers_pattern": null,
+ "layers_to_transform": null,
+ "modules_to_save": null,
+ "n_frequency": 1000,
+ "n_frequency_pattern": {},
+ "peft_type": "FOURIERFT",
+ "random_loc_seed": 777,
+ "revision": null,
+ "scaling": 300,
+ "target_modules": [
+ "v_proj",
+ "q_proj"
+ ],
+ "task_type": null
+}
\ No newline at end of file
diff --git a/peft/method_comparison/MetaMathQA/experiments/fourierft/llama-3.2-3B-n_frequency-5000/adapter_config.json b/peft/method_comparison/MetaMathQA/experiments/fourierft/llama-3.2-3B-n_frequency-5000/adapter_config.json
new file mode 100644
index 0000000000000000000000000000000000000000..40d40246c48487419ea0d21eb369bea60c729496
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/experiments/fourierft/llama-3.2-3B-n_frequency-5000/adapter_config.json
@@ -0,0 +1,23 @@
+{
+ "auto_mapping": null,
+ "base_model_name_or_path": null,
+ "bias": "none",
+ "exclude_modules": null,
+ "fan_in_fan_out": false,
+ "inference_mode": false,
+ "init_weights": false,
+ "layers_pattern": null,
+ "layers_to_transform": null,
+ "modules_to_save": null,
+ "n_frequency": 5000,
+ "n_frequency_pattern": {},
+ "peft_type": "FOURIERFT",
+ "random_loc_seed": 777,
+ "revision": null,
+ "scaling": 300,
+ "target_modules": [
+ "v_proj",
+ "q_proj"
+ ],
+ "task_type": null
+}
\ No newline at end of file
diff --git a/peft/method_comparison/MetaMathQA/experiments/full-finetuning/llama-3.2-3B-lr_0.00001/training_params.json b/peft/method_comparison/MetaMathQA/experiments/full-finetuning/llama-3.2-3B-lr_0.00001/training_params.json
new file mode 100644
index 0000000000000000000000000000000000000000..6d6c3b0f9114a63d0739eef0c996f4c1c0c0e36c
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/experiments/full-finetuning/llama-3.2-3B-lr_0.00001/training_params.json
@@ -0,0 +1,6 @@
+{
+ "optimizer_kwargs": {
+ "lr": 1e-5
+ }
+}
+
diff --git a/peft/method_comparison/MetaMathQA/experiments/ia3/llama-3.2-3B-default/adapter_config.json b/peft/method_comparison/MetaMathQA/experiments/ia3/llama-3.2-3B-default/adapter_config.json
new file mode 100644
index 0000000000000000000000000000000000000000..0c8e514faa808ac0874e71f21bad7a576d15349d
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/experiments/ia3/llama-3.2-3B-default/adapter_config.json
@@ -0,0 +1,14 @@
+{
+ "auto_mapping": null,
+ "base_model_name_or_path": null,
+ "exclude_modules": null,
+ "fan_in_fan_out": false,
+ "feedforward_modules": null,
+ "inference_mode": false,
+ "init_ia3_weights": true,
+ "modules_to_save": null,
+ "peft_type": "IA3",
+ "revision": null,
+ "target_modules": null,
+ "task_type": null
+}
\ No newline at end of file
diff --git a/peft/method_comparison/MetaMathQA/experiments/ia3/llama-3.2-3B-lr_0.001/adapter_config.json b/peft/method_comparison/MetaMathQA/experiments/ia3/llama-3.2-3B-lr_0.001/adapter_config.json
new file mode 100644
index 0000000000000000000000000000000000000000..0c8e514faa808ac0874e71f21bad7a576d15349d
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/experiments/ia3/llama-3.2-3B-lr_0.001/adapter_config.json
@@ -0,0 +1,14 @@
+{
+ "auto_mapping": null,
+ "base_model_name_or_path": null,
+ "exclude_modules": null,
+ "fan_in_fan_out": false,
+ "feedforward_modules": null,
+ "inference_mode": false,
+ "init_ia3_weights": true,
+ "modules_to_save": null,
+ "peft_type": "IA3",
+ "revision": null,
+ "target_modules": null,
+ "task_type": null
+}
\ No newline at end of file
diff --git a/peft/method_comparison/MetaMathQA/experiments/ia3/llama-3.2-3B-lr_0.001/training_params.json b/peft/method_comparison/MetaMathQA/experiments/ia3/llama-3.2-3B-lr_0.001/training_params.json
new file mode 100644
index 0000000000000000000000000000000000000000..8a120ad9a80c36dc3666f4da481a5292a7dc8072
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/experiments/ia3/llama-3.2-3B-lr_0.001/training_params.json
@@ -0,0 +1,6 @@
+{
+ "optimizer_kwargs": {
+ "lr": 1e-3
+ }
+}
+
diff --git a/peft/method_comparison/MetaMathQA/experiments/ln_tuning/llama-3.2-3B-default/adapter_config.json b/peft/method_comparison/MetaMathQA/experiments/ln_tuning/llama-3.2-3B-default/adapter_config.json
new file mode 100644
index 0000000000000000000000000000000000000000..70b7363d3ac83e8ff2ee85634baafbee1f42b56a
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/experiments/ln_tuning/llama-3.2-3B-default/adapter_config.json
@@ -0,0 +1,11 @@
+{
+ "auto_mapping": null,
+ "base_model_name_or_path": null,
+ "exclude_modules": null,
+ "inference_mode": false,
+ "modules_to_save": null,
+ "peft_type": "LN_TUNING",
+ "revision": null,
+ "target_modules": null,
+ "task_type": null
+}
\ No newline at end of file
diff --git a/peft/method_comparison/MetaMathQA/experiments/loha/llama-3.2-3B-rank32/adapter_config.json b/peft/method_comparison/MetaMathQA/experiments/loha/llama-3.2-3B-rank32/adapter_config.json
new file mode 100644
index 0000000000000000000000000000000000000000..1137259fa26b3abeac269c7bdda56dbeb29e34f7
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/experiments/loha/llama-3.2-3B-rank32/adapter_config.json
@@ -0,0 +1,24 @@
+{
+ "alpha": 64,
+ "alpha_pattern": {},
+ "auto_mapping": null,
+ "base_model_name_or_path": null,
+ "exclude_modules": null,
+ "inference_mode": false,
+ "init_weights": true,
+ "layers_pattern": null,
+ "layers_to_transform": null,
+ "module_dropout": 0.0,
+ "modules_to_save": null,
+ "peft_type": "LOHA",
+ "r": 32,
+ "rank_dropout": 0.0,
+ "rank_pattern": {},
+ "revision": null,
+ "target_modules": [
+ "q_proj",
+ "v_proj"
+ ],
+ "task_type": null,
+ "use_effective_conv2d": false
+}
\ No newline at end of file
diff --git a/peft/method_comparison/MetaMathQA/experiments/lokr/llama-3.2-3B-rank32/adapter_config.json b/peft/method_comparison/MetaMathQA/experiments/lokr/llama-3.2-3B-rank32/adapter_config.json
new file mode 100644
index 0000000000000000000000000000000000000000..7d30dd77a4c5f185fde99a5d60f381961ac7c522
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/experiments/lokr/llama-3.2-3B-rank32/adapter_config.json
@@ -0,0 +1,27 @@
+{
+ "alpha": 64,
+ "alpha_pattern": {},
+ "auto_mapping": null,
+ "base_model_name_or_path": null,
+ "decompose_both": false,
+ "decompose_factor": -1,
+ "exclude_modules": null,
+ "inference_mode": false,
+ "init_weights": true,
+ "layers_pattern": null,
+ "layers_to_transform": null,
+ "module_dropout": 0.0,
+ "modules_to_save": null,
+ "peft_type": "LOKR",
+ "r": 32,
+ "rank_dropout": 0.0,
+ "rank_dropout_scale": false,
+ "rank_pattern": {},
+ "revision": null,
+ "target_modules": [
+ "q_proj",
+ "v_proj"
+ ],
+ "task_type": null,
+ "use_effective_conv2d": false
+}
\ No newline at end of file
diff --git a/peft/method_comparison/MetaMathQA/experiments/lora/llama-3.2-3B-rank32-dora/adapter_config.json b/peft/method_comparison/MetaMathQA/experiments/lora/llama-3.2-3B-rank32-dora/adapter_config.json
new file mode 100644
index 0000000000000000000000000000000000000000..255d09d2508a603fd8eea98152025c6cd8f0a789
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/experiments/lora/llama-3.2-3B-rank32-dora/adapter_config.json
@@ -0,0 +1,30 @@
+{
+ "alpha_pattern": {},
+ "auto_mapping": null,
+ "base_model_name_or_path": null,
+ "bias": "none",
+ "corda_config": null,
+ "eva_config": null,
+ "exclude_modules": null,
+ "fan_in_fan_out": false,
+ "inference_mode": false,
+ "init_lora_weights": true,
+ "layer_replication": null,
+ "layers_pattern": null,
+ "layers_to_transform": null,
+ "loftq_config": {},
+ "lora_alpha": 64,
+ "lora_bias": false,
+ "lora_dropout": 0.0,
+ "megatron_config": null,
+ "megatron_core": "megatron.core",
+ "modules_to_save": null,
+ "peft_type": "LORA",
+ "r": 32,
+ "rank_pattern": {},
+ "revision": null,
+ "target_modules": null,
+ "task_type": "CAUSAL_LM",
+ "use_dora": true,
+ "use_rslora": false
+}
diff --git a/peft/method_comparison/MetaMathQA/experiments/lora/llama-3.2-3B-rank32-lorafa/adapter_config.json b/peft/method_comparison/MetaMathQA/experiments/lora/llama-3.2-3B-rank32-lorafa/adapter_config.json
new file mode 100644
index 0000000000000000000000000000000000000000..8832c108fac1825c52774517fd3e5bf0fc7d8d64
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/experiments/lora/llama-3.2-3B-rank32-lorafa/adapter_config.json
@@ -0,0 +1,30 @@
+{
+ "alpha_pattern": {},
+ "auto_mapping": null,
+ "base_model_name_or_path": null,
+ "bias": "none",
+ "corda_config": null,
+ "eva_config": null,
+ "exclude_modules": null,
+ "fan_in_fan_out": false,
+ "inference_mode": false,
+ "init_lora_weights": true,
+ "layer_replication": null,
+ "layers_pattern": null,
+ "layers_to_transform": null,
+ "loftq_config": {},
+ "lora_alpha": 64,
+ "lora_bias": false,
+ "lora_dropout": 0.0,
+ "megatron_config": null,
+ "megatron_core": "megatron.core",
+ "modules_to_save": null,
+ "peft_type": "LORA",
+ "r": 32,
+ "rank_pattern": {},
+ "revision": null,
+ "target_modules": null,
+ "task_type": "CAUSAL_LM",
+ "use_dora": false,
+ "use_rslora": false
+}
diff --git a/peft/method_comparison/MetaMathQA/experiments/lora/llama-3.2-3B-rank32-lorafa/training_params.json b/peft/method_comparison/MetaMathQA/experiments/lora/llama-3.2-3B-rank32-lorafa/training_params.json
new file mode 100644
index 0000000000000000000000000000000000000000..985db872405905c31c93a10aa9cd3f77ed223437
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/experiments/lora/llama-3.2-3B-rank32-lorafa/training_params.json
@@ -0,0 +1,9 @@
+{
+ "optimizer_type": "lora-fa",
+ "optimizer_kwargs": {
+ "r": 32,
+ "lora_alpha": 64,
+ "lr": 1e-4,
+ "weight_decay": 0.1
+ }
+}
diff --git a/peft/method_comparison/MetaMathQA/experiments/lora/llama-3.2-3B-rank32/adapter_config.json b/peft/method_comparison/MetaMathQA/experiments/lora/llama-3.2-3B-rank32/adapter_config.json
new file mode 100644
index 0000000000000000000000000000000000000000..8832c108fac1825c52774517fd3e5bf0fc7d8d64
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/experiments/lora/llama-3.2-3B-rank32/adapter_config.json
@@ -0,0 +1,30 @@
+{
+ "alpha_pattern": {},
+ "auto_mapping": null,
+ "base_model_name_or_path": null,
+ "bias": "none",
+ "corda_config": null,
+ "eva_config": null,
+ "exclude_modules": null,
+ "fan_in_fan_out": false,
+ "inference_mode": false,
+ "init_lora_weights": true,
+ "layer_replication": null,
+ "layers_pattern": null,
+ "layers_to_transform": null,
+ "loftq_config": {},
+ "lora_alpha": 64,
+ "lora_bias": false,
+ "lora_dropout": 0.0,
+ "megatron_config": null,
+ "megatron_core": "megatron.core",
+ "modules_to_save": null,
+ "peft_type": "LORA",
+ "r": 32,
+ "rank_pattern": {},
+ "revision": null,
+ "target_modules": null,
+ "task_type": "CAUSAL_LM",
+ "use_dora": false,
+ "use_rslora": false
+}
diff --git a/peft/method_comparison/MetaMathQA/experiments/lora/llama-3.2-3B-rank64-rslora/adapter_config.json b/peft/method_comparison/MetaMathQA/experiments/lora/llama-3.2-3B-rank64-rslora/adapter_config.json
new file mode 100644
index 0000000000000000000000000000000000000000..dc1f8039ab02888675a12a1a1a017ebdd196b9d4
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/experiments/lora/llama-3.2-3B-rank64-rslora/adapter_config.json
@@ -0,0 +1,30 @@
+{
+ "alpha_pattern": {},
+ "auto_mapping": null,
+ "base_model_name_or_path": null,
+ "bias": "none",
+ "corda_config": null,
+ "eva_config": null,
+ "exclude_modules": null,
+ "fan_in_fan_out": false,
+ "inference_mode": false,
+ "init_lora_weights": true,
+ "layer_replication": null,
+ "layers_pattern": null,
+ "layers_to_transform": null,
+ "loftq_config": {},
+ "lora_alpha": 64,
+ "lora_bias": false,
+ "lora_dropout": 0.0,
+ "megatron_config": null,
+ "megatron_core": "megatron.core",
+ "modules_to_save": null,
+ "peft_type": "LORA",
+ "r": 64,
+ "rank_pattern": {},
+ "revision": null,
+ "target_modules": null,
+ "task_type": "CAUSAL_LM",
+ "use_dora": false,
+ "use_rslora": true
+}
diff --git a/peft/method_comparison/MetaMathQA/experiments/lora/llama-3.2-3B-rank64/adapter_config.json b/peft/method_comparison/MetaMathQA/experiments/lora/llama-3.2-3B-rank64/adapter_config.json
new file mode 100644
index 0000000000000000000000000000000000000000..75890c9dce9fef14eee47ce19f3baa86d4d4168a
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/experiments/lora/llama-3.2-3B-rank64/adapter_config.json
@@ -0,0 +1,30 @@
+{
+ "alpha_pattern": {},
+ "auto_mapping": null,
+ "base_model_name_or_path": null,
+ "bias": "none",
+ "corda_config": null,
+ "eva_config": null,
+ "exclude_modules": null,
+ "fan_in_fan_out": false,
+ "inference_mode": false,
+ "init_lora_weights": true,
+ "layer_replication": null,
+ "layers_pattern": null,
+ "layers_to_transform": null,
+ "loftq_config": {},
+ "lora_alpha": 128,
+ "lora_bias": false,
+ "lora_dropout": 0.0,
+ "megatron_config": null,
+ "megatron_core": "megatron.core",
+ "modules_to_save": null,
+ "peft_type": "LORA",
+ "r": 64,
+ "rank_pattern": {},
+ "revision": null,
+ "target_modules": null,
+ "task_type": "CAUSAL_LM",
+ "use_dora": false,
+ "use_rslora": false
+}
diff --git a/peft/method_comparison/MetaMathQA/experiments/miss/llama-3.2-3B-bat/adapter_config.json b/peft/method_comparison/MetaMathQA/experiments/miss/llama-3.2-3B-bat/adapter_config.json
new file mode 100644
index 0000000000000000000000000000000000000000..a3267da039aad22dcc2d70006dccc34c8759d359
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/experiments/miss/llama-3.2-3B-bat/adapter_config.json
@@ -0,0 +1,18 @@
+{
+ "auto_mapping": null,
+ "base_model_name_or_path": null,
+ "bias": "none",
+ "exclude_modules": null,
+ "inference_mode": false,
+ "init_weights": "bat",
+ "layers_pattern": null,
+ "layers_to_transform": null,
+ "mini_r": 1,
+ "miss_dropout": 0.0,
+ "modules_to_save": null,
+ "peft_type": "MISS",
+ "r": 64,
+ "revision": null,
+ "target_modules": null,
+ "task_type": null
+}
\ No newline at end of file
diff --git a/peft/method_comparison/MetaMathQA/experiments/miss/llama-3.2-3B-default/adapter_config.json b/peft/method_comparison/MetaMathQA/experiments/miss/llama-3.2-3B-default/adapter_config.json
new file mode 100644
index 0000000000000000000000000000000000000000..02ee9f74396d7372104f2adf9f462e1ac4653d93
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/experiments/miss/llama-3.2-3B-default/adapter_config.json
@@ -0,0 +1,18 @@
+{
+ "auto_mapping": null,
+ "base_model_name_or_path": null,
+ "bias": "none",
+ "exclude_modules": null,
+ "inference_mode": false,
+ "init_weights": true,
+ "layers_pattern": null,
+ "layers_to_transform": null,
+ "mini_r": 1,
+ "miss_dropout": 0.0,
+ "modules_to_save": null,
+ "peft_type": "MISS",
+ "r": 64,
+ "revision": null,
+ "target_modules": null,
+ "task_type": null
+}
\ No newline at end of file
diff --git a/peft/method_comparison/MetaMathQA/experiments/miss/llama-3.2-3B-mini/adapter_config.json b/peft/method_comparison/MetaMathQA/experiments/miss/llama-3.2-3B-mini/adapter_config.json
new file mode 100644
index 0000000000000000000000000000000000000000..d732e181b21e0961029723bc640c25d5917d217e
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/experiments/miss/llama-3.2-3B-mini/adapter_config.json
@@ -0,0 +1,18 @@
+{
+ "auto_mapping": null,
+ "base_model_name_or_path": null,
+ "bias": "none",
+ "exclude_modules": null,
+ "inference_mode": false,
+ "init_weights": "mini",
+ "layers_pattern": null,
+ "layers_to_transform": null,
+ "mini_r": 64,
+ "miss_dropout": 0.0,
+ "modules_to_save": null,
+ "peft_type": "MISS",
+ "r": 64,
+ "revision": null,
+ "target_modules": null,
+ "task_type": null
+}
\ No newline at end of file
diff --git a/peft/method_comparison/MetaMathQA/experiments/oft/llama-3.2-3B-rank32/adapter_config.json b/peft/method_comparison/MetaMathQA/experiments/oft/llama-3.2-3B-rank32/adapter_config.json
new file mode 100644
index 0000000000000000000000000000000000000000..e8cdb86ecd110a0176dd42b34e25b3c133cbab4a
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/experiments/oft/llama-3.2-3B-rank32/adapter_config.json
@@ -0,0 +1,27 @@
+{
+ "alpha_pattern": {},
+ "auto_mapping": null,
+ "base_model_name_or_path": null,
+ "bias": "none",
+ "block_share": false,
+ "coft": false,
+ "eps": 6e-05,
+ "exclude_modules": null,
+ "fan_in_fan_out": false,
+ "inference_mode": false,
+ "init_weights": true,
+ "layers_pattern": null,
+ "layers_to_transform": null,
+ "module_dropout": 0.0,
+ "modules_to_save": null,
+ "oft_block_size": 0,
+ "peft_type": "OFT",
+ "r": 32,
+ "rank_pattern": {},
+ "revision": null,
+ "target_modules": [
+ "q_proj",
+ "v_proj"
+ ],
+ "task_type": null
+}
\ No newline at end of file
diff --git a/peft/method_comparison/MetaMathQA/experiments/prefixtuning/llama-3.2-3B-lr_0.001/adapter_config.json b/peft/method_comparison/MetaMathQA/experiments/prefixtuning/llama-3.2-3B-lr_0.001/adapter_config.json
new file mode 100644
index 0000000000000000000000000000000000000000..77bff7fd16cd3f675655221218e69a55eaead91f
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/experiments/prefixtuning/llama-3.2-3B-lr_0.001/adapter_config.json
@@ -0,0 +1,15 @@
+{
+ "auto_mapping": null,
+ "base_model_name_or_path": null,
+ "encoder_hidden_size": 3072,
+ "inference_mode": false,
+ "num_attention_heads": 24,
+ "num_layers": 28,
+ "num_transformer_submodules": 1,
+ "num_virtual_tokens": 200,
+ "peft_type": "PREFIX_TUNING",
+ "prefix_projection": false,
+ "revision": null,
+ "task_type": "CAUSAL_LM",
+ "token_dim": 3072
+}
\ No newline at end of file
diff --git a/peft/method_comparison/MetaMathQA/experiments/prefixtuning/llama-3.2-3B-lr_0.001/training_params.json b/peft/method_comparison/MetaMathQA/experiments/prefixtuning/llama-3.2-3B-lr_0.001/training_params.json
new file mode 100644
index 0000000000000000000000000000000000000000..8a120ad9a80c36dc3666f4da481a5292a7dc8072
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/experiments/prefixtuning/llama-3.2-3B-lr_0.001/training_params.json
@@ -0,0 +1,6 @@
+{
+ "optimizer_kwargs": {
+ "lr": 1e-3
+ }
+}
+
diff --git a/peft/method_comparison/MetaMathQA/experiments/prompt_tuning/llama-3.2-3B-default/adapter_config.json b/peft/method_comparison/MetaMathQA/experiments/prompt_tuning/llama-3.2-3B-default/adapter_config.json
new file mode 100644
index 0000000000000000000000000000000000000000..efa055b03d6f3a6c6d0f7df76f11550891919b0a
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/experiments/prompt_tuning/llama-3.2-3B-default/adapter_config.json
@@ -0,0 +1,17 @@
+{
+ "auto_mapping": null,
+ "base_model_name_or_path": null,
+ "inference_mode": false,
+ "num_attention_heads": 24,
+ "num_layers": 28,
+ "num_transformer_submodules": 1,
+ "num_virtual_tokens": 200,
+ "peft_type": "PROMPT_TUNING",
+ "prompt_tuning_init": "RANDOM",
+ "prompt_tuning_init_text": null,
+ "revision": null,
+ "task_type": "CAUSAL_LM",
+ "token_dim": 3072,
+ "tokenizer_kwargs": null,
+ "tokenizer_name_or_path": null
+}
\ No newline at end of file
diff --git a/peft/method_comparison/MetaMathQA/experiments/prompt_tuning/llama-3.2-3B-lr_0.001/adapter_config.json b/peft/method_comparison/MetaMathQA/experiments/prompt_tuning/llama-3.2-3B-lr_0.001/adapter_config.json
new file mode 100644
index 0000000000000000000000000000000000000000..efa055b03d6f3a6c6d0f7df76f11550891919b0a
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/experiments/prompt_tuning/llama-3.2-3B-lr_0.001/adapter_config.json
@@ -0,0 +1,17 @@
+{
+ "auto_mapping": null,
+ "base_model_name_or_path": null,
+ "inference_mode": false,
+ "num_attention_heads": 24,
+ "num_layers": 28,
+ "num_transformer_submodules": 1,
+ "num_virtual_tokens": 200,
+ "peft_type": "PROMPT_TUNING",
+ "prompt_tuning_init": "RANDOM",
+ "prompt_tuning_init_text": null,
+ "revision": null,
+ "task_type": "CAUSAL_LM",
+ "token_dim": 3072,
+ "tokenizer_kwargs": null,
+ "tokenizer_name_or_path": null
+}
\ No newline at end of file
diff --git a/peft/method_comparison/MetaMathQA/experiments/prompt_tuning/llama-3.2-3B-lr_0.001/training_params.json b/peft/method_comparison/MetaMathQA/experiments/prompt_tuning/llama-3.2-3B-lr_0.001/training_params.json
new file mode 100644
index 0000000000000000000000000000000000000000..8a120ad9a80c36dc3666f4da481a5292a7dc8072
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/experiments/prompt_tuning/llama-3.2-3B-lr_0.001/training_params.json
@@ -0,0 +1,6 @@
+{
+ "optimizer_kwargs": {
+ "lr": 1e-3
+ }
+}
+
diff --git a/peft/method_comparison/MetaMathQA/experiments/prompt_tuning/llama-3.2-3B-sample_vocab-lr_0.001/adapter_config.json b/peft/method_comparison/MetaMathQA/experiments/prompt_tuning/llama-3.2-3B-sample_vocab-lr_0.001/adapter_config.json
new file mode 100644
index 0000000000000000000000000000000000000000..8b9f14279798195477b8a188feb12dfcd9605e00
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/experiments/prompt_tuning/llama-3.2-3B-sample_vocab-lr_0.001/adapter_config.json
@@ -0,0 +1,17 @@
+{
+ "auto_mapping": null,
+ "base_model_name_or_path": null,
+ "inference_mode": false,
+ "num_attention_heads": 24,
+ "num_layers": 28,
+ "num_transformer_submodules": 1,
+ "num_virtual_tokens": 200,
+ "peft_type": "PROMPT_TUNING",
+ "prompt_tuning_init": "SAMPLE_VOCAB",
+ "prompt_tuning_init_text": null,
+ "revision": null,
+ "task_type": "CAUSAL_LM",
+ "token_dim": 3072,
+ "tokenizer_kwargs": null,
+ "tokenizer_name_or_path": null
+}
diff --git a/peft/method_comparison/MetaMathQA/experiments/prompt_tuning/llama-3.2-3B-sample_vocab-lr_0.001/training_params.json b/peft/method_comparison/MetaMathQA/experiments/prompt_tuning/llama-3.2-3B-sample_vocab-lr_0.001/training_params.json
new file mode 100644
index 0000000000000000000000000000000000000000..8a120ad9a80c36dc3666f4da481a5292a7dc8072
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/experiments/prompt_tuning/llama-3.2-3B-sample_vocab-lr_0.001/training_params.json
@@ -0,0 +1,6 @@
+{
+ "optimizer_kwargs": {
+ "lr": 1e-3
+ }
+}
+
diff --git a/peft/method_comparison/MetaMathQA/experiments/ptuning/llama-3.2-3B-default/adapter_config.json b/peft/method_comparison/MetaMathQA/experiments/ptuning/llama-3.2-3B-default/adapter_config.json
new file mode 100644
index 0000000000000000000000000000000000000000..54469edf776f3de255d054c317887b1312aa7791
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/experiments/ptuning/llama-3.2-3B-default/adapter_config.json
@@ -0,0 +1,17 @@
+{
+ "auto_mapping": null,
+ "base_model_name_or_path": null,
+ "encoder_dropout": 0.0,
+ "encoder_hidden_size": 3072,
+ "encoder_num_layers": 2,
+ "encoder_reparameterization_type": "MLP",
+ "inference_mode": false,
+ "num_attention_heads": 24,
+ "num_layers": 28,
+ "num_transformer_submodules": 1,
+ "num_virtual_tokens": 20,
+ "peft_type": "P_TUNING",
+ "revision": null,
+ "task_type": "CAUSAL_LM",
+ "token_dim": 3072
+}
\ No newline at end of file
diff --git a/peft/method_comparison/MetaMathQA/experiments/randlora/llama-3.2-3B-default/adapter_config.json b/peft/method_comparison/MetaMathQA/experiments/randlora/llama-3.2-3B-default/adapter_config.json
new file mode 100644
index 0000000000000000000000000000000000000000..3dbdfaa6b123a057774dc5c46d86bfe4d4e35b55
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/experiments/randlora/llama-3.2-3B-default/adapter_config.json
@@ -0,0 +1,22 @@
+{
+ "auto_mapping": null,
+ "base_model_name_or_path": null,
+ "bias": "none",
+ "fan_in_fan_out": false,
+ "inference_mode": false,
+ "init_weights": true,
+ "layers_pattern": null,
+ "layers_to_transform": null,
+ "modules_to_save": null,
+ "peft_type": "RANDLORA",
+ "projection_prng_key": 0,
+ "r": 32,
+ "randlora_alpha": 640,
+ "randlora_dropout": 0.0,
+ "revision": null,
+ "save_projection": true,
+ "sparse": false,
+ "target_modules": null,
+ "task_type": null,
+ "very_sparse": false
+}
\ No newline at end of file
diff --git a/peft/method_comparison/MetaMathQA/experiments/road/llama-3.2-3B-lr_0.001/adapter_config.json b/peft/method_comparison/MetaMathQA/experiments/road/llama-3.2-3B-lr_0.001/adapter_config.json
new file mode 100644
index 0000000000000000000000000000000000000000..d0f74c40761246f57831661e4a86dae1d28399d8
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/experiments/road/llama-3.2-3B-lr_0.001/adapter_config.json
@@ -0,0 +1,12 @@
+{
+ "auto_mapping": null,
+ "base_model_name_or_path": null,
+ "group_size": 64,
+ "inference_mode": false,
+ "init_weights": true,
+ "peft_type": "ROAD",
+ "revision": null,
+ "target_modules": null,
+ "task_type": null,
+ "variant": "road_2"
+}
diff --git a/peft/method_comparison/MetaMathQA/experiments/road/llama-3.2-3B-lr_0.001/training_params.json b/peft/method_comparison/MetaMathQA/experiments/road/llama-3.2-3B-lr_0.001/training_params.json
new file mode 100644
index 0000000000000000000000000000000000000000..52d87e3ef6d143c29d2ba640028909a31befffa6
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/experiments/road/llama-3.2-3B-lr_0.001/training_params.json
@@ -0,0 +1,5 @@
+{
+ "optimizer_kwargs": {
+ "lr": 1e-3
+ }
+}
diff --git a/peft/method_comparison/MetaMathQA/experiments/shira/llama-3.2-3B-lr_0.0003-random_seed_42/adapter_config.json b/peft/method_comparison/MetaMathQA/experiments/shira/llama-3.2-3B-lr_0.0003-random_seed_42/adapter_config.json
new file mode 100644
index 0000000000000000000000000000000000000000..0d4565eef10746dd8c02364f737fb7a7143955d0
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/experiments/shira/llama-3.2-3B-lr_0.0003-random_seed_42/adapter_config.json
@@ -0,0 +1,15 @@
+{
+ "auto_mapping": null,
+ "base_model_name_or_path": null,
+ "fan_in_fan_out": false,
+ "inference_mode": false,
+ "init_weights": true,
+ "mask_type": "random",
+ "modules_to_save": null,
+ "peft_type": "SHIRA",
+ "r": 32,
+ "random_seed": 42,
+ "revision": null,
+ "target_modules": null,
+ "task_type": null
+}
\ No newline at end of file
diff --git a/peft/method_comparison/MetaMathQA/experiments/shira/llama-3.2-3B-lr_0.0003-random_seed_42/training_params.json b/peft/method_comparison/MetaMathQA/experiments/shira/llama-3.2-3B-lr_0.0003-random_seed_42/training_params.json
new file mode 100644
index 0000000000000000000000000000000000000000..92f18b8a3c5adb57d1d25314d50f1c8df85eb570
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/experiments/shira/llama-3.2-3B-lr_0.0003-random_seed_42/training_params.json
@@ -0,0 +1,6 @@
+{
+ "optimizer_kwargs": {
+ "lr": 3e-4
+ }
+}
+
diff --git a/peft/method_comparison/MetaMathQA/experiments/trainable_tokens/llama-3.2-3B-sos+eos/adapter_config.json b/peft/method_comparison/MetaMathQA/experiments/trainable_tokens/llama-3.2-3B-sos+eos/adapter_config.json
new file mode 100644
index 0000000000000000000000000000000000000000..bce0cd5b129fe4281eb46c7d17f05bb0fca3935d
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/experiments/trainable_tokens/llama-3.2-3B-sos+eos/adapter_config.json
@@ -0,0 +1,7 @@
+{
+ "auto_mapping": null,
+ "base_model_name_or_path": null,
+ "peft_type": "TRAINABLE_TOKENS",
+ "token_indices": [128000, 128001],
+ "task_type": "CAUSAL_LM"
+}
diff --git a/peft/method_comparison/MetaMathQA/experiments/trainable_tokens/llama-3.2-3B-sos+eos/training_params.json b/peft/method_comparison/MetaMathQA/experiments/trainable_tokens/llama-3.2-3B-sos+eos/training_params.json
new file mode 100644
index 0000000000000000000000000000000000000000..92e546e6cfeadce2db2ab6dbd124790a4fb0dbf4
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/experiments/trainable_tokens/llama-3.2-3B-sos+eos/training_params.json
@@ -0,0 +1,5 @@
+{
+ "optimizer_kwargs": {
+ "lr": 0.2
+ }
+}
diff --git a/peft/method_comparison/MetaMathQA/experiments/vblora/llama-3.2-3B-default/adapter_config.json b/peft/method_comparison/MetaMathQA/experiments/vblora/llama-3.2-3B-default/adapter_config.json
new file mode 100644
index 0000000000000000000000000000000000000000..b6cbc59e57c07e6b883ff34ed98090d51916d652
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/experiments/vblora/llama-3.2-3B-default/adapter_config.json
@@ -0,0 +1,26 @@
+{
+ "auto_mapping": null,
+ "base_model_name_or_path": null,
+ "bias": "none",
+ "exclude_modules": null,
+ "fan_in_fan_out": false,
+ "inference_mode": false,
+ "init_logits_std": 0.1,
+ "init_vector_bank_bound": 0.02,
+ "layers_pattern": null,
+ "layers_to_transform": null,
+ "modules_to_save": null,
+ "num_vectors": 256,
+ "peft_type": "VBLORA",
+ "r": 4,
+ "revision": null,
+ "save_only_topk_weights": false,
+ "target_modules": [
+ "v_proj",
+ "q_proj"
+ ],
+ "task_type": null,
+ "topk": 2,
+ "vblora_dropout": 0.0,
+ "vector_length": 256
+}
\ No newline at end of file
diff --git a/peft/method_comparison/MetaMathQA/experiments/vera/llama-3.2-3B-default/adapter_config.json b/peft/method_comparison/MetaMathQA/experiments/vera/llama-3.2-3B-default/adapter_config.json
new file mode 100644
index 0000000000000000000000000000000000000000..f4962c1b4fa1266ba29f31559fa3260483d8fac7
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/experiments/vera/llama-3.2-3B-default/adapter_config.json
@@ -0,0 +1,20 @@
+{
+ "auto_mapping": null,
+ "base_model_name_or_path": null,
+ "bias": "none",
+ "d_initial": 0.1,
+ "fan_in_fan_out": false,
+ "inference_mode": false,
+ "init_weights": true,
+ "layers_pattern": null,
+ "layers_to_transform": null,
+ "modules_to_save": null,
+ "peft_type": "VERA",
+ "projection_prng_key": 0,
+ "r": 256,
+ "revision": null,
+ "save_projection": true,
+ "target_modules": null,
+ "task_type": null,
+ "vera_dropout": 0.0
+}
\ No newline at end of file
diff --git a/peft/method_comparison/MetaMathQA/experiments/vera/llama-3.2-3B-default/training_params.json b/peft/method_comparison/MetaMathQA/experiments/vera/llama-3.2-3B-default/training_params.json
new file mode 100644
index 0000000000000000000000000000000000000000..8a120ad9a80c36dc3666f4da481a5292a7dc8072
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/experiments/vera/llama-3.2-3B-default/training_params.json
@@ -0,0 +1,6 @@
+{
+ "optimizer_kwargs": {
+ "lr": 1e-3
+ }
+}
+
diff --git a/peft/method_comparison/MetaMathQA/experiments/waveft/llama-3.2-3B-n_frequency-5000/adapter_config.json b/peft/method_comparison/MetaMathQA/experiments/waveft/llama-3.2-3B-n_frequency-5000/adapter_config.json
new file mode 100644
index 0000000000000000000000000000000000000000..6aad104d0f1dec10bf97eee02c9d22b2b49dbeb2
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/experiments/waveft/llama-3.2-3B-n_frequency-5000/adapter_config.json
@@ -0,0 +1,26 @@
+{
+ "auto_mapping": null,
+ "base_model_name_or_path": null,
+ "bias": "none",
+ "exclude_modules": null,
+ "fan_in_fan_out": false,
+ "inference_mode": false,
+ "init_weights": true,
+ "layers_pattern": null,
+ "layers_to_transform": null,
+ "modules_to_save": null,
+ "n_frequency": 5000,
+ "n_frequency_pattern": {},
+ "peft_type": "WAVEFT",
+ "proportional_parameters": false,
+ "random_loc_seed": 777,
+ "revision": null,
+ "scaling": 25.0,
+ "target_modules": [
+ "q_proj",
+ "v_proj"
+ ],
+ "task_type": "CAUSAL_LM",
+ "use_idwt": true,
+ "wavelet_family": "db1"
+}
diff --git a/peft/method_comparison/MetaMathQA/requirements.txt b/peft/method_comparison/MetaMathQA/requirements.txt
new file mode 100644
index 0000000000000000000000000000000000000000..ee25a1ced129a9c13938c22922aa0514230af60b
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/requirements.txt
@@ -0,0 +1,4 @@
+bitsandbytes
+datasets
+numpy
+tqdm
diff --git a/peft/method_comparison/MetaMathQA/results/.gitkeep b/peft/method_comparison/MetaMathQA/results/.gitkeep
new file mode 100644
index 0000000000000000000000000000000000000000..e69de29bb2d1d6434b8b29ae775ad8c2e48c5391
diff --git a/peft/method_comparison/MetaMathQA/results/adalora--llama-3.2-3B-rank32.json b/peft/method_comparison/MetaMathQA/results/adalora--llama-3.2-3B-rank32.json
new file mode 100644
index 0000000000000000000000000000000000000000..8b38ea15e8a213a05e1872f928958e601ce60370
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/results/adalora--llama-3.2-3B-rank32.json
@@ -0,0 +1,4071 @@
+{
+ "run_info": {
+ "created_at": "2025-06-19T23:12:19+00:00",
+ "total_time": 2209.243281380004,
+ "experiment_name": "adalora/llama-3.2-3B-rank32",
+ "peft_branch": "main",
+ "train_config": {
+ "model_id": "meta-llama/Llama-3.2-3B",
+ "dtype": "bfloat16",
+ "max_seq_length": 768,
+ "batch_size": 4,
+ "batch_size_eval": 50,
+ "max_steps": 5000,
+ "eval_steps": 250,
+ "compile": false,
+ "query_template": "Question: {query} Think step by step.\nAnswer:",
+ "seed": 0,
+ "grad_norm_clip": 1.0,
+ "optimizer_type": "AdamW",
+ "optimizer_kwargs": {
+ "lr": 0.0001,
+ "weight_decay": 0.1
+ },
+ "lr_scheduler": "cosine",
+ "use_amp": false,
+ "autocast_adapter_dtype": true,
+ "generation_kwargs": {
+ "max_length": 800,
+ "max_new_tokens": 300
+ },
+ "attn_implementation": null
+ },
+ "peft_config": {
+ "task_type": null,
+ "peft_type": "ADALORA",
+ "auto_mapping": null,
+ "base_model_name_or_path": "meta-llama/Llama-3.2-3B",
+ "revision": null,
+ "inference_mode": false,
+ "r": 8,
+ "target_modules": [
+ "q_proj",
+ "v_proj"
+ ],
+ "exclude_modules": null,
+ "lora_alpha": 8,
+ "lora_dropout": 0.0,
+ "fan_in_fan_out": false,
+ "bias": "none",
+ "use_rslora": false,
+ "modules_to_save": null,
+ "init_lora_weights": true,
+ "layers_to_transform": null,
+ "layers_pattern": null,
+ "rank_pattern": {
+ "model.layers.0.self_attn.q_proj.lora_E": [
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false
+ ],
+ "model.layers.0.self_attn.v_proj.lora_E": [
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true
+ ],
+ "model.layers.1.self_attn.q_proj.lora_E": [
+ false,
+ false,
+ true,
+ true,
+ false,
+ true,
+ true,
+ false,
+ false,
+ false,
+ false,
+ true,
+ false,
+ false,
+ true,
+ true,
+ true,
+ true,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ true,
+ false,
+ true,
+ true,
+ false,
+ false,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ false,
+ false,
+ true,
+ true,
+ true,
+ false,
+ false,
+ false,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ false,
+ false,
+ true,
+ true,
+ false,
+ false,
+ true,
+ true,
+ false,
+ false
+ ],
+ "model.layers.1.self_attn.v_proj.lora_E": [
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true
+ ],
+ "model.layers.2.self_attn.q_proj.lora_E": [
+ true,
+ false,
+ true,
+ false,
+ false,
+ false,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ false,
+ false,
+ true,
+ false,
+ false,
+ true,
+ false,
+ false,
+ false,
+ false,
+ true,
+ true,
+ false,
+ false,
+ false,
+ false,
+ true,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ true,
+ true,
+ true,
+ false,
+ false,
+ false,
+ true,
+ true,
+ false,
+ false,
+ false,
+ true,
+ false,
+ true,
+ true,
+ false,
+ true,
+ false,
+ false,
+ false,
+ true,
+ true,
+ false,
+ true,
+ true,
+ false,
+ false
+ ],
+ "model.layers.2.self_attn.v_proj.lora_E": [
+ true,
+ false,
+ false,
+ false,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ false,
+ true,
+ false,
+ true,
+ false,
+ true,
+ false,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ false,
+ false,
+ false,
+ false,
+ true,
+ false,
+ false,
+ false,
+ false,
+ false,
+ true,
+ true,
+ false,
+ false,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ false,
+ false,
+ true,
+ false,
+ true,
+ false,
+ false,
+ false,
+ true,
+ true,
+ false,
+ false,
+ false,
+ true,
+ true
+ ],
+ "model.layers.3.self_attn.q_proj.lora_E": [
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false
+ ],
+ "model.layers.3.self_attn.v_proj.lora_E": [
+ false,
+ false,
+ false,
+ false,
+ false,
+ true,
+ false,
+ true,
+ false,
+ false,
+ false,
+ false,
+ true,
+ false,
+ false,
+ false,
+ false,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ true,
+ false,
+ false,
+ true,
+ false,
+ false,
+ true,
+ false,
+ true,
+ false,
+ true,
+ true,
+ false,
+ true,
+ false,
+ false,
+ true,
+ false,
+ false,
+ false,
+ false,
+ false,
+ true,
+ false,
+ true,
+ false,
+ false,
+ false,
+ false,
+ true,
+ true,
+ true
+ ],
+ "model.layers.4.self_attn.q_proj.lora_E": [
+ false,
+ false,
+ false,
+ false,
+ false,
+ true,
+ false,
+ false,
+ true,
+ true,
+ false,
+ true,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ true,
+ false,
+ false,
+ true,
+ false,
+ true,
+ false,
+ false,
+ false,
+ false,
+ false,
+ true,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ true,
+ true,
+ false,
+ false,
+ true,
+ false,
+ false,
+ false,
+ true,
+ true,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ true,
+ true,
+ false,
+ false
+ ],
+ "model.layers.4.self_attn.v_proj.lora_E": [
+ true,
+ false,
+ true,
+ true,
+ false,
+ false,
+ true,
+ false,
+ false,
+ false,
+ true,
+ false,
+ true,
+ true,
+ false,
+ true,
+ false,
+ true,
+ true,
+ false,
+ true,
+ true,
+ false,
+ false,
+ true,
+ true,
+ true,
+ true,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ true,
+ false,
+ true,
+ false,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ false,
+ false,
+ false,
+ false,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true
+ ],
+ "model.layers.5.self_attn.q_proj.lora_E": [
+ false,
+ true,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false
+ ],
+ "model.layers.5.self_attn.v_proj.lora_E": [
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ false,
+ false,
+ true,
+ false,
+ false,
+ true,
+ false,
+ true,
+ false,
+ false,
+ false,
+ false,
+ true,
+ true,
+ false,
+ false,
+ false,
+ false,
+ true,
+ false,
+ true,
+ false,
+ true,
+ true,
+ false,
+ false,
+ true,
+ true,
+ true,
+ true,
+ false,
+ false,
+ true,
+ false,
+ true,
+ false,
+ false,
+ true,
+ true,
+ true,
+ false,
+ true,
+ false,
+ false,
+ false,
+ true,
+ true,
+ true,
+ true,
+ false,
+ false,
+ false,
+ true,
+ true
+ ],
+ "model.layers.6.self_attn.q_proj.lora_E": [
+ false,
+ false,
+ true,
+ true,
+ false,
+ false,
+ true,
+ true,
+ false,
+ false,
+ false,
+ true,
+ false,
+ true,
+ false,
+ true,
+ false,
+ false,
+ false,
+ false,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ false,
+ true,
+ false,
+ true,
+ false,
+ false,
+ false,
+ true,
+ true,
+ false,
+ false,
+ false,
+ false,
+ true,
+ true,
+ true,
+ false,
+ false,
+ true,
+ false,
+ false,
+ false,
+ false,
+ true,
+ true,
+ false,
+ false,
+ false,
+ true,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false
+ ],
+ "model.layers.6.self_attn.v_proj.lora_E": [
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ false,
+ false,
+ false,
+ false,
+ true,
+ true,
+ false,
+ false,
+ false,
+ false,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ false,
+ false,
+ false,
+ true,
+ true,
+ false,
+ false,
+ true,
+ false,
+ true,
+ false,
+ true,
+ true,
+ false,
+ true,
+ false,
+ true,
+ false,
+ true
+ ],
+ "model.layers.7.self_attn.q_proj.lora_E": [
+ false,
+ false,
+ false,
+ false,
+ false,
+ true,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ true,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ true,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ true,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false
+ ],
+ "model.layers.7.self_attn.v_proj.lora_E": [
+ false,
+ false,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ false,
+ false,
+ true,
+ true,
+ true,
+ true,
+ false,
+ false,
+ false,
+ true,
+ false,
+ false,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ false,
+ false,
+ true,
+ true,
+ true,
+ true
+ ],
+ "model.layers.8.self_attn.q_proj.lora_E": [
+ false,
+ true,
+ false,
+ false,
+ false,
+ false,
+ false,
+ true,
+ false,
+ false,
+ false,
+ false,
+ true,
+ true,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ true,
+ false,
+ false,
+ false,
+ false,
+ true,
+ false,
+ false,
+ true,
+ false,
+ false,
+ false,
+ false,
+ true,
+ false,
+ false,
+ false,
+ false,
+ false,
+ true,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ true
+ ],
+ "model.layers.8.self_attn.v_proj.lora_E": [
+ false,
+ true,
+ false,
+ false,
+ false,
+ true,
+ false,
+ false,
+ false,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ false,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ false,
+ false,
+ true,
+ true,
+ false,
+ false,
+ true,
+ false,
+ true,
+ false,
+ true,
+ true,
+ false,
+ true,
+ false,
+ true,
+ true,
+ true,
+ false,
+ true,
+ false,
+ false,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ false,
+ false,
+ false,
+ false,
+ true
+ ],
+ "model.layers.9.self_attn.q_proj.lora_E": [
+ true,
+ false,
+ true,
+ true,
+ false,
+ false,
+ true,
+ true,
+ false,
+ false,
+ true,
+ false,
+ false,
+ false,
+ false,
+ true,
+ false,
+ true,
+ false,
+ true,
+ false,
+ false,
+ false,
+ true,
+ false,
+ true,
+ false,
+ true,
+ false,
+ true,
+ false,
+ true,
+ true,
+ false,
+ false,
+ true,
+ true,
+ false,
+ false,
+ false,
+ false,
+ true,
+ true,
+ true,
+ false,
+ false,
+ false,
+ false,
+ true,
+ true,
+ true,
+ false,
+ false,
+ false,
+ false,
+ false,
+ true,
+ false,
+ true,
+ false,
+ false,
+ true,
+ false,
+ true
+ ],
+ "model.layers.9.self_attn.v_proj.lora_E": [
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ false,
+ true,
+ false,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ false
+ ],
+ "model.layers.10.self_attn.q_proj.lora_E": [
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ true,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ true,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ true,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false
+ ],
+ "model.layers.10.self_attn.v_proj.lora_E": [
+ true,
+ true,
+ false,
+ false,
+ false,
+ true,
+ true,
+ false,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ false,
+ false,
+ false,
+ true,
+ true,
+ true,
+ true,
+ false,
+ false,
+ false,
+ false,
+ true,
+ false,
+ false,
+ false,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ false,
+ true,
+ false,
+ false,
+ true,
+ true,
+ false,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true
+ ],
+ "model.layers.11.self_attn.q_proj.lora_E": [
+ true,
+ false,
+ false,
+ false,
+ false,
+ true,
+ false,
+ false,
+ false,
+ true,
+ true,
+ false,
+ true,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ true,
+ false,
+ false,
+ true,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ true,
+ false,
+ false,
+ false,
+ true,
+ true,
+ true,
+ false,
+ true,
+ false,
+ false,
+ false,
+ true,
+ true,
+ false,
+ false,
+ false,
+ false,
+ true,
+ true,
+ false,
+ true,
+ false,
+ true,
+ true,
+ false,
+ false,
+ false
+ ],
+ "model.layers.11.self_attn.v_proj.lora_E": [
+ false,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ false,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ false,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ false,
+ false,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ false,
+ false,
+ false,
+ false,
+ true,
+ false,
+ false,
+ true,
+ true,
+ false,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ false,
+ false
+ ],
+ "model.layers.12.self_attn.q_proj.lora_E": [
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ true,
+ false,
+ true,
+ false,
+ false,
+ false,
+ false,
+ false,
+ true,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ true,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ true,
+ true,
+ false,
+ true,
+ false,
+ false,
+ false,
+ false,
+ true,
+ false,
+ true,
+ false,
+ false,
+ true,
+ false,
+ true,
+ false,
+ false,
+ true,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false
+ ],
+ "model.layers.12.self_attn.v_proj.lora_E": [
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ false,
+ false,
+ false,
+ true,
+ true,
+ false,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ false,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ false,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ false,
+ true,
+ false,
+ true,
+ false,
+ true,
+ false,
+ true,
+ true,
+ false
+ ],
+ "model.layers.13.self_attn.q_proj.lora_E": [
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ false,
+ false,
+ true,
+ true,
+ false,
+ true,
+ false,
+ true,
+ false,
+ true,
+ false,
+ false,
+ true,
+ true,
+ false,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ false,
+ false,
+ true,
+ true,
+ false,
+ false,
+ true,
+ false,
+ true,
+ false,
+ true,
+ true,
+ true,
+ false,
+ false,
+ false,
+ false,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ false,
+ true,
+ true,
+ true,
+ false,
+ true,
+ false,
+ true,
+ true,
+ false,
+ false,
+ false,
+ true,
+ false
+ ],
+ "model.layers.13.self_attn.v_proj.lora_E": [
+ true,
+ false,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ false,
+ true,
+ false,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ false,
+ false,
+ true,
+ true,
+ false,
+ false,
+ true,
+ false,
+ false,
+ true,
+ false,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ false,
+ false,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true
+ ],
+ "model.layers.14.self_attn.q_proj.lora_E": [
+ false,
+ true,
+ false,
+ true,
+ true,
+ false,
+ false,
+ false,
+ true,
+ false,
+ false,
+ true,
+ false,
+ false,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ false,
+ false,
+ false,
+ true,
+ false,
+ true,
+ false,
+ true,
+ false,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ false,
+ true,
+ true,
+ false,
+ true,
+ true,
+ false,
+ false,
+ true,
+ false,
+ false,
+ false,
+ true,
+ false,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ false,
+ false,
+ true,
+ false,
+ true,
+ true,
+ false
+ ],
+ "model.layers.14.self_attn.v_proj.lora_E": [
+ true,
+ true,
+ true,
+ false,
+ false,
+ false,
+ true,
+ false,
+ false,
+ false,
+ false,
+ true,
+ true,
+ false,
+ false,
+ true,
+ false,
+ true,
+ true,
+ true,
+ false,
+ true,
+ false,
+ false,
+ true,
+ false,
+ true,
+ false,
+ true,
+ true,
+ false,
+ true,
+ false,
+ true,
+ false,
+ false,
+ true,
+ false,
+ false,
+ true,
+ false,
+ true,
+ true,
+ false,
+ true,
+ false,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ false,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ false
+ ],
+ "model.layers.15.self_attn.q_proj.lora_E": [
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ false,
+ true,
+ false,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ false,
+ true,
+ false,
+ true,
+ false,
+ true,
+ true,
+ true,
+ false,
+ true,
+ false,
+ false,
+ false,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ false,
+ true,
+ false,
+ true,
+ false,
+ false,
+ true,
+ true,
+ false,
+ true,
+ false,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true
+ ],
+ "model.layers.15.self_attn.v_proj.lora_E": [
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ false,
+ true,
+ true,
+ false,
+ false,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ false,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ false,
+ false,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true
+ ],
+ "model.layers.16.self_attn.q_proj.lora_E": [
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ false,
+ true,
+ true,
+ true,
+ false,
+ true,
+ false,
+ true,
+ true,
+ true,
+ false,
+ false,
+ false,
+ true,
+ false,
+ false,
+ false,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ false,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ false,
+ true,
+ true,
+ false,
+ true,
+ false,
+ false,
+ true,
+ true,
+ true,
+ false,
+ false,
+ true,
+ true
+ ],
+ "model.layers.16.self_attn.v_proj.lora_E": [
+ true,
+ false,
+ true,
+ false,
+ true,
+ false,
+ true,
+ false,
+ false,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ false,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ false,
+ false,
+ false,
+ true,
+ true,
+ true,
+ false,
+ true,
+ false,
+ false,
+ true,
+ false,
+ false,
+ false,
+ true,
+ false,
+ true,
+ false,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ false,
+ false,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ false,
+ true,
+ false,
+ true,
+ false,
+ false
+ ],
+ "model.layers.17.self_attn.q_proj.lora_E": [
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ false,
+ true,
+ false,
+ false,
+ true,
+ true,
+ true,
+ false,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ false,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ false,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true
+ ],
+ "model.layers.17.self_attn.v_proj.lora_E": [
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ false,
+ false,
+ false,
+ true,
+ true,
+ false,
+ true,
+ true,
+ false,
+ false,
+ true,
+ true,
+ false,
+ false,
+ false,
+ false,
+ true,
+ true,
+ true,
+ false,
+ true,
+ false,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ false,
+ true,
+ true,
+ true,
+ true
+ ],
+ "model.layers.18.self_attn.q_proj.lora_E": [
+ false,
+ true,
+ false,
+ true,
+ false,
+ true,
+ false,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ false,
+ true,
+ false,
+ false,
+ false,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ false,
+ false,
+ false,
+ false,
+ true,
+ false,
+ false,
+ true,
+ false,
+ true,
+ false,
+ true,
+ true
+ ],
+ "model.layers.18.self_attn.v_proj.lora_E": [
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ false,
+ false,
+ false,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ false,
+ true
+ ],
+ "model.layers.19.self_attn.q_proj.lora_E": [
+ false,
+ true,
+ false,
+ true,
+ false,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ false,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ false,
+ true,
+ false,
+ true,
+ false,
+ false,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ false,
+ false,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ false,
+ true,
+ true,
+ false,
+ true,
+ true
+ ],
+ "model.layers.19.self_attn.v_proj.lora_E": [
+ false,
+ true,
+ false,
+ true,
+ true,
+ true,
+ false,
+ true,
+ false,
+ false,
+ false,
+ false,
+ true,
+ true,
+ true,
+ false,
+ true,
+ false,
+ false,
+ false,
+ false,
+ true,
+ false,
+ true,
+ true,
+ false,
+ true,
+ true,
+ false,
+ false,
+ true,
+ true,
+ true,
+ true,
+ false,
+ false,
+ false,
+ false,
+ false,
+ true,
+ false,
+ false,
+ true,
+ false,
+ false,
+ false,
+ true,
+ true,
+ false,
+ false,
+ false,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ false,
+ true,
+ false,
+ true,
+ true,
+ true
+ ],
+ "model.layers.20.self_attn.q_proj.lora_E": [
+ false,
+ true,
+ false,
+ false,
+ false,
+ false,
+ true,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ true,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ true,
+ false,
+ false,
+ false,
+ false,
+ false,
+ true,
+ false,
+ true,
+ true,
+ false,
+ false,
+ false,
+ false,
+ true,
+ false,
+ true,
+ false,
+ true,
+ false,
+ false,
+ false,
+ false,
+ true,
+ true,
+ false,
+ false,
+ true,
+ true,
+ false,
+ false,
+ false,
+ false,
+ false,
+ true,
+ false,
+ false
+ ],
+ "model.layers.20.self_attn.v_proj.lora_E": [
+ true,
+ false,
+ true,
+ true,
+ false,
+ false,
+ false,
+ true,
+ true,
+ false,
+ false,
+ true,
+ true,
+ true,
+ false,
+ true,
+ false,
+ true,
+ false,
+ false,
+ false,
+ false,
+ true,
+ false,
+ false,
+ false,
+ true,
+ false,
+ true,
+ false,
+ true,
+ true,
+ true,
+ false,
+ true,
+ false,
+ true,
+ false,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ true,
+ false,
+ false,
+ false,
+ true,
+ false,
+ false,
+ true,
+ false,
+ false,
+ true,
+ true
+ ],
+ "model.layers.21.self_attn.q_proj.lora_E": [
+ false,
+ false,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ false,
+ false,
+ false,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ true,
+ true,
+ true,
+ false,
+ true,
+ false,
+ true,
+ false,
+ true,
+ false,
+ false,
+ false,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ false,
+ true,
+ true,
+ false,
+ true,
+ true,
+ false,
+ false,
+ true,
+ true
+ ],
+ "model.layers.21.self_attn.v_proj.lora_E": [
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ false,
+ true,
+ true,
+ false,
+ false,
+ true,
+ true,
+ false,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ false,
+ false,
+ false,
+ false,
+ false,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ false,
+ true,
+ true,
+ false,
+ true,
+ true,
+ false,
+ false,
+ false,
+ true,
+ true,
+ false,
+ false,
+ false,
+ true,
+ true,
+ false,
+ true,
+ true,
+ false,
+ false,
+ false,
+ false,
+ true,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false
+ ],
+ "model.layers.22.self_attn.q_proj.lora_E": [
+ false,
+ true,
+ false,
+ true,
+ true,
+ false,
+ true,
+ false,
+ false,
+ true,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ true,
+ false,
+ true,
+ true,
+ false,
+ false,
+ false,
+ false,
+ true,
+ true,
+ true,
+ false,
+ false,
+ true,
+ false,
+ false,
+ false,
+ false,
+ false,
+ true,
+ false,
+ false,
+ false,
+ false,
+ true,
+ false,
+ false,
+ false,
+ true,
+ false,
+ true,
+ false,
+ false,
+ false,
+ true,
+ false,
+ true,
+ true,
+ true,
+ false,
+ false,
+ true,
+ false,
+ false,
+ true,
+ true,
+ false,
+ true
+ ],
+ "model.layers.22.self_attn.v_proj.lora_E": [
+ false,
+ true,
+ true,
+ true,
+ true,
+ false,
+ false,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ false,
+ true,
+ true,
+ false,
+ true,
+ false,
+ false,
+ true,
+ false,
+ false,
+ false,
+ false,
+ true,
+ false,
+ false,
+ false,
+ true,
+ true,
+ false,
+ false,
+ false,
+ true,
+ true,
+ false,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ false,
+ true,
+ false,
+ true,
+ true
+ ],
+ "model.layers.23.self_attn.q_proj.lora_E": [
+ true,
+ false,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ false,
+ true,
+ false,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ false,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true
+ ],
+ "model.layers.23.self_attn.v_proj.lora_E": [
+ false,
+ true,
+ false,
+ true,
+ false,
+ false,
+ true,
+ false,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ false,
+ true,
+ false,
+ true,
+ true,
+ false,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ false,
+ false,
+ false,
+ true,
+ true,
+ false,
+ true,
+ false,
+ true,
+ true
+ ],
+ "model.layers.24.self_attn.q_proj.lora_E": [
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ false,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ false,
+ false,
+ false,
+ true,
+ true,
+ true,
+ true,
+ false,
+ false,
+ true
+ ],
+ "model.layers.24.self_attn.v_proj.lora_E": [
+ true,
+ true,
+ true,
+ false,
+ true,
+ false,
+ false,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ false,
+ false,
+ true,
+ false,
+ false,
+ false,
+ false,
+ true,
+ true,
+ true,
+ false,
+ true,
+ false,
+ false,
+ true,
+ false,
+ true,
+ false,
+ true,
+ true,
+ false,
+ true,
+ true,
+ false,
+ false,
+ false,
+ true,
+ false,
+ false,
+ true,
+ true,
+ false,
+ true,
+ true,
+ false,
+ false,
+ true,
+ true,
+ true,
+ true,
+ false,
+ false,
+ true,
+ true,
+ true,
+ false,
+ true,
+ false,
+ true,
+ true,
+ true
+ ],
+ "model.layers.25.self_attn.q_proj.lora_E": [
+ false,
+ false,
+ false,
+ false,
+ true,
+ true,
+ false,
+ true,
+ true,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ true,
+ false,
+ false,
+ true,
+ false,
+ false,
+ true,
+ false,
+ false,
+ false,
+ true,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ true,
+ false,
+ false,
+ false,
+ false,
+ false,
+ true,
+ false,
+ false,
+ false,
+ true,
+ true,
+ true,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false
+ ],
+ "model.layers.25.self_attn.v_proj.lora_E": [
+ false,
+ false,
+ false,
+ true,
+ false,
+ false,
+ false,
+ true,
+ true,
+ false,
+ false,
+ true,
+ false,
+ true,
+ true,
+ true,
+ false,
+ false,
+ false,
+ false,
+ true,
+ false,
+ false,
+ false,
+ true,
+ true,
+ true,
+ true,
+ false,
+ false,
+ false,
+ false,
+ true,
+ false,
+ false,
+ false,
+ false,
+ true,
+ false,
+ true,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ true,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false
+ ],
+ "model.layers.26.self_attn.q_proj.lora_E": [
+ true,
+ false,
+ false,
+ true,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ true,
+ false,
+ true,
+ false,
+ true,
+ true,
+ true,
+ false,
+ false,
+ true,
+ true,
+ true,
+ false,
+ false,
+ true,
+ true,
+ false,
+ false,
+ true,
+ false,
+ true,
+ true,
+ false,
+ false,
+ false,
+ true,
+ true,
+ false,
+ false,
+ false,
+ true,
+ false,
+ false,
+ false,
+ true,
+ true,
+ false,
+ false,
+ true,
+ false,
+ true,
+ true,
+ false,
+ true,
+ false,
+ false,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true
+ ],
+ "model.layers.26.self_attn.v_proj.lora_E": [
+ false,
+ false,
+ true,
+ false,
+ true,
+ false,
+ false,
+ false,
+ true,
+ false,
+ false,
+ false,
+ false,
+ false,
+ true,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ true,
+ false,
+ false,
+ true,
+ false,
+ true,
+ false,
+ true,
+ true,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ true,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ true,
+ true,
+ false,
+ false,
+ false,
+ true,
+ false,
+ true,
+ false,
+ true,
+ false,
+ false,
+ false,
+ true,
+ false,
+ false
+ ],
+ "model.layers.27.self_attn.q_proj.lora_E": [
+ true,
+ false,
+ false,
+ true,
+ true,
+ false,
+ false,
+ true,
+ true,
+ false,
+ false,
+ false,
+ true,
+ true,
+ false,
+ true,
+ false,
+ false,
+ true,
+ false,
+ false,
+ true,
+ true,
+ true,
+ true,
+ false,
+ false,
+ true,
+ true,
+ false,
+ false,
+ false,
+ false,
+ true,
+ true,
+ true,
+ false,
+ true,
+ false,
+ false,
+ false,
+ true,
+ false,
+ true,
+ true,
+ true,
+ false,
+ false,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ false,
+ false,
+ false,
+ true,
+ false,
+ false,
+ false,
+ true,
+ false
+ ],
+ "model.layers.27.self_attn.v_proj.lora_E": [
+ false,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ false,
+ false,
+ true,
+ false,
+ false,
+ false,
+ true,
+ true,
+ false,
+ false,
+ false,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ false,
+ true,
+ false,
+ true,
+ true,
+ false,
+ true,
+ true,
+ false,
+ false,
+ true,
+ false,
+ true,
+ true,
+ false,
+ false,
+ true,
+ false,
+ true,
+ true,
+ true,
+ false,
+ false,
+ true,
+ false,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true
+ ]
+ },
+ "alpha_pattern": {},
+ "megatron_config": null,
+ "megatron_core": "megatron.core",
+ "trainable_token_indices": null,
+ "loftq_config": {},
+ "eva_config": null,
+ "corda_config": null,
+ "use_dora": false,
+ "layer_replication": null,
+ "lora_bias": false,
+ "target_r": 32,
+ "init_r": 64,
+ "tinit": 200,
+ "tfinal": 500,
+ "deltaT": 1,
+ "beta1": 0.85,
+ "beta2": 0.85,
+ "orth_reg_weight": 0.5,
+ "total_step": 5000
+ },
+ "error_msg": ""
+ },
+ "train_info": {
+ "accelerator_memory_reserved_avg": 12361399900,
+ "accelerator_memory_max": 22793945088,
+ "accelerator_memory_reserved_99th": 18203426160,
+ "train_time": 1986.3603882369862,
+ "file_size": 35147440,
+ "num_trainable_params": 18353664,
+ "num_total_params": 3231103544,
+ "status": "success",
+ "metrics": [
+ {
+ "step": 250,
+ "valid accuracy": 0.0,
+ "train loss": 1.3241184422969818,
+ "train samples": 1000,
+ "train time": 35.95594502204767,
+ "eval time": 11.413120707002236,
+ "tokens / sec": 5888.289123542072,
+ "mem allocated avg": 7292959393.792,
+ "mem reserved avg": 12441731727.36,
+ "elapsed time": 100.98083375500573
+ },
+ {
+ "step": 500,
+ "valid accuracy": 0.38,
+ "train loss": 1.0195633232593537,
+ "train samples": 2000,
+ "train time": 37.64258231502754,
+ "eval time": 11.37802824100072,
+ "tokens / sec": 5525.524212428035,
+ "mem allocated avg": 7285510731.776,
+ "mem reserved avg": 12328493907.968,
+ "elapsed time": 197.93603045200143
+ },
+ {
+ "step": 750,
+ "valid accuracy": 0.28,
+ "train loss": 0.7883218789100647,
+ "train samples": 3000,
+ "train time": 37.909325722001086,
+ "eval time": 11.385932488003164,
+ "tokens / sec": 5655.626838954038,
+ "mem allocated avg": 7296095842.304,
+ "mem reserved avg": 12484438130.688,
+ "elapsed time": 295.9188707240028
+ },
+ {
+ "step": 1000,
+ "valid accuracy": 0.3,
+ "train loss": 0.7408825470209122,
+ "train samples": 4000,
+ "train time": 37.79932949803333,
+ "eval time": 11.34964040399791,
+ "tokens / sec": 5511.6321576772825,
+ "mem allocated avg": 7286506670.08,
+ "mem reserved avg": 12351948455.936,
+ "elapsed time": 393.33776786700037
+ },
+ {
+ "step": 1250,
+ "valid accuracy": 0.36,
+ "train loss": 0.7282904219627381,
+ "train samples": 5000,
+ "train time": 37.475317073069164,
+ "eval time": 11.342822429993248,
+ "tokens / sec": 5564.676066473135,
+ "mem allocated avg": 7287005519.872,
+ "mem reserved avg": 12349910024.192,
+ "elapsed time": 490.5430299360014
+ },
+ {
+ "step": 1500,
+ "valid accuracy": 0.38,
+ "train loss": 0.7161256531476975,
+ "train samples": 6000,
+ "train time": 37.660518338059774,
+ "eval time": 11.34013032400253,
+ "tokens / sec": 5558.367469107556,
+ "mem allocated avg": 7287642494.976,
+ "mem reserved avg": 12380570386.432,
+ "elapsed time": 588.017992052999
+ },
+ {
+ "step": 1750,
+ "valid accuracy": 0.34,
+ "train loss": 0.7056601424217224,
+ "train samples": 7000,
+ "train time": 37.636171496975294,
+ "eval time": 11.3171367870018,
+ "tokens / sec": 5562.600861695649,
+ "mem allocated avg": 7289782888.448,
+ "mem reserved avg": 12389051269.12,
+ "elapsed time": 685.2421731229988
+ },
+ {
+ "step": 2000,
+ "valid accuracy": 0.34,
+ "train loss": 0.7058932571411133,
+ "train samples": 8000,
+ "train time": 37.505602380944765,
+ "eval time": 11.37751964799827,
+ "tokens / sec": 5537.732680318789,
+ "mem allocated avg": 7287054886.912,
+ "mem reserved avg": 12336119152.64,
+ "elapsed time": 782.1823508529997
+ },
+ {
+ "step": 2250,
+ "valid accuracy": 0.3,
+ "train loss": 0.700018577337265,
+ "train samples": 9000,
+ "train time": 38.06487834800646,
+ "eval time": 11.33160761000181,
+ "tokens / sec": 5646.885247730137,
+ "mem allocated avg": 7297638139.904,
+ "mem reserved avg": 12521129902.08,
+ "elapsed time": 880.444039299
+ },
+ {
+ "step": 2500,
+ "valid accuracy": 0.34,
+ "train loss": 0.6984639673233032,
+ "train samples": 10000,
+ "train time": 37.400825600088865,
+ "eval time": 7.680036880999978,
+ "tokens / sec": 5507.017470745635,
+ "mem allocated avg": 7283608303.616,
+ "mem reserved avg": 12278598467.584,
+ "elapsed time": 973.4031999860017
+ },
+ {
+ "step": 2750,
+ "valid accuracy": 0.32,
+ "train loss": 0.691307947397232,
+ "train samples": 11000,
+ "train time": 37.97861938195274,
+ "eval time": 11.376824188999308,
+ "tokens / sec": 5578.954776346737,
+ "mem allocated avg": 7293332232.192,
+ "mem reserved avg": 12452821467.136,
+ "elapsed time": 1071.2981272770048
+ },
+ {
+ "step": 3000,
+ "valid accuracy": 0.3,
+ "train loss": 0.6851879090070725,
+ "train samples": 12000,
+ "train time": 37.862704559986014,
+ "eval time": 11.377599911000289,
+ "tokens / sec": 5512.839149387935,
+ "mem allocated avg": 7288929478.656,
+ "mem reserved avg": 12371468746.752,
+ "elapsed time": 1168.7257358770003
+ },
+ {
+ "step": 3250,
+ "valid accuracy": 0.34,
+ "train loss": 0.6939580011367797,
+ "train samples": 13000,
+ "train time": 37.79518606400961,
+ "eval time": 7.2029460159974406,
+ "tokens / sec": 5580.102176050141,
+ "mem allocated avg": 7290687285.248,
+ "mem reserved avg": 12403068633.088,
+ "elapsed time": 1261.9857917680056
+ },
+ {
+ "step": 3500,
+ "valid accuracy": 0.4,
+ "train loss": 0.6825792235136032,
+ "train samples": 14000,
+ "train time": 37.73422463506722,
+ "eval time": 11.28984081800445,
+ "tokens / sec": 5558.614282617983,
+ "mem allocated avg": 7289277476.864,
+ "mem reserved avg": 12381820289.024,
+ "elapsed time": 1359.695578400002
+ },
+ {
+ "step": 3750,
+ "valid accuracy": 0.34,
+ "train loss": 0.6795008780956269,
+ "train samples": 15000,
+ "train time": 38.156728624038806,
+ "eval time": 11.362600938999094,
+ "tokens / sec": 5679.286663570962,
+ "mem allocated avg": 7299185600.512,
+ "mem reserved avg": 12562561236.992,
+ "elapsed time": 1458.6053942910003
+ },
+ {
+ "step": 4000,
+ "valid accuracy": 0.32,
+ "train loss": 0.6967895623445511,
+ "train samples": 16000,
+ "train time": 37.352128309052205,
+ "eval time": 11.363241717001074,
+ "tokens / sec": 5471.522219805362,
+ "mem allocated avg": 7281535514.624,
+ "mem reserved avg": 12256066666.496,
+ "elapsed time": 1555.2909630150025
+ },
+ {
+ "step": 4250,
+ "valid accuracy": 0.34,
+ "train loss": 0.6776066061258316,
+ "train samples": 17000,
+ "train time": 37.65609644694632,
+ "eval time": 11.334564828997827,
+ "tokens / sec": 5613.672683726684,
+ "mem allocated avg": 7291894349.824,
+ "mem reserved avg": 12418562392.064,
+ "elapsed time": 1652.928281804001
+ },
+ {
+ "step": 4500,
+ "valid accuracy": 0.34,
+ "train loss": 0.6868188911676407,
+ "train samples": 18000,
+ "train time": 37.48494880297949,
+ "eval time": 11.33762150000257,
+ "tokens / sec": 5544.038517760537,
+ "mem allocated avg": 7285549684.736,
+ "mem reserved avg": 12333837451.264,
+ "elapsed time": 1749.9311109990012
+ },
+ {
+ "step": 4750,
+ "valid accuracy": 0.34,
+ "train loss": 0.6806062284708023,
+ "train samples": 19000,
+ "train time": 33.62080936400889,
+ "eval time": 11.34113016500487,
+ "tokens / sec": 6244.31725384755,
+ "mem allocated avg": 7068488509.44,
+ "mem reserved avg": 12120833916.928,
+ "elapsed time": 1843.633759463999
+ },
+ {
+ "step": 5000,
+ "valid accuracy": 0.28,
+ "train loss": 0.6862971596717834,
+ "train samples": 20000,
+ "train time": 33.47089828590106,
+ "eval time": 11.363945298006001,
+ "tokens / sec": 6222.7191580255185,
+ "mem allocated avg": 7065409925.12,
+ "mem reserved avg": 12064965787.648,
+ "elapsed time": 1937.0431615920024
+ },
+ {
+ "step": 5000,
+ "test accuracy": 0.3904473085670963,
+ "train loss": 0.6862971596717834,
+ "train samples": 20000,
+ "train total tokens": 4198051
+ }
+ ]
+ },
+ "meta_info": {
+ "model_info": {
+ "sha": "13afe5124825b4f3751f836b40dafda64c1ed062",
+ "created_at": "2024-09-18T15:23:48+00:00"
+ },
+ "dataset_info": {
+ "metamath": {
+ "sha": "aa4f34d3d2d3231299b5b03d9b3e5a20da45aa18",
+ "created_at": "2023-09-21T17:22:46+00:00"
+ },
+ "gsm8k": {
+ "sha": "e53f048856ff4f594e959d75785d2c2d37b678ee",
+ "created_at": "2022-04-12T10:22:10+00:00"
+ }
+ },
+ "package_info": {
+ "transformers-version": "4.52.4",
+ "transformers-commit-hash": null,
+ "peft-version": "0.15.2.dev0",
+ "peft-commit-hash": "5fe7f8f8abe914d313fc3751f2ea92de7718fbaf",
+ "datasets-version": "3.6.0",
+ "datasets-commit-hash": null,
+ "bitsandbytes-version": "0.46.0",
+ "bitsandbytes-commit-hash": null,
+ "torch-version": "2.7.1+cu126",
+ "torch-commit-hash": null
+ },
+ "system_info": {
+ "system": "Linux",
+ "release": "6.8.0-1029-aws",
+ "version": "#31-Ubuntu SMP Wed Apr 23 18:42:41 UTC 2025",
+ "machine": "x86_64",
+ "processor": "x86_64",
+ "accelerator": "NVIDIA L40S"
+ },
+ "pytorch_info": "PyTorch built with:\n - GCC 11.2\n - C++ Version: 201703\n - Intel(R) oneAPI Math Kernel Library Version 2024.2-Product Build 20240605 for Intel(R) 64 architecture applications\n - Intel(R) MKL-DNN v3.7.1 (Git Hash 8d263e693366ef8db40acc569cc7d8edf644556d)\n - OpenMP 201511 (a.k.a. OpenMP 4.5)\n - LAPACK is enabled (usually provided by MKL)\n - NNPACK is enabled\n - CPU capability usage: AVX2\n - CUDA Runtime 12.6\n - NVCC architecture flags: -gencode;arch=compute_50,code=sm_50;-gencode;arch=compute_60,code=sm_60;-gencode;arch=compute_70,code=sm_70;-gencode;arch=compute_75,code=sm_75;-gencode;arch=compute_80,code=sm_80;-gencode;arch=compute_86,code=sm_86;-gencode;arch=compute_90,code=sm_90\n - CuDNN 90.7.1 (built against CUDA 12.8)\n - Built with CuDNN 90.5.1\n - Magma 2.6.1\n - Build settings: BLAS_INFO=mkl, BUILD_TYPE=Release, COMMIT_SHA=e2d141dbde55c2a4370fac5165b0561b6af4798b, CUDA_VERSION=12.6, CUDNN_VERSION=9.5.1, CXX_COMPILER=/opt/rh/gcc-toolset-11/root/usr/bin/c++, CXX_FLAGS= -D_GLIBCXX_USE_CXX11_ABI=1 -fvisibility-inlines-hidden -DUSE_PTHREADPOOL -DNDEBUG -DUSE_KINETO -DLIBKINETO_NOROCTRACER -DLIBKINETO_NOXPUPTI=ON -DUSE_FBGEMM -DUSE_PYTORCH_QNNPACK -DUSE_XNNPACK -DSYMBOLICATE_MOBILE_DEBUG_HANDLE -O2 -fPIC -Wall -Wextra -Werror=return-type -Werror=non-virtual-dtor -Werror=range-loop-construct -Werror=bool-operation -Wnarrowing -Wno-missing-field-initializers -Wno-unknown-pragmas -Wno-unused-parameter -Wno-strict-overflow -Wno-strict-aliasing -Wno-stringop-overflow -Wsuggest-override -Wno-psabi -Wno-error=old-style-cast -fdiagnostics-color=always -faligned-new -Wno-maybe-uninitialized -fno-math-errno -fno-trapping-math -Werror=format -Wno-stringop-overflow, LAPACK_INFO=mkl, PERF_WITH_AVX=1, PERF_WITH_AVX2=1, TORCH_VERSION=2.7.1, USE_CUDA=ON, USE_CUDNN=ON, USE_CUSPARSELT=1, USE_GFLAGS=OFF, USE_GLOG=OFF, USE_GLOO=ON, USE_MKL=ON, USE_MKLDNN=ON, USE_MPI=OFF, USE_NCCL=1, USE_NNPACK=ON, USE_OPENMP=ON, USE_ROCM=OFF, USE_ROCM_KERNEL_ASSERT=OFF, \n"
+ }
+}
diff --git a/peft/method_comparison/MetaMathQA/results/adaptionprompt--llama-3.2-3B-lr_0.0005.json b/peft/method_comparison/MetaMathQA/results/adaptionprompt--llama-3.2-3B-lr_0.0005.json
new file mode 100644
index 0000000000000000000000000000000000000000..c35ccc865b46ea711763fef8f6cabfd1d77d5bd8
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/results/adaptionprompt--llama-3.2-3B-lr_0.0005.json
@@ -0,0 +1,341 @@
+{
+ "run_info": {
+ "created_at": "2025-06-20T04:48:22+00:00",
+ "total_time": 2260.6744696069945,
+ "experiment_name": "adaptionprompt/llama-3.2-3B-lr_0.0005",
+ "peft_branch": "main",
+ "train_config": {
+ "model_id": "meta-llama/Llama-3.2-3B",
+ "dtype": "bfloat16",
+ "max_seq_length": 768,
+ "batch_size": 4,
+ "batch_size_eval": 50,
+ "max_steps": 5000,
+ "eval_steps": 250,
+ "compile": false,
+ "query_template": "Question: {query} Think step by step.\nAnswer:",
+ "seed": 0,
+ "grad_norm_clip": 1.0,
+ "optimizer_type": "AdamW",
+ "optimizer_kwargs": {
+ "lr": 0.0005
+ },
+ "lr_scheduler": "cosine",
+ "use_amp": false,
+ "autocast_adapter_dtype": true,
+ "generation_kwargs": {
+ "max_length": 800,
+ "max_new_tokens": 300
+ },
+ "attn_implementation": null
+ },
+ "peft_config": {
+ "task_type": "CAUSAL_LM",
+ "peft_type": "ADAPTION_PROMPT",
+ "auto_mapping": null,
+ "base_model_name_or_path": "meta-llama/Llama-3.2-3B",
+ "revision": null,
+ "inference_mode": false,
+ "target_modules": "self_attn",
+ "adapter_len": 100,
+ "adapter_layers": 28
+ },
+ "error_msg": ""
+ },
+ "train_info": {
+ "accelerator_memory_reserved_avg": 11893757234,
+ "accelerator_memory_max": 22410166272,
+ "accelerator_memory_reserved_99th": 17907664814,
+ "train_time": 1989.2834085189897,
+ "file_size": 17210384,
+ "num_trainable_params": 8601628,
+ "num_total_params": 3221351452,
+ "status": "success",
+ "metrics": [
+ {
+ "step": 250,
+ "valid accuracy": 0.0,
+ "train loss": 1.3201356165409088,
+ "train samples": 1000,
+ "train time": 36.18721537806414,
+ "eval time": 13.46754032199533,
+ "tokens / sec": 5850.657415556191,
+ "mem allocated avg": 6848060076.032,
+ "mem reserved avg": 11943163199.488,
+ "elapsed time": 99.94861951399798
+ },
+ {
+ "step": 500,
+ "valid accuracy": 0.1,
+ "train loss": 1.153662922859192,
+ "train samples": 2000,
+ "train time": 35.6493088029747,
+ "eval time": 13.314302301005227,
+ "tokens / sec": 5834.474972559473,
+ "mem allocated avg": 6840933136.384,
+ "mem reserved avg": 11833045942.272,
+ "elapsed time": 193.4177081749949
+ },
+ {
+ "step": 750,
+ "valid accuracy": 0.22,
+ "train loss": 0.9016587936878204,
+ "train samples": 3000,
+ "train time": 36.424757257977035,
+ "eval time": 13.392894379001518,
+ "tokens / sec": 5886.133941305707,
+ "mem allocated avg": 6851972698.112,
+ "mem reserved avg": 11989870968.832,
+ "elapsed time": 288.2962625699947
+ },
+ {
+ "step": 1000,
+ "valid accuracy": 0.2,
+ "train loss": 0.8571369113922119,
+ "train samples": 4000,
+ "train time": 35.59983186099271,
+ "eval time": 13.363479856001504,
+ "tokens / sec": 5852.1624712581015,
+ "mem allocated avg": 6842572642.304,
+ "mem reserved avg": 11863001661.44,
+ "elapsed time": 381.66334240599826
+ },
+ {
+ "step": 1250,
+ "valid accuracy": 0.18,
+ "train loss": 0.84929132604599,
+ "train samples": 5000,
+ "train time": 35.52914607799903,
+ "eval time": 13.408120855005109,
+ "tokens / sec": 5869.490911551474,
+ "mem allocated avg": 6843078866.944,
+ "mem reserved avg": 11855409971.2,
+ "elapsed time": 475.2031378399988
+ },
+ {
+ "step": 1500,
+ "valid accuracy": 0.18,
+ "train loss": 0.8379741818904877,
+ "train samples": 6000,
+ "train time": 35.84657208897261,
+ "eval time": 13.451748254003178,
+ "tokens / sec": 5839.637873335062,
+ "mem allocated avg": 6844234328.064,
+ "mem reserved avg": 11880013758.464,
+ "elapsed time": 568.970056428996
+ },
+ {
+ "step": 1750,
+ "valid accuracy": 0.2,
+ "train loss": 0.8320568509101868,
+ "train samples": 7000,
+ "train time": 36.04748217701126,
+ "eval time": 13.354637482996623,
+ "tokens / sec": 5807.756529900249,
+ "mem allocated avg": 6845049858.048,
+ "mem reserved avg": 11894333112.32,
+ "elapsed time": 663.2131869919976
+ },
+ {
+ "step": 2000,
+ "valid accuracy": 0.2,
+ "train loss": 0.83651398563385,
+ "train samples": 8000,
+ "train time": 35.70882848704787,
+ "eval time": 13.407459709997056,
+ "tokens / sec": 5816.376756110452,
+ "mem allocated avg": 6842067818.496,
+ "mem reserved avg": 11843724640.256,
+ "elapsed time": 756.9679808469955
+ },
+ {
+ "step": 2250,
+ "valid accuracy": 0.18,
+ "train loss": 0.8321560187339783,
+ "train samples": 9000,
+ "train time": 36.077689886013104,
+ "eval time": 13.313609958000598,
+ "tokens / sec": 5957.92027369615,
+ "mem allocated avg": 6853360060.416,
+ "mem reserved avg": 12025841319.936,
+ "elapsed time": 851.5264306229947
+ },
+ {
+ "step": 2500,
+ "valid accuracy": 0.22,
+ "train loss": 0.830465945482254,
+ "train samples": 10000,
+ "train time": 35.51607862501987,
+ "eval time": 13.570960901000944,
+ "tokens / sec": 5799.260728488849,
+ "mem allocated avg": 6838232895.488,
+ "mem reserved avg": 11785499312.128,
+ "elapsed time": 945.1205676109967
+ },
+ {
+ "step": 2750,
+ "valid accuracy": 0.2,
+ "train loss": 0.8323929319381714,
+ "train samples": 11000,
+ "train time": 36.33290277811466,
+ "eval time": 13.340032396001334,
+ "tokens / sec": 5831.6562619276265,
+ "mem allocated avg": 6849506107.392,
+ "mem reserved avg": 11957667102.72,
+ "elapsed time": 1039.698461469001
+ },
+ {
+ "step": 3000,
+ "valid accuracy": 0.22,
+ "train loss": 0.8273163681030273,
+ "train samples": 12000,
+ "train time": 36.133581758025684,
+ "eval time": 13.486512909999874,
+ "tokens / sec": 5776.648476140576,
+ "mem allocated avg": 6844330549.248,
+ "mem reserved avg": 11874754101.248,
+ "elapsed time": 1134.0729920019949
+ },
+ {
+ "step": 3250,
+ "valid accuracy": 0.18,
+ "train loss": 0.8321007430553437,
+ "train samples": 13000,
+ "train time": 35.81564853595046,
+ "eval time": 13.383609317002993,
+ "tokens / sec": 5888.515456820645,
+ "mem allocated avg": 6845503963.136,
+ "mem reserved avg": 11903065653.248,
+ "elapsed time": 1228.1345331240009
+ },
+ {
+ "step": 3500,
+ "valid accuracy": 0.18,
+ "train loss": 0.8267617487907409,
+ "train samples": 14000,
+ "train time": 35.759473790014454,
+ "eval time": 13.568141147006827,
+ "tokens / sec": 5865.578482269809,
+ "mem allocated avg": 6844375582.72,
+ "mem reserved avg": 11893385199.616,
+ "elapsed time": 1322.3741278140005
+ },
+ {
+ "step": 3750,
+ "valid accuracy": 0.18,
+ "train loss": 0.822540352344513,
+ "train samples": 15000,
+ "train time": 36.6447854490616,
+ "eval time": 13.383382205000089,
+ "tokens / sec": 5913.610827418539,
+ "mem allocated avg": 6855454945.28,
+ "mem reserved avg": 12064244367.36,
+ "elapsed time": 1417.8726171529997
+ },
+ {
+ "step": 4000,
+ "valid accuracy": 0.22,
+ "train loss": 0.842738341331482,
+ "train samples": 16000,
+ "train time": 35.83419257100468,
+ "eval time": 13.484180120998644,
+ "tokens / sec": 5703.295800373884,
+ "mem allocated avg": 6837201041.408,
+ "mem reserved avg": 11769015697.408,
+ "elapsed time": 1511.8286734409994
+ },
+ {
+ "step": 4250,
+ "valid accuracy": 0.24,
+ "train loss": 0.8195172207355499,
+ "train samples": 17000,
+ "train time": 36.032976000991766,
+ "eval time": 13.43221827600064,
+ "tokens / sec": 5866.542913196561,
+ "mem allocated avg": 6847173238.784,
+ "mem reserved avg": 11924070727.68,
+ "elapsed time": 1606.2413196950001
+ },
+ {
+ "step": 4500,
+ "valid accuracy": 0.22,
+ "train loss": 0.8333091423511505,
+ "train samples": 18000,
+ "train time": 35.92476197002543,
+ "eval time": 13.364069708994066,
+ "tokens / sec": 5784.812163081199,
+ "mem allocated avg": 6842308513.792,
+ "mem reserved avg": 11840637632.512,
+ "elapsed time": 1700.1633438569988
+ },
+ {
+ "step": 4750,
+ "valid accuracy": 0.24,
+ "train loss": 0.8247289218902588,
+ "train samples": 19000,
+ "train time": 36.319470202004595,
+ "eval time": 13.367499373998726,
+ "tokens / sec": 5780.343128144329,
+ "mem allocated avg": 6845010323.456,
+ "mem reserved avg": 11893443919.872,
+ "elapsed time": 1795.0117048679967
+ },
+ {
+ "step": 5000,
+ "valid accuracy": 0.24,
+ "train loss": 0.8317011270523071,
+ "train samples": 20000,
+ "train time": 35.778475134953624,
+ "eval time": 13.382634160996531,
+ "tokens / sec": 5821.377216731123,
+ "mem allocated avg": 6841479706.624,
+ "mem reserved avg": 11840956399.616,
+ "elapsed time": 1888.9356832179983
+ },
+ {
+ "step": 5000,
+ "test accuracy": 0.22062168309325247,
+ "train loss": 0.8317011270523071,
+ "train samples": 20000,
+ "train total tokens": 4198051
+ }
+ ]
+ },
+ "meta_info": {
+ "model_info": {
+ "sha": "13afe5124825b4f3751f836b40dafda64c1ed062",
+ "created_at": "2024-09-18T15:23:48+00:00"
+ },
+ "dataset_info": {
+ "metamath": {
+ "sha": "aa4f34d3d2d3231299b5b03d9b3e5a20da45aa18",
+ "created_at": "2023-09-21T17:22:46+00:00"
+ },
+ "gsm8k": {
+ "sha": "e53f048856ff4f594e959d75785d2c2d37b678ee",
+ "created_at": "2022-04-12T10:22:10+00:00"
+ }
+ },
+ "package_info": {
+ "transformers-version": "4.52.4",
+ "transformers-commit-hash": null,
+ "peft-version": "0.15.2.dev0",
+ "peft-commit-hash": "5fe7f8f8abe914d313fc3751f2ea92de7718fbaf",
+ "datasets-version": "3.6.0",
+ "datasets-commit-hash": null,
+ "bitsandbytes-version": "0.46.0",
+ "bitsandbytes-commit-hash": null,
+ "torch-version": "2.7.1+cu126",
+ "torch-commit-hash": null
+ },
+ "system_info": {
+ "system": "Linux",
+ "release": "6.8.0-1029-aws",
+ "version": "#31-Ubuntu SMP Wed Apr 23 18:42:41 UTC 2025",
+ "machine": "x86_64",
+ "processor": "x86_64",
+ "accelerator": "NVIDIA L40S"
+ },
+ "pytorch_info": "PyTorch built with:\n - GCC 11.2\n - C++ Version: 201703\n - Intel(R) oneAPI Math Kernel Library Version 2024.2-Product Build 20240605 for Intel(R) 64 architecture applications\n - Intel(R) MKL-DNN v3.7.1 (Git Hash 8d263e693366ef8db40acc569cc7d8edf644556d)\n - OpenMP 201511 (a.k.a. OpenMP 4.5)\n - LAPACK is enabled (usually provided by MKL)\n - NNPACK is enabled\n - CPU capability usage: AVX2\n - CUDA Runtime 12.6\n - NVCC architecture flags: -gencode;arch=compute_50,code=sm_50;-gencode;arch=compute_60,code=sm_60;-gencode;arch=compute_70,code=sm_70;-gencode;arch=compute_75,code=sm_75;-gencode;arch=compute_80,code=sm_80;-gencode;arch=compute_86,code=sm_86;-gencode;arch=compute_90,code=sm_90\n - CuDNN 90.7.1 (built against CUDA 12.8)\n - Built with CuDNN 90.5.1\n - Magma 2.6.1\n - Build settings: BLAS_INFO=mkl, BUILD_TYPE=Release, COMMIT_SHA=e2d141dbde55c2a4370fac5165b0561b6af4798b, CUDA_VERSION=12.6, CUDNN_VERSION=9.5.1, CXX_COMPILER=/opt/rh/gcc-toolset-11/root/usr/bin/c++, CXX_FLAGS= -D_GLIBCXX_USE_CXX11_ABI=1 -fvisibility-inlines-hidden -DUSE_PTHREADPOOL -DNDEBUG -DUSE_KINETO -DLIBKINETO_NOROCTRACER -DLIBKINETO_NOXPUPTI=ON -DUSE_FBGEMM -DUSE_PYTORCH_QNNPACK -DUSE_XNNPACK -DSYMBOLICATE_MOBILE_DEBUG_HANDLE -O2 -fPIC -Wall -Wextra -Werror=return-type -Werror=non-virtual-dtor -Werror=range-loop-construct -Werror=bool-operation -Wnarrowing -Wno-missing-field-initializers -Wno-unknown-pragmas -Wno-unused-parameter -Wno-strict-overflow -Wno-strict-aliasing -Wno-stringop-overflow -Wsuggest-override -Wno-psabi -Wno-error=old-style-cast -fdiagnostics-color=always -faligned-new -Wno-maybe-uninitialized -fno-math-errno -fno-trapping-math -Werror=format -Wno-stringop-overflow, LAPACK_INFO=mkl, PERF_WITH_AVX=1, PERF_WITH_AVX2=1, TORCH_VERSION=2.7.1, USE_CUDA=ON, USE_CUDNN=ON, USE_CUSPARSELT=1, USE_GFLAGS=OFF, USE_GLOG=OFF, USE_GLOO=ON, USE_MKL=ON, USE_MKLDNN=ON, USE_MPI=OFF, USE_NCCL=1, USE_NNPACK=ON, USE_OPENMP=ON, USE_ROCM=OFF, USE_ROCM_KERNEL_ASSERT=OFF, \n"
+ }
+}
diff --git a/peft/method_comparison/MetaMathQA/results/boft--llama-3.2-3B-default.json b/peft/method_comparison/MetaMathQA/results/boft--llama-3.2-3B-default.json
new file mode 100644
index 0000000000000000000000000000000000000000..83ddbc7c63224c54a14f3d4eb0efdaabb159fb66
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/results/boft--llama-3.2-3B-default.json
@@ -0,0 +1,354 @@
+{
+ "run_info": {
+ "created_at": "2025-06-20T00:26:06+00:00",
+ "total_time": 11113.556226242006,
+ "experiment_name": "boft/llama-3.2-3B-default",
+ "peft_branch": "main",
+ "train_config": {
+ "model_id": "meta-llama/Llama-3.2-3B",
+ "dtype": "bfloat16",
+ "max_seq_length": 768,
+ "batch_size": 4,
+ "batch_size_eval": 50,
+ "max_steps": 5000,
+ "eval_steps": 250,
+ "compile": false,
+ "query_template": "Question: {query} Think step by step.\nAnswer:",
+ "seed": 0,
+ "grad_norm_clip": 1.0,
+ "optimizer_type": "AdamW",
+ "optimizer_kwargs": {
+ "lr": 0.0001,
+ "weight_decay": 0.1
+ },
+ "lr_scheduler": "cosine",
+ "use_amp": false,
+ "autocast_adapter_dtype": true,
+ "generation_kwargs": {
+ "max_length": 800,
+ "max_new_tokens": 300
+ },
+ "attn_implementation": null
+ },
+ "peft_config": {
+ "task_type": null,
+ "peft_type": "BOFT",
+ "auto_mapping": null,
+ "base_model_name_or_path": "meta-llama/Llama-3.2-3B",
+ "revision": null,
+ "inference_mode": false,
+ "boft_block_size": 4,
+ "boft_block_num": 0,
+ "boft_n_butterfly_factor": 1,
+ "target_modules": [
+ "q_proj",
+ "v_proj"
+ ],
+ "exclude_modules": null,
+ "boft_dropout": 0.0,
+ "fan_in_fan_out": false,
+ "bias": "none",
+ "modules_to_save": null,
+ "init_weights": true,
+ "layers_to_transform": null,
+ "layers_pattern": null
+ },
+ "error_msg": ""
+ },
+ "train_info": {
+ "accelerator_memory_reserved_avg": 14814855089,
+ "accelerator_memory_max": 24427626496,
+ "accelerator_memory_reserved_99th": 20103445872,
+ "train_time": 8291.859631775995,
+ "file_size": 3225360,
+ "num_trainable_params": 802816,
+ "num_total_params": 3213552640,
+ "status": "success",
+ "metrics": [
+ {
+ "step": 250,
+ "valid accuracy": 0.0,
+ "train loss": 1.291453486919403,
+ "train samples": 1000,
+ "train time": 168.6401632970519,
+ "eval time": 140.71104099299555,
+ "tokens / sec": 1255.4482625059293,
+ "mem allocated avg": 6794374191.104,
+ "mem reserved avg": 14862272954.368,
+ "elapsed time": 378.35506656600046
+ },
+ {
+ "step": 500,
+ "valid accuracy": 0.12,
+ "train loss": 1.0658165102005004,
+ "train samples": 2000,
+ "train time": 168.0782826189752,
+ "eval time": 140.55351014900225,
+ "tokens / sec": 1237.4888460248842,
+ "mem allocated avg": 6786098696.192,
+ "mem reserved avg": 14759126630.4,
+ "elapsed time": 750.4153373740046
+ },
+ {
+ "step": 750,
+ "valid accuracy": 0.38,
+ "train loss": 0.8760707340240479,
+ "train samples": 3000,
+ "train time": 168.35559053501493,
+ "eval time": 140.5371915020005,
+ "tokens / sec": 1273.5009233649919,
+ "mem allocated avg": 6796379451.392,
+ "mem reserved avg": 14898109087.744,
+ "elapsed time": 1123.1088362480004
+ },
+ {
+ "step": 1000,
+ "valid accuracy": 0.42,
+ "train loss": 0.8187176239490509,
+ "train samples": 4000,
+ "train time": 168.23626853094902,
+ "eval time": 140.51234973900137,
+ "tokens / sec": 1238.3536666570453,
+ "mem allocated avg": 6788017170.432,
+ "mem reserved avg": 14785978564.608,
+ "elapsed time": 1495.2035204040003
+ },
+ {
+ "step": 1250,
+ "valid accuracy": 0.44,
+ "train loss": 0.7968595073223114,
+ "train samples": 5000,
+ "train time": 168.06973706404096,
+ "eval time": 140.56398986800195,
+ "tokens / sec": 1240.7825682534333,
+ "mem allocated avg": 6786994073.6,
+ "mem reserved avg": 14784728662.016,
+ "elapsed time": 1867.293767313
+ },
+ {
+ "step": 1500,
+ "valid accuracy": 0.3,
+ "train loss": 0.7768308148384094,
+ "train samples": 6000,
+ "train time": 168.12391281103191,
+ "eval time": 140.47015122300218,
+ "tokens / sec": 1245.0995013141533,
+ "mem allocated avg": 6790023022.592,
+ "mem reserved avg": 14800616685.568,
+ "elapsed time": 2239.2391544300044
+ },
+ {
+ "step": 1750,
+ "valid accuracy": 0.34,
+ "train loss": 0.7639130955934524,
+ "train samples": 7000,
+ "train time": 168.4569528100401,
+ "eval time": 140.76006173399946,
+ "tokens / sec": 1242.780404772479,
+ "mem allocated avg": 6790166409.216,
+ "mem reserved avg": 14820103421.952,
+ "elapsed time": 2611.854956449002
+ },
+ {
+ "step": 2000,
+ "valid accuracy": 0.28,
+ "train loss": 0.7575103138685226,
+ "train samples": 8000,
+ "train time": 168.38565446306166,
+ "eval time": 140.82750502999988,
+ "tokens / sec": 1233.4542432506432,
+ "mem allocated avg": 6787659706.368,
+ "mem reserved avg": 14766038843.392,
+ "elapsed time": 2984.338527646003
+ },
+ {
+ "step": 2250,
+ "valid accuracy": 0.36,
+ "train loss": 0.7480558000802994,
+ "train samples": 9000,
+ "train time": 168.98983921804756,
+ "eval time": 140.92262020800263,
+ "tokens / sec": 1271.9581307054364,
+ "mem allocated avg": 6798715979.776,
+ "mem reserved avg": 14937929809.92,
+ "elapsed time": 3357.8442202950027
+ },
+ {
+ "step": 2500,
+ "valid accuracy": 0.36,
+ "train loss": 0.7452825582027436,
+ "train samples": 10000,
+ "train time": 168.30827127001976,
+ "eval time": 140.89225408899802,
+ "tokens / sec": 1223.7485326527044,
+ "mem allocated avg": 6783722676.224,
+ "mem reserved avg": 14710111993.856,
+ "elapsed time": 3730.0927005050034
+ },
+ {
+ "step": 2750,
+ "valid accuracy": 0.4,
+ "train loss": 0.7368131847381592,
+ "train samples": 11000,
+ "train time": 168.8352410539519,
+ "eval time": 140.97951381299936,
+ "tokens / sec": 1254.9571918595636,
+ "mem allocated avg": 6794155292.672,
+ "mem reserved avg": 14876869132.288,
+ "elapsed time": 4103.762088249001
+ },
+ {
+ "step": 3000,
+ "valid accuracy": 0.38,
+ "train loss": 0.7284122853279114,
+ "train samples": 12000,
+ "train time": 168.7332625999261,
+ "eval time": 140.92822863799665,
+ "tokens / sec": 1237.0471404616308,
+ "mem allocated avg": 6789107718.144,
+ "mem reserved avg": 14802571231.232,
+ "elapsed time": 4477.013831755001
+ },
+ {
+ "step": 3250,
+ "valid accuracy": 0.34,
+ "train loss": 0.7360657904148101,
+ "train samples": 13000,
+ "train time": 168.6564349730761,
+ "eval time": 140.91345744199498,
+ "tokens / sec": 1250.4770424779092,
+ "mem allocated avg": 6791307786.24,
+ "mem reserved avg": 14825665069.056,
+ "elapsed time": 4850.336532419002
+ },
+ {
+ "step": 3500,
+ "valid accuracy": 0.34,
+ "train loss": 0.7245372575521469,
+ "train samples": 14000,
+ "train time": 168.69712368501496,
+ "eval time": 141.10813598799723,
+ "tokens / sec": 1243.3525564528145,
+ "mem allocated avg": 6789542191.104,
+ "mem reserved avg": 14803175211.008,
+ "elapsed time": 5223.900597244006
+ },
+ {
+ "step": 3750,
+ "valid accuracy": 0.36,
+ "train loss": 0.7196882257461548,
+ "train samples": 15000,
+ "train time": 169.02741387199057,
+ "eval time": 140.85168583100312,
+ "tokens / sec": 1282.0583066135978,
+ "mem allocated avg": 6800711397.376,
+ "mem reserved avg": 14974772576.256,
+ "elapsed time": 5597.923287113001
+ },
+ {
+ "step": 4000,
+ "valid accuracy": 0.4,
+ "train loss": 0.7386573747396469,
+ "train samples": 16000,
+ "train time": 168.47688378201565,
+ "eval time": 141.17620621900278,
+ "tokens / sec": 1213.062560347618,
+ "mem allocated avg": 6781920968.704,
+ "mem reserved avg": 14703241723.904,
+ "elapsed time": 5970.573302798002
+ },
+ {
+ "step": 4250,
+ "valid accuracy": 0.36,
+ "train loss": 0.7167660998106002,
+ "train samples": 17000,
+ "train time": 168.66243355697225,
+ "eval time": 141.03309625500697,
+ "tokens / sec": 1253.3259217358275,
+ "mem allocated avg": 6792739334.144,
+ "mem reserved avg": 14838457696.256,
+ "elapsed time": 6343.574297415005
+ },
+ {
+ "step": 4500,
+ "valid accuracy": 0.36,
+ "train loss": 0.7278824989795685,
+ "train samples": 18000,
+ "train time": 168.825120675996,
+ "eval time": 141.10180295899772,
+ "tokens / sec": 1230.966097745832,
+ "mem allocated avg": 6787403542.528,
+ "mem reserved avg": 14768026943.488,
+ "elapsed time": 6716.868663600006
+ },
+ {
+ "step": 4750,
+ "valid accuracy": 0.34,
+ "train loss": 0.7206774606704712,
+ "train samples": 19000,
+ "train time": 168.64492384497134,
+ "eval time": 140.88104952100548,
+ "tokens / sec": 1244.8581031290848,
+ "mem allocated avg": 6790186668.032,
+ "mem reserved avg": 14817972715.52,
+ "elapsed time": 7090.485984892002
+ },
+ {
+ "step": 5000,
+ "valid accuracy": 0.34,
+ "train loss": 0.7268091850280761,
+ "train samples": 20000,
+ "train time": 168.56219975605927,
+ "eval time": 140.98389447200316,
+ "tokens / sec": 1235.6269691628356,
+ "mem allocated avg": 6787183779.84,
+ "mem reserved avg": 14761332834.304,
+ "elapsed time": 7463.428281595006
+ },
+ {
+ "step": 5000,
+ "test accuracy": 0.3646702047005307,
+ "train loss": 0.7268091850280761,
+ "train samples": 20000,
+ "train total tokens": 4198051
+ }
+ ]
+ },
+ "meta_info": {
+ "model_info": {
+ "sha": "13afe5124825b4f3751f836b40dafda64c1ed062",
+ "created_at": "2024-09-18T15:23:48+00:00"
+ },
+ "dataset_info": {
+ "metamath": {
+ "sha": "aa4f34d3d2d3231299b5b03d9b3e5a20da45aa18",
+ "created_at": "2023-09-21T17:22:46+00:00"
+ },
+ "gsm8k": {
+ "sha": "e53f048856ff4f594e959d75785d2c2d37b678ee",
+ "created_at": "2022-04-12T10:22:10+00:00"
+ }
+ },
+ "package_info": {
+ "transformers-version": "4.52.4",
+ "transformers-commit-hash": null,
+ "peft-version": "0.15.2.dev0",
+ "peft-commit-hash": "5fe7f8f8abe914d313fc3751f2ea92de7718fbaf",
+ "datasets-version": "3.6.0",
+ "datasets-commit-hash": null,
+ "bitsandbytes-version": "0.46.0",
+ "bitsandbytes-commit-hash": null,
+ "torch-version": "2.7.1+cu126",
+ "torch-commit-hash": null
+ },
+ "system_info": {
+ "system": "Linux",
+ "release": "6.8.0-1029-aws",
+ "version": "#31-Ubuntu SMP Wed Apr 23 18:42:41 UTC 2025",
+ "machine": "x86_64",
+ "processor": "x86_64",
+ "accelerator": "NVIDIA L40S"
+ },
+ "pytorch_info": "PyTorch built with:\n - GCC 11.2\n - C++ Version: 201703\n - Intel(R) oneAPI Math Kernel Library Version 2024.2-Product Build 20240605 for Intel(R) 64 architecture applications\n - Intel(R) MKL-DNN v3.7.1 (Git Hash 8d263e693366ef8db40acc569cc7d8edf644556d)\n - OpenMP 201511 (a.k.a. OpenMP 4.5)\n - LAPACK is enabled (usually provided by MKL)\n - NNPACK is enabled\n - CPU capability usage: AVX2\n - CUDA Runtime 12.6\n - NVCC architecture flags: -gencode;arch=compute_50,code=sm_50;-gencode;arch=compute_60,code=sm_60;-gencode;arch=compute_70,code=sm_70;-gencode;arch=compute_75,code=sm_75;-gencode;arch=compute_80,code=sm_80;-gencode;arch=compute_86,code=sm_86;-gencode;arch=compute_90,code=sm_90\n - CuDNN 90.7.1 (built against CUDA 12.8)\n - Built with CuDNN 90.5.1\n - Magma 2.6.1\n - Build settings: BLAS_INFO=mkl, BUILD_TYPE=Release, COMMIT_SHA=e2d141dbde55c2a4370fac5165b0561b6af4798b, CUDA_VERSION=12.6, CUDNN_VERSION=9.5.1, CXX_COMPILER=/opt/rh/gcc-toolset-11/root/usr/bin/c++, CXX_FLAGS= -D_GLIBCXX_USE_CXX11_ABI=1 -fvisibility-inlines-hidden -DUSE_PTHREADPOOL -DNDEBUG -DUSE_KINETO -DLIBKINETO_NOROCTRACER -DLIBKINETO_NOXPUPTI=ON -DUSE_FBGEMM -DUSE_PYTORCH_QNNPACK -DUSE_XNNPACK -DSYMBOLICATE_MOBILE_DEBUG_HANDLE -O2 -fPIC -Wall -Wextra -Werror=return-type -Werror=non-virtual-dtor -Werror=range-loop-construct -Werror=bool-operation -Wnarrowing -Wno-missing-field-initializers -Wno-unknown-pragmas -Wno-unused-parameter -Wno-strict-overflow -Wno-strict-aliasing -Wno-stringop-overflow -Wsuggest-override -Wno-psabi -Wno-error=old-style-cast -fdiagnostics-color=always -faligned-new -Wno-maybe-uninitialized -fno-math-errno -fno-trapping-math -Werror=format -Wno-stringop-overflow, LAPACK_INFO=mkl, PERF_WITH_AVX=1, PERF_WITH_AVX2=1, TORCH_VERSION=2.7.1, USE_CUDA=ON, USE_CUDNN=ON, USE_CUSPARSELT=1, USE_GFLAGS=OFF, USE_GLOG=OFF, USE_GLOO=ON, USE_MKL=ON, USE_MKLDNN=ON, USE_MPI=OFF, USE_NCCL=1, USE_NNPACK=ON, USE_OPENMP=ON, USE_ROCM=OFF, USE_ROCM_KERNEL_ASSERT=OFF, \n"
+ }
+}
diff --git a/peft/method_comparison/MetaMathQA/results/bone--llama-3.2-3B-bat.json b/peft/method_comparison/MetaMathQA/results/bone--llama-3.2-3B-bat.json
new file mode 100644
index 0000000000000000000000000000000000000000..069bbfe1077efd4cc4ea365424fc6d6d3c554ff7
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/results/bone--llama-3.2-3B-bat.json
@@ -0,0 +1,350 @@
+{
+ "run_info": {
+ "created_at": "2025-06-20T03:31:24+00:00",
+ "total_time": 2742.3845372959986,
+ "experiment_name": "bone/llama-3.2-3B-bat",
+ "peft_branch": "main",
+ "train_config": {
+ "model_id": "meta-llama/Llama-3.2-3B",
+ "dtype": "bfloat16",
+ "max_seq_length": 768,
+ "batch_size": 4,
+ "batch_size_eval": 50,
+ "max_steps": 5000,
+ "eval_steps": 250,
+ "compile": false,
+ "query_template": "Question: {query} Think step by step.\nAnswer:",
+ "seed": 0,
+ "grad_norm_clip": 1.0,
+ "optimizer_type": "AdamW",
+ "optimizer_kwargs": {
+ "lr": 0.0001,
+ "weight_decay": 0.1
+ },
+ "lr_scheduler": "cosine",
+ "use_amp": false,
+ "autocast_adapter_dtype": true,
+ "generation_kwargs": {
+ "max_length": 800,
+ "max_new_tokens": 300
+ },
+ "attn_implementation": null
+ },
+ "peft_config": {
+ "task_type": null,
+ "peft_type": "BONE",
+ "auto_mapping": null,
+ "base_model_name_or_path": "meta-llama/Llama-3.2-3B",
+ "revision": null,
+ "inference_mode": false,
+ "r": 64,
+ "target_modules": [
+ "v_proj",
+ "q_proj"
+ ],
+ "exclude_modules": null,
+ "init_weights": "bat",
+ "layers_to_transform": null,
+ "layers_pattern": null,
+ "bias": "none",
+ "modules_to_save": null
+ },
+ "error_msg": ""
+ },
+ "train_info": {
+ "accelerator_memory_reserved_avg": 14713983755,
+ "accelerator_memory_max": 25251807232,
+ "accelerator_memory_reserved_99th": 20472733368,
+ "train_time": 2430.7548372539895,
+ "file_size": 29367552,
+ "num_trainable_params": 7340032,
+ "num_total_params": 3220089856,
+ "status": "success",
+ "metrics": [
+ {
+ "step": 250,
+ "valid accuracy": 0.34,
+ "train loss": 0.8741071329116822,
+ "train samples": 1000,
+ "train time": 44.769113782072964,
+ "eval time": 16.53786130100343,
+ "tokens / sec": 4729.130914464948,
+ "mem allocated avg": 6898425409.536,
+ "mem reserved avg": 14773294989.312,
+ "elapsed time": 124.73039968500234
+ },
+ {
+ "step": 500,
+ "valid accuracy": 0.42,
+ "train loss": 0.6946564470529556,
+ "train samples": 2000,
+ "train time": 43.747789238033874,
+ "eval time": 16.4541177170031,
+ "tokens / sec": 4754.4116770858745,
+ "mem allocated avg": 6890118709.248,
+ "mem reserved avg": 14662749913.088,
+ "elapsed time": 242.48505929599924
+ },
+ {
+ "step": 750,
+ "valid accuracy": 0.42,
+ "train loss": 0.6668610339164733,
+ "train samples": 3000,
+ "train time": 44.788394879076805,
+ "eval time": 8.99262467600056,
+ "tokens / sec": 4786.9766393472355,
+ "mem allocated avg": 6900886024.192,
+ "mem reserved avg": 14820195696.64,
+ "elapsed time": 354.3122298879971
+ },
+ {
+ "step": 1000,
+ "valid accuracy": 0.42,
+ "train loss": 0.6476555281877517,
+ "train samples": 4000,
+ "train time": 43.08444309095648,
+ "eval time": 14.581032188005338,
+ "tokens / sec": 4835.527282090601,
+ "mem allocated avg": 6892210176.0,
+ "mem reserved avg": 14677799075.84,
+ "elapsed time": 469.41999823199876
+ },
+ {
+ "step": 1250,
+ "valid accuracy": 0.38,
+ "train loss": 0.6442477897405624,
+ "train samples": 5000,
+ "train time": 43.81069704208494,
+ "eval time": 16.504536090003967,
+ "tokens / sec": 4759.979048031958,
+ "mem allocated avg": 6892437598.208,
+ "mem reserved avg": 14675995525.12,
+ "elapsed time": 587.4669312400001
+ },
+ {
+ "step": 1500,
+ "valid accuracy": 0.48,
+ "train loss": 0.6370412122011184,
+ "train samples": 6000,
+ "train time": 44.041188616007275,
+ "eval time": 11.50742915799492,
+ "tokens / sec": 4753.07335197389,
+ "mem allocated avg": 6893869041.664,
+ "mem reserved avg": 14704349020.16,
+ "elapsed time": 700.887209352004
+ },
+ {
+ "step": 1750,
+ "valid accuracy": 0.44,
+ "train loss": 0.6277673766613007,
+ "train samples": 7000,
+ "train time": 44.32280573899334,
+ "eval time": 16.494074002999696,
+ "tokens / sec": 4723.414876595195,
+ "mem allocated avg": 6895170344.96,
+ "mem reserved avg": 14718215389.184,
+ "elapsed time": 819.4313268580008
+ },
+ {
+ "step": 2000,
+ "valid accuracy": 0.48,
+ "train loss": 0.6278820457458496,
+ "train samples": 8000,
+ "train time": 43.325528461049544,
+ "eval time": 16.452074027998606,
+ "tokens / sec": 4793.848047040501,
+ "mem allocated avg": 6891568050.176,
+ "mem reserved avg": 14656710115.328,
+ "elapsed time": 936.9070930559974
+ },
+ {
+ "step": 2250,
+ "valid accuracy": 0.44,
+ "train loss": 0.6160005252361298,
+ "train samples": 9000,
+ "train time": 45.04456213898811,
+ "eval time": 16.52133422600309,
+ "tokens / sec": 4771.896757188206,
+ "mem allocated avg": 6903412344.832,
+ "mem reserved avg": 14851812360.192,
+ "elapsed time": 1056.8185863660037
+ },
+ {
+ "step": 2500,
+ "valid accuracy": 0.5,
+ "train loss": 0.6121727240085602,
+ "train samples": 10000,
+ "train time": 43.16439942702709,
+ "eval time": 16.356938169003115,
+ "tokens / sec": 4771.686916395162,
+ "mem allocated avg": 6888002562.048,
+ "mem reserved avg": 14598350569.472,
+ "elapsed time": 1173.7929829869972
+ },
+ {
+ "step": 2750,
+ "valid accuracy": 0.52,
+ "train loss": 0.6007345867156982,
+ "train samples": 11000,
+ "train time": 44.3066304440581,
+ "eval time": 16.514935120998416,
+ "tokens / sec": 4782.151065798665,
+ "mem allocated avg": 6899352545.28,
+ "mem reserved avg": 14785458470.912,
+ "elapsed time": 1292.7444534430033
+ },
+ {
+ "step": 3000,
+ "valid accuracy": 0.52,
+ "train loss": 0.5899704934358597,
+ "train samples": 12000,
+ "train time": 44.07467572299356,
+ "eval time": 16.412788394998643,
+ "tokens / sec": 4735.848796979486,
+ "mem allocated avg": 6894036676.608,
+ "mem reserved avg": 14687865405.44,
+ "elapsed time": 1411.115336062001
+ },
+ {
+ "step": 3250,
+ "valid accuracy": 0.48,
+ "train loss": 0.5988378477096558,
+ "train samples": 13000,
+ "train time": 44.070030323957326,
+ "eval time": 10.250203846997465,
+ "tokens / sec": 4785.587812163363,
+ "mem allocated avg": 6895260303.36,
+ "mem reserved avg": 14725043716.096,
+ "elapsed time": 1523.332073521
+ },
+ {
+ "step": 3500,
+ "valid accuracy": 0.5,
+ "train loss": 0.5801258901357651,
+ "train samples": 14000,
+ "train time": 43.991991777089424,
+ "eval time": 16.38271237299341,
+ "tokens / sec": 4767.913238909897,
+ "mem allocated avg": 6893688922.112,
+ "mem reserved avg": 14703484993.536,
+ "elapsed time": 1641.7187374700006
+ },
+ {
+ "step": 3750,
+ "valid accuracy": 0.5,
+ "train loss": 0.5768071869611741,
+ "train samples": 15000,
+ "train time": 45.04501243098639,
+ "eval time": 16.454509290000715,
+ "tokens / sec": 4810.810083180938,
+ "mem allocated avg": 6905122422.784,
+ "mem reserved avg": 14891314315.264,
+ "elapsed time": 1761.645320085001
+ },
+ {
+ "step": 4000,
+ "valid accuracy": 0.52,
+ "train loss": 0.5858320169448853,
+ "train samples": 16000,
+ "train time": 42.547905418032315,
+ "eval time": 16.350580427999375,
+ "tokens / sec": 4803.36218650576,
+ "mem allocated avg": 6886491265.024,
+ "mem reserved avg": 14582730981.376,
+ "elapsed time": 1878.0724109930015
+ },
+ {
+ "step": 4250,
+ "valid accuracy": 0.54,
+ "train loss": 0.5723247408866883,
+ "train samples": 17000,
+ "train time": 44.19116178697732,
+ "eval time": 16.508775556001638,
+ "tokens / sec": 4783.513070305705,
+ "mem allocated avg": 6897152284.672,
+ "mem reserved avg": 14738381602.816,
+ "elapsed time": 1996.8971549050038
+ },
+ {
+ "step": 4500,
+ "valid accuracy": 0.48,
+ "train loss": 0.5789256048202515,
+ "train samples": 18000,
+ "train time": 43.87211918797402,
+ "eval time": 16.414912490006827,
+ "tokens / sec": 4736.903615473535,
+ "mem allocated avg": 6893093124.096,
+ "mem reserved avg": 14658832433.152,
+ "elapsed time": 2114.9650602839974
+ },
+ {
+ "step": 4750,
+ "valid accuracy": 0.48,
+ "train loss": 0.568240401506424,
+ "train samples": 19000,
+ "train time": 43.939464293958736,
+ "eval time": 16.460097985000175,
+ "tokens / sec": 4777.914418698651,
+ "mem allocated avg": 6894218592.256,
+ "mem reserved avg": 14710372040.704,
+ "elapsed time": 2233.517725938
+ },
+ {
+ "step": 5000,
+ "valid accuracy": 0.5,
+ "train loss": 0.57634852206707,
+ "train samples": 20000,
+ "train time": 42.787552905057964,
+ "eval time": 16.445046182001533,
+ "tokens / sec": 4867.770785166333,
+ "mem allocated avg": 6890906441.728,
+ "mem reserved avg": 14656718503.936,
+ "elapsed time": 2350.279711092
+ },
+ {
+ "step": 5000,
+ "test accuracy": 0.5170583775587566,
+ "train loss": 0.57634852206707,
+ "train samples": 20000,
+ "train total tokens": 4198051
+ }
+ ]
+ },
+ "meta_info": {
+ "model_info": {
+ "sha": "13afe5124825b4f3751f836b40dafda64c1ed062",
+ "created_at": "2024-09-18T15:23:48+00:00"
+ },
+ "dataset_info": {
+ "metamath": {
+ "sha": "aa4f34d3d2d3231299b5b03d9b3e5a20da45aa18",
+ "created_at": "2023-09-21T17:22:46+00:00"
+ },
+ "gsm8k": {
+ "sha": "e53f048856ff4f594e959d75785d2c2d37b678ee",
+ "created_at": "2022-04-12T10:22:10+00:00"
+ }
+ },
+ "package_info": {
+ "transformers-version": "4.52.4",
+ "transformers-commit-hash": null,
+ "peft-version": "0.15.2.dev0",
+ "peft-commit-hash": "5fe7f8f8abe914d313fc3751f2ea92de7718fbaf",
+ "datasets-version": "3.6.0",
+ "datasets-commit-hash": null,
+ "bitsandbytes-version": "0.46.0",
+ "bitsandbytes-commit-hash": null,
+ "torch-version": "2.7.1+cu126",
+ "torch-commit-hash": null
+ },
+ "system_info": {
+ "system": "Linux",
+ "release": "6.8.0-1029-aws",
+ "version": "#31-Ubuntu SMP Wed Apr 23 18:42:41 UTC 2025",
+ "machine": "x86_64",
+ "processor": "x86_64",
+ "accelerator": "NVIDIA L40S"
+ },
+ "pytorch_info": "PyTorch built with:\n - GCC 11.2\n - C++ Version: 201703\n - Intel(R) oneAPI Math Kernel Library Version 2024.2-Product Build 20240605 for Intel(R) 64 architecture applications\n - Intel(R) MKL-DNN v3.7.1 (Git Hash 8d263e693366ef8db40acc569cc7d8edf644556d)\n - OpenMP 201511 (a.k.a. OpenMP 4.5)\n - LAPACK is enabled (usually provided by MKL)\n - NNPACK is enabled\n - CPU capability usage: AVX2\n - CUDA Runtime 12.6\n - NVCC architecture flags: -gencode;arch=compute_50,code=sm_50;-gencode;arch=compute_60,code=sm_60;-gencode;arch=compute_70,code=sm_70;-gencode;arch=compute_75,code=sm_75;-gencode;arch=compute_80,code=sm_80;-gencode;arch=compute_86,code=sm_86;-gencode;arch=compute_90,code=sm_90\n - CuDNN 90.7.1 (built against CUDA 12.8)\n - Built with CuDNN 90.5.1\n - Magma 2.6.1\n - Build settings: BLAS_INFO=mkl, BUILD_TYPE=Release, COMMIT_SHA=e2d141dbde55c2a4370fac5165b0561b6af4798b, CUDA_VERSION=12.6, CUDNN_VERSION=9.5.1, CXX_COMPILER=/opt/rh/gcc-toolset-11/root/usr/bin/c++, CXX_FLAGS= -D_GLIBCXX_USE_CXX11_ABI=1 -fvisibility-inlines-hidden -DUSE_PTHREADPOOL -DNDEBUG -DUSE_KINETO -DLIBKINETO_NOROCTRACER -DLIBKINETO_NOXPUPTI=ON -DUSE_FBGEMM -DUSE_PYTORCH_QNNPACK -DUSE_XNNPACK -DSYMBOLICATE_MOBILE_DEBUG_HANDLE -O2 -fPIC -Wall -Wextra -Werror=return-type -Werror=non-virtual-dtor -Werror=range-loop-construct -Werror=bool-operation -Wnarrowing -Wno-missing-field-initializers -Wno-unknown-pragmas -Wno-unused-parameter -Wno-strict-overflow -Wno-strict-aliasing -Wno-stringop-overflow -Wsuggest-override -Wno-psabi -Wno-error=old-style-cast -fdiagnostics-color=always -faligned-new -Wno-maybe-uninitialized -fno-math-errno -fno-trapping-math -Werror=format -Wno-stringop-overflow, LAPACK_INFO=mkl, PERF_WITH_AVX=1, PERF_WITH_AVX2=1, TORCH_VERSION=2.7.1, USE_CUDA=ON, USE_CUDNN=ON, USE_CUSPARSELT=1, USE_GFLAGS=OFF, USE_GLOG=OFF, USE_GLOO=ON, USE_MKL=ON, USE_MKLDNN=ON, USE_MPI=OFF, USE_NCCL=1, USE_NNPACK=ON, USE_OPENMP=ON, USE_ROCM=OFF, USE_ROCM_KERNEL_ASSERT=OFF, \n"
+ }
+}
diff --git a/peft/method_comparison/MetaMathQA/results/bone--llama-3.2-3B-default.json b/peft/method_comparison/MetaMathQA/results/bone--llama-3.2-3B-default.json
new file mode 100644
index 0000000000000000000000000000000000000000..a473c5827e1b13156e94be30ac5baee3f7350ff6
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/results/bone--llama-3.2-3B-default.json
@@ -0,0 +1,350 @@
+{
+ "run_info": {
+ "created_at": "2025-06-20T04:17:11+00:00",
+ "total_time": 1867.121674144997,
+ "experiment_name": "bone/llama-3.2-3B-default",
+ "peft_branch": "main",
+ "train_config": {
+ "model_id": "meta-llama/Llama-3.2-3B",
+ "dtype": "bfloat16",
+ "max_seq_length": 768,
+ "batch_size": 4,
+ "batch_size_eval": 50,
+ "max_steps": 5000,
+ "eval_steps": 250,
+ "compile": false,
+ "query_template": "Question: {query} Think step by step.\nAnswer:",
+ "seed": 0,
+ "grad_norm_clip": 1.0,
+ "optimizer_type": "AdamW",
+ "optimizer_kwargs": {
+ "lr": 0.0001,
+ "weight_decay": 0.1
+ },
+ "lr_scheduler": "cosine",
+ "use_amp": false,
+ "autocast_adapter_dtype": true,
+ "generation_kwargs": {
+ "max_length": 800,
+ "max_new_tokens": 300
+ },
+ "attn_implementation": null
+ },
+ "peft_config": {
+ "task_type": null,
+ "peft_type": "BONE",
+ "auto_mapping": null,
+ "base_model_name_or_path": "meta-llama/Llama-3.2-3B",
+ "revision": null,
+ "inference_mode": false,
+ "r": 64,
+ "target_modules": [
+ "v_proj",
+ "q_proj"
+ ],
+ "exclude_modules": null,
+ "init_weights": true,
+ "layers_to_transform": null,
+ "layers_pattern": null,
+ "bias": "none",
+ "modules_to_save": null
+ },
+ "error_msg": ""
+ },
+ "train_info": {
+ "accelerator_memory_reserved_avg": 11170837063,
+ "accelerator_memory_max": 20248002560,
+ "accelerator_memory_reserved_99th": 16303469363,
+ "train_time": 1664.0814183089897,
+ "file_size": 29367496,
+ "num_trainable_params": 7340032,
+ "num_total_params": 3220089856,
+ "status": "success",
+ "metrics": [
+ {
+ "step": 250,
+ "valid accuracy": 0.34,
+ "train loss": 0.8771067566871643,
+ "train samples": 1000,
+ "train time": 29.468342912026856,
+ "eval time": 11.086663477995899,
+ "tokens / sec": 7184.625230948821,
+ "mem allocated avg": 6894354876.416,
+ "mem reserved avg": 11212691603.456,
+ "elapsed time": 88.56553585999791
+ },
+ {
+ "step": 500,
+ "valid accuracy": 0.38,
+ "train loss": 0.6947847135066986,
+ "train samples": 2000,
+ "train time": 29.13603712292388,
+ "eval time": 11.12908834600239,
+ "tokens / sec": 7138.753946615206,
+ "mem allocated avg": 6887297284.096,
+ "mem reserved avg": 11116172279.808,
+ "elapsed time": 169.94219922799675
+ },
+ {
+ "step": 750,
+ "valid accuracy": 0.42,
+ "train loss": 0.6673308206796646,
+ "train samples": 3000,
+ "train time": 29.74789179801155,
+ "eval time": 6.2111000180011615,
+ "tokens / sec": 7207.267037805055,
+ "mem allocated avg": 6897885888.512,
+ "mem reserved avg": 11257109282.816,
+ "elapsed time": 247.40845895299572
+ },
+ {
+ "step": 1000,
+ "valid accuracy": 0.44,
+ "train loss": 0.6480507221221924,
+ "train samples": 4000,
+ "train time": 29.01437903306214,
+ "eval time": 11.063560270995367,
+ "tokens / sec": 7180.439731713689,
+ "mem allocated avg": 6888501639.168,
+ "mem reserved avg": 11141564596.224,
+ "elapsed time": 328.43337820599845
+ },
+ {
+ "step": 1250,
+ "valid accuracy": 0.42,
+ "train loss": 0.6442041766643524,
+ "train samples": 5000,
+ "train time": 28.86099356606428,
+ "eval time": 11.061821620001865,
+ "tokens / sec": 7225.600169399779,
+ "mem allocated avg": 6888334700.544,
+ "mem reserved avg": 11139123511.296,
+ "elapsed time": 409.5306018880001
+ },
+ {
+ "step": 1500,
+ "valid accuracy": 0.52,
+ "train loss": 0.6375475705862045,
+ "train samples": 6000,
+ "train time": 29.36598393299937,
+ "eval time": 6.896059851998871,
+ "tokens / sec": 7128.349606047729,
+ "mem allocated avg": 6890338080.768,
+ "mem reserved avg": 11164893315.072,
+ "elapsed time": 487.1438905899995
+ },
+ {
+ "step": 1750,
+ "valid accuracy": 0.42,
+ "train loss": 0.6282199568748474,
+ "train samples": 7000,
+ "train time": 29.2208460940019,
+ "eval time": 11.139122824002698,
+ "tokens / sec": 7164.576936838726,
+ "mem allocated avg": 6891485964.288,
+ "mem reserved avg": 11174582157.312,
+ "elapsed time": 568.6407176649955
+ },
+ {
+ "step": 2000,
+ "valid accuracy": 0.44,
+ "train loss": 0.628275181055069,
+ "train samples": 8000,
+ "train time": 28.774674860083906,
+ "eval time": 11.096917715003656,
+ "tokens / sec": 7218.013791986054,
+ "mem allocated avg": 6889055956.992,
+ "mem reserved avg": 11126481879.04,
+ "elapsed time": 649.4662010969987
+ },
+ {
+ "step": 2250,
+ "valid accuracy": 0.5,
+ "train loss": 0.6164452042579651,
+ "train samples": 9000,
+ "train time": 29.666104338008154,
+ "eval time": 6.740810982002586,
+ "tokens / sec": 7245.575541396888,
+ "mem allocated avg": 6899385456.64,
+ "mem reserved avg": 11287358603.264,
+ "elapsed time": 727.5584506419982
+ },
+ {
+ "step": 2500,
+ "valid accuracy": 0.52,
+ "train loss": 0.6124898854494095,
+ "train samples": 10000,
+ "train time": 28.952800227045373,
+ "eval time": 11.054138113999215,
+ "tokens / sec": 7113.888756349109,
+ "mem allocated avg": 6884753041.408,
+ "mem reserved avg": 11077492408.32,
+ "elapsed time": 808.6757636719994
+ },
+ {
+ "step": 2750,
+ "valid accuracy": 0.48,
+ "train loss": 0.6010023313760757,
+ "train samples": 11000,
+ "train time": 29.36040201097785,
+ "eval time": 5.933361176998005,
+ "tokens / sec": 7216.556500853691,
+ "mem allocated avg": 6895703631.872,
+ "mem reserved avg": 11229007446.016,
+ "elapsed time": 885.2688505609985
+ },
+ {
+ "step": 3000,
+ "valid accuracy": 0.36,
+ "train loss": 0.590470621585846,
+ "train samples": 12000,
+ "train time": 29.152743853985157,
+ "eval time": 11.051910919995862,
+ "tokens / sec": 7159.909236861306,
+ "mem allocated avg": 6890226739.2,
+ "mem reserved avg": 11156563427.328,
+ "elapsed time": 966.2876440099935
+ },
+ {
+ "step": 3250,
+ "valid accuracy": 0.46,
+ "train loss": 0.5996054347753524,
+ "train samples": 13000,
+ "train time": 29.23224936202314,
+ "eval time": 11.06002619300125,
+ "tokens / sec": 7214.668888053154,
+ "mem allocated avg": 6892138940.416,
+ "mem reserved avg": 11182651998.208,
+ "elapsed time": 1047.7634995759945
+ },
+ {
+ "step": 3500,
+ "valid accuracy": 0.46,
+ "train loss": 0.5810788285732269,
+ "train samples": 14000,
+ "train time": 29.556202010979177,
+ "eval time": 7.767598452002858,
+ "tokens / sec": 7096.649289448104,
+ "mem allocated avg": 6891370110.976,
+ "mem reserved avg": 11166763974.656,
+ "elapsed time": 1126.3068484049945
+ },
+ {
+ "step": 3750,
+ "valid accuracy": 0.5,
+ "train loss": 0.5778432558774949,
+ "train samples": 15000,
+ "train time": 30.077826159038523,
+ "eval time": 11.010653469995304,
+ "tokens / sec": 7204.742751493022,
+ "mem allocated avg": 6901065279.488,
+ "mem reserved avg": 11319788961.792,
+ "elapsed time": 1209.0550349339974
+ },
+ {
+ "step": 4000,
+ "valid accuracy": 0.4,
+ "train loss": 0.5869229323863984,
+ "train samples": 16000,
+ "train time": 29.213863794990175,
+ "eval time": 11.144038623999222,
+ "tokens / sec": 6995.753845988955,
+ "mem allocated avg": 6883645001.728,
+ "mem reserved avg": 11058953584.64,
+ "elapsed time": 1290.3985370609953
+ },
+ {
+ "step": 4250,
+ "valid accuracy": 0.46,
+ "train loss": 0.5733816763162612,
+ "train samples": 17000,
+ "train time": 29.18649683901458,
+ "eval time": 11.153094029003114,
+ "tokens / sec": 7242.698607029438,
+ "mem allocated avg": 6893432758.272,
+ "mem reserved avg": 11193884344.32,
+ "elapsed time": 1372.1237251569983
+ },
+ {
+ "step": 4500,
+ "valid accuracy": 0.48,
+ "train loss": 0.5803762240409851,
+ "train samples": 18000,
+ "train time": 29.077459994943638,
+ "eval time": 11.118935573998897,
+ "tokens / sec": 7147.047920834147,
+ "mem allocated avg": 6888416004.096,
+ "mem reserved avg": 11124485390.336,
+ "elapsed time": 1453.4214935309938
+ },
+ {
+ "step": 4750,
+ "valid accuracy": 0.48,
+ "train loss": 0.5692038584947586,
+ "train samples": 19000,
+ "train time": 29.40723867896304,
+ "eval time": 11.099454375005735,
+ "tokens / sec": 7139.024588193769,
+ "mem allocated avg": 6890813089.792,
+ "mem reserved avg": 11168844349.44,
+ "elapsed time": 1535.6791463129994
+ },
+ {
+ "step": 5000,
+ "valid accuracy": 0.48,
+ "train loss": 0.5775641392469406,
+ "train samples": 20000,
+ "train time": 28.941933833950316,
+ "eval time": 11.18307958800142,
+ "tokens / sec": 7196.47834159849,
+ "mem allocated avg": 6887869800.448,
+ "mem reserved avg": 11118328152.064,
+ "elapsed time": 1617.277517963994
+ },
+ {
+ "step": 5000,
+ "test accuracy": 0.5079605761940864,
+ "train loss": 0.5775641392469406,
+ "train samples": 20000,
+ "train total tokens": 4198051
+ }
+ ]
+ },
+ "meta_info": {
+ "model_info": {
+ "sha": "13afe5124825b4f3751f836b40dafda64c1ed062",
+ "created_at": "2024-09-18T15:23:48+00:00"
+ },
+ "dataset_info": {
+ "metamath": {
+ "sha": "aa4f34d3d2d3231299b5b03d9b3e5a20da45aa18",
+ "created_at": "2023-09-21T17:22:46+00:00"
+ },
+ "gsm8k": {
+ "sha": "e53f048856ff4f594e959d75785d2c2d37b678ee",
+ "created_at": "2022-04-12T10:22:10+00:00"
+ }
+ },
+ "package_info": {
+ "transformers-version": "4.52.4",
+ "transformers-commit-hash": null,
+ "peft-version": "0.15.2.dev0",
+ "peft-commit-hash": "5fe7f8f8abe914d313fc3751f2ea92de7718fbaf",
+ "datasets-version": "3.6.0",
+ "datasets-commit-hash": null,
+ "bitsandbytes-version": "0.46.0",
+ "bitsandbytes-commit-hash": null,
+ "torch-version": "2.7.1+cu126",
+ "torch-commit-hash": null
+ },
+ "system_info": {
+ "system": "Linux",
+ "release": "6.8.0-1029-aws",
+ "version": "#31-Ubuntu SMP Wed Apr 23 18:42:41 UTC 2025",
+ "machine": "x86_64",
+ "processor": "x86_64",
+ "accelerator": "NVIDIA L40S"
+ },
+ "pytorch_info": "PyTorch built with:\n - GCC 11.2\n - C++ Version: 201703\n - Intel(R) oneAPI Math Kernel Library Version 2024.2-Product Build 20240605 for Intel(R) 64 architecture applications\n - Intel(R) MKL-DNN v3.7.1 (Git Hash 8d263e693366ef8db40acc569cc7d8edf644556d)\n - OpenMP 201511 (a.k.a. OpenMP 4.5)\n - LAPACK is enabled (usually provided by MKL)\n - NNPACK is enabled\n - CPU capability usage: AVX2\n - CUDA Runtime 12.6\n - NVCC architecture flags: -gencode;arch=compute_50,code=sm_50;-gencode;arch=compute_60,code=sm_60;-gencode;arch=compute_70,code=sm_70;-gencode;arch=compute_75,code=sm_75;-gencode;arch=compute_80,code=sm_80;-gencode;arch=compute_86,code=sm_86;-gencode;arch=compute_90,code=sm_90\n - CuDNN 90.7.1 (built against CUDA 12.8)\n - Built with CuDNN 90.5.1\n - Magma 2.6.1\n - Build settings: BLAS_INFO=mkl, BUILD_TYPE=Release, COMMIT_SHA=e2d141dbde55c2a4370fac5165b0561b6af4798b, CUDA_VERSION=12.6, CUDNN_VERSION=9.5.1, CXX_COMPILER=/opt/rh/gcc-toolset-11/root/usr/bin/c++, CXX_FLAGS= -D_GLIBCXX_USE_CXX11_ABI=1 -fvisibility-inlines-hidden -DUSE_PTHREADPOOL -DNDEBUG -DUSE_KINETO -DLIBKINETO_NOROCTRACER -DLIBKINETO_NOXPUPTI=ON -DUSE_FBGEMM -DUSE_PYTORCH_QNNPACK -DUSE_XNNPACK -DSYMBOLICATE_MOBILE_DEBUG_HANDLE -O2 -fPIC -Wall -Wextra -Werror=return-type -Werror=non-virtual-dtor -Werror=range-loop-construct -Werror=bool-operation -Wnarrowing -Wno-missing-field-initializers -Wno-unknown-pragmas -Wno-unused-parameter -Wno-strict-overflow -Wno-strict-aliasing -Wno-stringop-overflow -Wsuggest-override -Wno-psabi -Wno-error=old-style-cast -fdiagnostics-color=always -faligned-new -Wno-maybe-uninitialized -fno-math-errno -fno-trapping-math -Werror=format -Wno-stringop-overflow, LAPACK_INFO=mkl, PERF_WITH_AVX=1, PERF_WITH_AVX2=1, TORCH_VERSION=2.7.1, USE_CUDA=ON, USE_CUDNN=ON, USE_CUSPARSELT=1, USE_GFLAGS=OFF, USE_GLOG=OFF, USE_GLOO=ON, USE_MKL=ON, USE_MKLDNN=ON, USE_MPI=OFF, USE_NCCL=1, USE_NNPACK=ON, USE_OPENMP=ON, USE_ROCM=OFF, USE_ROCM_KERNEL_ASSERT=OFF, \n"
+ }
+}
diff --git a/peft/method_comparison/MetaMathQA/results/c3a--llama-3.2-3B-default.json b/peft/method_comparison/MetaMathQA/results/c3a--llama-3.2-3B-default.json
new file mode 100644
index 0000000000000000000000000000000000000000..dedfb5f28850701d45d209484d9fdff0b0bafa89
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/results/c3a--llama-3.2-3B-default.json
@@ -0,0 +1,350 @@
+{
+ "run_info": {
+ "created_at": "2025-07-31T13:35:43+00:00",
+ "total_time": 2124.5942297870006,
+ "experiment_name": "c3a/llama-3.2-3B-default",
+ "peft_branch": "main",
+ "train_config": {
+ "model_id": "meta-llama/Llama-3.2-3B",
+ "dtype": "bfloat16",
+ "max_seq_length": 768,
+ "batch_size": 4,
+ "batch_size_eval": 50,
+ "max_steps": 5000,
+ "eval_steps": 250,
+ "compile": false,
+ "query_template": "Question: {query} Think step by step.\nAnswer:",
+ "seed": 0,
+ "grad_norm_clip": 1.0,
+ "optimizer_type": "AdamW",
+ "optimizer_kwargs": {
+ "lr": 0.3,
+ "weight_decay": 1e-05
+ },
+ "lr_scheduler": "cosine",
+ "use_amp": false,
+ "autocast_adapter_dtype": true,
+ "generation_kwargs": {
+ "max_length": 800,
+ "max_new_tokens": 300
+ },
+ "attn_implementation": null
+ },
+ "peft_config": {
+ "task_type": null,
+ "peft_type": "C3A",
+ "auto_mapping": null,
+ "base_model_name_or_path": "meta-llama/Llama-3.2-3B",
+ "revision": null,
+ "inference_mode": false,
+ "block_size": 64,
+ "target_modules": [
+ "q_proj",
+ "v_proj"
+ ],
+ "bias": "none",
+ "modules_to_save": null,
+ "layers_to_transform": null,
+ "layers_pattern": null,
+ "block_size_pattern": {},
+ "init_weights": false
+ },
+ "error_msg": ""
+ },
+ "train_info": {
+ "accelerator_memory_reserved_avg": 11804454210,
+ "accelerator_memory_max": 22280142848,
+ "accelerator_memory_reserved_99th": 17825917829,
+ "train_time": 1924.4760333429977,
+ "file_size": 22027512,
+ "num_trainable_params": 5505024,
+ "num_total_params": 3218254848,
+ "status": "success",
+ "metrics": [
+ {
+ "step": 250,
+ "valid accuracy": 0.36,
+ "train loss": 0.8909663727283478,
+ "train samples": 1000,
+ "train time": 39.02584077800293,
+ "eval time": 13.030882289000147,
+ "tokens / sec": 5425.097724463024,
+ "mem allocated avg": 6868124932.096,
+ "mem reserved avg": 11851408605.184,
+ "elapsed time": 101.62553732800006
+ },
+ {
+ "step": 500,
+ "valid accuracy": 0.42,
+ "train loss": 0.7016348876953125,
+ "train samples": 2000,
+ "train time": 38.45351204700091,
+ "eval time": 7.171581626000261,
+ "tokens / sec": 5408.9987865288385,
+ "mem allocated avg": 6861684402.176,
+ "mem reserved avg": 11746811052.032,
+ "elapsed time": 190.13871278500028
+ },
+ {
+ "step": 750,
+ "valid accuracy": 0.4,
+ "train loss": 0.6737332336902618,
+ "train samples": 3000,
+ "train time": 38.979470817998845,
+ "eval time": 7.451876584000274,
+ "tokens / sec": 5500.356867364139,
+ "mem allocated avg": 6871526113.28,
+ "mem reserved avg": 11907578724.352,
+ "elapsed time": 279.83808459899956
+ },
+ {
+ "step": 1000,
+ "valid accuracy": 0.42,
+ "train loss": 0.654857279419899,
+ "train samples": 4000,
+ "train time": 38.61999764599932,
+ "eval time": 13.0494962570001,
+ "tokens / sec": 5394.5109450720465,
+ "mem allocated avg": 6862362261.504,
+ "mem reserved avg": 11770039107.584,
+ "elapsed time": 374.5986276450003
+ },
+ {
+ "step": 1250,
+ "valid accuracy": 0.36,
+ "train loss": 0.6510260388851166,
+ "train samples": 5000,
+ "train time": 38.424466599010884,
+ "eval time": 9.087004377000085,
+ "tokens / sec": 5427.2191251541835,
+ "mem allocated avg": 6862755778.56,
+ "mem reserved avg": 11764250968.064,
+ "elapsed time": 465.21620532700035
+ },
+ {
+ "step": 1500,
+ "valid accuracy": 0.44,
+ "train loss": 0.6443832906484603,
+ "train samples": 6000,
+ "train time": 38.60136020600203,
+ "eval time": 8.362256499000068,
+ "tokens / sec": 5422.891806995228,
+ "mem allocated avg": 6864079349.76,
+ "mem reserved avg": 11795154599.936,
+ "elapsed time": 555.3471686519997
+ },
+ {
+ "step": 1750,
+ "valid accuracy": 0.46,
+ "train loss": 0.6348284522294998,
+ "train samples": 7000,
+ "train time": 38.819046561000505,
+ "eval time": 12.987756649999938,
+ "tokens / sec": 5393.09999979052,
+ "mem allocated avg": 6865506678.784,
+ "mem reserved avg": 11806663770.112,
+ "elapsed time": 650.521843128
+ },
+ {
+ "step": 2000,
+ "valid accuracy": 0.42,
+ "train loss": 0.6368349348306656,
+ "train samples": 8000,
+ "train time": 38.522883960999025,
+ "eval time": 7.980172546000176,
+ "tokens / sec": 5391.496654567027,
+ "mem allocated avg": 6861885327.36,
+ "mem reserved avg": 11751290568.704,
+ "elapsed time": 740.3195631050003
+ },
+ {
+ "step": 2250,
+ "valid accuracy": 0.54,
+ "train loss": 0.625629832983017,
+ "train samples": 9000,
+ "train time": 39.25956673700239,
+ "eval time": 12.96675302299991,
+ "tokens / sec": 5475.047685572397,
+ "mem allocated avg": 6873176825.856,
+ "mem reserved avg": 11939161833.472,
+ "elapsed time": 836.2159785140002
+ },
+ {
+ "step": 2500,
+ "valid accuracy": 0.48,
+ "train loss": 0.6208862951993942,
+ "train samples": 10000,
+ "train time": 38.55282327599798,
+ "eval time": 13.027243182000348,
+ "tokens / sec": 5342.4621726271835,
+ "mem allocated avg": 6857644570.624,
+ "mem reserved avg": 11701781004.288,
+ "elapsed time": 930.913046529
+ },
+ {
+ "step": 2750,
+ "valid accuracy": 0.5,
+ "train loss": 0.6103025305271149,
+ "train samples": 11000,
+ "train time": 38.69634664399382,
+ "eval time": 8.820525846999772,
+ "tokens / sec": 5475.478136199886,
+ "mem allocated avg": 6868590700.544,
+ "mem reserved avg": 11873739079.68,
+ "elapsed time": 1021.7124050419998
+ },
+ {
+ "step": 3000,
+ "valid accuracy": 0.48,
+ "train loss": 0.5977142386436463,
+ "train samples": 12000,
+ "train time": 38.552098998990004,
+ "eval time": 8.200822365000022,
+ "tokens / sec": 5414.257729662615,
+ "mem allocated avg": 6864444424.192,
+ "mem reserved avg": 11782135480.32,
+ "elapsed time": 1111.412057769
+ },
+ {
+ "step": 3250,
+ "valid accuracy": 0.54,
+ "train loss": 0.6062814455032348,
+ "train samples": 13000,
+ "train time": 38.8476868979933,
+ "eval time": 9.795037900000352,
+ "tokens / sec": 5428.92040274589,
+ "mem allocated avg": 6865998022.656,
+ "mem reserved avg": 11821754875.904,
+ "elapsed time": 1203.456824805
+ },
+ {
+ "step": 3500,
+ "valid accuracy": 0.54,
+ "train loss": 0.5876059620380402,
+ "train samples": 14000,
+ "train time": 39.031564167995384,
+ "eval time": 12.945379363999564,
+ "tokens / sec": 5373.855864377278,
+ "mem allocated avg": 6864331821.056,
+ "mem reserved avg": 11797008482.304,
+ "elapsed time": 1298.7533704500001
+ },
+ {
+ "step": 3750,
+ "valid accuracy": 0.5,
+ "train loss": 0.5839143842458725,
+ "train samples": 15000,
+ "train time": 39.49590561498735,
+ "eval time": 8.033668121999654,
+ "tokens / sec": 5486.720626498778,
+ "mem allocated avg": 6875409352.704,
+ "mem reserved avg": 11980509282.304,
+ "elapsed time": 1390.233747202
+ },
+ {
+ "step": 4000,
+ "valid accuracy": 0.56,
+ "train loss": 0.591371684551239,
+ "train samples": 16000,
+ "train time": 38.53615990600338,
+ "eval time": 12.963392601999658,
+ "tokens / sec": 5303.408551825156,
+ "mem allocated avg": 6856836122.624,
+ "mem reserved avg": 11673922437.12,
+ "elapsed time": 1484.869673702
+ },
+ {
+ "step": 4250,
+ "valid accuracy": 0.56,
+ "train loss": 0.577637273311615,
+ "train samples": 17000,
+ "train time": 38.46427064899399,
+ "eval time": 7.68621369199991,
+ "tokens / sec": 5495.723600975878,
+ "mem allocated avg": 6867260166.144,
+ "mem reserved avg": 11833297600.512,
+ "elapsed time": 1574.4202131299999
+ },
+ {
+ "step": 4500,
+ "valid accuracy": 0.56,
+ "train loss": 0.584571166396141,
+ "train samples": 18000,
+ "train time": 38.4389222480022,
+ "eval time": 7.678759501000968,
+ "tokens / sec": 5406.447107418601,
+ "mem allocated avg": 6862379522.048,
+ "mem reserved avg": 11747851239.424,
+ "elapsed time": 1663.6057326830005
+ },
+ {
+ "step": 4750,
+ "valid accuracy": 0.58,
+ "train loss": 0.5745555943250656,
+ "train samples": 19000,
+ "train time": 38.87202309699023,
+ "eval time": 7.697188709000329,
+ "tokens / sec": 5400.773699793749,
+ "mem allocated avg": 6863993468.928,
+ "mem reserved avg": 11795691470.848,
+ "elapsed time": 1753.6286738400004
+ },
+ {
+ "step": 5000,
+ "valid accuracy": 0.56,
+ "train loss": 0.5808088963031769,
+ "train samples": 20000,
+ "train time": 38.65712555299615,
+ "eval time": 7.723833553000077,
+ "tokens / sec": 5387.8811996629975,
+ "mem allocated avg": 6861167886.336,
+ "mem reserved avg": 11749034033.152,
+ "elapsed time": 1843.4390854000003
+ },
+ {
+ "step": 5000,
+ "test accuracy": 0.510235026535254,
+ "train loss": 0.5808088963031769,
+ "train samples": 20000,
+ "train total tokens": 4198051
+ }
+ ]
+ },
+ "meta_info": {
+ "model_info": {
+ "sha": "13afe5124825b4f3751f836b40dafda64c1ed062",
+ "created_at": "2024-09-18T15:23:48+00:00"
+ },
+ "dataset_info": {
+ "metamath": {
+ "sha": "aa4f34d3d2d3231299b5b03d9b3e5a20da45aa18",
+ "created_at": "2023-09-21T17:22:46+00:00"
+ },
+ "gsm8k": {
+ "sha": "e53f048856ff4f594e959d75785d2c2d37b678ee",
+ "created_at": "2022-04-12T10:22:10+00:00"
+ }
+ },
+ "package_info": {
+ "transformers-version": "4.52.4",
+ "transformers-commit-hash": null,
+ "peft-version": "0.16.1.dev0",
+ "peft-commit-hash": "25e5c6b25c4589eb2683484ede1ba3d985d8a760",
+ "datasets-version": "3.6.0",
+ "datasets-commit-hash": null,
+ "bitsandbytes-version": "0.46.0",
+ "bitsandbytes-commit-hash": null,
+ "torch-version": "2.7.1+cu126",
+ "torch-commit-hash": null
+ },
+ "system_info": {
+ "system": "Linux",
+ "release": "6.8.0-1031-aws",
+ "version": "#33-Ubuntu SMP Fri Jun 20 18:11:07 UTC 2025",
+ "machine": "x86_64",
+ "processor": "x86_64",
+ "accelerator": "NVIDIA L40S"
+ },
+ "pytorch_info": "PyTorch built with:\n - GCC 11.2\n - C++ Version: 201703\n - Intel(R) oneAPI Math Kernel Library Version 2024.2-Product Build 20240605 for Intel(R) 64 architecture applications\n - Intel(R) MKL-DNN v3.7.1 (Git Hash 8d263e693366ef8db40acc569cc7d8edf644556d)\n - OpenMP 201511 (a.k.a. OpenMP 4.5)\n - LAPACK is enabled (usually provided by MKL)\n - NNPACK is enabled\n - CPU capability usage: AVX2\n - CUDA Runtime 12.6\n - NVCC architecture flags: -gencode;arch=compute_50,code=sm_50;-gencode;arch=compute_60,code=sm_60;-gencode;arch=compute_70,code=sm_70;-gencode;arch=compute_75,code=sm_75;-gencode;arch=compute_80,code=sm_80;-gencode;arch=compute_86,code=sm_86;-gencode;arch=compute_90,code=sm_90\n - CuDNN 90.7.1 (built against CUDA 12.8)\n - Built with CuDNN 90.5.1\n - Magma 2.6.1\n - Build settings: BLAS_INFO=mkl, BUILD_TYPE=Release, COMMIT_SHA=e2d141dbde55c2a4370fac5165b0561b6af4798b, CUDA_VERSION=12.6, CUDNN_VERSION=9.5.1, CXX_COMPILER=/opt/rh/gcc-toolset-11/root/usr/bin/c++, CXX_FLAGS= -D_GLIBCXX_USE_CXX11_ABI=1 -fvisibility-inlines-hidden -DUSE_PTHREADPOOL -DNDEBUG -DUSE_KINETO -DLIBKINETO_NOROCTRACER -DLIBKINETO_NOXPUPTI=ON -DUSE_FBGEMM -DUSE_PYTORCH_QNNPACK -DUSE_XNNPACK -DSYMBOLICATE_MOBILE_DEBUG_HANDLE -O2 -fPIC -Wall -Wextra -Werror=return-type -Werror=non-virtual-dtor -Werror=range-loop-construct -Werror=bool-operation -Wnarrowing -Wno-missing-field-initializers -Wno-unknown-pragmas -Wno-unused-parameter -Wno-strict-overflow -Wno-strict-aliasing -Wno-stringop-overflow -Wsuggest-override -Wno-psabi -Wno-error=old-style-cast -fdiagnostics-color=always -faligned-new -Wno-maybe-uninitialized -fno-math-errno -fno-trapping-math -Werror=format -Wno-stringop-overflow, LAPACK_INFO=mkl, PERF_WITH_AVX=1, PERF_WITH_AVX2=1, TORCH_VERSION=2.7.1, USE_CUDA=ON, USE_CUDNN=ON, USE_CUSPARSELT=1, USE_GFLAGS=OFF, USE_GLOG=OFF, USE_GLOO=ON, USE_MKL=ON, USE_MKLDNN=ON, USE_MPI=OFF, USE_NCCL=1, USE_NNPACK=ON, USE_OPENMP=ON, USE_ROCM=OFF, USE_ROCM_KERNEL_ASSERT=OFF, \n"
+ }
+}
\ No newline at end of file
diff --git a/peft/method_comparison/MetaMathQA/results/fourierft--llama-3.2-3B-default.json b/peft/method_comparison/MetaMathQA/results/fourierft--llama-3.2-3B-default.json
new file mode 100644
index 0000000000000000000000000000000000000000..f3bc26876c01612fe60f472439e877c9c3ab1fe8
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/results/fourierft--llama-3.2-3B-default.json
@@ -0,0 +1,354 @@
+{
+ "run_info": {
+ "created_at": "2025-06-20T10:18:57+00:00",
+ "total_time": 2823.832106703994,
+ "experiment_name": "fourierft/llama-3.2-3B-default",
+ "peft_branch": "main",
+ "train_config": {
+ "model_id": "meta-llama/Llama-3.2-3B",
+ "dtype": "bfloat16",
+ "max_seq_length": 768,
+ "batch_size": 4,
+ "batch_size_eval": 50,
+ "max_steps": 5000,
+ "eval_steps": 250,
+ "compile": false,
+ "query_template": "Question: {query} Think step by step.\nAnswer:",
+ "seed": 0,
+ "grad_norm_clip": 1.0,
+ "optimizer_type": "AdamW",
+ "optimizer_kwargs": {
+ "lr": 0.0001,
+ "weight_decay": 0.1
+ },
+ "lr_scheduler": "cosine",
+ "use_amp": false,
+ "autocast_adapter_dtype": true,
+ "generation_kwargs": {
+ "max_length": 800,
+ "max_new_tokens": 300
+ },
+ "attn_implementation": null
+ },
+ "peft_config": {
+ "task_type": null,
+ "peft_type": "FOURIERFT",
+ "auto_mapping": null,
+ "base_model_name_or_path": "meta-llama/Llama-3.2-3B",
+ "revision": null,
+ "inference_mode": false,
+ "n_frequency": 1000,
+ "scaling": 300,
+ "random_loc_seed": 777,
+ "fan_in_fan_out": false,
+ "target_modules": [
+ "q_proj",
+ "v_proj"
+ ],
+ "exclude_modules": null,
+ "bias": "none",
+ "modules_to_save": null,
+ "layers_to_transform": null,
+ "layers_pattern": null,
+ "n_frequency_pattern": {},
+ "init_weights": false
+ },
+ "error_msg": ""
+ },
+ "train_info": {
+ "accelerator_memory_reserved_avg": 13104129350,
+ "accelerator_memory_max": 23653777408,
+ "accelerator_memory_reserved_99th": 19017267937,
+ "train_time": 2424.3862988609762,
+ "file_size": 231416,
+ "num_trainable_params": 56000,
+ "num_total_params": 3212805824,
+ "status": "success",
+ "metrics": [
+ {
+ "step": 250,
+ "valid accuracy": 0.0,
+ "train loss": 1.3263031902313231,
+ "train samples": 1000,
+ "train time": 53.55340486107161,
+ "eval time": 19.578013352002017,
+ "tokens / sec": 3953.4180982374883,
+ "mem allocated avg": 6781303625.728,
+ "mem reserved avg": 13152850804.736,
+ "elapsed time": 119.84825310099404
+ },
+ {
+ "step": 500,
+ "valid accuracy": 0.0,
+ "train loss": 1.3399862418174744,
+ "train samples": 2000,
+ "train time": 52.85717789203045,
+ "eval time": 19.544192551999004,
+ "tokens / sec": 3935.03793231005,
+ "mem allocated avg": 6774035257.344,
+ "mem reserved avg": 13043463356.416,
+ "elapsed time": 233.5829256769939
+ },
+ {
+ "step": 750,
+ "valid accuracy": 0.0,
+ "train loss": 1.3045952091217041,
+ "train samples": 3000,
+ "train time": 53.35706212905643,
+ "eval time": 19.607110917990212,
+ "tokens / sec": 4018.2309790861696,
+ "mem allocated avg": 6783920330.752,
+ "mem reserved avg": 13205673869.312,
+ "elapsed time": 348.1469791559939
+ },
+ {
+ "step": 1000,
+ "valid accuracy": 0.0,
+ "train loss": 1.3111453976631164,
+ "train samples": 4000,
+ "train time": 52.95546973698947,
+ "eval time": 19.472347582006478,
+ "tokens / sec": 3934.1733919976355,
+ "mem allocated avg": 6776025266.176,
+ "mem reserved avg": 13077269446.656,
+ "elapsed time": 461.81266678999236
+ },
+ {
+ "step": 1250,
+ "valid accuracy": 0.0,
+ "train loss": 1.299716483592987,
+ "train samples": 5000,
+ "train time": 52.12036712520057,
+ "eval time": 19.626158429004136,
+ "tokens / sec": 4001.0846335572023,
+ "mem allocated avg": 6775331573.76,
+ "mem reserved avg": 13063344357.376,
+ "elapsed time": 574.6407375999988
+ },
+ {
+ "step": 1500,
+ "valid accuracy": 0.0,
+ "train loss": 1.2867344057559966,
+ "train samples": 6000,
+ "train time": 52.594848359090975,
+ "eval time": 19.54386943600548,
+ "tokens / sec": 3980.0666135738998,
+ "mem allocated avg": 6776458844.16,
+ "mem reserved avg": 13093568512.0,
+ "elapsed time": 688.0431025519938
+ },
+ {
+ "step": 1750,
+ "valid accuracy": 0.0,
+ "train loss": 1.2803141210079194,
+ "train samples": 7000,
+ "train time": 52.98738884186605,
+ "eval time": 19.568909612993593,
+ "tokens / sec": 3951.0344739725274,
+ "mem allocated avg": 6778496358.4,
+ "mem reserved avg": 13108768669.696,
+ "elapsed time": 801.9154772249894
+ },
+ {
+ "step": 2000,
+ "valid accuracy": 0.0,
+ "train loss": 1.2766506419181824,
+ "train samples": 8000,
+ "train time": 52.03297274692159,
+ "eval time": 19.525613270001486,
+ "tokens / sec": 3991.62279292005,
+ "mem allocated avg": 6774647097.344,
+ "mem reserved avg": 13051189264.384,
+ "elapsed time": 914.5343848449993
+ },
+ {
+ "step": 2250,
+ "valid accuracy": 0.0,
+ "train loss": 1.2596003375053406,
+ "train samples": 9000,
+ "train time": 53.934016149127274,
+ "eval time": 19.535415460006334,
+ "tokens / sec": 3985.388356870549,
+ "mem allocated avg": 6785830477.824,
+ "mem reserved avg": 13237223424.0,
+ "elapsed time": 1029.9007452719961
+ },
+ {
+ "step": 2500,
+ "valid accuracy": 0.0,
+ "train loss": 1.2684449093341827,
+ "train samples": 10000,
+ "train time": 52.006629903029534,
+ "eval time": 19.470633051998448,
+ "tokens / sec": 3960.3989026791724,
+ "mem allocated avg": 6771212331.008,
+ "mem reserved avg": 12996118052.864,
+ "elapsed time": 1142.5889472209965
+ },
+ {
+ "step": 2750,
+ "valid accuracy": 0.0,
+ "train loss": 1.2548872971534728,
+ "train samples": 11000,
+ "train time": 53.403087337108445,
+ "eval time": 19.463876378998975,
+ "tokens / sec": 3967.579601952513,
+ "mem allocated avg": 6781916252.16,
+ "mem reserved avg": 13168084516.864,
+ "elapsed time": 1257.0122518049902
+ },
+ {
+ "step": 3000,
+ "valid accuracy": 0.0,
+ "train loss": 1.253697858095169,
+ "train samples": 12000,
+ "train time": 53.20096563108382,
+ "eval time": 19.472515105997445,
+ "tokens / sec": 3923.443823321214,
+ "mem allocated avg": 6777045135.36,
+ "mem reserved avg": 13084844359.68,
+ "elapsed time": 1370.94780872899
+ },
+ {
+ "step": 3250,
+ "valid accuracy": 0.0,
+ "train loss": 1.248513156414032,
+ "train samples": 13000,
+ "train time": 52.962746563891415,
+ "eval time": 19.54665829600708,
+ "tokens / sec": 3982.06312328573,
+ "mem allocated avg": 6779038627.84,
+ "mem reserved avg": 13110345728.0,
+ "elapsed time": 1484.7621198889974
+ },
+ {
+ "step": 3500,
+ "valid accuracy": 0.0,
+ "train loss": 1.2477959940433503,
+ "train samples": 14000,
+ "train time": 52.93443578510778,
+ "eval time": 19.444701158994576,
+ "tokens / sec": 3962.4489595298505,
+ "mem allocated avg": 6776803573.76,
+ "mem reserved avg": 13097142059.008,
+ "elapsed time": 1598.8772237269877
+ },
+ {
+ "step": 3750,
+ "valid accuracy": 0.0,
+ "train loss": 1.228544222354889,
+ "train samples": 15000,
+ "train time": 53.31031796212483,
+ "eval time": 19.472959079008433,
+ "tokens / sec": 4064.9354249577,
+ "mem allocated avg": 6788200585.216,
+ "mem reserved avg": 13268999471.104,
+ "elapsed time": 1713.6814467679942
+ },
+ {
+ "step": 4000,
+ "valid accuracy": 0.0,
+ "train loss": 1.2609001460075377,
+ "train samples": 16000,
+ "train time": 51.9827769130934,
+ "eval time": 19.473652824002784,
+ "tokens / sec": 3931.552182017475,
+ "mem allocated avg": 6770180233.216,
+ "mem reserved avg": 12983610638.336,
+ "elapsed time": 1826.5604049959948
+ },
+ {
+ "step": 4250,
+ "valid accuracy": 0.0,
+ "train loss": 1.227214762210846,
+ "train samples": 17000,
+ "train time": 53.09942602888623,
+ "eval time": 19.547112297004787,
+ "tokens / sec": 3981.0034836347163,
+ "mem allocated avg": 6779591426.048,
+ "mem reserved avg": 13132760088.576,
+ "elapsed time": 1940.5098487799987
+ },
+ {
+ "step": 4500,
+ "valid accuracy": 0.0,
+ "train loss": 1.2504195840358734,
+ "train samples": 18000,
+ "train time": 52.23909889203787,
+ "eval time": 19.522137050997117,
+ "tokens / sec": 3978.207978462565,
+ "mem allocated avg": 6775933241.344,
+ "mem reserved avg": 13056079822.848,
+ "elapsed time": 2053.2267840139975
+ },
+ {
+ "step": 4750,
+ "valid accuracy": 0.0,
+ "train loss": 1.2349513354301453,
+ "train samples": 19000,
+ "train time": 53.36620609794045,
+ "eval time": 19.541859832999762,
+ "tokens / sec": 3933.931514912433,
+ "mem allocated avg": 6777532579.84,
+ "mem reserved avg": 13101604798.464,
+ "elapsed time": 2167.8329333979927
+ },
+ {
+ "step": 5000,
+ "valid accuracy": 0.0,
+ "train loss": 1.2480293517112733,
+ "train samples": 20000,
+ "train time": 52.46977503092785,
+ "eval time": 19.44991449599911,
+ "tokens / sec": 3969.5234042309344,
+ "mem allocated avg": 6773533165.568,
+ "mem reserved avg": 13049645760.512,
+ "elapsed time": 2281.220151823989
+ },
+ {
+ "step": 5000,
+ "test accuracy": 0.000758150113722517,
+ "train loss": 1.2480293517112733,
+ "train samples": 20000,
+ "train total tokens": 4198051
+ }
+ ]
+ },
+ "meta_info": {
+ "model_info": {
+ "sha": "13afe5124825b4f3751f836b40dafda64c1ed062",
+ "created_at": "2024-09-18T15:23:48+00:00"
+ },
+ "dataset_info": {
+ "metamath": {
+ "sha": "aa4f34d3d2d3231299b5b03d9b3e5a20da45aa18",
+ "created_at": "2023-09-21T17:22:46+00:00"
+ },
+ "gsm8k": {
+ "sha": "e53f048856ff4f594e959d75785d2c2d37b678ee",
+ "created_at": "2022-04-12T10:22:10+00:00"
+ }
+ },
+ "package_info": {
+ "transformers-version": "4.52.4",
+ "transformers-commit-hash": null,
+ "peft-version": "0.15.2.dev0",
+ "peft-commit-hash": "5fe7f8f8abe914d313fc3751f2ea92de7718fbaf",
+ "datasets-version": "3.6.0",
+ "datasets-commit-hash": null,
+ "bitsandbytes-version": "0.46.0",
+ "bitsandbytes-commit-hash": null,
+ "torch-version": "2.7.1+cu126",
+ "torch-commit-hash": null
+ },
+ "system_info": {
+ "system": "Linux",
+ "release": "6.8.0-1029-aws",
+ "version": "#31-Ubuntu SMP Wed Apr 23 18:42:41 UTC 2025",
+ "machine": "x86_64",
+ "processor": "x86_64",
+ "accelerator": "NVIDIA L40S"
+ },
+ "pytorch_info": "PyTorch built with:\n - GCC 11.2\n - C++ Version: 201703\n - Intel(R) oneAPI Math Kernel Library Version 2024.2-Product Build 20240605 for Intel(R) 64 architecture applications\n - Intel(R) MKL-DNN v3.7.1 (Git Hash 8d263e693366ef8db40acc569cc7d8edf644556d)\n - OpenMP 201511 (a.k.a. OpenMP 4.5)\n - LAPACK is enabled (usually provided by MKL)\n - NNPACK is enabled\n - CPU capability usage: AVX2\n - CUDA Runtime 12.6\n - NVCC architecture flags: -gencode;arch=compute_50,code=sm_50;-gencode;arch=compute_60,code=sm_60;-gencode;arch=compute_70,code=sm_70;-gencode;arch=compute_75,code=sm_75;-gencode;arch=compute_80,code=sm_80;-gencode;arch=compute_86,code=sm_86;-gencode;arch=compute_90,code=sm_90\n - CuDNN 90.7.1 (built against CUDA 12.8)\n - Built with CuDNN 90.5.1\n - Magma 2.6.1\n - Build settings: BLAS_INFO=mkl, BUILD_TYPE=Release, COMMIT_SHA=e2d141dbde55c2a4370fac5165b0561b6af4798b, CUDA_VERSION=12.6, CUDNN_VERSION=9.5.1, CXX_COMPILER=/opt/rh/gcc-toolset-11/root/usr/bin/c++, CXX_FLAGS= -D_GLIBCXX_USE_CXX11_ABI=1 -fvisibility-inlines-hidden -DUSE_PTHREADPOOL -DNDEBUG -DUSE_KINETO -DLIBKINETO_NOROCTRACER -DLIBKINETO_NOXPUPTI=ON -DUSE_FBGEMM -DUSE_PYTORCH_QNNPACK -DUSE_XNNPACK -DSYMBOLICATE_MOBILE_DEBUG_HANDLE -O2 -fPIC -Wall -Wextra -Werror=return-type -Werror=non-virtual-dtor -Werror=range-loop-construct -Werror=bool-operation -Wnarrowing -Wno-missing-field-initializers -Wno-unknown-pragmas -Wno-unused-parameter -Wno-strict-overflow -Wno-strict-aliasing -Wno-stringop-overflow -Wsuggest-override -Wno-psabi -Wno-error=old-style-cast -fdiagnostics-color=always -faligned-new -Wno-maybe-uninitialized -fno-math-errno -fno-trapping-math -Werror=format -Wno-stringop-overflow, LAPACK_INFO=mkl, PERF_WITH_AVX=1, PERF_WITH_AVX2=1, TORCH_VERSION=2.7.1, USE_CUDA=ON, USE_CUDNN=ON, USE_CUSPARSELT=1, USE_GFLAGS=OFF, USE_GLOG=OFF, USE_GLOO=ON, USE_MKL=ON, USE_MKLDNN=ON, USE_MPI=OFF, USE_NCCL=1, USE_NNPACK=ON, USE_OPENMP=ON, USE_ROCM=OFF, USE_ROCM_KERNEL_ASSERT=OFF, \n"
+ }
+}
diff --git a/peft/method_comparison/MetaMathQA/results/fourierft--llama-3.2-3B-n_frequency-5000.json b/peft/method_comparison/MetaMathQA/results/fourierft--llama-3.2-3B-n_frequency-5000.json
new file mode 100644
index 0000000000000000000000000000000000000000..3c7241b5f04142fdc9bb7a3702e4d08c1b91730a
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/results/fourierft--llama-3.2-3B-n_frequency-5000.json
@@ -0,0 +1,354 @@
+{
+ "run_info": {
+ "created_at": "2025-06-20T09:31:48+00:00",
+ "total_time": 2824.376998209991,
+ "experiment_name": "fourierft/llama-3.2-3B-n_frequency-5000",
+ "peft_branch": "main",
+ "train_config": {
+ "model_id": "meta-llama/Llama-3.2-3B",
+ "dtype": "bfloat16",
+ "max_seq_length": 768,
+ "batch_size": 4,
+ "batch_size_eval": 50,
+ "max_steps": 5000,
+ "eval_steps": 250,
+ "compile": false,
+ "query_template": "Question: {query} Think step by step.\nAnswer:",
+ "seed": 0,
+ "grad_norm_clip": 1.0,
+ "optimizer_type": "AdamW",
+ "optimizer_kwargs": {
+ "lr": 0.0001,
+ "weight_decay": 0.1
+ },
+ "lr_scheduler": "cosine",
+ "use_amp": false,
+ "autocast_adapter_dtype": true,
+ "generation_kwargs": {
+ "max_length": 800,
+ "max_new_tokens": 300
+ },
+ "attn_implementation": null
+ },
+ "peft_config": {
+ "task_type": null,
+ "peft_type": "FOURIERFT",
+ "auto_mapping": null,
+ "base_model_name_or_path": "meta-llama/Llama-3.2-3B",
+ "revision": null,
+ "inference_mode": false,
+ "n_frequency": 5000,
+ "scaling": 300,
+ "random_loc_seed": 777,
+ "fan_in_fan_out": false,
+ "target_modules": [
+ "v_proj",
+ "q_proj"
+ ],
+ "exclude_modules": null,
+ "bias": "none",
+ "modules_to_save": null,
+ "layers_to_transform": null,
+ "layers_pattern": null,
+ "n_frequency_pattern": {},
+ "init_weights": false
+ },
+ "error_msg": ""
+ },
+ "train_info": {
+ "accelerator_memory_reserved_avg": 13111221498,
+ "accelerator_memory_max": 23681040384,
+ "accelerator_memory_reserved_99th": 19054869872,
+ "train_time": 2421.913372163006,
+ "file_size": 1127472,
+ "num_trainable_params": 280000,
+ "num_total_params": 3213029824,
+ "status": "success",
+ "metrics": [
+ {
+ "step": 250,
+ "valid accuracy": 0.0,
+ "train loss": 1.3800132541656494,
+ "train samples": 1000,
+ "train time": 53.57064967796032,
+ "eval time": 19.631924207002157,
+ "tokens / sec": 3952.1454616053315,
+ "mem allocated avg": 6784830552.064,
+ "mem reserved avg": 13158731218.944,
+ "elapsed time": 119.20255395398999
+ },
+ {
+ "step": 500,
+ "valid accuracy": 0.0,
+ "train loss": 1.3702282276153563,
+ "train samples": 2000,
+ "train time": 53.00863014489005,
+ "eval time": 19.629790833001607,
+ "tokens / sec": 3923.7950392508,
+ "mem allocated avg": 6777176354.816,
+ "mem reserved avg": 13048941117.44,
+ "elapsed time": 232.4386439989903
+ },
+ {
+ "step": 750,
+ "valid accuracy": 0.0,
+ "train loss": 1.3024170677661895,
+ "train samples": 3000,
+ "train time": 53.97298614999454,
+ "eval time": 19.64192995200574,
+ "tokens / sec": 3972.3760957780855,
+ "mem allocated avg": 6787548153.856,
+ "mem reserved avg": 13211654946.816,
+ "elapsed time": 346.9217278779979
+ },
+ {
+ "step": 1000,
+ "valid accuracy": 0.0,
+ "train loss": 1.2704877371788026,
+ "train samples": 4000,
+ "train time": 52.95541349705309,
+ "eval time": 19.62998814698949,
+ "tokens / sec": 3934.1775701854103,
+ "mem allocated avg": 6779591346.176,
+ "mem reserved avg": 13082126450.688,
+ "elapsed time": 460.14450727400254
+ },
+ {
+ "step": 1250,
+ "valid accuracy": 0.0,
+ "train loss": 1.2236453666687013,
+ "train samples": 5000,
+ "train time": 53.36593960013124,
+ "eval time": 19.652927816001466,
+ "tokens / sec": 3907.698460152047,
+ "mem allocated avg": 6779029788.672,
+ "mem reserved avg": 13073486184.448,
+ "elapsed time": 573.5348878969962
+ },
+ {
+ "step": 1500,
+ "valid accuracy": 0.0,
+ "train loss": 1.1792121708393097,
+ "train samples": 6000,
+ "train time": 53.3776921518147,
+ "eval time": 19.616937039012555,
+ "tokens / sec": 3921.69446750581,
+ "mem allocated avg": 6779851802.624,
+ "mem reserved avg": 13098995941.376,
+ "elapsed time": 686.9838123609952
+ },
+ {
+ "step": 1750,
+ "valid accuracy": 0.02,
+ "train loss": 1.1485692322254182,
+ "train samples": 7000,
+ "train time": 53.188338823019876,
+ "eval time": 19.653264298991417,
+ "tokens / sec": 3936.1071361264494,
+ "mem allocated avg": 6782223466.496,
+ "mem reserved avg": 13116058370.048,
+ "elapsed time": 800.3354816049978
+ },
+ {
+ "step": 2000,
+ "valid accuracy": 0.06,
+ "train loss": 1.1230667443275453,
+ "train samples": 8000,
+ "train time": 53.074023688037414,
+ "eval time": 19.656479785000556,
+ "tokens / sec": 3913.3268135239105,
+ "mem allocated avg": 6778141935.616,
+ "mem reserved avg": 13055400345.6,
+ "elapsed time": 913.367253695993
+ },
+ {
+ "step": 2250,
+ "valid accuracy": 0.1,
+ "train loss": 1.094045166015625,
+ "train samples": 9000,
+ "train time": 54.34830153394432,
+ "eval time": 19.628162662993418,
+ "tokens / sec": 3955.008600696563,
+ "mem allocated avg": 6789509545.984,
+ "mem reserved avg": 13248556433.408,
+ "elapsed time": 1028.463336018991
+ },
+ {
+ "step": 2500,
+ "valid accuracy": 0.12,
+ "train loss": 1.077717797279358,
+ "train samples": 10000,
+ "train time": 52.1458756570355,
+ "eval time": 19.611369335994823,
+ "tokens / sec": 3949.823402231256,
+ "mem allocated avg": 6775024920.576,
+ "mem reserved avg": 13002233348.096,
+ "elapsed time": 1140.4990660109906
+ },
+ {
+ "step": 2750,
+ "valid accuracy": 0.12,
+ "train loss": 1.0569540388584138,
+ "train samples": 11000,
+ "train time": 53.227410834049806,
+ "eval time": 19.625236430001678,
+ "tokens / sec": 3980.6745562092756,
+ "mem allocated avg": 6785537161.216,
+ "mem reserved avg": 13177051938.816,
+ "elapsed time": 1254.066401210992
+ },
+ {
+ "step": 3000,
+ "valid accuracy": 0.12,
+ "train loss": 1.0361379137039184,
+ "train samples": 12000,
+ "train time": 53.65395914198598,
+ "eval time": 19.719437510997523,
+ "tokens / sec": 3890.3186892066865,
+ "mem allocated avg": 6780720910.336,
+ "mem reserved avg": 13092201168.896,
+ "elapsed time": 1367.8724600419955
+ },
+ {
+ "step": 3250,
+ "valid accuracy": 0.16,
+ "train loss": 1.0240549674034118,
+ "train samples": 13000,
+ "train time": 52.97706237102102,
+ "eval time": 19.7029277440015,
+ "tokens / sec": 3980.9870642311216,
+ "mem allocated avg": 6782688188.416,
+ "mem reserved avg": 13119816466.432,
+ "elapsed time": 1481.1549517469975
+ },
+ {
+ "step": 3500,
+ "valid accuracy": 0.18,
+ "train loss": 1.0098259932994842,
+ "train samples": 14000,
+ "train time": 52.869576787008555,
+ "eval time": 19.597270865997416,
+ "tokens / sec": 3967.3099870839346,
+ "mem allocated avg": 6780575592.448,
+ "mem reserved avg": 13102678540.288,
+ "elapsed time": 1594.3849144269916
+ },
+ {
+ "step": 3750,
+ "valid accuracy": 0.22,
+ "train loss": 0.9942408270835876,
+ "train samples": 15000,
+ "train time": 54.702630093932385,
+ "eval time": 19.623511597994366,
+ "tokens / sec": 3961.4731435744384,
+ "mem allocated avg": 6792074147.84,
+ "mem reserved avg": 13278612815.872,
+ "elapsed time": 1709.9712875620025
+ },
+ {
+ "step": 4000,
+ "valid accuracy": 0.16,
+ "train loss": 1.0123027296066285,
+ "train samples": 16000,
+ "train time": 52.456372838059906,
+ "eval time": 19.68401901901234,
+ "tokens / sec": 3896.056645603915,
+ "mem allocated avg": 6773958766.592,
+ "mem reserved avg": 12989172285.44,
+ "elapsed time": 1822.6668115109933
+ },
+ {
+ "step": 4250,
+ "valid accuracy": 0.24,
+ "train loss": 0.9849327182769776,
+ "train samples": 17000,
+ "train time": 53.25562528491719,
+ "eval time": 19.648335694990237,
+ "tokens / sec": 3969.3271625123257,
+ "mem allocated avg": 6783509901.312,
+ "mem reserved avg": 13139588415.488,
+ "elapsed time": 1936.0694442329986
+ },
+ {
+ "step": 4500,
+ "valid accuracy": 0.18,
+ "train loss": 0.9994378657341003,
+ "train samples": 18000,
+ "train time": 53.01732904899109,
+ "eval time": 19.688141086997348,
+ "tokens / sec": 3919.8127051621955,
+ "mem allocated avg": 6779470948.352,
+ "mem reserved avg": 13063528906.752,
+ "elapsed time": 2048.985867203999
+ },
+ {
+ "step": 4750,
+ "valid accuracy": 0.16,
+ "train loss": 0.9892346875667573,
+ "train samples": 19000,
+ "train time": 53.11992502908106,
+ "eval time": 19.68838914000662,
+ "tokens / sec": 3952.1704875348883,
+ "mem allocated avg": 6781060145.152,
+ "mem reserved avg": 13109733359.616,
+ "elapsed time": 2162.7099456459982
+ },
+ {
+ "step": 5000,
+ "valid accuracy": 0.2,
+ "train loss": 0.9978675174713135,
+ "train samples": 20000,
+ "train time": 52.76285280592856,
+ "eval time": 19.634052573994268,
+ "tokens / sec": 3947.4741967818154,
+ "mem allocated avg": 6777472888.832,
+ "mem reserved avg": 13055861719.04,
+ "elapsed time": 2275.669019541994
+ },
+ {
+ "step": 5000,
+ "test accuracy": 0.1197877179681577,
+ "train loss": 0.9978675174713135,
+ "train samples": 20000,
+ "train total tokens": 4198051
+ }
+ ]
+ },
+ "meta_info": {
+ "model_info": {
+ "sha": "13afe5124825b4f3751f836b40dafda64c1ed062",
+ "created_at": "2024-09-18T15:23:48+00:00"
+ },
+ "dataset_info": {
+ "metamath": {
+ "sha": "aa4f34d3d2d3231299b5b03d9b3e5a20da45aa18",
+ "created_at": "2023-09-21T17:22:46+00:00"
+ },
+ "gsm8k": {
+ "sha": "e53f048856ff4f594e959d75785d2c2d37b678ee",
+ "created_at": "2022-04-12T10:22:10+00:00"
+ }
+ },
+ "package_info": {
+ "transformers-version": "4.52.4",
+ "transformers-commit-hash": null,
+ "peft-version": "0.15.2.dev0",
+ "peft-commit-hash": "5fe7f8f8abe914d313fc3751f2ea92de7718fbaf",
+ "datasets-version": "3.6.0",
+ "datasets-commit-hash": null,
+ "bitsandbytes-version": "0.46.0",
+ "bitsandbytes-commit-hash": null,
+ "torch-version": "2.7.1+cu126",
+ "torch-commit-hash": null
+ },
+ "system_info": {
+ "system": "Linux",
+ "release": "6.8.0-1029-aws",
+ "version": "#31-Ubuntu SMP Wed Apr 23 18:42:41 UTC 2025",
+ "machine": "x86_64",
+ "processor": "x86_64",
+ "accelerator": "NVIDIA L40S"
+ },
+ "pytorch_info": "PyTorch built with:\n - GCC 11.2\n - C++ Version: 201703\n - Intel(R) oneAPI Math Kernel Library Version 2024.2-Product Build 20240605 for Intel(R) 64 architecture applications\n - Intel(R) MKL-DNN v3.7.1 (Git Hash 8d263e693366ef8db40acc569cc7d8edf644556d)\n - OpenMP 201511 (a.k.a. OpenMP 4.5)\n - LAPACK is enabled (usually provided by MKL)\n - NNPACK is enabled\n - CPU capability usage: AVX2\n - CUDA Runtime 12.6\n - NVCC architecture flags: -gencode;arch=compute_50,code=sm_50;-gencode;arch=compute_60,code=sm_60;-gencode;arch=compute_70,code=sm_70;-gencode;arch=compute_75,code=sm_75;-gencode;arch=compute_80,code=sm_80;-gencode;arch=compute_86,code=sm_86;-gencode;arch=compute_90,code=sm_90\n - CuDNN 90.7.1 (built against CUDA 12.8)\n - Built with CuDNN 90.5.1\n - Magma 2.6.1\n - Build settings: BLAS_INFO=mkl, BUILD_TYPE=Release, COMMIT_SHA=e2d141dbde55c2a4370fac5165b0561b6af4798b, CUDA_VERSION=12.6, CUDNN_VERSION=9.5.1, CXX_COMPILER=/opt/rh/gcc-toolset-11/root/usr/bin/c++, CXX_FLAGS= -D_GLIBCXX_USE_CXX11_ABI=1 -fvisibility-inlines-hidden -DUSE_PTHREADPOOL -DNDEBUG -DUSE_KINETO -DLIBKINETO_NOROCTRACER -DLIBKINETO_NOXPUPTI=ON -DUSE_FBGEMM -DUSE_PYTORCH_QNNPACK -DUSE_XNNPACK -DSYMBOLICATE_MOBILE_DEBUG_HANDLE -O2 -fPIC -Wall -Wextra -Werror=return-type -Werror=non-virtual-dtor -Werror=range-loop-construct -Werror=bool-operation -Wnarrowing -Wno-missing-field-initializers -Wno-unknown-pragmas -Wno-unused-parameter -Wno-strict-overflow -Wno-strict-aliasing -Wno-stringop-overflow -Wsuggest-override -Wno-psabi -Wno-error=old-style-cast -fdiagnostics-color=always -faligned-new -Wno-maybe-uninitialized -fno-math-errno -fno-trapping-math -Werror=format -Wno-stringop-overflow, LAPACK_INFO=mkl, PERF_WITH_AVX=1, PERF_WITH_AVX2=1, TORCH_VERSION=2.7.1, USE_CUDA=ON, USE_CUDNN=ON, USE_CUSPARSELT=1, USE_GFLAGS=OFF, USE_GLOG=OFF, USE_GLOO=ON, USE_MKL=ON, USE_MKLDNN=ON, USE_MPI=OFF, USE_NCCL=1, USE_NNPACK=ON, USE_OPENMP=ON, USE_ROCM=OFF, USE_ROCM_KERNEL_ASSERT=OFF, \n"
+ }
+}
diff --git a/peft/method_comparison/MetaMathQA/results/full-finetuning--llama-3.2-3B-lr_0.00001.json b/peft/method_comparison/MetaMathQA/results/full-finetuning--llama-3.2-3B-lr_0.00001.json
new file mode 100644
index 0000000000000000000000000000000000000000..4f15dc9eb28e5cde17637f1ebcfe00e9c01217ae
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/results/full-finetuning--llama-3.2-3B-lr_0.00001.json
@@ -0,0 +1,331 @@
+{
+ "run_info": {
+ "created_at": "2025-06-20T18:02:43+00:00",
+ "total_time": 3274.9747593409993,
+ "experiment_name": "full-finetuning/llama-3.2-3B-lr_0.00001",
+ "peft_branch": "main",
+ "train_config": {
+ "model_id": "meta-llama/Llama-3.2-3B",
+ "dtype": "bfloat16",
+ "max_seq_length": 768,
+ "batch_size": 4,
+ "batch_size_eval": 50,
+ "max_steps": 5000,
+ "eval_steps": 250,
+ "compile": false,
+ "query_template": "Question: {query} Think step by step.\nAnswer:",
+ "seed": 0,
+ "grad_norm_clip": 1.0,
+ "optimizer_type": "AdamW",
+ "optimizer_kwargs": {
+ "lr": 1e-05
+ },
+ "lr_scheduler": "cosine",
+ "use_amp": false,
+ "autocast_adapter_dtype": true,
+ "generation_kwargs": {
+ "max_length": 800,
+ "max_new_tokens": 300
+ },
+ "attn_implementation": null
+ },
+ "peft_config": null,
+ "error_msg": ""
+ },
+ "train_info": {
+ "accelerator_memory_reserved_avg": 33098872284,
+ "accelerator_memory_max": 37241225216,
+ "accelerator_memory_reserved_99th": 33573390254,
+ "train_time": 3111.3685010060144,
+ "file_size": 6425499648,
+ "num_trainable_params": 3212749824,
+ "num_total_params": 3212749824,
+ "status": "success",
+ "metrics": [
+ {
+ "step": 250,
+ "valid accuracy": 0.3,
+ "train loss": 1.0749022357463838,
+ "train samples": 1000,
+ "train time": 90.81602771116013,
+ "eval time": 10.388541491003707,
+ "tokens / sec": 2331.295535996918,
+ "mem allocated avg": 26069449254.912,
+ "mem reserved avg": 33116739600.384,
+ "elapsed time": 162.0596859770012
+ },
+ {
+ "step": 500,
+ "valid accuracy": 0.4,
+ "train loss": 0.7238605101108551,
+ "train samples": 2000,
+ "train time": 90.41340426202805,
+ "eval time": 10.403155545005575,
+ "tokens / sec": 2300.488535938847,
+ "mem allocated avg": 26062513567.744,
+ "mem reserved avg": 33090961408.0,
+ "elapsed time": 315.86630137299653
+ },
+ {
+ "step": 750,
+ "valid accuracy": 0.42,
+ "train loss": 0.6648618497848511,
+ "train samples": 3000,
+ "train time": 91.4961106939445,
+ "eval time": 5.590419113999815,
+ "tokens / sec": 2343.27993150631,
+ "mem allocated avg": 26071394062.336,
+ "mem reserved avg": 33094367182.848,
+ "elapsed time": 465.79339110500587
+ },
+ {
+ "step": 1000,
+ "valid accuracy": 0.42,
+ "train loss": 0.6407654472589492,
+ "train samples": 4000,
+ "train time": 89.8546926038689,
+ "eval time": 10.434167744999286,
+ "tokens / sec": 2318.5878662838986,
+ "mem allocated avg": 26063373086.72,
+ "mem reserved avg": 33094367182.848,
+ "elapsed time": 618.5050604129938
+ },
+ {
+ "step": 1250,
+ "valid accuracy": 0.46,
+ "train loss": 0.6343449921607971,
+ "train samples": 5000,
+ "train time": 90.3596406209981,
+ "eval time": 5.810965301003307,
+ "tokens / sec": 2307.86663787969,
+ "mem allocated avg": 26063789404.16,
+ "mem reserved avg": 33081876545.536,
+ "elapsed time": 766.6042792719963
+ },
+ {
+ "step": 1500,
+ "valid accuracy": 0.54,
+ "train loss": 0.6249808443784713,
+ "train samples": 6000,
+ "train time": 90.81503154609527,
+ "eval time": 10.435444819988334,
+ "tokens / sec": 2305.025901948283,
+ "mem allocated avg": 26066218485.76,
+ "mem reserved avg": 33089409515.52,
+ "elapsed time": 920.292813491993
+ },
+ {
+ "step": 1750,
+ "valid accuracy": 0.46,
+ "train loss": 0.6174132014513016,
+ "train samples": 7000,
+ "train time": 90.68820026615867,
+ "eval time": 10.286707318999106,
+ "tokens / sec": 2308.5142210956765,
+ "mem allocated avg": 26065828059.136,
+ "mem reserved avg": 33101774323.712,
+ "elapsed time": 1073.8488811849966
+ },
+ {
+ "step": 2000,
+ "valid accuracy": 0.42,
+ "train loss": 0.618268838763237,
+ "train samples": 8000,
+ "train time": 90.44998777209548,
+ "eval time": 10.380125819006935,
+ "tokens / sec": 2296.252383398064,
+ "mem allocated avg": 26062920781.824,
+ "mem reserved avg": 33096330117.12,
+ "elapsed time": 1227.2062568730034
+ },
+ {
+ "step": 2250,
+ "valid accuracy": 0.5,
+ "train loss": 0.6107994567155838,
+ "train samples": 9000,
+ "train time": 91.58726547904371,
+ "eval time": 10.372407121991273,
+ "tokens / sec": 2346.920162707366,
+ "mem allocated avg": 26073357961.216,
+ "mem reserved avg": 33114382401.536,
+ "elapsed time": 1381.3805919409933
+ },
+ {
+ "step": 2500,
+ "valid accuracy": 0.54,
+ "train loss": 0.6089532144069671,
+ "train samples": 10000,
+ "train time": 89.29193754095468,
+ "eval time": 10.391672718993505,
+ "tokens / sec": 2306.6696240691504,
+ "mem allocated avg": 26059719045.12,
+ "mem reserved avg": 33086842601.472,
+ "elapsed time": 1533.778675338006
+ },
+ {
+ "step": 2750,
+ "valid accuracy": 0.52,
+ "train loss": 0.6020698472261429,
+ "train samples": 11000,
+ "train time": 90.41624103189679,
+ "eval time": 10.369720178001444,
+ "tokens / sec": 2343.3953632871467,
+ "mem allocated avg": 26070059464.704,
+ "mem reserved avg": 33107805732.864,
+ "elapsed time": 1686.671367884992
+ },
+ {
+ "step": 3000,
+ "valid accuracy": 0.5,
+ "train loss": 0.5949549045562744,
+ "train samples": 12000,
+ "train time": 90.9437831780233,
+ "eval time": 7.315949440002441,
+ "tokens / sec": 2295.165130654474,
+ "mem allocated avg": 26064854972.416,
+ "mem reserved avg": 33098074947.584,
+ "elapsed time": 1837.2926549609983
+ },
+ {
+ "step": 3250,
+ "valid accuracy": 0.48,
+ "train loss": 0.6066494225263596,
+ "train samples": 13000,
+ "train time": 90.87308476005273,
+ "eval time": 5.963120047992561,
+ "tokens / sec": 2320.8302057410824,
+ "mem allocated avg": 26066388537.344,
+ "mem reserved avg": 33098318217.216,
+ "elapsed time": 1986.6408478410012
+ },
+ {
+ "step": 3500,
+ "valid accuracy": 0.48,
+ "train loss": 0.592242598772049,
+ "train samples": 14000,
+ "train time": 90.65281462905114,
+ "eval time": 7.1309342330059735,
+ "tokens / sec": 2313.7726154261322,
+ "mem allocated avg": 26065652588.544,
+ "mem reserved avg": 33100457312.256,
+ "elapsed time": 2137.073564691993
+ },
+ {
+ "step": 3750,
+ "valid accuracy": 0.48,
+ "train loss": 0.5925718579292297,
+ "train samples": 15000,
+ "train time": 91.80342563094746,
+ "eval time": 5.844810517999576,
+ "tokens / sec": 2360.5110431407275,
+ "mem allocated avg": 26075058659.328,
+ "mem reserved avg": 33131771985.92,
+ "elapsed time": 2287.0305021950044
+ },
+ {
+ "step": 4000,
+ "valid accuracy": 0.5,
+ "train loss": 0.6050453131198883,
+ "train samples": 16000,
+ "train time": 89.85742108603881,
+ "eval time": 5.86809825799719,
+ "tokens / sec": 2274.414261280792,
+ "mem allocated avg": 26058425257.984,
+ "mem reserved avg": 33098662150.144,
+ "elapsed time": 2435.1958582270017
+ },
+ {
+ "step": 4250,
+ "valid accuracy": 0.48,
+ "train loss": 0.5929686036109925,
+ "train samples": 17000,
+ "train time": 90.97368233802263,
+ "eval time": 5.8907580230006715,
+ "tokens / sec": 2323.6280489841133,
+ "mem allocated avg": 26067367372.8,
+ "mem reserved avg": 33099207409.664,
+ "elapsed time": 2584.8373482140014
+ },
+ {
+ "step": 4500,
+ "valid accuracy": 0.48,
+ "train loss": 0.6010294322967529,
+ "train samples": 18000,
+ "train time": 90.13679483698797,
+ "eval time": 6.106882603999111,
+ "tokens / sec": 2305.5845326632484,
+ "mem allocated avg": 26064599832.576,
+ "mem reserved avg": 33092253253.632,
+ "elapsed time": 2733.494644669001
+ },
+ {
+ "step": 4750,
+ "valid accuracy": 0.5,
+ "train loss": 0.5936577550172806,
+ "train samples": 19000,
+ "train time": 90.74229130300228,
+ "eval time": 5.885364143003244,
+ "tokens / sec": 2313.5739354319567,
+ "mem allocated avg": 26065537388.544,
+ "mem reserved avg": 33100717359.104,
+ "elapsed time": 2882.6415541759925
+ },
+ {
+ "step": 5000,
+ "valid accuracy": 0.5,
+ "train loss": 0.5987544150352478,
+ "train samples": 20000,
+ "train time": 90.54863398504676,
+ "eval time": 5.88336711798911,
+ "tokens / sec": 2300.2003545895063,
+ "mem allocated avg": 26062803286.016,
+ "mem reserved avg": 33083126448.128,
+ "elapsed time": 3031.523533478001
+ },
+ {
+ "step": 5000,
+ "test accuracy": 0.5003790750568613,
+ "train loss": 0.5987544150352478,
+ "train samples": 20000,
+ "train total tokens": 4198051
+ }
+ ]
+ },
+ "meta_info": {
+ "model_info": {
+ "sha": "13afe5124825b4f3751f836b40dafda64c1ed062",
+ "created_at": "2024-09-18T15:23:48+00:00"
+ },
+ "dataset_info": {
+ "metamath": {
+ "sha": "aa4f34d3d2d3231299b5b03d9b3e5a20da45aa18",
+ "created_at": "2023-09-21T17:22:46+00:00"
+ },
+ "gsm8k": {
+ "sha": "e53f048856ff4f594e959d75785d2c2d37b678ee",
+ "created_at": "2022-04-12T10:22:10+00:00"
+ }
+ },
+ "package_info": {
+ "transformers-version": "4.52.4",
+ "transformers-commit-hash": null,
+ "peft-version": "0.15.2.dev0",
+ "peft-commit-hash": "5fe7f8f8abe914d313fc3751f2ea92de7718fbaf",
+ "datasets-version": "3.6.0",
+ "datasets-commit-hash": null,
+ "bitsandbytes-version": "0.46.0",
+ "bitsandbytes-commit-hash": null,
+ "torch-version": "2.7.1+cu126",
+ "torch-commit-hash": null
+ },
+ "system_info": {
+ "system": "Linux",
+ "release": "6.8.0-1029-aws",
+ "version": "#31-Ubuntu SMP Wed Apr 23 18:42:41 UTC 2025",
+ "machine": "x86_64",
+ "processor": "x86_64",
+ "accelerator": "NVIDIA L40S"
+ },
+ "pytorch_info": "PyTorch built with:\n - GCC 11.2\n - C++ Version: 201703\n - Intel(R) oneAPI Math Kernel Library Version 2024.2-Product Build 20240605 for Intel(R) 64 architecture applications\n - Intel(R) MKL-DNN v3.7.1 (Git Hash 8d263e693366ef8db40acc569cc7d8edf644556d)\n - OpenMP 201511 (a.k.a. OpenMP 4.5)\n - LAPACK is enabled (usually provided by MKL)\n - NNPACK is enabled\n - CPU capability usage: AVX2\n - CUDA Runtime 12.6\n - NVCC architecture flags: -gencode;arch=compute_50,code=sm_50;-gencode;arch=compute_60,code=sm_60;-gencode;arch=compute_70,code=sm_70;-gencode;arch=compute_75,code=sm_75;-gencode;arch=compute_80,code=sm_80;-gencode;arch=compute_86,code=sm_86;-gencode;arch=compute_90,code=sm_90\n - CuDNN 90.7.1 (built against CUDA 12.8)\n - Built with CuDNN 90.5.1\n - Magma 2.6.1\n - Build settings: BLAS_INFO=mkl, BUILD_TYPE=Release, COMMIT_SHA=e2d141dbde55c2a4370fac5165b0561b6af4798b, CUDA_VERSION=12.6, CUDNN_VERSION=9.5.1, CXX_COMPILER=/opt/rh/gcc-toolset-11/root/usr/bin/c++, CXX_FLAGS= -D_GLIBCXX_USE_CXX11_ABI=1 -fvisibility-inlines-hidden -DUSE_PTHREADPOOL -DNDEBUG -DUSE_KINETO -DLIBKINETO_NOROCTRACER -DLIBKINETO_NOXPUPTI=ON -DUSE_FBGEMM -DUSE_PYTORCH_QNNPACK -DUSE_XNNPACK -DSYMBOLICATE_MOBILE_DEBUG_HANDLE -O2 -fPIC -Wall -Wextra -Werror=return-type -Werror=non-virtual-dtor -Werror=range-loop-construct -Werror=bool-operation -Wnarrowing -Wno-missing-field-initializers -Wno-unknown-pragmas -Wno-unused-parameter -Wno-strict-overflow -Wno-strict-aliasing -Wno-stringop-overflow -Wsuggest-override -Wno-psabi -Wno-error=old-style-cast -fdiagnostics-color=always -faligned-new -Wno-maybe-uninitialized -fno-math-errno -fno-trapping-math -Werror=format -Wno-stringop-overflow, LAPACK_INFO=mkl, PERF_WITH_AVX=1, PERF_WITH_AVX2=1, TORCH_VERSION=2.7.1, USE_CUDA=ON, USE_CUDNN=ON, USE_CUSPARSELT=1, USE_GFLAGS=OFF, USE_GLOG=OFF, USE_GLOO=ON, USE_MKL=ON, USE_MKLDNN=ON, USE_MPI=OFF, USE_NCCL=1, USE_NNPACK=ON, USE_OPENMP=ON, USE_ROCM=OFF, USE_ROCM_KERNEL_ASSERT=OFF, \n"
+ }
+}
diff --git a/peft/method_comparison/MetaMathQA/results/ia3--llama-3.2-3B-default.json b/peft/method_comparison/MetaMathQA/results/ia3--llama-3.2-3B-default.json
new file mode 100644
index 0000000000000000000000000000000000000000..50d2efa1f91faafd63fdf9ab606668fd2c40c3c6
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/results/ia3--llama-3.2-3B-default.json
@@ -0,0 +1,351 @@
+{
+ "run_info": {
+ "created_at": "2025-06-19T21:59:33+00:00",
+ "total_time": 2004.8640038169979,
+ "experiment_name": "ia3/llama-3.2-3B-default",
+ "peft_branch": "main",
+ "train_config": {
+ "model_id": "meta-llama/Llama-3.2-3B",
+ "dtype": "bfloat16",
+ "max_seq_length": 768,
+ "batch_size": 4,
+ "batch_size_eval": 50,
+ "max_steps": 5000,
+ "eval_steps": 250,
+ "compile": false,
+ "query_template": "Question: {query} Think step by step.\nAnswer:",
+ "seed": 0,
+ "grad_norm_clip": 1.0,
+ "optimizer_type": "AdamW",
+ "optimizer_kwargs": {
+ "lr": 0.0001,
+ "weight_decay": 0.1
+ },
+ "lr_scheduler": "cosine",
+ "use_amp": false,
+ "autocast_adapter_dtype": true,
+ "generation_kwargs": {
+ "max_length": 800,
+ "max_new_tokens": 300
+ },
+ "attn_implementation": null
+ },
+ "peft_config": {
+ "task_type": null,
+ "peft_type": "IA3",
+ "auto_mapping": null,
+ "base_model_name_or_path": "meta-llama/Llama-3.2-3B",
+ "revision": null,
+ "inference_mode": false,
+ "target_modules": [
+ "down_proj",
+ "v_proj",
+ "k_proj"
+ ],
+ "exclude_modules": null,
+ "feedforward_modules": [
+ "down_proj"
+ ],
+ "fan_in_fan_out": false,
+ "modules_to_save": null,
+ "init_ia3_weights": true
+ },
+ "error_msg": ""
+ },
+ "train_info": {
+ "accelerator_memory_reserved_avg": 12023227429,
+ "accelerator_memory_max": 23137878016,
+ "accelerator_memory_reserved_99th": 18398566154,
+ "train_time": 1782.9318781230104,
+ "file_size": 1157064,
+ "num_trainable_params": 286720,
+ "num_total_params": 3213036544,
+ "status": "success",
+ "metrics": [
+ {
+ "step": 250,
+ "valid accuracy": 0.0,
+ "train loss": 1.3155810165405273,
+ "train samples": 1000,
+ "train time": 30.56459548201383,
+ "eval time": 10.972947114001727,
+ "tokens / sec": 6926.936105684404,
+ "mem allocated avg": 6780994971.648,
+ "mem reserved avg": 12076433014.784,
+ "elapsed time": 90.53726772200025
+ },
+ {
+ "step": 500,
+ "valid accuracy": 0.0,
+ "train loss": 1.205229633808136,
+ "train samples": 2000,
+ "train time": 30.221456803970796,
+ "eval time": 10.954313254995213,
+ "tokens / sec": 6882.361805029583,
+ "mem allocated avg": 6773721065.472,
+ "mem reserved avg": 11963673346.048,
+ "elapsed time": 175.07058417100052
+ },
+ {
+ "step": 750,
+ "valid accuracy": 0.1,
+ "train loss": 1.0194582087993622,
+ "train samples": 3000,
+ "train time": 30.774312397006724,
+ "eval time": 10.944943730006344,
+ "tokens / sec": 6966.881899231445,
+ "mem allocated avg": 6784231882.752,
+ "mem reserved avg": 12126680776.704,
+ "elapsed time": 260.540154495
+ },
+ {
+ "step": 1000,
+ "valid accuracy": 0.24,
+ "train loss": 0.9196457831859589,
+ "train samples": 4000,
+ "train time": 30.61534244806535,
+ "eval time": 10.960088267995161,
+ "tokens / sec": 6804.95409624808,
+ "mem allocated avg": 6775492155.392,
+ "mem reserved avg": 11986893012.992,
+ "elapsed time": 345.30987053900026
+ },
+ {
+ "step": 1250,
+ "valid accuracy": 0.32,
+ "train loss": 0.8685842225551605,
+ "train samples": 5000,
+ "train time": 29.97266351111466,
+ "eval time": 10.924794500999269,
+ "tokens / sec": 6957.606551138459,
+ "mem allocated avg": 6775089207.296,
+ "mem reserved avg": 11983428517.888,
+ "elapsed time": 429.5542291879974
+ },
+ {
+ "step": 1500,
+ "valid accuracy": 0.32,
+ "train loss": 0.8332846148014068,
+ "train samples": 6000,
+ "train time": 29.98314001694962,
+ "eval time": 10.942266878999362,
+ "tokens / sec": 6981.6236685572,
+ "mem allocated avg": 6776724867.072,
+ "mem reserved avg": 12008594341.888,
+ "elapsed time": 513.8152235820016
+ },
+ {
+ "step": 1750,
+ "valid accuracy": 0.32,
+ "train loss": 0.8169269208908081,
+ "train samples": 7000,
+ "train time": 30.245623568014707,
+ "eval time": 10.940915298000618,
+ "tokens / sec": 6921.8278647558345,
+ "mem allocated avg": 6777912934.4,
+ "mem reserved avg": 12032065667.072,
+ "elapsed time": 598.2868188970024
+ },
+ {
+ "step": 2000,
+ "valid accuracy": 0.32,
+ "train loss": 0.8072074156999588,
+ "train samples": 8000,
+ "train time": 30.292844633964705,
+ "eval time": 10.95617212200159,
+ "tokens / sec": 6856.272578875894,
+ "mem allocated avg": 6775099170.816,
+ "mem reserved avg": 11967473385.472,
+ "elapsed time": 682.7948923380027
+ },
+ {
+ "step": 2250,
+ "valid accuracy": 0.32,
+ "train loss": 0.7952859619855881,
+ "train samples": 9000,
+ "train time": 31.20892413101683,
+ "eval time": 10.942549917002907,
+ "tokens / sec": 6887.388975590319,
+ "mem allocated avg": 6786161477.632,
+ "mem reserved avg": 12167709458.432,
+ "elapsed time": 768.9645714229991
+ },
+ {
+ "step": 2500,
+ "valid accuracy": 0.28,
+ "train loss": 0.7890167078971863,
+ "train samples": 10000,
+ "train time": 30.187670495011844,
+ "eval time": 10.954304017002869,
+ "tokens / sec": 6822.884860692832,
+ "mem allocated avg": 6771082014.72,
+ "mem reserved avg": 11910984499.2,
+ "elapsed time": 853.427360558002
+ },
+ {
+ "step": 2750,
+ "valid accuracy": 0.3,
+ "train loss": 0.7823473591804504,
+ "train samples": 11000,
+ "train time": 30.410061570059042,
+ "eval time": 10.93302121299348,
+ "tokens / sec": 6967.4636965751015,
+ "mem allocated avg": 6782254225.408,
+ "mem reserved avg": 12090903363.584,
+ "elapsed time": 938.3584665200033
+ },
+ {
+ "step": 3000,
+ "valid accuracy": 0.24,
+ "train loss": 0.7709820411205291,
+ "train samples": 12000,
+ "train time": 30.02989622000314,
+ "eval time": 10.940404225999373,
+ "tokens / sec": 6950.773271769175,
+ "mem allocated avg": 6776725577.728,
+ "mem reserved avg": 12003133358.08,
+ "elapsed time": 1022.4627897890023
+ },
+ {
+ "step": 3250,
+ "valid accuracy": 0.3,
+ "train loss": 0.7755767168998718,
+ "train samples": 13000,
+ "train time": 30.172652364024543,
+ "eval time": 10.940153044000908,
+ "tokens / sec": 6989.806446431653,
+ "mem allocated avg": 6778589339.648,
+ "mem reserved avg": 12038298402.816,
+ "elapsed time": 1107.0076802080002
+ },
+ {
+ "step": 3500,
+ "valid accuracy": 0.34,
+ "train loss": 0.7658302361965179,
+ "train samples": 14000,
+ "train time": 30.384311634006735,
+ "eval time": 10.941136569999799,
+ "tokens / sec": 6903.233567590308,
+ "mem allocated avg": 6777534660.608,
+ "mem reserved avg": 12020623605.76,
+ "elapsed time": 1191.893303306002
+ },
+ {
+ "step": 3750,
+ "valid accuracy": 0.34,
+ "train loss": 0.7585167481899261,
+ "train samples": 15000,
+ "train time": 31.250990667955193,
+ "eval time": 10.924158087997057,
+ "tokens / sec": 6934.276173913666,
+ "mem allocated avg": 6788426940.416,
+ "mem reserved avg": 12209652498.432,
+ "elapsed time": 1278.4574160839984
+ },
+ {
+ "step": 4000,
+ "valid accuracy": 0.26,
+ "train loss": 0.7766438691616059,
+ "train samples": 16000,
+ "train time": 30.222231689898763,
+ "eval time": 10.98030305699649,
+ "tokens / sec": 6762.339793335249,
+ "mem allocated avg": 6769563977.728,
+ "mem reserved avg": 11885533462.528,
+ "elapsed time": 1362.9405450319973
+ },
+ {
+ "step": 4250,
+ "valid accuracy": 0.34,
+ "train loss": 0.7542061095237732,
+ "train samples": 17000,
+ "train time": 30.273203028933494,
+ "eval time": 10.948997009996674,
+ "tokens / sec": 6982.710081849145,
+ "mem allocated avg": 6780103426.048,
+ "mem reserved avg": 12047483928.576,
+ "elapsed time": 1447.661586811002
+ },
+ {
+ "step": 4500,
+ "valid accuracy": 0.32,
+ "train loss": 0.7659628703594208,
+ "train samples": 18000,
+ "train time": 29.84466753601737,
+ "eval time": 10.942651322002348,
+ "tokens / sec": 6963.320993581165,
+ "mem allocated avg": 6775043430.4,
+ "mem reserved avg": 11968387743.744,
+ "elapsed time": 1531.5572027719973
+ },
+ {
+ "step": 4750,
+ "valid accuracy": 0.28,
+ "train loss": 0.7580052223205567,
+ "train samples": 19000,
+ "train time": 30.03731635398435,
+ "eval time": 10.927273799999966,
+ "tokens / sec": 6989.272860661278,
+ "mem allocated avg": 6776962899.968,
+ "mem reserved avg": 12017695981.568,
+ "elapsed time": 1615.9832882379997
+ },
+ {
+ "step": 5000,
+ "valid accuracy": 0.36,
+ "train loss": 0.7657463653087616,
+ "train samples": 20000,
+ "train time": 30.07570726004633,
+ "eval time": 10.953207714999735,
+ "tokens / sec": 6925.19042691597,
+ "mem allocated avg": 6774270615.552,
+ "mem reserved avg": 11958900228.096,
+ "elapsed time": 1700.4354192270039
+ },
+ {
+ "step": 5000,
+ "test accuracy": 0.34495830174374525,
+ "train loss": 0.7657463653087616,
+ "train samples": 20000,
+ "train total tokens": 4198051
+ }
+ ]
+ },
+ "meta_info": {
+ "model_info": {
+ "sha": "13afe5124825b4f3751f836b40dafda64c1ed062",
+ "created_at": "2024-09-18T15:23:48+00:00"
+ },
+ "dataset_info": {
+ "metamath": {
+ "sha": "aa4f34d3d2d3231299b5b03d9b3e5a20da45aa18",
+ "created_at": "2023-09-21T17:22:46+00:00"
+ },
+ "gsm8k": {
+ "sha": "e53f048856ff4f594e959d75785d2c2d37b678ee",
+ "created_at": "2022-04-12T10:22:10+00:00"
+ }
+ },
+ "package_info": {
+ "transformers-version": "4.52.4",
+ "transformers-commit-hash": null,
+ "peft-version": "0.15.2.dev0",
+ "peft-commit-hash": "5fe7f8f8abe914d313fc3751f2ea92de7718fbaf",
+ "datasets-version": "3.6.0",
+ "datasets-commit-hash": null,
+ "bitsandbytes-version": "0.46.0",
+ "bitsandbytes-commit-hash": null,
+ "torch-version": "2.7.1+cu126",
+ "torch-commit-hash": null
+ },
+ "system_info": {
+ "system": "Linux",
+ "release": "6.8.0-1029-aws",
+ "version": "#31-Ubuntu SMP Wed Apr 23 18:42:41 UTC 2025",
+ "machine": "x86_64",
+ "processor": "x86_64",
+ "accelerator": "NVIDIA L40S"
+ },
+ "pytorch_info": "PyTorch built with:\n - GCC 11.2\n - C++ Version: 201703\n - Intel(R) oneAPI Math Kernel Library Version 2024.2-Product Build 20240605 for Intel(R) 64 architecture applications\n - Intel(R) MKL-DNN v3.7.1 (Git Hash 8d263e693366ef8db40acc569cc7d8edf644556d)\n - OpenMP 201511 (a.k.a. OpenMP 4.5)\n - LAPACK is enabled (usually provided by MKL)\n - NNPACK is enabled\n - CPU capability usage: AVX2\n - CUDA Runtime 12.6\n - NVCC architecture flags: -gencode;arch=compute_50,code=sm_50;-gencode;arch=compute_60,code=sm_60;-gencode;arch=compute_70,code=sm_70;-gencode;arch=compute_75,code=sm_75;-gencode;arch=compute_80,code=sm_80;-gencode;arch=compute_86,code=sm_86;-gencode;arch=compute_90,code=sm_90\n - CuDNN 90.7.1 (built against CUDA 12.8)\n - Built with CuDNN 90.5.1\n - Magma 2.6.1\n - Build settings: BLAS_INFO=mkl, BUILD_TYPE=Release, COMMIT_SHA=e2d141dbde55c2a4370fac5165b0561b6af4798b, CUDA_VERSION=12.6, CUDNN_VERSION=9.5.1, CXX_COMPILER=/opt/rh/gcc-toolset-11/root/usr/bin/c++, CXX_FLAGS= -D_GLIBCXX_USE_CXX11_ABI=1 -fvisibility-inlines-hidden -DUSE_PTHREADPOOL -DNDEBUG -DUSE_KINETO -DLIBKINETO_NOROCTRACER -DLIBKINETO_NOXPUPTI=ON -DUSE_FBGEMM -DUSE_PYTORCH_QNNPACK -DUSE_XNNPACK -DSYMBOLICATE_MOBILE_DEBUG_HANDLE -O2 -fPIC -Wall -Wextra -Werror=return-type -Werror=non-virtual-dtor -Werror=range-loop-construct -Werror=bool-operation -Wnarrowing -Wno-missing-field-initializers -Wno-unknown-pragmas -Wno-unused-parameter -Wno-strict-overflow -Wno-strict-aliasing -Wno-stringop-overflow -Wsuggest-override -Wno-psabi -Wno-error=old-style-cast -fdiagnostics-color=always -faligned-new -Wno-maybe-uninitialized -fno-math-errno -fno-trapping-math -Werror=format -Wno-stringop-overflow, LAPACK_INFO=mkl, PERF_WITH_AVX=1, PERF_WITH_AVX2=1, TORCH_VERSION=2.7.1, USE_CUDA=ON, USE_CUDNN=ON, USE_CUSPARSELT=1, USE_GFLAGS=OFF, USE_GLOG=OFF, USE_GLOO=ON, USE_MKL=ON, USE_MKLDNN=ON, USE_MPI=OFF, USE_NCCL=1, USE_NNPACK=ON, USE_OPENMP=ON, USE_ROCM=OFF, USE_ROCM_KERNEL_ASSERT=OFF, \n"
+ }
+}
diff --git a/peft/method_comparison/MetaMathQA/results/ia3--llama-3.2-3B-lr_0.001.json b/peft/method_comparison/MetaMathQA/results/ia3--llama-3.2-3B-lr_0.001.json
new file mode 100644
index 0000000000000000000000000000000000000000..f1982e8ef38015c53cc79f7f134677ee584bdfeb
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/results/ia3--llama-3.2-3B-lr_0.001.json
@@ -0,0 +1,350 @@
+{
+ "run_info": {
+ "created_at": "2025-06-19T21:27:27+00:00",
+ "total_time": 1921.5641919770023,
+ "experiment_name": "ia3/llama-3.2-3B-lr_0.001",
+ "peft_branch": "main",
+ "train_config": {
+ "model_id": "meta-llama/Llama-3.2-3B",
+ "dtype": "bfloat16",
+ "max_seq_length": 768,
+ "batch_size": 4,
+ "batch_size_eval": 50,
+ "max_steps": 5000,
+ "eval_steps": 250,
+ "compile": false,
+ "query_template": "Question: {query} Think step by step.\nAnswer:",
+ "seed": 0,
+ "grad_norm_clip": 1.0,
+ "optimizer_type": "AdamW",
+ "optimizer_kwargs": {
+ "lr": 0.001
+ },
+ "lr_scheduler": "cosine",
+ "use_amp": false,
+ "autocast_adapter_dtype": true,
+ "generation_kwargs": {
+ "max_length": 800,
+ "max_new_tokens": 300
+ },
+ "attn_implementation": null
+ },
+ "peft_config": {
+ "task_type": null,
+ "peft_type": "IA3",
+ "auto_mapping": null,
+ "base_model_name_or_path": "meta-llama/Llama-3.2-3B",
+ "revision": null,
+ "inference_mode": false,
+ "target_modules": [
+ "k_proj",
+ "down_proj",
+ "v_proj"
+ ],
+ "exclude_modules": null,
+ "feedforward_modules": [
+ "down_proj"
+ ],
+ "fan_in_fan_out": false,
+ "modules_to_save": null,
+ "init_ia3_weights": true
+ },
+ "error_msg": ""
+ },
+ "train_info": {
+ "accelerator_memory_reserved_avg": 12023331867,
+ "accelerator_memory_max": 23135780864,
+ "accelerator_memory_reserved_99th": 18398356439,
+ "train_time": 1746.0246657649877,
+ "file_size": 1157064,
+ "num_trainable_params": 286720,
+ "num_total_params": 3213036544,
+ "status": "success",
+ "metrics": [
+ {
+ "step": 250,
+ "valid accuracy": 0.18,
+ "train loss": 1.1670710837841034,
+ "train samples": 1000,
+ "train time": 30.829080988976784,
+ "eval time": 10.962777282999014,
+ "tokens / sec": 6867.509286952213,
+ "mem allocated avg": 6781095491.584,
+ "mem reserved avg": 12075594153.984,
+ "elapsed time": 91.04478788100096
+ },
+ {
+ "step": 500,
+ "valid accuracy": 0.34,
+ "train loss": 0.8285422480106354,
+ "train samples": 2000,
+ "train time": 30.237734625952726,
+ "eval time": 10.93798775599862,
+ "tokens / sec": 6878.656836331916,
+ "mem allocated avg": 6773575256.064,
+ "mem reserved avg": 11961039323.136,
+ "elapsed time": 175.57074494799963
+ },
+ {
+ "step": 750,
+ "valid accuracy": 0.34,
+ "train loss": 0.7387537934780121,
+ "train samples": 3000,
+ "train time": 30.784141963005823,
+ "eval time": 10.918857135002327,
+ "tokens / sec": 6964.657330961239,
+ "mem allocated avg": 6784163356.672,
+ "mem reserved avg": 12124793339.904,
+ "elapsed time": 261.120397177001
+ },
+ {
+ "step": 1000,
+ "valid accuracy": 0.36,
+ "train loss": 0.7030822492837906,
+ "train samples": 4000,
+ "train time": 30.625773959025537,
+ "eval time": 6.545184372997028,
+ "tokens / sec": 6802.636246147914,
+ "mem allocated avg": 6775321157.632,
+ "mem reserved avg": 11986549080.064,
+ "elapsed time": 341.78445690100125
+ },
+ {
+ "step": 1250,
+ "valid accuracy": 0.34,
+ "train loss": 0.6953592277765274,
+ "train samples": 5000,
+ "train time": 30.090904191973095,
+ "eval time": 7.180137749001005,
+ "tokens / sec": 6930.266989305977,
+ "mem allocated avg": 6774968741.888,
+ "mem reserved avg": 11983218802.688,
+ "elapsed time": 422.45400445199994
+ },
+ {
+ "step": 1500,
+ "valid accuracy": 0.34,
+ "train loss": 0.6861299908161164,
+ "train samples": 6000,
+ "train time": 30.086008766014857,
+ "eval time": 10.923475695002708,
+ "tokens / sec": 6957.75241003254,
+ "mem allocated avg": 6776914077.696,
+ "mem reserved avg": 12007201832.96,
+ "elapsed time": 506.8615667560007
+ },
+ {
+ "step": 1750,
+ "valid accuracy": 0.34,
+ "train loss": 0.6775313948392868,
+ "train samples": 7000,
+ "train time": 30.329398032976314,
+ "eval time": 7.039293795001868,
+ "tokens / sec": 6902.708710946855,
+ "mem allocated avg": 6778176180.224,
+ "mem reserved avg": 12032417988.608,
+ "elapsed time": 587.730657346001
+ },
+ {
+ "step": 2000,
+ "valid accuracy": 0.36,
+ "train loss": 0.6783386437892914,
+ "train samples": 8000,
+ "train time": 30.340071335995162,
+ "eval time": 8.14293124300093,
+ "tokens / sec": 6845.600252547578,
+ "mem allocated avg": 6775202904.064,
+ "mem reserved avg": 11967733432.32,
+ "elapsed time": 669.6239550099999
+ },
+ {
+ "step": 2250,
+ "valid accuracy": 0.5,
+ "train loss": 0.6720720986127854,
+ "train samples": 9000,
+ "train time": 31.104124111985584,
+ "eval time": 7.4280358140022145,
+ "tokens / sec": 6910.594853149151,
+ "mem allocated avg": 6785809762.304,
+ "mem reserved avg": 12167885619.2,
+ "elapsed time": 752.2532132060005
+ },
+ {
+ "step": 2500,
+ "valid accuracy": 0.46,
+ "train loss": 0.6705386472940444,
+ "train samples": 10000,
+ "train time": 30.09476044199255,
+ "eval time": 7.5499184540021815,
+ "tokens / sec": 6843.948812850663,
+ "mem allocated avg": 6770963554.304,
+ "mem reserved avg": 11912058241.024,
+ "elapsed time": 833.2611769709983
+ },
+ {
+ "step": 2750,
+ "valid accuracy": 0.48,
+ "train loss": 0.6631126835346222,
+ "train samples": 11000,
+ "train time": 30.640666239018174,
+ "eval time": 10.92325482400338,
+ "tokens / sec": 6915.025879241109,
+ "mem allocated avg": 6781913962.496,
+ "mem reserved avg": 12090299383.808,
+ "elapsed time": 918.4276470139994
+ },
+ {
+ "step": 3000,
+ "valid accuracy": 0.38,
+ "train loss": 0.6557366658449173,
+ "train samples": 12000,
+ "train time": 30.612569437977072,
+ "eval time": 10.933225860997482,
+ "tokens / sec": 6818.473712992361,
+ "mem allocated avg": 6776591689.728,
+ "mem reserved avg": 12003032694.784,
+ "elapsed time": 1003.438990486
+ },
+ {
+ "step": 3250,
+ "valid accuracy": 0.44,
+ "train loss": 0.6655691808462143,
+ "train samples": 13000,
+ "train time": 30.508301533980557,
+ "eval time": 7.2082155700009025,
+ "tokens / sec": 6912.905320707402,
+ "mem allocated avg": 6778600480.768,
+ "mem reserved avg": 12040143896.576,
+ "elapsed time": 1084.7670880670012
+ },
+ {
+ "step": 3500,
+ "valid accuracy": 0.46,
+ "train loss": 0.6528272937536239,
+ "train samples": 14000,
+ "train time": 30.571383574966603,
+ "eval time": 7.452295711998886,
+ "tokens / sec": 6860.991406740058,
+ "mem allocated avg": 6777338779.648,
+ "mem reserved avg": 12021227585.536,
+ "elapsed time": 1166.2843480039992
+ },
+ {
+ "step": 3750,
+ "valid accuracy": 0.48,
+ "train loss": 0.6513591132164002,
+ "train samples": 15000,
+ "train time": 31.176262214954477,
+ "eval time": 6.50122426100279,
+ "tokens / sec": 6950.897400909496,
+ "mem allocated avg": 6788519866.368,
+ "mem reserved avg": 12209543446.528,
+ "elapsed time": 1248.1537826940003
+ },
+ {
+ "step": 4000,
+ "valid accuracy": 0.42,
+ "train loss": 0.6660103598833084,
+ "train samples": 16000,
+ "train time": 30.1621740100818,
+ "eval time": 10.007692241000768,
+ "tokens / sec": 6775.804686084222,
+ "mem allocated avg": 6769538811.904,
+ "mem reserved avg": 11886321991.68,
+ "elapsed time": 1331.4140659110017
+ },
+ {
+ "step": 4250,
+ "valid accuracy": 0.4,
+ "train loss": 0.648773505806923,
+ "train samples": 17000,
+ "train time": 30.627343150990782,
+ "eval time": 9.851157391000015,
+ "tokens / sec": 6901.969882201866,
+ "mem allocated avg": 6780366684.16,
+ "mem reserved avg": 12050411552.768,
+ "elapsed time": 1415.4855422520013
+ },
+ {
+ "step": 4500,
+ "valid accuracy": 0.42,
+ "train loss": 0.6574939725399017,
+ "train samples": 18000,
+ "train time": 30.04905582394713,
+ "eval time": 6.792122120001295,
+ "tokens / sec": 6915.957733167199,
+ "mem allocated avg": 6775072815.104,
+ "mem reserved avg": 11969042055.168,
+ "elapsed time": 1495.5897211369993
+ },
+ {
+ "step": 4750,
+ "valid accuracy": 0.4,
+ "train loss": 0.6505398267507553,
+ "train samples": 19000,
+ "train time": 30.326544256924535,
+ "eval time": 7.6139581239986,
+ "tokens / sec": 6922.615324100572,
+ "mem allocated avg": 6777039572.992,
+ "mem reserved avg": 12019256262.656,
+ "elapsed time": 1577.114852814997
+ },
+ {
+ "step": 5000,
+ "valid accuracy": 0.42,
+ "train loss": 0.6568749620914459,
+ "train samples": 20000,
+ "train time": 30.342653310064634,
+ "eval time": 6.5661308569979155,
+ "tokens / sec": 6864.264567492972,
+ "mem allocated avg": 6774530805.76,
+ "mem reserved avg": 11958866673.664,
+ "elapsed time": 1657.5746541439985
+ },
+ {
+ "step": 5000,
+ "test accuracy": 0.41243366186504926,
+ "train loss": 0.6568749620914459,
+ "train samples": 20000,
+ "train total tokens": 4198051
+ }
+ ]
+ },
+ "meta_info": {
+ "model_info": {
+ "sha": "13afe5124825b4f3751f836b40dafda64c1ed062",
+ "created_at": "2024-09-18T15:23:48+00:00"
+ },
+ "dataset_info": {
+ "metamath": {
+ "sha": "aa4f34d3d2d3231299b5b03d9b3e5a20da45aa18",
+ "created_at": "2023-09-21T17:22:46+00:00"
+ },
+ "gsm8k": {
+ "sha": "e53f048856ff4f594e959d75785d2c2d37b678ee",
+ "created_at": "2022-04-12T10:22:10+00:00"
+ }
+ },
+ "package_info": {
+ "transformers-version": "4.52.4",
+ "transformers-commit-hash": null,
+ "peft-version": "0.15.2.dev0",
+ "peft-commit-hash": "5fe7f8f8abe914d313fc3751f2ea92de7718fbaf",
+ "datasets-version": "3.6.0",
+ "datasets-commit-hash": null,
+ "bitsandbytes-version": "0.46.0",
+ "bitsandbytes-commit-hash": null,
+ "torch-version": "2.7.1+cu126",
+ "torch-commit-hash": null
+ },
+ "system_info": {
+ "system": "Linux",
+ "release": "6.8.0-1029-aws",
+ "version": "#31-Ubuntu SMP Wed Apr 23 18:42:41 UTC 2025",
+ "machine": "x86_64",
+ "processor": "x86_64",
+ "accelerator": "NVIDIA L40S"
+ },
+ "pytorch_info": "PyTorch built with:\n - GCC 11.2\n - C++ Version: 201703\n - Intel(R) oneAPI Math Kernel Library Version 2024.2-Product Build 20240605 for Intel(R) 64 architecture applications\n - Intel(R) MKL-DNN v3.7.1 (Git Hash 8d263e693366ef8db40acc569cc7d8edf644556d)\n - OpenMP 201511 (a.k.a. OpenMP 4.5)\n - LAPACK is enabled (usually provided by MKL)\n - NNPACK is enabled\n - CPU capability usage: AVX2\n - CUDA Runtime 12.6\n - NVCC architecture flags: -gencode;arch=compute_50,code=sm_50;-gencode;arch=compute_60,code=sm_60;-gencode;arch=compute_70,code=sm_70;-gencode;arch=compute_75,code=sm_75;-gencode;arch=compute_80,code=sm_80;-gencode;arch=compute_86,code=sm_86;-gencode;arch=compute_90,code=sm_90\n - CuDNN 90.7.1 (built against CUDA 12.8)\n - Built with CuDNN 90.5.1\n - Magma 2.6.1\n - Build settings: BLAS_INFO=mkl, BUILD_TYPE=Release, COMMIT_SHA=e2d141dbde55c2a4370fac5165b0561b6af4798b, CUDA_VERSION=12.6, CUDNN_VERSION=9.5.1, CXX_COMPILER=/opt/rh/gcc-toolset-11/root/usr/bin/c++, CXX_FLAGS= -D_GLIBCXX_USE_CXX11_ABI=1 -fvisibility-inlines-hidden -DUSE_PTHREADPOOL -DNDEBUG -DUSE_KINETO -DLIBKINETO_NOROCTRACER -DLIBKINETO_NOXPUPTI=ON -DUSE_FBGEMM -DUSE_PYTORCH_QNNPACK -DUSE_XNNPACK -DSYMBOLICATE_MOBILE_DEBUG_HANDLE -O2 -fPIC -Wall -Wextra -Werror=return-type -Werror=non-virtual-dtor -Werror=range-loop-construct -Werror=bool-operation -Wnarrowing -Wno-missing-field-initializers -Wno-unknown-pragmas -Wno-unused-parameter -Wno-strict-overflow -Wno-strict-aliasing -Wno-stringop-overflow -Wsuggest-override -Wno-psabi -Wno-error=old-style-cast -fdiagnostics-color=always -faligned-new -Wno-maybe-uninitialized -fno-math-errno -fno-trapping-math -Werror=format -Wno-stringop-overflow, LAPACK_INFO=mkl, PERF_WITH_AVX=1, PERF_WITH_AVX2=1, TORCH_VERSION=2.7.1, USE_CUDA=ON, USE_CUDNN=ON, USE_CUSPARSELT=1, USE_GFLAGS=OFF, USE_GLOG=OFF, USE_GLOO=ON, USE_MKL=ON, USE_MKLDNN=ON, USE_MPI=OFF, USE_NCCL=1, USE_NNPACK=ON, USE_OPENMP=ON, USE_ROCM=OFF, USE_ROCM_KERNEL_ASSERT=OFF, \n"
+ }
+}
diff --git a/peft/method_comparison/MetaMathQA/results/ln_tuning--llama-3.2-3B-default.json b/peft/method_comparison/MetaMathQA/results/ln_tuning--llama-3.2-3B-default.json
new file mode 100644
index 0000000000000000000000000000000000000000..2e8dabe44e54439aad25b203985f6b693c33004a
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/results/ln_tuning--llama-3.2-3B-default.json
@@ -0,0 +1,346 @@
+{
+ "run_info": {
+ "created_at": "2025-06-20T11:06:05+00:00",
+ "total_time": 1870.2496634349955,
+ "experiment_name": "ln_tuning/llama-3.2-3B-default",
+ "peft_branch": "main",
+ "train_config": {
+ "model_id": "meta-llama/Llama-3.2-3B",
+ "dtype": "bfloat16",
+ "max_seq_length": 768,
+ "batch_size": 4,
+ "batch_size_eval": 50,
+ "max_steps": 5000,
+ "eval_steps": 250,
+ "compile": false,
+ "query_template": "Question: {query} Think step by step.\nAnswer:",
+ "seed": 0,
+ "grad_norm_clip": 1.0,
+ "optimizer_type": "AdamW",
+ "optimizer_kwargs": {
+ "lr": 0.0001,
+ "weight_decay": 0.1
+ },
+ "lr_scheduler": "cosine",
+ "use_amp": false,
+ "autocast_adapter_dtype": true,
+ "generation_kwargs": {
+ "max_length": 800,
+ "max_new_tokens": 300
+ },
+ "attn_implementation": null
+ },
+ "peft_config": {
+ "task_type": null,
+ "peft_type": "LN_TUNING",
+ "auto_mapping": null,
+ "base_model_name_or_path": "meta-llama/Llama-3.2-3B",
+ "revision": null,
+ "inference_mode": false,
+ "target_modules": [
+ "input_layernorm",
+ "norm",
+ "post_attention_layernorm"
+ ],
+ "exclude_modules": null,
+ "modules_to_save": null
+ },
+ "error_msg": ""
+ },
+ "train_info": {
+ "accelerator_memory_reserved_avg": 11385589622,
+ "accelerator_memory_max": 21177040896,
+ "accelerator_memory_reserved_99th": 16903066091,
+ "train_time": 1657.2412179829698,
+ "file_size": 358288,
+ "num_trainable_params": 175104,
+ "num_total_params": 3212924928,
+ "status": "success",
+ "metrics": [
+ {
+ "step": 250,
+ "valid accuracy": 0.0,
+ "train loss": 1.3265725662708283,
+ "train samples": 1000,
+ "train time": 27.216289801202947,
+ "eval time": 10.492610957997385,
+ "tokens / sec": 7779.127924726981,
+ "mem allocated avg": 6780187711.488,
+ "mem reserved avg": 11433404268.544,
+ "elapsed time": 87.52968039299594
+ },
+ {
+ "step": 500,
+ "valid accuracy": 0.0,
+ "train loss": 1.3411514971256255,
+ "train samples": 2000,
+ "train time": 26.650248568999814,
+ "eval time": 10.469055254012346,
+ "tokens / sec": 7804.617636547848,
+ "mem allocated avg": 6772587255.808,
+ "mem reserved avg": 11331533012.992,
+ "elapsed time": 165.70980707599665
+ },
+ {
+ "step": 750,
+ "valid accuracy": 0.0,
+ "train loss": 1.2789560747146607,
+ "train samples": 3000,
+ "train time": 27.327283490114496,
+ "eval time": 10.448594682005933,
+ "tokens / sec": 7845.6755526965735,
+ "mem allocated avg": 6783227031.552,
+ "mem reserved avg": 11478560145.408,
+ "elapsed time": 245.043655957008
+ },
+ {
+ "step": 1000,
+ "valid accuracy": 0.0,
+ "train loss": 1.263298665046692,
+ "train samples": 4000,
+ "train time": 26.423721938888775,
+ "eval time": 10.48604148600134,
+ "tokens / sec": 7884.430531089723,
+ "mem allocated avg": 6773840521.216,
+ "mem reserved avg": 11353729269.76,
+ "elapsed time": 322.872066240001
+ },
+ {
+ "step": 1250,
+ "valid accuracy": 0.0,
+ "train loss": 1.2484543447494507,
+ "train samples": 5000,
+ "train time": 26.471019316944876,
+ "eval time": 10.449013539997395,
+ "tokens / sec": 7877.973926999808,
+ "mem allocated avg": 6774061203.456,
+ "mem reserved avg": 11347018383.36,
+ "elapsed time": 400.9208664790058
+ },
+ {
+ "step": 1500,
+ "valid accuracy": 0.0,
+ "train loss": 1.2315508608818053,
+ "train samples": 6000,
+ "train time": 26.742762298934394,
+ "eval time": 10.483759973009,
+ "tokens / sec": 7827.575837531978,
+ "mem allocated avg": 6775242500.096,
+ "mem reserved avg": 11381990490.112,
+ "elapsed time": 479.3449222920026
+ },
+ {
+ "step": 1750,
+ "valid accuracy": 0.0,
+ "train loss": 1.2309930021762847,
+ "train samples": 7000,
+ "train time": 26.920282723149285,
+ "eval time": 10.450218685000436,
+ "tokens / sec": 7776.849974163588,
+ "mem allocated avg": 6777141585.92,
+ "mem reserved avg": 11390496538.624,
+ "elapsed time": 558.0740258180012
+ },
+ {
+ "step": 2000,
+ "valid accuracy": 0.0,
+ "train loss": 1.2312077372074126,
+ "train samples": 8000,
+ "train time": 26.66103798917902,
+ "eval time": 10.460793553007534,
+ "tokens / sec": 7790.244328982917,
+ "mem allocated avg": 6774060457.984,
+ "mem reserved avg": 11331650453.504,
+ "elapsed time": 636.1544087350048
+ },
+ {
+ "step": 2250,
+ "valid accuracy": 0.0,
+ "train loss": 1.2250888612270354,
+ "train samples": 9000,
+ "train time": 27.347798306160257,
+ "eval time": 10.455188547988655,
+ "tokens / sec": 7859.791768011602,
+ "mem allocated avg": 6784883898.368,
+ "mem reserved avg": 11515327414.272,
+ "elapsed time": 715.6408126690076
+ },
+ {
+ "step": 2500,
+ "valid accuracy": 0.0,
+ "train loss": 1.237301394701004,
+ "train samples": 10000,
+ "train time": 26.43946731692995,
+ "eval time": 10.463690039992798,
+ "tokens / sec": 7790.134253881636,
+ "mem allocated avg": 6770695682.048,
+ "mem reserved avg": 11285622161.408,
+ "elapsed time": 793.5970988850022
+ },
+ {
+ "step": 2750,
+ "valid accuracy": 0.0,
+ "train loss": 1.2318837890625,
+ "train samples": 11000,
+ "train time": 27.072892207099358,
+ "eval time": 10.45099154500349,
+ "tokens / sec": 7826.3156510643585,
+ "mem allocated avg": 6780353579.008,
+ "mem reserved avg": 11444477231.104,
+ "elapsed time": 872.6363771199976
+ },
+ {
+ "step": 3000,
+ "valid accuracy": 0.0,
+ "train loss": 1.2326687624454498,
+ "train samples": 12000,
+ "train time": 26.88052615702327,
+ "eval time": 10.466728950996185,
+ "tokens / sec": 7765.138181473555,
+ "mem allocated avg": 6776020297.728,
+ "mem reserved avg": 11370128998.4,
+ "elapsed time": 951.0341247300094
+ },
+ {
+ "step": 3250,
+ "valid accuracy": 0.0,
+ "train loss": 1.2315667741298675,
+ "train samples": 13000,
+ "train time": 26.58970486979524,
+ "eval time": 10.440216451999731,
+ "tokens / sec": 7931.678859646707,
+ "mem allocated avg": 6777846503.424,
+ "mem reserved avg": 11400059551.744,
+ "elapsed time": 1029.1816804429982
+ },
+ {
+ "step": 3500,
+ "valid accuracy": 0.0,
+ "train loss": 1.232551732301712,
+ "train samples": 14000,
+ "train time": 26.459182894948754,
+ "eval time": 10.444537474992103,
+ "tokens / sec": 7927.304514004579,
+ "mem allocated avg": 6776805982.208,
+ "mem reserved avg": 11380858028.032,
+ "elapsed time": 1107.2912037770002
+ },
+ {
+ "step": 3750,
+ "valid accuracy": 0.0,
+ "train loss": 1.2162783181667327,
+ "train samples": 15000,
+ "train time": 27.070398101161118,
+ "eval time": 10.439593077011523,
+ "tokens / sec": 8005.164873829656,
+ "mem allocated avg": 6786829993.984,
+ "mem reserved avg": 11549276110.848,
+ "elapsed time": 1186.5560989549995
+ },
+ {
+ "step": 4000,
+ "valid accuracy": 0.0,
+ "train loss": 1.2475486118793488,
+ "train samples": 16000,
+ "train time": 26.172411711973837,
+ "eval time": 10.464052501003607,
+ "tokens / sec": 7808.71867098513,
+ "mem allocated avg": 6768875591.68,
+ "mem reserved avg": 11260808658.944,
+ "elapsed time": 1263.9761855469987
+ },
+ {
+ "step": 4250,
+ "valid accuracy": 0.0,
+ "train loss": 1.2161538779735566,
+ "train samples": 17000,
+ "train time": 26.80681787095091,
+ "eval time": 10.449379954006872,
+ "tokens / sec": 7885.643160543526,
+ "mem allocated avg": 6779425828.864,
+ "mem reserved avg": 11415653974.016,
+ "elapsed time": 1342.6529225870036
+ },
+ {
+ "step": 4500,
+ "valid accuracy": 0.0,
+ "train loss": 1.2418145356178283,
+ "train samples": 18000,
+ "train time": 26.542597533072694,
+ "eval time": 10.46835913900577,
+ "tokens / sec": 7829.602952049208,
+ "mem allocated avg": 6773693413.376,
+ "mem reserved avg": 11331625287.68,
+ "elapsed time": 1420.7107766840054
+ },
+ {
+ "step": 4750,
+ "valid accuracy": 0.0,
+ "train loss": 1.2255646660327912,
+ "train samples": 19000,
+ "train time": 26.923357297797338,
+ "eval time": 10.45829652599059,
+ "tokens / sec": 7797.653081593045,
+ "mem allocated avg": 6775938277.376,
+ "mem reserved avg": 11381587836.928,
+ "elapsed time": 1499.7020156110084
+ },
+ {
+ "step": 5000,
+ "valid accuracy": 0.0,
+ "train loss": 1.2370348122119903,
+ "train samples": 20000,
+ "train time": 26.415459764844854,
+ "eval time": 10.446229163004318,
+ "tokens / sec": 7884.776636641793,
+ "mem allocated avg": 6773129859.072,
+ "mem reserved avg": 11327984631.808,
+ "elapsed time": 1577.772203030996
+ },
+ {
+ "step": 5000,
+ "test accuracy": 0.0,
+ "train loss": 1.2370348122119903,
+ "train samples": 20000,
+ "train total tokens": 4198051
+ }
+ ]
+ },
+ "meta_info": {
+ "model_info": {
+ "sha": "13afe5124825b4f3751f836b40dafda64c1ed062",
+ "created_at": "2024-09-18T15:23:48+00:00"
+ },
+ "dataset_info": {
+ "metamath": {
+ "sha": "aa4f34d3d2d3231299b5b03d9b3e5a20da45aa18",
+ "created_at": "2023-09-21T17:22:46+00:00"
+ },
+ "gsm8k": {
+ "sha": "e53f048856ff4f594e959d75785d2c2d37b678ee",
+ "created_at": "2022-04-12T10:22:10+00:00"
+ }
+ },
+ "package_info": {
+ "transformers-version": "4.52.4",
+ "transformers-commit-hash": null,
+ "peft-version": "0.15.2.dev0",
+ "peft-commit-hash": "5fe7f8f8abe914d313fc3751f2ea92de7718fbaf",
+ "datasets-version": "3.6.0",
+ "datasets-commit-hash": null,
+ "bitsandbytes-version": "0.46.0",
+ "bitsandbytes-commit-hash": null,
+ "torch-version": "2.7.1+cu126",
+ "torch-commit-hash": null
+ },
+ "system_info": {
+ "system": "Linux",
+ "release": "6.8.0-1029-aws",
+ "version": "#31-Ubuntu SMP Wed Apr 23 18:42:41 UTC 2025",
+ "machine": "x86_64",
+ "processor": "x86_64",
+ "accelerator": "NVIDIA L40S"
+ },
+ "pytorch_info": "PyTorch built with:\n - GCC 11.2\n - C++ Version: 201703\n - Intel(R) oneAPI Math Kernel Library Version 2024.2-Product Build 20240605 for Intel(R) 64 architecture applications\n - Intel(R) MKL-DNN v3.7.1 (Git Hash 8d263e693366ef8db40acc569cc7d8edf644556d)\n - OpenMP 201511 (a.k.a. OpenMP 4.5)\n - LAPACK is enabled (usually provided by MKL)\n - NNPACK is enabled\n - CPU capability usage: AVX2\n - CUDA Runtime 12.6\n - NVCC architecture flags: -gencode;arch=compute_50,code=sm_50;-gencode;arch=compute_60,code=sm_60;-gencode;arch=compute_70,code=sm_70;-gencode;arch=compute_75,code=sm_75;-gencode;arch=compute_80,code=sm_80;-gencode;arch=compute_86,code=sm_86;-gencode;arch=compute_90,code=sm_90\n - CuDNN 90.7.1 (built against CUDA 12.8)\n - Built with CuDNN 90.5.1\n - Magma 2.6.1\n - Build settings: BLAS_INFO=mkl, BUILD_TYPE=Release, COMMIT_SHA=e2d141dbde55c2a4370fac5165b0561b6af4798b, CUDA_VERSION=12.6, CUDNN_VERSION=9.5.1, CXX_COMPILER=/opt/rh/gcc-toolset-11/root/usr/bin/c++, CXX_FLAGS= -D_GLIBCXX_USE_CXX11_ABI=1 -fvisibility-inlines-hidden -DUSE_PTHREADPOOL -DNDEBUG -DUSE_KINETO -DLIBKINETO_NOROCTRACER -DLIBKINETO_NOXPUPTI=ON -DUSE_FBGEMM -DUSE_PYTORCH_QNNPACK -DUSE_XNNPACK -DSYMBOLICATE_MOBILE_DEBUG_HANDLE -O2 -fPIC -Wall -Wextra -Werror=return-type -Werror=non-virtual-dtor -Werror=range-loop-construct -Werror=bool-operation -Wnarrowing -Wno-missing-field-initializers -Wno-unknown-pragmas -Wno-unused-parameter -Wno-strict-overflow -Wno-strict-aliasing -Wno-stringop-overflow -Wsuggest-override -Wno-psabi -Wno-error=old-style-cast -fdiagnostics-color=always -faligned-new -Wno-maybe-uninitialized -fno-math-errno -fno-trapping-math -Werror=format -Wno-stringop-overflow, LAPACK_INFO=mkl, PERF_WITH_AVX=1, PERF_WITH_AVX2=1, TORCH_VERSION=2.7.1, USE_CUDA=ON, USE_CUDNN=ON, USE_CUSPARSELT=1, USE_GFLAGS=OFF, USE_GLOG=OFF, USE_GLOO=ON, USE_MKL=ON, USE_MKLDNN=ON, USE_MPI=OFF, USE_NCCL=1, USE_NNPACK=ON, USE_OPENMP=ON, USE_ROCM=OFF, USE_ROCM_KERNEL_ASSERT=OFF, \n"
+ }
+}
diff --git a/peft/method_comparison/MetaMathQA/results/loha--llama-3.2-3B-rank32.json b/peft/method_comparison/MetaMathQA/results/loha--llama-3.2-3B-rank32.json
new file mode 100644
index 0000000000000000000000000000000000000000..7baa8eb00fbb4baea00d55b0bd56b06f286ec04d
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/results/loha--llama-3.2-3B-rank32.json
@@ -0,0 +1,355 @@
+{
+ "run_info": {
+ "created_at": "2025-06-19T16:12:05+00:00",
+ "total_time": 2590.9341236870005,
+ "experiment_name": "loha/llama-3.2-3B-rank32",
+ "peft_branch": "main",
+ "train_config": {
+ "model_id": "meta-llama/Llama-3.2-3B",
+ "dtype": "bfloat16",
+ "max_seq_length": 768,
+ "batch_size": 4,
+ "batch_size_eval": 50,
+ "max_steps": 5000,
+ "eval_steps": 250,
+ "compile": false,
+ "query_template": "Question: {query} Think step by step.\nAnswer:",
+ "seed": 0,
+ "grad_norm_clip": 1.0,
+ "optimizer_type": "AdamW",
+ "optimizer_kwargs": {
+ "lr": 0.0001,
+ "weight_decay": 0.1
+ },
+ "lr_scheduler": "cosine",
+ "use_amp": false,
+ "autocast_adapter_dtype": true,
+ "generation_kwargs": {
+ "max_length": 800,
+ "max_new_tokens": 300
+ },
+ "attn_implementation": null
+ },
+ "peft_config": {
+ "task_type": null,
+ "peft_type": "LOHA",
+ "auto_mapping": null,
+ "base_model_name_or_path": "meta-llama/Llama-3.2-3B",
+ "revision": null,
+ "inference_mode": false,
+ "rank_pattern": {},
+ "alpha_pattern": {},
+ "r": 32,
+ "alpha": 64,
+ "rank_dropout": 0.0,
+ "module_dropout": 0.0,
+ "use_effective_conv2d": false,
+ "target_modules": [
+ "q_proj",
+ "v_proj"
+ ],
+ "exclude_modules": null,
+ "init_weights": true,
+ "layers_to_transform": null,
+ "layers_pattern": null,
+ "modules_to_save": null
+ },
+ "error_msg": ""
+ },
+ "train_info": {
+ "accelerator_memory_reserved_avg": 13446820344,
+ "accelerator_memory_max": 23886561280,
+ "accelerator_memory_reserved_99th": 19247870771,
+ "train_time": 2340.7451966560056,
+ "file_size": 73429560,
+ "num_trainable_params": 18350080,
+ "num_total_params": 3231099904,
+ "status": "success",
+ "metrics": [
+ {
+ "step": 250,
+ "valid accuracy": 0.0,
+ "train loss": 1.2914833688735963,
+ "train samples": 1000,
+ "train time": 47.4107696449737,
+ "eval time": 14.298813604000316,
+ "tokens / sec": 4465.630943885038,
+ "mem allocated avg": 7073903032.32,
+ "mem reserved avg": 13501707845.632,
+ "elapsed time": 120.40146815400112
+ },
+ {
+ "step": 500,
+ "valid accuracy": 0.36,
+ "train loss": 0.9051123185157776,
+ "train samples": 2000,
+ "train time": 47.1910586300055,
+ "eval time": 14.155041256999539,
+ "tokens / sec": 4407.508668766131,
+ "mem allocated avg": 7065529796.608,
+ "mem reserved avg": 13391154380.8,
+ "elapsed time": 234.63223427900084
+ },
+ {
+ "step": 750,
+ "valid accuracy": 0.34,
+ "train loss": 0.7515897085666656,
+ "train samples": 3000,
+ "train time": 48.203471163995346,
+ "eval time": 14.26281827999992,
+ "tokens / sec": 4447.8332124791605,
+ "mem allocated avg": 7076336949.248,
+ "mem reserved avg": 13550454046.72,
+ "elapsed time": 350.3563782780002
+ },
+ {
+ "step": 1000,
+ "valid accuracy": 0.4,
+ "train loss": 0.7082941273450851,
+ "train samples": 4000,
+ "train time": 47.1758063940124,
+ "eval time": 14.148222272999192,
+ "tokens / sec": 4416.161925457669,
+ "mem allocated avg": 7067704416.256,
+ "mem reserved avg": 13415607173.12,
+ "elapsed time": 464.4216197680016
+ },
+ {
+ "step": 1250,
+ "valid accuracy": 0.32,
+ "train loss": 0.6994056793451309,
+ "train samples": 5000,
+ "train time": 47.32811543400385,
+ "eval time": 14.265782994998517,
+ "tokens / sec": 4406.218123998481,
+ "mem allocated avg": 7067674988.544,
+ "mem reserved avg": 13411052158.976,
+ "elapsed time": 578.864341718001
+ },
+ {
+ "step": 1500,
+ "valid accuracy": 0.38,
+ "train loss": 0.6889224811792374,
+ "train samples": 6000,
+ "train time": 47.48961014100678,
+ "eval time": 9.485757000999001,
+ "tokens / sec": 4407.932585221307,
+ "mem allocated avg": 7068496666.624,
+ "mem reserved avg": 13434196328.448,
+ "elapsed time": 688.8339757740014
+ },
+ {
+ "step": 1750,
+ "valid accuracy": 0.36,
+ "train loss": 0.6795901688337326,
+ "train samples": 7000,
+ "train time": 47.5112849769921,
+ "eval time": 8.524607335999463,
+ "tokens / sec": 4406.426812101222,
+ "mem allocated avg": 7070726457.344,
+ "mem reserved avg": 13451493638.144,
+ "elapsed time": 797.8088079910012
+ },
+ {
+ "step": 2000,
+ "valid accuracy": 0.42,
+ "train loss": 0.680127969622612,
+ "train samples": 8000,
+ "train time": 47.15311444799954,
+ "eval time": 14.09636382700046,
+ "tokens / sec": 4404.714353047605,
+ "mem allocated avg": 7067623004.16,
+ "mem reserved avg": 13389174669.312,
+ "elapsed time": 911.8939753530012
+ },
+ {
+ "step": 2250,
+ "valid accuracy": 0.42,
+ "train loss": 0.6731046036481857,
+ "train samples": 9000,
+ "train time": 48.44002798400652,
+ "eval time": 14.30888277199847,
+ "tokens / sec": 4437.404538060332,
+ "mem allocated avg": 7078766321.664,
+ "mem reserved avg": 13582146207.744,
+ "elapsed time": 1028.5093922580018
+ },
+ {
+ "step": 2500,
+ "valid accuracy": 0.42,
+ "train loss": 0.6711453741788864,
+ "train samples": 10000,
+ "train time": 46.86391301901131,
+ "eval time": 8.751619284999833,
+ "tokens / sec": 4395.002182520381,
+ "mem allocated avg": 7063469082.624,
+ "mem reserved avg": 13336376770.56,
+ "elapsed time": 1137.0856770440005
+ },
+ {
+ "step": 2750,
+ "valid accuracy": 0.44,
+ "train loss": 0.6645345565080643,
+ "train samples": 11000,
+ "train time": 47.92562343400823,
+ "eval time": 7.835686906000774,
+ "tokens / sec": 4421.037950434847,
+ "mem allocated avg": 7074535438.336,
+ "mem reserved avg": 13512352989.184,
+ "elapsed time": 1246.1237790820014
+ },
+ {
+ "step": 3000,
+ "valid accuracy": 0.4,
+ "train loss": 0.6566170369386672,
+ "train samples": 12000,
+ "train time": 47.50991778100797,
+ "eval time": 14.152554526999666,
+ "tokens / sec": 4393.419516365485,
+ "mem allocated avg": 7068629661.696,
+ "mem reserved avg": 13428215250.944,
+ "elapsed time": 1360.8028930970013
+ },
+ {
+ "step": 3250,
+ "valid accuracy": 0.42,
+ "train loss": 0.6667062133550644,
+ "train samples": 13000,
+ "train time": 47.62723316902702,
+ "eval time": 14.332656014001259,
+ "tokens / sec": 4428.1598146069355,
+ "mem allocated avg": 7071043653.632,
+ "mem reserved avg": 13457114005.504,
+ "elapsed time": 1476.0946507730005
+ },
+ {
+ "step": 3500,
+ "valid accuracy": 0.42,
+ "train loss": 0.6537795497179031,
+ "train samples": 14000,
+ "train time": 47.07006615899445,
+ "eval time": 14.135684340000807,
+ "tokens / sec": 4456.12290604184,
+ "mem allocated avg": 7069669969.92,
+ "mem reserved avg": 13439749586.944,
+ "elapsed time": 1590.4238928290015
+ },
+ {
+ "step": 3750,
+ "valid accuracy": 0.46,
+ "train loss": 0.6509792991876602,
+ "train samples": 15000,
+ "train time": 48.58318820000204,
+ "eval time": 14.298812560000442,
+ "tokens / sec": 4460.452432802484,
+ "mem allocated avg": 7081669246.976,
+ "mem reserved avg": 13624240242.688,
+ "elapsed time": 1707.3096692510007
+ },
+ {
+ "step": 4000,
+ "valid accuracy": 0.46,
+ "train loss": 0.6675102390050888,
+ "train samples": 16000,
+ "train time": 46.83876558602242,
+ "eval time": 14.188353157000165,
+ "tokens / sec": 4363.330191199334,
+ "mem allocated avg": 7062227976.192,
+ "mem reserved avg": 13316957143.04,
+ "elapsed time": 1821.413719397
+ },
+ {
+ "step": 4250,
+ "valid accuracy": 0.46,
+ "train loss": 0.6494157313108444,
+ "train samples": 17000,
+ "train time": 46.9989987980116,
+ "eval time": 8.258924301999286,
+ "tokens / sec": 4497.7341093688,
+ "mem allocated avg": 7072862310.4,
+ "mem reserved avg": 13470619664.384,
+ "elapsed time": 1930.0706906220003
+ },
+ {
+ "step": 4500,
+ "valid accuracy": 0.44,
+ "train loss": 0.6580193819999695,
+ "train samples": 18000,
+ "train time": 47.171681194990015,
+ "eval time": 9.717189478000364,
+ "tokens / sec": 4405.566957449713,
+ "mem allocated avg": 7068038127.616,
+ "mem reserved avg": 13393654185.984,
+ "elapsed time": 2040.1967968460012
+ },
+ {
+ "step": 4750,
+ "valid accuracy": 0.48,
+ "train loss": 0.6511869616508484,
+ "train samples": 19000,
+ "train time": 47.517527918005726,
+ "eval time": 14.28858694399969,
+ "tokens / sec": 4418.138089217562,
+ "mem allocated avg": 7069871403.008,
+ "mem reserved avg": 13443927113.728,
+ "elapsed time": 2155.4679406510004
+ },
+ {
+ "step": 5000,
+ "valid accuracy": 0.46,
+ "train loss": 0.6569721374511719,
+ "train samples": 20000,
+ "train time": 46.99870921700858,
+ "eval time": 9.378413720998651,
+ "tokens / sec": 4431.6110691104805,
+ "mem allocated avg": 7066192863.232,
+ "mem reserved avg": 13386213490.688,
+ "elapsed time": 2265.1425104650007
+ },
+ {
+ "step": 5000,
+ "test accuracy": 0.4184988627748294,
+ "train loss": 0.6569721374511719,
+ "train samples": 20000,
+ "train total tokens": 4198051
+ }
+ ]
+ },
+ "meta_info": {
+ "model_info": {
+ "sha": "13afe5124825b4f3751f836b40dafda64c1ed062",
+ "created_at": "2024-09-18T15:23:48+00:00"
+ },
+ "dataset_info": {
+ "metamath": {
+ "sha": "aa4f34d3d2d3231299b5b03d9b3e5a20da45aa18",
+ "created_at": "2023-09-21T17:22:46+00:00"
+ },
+ "gsm8k": {
+ "sha": "e53f048856ff4f594e959d75785d2c2d37b678ee",
+ "created_at": "2022-04-12T10:22:10+00:00"
+ }
+ },
+ "package_info": {
+ "transformers-version": "4.52.4",
+ "transformers-commit-hash": null,
+ "peft-version": "0.15.2.dev0",
+ "peft-commit-hash": "5fe7f8f8abe914d313fc3751f2ea92de7718fbaf",
+ "datasets-version": "3.6.0",
+ "datasets-commit-hash": null,
+ "bitsandbytes-version": "0.46.0",
+ "bitsandbytes-commit-hash": null,
+ "torch-version": "2.7.1+cu126",
+ "torch-commit-hash": null
+ },
+ "system_info": {
+ "system": "Linux",
+ "release": "6.8.0-1029-aws",
+ "version": "#31-Ubuntu SMP Wed Apr 23 18:42:41 UTC 2025",
+ "machine": "x86_64",
+ "processor": "x86_64",
+ "accelerator": "NVIDIA L40S"
+ },
+ "pytorch_info": "PyTorch built with:\n - GCC 11.2\n - C++ Version: 201703\n - Intel(R) oneAPI Math Kernel Library Version 2024.2-Product Build 20240605 for Intel(R) 64 architecture applications\n - Intel(R) MKL-DNN v3.7.1 (Git Hash 8d263e693366ef8db40acc569cc7d8edf644556d)\n - OpenMP 201511 (a.k.a. OpenMP 4.5)\n - LAPACK is enabled (usually provided by MKL)\n - NNPACK is enabled\n - CPU capability usage: AVX2\n - CUDA Runtime 12.6\n - NVCC architecture flags: -gencode;arch=compute_50,code=sm_50;-gencode;arch=compute_60,code=sm_60;-gencode;arch=compute_70,code=sm_70;-gencode;arch=compute_75,code=sm_75;-gencode;arch=compute_80,code=sm_80;-gencode;arch=compute_86,code=sm_86;-gencode;arch=compute_90,code=sm_90\n - CuDNN 90.7.1 (built against CUDA 12.8)\n - Built with CuDNN 90.5.1\n - Magma 2.6.1\n - Build settings: BLAS_INFO=mkl, BUILD_TYPE=Release, COMMIT_SHA=e2d141dbde55c2a4370fac5165b0561b6af4798b, CUDA_VERSION=12.6, CUDNN_VERSION=9.5.1, CXX_COMPILER=/opt/rh/gcc-toolset-11/root/usr/bin/c++, CXX_FLAGS= -D_GLIBCXX_USE_CXX11_ABI=1 -fvisibility-inlines-hidden -DUSE_PTHREADPOOL -DNDEBUG -DUSE_KINETO -DLIBKINETO_NOROCTRACER -DLIBKINETO_NOXPUPTI=ON -DUSE_FBGEMM -DUSE_PYTORCH_QNNPACK -DUSE_XNNPACK -DSYMBOLICATE_MOBILE_DEBUG_HANDLE -O2 -fPIC -Wall -Wextra -Werror=return-type -Werror=non-virtual-dtor -Werror=range-loop-construct -Werror=bool-operation -Wnarrowing -Wno-missing-field-initializers -Wno-unknown-pragmas -Wno-unused-parameter -Wno-strict-overflow -Wno-strict-aliasing -Wno-stringop-overflow -Wsuggest-override -Wno-psabi -Wno-error=old-style-cast -fdiagnostics-color=always -faligned-new -Wno-maybe-uninitialized -fno-math-errno -fno-trapping-math -Werror=format -Wno-stringop-overflow, LAPACK_INFO=mkl, PERF_WITH_AVX=1, PERF_WITH_AVX2=1, TORCH_VERSION=2.7.1, USE_CUDA=ON, USE_CUDNN=ON, USE_CUSPARSELT=1, USE_GFLAGS=OFF, USE_GLOG=OFF, USE_GLOO=ON, USE_MKL=ON, USE_MKLDNN=ON, USE_MPI=OFF, USE_NCCL=1, USE_NNPACK=ON, USE_OPENMP=ON, USE_ROCM=OFF, USE_ROCM_KERNEL_ASSERT=OFF, \n"
+ }
+}
diff --git a/peft/method_comparison/MetaMathQA/results/lokr--llama-3.2-3B-rank32.json b/peft/method_comparison/MetaMathQA/results/lokr--llama-3.2-3B-rank32.json
new file mode 100644
index 0000000000000000000000000000000000000000..07ae5b1b5a95ddd9a199e1bc5e3f5d6c01b2557f
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/results/lokr--llama-3.2-3B-rank32.json
@@ -0,0 +1,358 @@
+{
+ "run_info": {
+ "created_at": "2025-06-19T22:33:02+00:00",
+ "total_time": 2351.995087948999,
+ "experiment_name": "lokr/llama-3.2-3B-rank32",
+ "peft_branch": "main",
+ "train_config": {
+ "model_id": "meta-llama/Llama-3.2-3B",
+ "dtype": "bfloat16",
+ "max_seq_length": 768,
+ "batch_size": 4,
+ "batch_size_eval": 50,
+ "max_steps": 5000,
+ "eval_steps": 250,
+ "compile": false,
+ "query_template": "Question: {query} Think step by step.\nAnswer:",
+ "seed": 0,
+ "grad_norm_clip": 1.0,
+ "optimizer_type": "AdamW",
+ "optimizer_kwargs": {
+ "lr": 0.0001,
+ "weight_decay": 0.1
+ },
+ "lr_scheduler": "cosine",
+ "use_amp": false,
+ "autocast_adapter_dtype": true,
+ "generation_kwargs": {
+ "max_length": 800,
+ "max_new_tokens": 300
+ },
+ "attn_implementation": null
+ },
+ "peft_config": {
+ "task_type": null,
+ "peft_type": "LOKR",
+ "auto_mapping": null,
+ "base_model_name_or_path": "meta-llama/Llama-3.2-3B",
+ "revision": null,
+ "inference_mode": false,
+ "rank_pattern": {},
+ "alpha_pattern": {},
+ "r": 32,
+ "alpha": 64,
+ "rank_dropout": 0.0,
+ "module_dropout": 0.0,
+ "use_effective_conv2d": false,
+ "decompose_both": false,
+ "decompose_factor": -1,
+ "rank_dropout_scale": false,
+ "target_modules": [
+ "q_proj",
+ "v_proj"
+ ],
+ "exclude_modules": null,
+ "init_weights": true,
+ "layers_to_transform": null,
+ "layers_pattern": null,
+ "modules_to_save": null
+ },
+ "error_msg": ""
+ },
+ "train_info": {
+ "accelerator_memory_reserved_avg": 13173683073,
+ "accelerator_memory_max": 23565697024,
+ "accelerator_memory_reserved_99th": 18987698094,
+ "train_time": 2152.0406475960117,
+ "file_size": 1131984,
+ "num_trainable_params": 279552,
+ "num_total_params": 3213029376,
+ "status": "success",
+ "metrics": [
+ {
+ "step": 250,
+ "valid accuracy": 0.0,
+ "train loss": 1.2610720434188842,
+ "train samples": 1000,
+ "train time": 43.70352009194903,
+ "eval time": 12.492729608995432,
+ "tokens / sec": 4844.438149479918,
+ "mem allocated avg": 6786119440.384,
+ "mem reserved avg": 13227744296.96,
+ "elapsed time": 111.06800683099573
+ },
+ {
+ "step": 500,
+ "valid accuracy": 0.32,
+ "train loss": 0.9418708410263061,
+ "train samples": 2000,
+ "train time": 42.27786245904281,
+ "eval time": 12.404362346002017,
+ "tokens / sec": 4919.714193249426,
+ "mem allocated avg": 6777965645.824,
+ "mem reserved avg": 13119581585.408,
+ "elapsed time": 215.0703402069994
+ },
+ {
+ "step": 750,
+ "valid accuracy": 0.38,
+ "train loss": 0.7932645809650422,
+ "train samples": 3000,
+ "train time": 42.92248660406767,
+ "eval time": 12.39727676199982,
+ "tokens / sec": 4995.0740733571965,
+ "mem allocated avg": 6788190218.24,
+ "mem reserved avg": 13280533807.104,
+ "elapsed time": 319.9520932419982
+ },
+ {
+ "step": 1000,
+ "valid accuracy": 0.38,
+ "train loss": 0.7486661098003388,
+ "train samples": 4000,
+ "train time": 42.81222543502372,
+ "eval time": 12.462298920996545,
+ "tokens / sec": 4866.273544135012,
+ "mem allocated avg": 6778714585.088,
+ "mem reserved avg": 13136702734.336,
+ "elapsed time": 424.5020112219936
+ },
+ {
+ "step": 1250,
+ "valid accuracy": 0.3,
+ "train loss": 0.7329869548082352,
+ "train samples": 5000,
+ "train time": 42.917129570938414,
+ "eval time": 12.430814264000219,
+ "tokens / sec": 4859.085453403965,
+ "mem allocated avg": 6779904688.128,
+ "mem reserved avg": 13134379089.92,
+ "elapsed time": 529.3957975729936
+ },
+ {
+ "step": 1500,
+ "valid accuracy": 0.38,
+ "train loss": 0.7207228287458419,
+ "train samples": 6000,
+ "train time": 43.03383123301319,
+ "eval time": 12.441326129999652,
+ "tokens / sec": 4864.335663412017,
+ "mem allocated avg": 6779916724.224,
+ "mem reserved avg": 13160828370.944,
+ "elapsed time": 634.2579850239999
+ },
+ {
+ "step": 1750,
+ "valid accuracy": 0.34,
+ "train loss": 0.7103905143737793,
+ "train samples": 7000,
+ "train time": 42.76188673896104,
+ "eval time": 12.393813144997694,
+ "tokens / sec": 4895.831684836612,
+ "mem allocated avg": 6782196824.064,
+ "mem reserved avg": 13176313741.312,
+ "elapsed time": 738.7873818459993
+ },
+ {
+ "step": 2000,
+ "valid accuracy": 0.34,
+ "train loss": 0.709170572757721,
+ "train samples": 8000,
+ "train time": 42.39193291300762,
+ "eval time": 12.418300639998051,
+ "tokens / sec": 4899.422737486692,
+ "mem allocated avg": 6778828410.88,
+ "mem reserved avg": 13120303005.696,
+ "elapsed time": 842.8626621349977
+ },
+ {
+ "step": 2250,
+ "valid accuracy": 0.38,
+ "train loss": 0.7017016235589981,
+ "train samples": 9000,
+ "train time": 43.90131158899749,
+ "eval time": 12.417865242998232,
+ "tokens / sec": 4896.163513571884,
+ "mem allocated avg": 6790482182.144,
+ "mem reserved avg": 13307486404.608,
+ "elapsed time": 949.0399838449957
+ },
+ {
+ "step": 2500,
+ "valid accuracy": 0.36,
+ "train loss": 0.6999357705116271,
+ "train samples": 10000,
+ "train time": 41.90174934701645,
+ "eval time": 7.302261034004914,
+ "tokens / sec": 4915.474967268057,
+ "mem allocated avg": 6775840593.92,
+ "mem reserved avg": 13059930193.92,
+ "elapsed time": 1047.236226049994
+ },
+ {
+ "step": 2750,
+ "valid accuracy": 0.36,
+ "train loss": 0.694103113770485,
+ "train samples": 11000,
+ "train time": 43.541668150042824,
+ "eval time": 12.415209386999777,
+ "tokens / sec": 4866.166341396629,
+ "mem allocated avg": 6786276190.208,
+ "mem reserved avg": 13245360373.76,
+ "elapsed time": 1152.8413292650002
+ },
+ {
+ "step": 3000,
+ "valid accuracy": 0.4,
+ "train loss": 0.686756227850914,
+ "train samples": 12000,
+ "train time": 43.03442109594471,
+ "eval time": 7.144659414996568,
+ "tokens / sec": 4850.32666140987,
+ "mem allocated avg": 6781073500.16,
+ "mem reserved avg": 13155426107.392,
+ "elapsed time": 1252.4253450399992
+ },
+ {
+ "step": 3250,
+ "valid accuracy": 0.38,
+ "train loss": 0.6960614495277405,
+ "train samples": 13000,
+ "train time": 43.27108911598771,
+ "eval time": 7.294012983998982,
+ "tokens / sec": 4873.947115929577,
+ "mem allocated avg": 6783027929.088,
+ "mem reserved avg": 13189282529.28,
+ "elapsed time": 1352.4968370129936
+ },
+ {
+ "step": 3500,
+ "valid accuracy": 0.4,
+ "train loss": 0.6833453825712203,
+ "train samples": 14000,
+ "train time": 43.27389094301907,
+ "eval time": 7.8778488079988165,
+ "tokens / sec": 4847.03352134867,
+ "mem allocated avg": 6781185138.688,
+ "mem reserved avg": 13163252678.656,
+ "elapsed time": 1453.3269581979985
+ },
+ {
+ "step": 3750,
+ "valid accuracy": 0.38,
+ "train loss": 0.6804633007049561,
+ "train samples": 15000,
+ "train time": 44.034181773953605,
+ "eval time": 7.058443625996006,
+ "tokens / sec": 4921.245070759568,
+ "mem allocated avg": 6792035817.472,
+ "mem reserved avg": 13346417934.336,
+ "elapsed time": 1554.5450010249988
+ },
+ {
+ "step": 4000,
+ "valid accuracy": 0.36,
+ "train loss": 0.6990108703374862,
+ "train samples": 16000,
+ "train time": 42.4217994650171,
+ "eval time": 7.152937473998463,
+ "tokens / sec": 4817.6409906547,
+ "mem allocated avg": 6773882982.4,
+ "mem reserved avg": 13037876543.488,
+ "elapsed time": 1653.5999729619944
+ },
+ {
+ "step": 4250,
+ "valid accuracy": 0.4,
+ "train loss": 0.6789947774410248,
+ "train samples": 17000,
+ "train time": 43.347477565999725,
+ "eval time": 7.062385851000727,
+ "tokens / sec": 4876.615938681662,
+ "mem allocated avg": 6784096524.288,
+ "mem reserved avg": 13200808476.672,
+ "elapsed time": 1754.0244643159967
+ },
+ {
+ "step": 4500,
+ "valid accuracy": 0.36,
+ "train loss": 0.6891120710372924,
+ "train samples": 18000,
+ "train time": 42.82309688109672,
+ "eval time": 7.127946433000034,
+ "tokens / sec": 4852.941873331364,
+ "mem allocated avg": 6779667169.28,
+ "mem reserved avg": 13117727703.04,
+ "elapsed time": 1853.5914762979955
+ },
+ {
+ "step": 4750,
+ "valid accuracy": 0.38,
+ "train loss": 0.6815101335048676,
+ "train samples": 19000,
+ "train time": 43.26974187397718,
+ "eval time": 7.069867040001554,
+ "tokens / sec": 4851.866244347975,
+ "mem allocated avg": 6780809029.632,
+ "mem reserved avg": 13175080615.936,
+ "elapsed time": 1954.106976348994
+ },
+ {
+ "step": 5000,
+ "valid accuracy": 0.36,
+ "train loss": 0.6876721383333206,
+ "train samples": 20000,
+ "train time": 43.18727576800302,
+ "eval time": 7.149106363998726,
+ "tokens / sec": 4822.716790909798,
+ "mem allocated avg": 6778227302.4,
+ "mem reserved avg": 13118625284.096,
+ "elapsed time": 2054.7161079569996
+ },
+ {
+ "step": 5000,
+ "test accuracy": 0.3752843062926459,
+ "train loss": 0.6876721383333206,
+ "train samples": 20000,
+ "train total tokens": 4198051
+ }
+ ]
+ },
+ "meta_info": {
+ "model_info": {
+ "sha": "13afe5124825b4f3751f836b40dafda64c1ed062",
+ "created_at": "2024-09-18T15:23:48+00:00"
+ },
+ "dataset_info": {
+ "metamath": {
+ "sha": "aa4f34d3d2d3231299b5b03d9b3e5a20da45aa18",
+ "created_at": "2023-09-21T17:22:46+00:00"
+ },
+ "gsm8k": {
+ "sha": "e53f048856ff4f594e959d75785d2c2d37b678ee",
+ "created_at": "2022-04-12T10:22:10+00:00"
+ }
+ },
+ "package_info": {
+ "transformers-version": "4.52.4",
+ "transformers-commit-hash": null,
+ "peft-version": "0.15.2.dev0",
+ "peft-commit-hash": "5fe7f8f8abe914d313fc3751f2ea92de7718fbaf",
+ "datasets-version": "3.6.0",
+ "datasets-commit-hash": null,
+ "bitsandbytes-version": "0.46.0",
+ "bitsandbytes-commit-hash": null,
+ "torch-version": "2.7.1+cu126",
+ "torch-commit-hash": null
+ },
+ "system_info": {
+ "system": "Linux",
+ "release": "6.8.0-1029-aws",
+ "version": "#31-Ubuntu SMP Wed Apr 23 18:42:41 UTC 2025",
+ "machine": "x86_64",
+ "processor": "x86_64",
+ "accelerator": "NVIDIA L40S"
+ },
+ "pytorch_info": "PyTorch built with:\n - GCC 11.2\n - C++ Version: 201703\n - Intel(R) oneAPI Math Kernel Library Version 2024.2-Product Build 20240605 for Intel(R) 64 architecture applications\n - Intel(R) MKL-DNN v3.7.1 (Git Hash 8d263e693366ef8db40acc569cc7d8edf644556d)\n - OpenMP 201511 (a.k.a. OpenMP 4.5)\n - LAPACK is enabled (usually provided by MKL)\n - NNPACK is enabled\n - CPU capability usage: AVX2\n - CUDA Runtime 12.6\n - NVCC architecture flags: -gencode;arch=compute_50,code=sm_50;-gencode;arch=compute_60,code=sm_60;-gencode;arch=compute_70,code=sm_70;-gencode;arch=compute_75,code=sm_75;-gencode;arch=compute_80,code=sm_80;-gencode;arch=compute_86,code=sm_86;-gencode;arch=compute_90,code=sm_90\n - CuDNN 90.7.1 (built against CUDA 12.8)\n - Built with CuDNN 90.5.1\n - Magma 2.6.1\n - Build settings: BLAS_INFO=mkl, BUILD_TYPE=Release, COMMIT_SHA=e2d141dbde55c2a4370fac5165b0561b6af4798b, CUDA_VERSION=12.6, CUDNN_VERSION=9.5.1, CXX_COMPILER=/opt/rh/gcc-toolset-11/root/usr/bin/c++, CXX_FLAGS= -D_GLIBCXX_USE_CXX11_ABI=1 -fvisibility-inlines-hidden -DUSE_PTHREADPOOL -DNDEBUG -DUSE_KINETO -DLIBKINETO_NOROCTRACER -DLIBKINETO_NOXPUPTI=ON -DUSE_FBGEMM -DUSE_PYTORCH_QNNPACK -DUSE_XNNPACK -DSYMBOLICATE_MOBILE_DEBUG_HANDLE -O2 -fPIC -Wall -Wextra -Werror=return-type -Werror=non-virtual-dtor -Werror=range-loop-construct -Werror=bool-operation -Wnarrowing -Wno-missing-field-initializers -Wno-unknown-pragmas -Wno-unused-parameter -Wno-strict-overflow -Wno-strict-aliasing -Wno-stringop-overflow -Wsuggest-override -Wno-psabi -Wno-error=old-style-cast -fdiagnostics-color=always -faligned-new -Wno-maybe-uninitialized -fno-math-errno -fno-trapping-math -Werror=format -Wno-stringop-overflow, LAPACK_INFO=mkl, PERF_WITH_AVX=1, PERF_WITH_AVX2=1, TORCH_VERSION=2.7.1, USE_CUDA=ON, USE_CUDNN=ON, USE_CUSPARSELT=1, USE_GFLAGS=OFF, USE_GLOG=OFF, USE_GLOO=ON, USE_MKL=ON, USE_MKLDNN=ON, USE_MPI=OFF, USE_NCCL=1, USE_NNPACK=ON, USE_OPENMP=ON, USE_ROCM=OFF, USE_ROCM_KERNEL_ASSERT=OFF, \n"
+ }
+}
diff --git a/peft/method_comparison/MetaMathQA/results/lora--llama-3.2-3B-rank32-dora.json b/peft/method_comparison/MetaMathQA/results/lora--llama-3.2-3B-rank32-dora.json
new file mode 100644
index 0000000000000000000000000000000000000000..a2b645db9b84e0c51f55b54d3d912b9af5ce63d4
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/results/lora--llama-3.2-3B-rank32-dora.json
@@ -0,0 +1,365 @@
+{
+ "run_info": {
+ "created_at": "2025-06-19T18:37:24+00:00",
+ "total_time": 2286.5437473089987,
+ "experiment_name": "lora/llama-3.2-3B-rank32-dora",
+ "peft_branch": "main",
+ "train_config": {
+ "model_id": "meta-llama/Llama-3.2-3B",
+ "dtype": "bfloat16",
+ "max_seq_length": 768,
+ "batch_size": 4,
+ "batch_size_eval": 50,
+ "max_steps": 5000,
+ "eval_steps": 250,
+ "compile": false,
+ "query_template": "Question: {query} Think step by step.\nAnswer:",
+ "seed": 0,
+ "grad_norm_clip": 1.0,
+ "optimizer_type": "AdamW",
+ "optimizer_kwargs": {
+ "lr": 0.0001,
+ "weight_decay": 0.1
+ },
+ "lr_scheduler": "cosine",
+ "use_amp": false,
+ "autocast_adapter_dtype": true,
+ "generation_kwargs": {
+ "max_length": 800,
+ "max_new_tokens": 300
+ },
+ "attn_implementation": null
+ },
+ "peft_config": {
+ "task_type": "CAUSAL_LM",
+ "peft_type": "LORA",
+ "auto_mapping": null,
+ "base_model_name_or_path": "meta-llama/Llama-3.2-3B",
+ "revision": null,
+ "inference_mode": false,
+ "r": 32,
+ "target_modules": [
+ "q_proj",
+ "v_proj"
+ ],
+ "exclude_modules": null,
+ "lora_alpha": 64,
+ "lora_dropout": 0.0,
+ "fan_in_fan_out": false,
+ "bias": "none",
+ "use_rslora": false,
+ "modules_to_save": null,
+ "init_lora_weights": true,
+ "layers_to_transform": null,
+ "layers_pattern": null,
+ "rank_pattern": {},
+ "alpha_pattern": {},
+ "megatron_config": null,
+ "megatron_core": "megatron.core",
+ "trainable_token_indices": null,
+ "loftq_config": {},
+ "eva_config": null,
+ "corda_config": null,
+ "use_dora": true,
+ "layer_replication": null,
+ "lora_bias": false
+ },
+ "error_msg": ""
+ },
+ "train_info": {
+ "accelerator_memory_reserved_avg": 12490471636,
+ "accelerator_memory_max": 24553455616,
+ "accelerator_memory_reserved_99th": 19189150515,
+ "train_time": 2022.7454924520134,
+ "file_size": 37181760,
+ "num_trainable_params": 9289728,
+ "num_total_params": 3222039552,
+ "status": "success",
+ "metrics": [
+ {
+ "step": 250,
+ "valid accuracy": 0.36,
+ "train loss": 0.9800839998722076,
+ "train samples": 1000,
+ "train time": 35.42731901501611,
+ "eval time": 16.70931195599769,
+ "tokens / sec": 5976.150775345474,
+ "mem allocated avg": 6924859500.544,
+ "mem reserved avg": 12552201306.112,
+ "elapsed time": 105.33911871900273
+ },
+ {
+ "step": 500,
+ "valid accuracy": 0.44,
+ "train loss": 0.7162023800611496,
+ "train samples": 2000,
+ "train time": 35.53461015297944,
+ "eval time": 16.7331051809997,
+ "tokens / sec": 5853.307496678993,
+ "mem allocated avg": 6917484427.264,
+ "mem reserved avg": 12427118772.224,
+ "elapsed time": 204.02196035100133
+ },
+ {
+ "step": 750,
+ "valid accuracy": 0.42,
+ "train loss": 0.6790966511964798,
+ "train samples": 3000,
+ "train time": 35.395415813978616,
+ "eval time": 10.35499690800134,
+ "tokens / sec": 6057.309825848329,
+ "mem allocated avg": 6927996166.144,
+ "mem reserved avg": 12609050902.528,
+ "elapsed time": 296.3724143870022
+ },
+ {
+ "step": 1000,
+ "valid accuracy": 0.42,
+ "train loss": 0.6590274780988693,
+ "train samples": 4000,
+ "train time": 35.01134122798976,
+ "eval time": 16.638093278997985,
+ "tokens / sec": 5950.528962696411,
+ "mem allocated avg": 6919690883.072,
+ "mem reserved avg": 12464313860.096,
+ "elapsed time": 394.33112582000103
+ },
+ {
+ "step": 1250,
+ "valid accuracy": 0.42,
+ "train loss": 0.6542477097511291,
+ "train samples": 5000,
+ "train time": 34.85555366096378,
+ "eval time": 16.627405782997812,
+ "tokens / sec": 5982.920312453697,
+ "mem allocated avg": 6919055253.504,
+ "mem reserved avg": 12449952563.2,
+ "elapsed time": 492.1167898590029
+ },
+ {
+ "step": 1500,
+ "valid accuracy": 0.4,
+ "train loss": 0.6471435966491699,
+ "train samples": 6000,
+ "train time": 35.407848127983016,
+ "eval time": 10.318167828998412,
+ "tokens / sec": 5911.994404273457,
+ "mem allocated avg": 6921185224.704,
+ "mem reserved avg": 12477500751.872,
+ "elapsed time": 584.325913470002
+ },
+ {
+ "step": 1750,
+ "valid accuracy": 0.42,
+ "train loss": 0.6376023133993148,
+ "train samples": 7000,
+ "train time": 35.61810469696138,
+ "eval time": 10.057756549002079,
+ "tokens / sec": 5877.7692350896,
+ "mem allocated avg": 6922196224.0,
+ "mem reserved avg": 12495888580.608,
+ "elapsed time": 676.5556904380028
+ },
+ {
+ "step": 2000,
+ "valid accuracy": 0.36,
+ "train loss": 0.6404745506048203,
+ "train samples": 8000,
+ "train time": 35.01814225999988,
+ "eval time": 10.846777078000741,
+ "tokens / sec": 5931.097042724754,
+ "mem allocated avg": 6919877345.28,
+ "mem reserved avg": 12428771328.0,
+ "elapsed time": 768.7593245980024
+ },
+ {
+ "step": 2250,
+ "valid accuracy": 0.48,
+ "train loss": 0.6327905882596969,
+ "train samples": 9000,
+ "train time": 35.941867801058834,
+ "eval time": 16.654083295998134,
+ "tokens / sec": 5980.434884178939,
+ "mem allocated avg": 6930785019.904,
+ "mem reserved avg": 12637135962.112,
+ "elapsed time": 868.0876048490027
+ },
+ {
+ "step": 2500,
+ "valid accuracy": 0.44,
+ "train loss": 0.6293514591455459,
+ "train samples": 10000,
+ "train time": 35.19044898093853,
+ "eval time": 16.654415837998386,
+ "tokens / sec": 5852.923334725435,
+ "mem allocated avg": 6914962546.688,
+ "mem reserved avg": 12361175924.736,
+ "elapsed time": 965.9673830700012
+ },
+ {
+ "step": 2750,
+ "valid accuracy": 0.34,
+ "train loss": 0.6212090995311738,
+ "train samples": 11000,
+ "train time": 35.78923041201051,
+ "eval time": 12.364532577001228,
+ "tokens / sec": 5920.2446535116005,
+ "mem allocated avg": 6926067247.104,
+ "mem reserved avg": 12561110007.808,
+ "elapsed time": 1060.7434992320013
+ },
+ {
+ "step": 3000,
+ "valid accuracy": 0.48,
+ "train loss": 0.6132309092283249,
+ "train samples": 12000,
+ "train time": 35.434680095979274,
+ "eval time": 10.902270734000922,
+ "tokens / sec": 5890.585139604081,
+ "mem allocated avg": 6921261266.944,
+ "mem reserved avg": 12472811520.0,
+ "elapsed time": 1153.3681941970026
+ },
+ {
+ "step": 3250,
+ "valid accuracy": 0.5,
+ "train loss": 0.6223928620815277,
+ "train samples": 13000,
+ "train time": 35.475069620017166,
+ "eval time": 9.885322058999009,
+ "tokens / sec": 5945.048234126565,
+ "mem allocated avg": 6922737405.952,
+ "mem reserved avg": 12498002509.824,
+ "elapsed time": 1245.241280964001
+ },
+ {
+ "step": 3500,
+ "valid accuracy": 0.5,
+ "train loss": 0.605602259516716,
+ "train samples": 14000,
+ "train time": 35.607162244014035,
+ "eval time": 10.090815307001321,
+ "tokens / sec": 5890.668808780496,
+ "mem allocated avg": 6920974434.304,
+ "mem reserved avg": 12474329858.048,
+ "elapsed time": 1337.4724736530006
+ },
+ {
+ "step": 3750,
+ "valid accuracy": 0.48,
+ "train loss": 0.6031041693687439,
+ "train samples": 15000,
+ "train time": 36.209776319014054,
+ "eval time": 10.371932055000798,
+ "tokens / sec": 5984.6544781390285,
+ "mem allocated avg": 6933558140.928,
+ "mem reserved avg": 12681738190.848,
+ "elapsed time": 1431.2058649130013
+ },
+ {
+ "step": 4000,
+ "valid accuracy": 0.46,
+ "train loss": 0.6162525477409363,
+ "train samples": 16000,
+ "train time": 35.48366187599095,
+ "eval time": 12.394127589999698,
+ "tokens / sec": 5759.636666425441,
+ "mem allocated avg": 6914222096.384,
+ "mem reserved avg": 12349406707.712,
+ "elapsed time": 1525.3134414390006
+ },
+ {
+ "step": 4250,
+ "valid accuracy": 0.5,
+ "train loss": 0.6013483003377914,
+ "train samples": 17000,
+ "train time": 35.15769277801883,
+ "eval time": 16.63699178299794,
+ "tokens / sec": 6012.59591562743,
+ "mem allocated avg": 6924507731.968,
+ "mem reserved avg": 12521616441.344,
+ "elapsed time": 1623.6120678540028
+ },
+ {
+ "step": 4500,
+ "valid accuracy": 0.48,
+ "train loss": 0.6073888168334961,
+ "train samples": 18000,
+ "train time": 34.98748015804085,
+ "eval time": 12.561758541996824,
+ "tokens / sec": 5939.781860861995,
+ "mem allocated avg": 6918951696.384,
+ "mem reserved avg": 12432495869.952,
+ "elapsed time": 1717.352138276001
+ },
+ {
+ "step": 4750,
+ "valid accuracy": 0.5,
+ "train loss": 0.5993685643672944,
+ "train samples": 19000,
+ "train time": 35.57701125005042,
+ "eval time": 13.379837485997996,
+ "tokens / sec": 5900.973483254653,
+ "mem allocated avg": 6921678901.248,
+ "mem reserved avg": 12490880581.632,
+ "elapsed time": 1812.886111721
+ },
+ {
+ "step": 5000,
+ "valid accuracy": 0.48,
+ "train loss": 0.6068210340738297,
+ "train samples": 20000,
+ "train time": 35.678432397002325,
+ "eval time": 10.087769599998865,
+ "tokens / sec": 5837.700425916121,
+ "mem allocated avg": 6918288025.6,
+ "mem reserved avg": 12423931101.184,
+ "elapsed time": 1905.221841073002
+ },
+ {
+ "step": 5000,
+ "test accuracy": 0.4806671721000758,
+ "train loss": 0.6068210340738297,
+ "train samples": 20000,
+ "train total tokens": 4198051
+ }
+ ]
+ },
+ "meta_info": {
+ "model_info": {
+ "sha": "13afe5124825b4f3751f836b40dafda64c1ed062",
+ "created_at": "2024-09-18T15:23:48+00:00"
+ },
+ "dataset_info": {
+ "metamath": {
+ "sha": "aa4f34d3d2d3231299b5b03d9b3e5a20da45aa18",
+ "created_at": "2023-09-21T17:22:46+00:00"
+ },
+ "gsm8k": {
+ "sha": "e53f048856ff4f594e959d75785d2c2d37b678ee",
+ "created_at": "2022-04-12T10:22:10+00:00"
+ }
+ },
+ "package_info": {
+ "transformers-version": "4.52.4",
+ "transformers-commit-hash": null,
+ "peft-version": "0.15.2.dev0",
+ "peft-commit-hash": "5fe7f8f8abe914d313fc3751f2ea92de7718fbaf",
+ "datasets-version": "3.6.0",
+ "datasets-commit-hash": null,
+ "bitsandbytes-version": "0.46.0",
+ "bitsandbytes-commit-hash": null,
+ "torch-version": "2.7.1+cu126",
+ "torch-commit-hash": null
+ },
+ "system_info": {
+ "system": "Linux",
+ "release": "6.8.0-1029-aws",
+ "version": "#31-Ubuntu SMP Wed Apr 23 18:42:41 UTC 2025",
+ "machine": "x86_64",
+ "processor": "x86_64",
+ "accelerator": "NVIDIA L40S"
+ },
+ "pytorch_info": "PyTorch built with:\n - GCC 11.2\n - C++ Version: 201703\n - Intel(R) oneAPI Math Kernel Library Version 2024.2-Product Build 20240605 for Intel(R) 64 architecture applications\n - Intel(R) MKL-DNN v3.7.1 (Git Hash 8d263e693366ef8db40acc569cc7d8edf644556d)\n - OpenMP 201511 (a.k.a. OpenMP 4.5)\n - LAPACK is enabled (usually provided by MKL)\n - NNPACK is enabled\n - CPU capability usage: AVX2\n - CUDA Runtime 12.6\n - NVCC architecture flags: -gencode;arch=compute_50,code=sm_50;-gencode;arch=compute_60,code=sm_60;-gencode;arch=compute_70,code=sm_70;-gencode;arch=compute_75,code=sm_75;-gencode;arch=compute_80,code=sm_80;-gencode;arch=compute_86,code=sm_86;-gencode;arch=compute_90,code=sm_90\n - CuDNN 90.7.1 (built against CUDA 12.8)\n - Built with CuDNN 90.5.1\n - Magma 2.6.1\n - Build settings: BLAS_INFO=mkl, BUILD_TYPE=Release, COMMIT_SHA=e2d141dbde55c2a4370fac5165b0561b6af4798b, CUDA_VERSION=12.6, CUDNN_VERSION=9.5.1, CXX_COMPILER=/opt/rh/gcc-toolset-11/root/usr/bin/c++, CXX_FLAGS= -D_GLIBCXX_USE_CXX11_ABI=1 -fvisibility-inlines-hidden -DUSE_PTHREADPOOL -DNDEBUG -DUSE_KINETO -DLIBKINETO_NOROCTRACER -DLIBKINETO_NOXPUPTI=ON -DUSE_FBGEMM -DUSE_PYTORCH_QNNPACK -DUSE_XNNPACK -DSYMBOLICATE_MOBILE_DEBUG_HANDLE -O2 -fPIC -Wall -Wextra -Werror=return-type -Werror=non-virtual-dtor -Werror=range-loop-construct -Werror=bool-operation -Wnarrowing -Wno-missing-field-initializers -Wno-unknown-pragmas -Wno-unused-parameter -Wno-strict-overflow -Wno-strict-aliasing -Wno-stringop-overflow -Wsuggest-override -Wno-psabi -Wno-error=old-style-cast -fdiagnostics-color=always -faligned-new -Wno-maybe-uninitialized -fno-math-errno -fno-trapping-math -Werror=format -Wno-stringop-overflow, LAPACK_INFO=mkl, PERF_WITH_AVX=1, PERF_WITH_AVX2=1, TORCH_VERSION=2.7.1, USE_CUDA=ON, USE_CUDNN=ON, USE_CUSPARSELT=1, USE_GFLAGS=OFF, USE_GLOG=OFF, USE_GLOO=ON, USE_MKL=ON, USE_MKLDNN=ON, USE_MPI=OFF, USE_NCCL=1, USE_NNPACK=ON, USE_OPENMP=ON, USE_ROCM=OFF, USE_ROCM_KERNEL_ASSERT=OFF, \n"
+ }
+}
diff --git a/peft/method_comparison/MetaMathQA/results/lora--llama-3.2-3B-rank32-lorafa.json b/peft/method_comparison/MetaMathQA/results/lora--llama-3.2-3B-rank32-lorafa.json
new file mode 100644
index 0000000000000000000000000000000000000000..35c7a9981da710c1f025c69644ff65550b1e0edc
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/results/lora--llama-3.2-3B-rank32-lorafa.json
@@ -0,0 +1,367 @@
+{
+ "run_info": {
+ "created_at": "2025-06-19T17:29:01+00:00",
+ "total_time": 2025.9028512089972,
+ "experiment_name": "lora/llama-3.2-3B-rank32-lorafa",
+ "peft_branch": "main",
+ "train_config": {
+ "model_id": "meta-llama/Llama-3.2-3B",
+ "dtype": "bfloat16",
+ "max_seq_length": 768,
+ "batch_size": 4,
+ "batch_size_eval": 50,
+ "max_steps": 5000,
+ "eval_steps": 250,
+ "compile": false,
+ "query_template": "Question: {query} Think step by step.\nAnswer:",
+ "seed": 0,
+ "grad_norm_clip": 1.0,
+ "optimizer_type": "lora-fa",
+ "optimizer_kwargs": {
+ "r": 32,
+ "lora_alpha": 64,
+ "lr": 0.0001,
+ "weight_decay": 0.1
+ },
+ "lr_scheduler": "cosine",
+ "use_amp": false,
+ "autocast_adapter_dtype": true,
+ "generation_kwargs": {
+ "max_length": 800,
+ "max_new_tokens": 300
+ },
+ "attn_implementation": null
+ },
+ "peft_config": {
+ "task_type": "CAUSAL_LM",
+ "peft_type": "LORA",
+ "auto_mapping": null,
+ "base_model_name_or_path": "meta-llama/Llama-3.2-3B",
+ "revision": null,
+ "inference_mode": false,
+ "r": 32,
+ "target_modules": [
+ "q_proj",
+ "v_proj"
+ ],
+ "exclude_modules": null,
+ "lora_alpha": 64,
+ "lora_dropout": 0.0,
+ "fan_in_fan_out": false,
+ "bias": "none",
+ "use_rslora": false,
+ "modules_to_save": null,
+ "init_lora_weights": true,
+ "layers_to_transform": null,
+ "layers_pattern": null,
+ "rank_pattern": {},
+ "alpha_pattern": {},
+ "megatron_config": null,
+ "megatron_core": "megatron.core",
+ "trainable_token_indices": null,
+ "loftq_config": {},
+ "eva_config": null,
+ "corda_config": null,
+ "use_dora": false,
+ "layer_replication": null,
+ "lora_bias": false
+ },
+ "error_msg": ""
+ },
+ "train_info": {
+ "accelerator_memory_reserved_avg": 11106307276,
+ "accelerator_memory_max": 20187185152,
+ "accelerator_memory_reserved_99th": 16257394933,
+ "train_time": 1821.1390361119993,
+ "file_size": 36715216,
+ "num_trainable_params": 3670016,
+ "num_total_params": 3221924864,
+ "status": "success",
+ "metrics": [
+ {
+ "step": 250,
+ "valid accuracy": 0.26,
+ "train loss": 1.13827001953125,
+ "train samples": 1000,
+ "train time": 39.487167649953335,
+ "eval time": 11.352047874999698,
+ "tokens / sec": 5361.716542367662,
+ "mem allocated avg": 6857574733.824,
+ "mem reserved avg": 11147042357.248,
+ "elapsed time": 95.33382818899918
+ },
+ {
+ "step": 500,
+ "valid accuracy": 0.34,
+ "train loss": 0.8058450784683228,
+ "train samples": 2000,
+ "train time": 38.91575912100234,
+ "eval time": 11.306344865999563,
+ "tokens / sec": 5344.749908469542,
+ "mem allocated avg": 6850229934.08,
+ "mem reserved avg": 11051613552.64,
+ "elapsed time": 184.45338391399855
+ },
+ {
+ "step": 750,
+ "valid accuracy": 0.4,
+ "train loss": 0.725865609407425,
+ "train samples": 3000,
+ "train time": 39.53630301699741,
+ "eval time": 9.965407437997783,
+ "tokens / sec": 5422.889436774727,
+ "mem allocated avg": 6861271248.896,
+ "mem reserved avg": 11192013684.736,
+ "elapsed time": 273.0429774479999
+ },
+ {
+ "step": 1000,
+ "valid accuracy": 0.36,
+ "train loss": 0.69585602581501,
+ "train samples": 4000,
+ "train time": 38.42195282199464,
+ "eval time": 11.263002069001232,
+ "tokens / sec": 5422.316792829388,
+ "mem allocated avg": 6851626665.984,
+ "mem reserved avg": 11074279571.456,
+ "elapsed time": 361.40852819099746
+ },
+ {
+ "step": 1250,
+ "valid accuracy": 0.4,
+ "train loss": 0.6884716705083848,
+ "train samples": 5000,
+ "train time": 38.42177955799343,
+ "eval time": 11.356440440998995,
+ "tokens / sec": 5427.598679682052,
+ "mem allocated avg": 6851712622.592,
+ "mem reserved avg": 11075865018.368,
+ "elapsed time": 449.83568274799836
+ },
+ {
+ "step": 1500,
+ "valid accuracy": 0.38,
+ "train loss": 0.6801862429380416,
+ "train samples": 6000,
+ "train time": 38.768619330003276,
+ "eval time": 11.348457601998234,
+ "tokens / sec": 5399.495871084515,
+ "mem allocated avg": 6853521098.752,
+ "mem reserved avg": 11096006066.176,
+ "elapsed time": 538.7312806489972
+ },
+ {
+ "step": 1750,
+ "valid accuracy": 0.38,
+ "train loss": 0.6713097202777862,
+ "train samples": 7000,
+ "train time": 38.99274470796445,
+ "eval time": 8.222045223003079,
+ "tokens / sec": 5369.0757490389815,
+ "mem allocated avg": 6854799144.96,
+ "mem reserved avg": 11113831858.176,
+ "elapsed time": 624.957832287997
+ },
+ {
+ "step": 2000,
+ "valid accuracy": 0.36,
+ "train loss": 0.6733613710403442,
+ "train samples": 8000,
+ "train time": 38.96502619797684,
+ "eval time": 9.028824541001086,
+ "tokens / sec": 5330.318500101101,
+ "mem allocated avg": 6852199981.056,
+ "mem reserved avg": 11058584485.888,
+ "elapsed time": 711.7122244169987
+ },
+ {
+ "step": 2250,
+ "valid accuracy": 0.38,
+ "train loss": 0.6658626307249069,
+ "train samples": 9000,
+ "train time": 39.83998639498168,
+ "eval time": 11.38518134900005,
+ "tokens / sec": 5395.282966940854,
+ "mem allocated avg": 6862685554.688,
+ "mem reserved avg": 11223865229.312,
+ "elapsed time": 802.4390404449987
+ },
+ {
+ "step": 2500,
+ "valid accuracy": 0.38,
+ "train loss": 0.6645791643857956,
+ "train samples": 10000,
+ "train time": 38.493957691986,
+ "eval time": 11.311897349998617,
+ "tokens / sec": 5350.631952372099,
+ "mem allocated avg": 6848127772.672,
+ "mem reserved avg": 11012925292.544,
+ "elapsed time": 890.7464078919984
+ },
+ {
+ "step": 2750,
+ "valid accuracy": 0.44,
+ "train loss": 0.658472005367279,
+ "train samples": 11000,
+ "train time": 38.51331885699619,
+ "eval time": 7.521690310000849,
+ "tokens / sec": 5501.499384842303,
+ "mem allocated avg": 6858912532.48,
+ "mem reserved avg": 11161915359.232,
+ "elapsed time": 975.6010923279973
+ },
+ {
+ "step": 3000,
+ "valid accuracy": 0.4,
+ "train loss": 0.6503657740354538,
+ "train samples": 12000,
+ "train time": 38.378428091957176,
+ "eval time": 9.959380172000238,
+ "tokens / sec": 5438.758447841249,
+ "mem allocated avg": 6853735892.992,
+ "mem reserved avg": 11091962757.12,
+ "elapsed time": 1062.3718837759989
+ },
+ {
+ "step": 3250,
+ "valid accuracy": 0.48,
+ "train loss": 0.6599743469953537,
+ "train samples": 13000,
+ "train time": 38.74303203701493,
+ "eval time": 9.720565422001528,
+ "tokens / sec": 5443.585308411229,
+ "mem allocated avg": 6855708461.056,
+ "mem reserved avg": 11117246021.632,
+ "elapsed time": 1149.5592005079998
+ },
+ {
+ "step": 3500,
+ "valid accuracy": 0.4,
+ "train loss": 0.6468936309814454,
+ "train samples": 14000,
+ "train time": 38.947772975978296,
+ "eval time": 10.49309463499958,
+ "tokens / sec": 5385.417033455723,
+ "mem allocated avg": 6854553325.568,
+ "mem reserved avg": 11102364631.04,
+ "elapsed time": 1237.83959684
+ },
+ {
+ "step": 3750,
+ "valid accuracy": 0.44,
+ "train loss": 0.6447412570714951,
+ "train samples": 15000,
+ "train time": 39.208677324022574,
+ "eval time": 11.265130790001422,
+ "tokens / sec": 5526.914315654032,
+ "mem allocated avg": 6864447199.232,
+ "mem reserved avg": 11258292076.544,
+ "elapsed time": 1327.6204509749987
+ },
+ {
+ "step": 4000,
+ "valid accuracy": 0.48,
+ "train loss": 0.6609537017345428,
+ "train samples": 16000,
+ "train time": 38.373366451996844,
+ "eval time": 8.435534727999766,
+ "tokens / sec": 5325.907495128434,
+ "mem allocated avg": 6846769313.792,
+ "mem reserved avg": 10994319360.0,
+ "elapsed time": 1412.8209538019983
+ },
+ {
+ "step": 4250,
+ "valid accuracy": 0.46,
+ "train loss": 0.6430994077920914,
+ "train samples": 17000,
+ "train time": 38.840016363014,
+ "eval time": 8.356262703997345,
+ "tokens / sec": 5442.556924391474,
+ "mem allocated avg": 6857134465.024,
+ "mem reserved avg": 11130768457.728,
+ "elapsed time": 1498.7970963499974
+ },
+ {
+ "step": 4500,
+ "valid accuracy": 0.5,
+ "train loss": 0.6519971441030502,
+ "train samples": 18000,
+ "train time": 38.99225058195225,
+ "eval time": 9.193580140999984,
+ "tokens / sec": 5329.725699295479,
+ "mem allocated avg": 6851737821.184,
+ "mem reserved avg": 11062996893.696,
+ "elapsed time": 1585.3292836179971
+ },
+ {
+ "step": 4750,
+ "valid accuracy": 0.42,
+ "train loss": 0.6448501836061478,
+ "train samples": 19000,
+ "train time": 39.31173135296194,
+ "eval time": 8.482506923999608,
+ "tokens / sec": 5340.365147366681,
+ "mem allocated avg": 6853984409.6,
+ "mem reserved avg": 11104352731.136,
+ "elapsed time": 1672.2648903240006
+ },
+ {
+ "step": 5000,
+ "valid accuracy": 0.46,
+ "train loss": 0.6509636770486832,
+ "train samples": 20000,
+ "train time": 38.96172000500519,
+ "eval time": 11.401191647000815,
+ "tokens / sec": 5345.759888763726,
+ "mem allocated avg": 6850959237.12,
+ "mem reserved avg": 11055900131.328,
+ "elapsed time": 1761.553419697997
+ },
+ {
+ "step": 5000,
+ "test accuracy": 0.42987111448066717,
+ "train loss": 0.6509636770486832,
+ "train samples": 20000,
+ "train total tokens": 4198051
+ }
+ ]
+ },
+ "meta_info": {
+ "model_info": {
+ "sha": "13afe5124825b4f3751f836b40dafda64c1ed062",
+ "created_at": "2024-09-18T15:23:48+00:00"
+ },
+ "dataset_info": {
+ "metamath": {
+ "sha": "aa4f34d3d2d3231299b5b03d9b3e5a20da45aa18",
+ "created_at": "2023-09-21T17:22:46+00:00"
+ },
+ "gsm8k": {
+ "sha": "e53f048856ff4f594e959d75785d2c2d37b678ee",
+ "created_at": "2022-04-12T10:22:10+00:00"
+ }
+ },
+ "package_info": {
+ "transformers-version": "4.52.4",
+ "transformers-commit-hash": null,
+ "peft-version": "0.15.2.dev0",
+ "peft-commit-hash": "5fe7f8f8abe914d313fc3751f2ea92de7718fbaf",
+ "datasets-version": "3.6.0",
+ "datasets-commit-hash": null,
+ "bitsandbytes-version": "0.46.0",
+ "bitsandbytes-commit-hash": null,
+ "torch-version": "2.7.1+cu126",
+ "torch-commit-hash": null
+ },
+ "system_info": {
+ "system": "Linux",
+ "release": "6.8.0-1029-aws",
+ "version": "#31-Ubuntu SMP Wed Apr 23 18:42:41 UTC 2025",
+ "machine": "x86_64",
+ "processor": "x86_64",
+ "accelerator": "NVIDIA L40S"
+ },
+ "pytorch_info": "PyTorch built with:\n - GCC 11.2\n - C++ Version: 201703\n - Intel(R) oneAPI Math Kernel Library Version 2024.2-Product Build 20240605 for Intel(R) 64 architecture applications\n - Intel(R) MKL-DNN v3.7.1 (Git Hash 8d263e693366ef8db40acc569cc7d8edf644556d)\n - OpenMP 201511 (a.k.a. OpenMP 4.5)\n - LAPACK is enabled (usually provided by MKL)\n - NNPACK is enabled\n - CPU capability usage: AVX2\n - CUDA Runtime 12.6\n - NVCC architecture flags: -gencode;arch=compute_50,code=sm_50;-gencode;arch=compute_60,code=sm_60;-gencode;arch=compute_70,code=sm_70;-gencode;arch=compute_75,code=sm_75;-gencode;arch=compute_80,code=sm_80;-gencode;arch=compute_86,code=sm_86;-gencode;arch=compute_90,code=sm_90\n - CuDNN 90.7.1 (built against CUDA 12.8)\n - Built with CuDNN 90.5.1\n - Magma 2.6.1\n - Build settings: BLAS_INFO=mkl, BUILD_TYPE=Release, COMMIT_SHA=e2d141dbde55c2a4370fac5165b0561b6af4798b, CUDA_VERSION=12.6, CUDNN_VERSION=9.5.1, CXX_COMPILER=/opt/rh/gcc-toolset-11/root/usr/bin/c++, CXX_FLAGS= -D_GLIBCXX_USE_CXX11_ABI=1 -fvisibility-inlines-hidden -DUSE_PTHREADPOOL -DNDEBUG -DUSE_KINETO -DLIBKINETO_NOROCTRACER -DLIBKINETO_NOXPUPTI=ON -DUSE_FBGEMM -DUSE_PYTORCH_QNNPACK -DUSE_XNNPACK -DSYMBOLICATE_MOBILE_DEBUG_HANDLE -O2 -fPIC -Wall -Wextra -Werror=return-type -Werror=non-virtual-dtor -Werror=range-loop-construct -Werror=bool-operation -Wnarrowing -Wno-missing-field-initializers -Wno-unknown-pragmas -Wno-unused-parameter -Wno-strict-overflow -Wno-strict-aliasing -Wno-stringop-overflow -Wsuggest-override -Wno-psabi -Wno-error=old-style-cast -fdiagnostics-color=always -faligned-new -Wno-maybe-uninitialized -fno-math-errno -fno-trapping-math -Werror=format -Wno-stringop-overflow, LAPACK_INFO=mkl, PERF_WITH_AVX=1, PERF_WITH_AVX2=1, TORCH_VERSION=2.7.1, USE_CUDA=ON, USE_CUDNN=ON, USE_CUSPARSELT=1, USE_GFLAGS=OFF, USE_GLOG=OFF, USE_GLOO=ON, USE_MKL=ON, USE_MKLDNN=ON, USE_MPI=OFF, USE_NCCL=1, USE_NNPACK=ON, USE_OPENMP=ON, USE_ROCM=OFF, USE_ROCM_KERNEL_ASSERT=OFF, \n"
+ }
+}
diff --git a/peft/method_comparison/MetaMathQA/results/lora--llama-3.2-3B-rank32.json b/peft/method_comparison/MetaMathQA/results/lora--llama-3.2-3B-rank32.json
new file mode 100644
index 0000000000000000000000000000000000000000..f3d348c07ec5957e5cdaad74b5c6d9071763afb1
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/results/lora--llama-3.2-3B-rank32.json
@@ -0,0 +1,365 @@
+{
+ "run_info": {
+ "created_at": "2025-06-19T19:15:35+00:00",
+ "total_time": 1993.494420946001,
+ "experiment_name": "lora/llama-3.2-3B-rank32",
+ "peft_branch": "main",
+ "train_config": {
+ "model_id": "meta-llama/Llama-3.2-3B",
+ "dtype": "bfloat16",
+ "max_seq_length": 768,
+ "batch_size": 4,
+ "batch_size_eval": 50,
+ "max_steps": 5000,
+ "eval_steps": 250,
+ "compile": false,
+ "query_template": "Question: {query} Think step by step.\nAnswer:",
+ "seed": 0,
+ "grad_norm_clip": 1.0,
+ "optimizer_type": "AdamW",
+ "optimizer_kwargs": {
+ "lr": 0.0001,
+ "weight_decay": 0.1
+ },
+ "lr_scheduler": "cosine",
+ "use_amp": false,
+ "autocast_adapter_dtype": true,
+ "generation_kwargs": {
+ "max_length": 800,
+ "max_new_tokens": 300
+ },
+ "attn_implementation": null
+ },
+ "peft_config": {
+ "task_type": "CAUSAL_LM",
+ "peft_type": "LORA",
+ "auto_mapping": null,
+ "base_model_name_or_path": "meta-llama/Llama-3.2-3B",
+ "revision": null,
+ "inference_mode": false,
+ "r": 32,
+ "target_modules": [
+ "v_proj",
+ "q_proj"
+ ],
+ "exclude_modules": null,
+ "lora_alpha": 64,
+ "lora_dropout": 0.0,
+ "fan_in_fan_out": false,
+ "bias": "none",
+ "use_rslora": false,
+ "modules_to_save": null,
+ "init_lora_weights": true,
+ "layers_to_transform": null,
+ "layers_pattern": null,
+ "rank_pattern": {},
+ "alpha_pattern": {},
+ "megatron_config": null,
+ "megatron_core": "megatron.core",
+ "trainable_token_indices": null,
+ "loftq_config": {},
+ "eva_config": null,
+ "corda_config": null,
+ "use_dora": false,
+ "layer_replication": null,
+ "lora_bias": false
+ },
+ "error_msg": ""
+ },
+ "train_info": {
+ "accelerator_memory_reserved_avg": 11868689976,
+ "accelerator_memory_max": 22273851392,
+ "accelerator_memory_reserved_99th": 17710763212,
+ "train_time": 1796.1857790169925,
+ "file_size": 36715216,
+ "num_trainable_params": 9175040,
+ "num_total_params": 3221924864,
+ "status": "success",
+ "metrics": [
+ {
+ "step": 250,
+ "valid accuracy": 0.34,
+ "train loss": 0.9827028260231018,
+ "train samples": 1000,
+ "train time": 31.395267726013117,
+ "eval time": 11.27943390099972,
+ "tokens / sec": 6743.659644748829,
+ "mem allocated avg": 6925580957.696,
+ "mem reserved avg": 11920245522.432,
+ "elapsed time": 94.68654379600048
+ },
+ {
+ "step": 500,
+ "valid accuracy": 0.44,
+ "train loss": 0.7164744178056717,
+ "train samples": 2000,
+ "train time": 30.728173206967767,
+ "eval time": 11.244831023999723,
+ "tokens / sec": 6768.869681873444,
+ "mem allocated avg": 6918363699.2,
+ "mem reserved avg": 11811654991.872,
+ "elapsed time": 182.6767855429971
+ },
+ {
+ "step": 750,
+ "valid accuracy": 0.38,
+ "train loss": 0.6791989279985428,
+ "train samples": 3000,
+ "train time": 31.248708018982143,
+ "eval time": 6.873092081001232,
+ "tokens / sec": 6861.115661798283,
+ "mem allocated avg": 6929003134.976,
+ "mem reserved avg": 11970174517.248,
+ "elapsed time": 267.2763524209986
+ },
+ {
+ "step": 1000,
+ "valid accuracy": 0.42,
+ "train loss": 0.6590347054004669,
+ "train samples": 4000,
+ "train time": 31.016855426081747,
+ "eval time": 7.663122134003061,
+ "tokens / sec": 6716.864012746194,
+ "mem allocated avg": 6919503566.848,
+ "mem reserved avg": 11835008876.544,
+ "elapsed time": 351.92747904299904
+ },
+ {
+ "step": 1250,
+ "valid accuracy": 0.4,
+ "train loss": 0.6547032891511917,
+ "train samples": 5000,
+ "train time": 30.914218463025463,
+ "eval time": 11.249955232000502,
+ "tokens / sec": 6745.698593332356,
+ "mem allocated avg": 6919763681.28,
+ "mem reserved avg": 11832551014.4,
+ "elapsed time": 440.29597954699784
+ },
+ {
+ "step": 1500,
+ "valid accuracy": 0.42,
+ "train loss": 0.647298491358757,
+ "train samples": 6000,
+ "train time": 31.093457819981268,
+ "eval time": 11.25276822899832,
+ "tokens / sec": 6732.316528188762,
+ "mem allocated avg": 6920362313.728,
+ "mem reserved avg": 11859000295.424,
+ "elapsed time": 529.2981231249978
+ },
+ {
+ "step": 1750,
+ "valid accuracy": 0.46,
+ "train loss": 0.6378061240911483,
+ "train samples": 7000,
+ "train time": 31.079548971014447,
+ "eval time": 11.2527706639994,
+ "tokens / sec": 6736.101614449091,
+ "mem allocated avg": 6922653980.672,
+ "mem reserved avg": 11870048092.16,
+ "elapsed time": 617.7172930779998
+ },
+ {
+ "step": 2000,
+ "valid accuracy": 0.4,
+ "train loss": 0.641120473742485,
+ "train samples": 8000,
+ "train time": 30.851661891996628,
+ "eval time": 7.384566520999215,
+ "tokens / sec": 6732.084667823985,
+ "mem allocated avg": 6919747647.488,
+ "mem reserved avg": 11816562327.552,
+ "elapsed time": 702.0775224069985
+ },
+ {
+ "step": 2250,
+ "valid accuracy": 0.46,
+ "train loss": 0.6332860335111618,
+ "train samples": 9000,
+ "train time": 31.288193090975255,
+ "eval time": 11.258606130999397,
+ "tokens / sec": 6869.939704571801,
+ "mem allocated avg": 6930711803.904,
+ "mem reserved avg": 12003997384.704,
+ "elapsed time": 791.1291831710005
+ },
+ {
+ "step": 2500,
+ "valid accuracy": 0.44,
+ "train loss": 0.6298432033061981,
+ "train samples": 10000,
+ "train time": 30.668521790059458,
+ "eval time": 11.22552015600013,
+ "tokens / sec": 6715.908950876132,
+ "mem allocated avg": 6916224055.296,
+ "mem reserved avg": 11759050031.104,
+ "elapsed time": 878.9048607999976
+ },
+ {
+ "step": 2750,
+ "valid accuracy": 0.4,
+ "train loss": 0.6213459351062774,
+ "train samples": 11000,
+ "train time": 31.198134894020768,
+ "eval time": 7.820672179997928,
+ "tokens / sec": 6791.463679471677,
+ "mem allocated avg": 6926273599.488,
+ "mem reserved avg": 11930135691.264,
+ "elapsed time": 964.4001106439973
+ },
+ {
+ "step": 3000,
+ "valid accuracy": 0.46,
+ "train loss": 0.6136174714565277,
+ "train samples": 12000,
+ "train time": 30.652901480014407,
+ "eval time": 8.59450396900138,
+ "tokens / sec": 6809.502197894445,
+ "mem allocated avg": 6921910312.96,
+ "mem reserved avg": 11851509268.48,
+ "elapsed time": 1049.6233134680006
+ },
+ {
+ "step": 3250,
+ "valid accuracy": 0.46,
+ "train loss": 0.6227310271263122,
+ "train samples": 13000,
+ "train time": 30.898520497004938,
+ "eval time": 11.247846516002028,
+ "tokens / sec": 6825.601893153528,
+ "mem allocated avg": 6923552774.144,
+ "mem reserved avg": 11884266782.72,
+ "elapsed time": 1137.9473550990006
+ },
+ {
+ "step": 3500,
+ "valid accuracy": 0.52,
+ "train loss": 0.6058980323076248,
+ "train samples": 14000,
+ "train time": 31.043968706952,
+ "eval time": 7.071496761000162,
+ "tokens / sec": 6756.545916535101,
+ "mem allocated avg": 6922457063.424,
+ "mem reserved avg": 11865602129.92,
+ "elapsed time": 1222.3722963839973
+ },
+ {
+ "step": 3750,
+ "valid accuracy": 0.5,
+ "train loss": 0.6032638043165207,
+ "train samples": 15000,
+ "train time": 31.41906641800597,
+ "eval time": 6.834270917999675,
+ "tokens / sec": 6897.18138397039,
+ "mem allocated avg": 6932064409.6,
+ "mem reserved avg": 12041553182.72,
+ "elapsed time": 1307.517348808
+ },
+ {
+ "step": 4000,
+ "valid accuracy": 0.48,
+ "train loss": 0.6166473155021668,
+ "train samples": 16000,
+ "train time": 30.82234557695483,
+ "eval time": 6.627715251001064,
+ "tokens / sec": 6630.676419149782,
+ "mem allocated avg": 6914480900.096,
+ "mem reserved avg": 11738338557.952,
+ "elapsed time": 1390.9289551410002
+ },
+ {
+ "step": 4250,
+ "valid accuracy": 0.44,
+ "train loss": 0.601645546555519,
+ "train samples": 17000,
+ "train time": 30.811621871023817,
+ "eval time": 11.241402788000414,
+ "tokens / sec": 6860.690452611215,
+ "mem allocated avg": 6925075550.208,
+ "mem reserved avg": 11899366277.12,
+ "elapsed time": 1479.325017957999
+ },
+ {
+ "step": 4500,
+ "valid accuracy": 0.46,
+ "train loss": 0.6076700875759125,
+ "train samples": 18000,
+ "train time": 30.499847401017178,
+ "eval time": 11.232504903000518,
+ "tokens / sec": 6813.73900884072,
+ "mem allocated avg": 6919328847.872,
+ "mem reserved avg": 11814020579.328,
+ "elapsed time": 1567.0791362639975
+ },
+ {
+ "step": 4750,
+ "valid accuracy": 0.46,
+ "train loss": 0.5997640329599381,
+ "train samples": 19000,
+ "train time": 30.974938084971654,
+ "eval time": 11.246996836001927,
+ "tokens / sec": 6777.705234602477,
+ "mem allocated avg": 6921498724.352,
+ "mem reserved avg": 11864662605.824,
+ "elapsed time": 1655.6881185989987
+ },
+ {
+ "step": 5000,
+ "valid accuracy": 0.5,
+ "train loss": 0.6069052599668503,
+ "train samples": 20000,
+ "train time": 30.736502733019734,
+ "eval time": 11.28520023999954,
+ "tokens / sec": 6776.307695418065,
+ "mem allocated avg": 6918408683.52,
+ "mem reserved avg": 11806051401.728,
+ "elapsed time": 1743.785376189
+ },
+ {
+ "step": 5000,
+ "test accuracy": 0.48218347232752085,
+ "train loss": 0.6069052599668503,
+ "train samples": 20000,
+ "train total tokens": 4198051
+ }
+ ]
+ },
+ "meta_info": {
+ "model_info": {
+ "sha": "13afe5124825b4f3751f836b40dafda64c1ed062",
+ "created_at": "2024-09-18T15:23:48+00:00"
+ },
+ "dataset_info": {
+ "metamath": {
+ "sha": "aa4f34d3d2d3231299b5b03d9b3e5a20da45aa18",
+ "created_at": "2023-09-21T17:22:46+00:00"
+ },
+ "gsm8k": {
+ "sha": "e53f048856ff4f594e959d75785d2c2d37b678ee",
+ "created_at": "2022-04-12T10:22:10+00:00"
+ }
+ },
+ "package_info": {
+ "transformers-version": "4.52.4",
+ "transformers-commit-hash": null,
+ "peft-version": "0.15.2.dev0",
+ "peft-commit-hash": "5fe7f8f8abe914d313fc3751f2ea92de7718fbaf",
+ "datasets-version": "3.6.0",
+ "datasets-commit-hash": null,
+ "bitsandbytes-version": "0.46.0",
+ "bitsandbytes-commit-hash": null,
+ "torch-version": "2.7.1+cu126",
+ "torch-commit-hash": null
+ },
+ "system_info": {
+ "system": "Linux",
+ "release": "6.8.0-1029-aws",
+ "version": "#31-Ubuntu SMP Wed Apr 23 18:42:41 UTC 2025",
+ "machine": "x86_64",
+ "processor": "x86_64",
+ "accelerator": "NVIDIA L40S"
+ },
+ "pytorch_info": "PyTorch built with:\n - GCC 11.2\n - C++ Version: 201703\n - Intel(R) oneAPI Math Kernel Library Version 2024.2-Product Build 20240605 for Intel(R) 64 architecture applications\n - Intel(R) MKL-DNN v3.7.1 (Git Hash 8d263e693366ef8db40acc569cc7d8edf644556d)\n - OpenMP 201511 (a.k.a. OpenMP 4.5)\n - LAPACK is enabled (usually provided by MKL)\n - NNPACK is enabled\n - CPU capability usage: AVX2\n - CUDA Runtime 12.6\n - NVCC architecture flags: -gencode;arch=compute_50,code=sm_50;-gencode;arch=compute_60,code=sm_60;-gencode;arch=compute_70,code=sm_70;-gencode;arch=compute_75,code=sm_75;-gencode;arch=compute_80,code=sm_80;-gencode;arch=compute_86,code=sm_86;-gencode;arch=compute_90,code=sm_90\n - CuDNN 90.7.1 (built against CUDA 12.8)\n - Built with CuDNN 90.5.1\n - Magma 2.6.1\n - Build settings: BLAS_INFO=mkl, BUILD_TYPE=Release, COMMIT_SHA=e2d141dbde55c2a4370fac5165b0561b6af4798b, CUDA_VERSION=12.6, CUDNN_VERSION=9.5.1, CXX_COMPILER=/opt/rh/gcc-toolset-11/root/usr/bin/c++, CXX_FLAGS= -D_GLIBCXX_USE_CXX11_ABI=1 -fvisibility-inlines-hidden -DUSE_PTHREADPOOL -DNDEBUG -DUSE_KINETO -DLIBKINETO_NOROCTRACER -DLIBKINETO_NOXPUPTI=ON -DUSE_FBGEMM -DUSE_PYTORCH_QNNPACK -DUSE_XNNPACK -DSYMBOLICATE_MOBILE_DEBUG_HANDLE -O2 -fPIC -Wall -Wextra -Werror=return-type -Werror=non-virtual-dtor -Werror=range-loop-construct -Werror=bool-operation -Wnarrowing -Wno-missing-field-initializers -Wno-unknown-pragmas -Wno-unused-parameter -Wno-strict-overflow -Wno-strict-aliasing -Wno-stringop-overflow -Wsuggest-override -Wno-psabi -Wno-error=old-style-cast -fdiagnostics-color=always -faligned-new -Wno-maybe-uninitialized -fno-math-errno -fno-trapping-math -Werror=format -Wno-stringop-overflow, LAPACK_INFO=mkl, PERF_WITH_AVX=1, PERF_WITH_AVX2=1, TORCH_VERSION=2.7.1, USE_CUDA=ON, USE_CUDNN=ON, USE_CUSPARSELT=1, USE_GFLAGS=OFF, USE_GLOG=OFF, USE_GLOO=ON, USE_MKL=ON, USE_MKLDNN=ON, USE_MPI=OFF, USE_NCCL=1, USE_NNPACK=ON, USE_OPENMP=ON, USE_ROCM=OFF, USE_ROCM_KERNEL_ASSERT=OFF, \n"
+ }
+}
diff --git a/peft/method_comparison/MetaMathQA/results/lora--llama-3.2-3B-rank64-rslora.json b/peft/method_comparison/MetaMathQA/results/lora--llama-3.2-3B-rank64-rslora.json
new file mode 100644
index 0000000000000000000000000000000000000000..dbeb788d4e2455d909eca39139320edbbf9fd173
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/results/lora--llama-3.2-3B-rank64-rslora.json
@@ -0,0 +1,365 @@
+{
+ "run_info": {
+ "created_at": "2025-06-19T18:02:52+00:00",
+ "total_time": 2068.5078051540004,
+ "experiment_name": "lora/llama-3.2-3B-rank64-rslora",
+ "peft_branch": "main",
+ "train_config": {
+ "model_id": "meta-llama/Llama-3.2-3B",
+ "dtype": "bfloat16",
+ "max_seq_length": 768,
+ "batch_size": 4,
+ "batch_size_eval": 50,
+ "max_steps": 5000,
+ "eval_steps": 250,
+ "compile": false,
+ "query_template": "Question: {query} Think step by step.\nAnswer:",
+ "seed": 0,
+ "grad_norm_clip": 1.0,
+ "optimizer_type": "AdamW",
+ "optimizer_kwargs": {
+ "lr": 0.0001,
+ "weight_decay": 0.1
+ },
+ "lr_scheduler": "cosine",
+ "use_amp": false,
+ "autocast_adapter_dtype": true,
+ "generation_kwargs": {
+ "max_length": 800,
+ "max_new_tokens": 300
+ },
+ "attn_implementation": null
+ },
+ "peft_config": {
+ "task_type": "CAUSAL_LM",
+ "peft_type": "LORA",
+ "auto_mapping": null,
+ "base_model_name_or_path": "meta-llama/Llama-3.2-3B",
+ "revision": null,
+ "inference_mode": false,
+ "r": 64,
+ "target_modules": [
+ "v_proj",
+ "q_proj"
+ ],
+ "exclude_modules": null,
+ "lora_alpha": 64,
+ "lora_dropout": 0.0,
+ "fan_in_fan_out": false,
+ "bias": "none",
+ "use_rslora": true,
+ "modules_to_save": null,
+ "init_lora_weights": true,
+ "layers_to_transform": null,
+ "layers_pattern": null,
+ "rank_pattern": {},
+ "alpha_pattern": {},
+ "megatron_config": null,
+ "megatron_core": "megatron.core",
+ "trainable_token_indices": null,
+ "loftq_config": {},
+ "eva_config": null,
+ "corda_config": null,
+ "use_dora": false,
+ "layer_replication": null,
+ "lora_bias": false
+ },
+ "error_msg": ""
+ },
+ "train_info": {
+ "accelerator_memory_reserved_avg": 12128059444,
+ "accelerator_memory_max": 22538092544,
+ "accelerator_memory_reserved_99th": 17953927987,
+ "train_time": 1871.457509397991,
+ "file_size": 73415408,
+ "num_trainable_params": 18350080,
+ "num_total_params": 3231099904,
+ "status": "success",
+ "metrics": [
+ {
+ "step": 250,
+ "valid accuracy": 0.36,
+ "train loss": 0.8666043817996979,
+ "train samples": 1000,
+ "train time": 31.633613975991466,
+ "eval time": 11.220254406001914,
+ "tokens / sec": 6692.848947347132,
+ "mem allocated avg": 7072427177.984,
+ "mem reserved avg": 12177985503.232,
+ "elapsed time": 97.06891104899842
+ },
+ {
+ "step": 500,
+ "valid accuracy": 0.32,
+ "train loss": 0.697043846487999,
+ "train samples": 2000,
+ "train time": 31.400947067988454,
+ "eval time": 11.24747418500192,
+ "tokens / sec": 6623.844801548661,
+ "mem allocated avg": 7064966957.056,
+ "mem reserved avg": 12070787481.6,
+ "elapsed time": 188.02626212299947
+ },
+ {
+ "step": 750,
+ "valid accuracy": 0.38,
+ "train loss": 0.6723507121801376,
+ "train samples": 3000,
+ "train time": 31.849995732016396,
+ "eval time": 11.249978227999236,
+ "tokens / sec": 6731.586459350098,
+ "mem allocated avg": 7075822055.424,
+ "mem reserved avg": 12225037205.504,
+ "elapsed time": 280.16055655299715
+ },
+ {
+ "step": 1000,
+ "valid accuracy": 0.38,
+ "train loss": 0.6529685587882995,
+ "train samples": 4000,
+ "train time": 31.612207354013663,
+ "eval time": 11.24677863100078,
+ "tokens / sec": 6590.365477074112,
+ "mem allocated avg": 7066256992.256,
+ "mem reserved avg": 12092287483.904,
+ "elapsed time": 371.5183315869981
+ },
+ {
+ "step": 1250,
+ "valid accuracy": 0.38,
+ "train loss": 0.6472815409898758,
+ "train samples": 5000,
+ "train time": 31.26670297003875,
+ "eval time": 8.06907803500144,
+ "tokens / sec": 6669.651104557813,
+ "mem allocated avg": 7066435080.192,
+ "mem reserved avg": 12087824744.448,
+ "elapsed time": 459.33407214199906
+ },
+ {
+ "step": 1500,
+ "valid accuracy": 0.44,
+ "train loss": 0.6395461517572403,
+ "train samples": 6000,
+ "train time": 31.471468601008382,
+ "eval time": 6.4898526670003776,
+ "tokens / sec": 6651.4531830043925,
+ "mem allocated avg": 7067292080.128,
+ "mem reserved avg": 12121664389.12,
+ "elapsed time": 545.9371380269986
+ },
+ {
+ "step": 1750,
+ "valid accuracy": 0.5,
+ "train loss": 0.629749027967453,
+ "train samples": 7000,
+ "train time": 31.650018079009897,
+ "eval time": 11.247470542999508,
+ "tokens / sec": 6614.688164707337,
+ "mem allocated avg": 7069213276.16,
+ "mem reserved avg": 12130329821.184,
+ "elapsed time": 637.2524904149977
+ },
+ {
+ "step": 2000,
+ "valid accuracy": 0.4,
+ "train loss": 0.6293291836977005,
+ "train samples": 8000,
+ "train time": 31.45956211398152,
+ "eval time": 11.187045163998846,
+ "tokens / sec": 6601.999075749819,
+ "mem allocated avg": 7066587928.576,
+ "mem reserved avg": 12076634341.376,
+ "elapsed time": 728.2233991199973
+ },
+ {
+ "step": 2250,
+ "valid accuracy": 0.4,
+ "train loss": 0.6171289530992508,
+ "train samples": 9000,
+ "train time": 31.87981533700804,
+ "eval time": 6.866186073002609,
+ "tokens / sec": 6742.448089104055,
+ "mem allocated avg": 7077788481.536,
+ "mem reserved avg": 12265227026.432,
+ "elapsed time": 815.9717469499992
+ },
+ {
+ "step": 2500,
+ "valid accuracy": 0.44,
+ "train loss": 0.6119417071342468,
+ "train samples": 10000,
+ "train time": 31.067599171023176,
+ "eval time": 10.55572699700133,
+ "tokens / sec": 6629.640058962326,
+ "mem allocated avg": 7062992943.104,
+ "mem reserved avg": 12015850487.808,
+ "elapsed time": 905.6140671029971
+ },
+ {
+ "step": 2750,
+ "valid accuracy": 0.48,
+ "train loss": 0.5985908216238022,
+ "train samples": 11000,
+ "train time": 31.864849751029396,
+ "eval time": 6.1964339680016565,
+ "tokens / sec": 6649.364477017663,
+ "mem allocated avg": 7072847513.6,
+ "mem reserved avg": 12192229359.616,
+ "elapsed time": 992.5055643979977
+ },
+ {
+ "step": 3000,
+ "valid accuracy": 0.48,
+ "train loss": 0.5865949945449829,
+ "train samples": 12000,
+ "train time": 31.337576934987737,
+ "eval time": 7.105518241998652,
+ "tokens / sec": 6660.725570232467,
+ "mem allocated avg": 7068560369.664,
+ "mem reserved avg": 12111589670.912,
+ "elapsed time": 1079.4884613180002
+ },
+ {
+ "step": 3250,
+ "valid accuracy": 0.56,
+ "train loss": 0.5926763614416123,
+ "train samples": 13000,
+ "train time": 31.477448584984813,
+ "eval time": 11.220603736997873,
+ "tokens / sec": 6700.066539084199,
+ "mem allocated avg": 7070318487.552,
+ "mem reserved avg": 12143046950.912,
+ "elapsed time": 1171.2174267509981
+ },
+ {
+ "step": 3500,
+ "valid accuracy": 0.54,
+ "train loss": 0.5736529529094696,
+ "train samples": 14000,
+ "train time": 31.59231336902303,
+ "eval time": 11.215632880001067,
+ "tokens / sec": 6639.273216556042,
+ "mem allocated avg": 7068978995.2,
+ "mem reserved avg": 12124969500.672,
+ "elapsed time": 1263.2709914519983
+ },
+ {
+ "step": 3750,
+ "valid accuracy": 0.54,
+ "train loss": 0.5691816571950913,
+ "train samples": 15000,
+ "train time": 31.92663248500321,
+ "eval time": 6.89942428699942,
+ "tokens / sec": 6787.530758271833,
+ "mem allocated avg": 7079011248.128,
+ "mem reserved avg": 12298890510.336,
+ "elapsed time": 1351.894684084
+ },
+ {
+ "step": 4000,
+ "valid accuracy": 0.56,
+ "train loss": 0.5762648656368256,
+ "train samples": 16000,
+ "train time": 31.08475098094641,
+ "eval time": 6.668889390999539,
+ "tokens / sec": 6574.7028221416895,
+ "mem allocated avg": 7061224237.056,
+ "mem reserved avg": 12000969097.216,
+ "elapsed time": 1437.9300296759975
+ },
+ {
+ "step": 4250,
+ "valid accuracy": 0.52,
+ "train loss": 0.562865238904953,
+ "train samples": 17000,
+ "train time": 31.594970259979164,
+ "eval time": 11.218020562002494,
+ "tokens / sec": 6690.590250935068,
+ "mem allocated avg": 7071853715.456,
+ "mem reserved avg": 12157852844.032,
+ "elapsed time": 1529.7590418299988
+ },
+ {
+ "step": 4500,
+ "valid accuracy": 0.5,
+ "train loss": 0.568256908416748,
+ "train samples": 18000,
+ "train time": 31.334908029966755,
+ "eval time": 11.24515695700029,
+ "tokens / sec": 6632.156054240077,
+ "mem allocated avg": 7066128418.816,
+ "mem reserved avg": 12073245343.744,
+ "elapsed time": 1620.988001589998
+ },
+ {
+ "step": 4750,
+ "valid accuracy": 0.52,
+ "train loss": 0.5585172891616821,
+ "train samples": 19000,
+ "train time": 31.425996138961636,
+ "eval time": 11.202903266999783,
+ "tokens / sec": 6680.4246736261675,
+ "mem allocated avg": 7068498065.408,
+ "mem reserved avg": 12124491350.016,
+ "elapsed time": 1712.544705993998
+ },
+ {
+ "step": 5000,
+ "valid accuracy": 0.52,
+ "train loss": 0.5657225311994553,
+ "train samples": 20000,
+ "train time": 31.088545892969705,
+ "eval time": 11.224285021999094,
+ "tokens / sec": 6699.573557317776,
+ "mem allocated avg": 7064964919.296,
+ "mem reserved avg": 12070275776.512,
+ "elapsed time": 1803.3861051699969
+ },
+ {
+ "step": 5000,
+ "test accuracy": 0.5299469294920395,
+ "train loss": 0.5657225311994553,
+ "train samples": 20000,
+ "train total tokens": 4198051
+ }
+ ]
+ },
+ "meta_info": {
+ "model_info": {
+ "sha": "13afe5124825b4f3751f836b40dafda64c1ed062",
+ "created_at": "2024-09-18T15:23:48+00:00"
+ },
+ "dataset_info": {
+ "metamath": {
+ "sha": "aa4f34d3d2d3231299b5b03d9b3e5a20da45aa18",
+ "created_at": "2023-09-21T17:22:46+00:00"
+ },
+ "gsm8k": {
+ "sha": "e53f048856ff4f594e959d75785d2c2d37b678ee",
+ "created_at": "2022-04-12T10:22:10+00:00"
+ }
+ },
+ "package_info": {
+ "transformers-version": "4.52.4",
+ "transformers-commit-hash": null,
+ "peft-version": "0.15.2.dev0",
+ "peft-commit-hash": "5fe7f8f8abe914d313fc3751f2ea92de7718fbaf",
+ "datasets-version": "3.6.0",
+ "datasets-commit-hash": null,
+ "bitsandbytes-version": "0.46.0",
+ "bitsandbytes-commit-hash": null,
+ "torch-version": "2.7.1+cu126",
+ "torch-commit-hash": null
+ },
+ "system_info": {
+ "system": "Linux",
+ "release": "6.8.0-1029-aws",
+ "version": "#31-Ubuntu SMP Wed Apr 23 18:42:41 UTC 2025",
+ "machine": "x86_64",
+ "processor": "x86_64",
+ "accelerator": "NVIDIA L40S"
+ },
+ "pytorch_info": "PyTorch built with:\n - GCC 11.2\n - C++ Version: 201703\n - Intel(R) oneAPI Math Kernel Library Version 2024.2-Product Build 20240605 for Intel(R) 64 architecture applications\n - Intel(R) MKL-DNN v3.7.1 (Git Hash 8d263e693366ef8db40acc569cc7d8edf644556d)\n - OpenMP 201511 (a.k.a. OpenMP 4.5)\n - LAPACK is enabled (usually provided by MKL)\n - NNPACK is enabled\n - CPU capability usage: AVX2\n - CUDA Runtime 12.6\n - NVCC architecture flags: -gencode;arch=compute_50,code=sm_50;-gencode;arch=compute_60,code=sm_60;-gencode;arch=compute_70,code=sm_70;-gencode;arch=compute_75,code=sm_75;-gencode;arch=compute_80,code=sm_80;-gencode;arch=compute_86,code=sm_86;-gencode;arch=compute_90,code=sm_90\n - CuDNN 90.7.1 (built against CUDA 12.8)\n - Built with CuDNN 90.5.1\n - Magma 2.6.1\n - Build settings: BLAS_INFO=mkl, BUILD_TYPE=Release, COMMIT_SHA=e2d141dbde55c2a4370fac5165b0561b6af4798b, CUDA_VERSION=12.6, CUDNN_VERSION=9.5.1, CXX_COMPILER=/opt/rh/gcc-toolset-11/root/usr/bin/c++, CXX_FLAGS= -D_GLIBCXX_USE_CXX11_ABI=1 -fvisibility-inlines-hidden -DUSE_PTHREADPOOL -DNDEBUG -DUSE_KINETO -DLIBKINETO_NOROCTRACER -DLIBKINETO_NOXPUPTI=ON -DUSE_FBGEMM -DUSE_PYTORCH_QNNPACK -DUSE_XNNPACK -DSYMBOLICATE_MOBILE_DEBUG_HANDLE -O2 -fPIC -Wall -Wextra -Werror=return-type -Werror=non-virtual-dtor -Werror=range-loop-construct -Werror=bool-operation -Wnarrowing -Wno-missing-field-initializers -Wno-unknown-pragmas -Wno-unused-parameter -Wno-strict-overflow -Wno-strict-aliasing -Wno-stringop-overflow -Wsuggest-override -Wno-psabi -Wno-error=old-style-cast -fdiagnostics-color=always -faligned-new -Wno-maybe-uninitialized -fno-math-errno -fno-trapping-math -Werror=format -Wno-stringop-overflow, LAPACK_INFO=mkl, PERF_WITH_AVX=1, PERF_WITH_AVX2=1, TORCH_VERSION=2.7.1, USE_CUDA=ON, USE_CUDNN=ON, USE_CUSPARSELT=1, USE_GFLAGS=OFF, USE_GLOG=OFF, USE_GLOO=ON, USE_MKL=ON, USE_MKLDNN=ON, USE_MPI=OFF, USE_NCCL=1, USE_NNPACK=ON, USE_OPENMP=ON, USE_ROCM=OFF, USE_ROCM_KERNEL_ASSERT=OFF, \n"
+ }
+}
diff --git a/peft/method_comparison/MetaMathQA/results/lora--llama-3.2-3B-rank64.json b/peft/method_comparison/MetaMathQA/results/lora--llama-3.2-3B-rank64.json
new file mode 100644
index 0000000000000000000000000000000000000000..5dd3d50954761111762cc831de93cf4f76995044
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/results/lora--llama-3.2-3B-rank64.json
@@ -0,0 +1,365 @@
+{
+ "run_info": {
+ "created_at": "2025-06-19T16:55:20+00:00",
+ "total_time": 2017.2277705579982,
+ "experiment_name": "lora/llama-3.2-3B-rank64",
+ "peft_branch": "main",
+ "train_config": {
+ "model_id": "meta-llama/Llama-3.2-3B",
+ "dtype": "bfloat16",
+ "max_seq_length": 768,
+ "batch_size": 4,
+ "batch_size_eval": 50,
+ "max_steps": 5000,
+ "eval_steps": 250,
+ "compile": false,
+ "query_template": "Question: {query} Think step by step.\nAnswer:",
+ "seed": 0,
+ "grad_norm_clip": 1.0,
+ "optimizer_type": "AdamW",
+ "optimizer_kwargs": {
+ "lr": 0.0001,
+ "weight_decay": 0.1
+ },
+ "lr_scheduler": "cosine",
+ "use_amp": false,
+ "autocast_adapter_dtype": true,
+ "generation_kwargs": {
+ "max_length": 800,
+ "max_new_tokens": 300
+ },
+ "attn_implementation": null
+ },
+ "peft_config": {
+ "task_type": "CAUSAL_LM",
+ "peft_type": "LORA",
+ "auto_mapping": null,
+ "base_model_name_or_path": "meta-llama/Llama-3.2-3B",
+ "revision": null,
+ "inference_mode": false,
+ "r": 64,
+ "target_modules": [
+ "q_proj",
+ "v_proj"
+ ],
+ "exclude_modules": null,
+ "lora_alpha": 128,
+ "lora_dropout": 0.0,
+ "fan_in_fan_out": false,
+ "bias": "none",
+ "use_rslora": false,
+ "modules_to_save": null,
+ "init_lora_weights": true,
+ "layers_to_transform": null,
+ "layers_pattern": null,
+ "rank_pattern": {},
+ "alpha_pattern": {},
+ "megatron_config": null,
+ "megatron_core": "megatron.core",
+ "trainable_token_indices": null,
+ "loftq_config": {},
+ "eva_config": null,
+ "corda_config": null,
+ "use_dora": false,
+ "layer_replication": null,
+ "lora_bias": false
+ },
+ "error_msg": ""
+ },
+ "train_info": {
+ "accelerator_memory_reserved_avg": 12128055669,
+ "accelerator_memory_max": 22540189696,
+ "accelerator_memory_reserved_99th": 17953927987,
+ "train_time": 1853.4967184819961,
+ "file_size": 73415408,
+ "num_trainable_params": 18350080,
+ "num_total_params": 3231099904,
+ "status": "success",
+ "metrics": [
+ {
+ "step": 250,
+ "valid accuracy": 0.38,
+ "train loss": 0.9425119986534118,
+ "train samples": 1000,
+ "train time": 31.823601707994385,
+ "eval time": 11.233909951999522,
+ "tokens / sec": 6652.892464614218,
+ "mem allocated avg": 7072427177.984,
+ "mem reserved avg": 12177985503.232,
+ "elapsed time": 97.04379223199976
+ },
+ {
+ "step": 500,
+ "valid accuracy": 0.4,
+ "train loss": 0.7080548154115677,
+ "train samples": 2000,
+ "train time": 31.45184341498316,
+ "eval time": 8.232533225000225,
+ "tokens / sec": 6613.125890767804,
+ "mem allocated avg": 7065105152.0,
+ "mem reserved avg": 12072179990.528,
+ "elapsed time": 184.765658884
+ },
+ {
+ "step": 750,
+ "valid accuracy": 0.48,
+ "train loss": 0.6735224899053573,
+ "train samples": 3000,
+ "train time": 31.813968455000577,
+ "eval time": 7.057446101998721,
+ "tokens / sec": 6739.20954888921,
+ "mem allocated avg": 7075631579.136,
+ "mem reserved avg": 12224064126.976,
+ "elapsed time": 272.18349517599927
+ },
+ {
+ "step": 1000,
+ "valid accuracy": 0.38,
+ "train loss": 0.6520720717906952,
+ "train samples": 4000,
+ "train time": 31.539530114994704,
+ "eval time": 6.8677342959999805,
+ "tokens / sec": 6605.551802464924,
+ "mem allocated avg": 7066230261.76,
+ "mem reserved avg": 12094502076.416,
+ "elapsed time": 358.6604399049993
+ },
+ {
+ "step": 1250,
+ "valid accuracy": 0.32,
+ "train loss": 0.6483409875631332,
+ "train samples": 5000,
+ "train time": 31.15382274799049,
+ "eval time": 6.63156994000019,
+ "tokens / sec": 6693.817374737786,
+ "mem allocated avg": 7066402795.52,
+ "mem reserved avg": 12090886586.368,
+ "elapsed time": 444.47985113600043
+ },
+ {
+ "step": 1500,
+ "valid accuracy": 0.44,
+ "train loss": 0.6400664356946946,
+ "train samples": 6000,
+ "train time": 31.237405868998394,
+ "eval time": 6.19883855199987,
+ "tokens / sec": 6701.292702661678,
+ "mem allocated avg": 7067143219.2,
+ "mem reserved avg": 12125288267.776,
+ "elapsed time": 529.970450933999
+ },
+ {
+ "step": 1750,
+ "valid accuracy": 0.42,
+ "train loss": 0.6309183040857315,
+ "train samples": 7000,
+ "train time": 31.58418034899296,
+ "eval time": 11.217398733000664,
+ "tokens / sec": 6628.476588175104,
+ "mem allocated avg": 7069430339.584,
+ "mem reserved avg": 12128735985.664,
+ "elapsed time": 620.7944932609989
+ },
+ {
+ "step": 2000,
+ "valid accuracy": 0.38,
+ "train loss": 0.6333342634439468,
+ "train samples": 8000,
+ "train time": 31.370570010996744,
+ "eval time": 11.2056582969999,
+ "tokens / sec": 6620.727641454827,
+ "mem allocated avg": 7066754975.744,
+ "mem reserved avg": 12075980029.952,
+ "elapsed time": 711.143019907
+ },
+ {
+ "step": 2250,
+ "valid accuracy": 0.42,
+ "train loss": 0.6244297958612443,
+ "train samples": 9000,
+ "train time": 32.090800706988375,
+ "eval time": 6.320641570999214,
+ "tokens / sec": 6698.118939524966,
+ "mem allocated avg": 7077559773.184,
+ "mem reserved avg": 12266535649.28,
+ "elapsed time": 798.2718276069991
+ },
+ {
+ "step": 2500,
+ "valid accuracy": 0.48,
+ "train loss": 0.6205919095277787,
+ "train samples": 10000,
+ "train time": 31.211024427002485,
+ "eval time": 7.8215817759992206,
+ "tokens / sec": 6599.1746115775,
+ "mem allocated avg": 7063100512.256,
+ "mem reserved avg": 12017771479.04,
+ "elapsed time": 885.0132823740005
+ },
+ {
+ "step": 2750,
+ "valid accuracy": 0.38,
+ "train loss": 0.6116842222213745,
+ "train samples": 11000,
+ "train time": 31.752687646014238,
+ "eval time": 11.215984603999459,
+ "tokens / sec": 6672.852464084136,
+ "mem allocated avg": 7072850802.688,
+ "mem reserved avg": 12190207705.088,
+ "elapsed time": 976.3748101059991
+ },
+ {
+ "step": 3000,
+ "valid accuracy": 0.48,
+ "train loss": 0.6028307398557663,
+ "train samples": 12000,
+ "train time": 31.220882691013685,
+ "eval time": 10.851913497001078,
+ "tokens / sec": 6685.621353687066,
+ "mem allocated avg": 7068516059.136,
+ "mem reserved avg": 12110624980.992,
+ "elapsed time": 1066.2028727340003
+ },
+ {
+ "step": 3250,
+ "valid accuracy": 0.54,
+ "train loss": 0.6109937611818314,
+ "train samples": 13000,
+ "train time": 31.23074521200033,
+ "eval time": 6.857214526000462,
+ "tokens / sec": 6752.992878279506,
+ "mem allocated avg": 7070265374.72,
+ "mem reserved avg": 12142795292.672,
+ "elapsed time": 1152.2392765660006
+ },
+ {
+ "step": 3500,
+ "valid accuracy": 0.54,
+ "train loss": 0.5937278937101365,
+ "train samples": 14000,
+ "train time": 31.52822203695905,
+ "eval time": 6.510061502001918,
+ "tokens / sec": 6652.7696916787745,
+ "mem allocated avg": 7069306679.296,
+ "mem reserved avg": 12124390686.72,
+ "elapsed time": 1238.6433643029995
+ },
+ {
+ "step": 3750,
+ "valid accuracy": 0.6,
+ "train loss": 0.5906780579090118,
+ "train samples": 15000,
+ "train time": 32.31397023300451,
+ "eval time": 8.545268227000633,
+ "tokens / sec": 6706.170688325575,
+ "mem allocated avg": 7078981097.472,
+ "mem reserved avg": 12299846811.648,
+ "elapsed time": 1328.641089326
+ },
+ {
+ "step": 4000,
+ "valid accuracy": 0.52,
+ "train loss": 0.6025177363157272,
+ "train samples": 16000,
+ "train time": 31.170676869962335,
+ "eval time": 6.8420828330017684,
+ "tokens / sec": 6556.57882735759,
+ "mem allocated avg": 7061331572.736,
+ "mem reserved avg": 12001287864.32,
+ "elapsed time": 1414.365250592
+ },
+ {
+ "step": 4250,
+ "valid accuracy": 0.54,
+ "train loss": 0.5884622411727906,
+ "train samples": 17000,
+ "train time": 31.543792515007226,
+ "eval time": 6.748535185997753,
+ "tokens / sec": 6701.445297024126,
+ "mem allocated avg": 7071957172.224,
+ "mem reserved avg": 12155780857.856,
+ "elapsed time": 1500.9030026039982
+ },
+ {
+ "step": 4500,
+ "valid accuracy": 0.54,
+ "train loss": 0.5941844927072525,
+ "train samples": 18000,
+ "train time": 31.45958714898734,
+ "eval time": 6.4977734870008135,
+ "tokens / sec": 6605.871813123572,
+ "mem allocated avg": 7066011588.608,
+ "mem reserved avg": 12069847957.504,
+ "elapsed time": 1586.8870083309994
+ },
+ {
+ "step": 4750,
+ "valid accuracy": 0.56,
+ "train loss": 0.5860341912508011,
+ "train samples": 19000,
+ "train time": 31.656771414985997,
+ "eval time": 6.746858504000556,
+ "tokens / sec": 6631.724923806254,
+ "mem allocated avg": 7068472178.688,
+ "mem reserved avg": 12124852060.16,
+ "elapsed time": 1673.7380427649987
+ },
+ {
+ "step": 5000,
+ "valid accuracy": 0.58,
+ "train loss": 0.5928755496740341,
+ "train samples": 20000,
+ "train time": 31.260896800042246,
+ "eval time": 6.4877336810022825,
+ "tokens / sec": 6662.636754545011,
+ "mem allocated avg": 7065262428.16,
+ "mem reserved avg": 12067549478.912,
+ "elapsed time": 1759.6036715839982
+ },
+ {
+ "step": 5000,
+ "test accuracy": 0.4890068233510235,
+ "train loss": 0.5928755496740341,
+ "train samples": 20000,
+ "train total tokens": 4198051
+ }
+ ]
+ },
+ "meta_info": {
+ "model_info": {
+ "sha": "13afe5124825b4f3751f836b40dafda64c1ed062",
+ "created_at": "2024-09-18T15:23:48+00:00"
+ },
+ "dataset_info": {
+ "metamath": {
+ "sha": "aa4f34d3d2d3231299b5b03d9b3e5a20da45aa18",
+ "created_at": "2023-09-21T17:22:46+00:00"
+ },
+ "gsm8k": {
+ "sha": "e53f048856ff4f594e959d75785d2c2d37b678ee",
+ "created_at": "2022-04-12T10:22:10+00:00"
+ }
+ },
+ "package_info": {
+ "transformers-version": "4.52.4",
+ "transformers-commit-hash": null,
+ "peft-version": "0.15.2.dev0",
+ "peft-commit-hash": "5fe7f8f8abe914d313fc3751f2ea92de7718fbaf",
+ "datasets-version": "3.6.0",
+ "datasets-commit-hash": null,
+ "bitsandbytes-version": "0.46.0",
+ "bitsandbytes-commit-hash": null,
+ "torch-version": "2.7.1+cu126",
+ "torch-commit-hash": null
+ },
+ "system_info": {
+ "system": "Linux",
+ "release": "6.8.0-1029-aws",
+ "version": "#31-Ubuntu SMP Wed Apr 23 18:42:41 UTC 2025",
+ "machine": "x86_64",
+ "processor": "x86_64",
+ "accelerator": "NVIDIA L40S"
+ },
+ "pytorch_info": "PyTorch built with:\n - GCC 11.2\n - C++ Version: 201703\n - Intel(R) oneAPI Math Kernel Library Version 2024.2-Product Build 20240605 for Intel(R) 64 architecture applications\n - Intel(R) MKL-DNN v3.7.1 (Git Hash 8d263e693366ef8db40acc569cc7d8edf644556d)\n - OpenMP 201511 (a.k.a. OpenMP 4.5)\n - LAPACK is enabled (usually provided by MKL)\n - NNPACK is enabled\n - CPU capability usage: AVX2\n - CUDA Runtime 12.6\n - NVCC architecture flags: -gencode;arch=compute_50,code=sm_50;-gencode;arch=compute_60,code=sm_60;-gencode;arch=compute_70,code=sm_70;-gencode;arch=compute_75,code=sm_75;-gencode;arch=compute_80,code=sm_80;-gencode;arch=compute_86,code=sm_86;-gencode;arch=compute_90,code=sm_90\n - CuDNN 90.7.1 (built against CUDA 12.8)\n - Built with CuDNN 90.5.1\n - Magma 2.6.1\n - Build settings: BLAS_INFO=mkl, BUILD_TYPE=Release, COMMIT_SHA=e2d141dbde55c2a4370fac5165b0561b6af4798b, CUDA_VERSION=12.6, CUDNN_VERSION=9.5.1, CXX_COMPILER=/opt/rh/gcc-toolset-11/root/usr/bin/c++, CXX_FLAGS= -D_GLIBCXX_USE_CXX11_ABI=1 -fvisibility-inlines-hidden -DUSE_PTHREADPOOL -DNDEBUG -DUSE_KINETO -DLIBKINETO_NOROCTRACER -DLIBKINETO_NOXPUPTI=ON -DUSE_FBGEMM -DUSE_PYTORCH_QNNPACK -DUSE_XNNPACK -DSYMBOLICATE_MOBILE_DEBUG_HANDLE -O2 -fPIC -Wall -Wextra -Werror=return-type -Werror=non-virtual-dtor -Werror=range-loop-construct -Werror=bool-operation -Wnarrowing -Wno-missing-field-initializers -Wno-unknown-pragmas -Wno-unused-parameter -Wno-strict-overflow -Wno-strict-aliasing -Wno-stringop-overflow -Wsuggest-override -Wno-psabi -Wno-error=old-style-cast -fdiagnostics-color=always -faligned-new -Wno-maybe-uninitialized -fno-math-errno -fno-trapping-math -Werror=format -Wno-stringop-overflow, LAPACK_INFO=mkl, PERF_WITH_AVX=1, PERF_WITH_AVX2=1, TORCH_VERSION=2.7.1, USE_CUDA=ON, USE_CUDNN=ON, USE_CUSPARSELT=1, USE_GFLAGS=OFF, USE_GLOG=OFF, USE_GLOO=ON, USE_MKL=ON, USE_MKLDNN=ON, USE_MPI=OFF, USE_NCCL=1, USE_NNPACK=ON, USE_OPENMP=ON, USE_ROCM=OFF, USE_ROCM_KERNEL_ASSERT=OFF, \n"
+ }
+}
diff --git a/peft/method_comparison/MetaMathQA/results/miss--llama-3.2-3B-bat.json b/peft/method_comparison/MetaMathQA/results/miss--llama-3.2-3B-bat.json
new file mode 100644
index 0000000000000000000000000000000000000000..fc788b3e6208118bac0eec843b00fdec8b96288b
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/results/miss--llama-3.2-3B-bat.json
@@ -0,0 +1,352 @@
+{
+ "run_info": {
+ "created_at": "2025-08-14T11:55:49+00:00",
+ "total_time": 2808.721444314,
+ "experiment_name": "miss/llama-3.2-3B-bat",
+ "peft_branch": "main",
+ "train_config": {
+ "model_id": "meta-llama/Llama-3.2-3B",
+ "dtype": "bfloat16",
+ "max_seq_length": 768,
+ "batch_size": 4,
+ "batch_size_eval": 50,
+ "max_steps": 5000,
+ "eval_steps": 250,
+ "compile": false,
+ "query_template": "Question: {query} Think step by step.\nAnswer:",
+ "seed": 0,
+ "grad_norm_clip": 1.0,
+ "optimizer_type": "AdamW",
+ "optimizer_kwargs": {
+ "lr": 0.0001,
+ "weight_decay": 0.1
+ },
+ "lr_scheduler": "cosine",
+ "use_amp": false,
+ "autocast_adapter_dtype": true,
+ "generation_kwargs": {
+ "max_length": 800,
+ "max_new_tokens": 300
+ },
+ "attn_implementation": null
+ },
+ "peft_config": {
+ "task_type": null,
+ "peft_type": "MISS",
+ "auto_mapping": null,
+ "base_model_name_or_path": "meta-llama/Llama-3.2-3B",
+ "revision": null,
+ "inference_mode": false,
+ "r": 64,
+ "miss_dropout": 0.0,
+ "mini_r": 1,
+ "target_modules": [
+ "v_proj",
+ "q_proj"
+ ],
+ "exclude_modules": null,
+ "init_weights": "bat",
+ "layers_to_transform": null,
+ "layers_pattern": null,
+ "bias": "none",
+ "modules_to_save": null
+ },
+ "error_msg": ""
+ },
+ "train_info": {
+ "accelerator_memory_reserved_avg": 14713719934,
+ "accelerator_memory_max": 25251807232,
+ "accelerator_memory_reserved_99th": 20472733368,
+ "train_time": 2466.149786608999,
+ "file_size": 29367552,
+ "num_trainable_params": 7340032,
+ "num_total_params": 3220089856,
+ "status": "success",
+ "metrics": [
+ {
+ "step": 250,
+ "valid accuracy": 0.32,
+ "train loss": 0.8741402707099915,
+ "train samples": 1000,
+ "train time": 44.507981576001725,
+ "eval time": 16.603345405999903,
+ "tokens / sec": 4756.8771376088835,
+ "mem allocated avg": 6898417197.056,
+ "mem reserved avg": 14772422574.08,
+ "elapsed time": 128.87205576299993
+ },
+ {
+ "step": 500,
+ "valid accuracy": 0.42,
+ "train loss": 0.6949697629213333,
+ "train samples": 2000,
+ "train time": 43.6579733309992,
+ "eval time": 12.170993550999924,
+ "tokens / sec": 4764.192749467687,
+ "mem allocated avg": 6890132037.632,
+ "mem reserved avg": 14662515032.064,
+ "elapsed time": 244.05737383899998
+ },
+ {
+ "step": 750,
+ "valid accuracy": 0.38,
+ "train loss": 0.667268633723259,
+ "train samples": 3000,
+ "train time": 44.76929137299828,
+ "eval time": 8.243386759000032,
+ "tokens / sec": 4789.0192903368525,
+ "mem allocated avg": 6900972326.912,
+ "mem reserved avg": 14823525974.016,
+ "elapsed time": 357.2643382499999
+ },
+ {
+ "step": 1000,
+ "valid accuracy": 0.48,
+ "train loss": 0.6478440872430802,
+ "train samples": 4000,
+ "train time": 43.91589877199954,
+ "eval time": 9.950706549000074,
+ "tokens / sec": 4743.976687842116,
+ "mem allocated avg": 6892131758.08,
+ "mem reserved avg": 14678444998.656,
+ "elapsed time": 470.61746281599994
+ },
+ {
+ "step": 1250,
+ "valid accuracy": 0.4,
+ "train loss": 0.6435494017601013,
+ "train samples": 5000,
+ "train time": 44.14956537599949,
+ "eval time": 16.547810228000117,
+ "tokens / sec": 4723.444007296278,
+ "mem allocated avg": 6892566360.064,
+ "mem reserved avg": 14674737233.92,
+ "elapsed time": 591.057877963
+ },
+ {
+ "step": 1500,
+ "valid accuracy": 0.44,
+ "train loss": 0.6368351166248322,
+ "train samples": 6000,
+ "train time": 44.08414804900008,
+ "eval time": 16.39257521799982,
+ "tokens / sec": 4748.441543371237,
+ "mem allocated avg": 6893236697.088,
+ "mem reserved avg": 14706580389.888,
+ "elapsed time": 711.4482007859999
+ },
+ {
+ "step": 1750,
+ "valid accuracy": 0.48,
+ "train loss": 0.6278127529621125,
+ "train samples": 7000,
+ "train time": 44.35628801999951,
+ "eval time": 16.51757288099998,
+ "tokens / sec": 4719.849413584954,
+ "mem allocated avg": 6894834587.648,
+ "mem reserved avg": 14716881600.512,
+ "elapsed time": 832.303061434
+ },
+ {
+ "step": 2000,
+ "valid accuracy": 0.44,
+ "train loss": 0.6281237225532532,
+ "train samples": 8000,
+ "train time": 43.95804043099747,
+ "eval time": 16.465996583000106,
+ "tokens / sec": 4724.869397352412,
+ "mem allocated avg": 6891602710.528,
+ "mem reserved avg": 14655669927.936,
+ "elapsed time": 952.480474365
+ },
+ {
+ "step": 2250,
+ "valid accuracy": 0.42,
+ "train loss": 0.6159191156625747,
+ "train samples": 9000,
+ "train time": 44.99231110500091,
+ "eval time": 16.5404373570002,
+ "tokens / sec": 4777.4385160692145,
+ "mem allocated avg": 6903352731.648,
+ "mem reserved avg": 14850520514.56,
+ "elapsed time": 1074.326083797
+ },
+ {
+ "step": 2500,
+ "valid accuracy": 0.44,
+ "train loss": 0.6119081476926803,
+ "train samples": 10000,
+ "train time": 43.74939265700118,
+ "eval time": 16.33099729599985,
+ "tokens / sec": 4707.882498273705,
+ "mem allocated avg": 6887975004.16,
+ "mem reserved avg": 14597494931.456,
+ "elapsed time": 1194.094911997
+ },
+ {
+ "step": 2750,
+ "valid accuracy": 0.44,
+ "train loss": 0.6010881408452987,
+ "train samples": 11000,
+ "train time": 43.686495668999896,
+ "eval time": 11.229614545000004,
+ "tokens / sec": 4850.0342441142875,
+ "mem allocated avg": 6899207546.88,
+ "mem reserved avg": 14785391362.048,
+ "elapsed time": 1308.783695182
+ },
+ {
+ "step": 3000,
+ "valid accuracy": 0.5,
+ "train loss": 0.5899516706466674,
+ "train samples": 12000,
+ "train time": 43.49030302700089,
+ "eval time": 16.45857661900004,
+ "tokens / sec": 4799.483688821613,
+ "mem allocated avg": 6894123913.216,
+ "mem reserved avg": 14693427052.544,
+ "elapsed time": 1428.4006117669999
+ },
+ {
+ "step": 3250,
+ "valid accuracy": 0.52,
+ "train loss": 0.5989595657587051,
+ "train samples": 13000,
+ "train time": 44.46332806799887,
+ "eval time": 16.496417500999996,
+ "tokens / sec": 4743.257177633304,
+ "mem allocated avg": 6895596777.472,
+ "mem reserved avg": 14723995140.096,
+ "elapsed time": 1549.445265484
+ },
+ {
+ "step": 3500,
+ "valid accuracy": 0.46,
+ "train loss": 0.579978278040886,
+ "train samples": 14000,
+ "train time": 43.63575344299579,
+ "eval time": 10.30441635599982,
+ "tokens / sec": 4806.838050224342,
+ "mem allocated avg": 6893774680.064,
+ "mem reserved avg": 14699450073.088,
+ "elapsed time": 1663.316950223
+ },
+ {
+ "step": 3750,
+ "valid accuracy": 0.44,
+ "train loss": 0.5772325273752212,
+ "train samples": 15000,
+ "train time": 45.25726027099972,
+ "eval time": 16.524598716000128,
+ "tokens / sec": 4788.2483098266675,
+ "mem allocated avg": 6905177583.616,
+ "mem reserved avg": 14889795977.216,
+ "elapsed time": 1785.1977310290001
+ },
+ {
+ "step": 4000,
+ "valid accuracy": 0.4,
+ "train loss": 0.5859311088323593,
+ "train samples": 16000,
+ "train time": 43.383903580999686,
+ "eval time": 16.386461492000308,
+ "tokens / sec": 4710.802466597467,
+ "mem allocated avg": 6886734053.376,
+ "mem reserved avg": 14584660361.216,
+ "elapsed time": 1904.6209389110002
+ },
+ {
+ "step": 4250,
+ "valid accuracy": 0.5,
+ "train loss": 0.5724418247938157,
+ "train samples": 17000,
+ "train time": 44.42285394400233,
+ "eval time": 9.048803244000283,
+ "tokens / sec": 4758.564145078759,
+ "mem allocated avg": 6896789555.2,
+ "mem reserved avg": 14740688470.016,
+ "elapsed time": 2018.321323589
+ },
+ {
+ "step": 4500,
+ "valid accuracy": 0.46,
+ "train loss": 0.5792494393587112,
+ "train samples": 18000,
+ "train time": 43.636566284001674,
+ "eval time": 16.3964514889999,
+ "tokens / sec": 4762.4737163655245,
+ "mem allocated avg": 6892818855.936,
+ "mem reserved avg": 14655921586.176,
+ "elapsed time": 2137.859151554
+ },
+ {
+ "step": 4750,
+ "valid accuracy": 0.46,
+ "train loss": 0.5680228790044785,
+ "train samples": 19000,
+ "train time": 43.96985955700529,
+ "eval time": 16.500367100000403,
+ "tokens / sec": 4774.61156608476,
+ "mem allocated avg": 6894185185.28,
+ "mem reserved avg": 14706722996.224,
+ "elapsed time": 2258.0618387639997
+ },
+ {
+ "step": 5000,
+ "valid accuracy": 0.44,
+ "train loss": 0.5760680929422378,
+ "train samples": 20000,
+ "train time": 43.83249596400128,
+ "eval time": 16.474086973999874,
+ "tokens / sec": 4751.7257555001215,
+ "mem allocated avg": 6891346642.944,
+ "mem reserved avg": 14655552487.424,
+ "elapsed time": 2377.7959423069997
+ },
+ {
+ "step": 5000,
+ "test accuracy": 0.5049279757391963,
+ "train loss": 0.5760680929422378,
+ "train samples": 20000,
+ "train total tokens": 4198051
+ }
+ ]
+ },
+ "meta_info": {
+ "model_info": {
+ "sha": "13afe5124825b4f3751f836b40dafda64c1ed062",
+ "created_at": "2024-09-18T15:23:48+00:00"
+ },
+ "dataset_info": {
+ "metamath": {
+ "sha": "aa4f34d3d2d3231299b5b03d9b3e5a20da45aa18",
+ "created_at": "2023-09-21T17:22:46+00:00"
+ },
+ "gsm8k": {
+ "sha": "e53f048856ff4f594e959d75785d2c2d37b678ee",
+ "created_at": "2022-04-12T10:22:10+00:00"
+ }
+ },
+ "package_info": {
+ "transformers-version": "4.52.4",
+ "transformers-commit-hash": null,
+ "peft-version": "0.17.1.dev0",
+ "peft-commit-hash": "47961bb54706e45fd3b5460baa4921a48bcdce35",
+ "datasets-version": "3.6.0",
+ "datasets-commit-hash": null,
+ "bitsandbytes-version": "0.46.0",
+ "bitsandbytes-commit-hash": null,
+ "torch-version": "2.7.1+cu126",
+ "torch-commit-hash": null
+ },
+ "system_info": {
+ "system": "Linux",
+ "release": "6.14.0-1010-aws",
+ "version": "#10~24.04.1-Ubuntu SMP Fri Jul 18 20:44:30 UTC 2025",
+ "machine": "x86_64",
+ "processor": "x86_64",
+ "accelerator": "NVIDIA L40S"
+ },
+ "pytorch_info": "PyTorch built with:\n - GCC 11.2\n - C++ Version: 201703\n - Intel(R) oneAPI Math Kernel Library Version 2024.2-Product Build 20240605 for Intel(R) 64 architecture applications\n - Intel(R) MKL-DNN v3.7.1 (Git Hash 8d263e693366ef8db40acc569cc7d8edf644556d)\n - OpenMP 201511 (a.k.a. OpenMP 4.5)\n - LAPACK is enabled (usually provided by MKL)\n - NNPACK is enabled\n - CPU capability usage: AVX2\n - CUDA Runtime 12.6\n - NVCC architecture flags: -gencode;arch=compute_50,code=sm_50;-gencode;arch=compute_60,code=sm_60;-gencode;arch=compute_70,code=sm_70;-gencode;arch=compute_75,code=sm_75;-gencode;arch=compute_80,code=sm_80;-gencode;arch=compute_86,code=sm_86;-gencode;arch=compute_90,code=sm_90\n - CuDNN 90.7.1 (built against CUDA 12.8)\n - Built with CuDNN 90.5.1\n - Magma 2.6.1\n - Build settings: BLAS_INFO=mkl, BUILD_TYPE=Release, COMMIT_SHA=e2d141dbde55c2a4370fac5165b0561b6af4798b, CUDA_VERSION=12.6, CUDNN_VERSION=9.5.1, CXX_COMPILER=/opt/rh/gcc-toolset-11/root/usr/bin/c++, CXX_FLAGS= -D_GLIBCXX_USE_CXX11_ABI=1 -fvisibility-inlines-hidden -DUSE_PTHREADPOOL -DNDEBUG -DUSE_KINETO -DLIBKINETO_NOROCTRACER -DLIBKINETO_NOXPUPTI=ON -DUSE_FBGEMM -DUSE_PYTORCH_QNNPACK -DUSE_XNNPACK -DSYMBOLICATE_MOBILE_DEBUG_HANDLE -O2 -fPIC -Wall -Wextra -Werror=return-type -Werror=non-virtual-dtor -Werror=range-loop-construct -Werror=bool-operation -Wnarrowing -Wno-missing-field-initializers -Wno-unknown-pragmas -Wno-unused-parameter -Wno-strict-overflow -Wno-strict-aliasing -Wno-stringop-overflow -Wsuggest-override -Wno-psabi -Wno-error=old-style-cast -fdiagnostics-color=always -faligned-new -Wno-maybe-uninitialized -fno-math-errno -fno-trapping-math -Werror=format -Wno-stringop-overflow, LAPACK_INFO=mkl, PERF_WITH_AVX=1, PERF_WITH_AVX2=1, TORCH_VERSION=2.7.1, USE_CUDA=ON, USE_CUDNN=ON, USE_CUSPARSELT=1, USE_GFLAGS=OFF, USE_GLOG=OFF, USE_GLOO=ON, USE_MKL=ON, USE_MKLDNN=ON, USE_MPI=OFF, USE_NCCL=1, USE_NNPACK=ON, USE_OPENMP=ON, USE_ROCM=OFF, USE_ROCM_KERNEL_ASSERT=OFF, \n"
+ }
+}
\ No newline at end of file
diff --git a/peft/method_comparison/MetaMathQA/results/miss--llama-3.2-3B-default.json b/peft/method_comparison/MetaMathQA/results/miss--llama-3.2-3B-default.json
new file mode 100644
index 0000000000000000000000000000000000000000..89af4592383509c5f08d994cb24616421c056bf7
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/results/miss--llama-3.2-3B-default.json
@@ -0,0 +1,352 @@
+{
+ "run_info": {
+ "created_at": "2025-08-14T12:42:42+00:00",
+ "total_time": 1917.9635583239997,
+ "experiment_name": "miss/llama-3.2-3B-default",
+ "peft_branch": "main",
+ "train_config": {
+ "model_id": "meta-llama/Llama-3.2-3B",
+ "dtype": "bfloat16",
+ "max_seq_length": 768,
+ "batch_size": 4,
+ "batch_size_eval": 50,
+ "max_steps": 5000,
+ "eval_steps": 250,
+ "compile": false,
+ "query_template": "Question: {query} Think step by step.\nAnswer:",
+ "seed": 0,
+ "grad_norm_clip": 1.0,
+ "optimizer_type": "AdamW",
+ "optimizer_kwargs": {
+ "lr": 0.0001,
+ "weight_decay": 0.1
+ },
+ "lr_scheduler": "cosine",
+ "use_amp": false,
+ "autocast_adapter_dtype": true,
+ "generation_kwargs": {
+ "max_length": 800,
+ "max_new_tokens": 300
+ },
+ "attn_implementation": null
+ },
+ "peft_config": {
+ "task_type": null,
+ "peft_type": "MISS",
+ "auto_mapping": null,
+ "base_model_name_or_path": "meta-llama/Llama-3.2-3B",
+ "revision": null,
+ "inference_mode": false,
+ "r": 64,
+ "miss_dropout": 0.0,
+ "mini_r": 1,
+ "target_modules": [
+ "q_proj",
+ "v_proj"
+ ],
+ "exclude_modules": null,
+ "init_weights": true,
+ "layers_to_transform": null,
+ "layers_pattern": null,
+ "bias": "none",
+ "modules_to_save": null
+ },
+ "error_msg": ""
+ },
+ "train_info": {
+ "accelerator_memory_reserved_avg": 11170868939,
+ "accelerator_memory_max": 20248002560,
+ "accelerator_memory_reserved_99th": 16301393182,
+ "train_time": 1713.3205038909991,
+ "file_size": 29367496,
+ "num_trainable_params": 7340032,
+ "num_total_params": 3220089856,
+ "status": "success",
+ "metrics": [
+ {
+ "step": 250,
+ "valid accuracy": 0.36,
+ "train loss": 0.8771686832904816,
+ "train samples": 1000,
+ "train time": 29.625120898993828,
+ "eval time": 11.058316758999808,
+ "tokens / sec": 7146.603746254777,
+ "mem allocated avg": 6894354876.416,
+ "mem reserved avg": 11212691603.456,
+ "elapsed time": 89.49706801999992
+ },
+ {
+ "step": 500,
+ "valid accuracy": 0.42,
+ "train loss": 0.6949640859365463,
+ "train samples": 2000,
+ "train time": 29.06092399400177,
+ "eval time": 5.4939734129998214,
+ "tokens / sec": 7157.205326400859,
+ "mem allocated avg": 6887297284.096,
+ "mem reserved avg": 11116172279.808,
+ "elapsed time": 166.80778670399968
+ },
+ {
+ "step": 750,
+ "valid accuracy": 0.42,
+ "train loss": 0.6677889958620071,
+ "train samples": 3000,
+ "train time": 29.654036860997167,
+ "eval time": 6.225696284000151,
+ "tokens / sec": 7230.078016190556,
+ "mem allocated avg": 6897885888.512,
+ "mem reserved avg": 11257109282.816,
+ "elapsed time": 245.76960384799986
+ },
+ {
+ "step": 1000,
+ "valid accuracy": 0.38,
+ "train loss": 0.6483739440441132,
+ "train samples": 4000,
+ "train time": 28.837856293007462,
+ "eval time": 10.98694702900002,
+ "tokens / sec": 7224.392752470884,
+ "mem allocated avg": 6888501639.168,
+ "mem reserved avg": 11141564596.224,
+ "elapsed time": 328.02559429799976
+ },
+ {
+ "step": 1250,
+ "valid accuracy": 0.46,
+ "train loss": 0.6433384964466095,
+ "train samples": 5000,
+ "train time": 28.81160366599852,
+ "eval time": 7.707165779999741,
+ "tokens / sec": 7237.986556302045,
+ "mem allocated avg": 6888334700.544,
+ "mem reserved avg": 11139123511.296,
+ "elapsed time": 407.06604839199963
+ },
+ {
+ "step": 1500,
+ "valid accuracy": 0.5,
+ "train loss": 0.6369507477283478,
+ "train samples": 6000,
+ "train time": 28.99961056100119,
+ "eval time": 8.123675749000085,
+ "tokens / sec": 7218.407280320836,
+ "mem allocated avg": 6890289985.536,
+ "mem reserved avg": 11163484028.928,
+ "elapsed time": 486.7935630989996
+ },
+ {
+ "step": 1750,
+ "valid accuracy": 0.42,
+ "train loss": 0.6278414962291717,
+ "train samples": 7000,
+ "train time": 29.449354215004405,
+ "eval time": 11.046255440000095,
+ "tokens / sec": 7108.984410032798,
+ "mem allocated avg": 6891426932.736,
+ "mem reserved avg": 11175706230.784,
+ "elapsed time": 570.2098619899998
+ },
+ {
+ "step": 2000,
+ "valid accuracy": 0.42,
+ "train loss": 0.62835728931427,
+ "train samples": 8000,
+ "train time": 28.844003398995028,
+ "eval time": 11.063917559999936,
+ "tokens / sec": 7200.664801170994,
+ "mem allocated avg": 6888937164.8,
+ "mem reserved avg": 11125752070.144,
+ "elapsed time": 652.66749592
+ },
+ {
+ "step": 2250,
+ "valid accuracy": 0.46,
+ "train loss": 0.616273587346077,
+ "train samples": 9000,
+ "train time": 29.490800742004012,
+ "eval time": 8.136742810000214,
+ "tokens / sec": 7288.645767215389,
+ "mem allocated avg": 6899370121.216,
+ "mem reserved avg": 11286914007.04,
+ "elapsed time": 733.5518891469997
+ },
+ {
+ "step": 2500,
+ "valid accuracy": 0.48,
+ "train loss": 0.6127588752508163,
+ "train samples": 10000,
+ "train time": 28.812003271001686,
+ "eval time": 11.006928690999757,
+ "tokens / sec": 7148.652527306175,
+ "mem allocated avg": 6884932614.144,
+ "mem reserved avg": 11077299470.336,
+ "elapsed time": 815.9489541349999
+ },
+ {
+ "step": 2750,
+ "valid accuracy": 0.48,
+ "train loss": 0.6011098005771637,
+ "train samples": 11000,
+ "train time": 29.451534630989954,
+ "eval time": 11.065294603999973,
+ "tokens / sec": 7194.226129630993,
+ "mem allocated avg": 6895703631.872,
+ "mem reserved avg": 11229007446.016,
+ "elapsed time": 899.4794512619997
+ },
+ {
+ "step": 3000,
+ "valid accuracy": 0.5,
+ "train loss": 0.590887265920639,
+ "train samples": 12000,
+ "train time": 29.118879764002486,
+ "eval time": 11.043336514999282,
+ "tokens / sec": 7168.235924310477,
+ "mem allocated avg": 6890226739.2,
+ "mem reserved avg": 11156563427.328,
+ "elapsed time": 982.334967583
+ },
+ {
+ "step": 3250,
+ "valid accuracy": 0.52,
+ "train loss": 0.6000960898399353,
+ "train samples": 13000,
+ "train time": 29.13528394500463,
+ "eval time": 11.077541423999719,
+ "tokens / sec": 7238.680096548703,
+ "mem allocated avg": 6892138940.416,
+ "mem reserved avg": 11182651998.208,
+ "elapsed time": 1065.5038535119998
+ },
+ {
+ "step": 3500,
+ "valid accuracy": 0.46,
+ "train loss": 0.5813224712610244,
+ "train samples": 14000,
+ "train time": 29.210709365002003,
+ "eval time": 11.022432370000388,
+ "tokens / sec": 7180.585633134473,
+ "mem allocated avg": 6891394273.28,
+ "mem reserved avg": 11167116296.192,
+ "elapsed time": 1148.6551861069997
+ },
+ {
+ "step": 3750,
+ "valid accuracy": 0.5,
+ "train loss": 0.5779635999202728,
+ "train samples": 15000,
+ "train time": 29.93350169399855,
+ "eval time": 11.012248770000042,
+ "tokens / sec": 7239.48043951862,
+ "mem allocated avg": 6900874864.64,
+ "mem reserved avg": 11322674642.944,
+ "elapsed time": 1233.146194169
+ },
+ {
+ "step": 4000,
+ "valid accuracy": 0.5,
+ "train loss": 0.5870059201717377,
+ "train samples": 16000,
+ "train time": 28.73894150599881,
+ "eval time": 11.028763495000021,
+ "tokens / sec": 7111.361424266106,
+ "mem allocated avg": 6883623936.0,
+ "mem reserved avg": 11058022449.152,
+ "elapsed time": 1315.630321268
+ },
+ {
+ "step": 4250,
+ "valid accuracy": 0.48,
+ "train loss": 0.5732149496078491,
+ "train samples": 17000,
+ "train time": 29.274482168998475,
+ "eval time": 11.023004681000202,
+ "tokens / sec": 7220.930460175991,
+ "mem allocated avg": 6893432758.272,
+ "mem reserved avg": 11193867567.104,
+ "elapsed time": 1399.0288222240001
+ },
+ {
+ "step": 4500,
+ "valid accuracy": 0.48,
+ "train loss": 0.5802423723936081,
+ "train samples": 18000,
+ "train time": 28.807760504997532,
+ "eval time": 11.07264679400032,
+ "tokens / sec": 7213.958890138232,
+ "mem allocated avg": 6888416004.096,
+ "mem reserved avg": 11124485390.336,
+ "elapsed time": 1481.5334540769995
+ },
+ {
+ "step": 4750,
+ "valid accuracy": 0.52,
+ "train loss": 0.5696245921850205,
+ "train samples": 19000,
+ "train time": 29.20943511798214,
+ "eval time": 11.082792330000302,
+ "tokens / sec": 7187.369394581538,
+ "mem allocated avg": 6890813089.792,
+ "mem reserved avg": 11168844349.44,
+ "elapsed time": 1565.0750862589998
+ },
+ {
+ "step": 5000,
+ "valid accuracy": 0.5,
+ "train loss": 0.5774132673740386,
+ "train samples": 20000,
+ "train time": 29.084354959996745,
+ "eval time": 11.092419973000688,
+ "tokens / sec": 7161.238414483417,
+ "mem allocated avg": 6887869800.448,
+ "mem reserved avg": 11118328152.064,
+ "elapsed time": 1648.4280528519998
+ },
+ {
+ "step": 5000,
+ "test accuracy": 0.5087187263078089,
+ "train loss": 0.5774132673740386,
+ "train samples": 20000,
+ "train total tokens": 4198051
+ }
+ ]
+ },
+ "meta_info": {
+ "model_info": {
+ "sha": "13afe5124825b4f3751f836b40dafda64c1ed062",
+ "created_at": "2024-09-18T15:23:48+00:00"
+ },
+ "dataset_info": {
+ "metamath": {
+ "sha": "aa4f34d3d2d3231299b5b03d9b3e5a20da45aa18",
+ "created_at": "2023-09-21T17:22:46+00:00"
+ },
+ "gsm8k": {
+ "sha": "e53f048856ff4f594e959d75785d2c2d37b678ee",
+ "created_at": "2022-04-12T10:22:10+00:00"
+ }
+ },
+ "package_info": {
+ "transformers-version": "4.52.4",
+ "transformers-commit-hash": null,
+ "peft-version": "0.17.1.dev0",
+ "peft-commit-hash": "47961bb54706e45fd3b5460baa4921a48bcdce35",
+ "datasets-version": "3.6.0",
+ "datasets-commit-hash": null,
+ "bitsandbytes-version": "0.46.0",
+ "bitsandbytes-commit-hash": null,
+ "torch-version": "2.7.1+cu126",
+ "torch-commit-hash": null
+ },
+ "system_info": {
+ "system": "Linux",
+ "release": "6.14.0-1010-aws",
+ "version": "#10~24.04.1-Ubuntu SMP Fri Jul 18 20:44:30 UTC 2025",
+ "machine": "x86_64",
+ "processor": "x86_64",
+ "accelerator": "NVIDIA L40S"
+ },
+ "pytorch_info": "PyTorch built with:\n - GCC 11.2\n - C++ Version: 201703\n - Intel(R) oneAPI Math Kernel Library Version 2024.2-Product Build 20240605 for Intel(R) 64 architecture applications\n - Intel(R) MKL-DNN v3.7.1 (Git Hash 8d263e693366ef8db40acc569cc7d8edf644556d)\n - OpenMP 201511 (a.k.a. OpenMP 4.5)\n - LAPACK is enabled (usually provided by MKL)\n - NNPACK is enabled\n - CPU capability usage: AVX2\n - CUDA Runtime 12.6\n - NVCC architecture flags: -gencode;arch=compute_50,code=sm_50;-gencode;arch=compute_60,code=sm_60;-gencode;arch=compute_70,code=sm_70;-gencode;arch=compute_75,code=sm_75;-gencode;arch=compute_80,code=sm_80;-gencode;arch=compute_86,code=sm_86;-gencode;arch=compute_90,code=sm_90\n - CuDNN 90.7.1 (built against CUDA 12.8)\n - Built with CuDNN 90.5.1\n - Magma 2.6.1\n - Build settings: BLAS_INFO=mkl, BUILD_TYPE=Release, COMMIT_SHA=e2d141dbde55c2a4370fac5165b0561b6af4798b, CUDA_VERSION=12.6, CUDNN_VERSION=9.5.1, CXX_COMPILER=/opt/rh/gcc-toolset-11/root/usr/bin/c++, CXX_FLAGS= -D_GLIBCXX_USE_CXX11_ABI=1 -fvisibility-inlines-hidden -DUSE_PTHREADPOOL -DNDEBUG -DUSE_KINETO -DLIBKINETO_NOROCTRACER -DLIBKINETO_NOXPUPTI=ON -DUSE_FBGEMM -DUSE_PYTORCH_QNNPACK -DUSE_XNNPACK -DSYMBOLICATE_MOBILE_DEBUG_HANDLE -O2 -fPIC -Wall -Wextra -Werror=return-type -Werror=non-virtual-dtor -Werror=range-loop-construct -Werror=bool-operation -Wnarrowing -Wno-missing-field-initializers -Wno-unknown-pragmas -Wno-unused-parameter -Wno-strict-overflow -Wno-strict-aliasing -Wno-stringop-overflow -Wsuggest-override -Wno-psabi -Wno-error=old-style-cast -fdiagnostics-color=always -faligned-new -Wno-maybe-uninitialized -fno-math-errno -fno-trapping-math -Werror=format -Wno-stringop-overflow, LAPACK_INFO=mkl, PERF_WITH_AVX=1, PERF_WITH_AVX2=1, TORCH_VERSION=2.7.1, USE_CUDA=ON, USE_CUDNN=ON, USE_CUSPARSELT=1, USE_GFLAGS=OFF, USE_GLOG=OFF, USE_GLOO=ON, USE_MKL=ON, USE_MKLDNN=ON, USE_MPI=OFF, USE_NCCL=1, USE_NNPACK=ON, USE_OPENMP=ON, USE_ROCM=OFF, USE_ROCM_KERNEL_ASSERT=OFF, \n"
+ }
+}
\ No newline at end of file
diff --git a/peft/method_comparison/MetaMathQA/results/miss--llama-3.2-3B-mini.json b/peft/method_comparison/MetaMathQA/results/miss--llama-3.2-3B-mini.json
new file mode 100644
index 0000000000000000000000000000000000000000..66e5f975921692c2d4349a18e3d5975511344864
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/results/miss--llama-3.2-3B-mini.json
@@ -0,0 +1,352 @@
+{
+ "run_info": {
+ "created_at": "2025-08-14T13:14:44+00:00",
+ "total_time": 1939.2463944070005,
+ "experiment_name": "miss/llama-3.2-3B-mini",
+ "peft_branch": "main",
+ "train_config": {
+ "model_id": "meta-llama/Llama-3.2-3B",
+ "dtype": "bfloat16",
+ "max_seq_length": 768,
+ "batch_size": 4,
+ "batch_size_eval": 50,
+ "max_steps": 5000,
+ "eval_steps": 250,
+ "compile": false,
+ "query_template": "Question: {query} Think step by step.\nAnswer:",
+ "seed": 0,
+ "grad_norm_clip": 1.0,
+ "optimizer_type": "AdamW",
+ "optimizer_kwargs": {
+ "lr": 0.0001,
+ "weight_decay": 0.1
+ },
+ "lr_scheduler": "cosine",
+ "use_amp": false,
+ "autocast_adapter_dtype": true,
+ "generation_kwargs": {
+ "max_length": 800,
+ "max_new_tokens": 300
+ },
+ "attn_implementation": null
+ },
+ "peft_config": {
+ "task_type": null,
+ "peft_type": "MISS",
+ "auto_mapping": null,
+ "base_model_name_or_path": "meta-llama/Llama-3.2-3B",
+ "revision": null,
+ "inference_mode": false,
+ "r": 64,
+ "miss_dropout": 0.0,
+ "mini_r": 64,
+ "target_modules": [
+ "q_proj",
+ "v_proj"
+ ],
+ "exclude_modules": null,
+ "init_weights": "mini",
+ "layers_to_transform": null,
+ "layers_pattern": null,
+ "bias": "none",
+ "modules_to_save": null
+ },
+ "error_msg": ""
+ },
+ "train_info": {
+ "accelerator_memory_reserved_avg": 11076096963,
+ "accelerator_memory_max": 20189282304,
+ "accelerator_memory_reserved_99th": 16251103477,
+ "train_time": 1757.4722608399989,
+ "file_size": 924568,
+ "num_trainable_params": 229376,
+ "num_total_params": 3212979200,
+ "status": "success",
+ "metrics": [
+ {
+ "step": 250,
+ "valid accuracy": 0.34,
+ "train loss": 1.0204485692977905,
+ "train samples": 1000,
+ "train time": 30.37152520300151,
+ "eval time": 11.248587610999493,
+ "tokens / sec": 6970.970294869372,
+ "mem allocated avg": 6780477966.336,
+ "mem reserved avg": 11118412038.144,
+ "elapsed time": 90.66597219600044
+ },
+ {
+ "step": 500,
+ "valid accuracy": 0.34,
+ "train loss": 0.747962894320488,
+ "train samples": 2000,
+ "train time": 29.572977570002877,
+ "eval time": 11.171488900999975,
+ "tokens / sec": 7033.278928631729,
+ "mem allocated avg": 6773512382.464,
+ "mem reserved avg": 11022605746.176,
+ "elapsed time": 174.9062917200008
+ },
+ {
+ "step": 750,
+ "valid accuracy": 0.36,
+ "train loss": 0.7062408643960952,
+ "train samples": 3000,
+ "train time": 30.206997992999277,
+ "eval time": 8.297702855000352,
+ "tokens / sec": 7097.726164304351,
+ "mem allocated avg": 6784103079.936,
+ "mem reserved avg": 11160933892.096,
+ "elapsed time": 257.1565456070002
+ },
+ {
+ "step": 1000,
+ "valid accuracy": 0.42,
+ "train loss": 0.688418450832367,
+ "train samples": 4000,
+ "train time": 29.89673271099673,
+ "eval time": 8.431126997999854,
+ "tokens / sec": 6968.520674614356,
+ "mem allocated avg": 6774552799.232,
+ "mem reserved avg": 11046932709.376,
+ "elapsed time": 338.98425150300045
+ },
+ {
+ "step": 1250,
+ "valid accuracy": 0.26,
+ "train loss": 0.6864906589984894,
+ "train samples": 5000,
+ "train time": 29.511754502003896,
+ "eval time": 11.189089829000295,
+ "tokens / sec": 7066.269136450018,
+ "mem allocated avg": 6774476697.6,
+ "mem reserved avg": 11043107504.128,
+ "elapsed time": 423.2539680640002
+ },
+ {
+ "step": 1500,
+ "valid accuracy": 0.34,
+ "train loss": 0.6819815402030944,
+ "train samples": 6000,
+ "train time": 29.53373699200074,
+ "eval time": 10.82430943000054,
+ "tokens / sec": 7087.860234439605,
+ "mem allocated avg": 6776410671.104,
+ "mem reserved avg": 11066327171.072,
+ "elapsed time": 507.00703521000014
+ },
+ {
+ "step": 1750,
+ "valid accuracy": 0.24,
+ "train loss": 0.6748508417606354,
+ "train samples": 7000,
+ "train time": 29.92787808700814,
+ "eval time": 11.135467017999872,
+ "tokens / sec": 6995.317188587526,
+ "mem allocated avg": 6777799206.912,
+ "mem reserved avg": 11081728655.36,
+ "elapsed time": 591.3889150910009
+ },
+ {
+ "step": 2000,
+ "valid accuracy": 0.32,
+ "train loss": 0.6793494290113449,
+ "train samples": 8000,
+ "train time": 29.828631155996845,
+ "eval time": 7.671241181000369,
+ "tokens / sec": 6962.974563391727,
+ "mem allocated avg": 6775091949.568,
+ "mem reserved avg": 11030155493.376,
+ "elapsed time": 672.1807907450002
+ },
+ {
+ "step": 2250,
+ "valid accuracy": 0.36,
+ "train loss": 0.6712708432674408,
+ "train samples": 9000,
+ "train time": 30.12409129900061,
+ "eval time": 7.389505904999169,
+ "tokens / sec": 7135.418554754249,
+ "mem allocated avg": 6785428178.944,
+ "mem reserved avg": 11193422970.88,
+ "elapsed time": 753.4013944540002
+ },
+ {
+ "step": 2500,
+ "valid accuracy": 0.36,
+ "train loss": 0.670761358499527,
+ "train samples": 10000,
+ "train time": 29.392454811994867,
+ "eval time": 11.273840481000661,
+ "tokens / sec": 7007.478664760802,
+ "mem allocated avg": 6770948311.04,
+ "mem reserved avg": 10981837111.296,
+ "elapsed time": 837.4394236850003
+ },
+ {
+ "step": 2750,
+ "valid accuracy": 0.36,
+ "train loss": 0.6636076529026032,
+ "train samples": 11000,
+ "train time": 30.132865259004575,
+ "eval time": 7.065399131999584,
+ "tokens / sec": 7031.558339334618,
+ "mem allocated avg": 6781682612.224,
+ "mem reserved avg": 11132194521.088,
+ "elapsed time": 918.3523091420002
+ },
+ {
+ "step": 3000,
+ "valid accuracy": 0.3,
+ "train loss": 0.6547267787456512,
+ "train samples": 12000,
+ "train time": 29.80804876098864,
+ "eval time": 6.651864860000387,
+ "tokens / sec": 7002.504648112936,
+ "mem allocated avg": 6776379066.368,
+ "mem reserved avg": 11060597751.808,
+ "elapsed time": 998.1520945420007
+ },
+ {
+ "step": 3250,
+ "valid accuracy": 0.36,
+ "train loss": 0.6653184123039245,
+ "train samples": 13000,
+ "train time": 29.843793005994485,
+ "eval time": 11.134645372000705,
+ "tokens / sec": 7066.829607001965,
+ "mem allocated avg": 6778676955.136,
+ "mem reserved avg": 11088607313.92,
+ "elapsed time": 1082.892349787
+ },
+ {
+ "step": 3500,
+ "valid accuracy": 0.4,
+ "train loss": 0.6504588623046875,
+ "train samples": 14000,
+ "train time": 30.091547277996142,
+ "eval time": 11.186960818999978,
+ "tokens / sec": 6970.395974067295,
+ "mem allocated avg": 6777435619.328,
+ "mem reserved avg": 11074858385.408,
+ "elapsed time": 1168.1813894270008
+ },
+ {
+ "step": 3750,
+ "valid accuracy": 0.38,
+ "train loss": 0.6486766980886459,
+ "train samples": 15000,
+ "train time": 30.235947965997184,
+ "eval time": 6.424060680000366,
+ "tokens / sec": 7167.064854182855,
+ "mem allocated avg": 6787226097.664,
+ "mem reserved avg": 11226214039.552,
+ "elapsed time": 1249.1344440330004
+ },
+ {
+ "step": 4000,
+ "valid accuracy": 0.34,
+ "train loss": 0.6649546232223511,
+ "train samples": 16000,
+ "train time": 29.315789502004918,
+ "eval time": 6.29557701000067,
+ "tokens / sec": 6971.430872977951,
+ "mem allocated avg": 6769964711.936,
+ "mem reserved avg": 10964573356.032,
+ "elapsed time": 1328.0223749040006
+ },
+ {
+ "step": 4250,
+ "valid accuracy": 0.38,
+ "train loss": 0.6468708947896957,
+ "train samples": 17000,
+ "train time": 29.780288893992292,
+ "eval time": 6.263248704000034,
+ "tokens / sec": 7098.2857403591015,
+ "mem allocated avg": 6779703865.344,
+ "mem reserved avg": 11102406574.08,
+ "elapsed time": 1408.0423461730006
+ },
+ {
+ "step": 4500,
+ "valid accuracy": 0.36,
+ "train loss": 0.6554104331731796,
+ "train samples": 18000,
+ "train time": 29.55899746599971,
+ "eval time": 8.381054077999579,
+ "tokens / sec": 7030.617335349179,
+ "mem allocated avg": 6774673686.528,
+ "mem reserved avg": 11030071607.296,
+ "elapsed time": 1489.5959585560004
+ },
+ {
+ "step": 4750,
+ "valid accuracy": 0.3,
+ "train loss": 0.6466003597974778,
+ "train samples": 19000,
+ "train time": 29.626044395983627,
+ "eval time": 8.314826920000087,
+ "tokens / sec": 7086.298703733166,
+ "mem allocated avg": 6776780376.064,
+ "mem reserved avg": 11071855263.744,
+ "elapsed time": 1571.4978439640008
+ },
+ {
+ "step": 5000,
+ "valid accuracy": 0.36,
+ "train loss": 0.6535431078672409,
+ "train samples": 20000,
+ "train time": 29.328363572000853,
+ "eval time": 8.339948383999399,
+ "tokens / sec": 7101.657734454723,
+ "mem allocated avg": 6774118805.504,
+ "mem reserved avg": 11025097162.752,
+ "elapsed time": 1652.8993119440001
+ },
+ {
+ "step": 5000,
+ "test accuracy": 0.3912054586808188,
+ "train loss": 0.6535431078672409,
+ "train samples": 20000,
+ "train total tokens": 4198051
+ }
+ ]
+ },
+ "meta_info": {
+ "model_info": {
+ "sha": "13afe5124825b4f3751f836b40dafda64c1ed062",
+ "created_at": "2024-09-18T15:23:48+00:00"
+ },
+ "dataset_info": {
+ "metamath": {
+ "sha": "aa4f34d3d2d3231299b5b03d9b3e5a20da45aa18",
+ "created_at": "2023-09-21T17:22:46+00:00"
+ },
+ "gsm8k": {
+ "sha": "e53f048856ff4f594e959d75785d2c2d37b678ee",
+ "created_at": "2022-04-12T10:22:10+00:00"
+ }
+ },
+ "package_info": {
+ "transformers-version": "4.52.4",
+ "transformers-commit-hash": null,
+ "peft-version": "0.17.1.dev0",
+ "peft-commit-hash": "47961bb54706e45fd3b5460baa4921a48bcdce35",
+ "datasets-version": "3.6.0",
+ "datasets-commit-hash": null,
+ "bitsandbytes-version": "0.46.0",
+ "bitsandbytes-commit-hash": null,
+ "torch-version": "2.7.1+cu126",
+ "torch-commit-hash": null
+ },
+ "system_info": {
+ "system": "Linux",
+ "release": "6.14.0-1010-aws",
+ "version": "#10~24.04.1-Ubuntu SMP Fri Jul 18 20:44:30 UTC 2025",
+ "machine": "x86_64",
+ "processor": "x86_64",
+ "accelerator": "NVIDIA L40S"
+ },
+ "pytorch_info": "PyTorch built with:\n - GCC 11.2\n - C++ Version: 201703\n - Intel(R) oneAPI Math Kernel Library Version 2024.2-Product Build 20240605 for Intel(R) 64 architecture applications\n - Intel(R) MKL-DNN v3.7.1 (Git Hash 8d263e693366ef8db40acc569cc7d8edf644556d)\n - OpenMP 201511 (a.k.a. OpenMP 4.5)\n - LAPACK is enabled (usually provided by MKL)\n - NNPACK is enabled\n - CPU capability usage: AVX2\n - CUDA Runtime 12.6\n - NVCC architecture flags: -gencode;arch=compute_50,code=sm_50;-gencode;arch=compute_60,code=sm_60;-gencode;arch=compute_70,code=sm_70;-gencode;arch=compute_75,code=sm_75;-gencode;arch=compute_80,code=sm_80;-gencode;arch=compute_86,code=sm_86;-gencode;arch=compute_90,code=sm_90\n - CuDNN 90.7.1 (built against CUDA 12.8)\n - Built with CuDNN 90.5.1\n - Magma 2.6.1\n - Build settings: BLAS_INFO=mkl, BUILD_TYPE=Release, COMMIT_SHA=e2d141dbde55c2a4370fac5165b0561b6af4798b, CUDA_VERSION=12.6, CUDNN_VERSION=9.5.1, CXX_COMPILER=/opt/rh/gcc-toolset-11/root/usr/bin/c++, CXX_FLAGS= -D_GLIBCXX_USE_CXX11_ABI=1 -fvisibility-inlines-hidden -DUSE_PTHREADPOOL -DNDEBUG -DUSE_KINETO -DLIBKINETO_NOROCTRACER -DLIBKINETO_NOXPUPTI=ON -DUSE_FBGEMM -DUSE_PYTORCH_QNNPACK -DUSE_XNNPACK -DSYMBOLICATE_MOBILE_DEBUG_HANDLE -O2 -fPIC -Wall -Wextra -Werror=return-type -Werror=non-virtual-dtor -Werror=range-loop-construct -Werror=bool-operation -Wnarrowing -Wno-missing-field-initializers -Wno-unknown-pragmas -Wno-unused-parameter -Wno-strict-overflow -Wno-strict-aliasing -Wno-stringop-overflow -Wsuggest-override -Wno-psabi -Wno-error=old-style-cast -fdiagnostics-color=always -faligned-new -Wno-maybe-uninitialized -fno-math-errno -fno-trapping-math -Werror=format -Wno-stringop-overflow, LAPACK_INFO=mkl, PERF_WITH_AVX=1, PERF_WITH_AVX2=1, TORCH_VERSION=2.7.1, USE_CUDA=ON, USE_CUDNN=ON, USE_CUSPARSELT=1, USE_GFLAGS=OFF, USE_GLOG=OFF, USE_GLOO=ON, USE_MKL=ON, USE_MKLDNN=ON, USE_MPI=OFF, USE_NCCL=1, USE_NNPACK=ON, USE_OPENMP=ON, USE_ROCM=OFF, USE_ROCM_KERNEL_ASSERT=OFF, \n"
+ }
+}
\ No newline at end of file
diff --git a/peft/method_comparison/MetaMathQA/results/oft--llama-3.2-3B-rank32.json b/peft/method_comparison/MetaMathQA/results/oft--llama-3.2-3B-rank32.json
new file mode 100644
index 0000000000000000000000000000000000000000..b57f300fa300c0d85a3554971d8da372e1baa254
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/results/oft--llama-3.2-3B-rank32.json
@@ -0,0 +1,358 @@
+{
+ "run_info": {
+ "created_at": "2025-07-31T14:11:12+00:00",
+ "total_time": 2493.9155955019996,
+ "experiment_name": "oft/llama-3.2-3B-rank32",
+ "peft_branch": "main",
+ "train_config": {
+ "model_id": "meta-llama/Llama-3.2-3B",
+ "dtype": "bfloat16",
+ "max_seq_length": 768,
+ "batch_size": 4,
+ "batch_size_eval": 50,
+ "max_steps": 5000,
+ "eval_steps": 250,
+ "compile": false,
+ "query_template": "Question: {query} Think step by step.\nAnswer:",
+ "seed": 0,
+ "grad_norm_clip": 1.0,
+ "optimizer_type": "AdamW",
+ "optimizer_kwargs": {
+ "lr": 0.0001,
+ "weight_decay": 0.1
+ },
+ "lr_scheduler": "cosine",
+ "use_amp": false,
+ "autocast_adapter_dtype": true,
+ "generation_kwargs": {
+ "max_length": 800,
+ "max_new_tokens": 300
+ },
+ "attn_implementation": null
+ },
+ "peft_config": {
+ "task_type": null,
+ "peft_type": "OFT",
+ "auto_mapping": null,
+ "base_model_name_or_path": "meta-llama/Llama-3.2-3B",
+ "revision": null,
+ "inference_mode": false,
+ "r": 32,
+ "oft_block_size": 0,
+ "module_dropout": 0.0,
+ "target_modules": [
+ "v_proj",
+ "q_proj"
+ ],
+ "fan_in_fan_out": false,
+ "bias": "none",
+ "exclude_modules": null,
+ "init_weights": true,
+ "layers_to_transform": null,
+ "layers_pattern": null,
+ "modules_to_save": null,
+ "coft": false,
+ "eps": 6e-05,
+ "block_share": false,
+ "use_cayley_neumann": true,
+ "num_cayley_neumann_terms": 5
+ },
+ "error_msg": ""
+ },
+ "train_info": {
+ "accelerator_memory_reserved_avg": 12057354384,
+ "accelerator_memory_max": 22294822912,
+ "accelerator_memory_reserved_99th": 17939310837,
+ "train_time": 2214.446992367006,
+ "file_size": 32693568,
+ "num_trainable_params": 8171520,
+ "num_total_params": 3220921344,
+ "status": "success",
+ "metrics": [
+ {
+ "step": 250,
+ "valid accuracy": 0.36,
+ "train loss": 0.9631057088375091,
+ "train samples": 1000,
+ "train time": 43.418166981995455,
+ "eval time": 16.96007740999994,
+ "tokens / sec": 4876.276791873667,
+ "mem allocated avg": 6903823460.352,
+ "mem reserved avg": 12108561383.424,
+ "elapsed time": 113.91408998500083
+ },
+ {
+ "step": 500,
+ "valid accuracy": 0.36,
+ "train loss": 0.7144306401014328,
+ "train samples": 2000,
+ "train time": 42.455775934988196,
+ "eval time": 16.150497423999695,
+ "tokens / sec": 4899.097835792689,
+ "mem allocated avg": 6896105342.976,
+ "mem reserved avg": 11994249822.208,
+ "elapsed time": 220.49977440600014
+ },
+ {
+ "step": 750,
+ "valid accuracy": 0.52,
+ "train loss": 0.6711842056512832,
+ "train samples": 3000,
+ "train time": 43.15603912099323,
+ "eval time": 10.51256339000065,
+ "tokens / sec": 4968.041654585135,
+ "mem allocated avg": 6906686986.24,
+ "mem reserved avg": 12155101380.608,
+ "elapsed time": 322.5515955810006
+ },
+ {
+ "step": 1000,
+ "valid accuracy": 0.48,
+ "train loss": 0.6508683092594146,
+ "train samples": 4000,
+ "train time": 42.42713372799517,
+ "eval time": 16.934662378998837,
+ "tokens / sec": 4910.442485595753,
+ "mem allocated avg": 6897939019.776,
+ "mem reserved avg": 12025262505.984,
+ "elapsed time": 429.7382754350001
+ },
+ {
+ "step": 1250,
+ "valid accuracy": 0.4,
+ "train loss": 0.6453732433319092,
+ "train samples": 5000,
+ "train time": 42.549762738994104,
+ "eval time": 16.92903551499876,
+ "tokens / sec": 4901.03790423462,
+ "mem allocated avg": 6897900118.016,
+ "mem reserved avg": 12017234608.128,
+ "elapsed time": 537.135011331
+ },
+ {
+ "step": 1500,
+ "valid accuracy": 0.5,
+ "train loss": 0.636857116818428,
+ "train samples": 6000,
+ "train time": 42.7670685170051,
+ "eval time": 16.97714005600028,
+ "tokens / sec": 4894.677312679627,
+ "mem allocated avg": 6899436058.624,
+ "mem reserved avg": 12045822984.192,
+ "elapsed time": 644.8122739440005
+ },
+ {
+ "step": 1750,
+ "valid accuracy": 0.48,
+ "train loss": 0.6280697054862976,
+ "train samples": 7000,
+ "train time": 42.93359049599712,
+ "eval time": 11.770931148001182,
+ "tokens / sec": 4876.251848060996,
+ "mem allocated avg": 6900382935.04,
+ "mem reserved avg": 12059630632.96,
+ "elapsed time": 747.525349122001
+ },
+ {
+ "step": 2000,
+ "valid accuracy": 0.4,
+ "train loss": 0.6299525223970414,
+ "train samples": 8000,
+ "train time": 42.82682755300084,
+ "eval time": 11.5680384089992,
+ "tokens / sec": 4849.670448808364,
+ "mem allocated avg": 6896952041.472,
+ "mem reserved avg": 12003611508.736,
+ "elapsed time": 849.5279627600012
+ },
+ {
+ "step": 2250,
+ "valid accuracy": 0.42,
+ "train loss": 0.6208749743700027,
+ "train samples": 9000,
+ "train time": 43.43083962600576,
+ "eval time": 16.986704689999897,
+ "tokens / sec": 4949.20203825146,
+ "mem allocated avg": 6908628027.392,
+ "mem reserved avg": 12188169273.344,
+ "elapsed time": 958.0240945160003
+ },
+ {
+ "step": 2500,
+ "valid accuracy": 0.42,
+ "train loss": 0.6179436918497085,
+ "train samples": 10000,
+ "train time": 42.63891591101674,
+ "eval time": 17.232789900999705,
+ "tokens / sec": 4830.493355643306,
+ "mem allocated avg": 6893492830.208,
+ "mem reserved avg": 11953867063.296,
+ "elapsed time": 1065.2266578140006
+ },
+ {
+ "step": 2750,
+ "valid accuracy": 0.42,
+ "train loss": 0.6097300077676773,
+ "train samples": 11000,
+ "train time": 43.157022238001446,
+ "eval time": 17.135427543998958,
+ "tokens / sec": 4909.537058222485,
+ "mem allocated avg": 6904392247.296,
+ "mem reserved avg": 12124977889.28,
+ "elapsed time": 1173.5244531360004
+ },
+ {
+ "step": 3000,
+ "valid accuracy": 0.42,
+ "train loss": 0.600518134355545,
+ "train samples": 12000,
+ "train time": 42.90499155000907,
+ "eval time": 17.038416949999373,
+ "tokens / sec": 4864.958422301702,
+ "mem allocated avg": 6898886381.568,
+ "mem reserved avg": 12038994657.28,
+ "elapsed time": 1281.100714346001
+ },
+ {
+ "step": 3250,
+ "valid accuracy": 0.54,
+ "train loss": 0.6095727566480637,
+ "train samples": 13000,
+ "train time": 42.991201876006016,
+ "eval time": 17.145920277998812,
+ "tokens / sec": 4905.678157318666,
+ "mem allocated avg": 6900920473.6,
+ "mem reserved avg": 12070426771.456,
+ "elapsed time": 1389.080374264
+ },
+ {
+ "step": 3500,
+ "valid accuracy": 0.54,
+ "train loss": 0.59402192902565,
+ "train samples": 14000,
+ "train time": 43.139979139998104,
+ "eval time": 10.18719298600081,
+ "tokens / sec": 4862.079309758545,
+ "mem allocated avg": 6899826102.272,
+ "mem reserved avg": 12054404530.176,
+ "elapsed time": 1490.7450829120007
+ },
+ {
+ "step": 3750,
+ "valid accuracy": 0.58,
+ "train loss": 0.5927710949182511,
+ "train samples": 15000,
+ "train time": 43.49427866901169,
+ "eval time": 10.884315328999946,
+ "tokens / sec": 4982.333461582249,
+ "mem allocated avg": 6910839183.36,
+ "mem reserved avg": 12223619530.752,
+ "elapsed time": 1593.6702795590008
+ },
+ {
+ "step": 4000,
+ "valid accuracy": 0.52,
+ "train loss": 0.6036465883255004,
+ "train samples": 16000,
+ "train time": 42.54699739801072,
+ "eval time": 10.508950370000093,
+ "tokens / sec": 4803.464697829781,
+ "mem allocated avg": 6892073494.528,
+ "mem reserved avg": 11931788247.04,
+ "elapsed time": 1694.1543825910012
+ },
+ {
+ "step": 4250,
+ "valid accuracy": 0.5,
+ "train loss": 0.5904108211994171,
+ "train samples": 17000,
+ "train time": 42.904117188016244,
+ "eval time": 10.362485865000053,
+ "tokens / sec": 4927.009663749569,
+ "mem allocated avg": 6902539771.904,
+ "mem reserved avg": 12087044603.904,
+ "elapsed time": 1795.3652429800004
+ },
+ {
+ "step": 4500,
+ "valid accuracy": 0.56,
+ "train loss": 0.5975252593755722,
+ "train samples": 18000,
+ "train time": 42.7045542899923,
+ "eval time": 9.970661539999128,
+ "tokens / sec": 4866.413043179837,
+ "mem allocated avg": 6897064284.16,
+ "mem reserved avg": 12006883065.856,
+ "elapsed time": 1895.7771126360003
+ },
+ {
+ "step": 4750,
+ "valid accuracy": 0.54,
+ "train loss": 0.588557964682579,
+ "train samples": 19000,
+ "train time": 42.698231221012975,
+ "eval time": 10.72399718899942,
+ "tokens / sec": 4916.8078863342525,
+ "mem allocated avg": 6900484192.256,
+ "mem reserved avg": 12052575813.632,
+ "elapsed time": 1997.1282366079995
+ },
+ {
+ "step": 5000,
+ "valid accuracy": 0.56,
+ "train loss": 0.5946548076868057,
+ "train samples": 20000,
+ "train time": 42.98944765599845,
+ "eval time": 10.321189939999385,
+ "tokens / sec": 4844.909887343902,
+ "mem allocated avg": 6896923324.416,
+ "mem reserved avg": 12004861411.328,
+ "elapsed time": 2098.129397994
+ },
+ {
+ "step": 5000,
+ "test accuracy": 0.5056861258529188,
+ "train loss": 0.5946548076868057,
+ "train samples": 20000,
+ "train total tokens": 4198051
+ }
+ ]
+ },
+ "meta_info": {
+ "model_info": {
+ "sha": "13afe5124825b4f3751f836b40dafda64c1ed062",
+ "created_at": "2024-09-18T15:23:48+00:00"
+ },
+ "dataset_info": {
+ "metamath": {
+ "sha": "aa4f34d3d2d3231299b5b03d9b3e5a20da45aa18",
+ "created_at": "2023-09-21T17:22:46+00:00"
+ },
+ "gsm8k": {
+ "sha": "e53f048856ff4f594e959d75785d2c2d37b678ee",
+ "created_at": "2022-04-12T10:22:10+00:00"
+ }
+ },
+ "package_info": {
+ "transformers-version": "4.52.4",
+ "transformers-commit-hash": null,
+ "peft-version": "0.16.1.dev0",
+ "peft-commit-hash": "25e5c6b25c4589eb2683484ede1ba3d985d8a760",
+ "datasets-version": "3.6.0",
+ "datasets-commit-hash": null,
+ "bitsandbytes-version": "0.46.0",
+ "bitsandbytes-commit-hash": null,
+ "torch-version": "2.7.1+cu126",
+ "torch-commit-hash": null
+ },
+ "system_info": {
+ "system": "Linux",
+ "release": "6.8.0-1031-aws",
+ "version": "#33-Ubuntu SMP Fri Jun 20 18:11:07 UTC 2025",
+ "machine": "x86_64",
+ "processor": "x86_64",
+ "accelerator": "NVIDIA L40S"
+ },
+ "pytorch_info": "PyTorch built with:\n - GCC 11.2\n - C++ Version: 201703\n - Intel(R) oneAPI Math Kernel Library Version 2024.2-Product Build 20240605 for Intel(R) 64 architecture applications\n - Intel(R) MKL-DNN v3.7.1 (Git Hash 8d263e693366ef8db40acc569cc7d8edf644556d)\n - OpenMP 201511 (a.k.a. OpenMP 4.5)\n - LAPACK is enabled (usually provided by MKL)\n - NNPACK is enabled\n - CPU capability usage: AVX2\n - CUDA Runtime 12.6\n - NVCC architecture flags: -gencode;arch=compute_50,code=sm_50;-gencode;arch=compute_60,code=sm_60;-gencode;arch=compute_70,code=sm_70;-gencode;arch=compute_75,code=sm_75;-gencode;arch=compute_80,code=sm_80;-gencode;arch=compute_86,code=sm_86;-gencode;arch=compute_90,code=sm_90\n - CuDNN 90.7.1 (built against CUDA 12.8)\n - Built with CuDNN 90.5.1\n - Magma 2.6.1\n - Build settings: BLAS_INFO=mkl, BUILD_TYPE=Release, COMMIT_SHA=e2d141dbde55c2a4370fac5165b0561b6af4798b, CUDA_VERSION=12.6, CUDNN_VERSION=9.5.1, CXX_COMPILER=/opt/rh/gcc-toolset-11/root/usr/bin/c++, CXX_FLAGS= -D_GLIBCXX_USE_CXX11_ABI=1 -fvisibility-inlines-hidden -DUSE_PTHREADPOOL -DNDEBUG -DUSE_KINETO -DLIBKINETO_NOROCTRACER -DLIBKINETO_NOXPUPTI=ON -DUSE_FBGEMM -DUSE_PYTORCH_QNNPACK -DUSE_XNNPACK -DSYMBOLICATE_MOBILE_DEBUG_HANDLE -O2 -fPIC -Wall -Wextra -Werror=return-type -Werror=non-virtual-dtor -Werror=range-loop-construct -Werror=bool-operation -Wnarrowing -Wno-missing-field-initializers -Wno-unknown-pragmas -Wno-unused-parameter -Wno-strict-overflow -Wno-strict-aliasing -Wno-stringop-overflow -Wsuggest-override -Wno-psabi -Wno-error=old-style-cast -fdiagnostics-color=always -faligned-new -Wno-maybe-uninitialized -fno-math-errno -fno-trapping-math -Werror=format -Wno-stringop-overflow, LAPACK_INFO=mkl, PERF_WITH_AVX=1, PERF_WITH_AVX2=1, TORCH_VERSION=2.7.1, USE_CUDA=ON, USE_CUDNN=ON, USE_CUSPARSELT=1, USE_GFLAGS=OFF, USE_GLOG=OFF, USE_GLOO=ON, USE_MKL=ON, USE_MKLDNN=ON, USE_MPI=OFF, USE_NCCL=1, USE_NNPACK=ON, USE_OPENMP=ON, USE_ROCM=OFF, USE_ROCM_KERNEL_ASSERT=OFF, \n"
+ }
+}
\ No newline at end of file
diff --git a/peft/method_comparison/MetaMathQA/results/prefixtuning--llama-3.2-3B-lr_0.001.json b/peft/method_comparison/MetaMathQA/results/prefixtuning--llama-3.2-3B-lr_0.001.json
new file mode 100644
index 0000000000000000000000000000000000000000..9c1717d39a8e3e171f29ff94bad443c9e912c558
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/results/prefixtuning--llama-3.2-3B-lr_0.001.json
@@ -0,0 +1,345 @@
+{
+ "run_info": {
+ "created_at": "2025-06-19T20:20:55+00:00",
+ "total_time": 1959.214138561998,
+ "experiment_name": "prefixtuning/llama-3.2-3B-lr_0.001",
+ "peft_branch": "main",
+ "train_config": {
+ "model_id": "meta-llama/Llama-3.2-3B",
+ "dtype": "bfloat16",
+ "max_seq_length": 768,
+ "batch_size": 4,
+ "batch_size_eval": 50,
+ "max_steps": 5000,
+ "eval_steps": 250,
+ "compile": false,
+ "query_template": "Question: {query} Think step by step.\nAnswer:",
+ "seed": 0,
+ "grad_norm_clip": 1.0,
+ "optimizer_type": "AdamW",
+ "optimizer_kwargs": {
+ "lr": 0.001
+ },
+ "lr_scheduler": "cosine",
+ "use_amp": false,
+ "autocast_adapter_dtype": true,
+ "generation_kwargs": {
+ "max_length": 800,
+ "max_new_tokens": 300
+ },
+ "attn_implementation": null
+ },
+ "peft_config": {
+ "task_type": "CAUSAL_LM",
+ "peft_type": "PREFIX_TUNING",
+ "auto_mapping": null,
+ "base_model_name_or_path": "meta-llama/Llama-3.2-3B",
+ "revision": null,
+ "inference_mode": false,
+ "num_virtual_tokens": 200,
+ "token_dim": 1024,
+ "num_transformer_submodules": 1,
+ "num_attention_heads": 8,
+ "num_layers": 28,
+ "encoder_hidden_size": 3072,
+ "prefix_projection": false
+ },
+ "error_msg": ""
+ },
+ "train_info": {
+ "accelerator_memory_reserved_avg": 11766684083,
+ "accelerator_memory_max": 20912799744,
+ "accelerator_memory_reserved_99th": 16945051074,
+ "train_time": 1661.6597991429953,
+ "file_size": 45875328,
+ "num_trainable_params": 11468800,
+ "num_total_params": 3224218624,
+ "status": "success",
+ "metrics": [
+ {
+ "step": 250,
+ "valid accuracy": 0.0,
+ "train loss": 7.371294965744019,
+ "train samples": 1000,
+ "train time": 27.91846932898261,
+ "eval time": 15.451216622001084,
+ "tokens / sec": 7583.474491569318,
+ "mem allocated avg": 7053410574.336,
+ "mem reserved avg": 11800925962.24,
+ "elapsed time": 86.14553656399949
+ },
+ {
+ "step": 500,
+ "valid accuracy": 0.0,
+ "train loss": 3.853111123085022,
+ "train samples": 2000,
+ "train time": 27.30431010902612,
+ "eval time": 15.427179872000124,
+ "tokens / sec": 7617.661796598262,
+ "mem allocated avg": 7047124914.176,
+ "mem reserved avg": 11721854943.232,
+ "elapsed time": 164.76258564100135
+ },
+ {
+ "step": 750,
+ "valid accuracy": 0.0,
+ "train loss": 1.7293416724205017,
+ "train samples": 3000,
+ "train time": 28.03611285903753,
+ "eval time": 15.425274275999982,
+ "tokens / sec": 7647.31548478152,
+ "mem allocated avg": 7057104787.456,
+ "mem reserved avg": 11848237711.36,
+ "elapsed time": 244.72437485599949
+ },
+ {
+ "step": 1000,
+ "valid accuracy": 0.0,
+ "train loss": 1.1541715533733368,
+ "train samples": 4000,
+ "train time": 27.01217528603229,
+ "eval time": 15.417352960001153,
+ "tokens / sec": 7712.670223479868,
+ "mem allocated avg": 7050079920.128,
+ "mem reserved avg": 11745879916.544,
+ "elapsed time": 322.8701755410002
+ },
+ {
+ "step": 1250,
+ "valid accuracy": 0.08,
+ "train loss": 1.01127068066597,
+ "train samples": 5000,
+ "train time": 27.13179545197636,
+ "eval time": 15.418993674997182,
+ "tokens / sec": 7686.111314273877,
+ "mem allocated avg": 7048705087.488,
+ "mem reserved avg": 11725462044.672,
+ "elapsed time": 401.46412933300235
+ },
+ {
+ "step": 1500,
+ "valid accuracy": 0.08,
+ "train loss": 0.9543052833080292,
+ "train samples": 6000,
+ "train time": 27.5597544680204,
+ "eval time": 15.42255902100078,
+ "tokens / sec": 7595.532109798078,
+ "mem allocated avg": 7050476988.416,
+ "mem reserved avg": 11746567782.4,
+ "elapsed time": 480.1674746890021
+ },
+ {
+ "step": 1750,
+ "valid accuracy": 0.18,
+ "train loss": 0.9019801757335663,
+ "train samples": 7000,
+ "train time": 27.391848403010954,
+ "eval time": 15.41637391599943,
+ "tokens / sec": 7642.967240465137,
+ "mem allocated avg": 7051827261.44,
+ "mem reserved avg": 11769468682.24,
+ "elapsed time": 559.677030461
+ },
+ {
+ "step": 2000,
+ "valid accuracy": 0.12,
+ "train loss": 0.8851136872768403,
+ "train samples": 8000,
+ "train time": 27.14071328902719,
+ "eval time": 15.419172215999424,
+ "tokens / sec": 7652.562325396589,
+ "mem allocated avg": 7048325701.632,
+ "mem reserved avg": 11717526421.504,
+ "elapsed time": 638.8433813260017
+ },
+ {
+ "step": 2250,
+ "valid accuracy": 0.1,
+ "train loss": 0.8607708604335785,
+ "train samples": 9000,
+ "train time": 28.18215358697489,
+ "eval time": 15.430102889000409,
+ "tokens / sec": 7627.096323090928,
+ "mem allocated avg": 7058774517.76,
+ "mem reserved avg": 11887655780.352,
+ "elapsed time": 719.1557081280007
+ },
+ {
+ "step": 2500,
+ "valid accuracy": 0.16,
+ "train loss": 0.8404088478088378,
+ "train samples": 10000,
+ "train time": 26.82789152296391,
+ "eval time": 15.41505262499777,
+ "tokens / sec": 7677.3457885685175,
+ "mem allocated avg": 7045414729.728,
+ "mem reserved avg": 11679693799.424,
+ "elapsed time": 797.9182705759995
+ },
+ {
+ "step": 2750,
+ "valid accuracy": 0.14,
+ "train loss": 0.8259119842052459,
+ "train samples": 11000,
+ "train time": 27.303442178006662,
+ "eval time": 15.412094721999892,
+ "tokens / sec": 7760.230326221408,
+ "mem allocated avg": 7055038418.944,
+ "mem reserved avg": 11819196350.464,
+ "elapsed time": 877.4897030700013
+ },
+ {
+ "step": 3000,
+ "valid accuracy": 0.22,
+ "train loss": 0.8099327564239502,
+ "train samples": 12000,
+ "train time": 27.035110770961182,
+ "eval time": 12.827202022002894,
+ "tokens / sec": 7720.737738726083,
+ "mem allocated avg": 7049757696.0,
+ "mem reserved avg": 11756390842.368,
+ "elapsed time": 953.558885925002
+ },
+ {
+ "step": 3250,
+ "valid accuracy": 0.22,
+ "train loss": 0.8175602672100067,
+ "train samples": 13000,
+ "train time": 27.43706444997588,
+ "eval time": 15.41863539300175,
+ "tokens / sec": 7686.718831911532,
+ "mem allocated avg": 7051605612.544,
+ "mem reserved avg": 11776833880.064,
+ "elapsed time": 1033.2767371779992
+ },
+ {
+ "step": 3500,
+ "valid accuracy": 0.18,
+ "train loss": 0.7965063021183014,
+ "train samples": 14000,
+ "train time": 27.750962379970588,
+ "eval time": 15.41753050600164,
+ "tokens / sec": 7558.296434122523,
+ "mem allocated avg": 7051713462.272,
+ "mem reserved avg": 11763227557.888,
+ "elapsed time": 1113.7006878970024
+ },
+ {
+ "step": 3750,
+ "valid accuracy": 0.26,
+ "train loss": 0.788856605052948,
+ "train samples": 15000,
+ "train time": 27.955327479998232,
+ "eval time": 11.66996129099789,
+ "tokens / sec": 7751.760381095479,
+ "mem allocated avg": 7061477945.344,
+ "mem reserved avg": 11919800926.208,
+ "elapsed time": 1190.2235273900005
+ },
+ {
+ "step": 4000,
+ "valid accuracy": 0.26,
+ "train loss": 0.8037499711513519,
+ "train samples": 16000,
+ "train time": 26.957003097031702,
+ "eval time": 15.42233503099851,
+ "tokens / sec": 7581.443651742726,
+ "mem allocated avg": 7042861262.848,
+ "mem reserved avg": 11658604838.912,
+ "elapsed time": 1268.9300010120023
+ },
+ {
+ "step": 4250,
+ "valid accuracy": 0.28,
+ "train loss": 0.7835113587379455,
+ "train samples": 17000,
+ "train time": 27.92120910200174,
+ "eval time": 10.70234186000016,
+ "tokens / sec": 7570.911389537389,
+ "mem allocated avg": 7053768085.504,
+ "mem reserved avg": 11783242776.576,
+ "elapsed time": 1344.1117449459998
+ },
+ {
+ "step": 4500,
+ "valid accuracy": 0.28,
+ "train loss": 0.7824292014837265,
+ "train samples": 18000,
+ "train time": 26.99022845998479,
+ "eval time": 12.42347607800184,
+ "tokens / sec": 7699.749570779183,
+ "mem allocated avg": 7048212195.328,
+ "mem reserved avg": 11725470433.28,
+ "elapsed time": 1419.3379556770014
+ },
+ {
+ "step": 4750,
+ "valid accuracy": 0.28,
+ "train loss": 0.7803363995552063,
+ "train samples": 19000,
+ "train time": 27.08754148402295,
+ "eval time": 15.42501401300251,
+ "tokens / sec": 7750.389607112494,
+ "mem allocated avg": 7051630567.424,
+ "mem reserved avg": 11771876212.736,
+ "elapsed time": 1498.5280245210015
+ },
+ {
+ "step": 5000,
+ "valid accuracy": 0.26,
+ "train loss": 0.7887116296291351,
+ "train samples": 20000,
+ "train time": 26.98893836600837,
+ "eval time": 15.411349758000142,
+ "tokens / sec": 7717.235749529201,
+ "mem allocated avg": 7048690728.96,
+ "mem reserved avg": 11715764813.824,
+ "elapsed time": 1577.725424725002
+ },
+ {
+ "step": 5000,
+ "test accuracy": 0.1470811220621683,
+ "train loss": 0.7887116296291351,
+ "train samples": 20000,
+ "train total tokens": 4198051
+ }
+ ]
+ },
+ "meta_info": {
+ "model_info": {
+ "sha": "13afe5124825b4f3751f836b40dafda64c1ed062",
+ "created_at": "2024-09-18T15:23:48+00:00"
+ },
+ "dataset_info": {
+ "metamath": {
+ "sha": "aa4f34d3d2d3231299b5b03d9b3e5a20da45aa18",
+ "created_at": "2023-09-21T17:22:46+00:00"
+ },
+ "gsm8k": {
+ "sha": "e53f048856ff4f594e959d75785d2c2d37b678ee",
+ "created_at": "2022-04-12T10:22:10+00:00"
+ }
+ },
+ "package_info": {
+ "transformers-version": "4.52.4",
+ "transformers-commit-hash": null,
+ "peft-version": "0.15.2.dev0",
+ "peft-commit-hash": "5fe7f8f8abe914d313fc3751f2ea92de7718fbaf",
+ "datasets-version": "3.6.0",
+ "datasets-commit-hash": null,
+ "bitsandbytes-version": "0.46.0",
+ "bitsandbytes-commit-hash": null,
+ "torch-version": "2.7.1+cu126",
+ "torch-commit-hash": null
+ },
+ "system_info": {
+ "system": "Linux",
+ "release": "6.8.0-1029-aws",
+ "version": "#31-Ubuntu SMP Wed Apr 23 18:42:41 UTC 2025",
+ "machine": "x86_64",
+ "processor": "x86_64",
+ "accelerator": "NVIDIA L40S"
+ },
+ "pytorch_info": "PyTorch built with:\n - GCC 11.2\n - C++ Version: 201703\n - Intel(R) oneAPI Math Kernel Library Version 2024.2-Product Build 20240605 for Intel(R) 64 architecture applications\n - Intel(R) MKL-DNN v3.7.1 (Git Hash 8d263e693366ef8db40acc569cc7d8edf644556d)\n - OpenMP 201511 (a.k.a. OpenMP 4.5)\n - LAPACK is enabled (usually provided by MKL)\n - NNPACK is enabled\n - CPU capability usage: AVX2\n - CUDA Runtime 12.6\n - NVCC architecture flags: -gencode;arch=compute_50,code=sm_50;-gencode;arch=compute_60,code=sm_60;-gencode;arch=compute_70,code=sm_70;-gencode;arch=compute_75,code=sm_75;-gencode;arch=compute_80,code=sm_80;-gencode;arch=compute_86,code=sm_86;-gencode;arch=compute_90,code=sm_90\n - CuDNN 90.7.1 (built against CUDA 12.8)\n - Built with CuDNN 90.5.1\n - Magma 2.6.1\n - Build settings: BLAS_INFO=mkl, BUILD_TYPE=Release, COMMIT_SHA=e2d141dbde55c2a4370fac5165b0561b6af4798b, CUDA_VERSION=12.6, CUDNN_VERSION=9.5.1, CXX_COMPILER=/opt/rh/gcc-toolset-11/root/usr/bin/c++, CXX_FLAGS= -D_GLIBCXX_USE_CXX11_ABI=1 -fvisibility-inlines-hidden -DUSE_PTHREADPOOL -DNDEBUG -DUSE_KINETO -DLIBKINETO_NOROCTRACER -DLIBKINETO_NOXPUPTI=ON -DUSE_FBGEMM -DUSE_PYTORCH_QNNPACK -DUSE_XNNPACK -DSYMBOLICATE_MOBILE_DEBUG_HANDLE -O2 -fPIC -Wall -Wextra -Werror=return-type -Werror=non-virtual-dtor -Werror=range-loop-construct -Werror=bool-operation -Wnarrowing -Wno-missing-field-initializers -Wno-unknown-pragmas -Wno-unused-parameter -Wno-strict-overflow -Wno-strict-aliasing -Wno-stringop-overflow -Wsuggest-override -Wno-psabi -Wno-error=old-style-cast -fdiagnostics-color=always -faligned-new -Wno-maybe-uninitialized -fno-math-errno -fno-trapping-math -Werror=format -Wno-stringop-overflow, LAPACK_INFO=mkl, PERF_WITH_AVX=1, PERF_WITH_AVX2=1, TORCH_VERSION=2.7.1, USE_CUDA=ON, USE_CUDNN=ON, USE_CUSPARSELT=1, USE_GFLAGS=OFF, USE_GLOG=OFF, USE_GLOO=ON, USE_MKL=ON, USE_MKLDNN=ON, USE_MPI=OFF, USE_NCCL=1, USE_NNPACK=ON, USE_OPENMP=ON, USE_ROCM=OFF, USE_ROCM_KERNEL_ASSERT=OFF, \n"
+ }
+}
diff --git a/peft/method_comparison/MetaMathQA/results/prompt_tuning--llama-3.2-3B-default.json b/peft/method_comparison/MetaMathQA/results/prompt_tuning--llama-3.2-3B-default.json
new file mode 100644
index 0000000000000000000000000000000000000000..013c9ebf413306dd841d2bf777f0c7084b56e13d
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/results/prompt_tuning--llama-3.2-3B-default.json
@@ -0,0 +1,348 @@
+{
+ "run_info": {
+ "created_at": "2025-06-20T08:46:44+00:00",
+ "total_time": 2700.1305744579877,
+ "experiment_name": "prompt_tuning/llama-3.2-3B-default",
+ "peft_branch": "main",
+ "train_config": {
+ "model_id": "meta-llama/Llama-3.2-3B",
+ "dtype": "bfloat16",
+ "max_seq_length": 768,
+ "batch_size": 4,
+ "batch_size_eval": 50,
+ "max_steps": 5000,
+ "eval_steps": 250,
+ "compile": false,
+ "query_template": "Question: {query} Think step by step.\nAnswer:",
+ "seed": 0,
+ "grad_norm_clip": 1.0,
+ "optimizer_type": "AdamW",
+ "optimizer_kwargs": {
+ "lr": 0.0001,
+ "weight_decay": 0.1
+ },
+ "lr_scheduler": "cosine",
+ "use_amp": false,
+ "autocast_adapter_dtype": true,
+ "generation_kwargs": {
+ "max_length": 800,
+ "max_new_tokens": 300
+ },
+ "attn_implementation": null
+ },
+ "peft_config": {
+ "task_type": "CAUSAL_LM",
+ "peft_type": "PROMPT_TUNING",
+ "auto_mapping": null,
+ "base_model_name_or_path": "meta-llama/Llama-3.2-3B",
+ "revision": null,
+ "inference_mode": false,
+ "num_virtual_tokens": 200,
+ "token_dim": 3072,
+ "num_transformer_submodules": 1,
+ "num_attention_heads": 24,
+ "num_layers": 28,
+ "prompt_tuning_init": "RANDOM",
+ "prompt_tuning_init_text": null,
+ "tokenizer_name_or_path": null,
+ "tokenizer_kwargs": null
+ },
+ "error_msg": ""
+ },
+ "train_info": {
+ "accelerator_memory_reserved_avg": 15297773830,
+ "accelerator_memory_max": 24379392000,
+ "accelerator_memory_reserved_99th": 20669781770,
+ "train_time": 2379.557773831024,
+ "file_size": 2457728,
+ "num_trainable_params": 614400,
+ "num_total_params": 3213364224,
+ "status": "success",
+ "metrics": [
+ {
+ "step": 250,
+ "valid accuracy": 0.0,
+ "train loss": 3.462425223350525,
+ "train samples": 1000,
+ "train time": 46.206722402057494,
+ "eval time": 15.901069569998072,
+ "tokens / sec": 4581.9956273412845,
+ "mem allocated avg": 7082871494.656,
+ "mem reserved avg": 15331489742.848,
+ "elapsed time": 119.40567356300016
+ },
+ {
+ "step": 500,
+ "valid accuracy": 0.0,
+ "train loss": 2.259350722312927,
+ "train samples": 2000,
+ "train time": 45.66361523300293,
+ "eval time": 15.856271529002697,
+ "tokens / sec": 4554.939396249854,
+ "mem allocated avg": 7075523266.56,
+ "mem reserved avg": 15240674672.64,
+ "elapsed time": 232.12755202699918
+ },
+ {
+ "step": 750,
+ "valid accuracy": 0.0,
+ "train loss": 1.758247773170471,
+ "train samples": 3000,
+ "train time": 46.58154148896574,
+ "eval time": 15.854417883005226,
+ "tokens / sec": 4602.70298377282,
+ "mem allocated avg": 7085465481.216,
+ "mem reserved avg": 15376771448.832,
+ "elapsed time": 346.0752758900053
+ },
+ {
+ "step": 1000,
+ "valid accuracy": 0.0,
+ "train loss": 1.6028480381965637,
+ "train samples": 4000,
+ "train time": 45.41573346107907,
+ "eval time": 15.861826895998092,
+ "tokens / sec": 4587.30893729906,
+ "mem allocated avg": 7077486481.408,
+ "mem reserved avg": 15288170971.136,
+ "elapsed time": 458.6240012299968
+ },
+ {
+ "step": 1250,
+ "valid accuracy": 0.0,
+ "train loss": 1.5049157681465148,
+ "train samples": 5000,
+ "train time": 46.04039786210342,
+ "eval time": 15.877354786993237,
+ "tokens / sec": 4529.456948321703,
+ "mem allocated avg": 7076584331.264,
+ "mem reserved avg": 15265983102.976,
+ "elapsed time": 571.9228152269934
+ },
+ {
+ "step": 1500,
+ "valid accuracy": 0.0,
+ "train loss": 1.4375499501228333,
+ "train samples": 6000,
+ "train time": 45.70124057796784,
+ "eval time": 15.84707298700232,
+ "tokens / sec": 4580.4227052190045,
+ "mem allocated avg": 7078481408.0,
+ "mem reserved avg": 15279463596.032,
+ "elapsed time": 684.8850296739984
+ },
+ {
+ "step": 1750,
+ "valid accuracy": 0.0,
+ "train loss": 1.3827230257987977,
+ "train samples": 7000,
+ "train time": 44.976750778907444,
+ "eval time": 15.845691901995451,
+ "tokens / sec": 4654.7382008346485,
+ "mem allocated avg": 7079360505.856,
+ "mem reserved avg": 15298052751.36,
+ "elapsed time": 796.8428356289951
+ },
+ {
+ "step": 2000,
+ "valid accuracy": 0.0,
+ "train loss": 1.3338124525547028,
+ "train samples": 8000,
+ "train time": 45.10262611102371,
+ "eval time": 15.857041016992298,
+ "tokens / sec": 4604.964675199615,
+ "mem allocated avg": 7075931449.344,
+ "mem reserved avg": 15257242173.44,
+ "elapsed time": 908.9726742479979
+ },
+ {
+ "step": 2250,
+ "valid accuracy": 0.0,
+ "train loss": 1.2829065501689911,
+ "train samples": 9000,
+ "train time": 46.84363810600189,
+ "eval time": 15.872781344005489,
+ "tokens / sec": 4588.627371631486,
+ "mem allocated avg": 7087554078.72,
+ "mem reserved avg": 15416986435.584,
+ "elapsed time": 1023.331907868007
+ },
+ {
+ "step": 2500,
+ "valid accuracy": 0.0,
+ "train loss": 1.2462495183944702,
+ "train samples": 10000,
+ "train time": 45.55510413390584,
+ "eval time": 15.84976143699896,
+ "tokens / sec": 4521.271631705095,
+ "mem allocated avg": 7072915062.784,
+ "mem reserved avg": 15202909159.424,
+ "elapsed time": 1136.1328145180014
+ },
+ {
+ "step": 2750,
+ "valid accuracy": 0.0,
+ "train loss": 1.2045790712833404,
+ "train samples": 11000,
+ "train time": 45.34144312601711,
+ "eval time": 15.8525270359969,
+ "tokens / sec": 4673.009621928461,
+ "mem allocated avg": 7083153442.816,
+ "mem reserved avg": 15344005545.984,
+ "elapsed time": 1248.7101804669946
+ },
+ {
+ "step": 3000,
+ "valid accuracy": 0.0,
+ "train loss": 1.1678078708648683,
+ "train samples": 12000,
+ "train time": 45.599694666831056,
+ "eval time": 15.870247816987103,
+ "tokens / sec": 4577.464860786221,
+ "mem allocated avg": 7077996111.872,
+ "mem reserved avg": 15283892781.056,
+ "elapsed time": 1361.5449211609957
+ },
+ {
+ "step": 3250,
+ "valid accuracy": 0.04,
+ "train loss": 1.1313301923274994,
+ "train samples": 13000,
+ "train time": 45.95094640579191,
+ "eval time": 15.868188906999421,
+ "tokens / sec": 4589.698722144641,
+ "mem allocated avg": 7079686449.152,
+ "mem reserved avg": 15301248811.008,
+ "elapsed time": 1474.734694629995
+ },
+ {
+ "step": 3500,
+ "valid accuracy": 0.06,
+ "train loss": 1.1092858843803406,
+ "train samples": 14000,
+ "train time": 45.96525488591578,
+ "eval time": 15.86030059499899,
+ "tokens / sec": 4563.229346178814,
+ "mem allocated avg": 7078805225.472,
+ "mem reserved avg": 15302347718.656,
+ "elapsed time": 1588.1363447299955
+ },
+ {
+ "step": 3750,
+ "valid accuracy": 0.06,
+ "train loss": 1.079538120508194,
+ "train samples": 15000,
+ "train time": 46.46510764303093,
+ "eval time": 15.86466599200503,
+ "tokens / sec": 4663.779145091515,
+ "mem allocated avg": 7089610215.424,
+ "mem reserved avg": 15446287843.328,
+ "elapsed time": 1702.2553167559963
+ },
+ {
+ "step": 4000,
+ "valid accuracy": 0.04,
+ "train loss": 1.0899075508117675,
+ "train samples": 16000,
+ "train time": 45.08557640206709,
+ "eval time": 15.860410296008922,
+ "tokens / sec": 4533.001822521445,
+ "mem allocated avg": 7071494891.52,
+ "mem reserved avg": 15189319614.464,
+ "elapsed time": 1814.3939928110049
+ },
+ {
+ "step": 4250,
+ "valid accuracy": 0.04,
+ "train loss": 1.0607522547245025,
+ "train samples": 17000,
+ "train time": 46.2303190480452,
+ "eval time": 15.875090683999588,
+ "tokens / sec": 4572.518735601033,
+ "mem allocated avg": 7082239875.072,
+ "mem reserved avg": 15329283538.944,
+ "elapsed time": 1928.1608909490024
+ },
+ {
+ "step": 4500,
+ "valid accuracy": 0.04,
+ "train loss": 1.068591582775116,
+ "train samples": 18000,
+ "train time": 45.96484722109744,
+ "eval time": 15.854171614992083,
+ "tokens / sec": 4521.237697155087,
+ "mem allocated avg": 7076175783.936,
+ "mem reserved avg": 15251420479.488,
+ "elapsed time": 2041.5032397750037
+ },
+ {
+ "step": 4750,
+ "valid accuracy": 0.06,
+ "train loss": 1.0587167317867279,
+ "train samples": 19000,
+ "train time": 45.48911916205543,
+ "eval time": 15.858397545001935,
+ "tokens / sec": 4615.147619194169,
+ "mem allocated avg": 7079419088.896,
+ "mem reserved avg": 15298539290.624,
+ "elapsed time": 2154.3035376479966
+ },
+ {
+ "step": 5000,
+ "valid accuracy": 0.02,
+ "train loss": 1.0654937489032745,
+ "train samples": 20000,
+ "train time": 45.758550852071494,
+ "eval time": 15.85034008299408,
+ "tokens / sec": 4551.7175723796145,
+ "mem allocated avg": 7075618770.944,
+ "mem reserved avg": 15251386925.056,
+ "elapsed time": 2267.4055672899995
+ },
+ {
+ "step": 5000,
+ "test accuracy": 0.050037907505686124,
+ "train loss": 1.0654937489032745,
+ "train samples": 20000,
+ "train total tokens": 4198051
+ }
+ ]
+ },
+ "meta_info": {
+ "model_info": {
+ "sha": "13afe5124825b4f3751f836b40dafda64c1ed062",
+ "created_at": "2024-09-18T15:23:48+00:00"
+ },
+ "dataset_info": {
+ "metamath": {
+ "sha": "aa4f34d3d2d3231299b5b03d9b3e5a20da45aa18",
+ "created_at": "2023-09-21T17:22:46+00:00"
+ },
+ "gsm8k": {
+ "sha": "e53f048856ff4f594e959d75785d2c2d37b678ee",
+ "created_at": "2022-04-12T10:22:10+00:00"
+ }
+ },
+ "package_info": {
+ "transformers-version": "4.52.4",
+ "transformers-commit-hash": null,
+ "peft-version": "0.15.2.dev0",
+ "peft-commit-hash": "5fe7f8f8abe914d313fc3751f2ea92de7718fbaf",
+ "datasets-version": "3.6.0",
+ "datasets-commit-hash": null,
+ "bitsandbytes-version": "0.46.0",
+ "bitsandbytes-commit-hash": null,
+ "torch-version": "2.7.1+cu126",
+ "torch-commit-hash": null
+ },
+ "system_info": {
+ "system": "Linux",
+ "release": "6.8.0-1029-aws",
+ "version": "#31-Ubuntu SMP Wed Apr 23 18:42:41 UTC 2025",
+ "machine": "x86_64",
+ "processor": "x86_64",
+ "accelerator": "NVIDIA L40S"
+ },
+ "pytorch_info": "PyTorch built with:\n - GCC 11.2\n - C++ Version: 201703\n - Intel(R) oneAPI Math Kernel Library Version 2024.2-Product Build 20240605 for Intel(R) 64 architecture applications\n - Intel(R) MKL-DNN v3.7.1 (Git Hash 8d263e693366ef8db40acc569cc7d8edf644556d)\n - OpenMP 201511 (a.k.a. OpenMP 4.5)\n - LAPACK is enabled (usually provided by MKL)\n - NNPACK is enabled\n - CPU capability usage: AVX2\n - CUDA Runtime 12.6\n - NVCC architecture flags: -gencode;arch=compute_50,code=sm_50;-gencode;arch=compute_60,code=sm_60;-gencode;arch=compute_70,code=sm_70;-gencode;arch=compute_75,code=sm_75;-gencode;arch=compute_80,code=sm_80;-gencode;arch=compute_86,code=sm_86;-gencode;arch=compute_90,code=sm_90\n - CuDNN 90.7.1 (built against CUDA 12.8)\n - Built with CuDNN 90.5.1\n - Magma 2.6.1\n - Build settings: BLAS_INFO=mkl, BUILD_TYPE=Release, COMMIT_SHA=e2d141dbde55c2a4370fac5165b0561b6af4798b, CUDA_VERSION=12.6, CUDNN_VERSION=9.5.1, CXX_COMPILER=/opt/rh/gcc-toolset-11/root/usr/bin/c++, CXX_FLAGS= -D_GLIBCXX_USE_CXX11_ABI=1 -fvisibility-inlines-hidden -DUSE_PTHREADPOOL -DNDEBUG -DUSE_KINETO -DLIBKINETO_NOROCTRACER -DLIBKINETO_NOXPUPTI=ON -DUSE_FBGEMM -DUSE_PYTORCH_QNNPACK -DUSE_XNNPACK -DSYMBOLICATE_MOBILE_DEBUG_HANDLE -O2 -fPIC -Wall -Wextra -Werror=return-type -Werror=non-virtual-dtor -Werror=range-loop-construct -Werror=bool-operation -Wnarrowing -Wno-missing-field-initializers -Wno-unknown-pragmas -Wno-unused-parameter -Wno-strict-overflow -Wno-strict-aliasing -Wno-stringop-overflow -Wsuggest-override -Wno-psabi -Wno-error=old-style-cast -fdiagnostics-color=always -faligned-new -Wno-maybe-uninitialized -fno-math-errno -fno-trapping-math -Werror=format -Wno-stringop-overflow, LAPACK_INFO=mkl, PERF_WITH_AVX=1, PERF_WITH_AVX2=1, TORCH_VERSION=2.7.1, USE_CUDA=ON, USE_CUDNN=ON, USE_CUSPARSELT=1, USE_GFLAGS=OFF, USE_GLOG=OFF, USE_GLOO=ON, USE_MKL=ON, USE_MKLDNN=ON, USE_MPI=OFF, USE_NCCL=1, USE_NNPACK=ON, USE_OPENMP=ON, USE_ROCM=OFF, USE_ROCM_KERNEL_ASSERT=OFF, \n"
+ }
+}
diff --git a/peft/method_comparison/MetaMathQA/results/prompt_tuning--llama-3.2-3B-lr_0.001.json b/peft/method_comparison/MetaMathQA/results/prompt_tuning--llama-3.2-3B-lr_0.001.json
new file mode 100644
index 0000000000000000000000000000000000000000..2ce456649c41cd57278667f453ef1b9e9e8406f5
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/results/prompt_tuning--llama-3.2-3B-lr_0.001.json
@@ -0,0 +1,347 @@
+{
+ "run_info": {
+ "created_at": "2025-06-20T08:01:25+00:00",
+ "total_time": 2714.5956150429993,
+ "experiment_name": "prompt_tuning/llama-3.2-3B-lr_0.001",
+ "peft_branch": "main",
+ "train_config": {
+ "model_id": "meta-llama/Llama-3.2-3B",
+ "dtype": "bfloat16",
+ "max_seq_length": 768,
+ "batch_size": 4,
+ "batch_size_eval": 50,
+ "max_steps": 5000,
+ "eval_steps": 250,
+ "compile": false,
+ "query_template": "Question: {query} Think step by step.\nAnswer:",
+ "seed": 0,
+ "grad_norm_clip": 1.0,
+ "optimizer_type": "AdamW",
+ "optimizer_kwargs": {
+ "lr": 0.001
+ },
+ "lr_scheduler": "cosine",
+ "use_amp": false,
+ "autocast_adapter_dtype": true,
+ "generation_kwargs": {
+ "max_length": 800,
+ "max_new_tokens": 300
+ },
+ "attn_implementation": null
+ },
+ "peft_config": {
+ "task_type": "CAUSAL_LM",
+ "peft_type": "PROMPT_TUNING",
+ "auto_mapping": null,
+ "base_model_name_or_path": "meta-llama/Llama-3.2-3B",
+ "revision": null,
+ "inference_mode": false,
+ "num_virtual_tokens": 200,
+ "token_dim": 3072,
+ "num_transformer_submodules": 1,
+ "num_attention_heads": 24,
+ "num_layers": 28,
+ "prompt_tuning_init": "RANDOM",
+ "prompt_tuning_init_text": null,
+ "tokenizer_name_or_path": null,
+ "tokenizer_kwargs": null
+ },
+ "error_msg": ""
+ },
+ "train_info": {
+ "accelerator_memory_reserved_avg": 15297364466,
+ "accelerator_memory_max": 24408752128,
+ "accelerator_memory_reserved_99th": 20650676715,
+ "train_time": 2394.4007484640024,
+ "file_size": 2457728,
+ "num_trainable_params": 614400,
+ "num_total_params": 3213364224,
+ "status": "success",
+ "metrics": [
+ {
+ "step": 250,
+ "valid accuracy": 0.0,
+ "train loss": 2.454602773666382,
+ "train samples": 1000,
+ "train time": 46.58359175696387,
+ "eval time": 15.906975480989786,
+ "tokens / sec": 4544.926486231061,
+ "mem allocated avg": 7082736850.944,
+ "mem reserved avg": 15330147565.568,
+ "elapsed time": 120.51601758999459
+ },
+ {
+ "step": 500,
+ "valid accuracy": 0.02,
+ "train loss": 1.4034885478019714,
+ "train samples": 2000,
+ "train time": 45.99672341402038,
+ "eval time": 15.859127072995761,
+ "tokens / sec": 4521.952534049426,
+ "mem allocated avg": 7075398952.96,
+ "mem reserved avg": 15237637996.544,
+ "elapsed time": 234.56530582100095
+ },
+ {
+ "step": 750,
+ "valid accuracy": 0.1,
+ "train loss": 1.051814435005188,
+ "train samples": 3000,
+ "train time": 45.34941398198134,
+ "eval time": 15.839738530004979,
+ "tokens / sec": 4727.756792738001,
+ "mem allocated avg": 7085216630.784,
+ "mem reserved avg": 15378130403.328,
+ "elapsed time": 347.9996997119888
+ },
+ {
+ "step": 1000,
+ "valid accuracy": 0.2,
+ "train loss": 0.9425526282787323,
+ "train samples": 4000,
+ "train time": 44.85872337181354,
+ "eval time": 15.849193180998554,
+ "tokens / sec": 4644.269482954245,
+ "mem allocated avg": 7077280739.328,
+ "mem reserved avg": 15280109518.848,
+ "elapsed time": 460.8599872249906
+ },
+ {
+ "step": 1250,
+ "valid accuracy": 0.2,
+ "train loss": 0.9085307500362396,
+ "train samples": 5000,
+ "train time": 45.535731699026655,
+ "eval time": 15.864107311004773,
+ "tokens / sec": 4579.656287909338,
+ "mem allocated avg": 7076838449.152,
+ "mem reserved avg": 15263508463.616,
+ "elapsed time": 574.5614464429964
+ },
+ {
+ "step": 1500,
+ "valid accuracy": 0.18,
+ "train loss": 0.8753413548469543,
+ "train samples": 6000,
+ "train time": 45.47140344994841,
+ "eval time": 15.851111587006017,
+ "tokens / sec": 4603.5746451155,
+ "mem allocated avg": 7078501443.584,
+ "mem reserved avg": 15280914825.216,
+ "elapsed time": 688.3081236659928
+ },
+ {
+ "step": 1750,
+ "valid accuracy": 0.18,
+ "train loss": 0.8501973593235016,
+ "train samples": 7000,
+ "train time": 45.876367467062664,
+ "eval time": 15.86328411300201,
+ "tokens / sec": 4563.460700115549,
+ "mem allocated avg": 7079126001.664,
+ "mem reserved avg": 15302154780.672,
+ "elapsed time": 802.3839824919996
+ },
+ {
+ "step": 2000,
+ "valid accuracy": 0.3,
+ "train loss": 0.8353641645908356,
+ "train samples": 8000,
+ "train time": 45.395122604924836,
+ "eval time": 15.847279680005158,
+ "tokens / sec": 4575.293293237354,
+ "mem allocated avg": 7075813670.912,
+ "mem reserved avg": 15257200230.4,
+ "elapsed time": 915.8055839799927
+ },
+ {
+ "step": 2250,
+ "valid accuracy": 0.26,
+ "train loss": 0.8205823216438294,
+ "train samples": 9000,
+ "train time": 46.531550297062495,
+ "eval time": 15.857669960998464,
+ "tokens / sec": 4619.403364550472,
+ "mem allocated avg": 7087054014.464,
+ "mem reserved avg": 15417707855.872,
+ "elapsed time": 1030.8605109579948
+ },
+ {
+ "step": 2500,
+ "valid accuracy": 0.24,
+ "train loss": 0.8074139108657837,
+ "train samples": 10000,
+ "train time": 45.232053409854416,
+ "eval time": 15.864067172005889,
+ "tokens / sec": 4553.562893413265,
+ "mem allocated avg": 7073174814.72,
+ "mem reserved avg": 15210467295.232,
+ "elapsed time": 1144.3065934619954
+ },
+ {
+ "step": 2750,
+ "valid accuracy": 0.22,
+ "train loss": 0.800323983669281,
+ "train samples": 11000,
+ "train time": 46.27672885800712,
+ "eval time": 15.85089660200174,
+ "tokens / sec": 4578.564760921707,
+ "mem allocated avg": 7083499849.728,
+ "mem reserved avg": 15345020567.552,
+ "elapsed time": 1258.9190711479896
+ },
+ {
+ "step": 3000,
+ "valid accuracy": 0.28,
+ "train loss": 0.7878623747825623,
+ "train samples": 12000,
+ "train time": 45.57083585388318,
+ "eval time": 15.872650785997394,
+ "tokens / sec": 4580.3636490071885,
+ "mem allocated avg": 7078042595.328,
+ "mem reserved avg": 15285402730.496,
+ "elapsed time": 1372.7267461329902
+ },
+ {
+ "step": 3250,
+ "valid accuracy": 0.3,
+ "train loss": 0.7943042907714843,
+ "train samples": 13000,
+ "train time": 45.666222987070796,
+ "eval time": 15.852009978989372,
+ "tokens / sec": 4618.314942746877,
+ "mem allocated avg": 7079504875.52,
+ "mem reserved avg": 15299428483.072,
+ "elapsed time": 1486.5100108069892
+ },
+ {
+ "step": 3500,
+ "valid accuracy": 0.28,
+ "train loss": 0.780832305431366,
+ "train samples": 14000,
+ "train time": 45.84015418085619,
+ "eval time": 15.86955204399419,
+ "tokens / sec": 4575.6826901685245,
+ "mem allocated avg": 7078824071.168,
+ "mem reserved avg": 15300871323.648,
+ "elapsed time": 1600.7413567879994
+ },
+ {
+ "step": 3750,
+ "valid accuracy": 0.32,
+ "train loss": 0.7758122501373291,
+ "train samples": 15000,
+ "train time": 46.99727132692351,
+ "eval time": 15.8490629579901,
+ "tokens / sec": 4610.969826153641,
+ "mem allocated avg": 7089586788.352,
+ "mem reserved avg": 15444173914.112,
+ "elapsed time": 1716.2785189549904
+ },
+ {
+ "step": 4000,
+ "valid accuracy": 0.36,
+ "train loss": 0.7912874612808227,
+ "train samples": 16000,
+ "train time": 45.15887627698248,
+ "eval time": 15.855249352011015,
+ "tokens / sec": 4525.644056031772,
+ "mem allocated avg": 7071318118.4,
+ "mem reserved avg": 15188732411.904,
+ "elapsed time": 1829.5188424160006
+ },
+ {
+ "step": 4250,
+ "valid accuracy": 0.36,
+ "train loss": 0.7664959132671356,
+ "train samples": 17000,
+ "train time": 46.26589757904003,
+ "eval time": 15.853440922001028,
+ "tokens / sec": 4569.002463182864,
+ "mem allocated avg": 7081992153.088,
+ "mem reserved avg": 15327354159.104,
+ "elapsed time": 1944.2481972599926
+ },
+ {
+ "step": 4500,
+ "valid accuracy": 0.34,
+ "train loss": 0.7785169410705567,
+ "train samples": 18000,
+ "train time": 45.61058669183694,
+ "eval time": 15.866839458991308,
+ "tokens / sec": 4556.354457882774,
+ "mem allocated avg": 7075963725.824,
+ "mem reserved avg": 15250623561.728,
+ "elapsed time": 2058.0909812989994
+ },
+ {
+ "step": 4750,
+ "valid accuracy": 0.32,
+ "train loss": 0.7709811532497406,
+ "train samples": 19000,
+ "train time": 45.832340708962874,
+ "eval time": 15.847010081997723,
+ "tokens / sec": 4580.586475674911,
+ "mem allocated avg": 7079141249.024,
+ "mem reserved avg": 15295871713.28,
+ "elapsed time": 2172.3217773149954
+ },
+ {
+ "step": 5000,
+ "valid accuracy": 0.3,
+ "train loss": 0.7790318930149078,
+ "train samples": 20000,
+ "train time": 44.844002045996604,
+ "eval time": 15.846091532002902,
+ "tokens / sec": 4644.545323728393,
+ "mem allocated avg": 7075675734.016,
+ "mem reserved avg": 15251831521.28,
+ "elapsed time": 2285.3788618499966
+ },
+ {
+ "step": 5000,
+ "test accuracy": 0.25246398786959817,
+ "train loss": 0.7790318930149078,
+ "train samples": 20000,
+ "train total tokens": 4198051
+ }
+ ]
+ },
+ "meta_info": {
+ "model_info": {
+ "sha": "13afe5124825b4f3751f836b40dafda64c1ed062",
+ "created_at": "2024-09-18T15:23:48+00:00"
+ },
+ "dataset_info": {
+ "metamath": {
+ "sha": "aa4f34d3d2d3231299b5b03d9b3e5a20da45aa18",
+ "created_at": "2023-09-21T17:22:46+00:00"
+ },
+ "gsm8k": {
+ "sha": "e53f048856ff4f594e959d75785d2c2d37b678ee",
+ "created_at": "2022-04-12T10:22:10+00:00"
+ }
+ },
+ "package_info": {
+ "transformers-version": "4.52.4",
+ "transformers-commit-hash": null,
+ "peft-version": "0.15.2.dev0",
+ "peft-commit-hash": "5fe7f8f8abe914d313fc3751f2ea92de7718fbaf",
+ "datasets-version": "3.6.0",
+ "datasets-commit-hash": null,
+ "bitsandbytes-version": "0.46.0",
+ "bitsandbytes-commit-hash": null,
+ "torch-version": "2.7.1+cu126",
+ "torch-commit-hash": null
+ },
+ "system_info": {
+ "system": "Linux",
+ "release": "6.8.0-1029-aws",
+ "version": "#31-Ubuntu SMP Wed Apr 23 18:42:41 UTC 2025",
+ "machine": "x86_64",
+ "processor": "x86_64",
+ "accelerator": "NVIDIA L40S"
+ },
+ "pytorch_info": "PyTorch built with:\n - GCC 11.2\n - C++ Version: 201703\n - Intel(R) oneAPI Math Kernel Library Version 2024.2-Product Build 20240605 for Intel(R) 64 architecture applications\n - Intel(R) MKL-DNN v3.7.1 (Git Hash 8d263e693366ef8db40acc569cc7d8edf644556d)\n - OpenMP 201511 (a.k.a. OpenMP 4.5)\n - LAPACK is enabled (usually provided by MKL)\n - NNPACK is enabled\n - CPU capability usage: AVX2\n - CUDA Runtime 12.6\n - NVCC architecture flags: -gencode;arch=compute_50,code=sm_50;-gencode;arch=compute_60,code=sm_60;-gencode;arch=compute_70,code=sm_70;-gencode;arch=compute_75,code=sm_75;-gencode;arch=compute_80,code=sm_80;-gencode;arch=compute_86,code=sm_86;-gencode;arch=compute_90,code=sm_90\n - CuDNN 90.7.1 (built against CUDA 12.8)\n - Built with CuDNN 90.5.1\n - Magma 2.6.1\n - Build settings: BLAS_INFO=mkl, BUILD_TYPE=Release, COMMIT_SHA=e2d141dbde55c2a4370fac5165b0561b6af4798b, CUDA_VERSION=12.6, CUDNN_VERSION=9.5.1, CXX_COMPILER=/opt/rh/gcc-toolset-11/root/usr/bin/c++, CXX_FLAGS= -D_GLIBCXX_USE_CXX11_ABI=1 -fvisibility-inlines-hidden -DUSE_PTHREADPOOL -DNDEBUG -DUSE_KINETO -DLIBKINETO_NOROCTRACER -DLIBKINETO_NOXPUPTI=ON -DUSE_FBGEMM -DUSE_PYTORCH_QNNPACK -DUSE_XNNPACK -DSYMBOLICATE_MOBILE_DEBUG_HANDLE -O2 -fPIC -Wall -Wextra -Werror=return-type -Werror=non-virtual-dtor -Werror=range-loop-construct -Werror=bool-operation -Wnarrowing -Wno-missing-field-initializers -Wno-unknown-pragmas -Wno-unused-parameter -Wno-strict-overflow -Wno-strict-aliasing -Wno-stringop-overflow -Wsuggest-override -Wno-psabi -Wno-error=old-style-cast -fdiagnostics-color=always -faligned-new -Wno-maybe-uninitialized -fno-math-errno -fno-trapping-math -Werror=format -Wno-stringop-overflow, LAPACK_INFO=mkl, PERF_WITH_AVX=1, PERF_WITH_AVX2=1, TORCH_VERSION=2.7.1, USE_CUDA=ON, USE_CUDNN=ON, USE_CUSPARSELT=1, USE_GFLAGS=OFF, USE_GLOG=OFF, USE_GLOO=ON, USE_MKL=ON, USE_MKLDNN=ON, USE_MPI=OFF, USE_NCCL=1, USE_NNPACK=ON, USE_OPENMP=ON, USE_ROCM=OFF, USE_ROCM_KERNEL_ASSERT=OFF, \n"
+ }
+}
diff --git a/peft/method_comparison/MetaMathQA/results/ptuning--llama-3.2-3B-default.json b/peft/method_comparison/MetaMathQA/results/ptuning--llama-3.2-3B-default.json
new file mode 100644
index 0000000000000000000000000000000000000000..5ad6db218199541d2a426111594958057bc70943
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/results/ptuning--llama-3.2-3B-default.json
@@ -0,0 +1,348 @@
+{
+ "run_info": {
+ "created_at": "2025-06-19T19:48:53+00:00",
+ "total_time": 1918.2703526590012,
+ "experiment_name": "ptuning/llama-3.2-3B-default",
+ "peft_branch": "main",
+ "train_config": {
+ "model_id": "meta-llama/Llama-3.2-3B",
+ "dtype": "bfloat16",
+ "max_seq_length": 768,
+ "batch_size": 4,
+ "batch_size_eval": 50,
+ "max_steps": 5000,
+ "eval_steps": 250,
+ "compile": false,
+ "query_template": "Question: {query} Think step by step.\nAnswer:",
+ "seed": 0,
+ "grad_norm_clip": 1.0,
+ "optimizer_type": "AdamW",
+ "optimizer_kwargs": {
+ "lr": 0.0001,
+ "weight_decay": 0.1
+ },
+ "lr_scheduler": "cosine",
+ "use_amp": false,
+ "autocast_adapter_dtype": true,
+ "generation_kwargs": {
+ "max_length": 800,
+ "max_new_tokens": 300
+ },
+ "attn_implementation": null
+ },
+ "peft_config": {
+ "task_type": "CAUSAL_LM",
+ "peft_type": "P_TUNING",
+ "auto_mapping": null,
+ "base_model_name_or_path": "meta-llama/Llama-3.2-3B",
+ "revision": null,
+ "inference_mode": false,
+ "num_virtual_tokens": 20,
+ "token_dim": 3072,
+ "num_transformer_submodules": 1,
+ "num_attention_heads": 24,
+ "num_layers": 28,
+ "encoder_reparameterization_type": "MLP",
+ "encoder_hidden_size": 3072,
+ "encoder_num_layers": 2,
+ "encoder_dropout": 0.0
+ },
+ "error_msg": ""
+ },
+ "train_info": {
+ "accelerator_memory_reserved_avg": 11867101593,
+ "accelerator_memory_max": 20937965568,
+ "accelerator_memory_reserved_99th": 17215688540,
+ "train_time": 1707.340225783013,
+ "file_size": 245880,
+ "num_trainable_params": 28382208,
+ "num_total_params": 3241132032,
+ "status": "success",
+ "metrics": [
+ {
+ "step": 250,
+ "valid accuracy": 0.06,
+ "train loss": 0.9461167964935303,
+ "train samples": 1000,
+ "train time": 29.476242057011405,
+ "eval time": 11.075081511000462,
+ "tokens / sec": 7182.699870305862,
+ "mem allocated avg": 7263395393.536,
+ "mem reserved avg": 11910330187.776,
+ "elapsed time": 89.09710205499869
+ },
+ {
+ "step": 500,
+ "valid accuracy": 0.3,
+ "train loss": 0.7913461194038391,
+ "train samples": 2000,
+ "train time": 28.956617519994325,
+ "eval time": 11.047425028998987,
+ "tokens / sec": 7182.986751003671,
+ "mem allocated avg": 7255670497.28,
+ "mem reserved avg": 11810254094.336,
+ "elapsed time": 171.9022758780011
+ },
+ {
+ "step": 750,
+ "valid accuracy": 0.26,
+ "train loss": 0.7562740923166275,
+ "train samples": 3000,
+ "train time": 29.73533859500094,
+ "eval time": 11.056799476999004,
+ "tokens / sec": 7210.309689765724,
+ "mem allocated avg": 7266187038.72,
+ "mem reserved avg": 11954009669.632,
+ "elapsed time": 255.8485612350014
+ },
+ {
+ "step": 1000,
+ "valid accuracy": 0.3,
+ "train loss": 0.7289484927654266,
+ "train samples": 4000,
+ "train time": 29.176458327034197,
+ "eval time": 11.069810884997423,
+ "tokens / sec": 7140.551387861937,
+ "mem allocated avg": 7258589235.2,
+ "mem reserved avg": 11838347542.528,
+ "elapsed time": 338.5030210529985
+ },
+ {
+ "step": 1250,
+ "valid accuracy": 0.4,
+ "train loss": 0.7231850942373276,
+ "train samples": 5000,
+ "train time": 29.15449026899296,
+ "eval time": 11.055301014999714,
+ "tokens / sec": 7152.860436794844,
+ "mem allocated avg": 7257714087.936,
+ "mem reserved avg": 11824925769.728,
+ "elapsed time": 421.85765765199903
+ },
+ {
+ "step": 1500,
+ "valid accuracy": 0.38,
+ "train loss": 0.711922277212143,
+ "train samples": 6000,
+ "train time": 29.099172437985544,
+ "eval time": 11.07098460600173,
+ "tokens / sec": 7193.709733364892,
+ "mem allocated avg": 7259322730.496,
+ "mem reserved avg": 11860233420.8,
+ "elapsed time": 504.97678817400083
+ },
+ {
+ "step": 1750,
+ "valid accuracy": 0.44,
+ "train loss": 0.7051182547807694,
+ "train samples": 7000,
+ "train time": 29.301267419017677,
+ "eval time": 11.044947161997698,
+ "tokens / sec": 7144.912778213831,
+ "mem allocated avg": 7260392302.592,
+ "mem reserved avg": 11872371736.576,
+ "elapsed time": 588.3443257949984
+ },
+ {
+ "step": 2000,
+ "valid accuracy": 0.38,
+ "train loss": 0.7055468891859055,
+ "train samples": 8000,
+ "train time": 29.128185330951965,
+ "eval time": 11.045154800998716,
+ "tokens / sec": 7130.413296955362,
+ "mem allocated avg": 7257253203.968,
+ "mem reserved avg": 11821100564.48,
+ "elapsed time": 671.2971968860002
+ },
+ {
+ "step": 2250,
+ "valid accuracy": 0.3,
+ "train loss": 0.699348534822464,
+ "train samples": 9000,
+ "train time": 29.44214156106318,
+ "eval time": 11.039785496999684,
+ "tokens / sec": 7300.691750095574,
+ "mem allocated avg": 7268387997.696,
+ "mem reserved avg": 11993788448.768,
+ "elapsed time": 755.1838785660002
+ },
+ {
+ "step": 2500,
+ "valid accuracy": 0.4,
+ "train loss": 0.6970288401842117,
+ "train samples": 10000,
+ "train time": 28.56064905500898,
+ "eval time": 11.062792377000733,
+ "tokens / sec": 7211.565801718971,
+ "mem allocated avg": 7253500915.712,
+ "mem reserved avg": 11774535401.472,
+ "elapsed time": 837.4507786270005
+ },
+ {
+ "step": 2750,
+ "valid accuracy": 0.38,
+ "train loss": 0.6885807738304138,
+ "train samples": 11000,
+ "train time": 29.626391561985656,
+ "eval time": 11.040969151999889,
+ "tokens / sec": 7151.765329121947,
+ "mem allocated avg": 7264164755.456,
+ "mem reserved avg": 11929330384.896,
+ "elapsed time": 921.4017121549987
+ },
+ {
+ "step": 3000,
+ "valid accuracy": 0.32,
+ "train loss": 0.6827223267555237,
+ "train samples": 12000,
+ "train time": 29.296160228008375,
+ "eval time": 11.056816091997462,
+ "tokens / sec": 7124.85862909926,
+ "mem allocated avg": 7259324233.728,
+ "mem reserved avg": 11842046918.656,
+ "elapsed time": 1004.5840267519998
+ },
+ {
+ "step": 3250,
+ "valid accuracy": 0.5,
+ "train loss": 0.6894591153860092,
+ "train samples": 13000,
+ "train time": 29.611147850035195,
+ "eval time": 11.049655115999485,
+ "tokens / sec": 7122.351388338677,
+ "mem allocated avg": 7259635709.952,
+ "mem reserved avg": 11876809310.208,
+ "elapsed time": 1088.4846693049985
+ },
+ {
+ "step": 3500,
+ "valid accuracy": 0.42,
+ "train loss": 0.6757243422269821,
+ "train samples": 14000,
+ "train time": 28.982272775025194,
+ "eval time": 8.037888349997957,
+ "tokens / sec": 7237.182591861713,
+ "mem allocated avg": 7260029884.416,
+ "mem reserved avg": 11864100569.088,
+ "elapsed time": 1168.5907526180017
+ },
+ {
+ "step": 3750,
+ "valid accuracy": 0.44,
+ "train loss": 0.6726652181148529,
+ "train samples": 15000,
+ "train time": 29.461453213014465,
+ "eval time": 11.036738884999068,
+ "tokens / sec": 7355.475591552708,
+ "mem allocated avg": 7270358327.296,
+ "mem reserved avg": 12018115411.968,
+ "elapsed time": 1252.6760096750004
+ },
+ {
+ "step": 4000,
+ "valid accuracy": 0.44,
+ "train loss": 0.6872537672519684,
+ "train samples": 16000,
+ "train time": 28.49340438899526,
+ "eval time": 11.04012111100019,
+ "tokens / sec": 7172.642384527876,
+ "mem allocated avg": 7252451676.16,
+ "mem reserved avg": 11753454829.568,
+ "elapsed time": 1334.9961819890013
+ },
+ {
+ "step": 4250,
+ "valid accuracy": 0.46,
+ "train loss": 0.6691881531476974,
+ "train samples": 17000,
+ "train time": 29.36704957404436,
+ "eval time": 11.048986494999554,
+ "tokens / sec": 7198.169481309866,
+ "mem allocated avg": 7262467567.616,
+ "mem reserved avg": 11896405098.496,
+ "elapsed time": 1418.9507249929993
+ },
+ {
+ "step": 4500,
+ "valid accuracy": 0.5,
+ "train loss": 0.6769082483053207,
+ "train samples": 18000,
+ "train time": 29.086171291994106,
+ "eval time": 8.132250926999404,
+ "tokens / sec": 7144.907382746569,
+ "mem allocated avg": 7257195100.16,
+ "mem reserved avg": 11816553938.944,
+ "elapsed time": 1499.0322536989988
+ },
+ {
+ "step": 4750,
+ "valid accuracy": 0.46,
+ "train loss": 0.6686601461172104,
+ "train samples": 19000,
+ "train time": 29.45103387799827,
+ "eval time": 7.564945229998557,
+ "tokens / sec": 7128.408492200246,
+ "mem allocated avg": 7260019183.616,
+ "mem reserved avg": 11863848910.848,
+ "elapsed time": 1579.1494789060016
+ },
+ {
+ "step": 5000,
+ "valid accuracy": 0.48,
+ "train loss": 0.6739867876768112,
+ "train samples": 20000,
+ "train time": 29.24236888399173,
+ "eval time": 6.952750485001161,
+ "tokens / sec": 7122.541980995923,
+ "mem allocated avg": 7256318291.968,
+ "mem reserved avg": 11821469663.232,
+ "elapsed time": 1658.0220765080012
+ },
+ {
+ "step": 5000,
+ "test accuracy": 0.3707354056103108,
+ "train loss": 0.6739867876768112,
+ "train samples": 20000,
+ "train total tokens": 4198051
+ }
+ ]
+ },
+ "meta_info": {
+ "model_info": {
+ "sha": "13afe5124825b4f3751f836b40dafda64c1ed062",
+ "created_at": "2024-09-18T15:23:48+00:00"
+ },
+ "dataset_info": {
+ "metamath": {
+ "sha": "aa4f34d3d2d3231299b5b03d9b3e5a20da45aa18",
+ "created_at": "2023-09-21T17:22:46+00:00"
+ },
+ "gsm8k": {
+ "sha": "e53f048856ff4f594e959d75785d2c2d37b678ee",
+ "created_at": "2022-04-12T10:22:10+00:00"
+ }
+ },
+ "package_info": {
+ "transformers-version": "4.52.4",
+ "transformers-commit-hash": null,
+ "peft-version": "0.15.2.dev0",
+ "peft-commit-hash": "5fe7f8f8abe914d313fc3751f2ea92de7718fbaf",
+ "datasets-version": "3.6.0",
+ "datasets-commit-hash": null,
+ "bitsandbytes-version": "0.46.0",
+ "bitsandbytes-commit-hash": null,
+ "torch-version": "2.7.1+cu126",
+ "torch-commit-hash": null
+ },
+ "system_info": {
+ "system": "Linux",
+ "release": "6.8.0-1029-aws",
+ "version": "#31-Ubuntu SMP Wed Apr 23 18:42:41 UTC 2025",
+ "machine": "x86_64",
+ "processor": "x86_64",
+ "accelerator": "NVIDIA L40S"
+ },
+ "pytorch_info": "PyTorch built with:\n - GCC 11.2\n - C++ Version: 201703\n - Intel(R) oneAPI Math Kernel Library Version 2024.2-Product Build 20240605 for Intel(R) 64 architecture applications\n - Intel(R) MKL-DNN v3.7.1 (Git Hash 8d263e693366ef8db40acc569cc7d8edf644556d)\n - OpenMP 201511 (a.k.a. OpenMP 4.5)\n - LAPACK is enabled (usually provided by MKL)\n - NNPACK is enabled\n - CPU capability usage: AVX2\n - CUDA Runtime 12.6\n - NVCC architecture flags: -gencode;arch=compute_50,code=sm_50;-gencode;arch=compute_60,code=sm_60;-gencode;arch=compute_70,code=sm_70;-gencode;arch=compute_75,code=sm_75;-gencode;arch=compute_80,code=sm_80;-gencode;arch=compute_86,code=sm_86;-gencode;arch=compute_90,code=sm_90\n - CuDNN 90.7.1 (built against CUDA 12.8)\n - Built with CuDNN 90.5.1\n - Magma 2.6.1\n - Build settings: BLAS_INFO=mkl, BUILD_TYPE=Release, COMMIT_SHA=e2d141dbde55c2a4370fac5165b0561b6af4798b, CUDA_VERSION=12.6, CUDNN_VERSION=9.5.1, CXX_COMPILER=/opt/rh/gcc-toolset-11/root/usr/bin/c++, CXX_FLAGS= -D_GLIBCXX_USE_CXX11_ABI=1 -fvisibility-inlines-hidden -DUSE_PTHREADPOOL -DNDEBUG -DUSE_KINETO -DLIBKINETO_NOROCTRACER -DLIBKINETO_NOXPUPTI=ON -DUSE_FBGEMM -DUSE_PYTORCH_QNNPACK -DUSE_XNNPACK -DSYMBOLICATE_MOBILE_DEBUG_HANDLE -O2 -fPIC -Wall -Wextra -Werror=return-type -Werror=non-virtual-dtor -Werror=range-loop-construct -Werror=bool-operation -Wnarrowing -Wno-missing-field-initializers -Wno-unknown-pragmas -Wno-unused-parameter -Wno-strict-overflow -Wno-strict-aliasing -Wno-stringop-overflow -Wsuggest-override -Wno-psabi -Wno-error=old-style-cast -fdiagnostics-color=always -faligned-new -Wno-maybe-uninitialized -fno-math-errno -fno-trapping-math -Werror=format -Wno-stringop-overflow, LAPACK_INFO=mkl, PERF_WITH_AVX=1, PERF_WITH_AVX2=1, TORCH_VERSION=2.7.1, USE_CUDA=ON, USE_CUDNN=ON, USE_CUSPARSELT=1, USE_GFLAGS=OFF, USE_GLOG=OFF, USE_GLOO=ON, USE_MKL=ON, USE_MKLDNN=ON, USE_MPI=OFF, USE_NCCL=1, USE_NNPACK=ON, USE_OPENMP=ON, USE_ROCM=OFF, USE_ROCM_KERNEL_ASSERT=OFF, \n"
+ }
+}
diff --git a/peft/method_comparison/MetaMathQA/results/randlora--llama-3.2-3B-default.json b/peft/method_comparison/MetaMathQA/results/randlora--llama-3.2-3B-default.json
new file mode 100644
index 0000000000000000000000000000000000000000..1025019a88057969667507acf0070f182c663d90
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/results/randlora--llama-3.2-3B-default.json
@@ -0,0 +1,356 @@
+{
+ "run_info": {
+ "created_at": "2025-06-20T07:20:24+00:00",
+ "total_time": 2457.3893872150074,
+ "experiment_name": "randlora/llama-3.2-3B-default",
+ "peft_branch": "main",
+ "train_config": {
+ "model_id": "meta-llama/Llama-3.2-3B",
+ "dtype": "bfloat16",
+ "max_seq_length": 768,
+ "batch_size": 4,
+ "batch_size_eval": 50,
+ "max_steps": 5000,
+ "eval_steps": 250,
+ "compile": false,
+ "query_template": "Question: {query} Think step by step.\nAnswer:",
+ "seed": 0,
+ "grad_norm_clip": 1.0,
+ "optimizer_type": "AdamW",
+ "optimizer_kwargs": {
+ "lr": 0.0001,
+ "weight_decay": 0.1
+ },
+ "lr_scheduler": "cosine",
+ "use_amp": false,
+ "autocast_adapter_dtype": true,
+ "generation_kwargs": {
+ "max_length": 800,
+ "max_new_tokens": 300
+ },
+ "attn_implementation": null
+ },
+ "peft_config": {
+ "task_type": null,
+ "peft_type": "RANDLORA",
+ "auto_mapping": null,
+ "base_model_name_or_path": "meta-llama/Llama-3.2-3B",
+ "revision": null,
+ "inference_mode": false,
+ "r": 32,
+ "target_modules": [
+ "v_proj",
+ "q_proj"
+ ],
+ "projection_prng_key": 0,
+ "save_projection": true,
+ "sparse": false,
+ "very_sparse": false,
+ "randlora_dropout": 0.0,
+ "fan_in_fan_out": false,
+ "randlora_alpha": 640,
+ "bias": "none",
+ "modules_to_save": null,
+ "init_weights": true,
+ "layers_to_transform": null,
+ "layers_pattern": null
+ },
+ "error_msg": ""
+ },
+ "train_info": {
+ "accelerator_memory_reserved_avg": 12743670025,
+ "accelerator_memory_max": 22798139392,
+ "accelerator_memory_reserved_99th": 18436063232,
+ "train_time": 2213.072415724004,
+ "file_size": 2211281240,
+ "num_trainable_params": 9289728,
+ "num_total_params": 3222039552,
+ "status": "success",
+ "metrics": [
+ {
+ "step": 250,
+ "valid accuracy": 0.38,
+ "train loss": 0.9159075767993927,
+ "train samples": 1000,
+ "train time": 50.62416129904159,
+ "eval time": 13.32173753400275,
+ "tokens / sec": 4182.172989481373,
+ "mem allocated avg": 6983776778.24,
+ "mem reserved avg": 12791771561.984,
+ "elapsed time": 114.85611474100733
+ },
+ {
+ "step": 500,
+ "valid accuracy": 0.34,
+ "train loss": 0.7009325810670852,
+ "train samples": 2000,
+ "train time": 49.47734279213182,
+ "eval time": 13.318595108998124,
+ "tokens / sec": 4203.843380875268,
+ "mem allocated avg": 6975756310.528,
+ "mem reserved avg": 12690437177.344,
+ "elapsed time": 222.717683150011
+ },
+ {
+ "step": 750,
+ "valid accuracy": 0.38,
+ "train loss": 0.6809726172685623,
+ "train samples": 3000,
+ "train time": 50.701564677088754,
+ "eval time": 6.592474952994962,
+ "tokens / sec": 4228.6860645325305,
+ "mem allocated avg": 6985956540.416,
+ "mem reserved avg": 12840031223.808,
+ "elapsed time": 325.2694208340108
+ },
+ {
+ "step": 1000,
+ "valid accuracy": 0.32,
+ "train loss": 0.6661903276443482,
+ "train samples": 4000,
+ "train time": 49.452677299879724,
+ "eval time": 13.326040301006287,
+ "tokens / sec": 4212.835611238114,
+ "mem allocated avg": 6977344550.912,
+ "mem reserved avg": 12711484194.816,
+ "elapsed time": 432.82023598300293
+ },
+ {
+ "step": 1250,
+ "valid accuracy": 0.44,
+ "train loss": 0.665697453379631,
+ "train samples": 5000,
+ "train time": 49.56871296803001,
+ "eval time": 6.698036557994783,
+ "tokens / sec": 4207.0489127789,
+ "mem allocated avg": 6977509738.496,
+ "mem reserved avg": 12708397187.072,
+ "elapsed time": 534.2725243740133
+ },
+ {
+ "step": 1500,
+ "valid accuracy": 0.44,
+ "train loss": 0.658678293466568,
+ "train samples": 6000,
+ "train time": 49.71162069692218,
+ "eval time": 13.42559558400535,
+ "tokens / sec": 4210.906767176883,
+ "mem allocated avg": 6978434217.984,
+ "mem reserved avg": 12733680451.584,
+ "elapsed time": 642.8949007330084
+ },
+ {
+ "step": 1750,
+ "valid accuracy": 0.44,
+ "train loss": 0.6513392345905304,
+ "train samples": 7000,
+ "train time": 49.957065908936784,
+ "eval time": 8.692238900999655,
+ "tokens / sec": 4190.698476600257,
+ "mem allocated avg": 6980155148.288,
+ "mem reserved avg": 12746875731.968,
+ "elapsed time": 746.9297674360132
+ },
+ {
+ "step": 2000,
+ "valid accuracy": 0.36,
+ "train loss": 0.6511732361316681,
+ "train samples": 8000,
+ "train time": 49.75638979690848,
+ "eval time": 13.350251003997982,
+ "tokens / sec": 4174.257835983607,
+ "mem allocated avg": 6976487055.36,
+ "mem reserved avg": 12692744044.544,
+ "elapsed time": 855.1831161730079
+ },
+ {
+ "step": 2250,
+ "valid accuracy": 0.38,
+ "train loss": 0.6382467728853226,
+ "train samples": 9000,
+ "train time": 51.20128064297023,
+ "eval time": 13.277926524999202,
+ "tokens / sec": 4198.098119827237,
+ "mem allocated avg": 6988260448.256,
+ "mem reserved avg": 12868644765.696,
+ "elapsed time": 965.4057929810078
+ },
+ {
+ "step": 2500,
+ "valid accuracy": 0.42,
+ "train loss": 0.6324679807424546,
+ "train samples": 10000,
+ "train time": 47.79617171884456,
+ "eval time": 13.268003197008511,
+ "tokens / sec": 4309.278182603765,
+ "mem allocated avg": 6973276801.024,
+ "mem reserved avg": 12640810172.416,
+ "elapsed time": 1071.8066454930085
+ },
+ {
+ "step": 2750,
+ "valid accuracy": 0.42,
+ "train loss": 0.6214727911949157,
+ "train samples": 11000,
+ "train time": 49.63376283789694,
+ "eval time": 8.245235234993743,
+ "tokens / sec": 4268.888512281446,
+ "mem allocated avg": 6983764305.92,
+ "mem reserved avg": 12802987130.88,
+ "elapsed time": 1175.2128759590123
+ },
+ {
+ "step": 3000,
+ "valid accuracy": 0.46,
+ "train loss": 0.6079807863235474,
+ "train samples": 12000,
+ "train time": 49.776777152961586,
+ "eval time": 13.29031453501375,
+ "tokens / sec": 4193.340990289104,
+ "mem allocated avg": 6978680711.168,
+ "mem reserved avg": 12727900700.672,
+ "elapsed time": 1283.6379908250092
+ },
+ {
+ "step": 3250,
+ "valid accuracy": 0.5,
+ "train loss": 0.6133705099821091,
+ "train samples": 13000,
+ "train time": 50.014745363077964,
+ "eval time": 7.092912267995416,
+ "tokens / sec": 4216.77644200688,
+ "mem allocated avg": 6980747913.216,
+ "mem reserved avg": 12754257707.008,
+ "elapsed time": 1386.1836155580095
+ },
+ {
+ "step": 3500,
+ "valid accuracy": 0.52,
+ "train loss": 0.5912622555494308,
+ "train samples": 14000,
+ "train time": 49.560089439110016,
+ "eval time": 13.321606318990234,
+ "tokens / sec": 4232.236107194697,
+ "mem allocated avg": 6979099045.888,
+ "mem reserved avg": 12738579398.656,
+ "elapsed time": 1494.848658177012
+ },
+ {
+ "step": 3750,
+ "valid accuracy": 0.48,
+ "train loss": 0.5849999967813492,
+ "train samples": 15000,
+ "train time": 51.10861245104752,
+ "eval time": 13.350408840997261,
+ "tokens / sec": 4240.048586870968,
+ "mem allocated avg": 6990205292.544,
+ "mem reserved avg": 12906016014.336,
+ "elapsed time": 1605.1250539940083
+ },
+ {
+ "step": 4000,
+ "valid accuracy": 0.52,
+ "train loss": 0.5914600425958634,
+ "train samples": 16000,
+ "train time": 48.92153307204717,
+ "eval time": 13.309209176004515,
+ "tokens / sec": 4177.567364845621,
+ "mem allocated avg": 6971749750.784,
+ "mem reserved avg": 12621868695.552,
+ "elapsed time": 1712.7276146870136
+ },
+ {
+ "step": 4250,
+ "valid accuracy": 0.54,
+ "train loss": 0.575433883190155,
+ "train samples": 17000,
+ "train time": 50.056106529867975,
+ "eval time": 13.322275185011677,
+ "tokens / sec": 4223.041196259767,
+ "mem allocated avg": 6981706383.36,
+ "mem reserved avg": 12772226105.344,
+ "elapsed time": 1821.8377219670074
+ },
+ {
+ "step": 4500,
+ "valid accuracy": 0.48,
+ "train loss": 0.5807004086971282,
+ "train samples": 18000,
+ "train time": 49.559131018977496,
+ "eval time": 13.371259606996318,
+ "tokens / sec": 4193.334219690434,
+ "mem allocated avg": 6976847835.136,
+ "mem reserved avg": 12694061056.0,
+ "elapsed time": 1929.8977656790084
+ },
+ {
+ "step": 4750,
+ "valid accuracy": 0.52,
+ "train loss": 0.5704656873941422,
+ "train samples": 19000,
+ "train time": 49.80019182183605,
+ "eval time": 13.346957685993402,
+ "tokens / sec": 4215.62633234572,
+ "mem allocated avg": 6979789905.92,
+ "mem reserved avg": 12742303940.608,
+ "elapsed time": 2038.7162974260136
+ },
+ {
+ "step": 5000,
+ "valid accuracy": 0.52,
+ "train loss": 0.5784689987897873,
+ "train samples": 20000,
+ "train time": 49.38921916205436,
+ "eval time": 13.307282750000013,
+ "tokens / sec": 4217.114656471855,
+ "mem allocated avg": 6976297842.688,
+ "mem reserved avg": 12688323248.128,
+ "elapsed time": 2146.6737093550037
+ },
+ {
+ "step": 5000,
+ "test accuracy": 0.5072024260803639,
+ "train loss": 0.5784689987897873,
+ "train samples": 20000,
+ "train total tokens": 4198051
+ }
+ ]
+ },
+ "meta_info": {
+ "model_info": {
+ "sha": "13afe5124825b4f3751f836b40dafda64c1ed062",
+ "created_at": "2024-09-18T15:23:48+00:00"
+ },
+ "dataset_info": {
+ "metamath": {
+ "sha": "aa4f34d3d2d3231299b5b03d9b3e5a20da45aa18",
+ "created_at": "2023-09-21T17:22:46+00:00"
+ },
+ "gsm8k": {
+ "sha": "e53f048856ff4f594e959d75785d2c2d37b678ee",
+ "created_at": "2022-04-12T10:22:10+00:00"
+ }
+ },
+ "package_info": {
+ "transformers-version": "4.52.4",
+ "transformers-commit-hash": null,
+ "peft-version": "0.15.2.dev0",
+ "peft-commit-hash": "5fe7f8f8abe914d313fc3751f2ea92de7718fbaf",
+ "datasets-version": "3.6.0",
+ "datasets-commit-hash": null,
+ "bitsandbytes-version": "0.46.0",
+ "bitsandbytes-commit-hash": null,
+ "torch-version": "2.7.1+cu126",
+ "torch-commit-hash": null
+ },
+ "system_info": {
+ "system": "Linux",
+ "release": "6.8.0-1029-aws",
+ "version": "#31-Ubuntu SMP Wed Apr 23 18:42:41 UTC 2025",
+ "machine": "x86_64",
+ "processor": "x86_64",
+ "accelerator": "NVIDIA L40S"
+ },
+ "pytorch_info": "PyTorch built with:\n - GCC 11.2\n - C++ Version: 201703\n - Intel(R) oneAPI Math Kernel Library Version 2024.2-Product Build 20240605 for Intel(R) 64 architecture applications\n - Intel(R) MKL-DNN v3.7.1 (Git Hash 8d263e693366ef8db40acc569cc7d8edf644556d)\n - OpenMP 201511 (a.k.a. OpenMP 4.5)\n - LAPACK is enabled (usually provided by MKL)\n - NNPACK is enabled\n - CPU capability usage: AVX2\n - CUDA Runtime 12.6\n - NVCC architecture flags: -gencode;arch=compute_50,code=sm_50;-gencode;arch=compute_60,code=sm_60;-gencode;arch=compute_70,code=sm_70;-gencode;arch=compute_75,code=sm_75;-gencode;arch=compute_80,code=sm_80;-gencode;arch=compute_86,code=sm_86;-gencode;arch=compute_90,code=sm_90\n - CuDNN 90.7.1 (built against CUDA 12.8)\n - Built with CuDNN 90.5.1\n - Magma 2.6.1\n - Build settings: BLAS_INFO=mkl, BUILD_TYPE=Release, COMMIT_SHA=e2d141dbde55c2a4370fac5165b0561b6af4798b, CUDA_VERSION=12.6, CUDNN_VERSION=9.5.1, CXX_COMPILER=/opt/rh/gcc-toolset-11/root/usr/bin/c++, CXX_FLAGS= -D_GLIBCXX_USE_CXX11_ABI=1 -fvisibility-inlines-hidden -DUSE_PTHREADPOOL -DNDEBUG -DUSE_KINETO -DLIBKINETO_NOROCTRACER -DLIBKINETO_NOXPUPTI=ON -DUSE_FBGEMM -DUSE_PYTORCH_QNNPACK -DUSE_XNNPACK -DSYMBOLICATE_MOBILE_DEBUG_HANDLE -O2 -fPIC -Wall -Wextra -Werror=return-type -Werror=non-virtual-dtor -Werror=range-loop-construct -Werror=bool-operation -Wnarrowing -Wno-missing-field-initializers -Wno-unknown-pragmas -Wno-unused-parameter -Wno-strict-overflow -Wno-strict-aliasing -Wno-stringop-overflow -Wsuggest-override -Wno-psabi -Wno-error=old-style-cast -fdiagnostics-color=always -faligned-new -Wno-maybe-uninitialized -fno-math-errno -fno-trapping-math -Werror=format -Wno-stringop-overflow, LAPACK_INFO=mkl, PERF_WITH_AVX=1, PERF_WITH_AVX2=1, TORCH_VERSION=2.7.1, USE_CUDA=ON, USE_CUDNN=ON, USE_CUSPARSELT=1, USE_GFLAGS=OFF, USE_GLOG=OFF, USE_GLOO=ON, USE_MKL=ON, USE_MKLDNN=ON, USE_MPI=OFF, USE_NCCL=1, USE_NNPACK=ON, USE_OPENMP=ON, USE_ROCM=OFF, USE_ROCM_KERNEL_ASSERT=OFF, \n"
+ }
+}
diff --git a/peft/method_comparison/MetaMathQA/results/shira--llama-3.2-3B-lr_0.0003-random_seed_42.json b/peft/method_comparison/MetaMathQA/results/shira--llama-3.2-3B-lr_0.0003-random_seed_42.json
new file mode 100644
index 0000000000000000000000000000000000000000..1263cd479fe1109dc2001db4d0431c99cfc5b36c
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/results/shira--llama-3.2-3B-lr_0.0003-random_seed_42.json
@@ -0,0 +1,348 @@
+{
+ "run_info": {
+ "created_at": "2025-07-31T14:52:50+00:00",
+ "total_time": 2084.7194732099997,
+ "experiment_name": "shira/llama-3.2-3B-lr_0.0003-random_seed_42",
+ "peft_branch": "main",
+ "train_config": {
+ "model_id": "meta-llama/Llama-3.2-3B",
+ "dtype": "bfloat16",
+ "max_seq_length": 768,
+ "batch_size": 4,
+ "batch_size_eval": 50,
+ "max_steps": 5000,
+ "eval_steps": 250,
+ "compile": false,
+ "query_template": "Question: {query} Think step by step.\nAnswer:",
+ "seed": 0,
+ "grad_norm_clip": 1.0,
+ "optimizer_type": "AdamW",
+ "optimizer_kwargs": {
+ "lr": 0.0003
+ },
+ "lr_scheduler": "cosine",
+ "use_amp": false,
+ "autocast_adapter_dtype": true,
+ "generation_kwargs": {
+ "max_length": 800,
+ "max_new_tokens": 300
+ },
+ "attn_implementation": null
+ },
+ "peft_config": {
+ "task_type": null,
+ "peft_type": "SHIRA",
+ "auto_mapping": null,
+ "base_model_name_or_path": "meta-llama/Llama-3.2-3B",
+ "revision": null,
+ "inference_mode": false,
+ "r": 32,
+ "mask_type": "random",
+ "random_seed": 42,
+ "target_modules": [
+ "v_proj",
+ "q_proj"
+ ],
+ "fan_in_fan_out": false,
+ "init_weights": true,
+ "modules_to_save": null
+ },
+ "error_msg": ""
+ },
+ "train_info": {
+ "accelerator_memory_reserved_avg": 12240924809,
+ "accelerator_memory_max": 21743271936,
+ "accelerator_memory_reserved_99th": 17637383864,
+ "train_time": 1867.0518525470034,
+ "file_size": 110115520,
+ "num_trainable_params": 9175040,
+ "num_total_params": 3221924864,
+ "status": "success",
+ "metrics": [
+ {
+ "step": 250,
+ "valid accuracy": 0.38,
+ "train loss": 0.9357188057899475,
+ "train samples": 1000,
+ "train time": 31.692333374005102,
+ "eval time": 12.883808001000943,
+ "tokens / sec": 6680.448470028325,
+ "mem allocated avg": 6994551982.08,
+ "mem reserved avg": 12283740684.288,
+ "elapsed time": 96.08096698400004
+ },
+ {
+ "step": 500,
+ "valid accuracy": 0.36,
+ "train loss": 0.7029980063438416,
+ "train samples": 2000,
+ "train time": 30.742395647013836,
+ "eval time": 12.860161713999332,
+ "tokens / sec": 6765.73818085656,
+ "mem allocated avg": 6987138160.64,
+ "mem reserved avg": 12187783397.376,
+ "elapsed time": 185.3151257690006
+ },
+ {
+ "step": 750,
+ "valid accuracy": 0.46,
+ "train loss": 0.6642508600950241,
+ "train samples": 3000,
+ "train time": 31.300478177990954,
+ "eval time": 10.545964175000336,
+ "tokens / sec": 6849.767558846972,
+ "mem allocated avg": 6997475934.208,
+ "mem reserved avg": 12327495663.616,
+ "elapsed time": 273.0391829120017
+ },
+ {
+ "step": 1000,
+ "valid accuracy": 0.36,
+ "train loss": 0.6439496507644653,
+ "train samples": 4000,
+ "train time": 31.05783393001184,
+ "eval time": 12.813238828999602,
+ "tokens / sec": 6708.00160981866,
+ "mem allocated avg": 6989375735.808,
+ "mem reserved avg": 12216002674.688,
+ "elapsed time": 362.4678097830001
+ },
+ {
+ "step": 1250,
+ "valid accuracy": 0.32,
+ "train loss": 0.6386180140972137,
+ "train samples": 5000,
+ "train time": 31.162159604989938,
+ "eval time": 9.70755834100055,
+ "tokens / sec": 6692.026568229476,
+ "mem allocated avg": 6988624240.64,
+ "mem reserved avg": 12208931078.144,
+ "elapsed time": 449.31565678900006
+ },
+ {
+ "step": 1500,
+ "valid accuracy": 0.5,
+ "train loss": 0.6296385749578476,
+ "train samples": 6000,
+ "train time": 31.37457448001078,
+ "eval time": 12.791106022999884,
+ "tokens / sec": 6671.994870667266,
+ "mem allocated avg": 6990819698.688,
+ "mem reserved avg": 12231488045.056,
+ "elapsed time": 539.3741775020007
+ },
+ {
+ "step": 1750,
+ "valid accuracy": 0.52,
+ "train loss": 0.6209055181741715,
+ "train samples": 7000,
+ "train time": 31.12063506498089,
+ "eval time": 11.802694226998938,
+ "tokens / sec": 6727.208476397092,
+ "mem allocated avg": 6991199850.496,
+ "mem reserved avg": 12244775600.128,
+ "elapsed time": 628.1649310410012
+ },
+ {
+ "step": 2000,
+ "valid accuracy": 0.42,
+ "train loss": 0.622630435705185,
+ "train samples": 8000,
+ "train time": 30.90304242698403,
+ "eval time": 12.802878865999446,
+ "tokens / sec": 6720.8916562416925,
+ "mem allocated avg": 6988364103.68,
+ "mem reserved avg": 12193303101.44,
+ "elapsed time": 717.7866772650013
+ },
+ {
+ "step": 2250,
+ "valid accuracy": 0.5,
+ "train loss": 0.6117782632112503,
+ "train samples": 9000,
+ "train time": 31.835284770990256,
+ "eval time": 12.896296490000168,
+ "tokens / sec": 6751.8792919945945,
+ "mem allocated avg": 6999611363.328,
+ "mem reserved avg": 12359498203.136,
+ "elapsed time": 808.9164720260014
+ },
+ {
+ "step": 2500,
+ "valid accuracy": 0.48,
+ "train loss": 0.6087703567743301,
+ "train samples": 10000,
+ "train time": 31.106087331994786,
+ "eval time": 8.24222338599975,
+ "tokens / sec": 6621.437077627842,
+ "mem allocated avg": 6984549638.144,
+ "mem reserved avg": 12142711406.592,
+ "elapsed time": 894.0944889150014
+ },
+ {
+ "step": 2750,
+ "valid accuracy": 0.54,
+ "train loss": 0.5988683942556381,
+ "train samples": 11000,
+ "train time": 31.549549333021787,
+ "eval time": 10.239751285998864,
+ "tokens / sec": 6715.817007827485,
+ "mem allocated avg": 6995372679.168,
+ "mem reserved avg": 12298949230.592,
+ "elapsed time": 981.9011422450003
+ },
+ {
+ "step": 3000,
+ "valid accuracy": 0.5,
+ "train loss": 0.5887085427045822,
+ "train samples": 12000,
+ "train time": 30.952114122006606,
+ "eval time": 6.788169478999407,
+ "tokens / sec": 6743.6750580986845,
+ "mem allocated avg": 6990271899.648,
+ "mem reserved avg": 12226782035.968,
+ "elapsed time": 1065.3513825200007
+ },
+ {
+ "step": 3250,
+ "valid accuracy": 0.5,
+ "train loss": 0.5973232421875,
+ "train samples": 13000,
+ "train time": 31.107180875995255,
+ "eval time": 8.763070525999865,
+ "tokens / sec": 6779.81720171717,
+ "mem allocated avg": 6991821465.6,
+ "mem reserved avg": 12247829053.44,
+ "elapsed time": 1151.3527770540004
+ },
+ {
+ "step": 3500,
+ "valid accuracy": 0.58,
+ "train loss": 0.5808243087530136,
+ "train samples": 14000,
+ "train time": 31.351620633020502,
+ "eval time": 12.858672252999895,
+ "tokens / sec": 6690.244260581693,
+ "mem allocated avg": 6991037339.648,
+ "mem reserved avg": 12237720780.8,
+ "elapsed time": 1241.8340592570003
+ },
+ {
+ "step": 3750,
+ "valid accuracy": 0.54,
+ "train loss": 0.5781804740428924,
+ "train samples": 15000,
+ "train time": 31.949568995005393,
+ "eval time": 10.286192837000272,
+ "tokens / sec": 6782.658008121384,
+ "mem allocated avg": 7002176088.064,
+ "mem reserved avg": 12393589506.048,
+ "elapsed time": 1330.699673422001
+ },
+ {
+ "step": 4000,
+ "valid accuracy": 0.52,
+ "train loss": 0.5873791750669479,
+ "train samples": 16000,
+ "train time": 30.883606043998952,
+ "eval time": 12.840774923999561,
+ "tokens / sec": 6617.523863917831,
+ "mem allocated avg": 6983247890.432,
+ "mem reserved avg": 12128861814.784,
+ "elapsed time": 1420.291728133001
+ },
+ {
+ "step": 4250,
+ "valid accuracy": 0.54,
+ "train loss": 0.5750357346534729,
+ "train samples": 17000,
+ "train time": 31.41448626901547,
+ "eval time": 7.603731496999899,
+ "tokens / sec": 6729.029346199935,
+ "mem allocated avg": 6993511036.928,
+ "mem reserved avg": 12266485317.632,
+ "elapsed time": 1505.506280988
+ },
+ {
+ "step": 4500,
+ "valid accuracy": 0.54,
+ "train loss": 0.5816998761892319,
+ "train samples": 18000,
+ "train time": 30.81339496200053,
+ "eval time": 6.927671567998914,
+ "tokens / sec": 6744.404511618528,
+ "mem allocated avg": 6988376672.256,
+ "mem reserved avg": 12194603335.68,
+ "elapsed time": 1588.958452021001
+ },
+ {
+ "step": 4750,
+ "valid accuracy": 0.58,
+ "train loss": 0.5723758825063705,
+ "train samples": 19000,
+ "train time": 31.16517290099182,
+ "eval time": 7.508142915999997,
+ "tokens / sec": 6736.333556272963,
+ "mem allocated avg": 6991473983.488,
+ "mem reserved avg": 12240195420.16,
+ "elapsed time": 1673.9547475400013
+ },
+ {
+ "step": 5000,
+ "valid accuracy": 0.54,
+ "train loss": 0.5789329997301101,
+ "train samples": 20000,
+ "train time": 31.123193277984683,
+ "eval time": 7.151714429001004,
+ "tokens / sec": 6692.115366816459,
+ "mem allocated avg": 6987954006.016,
+ "mem reserved avg": 12187749842.944,
+ "elapsed time": 1758.2295099830008
+ },
+ {
+ "step": 5000,
+ "test accuracy": 0.5072024260803639,
+ "train loss": 0.5789329997301101,
+ "train samples": 20000,
+ "train total tokens": 4198051
+ }
+ ]
+ },
+ "meta_info": {
+ "model_info": {
+ "sha": "13afe5124825b4f3751f836b40dafda64c1ed062",
+ "created_at": "2024-09-18T15:23:48+00:00"
+ },
+ "dataset_info": {
+ "metamath": {
+ "sha": "aa4f34d3d2d3231299b5b03d9b3e5a20da45aa18",
+ "created_at": "2023-09-21T17:22:46+00:00"
+ },
+ "gsm8k": {
+ "sha": "e53f048856ff4f594e959d75785d2c2d37b678ee",
+ "created_at": "2022-04-12T10:22:10+00:00"
+ }
+ },
+ "package_info": {
+ "transformers-version": "4.52.4",
+ "transformers-commit-hash": null,
+ "peft-version": "0.16.1.dev0",
+ "peft-commit-hash": "25e5c6b25c4589eb2683484ede1ba3d985d8a760",
+ "datasets-version": "3.6.0",
+ "datasets-commit-hash": null,
+ "bitsandbytes-version": "0.46.0",
+ "bitsandbytes-commit-hash": null,
+ "torch-version": "2.7.1+cu126",
+ "torch-commit-hash": null
+ },
+ "system_info": {
+ "system": "Linux",
+ "release": "6.8.0-1031-aws",
+ "version": "#33-Ubuntu SMP Fri Jun 20 18:11:07 UTC 2025",
+ "machine": "x86_64",
+ "processor": "x86_64",
+ "accelerator": "NVIDIA L40S"
+ },
+ "pytorch_info": "PyTorch built with:\n - GCC 11.2\n - C++ Version: 201703\n - Intel(R) oneAPI Math Kernel Library Version 2024.2-Product Build 20240605 for Intel(R) 64 architecture applications\n - Intel(R) MKL-DNN v3.7.1 (Git Hash 8d263e693366ef8db40acc569cc7d8edf644556d)\n - OpenMP 201511 (a.k.a. OpenMP 4.5)\n - LAPACK is enabled (usually provided by MKL)\n - NNPACK is enabled\n - CPU capability usage: AVX2\n - CUDA Runtime 12.6\n - NVCC architecture flags: -gencode;arch=compute_50,code=sm_50;-gencode;arch=compute_60,code=sm_60;-gencode;arch=compute_70,code=sm_70;-gencode;arch=compute_75,code=sm_75;-gencode;arch=compute_80,code=sm_80;-gencode;arch=compute_86,code=sm_86;-gencode;arch=compute_90,code=sm_90\n - CuDNN 90.7.1 (built against CUDA 12.8)\n - Built with CuDNN 90.5.1\n - Magma 2.6.1\n - Build settings: BLAS_INFO=mkl, BUILD_TYPE=Release, COMMIT_SHA=e2d141dbde55c2a4370fac5165b0561b6af4798b, CUDA_VERSION=12.6, CUDNN_VERSION=9.5.1, CXX_COMPILER=/opt/rh/gcc-toolset-11/root/usr/bin/c++, CXX_FLAGS= -D_GLIBCXX_USE_CXX11_ABI=1 -fvisibility-inlines-hidden -DUSE_PTHREADPOOL -DNDEBUG -DUSE_KINETO -DLIBKINETO_NOROCTRACER -DLIBKINETO_NOXPUPTI=ON -DUSE_FBGEMM -DUSE_PYTORCH_QNNPACK -DUSE_XNNPACK -DSYMBOLICATE_MOBILE_DEBUG_HANDLE -O2 -fPIC -Wall -Wextra -Werror=return-type -Werror=non-virtual-dtor -Werror=range-loop-construct -Werror=bool-operation -Wnarrowing -Wno-missing-field-initializers -Wno-unknown-pragmas -Wno-unused-parameter -Wno-strict-overflow -Wno-strict-aliasing -Wno-stringop-overflow -Wsuggest-override -Wno-psabi -Wno-error=old-style-cast -fdiagnostics-color=always -faligned-new -Wno-maybe-uninitialized -fno-math-errno -fno-trapping-math -Werror=format -Wno-stringop-overflow, LAPACK_INFO=mkl, PERF_WITH_AVX=1, PERF_WITH_AVX2=1, TORCH_VERSION=2.7.1, USE_CUDA=ON, USE_CUDNN=ON, USE_CUSPARSELT=1, USE_GFLAGS=OFF, USE_GLOG=OFF, USE_GLOO=ON, USE_MKL=ON, USE_MKLDNN=ON, USE_MPI=OFF, USE_NCCL=1, USE_NNPACK=ON, USE_OPENMP=ON, USE_ROCM=OFF, USE_ROCM_KERNEL_ASSERT=OFF, \n"
+ }
+}
\ No newline at end of file
diff --git a/peft/method_comparison/MetaMathQA/results/trainable_tokens--llama-3.2-3B-sos+eos.json b/peft/method_comparison/MetaMathQA/results/trainable_tokens--llama-3.2-3B-sos+eos.json
new file mode 100644
index 0000000000000000000000000000000000000000..eff36db4db861519316e19d0696797c8eb04da97
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/results/trainable_tokens--llama-3.2-3B-sos+eos.json
@@ -0,0 +1,344 @@
+{
+ "run_info": {
+ "created_at": "2025-07-31T11:51:03+00:00",
+ "total_time": 1813.5205606600002,
+ "experiment_name": "trainable_tokens/llama-3.2-3B-sos+eos",
+ "peft_branch": "main",
+ "train_config": {
+ "model_id": "meta-llama/Llama-3.2-3B",
+ "dtype": "bfloat16",
+ "max_seq_length": 768,
+ "batch_size": 4,
+ "batch_size_eval": 50,
+ "max_steps": 5000,
+ "eval_steps": 250,
+ "compile": false,
+ "query_template": "Question: {query} Think step by step.\nAnswer:",
+ "seed": 0,
+ "grad_norm_clip": 1.0,
+ "optimizer_type": "AdamW",
+ "optimizer_kwargs": {
+ "lr": 0.2
+ },
+ "lr_scheduler": "cosine",
+ "use_amp": false,
+ "autocast_adapter_dtype": true,
+ "generation_kwargs": {
+ "max_length": 800,
+ "max_new_tokens": 300
+ },
+ "attn_implementation": null
+ },
+ "peft_config": {
+ "task_type": "CAUSAL_LM",
+ "peft_type": "TRAINABLE_TOKENS",
+ "auto_mapping": null,
+ "base_model_name_or_path": "meta-llama/Llama-3.2-3B",
+ "revision": null,
+ "inference_mode": false,
+ "token_indices": [
+ 128000,
+ 128001
+ ],
+ "target_modules": "model.embed_tokens",
+ "init_weights": true
+ },
+ "error_msg": ""
+ },
+ "train_info": {
+ "accelerator_memory_reserved_avg": 12730137942,
+ "accelerator_memory_max": 20956839936,
+ "accelerator_memory_reserved_99th": 16957675929,
+ "train_time": 1571.9034050299992,
+ "file_size": 49424,
+ "num_trainable_params": 6144,
+ "num_total_params": 3212755968,
+ "status": "success",
+ "metrics": [
+ {
+ "step": 250,
+ "valid accuracy": 0.2,
+ "train loss": 0.9600473783016205,
+ "train samples": 1000,
+ "train time": 28.046887916000458,
+ "eval time": 11.940005464000023,
+ "tokens / sec": 7548.751955443032,
+ "mem allocated avg": 6772620728.32,
+ "mem reserved avg": 12816987717.632,
+ "elapsed time": 79.72835956
+ },
+ {
+ "step": 500,
+ "valid accuracy": 0.1,
+ "train loss": 0.9827968046665192,
+ "train samples": 2000,
+ "train time": 27.568676805000052,
+ "eval time": 11.946740159,
+ "tokens / sec": 7544.613093736749,
+ "mem allocated avg": 6765130303.488,
+ "mem reserved avg": 12640885669.888,
+ "elapsed time": 153.151956972
+ },
+ {
+ "step": 750,
+ "valid accuracy": 0.26,
+ "train loss": 1.078141197681427,
+ "train samples": 3000,
+ "train time": 28.346493393999594,
+ "eval time": 11.913883551000026,
+ "tokens / sec": 7563.581040517151,
+ "mem allocated avg": 6775356669.952,
+ "mem reserved avg": 12829595795.456,
+ "elapsed time": 227.42617082600003
+ },
+ {
+ "step": 1000,
+ "valid accuracy": 0.18,
+ "train loss": 0.9337297527790069,
+ "train samples": 4000,
+ "train time": 27.80469767599925,
+ "eval time": 11.935028867000028,
+ "tokens / sec": 7492.834571613906,
+ "mem allocated avg": 6767140114.432,
+ "mem reserved avg": 12714495705.088,
+ "elapsed time": 301.119469732
+ },
+ {
+ "step": 1250,
+ "valid accuracy": 0.06,
+ "train loss": 1.1530333435535431,
+ "train samples": 5000,
+ "train time": 27.832769999000448,
+ "eval time": 11.899406999999997,
+ "tokens / sec": 7492.534879118722,
+ "mem allocated avg": 6766889218.048,
+ "mem reserved avg": 12706635579.392,
+ "elapsed time": 374.949399381
+ },
+ {
+ "step": 1500,
+ "valid accuracy": 0.16,
+ "train loss": 0.9257006254196167,
+ "train samples": 6000,
+ "train time": 27.848633210000685,
+ "eval time": 11.963534283000058,
+ "tokens / sec": 7516.7423270463205,
+ "mem allocated avg": 6768338049.024,
+ "mem reserved avg": 12713531015.168,
+ "elapsed time": 448.64371043399996
+ },
+ {
+ "step": 1750,
+ "valid accuracy": 0.04,
+ "train loss": 0.9480950233936309,
+ "train samples": 7000,
+ "train time": 28.10500999800047,
+ "eval time": 11.907140037999966,
+ "tokens / sec": 7449.027771735166,
+ "mem allocated avg": 6769886017.536,
+ "mem reserved avg": 12724176158.72,
+ "elapsed time": 523.0294692360001
+ },
+ {
+ "step": 2000,
+ "valid accuracy": 0.22,
+ "train loss": 1.099897492647171,
+ "train samples": 8000,
+ "train time": 27.50086192600054,
+ "eval time": 11.908490246000042,
+ "tokens / sec": 7552.345106814087,
+ "mem allocated avg": 6767001008.128,
+ "mem reserved avg": 12671663472.64,
+ "elapsed time": 596.5166793630001
+ },
+ {
+ "step": 2250,
+ "valid accuracy": 0.2,
+ "train loss": 1.0596771531105043,
+ "train samples": 9000,
+ "train time": 28.679387931000633,
+ "eval time": 11.905819370000017,
+ "tokens / sec": 7494.860089662325,
+ "mem allocated avg": 6777668958.208,
+ "mem reserved avg": 12765641048.064,
+ "elapsed time": 671.4013165209999
+ },
+ {
+ "step": 2500,
+ "valid accuracy": 0.28,
+ "train loss": 0.8838931715488434,
+ "train samples": 10000,
+ "train time": 27.525735084001553,
+ "eval time": 11.918955123999922,
+ "tokens / sec": 7482.70661515273,
+ "mem allocated avg": 6762954442.752,
+ "mem reserved avg": 12636850749.44,
+ "elapsed time": 744.8136404429999
+ },
+ {
+ "step": 2750,
+ "valid accuracy": 0.28,
+ "train loss": 0.8453443908691406,
+ "train samples": 11000,
+ "train time": 28.56140573299922,
+ "eval time": 11.910845225000003,
+ "tokens / sec": 7418.437382975074,
+ "mem allocated avg": 6773394008.064,
+ "mem reserved avg": 12781445185.536,
+ "elapsed time": 819.4217107059999
+ },
+ {
+ "step": 3000,
+ "valid accuracy": 0.28,
+ "train loss": 0.8956673395633697,
+ "train samples": 12000,
+ "train time": 27.520784680998986,
+ "eval time": 11.922119511000119,
+ "tokens / sec": 7584.485777548084,
+ "mem allocated avg": 6768260833.28,
+ "mem reserved avg": 12729855246.336,
+ "elapsed time": 892.9293128969998
+ },
+ {
+ "step": 3250,
+ "valid accuracy": 0.28,
+ "train loss": 0.8384639675617218,
+ "train samples": 13000,
+ "train time": 27.425537425002176,
+ "eval time": 11.90852308500007,
+ "tokens / sec": 7689.9495799026545,
+ "mem allocated avg": 6769824622.592,
+ "mem reserved avg": 12732145336.32,
+ "elapsed time": 966.4361498369999
+ },
+ {
+ "step": 3500,
+ "valid accuracy": 0.28,
+ "train loss": 0.8318528242111206,
+ "train samples": 14000,
+ "train time": 27.599476771002628,
+ "eval time": 11.926854094000191,
+ "tokens / sec": 7599.781754572018,
+ "mem allocated avg": 6769281437.696,
+ "mem reserved avg": 12748083691.52,
+ "elapsed time": 1040.349463558
+ },
+ {
+ "step": 3750,
+ "valid accuracy": 0.3,
+ "train loss": 0.825278183221817,
+ "train samples": 15000,
+ "train time": 28.668002616999956,
+ "eval time": 11.920088525999972,
+ "tokens / sec": 7559.054702733158,
+ "mem allocated avg": 6780301985.792,
+ "mem reserved avg": 12867151593.472,
+ "elapsed time": 1115.464965257
+ },
+ {
+ "step": 4000,
+ "valid accuracy": 0.34,
+ "train loss": 0.8279166626930237,
+ "train samples": 16000,
+ "train time": 27.677960625997912,
+ "eval time": 11.956045786999994,
+ "tokens / sec": 7383.961656771504,
+ "mem allocated avg": 6761672556.544,
+ "mem reserved avg": 12607280906.24,
+ "elapsed time": 1189.311786065
+ },
+ {
+ "step": 4250,
+ "valid accuracy": 0.26,
+ "train loss": 0.7829471210241318,
+ "train samples": 17000,
+ "train time": 27.69402594300027,
+ "eval time": 11.900985279999986,
+ "tokens / sec": 7633.018053607661,
+ "mem allocated avg": 6771771314.176,
+ "mem reserved avg": 12787006832.64,
+ "elapsed time": 1263.137991501
+ },
+ {
+ "step": 4500,
+ "valid accuracy": 0.36,
+ "train loss": 0.788821615934372,
+ "train samples": 18000,
+ "train time": 27.622178668999823,
+ "eval time": 11.941970926000067,
+ "tokens / sec": 7523.591911062131,
+ "mem allocated avg": 6766746431.488,
+ "mem reserved avg": 12679666204.672,
+ "elapsed time": 1336.699760115
+ },
+ {
+ "step": 4750,
+ "valid accuracy": 0.3,
+ "train loss": 0.7817396788597107,
+ "train samples": 19000,
+ "train time": 28.053782109000622,
+ "eval time": 11.908781481000005,
+ "tokens / sec": 7483.447300770342,
+ "mem allocated avg": 6769035872.256,
+ "mem reserved avg": 12704303546.368,
+ "elapsed time": 1411.011856929
+ },
+ {
+ "step": 5000,
+ "valid accuracy": 0.32,
+ "train loss": 0.786205664396286,
+ "train samples": 20000,
+ "train time": 27.865934093999613,
+ "eval time": 11.930896392000022,
+ "tokens / sec": 7474.359169063313,
+ "mem allocated avg": 6766191118.336,
+ "mem reserved avg": 12745357393.92,
+ "elapsed time": 1484.8831304389998
+ },
+ {
+ "step": 5000,
+ "test accuracy": 0.2880970432145565,
+ "train loss": 0.786205664396286,
+ "train samples": 20000,
+ "train total tokens": 4198051
+ }
+ ]
+ },
+ "meta_info": {
+ "model_info": {
+ "sha": "13afe5124825b4f3751f836b40dafda64c1ed062",
+ "created_at": "2024-09-18T15:23:48+00:00"
+ },
+ "dataset_info": {
+ "metamath": {
+ "sha": "aa4f34d3d2d3231299b5b03d9b3e5a20da45aa18",
+ "created_at": "2023-09-21T17:22:46+00:00"
+ },
+ "gsm8k": {
+ "sha": "e53f048856ff4f594e959d75785d2c2d37b678ee",
+ "created_at": "2022-04-12T10:22:10+00:00"
+ }
+ },
+ "package_info": {
+ "transformers-version": "4.52.4",
+ "transformers-commit-hash": null,
+ "peft-version": "0.16.1.dev0",
+ "peft-commit-hash": "25e5c6b25c4589eb2683484ede1ba3d985d8a760",
+ "datasets-version": "3.6.0",
+ "datasets-commit-hash": null,
+ "bitsandbytes-version": "0.46.0",
+ "bitsandbytes-commit-hash": null,
+ "torch-version": "2.7.1+cu126",
+ "torch-commit-hash": null
+ },
+ "system_info": {
+ "system": "Linux",
+ "release": "6.8.0-1031-aws",
+ "version": "#33-Ubuntu SMP Fri Jun 20 18:11:07 UTC 2025",
+ "machine": "x86_64",
+ "processor": "x86_64",
+ "accelerator": "NVIDIA L40S"
+ },
+ "pytorch_info": "PyTorch built with:\n - GCC 11.2\n - C++ Version: 201703\n - Intel(R) oneAPI Math Kernel Library Version 2024.2-Product Build 20240605 for Intel(R) 64 architecture applications\n - Intel(R) MKL-DNN v3.7.1 (Git Hash 8d263e693366ef8db40acc569cc7d8edf644556d)\n - OpenMP 201511 (a.k.a. OpenMP 4.5)\n - LAPACK is enabled (usually provided by MKL)\n - NNPACK is enabled\n - CPU capability usage: AVX2\n - CUDA Runtime 12.6\n - NVCC architecture flags: -gencode;arch=compute_50,code=sm_50;-gencode;arch=compute_60,code=sm_60;-gencode;arch=compute_70,code=sm_70;-gencode;arch=compute_75,code=sm_75;-gencode;arch=compute_80,code=sm_80;-gencode;arch=compute_86,code=sm_86;-gencode;arch=compute_90,code=sm_90\n - CuDNN 90.7.1 (built against CUDA 12.8)\n - Built with CuDNN 90.5.1\n - Magma 2.6.1\n - Build settings: BLAS_INFO=mkl, BUILD_TYPE=Release, COMMIT_SHA=e2d141dbde55c2a4370fac5165b0561b6af4798b, CUDA_VERSION=12.6, CUDNN_VERSION=9.5.1, CXX_COMPILER=/opt/rh/gcc-toolset-11/root/usr/bin/c++, CXX_FLAGS= -D_GLIBCXX_USE_CXX11_ABI=1 -fvisibility-inlines-hidden -DUSE_PTHREADPOOL -DNDEBUG -DUSE_KINETO -DLIBKINETO_NOROCTRACER -DLIBKINETO_NOXPUPTI=ON -DUSE_FBGEMM -DUSE_PYTORCH_QNNPACK -DUSE_XNNPACK -DSYMBOLICATE_MOBILE_DEBUG_HANDLE -O2 -fPIC -Wall -Wextra -Werror=return-type -Werror=non-virtual-dtor -Werror=range-loop-construct -Werror=bool-operation -Wnarrowing -Wno-missing-field-initializers -Wno-unknown-pragmas -Wno-unused-parameter -Wno-strict-overflow -Wno-strict-aliasing -Wno-stringop-overflow -Wsuggest-override -Wno-psabi -Wno-error=old-style-cast -fdiagnostics-color=always -faligned-new -Wno-maybe-uninitialized -fno-math-errno -fno-trapping-math -Werror=format -Wno-stringop-overflow, LAPACK_INFO=mkl, PERF_WITH_AVX=1, PERF_WITH_AVX2=1, TORCH_VERSION=2.7.1, USE_CUDA=ON, USE_CUDNN=ON, USE_CUSPARSELT=1, USE_GFLAGS=OFF, USE_GLOG=OFF, USE_GLOO=ON, USE_MKL=ON, USE_MKLDNN=ON, USE_MPI=OFF, USE_NCCL=1, USE_NNPACK=ON, USE_OPENMP=ON, USE_ROCM=OFF, USE_ROCM_KERNEL_ASSERT=OFF, \n"
+ }
+}
\ No newline at end of file
diff --git a/peft/method_comparison/MetaMathQA/results/vblora--llama-3.2-3B-default.json b/peft/method_comparison/MetaMathQA/results/vblora--llama-3.2-3B-default.json
new file mode 100644
index 0000000000000000000000000000000000000000..ccf041765e8ee3c837eefb23eadba2249638e909
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/results/vblora--llama-3.2-3B-default.json
@@ -0,0 +1,357 @@
+{
+ "run_info": {
+ "created_at": "2025-06-19T23:49:12+00:00",
+ "total_time": 2210.184595478997,
+ "experiment_name": "vblora/llama-3.2-3B-default",
+ "peft_branch": "main",
+ "train_config": {
+ "model_id": "meta-llama/Llama-3.2-3B",
+ "dtype": "bfloat16",
+ "max_seq_length": 768,
+ "batch_size": 4,
+ "batch_size_eval": 50,
+ "max_steps": 5000,
+ "eval_steps": 250,
+ "compile": false,
+ "query_template": "Question: {query} Think step by step.\nAnswer:",
+ "seed": 0,
+ "grad_norm_clip": 1.0,
+ "optimizer_type": "AdamW",
+ "optimizer_kwargs": {
+ "lr": 0.0001,
+ "weight_decay": 0.1
+ },
+ "lr_scheduler": "cosine",
+ "use_amp": false,
+ "autocast_adapter_dtype": true,
+ "generation_kwargs": {
+ "max_length": 800,
+ "max_new_tokens": 300
+ },
+ "attn_implementation": null
+ },
+ "peft_config": {
+ "task_type": null,
+ "peft_type": "VBLORA",
+ "auto_mapping": null,
+ "base_model_name_or_path": "meta-llama/Llama-3.2-3B",
+ "revision": null,
+ "inference_mode": false,
+ "r": 4,
+ "num_vectors": 256,
+ "vector_length": 256,
+ "topk": 2,
+ "target_modules": [
+ "v_proj",
+ "q_proj"
+ ],
+ "exclude_modules": null,
+ "save_only_topk_weights": false,
+ "vblora_dropout": 0.0,
+ "fan_in_fan_out": false,
+ "bias": "none",
+ "modules_to_save": null,
+ "init_vector_bank_bound": 0.02,
+ "init_logits_std": 0.1,
+ "layers_to_transform": null,
+ "layers_pattern": null
+ },
+ "error_msg": ""
+ },
+ "train_info": {
+ "accelerator_memory_reserved_avg": 11735344663,
+ "accelerator_memory_max": 22181576704,
+ "accelerator_memory_reserved_99th": 17635223797,
+ "train_time": 1961.761054087001,
+ "file_size": 4864912,
+ "num_trainable_params": 1212416,
+ "num_total_params": 3213962240,
+ "status": "success",
+ "metrics": [
+ {
+ "step": 250,
+ "valid accuracy": 0.0,
+ "train loss": 1.308416832447052,
+ "train samples": 1000,
+ "train time": 40.12101128498034,
+ "eval time": 12.847303112997906,
+ "tokens / sec": 5277.010554299236,
+ "mem allocated avg": 6798303909.888,
+ "mem reserved avg": 11786547888.128,
+ "elapsed time": 101.0704645309961
+ },
+ {
+ "step": 500,
+ "valid accuracy": 0.38,
+ "train loss": 1.0353211228847503,
+ "train samples": 2000,
+ "train time": 39.44148263899842,
+ "eval time": 12.918682472998626,
+ "tokens / sec": 5273.508653408011,
+ "mem allocated avg": 6790843463.68,
+ "mem reserved avg": 11678368399.36,
+ "elapsed time": 195.96383863499796
+ },
+ {
+ "step": 750,
+ "valid accuracy": 0.3,
+ "train loss": 0.8149400608539581,
+ "train samples": 3000,
+ "train time": 39.73428049797076,
+ "eval time": 12.816220013999555,
+ "tokens / sec": 5395.869695210651,
+ "mem allocated avg": 6801506754.56,
+ "mem reserved avg": 11833448595.456,
+ "elapsed time": 291.3562671039981
+ },
+ {
+ "step": 1000,
+ "valid accuracy": 0.34,
+ "train loss": 0.766725031375885,
+ "train samples": 4000,
+ "train time": 39.66955411599338,
+ "eval time": 12.954798815000686,
+ "tokens / sec": 5251.785774824381,
+ "mem allocated avg": 6791902521.344,
+ "mem reserved avg": 11700715651.072,
+ "elapsed time": 386.48246048299916
+ },
+ {
+ "step": 1250,
+ "valid accuracy": 0.4,
+ "train loss": 0.7548577107191086,
+ "train samples": 5000,
+ "train time": 39.58740361595119,
+ "eval time": 12.921318173001055,
+ "tokens / sec": 5267.786744063522,
+ "mem allocated avg": 6792241373.184,
+ "mem reserved avg": 11698584944.64,
+ "elapsed time": 481.6297270110008
+ },
+ {
+ "step": 1500,
+ "valid accuracy": 0.42,
+ "train loss": 0.744083244919777,
+ "train samples": 6000,
+ "train time": 39.58100679998461,
+ "eval time": 7.990361490003124,
+ "tokens / sec": 5288.672950079719,
+ "mem allocated avg": 6792975718.4,
+ "mem reserved avg": 11729908006.912,
+ "elapsed time": 571.7995823969977
+ },
+ {
+ "step": 1750,
+ "valid accuracy": 0.4,
+ "train loss": 0.7353366105556488,
+ "train samples": 7000,
+ "train time": 39.89848869200068,
+ "eval time": 9.013003496002057,
+ "tokens / sec": 5247.191231129864,
+ "mem allocated avg": 6795538806.784,
+ "mem reserved avg": 11737281593.344,
+ "elapsed time": 663.3418345429964
+ },
+ {
+ "step": 2000,
+ "valid accuracy": 0.36,
+ "train loss": 0.735884799003601,
+ "train samples": 8000,
+ "train time": 39.573877232054656,
+ "eval time": 13.005171182994673,
+ "tokens / sec": 5248.3106161699825,
+ "mem allocated avg": 6792414906.368,
+ "mem reserved avg": 11683577724.928,
+ "elapsed time": 758.2818646219966
+ },
+ {
+ "step": 2250,
+ "valid accuracy": 0.34,
+ "train loss": 0.7294247032403945,
+ "train samples": 9000,
+ "train time": 40.16309046502283,
+ "eval time": 12.827437616993848,
+ "tokens / sec": 5351.878989172747,
+ "mem allocated avg": 6803159742.464,
+ "mem reserved avg": 11872145244.16,
+ "elapsed time": 854.2901024749954
+ },
+ {
+ "step": 2500,
+ "valid accuracy": 0.36,
+ "train loss": 0.7273153622150421,
+ "train samples": 10000,
+ "train time": 39.40831322706072,
+ "eval time": 12.578817460002028,
+ "tokens / sec": 5226.48606686793,
+ "mem allocated avg": 6788682082.304,
+ "mem reserved avg": 11624815525.888,
+ "elapsed time": 948.6046375669976
+ },
+ {
+ "step": 2750,
+ "valid accuracy": 0.3,
+ "train loss": 0.7221734907627105,
+ "train samples": 11000,
+ "train time": 39.99460277392063,
+ "eval time": 12.831681943003787,
+ "tokens / sec": 5297.739827488966,
+ "mem allocated avg": 6798795204.608,
+ "mem reserved avg": 11800045158.4,
+ "elapsed time": 1044.2291650330008
+ },
+ {
+ "step": 3000,
+ "valid accuracy": 0.44,
+ "train loss": 0.7163265677690506,
+ "train samples": 12000,
+ "train time": 39.72457089692762,
+ "eval time": 9.721318816998973,
+ "tokens / sec": 5254.455750864856,
+ "mem allocated avg": 6794274019.328,
+ "mem reserved avg": 11717786468.352,
+ "elapsed time": 1136.276137433997
+ },
+ {
+ "step": 3250,
+ "valid accuracy": 0.24,
+ "train loss": 0.7239821909666061,
+ "train samples": 13000,
+ "train time": 39.57894092098286,
+ "eval time": 12.939295003001462,
+ "tokens / sec": 5328.616559524724,
+ "mem allocated avg": 6796102031.36,
+ "mem reserved avg": 11749923225.6,
+ "elapsed time": 1231.5789504099957
+ },
+ {
+ "step": 3500,
+ "valid accuracy": 0.3,
+ "train loss": 0.7123430745601654,
+ "train samples": 14000,
+ "train time": 39.774808847985696,
+ "eval time": 12.81972120499995,
+ "tokens / sec": 5273.438291096208,
+ "mem allocated avg": 6794877718.528,
+ "mem reserved avg": 11727257206.784,
+ "elapsed time": 1327.2042175199967
+ },
+ {
+ "step": 3750,
+ "valid accuracy": 0.32,
+ "train loss": 0.7080619329214096,
+ "train samples": 15000,
+ "train time": 40.429172475058294,
+ "eval time": 12.810948685997573,
+ "tokens / sec": 5360.065188910042,
+ "mem allocated avg": 6804612114.432,
+ "mem reserved avg": 11907847159.808,
+ "elapsed time": 1424.0900874009967
+ },
+ {
+ "step": 4000,
+ "valid accuracy": 0.42,
+ "train loss": 0.7257569855451584,
+ "train samples": 16000,
+ "train time": 39.64596449997771,
+ "eval time": 12.844434396996803,
+ "tokens / sec": 5154.950890401844,
+ "mem allocated avg": 6787030419.456,
+ "mem reserved avg": 11605689499.648,
+ "elapsed time": 1519.344677588997
+ },
+ {
+ "step": 4250,
+ "valid accuracy": 0.38,
+ "train loss": 0.7041294666528701,
+ "train samples": 17000,
+ "train time": 39.938396073041076,
+ "eval time": 12.83599700799823,
+ "tokens / sec": 5292.876549508964,
+ "mem allocated avg": 6797280624.64,
+ "mem reserved avg": 11765333098.496,
+ "elapsed time": 1614.829351510998
+ },
+ {
+ "step": 4500,
+ "valid accuracy": 0.38,
+ "train loss": 0.7148806138038635,
+ "train samples": 18000,
+ "train time": 39.55479707601626,
+ "eval time": 12.901207727001747,
+ "tokens / sec": 5253.926586972907,
+ "mem allocated avg": 6791958038.528,
+ "mem reserved avg": 11679299534.848,
+ "elapsed time": 1710.0793527279966
+ },
+ {
+ "step": 4750,
+ "valid accuracy": 0.32,
+ "train loss": 0.7083848255872727,
+ "train samples": 19000,
+ "train time": 39.88160159892141,
+ "eval time": 12.8585010780007,
+ "tokens / sec": 5264.056396513368,
+ "mem allocated avg": 6794248144.896,
+ "mem reserved avg": 11730923028.48,
+ "elapsed time": 1806.240128286001
+ },
+ {
+ "step": 5000,
+ "valid accuracy": 0.36,
+ "train loss": 0.7142883945703506,
+ "train samples": 20000,
+ "train time": 39.631631882970396,
+ "eval time": 12.818420095005422,
+ "tokens / sec": 5255.398026885119,
+ "mem allocated avg": 6791235981.312,
+ "mem reserved avg": 11677395320.832,
+ "elapsed time": 1901.3912653839943
+ },
+ {
+ "step": 5000,
+ "test accuracy": 0.36997725549658833,
+ "train loss": 0.7142883945703506,
+ "train samples": 20000,
+ "train total tokens": 4198051
+ }
+ ]
+ },
+ "meta_info": {
+ "model_info": {
+ "sha": "13afe5124825b4f3751f836b40dafda64c1ed062",
+ "created_at": "2024-09-18T15:23:48+00:00"
+ },
+ "dataset_info": {
+ "metamath": {
+ "sha": "aa4f34d3d2d3231299b5b03d9b3e5a20da45aa18",
+ "created_at": "2023-09-21T17:22:46+00:00"
+ },
+ "gsm8k": {
+ "sha": "e53f048856ff4f594e959d75785d2c2d37b678ee",
+ "created_at": "2022-04-12T10:22:10+00:00"
+ }
+ },
+ "package_info": {
+ "transformers-version": "4.52.4",
+ "transformers-commit-hash": null,
+ "peft-version": "0.15.2.dev0",
+ "peft-commit-hash": "5fe7f8f8abe914d313fc3751f2ea92de7718fbaf",
+ "datasets-version": "3.6.0",
+ "datasets-commit-hash": null,
+ "bitsandbytes-version": "0.46.0",
+ "bitsandbytes-commit-hash": null,
+ "torch-version": "2.7.1+cu126",
+ "torch-commit-hash": null
+ },
+ "system_info": {
+ "system": "Linux",
+ "release": "6.8.0-1029-aws",
+ "version": "#31-Ubuntu SMP Wed Apr 23 18:42:41 UTC 2025",
+ "machine": "x86_64",
+ "processor": "x86_64",
+ "accelerator": "NVIDIA L40S"
+ },
+ "pytorch_info": "PyTorch built with:\n - GCC 11.2\n - C++ Version: 201703\n - Intel(R) oneAPI Math Kernel Library Version 2024.2-Product Build 20240605 for Intel(R) 64 architecture applications\n - Intel(R) MKL-DNN v3.7.1 (Git Hash 8d263e693366ef8db40acc569cc7d8edf644556d)\n - OpenMP 201511 (a.k.a. OpenMP 4.5)\n - LAPACK is enabled (usually provided by MKL)\n - NNPACK is enabled\n - CPU capability usage: AVX2\n - CUDA Runtime 12.6\n - NVCC architecture flags: -gencode;arch=compute_50,code=sm_50;-gencode;arch=compute_60,code=sm_60;-gencode;arch=compute_70,code=sm_70;-gencode;arch=compute_75,code=sm_75;-gencode;arch=compute_80,code=sm_80;-gencode;arch=compute_86,code=sm_86;-gencode;arch=compute_90,code=sm_90\n - CuDNN 90.7.1 (built against CUDA 12.8)\n - Built with CuDNN 90.5.1\n - Magma 2.6.1\n - Build settings: BLAS_INFO=mkl, BUILD_TYPE=Release, COMMIT_SHA=e2d141dbde55c2a4370fac5165b0561b6af4798b, CUDA_VERSION=12.6, CUDNN_VERSION=9.5.1, CXX_COMPILER=/opt/rh/gcc-toolset-11/root/usr/bin/c++, CXX_FLAGS= -D_GLIBCXX_USE_CXX11_ABI=1 -fvisibility-inlines-hidden -DUSE_PTHREADPOOL -DNDEBUG -DUSE_KINETO -DLIBKINETO_NOROCTRACER -DLIBKINETO_NOXPUPTI=ON -DUSE_FBGEMM -DUSE_PYTORCH_QNNPACK -DUSE_XNNPACK -DSYMBOLICATE_MOBILE_DEBUG_HANDLE -O2 -fPIC -Wall -Wextra -Werror=return-type -Werror=non-virtual-dtor -Werror=range-loop-construct -Werror=bool-operation -Wnarrowing -Wno-missing-field-initializers -Wno-unknown-pragmas -Wno-unused-parameter -Wno-strict-overflow -Wno-strict-aliasing -Wno-stringop-overflow -Wsuggest-override -Wno-psabi -Wno-error=old-style-cast -fdiagnostics-color=always -faligned-new -Wno-maybe-uninitialized -fno-math-errno -fno-trapping-math -Werror=format -Wno-stringop-overflow, LAPACK_INFO=mkl, PERF_WITH_AVX=1, PERF_WITH_AVX2=1, TORCH_VERSION=2.7.1, USE_CUDA=ON, USE_CUDNN=ON, USE_CUSPARSELT=1, USE_GFLAGS=OFF, USE_GLOG=OFF, USE_GLOO=ON, USE_MKL=ON, USE_MKLDNN=ON, USE_MPI=OFF, USE_NCCL=1, USE_NNPACK=ON, USE_OPENMP=ON, USE_ROCM=OFF, USE_ROCM_KERNEL_ASSERT=OFF, \n"
+ }
+}
diff --git a/peft/method_comparison/MetaMathQA/results/vera--llama-3.2-3B-default.json b/peft/method_comparison/MetaMathQA/results/vera--llama-3.2-3B-default.json
new file mode 100644
index 0000000000000000000000000000000000000000..690c35072932a4de9167712c9a2634f92db6f29d
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/results/vera--llama-3.2-3B-default.json
@@ -0,0 +1,353 @@
+{
+ "run_info": {
+ "created_at": "2025-06-19T20:53:39+00:00",
+ "total_time": 2024.6820476150024,
+ "experiment_name": "vera/llama-3.2-3B-default",
+ "peft_branch": "main",
+ "train_config": {
+ "model_id": "meta-llama/Llama-3.2-3B",
+ "dtype": "bfloat16",
+ "max_seq_length": 768,
+ "batch_size": 4,
+ "batch_size_eval": 50,
+ "max_steps": 5000,
+ "eval_steps": 250,
+ "compile": false,
+ "query_template": "Question: {query} Think step by step.\nAnswer:",
+ "seed": 0,
+ "grad_norm_clip": 1.0,
+ "optimizer_type": "AdamW",
+ "optimizer_kwargs": {
+ "lr": 0.001
+ },
+ "lr_scheduler": "cosine",
+ "use_amp": false,
+ "autocast_adapter_dtype": true,
+ "generation_kwargs": {
+ "max_length": 800,
+ "max_new_tokens": 300
+ },
+ "attn_implementation": null
+ },
+ "peft_config": {
+ "task_type": null,
+ "peft_type": "VERA",
+ "auto_mapping": null,
+ "base_model_name_or_path": "meta-llama/Llama-3.2-3B",
+ "revision": null,
+ "inference_mode": false,
+ "r": 256,
+ "target_modules": [
+ "v_proj",
+ "q_proj"
+ ],
+ "projection_prng_key": 0,
+ "save_projection": true,
+ "vera_dropout": 0.0,
+ "d_initial": 0.1,
+ "fan_in_fan_out": false,
+ "bias": "none",
+ "modules_to_save": null,
+ "init_weights": true,
+ "layers_to_transform": null,
+ "layers_pattern": null
+ },
+ "error_msg": ""
+ },
+ "train_info": {
+ "accelerator_memory_reserved_avg": 11489715316,
+ "accelerator_memory_max": 21596471296,
+ "accelerator_memory_reserved_99th": 17291123097,
+ "train_time": 1819.9693055349999,
+ "file_size": 6821968,
+ "num_trainable_params": 129024,
+ "num_total_params": 3212878848,
+ "status": "success",
+ "metrics": [
+ {
+ "step": 250,
+ "valid accuracy": 0.0,
+ "train loss": 1.3017588877677917,
+ "train samples": 1000,
+ "train time": 32.843521857023006,
+ "eval time": 11.480974874997628,
+ "tokens / sec": 6446.294064372017,
+ "mem allocated avg": 6784826523.648,
+ "mem reserved avg": 11538438029.312,
+ "elapsed time": 95.45296428899746
+ },
+ {
+ "step": 500,
+ "valid accuracy": 0.28,
+ "train loss": 1.0202219936847687,
+ "train samples": 2000,
+ "train time": 32.35236015598639,
+ "eval time": 11.4980273259971,
+ "tokens / sec": 6429.051821788439,
+ "mem allocated avg": 6777359808.512,
+ "mem reserved avg": 11429948162.048,
+ "elapsed time": 183.95939499299857
+ },
+ {
+ "step": 750,
+ "valid accuracy": 0.38,
+ "train loss": 0.8040032889842987,
+ "train samples": 3000,
+ "train time": 32.52055500800634,
+ "eval time": 11.426841341002728,
+ "tokens / sec": 6592.784162115804,
+ "mem allocated avg": 6787965165.568,
+ "mem reserved avg": 11585061912.576,
+ "elapsed time": 272.8589564269969
+ },
+ {
+ "step": 1000,
+ "valid accuracy": 0.3,
+ "train loss": 0.7544035723209381,
+ "train samples": 4000,
+ "train time": 32.27830113501477,
+ "eval time": 11.54098314699877,
+ "tokens / sec": 6454.3669485133405,
+ "mem allocated avg": 6779215933.44,
+ "mem reserved avg": 11460172316.672,
+ "elapsed time": 361.1500098109973
+ },
+ {
+ "step": 1250,
+ "valid accuracy": 0.44,
+ "train loss": 0.7379197257757187,
+ "train samples": 5000,
+ "train time": 32.060909217962035,
+ "eval time": 11.406497389998549,
+ "tokens / sec": 6504.431879404317,
+ "mem allocated avg": 6779128844.288,
+ "mem reserved avg": 11454770053.12,
+ "elapsed time": 449.3482204989996
+ },
+ {
+ "step": 1500,
+ "valid accuracy": 0.4,
+ "train loss": 0.7252234178781509,
+ "train samples": 6000,
+ "train time": 31.98088176901365,
+ "eval time": 11.480169268001191,
+ "tokens / sec": 6545.504326988923,
+ "mem allocated avg": 6780286265.344,
+ "mem reserved avg": 11479667441.664,
+ "elapsed time": 537.3097453219998
+ },
+ {
+ "step": 1750,
+ "valid accuracy": 0.4,
+ "train loss": 0.7148357192277909,
+ "train samples": 7000,
+ "train time": 32.29452324002341,
+ "eval time": 11.44221062500219,
+ "tokens / sec": 6482.678144650271,
+ "mem allocated avg": 6782215264.256,
+ "mem reserved avg": 11493600919.552,
+ "elapsed time": 625.780868398997
+ },
+ {
+ "step": 2000,
+ "valid accuracy": 0.4,
+ "train loss": 0.7139411936998368,
+ "train samples": 8000,
+ "train time": 32.33002986999054,
+ "eval time": 11.472246884000924,
+ "tokens / sec": 6424.243987253105,
+ "mem allocated avg": 6778636718.08,
+ "mem reserved avg": 11439217573.888,
+ "elapsed time": 714.3076436519987
+ },
+ {
+ "step": 2250,
+ "valid accuracy": 0.38,
+ "train loss": 0.7067342863082886,
+ "train samples": 9000,
+ "train time": 32.69249906902769,
+ "eval time": 11.424881449998793,
+ "tokens / sec": 6574.841511692143,
+ "mem allocated avg": 6789716504.576,
+ "mem reserved avg": 11617542602.752,
+ "elapsed time": 803.4051666009982
+ },
+ {
+ "step": 2500,
+ "valid accuracy": 0.4,
+ "train loss": 0.7048580280542374,
+ "train samples": 10000,
+ "train time": 31.796681229010574,
+ "eval time": 11.401134708998143,
+ "tokens / sec": 6477.625715607085,
+ "mem allocated avg": 6775192217.6,
+ "mem reserved avg": 11386755219.456,
+ "elapsed time": 890.7853266579987
+ },
+ {
+ "step": 2750,
+ "valid accuracy": 0.36,
+ "train loss": 0.6994425257444382,
+ "train samples": 11000,
+ "train time": 32.589996781029186,
+ "eval time": 6.453208308001194,
+ "tokens / sec": 6501.412118068606,
+ "mem allocated avg": 6785945655.296,
+ "mem reserved avg": 11552530890.752,
+ "elapsed time": 974.6122346880002
+ },
+ {
+ "step": 3000,
+ "valid accuracy": 0.4,
+ "train loss": 0.6912879683971405,
+ "train samples": 12000,
+ "train time": 32.34826778500428,
+ "eval time": 11.457833226999355,
+ "tokens / sec": 6452.617536966281,
+ "mem allocated avg": 6780318763.008,
+ "mem reserved avg": 11474030297.088,
+ "elapsed time": 1062.897270567999
+ },
+ {
+ "step": 3250,
+ "valid accuracy": 0.4,
+ "train loss": 0.700449936747551,
+ "train samples": 13000,
+ "train time": 32.51472582996939,
+ "eval time": 8.004199169998174,
+ "tokens / sec": 6486.322569744963,
+ "mem allocated avg": 6782387701.76,
+ "mem reserved avg": 11501452656.64,
+ "elapsed time": 1148.3985279560002
+ },
+ {
+ "step": 3500,
+ "valid accuracy": 0.36,
+ "train loss": 0.6886729755401612,
+ "train samples": 14000,
+ "train time": 32.572147220984334,
+ "eval time": 11.456443364000734,
+ "tokens / sec": 6439.550901479111,
+ "mem allocated avg": 6781381988.352,
+ "mem reserved avg": 11484943876.096,
+ "elapsed time": 1237.2252680229976
+ },
+ {
+ "step": 3750,
+ "valid accuracy": 0.38,
+ "train loss": 0.6851948540210724,
+ "train samples": 15000,
+ "train time": 32.8770313250061,
+ "eval time": 8.042231839001033,
+ "tokens / sec": 6591.318962402083,
+ "mem allocated avg": 6791807023.104,
+ "mem reserved avg": 11653781389.312,
+ "elapsed time": 1323.4750151669978
+ },
+ {
+ "step": 4000,
+ "valid accuracy": 0.36,
+ "train loss": 0.7032276903390884,
+ "train samples": 16000,
+ "train time": 31.65130396198947,
+ "eval time": 7.9955749260007,
+ "tokens / sec": 6457.016754994822,
+ "mem allocated avg": 6773653422.08,
+ "mem reserved avg": 11367989903.36,
+ "elapsed time": 1407.2714081800004
+ },
+ {
+ "step": 4250,
+ "valid accuracy": 0.36,
+ "train loss": 0.684476065993309,
+ "train samples": 17000,
+ "train time": 32.02934406197164,
+ "eval time": 8.007123895000404,
+ "tokens / sec": 6599.854170943876,
+ "mem allocated avg": 6784119472.128,
+ "mem reserved avg": 11519949537.28,
+ "elapsed time": 1492.0019941529972
+ },
+ {
+ "step": 4500,
+ "valid accuracy": 0.38,
+ "train loss": 0.6939880999326706,
+ "train samples": 18000,
+ "train time": 31.936327281997364,
+ "eval time": 9.855819755000994,
+ "tokens / sec": 6507.260467522446,
+ "mem allocated avg": 6777879162.88,
+ "mem reserved avg": 11436331892.736,
+ "elapsed time": 1578.2498042659972
+ },
+ {
+ "step": 4750,
+ "valid accuracy": 0.36,
+ "train loss": 0.68637368786335,
+ "train samples": 19000,
+ "train time": 32.33460194401778,
+ "eval time": 6.469711448000453,
+ "tokens / sec": 6492.704019164238,
+ "mem allocated avg": 6781104441.344,
+ "mem reserved avg": 11484004352.0,
+ "elapsed time": 1662.171022565999
+ },
+ {
+ "step": 5000,
+ "valid accuracy": 0.38,
+ "train loss": 0.6926896897554398,
+ "train samples": 20000,
+ "train time": 32.14674746405217,
+ "eval time": 8.441190715999255,
+ "tokens / sec": 6479.038049896257,
+ "mem allocated avg": 6777818853.376,
+ "mem reserved avg": 11434117300.224,
+ "elapsed time": 1747.4833575960001
+ },
+ {
+ "step": 5000,
+ "test accuracy": 0.3684609552691433,
+ "train loss": 0.6926896897554398,
+ "train samples": 20000,
+ "train total tokens": 4198051
+ }
+ ]
+ },
+ "meta_info": {
+ "model_info": {
+ "sha": "13afe5124825b4f3751f836b40dafda64c1ed062",
+ "created_at": "2024-09-18T15:23:48+00:00"
+ },
+ "dataset_info": {
+ "metamath": {
+ "sha": "aa4f34d3d2d3231299b5b03d9b3e5a20da45aa18",
+ "created_at": "2023-09-21T17:22:46+00:00"
+ },
+ "gsm8k": {
+ "sha": "e53f048856ff4f594e959d75785d2c2d37b678ee",
+ "created_at": "2022-04-12T10:22:10+00:00"
+ }
+ },
+ "package_info": {
+ "transformers-version": "4.52.4",
+ "transformers-commit-hash": null,
+ "peft-version": "0.15.2.dev0",
+ "peft-commit-hash": "5fe7f8f8abe914d313fc3751f2ea92de7718fbaf",
+ "datasets-version": "3.6.0",
+ "datasets-commit-hash": null,
+ "bitsandbytes-version": "0.46.0",
+ "bitsandbytes-commit-hash": null,
+ "torch-version": "2.7.1+cu126",
+ "torch-commit-hash": null
+ },
+ "system_info": {
+ "system": "Linux",
+ "release": "6.8.0-1029-aws",
+ "version": "#31-Ubuntu SMP Wed Apr 23 18:42:41 UTC 2025",
+ "machine": "x86_64",
+ "processor": "x86_64",
+ "accelerator": "NVIDIA L40S"
+ },
+ "pytorch_info": "PyTorch built with:\n - GCC 11.2\n - C++ Version: 201703\n - Intel(R) oneAPI Math Kernel Library Version 2024.2-Product Build 20240605 for Intel(R) 64 architecture applications\n - Intel(R) MKL-DNN v3.7.1 (Git Hash 8d263e693366ef8db40acc569cc7d8edf644556d)\n - OpenMP 201511 (a.k.a. OpenMP 4.5)\n - LAPACK is enabled (usually provided by MKL)\n - NNPACK is enabled\n - CPU capability usage: AVX2\n - CUDA Runtime 12.6\n - NVCC architecture flags: -gencode;arch=compute_50,code=sm_50;-gencode;arch=compute_60,code=sm_60;-gencode;arch=compute_70,code=sm_70;-gencode;arch=compute_75,code=sm_75;-gencode;arch=compute_80,code=sm_80;-gencode;arch=compute_86,code=sm_86;-gencode;arch=compute_90,code=sm_90\n - CuDNN 90.7.1 (built against CUDA 12.8)\n - Built with CuDNN 90.5.1\n - Magma 2.6.1\n - Build settings: BLAS_INFO=mkl, BUILD_TYPE=Release, COMMIT_SHA=e2d141dbde55c2a4370fac5165b0561b6af4798b, CUDA_VERSION=12.6, CUDNN_VERSION=9.5.1, CXX_COMPILER=/opt/rh/gcc-toolset-11/root/usr/bin/c++, CXX_FLAGS= -D_GLIBCXX_USE_CXX11_ABI=1 -fvisibility-inlines-hidden -DUSE_PTHREADPOOL -DNDEBUG -DUSE_KINETO -DLIBKINETO_NOROCTRACER -DLIBKINETO_NOXPUPTI=ON -DUSE_FBGEMM -DUSE_PYTORCH_QNNPACK -DUSE_XNNPACK -DSYMBOLICATE_MOBILE_DEBUG_HANDLE -O2 -fPIC -Wall -Wextra -Werror=return-type -Werror=non-virtual-dtor -Werror=range-loop-construct -Werror=bool-operation -Wnarrowing -Wno-missing-field-initializers -Wno-unknown-pragmas -Wno-unused-parameter -Wno-strict-overflow -Wno-strict-aliasing -Wno-stringop-overflow -Wsuggest-override -Wno-psabi -Wno-error=old-style-cast -fdiagnostics-color=always -faligned-new -Wno-maybe-uninitialized -fno-math-errno -fno-trapping-math -Werror=format -Wno-stringop-overflow, LAPACK_INFO=mkl, PERF_WITH_AVX=1, PERF_WITH_AVX2=1, TORCH_VERSION=2.7.1, USE_CUDA=ON, USE_CUDNN=ON, USE_CUSPARSELT=1, USE_GFLAGS=OFF, USE_GLOG=OFF, USE_GLOO=ON, USE_MKL=ON, USE_MKLDNN=ON, USE_MPI=OFF, USE_NCCL=1, USE_NNPACK=ON, USE_OPENMP=ON, USE_ROCM=OFF, USE_ROCM_KERNEL_ASSERT=OFF, \n"
+ }
+}
diff --git a/peft/method_comparison/MetaMathQA/run.py b/peft/method_comparison/MetaMathQA/run.py
new file mode 100644
index 0000000000000000000000000000000000000000..0d159220eb881ade49ff4fb8ad5d12d8cd7e9c69
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/run.py
@@ -0,0 +1,473 @@
+# Copyright 2025-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""
+Main entry point to run the experiments. Contains general setup and the proper training code.
+"""
+
+import argparse
+import datetime as dt
+import gc
+import json
+import os
+import random
+import sys
+import textwrap
+import time
+from contextlib import AbstractContextManager, nullcontext
+from functools import partial
+from typing import Any, Callable, Literal, Optional
+
+import torch
+from torch import nn
+from torch.amp import GradScaler, autocast
+from tqdm import tqdm
+from transformers import GenerationConfig, set_seed
+from utils import (
+ FILE_NAME_TRAIN_PARAMS,
+ BucketIterator,
+ TrainResult,
+ TrainStatus,
+ get_accuracy,
+ get_base_model_info,
+ get_dataset_info,
+ get_file_size,
+ get_model,
+ get_optimizer_and_scheduler,
+ get_peft_branch,
+ get_tokenizer,
+ get_train_config,
+ init_accelerator,
+ log_results,
+ validate_experiment_path,
+)
+
+from data import get_train_valid_test_datasets
+from peft import AdaLoraConfig, PeftConfig
+from peft.utils import infer_device, CONFIG_NAME
+
+
+# # suppress all warnings
+# warnings.filterwarnings("ignore") # FIXME?
+
+dtype_to_bytes_linear = {"float32": 4, "float16": 2, "bfloat16": 2, "int8": 1, "int4": 0.5}
+# if lr scheduler with warmup is used, the ratio of warmup steps to total steps
+BUCKET_FACTOR = 20 # number of batches per bucket, increasing this further has diminishing returns
+
+
+def get_generation_config(*, seq_len, generate_kwargs) -> GenerationConfig:
+ # filter out None values so that we don't depend on setting correct defaults in the config
+ generation_kwargs = {k: v for k, v in generate_kwargs.items() if v is not None}
+ if ("max_length" in generation_kwargs) and ("max_new_tokens" in generation_kwargs):
+ # transformers does not support setting both max_length and max_new_tokens, but what we want in this case is to
+ # take the smaller of the two values
+ new_max_length = min(generation_kwargs["max_new_tokens"] + seq_len, generation_kwargs["max_length"])
+ del generation_kwargs["max_new_tokens"]
+ generation_kwargs["max_length"] = new_max_length
+ generation_config = GenerationConfig(**generate_kwargs)
+ return generation_config
+
+
+def evaluate(model, tokenizer, ds, batch_size, generate_kwargs, use_tqdm: bool = False) -> tuple[list[str], list[str]]:
+ with torch.inference_mode():
+ predictions = []
+ responses = []
+ pbar = range(0, len(ds), batch_size)
+ if use_tqdm:
+ pbar = tqdm(pbar)
+ for j in pbar:
+ sliced = ds[j : j + batch_size]
+ responses += sliced.pop("response")
+ batch = tokenizer.pad(sliced, return_tensors="pt", padding_side="left").to(model.device)
+ seq_len = batch["input_ids"].shape[1]
+ generation_config = get_generation_config(seq_len=seq_len, generate_kwargs=generate_kwargs)
+ outputs = model.generate(**batch, generation_config=generation_config, pad_token_id=tokenizer.eos_token_id)
+ predictions += tokenizer.batch_decode(outputs, skip_special_tokens=True)
+ return predictions, responses
+
+
+class DummyGradScaler:
+ # if no mixed precision is being used
+ def scale(self, loss):
+ return loss
+
+ def unscale_(self, optimizer):
+ pass
+
+ def step(self, optimizer):
+ optimizer.step()
+
+ def update(self):
+ pass
+
+
+def train(
+ *,
+ model: nn.Module,
+ max_steps: int,
+ batch_size: int,
+ batch_size_eval: int,
+ tokenizer: Any,
+ accelerator_memory_init: int,
+ eval_steps: int,
+ generation_kwargs: dict[str, Any],
+ grad_norm_clip: float,
+ optimizer_type: str,
+ optimizer_kwargs: dict[str, Any],
+ query_template: str,
+ lr_scheduler_arg: Optional[Literal["cosine"]],
+ use_amp: bool,
+ is_adalora: bool,
+) -> TrainResult:
+ accelerator_memory_allocated_log = []
+ accelerator_memory_reserved_log = []
+ losses = []
+ durations = []
+ metrics = []
+ sample = 0 # keep count of the current sample
+ total_samples = 0 # total number of samples over all epochs
+ total_tokens = [] # total number of tokens over all epochs
+
+ device_type = infer_device()
+ torch_accelerator_module = getattr(torch, device_type, torch.cuda)
+ if use_amp:
+ grad_scaler: GradScaler | DummyGradScaler = GradScaler(device=device_type)
+ autocast_ctx: Callable[[], ContextManager[Any]] = partial(autocast, device_type=device_type)
+ else:
+ grad_scaler = DummyGradScaler()
+ autocast_ctx = nullcontext
+
+ optimizer, lr_scheduler = get_optimizer_and_scheduler(
+ model,
+ optimizer_type=optimizer_type,
+ max_steps=max_steps,
+ lr_scheduler_arg=lr_scheduler_arg,
+ **optimizer_kwargs,
+ )
+ # print this after getting the optimizer, in case it modifies requires_gard
+ if hasattr(model, "get_nb_trainable_parameters"):
+ num_trainable_params, num_params = model.get_nb_trainable_parameters()
+ else:
+ num_params = model.num_parameters()
+ num_trainable_params = num_params
+ print_verbose(
+ f"trainable params: {num_trainable_params:,d} || all params: {num_params:,d} || "
+ f"trainable: {100 * num_trainable_params / num_params:.4f}%"
+ )
+
+ status = TrainStatus.FAILED
+ tic_train = time.perf_counter()
+ eval_time = 0.0
+ error_msg = ""
+
+ ds_train, ds_valid, ds_test = get_train_valid_test_datasets(
+ tokenizer=tokenizer, query_template=query_template, print_fn=print_verbose
+ )
+ # note: bucketing by length is only really worth it for the train dataset, since it's length is big compared to the
+ # batch size
+ iterator_train = BucketIterator(
+ ds_train,
+ batch_size=batch_size,
+ bucket_factor=BUCKET_FACTOR,
+ delete_cols=["response"],
+ )
+ try:
+ pbar = tqdm(range(1, max_steps + 1))
+ for step, batch in zip(pbar, iterator_train):
+ tic = time.perf_counter()
+
+ # create the batch
+ tokens_per_sample = [len(i) for i in batch["input_ids"]]
+ total_tokens.append(sum(tokens_per_sample) + len(tokens_per_sample)) # add EOS token
+ batch = tokenizer.pad(batch, return_tensors="pt").to(model.device)
+ actual_batch_size = len(batch["input_ids"])
+ total_samples += actual_batch_size
+ sample += batch_size
+ if sample >= len(ds_train): # new epoch
+ sample = 0
+
+ # add labels, they are automatically shifted by transformers
+ labels = batch["input_ids"].clone()
+ # We want to ignore the padding tokens except for the first EOS token; if we don't ignore them, the loss
+ # will be dominated by padding tokens; if we ignore all, the model will not learn to predict the EOS token.
+ # TODO: Note that the longest sequence in the batch won't have any PAD/EOS token at the end, this is fine if
+ # the batch size is > 1 but should still be fixed eventually.
+ for i, num_tokens in enumerate(tokens_per_sample):
+ labels[i, num_tokens + 1 :] = -100
+ batch["labels"] = labels
+ num_items_in_batch = batch["attention_mask"].sum().item()
+
+ # train step
+ optimizer.zero_grad()
+ with autocast_ctx():
+ outputs = model(**batch, num_items_in_batch=num_items_in_batch)
+ loss = outputs.loss
+ grad_scaler.scale(loss).backward()
+ if grad_norm_clip:
+ grad_scaler.unscale_(optimizer)
+ torch.nn.utils.clip_grad_norm_(model.parameters(), grad_norm_clip)
+ grad_scaler.step(optimizer)
+ grad_scaler.update()
+ lr_scheduler.step()
+
+ if is_adalora:
+ model.base_model.update_and_allocate(step)
+
+ losses.append(loss.item())
+ pbar.set_postfix({"loss": loss.item()})
+ accelerator_memory_allocated_log.append(
+ torch_accelerator_module.memory_allocated() - accelerator_memory_init
+ )
+ accelerator_memory_reserved_log.append(
+ torch_accelerator_module.memory_reserved() - accelerator_memory_init
+ )
+ toc = time.perf_counter()
+ durations.append(toc - tic)
+
+ # every couple of steps, evaluate; this can be slow due to generation
+ if step % eval_steps == 0:
+ tic_eval = time.perf_counter()
+ loss_avg = sum(losses[-eval_steps:]) / eval_steps
+ memory_allocated_avg = sum(accelerator_memory_allocated_log[-eval_steps:]) / eval_steps
+ memory_reserved_avg = sum(accelerator_memory_reserved_log[-eval_steps:]) / eval_steps
+ token_sum = sum(total_tokens[-eval_steps:])
+ dur_train = sum(durations[-eval_steps:])
+ tokens_per_sec = token_sum / dur_train
+
+ model.eval()
+ predictions, responses = evaluate(
+ model=model,
+ tokenizer=tokenizer,
+ ds=ds_valid,
+ batch_size=batch_size_eval,
+ generate_kwargs={**generation_kwargs},
+ )
+ model.train()
+
+ example = random.choice(predictions)
+ example = textwrap.shorten(example, width=750)
+ example = textwrap.indent(example, " ")
+ print_verbose(f"\nExample prediction:\n{example}\n")
+ accuracy = get_accuracy(predictions=predictions, responses=responses)
+ num_tokens_generated = sum(sum(mask) for mask in tokenizer(predictions)["attention_mask"])
+
+ toc_eval = time.perf_counter()
+ dur_eval = toc_eval - tic_eval
+ eval_time += toc_eval - tic_eval
+ elapsed = time.perf_counter() - tic_train
+
+ metrics.append(
+ {
+ "step": step,
+ "valid accuracy": accuracy,
+ "train loss": loss_avg,
+ "train samples": total_samples,
+ "train time": dur_train,
+ "eval time": dur_eval,
+ "tokens / sec": tokens_per_sec,
+ "mem allocated avg": memory_allocated_avg,
+ "mem reserved avg": memory_reserved_avg,
+ "elapsed time": elapsed,
+ }
+ )
+
+ log_dict = {
+ "step": f"{step:5d}",
+ "samples": f"{total_samples:7d}",
+ "lr": f"{lr_scheduler.get_last_lr()[0]:.2e}",
+ "loss avg": f"{loss_avg:.4f}",
+ "valid acc": f"{accuracy:.3f}",
+ "gen valid tokens": num_tokens_generated,
+ "train time": f"{dur_train:.1f}s",
+ "eval time": f"{dur_eval:.1f}s",
+ "train tokens / sec": f"{tokens_per_sec:.0f}",
+ "mem allocated": f"{memory_allocated_avg:.0f}",
+ "mem reserved": f"{memory_reserved_avg:.0f}",
+ "elapsed time": f"{elapsed // 60:.0f}min {elapsed % 60:.0f}s",
+ }
+ print_verbose(json.dumps(log_dict))
+
+ # # TODO is this needed?
+ torch_accelerator_module.empty_cache()
+ gc.collect()
+
+ print_verbose(f"Training finished after {max_steps} steps, evaluation on test set follows.")
+ # test set evaluation
+ model.eval()
+ predictions, responses = evaluate(
+ model=model,
+ tokenizer=tokenizer,
+ ds=ds_test,
+ batch_size=batch_size_eval,
+ generate_kwargs={**generation_kwargs, "pad_token_id": tokenizer.eos_token_id},
+ use_tqdm=len(ds_test) > 100,
+ )
+ accuracy = get_accuracy(predictions=predictions, responses=responses)
+ metrics.append(
+ {
+ "step": step,
+ "test accuracy": accuracy,
+ "train loss": sum(losses[-eval_steps:]) / eval_steps,
+ "train samples": total_samples,
+ "train total tokens": sum(total_tokens),
+ }
+ )
+ print_verbose(f"Test accuracy: {accuracy:.3f}")
+
+ except KeyboardInterrupt:
+ print_verbose("canceled training")
+ status = TrainStatus.CANCELED
+ error_msg = "manually canceled"
+ except torch.OutOfMemoryError as exc:
+ # ouch, still let's try to log some results
+ print_verbose("out of memory error encountered")
+ status = TrainStatus.CANCELED
+ error_msg = str(exc)
+ except Exception as exc:
+ print_verbose(f"encountered an error: {exc}")
+ status = TrainStatus.CANCELED
+ error_msg = str(exc)
+
+ toc_train = time.perf_counter()
+ train_time = toc_train - tic_train - eval_time
+
+ if status != TrainStatus.CANCELED:
+ status = TrainStatus.SUCCESS
+ train_result = TrainResult(
+ status=status,
+ train_time=train_time,
+ accelerator_memory_reserved_log=accelerator_memory_reserved_log,
+ losses=losses,
+ metrics=metrics,
+ error_msg=error_msg,
+ num_trainable_params=num_trainable_params,
+ num_total_params=num_params,
+ )
+ return train_result
+
+
+def main(*, path_experiment: str, experiment_name: str, clean: bool) -> None:
+ tic_total = time.perf_counter()
+ start_date = dt.datetime.now(tz=dt.timezone.utc).replace(microsecond=0).isoformat()
+
+ peft_branch = get_peft_branch()
+ if peft_branch == "main":
+ print_verbose("===== This experiment is categorized as a MAIN run because the PEFT branch is 'main' ======")
+ else:
+ print_verbose(
+ f"===== This experiment is categorized as a TEST run because the PEFT branch is '{peft_branch}' ======"
+ )
+
+ # load configs
+ peft_config: Optional[PeftConfig] = None
+ if os.path.exists(os.path.join(path_experiment, CONFIG_NAME)):
+ peft_config = PeftConfig.from_pretrained(path_experiment)
+ else:
+ print_verbose(f"Could not find PEFT config at {path_experiment}, performing FULL FINETUNING")
+ path_train_config = os.path.join(path_experiment, FILE_NAME_TRAIN_PARAMS)
+ train_config = get_train_config(path_train_config)
+ set_seed(train_config.seed)
+
+ # initialize objects
+ accelerator_memory_init = init_accelerator()
+ tokenizer = get_tokenizer(model_id=train_config.model_id, max_seq_length=train_config.max_seq_length)
+
+ model_info = get_base_model_info(train_config.model_id)
+ metamath_info = get_dataset_info("meta-math/MetaMathQA")
+ gsm8k_info = get_dataset_info("openai/gsm8k")
+ model = get_model(
+ model_id=train_config.model_id,
+ dtype=train_config.dtype,
+ compile=train_config.compile,
+ attn_implementation=train_config.attn_implementation,
+ peft_config=peft_config,
+ autocast_adapter_dtype=train_config.autocast_adapter_dtype,
+ )
+ print_verbose(model)
+
+ # train model
+ train_result = train(
+ model=model,
+ max_steps=train_config.max_steps,
+ batch_size=train_config.batch_size,
+ batch_size_eval=train_config.batch_size_eval,
+ tokenizer=tokenizer,
+ accelerator_memory_init=accelerator_memory_init,
+ eval_steps=train_config.eval_steps,
+ generation_kwargs=train_config.generation_kwargs,
+ grad_norm_clip=train_config.grad_norm_clip,
+ optimizer_type=train_config.optimizer_type,
+ optimizer_kwargs=train_config.optimizer_kwargs,
+ query_template=train_config.query_template,
+ lr_scheduler_arg=train_config.lr_scheduler,
+ use_amp=train_config.use_amp,
+ is_adalora=isinstance(peft_config, AdaLoraConfig),
+ )
+
+ if train_result.status == TrainStatus.FAILED:
+ print_verbose("Training failed, not logging results")
+ sys.exit(1)
+
+ file_size = get_file_size(
+ model,
+ peft_config=peft_config,
+ clean=clean,
+ print_fn=print_verbose,
+ )
+
+ time_total = time.perf_counter() - tic_total
+ # log results: print and save to file
+ log_results(
+ experiment_name=experiment_name,
+ train_result=train_result,
+ accelerator_memory_init=accelerator_memory_init,
+ time_total=time_total,
+ file_size=file_size,
+ model_info=model_info,
+ datasets_info={"metamath": metamath_info, "gsm8k": gsm8k_info},
+ start_date=start_date,
+ train_config=train_config,
+ peft_config=peft_config,
+ print_fn=print_verbose,
+ )
+
+
+if __name__ == "__main__":
+ parser = argparse.ArgumentParser()
+ parser.add_argument("-v", "--verbose", action="store_true", help="Enable verbose output")
+ parser.add_argument("path_experiment", type=str, help="Path to the experiment directory")
+ parser.add_argument(
+ "--clean",
+ action="store_true",
+ help="Delete training artifacts after run finishes (logs are still saved)",
+ )
+ args = parser.parse_args()
+
+ experiment_name = validate_experiment_path(args.path_experiment)
+
+ if args.verbose:
+
+ def print_verbose(*args, **kwargs) -> None:
+ kwargs["file"] = sys.stderr
+ print(*args, **kwargs)
+ else:
+
+ def print_verbose(*args, **kwargs) -> None:
+ pass
+
+ main(
+ path_experiment=args.path_experiment,
+ experiment_name=experiment_name,
+ clean=args.clean,
+ )
diff --git a/peft/method_comparison/MetaMathQA/temporary_results/.gitkeep b/peft/method_comparison/MetaMathQA/temporary_results/.gitkeep
new file mode 100644
index 0000000000000000000000000000000000000000..e69de29bb2d1d6434b8b29ae775ad8c2e48c5391
diff --git a/peft/method_comparison/MetaMathQA/utils.py b/peft/method_comparison/MetaMathQA/utils.py
new file mode 100644
index 0000000000000000000000000000000000000000..d48a301b35b7759d947f18a121d906fce55b3fb4
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/utils.py
@@ -0,0 +1,709 @@
+# Copyright 2025-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""
+All utilities not related to data handling.
+"""
+
+import enum
+import json
+import os
+import platform
+import subprocess
+import tempfile
+import warnings
+from dataclasses import asdict, dataclass
+from decimal import Decimal, DivisionByZero, InvalidOperation
+from typing import Any, Callable, Literal, Optional
+
+import bitsandbytes
+import datasets
+import huggingface_hub
+import numpy as np
+import torch
+import transformers
+from torch import nn
+from transformers import (
+ AutoModelForCausalLM,
+ AutoTokenizer,
+ BitsAndBytesConfig,
+ get_cosine_schedule_with_warmup,
+)
+
+import peft
+from peft import PeftConfig, get_peft_model, prepare_model_for_kbit_training
+from peft.optimizers import create_lorafa_optimizer, create_loraplus_optimizer
+from peft.utils import infer_device, SAFETENSORS_WEIGHTS_NAME
+
+device = infer_device()
+
+if device not in ["cuda", "xpu"]:
+ raise RuntimeError("CUDA or XPU is not available, currently only CUDA or XPU is supported")
+
+ACCELERATOR_MEMORY_INIT_THRESHOLD = 500 * 2**20 # 500MB
+FILE_NAME_DEFAULT_TRAIN_PARAMS = os.path.join(os.path.dirname(__file__), "default_training_params.json")
+FILE_NAME_TRAIN_PARAMS = "training_params.json" # specific params for this experiment
+# main results
+RESULT_PATH = os.path.join(os.path.dirname(__file__), "results")
+# testing results
+RESULT_PATH_TEST = os.path.join(os.path.dirname(__file__), "temporary_results")
+# cancelled results
+RESULT_PATH_CANCELLED = os.path.join(os.path.dirname(__file__), "cancelled_results")
+hf_api = huggingface_hub.HfApi()
+WARMUP_STEP_RATIO = 0.1
+
+
+@dataclass
+class TrainConfig:
+ """All configuration parameters associated with training the model
+
+ Args:
+ model_id: The model identifier
+ dtype: The data type to use for the model
+ max_seq_length: The maximum sequence length
+ batch_size: The batch size for training
+ batch_size_eval: The batch size for eval/test, can be much higher than for training
+ max_steps: The maximum number of steps to train for
+ eval_steps: The number of steps between evaluations
+ compile: Whether to compile the model
+ query_template: The template for the query
+ seed: The random seed
+ grad_norm_clip: The gradient norm clipping value (set to 0 to skip)
+ optimizer_type: The name of a torch optimizer (e.g. AdamW) or a PEFT method ("lora+", "lora-fa")
+ optimizer_kwargs: The optimizer keyword arguments (lr etc.)
+ lr_scheduler: The learning rate scheduler (currently only None or 'cosine' are supported)
+ use_amp: Whether to use automatic mixed precision
+ autocast_adapter_dtype: Whether to cast adapter dtype to float32, same argument as in PEFT
+ generation_kwargs: Arguments passed to transformers GenerationConfig (used in evaluation)
+ attn_implementation: The attention implementation to use (if any), see transformers docs
+ """
+
+ model_id: str
+ dtype: Literal["float32", "float16", "bfloat16", "int8", "int4"]
+ max_seq_length: int
+ batch_size: int
+ batch_size_eval: int
+ max_steps: int
+ eval_steps: int
+ compile: bool
+ query_template: str
+ seed: int
+ grad_norm_clip: float # set to 0 to skip
+ optimizer_type: str
+ optimizer_kwargs: dict[str, Any]
+ lr_scheduler: Optional[Literal["cosine"]]
+ use_amp: bool
+ autocast_adapter_dtype: bool
+ generation_kwargs: dict[str, Any]
+ attn_implementation: Optional[str]
+
+ def __post_init__(self) -> None:
+ if not isinstance(self.model_id, str):
+ raise ValueError(f"Invalid model_id: {self.model_id}")
+ if self.dtype not in ["float32", "float16", "bfloat16", "int8", "int4"]:
+ raise ValueError(f"Invalid dtype: {self.dtype}")
+ if self.max_seq_length < 0:
+ raise ValueError(f"Invalid max_seq_length: {self.max_seq_length}")
+ if self.batch_size <= 0:
+ raise ValueError(f"Invalid batch_size: {self.batch_size}")
+ if self.batch_size_eval <= 0:
+ raise ValueError(f"Invalid eval batch_size: {self.batch_size_eval}")
+ if self.max_steps <= 0:
+ raise ValueError(f"Invalid max_steps: {self.max_steps}")
+ if self.eval_steps <= 0:
+ raise ValueError(f"Invalid eval_steps: {self.eval_steps}")
+ if self.eval_steps > self.max_steps:
+ raise ValueError(f"Invalid eval_steps: {self.eval_steps} > max_steps: {self.max_steps}")
+ if self.grad_norm_clip < 0:
+ raise ValueError(f"Invalid grad_norm_clip: {self.grad_norm_clip}")
+ if self.optimizer_type not in ["lora+", "lora-fa"] and not hasattr(torch.optim, self.optimizer_type):
+ raise ValueError(f"Invalid optimizer_type: {self.optimizer_type}")
+ if self.lr_scheduler not in [None, "cosine"]:
+ raise ValueError(f"Invalid lr_scheduler: {self.lr_scheduler}, must be None or 'cosine'")
+ if "{query}" not in self.query_template:
+ raise ValueError("Invalid query_template, must contain '{query}'")
+
+
+def validate_experiment_path(path: str) -> str:
+ # the experiment path should take the form of ./experiments//
+ # e.g. ./experiments/lora/rank32
+ # it should contain:
+ # - adapter_config.json
+ # - optional: training_params.json
+ if not os.path.exists(FILE_NAME_DEFAULT_TRAIN_PARAMS):
+ raise FileNotFoundError(
+ f"Missing default training params file '{FILE_NAME_DEFAULT_TRAIN_PARAMS}' in the ./experiments directory"
+ )
+ if not os.path.exists(path):
+ raise FileNotFoundError(f"Path {path} does not exist")
+
+ # check path structure
+ path_parts = path.rstrip(os.path.sep).split(os.path.sep)
+ if (len(path_parts) != 3) or (path_parts[-3] != "experiments"):
+ raise ValueError(
+ f"Path {path} does not have the correct structure, should be ./experiments//"
+ )
+
+ experiment_name = os.path.join(*path_parts[-2:])
+ return experiment_name
+
+
+def get_train_config(path: str) -> TrainConfig:
+ # first, load the default params, then update with experiment-specific params
+ with open(FILE_NAME_DEFAULT_TRAIN_PARAMS) as f:
+ default_config_kwargs = json.load(f)
+
+ config_kwargs = {}
+ if os.path.exists(path):
+ with open(path) as f:
+ config_kwargs = json.load(f)
+
+ config_kwargs = {**default_config_kwargs, **config_kwargs}
+ return TrainConfig(**config_kwargs)
+
+
+def init_accelerator() -> int:
+ torch_accelerator_module = getattr(torch, device, torch.cuda)
+ torch.manual_seed(0)
+ torch_accelerator_module.reset_peak_memory_stats()
+ torch_accelerator_module.manual_seed_all(0)
+ # might not be necessary, but just to be sure
+ nn.Linear(1, 1).to(device)
+
+ accelerator_memory_init = torch_accelerator_module.max_memory_reserved()
+ if accelerator_memory_init > ACCELERATOR_MEMORY_INIT_THRESHOLD:
+ raise RuntimeError(
+ f"{device} memory usage at start is too high: {accelerator_memory_init // 2**20}MB, please ensure that no other "
+ f"processes are running on {device}."
+ )
+
+ torch_accelerator_module.reset_peak_memory_stats()
+ accelerator_memory_init = torch_accelerator_module.max_memory_reserved()
+ return accelerator_memory_init
+
+
+def get_tokenizer(*, model_id: str, max_seq_length: int):
+ tokenizer = AutoTokenizer.from_pretrained(model_id)
+ tokenizer.model_max_length = max_seq_length
+ if not tokenizer.pad_token:
+ tokenizer.pad_token = tokenizer.eos_token
+ return tokenizer
+
+
+def get_base_model(
+ *,
+ model_id: str,
+ dtype: Literal["float32", "float16", "bfloat16", "int8", "int4"],
+ compile: bool,
+ attn_implementation: Optional[str],
+) -> nn.Module:
+ kwargs: dict[str, Any] = {
+ "pretrained_model_name_or_path": model_id,
+ "device_map": device,
+ "attn_implementation": attn_implementation,
+ }
+ if dtype == "int4":
+ quant_config = BitsAndBytesConfig(load_in_4bit=True)
+ kwargs["quantization_config"] = quant_config
+ elif dtype == "int8":
+ quant_config = BitsAndBytesConfig(load_in_8bit=True)
+ kwargs["quantization_config"] = quant_config
+ elif dtype == "bfloat16":
+ kwargs["torch_dtype"] = torch.bfloat16
+ elif dtype == "float16":
+ kwargs["torch_dtype"] = torch.float16
+ elif dtype != "float32":
+ raise ValueError(f"Invalid dtype: {dtype}")
+
+ model = AutoModelForCausalLM.from_pretrained(**kwargs)
+
+ if dtype in ["int8", "int4"]:
+ model = prepare_model_for_kbit_training(model)
+
+ if compile:
+ model = torch.compile(model)
+
+ return model
+
+
+def get_model(
+ *,
+ model_id: str,
+ dtype: Literal["float32", "float16", "bfloat16", "int8", "int4"],
+ compile: bool,
+ attn_implementation: Optional[str],
+ peft_config: Optional[PeftConfig],
+ autocast_adapter_dtype: bool,
+) -> nn.Module:
+ base_model = get_base_model(
+ model_id=model_id, dtype=dtype, compile=compile, attn_implementation=attn_implementation
+ )
+ if peft_config is None:
+ model = base_model
+ else:
+ model = get_peft_model(base_model, peft_config, autocast_adapter_dtype=autocast_adapter_dtype)
+ return model
+
+
+class DummyScheduler:
+ # if no lr scheduler is being used
+ def __init__(self, lr):
+ self.lr = lr
+
+ def get_last_lr(self):
+ return [self.lr]
+
+ def step(self):
+ pass
+
+
+def get_optimizer_and_scheduler(
+ model, *, optimizer_type: str, max_steps: int, lr_scheduler_arg: Optional[Literal["cosine"]], **optimizer_kwargs
+) -> tuple[torch.optim.Optimizer, Any]:
+ if optimizer_type == "lora+":
+ optimizer = create_loraplus_optimizer(model, optimizer_cls=torch.optim.AdamW, **optimizer_kwargs)
+ elif optimizer_type == "lora-fa":
+ optimizer = create_lorafa_optimizer(model, **optimizer_kwargs)
+ else:
+ cls = getattr(torch.optim, optimizer_type)
+ optimizer = cls(model.parameters(), **optimizer_kwargs)
+
+ if lr_scheduler_arg == "cosine":
+ warmup_steps = int(WARMUP_STEP_RATIO * max_steps)
+ lr_scheduler = get_cosine_schedule_with_warmup(
+ optimizer, num_warmup_steps=warmup_steps, num_training_steps=max_steps
+ )
+ elif lr_scheduler_arg is None:
+ lr_scheduler = DummyScheduler(optimizer_kwargs["lr"])
+ else:
+ raise ValueError(f"Invalid lr_scheduler argument: {lr_scheduler_arg}")
+
+ return optimizer, lr_scheduler
+
+
+class BucketIterator:
+ """
+ Iterator that yields batches of data from a torch Dataset, grouped in buckets by sequence length
+
+ The iterator will yield batches of size `batch_size`, where the samples in each batch are sorted by sequence length.
+ This is done to minimize the amount of padding required for each batch. To avoid sorting the entire dataset and thus
+ introducing a bias, the dataset is first split into buckets of size `batch_size * bucket_factor`.
+
+ Args:
+ ds: The torch Dataset to iterate over
+ batch_size: The batch size
+ bucket_factor: The factor by which to multiply the batch size to determine the bucket size
+ delete_cols: The columns to delete from the dataset before yielding a batch
+ """
+
+ def __init__(self, ds, *, batch_size: int, bucket_factor: int, delete_cols: list[str]) -> None:
+ self.ds = ds
+ self.batch_size = batch_size
+ self.bucket_factor = bucket_factor
+ self.delete_cols = set(delete_cols)
+
+ assert self.bucket_factor > 0, "bucket_factor must be greater than 0"
+
+ def _batch_iterator(self, bucket):
+ tokens_per_sample_bucket = torch.tensor([len(i) for i in bucket["input_ids"]])
+ # sort long to short instead to encounter possible OOM errors as early as possible
+ sorted = torch.argsort(tokens_per_sample_bucket, descending=True)
+ cls = type(bucket) # conserve the type returned by the ds
+ bucket = {k: [v[i] for i in sorted] for k, v in bucket.items() if k not in self.delete_cols}
+ num_samples = len(bucket["input_ids"])
+ for j in range(0, num_samples, self.batch_size):
+ batch = {k: v[j : j + self.batch_size] for k, v in bucket.items()}
+ yield cls(batch)
+
+ def __iter__(self):
+ bucket_size = self.batch_size * self.bucket_factor
+ for i in range(0, len(self.ds), bucket_size):
+ bucket = self.ds[i : i + bucket_size]
+ yield from self._batch_iterator(bucket)
+
+ # if there is a remainder, we yield the last batch
+ if len(self.ds) % bucket_size != 0:
+ bucket = self.ds[-(len(self.ds) % bucket_size) :]
+ yield from self._batch_iterator(bucket)
+
+
+def get_file_size(
+ model: nn.Module, *, peft_config: Optional[PeftConfig], clean: bool, print_fn: Callable[..., None]
+) -> int:
+ file_size = 99999999 # set a default dummy value
+ if peft_config is not None:
+ try:
+ with tempfile.TemporaryDirectory(ignore_cleanup_errors=True, delete=clean) as tmp_dir:
+ model.save_pretrained(tmp_dir)
+ stat = os.stat(os.path.join(tmp_dir, SAFETENSORS_WEIGHTS_NAME))
+ file_size = stat.st_size
+ if not clean:
+ print_fn(f"Saved PEFT checkpoint to {tmp_dir}")
+ except Exception as exc:
+ print(f"Failed to save PEFT checkpoint due to the following error: {exc}")
+ else:
+ print_fn("Not saving the fully fine-tuned model because it's too big, estimating the size instead")
+ try:
+ num_params = model.num_parameters()
+ dtype_size = next(model.parameters()).element_size()
+ file_size = num_params * dtype_size
+ except Exception as exc:
+ print(f"Failed to determine file size for fully finetuned model because of: {exc}")
+ return file_size
+
+
+##################
+# ANSWER PARSING #
+##################
+
+
+def parse_answer(text: str) -> Optional[str]:
+ """
+ A label/prediction can look like this:
+
+ Question: If the magnitude of vector v is equal to 4, what is the dot product of vector v with itself?. Think step
+ by step
+ Answer: The dot product of a vector with itself is equal to the square of its magnitude. So, the dot product of
+ vector v with itself is equal to $4^2 = \boxed{16}$.The answer is: 16
+
+ We want to extract '16' from this string.
+
+ """
+ # This implementation is based on sampling meta-llama/Llama-3.1-8B-Instruct. It may not work for other models.
+ candidate_delimiters = [
+ # MetaMath:
+ "The answer is: ",
+ "The answer is ",
+ "The final answer is: ",
+ "The final answer is ",
+ # GSM8K:
+ "#### ",
+ ]
+ text = text.strip()
+ text = text.rstrip(".!?")
+ for delimiter in candidate_delimiters:
+ if delimiter in text:
+ break
+ else: # no match
+ return None
+
+ text = text.rpartition(delimiter)[-1].strip()
+ # if a new paragraph follows after the final answer, we want to remove it
+ text = text.split("\n", 1)[0]
+ # note: we can just remove % here since the GSM8K dataset just omits it, i.e. 50% -> 50, no need to divide by 100
+ text = text.strip(" .!?$%")
+ return text
+
+
+def convert_to_decimal(s: Optional[str]) -> Optional[Decimal]:
+ """
+ Converts a string representing a number to a Decimal.
+
+ The string may be:
+ - A simple number (e.g., "13", "65.33")
+ - A fraction (e.g., "20/14")
+ """
+ if s is None:
+ return None
+
+ try:
+ s = s.strip()
+ # Check if the string represents a fraction.
+ if "/" in s:
+ parts = s.split("/")
+ if len(parts) != 2:
+ return None
+ numerator = Decimal(parts[0].strip())
+ denominator = Decimal(parts[1].strip())
+ if denominator == 0:
+ return None
+ value = numerator / denominator
+ else:
+ # Parse as a regular decimal or integer string.
+ value = Decimal(s)
+ return value
+ except (DivisionByZero, InvalidOperation, ValueError):
+ return None
+
+
+def get_accuracy(*, predictions: list[str], responses: list[str]) -> float:
+ if len(predictions) != len(responses):
+ raise ValueError(f"Prediction length mismatch: {len(predictions)} != {len(responses)}")
+
+ y_true: list[str | float | None] = []
+ y_pred: list[str | float | None] = []
+
+ for prediction, response in zip(predictions, responses):
+ parsed_prediction = parse_answer(prediction)
+ parsed_response = parse_answer(response)
+ if parsed_response is None:
+ raise ValueError(f"Error encountered while trying to parse response: {response}")
+
+ decimal_prediction = convert_to_decimal(parsed_prediction)
+ decimal_answer = convert_to_decimal(parsed_response)
+ if decimal_prediction is not None:
+ y_pred.append(float(decimal_prediction))
+ elif parsed_prediction is not None:
+ y_pred.append(parsed_prediction)
+ else:
+ y_pred.append(None)
+
+ # we convert decimals to float so that stuff like this works:
+ # float(convert_to_decimal('20/35')) == float(convert_to_decimal('0.5714285714285714'))
+ if decimal_answer is not None:
+ y_true.append(float(decimal_answer))
+ elif parsed_prediction is not None:
+ y_true.append(parsed_response)
+ else:
+ y_true.append(None)
+
+ correct: list[bool] = []
+ for true, pred in zip(y_true, y_pred):
+ if (true is not None) and (pred is not None):
+ correct.append(true == pred)
+ else:
+ correct.append(False)
+
+ accuracy = sum(correct) / len(correct)
+ return accuracy
+
+
+###########
+# LOGGING #
+###########
+
+
+def get_base_model_info(model_id: str) -> Optional[huggingface_hub.ModelInfo]:
+ try:
+ return hf_api.model_info(model_id)
+ except Exception as exc:
+ warnings.warn(f"Could not retrieve model info, failed with error {exc}")
+ return None
+
+
+def get_dataset_info(dataset_id: str) -> Optional[huggingface_hub.DatasetInfo]:
+ try:
+ return hf_api.dataset_info(dataset_id)
+ except Exception as exc:
+ warnings.warn(f"Could not retrieve dataset info, failed with error {exc}")
+ return None
+
+
+def get_git_hash(module) -> Optional[str]:
+ if "site-packages" in module.__path__[0]:
+ return None
+
+ return subprocess.check_output("git rev-parse HEAD".split(), cwd=os.path.dirname(module.__file__)).decode().strip()
+
+
+def get_package_info() -> dict[str, Optional[str]]:
+ """Get the package versions and commit hashes of transformers, peft, datasets, bnb, and torch"""
+ package_info = {
+ "transformers-version": transformers.__version__,
+ "transformers-commit-hash": get_git_hash(transformers),
+ "peft-version": peft.__version__,
+ "peft-commit-hash": get_git_hash(peft),
+ "datasets-version": datasets.__version__,
+ "datasets-commit-hash": get_git_hash(datasets),
+ "bitsandbytes-version": bitsandbytes.__version__,
+ "bitsandbytes-commit-hash": get_git_hash(bitsandbytes),
+ "torch-version": torch.__version__,
+ "torch-commit-hash": get_git_hash(torch),
+ }
+ return package_info
+
+
+def get_system_info() -> dict[str, str]:
+ device = infer_device()
+ torch_accelerator_module = getattr(torch, device, torch.cuda)
+ system_info = {
+ "system": platform.system(),
+ "release": platform.release(),
+ "version": platform.version(),
+ "machine": platform.machine(),
+ "processor": platform.processor(),
+ "accelerator": torch_accelerator_module.get_device_name(0),
+ }
+ return system_info
+
+
+@dataclass
+class MetaInfo:
+ package_info: dict[str, Optional[str]]
+ system_info: dict[str, str]
+ pytorch_info: str
+
+
+def get_meta_info() -> MetaInfo:
+ meta_info = MetaInfo(
+ package_info=get_package_info(),
+ system_info=get_system_info(),
+ pytorch_info=torch.__config__.show(),
+ )
+ return meta_info
+
+
+def get_peft_branch() -> str:
+ return (
+ subprocess.check_output("git rev-parse --abbrev-ref HEAD".split(), cwd=os.path.dirname(peft.__file__))
+ .decode()
+ .strip()
+ )
+
+
+class TrainStatus(enum.Enum):
+ FAILED = "failed"
+ SUCCESS = "success"
+ CANCELED = "canceled"
+
+
+@dataclass
+class TrainResult:
+ status: TrainStatus
+ train_time: float
+ accelerator_memory_reserved_log: list[int]
+ losses: list[float]
+ metrics: list[Any] # TODO
+ error_msg: str
+ num_trainable_params: int
+ num_total_params: int
+
+
+def log_to_console(log_data: dict[str, Any], print_fn: Callable[..., None]) -> None:
+ accelerator_memory_max = log_data["train_info"]["accelerator_memory_max"]
+ accelerator_memory_avg = log_data["train_info"]["accelerator_memory_reserved_avg"]
+ accelerator_memory_reserved_99th = log_data["train_info"]["accelerator_memory_reserved_99th"]
+ time_train = log_data["train_info"]["train_time"]
+ time_total = log_data["run_info"]["total_time"]
+ file_size = log_data["train_info"]["file_size"]
+
+ print_fn(f"accelerator memory max: {accelerator_memory_max // 2**20}MB")
+ print_fn(f"accelerator memory reserved avg: {accelerator_memory_avg // 2**20}MB")
+ print_fn(f"accelerator memory reserved 99th percentile: {accelerator_memory_reserved_99th // 2**20}MB")
+ print_fn(f"train time: {time_train}s")
+ print_fn(f"total time: {time_total:.2f}s")
+ print_fn(f"file size of checkpoint: {file_size / 2**20:.1f}MB")
+
+
+def log_to_file(
+ *, log_data: dict, save_dir: str, experiment_name: str, timestamp: str, print_fn: Callable[..., None]
+) -> None:
+ if save_dir.endswith(RESULT_PATH):
+ file_name = f"{experiment_name.replace(os.path.sep, '--')}.json"
+ else:
+ # For cancelled and temporary runs, we want to include the timestamp, as these runs are not tracked in git, thus
+ # we need unique names to avoid losing history.
+ file_name = f"{experiment_name.replace(os.path.sep, '--')}--{timestamp.replace(':', '-')}.json"
+ file_name = os.path.join(save_dir, file_name)
+ with open(file_name, "w") as f:
+ json.dump(log_data, f, indent=2)
+ print_fn(f"Saved log to: {file_name}")
+
+
+def log_results(
+ *,
+ experiment_name: str,
+ train_result: TrainResult,
+ accelerator_memory_init: int,
+ time_total: float,
+ file_size: int,
+ model_info: Optional[huggingface_hub.ModelInfo],
+ datasets_info: dict[str, Optional[huggingface_hub.DatasetInfo]],
+ start_date: str,
+ train_config: TrainConfig,
+ peft_config: Optional[PeftConfig],
+ print_fn: Callable[..., None],
+) -> None:
+ # collect results
+ device = infer_device()
+ torch_accelerator_module = getattr(torch, device, torch.cuda)
+ accelerator_memory_final = torch_accelerator_module.max_memory_reserved()
+ accelerator_memory_avg = int(
+ sum(train_result.accelerator_memory_reserved_log) / len(train_result.accelerator_memory_reserved_log)
+ )
+ accelerator_memory_reserved_99th = int(np.percentile(train_result.accelerator_memory_reserved_log, 99))
+
+ meta_info = get_meta_info()
+ if model_info is not None:
+ model_sha = model_info.sha
+ model_created_at = model_info.created_at.isoformat()
+ else:
+ model_sha = None
+ model_created_at = None
+
+ dataset_info_log = {}
+ for key, dataset_info in datasets_info.items():
+ if dataset_info is not None:
+ dataset_sha = dataset_info.sha
+ dataset_created_at = dataset_info.created_at.isoformat()
+ else:
+ dataset_sha = None
+ dataset_created_at = None
+ dataset_info_log[key] = {"sha": dataset_sha, "created_at": dataset_created_at}
+
+ peft_branch = get_peft_branch()
+
+ if train_result.status == TrainStatus.CANCELED:
+ save_dir = RESULT_PATH_CANCELLED
+ print_fn("Experiment run was categorized as canceled")
+ elif peft_branch != "main":
+ save_dir = RESULT_PATH_TEST
+ print_fn(f"Experiment run was categorized as a test run on branch {peft_branch}")
+ elif train_result.status == TrainStatus.SUCCESS:
+ save_dir = RESULT_PATH
+ print_fn("Experiment run was categorized as successful run")
+ else:
+ save_dir = tempfile.mkdtemp()
+ print_fn(f"Experiment could not be categorized, writing results to {save_dir}. Please open an issue on PEFT.")
+
+ if peft_config is None:
+ peft_config_dict: Optional[dict[str, Any]] = None
+ else:
+ peft_config_dict = peft_config.to_dict()
+ for key, value in peft_config_dict.items():
+ if isinstance(value, set):
+ peft_config_dict[key] = list(value)
+
+ log_data = {
+ "run_info": {
+ "created_at": start_date,
+ "total_time": time_total,
+ "experiment_name": experiment_name,
+ "peft_branch": peft_branch,
+ "train_config": asdict(train_config),
+ "peft_config": peft_config_dict,
+ "error_msg": train_result.error_msg,
+ },
+ "train_info": {
+ "accelerator_memory_reserved_avg": accelerator_memory_avg,
+ "accelerator_memory_max": (accelerator_memory_final - accelerator_memory_init),
+ "accelerator_memory_reserved_99th": accelerator_memory_reserved_99th,
+ "train_time": train_result.train_time,
+ "file_size": file_size,
+ "num_trainable_params": train_result.num_trainable_params,
+ "num_total_params": train_result.num_total_params,
+ "status": train_result.status.value,
+ "metrics": train_result.metrics,
+ },
+ "meta_info": {
+ "model_info": {"sha": model_sha, "created_at": model_created_at},
+ "dataset_info": dataset_info_log,
+ **asdict(meta_info),
+ },
+ }
+
+ log_to_console(log_data, print_fn=print) # use normal print to be able to redirect if so desired
+ log_to_file(
+ log_data=log_data, save_dir=save_dir, experiment_name=experiment_name, timestamp=start_date, print_fn=print_fn
+ )
diff --git a/peft/method_comparison/README.md b/peft/method_comparison/README.md
new file mode 100644
index 0000000000000000000000000000000000000000..c34fec0f9d0ef4de9342c539ca1e29642f4f6133
--- /dev/null
+++ b/peft/method_comparison/README.md
@@ -0,0 +1,116 @@
+---
+title: PEFT Method Comparison
+sdk: gradio
+app_file: app.py
+pinned: false
+emoji: ⚖️
+---
+
+# Comparison of PEFT Methods
+
+The goal of this project is to provide replicable experiments that produce outcomes allowing us to compare different PEFT methods with one another. This gives you more information to make an informed decision about which methods best fit your use case and what trade-offs to expect.
+
+Visit our [Gradio Space](https://huggingface.co/spaces/peft-internal-testing/PEFT-method-comparison) to check the results.
+
+## Community Contributions
+
+We envision the PEFT method comparison project as an ongoing endeavor with heavy involvement from the community. As maintainers, it is impossible for us to know all the perfect hyperparameters for each method or to predict all the use cases that PEFT users may have. As a consequence, community contributions are very welcome.
+
+Below, we outline all the ways you can contribute to this project.
+
+### Creating New Experiments
+
+Creating a new experiment requires setting up a new PEFT configuration for us to test. This will result in one more data point being added to the total comparison.
+
+Working on this is especially relevant if:
+
+1. You are the author of a paper whose method is introduced in PEFT, or worked on the PEFT integration, and know what hyperparameters work best.
+2. You have experience with a specific method and want to share your knowledge with the community.
+
+Of course, you can contribute even without meeting these criteria. Please follow the instructions below.
+
+#### How to Add New Experiments
+
+Start by navigating to one of the existing experiment folders, e.g. `peft/method_comparison/MetaMathQA`, if your experiment involves using the [MetaMathQA dataset](https://huggingface.co/datasets/meta-math/MetaMathQA). There, create a new directory inside the `experiments/` folder using a descriptive name. For example, if you want to test LoRA with rank 123 using Llama-3.2 3B as the base model, you could name the folder `experiments/lora/llama-3.2-3B-rank123`.
+
+Inside this directory, you will find a default configuration file called `default_training_params.json`, which contains the default parameters used in the `run.py` training script. Create a new JSON file containing all the parameters you want to modify compared to the defaults, and save it as `training_params.json` in the newly created folder. If you are satisfied with all the default training parameters, you can skip this step.
+
+Finally, you need to create a PEFT configuration file for the PEFT method you want to add. This should be a JSON file called `adapter_config.json`, placed in the same directory. Below is an example of how this could look:
+
+```python
+from peft import LoraConfig
+config = LoraConfig(r=123)
+config.save_pretrained("experiments/lora/llama-3.2-3B-rank123/")
+```
+
+Once you've created the configuration files for your experiment, please [create a PR on PEFT](https://github.com/huggingface/peft/pulls). After it is reviewed and merged, we will run it on our hardware to ensure that the results are comparable. Of course, it is best if you run the experiment at least once on your hardware to verify that the proposed settings work well.
+
+#### Considerations When Adding New Experiments
+
+When adding a new experiment, please consider the following points:
+
+1. Avoid changing too many training parameters at once, as this would make it difficult to compare results with existing ones. For example, if all existing results were created with 5000 training steps but your result uses 10000 steps, it would be unclear whether an improvement in the test score is due to the PEFT method itself or simply due to longer training. Similarly, using a completely different base model, especially if it is significantly more capable, does not contribute to a fair comparison.
+2. Avoid suggesting configurations that are very close to existing ones. For example, if there is already an experiment with LoRA and rank 123, do not add an experiment with LoRA and rank 124.
+3. Experiments for less-tested methods are more valuable than additional experiments for widely tested methods.
+4. Do not edit existing experiments, always create new ones.
+5. If you found hyper parameters that work especially well with a given method but are not trivial to find out, consider updating the PEFT documentation of that method so that other users can benefit from your findings.
+
+### Updating the Training Script
+
+We provide a training script that includes features typically useful for improving training outcomes, such as AMP support, a cosine learning rate schedule, etc. However, there is always room for improvement. For example, at the time of writing, the script does not support gradient accumulation. Therefore, PRs that extend the training script are welcome.
+
+#### How to Update the Training Script
+
+Follow the same process as when contributing to PEFT in general (see the [contribution guidelines](https://huggingface.co/docs/peft/developer_guides/contributing)). If the same training script is used across multiple datasets, please ensure that all relevant scripts are updated accordingly.
+
+#### Considerations When Updating the Training Script
+
+1. Updates should be backward-compatible. By default, any new features should be disabled to ensure that existing results remain valid. For example, if you add gradient accumulation, ensure it is disabled by default so that new experiments must opt in.
+2. Before adding a bug fix that could invalidate existing results, consider whether the trade-off is worthwhile. If we already have many experimental results, rerunning all of them can be expensive. If the bug fix is not critical, it may not be worth invalidating previous results. However, if you discover a significant bug that could meaningfully impact outcomes, it should be addressed.
+3. Avoid unnecessary complexity. While we could add support for DeepSpeed, FSDP, etc., doing so would add significant complexity, exclude users with limited hardware, and is unlikely to alter the relative performance of different PEFT methods.
+4. Minimize reliance on specific training frameworks. For example, we deliberately avoid using the `Trainer` class from transformers or PyTorch Lightning. This ensures transparency, making it easier to understand the training process and replicate results over time. If a training framework were used, we would have to pin the version or risk future incompatibilities.
+
+### Adding a New Dataset
+
+Adding a new dataset increases the breadth and usefulness of the PEFT method comparison. The goal is not necessarily to outperform benchmarks or replicate paper results, but to fairly compare different PEFT methods in a way that is useful for PEFT users. If this involves replicating an experiment from a paper, that is great, but it is not a requirement.
+
+#### How to Add a New Dataset
+
+The easiest way to add support for a new dataset is to copy an existing setup, such as `method_comparison/MetaMathQA`, rename it, and modify `data.py`, as well as any other necessary parts of the code. Ideally, as much existing code as possible should be reused. The general folder structure and experiment logging format should remain consistent.
+
+After adding the dataset, ensure it functions correctly and produces meaningful results by running at least one experimental setup, such as using LoRA with default settings.
+
+#### Considerations When Adding a New Dataset
+
+1. Before beginning, it is best to open an [issue on PEFT](https://github.com/huggingface/peft/issues) to share your plans. This allows for early feedback and prevents wasted effort on impractical ideas.
+2. The most valuable new datasets are those that test different capabilities than those already present. Bonus points if the task is similar to what users may face in the real world. Task ideas that would be great to add:
+ - A task involving both language and image modalities.
+ - An image generation task (like stable diffusion)
+ - A task involving audio (like whisper)
+ - A task that requires knowledge preservation (checked, for instance, via an auxiliary test set)
+ - Learning something completely new (e.g. a new language)
+ - A reinforcement learning task (e.g. using [trl](https://github.com/huggingface/trl))
+3. Training should be reasonably fast. Running dozens of experiments is impractical if each one takes multiple days and incurs high costs. Ideally, training should take a few hours at most on high-end consumer hardware.
+4. The chosen base model should not be too large, to avoid VRAM constraints. Morevoer, if the base model is too powerful, there is little room for improvement through further fine-tuning.
+5. Test scores should be informative and have a broad range:
+ - Besides loss, there should ideally be at least one additional metric, such as accuracy.
+ - Comparisons are not meaningful if all methods score near 0% or near 100%. The dataset should yield a range of scores to facilitate meaningful differentiation between methods.
+6. The dataset should be publicly available and have a track record as a useful dataset. The license should permit the intended usage.
+
+## Result dashboard
+
+For convenience, we included a [Gradio](https://www.gradio.app/) app that shows the results of the experiments. It allows you to filter down the task and base model and show the experiment results for this selection. Give it a try [here](https://huggingface.co/spaces/peft-internal-testing/PEFT-method-comparison).
+
+### Local deployment
+
+This app requires additional packages to be installed, please install the packages listed in `requirements-app.txt`, e.g. via:
+
+```sh
+python -m pip install -r requirements-app.txt
+```
+
+To launch the demo, run:
+
+```sh
+python app.py
+```
diff --git a/peft/method_comparison/__init__.py b/peft/method_comparison/__init__.py
new file mode 100644
index 0000000000000000000000000000000000000000..e69de29bb2d1d6434b8b29ae775ad8c2e48c5391
diff --git a/peft/method_comparison/app.py b/peft/method_comparison/app.py
new file mode 100644
index 0000000000000000000000000000000000000000..96444b6c155091ba2eee0da73cc0b7142cf6f4f7
--- /dev/null
+++ b/peft/method_comparison/app.py
@@ -0,0 +1,379 @@
+# Copyright 2025-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Gradio app to show the results"""
+
+import os
+import tempfile
+
+import gradio as gr
+import plotly.express as px
+import plotly.graph_objects as go
+from processing import load_df
+from sanitizer import parse_and_filter
+
+
+metric_preferences = {
+ "accelerator_memory_reserved_avg": "lower",
+ "accelerator_memory_max": "lower",
+ "accelerator_memory_reserved_99th": "lower",
+ "total_time": "lower",
+ "train_time": "lower",
+ "file_size": "lower",
+ "test_accuracy": "higher",
+ "train_loss": "lower",
+ "num_trainable_params": "lower",
+}
+
+
+def get_model_ids(task_name, df):
+ filtered = df[df["task_name"] == task_name]
+ return sorted(filtered["model_id"].unique())
+
+
+def filter_data(task_name, model_id, df):
+ filtered = df[(df["task_name"] == task_name) & (df["model_id"] == model_id)]
+ return filtered
+
+
+# Compute the Pareto frontier for two selected metrics.
+def compute_pareto_frontier(df, metric_x, metric_y):
+ if df.empty:
+ return df
+
+ df = df.copy()
+ points = df[[metric_x, metric_y]].values
+ selected_indices = []
+
+ def dominates(a, b, metric_x, metric_y):
+ # Check for each metric whether b is as good or better than a
+ if metric_preferences[metric_x] == "higher":
+ cond_x = b[0] >= a[0]
+ better_x = b[0] > a[0]
+ else:
+ cond_x = b[0] <= a[0]
+ better_x = b[0] < a[0]
+ if metric_preferences[metric_y] == "higher":
+ cond_y = b[1] >= a[1]
+ better_y = b[1] > a[1]
+ else:
+ cond_y = b[1] <= a[1]
+ better_y = b[1] < a[1]
+ return cond_x and cond_y and (better_x or better_y)
+
+ for i, point in enumerate(points):
+ dominated = False
+ for j, other_point in enumerate(points):
+ if i == j:
+ continue
+ if dominates(point, other_point, metric_x, metric_y):
+ dominated = True
+ break
+ if not dominated:
+ selected_indices.append(i)
+ pareto_df = df.iloc[selected_indices]
+ return pareto_df
+
+
+def generate_pareto_plot(df, metric_x, metric_y):
+ if df.empty:
+ return {}
+
+ # Compute Pareto frontier and non-frontier points.
+ pareto_df = compute_pareto_frontier(df, metric_x, metric_y)
+ non_pareto_df = df.drop(pareto_df.index)
+
+ # Create an empty figure.
+ fig = go.Figure()
+
+ # Draw the line connecting Pareto frontier points.
+ if not pareto_df.empty:
+ # Sort the Pareto frontier points by metric_x for a meaningful connection.
+ pareto_sorted = pareto_df.sort_values(by=metric_x)
+ line_trace = go.Scatter(
+ x=pareto_sorted[metric_x],
+ y=pareto_sorted[metric_y],
+ mode="lines",
+ line={"color": "rgba(0,0,255,0.3)", "width": 4},
+ name="Pareto Frontier",
+ )
+ fig.add_trace(line_trace)
+
+ # Add non-frontier points in gray with semi-transparency.
+ if not non_pareto_df.empty:
+ non_frontier_trace = go.Scatter(
+ x=non_pareto_df[metric_x],
+ y=non_pareto_df[metric_y],
+ mode="markers",
+ marker={"color": "rgba(128,128,128,0.5)", "size": 12},
+ hoverinfo="text",
+ text=non_pareto_df.apply(
+ lambda row: f"experiment_name: {row['experiment_name']}
"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "ngqdEv0rP01q"
+ },
+ "source": [
+ "## Introduction\n",
+ "\n",
+ "In this notebook, we are going to fine-tune the LayoutLM model by Microsoft Research on the [FUNSD](https://guillaumejaume.github.io/FUNSD/) dataset, which is a collection of annotated form documents. The goal of our model is to learn the annotations of a number of labels (\"question\", \"answer\", \"header\" and \"other\") on those forms, such that it can be used to annotate unseen forms in the future.\n",
+ "\n",
+ "* Original LayoutLM paper: https://huggingface.co/papers/1912.13318\n",
+ "\n",
+ "* Original FUNSD paper: https://huggingface.co/papers/1905.13538\n"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "6K4S2s33ebY0"
+ },
+ "source": [
+ "## Install libraries\n",
+ "\n",
+ "Currently you have to first install the `unilm` package, and then the `transformers` package (which updates the outdated `transformers` package that is included in the `unilm` package). The reason we also install the `unilm` package is because we need its preprocessing files. I've forked it, and removed some statements which introduced some issues."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 1000
+ },
+ "id": "5cngOTr6SqEf",
+ "outputId": "6c7a2f76-682b-4f93-a3db-59ab010e5ffe"
+ },
+ "outputs": [],
+ "source": [
+ "! rm -r unilm\n",
+ "! git clone https://github.com/microsoft/unilm.git"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "RGMkEG5aRB0D"
+ },
+ "source": [
+ "## Getting the data\n",
+ "\n",
+ "Here we download the data of the [FUNSD dataset](https://guillaumejaume.github.io/FUNSD/) from the web. This results in a directory called \"data\" being created, which has 2 subdirectories, one for training and one for testing. Each of those has 2 subdirectories in turn, one containing the images as png files and one containing the annotations in json format."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "colab": {
+ "base_uri": "https://localhost:8080/"
+ },
+ "id": "DTFnEZagQm4v",
+ "outputId": "97ce03ba-a6bb-4444-8eba-77eceece44e0"
+ },
+ "outputs": [],
+ "source": [
+ "! wget https://guillaumejaume.github.io/FUNSD/dataset.zip\n",
+ "! unzip dataset.zip && mv dataset data && rm -rf dataset.zip __MACOSX"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "UrNMR64LsJXm"
+ },
+ "source": [
+ "Let's take a look at a training example. For this, we are going to use PIL (Python Image Library)."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 5,
+ "metadata": {
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 1000
+ },
+ "id": "eG-eGcj3sNPs",
+ "outputId": "69ead0ea-15d6-4d5e-af61-a99a7533d31b"
+ },
+ "outputs": [
+ {
+ "data": {
+ "image/jpeg": "/9j/4AAQSkZJRgABAQAAAQABAAD/2wBDAAgGBgcGBQgHBwcJCQgKDBQNDAsLDBkSEw8UHRofHh0aHBwgJC4nICIsIxwcKDcpLDAxNDQ0Hyc5PTgyPC4zNDL/2wBDAQkJCQwLDBgNDRgyIRwhMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjL/wAARCAPoAvoDASIAAhEBAxEB/8QAHwAAAQUBAQEBAQEAAAAAAAAAAAECAwQFBgcICQoL/8QAtRAAAgEDAwIEAwUFBAQAAAF9AQIDAAQRBRIhMUEGE1FhByJxFDKBkaEII0KxwRVS0fAkM2JyggkKFhcYGRolJicoKSo0NTY3ODk6Q0RFRkdISUpTVFVWV1hZWmNkZWZnaGlqc3R1dnd4eXqDhIWGh4iJipKTlJWWl5iZmqKjpKWmp6ipqrKztLW2t7i5usLDxMXGx8jJytLT1NXW19jZ2uHi4+Tl5ufo6erx8vP09fb3+Pn6/8QAHwEAAwEBAQEBAQEBAQAAAAAAAAECAwQFBgcICQoL/8QAtREAAgECBAQDBAcFBAQAAQJ3AAECAxEEBSExBhJBUQdhcRMiMoEIFEKRobHBCSMzUvAVYnLRChYkNOEl8RcYGRomJygpKjU2Nzg5OkNERUZHSElKU1RVVldYWVpjZGVmZ2hpanN0dXZ3eHl6goOEhYaHiImKkpOUlZaXmJmaoqOkpaanqKmqsrO0tba3uLm6wsPExcbHyMnK0tPU1dbX2Nna4uPk5ebn6Onq8vP09fb3+Pn6/9oADAMBAAIRAxEAPwDa/wCGb/DH/QX1f/vqL/4ij/hm/wAMf9BfV/8AvqL/AOIr2WigDxr/AIZv8Mf9BfV/++ov/iKP+Gb/AAx/0F9X/wC+ov8A4ivZaKAPGv8Ahm/wx/0F9X/76i/+Io/4Zv8ADH/QX1f/AL6i/wDiK9looA8a/wCGb/DH/QX1f/vqL/4ij/hm/wAMf9BfV/8AvqL/AOIr2WigDxr/AIZv8Mf9BfV/++ov/iKP+Gb/AAx/0F9X/wC+ov8A4ivZaKAPGv8Ahm/wx/0F9X/76i/+Io/4Zv8ADH/QX1f/AL6i/wDiK9looA8a/wCGb/DH/QX1f/vqL/4ij/hm/wAMf9BfV/8AvqL/AOIr2WigDxr/AIZv8Mf9BfV/++ov/iKP+Gb/AAx/0F9X/wC+ov8A4ivZaKAPE2/Zs0HexXXdSClgVBRCQuOQTjk578Y9D1qrJ+zRYkjy/E1wo5zutFPfj+Idsf54r3aigDw+H9mvSFiUT+IL55Nx3MkKKCOwAOcHrzn8Knh/Zt8PLHifW9Ud8nmMRoMduCp/nXtNFAHisf7Nvh8TSmTW9TaIkeUqiMMoxzuODu59APxqvP8As1aWzubfxHeRqfuiS3VyOe5BGeMen9K9yooA8JX9miyAXf4muCd2Ti0UZX0+919/0ph/ZntcnHiibH/XkP8A4uveaKAPBv8Ahme2/wChpm/8Ah/8XR/wzPbf9DTN/wCAQ/8Ai695ooA8G/4Zntv+hpm/8Ah/8XR/wzPbf9DTN/4BD/4uveaKAPBv+GZ7b/oaZv8AwCH/AMXR/wAMz23/AENM3/gEP/i695ooA8G/4Zntv+hpm/8AAIf/ABdH/DM9t/0NM3/gEP8A4uveaKAPBv8Ahme2/wChpm/8Ah/8XR/wzPbf9DTN/wCAQ/8Ai695ooA8G/4Zntv+hpm/8Ah/8XR/wzPbf9DTN/4BD/4uveaKAPBv+GZ7b/oaZv8AwCH/AMXR/wAMz23/AENM3/gEP/i695ooA8G/4Zntv+hpm/8AAIf/ABdH/DM9t/0NM3/gEP8A4uveaKAPBv8Ahme2/wChpm/8Ah/8XR/wzPbf9DTN/wCAQ/8Ai695ooA8G/4Zntv+hpm/8Ah/8XR/wzPbf9DTN/4BD/4uveaKAPBv+GZ7b/oaZv8AwCH/AMXR/wAMz23/AENM3/gEP/i695ooA8G/4Zntv+hpm/8AAIf/ABdH/DM9t/0NM3/gEP8A4uveaKAPBv8Ahme2/wChpm/8Ah/8XR/wzPbf9DTN/wCAQ/8Ai695ooA8G/4Zntv+hpm/8Ah/8XR/wzPbf9DTN/4BD/4uveaKAPBv+GZ7b/oaZv8AwCH/AMXR/wAMz23/AENM3/gEP/i695ooA8G/4Zntv+hpm/8AAIf/ABdH/DM9t/0NM3/gEP8A4uveaKAPBv8Ahme2/wChpm/8Ah/8XR/wzPbf9DTN/wCAQ/8Ai695ooA8G/4Zntv+hpm/8Ah/8XR/wzPbf9DTN/4BD/4uveaKAPBv+GZ7b/oaZv8AwCH/AMXR/wAMz23/AENM3/gEP/i695ooA8G/4Zntv+hpm/8AAIf/ABdH/DM9t/0NM3/gEP8A4uveaKAPBv8Ahme2/wChpm/8Ah/8XR/wzPbf9DTN/wCAQ/8Ai695ooA8G/4Zntv+hpm/8Ah/8XR/wzPbf9DTN/4BD/4uveaKAPBv+GZ7b/oaZv8AwCH/AMXR/wAMz23/AENM3/gEP/i695ooA8G/4Zntv+hpm/8AAIf/ABdH/DM9t/0NM3/gEP8A4uveaKAPBv8Ahme2/wChpm/8Ah/8XR/wzPbf9DTN/wCAQ/8Ai695ooA8G/4Zntv+hpm/8Ah/8XR/wzPbf9DTN/4BD/4uveaKAPBv+GZ7b/oaZv8AwCH/AMXR/wAMz23/AENM3/gEP/i695ooA8G/4Zntv+hpm/8AAIf/ABdH/DM9t/0NM3/gEP8A4uveaKAPBv8Ahme2/wChpm/8Ah/8XR/wzPbf9DTN/wCAQ/8Ai695ooA8G/4Zntv+hpm/8Ah/8XR/wzPbf9DTN/4BD/4uveaKAPBv+GZ7b/oaZv8AwCH/AMXVe7/ZoYQj7H4mDS7uRNabRj8GPNfQNFAHzj/wzVqv/QxWf/fhv8aP+GatV/6GKz/78N/jX0dRQB83Tfs36pDBJKfENmQilsCBucDPrXpHwJ/5JRp//Xaf/wBGNXoN/wD8g65/65P/ACNeffAn/klGn/8AXaf/ANGNQB6TRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAV7/wD5B1z/ANcn/ka8++BP/JKNP/67T/8Aoxq9Bv8A/kHXP/XJ/wCRrz74E/8AJKNP/wCu0/8A6MagD0miiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAr3/APyDrn/rk/8AI1598Cf+SUaf/wBdp/8A0Y1eg3//ACDrn/rk/wDI1598Cf8AklGn/wDXaf8A9GNQB6TRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAZ+vXaaf4d1O9kVmS3tJZWVepCoTgflXDfAn/klGn/8AXaf/ANGNXbeI4hceGNWhMDTiSzmQxK20yZQjaD2J6ZrifgT/AMko0/8A67T/APoxqAPSaKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigCpqsMdxo97DMgeKS3kR1PQgqQRXA/An/klGn/9dp//AEY1eg3/APyDrn/rk/8AI1598Cf+SUaf/wBdp/8A0Y1AHpNFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRXP65410Lw/ObW6uzNflcpY2qGa4fjPCLk9O5wKAOgoriYvE3jDVlH9l+D/ALBHkAz6zdCPHPOI0DMRjnJI/Gs3VNW8cWdyBN4i8D2AcZSKd5MkdCQSRnmgD0iivO7HUPiFNA11b6l4O1WM/KiW7yqGbP8AeBI49KtyfEK70hwPE/hbUtLhXiS9hIurZOTg7k5wQM8qMd6AO5oqlpWsabrlkLzS76C8tyceZC4YZ9Djoau0AFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAVNVmS30e9mlbbHHbyOxxnACkmuB+BP/ACSjT/8ArtP/AOjGruddhjuPD2pwzOEiktJUdycbQUIJzxiuG+BP/JKNP/67T/8AoxqAPSaKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKRmVFLMQFAySTwBS1wfiqQ+LNZk8KR3Bg0e1jE+uXaSbSF6rb7s8FgMt6Lj1oAr3viDUfF8NxJpN6+ieFYELza82FknAzuEIb7q/8ATQjtwK8s1T4uaP4WmurPwHo8LSsPLk1q8y81we7HPzHnkbjj27Vz3xR+JL+Lb5dM0dpLXw9Zr5UMCnas2P42UduBgHoBnqa84AycCgDrI9d8deN9TWxh1LVtSuZCWEEcrbRngnaCFVfyArrtN/Z58X3tuk11Pp1iW6xSyszjjP8ACpHt1rduDqXwX0fQrGxm0y31HU4bi41C6u4Wkw6qpWJSvOP4fQk5q943+K3imx8P+GZrOe00++1Gza7uooohK8Yz+7Yh8hUYHPr19KAPPNe+D3jXwtFJf/ZUuYLb94bixm3FAMHdjhuPp2NVfDvxb8Y+HrlXXVZb+3ACtbXzGVCo7DJyv4EV7XqXi/xHqfxA0rR/Dmvab5Fxo7zu3krPbyXCNIG+YYYDK4yDx1wa8g+IOnR6ro1n40trCGzkubqWy1KG2O6H7Qh/1iEZG1x+oPXOaAPQ/CWv+H/Fl1DL4UuP+ES8TJ8zWEY/0O+I5AdQAG6kZ4YZ74Fep+FvFT61Jc6bqlkNM12zwbixaTf8h6SIf4kPqOnQ18TxyPDKksTskiEMrqcFSOhB7GvoTwN4ln+I2kIxnhg8c6EvmWV0QB9rjxjZJ6qclW9Mhh3oA95orK8Oa5D4i0K31KKN4mfKSwyDDRSKSrow9QwIrVoAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigCjrUvkaFqEweNPLtpG3ynCLhScsfT1rhPgT/ySjT/+u0//AKMau08T2xvPCes2obYZrGePcQTjMbDOByetcX8Cf+SUaf8A9dp//RjUAek0UUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQBT1XUrfRtIu9Su3CW9rE0sh9gM189+ONVuPDnwlt7G4kk/tjxZctqd5nI2I207efby1x7GvW/i1JOnw01ZLZC8s5htwgXcWEkqIQB6kMa8L/aAu/M+IEFgkflwWNjFFGgPy4OWyB26gfgKAOC8LeGdQ8XeIbbRtNVTPMSS7cLGg5Zj7Af4V9M+FPgd4V0CCJ9Qtxq98p3NLcD93njpHnGOO+etZH7O+gQ2nhC61tocXV7cNGsjKQfKTAwD3G7d07j2q/8AEb4i6z4e8WWuhaJHbm7Nstykc6bxdlnZfKGCCrfLkY65xxxkA63xH4G0zxRrmkalqDOy6csy/Z9oMcyyLtIbI9q8y8ZeE/AngyOyi1HUvElzcGB4Vt7a6VpGtF+Yo/AxEOfQ8nrji94P/aA0/VLyPT/Edj/Zlyx2CeMlot3+0D8yc8d/c1wvjS+k1XXdZ1W+ilkt7mOeGxu9vlSWkiRMDaSKcjoScdSSCDywoA9Ps/hD4S1W0stQ0zWtZNkbdo7c296NhgdmYxg7c7TuYEZ7nPNdrF4N8PR+GYPDraXbzaVAMRwTLvAPPzZPO75j83XmvDPg/wDFC08MeEtWstcuWa3ststlEoy7Fs7kX8cHJ4Gatn41eI/FEl4+nJaaDpFlH5t1ePiaVVzwq7sKXY8KuOvfHNAGh8QvgNYtpsuo+D4ZIryLLvYmQssq9TszyG9s4OMcHr4d4a1u58KeKrHVo0YS2U4Z42GCR0ZT6ZGRX2P4K12TxN4P03WZYxG91GW2ZzgBiBk9zgDPA59K+a/jp4et9C+IkklpGkcOoQi7KKScOWYMfbJBOPegD3DQLmDTPiNILMudK8VWS6nbFjgCdQN+AR/EjIccnivQ68I8JXy6j4T+GupWaFZtM1ZtNmcn7okRgwAPUMNv0r3egAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAKOtXAtNB1G5MbyCG1kk2RjLNhScAetcJ8Cf+SUaf/wBdp/8A0Y1d7qwLaNfKJjCTbyDzRjKfKfm544681wXwJ/5JRp//AF2n/wDRjUAek0UUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQBx/xPmktfAd3eRwmY2txa3LIDjKx3EbnntwprwP9oG1kg+JhmfbsubOKSPB7DK8/ipr6b1/SYte8P6hpM3Ed3bvCT6ZGAfwPNfO/xM08eIvh1ofimOF1v9KxpOpxgcIyZGcZPAfOPZxQB6n8DLmKf4UaZHG2WgkmjkGDw3mM2PyYfnVL41WWpR6Zput6VFpxktJWjna9t4HUI2NpLSjAww/Nq4L9nzxrFp2oXPhe/nCQ3jebZl2wBL0KD3YYx7r719FXdrBfWc1pcxrLBOhjkRujKRgigD5U8ReFtT8S6bca3NHYf8JDFhrm3sby2lF5GAS0qpExIcYG4Yweo5yKpeFPED3sUkN8ftDi1ltpUlCv5yeS4hbB/jibGG67WxkAYPc+LfhXpngq9TWNL0rxHdW8LrMk9hfxBrdw3HyGItwcc5PvXP6NLa6p4huta8KWjpJe209jf6SygyR+ZEVEybQBtLBcgAbWOOjCgDjvCFpJe2usWiLABeQR2gmn4SEmVZC5PYBInJPoD6jPQ3A1CSa08LeFLjSm05ZljQiWGR72Ynb57qdzd+Bj5V/Gp9Gk06HQZfBVppWs6lfXMqvqU2kTxhZWBJWLcUfKL6jALA9QAT7H8OvhRo3haVNaksblNTdPkiu7hJzbZ64Koo3dj1x2PJoA77R7H+zNFsbHj/R4EiJAAyQoB6AD8gK+ev2k7sv4n0Wz2KBFZtLuHU73Iwfps/U19HXFxDaW0lxcSpFDEpeSRzhVUckk9hXxr4p1a8+JXxKkks0Be+uFtbNDwFTO1M/zJ9zQB6r4RtG0/wAG/DXT4Chm1DWGv5UQcuqByWP+6u3Ne815zoFhHc+PrSxt/Lew8IaYtmr7MlrmVQGwcAZCIM+7+9ejUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFNCnzC287SAAuBgHnn/PpQA6iiigAooooAKKKKACiiigAooooAKKKKACiiigDD8Z/wDIi+If+wZc/wDopq5L4E/8ko0//rtP/wCjGruddgS58Palbyqzxy2sqMqjkgoQQK4b4E/8ko0//rtP/wCjGoA9JooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigArzjxBpttomv3kGowxN4U8UsIb0ltv2a7KkB89AHCqM9mAP19HqpqWmWWsafNYahbRXNrMu14pVDA/n37g9qAPjLxh4V1P4f+LGspXfdC4mtLtFKiRc5Vl9wevoRXvHwz+NVjr1mmm+JrqG01dSESZsJHc5OAeOFbPUcDuPQO8T6TbaXpseheNorrVfDnzC010jfcWTkcCUjnA7Pgg8ZHFePeIvhH4g0qE6jpKrrmiuokivbEhtynuUBJ/LIoA+pPFd99j8Ozuiyu8pWKMQXaW8hLHA2O5A3eg79MGvnn4mw3Vtplhqlw/iO1v8Af5AmvbO2h3oyYZTLDhnOBj5s5Gema8+tfGGv2dmtidQkuLFCpFneKLiEbTkfu5AVHPoKo6prF7rF1JPdyj523eVGNkanp8qDhfwFAHvvhZv+Ef0nSZNKj8StpI23CSXP2Swtip+YvK4+Z1I7MSQOK9pvdSstO0+S/vLuGC0jTe0zuAoXrnNfEmleKdT0eNktzby9PLa6tknMBHQxlwdh+noKi1fxJrevlTquqXd2qnKJLISif7q9F6dgKAPTfi78Xl8UI+gaA7DR8gzzlSGuSDkAA8hQQPckenV/w+8OP4K0pfF+q2wbWrwfZ/D+nSqQ0szgBXPTg7h17ZPpXjVekeGfibG2nQeH/GdkNW0dMrFdNzdWYIwDG5544x0I9ccUAfSvgvw5/wAI14dit5xG+pTk3GoTqOZp25ck9+Tgew7V0VeS6L4t1DwrpNpdyX58T+D2JDayhLXNkDjCzLyWAyMnqO44APqVhf2mqWEF9YzpcWs6B4pUOQwNAFiiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAp6sYl0e+NwUEIt5DIZMbdu05znjGK4L4E/8ko0//rtP/wCjGrr/ABgpfwRr6AgFtOuACxAH+rbqT0rkPgT/AMko0/8A67T/APoxqAPSaKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAGyRpNE8UqK8bgqyMMhgeoI71xVz8Pm065e+8IavcaJcMdxtQPNs39QYjwuT3XHU129FAHkuo6H4gljdPEvw/wBA8QqQzNd6dKIZWzxkq4B3nrkHjPHIrEbwH4XvbZRP8LvEdhMr5xaXSSBhjuWl/p+Ne60UAeK6b4QWK4judI+EdrbTbtpk1bU96x9CG2ZfIB9BntUPijRobq3h0r4gaDpmlCb93p2uaKjeRbOf4Zc4wCfXg5PTBNe4VXvrG01Oxmsr63juLWZSkkUi5Vh7igD4r8Y+CNZ8EamtnqkSMki74biElopBz0OOvHTrWt4I+HkviG0l17WLldM8M2jZubyQ4MgHVYxjk5wM+p7niva9f8N3nhjS7nTJdIm8TeC533ixQlruwPJ/dnOWTPTnIz9c6OheELvxJNaah4m0+Ox0mxYNpGgoAFgUcbpgB8zcKQM4HcUAUPDvh1/F2jxWENpPovgWIJ5FpkLc6kRyWlYEkIfTqcdq9Vt7eG0t47e3iSKGJQiRouFVR0AHYVJRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFAFHWrWO+0HUbSbPlT2skT4ODtZSD/ADrhPgT/AMko0/8A67T/APoxq9Bv/wDkHXP/AFyf+Rrz74E/8ko0/wD67T/+jGoA9JooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAKWsLM2iX627hJzbSCNiMgNtOD+dcH8Cf+SUaf/12n/8ARjV3OvSGLw7qciy+SyWkrCTj5MIeeQenXoa4b4E/8ko0/wD67T/+jGoA9JooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKwdU8X6Vo2qNp979pjkWD7S8gt2MaxBgrOWAxhSwz6ZyeKs/8JBYnxCNEQXEt55QmcxwO0candt3uBtXO1sZPOKANWisCPxjpMmqtpxNzHIt0bIyyQMIvPADbN+MZIYEeueK2Ly8t9PsZ727lEVtbxtLLIeiqoyT+QoAnorjW+JOlppV/qD6fqaR2lul2sbRIHuLd2wJYhvwV7nJBGRkcircfjixDa4Luxv7FdFhWa5e5RACrAsNu1zkkDvjtQB09FcbrvxBh0rRNC1az0u41C21iWKKIxyIuxpACgbk8nkcccHmrnjDxXP4Vhs5o9Hkvo7mdbfetwkQSRyAgO49z36CgDpqK871L4mahpl3LbS+EbtniD79t3H95IFmkC/3sK3UdSMCpLX4lXU2vxaHN4ZuLfUpJolFu11GWMTqzGYeqKF5I78daAPQKKZKZBE5iVWkCnYGOAT2yecCvOG+IXiODQNe1e68PafHFotybedF1BmZypG4r+79GGM4z7UAelUV5lefFpW0TxHrOj2EF7YaPJbxiRrgqZjJgNjCkDaSB155/Ft38Ur61sbSdrPRF825urd5pNUKwBoVDfLJ5fzbuQOBzgUAen0VxVx401W6toW0LRI7u5XTYtRuoLi5MLRrKCURPlO5ztfrgDA55rOu/iRfoLiS002zmRo7SbT0a4cSXcdw21CAEO0g5BHPSgD0aiuITxjqk/i278O29npz3ltMoZDcSA+SVRmk+5jI3gbc5ODXOaP8UNZ8SzabpOkx6WmtOl016LiKUwp5TYQLhgRuHPfAoA9aoryDS/ih4g1DwnqmtRxaRcPZ20MphiilQpJI6gRtub5sgt8w4BXvW1ZeNPEOvaxc22iR6YLaKOGWQ3MUnm2wZZg8cihx86yQhT0+90oA9FormvA+s6vr/h2HU9XgtYjcpHNB9mDBWjeJG5DEnIYsPwFdLQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFAGX4lnjtfCur3E0KzxRWUzvE3R1CElT9elcV8Cf+SUaf/wBdp/8A0Y1dxr8ltF4c1SS8UNapaStMCuQUCHdx34zXD/An/klGn/8AXaf/ANGNQB6TRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRSMdqk4JwM4HU0AedeOvDOreIPFVm1pYytbJp0sQuftCpCJWkRwkqbtzxkRlWG1h84444zdf8J+M9U1abVrBRZXVwiKNmqNH5UQjCvbkKhDAtvZXBBUtng1o23xB1q90TWNVh0vT1is7Ka4WE3LG4hkQjEU8RUFGK5PGRx15FOh8Y+JYLQX17b6TLb3NjZSWscIkRhPcuI1DkkjYGySQM4x1oAgHhLxJfalNa3NvbWemy64mrG6jvWkmCxoirGF2jkmMZYnueDXe65paa3oGo6U8hiS9tpLcyKMlQ6lc49s1yP/AAlPieKJNMmtdGOsz6h9hguIpma2OImkZ2QEuuAjDaTknuBzWX4l8f694e0bSbqa40UvObtbqWG3kuEJiyyeWFkGNygfePBPJAFAEFr4d1rWr/U9D8QobS5XQk061vLeNpIrhN2WlLYAVtyr8hweT161auvA3ibW9MvG1O6sIr/UL20e7WCRwhgg9CBncx5xjAqbXfF/ifSIdPhml0GxuJrEzvdXkU32WWbPEauGAj4xy55LACq/iHUfiJF4htrbTL7TIxeLIbO3MIZJfKijckuTkBmZwOmAB60AV/8AhXHia20C10W0vtMa00/Wl1KxNw8jMI1ZmEbEL6kdPU1qa54Y8ba7pEUM9/pAul1RL5SDKEiSMJsRMLn7wckn1q2154jh+Ic1lLrMR0yOx/tD7Mtmu7G4qY9+c9s7qwrfxp4lm0ez1iS5tlt9bsbua1ijgVjYyRIzoCc/vAVU5yBgjtnFAHR6xo3iu/1rw7qdvJoySacrtcJIZcO7qUcLgfdxyM8561Jc+F9Sm+J9r4njmsEs4bFrRk2N5zgtk5PTjsffpXP/AA78Za14i8QTWmqXOz7LpkUt1bNAq7ZmPDK46oUww/3/AGFNuvE/iS806XX9Lmk/s271NILaGOFHl+xxhg8sSNy7O2TjJO0DAPNAHqD7tjbCA2OCRkZrz9/AGsTaL4j06TW7ADWrg3LSJpzAxuWUkH978w2rgdMdfamWGta1rr6Hptnr8YlmtLq7uL6K0CmXy5VRE8tx8hBYbhjsQOoNM0XU9a1XX/Ck1zrMqx3umz3F1bWwjMEkkTRrlSVJ2t5hJwewxigCfW/h7qOq6brmm2+sWVjZ6mkMaRW+nbRCqHcw4cZ3En8z1rS1rwQuvNoi3tzbtBYiQXUC2g2XW9NrADPydzxkjjB4rnNY1PWYLjxS0OvXYjtNQ077L5YjwsU7IHT7pyP3hwevA/GbTbPxfD46TTrrxRNOsUC3s0LJH5bxtPKm0ERhgQgQ/wC8D2oA0rr4e3VxarGnie/glNkdPnmjijLXEA+6HJB+YZYb+vzH3zpN4G0san4evYWmh/sOEwQRo3yyJtAUP64IBHvXJyX+taNF45uzqd7cS6ICLBLiTeipJEsm5lGN5BORu6Diqviu/wBT03Ttb0vTfEN1LItpY3ttePcfOs01wYyAw/5ZsADs5HJxxxQB0z+AL5tcuNTXxXfxm4vUvJI44IlyUCqqbgM7dqKpGfmA5zVe2+GUlkulm28S3sM2nrOizJbwhnWXqD8vbtnOKPhpqM2qXXiOea41FmjvEhe2vZmf7NIsYMiJkn5d5bBGOMccCovie95BdeH3sLjUTPPcyQmzs9Ra1+0KIXfGR33KvbPbvQAsPwtdNHk0qXxLfSWpshZxIIY02AMjKx2gb2XywAWzgE+tb8Xguwt7jV7q1ury2vNWiiju7mBkVmMYI3gbcBmycnH5GuO1iS506XU7K+8SanaSaPpS3GmymdlN053lmkH/AC3KlUXac5zzknNZSTtB8Ubu4a6e1jW/tvtF094xRFktgXgaLOArOfvHhTjkcUAereHtDh8N6Jb6TbXNzPb267ImuXDMq9lyAOAOBWpXgWl6jeWninSrOS/tx4Wh8T3Edqy3bNIW/eCNH5JKgqCCTg7xnPb32gAooooAKKKKACiiigAooooAKKKKACiiigAooooAKrXVxNBLbLFZy3CyybJHRlHkrgnedxGRkAcZPPSrNFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFAGfr0c0vh3U47ckTPaSrGQcYYocc4OOfY1w3wJ/wCSUaf/ANdp/wD0Y1d9qsKXGj3sMgJjkt5EYAkZBUg8jkVwPwJ/5JRp/wD12n/9GNQB6TRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABSMu5GXJGRjI6ilooA4jTfh6YplfWdXfVRHYPp6M0AjkeJ8bvNbJ808cZ4GScE81PB4BjXQptLu9av7rMdvHbzsscb2wgbdFt2KASrc5bOe9dhRQBxkHw8ht7ObZq94NTlv/wC0f7RWGFZFm27CQoTbgqSCCCOSe5qOP4cRWdno8Gma1d2L6YZ3WWKCAmV5vvsyshXoSAAMAfQV29FAHFXXw8F7B5Fx4i1Z45bQWd4rNGwuowzsc7lO1iXPK4OBWxd+FrW61DSbxLu8tm0pClskLrtAI2kHcpLZAA5Pb15rdooA52fwhBceJxr7apqa3QQReUkqiIxg58srt5XJPXn3qpB8OtEtobiCGW+WB7eW2gi+0EraRyf6wQgj5c++fautooA4a98ANZ6TNF4evpYdQuLWLT5Lu6fe32dXJPQffCsVB7AD0zW/feE9G1DTdOsJ7VhBpzI9p5UrxNCyDapVkIIwK2qKAOam8A+HZtNgsGtJxFBJJIjpeTLKWk/1haQNvbdnnJOeKZd/Dzw1eLp6vZzxjToDbWvkXk0XlRnqBscde5PJ711FFAHNx+A/DkWoWN9HYMs9lFDFDieTbtiBEe5d2HK54LAn3q3H4V0mLxPL4jSGYapKgjeX7TJtZQMAFN23A+nXnrWzRQBzGm/D3wzpWr3Gq21hIb25R45pJ7mWbzFb7wYOxBzip4/A3heLSptMTQ7JbKd1klhEfDsvQn6dq6CigCpY6XY6Z5n2K1jg83bv2DG7aoRc/RVUfhUGqaBpOtS2kupWEF1JaP5lu0i5MbcHI/IflWlRQBQ1HQ9K1eW2l1HTrW7ktn3wtNEHMZ9Rn/PApr6Bo0s888mk2DzXClZ5GtkLSg9QxxyOB19K0aKAMlPC/h+MKE0LTFCuHULaRjDDoRx1961qKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAr3/wDyDrn/AK5P/I1598Cf+SUaf/12n/8ARjV6Df8A/IOuf+uT/wAjXn3wJ/5JRp//AF2n/wDRjUAek0UUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFAFXUlD6XdoSQGhcEqSD909COlcB8Cf+SUaf/12n/8ARjV3etXH2TQtRuSjP5VtJJsXGWwpOBmuE+BP/JKNP/67T/8AoxqAPSaKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooJABJOAOpNNR1kQOjBlPIIOQaAHUUUUAFFFFABRRRQAUVTv9X03SzGNQ1C0tDJnZ9omWPdjrjJ5q0jrIiujBkYAqynII9RQA6ik3LvCbhuIzjPOKWgAooooAKKKKACisfXfEdtoPkJJbXd3PMGZLe0QPJsXG58Ej5RkZ+oq4dUsxo51YTq9j5H2kSpyDHt3bh68UAXKK5xvGNpHfafbSafqca3vkhZ5bbZHG8oYqjFiPm+UggA4JAPJrW1PVINKhhkmDuZp47eOOPBZ3dgBgEjOMkn2BPagC7RXP2Pi/T795NkN1HAFneO4dBsnWF9shTBJ4PqAT2qbQvEtrr8k6QWt5btFHFMBcxbPMjkBKOvJ4O08HBGOQKANqiiigAooooAKKKKACiiigAooooAKKKKACiiigCvf/8AIOuf+uT/AMjXn3wJ/wCSUaf/ANdp/wD0Y1eg3/8AyDrn/rk/8jXn3wJ/5JRp/wD12n/9GNQB6TRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFUNS1rT9HezXULgQfbJxbwFlYhpDnCkgYGcHrgVfrjPiRo0uvaRpllHb3Msf9pRSTNbffiQBsuPcEg0AdBoviHS/EMVxJplw0y28phlLQvHtcdR8wGfwrTrx7VNP8bR+H7XT7jTZ7meW/uZ7+bTpNqzYQrH8okRtrsQ5wwwV6dqyn0LXruzsZtQ0LxPJfR2dtHceReGMSSIxV+koGDGF5AGT7kmgD3as/VtZtdGS0a53lru6itIUQZLO5wPwAyx9ApNeProfjy91LSJ7xNWDQ29mItjqoV4wvnCVvOGNzBjkq5YHoK9BsQfEvjefUZIlbTdEJtrJzj57ogiZx7KMIM991AFJ/izonlXjRWGrSPbeepU2u3e8IzIikkAsq5YjrgGu1sruO+sYLuMEJNGsig9QGGRn868m0LwNeS2fi25vtM1GPU5Lq/fTY5rhRD+/VlDKofG7BIJPYjFOg8Aa1aWd1aaNp0OlWt5oEMNxEtwBvvI5csCykn54yyl/Rh6YoA9ZjuYJoFnimjeFhlZFcFSPUHpUD6rp0dil8+oWq2b4C3BmURtnphs4NeU6j8PNQutDj+z+HbW3Q67b3y6QJ0KwQJGEkXd935yuSB6880av8P8AxJd3VxFaQQRaRbajcS2tgrw7XSZAN43xuowxfKsvAc7TwAQD2LqMiuV1DxsLDxLLow0W/nMXkF7iN4QgExIUgM4Y8q3ABPynitbw5Y3GmeHNOsLvb59tAsTbZjL90YHzlVJ4A5wK4zxH4P12/wDHcmv2dlp0wjjtxZvNqEsRikj3nc0axlX5k6E/w9Rk0Ad3Hq2mzOiRahau7yNEqrMpLOoyyjnkgckdqoab4v0HVtRl06z1O3e+ikkia334fMZw2B3A9RXO23hXWbXxzJr0dppJt5ruQNB5rARxlUH2hRsx57bSG7EBRnqTqeHdJ1/R7qaznfTpdM+1z3C3GXNxIsrM4UjopVmxnJyB0FAHTTTR28Ek0zqkUal3djgKAMkmmWd5b6hZw3dpMk9vMgeOVDlXU9CDVezOqNbXX25LMTedILcQsxUxZ/d78j72MZxx6U/SlvE0q1XUI7aO7WJRMlrnylbHITPO30oAt1wvjH4lWnhGXU7aW0M13bWkdzboGIE+5ipXO35SoG49fl54wa7qvM/HFje6pfazZvoV/ew3FmkNpcW1qr+RJtlVmO+VN3yzMBgcZ70AejWjyyWcD3ARZmjUyCMkqGxzjPOM0XZnFpMbXy/tAQmMS52bscZxziuMj8Va6l7aE+FtdNnHblJ4hawBnl+XDKfPOFwG49xyauyeML5onVPBviNWIIBMNuQD9POGaAM7w54/m1u70dZBYLDd6TJqFz5Mpd4GRlGwjtw69eeG4q1cfE7w/bac15ImogefHCsJs3WV/M3eW4UgHa21sE4zjFchY6dqtrb6ZbLpPiSMWWlz6WssNjbxuVk24k3faTtZSinp2NVB4K8U2139qh0iZrh5rWeSSNraIM8LSckb2yWWTBJP9MAHoNj8RNE1PSrnULKLUZ0geJPKSzcySeZ9xkXHKnnn2p0/j/TIDYp9i1SSW+tnuYYo7QliqHDg+jL3B/mQK8303wL4mtIYorzR9Ru44hAoi+2WixOIkZEEiHIcAEYz0IzzW3pujeJtMm0mSHw/qbf2ZDNbwqdQs1DRykEqdqjGCq4xjGKAN+9+KOjWhYpY6rcRJaR3zzRW3yLbOMiXJI49uvB44NduDkAjvXjr+GfFH2OW0Hh/Up4bnTV0q5M2qWgYwKXKsCE++N5HPBHXJ5retLj4mi70+WTR7ERRwmGeGbU0xI3aRisOQRg8Lwc9OKAPRCCQQDg+vpXl/gTxP4i1nWrGKbUZtQt9l0uoh9PEMcDJIViKSAAMWxyBuxz+HT/bfHf/AEA9A/8ABrL/APGKx/DeleNPDOl/YLbTNJni3vJmfVXyCzFj922Hdu+aAPQq47x5rt3oV14blga+aCfUhDcW9lEskky+W7AAEZxlRnGOM1Dpkfj3TYJY2sNKuzJM82+51iViu452r+44UdAKW/0bxF4hn02bVbDTLd9OuhdW/wBn1CRhvAOCcwjPcY9zQBTXxjP4f8IwahPHdX811eXKoNSnjtnjCyOAjfLwcKAAFPJxxkVo6j4w1I3OlW+h6RDfHVrFry0lluvKX5dhIYFcgYkUg9T0wKpXPgvU5I1aE2gulecrNNe3LfLM26RCEKEqSAQM8ED8a8Hg3xPbS6fJDNoSNp8Xk2uHvv3UZxlQPP5HyqMHsAOgoAv2/jy9l1+/01tB/d2GowWNxNHdbivnfckC7B8uSuecjPel0vx+2q+Jl0q3012hlkuIkuF8zEbRFl/eEoFAYo2NrEjjI5rFh8AeJ08RXutzXehXFxdXUV35ckVyIo5Y12qwQSAEjr82cHpitGy8FavFqS38zaGs/wBpafCR3TIjN950jabar5zyAOp9TQBq+Ftc1/XZZJbux063s7eWa0maOd2kaaJyjFAVA2ZHGTnjpXVZzXFaf4Iv9EE/9h6vbWD3DbpmNrNPubOScSzsASSckdc81FpHgzxNodrLbWPi+BYZJ5Lgq+lBtrO25sZl4GSTj3oAteP47n7Pok9q14WXVIY5YrW8MBljfKsp+ZQ3O36Yz61p+EtP1LS9D+z6rcPLL58rxiW4ad44mYlEaRuWIBxnn61z2s+BNd8QxQR6r4lsrlLeUTRBtJ27XHQ8SiptQ8G+ItVtIrW+8T2U9vFIkqRtpAwGQ5U8S84I6GgDuK8V1qx15PFlpEJg3hmbxMkrDzmDrKWCmLGeVJy+OmfTv2914b8a3KgL48W3x3h0ePJ/76c1hQ/CK5kkmOo+KWuUluftbhNJtULTc/Ocq2W5649fWgC7a+NdTufHEOlmeyOmX091b2sqQMrAxLncHZsSfMCpAQAEYDHFP8IXviPXbC+vrrxHbSwQNdWUaW9sm5njcqs7Hs2BnaPlxg96tf8ACv5/tRuv+EnvvtJJYzfYLLfk9Tu8jPNOtPANzYOz2Xim/tmYYLQWNkhI9DiAUAc/4duL3UPhTczXXjCK+lfSEd45Y4na2+TLCQ5y2RlSX579abbeIbg+C/BH9h63YWAvHh0+4it4UdUZ4ycgNyrKV6d93OeK6Bfh/OkU8SeJ75YpzmZBYWQWU+rDyPm/Gp7DwFHZnEmsXMyK4kRPsdpGEkH8Y2wj5uOtAHPah4x1cmz0q11W2S7WG9WW8PkxiSeGTy1Qh/lXqHZRzg8YFS614rvYtbtLVPE9tYNJbwXVzH5CNHbxdHALDdI7sQEUYwASe1dcnhhYs+Vq2oR7pDK/l+Su9z1ZsR/MT7+1Un8DRySM7eJPEuWJPGpMAM+gA4oA6qioraH7NawwCSSQRoE3ytudsDGWPcnualoAKKKKAOQ8d3EdrN4auJlkMMGrCaUxxNIVQQTAnCgnqwH4iuF1bVNW07whY21vFqdmXF5eWXlJNGoXzmMERESFtwQghG2p0DZ7e00UAeVawltd+I9A8Q3zeIPs9zpDxj7CLiKR598TBDHHym4buDhTgc8CrMNxrUnxHukv5dUhMV3GbKKGOZoJbUqoOcER8EncXyQenQCvTKKAMm1Np/wk+oLGl4Lv7PCZWff5JXL7dmfl3dc7fbNa1FFACEgdSB9aqXOrabZE/atQtIMEA+bMq4JGR1NRavoOk6/BHBq+n297FG29EnQMFbGMjPsayP8AhW/gr/oV9K/8BloAzPGGpaLdww3djqkT6nHHLbwyWl/bpsWUAMHMhI25CkkAsNvHoc68vNAksfDvguLxFYC0tYYZb1/tCESQwbQqbsgZZwvvhW4rqrXwF4RspfNt/Delo+NufsqHj8RU0fg3wxDPLNH4e0sSS43t9lTnHTtQByPjDWtP1bVNNjsJLf7VZ3Ec1tqv9p24gt8nEhMZk3P8m4Y2nr1FaEHiLQtZ8aSX02sWC2ejqbe1El1GBJO6gySKM9ApCA/7T49+k/4Rfw9/0AtM/wDASP8Awo/4Rfw//wBALTP/AAEj/wAKAON0e40XT/Ect7Bf2dvp1nBcRW1tLqcUhlkkkDl4xvKop28ZOTv5wBy/wZ4ms3vdRvtaW20/Ur0hpp5NSt3jZVLCONAsrEbVPJwMkk966/8A4Rfw9/0AtM/8BI/8KP8AhF/D3/QC0z/wEj/woAcPEmhMMrrWnEeouk/xqzY6pYamJjYXkF0IX8uQwyBwrYBwSO+CD+NPtrCys4BBa2kEEQJIjijCqM9eAKnChRhQAPYUALRRRQAUUUUAFFFFABRRRQAUUUUAFFFFAFe//wCQdc/9cn/ka8++BP8AySjT/wDrtP8A+jGr0DUWVNMu2YhVELkknAA2mvP/AIE/8ko0/wD67T/+jGoA9JooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKZFDHAmyKNI1yW2ooAyTkn6kkn8afRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQBW1ABtNulYAgwuCD34Nef/AAJ/5JRp/wD12n/9GNXoN/8A8g65/wCuT/yNeffAn/klGn/9dp//AEY1AHpNFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUU2SRIYnlldUjRSzMxwFA6kmgB1FUdK1nTdcs/telX1veW4YoZIHDKGHUZHfkVeoAKKKKACiiqFhrNhqd5f2lnOZJrCUQ3K+WwCORnGSMHgjpnrQBfoopCQOpxQAtFIWVVLFgFHJJPArmF+IXhw6bcXr3jxrBZrevHJCyv5LHCsoIw2TwME8ketAHUUVHFKJYo3wyF1DBHGGGR0I9aeHUnAYE/WgBaKjS4gklliSaNpIseYqsCUyMjI7cVXh1bTri3kuINQtZYIlLSSJMrKgGckkHAHB/I0AXKKpPrGmxw2szX9sIruQR27+aCsrHOAp7ng9PSq6eJdEk0xdSTVbRrFpfIFwJQUMmdu0H1zxQBq0UUUAFFcyfFU6/ERPCh0vCNZG9F59oH3Adv3Mf3uOvvXTUAFFZXiLW4/D2jvqEkXmKJEj5fYil2Chnb+FQTy3OBTtC1K61Wwe5urKK2/essRiuVnSaMdJFYAcH0IzQBp0UVwN7431a1uvFdsLbTRcaQA1pA8kgkuh5fm9MY+4GHGfmU545oA76iudtNeu5vE9to00MEcv9nC7uhiQFXJUYQldrLknvmpoPF2i3OsJpUN1K148ssKL9mlCs8X+sAfbt+XvzQBuUVyzeP9FVNQcx6gFsrYXb7rKRS8JOC6AgEgEHPAxg9qd/wnujAXPmLeRSQ+Tsilt2V5xMxWIxg9dxU4zjGOcUAdPRXMeENf1HXLnxBFqNqtsbDUmtoY9m1/K2KyluSCSGzkcdK6egAooooAKKKKACiiigAooooAKKKKACisLxmzJ4N1aRZZ4mjt2kD28xicFeeHBGOnqK4S01jUofDetWMMl+t5caqmnWFnd3pe4tyUViJJskgMA7BlZsBhg+gB6xRXlb6va+IJvDmmW17q1qtrqMum34+3ukm8W0rMjOr7mKsi4c9exPNdb4B1i91vwyLq9PmFbiWGC527ftMKsQkvb7w7jg9RQB09FeV67ravqXi5Nb1K+05rEQx2SWVyUdISM+eqb13ks2D16AYznPQW2v6rceO7rSDq2ixWkHlSC3dCbpw6sTHgSYDDbnODwelAHaUV5voXj7VNamtlCWSXF4L1TYIpaaxMOQrSfN8wLKBjC8uMH1rah8TZZbK7uNHv8AT3kh0Aan5D27MwlDYdGIcY9NvUck0Aeo0Vx+j+IbnVf7fhOqWhtbSCJ4NVgiAjUujMxOWKnZgE89+a6fTpRNplpKt2t2HhRhcqABNlR84A4GevHrQBZooooAjSeGSRo0ljZ1+8oYEj8KRLq3kuZbZJ4muIgrSRK4LIDnBI6jODj6VwsGqeG/Dni/xRdRrA1zsgaaKxtA0287ywIQZYkkMSfXnpUujTCx8d+KwGknluBA1sZYgpdwsm6MOFGVXCjknGetAHdUV5fpep+JZNG1e9tNW1C+1ddMDPpt3prRLb3fcRuUVWA5AUFskZyap3V/rw8E6lewa9rDrHdW/wBkdLZ2uMFtsqtutk3LgkjC8bRz2IB65RXm97P4ijtdV0uwv78yWepW5iuriF3aeBoVdlLRxkgbtw3KpI4BxnNRu3iPUfDugR3b6tZMftBu5AJDMJFI8osIhu2kbiAQAcDcD0IB6ZRXmmtR+K7vULGOa5uIIo9PV4bq0SRd95n5vNjjkxjgEK5KcnJ9PRIbhXgjeRlR2UFlJAIOOR1P8zQBPRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAV7/8A5B1z/wBcn/ka8++BP/JKNP8A+u0//oxq9Bv/APkHXP8A1yf+Rrz74E/8ko0//rtP/wCjGoA9JooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACsDxtbwXng7Ura6tb66gmjEckViMzbSwBKjvjqRg5AIwelb9FAHk2jvrtjaxap9kv/sVprG6Y29g9tcahA0OwySWygbir7OQOQpIHAzj3Mk9zDoiaz/wlccTahfwT20QnEs8R8yaFlVfmbAMYz22kHpXuNZ9/oWl6pfWV7fWUc9zYsXtpHzmJjjJH5D8qAPI9btfHZt9AVlvjjTVEckKyySQ3QZipkVHVd+zYMyZTIbPXNb9/4ekvfiBG+oWGvz6fcWcKTyW108UH2nkF2VZQQAu37mRnPXk16bRQB53a+DL2x8Y2trCJpNBhuG1ETzXcjOjbNgt+Wyw3ASfMSMDFXNJlnS88QWUfhvWrOG9eSVJ3MYUkRKhwfMYqSV+XjHI6V3FFAHk2k+GvFg0PVrTy5QkkdqImuZBBLOIpD5kZCSOFLrkeYCCdw47ifW/B2qahoGsQjSHlWfU4LnTrKS5TfaqmzzG37vk3BXACk43e5x6lRQBwmqWsLWlj4R0exOltqcjT30SMFaG1DDzWLIT8z8ICD/ETnisvxD4Ek1XxJq12dCWa3t9Mhh0rbcoitKiyDaVzwB5gIzxmMV6dgZzgZ6ZpaAPMtQ8LeKdT8UQeIFtdPtpBc2sphacFxDGAWjZ/LbDbiw+QqpB5zmn6d4AvdKvUu7Cy023nXX5L8SpKdwtXQqY87M9/u5x716VRQB5KnhbX/D9rq2pXNpZeQdEuoJ4tPb5pJWYuGSNY14HIG4kjJ5Peno/hVb7wxqHh/TXsjqbJa3VxeW7ZgkaPYBCSqAKrCPOPmOSSRk17NRQB5qfA2sw+A59Gt4dOeebUorzyJrmRo0RZEdlLlPmyUxwij5jx69bc2epJ4fsodO07SIruOSJ3tpMm3iwwL7CFByOSpwOea3aKACkPQ9fwpaKAPLdMuNYg8Xt4g1Tw94gvLiOx/s+Ax2cEZMe/eWf9+QXJ9ABgdBnFbtl4t1uOW7N74U16aN5i1ssdtApjjwMKx875jnPPHWu1ooA4XWtf1bVtONnZeHfEunzu6ETm1tpFwGBKspm5UjgjI4NO0ay1XRfDdxp9hp+oRXcsskv2lorYRpIx5KQibATjhc+9dxRQBg3Gsa1DaKbfwzeXNwMAh7i3iDepz5hx9K4bXPDuoeINfXWb3wPfC6WOOMCHWYY1IRiecHncCUOf4emOter0UAecTr4sl8Upr6eG7+GZbf7N5K6haGMx7gxByM5JHXNUNJ0jxfba3LqH/CPLHc3l7JNO9xewNHFE5wyRlBvU7VXkdWyTnNerUUAeaweAry1guo47Tc11ZyWErm+RSYH3Zztg+ZhuJDHk4GSaW58MeI57nzf7G0x3SCC3jmbWJFcCBi0UnFvgOCzcjjkjBFek0UAef6PpfjHRLrULmDS9Mnm1CUTXDXOtSvlwu3IAtwBwAOOwHpWv9t8d/wDQD0D/AMGsv/xiupooA5Ca7+IjPGYNI8NoozvD6hM5bjjBEQxz9c+3Wqtu/wAUnlC3EfhGKPuyG4c/lx/Ou5ooA5XyvH//AD9+Gf8AwFn/APjlHleP/wDn78M/+As//wAcrqqKAOMu7L4jXGzydZ8PWu3OfLspW3f99OaS00f4gszfbPFmloMfL5Ol7s/XLiu0ooA5T+xfGX/Q42v/AIJ1/wDjldFp8N3BYQxX10t3cqMSTrF5Yc+u3Jx+dWaKACiiigCtqGn2eq2Mtlf20VzaygCSKVdysAc8j6gVWn8PaNdWTWc+l2clu8SwtG0KkGNfuqeOgwMDtWlRQBlReGNBgt0t49F05YU+6gtkwOMenpWmiJHGscaqqKAFVRgADsBTqKAK02n2VxdRXU9nby3EP+rleJWdPoSMimf2Tpv2/wC3/wBn2n2zOftHkr5mcYzuxnpxVyigCGO0tobiW4it4kmmx5sioAz44G49Tj3qrqmjWWr6Re6Zcx7be8jaOby/lYhhgnPr71oUUAQw26xWi27s0yhdrNIAS/1wAP0qSONIYkiiRUjRQqoowFA6ADsKdRQAVzl74G0HUL2a7uIb0zTNvcpqVygz7KsgA+gFdHRQByw+HfhtSSINQBPXGq3X/wAco/4V54cxjydQx/2Frr/47XU0UAYsXhPRYUCLZlgMAb5pHPAA6lie39epqT/hGdHzn7EufXe3+Na1FAHO3PgLwpey+bd6BY3EmNu+aLe2PTJqH/hW/gv/AKFfS/8AwHWuoooAwrLwX4X04OLTw/psQfBbFsnOPqKtf8I5of8A0BtO/wDAVP8ACtOigBFVUUKqhVUYAAwAKWiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAr3/8AyDrn/rk/8jXn3wJ/5JRp/wD12n/9GNXoN/8A8g65/wCuT/yNeffAn/klGn/9dp//AEY1AHpNFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFQ3V5bWMPnXdxFbxbgu+Vwi5JwBk9yeKAJqKKiubq3sraS5up4oIIxueWVwqqPUk8CgCWikLAYyRz0oJAIBIyegoAWiiqs+o2dtfWtlNcIlzdlhBET80m0bmx9BzQBaooooAKKKKACiiigAooooAKKKKACiiigAooooAr3/APyDrn/rk/8AI1598Cf+SUaf/wBdp/8A0Y1eg3//ACDrn/rk/wDI1598Cf8AklGn/wDXaf8A9GNQB6TRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFBIAJJwB1NFZ3iCOGXw3qkdyZRA9pKshhGXClDnaPXHSgCey1Kw1FXaxvba6CHDmCVX2n3weKtV4/4VdtP0nUrjRDm3026sjLeafYGL+0bdVxIhifOGVSSSmCcDv1nuPFHiIafq1xBPqTxnWoV09DaCOa5tHUErDuTDDOTuwSFUnjrQB6zRXkGqeItdfQtC06x1a51DVZ5bmK++yIUlikQAgtiPKrGWQEbRuBHrgrq+o+KbiSxm0rU9SurVbJRbXdpbM6zXiyMsoljCAAcbQHKqOuQc0AevU1XRmZVZSyHDAHkHGefwrzi/1DXW+IMMMcOtzW/2i3Xy0gkgghXbmRhIMxyJ1yHw2eFPHN/Q7CbTPG2t/aLDWZDdXyywXIuHa3EJgUDdl8HDK4xgkbl7YwAdfZ6pZahNdw2lyk0lnN5Fwq/8s3wDtP4EVbrg7KHVIdN8VafptnqUDTGSXTZLl2zloVBxIzMQfM3EZ6fSsKfSNaGg6i2n2GvwQJNZSWdrNeM1wZFfNwwbzOFKEjBONwJGOKAPWaK89tNLlstL8WaVPourXulvIktlbG6ctNG0Ue6NZGfcpEgYnJGM8Z6V38P+oj+Ur8o+UnJHHTNAD6KKKAOe0bxppGt3jWcLXFvc+ZLGsV1A0RkMTbX2k8Ng8EA54PFX9K1u01lr8WolxZXT2kjSJtBdcbtp7jnGa4vw/oGvvrFqNS0sWNrZare6ok32hJPOMxkCxhVORgSkkn+771Fo2k+Io9A8S6Nc+FYoLfUJLmaBRqEaqVlIHlfICVOC3zAY4FAHpDzRRxPK8iLGgJZ2YAKB1JPaoJdTsIbFb6W+to7RwCs7SqIyD0w2cc159Y+BtWh8P3dkbbTVH2u2mjtZdu26jhA+SZkjCjJAIYITgLnvVmXwfqLWGnvHomiI1peT3DaSbl3tZTIuN+4x8MCWIATHPGKAO1udY0uzdkutSs4GVQxWWdVIBzg8nocH8qr3HiXRbTU00+41O0iuXhMwV5lGFBUZOT33DHrzXGWXgHU7K80gyJpl2lrpt5aSyys27MrZjRQVYmNAAgy2drH6G9pfhfXtOj0K736fLqNnpP8AZlws0jshwVIkDbcsfkGQQOvXigDpRrtu3iOXRkUNJDai5mlEseIstgKy7twJ65xjHenDxFohhllXWLBo4o2lkZblCFQdWOD0HrWcdG1VPHTa5E9kbSSzjs3ibd5mFcvuB6Z+YjH05rGh8AXI06zsZbi2WCO9vpZkhDKHhuVlBQehXzeO3yigDrv7b0vMw/tC2zBbrcy/vB8kRyQ59FODz7U/TdW0/WLb7Rp15BdQg4LROGAPofSuRbwPq93po0++1yEwixSy8yG2ZJD5bhkckP3wAwH4EZzW54Y8PyaHHeSXEkEl1eyiadofNIL7QucyO7HgDuPpQBp3+p2WlxJJe3McCyNsTeeWbBOAO5wCfwqhfeLdB06G1ludTgEd0oeFkzJuQ/xnaDhPVzhR3NO1bRHv9S07Ura6W3vLDzBGZIvMRlkUBgVBU9lIIPbvmsDUvAV3f25RNaigefTG0u8ZLBQskRYkbFDARkbmHfqPSgDob/xNpGm39vY3V3tuLjbsVY3cAMcKWZQQgJ4BYgHnHSse08Rav/ws+68NXkNl9i/s37fbSw7vMx5uzD54z7D0684GbrPw2utQ+yxWfiOa2tLNLZLWGWAyiLydpGAHVTkopJKk8HBAOK15vDOry+MLTXhr0SpBb/ZjbixHzxkozjdv4JZBg4496AOmlkEMLylXYIpYhFLMcegHJPtXL6X8Q9C1a0nvIftkdnb27Tz3M1q6xRbSdyM2Mbxjp/XiuqYMUIU7WI4OM4NcbpHga5tfCV74Z1TWvt2nXEDwp5VqIHjDlixzubJy3HHGKAJ7/wAfWNp4Vv8AXI7DUJDZOsctm9u0UyuxXaCG7EMpzyMH14p174+0zTNEi1PULPUrNZZzBHb3FtsmZgu4kKTyMA8+1Oi8FW48O6ho1zfTzw3gHziGGExkAYZRGignIB5B5HpxTNR8ELq1haR32sXVxe2ru0d7Nb27vtcAMm0xlMcL/DnjrQBDJ8StG3QfZ7XU7uOeyN9HLbWpZGhABZs5/hyAR1BOOtLN44lfxBb6dpmg32owzWKXyzwvEgaNyArAO6nHXPGc9qll8CWzPaNFqV7B5FnPZMI1iAljmOWyNmBhgCNoGMelPi8FQ26aYbbVtQgmsrNbFp4igeeBeitlcDB7rg+9AD7TUNVuPH19aSGW30y1s0ZYZYEIndmb94kgYnA24KkD171TtfiHaXcUk0elX4heKaWxkbywL9Yid3l/PxwNw3bcjkZrXbw+7eIW1f8Ate/DEKn2cGPyvLHJTG3JBPOScjkAgHFVLTwNpFkoSF7vyo45o7WJpty2qyjD+UCOOOBnOBwMDNADvD3i+DX7mKAWF1ZvPZR39uLjYfNhY43Daxxg44OD8w98aGvazHoGkvfywSTKronlxsqklmC9WIHfPXoKr6b4XsNKurG4t3nL2VgNPj3uCDCCCAeOSMDmpdS0/TPEtqLeScv9nnWVXtp9rxSKeCCp4PUUAYUPxBS/s9Km0zSLi7bVJLiG2AmjVd8RcNubJ+UhCQwzwRx2qvqHxMt7Pw5p+rxaa8n2uOWVoZLmOMxJGcPyTyeDgDrjkit208HaHYm3NtbTIba5e7iP2qUlJXBDnJbo2TkdDk8c1lXvhjwNazQaVdmC2mvIWtY7ZtQkje4jZyxTG8FxuY4HOMnFAFnV7i7tvHfhpYb24W2vhcJPbEgxtsi3KcYyDn0NNPjC6TW10V9Nt/7SN4kX2dbwk/Z2Qt9oGUGVG1hj1GM9K0Z/Cmk3NxYTypdtLYAC1b7bMDHxt7PySOCTnPfNZun3ekaj44luJNb0m51K3he1t7K2lRpYV3ZkLfxbjtUEYwu0+poAkg8ZhtV1G0uLBrdbMXBXzJMSzCLacqhUAqwbIKsenOKzNH+Ic+saXqd7baPNN5Fst1apGsieaGztjJkRRv6fdLA54J77+meDtB0e6kubOxKyOHH72aSVVDnLbVdiFyeu0DNFr4N8PWVtdW0GlwiC6UJLE5Z12A5CKGJCrnnauBntQBD4N8QXPiHS5pr1bWO6im2PDb+YCg2ggMsiqynJPbBABBINM8T+Ir3TNT0rSNLt7eS/1Ayssl4zJAiRpubcygnPTAx61tafpOn6UJvsNpFAZ38yUovMjYxlj1JwB1pmsaXpWsWQtNYtLa6ti6kR3Chl3dB178/rQBxMPj3WtVe1fSLDTVgm0htTJvJ2UjaxRlBAxjIGGPbn2rvbC6F9p1tdhdgniSULnONwBxn8ayNW0/wzbT2E2pWVoJSPsFoTDuIDgr5agDgEEj0xWzaWlvY2kNpawpDbwoI440GFRQMAAelAHIWVnbaf8XL37ODH9r0lZ5lMjENIZiN2CcA4AHFQaHeTWHiXxxJcSreXVsIZwkTOu9fJyqhCzY6YyByc+wHXNoulvetevp1o10zBzO0Kl9wAAO7GcjA/Klt9I0y0uTc22nWkM5yDLHAqsc9eQM0Acdc+L9RtvBuq6zbalo2q3ENrFNBDaK37pmOG3gvkqMggnaeDnFUpfGuuNodlctNYWLyaxHZPPKI5EMLqfmIjlZVIP+32Hriu9sbPSkSeSwtrNUnZhM0EagSMCQ27HUg7gc9805tJ057JLJ9PtWtIyCkBhUxqR0wuMCgDzvVfE3iKy0cWsOs2M97a6jNBdzw+Stw0KjKlI5GWPf8AMoYZHsDUV9421p7LRFttQhtZptJ/tBp7qGOFLl8gbGV2+Qd22En5hivRbmXSNFiM1ybSzS4nALMFQSSucDPqxpt9q9laCx3Brj7ZMsMIgUP1/i9lHc9qAON1jxVq6eIEit7qGzgiS0fypjGsd0JGzIVZvnYAfKNg+91r0SopZreMgyyRIQQAXYDk9Pzps17aW8ixz3MMTsMhXkCk/gaAPPdN8T6prOt3VhaazvlkS68o29ujxwD/AJYmRWUSRsMEEOCrEHBHFc94z8RazrHh24t7Y3jmbRI7mS1+xENBeJPDwCF+9jeSuTjbmvacAZOAKx9C8SWniD+0JLRR9ms7hrfzxNG6SlQCSNjHA574PtQBwV5rGuKPstpqeqT6empWkYvhCDKQ8UhkjJCcqGEfzY434zxxn/8ACQarqPw71x7281BtQEEE1sn2Z1k+0PCC8YXbyglDYGOMcnGK9X0zW9K1pJH0rUrS+SJtsjW0yyBD6HaTik1TXdI0QRHVdUs7ESkiM3M6x78dcbiM4yPzoA5Dxnc21/beHdYhuNQ+x2mqAXD2iS/IvlyAsUVSThtoBwfvccGs7xJDavqfhTVHPiVtLW1uYvMtmuBNuPlmLeF+cF8MOevGenHc3finQbHSY9VudXs0sJGKxz+aCrkEghSOpGDnHTB9Ko61488P6Dc6dDe3bEaghlhkhjMieWFzvJXPyngAjPLDtzQBzE+peI2+IcqvFqMNqJbd7QRRSsktuwXzVZf9WCGzlmII3cdOY1tdUTxxo99f22t3d7bancxylUc2i28iyCJ15CKArICR83BzXpsUqTwpLGco6hlOMZB5FPoAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAK9//wAg65/65P8AyNeffAn/AJJRp/8A12n/APRjV6Df/wDIOuf+uT/yNeffAn/klGn/APXaf/0Y1AHpNFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFZmtaBp+vwRRX8TkwyebDLDK0UkTYxlXUhl4JHB5FadFAHOSeBtEktoIQt7G8O/FxFfTJO4Y5YPKG3sCQDgk9B6VsaZplno+mwafYQLBawLtjjXsP6knJJPUnNW6KACiiigAooooAKKKKACiiigDm7Dxrp2o3n2eO2voy9xPaQvNEEWaaLO9Fycg4VsbgAdp9KZB40gms7nUH0nUrfTbSKd7m6njVRGYidy7d25vutyoI461keE/Bl9Z67qd/rM9wyR6vdXmm2wlRoUWXP7wADcGwzggnHzZxnmt2y8JxwWGpWF7ql/qVpqAkWSG5MYVRIWL7diKRncepPtQBGfGlmIrsGxvlu4PJC2jIvmSmbPlbSGK4YgjJIAIOcYrP8LeK9Rvb28s9Ys5opzqslnCm1MwqLdJgHKMQerYIJ7ZxWivgnS/sN3bSS30rXSwq9w9y3nKIeY9rjBG08/Uk9zVW38GaBd2VzHb395O73oupLuO/ZpknVNmQ4OVO35TjHBxQAlt48W/tIPsGjXlzqEnns9irxh4kikaJmZi23l1wACSc+gJFjVtd16DWbCy0nRrS6E9q9zKtze+Q6YKjAAVum8fX8KYvw90KGzitrb7da+TJI8UsF5IkqLIdzoHzu2FuSuevPWrd94O0e/tLC1dLmKGyVkiWC6kjJRgNyMQcspwM5PagDf7VyVl4zmuvF91okumLaxQ+b5cs9yFlmCBcuse3BQ5IDBj05Arq40WKNY0UKigKoHYCsKDw74bsNXMiwQi+uPNZY5p2fO8kyFEZiBnnO0DjI6UAYlj8QLq/tb+ZNEVGt7ZLmNXuTh1LlcbwhQ4UbsoXHOM06XxxqkFtLJNodskkd3DamP7cT/rLh7cNny/7ybseh9eKuXvhDwbpemXE19aw2tksRilllupEVUZgcFi3AyBj06Dg4qvrXw+0680q6TRo4bW8uZ4p3lnMkySbJhNhl3cgkHoR1NAGT4q1K61z4deJZpzcaZqehyypvsLx1VpERXDAjaSpDj5WH8ga6DxP4l1DSLmzs9LsY7u6khe5ZJDJ8yJtBVdisQxLD5iMDvWp/wjejyaYLC40yze3ZvMkiEQ8tnIwSQeuffNOuPDeiXcFvDcaVaTR24YQrJEG8sN94DPQHv60Acx4i8b6hp8MFxY21nHbNZxXUsl2zvsMjAKjiMExjBPzt8pxx0Nd0WUMFJG49Bnk1mT+G9EuruO7n0mykuI0WNJHhUkKpyq9OgPIHarcmn2c1/DfyWsL3cCskU7IC6K33gD1ANAFmkJwCQM0B1LMoYFl6gHkUjuI42chiFBJCgk/gByaAPLb64vbz4a6Zq0V/LZatquqWkk0yysPJkeZUKYz91B8pX/AGTkZzT9P8UTafaPv3aSbrWms7qbUZmmjsmW3VmALNjazgheQPnBx2rqtBk8Pa3pV9qFrA8trLdySTwXkJ/dTKNrjy2HyngkgDkknqTWvZyadrmjxXEdustndqJNk0G3cOMblYdRgdR2oA4G48W6lcxeDb+51eDS7O+kuRcTrCRBKygiIkvjarAFgCR25OKdrXxHu9M1K2gtEgvbZrSG5juRJGi3YZyrbVLbzjAwI1dsnp0z6NPZ21zb/Z57eGWHj93IgZeOnB4oktLaaWKWW3ieSHmJ2QEp/unt+FAGc1+n/CSWcH9qogntGdNPaIB5MEfvMnkYHGPetemeVH5wl2J5oXaHx82OuM+lCyxtK8SyIZEALoGGVz0yO2cGgDE8arqD+C9XXShMb9rZhCIM793+zjnP0rkZdV0ix0q7ufBFp9jtxPZx3t9Z2PyLGZCJCFK/M6LncSpxkZ5HHo8dxBK8qxzRu0R2yBWBKHrg+hplrfWd8rNaXcFwFOGMMgfH1xQB5xfa5rT+CybS81W5D6g8dvfpbiGSW2Vd2WIjfGeVV1TLELwM1VuNburzwR4Qv9Ytb+TUl1SKW4I0+VpESKQ7iQqcfLt7Dd2HWvWaKAIra4ju7WK5h3eXKgddyFTg+oOCD7GvJFtvL8VXt/JDdzafZ+IDdyLBpkqyozRhRIHZcvGCrhlQE9DkgjPoGr+LbXSLq6ia0ubiOxtxdXs0GwrbRknBYFgScKzYAJwp9s2D4o0Yas+lm+jF4sccnltkZEmdnPqcfyoA5XQovEreKJJtTmvITLc3Ec9ukMjwNDg+UyyFgiYAH3RuJPzc9KGnaFqWleG9YttFg1uHxB5d0IpLq6kkhH74lShc7NzKQQQCRzuOeT2Gg+LbPWJJ7WZ7e11CG6mtja+eHZjE20leASO/TpWj/bulZulF/blrVd06q4JjGSMkDnqCPwoA4BLTVU8LTbP+EjcpeWk0Uf72OZcsvnLuZ3dhtLEg/LkfL7WJdJvbyy1LT30rU7u1s9fhuLZJrlkeSEFCzI7MMqrbyoz0A7nNdppXiDS9bJ/s27FwBEkpKowAVs45Ixng5HUdwKg8S6+PD1raTtDE6XF0ls0k03lRQ7gxDu+DgZAXp1YUAY+t2d9dWehPZaTqSGz1BJXh+0IW8pG535lw2eCOWPHaqPiPS/El9e6jc2MV8s9xb240x0u1iSykViXMq7sNyQTgPkDbnpWg/jyIWXhqUWBjl18kQC5nWJIyF3AM3JO7+HC85HTIp2oeJ9Ws7vxHD9isI006GOa0kuLhkFzuVmYH5eMBH6Z5H1wAY99outJqd/dWdhqbXCaray20329Sht/3XnhUMnyg7ZPlI5yOnb0aoLWWWSxglnRVlaNWkWMlgGxkgcZI/CsCPxjYaqz2WkXDJfSxyC1lu7KZYXkXO5eQuSuMlQQcUAc9b+GtUTw3q2i2GhW2lXgjmSHU45EH2jMm5QNuXAZeCTjHYHtEnh/xC3hHVLJ7C7QXdzE8dsk9vG0CqQWCIoMZT5V+Vj84Zt2DnOt4e+IdtqHhWPUtRtrqK6jsEvJ0is5Asi4G5oc/fVSRkgnGa0ovHGjS2t1dA3K21tbQ3LzNAQpWVQ0YU92IYcDpQBzsnhHUdS8EWlpd6PpwuYNVS++xOFVHjEmSrY3IHZSQdvy8kDitS+0e5aw0VrLwrpkVzZXfmJGkyKLWMPk+WwTguAMgADsSeps6/wCK5rDwdqOs2NhcCa13qY7mAjyyv3nZdwJUDJ4PPatHVPEVrpL20MkN3czzxPMkdpbtIdiAFmIHQcgepJAGTQBx/ijwRd67f65cR6VYZ1HR44oZJWXfBdoXOfu+jqN4OflFc54lmhk+IEl1qek2d4bK4ssWZKG4eQxHcI8oWljG/dgYBaMnjHPoWtePtH0S2tbi4S6eK5tvtYZYwu2HjLEMQcjcPlGW56VJJqGow/EW0083avpt3ps04g8oAo8bxLnf1ORIePagDpa4nRtB1mzg8Sxtp2lwR6rcyzxxC5cqpMSxgMFQcNs3Eg5G49TzXbUUAcp4K8N6j4cS7ivLiB7ZxEttDGd5iCqQQZCqsw6BQc4A6kk1P4v8P3WvLo5tBZb7HUortjdAn5EzkLgHk9K6SigDgrfwTqtvql1fLdac7C9upbWGeFpIxFcFS+4ZGHG3AxxgsD97Is2fgi80u38Nf2fq0az6LbzW5M1tuSdZAuflDArgqpGD0GK7SigCO3WZLaJbiRZZggEjqm0M2OSBk4Htk1JRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAV7//AJB1z/1yf+Rrz74E/wDJKNP/AOu0/wD6MavQb/8A5B1z/wBcn/ka8++BP/JKNP8A+u0//oxqAPSaKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooA85sfF+uDxiNPvLjT5YG1aXTfs0FuwkVFh84TZ3k4+ZVIxgZzmovC3ju+126nguNRsbd7q2mkhR44xJYSIfuyIJSzADJJYR/c967TR/Dtpot7qd3DLLNNqNy1zK8wUlSQBtUhQdoCrgHPStAWdoHmYW0O6UYlIQZcf7Xr+NAHnXhrX9Q1nwPfa5f8AjTTkElqIvkgiVbKXJG5yWOWbjg4HIwKqaW0Oh+B7CbRNctyt7dQRahqtrb25+xJ5ecMsabSd2Fy4JHmZOcCvTlsLFYXhS0txExy6CNdpPuKfbwW1vGVtoookJyRGoUE/hQB5pf8AirWD4d8NX7a9HYve6jLZTTpaDypYdzqs4VxlThFI52/Pk7hVDxH4i1rRvENxp6+Mbtkt7SF0As4GaaVkmbHEf+xF04+evWZry1t2jWa5hjaUlYw8gBcgZIGevFRHVtNW2guW1C0EFwwWGUzLtkJ6BTnBP0oA84tPGmsahq1gpujb+aLOSOBYSwuoWRGmdUEZY/MzrncAuzJ71JPc6q/jPQ7jUotSmlt9auUMEVnmKC3aKRInDqnKkMhJLHGTxxgd9Jr+jQ3DW8urWCTq21omuUDA+hGc5qdtTsEuZLZ722WeNS7xGVQyqBkkjOQMc5oAyPHlvNd/D/xBb28LzTSafMsccalmZihwAByTWEg1TXdL1W0sNV1e2EEFvLa3l1B9nImwxZPupuTAQNkcEn046q28S6He3FxBa6vZTy28XnSrFOrFE/vHB6VjxeK/B3i7R7grq9vNZxRGa5X7QYikfIJcAghT6HrnpQBN4Ilvr7RpdYvmmU6nMbqG2llMn2aIgBUB6EcFsjj5sdqo+Lkvn1iBrVta8uK3SRo7BnVZP38YYHHG7Zv7g4/Cuk0bV9K1mx8/Rry2urWNvK3W7BlUgD5eOmARxT9S1jTtISJtQvIbYStsj8xsFzgkgDvwCaAPOM+NZvD6GcaquoDTQll5Qxi7EjAmYcAgr5WC3y4355qzrNt4jn8Z6dcm1v50t5bVXSOWSKEd5HQodjJk/MJF3fLgcHjrNW8a+HdEtrW4v9TRIrqLzoWjR5d0eAd+EBIXkfMeOetbkUqTRJLE4eN1DKynIIPQigDz2x0M6T8R9Tujo+sXP2y6jnt7mG6b7NGpiVX8wNIASGDkDaeNoHYD0KaQwwSSiN5CiltiDLNgdB71lHxTow1ltJ+2f6YpKlRE5XcBnZvxtL45253e1U9M8feGtX2Gy1BmR1lZXktpY0IiAMnzMoHygjNAHP8AhxpptE8T22qeGNX8m5u7i7FvLGimeORshFw/3sdRkfU1Q03Std1D4f8Ah+wu9FvXTT7gJqGnXUyxtdRbWA2tu+ZVLKcMQG2YrodP8fWl5q2oMWQaJb6Ympx3vkyoxiJYMSrKMj5SQVzke9dRYahb6lAZrbztgbb+9heI9AejAHGCOelAHnGseFNSu9E0eCDQ7j7FapPH/ZTXMMklu7MCkgkZtvygMBgkqCPeqmueBdSvZZjJokuoSnQPs0dxLeRswvVyI3JJXLBSPmC9frmvRda8R6foMlpDdGZ7m9dktbeCIu8zAZIGOBgc8kVm3HjVE1PQ7S00jULsarby3IZUCNEiAZ3K5BzllGDjr36UAcpJ4X1+88aaXqkmkTrtaza5luLqGSNRGmWK4/eKwYsMAlWPJzni3oHg7W9O8VXV7cgyyNdXMi6kbhBujlBCAoELuVwo2swUcbc12GoeJrPTdRtLG4huRJcvHGriMbFaQkKpOeTwcgZx1OMisDw14unFxNp2tvPNO+r3Gn214tuqxOUyyodp4O0HqOcdaAKXh/wTqGiWV2iWtubmTTWtGkF35aXEnOGIjiUjJ53ElhuIHrWv4G8Mz+G0v1lt7aGOdo/LWMR7wFXGGZEQMB0BILHkk84Euj6tqus6h4msHcWUtlOILctbqWjDJuVziRg+QQRwvuKj8M6trEvhrVJLpn1S/sr66tUMcccbTCOQqvGVUHA9R9aAOms3uZLOJ7yGOG5K5kjjkLqp9AxAz+QqeuDXxdqNl8MdN16KJ9XvrtoUQSqluWaWQIMhSQMFgOD9T1Nbep+Kf7G+wNqOmz28V27xmZpY/LhcKWUOd3G7bgEZGeuKAKmreHNVfUNaudJubVDq9pHbStcA5gKBl3KACG+VzwccgdRxSy6DrVj4ll1LRrjT/JuLS2tZVvEcsgiZzldpGSRIeuORWx4d1SfW/D1jqlxZNZSXUQl+zs+8op+7k4HUYPTvWF4j8exeH/ENrpRsfPEjwLLILhQ0Ylk8tSE5JAPUnaORgknFAFODwdrMV/ZSibTxFBr0+qvy5ZklDjYOBggSHnvgU/wx4L1Pw5NK63lrP9ms3tbBnaZiwLbh5gLlVwQMhAM+2MVYk8aX9vqcMNz4eeKyfUxpz3f2tG2u2PLYIBkgkgHpgnuOag0zxBf6x4x0e6hYxaLfWF08Ufm7vN2SRhJCu0FSQx4yeCOhFAG34T03VNI0OKw1RtPLQAJF9ijZV245Lbj94nJOKf4j0a81hLD7HfQ2j2l0tzmWAyh8AgKQHXj5j1z271pXxulsJzYrC10EPlCZiqFscbiASB9BXE6T4h1G08AeE7u1iju5dQMMLtqN8Q4MgJB37SXOcds47UAEvw6uTo62EOsQBpLae2unlsA6uJJDIDEN4MW1mOACRwvoKhn+FUV7ptjZXusTTLaWvkArGUEjBztdgGwTseVGz97zWPHFTz+NdbFhBFbaVZy6ot3Pa3uJZHhgMQB3AKpkYMGTkKQu75iKhfxzrZW0mit9I+zz6KdWDvPIAQmzeudvA+f5Tg9OQKAPQgAoAAwBwBXF6L4Ymk1O7ursXdtHbandXNjC/llA8gZfNBBLEEM52tjG88cDCXvjPUYvEM1pa6fbvZWstrHcyTzLEVWYZLAsQMAEY4O4hh1FXrPxLdXmrMqrYx2I1CWwKyzFJwyA/MAeCSw4Uc7SGz2oArweGo/C1lpV7bG+1B9GsXskt4kQyTxuyHpwNw2L3GcGlsfCU0nhGfT5bya0nvbhrqUiOOTy1ZsrCVcMhVUCpjGPl4pPCup3lze6lBeeILK5kW+u4ktfJ2SxFH+UDLfMoXB6fxDmsuw8Vy6b4D1TUWuIbi9g1OeGVpJXdYgboxCRlLEqirhtoIGBxgUAa8ngVG8GXHhuPV7qGO6aQ3E8cMKtIHzvXaE2qDn+ECri+Fi/9mz3Gs38mo2CSxpeoI0Z0cjKsgTYR8q/w/wg1zl346vraKOOO502XGsW+ni+CkwXCSg/cw3DpkFhkj5e2eOn8L63NrEGoxXRiN1p19LZytEMB9uCG25JXII4yaAKfiDwTpOuJI9/d3cYe0FpJIJVyY85+8ynaSTyVxu6HOBV+48OJcaza6r/AGlfR3NtbtboUMeNjFS2QUPJKLn6cYrlPiT5U+ueGNPutXs7ezurmUTWl3EkkT4hkIkdWI3BW2gA8bip6gVDr3iu80PV49P03ULFGt0tUtNKW1LNqAkOGZCPuhRnG0kDB3cYoA9Lorg4NeuZviXeaAfFNqqQmKeKyFuhlkBVy8O70AVWz975vSu4uJPJtpZc42IWztLdB6Dk/QUASUhIVSzEAAZJPavK9M8U+LLjS9a+z/aNQ1G1s0aPEMYg3seXU7FbeFO7yWXPAGSTSy3+oXPhjxNBc6jq02jiJP7P1MwbbmeR0O+LyxHkruIH3OASM8ZAB6Np2taVrAkOmanZ3wiIEhtp1l2Z6Z2k46Gr1eZXllG/gazutF1LWZobfUoJrubyDDM8KyL5gZBGjMqrkgBc8d673RXik0mGSC4vJ4nyyyXiMkjAkkZDKpx6ZHTFAGhRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAV7/AP5B1z/1yf8Aka8++BP/ACSjT/8ArtP/AOjGr0G//wCQdc/9cn/ka8++BP8AySjT/wDrtP8A+jGoA9JooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigDyS38LeJ4fEcF0NOuxCt7LIX+3J8iG7EiHbv8AmxCCm0jvWjofhLxHpF5NdRLB9vMdwtxNJOBDeuwJiZgFLkA4zkqUGQpYV1U/jLS4dfbRlS8nuY3WOVre1eRInZdyqzKOCRz6etV9L8eaXqd39nNtqFkG83ypb23MSS+USJApJ6rgkg46UAc5Y+EfEcVnrFvLBbJFqFlDbAQ3nlSI6M4d9yxnJKtkFtx+UAn0v6Z4T1TT9Pylrpa3Nvqsd5bovyhoxEsTbiqACQrvGQuOme9aum+OdP1iC6awtL15o7Y3UEM0XlNdxdA8ZYgFSccnHUetNPjI2nhI6/qukXVlGIYX8vzI5NzSYGFYNjAJHzNt6+1AHJS/D/XJ9EtYW0/RIbqHxCdT2QzMIxATlowSmcn7pGACBWj4r8C3+sXVnLYQ2S2osHs3sHlEUVsWYMZIyImJPUHG08DBGTXX+HPEFv4l0kahbQyxR+Y0RWQqcspw21lJVhnIyDg4qh4w1O+0/wDsWOynltlu9Tht5Z44kkwrH7pDHgN03DJHpQBxurfDbWL3UL26jTTJpJ/MHnTSOHcNZpBydhIIkQsOT1z1rVs/h7dWvitdSN60toL5r8pNdSt87IVI2DAyOBuJOV4K8c62ueNJtDutRSTw/qE1tp8CXM11G8ZTyTnLgbs8FXyMZwpPpnqkkSSJZFOUZQwPtQBxOgeB7rRv+Ed/fWgGlyXjSrEhUSCckjHuOBz6UWnhDWbfwbd+GpbjSLizWIQWglt5CWj3ZPmkOMnHGVxg8itvQfEo1/E9tYyrp8hlEF2XUrL5b7M4HIB5Iz2BrH0fxJLZeG/EusaiL64bTr258y33JI0apg7YyAuVxg89OeuM0AafgzQL/wAPaTcW+pagL24nuWnLjcQgKqoXLEscbepOeaj8W+GLnxG1kIL8WyQ+YsineNwdcZBR1YEY6ZwcnNULPx7Ld+GrzVRpKq8MyW8Mf2xSlxI23AR8cgBxnAJyGABI5mufGF7F4bsdVh023eS4vxYvD9pYAMZjCpVig4LYJyBgE8HpQBU1L4eTaloOn6a+rRxzWVmtpHex27pKAuBnKyjOQBlW3KSM4rtoIjDbxRGR5CiBS7nLNgdT71xOveO73wzLaWF7paXWpSWkt1Itn5zphWwqrtjY5b1YADHXmo9T8R+JpfG1jp2j/wBnQ20+kG9MWoh153oOWVfvDONoJ7k9qALtt4Ags9ekvre8At3vft/kyQCSRZj97EjE4U8/w5GThhUNt4BuINL03TW1iN7eze5D/wChgPLDNndHu3/KRuPzDrxxxQda8Sn4galp0U+kLpVtHZuVuWZXAkLhthA5YlSACcfd9TUOgePb/VvET21xpS22lSNOsNzITGyNEWBV93BYhS2B90DnNAFy38BtbSCRdfvmYacumjdDAwMKnK5BTBPJHTBB6Vs+HvD0Hh23ngt5pHilkDiLAWOLgDCIoAUcZOOpJNYng/xffa9qLWeow2tvMbX7SIIdzELvKgiQEpIhGMMp654xzWt4u8RReGNBe/keNHaRYYvMUspdj049s9SB6kdaAH+IfDy+IEgSS8eGOLfuj8mKVJNwxysisMjsRg8nsazJvAcH2TQo7LV9RsrnRoWgt7uNkeRkZQrBg6lTnaD04wMYrl5PiHqcvhW0v7fVdFiuk1g6bctOoMbqZNqyfLIQgC/N1YEDrjmrfifxd4k0KPS7azuNLvbmaBrg3TrHBBdDdhUQyTqF4IyQXPIIFAGrqnw4t9T1M6gdc1OG5PkuZE8pmEkX3XVmQlfdVIUknircHgqxs9WbU5tRvJIY7yXUUtpHVYYpnBDPwATgMQMkgV0dnObmygnYANJGrkA5AJGeK4iV7p/HmpWOpeJWSwkNusWlT2kTR3McgYFAWBZgSCDjp344ABtaR4a+x65f61Fr17crqEnmyRHyfKOF2KAVQHCrgDn+EZzzT7LwjBp9rqFvb6rqiJfSPLKROoZZHILOhC/KT7ccnjNef+DPEGo6Fo3h+1S6gvLe7sb0QWKxhCk8JDJEGBJ3MHIIPoMAd7X/AAkfi5dIn+yX0upzJYw6jJNFYqjwOJFEtqU24yULEKf3g2nPUUAdfbeAtHt/C0/hyR72602XG1Li4LmLGCuw/wAOCARjvWfqfh+Nkt/C0dza3Ftev9ou31O8ae7kCld3lowI5UAbsgL6ZNZuseN500fW7vSdTmuAtxafZGFqCwjlZFZYsqA5zuCk5GcgnioXt9UuPFHhg3WsXA1CJ7xbueKGCSS3V9hjhk2KUUle5HXODigD1ADAwOlc7qvgXw7rWoSX1/YyPcSlDI0d1LGHKY2llRgCRgYJGeB6Vxl1eahrFv4Q1K7vtds4ke7gvZre3Mb7tjKkjRhDtLYyPl43djXptjcx3dhBcRed5ciBl86NkcjH8SsAQfYgUAZNz4N0K7klea0kYy3iXzYuZVHnp91wA2B9BwepFSx+FNDi1n+1109PtwYskrOzeWSMHYCcJnvtAz3zXNwxpZfFDVZLw6sn277L9jMKztBJtQh9xUFAAcfex1pujX2uP4utbYnVH2y3Y1VbmEiCNMkwGNuFJxtA2E8E7sEUAdfrN/pthYZ1WVY7Wd1t8sCQzOdoXj1JxVZfCegJaRWq6VbC3ilSaKPb8sbpnayjsRk4x61mfEzTr7Vvh5q1npkU0t6yxvCkP3yyyK3HI5+X6+mTxWFqY8UPpuoDT01CXTBeWwVZ/MW6aEqRPswVkwCVI5BOHAOMUAddP4Q8PXMzSz6PaSSNI8rOyZJdwA5z6sAAfUCq174N0+/8R2Gp3EdvJa2Vm9rHYvbI0Y3Mp3DPTG0DAFSeDU1GLQjDqT3UjRzyLBJdR7HaHPyZBZm4HGXO44yRXOfEePWHvrJtMttXugLWdBBZ71iaRtoQs6SIUYc4Y7gOeKAO3m0nTbm5W5n0+0lnTG2V4VZhg5GCRnjtWTe6loNr4ojt5NOafVtiSGaCwaVolYlFZnVTtBwwznoD2rn/ABba+JDbaxZaXp+pXEl9HBNa3FvfKgilTaHQ7nXYMKDxw2T3zlYfC8T/ABPvNdufDM/lPDbeRdebGQs6ly7kCTOACg6fwnA9QDeTVNCbxRcWcGmyS6iGEFzdRWDMqlkDbXlC4Hy7epxyParOjwaFcJePpumW8KLK9pMRZiISbThhyBuXPGeQcGuW8K+Gl0vxlr99L4VlgW7uXe2u2liceWY1DDbvJG5lY9P4ucVBpuleI38Ma5odtos2iI87T2LvdIQYi6kw5jkZkLAONwwACMc0AdpqcOi6VoUk15Y2w06wUziMW4ZY9uTlUA69enPNWbN7AWf9oW8cUEV0qzu5QRltwGC3TnGOvNcgNFdvBetWSeD/ACo7kGSDTpbqOYtIw2k4Y+XHggMAGI6ng1mXXhfX9c8N+E7e5sXto9KIivdOnlhcXAWIIJBw6HBzgN654IFAHot1HYFlmvEti0PKvMFymSOQT05A/IVDca1pVnqMdhc31vDdvE0qRu4B2KQCfb7wrhpvAE1xrOgyXdjb3unWeky2NxFcursx/wCWeflAOPXsT+NTN4X1T7ZoOqTaHpl7cWelmymtppR/rQ8ZV/MKHIGwkfLkFvfgA9BAT7w2+uarxalYTyLHDe20kjdFSVST+ANWV+6MgA46DpXmtt4B1BNV0q6itNNsPsgjaWaE/vGYC5QkELycTI/PcY7ZoA9FiuracyCGeKQxnEgRwdp98dOlMGo2LW0tyt5bmCEFpJRKpVABkknOBxXEaR4J1bTNPmij/s2O7bS/sQuGkknDsDnJjYBQpySRhuT3HFQReCNbij8QRBNJaDUmtnihlnmbZ5W0YLKqkcDII6EAYxQB3MWtaXMsDRajaOJ5PKiKzKfMfG7aOeTjnHpSPrmkxqjPqdoqu7xqxmUBmQkOo56qQcjtiuWfwnrb6fHKbuzbUbTVTqFmkuXjC7Cmx5Aqu3DMdxBPAHQVnHwd4rXSLS0SbRHmttZbVVZzKFJZmk2EYP8AHIRn0A7ngA7hNe0l4rWQajbBbvP2fdIFMmDg4B5PJA/GpZtV0+3vo7Ga+t47uTGyFpAHbOcYHXnB/KuP8W+BL3xHqkGoxXcCSyWYsruGSWdYiu4tuAjdd4ySNjcEY5GOZ28Har/wmMutx6tDCkptw/lRMrskYG5GXdsfcd2GYFlDcGgDtaKKKACiiigAooooAKKKKACiiigAooooAKKKKAK9/wD8g65/65P/ACNeffAn/klGn/8AXaf/ANGNXoN//wAg65/65P8AyNeffAn/AJJRp/8A12n/APRjUAek0UUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQByU/gCxuvFsfiKbUb97iK4E8ce6MKuFxsDBd+zoSu7GRVTw/4Snmvbu78QQy4S5uhaWZmjeBI5mO5lCqGG5WIIYnvjGaLzU7vT/iDexXuumz05rS1a3ikiBV3aWRWVM9T9zJHI3DNQWXi3WpvEunWjRRv9qvLqC7sVjw9jFHny5GbqQwCnJAB3gCgDc0PwVpmhXP2iKW7uZEthZwG6l3/AGe3ByIk46e5yeBzwKenhK1jsJLNNR1cRMI1XF8/7tU6KvoOx/vDrmtHW9RGkaHfaiY5ZBbQtJtij8xuB2XIz9Mj615jpPxB1G68O+IFOrQm7tUgktry4gyq+ZgMG8pNoCtwDg4zyWxQB6VoWgWHh2xe009GWOSZ55C7ZLOxyT7duBgcVB4i8MWXiZLVL24vohay+dH9luWhw46MdvUjHB7VxEfifVZfBdrcwa3c+fNqZi+13FsnzQryyq8cTJzg4YoO68EZq/Z61q6aZpd5eXeuGHULGeLK6cjSQzh8xyMqJwWXIGRtOBwM0AdTceFtLuzcG6S4nNzZLYz+ZcyfvIRng4bqcnJ6nJ9TWtDClvBHDGCEjUIoLEnAGByeT+NeZXN9qOqap4e+0an4ksrK+01hefZbN49lwjKFz+7JjyfMJPGQB2IzeebxEfH4gFzdQJHOqonlTSW01rtGS2E2CQkn5t4Ix0x1AOvt/DulWt4LqGzVZVkaVPmYrG7Z3Mik7UJyclQM5OaydS8EWMuga3p+lyTWU2rI4mmaeWUM7DBYhm7gYJGCRXRXhuFsbg2iq1yI2MQboXxxn8cVyPhiPUEgP9qS6/JcSWAF7HOP3aTD7xiZeQTkgCM4wo6HFAEmgaVDraXF7fX9jqmnMUht7WBWaCBoWYFl3sfn3EjIxwq/Wtn/AIRXQPsa2n9j2f2ZZfOWLyhtEn94D175rhLea+0P4Of2attfWmpxFYYoWUxvM0k5xGjkj5mU4LA5XOeoqDztTu/DlrosS6pNeQXwOrBZ7gvbRsGaNP4JJFKYXKsvzKCT1oA9IvvD2j6nHbpfaZa3K2yMkIliDeWpABAz0BAAPqKS/wDDmiaqlsmoaTZXS2oxAJoFcRDj7uRx0H5V5yum6vc6J4Qj1iy8Rie2kmg1E207BmiCsBvKSZILFMHlsBufXd1rQ9Ra7xYWurPaw6bFHYyW96BJFMrknPmygFsBMl1bPr1BAOon0rQrvXYrmeysJtWt4w0cjxq00aZIBBPIGc/rUkGmaQuq3d/BZ2Y1B8R3E6Rr5h+UEBm6/dI/AiuWuNDvLbx7fa2NDk1AXVtaJDNHdJH5TIzb9wLDjBVuAQdvTNR6V4eudN8Z6pdy+HvtH2rUjdW+pC5TbEjQhDlC27IIYcL/AB9cUAdfp2jaXpAcabp1raBzlvIhVN31wKtT28N1C0NxDHNE33kkUMp+oNefeA/DWu6RrIudVS7WQ2Ziu5TdI8N1MGGJQoJZmwCNzbcDAx6aXxSt4p/A8rS26TiG8tZBG7hQ379ARk8DKlhzxzQBoajL4f0zUtJ0e40mE/2lK62+21QxK6puOfQkL+OPato6fYtHBGbS3KQENCpjXEZHQqMcfhXnZ8L6vPNozS6MVsf7ce9l04zRFLOAwmPaRnDfMzPtXj5mGDVS+8PytothZXS2tn4ka4uLW2iQRyMbOWRlyVGPlSM7gexQZ6kUAeove2kflb7qFfOz5e6QDfjk49fwqD+04zrg0tYZHkFuZ3lUrsT5gAp5zk5JHGMA81wPirwBfX13ax6TY6cbW2s4reP7VsZCVckhozGdowScxshY8HgAjpbmz1iDxpHqFjpOnPaSW629xctdGOYjcCTtEZ3bRnALd+1AHQrdWz3L2yTxNcIAzxBwWUHoSOoqGa+Vra7On+Te3VuCPs6TKCXxwrHnaT71yujeGNS03xM1zJp+kOqSTt/aoZhdTpJ8211AAJDY5LEYXgCqfg7wn4h0HVrrUbpdLD3NoIpYoW2h5lYkSDbGoAbPIIYj1NAGzp8lt8QPCcFzf2U9i/2iTCJPiW3likaMlZFxg5U8jsSKTULnSfh34cuLoMJJZGyDeXirLdy44BlkPJwOMngDirPhLSdS0PTpLG9+yMhnnnWSCRicyyvJggqOm/Gc84o8a6NqHiHwteaRpz2kcl2hieS6DEIhBBKhf4ulAFq/8UaJpDJHq2q2WnzNEJfKubhEYKTjPXkZ4yKjvfFui6fqFvZXF5iSe3NyjKhZDGMc7gMc54HU1lS+HdavNd0TV7w6RJPaWlxbXUfluUIkKlTHnkHCAHPZmp1l4c1+0tdDaLVbGG5sLJ7KZFtS8LKdu1lG4MCPLXvg5PAoA2pvEejW+tR6PNqMCahJjbAzYJJ5A9NxGSB1IBIHBqGLxboM2uS6LHqUTajESrQYbJIxkA4wxGRkAkjPNZh8Er/wk1zqv2i3eK4vIr1oprdnZJERV+Vt4UfdBBKkjn1rA0GxvrLxxeXTW95Jd3F9MfJuLWQxWls7/M0c27y/mCIxABOcDA5NAHXaf4z0HVpZYdOvHupYo2eRIraVim04Kt8vDZ/hPzdOOao2/jP7P4Fl8TatAhSNnHlafvlLYfYFAdVO7cMHIAHrWloWkX2kW15BJe204muJriIpa+XsaR2chvnO4AtjPB461k6d4Ini8I3vh3U9WF3bXG9kkitvJaJ2kaQsPmbPzsCAfTnOaANlvEumRfYRcPcWz303kQJPayoWkxnbyvB+vBwcZxVzTdTtNXsUvbJ3e3ckKzRsmcHB4YA9Qa5bxLpWq3WkyaSLi8vr29YNa3ohjjj090Aw5ZcMpzkgjJzkDA4rpBpbW+l2thp93JZpbeWFZVVyyLjKncD1AwT154NAGhQenFFFAHnFvr/jye+1K0mGh28lhFFNcKsEjGNJEkbAPmYZlKAdADkntitTw/4+sbnw7b3Oqme2u49Jj1G4M0JjV0K4Z0PQjd29x61ei8JSJretai+tXjjVYPIkgMcQWMAEIVIXOVDMBknOec8Vnx/DeyNtDa3mpXt1bppJ0ho3CLvhyCDlVBBGAPw5zzQBv6L4j0/XpLuKzdvNtComRsEruGV5BIORnv2qDxJ4mXw59gB0y+v3vZ/s8S2gj4cgkA72UcgH8qm0Lw9aeH4XitJJmRsfK21VXHoiKqgnqTjJ7ms/xnol9rg0SKzkEKW2pR3M0yzeXIiqrD5MqQT83Q/1oASfxosVrp08Oh6pdfbXkhEcIiLQzJuzG+XAByjDIJGR1qGfx5HZKy3mjagk1rZpeaksWx1sUb++xYbiAGOFycKfYVPdeB7GfT9PtItR1S0FlK86y21ztkllfO53ODuY7mOf9o1Nq3g3S9auY57t7sP5QhuBDOYxdxjoswXG4Z+nUjoSKAKbePIE1K4tn0q9WC2vIbSe6Zo9imbb5TABiSrb17ZG7kdaWx8bpfazbQLps6aXeTy2tpqLOAJpowxZdn3gvyPhu+2o7Xwhu8a6zqd/BHJY3EltNaqLl8b4owo3RfcOCMgnPb0Fa1t4T0a01dtTitnFyZXnAad2jSR+GdYydqseeQAeT6nIBz2lfEy31G61dJdMe0g062mum8y4Tz9sZIO+D76EgZGQeCPWn2HxItrrR9QvZdOnjktFg/doSySNMwRFV2VQTvOCRkDggkVrad4G8P6XdSXEFpLJJJA1sftV1LOBE2NyASMQAcAYHYVPaeEdFs7K4tFtZJoJwA63NxJNwDlQC7EqAeQBjB5FAFDwjqOo3eq+JrXUpw8lpqCrHEHDiFGhjcKCFUkZZsZGfriuqrM0jw/pmh+c2n23lyT7fOld2kkl2jClnYksQO5NadABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAV7/wD5B1z/ANcn/ka8++BP/JKNP/67T/8Aoxq9Bv8A/kHXP/XJ/wCRrz74E/8AJKNP/wCu0/8A6MagD0miiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAEJAOCRmjIzjIz6V5r4t8PeIL7x5ZatZ6Nb3kNrLbNFOZY1KRoxZ1+ckgknqoHAGSeg1rXQruHxqL6Xw9bTSLcTSrrL3p3iKQY2BMEkgbVCn5QBkEE0AdPba1pd5cyW1tqNrLPEzI8aSqWUrjcMZzxkZ9M1X0LxBba9ps1/DFLBbxzSRB5ioDhDjeCCflPvWB4a0K/0TWb2E6DpgtftFxMupIyLLKkrF1jVAvGCdpyQOARnPGfH4M1i48E6voTRWeni8vXu4o4pd0ex5fMMDgIMDHykr/LqAdx/bOl/Zorn+0rPyJSRHL567XxnODnBxg5+lWLe4gu4Entpo5oXGVkjYMrfQjg157c+BL+5ghlaw0kbdbi1AaaHPkQxJH5ZVW2cs2A5+UDP5113hzTJ9Kt7+CW3tbeJ76aa3S2YkeWzZBI2jaxJJIGR7mgC+2p2CzzQNfWwmgTzJYzKu6NcZ3MM5AwRyaq/27atr1vpMTJLJPam6DpMhwgIAO3duIOeCARwea5vxV4J1bWNcbUdH10aWJbYRTxrAG85xuUMx7jZJIMdM7TzitS80K+PifRtRtGtRbadbS2+yUtvcSbMngY4EYx657UAWbPXZ5/FuoaFPYCEW1tFcxXAm3ecjll5XA2kFG7ml0LXJ9VvtXsrqyS1n025WBtk/mrIGjWQMDtXHDjjFQx6RqMfji41rfam1ms4rTy8tvARnfd0xkl8Y9BTdD0fU9O1/XL66ktHg1K4EyiLcGjCxpGoOeD8qZJ9T0oA0ddi0ubRrldZgjnsAu6RJIy446EAAnOcYxznpWPouq+HdF8K6Vcg2WmWt+qNEqy7xI7KMAOQC7EAcnk4rpZ1leCRYXRJSpCs6FgD6kAjP5iuUs/Bt7Z6FoGlrq8JXRp0kjc2Z/eqiFArDzOvzE5Htx6gGrceLdCtdLg1KXUE+zTkrFsRndyDhgEUFiR3GOMHOMVHf+M9A02SCO5vjuuLf7TB5UEkoljz1QopDHvgZOOcY5rPPg68TVItRttWhingubmSFDZboxHOVZ0YbwWOVB3AjqeKnufDGoS6pod9Fq8IfSrd4gstluErOoVmO11AGAMKOlAFuXxfoUF/a2U16Y57pUaIPDIB8/3AzFcIx7KxB9ql/wCEn0j+3RopumF+XMYQwuFLBN+0PjaTt5xnOKwdT+HVpqPi9tf+0QxvKYnlVrNJJBJHwrRyNnZwFBGD0yMHmobn4dS3HjGLxH/bZS4gu/tEOLNDIEIIaJnJJK4JC4xtz3PNAHQweLNFuZbhIrpytvHJLJKYJBEFjYq5EhXacEEcHsfSl0TxHYeIhPHDDcwywhGe3vIDE+xs7H2nqp2nB9jWRafD2zivr+6vNQurz+0LSS0u0ZI4hcBzy7+Wq7nA+UN2BPqTWl4d8MR+HjKUvZLgOqphreCIAL0z5aKSevXPU0AM8cX+qaT4O1LU9Jnt4bmzge4PnwmRWVVJKgBhgn15+lTa34jsvD9jBe30M8hkBA8iLcVAXcxJ6KOO55OByam8SaIPEeg3WkPeT2kV0hjlkgClih4ZfmBHI46ZrI1DwLBq0OlLqOq3t1Jp4lXzJI4T5yycEMuzbkAAAgAgd+TQBk/8J8bLxDfXE7XV5oD6Xa6jDJBajFrHIXBZ+dxHyqe568YBrobnxda2+ttpws7uWOKaK3uLyNVMUEsgHlo3O4k7l6AgbhnGaqxfD/TIrNLVby/8r+z4tNlAlA86CMttViFyPvsMrg4rRufDFjc6ibwyXMe+WKaWGOTbHLJERsZhjORhehGdoznFAFO08XSXviC60eHQNS8yzuBDczExCOJWAZHzvyQynOACR3Apuj+N7TWdan0uKyuIp0hknj3vGfMVJAh4ViVOSCAwGQc1fsPDlvp2q6jqEd3eSSag++4jlkDIxwFGOMgBQAAD0qrpHgrS9FurG4tZbwvYwPa24knLKsLEHy8dwCARnngc8CgCvb+L7i38Kw6zrGky2/mRRMiW7rL5skpAREAOckso5x1pmpeORp+mXl0NIuJJ7C8itbu081FkQSFQjrzhgd645HfkYqyngPQf7PnsJobq5tJVVPJuLyV1jRWDKqAt8oBAII596sSeD9DmsprR7WQxTzrczn7TIHlkXBVncNubG1cZPGB6UAQ3nimTR7W0n1rTWsVuHkjMhnV4omALJvYdN4HXBAPHpnX0m7ub7SbW7u7QWk80Yd7cSCTyye24AZrO1rRp9UtbfSPLifSmKm6ead2lIRlZVHXOccsWyPfPG7QByGoeN5NP1nVLaTSs2OmPapPci4+c+eQFKx7eQCRnLCp7XxDq194g1HT4dMto7fSrhY7qd7hmMiNGJB5ahPvAMMg4HPBPZi+CoJfHV94hvSsySrAbeMSSL5bxgjLKG2P2IyDgitG28J6Naa/NrkFvMmoTuXlk+1SlXYrtyULbenA447UAYo+IUcFrBd3umvFDdadNqVssUvmStFGAxDpgbGKsp6kZyM8VnXfiXWNCk1bVriC1m3RWM/2RNQeRUheR0ZkyoAP3c4GD1z2rsrTw9o9jcTz2umWsUtwhjlZYxllJJK/TJJx05qK38J+H7RHSDRrJFeH7Ow8kHMWc7Of4c846UAYY8b3Et3e2EFlELtNXOmW7ySYiOIxJucjkcbgBj5jgDqSHah4g1yOHw4kX9nQ3l7qDWd4iuZ40KxythWGO8Y68jOK2IvCHhyCxnsotDsEtbiNY5olgULIqklQwxzgkkfWpm8N6I+i/2M2k2Z0zj/RfJXy+Dn7vrmgDIv5mu9S8MXTalaPam6ZWa2mdRJJ5UmMEPgrlcYIPWs7WPEXiWy1+50WA6f8AabqWBtKdrWRleJmYTB8PyUADEjAAI9eOsk0HR5Y4o5NKsXSFdkStboQi+g44FXDbwmSOQwx74gVjbaMoD1APboPyoA5TTbmyt/iNrUV1qdi9/PBb+REkhWQJmT5CpcgsMA5ABwRkVV8N6rrWp2mpQNrunnVIrq7jjtpbcb0CTMqFlDg7doHYcEcnv1Y0bS1vvto02zF3u3+eIF8zd67sZzS3OmxypdNasLK8uUCteQRp5ox0OWBBx2yDQBz3hHX9V1x7y7vhBBYWsaQOhhaOQXKqPPDEsQFVsrxkdfmOK1tbjsNY8L3bNcI1q0BmjuYpB8hUblkVxwCpAIPtVrTdJttM0xbGPdKh3NK8vzNM7El2b1LEkntz6Ul3oum3uknSp7OI6eQqm2UbEKgghcDHHHToehoAr+Fbu71Dwhot5fkm8uLGGWcldpLsgLcduSa16RVCqFUAKBgAdBS0AFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQBXv8A/kHXP/XJ/wCRrz74E/8AJKNP/wCu0/8A6MavQb//AJB1z/1yf+Rrz74E/wDJKNP/AOu0/wD6MagD0miiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAr3//ACDrn/rk/wDI1598Cf8AklGn/wDXaf8A9GNXoN//AMg65/65P/I1598Cf+SUaf8A9dp//RjUAek0UUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFAFe//wCQdc/9cn/ka8++BP8AySjT/wDrtP8A+jGr0G//AOQdc/8AXJ/5GvPvgT/ySjT/APrtP/6MagD0miiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiuc/wCEzsD4kbREtb95EnFtJdLB+4SXy/M2l88Hbjt3rYj1TT5Xt0jvrZ3uVLwKsykyqOpXn5gPagC3RWfba9o95JNHa6tYzvApeVYrhGMajqWAPAHvUcPiTQriGaWDWtNlihUNK6XSMIwTgFiDwM8c0AalFU5NX0yGyjvZdRtEtJDtSdp1CMfQNnB6H8qzdW8aeHdENj/aGq28SXyl4JN4KuoGdwI7dOfcUAb1FZc3iXRLe+tbGfVLWK7u1DQQySBXcHpwfXtnrVS78V2UPiGy0a3khuLiW4MFwolw0B8ppBxg5JC9MjAOaAN+io55fIt5JdjPsUttQZLYGcD3rlPDHjWXW9NutT1GwttO0+GBJxcJfLOvIJZHwo2OuBlT/eoA6+iuS1fxe8nhLUNY8Mi3vLixRpJ7a6WSORFVSxUx4DhiBwCBnOatWnjHTWg0SO+l8m/1Wx+2RQJE7ggRh3wQD0B6dTQB0dFc2/jXT2l0f7JbX17b6pFJNHPbWzuI1TGS4xuHLAYxkHrRP4jlHjXTdGjjMUFxbyyu9xA6eYwCkLGx4JAJLD09waAOkormv+E40k60dNWO9fEjwC6W2byGmUEmJX7v8p4HcYzniotE+IGka9qVrZW1vqMTXccjwSXFq0ccjR8SIGPVlPB7ccE0AdVRXJaP4tFz4Y1LxXdmQaQHkktYo4CZBBGSm49yWKsw9AR6E1I2t6h4i8LT3/h3da3sDhkS5VJEn2gMUDKxUqwO3cp4OfQ0AdTRWT/bTzeH7TVbGwmvftKROsELpuCvjnJIHGcnnsa1qACiivOdL13xDBrVxcXepR3mnf25LpbW8sccRhTG5HVgAWIPBBzxz2JoA9GorktH8XxeKcWcNpqNkt5atLBdom4BegO/BVWIIYZzkflUdvrx8N+BjeX013qUsF3LaRtNxLM32ho4wxwAO3OOgoA7GiuBvvHOqv4Tvby10pbLU7e9gsyLvcYCZZEQSI21S6/P6L0P43/EPjd/DclhZ3en+bqF75pjjtvNmjAQA4LJEWycjgLx345oA6+iqOjamus6NaaikE0AuIxJ5Uy7XQnqCPUVzeo+LNUXxNd6bpljZSW+mPb/AG97i6EchSXndGDhcKOcseegHHIB2VFcMnju5/4SIQPa2x0xtVOjgI7NcrOFJDsoGBGcfUAgnjNQaL44m8QeKJNEnjgGn3sFy1pPatKrlY3CElmC8kEkFOmOvegD0CiuP+HKJbaJqNlFNJJDa6teQxCSUyMqLK2Bkkk1c8barqWh6Iup6fc2EQgmjEyXoIWVWYLtDg/IeeuG+lAHSUV5x4l8VeI/DsdjYPe6ZLfXonmS+NuIrZQiriL55gCxY/e3Dj+E03WPEWtHVfDMo1/T9Ct77TpJZVuokngaYbPl8wSAE4YlcHopPOeAD0mivNZfHutSfEFdGtrW1XT4XhR2laNWuUcf66PMgYrzwFV845Izwui+K9bm1m4l1LV9L+x2+ty6S1qkYjO0BtshJYkOSowOhGepxgA9JpqSJICUdWAJUlTnBHUV574H1HUZry9i1jxRcS3ourqH+z7i3iQqEb5ZRhQwXZtPPy/Mfas7w/rLaN8OtVXSZ7a51C31C4DSQom4RfaNhuWReoCfNnBBwO1AHqtFeRXXjDXo7Q+Xrn+hW+r21nFqptYyuoQzAb8DbtDRncdy8HbgjrXbeCdTvtRstUhv7wXsthqc9mtz5aoZVXBBIUAZG4rx/doA3r7UbLTLf7Rf3cFrDnbvmkCLn0yfoamiljniWWGRZI3GVdDkEeoNeffEGKZ/GfguZZLyK3gnuGnlt4fMEQMWAx+VgMk459aml+0z/EE2EOs6rbaRNZRTCKGILH5wYYRX2fICgyQCM5PI6UAd9RXnFpqusnxdcQX9xq6zG8uImthaEWiWQV2jlWQLjecJzuLZJGKoeGNZ1lfEuhQTXGuyQ3EK/akvYGKIWt92CQvB8wHOTxkDjpQB6sTgZNULrWdOs7+xsri7RLm/LC2j5JkIG44x7c81Q8a2V5qPgrWLSwVnu5bVxEiOyFzj7oKkHnp75rh2tra60/w0LOw8SW1nDqkXni4Nw0kIa3mjwjElwqsQpYYHIOcc0AerUV5PNb+KJdDtLa8i1dba0vb2FmiaZ7iRQ2bd/kdGZdu5eSckKT149D8NHUz4csP7YLnUBEBMZEVGY+pVWYAkYJAJ/pQA8a7YnxCNDzML0wNcANA4RkUqDhyNpILL0Pepl1S0fWJNKDt9sjgFwybDjYSQDuxjOR0zmuU1u/urL4kabdromrXVrBp81u89tb70DyyRFecjgCNs+nFQ6Y8+n/FDXPJ0HVFs9QigX7UIx5JmTzC75LcAhkGR1K9KAO9qOCeG5hWaCVJYm+66MCD9CK888H6BrdvrN3JqtjOYrq2nL3F3IvmB3dcI6xzMjkqB8yqmAgAq18MvDknhvS/sdz4dOn3kcSxzXvnJIt0QTyoViQO/IHUcUAd7WX4g1618OaZ9uu0mlDSxwRxQgF5JHYKqrkgZye5FVfF+nS6poggSyN/EsyST2SzCI3CA52hiQM5wcEgHbgkZrhrzwvrP/CE6bYy+GzfvHrC3kVk9xFIbO2WUP5JeRgDlAVwCRzjOKAPTNNvTqOnxXZtbi1Mgz5NwFDrz32kj8ialmu7a3dEnuIomf7qu4Ut9M9ag0kbdJtgNO/s0BMfY/k/c/wCz8hK/ka4jxV4L1DW/FX9oQ2lpIitb7GudkiFUYM3Vd8eOf9WwDcZHXIB2w1rS21CWwGoW32uIqHhMoDLu+7x74NTm9tFeVDdQh4hukUyDKD1PpXPRaXqFn4uv7mLS7G4s76SKU3LyhHhKoFYbQhLH5QQSe+OABXMaZ4P8SQa//aF7ZaXKgkvjNGsyqlyJ8EHaIs/wgEOzfhigD0eG+tLksILqCUoMtskDbR74rOsfE2n3+rajp8bFWsI45ZJi6GNkcsFIYMf7jZBx2rgIfh3rX/COaTpiR2dlKmi3On3UkMpx5jPG6McKCwbyyG6HDnr31R4N1xpdVbydDt4b2zs7UW0AYx4hclhhkIAZXcDg4+XrzQB2kmuaRFawXUmqWSW9xIIoZWnULI5zhVOcE8HgelU7/wAVaTaeH31iG+s7m3Kv5DJdRqkzKDlVcnbn5TnnjB9K56Xwlq8vhe70mSLTZjPqS3QE9zIw8oSB9pYIDu+ULn0J/HR1zRdbupLK60uLR4547aa3mhug7Iok2klGUA5+XByBnNAG9o+pxazotjqkCOkV5bpcIr/eAdQwB9+au1leGNLn0TwtpWlXMkcs1laR27PGCFbYoXIzz2rVoAKKKKACiiigAooooAKKKKACiiigAooooAr3/wDyDrn/AK5P/I1598Cf+SUaf/12n/8ARjV6Df8A/IOuf+uT/wAjXn3wJ/5JRp//AF2n/wDRjUAek0UUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQB563hvXJviZ/akenWlnp4mLXF5FdFWvYfK2iOSEDDEMQdzdl+lVYPB2vabrOkXkkelSaZokl55SwbhcSW8ofagGwBSgIULuweuRivTKKAPnvwtJINJ122htrfU5LrR3gaW18xWs0ThIpAIl+YeYd2Gdjt57Vp+HfDd94l8O6vpsRtheNPb3p1SFZIYp5kIxCQYo2QAIpygON2ck17gFVc7QBk5OB1NLQB55D8Pb1NBhsTPaxSpfSXu9JpzKjupyVnLbt+4nLYAIJG3JzWhD4R1a0svDLQ6naS3+ixSxM8tuVjmDpt+6pGMYX68+tdnRQBwt98P573X7rU5b+3k+3JAbqOSKXYJYfuOiCUKR32tuwRn1Buz+F9ZbWDNba1bW9h9u+3hBZbpS5XayFi2CpGecZGfQV1tFAEc8bTW8sSyNGzoVDr1UkdRXExfDnMur3Fzq7G61G3giMtrbiELJE25ZmXJDvuwST7joa7qigDlIvCF1FZa4Tq4fU9Zws92bUBUQJsULGG7Ankk89fSq6+BrldM0NBrhXU9EDR2l8tomfKZNhRkJIPy98jkA4OK7OigDjrbwReWGk2NpZeJb2KeyaVIrpokZjBIQTGy42kjaCGxwR0xxVnUvCl9f6/pOqJ4guIhpqFY4jbxvvZgFdmOByy5HTAJyPSuoooA5mLwTZRa4uofbr1rZLp72PTmZPs8c7A5cDbuzks2N2AxJxmo9N8C22mXWlzRanfuumzXEsEb+XjE3LqcJkgEkjnPvXVUUAcnZ+DzbaNqPh5LiS10eSbzbR7OUpNGHcvJGflxt3EgdcqxB6c2E8K/2Z4d1LTtCuzaXN9IZHupFDFXYKrMFXaAdq8YwAea6SigDLutDjuNCh0mC8vbKOFY1jmtZtkoCEYG7uCBg+oJrUoooAKxbPwpo9leG7jtneczvcbpZ3kHmvwzhWJUNjjIGccVtV5jL4wvJfiX/ZMepXcdi909o8YjjIhPkkKQBGzcychmYdPu4oA7iw8NaTpjs1nbPDlWVQJpCsYY5IQFsIOf4cdvSqNx4e8M6RoGoRXqiLSZgWuhd3kjR/M2SxLsdpLHORg5rhvDHirVI7nRbzUdcv9RN4t7Bd232dMLLDgxoiqgwxBJz3yPQVb8AeKL681LUP7SubufTDYLeie5VnXeGIcK3lIowNuUUMAc4PWgDs9P0Lw1e+HHtbK2trrSb6PDMHMonXsS5JLY7HORU6+FNAS3SAaRabEl85cxgkSbQu/J53bQBnriuH0KC7l+GthHZXN/Zavoyee9qzNbLJ85by5Ny4IYKR7ZpL+41238GWGoC+1QT6jf8A28wLFNP5UDKWW2Z4gXRQNvzAdc9jQB6TZWNrptnHZ2NtFbW0QwkUSBVUdeAKp3nhrQ9Q1Bb+90ixuLsBQJpYFZ8A5HJHavLdabxnfaL4eQLqdnE9huMriaWaO83fKZPJwSduCN67OTuAPTQ8UDWb7xJYbE1rfHBbHyUimjQyA73KSRMY9xHysJRtG3g80AekLoulpq7auunWo1Jk8trsRL5pXpjd1xwKq2PhTw9pl19qsdE0+2uPm/exW6q3zDDcgZ571rOgkjZGztYEHBIOD7jpXj/gnT9XksjNpV3qw1CM6jbzzXty80JKsyQL8zFN4YIcqDwrZ6igD07SfDeiaC8r6TpNlYtKAJDbQLGWA6ZwOetP1ttJh0qa61tbY2NsPOdrhAypt/iwQef1rgtC0fWrfRNae7t9V819NWM2ryMd10u4lo2aZyxJI5G1TgY74qS+GZp/gvqlra6Jqf8Abt3axxXQu23XFzMmPmLFjlQS2OegxjtQB3+lT6Vr2kBYtMkjs1PywXdiYl9iqsoBHcEetaU1hZ3McUc9pBKkX+rV4wwT6AjiuEl0KfVtI8PCXRL46ZbCRbzSp5lR5WKDY5Bk2sFYHhm7g44FZ8vgvUpYPCZ1fSZdWktop4dSCXSljCcmKN2Zl83aSuexK5oA9PNvA1wtwYYzOqlVkKjcAeoB64pqWtvGWKQRKWfzG2oBl/7x9/evFvE/gDXZtZ1GXQ/DzxRGbdbSR3cSDYLYRrwXBB8wBhkcYyOtbun+FPEa/EQavewXDxC+kuo5/tEARIXTb5bYXzSVB2hc7MqDkUAeiyanbxazb6Y6yCe4heaNtnyEIVDDPr8w496tsyxozsQqqMlicACvOPCvhrXtF1ewW40Wyc2Znin1drvMt3HKwYPjBYsNoyrEAfwnFdh4r0mfXfC9/pttIiTTxgL5h+R8EHY2P4WxtPsTQBopfWckEc6XUDQynEciyAq554B79D+Rp9vcwXcKzW00c0TdHjYMp/EV5jP4B1Se0u7j+xtFglm1GzuYtMik/cRJCfnO7YPmkHynCDjGc113hLQ7jQJtatza2sFjcX7XVoLdsBUZVBUoAAuCvbOc0ASeI/E8vh/UNHgOlyXFvqN5HZm5WVVETuSBlep6H07c1Pe+JLa08VaZoCiOS5vUkkb9+itEqqSDsJ3NkgjgdjmqPjbTdY1O20xNHtbSd7a/hvH+03BiH7pgwAwjdeRnt71T1vS/Ed74r8Oara6bpRSwV2nMl0yvukQoyqRGcquc/wC1gdKAOk/tzSf7XGkf2laf2kV3C085fNx67c57VB/wlXh//Tf+J3p/+g/8fX+kL+45x8/PHPHNYWk+EdT0rxFez+fp1zp1zqMmorJcQu11E7qFKqc7QAMgH0PSsvwx8MX0KW5aae3ncQTW8FxvnaR1kySXVnKKScE7V5IzxQB2Nn4p0DULa5ubPWbCeC2TzJ5Y51ZY15+ZjngfK3PsaeviTRZNOmv49TtXtYXEckqSBgrEAheO53LgdTketcnbeBNRS3sIZ5dNmji0IaTPG8TsjlXUhsZGRgHPIOT2qxZ+Br6LRp7SbVwZWu47mBSsk0cOzjG538xsj1fg9OByAdBceKtDtdKi1OTUoTZyuY45I8yb2BIIAUEkjBzxxg5xg1p21xBeW0VzbSpNBMgeOSNgyupGQQR1BFcjJ4EIsrSK2urS2lgupp3EdowilEikMCvmbs9Du3ckc9a6XRtMi0bR7bToRGI4E2gRR+WvrwvYe1AEN34j0my1FbCe7xdFo1KJGz7DI21N5UEJuJwN2M1Hc+JdMigiZLoeZcXL2VuGjfD3ClgUPHHKnnoccVm6t4TvdT8QjUE1hba33wOY4rbbL+7JOPNDDcG44dWAGQOpplx4I87VftMeqzxW39pLqn2cRK2ZwoU5Y87cDoMc55oAi8PfEHTdR8NWeoalKbe5ks2u5o0tptqqhAk2kr820nBxnGCela1v4t0m/F2ljLNPcW8cjmH7NIrsUxuVQVBYjcvAyfmHrWNafDuG1sobU6tdPHbW1zBany0BhM5y79PmPJAB456Z5q3p3gv+y9RnvrbVJTPK8z5khRghlEe7bxnrGp60ARReNWi+Gr+Lrq0EuyFpmt7Xf2YrjLKCMY5JHHPpWhqvic6Zptldf2VfSyXd5HaJbhAJBuPLYyRgAE/h2qgngSI+C7rwrcancS2E8ZjVgoSSPLFycjryeh4xwc1ZufCtzfaGlje+IL+a7iuUuYL7y4kkidCCuFVApHUEEHOTmgB2qeNtI0VITqRmtpJI3mMLoN6RqcF2APT6ZJ7DrVDxX44TS9Jnk0hknuolt5Hd4i0MUcrqqlzuXBIJIGc8cjFM1b4c22tfYpr/AFW6nvreN4pLuWCB2mjdtxXayFFwehUAj1qfVvh5puqxtCb2/t4JreO2u0hkH+krHgxsxIOGUj7wwe3SgDrR0HOaWo7eH7PbRQeZJJ5aBN8jZZsDGSe5qSgAopkU0UylopEkAOCUYGn0AFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQBXv8A/kHXP/XJ/wCRrz74E/8AJKNP/wCu0/8A6MavQb//AJB1z/1yf+Rrz74E/wDJKNP/AOu0/wD6MagD0miiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAqmmrabJfGxTULRrwEg26zKZAR1+XOeKuV5VpehpqXxH8RCxsLGC3tdWt7tr3aVnjcRLuVFKYKuyurHcPvMcdKAPR4da0q4nSCDU7OWaQsqRpOrMxXqAAeSO9Pi1XTp0uHhv7WRbbPnskykRYzndg/L0PX0rjND8HXth4g12WXStIt7fULmWW3v7WQ/arcMgRQoMYCngtw3Vj1qC3+HM76Fe6bINMsDJYpYLLZQkmdVcN5ko+XlgMFcn7zfMc0AaMur+H/ABrfX2g3vmCC0liAYXirFe7wxCrsf5xhTlT+XFdE+vaNBp9xeNqdmlnauYppfOXZGw6qTnAI9K5WLwbqrajf6kx0i0mkWyFtBbwsyRm2diCScfeVivA4BA5xzJb+C9Ttr2bUEu7FrhtWOqLC0B8rc0PlMh7ggchxySTleaAN2+8XaFp0WnzXOoxLBqAZreZTuRlVC5bcOAAB1rWtrmC9tYbq2lSWCZBJHIhyrqRkEH0IrkpfCF/b2GitpU2l2t7pU00scQtGW2bzVZWG1X3DAcnOeT1611tqtwtrGt08TzhfnaJCik+wJJA/GgDPuPE2iWupDTp9UtY7wyJF5LSDdvf7i/U9h3qlY6t4S0f7XY6fcabZrA0stxFbhUCsmPMYheMjK7vTjNV5fB0j+KJtZh1BbczXEM0iRROC4jUDa37zYc4xuKbgDgHgGsr/AIV5qLTy3M/iJLi5mguIJJZrNmDLL/0z83ywQPRRnvmgDeHjnw01td3C6rE0VpE007KjHYikZPT/AGlPHUMD0INRP4qj1fQNRu/C0tvd3tmPmhu0kh2nG75lKhhleRxg+tcxqXw/1Wx8Oa8tpqaX8t3p8sS2/wBk2M8jW8UXytvwM+Sh5Bxk/Wt7S/DupNpl/fPqRi1fVLeGJ5ZbIAQIgIC+UHOW+d8nd1I7CgC5b+MNPi8IaRr2qObZdQghkWOON5WLum7aqoCx79ugqa88YaJZWtrcSXTyLdQPcwLBBJKzxoAWbaqkgDIznHJxXOTfDFb3wzpOl6jqUN5caOdtjcS2QMax7Amx4t2H4Gc5Bzg9uXat8NBfaNpulWuqxW1tYrMF3afEzK0jbt8ZXb5bLyAR65OTQB3cUizQpKudrqGGfQ0+swaZdRTaULfVbhLayQpPFIqyG7GzapdyMhgQGyOvOa06AGysUid1QuyqSFHU+1eeeHvH97Jo2qa1r5tVtrSFJZLG1t5FurMlmBWRXOWAXad4AB+Y9BXoUsfmwvGWKh1K5U4Iz6VwWr/D+dvD+uNHqN5q2sXeltp9vJeNGm1OoT5FUctgknJ460Aap8d2UVlqct5ZXdnc6fJHG9pcGNXcynERVt2zDH1bjBzjFMX4gWM2lQXNtYXlzez3bWSWEPltIZlXew3hvLwEG7cGxjvnipLXwZBcaXONWmuJtRvPIe4uPNUujxHdHsKooG05wdoJ71Y1LStKtLCGXU9Vlha2uDcQ31xcqjxOQQdpI2gbSV24xgnigDN1bxReXOgaBfafHe6b/aWoQ28pntkaSEM+0q6Mwxk8ZGcdcVqa34st9E1e00+S0nla42EyK8aqgaQRj7zAscnOFBOAadqHhqzutMtbe61C+WKzmW6Ez3ALGRDuVmZgehGccD2xVa48F6Rq14NQnu76cywJFMY7xkS5VCShfZjJBYkEYoAct5exfEddON5JJZTaW9z5DqmI3WVFG0gA9GPUmujkLLGxRQzgEqpOMn0z2rCPhGyPiWDXftmpfaoIhAqfa28soMfKR3BIBOTyRk1vMAylTnBGODg0AcfB40v49FvdZ1Xw89jp1nDI0ji7SV3dGKlUUDlcg4YlfpUqeNd1vc/8S1zdR3UNtCiyHypml+6RIVGAOd3BxjjPGZIdM8KWmhavpqzLLpsSsl/BJeSTiLOWYEFiVJ3E8YJz9KpRW3geDwXPqIkL6HdYd7iWeeViVbClWYmRSrZxjGDk8daAJdN8bTXuqW2nzaUsM0uoXVg5W53hHhj37h8gyGH0I96zpvilDHpunXA0t2uLy2nuPIVpJMCN9m0GOJiST3IUDuau6H4G0VvDstpLJ/aGmXl6dStTukRo94BXD7y547kgkEg1YXw14NW8i0CPT4I5oFa9jtow6BUchWIIwNpIAK5we4oAr6z4+Ol6vbWS6eAktuk7S3UjRKpdgAhZUYIw5zv2g8AE1Lbal4mm8d6jZK+kNpVv5GYmkcTIrBjuHy4LHgYJx8vB61sSeF9CluRcPpNoZQiJkRgfKhyq46EA9B2p134a0S/1aHVbvSrSfUINvlXMkQLptORg+xJNAGDo3jK81HxlPpFxbWlvakz/AGUl5PNmWNgu9Ts8tgeThWyMc11t19o+yyfZWiW42nyzKCUz2zjnFZun+FNA0rUX1Cw0eytryTduniiAc7jk8+9O8T3Wk2fhu+n12IS6Wkf+koYjICuR1UA5FAHD6GZ/CXhCDW5Egl1TU2hjkdruYwCSVv8AWylicDJ6gcdPejVfHniDTvCl3fIulT3um6pHY3DormC5VtnMZ3ZUjeAc7sFSOa7PTPC/hux0+eHTdHsYbS+QeckcICzKRxuHcYP60l5pXh/SPD5STSLb+zbIGZbeK08wKQCMqgBycE9s80AaGmLfpYRjU57ae7yd720RjQ88AAsx4GB159q5XX/EuqWviSawttQ0bS7a2hilLaqrA3W5jv8ALYMMBVGM4PzHGB1rq1lsdPtraPMFpFIyxQRnEYLHoijjnrxVbUn0NL+z/tMWP2v5mtjcKpcbeWKk8jHHP0oA5nUvF+oWniOe1hn090S/tbWKw8tzcSxyhC8oOei7yeFIwjZPpS0/x61z45+yz6nbrpk91NY28LIi5aMfezuL53KwywVSCMZJye/aGzN9HO0cH2zyyqSFR5mzIJAPXGcVl6v4m0rRdU0ywustcajci2jEahtjkErv5yAcdcGgDm/Ak2k2Xi3xhpGnS2EEK38TwWduoTH+jpvKgcEZU5AHBBz1r0CmhFByFAPriovttoEkf7VDsibbI3mDCH0PoaAJ6Kht7u2uwxtriKYLwTG4bH5VNQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAV7//AJB1z/1yf+Rrz74E/wDJKNP/AOu0/wD6MavQb/8A5B1z/wBcn/ka8++BP/JKNP8A+u0//oxqAPSaKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACucfxLqA8RSaQnhnUJNjIxuRNCI/KZivmcvnqp+XG7jpXR1kP4egbxGNbF7qC3GxUMS3LCFlAOAY+h+8T9TQBh6J8SdK17xTJodpDKSDIsdwJI2WQoeflDFlHBwSB+oo0bxnqFz4cvtd1XSI7bT7SO5kMkFxvdvJkdSuwgYOEPOetall4O0nT9XbUbb7WjGRplt/tcnkJIwIZxHnaCcntjmm2/gjQre6vJhbSOl2JVe3kmdoVEn+sCx52ru6nA70AYkHxKEnhy51htDu2WF4AkcDhxMszbUKOcKWBIDLng9yMEx+IvG+uaZ4Wur1NItrTU7fUYbQ289x5qMsmwghlHUhwOeAc9cDO/8A8IP4fOlT6Y1nK1nPs82NruZtwT7oyXzgemcVPceE9Eul1Bbmy85dR2falkldg5QAK2CflYADkYPHWgDA8XX3iEeGdNmeMaVcyarbQz/Y73eUieVU4Yxjdnd0wMcHJxirHijxnd6HqFxBY6bHdR6fZf2hqDyziLbCSyqsfBy5KMecDC4zkitG68E+Hr3SrfTLiwL2dvJ5safaJAQ/94sGyx9yTUreD9AeGzil02OVbMFYfNZnIU5+VixJYZOcNkZwewoA5XVviFrGmvPff2NaNokFxbJ5/wBpYyzRzY2lU2jaw3BiG9cepr0Q52nbjOOM1nXfh7R783Ju9MtZ/tRQz+ZGG8wrjaTnrjAx9Kspf2X9oNpqXMP2xIhKbcON6xk4DbeuM8ZoA4vS/EfiTT/D+r654gbTLqztUu5o47QuspMTsNmGAG0BSMnnpmmW3jPX20HWbqXT7B7q2hhlsSjvHHcmXICfvNpzkcEcMWAFdguhaSl3PdrptoLicESyeSu5weuTjv39aItC0mC1ktYtMs0t5eZIhAu1uc8jHPJNAHDXfjDV77wpNcRXltY3cetw6e1zHayFYVLR5MiSbSPvYPJHIweci34tuLqTSdIkm1SxuETXLeK5Fr5kYYNMq7crLwV3ZIbIOBkCuklGg6OLDQ/sdvDFfOY4LaO2/dsUXcc4G0YCjr6cVdOj6Y0CwHTrQwqxZYzAu0E9SBjrQByHizxVrWj3erSafcaS9tp2nJqHkSKzTSruYMvDAAfL97B7DBqJvFms6r4pg03S7mzt0MVtcSRyWxmKwyIWZmfeoU5AUDBJyDjFdt/ZWnYx9gtceX5X+pX7n93p09q43WfCnh6/8QHSLuW7J1LFw1tHCuxEiVQFEuzdGvyDChhyDjqaAO5ndo7eR0XcyqSF9TjpXmWleOtXu9AvtVj1PS769bSnvI9IiiYS2kyZyjDqV6Z3YORxwa9QAAAA6Coo7W3hnlnigiSWXHmSKgDPjpk96APN7HxbqbW+qTjXU1LTdPazuX1K3tF2lHbM0RAB4CYbIBIHU5p994k0LW/Cnio6nqdhqMFrM7WbTW4URh4h5O0EcndvAccnBNelIixqFRQqjoAMCloA888TeKbDU7ewSLV/I8O3sc0c9/DbLcLJICqiAhkYLuDNyRyVAHXB2PhojxfDjQ4ZYpopIrYRvHNE0bKykg5VgCOldXRQB53q+oavL8RLOK1utRbT47mKKSG2RolTgli4aMiVDxllcbRxgnqaJA9l8SNZivNR8QlpbwSWkDJI9rJGYE5LhNoCtuABYfdHB7+iUUAed+A9Ws7KfxJbyJqhaTUbi9SS4sJwZIdic7igyeCAv3jjoa0PDfibTBompO0Gpxx29zPM6y6dOCUkmcqUUplgQw4AyO4FdpRQBheD72O78MWEaRXMT21vFBIs9u8JDqi5ADgZHuOKy/Gemx32paa9wuteRHb3Q36S8iOHPl7QxjOcHacZ4yBmuxooA8nubDxpejTIdSbUYbqLT7eSK4six/0lTmZJNkqxknC4L5XGcHOc+roSyKWUqSMlT29qWigDzWKy1u88W3FuINYS3uHuvMubl2iWCN1KrsKyFJADgqAqsAc561TOkeMJNDg0qexv5nGgXlhdTSXcbJPcOAIm5kyejfMRn5ufb1aigDzSPR9fiiuRFpmpJZLHp6LaG+HmSMjsZ2U+b8oKFV+8M46d6x9N8N+KIvBviKxvdEvp76/06CGMS3cUu66Ebo825pDjnyznrwPSvY6KAOJ1yy1DU9G0O7/4RtLqewuUafT7sQtI6GMq2xi+zILA8nnb9Kz9a0K9vtS0HWH8GWd7DFZS2s+lSPCTbsxUoct8hUbSDjONxwDXo1FAHl+peEvEFx4ta+js4/KeO2ktWhnhjFi8ewNHvMZkKZBOFwGGQQM5JqPgvXbnxTaXZ0zSrk2+tjUF1Z5ylx9n3EiErsJIUHaPmIwo4FeoUUAVdTs31DSbyyjuHtnuIHiWdBloyykbh7jOa8wg+HOqN4d1Owm07SoGbSlsFjt5PkvplYMtzJ8o2twOu48nmvWaKAOP8MaDf6V4o1S+fT7GysL20tVSC2lz5MkakMgUKFK8nDYHTp6dhRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAV7/wD5B1z/ANcn/ka8++BP/JKNP/67T/8Aoxq9Bv8A/kHXP/XJ/wCRrz74E/8AJKNP/wCu0/8A6MagD0miiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigArznxD43fSfGYifU2t7C0ngt57YwofNMi7mYYDOwCspyNoBz97t6NRQB5RpPi7WYdUurrU9Ymnt7fxC2lfZFtUCeS+fLkLBdwIJx1x8uCM16RrdzeWeg6jc6dB9ovYbaSS3hxnzJApKrgdcnAq/RQB5jpGua7eeG9UvLrWb3zFto5YfsmnmaSGYZV05hQOS2PkxlcHJA5p9p4h8SSaGZL0anHd/2vtvhb2IJtLYkgCHKHzkyFywBYBie1el0UAee6xNrkuiaZHb6nqskb3Myz3iWht5NuSYtwWNmCj5VyFG7HOATWPf6h4gXUbC3vdR1dr99EmdIrKBkVrtZFRHZFXgHOTv8Al55wOK9aqjNo9hPrFvq0kGb62jaKKYOwKo3VcA4IPvQBxc9lfR+MYdY1Sz1V2OiQxv8A2e8m37QJGZ0wjY9OvFT20epQfFjUrtbfUf7MudNjgSV1doxOHJ4z91QG+nJru6KAPNdPg8VNpqpdSat9uTT7n+0mdjtkuAf3XkbcAc5I2ADbgHmr3hG31bT9btUuY9TNveaTDLdtcs8ii9yd/LE7OOwwvSu8ooA5nxvZteaVaAWF7exRXaSTQ2MpjmKBWBKsGU5GR0Iz071w2qad4un8M2FpDZamEkuLs28f2hmmt4zxAsxEi5wCTuZzt4yDivX6KAPK9R0nxTq+g+H7n+zb9tStNP2T29xdKqSTDCkkrKjI5wSJBuwGIxk1v6hpeo/8LE0bXLfSbkrHayQX8sVzHsbcBsUKzAsFbJzgfQ12tFAHnNl4f1v/AIWd/bEmjolss0rNeXMySPsKFFEbK24Lgg7GTAy3PSu7tbm6muruOexe3iicLDK0isJxjJYAHK4PGDirdFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQBXv/APkHXP8A1yf+Rrz74E/8ko0//rtP/wCjGr0G/wD+Qdc/9cn/AJGvPvgT/wAko0//AK7T/wDoxqAPSaKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigCvf8A/IOuf+uT/wAjXn3wJ/5JRp//AF2n/wDRjV6Df/8AIOuf+uT/AMjXn3wJ/wCSUaf/ANdp/wD0Y1AHpNFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABUe6X7Rt8tPJ2537/m3Z6Yx0x3z+FSUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAV7/8A5B1z/wBcn/ka8++BP/JKNP8A+u0//oxq9Bv/APkHXP8A1yf+Rrz74E/8ko0//rtP/wCjGoA9JooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKy7jxFpFrqNxp899Gl5b2pvJISDuEI6uOOQMds1a03UrPWNOg1CwmE9pOu+KQAgMPXnmgC1RRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFAFe//wCQdc/9cn/ka8++BP8AySjT/wDrtP8A+jGr0G//AOQdc/8AXJ/5GvPvgT/ySjT/APrtP/6MagD0miiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAMXUPFekaXqcmnXcs6XMdo94yraysPJT7zBgpBx6A5yR61oadqFtq2m22oWbs9tcxiWJmRkLKRkHDAEfjXE+MdH1PVPFsX2az1D7K+i3Vq11ayoirJIVZVYlt2P3fYdWX3xymu+HPF17aaIthpt9b3FnpFtChjmjCiVCDIGPmDYw2DaVDZ3EEgUAe10mQSQCMjqK4KXwTeS+KYriJlh0K5livrm2eZhLDPGrAKm042sWUsM4+Rv71N0Lwrqll4sGoX0LyTJc3DtepNEiTxuTsDKE3sVDYCscDaSDzigDv2ZUXczBR6k4pvnRZI8xMqMkbhwKp61babe6NdWusCA6fKmyYTsAmD6k9OcYPrivN9I8HX2teEZL10tWvru8t5EMwMQubKAqsaOU3Y3ou48dW6YxgA9UEsbbcSKd3IwetOVldQykEHoQa4aPwffWdzYahZWmmxTWuo3F0tkJmESxzRFGVX2Eg5+fAUDJPpWx4G0fUNA8J2ulaktqJ7dnANrIzIVLFh1VSPvYxjtQBs3Wo2NlJDHd3lvBJO2yJZZVUyN6KCeT7CkbUrBb/AOwNe2wvNnmfZzKvmbf723Oce9cZ4i8GX+peJL++istFvre9toIwdRMge1kjckFNgyV5zgMpJHXFQ3ngLUrvxD5xmsltW1WPVWvVLC6UqqgwqNuNny9d3Q4xQB2lrrukXzlLTVbG4YR+aRFcI5Cf3uD096z9G8a+G9fW4bTNXt5xbKzzHJXy1UkFjuxgcHnpjmueh8H6tHqGi3SWWi2z2GrXFzI1vK4LW0gYbcCMAt8/Q8fIvPJxeGgeKP7J1HSItQ0u1tZEmW2mjgZ5dzvu3OCdvRmUjBz1yM4oA24vFOgzaNNrEerWjadAxWW5Eg2IRxgn15H5iq19410Gw07Tr9r5ZrbUZlhtWgG/zWZscAdh39MGuXtvhxqQhuDdanaS3CXtvf2TtHLJtliXaFlLuWkTaOmRgkkY6V0E2gazLoixJqFjBqEd6LyHyrQi3X5slCm7cwOWJO7O4546UAX5vFmg29nbXcupwLBcxtLE/OGRSAzdOAMjJPrVLxV4ztPDUSqqLd3m+HNsGKlY5JNm8kKQBnOM4zjGaxde+Hd34jls7zUdVglvkt5La4Jt3WJo3bd8qpIpyvQbiwI6ip9X+Hs1+t1HZa19iiu4LaO4T7KJNzQEFGUlht6AY5oA7hmCIzHOAMnAzXPWnjjQL1rIQ3co+2GcRGS2kQAw/wCt3blGzbjndit9A0cKq7mR1UAtgAscdcDjmuN0bQU1XVdd1W4sZ7Ow1GLyIbWdSkgJBE0u3/lmX+Uep2AnqKANEePPDv2Oa6N5KsUQjZt9rKpKO+xHAK5KFuNw496sXvi3SNPh1KWeWbbpkiR3e2Bz5RYBgTx93BByOKx7T4dWvl3C6tqE2oM9kunQuEEPk26NuUYXhmDAHcfQcdcvm8Ard2usRXmu6hK2sJGt4wSFQSihcqNny5AGetAHSaZqSapbNPHbXcChygF1C0TMB0YA84Pb+lcf44+Ir+DL24tn05rovY+faFAcNNlso5HQbVLZ44Vh6V3FtFJDbpHLO87r1lcKC34KAP0rG1bwtDrL6j9pvZ/KvrT7K0YSMiNcMNyEqSG+d+ST96gCC58ZWemRWA1CK5MlxFA0ssMDeTEZWCLlj2LHGBkjqfWkt/HGnTX8tpJaX9v5N4tjLLPCFRJm+4pOc/MCuCBj5lzjNULn4a2N4yG51fU5QI4UIYxctFjY4Pl5VvlXO0gHHIq/L4Js5r28uXvr4/atSt9SaPcm1ZYdu0D5c7TsXIJ/hGCKALFv4u0248QPopE0V2FldRIoG9Y2CscAlgMngsAG5xmqcXj/AEh9IudXljuoNOt7RLtriRVw0bkhMAMWy2DgEA+uKbb+AtP0yaO80uaaK/t4pUtnlYMoMnJ34AZxuAPJzxwRWDoHgnUXsl0nVLCC20R4JIb62e5WZ7tztKyAqgK/NubJYtk9O9AG8njgTeG7jV7fR7m4a1b/AEm2hngdo02lt+4OUbgA4BLc4xWlHr7Q6Bd6vq+m3GlxWwZ2juHjZigGd3yMQM9ME5yKgbwdYSaXeWMl3qbi8RI5pjeP5hROAobPAxkHHXJzmmXPhaSf+xrM39xNpthObqYXMpkmnkU5iVnPVQSSc8/KvvQBzmqav4r03TrS5v5ZNMtGgmvL26ihW7a1kLEpAyKCfLVeDIATkdVFampeOzpNvq3maXPcPpVvbXEjrIiiaKXcPMXnjGxsggHjitLXfBmleINQW+upL2G4+zm1drW6eHzYiclH2nkZJ/OpNU8G+H9Zl8y/05ZWMKwNiV1DxrnarBSAwGTjOcZoAyh45mTWJLWfRZEtItTTS5LlbhWKzOEaM7MD5SHGSDkHseSF0jxzLq2sy2CaNPHHIspsrklzHKUJGJG2YiJ2kjluPQ4BdpXgS0sfFmo61cpDcedMk1pkyboCsax8gsVY/KCGxuGTzWra+E9EstSl1C3sdlzKWYsZXIUtncVUnCE5P3QOpoA5vSPGHi3VtAfWoPC1nJbeQWjhGoYlldWKuF+QjBxxnB496TV/GGoal4O8U3+hx2ywWVmz2uoJcEiQ+XvbC7eGRSPUbjjPBx1Og+GtJ8M20lvpFqbeGRtzIZncZ9txOPwp8vhzRptFm0dtNt106bdvt402IdxyT8uOSTnNAGDf+JbvT/BmjX2mxG8ku7eN/Oug7lU8veZHSMF2J4B2qcFsnArNn8farLbWEenWWnSXr6KNZuTNcMsZj6bI8AkknPJ4HGetdSnhHw8lraWw0i0MVoCLcMm4xZAU4J5GQoB9cVNceG9Eu7S2tLjSLKW3tVCwRPApWIDoFGOB7UAcw/i3Xr7xRZ6Zo9rpZtr3TY9SilvJHR0jJAKlRnLc8Y4HerZtL3/hY6GHULzasX2i4Esh8kwMCiQxxj5dwdS5fG4cDJB437nQNIvNSi1G5021lvYgojuHiBdADkAHqMHmrQsrVb974W8Qu3jETT7BvKAkhc9cZJOPegCeiiigAooooAKKK5u88G295eTXLa14giMrlzHDqkqIueyqDgD2FAHSVDd2lvfWslrdQpNBKu143GQwrmx4FtgQf7e8SnBzzq83+NdVQB5Npl7b2Gl+JNR0O6t9V1nRrX7DZpCM4t1+ZWKqPmbJIJHUpx15taV4w1zUPCeo3Md7BLcJcRJazxxvKCrY3AyLCEzww3bCE43CvT6KAMXwrqUuq6DFczi48ze6l51UFwGOGUqqhlx0baMgZxW1RRQAUUUUAFIzKi7mYKPUnFLVTUdMsdXsms9Ss4Lu2cgtDOgdSQcjg+9AE/2iD/ntH/30KckiSZ2OrY64Oa5z/hXngz/oVtH/APANP8K1NJ0DSNBSVNJ0y0sVlIMgtoVjDEdM469aAOM8V6JqN/4/iubG3mSYaUUtb4Rboo5Q7Fo5D2V0JX/gQPUCspfDfi6HRoLB4L3EOhWtvYfYr4RC0u0UBzJ843fMByAw2gjvz6zRQAgztGeveloooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigCvf/APIOuf8Ark/8jXn3wJ/5JRp//Xaf/wBGNXoN/wD8g65/65P/ACNeffAn/klGn/8AXaf/ANGNQB6TRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUANdFkUq6hlPUEZFOAwMCiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAK9/8A8g65/wCuT/yNeffAn/klGn/9dp//AEY1eg3/APyDrn/rk/8AI1598Cf+SUaf/wBdp/8A0Y1AHpNFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFU7jVtPtL+GxuLyGK6njeSOJ2wWVOWI9h3pdN1Oz1iwjvrCcT2sufLlUEBwCRkZ6jI69DQBbooooAKKMjOM81G08SRPK0qLGmSzlgAuOuT2oAkoqNJ4pXdI5UdkxuVWBK56Z9Kz9a1610SKLzY7i4uJiVhtbWPzJpccnavoByT0H4igDUorI0fxJp2s6PZ6nG7W0V47Rwx3YEUhdWZSu0nr8rce1WJNc0iK4NvJqlkk4cR+U1wgbcSAFxnOckDHvQBforNg8RaJc3gs7fWdPluixUQR3SM5I6jaDnIwfyqU6zpai6J1KzAtOLkmdf3P8Av8/L+NAF2ism68T6JaadfXzanayQ2MZkuPKmVyg56gHqSCB6nipLfxBo9zpi6lHqdp9jO3MzTKqqWxgNk8HkcHnmgDSoqlNrGmwaaNRkvrcWRZVFwJAYyWYKPmHH3iBV2gAoorhrX4jJd6lp+lR6cF1O41GexnhechYPKDNv3bcsGC/LwAeeflNAHc0VjDxVojNdKt+jG1R3k2qxyqHDlcD5wp4O3ODwagtPG3h29ivJIdRUJaQrPKZI3T903R13AblP94ZFAHQUVhN4x0RdFbVmupBbLMIGU28glEpIAQxbd+45GBtzgg9KhXxzoLadFfCe58qUyBENnMJGEYy7CMru2jucYzx1oA6OiuW1Lx7pWm39jafZdSu3v7b7TaPZ2plSdf7qkd8EHnAGRkjNdNDL50Ecux496htkgwy5HQjsaAH0UhOFJwTjsK5XRvHWn+Ip4LO2t9RspbyGZ7Wa5gCq5jba4Xk5ZTzg+lAHV0VwvhvxRPY+Ftdv/EmpfaRpeo3Ft9oeJIWdUICjaMLuJOB65FXoPHllJ4cvNWezuEazmEE1sskUjKx24O9XKbfmHzFgBg56UAdZRXJXPj21t/DljqwsZXa8keJIfPhVVZCwfMxcRADYcHdz2zUGo/EnTdOjsw9rM91NZrfSWwliDxQsQAclsOeThVJJAPtkA7SiiubtvFrXWsLaxaPfNYNcy2o1FdrRB4wdxIBJC7gy7iMZBoA6SiuNb4gRrFDMdIuhDdWk95auZE/exxYLcZypKkMOxHeq9349uW8O6vcw6YbW+t9H/ta2SeQOrRENtLbejZU/L9OeeADuqKwJ9cvbDQkvb62s1uJWiSGJLptrl8dygPGScAMcCs+DxwLxNKtrSyDapqS3DR28sjJGBCxVyXKZ5I4+XPPIFAHX0Vymo67rSeKNC0+ytbRUvLKe5niuJyCGTyxtDKrDgydRkHn2rqUbdGrHbkjPynI/A0AOorhv+Ey1VvG66QbWytrM3DQRm4Mm+cBSdyOoMecgjYTuG1sjinaJ43utTfw8s9rbR/2nZXNxKEkJMbxMo2gHsd3U+lAHb0V5x4e+IGsal4Z1nX76wsorO0skurcxtJhiULlWJHO0YBKjrnFPl8Y+ID4de9SCzD3WpR2VjMsLAeWxwZpEd125wQqkrzjJ5oA9EorznWvG+r2nhrTbqA2ENzNPMs8u6KbEUeQXSMTDcSdmVDkqCc9KffeJLufUfDV1b+JbTT9OvdMlnea4tgIJpP3e3l2VgfmJC8HCmgD0OivOpPHmqyeOjpNtZwrYxTQxh5ZYlNxG4y0qZkDEcjbsVgcHJ54s6XrV/f8AxB1bRx4ntDb2M6SLbCKIyyqyktFkHhUwcnG7JGTxggHeUVV1O7+waVeXmx3+zwPLsRdzNtUnAHc8dK8n0zxt4hvNI1f7Xrlra3VpZW1/5ojhkWJnZg8XykgoMJ33jdycmgD2KmRTRTxiSGRJEPAZGBH5ivNv+Ep1eyvr3R5dZF4lre2vn6qsEatBbSxs5JUApwUUbyMYlGema2/hmqR+FJYolkEaajd+WzRbA6NM7oy8AFSrKQVGOeKAOpvb+z023+0X13Baw5C+ZPIEXJ4AyamjkSaNZInV0YZVlOQR9a4TxtcW0PjHwwLvVbm0gb7QCiRo6bimFOGVvmJJABB74xzkvtZ1q21zU7S2aeP7NPapp1mlniK6jYIXLSbDjkuCQRt2gkeoB3tFcPaC5n8e6pbTa7rSW8M8MtvbmNVhkbYS6htnMY4GMjkHkmsPw3qnii61LT7DU7bV4RpsU8k93khb1oxsZSCpBJcqycj5aAPVKK8i0fxTq13NrMN6dea1/skXKSLbSrJ9oUncqMYowpwVG0KVPr1zq2t5cjwXDqVrc6/dzm4txq0kkUsc4RQDJ5UTKMDkA+WBkZwSRQB31hqVjqkDT6feQXUSuY2eCQOAw6gkdx6Vari/hxDNBYa15ttfxRzarNcQPfRlHljcKVbnn8wD6812lABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFAFe/wD+Qdc/9cn/AJGvPvgT/wAko0//AK7T/wDoxq9Bv/8AkHXP/XJ/5GvPvgT/AMko0/8A67T/APoxqAPSaKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooA8+8Z+F5vEPjbS5Tb3i20FhMgvbcj9zIzpkEbgTujWROOm8fUcje6L4pm8D6RosegarE9npskaGGZRsud2ELATIMAAEN8xG4/LXrmua/pvh2xF3qdwYo2cRoqoXeRj2VVBLHvwOgNZt74+8O2Fhp97LdyvDfxNPb+TbSSMY1GWYqqkqADyTjFAHCy+HNal1zWNTutG1afdaWVzYol5jbcgIJRt8wLu9c/Kdp/Gy2keKLv4m22uDTtQtrZLxfNBuF8s2xj2j/lqecnLKFABBwW79Te/ErwzYai9jPc3XmoyqWSymeP5k8wHeFK42ZbOegJ7U6P4i+HZdYGlJLeG6M5txixm2bw6ofn27cBmUE5wNw9aAPNvCwa68Y3c7TXMV7fzahFpdykibAzGVlkkUylyVUEBTGAB7810OleDNUs9E1mzm0ON0utOEL28l1Ey3FyCcSbQgGTnJdyW4Xjit+z8R+CItdujZW1uupr55aWGwIknMZ/ehGC5kIPUKSTg9cVcs/H2iajZzXFmbt9li9/GklpJEZoV6sm5RuGcDj1HrQA3wFoX9ieH4kuNFg03USiR3TxyLK1yyDHmM45JJLHnJGad4i0W8/4SDTfE2l2yXd7YxS27WjzeUJY5MchiCAVIzyOQT7Ulr44tJPC0eu3en39rE0UDCNocl2lwFVD0bkgZ4HIJwK29J1RNXsBdx29xbgsVMdwgVwR14BI/I0AcVrPgzXtYD3F9/Y+o3U+mtZslzvSO3cys4kTAJOFZV42k7AcjPEHiPwLrOqNfpaWuj7p2JjvJZmWUfuUTccRnDBk3de/rXV6z4jm0nXtI0yPSp7v+0PN/eRSIu0om7ADMMn6kD69KjuvGdhZ31xay215/oiRPezBF8u08zG0O27rggnbuwOelAHMf8IRrkmoWl59j0O3khvFumeCV95/0oylQfLHWNtv146VNp/w/wBRtbW5tp7ixuD9juLSO4mVpGlEvzbnThQd4BOd+ccEZNeiV51e+M9fvdH8VG10eWwXTPtccWpLPC4RoY9y5RskliPQgBvagC/D4NvxZeQktjYebof9mSraRk7XG7aykgAqNzcEfxHpVvVtA1rW9Ijs72608bLiKXECSx5CAnIcNuVt+1gR0245zVW38ffZdCur3W9Ku7E2tnFdL5rxk3CudoI2sQpLYGDjG4Vp+EPF9r4vsLi4t7We3e3l8qVJMMucZG1hwwwfwNAE1lpmq2Ph1LQXdpcX6ymTzZoPkIMm7BCkEsF43dSfmOelblcnrl9qV54utPDlhqR0tXsnvXuo0R5X2uECKrqVxzknBPTp3w9G+JN5cW0ltNpLzXlvpM1/5nnKi3HlTNC3bCk7S3tQB6RXIHwQx1PTdSF7AL2yu5J/NFqcyo3m4jPz/wAPnyYPuOOuWa348XStZsLGKxW4SdrcTyCcZiE0gRcKAe7A/NtBHQk8VZiL23xQmhF1dNHd6T53kNIWjVklClgCflOHHAwOuc8YAMqw+Gz2GsvqSa0zyPZT2j74Cxk8zne2XwGyFJ2hQcdBmrF14EvruZ7h/ELRXL6WummWC1CHCyB933j1xtI9CcEZrS0M6kdb8S/a7gM4njFtD5peOJPKUggEAgkkkiub8P6/451LwYNXVtBurhoTNHCFkV2AZgQQDjOBge/WgCrqXgXWdM0aa3s9QlvTfatBeTPbWkcTWuxR+8RdwzykY4YEDJHNS2ngG48R6TZDX1jgk0yWWGxWWyiffbtt3GSNi67iVypByOCckkHqvDOuX/iC5v71UtToW5Bp08e7zJxtBZmB4ABJXscg56VS8WXDz+JtA0O4u57XSr9bhrhoWaMytGqlIvNXBTOWbggnZjvQBbPg+JLjSJrbU7y3OlW7W9sqJEQFYAHIKeiqOMAY6Vp3VpqMuvafcwXpisIY5RcwcHzmIATtkY+Y5yPTBzxwp8Tz6Ho62ehX1rc2ljpsl8b7WHctcgSMAiHIJxtbLHPVP72akuPiFqkMGsytb6fB9m+wTWa3DFDLFcY3Bvm+8vI4x0zigD0iuB8EeDLrTk+06010Lu0luUsk+0K8UUcrli6BVGCc4+YsRjjAOKmg8VazJqF+WOlrZ2etJprIVcSGNtvz53YzlwMYwcE8dKTw54o1LWdat2bUdGa0uDOj6em4XVs0bEDv82QATlVAyMZyKALNr8PrCCw1Sz1DVNQ1Kz1GQzzxXZiAWXIPmKURSGyo7446VaufCWka7aQvc3t5fqtwl1DM10XUOgIUqv3Mcntz3rI8Fajo91aeJ7K5u9OnWDU7l7lWkVg0fy5kdSxAXIPPC8U/4Y6vpX/CvLVYb+0YWSStOkUqsYV8xyNwH3RgZHtQBrxeDLGCyFpHfaksYkmk/wCPknPm/fBBGCpOTjHBORikj8C6FbSWb2cNxaPawfZVa2uZIy8OSdjEHLDJJ9Qehrcsb621OxgvrOZZradBJFIvRlPQirFADIokhhSKMEIihVBJOAOByax4vCWiwaj9uitpUn+0G6wtzKE809W2btuT9K26KAMBPBXh6N3ddOALwyW4HnSYSOQ5dUG7CAn+7ipV8J6IoA+xllFmbEq80jBoOf3bAt8w+Y4znHatqigDml8AeGUsWsxp8nkmRZebqYsGUEAht+4cEjAOOaWPwF4Zi0kaWmmlbRZjOqi4l3I5GCVfduXI6gHBrpKKAMa78JaDfWdjaT6XAbexObVEBQRcYwNuOCOCOh7g1rQwx28KQwxrHFGoVEQYCgcAAdhT6KAMqLw1ocGqtqkWkWSX7OZDcrAokLEEFt2M5IJ596hufCWiTm5mj061tr2cu32yGFVmSRlKmRWxkNgnmtuigDz2z+Flta6ffWq3dtF9psBZbrPT0gzyCXkwf3hJUZB4wWH8RrZ8LeCLLw5BfK4tLh73YJlhsY7eIqudo8teCfmOSc9vSupooApyaTps0EUEmn2jwxZ8uNoVKpnrgY4qWaytbiFIZraGWKMgojxhlUjoQD0xU9FAEZt4WuFuDDGZ1UqshUbgD1APXFQx6bYxXTXUdlbJcsSTMsShznrzjPNWqKACjFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAV7//AJB1z/1yf+Rrz74E/wDJKNP/AOu0/wD6MavQb/8A5B1z/wBcn/ka8++BP/JKNP8A+u0//oxqAPSaKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAwPEfh2TWbnTL+zvPsepaZMZbeVk3oQw2urrkZBX3BBxVC88G3txNbXkPiGe31JLZrS4uVtYiJ4i27GwjCkEnBH45rrqKAPO7r4VJJIy2msvb2ojjjiha2WTYEtmthyTydjnr3xT7X4ZTWlzFcReIZY3jlkkAjs41X53ikKgc4AaFTx646V6DRQBxWmfDXTNJ1qXULSZYvnleBY7K3V4zIGDAyBNzAb/lGeMAHIqXSPAUemrpyT6rcXcdnpcml7GjRA8Tsp7DIICqOvb657CigDmk8HKmmJp41zVTbRpDFEhaLaiR9Fx5eGBGA24HIFaPh/QLLw3pn2CwUrCZHlIwqjcxycKoCqPZQB+Oa1KKAMnWtAg1prSVrm5tLq0cvBc2rhZEyMMPmBGCODx9MVRm8DaPcSSvMbt/tCRR3INwxFyIjlPN/v+hz1HByK6SigArnZfBWky3N/KWvVjv/ADftNul3IsMhkTY5KA4yR+R5HNdFRQBzreCdGkXbOlzOP7P/ALN/fXDsfJ3bu5+9kD5uvA54rQ0jQrPRVk+zPdSyShRJNdXMk8j4zjLOSeMmtKigDL1rw/Ya9FGt2sqTQ58m5t5Wimiz97bIpDAEDBGcHvWTa+BtOn0eysdctrS+ayRoIZI4jCDESPlYBsNnaNw6EjOBXVUUActN8OPCNwUMmixHYqKAJHUYThcgNyQAACeeB6Vcl8HaDNrqa3JYBtRjKlJ/NfK7cYAG7GOBxjFbtFAGDYeDPD+may+r2eniK/csWm81yTuznILY7ntxSS+GoLFbq58N2umaZqlwfnums9+4E5YEKynk89cZ5wcmt+igDP0PSINB0W10y3Z3jgXG9/vOxJLMfcsSfxqbUNMsNWtGtNSsre8tmIJiuIhIhI6HB4q1RQBTn0nTrqG3huLC1mityGhSSFWERHQqCOMe1SzWVrcSCSa2hkcDaGeMEgemT25qeigCs2n2T799pbtvIL5jB3EdCeOcVKlvDHM8yQxrLJje4UBmx0ye9SUUAV49PsoQ4itIE3rtfbGBuHoeORSw2drbo6Q20MaP95UQAN9cdanooAbHGkUaxxoqIowqqMAD2FOoooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigCvf/wDIOuf+uT/yNeffAn/klGn/APXaf/0Y1eg3/wDyDrn/AK5P/I1598Cf+SUaf/12n/8ARjUAek0UUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFNeRI0Lu6qqjJJOABQA6iqD65pEUjRyarYo6kqytcICCOoIzTf+Eg0X/oL2H/gSn+NAGjRWd/wkGi/9Bew/8CU/xo/t/Rv+gvYf+BKf40AaNFZ39v6N/wBBaw/8CU/xo/t/Rv8AoLWH/gSn+NAGjRWPd+LPDljGJLrXdNhQ93ukHp7+4oXxXoLorpq1qysMhlfII9QaANiisj/hKND/AOgpbf8AfdH/AAlGh/8AQUtv++6ANeisC68a+HbMAy6irZBP7qJ5ehA/hU+o/X0NU/8AhZHhb/n+uf8AwX3H/wAboA6uiuU/4WR4W/5/rn/wX3H/AMbrUi8S6fNGJI01BkPQjTbj6f3KANeiufvfF1pZlAuma5c7s8waVO2365UVV/4Tu2/6AHib/wAE83+FAHVUVyv/AAndt/0APE3/AIJ5v8K0IfERnhSVNF1cK4yA9sEb8VZgR+IoA2qK5+78S3duEMHhjWrrOciNYV2/XfIP0qr/AMJdqf8A0JHiD87X/wCPUAdVRXK/8Jdqf/QkeIfztf8A49WmuraiyBv+EdvhkZwZoMj/AMiUAa9FZP8Aauo/9C/ef9/4P/i6P7V1H/oX7z/v/B/8XQBrUVk/2pqP/Qv3v/f6D/4uqFtrHiqa6WOXwnDbxEn97JqiED6hUJoA6WisaG98QyJufRbKI5xtbUST9eIjUn2nXv8AoFWH/gwf/wCNUAatFZX2nXv+gVYf+DB//jVRXFz4l8h/s2l6X52Pl83UH2598Q5oA2qK5X7R4+/6Bnhv/wAGE/8A8Zo+0ePv+gZ4b/8ABhP/APGaAOqorn7STxhJv+22uhwYxt8m4llz65yi4/WrP/FRf9Qv/wAiUAa9Fc1cQ+N3nZra/wDD8UR+6klnM7D6sJRn8hUX2fx9/wBBPw3/AOC+f/49QB1VFc1b2/jfz0+06poHk/xeVp8278MzYrQ+za9/0FbD/wAF7/8Ax2gDVorBvdO8S3MSrB4htbRg2S8em7iR6fNIRVL+wfF//Q6p/wCCmP8A+KoA6uiuWj0LxYHBk8Zhk7hdKiBP45Naf9laj/0MF5/34g/+IoA1qKyf7K1H/oYLz/vxB/8AEUf2VqP/AEMF5/34g/8AiKANaishtJ1FlI/4SG9GRjIhgyP/ACHVS08MXtu7NP4r1u6UjAWRoFAPr8kQNAHRUVjroMqjB1vVWOScmVPXpwnbpS/2G/8A0GdU/wC/q/8AxNAGvRWR/Yb/APQZ1T/v6v8A8TR/Yb/9BnVP+/q//E0Aa9Fc7d+EY751ebXNeUqMDydQeIfiEwD+NV/+EEtv+g/4m/8ABxN/jQB1VFc5beDbW28zOra/NvXb+91ac7fcYYc1f/4R+y/57aj/AODK4/8Ai6ANSiuZufAPh28uHuLm2u5Zn+87ahcEnjH/AD0qL/hW/hb/AJ8bn/wYXH/xygDq6K5T/hW/hb/nxuf/AAYXH/xyprbwB4ZtJ1mj0+RnXOBLdzSLz/ss5B/KgDpaKzrbQNJs7hLi2sIIpkztdVwRxitGgAooooAKKKKACiiigAooooAKKKKACiiigCvf/wDIOuf+uT/yNeffAn/klGn/APXaf/0Y1eg3/wDyDrn/AK5P/I1598Cf+SUaf/12n/8ARjUAek0UUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQBl6z4d0fxCkKavp8F4sJLRiUZ2k9cVk/wDCtfBn/QuWP/fH/wBeuqooA5dPhx4NjkV18O2IZSGB8vPIrSXwt4fSMRjQ9N2+htUP9K1qKAMY+EPDLEk+HdJJPJJso+f/AB2k/wCEP8Mf9C5pH/gDH/8AE1tUUAYv/CH+GP8AoXNI/wDAGP8A+JrQg0ywtYEgt7G2hhQYWOOJVVR7ADirVFAEP2S2/wCfeL/vgUfZLb/n3i/74FTUUARC1tx0giH/AAAVKAAAAMAUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQBXv/wDkHXP/AFyf+Rrz74E/8ko0/wD67T/+jGr0G/8A+Qdc/wDXJ/5GvPvgT/ySjT/+u0//AKMagD0miiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACisvWdP1K/SEadrc2lshJdo7eOXzB2B3g4x7Vk/8ACOeJ/wDoebz/AMF9t/8AEUAdVRXMQ+H/ABGk6NN41vZIwcsgsbZdw9M7OK0/7KvP+hg1L/vi3/8AjVAGpRWX/ZV5/wBDBqX/AHxb/wDxqo5tEu54jGfEWqoCQcoLdTwc9RFQBsUVzEXg6SOTe/inxFKMg7XukA6g9kHpj6H1wa0P+Efh/wCghqn/AIGyf40Aa9FZH/CPxf8AQQ1T/wADZP8AGg+HoSCDqGqc/wDT9J/jQBr0VzMvgXS55DJJe65uOB8usXKjgY6B8Uz/AIQDSP8An913/wAHV1/8coA6miuat/A2k286yi51mQr/AAy6vcup+oMmDV1PDGmIgXF4cd2vpifz30AbFFczc/D7wteztPdaUs8zYzJLNIzHHA5LVF/wrTwd/wBAOD/vt/8A4qgDq6bJIkSb5HVFGBuY4HPArmIvhx4QhlSVNDt9yMGGWYjI9icGtN/C3h+Rdr6FprL6NaIR/KgC5JqenxPskvrZGGDtaVQeeR3pn9r6Z/0EbT/v+v8AjVB/BnhaRtz+GtHZvVrGIn/0Gk/4Qnwn/wBCxov/AIARf/E0AaH9saZ/0EbT/v8Ar/jR/bOl/wDQSs/+/wCv+NVrTwv4fsJTLZ6FpltIV2l4bSNCR6ZA6Vd/s2x/58rf/v0v+FAEf9s6X/0ErP8A7/r/AI0f2xpf/QSs/wDv+v8AjUn9m2P/AD5W/wD36X/Cj+zbH/nyt/8Av0v+FAGa3jHwyswhPiHS/NIUhPtabjkZHGe/apf+Eo0H/oMWP/f9f8a0Es7WI5jtoUOc5VAKmoAyf+Eo0H/oMWP/AH/X/Gj/AISjQf8AoMWP/f8AX/GtaigDn7nxv4atbZbiXV4DGx2jywztn/dUEjp6VT/4WV4R/wCgsf8AwFm/+IrrKKAOT/4WV4R/6Cx/8BZv/iKP+Fl+Ef8AoLH/AMBZv/iK6yigDFh8V6Tcb/Ja8k2NtbbYTnBwDg/J6EH8ar3njPT7SRU+wa3PkZ3QaTcOB7EhOtdFRQByv/Ce6f8A9AjxH/4Jbn/4ij/hPdP/AOgR4j/8Etz/APEV1VFAHO2njC2vWKw6TrgI/wCeumSxD83Aq3/bw/6BWqf+Ax/xrXooA52fxVPFDG6eGNemZiQY0gjDJ7ndIB+RNV/+ExvP+hM8S/8Afq3/APj1dVRQBz9n4kvb1nA8Ka3BtAOZ/s6A/T97Vv8AtW+/6F/UP+/tv/8AHa1aKAMr+1b7/oX9Q/7+2/8A8do/tW+/6F/UP+/tv/8AHa1aKAOfuda15Z40tPClxLGwO6Sa9gj2n6BmzVr7Zrv/AEB7T/wPP/xutaigDJ+2a7/0CLT/AMDz/wDG6Ptmu/8AQItP/A8//G61qKAMaS88Q+U/laPYmTB2h79gM9s4j6Vn/bfHf/QD0D/way//ABiupooA5b7b47/6Aegf+DWX/wCMUfbfHf8A0A9A/wDBrL/8YrqaKAOdiufGLeV5umaKmc+Ztv5W289v3Qzxz29PerMreJjE4ij0lZCp2s8kjAHsSMDI9sitmigDlnj8el2KXXhtUz8oa2nJA9zvGaTyvH//AD9+Gf8AwFn/APjldVRQBz1lD4xMjfb77QlTHy+RZzMc++ZRV3yNe/6CWm/+C9//AI9WpRQBl+Rr3/QS03/wXv8A/HqPI17/AKCWm/8Agvf/AOPVqUUAZT22vsjBdU05SRgMNPfj3/11U7bSPEabPtXigS43bvK0+OPPTbjJbGOc9c5HTHPQ0UAZ1tY6hDcJJNrE08YzmNoI1DceoGa0aKKACiiigAooooAKKKKACiiigAooooAKKKKAK9//AMg65/65P/I1598Cf+SUaf8A9dp//RjV6Df/APIOuf8Ark/8jXn3wJ/5JRp//Xaf/wBGNQB6TRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRUcs8UABllSMHgF2AzQBJRVf7fZ/8AP3B/38H+NJ/aVj/z+2//AH9X/GgCzRVb+0rH/n9t/wDv6v8AjTW1TT0Rna+tlVRkkzKAB69aALdFZF14r8O2Uoiu9f0qCQqGCS3kanB6HBPSof8AhNvCf/Qz6L/4Hxf/ABVAG7RWF/wm3hP/AKGfRf8AwPi/+KqWLxZ4cmTfFr+lyLnG5LyNhn8DQBsUVi3Pi7w7aW7zy63YeWgyds6sfyGSazv+Fl+Dv+g5B/3w/wD8TQB1dFcp/wALL8Hf9ByD/vh//iat2fjfw9qAJsr9rkL18m3lfHT0X3H50AdBRWIfFmkh5EDXjNGgdgtjOTg5wPudeOlU5fHekxSvGbTW2Kkjcmj3TKfoRHyKAOnorlv+E/0j/ny13/wS3X/xupofGunXCO8djrRCFQ27SbhepwMAoM/h070AdHRWOviKBwSNP1Xgkc2Mg5Bx6Uv/AAkEX/QP1T/wCk/woA16KyP+Egi/6B+qf+AUn+FQXficW0PmRaJrV02ceXDZkN9fnKj9aAN6iuY/4TGYzGNfCfiNhkgP9mjCn35kFaKaxeSRq48PaoAwBwzW4I+o83igDWorL/tW8/6F/Uv++7f/AOO0f2ref9C/qX/fdv8A/HaANSiuVPiLxNnjwNeY/wCwhbf/ABdH/CR+J/8AoRrz/wAGFt/8XQB1VFcr/wAJH4n/AOhGvP8AwYW3/wAXWmL7WyAf7EiHsb0cf+O0Aa9FYNzf+Jgh+yaDZO+BgTaiUHX2jPaqf9peOP8AoWtG/wDBw/8A8YoA6qiucs7/AMXyXkKXmgaVDbFwJZI9Ud2Ve5CmEZPtkV0dABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFAFe//wCQdc/9cn/ka8++BP8AySjT/wDrtP8A+jGr0G//AOQdc/8AXJ/5GvPvgT/ySjT/APrtP/6MagD0miiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAK9292kQNnBBNJu5WaYxgD1yFbn2xVPz9e/6Bum/+DB//AIzWpRQBy8svjvzn8mz8OCLcdge7nLY7ZxH1pvm+P/8An08M/wDgVP8A/G66qigDlfN8f/8APp4Z/wDAqf8A+N1JA/jhnIuIPDsa44Mc07nP0KiumooAxJI/E7J+7utIjbaRzbyMAccH744H6+1UPsXjv/oOaB/4Kpf/AI/XVUUAct9i8d/9BzQP/BVL/wDH6BZeOsjOuaDj20qX/wCP11NFAGOln4g2DfrFlvxztsDj/wBGVnz6F4plneRPGTQoxyI00yEqvsM5P5k11FFAHKf8I94r/wCh4l/8FkH+FH/CPeLP+h4l/wDBZBXV0UAZI0q/wM+IdQJxyfKt/wD41S/2Vff9DBqH/fq3/wDjVatFAGV/ZV9/0MGof9+rf/41VOTwzdzXouJPFOubQRmFHhSNsdsCIHn2IroaKAMj+wR/0FNU/wDAk/4Uf2CP+gpqn/gSf8K16KAMj+wR/wBBTVP/AAJP+FZ83geynmeV9W8Qb3OTs1e4QfgFYAfgK6eigDlf+EC0/wD6C/iP/wAHVz/8XT4vAunxSpJ/aniB9rA7X1m5Kn2I38iunooAyT4c08ggtfYP/UQn/wDi6yf+Fa+Ef+gSf/Aqb/4uusooA5P/AIVr4R/6BJ/8Cpv/AIuj/hWvhH/oEn/wKm/+LrrKKAMCz8FeG7GMpDpFuQf+euZD+bE+tWf+EX0H/oD2P/fhf8K1qKAMn/hF9B/6A9j/AN+F/wAKin8HeGbpQtx4f0yZQcgS2qMAfxFbdFAHO/8ACA+D/wDoVdF/8AIv/ia1f7G0v/oG2f8A34X/AAq7RQBS/sbS/wDoG2f/AH4X/Cj+x9L/AOgbZ/8Afhf8Ku0UAUv7H0z/AKB1p/34X/Cj+yNM/wCgdaf9+F/wq7RQBS/sjTP+gdaf9+F/wqzBbwW0fl28McSZztjUKM/QVJRQAUUUUAFFFFAEUFutv5u1pG8yQyHfIWwT2GTwPYcVLRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQBXv/APkHXP8A1yf+Rrz74E/8ko0//rtP/wCjGr0G/wD+Qdc/9cn/AJGvPvgT/wAko0//AK7T/wDoxqAPSaKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKoatrFjodn9r1CSSODcE3JC8mCenCAn8aw/wDhZHhb/n+uf/Bfcf8AxugDq6K5+x8a6HqRcWUt7OY8FtmnXBxnp/yzovfF1pZlAuma5c7s8waVO2365UUAdBRXK/8ACd23/QA8Tf8Agnm/wo/4Tu2/6AHib/wTzf4UAdVRXNW/jOG6lEceheIQx7yaZJGPzbAq9/bj/wDQG1T/AL9L/wDFUAa9FcxN4r1GOZ0Twbr0qKcCRfswDD1AMwP5imf8Jdqf/QkeIPztf/j1AHVUVyv/AAl2p/8AQkeIPztf/j1X7fW9SuIFlPhnUod2fklltww+oEhoA26Kyf7V1H/oX7z/AL/wf/F0f2rqP/Qv3n/f+D/4ugDWorJ/tTUf+hfvf+/0H/xdU7XVfE9xcOkvhiC2jAJWSXU1O7ngYVCQf85oA6Kisr7Tr3/QKsP/AAYP/wDGqPtOvf8AQKsP/Bg//wAaoA1aKxLq58T+Qfsml6V52RjztQk2+/SHNUPtHj7/AKBnhv8A8GE//wAZoA6qiuV+0ePv+gZ4b/8ABhP/APGau2r+K3hzdw6NDLk/LFLLIMfUqv8AKgDdorBu08WyRqLO40WF88tLDLKCPTAZcfXNU/s/j7/oJ+G//BfP/wDHqAOqorlfs/j7/oJ+G/8AwXz/APx6pYLfxt5h+06poHl7TjytPmznt1m6UAdLRWSLbX8DOq6fnvjT3/8AjtL9m17/AKCth/4L3/8AjtAGrRWS1rr5UgatYAkcEae3H/kWssaF4tCYPjMFsjn+yosY5yMZ+lAHVUVk/wBlaj/0MF5/34g/+Io/srUf+hgvP+/EH/xFAGtRWT/ZWo/9DBef9+IP/iKo3HhnU7iQuPGGtQ5OdsSWwA4AxzEfT9TQB0lFcr/wiOp/9Dv4g/K1/wDjNH/CI6n/ANDv4g/K1/8AjNAHVUVyv/CI6n/0O/iD8rX/AOM1ctfDlzBEUm8SazdNnO+R4lIHp8sYH6UAb1FYdz4a+1wGGTW9ZVSQcxXfltx/tKAf1qj/AMIJbf8AQf8AE3/g4m/xoA6qiuV/4QS2/wCg/wCJv/BxN/jWlD4as4Y9hutVk5J3SancE8nOPv8AbpQBsUVz174J0LUnR7yK8nZBhS+o3BwP+/lVf+Fb+Fv+fG5/8GFx/wDHKAOrorlP+Fb+Fv8Anxuf/Bhcf/HKvW3g3w/axlI9NQgkH967SHgAdWJPb+vUmgDdorI/4RfQ/wDoF23/AHxR/wAIvof/AEC7b/vigDWJCjJIA9TTDcQDrNH/AN9CsqTwl4fmQxy6RaOh6q8YIP4GqyeAfCEcqyr4Y0kSK24N9kTIPXPSgDcN1bjrcRf99ij7Xbf8/EX/AH2KoQeGNAtYzHBomnRoWLELbIBk9T0qT+wNG/6BNh/4DJ/hQBb+123/AD8Rf99ij7Xbf8/EX/fYqp/YGjf9Amw/8Bk/wo/sDRv+gTYf+Ayf4UAMufE2gWc7QXWuabBMuMxy3casM8jgmof+Ew8Mf9DHpH/gdH/8VVn/AIR/Rf8AoEWH/gMn+FH/AAj+i/8AQIsP/AZP8KAIF8W+G3OE8Q6Sx9Bexn+tOfxRoEcbO2t6cFUEn/SkPA/GrMGj6ZbOXg060icjBaOBVOM57D1A/KrmB6CgDlv+FleDP+hjsf8Avs/4Uf8ACyvBn/Qx2P8A33/9auqooA5ZfiP4Oc4TxDZMcE4DE8AZJ6elaKeKdGljWSO6Z0YBlZYJCCD0IO2tiigDJHiXSi6Ks0pZ2CAC2k6k4H8PTnr2rWoooAKKKKACiiigAooooAKKKKACiiigAooooAr3/wDyDrn/AK5P/I1598Cf+SUaf/12n/8ARjV6Df8A/IOuf+uT/wAjXn3wJ/5JRp//AF2n/wDRjUAek0UUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFAFe/8A+Qdc/wDXJ/5GvPvgT/ySjT/+u0//AKMavQb/AP5B1z/1yf8Aka8++BP/ACSjT/8ArtP/AOjGoA9JooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAK9/wD8g65/65P/ACNeffAn/klGn/8AXaf/ANGNXoN//wAg65/65P8AyNeffAn/AJJRp/8A12n/APRjUAek0UUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUVT1bUodH0e91O4DGG0gedwoySFBJx+Vc1oev+I9cgnEmnadaGbTory0Zbp3wZd20P8AIOgXnHce/AB2NFeYaRr2uaV8L/Dc1gsN5f3l4tnLLqE8jhS8jrvJ6kZA4yMA12HhjXp9X0+7/tCKGC8sLp7O5MLEws64+ZGPYgjjqDkHpQBv0VwHi/4gN4P16W11C4s4LSazElm7QSOxlyQd+CBsBAzjn5xgcVUufGXi3TYvtd7DoTWyRWczxJ5qyus7bCFySAVOeue30oA9KooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAK9/8A8g65/wCuT/yNeffAn/klGn/9dp//AEY1eg3/APyDrn/rk/8AI1598Cf+SUaf/wBdp/8A0Y1AHpNFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAIQGUqwBBGCD3rjLDwHDp/ifU5oY7WPQL+xFvJZI0gJcMTuOTgDBYDbjHYd67SigDh9X+G+nvoKaXoMdtYRfbYruVJ1kmjl8s5Cld4OCcZ5FdPNoOlT6PJpMlhb/YJeXt0TajHO48D35rRooAp3mk6dqIUXthbXIVGjUTRK+FbGQMjodq8ew9KyT4Ut5/GU+v3v2a7zBHFbRTWqM9sylslJDyAdxyK6KigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiimsxBUBCwJwSMfLx1P8AL8aAHUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFAFe/8A+Qdc/wDXJ/5GvPvgT/ySjT/+u0//AKMavQb/AP5B1z/1yf8Aka8++BP/ACSjT/8ArtP/AOjGoA9JooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAK9/wD8g65/65P/ACNeffAn/klGn/8AXaf/ANGNXoN//wAg65/65P8AyNeffAn/AJJRp/8A12n/APRjUAek0UUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFAFe/wD+Qdc/9cn/AJGvPvgT/wAko0//AK7T/wDoxq9Bv/8AkHXP/XJ/5GvPvgT/AMko0/8A67T/APoxqAPSaKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigCvf/8AIOuf+uT/AMjXn3wJ/wCSUaf/ANdp/wD0Y1eg3/8AyDrn/rk/8jXn3wJ/5JRp/wD12n/9GNQB6TRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRXIn4n+C0uJ7eXxBaQzQSSRyJKSpDISG6jnkHHr2pZPiV4XTQbfWUvzLbXNwba2VIyHnkBxtVTjv3OByOaAOtorDg8U2T+II9Cuobmx1KWEzww3Cr+9QdSrIzKcemc8Zxism6+Knguzs7a6n1uJY7iZ4VARi6spw25QMqB6kAcigDsqKxv+Es0A2l9dpq9nJb2Eay3MscoZY1YEqSRxyBxjrWfa/ELw7dTaTGtxPH/AGuSLB5raRFnx6EjHcdfUUAdTRWPrHijSdCvLKyvZ2+2XzlLa2hjaSSQjqQqgnA9TxTNH8XaJrmm3d/Y3oaCyZ1uvNRo2hK53B1YAjGD1oA26K4yD4s+Bp7IXS+IrVU2s2x9yvwMn5SM59PXtV2H4g+F5tMk1AarFHClp9tKygpJ5JLAMEOGOSvHHOV/vDIB01Fc3pXj7wzrVlZ3djqkbx3lz9khDKys0uCdu0jI4HXp0rI1H4u+FNNvbiBpb2eG1k8q6vLa0eSC3fsHcdycgYzQB3dFY2q+KtE0Xw8uvX9/HFprqjJNgneG5XaBySRzgVjaN8U/B+vapDptjqv+lzjMSTQSReZ6BSwAJP60AdlRRRQAUUUUAFFFFABRRRQBXv8A/kHXP/XJ/wCRrz74E/8AJKNP/wCu0/8A6MavQb//AJB1z/1yf+Rrz74E/wDJKNP/AOu0/wD6MagD0miiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKRmCqWYgKBkkngClqOeFLi3kgkzskUo2PQjBoA8sstGu/BHw/vLzTB4f16C2aa7MjQlWkXJZhvBYMw6duBjtVK507S/i74L0fWbNotD1mGZ/sEUkg8syKwLDaPvA4ByBke/e1/wrHxfpvhy48MaJ4ut4NDkLhFltP3wR8lkLDtyeRz9OlX7P4M6KfBmlaLqM873mns8sd9bN5bpI5yduc8ZxgH0oA4j4l3Pja18beCHv59MW4+0gWkdi8mwyb4wxcsAcNuAwO2R3ruda0P4f+AtDiN/omn3tzcTMtuLuGJprmViWwZGACjnqcADH46emfDtIvE8PiLXdau9c1K1Ux2jXEaRpAueMKgALDJ575zgcUfEP4eQ+PV0kyXfkHT7jzCjLlZUYrvU4IIOF4IoA898Y6Lqvhj4b6/qv9i6dZnVrm2WbTbRR5VnAmcElcB2LY3cY+bvirfxItpZvgT4ZvIbTzXtIrKZpEX5oV8oAkccDOB1HavX9X0ix13SLjStRh86zuE2SR7iuR16jkcgVwUnws1K8tdP0fUvFtzd+HbGRGSxNsEaRFPyxvIrAkAYGfbp0oA5TSryfUP2oJZbhHVRZ/uElTBRDArAfXLH9aVkH/C6fiBo0L2tnb6horB5JDsjR2ijG9j0HMhJPvXoHib4fRav4msPFGl3i6drtnkCdofNSVdpUBlyOQCcH+fGKNj8MpJ9P8RnxDq323VdeVYri7ghEflxrwqoOR2GfoPTNAGPEt98O/h9HqGp6F4d1Sy022jSOWylbzJQ7qN5LoRg5BODyfatS30XwV4qsIPiBq1tC1o9ggEV0wMNqi53DHTIJYfh0zWRcfDTxtP4K/wCERfxPpjaUI1iXdZt5m1WDL8271A/Cuvk8B2zfC/8A4QtLgxR/ZBB56qPv53Fse7cn60AeYaXpOjeOLmfVfBfhwaRZ6MbiSO+RxHLdztEdiKP4QG2tkngdMEnFj4LQQ3Xwd8TrcRJKslxcBxIobd+4Q85616d8PvCb+C/B1tok08VxLE8jvLGm0OWYnofYgfhXNar8MdVt2u7fwd4iOiabqLO99aGJZFLNwTHxlPl4wCOgoA8ps9Ov/E3wS0LTbN5rjVU1qVLC2BGHUIWYZPAC5JySB1p8nj3WL/VdI8M+NNMtrO8ttTt3bUHg8qW3RXBAAAxjBIyOMH8a9nv/AIfNaeGdH0/wrf8A9l3ukOWtbmVTKPnBEu5ScEtuJzjjtisXxD8OfE/jS70tPEutaXJp1nOsskNpaNG8mAA3zEkjIz7c+wwAep0UAYGBRQAUUUUAFFFFABRRRQBXv/8AkHXP/XJ/5GvPvgT/AMko0/8A67T/APoxq9DvEaSynRBlmjYAepxXF/CHRdR8P/Dqy07VbV7W7jllLROQSAXJHT2oA7qiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAP/2Q==",
+ "image/png": "iVBORw0KGgoAAAANSUhEUgAAAvoAAAPoCAIAAAAgFM2mAAEAAElEQVR4AezdeaB91fw+cA2SIWODsRBCipSkJJmJQgNFmTIlVMgQZShziQyJZMxchkSGMoRKRBoQSUSSKaGMvxfvb8v+nXPv+dx7P+feu++9z/nj3nXWXnvttZ61z34/63m/19pXu1o+QSAIBIEgEASCQBAYKwKf+9zn/t2nz4pj7V0qCwJBIAgEgSAQBIJA7xAI3endkKRBQSAIBIEgEASCwHgRWPl73/veeGtMbdNFYKWVVtp7773vf//777DDDu94xztWXXXV9ddf/8c//vE73/nOpz3taZ///OcvueSSFVf8HzG98sort9hiixe96EUf+9jH/va3v62yyiprr732+eeff9xxxz31qU/dZJNNZLY2qNzpe+2117rrrnvQQQf9/e9/r0PXuMY1jj32WH+PPPLILbfc8upXv/qJJ57oax1Vw1ZbbSX9la98hRi5yy67fOtb3/rpT3+qtlZzEkEgCASBILAIEPj+97/fTMMi6M5kXViBMZvsWPKDQBAIAkEgCASBRYwADmDSe9lll3Un1TPur5nzueee+5a3vEUNYnce+MAHzriqsZ+48thrTIVBIAgEgSAQBILAgkBghRVW2H333cfY1C9/+ctFd8ZY51iq+p+LZCzVpZIgEASCQBAIAkEgCPQNgdCdvo1I2hMEgkAQCAJBIAiMGYHQnTEDmuqCQBAIAkEgCASBviEQutO3EUl7gkAQCAJBIAgEgTEjELozZkBTXRAIAkEgCASBINA3BEJ3+jYiaU8QCAJBIAgEgSAwZgRCd8YMaKoLAkEgCASBIBAE+oZA6E7fRiTtCQJBIAgEgSAQBMaMQOjOmAFNdUEgCASBIBAEgkDfEAjd6duIpD1BIAgEgSAQBILAmBEI3RkzoKkuCASBIBAEgkAQ6BsCoTt9G5G0JwgEgSAQBIJAEBgzAqE7YwY01QWBIBAEgkAQCAJ9QyB0p28jkvYEgSAQBIJAEAgCY0YgdGfMgKa6IBAEgkAQCAJBoG8IhO70bUTSniAQBIJAEAgCQWDMCITujBnQVBcEgkAQCAJBIAj0DYHQnb6NSNoTBIJAEAgCQSAIjBmB0J0xA5rqgkAQCAJBIAgEgb4hELrTtxFJe4JAEAgCQSAIBIExIxC6M2ZAU10QCAJBIAgEgSDQNwRCd/o2ImlPEAgCQSAIBIEgMGYEQnfGDGiqCwJBIAgEgSAQBPqGQOhO30Yk7QkCQSAIBIEgEATGjEDozpgBTXVBIAgEgSAQBIJA3xAI3enbiKQ9QSAIBIEgEASCwJgRCN0ZM6CpLggEgSAQBIJAEOgbAqE7fRuRtCcIBIEgEASCQBAYMwKhO2MGNNUFgSAQBIJAEAgCfUMgdKdvI5L2BIEgEASCQBAIAmNGIHRnzICmuiAQBIJAEAgCQaBvCITu9G1E0p4gEASCQBAIAkFgzAiE7owZ0FQXBIJAEAgCQSAI9A2B0J2+jUjaEwSCQBAIAkEgCIwZgdCdMQOa6oJAEAgCQSAIBIG+IRC607cRSXuCQBAIAkEgCASBMSMQujNmQFNdEAgCQSAIBIEg0DcEQnf6NiJpTxAIAkEgCASBIDBmBEJ3xgxoqgsCQSAIBIEgEAT6hkDoTt9GJO0JAkEgCASBIBAExoxA6M6YAU11QSAIBIEgEASCQN8QCN3p24ikPUEgCASBIBAEgsCYEQjdGTOgqS4IBIEgEASCQBDoGwKhO30bkbQnCASBIBAEgkAQGDMCoTtjBjTVBYEgEASCQBAIAn1DIHSnbyOS9gSBIBAEgkAQCAJjRiB0Z8yAprogEASCQBAIAksWgTPPPLOffQ/d6ee4pFVBIAgEgSAQBBYeAoceemg/Gx26089xSauCQBAIAkEgCASBsSEQujM2KFNREAgCQSAIBIEg0E8EQnf6OS5pVRAIAkEgCASBIDA2BEJ3xgZlKgoCQSAIBIEgEAT6iUDoTj/HJa0KAkEgCASBILDwENhtt9362ejQnX6OS1oVBIJAEAgCQWDhIXDve9+7n40O3ennuKRVQSAIBIEgEAQWHgKHHXZYPxsdutPPcUmrgkAQCAJBIAgsPATOOOOMfjY6dKef45JWBYEgEASCQBBYeAjst99+/Wx06E4/xyWtCgJBIAgEgSCw8BBYd911+9no0J1+jktaFQSCQBAIAkFg4SGw995797PRoTv9HJe0KggEgSAQBILAwkNg22237WejQ3f6OS5pVRAIAkEgCASBhYfA1ltv3c9Gh+70c1zSqiAQBIJAEAgCQWBsCITujA3KVBQEgkAQCAJBIAj0E4HQnX6OS1oVBIJAEAgCQSAIjA2B0J2xQZmKgkAQCAJBIAgEgX4iELrTz3FJq4JAEAgCQSAIBIGxIRC6MzYoU1EQCAJBIAgEgSDQTwRCd/o5LmlVEAgCQSAIBIEgMDYEQnfGBmUqCgJBIAgEgSAQBPqJQOhOP8clrQoCQSAIBIEgEATGhkDoztigTEVBIAgEgSAQBIJAPxEI3ennuKRVQSAIBIEgEASCwNgQCN0ZG5SpKAgEgSAQBIJAEOgnAqE7/RyXtCoIBIEgEASCQBAYGwKhO2ODMhUFgSAQBIJAEAgC/UQgdKef45JWBYEgEASCQBAIAmNDIHRnbFCmoiAQBIJAEAgCQaCfCITu9HNc0qogEASCQBAIAkFgbAiE7owNylQUBIJAEAgCQSAI9BOB0J1+jktaFQSCQBAIAkEgCIwNgdCdsUGZioJAEAgCQSAILHEE3vjGN/YTgdCdfo5LWhUEgkAQCAJBYOEhcJ3rXKefjQ7d6ee4pFVBIAgEgSAQBBYeApdffnk/Gx26089xSauCQBAIAkEgCCw8BL73ve/1s9Er97NZaVUQCALLj8BZZ531l7/8ZYUVVhiu6t///vfVr371u9zlLhMeHS6fnCAQBILAVBB4zGMec+CBB06l5ByXCd2ZY8BzuSAwKwj885//XGmllfCbN73pTdKuseKKK37sYx/7wx/+MNn1Vl111Uc96lHXvva1MZ4Xv/jFa621VqjPZFglPwgEgSkiYCo1xZJzXGyF3rZsjoHI5YLAgkPgH//4x5e+9CV/EZ399tvvRz/6kfTf//73zTffXI7uXPOa10R6JuuX3/4VV1xx+umnX3bZZUjP9a9//de//vXXu971VLLlllv6OtmJyQ8CQSAITIbAl7/85a233trRz33ucw984AMnKzb3+VF35h7zXDEILC8CGMmpp55KMf7iF78ojdysvPLKu+2220Me8hD8Zptttim6M5XLnHTSSRSgc889V21qwJachTDtueee22+//SqrrDKVSlImCASBINBzBKLu9HyA0rwg8P8hwF2F6HzkIx/5/Oc/L/hml112IdI8+MEP5pbiw0J6/r/SU/7yr3/9S9nTTjvtrW9967Wuda1jjjnmN7/5zR3ucIfnPve5t7zlLe9zn/tMuaYUDAJBYEkj0Ft1J3RnSd+X6fwCQuBvf/vb3nvv/clPfvKXv/zl2muvfeihh970pjfdeOONh4WcP/3pT7/61a/IPKJz3vnOdx5//PHXuMY1Wk85sJ7ylKc86EEPuvLKK1Elh9TWjlbiBz/4wdve9rYPfOADv/3tb294wxve8573VM8aa6wxUCxfg0AQCAIDCBCJ3/e+98nsmzMrdGdgpPI1CPQRgc9+9rNvectbPvOZz2icsOJXvOIVw62k93zta1+zxxf559hjjx0uMGHO6quvzm9Fwnnc4x43UOCiiy56wAMecM4558jfdNNNtQH1GSiTr0EgCASBLgI87Pe///3lhO50YUk6CASBUQj89a9//e53v7vvvvvayuImN7nJK1/5yo022oioQ7ZxGu/V97///Ze//OXKyLn44ot///vfj6pu8mOCmtdZZx0V3uAGNxCwfNe73lXwsuLqFMj8xz/+caeddhLWI5PMI5B58ppyJAgEgSWNQG+dWTP09C/pwUzng8BcIbD//vsjH672pCc9Cc/oXlYQz2tf+9oPfehDFVzcPTSDNF7FgVUn3ute93roQx/6jGc8g8Prxv/9yOcRE8Fj8Zf4ZSLT3e52txlcJacEgSCw6BGw11c/+zjpItV+NjetCgJLBAGCzR577MGBtd1225199tkiaarjP/nJT7AN3nGEg4N8LFxnGNLjjjvOdak4HGR1CWHLLn344Yff/OY35+E6+uijL7300uETkxMEgsASR+ATn/hEPxFI7E4/xyWtWtII2E2HiMKFdOSRRz7xiU8sLIQVH3DAAR/+8IdJLFNEx0It0TZOFJVs9dYll1yCRfk6Yu/BgZrFQd/73vd23ebAEge94447nnDCCRxee+2116677jpwSr4GgSCwlBGwEuId73gHBBK7s5Rvg/Q9CCwbAYF+ts+xmw7xxnbs7YRnPvOZb37zm9vX0YnrXve6om1ufetbv+AFLyh5BnFBdCzX+vGPf8wLZrX5pz/96QsuuGB0PXVUODPG8+hHP1pCDvL0yEc+stxbVor19gXIU+laygSBIDBeBMyF+MHV2Te6czVPwHyCQBDoCQK2z8EedthhBzHI9sKpViEWXm41lT11RBwTXU488cQzzjhjmT0SrGOjnfvd735TfNjd9ra35cOqai1Q/9SnPmULZszMC5CXea0UCAJBYIkgIKCwHinoTq+6HLrTq+FIY5Y0AmiKnQMf8YhHkHYaEF/4whcoMVNkJEJ82olTTFh4JTZ5ivVvtdVWNuNpNVOJnGifeJHOLTOJIBAEljICt7rVrfpJdxKqPMXnfIoFgdlFQFCw8Bpc54Mf/GDtHCjUxjxJEM9UVjoIJcZ1nva0p023lauttprA5CnuqfOVr3xFsI4dDusqT3/6023rTCJ6+MMfLqZnupdO+SAQBILAnCEQujNnUOdCQWBSBE4++WTxv2Ji7KxTOyCLU0Z0dt55Z+rLpKd1DnitxAiuI3zHZsrqb2dIy6mwHoyHr93r06cShcPFZnPniiJSntiz++6789YL4mmVJxEEgkAQ6BsCoTt9G5G0ZykiICoZrXnve9+77rrrVv+tbsCBpojFs571rNvc5jYf/ehHP/7fD+rjjVd1LlFd7DPdyBvO73SnO9XmOt5HseGGG9pREMdCUxAd8TdeYkzmkTmVi4qbfsMb3lAl7XOo/qc+9anf+MY3pnJuygSBIBAE5gGBpexiTN+DQB8QeM5znuOX/653vas1hlgiCniKjwOe8vPPP9+2y93yQptRKBWW44l37EY3upECL3nJS2SSduoFWEKFavfke9zjHkiPQ5xT3XpGpC3yetOb3lRtxtWEPGuzLYIqJ3+DQBBYmggkdmfEYzOHgsDSRcD6poMPPpiW84QnPKFQEMRjiz/OrCmCYus/zxfRzVXeNjnWZ9lfxy7MfFVrrrmmfF4nUcbDFT75yU+mA3nP6De/+U3vzMJaNGYqS8BUxatFVbKCTJo7zIZAJCK+reGrJCcIBIGlg8B973vffnY2zqx+jktatSQQ8I6ql770pRxYz3/+86vDlm5yMImqmWL/H//4x+M3rbCAZWvFa2dCr9ZCXKxs9x4I5OmYY46RI7i4FZZAWXAjPix7NP/5z3/25lGFheZ0y4xOe59XBSnbz/CQQw4Re2Qn6NGn5GgQCAKLGIHubmG96mboTq+GI41ZWgiIm7FBzute9zr7AVbPxcRMMTZZeZoKd9Iqq6zSUDv33HO9XYtfjItKMM0KK6xgL0F75FQBC9q9Z5TTCstpp0igOJiKxE9/+lN/11577e7R0Wn8zNbPVYbYs/nmmx9xxBEzflPp6GvlaBAIAv1HwBOmn40M3ennuKRVix8B/ibbCZJbuK70FgV59rOfbcvj5ey5JeV2weHD4r3yGlHqDpfWne985zve8Y5CfG55y1t6FdfXv/71Wv9V17rwwgtL9VlvvfXk8HBtsMEGU2+GUOWvfe1rVV788plnnmkDoamfnpJBIAgsJgQ222yzfnYndKef45JWLX4EDjvsMJGML3vZy8T86i1/Fqlm6t2m3FSU8cAp3Fv8Sj//+c+PPfZYAT21+PxVr3rVfvvth1H97Gc/4zvjXK98Dfjd737n/eeIkUDj5z73uWrDhKzP4ghziYHKJ/xKy/FOie985zuObrTRRvbgsX7+y1/+8oSFkxkEgsDiRsBbhPvZwdCdfo5LWrXIEbAgnJupiI6u0lcsIZ9iny0pJwvtv//+1JrhnXJsVEhiQXRwDn6lqtMWPpxclT7llFNEJSM6vnJ7cV1VuLHAnbYK3UvXhTDTgXAXq7eW2TBvRz/vvPMUU3jTTTelJ1kXtsyzUiAIBIEgMGcIhO7MGdS5UBD4HwL2yMEnROrUgnBvxaq4mf+VmChlcx0lcRGni3EWZdwEGJJMrajyF7nhyVp11VW/9a1veQcFN5Y3hpKC6ElEF7vvCOIRtiyOx9WF/jzjGc+wNw+e1K6JRSFV9hLkhrdSzEbPt7jFLUbzHtJUbVooUHH99ddHpC6++OJWYRJBIAgEgXlGwCQvnyAQBOYSAS+FsEsN/nHqqae6LiVGhM3oBwGqQZ4RiTyinZaCv/GNb6wC/FaWffn46q+vPnWovv7n2FWfdmhE5Q615WMTNhXNoldVDQQkZWrjn9F15mgQCAKLDIGTTjqpHhF9e0Vo1J0JH93JDAKziMBFF11ETfEucX4flxHbO3otg1hmuwi+/e1vv/3tbz+iWTvttJO1UVWA6sNTVs4yfwktxCRsyVFf29H/lPjv1xHVtkMCgJ73vOe1rwMJpI3vDHOST0zCz7zDy/bNA8XyNQgEgcWNwC9+8Yt+djB0p5/jklYtZgS85EH3LGiqTopWprNM1mFvs+JLsqFOvTd0smIj8kXVeGn5Nttsg2CNKLbMQ0iSV6DXHtATFqbufPWrX3VIa+udEnImLJnMIBAEFisCwgr72bXQnX6OS1q1aBEQ1fue97zHVjckEJ0UWzPi5ZqCdWwPKEZnxnCQW4Qbe7eD615wwQXCdEZQq6lc5fWvf/0LXvCCyUo2+ed2t7udMlT6yUomPwgEgSAwlwiE7swl2rlWELjaJz7xiR/96Ef2thEsDA5xPCNA2WuvvZaH61i6JSrIXj6uVarMW9/61sZIRlx39CFereY1GyjJZVYOLBv5WA/f3FsDxfI1CASBxYqAV+L0s2uhO/0cl7RqqSAgWnmyrnpqEGMmOzqVfPspiwrCPwTotPL247H7Tvs6s4Q3iVq6NXyumpGhyud9O+200xK+M4xScoLAIkYg2wwu4sFN14LANBAQ0mtNVr3WChXwIs8JT/bWz2m9u2q4Ensrv/jFL0aYrDyXbsvCubS8V2u4/EDOH/7wB2vjvUhrIL++3v3ud3/AAx4w4aHawBDB8g52S9NtYzhhsWQGgSCwKBHo7U/+f3O+RYl7OhUEeoWASBrBOrw8XuYwumH2yJlsHRaGZNOdinceUYnNBm2Zg7XYwNCuOe09D0550Yte9P73v3+yc+2PLEDHRsne5GWDn8mK2Vmn+3bSgWLojkq46g444ICBQ/kaBILAIkagNmfvYQdDd3o4KGnSokUA+RCY3F7q6VUPE/p66jUOwygQS+yAbJtBTOIJT3iCNzagRIiLpez0m275YjlyPvCBDxx44IF2F3zsYx/bLTCw9P3yyy9Xs1AbexI+7GEPE99j84xHP/rRlCHUqntiS9OolnOpV6sqiSAQBBYNApaa9rMvoTv9HJe0akkggLX88Y9/HO6ql1h5tfhw/iWXXLLhhhtusskm++yzD+HES0Z/+MMf7rrrrt4A6r0QXf1GYA3usvrqq6vEdn/ilLvhOzK//e1vO7cuQQRChtRs9bi9eX75y1/Kt57LayW8raJeMVElB/62PZ27+SeccEJ7B3s3P+kgEASWAgK05H52M3Snn+OSVgWBiRHAMETkePmDV2J1S/A62VxHPE05zh/84Afzmnk7epVBQQbkH1uBeW+Xo5/61KdsYziwGJ4nS4XUHaHHI94d4SUYwx43vjCbKKrZYntbLS/nuvduH5MOAkEgCMwYgdCdGUOXE4PADBHwyqrRZ44oUIKK8J3yOnXrQWhQnPvf//7cW1ZF2dTY/oS27VlzzTV5wQbojhN/9atfiZj2ueKKK7r1qOFDH/qQV1LYyrmbP5zmdGuOue7Rgw8+2NeNN97YuzIGKu8WSzoIBIEgMGcIhO7MGdS5UBD4DwLUjmIDk8Hh1Z6vec1rJjta+YJ1rK7yhiwqzkBJ4srhhx/u7Z48WVjLPe95TzHFmI0gnpvf/Obdwvvttx932IDjic9r9913R5i4tywi65ZPOggEgSCwTAS+/vWvL7PMvBQI3ZkX2HPRJY0AUWR0/ycrcLOb3cyOxrZaXm+99X7/+9+LyLFBMzFmoDaPmz322IN/ijvpHve4hzXtXqflJecDoTarrbbawG6BNCH7ECrs5Q+2RRanfJe73GX0toSj3xs60LB8DQJBYNEjcOSRR/azjyv3s1lpVRAIAhMicNBBB62zzjqIiFhmr2jAYGzTbC3ViSee2C0vascuhUKh73Of+wg6Fkyz9tprb7HFFtaCtWKCnR//+Me/4x3v+MY3vlGZ0gKfaUt3u9vdvL5U/cSe9ddfv50ynBiO3VFGqPVwyeQEgSAQBOYRgdCdeQQ/lw4CM0GAACOC2PIHu/jY0+91r3vd0572tAG6o16MxwsorEIX2mzF+FlnnTX6JaOI1G677SY8ubtGfd11191zzz2n28rtt9/eKVaKfe5znxMbNN3TUz4IBIEgMHYE4swaO6SpMAgsAwE0ZRklRh62VMq2OtaHe/Gn92F5K5ZwH0HKw5v+2W5nq622outYh6XKAWcWl5kXmNf6LA6vHXfcUbxOl+s4BVWyv86I5ggJmuzoZZdd5tDAAvjJCic/CASBIDCrCITuzCq8qTwIDCJAYhFzM5g7ne+HHHJIt7iNCh/xiEf86U9/Ov7449daa63uIYvSqTXCfRw955xzBtQdtEmosjKCgU4++WT79Aht7p4+lXStOe+WtGH0hK/T6pZJOggEgSAwxwiE7swx4LlcELha21qQo2d4zbmImcneVFXYeQeFjwge/izvpZImwIjUsXOgxVYD+F500UVewC7i2DKugQhomhAaJGDZNoOEH74nL04nBfmoXP6hhx5qJflAhcv8akMgIdXLLJYCQSAIBIG5RCCxO3OJdq611BHAS4QYX3jhhQWE3ZDlCBnu4iIcZ99997VlTjezmxY7bFMc5OYGN7iBWOPa+YaDzMeycxLOwHvUrULnqxre7s8mgVZdeRkFdmUpFqdY21EQMfJOLvsWDqxd7zZjmemvfOUrylgatsySKRAEgkAQmG0EQndmG+HUHwT+hwAascsuu3hDp+CbER4fuwL+75yJUgQYL3w4//zz3/ve99q5mCCkFJ5017ve9ZWvfCX+hDBVpnz+JgqQJVcVwdPq05jb3va23m2+7bbbevl5y68EuWjCVVfdYnjSZLsI2rPn3e9+9/Wudz397Z6SdBAIAkFgXhAI3ZkX2HPRpYsAdmLLHPE3L3/5y2eMgk1xhCF7ZcTAjl6nnnoqWUg4jmVZba2WjQTf/va3Wy215ZZbtivSe0Qx86ZRm4a5DppilVYrPFnCGjGesu5RvjlL37s5SQeBIBAE+oBAYnf6MAppwxJC4CY3uYnecjz5y/Fkpfdw522lY83UcH43R+COtVTdnErTjfineLu8RnT4aMvxViyXfvWrX33KKae0zEqQgmxRaJOegfzhr9bDD2SKlW7hPtQmlE6E0ECZfA0CQWARI+D9Nv3sXehOP8clrVq0CGyzzTYbbbRRvcEK3eHYGu6qOBvCyXD+QM5LXvISzixbDgo0FsHTPrZa9jJz74Kwq3KdUsvF20J0C87tQOhFEy984Qu1oZ1IeaLrHHvssYSfgWsNf+VKe8tb3jKQr4bK8YZRC9GL2w2UydcgMGcIEDsn87fOWRuW2oWszexplzn48wkCQWAuEaiN+2yZUxd90IMeNPx0sDDqjDPOmEqruMa4q4TRdD8ynXvSSSdVzfYbtE/P1ltv7St/k2geRy0Qu/zyy9tZ0s669NJLp3JRZax+H26296s7hMx5tYXYIM61KdaWYkFgNhD4zW9+Y/IwGzWnzskQMNWpJ4NdRicrMy/5id0ZfmInJwjMLgLPfvazKSsibMqTxet0wgkn+P13r2qJuDLefN7NnDAt5Bl9ee1rX8tthGFUPf6Kd7ZJ4Gc+8xl7Lnt3hG11HFUDL5XwZAIPokPaqTpFFluWZSkWTWjCqwxk2qdneMcdZSyM9xe1su2hLX+8iWLgxHwNAnOJgBflzuXlci0I9Bbz0J3cn0FgrhHACSxBp45QX6yNsikOqmG3wIF2eNPe05/+9I033nggf/ir/ZSt+rZ0fCBw2IsjxDJ7E1YJSAiQ2rCr6173ugPsig/L6VOPMn7f+96HkA20BKMS+CyzoqS93WKgQL4GgSCw6BGwj1c/+5jYnX6OS1q1mBGwX451UjYA/NKXvqSfa6yxxt577z1hh0X2DLOK4ZIiZgTrIE9WYJWEU2UsubrXve5l0z+Xo+XQdYQy2G+wy3UEF3ur+emnn26dV4u8Gb5EN4cbDt3p5kgTmWrNuZCdww8/XKd40AbK5GsQCAKLHoHl2axrdsHx4MsnCASBOUaAM4jvyZs7iTou/b3vfW/g/Q/tZy/gRlTN1Jv38Y9/3Hoo68xbDVxmwoBsmmypVFe/wU6QJH6uqVeupD0SJ9yPx74+VY+Nf1z6sMMOm1a1KRwEgsDiQKCFDPYtdudqiwPf9CIILDgEHvrQh6IFl1xySbV8xD43FdkzrQ6KOLZyyvscbGrsJZ3eimUXZuHDrigI2lpxX+1GOK06q/Amm2zSiFRLoG6ecQrYyZDMYwnYMcccM4PKc0oQCAILHQEzn3oyhO4s9KFM+4PAeBCoDW8sCK/qfvjDHzb2MJDgkJr6JUX8PPzhD/da0FqQIl6nLUevahGgqs2lt9tuO+8rnXrlfGHtRRPdRqJuVYm18fLf9ra3Tb3OlAwCQWAxIdBbdSexO92HdtJBYO4QsDyK+iKO2BItV7VR8lFHHTUhmRBuzNVlG+WpNK4kHFHDFBef61znOr/+9a+7J1ocLt+FvP/civH2vtJumQnT9vh5zGMegz8NHBV27XIyL774Yl3YY489rAUbKJOvQSAIBIH5RSArs+YX/1x9SSPgDZ2bbbYZMcYbOq2N8r5Pi8+5mQZAodPwee2www48RJSegaMDX+22bJ/A73znO4JsuLFsIfjd735XyLPpo5JPfvKTd9ppJ24sdZJ5CD/oi9ggrGignoGvRx99tLdo1WbQA4e8kdR2gjZzoxVxZvU3UHGg3fkaBILAUkJghXoILqUup69BoEcI2JzGCx8oIrVD8QUXXGCF1HnnnTdhE4Xd2Een++qrgWJOVxvlxmosbzhvR1ElIcwieLo1H3/88T/5yU+sXbcw/qUvfWkrPJywDmuy0KLnPve5teDciy8srV9nnXUsB2vbNw9XlZwgEAQWNwJ06NrRVOyOrbz609moO/0Zi7RkKSLA+0No8ZdG4l0z9l+n9AgHprgMw2FROikIcbHRzvBROV5i9YY3vMGegVxUL3vZy+SYz1iabvmVNOmFB82KdCIN4Yf8o0KRxa961asmrE2mkGftsf3PhAX4torrqLDeeiEeKFxnQqySGQSCwPwiELozv/jn6ksdAZvTIAprrrmmEOODDz4YHOuttx5hxtcJoRHo46iXgIr18T7zgTLedSWA5txzz/3Yxz6G9DhK6TnnnHMsdJfmbzrttNMoSSKBHKUVIT2Wo0/2Zis79AgtOvvssweuUl+tv+Aak7armNhk2yjztU34ZokJT09mEAgCQWBOEVhMAeHpSxBYoAgceOCBfvZ77bVXLafCRZ761KeOfhAQUQ466CDeqG6XDz30UDvuWLhOtmn5xx13XLeqH/zgB3WIG+tb3/qWt4faZHlg3bjtmLGi7lkDaWE6rX7NdpRKNK39gdrpSQSBILCYEGivjunbQvSoOwOP8XwNAvOAgCVa4mOQFdHKFjp5lRXJRxDxu971rsla4/m43377UV+EHu+///6KXfva18ZyfvWrX/GX83nRbCy8slGygJ5uJd6CjpooTJXBeG5605vSZrw3FNOy5+Ef/vCHAw44APvx2tHuWQNp5VtO7ePsXGqTyrU//qwGThJBYKkh4LWsPe3yYiKV6UsQWLgICH+xUMtjglhSvcA/rKjyUq3Rzw4OKfSFU8zKKfHCvGAWXqmttsCZ7FwuM/sQupC3oHuNuXnYNttsoxJKz2SndPMRMlHJ1nypweV8ajNl7Iqvjdds4Q5EWh4EgsDyINC2dO+bupOVWd1neNJBYD4RsKaJMGPxFLWmAo21xguqvGuiu6JqdBMF63hTBMXFvoUjti5UideFWjROzvF60dF1TnbU6XSgDTbYwEY+ynh5BWVIQjzQu9/9bi2Z7MTkB4EgsFgRuPWtb+1Rpnd9W5kVurNYb7n0a0EiQHERxyO42AJ1b0qvFVi8UTYPxHv62aWHPexh9hXEyTTPO0o54AREP/KRj7RFkMxlqlP97FRaFQSCwMwQCN2ZGW45KwgsRQQsJt9nn30wHsu8a9c+ETkcVfxcQmR6iIjNDBEdgUfaJujHxhvieLwaff3117dRELdXD9ucJgWBIDAbCPSW7uQlErMx3KkzCCwXAvQSL73ykgc78ZSnSdyxzW8++tGPPvjBD16uqmfnZCSMwLPnnntSp2xauP3222sqD5dF7Bp80UUXzc5lU2sQCAK9Q8Dkp3dt+m+DQnf6OS5p1ZJGwPbHtv57z3veI+ZXNI+P12ZZnb7tttvaNJnSc8ghhxBOeoXRlVdeaWNoLfziF79oJ0N7Q9vVkEZlEyBNxYREXveqwWlMEAgCs4GA3Udno9ox1Lk8Adg5NwgEgVlF4MQTT7SkvH7nr3nNa7rXsp3g4YcfvsYaa1iZNYYHwdWuZvV4RRwvf202DWpNfeYzn1kV1nu7Wn4SQSAILEoEersyK/vuLP+zPTUEgdlCwKtntthiC5vZeHHE85//fKuoNtxwQ8LJDW94QzsjW3lue+XXvva13//+960h96pzWwhOtylWntszkPTiLaH2RLbfj20JPYWnW08rb7vn1VdfvX2tBK+cpg5k5msQCAJBYM4QyMqsOYM6FwoCM0fAsiyhPLWVjn38vGDL7oJeot6t0Z6B1nDxf3ltp7+115+/NsWpjb9simNTwTrFxjxOFwptzx6vRu/WY/dCGw/aj6ebOfU0FWrfffdVHmd6znOeI+wa1xGw7HVgU68kJYNAEFigCPQ2VDl0Z4HeUWn2UkTAFoJCYd7//vf/+te/tsAb6RElw1M+eumTUyybsjEgQaiIyDKx82auBz3oQV4xscyS3QJ3uMMdnvSkJ6E4Mr/61a/a8VlTZXqdlje0d0smHQSCwGJFwHOpXhicfXcW6xCnX0FgjhDwenP05b3vfW+955yn3CsdvD8L6eGQEuY8xXZYRYXWOPeDH/zgRz7yETsTCjcmID32sY9VwyWXXMLJdcopp0yxNrSGhFNue4+5HXbYwXIt0UVWmQkwmmIlKRYEgsBCR8A+FLzwehG6s9CHMu0PAr1A4MILL7QTz+mnn+5lW61BNunZcccdK/LGSi7kw9oofisFRDRjMFhRhTY7KkZn4HVainF4HX300SqR5gKzjPzb3/52q3+yBI5Fwil31Ze+9CU8ieykYcWcJjsr+UEgCCw+BEJ3Ft+YpkdBYP4REJdDofG6BgE3uAuygp1ceuml1TIOLHpPayXe4x2ivgro8dbi1VZbTZqb6dWvfrVQZbtl0HK8+uqMM86wdPzYY49de+211e/96qKhxUFPGL/srCOOOMJGOy7kunjSN7/5TSXtrdzf9agNkSSCQBAYNwKhO+NGNPUFgSAwEQLYBi8V3uMg2tHd7QbLQYDkE3hskFNvMh+ogwIkstjOyHe6050++9nPtj2dhQoRbAYKq1A4US25smqM3+rkk0/217tOt9xyy4HC+RoEgsBSQKC3dCcL0ZfC7Zc+LiEELLMaWGk1rc6Ls7Gjj7Vdb3zjG21viPHQeOzpLLjnsMMO44xvtWFURx11VLmr6Dr4E6blJV9eHxGu01BKIggEgZ4gMJ4NynrSmTQjCASB5USAYIPHHHzwwZZXeFMp+mLXH14wL/v89Kc/7U0RVb8yfFjFdcQjb7755riOl3yhR21fxOVsSU4PAkEgCIwRgdCdMYKZqoLAIkGAz+vNb37zoYceat2WyB6vJtUxFMd+PMV46Drlw7I9j5ddnHfeebiOGOdx7cu8SHBMN4JAEOgNAqE7vRmKNCQI9AyBZz/72daWC+XhxsJ4KgzIzoRnnXVWhSG/4hWvcFSoEAcWAkQZ6lkP0pwgEASCwP8hELqTWyEIBIFJEbCXz/HHH7/eeusJ5bGVjnd4WYFl3RZmYw3X/vvvLxpapoDl6DqTgpgDQSAI9ACBhCr3YBDShCDQYwSK8ey999421LG5jkgda9dPOukk0o51W95l0bd3s/cYyzQtCASBeUMgdGfeoM+Fg8BCQcBLcD75yU/ax1m8zq677lrNRnoIPxtssMFC6UXaGQSCwFJGIM6spTz66XsQmAYCu+2224c//OH73Oc+PFk777yzRVjhOtOAL0WDQBCYVwSi7swr/Ll4EFhQCAjfud/97nf22WdvttlmtWPhgmp+GhsEgsDSRSB0Z+mOfXoeBGaAwPWvf/0ttthiBifmlCAQBILAPCIQZ9Y8gp9LB4EgEASCQBAIAnOBQOjOXKCcawSBIBAEgkAQWAoIvPOd7+xnN0N3+jkuaVUQCAJBIAgEgYWHwPC7hHvSh9CdngxEmhEEgkAQCAJBYMEjsNZaa/WzD6E7/RyXtCoIBIEgEASCwMJDYNttt+1no0N3+jkuaVUQCAJBIAgEgYWHgPcK97PRoTv9HJe0KggEgSAQBIJAEBgbAqE7Y4MyFQWBIBAEgkAQCAL9RCB0p5/jklYFgSAQBIJAEFh4CPz973/vZ6NDd/o5LmlVEAgCQSAIBIGFh8CznvWsfjY6dKef45JWBYEgEASCQBBYeAg8/OEP72ejQ3f6OS5pVRAIAkEgCASBhYfAFVdc0c9Gh+70c1zSqiAQBIJAEAgCCw+BTTbZpJ+NDt3p57ikVUEgCASBIBAEFh4C3/nOd/rZ6NCdfo5LWhUEgkAQCAJBYOEhcNppp/Wz0aE7/RyXtCoIBIEgEASCwMJD4Ne//nU/Gx26089xSauCQBAIAkEgCCw8BA499NB+Njp0p5/jklYFgSAQBIJAEFh4COSdWQtvzNLiIBAEgkAQCAJBYHEgEHVncYxjehEEgkAQCAJBYP4ReNnLXjb/jZioBaE7E6GSvCAQBIJAEAgCQWD6CPzsZz+b/klzcUbozlygnGsEgSAQBIJAEAgC84hA6M48gp9LB4EgEASCQBAIAnOBQOjOXKCcawSBIBAEgkAQCALziEDozjyCn0sHgSAQBIJAEFhUCDz3uc/tZ39Cd/o5LmlVEAgC40Hg3//+93gqSi1BIAhMAYE73vGOUyg1D0VWnodr5pJBIAj0CYFf/epXF1100Yor/mfy869//esmN7nJX/7ylz/84Q/Xv/71b3vb28r88Y9//Pvf/37DDTf87W9/+8tf/rKVvOlNb3qjG93orLPOWmGFFerc9dZbb7XVVpNGMuT/7W9/k1511VXXX399Lw6U+c9//vOvf/2r8te85jWvfvWrq+Hcc891yhVXXPH3v//dBmXXvva1L7300kc/+tG77rrra17zGqdLf+tb33KuelZZZRVtU8mVV155yCGH3O1ud9t+++39ffvb3/7Zz3527733vsENbvC85z3v+c9/vl6o02edddbR5i9+8YsOqS2fIBAEliYCoTtLc9zT67lDAIFwMQbeR6J9bapDOyTHp8iEkl/60peOOeYYR+9whzs84xnPqBYr8IpXvAJBQReYfJ8nPelJn/jEJy677LKVV17ZuXLqkDQ+sdJKKz384Q8/+uijXZfIfJvb3Kbq6f5929veps6Wo9i3v/3tk046aauttvryl78sf8899zzhhBN+9KMfvfe97z3wwANbyRe/+MW77bbbJpts0nKe+tSnHn744b7+4x//eMADHnDxxRdLu+h555137LHHOtfMT4P14k1vetOFF17oKl//+tdf+tKX7rzzzpttthl+I/Ob3/zmmmuu+f73v/8pT3nKuuuuizbd6la3euQjH/nOd77zjDPO2H333e90pzshSW95y1u+8pWvAOeII45AiR784Aefeuqpr371q3Ey/MzR888//+lPfzoO9OQnP1l7WiOTCAJBYCki8J/naz5BYGkjQHj41Kc+RR74yEc+cuKJJ3bBYPiRCWa1MikQn/nMZ44//viPfexj8n/yk590Cw+njzvuOHIF/rHvvvs6+rvf/e7mN785MYNdRyboDdLK1InYAIpQ6T//+c9bbLFFPZLufe97t5q/8IUvOJEo4tDtbnc7ZT7+8Y/TPDbeeGOZ17ve9eqsO9/5zre+9a2Vka9H8l0Ib2j1dBP0Eh2k0yjzuc99zlefPfbYw+naRheRKI7yxz/+8cY3vjGVxdYamM1ee+2lnsc85jGbbropZF73utehKXJoKjvttJMa/vSnP334wx9GvF772tfKR1nuf//716VpRViU9OWXX64j3/3udwlIro57yXz84x/vol/96lc/8IEPSNTpmJD01772NZnve9/7KDpKIjoysaKf//znBksaF3zc4x7n0kiPr5jW0572tAsuuKCum79BIAjMKgKHHXaY352Pn/OsXmi6lf9Hc84nCCxxBBj7cqMceeSRG2ywwXve854C5PTTT0cC/G6xhwYRoYW9f/e7381LojA3UDvUTeArlA9iBmUFj6GyEBsUwBsQIMwDC9l88815fy655BL5XiN8y1veEjtplfz0pz91CVf/0Ic+1DIr8exnPxvtKBNem3ox7c961rPuda978R8RhPQIObjFLW5xz3vek4JCX6HTDFQy8JW+8qAHPahlvvCFL3RpT66HPexhEsVsHEXXsDe9e85znlOZeA9hxiGFi+5QWZyCdlRtsEJHUL1TTjll7bXX1veTTz4ZIK961asUwEv0GmtR5hvf+EadUnTnvve9b0lHRXcoWIbpHve4BxcbjadK0q4wPORJe84880zXhSf+Ss1CdHz19/vf/z5SVeXzNwgEgVlFgBbrd+fTN7rzH299PkFgiSOAJXCUeAQ88YlPxC1oA2QbmOAQfEO0CrynQcTcXuMa1xBZgm3gK7vssks71E2gHapCC9CI/fbbjwTCsaIA005EEcuy9dZbYyEYyRprrCH/05/+tArpE8hW1YP9YA/StJPKaX95qfiJTjvtNDnI02Mf+9gb3vCGIlp0wSHtV6eaMS3E4j73uc/tb397fWynT5jgC+Ouwrq6RxEaAk83p1xvSNvBBx/sWg5hP3gMhemZz3wmj1K3cKXREXj+5je/ufvd707CIaF973vfW2uttUTYKOC6cMYa1dPO5XsiVv3gBz+gM+lgeQDrKPBdt/ouR0mkkOTmPcxvfOMbsSg4bLTRRtpZ5RXg/FJJqzyJIBAEliACoTtLcNDT5QkQYESZSYIKTYKEwAYrtOWWWyINBx10EF3BV3oJu9vsqBw2nmjhxAlq/K8l3n///euQCjGnCYvJxI0IGDgEDxQ/F5I0WcnK5zkSiktT8ZX+xLPDL8auoztyjjrqKBEtEnxY+iWTWNJtdlUy8Fdf6E+EkMrXWpwMV+OBQptaRNETnvAEscY77rgjdYquo7CS6AXvlbTAYX8RFx8qS1WlRxLVNqKRqBqKFArYmoRQAuoFL3iBfuE9CqsTN/rgBz+IutFy5FdV8oUZiS7Cw37xi1/IVImO05zkEOeqWP4GgSAwXwi0h958NWCy64buTIZM8pcWAlQBphTbeMQjHkGDLS/SS17yEnaUfeVVET8r86Mf/Sgy1KDh1cIPqDgtp5tgicuf0s2cMP2ud72LssJ+YxKCcEUFTVhMzFCtdSJvoGWUmwmLtUy+NlG67evoBB2FM+t+97tfFUPsUBZESpTSXe9610ZNRCujUEJwqFPcTworeZ3rXEdk8UMf+lBRMnJcF0/icZM+55xzdMfiKd43X3n3hBLjdhiSr+3j6gQwIAOcDqSDKA66KeZJgj/OVT7/+c9jliBCubgXMVGxRBpJEoPG61//epU36imoWSyR+qlQfFvtQkkEgSAwqwhM8aE3q22YsPLQnQlhSeaSQ4CZJG+cffbZGI+/+k9yoGqw2TQDvhhUgN/qUY96FMPc0GGDpcsb1TJbAoWiT7SvlSDz8ENROLr5pXwgEAw86oBhdI9Wmr8GmSiVpchHXb2VdIjU1G1eO7TMhO4jGdgDN1NFBCMQNC21oReiguheP/zhDxEyoTZaK8jGSnXVUlaoOMKH+ZKsveJ94xCkEpGXLLkCph5ZWC7UhtSk/DbbbMOtBur6aoU5EonDKaCweSGiY0ma+GukU5gUpcpwUJIE8bzoRS9SAzeikuopEJQ3OuUX0wbMDBtTodcyC2BCs9SGSjoxnyAQBOYAgeGH3hxcdCqX+I9in08QCAJMOCJCHqAcWEqN1qAdMhlO9hsP2GeffcTDAoqBL7iwFuu5cBTLqYYBtGkNeiQQR+yL2BT8gLNGMcusbnazm6FQCISQ3gMOOABrsdTI1Vl0XidRKfIJS2oWvOIUtry2t6E/KSbCV6CP/He84x2WTdlmRrNFQ+MEGAndhY9JlLQC5A2KiIRFTMgBt5T08MdqL/RLVfjZXe5yFz3Fb6yoUhLHIp9UJVaEoUS0GfkuWplCgO1qQ+YhejkdX6FO6Sx/EwRQIiQMBxJdVNfVfvWLpNFmOQJ0hBg7F6pwwF18iEPWk2Ng4pddjmyjZhRHzBM25iwldQdn0jbeLkpPRVDpu09daDKFrI7mbxAIArOEAGX3la985SxVvjzVrlDTyuWpIucGgUWAANrBxHJLieoVb4vr8BzhHNwobDyrzOISaTEMv2RMRQFMiA1WrK1EGMDBj0t4MqohH5VRlbOk1UMrIp/wHBGQGG92nYiCpghkttkMk08x4lbDQjADEosyeINlTVY5KYA/yac/YRtvfvObnSXuR6tkigXmVCpqRd6wpY3auLTwAPxjoIX1FaXAS5zrqzZrJP5RkTdCghALopFDmuSK1B1pBUqekSYCIStipaXzCQLTRcD9g6k/8IEPRF6ne27K9xABfmr7SmgYgdaw9qeFoTv9GYu0ZN4QQFxs/YIoePJahEWNsMZHhCz+wU1jwZS4YIxHOIhFUhQUVp/24IPEOHFEuwUd26CPFkKesSKpNq1RnoOm6M6Ic3MoCCwFBES/0U1FyNm1cin0d9H3UWReOZdDdxb9WKeDCxIBfqJSOrlI6CjUFF8pOmPpDMJkNTglhsBjudNY6kwlQWBxIOCHZv5AIOSsXBw9WuK9sMUXRzwQ+kZ3EruzxO/MdP//EBDf2sUC4+l+Xc60HXRoPNxV4TrLiWROX3wI8JbGjbX4hrWHPQrd6eGgpEmLEIF61+Yi7FhvumQhmNkk20moE28uBquFOYuCEt4kBMqi9Ote97q1Qr43DU9DgsCiQsCb/vrZn9Cdfo5LWhUExoAA95n3Kggw4qGbrDpRz9ZVYQkK4Ae2ybF4imdB/LUtcMQnWWYlx+Y3iimsKp4+MdpWmzvLhzNCjp2LnWUtusVTVpWLbraird5BgX9YbiZq29Kwl7/85S5kOx+7AtYuzAKrRT2LibbpjgsNtFNsuLBrUdKioFzFJSy5srG1dgq+dmlB05/85CfJZl6wZXmaNlPmbI9koZldkSxhEyZlKRy6AwoLx2yhFLozAHK+BoExIlBxymOscGxVeV7kEwSCQBcBNlXwshx22sfXOsr2+8rwdwtXpvw6hUn+zzmdTztdgZZdmbbsq5dL4AeWjlvWrmZr1C2rRg5k2qqYwa7L2VTQV8XwDDnePCVtyRWW4F2bEkUyum2r96hjHupUWOS1ZdsCCauMl3H6KtTauZXZ3e/HArQqplqPG5vl2I+nXPKq2nbbbQeeQXbKsTTMzjfoi0OYjXeeW4OmEovSLb+3laJtoKtai9VREMVwlEMOOUSMFApSlxv4i6N4pbmSlphZlWaDAIgpoy8PechDrHoT4uq9Y9qGAOE3CJa1Y7iaRlZVmJm3WEjTeNSDvQ1cIl+DQBAYIwIiFP3QfKitY6x2+avKK0KXH8PUsLAREFVjzRRL743oesIAYxu2n7FNsIVUVmV7R2btrWe5lt+wXXbE4qE1Ctu/jhkmeDC0TpFj9ZZABKuyqQ5CLx1ijyufgRchJFMBNp7Jt0Scz0WdVpiTNxSuHQjL82XXYCTDSnWn89QQMCxfZ8gRFFvdoDtOca6Hi217qCzyMRuF62PzPaoJeiFmyOZ7mkTzcCE771UBvETviDHFJ1Qiv14iAYrG0vADegklxlE4qNM2YqiSq1u+LiyJZKKqer25MrUnEKzqKoQcjaxe2G+QL6neAF9vwNAkfBEsFJoqP/y3Jot2OPTOc5XrL04Domqh9XT6bi9BJ9qxkLtKAlA2/6iqkCENqO0NJUJ3hhFOThAYIwK9pTvjjMf0KMknCCwsBAgG1AIih51v6AEaTzthm1EEvIQ7hj9IJieLd4haXcmoc47QKmxFKJ+Yge540QHXDFsux27C3htqKbstfBwlLbDK8r03ijFmrW2Qo3I5lB5CUTli0AXCCfkHn9hjjz28cZM5Z7NtnMNs22zQ9hVqxkIwLRey1zD2Q95QDwOvjAtpbREgmT6UDzSCCkIW8hYFpG2HHXawS1ARLNsZoxFYgjXANmvGwFzaWauvvrq/uFFblcZzpEfaJh89ko/9oG4cTKiPr9bYQ6CVr5IK10e1WKMW+gpSaFiGc9XB/wCoNsgPnNUKSGAz/qrBNkVe8A58NEtOXdFmQqgYMOXoBSYETByo67HCI0GXV0mAKJ8gsGQRGPSUL1kg0vEliIBIFDGtDCQSQ5WRZoxZd1Cw5fw1PnQU+/hx0/D4oB2kAtxIPmLBU/PWt77VXy82dwphBo9hcX3FY+xViPQQjSxBt8UOboEtCTfxEUzDeFudbsNAtAZ1cCJfD5JB/FCVhEyyRw2KmrGusu7kGeyBROEQhclXYTG2Q6xNAqu8vyrnn7Lfj6qwBH4c+zsjKzxTPGgK8P6QgihS0mQhTKhoma/L/Ij55VarDcRMCjXemyI4jOpEQpeE/NH1iMXxulBsT1W2dcZRRpfXayBMWK09r4sSAQT3UgyH84bRqtCFbCBpo2ojawgmrGH0pXM0CASBRYBA1J1FMIjpwgwRIH5wOQmGZfsZfmG2VBx8BedgOKtSJMOnbCSRQCaygmFQg1h9XytTgtNKhRLsvc0JbS1KYyBdyLFLIX6D3BAnBKMgQPLpMQQYdtq1MBtKiZZgSMoPfOrqaFbl4zHe7YCsICgq3G677dTDCcU11k4UEawx9cJOmXxP3Gfcc6QRek8r1hLIWetyyxydaB2vYtVTaZoTHatxNR0kvYBiuDZAaSd/FrUGyMMFKqe6j3R63XpVC08ss15z4VwErhrjQt5WQQCjwKGA7XTI8KnxQqKh3m8/2YWSHwSCwCJGIOrOIh7cdG0ZCAiOYRopNMwzZsAh5QRcxxKkCaUOlpvpZaF5XrxAirKivEw2GNdhSjl9xIj4utZaa5ErhNeUqVbMjrHEleJVOBavVoX9OrTMj0sog6wgJRLIFtZCtkFQXJR0gSfJb4TDdalK3nuFUcm3DTTnl8tRqpAerjphQwNkxXushOAoPPARZ+Oi1YCBQ1P8ipAB09u7RBFxpeGIWI6YJ6FFquWwo8SggCNqQ0Md5Rzcb7/9qhiHIJ9jhUKTvrwzSyXCm37961/rOGHMaLpi8Ug7ZYvNsik2yiWHf9ArCzDOEVfMoSAQBBYfAv+ZeuYTBJYmArww6IigWoRAgAvvDCPK90E5GF4RXRApbwkSy81glyDBZsskUch0omIoCH+WF3my6N52KcAWAeIv47URqiIi2CUEzUwdc8xGe1Rbp4gUtppaWrWYhKO1ZXurUOgP6lOvzZLJZydyCDlg7ElBXgHG3gvlIVPx3wlVxnWQhuqyfjlFa71M44gjjiApuS7py9ouTMJ6MVxQtFNdC/+A2M9+9jOXqBxIiuORAw1rwi3NsECdKuM1n1gIBEhcGKFgRrwHR1R/vZpUX6qG4b+ooUyxON39PLxLFYzedKZVlmsJOXJp4U0EHsFMGuzNo8qLQ8eEKEC6wyOpy7yHrbXD10pOEAgCixYBT+p8gsDSRKDYCWlB9y38IfaI9pUW8sJGSuAHCAFWRA7xCGDdZXKLUICQAOaWxoNVyCSfoB0SPrQHMk+lLXpyljXSTmebZfJzUVZIKVVA3K5oHj4swUNEI5kMNjYgApc2gx/UmiYN48HZddddmXZtY9rZbAFGMrWW74Z0VIvJtYqgUk2tS6AyzLwGFEnCV3TcIWygyTZIAHIms2JoGtsToiQURg0kmXoIEpmqWpwGqSr/HaZYmWQnxRQuzxpqKF9sDW+a151SoYpiAoSoJodyo4C4JcFGVcPwX+0UGK6wXnePGh0BSdWXbn7SQSAIzCMCvV2ZlYXo83hX5NLzjEDRHZIAlw2BBF+phdz8Jqw1UoINUEGqlVZmtUwvCiUqyGduMYNyDAkHllOrposHFBXAbAgqFpDf8Y53lI9U0UiwHIVxJnvSYDCuIhhIRI5MdGrHHXckw/gIN3HU7n9Mu0YiEyiLSyhmnRFPEHaCA/lqPZdte5AJa9eF64qqltk+lkdZz8WZ5S/yUfnqVLNPN5Prx9fK9xcgipFeWo50nd4ylXdWZXZPl4+6tTYkEQSCwFJAoLd05z86fE3a8jcILDUEGGxrmPEVSoOFRXwrdBGMBA5+sUUL6DQCcQoZPiDmXFphykplckvVEm7ncqk4S3SISrAEBfy+LPy2nosygS3hKHQUsSZ17tj/8t3gQBw91KaxV54Kg0AQCALLREBAZAUm9u0VoaE7yxy7FFjMCBQp8ZeQM2Jx0EKBgAKEtInFoQktlDannUEgCCwmBHpLd7IyazHdZunLtBEoLaf+Tvvk/p1AduIRq60C+9e6tCgIBIEgMG8IhO7MG/S5cBAYOwLdXZXHXnkqDAJBIAgsXASyEH3hjl1aHgSCQBAIAkEgCEwJgdCdKcGUQkEgCASBIBAEgsDCRSB0Z+GOXVoeBIJAEAgCQSAITAmB0J0pwZRCQSAIBIEgEASCwMJFIHRn4Y5dWh4EgkAQCAJBIAhMCYHQnSnBlEJBIAgEgSAQBILAwkUgdGfhjl1aHgSCQBAIAkEgCEwJgdCdKcGUQkEgCASBIBAEgsDCRSB0Z+GOXVoeBIJAEAgCQSAITAmB0J0pwZRCQSAIBIEgEASCwMJFIHRn4Y5dWh4EgkAQCAJBoF8IHHXUUf1q0FWtCd25Con8DwJBIAgEgSAQBJYPgcc85jHLV8FsnR26M1vIpt4gEASCQBAIAksNgVVWWaWfXQ7d6ee4pFVBIAgEgSAQBILA2BAI3RkblKkoCASBIBAEgkAQ6CcCoTv9HJe0KggEgSAQBIJAEBgbAqE7Y4MyFQWBIBAEgkAQCAL9RCB0p5/jklYFgSAQBIJAEAgCY0MgdGdsUKaiIBAEgkAQCAJBoJ8IhO70c1zSqiAQBIJAEAgCQWBsCITujA3KVBQEgkAQCAJBIAj0E4HQnX6OS1oVBIJAEAgCQWDhIXDmmWf2s9GhO/0cl7QqCASBIBAEgsDCQ+DQQw/tZ6NDd/o5LmlVEAgCQSAIBIGFh8DWW2/dz0aH7vRzXNKqIBAEgkAQCAILD4GVVlqpn40O3ennuKRVQSAIBIEgEAQWHgI77bRTPxsdutPPcUmrgkAQCAJBIAgsPARWXnnlfjY6dKef45JWBYEgEASCQBAIAmNDIHRnbFCmoiAQBIJAEAgCQaCfCITu9HNc0qogEASCQBAIAkFgbAiE7owNylQUBIJAEAgCQSAI9BOB0J1+jktaFQSCQBAIAkEgCIwNgdCdsUGZioJAEAgCQSAIBIF+IhC6089xSauCQBAIAkEgCASBsSEQujM2KFNREAgCQSAIBIEg0E8EQnf6OS5pVRAIAkEgCASBIDA2BEJ3xgZlKgoCQSAIBIEgEAT6iUDoTj/HJa0KAkEgCASBIBAExoZA6M7YoExFQSAIBIEgMBkCf/rTnx760Ieus84622+//V//+tfhYuecc86zn/3sK6+8skre737322STTT7/+c8Pl7zsssvucpe7nH766Q49/OEPf9CDHvSQhzzkPe95T5X8wx/+8KEPfei+973vBhts8JGPfGT49OQsTQRCd5bmuKfXQSAILCQE/v3vf+MBWvz3/34WUtOvauuRRx652mqrPe1pT5Px/ve//6rs//1/2cte9olPfAITevvb3/7FL37xwAMPvPDCC3/5y1/+r8RVqb/85S+rrLLKLW95yy9/+cvf//73X/Oa17zlLW9529ve9uc//1mR1772tU95ylPe8IY3YEsu949//OOq8/J/SSMQurOkhz+dDwJLEIELLrjghBNOmNCO9hYNhn/33Xe/3e1uRxq5//3vjxCMbupvfvObr371q//6179GF5uzo7/97W8POOCAvfba64UvfOEee+zxohe96PLLL+9eHYPx+dznPnf9619fT3/84x9vttlmT3jCE9773vf+85//7JZ04pOe9KRtt9129dVX/8IXvnDta1/7zne+861udavb3OY2Z5xxhpIEpEc96lEbbrjhK17xio022uhvf/tb9/SklywCoTtLdujT8SAwiwhQI/gUGLA//vGPl156qWn3hP6LyVpwxRVX7LbbbuWtUOYDH/jAdttt97WvfW2y8hPmM/auO2Dyf/e732EM3B+f/exnJzyrn5lMOGfNJZdc8pjHPObDH/4w6YK/pjWV8IMENFqgy/icPgIf7AaiHQKskgNjcd5552EVrbbZSNCkeKBWWGEFlfuL/QyILo997GNvfOMb3+EOd1AA47n5zW/+1re+lU7z5Cc/eaWVVuo2ycB95Stfee5zn9vNlNY1PZV46lOf+o53vEPixBNP/Na3vkUHks4nCITu5B4IAgsPge985zsV0/DTn/70qKOOqkltr7rBpD396U/nvCBF7LPPPte5znU23XRTEsUUG7nyyiuzwTvssIPyQjrYwi996UtTPLcVo+KsscYaP/nJT1qOxA1veEMaw4tf/OInPvGJ3fyFksYS1lprLfzPp9xbCNy97nUvUL/pTW+qXhx99NF6h9Moea1rXesBD3gAquHQZz7zmXve855KUol+9KMftS5/7GMfe9zjHjerd5EbQCTNySef7KKnnHLKiiuu2K4u8b3vfe/Tn/70lltu2TJ/8YtfICu+fvvb326ZEnjbM5/5zMMOO2zVVVf1la6DSH3wgx+UqbybrRXGfp71rGep073UMpNY0giYhOUTBILAXCLw85///N73vrdQykc84hH3uc99iA1cD1NvAKfAjW50o2222cYpD3vYwzy/GO+pnz5nJUkLd7rTnYg0rmhGbsrOSk396my2rr3rXe869dRTJQSu1rnsPVtYH2mZxx9/PFNKDOABYc7vcY97nHTSSfK5Qpy48cYbs3n+cu7INPX39SUveYm0D5lhiy22qFAPZQyH0alDtKVHPvKR3CKgJlPJFPdq1LhakAkXeuUrX1kl5+YvS3+9611P1IvLnX/++bp21llnSWseqQMDZvvf+c53VmPEwVA1PvnJT37qU59CHGVy3t3gBjcgC+mXSJeXv/zlVdJfzAATIo20nNlIGDLIP/7xj3f3EnIwsHYVI7Xuuusai5YjQaP65je/ufnmm+tLyz/44IP5p37/+9+3HOE7H/3oRw2NO0SMc8t/1ateBatp/bLauUksDwJ+fW5OH67J5aln7OeG9ta45G8fEeC88Fg375xK40zlPd3MZX3EJ7773e+++OKLb33rW++0005TOX0uy4g28LymOjBFVHdz0zXXXJO1nmIbLEJhAKq80E7W9wUveMEyzz3zzDPxBq6BESWZT46DcigoRozBNoRQbL311m984xtpCQ984AOJNCNq6B667nWvyyVh8i2TY0WvB/xK3cLD6RIAaBg/+9nPukdZ9Ap3lWmU3R4Em9ve9rZ77rknh5dGolnsuqM3u9nN/BXSoQCpQ3t8XW+99fAesS+PfvSj73jHO5r63/Wud33f+96nGJ7E74Y7qlZJbiNcTf24KTZAavrhD3/oNhNF+4xnPINQwXIrNu8fxAUbM76/+tWvmpS1/vrr6xrYmytH0AxYrnGNa7gNfvCDH7jlWstluqna11lKGA7UxLAed9xxxpTIVBfScgqlcGPD1L00gdC9J9Nt2fJRN9MD1LnlbLXVVtLHHnssbtQ669Ghv/jTQJ3trCSWIgJjJ1CpcIoImOuwBMOF/UTpt0z18KGx53jqffeqDymbU3/sl5hWhYwQA8MyOcsEGnFhwKZYgye+ibjfsJmrU8zCpenbUzx9ZsUMYk2dp3u6UE2ChLNM2e9+97uzqVOvwYjp2te//vU6BVAiVKRNZJmNW9ziFkieGbwcRoUJR19e97rXWcbC/iFYJCWiCwaz6667YgkMedVDq+AT4fi4/e1vX9MyTgdygvIGBXExIz/iiCOq8BT/MqIYEpaw7777snam4FM8UTGhKiyWvnBbMI0aXOfuvPPO0BPFgshSCyqz1A5f/XyaPGNoAHXuuecOXBShkd9tDIj2339/xVRL/pEQy6K/1JGzzz4b3SHzyMQn/GQM+k1ucpPDDz98oNrZ/jqs7ugazcYAIV6AuulNb+pXXM3gn/LzQf5aq9BivabunHbaabgaF1g7NGcJMhK/lQVTxxxzTLuogeD3bF8lfv3rXxOrODFNYMQjG4I6SiN06w4INu4u3ZGPmlcxBVBYtzeepB7j1a086dlGoLfqztVmu+epf0IEPIj9IFmpN7/5zSIJnvOc55ib2nMC0fHw8lRqYvuEp48r0xTQtdrHlGhEzYSEroY8ouSMD3k6e0Z7UqvBxE7DpkUmyOPECUGaTi+Xf3vSebhDWORjtc2TEeweslZ2HHLIIXvvvXejegIgGDz6gUmwwqyaCABpZZT3sPYUlnje857HGKMsLB+txXO8ap7i30Z3+F/El1hpMsUTFdMGyKA1uqBTfDHFm0kOKIUGW7RSICiMzZglI4Jmz5QkOZrtdLeZND+IJS0SKAIfATPDPYSgkDpk+oAF2xiwRnVoKn9NxF2LpIRLEU6mckorY90y80ZVssRG9I/7oQ4ZSl9f+tKXAp/vqTK7zp1Ww2R0x9jZtaUVkximOwgiqoccWN1jRbRIqSoPIpbVmufu6XOT7tIdig4vD7UMtuSNaoBO6Vqli+4YTQ12M3NUcfkZC+RYASTJzYMaVmEkD6Ttx1KZY/9LfSGYaYMx7VYu4OYb3/hGN8fvVLH6VIPrqHhtzqxuSWk3sLmNp1PL9/B0rtu+avAbaYeSmAMEQnfmAOSxXcLUlijKQaBGTuXyNLfn3Vgu42FKQPb8qimXOD6zcD/Ogw46qEIW9ttvv7FcaHQl9QS0eIGgwtU9wtWqgKkzEcLslhY92s1PnVZmuuZNU7UELMxbeRMAMha6w7V/9atfnT4huEHgC75iHqxyD0omDdugjZe+ggYR24Vl0EJITZqE6yhJXWD5PFWRG/2idshUktkjYCAE3UCE0ZjXUQxJDWau+stuTQurojta7kSuJVbfjaRaZFTvzO9ZMkS2LoQJubus4mmtYlpcumQzRgLaDvHvYIoIt2p5nZj/Ko/ugK4pQK2SKSbcLdMSrrrVojsf//jHtZ9zisUqugMobIxdZzuNwoC6U7EsrZLJ6E6pO11MGt1Rv3AoNOL1r3+9GwNXUBvSgHg5RN0BLPXLRIVfpnGLdsVZTRh3dxouzuobrArTwc6luWw8piTck+hsNYNQpzyNyk2CyrhJ+OPccpx67mQdbK3F59wSZggtZzYSfiPcozhW3a51Cfcq+jhwOU8baCvpbxOoTEuAb2gGCrvtSw9u+YTeOr1qKO2zHZ0soRKjPN0f8mS1LeX83tKdxO74mQ9+6C5WLtDSqeWmj5aEeNQ2r/Bg6el/97tCazy2PJvQGo8tT1tGiAmU78fpScTM+GGXsbnmNa9ZF/HoZ5DYVx/n2k+CqMBeeg6qRyYFokpqvKc597yJVNfPPdBYj0g5ggSZeTM8Zp4qICiEj5/bQoKdoz8Jd+BAof14slAOrOmwDqItAxmo01dkTjCEEIfyKA0XmCzH44kJ118ImNVp1WQlJ8s3TBrmseX53sp4/EHGbh/66NEvrlNPSegAZzKRIVzWEiflmU/BIqI6rBMRpSGH8VAhLcFz2Y1hJgpwSglnh3zzZk4EoLVrTTHBggKZ5sHBpM4aiCmeW8WMLCYhTRliEoBmsPgpDj30UBXWitxlVoj0CHqoYowQc2LQ8Rs5brZKTFiJoy6KSE14tGUC2W3cvraE0/0KGOMRPyv1+y3Ah3l2q2ue040LTkyLMl4IB6tGeOMNdMM4yiK690zrYeur3wgGgCpV1I5BxO3cvbWE2yDylWD5fB+IkdXdhliP3Lc26sVu3fmoj8p1wU/AhMRdzbGCRvB8qUSi9WgOEtBArzXmbne7mxtGI11U71BwRlpnYQWlyneIgkhdQ9pKMJbjVmeKICAf75FTH7+OtddeG8W/KmNK/93DfllNRDGUhtt96AdimLS2HarqtNC4a6ET9UJ5aV4to6M93fukBq7OUsYhXbOdILpJp1RJt30OKeDTMov2ta8OqaR9RUSg596TaJmuCEPj61nqJmn5SSwmBEJ3JhhNDwhPNzNLDz4TOJae46AC4pRmVC666CKPBg87QaZ+ujL9sH08oLn52T85JATRFX5FSg5Yfc9KNMXaWsW6Pzlf62N6zZiJQVG5p61nhyap3Ck0ao88nAAJI4HwMihMe1CMHG2ib3mCJzJfPl5CrfEEb0rJVdUP/vegZ+TYclVpP5cHtuTqbCczo19OEOQBAZfmLpEz8MQZqJHJ4WEZ6PVAmQm/6gXkCfWmpLojEmXCYiMyNYzPXt+RM1hVSRTHQJDrmCgPR5ke03R1XFYal8VXqptGzUyX7RQQQDZvF0KPpIW24Bae45VfglwrM62Ey7H3MLcaaFontsKicIruyGE53KVuD83G1I2gjUlayQkTAJHvPgGUBLkL62UVDByNhBFVFRVE+A5I/RAwUXy60TKGDX1EOLjAJqyfjfELYsw0DO02KKS1VtINxgvDT1RCS8tvCQPkZ4LNaAbMkW+HBNCoEDvh/PUVN9U2to2JUhIable8n/ZjLqGAX6J7G6fRGPEiZcYIWmB3rt+g6QQc/AbV7Mbwc/O3UPWzdWkVKmawyCf+mmwg+jJ9zExGcLXWkTEm3G/Dt5xW1XL94Qv5wfoM5AuB8hnI5EE2QAOZy/xqksAZCv9WEs7a46tEy+wmtMctBHA4m05gro4Od8rpAzUYaPePgfOr6VYoXU/gbqbb2Keb002rym/fTWIQu/la7qHnGdjNTHoxIRC6M/FoFgshp/NlmDzVVzNmvxOeGssdzYNxDr4DSyFqmuJXZFojn4Wg2ZINKOFqJ8ULeOw+YjjOCfKmaO3arKzfPDODVch0OQ8Rxh7L8ZYZBsnjGLNRD4JFrfGUEYS7yy67MMwa4Jn+4Ac/GBER4Ox0goRZO4vC5rFnNOrJbGo9m8wCyTasvnN1gXlwCWTOQ1BoSz3TUSi12cajJsqt5RMmFCt7M+HR0ZnVd7aQHS3YR5cfOOoUM3tTzJq8MmaehuwBKkDUwQXLe6jjzJghc7pYEH/N9thXBhjzEwyL69TwVf2MvYT5JZKBAUPG18qU8GxVSa008RBXOcdZ1wxUJd2/5qkMqkc/oQKZbofcA/ynwGdNW+ZAwv0jB+f2FxEx0O4lio67BQVBdwSy8EnB0OjTDuWbtlK8UIG6wZzI5+Wo7iDWvuI6ZtjMOY4ouhPj3HHHHfXF/Y8JuSUQDgJkozvuELNhSthkdAcIBAN+H8igHSW3uFB9DJB7koB3VcZ/jBbywQKxZzVq7m1jJIpIpqsbWd3Ud82u+1YxCeUdQsSrKmbScPgB1lc8tX56LdPpdQ8oUKdTdBB0X3EmXAotluaG00gdx/+A46dH7HGT1KWrcvePscPq6utS+2s4eMO793kDpyW6mBgaD5n2APH7QoWV9Oir3063cNJBYOwIhO5MDKnJpTklwRyN8MSvp6enm583zcMv3E/ds54sTCjGgVgpM12CBF6iRj4Oj1cnkmRI6ExauwyGZL0MGtFyJEwpTFzYpzIAnvuqYqE96D1ziTSqtdaGoeVnYQN4GZgHDw6TTnTHelqPfubh+c9/vocINUiBMjCsRTNR3StWuviEaFmXQHQoRtQdz3SWz1QeZZnj+atWwU2nxNuyN75WCyVgYu6FRGKf1fjhv1W4+1cIkWmrYWK5eT0knEWfA53hQyU9bWHrilgpq+ao6yKazCc2w1obQZmYpfGl6yAZpCMcwj2AFVkSAi4FZJKIiFIOYSqIcteWK9D9oMvoIx6gsLFTeTuKdxroZo9bfjeBzTDJjIeFOZilmw270nj+O54par9D7gdI+svAaKocsPja6iF1DMh+nDs+bjk3T5kr9xiDVHqYE3WQN1CUj7tCGZZe90WVOqVV2024dV1FB+GGphe5bAXAjoRVpoahGnh5eamqTLVWs33KplYvWg3jSvjp+ZlP2AvNQxO1BBR4z8AVIdxdzj1wdNF/RaPhNuNuunXN+mZ8ek4MAtNFIHRnUsQ84F796lfzg5gHi7FQrkgPY8auePLWI1g+28BfbsbP2rENxBhGwjPatFslNNhmoVk4AbCoDEvQvbDYQ7a8m9PS7Irpo9mty9W0vkxRK9BNaJWHiBzqjgkrEibHLFxjJjyrdjRhX0n9SlrRwAOFImAVpvJUHwyMVmR2bjaPD5n9o2tsuUBR5t+FzK35BShP2GFrCecCKqDYsEzdykyY0GYMAKXTDAbStNtXNlhhO9RpD/dTA3O4BlHeoqDMwjFCOjmq568uOFdEix6hERxSzBs/BXUBVhrPfUYKYsi5sfj+cBFmTNAG0AyTvwI7ioSRTFBDJtCJOAclQD2uogDpi0SHa2IbeBXWQgoaMPCtwW4SJFgZ0ogy1JQ6VAYeC5HfMttZEgYR/cJg9IJ5VoNMyMvEQgwQUoiFSNRZA+NeX8sdgNrSgQy6zCqscl91R2dRPRTQuEvXUX91WQv9CurOVwCP4Tib8NZqdUq0S7SqJJzVzVczWMzyh+UivB9Kbumint1Klj+tyygLZXT5q0oNQSAI9BmB0J1JR8eDnoRjn65SPjADcxHPYvEfDHCtYnCyRzZOY76LJbAf0vRzxVgFhIAdxQ94HNgnRohowZp2p0QMc2uBJ28ZPM99Co34we7ckVUTN+CJrx4uMza7nWiWzBFjZs9FwmCw7kqyRibfbLB6hHC2wt1ErQ9qcyztd1RgBLcdlqbx2Ab2RvAwTVc/EuAvDQkfqnq0mVCBEXarZf4JD0xvN3Mqac4mSNIqFNY2DprmfNEjsJRZctEJayNHkTqMiA+5BX2RUFg+NEhoKCm+IsRYvsm6IePCVxWz7ai9YVyiW7N7gFWuQTGyqiq5S9ooIDcIFpcNS4zFNnnAKUa8W89wuiiCZkx4aML8Kin6QZvBa9TaFbuVCLvpfh1O645e6NowG5PJj6ZaI0gucicPn56cIBAEgsBCROD/e7gvxA7MRptNmvksiCJmzAIbuXWYN84OHi6G3+wZZXFdkRAsPac+44RnEBLIJAwGCYTZ5g1hCNkVIRqiRlhHZYSGiCMRUNyaTcOQdi49QyAFo4ujsM3Ks6A0gAqn1QBmjI2kGCmDcxQnMNF3CaKRSqwj4wvwUZLaRNXQQoyhOcvbRVtCABDb1kwvJckhvXY5woYG4Ell4OVjfiqX6OorCARvmga3OiX4wghg2FI3c5lpvfARhySaBLGAKhC0pMiNRuo4vQ3Cy6yqW0ANFIvaXYYsQcXpHl2eNN4AE/Vje+isGwOF0mz5nJUGGjUZryChcqNpaLDkWQ13EJe2PMjk3CAQBIJA3xD4//TkvjVuvtrDqFuuyb4KyxCwaRKP61A+EJEKRGXPfNhdXIHtqVkyrsAw+/BMmRYLE+HxoRZgHuy0vlBNKta1oj2qd3QFGoMaKEm8KvPV5T5cFxHBHeFZ9GtcTUJHjN103WrjunrqCQJBIAgsKQS4Nbb+7+o/jpHmOugDAqE7czQK4h74sATHCESYo0vmMkEgCASBIBAE5haBWuLqmn2jO/9bqTG3gCy5qxEtOJ56+LrKJTcS6XAQCAJBIAjMGgIj1gLP2jWnVHFid6YE0/IXEu8i7Gb560kNQSAIBIEgEAR6i0B3Q9FeNTLqTq+GI40JAkEgCASBIBAExo9A6M74MU2NQSAIBIEgEASCQK8QCN3p1XCkMUEgCASBIBAEgsD4EQjdGT+mqTEIBIEgEASCQBDoFQKhO70ajjQmCASBIBAEgkAQGD8CoTvjxzQ1BoEgEASCQBAIAr1CIHSnV8ORxgSBIBAEgkAQCALjRyB0Z/yYpsYgEASCQBAIAkGgVwiE7vRqONKYIBAEgkAQCAJBYPwIhO6MH9PUGASCQBAIAkEgCPQKgdCdXg1HGhMEgkAQCAJBIAiMH4HQnfFjmhqDQBAIAkEgCASBXiEQutOr4UhjgkAQCAJBIAgEgfEjELozfkxTYxAIAkEgCASBINArBEJ3ejUcaUwQCAJBIAgEgSAwfgRCd8aPaWoMAkEgCASBIBAEeoVA6E6vhiONCQJBIAgEgSAQBMaPQOjO+DFNjUEgCASBIBAEgkCvEAjd6dVwpDFBIAgEgSAQBILA+BEI3Rk/pqkxCASBIBAEgkAQ6BUCoTu9Go40JggEgSAQBIJAEBg/AqE748c0NQaBIBAEFgQC//znP7/61a+eeOKJX/rSl04++eSBNr/lLW+5853v/POf/3wgP1+DwEJEYOWF2Oi0OQgEgSAwMwT++te//utf/6pzr3Wta62wwgqtnr/85S///ve/W6aS2MDf//73a1zjGte85jW7JdspLfG3v/3tj3/8o9OvfvWrr7rqqsq3Q31OXHHFFQ9/+MN///vfa+TrXve6e97znq21l19++Sc+8Yk//elPl112WcucpQT0fOC28sr/M0mVueKKKxqRWbpuql1SCPzv3lpS3U5ng0AQWJoIPPjBDyZj4C6rrLLKIYccst122934xjcGxfe///373ve+DP8nP/nJhzzkIXK23nrrc845Z5NNNvnGN77xmc98xtHJEPvzn/+88847s8prrLHGWWed9bvf/e573/veZIV7la/NxJuf/OQnRxxxxHOf+9xu277+9a8/4AEPWHfddddff/1u/tlnn3366ac78WEPexiC4hBKBDTUcPPNN7/tbW+LQh177LEQRv7+8d/P7W53uy222EJJzOnTn/70lVdeudJKK8m8xz3uIROt3HHHHSG81157veENb6hrydxhhx2OP/74a1/72p/97Ge33HLLys/fIDBzBNyR+QSBILBwEfjNb35z4YUXmgov3C7MZcvf8573POpRj+K+YZIpB5/61Kfq6i94wQuOPPLIE0444ZRTTqmc9773vR6sZ5xxxsc+9jFW/KSTTpqsnewx83/JJZco8Na3vhV/kjj//PPRCNTHxwD97Gc/a6f7eu6556JWlfPTn/4UYZLGDX7xi18YUFX98Ic/lPZXSfUQmaowbnHve98bFaivY/n7xCc+cY899hioiuqj+xtttFE3f999973VrW5V2tXzn/98hzTsSU96kpzrXOc6d7jDHV75yldqIdqH7oCXXPTABz4QMapKHv/4x2OZH//4x9EXRLMyH/OYxzz72c/+7ne/+8hHPvJ5z3teZWJFT37yk/Gqj370o7vuumtl5u+CQMAvpRjJ5z73uV41OLE7NS75GwSWF4EPf/jDr3/96w866CAPbobqwAMPJB6YNFe9X/jCF/bff3/Wa3kvM3T+LrvssvbaazOKQ0eSMQECd7zjHekKlJsHPehBHE8ex60QDG9961vf/e53r5wNN9xQ4oY3vOH222+/33773ec+9/na177WCrfEd77znUc84hGGm42X6aynPOUpEjxB22yzzVZbbeVEA+RmkPnLX/7y5S9/OSbh60Mf+tDyIrkx3v/+9zt68cUX3/zmN6c/kYgY/nXWWefNb34z1vXYxz6Wp0kBH7pIdaG+juXvTW5yE9RkoCp0UFPxsJb/ox/9SObBBx9MEEJ6EEGH3vnOd9Jg+AGxHEoYHon3oGs0IXwIYn4XulkBQE6h6DgKlp122qlqRgc1QMm73OUuuvmVr3yFqOauhsa3v/1tVO9973tfs6CtMUkEgekiEGfWdBFL+QWAwEte8hIzck9wz1aP42m12IP1Fa94xY1udCNmjJ177WtfO8XT6fkf/OAHWcdb3OIWu+22G3eGNmy66aZl/Dy4UR/tWW+99aZY4RSLdQ32FE9ZysXQhV//+tf0FZaVMmG8Cg02+F3vetf1r399zIa3ReRKlwHc7GY3g7MhHvaqEIS4bzCnqofXphw3e++9N3b79v9+jDsipQChAiFg9Zl2BegZ7jeGX3scdZU999yTeIONaRv/Dva82mqr4VJHHXXUC1/4QmXoKCKI61rj+qtV73jHO4ZrK4dUy0dE/vCHP+B2cr785S9DSQJK8CTwKEzQuutd71rlffWRFvn0rW99S5f9Lt72trf5afhN6RR6RKMi9kBe2FN1WQ6JiMzmKEVt44035tXCfjC/qjZ/g8CMEVhxxmfmxAWNwJve9CZy8UAXzDg90AcyF9xX8QH8/SaUnpJ3u9vdptV+8Qoe3K9+9asZKc/xH/zgB1M/3VkKM2Ye6BLsh8f9q171KmlhDawd02Xi3q2QB6psBi+GMnXIfFoUxQEHHFARtSbHBksx3panP/3pnC9V7LzzzhPrwDZLdOtMejQCvE54ZwknNJUKzsUkLrjgAn4o6sW73/3uww47zMAp2aq66U1ver3rXa+NUcsfSNAhDIrP5z//eYfEAHGc4bsbbLCBe1IOlxa+ReyRZv65sSSYfFJQVU7dmVBDUmxuPiQcqkzdliOuqAu3uc1tFNDsNddcE0Fxw1vkdeihhw6f5YfgVpev+yQ0rAjbe+Mb31iaDeqD4ZkYoEomDD/+8Y/9Bm9/+9ufeuqpqA/FyE/AiAxXm5wgMD0EeuVa61tjGB5TN455Suzct83jgyw8S35rDxFu+Be96EXiDEzU9M6Dxq3DzM9lT2keQkRd0RPwuOOOM8etqwPcVzr2jBvDwOgOp9K0ahAowBDWWb/97W/NO6d+uke5K97vfvdzCp5EomfPzjzzTF9f9rKXMWOCGLq13ete91KYR2P11VdHy5hbR4VKyBcVaxKP8aBufC7sLnuA2ey+++4sh8pdixKAP1100UUCL1yXmNStPOnJEBAOgk0y56Q72EJYSWaVR0nCjWc4bnnLWypg7ABb96RfijSeNFwtP46xeOpTn+oQ8YMDiGJ06aWX+krSGPj9imJBo90bjopNMfoSKLLKWXe3HFZ0pzvdSWYRptNOO01aJVooUR/3J6Hlqm/L+99Nrl/QcEVsD49xv3n0aTyuhuf5JfpduNPwb0TEQ0kHcZTXvOY1ro3HPOEJT5B53etel6yFMsqkRekRGueuRuUdpWPJf8YznvG4xz1Ox7n5UEwVyhQsBQeZ4odc1KVlQpKmpQHkLvf28jwK1JbPXCJQLNYN0LfYnavNJQoL7lrUZmPmY8VBLVKdyy6Y07NtHkDTvaj5loc4fZge7iNBbO9WYhLmgW6FhYeL3m277baKmV2x9K0YMd9zUNSk2mR6EKvTpzLrkSSf1KzkPvvsY67WzqWsUDjYEhNl+VWYASDaM/kmglXSPI/PSEk2plw8hx9+eB0iemsYp1Krc7qJmdEdV8E2KDGev1wJ07qox7pnuhmqXjsdYt3wT6QEZelWyEbyShgaoj2DUYf4v775zW9KUx2YlsoUFFKGlp0DCxcJqup0FkiBolkChqpw/o5GgGNF7Iu70XorQgvDrDynCfFMwu3NbAP56KOPRjUk+DRpMNgncjlZzSJslBSjQ3sTlSJsRUkqxVprrWXsOGjIPEiqTPIhEuD2oPP5daP7Mv1e3HUmHoJ2UQ1iibb5kaoTyxHF4nT74tTV0Qts2OjX1+X/65az/Jt2Jcr4Qx/60Ec+8hG6r2q/+MUvAkFYMQ3MLV103I9dAR8EyG+/rs7xRIBRWJcrR0IZNTskR7W67xGKRLrhfTxwdMRRjxT50pUvXZn+IoU+fkcVu/2roY9AqKq/Lpq/PUGgt3QnsTseKRN//MKtiiQyM3uEFr9zj7xuUdNEDyOzMebHk8vkDDMoY1nFPMVKLWDj5bD6vkqIhaQY+xlXcIBnrh+/+T3zX795VtMvuTReMky7qOmmiyrsciZYJmQS7JwnuHmSerAHnnU8RrykYAITI88X8y3W0VSs1SP4kYrgoe9EmR7x97///V2xwgvkWKmrzbQHDyPzMLNh0gKa4pAnL1MBDdf1lVBPe1fSUQ0we5OJJopexJ+oEQDBAGjXuI4eeZTTpQFlMmeNq4mdQ2ZyZrQWo5oiO91HS3AFFqi+zuVf82ZD70n9nOc8x+ND96d4dd03WGwknQwFYQAQoBHnClaAM0DY1zbKGIzxMjpuKphMdjoASUdm3pMVSP5kCFgExMvpJ2agySrQhj8BA1nhjhRoYsUQeI0dwuGmpXf6xTn0rGc9a7I63fZIjJkJk69mt66SajBNUqEfdTtxs80280N75jOfiWGw5UWtBAxRWD1n3EJ+R2iEfPzGV5zDD9lX9VQlvjq9tJ9W7VQSKJSOdze2cZYHiN6JPpYma7miex7n8BOoXXBAoWuu7mcOLo8sNfjoHc+dwk6U6dmoKpBqthwFnO6o34IGi7x+9KMfrXKHpvJxUUzRA0FiRHkPN4873HFEmRwKAv9DwB2ZzzACnlCm1ywK0+6pVO4e1hcp8chQni2khWADMk3LiBPl6WfaPSwUOOaYY0zyzJkcZTvl0DDQEdCTiz2/8BUfOR4NDL8LldubffW8M6FEUDxEhAG25vGpU2VQBBNNps6UyCG8gV30lPEcV63W4lUccB5eHqMIFkWR7WyVcJFoQ622RdE8qmgzcmjLntqeIEriNx4iaBA+ZO8NOUWMPKz1zooJa1twJvnQMKN1UW3Ti7qKhSceVficakt10B5pOj/i5UEGpSpZZTwl6+ty/vUIVmFVMjN1B40joXvIqsROKgSqaTUJWXHPYHX6qL9oXzudVOPmaV8lymKZBGNIpeobLDdSuaVwYo9yE1ol1QY6iVJ3UElTbR3Ewt1UJAHXGu/K5G47F1naPe9uhPlAv8xAEA70gvkfODQvX90eCIR21vNk+dvg+YC11GOn+9cjyLPCp5s5YdrTzA8fq+OSMw+UmOLHI0JUwNQ/Bqg0zuXvdWqYewSi7nggL6SP54JFxX7VngLmUjVds1qS1SdF6AlDaErkecQ+oS90Fz9mhoo7xoOApTQppDlz5ViBjDGY65sp4jQ0FfMe1osPuxDhsrFIBGNAERg/E0QF0BrMgPnEXRpwqImvntcmTDiKv4QcNk/gi3WhCBAKIgSBfKJ5LCh1ihVsp0uwl7iXFShtta0fA4JFo9KkigJRjNij4+a7pmUaLIf8oFP0KgzMx0SNXi1fnKzAFEDhT9ojx8d0EMsxIUZrqO5yXMVfpytjVW0FOf6n6Fg/hkZfYGhEGC2E1VO7XYEfAe1rfWz53YRJLbpjWHFQ8juO0o76DRtinoVan9zyuwlDoIMvfelLFdMSY1FHVesOcfPIx02FYmBF7itHSXoGRc2uZbAQa9v2W4TMJ4K9uRkMtMYUPWVvBJGIY+AKMY48XCJLIFycu9uSeU+7/fwW+BrctAONMTSODmQOfFUGDpSSgfzl/0p0nLASLkWfCQ/NS6YnAD3pAx/4gEnIWBpmNlUTquXvTm3Js/z1pIYgMJcIxJk1KdoIAbc9174YGpMYBomVMkMqy82iO5O+YuMsTIUGw2vjQ/Jlbnl8TM7MvE2GCAZK4ijojgT5BNFpXEcOl5PZj/L0IcE0VbP84Q8FhbMfmxGOw6LjDaUPc52gO56JBCc2cvjElsMrj6BUSypTdxAazMZXaVdHcdAXQYJUBHaUBt5O7yZwMmRLVXQs/WWh+fhBgWFolbmyeAgLwkkdzrrBDW6AB6ifKkauBylkXJS1dlRhZ+FA6qxLwNDyFkJUc291Lz1Z2jxVJJARKRXEOibMrBXGV7SHm0wMTcscSDidTmbtOoEHzyjfXJUxNJilu2IE3VESX9Flupobpvou0zpkwhgOTbdzz4jnQGQRZWUIhHqtZlwHIUOy0SA5htKJ2C2Bx0xXVWK6tcqd46/bAAfiSQQpcqYkAuF2lZjiR2OQ7FpKg5syq3LauRop7W9V3vKnntAwg6upw6eYNuiOAsOHWg6gADIbdKddoucJP+dxsZOe9zTNCwJzg0DozqQ4swTiKhhIgSl88GbqfNVKdx/Tw5PUZn4kOFZ4iCRMcGvzlbpY1dBKogLMP8cHcYgxK5NfR/31qYsyPKb4uII1PtgAOmKtrAeitiElDtkult2qR6RZNXpBG+AQwWDK6rM9eoEk0XKqJdQgCf1CVtAappqB1192jrpDHBJjqHl64XKsKevLhtGo8AmCMzkKa0EBpcVAQEPzVOVCWAXdok5RjFahKgZM8+xcohlFsEgpGsAf5y81BQOohqFNzDxvWn2d+l86HOcORghww9cGyBCIlSFr4Totc7haS0iwNwV8Sksr/JVUs55CpvirHPxAICee2mWo0rqPdMJfok6X2eUNMkXtYMPGvUoKycJm6HkOOdHV5WONcOa3IrZhRRDGlYfbvJw5QlWGa6joddct3jNcYCo5A72uU8g2SAy/51RqSJkgEASCwLgQWKE9zcdV4+Koh9sFq2CVzcv5IMSyUCDMt5hnFp3VZJ8YJ14qEoj1NRw6nAsEAKdQRwjRPBoy/VUPBoCaMOrEFQK1WEVTczpHGftCTCgfkcY8vr7aiUt0MItbkoAZv01x1Ca8gOsKe2AL+cuIIgwhIcRZJJ+nPe1pTBQb6VykxBTZ1QUP1V55WBFCgxjVJfwlhPBJcfpwPInWtDSDVUabWH3VKoAYMb3qET4CEzk4BIvFbSSfR4btl2YUlXQvuZYuEHvEHLB29CosyiXoUsoL+vFXgJFPtQGtEZpQVMAlwFL5eBWyiGk1gaTyR//VGNt1oHrOUq1rtfLaBkn1y2+ZEybwDPqNAGqCHDJX/ZqwpNGh6mmnxIQFJsusxhhBwFYZOeKx4Anb7lnK+GA5LgHMLmfqFht7mjoFvWmBP/Y2pMIgEAQWIgKsjLmllgsbrWU6PelF6M6kA4GXEAkYSPYP2zARV5S2ISyGbsFTw91ACTC0zLklSCblbBWRBi9REikReYphsJ0V3SL8WQRPE1oYMJ6gZuCRKta67hKnm+uTRjAGhlC1loCJOaiFFZiWNVld18OkfegcEDtiHs9/QWLpZI8/afmGyBJN5bJB70Q4iUrpeoXGf8mragQUtyPutTy0wHALORIIDOdaeXdV9fkfBIJAEAgCy0AgdGcZAPXwMLOHoDCcCAcHU+MlZuScFL7iKywrIQS/QYY4HWgSJSFUd8yPaQlKln9qfvsoQkhoiNAiDZ7tlnC74Gp6TXCiBtUy19m+aOoPAkEgCASBeUcgdGfeh2C2GsDFQwwQh2Eljrjm7lKg2brkjOrFPHwEOM/o7JwUBIJAEAgCQWDZCPSW7iRUedmDN7qE0Ao+KW4UcTy95Tq6YA2zz+i+5GgQCAJBIAgEgUWJQOjO8g6rqNvuhsXLW13ODwJBIAgEgSAQBMaNwPRWlIz76qkvCASBIBAEgkAQCAKzjkDozqxDnAsEgSAQBIJAEAgC84tA6M784p+rB4EgEASCQBAIArOOQOjOrEOcCwSBIBAEgkAQCALzi0Dozvzin6sHgSAQBIJAEAgCs45A6M6sQ5wLBIEgEASCQBAIAvOLQOjO/OKfqweBIBAEgkAQCAKzjkDozqxDnAsEgSAQBIJAEAgC84tA6M784p+rB4EgEASCQBAIArOOQOjOrEOcCwSBIBAEgkAQCALzi0Dozvzin6sHgSAQBIJAEAgCs45A6M6sQ5wLBIEgEASCQBAIAvOLQOjO/OKfqweBIBAEgkAQCAKzjkDozqxDnAsEgSAQBIJAEAgC84tA6M784p+rB4EgEASCQBAIArOOQOjOrEOcCwSBIBAEgkAQCALzi0Dozvzin6sHgSAQBIJAEAgCs45A6M6sQ5wLBIEgEASCQBAIAvOLQOjO/OKfqweBIBAEgkAQCAKzjkDozqxDnAsEgSAQBJYUAv/85z//9a9/9aTLX/7yl1/72tf2pDFpxjwiELozj+Dn0kEgCASBRYjA17/+9Vve8pZvfOMbp963N73pTTe72c0uv/zy7im/+c1vfvWrX3VzpC+55JKLL754IHOyr3/5y1/23Xffd77znZMVSP7SQSB0Z+mMdXoaBILA/CPw9re/fdttt91pp50+8IEPdFvz73//+6Uvfenhhx/ezVyg6Xvd617Xv/718ZKpt3/11Vd/5Stfueqqq7ZT/vGPf+y2225f+MIX5Fx55ZWV//e//33XXXf97Gc/C66//vWv3cJ//vOf29dKqOFa17rWDjvs8Le//W3gUL4uQQRCd5bgoKfLQWBhI/D973//He94x/vf//6vfvWrC64nTK/P8ccfTwLpNl6nDjvssEMOOWRYz+gWWyjplVde+ayzzvroRz+K1elvNRt3ec973vO5z30OWZH/iU98Qv7vf/97mWefffZ5553nrCpJ5nnIQx6i5De+8Y0PfehD97nPfU455RSHnve8533+859/8pOfvOKKK2688cZV+Mwzz3zWs5615pprHnHEEb/97W8r83vf+94zn/nMFVZY4fnPf/51rnOdyszfpYxA6M5SHv30fZ4R8ND/5S9/2Z2kznODJrk8E/KABzzg8Y9//GWXXTZJkTnNvva1r/2HP/zBLJ8eMKcXHsfF2GBW/G53u1tTLNTKO7PWWmvd4x73oP3c5CY3addxb/zoRz/6yU9+wq1TmWJi8CHM4Pzzz6deyFTPy172Ml+/+c1vbrrppk972tNIIFX46KOP3myzze5+97vvscceLfNd73qXq2+xxRbnnHNOuxCiQJJ58IMfzPXTMidMKPmoRz3qSU96khq+9d+PE9/73vcq7O/mm2/uqDSd5lOf+tQb3vAGnGaTTTZRUOaLXvQiJ2rn9ttvf+qppz7lKU/54x//iOKQgtCX173udX/605/qorqmI2jKNa5xDX+f+9znrrbaag45/epXv7qvmNPb3va2KuwquilG54c//KE6ZZ577rnYko7LfOITn9j/n1h1JH9nFwEP3HyCQBCYewSYjZe//OWe3c94xjPm/uqTXdFUm4UYOPqLX/zCY4i9oaYMHJrHrwzbPe95zxk3gDH+yEc+0j395z//Of7kg3NgFd1D3bRDCij2ile84mc/+5lDOOtrXvOagw8++NWvfvVBBx105JFHdstPmL73ve/NDLdDKMgGG2xw05ve9DnPeU7LlNh5550f+chHIhZ3utOdKv/jH/+4sXjc4x6HZLioTNRHoIxMDrI999wTe3jrW98qvyjIjjvuqE6Z2izzwgsvRD722WcfBGjDDTf8wQ9+IPOnP/3pXe5yF9rSxz72sfXWW0+FMif8IFUuRDhxdLvttqPQSGg50UUC8ZJ5vetdTxrvURJXk37Qgx709Kc/XeIOd7gD3BAdoovCuvDUpz5Vvs8JJ5yw0kor4dP11V/xzqqi4bUcCaQN+6H3tEzyjwuBQvsRpvvf//4OfeUrX5GJpksbl3XWWaeVT2K2ETjppJOA71My3mxfbur1R92pccnfxYaAed53v/vdNqPtYfeue93rCtTQQka3qf3L306miDGbWcd5EBAacZ2s1BlnnEFU0B7z74suuogJR4O23HLL1kKWTxmfSy+9VCbjxKfgRBEb/A7SpT208gMJlZ922mlKcnl4YJmOs4IcOqeffvpd73rX17/+9b/+9a/rFCyEwaZ5cGB1K2Ey21fl2U42++STT9YGMommVvuPO+445pYqgDeUoKLBHsS4JhtJiiisNJvkwF7qvtpGLCxC/g488EBsVXvQDjoTjviSl7yEdHHMMce4hGs14aG1cHSCUsVI3OY2t+nG6tIwoOr2QHHud7/7VQ3ve9/70JQXvOAFAn0+85nPaLaz7njHOyrwwQ9+kMnHZqpH5enDgZ797GeTWB796EerYf/991977bWRD9oJrva1r31NJrqDTiEKaAHqNuBl67Z8lVVWuf3tb889ZNxRHJqKoxheuZAc1ZHuvVdjRBfUbCV9rZyq85rXvKYrduufcfqAAw4QpuN3xKulEtT8Rje6UQ0iyUqXATXjynPiIkFg6swoJYPAMAKeYiaUnvVXXHHFwFH2wCOVbRjIH/vXD3/4w8N1snx+onNw9eFLTz2Habzhfz8SI85CCCgZjBlNnukiKpT24Ovee+/94he/uJ1rXl724xGPeATRiPGuQ2Ij1GAmbQ4tx+TY0DBXxk4N6qx5MC2h+1yjQFThyvzOd77TLoTNNJ8LV4J8fEgxAadbbbXVQx/6UDN1PpdWfiDBtcEgsdAuXXP6T37ykw984APVwOiq8Ha3ux12UmexxNtss42m8o90Z/+601V30IWa2TsLv9GXOt16H0uEpCGAl0jouNujjooaPuqoo6Rf+MIXunqlv/SlLzGcVWDgL6upbUJJKh+32GuvvaRJNQWXNAEDHRk4ceDrgLpTR3WnqR1ykJJhDMtVVCNy4xvfGEFUsttfoS0CgGSim6SdVhL7lwkibJLggbFhdVimzK233pp7y9fKNFWQOeLz7ne/m45FMSrpxV3nKlUVfQjtcG6pOyUUud9IMjLRsle96lWl7nhiuEsF99SFRqs7CLc7RElc6gY3uIF+SWOrn/70p/m/7nznOxPGCFcItFHm53IUkvirvljzpXnor5J1rfydVQSi7tSPLn/HgICftF+7OfcY6lruKkyg3/zmN3voMACe4N36mGdkaIy6RbfyljZDFaDQvrbEfvvtR9Bm6lrOcMJjt57U2AML1+Z/OqVHBIDuPHX4dDmEBBN6H4ykFfDc51xgivCDlikSExExnbVOxIO+5U8lQUXgmMAn2GYJDdNaxsy6FX1kJ5AMXglVMedEEZdGX0RIVHAGwYCvRANwFAZGmIgyhAE2DwLIhJGiUjhdjvk6g0r/uOCCC/BImdwTTtSjrlrDi6EXjBA1Ba/1gKMiMPPUCO2Enm4iKJP1jvsDHWGZRFc4Bc66JjxIy1k1BIIBa3fOwx/+cM1TABsoeWbCat1+BDOhJ6yaQBCSQxUTzkKNcCuiUxX/gTax/WussQYBgPZTygTZgzJB8jFGhCtOxgmvQmoy6JMdrVPICRow4enTynRDUowGTrGyGhTA12x+HF0eKNC+svTGAkGkVxl0zw2HoC2kF8v0A6GHlXOKYIMuIL4ySxWb7M7XtV122UV5v/cnPOEJ5S+DKvkEzTJ2SLZfk5sNi3W5L37xi8cee6zIYrKTr5gQhMuD5oahKrm3hSU5URmnuLcf9rCHkY4UhiEShkcaJl4wspNM4hBuR2jUcb3TL0Rq9913F86FwqocQcTnlKR+/e53vzMZIFa5c1AfJeXns2QR+L8w+CXb/9EdZ0rN+TxZcGFzVk/h0eXHftQz2m/bc7lbsxmVKRR92JS3mz/FtL6wGd0Fn1M8ccJi9HZ2xTSLy59Z8ij0XPN4YnKI/B6It7rVrepE17VS1NOWJsGiePCxGTJZNZaGQT300ENve9vblp2wbkX8gbR5uRpYbo8t1sjT2eOMGeDd8LAWjsDW/vjHPxb+yRirVktchdrkMaphyrg6oy7fUc9lj1Rtc7pLO1rtZ+8f+9jHYi3YgIcvYD1V+Qhc3WS0hKLh7msMw4NzeNS6N7QZdXBpE1btgbAHujq5HtACrgQzfvSLfuD5e9/73leFrqIYQIYr7+ZABpgUGlfBSHAFR1kXPg7ylVhOF9IpmcwDyURPeUBaDUwIVmRoIMNYEofe8pa3aImWIyscEMxPLfcl2GiP7hhBn6pBjiuaK7d2uhb9QD1spA8YjSC3CNZlxr/uuus6USVlSlszugl2WiVwoBNoQDukLxrfvkpgTpqnKg12CQW6RwfSfq0QgAx468ZzV/AYso7uJfcDAQCGMv2mDK470G/BoKsH76FYIIJMtZLKEMAG6veVpYdwQXHiiSe6bzEA+YbSKW4qCffk6Ha6511XJUAwKPhHDZ9zixy4kdQAczcSO+1Xo2YtJ8OIuXH3GjtAGSOOM1c3RkaZH4eSgdx8+9vf1kHNc6IoYPxD9A9dR0lER4UYrcFCx1FSzMb94Mfl9+sGQARdVMkJPyZaWuhewoZph1xIigmyhp57CXp+aJqKY2Ebbk499YMi19XV3TN+vBqDJ7muu0XbkBInYiq+4uukwcZ0FbPm3CWQGwRawu/X9IafzqRCg11apl4g5TL9yopmyUSdISCRTxD4PwTcmvlMhoDnGphMCv1y/AgnKzZL+R4ZJqzdoDwX8lxg/NiAgYuyBMIFmu9GSITHn0cJbsTwd90QvPiqLefFQCUz+Eo5YDNIBc6tlaIsiuc+f4EwQ/PFVieD7RHsIethiuvQhBzypPMgM/fyLPPIrmhK0gJjaZaJTFhrit/wfWgzY4CUqMeImM85nc0w/aWa6I5ipnq67Oq+mm6yXnV1D31GwlAye+w9a+T56BBpnRgg4cnr0hV3ia6VJwKAThHQWpUM/8VjypHEbnnOmpIqw9hbJiOhnZDBAqU1iT1jEpgifUc+ZNbHReXoyFUZE/9nZvS6e4xR1zwWkZHj9aiYWQXcqCX1V2FdY00hTE1h5B7zmMewQw6V06Gu23XuwLkbQtuuiPa1Zrszda3Bqw3qVxKwhrhO6Tp3WiWVMBz4mQ9YimbV/YzJGcoqowuMGQz1sRpc/S1nXJUxpje/+c1RyfpafyHslBaDbCzwHvc8/YDjqfxu+u5ecg9gqLgaHulcxFdtDmEValBPt9pumjHmaFPGB6R64ajafK3uu3WlS8PonlhpdwJNy3TFp2Jo5PidIi5ELB3HPModo7z+mvAYU/W3m0Sz8R6/dydWnaibMviZr35ffk1+huZpfhQ+dBG/0yrpB+Isj5FupkM65eczkFmndP8aO9WiaO4BVXUPJR0ECoHeOrOulhEagQBby4wpIPbThEaCUanHqx88P4gpDvMp38NCmu+AH4TYUI8hmXRvqq85Cg28POKmL+Yx5ojmKO1pxep7prsWDaniLRCImg9RcWn+noCqdaHacKJrz2R6Snqm4w2iCjymXYIgYVbHoiBqJFxTcM1T0gdRYKvQo/q6nH+7dMe80FO+2V1uEc/oVr9WmXgVP2DjCdEOmRx7TBeGrFFlsjeIZj3cN9poI6TEE9YDWuV0Gmdx5TBXKpRmdG9961tLDHxkNnvsUCkNFRXL8pk6yzS+sK0T2Rsfac1Yf/31tZwkjpw1G1/Fun9pUWar3Rzpdl3No1uU/SZjsIv0CfIDEExD21ld2tEyhxNGHFDdfIaQYqFfgEIQmbc66mZQ0pTaiNegk15IZTiZ2wwhJl0oSRkCgnuYASPCAbnMdk39VUjkcKKSOAcriAJiBip0J8vktzIcuu/RRgYzIjJ9xXFN36XdZsYO2ZIe/iBYjrpW3aLuWx2BP5LK6vtxETBk+kFB7Ba3uAVGVVN5PwdtcDnyBo5lgPxkSETtEq5uBbKeVo65gSaJj8Ipxaa0YgKiURYAVpiLfL8vfJQa5/boDlA7pZsAL85BeGgXQm7kkBMUU7lDjWF0T5T2WIDtQGa+BoFFg0DozoIcSl5/Szzwkmq9J6lHvKewr8yGJ6+vHpG+4ijS/NYyPZ09u2WiNZ7Inte4iEl/8RgFBPExJKaSptpVM8PJlrA3Hr5tbu2Zrk6Ts5pOMUsKe1aK2sEk8Ko6119zShNrCfaGmE/bUJjQXWIJ/qEeXKSVH2Ni6nSHuWUjES/dN8mmt2tGN8SytQrXYczqK7ah8SxugT9GumNuWja7ZuHEjxLSOG5M9OvqQBthmRSjheiXQSF+mGE7i6BlKMkV5U4yfZdpfGkzyBa2pzvIK+VfPsWCycc+ucBM1uuiw3+xDSqRD08B94FbQhlWH89QW/liqFx1IppFG5PvU3yFIa+FynLcHqWrETz+U+JqV2OYMQYJKqAadEcMja/usWoSBNxggmlcAkcBWl2Ik8gNT0soG4+zivwgNbH6Cqif2IDOVuHhv+pBuUohwIqKbLlvcZ3hTLeZX4FKqqS/copLya9DjmIhiD6VaPhyyQkCQWBuEAjdmRucx3wVEQZkGPN10/3aasIEUbouw8KxCqXDlx4g32y1zcLZJ55ymQySuakEIsI7zkKwVSXeiB+Ub+7OdJlusq/iVOT4kATUX3Plyqm/7AHS0CagrLUrslKOImFOKSZhRlvLTOaM7nDqs4tkmGonWsOWt5YLS+RuZ3opCtwrNatmEYU+mMRrs0/1nYIlXFFhaLCyTDV7VtuUlZOCGdbNMqU8EQbIUUyIVGO2jXwYOBTTtN5MveoszxT7qj0yna5+NIKqAT1MFA1FSggMXHLsvQHVMAmxlq0LwwkihFFDzjSyfCKGA7XFFXBlXKdMMkrhRlKhSxCNaBiiJQDFqeEmkeP0AV9V91qa5ES+MzcJuagxMCPLTanj/tYN4Cy8wWod0HGutUzgK+NTVEkxpFkBOcpoCUHCzVkXRRp8beMo05CVqAOxVmcV7slfrfJ7ccMbUNJUT1qVZgSBJYhA6M4CHnRPf7aQrao+8LgzqNK1bqViO0y7WTg+LyVbtA0hnVllCz2C+SycUi/mxX4YbAbPBBfvqWqFlYgaYc/aAtqiO2V1StqpkrzmHC7cZPWVCMS+4gq+8lOwoLQQaXTHehyJojsVWeIrtsRb1E6XszyfCpUAjkAKfWcm1cb24AE4me4LI6ABsPq8gb7qHZGAZ6G0EP0iccmvD3okx+Se66dyiCXIkDqREjnFNblCpJWplhsIwY86BXAXgg8mik4hMRAuXiUYWWYxEtqbBbclQqiB2oEtSSAlzZYbC1Sg6s/f/iNA0yJtdr1a/W/z/LawJLTxtsFTbiCUarz1V21a3n0ezsYlUufyIBC6szzozdu5bG0xG5SFh6Xa0fR80QmMbjmzah0yFkLDb821QkcB7oMWWUylMDsnQpR3n9Jjam7ebO4uZpZcwWzLNBdXiVgfO0xYY8Kbhh8oKVPEhsAX7g9ra12rQgesJBKpQzRyuXJAqEooD6cGbcOMXD4fXFWLrvnqjlTb8n/wCb4b3hBiRouDwajoIoKW+KqEbfpQDhA7/IPugpMJimyRDRIQoEv5O5xZ6oh2VnhKkT8wClVpaoSjGF4rufydSg1BYHEjYMmn58B4fzImWh4sZnSzDZ1nIO22eTBn+3Kpf7oI9JburKAn7tF8JkSAtTaNEOrLSIvSKDmHQsDGi3IlkPAa8F55dpAHqDu8MMI/RdUIYhD0w0nBBYYEWHOEl6iHoiMYhdUXiczVIkH8YMKpI+y9WQt+gxs5t9ojoFgIsweTYRKAKTDT/Ilpt6Dar12MKk+KTA4vjwBeDIqO1UzCeLWnQlI8FzyGuJnoFtiYBa6iRsgbusajNGGvkxkE+oOAm1xUkPag+CP2TfHboepVs/1YlFR+jnvhuiKrzHz8rgmu47q67ltz7kc9gwoRmgqxEpTdPd0MhPjqwdXdBaBbYLpp00KqtqZ6WHnctdPbAq4RI2LFhsesUwCoHp01VasajL6Hrcke7dajVabVDGZ0tGpPMIVdrisPt+smMY8I8FRYOagBQgj46OexJYOXdoflMxkCXB5ibjASq126AQGcRH5+fttkDIIEb4v4VjQFpeD5QoyswaGv0GxkKuZH6ycqdrgu5KtfuHPbdZVRj08301EP8UxiGkpJLFwEOFtxfQvERsdCDXdQVHs9s1pI3HAZORg8ftP27GnB5hMWXv5MSqRpz4A64jlgTiIOffnrbzXolzo9MVrO1BM4hAeXxw6PM/AFqznXE8ZXHt5yf1dtZlAVRChKzM493WUQ5leeXYKi/GXGJry65x6BGR3x3Os+JwWQ0apr+DigJzxXpqkjNoYkUaMF/JmhVUmNMa8Te24/Ho7yyizvOTmZW1yEnynoZNUmf74Q6K268x9Cnc9yImBVlJ+0hS3iQAktIkg8o62KEojjq9AZkZ74kFDT5bxQTu8VAowQw8Ag8dPNbzABOaECtymOFQ2mYayvr13zM1/omYsLJ2d3TdMFrk2rGbyWNE6GjZ939Il4hhhwPt9iSEK1Wnk/wxajXZlYF5NJnQUXHtCmGUr6tZp+VDHo8QWbddBsOJfLd+yQn7wNBVyLfFs1K+NEOd3NF2T6+QstZ/hrXExpnOKeMUAC/oTey2ntHEigUxY0EGDsFOBjzWZtvmC6BRBURrXtFHFLtF7L+Hnb680MvL3kXrKQBQSc3SWHmI+hIOqkmtS5iA4qaaGoS9CVsRaydM2ykAnisY9K9Neyu3a5bkIXbBSElygGwHaIw53KBV4eru5wtAKVoD070ek0ac3znKzAPrKNQTcztKOEB2wtPoUJoajFRw5Ula99QCB0pw+jMIttsJtZTWL8xXIqSsbq4pYpdMaDbxZbkKrnHAF2q8bXHJRoP+fX/78Lsg0iuNkJ32uPXZqieC9OTA2rWfuEbWPjxVHxok54dFyZeBibp0kqZK1rf8iqnOmyz83AhTwrxbkPxInjEJzFAyUHvlp13zQApr2F/AsUs1aAZiAmvZa7Uym6fjGr/yomjEE1LTGmtV+f1hIeKBZQUjmrT9OtixbO2ulDsZeJ7zLqPERYSGsYQoxn2PDX6drAJ4481WvCaMZ2JWDRBec1dtVObAmuKFtrajb+URTEJl5W+dU2S1wGNb6YjWaX+oJYWOVQNbg3tL/S0Ea/Kk04qc0w6yvu5fRaw2hzBMym7mfytjYrw/Neu1JV+Qn/Dq8ktQcH0LRneJQHauiOr4GGKnKpSe3m5Igv8EN3BqDr4dfQnR4Oyjib5ElkpmgK6OFO6K6qabzDmeO86iKqy3PNYih2ZQH1yaCbuGMVdPj5ojvcEJwdpRyArtbby2F9mfC2eI29ZLdIGs1+aDAxgEVBAoRzmZ2zxGpgoT2tfG111oiImSAbzGDdDQeWvS6rEs2oGjAJTn27UpnTW4rfVArMAJjoETWo65DqmsOqavivKDemHQfFWpzOVFcZUfPaQKchFdAbZFIglCEFkRP8Zqvj/Ds0BhoJCQdVss5LSQVso0WvlZZpNUDVaUeDVn/l1N8uzZJjb0beGRZa2iaiOBb8Iaydtc+nqxsCYk+3km6aSEz86OYIziP5WFeo/c7le3KUBGJCpX4CjKA98NYpXbrTrWSA7miVqsq9JQqw0R2/RzwDi0Lj5HdrGE4P0x182koO0z+CjQUNRn/4rMrpji+6Y42IQRHIWARO71Ri3avCwEShED4JSNqPY4Q8Ntnlkj+rCPSW7vx/8Wvu+HxmhgAFWBSwSbbZIVm4KvHgHs6cWf2L/izWiC/AfJdKMd3O2s7RGnJneZ6OPhcJUMbHr72VFPDI9pdNkqlMhVIpJt9RHw9cXz1eBTFoap1r0E3ZXd25rTYJJT2vrcz3uG/5ysi0E494dqe0/OVJaKodmzz6LferekzfhbCIhDBHF4reYlmYPVdHd8RYoJUKs4jMW62mMa0nElS/hKQgH7ZH0lOEqTUPCSgVpOXMIMGOMpxOtLrQBgpaxZ4hGU0HtVsB1sIHZz0jsz2tS+g15Nl7iwMILZYLOB0tIF0QVlEWXic0hR3l3EFi0Cm23G+24kscZUeRPOfy9eiv040vbkGPkUaArDNAlaTdPy0qxdf28ZPXnfbVtfjvhJ7IEcXMMKPI7iKjgOq1YiMSziXUVQGDK6FtJlTUHdoJqgoomYgO/YyOosEUKfAO1KnBwGmZqnLztK+VaDkKV1pfqCyUNnwRaxwoP/C1TvFL0U13O1HN3W4QjaZtpRC77o+ue66SuBTfq/Wq8v2sqEFGyv5YfkREHSTY6LjVHQWIdbLqNHy8b1CdrNruJZIOAv9BwL2STxCYPQTID7UubMQlzHSZZ/NUNyS6wx7Uw9EpLLRVbAhHnW4yJ9zBo7AkNE/Y2g6ADWBXWKARKgsPY7150ROzfCueyxbzi+Hw3CTX1048Is1FMPA1oAserMIaSCYi1n3levDVhWq6X03qzoblsGcW61mWrx5GqNwKLkRKwS14BGrjxDp3Of/qLALRnXbDigNLp9BuGJbnSAGZjIrL0SdaDFl39+pqiU2kLIrRX1KQIBtdaC3UBePSvk490VV3jGPFGHVVB3pP83BpuRAf03p3QpOmXKs7+5/s0mx8xfdQbpRnp5UsZompsJcQQOkMkHw0CyZNBZHDfKI7LC4moUmkWZloAX5W8bA4k1aVEEW00MhyQrHoLabH+KKzTqyPmCpxMHXUvgwmQtgSENxs5QJbprpjx2pcgfl3c9qVStsoMUJ6/ViQVDDWGMHK6k6/DhNrDcNoqwGu4g5xG4sTMrL66+p+j7x+qAy2JK2P+qtr/H0SNTXnrVMD5icf28OivIxzhGO0wmvcdYaS9802V7gySkfuUpWfWHsL2P9B0/mHW/PK6YiHgGw8lSRWTjTjhQq7ZyTaGUZQO82OnIhdtfwkeoJAb9Wd0J2e3CELtRnmr2bkAifFUdpO0MNUT4RSMvlmZjwgtRCxAhWRDIW9/0hmcQuFPXA9iGkSWAjWwoQLomymjqfD87q22GF1FHCIWbJAw7nkE0bOg9IhT1irSEqkGUYT6yqe4afoeYowKeOJqXKNl/ZQrvhHa1j4KfhENMnDlFTA8nFaee6X08F0UwQoplVXGaA7jJDeedYzcjiTObFiOkUkEJGgweJ2W9+rhhn/nZDuaDYDpg3In78qN0s2Yy77rXmkhbqiJhmm7tVrp6gaDiYZyKrqFphBGt2hphRVwmUxTnKLkBQerhosaNfu2+4EPguMjcKEk3HJ1eXIEkaHEoNeTGbelDHE+Cha5m5hnokBTicDsNPojl2kxczqbw0iHNxL7CjCgYniEOgRxLATppTKKPAZpXY5aNROlcbdPVBvzMDCcY665zWsOBzXFTec28ydr8HFL91s7k86B7JLwNAkshkejGsaF+KEZnTDaIYRRrVdFzKIvkEEGrLlKjJBV93xyyKB8DbK1NpumKAGC/fxMbh+nmqQ9mNRG5z9fFQo0y/CunQQQU8mZqPvWJG4bz8uNzlk6gWCwy2UA0a1GdkJjyZzSSEQurOkhnsJddaz2xPWo5YhtwcGy1E2DGnAJIRtil7ykHWUvfFkZ9J8RVlQATB5kgqzqLci1I8ESzBp8zRngRRgV9TvyevpjPogKDJNwRWWqI/rTsUq282Z3TX/tqS26nE6s+cVS+VZ0DY5wjXqVVNMFNYyTHfUgAqMoDvMG8tHR+E/kqhGssfoDgMJhK44VEdn9ncyusN6mQ0jFiJj1EyzgSHEtJk6xTzX5Yya/Nq+UswKZmCw+MVqIi6gB0kqWqm8Q5rd9uaeeoPVg3XRHuDm0kQO58rk9xGGwiOjDWyqTFKEvRtQZJ6mcgmVBMLQKlMfPTIow1dn9asA0uwWcluy/XQRJZlw5MNwEB7clu1cF6LEyHQ/VCabzaIbdx6xWmFEbaJVGEc3GAEDWS/iDkncC8gInBu7bj9EAdlyr8p0yIirVkmaipySguQoIy2zCksbx9aq4QSmqMyAtOarUW63vYTf3UDmcFXTyik1qxDDzDDIFv09rXpSeKkhELqz1EZ8qfTXI5ucYEauw3R+Jqdmlh79rGk5DgoLz3c2TMSGr0yskkwC+ZrYUwUq1NGJZtXsU2XWK0LVYzbcJJ86VH9dmu+pmzNhmjEwt9ZCNYtoqbdI4jo4ASKFb/F6mPI6F92hn0twiMyA7pgWcwrU0rzSCVTl0hpZmWQDTo3WSADyhpRxbZlTT3BSEGlaeaoJlolMyOHvYPIlcE2eKSoFi0VXMFOv8pqK/xEk8AkLiNAR+RgqL4+IEHICQNjpKkwzMGSkmvo6rb+MMbaB32CcTQDQa1RDXKpmFEVWp3AiA8rTxL/pb7mBZFaOm8EN05rUbQPb7yhvjk8xA+Ab326ZpKeLADLqZubqJcUJW+6KRtOtKuWXDgKhO0tnrJdWTyejO1CgZDC0DY5husPG+xD5ecQUK7rDmGE8LGtFvYgbQJJcxbZGMkuKMJWXTxmqygkGDJuwBpm140i7aEswrggHdxW+xZtTThw+DubWfF2MAi4lzoDy77EuBIQkgATwX+BD1BFqkKuz2Y46XdfUzFtBB+JA0UKRH0WhcDjSFI3EvmqkiMpk0Z1u7YxiIkm7GgP9wKFa+dxaO60EZ1y9uA2rwH54T1y6fBxtATB5QFPhU3Sz1a9h+kh2ahyCOMGVQ94or00riUaUT6flJLEUEHBToY/+LoXOpo9jQSB0ZywwppLeIYCIEAzIBgwnD4K4TgxGK5Eb/gsm07y8ljSjPtYQ8VbIYfjLy+N0meQW9rXWmGAeTrc8R2yE9boYA89R0QvSgugKl7AEFxfhXik4+MW4XXgu+EoqPGIYJoxKVRiPBbEISsUYKSb6oVYaC1zQAMKSuSxRhGNLp/g1eMrwofKVYBW8ORaqFI3DIdAvObgUTUi4T10XAoI5HCIwVA7tAX/SYCgVt2stRC/kC6RtOdNNWFRMYFP/dE9M+SAQBILA2BHoLd1ZQVdNLvMJAjNDgOHnmhEl6nRrl4gH5BDxCoJ4kIPKFAsi8lRaNChXBS3EXSeGV0mZuIJl5DItJMZ7hEr4i7XUohL+DrwBKxLnoTBFh4rD/6J+X+tDDRImSXXnsrkqb8z/ebu0FulxlTFXvdzVAQfRFFchgnu5K0sFfUGAoCL6R2tEI/lpzLhZfmt8hQixn9h0KxFTbxogMJ+oyd053dNTfmkiYELbz3dmhe4szRtybL1Gd/j1KTH0DI/UWkLsSU2uEJPrUdsyx3bJ+aio6I4re/ojZPPRhFxzgSGAhXvu+wlYVk2SNOXlMbRMzKrsqfREeRsu2/UA5yBJTuWUCcvYtoc46gY2SZiwwIhMSx3FtFEfrRsgtY4omUNBoCHQW7rzn/2v8gkCy4kAOccctLiOqkxGF9nDkftMHIxZcu3Lt5xw5fTlR4DyIZCZP1EENMI9YYW8ioKjMW9BVwKzJiwzg0wMRsC7iBYypNteeBa6rx4ym8VrvIr8quQQQdncrPKtEkd3BIphMOLMKKBTuSg1kWjHl+pCUyk/WRlMxVL2KaqSugDYJuRov4WTos0mqzz5QWAhIeCnm08QmDECnsWW6Xoot6jYGVeVE6eLAPAtoiY4DZ/IstZC6OFDiyPn9a9/veesbQLQAnyidUqEO9dqfcXChUaJ96o3LbQyy5lQLUJQS/SFebn/VYgKU27kW83nonUJUWK18L6+eoWFGK8RV3eiNfltpb0F6sTReic5kaZO5PlFqmyN46u/yFZtoOCrOH2hb3JoOb7igsLd+JrtPuBWqdP9pdYoI/DcX67kyhd55l4SpI8YuaNacJtlcXCuXSFaDUkEgREIePgUB6qNJEaUnONDV5vj6+VyQaDnCAisFjnUNQ+9bTD7ZNG4J4vtcbuNtEuKzNrMppu/aNL8RNbHYTbcpgiEjZhrQyBUwNJ68WHCyYV8Fe1g7/EDuwoNhLHbF0CUdwvxRjKoKYLZmXbL3UXQD5TvoudorVMT/95eLW7BHbGnu1rbQjwB++1EUtOEGxdpm+uKbxOgprUElWIz6A5nlk2hiIu4VC1FtHGDwUVKVItLUZiswJe2w7JK+BGcXvTOPewr7qJ822jKGgLLBm1/7JB1A+qh6Djdmj6XEF1nLwMcq20FFLrThi+JKSLQW7oz8wg4P6F8gsC4ELCdoGXS9vkQDDSuOieshxLACFlsVXGgw2VsNGdNloDo4UNzlmN/oHq9wOgrWr5uqRcfoo0ZuyWtNSMk1Ma73fzlTBMwCBvdSvhlmMlujrSHnRVtta1AHeJ1MrKWx++777728hkoP4OvRAsUQUyM8Fv7A6nfRz0Mv/gY9xLCR/OoHQ3EkImap5HQWigx2IySSIm3b9qCiL+GMClH8BkYUQT3ho2LMA9LAidrG67jLhJbY98BXatiqIybCg/jPpODitkUwFgAzUpDA2oxv8YM14l2GC+R5lYFWhtolwScQ0s4hf1VidbasAC79dUhcfoS6sGQ+Mjq7Ztm0riXwCDdL5era/lquWL3ingMz5olkw5hdXaBqjhosaVYI33I2xts3dQ9JekgsEgQmCJfS7EgMHsImGebLgsR8LfWnM/etdgnGr45scXhE16FyfTbbrPhCcuMMVN7arm+raJVa/JNojDFF/xBn2C62r58k13U1kF2RGxH8QxTdvP+7uJ2a8rspsN+8+w0hdlmRSyfTKEt2IMaXBRJskcAp4z1OHZD1h75Nv1jtplhDMPOwnUt8oB9rtlau0hLVyaySIowlCijllQmtsGWs8G0inplR+XP+C8bjyK0072EwXsVfIWYset2XKaWo1kSXDyO1suYdLN2PyJ+eFtF2w/TAjdcrdU8WQIlIupgTtCo8uB1rtHUGJV7fTc+hLujpBgGAmETZ+RssvtKA4xaeeVqu068hzfKibUtZFdlUS3eZshcvXnunAt2QUUih+yc2VpOvurezzZHMLLl7WplJDTb21LLTUajirrTBSfpaSEQdccvLp8gcDUKARRMfMvAFCJm5Cas7L0HvelmZYoe6Jbxe/O1JrX+SqvKR6I+NHmfBjE2w/YwBq5VmSbZ7ATvjzBqtbWSAwnL6eUw85747XQvEGDs8SSHbMqnkSUJDJzrK0No6Za3E5ipe4kY/0XJSBppbyG8xNJ6XpI60SElUROMgfYgUyPtB8iOmtPjBzY/9I6C4auMyAEOpwYKxaPRirkuFw8Dz4uhSZXvRZKYDZGD4dQ7QGEqICJC6Cnqg8R4lZLCmoSveNcSumNzRTkGS/Cv3QSwQ/aVsa86tZZnzVGigi5UpjdDwYTnCO8BQmWO8S9ZYsSA6lcFzvNzuWiVNLJ0JjRII41C3VeOkspasydroQqpO1iUau3bRHThAHUrWsSkJcbdfaiAkaWvEI3cBhL2yaQYOWvCao27DZn8dVRV/o5YN441YlH15paSoIiRkAe7iCIvIFOVGrTTXed3JK2DVTn+pO80OZ4+dzi2Z8QRRGOkhUaHjOTSMqsGhSX8HCS6vy+Z+QSBhYVAnFkLa7z62FpKOy8AGZxs0G0fY+lhSjCvTA9xFEFQs+kmTmCKyfixPU7EAMyVbRXIIJliKs/em6rSYEw3TXPlWGVDcqgNAPkvHGLCvfFAPfWx8aDXKdTEQnu23HJL74JAF5olVhVjY85tnj2hT6HbePae2bOkhQ2TTwDQnYqJsaCXSZhsObEWmojjAUgDYgSTqsEbK5lVtEloBXIjRFS14jBYKSBYbOwtGXLYS+qO5nmlg8k9aUeF3YYtM80rIfKDwMDUVWFt0BhCEUaFvng/tnxyiOEAOP7HfGI8gmCQEsJSaWwMqvdOMJkKi2Bltq0/ohKV70aQh/pVSxnCLEWoKKbN8Hch/WJf22IouHE24ZEs8TKRrzZP/S+bzROkC1M/RUkkAPkwNCgCVaaowBRr4P1xilHGKuDpfsA5DKu7EdT4BHVEVbxpblp3KT+aktrp3naTT3gV7cc+qTV+MggTJHEp8piGEeHaKaSpSguv8TtqzNW1jJ1FanXn1I9IHwUp83A5xV3k1jIKAnRoPxrmh8B97LdjWGl+AoOwYYNeA4ccO4uz0ut+jZrAIHqSjtTV8zcILEgEPGrzCQIzRkB0p8e91TFMoycpV4UnqdpM+ukBnr84Cmsnx+yQcVWMwODh7qhHqnxHnU7dIdoT5D1tZZIWKA3l1vG8ZlA9u9kSRMfPzBTWWQywHF9Fcngiqw25sdOg09m/Wjgjk2FgmIVxECG8CLOuyOqoU3r40xX/9YUhN6lVjMLBZkiYzQv2xAOGz5Wj48icBJNvAr3ppptSUMqNUk4W9E6bkTBldEHvqDuImvUyVaGGaV6BVjmj/w44s6owccXbISqtKiC010RUJmTYOWYS7wGjGCB81CFUrPkTjdcRRxwhEycjF7G+xhf1kVOqD5MpbcgAhcyhWQwntGX6S3IAnY/R1CmXEHfCojvaPgKECQnt6xQT1BRjQUZyXb4k1NZVnFtuIBIFHmCPbHRTPpqFubp/DATkiSJKaglOgJWS0PCeOh0ddA/TxlTofSOTNYYshDpY/V7b4VSosu5z7WEPBDBck7TD3aZ5sK2wYjwG2Z2sTvluTg1GKZCMKkYPM0CosK+GAD3FL+sQHmxMkc76qncGFAtXvpVxiJvYWYbYPdB+XHVK/gaBWUKgt86s/8xC8gkCM0aAaGGJLDPjcSxUk8TCzqmNOTEvZB3NR0VamOibAXv6M8MlFTAPNQlmbExkPZTZnmoGw8w+iRexJoWRIFfQORgSoSQe8YiCAIUqKVMCXTB7xplQEHUS3mn1GI/ZqmAOfAV7QDXYyIGwzapkxF/2XnRLTf0FNzAeFYjKho3wNYyo0CFsDwWsOjEMNttUHtcBCyWsgkxbDdVsBrjlTCXBFuos4lKFywyD17SeUcQ8YEKvYvjZS+MCNPgjXqgDhAkeKIgmGVMURz3EDP47VJU8UJGt6KnREdLLA4LyqgfPQ2X46chUlAbUh1DERYIMMfN21ibsyTTc3S5gBnik63Yzl5lGN9EC1eqp+w23qJ1v1Iam4M0uqtfycSwSnWbrOwEGkyvHFjJKCNEqMUYWb+u1izqkee5MmAy0s9skFeq+G8DwqaQAIeoIRmY/ZLrfHJWWCXbKmdNxKTndegbSmo2vG5SW370ZgF+bhlMZIY/TYF1exlKFtd+AthNbAsX3aV+TCAJLGoFZ4nepdukgwFozD/pr6w6/JWaPBeJsIqTbFkVQiGl020qkqzo0iPAk0/H2FStSTwW6MlTWv2AzdfQOd7gD69hK1iobjiEciE8N9/Kp9Tgsq2p5HFhiMoOIEySDXORc01z1i6hgFFtVLVHqDqMiR7QKa9GK4QFO1KNWeDjhdRZqZjJ5uxhXIoToXV+5CZgrTbVACSDiijjpEAIWTu94iDRPO6tCBph+oBg1C9vQo+ELyRF6QjkAtYgTCZeWieRhadqJCzL/JRXgo1xUTC+LrmEQVlJ3nEVF4+NjOykcihkgOciidewSOBBgWXe0z1ftqVBfp2NU+kJE4W1pMgOs8FQXNXwkB8V8QMo8y3RuaUiV768V4+3eaJlLMIGDgpcyhJaN7j5OSUIziKOL5WgQmC8Eou54/OazJBAwx+VeoV54KAuD1WfKgcgAQR5T7D/jbW7NA8JXQp/nRjFddm699twkWFV8YXJM5f0VqWOazmq6NB1IggaD2VAa6BbkfcabkSBsmO6zuBU3wyrjUsMb8pZsQ8wgUdAPSgaolgsnIlGYW9fXCf8y7drjEkQpjxuePlzHhbjA7IyHVWAnxCFsxulcRSWQ6CBFqsWx6j5lRQEYIk8TXkgmTxlpwStaXQhZ4T2RKfKjzkU6cRTSl0y8R8MU64pSulOvPm31W9hMDillwl/usDpUrqtWrBIkFrRsIJPaMYwPpuUzULK+ooMT5i+1TG5foWzQQ+hH9x2hN6wj7orRp+doEFi6CMwXAcx1Fw0CdBTWGplg5wQ91GQdv2GGGXW8hF0UFKm/NBi/NPae66Fia/AANp6wIZqHJkF7IHsoabJLRKFGYE4lWshEbmgPZsAidUr7EaXB0UN7oDHgJVxgXEUMNoZBSuGnED1KRGlxNoQKAgYaxAkyEMui/vrQJJAAC4YF1iAu3cgS1ARF6OZcddL//mt5Ld7+X1ZSQWDhIOAmNzv3C5r7JtNiPQE8MXju0PS5b0CuOBYEeqvu/MfBvHS5Xno+DgTE7mAVljJ5VCEirUoyjGAXVAMHwkK4OQTiVKAD4YEaz1kjE1siBYly8IT1V4iDmW6rpCcJcdY6Qu/RwRY51JO2pRmzjYCHJNXQben+nO1rTbH+apKfDD/yFE+ZSjGOaeogYU+0Fv+y+KepnDWuMsRXDwqh5dA2BTKNUbN1lGY+tXv4uC6UemYVAZEAtG2XIGMLuJzVa02r8oQqTwuuFJ4AAetHzMYsuC0q00oM3OgUIAvO29FKyBTgMpDZw68ir2lCXELhOj0cneVpkkcz/Y/3s8LeJ6yKo7AUSpHXExaY1UwL+7XNIoDuVeiUIq/FTg3vat0tNq209YPmLULURUATWRGOaZ0+rcIc035QQuY55pxoEwR6qmgwAfs8ekiPuZDYO1MpsWgEV5KwYuK4ebqndaEUDgINgRVbKokgMAMEeHYsc8VahFjO4PSFcoo1zMKWrTBfKA2e7XYS6jgQzbyHL2T5vRBywh7twVHePQFPnJKWbfN4dstzZYrUFottT5pu/lym7WJgIyLOzREXxeMtUJ9V8z/i6gLSSafi2UEq0FtJCHOYigarpfXtXBHoIrR4kyuHHmkPZaMg1F0sOcmklRxOWOlGuXSKsbC03t8SWa1tFF9lMmOwyhVg6PF+3moh/3jJaL4FW25l0fromo2v6rpIFcFGnaY6NfSuJVqfE4TX2y2hciXB7kenSdieLpMKpru70nA3k7OUEYi6s5RHfwx9F4UjwMUjqVZWj6HGVDFNBBgMNpsDQqjT3ET+ckGKxba+uvYTGmivpfX8IHYSEnsrVJxa4K+GidaiSXQLWxpmZZYVfF0nkZV9TDtnSrfk7KVtoGcnpBE+fZIDFw8LXevAtURhah+0kQ+x5xI0iWoh6i84jD6hy5YlEj5FkjHSvLcKW2Mo8kxJPxnTA+bcr8bpiGOdLhMvMZRkD1FiMmuBoemEcHsL95h8a84JIbbMdmkMsqkdiE5xRyvgHBJ1juVY7YVV4GqaoRL5AxJsXddfETNEHVe3rYAy5BZfBdPwbXFMiGZTwIAaLNH9VhRiMHxPWl7yTKunmzCUIoF0CpupfagdtUbPR6aoOwE6PhqMNrk37Edga1AV1nAgVTazALuLes7oCGS69ScdBKaHgBsrnyAQBBY0AuiFnz2LMpZemK/bMGmZVU24vSGjziSX72+gBqFduEXLRIN86D0m7i3TCjsR7uwcQ2vpnCVmdh5ieu1xgFIrL1ad9ZVup3QTBAwUig0W/y6M3SHMyfo1GxbbH4hDSvS6CHT5NA/G1SonZht02EC3nm5aUDy6oIy2VT4Kwu66BFJi6Zx4fLqLQ8gEq1xr+5XHTuw4JYerl4HH/yzT4zirkpb0a4lMp+ujTGsJcRT8AC8UkVOZuKwNdbANXbOZgmL1qSV1tdOPHMW0p3bRtIwOU4GVfMoQPkTjkbb3ld0Q6vQJ/yJqmo12tKPaj474yp2EnaBTdcjyRoxnmSH5EHC6rRxwJoKf0dRsRBBLq3rK322s66sRqV7XV3/dHuhdbQLZMpPoOQK9DVWOM8sPPJ8gMIiAaS47N5g739895pg9xr7bEKbIon1WVqLlE2D4GQdKtqPdhP11WEEREpVJmyEksGecCzwLtdWQQx5hCIQZdm0uIIeGIfDFajuZyESdzpyXWTVlr5zJ/mJF5vSCZmo3gSrmcmwb4y1gxYeB5KBRIQIkQWhRwFmTzfKZf3yIGMC+0j84Ynh2UBw7F2AkouDFixAMXEvL2XUag+77CtjJ2kmPoabQnxqYNjWwDJD5t98x+61t9WIp+ChG8RJ0wu+J6ADHukLUyoaB9pBEF2pTKJ4ju2ISS8TfyKH9uDrk0QtCkW0IbMFQ0SpCdKkp+JavxbombCeWCXn3gKMifDFR73yQRjFpSyXA4D0AnPD0yTLhrEmO4hxoWUNAwq4H1cLJzpWPgfFGgYWIhR7ZMQvjBFd5OUecOOGh4Tt/wmLJDAKTIRC6MxkyyV9CCHAEcEMwqNVnptHEnRk2KTfnrn16HDLzttyM3SI8jDCQSirAmPl0ORN7ZqLPbIhjqNn5ZBDbz4axpHNwo9R12SqOCdaC8SAMiNuQz/azcCQKfMUM3rxZJq5gcs8ZhIXssMMOk11Cvshx1WI2KlRYTIbM8rb4K66Ct8IhmSpXWLwFo8VUV52MFpvtRJVw3NTmjSwcQYV97XKvKj/w16Y+LDQXCVPdDlGVpHmXyBIvfelL1UbwADiTT3vQWWoKKtPKDyQUsJURyaR2vFSzbRKtp+MiwQh91Fl7CIER03I6nG11M10DbOfoUia4aSw8rD2l8CedAprKuYRq96OBFvrK9uNJro5+oTXoDv2DLdfNGkE7MuBJbckVsjXFoDFkTv2YrvFCCqU5HLuOwuHGdHPq9G4OumPc3cNIoR9Ic5WqFv2tF1Y0DtQ9sdJeSaab9qeoHaGIW9xkTtQ1PMyd4yYBmmpxRMyPrGUsQNpCwv0MQWr03Ql77LFHvZ52+ELJCQJTQqDnsliat3AR8FhneoeFaM4Ljy1PutY1T0wrQUzEHZL2cSILpABjwGwId5XmLCDs4x/MPJHcrn1VA7JiQk8DwEXkeDQzzFz+eIAgWQGYyIF8FdItzMvNzmkPcuwiqJgdBT1q/VpUUheqp61Hc5kK1kth4ZMexCQNJT2s9U7mhB9PbWX22WcfJ+IoVYZ/R6aaGXKJ7t7QA5Xw+BADvOSIYbY+RYItrPcJsNYKYzPm3BLspapswyitC7ojwcXAStFOpEf4aByFj9NZWchYAiOgRCZvgky6iHT7qFMcBpvEetU7pxxqzixQMGCYWSuPlomubV8rMeDMqkyWTOBRK0mecXX8suVUgmkU0UwdQeMGDnW/aqTT8Q+iggS26qgONjcfbDE2mcalrksD4/yiJHXrGUi7G90JdXfVIbTMTgp1ixpKApJ8pNOCI4niDW5LaYMoaKaCiI1RZZLNuORoQvxZ7rrCih6DqPkhuL1xqdZmN7Y2o85uftG+6vTbERWkg67ovkI+ZNp40IXc7W4VVFWOnaXwJy0nYvnqt6AA5Ul6+EPuQq8VNr4YG7qmDI2zvYPCKrA6C56GG010m2Fm9ZMZrlCOwCzsU+90Vvv9rquYe4wc6FfJw1U5ukM1NGqu6xD3ZasQe6OQVXxVy0yizwhgtG5On3oK9aep/5kO5hMEZowAA0MLYfCQA89Wzz5zOCGZ3Pb4AdPuSY1bsNAu4bmsvKcwRcGDklvBE5PAztaaOyrpb8UZsIKkFFEXXCqemCboHnlskqo8Z031ah5cdTrKvnpYm8TzBbAZZTlYTZv5mlyKaTBJ9dj1zGWz2XKRp56q4jZQE01lk1gdFIod8tg1t65lL76ia4yEC3kEuwRTpP1Mu5ZPBhooyDNqY7y1gVHUWkoDo2jyylZZ+TKwpqZVhdtRWZTxYR5ci6rBu8E8WxlUPAzPqPJoELvLlrTTJRAylA4tEOta5btHu2kIUJvQKY3xSOoum2K2gd8KQx5RoJQU/2v5s5QwoUdqCWCsoI6AGoMh2BBFRi+hYqcBgsa5IbXNLeRE4oSBQAJIVoYPyWDF3WnuT1E46IWRxYD1sRSRgU4Rq+h88HF1cpRVQiiyelB2j3Uyj9ATw4Ti0Lfcpdi2m4quhhOoSuMNvdds+YpXUcJk4ql+Ne5t94a7xb0nE79BZzFypyDWBr1aojbUmahmZCvTFd2l2qwvyK5bhXxCO1Q5guuGNxNwrvIu5I7SeF/la7MrVrUDf91USJIWorZoZd3zfragK5rSVkXx4vnN1p1QTR2oqn0l2/i4OmFGj1q+X7ffY/sqYXR8ujktrReWd7WvSQSBmSPgXswnCMwYAcTFzXfggQd6fuEcLE3FIZqlsdAMSS1bJci7hMmc5z7Sg0OgRB6aMk1PRQYw6kyUGWrFKnKOlACDP6nQbjfVQo9jl2MIW4OZahditEw60RFTbbZHGVoFccW5jIH6MSo8TLQBPkQnEBLhWioR5MvIVW1MlwdrpQdUB5lMnZI2XnO6zrapapXv/mWfTMSLHJgct0Om5ria5z5nFlhafjdRs3aWiTKBf1AUIKMAYBnFKsl+A1xalAZuV5l6x1JKgwK8WB1myblTprrKDPzF/you1SwcRAZCAegxzGpj5h3FBVlQpk6XHWXLdYHplcYe8EXW1MtTAY5KymTanUjIscO14a5Ve7WSyzBBQ211M7hzjKbraiRAUJM6HWVxCcMEauzQXSHfR/1YbKUn+4u+oCPchT7cXiyokoaD8TayhBxEGWtERuVjvaJhNAnIoMaBJqyWMKO/4pQ1QALFUczoYD+UEmE3zvXRU+NiOos6Q75V5RQ3m3ueTtkykwgCixiBqDueh/ksQgSEVrBY5tCe6e5ysrm0GSHzQHUobd8UkN6AvrCCZr1eocWIMgk1gzStRFNQEyq62SS9AUxUmZqgIwdmrk3PGECQFMSDYxtWS2/QGpZSNEmd2EoywKypdrJtaIS/crTN3LqVGZ3wYNIFbWah9cu1WD7Ta5nDJ9qehJdEN9VPPmH1q4wTec3IRayvdrJ/w+fKYaEpBIiI2b+gTsoWM0x4gBUwUS4Gm00FNe7lKqb4Yln0GsWxokom02v2j8yZx5sZs/oTXkgmm/2c5zxH3AllAqEpKimYBpeSWfGtBsVry/jOlNRyFMdw08bQVpVzzRgdPIZ+VmE3Wliewde97nXMPw3PLcFHCQqaAeTRL3QKK9VI41IuIUSkdrUhg+kyCoLRYjzdMB39qhZO1h350PAZKIAr+1SmQWxHyVdTiQXRBR6idlYl3OQtB7WtNI7YMluCTKX7BrEknJafRBAIAnOMQJxZcwz4Yr4cWR7/wFfMsE3WaQ+MmZm96TtrTadhJFg1i4D4AmqrGHBQxYlAqIPwXuEFnBdMr0yeKdIFYmEvOxyCujCMHf7EMUQpwSRYSqGRam7OHe1xImagAYJgVG6qzV8gTIFFxxtYUwKGyAwzb3qAixIkmGQWHeFA0fyl4ghxFbOCo9D5sQHyCYuu8uH2yNF98g9mgJ2o0KXpClYJVZddhYklIwlGmfB0mcqjblrIu1fxwjKxCvhgCWQz7ESzsUYkA79BdDC8cpPTRWBOIVMDlsbElhtxwmtRm6BBn9AXDWvW2hDghUZE3yl2zsV+tNlVAA4ElTsFg3E56PGhYJx1CQXIUc5VALMsn6PKy73SbcYIBGpdfRUmrvi4W8hCtKVuDQsijb9yw40YhQXRizQyCCwCBFbwTFwE3UgX5gsBfIJVEwlhnw+yBEuPu/DIiG5BQZAVhtM0neU2O6fi4EDMKlbEVCMQwm4svhAMwR5wBwhG5goxn+aL4SixA5v4HgEKSAOOgmfIQU1M1jmbCCe1FNbaY1IBBFRO1RAiQ9LAURhm8RnCOZUU4oAGIUYMp/bQD5RUM17CqKtWkIHYC5YJB2KzNUPgpF8H1UrkAeNNq9AG9lt5EkLxgAlhd5ZIF1wNx5qwQDKnjgBOxodlgNCjEpCmfm5KBoEgMPcIeE7WnNMcbOBVQnPfmO4VQ3e6aCQ9bQRILwImOD6IIiJnqTike74PngIRIRQaISxkEjIAyaciOvEGAgYCQZbAWqg+EhXPS9eR45B2WKiFrziRRkIiKicUgoJw8H0oYI10lTT7pzfIcQk1ECFqeRGmolWkBdyFKlO+M7Em6izVYdq9zQlzjoB7w5ARBY3anF98Hi5ItyOPodQ4d4sWF+WGiNPMfJD7clCaHrjPu261CZsLQObH/T+ZR3jCs5IZBGaMQG/pztXMRPMJAkEgCPQWAewW352X5hEXCUvciHNzdcROkBlXKecpFyEHqOsi/WRC5L7ELYKlTDMH+iLqs8yGCQxnt1pI+zLLDxQQRCVEbG7irDEzsV+G2xSommF6U0NvDgMHkyL5Zi+EXgmOVJ5xcnIVNtFyOmdxfe1mkpM5bbv5Sc8eAglVnjFTzIlBIAgsAAQIbHQ+chobLAZ5LC1m+SypE2DEn2VHvrHUOa1KRHFZ8cflyic7rRNnVpjBthMPlmMTgTLz6mHU+XZJPkLXZRI7ZbJV/AVk1GVeSFC89YnDfkCxZQRUIedVA2e0ACwaKsANInetvltzwP8r4k17uJgNh6htstPARZESAemUJ6KUs9wJ1FNB7k5BPpyuPOW19hSQJkpZv6a8Ym6VikDHqJyC1Ylk5/XmjBb/h2vyettGS4y58DXgWKyH4vCScDrLxG/g45ZzIW3DC2m6QumxRhdCjATIS4vJI5W1dQMD7c/XpYLA7FG81BwEgsDSQYAyISLKc7N28RlLx83yrRJnhhm/4QrZsAnzh0tavsejWtrA8NHRORVnPVyG3mD1HIs7fGggB6uw/RI+QSnBJBx1Iuoggb7wSbHK0ngViw5ANhuzqY0SLOyqja0tvhNeVkvouYNtfiNODmVp1+JKttROJBynFVGq8q1/NCiIhXi1bkmEwHo6TjGqjxM1BhuotX5VHsVUnmcNvUCwbPyD5RCWJpR5QGGjBJyjlsUhprzMljGqQbC8Xaz4tdVv5WC1QTHrFi3jF2bnPVmV6XSR+NJC6NA4CYjhQzi0NOggg35VYeoXBLS8vmqA00V3oT5A4Lkj5zgEDW5QaYSscqp8/s4qAr1VdyZeXeLGyicILHEE7L9n1fQSB2F099ldC/KrjCVprDirU2+AGn1i96gnb/erdD2LJYRbmd+b7pMNfK2/VZjdZfPsrUf2QHpcuvKH/wrtMo7aKXbeejex6lXGxjliy3zwjOGzWo5oMLtlEga6JQXTMNiICDaAUrTCwwklWXoag22NeKkQCLbZPgs2F1CYp0klxRKwOiZcJq5jeV3FuZNbKuZGpq2qrNRTwHYAot+YcCJHuyIZhopDBlOJYrX7FJYDGfwDoWklLfUXhm9ZADcQKkZS0kd8Bb2gtShvj00kTHmUyJoDDUZ3kEsqC5Gm1dMSyI0eQVjNVgZgLSXzWLKg+6QaEFF0irI4C4OhltmaAUWu8DuZNBjijYWWTsGQ5CBDAraGbw+HNAktay/tQmQBq9luFSAYFBdVTJw7nyCiZhsFPZWTz5JGYFZZXioPAnOAAPHcxI61sDZ7XJfzaLaazDSxTSjHVfNAPWwtT4EudPPN6Sn8M1MjuvUMpIkl9ADr2Cufm8MUnKOEJZNg/Ep74Bfw1S58o8MdLHZDccy/GR5Wud7pYd011w96AT29YJLrWuiCIHQr7CoehW2GLfvkqMVxThfeKM1MskyUDHaarWXUZVI18B6WuDSJkjRs+cNI25aJfkAUGXjrRV20/oLR8hAkQE/1S8yvfHqDeT+La8EgG0lR6J7STeuIHYYYbN1xIX8dtUMBBUIEiWYDwcrE7indtHuSgSE5yASRXaElvAOrQnCkbXyMD9UpBkJhywzra/1lyGVidd1MaQKMt1ZVJlUDvNxGvmI2btruzeP9D1YMVEk0CPIEG++msOTQisgauFrkX+oRatJEl1rzqGF1+mR/cUElBd+gOxqjwXDGe+wV6X4zZPQtqzidTg9DYa3idPtpVbuQX5wxJfm4fyx9qLdtGJp6OcmAuqPxXGOtMTpLmrJdAp1M342Rv5QzTBHBdT+burhbeL7aKUnMHgK9VXey744fZj7zjIAfnumaRzDVfQZN8VxjyUz1ymE/gxqGT2GYTVW1pybZrYB2Slf8RGVqvKctosAkV74y5rXSnrZskjk9s62wfARCYU1lQeX4atNCj3i7SJvmMvbsjYgH0Qnssa2GZKpfJhOlTmKGar0aQp11dWaebMByIxau0vYcqqPdv+QEO+WIscBIVOUQK8gMqBmxcDnUgZ1jFWwBwIproYX9pvWTbe5HFWCnSQIUheq+Op3OPvGSOJH6gveQDWyyR4Dh5NJO1t2+hZDB8Bgnp9hWwOVQB2mmEZNAhoCgvLm+TCXpGSrEbMgkdB2Z5ARqjXHHVHwd8YEYOgV8akErphKeDpsJwRxoXluh8na0mwCLUUC5BIVA2EaRusMvI0evSUes+whtCc2qxYnqN/S4kcqZ87qRpPVUhd0rTjGt5TYoquAbLaFeIKDiVwyBm9bRCesxBJQVJNte2IYP/4PkcMl2ulCedtTtit36tJxuQo/cM0gzRgtzyo22uRlARKxy67rPUSs3PMoFScVQH3cRLuUQYN1v2Il7GymsXS7dG9Q4QTyokmuR2XRZF1Arw2EnLZfwcTnsUwLCrqvNLme4AUsxci7Gow1u9W6Dk15qCKy41Dqc/vYQAfZPhES9DsmksLWQ8RvtKaiSnrCYgcdibZRHw1BhyRjm0Cx6t85WeUuwtV5ASNuviXvle4ERLUGrWjEJdZqYehkW6qC8pSIybSFIWBIDwf5VYVfHJCzRp6trm8o9bR1ihDzQOUFY2bJwpv7lNTB5rQ+7pSTbz94wopVZPAmrYCc8u9l+fEgx83hGFEehnaAOrlUNGP4rysH+hMJBUEN2UduUQX3wCdeCnr5wIjAk1A6+AI4eWwfpCGsxXFvleH+T8BGmxY7YJJnaNtD8Xm34mUx2t6ymGb9LkzSYK0yI1sKDQxNqJh96DFW7EKGCDwJLqKhYdAfmRUeULL2hFZ5ZQsPK+KEy1nJ3rz5QIQ9Oa2c7ZKwJNnQIAgbGQFpohwYSQne5Ztw54KKgYKUKoFAwwRSl3QCGACeQJuH4O/CpTIWVBG8dRU/pH7iC8UJ5+Zjc6uKc7HTFw8XthfdUSayCjoIEKOkOQVYMEEj5nowv6cgPpF2xfiluTlwfpZOv+zbkdD8ghW6Mkppa+ZYAkSHWWee6b93naCiU/ATcSAKnXEs9hhVi5Ew8BvXBpFFtIh8ugntpqkp4SB0tXoj7qkFnzSUEJPkduXvJgVx7lDaKUf0GNcPe1r6WJgRM8JqrOEVMND7HXUgJA3trcBJLEYHZU7RS89JBwNOTNbVtIDvq2coMe8qY3NOcWcSSowsN9pvd8nRDFyqHJWB4zM88ktgPn8onj3uieY6bhY+OSCVv+Ol6xNeJpoweux6sjJDnpkPkijo0/FfLPXDpBBwBzLCZepVhMzyLNbWdooOqMgdl2skzelriPBtAbvEU1t/m/WEeFC4XRtWAoHjs1uuiqFDt/dL0D7QAC2kXkpAp+AD1aZlsA1LFaQIfFkvsrUNaaxJMKWEwRGIO+zva6apyLpPAnDhdY+oQU4RStGISQODgQEfYBpN1bKZ7dCBtSt3Gqw6J3aGUSLuiLuiINLPH0VAFqr/SzCfGg8BJo6rl3HHnGEc95bqiQNQpbgMXqrRZOw5aaSat3EDF4Vi+yh/+S0tgNY0OUYfJVMBdp3fuRg4O/XW54bMqB4dmayvW2Fgbd/neiGJ8SREoiOYZgslOZ2WVdCP5IbgtXVFJvdZyNx5aACUjAhZEgePMVwzDfYsbKYkBGGKZsHLb2DdcJn5Dr3IToqcqp2rI9FGJrxrpx9UWzyNzrlsl2w9B+4XvWPQkjKbuPT9bpxtuKCEc8ptrGAfCG5Qf4THkPPKT0Qb9Xabn67+NzZ9Fi0BvnVlXW7SQp2NziABGwpbXhJJNNZOrhyz/Oibh+VuMx7SP8WAeqND1UNZGE2uPV6+39Ng1za2HL+vCbe/hbqJmUljWfUSHWL5mckzc2VrmpJ7XwhXZACrRhKeba4oUqUPiCZjbVkzj0bX2tWyJvx7o2mY6W4fMNQk8/EQ6Xo2XbybNxpiLt9NL/GjzS2TOIeXxOZ92YpV3FRauS3f4gJAATILmZAluvT+1CpuFm69TRBizgXra1ZlVxpXMAG3mE8upQ8N0R8PU1k7kH+n2ouVXAgsxmtIm/SiLBI7Y6A4TW5EZtQCYOVcAdHQOidI2DDH02HsGnmkvhY98pZ3K1IcqRg9jTWlUYlexw3qfaI0Ikg0TQ0zYuOqMwf/MP7qjjA/CV4cJGL6iMhxkRUMHT/vvd8YeWzJ8WugOaWVQRoMis8vm29GWqGAU95Lda9w5LV/CV15FPaVHup3wDGqNv2g0PkSPUaZlGgU5CshUXsLf+rRBd+fLaV/rWr5eVfCvyH1l5m8QmD0EQndmD9vUPM8IcC6YaLKRZBUSQgVjmiyaztaTl5QtXEArBbKw4kyjtPIUaU9zaSaBS77bDQ4as3/T7poEm0N3jw6nWaNGdxz13MeoqphJP1m7yw/a6eb6QikJEpXDGJTYUF8H6I5MxIslxoFYyirD50UYYKdJ9xwuzdIM0x0ddC12F1ymzk6pGrh4oMdtBzdT5AKE1CET54OVE/1VAC1TLUXH04SSxPbjWBQsPjgdwWbQoKpz+K/YIOQDB+VHwMMwJzIJG69HqIaaUdVStvBLdeqUDx7gEsAcrrByeNCQPFCjIyU8AA2epcYZESJEySHEBu4tJbW2VDHtx1qwXkIXTEgaCBDHIjajg+p3V6jBq0bxJFzHO7NkYsYYGGSqAfQGHhyfOlqZE/7FpJ2o5qIRymAYauOKGtHBCatKZhAIAiMQ8Cv778ziaiX4jSg5x4ei7swx4IvzcsJTBLW4xck8NYVluiyuqdkkusPQ6rm9zkgLBYFMqkbN+Lt0h+1p5gdHIUjQD0oPGIHdAN1Rkr+srCYqoGHW4Ex4Oo+J0EiTbEcxAIa/nB2+0qVYa7ytnSiqtDSMlkPJIKvQSMzdERTUhC1nVrEHQSEMebkklCfVqI2WgN+oRwRPVYLJCYuupwOUinO4aL2Ti5tPSV1QWFgu9JQkKqAFcnjQgIyyYBiAYrmrzuG/uAUdy4JkTaK1+MjBujjmnChTRwR21IlYCGqicINiuMKWY7CQvK4QRa5oKoKjTaeR2ehgO30ggf1oZ2UKG+LB4RUdKJOvQSAI9BmB0J0+j07atlwIcCKYhaMmQl8ZYxP9qo5VFtKLyogtKOFBRAuhRfgLeqRki+fg7MdpKB8YBvJBdeCnwB6szVGnsB5WeUQTcSyKhVAM/KnqJCEQMwgPxBJxLWSk5sIYrkertNmltYq+Uv4Cl67oY5WjBc4SPaPNuqlHVBbOO4qLyFPEjrQgU5ikhCsKByHeUCAQCDa7rsjwYzZOqcyujKT7qIxPN1MlcirUo7WZfqaFfBOVg2QQY2g/U+ElrZI+JzA2dwJW5yOoOVynz4M1S21zhwt667qVZ+lCqXaWEOgt3VlBhz3E8wkCM0aA50XUCB6DGXArCOlFHdSGLtReapYiC4HkNJFJ3rTaAkUQ5ik2meeirosoUCwoImiEuE4F6C6IjvtTGU4QushkLcSTEAWMh2JBnhFsq6SfHHfYZKfMIN/CKLIHsuJci5hIMlwwPD4zqCqnjEAA4xFHrICQHX7DESWXwqGSx/RUgvcNp5cQiOaXZfnbokSgnhtCpsa4r8SiBKq3nfIkr2evp309jXvS1NCdngzEAm4GD4V4CHSHsCEU18IZrEXwja1dERHPaDpNozX6ad7mFErMwuqziFQ0jtMHrxKmylnG+dX2v1lYfUlrp4UAfxy9kKjG1zZizfm06pxiYa493k8/Ky5LYdrUQUqkcDRR//S/KVaysIrx5Ipys8yQKLuwWp7WFgK9pTsTbxiVYQsCU0eA7iL0daC82SdqL4TFwqWB3Ws8tX0Gyvf/qxXXgm/ISJrK7UXKwvD63+wRLcREmXDB4yPKLPMQKsD6FsddZuFuAdbaiip3AjYsnNmucd2jw2l3FH5pkzqGf/jorObg8byxIqjEPDW6Q3cU/sxniv7O0tX5VS27E+DPMcoravdFW0SaRZgwoN0zvqhBV3Pdvf4aO3/NWIij+mIgeEgFb9lewdZHxlc4mvmJGYuS5T/1kycyEVBJtgLyaE7VGCsoxewboNr6sjJ5gfm7MTbhfQLCZHJXab9iKjGgtcWOfDsfCtiXKb3Qf1zV9/ztFwKz5L1LtUscAUtmeKC4q4SbLHEo+tl9dsWac5pzrZOacSNr4+MZbLViVRcGiWwxlhWLPboNFpx7dGLPo4vhcMoscynf6EqGj1rD1cKw6igTrj3C0ocLjysHL/GeB7FZSE8t+OfzJXvgPQiHHRYsDBQ738Jc7LzAw8VZLNO5EzYDX6kNI3iKtZ8Qa5tBJYXLoB3ojrV1ZaIqur9C1qw6VJJ/WbX2iVbA9kj2uUaALMWvCyEr6JE1gIRbG0NUJq6mMLIoGMtCS4MuX/S9qHyh647aIKDC821FIS0YDhlyyohNpKrm/O0tAr2N3cnKrN7eM2lYHxGwlMzWwG3l0ew1kTeQ5R6of8LMgTJT/MrGkArYlRHruaZSle0ZyQBTKTlhGfvXacNoukNcIW/YWte2Nw15QdzGgnXk3/Epk0+KIEuokMwg0JuEIMd16U8uZBE+ytJ4ACLOvqIRaJ9YMbodkmSNm1B6UVlUHLEjItNlCrq38g5LIDxUL4SlW5FHsZDJxVmL8IlVIs8QDnvkCJO3uSJVf8JeTzez7W9UJ9aOl6Lvbf2nsxWe76KEFmE9ouZdvRGOgWsB04hb8kYlQimQtsZXBOBjnwLzzVWEqVF0OKOpLHiMu8VRIq6QGmAiNJiWmkVZYTzWFmBgWqK8TNRQJvyl4YknGSCkSn41BnR0MhSqonOMrHx16pcEeqeq0J3CaiH+7S3diTPLLyufIDBVBARS2IvWk3q2Q/BM621749NtGSNh0fuM3U8enSb3ZvBsGJ+FvQBqn1yXqHzmHD8gt2BaMgkAthUQpVSBVi5tdm6dHTPPlivAnLOLAtW7jZQmMDBa9kyi37RDdtDBMNi/2hWw8uu9H63MhAm0psI47JT9iEc8opxHmoG7iGXmM3UWjkLtsDKfcRU/rjvMtr2ISsPgQ+ELs1sg+2rVfQX5YjlCzu33g0wIhbEjok2VBKQjN5xr8LfHsYEGmrAtOWhu87CgNcgT/46VgxCrfEv67S/FzPPQaYN80E3Yo+XM1Dt7GXDtqccQ4GoS+muhgHGBj+5MdgmyEHmGA1HvoGq/AxILSmcfbSQJCBSa9nKxyhc/pDbgYIT8dzB084BFJsEGVUWGXBFBrDsBg5RZr8uw4yjobD6Jjxp6qyC13KCQcPi2dAT+hJ/h1rrxErszDEtylgeBFZfn5JwbBJYUAqQFPiAOoAGu81994ZwBKAgAPB21ksuh9hVjMPsxCxcqIZ9hUIwZwDxaDXbr8bhnZRVjzgkSDqELJArqhTk9m+GtETK5oqx6sz2PTCEXrYaBBE8QoyIC1FQeRWC0FLACDjngs8B7CAOuiFiwWFaAkysE59qLmY2vzYuRAwEZ1A4lnch6qUH8DcXFrL17OT4OJbWcfsAA1yE98pImqoleuGK3/DLTmo0nmfqLOGmF+XekqQh6zaDWGyf0kRTB5GMetjrEXZShE4AIy9FyPapNEORjdWgZx4o0gYQ5l1AGSaJSqF+mnKIyRZt8bZ9GfcSv1FGMAXrGlxXn3WPIW+E5SGiP+xMOOmvjhtbN0ZfWcjdS3TnIrgHt9hQZcofUrlQiiKHto0KZfggSbhj3HgqFUBodt40YIH4xOhBuqoDpgbvF/UANsjsDfilTgL9ldzbTwlmdVXcyBkk6cofYkVKZ8hVK5BMExobAQtTK0ua+IUDf5p73LJtxw1gI5r9cD60SmSy9T3NheCL7auLYMiXo806hvZtlVkl/0QK2lgDAwvE4lLRutsorIYcm0a4yYUJ5+z77sHlVv2K++uFRXLqn4DqsrDdPiVowOfbsdpTJ5y9QmE2td1ngNEQRH6pA/Xo5aJT0xFeGcGIuyzFUNfNEMCHWf3nBgkP6Jd/VnS6000dwBucFDYb8oIU0Bg4Cc2jGo2oY+GsDGxdFBeSbzXNjwbZsT2UiN2y/o4aAguJa0gw2QyXBeDudKZLGbxjUNiJoDZMmvz7onaiOci3Z+7G2LHIIJeKJc6Itmljiq4r/2+lqHu3MqsJGkyUuKORojBNbzJDbr4bJVag4rX4JvhslaT9ws0k0p0wdFVvGeG+33XbWOjHSlcnwI3/d0yuNbJG4uvlQciNVjkvDs9KqNZRokzuzlYdqu4ta5tQT3IW4lJvfx1n6gu/WWAuP45KTifPpZt1C0gDBHia7BEaIcIAU98VKq5i7Vw1a7lxCTmXiqTL9ajAY+ZVZ8g8Obd8HlVQmByLKRdAiL9GcKpP84/TahMKNUTgbbsqffG8U0Ze6FppIdVMDJ532tzd2VT35u4AQ6K0zK7E7C+gu6mlTuS0qnpHhZM88qsz8tJXNY+24fsgD3Uf/cDfYzpLBu5sBslKV6bEoPKLOInjwFLDxMj1t8R4TTfNyRwUQkCXq2c1zwaJ77GIh3rdAj6lHv+YRZjzQPaZbJMFweygxzAkdQj2e1PhElWFgTEmd3j2FU0BsLLNtlbKOl9ljgeCgGLtCY6jyJZOI7YWMJz6yUjRRQgG0RqcQMmkleayaBa3T9b37ri6ZbD+qRMlAVmgSTm/mv05pf13OUY2UU2KMc1kamRW74xAHh/Yo4E0g5t9m8/Bsr8uw4qbm67pm+t7a5sQu3aEr+NR19av4q/HFn4xmDSgZqQr463RtGCPdccupkA9F5eWqA6lFQEQyOSJ+YFVXZ7yB7IbBsyvHXyTSDVZaUcuUcA9wXZHQ2iFQA584hGu6WxDTKk/E0gAj2D0dPTV2vE7dzCmmrQFUoY8BwgkwntrBHLsVplPMoyAlsWBguDKcEf0RBIuvjXLjZ+V+5gGslpgh+OpyeAle2Jqn8X5i7oo26M61b5a7BTtsxRylGqL7dRdVvl+owfVxqEhw5cNZTrekfF1TsjHpVnMSCwuB3tKdxO7UkyR/Z46AObfnvvP9pUl4ZtVkTqCoJ6kpIx2btlFmYMLLCElhY2jdEpwOeIZiqA+d3C/HM7H9fsz/vIqLT4fFNb9nQswCMSrlTX+LWkl7XrPNdBQXRXfk+DCEDLzJKBpk50OGgUpfGkwVaH/Voy+MgZXnLsTM1CHWUQdRt1ZSQmc96Jl21TID0GDjNV5fxGAiQMSDKs8o+ogyYTh9ZDqFOKQkzwtixJRiGN3Kp5LWJFeHiakzQJZ5ikcntA2TDhojX+sU/ZIpDTE+MpxSNAb7J4eVpZpw8ZCXeBn0iK0SwKGn7BMWiDw5HVwUHcaYoTXXR2XEl/DTcUVhhMYXPr7qLPNJWVFtOTKwEKNsZRB8Jmw/1xJ9RfOwVcQOmShfEkeJXbMZSPIV0+sq1A71Y97aiYgjrMKDDDftDU91zxDn2u6F2LD7xIiAjgRIzUKIDT3uorNksCKRLgFeQgXOhAXaB08jdRapKo1NAQSiWm4sKG0DQVc4BHGo2jxhB0dkciMSnNxXRkprVYJJY3KIDoaNbJEJSyypH86IqloL9ZcKpYPdwkW4uzmV9hP26eZrg3ve3Wsdfsv3QyhXV8uRmOyGdAf6dEtKq7aixAby8zUIjAeBhUUb09p+ItB1dlQLuTw8+2pyz6a6WW2+PFnjGSqeFA9xBIVhqGIEfGd5IstnSiuTkiHTX06WNk334GYIFWCSPZer5ICzQ6bAAhYat7Dk1UTWWpIqOfwX5RKwOZwvh+FkYruHWiRKOYAcYvIp/96fxSQIzyxKIZ/VF8paen7VwFhSoUzEfWXveVvMhqXZMN3EEdEI2klJBegam0dI42hj/rktwILrsIV4lck3Mzzw0om6ir9IiXOF35qp0zPQPpklhNS6Kq11RTa+TlHeWKBi9bXGl+1HHxkwMa01shXz60Qflk93lNeSIojIBKce869TpAhlUCg5xgs7kWkUUA1wgcjATfbKCKwItj5KOpeG4SqiTMgYQqGF5vCgYTmYSrXWX+zEWU0n0AYMzBWbwICIGwv9UsZR8SLl1AOpHB1RuPqotsr0VcmW2a41kMDwBDsPZPbqq9vMWOB8XVlrWi0sSanuommdmMJLAYE2Oy1JtT9dvlp/mpKWLFwEhulON9ah6M6AvN86a4osjMA8FW/AJGgDdci830yaDeOJQFBkssFy2GD2nn+K8FAlGWacgD3z60JHzOnlF90xuS8bLEcjneKomBWV+FqnD/9lD6gsbDkXGFLFfVNhSQIzXZeZlM8HVLbTUQ41YoZ4oIoQ0hg5yITgG66u4liuQr9hZsgM2sZay2FZzcsxPLactIAfWOEiX83EBod4JWSWA0VHhFBoGIUDJqKGlbTCxekCYmgPZAA5E34IMAJ+qWVqwzlQK8W0RD2kGmmeMjWU98dX/UX48DNpH3FRdnyx6hgD4wsj7VQ+SiHTWXQy4g02UPm8NvABV33112jCp/lNWv58JXSHwAZD0kjdTojg8jQGDbKXjEVJnJUjvEjLc4lxnesNa8YLw5sx3TG+Br2xyXE1LPUsDgR6S3fizGKA8hkPAh5/KqITsNxIAHWHSiHt6c/QIiUTXoYJRGJM+j1/WVmWmNLD2SG0Qhgp3sC3Ui4PeoxQCdIL2RxrYY+rQm4p+SyxfL80j3J2uoJz2XJsgP6hKpbeKfwpzhJnKlPOhE2iInB8CF9AxXTK6qQ6C51Cd8gk8pk3r83i3OH7oLV4TskkvXi3KLpD3ihjL+SF2lFb5JEikBiSDwechmFC3AGNYWiJzlZ7WOKKOVVtyyT+13IbmWT/Kokpcg91cybsERHI5QgPrtsKdN2LBAkfh/QLjIZADDUyVIX1seSZdm4lcC+fgUxfhUYNZIrm9hnInMevumO88FFjQYHD/GqMZtwkI4KsQ4/4ZFhnXM8cnMgN57M8Fxoe3+WpLecGgblBYAUPyrm5Uq6yuBFgO8kzPB0cK4In+Dv4aKgyrKyVF6a8JYAPg0A54GQheLCyWIKvYnvRERZIDTIZD0qJ4FkSBTOMbcjBpYRH1PbzGAmpBqlinrElhkeCW8e1cAVKiWJluVWOObnnRVcMhw4Mt22ZObid/dNQFmE9TB0246+1P8s8cY4LUIaYKBy0NqYbcXUjxe1obxVqB11qRMlFcMi9wQEqIGY46GQR9G5EFzhJaaX4+ogyORQEZoaAdXmmhc41PyRFz6yS2TgrdGc2UE2dSwUBRId6JBiWJwjf8iHAVBhy3yCw3Aztm0zQaq1lCDl36kUBLTOJQoAyh8620PXlhEVVYquFUhHPRlfFbIiGNgFocfejyy/zKG8s2ZVZmlCcW+bpKRAERiDQW7rzf+L5iKbnUBAIApMhINBYJARvGtGIRmU1UD+5jvaLjlom11EMJQrXmXC4sROC4hg3SsZ1BGjXxjYTXrFlYidurVo31zKxUgpN+zqthJ2BxImTYCvqblrnpnAQWKAIhO4s0IFLs/uCgKm5yCETGqvfOdr60qwptIP9FuQkplgIy4jiPIDWQInDtYHNiGKL/hAcKDET7lywzL6L3LeCbKCYmHcLDIWfV771XwLYLdzz1V9ERCS4ND6NVYtFE0/WahAsTOkR/c1pK9raOjL7ThlNoe4kqDq94uvbKQMJeyUoKd6IJDlwKF+DwKJEIHRnUQ5rOhUElo0AtYB/ZIstthCaPYLKiLnm4WJZ/V12pdMsIR5chNY0TxpzcdFmXgslwn10vdag2RWmQMAk7M2DLjjFid2IKEqMLQ9sgSOMrCp0FE8S3CaS3SEF5Av5Ep6PaLa3hlEHLfXHPyxws9BPtJn3KriExYkiIUStdZsnPky0vmhr1fJzYTxWPoq5tpRPvJqdGpzubwtp757b0jbaAX7oTgMkiUWOgLDNfIJAHxCwOLxtXT977TEbtgjZbLhdwta0zAzTYlVXyyTY8OlYV2y9WMucLCEQ2OlTKTlZDfOVzyTXai/awIg2lMsDULwnRIhuSYuZhZnXPtrySSDYQ9VmkbxDbTU7kyzUSU7beUi1duuxlMkptnNsmwY5EZjoheB0dVKhLKMTBu4qFsEJo2bpXRfPqFMoH2LPEYJuw1pak/A5Q2mtGQWuNiC2GHDnnXe2Ug9dsD2BlYO1EB23s1DfvgB2s2yvm3BnyhTojRpa0qVm+x0wDLXy39ZQuAUaJF/LXUiovijvtlECpqgwZlMr+QVHK0mekS+ApraM0kfyj1PsKaDXlvrXSjolReLbWIgfTbp9dFydLtdyJFAoOpyEVY22PdTx7tHhtHX4+JB7YPhQcoLAjBHo7UL07Lsz4zHNieNEwGbHFmHZdGeZz+jlvGrtCmiFfKuH0a3dCwde08MusihiJlrJyRLmx6bj5TuYrMy48hm/tr1N1cleWmE0kGni7m2gNIZlXlcIs24O0B07yKEIIksYWjUU3bELMwrIQjPMVS1SIm7J6RaZ155DZYYFwJIuKowJdVC4xldYt0xbAtbpzC3ugsF4IwF9RUCufEv3LeIjhGAnrijHVgUohaAiK/IwDCW5DnECmz6TPRRAHYSKt9c7VOXtr00srUrDSLiKlKSm1GueECYLCe3jDNIqjEXZncie2r7iUhYDYiSislRem1KC2j6HjgLE3gTVEWvZIMAtxfdka++6tbC39v4NDVBgwpeWqK07cIWzRtpcgMzTutCu23ImpDsG0YV009iRfFrhyRKhO5Mhk/zlQSB0Z3nQy7mLCgFz9HpPU7dXzIkg0LI03fyxp03rzdpNprs141jMcNvqpg6RMWxXY8bcLTmcrqgdTgSkp45yEDBXbCqqxGjhE+0s5tOyZ+azZAnXZX3pASw92YA5Fz2qMPGJnGAFEPnBfkK1HRyrKYCGw4IZtla/VAF6mEuwmjK5Wlhcp7O41CahIcw8mapdfcLEMN1hp1lNaoeabQ8NhwoiQVaYUlsiITfVpMc97nEYqtbaxZi+oiTjrbDGoBe0B9IOQch1FbCxjYTttkFdpNbfYg+tYQy2+CduHTmApXAUi/LVWvEB/UbfqTKg49MZGLtWYSW8NNSGQ5VGkmwfIK21tk3SsFZ4wPwbF6wLTdGkEm+6tAM4NB7n2pYay5Ew3G4Y1bYKKzF1uuPdHaATwiygp+BqVdk4qsunJ6Q7CttayeiQiJqE1moYTgz0d7hAcoLADBDoLd1J7I4Hez5jQMAUmUkw52YIW3UyyfIy2YDK9Mhm0b1w0WyYRSfvyyfvs1g8SgMbgYhaEI9JTlCJYmiKcxm2ehXiQDRDuyhxnrBBGDDH1SRtoPDb/U8BlpiVst2fCXQrv5wJddIhRE6Y0FdV+stcyTRZRw4k6BMOWQvDhhEzWF8bC7FtwpwJMGQt6oW9p83ItVlJ3hlGS3QIhgElwaoydURJ5dVjOQ/mIRMmuCOCYm9Dp2M8oj0YaV9JL2qQqNMVnuIHo/I2CWqKFrKaqGGFgNBg8A8Vlu3XO9zF3tM0En3EzAy9wBHSDtKjO7ZARHo0yXWV0XiZxnTEumsEyLmUIaegvxQUXahme+xWVa0XuA5iJBqGvjJwqJUZTmhha4A6uzvu2Paat0vvnEVkEs+EgEKDY6hevGAIcDjgKACTit3RYOTD/t28XWogjMkHhXgdo6OkK6pHDiQFS8n3cwCsu5qbzDtS4Fw/EFSYRlX3qtGsxpsekNCokn4LopXLNWYgaEvkNz4+rit+xiosAFnD+OkMX+X4q8F8c1rYciQ0G7Z+Kd33XnULJB0EFhkC2VV5kQ3o/HTHo5Mhr4BNT2TTXO3wcDf7Z5XNjwUlkElkKiM8gnVkpJvVqcIEHrNSNqP6oKTTTcrVY19js3CTbPMGb3VAd0RR+Gs9bXeb4DqRzeChwIo4YhgnhIOCUmuw5SMBvmoD81zll/Mv04LfMORsZ1XlilrFOLFtuJd+oTv2saVdsZo6RfNgrspC4z10FOSG9arTqUTkB0aXxdX31jzdVy3CV+Sj8tXGKkOSaMGh5hDDydmEiFBHmGfGdVr7xBAwkCd22juVXLFdvSW4e2yQjZdgMAhNt4WtzECCwWaVhUzBHN0pg60MAsRVRNEpfQvzUKd8VpzVF1TkzhG1M1Bb96sXXamWSFPbmnUPddMuBHNWX7OxseIT3FW+UjhAbZdI96Q7B7zoNa2OfoYKYJbqwY+92wspoWARwwyiMngzoADuJsRKwYW1a7Y3l1HUUBy3AZbjdP0ylBgwiuP2dqsYETeDiCUdx5KFNHH5ufkVdnMaU8pcA9+vSTupO6AuKqaYmv1ANA/p1J3uPEEHaXvKjP4QpWiQbpLRxXI0CCweBGYgVeWUIDCAgAe9Bbp24/XxWK+jNBVmQxgvQtAyGWB8SLzqQA2+YiQiTirf/Ngju8IzBaaonHFyiHdGbVUG3RmItql8f822sQ1KEuOBV9GBvMmhjqqZbRt4gRdzMmNnlmoZIcapIkLqKibTCEelmWT2TLp7XZbPRasAEkPvqbS/8pEhAhhDTv0SQlTuMBoGE2VdD33FA8iEXmHWDmNA7EgvMklN6A77iu3hoNxMCrRg4XaJlkCt2Hsnent5hdD66yvmZOBKxuD+K30I/0BexfbycBkUlTD8dk1VP8bGypY7j/6kBiYfy9FNxQwEQobxGBe3hKO6UG0QDMR9Y7AYbK8HkYk3c/a5echa5Ac5LgofQ4lSoALNvVU14AFoZaUn+1ucCSy20m4OUwxGjr4YF9SkzkUpUBaY85EZ1pbJpUhyc2n3Yb3XzCHI4yLoJqyMfnUf4GiE02V22+NE+YVbN39caZzbMAEWD1tmnUpa3N5+FMssnwJBYOoI9NaZFXXHszef5UWAFTE99QxlZc1rqzrMhlCPRpjQtwswBma6ZbBb5nBC+IKFPCV4qJANLn8QE25CXOXtm0eKGD5XDtvJRtYWKTw7PGUDSv6EZ80404PAufVXQiNxEdpAVaiRuux9n0w+AsHECsFhk4RZCNRlO0lQHHlVA7VAsUMOOQSr4wkiA4AUHxJMjTMRP0gjuIXC1AiHaAnq59Ap34c0qQODoXbgjpiKsBLUgT5Rjfl/7d15oHXl+P9xzYMmpXlQJA3mIlMlIukbmSNTKRRKQsoYDeZMISoiZEgqkoqilMwkaUBRaVBK8/x76fJd3/3b+5x99tnPfp6z9z6f/cc+a9/rXve67/e9zro+67qutVbbt+fBcKUoFDmyIc66Jx2Hw4Bt1gj/DQcAtcHBRn75mFa23LTaSuiN/RZZs19eN5krXCBEwJ577kk3VKyE20lMiruIXOAOMbMCRvZVPSFG6ULCgumtEnUAJB24ZDSokOvL6KAgVX2abas+j8v73ve+Wp7smwTEsLLUmzqiTj7Nz1ogWyHtLJzQe6RjPlUZtFqg2n3aWvCTvOgsHGAJBU8pcryRa1M2W27Ocj5NWTkVQmA8CETujMc8zvAo2EImlk1iDtnv6g0bw/KVOuGTqDQOtopBVYcdlUCjjhN047dvhsE8cxK4U4bZ86ptZl6gwVrShwOjqhE0jW+/2bBZYGK1z55xAvEKMOdWueAmGlhT/hJX2wSTll0WW1YokYKhcluQvAcuFj4D32pyAOjtZC+QshW1IaLhETKEHXVFH5Av3vNFBHBp2CP/B3+PFGag3v72t3PeCMbROrpEx+iDsZBHJIJUGGEvDjBSj14hVogJe1dTnoou1S0/QnI8DRwewj06CSNFRR/oqpo6w98jRxgumk+Oi8IJP5JtmWH8aTWVjdGyUfDHmC+tsaC+2UUpRxO24LVoreUidBM+Jpja8KmalHHrJhw2rT8t60PrG810rNQVIehTlaXCcKtQseaL8W5roe0nqaSmQ5TSals1Nj/l98gccgD3ksYEqc/YjD0DCYFeCMzXXJL2Ujt1QmBCAmJV5IicRxfQJA6r7NEjoh6CHS6L+QNcsjOiPBY2t0pchpFTwY05PEBusXGBLheB9JHeIfVS0EpAgX5yNU89iJHJlrCt/AbqgenlP7A75pm7aMITt9thjjzySJmbLnZVEC6xOe+F3QleaJaQsiPKQ4c5OaqQdFDIZmhW1EOhzvvQIoI1E449hTNCQOKLo8VhQJBJJ+reB6EoulAcrXENdq+ftSEQAn0TcMYubyg3cF4R2jfGbDikBGSbSoklnUUfKAkWyI1R+ur2K8ELl+YCN2xSxSa4IuRSSOwgd2RpuF637N5pF/0cLQQHvwKdYXPOG6rF5gIWpWkIIzLFMkXCzWPBqiGFkm7NTQIOM/FNGrTTNTg3d5u2QyAEpiAQuTMFoKwOgRAIgRAIgRAYdQJDK3cSvh31Qyv9D4EQCIEQCIEQmIJA5M4UgLI6BEIgBEIgBEJg1AlE7oz6DKb/IRACIRACIRACUxCI3JkCUFaHQAiEQAiEQAiMOoHInVGfwfQ/BEIgBEIgBEJgCgKRO1MAyuoQCIEQCIEQCIFRJxC5M+ozmP6HQAiEQAiEQAhMQSByZwpAWR0CIRACIRACITDqBCJ3Rn0G0/8QCIEQCIEQCIEpCETuTAEoq0MgBEIgBEIgBEadQOTOqM9g+h8CIRACIRACITAFgcidKQBldQiEQAiEQAiEwKgTiNwZ9RlM/0MgBEIgBEIgBKYgELkzBaCsDoEQCIEQCIEQGHUCkTujPoPpfwiEQAiEQAiEwBQEInemAJTVIRACIRACIRACo04gcmfUZzD9D4EQCIEQCIEQmIJA5M4UgLI6BEIgBEIgBEJg1AlE7oz6DKb/IRACIRACIRACUxCI3JkCUFaHQAiEQAiEQAiMOoHInVGfwfQ/BEIgBEIgBEJgCgKRO1MAyuoQCIEQCIEQCIFRJxC5M+ozmP6HQAiEQAiEQAhMQSByZwpAWR0CIRACIRACITDqBCJ3Rn0G0/8QCIEQCIEQCIEpCETuTAEoq0MgBEIgBEIgBEadQOTOqM9g+h8CIRACIRACITAFgcidKQBldQiEQAiEQAiEwKgTiNwZ9RlM/0MgBEIgBEIgBKYgELkzBaCsDoEQCIEQCIEQGHUCkTujPoPpfwiEQAiEQAiEwBQEInemAJTVIRACIRACIRACo04gcmfUZzD9D4EQCIEQCIEQmIJA5M4UgLI6BEIgBEIgBEJg1AlE7oz6DKb/IRACIRACIRACUxCI3JkCUFaHQAiEQAiEQAiMOoHInVGfwfQ/BEIgBEIgBEJgCgKRO1MAyuoQCIEQCIF77rnn7ns/FmaExu23337zzTfrQn97t/lb3vKWs846q7/Ns9UYEIjcGYNJzBBCIATGnMAZZ5xx4okn3nrrrW3j/NOf/kQEtBUO/OeNN9747Gc/e4kllrjvfe/7kpe85Lbbbhv4LqZs8Ec/+tELX/jCBzzgAVdfffWUlTsrfP/73//e9773nOc854Ybbuhcm5LZQCByZzbMcsYYAiHwHwIu8S+//PKrrrqqbyfBdDna0Tve8Y7/+Z//ufDCC6e7bdW/9tprX/e61z33uc/daqutrrnmmtZG/vKXv2y66ab77rtva+GEy3fcccecaJTTTz/9+OOP/9znPnfkkUduueWW0xVYP/nJT374wx9O2LHeC5/xjGe8613vuvTSS++6665mK/qv+cntdN111/373/+21rflxhF1/fXXP/nJTz7ooINMfVO/aSQLs4TAgrNknBlmCITACBG48847v/rVrz7lKU9ZbbXVBtVtxm+XXXZhBZlMxu9Vr3rVOuusM6jGW9shUC6++OJHP/rRCv/4xz+ec845/Apvf/vbH/zgB7dW63F5mWWWOfDAA7fbbjvKpnOTLbbY4v73v39neVvJfvvtt8oqq7zmNa9pK+/xJ72iJs8K784jHvGIBRZYYLINL7nkEoNdaKGF0N54441VPvPMM7/whS8cddRRH/rQh+aff37lL3vZy5Zaaqm//vWv/FUm2hRzupiUY489VvtKqFKi5KlPfer6669vRxdddNHJJ59spxaa/ZKPRNi3vvWthz70ocb1oAc96J///OfKK6+stXe/+91vfetbKZ5//OMfyy677HnnnYfeE57whK985SuLLrpo00IWZh0BB18+IRACs4EA38AHP/hBwYhbbrllyMfrOt65WPBigP1kArV59tlnc/B8+9vfZpgH2HjTFCfKtttu++pXv5pHAXDeHR4F+5U1ctNNNzHqTU0Ll112GROuP62FEy7/6le/0kjr5ocffjgxYV/UVesm/CiPetSj1CdxBKGs+uxnP2tbYuWxj32sVV/+8pdb67ctP+95z3vkIx+p2g9+8INa9bWvfY3k0gIB9/CHP/wb3/hG2ybNzyuvvJImu9/97rfCCiuoz+1k1S9/+UvixjLJwkXk4/AjaDbYYINVV131hBNOIDrtgv+J+8pWD3zgA+36Ix/5yJprrokhROutt57lk046SaEKRIxmP/OZz1A2hklFfexjH1OizZ/+9KdrrbXWC17wArG/U089lWaibmmmL33pSyp86lOforf+9a9/Wc5n7hFA3jT5kLNzby99tBzvTs1LvkOgfwIuMX/96187+e666679tzL3t5R+wQzYzyabbPLa1752UDss++oyur8GXdMLSbzoRS9q3dwl+5ve9Kadd965tXCyZSc+q+abb77JKlT5+eefb4HzgA+AO8HCAQccsNhii+2xxx4UyUc/+lFm9RWveIU6HAOMqGo1od/5znfML9vJ28QnQZ3YZMkll+zcnTrUpPpWnXLKKcsvv/xOO+1EtLGyLC5PzwUXXEB18UbY7+9+97unP/3pdu3IIQXWXXfdzga7lFAAlIF9tUapuGHe8IY3PP/5z+cQ0gHJuVpQc8EFF+T/IGLsV38ma5akOPfccx0nxisAx1wZMteIwSJ22mmnSd/pEge0u4UXXpj80j7twqFiYcMNN/zkJz+5yCKLcEQ1+yVNNMjNQ+vsvvvuNJ8efv3rXyeV6BhYuKz23HNPMwu1w4OLyHQsvfTSTQs02Te/+U0Ont///vePecxjlHMp2aMe8qI98YlPrJoSfbRmR36a3zpUmkayMLsI9CGRskkITIvA3/72tzl0J7h6636h8J73vMdJTRLitDrWpfLPf/5zV8Ms0IorruhKnWmcrDJX+eMe97jllluO0ZqsTmu5K+Df/OY3rSXzbFmqB4vLBn/iE5/ostMrrriCKwIBF9w2YWmaDptKP12vN0BcnbNkfAy//e1vbeVyvFoWzVHTxTcFoIRbwloG3q7ZXZGIqsYEil8IMTDJK620kkaU23CNNdbgSLBJVfPNqFMSOs9m64aS9773vUwgySKrg+Nh7bXXbppttmoWGEVT6eS+9dZb77DDDkSG0bGOHA/6wzY/5CEPoRXUL7cB0+gAkHajRLfNLwHEIcFIcx68+MUvblpuXTBYwoVEsDtbAQWgIIv9SnzRvSOOOIIs4/Wx1W677carYVlCDHfIH/7wh9am2pY7vTsq8FRpubwdfmrKEauT1IMU5r///e+kSbWD7ac//em2Njt/Uhj6rxxt7VBOVafiU+Ur6tyqKXFsP+lJT/KPYF4+8IEPVPaMpsTRyLKmmgXd819TbjDHz/vf/36FVKaIVXmVarxakLTkIKlta7z2opwme9vb3kaWbbTRRq3Hs4OExGn2hT+5VgchXQ5+vDsNnLm0MLTenfvMpQGn2Rkk4BznVN69A8yVOvXpUtPtDC6MXIzK8utSrcsqvmjXoKLpXep0X+Uk64TIB9Cl2o9//GPXds985jMbM9ylci+rnDEf9rCHMR6slGYR6L6Vq3bpIM7srdVqIupUW+WVMskeGJTlpr4FZ3AZoK2bT7YM5stf/nJXzE0F1shZXjIKy9oU1ty99KUvbbNzIggf//jHm2qdC1pmRF1tMzw0hGWbqEYGkSB++nz+85+vDV1k31vw3y9nOuUMLXqKTFzFEUiTqqGF973vfeIL6qgpo0U5ycK5wkCW5bZKHeW0VO3FtwGKsxjLXnvtpRGmnTqhkxgw/RTZUZ/9a+p3LjCQ6tBSraue9rSnaa2JB5kXbfI3qGOChGb+/Oc/Oxgk/SgRHiJiyBRGvbWR1mU9pC1aSyqYJc6i0IGqD3ZXhf65zKahKTRTrVu1Lfcid2xCZjm6tOafDsP6d3CpoOSQQw5pa7PzJ/cM706VkyOvf/3ra7lHuSNQReE5fhwehOk73/nO2tzQeG4sc+qUIDZkiraOAXLTYWCtfwFuMMet5RqvQ06bOr/99ts7WZW3T0BWTYdQdRVDrqzakZFSWkcffXTFyxRqgYTiqeLOrGCZ/+iqnO+5RCByZy6BTbMTEDj00EN5dFvD/G2VXB65ruV25qNmyfxsq1A/nfqdlVw8Od10Ob832zrKOy+vXWiyKHvvvXdTbVoL+vCsZz1LXKNtK6f1No8R4+cisi7Qm8qGVpGmpqT3BVfw3Abqf/e730Wg8gO4H7jQXZT7rhN30+COO+4oOaP56Vz8xje+0YbaYQOqnGosmDxGbECJA74T+kMJn3yXxAgtsOuyKNghBpUUYzIV6p5lHgVz6jq4Lm0lptB/ckU333zzxz/+8eVOqD5MKXdoL11ijRxFhlm22ba6V2bJjPCmlC/NYWan3DD2K8pD2/HrsLWkCaFDx1irJjun0NhdbYtN6HDNVJn/1u5VJ827/rOy9dO3YJmMVwuGph3i0rJ0ZodxYXeQMIEKJ/tMKHe0Y+KaTdr2y/zz3vEH8AkZmuFMKXdYet1jkps2W+WO4Iu1IlyECH8SW+4QNXw2vrv/sovcKXeI3eGsweOOO07j4C+++OKlp/Wf+CDZ1fTvoKmmb20LPFuOGV4Q/7D6edhhh6lAyu+zzz5Eg4PzmGOO4SBs26r5iaTThSCaHXEOldK11lGkNX4aR6lwIciycMyvA8xBpZA4dtaiKVUTirIJt41lvjTXDDbku6Xm/T/KX+ZyI33MiP8sJN0p5mDTc4UcOSqoTwM1pwIHidjWZpttZkf8SY7ApsNZmBsEInfmBtV51yZr5F/FxcE222wjA2De7fjePTkh1nmnx/26jvRf3aWfzixOha6B+JBZiyZT0lmSe6DNinM7O+80csdJ39nZ1ZXOsGGWy2HOhjl9yxMkRMQatKMmW+gky643V8+2clZywnWSYgidGZXYxInMZbRL/DohNn1wfW/v9tKMncqhDOzIGJ1ea++11iWgM11T04JcBJs7UbYW9rjcyB31ncTLQUX/OXVy+FuQA2GM1Rq74lTbqsCcjg2QeTP88kCoaSD6w8a39oELQWtKVHZpXkxaKzTLbLPKsNNSzH/lnDZX4TpDDNVFPIAHH3ywmfVtj60qakq5U7tj6VtzWisfhS2kKmgdbTKKanaaYZrAWpaMmOYiwqGEEf3kCrsaN9GmxjKbpPL+++9f5c13m+xgpFUr81lyR0hL5Vavg+zmSs5oGmlb6EXucLDJGvGfrs8gk2iSdRQy9v6tGGkOBr4fOb9tjTc/uTMdnD7MKp8WD4cYjc5TpepU7hTzbNlMcSzRcDKEBLMcJ00jbQv+VY1XIw4A+lU3VDCn5VojZagBRp2zxJEmBkdnw67zJXdUlqVrLnwkx7T5t9r25ZxgR7wstRdr3/zmNytxvPHVWWh8Nm0b+kmjmCMBO4Nq9cw5D+iew6nRr041jigl5KOTCU1pc6LZhQTFZplEs0nbf0rnHlMyhASGVu4s6PDNpzsBAWMnuLJtzjt13dN9kwGudXJ3+pAk6LB22uXAcK7UvuUvfvGLzkGsbLM7F4hUjkIW0YmvKW9bIBEkTFAGyp0TnQSrAlFFnay++uqOVx7mtq3qpxtKqQonX6c2GTNsm6tJKhAlZ1tb0VKkj2RY7Ut3UOjE5+Tb9JOHQ7Ymg0FySVB17Wt0XAK2ZbmlUhqvjArxeHtkXFma1p6QHQb+s5/9zBnTtR3xRLFVBT7tsrVNfY4lZ96yc01hHwusBRXCeJgObeozbcHekEFkgQadtSvdsho3Ec7sjDrlZ6bMnUtkNqlz14J0TD7r4kRvIgyHfe2sViWG7KLZZTE3Bm+KrdpqCsRIv6AC2QyQaRElbXV6/2kem8rVjqCAa2tjb9s1odbMLzFkLf3qUDF3bsNmz6gfByQ52DRYC3WU1qU8hpxnlSzcVs1+HU4GRVLjbK2Ldd/MIWKEiElxBCLTtmHzkwoxBX6We0PIw/+RI83xaZhEISVnNh1+Js7uKhPZUaqmqTdkBpg9duARVRKbRGfa0qtrX/5DxYD8K9lWGJQiMXZXC9Q5hecgB6o6T7U77P2vweIeaeK46W3bgiPc/6mcX8eS3vrHUUGh1nhH/LPjTKIRuyr47/btWDKW5l+D44TotxXgpVradtH8dDw73VX7VejfqmKL9bM5XTSbNAtOCz7Nz2aBwnbx0Py0oMOt/5WVg+zf36eqGUvbJq2bZzkE+iEwhNpw2LrkZIqsk6yOOdc7qzrxOb1W8h23v3/R5srMdSpHvf95Z0/ntRqLmzCr0FnPglObchkANIEzJgtd1RgzzxNz+a41NoNlVc5w2rszl9Ou685KYaEPnEZFNFwxa7PcM5466iTyyle+0gWWM5ozaTXb+c3XQn+4J4JwEdt2KlfHcNzX6mwu9O56scIWtS2p51Rbyxwb+lNRAzEal5s0R61ikKrP9bO+NW5fBlU/7Y494PDn53DiFmdxUW4VsBwbwCp0yWsUVV8h+1fL9c0JpOe8327ZcJ3K2jVrjYspqivFprDvhVbvDlvlqpeRM3YzAgJDS0wYTtM+kdEEs6xlkySU6KGt/KxE1PLu8O3bipEzFm4YbB0tqjmWzB3j2uqyatq34KijUxndMpCVoekQYhtoJoeog6QuyoE1NfyCDkh9Jrxszi5yOcjYdYHOzPOgtDbeuky+cAM4jHk4yK9aJYYl0KC3jj2HLrefcvNr3plAhay4xBqFbvM2fHPBpLGU3BsKKRU9+fCHP2xZ9xwSdDAFKfAhAOEo4jarcJWWDcq+bC5LqdwJhmwWHHgqkwhQo0Sg8ItwPxB/FvRE4xN+zBSwnCs0B0eL41w1JZryj0NImYtmQ5Ol3KciwnSYOv7LlJhKbi3/gBVJbDZpW/Df10QwrSK2ao9t1fIzBMaPgH8T/+k+TpVDNbr7DFVvhrMzLJaZk7PJLUGR6KTznZKKGshMtFzmnwlhql0bkTIK69TvxMc2cy+7zUEhI8qqVQvMnvOpwnpABTeJZVefTD4JJcRTQFz2Oem3whGZZo2UOC/bpCwcn0ejulyiMVStm7Qts7u6xw/kao9RtJYpdfa34DxOk7lYbDbRGmNWPyWT2mONVwld0mStWp7QTvMY0WS1OXNr8+YmFD4AQKySHIBS1Wkdr4taV6h6W6vqW2yRY4n1Zd1Lq1W5vrlibq05J8s6JuKmBXpXN3wDRRGaXxPNmOlzY8PMqUvtUsDVJaaXLCOSfExf5XoTZ7pNCphxuHhByJ1KsxXoIQU4FbgWWjVc6xA4mdAjAR0exK7MWTXpgMYxoELVp3XU9BH7oJUrWFZ+kSr3Xb1tbb9ZJnaJD7EYSoKTpiknFAzfx81ETaG8k3IJiD40hWqK0VCETYlZI1wqCgl5rAAAoTtJREFUTEmctapSxBzz9c+lvp8VhTE6C1Ra04hVPs3PLIRACAwbgcidYZuRafTH2VaEyDUlj6tAT90ryw3e5M86ibuNVou/+MUvXGe7NmULmZM617OICuXwcgspdKWoJoFimYFktCw0V6UMCWPG/0EiNK6CVvNvW+aN1iEC3E/LjHEM1I74z0mlGlh3ucMsOSLVdGFt74wxS2OnTYYQJ7zISzXlu1Xu+Ekn1XiRcZXvErxqknqCApZZssaYMU7sd+PdsZarn58fB5Xd31vOA/YV20rxsWtDLuMnZKCHjdzBti7izQi3ELnWavxA88SR6kx9G6ZZ637DTmv9ZtmsmR1yh9dBZ4CqVXrLo2C+rBJ+qjuhCD4/KUKSkcOsKtMWfBhUsr0L6DTZSwINwig1QYZjmD6GYxI5eCr003SjbYH5V5NYdBDWzdhVAR/qFvNGJ1krpVShVXpS/hXSQR079W1VpdS07aJ+OsZqaBOuTWEIhEAITEYgcmcyMiNQzjyUOBBIYno5e3SaT9uy4AsT4jq47iZQztrRK5wBFEMTLOCZF3WSvcjwl4gRiLG51BZX9p55WjERHgJXvS6mXbVbW0/Z0iZzq1kL7KI0CCbNdTMJ5YKYN4Ul04i1FBhniQWmTuCAARb18LPzwy8l20bP+ULsqK7U5dxYJpiqsJSTPTKWohIElvJy4It2cRhIBahkFEOrcAPnRD3QXbjEkO2Xz1+XNKsOz1PtiNBpHnvfPNijYi6gMeTo2aQ4s9Y8GRUB0SALbVwwiq/xqwn9NP4kJrzxrzRD5u/RWjmQmsJeFvjkStf2Ujl1QmBICPiHbf4jZrBLTk1kvROg/sxgN7LrGSEwtHJnQXYln+4ExOwpCSLDJW9Ts1Ishfz9PwtzcNKQBS7lJUuKT1UKjut1Xg0WWuSeBGHa+UIU+hbIoFG4EGgaCxwAUgo4AGQn8BmUGqBsanfklNgH3wmhQGBJhiA1XLtTPGQTqcThoSZjL1IgUCK9g8uHDCKtmg63Luink5FOUgNu9SQyrOUr4jZwr4RVomyVEG1oVAVfjk3IPsm5tuJEcc+zgB0/BwXD/2F3WjAWyUNcR24Kla+jRAVkNEX9cB1VhMVAJI3iqUKlKFoQ7NMOmPI6JY7AaHTK+W90xiqhLr4Ta+WFKBcGakvCpavsSwzO2uajRBpsTVZT2MuC21t8eqmZOiEwJAT843iojAwq/y+9dEnCE8vkn84/JuduL5v0WIefW+aiixwxTf/CPW6VaiEwdwnMiPobrZ1W7o5pYGKZW//J+u/CRRIGO8pnIzpjgatGuX9ygoOp9s0ei2s4BxEBFAnTziniQySpyZGjhCuIPpAIqYRwEbshIJR4vkUTa+CG4ViS4EwJNR4j2osOaG7stLlPKRWJtPVzbL4lMkvTaSI1E44L1c5E6QlrpnC2EeDwoOzlIVHMPKNtw/cf5/bytsJR/MnZ6TRV6d699F/itpi4Rz+0Bi75mF0COZO0tiA6L4DLZ9Na2H3Z9Ynktu51snYsCcS7M3dF21xtnYeAN4VkqRfd0St2x4PipnSnUUKHDJKL48Th1l/eFy6WuldTRMm5g89G8EgL1Uk+GGkTwjF8PGJDNm/unhUDEqPpHIuWSau2clpKnkpbob51FrbVGcWfnFviZV3ugDUoSEdxaEPeZ9KZP1I0cG77uuRNuzdKGpm7AgfORIKXRDFOVsPhZ21t3zWGMKvU+9bCEV2WK6bngr899l8emGx02fdS6JpNXFO51pJX7oynKacpq6rQkzbd8gkm57RNBHxdcTmDySBsnEPuRXBidCLiFNdC02wWQmDGCSSYNfUU8N9UXktb1VbrW//Ykm1dWr373e/mmHG7Cpki38W5w4Mr6iky/MZSSdyxXE2p0NZmfk5IgKAcOVZO98KRjAH73eQqTTi64Sx0xe9AFTPlUOR9FB+ZUIsPqvMQeeKAO/jmhtzxryoE7DqEP4O1bu0zN4ZM87YJ8n8qNu1ixqVOE4txO54AsescsV0tmF8NOjJdoHN7MPCuZOqcoKacM5tzBiusk4P6TgIUCbcH7ViF+mPUMvfdvufsobXWvjXLzieSBeXMadC8uK/TlZLoLaevs5NVrqY8WYdr2SZmTQodGWdo7rV0naCaPHqb6BLHsz5U7qD4Mte1aa0Eu9qdE5dRSNdzQWX4VWiPuqfn/g01wnXtLkUJhZSisdcDCBwhxihszTlEJKmDTDOELITAzBMYS2faTA1KMEX+Cm+Ns5Jbb6SwVE+kvHCkc+26p4lTfaa6l/3OSwLO+/Xv3fcLNOZlbzv3VY/TrMgI8996B1xn5c4Sm7CLPhZa14rMdjZViXEiTSK/rZXblvkSJMA1j2B2Y6BLC4KM/0kmGd9qpdK3bdX8VJ9dpw+aEu4N+SWmST5ZUyiDTcCLTlXuLoEK6/DIelaeEkFVHhFD4PGq+VVT4j/5Uv/aEuzk9YsQ6Sr5Ul0SAfd8SJc9NIGaxJDduVWTV8ljtzhLyAiO4aYPbQs25FaRO89BJU+OzJKWJ39OXpqavGIcw3LvLNMZnpZkQea++yc4WqhVm6jj6RWy9MgUFZqzkNedcou27k78XQ/rVr6mnITynIvmpwXPTSCGuF09EoKEqoOccw6xqubJYXRVE5Fv3TbL400gwaw6M4z5t1Ond+XUudJZtRmtc4pP8zMLs4EAz790LqnTLn/7Hq9gKMPDXLXmZTNyCllZxnJCXwiTJq+c0SrBIW+sCdYI5cgTd7aVNOYKXsfcvsd2uhaXDSaFhfeCwVaBe8NaN8a7shfv4P9g+JlthzcLKiWWMRPeZdeJBrZQiaeKecivi3uuFNbdvwA/AfUgvZ0ngNrg7ERDiWoivGy8ZU8k0iBlINJUN+hNiEs/NeJRRgbOzyFPhSmlxnheWVYOFUPT23rryIQtuA4hawiXZi2DTUJxbxBhTaF7EmXzGL57DmhWMLlz3C8pKu2WBbrBExBEedxhgKrOe3yACtSPdHvV9BNJlze6WtJKy5woQBFbFnTYtRDPCteO2wwdIa6OAHQthEnTjdYFk2VbekgfKDwHA3TUISeNmx85jCkYeG3CB1MD9OgsPiR+HTk3HqLhSEDYh2xyVaadxnPTuiPLDo+Seq3lNqzjoSlUoj9cQdDh4NOsahb0s9xdTUkWQmAGCUzsO53BDo36rp0FnH1atc6oj2g299+pnI2nLcqWWGCtuSJcHDOEJEUDhz7w+AA31jGHVcicsD1iHFYpYW8YOeEGwQuGmYaw4KJZm9YKOljFH6CQh6NaoB5crLtrph5MoFB0TMzC/f8eHqjc3XxVs+2bEbLWtqIMavp4ZKU6PA3umHNjHTkibERqKHR7jleRu/uP3dU4H4lj2DBZRGtLOdUtfp6NpFnxCy5M1pe1VsGTongRdEnevWc3u+i3U/LFjiTjS6WXTKZNNWkd/ScIuDlZdy4ZhYi5GdCzGGSHuIOvizTUuF0TNDakb2gLhpwD1aBsSxe6Y0A2iTa7fHhoTERTgVwTSOIZavZrpJ56QPxRMG6rJBcEsxQSr0QA3wxnDKkBDlvOp0JTVrjK8yGx0jIyMuv5UYhU/VFZoW0Zfj23dzqJF6QKCSNZwHQYCMRc07G2BQMnjwgR/XHhBKMKjitjr5q8TaVRhLpMXxXaV+UFcrA11UyNY2xCdVJ1HAy6Wse5g7O25a+i3euQcDuFSBnZhADpRnxzbjmeqR/Hs2Pb1PjH0Q1X+UJp1Wy+Q2DGCUTuzPgUpANDSsAZ3+33dWFNDeili2nnfX4OSehcC6IJlZJlmZeFX4FtkLZZT45uG5Wzv4tswQhuCa4I1/quy+s1T+wEg6E+WaORUiHu4LU7V+qcDXwebtZTgd2lDKxi6uiJVp9E6+4ER/RNCV8C88a2cUv4SU+INRBk9kLGMZ8KZcEzzBYkmRFkQh6W+XjoAAvq881UnrKtxCx8qCJqidBRwUMmeYlUZvk4h3hKeFD4kygGAqW1hx67QMApJ4lsWObZiKT5o6qEy6QxzH62feQPEXAKmXCOpXqQQVudgf80LpKIbnAwGK/h4ElkkDhd9oWDTchWIkaMSU3zBakDgCbjKmt8HoQpBw/PkEEREJO1iaRnOpBQjhPi0iGhpgQdezFr1CTHWPlsiE761cMa9JaQknHMK8PlzGOnA3bnBkaPyqROlLjZ01acWBQMP1mpGQ/mNthS6gSfuJt90WdaNq36Sa3aL1VkFvSBnhOs564ziZSu49OR4E0j3EvCZDXLk40r5SEwLwkkVXle0s6+RokAjw5TxCeh0+IXvokbmSJMMgvNEhA95ZthSJziK3xAW4iPCEx0DtV1vw9j7+K4zIAHc3P/uMR3ocxXZENPOZIQalt3EjE/KpdzqHQDX4LcEc4VptG9MDRT516qpBwMTLW+udpmrvRZz2kszgwig3Gqt2Cqb6RSWetRSZM1qFxPiBULbB5/A2dPVVZePozWbQ3QrltLDIE2EgtjLPknqikOEuiIJAtUI+Oqk40aaN2cUedi4UYiONjmyqRRgWPDLNiXPRqInyi1btgsW6umvRME6nDb0Hy8EVKV7ZFfhISC19zxfhXbitYBaLD8OhSb+UK+YtO20pT+8/qYQWyl1/hQOeQv0WAqSUMdUJ9wpDYoSxq0YnZGbSC+9YSq5nVrutq2YLqJEqrI4ccFiGG1CQLZ4SilRO0OVS4igtX80qPUBiy8jNQPjW4reots0n8QEDBxtIumHIF2UcckZc+HpNBEOKTNi2WyhlTlrLIJdVv3YdHQxqKEymkSurkSaSnHg/iaDfMJgeEhELkzPHORngwXAfaYbXDuJh2c7nWO8XDVyzbQOn460VePeW5cXpMU6jfxi8kGwwy4j4aNFA6rxxMwFcwVGyl1wxU5K8LMMEjkiPwPNph/pTQQ0+XmF4mrjDQfEmNTdwl17ku4rSlkCAkFP7XJQkv+cBcxH1IT9Whqdl8Q7eKx0B+6gWaq+4Bsok2OIj6DiuEK2dBzZAcmbKoPd4hCWode5Aawd+NlgIWiuB8EyKhAVp9zSw+pCg6kzp5QDPiUyuFA4lFQxy5swu0hsmZ2OK60I15GkHW2YFUZcl4KasBYTBb9xOWmMoFChTD/plvurYwcLYvEEQ3WgkYgkjucK/QQ0aOQtCX7yjXFzMsgNlhzJ6EHEPE1Sc1K1KSixBNx8yEsaCOFxqIOFWhHJdcUTvihmYgh20LdOjQ+PN4dMqWUim1F0ttakBgkm6oKJVRZqOxsC3VUt9U3L52PvVDHcevTWhlGscjWklouZ2FneUpCYIYJOGXnEwIh0EmA9XXNLYrEBFbOqTqMLvtXlVk+bgDLnDSsphCVh1DTKGIHTWsEEN9A89MCo+hy3L+9e2eq3FZSHPgJuAe4E1hi5QIibKrsB+W8PuyKQs4eYRSJPrwgtILgDvFRjbR910OxJbUw26InLs1V0D65JuVF0IpN4mxQyOSLUzDALKUISLUjDaXSO1zcu9znT1LOKovFsJ2EGn8GFaXQqIk/2xJD/Ap0mJzligBqgYGkRey03pDKbDP82pTkUT3n0SE79JCek+TrQ3xUHzq/qZmqYy/VH/rDACUJoUpj+Un3VMc6NydBbK6+b26SqiDPuhoRWJxsw86mUhICITAZgaG9M2s+PZ5hwZXdh8BQEmCbXU+z3CwoGykWQADxx1Ab3C2iG3wMrrYteEQeR4u8Ct4L/1DCFtJrjImjgu1n7IkhoQFuA5faymXkaFwab4WT5K6Wm8cqYQJ3ArvsFo8Qz+KV4aepi3uawE+uCyXsPf+KK/4SJZ38+FpIEEqLlCHLWtNg3dZELbl1qDojiGNHBiJIJKRFylRrzlnlyyFE+EWaXRA9lls9Q4bMu1DnvnsdDfOpUIWtC00LWQiBEBhjAi6rODsN0FVWXdoNyWATzBqSiUg3ho4AuSCtmNDh0SFZiANxBELEzUH8MborVVOMRjU3rYjs8NZI/PQtTiRgQVKIU9icG0OIikApecFb47lwPCJN6ow7ZWSKlFzg0eH/0LjohmwVsRIuB9EHckQhmaWyEgG1pnBCcLqhXLOVBN1aR/JH60/BC5Ga1pJadsKqc1bbqlahU6sqktIIndZCy7W2rZH8DIFOAgKgLi18WyVJvP5fOqulJAT6IxDvTn/cslUITJsA9SOTQxBKLEnohLdm2k30vIGkVLcyiViJ1PS8USrOOgKCiSKV/IUyq2jrSiqaKQo6w5la6f9uHOM9nameZL9zQiDenTmhl21DYBwICDCJc/GO1N3Ic3VIcnJ5lconNFd3NK6Nc4/xe034FMdxGrKYpsww4piHksIQ6JzB0XHnyMT3byJ+ytk5gz3JrseSQIJZYzmtGdQwEnDPjvtoRMSkyMzt/g0kECBqJrIgrDa3e9vZPmsn9ViekAWpza23I3VW7r3Ejd+8a9KwPJposq3EHz0OgO13W5wH0kxWbRjK5VmTzm5Sq7vD+uiShK3jjjtOzrs08KYRzMkOak9MttqsuZBYJtNLINUdgpPNiGNGHRFMjcgbq4itTRRKR1NSsVrNcnbqv+x7dxdKX+NYspWDTba+tR5G1cdwskkIdCGQxwx2gZNVITBgAm7DngdaZ847zTi53JdA7d6uOW+tjxbkcUtOEtqQNVXPXeyjkbZNJJ7zZEi3qmfJtK1tfnpkM1XkBjQ1m8JhWBCdrCcBVmckhHn8oMR5T1SSFC8ttMpFprxw1NMKCLvKK5+w85LraT7zKyHdDYZu0Ktn50gy85Qp2D1xqiKhduHORI/ctCOPgjQv9YDKCZsVqLVtTVw9/kA1D8zUgrR9t+m5R89tdAo9DUg8V7zV0488j6CtNXc7tpXkZwjMKQEaPJ8QCIG5R8BN3R6077Erk900Pvd23XfL7JknKbNbPBwuyvtup78N4eJXcD8ak+whPV7U1bTD3jPzfA9NiVvesCVNOgvroX/8DVXZ84UpBoqn2daCSeHIkUqlMn9Ds4pikITe/JxwwQs4Rbs8XMeNeFgx3nqupnCMZxO7Ha/1kQR2LfXbg3w0+7a3vU232X4PBVCfk8MDC2Sm117cpe9OOlpEmrlEFoUOIeLAXEivcW+/CJRCaoYjhLPEnXfcLdqszb1LS7lCHj6vnqjCzm/PLfR8Rc8D1CWcwVEHQ54eSTPepMHZ41FSCj0agEZhaVT2NjG0eWs6G1TCReRhPJo1IrfkCI0pdPxwC8n6t0zFascjoyx79pLXi5JZxKUnHimpj3x/dURj/7cgf0eMwNDeiP6f+0XzCYEQmHsEXHk7fUujcdk93b0IplRAZ7obDqS+QIncamGFKVtjvOkGN6w1z7OZcpMuFSgDxDxuUR0OBo/2scA0suj16GcOGP6naoFFV9mH58zdcFXIkVCFvr21uwqZVT+FFOtnffNYKCQ7fJcZrvJe5I579CCyoQcGEj08JbYVC+MIISD4MPSTh0OhUVA5bjvSQ2vpGIUkBU1pwaeeZ2iBqXDX3r1l93ghSW2uTVKDv0053SP8VBWAqsL6Wd86U0854u+ZTJc09cX16J7mp+Hw39TPkh1UoJ/lOqLAmpoTLpBHstPaVpkpjqIqLEcdOeioJnE4gdzeaKd8Uc1WrfttCrMwQgSGVu4kmOVklU8IzEUC3PuMmUvztiQYjgqBg2bHLoI994/rokqc3Tw1x10zPAeMjYc7kxRN5bYFFsJ1s8f/eGaPc03dyuu6uQo1a19Eg+tprXliIbtLOpQO8wImF9+8FNIsmGF3xzSNCzToRvPTgk34DDgPPHhXDEKJCBEj58UCkjA8H1mSR2v9/pZ1hmvBLffekCDwxChqx7gqasNksqCeDqBQb6VD8SVw4XiVQT0OmAhgX6kc2ovzo56BpDJrTTPh3NorHaZs+Gnq3Rqtq6Zc9lQCjz7ihbIjD4qsx0zzM3nWAK3DY+TpzOBrh9zxRGMPbBQwIstIQ4Wtt+g3y56z7KmJ8ma4tegn8khNm3iDhClzCBksFVV940yqhdZvk6gFc+rg4W5pXTW3lx0GXmRRt1bZF4+R3CB9dox5/rWSkjukP0oeWMX7RRc6bIhFFwOt3Uswq5VGlgdCIKnKA8GYRsaQgGcGkgUuQ5lSYsVlNFeHQpLCad1zQXgL5Fdy3TNOTGxdUrNqzCfrRQ14wg17zOIyAJz83oolSYI18sRkjciQUI0V96wdgsa7FTnw5XKyDXWJzABohO1k5yy4Cmc+O0GzrNrUSY8xZNFVYMLV92BlxlJnPOyYp8QLB+TieHejngtYGAhLzO5SQnZEWBAZOiyMwnlQe2EyW+UO54d22CHZG/qvz5wiHpno9RfecE6dtOm5zq72WEJGEGp8ABwAsoZJPR4Rz7YW/ZECQpYBKDiiNRNEzdBD3vjBcFb7TKxYmNiQ2aHw6h0RtYqKaktn4Qu58MILKUtNeaxRjz1squFjyiq7tgrNKWHKJWZHnj1NtVR5a50q4bCxoAWbmIiSs44xs+xYclTwzYhMqWOMKoNslVkWfaucKtE3ecrmFxMHAC0lVEcgem6kqBNtJ7mn8X7VTpvveiyC/cLlaLEvmzt+HJDEotQl0tbLPRz5NtG4b3UcyXprd007rQsOVIcT75T5kssMrG5wpznwvBhE9I388l7S+l/QiN7S9x5cDoIpIIC0Zr8OJOFUUtItWuU/a91LlkOgTwKOs3xCIATaCPCXOGX7p+Lb50hgPisPgyFxClYuN4Ke4CnhaWAtmIqq6SxfKQsEgWr8Da5367qfCnHBzaLYF/tR73mgSJhGWzFpDB5zblmhOpwZFexgkJgZ5rOtk/WznP8sDf+Ni2bmqsrZEg4GLh/mkI1RKEuaE4Kx1DEN8sdombfAT5ZJBQaVEWICqwU6g21rglmcPWry7jDwLtCb1JZ6biFzLoTU5RUQ1WYv34SdXqnJdtJnUkks40kK6LZlqhF/C1SRntipWaAsq+dUo/lim1Vo+0iJpW+aQspSt9FGnlllj5tVZGIzwKawc4HYpUgcAM0qshUiLeNPalQcR7avDtPHZIo0neY9JISdJ1Y3j3kkZbRTr+Ii1KgNRw4alTojp4cSNQtETO1OkMuMwOJb+yCIClWJeXQg6V7TsbaF0hbmtzbXkwq20h/kiEb0UyzVVhx4JLLImkOXcHFEtTXV+tPmRudDrJTmq7XGSMQL/9VPB7P58jI12ULlELJ3U+ZjwSwrtMoB0Np4lkeCgFOQ48fHFdFQdfg/1xb5hEAIdBIQVvAfW3kSDJWrz6pDOjCxrUkqLIcXXVVKL5NZiQie2yYvwenbVmSHppzcGWZmtdqpRzM7oUvFJX3KVPMxiETUciN3OvvWVuI6nokVzSnfjLWshZt7vceKP4Pngw9AIY+Oml3kjjdUaGcyuePpLEYhd4SVpTNKQgmciVM4wZ100kkeKdQ8HtruyC+fyVRa2xBaf1J+BA0V4uE3XjsvBmQtuaN9nacaCSzOKoXkmgVeGaYR9sr2ZSwNXHCKUFDI9eW5ZypTA0Qh5wctxe5SnPxbjD0BQbLweHkfmaZ0WC4wk08zMfk1m63da5a9e4s85dszfWQN5laZ5XpkNvJcO56gXfWpBBKknD3qV6FIHOAGKNpFida+pMt4lQedhyodpqa4JMtx/PHHC7qhjXltzrEHiw9tJE6kkAfOoJSob9RNzarf+s19YiuzVptzPTZrwTEFpbkV6kM13lTIQgh0ITC0cifBLCfwfEJgAgKc8Aye/2rrJE/ssMMOLCjzpoSznRluthHQYfOoCiUuzSuqwtIIsrQ+ptaGLrjlW7jRhtFlvdSnnJg6gRumiy1k+cTFiCSmsWnfQnXDtXhrYS27StasPAlt0iJMqTiFMJN27MuNPLw7LtBVJlCMiAizTK+w9JqtlllHXiuhB+JAl1RwfzKRZy23lht/jN21vruN9FYwy1ofV/z0B63g2l3LhAI+1Ss2UoqJ/VInrRBqbfdveNl+H9V4pGgCC7SO9t2aZLAocZ8oVFPqDNkhpRc0zjOF0PGsEHZ8OVAQeZxkyplwdWQaeR29ctKQ+4RHynypUJ4VGghko+DSE07y07zbdsIPMcQrBqNq+qa+amKCJE5nffKXDlMOGrdHVeAdNH21XM4zy+7wojursL51z6e1pJa5psxIa7me+7SWTLbMG+Qz4VqeHp9mlQHWq9SbkiyEwEgS+M/ZLp8QCIEOAkwjAyZwwBnAfDY3+LgEd0XOJePDltvOhTJ7wJvC9gtp1S1FkhXcnCyaoJBacnYQH+E4oRXYZg4StyXTN3w8XBTiNbwUBAS3BAdJXVizeTInhFSYOoWHHHJIRx//U8BjJO7GPAs0uHGp4heyWyQYyW8VgKBjpGLII+HAsEw9+LY7twpTQkSAvlFFeq4+HaBNAQWV7Z1k0QG+q/ITcKKIa5B0PAdcL2r6NnY1dZJrpPEMWSWnR5ukgOVpfQDhWuPkINea6Bg/hH76xryL02JaO5r3lalSMGFxO/e833v2GALzgMDQenfmM/iRlGnpdAjMZQLstDwPwSb7YdHrphIRKz4bYYvaOc+HG68su8oXwiBldt99d5fvtVbAS64P34+LeM4JcoQ3QjuSS7gQRGR4SrRfLyEnDiRyuuDmdajNfYu/cD+w7lqgUZryAS6IYhBG+l+5SgNsebBNSX/hRtJJ0RzP4R1s42ltZgnwjfkHmdk+ZO+DIuBayLWc1viMh+qN6JE7g5ritDNuBMgd6ReyTYU8OC2EiozQ5QHvgrNzLbtThqenRu4WKnEWJfWzvm3IS9R5V05rnZldLrnDvSTnw61YM9uZLnvn6ZEjxdnGjVRxwy6Vs2pKAuZdTK0im1NWVkF0kuLkp6z0o1426bEOoe+xyyKtQ2Uae+x8qnUSGFq5E0HdOVkpCYH/EBA8onici911VVpHIa+MG8t5fXy4eRqtY5WkjTato5AAGmato4cG4nYhidhNEonCIfwIqxFkHFE9ah1RucqVmdtjcZBw0dld7YjA5eEjkT1ooNm1HCbOPIUyiprCzgVBTDfbS5TuXDXYEtLcs6DknkuN77FlXkaR1vJxNptwdrorrflZC24VdItfW2GXn9AZuIcudqmTVSEw5wT+k5OYTwiEQCcBCbZuEqZ1xJJka3ZWGI8Sib11n/x4DMco3Mck4CVfWHJV3WbfOjSBSDnXQieebjdZrm5r/SmXxSsJFE8fqCfE2KlUdMFBGsjT82pzqVoUhhwvCeldFA8xLV1MC1PudA4rkOZ77bWXrG39lEvUS2vSvzg73f3XWlng1VMJJKs1hbK+ZE9jK3HNeFUouU8VuXKQQW/XTWX61d1zyDQlky3Q4kQ5D5MOiCyTmDLbuFqV0JdmU/aY/LbJNk95CPyHwDxIXMouQiAExpsAI+dGqtab82dwvASNLB9W1u1Fnd1gg91o5tRXOd2dFbqUuNVLJlZbBfJFgyROazkZ0dxt3pSLH/GpND8nW5D7JaPZLeV0W5OUzQUitasKxVIn21Y5KWAiJMiTerwmNpROblu+LmvdA+hW+dqcz5ILSlflTcsSU2geVfaTh8YDEdx6Jr1MuVvTCRd6Qgp5bUtnEHk0jTqy4Ckn21rl1jmijRNOPjslLf6oUHRDoMq9/R69421iTQsez2OaqCjT0fn2iarmWwqIVHo6ybWH29ZAoH7cC2lHImtUlG3d18aF1myShRkkMLSpypE7M3hUZNchMAUBEQQGqW4In6LqPFnNoriTq21XTLKIGItVj8dtWzuDP92Vxth3dsAdcPwBngfYuaopcXc6/wf4NShBHK+XMkZPz3OPntvulKhsrVvV2OBmw2ZB6jqnTvPTgs7UQyZbCzuXm3dE6GQ9MEkdD5C0dx+ORo8b6NyqKZE7z/zvt99+MrE8DYguqQSdkneSn7Rf4sas8cR4iID7+NRxQ5zHE1AqWqAk6Bu37zWSUcqavXvyZLMjC9qn84yLxioRRk1qwRMNqhrXiwXuQ/c2WqhR0F6W3UtYTyykzLQ8mdxxdNGI9YBvW3nWIteRBY/bpjIt+LgJgPqx6/qZ75klMLRyJ7k7/zmD5BMCM06A+eTYb+sG8yMgUvdgt63q+6eMDWmh/W3uRnSX8p5kY3N+gkrZ9ixBxpWFY8CaZr0OjKljgdi2ptBZWKTGvfe+uQ3cZN6salvQMivISUNkMHi1Vn2v8pAgJQ/GJb5CD3V0wxpza9nbLQRc2tpp/cnWeiaNpGyba79LgFLfDJOwk1DiIT0akR9dLzgzF9wJxqVEOfcGf089qah1X9rneOjvDjIqx9szUCWtPBrAc4rFxYgVzh7agopqeypP634tWyuhmFtFV8V9DJOSaOpoUNJ3TQrxSknwTlE8nl3EGyS7yDONPONRH5AXeyq2NvdcJRqoaceC+BTZJDvNCy6ateUZao4EZCghTzIkjPTc46HrQUpEGK1jW+2YEQ9EaHuXWbMjTimP+qyaTaEFmXNN0rQjTbMDCU227iLLY0YgcmfMJjTDmRkCnpvMGcDIsc2+m04w8M7svpuSWlBHeVOTt99TdCVHW+vc7WauqsaRYIHxq5/1zRAyxixfUygHQiFPgMto1rEpb1sQxXAdzJYLKLigl56sD1WHu8JLr/gehC2qxFMQVWbzGCqBqhoCj4irfFf/njooPMFiqSzE41l8Mlca0+j+fG4DnZTcqlq9i1RNL7rSoJo8ItwJnlRU+2r7FsrRGe+4kKhB0Mj8VYG+EbAgqigehrneBsrQCnDYr4/n9JQGamut+cmxwax6sDIFwww3Kqqp0CwYoMcOEaDkppEql5MuR8eCpxaJ/njIYWWpS3zxbMPOdF0zK6mlNU+laXzKBQ4V08Gce5GZykQJgUWhcvLJEKIyaYsujajDfWVGLEirV7OLsGttR7OEhfmldVrLJ1vm6eFnquc2GW8dIbZFox4CqdDH5r4dD1SUgfB4wQK+uSvZ7Ugmf9u0VLNT6lZ0j9b0+AaF9lLdExoTLPPPolBTDvt6DHqzYRZCoJ2AoyefEAiBTgLMp7O2ZxO7FPbwfmfbek0EH4yfzB6fbbMV6eBfyxN0PIuZaHA2t4ovhIJhRbhDyBElHBskgkRaddRnVhW6/HXh66ezNiMqRdpzCJXTQFz0yllxP+ujHVkRnAqsqVCLwjL8NmQmXSi75GU8/rf6//dXz1nxCmFY8CwfcseHrKE/6BJhCA+2UWIzL2RggQRrPBOPaakRyf/1JEMZIUy+9I6KiZQ91nnRkNqf+31YKXIHMa/CMIR645gdMeTqeFSjzFMb/n/9+98f5QwnkhSQRDSKBR4C7RiCZfrPMJlAy1wglYzCDSD+oqT5gEwG1U9WWY4I1PVTHEQ0pKnZtqBlySImTnZLM8v1bjJHRVtls4BbWyEzbO9thTrTWdhWx0916AMLRkSpOGY4RcyvBR3DXGoOUdK5oRIbyhAyTDeZO7oQczCYOwdSjZcyVlhRNrJDtNRWJVnIBZnUDgNq0kFI3tFbUoBrR/WoaJKxdb+yeQg+q8hTj2ywSsu4ccsp5ONxYCssD5nZJ14dVB6ErdArLBzDUrPrVrsux61BmWXdVlkkruadu0uJfvovK0nKt9fatyzPFIH6/zU7kq5mqg8T7vc/YjmfEAiBTgK8C/5jmRkRAc4A5lw0QTUO/8qvJALqjVoKncHV5HtgxV2zusBly3kjPHiQnRb4EO5RjV2pq1iGmQ5gGFzaKqce2B7naypKlkNjpMv/0cgd1khnhEic8UkiV7csPQMjK9aO5Ip6Moo+d7GpnWZYaqpNNGIVE1JXzLokxiGCwCbpm/uKywBzzFA/1rZ9eEFUbuSOtfSfDS2UWSr/EAllQUxK6EH0pK2R5ie3gS65YacpsQAj21/5tvwuaJfp5abi8FCBtCph1GyFQ0PSTJk1ppHtV2juBKqamq0L1tqLcJWTNe+U4E6tLbkjgdcwqY0arNaoCprA3gmR2p1pEn4yRnJZUm1TaCv3+qlmwRHSutPWZYcNaSLh2nstHHi0o257trX3ljgSCBSxKhPdukmzbJgOD04+qpTmIIV1wFqCifIgC8hZz7pULtQly5heUciTRPuaYlqcBFGTW4gipIl9mw4RVWPEHDfZM6VENWuV+qbef4eDpLqhZajNoMHqvEL9J3SIFd5KTJrjhBfKP4sb5XyArc0n/LYJ56X/ryZBx6T7X/NBngbVjuNqwm1TOI8JRO7MY+DZXQjMKYHyPXgOimCNtgSYfNMrjA1vjUK2360lZcwEGkRVWnfp8poZELuRS1HhGNKEDSN3XOZWTW9dKFNtc+aheU9F0w67rryRO5XcU84bOokF4k9SmZbiCrLAQqvfRe4wP0bUtG+h5A5PjEe9GRHvSzlyrNpnn33YNgKI36gKDYQhZPhbW7DcRe4QUlSdplTj1sKE/4Ddamuh9WedLmWZKBRco0tkhIAgOYOXiOiUcUL21SY0okxhDRoX28yRQEmYFAuUmYBOczuVyQKH3ip/GMcAN1Xrfmu5MmNoBbqTGqieW0XE8IFpwYfXR2qRQmmz9xb894stV8jh0VpIQyisfGHCl3NOP/lgFE74kUnDWWIuCG6yqYSmAJ+Yjmky0Qx8FXZuThbwstAW5IsoZCOq1HfsUZAq8P0YeFFqColdrWnZx0itrQXflnWDbLKhZY3YqnatWf8X9Wm61BRWm601m0Ors+cpGRsCQyt3Fmz9t8xyCIRAQ4Bhtsy6Uw8WWEffLjFlvLIHzIZzN6eO61rlE35cmqtvlUQKjXDXsxbuMfEazqrPXeEcZ5kh8V2On1rV5Zt7wFoKwJUuG181q7ddtqpVghqskW7Yl5iF0VVihxI2kn+IM0YFkoIm4FvyknA/622mWiB3VHAdz48iZ4We4LBhOxljA9EllPiZ9FCWj2t6V+3WEh/Emc2lejCBXpbJZUJmsfp1E3JbtzWrfcqM+0HwTp+pOh4IXSI+ODBoRL2trcgXQROy0r3QdiRF109ah0OCG0PYi8EWWSMy6B4JUsQTuUmEkbOUXNuu/SRxnK+NWmv8K+5Oqjo8FvrPZeWnqax3evCxsf0Yqu94qEKpUcSu2cdEZFCE0SYcNkQDnWSmtNz6itlqv/nmV2uWmwUTUZkuTcmEC4ZMoVpVvsmmjunmhml+EqC13Hb0TvYIR46ZZtvWZc3W/0Wz1kLvha1bZTkE5jaB+epsO7d3k/ZDYEQJuJ4WNCnnvCHwIsg7YVw5ZoQk2DBPH7FWEq4rcmaSI4Srn1nldWDLXWS7TKdLKAm3DrEuSsgC0Sibu2VGUoIbhaRNsLJMsoxOykOCAgPPiyN/wjPc7I5h1iadZO+8BRohF9hXWUSkEtFDuHDMuPKudgQU6ubwTuzCTISOPgvZWOZ1MEDpIH4KozDGbDx1opAzSbCAoBFo03lmTGticBSMZf3Uf0ETAS8uB2ZPf2gIASCuF9X8ZHTpQo1Us9KEWXqt4WBo7pPSzwk1hx1xn9BbDDO3k9HVQGSk2hHIneNqLSEyqI3WkiyHQAjMGwLOBsP5zqz7kDv5hEAITEiAJ8BtIPIVSI1KkOS3dyM3C81JIzDhwp0Pw7asuOALK67QJb4btRSy1uJNFIw0Dq9DV8IZwFRTFaI/9Ap9Y7myX20iKCNe486jymuWJuwnOaJcykXlNWvE2YRvgFCgJPwkdygD2ohGIUE06yf/k1UTfgzBrch0Q2V1VB0b6kZr9EE5v0iJqgnbmW6hPXIM6KQN7drYSa4a6XSbSv0QCIGhJTC0wax4d+aN3s1eRo8AD4GYCBeFD6eF/M0mdYNY4Q7hPmlefm54xAd9w3VB94zeaOd+j4VyOKWk3ELkZngaTnJJBXrm/s6zhxAIgXlEYGi9O5E78+gIyG5CIAQ4daT1uCoV2xKfSrwph0QIjB+BoZU7CW+P38GWEYXAkBIQBPQZ0s6lWyEQAmNNoKenZ441gQwuBEKgVwKCUO456rX2JPXczO/hjZOsTHEIhEAIzBUCkTtzBWsaDYFhICCLWY5RPa1nzvvj4XUesSgJek6acgub+8vcoD4njWTbEAiBEJgugcid6RJL/RAYGQKe0eee8LZHsPTde7e4u1NMBnffLUj6dvu9G909J7DvRrJhCIRACPRBIHKnD2jZJASGjoCnAHtHaVu33K/utnnPAWorn/CnhwN5J4D7pyZcq9CNVB6n4cH/Xt7kXlOP12tqemqfJyZLUWx8P/KRPUzInWsezecW9KrpIdHurhfJIpuabS24P98zijy7zwOXW8uzHAIhEAKDIpBU5UGRTDvjSYDZ9kwdT9VrHkQrQuTGIo+oMWD3FnW/vci2bkfysFqbe/auZR4OPz2hxyqNK9e4Qj89/EZrHk5jbT3Tz9tJPcbQY3u8h1KJOl4T4eUG6vCyeI5wPc6L+JBV4z1KHjNoWy8xeOlLX0q7eNmFb0/oqfu97U63vXHCcwI9U8cTDptnDHp2H7Fy7rnn8rt4i0I9annCGa2H9lpFynjool7VIxbt0Qu/vL3LcxGt9eRlNXXeE5n1wVOLFNqpJxi5Xd+7J5vHInvYsXY8sNHo3OE/4U5TGAIhEAJzSCDenTkEmM3HmUC92tDT9z0t0HsSDJWw8DYDjxj2NgCag8PD2wMmQ+CdhZ477LUG3tpYL22mVDx10EOTbeL9i16PUG+EIBG8UcHLkrxuQvvlOPEySEKHRqFjFJJZNIT3anGQeAiQmt6OSaNoimrxngSSyHMRPbnYc40VelGDtyVYqDoWvHtBNe/E9moFusRjoHllPLKZuDGuM8880y48BtBTjFWe7MO1w4VDmQFiX6rZyhsbPNPZS6l0tTZUx3vCvQ7Ceyfstwq9kMHTqCk88q5p3+ae5eiNY7w7NFNTnoUQCIEQGCCByJ0BwkxT40aAy4QvhEPF+6G8CcHweF8Y8i9/+ctcGt7RTZeUDOocOSvuBQt0iUiN7BneC2krHB5eAeHN0nwbPD3eUOGZe7aVTUyseK+CNzY0TanAAUPc0B+El5iUn14u4d0LXimlZY9v5hpRn2+GU4fTiGggreiGKmzevVBtUmYeqUx+ET3yhT0A2h5tS8/Z3DOOywXFB9P0oXPBtmqSejQK0aMCP5O4lYcrGpp2ahOvpzBqr6+iqyiqqmkVqUfnceQ0LROCEHnphLfE009G3azKQgiEQAgMikDkzqBIpp0xJPDc5z7XK7Xd3MQ/UdEl1po+IAvIBX4a2kKoaMKRkzteJ0mjeGk2ZwaHkNc3quntE2I3FADdwMwrEYHi16lXUfLT+FkvzuR0oXI4TqTLcIpQORPuaLqF2q9NqBbKY1qbUzY1XkC8otyIZPzom1dheHOFhyZ7NRiNqE2pPKuvvjqBRcFwU3mHRu3IWyO8mKKJAHpLvHjcj3/8Yx4pKczqnHXWWVXTi73e9773Na6pKsx3CIRACPRHILk7/XHLVuNPgAeCe4b/RgYMu175trwXJA4jXeOXCuM91V4COiEOLXiDt3ddUTaCVqSAh+zxncgp5mKR6UJLeT+oNrlhyAJpLrSUF4iqL5mXVqAqZLpo3N5pAgtUlxYk2dhK35qXZdJGl1xyiVxgjiLvDOf14SbRlE1U430hobx4i/fIKtKKjKA86mXvRJXKXoIhJ8ljdYyOy0rlzkHZCwly2GGHqSP6xjFDvblB3WvSxeMqRMWD5QVeYl7uNucYsxe5RHV3GJ2nGrFoXOJWNkTYy7NwUAgXpxcRWfslpEok0YudPUlJCIRACEyLQOTOtHCl8iwiIGnmjDPOIEpoFDcTCWDRBGI00n4FmCTV1m1KknA5NrwBqg0N34k4zkEHHUQSseWerSfRRw6QaBQHifgUUUIucB3J55U6Q4LwGK2xxhqUBH8JuePGb3rFLVcSgLhVKt1YCMkLvDRF3BBSu+yyS+2XhCJ03AblJ2XDhaNjF198MfeSgXhxOgcMoSZH2FurvvGNb2hQPI6XhQ5zAxdxozKxxUNjF3wzE8qdZz3rWeJTek51SQyidezOgpaNl2LTpkLq8D3veQ+XlV2r6VOdFK7y8VN5s6r0XFVo/Uaje1ittXKWQyAEQqA7gbwzqzufrJ29BKgKeoXlFpaSdEyyCCeRL9wS7mxitkkfrg7ZxzREZQe3wZIo4zXj4lYHHnggoUMTsPEcJ/SEdBmCQ8t8KqUV+H64YThI/JTcU02RSiJiVAiNUiX2xZWiWdqrLTWnbe/5GQIhEALzngDPcd0xyrk7VI+WiNyZ9wdD9hgC/ROQ0ssbxD3Dy9J/K9kyBEIgBOYOgaGVO0lVnjsTnlZDYO4QcHe3fJdjjz12zt9dNXc6mFZDIARCYBgJJHdnGGclfQqByQg8897PZGtTHgIhEAIhMCGBeHcmxJLCEAiBEAiBEAiB8SEQuTM+c5mRhEAIhEAIhEAITEggcmdCLCkMgRAIgRAIgRAYHwKRO+MzlxlJCIRACIRACITAhAQidybEksIQCIEQCIEQCIHxIRC5Mz5zmZGEQAiEQAiEQAhMSCByZ0IsKQyBEAiBEAiBEBgfApE74zOXGUkIhEAIhEAIhMCEBCJ3JsSSwhAIgRAIgRAIgfEhELkzPnOZkYRACIRACIRACExIIHJnQiwpDIEQCIEQCIEQGB8CkTvjM5cZSQiEQAiEQAiEwIQEIncmxJLCEAiBEAiBEAiB8SEQuTM+c5mRhEAIhEAIhEAITEggcmdCLCkMgRAIgRAIgRAYHwKRO+MzlxlJCIRACIRACITAhAQidybEksIQCIEQCIEQCIHxIRC5Mz5zmZGEQAiEQAiEQAhMSCByZ0IsKQyBEAiBEAiBEBgfApE74zOXGUkIhEAIhEAIhMCEBCJ3JsSSwhAIgRAIgRAIgfEhELkzPnOZkYRACIRACIRACExIIHJnQiwpDIEQCIEQCIEQGB8CkTvjM5cZSQiEQAiEQAiEwIQEIncmxJLCEAiBEAiBEAiB8SEQuTM+c5mRhEAIhEB3Ah/+8IePOOKI7nWyNgTGksCCYzmqDCoEQiAEQqCTwGtf+9r5589VbieYlIw/gcid8Z/jjDAEQiAEisASSywRFCEwOwlE5s/Oec+oQyAEQiAEQmAWEYjcmUWTnaGGQAiEQAiEwOwkELkzO+c9ow6BEAiBEAiBWUQgcmcWTXaGGgIhEAIhEAKzk0Dkzuyc94w6BEIgBEIgBGYRgcidWTTZGWoIhEAIhEAIzE4CkTuzc94z6hAIgRAIgRCYRQQid2bRZGeoIRACIRACITA7CUTuzM55z6hDIARCIARCYBYRiNyZRZOdoYZACIRACITA7CQQuTM75z2jDoEQCIEQCIFZRCByZxZNdoYaAiEQAiEQArOTQOTO7Jz3jDoEQiAEQiAEZhGByJ1ZNNkZagiEQAiEQAjMTgKRO7Nz3jPqEAiBEAiBEJhFBCJ3ZtFkZ6ghEAIhEAIhMDsJRO7MznnPqEMgBEIgBEJgFhGI3JlFk52hhkAIhEAIhMDsJBC5MzvnPaMOgRAIgRAIgVlEIHJnFk12hhoCIRACIRACs5NA5M7snPeMOgRCIARCIARmEYHInVk02RlqCIRACIRACMxOApE7s3PeM+oQCIEQCIEQmEUEIndm0WRnqCEQAiEw7wn89Kc/ffrTn/7Zz362dv2a17xmm222+dCHPjTve5I9zmYCkTuzefYz9hAIgRCY6wQWWWSRX/7yl7vsssuvfvUrO/vXv/713e9+d67vNTsIgf+fQOTO/88jv0IgBIaGwF133fWXv/zlsssuG5oe9d+RAw888GlPe9omm2zy85///Nxzz33KU56y1VZbXXLJJf23ODpbbrTRRo9//OP196CDDvL92te+dr755tt5551rBH//+99///vfX3TRRTfeeOPojCk9HT0CkTujN2fpcQi0Evje9753++23t5bMyPJtt932wQ9+8OMf//gA93744Yc/6EEPevjDH843MMBmZ6Spvffem5lfbLHFHvvYx26wwQZ33333iiuu+IAHPKA6c8+9n7aOKVPNd1v5KP68+eabxbBuueWWX/ziFwsvvLAhzD///Ao/8IEPPOtZz/rqV7/60Ic+VIVRHFr6PCoEIndGZabSzxCYmMCnPvUp1sI6rgLKwIdllS0xce25VsqSveMd7/j6178+qD0ce+yxb3/7288777zPfe5zW2655ZVXXjmolmeqnec973m0y0c/+tHvf//7N9xwwwEHHFA9OfLII6W2POMZzyDvmr4dccQRW2yxBReINBderqZ8dBfomz322IO4caAueO/nd7/73dve9rb3vve973//+2X2fOMb34BldAeYng85gQWHvH/p3uwk4KLWx/nRZwYJ/OY3v6EkmKWFFlqIoXr3u99900037bfffq7RZ7BXrbs+++yzr7322le+8pWXX345u/g///M/q6222oknnrj55pu3VrOMpwiCj4H4WGBEGZ2m2r3I7/azKbzzzjuPPvpoZlj9ffbZ581vfvNKK60EhW3VgaIWbOJ6/bDDDrvjjjv233//pkEL//73v9/61rcqX3TRRd/1rnfxZyiUurHXXnuRRy9+8Yuf+cxn2ovGr776aobwwgsvxPxRj3qUrdZZZx2GcN111+W7Mkbeo9aWR3TZ4bT11ls/4hGP+Pa3v73KKqsYxTHHHLPvvvty0QFL9AD78pe/HHYkjzvuOMM/9dRT8R/R8bZ220Q/6UlPIsc/9rGPGabx+ldSYdVVV/VN0T7ucY8bBj9la5+zPE4EZtKWjBPHjGWwBFzmOhsONjLSRw+dmk8//XS22bYuQN/3vvex93NV6/zwhz88/vjjm5P+T37yE5aP/19yg4WTTjqp1fIRHLQIFaJ722677TnnnPO6171u1113lRO6/PLL//nPf7YJRwJZ8+tf//oNb3jDIYcccvHFFxNtLql9Ex8qXHfddUVmzz33xFx4xb6qRHBhu+2223HHHZ/znOd85jOfkXfyxje+cfXVV3/IQx5CwZgj5nmttdYiuWTYMNi2IoBqW99kDUHzxz/+8U9/+tOnP/1pPxWSYjYha84///znP//5+sPySexwZf+iF72I7ZfJ8Y9//EPN9dZbT/Tnb3/720tf+lJaao011mhaHt0F8/LsZz/7mmuuacJYUnmkrSBA5BlsuTee+tSnCng5/KT4LL744hCN7pCbnpeP6jvf+c7SSy9N+pDXBmjtb3/7W98O1z/84Q/jMdJmyFkYLgLOnvlMScDFpavPf/7znwyMf1pnK8u33nrrlBuOTQXmzaidofobkTsyXvjCF/ZOjAFYeeWVBUcm3B01gL+PXvEfCHPom3lRmQ/gqquu4upwPvVTTRMnBdLy9ddfr2b1wfKXvvQlIoANZtG/+MUvTrgjhfQEiXPyySezvv51v/CFLyi0Ly3svvvuvCmkg5If/ehHT3jCE1hlooF5Fk5SWB+FSjhgXMT/b9k9QhUKhSoIAptUbzXOti2wwAKSYKrmE5/4RDtdYYUVHvjAB1ogFGqYtfYjH/kI79dpp53mp4gPFwtNQ77omxI6o/wH4PzgBz+wOZlCZOiwZbEDHaNOXvKSl6hMkXA5CEUJtbDElJNC7VQHTAQrpRGFZB/BR5FYfuc732krCz5IslUVr6kSuo1TB39zBLKwlHKGXPvGa+64owiaqsznoVdmpH7Wtzbl7nzyk59sLRz1Zcftq1/96mYU5TPj7HGz0je/+U24HMOO20svvVQ474QTTnjYwx528MEHN/VHdMH/0TLLLEOL6z8Rv9xyyzkqLJPUlsl03h0oRnR06XYrAf5I/8s+rm1ay2d8+T4z3oOR6MBXvvIVF77mb7fddnP1ee9U3ufzn//8SHR+IJ3k2EDgwx/+MNvD4dG0yRvB6LoqbUrcR6OOj4UqdP3q/M6K25zD5mc/+5lyyunLX/6ynz5HHXVU1WTL5TFwPDg58iKwpk2zrQvNv9OPf/xjjd///vdntiUEqOPsSTHIBn3LW96i5JRTTjFZVIVVJAtBINPFMrXhepoC8/2KV7zCViWJWvdSy+RIXYM+5jGPqZCNcqZIs+SOnlv41re+5QqVq8My+60pMRouFjVdrOvMmWeeSWYttdRS7JlCvg01ScArrrjiZS97GQ2t0OGksDRB5TEoZPmsJSn4dRBr1YtU3ZOf/GRHo2r1ER5iMOgD7SCj8IwzzrBc0gRnuk1hpfXY3LK5E/yyQJ+Rbl/72tfcRGMTJlahzwte8AI3ENVy8y299FWvepXOI9NMPWmCDynTVLNAwJVg4nySl0riLLnkkmxb1TFHj3zkI2vZWLiRWre1zCIaex0wbatG9Ke5cIsWZeyUUsqV0KFZHYE8bbAL4Tl+KGDeLP8gPnJ4S2SP6JCr25/4xCccSyVoDNyxWuWEryOcyHP8tEr5kR7sLO98c36O3BnVI8FFrYvXska87q62uXymOxib8N532Yo9cJPqBRdcoKazgGV7FFywiQs+zl7Jfby+zgv1s2w8q+BynPnp0jLzJkNi/fXXdzdsY6KIFSXyA7g67I7t5MNgdZyVNt54Y6cndl2bruw54VlBbgY2Wzu1IwaSKHFxJlPECUshR4Lw/H3v/fDDVzXyhdZZc801uQfY/ve85z3KiSGtuWwF1pm9YOrA/e53P1kL4iPM8GTeHV4HV70kjm9N6X9ZSn6LzTbbDCVGhQairqxlv81X9YQxZuBrWXRmiSWWaFBUYec3f4lOGrsMHs4VThR1nKNdeTPDnCKAlHPIXKhG96hQqRiQWqY8qKvSTCV31LRrnac8dthhh9qpxAWbi++QhtSeU0aVkzhNnSqpb1PGAVa7UOK4YjAsyH0RpaLzLMOozZI7wkmdcocGkjmhJizUm6gZ+aiF5jzlGDDLKrR+7Gjttdd25NArTXmn3KEFCUEqhyHXDaxUNlnGzv3GC0UzGWm1QFQ5ahzqBGLTpgUHGwXcWjLSyybX/4sD3hyZwRoLTeP/i/PDfdqlXwUH/W8CyCtGFs/4kB1m/IJkevePE5eZnfHepgMzS2Bo5c44hISdSefBx/ndxWvFFJyt/PMzzPbrlERqML0suiQPLgSX8oQRp70rV0l5pAmbYVmkgGtBiIEFdQ0niDBht53fmVJJmu5iEBpwGWSBuGGeCR0dkDPh/CgUwtXEWjsBMf9iAex62ZXOZtkw/SE1dEOypKRR14su/V1nyw/VWxf3YiIsIqtjCBwVb3rTm5gZW/HlyDZgiqgH/naVm/ZduGuK20NWB03jZK0+HcPkEwQkCPXGJ0TfuGzVSc361OYGiJhC/5ksnEes0hPuxNlwww0RUAde/oxmX60LFIZ+Pve5z3VlbEHIRnanCgyqrSQ9WCZ3BFNcJVs7YTv2y+6Sa60tdy6z1uJQWnCRXbpHHYkm5IV5V84SmP3ODZV4uhoZYTYpBoGbkq3KHT/wbr/99maWH6h1WxAe/OAHa1kWy6abbjpZpjY5wt/G5cOVVZvTDYQLCWWKSVX8lVfHzBplSXkQow5OvbLKjrAy6Q5OP21FjDKxjjQ/6TDBBWJXdEkj5sVcN12VeyHRxMEm8qWyjyPTse1QJ2JUJivZdfqJijWbEKkDuG/S2XFC1dF8qhmIQsew/wvVZCjrgBRdx5tyx5J+1vHg5xh8HEIyqAwEjeaw9L/s0zo6wtpHCaXeWj5Ty04CDrBe9u5cYYp7qZk6ITCPCfyf6ZrHOx653TnpOxEzD9wYbJggSA3BJRrd4CzGsrq4oRgYide//vXMJPeGqzRea3ZLVEJNQQpXdcIc9O+EcoeYEFBgyJ36GWN7IReYDVpHpgWNwvRSXSyN8yOJw0WsGxwhLBxhNBlVCsa1I7PH1DEkrvLVVGhQAhOWCQUqSrcNjS+BslHIN0AxSKNx6cl82l2r1uFMohXEg0RP2H6G1sAZLd4d0tDmDHZTX3mbsKB1WF96BRniz0W/Tab1AYqniocDYU6dtm21zzdmFjTOZps73KiHv/71r201p/xp7MioZqE2N4+YQMelQagZnbX1DZf4i2X78iEyDJx0IOmYeVfqZgoWOpg4Vm6izzrrLBMt/Mei0IjUISFLoJCSdACdoY65EwEhQB0VLCWTqQMUWNN5bjnACQhrOYSoSasoUULWkWPZvGBFctWhSyrVnJpxa/nnyLLK5qEgDz30UIXcQuSU/BtK3fHTyB2HjdAbIVITrabeCld5Og4lZEEnFfq/oHd1HgeOnLpUkD/kn6W8pJSo2JaaHB6ONAdnHcPNYeOfRU1+QXVm/MPRwmeGRveeGDLBWmHEzprN0DB0iHZWGM4SB4//JvPYvXsEnEuR7nWyNgRmikDkTq/knZ6YB7Ekp3LODHa0tmTvXac60TtlVyyGy8TlqUscJscJ3cmdVaN1XMjy/5MvPEPKJ9uxPFB2kbtCZIGdJiPUdA517U7rWHb35nSvd5lAzfrYXDimLiuNyM/61DLL9L8F//krNuTy3bZVaPgWfNucdGAmxWhUcKHvYp25IuAoOSGeqq/NnXbaSW9ZWaE0F4j8GfI0RcqIQi0wbzQWxw9QZSBpOC2owPpyGBBDlBlnWDXY9o0k1PizxLWKUNPn8io5NdOUrDU5ghslwW9k1jghKANagVoiC+gYco2Xpa1xPzGXXMwxRsgaBZcVPhIv6CcC1JCJTsLU7jjw1a9vFfjkLBudFrg6CCCJzCogpgUKmDigOfRBnEsPzYhuaMddVLI4SSJ9Lm3hoDLXWMFOsaEHlGCTo8sR1dpnjXCtmRo7NSMkV60lSlqrWebg8U2460CzymQJbPk0JRaoJfKotaRZJmt8mp9UC8VpipsSC40Yai20zMy3CjUly977aavmJ3HQhw7ubGcgJRwt/KONXpmsTVNgNJOtHdFy10jOXSPa+XQ7BP5LgDHLpxcCLtNZJq4IlZsUS54eQQpqprJYXANVUy5J8WVEKYxK1uGYYZVZfZKI0XIV232ndfMzC10ptC79nXHoJFu5xCQLLFAYPN6sKStegSqhhAmbZR2Zf7dFcMlINGGJeW5czTP8VvEcyCxhv20r8cUoFDpr1+08HEjKGWYtiNxZa2i8QZwQFhh+F99lA2hB4QxAGGlCR2Fzh5FVoksECksgKZVAZPiNguFn+QCsZEymmmbisyFiIFXOtE84oiqkD/hOinCV6LkeMr2VQ1OFJVzQM3w3Z5kFH3FAy0RVk1JdlZtvBLRsLYFCanDk8HZowbZW+bY58g6Jmk1jV1JJSAqrWtNa64LJarJehPMYkgmzc1o3aV1+9KMfTdW1lkxrueQOKaOH09owlUMgBEJgSgJDm7vznxByPr0QoBJol0rdlWHARNmKk58KqUt2DhvZM8whW+hT4Q/36bCCaipn5rmFXLsLZEiY4Dbosl/WmiihcqqO/VIk1A9/Rt2nU+XaZLc8FoUPWU+4TyZrkwJQwTfBwTFQmcVCEi616RgjEn+xLecEmUKZMeSUB78C46qcFRczshfOBpKCkaZ4SEA+Eum3wiiWCQI1mXyqSIYQv5SfzYezSmUCpSmxwB9AeLWWTGtZei/Xy7Q2GYbK+HBaSGPic+KSEbJxVPTeMTeLgd97/baaYoj8UiZoyjTttg3zMwRCIASmJDC0cmc+XXeNnk93Ai7u5ceQCKpx73OrCFII5ZAvMipIGY59IQzXzTJ/uT0II4pHBTGpJkJPB1AV3P4CE5w38lWbVZ17d7+SduppLrXWVnwGekIG8TM1hSIy9lUpBdbSNK1RqqZlHg7VfNucl6XKzb4SyyQO0WOBOPOxUAEUm2itqa/9pma1MCPfxB+BJeVFf4itCcc7Ix3rfafidKWV3YbGxdXlSOhs05FgFjrLUxICIRACM05AoFw2gm7I3+Chn/H+NB2I3GlQdFsgC2TnlGLg7eDGEEJyge663HW2oAC3h3tbREbqqSfd2uptnRQWmc5110xvW8yiWjxP8kZNCq0zZeroLOKSoYZACITATBOI3JnpGRiR/TPk7oqS2uImL8Ggum9lRPqeboZACIRACMx2AkMrd+ISH65DU6TJgyv4LYS6onWGa27SmxAIgRAIgZElELkzXFMnh6O5hXi4epbehEAIhEAIhMDIEvhPdmo+IRACIRACIRACITDGBCJ3xnhyM7QQCIEQCIEQCIH/EIjcyXEQAiEQAiEQAiEw5gQid8Z8gjO8EAiBEAiBEAiByJ0cAyEQAiEQAiEQAmNOIHJnzCc4wwuBEAiBEAiBEIjcyTEQAiEQAiEQAiEw5gQid8Z8gjO8EAiBEAiBEAiByJ0cAyEQAiEQAiEQAmNOIHJnzCc4wwuBEAiBEAiBEIjcyTEQAiEQAiEQAiEw5gQid8Z8gjO8EAiBEAiBEAiByJ0cAyEQAiEQAiEQAmNOIHJnzCc4wwuBEAiBEAiBEIjcyTEQAiEQAiEQAiEw5gQid8Z8gjO8EAiBEAiBEAiByJ0cAyEQAiEQAiEQAmNOIHJnzCc4wwuBEAiBEAiBEIjcyTEQAiEQAiEQAiEw5gQid8Z8gjO8EAiBEAiBEAiBBYMgBEIgBEJgXAnccMMNCy200KKLLjojA7z66qsXXHDBhRde+L73ve+MdCA7DYGGQLw7DYoshEAIhMBoEPje9773uc997rrrruvS3VtvvfXLX/7yuuuu+5znPOezn/3seeed16XyXFr1jne8Y9lll33Na14zl9pPsyHQO4F4d3pnlZohEAIhMBQEDjnkkOOPP/6JT3ziMsssM1mH6JtvfvObX//612+66aZbbrllHvhX+HLuuuuulVZaqenSpz/96Ysuuuhf//pXU5KFEJgpApE7M0U++w2BEBhJAj/84Q8f9ahHcVrMYO8/9rGPkTvdO/CWt7xl1VVXfdKTntRW7e6771Yy//z/de3//ve//9rXvrbllls+7GEP++AHP7jBBhu87GUv+/CHPywCtfvuu19xxRUHH3zwfPPN98IXvvChD32oDX/yk5/Y9fOf//yNN96YijrooINuvPHGrbfe+oILLrD5WmutdcIJJ6h2xBFH/PnPf15iiSWuvPLKBz7wgW19yM8QmPcEEsya98yzxxCYmMBHP/pRV8YPetCD9thjj4lrDHGpy/pf/OIX//73v/vu4xe+8IWf//znfW8+hxteeumlP/3pT//5z3+2tvP3v//9Z/d+/vKXv1T5d77zHab9la985VlnnXX66ac3fotLLrnklFNO0f977rmnam6++ebrrbfexRdfrHz11Vf/yle+0tpy6zK5QEOIOj3ykY+0N6ve//73L7fcch/4wAce8YhHOCT23HPP0ijiUy996Utf/OIX77XXXq0ttC3feeedb3rTm/7whz8Y0c477/yKV7ziqquuUufcc8/dbrvtqJltt932bW97mxKzZl8OvG222Ua1b33rWwalcJ999ll88cWNbrHFFjOn73vf+3hufvOb32y00Ub777//yiuvLD5luq39n//5n1//+tdPfvKTv/3tb3MmcTtp9qtf/eq73vWu5z73uauttpqdSt9p62F+hsAMEPDPmU8IjBwBJ3Sf6jZLcMcddzgp33777SM3kNYOM5avfvWrnQWe97zntZYP5zLs7GLTt3/84x967rr/tttuk1Piu1apJlv25ptvbmpaqDqthddee+3jH/94MoLDwObdp1Lmyvbbb7/jjjvutNNOv/rVrzR4wAEHHH300RYEbojFKvRTTfrgta99rcqsshIfNVnr3XbbDe29995bCZVDaug/s33kkUfeW+seEuHhD3+4Qh+7q8IDDzzQT9Lkve9972Me8xjOD+V/+9vf6BK64XGPe9yhhx5aNembTTfd1KCkCdvq8MMPr/LO7x/96Efa5CbRggXuFv3fYYcdOGCU0A0KSQ0bcrEQKxb++te/KiRoOltrSggRCqb5WfGs173udUrMyGabbUaI1FqeGP0kbuqnf6UFFliAVPrIRz5C/ZgL9GqV+TVrxkuUP/OZz6xC3aDtiLb66dt4dbt+EmfPeMYzmlVZGHsCp556qoPT58QTTxyqwUZ017zke8QIuGZ1wX3ccccttdRSchQ22WQTJ1zeew72ERtJS3eZT59rrrmGRWkpvg9jfNpppwkTbLjhhq3l7Ld4AQu9/PLLVzkLzUoJPcDylKc8pQpFE2y+yCKLsL5dQjB0CT/E9ddfL4pxv/vdT2WbEzQ/+MEPFLpA52bAmcEjNF3WC15o9q1vfSsbr6Yre99yNcoistbVAW4GNQ3qjW98I9dCtUkT6DwTbvMXvehFCiXe8pc4OQqgGP4uu+zyhCc8QXnnx6RLgF1llVVoXEJhq6220uH3vOc92udOOOaYY+gGxvvRj340z4qYCyHC9cKW00Za05m3v/3t3Bj0CocEb41CqohOYsW5T97whjfw38iJsYry+NOf/rT00ktrtnry+te/HqUPfehD4lm6irO9PPWpT7U7mTQ8IhwbRMmSSy75kpe85KSTTjJB/CLyZkxKtTDZt4gPztYal9ae/exnr7/++m9+85uV6BV9dvbZZ5sLoSUlQE3WTlOuG2eeeWbz04KJe/rTn25BjMkuqL0zzjjDT4P1j9OkATlUQCN0LrzwQuJPeKsOsApsHXvssQ5I4ypxZvNf/vKXjoEmN0hv4XrVq15lVT4hMEQEhkp8jVZnnB9br26HqvP65mzr1Oak6UQ5j/vmNhChgbm6U85//0VMrL2QPpaZtGaP7CWb0fx0/nWF6uqW4fHdlDv7O3GzMU2JBT8VMs++XQTXKsaSVbO5ppRYeNaznuXqmdUUfWBcZS20NtJ9GRzbCigw/4IIlEHTW6vWWGMNjbe2wG4ZIANvpESJVfrjgltmhvLGFWRoWmNW68ZjJkdNR8LTnva0l7/85QQKYdHabNvyJz/5Sa3ZBWvn2h1DFcRTKDBNcW9omdRg7EvfiHcY/oMf/GD2T01dUkFeS2uzXD52ChpKNEStoksoD8vMJDlSheUcYtFbN59weYstthBMIXZN38knn3zZZZepJsiiWQtIsuVHHXWUZdbaiASk7M5W1ZqdlkfHiBp0XDvVAgUAVF2VfvGLX9SUDfGnI2uO+F202Xp4cywpIbl4cThFDLM5bGBv9lt7n/AbBC2QrTxAFso1hbnAUNUXS1pnnXUsE17lfKrgWndcdq0DzR4dHnpIjVUJ3XbYYYfVsvyetrOEvegJPg95yEMs1Hj9X/Oc2eTHP/6xQsdVbS6nh0Y0y/5r6vjUsgpm4Xe/+52oHIywV+V8jz2BofXuJHfHf2VPH9aUPXDpXLVd+bFJrpt72njeVmLhmFLRAZdrTFFlDs6zLpACLq9lG/SyR0EN5/TLL7+8l8qtdVybOoe6vFZYFqhZyx67ytcB1+UKOQCEM2Qq0H8uUp3WiVTlrvK5BO5///s7WbtUrc3dRaJlhWr6FltRrh2OCsmhMjCcwZUQBKzsd7/7XYYKagkKzaVttdP9m9WxR1fqpSGEEprjir1sS3Rw/V0ai7Zj3hhdjXOrMMmcE06dTGB5g9h7k87e0HacJSII7G6ZW7v4/ve/LwKi/mR9427Zd999bVjuGRf3aop3MPbGyP6tvfbarBdPBrVBV8nhYA7B7HKHs76x4m6H5kqp9BGCCckaI2eV+4Ym689k5d/4xjf861EnVN0f//hH452sZpXbu7nGoX6aKaEWUSqsPv7xj1eh49C1gRQWh66gTLlARKyEdSghUmbFFVfEvCq3fTtglNC79AQFpvHu94e3be4n9UBJMBIO6WYtRKXptcnvZbBWge8/WtJMeWVIlqZ+24L/KdN9/vnnUx6f+MQniHhHHQi09ac+9SlONYec6bOVM5uPgJSpd4pzzCikchzktKyb2JuWleBD1AqEKaQ1HYTSnG1rQ+07MFwkWEWLc7VS8zrs4DFftmrayUIIzAiBBWdkr6O409/+9reC/f6BuazlVPp/dsrw7z2QsThROuE2zmRtOhc7cTB+a665pm8lZIQzl2vlFVZYwRmf29xy595ZPmcoHgLxAmtZFJkKVY294exxpctIs0N0BinAVDsVOs8yh1z6ToJO+s5NdXplOF0O8mZrwYWda3Tn/c985jMG7gSnBakALuh1hkX50pe+5BoUFlfV2rcjg3LtSyWw0+hxzjuZOpPut99+dfpjWrjr6RWn2s6xdCmhAFhcFXganLWZ6qpMghA0TALDzGidc845UOgzP4RcCgrAWgEdZ21jYXrZSw5/16nqC0A4ffNSMCcMjBE5ZeuwrVz0My0speEw/2rCxRC6n4WrgFXo0tXOVa53zRFVwcdDSHEOcSSUCXEMYFuCzIbCK6QbVjrgMMDZ1FNvOixIpEsOBhf6LI3KJJ1qJJqxkCZm2RAMBH/lhM4DHvCAyayOwxuNEi4aBwc382jh3e9+t8YdopjX5pqqY7JzaK0lZt/hYSym3rjKYVC6sFFdBihw5mipDUsS2ZdBURsT7sXhhzkjqn1TT5USsgJtRIZoixbskRilVOrmI8cYGy8M5zKgUaUmkW/M5HLa+RcTnHJ4S0aBFzHT4VhF2JANgdCheGpbOkkmECvO9uu5w09Mx9HF12UrhOmwUuH6RhAYl6boWhG0Vjity/ZOkwntORT1CigSygUVQez/wgEgpuY/1H+rf0ZHuPa5oPRKKK21ndZl/1MOAC4i/6ekWP0766GmcOO9448p7Iam3MzW/FZNo/A/q31gYalglgWarKj6xtnNXNSYnvhpTjXSnMRIZ/UhEhdr7ViWQ2DGCDhG8+mFgLNPTZLzhetay5///OebDaUsODk6ayhhbJhwIsCpiu33sUnVdDpjQX2c0aqEcdUaA8Zwui5kTSkMq1wN1+6aDMeKIHBa1NWk01ATAamm6psht2FnbEU7wvPO1AwhwUFLuaa08M53vpNuIIMYOV11OiNZnJr55Jlkp3V71LLhMBj0kMtQ7hDddiovK0v8lXumnPAqS7xgb3TPibWc2zZ0GiXF2CRWuRI81fTT6bt6Pq1vVo0d4jx3hjU0365QtcBmgA+jkeJQTnjpDrSFtbYyZDKo9kU+qkkAOVlbpZBtIA4sGIKLYAuCLK6zywZokNUxduU+VI4oQy1P95t1ZCpqq7agQ2tqp+tmO+UgqZpgsi7mjtIiRwhTNolaqmPG3Okb5gbFzEhwIeZsXlEk2wrryCaZsKtW6Q9VxL+lTZPOhqnJZtfm7kzWVB1XjhafakfGiQPYsl0znJSHHFVyBBkSSpsOKhExmUB0CRPoqKBX9J+KcpgBSzTbnK31L8C+qkPHOyaNtHbR9l1+GplMLjwIWb43FWgayVs1WP9NFlh6WsqCY8PHQkXQyufXFDb/R5ygRk30UO21R4eNnw5XbrMKm1Y5kvQ6udAEhpQ7PzhmyO6q4xsr908ZI7VXadTNqs4FWBAgIKyq/+vWb4U19bWhalWzs52UhMCME3Ai8u/mU0HhGe9P04H7NEtZ6E7A2dP8sYXO5i59LFMzNmEmXR2645QfxQWfi34uaCdTV04uBF3ZuDCqEyhNoJABYJ/UdHq1ecXgXYdVZl+ZQNrCtqLd3NE2LxNlRwyz/ZJWtnLl7QzY2efJ5A6VQ5DVHl2DEiuWeQJ8C9C4PKXVnPq1WYUEmTM4Scf9o47RMQbO5gIoLuDqng51GC1rfTRedsulOZ0kzFfl9W0sWuCKoCFolNZV/S2jQdDYlkCBF5aSO36yxNJIeaTMQpvcUZ9brtQDI81w2oo33uYld1A1Zewi1KUhKqeEEiUyCFntU1TV5wnlDrvrAKAzqs5k36ygw4bzqeIp2leT1HBzFt1J2vIwVeyJHtUl2tSHS4OeEK3jXsKTGKp0Ud4LmzPA0nu1QF6YbsJUIdFD4XEw6DlnUmm4CXtFJLnop29UIyZKzTvSRCJAc6XOzWByyQWOKE4pql07/BYwOuos051cMo5hZPRBCVVnmT7W28c+9rGUOrelcp1Rbo4c6lwsSnyge8ELXqC3zpKWq7Dzm4iB19jJKSqtqWCC8CSgeXEEcZTLYi7lbZZdcugnDWH2ecV0w/+jqSTo1W8ayUIIhMAcEhhauZNgFkvX08fllEtPasZ1qss1Z1VXn7bk4pbdSSIwM8y8cyjbwH/AEc3tUU5pplRNjgFGzgnaZRyHuRaaHbt0ds8nYaF9hYwEjwKBxR0i0qS+QrpHB1wWO4M3G3YuuES2o+qbtXbkylL7dAy1oYQlc8FdbXZuPlmJIZAO7L0uGRpbpSafTYVgLOteSTfGXiypchVBsyMhGCkaLBxDxVi6KOc5cF1e+6IqXOLX9fdke+8sr9iKbZkuY1SB1cTK5TjpRvGYI5pMN8hTRo7xZu2IMKa0YmoSd0SpXIKXD4CvyLKOsaPkLFxVYlzcLaSAieOy4sBgpEGgQsxgBb/EXDgzSFjdYGgdIWbBqs5uNyUqC6NQBlqjGu3CKvFKXarbgCUIGxpo/HxoUz8qECKOLqwoYD4Y39rhhABZZygPQlZWB2eVgVQis45R0hQtGaHBpgOdC1wyPm3ljhaz2VqoHY03JTrfLFNdPs1PCzSlT2tJLetJZ2f8K4kldVZuK3HJ0VZSP4UIfWqZh9ICTSNHykRTihKG6C3/Vo4Nssx/onO6ucbZ8TlhgykMgRAYJwKRO9OYTRqCcfLcCyfTRk84k4qpUwMCNNrqYrZV41NxXd4pNZgQl8WuzstEseIu03nRGXWeBtesTs1dWm4dAz+TE7oL39qEneO9IHec6F3gqkmOiP2TLJbZV/qMyWRNORvIDtZawge7zhKIVZVCUpPMIrYYP33j1tIZAoLZk0PAYFB1lJBQHctK6gl/uLBmUaTLCGHwKDAw5Aj3gAYt0B/VZwaJ9RK/EIGqkh6/kbQt1wWNYix8DxQJ/xMFZl++eWVoDr3FwcDt0ailXlEYxuVyn+/KtuQXsaK3hILwEPeVsZTPgLIhQEUxxCyUc1+RpBwtSJJxrDXV6DAQPNJCE+2yuSmDpftAHANUl45xLQBblTl1SEaN+6nbjRl2yLW1pqZPW6FgpU9boZ9m1rHUWT72Jdx+VK+IEh1s0gsjB5KLCge5Y0N81mEz9hwywBAIgf8QcFbNpxcCfCRkQROIkU/KWNpQxoDTKGcAu8UTIJ1CoWt0bKkBy5IQpSJaEMPiB7IgymCtC3fL5RFxVV2OE/pDoWtcwQjGW2sEFkGgfaaR9aWWOFToA9Um+zClomOuZflRmHyCTE1ahNqQFaFlisS5nm+AFtGaEIkFTn5qRif5BjgMGGMfaRZCV8yD0bm7h2GmSygAUkObhsCuUx7EhD7TVRXkEroiEQzcN0ujJkVirRIWqDXQQysAK0l2srHMy/JywvHE1k6JG26eZsZ77AmlSHPwGHWvLwhIJIkT8cp0r5m1IRACITBCBIY2mDUfiP9RPflMRcDVPBFAQ8ic4AIR8hd0kGbLlyCdpdmaQ17OJgEhNYcngJeF24Dx4/bgV5DzqCZJIYmHP4CZF9EgMggpfgKX9UI8SlyJEgGCWRwJknj4FWzFQ8PjoiYB4TkZnbGApg8WNEUtSYDgwxfbqlUKeVY4LTTC1paTyX4dAwpJFl3y07e1BJatLFAkfDm65CeRpEv0UDWojvq2rZ+j/g0IdUhWir+4R4lTyh28XG7TGhcgiNVdPF02dHgI8IFpgkjYLjWzKgRCIARGiIDr/LpvQEDfGXV4eh6509NcsOu8IyURXPFLihTvIALc0szYywhpFIA6JBE9xE/DF0LxuF9JqgdvkJiCmBFzKBZGcJAOIjsyQ8UsXOuztbSIRBOpJ3WDaE89S6WBEjCV5s5cmEcyUYItRTLQPaSxEAiBEBhnApE74zy7czI2t+RIInHbLReLHB1yWEilXClz0my2HScCEowEQIUm5Z2M07gylhAIgfEjMLRyJ1euM3ywuaVL0IpHh6+I48edRNE6vU8JD5kblNx23gTset92ujXdFi7OyI3ndn2p5dPdvMf6HIEeG+MOI5ngtYlQqYQnwS9J5ZE7PWJMtRAIgRBoIxC50wZkXv8U5HIH+7ze6yD2R5xJ9xHLE/fpuz0t1I1IYkbTDRt5aIp8JtnQnvzbekeSUKObsGREeRZc0zHOMzua7i6azd3J5e4tcS4l0r3rVRLN2gEuyPsha5r7vLQswdzHU4DdpjfAHaWpEAiBEJhVBP6bczqrxpzBDoSA58HIOurlQSmT7U5Ot/vC3Nvlw6VB+kxWc8Jyt9y7EV0CuGcBt1agaeoJja2FHg/Tqn5aV0257MZ76VbunqOZ3EvFATPlJj1W0E93q9E3TX1PzXEfu8T2piQLIRACIRACc04g3p05ZzjvWmBu3Q7WdyKzbblkpFf312O3WAu6cZzU5h7v61b8vm2/vGwPzXOTmjRtgTxv+JIMTv2UD4MAshd3lsnpblwd9uW2bcOv+55E/dz1ZrlV7rhhXtSJw6luZ6uuulXe0/kEoYgJjXhMgDa9VsLTfkkZmTGeziIuRg+55a0NDmgeGez+uFe84hVW6W25o9R3c5zUZg0KpbmTzlMDPO9HTQ9K5rHTpuf+2S/tQtjJW0ceQw9NxtBWHtvjGUjutnPDv6bqrRcUpC65Qc/DAtp6kp8hEAIhEAJ9E4h3p290M7Chl1SX0e1v3541JyzS37YiRB4eKGHW7dkeIySbxHMRKQ9W39snvDGgXtFcjXtOjxTsJvtkwj3qDEtPDbhTkWn34GAvJaASiAO30NuEgOBK8VaH2lzyiocEegwjDSHiU4XEAe1S73moEo+PIzvcRt6IJOWkBv2kt5455D0JxIR26CoyyFoSygLR07zdsJqqb7rEKs8gqJ+eIuixipaVGCBPDMVmILrnWUdy9OpF4vYl8mU41JiheXiBcXnJhnu+KnaJj6dTuOldfjoN5Pa9at8DDnSSKq2f+Q6BEAiBEBgIgXh3po2R84BnwrNSZIfUxp65x2JxUbjKd7e55+J40E5za7qb2BWK1Mj/aH1EDQ+EEIlqlIT3M6jmWX8e7OvOrMre0CDrKDRjR/VoFm+l8ER/D/ezSjl/AMPvRUu77rorr4aH/Xh9gc+EQxJ78lxBPfeoQ1txddRjEj1zlt0lAjwjkVui6XZbIzrPqOu/h+/ZnF/k5S9/OQ3hznlignTQmhyaet2Bxwvpnqa83ku0S2Fba34aGungIYq1ijrxoEVW371ptSEp4+0Q2lHBQ43106OTeUHII3wa+Hw83CFeu1HtSFsWHiIyyJQq8S2zR3Ixz029UKzK+ZZE0Op5ifwu9mtQzSZtC028iRCxid4arwfnuKXOh2TxDEayj2Ayj7a1O2+Vkphl2XD8rCdPwuVxi9V4OaUQIIAMtm2P+RkCIRACITBAAvHuTA8mu+uxOp6m4xH+HiFoY7afv0EIQxKJC33v6PGyCD/ZzvpY9pYrr5jwbof/LfvPX5W5RlhlMqXe8cQq01ICH7JiVWAI5abYkZc32RGlwmHAM2HBQ33oG4V2p6YNWW6JIBwVCif8MLQ8B5QHnwTDXK+W5GLhqiGA5N7yozRPw+xswRNoZMsKNukh2085qUPDuTtaH4ghFTyAWCEfBtHmeULkBUT8QJ2tdZZoiiYAipITs0MGBAGpUi2EkWW6oe39TZ3tVEk9h3qytVVO4ngWFvKkqhCVt2R0qe+FGLUWOs+V1kkTyg3TbEIG0Vj8Uo3MEoaTXdRUqAXCtwQcVVSvFVNO5jqu2mpO9lMorRSVCqSkuBi9O1nllIdACIRACBSByJ1pHAm8Fy7ZGXgBHcasohI//elPGXXvkeCh4SPhafCiULZf1EloQ+vyOagB9ptDQkTDK6AVMm8MrULZG1rgDqk3+0jsYPXr7eskhRAJj4tbkdXk4CEgOAx4MrxEoiI+CldZZRUuDa+A8BJvC13Gw0j7qEA3+FhgLzVVbgaRoyYvp0sjratoFBEuJbwdyHByWOYmccO28I07pxQaZusmzTJ1iE+9ErUptGD4zHn1k7SqYJb4FG8KgUJytVbusiwC1bqWL80sVNxKCKlWmTVagQuq8mZa6zfL3GAEnJHqrewiN4KZAl4cW5GJps+Tlz05qdRS+ZxMsTcxqVyOHHBqv8YlymZEyJQSkntkHpt7vuyUGLUVxcxT2LywU/hMaM/x4AZ1arsJ3nkqt72j3fQ2CyEQAiEQAhMSSDBrQiwTF4oHuTqvmAWXjCRW9bxxWpClrtRV8NptGa8u9GVveMWVCuyl8BbVIhLETFYhO8ee0RysuG8KhkEVl2HmXb6LK9mw3vzMxvN2TNyhe+swrlJqJA6rQ77UVpPVb8o5pSg2faDGuCsEUygq/WwqdC7oW+WUcCzps0iWEltVTf2XwUMB0HmehUP0cGNIbRbx8RzqztaEpdxGLjTGY8ShpRtKVINCeEjmsiwchp8eIum0LJ+Xc8v7v9QRvINds77pD/nCcpJIPW8plzojYkVSEAFe8aFOxbm8C0LHJAl5sLUwljxl7ZgayUOWW4OMnV0lB01BPRadMNIZdTiiOLF4ffi6+MYqKYqfD0kvBRPgQ4A+rr6ZULqKJMXN6FTgjdMZIgZSSc2Oh9qvI4fiIc7EBxuHE0kka7sKObrqPbLq6xgF3AQEO3uekhAIgRAIgSIQuTONI6HyS7gcWFYmp6wOo84MC2FMln7BKLJznCisbNvOmDp+C8aM/6aSW4WTWLUu+qZakBvkWp/lIyx4EeT0kE0sMbvb5Ul0fE4MsBd80iicE5Jt6ST2kn01tD322IOFbuth60816Qz6gMKQp8ynZcg0igCZngiWcdioz5DrjwYJNeGzyl9pbaeWcfN6VHqF5DJeuqGcTCgp5BwCx47IFzXFsAAUPwKHsCA66RgeMg42PREuJJgIOC0Ti2SoLnGf8KlUofIXv/jFVKmRykrWYPWBRJOQ5OXz9bPLt5Rkj9vRT3KkqcazxX1lj4bQFPLtNcv6Zln8kVarQt47n1r2ChGaqalcCyVb2wrlaLeV1M97M7UmTtWasH4KQyAEQmD2EnAGz6dHAiIXrJ2gj2wPMRrCgr3kb+B+YHF5KaTRvOc972H/5OVIyKAnWP16qbgsGcaJhXNB72jjBHJBz67LwnHpL0JBGbjcZ8h1pjJFWHR7rPANl5JyDg974UFhMjUleMR3Yu/MIZHBbcDSdx+LF1LaO8PPm8LHwGcgXqZL3DCcHJW3O1kLxkWFCLSpqWOqGTshQnPgoEFRudpW0rFyEZnJmmrKCS/6gy8HQHnK8pebVXN1gUtGSMgouLjkHs3VfaXxEAiBEJg9BJocUNfPQzXqvCJ0ekqXd4QocbEu0EDu0Ci2ZzXdmGNBOVcNtwf7LdDDi+BbxgZHhQURE9ZdvMMj79SsAAq3gQ25LkgoUTAixk9pQG5UFpYikgRfKsOmvEeaEubQckW+VNa+EkeVCmIlSrp86uDTGZ8u1eb9KnFA+cKkYZc0mgH2SjqOHYnH8avVPVMDbDxNhUAIhMCsJSDNMW9EH5PZl20q8CRBeEzGMxzD4GsRoZPrzSs2D3pENfKNUZxJfJkHtLOLEAiB2UNgaOVOcnemfRB23l087SayQQcBKT6TZfl01B1AAfdY97vYBrCPNBECIRACITA0BKaIfQxNP9OREAiBEAiBEAiBEOiTQOROn+CyWQiEQAiEQAiEwKgQiNwZlZlKP0MgBEIgBEIgBPokELnTJ7hsFgIhEAIhEAIhMCoEIndGZabSzxAIgRAIgRAIgT4JRO70CS6bhUAIhEAIhEAIjAqByJ1Rman0MwRCIARCIARCoE8CkTt9gstmIRACIRACIRACo0IgcmdUZir9DIEQCIEQCIEQ6JNA5E6f4LJZCIRACIRACITAqBCI3BmVmUo/QyAEQiAEQiAE+iQQudMnuGwWAiEQAiEQAiEwKgQid0ZlptLPEAiBEAiBEAiBPglE7vQJLpuFQAiEQAiEQAiMCoHInVGZqfQzBEIgBEIgBEKgTwKRO32Cy2YhEAIhEAIhEAKjQiByZ1RmKv0MgRAIgRAIgRDok0DkTp/gslkIhEAIhEAIhMCoEFhwVDqafoZACIRACIwugbvv/ej//PPPb3HCgVj1r3/966Mf/eiEa/sunG+++bQ84eZ77rnn0ksvPeGqFI4ZgcidMZvQDCcEQmDMCVx11VXnn3/+AgssUOO86667br311mbMiyyyyG233db8nBsLiy666KGHHnrCCSfYV4/t6+Saa665wQYb3HHHHeedd95DH/rQe+65p3NbukTnzznnnM5VfZfceeedD3jAAw444AB96GxkscUW6yxMyVgSiNwZy2nNoEJgbAkwk0xm38OjDCZzLbS2ueCCC/7tb3/bf//9LbSWd1/WN1JAnblnRBdaaKHf//73J598ctOT9ddff9ddd7399tuVGNrXv/717bffvpcxNi30sfDoRz96ww037H1DU7bRRhttttlmNMepp566xRZb9L5taobAQAhM4z95IPtLIyEQAmNJ4Oyzz7744ounJQ5aORAKvfgkuDSuvvrqt73tba3b9r7M1m611VYrrrjihBf6re2Um+HKK6+00FrefdkQnv70p+vkC17wgsb70n2T6a4FiuIhpyzY1jcXS2s45tWvfvWSSy453WbnWX1YonXmGe3sqJVA5E4rjSyHwDQISDJwzTotc1itlyllGvvYtpf+LbzwwgceeOAf/vAHdrHqS1xYffXVWRp9VuLnUkstVfaylwanrEPl/PjHP/7zn//cn9zhilhmmWU++MEP6mH3XpEpyy233Je+9KUpuzRhBZuztcsuu+yEa8ejcJi1zngQzihGlEDkzohOXLo9BQE+gCOPPHJOrrDZ4C6ml11nni+99NIp+jHJ6sc+9rGbbLLJnARlJmn4P8VU1C233LLGGmuUnDKQJZZY4r3vfS9DePzxxyvkD2D1e/GmdNlL2yptzgltvWrEWVvL+RkCIRACc04gcmfOGY5tCzIiGTD+fM4Al8Us6KCGyrbJH9xtt92e//znH3PMMTfccEMZ5h7bZ7/ZclrBt+XOrXT4+uuvP/PMMy10ru2lRIbHLrvs8rSnPa2LJvja177WX/tgStvkbumlJ4OtI8jSNDj38kuaXWQhBEIgBIaEQOTOvJgIpr1209hm1p09PuOMMzbddFNxh2kZ+8l6zPTOyeV1W7O8FyeeeOLiiy9+2mmnWUVY7LTTToP1RnAw/Pvf/958883bdj3lT93Yeuutb7zxRt8N27atIB0gjbbG8zMEQiAEQmC0CETuTGO+dthhB66I6V4Tu5R3S4JvAmLllVe2ULtks7lPjj76aDkW0+jEJFU5IQRH3vjGN3bxRkyy6aTF2223XSVCUmlGvdpqq01adeZW9JcsMnP9zZ5DIARCIARmgEDkzjSgv+hFL3L75XTtK1mzzTbbcELYcK211prG/lI1BEIgBEIgBEJgEAQid6ZB8Rn3fqaxQaqGQAiEQAiEQAgMAYE+EzmHoOfpQgiEQAiEQAiEQAj0RCBypydMqRQCIRACIRACITC6BCJ3Rnfu0vMQCIEQCIEQCIGeCETu9IQplUIgBEIgBEIgBEaXQOTO6M5deh4CIRACIRACIdATgcidnjClUgiEQAiEQAiEwOgSiNwZ3blLz0MgBEIgBEIgBHoiELnTE6ZUCoEQCIEQCIEQGF0CkTujO3fpeQiEQAiEQAiEQE8EInd6wpRKIRACIRACIRACo0sgcmd05y49D4EQCIEQCIEQ6IlA5E5PmFIpBEIgBEIgBEJgdAlE7ozu3KXnIRACIRACIRACPRGI3OkJUyqFQAiEQAiEQAiMLoHIndGdu/Q8BEIgBEIgBEKgJwIL9lQrlUIgBEIgBEJgzgjcc889c9bA1FvPN998p5122o9+9KOFF15YbT/t1PdkW77hDW9YaqmlJlub8nEiELkzTrOZsYRACIw5gbvuuuucc865++67BzVOUuDmm2+ef/75F1100dtuu81P322NW3vjjTfuvvvuL3vZy4488sg77rijrcKUP3V79dVXf8hDHmJhyspzUmGBBRb461//evHFF995552bbrrpDjvssPPOO++77752PWG3F1lkkTnZXbYdIQKROyM0WelqCMx2AuUeqIt1y/WzRyis+FyytUzmUUcddeqppy600ELlVJhLRtTAb7311kMOOWRCy90jh85qr3nNa6666qpjjjlmiy22IH223XbbCUHtuOOOgBMQnS1MWaLDG2+88dOe9rQpaw68wp///OeBt5kGR5FA5M4ozlr6HALDQuD000+//vrrXf3PYYfYUZfjnBaT+S1Y+uuuu+6EE05Q4QUveIEAxBe/+MXvfve7PQoLjW+yySYcDBMa8jnsvOFfccUV1157LaO+5ZZb+vmiF72Im2EOm51wcxz22muvEnwTVphuIfIrrLCCnl9zzTX3u9/94F166aWn20jqh8DwE4jcGf45Sg9HmIBr5cUXX/yGG25gZVncGokL9IGYK5b+lFNOYfg32mgj5ord2nvvvRndORcf1U8NLrfccrr6r3/9a+WVV+6cBjv69re/ffXVV8+haWdiV1xxxSc+8YkPfOADN9hgA2Pp3JcSPXnWs55l4ZZ7P9tssw0/xIQ1OwvBf+pTn7raaqt1rkoJApxS973vfYMiBMaYQOTOGE/u7Bral7/85Yc97GEspW/L/Q1+MkPbX2tEwBFHHLH99tsfcMABl19++YMf/GB2XeFWW201kB0x/+y+bz4P0kQnNTtAoyX685KXvESH8Xzve99rR50cPvCBDwxEXWlkwQUX9D2HyqmzhykJgRAIAQT+k7UeECFQBG6//fbyRlx66aUT2rZeQN10002MuotFh1bjz2jdkD3bZ599LrnkEuattbz3ZVmHHBtth+5JJ53EN2CPvi333lrVLB/+Rz7yEekXbS1Pt6nW+jigKglUIQeJvbDoHBitdbIcAiEQAmNDwJ1xm2++ueGceOKJYrvDM64+7c3wDGD4e8J2zrn5ZCMPPvjgdddd94ILLrjsssuaK2Dl5TCYcw7a1PL5559vL5/+9Kf7bnDXXXddfvnlzz77bG6G9dZbb0LFQ5GstdZa/e0CTLkLdtGWhEFYKKHSfFvur/FsFQIhEAIhMJYEInemMa2vfvWrjz322MUWW6z3bWgR2Q8bbrhhm23uvYWqSdb87ne/k0goi4L7pFwvDP9OO+102GGHffCDH1xppZXmcBd2ZC88LgQKyTLdHjb111lnHQ4S/dTUkksu2ZQPfKHTOVQljRYc+B7TYAiEQAiEwIgSiNyZxsRtvfXWD3rQg9jy3rep2Mrzn//83jeZbs0999xzupvMg/qU2TzYS3YRAiEQAiEQAr0QiNzphdJ/6zz73s80NkjVEAiBEAiBEAiBISAwp0/LGIIhpAshEAIhEAIhEAIh0I1A5E43OlkXAiEQAiEQAiEwBgQid8ZgEjOEEAiBEAiBEAiBbgQid7rRyboQCIEQCIEQCIExIBC5MwaTmCGEQAiEQAiEQAh0IxC5041O1oVACIRACIRACIwBgcidMZjEDCEEQiAEQiAEQqAbgcidbnSyLgRCIARCIARCYAwIRO6MwSRmCCEQAiEQAiEQAt0IRO50o5N1IRACIRACIRACY0AgcmcMJjFDCIEQCIEQCIEQ6EYgcqcbnawLgRAIgRAIgRAYAwKRO2MwiRlCCIRACIRACIRANwKRO93oZF0IhEAIhEAIhMAYEFhwDMaQIYRACIRACMxmArfccsv8889/9913X3fddfPNN1+PKO65555FFllk2WWX7bF+qo00gcidkZ6+dD4EQiAEhpfA4Ycffu211xIic9hFusRnskYWXnjhs88+2/ett9561FFHTVZtwvItttji5JNPnnBVCseMQOTOmE1ohhMCITADBK644gpOAhbXvi+77LJVV131oosuYn179zQ0nb755pt5Ke573/vefu9n0UUXve2225q1c76w0EILvfOd77zgggsIiFe96lXf/e53r7nmmlIk9rvccsstsMACd91113rrred7TnZn7GeddZbh9AGhdb8w6PDDH/5wC63lrcuPetSjDMeO3vSmN3URRq2bWDbeZZZZpq0wP8eVQOTOuM5sxhUCs44AO9fFIsLB0n/84x//y1/+suCCfZ76tGAvbZvTByeccMLGG29cYZHjjz/+mc985qGHHkpG9DEHr33ta1dbbbX9999/yy23fMITnvC1r31t6623tt8+mppsk8c85jEbbbSRtXBxbzTV7rjjjoc97GH2ZeHFL34xNdCs6m9hzv06/e03W4VAJ4H5ehfCnRunJARCYPwIXHrppeeddx4TPtnQnDT4Lebw1CFngiFndNddd92f/OQnBx10kJLJ9thLOdtMbWy66aZdjDTre+GFF9500019+xu23357Po9tttmm8bjw6JxzzjmXX345iSODRFcNxNrFF1+8D2OPKq2jzUsuuYSjZYkllvjnP/9poe8O94IudUJggAROO+20zTffXIMnnngiyT7AluewqcidOQSYzceWAIt155139j08dquMX1sLZITAx7ve9a4+bGFbU/XTjgQ+fDONE1aYVqEr+1//+tenn376ZPbVjhZbbLH99tvPt+VpNd5WGQrSRCNQdFFXbVtN9pMKWWmllbbddtvJKsylcvs10QOBP5d6mGZDYF4SGFq506dHd16yy75CYDICp5566t///veylAwnD/xkNadb7gJdMML/bX9BBCZcC9ttt53N2zQBGaGfjW9guh3rrK+pTTbZRJt217l2uiV6y7Wg823dbm3HEJZaaqnJ9FBrzdmwfMABB9CvBx988GwYbMYYAqNLIHJndOfuPjfeeCNryjJdeeWVrN2cmx+KgT/DpzMcYC+f+9znTjnlFAt9I2NBV1999XJF9N1Is6H8CXJEEIHckYLwyEc+cu+99+6eutFs28vCHnvs8Za3vKWXmp11SjQ85SlPmXOnRWfjKRkqAlTm8ssvP1RdSmdCIAQ6CUTudDKZoxKyw3Vef3dkdNlx56W2S3DiQ5j/IQ95iOtLd3t22bzHVSussMLaa6/9wAc+cJVVVmm7KYOWMii3P8yJqAJnt912k6thoccuda9GezV6QsfmpG/dd5S1ITAZgQc/+MGTrUp5CITA8BCI3JnGXNxwww3ucuzuR6ESPAGie51p7PLeWyWpEJlfZM25557Lh7HWWmvZCwH0+Mc/nhvG8g9+8IM5TwTRoORKt2UuvfTSFqbVyelWnhMX0XT3lfohEAIhEAIhELkzjWNgySWXFNCZcoP4GKZElAohEAIhEAIhMC8JRO5Mj3akzPR4pXYIhEAIhEAIDAGBOX229xAMIV0IgRAIgRAIgRAIgW4EIne60cm6EAiBEAiBEAiBMSAQuTMGk5ghhEAIhEAIhEAIdCMQudONTtaFQAiEQAiEQAiMAYHInTGYxAwhBEIgBEIgBEKgG4HInW50si4EQiAEQiAEQmAMCETujMEkZgghEAIhEAIhEALdCETudKOTdSEQAiEQAiEQAmNAIHJnDCYxQwiBEAiBEAiBEOhGIHKnG52sC4EQCIEQCIEQGAMCkTtjMIkZQgiEQAiEQAiEQDcCkTvd6GRdCIRACIRACITAGBCI3BmDScwQQiAEQiAEQiAEuhGI3OlGJ+tCIARCIARCIATGgEDkzhhMYoYQAiEQAiEwbQL33HPPTTfdNO3NssFoElhwNLudXodACIRACIwVgR/+8IfnnnvuQgstNCejuvvuu+eff3465q677pqynTvuuOOrX/3qUUcdtfbaa09ZORVGnUDkzqjPYPofAiEwiwj84x//YM4Z9RtvvHG++eZrHfnNN9+84IILLrLIIrfeeuvtt9/etra15pwsL7DAAnvvvfcll1xiX9NqR5/XX3/96667bplllllsscUoktbNNfub3/zm73//u4XW8mkt28XOO+/8uc99bt11133Pe94DwpSbH3jggYsvvviU1VJhDAhM73gdgwFnCCEQAiFQPoA777xzQhQM+emnn37cccctvPDCE1bopbBEyZwY78696M+XvvQlWuGWW2658MIL2yq86lWv+utf//qjH/3oGc94xuMe97hejH1bCz3+3GCDDQiXHis31dDec889zznnHJuvssoqnd4X2EFr6ve9sN9++/W9bTYcYwKRO2M8uRlaCMxFArfddtuvfvUrUYCLLrpoLu2GA4DHYrLG2X4dcHXOnzFZnQnL2VRX/+edd95mm22mkTY3g01UuOKKKzgw+ra+NnzlK1/5xS9+8aCDDlp66aWpqwl7Mt1CXd12221rqzbnilVrrbUWXJdffvlqq63GgzLdxudN/VVXXbV2NFghOG86n72MNIHInZGevnR+JgkwMGL/A+mBC1/qgel1yTuHplEjZ5xxxuGHH14iQESDM6BEAxu81FJLDaTDmrr++uu/8IUvbLHFFqeccspA2uxshFB417ve1SUooxvvfOc7OzfsXmKrpzzlKbwgO+2006KLLtq98pysfeMb3zgnm/exreEsu+yyfWyYTUJg7AlE7oz9FM/qAV555ZWnnXZa23Vw70SIj8kEjTYvvvhixrjvxptu0DrrrbfeJptscvbZZ6+xxhrLLbfcnCge4uCGG264+uqrGXWCjNZ54QtfeNhhh/m58sorv+lNb5qTxps+W7CjD3zgA1TadJ0rrY10X9ZnNLrX6XttH+GYvveVDUMgBGacQOTOjE/BXO+Aq3A2qcslcu89cNMmC9p7/R5rspdHH330N7/5zTKcvNy88XPeYe1ceumlJ598cn+KROqDBIjdd98dvc6B0Cirr7662zo6V023RFPrrLPOox71KLelcPXPjTDEy172sun2KvVDIARCYJwIRO7M69l02X3kkUcOKm5dV+pdJIjQxic+8YkLLrhgzsdJNOy4446dt1TMecuUjdTLNddc04IRCbjsu+++7kftMq4ed4rznPgeeBf6k0o9dq+tmhTOtpL8DIEQCIEQGAiByJ1pYOTb2H777d0Q0YtYYap5y+973/u22mzmk6/lzDPPtDCNHU9SVcuu2vkenvOc50zogajtDj300F46PMlO/q9YnzfaaKN5af7/b99ZCoEQCIEQCIE5IBC5Mw14tMtee+317W9/m8tkys1EKF7/+teLd1horcyBMRDx0dpmlkMgBEIgBEIgBLoQiNzpAmeCVY+/9zPBismL4g6ZnE3WhEAIhEAIhMC8IDCAkMq86Gb2EQIhEAIhEAIhEAL9Eojc6ZdctguBEAiBEAiBEBgRApE7IzJR6WYIhEAIhEAIhEC/BCJ3+iWX7UIgBEIgBEIgBEaEQOTOiExUuhkCIRACIRACIdAvgcidfslluxAIgRAIgRAIgREhELkzIhOVboZACIRACIRACPRLIHKnX3LZLgRCIARCIARCYEQIRO6MyESlmyEQAiEQAiEQAv0SiNzpl1y2C4EQCIEQCIEQGBECkTsjMlHpZgiEQAiEQAiEQL8EInf6JZftQiAEQiAEQiAERoRA5M6ITFS6GQIhEAIhEAIh0C+ByJ1+yWW7EAiBEAiBEAiBESEQuTMiE5VuhkAIhEAIhEAI9EsgcqdfctkuBEIgBEIgBEJgRAhE7ozIRKWbIRACIRACIRAC/RKI3OmXXLYLgRAIgRAIgRAYEQKROyMyUelmCIRACIRACIRAvwQid/oll+1CIARCIARCIARGhEDkzohMVLoZAiEQAiEQAiHQL4HInX7JZbsQCIEQCIEQCIERIRC5MyITlW6GQAiEQAiEQAj0SyByp19y2S4EQiAEQiAEQmBECETujMhEpZshEAIhEAIhEAL9Eojc6ZdctguBEAiBEAiBEBgRApE7IzJR6WYIhEAIhEAIhEC/BCJ3+iWX7UIgBEIgBEIgBEaEQOTOiExUuhkCIRACIRACIdAvgcidfslluxAIgRAIgRAIgREhELkzIhOVboZACIRACIRACPRLIHKnX3LZLgRCIARCIARCYEQIRO6MyESlmyEQAiEQAiEQAv0SiNzpl1y2C4EQCIEQCIEQGBECkTsjMlHpZgiEQAiEQAiEQL8EInf6JZftQiAEQiAEQiAERoRA5M6ITFS6GQIhEAIhEAIh0C+ByJ1+yWW7EAiBEAiBEAiBESEQuTMiE5VuhkAIhEAIhEAI9EsgcqdfcpNs96c//emPf/zjJCtTHAIhEAIhEAIhMAMEFpyBfY7vLi+88MLNNttsoYUWOu2009Zee+3xHWhGFgIhEAIhEAKjRCDenUHO1l133TXffPPtvPPOD3rQgwbZbtoKgRAIgRAIgRCYAwLx7vQJ79///vfBBx/83Oc+99hjj33lK1+5wgorXHvttfvuu+8999yz6KKLEj3V7ic/+cnjjjtO4e23377ffvttuummE+5v7733/tWvfqXaxz72sZtuummfffaZf/75l1lmGXvR1K233nrnnXdyF336059ebLHFJmwhhSEQAiEQAiEQApMRiHdnMjLdyn/xi1+svvrqxxxzzIYbbrjXXnu9733vU/uss85afPHFF1xwQWtr49///ve77bbbKaec4ucCCyyw5ZZb/vSnP52w3a222urkk09+6lOfusEGGzz2sY999KMffcUVV+y+++6iYxpZZ5111ltvvW9+85sf+tCHJtw8hSEQAiEQAiEQAl0IxLvTBc6kqz7zmc8sv/zyBMpll1321re+dZdddlF163s/L3zhC2+55Zba8uEPf/jznve8884777vf/e7dd99tlQ2f+MQndrb7pCc9ydptttnmzW9+89JLL73ttttKAFKTovrIRz5yyCGH2ORnP/vZbbfd1rltSkIgBEIgBEIgBLoTiHenO58J1p5//vlf+MIXVl55Zbpk/fXXX2mllVZbbbUJ6t1bpNpSSy0lvMXx8/SnP/0rX/kKb01nZaGrZZdd9pnPfCZhdPTRRz/nOc8R2FJtjTXWWHjhhTvrpyQEQiAEQiAEQqB3ApE7vbP6b80lllji/ve/v6zkXrYUnJJ5c91116l81FFHvfSlL+XyqQ3POeecc889t2lk3XXX/dvf/kbl/OEPf7jqqqsEsKwig/75z3+efvrpomDXX3+9n039LIRACIRACIRACPRIIOazR1D/V23VVVf9wQ9+cOONNwo/+UgxrnVSkv2UwaNECvMRRxyhfMUVV/zd734npLXHHnvQPa973euahuQ1S9a5+OKLq8QqjqL9999/1113pXWkPyvnFiJ0JDiLdr343k9VzncIhEAIhEAIhEDvBCJ3emf1fzWlEh9++OF8Nm6Y+stf/kK4WLf55pu7bWqjjTaSc+OOqjvuuEMhx4wsHOnMbrb64Q9/+LjHPa5pZeONN37DG96w5pprVokcZ48ofPazn/3hD3+4SXY+44wzSCJ5P277cmOX2FmzeRZCIARCIARCIAR6JJBU5R5BtVcja0466SSl/C7CTBaWXHLJ8ui0ViV6RK/U4adpC0W95S1vaa1pWTJQlTT5OuJfPttttx0Z1FY5P0MgBEIgBEIgBHokEO9Oj6AmruaJgoJNso+vueaazhpk0G9+85tf/vKXolSeptNZYcoSYSzun1//+tc9pgpN2WAqhEAIhEAIhMAsJBDvTv+TToK8/vWvF7dy7xXXTmdDnrXjSTmLLLKIBXdmdVaYskS6DsXj/qwpa6ZCCIRACIRACITAZAQidyYjM3U5EfOIRzzi61//+mRV3cP1+Mc/frK1vZTbRbROL6BSJwRCIARCIAS6EEgwqwucrAqBEAiBEAiBEBgHApE74zCLGUMIhEAIhEAIhEAXApE7XeBkVQiEQAiEQAiEwDgQiNwZh1nMGEIgBEIgBEIgBLoQiNzpAierQiAEQiAEQiAExoFA5M44zGLGEAIhEAIhEAIh0IVA5E4XOFkVAiEwKwjcdttts2KcGWQIzGICkTuzePIz9BAIgXsJfOUrX7nnnnsCIwRCYIwJ5DGDYzy5GVoIhEBPBHbcccee6qVSCITAyBKId2dkpy4dD4EQCIEQCIEQ6I1A5E5vnFIrBEIgBEIgBEJgZAlE7ozs1KXjIRACIRACIRACvRGI3OmNU2qFQAiEQAiEQAiMLIHInZGdunQ8BEIgBEIgBEKgNwKRO71xSq0QCIEQCIEQCIGRJRC5M7JTl46HQAiEQAiEQAj0RiBypzdOqRUCIRACIRACITCyBCJ3Rnbq0vEQCIEQCIEQCIHeCETu9MYptUIgBEIgBEIgBEaWQOTOyE5dOh4CIRACIRACIdAbgcid3jilVgiEQAiEQAiEwMgSiNwZ2alLx0MgBEIgBEIgBHojELnTG6fUCoEQCIEQCIEQGFkCkTsjO3XpeAiEQAiEQAiEQG8EInd645RaIRACIRACIRACI0sgcmdkpy4dD4EQCIEQCIEQ6I1A5E5vnFIrBEIgBEIgBEJgZAlE7ozs1KXjIRACIRACIRACvRGI3OmNU2qFQAiEQAiEQAiMLIHInZGdunQ8BEIgBEIgBEKgNwKRO71xSq0QCIEQCIEQCIGRJRC5M7JTl46HQAiEQAiEQAj0RiBypzdOqRUCIRACIRACITCyBCJ3Rnbq0vEQCIEQCIEQCIHeCETu9MYptUIgBEIgBEIgBEaWQOTOyE5dOh4CIRACIRACIdAbgcid3jilVgiEQAiEQAiEwMgSiNwZ2alLx0MgBEIgBEIgBHojELnTG6fUCoEQCIEQCIEQGFkCkTsjO3XpeAiEQAiEQAiEQG8EInd645RaIRACIRACIRACI0sgcmdkpy4dD4EQCIEQCIEQ6I1A5E5vnFIrBEIgBEIgBEJgZAlE7ozs1KXjIRACIRACIRACvRGI3OmNU2qFQAiEQAiEQAiMLIHInZGdunQ8BEIgBEIgBEKgNwKRO71xSq0QCIEQCIEQCIGRJRC5M7JTl46HQAiEQAiEQAj0RiBypzdOqRUCIRACIRACITCyBCJ3Rnbq0vEQCIEQCIEQCIHeCETu9MYptUIgBEIgBEIgBEaWQOTOyE5dOh4CIRACIRACIdAbgcid3jilVgiEQAiEQAiEwMgSiNwZ2alLx0MgBEIgBEIgBHojELnTG6fUCoEQCIEQCIEQGFkCkTsjO3XpeAiEQAiEQAiEQG8EInd645RaIRACIRACIRACI0sgcmdkpy4dD4EQCIEQCIEQ6I1A5E5vnFIrBEIgBEIgBEJgZAlE7ozs1KXjIRACIRACIRACvRGI3OmNU2qFQAiEQAiEQAiMLIHInZGdunQ8BEIgBEIgBEKgNwKRO71xSq0QCIEQCIEQCIGRJRC5M7JTl46HQAiEQAiEQAj0RiBypzdOqRUCIRACIRACITCyBCJ3Rnbq0vEQCIEQCIEQCIHeCETu9MYptUIgBEIgBEIgBEaWQOTOyE5dOh4CIRACIRACIdAbgcid3jilVgiEQAiEQAiEwMgSiNwZ2alLx0MgBEIgBEIgBHojELnTG6fUCoEQCIEQCIEQGFkCC45sz9PxEAiBEAiBeUrg9ttvv+CCCx784AcvssgirTu++uqrL7/88tVXX33ZZZdV/u9///vMM8/8+Mc/vsoqq/h52WWXbbfddk94whNUWGyxxZT8/e9/v+eee9ZYYw3Lt95660UXXVQ/l156aSVtn+uuu+7SSy+94447brvttvnmm2/xxRdfaKGFHvKQh1hurXnnnXfq21133XXzzTers+CCC66zzjoLLLBAU+emm27685//rIerrbZaU2hB49dee+2iiy6qvq6uuuqqCrWjtbvvvlvHmvEa44orrlht2osNf/7zn3/oQx/Sk/e+973rrrvummuuufDCC7c2fuWVV1511VXzz/9fz4LWEHjQgx7UWifL84gA+vmEQAiEQAiEwJQE/vKXv7BMO+200zve8Y699trrAx/4AFmz9957b7rppso/85nPaIEo2Xrrrf3cd999q8Hzzz//AQ94gBLioEpe8pKXrLzyyn/961/9fOc732mVzwte8AIiQ8mPfvSjj3zkI1WTiHnOc55j7SabbPL+97//3e9+933ve1/y4utf/3pVaL4POeQQ1e5///vvv//+NI06u+66q103FU499VQV1ltvvbe97W0nnnii+vvss8/vfvc7MkU57UXcvPKVr6z6//rXv+xIuU8zkBe+8IVf+MIXqsKee+5Za1u/DzzwwGZ3FqiojTfeuLWC5RVWWAE97bfWHKfl4mykIA/VuO4zVL1JZ0IgBEIgBIaWwAknnNBqvDktllhiiaak5M6rXvWqKuHwaAbypje9SeFmm21WJVSFnw9/+MMpj6rsW2u8QbZaZpllHvnIR1bN173udVXh85//vBI+npVWWknJM57xDLqq6vg++OCDy4Ny3HHH+fntb3+7tmpkk8LHPvaxVei7XEQWllxyySq04aGHHmqZ68UwKZsq982TdPbZZ3/iE5+wvOOOO2qqlv182tOeRrh88YtfLHfX+uuvf80116hQn2c+85nVCIcQuca/1XikuLv+t9a4/Y3cGbcZzXhCIARCYLYRePKTn8x+c4cceeSR/ByHH344iWDB53Of+xzfzx//+EfhnrLxrXKHk4bzhiL5zne+A1rJHfEmOoDy4Eepj0hQhYoe9ahHFdtnP/vZWltrrbUa1I03qPHE2HvJCE6m66+/Xk0SZPPNN7ehPX7pS1+qbTWihOj52te+dthhh6lgw+o/LSUed8455yy//PLVefEyCqaJTDUy5TWveY1Q3SMe8YiqVsPRPhRVApHwnBJWv7QgDUR+iQOKf+G23377qXm/+92v8XVV98bme2jlTnJ36hDNdwiEQAiEQE8EvvKVrzz60Y+esOqxxx4rW6VzFf0hRCVa9KIXvUgGDPVACpxyyikPe9jD6IDW+twtBMFXv/pVhRdeeOG5557LEfK3v/3NtuW/oaJ++9vfHn/88WeccUZtyPVCK1gmLJZaaikL/EPf+ta31l57bfulKl72spcprDpa8/HTN6VlofkIkBE9HEs23G233W655RbpPgpl5AjYyeyRhUMAkVlCYLayzGFTm++www7nnXeePJ6f/OQnp5122pZbbvmHP/zhxhtvtNZ+n/SkJ9FPPttvv70SiD75yU/KDXrMYx5Tm+d7HhD4b/7UPNhTdhECIRACITAGBHgvJhvFE5/4RPpAAo0KfCd/+tOfLLD3NIooj2URKJKCL+d5z3uevBaCgzRp/XDPHHHEERKHVZYjTFf985//lNPjZ/NpnC5KSKJjjjmmWdUsaLlcMqU5lOsGf1JpHT/btI4S2oWy4b/55je/Kfb09Kc/XdrQUUcdJWdIDjXFo46u0kAWOj/VZ7KMr8jaJsxHBj3lKU/ZYostyLvaivwi3doG1dlgSgZLIN6dwfJMayEQAiEw5gR4aHbffXfxKeMkIMp78fjHP95PQkfWi7Rf2coykbfaaispvbwvgjgNlF122YWnx1ZNSbPA4SEPxoaV0/PmN7/5G9/4hrXiUOXaaWo2C1TUhP6kpoIGJQBttNFGWtBnXXrFK17BcyNXmkumqWZBlEoghuJpLWyW3U1GIdFtMpCawi4LnECf/vSnf/GLX6jD0+Pzq1/96l3vehdVJLZFNjURsS6NZNUACUTuDBBmmgqBEAiBcSYgQYcmoFSkoUhtOeigg77//e8roXKkwkiIqczfxz3ucUcffXRlGX/0ox8VxBFm4uQoiVPfTTZM8ZKD/MY3vpEOuOKKK97ylrcccMABqvGsdNIU3vrpT3+qnJPphhtumEwGtW5Ye5Ry5CZwsTOBJLvTSbe4f/azn9U9ST9um+/UMSrzHvHrSEsiwj71qU9plv+mtfEuy4JiJXeqjt1VyrafnD2RO13QzY1VkTtzg2raDIEQCIExJCC61DoqckTgiRtDvEkASMjmta99bVWQsUuXNJWJGA/dKYeQnOWmvFl4wxve4M5wCoDQKafLZKpigw02EDIjpzz2hnDZZpttmka6L7TdVqbyD3/4Q42Qbrr63Oc+lwRpa4Gea+4d4yXiFmqr0P2nm967V8jaeUkguTvzknb2FQIhEAJjRUAMi46Z1pCEk1rr8/pwDp1++unCPT/+8Y+bABO3zQc/+MHWms3yoGTEU5/61Eoz0rJ7ypr2a8HzexqtI4bVaJ0Pf/jDbTUn/EkeCV25OZ9Tx+YynVuryeOR1t1akuW5TSByZ24TTvshEAIhMA4EKJLnP//5Un15RJrxyBqWvlM/Kz5Fo8jwde9Sq3um7s1WTf228JMIkfwbakOgRwpz07IFD9eRc9NaUsvUg1ucVN522205nOr2eKvabvJqNlSTtpAc7ZlAfDlNeeuCJ/S0/uTX8TDAKpGK9NKXvrRZu9xyyzXLEy5UzrJnDHq4IneXNGc3z7tda8MNN7Sq7rS3YcXUJmwhhXODQOTO3KCaNkMgBEJg3Ah4A4MQkhuv3DzVjE1ib711QYnMGOEhT1v2NBq3c7sru6km6bhuRJIHU09Yblb97Gc/q+WzzjpLBnFTbsHDkSd838LJJ5/sbiwP+JESREDUY5HV9/Cb1lyZaurVr361atKlJQYJvTW3r7fuqHNZ/aaQqKpn9lSJR+Y89KEPbda2LUhpmtApJTOaXuTpaeJ97pDvco9bW7P5OecEInfmnGFaCIEQCIFZRKBuKTdgmcIekOOGoxq8m8w5WppYlVyc3/zmN9J6PLD4pJNOUkdqjhdQTEaKuGk8H00dz/0jaKQJf+xjH6vXZtE6bv7ipGkeCfj617++kVCVHsTN41E9lt0N7iaypjWSq3keYFNYCxO+FKJWEUytlXl3vve975Ev9iLg5WE8niQEAi3FcaUndkq3SRWi/7yES4Xa3E9iqB69o2TC8bbuKMuDJfBfJ+RgG01rIRACIRACY0bAk445VNz1LbKzxx57MO1uxfIk4homEaACvSJn2auj/vGPfxAWrU8j9ETBH/zgB80zlzvhkA6dz8IR8aGQPLXPHrmObMUJxL0kfYerqRqRvExOeZ8DiUNzcMx4VZZbrqyVcMO107ovjwJyE1YT9nJbWa1tq9a6Seey8JbQm6CeR+xorangcYJcOH66F0x2jic4ex3pAx/4QJXdfs8j5Q6vpv6E422aysLgCZiVfEIgBEIgBEJgSgICTzRN5aa0WSM5Pa2bC9NIxyF93Iy98847W+bnaK3QLBMxlJDWvvzlLzeFbQv2yzNE1ni/Jl3iI32nrc7vf/97DykWXOM14USRSCSth/ioapxMwnDNG7LaOs8jxfHT2iDBpOdVTQ5166rW5bo1varpm362rpXqVKt0RjisVczpKg9Qa+WxWR7al0jMB3HbxOdnCIRACIRACExGgC4RoGkNPMlKdkeVpJbJNpmynDPGw2/omO413bpF93hG32TVOJ9Evi666CIRN89HblNmnEByqD1op3VzMTJ6S1p0a6FlEk3QyjC5iCZLT5bPJCVIgxrR/7b3n+tDRbi0JtKnWqVpi7Jx+bj1vW2P4/FTUna9sMwb0bnlhmdQkTvDMxfpSQiEQAiEQAiMNoGhlTvJ3RntAyu9D4EQCIEQCIHhIcBF5yWyAkf8cMPTKz2Jd2eopiOdCYEQCIEQCIEQGDyB3Ig+eKZpMQRCIARCIARCYKgIRO4M1XSkMyEQAiEQAiEQAoMnELkzeKZpMQRCIARCIARCYKgIRO4M1XSkMyEQAiEQAiEQAoMnELkzeKZpMQRCIARCIARCYKgIRO4M1XSkMyEQAiEQAiEQAoMnELkzeKZpMQRCIARCIARCYKgIRO4M1XSkMyEQAiEQAiEQAoMnELkzeKZpMQRCIARCIARCYKgIRO4M1XSkMyEQAiEQAiEQAoMnELkzeKZpMQRCIARCIARCYKgIRO4M1XSkMyEQAiEQAiEQAoMnELkzeKZpMQRCIARCIARCYKgIRO4M1XSkMyEQAiEQAiEQAoMnELkzeKZpMQRCIARCIARCYKgIRO4M1XSkMyEQAiEQAiEQAoMnELkzeKZpMQRCIARCIARCYKgIRO4M1XSkMyEQAiEQAiEQAoMnELkzeKZpMQRCIARCIARCYKgIRO4M1XSkMyEQAiEQAiEQAoMnELkzeKZpMQRCIARCIARCYKgIRO4M1XSkMyEQAiEQAiEQAoMnELkzeKZpMQRCIARCIARCYKgIRO4M1XSkMyEQAiEQAiEQAoMnELkzeKZpMQRCIARCIARCYKgIRO4M1XSkMyEQAiEQAiEQAoMnELkzeKZpMQRCIARCIARCYKgIRO4M1XSkMyEQAiEQAiEQAoMnELkzeKZpMQRCIARCIARCYKgIRO4M1XSkMyEQAiEQAiEQAoMnELkzeKZpMQRCIARCIARCYKgIRO4M1XSkMyEQAiEQAiEQAoMnELkzeKZpMQRCIARCIARCYKgIRO4M1XSkMyEQAiEQAiEQAoMnELkzeKZpMQRCIARCIARCYKgIRO4M1XSkMyEQAiEQAiEQAoMnELkzeKZpMQRCIARCIARCYKgIRO4M1XSkMyEQAiEQAiEQAoMnELkzeKZpMQRCIARCIARCYKgIRO4M1XSkMyEQAiEQAiEQAoMnELkzeKZpMQRCIARCIARCYKgIRO4M1XSkMyEQAiEQAiEQAoMnELkzeKZpMQRCIARCIARCYKgIRO4M1XSkMyEQAiEQAiEQAoMnELkzeKZpMQRCIARCIARCYKgIRO4M1XSkMyEQAiEQAiEQAoMnELkzeKZpMQRCIARCIARCYKgIRO4M1XSkMyEQAiEQAiEQAoMnELkzeKZpMQRCIARCIARCYKgIRO4M1XSkMyEQAiEQAiEQAoMnELkzeKZpMQRCIARCIARCYKgIRO4M1XSkMyEQAiEQAiEQAoMnELkzeKZpMQRCIARCIARCYKgIRO4M1XSkMyEQAiEQAiEQAoMnELkzeKZpMQRCIARCIARCYKgIRO4M1XSkMyEQAiEQAiEQAoMnELkzeKZpMQRCIARCIARCYKgIRO4M1XSkMyEQAiEQAiEQAoMnELkzeKZpMQRCIARCIARCYKgIRO4M1XSkMyEQAiEQAiEQAoMnELkzeKZpMQRCIARCIARCYKgIRO4M1XSkMyEQAiEQAiEQAoMnELkzeKZpMQRCIARCIARCYKgIRO4M1XSkMyEQAiEQAiEQAoMnELkzeKZpMQRCIARCIARCYKgIRO4M1XSkMyEQAiEQAiEQAoMnELkzeKZpMQRCIARCIARCYKgIRO4M1XSkMyEQAiEQAiEQAoMnELkzeKZpMQRCIARCIARCYKgIRO4M1XSkMyEQAiEQAiEQAoMnELkzeKZpMQRCIARCIARCYKgIRO4M1XSkMyEQAiEQAiEQAoMn8P8AZJA4DPH5A3EAAAAASUVORK5CYII=",
+ "text/plain": [
+ ""
+ ]
+ },
+ "execution_count": 5,
+ "metadata": {},
+ "output_type": "execute_result"
+ }
+ ],
+ "source": [
+ "from PIL import Image, ImageDraw, ImageFont\n",
+ "import os\n",
+ "\n",
+ "base_path = \"./data\"\n",
+ "\n",
+ "image = Image.open(os.path.join(base_path, \"training_data/images/0000971160.png\"))\n",
+ "image = image.convert(\"RGB\")\n",
+ "image"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "uAVffmnZyUvw"
+ },
+ "source": [
+ "Now let's plot its corresponding annotations. Basically, if you type `data['form']`, you get a list of all general annotations. Each general annotation has a label, a bounding box, and one or more words, which in also have their own bounding box. The bounding boxes are in [xleft, ytop, xright, ybottom] format.\n",
+ " "
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 6,
+ "metadata": {
+ "colab": {
+ "base_uri": "https://localhost:8080/"
+ },
+ "id": "JPKkuJQ4sdZc",
+ "outputId": "c95bf306-98bb-4480-cc6b-ebb3aea548b3"
+ },
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "{'box': [292, 91, 376, 175], 'text': 'R&D', 'label': 'other', 'words': [{'box': [292, 91, 376, 175], 'text': 'R&D'}], 'linking': [], 'id': 0}\n",
+ "{'box': [219, 316, 225, 327], 'text': ':', 'label': 'question', 'words': [{'box': [219, 316, 225, 327], 'text': ':'}], 'linking': [], 'id': 1}\n",
+ "{'box': [95, 355, 169, 370], 'text': 'Suggestion:', 'label': 'question', 'words': [{'box': [95, 355, 169, 370], 'text': 'Suggestion:'}], 'linking': [[2, 16]], 'id': 2}\n",
+ "{'box': [482, 268, 518, 282], 'text': 'Date:', 'label': 'question', 'words': [{'box': [482, 268, 518, 282], 'text': 'Date:'}], 'linking': [[3, 12]], 'id': 3}\n",
+ "{'box': [511, 309, 570, 323], 'text': 'Licensee', 'label': 'answer', 'words': [{'box': [511, 309, 570, 323], 'text': 'Licensee'}], 'linking': [[13, 4]], 'id': 4}\n",
+ "{'box': [211, 651, 217, 662], 'text': '', 'label': 'question', 'words': [{'box': [211, 651, 217, 662], 'text': ''}], 'linking': [], 'id': 5}\n",
+ "{'box': [461, 605, 483, 619], 'text': 'Yes', 'label': 'question', 'words': [{'box': [461, 605, 483, 619], 'text': 'Yes'}], 'linking': [[19, 6]], 'id': 6}\n",
+ "{'box': [545, 603, 563, 617], 'text': 'No', 'label': 'question', 'words': [{'box': [545, 603, 563, 617], 'text': 'No'}], 'linking': [[19, 7]], 'id': 7}\n",
+ "{'box': [525, 904, 641, 926], 'text': '597005708', 'label': 'other', 'words': [{'box': [525, 904, 641, 926], 'text': '597005708'}], 'linking': [], 'id': 8}\n",
+ "{'text': 'R&D QUALITY IMPROVEMENT SUGGESTION/ SOLUTION FORM', 'box': [256, 201, 423, 230], 'linking': [], 'label': 'header', 'words': [{'text': 'R&D', 'box': [257, 203, 279, 214]}, {'text': 'QUALITY', 'box': [285, 203, 334, 216]}, {'text': 'IMPROVEMENT', 'box': [341, 201, 418, 211]}, {'text': 'SUGGESTION/', 'box': [256, 215, 324, 229]}, {'text': '', 'box': [324, 216, 332, 230]}, {'text': 'SOLUTION', 'box': [331, 214, 387, 228]}, {'text': 'FORM', 'box': [395, 215, 423, 228]}], 'id': 9}\n",
+ "{'text': 'Name / Phone Ext. :', 'box': [89, 272, 204, 289], 'linking': [[10, 11]], 'label': 'question', 'words': [{'text': 'Name', 'box': [89, 274, 118, 289]}, {'text': '/', 'box': [117, 274, 127, 288]}, {'text': 'Phone', 'box': [128, 274, 163, 289]}, {'text': 'Ext.', 'box': [169, 272, 196, 287]}, {'text': ':', 'box': [196, 274, 204, 288]}], 'id': 10}\n",
+ "{'text': 'M. Hamann P. Harper, P. Martinez', 'box': [215, 271, 451, 287], 'linking': [[10, 11]], 'label': 'answer', 'words': [{'text': 'M.', 'box': [215, 272, 230, 287]}, {'text': 'Hamann', 'box': [237, 272, 287, 286]}, {'text': 'P.', 'box': [293, 272, 307, 286]}, {'text': 'Harper,', 'box': [314, 274, 363, 285]}, {'text': 'P.', 'box': [370, 272, 384, 285]}, {'text': 'Martinez', 'box': [390, 271, 451, 282]}], 'id': 11}\n",
+ "{'text': '9/ 3/ 92', 'box': [543, 264, 590, 279], 'linking': [[3, 12]], 'label': 'answer', 'words': [{'text': '9/', 'box': [543, 265, 560, 279]}, {'text': '3/', 'box': [560, 264, 575, 279]}, {'text': '92', 'box': [575, 264, 590, 279]}], 'id': 12}\n",
+ "{'text': 'R&D Group:', 'box': [420, 310, 491, 323], 'linking': [[13, 4]], 'label': 'question', 'words': [{'text': 'R&D', 'box': [420, 310, 442, 323]}, {'text': 'Group:', 'box': [448, 310, 491, 323]}], 'id': 13}\n",
+ "{'text': 'J. S. Wigand', 'box': [236, 313, 327, 327], 'linking': [[15, 14]], 'label': 'answer', 'words': [{'text': 'J.', 'box': [236, 313, 251, 327]}, {'text': 'S.', 'box': [256, 313, 273, 326]}, {'text': 'Wigand', 'box': [278, 313, 327, 327]}], 'id': 14}\n",
+ "{'text': 'Supervisor / Manager', 'box': [91, 316, 218, 331], 'linking': [[15, 14]], 'label': 'question', 'words': [{'text': 'Supervisor', 'box': [91, 316, 161, 330]}, {'text': '/', 'box': [163, 318, 169, 331]}, {'text': 'Manager', 'box': [169, 317, 218, 327]}], 'id': 15}\n",
+ "{'text': 'Discontinue coal retention analyses on licensee submitted product samples (Note : Coal Retention testing is not performed by most licensees. Other B&W physical measurements as ends stability and inspection for soft spots in ciparettes are thought to be sufficient measures to assure cigarette physical integrity. The proposed action will increase laboratory productivity . )', 'box': [190, 346, 594, 447], 'linking': [[2, 16]], 'label': 'answer', 'words': [{'text': 'Discontinue', 'box': [190, 355, 268, 366]}, {'text': 'coal', 'box': [274, 353, 303, 366]}, {'text': 'retention', 'box': [309, 352, 375, 365]}, {'text': 'analyses', 'box': [381, 351, 435, 365]}, {'text': 'on', 'box': [443, 352, 458, 363]}, {'text': 'licensee', 'box': [464, 348, 520, 362]}, {'text': 'submitted', 'box': [527, 346, 594, 361]}, {'text': 'product', 'box': [190, 369, 240, 383]}, {'text': 'samples', 'box': [247, 367, 301, 380]}, {'text': '(Note', 'box': [318, 365, 352, 379]}, {'text': ':', 'box': [352, 367, 359, 380]}, {'text': 'Coal', 'box': [373, 366, 402, 376]}, {'text': 'Retention', 'box': [408, 366, 472, 376]}, {'text': 'testing', 'box': [479, 365, 529, 376]}, {'text': 'is', 'box': [536, 363, 549, 374]}, {'text': 'not', 'box': [554, 363, 578, 374]}, {'text': 'performed', 'box': [190, 383, 256, 394]}, {'text': 'by', 'box': [261, 381, 275, 394]}, {'text': 'most', 'box': [282, 383, 311, 393]}, {'text': 'licensees.', 'box': [318, 380, 386, 391]}, {'text': 'Other', 'box': [401, 378, 437, 389]}, {'text': 'B&W', 'box': [443, 378, 465, 389]}, {'text': 'physical', 'box': [471, 377, 528, 391]}, {'text': 'measurements', 'box': [191, 398, 275, 406]}, {'text': 'as', 'box': [282, 397, 297, 405]}, {'text': 'ends', 'box': [304, 394, 332, 405]}, {'text': 'stability', 'box': [339, 394, 402, 405]}, {'text': 'and', 'box': [409, 392, 430, 402]}, {'text': 'inspection', 'box': [437, 392, 508, 403]}, {'text': 'for', 'box': [515, 391, 535, 402]}, {'text': 'soft', 'box': [542, 391, 571, 401]}, {'text': 'spots', 'box': [193, 411, 228, 422]}, {'text': 'in', 'box': [235, 409, 250, 420]}, {'text': 'ciparettes', 'box': [256, 409, 327, 419]}, {'text': 'are', 'box': [332, 408, 352, 418]}, {'text': 'thought', 'box': [360, 406, 410, 419]}, {'text': 'to', 'box': [415, 406, 430, 416]}, {'text': 'be', 'box': [436, 404, 453, 417]}, {'text': 'sufficient', 'box': [458, 405, 529, 415]}, {'text': 'measures', 'box': [535, 405, 592, 415]}, {'text': 'to', 'box': [193, 425, 208, 433]}, {'text': 'assure', 'box': [214, 423, 255, 431]}, {'text': 'cigarette', 'box': [261, 420, 325, 434]}, {'text': 'physical', 'box': [331, 419, 390, 432]}, {'text': 'integrity.', 'box': [395, 418, 463, 431]}, {'text': 'The', 'box': [478, 416, 500, 429]}, {'text': 'proposed', 'box': [506, 418, 566, 431]}, {'text': 'action', 'box': [193, 436, 236, 447]}, {'text': 'will', 'box': [240, 436, 269, 447]}, {'text': 'increase', 'box': [277, 434, 333, 445]}, {'text': 'laboratory', 'box': [339, 433, 410, 446]}, {'text': 'productivity', 'box': [418, 430, 502, 445]}, {'text': '.', 'box': [503, 433, 507, 444]}, {'text': ')', 'box': [508, 430, 514, 444]}], 'id': 16}\n",
+ "{'text': 'Suggested Solutions (s) :', 'box': [95, 486, 250, 504], 'linking': [[17, 18]], 'label': 'question', 'words': [{'text': 'Suggested', 'box': [95, 489, 159, 504]}, {'text': 'Solutions', 'box': [165, 487, 222, 501]}, {'text': '(s)', 'box': [223, 486, 241, 503]}, {'text': ':', 'box': [243, 489, 250, 503]}], 'id': 17}\n",
+ "{'text': 'Delete coal retention from the list of standard analyses performed on licensee submitted product samples. Special requests for coal retention testing could still be submitted on an exception basis.', 'box': [263, 483, 593, 553], 'linking': [[17, 18]], 'label': 'answer', 'words': [{'text': 'Delete', 'box': [263, 486, 306, 500]}, {'text': 'coal', 'box': [313, 486, 341, 499]}, {'text': 'retention', 'box': [348, 486, 412, 497]}, {'text': 'from', 'box': [416, 485, 447, 498]}, {'text': 'the', 'box': [453, 485, 475, 498]}, {'text': 'list', 'box': [480, 483, 508, 496]}, {'text': 'of', 'box': [515, 483, 532, 494]}, {'text': 'standard', 'box': [536, 483, 593, 494]}, {'text': 'analyses', 'box': [264, 501, 320, 514]}, {'text': 'performed', 'box': [324, 501, 392, 512]}, {'text': 'on', 'box': [397, 501, 412, 511]}, {'text': 'licensee', 'box': [419, 499, 475, 512]}, {'text': 'submitted', 'box': [482, 499, 546, 510]}, {'text': 'product', 'box': [264, 517, 314, 528]}, {'text': 'samples.', 'box': [320, 514, 374, 528]}, {'text': 'Special', 'box': [390, 513, 439, 526]}, {'text': 'requests', 'box': [446, 513, 502, 524]}, {'text': 'for', 'box': [508, 511, 530, 522]}, {'text': 'coal', 'box': [538, 510, 566, 523]}, {'text': 'retention', 'box': [263, 529, 330, 540]}, {'text': 'testing', 'box': [335, 527, 387, 540]}, {'text': 'could', 'box': [390, 527, 428, 538]}, {'text': 'still', 'box': [433, 525, 468, 536]}, {'text': 'be', 'box': [473, 525, 488, 535]}, {'text': 'submitted', 'box': [496, 524, 560, 537]}, {'text': 'on', 'box': [566, 524, 584, 537]}, {'text': 'an', 'box': [264, 543, 281, 553]}, {'text': 'exception', 'box': [286, 539, 350, 553]}, {'text': 'basis.', 'box': [355, 541, 397, 551]}], 'id': 18}\n",
+ "{'text': 'Have you contacted your Manager/ Supervisor?', 'box': [96, 608, 398, 624], 'linking': [[19, 6], [19, 7]], 'label': 'header', 'words': [{'text': 'Have', 'box': [96, 612, 127, 623]}, {'text': 'you', 'box': [131, 613, 156, 624]}, {'text': 'contacted', 'box': [161, 612, 225, 623]}, {'text': 'your', 'box': [229, 610, 260, 623]}, {'text': 'Manager/', 'box': [264, 609, 314, 622]}, {'text': '', 'box': [314, 608, 322, 622]}, {'text': 'Supervisor?', 'box': [323, 608, 398, 621]}], 'id': 19}\n",
+ "{'text': 'Manager Comments:', 'box': [98, 651, 211, 665], 'linking': [[20, 21], [20, 22]], 'label': 'question', 'words': [{'text': 'Manager', 'box': [98, 654, 150, 665]}, {'text': 'Comments:', 'box': [154, 651, 211, 664]}], 'id': 20}\n",
+ "{'text': 'Manager, please contact suggester and forward', 'box': [232, 644, 547, 662], 'linking': [[20, 21]], 'label': 'answer', 'words': [{'text': 'Manager,', 'box': [232, 648, 288, 662]}, {'text': 'please', 'box': [296, 649, 338, 662]}, {'text': 'contact', 'box': [344, 648, 394, 662]}, {'text': 'suggester', 'box': [401, 648, 464, 661]}, {'text': 'and', 'box': [469, 647, 491, 658]}, {'text': 'forward', 'box': [497, 644, 547, 657]}], 'id': 21}\n",
+ "{'text': 'comments to the Quality Council.', 'box': [99, 662, 323, 677], 'linking': [[20, 22]], 'label': 'answer', 'words': [{'text': 'comments', 'box': [99, 666, 155, 677]}, {'text': 'to', 'box': [162, 665, 177, 676]}, {'text': 'the', 'box': [183, 665, 205, 675]}, {'text': 'Quality', 'box': [211, 663, 261, 676]}, {'text': 'Council.', 'box': [267, 662, 323, 676]}], 'id': 22}\n",
+ "{'text': 'qip . wp', 'box': [102, 823, 145, 838], 'linking': [], 'label': 'other', 'words': [{'text': 'qip', 'box': [102, 824, 123, 837]}, {'text': '.', 'box': [124, 824, 130, 838]}, {'text': 'wp', 'box': [130, 823, 145, 837]}], 'id': 23}\n"
+ ]
+ }
+ ],
+ "source": [
+ "import json\n",
+ "\n",
+ "with open(os.path.join(base_path, \"training_data/annotations/0000971160.json\")) as f:\n",
+ " data = json.load(f)\n",
+ "\n",
+ "for annotation in data[\"form\"]:\n",
+ " print(annotation)"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "Hs4L3S5a2Gfb"
+ },
+ "source": [
+ "The PIL library has a handy ImageDraw module, which -you guessed it- allows to draw things (such as rectangles) on an image:"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 7,
+ "metadata": {
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 1000
+ },
+ "id": "gWaHFM_LtKPP",
+ "outputId": "c498e560-035f-4170-b0b9-85ba3956711c"
+ },
+ "outputs": [
+ {
+ "data": {
+ "image/jpeg": "/9j/4AAQSkZJRgABAQAAAQABAAD/2wBDAAgGBgcGBQgHBwcJCQgKDBQNDAsLDBkSEw8UHRofHh0aHBwgJC4nICIsIxwcKDcpLDAxNDQ0Hyc5PTgyPC4zNDL/2wBDAQkJCQwLDBgNDRgyIRwhMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjL/wAARCAPoAvoDASIAAhEBAxEB/8QAHwAAAQUBAQEBAQEAAAAAAAAAAAECAwQFBgcICQoL/8QAtRAAAgEDAwIEAwUFBAQAAAF9AQIDAAQRBRIhMUEGE1FhByJxFDKBkaEII0KxwRVS0fAkM2JyggkKFhcYGRolJicoKSo0NTY3ODk6Q0RFRkdISUpTVFVWV1hZWmNkZWZnaGlqc3R1dnd4eXqDhIWGh4iJipKTlJWWl5iZmqKjpKWmp6ipqrKztLW2t7i5usLDxMXGx8jJytLT1NXW19jZ2uHi4+Tl5ufo6erx8vP09fb3+Pn6/8QAHwEAAwEBAQEBAQEBAQAAAAAAAAECAwQFBgcICQoL/8QAtREAAgECBAQDBAcFBAQAAQJ3AAECAxEEBSExBhJBUQdhcRMiMoEIFEKRobHBCSMzUvAVYnLRChYkNOEl8RcYGRomJygpKjU2Nzg5OkNERUZHSElKU1RVVldYWVpjZGVmZ2hpanN0dXZ3eHl6goOEhYaHiImKkpOUlZaXmJmaoqOkpaanqKmqsrO0tba3uLm6wsPExcbHyMnK0tPU1dbX2Nna4uPk5ebn6Onq8vP09fb3+Pn6/9oADAMBAAIRAxEAPwDa/wCGb/DH/QX1f/vqL/4ij/hm/wAMf9BfV/8AvqL/AOIr2WigDxr/AIZv8Mf9BfV/++ov/iKP+Gb/AAx/0F9X/wC+ov8A4ivZaKAPGv8Ahm/wx/0F9X/76i/+Io/4Zv8ADH/QX1f/AL6i/wDiK9looA8a/wCGb/DH/QX1f/vqL/4ij/hm/wAMf9BfV/8AvqL/AOIr2WigDxr/AIZv8Mf9BfV/++ov/iKP+Gb/AAx/0F9X/wC+ov8A4ivZaKAPGv8Ahm/wx/0F9X/76i/+Io/4Zv8ADH/QX1f/AL6i/wDiK9looA8a/wCGb/DH/QX1f/vqL/4ij/hm/wAMf9BfV/8AvqL/AOIr2WigDxr/AIZv8Mf9BfV/++ov/iKP+Gb/AAx/0F9X/wC+ov8A4ivZaKAPE2/Zs0HexXXdSClgVBRCQuOQTjk578Y9D1qrJ+zRYkjy/E1wo5zutFPfj+Idsf54r3aigDw+H9mvSFiUT+IL55Nx3MkKKCOwAOcHrzn8Knh/Zt8PLHifW9Ud8nmMRoMduCp/nXtNFAHisf7Nvh8TSmTW9TaIkeUqiMMoxzuODu59APxqvP8As1aWzubfxHeRqfuiS3VyOe5BGeMen9K9yooA8JX9miyAXf4muCd2Ti0UZX0+919/0ph/ZntcnHiibH/XkP8A4uveaKAPBv8Ahme2/wChpm/8Ah/8XR/wzPbf9DTN/wCAQ/8Ai695ooA8G/4Zntv+hpm/8Ah/8XR/wzPbf9DTN/4BD/4uveaKAPBv+GZ7b/oaZv8AwCH/AMXR/wAMz23/AENM3/gEP/i695ooA8G/4Zntv+hpm/8AAIf/ABdH/DM9t/0NM3/gEP8A4uveaKAPBv8Ahme2/wChpm/8Ah/8XR/wzPbf9DTN/wCAQ/8Ai695ooA8G/4Zntv+hpm/8Ah/8XR/wzPbf9DTN/4BD/4uveaKAPBv+GZ7b/oaZv8AwCH/AMXR/wAMz23/AENM3/gEP/i695ooA8G/4Zntv+hpm/8AAIf/ABdH/DM9t/0NM3/gEP8A4uveaKAPBv8Ahme2/wChpm/8Ah/8XR/wzPbf9DTN/wCAQ/8Ai695ooA8G/4Zntv+hpm/8Ah/8XR/wzPbf9DTN/4BD/4uveaKAPBv+GZ7b/oaZv8AwCH/AMXR/wAMz23/AENM3/gEP/i695ooA8G/4Zntv+hpm/8AAIf/ABdH/DM9t/0NM3/gEP8A4uveaKAPBv8Ahme2/wChpm/8Ah/8XR/wzPbf9DTN/wCAQ/8Ai695ooA8G/4Zntv+hpm/8Ah/8XR/wzPbf9DTN/4BD/4uveaKAPBv+GZ7b/oaZv8AwCH/AMXR/wAMz23/AENM3/gEP/i695ooA8G/4Zntv+hpm/8AAIf/ABdH/DM9t/0NM3/gEP8A4uveaKAPBv8Ahme2/wChpm/8Ah/8XR/wzPbf9DTN/wCAQ/8Ai695ooA8G/4Zntv+hpm/8Ah/8XR/wzPbf9DTN/4BD/4uveaKAPBv+GZ7b/oaZv8AwCH/AMXR/wAMz23/AENM3/gEP/i695ooA8G/4Zntv+hpm/8AAIf/ABdH/DM9t/0NM3/gEP8A4uveaKAPBv8Ahme2/wChpm/8Ah/8XR/wzPbf9DTN/wCAQ/8Ai695ooA8G/4Zntv+hpm/8Ah/8XR/wzPbf9DTN/4BD/4uveaKAPBv+GZ7b/oaZv8AwCH/AMXR/wAMz23/AENM3/gEP/i695ooA8G/4Zntv+hpm/8AAIf/ABdH/DM9t/0NM3/gEP8A4uveaKAPBv8Ahme2/wChpm/8Ah/8XR/wzPbf9DTN/wCAQ/8Ai695ooA8G/4Zntv+hpm/8Ah/8XR/wzPbf9DTN/4BD/4uveaKAPBv+GZ7b/oaZv8AwCH/AMXR/wAMz23/AENM3/gEP/i695ooA8G/4Zntv+hpm/8AAIf/ABdH/DM9t/0NM3/gEP8A4uveaKAPBv8Ahme2/wChpm/8Ah/8XR/wzPbf9DTN/wCAQ/8Ai695ooA8G/4Zntv+hpm/8Ah/8XR/wzPbf9DTN/4BD/4uveaKAPBv+GZ7b/oaZv8AwCH/AMXVe7/ZoYQj7H4mDS7uRNabRj8GPNfQNFAHzj/wzVqv/QxWf/fhv8aP+GatV/6GKz/78N/jX0dRQB83Tfs36pDBJKfENmQilsCBucDPrXpHwJ/5JRp//Xaf/wBGNXoN/wD8g65/65P/ACNeffAn/klGn/8AXaf/ANGNQB6TRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAV7/wD5B1z/ANcn/ka8++BP/JKNP/67T/8Aoxq9Bv8A/kHXP/XJ/wCRrz74E/8AJKNP/wCu0/8A6MagD0miiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAr3/APyDrn/rk/8AI1598Cf+SUaf/wBdp/8A0Y1eg3//ACDrn/rk/wDI1598Cf8AklGn/wDXaf8A9GNQB6TRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAZ+vXaaf4d1O9kVmS3tJZWVepCoTgflXDfAn/klGn/8AXaf/ANGNXbeI4hceGNWhMDTiSzmQxK20yZQjaD2J6ZrifgT/AMko0/8A67T/APoxqAPSaKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigCpqsMdxo97DMgeKS3kR1PQgqQRXA/An/klGn/9dp//AEY1eg3/APyDrn/rk/8AI1598Cf+SUaf/wBdp/8A0Y1AHpNFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFMmlWGIyNkgYGB1JJwB+dUdRu7uG7tLazEBeffzMDgbQD2/GoZotcniMbf2cAcEEb8gg5B/OtI09m2bRpXs20kya41NoxII4WDJDI7b8fKygEA4PT5h09RUr6lFGD5qPGw24V9oznOOc4/hPX0rLfTtZcPuksizq6u2WywYAHt/sj8qw/EPipdEvTFdXti+plVMdlZpJNcHAYjEYBPIY9eMVryQ7o19nTstV952Ud9HM0IjV280MQRjA2kA559T2zVquJ0PV/EmqMkzeH7mxWNWQPfhE3biCTtEhbt6AelXb/WLmxlVbzXdDs2cZVJZwmR6jdzUSpro0ZypR6NfedTRXN2moancwfaLPUNK1CM/Kvkyhgxz2IwM/jWDqXj7V9EuWXV/D93ZWinDXzW/mwKOxJidiBx6cd8VPs/NE+y/vL7z0Kiue0rWLzXLIXml32jXluTjzIXdhn0OOhq7/xPv+ob/wCP0ez80Hsv7y+81KKx55tct7eSZxpxWNC5A35wBmtKzma4soJnADSRq5A6ZIzSlBpXuKVNxV7k1FFFQZhRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQBU1WZLfR72aVtscdvI7HGcAKSa4H4E/8AJKNP/wCu0/8A6Mau512GO48PanDM4SKS0lR3JxtBQgnPGK4b4E/8ko0//rtP/wCjGoA9JooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigDLvv+Q9pP/bb/wBBFabMqKWYgKBkkngCsy+/5D2k/wDbb/0EVy/iqQ+LNZk8KR3Bg0e1jE+uXaSbSF6rb7s8FgMt6Lj1rSfwx9P1ZrU+GHp+rK974g1HxfDcSaTevonhWBC82vNhZJwM7hCG+6v/AE0I7cCvLNU+Lmj+Fprqz8B6PC0rDy5NavMvNcHuxz8x55G449u1c98UfiS/i2+XTNHaS18PWa+VDAp2rNj+NlHbgYB6AZ6mvOAMnArMyOsj13x1431NbGHUtW1K5kJYQRyttGeCdoIVV/ICuu039nnxfe26TXU+nWJbrFLKzOOM/wAKke3Wt24OpfBfR9CsbGbTLfUdThuLjULq7haTDqqlYlK84/h9CTmr3jf4reKbHw/4Zms57TT77UbNru6iiiErxjP7tiHyFRgc+vX0oA88174PeNfC0Ul/9lS5gtv3huLGbcUAwd2OG4+nY1V8O/Fvxj4euVddVlv7cAK1tfMZUKjsMnK/gRXtepeL/Eep/EDStH8Oa9pvkXGjvO7eSs9vJcI0gb5hhgMrjIPHXBryD4g6dHqujWfjS2sIbOS5upbLUobY7oftCH/WIRkbXH6g9c5oA9D8Ja/4f8WXUMvhS4/4RLxMnzNYRj/Q74jkB1AAbqRnhhnvgV6n4W8VPrUlzpuqWQ0zXbPBuLFpN/yHpIh/iQ+o6dDXxPHI8MqSxOySIQyupwVI6EHsa+hPA3iWf4jaQjGeGDxzoS+ZZXRAH2uPGNknqpyVb0yGHegD2/U/+QVef9cH/wDQTRpn/IKs/wDrgn/oIrK07XIfEXg2TUoo3iZ4JUlhkGGikXKujD1DAitXTP8AkFWf/XBP/QRWn/Lv5mv/AC6+ZaooorMyCiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigCjrUvkaFqEweNPLtpG3ynCLhScsfT1rhPgT/wAko0//AK7T/wDoxq7TxPbG88J6zahthmsZ49xBOMxsM4HJ61xfwJ/5JRp//Xaf/wBGNQB6TRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFAHP8AiTUrfRp7TUrtwlvaxXEsh9gma8P8carceHPhLb2NxJJ/bHiy5bU7zORsRtp28+3lrj2NekfGZ518IMlsheWb9wEC5LCSSNCAPUhjXj37QF35nxAgsEj8uCxsYoo0B+XBy2QO3UD8BWk/hj6fqzWp8MPT9WcF4W8M6h4u8Q22jaaqmeYkl24WNByzH2A/wr6Z8KfA7wroEET6hbjV75TuaW4H7vPHSPOMcd89ayP2d9AhtPCF1rbQ4ur24aNZGUg+UmBgHuN27p3HtV/4jfEXWfD3iy10LRI7c3ZtluUjnTeLss7L5QwQVb5cjHXOOOM5mR1viPwNpnijXNI1LUGdl05Zl+z7QY5lkXaQ2R7V5l4y8J+BPBkdlFqOpeJLm4MDwrb210rSNaL8xR+BiIc+h5PXHF7wf+0Bp+qXken+I7H+zLljsE8ZLRbv9oH5k547+5rhfGl9Jquu6zqt9FLJb3Mc8Njd7fKktJEiYG0kU5HQk46kkEHlhQB6fZ/CHwlqtpZahpmtaybI27R25t70bDA7MxjB252ncwIz3Oea7WLwb4ej8MweHW0u3m0qAYjgmXeAefmyed3zH5uvNeGfB/4oWnhjwlq1lrlyzW9ltlsolGXYtnci/jg5PAzVs/GrxH4okvH05LTQdIso/Nurx8TSqueFXdhS7HhVx1745oA0PiF8BrFtNl1HwfDJFeRZd7EyFllXqdmeQ3tnBxjg9fDvDWt3PhTxVY6tGjCWynDPGwwSOjKfTIyK+x/BWuyeJvB+m6zLGI3uoy2zOcAMQMnucAZ4HPpXzX8dPD1voXxEkktI0jh1CEXZRSThyzBj7ZIJx70AezWdzBpnjHUBZlzpXirSzqdsWOAJ1X58Aj+JGQ45PFeh6Z/yCrP/AK4J/wCgivCNEvl1H4feAdSs0KzaZfy6bM5P3RJGwYAHqGG36V7vpn/IKs/+uCf+gitP+XfzNf8Al18y1RRRWZkFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFAFHWrgWmg6jcmN5BDaySbIxlmwpOAPWuE+BP/ACSjT/8ArtP/AOjGrvdWBbRr5RMYSbeQeaMZT5T83PHHXmuC+BP/ACSjT/8ArtP/AOjGoA9JooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigDz34uTva+H7a7jhMxtZ47goDjKxzROee3CmvFf2gbWSD4mGZ9uy5s4pI8HsMrz+KmvofxbpMWvJDpM3Ed3b3MJPpmPAP4HmvC/iZp48RfDrQ/FMcLrf6VjSdTjA4RkyM4yeA+cezitJ/DH0/VmtT4Yen6s9T+BlzFP8KNMjjbLQSTRyDB4bzGbH5MPzql8arLUo9M03W9Ki04yWkrRzte28DqEbG0lpRgYYfm1cF+z541i07ULnwvfzhIbxvNsy7YAl6FB7sMY9196+iru1gvrOa0uY1lgnQxyI3RlIwRWZkfKniLwtqfiXTbjW5o7D/hIYsNc29jeW0ovIwCWlVImJDjA3DGD1HORVLwp4ge9ikhvj9ocWsttKkoV/OTyXELYP8AHE2MN12tjIAwe58W/CvTPBV6msaXpXiO6t4XWZJ7C/iDW7huPkMRbg45yfeuf0aW11TxDda14UtHSS9tp7G/0llBkj8yIqJk2gDaWC5AA2scdGFAHHeELSS9tdYtEWAC8gjtBNPwkJMqyFyewCROSfQH1GehuBqEk1p4W8KXGlNpyzLGhEsMj3sxO3z3U7m78DHyr+NT6NJp0Ogy+CrTStZ1K+uZVfUptInjCysCSsW4o+UX1GAWB6gAn2P4dfCjRvC0qa1JY3Kam6fJFd3CTm2z1wVRRu7HrjseTQB32j2P9maLY2PH+jwJESABkhQD0AH5AV89ftJ3ZfxPotnsUCKzaXcOp3uRg/TZ+pr6OuLiG0tpLi4lSKGJS8kjnCqo5JJ7CvjXxTq158SviVJJZoC99cLa2aHgKmdqZ/mT7mgD0vRLRtP+HHgHT4Chm1DUpb+VEHLqiOSx/wB1dua950z/AJBVn/1wT/0EV5zZ2Edz4pNjb+W9h4Q0Y2avsyWuZYwGwcAZCIM+7+9ejaZ/yCrP/rgn/oIrT/l38zX/AJdfMtUUUVmZBRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFNCnzC287SAAuBgHnn/AD6UAOooooAKKKKACiiigAooooAKKKKACiiigAooooAw/Gf/ACIviH/sGXP/AKKauS+BP/JKNP8A+u0//oxq7nXYEufD2pW8qs8ctrKjKo5IKEECuG+BP/JKNP8A+u0//oxqAPSaKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAy77/kPaT/ANtv/QRXGeINNttE1+8g1GGJvCnilhDektt+zXZUgPnoA4VRnswB+vZ33/Ie0n/tt/6CKs6lpllrGnzWGoW0VzazLteKVQwP59+4PatJ/DH0/VmtT4Yen6s+MvGHhXU/h/4sayld90Lia0u0UqJFzlWX3B6+hFe8fDP41WOvWaab4muobTV1IRJmwkdzk4B44Vs9RwO49A7xPpNtpemx6F42iutV8OfMLTXSN9xZORwJSOcDs+CDxkcV494i+EfiDSoTqOkquuaK6iSK9sSG3Ke5QEn8siszI+pPFd99j8Ozuiyu8pWKMQXaW8hLHA2O5A3eg79MGvnn4mw3Vtplhqlw/iO1v9/kCa9s7aHejJhlMsOGc4GPmzkZ6Zrz618Ya/Z2a2J1CS4sUKkWd4ouIRtOR+7kBUc+gqjqmsXusXUk93KPnbd5UY2RqenyoOF/AUAe++Fm/wCEf0nSZNKj8StpI23CSXP2Swtip+YvK4+Z1I7MSQOK9pvdSstO0+S/vLuGC0jTe0zuAoXrnNfEmleKdT0eNktzby9PLa6tknMBHQxlwdh+noKi1fxJrevlTquqXd2qnKJLISif7q9F6dgKAPTfi78Xl8UI+gaA7DR8gzzlSGuSDkAA8hQQPckenV/w+8OP4K0pfF+q2wbWrwfZ/D+nSqQ0szgBXPTg7h17ZPpXjVekeGfibG2nQeH/ABnZDVtHTKxXTc3VmCMAxueeOMdCPXHFAH0X4d8Of8I14Imt5xG+pTwyXGoTqOZp2BLknvycD2Haui0z/kFWf/XBP/QRXl2k6/rGkaLbRQXh8VeGLvMEerI2bi0Z/lVJlzyAWGT1Geegz6fpMiS6RaNG6uBEqkqc8gYI/AgitP8Al38zX/l18y5RRRWZkFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFAFPVjEuj3xuCghFvIZDJjbt2nOc8YxXBfAn/klGn/8AXaf/ANGNXX+MFL+CNfQEAtp1wAWIA/1bdSelch8Cf+SUaf8A9dp//RjUAek0UUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQBl33/Ie0n/ALbf+gitSsbV7mK01bTJ532Rr5uWwTjKgdql/wCEi0r/AJ+v/Ibf4Vu4SlGLir6fqzolTnKEXFN6fqzSkjSaJ4pUV43BVkYZDA9QR3rirn4fNp1y994Q1e40S4Y7jagebZv6gxHhcnuuOpro/wDhItK/5+v/ACG3+FH/AAkWlf8AP1/5Db/Co9jU/lf3Eewq/wAr+4851HQ/EEsbp4l+H+geIVIZmu9OlEMrZ4yVcA7z1yDxnjkViN4D8L3tson+F3iOwmV84tLpJAwx3LS/0/GvYf8AhItK/wCfr/yG3+FH/CRaV/z9f+Q2/wAKPY1P5X9wewq/yv7jynTfCCxXEdzpHwjtbabdtMmranvWPoQ2zL5APoM9qh8UaNDdW8OlfEDQdM0oTfu9O1zRUbyLZz/DLnGAT68HJ6YJr1z/AISLSv8An6/8ht/hVe+1Tw/qdjNZXzR3FrMpSSKSFirD3GKPY1P5X9wewq/yv7j4/wDGPgjWfBGprZ6pEjJIu+G4hJaKQc9Djrx061reCPh5L4htJde1i5XTPDNo2bm8kODIB1WMY5OcDPqe54r2HUNOTSrebQksx4m8I3Tl0sXk8u5sDyf3buVBXPT5gRn65t6Rptvrt5b3fimKCy0vTnH9k6DCu6OEDjdKVUhzwpABIFHsan8r+4PYVf5X9w3QdKu9c0NP7Ot59B8HWKLNZ2/AudQdPm3ynnCZA46nFeo6YANKs8AD9yn8hWdfa9pk2n3MUdzl3iZVHlsMkg47VpaZ/wAgqz/64J/6CKqUZRp+8ralShKNL3lbUtUUUViYBRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQBR1q1jvtB1G0mz5U9rJE+Dg7WUg/wA64T4E/wDJKNP/AOu0/wD6MavQb/8A5B1z/wBcn/ka8++BP/JKNP8A+u0//oxqAPSaKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigClrCzNol+tu4Sc20gjYjIDbTg/nXB/An/klGn/9dp//AEY1dzr0hi8O6nIsvkslpKwk4+TCHnkHp16GuG+BP/JKNP8A+u0//oxqAPSaKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACs66nuILq6kjZTHFbLIVYE55fpzxnHX6VxLa7FbSpDe6zqUEhgNy7CCR40iD7GcuDjAJGfTOTxzWiyLJ4hOiDWb+a8eBZJSltI8aId20O4O0Z2tgE88148sVia9OM6dF2eqfNHqtOvmdyo0acnGU122ff0OkOoSiR2aNVhVpFy2BjaDz1yenTb3pIr64lkMJ8pJFLZZlOMBVPTPB+f17Vxcuo2cd9dQnV75Z45ntGlktnWNplUN5ZkzjJBXGeueM1u6vpVppdgJpNSuILZGaSWSRtyxqsbMWwMdlrH22OV7welvtLW+nT+kaezw/SX4Pp/XzNOzv7hobcbNyhYldmIyxZVOcls9/Q5xV+0lkmSR5NmBI6KFHZWI5/KvMj4itItMvNSafWEWxto7qNDbqHntmO1ZYv3vKeuSCARkcir0OrhDrq3N7q9gmjRCe6aeNQpDAsNu2U5JwTzjrWlCpjoW5qTf/AG9H/MipHDy2ml8mej0V5drviK60rRNC1azudR1C21iWKKIxyBdjSAFA3znk8jjjg81d8YXmr+FYbOaOW+vo7mdbfes6xBJHICA7n7nv0FdX1rFf8+H/AOBR/wAzL2NH/n4vuf8AkeiUV45qXi3X9Mu5baXTtUZ4g+/bdL95IFmkC/N82FbqOpGBU9h4r1ObxJDod/HqFnfSSxqIXugWaNkZvMXBOV+ULnsWANJ4zExV3Qdv8Uf8wVCk3ZVF9zPXKKwrvS5ofJWDUb9nkdlAe5IGdjMOQOOQOxrz5vE/iODQNe1e6smji0W5NvOi6wzM5UjcV/dejDGcZ9q0WIrttKnt5oh0qat7/wCB69RXj158QFbRPEes6PJd3tho8lvGJG1AqZjJgNjCEDaSB155/Fl343vrWxtJ2ntl825urd5pNcKwBoVDfLJ5XzbuQOBzgVXtsR/z7/FC5Kf8/wCB7JRXmtxrOq3VtC2hW99d3K6bFqN1BcagYWjWUEoifIdzna/XAGBzzWdd+Lb9BcSWjTTI0dpNp6NfuJLuO4bahAEZ2kHII56Ue2xH/Pv8UHJT/n/A9borzRNW1Sfxbd+Hbe4L3ltMoZDfyA+SVRmk/wBXjI3gbc5ODXOaP411nxLNpuk6TfqmtOl016Lh5TCnlNhAuCCNw574FHtsR/z7/FByU/5/wPbqK8M0vxr4g1DwnqmtR38dw9nbQymGJpUKSSOoEbbm+bILfMOAV71s2Ws+Ide1i5ttEvwLaKOGWQ3LSebbBlmDxyKGHzrJCFPT73Sj22I/59/ig5Kf8/4HrVFee6Dd6jqXgeLW7q/uRcyRQyhYpWCASKrYwSTwH9a9Cow+JdWcoSjZq3W/Vr9GFWkoRUk73/4D/UKKKK6zEKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAMvxLPHa+FdXuJoVniispneJujqEJKn69K4r4E/8ko0/wD67T/+jGruNfktovDmqSXihrVLSVpgVyCgQ7uO/Ga4f4E/8ko0/wD67T/+jGoA9JooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAoopGO1ScE4GcDqaAPF/EFlNqup6bHFDL5UOnTxGfztsIlaVXVJUBzJGQm1hhh84444j8QW2u6pq02rWFwLK6uERRs1CSPyohGFe3IWMhgW3srggqWzwa6iHxRq+m6Nq5tLXTbm30yxluEKXRaVZVwwjljwCu4MxBBOQB0zRD4x8SwWgvr230mW3ubGyktY4RIjCe5cRqHJJGwNkkgZxjrXl4KGJ+rU+Wcbcq+y+3+I7MRKj7aV4vd9V39Dnri01HULi8tJRZ21jLrK6qJ1uJJJCI40VY9pQcsYxli3QnrXoniVNP13SJNLbUYI47tJYHkWRSUDwyLu6/7VYn/CU+J4ok0ya10Y6zPqH2GC4imZrY4iaRnZAS64CMNpOSe4HNY/irxvrGjaHpE96+hSmZrsXLpayXMZMQLIY1WTjco/iPBbkgZrZ0MQ7tyTen2Wtnf+ZmaqUlZJPr17/JFO10691q81PRvENzBaTroaaba31ufMhnXdkyluArblX5CQeT1HNWbrwzq+t6ZeNqesaPFf6he2j3awXRCGCD0IGdzHnGMCptd1zV9Ih0+Ga38MWNxNYmd7q8tZPsss2eI1cECPjHLnksAKr+IV8aReIba20z+w4xeLIbO3NmjJL5UUbklzyAzM4HTAA9av/a/7v4k/ufP8Cv8A8IVq9toFrotprmhtaafrS6lYm4uXZhGrMwjYgepHT1NaeuaX4m13SIoZ9d8Pi6XVEvlIncJEkYTYiYGfvBySfWrjQapD8Q5rKW7sTpkdj/aH2ZdOj3Y3FTHv69s7qwbfxDqs2j2esSR6atvrdjdzWsUdmjGxkiRnQE5/eAqpzkDBHbOKP9r/ALv4h+58/wADqNSsvEOr674e1CxvNAabTUd7iPzZGDM67H24GdoBGCe/Wota0K7PxOs/EPm2otoLVLdo0gkaZg0oIyQNvVTjn1GO9ZHw612XxHrFzb6rBAstpp0ElxA1qiBJXJJYEDlWUI49NxFUrnxBqt3J/a+j2iR2U18BbCG2R5Ws1O0yRxn7zlkZh32njOMVhWq13HkaV2+W+vVdv+Ca04U+bmTeiv8AceoXVys3ktCZ0kifeN9nKwPylccAf3q5WXwrFNpWt6e13OsesXDXNwy2D7g5KnCnb0G0AZzVew1rWtdfQ9Ns9fjEs1pdXdxfRWgUy+XKqInluPkILDcMdiB1Bpmi6nrWq6/4UmudZlWO902e4ura2EZgkkiaNcqSpO1vMJOD2GMV0OhNtvm39V/7cZKpFK1vy/yLOqeEoNT0vVdNF1PaWmopHG8dppzRBFRt2FwvGSTnOc5PSp9Z8MWmvHT1vpGaGzEgMK6Y4SUOm1gwx6d12kHkGsXWNT1mC48UtDr12I7TUNO+y+WI8LFOyB0+6cj94cHrwPxm02z8Xw+Ok0668UTTrFAt7NCyR+W8bTyptBEYYEIEP+8D2pfV5/zf+lf/ACQe1j2/L/Is3Pg5riARr4j1mBmsP7PmljsfnnhGcByUOWGSAwweTzyasnwnYDUNAvIpriJ9EhMFskdjKFdNoAVx/FjAI6c1iyX+taNF45uzqd7cS6ICLBLiTeipJEsm5lGN5BORu6Diqviu/wBT03Ttb0vTfEN1LItpY3ttePcfOs01wYyAw/5ZsADs5HJxxxR9Xn/N/wClf/JB7WPb8v8AI6CPwXPdazdX8XirU4p5buO9ljFqkQJUBVXJQNsKxhSM8hec1XT4fQ6W2nBPFtxaz2KTLDJ5UCuyy/eDZXkdcelT/DTU5NUn8Ryyy3xkivUieG8kLtbyCNfMjUkn5BIXx0GD0qj8TJr2HW9FFhNfmaWTyjaWd+1qbhfLmfGR1IZFx35wPvVCi3Fa6ttby6X6X8u5Tau9NLJ9PLyCPwDYJpDaW3jKd7T7ILNU/crtUMjK3ygbmGwAFs4BPrWpH4asLe41e6tPEMNreatFFHdXEIRXYxgjePmwGbJycfQA1haxJc6dLqdlfeJNTtJNH0pbjTZTOym6c7yzSD/luVKou05znnJOayknaD4o3dw109rGt/bfaLp7xiiLJbAvA0WcBWc/ePCnHI4q/q8/5v8A0r/5In2se35f5HaWum2Ph3wQ+jW2qreiPaIy8il9oKgLwecAY+grtq+fbW71aPWrbT4Lu3fw3Frt6lsEujJKcRy7UbJJKgLkEn+Ide30FWeHg4YmcX/LH8592y6sualF+b/KIUUUV3nMFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFVrq4mgltlis5bhZZNkjoyjyVwTvO4jIyAOMnnpVmigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigDP16OaXw7qcduSJntJVjIOMMUOOcHHPsa4b4E/wDJKNP/AOu0/wD6Mau+1WFLjR72GQExyW8iMASMgqQeRyK4H4E/8ko0/wD67T/+jGoA9JooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigApGXcjLkjIxkdRS0UAecW3h9ZdQku9WtL2dDZy2SQQ2WzEcn3g75zJ3IBAC5PBPNOg8NxroU2l3c3iG6zHbx287W0cb2wgbdFt2AAlW5y2c969ForhpYWtShGnGpolbZdDonWpzk5OGr8zzeDwvDb2c2yTXhqct/wD2j/aK2UKyLNt2EhQu3BUkEEEck9zUcfhOKzs9Hg0ybXbF9MM7rLFYQEyvN99mVlK9CQABgD6CvTKKv2OI/wCfn4Innp/yfiebXXhcXsHkXF94oeOW0FneK0MbC6jDOxzuB2sS55XBwK2LuxtbrUNJvEt9etm0pClskMS7QCNpB3AlsgAcnt6812NFHscR/wA/PwQc9P8Ak/E4mfS4LjxONfY+JVuggi8pFURGMHPllccrknrz71Tg8KaJbQ3EENh4hWB7eW2gi5K2kcn+sEIP3c++favQqKPY4j/n5+CDnp/yfieY3vhyez02WDw7HqsF3cWcdhNd3cW9/JV88ED7wRnUHsNvpmtDU9Hsb59Pi/sG/a00+OMWqKZIGhdMhWVk54Bx+Nd9RWM8FWn/AMvet9luaRrwj9jpbdnnc2gaZNpsFg3hjUBFBJJIjpeXCylpP9YWkHztuzzknPFMu/Dek3i6er+FtQjGnQG2tfIvbiLyoz1A2Y69yeT3r0ein9VxX/P9/wDgMf8AIPbUf+fa+9/5nnsehaXFqFjfR+E7tZ7KKGKHFxNt2xAiPcuMOVzwWBPvVqO0gi8Ty+I08O6gNUlQRvL9qm2soGACn3cD6deetdxRR9VxX/P9/wDgMf8AIPbUf+fa+9/5nnOm+HNI0rV7jVbbwnem9uUeOaSe6nm8xW+8GD5Bzip49F0aLSptMTwNGtlO6ySwiM4dl6E/L27V39FH1XFf8/3/AOAx/wAg9tR/59r73/mcvpMsemz3Lw6BdWqzLECkMRbJRdoJzj+EIPotVdYt7PV9TgvLzwzNetbhTAbiIgxOGJyuAfb8q7Kil9Tr8qXtno73sut/l1D29O9+T8WcjqLw6vLbS6j4RF3JbPvhaaLeYz6jKf5wKR/s0s888ngyF5rhSs8jW4LSg9Qx2cjgdfSuvop/VcV/z/f/AIDH/IPbUf8An2vvf+Zws9lam1aKz8Hw2cmQyyw2oUoehIwg5IyPoa7qiitcPhp0pynUnzN2WyW1+3qZ1asZxUYxslf8bd/QKKKK6zEKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAK9//AMg65/65P/I1598Cf+SUaf8A9dp//RjV6Df/APIOuf8Ark/8jXn3wJ/5JRp//Xaf/wBGNQB6TRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAVdSUPpd2hJAaFwSpIP3T0I6VwHwJ/5JRp/wD12n/9GNXd61cfZNC1G5KM/lW0kmxcZbCk4Ga4T4E/8ko0/wD67T/+jGoA9JooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAori/GmuXelpqXlap/Zxt9MNzafu0b7TN8+V+cHO3anAx9/J4FSaj4klsr6/snvUjuv7XsobWEqu428htw5AxypLTDd2PGRgV2QwNWcYyXX18vLzX4k8yOworzm28R65PZTzS6nZwObdZJkLhjZyGVAUb9ziLguPnL4IB6AksttXuZtQa7/ALSmlaVNNRI5o4sMDfyROwABB+XA3qcHeCMZXG39mVVe7Wjt18vLzFzo9Jorzv8A4SLWJbS3Fvqmbq4Fv9rXyYz/AGfK91DGYsY7rJIMNk/u855rrNCuLp59WtLm5e5NleCGOWRVVmUwxSfNtAGQZCOAOAKwq4OdKLk2tPXy8vP+kNSubFFFFchQUUUUAFFFFABRRRQAUUyWWOCF5ppEjijUs7ucKoHJJJ6Csz/hKvDv/Qe0v/wMj/xpOSW7JcordmtRXmd54utXutZ8jXETNjehB9ryBIpURFDnbkjcQE59ST0san4g0u1uZoIPEoa1CQSbhfNJvc+cHG5G3qOIz8ucHbxgmsPrETn+tQ/pnolFeYN4sVE3x63HmAZVJL1GMhnQYDEHB8tyc46D0FXtM8SWMeuIk/ie2ZY5pVdWnyjQgERkuZNhJ+Q/Ku7Oc9zQsRFuwLFQbseg0VyvhzxJokPhzTxdeIbNrlreNpjcXys+8qNwO5sjntWp/wAJV4d/6D2l/wDgZH/jWqqRavc2jVg0ndGtRWT/AMJV4d/6D2l/+Bkf+NH/AAlXh3/oPaX/AOBkf+NPnj3H7SHdGtRWT/wlXh3/AKD2l/8AgZH/AI0f8JV4d/6D2l/+Bkf+NHPHuHtId0a1FZP/AAlXh3/oPaX/AOBkf+NH/CVeHf8AoPaX/wCBkf8AjRzx7h7SHdGtRWT/AMJV4d/6D2l/+Bkf+NH/AAlXh3/oPaX/AOBkf+NHPHuHtId0a1FZP/CVeHf+g9pf/gZH/jR/wlXh3/oPaX/4GR/40c8e4e0h3RrUVk/8JV4d/wCg9pf/AIGR/wCNH/CVeHf+g9pf/gZH/jRzx7h7SHdGtRWT/wAJV4d/6D2l/wDgZH/jR/wlXh3/AKD2l/8AgZH/AI0c8e4e0h3RrUVk/wDCVeHf+g9pf/gZH/jR/wAJV4d/6D2l/wDgZH/jRzx7h7SHdGtRWT/wlXh3/oPaX/4GR/40f8JV4d/6D2l/+Bkf+NHPHuHtId0a1FZP/CVeHf8AoPaX/wCBkf8AjR/wlXh3/oPaX/4GR/40c8e4e0h3RrUVk/8ACVeHf+g9pf8A4GR/40f8JV4d/wCg9pf/AIGR/wCNHPHuHtId0a1FVLHVdO1PzPsF/a3fl43+RMsm3OcZweM4P5Vbppp6opNNXQUUUUxhVO/1Wz0wR/apHBkzsWOJpGIAyTtUE4Hc9BXD678TLzS/FOpaJaaDa3P2Hyt01xrEVru3xhxhZBzjnoT07Zqtf6x8Qb66s9RsPA0cM0UUkau2rwSo8cmwnAGOcohBz+BzXpUstqNr2jik1fWcE9VdaN3V9OhDmuh3KeItKexlvVus28VkmoO/ltxA4Yq+MZ5CNx146dKJvEOl280sc10Y/KDlpGjcR/IpZwHxtJABJAORg+hryma0+IX9jnSrbwjHD52jxaXOz6lA7OkauodRuG3/AFjZBz1HTrVkWnjZL65uI/h7aIJXnlV/ttq0weUNndIwO5QXbC4HGASQMHs/sqhr+9j5e/Dy8+9/kT7R9vwO+uPGemwz+Won2i1uLmSSS3lQRCHYWDgpleHz09P7y5u3HibSLV7lZrooLZJHlcxPtxGu5wGxhmUZJUEng8cV5Ncy+LLJ7Gy1vw6mn22qvNo6yrepKkAuhGo8uMMWAUxbsE4OWHy5GPRdQ8HPqFpdWTaiEs5DdSQp5GWjlnSRWYtu+ZR5shC4HUc8VniMFhaHJzy0d9U0+vdJr5f02pSZuafq9lqbSpayOzxBWZZInjO1s7WAYDKnBwRwcH0q9VGLTvK1u61Lzc+fbQ2/l7fu+W0rZznnPm9Mcbffiv4q/wCRQ1r/AK8J/wD0W1ePWcItuG1v01/Epu0W2a1cVeeIr1LrWVt7wHyLG9lRGVMwyQlQp24zg5J+YndwcAcVzy+HvBun+HNEuLzQbu/vr2zSZorSSRpGARTJJt3gBQWGcf3hgVunwN4DGjnVhpyvY+R9pEqXMxBj27tw+bniuWXtZpNJL5v/ACOaXt6kU4pL5v8AyLep6hqOnXM1q2q/KiQSmaRY42+fzgyqxXYOY1I3e4zkiqjeI9UjTeJGkWAbpA8IQyeegMAx/Dhztxn65rntO0TwYlvodvf+Hr9576C2D3oaRYPNlQkAtvHJKn7oIGVHGRWh4w8HeDvD/hi9vRpbLceWY7fZcSFvMIwpAL4IH3j14UnBxWbVa3Mvzf8AkZtV+XmVrb7v/I6DTNS1STXEtbi7hbbNLFLAWG/YoO2TYIwV3YU5LY+bAHTGt4cmubnw5p91d3DTz3FvHM7lVXllBwAoAxzXDWOhfD+/eTZoV1HAFneO4eaTZOsL7ZCmJCeD6gE9qyZbTwuL/Q7jRNHvLC5XVrElrnf+9hl3MjKCzDB2exGMECrvVgry/N/5F3rU1zSSa9X5eR7HRRRXSdgUUUUAFFFFABRRRQAUUUUAFFFFABRRRQBXv/8AkHXP/XJ/5GvPvgT/AMko0/8A67T/APoxq9Bv/wDkHXP/AFyf+Rrz74E/8ko0/wD67T/+jGoA9JooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACvArfwV4U13Wde1DxDqV/ZzT+JrrT7cQEBHbO5QSUbBOTySB0r32vFF0aXXtI1yyjt7mWP8A4TeeSZrb78SADLj3BINergMTVw9CtUoys/d1+ZE0m0mP0X4ReAfEMVxJpmsa3MtvKYZSxWPa46j5oRn8K0/+FA+Ff+ghrP8A3+i/+N1T1TT/ABtH4ftdPuNNnuZ5b+5nv5tOk2rNhCsfyiRG2uxDnDDBXp2rKfQteu7Oxm1DQvE8l9HZ20dx5F4YxJIjFX6SgYMYXkAZPuSaP7czH/n6xeyh2G+LvhB4f0D+wvst5qb/ANoaxb2EvmyxnbHJuyVwg+bgYzke1O8bfCnwh4R8L3Opm+1l7jBjtozJGweUglcgIDtGCTg9AaztcsfGI1Pwnc6zHej9/p1vbCRwAs6riQMQ5w5cEhipyD1GMHvPE4PiWPxRqMkStpuiabdW1k5x890YnEzj2UYQZ77q9GOb47loP2j95u/nqifZx10PLNK0PwBe+Ho72Q+KZLpLZnlWFIljkljQNMkbMmCVGWxnO0Zr0Ky+BfhG+sYLuO/1oJNGsigzRZAYZGf3fvWJ8NvA11L4C1K5u9Pv/wC0JIrh9LWS4AgYTw7Q6LuxuIOCWHQitmDwBrVpZ3Vpo2nQ6Va3mgQw3ES3AG+8jlywLKSfnjLKX9GHpiuTEZ1mEa04qq7Jv8ylThbYkj+BXg6aBZ4tW1V4WGVkW5hKkeoPl4qF/gt4EjsUvn1+/WzfAW4N5AI2z0w2zBpuo/DzULrQ4/s/h21t0Ou298ukCdCsECRhJF3fd+crkgevPNGr/D/xJd3VxFaQQRaRbajcS2tgrw7XSZAN43xuowxfKsvAc7TwAcf7czH/AJ+sPZQ7FnR/hB4Rt/Empadc29zqEMdnazxtcXDKys7zq2DHtBGI165rA07QPBQ1K70u48GX91LBfSRNdR3u1BG11LFFgGYM2BGRgKT8hPPU+keErG40zWJrC72+fbaLp8TbZjL92S6A+cqpPAHOBXmzWyL4tv8AVG1Dw2k9vfzi2S91s28kEiXdywZ4gpDZ83gHsBgjca6amPx9SMnCpJv3Nm+sXfYShBdDtY/hp8MpnRIrK1d3kaJVXUZSWdRllH7zkgckdqoab4N+EurajLp1na2730UkkTW/26YPmM4bA38geoqG2u9NtfHMmvR634QNvNdyBoP7TUCOMqg+0KMY89tpDdiAoz1J1PDuv2mj3U1nP4p8Ky6Z9rnuFuP7QU3EiyszhSM4UqzYzk5A6Cub61mv89T75D5YdkZGvfCXwadesLSOK40y0Njd3U8kFyST5bQAZMm4AASP0xTPAnhvR/DXxUEOhXk15Y3fh43STSyK+7dOo4KqBjCium0zWxrPjK38rUNHvZorLUBGLC581ViM1t5XmYzhiBz24OKqaUt4nxhtV1CO2ju18KKJktc+UrfaeQmedvpXbHG4udKVGtNtcjbT9X31J5Y3uu513ir/AJFDWv8Arwn/APRbV5je+JvC/hjw3HHd+GdPur+HR7W8i3W6n7SzjDAtsOGGNx65HPrXp3ir/kUNa/68J/8A0W1eKar4n0i80Z9MuYZrkPo9va28sFsGNtMsUkbk75U3HErgYGPrXys3BVPftt1M6kqaq/vGtuvqeo6p4e0ddCs5n0PSorh7myEnk2yY+aeMMAduSpBI56g0a/4c0mGbShZaJpKzPdOoV7VAj4tpmAfAyV3AH8Ae1cPqPxXgvWsIo7S/W0hMLzxtbxBnkjmjfKnzjgYRwB6kZPcXdS+LukXs+nyw6Xq0ZtZ2mPmRwnIMMkYwBLycyA8kcA85xUSnRvuunbuZyqYe+66du5Y8Oaroet3ejrJ4f8OLDd6TJqFz5MCO8DIyjYRjjh1688NxVq48S/D2205ryTw8gHnxwrCdHCyv5m7y3ClQdrbWwTjOMVwll4r0u0ttMt1l1uNbLSp9LEsNlAkhWTbiTd9oOGUop4HY+tZI1iC2u/tUJma4ea1nkkjgjiDPC0nJGWyWWTBJP9Mac9DuvwNfaYbvH8D1ex1rwHqelXOoWXhxJ0geJPKTRwZJPM+4yLt5U88+1On1XwVAbFP+EU8yW+tnuYYo9IQsVQ4cHjhl7g/zIFeQ6bqdtaQxRXg1G7jiECiLfEsTiJGRBIhUhwARjPQjPNbem+NLXTJtJkht9Tb+zIZreFTPAoaOUglTtiGMFVxjGMUc9DuvwD2mG7x/A7a98UeBbQsU8JG4iS0jvnmi0qPYts4yJcnHHt14PHBro/EfhvQYfCurzw6Lp0ciWUzo6WqBlIQkEEDg140/ie3+xy2gt9SnhudNXSrkzXcQYwKXKsCIvvjeRzwR1yea0rv4la5f2K28v2VYJLGW0uIjcFjIWXAkOIBhhzwCAcjp1qZzo8rs1+BM6mH5XZx/A9T1bw1oSahoqR6LpyCW9ZHC2kYDD7PMcEY5GQDj1Arg/Aif2zrVjFNY2GoW+y6XUQ+hxQxwMkhWIpIEAYtjkDdjn8Jb34nXVzdafKY9EBtrgyjZdXJGTFInzZtxgfP2BOccYyRS8N+OJPDOl/YLaXSZ4t7yZnvLjILMWP3bQd275ojOjd6r8AjUw93rH8OyPRYPDehHxTfwnRdNMS2VsyobVNoJecEgY6naPyHpXF+Lbax0zWYTHpwNq+spYm2sNMt3k2G1WXKgxkk7zzkkYzxWdo/j680rUb64a4067e5C5e6vrlgoDysFU/Zs4HmYxgAADBJJxSv/ABvBfaslzfWSSNBqCahC9lcNsWRYkjH30UsMJ3A+8euATDnRsrtbv9TJ1MPZXa3f69jVu4NN0rwxb6p9jZnurq4jSG7gsbcpsdwA2+BmDEKBgA/MccZFWdR05Tc6Vb6HpsN8dWsWvLSWWGyiX5dhIYG1yBiRSD1PTArnLnxhYyRq0Nnci6V5ys01xK3yzNukQhJEJUkAgZ4IH41oPGUttLp8kMFsjafF5Nrhbr91GcZUD7VyPlUYPYAdBRz4buP2mE7r8TpreKCXX7/TW0f93YajBY3E0cNkxXzvuSBfso+XJXPORnvS6Wum6r4mXSreydoZZLiJLhdPtsRtEWX94TaBQGKNjaxI4yOa46HxLMniK91uYW1xcXV1Fd+XJbSiKOWNdqsEFwASOvzZwemK0rLxfaxakt/NaW6z/aWnwltMyIzfedI2utqvnPIA6n1NHPhu4e0wndfidX4W8NXeuyyS3dvp1vZ28s1pM0dtatI00TlGKA2wGzI4yc8dK6fTPC+kQa7f2M9jZXsUdtBMhnsbcFWZpg33I14+Retebaf4t03RBP8A2Hd3dg9w26ZjYNPubOScS3bAEknJHXPNN8L65FpdzqBt/GDaek5D5utHMm9i8jsqqsjbQC5PXnf045OfD3Vmg9pheZWa/pHReKfDGmPdGW30iJvI8Q28JhtmWDfC9vFuTqoI3NnHbJPrXS+E/A1hpeifZ9V0nTpZfPkePzY1neOJmJRGkZcsQDjPP1ry/WtatNSu54r/AF038Qu0uo5o9HAV3EaKGwZkK42hcYIO3PfFWNQ8ZnVbSK1vtbnnt4pElSNtDiwGQ5U8XHOCOhpxq0Fu0ONfDJWbXX8zvodA0Y+BdCuDpFgZ5f7O8yT7Mm590sQbJxk5BIPrk1wuseF7mDxjaeXZWP8Awjs3iJNxUbZEYkIYOOTGeX2/d7cd7UGuLcaJp1pN8Q0tI4I4SLVdEZ/LZNrKpfPzbWUcjGcVDDB4TkkmOo+MYblJbn7W4TQQhabn5zlGy3PXHr60ozpK22y7ChUoK22y6r/M27W7sLnxxDpZ0jw8dMvp7q3tZU0xVYGJc7g7HEnzAqQEABGAxxTvCGhNrthfX1zLoUsEDXVlGlvpUG5njcqs7HHDYGdo+XGD3pv9reEftRuv+Evl+0kljN/ZMe/J6nd5GeaW01nwnYOz2XjGe2ZhgtBpUaEj0OIBV+1o+X4f5l+3w/l98f8AMoeF9FsLj4YTXz6vpN1djSkm+axtmktGCbjvbG4k4xlue/Wlzp1/4V8G3WnSaBBPqEsVjd7bCGbEjxk5+cZDqV6Hru5zxV1dW8IpFPEni+ZYpzmZBpMYWU+rDyPm/GiHU/BUQVf+ErnVEkEqCLSok2v/AHh/o/X360e1o+X4f5h7fD+X3x/zKOoXFqTZ6Va22hJdrDerLeG0tYxJPDJ5aoQ42r1Dso5weMCptaOlRa3aWqXGhWDSW8F1cx/2bA0dvF0cAsm6R3YgIoxgAk9q0k8Q+EYt3leNdVj3SGV/LtVXe56s2Lf5ifeqb6h4Okdnb4g+KMkk8XEwA+gEfH4Ue1o+X4f5h7fD+X3x/wAzqPC1rb2Xjrxdb2lvFbwJ9j2xxIEVcxMTgDjqSa7OvPvh7c2t34k8TTWWoT6hbFbNUubgYkkCxsPm+VckYxkjJxnnrXoNXQacLru/zZphmnTutrv82FFFFbHQeL6ncR2vxZ1i4mWQwwatps0pjiaQqgspwThQT1YD8RSatqmrad4Qsba3i1OzLi8vLLykmjUL5zGCIiJC24IQQjbU6Bs9u41P4d2mo6/fazDr+v6dc33l+eun3ghRtihV4C5PA7k9TUH/AArX/qdvGX/g1/8Asa9Sv9WryjN1Le7FW5X0ik/yIXMtLGFrCW134j0DxDfN4g+z3OkPGPsIuIpHn3xMEMcfKbhu4OFOBzwKsw3GtSfEe6S/l1SExXcZsooY5mgltSqg5wRHwSdxfJB6dAK1P+Fa/wDU7eMv/Br/APY0f8K1/wCp28Zf+DX/AOxrH2GF/wCf3/krHeXYyfiAbT/hJ9AWNLwXf9vaYZWff5JXM23Zn5d3XO32zXp1cPH8MbT7fY3V14l8TX32K5juooby/EsfmIcgkFPqOMHBNdxRip0vZU6dOXNy36W3YRvdtiEgdSB9awPF2o2MPhbWIZby3SVrOZFRpVDFjGcADPU9hV/V9B0nX4I4NX0+3vYo23ok6BgrYxkZ9jWR/wAK38Ff9CvpX/gMtcEldNBJcyaOEv8Axb4b/wCEV0byLy9/tq0sBZq1ouwx741Vw5kUrtyqklQT8ox7z3fiTwvJoPh3w1FrZGmWnki9k+zykyRwhdsf3QfmYLk46KemRXdWvgLwjZS+bb+G9LR8bc/ZUPH4ipo/BvhiGeWaPw9pYklxvb7KnOOnaslGola6+7/gmUYVkrcy+5/5nlWo+M9GudP8M2MEd0moaYlsY9Tz+5tWCqsuUzl8LuGNpzng961fEPjLw9rl/qUr3x8q006aDTkaJ8TTyxkNIPl+XAwgLY+8/Y5Po3/CL+Hv+gFpn/gJH/hR/wAIv4f/AOgFpn/gJH/hRyVOXluvu/4IvZ1eXl5l9z/zPNtH8WeFtP8AEct7Bcz2+nWcFxFbW0gkkMskkgcvGMFUU7eNxB+fnaBzh2njGy1vUrC5vLOez1SbWbW5u55pF8kQxs4RF+c4CK4ycDJLHvXsv/CL+Hv+gFpn/gJH/hR/wi/h7/oBaZ/4CR/4UShUkrNr7v8AghKnVmuVyX3f8EcPEmhMMrrWnEeouk/xqzY6pYamJjYXkF0IX8uQwyBwrYBwSO+CD+NPtrCys4BBa2kEEQJIjijCqM9eAKnChRhQAPYVsdAtFFFABRRRQAUUUUAFFFFABRRRQAUUUUAV7/8A5B1z/wBcn/ka8++BP/JKNP8A+u0//oxq9A1FlTTLtmIVRC5JJwANprz/AOBP/JKNP/67T/8AoxqAPSaKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigArjr34V+C9Rv7i+utG8y5uZWmlf7VMNzsSScB8DknpXY0VtRxNag26M3G/ZtfkJpPc4f/hT3gP8A6AX/AJNz/wDxdH/CnvAf/QC/8m5//i67iiuj+1Md/wA/p/8AgT/zFyR7HD/8Ke8B/wDQC/8AJuf/AOLo/wCFPeA/+gF/5Nz/APxddxRR/amO/wCf0/8AwJ/5hyR7HD/8Ke8B/wDQC/8AJuf/AOLo/wCFPeA/+gF/5Nz/APxddxRR/amO/wCf0/8AwJ/5hyR7HD/8Ke8B/wDQC/8AJuf/AOLo/wCFPeA/+gF/5Nz/APxddxRR/amO/wCf0/8AwJ/5hyR7HD/8Ke8B/wDQC/8AJuf/AOLo/wCFPeA/+gF/5Nz/APxddxRR/amO/wCf0/8AwJ/5hyR7HD/8Ke8B/wDQC/8AJuf/AOLo/wCFPeA/+gF/5Nz/APxddxRR/amO/wCf0/8AwJ/5hyR7HD/8Ke8B/wDQC/8AJuf/AOLrV8P+A/DXhe/e+0bTfs1zJEYWfz5HyhIJGGYjqo/KujoqKmYYupFwnVk0+jk7fmChFbIKKKK5CgooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiori5htYxJPII0LpGCe7OwVR+LED8aejiRNyhgMkfMpU8exp2drgOooopAFFFFABRRRQAUUVWbULJXnRry3D2675lMq5jXGctzwMdzRewm0tyzRVL+19M8h5/7RtPJRtjyeeu1W9Cc8H2qVb6zcoFu4CXLBcSD5tv3seuO/pS5kHMu5YoqtFqFlPP5EN5byTFQ/lpKpbaeQcA9ORz70+2ure8hE1rcRTxHo8ThlP4ii6C6ZNRRRTGFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQBW1ABtNulYAgwuCD34Nef/An/klGn/8AXaf/ANGNXoN//wAg65/65P8AyNeffAn/AJJRp/8A12n/APRjUAek0UUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRXF+JPGup6R4nGh6X4dXVJV0/wC3ySNfpbCOPeUOd644wO/fpxW1DD1K8uWn66tJW9W0hNpbnV31/badAJbl2VWYIoRGdmY9AqqCSfYDsar2OuadqRgFpcFzOszRgxspIicRydQMYZgOevbNedf8Jh4t8V2Vrf6H4PtpTZ3PmRTx63BNGHCMjKwGM/LIe46g1Xtj8SLNbWS38HILuE3m+Z9SgKutxMJWwuRgghcHJHB4549KGVxdP3pxUv8AHDs/Pvbr1enUhz12/A9Jh8SaTcC2MVyzpcrG0cghfZ+8AKBmxhSwIwGIPI45FVf+Ev0yW4sIbTz7g3s4hRhBIAMxu6vyvKHYcMOOpzhTjzbTtL8a6e9kR4AtZfIW23yyX1s0zPDGiAo5zsU+Wpxgkc4IzmprGL4h2d1az/8ACFxkW9yk6xJqUKR8Ryxt8ucKzCUklcLlR8vXPQ8rw6vapF6ae/Df7xc77fgelWvibSrr7IEuctdRxuhWNyn7xdyAuVAUkdA2CcjjmpNL8RaXrJjFhcPJ5sPnxl4XjEicAspZRuAJAOOmRmvMdPtvH+n2trZDwUHs4zayTJ/akAaSWBI1Vg2flU+VGSuD0PPNHhzxB4s+12dpZ+CTcTeHbI6Vcr/akSAuwhOckY6RA4GfvdeOc6mV0knyTjfp+8h2fn3svx9BTfb8GexUVw//AAlHjz/onP8A5W4P8KQ+KfHY6/DrH/ccg/wrh/s6t3h/4Mh/8kXzr+kzuaK8pl+LHiKKeSEfD28meIMZBb3hmCbZHjO4pEQPnikHPXaSOOaqQfG3ULmxuL2LwevkW9uLmRm1VFPllym4AoC3zgrwCc/UVrPKMVBc01FLznD/AOSF7SLPYaK4RPFnjl1Vh8OSNwyA2tQg/kVyKUeK/HJOB8OwT/2HIP8ACsv7Ord4f+DIf/JD51/SZ3VFcEnjDxrJLLEnw/jaSLHmKuvW5KZGRkY44qCHx94quLeS4g8E2ssESlpJE8Q2zKgGckkDAHB/I0f2dW7w/wDBkP8A5IOdf0meiUV5y/xA8Uxw2szeCLYRXcgjt3/4SC3Kysc4CnHJ4PT0rDtPjjeX19NZ2/hWBpYThy2sxqn3wnDlArZZgBgnOeK0hlWJmnKPK0t/fhp6+8L2kUes31/badAJbl2VWYIoRGdmY9AqqCSfYDsar2OuadqRgFpcFzOszRgxspIicRydQMYZgOevbNYmiajJ478KaRr8CLp1ys7zwo/79VKmSEhvu7gVLemMj0rmdS0XVf7S8NaSdSuNPu7m61VnurdtrMjTecPut0YBTjPGRnkVz1qVOhBqp8alytX9V2eidtU/lsyalRxjzJX2/FpHaXPiqwNhHNYzmV7hImgf7PKyfvMFAxC4UkMMKxUnI6ZzXPQeP5b+60SzsjAZ9Re4iZzbSMqlCfLcAN9xgrZIJA55+U1xZ8Cxn4mWnheee8eAaat1Jd+aoZ1QCMbBg7QGCqFOcAda37D4ayQ641kPEmoILBYrmB4fkMaymVZFX5jtYiMfMPU5Brnn7NT91O1u/X7jnnKu5L3dPX5/kbTeOpwsUzi1ijeCGUI0bsDvjEhXzAcB8bwEYAng5OcUQePnvPMW0iSRtxkizE6b4GdEjcbiATuk55x8p6ZzXI3fgu0sfDOneIp9W1AwzW9r5sXmBdrsECkyniONTs5KttCj2rV8N/D59Ssoru+1XU7dkhez3W1+kqXEQK7WjcD5Yjhv3ZB7c8c86UnG63fn/wAD+vMmLxLV7fidhHrGqSfZYGit4riTUDauXUH5BC0udqyNtbjGNx9e/HR15fF4QWDQ4riLXtdjMOqm2jRLzCoDdmAsBt4bYTyO5PY4rEvY9WtbrxXbDxFqwuNIAa0gfVZBJdDy/N6bMfcDDjPzKc8c1MJz7fiaU6lTrH8T2uivMLTQrubxPbaNN4l8Qxy/2cLu6H2+QFXJUYQmPay5J75qaCy0W51hNKh8aeLWvHllhRftEoVni/1gD+Xt+XvzV80/5fxNeep/L+J6TRXlLSaKqag58T+OAtlbC7fdJIpeEnBdAUBIBBzwMYPanbtGAufM8UeNIpIfJ2RS3DK84mYrEYwV53FTjOMY5xRzT/l/EOep/L+J6pRXiDLrMfh7xZfza54hguNI1EW1vDLesMxny8FwCckiTOQQOle304Tbbi1YcKjlJxkrWt+N/wDIKKKK0NQooooAKKKKACiiigAooooAw/EXjDQfCf2b+27/AOy/ad3k/uXfdtxu+6px94dfWuP8Q/FbwXe6JNBba15jl42aL7NMvmorqzx5KY+ZQy88c1V+LbMniHwxIss8TR2+pSB7eYxOCsCnhwRjp6im2msalD4b1qxhkv1vLjVU06ws7u9L3FuSisRJNkkBgHYMrNgMMH09SKwuHhSqTjKUmubSSS0lJbcr7dyPed0jGsviR4RspzeW7NBDHrZvI7KOBg3lGy8gkcbAd5JxkcA47Zz5PHPh27jZrrUrhWla4aKOGEf6NI91NJvLPGxXKvGd0fzDb0ziutfV7XxBN4c0y2vdWtVtdRl02/H290k3i2lZkZ1fcxVkXDnr2J5rY+FepXGr6Xrl5czfaHbVnRZ9u3zo0hhRH/4Eiq2Rwc5HFd1PMsM1KXsndJfbXR2/k8733IcJdzgL7xz4Pnvr5tyzwvdx3DGa2Zml23UchCnaNwMYfiQAr90Eg06fx74XZL1WvfOlnNyLKXyJP9Bke6mkE3K5GVeJvly3yYIqxpGtq/ha9TW9SvtOax0uwjsksrko6QmFT56pvXeSzYPXoBjOc97ba/qtx47utIOraLFaQeVILd0JunDqxMeBJgMNuc4PB6UVczw9OTp+yk+V/wA66afyeQKDetzi9O8e+CbK+sb1NQSO6OsXs11MLWXcbeQ3BQE7OVJaE7ex5xwa7D/hcPgP/oO/+Sk//wARWfoXj7VNamtlCWSXF4L1TYIpaaxMOQrSfN8wLKBjC8uMH1rah8TZZbK7uNHv9PeSHQBqfkPbszCUNh0Yhxj029RyTXDWxeErS5p05f8Aga7t/wAnmWoyXX+vvNn/AIXD4D/6Dv8A5KT/APxFbnh3xhoPiz7T/Yl/9q+zbfO/cum3dnb95Rn7p6elZej+IbnVf7fhOqWhtbSCJ4NVgiAjUujMxOWKnZgE89+azfA0om+IHjKVbtbsPDpjC5UACbNufnAHAz149alQwtWlUlTjJOKT1kmviituVd+4XkmrnoVV9QvY9O026vpldoraF5nCDLEKCTjPfirFZPir/kUNa/68J/8A0W1eXJ2i2ObtFtGDb/Ee1u1Vrbw74imDKGBjsg2R68N0rlJ/EN1fahq9uPD+tNK9ldwiNbU7k89lMZaMfcGEIJ5LHnntZ8Hap4b8OfbrqNYGuf7NsWmisbQNNvMZLAhBlmJIYk+vPStzRphY+O/FYDSTy3Aga2MsQUu4WTdGHCjKrhRyTjPWsfZynFNy/A5nSnUim5fgZepa9cT6g9za+EvEIURQJEps2jZCnnAkEZA4lA5BBG4EdDWfJf37I+PDuvhwqCEpppQIXQJOQAeMjLKB39KvaXqfiWTRtXvbTVtQvtXXTAz6bd6a0S2933EblFVgOQFBbJGcmqd1f68PBOpXsGvaw6x3Vv8AZHS2drjBbbKrbrZNy4JIwvG0c9inh2/tA8LJ7y/Au2Oty2mqpMfCniUwRXEs8bfZpSfn3YUR7ti43kZ54HTnNami+LX03QtPsZPCviUyW9vHE5TT/lLKoBI+b1zVK9n8RR2uq6XYX9+ZLPUrcxXVxC7tPA0Kuylo4yQN24blUkcA4zmo3bxHqPh3QI7t9WsmP2g3cgEhmEikeUWEQ3bSNxAIAOBuB6Go0pR2l+BUaEo7S/BG/wD8J3/1Knij/wAF3/2Va/h/xBb+I7Oe4t7e6t/IuGt5I7pAjq6gEggE464/OuK1qPxXd6hYxzXNxBFHp6vDdWiSLvvM/N5sccmMcAhXJTk5PpsfD+cNB4heUhHbW7lirYBBIX3P8zT9+M0m73H78ZpN3Tv0OzooorY6AooooAKKKKACiiigAooooAKKKKACiiigAooooAr3/wDyDrn/AK5P/I1598Cf+SUaf/12n/8ARjV6Df8A/IOuf+uT/wAjXn3wJ/5JRp//AF2n/wDRjUAek0UUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABXk/ja3gvPiLqVtdWt9dQTeFhHJFYjM203YBKjvjqRg5AIwelesVx3iDwdq2o+LE8Q6N4l/si5FiLJh9hS43J5hc/ebA5I7duvNduBlTUpxqS5bxau72v8k3+BMr9Dl9HfXbG1i1T7Jf/AGK01jdMbewe2uNQgaHYZJLZQNxV9nIHIUkDgZx7mSe5h0RNZ/4SuOJtQv4J7aITiWeI+ZNCyqvzNgGMZ7bSD0ruf+EX8ef9FG/8okH+NZ1/8OvFGqX1le33jqOe5sWL20j6HDmJjjJHzew/Kn9Uo/8AP+H3T/8AkA5n2/I5zW7Xx2bfQFZb4401RHJCsskkN0GYqZFR1Xfs2DMmUyGz1zW/f+HpL34gRvqFhr8+n3FnCk8ltdPFB9p5BdlWUEALt+5kZz15Nav/AAi/jz/oo3/lEg/xo/4Rfx5/0Ub/AMokH+NH1Sj/AM/4fdP/AOQDmfb8ina+DL2x8Y2trCJpNBhuG1ETzXcjOjbNgt+Wyw3ASfMSMDFXNJlnS88QWUfhvWrOG9eSVJ3MYUkRKhwfMYqSV+XjHI6Uf8Iv48/6KN/5RIP8aP8AhF/Hn/RRv/KJB/jR9Uo/8/4fdP8A+QDmfb8jntJ8NeLBoerWnlyhJI7URNcyCCWcRSHzIyEkcKXXI8wEE7hx3E+t+DtU1DQNYhGkPKs+pwXOnWUlym+1VNnmNv3fJuCuAFJxu9zja/4Rfx5/0Ub/AMokH+NH/CL+PP8Aoo3/AJRIP8aPqlH/AJ/w+6f/AMgHM+35HHaTbvcaxd+GtOt3s/7UJa72ttMNrFf3olG5SfmIKRjB/iznisg6XocmreITff2XGbQXMOmwy6pDCfNW5ucKyMwIH71SN3HyA+ldzY/D7xZp11Pc2nj7y5p8+Y39jRHdmSSU9W4+eWQ8f3sdAAJ7TwX40sYWhtviHsjaWSYj+xYT87uXY8t3Zifxr0K8cJVnNutGza/nWya/kZC5lbT+vvOW1C7Gp+KIPEC654WtpBc2sphbVoS4hjALRs+1sNuLD5CqkHnOafp1poWlXqXdhrPhS3nXX5L8Spqce4WroVMecZ7/AHc49667/hF/Hn/RRv8AyiQf40f8Iv48/wCijf8AlEg/xrm+rYL/AJ+r75//ACofNLt/X3nBQ3FtocGqX82s+GnjfRbm2lg03UIi8szMWUxxqi5HYBiWGTye8dlb6Cvhi98Pxa5oNvqkqW11LeC8RYJmi2ARZCqApEfQbjkkkZPPoP8Awi/jz/oo3/lEg/xo/wCEX8ef9FG/8okH+NH1bBf8/V98/wD5UHNLt/X3nImLTofAc+jW/iDwq882pRXnkTauGjRFkR2UuR82SmOEUfMePXgfDniK30D4ha1qDnR4VkkkEe9ZJ7Zf9IRj5RjXJwqko2AOB0r2z/hF/Hn/AEUb/wAokH+Navg3wxP4XsL+G61P+0bm+vpL2WfyBDl3Cg/KCR1UnjHXpXXQrYPCUKsVLn50lZNp793TS/MTUpNf1+plfB7/AJJXo3/bf/0fJSeNNTs9H8Y+FL+/m8m2i+2b5ApbGY1A4AJ6kV3NFeHjajxNWdVac0ubvbW/kE6blDlT7fg7nhemfEPT4PFzeIdUh1a8uI7EafAY7WGMmPfvLP8AvyC5PoAMDoM4rR034t2lvr2q6hfWOpTQ3KxR2qRQwq8UaFzh8y4JzJ1B/AY59jorlcaj6r7v+CS4Vnb3l9z/AMzxZ/idYN4RstFgj1izureGCJrmO3gljbYFDAq0oLI2CCODg/hUuj+PtF0Tw3cadYz38V5LJJL9pNjH5aOxySkIkwq+i5r2SihRqJWuvu/4IRhWStzL7n/meNP8StOj8Oi0S2up7oaj9rJZVRWX7UZ/U4JGB7E+1YGueK9A8Qa+us3vh6+F0sccYEOoeWpCMTzhedwJQ5/h6Y619CUUKFRdV93/AARRp1Y7SX3P/M8Ln+JaS+KU19LK/hmW3+zeSs8RjMe4MQcx5ySOuaoaT42+za3LqH2VY7m8vZJp3uJA0cUTnDJGUj3qdqryOrZJzmvoOinar3X3f8ErlrfzL7n/AJnhEGoeG7WC6jjvNzXVnJYSuZWUmB92c7bX5mG4kMeTgZJpbnxNZT3Pm7dMd0ggt45mv7lXAgYtFJxa4Dgs3I45IwRXu1FFqvdfd/wQ5a38y+5/5nz3qHiMNo2t2ySWksmrSxzXD/briVy6lcFVa3RRwoB5HAHoBXrf23x3/wBAPQP/AAay/wDxiupopwhJScpP+tfN9xwhJScpO97dLbX833OQmu/iIzxmDSPDaKM7w+oTOW44wREMc/XPt1qrbv8AFJ5QtxH4Rij7shuHP5cfzruaK0NTlfK8f/8AP34Z/wDAWf8A+OUeV4//AOfvwz/4Cz//AByuqooA4y7sviNcbPJ1nw9a7c58uylbd/305pLTR/iCzN9s8WaWgx8vk6Xuz9cuK7SigDlP7F8Zf9Dja/8AgnX/AOOV0Wnw3cFhDFfXS3dyoxJOsXlhz67cnH51ZooAKKKKAOM8eeA38aT6ZNHqcVk1iJhiWyW5WQSBQcqxA4C9wevbFY8/w28R3Vk1nP4ys5Ld4lhaNvD1sQY1+6p56DAwO1el0V2Qx9aEI0/daW14xfVvdpvdslxV7nmMXww12C3S3j8WacsKfdQeGrXA4x/Krtp4I8ZWL3DW3xAWI3EgkkC6JDgsEVBgbsD5UUYGBxXoNFWsyrrZR/8AAIf/ACIci/ps83g+Hfie3iso4/G9ufsMSw2zPoFu7xIoAADMSew70/8A4QHxV9v+3/8ACbWn2zOftH/CO23mZxjO7OenFei0UPMq7d2o/wDgEP8A5EORf02cDH4M8Zw3EtxF4+iSabHmyLoNuGfHA3HOTj3qC/8AAPi3U9NutPu/Hqva3aMk6LokKbw3XlWB59c5r0Wil/aNbtD/AMFw/wDkQ5F/TZwY8JeOBF5X/CxAY8bSp0OA5Hvk81f8H+D7vw1qGrX19rK6lcaisCsy2a24QRKyqAqkjG0gcAdK62ipnj604Sp+6k97Riuqe6Se6QKKvcK5bWPAOi6v9tmYXcd3cq370Xs5RXIwD5fmBSB/dxg11NFcTV1ZjaTVmeUL8GrpOE8X3yDphFkUAegAl4FL/wAKcvcY/wCEy1DH/bX/AOPV6tRWfsY+f3v/ADMlh4Lv97/zPOIvhpqsKBF8WFgMAb7BXPAA6lye39epqT/hXOsZz/wla59f7MT/AOKr0Oij2UfP73/mHsI9397/AMzzC5+Ect7L5t3rNjcSY275tFhdsemSah/4UvF/0ENL/wDBDB/jXqtFHso+f3v/ADD2Ee7+9/5nmtl8K7jTg4tNY02IPgtjQLfnH1roPDvgaw0izuIr+Oy1Oee4aczPZIm3cB8oXkAZBOBgc9K6qimqUU7/AKscaMYvm1+9v82IqqihVUKqjAAGABS0UVoahRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQBXv/wDkHXP/AFyf+Rrz74E/8ko0/wD67T/+jGr0G/8A+Qdc/wDXJ/5GvPvgT/ySjT/+u0//AKMagD0miiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiisVfEtu+qW9ktpdlLi5ktY7ravlGSNXZx97dx5bDOOo/GrhTlO/KthXNqisCTxhpkOnWN9MJo4b2y+2xFwowuYlCsc4DEzIOuOuSKgi8cabOIRBBczSSSvGY4TG5UoELchyrcSKcIWJ544ONlhK7V1H+luHMjpqK5a28YqU3XtnNAzSXaRxKqsZDDcJAoBD9WaRRgjrnkDBNk+LITdx2UemahLet5u+2RY90Zj8skMS4XkSoRgkEH14oeDrJ2t3/Df7hcyOgoqvY3kOo6fbX1sxaC5iWaMkYJVgCOPoasVztNOzKCiiikAUUVzvjrU7zRvBt/f2E3k3UXl7H2hsZkUHggjoTUykoxcn0JnNQi5PodFXNL4rd4bpksVeSJ7cRqs+RIJpTGp3bcZBBPGR7+lf/hH/ABh/0PH/AJSYf8azIPh9rlsrLF4wYKfJ4Onq2BE2+MDLcBW6AcdulYynUfwxf4f5nPOpVfwwf4f5m9N4luLd3jl0+NXinMMz/aCIlO1HGHK9SJBjdtGQRnplq+K90ixfYf3hiHHm8CfzRGYs47Eg59O1Ytz4C167klkm8YsWmYtKV05F35VVIOG5UhEBXocdKUeBNeEwlHi8bxcm7B/suP8A1pGC33vTt0zzjNTzVr7P8P8AMjnxF/hf/kv+ZsR+LTLYXV6unTeRHZSXkLEOokVQCFJZAASCMbSw6/j0MDSvCjTRrHIR8yK24D8cDNcIPAOurFcRf8JgTHPE0LqdOQgRt95V+b5AfRcdvStL/hH/ABh/0PH/AJSYf8aqE6i+KL/D/MuFSqvii/w/zOtorkv+Ef8AGH/Q8f8AlJh/xo/4R/xh/wBDx/5SYf8AGr9pL+V/h/mae1l/I/w/zOtorkv+Ef8AGH/Q8f8AlJh/xo/4R/xh/wBDx/5SYf8AGj2kv5X+H+Ye1l/I/wAP8zraK5L/AIR/xh/0PH/lJh/xo/4R/wAYf9Dx/wCUmH/Gj2kv5X+H+Ye1l/I/w/zOtorkv+Ef8Yf9Dx/5SYf8aP8AhH/GH/Q8f+UmH/Gj2kv5X+H+Ye1l/I/w/wAzraK5L/hH/GH/AEPH/lJh/wAaP+Ef8Yf9Dx/5SYf8aPaS/lf4f5h7WX8j/D/M62iuS/4R/wAYf9Dx/wCUmH/Gj/hH/GH/AEPH/lJh/wAaPaS/lf4f5h7WX8j/AA/zOtorkv8AhH/GH/Q8f+UmH/Gj/hH/ABh/0PH/AJSYf8aPaS/lf4f5h7WX8j/D/M62iuS/4R/xh/0PH/lJh/xo/wCEf8Yf9Dx/5SYf8aPaS/lf4f5h7WX8j/D/ADOtorkv+Ef8Yf8AQ8f+UmH/ABqve6f4j06ETX3xDt7WJm2h59OgRSeuMluvB/Kh1Gt4v8P8xOtJauD/AA/zO1orzz7Vff8ARVtL/wDAW2/+Ko+1X3/RVtL/APAW2/8Aiqn2/l+K/wAyfrK/lf3x/wAz0OivPPtV9/0VbS//AAFtv/iqPtV9/wBFW0v/AMBbb/4qj2/l+K/zD6yv5X98f8z0OivPPtV9/wBFW0v/AMBbb/4qj7Vff9FW0v8A8Bbb/wCKo9v5fiv8w+sr+V/fH/M9Dorh7G01/U/M+wfEe1u/Lxv8jT4JNuc4zhuM4P5Vb/4R/wAYf9Dx/wCUmH/GqVRvVRf4f5lKtJq6g/w/zOtorkv+Ef8AGH/Q8f8AlJh/xo/4R/xh/wBDx/5SYf8AGj2kv5X+H+Y/ay/kf4f5nW0V5np9p8TdR021vofEWmrFcwpMgeJQwDAEZxF15qz/AGP8Uf8AoZNL/wC/a/8AxmpVdvXkf4f5maxLauoS/D/M9Dorzz+x/ij/ANDJpf8A37X/AOM0f2P8Uf8AoZNL/wC/a/8Axmj2z/kf4f5j+sP+SX4f5nodFeef2P8AFH/oZNL/AO/a/wDxmj+x/ij/ANDJpf8A37X/AOM0e2f8j/D/ADD6w/5Jfh/meh0V55/Y/wAUf+hk0v8A79r/APGaPK8Yf8Ih/b3/AAmH/Lh9t8j+zIf+ee/bu/TOPwo9u/5X+H+YfWH/ACP8P8z0OiuS/wCEf8Yf9Dx/5SYf8ahutL8TWMPnXfxAit4twXfLpkCLknAGSepPFV7SX8r/AA/zL9rL+R/h/mdnRXJf8I/4w/6Hj/ykw/41Fc6T4osraS5uvH8UEEY3PLLpkKqo9SScCj2kv5X+H+Ye1l/I/wAP8zsqK5E6D4uGM+ORz0/4lUP+NB0DxcCAfHIyeg/sqH/Gj2kv5X+H+Ye1l/I/w/zOuorkv+Ef8Yf9Dx/5SYf8aqz2HiS2vrWym+ICJc3ZYQRHSot0m0bmxz2HNHtJfyv8P8w9rL+R/h/mdvRXMeCL/Ur2z1WPVL37ZPZ6nNaLN5Sx7lQL/Cox1JPfrXT1cJc0bouE1OKkgoooqiwooooAKKKKACiiigAooooAKKKKAK9//wAg65/65P8AyNeffAn/AJJRp/8A12n/APRjV6Df/wDIOuf+uT/yNeffAn/klGn/APXaf/0Y1AHpNFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAVm+IdQl0nw1qupQKjTWlnNPGsgJUsiFgDgg4yPWtKsPxp/wAiJ4h/7Blz/wCimrbDxUq0IvZtfmJ7HI6JrvxE8Q6bBfafceCpEliSRow9wXi3DIVwCdreo9qrJ4a+JkepwXi3fhgJBdSXcdtun8pZJFdXP3d3PmMevU8elZPgS5uIPCs9/pkRhFi+nyXU9jaEG+iCDzYmV8gsgZsumC2Ae/OhceKPEQ0/VriCfUnjOtQrp6G0Ec1zaOoJWHcmGGcndgkKpPHWvQqZg6NScIU42u1t8iFC6V2RJ4J+I6CBWvvDkiW1t9mtUZ58W6B43XbhQcq0SYJz05zU954U+J1/Zm2udS8OyLIzGZmec+bu29Rt2rgKMFApHOCCTmvqniLXX0LQtOsdWudQ1WeW5ivvsiFJYpEAILYjyqxlkBG0bgR64K6vqPim4ksZtK1PUrq1WyUW13aWzOs14sjLKJYwgAHG0ByqjrkHNP8AtmtdPkjp/dD2aJn8I/EaRiWuPC5w1w8fzXA8ppZknJX5eokjDLnOMnORjE9hoXxJtNT+3LdeE7i8QSrM8jTkuZPKJLBQACFhjAxgY7HrVi/1DXW+IMMMcOtzW/2i3Xy0gkgghXbmRhIMxyJ1yHw2eFPHN/Q7CbTPG2t/aLDWZDdXyywXIuHa3EJgUDdl8HDK4xgkbl7YxLzeq1Zwj16d9/vH7NGXoEvxCjsBpOm3fgy4XSQljJk3JZGRFwG4AzjHTitb/i6n/Um/+TVR2UOqQ6b4q0/TbPUoGmMkumyXLtnLQqDiRmYg+ZuIz0+lYU+ka0NB1FtPsNfggSayks7Wa8ZrgyK+bhg3mcKUJGCcbgSMcVjLHuTbdON35ByeZ0H/ABdT/qTf/JqtbwH4gu/FHgvT9Zvo4Y7m58zesCkINsjKMAknoo71gWmly2Wl+LNKn0XVr3S3kSWytjdOWmjaKPdGsjPuUiQMTkjGeM9KtfB7/klejf8Abf8A9HyVpOca2EnNwSalFaK2jU7/AJIErSsdxXJfE3/knmqf9sv/AEaldbXJfE3/AJJ5qn/bL/0alePW/hS9GRiP4M/R/kVdG8WXWt3jWcOrWdvc+ZLGsV1o00RkMTbX2kz4bB4IBzweKv6Vqer6y1+LXU7DFldPaSNJpciguuN20+fyOcZrivD8movrFqNS0TU7G1stVvdUSb7FNJ5xmMgWMKqZGBKSSf7vvUejX2qR6B4l0a58HX8FvqElzNAoimVSspA8r5IiVOC3zAY4FHud/wAQvT/m/H/gno7rrscTyvrGkLGgJZ209wFA6knz+Kglu9ShsVvpfEWhR2jgFZ2s2EZB6Yb7RjmvP7HSbiHw/d2R09lH2u2mjtZdKn23UcIHyTMluFGSAQwQnAXPerMtk7WGnvH4dgRrS8nuG0k2d69rKZFxv3G34YEsQAmOeMUe53/EL0/5vx/4J2lzqF9ZuyXXibw/AyqGKy2jKQDnB5uOhwfyqC4124tNTTT7jxPoEVy8JmCvZsMKCoyc3HfcMevNcXZaJLZXmkGS1N2lrpt5aSyy6ZebsytmNFBhYmNAAgy2drH6G/pcWoadHoV35ckuo2ek/wBmXCzadeMhwVIkDeVlj8gyCB168Ue53/EL0/5vx/4J0o1XWW8Ry6MmpaU0kNqLmaUWfEWWwFZftO4E9c4xjvThrUxhllXxZ4caOKNpZGW2JCoOrHFx0HrWVPqD2vjSbxEfMj0/7CltMsumXasqI5cvu8vAxubg+g5FcnDfeGBp1nYy6/bLBHe30syQ2s6h4blZQUHycFfN47fKKTlSW8vx/wCCS50VvL8f+Cei/wBp3uZh/wAJJoWYLdbmX/Qn+SI5Ic/v+FODz7UaLr0uo6rBCmq6ZqVrNbzSeZZwMhRkaIYOZG6iTPQdBXnraro93po0++8ZwmEWKWXmQ6bOkh8twyOSPXADAfgRnNafhHVvD9p4l+1f23YtLPbzyXUp86JfMYwADdO5LEhD0PQdKl1KfSX4kurS+zPX1/4J1E7aaNS1efV9Ru4FW+SCBU1CaJf+PeJ9qqjgE5LHp61HfXXhPTobWW51q+Ed0oeFk1W6k3If4ztc4T1c4UdzXP33iDw5H4pudQ/4SCC3vLa8Z7dxA9zDJFJbQowOzjqnZuCp9ay9S1Dw1f25RPGMUDz6Y2l3jJo8gWSIsSNijAjI3MO/UelCnR6tdewo1KGvM1e77dzuL9vDWm39vY3Wp6otxcbdirqN44AY4UsyuQgJ4BYgHnHSuW1S5v7LxZr2iSSTpBBoMup2U8OqXZkBVio3hpMZz2wRx74GPrMnhnUPssVn46mtrSzS2S1hl0+eUReTtIwAVU5KKSSpPBwQDirmt6na6/qs13pfiv7Rdtpk1jFYQ6NKzTKyhnG7sSyA5x8o/OiU6NnZr8AnUw7i7NX+R6F4nhtp5dGjvLZbm3+2uzwtF5gfFtOfu4OTkcD1rndL1rwBq1pPeQ6Dbx2dvbtPPczaUFii2k7kZtuN4x0/rxXU69HdmTTLi0tZblra6aR0iKBgphlTI3soPLrxmuIsdH1HSfBt54e1uDVLzS7pBaRmKC1heNpXI6idsktIMZGBVvlTbkvwNHyJtyX4eRcv9U8H2nhW/wBcj8JRyGydY5bN9LWKZXYrtBDL0IZTnkYPrxT73VPBemaJFqeoeFVs1lnMEdvcaXGkzMF3EhT1GAefanRaDMPDuoaNc6Vrc8N4B84WwhMZAGGURuoJyAeQeR6cUzUdAvNWsLSO+s9euL21d2jvZo9Nd9rgBk2klMcL/DnjrR7nb8B2p/y/h/wCCTxB4E3QfZ/C4u457I30cttpKMjQgAs2cfw5AI6gnHWnTX+hP4gt9O0zwHDqMM1il8s8NtbIGjcgKwDspx1zxnPapJfDkrPaNFp3iGDyLOeyYRtYgSxzHLZG/AwwBG0DGPSnxaDcW6aYbax8SQTWVmti08UtkHngXorZkwMHuuD70e52/ALU/wCX8P8AgElpotlcePr60k0Kwt9MtbNGWGXTICJ3Zm/eJICTgbcFSB696pWus+E7uKSaPwZEIXimlsZGs7cC/WInd5fPHA3DdtyORmmx+JdMuNbXXF1DUV8xEC2zX2nogj67Cpk3cnnn5hyMjkVetPDttZKEh8Pa/wCVHHNHaxNdWzLarKMP5QMvHHAznA4GBmknSey/AmMqMtlf5GdJd+GtY8PakIfC0Gn3D6K+o2jy2sIZ4mVsOpTO0g7euDyMd8dN401ZNDj0bUZIJJli1DHlxlQTuglUcsQP4s9elc5q9pDpGkIkWg68LhtLfRbQEwTblKFlDKjljgJnIHQGrninV9N16309La21q8S0v1mmWwspklTbHIFIYqoBDFe+etS5QTdtNvzJcoJu2m35luH4gpf2elTaZpFxdtqklxDbATRqu+IuG3Nk/KQhIYZ4I47VX1D4mW9n4c0/V4tNeT7XHLK0MlzHGYkjOH5J5PBwB1xyRWfaXOh2JtzbeC/FyG2uXu4j5MpKSuCHOTJ0bJyOhyeOay7zUvA9rNDpd34W8Q2015C1rHbNvie4iZyxQL5oLjcxwOcZOKv20O5p9Yp9ztdXuLu28d+Glhvbhba+Fwk9sSDG2yLcpxjIOfQ00+MLpNbXRX023/tI3iRfZ1vCT9nZC32gZQZUbWGPUYz0rPthputy2t1H4Z8SNLpTiGHzbvyXhbYP4WnBJKsMkg5B5zWBpfxJ0bVvGTXws7+8vooHt7S0tLaOSSNN2XYkPuJOFBGMLtPqaftYdx+3prqdlB4zDarqNpcWDW62YuCvmSYlmEW05VCoBVg2QVY9OcVmaP8AEOfWNL1O9ttHmm8i2W6tUjWRPNDZ2xkyIo39Pulgc8E96OmXWg6PdSXNn4G8UrI4cfvbWSVVDnLbVeQhcnrtAzRa3Ph6ytrq2g8AeIhBdKElifT2ddgOQihnIVc87VwM9qXtodxfWKfc0/A2u3niDWNWur6O2iuI7e2iaOASDZhpjhhIqsG+b0xjBGQaoeLLxP8AhP7fSotI0y/vr2xjaF9TTMMKRmdny20kE/LjA5wc9Kt+Hb/T7LWdTuofD+saZBcxQArJpkpaWRTLuY7A3ZkGSe3tSeIU03WLqWS4jMltPHDE0GoeHrqddyNIVK/dwT5hHeo5otL1f6mfPBxXXV/r3MCHU7fVXtX0jwl4ZWCbSG1Mm8jCkbWKMoITGMgYY9ufau38H/ZjDqb2drFa28l1HKkEShVTdawNgAADqa52/ew+0Wct+dPWZYzZ2pl8L3anaylTEmX7gkbR2rZ8P3NlodrPD5d4RLKrqltod1DHGqxpGqqpVuAIx3701KF1bT7hqVPmTSS+4wfBNnbaf4tsvs4Mf2vw1bTzKZGIaQuBuwTgHAA4q/od5NYeJfHElxKt5dWwhnCRM6718nKqELNjpjIHJz7ARW+kaLamJorjXRJEECSNoIZxsUKvzG1JyAoGc9q0E0awsNKk8RWmqXYjFq1150FnaJI8e3fx+4ByR2OPenGaUbdvT/MqFRKKVtl5f5lK58X6jbeDdV1m21LRtVuIbWKaCG0Vv3TMcNvBfJUZBBO08HOKpS+NdcbQ7K5aawsXk1iOyeeURyIYXU/MRHKyqQf9vsPXFaFjZzok8lhba4qTswmaCPSgJGBIbdjqQdwOe+ac2k3T2SWT6frzWkZBSAw6UY1I6YXGBT9r5Mftv7r+4yNV8TeIrLRxaw6zYz3trqM0F3PD5K3DQqMqUjkZY9/zKGGR7A1FfeNtaey0RbbUIbWabSf7Qae6hjhS5fIGxldvkHdthJ+YYrYuZZdFiM1ydds0uJwCzDSkEkrnAz6sadcanewfZBJL4mf7VII4PLTTZNxPf5QcD/aPA9aPa+TD2391/cVtY8VauniBIre6hs4IktH8qYxrHdCRsyFWb52AHyjYPvda1/8AmkP/AHAf/aFRSzapGQZZPEaEEAF20scnp+dTG+gstGi0K50PUPs/2UWuya6tVd49uztMOo7jFS5c3R7MmUufo1o+hhab4n1TWdburC01nfLIl15Rt7dHjgH/ACxMisokjYYIIcFWIOCOK57xn4i1nWPDtxb2xvHM2iR3Mlr9iIaC8SeHgEL97G8lcnG3NekaZpWnalZfakOsQfvJI2jl1W43KyOyMDtlI6qehNcl4SN74s02e9i1JreOFxG5a5unG7aGYZW8OMZx8wB9hVc8tLIp1J6WV7+f/AILzWNcUfZbTU9Un09NStIxfCEGUh4pDJGSE5UMI/mxxvxnjjP/AOEg1XUfh3rj3t5qDagIIJrZPszrJ9oeEF4wu3lBKGwMcY5OMV0unC1vb+xFr4kh1W2muWt5vsOoXWYz5Ukg+YXLgfc6Ed6TUTaWOo3qXXiaDSbeK4EEIv8AULrdJ+6jkYhjcoDzJ0A9KPaS7fiL2s/5fx+Y/wAZ3Ntf23h3WIbjUPsdpqgFw9okvyL5cgLFFUk4baAcH73HBrO8SQ2r6n4U1Rz4lbS1tbmLzLZrgTbj5Zi3hfnBfDDnrxnpxcu1tLHSY9VufGdmlhIxWOf7TeFXIJBCkXfJGDnHTB9Ko61qFnoNzp0N74mYjUEMsMkP26RPLC53krdn5TwARnlh25o5p/y/iPnqfy/iTT6l4jb4hyq8Wow2olt3tBFFKyS27BfNVl/1YIbOWYgjdx05jW11RPHGj31/ba3d3ttqdzHKVRzaLbyLIInXkIoCsgJHzcHNdHoWlx3y3y3V5ezNb3CxpLBf3cSurRRyA7WmYg/vCOvatf8A4Ryx/wCe+qf+DW5/+OVSlJq9v6+4qMptXt+P/AMjwJ/zMv8A2Hrr/wBlrra4/wCH8aww+IolLlU1y5UF3LNgbepOST7nmuwqaPwInD/w0FFFFamwUUUUAFFFFABRRRQAUUUUAFFFFAFe/wD+Qdc/9cn/AJGvPvgT/wAko0//AK7T/wDoxq9Bv/8AkHXP/XJ/5GvPvgT/AMko0/8A67T/APoxqAPSaKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAqpqmnxatpN5ps7OsN3A8EjRkBgrqVJGQRnB9Kt0U4ycWpLdAcHB8L4raCOCDxj4vihiUJHHHqYVUUDAAATAAHao7j4T2l3LBLc+LPFk0lu2+FpNRDGNsYypKcHBIyK9AorueZ4p6uf4L/ACJ5Inni/CKwS5NwnijxSs5BBlGoKGIJBIzszyQCfoKktPhTa6fapa2Xi3xZbW6Z2RQ6iERcnJwAmBySfxrv6KX9pYr+b8F/kHJE4f8A4Vr/ANTt4y/8Gv8A9jR/wrX/AKnbxl/4Nf8A7Gu4oo/tLFfzfgv8g5InD/8ACtf+p28Zf+DX/wCxo/4Vr/1O3jL/AMGv/wBjXcUUf2liv5vwX+QckTh/+Fa/9Tt4y/8ABr/9jXR+G/D9p4X0C10axkmktrbfsadgXO5ixyQAOrHtWrRWdbG160OSpK636b/0wUUtUFcl8Tf+Seap/wBsv/RqV1tcl8Tf+Seap/2y/wDRqVwVv4UvRmeI/gz9H+RRsNS0HUbz7PGviKMvcT2kLzahcIs00Wd6LmXIOFbG4AHafSmwajpc1nc6g9h4mt9NtIp3ubqfUZ1EZiJ3Lt87c33W5UEcdax/Cdrpdnrup3+s+JbNkj1e6vNNthqMDQosuf3gAO4NhnBBOPmzjPNb1kvhmCw1KwvfGUWpWmoCRZIbm9twqiQsX27ApGdx6k+1H7ryD9z5fgRnUNFEV2DB4iW7g8kLaNqU/mSmbPlbSJiuGIIySACDnGKzvC1w97e3lnrEWtRTnVZLOFP7TmzCot0mAcpMQerYIJ7ZxWktl4J+w3dtJ4khla6WFXuH1VfOUQ8x7XDAjaefqSe5qL+y/A/2SeE+JkMs12L1rr+2B5yyhNm5X3ZX5fl46jij915B+58vwIbbWNPv7SD7BpviC51CTz2exXWJQ8SRSNEzMxm28uuAASTn0BIn1aHUINZsLLSdNuboT2r3Mq3PiG6gdMFRgAM3TePr+FNXR/AENnFbW2vQ2vkySPFLBrGyVFkO50D792wtyVz1561bvoPA1/aWFq+t2kUNkrJEsGreWSjAbkYh8spwM5Paj915B+58vwLcssk/wneaaR5JZNDLO7nLMTBkkk9TTLLxnNdeL7rRJdMW1ih83y5Z7kLLMEC5dY9uChyQGDHpyBVS11jRrr4cQaX/AG5pcN1LpC2+2a7RdjmHbhucjB68VQtZtDtL6S9ij8LGeQyEmXxE8ijzDl9qtGVXdk5wBwcdKmNSK1b6IzhVgrNvoi7Y/EC6v7W/mTRFRre2S5jV7k4dS5XG8IUOFG7KFxzjNOl8capBbSyTaHbJJHdw2pj+3E/6y4e3DZ8v+8m7HofXisPW7DStA0WK7n8NaVJZXY+zq8WuyKpRgZPvuiqF+Tjn2HBxVXVvDutXunXKaX4Gjs7m5ninknl1VbhZCkwmwyFhkFgehHU4q/ax8/uf+Ro68PP7n/kanirUrrXPh14lmnNxpmp6HLKm+wvHVWkRFcMCNpKkOPlYfyBroPE/iXUNIubOz0uxju7qSF7lkkMnzIm0FV2KxDEsPmIwO9ZlhBdajBcaLd+CdJt1iVLiW3nvQUkMm9d2EjcHOxhyc9KXUX01DFYanpvhFWtARHDc6rhogwyQA0OQCCPrR7WNr/ox+2ha/wCjF8ReN9Q0+GC4sbazjtms4rqWS7Z32GRgFRxGCYxgn52+U446Guk1gj+1fD65GftznH/btPXKz32iXV3Hdz2fgqS4jRY0kfV1JCqcqv8AqegPIHarD6vp1/r+lajeXnhiB7F3Pnxasssuxo3UoMxrwWZSef4amVWD0TIlWg1ZPt+Z3NZHiU40qIgZ/wBPs/8A0pipf+Eq8O/9B7S//AyP/Gq/jF54/DjPahDcrdWpiEgYrv8AtEeMheSM46c+lVOScHYuck4Ss76HE31xe3nw10zVor+Wy1bVdUtJJpllYeTI8yoUxn7qD5Sv+ycjOafp/iibT7R9+7STda01ndTajM00dky26swBZsbWcELyB84OO1M0GTxHrelX2oWsHhqW1lu5JJ4LyG5/dTKNrjy2HyngkgDkknqTWvZyeMtc0eK4jt/CstndqJNk0Fwu4cY3Kw6jA6jtS9r5MXtv7r+4zrjxbqVzF4Nv7nV4NLs76S5FxOsJEErKCIiS+NqsAWAJHbk4p2tfEe70zUraC0SC9tmtIbmO5EkaLdhnKttUtvOMDAjV2yenTOzPZ+Orm3+zz2/hGWHj93Ik7Lx04PFElp46mlillt/CTyQ8xOyTkp/unt+FHtfJh7b+6/uKE12sfgm2tG1WNDL4Ydl08xjdJiEZkDdeOmOnNehVx/8AY+u/8IsNG/s/SPNGnfYBdfbX3Y2bc48np3xmtdb7XWleJdP0gyIAXQam+Vz0yPI4zg0oO2/ZdCacrbp7LozE+Ji6g/h63XShMb9ppRCIM7932af7uOc/SseXVdIsdKu7nwRafY7cT2cd7fWdj8ixmQiQhSvzOi53EqcZGeRx1Fyb7V0e3utG8P3qQPl45dQaQRvjuDAcHB/Ws610yzvlZrTwv4QuApwxhug+Pri3p8zTdl+f+Q+dpuy39f8AIxb7XNafwWTaXmq3IfUHjt79LcQyS2yruyxEb4zyquqZYheBmqtxrd1eeCPCF/rFrfyakuqRS3BGnytIiRSHcSFTj5dvYbuw612WlaLo16b2K78MaNbz2lwIWWKFJVbMaOCCY1PRwOnatH/hFfDv/QB0v/wDj/wqlKTV0v6+4tSk1dL8f+AQ+HriO7utauYd3ly3kbruQqcG1g6g4IPsa8l8KWpiSyvpYbufT7LUYruRbfTJBKjNAiiQOVzJGCrhlQE9DkgjPWQ6rDpKamtrPqNvb2ctxPerplvZpDaRLM8algybidkeeNxIU+wqU6N4SGrPpZ1OMXixxyeW2n2QyJM7Ofs/U4/lWactGl/TMoueklHv+Oo/QovEreKJJtTmvITLc3Ec9ukMjwNDg+UyyFgiYAH3RuJPzc9KGnaFqWleG9YttFg1uHxB5d0IpLq6kkhH74lShc7NzKQQQCRzuOeS/QdK8P6xJPazXFva6hDdTWxtfs9i7MYm2kr/AKOCR36dK0f+Eb8L5ulGq25a1XdOq2ViTGMkZIEGeoI/Cq5p/wAv4l89T+X8TNS01VPC02z/AISNyl5aTRR/vY5lyy+cu5nd2G0sSD8uR8vtYl0m9vLLUtPfStTu7Wz1+G4tkmuWR5IQULMjswyqtvKjPQDuc0mn2Hhi61XSl06a21KK4lAljl022CbGhldeVhUhsxjjOR3HNReLLLStL1lUSwsLa1ItYywtraOKNpWny8jvC+B+6RR7sPWj2ku34i9rP+X8fmbet2d9dWehPZaTqSGz1BJXh+0IW8pG535lw2eCOWPHaqPiPS/El9e6jc2MV8s9xb240x0u1iSykViXMq7sNyQTgPkDbnpWE8WjCy8NSi2McuvkiAXNtYRJGQu4Bm+zknd/DhecjpkU7UNFazu/EcP2ewjTToY5rSS4t7RBc7lZmB/0bjAR+meR9cHNP+X8R89T+X8TVvtF1pNTv7qzsNTa4TVbWW2m+3qUNv8AuvPCoZPlB2yfKRzkdO2z/wA0h/7gP/tCsiDRdOm+Gmo3d1pOmm/it71TMlpECGRpFUgqi8jaOQB0zTo5PDOq2z6NpFxqKSSwSRWq3ct8ts5UENHguoO0DlARxU3lPZdPz+RDc6my6d+/y8iK38NaonhvVtFsNCttKvBHMkOpxyIPtGZNygbcuAy8EnGOwPaJPD/iFvCOqWT2F2gu7mJ47ZJ7eNoFUgsERQYynyr8rH5wzbsHOcjw9a+BtQ8Kx6lqPh+6iuo7BLydIkugsi4G5oct86qSMkE4zWlFpfw3ltbq6Gk3K21tbQ3LzM04UrKoaMKd3LEMOB0qr1ey+/8A4BfNW/lX3v8AyLcnhHUdS8EWlpd6PpwuYNVS++xOFVHjEmSrY3IHZSQdvy8kDitS+0e5aw0VrLwrpkVzZXfmJGkyKLWMPk+WwTguAMgADsSep5vX/D3hWw8HajrNj4ZuBNa71Mdy0w8sr952XzASoGTwee1aOqeFPAukvbQyaFd3M88TzJHaGeQ7EALMQH4HIHqSQBk0Xq9l9/8AwA5q38q+9/5DPFHgi712/wBcuI9KsM6jo8cUMkrLvgu0LnP3fR1G8HPyiuc8SzQyfECS61PSbO8NlcWWLMlDcPIYjuEeULSxjfuwMAtGTxjnV1qx+HGiW1rcXGi3TxXNt9rDLLKu2HjLENIDkbh8oy3PSpJPAWgQ/EW0082avpt3ps04g8yQFJI3iXO7fk5Eh49qL1ey+/8A4Ac1b+Vfe/8AI7vw5/yC5v8Ar/vf/SmWvPfB0eoaN4d1WxuNIaI3+XEZs7s7W8hIsOEh/iKFiQ2RuPXqfQPCMUcPg7RVijRFNlCxCjAyUBJ+pJJPua2aIpuKa7BCLcYtdjzLwlpl7p+qWFu/2h7ZLpGijNlMot41tpkOZpIk3DcyhQckDHJJNT+J7CW71VlW1bfb67b6gHk0+4mVokgiUhGjRhklSOvY16NRT5XvcfI9763/AEseWW+mT2+qXV8ru7C9upbWGfRLySMRXBUvuGwYcbcDHGCwP3sizZ6Wul2/hr+z7/UFn0W3mtyZtBumSdZAuflCgrgqpGD0GK9KoqrS7/195Vp9193/AATB8MmaT+1J5xMTLdowkltnt/MxbwqWCOMgblb8u9b1FFOKshxVlY5LwJ/zMv8A2Hrr/wBlrra5LwJ/zMv/AGHrr/2WutrOj8CM8P8Aw0FFFFamwUUUUAFFFFABRRRQAUUUUAFFFFAFe/8A+Qdc/wDXJ/5GvPvgT/ySjT/+u0//AKMavQb/AP5B1z/1yf8Aka8++BP/ACSjT/8ArtP/AOjGoA9JooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACuS+Jv/JPNU/7Zf+jUrra5L4m/8k81T/tl/wCjUrKt/Cl6MxxH8Gfo/wAjGsfF+uDxiNPvLjT5YG1aXTfs0FuwkVFh84TZ3k4+ZVIxgZzmovC3ju+126nguNRsbd7q2mkhR44xJYSIfuyIJSzADJJYR/c96v2Nlp+m3V5dWmp+Jo57yYzTyf2OWZ3IA6m2OBhV4GBx0qwPsgeZhqniLdKMSkaGMuP9r/Refxo9qv6t/mHt4/01/mY/hrX9Q1nwPfa5f+NNOQSWoi+SCJVspckbnJY5ZuODgcjAqppbQ6H4HsJtE1y3K3t1BFqGq2tvbn7Enl5wyxptJ3YXLgkeZk5wK6FUsVheFNS8QCJjl0GhLtJ9x9lp9vLbW8ZW21jxHEhOSI9ECgn8LWj2q/q3+Ye3j/TX+Zg3/irWD4d8NX7a9HYve6jLZTTpaDypYdzqs4VxlThFI52/Pk7hVDxH4i1rRvENxp6+Mbtkt7SF0As4GaaVkmbHEf8AsRdOPnrrJtYtbdo1m8TeIo2lJWMPpQBcgZIGbbnioj4i01baC5bxbroguGCwynTF2yE9Ap+zYJ+lHtV/Vv8AMPbx/pr/ADMW08aaxqGrWCm6Nv5os5I4FhLC6hZEaZ1QRlj8zOudwC7MnvUk9zqr+M9DuNSi1KaW31q5QwRWeYoLdopEicOqcqQyEkscZPHGBoyeKtGhuGt5fGespOrbWibT0DA+hH2bOanbXrBLmS2fxVr6zxqXeI6WoZVAySR9myBjnNHtV/Vv8w9vH+mv8zI8VW8138JNFt7eF5ppNPZY441LMzHT5sAAck1oINU13S9VtLDVdXthBBby2t5dQfZyJsMWT7qbkwEDZHBJ9OEh8S+Er2ysdN07Xb4SaPGsqvbWjySIixmPc4MTDG1jk4H4VnSeKPCniLTbmNvG+r3FrEhkuRDbphE5BLlIOFOe5x61MJqKt/l2IhNQVv1Xb1NbwBPf3+p6rqt+ZVOpW9vdwW0knmfZomecKgbuPlLccfPxWfqyXz+K9Za1bWvLinikaOwZ1WT5bUMDjjds39wcfhW94N1TQdYmvbrRtcm1VkjhhkZ4lRYlUuUVQsaD+J/XtVPXNT0TT9VvHuLXVlke4WKSS31L7Oksvko2FTz0yRHtyQvanfRNd3+va47+6mu7/Xtcw8+NZvD6GcaquoDTQll5Qxi7EjAmYcAgr5WC3y4355qzrNt4jn8Z6dcm1v50t5bVXSOWSKEd5HQodjJk/MJF3fLgcHhNW8U+HdEtrW4v7XxKkV1F50LR6s8u6PAO/CXJIXkfMeOetdRpFhpes6ZHfQSaxHG7Ou2TVbgkFXKn7spB5U9CapTbdrfn/kWqkm7W/P8AyOI1zQzpOs+Lbk6PrFyLyJ57e5iun+zRKbfa/mBpACQwcgbTxgDsB33i+5jsvDxu5c+XBd2kj4IHC3EZPUgdu9cNpdpo2sWtnY3njLxG95d2qGaAXTmIs0YZo9xQqWwT8mS2O1bemeJtI1fYbLxpqzI6ysryWUcaERAGT5mtwPlBGahOUk3bdGac5pvl3Xl5mB4c8WaJNonie21S2fybm7uLsW8txCpnjkbIRcSfex1GR9TWfpuqxah8P/D9hdyQOmn3ATUNOutShja6i2sBtbf8yqWU4YgNsxXQ6f4me81bUGPibURolvpianHe/ZYkYxEsGJVrcZHykgrnI966PSL6WXXLaOPVNQvLWa1ndlvbZISGRodpGI0OMSH1H5VXNPr/AF+JfNNb/l/wTz7WF0+70TR4IGs/sVqk8f8AZTaraySW7swKSCRn2/KAwGCSoI96qa5p+n3ssxkew1CU6B9mjuJdYt2YXq5Ebkl1ywUj5gvX65rv/EXiFNP8Trp02q6hbvNbRG0tbG3jkeeQtLv+/G2MKinkgcGqVxr12mp6HaWl54kuxqtvLchlgtUaJEAzuV4gc5ZRg469+lHNPp/X4hzTe35f8E5SRkvPGml6pJPZLtaza5luNWtZI1EaZYrhvMVgxYYBKseTnPFzQIINO8VXV7c67pksjXVzIupHVIBujlBCAoAXcrhRtZgo425rr9Qvm03UbSxuNe10SXLxxq4t7XYrSEhVJ8rk8HIGcdTjIrH0PXdSmvZLHV9d1VJW1WfTre5gtLcQyNGCQD+7YqxAPXjii8+39feHNU7f195meH7PTtEsrtE1TQzcyaa1o0g1eONLiTnDERopGTzuJLDcQPWtbwM+i+G0v1l1bQoY52j8tY7u33gKuMMyKgYDoCQWPJJ5wLWhv4g1bVPEVlL4h1C2k0+5WGBZLO2yFK7lZioO8EEHjYR3GaTRZvEN9oeq3MutahdXllfXNrHFawWqeaI3KggOmMkDPLAfSi8+39feHNU7f195s+Er06iNYuy1sWkvVLfZZ/OjyLeEEK+Bu5HoK6OvM59d1uH4c6f4jttW1K+u7xoESHyrWAbpZAgyDG2OSB94/UVq6nqN9o32BtR1LW7eK7d4zM32Ly4XCllDny+N23AIyM9cU4tpbfl/mOLkla35f5mRNoniXT7rxD/ZmlSudXMsbzPJBiIedKVdAZPmykvRgMEdxxV2WDxRY+JZdS0bQ5PJuLS2tZVvDCWQRM5yu2cZJEh645Fa/gLWNQ1vRJ7vUVnSQzKY45yhdI2hjcAlEQH75PTvjtXI3OvaDpmrCzvPDVhfzT6lKtxcSCIyKJbySNDtILMAQMlto6AEnipV9FF/l0+RC5tFF/l0+TJYNG8TxX9lKNCkEUGvT6q/72EsyShxsH70YIEh574FP8MaF4h8OTSuuj3U/wBms3tbBnmRiwLbh5gNwVXBAyEAz7YxVmS70y31OGG58AadFZPqY057vEDbXbHlsEC5IJIB6YJ7jmsec2t34l8Palp2lWNnpl5teDyY0DPsvLdVkICAoSrtxuPB5xQ+dK/9fkOXtEr3/r7jo/DFl4jig0Sx1XSEtksLln82Dy1TZ5EiZIErEsWcdBjvU3irSNZu/EEV1p0EhjjFtKHWOOQM8ZnyrK00fGJQe/4EVpeMLZryPSoEtrS5drx9kN2MxMwtpyN3B4yB2NcfpNtp9p4A8J3dr4c0e8l1EwwyNqLIHzICQd+wlznHbOO1HK7u3f8AT0Dlld27/p6BL4S1c6OthDaXoaS2ntrp5bS1dXEkhkBiH2kGLazHABI4X0FQz+Arm902xsr2z1qZbS18gFfsyCRg52uwFxgnY8qNn73mseOKmnu4RYQRW3gzw/Lqi3c9re4g3wwGIA7gFjMjBgychSF3fMRUL6hAVtJovDHhT7PPop1YO8WAQmzeudnA+f5Tg9OQKdp9/wCvuHy1O/8AX3HX3NvPbfDrW0uLdreR4b+XymKkqrtK6g7SRnDDoTXPaK+iSand3V3r1tbR22p3VzYwveQFA8gZfNBDFiCGc7WxjeeOBgvbnT4vEM1pa+EdDeytZbWO5kniiiKrMMlgWwMAEY4O4hh1FXrOLR7zVmVfD/h2OxGoS2BWWFEnDID8wBGCSw4Uc7SGz2pKM1tYSjUj8NtitBJ4a8LWWlXttr8OoPo1i9klvFcwGSeN2Q9NwG4bF7jODS2MehyeEZ9Pl8V2NpPe3DXUpFxbyeWrNlYSrlkKqgVMYx8vFHhXSNJub3UoLxvD1zIt9dxJa/2bGksRR/lAyfmULg9P4hzWXYNoem+A9T1FtJ0a4vbfU54JGkgDrEDdGISMrElUVcNtBAwOMCn+98h/vvL8TWk07w03gy48Nx+NbWGO6aQ3E8c1qrSB8712gbVBz/CBV1T4ff8As2e48bxSajYJLGl6l3bozo5GVZANhHyr/D/CDXOXeo6XbRRxx6V4ZlxrFvp4vhYoYLhJQfuYPDpkFhkj5e2eNvwlNaS+KHihsLC1urIX1ncNZwLEJdkluVYqORw3Qk9/Whuot7Cbqre34jtd0/wX4h3/AGzxPArSWgs5GS/hLNGCT1bJUnJyVxnoc4FXLibw1caza6r/AMJhDHdW1u1uhS8t8bGKlsgqeSUXP04xXMfELyZ/iJo+n3WpWltaXUcYmgvI0kikAS6IdlYgMFbbgHjLKeoFXde8V3mh6vHp+m6hYo1ulqlppS2pZtQEhwzIR90KM42kgYO7jFNcz6/195UXNq9193/BOh8N+JNCg8LaRDNrWmxyx2UKuj3SBlIQAggng10l1dW9lbvcXdxFbwJjdJK4RVycDJPHUgV5n4j165m1zxNoB8U2qpDYtPFZC3QyyAwyF4d3oAqtn73zeldv4rk8nQxLnGy8tGztLdLiPsOT9BSTcU12Qk5Qi0+iJf8AhKvDv/Qe0v8A8DI/8aP+Eq8O/wDQe0v/AMDI/wDGuA0zxT4suNL1r7P9o1DUbWzRo8QxiDex5dTsVt4U7vJZc8AZJNLLf6hc+GPE0FzqOrTaOIk/s/UzBtuZ5HQ74vLEeSu4gfc4BIzxkXaXf+vvLtPuvu/4J33/AAlXh3/oPaX/AOBkf+NW7HVdO1PzPsF/a3fl43+RMsm3OcZweM4P5V57eWUb+BrO60XUtZmht9Sgmu5vIMMzwrIvmBkEaMyquSAFzx3rp/DjxSazdyQXF5PE9hbMsl4jJIwMtyRkMqnHpkdMUryTVxXkmr/1+J01FFFWaHJeBP8AmZf+w9df+y11tcl4E/5mX/sPXX/stdbWVH4EY4f+GgooorU2CiiigAooooAKKKKACiiigAooooAr3/8AyDrn/rk/8jXn3wJ/5JRp/wD12n/9GNXoN/8A8g65/wCuT/yNeffAn/klGn/9dp//AEY1AHpNFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAVyXxN/5J5qn/bL/wBGpXW1yXxN/wCSeap/2y/9GpWVb+FL0ZjiP4M/R/ked28Wsw+I4LoaPr4hW9lkL+TP8iG7EiHbj5sQgptI71oaHa6rpF5NdRWt79vMdwtxNJY3IhvXYExMwEJcgHGclSgyFLCuij8b3V1rlxpkF1H5sV3LbMsejzTrCQ7BA7rKBkqobOMc0ul+M73U7v7ObyOyDeb5Ut7oskSS+USJApNx1XBJBx0oUpvVf1+IlKo1dfl/wTm7G11WKz1i3lsbtItQsobYCG2uopEdGcO+5bc5JVsgtuPygE+mhpltNp+n5TTttzb6rHeW6LpVyoaMRLE24rAAJCu8ZC46Z71qab4x1LWILprC5geaO2N1BDNpDxNdxdA8Za4AKk45OOo9aQ+KvEVp4SOv6qlrZRiGGTy/sPmbmkwMKwucYBI+ZtvX2ovPt/X3j5qnb+vvORl0K+n0S1hbSIIbqHxCdT2Q2F4IxATlowTBnJ+6RgAgVpeK9IOsXVnLYWU62osHs3sH0+4iitizBjJGRbMSeoONp4GCMmur8J+KL3Xri3aVoGt54rg/JbeWVeJ40OGEsiuuXYZH92svxtNeHxVY2sV9qNrBLNYws9rOyhfMknDAqHX721RuwSMUc0+n9fiLmn03/p9zldW8M3V7qF7dR2pmkn8wedNp94HcNZpByfJJBEiFhyeuetatnoEdr4rXUjNq0toL5r8pNaXzfOyFSNgjAyOBuJOV4K8c6+uajb6HdaikmjeJJrbT4EuZrqPWJSnknOXA87PBV8jGcKT6Z6bw9tSTV4o555beK8URGeZ5Sqm3hbG5yTjLE9e9F6l9bDvVTSdjjdA0uPRv+Ed4uQNLkvGlWLSLtRIJySMfu+o4HPpSWlpd2/g278NSlLizWIQWgl0K+JaPdk+aQBk44yuMHkVoeDCniDR7Ce4t9aVZIWBu21efEkkZCOdqyfLltxHsDwKq6XJBbeG/EesalL4guG0y7uVe3XVJWZFjwdqFWXIwc5bnrycZpJ1Gr6Ci6zV9PxLXw50i+0y+1l765ubprhYGE01tNEAQZRsBmG5sDacnP3sVD4o8O6xqWrXJt7W8Nu900m+F0AdGt4o8gieNwysh4zg55zUNnrVtd+GrzVRYakrwzJbwx/8ACQzlLiRtuAj7+QA4zgE5DAAkczXN4IvDdjqsNpePJcX4sXh/t67ADGYwqVYkcFsE5AwCeD0p8s7f1/kHJOy/r9CnqXhTVNS0HT9Nex1COays1tI72OOFJQFwM5W7GcgDKtuUkZxXc+GLS5sdCSG7SVJvPnkImZWfDTOwLFSRkhgTg1w+vawPDMtpYXtlqN1qUlpLdSLZ6rfumFbCqu0Mct6sABjrzUWp/wBsS+NrHTtHneG2n0g3pi1HVL1ed6Dllb7wzjaCe5PahKd7/wBfkNRmnd/n/wAAPD3g280R7NhpOobYpY7p49lrIwuAoDlZGm4U4P8ACCAeCOlWLbwzq0Gl6bprWeoPb2b3If8A0e1DywzZ3R7vtHykbj8w68ccUhttXPxA1LTor5F0q2js3K3OrXiuBIXDbCH5YlSACcfd9TUOga02reIntrix1K20qRp1huZNWu42RoiwKvukwWIUtgfdA5zQozStf+vuEoVErJ/j/wAAu2/hrULaQSLF4iZhpy6aNy6ewMKnK5BfBPJHTBB6Vp+F9Am0rW0kjsb62tFgmG24aARxsxhwsaROQoxGxPA5PvXMafqs2oabqwuJLqzvYdKlvYo4dTu3KYLBWD+YY5E4GGB5IPGK3/iHqWm6Vd6fc6lb2k6/ZrhIUu4PNTzDJbgcdM43dSB2yM5pPm6+X5+gnzbPy/P0JvFGgXep+IHnFtezWjWkce23S1kRmDS53LOeoDggj1PPUVSm8Nz/AGTQo7Ky8S2Vzo0LQW93HNZvIyMoVgweQqc7QenGBjFctJrVhL4VtL+3tvCMV0msHTblp7GIxupk2rJ8rkIAvzdWBA645q54nkbQo9LtrPSfC97czQNcG6ext4ILobsKiGSZQvBGSC55BAp8s+n9fgVyzW35/wDANTVPCE2p6mdQNv4nhuT5LmRJLBmEkX3XVmclfdVIUkniqNnd6ZFqA1k6T4yuLT7XJqcMLWaeQksgOZAVIJG1jjJI5zXofhX/AJFDRf8Arwg/9FrXA+Gnunvbex1LxKyWEljYLFpU9pE0dzHJFgoCwLMCQQcdO/HAXvO1nuT78rWluvLyJNI1b7Hrl/rUVl41uV1CTzZIjp0PlHC7FAKgHCrgDn+EZzzT7K9g0+11C3t9J8eIl9I8spFqoZZHILOhH3Sfbjk8ZrM8GeINR0LRvD9ql1BeW93Y3ogsVjCFJ4SGSIMCTuYOQQfQYA72v+Ej8XLpE/2S+l1OZLGHUZJorFUeBxIoltSm3GShYhT+8G056inyz/m/ArkqfzfgOtl0e38LT+HJPDHjW602XG1Li2LmLGCuw7vlwQCMd6oalrUbRQeF4/D2uz214/2i7bU4mnu5ApXd5aMSPugDdkBfTmtrWPG86aPrd3pOpzXAW4tPsjC1BYRysissWVAc53BScjOQTxUL2+qXHijwwbrWLgahE94t3PFDBJJbq+wxwybFKKSvcjrnBxRyz/m/AOSp/N+B0eh6/EJtVuLjTNZtBc3Ykjil0yYttEMSZOxWHVD3rAvPAfhTWW1XWpNS1qBI5nnvEG6AI4/fZMZjDHG4EEgnGMHgVWurzUNYt/CGpXd9rtnEj3cF7Nb25jfdsZUkaMIdpbGR8vG7sa6CS5ju/CvjK4i87y5Edl86Nkcj7FF95WAIPsQKmScVq+/+ZEouC1d9/Lz7mTc+GdCu5JXm1HxYxlvEvmxp8qjz0+64At8D6Dg9SKenhzw1/b9tqlxd68919rieN7rTmSNZN67QCYAIwzYB2lc55q3DGll8UNVkvDqyfbvsv2MwrO0Em1CH3FQUABx97HWsa6vtcfW9OtidUfbqijVVuYSII0+1IYDG3Ck/dA2E8E7sEU5QaTd/z/zHKDUW7/n/AJnQ+P8AUHtpNIt43sY2eV5A98ZPKPAhCEICcsbgYOQBis5fCfiRLSK1XSvBwt4pUmij23G2N0ztZR2IycY9af8AFTTr7VtLls9MimlvW06d4Uh++WW4tG45HPy/X0yeKh1MeKH03UBp6ahLpgvLYKs/mLdNCVIn2YKyYBKkcgnDgHGKfJeTd3/SH7PmlJ3a/wCGQk3hrVW1WzXVdL8KYvbqX99FbzSuJGiZnYgsv3hHtPPp1pL/AEK+v/Ey3H2O3vxpMRsVhTS4fsy7ljk4WS5DZAKDIwOorU0RNRitdAh1J7qRo9WmWCS6j2O0P2efZkFmbgcZc7jjJFcf481Z7HxPqMcV1d+YXl22sU5iR3a3twjMyyoUIIbDEMBzxUNW0be/fyIcbaOT37+R100GvXNytzP4ftJZ0xtlfS7dmGDkYJvM8dqzbvXb+38SLDLook1cIkvmRaEsrorEorM63R2g4YZJHAPaqXi3X3NtrFlpd8txJfRwTWtxb61EgilTaHQ7pF2DCg8cNk985IW8Mv8AE+8125gsvKeG28i6/tG3IWdS5dyBLnABQdP4TgertH+b8R8sP5395dj1/UH8RXNvDou/U1cQXE0Wgq2CyBtryi62j5dvVvT2qbSZtRnjun0zw/bRoJHtZyuiwxbypwy83Y3LnjIyDzWX4Vl8N6X4y1++ls7CBbu5d7a7bUbZx5ZjUMNvmkjcysen8XOKr6bqjP4Y1zQ7aSx0RHnaexd9WgIMRdSYcxysyFgHG4YABGOaLR/m/EOWH87+839QuNV0zRGkvdEtY9NsVM+z+yYWWLGTlUF4eeT0Geas6XcX63sevT6PL5Ulu5Bgtbe2L+aY23uWuWJOI1HIB5rGF/oDeC9ask03S4o7kGSDTpdWt5i0jDaThn8uPBAYAMR1PBrLumTXPDfhO3udQ062j0oiK906fUbVxcBYggkHLocHOA3rnggUWj/N+IcsP5/xOy1WNrjUzqkmmaxZzLCkZYNp7AKrMVP7xmKnLHoRnA9KrXGtTWeox2FzfeIIbt4mlSN30sHYpAJ9vvCudm0nQ7jWdBku9R0O906z0mWxuIrm+hdmP/LPPQHHr2J/GpmNj9s0HVJm8MXtxZ6WbKa2m1GL/Wh4yr+YQcgbCR8uQW9+C0f5vxDlh/P+J1E0Iv8Awrf311rGtC0ENwlzA0dp5hVN6SLlY8Z+VsEN+NWLnXLfWIfsMmj30wdlYJDe2yvuVgwIKzhgQVB49KriWOf4a65LE6PG66kyNG25WBlmIIPce9cfbaXpqarpV1Fqfhmw+yCNpZobyPzGYC5QkEDk4mR+e4x2zSjbq90v61FHltq90vn9510S205kEOleI5DGcSBNcB2n3xdcdKYJrFraW5XT/EBghBaSUa8pVABkkn7VgcVz2kWdnpmnzRR694Zju20v7ELhtQ88OwOcmNsKFOSSMNye44qGKxhij8QRDW/CrQak1s8UMups2zytowWXaRwMgjoQBjFPlp9/yHy0v5l+H+R0UV9pcywNFaa64nk8qIrr6nzHxu2j/SuTjnHpU9prumaTI9xHp2oB7kmEy3GpwSljEWygL3B+6S+QOhzmsV0gfT45T4q8PtqNpqp1CzSW8R4wuwpseQBXbhmO4gngDoKzjBdLpFpaJ4k8IPNbay2qqz3pCkszSbCOf45CM+gHc8CUFqn+Q1GmndS/L/I7hPG1u8VrINMuwt3n7PuuLVTJg4OAZsnkgfjUs3i1be+jsZtJvI7uTGyFrm0DtnOMDzs84P5Vx3i3TdK8R6pBqMXinRElksxZXcMmousRXcW3ARyLvGSRsbgjHIxzO1vZ/wDCYy63H400WFJTbh/KnVXZIwNyMu/Y+47sMwLKG4NVdfzfkVzR/n/I1/hrex6jpuuX0KusVzrE8yBxhgGCEZx35rta88+Df/IoXf8A1/v/AOi469DpYd3pJk4R3oxbCiiitjoCiiigAooooAKKKKACiiigAooooAr3/wDyDrn/AK5P/I1598Cf+SUaf/12n/8ARjV6Df8A/IOuf+uT/wAjXn3wJ/5JRp//AF2n/wDRjUAek0UUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABXJfE3/knmqf9sv8A0aldbXJfE3/knmqf9sv/AEalZVv4UvRmOI/gz9H+Rztr4Z0uPxO+tahLr4vYNTuLiOGLT5GjA8x9oDrEWKMCrFd5BPNL4ftYJr27u/EFlrOEuboWlmbCZ4EjmY7mULCGG5WIIYnvjGaqwSTSeMtSGreJL+0sGcm2jN1Kiu/2ueIom1xnASMYHTI4HWn2V1eTeJdOtGbUH+1Xl1Bd2K6jdB7GKPPlyM3mZIYBTkgA7wBSj7SytYmHteVWtY1tNg8LeFS+oTS60yRWws4pb+yuSttb5GIlJjAAzjk5J4GeBVFNf8Cx2ElmninVxEwjVcS3P7tU6Kvy8Dsf7w65rW1bU3s/hRYatO8kskMFhcuxUyO5EkTE4yCxOPUZ9a5fTviNevomtW82tW6ajGsLWNxdxdS+N6ny02naeMgNjOTuAzS55X3S+X/BF7SbfxJaJ6r/AIJreHNY8GadrdvFpGqRR2ywXcs8lyzRZlkkgPVwoydp4HQLSeKodF1/WkuxrumNCkUOwR68bRkljaRg3yK2cbxg8YOfWs8eOZz4XgSPxRt1FtS2PJdRxiTyFALAGOMqAR91mQddvB5qW08ewx6fp1xe+JbrZe2M8LgQQtLbzq+Y5HVFypK5HI2nA4GaXrJf18xes1f+l3L9xc6Xdm4N1P4fnNzZLYz+Z4nk/eQjPBxH1OTk9Tk+prY0DWtHsEvTda1osRnnV0jh1JZgqLDHGAWbaSf3eeneuKufGNpquqeH/P8AFmp2Vle6awvfsq+WUuEZQu75CY8kyEnjIA7EZg8T+KJrjVdWtYfEMKgRSRRRJK8tvcWxi74XZ5pYkZ3gggfKR1G7a8ydgcmlzOadjqP+Ea1LwyukQaW2kXNw0/kwG6t5lWNvKdmkGJWCswQ52qMljmqU3gnxY+matYQf2HbJqoYXbxXV2zOW4Y/OWAJAwTjpXZeJDcLNpBtFVrkXcpiDdC/2WfGfxxWP4Yj1BID/AGpLr8lxJYAXsc4/dpMPvGJl5BOSAIzjCjocVSp6tJvQpUrtpNq3n5GLZab4m12NryC48L6jp52wx27yTyQRPCzDcgP3XycE5/hGPe1/wiviT7Gtp/Y/gv7MsvnLF5U+0Sf3gPXvmqNvNfaH8HP7NW2vrTU4isMULKY3maSc4jRyR8zKcFgcrnPUVB52p3fhy10WJdUmvIL4HVgs9wXto2DNGn8EkilMLlWX5lBJ60/ZebK9j/ef3m3feHvFepx26X2meDblbZGSESxTt5akAEDPQEAA+opL/wAOeKNVS2TUNJ8FXS2oxAJoJnEQ4+7kcdB+VYy6bq9zonhCPWLLxGJ7aSaDUTbTsGaIKwG8pJkgsUweWwG59d3WtD1FrvFha6s9rDpsUdjJb3oEkUyuSc+bKAWwEyXVs+vUE9l5sPY/3n95FPpXia712K5nsvBE2rW8YaOR45WmjTJAIJ5Azn9akg0zxYuq3d/BZ+CxqD4juJ0jm8w/KCAzdfukfgRUlxod5bePb7WxocmoC6trRIZo7pI/KZGbfuBYcYKtwCDt6ZqPSvD1zpvjPVLuXw99o+1akbq31IXKbYkaEIcoW3ZBDDhf4+uKPZebD2P95/eVl0TX7JBpDWfhfTrXVzJaSS6daybxmJ2JwSoPCHv1I4Na+v6VqGv+IzbWupQ2KWdkpO+yW480TSNkEOcYBt0I4z1rlPDXhvXNH8WaDc6sl2spZ4rqU3KPDczCGXEoUEsW2gjc23AwMemh8SreKe21dpbdJxCmlSCN3Chv9LlBGTwMqWHPHNTyK9m+v6XM/Zq/K29+/lf8yHUdEv8ATNS0nR7jxFCf7Sldbfb4ftzErqm4554JC/jj2raPg/xE0cEZ8WW5SAhoVOiwYjI6FRnj8KyD4X1eebRml0YrY/2497LpxmiKWcBhMe0jOG+ZmfavHzMMGql94flbRbCyultbPxI1xcWttEgjkY2csjLkqMfKkZ3A9igz1IqvZR8/vf8Amaewj3f3v/M7Kyt9T0rTrCxTX9HESQrFAZLJt0iooGR+/GTgc4qCwXWtPurTw7b6hZSC1slPnnTiQirhFVv9IB3Ec9McGsDxV4Avr67tY9JsdONrbWcVvH9q2MhKuSQ0ZjO0YJOY2QseDwAR0tzZ6xB40j1Cx0nTntJLdbe4uWujHMRuBJ2iM7tozgFu/aq9nFf8OylSiv8Ah2W1bWXuXtk1vRmuEAZ4hYOWUHoSPPyKgmm8QNbXZ0/VNFvbq3BH2dLNgS+OFY+edpPvWZo3hjUtN8TNcyafpDqkk7f2qGYXU6SfNtdQACQ2OSxGF4Aqn4O8J+IdB1a61G6XSw9zaCKWKFtoeZWJEg2xqAGzyCGI9TT5F/TY/Zrz+9lc3OseMPBVrf3z2Vq7X6QCJLaRZbaUXHkF1kWbggknjqMjvWfrP9qeCYb9YPFNvbvHBFNmWGPzL6Z2lADSTyMSwWL+9jAwAMc9Fa6TqWh+G1sb37IyHVop1kgkYnMt8smCCo6b8ZzziqnjuMX02taQupaVYSX+m28XmajLsATfcBig7sMj6ZrKaXNZvT1fmYziuazbt6vz8xL+41TSGSPVvibZafM0Ql8q5sbdGCk4z97kZ4yKXzLXTLmXT9X8YXVxPqcbXjtDYwiGSLYkfIMbg5AAAB59O5ZLcW95ruiavea/4UkntLS4trqP7QChEhUqY8tkHCAHPZmpbKdLS10NovGfh2G5sLJ7KZFZHhZTt2so3hgR5a98HJ4FHLT7/i/8wUKP83/kz/zJJtB8J2+tR6PNq8CahJjbA1jZAknkD/UY3EZIHUgEgcGmWth4SHiJtLtdbVdWtnyETT7RWV1wflb7PgsMjODkcVn3d/4RtPF13fSeILKVJbyG9eM2cs+yREUDZIjbP4VOcEqc/hj6L4q0fTfElzrb6k0r3d/MBBPbyMLS3d/mZGDYG4IjEbSc4GByan9wuq+8n/Zk/iX3/wDBOpEmieKLsfZvGGv3F1aRSEmzj8to1yA6N5cIO7Kr8h+bgcVk29v9n8Cy+JtW8SeJSkbOPK0/UHlLYfYFAeNTu3DByAB61paF428PaRbXkEniS2nE1xNcRFNMmj2NI7OQ3XcAWxng8daydO1bwtF4RvfDup+LRd21xvZJItNlhaJ2kaQsPvZ+dgQD6c5zQ3Qera+8G8M3dyX3/wDBNyPTdMsrvS7ifxR4pjnnuDFZrfbm/fFCMbZIiAdrMAT74PFaNxcXE3hS+1vTPEuqSpDbzSxGW2gQMyA9Q0IOMiuS8R+MtHvtDuNNTxBcX13csrW159j8pdPdcYfhQ2c5OVDHOegrQ1zxj4Wk8FXGj6TrskDJamKJVtnJkAUjYSyYG7oTwec5FJyoqL5ZL7xOeHjF8sl9/wDwT02sXxTFHPoqQyxpJHJe2aujgFWBuYwQQeoNSf8ACR2P/PDVP/BVc/8AxusvxBrsM+lAW1jq88sdzbzeUmmXAZgkyO2CyAZwp6kVrOceV6m1SpBwav0OLt7TWp77UrSbQPB9vJYRRTXCrpu4xpIkjYB3YZlKAdADkntitTw/qvhC58O29zquhWVtdx6THqNwZtNSNXQrhnQ4wRu7e49arxX0ia3rWovp3jRxqsHkSQHSogsYAIQqRzlQzAZJznnPFZ8dlZG2htbzR/Gt1bppJ0ho305F3w5BByuCCMAfhznmp56P9Ij2lDy+46rQL7w9d+M44tEs7e1lgsZxcpDCiHloCmSnB4J78c1Hr/iG903VJ187W5Vk1FLG2g02O1IDGCOQAmZc5JZ+/btVPw1NY6Zr9q0ema9YWvkPbhr+x8qPzJJIQgURrtUkqcsQMkjJPFUfGmoWces/ZJ9TSyaLX4byR0ZvNSNbWJcqFRupbvgHBHPOFzQ3vZX9OhPPTWt7K/p0NifXLyK106eGfxRdfbXkhEcMViWhmTdmN8oADlGGQSMjrUE/iS6slZby68SJNa2aXmpLFHZOtijf32MY3EAMcLk4U+wpEHgrVtJsYbTxZcWSWE7yrIt6LeWWVhlpH8wAsTubnGMsfwv6tb+CtauY57vxDbB/KENwIdTSMXcY6LMFI3DP06kdCRVp03s/xNE6T1Uvx/4JSbxJOmpXFs9/4hWC2vIbSe6ZbHYpm2+UwAjJKtvXtkbuR1p1j4gu77WbaBdR1tNLvJ5bW01FhaATTRhiy7PJ3BfkfDd9tRWsPh5vGus6nf6vo8ljcSW01qo1UY3xRhRuizsOCMgnPb0Fa1svgW01dtTi1XThcmV5wG1INGkj8M6xl9qseeQAeT6nJ7nf8R3p/wA34/8ABOf0rxpNqN1q6S6jq9pBp1tNdN5kln5+2MkHfB5O9CQMjIPBHrT7DxjLdaPqF7LqWtxyWiwfu0S3ZJGmYIiq7W6gnecEjIHBBIrV06w+Hul3UlxBqdhJJJA1sftWqmcCJsbkAkcgA4AwOwqe0j8B2dlcWi6rp80E4AdbnVPO4ByoBdyVAPIAxg8ij3O/4hen/N+P/BM3StR1wXmsLd6xOZdP1i0tfs4MMitHL5Gdx8pTz5jYxt6e2T6JXCuPCVhaLBol7YPd3V/Y+YUvBNNPsuI8FiWLMQM8nPFd1Tg1d2Y4Ncz5Xfbz7hRRRWhqcl4E/wCZl/7D11/7LXW1yXgT/mZf+w9df+y11tZUfgRjh/4aCiiitTYKKKKACiiigAooooAKKKKACiiigCvf/wDIOuf+uT/yNeffAn/klGn/APXaf/0Y1eg3/wDyDrn/AK5P/I1598Cf+SUaf/12n/8ARjUAek0UUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABXJfE3/knmqf9sv/AEaldbXJfE3/AJJ5qn/bL/0alZVv4UvRmOI/gz9H+RDBYXF69zPZaeI4Wu7hQP8AhILuHcyyurNsRSq5YE4HrUv9i6nnH2MZ9P8AhJ73/wCIryTU/EVs/i221GKK3uUt9R86GYoQUh+0yyEZZSVLbwflA4wDk8Dp7Xxh4ah8ai+ltbaaRbiaVdZeSbeIpBjYE2EkgbVCn5QBkEE1jGVJpNyX4HPGdBpNzX/kp3Gl6zOEXTNOh0FvsgMAgTWHZkEYAI/1Ofl4B/Wm6H4o1jXtOmv4NGsYbaOV4w8+pMA4Q8uMRH5T2Jx9K4nw14w8PaJrN7CYNMFr9ouJl1JIHWWVJWLrGqCLjBO05IHAIznjPj1rR7jwTq+hNqVnp4vL17uKOKOZo9jy+YYHAiGBj5SV/l109pT/AJ/xRqqtJf8ALxfej07/AISG++zRXO3w/wCRKSI5f7Zba+M5wfJwcYOfpVnTtaurvULe3mt7Hybm3knins70zq2xkUjmNR/y0HIJ6GvJrnUvD9zBDK1xpI263FqA00QTeRDEkfllVbyeWbAc/KBn863dC8YeHNM1wyPeWsFmHvjELaGYgLLJC6ZBjGGO1yQMgY680nVgvt/ihOvTWqqL70ddY+KL6/tY547fRELW63LRSasweKNlDZceTxwR7UDxLqr63b6VFp2kyzz2xulZNXyBGCADjytxBzwQCODyK8yu73S7u306aw8ZDSJV0uC2u4FsHfzJUQplm2nICSSDHTIU84rpbzxf4ePifRtRtNatRbadbS2+yW3n3uJNmTxHjgRjHrntRGrBpXn+Qo16bim6i+9G1e6hrer+If7FGnQ2V7p6Jfx3EWogqyuJIhjdA3+2CCo7VV07VNcuvEEulXV9eweTeCzkkS4t5PnNuZwVH2UZXaMckHJ6VTj8baBH44uNa/tq1NrNZxWnl/Z594CM77vuYyS+MegrNtPFej23i6XUptYtJba61P7W3lW84aJVtWhUEFOf4c47npiplOnvz/iiZVKW6qduqOp8WaeI7K0g1XW724065nMdws1tbyYURSSAqBDnduRcYBPpziquirpei+FdKuR4ln0y1v1RolU2ziR2UYAcwAuxAHJ5OKg8RfEfw8406ewvmnlt7ppGVbZyQDDKgOG2A8uvG4Vyln4z0qz0LQNLW6viujTpJG505P3qohQKw8/r8xOR7cep7akm7y/EPb0E3ef4s9BuNWsLXS4NSl8aaj9mnJWLZBA7uQcMAiwFiR3GOMHOMUy/1vTtNkgjufGWq7ri3+0weVaRSiWPPVCluQx74GTjnGOa4I+M9JTVItRtrq+ingubmSFDpsbRiOcqzow84FjlQdwI6nip7nx9p0uqaHfRXd8H0q3eILLpsbCVnUKzHbMoAwBhR0p+2o/zfix/WMP/AD/izuJdYsIL+1spvGOqxz3So0Qe1hA+f7gZjb4Rj2ViD7VL9vtv7dGinxdqwvy5jCG1hClgm/aH8jaTt5xnOK8z1PX/AAlqPi9tf8q+jeUxPKradBJIJI+FaORnOzgKCMHpkYPNRXOv6FceMYvEf27VUuILv7RDjToDIEIIaJnMhJXBIXGNue55o9tR/m/Fh9Yw/wDP+LPSFu9N1G63f8JXq7nT/NuRMbWJYk2bonYSeQEbGXGMnv6ZqhaTaXr+t6e07XV5OZ/Jmt9Y063WTyWhmkRh+6DbSyHBBxw3FchaeI/CMV9f3V4+vXn9oWklpdo1vbxC4Dnl38srucD5Q3YE+pNWtC8V+G9P1XTmW71FYop98klzZW8aqoglQf6hdzHLjrnqelTKrQf2vxJlXw72l1XVmn4/8MadFb69e2Gn2EEmm6XDdInksqH5pywxGyfMdi8nOMdK0Nb8L+BPD+nQXd7odw4lB4gkmbGFLEk78KMDufQVT13xR4U8QS6xZy+IJ7SzvrGC2aaC2YswDTb0w0Zxw68478GodQ1LwTq0OlLqPiy9upNPEq+ZJZA+csnBDL5O3IAABABA78mhPDve34BF4V6vl69u5k/YPCFl4hvrifSrq80B9LtdRhkgEuLWOQuCz/PuI+VT3PXjANdDc6B4Ft9bbTh4cu5Y4pore4vI55DFBLIB5aN+83EncvQEDcM4zVWK9+HsVmlqviO/8r+z4tNlAjkHnQRltqsRHkffYZXBxWjc+JvANzqJvDrdzHvlimlhjimWOWSIjYzDZnIwvQjO0Zziq/2b+7+BX+x/3fwKdpoHhS98QXWjw+CdS8yzuBDczG6xHErAMj587JDKc4AJHcCm6PpPgTWdan0uLw3cRTpDJPHvvCfMVJAh4WUlTkggMBkHNX7DxV4H07VdR1CPxFeSSag++4jlikZGOAox+7yAFAAAPSqukax8PNFurG4tdcvC9jA9rbiRZ2VYWIPl42cgEAjPPA54FH+zf3fwD/Y/7v4EVlo3hyw8N22v6l4Wns5SkMkP2W+kdnlkZRGseHyCSy8nGK0dS1ax0/TLy6Gn65JPYXkVrd2n9tTLIgkKhHX97hgd645HfkYqimo/DH+z57CbUbq5tJVVPJuHu3WNFYMqoCPlAIBBHPvViTXfhpNZTWj3shinnW5nP+lB5ZFwVZ3A3NjauMnjA9Kalh1s1+BSlhVs4/gaF5Na6Pa2k+tWmrWK3DyRmQ65O8UTAFk3sJON4HXBAPHpnV8Fz3M9lfm6ingcXKEW8121yYQ1vC+3zG5PLE/ia5rWvGnhbVLW30j+04n0pipunmW5aUhGVlUfIc5xyxbI988XNN+IfhW3v9Xkl1TalxdrJEfs8p3KIIkz93j5lYc+lDqUU1Zr8AdWgmnGS+9dh7+KpNF8R+JUk08SWNvd2jz3Anw6+dHHEu1NvzYKgn5hwfatO18Q6tfeINR0+HTLaO30q4WO6ne4ZjIjRiQeWoT7wDDIOBzwT286k8U+FU+Iuq67dR3l9BJ9ma0NuHUBo05LKzqG56blOCuQav23jjwJaa/NrkGla0moTuXlk80lXYrtyUM23pwOOO1KOIpLRy7iji6CVnJbv8zqh8Qo4LWC7vdNeKG606bUrZYpfMlaKMBiHTA2MVZT1IzkZ4rOu/EusaFJq2rXEFrNuisZ/siag8ipC8jozJlQAfu5wMHrntWdafEPwLY3E89roF1FLcIY5WW2iyykklfv9MknHTmobfxz8PbRHSDwzOivD9nYfZIjmLOdnL/dzzjpVfWaP8xX1yh/MjqB43uJbu9sILKIXaaudMt3kkxEcRiTc5HI43ADHzHAHUkO1DxBrkcPhxIv7OhvL3UGs7xFczxoVjlbCsMd4x15GcVycXjX4dQWM9lF4XlS1uI1jmiWzhCyKpJUMN/OCSR9amb4geAn0X+xm8O3B0zj/RfskXl8HP3d/XNH1mj/ADB9cofzI62/ma71LwxdNqVo9qbplZraZ1EknlSYwQ+CuVxgg9aztY8ReJbLX7nRYDp/2m6lgbSna1kZXiZmEwfD8lAAxIwACPXjHk+I/gaWOKOTw7M6QrsiVrKAhF9B83Aq4fi54XMkch03UN8QKxt5EWUB6gHfx0H5UfWaP8wfXKH8yNnTbmyt/iNrUV1qdi9/PBb+REkhWQJmT5CpcgsMA5ABwRkVV8N6rrWp2mpQNrunnVIrq7jjtpbcb0CTMqFlDg7doHYcEcnvjj4l+CVvvto0C4F3u3+eLOHzN3ru3ZzRc/FPwzKl01ra6nZXlygVryC2g80Y6HLMQcdsg0fWaP8AMH1yh/MiLV/EWt6z4I1u+lKW1vaC1iUJC0cy3iyRmbndwEf5RjPP8RxVzULPT7rxVdWyX08unHw891FO1883lP5wIljd2baRsQ5Bx8orn9W8a+Hr3wXN4dsE1CKS4dC11eIpDOZVd5JCrEkk7icKfYUt34g8P3usm5nGjHTzp62JsFkukQqJRIDkW444xtxg9/SsJ1qbqXv2/U5p4ik6vMpLp+t/0O7+Ht3d6hok15fkm8uDbSzkrtJdrO3LcduSa66vPdF+IPhu1bUJrzUreJ7q5EqxW8c8iooijjAyYl/uE9O9av8Aws3wf/0F/wDyWm/+IreFanb4l950wxFG3xLr1Xc62iuS/wCFm+D/APoL/wDktN/8RR/ws3wf/wBBf/yWm/8AiKr21L+ZfeX9Yo/zr70dbRXJf8LN8H/9Bf8A8lpv/iKP+Fm+D/8AoL/+S03/AMRR7al/MvvD6xR/nX3o62iuS/4Wb4P/AOgv/wCS03/xFH/CzfB//QX/APJab/4ij21L+ZfeH1ij/OvvR1tFcl/ws3wf/wBBf/yWm/8AiKP+Fm+D/wDoL/8AktN/8RR7al/MvvD6xR/nX3oPAn/My/8AYeuv/Za62uM+HV1De2ev3du++CfWriSNsEblYIQcHnoa7Oij/DQYd3pIKKKK1NgooooAKKKKACiiigAooooAKKKKAK9//wAg65/65P8AyNeffAn/AJJRp/8A12n/APRjV6Df/wDIOuf+uT/yNeffAn/klGn/APXaf/0Y1AHpNFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQBXv/8AkHXP/XJ/5GvPvgT/AMko0/8A67T/APoxq9Bv/wDkHXP/AFyf+Rrz74E/8ko0/wD67T/+jGoA9JooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACioLe8gus+Q/mAM6FlU7QyMUYZ6ZDAjHsanptNOzAKKKKQBRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUVjXHiWztZr6KWG4DWlvLctwvzpHjdtGc9xjIAOeMimy+JreAlJbO7jn3RhYXCBmDhypyW2jPluOSDkYxkjMe0j3I9pDubdFYn/CUWKtEskdxEXMwIkQAp5a7juGeMryP1xS2fijT73UY7FN6zOzIAzJkOoJZSoYsCMNyRjjr0ye0j3F7WG1zaoqnpeoJqumwX0cM0MU6CRFmADFSMg8E+tXKpO6ui001dBRRRTGFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQBXv/8AkHXP/XJ/5GvPvgT/AMko0/8A67T/APoxq9Bv/wDkHXP/AFyf+Rrz74E/8ko0/wD67T/+jGoA9JooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACoL28g06wuL66k8u2tommlfBO1FBJOByeAelT1h+NP8AkRPEP/YMuf8A0U1aUYKdSMH1aQnojD/4XD4D/wCg7/5KT/8AxFcXF8RfB6+J7C6kud0sOp3FxNqX2eT54XimEa427jt3xrjHG3jjJrV8I3mgXNhomlbPErTG2t4ZbmG/u0to5jbrLsyJQF+UjgDHIArsI9G8PSvbpHq+oO9ypeBV8QXRMqjqV/ffMB7V7arZbhpTpqM3ut4+a7f8AztN2eh5SfiJoU2m6VYi+lt/7O0k2ckoiY+cwktiyoNp4dIXA3DHOGA7k/jnwktlGbe5nlZZppIILiAbYtwjA3IiIqZKMd0RLLknncRXqNtY+FbySaO11+7neBS8qxeI7ljGo6lgJuAPeo4bfwhcQzSweI7iWKFQ0rp4kuGEYJwCxE3AzxzW6zXL1a1OfV7rr8hck+55qfHHhOMFLa7SKNZL9pFS2dRcJJeQSqnC/wAcKMnOMYwcDGbdl438B3OuQzX08aaUq3Zis5bSRlt9/wBmCqVCleTHM/GQM9jivRpNK8Nw2Ud7LrV8lpIdqTt4hugjH0Dedg9D+VZurXHgzRDY/wBoa9qMSXyl4JP7duyrqBncCJenTn3FS8zwDXwz6/aXXfoHJLyKHh74teDrXw1pVvf66wvIrOFJ91tMx8wIA2SEOec81pf8Lh8B/wDQd/8AJSf/AOIqea38J299a2M+u38V3dqGghk167V3B6cGXv2z1rA8ZXekaRaXlppuoanJqKQ3CsRr13utpFt3lQ7S5DH5B8pxxz7Vyp5ZWq25Z3k+8ev/AG6V76XQ2P8AhcPgP/oO/wDkpP8A/EUf8Lh8B/8AQd/8lJ//AIitjxLL5Go+HJdjPs1CRtqDJbFncnA96oeGPGsut6bdanqNhbadp8MCTi4S+WdeQSyPhRsdcDKn+9XPN4GKi/Zz1V/jXdr+TyH73f8Ar7yt/wALh8B/9B3/AMlJ/wD4ij/hcPgP/oO/+Sk//wARVvV/F7yeEtQ1jwyLe8uLFGkntrpZI5EVVLFTHgOGIHAIGc5q1aeMdNaDRI76Xyb/AFWx+2RQJE7ggRh3wQD0B6dTWftMD/z7n/4Gv/lY7S7/ANfeZX/C4fAf/Qd/8lJ//iKP+Fw+A/8AoO/+Sk//AMRWo/jXT2l0f7JbX17b6pFJNHPbWzuI1TGS4xuHLAYxkHrRP4jlHjXTdGjjMUFxbyyu9xA6eYwCkLGx4JAJLD09waPaYH/n3P8A8DX/AMrC0u/9feZf/C4fAf8A0Hf/ACUn/wDiKP8AhcPgP/oO/wDkpP8A/EVp/wDCcaSdaOmrHeviR4BdLbN5DTKCTEr93+U8DuMZzxXA/Eb4gaRr3w9v7K2t9Ria7jR4JLi1aOORo54xIgY9WU8HtxwTW+Fhga9eFHkmuZpX511dv5CZcyTd/wCvvOr/AOFw+A/+g7/5KT//ABFH/C4fAf8A0Hf/ACUn/wDiKt6P4tFz4Y1LxXdmQaQHkktYo4CZBBGSm49yWKsw9AR6E1I2t6h4i8LT3/h3da3sDhkS5VJEn2gMUDKxUqwO3cp4OfQ1h7TA/wDPuf8A4Gv/AJWVaXf+vvKH/C4fAf8A0Hf/ACUn/wDiK6Pw/wCJNJ8UWD32jXf2m2jlMLP5bphwASMMAejD86888OXP9tR3l9HBq11Cw8+G0sdRkt9vnX97uY7JFU4AXJOeF4rc+F8K28HiuFC5SPxHdopkcuxACDlmJJPuSSa7MXhMJCnU9kpKULbtNa+kUyYyldXOu1q9k07QtRvoVRpba2kmQOMqSqkjOO3FcJa+K/Gd3ZwXKW+lhJo1kUf2ZqDcEZ6qhB+oJHoTXZ+Kv+RQ1r/rwn/9FtXnXgPXvEEWmadc3Wox3emG+GmG2kSOIwR+UrI6MACxHQg5457E189NSlOydtDKopSqcqlbQikh8VSPeFjabbqG4hZP7Lv8IJyGcj9znOVGMk46dKtXtz4wvbiacmyieWOOJtml35UqnmYBVoSDnzGzkHoOhFdTo/i+LxTizhtNRslvLVpYLtE3AL0B34KqxBDDOcj8qjt9ePhvwMby+mu9Slgu5bSNpuJZm+0NHGGOAB25x0FT9X/vEfVH/N/X3nHG18SGKWPyrPbIsKn/AIluonAjAXqYv4lAVvUelX4L3xjb3hnQ2fl+Y8q2/wDZmoeWrvncf9Vk5JJwSRknitW+8c6q/hO9vLXSlstTt72CzIu9xgJlkRBIjbVLr8/ovQ/jf8Q+N38NyWFnd6f5uoXvmmOO282aMBADgskRbJyOAvHfjmhYe20gWEa2l/X3mdoM/jZtLjtLB/DzRWKrakXEN1FICqKRuDKpztKnpjmmHxJ4z3yIi6NJ5cjRs0WnahIu5WKsAyoQcEEcHtW/4P1NdZi1TUUgmgFxdxyeVMu10JtoMgj1Fc3pnizVF1PUdN0yxspLfTNSk+3vcXQjkKS3Mh3Rg4XCjnLHnoBxyKm9EpPr+ARpy0Sk+v4OxL/wkfjX/nhpf/gq1H/43R/wkfjX/nhpf/gq1H/43VpPHdz/AMJEIHtbY6Y2qnRwEdmuVnCkh2UDAjOPqAQTxmoNF8cTeIPFEmiTxwDT72C5a0ntWlVysbhCSzBeSCSCnTHXvVeyl/MX7Cf87/r5iQeIPGs93DbBdDjlnYrH59jfRKxCliNzoBnCk9e1TX+r+ONOmhhn/wCEeaWZWZEgtryZiF2hjhFOANy9fWqfhFEtoLGyimkkhtfEt9DEJJTIyosdxgZJJNXvHurX+h3+m6lYT2MTwwTeYt7kJIjTWylQwPynkHOD06VPJKz957/5E+zlZ+891+hV/wCEj8a/88NL/wDBVqP/AMbo/wCEj8a/88NL/wDBVqP/AMbqPxL4q8R+HY7Gwe90yW+vRPMl8bcRWyhFXEXzzAFix+9uHH8JpuseItaOq+GZRr+n6Fb32nSSyrdRJPA0w2fL5gkAJwxK4PRSec8V7KX8xXsJ/wA7/r5k3/CR+Nf+eGl/+CrUf/jdH/CR+Nf+eGl/+CrUf/jdQS+Pdak+IK6NbWtqunwvCjtK0atco4/10eZAxXngKr5xyRnhdF8V63NrNxLqWr6X9jt9bl0lrVIxGdoDbZCSxIclRgdCM9TjB7KX8wewn/O/6+ZN/wAJH41/54aX/wCCrUf/AI3TU8T+MpASkeksASpK6XqJwR1H+rpfA+o6jNeXsWseKLiW9F1dQ/2fcW8SFQjfLKMKGC7Np5+X5j7VneH9ZbRvh1qq6TPbXOoW+oXAaSFE3CL7RsNyyL1AT5s4IOB2o9lL+YPYT/nf9fM0v+Ej8a/88NL/APBVqP8A8bqWz1vxte3gtIhoKTmNpAs9new7lUgEguoBwWXp61gXXjDXo7Q+Xrn+hW+r21nFqptYyuoQzAb8DbtDRncdy8HbgjrXQeEdTvtR8RPDf3gvZbCTUbNbny1QyqslsQSFAGRuK8f3aTpyX2hOlNa8zMqTxl4+h0uDUp9J0SCynVXjmmnWNWDDI+9MO3OKuRa78TZ4llh8P6TJG4yrpMpBHqD51ZerxTPJ8MZlkvIreC3LTy28PmCIG3UBj8rAZJxz61uS/aZ/iCbCHWdVttImsophFDEFj84MMIr7PkBQZIBGcnkdKI0m0nzv8P8AIUKEnFPnl+H+RF/bHxR/6FvS/wDv4v8A8eqG68Q/Euys57u48PaWkEEbSSNvB2qoyTgTZ6CnWmq6yfF1xBf3GrrMby4ia2FoRaJZBXaOVZAuN5wnO4tkkYrmW1nWVtVgmuNdkhuNKl+1JewMUQtaFsEheD5gOcnjIHHSiVJpN87/AA/yCdCSi3zy/D/I7LU9T+IWmrbAWvh65kuZfJjjgMoJOxnJy7KAMIe9ZF14x+IFnf2NlcaNpCXN+WFtH5gJkIG44xL6c81vfE2yvNR8OwWlgrPdyyyiJEdkLn7LP8oKkHnp75xXOtbW11p/hoWdh4ktrOHVIvPFwbhpIQ1vNHhGJLhVYhSwwOQc45o9k237zH7Fyb99/wBfI0/7Y+KP/Qt6X/38X/49Uun6r8RL28uLSWw0GzngjjkKzmQ7lcuAQUdh1RuuKxZrfxRLodpbXkWrrbWl7ews0TTPcSKGzbv8jozLt3LyTkhSevHW+EjqZvH/ALYLnUBpdoJjIiozHzLjkqrMASMEgE/0o9k017z/AK+QOi0177/r5GFp/irxjqWoWtjCNAS5urIX0aywXSqYztz82NpI3rkAnGavrqnjh9Yk0oP4Z+2RwC4ZNlzjYSQDuxjOR0zmsqwv7qy1nwndromrXVrBoAt3ntrfegeXyCvORwBG2fTitHTHn0/4oa55Og6otnqEUC/ahGPJMyeYXfJbgEMgyOpXpVRp3indlQpXim5P7zQ/4uH/ANSv/wCTFU01TxzNeW1vC/haX7RDJNHJGZ2QqjIp5z1y4/I1R8H6BrdvrN3JqtjOYrq2nL3F3IvmB3dcI6xzMjkqB8yqmAgAqt8OfD0vhvVLCxudBbTruPTZ0mufOSRbwrJD8yhWJAGe4B+aiVOy3YSpWXxPp1NtL3x++pT2IXwz5sMMczEifaQ5cDHv+7P6VT8Qa9458OaZ9uu08OyhpY4I4oRMXkkdgqquSBnJ7kVJ41idr+7WTS77ULWSC0Mltbwyn7SqSTlk3qpAILI2GIB6Z5rj7uK7PgrTrCXwpqt+8esLeRWT2ckhs7ZZQ/kl5FAbKArwSOcZxUqK6yf3kqMftTf3nW2GtfEC9azRrPQbWa6gknWK4WYMioyKQ21iMnepGCRjvUtrrHja5sLK7M/hSFbyJJokmeZWIYAgYz15HStDQ7tL/VNKkt9GvNLig0+4R7aazaFYCzw7UBwFJwrH5SelefXei3F7Ppkr6VcmS2trKIi50uaZMxhS45i3x4Ib/VthuM98qyv8Tt6+hKS5tZu3r6HYjWvF7ahLYDUPB32uIqHhMswZd33ePfBqc3vjhXlQ3XhEPEN0imSfKD1PpVSK/az8XX9zFok1xZ30kUpuX0+4R4SqBWG0QEsflBBJ744AFcxpllq0Gv8A9oXul+agkvjNGthcKlyJ8EHaLbP8IBDs34YqrR/m/Evlh/O/vOxhvvHFyWEF14QlKDLbJJm2j3xWdZeJvGd/q2o6fG3hhWsI45ZJi8pjZXLAEMGP9xs5x2rl4fD15/wjmk6YlpcWUqaLc6fdSQ2F1jzGeN0Y4hBYN5ZDdDhz176gsL9pdVb7Fb28N7Z2dqLaDSrsx4hclhhoCAGV3A4OPl680Wj/ADfiHLD+d/eb0mueLYrWC6k1TwUlvcSCKGVp5gsjnOFU5wTweB6VVu/FPiq10P8AtddQ8Gz2bBvKeK4kxKVzlVZmCkja3fsapy2t1L4Xu9Jks2mM+pLdAT2d8w8oSB9pYQA7vlC59Cfx0Ncub26ksrrS7OOOeO2mt5obrSrxkUSbSSjLEDn5cHIGc0Wj/N+IcsP539503g/WbjxB4VstUu0iSeffuWIEKNrsoxkk9AO9blcl8Mv+SeaX/wBtf/Rr11tXSbdOLfZGlBuVKLfZBRRRWhqFFFFABRRRQAUUUUAFFFFABRRRQBXv/wDkHXP/AFyf+Rrz74E/8ko0/wD67T/+jGr0G/8A+Qdc/wDXJ/5GvPvgT/ySjT/+u0//AKMagD0miiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKw/Gn/ACIniH/sGXP/AKKatyo54IrmCSCeJJYZVKSRyKGV1IwQQeCCO1aUZ+zqRm+jTE9UeGeE7m2j1jQrx9Q8Padaw2kAu7gauiSXcYtgvkywA4LK56tzhcegq/bvaadrWkXb+IfCMum6JJd+UtvfoLiS3lD7Y1GAAUDBQucHrkYr0z/hC/Cv/Qs6N/4ARf8AxNH/AAhfhX/oWdG/8AIv/ia7ak8FObm+bV36EpSSPCdC1zT9N0nV7a4udLuZNQ0doUljnaJreMcRxuPLXc37w7trOx2d+Kt6PJpusaBq2kza7odvfvNb3/8AaQufs0dxKhAERVo42RcRqcoDgnOSeK9r/wCEL8K/9Czo3/gBF/8AE0f8IX4V/wChZ0b/AMAIv/iaj/Yf7/4D9487hstCTQYbE+LfDkUqX0l7vTVWMqO6nJWcybt+4nLYAIJG3JzWhDNpdpZeGWh8c+G5b/RYpYmeWaNY5g6bfuq4xjC/Xn1rtP8AhC/Cv/Qs6N/4ARf/ABNH/CF+Ff8AoWdG/wDACL/4mj/Yf7/4B7xwl9Z+HL3X7rU5fGvh6T7ckBuo5Lr5BLD9x0QTBSO+1t2CM+oNbxjPY3Oka59h8c6ALSQT3qW0ZjeeSQwshi3eZgggkA7d2SPQCvRP+EL8K/8AQs6N/wCAEX/xNH/CF+Ff+hZ0b/wAi/8AiaunPBU5qa5tHfoJ8zOe8VeK9CmGlT2Ot6dctbXbySLbalbLIqtbzR7l3yKOGkXvXFRXmjGXV7i51BjdajbwRGW1vNNhCyRNuWZl+1kO+7BJPuOhr1b/AIQvwr/0LOjf+AEX/wATR/whfhX/AKFnRv8AwAi/+JrRVsByqMoydv8AO/RruK0jziLxHYRWWuE6gH1PWcLPdm600KiBNihYxd9gTySeevpVddZsF0zQ0GqldT0QNHaXy3Ol58pk2FGQ3RB+XvkcgHBxXp//AAhfhX/oWdG/8AIv/iaP+EL8K/8AQs6N/wCAEX/xNHtsu/59v+vmFp9zzK21uysNJsbSy169insmlSK6a/0tmMEhBMbL9p2kjaCGxwR0xxVnUvE9pf6/pOqJrNxENNQrHEbzSn3swCuzH7QOWXI6YBOR6V6J/wAIX4V/6FnRv/ACL/4mj/hC/Cv/AELOjf8AgBF/8TR7bLv+fb/r5hafc88i1zw1Fri6h5961sl097Hpzatpn2eOdgcuB5+7OSzY3YDEnGa5XxgNFvfB32OwvrtpLF5p7dJ9T01lxI4eRSI5S7YwSoAJzgc17b/whfhX/oWdG/8AACL/AOJo/wCEL8K/9Czo3/gBF/8AE1rQxeAo1Y1Y03eLT+7XuDjNq1zk7OTwtbaNqPh5PF2k2ujyTebaPZ6pGk0Ydy8kZ7bdxIHXKsQenNhLrwrpnh3UtO0Lxjo9pc30hke6kvImKuwVWYKrKAdq8YwAea6T/hC/Cv8A0LOjf+AEX/xNH/CF+Ff+hZ0b/wAAIv8A4muP/Yf7/wCBXvHnPhq88NqdV04+KYdNt1VVguIdRSJyEv71wAxPIKshPqrj1FdN8L54rmDxXPBKksMviO7eOSNgyupCEEEcEEd66D/hC/Cv/Qs6N/4ARf8AxNaOn6Xp+kwNBptjbWcLNvaO2hWNS2AM4UAZwBz7V0YrGYepGp7NO87b2toTGLVrlTxV/wAihrX/AF4T/wDotq8/8LWWpafpWnXNn4Ea5xGJ455NZXa7ugBkEbZCkrx0yBxXoHir/kUNa/68J/8A0W1eYeGvGF5LrmiaTHqV3HYvFHaPGI4yIT9lAUgCNm5k5DMw6fdxXhSi3U0dtDKcXKto7aeXfzTOisIdZ0x2az+Hzw5VlUDXFKxhjkhAThBz/Djt6VRuBdaRoGoRXvgURaTMC10LvxCGj+ZsliXJ2ksc5GDmqfhjxVqkdzot5qOuX+om8W9gu7b7OmFlhwY0RVQYYgk575HoKt+APFF9ealqH9pXN3PphsFvRPcqzrvDEOFbykUYG3KKGAOcHrVezl/M/wAP8i/ZS/nf4f5E2nvdXvhx7Wy+H1tdaTfR4ZhrMUonXsS5yWx2Ocip1tNRS3SAfDC02JL5y51GEkSbQu/JGd20AZ64qpoUF3L8NbCOyub+y1fRk897Vma2WT5y3lyblwQwUj2zSX9xrtv4MsNQF9qgn1G/+3mBYpp/KgZSy2zPEC6KBt+YDrnsaPZy/mf4f5B7KX87/D/I3/DQ1DRre9jPg+eyjmuBLFbWc9s0caiKNMZLryShPTvWVJ4eu3vpLpvC9tPKZ5JUlutNtpZVDSNIAW+1jOCxxwKwNabxnfaL4eQLqdnE9huMriaWaO83fKZPJwSduCN67OTuAPTQ8UDWb7xJYbE1rfHBbHyUimjQyA73KSRMY9xHysJRtG3g80ey82Hsf7z/AK+RsL9qbUtP1qzstOudU1KzM6TxaSqzCICPhme5X++gwCagsdDv9MuvtVj4U0+2uPm/exaTbq3zDDci8zz3rW0FBJH4VRs7W0CQHBIOP9F7jpXGeCdP1eSyM2lXerDUIzqNvPNe3LzQkqzJAvzMU3hghyoPCtnqKmEeZXu/6REIOavd/f5I3tI0C40nU7a6t/C0VqkMplddPsLa3aU+W6AFvtTcDzCelX/FUmmXdh/aHiLwzqYtbBGk81rqFBGDgk/LOM8qvryOKxtC0fWrfRNae7t9V819NWM2ryMd10u4lo2aZyxJI5G1TgY74qS+GZp/gvqlra6Jqf8Abt3axxXQu23XFzMmPmLFjlQS2OegxjtV+z0tctUVa13+H+Rrafb6RrWmCODwr4oayXG2K4unhX1BVZJxke4FXptEs7mOKOfwv4hlSL/Vq+qhgn0BueKoy6FPq2keHhLol8dMthIt5pU8yo8rFBscgybWCsDwzdwccCs+XwXqUsHhM6vpMurSW0U8OpBLpSxhOTFG7My+btJXPYlc0vZL+rf5B7CP9Jf5HRHTIGuFuD4d8SGdVKrIdXG4A9QD9qzimppNvGWKeG/Ealn8xturAZf+8f8ASevvXB+J/AGuzazqMuh+HniiM262kju4kGwWwjXguCD5gDDI4xkda3dP8KeI1+Ig1e9guHiF9JdRz/aIAiQum3y2wvmkqDtC52ZUHIo9kv6t/kHsI/0l/kbcklrFqUGnvo3ikXU8byRr/azYZUIDfN9pxxuHGc81YlXSo9K03UIo9dmXUAphjTVZlYAxtJ8xaYKMKpzzWL4V8Na9our2C3Gi2TmzM8U+rtd5lu45WDB8YLFhtGVYgD+E4pviOzW/+Gfhe1a7t7USRwjzLl9kR/0SQ7HPZW+6fZjUyio/0vIicIx/4Zd15GsjWckEc6ab4haGU4jkXXQVc88A/aueh/I1c0GbTpdXheGz1JJpLaUwz3V+LpGQPGHCkTSAHJTsOlefT6VYz2l3ced4Rglm1GzuYtMi1CPyIkhPzndtHzSD5ThBxjOa6PwZb21l40vbexm0uSxk+13VuthcK4jRzbDayKMJyhx65PpRaC2f5BaCaaa/ApeIbzxB4Y13RtC0nWbtdNkNpZiWW3gkMJkaRE/hUkYi/wATV29k8T2nirTNAXxtHJc3qSSN/oFsrRKqkg7C25skEcDsc1Y8W6brGp+Jgmj2tpO9t/Z14/2m4MQ/dTTsAMI3XkZ7e9W9b0vxHe+K/Dmq2um6UUsFdpzJdMr7pEKMqkRnKrnP+1gdKcaUWuv3v/McaMWt316v/MrbNa/tcaR/wsq0/tIruFp/Z8Hm49du7PaqV39qvbPVLW4+KGnvBBG0V8v2OAeUp+UhyGyvXHatbSfCOp6V4ivZ/P0650651GTUVkuIXa6id1ClVOdoAGQD6HpWX4Y+GL6FLctNPbzuIJreC43ztI6yZJLqzlFJOCdq8kZ4p+xj5/e/8ynh4Pv97/zLs183iK1+1WXjjRETTW+1Pc2loGEQKOmWLTMu3BfqO3tUKyarJp01/H8S7V7WFxHJKmmwsFYgELwep3LgdTketLbeBNRS3sIZ5dNmji0IaTPG8TsjlXUhsZGRgHPIOT2qxZ+Br6LRp7SbVwZWu47mBSsk0cOzjG538xsj1fg9OBy3Si9dfvf+Y3Ri3fX73/mUri61O10qLU5PiVCbOVzHHJHpMcm9gSCAFySRg544wc4wa2fCqXa61fy3etJrHn2NpLDdRwpEpjLT4ACkgjqc+9QSeBCLK0itrq0tpYLqadxHaMIpRIpDAr5m7PQ7t3JHPWr3h7TItG1i406ERiODTbRQIo/LX/WXB4XsPap9moyTV/vfYn2UYyi1f72+j7s5+7TRE8Q32mraeHbVoLiGFI30Np2/eJHtZ2RgFDO5UZA+6eeDSz2elwxQsB4WLXF09lAp8PON86lgUz5nHKkZPHHGaZqekzyeNNSu5b2+tLc3dtKq2ulTyu4jjQ5E0fykE/KVYMBtPA3GpLjS7GbVftMd9rcVt/aS6p9nGiztmcKFOWMeduB0GOc81KjT6kKFHXm8+vmY+i6jo+p6DbaldW3huzkltGu5IT4clfYqECTa24b9pODtHHPYVtaVd2qS3j6HNoiXkEUm+ODw9NDI4TaWQfvAWIJTKjJyRx0qraeHtLtbKG1N/rzx21tcwWp/sacGEznLv/qvmPJAB456Z5pI5dA8Mai99Nrl/az3LzvGbvSpFAMgj37Mxg9Y1PU9adqK1v8AiPloR1ul8yz/AMJdr6fDiTxfJNprIkDSm2gsJmPDFcZaRSOnJKjHPpV3Vdf8RaZptldYhlku7yO0S3GluJBuPLY88jAAJ/DtXNJqXgs+C7rwrceKriWwnjMasLSRJI8sXJyE55PQ8Y4Oas3PiPwxfaGlje+N7+a7iuUuYL77FskidCCuFWIKR1BBBzk5o9pR/m/H/gh7Wh/Ov/Av+CbOqeLbvRUhOparY20kkbzGF9KfekanBdgLjp9Mk9h1qvr/AIy1PSLKaa2v9PvmhSCSXy9OkVIklcKpdzN8uQS2MZwO2c1mXOmeHPFkNneHWtX1G6tVkt5b5dIM/mqxDFCpgKIRkYKgEA1c1PRfDetCa3W68QwxNBHaX0VvYXBM/lhWjLkxEh14IIwcH0qr039r8SlKk9pfj/wTtNGu7y4fUYL6S3kltLkQiSCIxqymKN87Szc/OR17VqVyei6pb6fLqSyQ6wySXCNFJJptyzSKtvEm4ny+u5G6+lav/CR2P/PDVP8AwVXP/wAbpxnG2rKhUjbVmvRWLF4q0qZkCNeAPIsQd7CdU3sQqgsUAGSQOT3raq1JPZlqSlswoooplHJfDL/knml/9tf/AEa9dbXJfDL/AJJ5pf8A21/9GvXW1lR/hR9EY4f+DD0X5BRRRWpsFFFFABRRRQAUUUUAFFFFABRRRQBXv/8AkHXP/XJ/5GvPvgT/AMko0/8A67T/APoxq9Bv/wDkHXP/AFyf+Rrz74E/8ko0/wD67T/+jGoA9JooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAyfFX/ACKGtf8AXhP/AOi2ri/DurTSaVpljb6hrDXAtYwtvBNphIAQfdVjvwB/e5x1rtPFX/Ioa1/14T/+i2ryrwFoi6nrNx9isbGGC2nsLt77aVuEcW0ZZUBTBV2Vwx3D7zHHSsJR5qm/Q5pw5q29tP1Owh1qe4nSCDU9clmkLKkaT6UzMV6gAHkjvT4tVu50uHhv9ekW2z57JNpREWM53YPy9D19Kh0Pwde2HiDXZZdK0i3t9QuZZbe/tZD9qtwyBFCgxgKeC3DdWPWoLf4czvoV7psg0ywMlilgstlCSZ1Vw3mSj5eWAwVyfvN8xzVey82X7H+8/vM+7vrPxY8+j3V74huY43jDRR3VgiSlwSqkqQsgIB+XLDjkVrPrzwafcXjanriWdq5iml87StkbDqpOcAj0p8Xg3VW1G/1JjpFpNItkLaC3hZkjNs7EEk4+8rFeBwCBzjmS38F6nbXs2oJd2LXDasdUWFoD5W5ofKZD3BA5DjkknK80ey82Hsf7z+8o3nixdPhsZ7nU/EKQ3ys9tKP7NZJFVdzHcAQAF5ycVuaHJNr1pJc2+vazGiOq4kSzbcGRZFYFI2BBV1PWq8vhC/t7DRW0qbS7W90qaaWOIWjLbN5qsrDar7hgOTnPJ69a1vDy3C3WtrdPE84vk3tEhRSfs0HQEkgfjRyWa1YvZ8rWr+85Cwj8P3ukaHY6p4kVroW1vHFazQ2knlPJGpVF3wkgkAYBOSB3qY6N4NSa5gOt2vmWwkaZfsdidgjxvz+4/hyM+mak8N+DpHt9K1mHUFtzNBZTSJFE4LiOJBtb95sOcY3FNwBwDwDSS+Ab2I3F/e+JopJGt7mOe4ubVtuyUckp5ojXaO4UZ75pRpQcU2KFGm4ptdCmLfwM1td3C63E0VpE007LplodiKRk/wDHt/tKeOoYHoQaifSNH1fQNRu/C11b3d7Zj5oLvTbaHacbsMptgwyvI4wfWs/UtIs7Hw5ry2njHSL+W70+WJbfMaM8jW8UXyt5uBnyUPIOMn61u6Xcae2mX98/jHTItX1S3hieWURAQIgIC+UJDlvnfJ3dSOwpclH+mL2dDy+8q2+neHI/COka9qlwbZdQghkWOPS7WVt7pu2qq25Y9+3QVNead4QsrW1uJNQeRbqB7mBYNItpWeNACzbVtiQBkZzjk4qnN4b8N3vhnSdL1Hxhot5caOdtjcSrEY1j2BNjxeZh+BnOQc4PbldW8O+Hb7RtN0q18Z6NbW1iswXdHbsytI27fGVZfLZeQCPXJyaOSj/TD2dDy+82rzwjpllZ2t9EI5le5tUMc2n2e1kkmRCDthB6MehFdL/wivh3/oA6X/4Bx/4VzGvalphtNESz8X2pgsbq2E8BuIpWukEsfzO2dwK43kj0Ofbp/wDhKvDv/Qe0v/wMj/xoSpqT2FFUVJrT+rmN4p8M6Cmhny9DsVZrq2Q+TbrG5Vp41IDKARkEjj1rj/DGrxJoOo6rrMtxDY2FvG7adZXd6lxY/Mw2OjS8gKFIYAAgNgYFdr4l1vSLvw1PPDqltNBb3No9xJbSiQxL9oQ5+XJ6A4+leeave+Fm8P640fii81bWLvS20+3kvICm1OoT5I1HLYJJyeOtJuipa228vMG6EZ+9ZaLt5nWHWNEistTlvIdfs7nT5I43tLjVpldzKcRFW87Zhj6txg5xio113Q5tKguba38QXN7PdtZJYQ6rM0hmVd7DeJvLwEG7cGxjvnis211rwRcaXONW124m1G88h7i48uQujxHdHsKxKBtOcHaCe9aMvijwNPbwLL4ivHuLe4NzDdtHL5sbkEHb+72gbSV24xgninz0O6/AftMN3j+BmeI9K0jW9G8P6oun6pbyahfQWjyX0kkssCtIVKMskuQCcjIzjOcc1c1vw94I0TV7TT5PDk8rXGwmRbxlVA0gjH3pQWOTnCgnANSXviXwPf2FnaTeJdQK2s63KyFZWdpFO5WJaM9CM4GB7Yo87wR4i1Vp01PWL65a3SO5itkuR56ITtaRY0HKluCMckUv9nb+z+BP+ySf2fwMbXvBWh6Z4i1K3gt3MA0C5voo3lYiKVGUKVOckcnhia7PxR4X0JdExDoenq73VtH+6gWJiGnjUgMoyMgkZHrXKa49hqt3fX9lpXjOa6FpNp8LrHJ9nYAFMMCdxG4AkHnI5GeK7LXbvVr/AEsw2vhvUDMs8EyiS4t0U+XKjkbhKSMhSM4NRal73KunRepFqLUuSPTovXyOJg0fw/Hot7rOq+B3sdOs4ZGkcao8ru6MVKooblcg4YlfpUqaP4Qa3uf+KWc3Ud1DbQot7N5UzS/dIkJGAOd3BxjjPGZIb2W00LV9NXwasumxKyX8EniITiLOWYEEkqTuJ4wTn6VSi1e3g8Fz6iPBZfQ7rDvcS66ZWJVsKVZsyKVbOMYwcnjrVWo/yf8Akr/yKth/5P8AyV/5Eum6R4WvdUttPm8JrDNLqF1YOV1KZwjwx79w6ZDD6Ee9Q2+teGtI02xuNP0O9trjULaa4eC11C85ET7AuYgxYkk4LBQPXmpfDOj3dzpzaNe+HIJLG/nk1iyefVXUqvyDiRA7kgOvJIyGP0p8LWst7/YNj8PrVzaPNPHHBqYjXHmeVIVyq/IWTBU8HAyKF7FaqP8A5K/8hr6utVD/AMlf+RoazrVlper21ktvqYSW3SdpbrWbuJVLsAELKWCMOc79oPABNTW2naxN471GyW6RtKt/IzE2s3gmRWDHcPmwWPAwTj5eD1pZLfUpbkXD/DG0MoREyNShHyocquMYIB6DtWhHp7eIZdP8Ry+FNDlu2hjmt557xjLGuNy8+QcEZ/OrTpvS34P/ACLUqTduX/yV/wCRzaa7MPFIsQZraL7dGloX1S8d50W5jjZgGzE6sC3AYkDrXeal9o/4SWy+ytEtx/Z135ZlBKZ8y3xnHOK5mx8NreWlrrGleFdBsZ7poLwTrdMJCvmJMVOIep24PPfvUnjaO9OjzalrFraQWVtBJHP5N2Zg0TshYMjWr5GUU5A45pXW8Vpp0E2t4rTTp5mfoZn8JeEINbkSCXVNTaGOR2u5jAJJW/1spYnAyeoHHT3o1Xx54g07wpd3yLpU97puqR2Nw6K5guVbZzGd2VI3gHO7BUjmptM8EXljp88Om29jDaXyDzkjngCzKRxuH2LkYP60l54b1DSPD5SS3tv7NsgZlt4nhkCkAjKoLE5OCe2ear2vky/bf3X9x1HhVb5ZNaGpT28139vHmSW0ZSM/6PDjAJJ4GB15xnjpXM3mv6nY+M9fs7XVdD063imguG/tMNun3RRhghDADaqZ6Nyw6VsaXFqfh212G30wC9uFKm41Hyi0hRVVFVbZQDhBwBnrWVqdvrdrr7Tyx+EI57ub7RbrfvJLJGUjRWKNsXA+RTnAwT16VPNZLR7/AOZHNZJ2e76epa1LxfqFp4jntYZ9PdEv7W1isPLc3EscoQvKDnou8nhSMI2T6UtP8etc+Ofss+p266ZPdTWNvCyIuWjH3s7i+dysMsFUgjGScnSaHxub6Odo/CH2zyyqSFZvM2ZBIB64zisvV/E3i7RdU0ywuv8AhGGuNRuRbRiNZm2OQSu/nIBx1war2vky/bf3X9xR0ebSbLWvFWkadLYQQrr2nPBZ26hMc2+8qBwRlTkAcEHPWvV64i5l1u+8MaZqck2mOLiaxnFulq8R3NNEQvmeY2BkjJ2njtWz/a2rhJH+y6LsibbI39qvhD6H9zwaFNOV/T9RRqJyvZ7L9exvUVh2+p6zdhjbWejTBeCY9VdsflBWjpV9/aej2V/5fl/areObZuzt3KDjPfGatSTdjVTTdjnfhl/yTzS/+2v/AKNeutrkvhl/yTzS/wDtr/6NeutqKP8ACj6Izw/8GHovyCiiitTYKKKKACiiigAooooAKKKKACiiigCvf/8AIOuf+uT/AMjXn3wJ/wCSUaf/ANdp/wD0Y1eg3/8AyDrn/rk/8jXn3wJ/5JRp/wD12n/9GNQB6TRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQBk+Kv+RQ1r/rwn/wDRbV5poeg6LeLp9nL4F1CeeS1t5pbsXyrGUkGDLjzQRyG+XGeOlel+Kv8AkUNa/wCvCf8A9FtXAaFdQQjS9UGraZHcR2MEJhfxG0aFVTAV4fKIB5Jxzgk81zVOT2nvroclX2ftV7RX07X6lTRI/h1r3imTQ7TQpSQZFjuBesyyFDz8okLKODgkD9RRo2i+H7nw5fa7qvhGO20+0juZDJBqMru3kyOpXYSMHCHnPWtSyOk6fq7ajbXWhIxkaZbf/hKJPISRgQziPy9oJye2OaJtF8ixutS03TdIni1CTyFB1aa5tV8+VY5NsQRVAYsd2D6/QlqHSK+4VsNbSK+7/gGFAng6Tw5c6w3gu7ZYXgCRwXkjiZZm2oUcsFLAkBlzwe5GCY/EWk6Zpnha6vU8IW1pqdvqMNobefUZpUZZNhBDKepDgc8A564Gd/8A4QfxGdKn0xrPw41nPs82Nru+bcE+6Ml84HpnFT3HhPxRdLqC3Nl4XmXUdn2pZJbtg5QAK2CflYADkYPHWjlpf8+/wDlo/wDPr8EYvibwRaWvh3TrgaFFpl3Lqltb3At9RefZE8qocF1wxO70GODk4IOjrn2Dwld3Nloek3H2awtP7S1HGsT26iMllAQB/mc7GPIxhQM8jD7rwT4ivdKt9MuLDww9nbyebGn2i8BD/wB4sGyx9yTUreD/ABI8NnFLpvhOVbMFYfNa6chTn5WLElhk5w2RnB7ChKmtofgNKktVT/A5XVrTSNNee+/4Q+0bRILi2Tz/AO0pzLNHNjaVTjaw3BiG9ceprr5vC+hWPh/xhHBpVr/ovm+Q8kYkeP8A0SN+HbLD5iT14zUl34e8V35uTd6Z4Nn+1FDP5kc7eYVxtJz1xgY+lPSx126h1zR7jV9Aj1O/iaWSzhikciNolhDZLgqDsxna2Dzz0EyhF/DD8CJQg/gp2+SXQx9LgbT/AA/q+ueIND8MXVnapdzRx2loFlJidhswyAbQFIyeemabbXStoOs3UvhHw491bQwy2JS2EcdyZcgJ+8VTnI4I4YsAK2V0Lxal3PdrpvgwXE4Ilk8mbc4PXJx37+tRPYeJNIswk2keEDYTXEMU0EEUq+ZvlCjqCOr9SDj0PStOaC3j+Bq5QWrh+Bg3c1pfeFJriLTdCsbuPW4dPa5j0nKwqWjyZEkCkfeweSORg85F7xRoemJpmkT+ToEgTW4ILn7Ha+SGVpQmzKPkFQ3IbIOOQKv32vTaDqFp4Vg8G6fL9pjVo7e1ugIT97AO6JQDiI9fQVZNxrjQLAfhtaGFWLLGb+32gnqQNvWjmp9vwf8AkHPR/l/8lf8AkZPieaPQNR1O50nTfC4j0uwj1NIzZr574ZgQCCNo+XIYZxxwavt4s1nVfFMGm6Xc2duhitriSOS2MxWGRCzMz71CnICgYJOQcYqz9r17GP8AhXFrjy/K/wCQhB9z+793p7Vx+r2N7qGuPpV34Pud+o7bg2iX8G0JGqqFWUR5iX5B8oZec46mmqkFsn9z/wAilVprZP8A8Bf+R2/iJ2j1TUHRdzKukkL6n7ZJxXP6V461e70C+1WPU9Lvr1tKe8j0iKJhLaTJnKMOpXpndg5HHBrY265qNzey6j4bv7ISx2qxGzvLaVlaGV5A2XYDqy8YPQ1NbwXUOqQpJJr1jLfyGP7Q8WnfOyoz4YorMeEbtUxnZ3s9f82RCpZ3s9fLzfcxLHxbqbW+qTjXU1LTdPazuX1K3tF2lHbM0RAB4CYbIBIHU5p994k0LW/Cnio6nqdhqMFrM7WbTW4URh4h5O0EcndvAccnBNdmmi3kahU8RamqjoBFagf+iaX+x77/AKGTVP8Av3bf/Ga25n2/I35n/K/w/wAzk/E3imw1O3sEi1fyPDt7HNHPfw2y3CySAqogIZGC7gzckclQB1wXfDxHi0fwjDLFNFJFo91G8c0TRsrLLADlWAI6V1f9j33/AEMmqf8Afu2/+M0610d4NSS+n1O9vJY4XhQTiIKocqW+4i8/IvWk23pYTblpb8jzu2vdZbxlBBbXWoPYR6vNG8NqrRqgNxKzFw0ZEqnjLK429MZ66miQPZfEjWYrzUfEJaW8ElpAySPayRmBOS4TaArbgAWH3Rwe/YS+G9CnmeabRdNklkYs7vaoWYnkkkjk03/hFfDv/QB0v/wDj/woXMla39fcEVOKSsvv/wCAcj4D1azsp/ElvImqFpNRuL1JLiwnBkh2JzuKDJ4IC/eOOhrQ8N+JtMGiak7QanHHb3M8zrLp04JSSZypRSmWBDDgDI7gVvf8Ir4d/wCgDpf/AIBx/wCFH/CK+Hf+gDpf/gHH/hTvLt/X3DvPsvv/AOAYPhi9ju7jw/GkVzE9tpE0Eiz27wkOv2XIAcDI9xxXN61e6EZ7aLUtUu4PIn1UMun3hilR2uMoH2MGwQCRnjIGeK9KstF0rTpjNY6ZZWsrLtLwQKjEdcZA6cD8qvVPLK9/66EqEr839dPTseIXOtanejTIdS8QJDdRafbyRXFleqf9JU5mSTZMsZJwuC+VxnBznPrPhX/kUNF/68IP/Ra1rUVSTvdlKLvds8g8J2OtXR0+2WLVxbT2j+Zd3DvEkMbw7V2FZCsgBwVG1WAIOetWTpHjCTQ4NKnsb+ZxoF5YXU0l3GyT3DgCJuZMno3zEZ+bn272LwvpsEKQwvqUcUahURNTuQqgcAACTgU//hHLH/nvqn/g1uf/AI5Ux5kkrf19xMedRSsvv/4BxUej6/FFciLTNSSyWPT0W0N8PMkZHYzsp835QUKr94Zx071j6b4b8UReDfEVje6JfT31/p0EMYlu4pd10I3R5tzSHHPlnPXgelem/wDCOWP/AD31T/wa3P8A8co/4Ryx/wCe+qf+DW5/+OVV5dv6+4q8+y+//gHP65ZahqejaHd/8I2l1PYXKNPp92IWkdDGVbYxfZkFgeTzt+lZ+taFe32paDrD+DLO9hispbWfSpHhJt2YqUOW+QqNpBxnG44BrsP+Ecsf+e+qf+DW5/8AjlH/AAjlj/z31T/wa3P/AMcovLt/X3BefZff/wAA4XUvCXiC48WtfR2cflPHbSWrQzwxixePYGj3mMyFMgnC4DDIIGck1HwXrtz4ptLs6ZpVybfWxqC6s85S4+z7iRCV2EkKDtHzEYUcCu6/4Ryx/wCe+qf+DW5/+OUf8I5Y/wDPfVP/AAa3P/xyi8u39fcF59l9/wDwDnry0fUPhPpVlHcPbvcQafEsyDLRlpIgGHuM5rnYPhzqjeHdTsJtO0qBm0pbBY7eT5L6ZWDLcyfKNrcDruPJ5r0uTR7GTSItLMTiziWNY0SV1ZRGQUwwO4EFRznPFV/+Ecsf+e+qf+DW5/8AjlSoyj9yJjGUduy/rYxfDGg3+leKNUvn0+xsrC9tLVUgtpc+TJGpDIFChSvJw2B06em14V/5FDRf+vCD/wBFrR/wjlj/AM99U/8ABrc//HK0LW1hsrOC0t02QQRrHGuSdqqMAZPPQU0ne7KSk5XZzHwy/wCSeaX/ANtf/Rr11tcl8Mv+SeaX/wBtf/Rr11tTR/hR9ERh/wCDD0X5BRRRWpsFFFFABRRRQAUUUUAFFFFABRRRQBXv/wDkHXP/AFyf+Rrz74E/8ko0/wD67T/+jGr0G/8A+Qdc/wDXJ/5GvPvgT/ySjT/+u0//AKMagD0miiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigDJ8Vf8ihrX/XhP8A+i2rzm38bvpMmiRPqbW9haW9jbz2xhQ+aZIlZmGAzsArKcjaAc/e7erXVrDe2c9pcJvgnjaORckblYYIyOehrmP+FZeD/wDoEf8AkzN/8XWUlPn5o/1+DMZxmp80Unp3t+jOV0nxdrMOqXV1qesTT29v4hbSvsi2qBPJfPlyFgu4EE464+XBGa3NauLuz+HWo3Onwefew6rJJbw4z5kg1AlVwOuTgVe/4Vl4P/6BH/kzN/8AF0f8Ky8H/wDQI/8AJmb/AOLqZKq+i+//AIBE1Wl0Wz6v/I57SNc1288N6peXWs3vmLbRyw/ZNPM0kMwyrpzCgclsfJjK4OSBzT7TxD4kk0MyXo1OO7/tfbfC3sQTaWxJAEOUPnJkLlgCwDE9q3v+FZeD/wDoEf8AkzN/8XR/wrLwf/0CP/Jmb/4uqvV7L7/+AXzVv5V97/yMrWJtcl0TTI7fU9Vkje5mWe8S0NvJtyTFuCxswUfKuQo3Y5wCax7/AFDxAuo2Fve6jq7X76JM6RWUDIrXayKiOyKvAOcnf8vPOBxXW/8ACsvB/wD0CP8AyZm/+Lo/4Vl4P/6BH/kzN/8AF0Xq9l9//ADmrfyr73/kZU9lfR+MYdY1Sz1V2OiQxv8A2e8m37QJGZ0wjY9OvFT20epQfFjUrtbfUf7MudNjgSV1doxOHJ4z91QG+nJq9/wrLwf/ANAj/wAmZv8A4uj/AIVl4P8A+gR/5Mzf/F0Xq9l9/wDwA5q38q+9/wCRhafB4qbTVS6k1b7cmn3P9pM7HbJcA/uvI24A5yRsAG3APNV7S31bT7jT0uY9TNveQabLdtcs8ii9+1R7+WJ2cdhheldL/wAKy8H/APQI/wDJmb/4uj/hWXg//oEf+TM3/wAXSl7Vpqy+/wD4BMvbSTXKvvf+RiePLmxg1pxfl3iEdnI0MF2LeZ0VroMUbepyNy9COuO9clqms3k/hmwtIdRASS4uzbx/2orTW8Z4gWYiZc4BJ3M528ZBxXpH/CsvB/8A0CP/ACZm/wDi6P8AhWXg/wD6BH/kzN/8XUr2y2S+9/5Er6wtkvvf+RwWo6pPq+g+H7n7bE2pWmn7J7e41WFUkmGFJJWdGRzgkSDdgMRjJre1DVtP/wCFiaNrlvcWhWO1kgv5YtUt9jbgNihWkBYK2TnA+hrf/wCFZeD/APoEf+TM3/xdH/CsvB//AECP/Jmb/wCLp3r9l+P+Q74ntH73/kcfZXUH/Czv7Ykm0hLZZpWa8udSgkfYUKKI2V9wXBB2MmBlueldcfEdprHiPTLWCW2byNQYxNFdxSmZPss2XCoxKgE45xTv+FZeD/8AoEf+TM3/AMXR/wAKy8H/APQI/wDJmb/4uk/bPdL73/kJ/WHuo/e/8jraK5L/AIVl4P8A+gR/5Mzf/F0f8Ky8H/8AQI/8mZv/AIurvV7L7/8AgGnNW/lX3v8AyOtorkv+FZeD/wDoEf8AkzN/8XR/wrLwf/0CP/Jmb/4ui9Xsvv8A+AHNW/lX3v8AyOtorkv+FZeD/wDoEf8AkzN/8XR/wrLwf/0CP/Jmb/4ui9Xsvv8A+AHNW/lX3v8AyOtorkv+FZeD/wDoEf8AkzN/8XR/wrLwf/0CP/Jmb/4ui9Xsvv8A+AHNW/lX3v8AyOtorkv+FZeD/wDoEf8AkzN/8XR/wrLwf/0CP/Jmb/4ui9Xsvv8A+AHNW/lX3v8AyOtorkv+FZeD/wDoEf8AkzN/8XR/wrLwf/0CP/Jmb/4ui9Xsvv8A+AHNW/lX3v8AyOtorkv+FZeD/wDoEf8AkzN/8XR/wrLwf/0CP/Jmb/4ui9Xsvv8A+AHNW/lX3v8AyOtorkv+FZeD/wDoEf8AkzN/8XR/wrLwf/0CP/Jmb/4ui9Xsvv8A+AHNW/lX3v8AyOtorkv+FZeD/wDoEf8AkzN/8XR/wrLwf/0CP/Jmb/4ui9Xsvv8A+AHNW/lX3v8AyOtorkv+FZeD/wDoEf8AkzN/8XR/wrLwf/0CP/Jmb/4ui9Xsvv8A+AHNW/lX3v8AyOtorkv+FZeD/wDoEf8AkzN/8XR/wrLwf/0CP/Jmb/4ui9Xsvv8A+AHNW/lX3v8AyOtorkv+FZeD/wDoEf8AkzN/8XR/wrLwf/0CP/Jmb/4ui9Xsvv8A+AHNW/lX3v8AyD4Zf8k80v8A7a/+jXrraqaZplno2nRWFhD5NrFnYm4tjJJPJJPUmrdVTi4wUX0RVKDhTjF9EgoooqzQKKKKACiiigAooooAKKKKACiiigCvf/8AIOuf+uT/AMjXn3wJ/wCSUaf/ANdp/wD0Y1eg3/8AyDrn/rk/8jXn3wJ/5JRp/wD12n/9GNQB6TRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAV7//AJB1z/1yf+Rrz74E/wDJKNP/AOu0/wD6MavQb/8A5B1z/wBcn/ka8++BP/JKNP8A+u0//oxqAPSaKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACo90v2jb5aeTtzv3/Nuz0xjpjvn8KkooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAr3/APyDrn/rk/8AI1598Cf+SUaf/wBdp/8A0Y1eg3//ACDrn/rk/wDI1598Cf8AklGn/wDXaf8A9GNQB6TRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRWXeNLHdXk0UpQxWqPgAHcQZDg57cVlWq+zSbV/+Gb/QuEOd2NSisk3twtxLudQEMmYx8zBVBwduO+B1OOabDfSuSsl0FjDsPOG05O1CBnGP4m/KsPr1O9rP+vmafV5mxRWHZXNwI7SIOiqEhUITy6lRk425PfnI6Vp2TySRyPJIW/eyKBgDaA5AH6VVDFRrWSTFUouG7LNFFFdRiFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFYfinxTaeE7C2urq0vbr7TcraxQ2cYeRpGDEAAkZ+6RxzkitKVKdWahBXbE3bVm4TgZPSqMGtaVdK7W+p2cwRkVjHOrbS7bUBweCzcD1PAridV8enUtHvrAeDvGcRubeSESDSuU3KRn7/AGzXNyeKdXupr66l8DeIYJpEsPJih05yha2maXDHggNkAEA4Hrjn06OUVZxbno9Oq7rz7X9LeZDqLoeu3Gq6daJI9zf2sKxyCJzJMqhXKhgpyeDtIOPQg1X1HxDpOlwXMl1f26tbQG4kiEqmTYBnIXOTnt65Fec+HLq98X65rNx/Z1zY39rcb5bK7nltNqTQRKh3J8xI+znggAh8/TfuvBeoNa3FlaPZQ28tk1uW3udzfZfJU7GDbSDj51bJUbSD1pSwNGjNU60rOyb28n59Nu9/UOZtXR1R1zS0haeXULSKEOIxI9wgViVDjBz3VgQDzg56EVIdX00XosjqFoLsttEBmXfnAbG3Oc4IP0Irn20DVU1i51aNLCSaeRz9mllbywrwW6E7tnJDQEdOVbtnFMsvCE9lpk1qs0MkjX1hOszZDNHbrbht3H3j5MmByPmHIycYeww9k3Povv0v92/n0Kuzr6KKK4CgooooAKxda8S2+iLcl7S7uvstsbq4+zKp8qP5sE7mHXa2AM/dNcBF4/8AFWpa94gsNOufC0A0q4uAYr1bgTGGJseZ8hII9cc57dKjuNM+IHjLTWv7PUfC6Wmo2Zt3ktTcKJ4ctjO9SRgs+CMfePUV61HL4QqWxE4r5/10/Ezc9NEeky69aw/a90cx+y3sFi+AOXl8raRz9398ue/B4PGcpPH+iypM8TPIscYkQo8TeYpdUzw/ycuv39vBz2OOb8Mwavrni3xHp3iK4ghm0+6sLx4tLJEMsu0OrEyAseIowQMDg9+a7GHwxDb2xt4tR1BIkjEVuokUC3QMGCqNuGHygfPu4GOhOVUoYbDvkqav3Xo9LNJ9vP7vMabeqKg8WO2oyQvp9zBAqWbB5FUtunnaHaQH6ZAIYZGAx5G3c+TxpYx2y3DWd95cqxvbYRSblHlSMMg3dN0iH5sHDDinW/g2wtlVY7i6CjyCy5QBjFcG4Q4C8fOzDC4G04AGBhyeELFFhRrm7eO2MQtkZlxAiSpKEXC/dLRoDnJwoGRUN4K/ldd9rL8b/h5h7xpabqaaktwBBNbzW03kzQzbdyNtVxypIOVdTwT1q9VW1sIrO5vp42cteTieQMRgMI0jwPbEY9ec1argqcvN7u39X/EtBRRRUAFFFFABRRRQAUUUUAFFFFABRRRQBXv/APkHXP8A1yf+Rrz74E/8ko0//rtP/wCjGr0G/wD+Qdc/9cn/AJGvPvgT/wAko0//AK7T/wDoxqAPSaKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooA85h1TRLXFpe2pa6W0lvGJFx80KE7mGxCvHTAOenc1vadYWGrabbahZ6dA9tcxiWJmuZkLKRkHDICPxri9StZ77U7KONblIG0W8tXuLe5ijCySSBlVssGxhOw/iX3xja7p+v3tpoi2EUtvcWekW0KGO7iCiVCDIGPmjYw2DaVDZ3EEgV4OEwuDlh6bly3sukO3oelXrV1Vkle131f+Z6t/YEP/QLtv8AwMk/+JqOfR7aCCWVtMtiIkLsFvJM4Az/AHa5qXw4kvimK4iv7SHQrmWK+ubZ7vEsM8asAqbWxtYspYZx8jf3qqWeizWus3V9dzxTXCvdsbuO7hVbhJA2wMqr5jFQ20KTgbcg8gVrVwuCjBtct7dof5EQrV3JJ3++X+Z2k+k6TDM0Q02WQqquzLLgAEkD7zj0NM/s3S8kf2RNlRkj7QvA/wC/lSX40bVzf2OoS2k9lc2yRujyKVbl8/iMg+3Fef6d4bk1LwxcT3U2npqc99A225cQma0t2VUjk2kld6Jk8dW5HHDjhsFO7fKtX0h39BOriI6a/fL/ADO9GmaY23GkTndyMTrz/wCRKdBpOkzTLEdNljLIXVmlyCAQD91z6iuZj0JbO5sNQsn0SKa11G4ulshdkRLHNEUZVfaSDn58BQMk+laHgqB9A0bTtN1K600S20c67rW43xkNIrDkhcHkjHtRLDYKFmuV6rpDv6AquIlpr97/AMy3NbaPBJGs0FhAZpmhhW41Bo2lYMVwARyeOgzStZaUt/8AYGg00XmzzPs51F/M2/3tuM4965jVPDh1DXdRvUHh29gvUVF/tKZg9s8czsGTaMlSGDYDLkgc4p954Va78Q+cdT0lbVtVj1Vr1ZsXSlVUGFRjGz5eu7ocYpU8LgpQUny3a7Q/yHOtiFJpX++X+Zv2qaFfOUtDpFwwj80iLVGchP73A6e9UNG1bwrr63DaY+nTi2VnmP22VfLVSQWO5RgcHnpjmqMOhTx6hot0h8OWz2GrXFzI1vdsC1tIGG3AQAt8/Q8fIvPJxeFnrP8AZOo6RFrug2trIky200al5dzvu3OC23ozKRg565GcVf1PA/3fuh/kT7fEef3y/wAyeK68NzaNNrEbaW2nQMVluRqD7EI4wTt68j8xVa+1bw1Yadp1+0NnNbajMsNq0F5I/mszY4AXoO/pg1mW3gtxDcG68Q6XLcJe29/ZOxeTbLEu0LKXkLSJtHTIwSSMdK6CayuZdEWJNe0iDUI70XkPlRAW6/NkoU3bmByxJ3Z3HPHSj6ngf7v3Q/yD2+I8/vl/mQzXvhu3s7a7lGnrBcxtLE/2yXDIpAZvucAZGSfWodf1HQvDvyXenxSz/uz5EFzI7BXfYrH5QAM55JHTjJ4qnr3g6PxHLZ3mo+I9Olvkt5La4JUrE0btu+VUlU5XoNxYEdRU+r+ELa/W6jsvFFtZRXcFtHcJ5SSbmgIKMpLDb0AxzR9TwP8Ad+6H+Qe3xHn98v8AM3ZNG0+WC3b7O1uWneOTypGc4UP0z15UdqxbS68IXrWQh1G+H2wziIyQOgBh/wBbu3INm3HO7FdDb3ttFDZrJexSPHdSs7F1BIxJ8xHQZyPbmuf0a003VdV13VbjbZ2GoxeRDazyBJASCJpduf3Zf5R6nYCeorGhhcBUjecY307Lou1uppUrYmLtFv8ApsjF94O+xzXR1K+WKIRs2+B1JR32I4BjyULcbhx71ZvR4Z0+HUpZ7u/26ZIkd3tjJ8osAwJ+X7uCDkcVFaeDdG8u4XVteTUGeyXToXDpD5NujblGFOGYMAdx9Bx1zJN4U067tdYivPFc8rawka3jBrdQSihcqNny5AGetbfUct/lj9//AATP6xi+7Lukabpl9OrLa36xMsgC3sbRM20phgMA4Ibv+QNcn4q8Taf4SQRzaK13JNpiXNqyPIA8/wA2UfBwBtUvnjhWHpXoUV5bRXdqJdTiuCkMoaZ3QEksmM7cAdP0rnLi10bU7K4ivdWnVbvT0s5IhApEQCsNyEoTu+d+cn71YRpZdTqtSUEtd7do9/maOeKlC6cr/PzFub/w9pkVgNQ0+5MlxFA0ssKSeTEZWCLli3QscYGSOp9aS31XwxNfy2kmlX9v5N4tjLLOrKiTN9xSd2fmBXBAx8y5xmqFz4Y8N3jIbnxDqcoEcKEMictFjY4PlZVvlXO0gHHIq/Lpnh2a9vLl9Zvj9q1K31Jo9vyrLDt2gfJnadi5BP8ACMEVv/wlf9O//JTP/bf734lm3u/C9x4gfRTZzRXYWV1EjEb1jYKxwGLAZPBYANzjNU4tc8JPpFzq8tjdQadb2iXbXEjcNG5ITADlstg4BAPrimW+i+GdMmjvNL1CaK/t4pUtnlVmUGTk78KGcbgDyc8cEVhaBpkb2S6TqkcFtojwSQ31s8pme7c7SsgKxgr825sli2T070f8JX/Tv/yUP9t/vfibqarpE3hu41e38O3Nw1q3+k20N5G7RptLb9wkKNwAcAlucYrQt49Li0PUNX1bS5tPjtiztBNNl40CA8lWIyeuM/xY9qjax8NSaXeWMmram4vESOaY3E3mFE4ChscDGQcdcnOaqNbafJNp9q+rzyaZZ3n2uT7Q0ks1w6qnlBmI5UNuJzz8q9qzn/ZfNG3s9/7vZlR+uWd+b8e6Ocv01W1gWbURJplvHE9zezQw/afsjEBo4mC5JTBYFwCfkHIzW5qWsaXpNvq3maBPcPpVvbXEjrcbRNFLuHmL83GNjZBAPHFWdV0zSPEOrXN3c3N6IinkobW9+zeYjKu9XBZSynav5GrmqaV4W1mXzL/TFlYwrA2LxFDxrnarBZQGAycZzjNZ4ZZfyPmjF6y+zfTmdum1rW8i6rxPNo3suvkr/iZY1bT01iS1n8NyJaRammlyXK3m4rM4RozsyPlIcZIOQex5IXSNW07VtZlsE8OTxxyLKbK5MsxjlKEjEjbcRE7SRy3HocArpWg6XY+LNR1q5ihuPOmSa0zcrugKxrHyDKVY/KCGxuGTzWta2Phuy1KXULfT9lzKWYsbxCFLZ3FVMuEJyfugdTXRbLf5I/8AgP8AwDK+L/mf3/8ABOb0i91fVtAfWoPBdnJbeQWjhGqOJZXVirhflIwccZwePel1PUI77wl4n1PQbC1ENhaGS01AXTusjeXvbCFfvIMcHI3HB6Gun0GDQPDNtJb6RZm3hkbcyG9Rxn23SnH4U6WLw7Nos2jtpduunTbt9vHJCiHcck/K45JOc0Wy3+SP/gP/AAAvi/5n9/8AwTD1KW2s/CGkajp2n/a5r2COQy3BkO1DHvLtHFlmzwMIvBbPAFZc+t+bbWEenaRp0l6+ijWbkzXkixmPpsjxkkk55PA4z1rqU07wqlraWw0W0MVoCLcNJCxiyApwS+RkKAfXFT3EPhu7tLa0uNGspbe1ULBE/wBnKxAdAo38D2otlv8AJH/wH/gBfF/zP7/+Ccu91c33iiz0zR9L0s217psepRS3lxKjpGSAVKgnLc8Y4HetSa1j03xjBYxLM6tJHcb3ICxqzBVjUdWwUdiSeNwHOeNa5Xw/ealFqNzpVrLexBRHcO8BdADkAHfkYPNMvpdPu9UsrqK1iW8a4ijafdEzlASQuVYnGWJ9OawxKwHs37OMVLS3u26+hpSeJ5/ebt6/8E6miiivdPOCiiigAoorm7zwbb3l5NctrXiCIyuXMcOqSoi57KoOAPYUAdJXBfFKCK6tvCtvPGJIZfEdokiN0ZSHBB/CtMeBbYEH+3vEpwc86vN/jU/jLwxP4osLCG11P+zrmxvo72KfyBNh0DAfKSB1YHnPTpXXgKkKeIjKbsu/y8iZK60OJ0y9t7DS/Emo6HdW+q6zo1r9hs0hGcW6/MrFVHzNkkEjqU4682tK8Ya5qHhPUbmO9gluEuIktZ443lBVsbgZFhCZ4YbthCcbhWt/wi/jv/oo3/lEg/xpf+EX8ef9FG/8okH+NX9Uo/8AP+H3T/8AkA5n2/IyPhhfS6l4z8aXc7TNJIbLLShckCNwCCqqCuAMHAyMHHNen1yvhPwnf6Bqusanqeuf2teap5HmSfZFg2+UrKOFJHQjsOnfNdVU4+cJ1v3crpRir69IpPdJ7rsEU7ahRRRXGUFIzKi7mYKPUnFLVTUdMsdXsms9Ss4Lu2cgtDOgdSQcjg+9AE/2iD/ntH/30KckiSZ2OrY64Oa5z/hXngz/AKFbR/8AwDT/AArU0nQNI0FJU0nTLSxWUgyC2hWMMR0zjr1oA8U0DRNRv/H/AIqubG3mSYajepa3wi3RRyhwWjkPZXQlf+BA9QK6NfDfi6HRoLB4L3EOhWtvYfYr4RC0u0UBzJ843fMByAw2gjvz1F78K/Beo39xfXWjeZc3MrTSv9qmG52JJOA+ByT0qD/hT3gP/oBf+Tc//wAXXqYieCr1HUc5K9tORPp/jX5ELmStb+vuE8LZ/wCFpePc9f8AiXZ/78Gu5rD8O+D9B8J/af7EsPsv2nb537533bc7fvMcfePT1rcrmxtWFWrzU72SitdH7sUtrvt3HFNLUKKKK5CgooooAKKKKACiiigAooooAKKKKACiiigAooooAr3/APyDrn/rk/8AI1598Cf+SUaf/wBdp/8A0Y1eg3//ACDrn/rk/wDI1598Cf8AklGn/wDXaf8A9GNQB6TRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFAFX+zLD/nxtv+/S/wCFH9mWH/Pjbf8Afpf8KtUVl9Xpfyr7kX7SfdlX+zLD/nxtv+/S/wCFH9mWH/Pjbf8Afpf8KtUUfV6X8q+5B7SfdlX+zLD/AJ8bb/v0v+FH9mWH/Pjbf9+l/wAKtUUfV6X8q+5B7SfdlX+zLD/nxtv+/S/4Uf2ZYf8APjbf9+l/wq1RR9Xpfyr7kHtJ92Vf7MsP+fG2/wC/S/4Uf2ZYf8+Nt/36X/CrVFH1el/KvuQe0n3ZV/syw/58bb/v0v8AhR/Zlh/z423/AH6X/CrVFH1el/KvuQe0n3ZV/syw/wCfG2/79L/hR/Zlh/z423/fpf8ACrVFH1el/KvuQe0n3ZV/syw/58bb/v0v+FH9mWH/AD423/fpf8KtUUfV6X8q+5B7SfdlX+zLD/nxtv8Av0v+FH9mWH/Pjbf9+l/wq1RR9Xpfyr7kHtJ92Vf7MsP+fG2/79L/AIUf2ZYf8+Nt/wB+l/wpG1O0XUFsDKftDcBdjYzgtjdjGcAnGc45qpD4m0meATx3LmNkEiEwSDzFJCjYCvzcsowMnJA71PsqH8q+5EvENfa/Euf2ZYf8+Nt/36X/AAo/syw/58bb/v0v+FV49f0yQIVucb51twGjZT5jDIXBHH9CCOopU1zTpJERJ2bewQMIn2hicAFsYBJ6ZPORjqKPZUP5V9yD6w/5vxJ/7MsP+fG2/wC/S/4Uf2ZYf8+Nt/36X/Cls7+2v/O+zOziGRonJRlAdSVYAkc4IPSrNNUKL2ivuRSqzeql+JV/syw/58bb/v0v+FH9mWH/AD423/fpf8KtUU/q9L+Vfcg9pPuyr/Zlh/z423/fpf8ACj+zLD/nxtv+/S/4Vaoo+r0v5V9yD2k+7Kv9mWH/AD423/fpf8KP7MsP+fG2/wC/S/4Vaoo+r0v5V9yD2k+7Kv8AZlh/z423/fpf8KP7MsP+fG2/79L/AIVaoo+r0v5V9yD2k+7Kv9mWH/Pjbf8Afpf8KP7MsP8Anxtv+/S/4Vaoo+r0v5V9yD2k+7Kv9mWH/Pjbf9+l/wAKP7MsP+fG2/79L/hVqij6vS/lX3IPaT7sq/2ZYf8APjbf9+l/wpV06yR1dLO3VlOQREoIP5VZoo9hSX2V9we0n3YUUUVqQFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAV7/AP5B1z/1yf8Aka8++BP/ACSjT/8ArtP/AOjGr0G//wCQdc/9cn/ka8++BP8AySjT/wDrtP8A+jGoA9JooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigArP1HVU0+aCBba4uriZXdYbcKW2Ljc3zEDA3KOucsMA15z4h+IviCy8eap4f059FjW0WNolurW7mlkUxK7keSG4XPOQOCOvNZUviLxvr6WmpWVxpICo6w3VlpOpsHjfG5QTCwIJVTkc5UYIr2KGUVW4ym1Zq/XqrrZehm6i6Hpsfi2wk0q41FYrnyYNLi1VgVXcYpFkYAc/exG2R05HNQzeONHhvri1Z3ZoPODFGRiWiVmdQgbfkBG5KgEjryM+Uz2vjWbSxpyS2sEB06PTZfK0jUszQoGC7iYDyNzcjGdxzxxV0XXj1ZpmSW0jhkaWRYI9K1VFjeTO91Ih3ZyzHkkAnIHSu3+x6Ku7/i/Ly73+XmT7RnoFz40MRWRdNuUtRYXV48rCN8CHyz8u2TDgh+oPUgZ4bF288X2NjHdTTW939mgE4E6quyV4VZpET5s7gEfqADtPNeSNa+NHiuI2eyLXEVzDO40XUVLrOqK/AtwoP7tCMAcgk5ycuvpPF93bXouJdOWykFwxiGk6mI4HlVlkkU+RkHDv94kDceKt5RRdtV1vv8A5f0vMXtGe0adrCahcz2xtbm1nhSOUx3AUEo+4Kw2sepRhg4IxyK0a8dt/EvjY65LdrJ4fS4uVtrNhLpupJGp3v5eS0YClmmIyTjpVu/8W/EWwkuoDD4YnuoLn7MtrbxXMkszeUkpKKDyoWQZJxjn2z5tbK5Rd1KKVur9L7ruy1M9XorzDR/EnxE1nR7PU438H20V47Rwx3YuYpC6syldpPX5W49qnk1zx9FcG3k1T4fpOHEflNcThtxIAXGc5yQMe9c/1H/p5D7yubyPSKK80g8ReObm8Fnb6z8PZbosVEEd1OzkjqNoOcjB/KpTrPxAUXROpeAQLTi5Jnn/AHP+/wA/L+NH1H/p5D7w5vI9GorzC68T+OrTTr6+bU/AUkNjGZLjyprhyg56gHqSCB6nipLfxB49udMXUo9T8BfYztzM01wqqWxgNk8HkcHnmj6j/wBPIfeHN5HpdU9R1GPTo4S0Us8s8oihhhA3SNgtgbiBwqseSOAa8li+I/jKXxJe6N9p8HIbOJJXvGac27BjGqhXDEk5lUdOua7bwpfT+OvA+k6xfsLS+MskySWY2+WyvJHlQ+4crkHOfvGtauXTw8VUqtOOmzv8Sbj8nYSmnojY0zxFa6pLbRRwXMUk63LBZlUFPIlWJw2CedzDHXjPSuKs/ivd6gqG28PQOzypCsZ1WNXZ2IAAUqG6kc4xXUWHhRoLOFZdQuYrqCa82zwOpZ4p5zIVbcp5ICEkAEEcGvLvCg8P3Efh2x+wreajeXkkVzFLsWNditIHYlGfBXACghWKsD0auKuqHtuWEnb3tvJ6bp9PxMKrqucYxdtH28vJ9zcj8ReIdS17T9Vg8OLJHNPutla8UksbeQeWH4CgBXcqQCCMHkioLfXdbu9G0z7P4bjkhtbSGwEkl1GySNN9nePcpHG4KnGcjzByCBW3baF4FimlYXKztYHzWDW8bAxxbkZQBHiRQXIYjc24LlsqMQ6Zp/w9mVpYblXh023hmnS4t1USoFwsxLRhmDY5KHax6g5OcpYajraT+9fP7Hp8zL6vU/m381/8iZNnfeI9SWzkt9AkklvLBp7V3vlGdkgZJRu5wnmqoUnJBHPGa04bPxPb3kUsfgm3KIYWJkvIHlzGqqNrn7oOxc8E9cEZq9b2vgKz0W01ZreOS2sk/s9lmsMyySsYwPMi8veZflGPlBw7HGGqwt/8P206K+GkWnlSmQIh0dhIwjGXYRmPdtHc4xnjrXPUw8b+43b1Xd/3ew1hZ9/xX/yIunan4vsLZ4f+EL37p5ps/wBqQj/WSM+Onbdj8Kt/8JB4w/6Ef/yrQ/4Vm6lqngnTb+xtP+EXW7e/tvtNo9npKypOv91SB1wQecAZGSM10sPhrw9NBHL/AMI7p0e9Q2ySyjDLkdCMcGkqdRK3N+X/AMiaKlVSspP8P/kTM/4SDxh/0I//AJVof8KP+Eg8Yf8AQj/+VaH/AArW8LnHg7RTgnFhBwP+ua1xfhbVNK1+006wkl8QwX93ZuyXUt9Osc0keEkKYlwSGycYHHbFFpu1pPX0/wAg5ajtaT19P/kTe/4SDxh/0I//AJVof8KP+Eg8Yf8AQj/+VaH/AArnPDcsFj4W12/8SazqlyNL1G4tvtD6hNCzqhAUbRIF3EnA9cir0Gs6JJ4cvNWeLXEazmEE1susSyMrHbg71mKbfmHzFgBg56U+Sp/N+X/yI/Z1f5n+H/yJq/8ACQeMP+hH/wDKtD/hR/wkHjD/AKEf/wAq0P8AhWRc61o9v4csdWEGsu15I8SQ/wBuSKqshYPmYziIAbDg7ue2ah1HxL4f06OzDprT3U1mt9JbDWpQ8ULEAHJmw55OFUkkA+2Tkqfzfl/8iHs6v8z/AA/+RN3/AISDxh/0I/8A5Vof8KP+Eg8Yf9CP/wCVaH/CtTQYzBc6zbCa4kigvVWPz53lZQYIWI3OScZYnr3rivCc+iahp+jxN4LSW2kQW76o1pC6GVIwXLYywG4Mu4jqDmlab2k/w/yJ5ajslJ9e3T/t06H/AISDxh/0I/8A5Vof8KP+Eg8Yf9CP/wCVaH/CsNtW8NLFDMfBVqIbq0nvLVzbwfvY4sFuOqkqQw7Ed6r3ep6O3h3V7mHwdplrfW+j/wBrWyT28Tq0RDbS20cNlT8v0554fJU/m/L/AORK9nV/mf4f/InSf8JB4w/6Ef8A8q0P+FH/AAkHjD/oR/8AyrQ/4VWnstKsNCS9vvDHh9biVokhiRV2uXx3MYPGScAMcCqEF/4cvE0q2tPCelNqmpLcNHby26pGBCxVyXMeeSOPlzzyBRyVP5vy/wDkQ9nV/mf4f/Imx/wkHjD/AKEf/wAq0P8AhR/wkHjD/oR//KtD/hWVqNnbp4o0LT7LwvoCpeWU9zPFcRICGTyxtDKjDgydRkHn2rpPDdtb2lxrcNrBBBCt8pWOBQqLm2gJwAAOpJo5Z3V5P8P8g5KiaTk9fT/5Eof8JB4w/wChH/8AKtD/AIUf8JB4w/6Ef/yrQ/4VyVhdxTeMZdMu9B0NoZdTukE97auZbgeZI2Uk2FCQfl2k7sITjAq7ol9pGpv4eWfwtoUf9p2VzcShLdCY3iZRtAK9Du6n0pKNRq/N+X/yIowqtX5n+H/yJ0H/AAkHjD/oR/8AyrQ/4Uf8JB4w/wChH/8AKtD/AIVx/h7V7XUvDOs6/feEfD0VnaWSXVuY7XhiULlWJTnaMAlR1ziny3APh171PDPh8PdalHZWMy6aoHlscGaRHK7c4IVSV5xk80+Sp/N+X/yI/Z1f5n+H/wAidb/wkHjD/oR//KtD/hR/wkHjD/oR/wDyrQ/4VyGtXtpaeGtNuoNC8OQ3M08yzy/ZbabEUeQXSMSjcSdmVDkqCc9KffQ6TPqPhq6t59A0/Tr3TJZ3muNKiEE0n7vby+1gfmJC8HCmjkqfzfl/8iHs6v8AM/w/+ROs/wCEg8Yf9CP/AOVaH/Cj/hIPGH/Qj/8AlWh/wrkJNSs5PHR0m28KaKtjFNDGHlgtlNxG4y0qZYMRyNuxWBwcnni1pdhpt/8AEHVtHFzoBt7GdJFthp1uZZVZSWiyBwqYOTjdkjJ4wTkqfzfl/wDIh7Or/M/w/wDkTdvfF/iPToRNfeEre1iZtoefWoEUnrjJHXg/lVH/AIWTff8AQF0v/wAKK2q4bv7B4O8I3mx3+zwCXYi7mbbYzHAHc8dK5TTPG3iG80jV/teuWtrdWllbX/miOGRYmdmDxfKSCgwnfeN3JyamMZy1U3+H+RMYVJ6qbXyXb0N//hZN9/0BdL/8KK2q3Y+Ndf1PzPsHha1u/Lxv8jXIJNuc4zjpnB/Ksv8A4SnV7K+vdHl1kXiWt7a+fqqwRq0FtLGzklQCnBRRvIxiUZ6ZqX4VqkcmrxRLII0Y+WzRbA6NdXboy8AFSrKQVGOeKfJUTV5v7l/kP2dVNXqP7l/kXJPHOuwWTXk/hWCC2WVoTLPrMMah1coVywH8QI9+1XI/EniyaNZIvBSujDKsurwkEfXFc1qdxbQ694eF3qtzaQNf6oCiRo6bjNIFOGVvmJJABB74xznXvtZ1q21zU7S2aeP7NPapp1mlniK6jYIXLSbDjkuCQRt2gketRhJpPmf4f5FQhNxT53+H+Rof8JB4w/6Ef/yrQ/4Uf8JB4w/6Ef8A8q0P+FVLQXM/j3VLabXdaS3hnhlt7cxqsMjbCXUNs5jHAxkcg8k1h+G9U8UXWpafYanbavCNNinknu8kLetGNjKQVIJLlWTkfLT9nL+Z/h/kV7KX87/D/I6f/hIPGH/Qj/8AlWh/wo/4SDxh/wBCP/5Vof8ACuP0fxTq13NrMN6dea1/skXKSLbSrJ9oUncqMYowpwVG0KVPr1zq2t5cjwXDqVrc6/dzm4txq0kkUsc4RQDJ5UTKMDkA+WBkZwSRR7OX8z/D/IPZS/nf4f5G/wCEPGDeKZ9RhexitmsjGGMV2twrFt3G5Rjjbg8nnjjFdTXmnwujMeveLSVuwslzHKn2tSspR2lZSwIBGVIPPPPPNel06Tbjq+r/ADHRbcPed9X+DaCiiitDUKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigCvf8A/IOuf+uT/wAjXn3wJ/5JRp//AF2n/wDRjV6Df/8AIOuf+uT/AMjXn3wJ/wCSUaf/ANdp/wD0Y1AHpNFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAfPniiDTj8cNbn1We4tLcQRpFdwDcYpDDDkEA5wyb046b88YyMu/8SC88F6LoKQ3Ea2mnyRuRI2EnydnCyAH7q4b5sB24yMHs/iBonhaf4gSNr8tzbW89glwxtizSTTh/KUKuGJ+Reij+HPrWfe+BfhhYWGn3supay8N/E09v5KtIxjUZZiqxkqADyTjFdFSpSxT5qk3FpKOkE/hilu6ke3Y4W68uaMbWu/63MWTUdGmfUri5N3NdmytDZyLLINtwscav/EOh3Hnj5WxyRll34iVfHK+INPkuEzftO6SMT+62kAA7j1ycrgAAcFq1b3wh8K7DUXsZ9Q17zUZVLJC7x/MnmA7xEVxsy2c9AT2p0fgz4Xy6wNKS88QG6M5txiF9m8OqH5/K24DMoJzgbh61j9Wwv8Az9l/4Lj/APLTP2Nfy+7/AIJztpf2UGs3EjSXKKr3EcEscSvGyEvseQOxJP3MDaBj0PNXNIvNAtbS9W5tA/maXLCIJiHSS5Zhh8CMYOCcs2ThQP4Rnbj8C/DCa/nsotR1mS4iE2FXJ80xf6wR/u/nK+i5PB9KbZ+BfhtqNnNcWdxr77LF7+NJEaIzQr1ZN0Y3DOBx6j1oWGwq/wCXkv8AwXH/AOWjjRrra33f8Et6H4k8L2Xgy0tvJgsdVF3YNdtGju1wIZ4naVn2DJwHOCSe3elvPE+h23jK78V2N2lzdR3LLHauskYuIXtrdCwbYdpV424I5GfbNK1+H/geTwtHrt3beI7WJooGEbFSXaXAVUO3DckDPA5BOBWx4W+GfgvUL+9jk0rUJIUt4ZFS/maORGZ5lYfuyAR8i+v1rqjOgoez9pKzv/y7Xk/+fv8AdNb4i6vb7v8AgmfrOtabrAe4vtX0fUbqfTWs2S5trhI7dzKziRMRknCsq8bSdgORniDxHqekao1+lpe6PunYmO8lS4WUfuUTccQHDBk3de/rWnL4S8Jad4r/ALGHg576O4u3iidLogxqttFKVG6QbjlmPJHB4Jxir914a+HFnfXFrL4Xn/0RInvZg7eXaeZjaHbzOuCCdu7A56VxuMW3yz0/w/8A2408S9nH8f8AM53+1tLk1C0vPteh28kN4t0zwR3G8/6UZSoPkDrG2368dKm0+90C1tbm2n1+xuD9juLSO4mtLiRpRL82502BQd4BOd+ccEZNbM3w18IjwjrGpDR1F3bfbjE4nlwvlSSKny7sHAVeo5xzmsC98N6Ne6P4qa18EfYF0z7XHFqK3gkCNDHuXKM5J3EehADe1Nqm0uSo9tbwt/7e7/gJSxMtnH7n/makOt+HhZeQmuWNh5uh/wBmSraWUx2uN21lJQAqNzcEfxHpVvVvF2la3pEdne+IdPGy4ilxBZ3UeQgJyHHzK2/awI6bcc5rPt9F8D2uh3V7rfguaxa1s4rpfNucm4VztBG2QhSWwMHGNwpdE8PeAvFa2DWnhp7UHUDbXSPM5DD7PLINrq+CMqpyCDxj6pRSa5p6f4f/ALcbeJW7j+P+ZymmeIm8OfEHV9ZSUaolxAscVwtsMMd8THKMyHICMu7qWAYg5Nd38N/Gvh7QPAGmaZqeoeReQeb5kfkyNt3Suw5VSOhHerNv4fi0Dx23hrwvdnQra805b2Z4yJpXdJGTC+dvGCHyeP4RjGTU2jfEm8uLaS2m0l5ry30ma/8AM85UW48qZoW7YUnaW9q68Vj61en7JNcq5Vflab5E4q652urvYdOFbfmXXo+/qbf/AAs3wf8A9Bf/AMlpv/iK8q0TxHothb6DNOtzHqOlzO7SRWiuJUPmhUJMq9POkOcdSOOOfUNb8eLpWs2FjFYrcJO1uJ5BOMxCaQIuFAPdgfm2gjoSeKsxF7b4oTQi6umju9J87yGkLRqyShSwBPynDjgYHXOeMea6dRtS5l93/BHKlWclLmSt5d7efkeT2Gt6DYay+pJfas8j2U9o++zRjJ5nO9sz4DZCk7QoOOgzU914q0y7me4fVNWiuX0tdNMsFhEhwsgfd/rj1xtI9CcEZr1bQzqR1vxL9ruAzieMW0Pml44k8pSCAQCCSSSK5vw/r/jnUvBg1dW0G6uGhM0cIWRXYBmBBAOM4GB79aOSt/P+H/BD2df+dfd/wTz1tdsotNubK31G/JvNShvpZvsEUX2cxqOY1WQ5YlIx1XAyc56ySa3oWq2dlBrQnlbTHeOyePToHV4HC7hJHI5XfleGHTgktzn0yw1y/wDEGu6feqlqdC/tHGnTx7vMnH2SYszA8AAkr2OQc9Kp+JZ3n+KVjok95Pa6Zf6erXLQs0ZlaNpikfmrgoDl2yCCdmO5qbVr25vw8vUi1e9udb9vK/c50+NPDKXGkTW0/iC3OlW7W9sqW9sQFYAHIPsqjjAGOlaV18WdOl17T7mA6rFYQxyi5t/KiPnMQAn8WRj5jnI7DBzxaPiefQ9HWz0K+tbm0sdNkvjfaw7lrkCRgEQ5BONrZY56p/ezUlx8QtUhg1mVrfT4Ps32CazW4YoZYrjG4N833l5HGOmcVXJW/n/D/gl+zr/zr7v+CVdF+LGhadoWnWM1pqTS21tHC5SNCpKqAcZfpxXJeCfE+i6FbW8msf2vcXlp56WgieNoYElYlig+Uhjnndu6cHnA9Hg8VazJqF+WOlrZ2etJprIVcSGNtvz53YzlwMYwcE8dKTw54o1LWdat2bUdGa0uDOj6em4XVs0bEDv82QATlVAyMZyKSpVVb3/w/wCCSqNZW9/by/4Jwtn4i8IRWOp2N/N4k1O01GQzTRXcdvgSkg+YpTaQ2VHfHHSrt/4x8GapFGmoR+I7porhLmN5XRtjqCFwu/Zjk8bec811PgrUdHurTxPZXN3p06wancvcq0isGj+XMjqWIC5B54Xin/DHV9K/4V5arDf2jCySVp0ilVjCvmORuA+6MDI9qfJW/n/D/glezr/zr7v+Cc7pmuaBeWTWml2PjC5jiklkk8hRLjzs7gwDEbSckAjrkircZ0K2ks3s/B3jC0e1g+yq1tbyRl4ck7GIfLDJJ9Qehrc8I31tqfjTxVfWcyzW06WMkUi9GUwnBFdrSpqpJXcu/TsxU1VlG7l1fTs7HA6X4qbT5tQP/CK+JvKnuFkiAsCSqiGOPBy3XKH14xWRoL6VpFnp5Pg3xULy3CSOYoJfKMwQKzhPMC88/wAP4V6rRVKnNfa/ApUpp35vw7nmaTeHo3d18CeJwXhktwPskmEjkOXVB5mEBP8AdxUq32iKAP8AhCPFLKLM2JV7WRg0HP7tgZPmHzHGc47V6PRT5Z/zfgVyVP5vwPLVj8MpYtZjwJ4s8kyLLzDMWDKCAQ3m7hwSMA45pY18MxaSNLTwF4pW0WYzqotpdyORglX8zcuR1AODXqNFHLP+b8A5Kn834HnN3faDfWdjaT+APEJt7E5tUTTSgi4xgbWHBHBHQ9wasaX4p/s6bUNnhLxGkE86vDHHp2AiLDHGBjOByh4HbFd9RQ4Tf2vwE6dR/a/A8z0m/wBMsbuXUZfAettqb3U8/wBrXSgZMPI5X5ic5CMF/TpUlzfaJObmaPwHr1tezl2+2Q6QqzJIylTIrZyGwTzXpFFChNK3N+AKnUSspfgeIWejW1rp99aroGvxfabAWW6z8PpBnkEvJh/3hJUZB4wWH8RrZ8LPZeHIL5X8J67cPe7BMsOgR28RVc7R5anBPzHJOe3pXq1FHLP+b8B8lT+b8DhpPEumzQRQSeBNdeGLPlxtpClUz1wM8VLN4utbiFIZvBfiKWKMgoj6WGVSOhALcYrtKKOWf834ByVP5vwOOPjOFrhbg+DvEhnVSqyHTBuAPUA7s4qGPxTYxXTXUfgfxAlyxJMy6Soc5685zzXb0Ucs/wCb8A5Kn834Hm1vrj/2DotlLoHi23utNjjxNa6ep+dYjGcb8gghm6j0qX/hI73/AJ9/Hn/gqtv/AI3XolFT7GX8xCoTX2jzv/hI77/nh48/8FVt/wDG6m0/xKbK8uLuXQ/GV5PPHHGWn02MbVQuQAECjq7dc131FCpSvfmBUZp35zzw6vp++R08L+N4/MkaRli+0RruZizEKsoAySTwO9H9sWP/AELfjz/v5c//AB6vQ6KPYvv+CD2D7r7keef2xY/9C348/wC/lz/8eo/tix/6Fvx5/wB/Ln/49XodFHsX3/BB7B919yPPP7Ysf+hb8ef9/Ln/AOPUf2xY/wDQt+PP+/lz/wDHq9Doo9i+/wCCD2D7r7kcP4GilbxD4jvf7P1Sztbj7N5I1JX8xtqMG+ZySefc4BFdxRRWlOHJGxrSp+zjy/1q7hRRRVmgUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFAFe/wD+Qdc/9cn/AJGvPvgT/wAko0//AK7T/wDoxq9Bv/8AkHXP/XJ/5GvPvgT/AMko0/8A67T/APoxqAPSaKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooA818caB4lufG+na74fs/NksrdBG5mjVd+59ysrEFgUcjjHJBzxis6803x7cTW15DpM9vqSWzWlxcreWpE8RbdjYVwpBJwR+Oa9borL2bu2pNfd/kY+xabcZNX9P8AI8OuvBXiySRltNAe3tRHHHFC17BJsCWzWw5PU7HPXvin2vhLxraXMVxFpEsbxyySAR3Vsq/O8UhUDBwA0Knj1x0r26ij2cv5n+H+Qeyl/O/w/wAjx3TPCuu6TrUuoWng1YvnleBY7myV4zIGDAyCLcwG/wCUZ4wAcipdI0LxZpq6ck/hy4u47PS5NL2NqVugeJ2U9lyCAqjr2+ufXaKPZy/mf4f5B7KX87/D/I8tTTvFyaYmnjQ9VNtGkMUSHWLTaiR9Fx5WGBGA24HIFS+G7LxF4XlufsHgkiGdEBj/ALTgUKweRiQFUKoPmY2qoAx3JNem0Uezf8z/AA/yE6Mn9t/h/keY31l4o1C7lu28KXNvdfa/tME9rq8CSQ5hSJlyysCGCc8d+MYzTJtG1e4klebwRdv9oSKO5B15CLkRHKebx8/oc9RwcivUaKFTa+0/w/yBUZLab/D/ACPPHl8YP4e1DSf+EPx9s+1fvf7Th+TzndunfG/HXnHaudl0Lx3Lc38p8OwLHf8Am/abdL9lhkMibHJQT4yR+R5HNey0VPsH/M/w/wAifq7/AJ3+H+R402g+OJF2z+GLScf2f/Zv769LHyd27vP97IHzdeBzxVzR9P8AHOmXtrPN4bW5EMvmuz6mXllIjkRQXklfgCU9uwr1mij2D/nf4f5B9Wf88vw/yPM9WsvEGtanLfXfgmVZTBHDDLb6zHDNBtaQsVkXDAMHwR0O3nPatBo2uTaRZWOs+ALbUDZRtDFImoRwZiJHysqnDZ2jPYkZwK9VoqlTa+0/w/yKVGS2m/w/yPKZvDBuChk+FsR2KigDWlUYThcgHkgAAE88D0q5Lp2oza6mtyfDgNqMZUpP/ba5XbjAA6Y4HGMV6VRR7OX8z/D/ACH7KX87/D/I80sNM1DTNZfV7P4biK/csWm/ttSTuznIPHc9uKV4fE1j9pufD3w/03S9SuD+8ujcQybgTkghSh5PPXGecHJr0qij2cv5n+H+Qeyl/O/w/wAjzfT4vFOmafo1lb+DnMemStLufVIS0zNHIrE8DBLSFv0xU15/wkOp3l1JqXw/t722uIYYjbXGoQOgMbSMG5BB/wBZ6cY969Copeye/M/w/wAifYO9+d/h/kcNPda9dQ28Nx8OLWaK3IaFJNQgYREdCoK8Y9qlm1PxLcSCSb4fQyOBtDPqUBIHpkjpzXaUU/Zy/mf4f5Feyl/O/wAP8jiW1DxG+/f8PLdt5BfOowHcR0J+XnFSprHimOZ5k8BRrLJje41SEM2OmTjmuxoo9nL+Z/h/kHspfzv8P8jio9Q8RwhxF8PIE3rtfbqMA3D0Py8ilh1TxNbo6Q/D6GNH+8qalAA31wOa7Sij2cv5n+H+Qeyl/O/w/wAjkPCFhqsWva9qWo6SumJei2EMCzpKAI0ZTgr+HYda6+iirhHlVi6cOSNr3/4OoUUUVRYUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAV7//AJB1z/1yf+Rrz74E/wDJKNP/AOu0/wD6MavQb/8A5B1z/wBcn/ka8++BP/JKNP8A+u0//oxqAPSaKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiimvIkaF3dVVRkknAAoAdRVB9c0iKRo5NVsUdSVZWuEBBHUEZpv/CQaL/0F7D/wJT/GgDRorO/4SDRf+gvYf+BKf40f2/o3/QXsP/AlP8aANGis7+39G/6C1h/4Ep/jR/b+jf8AQWsP/AlP8aANGise78WeHLGMSXWu6bCh7vdIPT39xQvivQXRXTVrVlYZDK+QR6g0AbFFZH/CUaH/ANBS2/77o/4SjQ/+gpbf990Aa9FYF1418O2YBl1FWyCf3UTy9CB/Cp9R+voap/8ACyPC3/P9c/8AgvuP/jdAHV0Vyn/CyPC3/P8AXP8A4L7j/wCN1qReJdPmjEkaagyHoRptx9P7lAGvRXP3vi60sygXTNcud2eYNKnbb9cqKq/8J3bf9ADxN/4J5v8ACgDqqK5X/hO7b/oAeJv/AATzf4VoQ+IjPCkqaLq4VxkB7YI34qzAj8RQBtUVz934lu7cIYPDGtXWc5Eawrt+u+QfpVX/AIS7U/8AoSPEH52v/wAeoA6qiuV/4S7U/wDoSPEP52v/AMerTXVtRZA3/CO3wyM4M0GR/wCRKANeisn+1dR/6F+8/wC/8H/xdH9q6j/0L95/3/g/+LoA1qKyf7U1H/oX73/v9B/8XVC21jxVNdLHL4Tht4iT+9k1RCB9QqE0AdLRWNDe+IZE3PotlEc42tqJJ+vERqT7Tr3/AECrD/wYP/8AGqANWisr7Tr3/QKsP/Bg/wD8aqK4ufEvkP8AZtL0vzsfL5uoPtz74hzQBtUVyv2jx9/0DPDf/gwn/wDjNH2jx9/0DPDf/gwn/wDjNAHVUVz9pJ4wk3/bbXQ4MY2+TcSy59c5RcfrVn/iov8AqF/+RKANeiuauIfG7zs1tf8Ah+KI/dSSzmdh9WEoz+QqL7P4+/6Cfhv/AMF8/wD8eoA6qiuat7fxv56fadU0Dyf4vK0+bd+GZsVofZte/wCgrYf+C9//AI7QBq0Vg3uneJbmJVg8Q2towbJePTdxI9PmkIql/YPi/wD6HVP/AAUx/wDxVAHV0Vy0eheLA4MnjMMncLpUQJ/HJrT/ALK1H/oYLz/vxB/8RQBrUVk/2VqP/QwXn/fiD/4ij+ytR/6GC8/78Qf/ABFAGtRWQ2k6iykf8JDejIxkQwZH/kOqlp4Yvbd2afxXrd0pGAsjQKAfX5IgaAOiorHXQZVGDreqsck5MqevThO3Sl/sN/8AoM6p/wB/V/8AiaANeisj+w3/AOgzqn/f1f8A4mj+w3/6DOqf9/V/+JoA16K5278Ix3zq82ua8pUYHk6g8Q/EJgH8ar/8IJbf9B/xN/4OJv8AGgDqqK5y28G2tt5mdW1+beu397q052+4ww5q/wD8I/Zf89tR/wDBlcf/ABdAGpRXM3PgHw7eXD3FzbXcsz/edtQuCTxj/npUX/Ct/C3/AD43P/gwuP8A45QB1dFcp/wrfwt/z43P/gwuP/jlTW3gDwzaTrNHp8jOucCW7mkXn/ZZyD+VAHS0VnW2gaTZ3CXFtYQRTJna6rgjjFaNABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFAFe//wCQdc/9cn/ka8++BP8AySjT/wDrtP8A+jGr0G//AOQdc/8AXJ/5GvPvgT/ySjT/APrtP/6MagD0miiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAMvWfDuj+IUhTV9PgvFhJaMSjO0nrisn/AIVr4M/6Fyx/74/+vXVUUAcunw48GxyK6+HbEMpDA+XnkVpL4W8PpGIxoem7fQ2qH+la1FAGMfCHhliSfDukknkk2UfP/jtJ/wAIf4Y/6FzSP/AGP/4mtqigDF/4Q/wx/wBC5pH/AIAx/wDxNaEGmWFrAkFvY20MKDCxxxKqqPYAcVaooAh+yW3/AD7xf98Cj7Jbf8+8X/fAqaigCIWtuOkEQ/4AKlAAAAGAKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAr3/8AyDrn/rk/8jXn3wJ/5JRp/wD12n/9GNXoN/8A8g65/wCuT/yNeffAn/klGn/9dp//AEY1AHpNFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFZes6fqV+kI07W5tLZCS7R28cvmDsDvBxj2rJ/4RzxP/ANDzef8Agvtv/iKAOqormIfD/iNJ0abxreyRg5ZBY2y7h6Z2cVp/2Vef9DBqX/fFv/8AGqANSisv+yrz/oYNS/74t/8A41Uc2iXc8RjPiLVUBIOUFup4OeoioA2KK5iLwdJHJvfxT4ilGQdr3SAdQeyD0x9D64NaH/CPw/8AQQ1T/wADZP8AGgDXorI/4R+L/oIap/4Gyf40Hw9CQQdQ1Tn/AKfpP8aANeiuZl8C6XPIZJL3XNxwPl1i5UcDHQPimf8ACAaR/wA/uu/+Dq6/+OUAdTRXNW/gbSbedZRc6zIV/hl1e5dT9QZMGrqeGNMRAuLw47tfTE/nvoA2KK5m5+H3ha9nae60pZ5mxmSWaRmOOByWqL/hWng7/oBwf99v/wDFUAdXTZJEiTfI6oowNzHA54FcxF8OPCEMqSpodvuRgwyzEZHsTg1pv4W8PyLtfQtNZfRrRCP5UAXJNT0+J9kl9bIwwdrSqDzyO9M/tfTP+gjaf9/1/wAaoP4M8LSNufw1o7N6tYxE/wDoNJ/whPhP/oWNF/8AACL/AOJoA0P7Y0z/AKCNp/3/AF/xo/tnS/8AoJWf/f8AX/Gq1p4X8P2Epls9C0y2kK7S8NpGhI9MgdKu/wBm2P8Az5W//fpf8KAI/wC2dL/6CVn/AN/1/wAaP7Y0v/oJWf8A3/X/ABqT+zbH/nyt/wDv0v8AhR/Ztj/z5W//AH6X/CgDNbxj4ZWYQnxDpfmkKQn2tNxyMjjPftUv/CUaD/0GLH/v+v8AjWglnaxHMdtChznKoBU1AGT/AMJRoP8A0GLH/v8Ar/jR/wAJRoP/AEGLH/v+v+Na1FAHP3Pjfw1a2y3EurwGNjtHlhnbP+6oJHT0qn/wsrwj/wBBY/8AgLN/8RXWUUAcn/wsrwj/ANBY/wDgLN/8RR/wsvwj/wBBY/8AgLN/8RXWUUAYsPivSbjf5LXkmxtrbbCc4OAcH5PQg/jVe88Z6faSKn2DW58jO6DSbhwPYkJ1roqKAOV/4T3T/wDoEeI//BLc/wDxFH/Ce6f/ANAjxH/4Jbn/AOIrqqKAOdtPGFtesVh0nXAR/wA9dMliH5uBVv8At4f9ArVP/AY/41r0UAc7P4qnihjdPDGvTMxIMaQRhk9zukA/Imq//CY3n/QmeJf+/Vv/APHq6qigDn7PxJe3rOB4U1uDaAcz/Z0B+n72rf8Aat9/0L+of9/bf/47WrRQBlf2rff9C/qH/f23/wDjtH9q33/Qv6h/39t//jtatFAHP3Ota8s8aWnhS4ljYHdJNewR7T9AzZq19s13/oD2n/gef/jda1FAGT9s13/oEWn/AIHn/wCN0fbNd/6BFp/4Hn/43WtRQBjSXniHyn8rR7EyYO0PfsBntnEfSs/7b47/AOgHoH/g1l/+MV1NFAHLfbfHf/QD0D/way//ABij7b47/wCgHoH/AINZf/jFdTRQBzsVz4xbyvN0zRUznzNt/K23nt+6GeOe3p71ZlbxMYnEUekrIVO1nkkYA9iRgZHtkVs0UAcs8fj0uxS68NqmflDW05IHud4zSeV4/wD+fvwz/wCAs/8A8crqqKAOesofGJkb7ffaEqY+XyLOZjn3zKKu+Rr3/QS03/wXv/8AHq1KKAMvyNe/6CWm/wDgvf8A+PUeRr3/AEEtN/8ABe//AMerUooAynttfZGC6ppykjAYae/Hv/rqp22keI02favFAlxu3eVp8ceem3GS2Mc565yOmOehooAzrax1CG4SSbWJp4xnMbQRqG49QM1o0UUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAV7//AJB1z/1yf+Rrz74E/wDJKNP/AOu0/wD6MavQb/8A5B1z/wBcn/ka8++BP/JKNP8A+u0//oxqAPSaKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKjlnigAMsqRg8AuwGaAJKKr/b7P/n7g/wC/g/xpP7Ssf+f23/7+r/jQBZoqt/aVj/z+2/8A39X/ABprapp6IztfWyqoySZlAA9etAFuisi68V+HbKURXev6VBIVDBJbyNTg9DgnpUP/AAm3hP8A6GfRf/A+L/4qgDdorC/4Tbwn/wBDPov/AIHxf/FVLF4s8OTJvi1/S5Fzjcl5Gwz+BoA2KKxbnxd4dtLd55dbsPLQZO2dWP5DJNZ3/Cy/B3/Qcg/74f8A+JoA6uiuU/4WX4O/6DkH/fD/APxNW7Pxv4e1AE2V+1yF6+Tbyvjp6L7j86AOgorEPizSQ8iBrxmjQOwWxnJwc4H3OvHSqcvjvSYpXjNprbFSRuTR7plP0Ij5FAHT0Vy3/Cf6R/z5a7/4Jbr/AON1ND41064R3jsdaIQqG3aTcL1OBgFBn8OnegDo6Kx18RQOCRp+q8EjmxkHIOPSl/4SCL/oH6p/4BSf4UAa9FZH/CQRf9A/VP8AwCk/wqC78Ti2h8yLRNaumzjy4bMhvr85UfrQBvUVzH/CYzGYxr4T8RsMkB/s0YU+/MgrRTWLySNXHh7VAGAOGa3BH1Hm8UAa1FZf9q3n/Qv6l/33b/8Ax2j+1bz/AKF/Uv8Avu3/APjtAGpRXKnxF4mzx4GvMf8AYQtv/i6P+Ej8T/8AQjXn/gwtv/i6AOqorlf+Ej8T/wDQjXn/AIMLb/4utMX2tkA/2JEPY3o4/wDHaANeisG5v/EwQ/ZNBsnfAwJtRKDr7RntVP8AtLxx/wBC1o3/AIOH/wDjFAHVUVzlnf8Ai+S8hS80DSobYuBLJHqjuyr3IUwjJ9siujoAKKKKACiiigAooooAKKKKACiiigAooooAr3//ACDrn/rk/wDI1598Cf8AklGn/wDXaf8A9GNXoN//AMg65/65P/I1598Cf+SUaf8A9dp//RjUAek0UUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQBXu3u0iBs4IJpN3KzTGMAeuQrc+2Kp+fr3/QN03/wYP/8AGa1KKAOXll8d+c/k2fhwRbjsD3c5bHbOI+tN83x//wA+nhn/AMCp/wD43XVUUAcr5vj/AP59PDP/AIFT/wDxupIH8cM5FxB4djXHBjmnc5+hUV01FAGJJH4nZP3d1pEbbSObeRgDjg/fHA/X2qh9i8d/9BzQP/BVL/8AH66qigDlvsXjv/oOaB/4Kpf/AI/QLLx1kZ1zQce2lS//AB+upooAx0s/EGwb9Yst+Odtgcf+jKz59C8UyzvInjJoUY5EaaZCVX2Gcn8ya6iigDlP+Ee8V/8AQ8S/+CyD/Cj/AIR7xZ/0PEv/AILIK6uigDJGlX+BnxDqBOOT5Vv/APGqX+yr7/oYNQ/79W//AMarVooAyv7Kvv8AoYNQ/wC/Vv8A/GqpyeGbua9FxJ4p1zaCMwo8KRtjtgRA8+xFdDRQBkf2CP8AoKap/wCBJ/wo/sEf9BTVP/Ak/wCFa9FAGR/YI/6Cmqf+BJ/wrPm8D2U8zyvq3iDe5ydmr3CD8ArAD8BXT0UAcr/wgWn/APQX8R/+Dq5/+Lp8XgXT4pUk/tTxA+1gdr6zclT7Eb+RXT0UAZJ8OaeQQWvsH/qIT/8AxdZP/CtfCP8A0CT/AOBU3/xddZRQByf/AArXwj/0CT/4FTf/ABdH/CtfCP8A0CT/AOBU3/xddZRQBgWfgrw3YxlIdItyD/z1zIfzYn1qz/wi+g/9Aex/78L/AIVrUUAZP/CL6D/0B7H/AL8L/hUU/g7wzdKFuPD+mTKDkCW1RgD+IrbooA53/hAfB/8A0Kui/wDgBF/8TWr/AGNpf/QNs/8Avwv+FXaKAKX9jaX/ANA2z/78L/hR/Y+l/wDQNs/+/C/4VdooApf2Ppn/AEDrT/vwv+FH9kaZ/wBA60/78L/hV2igCl/ZGmf9A60/78L/AIVZgt4LaPy7eGOJM52xqFGfoKkooAKKKKACiiigCKC3W383a0jeZIZDvkLYJ7DJ4HsOKloooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAr3/wDyDrn/AK5P/I1598Cf+SUaf/12n/8ARjV6Df8A/IOuf+uT/wAjXn3wJ/5JRp//AF2n/wDRjUAek0UUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUVQ1bWLHQ7P7XqEkkcG4JuSF5ME9OEBP41h/wDCyPC3/P8AXP8A4L7j/wCN0AdXRXP2PjXQ9SLiylvZzHgts064OM9P+WdF74utLMoF0zXLndnmDSp22/XKigDoKK5X/hO7b/oAeJv/AATzf4Uf8J3bf9ADxN/4J5v8KAOqormrfxnDdSiOPQvEIY95NMkjH5tgVe/tx/8AoDap/wB+l/8AiqANeiuYm8V6jHM6J4N16VFOBIv2YBh6gGYH8xTP+Eu1P/oSPEH52v8A8eoA6qiuV/4S7U/+hI8Qfna//Hqv2+t6lcQLKfDOpQ7s/JLLbhh9QJDQBt0Vk/2rqP8A0L95/wB/4P8A4uj+1dR/6F+8/wC/8H/xdAGtRWT/AGpqP/Qv3v8A3+g/+Lqna6r4nuLh0l8MQW0YBKyS6mp3c8DCoSD/AJzQB0VFZX2nXv8AoFWH/gwf/wCNUfade/6BVh/4MH/+NUAatFYl1c+J/IP2TS9K87Ix52oSbffpDmqH2jx9/wBAzw3/AODCf/4zQB1VFcr9o8ff9Azw3/4MJ/8A4zV21fxW8ObuHRoZcn5YpZZBj6lV/lQBu0Vg3aeLZI1FncaLC+eWlhllBHpgMuPrmqf2fx9/0E/Df/gvn/8Aj1AHVUVyv2fx9/0E/Df/AIL5/wD49UsFv428w/adU0Dy9px5WnzZz26zdKAOlorJFtr+BnVdPz3xp7//AB2l+za9/wBBWw/8F7//AB2gDVorJa118qQNWsASOCNPbj/yLWWNC8WhMHxmC2Rz/ZUWMc5GM/SgDqqKyf7K1H/oYLz/AL8Qf/EUf2VqP/QwXn/fiD/4igDWorJ/srUf+hgvP+/EH/xFUbjwzqdxIXHjDWocnO2JLYAcAY5iPp+poA6SiuV/4RHU/wDod/EH5Wv/AMZo/wCER1P/AKHfxB+Vr/8AGaAOqorlf+ER1P8A6HfxB+Vr/wDGauWvhy5giKTeJNZumznfI8SkD0+WMD9KAN6isO58Nfa4DDJresqpIOYrvy24/wBpQD+tUf8AhBLb/oP+Jv8AwcTf40AdVRXK/wDCCW3/AEH/ABN/4OJv8a0ofDVnDHsN1qsnJO6TU7gnk5x9/t0oA2KK5698E6FqTo95FeTsgwpfUbg4H/fyqv8Awrfwt/z43P8A4MLj/wCOUAdXRXKf8K38Lf8APjc/+DC4/wDjlXrbwb4ftYykemoQSD+9dpDwAOrEnt/XqTQBu0Vkf8Ivof8A0C7b/vij/hF9D/6Bdt/3xQBrEhRkkAepphuIB1mj/wC+hWVJ4S8PzIY5dItHQ9VeMEH8DVZPAPhCOVZV8MaSJFbcG+yJkHrnpQBuG6tx1uIv++xR9rtv+fiL/vsVQg8MaBaxmODRNOjQsWIW2QDJ6npUn9gaN/0CbD/wGT/CgC39rtv+fiL/AL7FH2u2/wCfiL/vsVU/sDRv+gTYf+Ayf4Uf2Bo3/QJsP/AZP8KAGXPibQLOdoLrXNNgmXGY5buNWGeRwTUP/CYeGP8AoY9I/wDA6P8A+Kqz/wAI/ov/AECLD/wGT/Cj/hH9F/6BFh/4DJ/hQBAvi3w25wniHSWPoL2M/wBac/ijQI42dtb04KoJP+lIeB+NWYNH0y2cvBp1pE5GC0cCqcZz2HqB+VXMD0FAHLf8LK8Gf9DHY/8AfZ/wo/4WV4M/6GOx/wC+/wD61dVRQByy/Efwc5wniGyY4JwGJ4AyT09K0U8U6NLGskd0zowDKywSEEHoQdtbFFAGSPEulF0VZpSzsEAFtJ1JwP4enPXtWtRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQBXv/wDkHXP/AFyf+Rrz74E/8ko0/wD67T/+jGr0G/8A+Qdc/wDXJ/5GvPvgT/ySjT/+u0//AKMagD0miiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAr3/wDyDrn/AK5P/I1598Cf+SUaf/12n/8ARjV6Df8A/IOuf+uT/wAjXn3wJ/5JRp//AF2n/wDRjUAek0UUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFISAMkgduaFZXGVYEZIyD3HBoAWiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAK9//wAg65/65P8AyNeffAn/AJJRp/8A12n/APRjV6Df/wDIOuf+uT/yNeffAn/klGn/APXaf/0Y1AHpNFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUANkljhjMkrqiDqzHAH41X/tOw/wCf22/7+r/jVXxF/wAgG5/4D/6EK5jQ7zVNcgnEmg6LaGbTory0ZZC+DLu2h/kHQLzjuPfjRRjy80jVRgoKUr7v9P8AM13v7eSKMPeZI2NODMfvB1+7z0xu6e1SfbYYot8F7H5rzT/KZhtAO8rxnA528+/vXEaXfX+m/DHw5cWVjY3uo3l4tnLNqLNIAWkdd5P3iMgcZGAa3fDF/Hq+qXceoWFlBcWIktblYVzA0qOPmTI6EMPcHI7VupwkmtTojUpyTWumptLqEDQSAaipDPEB85Uj5xuxlienXt+tao1KwAA+3W/HrMv+Ned+KvGOn+EvEV7Z30WnQWsluHtWktGkbzcAHOCAIx8ucfMS/FRXOv69psX2u90zwy1skVnM8SROsrrO2whckgFTnrnt9Kzm6b7mdSVN9/w7I9SjljmjEkTq6HoynIP406svw7/yAbb/AIF/6Ea1KynHlk49jGpHlm49mFFFFSQFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAV7/8A5B1z/wBcn/ka8++BP/JKNP8A+u0//oxq9Bv/APkHXP8A1yf+Rrz74E/8ko0//rtP/wCjGoA9JooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigDO16KSbRbiOJGdztwqjJPzDtXEWHh2HT/E+pzQ6RcR6Bf2It5LJIZAS4YncctgDBYDbjHYd69IorRTXLytXNY1Fy8slf+v8AgHmer+EdPfQU0vQdIuLCL7bFdypPbSTRy+WchSvmA4JxnkVtTWGnTtJayeHrj+y5bfyntktdoZvM3k4B9ea7KimqkVtEqNWC2j+JzMwsL2Sc3/h6e5VyQglsw+1CqArz2JQcewrPOnW8/jKfX73TLm7zBHFbRTaajPbMpbJSQnIB3HIrtqKHOL+z+InUg/s/iZ2gxSQ6LbxyoyON2VYYI+Y9q0aKKiUuaTl3M5y5pOXcKKKKkkKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKazEFQELAnBIx8vHU/y/GgB1FFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQBXv/wDkHXP/AFyf+Rrz74E/8ko0/wD67T/+jGr0G/8A+Qdc/wDXJ/5GvPvgT/ySjT/+u0//AKMagD0miiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAr3/wDyDrn/AK5P/I1598Cf+SUaf/12n/8ARjV6Df8A/IOuf+uT/wAjXn3wJ/5JRp//AF2n/wDRjUAek0UUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFAFe/8A+Qdc/wDXJ/5GvPvgT/ySjT/+u0//AKMavQb/AP5B1z/1yf8Aka8++BP/ACSjT/8ArtP/AOjGoA9JooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAK9/wD8g65/65P/ACNeffAn/klGn/8AXaf/ANGNXoN//wAg65/65P8AyNeffAn/AJJRp/8A12n/APRjUAek0UUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRWTr8aTRWMUgyj3kasM9Qc5qoR5pWLpx5pKJpXDvHbSvGu51QlV9TjgVmeez3dsBdmSESr+8G0Ako+VPHsP++vpXKHxb8NkuJ7eXVrSGaCSSORJZZFIZCQ3XryDj17UsnijwEmg2+spKZba5uDbWyp5geeQHG1VJHfucDkc1rF00t39y/wAzWLoxW7+5f5nTQz3FtYWgWTeHtg2GAATBQZ6dgx656VYjnuJFgXzwQ9wU3phsqEJ67QDyOoFYUE/h1/EEehXWnXNjqUsJnhhuG/1qDqVZHZTj0znjOMVk3XjL4bWdnbXU+oxLHcTPCoBlLqynDblHKgepAHIqnOk/+GX+ZbnRff7l/mejUVyX2rwWbS+u0vbOS3sI1luZY7kssasCVJIOOQOMdaz7XxB4IuptJjVZ4/7XJFg80UyLPj0J47jr6isrU+7+7/gmNqXd/d/wTvaK5PWJvCmhXllZXqN9svnKW1tD5kkkhHUhVycD1PFM0e88H65pt3f2LhoLJnW680yRtCVzuDq2CMYPWi1Pu/u/4IWpd393/BOvorziDxt8MZ7IXS6xaqm1m2PJIr8DJ+U859PXtV2HX/AU2mSagLuKOFLT7aVleRJPJJYBghIY5K8cc5X+8Mlqfd/d/wAELUu7+7/gndUVw+la54E1qys7uxuo3jvLn7JCGaRWaXBO3aeRwOvTpWRqPjv4f6be3EDRXs8NrJ5V1eW0EskFu/YO4PUnIGM0Wp9393/BC1Lu/u/4J6fRXJarceD9F8PLr1/JHFprqjJNvc7w3K7QDkkjnArG0bxj8Ote1SHTbG7/ANLnGYkmSaLzPQKWwCT+tFqfd/d/wQtS7v7v+CejUVl+Hf8AkA23/Av/AEI1qVM48snHsTOPJJx7BRRRUkBRRRQAUUUUAV7/AP5B1z/1yf8Aka8++BP/ACSjT/8ArtP/AOjGr0G//wCQdc/9cn/ka8++BP8AySjT/wDrtP8A+jGoA9JooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACsrXGCrp7MQFF7GSSeAOa1ax/EUBuLKBPJlmT7QpkWJcttwc1pS+NGtH+IjgLLRrvwR8P7y80weH9egtmmuzI0JVpFyWYbwWDMOnbgY7VSudO0v4u+C9H1mzaLQ9Zhmf7BFJIPLMisCw2j7wOAcgZHv3q/8IX4v03w5ceGNE1u5g0OQuEWXTP3wR8lkLA9OTyOfp0q/Z/DPRT4M0rRdRs9Ye809nljvraLy3SRzk7ck8ZxgH0o9lPsHsZ9jnPiXc+NrXxt4Ie/n0xbj7SBaR2LybDJvjDFywBw24DA7ZHeu51rQ/h/4C0OI3+iafe3NxMy24u4YmmuZWJbBkYAKOepwAMfimmeFUi8Tw+Itdn13XNStVMdo1xaJGkC54wqYBYZPPfOcDij4h+F4fHq6SZLfUoDp9x5hRrXKyoxXepwwIOF4Io9lPsHsZ9jkfGOi6r4Y+G+v6r/YunWZ1a5tlm020UeVZwJnBJXAdi2N3GPm74q38SLaWb4E+GbyG0817SKymaRF+aFfKAJHHAzgdR2r0vV3sdd0i40rUdG1KazuE2SR+UVyOvUHI5ArgpPA+pXlrp+j6lrWtXfh2xkRksTp4RpEU/LG8iuCQBgZ9unSj2U+wexn2MjSryfUP2oJZbhHVRZ/uElTBRDArAfXLH9aVkH/AAun4gaNC9rZ2+oaKweSQ7I0dooxvY9BzIST711nibwxFq/iaw8UaXBqGna7Z5Anay81JV2lQGXcOQCcH+fGKNj4Mkn0/wARnxC+pXuq68qxXF3BYiPy414VUGSOwz9B6Zo9lPsHsZ9iOJb74d/D6PUNT0Lw7qllpttGkctlK3mSh3UbyXQjByCcHk+1alvovgrxVYQfEDVraFrR7BAIrpgYbVFzuGOmQSw/DpmuUuPB3jafwV/wiL6oG0oRrEu7TG8zarBl+bd6gfhXXyeHrZvhf/whaWmpxR/ZBB562o+/ncWxnu3J+tHsp9g9jPscJpek6N44uZ9V8F+HBpFnoxuJI75HEct3O0R2Io/hAba2SeB0wScWPgtBDdfB3xOtxEkqyXFwHEiht37hDznrXdfD7TX8F+DrbRJrO9uJYnkd5Y7XaHLMT0J9CB+Fc1qvgvVbdru38HX+p6Jpuos731obJZFLNwTH3T5eMAjoKPZT7B7GfY89s9Ov/E3wS0LTbN5rjVU1qVLC2BGHUIWYZPAC5JySB1p8nj3WL/VdI8M+NNMtrO8ttTt3bUHg8qW3RXBAAAxjBIyOMH8a9Tv/AAw1p4Z0fT/Cseo6Xe6Q5a1uZbYyj5wRLuUnBLbic447YrF8Q+E/E/jS70tPEs6yadZzrLJDaaa0byYADfMWJGRn259hg9lPsHsZ9j1Pw7/yAbb/AIF/6Ea1KztBikh0W3jlRkcbsqwwR8x7Vo0Vf4kvVhX1qy9WFFFFZmQUUUUAFFFFAFe//wCQdc/9cn/ka8++BP8AySjT/wDrtP8A+jGr0O8RpLKdEGWaNgB6nFcX8IdF1Hw/8OrLTtVtXtbuOWUtE5BIBckdPagDuqKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooA//Z",
+ "image/png": "iVBORw0KGgoAAAANSUhEUgAAAvoAAAPoCAIAAAAgFM2mAAEAAElEQVR4AezdB5wkRfUH8D44kmSJShABRSUHyUklJ0GC5KigBBHJIJKUJAKSM0gSFAlKzjmLZFAySJQ/OR3p/t+5d9cMM7N7s7uze7O7r+GzV11d8Vc99X713qvqosgrEUgEEoFEIBFIBBKBliJwxRVXDG+na6yW9i4LSwQSgUQgEUgEEoFEoO0QSLrTdkOSDUoEEoFEIBFIBBKB1iIw9P77729tiVlaVxEYe+yxd9hhh2WXXXattdY66aSTxh9//Nlnn/2JJ544+eSTf/azn1111VWvvvrqWGN9TkyHDRu22GKL7bHHHueff/5HH3007rjjzjjjjE899dQll1yy1VZbLbDAAiLLNihc9l/+8pezzDLL7373u48//jgejTfeeBdeeKG/p5xyyhJLLDHOOONcd911buOpEpZaainhG2+8kTJy/fXXv/vuu59++mmllSVnIBFIBBKBRGAAIPDggw+WomEAdKejLgwhzDp6lvGJQCKQCCQCiUAiMIARwAEset9+++3qRXW3+2vl/Oijjx5zzDFK4Luz/PLLd7uolmcc2vISs8BEIBFIBBKBRCAR6BcIDBky5Cc/+UkLm3rDDTcE3WlhmS0p6nMTSUuKy0ISgUQgEUgEEoFEIBFoNwSS7rTbiGR7EoFEIBFIBBKBRKDFCCTdaTGgWVwikAgkAolAIpAItBsCSXfabUSyPYlAIpAIJAKJQCLQYgSS7rQY0CwuEUgEEoFEIBFIBNoNgaQ77TYi2Z5EIBFIBBKBRCARaDECSXdaDGgWlwgkAolAIpAIJALthkDSnXYbkWxPIpAIJAKJQCKQCLQYgaQ7LQY0i0sEEoFEIBFIBBKBdkMg6U67jUi2JxFIBBKBRCARSARajEDSnRYDmsUlAolAIpAIJAKJQLshkHSn3UYk25MIJAKJQCKQCCQCLUYg6U6LAc3iEoFEIBFIBBKBRKDdEEi6024jku1JBBKBRCARSAQSgRYjkHSnxYBmcYlAIpAIJAKJQCLQbggk3Wm3Ecn2JAKJQCKQCCQCiUCLEUi602JAs7hEIBFIBBKBRCARaDcEku6024hkexKBRCARSAQSgUSgxQgk3WkxoFlcIpAIJAKJQCKQCLQbAkl32m1Esj2JQCKQCCQCiUAi0GIEku60GNAsLhFIBBKBRCARSATaDYGkO+02ItmeRCARSAQSgUQgEWgxAkl3WgxoFpcIJAKJQCKQCCQC7YZA0p12G5FsTyKQCCQCiUAikAi0GIGkOy0GNItLBBKBRCARSAQSgXZDIOlOu41IticRSAQSgUQgEUgEWoxA0p0WA5rFJQKJQCKQCCQCiUC7IZB0p91GJNuTCCQCiUAikAgkAi1GIOlOiwHN4hKBRCARSAQSgUSg3RBIutNuI5LtSQQSgUQgEUgEEoEWI5B0p8WAZnGJQCKQCCQCiUAi0G4IJN1ptxHJ9iQCiUAikAgkAolAixFIutNiQLO4RCARSAQSgUQgEWg3BJLutNuIZHsSgUQgEUgEEoFEoMUIJN1pMaBZXCKQCCQCiUAikAi0GwJJd9ptRLI9iUAikAgkAolAItBiBJLutBjQLC4RSAQSgUQgEUgE2g2BpDvtNiLZnkQgEUgEEoFEIBFoMQJJd1oMaBaXCCQCiUAikAgkAu2GQNKddhuRbE8ikAgkAolAIpAItBiBpDstBjSLSwQSgUQgEUgEEoF2QyDpTruNSLYnEUgEEoFEIBFIBFqMQNKdFgOaxSUCiUAikAgkAolAuyGQdKfdRiTbkwgkAolAIpAIJAItRiDpTosBzeISgUQgEUgEEoFEoN0QSLrTbiOS7UkEEoFEIBFIBBKBFiOQdKfFgGZxiUAikAgkAonAoEXggQceaM++J91pz3HJViUCiUAikAgkAv0PgSOOOKI9G510pz3HJVuVCCQCiUAikAgkAi1DIOlOy6DMghKBRCARSAQSgUSgPRFIutOe45KtSgQSgUQgEUgEEoGWIZB0p2VQZkGJQCKQCCQCiUAi0J4IJN1pz3HJViUCiUAikAgkAv0PgY033rg9G510pz3HJVuVCCQCiUAikAj0PwSWXnrp9mx00p32HJdsVSKQCCQCiUAi0P8QOOqoo9qz0Ul32nNcslWJQCKQCCQCiUD/Q+Bf//pXezY66U57jku2KhFIBBKBRCAR6H8I7Lnnnu3Z6KQ77Tku2apEIBFIBBKBRKD/ITDLLLO0Z6OT7rTnuGSrEoFEIBFIBBKB/ofADjvs0J6NTrrTnuOSrUoEEoFEIBFIBPofAquttlp7NjrpTnuOS7YqEUgEEoFEIBHofwh873vfa89GJ91pz3HJViUCiUAikAgkAolAyxBIutMyKLOgRCARSAQSgUQgEWhPBJLutOe4ZKsSgUQgEUgEEoFEoGUIJN1pGZRZUCKQCCQCiUAikAi0JwJJd9pzXLJViUAikAgkAolAItAyBJLutAzKLCgRSAQSgUQgEUgE2hOBpDvtOS7ZqkQgEUgEEoFEIBFoGQJJd1oGZRaUCCQCiUAikAgkAu2JQNKd9hyXbFUikAgkAolAIpAItAyBpDstgzILSgQSgUQgEUgEEoH2RCDpTnuOS7YqEUgEEoFEIBFIBFqGQNKdlkGZBSUCiUAikAgkAolAeyKQdKc9xyVblQgkAolAIpAIJAItQyDpTsugzIISgUQgEUgEEoFEoD0RSLrTnuOSrUoEEoFEIBFIBBKBliGQdKdlUGZBiUAikAgkAolAItCeCCTdac9xyVYlAsWHt34YKLx5yJsJRyKQCCQCiUBPEEi60xP0Mm8i0IsIlHSnF+vIohOBRCARGBwIDB0c3cxeJgLtjsBn7372/j/eH/7R8CHjDvnSql8a9s9hwu+e/e5EG0yk6R9c/8Enz30y/MPhEyw1wTjfGkfg/Svel6X4tJhg2QmGfrXyQ6YE8mjotEPHW3C8du9tti8RSAQSgb5FIOlO3+KdtSUCHSDwwdUfjDv7uOPONe5HD3z0wTUfTLj6hMPuHBZcB6cZ8qUhE28y8af/9+m7Z7076bcmlWC87443dLqhn7312bvnvTvJlpNUSv20UMI4s4zTQQ0ZnQgkAolAryPwxz/+sdfr6FYFSXe6BVtmSgRajcAnz34y4WoTKhVl+eC6D6qLHz58+HhzVxQ2Y08x9vBhwwU+fvLjT1//NNIM/3h4IW5I5f9xZk6uU41chhOBRKCvEZhooopCug2vpDttOCjZpEGJQIXGNL6GjD1kyPjoTNX1WTHR+hMNGToE0fnk+U8qXMfFE++LqaoyZDARSAQSgb5A4N133+2LarpeR7oqdx2zzJEI9AICQ2ca+tEjHynY36FfG7EOQYCCA9WRmKEzDP34sY8l/viJjz+8ZeQGrl5oVBaZCCQCiUDXELj//vu7lqGvUqd2p6+QznoSgU4RmGCZCbgqD7t32JBxhnxptS9JO3TGofxyJlq3gWZ4guUmeP+S97kz0+hMuErFBNbweuihh95///0hQ+roEh41fPg444wzzzzzNHzasLSMTAQSgURgtAhssMEGv/3tb0ebrO8TJN3pe8yzxkGKwBv7v9Fkz986/K0yZeSqzlsdluyto2sTl3mnK6Yrww0Db17yZsP43oicfK/Je6PYLDMRSATaCgFLqbZqT9mYNGaVUGQgEUgEEoFEIBFIBHqEwDLLLNOj/L2WObU7vQZtFpwINEKgJUqOTz755M4776Qxvuaaa4THHnvsoUOHbrzxxiuttNJYY4218sori2lUeYO466+//s0333z00UeVpqiPP664BC266KLbbrvtmmuuOe644zbI08WoGnVUF3Nn8kQgEUgEWoBA0p0WgJhFJAJ9hgB3HETnL3/5y1VXXcX5hpmc6njFFVf88Y9//OmnnyI9XW3J9773PVl++MMf7rbbbnfdddexxx77pS996YILLlh//fW//e1v77TTTjPNNNP3v//9rhab6ROBRCARaCsEujw5tlXrszGJwOBB4KOPPtphhx0uvvjiF198ccYZZ7zwwgu/+tWvzj///KUip+Q677zzzksvvUTNM/7445988smXXXbZeON9fs7yhx9+uOWWW66wwgrDhg2rnOgz3nhKkxiSC4+4BH75y18ed9xxZ5999hZbbPHlL3958cUXV85UU001eNDOniYCiUD3EDj11FO7l7G3cw1pW6+i3u55lp8I9DECYdPpnjHr8ssvP+aYYy699FJt/vWvf73//vvXN56+5+abb3bGF/UPMlSfoGHMlFNOyW5FhbPJJpvUJHjhhReWW265Rx55RPyCCy6oDahPTZpmbnvS8WbKzzSJQCLQPgiwsC+77LLac8UVVyy//PLt07DU7rTPWGRLEoFaBD744IP77rtvl112cZTFV77ylfPPP3/eeeel1Il0rFcPPvjgfvvtJw1Fzssvv/zGG81u/ipreu211/bZZ58JJpjgoIMOUuDkk09+6KGHzjfffBNOOOF000137bXXvv3222+99dY666wz11xziaTmWWKJJcrsGUgEEoFEoBqBUs1cHdkO4aQ77TAK2YZEoDECv/nNb5APzxiV8IzqRJx4DjnkkHPPPTeci6sfdSOMVz322GORcckll1xllVW22WYbBq9pR1ziWcR48PznP//hv0zJ9N3vfrcbtWSWRCARGPAIOOurPfuYG9Hbc1yyVYMdAQqbrbfemgGLE/HDDz/MkyYQefLJJ7ENm7AQjjPPPLMlXKce60suuUS9tDgMZFEFt2VVH3/88dNPPz0L1znnnEMtVJ8xYxKBRGCQI3DRRRe1JwKp3WnPcclWDWoEmJAoUZiQTjnllM033zyw4Ga39957n3feeVQsTaJDq8zbRkZeyXZvvfrqq1iUWzvPR1sCz+hbbrnFzvall15avaiPHVtbbbWVHVtrr722HWEMXjyaN9poo9EWlQkSgUQgERjjCCTdGeNDkA1IBL6AAEc/JMMROGeddRZWUT77xS9+cfTRR5e3nQcmmWQS3jYzzzyz7eWhnrGBC9GxA+uJJ55gBcNd/vGPfzzzzDOdl8ObB/fiOYTxrLvuuvyaJ554YrvDfvSjHzFvnX766WussUbbfgC5867l00QgEegNBCzVTjrppN4ouadlmgHzSgQSgT5A4PX9Xvd/5xU5Pgd7WGuttfggf/bZZ5EYsfBxq2YcAHkcU7pcd911//rXvzqvyFPOOg7aaf4I1G984xtsWFHs//3f//3973+fdNJJMTMfQO68rmY63nkJ+TQRSAT6CwIcCoOX2JnVVm1O352e8sXMnwi0CgEHHDvfzx5O88Ucc8wRH++k7MF+GKHoe0Zb0WGHHfbPf/7TyYHo0WgTzzbbbByA1Mg3ebSJJXj88cdPOOEEjEeYjWzVVVfdc889UTGLOWf5NFNCpkkEEoEBj8Duu+/enn1MutOe45KtGnQIcArmXsM29Oc//zlODuRqg/cgE83sdOBKzJ35Zz/7WVeBY5zimNzkmTo33ngjZ50jjjgiavn5z3/OlYeKaPXVV3e2YVerzvSJQCKQCPQZAkl3+gzqrCgR6BABTsH8fzkUH3DAAXECMj9lRGe99dZz7E2H2aoe+KxEJ1yH+w4FjPLLHMJiwq0H47Hn3KE+zXjhMLE53Dm8iKR38vJPfvKTK6+8kkNPWXgGEoFEIBFoNwSS7rTbiGR7BiMCtpSjNWecccYss8wS/fedBxyoSSx4Mc8666x//etf/zbiQn3+97//RV62c+YweqPJJpuMgSwO17HrypmBThTEsdAURIf/DRMYNY/IZirdbrvtDj/88EjpnEPl27R12223NZM30yQCiUAiMAYQaCtPomxMIjCAEejIY3fHHXf0y/ehmbLvlCW8gJucDr7+9a8/9dRTNk9Vp+e7g0IpMAxPrGNTTDGFBHvttZdIqp34AJaPjDooWfwiiyyC9HjEOFVdTidhm7yOPPLIaDOuxuVZmx0RFDHVfzvqeHWaDCcCicDAQMCMFPNGuip3Mn/mo0Rg0CFgf9Mf/vAHupzNNtssOs+JxxF/jFlNYuHoP/NL6cjsmBz7s7g2O4WZrWrqqadWDqvTUkstVV/gT3/6U3og3xm9/fbbfTMLa9GYZraAKYpVi1bJDjJh5jAHAlERsW3V15IxiUAiMHgQ+MEPftCenU1jVnuOS7ZqUCDgVBvfq2LA2nXXXaPD1kMMTM1vdNp0003xmxIsDst2TsXJhD6thbjY2e47EMiTHVhiOBeXiQVQFtyIDcsWrffee8+XRyXmmlOdpvOw73mFk7K9WvaF8T1yEnTnWfJpIpAIDGAEqk8La6tuJt1pq+HIxgwuBPjNOCDn97//vfMAo+d8Ypr0TZaeToU5adxxxy1Re/TRR31di12MiYozja3szhJ0Rk4kcLRgfGcUyymzCKA4mIrA008/7e+MM85Y/bTzMH7m6OdIQ9mz6KKLnnjiid34UmnnteTTRCAR6C8IMIu3Z1OT7rTnuGSrBj4C7E0O1KFuYbrSWxRk++23d+RxD3tuS7nvfbJhsV75jCjtDpPW3HPP/Z3vfIeLz0wzzeRTXLfeemvs/4q6nnvuudD6OIlHDAvXnHPO2XwzuCrffPPNkZ7/8gMPPOCcw+azZ8pEIBEYSAgsvPDC7dmdpDvtOS7ZqoGPwFFHHcUzcd999+Xzq7fsWVQ1zXeb5ia8jGuyMG+xKz3//PMXXnghh57YfH7ggQc6EhCjevbZZ9nOGNcjXgNef/113z9HjDga77TTTkrDhOzPYgiLcw5ryq+/pcvxTYl7773Xo3nnndcZPPbP33DDDfUpMyYRSAQGPAK+ItyefUy6057jkq0a4AjYEM7MFERHV+lXbCFvss+2lFML/eY3v6GtqT8px0GFVCyIDs7BrhRlOsKHkSvCd9xxB69kRMctsxfTVbgbc9wpd6H76DoXZnog3MXurdE2zNfRnbksmcQLLrggfZJ9YaPNlQkSgUQgEegzBJLu9BnUWVEi8DkCzsjBJ3jqxIZwn2IIv5nPUzQKOVxHSlxEdj7OvIxLBQyVTOyo8he5Yckaf/zx77777quvvpoZyxdDqYLokyhdnL7DiYfbMj8etXP92WabbZzNgyeVdWJRSJWzBJnh7RRz0PMMM8zQOe+hmopDCzkqzj777IjUyy+/XBaYgUQgEUgExiwC+UX0MYt/1j4YEeBbc9NNN+EfcciN/VmjNf2gGhtvvDFj07e+9a2GkGEYNoFjGL7ZKYHPb4X+hgKJ8iZYUfx1Qo9API2i3LoaFuvAntj55XPoPq5+8MEHN0wm0qckHBfELkZdxHmZ/R6F2nDDDTtKn/GJQCKQCPQlAqnd6Uu0s65EoILACy+8gArgJew+bvn2dr6XgS8zjuLznB1xnYB1nXXWsTcqwugLouNy6y8aRJlk31bclk9HJBmrI64TRZV/OQDtvPPO5W1NgPmM7Sz2fFEm4We+4eX45ppkeZsIJAIDG4H//ve/7dnBpDvtOS7ZqoGMgI886J4NTdFJ3soUPB112Nes2JIcqBPfDe0oWSfxvGqWX375lVdeORQ/naTs/BFWdMghh8QZ0A1T8kaitfJIa+ObEmIapszIRCARGKgIcCtsz64l3WnPcclWDVgEePX+6U9/ctQNFYhO8q3p5OOanHUcD8hHp9twULdwN/ZtB/U+88wz3HQ6oVbN1HLooYeyanWUslT/fPOb35Sm2mTWUZaMTwQSgUSgDxBIutMHIGcVicDnCFx00UX/+c9/nG3DWVjs+++///mzutAvf/nLnnAdW7ecu+MsH3WFVubYY48tGUldbc1GsGqVVrOaPExmYcBykI/98KV5qyZZ3iYCicBARcAncdqza0l32nNcslWDBYE777yzo66aNShjOnraTLzzlHkF4R/hxBNZnMfj9J1msneShpO1rVv1CZSMDEU86xv/5XTfqUcpYxKBAYxAHjM4gAc3u5YIdAEBLr32ZMVnrVABH/JsmNlXP7v07ar6Quz/+vWvf40w2XkuXG4LZ9LyXa369DUxb775pr3xPqRVEx+3Cy200HLLLdfwURxgiGD5Brut6Y4xbJgsIxOBRGBAItC2P/nU7gzI9y071b4IcNZh5fExh86b6IycjvZhYUgO3Ql/504KcdigI3OwFgcYOjWn/M6DLHvsscdZZ53VUV7nI3PQcVCyL3k54KejZE7Wqf46aU0ydEchTHV77713zaO8TQQSgQGMQBzO3oYdTLrThoOSTRrICHBMLj/q6VMPDW098RmHehQoSxyi45hBTGKzzTbzxQaUCHGxlZ3+pjp9sBwxDuP57W9/61yfmiNwara+v/vuu0rmauNMwlVXXZV/j5N7nLVDM4RaVZdchumoerjVqywqA4lAIjBgELDVtD37knSnPcclWzUoEMBa3nrrrfquOqzPp8Xr41999dW55pprgQUW+NWvfkVx4iOj//73vzfaaCNfAPVdiGr9Dcca3GXKKadUiO858FOudt8R+c9//lPeqIISCBlSst3jzuZ58cUXxdvP5bMSvlYRn5iIlDV/Gx7Y47DB8hvsNenzNhFIBAY8AnTJ7dnHpDvtOS7ZqkSgMQIYBo8cH3/wSazqFKxODtfhTxOG8xVXXJHVzNfRIw0KUqP+cRSY73Z5+ve//90xhjWb4VmyFEi7w/W4k29H+AhGvcWNLcwhikq22d4XLXq47726jxlOBBKBRKDbCCTd6TZ0mTER6CYCPlnVec5OEoRChftOWJ2qy0FoUJxll12WecuuKIcaO5/QsT1TTz01K1gN3ZHxpZde4jHt+vDDD6vLUcK555573nnnOcq5Or4+zOhWGuaqn/7hD39wO//88y+zzDI1hVcny3AikAgkAn2GQNKdPoM6K0oEKgjQdgQb6AgOn/bs5NNUkYuzjt1Vf/zjH2lxasqhXDn++ON93ZMlC2tZfPHF+RRjNpx4pp9++urEe+65J3NYjeGJzesnP/kJwsS8ZRNZdfoMJwKJQCIwWgRuvfXW0aYZIwmS7owR2LPSQY0ApUjn/e8owXTTTedEY0ctzzbbbG+88QaPHAc0U8bUlGa62XrrrdmnmJMWWWQRe9p9TstHzmtcbSaeeOKa0wLphJxDKLGPPzgWmZ/yPPPM0/mxhLvuumtN7XmbCCQCgxkBXwhuz+7nF9Hbc1yyVYlAYwR+97vffe1rX0NE+DL7RAMG45hme6muu+666gy8dpxSyBX6+9//PqdjzjQ+VL7YYovZC1Ym4+y86aabnnTSSbfddltECnN8plv67ne/6/Olyqfs8a31Mkt9oN53Rxqu1vUpMyYRSAQSgTGIQNKdMQh+Vp0IdAcBChgexLY/+B6WM/1+//vf/+xnP6uhO8rFeHyAwi50rs12jD/00EOdf2QUkdp44425J1fvUZ9lllm23XbbrrZyzTXXlMVOsSuuuIJvUFezZ/pEIBFIBFqOQBqzWg5pFpgIjAYBNGU0KTp9bKuUY3XsD/fhT9/D8lUs7j6clOsP/XPczlJLLUWvYx+WImuMWUxmPmAe+7MYvNZee23+OtVcRxZUyfk6nTSHS1BHT99++22PajbAd5Q44xOBRCAR6FUEku70KrxZeCJQiwAVC5+b2tiu3B922GHVyR1UuMYaa7zzzjuXXXbZNNNMU/3IpnTaGu4+nj7yyCM12h20iauyNJyBbrnlFuf0cG2uzt5MOPacV6d0YHTDz2lVp8lwIpAIJAJ9jEDSnT4GPKtLBIryaEGGnvo95zxmOvpSVWDnGxQuHjzsWb5LJUwBw1PHyYE2W9Xg+8ILL/gAO49j27hqPKDphNAgDsuOGaT4YXvy4XSqIJfCxR9xxBF2ktcUONpbBwJxqR5tskyQCCQCiUBfIpC+O32JdtaVCBRcjJ977rkAwmnImAqX4WpcuOPssssujsypjqwO8x12KA5yM/nkk/M1jpNvGMhctp1T4dR8R90udLaq+uP+HBJo15WPUWBXtmIxipUnCiJGvsnl3MKavevVzRht+MYbb5TG1rDihdGmzQSJQCKQCPQuAkl3ehffLD0RqEFg/fXX94VOzjedWHycCliTq+aWAsYHH5566qkzzjjDycUUQhLgSfPNN98BBxyAPyFMESmevYkGyJar8OApi8JpvvGNb/i2+Wqrrebj52V8BKiLGu66qk6GJ3V0iqAze04//fRJJ51Ufz/4/QfVuTKcCCQCiUDfI5B0p+8xzxoHNQLYiSNz+N/st99+3QbCoTjckH0youZErzvvvJNaiDuObVnlXi0HCZ5wwgl2Sy2xxBJljfQ9vJhZ02ib6rkOmmKXVpm4o4A9Yixl1U/Z5mx9r47JcCKQCCQC7YBA+u60wyhkGwYRAl/5ylf0luHJX4YnO73rO+8oHXum6uOrYzju2EtVHRNheiP2KdYunxGtf1rG+CqWqg866KA77rijjIwAVZAjCh3SUxNff2s/fE0kX+nS3Ye2CaXjIVSTJm8TgURgACPg+zbt2bukO+05LtmqAYvAyiuvPO+888YXrNAdhq36rvKzoTipj6+J2WuvvRizHDnI0ZgHT3k5atnHzH0LwqnKkSW2i5cb0W04dwKhD03svvvu2lBmpHmi17nwwgspfmrqqr9lSjvmmGNq4pUQMb4waiN6cLuaNHmbCPQZApSdHdlb+6wNg60iezPbs8tJd9pzXLJVAxkBihPGrCeffFInHYi8wgor1PfWrnK7xOvjq2N4FvPIsaPqtddeYyArLy41++6777e//e3S39lxf44ZDC7C3sTBWTnMVe+++65tYpGRCex///ufVi255JLVtXQU3mmnneofxefACJjTTjuNb5AdXvVpMiYR6DMEfGIFm++z6rIiCNQfANYmsKTvTpsMRDZjECGw/fbb06ygF2HJYnW68sorS8/iAMIWcWl8+Xy0uHB55ox8yCGHMBthGFGOv/ydHRJ46aWXOnPZtyMcq+Op0pAt7skUPFgR1U6Uz7MYebIVi05otDVK4Jye+hN3xNsY768jEB176MgfX6JoprRMkwj0EgI+lNtLJWexHSHQtpgn3eloyDI+EegtBHACW9CdDXj99dfbG+VQHFTDaYE19fnS3s9//vP555+/Jr7+1nLKrm9bx2sch2l0+DL7ElYokBAgpWFXk0wySQ27YsOSvXkv4zPPPBMhq2kJRsXxWWR4Sfu6RU2CvE0EEoEBj4BzvNqzj2nMas9xyVYNZAScl2OflAMAr732Wv2caqqpdthhh4Yd5tlTzyrqU7JScdZBnuzAChVOpLHlimXKoX+qo8uh12Hect5gNdfhXOyr5vfcc499XqXnTX0V1TG+XIHuVMcIUzLZcy7AZef444/XKV/sqkmTt4lAIjDgEejJYV29Ck5qd3oV3iw8EWiMAD2KA3Ic7rfFFltQ7SAKTql55ZVXalJbJ/3whz+UrPMPV0UuZyI7LIcm2be0uM7E9nLUxBfRfQmLmw7T0oorrlhuUFcp/x5+PF2antjF+BuFq3V1a0VGI/kvP/PMM0cddVQYtqrTZDgRSAQGPAK5M2vAD3F2MBHoAgIULTZs80e2b1y2ueaai99Mw/x0NjWH6zRMVkbaYW7H1t13323nlO85ONQY77FlnYfyKqusguv4OoSqHcrMMYhzT5e4jlqUH18VLWsU4DYUXz6nsuJFZAtYfkeiGp8MJwKDB4FTTz21PTubxqz2HJds1cBHANXQSTvJo6v1n7sqIfjd735XhkcbMNfwCrLP3K6oc845x/k9U089NR0Prx3uw7LbuC7g/GV73Sl+Gm6w6qgW3xC9//7765/iT7EdgzUNgVOyNtQny5hEIBEY8AjEyqcNu5l0pw0HJZs0KBCwPYr2hR+xLVo67KBkFiiGrfrO0+7wsHGMcv2j+hg7b0XyGqZxcU000UQ1NjInL4tXEe7CJlV+r7S+qJoYzGyDDTao/8AFt2vVSfzyyy/rwtZbb20vWE3evE0EEoFEYMwikL47Yxb/rH1QI+ALnQsvvDAVC+8ce6O40dh8zsxUA4pTB1999dW11lrrggsuGO2hOE5bdk7gvffe60OkY401lkNHnN/D5Tnck3/605+us846PqqlTHYu5xCiL9x6sKKaSmtuKYo4BsVh0DWPfJHUcYLO2uFm5LNcXbWO1ZSWt4lAIpAI9AYCSXd6A9UsMxFoCgHHKzP6+OADOhInFPMptkPq8ccfr8/v01ecb5yjU/3pq5pkfISVRnPDdcYXzuOpXeg2Xv3tb3+bddZZQw0T8TyHHCpo7zqf4n322aemqOpb+7A6+oQWWxgKJbGTDO+66y4WtN122606b4YTgUQgEWgHBJLutMMoZBsGLwKsPxQt/tKR2NHg/HWangUWWIDGpR4Um9KpghCXjs4t9RGrww8/3JmBTFQOVlYCpY6t6bZTCVO9sKDZkU5JQ/FD/aNAG8gPPPDA+roixnnN2uP4n4YJ2LbicB0Fxlcv+AyVn6pomCUjE4FEIBEYIwgk3RkjsGelicBIBBxOgyjwJnaoYHyBYbbZZqOYcdsQI44+nvoIKF+fepdA37riQPPoo4/SEiE9SqDpeeSRR8K/mL2JAoZvDU8gT23RQnpsR+/oy1ZO6OFaZFt7w5b4fkXodeyWP+6447g/s7Wlh3JDrDIyEUgExjwCFn95JQKJQB8g8Pp+r/u/YUW//e1vzQW//OUvaXokwEW22mqrzmcHShQ7tlijqgs84ogjvv71r/skBbVNGX/JJZdUF2UbeTxixrJf3ddDHbKMqZTpBRzHjBVV56oJc9Mp02u2p7RENFJlZHWgk45XJ8twIpAIDAAEyk/HMHC3VXdSu1MzjedtIjAGELBFi38MssJb2UYnn7Ki8uFE3MkJFuYRe9dpX7ge/+Y3v9Fop/xhOS+99JIjfNi86GxsvHJQMoee6i75CjpqIjGtDMbjcEK6GafyYFo+ZGEb+d577439cBWqzlUTlr6MiXOc5aVtUrj2pz2rBCcDicBgQ8CXhtu0y21FvrIxicAARqBzJQf3Fxu1TBOUJQEC/sGF2Ue1Op87GKTQF0YxO6cuuugiVjAbr5TmsMFOMjKZOYdQRT6H/ve//906bOWVV1YITU8nucpHCBmvZHu+lKA6l0OiPcWu2NpYzarHsfOOV6fMcCKQCPR3BCiYY6JoN+3OEMiWU1gGEoFEoPcQeGP/NxQ++V6Td1SF448pZmzLoq0JR2MpnRC40korNdyr1bAczjq+UEHj8u8RV8M0EengQZvGqXN8XrSTZJ08kp0eaM4553SQj2T77bcfzZBAfBNDSyLvaDveSRX5KBFIBPoXAjPPPHN8wQbd6eiw+DHSozRmjRHYs9JEoAECVkUmCH48nG98RtSX0u3Asnuc1cnhgXhPgzx1UUxgstdFN4hwwE/9GT8N0nUcZasXO72vZTlXECfD0jhBM8A5pIeCxxFBIkerneq4+HySCCQCiUDLEMhTlVsGZRaUCPQcAQsjdIE9yDfSfZABn1Cm3em+BcGbx5mBPa+i5SXYqW5Dlk+cKpmHteN87Au75pprWOXE2xvf8hqzwEQgEUgEuopA0p2uIpbpE4FeR4C+xGF9PvLgJJ6wNPE7dvjNX//6V5807/Xqu14BP2UKnm233ZY/kEML11xzTU1l4bKJvT0b3PUuZo5EIBFoCoH2XJVpetKdpsYvEyUCfYkAA5aj//70pz8xCTF+u3w2y+701VZbzaHJ9l4ddthhs88+e182abR1DRs2zMHQWkiv4yRDZ0NTTf3qV79yCFDk5Xk92kIyQSKQCPR3BJw+2p5dSLrTnuOSrUoECt9t4IVDO8J3Z/HFF0dxgOJsQB+6Yuq69tprjz/++KmmmsrOrJaAZfd4eBz3pDTqHG5GO+64o0KoeRycuN1220WBsVu+J4Vn3kQgEWh/BJwR356NTFfl9hyXbFUiUEHge9/73mKLLeYwGx+O2HXXXe2immuuuShOvvzlL3MKtvPc8cqHHHLIgw8+aA+5T507QrCrwNl57sxAqhdfCeVqw0PIsYQ92bDpuOcpp5yyvhmaWh+ZMYlAIpAI9A0CuRG9b3DOWhKBoif7sW3L4soTR+k4x88Htpwu6CPq1bA6M9CJguxfPtvpb5z1569DceLgL4fiOFQwsjiYR3ZfvHJmj0+jV5fj9EIHDzqPpzqy+fDBBx+8yy67SI8zUfP4hpdzd9x2sgO/+cIzZSKQCLQ5Am27ET3pTpu/Odm8gYNAT+hOoOAIQa4wZ5111iuvvGKDN9LDS4al3Il/ncAki01eDgakEAoi0knieOTLXL6j7hMTo01ZneDb3/72FltsEZYsW8mc+KypIm9d71bJku5UY5XhRGCgImBeoiTWu3Y7dyfpzkB95bJfbYdAz+lOdMnnzdGXM844I75z7rQen3Tw/Sykh0GKm3OTPbeLCq2R989//vNf/vIXJxNyN6ZA2nDDDZXw6quvMnLdcccdTZaG1lx66aVxoKppbq211rJdi3eRXWZDj68YzZPuNIlkJksE+jUCN9xwAyu8LrQb3UnfnX79XmXjByMCM8wwg6MI45MR99xzj49tQcFHsvx1zPHaa68dnjd2ciEf9kaxW3nEoxmDwYrCtdlTPjo1n9OSjIcN3qMQH2n3cQmO0s0cRYhjOW7H+UBK4EON61A7aVgwpzeKbtrFlJZXIpAIJAItQSC1Oy2BMQtJBEaPQKu0O9U18cuhofG5Bg43uAvvHOzktddeizQMWPQ9ZXq8xzdE3XLocRqyTV7C00033UEHHcRV2WkZdDk+ffWvf/3LLvcLL7xwxhlnVL7dYbyh+UE39F+W68QTT3TQjorUiyfdfvvtUjossdyP2hsdLzuVgUQgEWgrBFK701bDkY1JBAYIAkxRLp05+eSTo0vYBisV3uMW7ag+7QbLQYDEU/A4ICe+ZB654i/D00ILLeRsw3vvvdcXQy+//HLqItu1Fl54Ya5CFDbViYUVyFy1ySabCNs1JuUtt9yiEN86XWKJJWoS520ikAgkAmMQgTRmjUHws+pEoPUI2GZVs9OqS3U4yOfll1+2t+uPf/yj4w0xHjoeZzpz7jnqqKMY48vSMCoHbIS5il4Hf8K0fORr8803T65TopSBRCARaBMEWnNAWZt0JpuRCCQCPUSAwgaPcTyg7RWPPPII+uLUH1YwH/v0bSxfiojypWHDCq5DwbPoooviOuuuuy56FF5EPWxGZk8EEoFEoLUIJN1pLZ5ZWiIwEBBg8zr66KOPOOIIljKePT72qVcojvN4gvHQ68SxgY7n8bGLxx9/HNfxIfSen8s8EODLPiQCiUD7IZB0p/3GJFuUCLQHAttvv7295Vx5mLEwnnADcjLhQw89FG7I+++/v6dchRiwECCaofZoeLYiEUgEEoFaBJLu1CKS94lAIlAi4CwfO8xnm202rjy2l1933XV2YNm3hdnYw+UzWLyhRTr/MPU6JWgZSAQSgTZEIF2V23BQskmJQBshEIwnPkp69dVX89Sxd/3666+n2rFvy7cs2u3b7G2EXTYlEUgE2gaBpDttMxTZkESgXRHwEZyLL77YOc78dTbaaKNoJtJD8TPnnHO2a6uzXYlAIpAIfI5A0p3PschQItAHCMSZe31QUcurWLVY9bV9Rh5gOLLwi4o3LsoTk1uOdBaYCCQCrUcgfXdaj2mWmAgkAolAIpAIJAJthUBqd9pqOLIxAxmB/EbmQB7d7FsikAi0NwKp3Wnv8cnWJQKJQCKQCCQCiUCPEUi602MIs4BEIBFIBBKBRCARGIFA+f2+dsMj6U67jUi2JxFIBBKBRCAR6K8I1H9LuE16knSnTQYim5EIJAKJQCKQCPR7BKaZZpr27EPSnfYcl2xVIpAIJAKJQCLQ/xBYbbXV2rPRSXfac1yyVYlAIpAIJAKJQP9DwHeF27PRSXfac1yyVYlAIpAIJAKJQCLQMgSS7rQMyiwoEUgEEoFEIBFIBNoTgaQ77Tku2apEIBFIBBKBRKD/IfDxxx+3Z6OT7rTnuGSrEoFEIBFIBBKB/ofAL37xi/ZsdNKd9hyXbFUikAgkAolAItD/EFh99dXbs9FJd9pzXLJViUAikAgkAolA/0Pgww8/bM9GJ91pz3HJViUCiUAikAgkAv0PgQUWWKA9G510pz3HJVuVCCQCiUAikAj0PwTuvffe9mx00p32HJdsVSKQCCQCiUAi0P8QuOuuu9qz0Ul32nNcslWJQCKQCCQCiUD/Q+CVV15pz0Yn3WnPcclWtQ0Cf52sR03pYfYe1Z2ZE4FEIBHoawSOOOKIvq6yufqS7jSHU6ZKBBKBRCARSAQSgdEh0LbfzBo6upbn80Rg0CNw/57F/24pPnq9mHO/YoY1io/eKO7Zrvjw5eKzj4p5Dy2mWLB46+Hirq2Kj94sZtmi+NYOxYevFHf+tJJs4llGYlefxQOKH6VNPm8xW5ueyjXoBz4BSAQSgYGDQNKdgTOW2ZNeQeCzYcV4UxbL3Fi885/i2mUqBOVfOxezbVdMsVDx3nPFTasVK95X/OfoYu4Di8lmLy6do0J37t2p+NqPi5k2KP57UfHMuZVW1WcRqeSvrVt8ZfleaXYWmggkAonAmEBg3333HRPVjr7OpDujxyhTDGoEhg8vZt6sgsDE3yw+fqsSeOnK4p0nKgHXJ+8Vwz8t5jmkePbc4sVLio/frkS+ekOx8MmVwHSrFGONXQnUZxkyduH/aZetPM0rEUgEEoGBgsCzzz7bnl1JutOe45KtahsExh63GHeyUa0ZUgl89knxvSuKsccvhn9WMXJhLbesXcywZvHN7YrHjxuR4KOR6SXAlhpmETlkaDEknedGQpX/JAKJQCLQqwjkbNur8GbhAwCBut/IVIsV/72w0rGXLi8ePrASeP2e4mvrFJ9+WHw6rHI75aLFfy+uBJ6XbATdqc9SeZxXIpAIJAKJQB8hkNqdPgI6qxk4CMx/eHHnlsXjx1fUMwudVOnXN7Yurlq0mGzuih6IR858hxV3bFJx6MF7xhqvkqA+SyU2r0QgEUgEEoE+QmDI8FC291F1WU0i0GYInDPCPtVmjcrm9DoC64/QuvV6NVlBIjDoEDj22GO32WYb3b7iiiuWX76NtmLUKeoH3dBkhxOBRCARSAQSgUSgNQh85zvfaU1BrS4ljVmtRjTLG5wI1GgL2lNpVNNII6Wd6w9/6aWXXnjhhbHGqix+Pvvss6985Svvv//+m2++Odlkk33jG98Q+cQTT7zxxhtzzTXX//3f/7344otlyq9+9atTTDHFQw89NGRIRUkm72yzzTbxxBMLUxuL/+ijitf2+OOPP/vss/twoMhPP/30gw8+kH6CCSYYZ5xxlPDoo4/K8uGHH3788ccOKJtwwglfe+21ddddd6ONNjr44INlF7777rvlVc64446rbQoZNmzYYYcd9t3vfnfNNdf094QTTrj88st32GGHySeffOedd9511131Qpmur33ta/9Y75I3VnzdI6VVupxXIpAIDD4Eku4MvjHPHtcjUM8D6tN0EtNQgo4qEwmQlYB3CZS3pR25fCTGFWRCymuvvfaCCy7w9Nvf/nYoh0VKsP/++yMo6AKR79piiy0uuuiit99+e+jQofKKiUfC+MTYY4+9+uqrn3POOccufhzWMuussyqk5jruuOOUWUbutNNO//znP6+//vqlllrqhhtuEL/tttteeeWV//nPf84444zf/va3Zcpf//rXG2+88QILLFDGbLXVVscff7zbTz75ZLnllnv55ZeFVfr4449feOGF8lr5abBeHHnkkc8995xabr311n322We99dZbeOGF8RuRt99++9RTT33WWWdtueWWs8wyC9r09a9//Uc/+tHJJ5/8r3/96yc/+ckcc8yBJB1zzDE33ngjcE488USUaMUVV7zzzjsPOuggnExPPX3qqad+/vOf40BFcYn2lI3MQCKQCAxGBCrza16JwKBF4Oxi+NkFxcPf//536oG//OUv1113XTUYBD8yQaxGJA3EpZdeetlll51//vnin3zyyUq8QmquUTGXXHIJdQX+scsuu0jy+uuvTz/99JQZ5DoyQd8gLE3kxgZQhAi/9957iy22WExJSy+9dFn81VdfLSOliEff/OY3pfnb3/5G5zH//POLnHTSSSPX3HPPPfPMM0sjXo/EayTeUJYzMjCinfQlOkhPozHM7W5dW2+9tezads011wgER3nrrbemnXZaWhZHa2A2v/zlL5WzwQYbLLjggpD5/e9/j6aIoVNZZ511lPDOO++cd955iNchhxwiHmVZdtllo2q6IixK+N1339WR++67jwJJ7biXyE033VSlN91009lnny0Q2TEh4ZtvvlnkmWeeSaMjJaIjEit6/vnnDZYwLrjJJpuoGulxi2np+zPPPBP1VgZr1OiMjMl/EoFEoHUIHHXUUX53Lj/n1pXagpLSdyfGJf8OagSIRlJzrbXWEth+++3pMAIO4hP/oB35xS9GfueBBgXXIbYJaSk9YtxpiB3GQOhiOSeddNKee+75hz/84emnn8Zv+O5R8Ky88sp77703zQSOgiso4dVXX6W9oJmI0ph1qDcYYtz+7Gc/K6tYZpllaFzWXntttOOqq6665ZZbKFfYjLAK7cdy6EsohOhOJJthhhkwLbdTTTWVEliUynKqA9IsueSSeooqaZ5bF4YkjTb/8Y9/FMCE/J1kkkkgoMApp5xyookmikIEEBrxaFDE3H///YjjXnvt5RHec+qpp6Im2Aw0/v3vfz/88MM0Ov5ON9100pvGFE4royPKr+6s41kPP/zwKNNfxjWwKIQ2CD+j+xGJWmk2TunDhLRZYii0DI0YJZd5NbgMZyARSAR6DwFW5t4rvCclJ93pCXqZd4AgQNijGqTj5ptvfu6556Ip1Db6Rj3ANkSg3nPPPWVXF1lkkfHGG49nCYXBoosuuv7665ePqgMoiKIoaZhp0B0qEIYVCahbSHfM43vf+x4rD0YSXOQf//iHAhGsP/3pT1HOTDPNRFkiHHyounBynZ3orrvuEkmub7jhhl/+8pd5tOiCR9qvTCWzYeFD3//+97/1rW9VZ28YxleYq1555ZXqp/Q3FDzVMbiOi7IHgQt6gRvdcccdNEzbbbcdi1J14gijI/D83//+t9BCCyE9mBA+NM000/CwkUC9cOY8pJwyL9sTIvjYY49hjToYFsB4Cnz1Rt/FSIkUUrmhO5gZrgOHeeedVyMjfZixFFIWnoFEIBEYhAgk3RmEg55dboAAIUpMUmYwhVAhkMESLbHEEkjD7373O54xbhlTyN1Sjooh49mnGhQ3Ioqg/c1vfhNPFYg5dZQSN2KvwSFYoNi5kKSOUkY8yxFXXM4ubhmhWHbojVQX+ozTTjuN3sgjGhr9Ehm2oc7L1BfOLg8++GAk01qcDFejykKb6G8ifrPNNuNrTL3ERsaeJVJK9IIWR5jjsL8V7dAEE9BXRRY9Eoi27b777rxq2MJQwBJJhBJQu+22m37hPRIrEzf685//jLpxlxYfRYnnZsS7CA/773//K1IhOs5EKOaUU06JZPk3EUgExhQC5aQ3phrQUb1JdzpCJuMHFwK0AkQptrHGGmswOYcViTmGHCVff/CDH/CfFfnXv/4VGSqhYb4p+UEZWQZIYo4j5W0nAeYemhXyG5PghMsrqGFidrTY60S9gZbR3DRMVkbOOeecP/3pT8vbzgP0KCussAJjWSRD7FAWRIqX0nzzzVdSE5Y+FIoLDu0UjxmJpWS0YnpbZZVVwhSlXjyJRcnTRx55RHdsnmJ9c8tVmcEOt8OQoqL4q3YKMCADnB5IB1EcdJPpSoCFTi2MdygpiFAuZjtMlC+RRlKJQePQQw9VuARRIKdmvkTCtFDVFWU4EUgEehWBJie9Xm1Dw8KT7jSEJSMHHQLEJPUGhxKMx1/9p3Kg1SCz6QzYYlABdqsf//jHBHOJDhlchusDKBT9RE08NQ87FA1HdXxoPhAIAh51wDCqn0aYvQaZCC1LkI+a2j2iaqpuXn0hHcXoPpKBPTAzhUcwAkGnpTT0gusSvRe3G4SMe5PW3nbbbXaqK41mhRaH+zBbkr1XrG8MgrRE1EscdICpRzaW204VzkCclpgOQR23dpgjkTicBBJbFyI6tqTxv0Y67UejqTIcNEk8e/bYYw81MiNKqZwAQXqjE3YxbcDMsDEF8vvh34NmKa2jXmd8IpAItByB+kmv5VV0r8A8Vbl7uGWugYJA7CFffzj5ak81KxL/DyKWOgHt4GTjp0vfw2H2V7/6FXdaYpV6g/hHLIh5kps24rqfXO/0mi8gMuI8G0oIjjj2fPFN4avLWMM0Y+mD1qAFXGq4xXBYRqGUYxM1AW+LNRMVPRPDlmRcodELlqM43iZ8aw488EBt4Ndii5Yd2o6ZodWwq4t+BSPhTsTGpC/aQ73BJ0kuypirNr26tpFSNNxC/4WeDJSbcoBGjfhA6Vj2IxFoLwTYqQ844ABtMqG11anKFQeFvBKBROCBBx6gqKCfsEEJuaGTYDlCRGh3KHW4zfIgwVfQDr9kWhDKCSoEaoaKv8jtMzcEkImKpmHVVVf1lHIi/FqUg0vRFTlqneXIU5u87EhafPHF6VcoVHgo01hQkLDX8GvmY0s7glqJDEdgihaOO9yc6Z+QHtoX5YuMRvIFLjeL8XHWC+qTiknr46sbNHIECWBdoqoJZ16aGzyPwU6N0nMJokQJ/yTuz2pEv8RLEOoZYW0GHV/pBuVnVCIwOgS8P7R3sSVwdGnzeT9AwJzTnq1M7U57jku2qq8QGLHW/2itYY5+QRTMvDZhUb3Q8eAl1CTMNDZMoRfIBHcQBIIGhdRn/XEhMTLG2cRfaPEI7Y4Y6iIH9FHA4El2JMWhNeIZaFiLSkeZL+TtpZtRTeql4vtNsandabOh4v3mECYeck6tbLOmZXO6gwDPvDAut5t2J+lOd4Yz8wwcBEL49bw/pa0kivoit0CYmK5oceh1Ojr8pudNaFxCqzrYuPSWxtZg2NKyPy8s6c7nWLRFiELR+oGCMM52aos2ZSN6gIATvxjiFdBudCeNWT0Y1cyaCJQI1LOKqpiZiuKp345Iev8cxf1lnl4INGQMEak9DZ/2Qiu6U2QVXF/I3lH8FxLlTT9GgLXU9rp+3IFsej9BIOlOPxmobGavItByHjCmhHTDehtG9iqerS28udGxEcxqkuzk6M1J3MmKfJLsTrc/jrM5Lyi7zGxK32uWkSchtbaNWVoikAgEAr70155QJN1pz3HJVvVzBJqT0C3uJFrzxXqZzyb6+8SVWr4YX12vXWOOz8ESROIHjsmxVZ5lwZ4vm874J9lzLsbhN5JJbA+5DfB8tDlTy+VijBBjT5lcfL1tZbernHezHem+nsMXG/9wCLJDpZ1YuN9++6nIcT5OBYxTmJ3Ww+v5if0qe9pVVN22CHN74iXNC0ot0jjFx8HW2hmf3+I0ffHFFzMR+sCW7WnabEO+45F86supSM6q5iblaxXoDm90G933Oru+hoxJBBKBliHg+3ctK6ulBaXvTkvhzML6HQKh+fgiGyDjSVY7oeJMP+oBl56FuCVNq6VyRHpK8MtC9pdHAAcYZXbxnlZHkvocmW3L8khdPnqFHNjP5agYDEAk12nHzCAEctFe+BIWEe6LUbgIKc4l0M4vrMInM1GKE5c+6Y0VX7eXKqrw1zc4j160csDPqR+e4hAaJgNOEpgB12mRPl3u4w9O9rOhnV+2SLvxtSGy24DmBGRhu7rsZrdV3kZ3G+m5H9nlbieXDfaRMv7K68wbzAPPsMEes/FlU1vJ7CBTMgdwuXy6fLXVVlOsDWXctB2gjKN4JMEnZ3zamJOdM+RX9+xgr5xe27PmM67A1xJHEPkm6A9/+EM7yNz6cipupwH23jtCmuurvXXxOQ4sjae5Ixk1CRvzfdDK9cURjy7k30QgEeg5Am3ru1M52T2vRGDwIjDi+9j2TDnZjyiFAwFs5/k888xDiNpIZVc2ChJn68XHMu1U93vGciR2pA0xTOGBhcgixu4trMKubFoHrpce2XIS8XQM2IlICXxFz+nJ6FF8zWrGGWdEUySOEwiRD5OOU4ORDEcdyo7roCm2ryM69oLZau7z5sFs8A90p6JlObugU5E4Lofv4UzxAXA8QJPoPFTk5L1IgEXpHWXMDjvsoDqFiI9DokFBjxLJaHcwPJoYt3BQprOIfLdc7UgPCkJloqj4vLk0FCpKg1VkR+ncRi/sqMftkCGP4gsYmoRcgqXDr5SfXcRi0QmH+I3C9ZfSCETRQvvp9B1BVKYt98xVAoByrHM0YLbZZtOAON5QIACJR/k3EUgEWo6AX6gfmotxueWF96TAsaJZ+TcRGMwIUFr4InoczcdGQzY7zAYvoTihM4AMjQINh92VhDq1Cr0F1Yh4x/iiOz50wDRDlotxmrCD/mxl931QTxl9SGXxvhtFGJPWzg+Mk3LoY+hvwhCDLtjLQMGDT2y99daULsQ5mU0lQ2zThTiVRMlYCKalIgchYj8rrbSSkgl4aVQkXK3acbAhGiHSde+99yJtNDeOxAiC5ThjNAJLoAihKcHA4kCd+HI4bhQKLXlZjvRI24TRI/HYD+rGwIT6uGVsgkCZPlJWah1xKRZr1EJ3IIUGDdPIZyMAVFogX0bWBLAZMUqgEHI6EfDRLDFRo8+ko2LAFKMXmBAwcaD4hIVIFx4JOiDEbf5NBBKBQYhAA0v5IEQhuzw4EeCJMuuInnNipZXh30oYk+7iyHJmFxc9ytFHH+0QPzYdtIOqADcSj1g4H9lRgf6y18hCMYPHkLhu8Rh2HKSH0sgWdEfs4BbYEncTl9N6CG+707fccku0BnWQkQ0LyaD8UJSASGqPEa2rlIx1hXSnnsEeaFw8omFyyy3Gt71qvvitcKYuRiJHK0vJV5dlB1nhVeNEZjG+FEEVRCMlTF2ECQUtczvaC1w+CBrnpVpsaTzLkc+eR0aKLgHxnZfDF4dVC9tTFFPUiUt3nrzQayA0LNapj0GJAIJ7SYbD+cJolKgix2E7tNrIjjgOpEKM8koEEoHBhkBqdwbbiGd/P0egVH6Q/QQ/xw5aHHwF5yA4Ix2S4QopS0kgElnBMGiDSH23ESnAaBUFkvcOJ/QJTDoGqguP+I7gN8gN5QSHWQRIPH0MBQw5rS7MhqbkpJNOwpCkr7midjQr4vEY389CVhAUBfJfUU7Nl0p5BGtMfLBTLrYn5jPmOaqR+Ix5TRXIWdnlmkcd3ZYdjwTRU2E6J3qskqvpINULKOrLAZR2smeFtqY+QcRE95FOx1JHsfDEMs877zwJ5EXgojEq2nDDDSnAaOBQwDI7oyGbGiskGtpRLRmfCCQCAxuB1O4M7PHN3nWGAOeYeEw8YwYMUm5xHc6tDVUdJDfRS0Kz13DvpVmRXiQZjOsQpYw+fETcTjPNNEwq3GtCVEvmxFjKleBV3HpYteIkLo9Ge6lCGmQlPiKBbGEtNEAIikqpLvCk6kLUS6vkw14VC9cdlSdcfVVHU4X0MNVxG6ohK74IxgWnupAI87NRaTSg/mkzMQgZMHkQ831mSsMRsRw+T1yLFMtgRxODAnZSFBrqKeOgb/FEMgZBNkeO20gP1ZevbSiEe9Mrr7yi4xRjRlONwSO5e/PNcig2ytVVStdJq/JRIpAI9C8EUrvTv8YrW9tKBMKHRom+C2HnDusMIcr2QYhW772qrhJ9sQWJ5CawaX08IrNFUlGIlFEMCsKe5UOeJPqcc87JwRYB4vTDasObh0ewKjjNVBfbeRiz0Z5SM8FT+Ac/+IEsisUkPI0j28tCuP7QtfjCVxnDcwg5IOypgnyZyyeKuPJQU7HfcVXGdZCG6LJ+yaW1NkzZSEWlpF6qL58GwyRsJscFN9hggygZ/4DYs88+yywYMZDkxyMGGvaE81W0QZ1Wxvk3WAgEqLgwQs6MeA+OqHw7uQLJsrU1AdRQDF+c6vM8bL8Cow+sapVPm3E5UjX3JgoezkwavOOOO0pv4xsmRAOkOyySulxTeN4mAonAYEHATJ1XIjA4EcBOyn06Nv5Q9vBNBgWXFzJSAD9ACLAi6hAzAukuklmEBggJIG7peLAKkXyH0Q4BF90DNU+EbXqSyyExspPNItm5aFaoUiIBv13ePGxYnIcojUQS2NgAD1y6Gfwg9jRpGAuOTelEu7YR7RgGByORWst2Q3UUm5u0ikIlmlqpYsTWsxDzQZLwlUrHhw/HBkq1DRci5EwkpZSmlmyPixJXGGSISibmREqmSrHDh+M0SFXY7zDFiKR2kkxi9iMB1FA83xrWtGOOOYYWCphiAMLtSUxlZ/jw4fyWovHCtdfZhXZyDJdYr6ufGh0OSdGX6vjRhEcAMpo0+TgRSAS6i0Db7szKjejdHdLM1/8RKOkOkw0FCb4SG7nZTUhrpAQboAWJjtqZVUb6UCilgnjiFjMIwxB3YDGxazp4QFABzIZCxQby73znO+KRKjoSLEdinGmnnXbCYNTCGYhHjkh0au2116aGcXE38dTpf0S7RiITKIsqJLPPiCUIO8GB3NrPhTEgE/auc9flVS2yco2Q7rZH2c/FmOUv8hFPlKlkV3Uk04/biPcXIJJRI5UxwpG9jJReroiszi4edYv40f/VzoZXR/ENEzcTmXSnGZQyTSLQXQTalu5U9PCxaMu/icBgQ4DAHvu8ivva0I3HtrGIbYVeBCMR4xcbtICehiNOIMMGRJwLS0yzEpHMUrGFW14mFbnsHlcIliCB35eN3/Zz0UxgSzgKPQpfk8jb4r/nDLlyiitwIIYe2qaRhTc6R7HF9bakuLojoT9vf2uPBOwvgLQE1SwkEehzBOwVCMfE/ERon2OfFSYCHSBQuozQtVDklLeSN/QjtqOqvqSwEJXxNljZpl7eloE47K7iO9ybF3URzRPGU1tJyPja2H5y368b308wzmYmAgMegdyZNeCHODs4egSG/qXiaDIArlXeXnWV7fkwr1ucs27/607Smv43ZtniRKDfIFDR2+eVCCQCiUAikAgkAonAAEYgtTsDeHCza00g0Fq/kCYqzCSJQCKQCCQCfY9Aanf6HvOsMRFIBBKBRCARSAT6FIGkO30Kd1aWCCQCiUAikAgkAn2PQNKdvsc8a0wEEoFEIBFIBBKBPkUg6U6fwp2VJQKJQCKQCCQCiUDfI5B0p+8xzxoTgUQgEUgEEoFEoE8RSLrTp3BnZYlAIpAIJAKJQCLQ9wgk3el7zLPGRCARSAQSgUQgEehTBJLu9CncWVkikAgkAolAIpAI9D0CSXf6HvOsMRFIBBKBRCARSAT6FIGkO30Kd1aWCCQCiUAikAgMYAROO+209uxd0p32HJdsVSKQCCQCiUAi0P8Q2GCDDdqz0Ul32nNcslWJQCKQCCQCiUD/Q2Dcccdtz0Yn3WnPcclWJQKJQCKQCCQCiUDLEEi60zIos6BEIBFIBBKBRCARaE8Eku6057hkqxKBRCARSAQSgUSgZQgk3WkZlFlQIpAIJAKJQCKQCLQnAkl32nNcslWJQCKQCCQCiUAi0DIEku60DMosKBFIBBKBRCARSATaE4GkO+05LtmqRCARSAQSgUQgEWgZAkl3WgZlFpQIJAKJQCKQCCQC7YlA0p32HJdsVSKQCCQCiUAi0P8QeOCBB9qz0Ul32nNcslWJQCKQCCQCiUD/Q+CII45oz0Yn3WnPcclWJQKJQCKQCCQC/Q+B733ve+3Z6KQ77Tku2apEIBFIBBKBRKD/ITD22GO3Z6OT7rTnuGSrEoFEIBFIBBKB/ofAOuus056NTrrTnuOSrUoEEoFEIBFIBPofAkOHDm3PRifdac9xyVYlAolAIjCQEXj4fw8vfuricxw7x+F3HB79nOygyfa8bs+lTl9q7uPnvvCxC0UedddR854w73wnzHfVk1fNdvRsz771rMjlz1p++yu2F7jhmRvW+9t6b3z4xoYXbLjMGcssedqSd71wV1nUZhdvduSdR8Zt/k0EINCmLCzHJhFIBBKBRGAAI3D0XUcfuMyBs081O8azw8I76OlHn3405ZemvHHTG59646mlT196jW+tsf+N+z+5/ZMvvP3CATcfsMKsK9z07E0bzLnBZ8M/u+/l+6R3u+KsK+581c7bLbTdQtMt9Nxbz63259Xu+1nl0bBPh607x7rLz7K8cF6JQCCQ2p18ExKBRCARSASKgw6qgPDww8Vxx/UFGocse8hjrz128K0Hvz3s7agPj9lsns2EZ5585reGvSWw0jdW2vjCjZ9/+/kz1jgj6M5Drz4077Tzjj90/Hc+egfdWX7W5a988spdr94VPZLyvY/f+3T4pzKOPWTsZWdeNorNv4lAIJB0J9+ERCARSAQSgZF0Z/bZi5//vC/QWPsva6tmuwW3G2vISDE07tjjTjb+ZFH3kGKIwOmrn07xc9zdx7FMLT3T0ne/cPdtz9+2+IyLLzz9wixZVDjTTDjNJ599csWGV9yw6Q3XbXLdKaudgujIOHSsoWWxUWD+TQSS7uQ7kAgkAolAP0bglVeK1VYrllii2HTTYrLJRnakDLiP8BtvFBtuWCyzTLHkksVdI1xcjjqqmHfeYr75iquuKvbeu3j33WK55SrZI/3LLxcrrVRJ7K9wxO+5Z7HUUsXccxcXVlxrenTd8+I968y+zoeffIi1REE1BIWChx/PIjMscuaPzrzs8csmGDrBtBNNe8GjFyw242IYz2G3H7bU15aScbEZFgtHn8ufuPzAWw7sUZsy84BGIOnOgB7e7FwikAgMdAR22qn48Y+Lm28uVl+9+PDDDnu7887FdtsV11xTnHVWseWWlWT771/cdFNxzjmVmH33LSaaqMJ7ymvHHYv11qsk8FcVro8+KqacsrjxxgrX2b7iK9yja+vvbr3oKYv+5vrf0OiUjKe6xEnHm3SVb66y8MkL82jea8m9PGLPeuGdF6aYYAranZufvdmtyMNXOPyM+89AjBCgY1Y6prqEDCcC1QgMGT58ePV9hnsbAQby3XarGMjNI32jNO7tHmX5iUAiMAYRmGGG4oknivHGKz75pJh00uK99yptoaF5882RjZpkkuLttwvJZpllZMwLLxSPPVZssUXx1lvF1lsXy47wcimzRGC66YqnnqoUO2xYMfPMhSzjj19R84TuR0Xydn4N2bdikGqfa/jeKez6YjRuuOGGOFj5iiuuWH75NvIWT+1OXwx/dR3hD9hnBvLqqvtpODes9tOBy2b3DQKULnF99llRrl6F40J6IgEydMUVxQ03FNddV5xySuHk29NPL3bYoeKYvNlmIxNX/1MWVUaOO+5IriNmSHsxmbKNGUgEOkQgN6J3CE3NAwbyn/60YP+2QrroopErp3I9JHGEJaAxtgYyxRx6aLHgggUD+amnVmYHROfWW0cayCmNI72Um29eiaRJlmzaaSvx22xT3HJLpYp99inWWKOmIYPuNjesDrohzw53BYFFFy0uvrhwki0bU8lRaF+okC2rzj57JDVZbLFKApapyy8vjj664n/D44dta/75K8obF4bk/7FGLYF9+Oj884sNNqj8XXrpSoLyUeWm6atLOhUKoebTN5+43fRMTYOXCVuJwKhXu5VlDsyy+qmBfAAMRm5YHQCDmF3oPQQOO6xCX/gU/+tfFdtTXEceWSFAKMtzz42MPPzw4owzKo7G0h9zTMXstcoqxcILF4svXuxVcYypODsjQOX1+99XfHoU66+VW16JQH9HILU7zY4gJfDJJ1cSmyMafgEttMdXXlmxo8fFiP7pp5V9DRtvXDGQm2vqL8VS6rjMTXx6XMoJ3bIl12it45UMA/2yYXXN76xpw6r9qNHXhhtWHcJxxB1HnPPgOceufOzu1+weG1YnGGeCmg2rTuxwvMctz92SG1YH+oszcPrXpOWIt7KrOvEjj1SsVzWRbksnnsozu8G3q/wfl+yhIvrqVyt6oOqrdAYSWR2uTpPhRKBtEUjtTrNDkwbyZpFqdbrcsNpqRLO8RGAMIPDOO++sssoqX/va19Zcc80PPvigvgWPYGcORB42LFIus8wyCyywwFXVu8VG5Xn77bfnmWeeuFt99dVXWGGFlVZa6U9/+lPEvPnmm+eee+4PfvCDOeec8y9/+cuoTPnvYEcg6U6zb0AYyKWuN5CLrDGQi7EwOvDAinqG9niRRYozzywuu6xSVxjIK6ERVxjIBXtoIB9Z3ED8JzesDsRRzT51GYEPPxxG7/LRRx/7X6A3/u9ym7qS4ZRTTpl44ol/9rOfyXQWC1ndta/d8EWBCZ1wwgnXXHPNb3/72+eee+7FF1+sS1i8//7743Kc9tmsG2548MEHDz744GOOOea44457b8S2tEMOOWTLLbc8/PDDsSXVfcJJO69EgOIzN6I3+Ro8/XSxySaVtHjP8ceP1OWiPr/+dTH11BWX5BNOqEQ+/3zlTIv33y98FPakkyo+gEzg555bYTm2fW67bbHyyhVt8yWXjHRV9lsW70c64YQVq9ZXvjIyPlpV7QrdZDv7Y7J0JOyPo5ZtrkGgeR/bmoyjvQ371IYbbnTnnXd+61vfottYb731ttpqq04y/u9//3v00UcXX3zxsbriYBwVhTGrk8KbfBS/64Dl//7v/2aeeWaqmoUWWujaa69dd911n3766Yls0Bh1YTA//vGPL1ngEumpZ959993pp59+1113vfvuu6+++uqxqxwIPJJykUUW2evTvfb4aI9//OMfDzzwgGI23HBD5EaXsaV77rnnpJNO+u9//7vJJptIMOHvJ5Sg9wZoVCfy3woCOGh7bkRP353PX9D4qX9+30GoVQZyxdfUyFgeV3V8dbiDFvWD6FZNoP2gq9nERKB3EGCs+fKXv7z//vsvvfTSSy211KSTToo0RFUMQB9//PEEE0wQtOCzzz678soraTheeOGF8ccf31NqlXj04Ycf0nYIS1w28/HHH7/99ts35mPYa5fmYWlDRkxn/mI/NUoXZGVaG1NHXJONuI499lh6mnPOOaea63h++eWX33jjjX/729/2OniEi/WoNusanuQOEQwueN1112FLoQcalSr/HcQI0O7kFQhg//l/LyHQ+TtW7FP4v/M05dOGKRtGllnGVKC+VfUxHbWt85T//Oc/yTN5n3rqqVNPPfXee+/tqJwxEh+NJ4ypFr773e9utNFGptg55pjj2WefrWlPfTcjhnRceOGF+XlI/7Ad1QX154Q33XRTTfbOb5988klC/T//+U9NsjPOOOPXv/41TlAT3+1bba7vSLdLq88Yv8pPP/0UxWEGkoD2gh8MAS+MOixIvVzYcnVY5D3zzDPHGWccMfHXELz++useXXLJJfPbd14UFCf//ve/I7G/BxxwgEhvUVRUxvcwUA0LdxyeNH/4wx+U+bvf/Q6DeeONN8ry77vvvqFDh1acb0bNA88//zwXH63acccdy2QCSNI000zjnReW+LzzzqPuQom23XbbySefPACJ9Ixi4OLTEynLkuNp/u09BK6//noD53LMYO/V0o2SU7sT4zIo/taoWCy0amJ6iMLAUET1EIRmstOxYwBm/EkmmeStt94yTR9//PFTOp9/dFet1e/2URmeK4q/jwr3+b8d2QjYFB566KFvf/vbxNj666/P/vL3v/+dWGqmgYTfL37xC7lOO+202Z0eU3CAW2QJW6ULux0/fTm+4VQ4p2paMFrus3r8/Oc/X2655TbddFMJyG8qEM4fZJ56v/SlL7GVcOZQAnsHl1hPQ9OAB6y22mqq0E5MgoDUWmxARTilcjAG1pO//vWvmJO/OvX1r38dVcKiiNLdd9+9me60PA01D+7yxBNPaDmtzJJLLukV2myzzbxRW2yxBU0JHoxVaLBu6pp37KWXXvLW/eY3v9EFRjFEYa/YgF4Uv/rVr+aee27Gppa3syyQ3cowGQuuNqxLU001VbXO5o9//CNqi8AVR43MYQg0XjvRnf3220+z44GUX/3qV9cYdRzZOuusg/2w3EHgsccew5LHG7UX/4gjjuDQ01an+pZoZGCMIJB0pxb23mAAHZUZ/KCjp7Ut69l933CR+r70pN6bb77ZrM363kzXn3nmGeKKYHMRaaeffjqhaAY3ITaTvS/TUFRY2tI9EP88DP785z9PPfXUVPfNtAG3uOuuuzhA0JTMOOOM5O5PfvKTo446SpmdZ+ffQHj81FmZHV/YCSFEOkYSjqKW0bQsLPHEDJsI4RGKhLKMWgZWPigKopfQIoHE2TujhVpb9Xw0wXA6Ofvss/W0OunJJ59sfCPGKHs9yP5vfOMbiNQPf/hDjQwGKcF0voNQFLPOOqsEeI/2uJ1tttloiYh8yqfvfOc7eNV8881HHSIZRvXaa69R/ChWyg022ACTUD5udOmll6611lo0Il4zXrTbbLPNLbfcglpJNsYvbACZM74IjZcq2oMG6RrYS1MOZob0YANeA8zAK1e2XCTqVt72UsBw8OowrIiaMWVfi4q0HKnlbmyYqqtG1Lx7Ir2WZTy7G60PY1cZw64nfOGFF7LHlZ01degvvVdNmWWuDAxCBJLujLFBZ1Y3IddXb7lpSjU1WLXUP21tjOmb+jfKpBskM0YrNVvbgJrSTjzxxFtvvZUo4nBgkWo36bLLLtsk3QGXadGa1ZJOsagPj0jG+5oqWntrEMlRkrJLxZI6K6+8sjUuGmGyRumIq+ZLiPUrFRG6Q3iQCi7ZiWqCxDqYQsL+W2YLfIVQ59Cw+eabg0UW6hCihcywvMZF7rjjDovgEHUHHngg5TPk5RKJ2RCfAt///vcRMkiyI8heQ3c6b7bmeZ8pQuzKkfIrXPGbvhAXEsuA2ptDNNLZRFZ+G3vssccvf/lL/EaxXg/k79BDD73gggsgoAvADPWMRxQ8++yzD3tHWe0OO+ygSeLZyNAdHOjII4/EYIBgZxA9Qeg8ECC0iQHOX6VBAN3BLNdee22DTrjSpnhFy2LHSAA3NUb6QimFw+E3nZB7b4U3DaqLLbYYXY6+932bcV9zDpyNYFm7GJq5XXbZpYx59dVXgexVZF/zihrxeGRwsczSVhKR3i6j5rVH+oPueA28HlRZwMGrqoldWUUGBiECYw3CPrdDl2mhqdCjJebfnXbaabvttvMT9fM2pRJUIbN7u6nWSY6viGveeef9l2NZO74uvvji8ATsOElPn1gun3/++VbSCmJxILeIsSYLZWugKSEAgnxwcpTxm9/8ZmSnTYHw722TG3ER+WDfeuutyTk2Dsr82MLqoUmT8sD8S4niFvfafvvthaWR3krUhhcBs7Mpe8UVV6RFt7wmRaLkrv61P4UQIqiazxjkBo/RBZ0iLWKWJ9dpJvbcc09C2rpWgfiQGEt5rh56ZKfuqquuSvbjhdbHXFjgE9YlTIjtwHXZZZcxK0QkGkHqsEEgwXwpCI/OlUP1XTAofIwMouruv/9+XKE+TUcx2BVsga+R6kUrI6WfBo5OGWYgwjelLEEHreaD65SR9QGD5Z3vvDGvvPKKGg0NFuUAmNAnYXuoKpUJ4RrOsPWF900MNr/ooovSVO29997Ym/eZXodc58VS3QA/B9TB0CNtP/rRjzxiS+LKQ+vppZUxEqMLbEbGujpvy8OIC4KIaSEipTVKLX62YqqrY0+kckPIWOXMkyUzMwoMdjVmX8MBBJzPoygEfzWRgsgPQTkHxXcKqyvI8KBEoAuT7ODBxwTtN0a8We9aFrM4mFXJBpqGVoFw0UUXhQOmAi2gGbb58VHGmrDMwtaOXVL7d7tVxL9Frc0L5gXNKEV+fYEEDDdDDbPgxtXs9rSgrE8WMaZUGgKK6CmmmKKjNA3jkQmLeBMxbwmTY8M03YhEoXiBUP9ojz7axYoE0BlwwiAecAWLTlM/EwaxgXQSJMQ//keTgXWZPcVrFd2JuVXvFEKyUl0QvZQ03hPMo3QaaKaFEiuHioULJ3ZLk99Mruo09rkgYTgBqawlHpnxSQIcBb/x9oYJgDsLskK66HVkx3g0OF4wNILkFo91AZ+rChCUiSeVdRmRilNFty7uI95tSrtu5a4cr4JZIsE4XJSAxrEx4SLwx0U0uxslA59vLL1RiUlZCCS9GDSdOKUXw2vjJwkBe6FV7T1BfdwyclE54OXBqsvsvRowoIgaMw00vJ+IuEaaNxgcvdjCViMGEXU2jlYyYAc+omk0/aCo6yiozGZ+uRgPpl4aeqTk5gzYhvrmHnbqC+bOb1R8urd/Y/vt993+82IXK66+6uriqpERI9PvM/L2VAd07HvqyJvNih3f2XHHfXcceWtz675Dik2Kp4unr73v2uK+UdFjj/Acr2w9qVxH+6+JyxTH1kb1VVrZmsiUSfoTAkl3GoyWBYEFpRUGzTBNPpsIyR0L6Aapux5FPhEDVoe+axMXb4nbbruNjlc8UWo1bHoikPzFtCyRI5nZ1mIXQXGZlz/66CM/UXO3dbMZUCShGyk1niXITM3lotrOPbK+Uf8EHZllllnMmFaBSAyqZ91sCWsGFDChH3300RaRxIN5lo4EEaQ9plRAAkYVU/svFsUWQHHiYNPaZ53ekyiohv5CANHUqk6TN3homDSMQoI8KB+TmqHL0UcMhi5NT5l7AE5uUWk4DiQEJ1dWziIUJ0gMk6IS0DsFUpygQV4MlBfg2An6K95y00IZaGVdTQZQCiATS4STMrvKC9ViZMPMZ8VMCgLNYCFAaKsCm9TDcXZBYaPNpDiHD4MeKhMvW43upLprnqqUNK2OrA8DuSFxl92vgLWiPksZo3y/BfiwN3nVNc8j44KdUzUZL8KJ2YInShizPCWzvXsEP2zd+o1Qb9BUhdeOQZxrrrm8vX4anhpECgDMj26DdQ/7McR65L11UC+dnzcfNVS4LvgJ8OzxVlulYJA4okIElNNnV5BsjUFWvDAaqWq9YyLEfXUWVlCKeI9oH5EelLpUpXjVWYIgIL5aR+LXgRLNNNNMcjV/eYf9sqAdWfz0DLf30A/EMGltMVK12nyRvZsycMBloefdEyjrgx4Mja+51EtSxmdgICGQdKfBaJogzG7OdTDx7bzzziT9DDPMEA5xUhMqtL6mBpMdi77fvEi/eZcJmldjbHCgFeCGUhQ/ra/AXImm0NN2RBgsxwkzmgOFm23NHZqkcFkoKqxrcQIkzEKcmlpiyxHJLOgt9aw+zcgWxHgJU7cZXLL6NlTHmOgJObJcUdpPt4wtqZ3sJGb0S2JuPRBQNaciMcRVdQk1YSLHIqmrXEchegF5ehRWA92hU6kpebS3GkYxru/IGawiPYpjOtttt92IKCJBpGnaWhaXFcZl8ZXoplGjI0G2WIhos8rq0CNhthXcojKPj7jIvzJBVwOqI+9hTrXT1byR3jK99GoiabylXg/NxtSNYOnu0FHhAPHIewIoAbtdsF7C0sDRIhCiiqIDo2MDqR8CJopPl7SMYKN3QTg6Kp9U9gtiCdIwtNugsGKUib1gFEuOkCljagIGyM8Em9EMmId+iDlGgWF5kR431TaEhoiSEhpeV7yfoSosTX6J3m2cRmMcsBtijGIV7PL6DVpOwIHYU7IXw8/N30DVD1zVCpTMYFGE+GuxgeiLdFmZtHAJVNP9hrfet/pXTqvobBqm94N11TziLuaqieTdX2NOqknQ8NYigQsa/MuncNYetwJlZHVAe7xCnspFAYy5ekrtZObpKEtkN0ZYlFx+NdUFdiPsnfHb95IYxOrsWm7S05LqyAwPJASS7jQezSD+HCHthrV4ilsrZr8T6mIGCOtgnIPNmMncrEdO+BX5QYonIfySqQ2o3IPuWFFVTzG05X7hlmhl3aSsiYyYwSpEqs4Pm7DHctgRCCTTMWbDewbBoq0xy3AdpWknmDXAnE41jYjEBl0KCat2EoXMI8/sp+1IpsbcZBVIbUPqq1oXiAdVIHMmQTr8mNNRKKWxB8VCuWx5w4Bk3fZsiL6ThWxJAXvDKjqKlMXK3hIzFq+EGRlGHqAClDq4INcoeXWcGDNkwuHBYLVHvhLAmJ/tsrjOiOEbWQ9hL8T8hGRgwJBxG5ECRl8hoQOnE1I495FqMTCylKp/+MEQqKZ+igpkunziHeCCUFEbjFvG1Qa8P6LC0wIRMdDeJRodbwsKgu6w8jBYwNDo28ck3rKVxgsViBdMdn5anuoOYu0W17HiJ85xRH4PGCejqr54/zEhrwTCQQFZ0h1viNUwTVgxcW3z4h4IFAb8hCCDdoS6pUxqgLyTFHh7nbRXRBom5CMkEEzcereNEU8skWo3srqp75od763BFSD/PELEoxxS03D4AcYtnho/vTJS9ngHJIjsNDoIulucCZdCi4UZBDVSx/E/4PjpUfZ4SaLqKNz7Y+ywurjt7b8jiERvV9KF8g0HT6/q97wEpwxUF2doTDLlBOL3hQpLaepL+1E1UBnuJQSS7jQG1uLSmpLCHI0w48fsaXbz86bz8Av3UzfXUwtTkOJApJSVLoUEXqJENg7Tq4yx28D0XVaDIdksgEaUMQKWFFac5BMB4Na8rygS2kRvzqWkUSxvU4KWnYUMYGUgD0wcFp3oDlc+Uz/x4PQRkwhtkAQhYEiLUkRV1xjh4BN8cVSB6NAY0e6Y00k+S3mUpY/Xr1oFN52y7YW8cRstFICJtRcSGS1v+DcSV//lbWPZaphIblYPARnp50Bn+FBJsy1s1ciXk1TzVL2IJvGJzZDWlGoiMUvjS6+DZFAd4RDeAazIPhFwSSCSiohSyiPrfkQ5htKj+gtdRh/xAImNncLLNHinga7I45fLuNoANkMkEx58dTFLLxt2pfHsdyxT/FE88j5A0l8CRlPFgMVtWRZVR43aj3HH5ZXz8oS48o4RSKEPk1EHWQPtAPJWSEPS636xYsVnqCy2DADBq6sWHYQbmh7kskwAdiTMrewahmrg5ZVfyibFjKfOWCb7Ag5//zy670I3F4X/XT9sUOfdxd1f8E1pkGTARqHRpsdud8+ra9XX7eyZMRHoKgJJdzpEzFzPpZ8dxDqYj4V0QXrM4+QK+VEua8gG9nIrftKObKCMISRIF8vuothZxnL/LQnHwRCVIQmqK7YXhiyvjinD5Irlo9Wt6mJZH6KoTFAd0CqTiBjaHQtWJEyMVfgIBlBRMtdccaIJ+UrVL6UtuCxQKAJWYSlP64OB0RVZnVvN40NW/+gaWc6rmvhXmrU1uwDNE3ZYFs64gApIVq97L9M0DGgzBoDSaQYBadntlgyW2IYp7QnzU8O8Ivkd84KyCscI6clRPX91QV4eLXqERjBIYZbsFLQLsNJ45jOqIIKc3GX7w0UQBU4bQDNM/nLsCBJGZYIaEtsy4hw0AcpRiwRUX1R0uCa2gVdhLVRBmkRTUtNaMV4SfiTS0GAprUwTdAQLEV9c2CCvougOMRi9wEuUIAbyOBkWYoCQQixEICrV+Oq3JW7DHIDa0gMZdJGRWEq3uqOzqB4KaNyF46m/uqyFfgXx5ksQdj1uTGWakYENioiM2ssqqpN5VIkflVLJYLHKn/fieauTCeP9UIozdWoe9fxWl9naaEZ7UlRvM55RQ9STNmbeRGCwI5B0p8M3wERPhWMnTmg+MANrEXKI/wcBbCUak7i/iJH1LpZAfgjTn0tGKiAEU01VKZ/FgXwihCgtSNOOlkRm3hB45n0aGv6DJuKyfaQavwGCTTlMZmR2+cgqmSHGyp6JhMAg3aUkjSy+yWDlcOEsE1cH+Oq6LddY2u/WllRmO54WSAC2gb1ReFimKx8J8JcOqdSyaDNFRc0OduKf4oHora6rmTBjEyRjI7G2MdCUxhc9AkuIJZXWlyaSOoqqw4i4qFvQF4GIhwYVGkqKr3AxFs9IYciY8BVFbHtqb7kqqkv2DpDKMShGVlGh7hI2CsgNgsVkQxJjsfhH5JXFiFfC+xS1ZsRRMaPnAaNSVrdHgfQ62gxeo1bWWJ0m9pBXx9SEdUcvdK1G3SKZSHY0xRpB6iJvck3e+luSPnRm1Y8aRlYnKMPNpyyzZCARSAQSgW4g8IXJvRv5B2QWi2Y2C0oRK2aOjcw6xBtjBwsXwW/1jLLoOE8Ikp5Rn+zEMygSqEkIDCoQYps1hCDkFCslD2LSURquIfxI3NbgJi99BkcKQhdHIZulJ0HpAEKfoQHEGBlJYyQNzhGcwEKf6KI0UqB9ZGwBLilpm2g1tBBjKI3lNZW65QBEtpWilyZJpF6rjmJDA/CkEPDiMT+FC5TKKmEEgjVNg4XLiy2MAiy8Z8rI0Qb0wsUPiTcJYgFVIGiJsLwaqeOVIzR+UdRUVyl5h0aRI6pUAo2FPecKpJagxRkR3YI/eANMlI/tobNeDBRKLeIZKw30Wg+tBYfqmqY/efqamOqn1eGGKUXe+D1nrt1YLFpc9c5V1em7Fq68lY2vPS/dc+SDZ4ri2sZpmontbYVHM23INIlAIpAIlAiM0CeXd4M7EJ6A9MaEOudi8pVbBodNi3hch+YDEQlHVPLMhdngCmhBrJJxBYLZxTJlWWzJy+Kz6aabADV00bQm4esa3h7io8Zzzz1PCTRJrCq9NwLqqlGJ18f0sPaGBUYfa6quqShFYw0gedsfEejo22H9sS/Z5kSg2wgwa8T+AIaR0nTQ7dJamDHpzudgNiOYP0/dXKgsk98DGxbnGI4IZdbyaRnTewF11XCOqL21NdZUofBm+ph0p7WjkKWNEQSS7owR2LPSdkMgtrhqVbvRnTRm1b4qvUECRpQ5c1H821HpXzwtvVJ7b9RY26sR931QUfeqSDnRcLwyMhFIBBKBfodAJ3uBx2xfxhqz1WftiUAikAgkAolAIjBgEKg+ULStOpXanc+Ho94Q8/mzDCUCiUAikAgkAolAv0UgtTv9duiy4YlAIpAIJAKJQCLQHAJJd5rDKVMlAolAIpAIJAKJQL9FIOlOvx26bHgikAgkAolAIpAINIdA0p3mcMpUiUAikAgkAolAItBvEUi602+HLhueCCQCiUAikAgkAs0hkHSnOZwyVSKQCCQCiUAikAj0WwSS7vTbocuGJwKJQCKQCCQCiUBzCCTdaQ6nTJUIJAKJQCKQCCQC/RaBpDv9duiy4YlAIpAIJAKJQCLQHAJJd5rDKVMlAolAIpAIJAKJQL9FIOlOvx26bHgikAgkAolAIpAINIdA0p3mcMpUiUAikAg0gcBBB1USPfxwcdxxTaTOJIlAItBXCCTd6Suks55EIBEYBAgE3Zl99uLnP+/fvX34fw8vfuricxw7x+F3HB49meygyfa8bs+lTl9q7uPnvvCxC0UedddR854w73wnzHfVk1fNdvRsz771rMjlz1p++yu2F7jhmRvW+9t6b3z4xoYXbLjMGcssedqSd71wV1nUZhdvduSdR8Zt/k0E+gCBpDt9AHJWkQgkAu2OwCuvFKutViyxRLHppsVkk41sbRlwH+E33ig23LBYZpliySWLu0bI7qOOKuadt5hvvuKqq4q99y7efbdYbrlK9kj/8svFSitVEvsrHPF77lkstVQx99zFhRXO0KbX0XcdfeAyB9602U2/v/X30cSPPv1oyi9NeeOmN1744wu3v7xCaPa/cX8JzlnznLMeOGuFWVe46dmbPhv+mf/ve/k+T92uOOuKO1+183YLbXfNxtec9aOztvzHllHUsE+HrTvHur9Y6Bdxm38TgT5AIOlOH4CcVSQCiUC7I7DTTsWPf1zcfHOx+urFhx922Nqddy6226645prirLOKLUfI7v33L266qTjnnErMvvsWE01U4T3lteOOxXrrVRL4qwrXRx8VU05Z3HhjhetsX+EMbXodsuwhj7322MG3Hvz2sLejiXjMZvNsJjzz5DO/NewtgZW+sdLGF278/NvPn7HGGUF3Hnr1oXmnnXf8oeO/89E76M7ysy5/5ZNX7nr1rkufvrSU73383qfDP5Vx7CFjLzvzslFs/k0E+gaBoX1TTdaSCCQCiUA7I3DDDcXJJ1cauMoqxdhjN2jpZ59VIq+8snjiiZFP33uv+PTTitpm442LrbcuzjijQS7FnnpqJX6ddYrddqsElLNZhTMUM89cvFXhDG16rf2Xtdf8zprbLbjdcXeP9EIad+xxJxt/smjukGKIwOmrn47THHHHEec8eM6xKx+7+zW73/b8bYvPuPgE40zAkkWFM82E03zy2SdXbHgFAoQt3fLcLYiOjEPHGjrWkFxsB5b5t48QyBeuj4DOasYUAumCMKaQ71/1UrrEhY4MH/55OEJvvlnRyrg++aS44ooCibnuuuKUUyrE6PTTix12qDgmB4kZmXPUP2VRoyKKccf93Fg2pMIZ2vS658V71pl9nQ8/+RBriSbWEBQKHn48i8ywyJk/OvOyxy+bYOgE00407QWPXrDYjIthPIfdfthSX1tKxsVmWCwcfS5/4vIDbzmwTXubzRoECCTdGTODnNs3+gz3hi4I999ecUE4ZL4Ltzg/XRD6bCjauqJFFy0uvrjSQjamkqNMOmllj5Xr7LOLoCaLLTbS4ebyy4sDD6yoZ3jhLLJIceaZxWWXVVJiS6EHqtwUxfe+V5x/fiXg79JLVwJj9ZNJd+vvbr3oKYv+5vrf0OiUjKfSgVHXpONNuso3V1n45IV5NO+15F6i2bNeeOeFKSaYYuHpF7752Zvdijx8hcPPuP8MxAgBOmalY0blzn8Tgb5GYMjw8pfd11UP6vq4MVov5tUHCPAhOPehc594/Ylj7jrm3T3eVeP4vx1/vKNefuuVyYQnPWjSt3Z7a9OLNrVUNb/zJ7AGtUKlw+d9ef8r95+/zvlrnLvG2WuevcCJC8wy+SzRYHP6Y9s+Ri0/0QETvb372zWr3kiTf/sXAk8/XWyySaXJeM/xx4/8eaI+v/51MfXUxYILFiecUIl8/vmKy8777xdDhxYnnVQxSP3+98W551YozhZbFNtuW6y8coUYXXJJRYUj/YsvVuKZvSacsGLV+spXRsYHOGN2Hhiybxsrlzp4e4bvPUrz1kGCjB7jCNxwww3fQ/MLetArll9++THenrIB6btTQtFUwPaNn/60sDtjllmKiy4aOSdWz1kRloA/o40YFOCHHlqZK23fMNmZB+l1br115PYNLo2RXsrNN69E8nOUbNppK/HbbFPcckulin32KdZYo6nmDfhE3cD/4x+vvfkia0708HYffHCc7TPwH/7puO/932S2z8D/nbcrM/5BC5+++vY3rXfzEeMX59yy27F3v7D7wmvftspSi//7+QnmOuuGCZZJF4SB8Gb59TVz8VZ2VSd+5JGK9aom0q1JoPryk/d/XJG9uhDxX/3qF55Wpxz5oFv/5Iq1W7BlpsGHAO1OXs0jsOGGw886q5L8wguHjzfeyHyTTjoy4J8Ib7HF8DvuqEQ+++zwueeuBKaaavjbbw9/9NHhG21UuS2zRGD99YefcUYl3t8NNqgEJphg+GGHVQJPPjl8hhkqgbwg0A38h+4xxZsfvvnlWR8fd/9xA/9JD5y0xH/I7pN6OvWuS572p4/e/ejdSfafGv7Ln7n8WJsuu/8fXnOayELHLT3J6nuqes3z1uSPKXDJfy5Z4awVYjgUFYH82/4IFAXFwAD8v9vIF/sU/r/xxhuvvfbaa6655uabb64p6uijj55rrrmee+65mvgxchutHSNVZ6VdQuD6668PJkW706WMvZ04tTtdY7gWebl9o2uQtTR1N/CfZMqtFz150UlXn/u9YZM99eywM84Yb7KDvtAmLggfPrDKkV9f+I+nfrbv9/f6/XHFztuucNWdJ227+RRjf2nhe169efx/7y8DFwSnhhx/z/E2lZy06klfKCJv+g8C77//wWejnGu+9KUvDanSwLz//vsm3DLygw8++PTTTz/++OPxxhtvggkmkFLaGlVKGfPRRx+99dZbso8zzjjjjz++9H0ASVXbu1/b6quv/gZ1dMEq9/vFF1+8LOjdd9+96KKL3nnnnbfffruM7KUA9FxwG8pGOOqKyLHGGsuIjIrLfxOB7iOQvjtdw26aaYrnnivGG69ipWJvYsJ3TTJJERMCwxM7lEM7WOi5Aow/fsWizyDlkDGXszeOOKLg/HjaaZ/b78OYRcstvWKHDat4A7zwwudlyhhpKkUM+qsh/v3RBaG3RzJdHOoRDnKw1FJL33LLLZjLuOOOe9hhh/3whz+c1o+2KB588MEf/OAHBP/FF1+8ks3lRbHwwgs/8sgjCyywwG233XbppZd6WpKbsvCIee+999Zbbz1SeaqppnrooYdef/31+++/v0zTe4HoUQ0Da766+OG8u9O7Tz755IknnkiXU533yiuvfOCBB2aZZZYf/ehH1fEPP/zwPffco7OrrroqguIRSgQ01HDRRRf9xje+8eGHH1544YUQRv4+GXF985vfXIyPd2GefPsf//jHsGHDxh57bJGL8PEuCrRy7bXXhvAvf/nLww8/POoSudZaa1122WUTTjjh5ZdfvsQSS0Rr88UOfNr5b/rutPPodKFtsX3DERr12zccG1+zfcPBYrZvmEMcn+rAVkeTzT9/hc240CD/l3s0YvvGBhv0v+0bXcCuFUkb4t+KgrOMwYLA5ptvjt9stdVWlDFrrrnmV7/6VWJb588555yDDjpo+umnZ+kMLLbZZpuNN94YJcIGfv7znyMERbF0Q5iYgdiDnnnmGXTnuOOO22+//SR7+umnyfvJJ59cmKZEeMYZZ4zszz//PIakGZNZyhSFjFNPPTUCgTG8/PLLlEkSI14kvWR0UZiZvKH5UJQGTznllH/961+jtB7+Vcsf//jHIC7VRR1//PG0O/POO2813dl1113Vq5HoiDDE8JkddtgBehjMDDPMsNFGG2233Xbbb7/9a6+9hvEgQMrX/r///e8KFy/ln//85yOOOOLLX/6y8kX+9Kc/nXXWWe+77z647bLLLocccohIeE433XR4FRhPOukkdEdkXolATxD4XHPYk1IGT97DDqts38BgyF3KmLiOPLJyhlhs34hISxTbN+zviO0b5k9nly28cIXi7FXZsFk5qx4Bsn0jLps7bN+w9SO2b4yMzX/qEGiIf6Ra+obhzWyfuW/1IRaI5fYZS0a3Xdo+E1nKppW35513HjFm5bryyiuTRqeffjoBNtFEE2054vDdq6++mlDcYIMNZptttjJvSwLLLbecwqkTuFkoMBbBLSl5QBbyne9854knnrBzhBKC4QmxKLv56KOPLrnkkkRvxASepPI888yDZHz/+9+3TikTl4F77713jTXWOOCAA3AdkXLFiJPlGJIq8ACynKQn41988cWTTz6ZLmT++eenOqLqwId+85vfsCLJhUbgW/RJRL7EFB5bb721V8hyGcXZfffdla80XQieVLahh4GvfOUryF9NITQ0+++//1nOih51/ec//xH5hz/8AUrf/e53//Wvf3miO3Qw7IDC2OF1112nna+++uqcc86pzWBR8iqrrOKngQzJQqPj6VJLLfXtb387CqYMk9ivA86g8POB5Prrr7/00kv/85//RPvOPPPMzRoeajSqYflvItAMAkl3alEK/XBtbN19v9u+UdeD/hRRiqSvf71iE4wLm6y+wj3u4IMrcSeeuNczz5zP6m9unXnmylm5zv73v2vIvpW/l15a+VtejIn0cHHxs9tgg/2XXXaKWWa51+qf4GGjbOYiwyxbSUfTunkf/zj//PMXXHDBEH4mbsJPe1pOd6oFdjPtHORp0IVXXnmF+y1XFX45xisAIYNPPfVUNGLPPffEWfEb70+JFU1DRzgz+gRzisSsNmG4ofP497//fcKIa8R7OLMElB8IAalPtEtAceJ9W2eddbTHU7Vsu+22xDw2pm3ozu9+97uJJ574t7/97WmnnRZ0h1fQMce0+PQaraJBKTtbBsIgVd5yan7zzTdxOzEYGJQEoATPLbbYQuKnnnpqPrsfR1xuXYKUVXfffbcu+11Qfflp+E3pFBMYcxXFD+RRouiyGDTolFNO8ZRdDCmkRsILv/a1rxU3RcH5NxHoJgJJd7oJXGZrWwT4B9CfWxSahX/xi190qZ233nqrifvcc8+1xF9ooYUee+yx5rNT7KM7hNncjJeFQ1lO+tvf/nago+gKnxr4dOaZZya6VlxxxeoCOWMSouQBiwDZQBJ7yn6x995764K/ZAmlkY4wvrglFZSwGsVgUTz++OPEnmQC1WVmuHMEqNzwTpdkDCvhnItJsCgde+yxBC3OwRBD0cKAVRbF5sXIVacBKZ+PDNBD4LVueP/QuvmLHwTfjRTPPvusUQ6rFvFPWSKeyKcKMsQe0e7Qc+DZI0vs83+ocIDAruS17KRyXQj+591miZPFbcTU5/Jue9XF6z4VGqvcJptswoLmZXYuC+qD4VkYYDZ+L/iQ3+Chhx565513Ui/5Cfhl9Y3rd33LM2YgITDWQOpMC/tCneD/9957/8orr7r88iuef/6/EdOXf0866eSJJpp4o4027mGlYFFCw2uPPfacdtqv3HDDjRL8+c/n0n2ccMKJPayuS9n/+c97H3zwIVmeeurp6hYC/JJLLn3yyaeqI2vCHSldJplkkt12280ULD0tek2uzm9feuklrhIEnkW/2dYk3nn6+qc7jfgOpGW9qZ/oCgMHorPjjjvWOFvQ59PbW85Kw8Xhv//9r9IsjslItg+6ByLHGpdRjDBeYYUVCAmsyD4ahVMGWA3rI/8SLrT1zciYjhCgtjFGNBMoxRlnnAFhKWnm8B78Bu3Yeeed8UhWmDDQhIri7LPPrjf3RBUcbL0wPJTdYqJTTDEF0kMt4RYnQGUiWfxlh/JiRJnINCOOeAYv5kg8iVmHgOe2IlIaTCIINwpSvWXphRdeuKlUclaX3q3w//73P6Vhe9qg+8suuyyfZVV7CXUK+aZkoqdkhvvJT36ig9iJPvqVeUVVKBJrEUkxxshFmSXSS8v1G2XBb/RO460ExHMSlx7/+7//+z9vNUYoEps56qijRBoX6i7MUuQdd9yhWI5WhkMkX2aReSUCPUKgQsjzqkIgTuaICNrmAJc0MvdVpeqL4JFHHmnKs/7ramWmKhoOszN9uEuPKNsrnGfUZXabaaaZxNAw66ApTDKrKxrjUUmGkwqUzKZCpYk0PSnTFZEmwUhpQSblr371K2u1Mi/NiiUaCW3WEx+JrZgp7S3myoWgdZ55U0p2/REmHqRs5P+U3hpm6o+YsuSGgWKfyvEhNY9CkOAQNfE1KWtuJTZl08TgSWb5mrxxW5OlvMVFzMv4il7LDjGOF2UJJm5L2PJWgIwkVg0NpT3XhHhErtx+++3CpK81bkTiQ7QRwkGJ0B0enbITeyJJFFgRTpFYe8omRUz+HYnMiLeLYQXn8Dbab0WbwkjkKXaCIgt4vQlyeFL83HXXXQJcc3jL0i7grN7GmitiYk8T5x4OuVjs7LPPLhkPoWmmmcbYYbQoLOIikvoQAfJ6kOV+3SiOSL8Xbx3PZa5dlE9YrLYFoWHZ4cUiOw4UVVOTILhG320zv47I1fBvvCpeOXSE7grDo9f8y1/+wqNIeifxAIGGkvuOVxofEunHLoELd/fbj2JRRjpIiXU5YgSkUbJHYhSr+6ZQLNML7zLh6IinphTxwhEvHJH+In8uvyOzkHGJ1lqQlBcGFuVHpfm3TRDIc3fMG/3s8gu3K9Jyh9hjmPA7r1Go2jVgMmJNIH7MXJQBmEEIy+iqWcykgEPEQdqkfqzvWUks1/yMwznAnOvHz/WP+I/fPKnplxw6Xn6LJXD2hapUYtVRP1ieCpBzZnA6CeVgDyzrdoryl7So4gcwwr5+DAfAoji4LMei1oaLZ54pFCXSVGJJp0ZiPtJYhGnzMsssYzKigbDq4tAQqg4zL1EBDfVKbE1G9y6lpxpA2SASTeS9iD9ZyQEEA+CpgOvokancSg5QtmPY42oN5xGF/xxzzPHvf0fllb9agiuQQOHZ/fmD3g9xUDD0Zmr6GNOH7jdZp+4bLDLSQhYFIQAQoE7yUs/AGSDkaznKGAyTitHxUsGko+wAZAqJdXBHaTK+IQJchvmC+IkZaJZHaMP/kksuQVaoGVhwbE0Hr7FDOLy01BV+Jh4xjO65Z8MiHYC+DRJjZULkK9mrK50SLJMU6EddZrO53Q/N3iUMgywPakUvwhXGPOMV8jtCI8TjN25xDj9kt6Vpya3sVzkRvIsXCqXj1VqiKMA0xftYmH+9Gr3zOIefQJyCAwpdU7ufObhMWUpw6R0llsQyijQ3motAGqopCWT31G9Bg2mJ1l13XYU32WSVYoo0OgKfZ5mmEqTyLGNMbqa7rmpwy+wZGHQIeCPzqkYgFkxmKMtrEoVoNyuZjKQhfZESU4YwWYjHYAMiLcsoJyzLvD1Eu8lCggsuuMAiz5rJU7JTDB0GOiINFbf5C19xiTE1EPwqshfDU/LVfGdBefDBB5tE+G3IG5edn7QyKIKFJlFnSSQebyAXzTLmccVqLV7lpAqTl2l0BMEaTnaWC1MuIGpRiBgUzVRFNyOGbtmsbQZRJn5jEkGDECkKZzEC0pis9Y5bgzMzcCbx0LCiVam26YUYF4OLqQqfkyW0DtojbKqiljCRQSlSRhqzpNtAPv7G0zKyvG0YiGWfR6ZgBUaa7ml30DhuoSZZhThJhYKqvkbVVUdW3yIr3hmsTh/1F+0rU1LVeHnKW4GQWBbBGBK2KsZgeZH4OAvjxKZyC1lhpYFOILQ7qKSltg5i4V4qKgF1USFI4CrRiNv8WyIQr5Z33tsI8zI+AlYgCAd6gdzUPCpvlVBz1cfUJOj2rdcDgdDOmE8alhM9avioPtL8gLXEtBN/41UxBZkrXNWPGobNZn74WJ0tV9aBAk1epggO3c1fBih0nNW9yBe7Go12Dqd2x4Tcny7zAsOzX7VZwFoqlmu2a5L6VBF6QhBaEpmPyCf0hd7Fj5mgisMqSEqLQjpnphwWcYzBWt9KEaehSLfuIb046wUiTDas4BgDikD4WSBKgNZgBsQn7lICh5q4NV9bMOEo/lLkkHk2RHz9619HgFAQihzqE80jQWmnSEHZTVJRCHmJe9mBQppGjJ8NgkVHpUkMLhFJ2aPj1ruWZRoskvpBpywEMTCXhRp9tXh+svvuuy+g8CftieyWg1iOBTFaQ+suUi3+yi7NhhtuWO71jfSt+mto9AWGRoTQQljN2mXh7AgjaF8Z0SBgUYvuGFYclPodRykT+Q0bYpaFMqY+YAh0cJ999pFMS0Yo1SqpFOsN8fKIx01thMGKvFceUekZFCWry2Ah1jyd+SuwiWBvXgYDrTHghSF5s8ceezgGhinEOLJwceKBcHDu+vaMwRivn98CW4OXtqYZhsbTmsiaW2ngQFNSE9/z24UWWrCDQr5RFP4fzTVis9EX0tTHfOFx92+Wte/d2QqtuqymYkFVFhhnFvzfdpVlSZPXW8Vba9y/RjF/8Y/7/tFklu4nu7L7WTNnIlCPwND6qIwJBBACZnumfT40FjEEEillhRSSm0SXjH5l0003xVToYFhtXFS+xC2Lj8WZlTeeQWEgJY6C7ghQnyA6JdcRw+Rk9SM9/RBnmihZfP1Fg8LYj83wyyHR8YbQDzOdoDtcQCicyMj6jGUMqzyCEi2JSN1BaEacKVIhJWpHcdCXH//4x7QI5CgdeJm9OoCTIVuKosfSXxKajR8UGIZWWSvzh9hrr72oOuRyuAgeoHxaMep6kEJGpbH/VuIRvORz2w0MeYCOUERtVV1p52HrVJ5ARiS0IDxPMbMyC76iPcU+ZUSDgOz0ZI4SoeDBM8I2F+kMDWZZ0sQGmUdE4Su6TK/mhYm+i7YPmWIMh6a3887w50BkEWVpKAghqWRcByFDstEgMYZSRuyWgsdKV1F8P7XKm+Ov1wAHYkkEKXImJQLhdR3RhMqf6nAZWR3QGCSbvYYIxE254oopE2iksL9ReBnffEDDDK6m1mexbNAdCeoflTGAAkhv0J2yigwkAonAoEIg6U6Hw00S8KsgIDmmsMFbqbNVS109TdcvUkvxI8CwwkIkYIFLMpU1RQllSlSA+Gf4oBwizIi6qIWkkcZV3lri4wr2+2AD6IhNm2SVtiElHv3pT38it2IBZ1WNXtANjDgkY9KomuzRCySJLidiaIME9AtZQWuIagJef8k52h3KIT6GmqcXqiNBSV8yjI4Kn6Bwpo7CWlBAYT4Q0NA8RamI8w29RWSRjK5CUQSY5jkgVTOCYFGlaAB73Ij2fC7/0CZivuKf2MWLHo5xJzZ6GL5ygAwBXxlqrc2f27yMjLKrbx3phr2JcYUuLfCXUsl6WuEBD1QOyRWDH3DkFPjZz34WRfmLL+o+0gl/gcguspo3iOS1gw0b90jJJQuboc/zSEa1i8ca4cxuRdmGFUF4hCdWWVUHgX0q8bEzqIMUX4jmqvKF+xE34b2u3uA99QmaianpdWShtkFi2D2bKaG1aTrlV62tqn+UNnzvz39x/aPF2cpEoAcIJN1pDB6zC3sBqRz+KxLhFlQFDE/oAqlJPokkWalArLPRC8oDCgCCn3aE0YFmgpWHeQU7wQCIRkKdcoUYQ6E8oucIYa8cq3/WKxKR/j8aZOXNO5jEZQex0rXid5i9Vf6vf/1rpivsAXXQPInVSBHCDkXlQ0XkERkpL4EXGYuiwmlcIokZjCRu/SW2HYkWDjQYhmU3woR4oRrkqwQaSfQqh/uIz9uKQYP0jmwWzyKDFOojoYhyEdUclei3YMLngLSjr8KiUDGt4tCjYXJxMHJFG5hjEKCgAtNPH3GVvxRpNEYjDpz9PHK0Id351re+ZSwoD8ClrjKLthkCI1VsVVRbuIodvng7wsOUozcHago5ZA41lLcspxKYsXIWvn+NDq0exT4t1xcSjO5GgboGSShFWjHeDXhiA9W5MR4XlqMu2qZqzlSdrDo8/ckVHEFdHdnVMO0U9ErtVFezZ/pEIBFIBNoNgYr+oN3aNGbbE5Z4qNiIQUlAQCIo2IaFuIbRbXCLobdAJpgbaAJoRHix2IJkUU5W4QoErZRICc9TJIDsDO8W7s88eMK8Yt1PgLEEVQTwiItjB2lNAxG3+ATVCMZggBRrC5iNTrGxAtOyJ6va9BBZOvqrR7rj70wzfR2LwpMiZcR3lKvb8bZvYIqaymRDhPNw4pVSbRXqqORAvuHTzl/S/GxCPWi5cK/HJGMSgUSgDxAgE0OQWSHHruQ+qLSZKpLu1KIUQpd8xXIQFOtphIOBqeQlVB3Iilt8hVaD+QO/QYYYHdh6RqoQRpRqfWxXhZRhn6qtqa/ug9b4O88881K9aHDU3Am96KumNVtP0p1mkRqVLunOKCTy30QgEehTBNqW7qQxq8P3AE0pmUF1omrvV9oXZi9KILYDPhD8mku3GFnwoYYlVJfWl2FHx9a0p3Ma0ZdtU1dJNLtab4r2riKW6ROBRCARGGwIJN3p6YhzrWCTYm+y2/wLTiE9Lbj1+W3man2hWWIikAgkAolAItD2CCTdaTxEXTH08Lo9WCmHH964qHaIje7Ud6o+ph1am21IBBKBRCARSARai8BYrS0uS0sEEoFEIBFIBBKBRKDdEEjtTu2ItJU7S23j8j4RSAQSgUQgEUgEuo5Aane6jlnmSAQSgUQgEUgEEoF+hUDSnX41XNnYRCARSAQSgUQgEeg6Akl3uo5Z5kgEEoFEIBFIBBKBfoVA0p1+NVzZ2EQgEUgEEoFEIBHoOgJJd7qOWeZIBBKBRCARSAQSgX6FQNKdfjVc2dhEIBFIBBKBRCAR6DoCSXe6jlnmSAQSgUQgEUgEEoF+hUDSnX41XP2nsQ//7+HFT118jmPnOPyOkadNT3bQZHtet+dSpy819/FzX/jYhbpy1F1HzXvCvPOdMN9VT14129GzPfvWsyKXP2v57a/YXuCGZ25Y72/rvfHhGxtesOEyZyyz5GlL3vXCXQGAoja7eLMj7zwybvNvIpAIJAKJQCLQOQJ5zGDn+OTTbiJw9F1HH7jMgbNPNTvGs8PCOyjlo08/mvJLU9646Y1PvfHU0qcvvca31tj/xv2f3P7JF95+4YCbD1hh1hVuevamDebc4LPhn9338n3Su11x1hV3vmrn7RbabqHpFnruredW+/Nq9/2s8mjYp8PWnWPd5WdZXjivRCARSAQSgURgtAgk3RktRJmgOwgcsuwh5z507iX/ueTtYW9Hfjxms3k2E5558pnfGvaWwErfWGnjCzfe+rtbn7HGGZc/cfkFj14w9zRzzzvtvPe/cv87H72D7my1wFYUQk+8/kSU8N7H7306/NOxh4zt/2VnXjYi828ikAgkAolAIjBaBJLujBaiTNAdBNb+y9prfmfN7Rbc7ri7j4v844497mTjTxbhIcUQgdNXPx2nOeKOI8558JxjVz5292t2v+352xafcfEJxpmAJYsKZ5oJp/nks0+u2PCK8YeOjy3d8twtiI6MQ8caOtaQtMMGlvk3EUgEEoFEYPQIpMwYPUaZohsI3PPiPevMvs6Hn3yItUT2GoJCwcOPZ5EZFjnzR2de9vhlEwydYNqJpqXgWWzGxTCew24/bKmvLSXjYjMsFo4+1D8H3nJgN1qSWRKBRCARSAQSgdTu5DvQKwgwUS16yqKMUzQ6GM94Y49XU82k4026yjdXWfjkhalt9lpyL0+575x070lTTDDFwtMvfPOzN+//vf1FHr7C4Vv+Y8vj7zmeRuekVU+qKSRvE4FEIBFIBBKBZhAYMjy/AN4MTpmmDoEh+1YMUnklAolAItDvEBi+9/B+1+b+0uAbbrjhe9/7ntZeccUVyy/fRhtK0pg15l+hgw6qtOHhh4vjRnq5jPkmZQsSgUQgEUgEEoGBhEAas8b8aKI7u+1WzD575f9+d+Uiqd8NWTZ4DCLQj3Si9T9tja+PHINgdq/qfjQE3etg5uoIgaQ7HSEz+vhXXil++tPijTeKWWYpLrqoePPNSpbJJhsZKMMSbLdd8fLLxUcfFYceWiy4YHHUUcWppxZDhhSIzq23Fu++Wyy3XHHVVSPzSrn55pXIiSaqJJt22kr8NtsUt9xSKXmffYo11qhUlFcikAj0RwT6BWNITtAfX61sc+cIpDGrc3w6e7rTTsWPf1zcfHOx+urFhx92mHLnnSt055prirPOKrbcspJs//2Lm24qzjmnErPvvhVag+uU1447FuutV0ngrypceNKUUxY33lhceGGxfeXA4bwSgUQgEWhfBD799NPPPvusTdrHleSQQw5pk8ZkM8YgAqnd6T74N9xQnHxyJfsqqxRjV46Dqb3i937llcUTI8/JK957r/j002KllYqNNy623ro444zaLO4VS6njWmedipHLpZzNNqsEZp65eOutSiCvRKBfI9AvlAf9Qg3Tnq/BrbfeuuGGG+64447bN70+O/LIIw8++OB///vfE1n/jbr+97//ffLJJ1/5yldGRVT+ffXVV3Gpaem9m7jef//9XXbZ5c033/S3ieSZZCAjkHSn+6NL6RIXOlLubyuXNAxPkeCTTzioF+OPX2EtDFKI0emnV5Q3RxxRUfCcdlptA8qiygfjjluxZ8XFBJbX4EGgX9CCZoajnjrUxzRTTp+l6Qj5juI7alh9N0844YRLL710/PHH/+EPf7jBBhuUGW2S3XfffUnxn/3sZ2VkPw0sueSSk002GV7SfPunnHLKAw44ACxlFkRn4403Xm+99fwdNmzYeONVDrP4+OOPN9poo3XXXXfTTTf98MMPJ5hggkgvsTQTTjhhmV1A5Je+9KW11lrr2GOPrY7P8OBEIOlO98d90UWLiy+u6GDYmEqOMumklT1WnI7PPrvineNabLFKApapyy8vjj66mHvuYrXVKrat+eevaGtcaJD/xxplV7SD7/zzC9Ogv0svXUlQPqrc5NUGCHRV5jXf5HrpWB/TfGltkrLlcD344IN33HEHUTfjjDOSrH3czeZHpGHHPxpxXXfddQR8Nd3RqaOOOmqKKaZAg2r0GX3cwZZUN3To0Iceeuivf/2r7q699trjWrQVxdVXX/3iiy9OM8009iefc8452Mnqq6/+xhtv/P3vf//Pf/4zZMgQuaL2d99990c/+pH0X/va1+SFzB/+8IeFF1545513vuqqq6699trNN9/829/+9iOPPCL9Aw88cPzxx//pT386/PDD11xzTRiKvP/++0W6hGfvj9tAAoj820IELCny6h4CTz01fIklKv/vuuvwSScdWcYFFwz/zneGL7308F12GRn53HPDV1hh+JJLDv/+94c/+WQl2SGHDJ9vvuHzzDP8qKMqtyutNHzllSuBKOSFFyrpFevviy9+Hl8JjUoT4TH7t9in8P+YbcOYqr1VHaeTf+GFF+jboyP1xdbHjJEuv/baa8suu+wmm2zy1ltvdaMB9b2oj+lSsU8++WR4Y5CaXcrYfOKOWthRfMOS6xOXMUsvvTSBXeZ66aWXXn755ZVXXhkNKiMFvBvsO0888QRNScRzi8EYkAMgUHWIpOTYZ5993N52223f/e53t9pqKwwjEp999tkLLbTQggsu+POf/7yMPOWUUxZYYIFFF1304YcfjmT+0jktscQSK6ywAj7htmxnmaCMlHKdddbReCXcNeKSEdWQwN9FFlnEU2EBcspfypU555xTQpHqHXvssX/zm9+sscYa22233VRTTcXM9Pbbb1900UW//vWv0RphyVw40N/+9jeGrV/84hf/+Mc/LrjgAuRJPGYzzjjj7LrrrpgQp5wRaYfT9KhaFb/61a+QJJFo0Fe/+tXTTjtNGk2deeaZI6W/utawd2WCDPQQgeuvvz4oinN3elhUa7OndifGpfHfJi1HvJVd1YktObjg1ES6tYer+uLC7P+4Int1IeK/+tUvPK1OOfJBz/4plVLdLqbh+rXbpbVtxuYX9M134aSTTiLh9t9//y233PJoer/2uIgfy+KlllqqujkEKuky8cQTb7HFFmRb9aMxEia9SGUkIBb33WsDIapfFA9l9v/+979nnnmm21APlPE1AVOwsfu///s/zIOdhYYJWZGRZgL/EMkgRcTW5Or89vLLL6eZUCY7VxzRFukBzkbzyiuvIJrUPyIxAwoM1PPpp59Gj7ikPP/886effjrGg2cgN/QZc889N36jSZqng1r4xz/+cZ555vGmSXzcccdRiek7O9Ff/vKX2Wab7ZlnnhGpLlqlPffcU7KOWqtSdMobMtdcc1HMPP744+uvv753BheRhY0JL7mSu2JlPqwot7GQb3zjGyuuuCLmgYq99957Xvgf/OAH/mqAchAXDabQoqs78MADy3rZwpSPG+Fqq/COHHXR6LBqzTvvvMsss0zE3X777bovHlXS/kCJ0w9SuNpqq335y1/+5z//SRs0qoD8d/AikHRn8I59S3reGzygJQ2zJv7ggw8osa0Fe1hgL1G6SSaZhIgiIImcww47LLT9PWyq7EQIGcPrsxsdZ0G46aabGCCIDZJJC2eZZRaClgqKSoC8nG+++coWPvXUUx65nWGGGdhliHnaAr4XBJVHfCa+853vlLaJMlcZoI0g3em3rOAN02OPPUZcyUW6E7eEKBcNVg/pSegjjjiC7WO//fb7qbMfRl0hUOPu0EMPZRBRAuI49dRTYwOqJgW1/5JLLhE53XTTURj8+c9/Jiwpq+655x6lIS7nn3/+WWedBSvqEzSC/J588slJ2eJzp5pR9Y36Fyv67W9/K43Gk6MXXnihkvfaay/twTMoSIKjIByjcoz+X50lm2kmDEGZeqeddoKq10ODD4rTSIsCiUE1dtttNxzL+0OxMeuss4LaX70ba6yxdM1LpRBD6W9wIBQqeCrNCvajbX4ddD8333wzuoPEzDHHHBR477zzDpbA0bhsQ03AW/qtb30LR+Fng3GG0e13v/sdEialpzqCGZe5Yow08ic/+QkHGrcREwlQHLaqMnFPAnvvvfcxxxzjBaANUg5qjrMaIGFkS/OMrxejJ1Vk3v6OQNKd0Y9gz1Ugo6+jz1PUqJG6XT9Rceedd5IQFoXhS1gWZQV877330lGTNGVkbwTIA3N6TckWmvfddx/J1Nu119Tb/O2Pf/xjKn0Cg0jrPBcaYd8KiWW9S87hFtAmNqyP99hjDw4Q1spRAoWHhfKzzz5rvU6ZP9NMMxGZHp1xxhlkmCwE6nLLLXfeeedR8hMJZB5JTyqQgtbBeAaRKb1h9XfppZeml6aRBqZbo+lvXNbQDEkkrltqiV/+8pc4FjGvbbiLkqkrgN/J9hkLdKoIiXERdAHPIA4pBghdOgnKBqt25gzlr7TSSoQimwhJpiUKH9mIqn90k6GEDF588cVFo1zeSVxHmOcvFYi81BL66y1lCCOS//Wvf3kKLlKfPMaoWEMoIYRZlH5w8w+qiv9CkF6BxiIUBjQW/IshYCMSkhdqfJzvueee+0Ke0d0gZ6V4LtOyZNHK4FVonyoiXvsZdCgz3II3pLgRZBjCdUSicaFroTXBR0N9JaVxxMYwVywTNQQFihZweX/QLLzQG4U3VOxQz0RttX/9mh599FFjzYHGTxuhpGnTGFwN+8GEajN0fI9rYreQ7DjJ50+QMDROLaK8sV4MPx/jiOd5S/WLOsebQ1168sknw98YeWEMvVfimmuuwercXnbZZdXbvj4vPUODA4HKzyOv/oWASdkUFgvrMd5ya3Tiil3g+9//vnmnuj0Ep5Uoj4HqyJaHiXbr/vpiEYIbb7yxc66DqJGy8sYyneSIcnRKj4iHWCXXF17GcKGgvXeFgIl48gDPIGCq+QHKQmZbzpp2CZWyhGYCiCO+Qr9iuhfQMLI29q3oI4qAZNCOKApvYPhQNZGGLoSthyQ79dRTNYCYRLCIBGkYTfh+QsCy3khRh8ge3qAECXUCwoQViUQIZNQjNZatRRH0guy85ZZbTjzxRGIe4yRaUDfthJ5ubrvttmX6+gBLCnaF8cgCZ13Dw7T84osvRp4IsPLNQfI0TwKyme6nvqiI8fpRR2E2VBQEP5VDxLOG0EZ4FfGzoErEISqMH2AYZDyspET4aCZwBWOEuHRUi3iD3rnmjDohmEcnhTTzyAuJztakxIFAAXzN5qyjyzUJylsKTmNB4YEBGHTzhkfQpuSwP9wPhEkreoqmIMc77LCDSEog739ZSE1A1yjepPd732yzzbyNEkCVxggBMnbbbLONX5OXraIhK+zJuIb2i06Or7Fb/AbC3lVcxwtDq+TdxlRklEYW7/aqq64aTBSG2CSzoGHCqDAeJaDs9GfIuo7rnX5hMFRHSD/to8JR8NBBUn29/vrrOBmi782hukuuA8DBfKV2Z/SjH75vvBnMwqNP3dIU5mi/bfNydalW3jTw1qAs99XxTYZNNCNkxvhNpu88mVU1ucJ0QiVOLJkKY3cJkcOib0L8+te/HiWol33EbGtZSaKY+MgMkaQaSUOgWl5b6oWcsA6z1he2ulUCyW3aIo3MzqYzYsCRHiZrXpNkLZUGt0fCWLFaohbLVtOohsW2HUJdvKfmZVOqtsmuak+j/eS91TnWgg2YfAFrVmUdUHu1P0ENFBpD8FBFmGq9G9qMOqiaMUh7yFQTujKZHtACagmKGfSL/sD8y31BaWqRDCA1JdfcQgaYltRqwUg4fkpAuljj0qBY7qtIp0QSD9a1ekrjVRZChGBFhgYyhKWlPLW/lmg5ssIAQfyEAYKqSXt0h4BxRQli1BiqkYhRF+ubcshIFxiNoAU01kVLEToVhYQoLZtRE1AIHKgHqq14+qLx1SkxJ81TlAarQoLqpzXh3XffHQKQAW+8eN4KSg7S0bvkfaB0gaFIvymD6w30WzDoysF7GIwQQaJaymLdmrI/v4VwDBklkPcWA/DMUCrWSyXgney8nd559SoECAYF/4jhkzfIgRdJCTD3IpHTfjVK1nIavq233trba+wAZYxo1NRujIwyDRYtIHLDW0UHNU9Gii78Y7HFFqP8kBLRUSBGa7DQcZQU1/Q++HH5/XoBEEGVft7bL4YstLTQu4QN//73v6cK8pzyCXreJej5oWkqjoVteDn11A+Kaipq98748WoMnqReb4u2ISUyYipu8XWeOiXTlYyaUBXIDQIt4PdrecNOZ1GhwWHu1AukXKRfWdAsKVFnCAjklQgEAkl3Rv8mkBD8IcxlppvRp25dCjOgRTlhYG4qSzVZECdkQA3XMddQMFgYhT6DgCcgLZdNDWbV+eefn+0gCqHHJj6L4vqyzJ4HgEN1Qa7YKWq+M8Oa14ioan2PGRCbMRVa1luWUURbCGoktQFCYG6yOCOBrPgtW8lvSzT2CNOrmZRYMi1a59m4S5kEEESQlEWnCDCaBgYFUyRpYcbEadzqplZF14hA8zj+ROxZ6+OLRAJahtBEGgWSOiHDqDTIPyyH1gTXJF06wkcyzbP+ttS2LzqKwpyIIgKJ+s1yWUdIa73D2HAOi1HCWHyUqV9kRrU/Skd1eQkpJ0qLhmQ6CxM9JRe/+c1vxrxfn12r4Gx1C3lCEYBj3INBs7WTJEbdyDaCkJai2h01emEoYYhQEpzEKkIGKzB6qyMBwUboWvSjXBHjPUdzrfVpKSKGwgmjghu4gkmLlwyzUSkzmddASwyZn4xx8dPAFQxZZG/4F68lVhXoqTcnRD7y4TdoFPxC/RIxs46Oz6FsQ5jCGkXtZFz0y0tOQ8Yw5FXxK9AeaSCDvmg8KPxMsAQ1eicji1cLRw+NBRpkoEMZqQ1+7JZnXk7sQRbp0QUEVNgUIdLrpNdlpHgsHO0wNBG50b4biay/rLK8QvK6VB0gSIYQu+rT18RofMQEJy6fWiyV4eqAn21Dp2+/fVd1Sg5k1bv6qx9lOBEIBJLujP5NsGwivQgqSQlXU4/p1XxhniWuCA8znYnGrUiyx+RixjEXiDQdm/XMEeYjT4klAt4Mi4VYEJt6YrYyAZnXTLJUF+Z9KgdTqpmXeLbusUYhic2q5ghKDlzB+qxaPCjfygZLMDNS5nuqUlUTDOJNr6Ywk3t4BZpYrapH3+2upyBNZdJ9cgibMePH/BsliTefWn9jQlgRiiDe+s+0RRUBQ6QEtiL5gfIeYG1B9ZAeK3XLUCwEqtadk046qT4SBoQEXqVrquN3ErX4G7dRVESScyBFd6xoVaQcQtEoCBsOaSQmDLRQmBIF2kCDmPSqi0Lq/0pmuMXrOJYTCRQSkQKEQXSTKDW+xCExZllfCglZInF94fUxXrbqSOXrF3mJ4GLG3q54asXvTWCNQuDEGHQvAyGKGmqwZDooXhtILO8zESsxsugWdLLLqAQvHszRKZxDLn8prqy2pZl++unFU1YZX0SKZY2aTZmyxGqeakHbZCGDqwciWhi0gxkRV1Catvl9ceIxLjqFrMCKcQSn95vywnjh/S4ULoElh+U+a4te4NPgpWnQtTDGKR89QmK8HlGX4fPWEZlS0h/EisUP5O6778aE/Ij4OBsUiaGEnWu/nyqF7pLXfUGaRmnx10Dor3bCkDFOF8RTMKg3fgJ+hlQaUKrOVYaNuGUMp5MyRoCobiit/YRd1SmF6ZNCpVTG0+u44hZ6ZTxsy3AEtNmcE9NO9SOdAm91TMPw2PtXOptXItAfEUi6M/pRI8ksQ6UzhREeKAujOIJiYqVQxR4oWizIeOpZRqMmJKV1vAnFCtJSni0cUyEezKeErsMqKC2szMhsEj18Qk2a1jHymqrCCySmTitakdITRTGTUjuboC30zfUEVbQeN6J+pyRAFEzEtA5WqHgYokBiEWmaTa4H3SHpXSOWpqPvewtTaD+iQzejR9adsTgDgt6hHSoigaI6CCCUYePA+axTyapqitCSVpGsxB7djLM6LC6NBX24ktERsgSXEqbVqyEZ1VVLT9IbUwLPG8I8R+SINByEN25BdhpHWfBRg0VddO655xpK+BP5FuvG19uFNBi4UkVRXUWECXtGE2EkEvMI+qLNynQZbvYFHamYYIoCYgRtGEBRai9eqApCTYVTBjPQZj2lb8MevEu8fKzviXAvpC7geShppGSJwwM0z3seCi0UxIViclhmrWO7QRH01zDJwqUUgJgEouMH0tGi3zugCwo0sliRv8xPNH8K8T54yf18RCIlwFG40hCFSInh+cm4FakXJWJ4G3LALuOliki2G1eZoAxQ8IQfdBljLeEqb4vrPg/Wh+BTQzj0xRUpFV6fpYwZ94Bxy3D/CrTtNswuwdhLGy271IZMPEYQSLozetgpVAgS+hg2F7MwqSCPCZcUMemTmm4pzC3vKAwsWAmk8BtgZKG8NV9T20hGLlpooh2Wnpab1PISmItJIHYc3nk4EPlU2RYx4gp+QyyZ1iPGX9KXdMRgCCGiTgzuZeo3xQtb5lqC0+tQiqix2iuiLKH3AhwPSdlotlpIdHK6rI56jGzTRw0j6f3VSCp6vsaEInkmJX5AykJPYqCRZAiENMoMn2KJWaP4ispufzLtDpooIxFLD08NQEYimm4lYJBiMkD7lCmLZLBCRASULIyFkO7GBaPisiAXaYqLGAXOExQMqAlCJn3DCyWS16JcjbRoiIVk/C3QAi+M9tjuG0ttfxlK4qgYvcaGNQnVMFjeB4SAba4iLEeOfG1thltpSIC2GX0YWrUjr8gWNYwY5YRxRE62PJY1LYdA7JQhxRlKEHRPwRUrfgTFKyeNjJoEzHhpQe21hDPrQJi96CEousRjUV7ykknoaXVDNQ8vKWNwJld5Wx/w2ykjsZYIe2ewxghXR4YhRnwZWQbi14EkUQEaZa9Qqekpy29toCfycmAwhno8m8ekGoHmc9XXWBNTXWzNo7xNBEYiYL7LqyMEWGb8T6lDJFjMRTIy0pQqTHECRD4iwhxWCDB6Aimt4COldbYEWBGBwblYpNW5GFLfPlt6GkwINYnE7FbYEm8SC9yICZMTHb7bkF4RzwnGntsQ+WLIPPKMOkeYlEV9SFBhi286cwGiS6Uh29wyVYxQ6Ve61pOr2KdyOCknGIUDh/JA34Nn4C7ME6Gu4GBI6UUkMzpIqXf0EEQafZja9atah0/dIoZoxxoldmEJFA9ShvEOWRHGGzySJtpvIPAnnQK4iuCD6PClRUcgLCAZJYpIFhBhygyCmQ4mslM4USwJ03NoeUQaC+IzwroZgfJvfUz5qCeB+mLrY3pS/pjKW9+L+pgetg2Zozu06uhhOWX2lrewLLlNAn5lLWxJwGWWswzrpNgaVGtuO8lY/UjLq+dDj7pUjsRdSl9ddYabQcDiqjJ3Fz4WeUUz6fssTWp3Ylw6+0txTQHDjSASMXDQ8VibskSICUcEC3peFHQDZGq5qA2vYaoLZCikNV0FlkMFokAsio6HvYn+xq5OHIjjIaqE9+BAVBrqtZLGEmy+YGXwDlFssI7R2GsDTQY9EJOQvBbxyqHgIaQRKf4KrAwaw9MFBQkbFnLAmKJY5INUcFpKZ31u+hnHTG2g0EJ0mO1CjW8+0gCtog9D11woCObBgxIv0RGEI7wHoMf6FmYLL73+Bp56B2S2DP4EsY7XZrXEUp5g07VyxU/bwbrnNlJSb3ArqekB39IyhhqjdGUVCZB4VPpRuqXGKNOP2UALV8BjtiM1tfdKv54pNt1305qK+u9tr0DUCjgaqlKs9/ioWdHFaqQV9TQuw8TLnmterVZ7N06asYlAFQJJd6rA6CCIiFDmc1+I58xPJDdxTr/CWoSg4DokMTlN2HNMYXEgTXERySKSAsbmZAIe16FgoHWgnkFKBFg0sAE6CUoIAp6856GJlKiLk5DjKGxLQVyQmDBd4Q3qYvugvZfRKkdKWhxURjKHh/IoEuMppQUCoWTOpxpJb8GpyCPkiSFjxDEr7np67fHRHsX3RxZyV3HXifueOPJm0S+UPMVRU4y8v6ry757H7/mFx/3wpm9EUUO5EmhpQCdPW4VoD2spUSoDrWpYTd9bXr529kaZnXS/pkeRUqTfO0Mh6t9J3o4e+fnbL4nQxyqiTGZlQvlqGumGvbsjWOh3ab5dZS0C5qtQI5n9OnKD42gf85j5iuJcZ+0/iEIYnc2ilMF0t0FuLIRMhjTW3MklVl21eri66gwnAjUIJN2pAaTBLZ0BY014K3vMM8APmOuoH15o4awzcAjUhFMOSsEH08UyIiwy9DcYCR8gdIebCCbkh2oCCjcFFIe9RpkKN6lFZLTDthc2l+pFTBw+UdNKPhbhu1PG0x65ytvSNiRGma5W0Z2Gc3RZb5sEOpqgm29ez0sYbV1ti2TDvjff2kjJMsijyOuNxPtFjBaNMgEDZezbpx+1Eoj4hk0a53fj+Kmi9dLwqbKWKAtpecCOQgsbmtdQKEb55gH1Wl3E4XtdqrRhj5TAH46ikSt6N3iJKcX2BXspTCl4Q6iBkSeGXVzBRFSWaQ+dxZsZg3rGaYTWb7G40gAO3fTQPLesoKiK5arvl0ciHSFBIW3qkzjSUEKbOcOBj8onTPn12cONTGPouR0vKT3tr2QaYys+S729C1aJcWameIZ7zbBcNMF2RKHqa8mYRKDWKSHkd/4NBMJ3Z7Ro2JniTaLU8UNl3DFB24nKRsMRx62FCDdb7qgsO6Mtqs8SNNm1TtrTj0zgvWSqJ0LsiDY1Mz7WOBN0glvDR91oYXUWoh3/VjKhFd5gGkY8uGX6bFhjk5HVtZRZGkaWT6sDkZLfGPGJB5C7dKXVCUYb5qbtRANHNoR7e6Svb4AYjJ93ORnp1+f3yKxcFu5n6LdZ3go47ZfIpKMFF5rCoS2eSunXihPELfRYsfEGEpdvu60GEe8nTzari0SPkqWRUQx2Emn8Fenn79xCjvAxLiS0LN4ZA8TG7QgGMVLW9ygiyXs8wBYEF9s3FyXx1k4Ase5SrNu4WHuRGOsuJmO6ZJHc2DnwoZis55z62WqtsnAX7urKpDWJjPgNKskPXRVWYhZXXNcxGE95xWEwLoXoL1u8yPqm6oJI+y0kA2AU6y/7PrICXkQnhqMmb9wiczLKzoVO88yT4dhHbWPQ6X4Yuw0ozJVJX0VRVPpHRl01xZYNaBiQuEvpGxaSkZ0gkL47Xtf+ejWhRf5pUVSfFbf9qK5uWfVNugdENlHUqKz95N+OVqVjsPnNKx562Eh7xyxGFcJbiIemvz0ssHvZbfsi6sKIQIJSOtKCEBJkBsbDkIpnNCyZUEfNSc1wMmuYpueRKAWVpMaQqZzoqx07mF81FQGqroXvGoUEURcHY9og5iJ3CcLqZPVhLlkcyPi3udh2Y+u+ZGy+FBu0Ptzn+XwQ23bGOZCXkI5N8gaRSxwqZsXC+02DJWMx0Vo+YTYJMtOgts5t4l0XXAqtQXDj6GqMxGY3sz+xDU+3ZdvIZoXjVf5y4+XXz06NrDA06zXnNtpf66JSa1VmLAOc97mvaRisROIiLFDYgwaDRb+MOK0MHuYFAJ26kIPYJYDrOAJDYrooeZWg77gLAqf9IIpaZDc6eAn1DP8bnjFUMoiRuhA4WzFwIGyJZrojs1F40UmAnZQtF6DApjdiYbfrsGaUq5MZC+Y2Y8fEL95A4LiYuh2CWo7coE3QK7U71XkznAg0j0Aas5rHKlM2QKBV3AJdIC1Y+u3balBN01F9Sb9M4hbu1tzW6003sMUJiRNyy6FBxJiimRLCuYEEZTOyHA+bJtlsEY/fELFBbvAhAtKpOYwCFtbYgF1v1v3kHE81opFXWTi5R4tDSCMiIUqb74bDFelOwlUfI4zt+pgE53HxOAevf2wGIVAmyac7WuhloKvokkGKcPX+YDlkOWFpXKKRtkbSuPBnt4fAfntswE5JrnJ257HU8BRBC5iD8Rh8yDETvN9IX09Znzm+aAZx7rUk+8PFRLGOU6pxeFc7JsfCBcASHGwjdmWyeWmSM4FQZPyD8OYCyKbs/XHkQRxhWuaqDlB7YDxoiivi5UV0aJtkRwuYCA0xbQ0rIZD1GjlreGBgtd2tugrhMJcrRBhvK5+q3SvEpxACVERlfJMBACJA3G4wGEQQOE1mpBXzqrDy+z6Ml8FL4oWBcGRnLOPRCBbJjDVdVJPFZrJBjsDIF2iQo9BR9/3wB/b/HXW87+NZDYgT8+NoF/H1bXNaLk8p8bECrk9QxhBX0riq53TyiZi0EI9IadACM6xk4j11IQduLfGJQ02NAgkJwkzt8pZVCEjJ3YTUIc7LeGlEOomHGlCWMr4nAU3FbzCYkpcQALwZCAarfyKcLI/yLd/VzoLDLYMCQySzCB8IxxYIOwIKGYp+cZJgIiFm9JRepGwe/QFGUh1TPmo+QGYHW7Jwp3bSKgoJMtW5QVEIbxiSDDMgwjGD5kuWUq8hTzzTUqAUsfmO6xuzEYsSccvqhN/QbZDcGAM/G+qEIHmye4oyMjnJS/Drr0jjS1sTBxXaD0gtxFgj3qsSBz4JV18kse6UMeoi6YNnoD5eKkYib5FRQFbKZJ0E5HXiVyQwuALahrQhOmgiLVHQWSoQBJfBSINtmABvTZkaDJwyUlEldSsjyxiJI6wvTHj8rmi26g93LjNGILL4peimtx2H87YbRKNJp4Wfxe+rJpdbKXFcyhsKHrd+Vli4kaL68iPClvBUo+NV9xQg+KsyDR/rG1Q7Kra+oowZ5Agk3RnkL0Cvdz+02eHM2FFlFACkCFcnM5cZFr2w6o3EhCKJVfIJbhz8EsyGoZ83a2MPpjxaAQtQrhsdVSGeJKPGIBiQAOoQMeiIKdU8bkolAp0SIZK/uctMallpu7tFJFO0GdYtxwhV4xbkdEcVEWZ0/hQkXBbYOASiIsoMrIKQ46AQJ1V2VELz8WiZFTODS5kFgCSuYwucjgjDELSoDw6hp8ShUwPiqCRY0d9QUNFkkBy0Fyw7RKYwj1TMhpqkevc+0cXsEgamsrquBowjU5FcRCMNhHU53ZIhLrURRB2NDtpB3xMmkuarYI7xCuFPnDz8JRHlRenQHYOum8aCLiRMe94BfIjOoCwfdC4KEiKWX4vLI8m8FWG0wiNhQu6KBzKgwi0aIYgjHMUz21U3G6RoUzzVAP4x9hzJq3cEfFl1JwE6JC8MXRdCT0GF6OBt/vqNeJnBGKc1GinvsFEzoPiQjkSZbpEJ9kqo6rj+GgLWJW8y9sb8JCxxUDQbGvAz2f2s9E4J3h/0BVn0eniZtaSTpnq19Nc75lVBVrBPLkoYtl+oSUCX422sL8HPEDJehgDKb8RvDWmzfczpnRDTZW1gaIu8hgYCNHaWDWxtBre+zIxJBOoRSGNWPSYZ0wUEzP5mRnMiukA2sAiQCsQ5IUFombOICjO7SdBZOEwhdoVQU2MeVsxcBNRkwjUdkxymXVMtgWcTHPMQb0RPCQmaBmSIxUFR3FE5ARCQTBKmbCzKtg4JzLDmaFWv9dBaDVtvwkWJrDs1zBRMWkim8dgMwwRLjdmZLkekRaRplyuopT95wMDBH4IygBqAhCB+qEnMs5iQLPV1cctVF96gMdQMbDe6r20gMo9rvHJCZNbnbUkMTJhjuJ5QS/D6VKYY/UUshKlPYtuLMCFXQ0NxNSAQq4aDWsJA3PDfG6R0VUvxiGn+L6msAQYXMhqAeBllkfQNRKC3JeScN4E9yLYmeiZVQyyqkFJ7JPZXuCPxRmWCGZOdxpSApIjywuABBlE5ukOWY8beHIOoATpLarKiOkSb/xOpTCliyIxdbHUmVvmseGekUUJ47YTWB2XRIxLXO8+e4v1hecE84rwJL63Cnfnpp4FhMIdhkBqGd/qZcLTSCxYiaShOwMIdpyMwvd5ojRIwOe2RHWKoA65Gj8Xipmp5ORVhsX5TXj92ujiNQjwqzBcn1gasnAZR1YDVZZo2eGLMYvy4EBRho++dgQMqrOOGRq8p5PxG9E7Jfr8dNZVe0BtebumSzOKko8TV8XhqtZ1Lp8qnKFq9KtTYddWiWhaYgcGMQNKdwTz6Leg7WU7ZTtvMRGKWJ13MxVQjZlLTsVnYtE5+WFOaSckhT4klrMU0je4QSKZRag9KeCtykzupRtxKRsZY5JFVdC1EAkFijqaxMO9bsocsJMOITxM6jhIr1OKhxp0i7NXL5VOxlpLBAxRFsWTRbx0pEP4lHF01WAI6EgKgvjg0qHP1DDFGSBBvSJKpWQkYntU5j0skyWcrmEuC6tUX3pIYDSCxll566bA9QUYMxYb1NxlcGqSgB398TpfJKl9zC7sYwQlzh3pXdozvPrJFjBFYJuZH+napkZC0cMc1Kb2wECY2EpHDCh7gfUD+UOFgEqiDptJG0EWR0FQp3i4CW/PQApVqsNpFNmwAaiLem4Mco00YDFpjI7f3ykvITuqd1H6RklEV4DReWiQbL/SmifQikbUuVBXfwi0wM9QBK5KMesPLhtx4S12srl6P4OjGV3aVqkUMEqkj0R7S2pvvrUY1dFAy7yo9ihFRC19jb4Wnex+2t0cNLz3CSLATv4JI4E3WZhza2xWvvRgbr8RUR0ZiTa0uVqU1h1Z4ikJhVGUy3RRmL6OhVKnfIyVKdKpMUx/Y5OlNiqfro0cT05fOdqNpSj4e8Aj4ceaVCHQDgWKfyn5OS0ATKNuQEvh8+L1QOwvbBIsDmSLLkq3gTc1EphgyQ0qLeOtdn16KNPHRDBlJF5qbiOQtIaVyCGBCoiytDKjazpHyVpPKcBkQiW9xDtBCJZM6hJmnaBa5S+RjUcSSlatIGnuuJALW7piB5T4xGcY1ehHx+AryRAIJu0hfoohIi1tOMCFl3aJWIf9UrZFEr0jCBt+KxP4CsOKk0qjZZZqGgchiYw7JVybgWqsxqJsY8p7tSQDxolViFMApqUY0ONJrKolubY2OkM36JZ6mjfDmEYILVpbyoxpmZW8g+HBIU0ZGOZ38jZRkMJ5HI8ImwrQU6fUaoUQ7NMPoRCQia0ARFIoBf6lSxIuMGC+DF6bi3TWqVWXVYjxl+3BhEuKBb3zLBG0eqO+RBjeM7MuOWIp4ma1eUD1EOX7aY7xVPURA+/t7F3qIQG9nz43opsq8BhEC1OMU0ThBJ30mBS3WcQvGndLxU6RFPMW7PSb0DXxlkCTLX1yHucFXyaz18QbeM55ad1Kz4y5UFxboAsXkjSskZREd2n4rV/qD4FusWsS/R4xrCA01DycSMpJqXTK3FA/+WvQzRiiXEiLccaglWLKQIeJfdm3GlnRB86guEAuaFW2TMVbSOI1iKSqoClAfUqRspTbQfFSm4G5dfHSQG+oo1jezGGsRoyGdBG0/hoFXKRWelD2MOJ5qAI1CVIXT4BaUcxgSDhR7u3i/Ukphb1pFMbDevutFYjotjIfRsKvNHLl8n6IodisOKA444MyKT8zIS+umLxa8bMHislExNf/eUHM/4va2RpFFsdT1S418cF1Vgiurwv0wOIaVH1STFZXN08XPij0/3nPP0/bshxBmkxOBkQikMStfhZ4iQKNOjU9PgDGQsqGxZ6pAYrAKtMC+DO69tOIcJ51owqJEZUIqy0LxQAZTMKAyCIGmsBMpjTmDBzGVgzTYA7sYAkQHQAZjP3TvZDPdQDQdtUIvsI2KwF6lcXcUQkmDJNFFEedhjaJ6URrKwqDDkkUdwmWBIwUjBd0DlRI9ATGvX5RAyqVHkZcdSkfcKpMRQb8wNsa1sDUgeVgORqU63qPhZMCFk10AaROJEpXcTiEMRrx35/zbnI3b3UQsNw7GOKYfpqia77eXh50YlNgBXlMexuOqjsT/uChVx0RYFa76+M5jhu89vPMErXraZxW1qsHV5QSnGcPMprpBnYb7NdSd9iwfDnAEhlgRDvAuZvd6B4GYnd/d6V0qBORGJdwy2KowA0odrgDs/RFJ/IevjD0s1AkYhrcOmwkOgVjwaxGJGJHK3H38pQLhU0zrgNPgTLQj4X3Jj4FLAXpU7WrA/sX1hNaddNeq+um4YWSXUAnGw5illi5lbDJxN1pYZgEO9uZT86GeabLGJpOVtVSnbxhZnaBXw2rv1fJrCq95nVpSe32ZNTHaQGWIHwsg934aNa1q/tZvzToBy/cTaz5XpOT6jf1bTrBkhSvSmB36rra/YfoYwXrAGybOyG4gwPQcHmPmcCrtbpTQS1lSu9NLwA6iYk3KbEC0C6ZU+1P0PFQmPF5NtWWkeEqR0ItUo0Mn4aqOEeZl4orI0vjilkmrJqVbChUqk/r4lscwVJn9EbKWl9y9AqtF7y+O+UX3CumPufpMVlUjXALVZO1YuHnfT4DVlZKPQwOvI7+UpW9YuiyqkwBXJJo/hkicg495Jyk7f8QBi10YX7dI6Dxl/VNqThlpHzldBd2pT5MxiUB/QSDpTn8ZqbZuJ3WONWhwHQ21GI2tLu3T6IZyq2vN26eSfKMnN9po3426lrGfp24IXcPInnS0SQ5RVoFkc2Qmj3lAc6gq46sDtmiR04yq3JhsXKp+1JMwBsMPjKGTGtJrz2MsdulTs9l6xmrJeksdwqkrPujLswrdYSLEeCrcvTnqQvdJaefkaxX1pLX2uDEBN6mV1AXAlsxG+1F8x0n0pAGZNxFoEwSS7rTJQPTXZlDecLux68pitPQUabfONC9KuyTFmy+2lwAZtvsw+/l529QrnOgVuNqwBvZS1a0ttkuwR9XcsJxqwwksPMrjEAGP3NrcHocMse7hH76u4MDu1tId5/7Z3I702NTGc4sTN5ZgLxtqwmJLJaMlfOrtvUe2om383/mrIRDfvfQLzlLVSGIbdKLc5NmFea2x2PpxcRu34U6P2CslZiBQhaeScTPnJYaRVLzdi8L3JXjxG3SdpRzlKOaMH5vtbQjQvPAtk8yZAja4hU2Z81koXGlnQWd3ntOJ+N1To/ppS5xXIjBgEEi6M2CGcsx0xBwaW5THTPW9UOszmz5DZ0DzX4qHhpV0Q0I3LKcnkbgO32Re0ty9HXpUFsVryikA9pHxlS4jB1KAXoemxMkFtvfbpk662+BGqKMCzr8m4zmDc1gh8nFB4p8fDMZD5McOu4DCdjx769CIsKVSBTEbOZHZCU9cx3jH2xXYEDTKS/okLMRTmh7MQ4Cax7lQtv7xcEdWIqNmxLGEcaslkkW45i+DF7d9aiEnDCEoVEHYjDQ4B8bGXw2Rkt12P4cxOt6atkYC/vsc/PVaSo72Tua0l5DpSi59l95fMbYHKgEbk4ybHfrFy14tuJSNeGxVtFMK8UO2jR+wSvD+JN2pGaO87e8INP7t9fdeZfv7DIF2kPo1ne1qk2qUNE5KtK2ddAzxUFN457ddrbrz0qqf1jQyHtnmZksaSelc6erEto85vC4+ulkd38MwAkHSE6JlOTzTfedIXWWMAHnpKCMKp/L72ES+jxhgGzQKjgIKLUV1lq6GbabzjQgdl9EwKd8lTMXIPwb1Ic7xA44y6A7aiv+hsHiMYwbtwuNc7wgZpIE1SlMpM+hRqDfAKBd+wBuMa3yoiBq2DTNAGpwS7uyo8lgBJxrrI30J3Qmig2PZNAccpl70hV4Hmejoo+KS4StOuHGIgAKpc+KwA+1RCD7nnRSPhXikj241zA4ABzHw7FEvvoLw6aDuV44mGvF1LbeVU52qLiyNZQ0gVF/ayV4WftB8S/n7gwiw1UNclTWDiUA/R8DqJK9EoBsIFPu07LQuGngrbC4C/lpZdqMxzWeJDxSQc1T9culFdV63RKbfNLpTHV8frskYCRpG1uetjtEeZg62J7xBPLOgfWrkMecPW9KILi4gDYstI53U50TEskw6D0t/PiLMKGWkPWV23ZPfxDC5GPEUAySfSK4thJxIlSJJbC68N+zHsatCe8Q79A+FolrAMCgVIrs2s4OQtSiXcEQii77GZSjpFbQkIkO4+hwpK0+cDxTx5d+yL2VMJwGJsQdHBpRp7LHHPNzGcUrVHRep5XRgArxujSyTjbBuOrBbgO85xkAlI+xCxZwtFGF/6xsWMSiRTzpwi4FGpAevvEZTYxTOd56tjcIGJcUwEAiaGGzPe9WwTA0warx8VBrHdTpsE0WTMY6FpMTSeDVKoFhfMjFkaqetidbKC3b2NSoiHC4i/eVLVP0+O33RyIKiTBABzWYEpElyRBMVlDZHfHW9YuobX1NO+9/qwgDoRTvjbMHjlXOVU02btHasaFb+TQT6BgEaAhVZ+IaAiUotRi2vyXsTfZzLJ943iarT+MG4tdj1yF9hRbkE4uL34IoC/cVmyB7CQF0RaZFNTjgymBu10sqUNYGwRBDzZvwyuzP6CPvKMYZFQT1QNrImr1uCkGKDmcBKnYGJq6yVt3iNZB/BS2ytZyuJjB5JiZpgDLHu10g2EVLNmh4/4ELBUFVfSycxwGHiQaFoC8pk6nUEAAHvBCBNinjmDMyGkoPg1DtAYSogooTQU9QHifEpJYk1iTLA16zQHc4iYgwWlYPTBLBD8pWwjzK1ln3EU+cV6UJE+lIVTCgk8B4gRGQL/1LGdDKg+hWO82F1ipRG1pYlNEgjjUK8V5rE3b5sdkctVCDtDhalWF+c8DEKdjGvIi2Rlhh376EERpZiidLIayDguCkaI7kaFmvcOc3466mi/MWNGqYUiTViUTQ9BitUUGxVkAc71x9qIUVJpp3eOr8jYR2MwvEnfXcYNxuoNxzbUwiCaIy00OgwlqlaZJQgsYCfg0D170tkXolA/0Ig6U7/Gq92bC27ACsANTguX90+wtJkSmEekSZxzhB2mlhu4gSWmIQf2SMjBmCt7LhCAskSU3ry3lKVDsZy0zJXDNcKKgemEF6i7BceEeG+eKCcuDiNOgYwFhbaw1GXDym6UEpiRRE21tzW2Z375aiOvCf2eICSYW4pAHSHoUGYWw+RINDw0kILYjwAaUCMYBIl+FISsYo2cSxFbsLE4AMapBQQeI34SoYCyUvaHc3jNGpxT7WjwIYVdRTJKmGBTsFA1EUabdAYiiKMCn3h3SKeOsRwABz/Iz4xHl/PQEoolkLHRqAyCRGZEjNLEds8PGiJwnbDW1b5iqUZwizjE2DaDH8V6Rf5ig9FA+DG2IRHksSjRT6yNP+XzGYJCu/g5nMhAciHoUERaGWCCjSZnfVHFqOMVcDT+4BzGFZvI6jxiXDQ8aJ6ab2lPIil1E7vdnxDrb4i7cc+aWv8ZBAmSOJS1GMaFsdvRhaqqQhwrPE7KpmruoydTWrx5sSPSB9Z3Fi4ZPEWebWMAgMf3Y+G+SHwNPLbMax0fk60woYNegwcciwXYyX/MKPGMZw+SUei9vybCPRLBEy1eSUC3UCg2KeiE2b7N93bNEs0mkmZKsykSrPopw8w/+IopJ0Yq0PCVTIKBpO7p6ZU8Z7KTrtDaU8hb7YVSbVA0xBmHfM1gWruJkvCn8YSVi4CWIxfHU8OM7LSkBu7w2Qn/6QREEkwEMwOQaGE4MQaNZI6yhTWBX/Ly2218l9fCHKLWgloOMgMAat5h0TXZIwSROo4MueWyLeAtj2HBiXMKGFkQe+0GQmTRhf0jnYHUeMxGoVomOYFaGWxEaj+WzagxpgVaShX+ClHWFFAoEKrzg4Zco6YxHvAWH64ChUr7YnGi+uuXDgZdRHpa3xRHzGh9SEyhQ0ZoJA5NIvghLZIf6kcQOcymjqlCn4nJLqn5cVZuKJI+OIolE8bBiSmTTEW1EjqZUtCbdUicZiBqCjwAKdFo5vi0SzM1ftjICBPKSKlluAEWCkVGt4T2dFB7zDdmAK5/UpW3zAx1EKoA2/lOA4HU5dS95n2sAcKMFyTaoe5TfNgy0olAR6D7HZUpngvpwajFPFdOTH0YQYIFRY2BOgpfinswoONKdIZt3pnQLFw6cs0HjETy2WIvQPljyuydO9vPSDdK2cM5tKFAdCLMQjgaKtuW2NWuiqbAPPqPgKUFnbDEjOmY66aVCzknOKIE+tC0tF6lKeFhb4VsNmfGA5VAfEQi2DCxkLWpEz2RDsIZvKJv8jiiy9OSFBX0HMQJFxJTPGIAgeFSClSAF2wesaZqCKUSfFOV4/xWK1y5sBXsAdUg4xUe2Rs8i95z7sllv6cGwgPjqiKIsO+fd63myykJhm2hwJGmTReZLalPK4DFpow0rc6fTS7OqaZMFmos4hLJA4xDF7LekIR84AJfRXBT14aF6DBH/FCHSBM4YGCaJIxRXGUQ5nBfoeqUg+EZyt6anR8rosFBOVVDp6HyrDTUVPRNKA+FEVMJMgQMe9kbYo9kYa7uguYAR5ZHdNMGN1ECxSrp9433AJ1k1FpaArerFK9Fo9jUdFptr5TwGByYdhCRilCtIqPkQ/U67XsHmmeNxMmNe2sbpUCdZ/Fx/ApJACh1LHBmyQQ6X3zVFgk2GnOZMelxFSXUxPWbHzdoJTx1S8D8OOgB1pGyOM0WJc99pFY+w1ombEMoPiu8jYDicBgRiDpzmAe/Rb0nZihwydUlGVy9xcnsJ620KTbsKyk1GGN8jd8YoiBEA/BdaIFkbGmNZGMAHO2LOlVPo348rY+EELFphWSzErd3hwNYPxCMgSs6ZWgQJoJDhb12SOGRydNErJlqU1HFZGU/wgTN5fYutwwL57BEofNMFdJT/iJIXqZCbbeemuKH6Y0YtU6XjKyDcuxY5whgwYItVKm6hBEgpn+QDuRhmLphlUVKB1dEWcabAOP8aExhiq6LgF+S+gmca6P6CBRyomYE4la9Cv4IndabFVTIUbk46b3339/eGlogNpdYghv9EICQ0a68+CJ1mBpCCW6w0kI7wzRi7t4GSgbcBH6laARYlBYUKChNZ/oorqAxtbHbd24hx3EjtwBN92Ix5MWpz112sb7bvx52q+NDJ517lmVUAXU4rgnjqv8M2Plz/777l/5xzVb5c8RBxxR+cf1pRH/jwgeccgRI/5t8GeCgydoENuzKKQNs2QXBp1B6aQwgKOV0MZ7OkmWjxKBRKAGgaQ7NYDkbU8RsMZlXiFE2TW4wSqO5oBnACePJovmLmptzQKCkaBNzCgkrrycGNhHSG5FsYWJsZT3l6cOuc4somp6IAE6GIYwmgYSmnofLSAhEALLfdqm8JuhPbLor28SQiaSMoOKgswONUAk405ERWFtXZ+rjGEL0x5VUEqhESx9tAUqYgJzMJ0VOeJFOcQaIgtTUShIdBAVKP1YdZ9mRQIY4igd7W9nKUPd8DkVMcewnsjC8yPykqD4E64jEmvUMMmid2JcusMXJ8LxF0dETUIz4W95bE+YrqpTCgcHqonEh+rxwQ47Iohd9UxSXcM9+TXN6L3bXqodx+XKBr3qk4Ea9gIZMqzeioZPMzIRSAQ6QqCice3oWcYnAp0gEDLY7M+YRRWB01BdkJGsDBQ5bAdUCKHVpwGi/+cpzHfYThbynpDm/CgBXQJJTA9kUSuZ6Z46ARUgqimN6IQ4eLKwhHctzoQxSIME0ExwkqA+4WDrltqGHQ0HIjOoT4RJBToPugQ10h+EmMeW1KgEDWMdkF4vqgWY24/2+CjUM4w+fIwUXrrBWn+rkR1BTE3GAErkB7t+oPE0SZ1A19VHHdXV1XLaOX31KLRzO3ujbca3N4rtyzLrh6/3OlVfV5d6Gg3rYSFdqnGwJaZ3tNjTa+u6/EToYBv9gd9fuhwqDcoALsPRWxYfDhAMW/xpOH5yWGGXoQ/ARSRACGiABPAGlhfZ2bNoQfwNJwyLXeSmBjieDa7qSJyp+lYYuYkY9KvmkVvuz676+OoY9he+pdUxwoiXjlA44V4l+6lJE7da7mr4qLWROV/X4Nlz+VoPac/LrGlkm9w27KlIBkraQWsD3lrcvRlhm2lwRyjV19J5aZSvJgqLJTpaCwYOUtKbMUwm9g9G3o7q6rzkfJoIQCCNWfka9BQB+0doSmy4rfGqqeH1FCo2nNdUJpJmqCayDW95XjONUUSVXtIdNTKn446Q6YP4rspXTbISpRpk/ZziqIp5sf5SJu0jpk6xx/O6PkFvx9jYzzWKwrK6Ig5hPK933nlnNtDq+GbCHb2i/LqoVLmocwzi+9VaDWVNwxim/aC4zIe/Gh2tAxh1iisb5SvSw8fO1geaY/5hVL9Uwkqo9uOuKTBvE4HRIpB0Z7QQZYLOEKhMncTEL4qx9x+7s3T951lHwqCYpdKHg/Y9qJOudEPc1pTWUe0dxddk7+i2vmE9LLCjivosvr5H3auaZzd37/C176gEPN4G9V4V/x1VLd5ZiBx6fIUj/NZpH9EvNlneYNQe1RntfHTgAm6kteLpI+3sE+bLhb7wDOtcMUk1Kwvzsa31HNs5qivE3kZe9liIM4o41VH88N9nU6b7UZq/XNyq21ATZobWWqsa29OEwxsMqeKQp0m+ccHqbbFEIeo8J/sDDATVjrDqwM4vXpP0SNeYkumcasrP20SgeQSS7jSPVaZsgACpYz5yMUiZ1Bqk6FdRrRKiPel0V9tAPpHZ5JA9zw09fztiNl2tqOwUuUsa2UJP11W/u40LFynoJCF+VMQYAcYjm5B2EhLjo+1pZTk23nO5dRQeE2QYMT2yod2xAp0Lto56VJbcfECT0J1OXBipHJh4SOjYB65kiWn7oG2vGd9zAWwgarQV0aEM9BN85H2tneJT99EC1luJ7THkcCYlyy8xT5z71che7lYTyeHMUFJ7cCSX0tZ9Sg6/LO72PM84Q0CSIsRuOFU7+AcFiaq5ojP1OjXAXkKPeJ2jPky31K4Yj2YoRLxKI339X0odtcdXtKhb3DpKkW2LHwaX9nCMM1hokN2C+BDbk5ZX1DNf8Hf/vGBDyRNfp7wG3pPwxOf65hJp1yQ/epcGU+fYlcZSzL1PgTEclKl2F4JdpV4PHYHM56VnKBHoKgJerLwSgW4gUOyTp3V1A7bRZIHqaFI0eoxe+OGTKI0eNjgrT7JOKmIfsSm9YVHVkQ2PNyTUieSw/VUnFuYwjluUkYwmLtvlrP7LSDvsbDQj5whaW+eoJegniF4O7Ci19A4CqHhBNkJJJMWAQ4PIYJLVYYOKxZzsX7PP3/5tBilnEzjaUTxHMcKVPzuxDTpsoKMyKRVCWaJt0U4UhNxVBVLCk51nPR81j5AJUpnjV/iHYSf284uhvSDg8T/b9BjOIqXjALREpOz6KNJeQhwFP8AL+b1FJC7rQB1sQ9ecOCBZXLGlLk76ESOZ9sQpmrbRYSqwEk8zhA/Rmgg7+4qeRqCjnsYhjWiHNHFpPzoizJyEnaBTEW97I8ZDwxS3HRUIAdkd/IMzcf83mpqNCGJpkTHs3cY6bo1I9Dpu/fV6oHdxCGRENqyrTN9MQAk9L6SZigZtmjxm0JSSVyLQbxCwzKVsL1ftTba7q1qHrupXTKD2i1krV6/RiSI+1GStQNlOChgSPTbBlZENA0790VnL69jbTGdDkUAGMygQsTbkx9mMpjBb+nEOKW3OVxQdBscXpz7y40ZQrPVFEufx7QgMo/M91VgR1xNZEJHSqQtZIdsIbw4rakdQyFQFUlQQ9hQtEuAx1xfXN+wL8Y/cOBCS1oT+yekDVBoojpMLMEIH/THTUBjospaT66SpYkceoNywxKKgj6FNQRr0PZIoNk4x4E1PbcPvBwIeaRhfex4wxohCC9EBDhAYcRwYSJXl8EwdQRTsXnQqJu0X/xssSiGyQx698MohK6R+eKtw0aVNwbfcRky0oeYvlgn5cLHn4esMZd98UDKKSbcU/jG6AMCajJ3fYnWaJA3O4ZUoERBw6kEn7YliMTDWKIocREqvOT9h5F4Vb2bn9TZ86n3w5jd8lJGJQDMIpDGrGZQyTYcIdFXAd1hQez64prNmNSQrEUkcktMyExIlZyLPCF2SgxQn8GY5c4Q3UKManOlHZhM21CR8I6z4qVticwrbB78HRMFSmOynn6ASoGOwgrduVhiugKCQpjQE1tMNd6hFnUgGTYBDkAljlgJKCOQmrC3+ciEPZxGJFS7xn/70Jy3R8qA7hJZaZORMynBDKmskCUehogHV3KtRFwtuHDQrrG9EdZlACWgW61KYcsQrEFFAKYhM4lxPqQqOvPjIMkt1QAI8Q6vCgVfJugZAhWA/UqJodvqgO6hJ0DukBCPpqgAGGmwVSADbeIhOGXH8yUFNQftopOhCOJ1UNy/CqJjDFVmjFKJeDEwyslw3w9LnLG88qcyIbLEPBu0oIxsGOP9SnBg14+WtkIbHTMMzPDvKXhPvDTTu+CjtFzudpkYCxQb9RaTqj1kqC4G510/2+OAo5RaaLiNk8DBWKi8J0IwOjmjoaYCwdmQR4fb+K4f+zHvi1eI4xRRYNqCsIgOJQPMIJN1pHqtM2QCBhiI/0lkCmuZMcCRKdU7Ld/GmeII/4iktHMRHDFiJRmJphM3U4klxUopcsQrnJkm0kAe09JT8ziZWgjP9iH+Sw4oWG3DAj30fRJ2MSmMrIVeo8ZVveW0hLobTCTU7ocgTk/WEwYKanYsAQasie+PNtlpuupeLaGSFsUjlwKFT5miT9Qs/faG6U9VhApWQcDKQJjkm0YTuqRMXtdzWHrM5NoM6FGNVZ/o8TBASEuZ92R1SjIUwedgSrKkapgRhSgIZ9NR6nbqCfcdSXnqRWsg1hHKFpYDQ/bzcuhBiBA1MBRR6RC8iSWgCiNs4tDAygZFLhyFDd8rRVBF/DqIIVqpTmsQwx0jKka2r8/MIKa34/f08alTIiIwKVv61KWmttdbCJCg5+Kb42EVxcfXzz8Pkve7gHzhHfHTMM+0sHVwEvGwivWAGV8A7pjqD8nkpTYQMn/56H2SPt1cmIy6GjY8bDZUS2iEyXiHcyJB5gRFKWTTSniNUlblHFsMnL+JoQPEzY+pFNXzeZyUAnJXK6ITDEB2Jd5vrrkcIdHxzzWBhb5gBrRjSYFsTPQr1pLdO87zV6qLoQjXCYiVv/aVV2uZttxUc33WiJtiRlSA0fmKYqFzeNA3TKlouL4Au1BcVMRiMlwERRNCpsvy+xGPt3ljkyeuqQC+eSMPhi2bURX5u4itDPOKCHr8u/NVsoDERmX8Tge4h0GCu6V5BmWtwIsAbkeOCSQo5ILqIDWs46zCTIFU/UkKkcUWkn4ePRaH0vifA9o+ymPVMZyZ3U7/pT0p/w8+AECVZTfEmROt1C3QCxlSuKPOs5WApJpXpKX0JocXPkSoFOTAd+4sGOczXZE1a4B8+cm7OtY7EG8gY8zjtAj8JTaXkMBeT+mQJCUHY2/Zi/nVrIiYnNB51UAWFivbzXf1j8ceORhwUCI3S2Fa0wfSttUQUEUiRgC1ZpCo89A31haB00rjIaXWRTw5Z5g5igRsboePIIhmpBEiUii9L1YUa0r5w9aUg6XzjNARwKbRAYwhFlp2yGHwx2E/EQB7hI4SIwzJN7wWIbY4sCChXXx3xkmAw3HcoRXwkq5N6sRyAEO1eSMm8QjLisgYCjSDCDR+Gx3jnTfN+8sLBCYwsyV1s3bhgyqqwdqmdwQjno5ZQDisY9oBJcz0xTJiWb3B6S6mOvFRkM+2aEjXe0Dtm0y2noiBezGp+Nd5t74a3JXgAgoLOUmzIgnOXH+1SGjJEqWZkI1KN3lJt1hdMwquC7qA+CqeG8cLbOaVq6VWEaQXDE6/Namzcz6Kgz9NCWknal3jn/WxB5z1UAsIRGTnx+M3GmxBN7ahAqjuXvLRWelQm8+v2eyxvBYyOqzqmDOtFnDJaxmQgEegmAt7FvBKBbiBQ7FPx+ENcvHlWYOYvnIOkCT9EygASmiAhvFnrKeRVYd1p3kdQcAiUyKQp0pqVMoBQJ6KsUMNX0UITs/EUf1IgZUy00HSsOoIwbv0lqlVEaLEFoCPUIWSPNDQc1qnyEgbKx6jwMMtHfIiGwBJTXbKzLnFGidKILhNrhM3ItjtFOP4SdVLSrMhemaw78JaVmHyieQpywE+zLMTaHVcz71NXgKWjEjSeZOLcin/4YgZklABYQjGKIr8BLsxLA6uLSL0jKYVBAV6sDrNk3CGqO6oI/6N5kuXee+8FkYEQhh7BrDRi3lNckAQl6nTZU7JcF4heYewBXyRNw+6ASook2mW0ZKefMNxGgbCk50D7DBM0lBYvgzfHaKpXIwGCmkR2lEUVhgnU2KG3QrxL+VhshDvqEfqCjjAguugVSFDpDQfhbWTpFBFlrBEZFY/1UhdpEpArVK+DAaVH0V8qDQ0QQHHkNTrYjz1T3G7kdempceGQhDpDXpq4ZPGyeedpd0bFjeF/O+ppt5vVUYHie+P/brczMkaTelhIZu8EAb8Rk5jLz6GTZH3/KLU7MS75t5sIcBEgsayhzenechYfYStC4oHWgZLAO20JSN+AvpCCVr0sNYQokRArSLoKNAU1cYaY1SR9g6bQysQCHTmwci31GTWtpApi46B7Z0xBa0hKeu/IWKYkgElT7STb0Ah/xWhbaObLZJ0EogvaTELrl7pIvo6UAaxveJJuKp/6hNSPkmVkyKAuIn21k/wrOlCU0BAgIlb/aCLNFlUE5QqsgIlyEdgmEVDjXmqxxOfLotcoDtucSKLX6h+Zs463Mib1i8cad47MZg1kYqOZQGiCSjJP4FIiw6plUNjjOI5IqeUojuGmG0NbFc5qY3TwGPozahXVaCH3WwHnxBD/dHheCdZDUNAZQB79QqewUo00Lk5e0U5EJE61oQbTZRQEo8V4dK1sun5FC8uY+sAGj2/gCKjyeql4aaRv2e7FGcUZZ/z+jGKLysNd3t9ll313qYR+Xvmz/O3LV/7p4NKF8qzwMomXvAyjthHGEcvIMkBNpfsGMVQ4ZXwbBlrrhzd874rRMK9EoH0QSLrTPmPR71tCLY9/4Cvh5EH3QJhZ2Vu+k9b0NIQEqcazlS0gjorRZ1pxSiCUiI2fuwDjBdErkmWK6gKx4AqDQ1QUKnUX/sQwRFOCSZCUzENKLo072iMjZqABvBkUbqnNXmBXDomON5CmFBicMKy86QNUSiFBJJPoCAeK5i/lhH1PXGVxFHp+bID6hER/tag4T9Rfuk/9gxlgJwpUNb0Cd5zosloYFKiROGrsf9z+9dnFSI+6aSHrHvuCekViFfDBEqjNsBPNxhqRDPwG0cHwYiFFLwJzGjIlYGlEbMWMOHKtVVsbbRM06CcApWGltDYEeKER0XcaO9mwH21WC8CBoHBZMBjVQY8NBeOM0iWgjpJXAswybI4KD/NKdQsgUH1bHY599RFDueLytlAL0S1VJ6sJ95J87SkJmKGi4Vj1n6sW/6xpb3vd9hJ67dXJbM3gRiDpzuAe/x73HpshVlEZIhCnoWtBHSgGUAQUhP8KwUkZQHJjIc4CwYGwE6xIzQgNtxubLzhDkMrMASEdPWLqIk1pFPj3uCVBKVfwDIt+twpnbKI4YZyiRGE+cIqJeIVzVgjvBJ4ZSmNq4fNBo8A6hjfQFZHl1Aa8Q7AfkpsGBWNQOJFMIyIx4UpmoyzK1zVaK2oJwpvWAU9SJhJApzLT6TOpsf6SgGjHpXA1HKtM0LwySRbcrobeITquKA1pK4ul1ynDZQDaZbiTACVKw6egcFU/wv9ip4/IktkE5hXtUdVF5QPSqoieBlkh2bB4oDOZjXbnc08r+2L+7hGd5A1fRDHvEoF2QWCICb1d2pLt6FcIhDA4efqTOUzgN5QiPGcxHqp7tg+OrjxCEBouLNQk1ABUPuHRycZBgYFAUEtgLaiSAI6CKNDriPEIEq+88go6IiMdCVIVRii+mZKxfUhA3EZKBAXZEqMKJVBCUG+4xVS0iuTmTUIro20iESBlKkS4J5fu1wu2rgrInpfQZBf6rKIm29PzZPU96nmZNSU0HOKaNDW3NVm6+j7UlNa2tzXg98du1nShbaHujw2zLAwVO5VzzZcTx2x3ku6MWfz7ce39cY5rLdyDecZs29GvHpSuNrI6r1dF9lNnPJVqEGunpGzm5ZGlupCa29GWwDLI4Iv989EORzHb61B8tWP8Im3+orb0qSyaTocb8StiCO68WEpTllC6Rr78nads+JQPmf2VNoJZS0SC+k7VxzQsarSRljFWOCqyjImdXBYnVHpUhlSqwLGAsfixmBFjGWNlRVVsZQUKhcMNVjSRlkZlXRGpQOkteDQ1HlUPU5k4Ay1BoG3pTk/XuC1BJwvpvwjkrNF/x66HLa8Zego2ej7qNLKHD3IPC4/s5B9jFgcj9qyddtpptGWWwqxMWdPIMr4+UJ9XGrITS2BybZLu1BfbpRjy25cluHlhOWEmlp2Yt8+OPZeVUCR5L5JW3gK6mbMHOcXbnxiO5NWN4VtGgcrlPCIZmpkpEQWAG0TmWn235wCfYDzVHtTKcNR7bUd2pt5w9pLLm0B7ysldFp5qYXtFYuJMAenxFQZo6SXzqoQHOiO4LFS2PNntXWCwtlmPEZODGnrH3Iy0AQfn4/xHbcDxTiTXePh45VSkbczHKBHredheqXVZooX55GFF5b6BaHP+HWwIJN0ZbCOe/R10CDQU5M2j0CRj4PLMVdzhAo4GaBXdIdr5SjN0hrGyps08wOxiq/ZrrklQ3tqzRktBTAZXKONHG0B0uHmxltanpG8gbhXIT6v+aXWM7JQWOAQrqsRkPJRwC4ZX/SKwBbhA2bvHe0xG0loaBMtROuQ6P3GRWoJJYAyO+6P4Qf7oKkjx0k+LURhPcv6yuniqxaY2m++UybGdhTfKUZSUjuTmwq9JfMDjPEa+YuJt/leI9Fro0CZ+9/RJ+sgMrTFOBurIfcrmQQjzwMOWtE1KzAPd4TDHnM2pzjmfWktRpAESGFYkhqcdz/qgOz4VYo8bDy1HIuF2ktnWoIXhiofeCcBcPC9+CXBrmz2jPeLxOfs3bVzwiOcfJzwWdp3C2OjDII+ryZvXYEYg6c5gHv2B0PeuyvIa4d3V7P0Fsppu1tw234vO8eGGRZzwzVIg0UjgEV3xBajmqyDJLPSr04dDoUgS3frecj/knL/hrSUxZYDtcpgEGWmPOm2ETXDVhZRhaRikSEFqACc9UjPEtxocnEPDIRn7kVrK9DUBXISQtsVP1WVKbMBBlDbusbmoncyuyVXeSsntneRGX/AtpiUe4s5ZsD/fmYGOIOJsLgHygQA5wU8MLQ5XM2kUQt1CisslEiWyU0+k4wB4vzEwIUPlGQ3UMAaCLsrWd8lsysM2eOWHNQqXKptEE+NTVnQnOAf0qJRU7WAnRAqdcgSzkj2V3hEDTtSk2nHOoc6WJdQHtBbNxZa8BnzqeesjZ06J1H0dd+oEjU7sM5AXUwG+JrFVlQNKB0N5g68oIb6hYbDQlHgZamrE3sBYci9MCEVzDBKEpTdM9EOy/D97dwKo21T+D3zfa56ViFBRpFQyVIZMRaSSkikUiYZ/kjTJj0ilVJQ0UzKlASkhyZyiUZISZY6UeZ7O//Oe51q2d7rvOec9577n3Gd3e6299hq/a539fNfzPGttew+xKDsPHNyF9sXZCk1F5e1shIDJkVciMAoEqv0bO2xHkbG/WbTBEtmuZq9se7O7F97a4NaYKMGr2bqZ1CHOu5c5xqfkE3GiC/VySCy8wUu8Htl7uKlT5dbynYC3jz2KYuagJ2AosewW4AViMe0Ru4Bbp/A1iEuHIRbvPF+SiR6C4CGVSTh5nexHD4FeQE8v+FJEXewInNAxEsoDMWQzbDEGYZv2ZWfvF0ZobMfDAMhpspZQF+lkXryHxojaQ6QuiHTkDyKCbZDrzBxaK7KptXELRv6SmISe6pd1v5T86FEQEhdZQafoMJryltJ0hKcIga07KvLrEdnPkMSBRrOBQCEh0tVUiFtzkjihZfEURE6FFqCDoXJoZBgaouFgZ4mwgZDYiURxG78EuUh0rR4pzMbno60RicmBl9nILTWGSVufPHgMFUukpKeBPIUNHoD20cfEwMUm/ziAETWh/on0GqN2DYtbv019jBjuTVJylKHF0RhZ4Iz3IEDmmyFzziTKKDGVGHJJLWf6aVWpyF+cMUVZzB+8RFhiQ4NvCQRVKn+MGo+ZiY9LZ+2vpL5ivZLGGPll+MMFqYLMZxoss4UiTePj3+NZ87/9RwB3NwFc6Hj/Sx9DiandiXHJ39Ej0F0BMPpy2+Vsq6XwXiPJLPXKZul2WUcWRzCHO0J9M7kiLCv9khalOH993raIApEc8dJY1wp725JJDukhtiMvAiGxppKgYtw6tNArnvXBMpewJ28syi1SyWOqeJHKF0lEKZNBQbGsDHGUnxKIeachk9yIhVpiQ0RpWz3A3GBvP6UCRqIoj0hBYkDJOITqUAdyjlRwVjIproVsEFVDxdD+ohUgp/l8cKyJ7ksnO/lED0EfQPuC91AbOGSPK4bVv3aS7s4thAyGRzjJYuWtOtRBmGjEJJAhIEhvrS9SSvoMBWI2XDHodURSJzjpwLg3mErXC2LolEGhLSgJFeIEBIcJwRxoLFbVjuXhkwJgMQooF6cQCDsoUndYx8ToNdUR6U6D8qQ8tRs0KzYnaryhx408JM5jIgnrqQJrOXoNajlDXjjfaAlHHASU/4ohMGk9bVtQ6JmQbGYjw4f/hRqpKXHJzjhVHpmu2G25bQrokTmDNGO0MKe50TaTAUS0X6aueY5amfAoFyQlQ33MIlzKI8Cab9iJuY0UhibG3GBuo2pClVRHzabLuoBaGQ5nSajCpTrsUwDC6tVm1RluwNIYyYvxaIOp3tTmvJ2tEOg4d2crFLKzY0SgLQvpvUyLVG8urzCOihaF5eAWws+bsVgKOvEqb1jMwEswDsqjw/BZABLO0pAwJq6oH0qZra0ia9XiRakEq8YwrHA+cIaQpX89vUUqNbuU1rKySOyEPUcI4jTereFnKj1xTmYTOd7OXsr6ZTlr8S2G+UAjLT0xDwtfS392ClksXoPukFtuyX7yhhDVGHSHICFpsArCkkQh+zWAct46nhClHHKEMRoBh050xxkBzieUBZNQr5MbCRLURzvJDz431spYIwSMBW9QLadUUGP10ToATwqzxYDXeUJOVyoPrO+NBX6mzRb3ITWt+FVNpaEvFnx0LQo3KEXk2zcE1VIIrPQUS2CGEInuqEJPhaWEJyJVEo8uoGEh/MDO9kHcdiqHiwl4m57iOhQ2JDejCcmthU0Jyi2bjjmDV8FKRRQq6jUnObVQYtFJmACGGyegnqTCKRlLICJlZ9mBTJhp0FP6D1POFFUgCktdZCwcy2mGaDAADaVCsAp6FCRASlXQGhog6igWK3TTHwtOUE6v9tcnixhcH+P3WRLdN0/YnnAIlimkuTSsHjCUhthRkPKat4gLGmoa8JL2tTV5MRhWLX8vZgXvItPP7NUY0FHyqQj30lSFmBueBi80P3UKjTNpHcGFxGB1lFj+nFEcGiNFRTNY5dyaaag2MJks/e3IAmpKHfPHEFiQ1Nuc4dkOAS+gvBKBUSBQdMIC3lmkqTc4Oerd6kVm5wWZhBDwSwh1dFRBrpNbGIwvfkcMDuF97eXF/YIe2xXxJDrbgdeWVTjdgEgVxaP6r0jqDX+3/BMj3pKRjPFiJUu8Nz2irohHrSWIodugJ/AOJYat1CMlqexdrKmlLh1UlDUoawv1TJz17ClyQN3iLay/SEmkJx4kDhNGxFDYWEbH56JooWhWIp7+w3Ic1YjbEkmqoT4l0rKYrCKl4GOFjYp5pLUWwTQlBAa/3WLvaOqmW0XJSyQQJ7KHi4MSiCKUotQiAAQGDryTnCA4m4oqKSPekrqMVzyyR4amRFiNuqB3wsgBQ0MkiP4KY2YYD9YobAUfxh0zxzjqKdMVDURkMQ1UFGECz47iCJNtYQaCHvwbku/JM6TcYiTkrtGh1LHQl92s0zuzkSzU34Zv9ZPzShMx6CkxSZQiHMbauHvESdb4UkUgK5pnCKJJTYW4Dc5hIvlDMC3VKKVea7mJhxZAyYiABVFgOHOLYZi3rEtSYgCGWCSsTBvEVGR87cskRE81g1ZDpEshbjXSH5czuCMSx1JvpCx/CNrPfcemJ240Mff82cqOl0CJS5b4YhrGgfAG6dtaDNWimxh8WC70t275ijYMzq+mxr/BadLUa8nAGrPayI+ph372aDwQKG8NAYyELI9NqmQq9Ua8ZOkMMAnv32A8ln2EB/FAlxMvZQ2zrPd6tbzz2rXMjZcv6UI34+VuoWYzS0h3FbV2JCJJviJyLNzJWuIk3tfcFcmA+GpjawliLLKjWP4ExG2pQuPRtXIbssSvF7q2Wc7GI64nFDy0NToejRdvJU3GUHWU7PHNBBxCY1zInEfS43OukjHSq4WEq9MdyhskAJPgv2ItTlyVkhlWrNet+wmzKKepm26JVcI1VFPEJ5YT2VvpjoYprRQub70X9XhhLMRoCliRoywCOGKhO0RseGbEBmDiXALQUQsJYA9wMMTQI+8JeKI9PnhOfWVWSBMXrZilOWlKR0XDgR2ybngUI4Jkw0RRjQ+ZPXmGlFviH91p4F5VCF8US4HhFpVhIENDS+IZtT5Odwh7bMnwaaEZUp6ijAZFZJ3NNxXilt4IIzSXfODMzCnZBdyyKuopFYvphGfQ1vhlfMGH6GOkKZFGQYwEIqUX8BtXmTxmvphyG3W5fTxh4+jziBzLb1MfFdUaM5byxzWvpsa/ca1lNi98YOlOGrMab8C8xogAe5BXPzU1SYzHsL4z7vBHsXy0hsZFKGAkIC2swvlbEL2kFBLj8xHkDQFGuyOlhXu0hFC04CZI6CQopYmK7i0kL0sC6ZWmAQoXSRYyytRtJSVlOAQUCkImkSgaUxLUA4QilQzZTM3OWMAI4qkluEYSnLxeSKZ6+qawXBTyzF50CcicsAS6rEwin5iHA7FErSKgC+SfSCt4Rgc7bjAGcpcpB49kzaHs4RRiCa49TAYICl1IcQlqqtot/RlVEM7H6kGU0paBiCJHOUaEGkx7qK+Y3qhh6FcYyORCZarnN9xxWguMGMKemsSgW9AHn9B+XITPDRsZBoxx0vfQgiCO+IE24CjaIDviK6VpQPNBbYC06Xjsyo7mUVZhSzi0QhBlpFAHdZP81h0lGBEGF05LwkgMplX9QbDNhQiCjhsHYBuKnOFL4xEpMYiy3zbZhqPoVMzb1qfMUq7W+KaYVU9ZtXrujLgfXfqjqmEsql1uz6jdTtpgJ0PzpO1QNnwKIvCEkJiCncsuTRQCFN3UG0gMNQ+Wg+6QSZQTRYpEgJwm9SXTLuKWbKMVIP7rzbQwcktXwWDvslBg5uCmyqm2nqx7WHUEJBLGgmDJq0y/rVlIUJFID3FLBmMtaBnvBH4/4lEoS3Pr/obUH74QGit1Mjhu/TKccYCgnWI7IPi5fzpThJym/MdX3FKlNNxgq0qYHYRaC+PhGISgBKXgyate5EwaVIZaiNRn/aHLQRfIdYSApgdocCCzVYc4IklkPzUJQglwDaaBoF5SSNuLiguktCOQwTyksVeZdoHdRDkxWLQvqAnPWaYx7hqomL58/+vfL4PYWjI/CXzUQCN/wThZQ3Q80AZIQZ7fBoTdKjbKUa/tV9yz4lbvBOCgUqMmbIYwPJlLZkiZJBQ/kT5+6fDqt63hNmL4vJZUZ7bE9Cli6OONyTy6q03LR17QWBrQe20TU0vv7emesi/Adq8inw4mAkl3BnNcJlmreBRakRPhxCfhx5mAhYi3AecVChv6A4t+XUIUOLgQ/4QfpQVFQogxItZpH3QMXF5QB47GiBGdAUcZa3EuruR6F0SIeRyFVFYXKkDhwfBBF0IHQwVCcnNsZF9jEGlbCHcQVh6SWy10D8wlknGQJGuRFW1AcfgV6SO9CC0INoNz8OChdcBdKAloZeg2WHaYGOhC0CPZAeIWd4lKCW9dY01gLwOC6iKekgNVolVyi+LQrwgogeaDLgQnoMCIlKgA24dIWUIjha6hLGpXS1C0SNn6qxx8qylep1xNkW6xEFdrfNsYsBcGEwn01BVhT0uYda9tCfVIjJA2jn1QJG5kaJjh6glGFB67GJ61onGM7Z+1jR/RSNUT0/5agVgMdFEr1tNnOBHoEYGkOz0Clcm6IUAMIxNUO2QbNUMkxXKCYYQCQ6QECA3egFXQBhVZy1uWSYgyhuEAYcKNiHDsQWmsJIwglCJdquceRGNBmtJeoFlSusVFYpsSU5qrS3atcjUlwLGaYrSE8iN2IfFKYZDSSEY3V1NKDqeupkiCH01pioxb3Xc1PWotQYKmA3wpVDDFpoxtbyeL5ENP6auohfSCpck4jrTlI03fFq6xRHZvwEgZDD1Z2GEFqM0wSwFGSfyeEXOk7ezetpGWNr7pz36i+JGC9kTODCUCNQSS7tTAyOBoEcBsiHO2HlqH8L/hy0IY2yzjHU21EJYOxRNgTDasJ2FIKhWyStQNEzQ9rvK0e4DPTWuCTluyW1P2KgMWrarXNT4bOaOE/avVf7p69dPW8gYr5okGj7ZdnUroFD/aelryXexYoZbImUWMh2hEOJxch93yS+t9Wra2dBSIUR9i3v6sMF16R7Y/Swh/Vmy1o6A7mjQe+LT2dCwx9oiFDjUOjxgFaGOpPfNOYQSS7kzhwZ24rrHCNFVm9cmixM+UYaI4IEcab21XU/qx3I7lhdj09h9LUWPpQh/zNvVIya0xUR0mSoRzDBpL7agA6WuIw3e796J4brFbmQnYMBtWWPFkNwT1BpdbM4pty1E3TSqu3mscdUo8nmnVJnYO44XusLXZSEjP14uRbnRVM4by4MZ4qBL5WTszif8Tpyv20HAIG12xBl3J1iey+zV2fplTKUf1xUDYDvm+973P8QqOPjK+TEvWJ0xLUjJVe8p4SsnEr84yxseqijXT5gPH7RggPnCx9V0V3OFtmsPYnD7FMUuMXevaL5lCDGgcsSOevZV7vshomN+8EoF+IuCPNq9EYBQIVPs3tnTKGL9NJXD+ZYFiruLM2/Ro1LdtKxp1aW0zTkAVbevtV2Rr+1tjoi5yxZ5zOjDCbCy1x8HHozhqhf8Tpyhki7DEJEobmhpcbrlse/FhzyVl2wAOJ43jcNo+HXUkvyuEo569se+9anxJox7ZPVz60j1ZPJUYL7H5izs/0sOdS7xz/LiO4T0IB/dzPu/2/5fTExhwqXwYi0XK21qdGHwlDowInyokNT4Rys0O7UB3iq7UFzbUiKzoJhuulLbFKZbBUYztezYQIEB816LByAp6xHGe4pb5OCJxNYmRRW5wHPUMuniebVS8/Ng85fTGHU2koyiE7bNDhmTRzSihtRcRP+pfBfa9zFE3ZkpmHNiN6G0OMpmSA5Cd6jsC5a0RgYn57Xsvmgqc6XvQ9iUnDvfl/JKmqptuWQNJ7l4i62la298aE+nJmNgQ7jMC9RJGGnY8IzXASHOV9LawkW3d6Q7lCvWGc4RtCC/IO6/PWJCO7DuuEPlUEdQSCqRm4PFKhSBGXfRPKuL9irIQ2FE7Ik6+ohFon0OA+KEjSdyzOKfzlKfF4UnmfCOR/N8dhYAlUDxEXica2+lGYyGS61ic/kdZZTMdwuGMHO7zttdxRys9Feg0FvU0JVxPzI8t6E48jRMv7b23I1Jn4whHlVK0cOuxnVDtDX+14dVIKVBADDCNuG0EtEQoBdJW+Ipdgdin0w2sVXjK0+g4r4jiB48xW+JQZjsAgInQYFoK5GWF8di9iIFpSZwdihqKhL8E8MSTDBBSJT4aAzp6MhQKwnIZWfHK1C8B9E5k0p3AajL+DizdSWOWv6y8xoRA3fQwioJYK3rPNaLEvRQ70sZzpOBL603t0Jpeyh91Gst658q46iUQEg4GHLX5yavT4t4Kngxjs3CcD8EmUhURT5zjB9QtmJZICgA7vxyBHY5WqrY6t+2OmCfLJSDOyUWn2tQbKUzBQGhxxqK/KY9slMMwyD+0oER2ct8uCQTQmnDjcFK2s5TCeKQZuAtXMDZTaXAU2g4+ZISr3Xy6Q2zbvR86DDYUtjBO9OSrPfzh9YLl+CoC13hkgiuMbYN2uTuiCblhXIM/b3EDDR9+9GLQXLhFw9Ca2Dpk3x/EIt7+PlsOiXkWOm0QD7p6R/oV1jsu6kx7CjQEcWCj/trSaFzgozuNupZsUyG1EPUMA6LeQdVXTahYUDr7A5AkINDQxLEIMke887SEgYMRst/B0OSJaUNhg6oiQ2pEEGMmYGYi4zwkOyJB50gkfNTQ26mg5QaFCodtS0fgT/HT2lATLwa99VHGJAKjQyDpzuhwy1z9RGCknKNfdY+UPFEtsAExADVxHYtXTSpCIppHAUBDQzA0jr+rqnJrExb5TSqL5w9BMFgxW3NbEIe6RWKnF3rdEwbWwbQRpCb5hC5QURAzG2ywgW3wlr+KYooi76k0rLbJ/qi69ZclKNbuquB7QTQ60cf5fprBZkFrgp1gP6Q4RmXJziSheaojSjEAsh85oMghyEkvIpM/qTD/G3k5YZSWq5qNgwOHrnHgINsCKz1y9AAfLys/4s0BQq2N7BTDcRVPomgJe1YkY9+xnw5ouqM6NhfIKJkqQgMwj1IaoJwGBD30Cxdx5EHQHawOLUNo5KUgCU95ChIkyWZA4EQJQWWCNpUyBQr1KW74GAN5bzIYONa90DPVs4xrWHvMT/YmXjimB5vUAp+buYecfvn8CAw1Htk1oPWeIkNmiH2XxteIQ9ulFyL9IQiYySaS+YBQmi20XHgnu5iBxk0lsDygRnJ4EqpkXPBLU8KtbXfOfcCqUUkNcIyCuecPgV6NJk9GaqcwhAnnlQj0BYGkO32BcbYuZKSkoS25sRQmJEig+ttWpAu4ImNNT6TRsbu8YSMSUfCid+tdL57iQUpFef/G8TZemhJ4EaMj3tG+s+217s3b/WgZQouEVnXwDOULMx84I6dJ44LHEN6qUJ0mEbSEbpzK4+WuR3bd00k4xUcChXjRe6cLeK0T5A4rsuQljB1DjFKEXwXRokbiPPxFoqki9Y7awGJad7iC6ohN/gp0MCDh2ljuN2pocymKRwsqYKXulyynleGaqgQtR0RwJl3WTmxAmbQ40rBQgBENIpCcjKzZamdAgbB+qYYdh0RkHClV+hCENpNb6A4OgczFI/KSAMZ1nIoUhwyVLDMNgAKjgmpoFCJ9eMcjPcQngao7JoCUOmX062Xiiy4TiSoLDmw38VQyFh/6GHudyNqINJ2kKVynXk5TGAihAxNv4hl6vIeGiZ8Kpogz2cZVskgZM7nEjCggr75H942XPsrOekXPp8EG0a0G+DVephDm0fhoybM6VmIi+aqdeWWSm5ZxeKMs5io1DAaDEfo1vkaQNogtD4nBBUPj4o+CexAAMWPU2QxUEzDjc57mAw4d3RfAHSGjC9x9THgpqXyAzOvLIQ5mI6xEItOoD+hwa5Q62FLHDuSDRGAUCMRfUf4mAiNFgB9AOAf4DX9Gby7LaK8qrEJp3ptehUw/3qHkTZQfWep1iSGoQg1evmckgZdmsZJ47UYWL0RKBStyU91an8LcQtPL2lMOBM7uI/mEWS7IVwKJ/sPbnD6GABaveZQN3tqO5+FJ0LYxkmEwhCgKohxv6vCNEG8/iyWp7MLlYhTAJPhMeL/rOBngEacQOAgwLtCORGI4aLa3PGRIESKQGwTpKCABU5GnzAfCUpJkUVTk9avvxEMkjki8B+1AsGyTDpnRqUdBOzRSxkbHq0peslkAziI9IsO0R9hBydbf2BU8nfgsxkWDEhJI10i+0jYZreAjjV88zxW3mhpy2vhidUYzBpTiqqSXXRs0r8Q0daHcstSQ6JodKYMyFhdpMBL8HplyCiRQhcNUB1JsCZ8Tw+MHVlGCLEA2YbCHiPGLQ5hgdCQlJgLmAAKH6pVHqgY+Ac+eZbagcZESd9QAI1gvATlonM/U4kxTT9MULokxAwW6DBAaitwwA7nFDLjphE4xIMV1nMqIdsAZ6SwllJJLDNqKp/qzMp9ZACMBxuxWdXiJY7FKLo33JxbHZ0ekvOiv2UItVJKZEkxdmHHMooj3F2pwXR6Z9iUxnMXUU3qka1KaLSWZQGlzPXIsYQX2vcyxtGfq5U3fncafa15TFYFY6/u1vPbOCvU+R1FvUt4A7Cw2sIQYaIsAAwoZQzEgwLUCz5AM9bG+9JfjnVj+fiw6mXIsXklcAo8IsRsFo5KeNj6olbD3NdnMu0KloVMRSRAS8KQmGkSB0Tiu992i21zK0RfCgI5dRcRMJCIddRB1q+fRWS96ol2xxACRTMZrvL7wwUSA4qxFWQhFF20/wekSIwudipSOYEaMiNJy2nK9iu5hTVI7TGhNtrxsy+6JPfV6hbZh0kFj5Day6JdIYYixkeGUvDHIPzGkLMMcR1RaAVYGPSKr2On0lHzCArEQ2cFFQ0AYYx6chVEZCie6K6YojND4wsetzhKfzCKKJR2Vj4UYZTuD4BONafqlxeHHqnnYKmKHTFBySEMNQ7NFQNJVEL1qsRlQ+Zi3drLQIazcgww38xyeas5QzhWrHzZsnhiRBnRbbsmPBCE29LiLztILBolUBXj5qeBMWGBY4nQWqSK2gS8BAhFtdssE2aQCxCH4P237t22b+tXLLZ0fBZt5ZaS0VscxaUwO0cGwkS1qwrDExR/OE2We9ESwHtJC/Y3vmdTjg3DXYyLsT9hVj9cGc97sLbvNPfWHEKauesoGyWt3mYGupieKDS+xpvi8TQT6gkAas/oC4+xeCOpgaUjOlZe+dTAigu54TWMYeAYKQpy0RQrFYTehgCFEeVdEGoKW0KJvtzQPZwvxIi0rndVBpxJ+oG94wxtiKe9dyYlSuF4Fv8tyG3t5cC9CmlKdF+2OV+9YntYDxCq5S56JjG239adNYevgkH8UGDrrKXUOIeRW+4klgiGycOFUr9qbSiCh6ahwC/qbkFtuyVGGM96dbAG+I0F86qBI1gey01KbFMdLRFIzCKAOfGWqdZrKfuJW23yXCrxoB0JADhHtHuNYyIcxinAoYBRI+Bm1AIGgRRfIfsyMrEV3gq5pDAdeGamsSD4tseVHJHqh2ciEZsuLtlJF6AsKBRZciu3JfKAU1H4MCRNlD1Js209GYFo0NLYuwxkCSlOjAaLGcIuMErR4jwvP8EgfcSOcJlKKwQO0EAkjoaPluBF1IH8gRjHIUHFh5FKigHgA/mSYsFsxLnogzTYoWlvYoUqL3iWSxa/Jo2v1GGGwuLY9YDR0p3UGmvyuqIIhKWxJTTV2uUXOsHAzE0MtVL5L+tZHMDS3gym2Ps2YRGAwEUi6M5jjMulb5aVPMIT4j84UOdHaN8Ym6S2p6TZImkhAvtojQzY7kMOSmraAmLS5BjlQFBlJuxDLdO60Vv9IRhAmuoQZlp1h/xhiONaRzBZKU6zs7BeNw80a3pZtLtkRNTKSLgGNYKzB3mgmNAMhQ19YCmjm+TF479vXQxCSprxAqGqsuYl5yQghliAuO/iBBmBpmBnrA25nsU7KklgUCRqjg7JQkDAzkdmICLZB2cDNiFEJ6YmNx7LzreFdyx9CRVRQdC3UFQrk7gAc3OIX1S/a9Gf40+u0X0iY/cAol0Iko31BJcO2pdm0F6qL7BQ2dABF3uMWTnwRQ0BSzyghRhZlxEJ0Xy+I/5CdGi+xEqz1lalAPUJDbd5B+MLnJmrppE6Ip+XXrMApy20EoEdsl8iwYZVbBKWEBbSQDsxVIil+6N542iJM+sWlCUXzFKR+saKSskTWY1rDCjGNDbeqjXhrglHEjNQrrscq9BT7LCy8x1z1ZHizv6DYnVePz3AiMMgIJN0Z5NGZZG0LpsLllhaHhwdpR74KW1VbZzMtdeoPGsF3mFzn28uoQRjTNxAbBDxBRXyGyYMGiKsE6U6yEldFc0MlED6S4pm9bCTBeFg3VEdhYAmOXigKpZAF0pir3wAA4alJREFUaxGPN4js1B5ciuGDiCWkdYoCI3KxZRBpJL14q39KF9IRZUG2yHuR1BU4CnpE8BOlIrm80MTEliLkAIkhZui9NIzAJlbDv0RKjdHZaBIWxXNTpKtE4kz8iCUQSc0QKZEq/KPEHHjAgRHf9EvSq45pSb3lUd28iFm6PNIvMBoCO72RoUisjwRkyVgCiIir3JZAfLms3ApwNHbVYyYy3J43fLh61QWPq2HWr875zznvOeA9Y2rVcGEfe+hjH/vMxzqV074lnVKPOT6qG/r4DHtllLfk1xs6sMb1y/hP47cpzRMP2oVax7ddqoxLBAYLgSd0s4PVrmzNwCNQ3qQC3pVkJ62DdbxFM1uJMzyoQOgtSFl7UCk/wqcyEtc7F+XUYyYy3PSWb21e98bgdvQlKAtFCKKAzfi15bt7rvF72tr+iKHDIKJwUGqq7rUbKWt3ZkEOqvRn3ROPx9OmLrgdj1pmVZlN820CmlHHc5KC2V/QAoT+ljkB4ziJqnAWlGWhBlsfUpAPTstTuzM4YzG5W0JZ0qQvITLtgplpryb1e4fSiMeMv21WG0osXCcUMDPt9UQmmCHkdq6OqY455oBjZl71m6o/V38+9pBjZ55y/FP0ZXpAoC/l0MwZ4tH5u7RCpSi+1WyslGetT+sxxAbLHTssTWc9fqThAAEaf9riT9SuxFIo5/qFz0jbk+kTgYlEIOnORKI9ZeuaIVCnbP86dsx2d+4aTD9cfe2gsWus7q7UMdsEPugk5gd5yMbStk79HTvk2AnvKO7YPJPGXpoScB07nmySogTtXiCnNBvNuEvXk/HI5prduhmqnibCrXhyO7O3gAqWsZX+tTVLxiQCUw+BpDtTb0wnukfjJ2AmuifD9bXKhp6asWF13oXnVRf2lHZcE3Vqf+swPbzPwxyxyW8O1HbOd2qVPVO2asd2J/7OnZINQnynvvelbXCgiZmpNbBtXZzNOfYWb7NIw7edarB4U3ED5+HOg55FGAfi681ti8MTPo1V80XjT1YK557vlq+3DX3cy/AeJmMeWjym0Rd+xLLjZ+FzJlcZ/QKREacx4hrP160Um4FEYAojkHRnCg9udm3ECBSp0GNOwmOkWXosub/JipCrF2s3HPtIbEFnYu9EZfhc2zVm67jfeva+hPmDk+Xsnn0pbXSF8DbjZk7Vseaaa3YpwQnCToUJEPjUU7fQzXA2Rxf42tszGHlpYrhzMXhRxtiqLRJDwpNsm3d2ACLCAEq5Io29+qhMMQHbXme3HQ7ExmQfoovvlGONnBfg5EbO+/Vd+vzDeOtrti30rKhOrOY554AG7vNinDzJLZ3vuaMNuvQIW7K3X/YuafJRIjBlEEi6M2WGcpZ1pK0oneDWFM4xfo0pVbR2zaZ0h8qQ3GRV69OBjeEy4rw+B/HFHuxO7cRF7Ml37B5lg+3udo3Fbu1ITyfhEGq7/WMTO00DPRA5jTwJ0IjYxB47vNAmSgvbvjxqnAJQVTbc2fWGFjhcgDM1tQRpLV5GG/Sk5F7NB5zGgiqC5sPxSzas2XPOBKNYvvC2tctip5sEtuy17UJsGORcZRcbnYdtdzadOXTHh9y1HGVBHVAEXizoDuIiRl+c9KNAHEiZkslFWaIlUZpmc9LSJF/zwBftPLfXT6+1HJhO7nE8AYKI08gen0GlhnEqFbjiKCORGhBnMdtnp2RHPoLXgUDSOB8ZU7HLD51yoDMf8zi4vHSQWc1uRMnKoTsaj0XxlmNONSHV5WjEkr5toOzva/s0IxOBqYZAY6trXonAyBGo9n/iIxIjz92cg8wg3hxUSEA2P5vZvZaUJPVwiawHLIL9DdshXyJZc+KLkqRmiRRwML+UFvHCnYqNeOtja3Er/nr2cQoTt0RjvXBKGuKtKdLC3ceh0JRI2dr+EkOW6ybxXy/TAYMEPMH/29/+VjyIpHEEnyPvuLj66GYkdnZAqBzYXEh6kc5ylBJ1cLIAYiSMzYiP8XUogMg4OUmkU/5wKdv4HUrk5BsOuSJRGZv4SHekRI1inIHkgGMMieznICUl/QfigkBwEpeAZQebcV5i6ZTIciEQ4lEu37+UEs/QGE8pWpiN0CaQRmL6EkcKUbG4pbNBelAWnEzhDkEQCWpURgAg7ETREXvZdJNZimUQk4up5TDu8v2NRgOqyvlGUUv9V2n1gQucNdLhAsxMJWWpt8QEzr4rXmIEDKKKdNPYMVTFI32vw1K/hT/Gg1nWE9QLnJLhOgJTsoOzvFPlEPz4i57l7SkNmO7PI69EYCIR8KZmF2iqkUhwgDL5MdNdKk0ZR3pLSlnN1+0CzuMhRIlhQqVemjMMOUP4U6lHtoYd1me/DAYQR/pKQFxZZJO+JDcHi/jCc2Qk8xhEyFRn7okhaAlI0pQAdp6yvsfWG1oQJ/NqEocP7w7LfYk5Z1jlM2o4rA+ZiIZRMDhpmm5DJK9VBxBLSfFA2tGm+Fy5rfJRde+/1FQ0DTgHwak9yFyc/aMuspxIpvOIJnG2pZXxXSR8RYOlBC+pz5SjDVx6HYCEzagaaXCQEimuYUwwoSOhDKOEoClxWLNTehnU6FSwHB7fzDfaoO8OVKTCoQjBdXBK2hQpHahN6+McZFCDzhnBOEecbd3aTYRGJMxpj6iLoGrIxJD0uLXmKTlyqZ12h7HJLRMbNQnSg8UqPyIjmV9zBtmKk/oUYhDZpBxiCbHwsHH6Yv377SVj94C24VjONaCYqR9oFKQEG+ueXTPYsLRcS/wpdU+cTxOB2Q2BpDuz24iPV38JMG4N1twWzaUOkWSkyJCO4gkPwpJ+3mrYJwWC9xDSRKCzjMOWUbLzWiBuqRMUIhJNkZc5Iz6FGEcDl8QlYLVKsUExYI2rSdrAbYJdQAKS2KLZcX/EZEk/xoAySWhWIQv6KEp/fUFaJGaAnQjQT3hkLwwRSL7y82D7YLnAbyhgqLVoL0h3VECbpeSXSl/C0kEdAiUeHiJ1RErpleNDDSSryDDEUCQ421B2XIoMphpxS/WiBIHILnGPF8Mc0xVtihYiXow4YfXAaTAGBUIV2dI7dIqBiY5EH/nhGnrEiJwO0ww7C51KfAVJGo3XR2Oq151agjrIi8xJgNMgT7oQidUYRZW8zq7k74IA4TpNj0qa1oAWlgYos76zCblE2sI7B1XFfjAhaOBk3GIUZQgoVIAjDJOgOxqMwbMJIqNKoBgTDwr+OkZHSjUqRwwkOUuJ9+cAWLMamWMIg3P8gfD1wZJjrhrNaDyyhZ3TSvpbwKUonMQbCISG+s1RT3gkZ/NIjPhqGFeeMBdGpF8MUgvLrYBmw9ZfSv27V/UEGU4EphgC6bszxQZ01nTHq5Mgj00r3sgMQNrh5f62t72NVKbSoIEIPwZpaB1IR94SRepEYvYC/gdkRvRBStntW1EOBYD1rtW25T7FCbpDFeSXs0LZ2FJ6TmZY0GNFDDGEE8LBfmE5LoF4JMCtNjRtkynZRxogWvAbgjzULbKrUasIJ7IN99IvdIfHBisJqalTdB7EVUhovMeBfshNWY7TkVDJELokrr6X9ui+YhG+IB8RrzRSGZKUDZQfHhGcVE2ICIsP8Uy4juicGCou5ImcptxSY6m9BKhJHJCNl2AwCE29hSVNU4DAJpUpe2CO7oTAlgYBovVhgqGaovfGPJQpnhQn9emHzJziydtUZtzS9CiWLxGrVtsEJRLmaIpmY2PBJ2hu3DLogJquyJw0c8CLXvtwmG+SoAKYpRLwY3vTkBIKPLY/gygN3gwogJuEWCm4sHbNpmTiVYPimAahN9IvQ4kBozimt6liREwGLtI6jiVT5zD5haO0yWlM6b0K+P6atJN6CdRBxTRJyf5ANA/p1J36OkEHV1pppdLxTgEKM8o2k6RTgoxPBKYYAkl3ptiAzprusLN4azuNV/WkVDSCCkeArQETinWwW5KApp3xyIo5kvn1gqbdwQCK7BSgReCPSWtiWUysEgkkCnU9uU7DIRelBZ5RCqkHyEhEh2ygR8E2SI6Qo4RE72qAeoEjDas6/HlJULITg1ECPhSR9FhYDi5SJ3ylilAGkH8UVHikbpJ2ntrMLAshTUqBkfRVDrqAHJCFcEawqJrUyGeWhFYFfBibiowsVZSAkmVx65fIJ85ZFSneMCd6JkIaOyTFQ1VAh8GupHYin5mP5YXajB2K8cuHMuxIim+T0S0xu1BdSE8BIy9ao6fUWgYOreFp5EOthLSeap5h9WVveg6EgK7IbGFs0il2JeoHIJDoatEvE4x4xn3jhO7ohZZoVelRp4DSTEgDYT+ULJKZcoiICYZJcyFCd0QiEAxeWqid+EqURmVi1mGuaAQrFeZqRuGyGI9vlmkM3DAzPVUyzRwfal1DWQIQhbDTGSBDRmUFNzE6GIW3/jZ5JSNertZk2qAvJR6Smm2SaAwfuBIfgSZag39T9vBOK31sSp+3icDUQyDpztQb01nQI6914plgplPxoo8WkM0U9V7uFvSlTUQXIYrKlJi2AU4hXF5C4aFAEjfsQcS/BXFkISObvG1KURa7tEq+QS2G8CDYmjT5JWVfAqHXKdodjWRcoBuIwjVSl8M1h4KBiCUySUpuFqQsJx7MDHGRWAm0BZgBNkBpxBJEDQBSSh3O1Agf0kY1QhskMfHsEV2C8hl0wvYhjFHRWNB28FYm4xFEpKRTN0nHkLvEsIxw1jzCEhdBaxSCaJKUWCOSQY/iMqyoQMhslIiIZVlTL60bYU+iY2A8bxDWsJUgCuEvhQdQhxhZBqOgfVpFyUcRhZAhTNFIaQCIlyBJwUuovvQOFEizq+SN9KS7bVCdOljiYRhe6iWG1clVbiOAQ7T6AIlsqz3SMFdkLAyDHjFUiU0lc6lpiunvLd6GKVK80TDNtORQc4byaaaJM0EiMDUQSLozNcZxFveCLCRiySTiMJxwNYhVheQLdmLpH24cZBWBKg05yoFGGi9o4qSpA5QTNAGUBMQebRAxb3EvDeoT2ghhhKaL3oKIVT55xuZFf0Ccy2IFjDSQpvQT1CQIk5KpQIRFUjAQVBbrlunUHpbvfqXsrjyQC9tg0aDkQOywK/wAfbFfGglgxFEjSwrnCYt+QFFU0GMxxuE6moTHaIO+oEcoAvUG5QGDIKqHryAryASspOSnokmx5YfSxU4ohg9KBY0EI0aFH0RTNYYhz5Et4ML5qFh2PGBHJbRedk2HTy6mJTG1kLHQCy5WxktpJKhfcpFupjW7mKYTgSnPNLg1JbbhinjMuJ6A7aZ+K6wNRS/iVsOCXSGCrkhM58eKh8Uar3BGbiqk6VZKUxTTaoqfMrf8e3gOmcC96C9B6poyfc+OJAK9IJB0pxeUMs1MEGDMwics+ikqUBwS3VdCxbCnWBbTB1iyE6I0FuxWNPOsVIScr4raiEsDJLsFOi7CvwfF4XrJoIA34E+8IrAHVgwaEY1gcKEeQKHoDyQgnsO7orV9kjm5hFWLpqe83DEbztE8WykJrPXRDlQDZ8JImG9EEorEPLqjSTZMkdwaL7K1/BJD3FpYl1sBHMJVYqg9ShgHKuEItMaIRwrDEaqemP4AC4kYBC4CwQLrySKMCbla45tiUE9Xl8i2ioqm9LPklvIPUTYNELJeGoCShgqtl8STMQ2W04XoNJ1H1XQ7GfubbU4ERopA0p2RIpbp2yDAOMUlloaA7MQVwlMS1RCDdlia0+5wcY2c9t3wFBbjQilEIhxoEJdVdISuAuEQiSpZi3MlkZ3BIvLSYdD3oC8UAAopPCae1n/pJGKDT2wMjkdqiSN26ilJ9NZITKgeue8B+9az1MMpOepoTFiYjYxKzIC2qgbbtmG/x/bb7/j92j6a8pFdTsic8n3PDiYCBYFpBFK5yUAi0DsCKeZ7xypTJgKJwEAhkBRw/IaDPj583ej7OemPX0UjLTnNtyNFLNMnAolAIpAIJAKJwCRDII1Zk2zABqe5uTwanLHIliQCiUAikAh0RyC1O93xyaeJQCKQCCQCiUAiMOkRSLoz6YcwO5AIJAKJQCKQCCQC3RFIutMdn3yaCCQCiUAikAgkApMegaQ7k34IswOJQCKQCCQCiUAi0B2BpDvd8cmniUAikAgkAolAIjDpEUi6M+mHMDuQCCQCiUAikAgkAt0RSLrTHZ98mggkAolAIpAIJAKTHoGkO5N+CLMDiUAikAgkAolAItAdgaQ73fHJp4lAIpAIJAKJQCIw6RFIujPphzA7kAgkAolAIpAIJALdEUi60x2ffJoIJAKJQCKQCCQCkx6BpDuTfgizA4lAIpAIJAKJQCLQHYGkO93xyaeJQCKQCCQCiUAiMOkRSLoz6YcwO5AIJAKJQCKQCCQC3RFIutMdn3yaCCQCiUAikAgkApMegaQ7k34IswOJQCKQCCQCiUAi0B2BpDvd8cmniUAikAgkAolAIjDpEUi6M+mHMDuQCCQCiUAikAgkAt0RSLrTHZ98mggkAolAIpAIJAKTHoGkO5N+CLMDiUAikAgkAolAItAdgaQ73fHJp4lAIpAIJAKJQCIw6RFIujPphzA7kAgkAolAIpAIJALdEUi60x2ffJoIJAKJQCKQCCQCkx6BpDuTfgizA4lAIpAIJAKJQCLQHYGkO93xyaeJQCKQCCQCiUAiMOkRSLoz6YcwO5AIJAKJQCKQCCQC3RFIutMdn3yaCCQCiUAikAgkApMegaQ7k34IswOJQCKQCCQCiUAi0B2BpDvd8cmniUAzApffevkrvv2KF371hYf+5tB4tuhnFt3n7H3WP2r9Vb6+ysl/O1nkly/58qrfWHW1b6x25tVnPu/w511757UiNzl2kz3O2EPg3GvO3e7E7W5/4PYdTtpho6M3Wu87611y4yWlqJ1P2fmwiw+L2/xNBBKBRCAR6AsCSXf6AuOYCvnMZxrZL7+8+trXxlROZp4YBA6/5PCDNjro/J3P/9yvPhc1PvToQ0+b/2nn7XTeyducvMfpDUJz4HkHSnD8lscf++djN33upudfe/5jQ4/596eb/+Sp29c89zUfOvNDu79897Peetaxbzp2t5/uFkU9+OiD275w2/e9/H1xm7+JQCKQCCQCfUFgzr6UkoWMBQF056MfrVZeufEvr8FH4OCNDz7hLyeceuWpdz14V7QWj9n5JTsLL/+U5e988E6BzVbY7K0nv/U9L33P0W88+vSrTj/pipNWefoqqy656qW3XHr3Q3ejO+9c450UQlfddlWUcO/D9z469Ogc0+bwb+PlN47I/E0EEoFEIBHoFwKp3Rk9krfcUm2+ebXuutVOO1WLLjqjnBJwH+Hbb6922KHaaKNqvfWqS4ZNFl/+crXqqtVqq1Vnnll9/OPVPfdUr351I3ukv/nmarPNGon9Ckf8PvtU669frbJKdXLDVJLXrERgqx9spfrdX7b79Gkz/nzmnmPuReddNNo0rZomcNQWR+255p5f++3XWKY2ePYGv73xtxddf9ErnvmKNZdZkyWLCufpCzz9kcceOWOHM87d6dyz33b2kZsfiejIOOf0OUuxUWD+JgKJQCKQCIwdgaQ7o8fwgx+sttmmuuCCaostqgce6FjOhz5U7b57ddZZ1bHHVrsNmywOPLA6//zq+OMbMQccUC24YIP3lGuvvarttmsk8KsK10MPVU97WnXeeQ2us0fDVJLXrETgdzf9buuVt37gkQewlmhHE0Gh4OHHs9ayax3zpmNO+8dp880535ILLknBs84z18F4Dvn1Ies/a30Z11l2nXD0of456MKDZmWXsu5EIBFIBKY6AmnMGv0In3tudcQRjeyve101R2Nl3nw99lgj5uc/r66aYbKo7r23evTRhtrmrW+t3vOe6uijm7O4V+y3v92I33rrhpHLpZydG6aSavnlqzsbppK8ZiUCTFRrH7k24xSNDsYzzxzzNLVmkXkWed2Kr1vziDUZufZdb19Pue986w/fWmy+xWh3Lrj2ggM3PFDkoZseymXn67/7Oo3Ot17/raZC8jYRSAQSgUSgjwhMGxoa6mNxs1VRT396dd111TzzNLQv7FD33dfo/cILV3fd1QjccUe15JINrc9SS1X/+lc177wN1nLhhQ0rlYvy5otfrBZZpPrOdxp5JXZF4BnPaKRX7IMPNvjNjTc+UWZJ00id17ghMO2AhkEqr0QgEZiSCAx9PKXeOA7sueeeu+GGG6rgjDPO2GSTTcaxphEWncasEQJWS7722tUppzTu2ZgKacRg7LFyHXdcNW1YaK6zzgyHm9NPrw46qKGe4YWz1lrVMcdUp53WSIkGhR6ocVNV5smPftQI+N1gg0Zgeo5SA4a8EoFEIBFIBBKBUSKQxqxRAifbIYdUb3tbdfjhFd5DGRPXYYc1jFBLLFG97GUzIg89tOGy8/WvV3POWX3rWw2NDuPXmms2KM6+DUNHw9mZy/Opp84o4XOfq3bZpfrGN6oFFphh1ZrxIP8zsQjkEnBi8R6X2sZbUdc0SfpSXb1MBcbthRdeeM8992ywwQbzUhTXrr/97W/PfOYz559//lrcTIKlzHq6tpElgarf8pa3nHXWWawBW2yxxVFHHTXPPPPUs9TDJVd/A1QFhx9++KWXXvqHP/xh8cUXH2nhp5xyyt57733FNleMNGOmnzIIJN3pNpShnumWYvgZb2VXPfFf/9pwwWmKdPuc5zQiy8WF2b+4Inu9EPEMW/WnreEZj/M/PSNQ9HAzzeENPtM045egLvOilnFqz4RVNH5YtZZc71Q9/NBDD/33v/+dc845n/a0p00fs9a07YjUq9Owxx57bL/99vvTn/506KGHrrDCCq1NbYppLfO2227bd999f/jDH95666033HDD0ksvXbL885//XG+99XbeeefPfvazJbJt4OGHH9YSHKXt05lGXnDBBT/96U+POeaY+eab7+67777vvvtGVNT555+vAa961atmWlGXBJtuuulTn/rUl7/85Y/yf3z8euCBB+aaa6455phDBCp25513GtaFF174rrvu0t9FFllk2vArVfwGG2xgCDb9zaaPZ83/znYIJN2Z7YY8O9wjAk1yq8dcfUnWKvOi2L43acIqGiksjzzyyPHHH//KV75ymWWWGWnejp0aGnr3u999xx13IA2E3y677LLiiiuOtPBe0iMo11xzzWqOmqiqv/71r5dddtnPfvazffbZpxe601r+oosuetBBB2277baYTevTjTbaCHVrjW+K+eQnP/mMZzzjne98Z1N8j7f4ipTPetazFlhggVVWWSXoRdu81157rc6iIMgHaiLxRRdd9J3vfOeEE0743Oc+h4uI33HHHTGSf/3rXxQ2BtoQv/GNbzQoFDDKF4OV4jTo0Qte8AK1XHXVVb/4xS9UKlAq/cc//oGE/ehHP3rhC1+oX895znMQ2aWWWkppH//4xz/84Q9jPP/+978xpCuuuAJ6a6+99nE8DPYqBWRgtkMg6c7Mh7x3fcDMy5rVKSx1Jkt3hldlo2ltpz5GgbN6BGZl/cTwkUceSdPgt8kmMiub1a7uAw888BOf+MTWW2/9/e9/v93z0cR99KMf/fa3v33xxRcvu+yyv/nNb8YJAaIakVpiiSVId5J75ZVXPuKII9xSM1CK3H777XX1zE033XT//fczRZHTnboU6go8oCkBDvGlL31pueWWe8c73lF/dPbZZ3/wgx9U6emnn/7+979fxm984xvARFZ0n5alekM9eXP4zW9+89VXX621n/nMZ149fCAYpvJ1xviqUpoe/d///d9WWzWOnmq9/vOf/7z1rW9F79Ad4QMOOADdoQc66aSTGJJWWmklyhi55p57bs14/etfj3p+61vfUuyDDz6oXjxJm5dffvmvfe1rf/nLX1772tcyXbGjbb755lD65je/KVwq/eUvf/mpT30KQ9LfU089dY899sAL0bIddthBIT/+8Y9VIYZeR8mGHsdCjN773/eWEjIwuyGQdGfmIz6pxeRkITczH4YRppjIUbPE5E9gWfkepwsM8PWGN7yBC4gGrrvuuu9617v61VKCZ9VVV7WMHl2BJBYpuI0zrGoXyfSBD3xg1113rcV1DFIYeBZmi46Jqurvf/+7pwQ2bkGdIPDpT3+adWbPPfckmw855JDnP//5b+OOV9lceReyIlkMKNlpfOkbaJvoJHAUWRZaaKG2dfFxkd4jni5cTHARpA1lOfroo2l6rrzySooH2gj1kuX4hKrNHNoLbKBtgZ0in/3sZ2MG6sIVShryfvfddyfgKYQ04ENO/aoqKdnv6D8Mk3r/WP2xpG8KnHnmmZdffrl5or+ve93raF90mWpEZyFmx82CCy7ISNSUq9yqDpXBqsW85jWvoVARWH311b/85S8jPRRRJSVSqEAUhIINU6G20ULU9ilPeQquAxYqq7322svIgtr0oCIyHIxTpYSXvOQlDHwUPH/+859f+tKXisex1KiFtGjr2CEyfLEAKk1F7oxvdUFE5+/siEDu+Zn5qHuXTtJ/M+/bhKS4/vrrY1U36tqsYn/u/KLOl3WkHY/1xZ+0TaPWOXf7J4SE9+OSSy5JONXdBZpS8xX9whe+YOlJwDQ9antLvNGvtH003pEhccngxhK/60X58dvf/hYhIN1//etflwYbSre///3vCyBW0lbh9BmEt1yIQhTMqCElqRnS8cYbb/SUZCL5nvvc5xarxMYbb7z99tvvtNNOtBTkmUJkl5F+grS2+i/NJCClpCZhJNIM8TRADDRg32yzzdZYYw1CrhRbcpUAlYMGuEVx3v72t5OCwtQJ+++/v/ZoAN6APYikyaCSOfHEEw8++GBOM2LEf/WrXyWJCebTTjuN4qGLVQiPRBH09OSTT/7KV77CIgNtIKAaNC5UJmgcXYVi6VpM7P/9738i119/fTxDZO+Xvb6UFkH1IheeoWFoHxUL61VoWTzyp4E94ECf//zngdalCnTHAGkPfQkiErxN+qCSSJtAF0sWjugvnfLMuGhesBADR7XTpEszr4zvRz7yEQ2+7rrrMJVOrTIJETVzoyTQDDobjUSUGfjYqsojgRe96EUYUonR2ptvvrkLRSspMzDlEUi6MwWH2BvQO6J7x4graeLqktLyzqvTG/yLjgka1WUpvMEGG3g3jSp3I9O9997rtVhfwrYW5d16zjnn0BAUMdyaZqQx3AtkIR54Ffy///f/OmW3KCeeXaSmN3s9WQxE/VWLDWgkNb5OCZf0At7gIQXrJbQNk9CUEHaplKdkMCpAkUB2lsgYO+tay+WIRCkQOOvvuows6euBtdZay0KZmcDKWMBC39NbbrlFwC1uwZIS6T/2sY8ZGnLRalsu/EY8xPRRSlfDYWJYtHvKtEHk4xb0B9KI594BCs6873vf+0ippzvMqqrIS3odjIHpx21cHHJVhNdqkmYQ7eaVBHxiZHzve9+L6zDSPZ68+b+k4Jr2Q1aV9HgGzked8Ktf/UoDmHs0Em2l9NIYpW255ZY0MRpAWcIdmPCmocHAtttuO+ATvcG3musYvudTIq/qXvziF1NswDwmAAplhuDQwEca8K3DDjvMwMUvEjyWv5FoCQXbD37wAxNJRSig/VNRtaUCkd+FppSOYBI669YkodGZ6TwpGSNwySWXeFH4a2U7Q60sA6Io/C/+fjG/IMQSeDOgVgxtlFvcn6XUWjXW/16QJ+OOGDFReVmZPJJ997vf9QtncxuJNKWNmhiXnnoPGDUZg9MzFFICmW/ctjQpkuXv7IlA0p0pOO7e5lai1tOd+ubdalXkLe/96P3rtm1KLxF7MSyevJIsdtumqUfSdbcur4lwi7Mi1+vpewlrA+sAtsF+X09v5VrXGOkOkwolBKV3PZmuafkf/9hRe19P3BRmTwEOucuiAQELcQmoH5iueDP4LZoM8VQLdADeyKUQMs863rLVm5o6JOINDZQU65FORWs1m0aBjcMS36u5lNAasPg2st7pAjQHRUVB7U+ehUsmh00ZrZghxnRiGhjEsC+0FtgpBmLEHqlPdyJvAIjBuAgkJaNQoUujBmCkwPY0hgAzEPQ6OkI3QJnEadSvlPQQoTtBjJg8iDTre7XjLn4t8ZEMCNCluSX/3IKuLm6xNyyH0DIciIi2YSfwlOwVr3gFoQjSn/zkJ5161CmeUMTeoFoSYMzRKnwXGTJ1ESN4ajM2UJJ1CmiPsaDnaJsgStBTf3rPe97zsCjdIfUpycyTtllmGgmNSANn4FNEmYdombEL9q8X6B0matp0/0M2RlRfaC4WSxmGTCgZscALdR85M3xN2pR68yi0LI3wD3vj6eGKaza2geUbMrur8Fp/1IggP2IpX/ayl3EqMnCoKiWQWiRQZuiTDDfd4Zve9CazS8lYJm2ZvzvvLjySBsufp7/x3/3ud/6C9BrD492MvO62226hzEOgzX+0WLO7L5nqHcnw1ETACyWvTgiwhwxvbxwi6ixQWKO97nkAdEo/TvFW1d4FvRfu3eRsjGFPheZM0R2LJIseLz4LSss4UirSeV8QllaH9WxWvaY+iRKRXqBUCKwMbkkCYW8oYeTD69s7yMuXbFCOlFbwJJn3OJFZyiRgiH8KdmLSuk28LN6DHCT5T8CZ6kIbAnxvWLWrpWTHn7zLVKSPXs1Rezyl4fBmjD7Gr/e77EwtEkSBpZwugWr/yj9Lea2KZCQiyS2Me3EL4GkhQFbpYyTwJuXioG1x69drWgf5Fui+dzeOIlJHtOe8884ryQRQBKUJSEzSw0Tt9QQRFkmfITHYGT7IS+9xjygt6DYENIZvJmYmDEB8yMj6VaNFfxTil6us+Ry3nSryFCmJ8iNl2DUITqwi9hzhlx4FkzPQkcwva5EauVBQDyAKcLB2F08EkliRzEAbGmELcYn5nEZ8+SW58QbGpohBLiXDnNyS6MIksbAEkkksTEVEfArUO1UPE7oyopjSlAukZlG55U3M7uMvXZuBTPyjZSKpRvxZUVeQr0xahLQs9cKjBDH4pcnpohaiw2AOC1qMF0oTvlMEv7CRogGiJ8N4kAPzpLXMqMKfajAPraXI1AwpjSmNmh6hMviZjWzYgJmGPXD+BbvGm5ZSuugCjYWrQew6zK5IGUomtCxqEUmtpRbzLTaf61GkrJcTYYzKGNG+6JS/3Ejm1/TQPNOpDKhXjRklxvrBywQXkQxp/t73vmfHuzCCIkvTX0opcNQB7aw3e9TlZMYuCFCwmTAuS5QuySb+0ZzRrPztgoCtHF5wIdu8dyxBuiTu+yMvd68PKgGTw2s31txqEbaU8Q4iZUulpheWI5JEjOVReVQPoAiWR8PMoOGX4CUYT5Eq7IQpwXylkqlnKWGKDazCy9erzQqSbLMywwKh5G0rFy6F+lh5K98aV6QXn5dvaafTL6xuCQyUy5rP4kzvbNyVl+TmSqm/w4akw1RKuDYp4dEOHbd088ZkvkGeMLZonuVsyNrSWq4h3rwh50rkKAKkBRZCeBgOZWozbkHeoEHhDeqtTbNVkDQQ3uyEOuZnpIwdRUvoDJpq539A5JMuXvSy606oPZqSxa0us4kQ8Jaw1ruhKqin5CFB00N+kxlAxkWafCbqiWcaruvPohz6FRtz9L2pakStjC8y5CmmaKoYO3o48gz7MSFbrXUxS8MEBkOKrnAWbmqbek0nnUKpQ4NIgSQNcQgxRMSgmIGQacpYbrEQQ+AWcwILgxTOYaaZn7qJFGJyRtP0M3CqC09ks1RKQ6/LBDB5bOIhVaw2nbaM+QvFPv0pycuihJHou9UCdo7hmeSAisZj7aa9vzWwUEggx6W1TQEz3N8pjYi5pLX+cCQQqTT+Mf7Y4YyiIbsS+Ov2ay7pS/nToCZB+uUC+Lyfmbep/Lh9YgP//pWT3ve6e6+9Dtir8WjBBkW4zf+GrwMZeA84MML13yeyRyxSekn9+XD46qr67ZMjxbReM5ShVWXEZojO1kQZkwiMEIGJZ1iTqMbQB3iZAtVLVsu9671Vvfi8Xq1OxNDzE9KxMnNrncqZAxvw9vRei85yOIhIbz0BrzbxdLY4AXlPQkcywoyBw/JdaWQGySqe4FS7N5fXrnUn6SgSP/Aapfm3YlZmqGeooL31OEZYYFmHeZNqf9MVMXQt+AdzA+JC8e5VLpnucK3wNqdat17k4lDyonpetXFLsaE9xK1bOmTLTZwjHhFI0eaSUUDh6tKpiFQdeWD3KT2HFzd/DotyjwBLsQFYkZa8ehHgiyT/Im/8UgJpeTgkWqmTduWpfhFF0ce2fW+NLHnrgVgC1rU7ZJVVLyGn70YECAQtqak7JSOSQUsft56SSUwtWiiXW/6tHoV2h8VKmJDTF2oY2JotkplLxq6Ldsesw1MJ3RCQ3D6UYwrFFlxT1CSJRTlgDQ29oAmpzYiXlOQilQP1vgU6MU8p0nalKxJ9oQYwjWk40C95XWxYzBNaa+6ZutR+Io2vcSdcRZLi/DZE2nis+8YC0eT8RL0hElPREv4TwppnSuDBGCS9FwuFWURthpt6qmSdUpfsXMdCnaDLRsHEkxhFADW5jqDQi1A/IH8CWiJ7vVMlbKQAS7mCc1C0mOdSilGUPxxEyliIictgiXeF1goPk8ZfmRhDSa3lDxDlLYU/nu+Jqv31+eso8chW1FhiOgWaymy67ZRrRPHjUeaIGjALE+v77Nz9iUHen4m/dJdX5cTU2GMtqd2Jcen2GwtQq1VchD4DpfDuI/DsdJAtFnyhr/ZytOZjpoE+UUTeSIABWFDKTjBgEoSoV7YSJCD2vPdJdDKb1Pf2t8qU2OJS3mGDTmNXhWUfimAlWlpp7ahY0p004mJCMUALQpGgcAJDMktq8qCkbwqQZMSqjSdoB40xSUBUqJqkJHetI4VjwR0ZqcdjZexWdaU0ko8biiwRQyVDM1SeRsBCXwe1M26tO4kNvaaCEmNnKc8AAaJLq4htYY1xK+CyPNU70jrSi9E8A4EYaaEFOsyHEzZ+yE5i+MkbNcrD0QSMo2woC3MbLQ4cMEJuFuQrJkHVhwGEdy21BEFoVpDQGk+WG3EMCQdSAj8e1IFiBkSyIHBi0AijoCO6IxluxMMUM24s/ddo31qFq8KpJyAlUGkRUGS6Lto1NcpDC6U0AXyXSNY2tg9cmegVaYaoQgAFcYV9ym3r5T1llpp7phNKYZSlQbVpPjRAmFIh6IvxZd+hZsClzAQz0FN7jKm+zGcahbB8iWSyYeKUWNgpwCg16i9M6WWG+xPAmfxxiUF0IGPo9Q6Y8QdIvcQ1JCaGSiVz2T4WAb9GpIRbA6BwNcVjTk0xcWuk6vH4d9xik/X4LmFTxVUS+Pt1ldsRBZq1JiPKnIkTgUTgcQTmfDyQ/+2IgNc9C5GXNa5D7loI8i9BPqz55KEl5nPHCC2MN5AoYqybsRlKkYi0kiaEsBN0h8+mt6dyPBIOUhJFEVqsZuzuFD/CRIg0rRf9h+WpjGQkAU/GBK9Cpyx/W9O3xiAQXtyEsY4QaQQ5WYuRoFASk0MoBUnTmlEMlZIVfGjyiShrYgLb0twj/IMHK6DC3SeEGflkaVvkE58GQlrLMS1LbeIqJDGRxuShKKRHYpQoamefstAvLTEQ5DqFlnglhydEeWqAgFxuBYh8mBgR6evxvYSpW5AD4hmx0C+bjORCEbANAwp/KqhgD+x3SCrzB5qIwlJIEOHYpJ0jHqHFEI7D5Uh0Jh7xZohIE4C2RnqKDTFGELVCGRf94qJtW8jUSMEDdqOD/wW5VKbhMPfgFu2RF11QILpmvKCKQYqUnpMEqMVDj2qw+lPbeqpPzfWpauPqV4/9qmHI+Fu17QFPGEyrpwxnuara4YAdnsi8QFX5d2X1lgPe8kTkEtVXf/rV6qdPRFRzVAceemDtPoMzQWDo4w3CnVcikAiMHYGkOzPHkP4foaH35qRieU0/IY/1rjU6NTulPVVNOA0gRgw3lqoWpsz2sfxFR1AK60grV2qbEEihk+C5udhii1kWB02hIaCuoPlglWDcYfIvOycJQpX6JcMISGtoWhkyWEViyFpraGKPcFUCYaypFBK0iW27xw0T4yG/6SckIJu1jVultTh1C22/dbkyo0bCHrsiTclaWyGQIaoFK2kUR0WsHqQm1ZTsxLYmqRcnwMDIdQoPpIqqQBoynsKD+QyB8IiaRPmORAvNARiVxorHtKf7MI+WA5OtkI6BS4oYpIGaBGKQV4Vdr7H09wjHMkYUVPE9+ciOckE4aFzE9P4LnGhkPYvW1jUK8QgUrnoyYWwVd2mKdEvXEtjWHzHP1W87hQ1x25Soj6ueq65mK4/MluCg9ZSt4SkmYidYOzLB1TUNn1cE1lv+KJqeTtitZRg+7aKTC43dhFWdFSUCnRBIutMJmSfiaRrociypeQ+U2Hih0PRYZ3PusYYmpFEZvAeVocuhhODb4Re3oN6g9SHamVpE+qUYoFBhzifFBazykQyaCbwHEeGjoyLajqjO0p+Ng06IEshKnRkCL2ENYfqxXzdMUVKSr+xfeAM+hGOFfS1KaPrVTqRNI9E4dgfMTAJbebksUFN5REWBNonUNftayXhZ8AkWCrnwHlSJCgq9O/bYY0l61UmsL15twcPQPjESQEZRNDQMcKGF0hGmMXhKUI5JpdNSDjCRPBQKjMP6iMZ+EI3xiLMOxYan/EJk9E5vcsLFpdTFYdPTcomhcxrd27+V65RiZ1Vg1orSWdXrsdRbqNs4QTdOxTZ1eWJqaaq0v7dlIPpbbJaWCPSOQEOt3Xvq2S3ltGmNHl900a/DkEHEIhP8sEhxtgybh9EdVIBoZ8VgvIiDyGhWLKNpICxuuDvIQszTMVjxiFQg0kDNQ6izWLGAyEgq87GgMqEOwQNURAdAsUG6Sy8XBQktjnhZsBmRYdJSeJAVMS6EjHcFGiSvW+1vGt7WmOF8g/gT4Ef76XKwJZSReqNTW6mgEClqpOhja0/rBXYqJOIHQbqkeOg+RiN66i03/RPTP3jPBy0YOAb5a61nt3XA351zseuRsyps7rUOfdvI1hZaq9CwUoUOe/q3Pm+OsZhhzmYa9kbygorHdMw0tTDxCioZLNKoXa1kYi96ie8S8MfoZRWe8j22v0tp/XoUf9qtCPer/CwHAlwIiDMBYotlY3Aw6Sg8BqeJs7wluAhtCr0FP1NalngL4ByMHQgNzQEWwoaC4tj6S/tCxRJSmTHLXhs6GwdsKCE6QgfDSwbdoeOxuUP2snuWK2W4+zR1Wcn8W5si6TbCV7oer22tkfUEwiH1myIH/BbsGE8XrqP9IB3wXoyoefFe7iVLeXf3nqWXYmd5mtIvLRlp1+p5ZQ9bMCUrP2ukud41ylEmVH7Z9chJGmYH13LG3x7bzxMOs6HFLFxHRtplLuFOZvLGU5TXVIlkO0Z3gIlOycLMTfPqDWbhVxyxmaG9GL2IKMWV0GNLMlkiMAEIJN2ZOci8a/nEtKarS9/4w+YwYWnlYBgGLPt30BRHa3h38JPluawExhpewBx1ozQJWosd15gmZc+41jX2wgszQyhnAVYfH5Pi0+ueOZIw4O0U1smxA9JaQhMPaBLzrel7j7GLykRlM6VWtFJnT2zLxXsvsHtKXue0pEy6YRht6pe8vXetNW/8qXIsU0tQn9IYplte800D5O+UbdpixlKneD7xLWMgts4JbzPja2FjZlIdUbUS8FYyUZGUThyQnXZWZLwcpPcSwEiYZW3aikjt4QLohB4ubt4eSisNawpQXtrooEDjYie8lRLrLeWxtxPVlNUUf/w4+sio2T6JxukabzbrBMkcEyCLJlH9agMjuPJpTLmXGVZFleq8uPTCIQIWVLof8WrUPC33Z6gQSmWqaH54mKK+xwEEZog+MluzjyNJ0qTpoKCagYFAwIzMqxMC3rH5b4oh0Gms6/HV/n04nKNsKHMuZb3w/oY1tRRYD5fIUQfiOE30XQnEP5YwoqJkIRddAvWMTLqtRYVjHN8sFt5I3NSXuKVL4ABXjmBm5LW0QMiYWniS0a2S6LI35S0FSk+u4welPdQbrJ9exPhcieTBZnchniqeURhp8IhGNvbW2dJII6ILseVeGilZbdAXnnBSspfZXchIpKnoSzSJe7vN7ZY9OIGUyJCUTvCiVWIkoixBIyiGRXZqPLUKMxMFFTqIZjGms7DzS5PF7kiKYb53wngGX34BW/CY7ShasFVZpLFXgOEbTZEgmiqZbYbUogLlcgySFsZRSSUShXLeQbkVsM0CGaJ2tR0ShYpJzpQGsUhm8wReZeHntm2n6qVNWFhLBqcxE9brCa5oYM/dme7PNa9EIBHoOwI0/+wmhJzl76gLZwy1dm8qgZBjHRfvbL22JYcTGM2B85qlRAhKMk2y4mfTIQ4j0sFRYqzyreCpHq3gcRTinHpDAgc4iSeJSW6CX6V6RDlBKIYvPLmOByiQ4OSI5pYSwr53Yo/KgVc7AcwRRFHYBrlOIuIWZLNbkbiFZPQEYhTSxTVEOyXzJrWtD+eQmOccNoYkkbh6SgVLUxKdavvLaqxq9Ks8JbBRKN1BwkqkfXMc8HVfZzUPmB6plFXalgX7Cu1DhIkdBjYN0P04OIoG1wmH3O2ljEMgufE5VCLOVBQJXsggW6gGbJ1BINIA8WzgXI8ZQMP5DiI7XfIaBfwMw6N3oTvR8VDSGLXYrigvHYzhE7AFT7/odaijbAsVaQRdEI4juzpVZBtBUL16AhljPpRIMdpDFaQKpM1VHpWAdtZV4CU+A4nALEEg6U432C1L8t8UQ6DbeLc8IwXJeHI9ZLMA5kEVYXFMeRPHC0Um6ye79G2ss4yOGKKU7GHj8EgMeUPIMTcQyTgHeSlg0RykAeHwiD5AJA1HlMDRD1fYYIMNlBwxrGNsFg4O4Akonukn4pt+CSFP5WVlkNI1fCpBRdPAYISCkNMcVMlyGXEmh/7Z/UfuKpyOhCTTzTjBiLDXTboEKR20rVj2C1vwSF/SWiShTougSTbZOU3Kol+lNAoqQkE4znMmU6aUDLvajzf4/CRVAZWMSIhxsPV9Ry4jdvA1ETsJyqVwVaNfMuIHuAWGwT6lU/Lihc5z4k1S0rcNYGbBBuIpbzyGJJqhUq+e4ijIBIuVbZVkOUIjMo48oJuhjKGJAQ5ZTqdCERLmKlQviBFknCJBj0Knoj0SqwuBIPi1XO14Es4XkfYWOHcKDwMCMte2zRHJ8ISIaA9aGXs2zSt9j6coVHAUpi7DF5HqCr/AwvAkMzTmWFt2ErlMBk2NeW5yRl76Kh+EiSkRhzyhTRBAMZFvyq3gxOazuW1o/OFoBm7KlBbF5m8iMMsRSLozy4cgGzCgCHjj237vkCECDBvQSotp731+HpzQaelZE8IlS5iDjsOKyAZum+XQoHrHvP0tshkjHADIt8Nan94lPvNklUxgSIzWKCRYCF8N1bGhUDYw39gUIwG5ixl4RNThE3WdRL0uSpTYS0ipQLyRbXEkNz5B6YKQqQWNi5OyecGHuwwVBULG5KEoKgE8QEB6Rw/QEwjLxWbhwoqwJURHpJOo+HlITPLRfHAEoUGh3cEYEJR6Cx27gMCJR4lkDPGsR9z8oSqGY2wRzG6bLqdbIXAiiXBWkjjIoClN32/1CyXCG0wG/dUdeCIZKE6XuuAgC9qKxNBaSWm8QsuCk3ENLjoPxJSCh11Mp7potpRgNygKZZ4gl3FuEwcdtRg1bJKuK3Q2SCf+6rAGrUWkeBzTytj7ycSmAaqjEnOcN3YihtZNrjgLnp4s2IyDuXU2mDrCF589wc+UbFi1E1tVL1ZkFLQBn7OxyynbBhHTNT/NBOetUy8xk7Uqirrglo8SgXFFIF2VxxXeLHwSI0CjQxTRSegD+4Vf5IZhiEgmoUkCpCd0MwSJV3yYD3AL9pG2hgm0yUXYcyMNMeDTH9Q/lvgWypQoMjrliDlJXTZLEz8Sh3IoeANdAjsO5QrRaC8MzlR9tz3CoWAgqrXNapu40mYtx7EoM5AMwolCIjLrKVdW/Kl9WY/Hagmy4o7Mo2ih7Ikn4kOH8XjCxn91UNX1GF3AjbjFEJb0E1EUBQnokCQBrJFw1cjCBurZCXUqFmokhINsDk8aCWgsjIK61Kgjbuu56mFPpVQ7QgBJahucjzaCq7Ia6UVQKPAaO9qvBrZVBUABAOosvQ7GZrwgT8XiqVyK0n5aHyMIW+41LiwH/UUaDCVqKKX0iCO2gVnioLE9W691xK+WYNW0bvXWNoWREqzI9KMChGGUCQS0wyzFRFUHVSoihNX44qPYBlhoGbEfHF0uhBtt0n4gQMDA4S6KMgPNqJiTmD0dkkgDYUobF2G0BlWlrJIFu419WDi0vojBcnRBMhdVIi5lPrCvRUz+JgIDgkDSnQEZiGzGwCFAHpMN3t2og9e99hEeVr1kA67j1os+Gk1zY3mNUkhf7Bed+kMM8FYhI5nDBCQjKogrMtKBBVbkpAgxQyChI85QJoPpV4IDEV02v/B4JaTpkAibTrUwt5VHBCGi4FaZJDTnD7uI6ZCK1aOk7B5g7aKx0B68AWeKfUCyKJOiiM6AF7BbJht8Du2ACZnqog4Rievgi9QAatdfApgpivqBgQwLJPUpt7QQq6BAam0JxgCfYDkUSDQK0qhCFmoPljWjQ3GlnOrFrbkbMR6FIKelwAb0xWDhT1RuniIoWAjxb7j53vqEiJJZ4pAGT4GGIKI7lCv4ENIjErVF+0I1RczzINZZY3fooYcChH2NU7MYKbEo9kS4uRAL3EikvkiDBaoo6JrITpdZJy+occ2Shg6PdgdNCaYinh9PeRoBm7lslYowvyuB8M4WiFkdj8qvcWk99sJT89ZVkgmAkS2yHhPhUBa2xmdMIjCLEfDKzisRSATqCFT7N7ZvkL7W3KxIRGDZzkPokn+RmOSjBhCmpCE1maic24ajsB2U0hAguoFyK0AoWo77s+csHPFycXGgJ6AeoE4gicUziJCpvB/E0/qQKyIpe5hROPrQguAKDeNOh51ZcSg2pxZim/XE0lx25aNrXF4YrcgkygaRRD47BQFMUrKAiHFxQwn3Dot7y336JJGkMlsM2Ymo0WdgUSL1GvmTFxmiV8DDnNcXFkAlEJC4iEoxAImpOgh+ZXLyQJvE0OigHVqIz3HydSEf4uv9KrfYTKRRi0jtwT90kJMQVHEstw2PohomksUlEgWRXXq/1CQRz/k3CmFYjB49nmPW/LdT42dNa/pUa9tO9anskRWjJYPTmJE1ffKk9tYKWhOvncFpeJ6qHOOSv4nAEwjEwS3vuvld1tMkNwlKRrIFIED0MdgGdQvrBh2D1baAb4RRtPCroL3wt81swb1GcRQVZD9hjwwxDVAbWGqL55FD8HPjDXMS39VQ83jETGDTk2U3ewR7Fq0MPY3ELB04gVuuvmLIe/oVkSv/cOVyII1mlzBdCwqCaaEyaFndDdbOKWzJ1qFoDCOOinSEkYhJC5UJILyzQpeDiDRUJo9fSIZgXTOky7QL8VIbVjRMkyAi64HHC+jpv/W+yNB0272ItonbRnYvZ5Y8bdtOkbOkMQNSaZnVY29PINnHAsfepKlXgmUVZad+oTuxtBuQPqYxa0AGIpsxcAigC9yKER0aHZQFOWBHQERsDqKP0Vyummw0ktm0wrJDW8Px0y87EYMFSsFOITs1BhMVghL0grbGDmcakeI6Y6cMB5GgCzQ69B8KZ93grcJWQuXA+oCOiESzJBbDtFEi2wIX+8wVG07Q9TScP+q3jBcsNfWYCHthxTur6VGd6MSjsKQUolOPFI6nTYWM4nZ2Fvn9Fc99QbJtk5TcNr7H4WYAtbQI7ytO4vH30pfW9tiATDa1EUjtztQe3+zdaBCIN+xYXtxta8V+eHIwQrElMZ3Q1rRNNqLIuoCZYoKhv/hPInD62/HW6VSfM4yJLJX0hTyrcOtwKmrN0hRTL6H+qFN8PU2XsMZQpob7v41jtKcSj7HMpuqUJma8EW6qdHa7Te3O7Dbi2d9EoBkBBiZ2LtqR2I3c/HjM9/WXOMsUrRKdUNEhjbn4CSogBJLKSmCCKu5aTR3bSDh+zet7ya2NL31l0+QZZscWDSWGwdBZHk18gDqHJ74/E/ZTys6Jb0DWOLURSGPW1B7f7N3oEei71Gk0ZdfGzxeqL3zhgC80Qv24xqWd/WhYKaOLuC1p6gHpXVyP+QkJcG2ub0eqpxxp2MZv2jVuWI4m6pSX/dFxAGS/bXGO1JOsE8Ij7VenGkcdz88adbZJLXaHtS2nU+MjMVr8k5/8hM87N/BSCMzRDlZONtlIFmPBsYynF0Nq24oikqVVGhZMhfAbC7Yti0juaGLCVisxZaf28753oiP3NYoludhweet76jCqLrXko0RgNAiYlHklAolAHYFJtH1jnLaZcDCyv8yRic6kqSMzivBIWxjpnYYX7kpeavFlqFFU3ZSFfLV9jHbNNvimR/VbWjE0y9egbIKL+LZdaBtZL6fvYWcicAgrxfoOVxwKxVneFvrYZ+dpHFXATR5pa/jBtOxTixj+Z/zAMAx5bZjngB8l8z/jUy/ewQq2sIm02x8X4VXmvOkZ5yu2lBl5lYx+FTmk2IjnU8+M69hMvvAOn3Q+kPg4OZM3PTuaL6RGSr8aoAR7+iKmtf0l5SgCSutvgaNow5TPMrA7s6aXqZmBRCARGA8EnDrjeBUOzjZnjUf541GmtbXtWnZmsXE4i288quhSJrgceGMrvv1uDukJ39VIr2Hcw+unCnkKW5SoNZKGxoXlRF575nlNUdggPaV2g+JEHBodKW3EE49mEfYUG8RSSdY24Pg+Z884jMAmO57jZLmWS2lvP/TsSYFeyUgG8Bzn9o4xOFhIs53rGOcF2CHvOKJyNKVtetxoHMfs/BvuLEowhZyvY4OekwJ8QEMvRPJ/j8+H0e4wQvF/j7qQGCcz0WNxdfexjohs/XVStiMPqM20mY01PvMOQ1XT92g5xkkTJqMDBRRIQ+NEBiwwPkjSWmDEaAyKTG2j+6EuMn/i62aIDmrl1IY4vtnhRj52hu44ZKE+xFGOR52qyPhEYHQIpDFrdLhlrqmPQHcrwKzq/8QYUOxdJ7Pt4SLwkIA4AblLl4kr5ABpIOGcutslZS+PrP5xFN+UsPcNk3C4olwELUMJZiOGyPe9MExIvFMZYxs/xmDjaxzvyzgSmo/IGIdiY284hGMAcanSDGcH8NV1FhHu4uTGOCmxPO0eYO2yb1/hDgykwAAanQSlC62YPX1OIdpwww2dL4yj8Ex3UpFI4DjxyEkEtB3YT/jKKAfbiC+5cvOMr5Oq2vEBOiI7hYetf7gCVxu8J/RezEDO9Ub+RNbbqRxYoRFONHDe8S6f3aX+tIS1WZNwHSQmDm/0iE6IcgvzE8bMUCLshE99jKl+zTjR4KRSTHOAf7FixRqLeIYnOaoqPk4SXyPBJs0WVTtsUyN9caI0oBQXKcttBhKBsSOQdGfsGGYJUxOBfhEL+oM4/t9xdnXHYWtcnhPliFueDY7Lc7avkwkBSh5Q/p944olMEpbgLqJrrk89caJuHXTi0O53gorFgXy1y500xVeIVZEUFUSs8nEFZhoyhoB0MhAnCaLOB5gc4SMZMuGAYyaG0ki51F6viDh0sQdJSbWABiFDxJuuqZQ4J73GTneAgDbRUlA24BN262gD7QhlD5WGzyY4upAw9hUtyg/iny6BdGSCoQ6xk1k8rkPkS8MJV0+D7vDXAZRvbdZ7xCuFJYVmBasAUf3RTMNOJcByUD0lhMeJLPgHU6BjD1EcCgw2JiXDx4nG8eU1tCwcU0j9UkUJIwGmAb8ZE0CyMB7JYgp99KMfdWSAEymDOshLp1VKKAFHDyiBLRLzC9+j8mgCAqiqrVWBBt6GqnLHMcdQTJ9wj+/BoWtQYoMz2fTLJNcjw13cerQTzWK8m4AGZxWzDwJJd2afsc6ejgwB636yEz/AA6y/qfdxCJEh0Z0Lwl7Ap4HqnnAiYuPgYFKN8CO96PBpR8hjL3ECgNXDV7EYPkgjZhqFkMGSkeI4iqWwbyv6xAFfTrKBcYG0I+wVQnaScwK+mtS2AySrMjWSvA8PXCJceoYSrh4aQ5ZQgfjgAC2IlbSWc03VEZIYy8G6VIRDIBkabPnOlhEVcU3VjFIp5YdyyCEUTfu1mVIEo/L5C0YT4opgK4nHEkAjqHDs0KHPwLeIPd9qxcywHNoXbAyAqJUqDBA2gw8hXuWTGkgkhseUY3S46cQ3IqI9WJQBrbeNXuEf//gHXYiiHGtUf9RLGD6GrHAdWYwpgoupqAgRDBWU+HqaKDk+NKYEWQxE2DrNMSTJXDIr6EVQBIn1UWIge2SUaV+cly2eDozxyPjCxATAb2yz4tnNlHbssceyB7EfVc+M2pp/5VWXesFltqhLdvPHhEQWnZ2N1/q4h5kvp8L9SmMma21zWbV7Ci3E13gh6IDVDOo0E4/9jqaQQ7TvksbfgjZrLf6K9ADBECBASlKvicTAh0rGt1NqxWcwERgDAuZZXolAIlBHoNq/4c/ole0Pi0mFkoD4jE9DECTxCma5wCe4HdhyQloQFZHSW56FQmkIgez0Dda78XkpLITdhETxlPwIvw2MhGiUi0gj8Ihz4fBI9VFPSguJCSRipiGnW1xExYRrJ0rEN8WimbiSxUWWUDA48Zk4JGPEcC6hGwhThQJZQ5RMNaKdJJMEBCohRAQ28g8N4Rlkm+YN3w1R9khptzABb4HufMWIj3MLiXNHSMcnICI+flvbXH/aGpYesdMqj1Ax/Ix9RBiexLNmC2ON8BfAirREpUYBs4yWY43Gi2yWoOnyiS78pkRilpoNbcjzsSWPyyM0sXSwbRciEtnFSEyAkhFtBZGS4U+ThDp4xBFYg/FjNIX2rnyHBLFzYnU55hGVkTg+xYWoYRtmDjSwH8j78gYmahSQmKiO9VA8WPwqHwicbCLGOJpImtfa+IgJbmF8I7uWYL2KxT/QEYVoJ+WQGAo8FJkly9RFXMyo1jKjPeJl1zsXshKcLx7pIxJPvxi3JrPx4pPEsToUQmo3ZC4BoyzSo4aXT8ucjxJG96u0/hY4umZM7VxeQeaPy4pooHqa2p0Yl/xNBJoRIK64YlAq0J3gAcES7GG2wqbJIFOL1YaUIqLIYzoG0s6bWlnUElxPCAw6BmYpph82IKqREEjksTA1PnlD548Vce0keGhKSIImTUB3rQldi3W8XTP20dBzxFcgqHyIE/HMKNbxuqBJ5GVDfnS+NNXrqdPzOOWWWkUtdE7RTa3VeGoeVIN4ZuQqNohO6qhO5Zd4HxVn0wE1cYiQUZ7FI22j8qG9EE8XJZKBjySmDyC8iXbylZqKgoFbDPsUBQ88aX2wTCnRGqIUs6E5IMLxA8AyYFEaARwBpe5ibcFWZdRNGLIiBSstbasHYKtqOCOUtDgIMSIICuoKTkJ4mBHnEiRLHGwjGSWNZpQy8TaR6JqiULfwkZLdJEFMjSk9nFlB12KyQVizfclE76IZfHeCVTOomQbaYPSRWvXCymjKvuuBu9bbXMLmMOOaRkopO24XPlL4pRHEoc1eJF56pXEhis+Lzsj+p1JMc0B2jsnNsTjG/vvXI0170ylmVMTjZxGIZggDs54lw4nAGBFIujNGADP7lEWAEh4pCfFP7BFgfFziW6HEJElTes6gQySHrMJ7wqpChKAFRE5JpigLbv4WPsBJZodUIG+IOlKccCWuSCB2MWvc8vaP7NGMUlQ9QNwqFmdSJuFKlOI3hK5y1IWxEajEpCx0PHpEjAkTruSoYqNk6zBaK6YHxEiTJODYSxvhKSlOAuk76ubjX1pLsnrqsuLHAqk3rN2VjPoUV1+sgkNxo949643tKQxewt4lNeHNO0eA0FW+fUM6CyXqE5FS2q+E5/maGNDQGpGgQ1XJV7ocUDDbhd8r/Zk09lfzXhLPbIef0UgZr3D90VmkhyTWCyo95iS3xn3vr++t2NaL/oNWDIySaZv00uBhZZNUPYvt1pQWYoCGlsUj2kHDF+FQnglzDUaOIzJ+Nc9Vj4kwlmZE6vFa7qrHtA23ccNv6ImefP3uybcNvPNKBCYxAkl3JvHgZdPHGwEilrcBZYBPUHF9DUHCZoTKhJeob2khGQiB9TdyYGlLqUAAa1iwB5KV+iEOI5GAPKbzIMx40rA04TfU+wQqzQQdCc0EbQFJTForgdkFh+Csqjq/obZp7TJ5qWQaEcKPvYxWicCWniaDv5ESMBI6DFt+qBYIWpYXbaPDQAtoUKJYy3cpdZAeSxXKoS9By1AWLIcTjy5oLcZAQtO4qCXW62S8dT8bjWbzfUE7ooU4E5sL299vqt9ETO+/yCXtjl7gEOANRU7QMgY+ti0xhiYKRIBcTYWjQfreFEmf4WqKpPFyRaQag7OCpSlZ29vghR7VSW3blCXSdDJ/cEHjHlbR8mjCAv3ywW/b4DZEqm26jEwEJhyB/GbWhEOeFQ48AvHKvv8j9yMcYf0h0WNTCd5AZxN2HP1AdOIQFKt8HprUHrbhWL5HF20JJu/pflAE4pnfAzGsHIYwkpXLC02J8oNwMLuQhSwsM/b6DhfBG4P6Ad1RAumoYU2yqjVmpOhyoGYo0f7wVRpp9pmmH2kLO6Xn/kKNpJFOvYtDYmZadb8StG2SyH6Vn+XUEWid4fWnvYebyomMMWptH/VecqbsjkB+M6s7Pvk0ERhEBChCGICYPLhNRPus/pEYWge39A38eCIeTXH8GjtLiRHPsBVGlrovDp9QV+SKfTcRZnKKQP2XjYzzUD1mnMJMYDxXaHHGqfyxF8uPxEDQGIUj7dgL7FRCWx7TNrJTCb3H1+XuSKuo5y01KqRtfElQAmguVV9YNktklwCNFMZJ8UbJ1yXZKB4h+pzb/KFxX2sLQo89qlfdtpx6ggzPhgikMWs2HPTsck8IfOMb3+CT4V1ctDWy0crUTwepFxQ2l3qMMALkaoocqFsaLKYoTi3FiWSWN6+jrFqzOuMHZ8yS5nWRuCYJWkxvxxqobZixY43sLGPE9BWFaC0fJnZMKjTb94rTbms3//ve/2K9WDIn5e7dbM3bPX3TU57mDsJxsoDTGp2t3PS07S0tI2OlhTun75KAsrNYAEskN2d7c2zjKjHdA8yg3Ld1Gd3pnjKfJgJjQSDpzljQy7xTGQEOGTYJUyqwJXFHnQJdnYmMvG68ujiTeh+vtguleDzJeP23XrXW1m9nWiV7JX7DFyo8tJyqzOcJs2GmLHTHjnEMgxMYh/RCd1pLRh34Qimh9VF/Y1BzTma8trWzR7rDO82pRXWuo0kMr/ZPOY2pNI/HGO9pG/S4temvBKHaxAitHHjQ11cFFIpc2SBTsncK4OJIOQ2TBrAso5gc4KhXxeCXLMXOByob1joVkvGzOQJJd2bzCZDd74jAu25+V/WCxtOvf/LrHRMNwIMeycQsbGkv7KHei17Sd+kOSmFfFU9wrlQ8gptSEvC8rPhicw+Pzx3Uq25K3HRrk5fDY2hf6vEct+1cw4wjkhO6y0Y5JyGVZCiFi8rHmQUlsjWAWzubAEXgxUWEu5AGv1LSD2EG+JBb/WrNW2IoS6htkAB8nTHUZm+3vNTxDM7pztqmiBKmRuJ25lZT6fbYMVmpwMIvTV4khpLGWQmHH364LWMczhxEhMpw87JXTl3WADrIYZ8vuVMfNY+jPRzs4Yew5YFjGzll22Nv57ytarbWcz+3n44XWhznqAQO7w6AnulawmZ7pxTqviwAsVNP+zWeTghi7MX4Fj5kq+CAa1LLGGVgliCQdGeWwJ6VJgKjRKB32RwV1KmDvPXbUbSAIGT+8G3Lel6eTAQwwRbfBKg/miVholojVW3LGzFM0tebwcvKxjdKArKzHt8Utrk9jit0HoEPHfA3J5tdTs/DDGgXkJLYkuY8QCK/yaOISzWlBT0NZ5dSso1v9ZNmSnxTgFdNuI1jNnQYqJsECId9fwLIQWzca8pVbm3gRyzoV7TWcX9+bT3TnaB3uILjBuCD3MQhCCiUA/2UzwccfaGpkotpiQ0XdBghysjbzJ44bKac26QZ9r7ZWu/oIP5qFC2Bs7PC4wMR8NEk2he/DqNSDvOZ8vXCJ1od8wNVkY5j4PRm731pf2vA9kYKM4ctecTfX3cYy2jOXBiYSCY2g4W6GdzW7BmTCAQCSXdyJiQC7REYIzNoX2jnWPKG2LDtq57EUth7nGDAJOrxPYbbciNH3hEYIY16LKckIxeJKEttx/A4K8hhMESyRbwVvIV1COZIfN1113FykoZctCs+IglFp+4GBYmVOs+hUng9gEKRskQvAcZOpBBPg1H5sgTNBOdWItM5yMS5MvnNUEWoLg7pqRdVwsQwiUvDoTTlR5nlaT1gx5xu4gEK5G0Dfz3VI2kQBRmJZzFuKRswIZSonl1Y+fjE6HaQgVQfWZqcSqBqJElPkRXinKnLOcs4UOgdmyqNW0/tzHeOgMnjwECtpZFCd+KpAgFFe6R5BgIgdDOANfEonziDAxCD4RJuN75cPNgiI4QBUq+RfcrOQeNeJ5S4C7VQmQkYFWpIPeOKA5DiICUbGJ3OHP49ThYwoJRM9cLrYWdJtzrMabAuRDIsXLHJdeqgZbgVgYaaNK9EIBEYIwJMJ5whCDlS3G8pLdwL/JaYCEhj4VtSWp5a9YZo8e5mXIhkDvsRIPzq2dELwth6t0TygRDp80lkIdlf4lsDFsdkOQsFIecrRbH4lgyDcSYN8VOsP5bdEpN5PoNAYRBdsExn72BHQHc4lja+J1BVTvOjR+G5wowSNdqfz4FDI63jJSO2I95RxQqUkhuvPUEO+4n4pl+ST2N844IOBqEhGiVgkWFVoZmgVCCYHVMkkqBlzlCvy8lD0jQVVb8lwolVJhjaAmK4i3ZHB51HjIA6jFFPFUIrw0dHABtgrGGUCT0NExUfZIK/XpGwkaVkqvupNCXockuVYjiIc+YhyZASXi82LjldCfPDwMInulMJ0jDrGBGBYAldiF29EMUiFsYX36rHdwrjUo61dBSTBPobM0ReaMQhkCJd8dR8wKJ0hBsTWIBv7HTKUzOZGqyJS9UrpWfCNfF+kWqJ5lGnYa7+WEQqyrSn06rnynAi0IRAT9O6KU/eJgKzAwJO5+NIQW1OiHqtkwQh1SyF3ZL0OErBwZKajPdeJquwhHjL07RblJOL6AXPA4kd4OutbUOvNJbF4d5BVDuVmFRTgjc41067YCTm8WBdXqqIgHIswekYHOsc31pyXK/PIHAoIU4ch+hpF8ZDVHM4VQXGYBVOxhA8eIkjmEkdoogzafAAvhfkK6mPAGlPCDP0hSVLv5AAvQjHVVKZGKuLfKceK40Qkhe/oWmIQ/+IYXvviSWeHDxP694t9W7qI1qD0PB0QYniMGIcCPIsR4gaSw2pjOGBkTcJAIlqwHY5uA9xQQq1xBhhlpxaYozq9ZYwXRoo+L6gj1hLiZ9VAeC7MAbU0+AiQ11aQtVkaHxmyyjzKJIeW9XfYAZIobxN3CIiJeDt6xejMjlFmgklJbWNNsSnVKJ2B3BLb27wv6EvNFvEY2nGwmGVIqHngx5gZAhzWKVJgi57inD7ZZKL72bQXbHfmZCd5q05oOOUVY6B0IA4CdPUUo4+mo3iuRyZ/9Gw/E0E2iMw/HeUP4lAIvAEAtX+je8I0i74m0FWuGhQBhDerAkS4RNeskiD9SUOFNmcpCwlIU2KW7OS/egLbQSnFmp8hg/mHikthUN+sCWRAV76aIF4LMSS1+YXygNigPyOYkP/gW/FLSdcjWEisdjloYkbcWggmJ2aoyLvfXJOmylpIr1eRKDcEmblaURiSLIoxCPkLFbMHtlAROahF9pGwCAHIilmGHciY/2X3JKY026JpDqS0a0ylR/6IX6sAlgL0wNDSUksUJoqEF/d4vtSTwBGWgrURyS9C7Rpa4SxH+JZwKZoyhuBculpQdJIGTXGOCJcpLHjnhIpS9XlVi12FfmwBnqHukU8dqgjpLhuIlvRWaVRBdkWpHaWnajOMPFx0UdKDi60JVIu/EMygQY7bBmdqMi0YaEjv7E9Ew/v1GycAME1E9CLhj/Qk/NGRr/iTQ88AyvFLFFGDRCP/XDQRlJ5BXFVFo8x+wgGviISR0EmDDESj95JSS3EUwfZ9Ws4eMnoI8zhhtlQ10WNHklv6P11mCQRqWRQw0pnNV6k9tPSscTRVsKkzBP01x8LJuQCrJSt/YoYWSgv/X0Zl6jFoPtbc0EeM1OOeRWP2pYTj5TWWkXJlYG+IGCJaPRdg/aJ0Ce9DfvS1SwkEZjsCMQ7EV/REYoTxhoBBia/+AphwwtBJNnPqTOEmaUtq0q9485wIwboNih+whyDmpBh6A6dRKS0RSVEdayMCYN6CcLkurdGoTuhIqL59whPIoGcyCyMS1E1CXi/SF8ITdOb3S3xo0dSlivoDgUPbxg9ojkgwuOpEw7JNgSIyioidYQgJPhL9gh0oTuIFFanKCk5w8KEeYvcaiqhNFUgXpe8TKSxiMdLqBaAwDmDAgzp5HGC9kUJOCJPGgXqF9nMUIVJGBQBzIxBx0hxr5HYYAEH3wpDGK2DrT3iS9VRoFsXroB3YgPRco+QGDa4xrOq4ptMzSCSnmk4YsYPWS6ShaseiUOIjAP9EF96OO2kz2itVzIXpR1bnrFAuNGmIJqUW/RShslAE/BNeSOjX/E+w45boC80IqCIRwox9zBIvIEzjY4HSiUS2ZVSyS499TQCfoU1A22SUVghcpVi/V3EFe0ULxAxUWY9ZZlaEdn629qv1pjWXK0xnXKJ7/SotZCMGR0CA0t35qz/WWY4EUgECgIEszDpjj0IkI5+LTF5vJIHxIZ3N6WOda34tpelufQecaRQCM9K0sK+nvg+uXjqCi8UAYLEbzEcCHe5qAc8xQCsdMn4SBmt7ZIrHoURRzPUxXygd+HYIYaMpB+ijCGuUAqcgG6Jl7Hb8o1rdEcC63h6FD4r+ASFDdlJGOuIJkGJnkkLmS2s6a3aPUU+kDMNYAQkAlnfqEzQLFKfkqy1zYpVPmZG/cBipc1YHQ2EJiEf9DQ4otZGRvSFYyxaybdXRcxVbnEdCglqDG5PBDYfcCQD72HGQp7QTSQMncXkWmsX432t10qjX7GrPNLQWGg/lZVbQxmGMzo2sh+G0psPEcl2iewafZjwjuKKKwuFDdKAJxkpJdc/MRvl+53hWj6tqpabEff1w75enlYrNoJHnHtEde4Tca0hDFVk6CbLU8Ndt8ohoPGoafbGJ8NKrhKgmGkbVmz8XZSnAr1H1nNlOBEYbwSS7ow3wln+lELAop+HAeFKMcMkQYYxfBCE3CcJMytvihCqfmKV1oH8ox5gWaAJwCQoY8gGNg5fyyLyZWcLYFxwy35BJNPNkJqYhw9zEvC0OOEeS0ITzMrEk2z05RPNEoQu8LNhpECVlOPTFpoR0ossp9hvu+mJlHUxfkms5UxOtA7UCbJTfmiGEshpRIE1BD9gLEBoqHzIMANplxAagcHgExQVVCwiuWlTO0lD9YVDMACJ1yndRw4IeOYeMt6K36+N3GgQNw5dUxrDRyvngBKnZqDhWwQztRNapiI4ANNTIJdZ5ZPvyFa5jQAaqgFNkexBLHSupvjW2w3P2/CJyPOfCD4pdNKT7mbctE3cNrIl+9DHG8Q3r0QgERgnBKbF4nKcSs9iE4HJiEAssokf7jWEPe1CHG7mF7dAC/AJQprwtmLGUQhjYp7+hmuzMCaBDTB8MFE5nI0vBTMWOY2mIBAeIRNYC+mLdijHhizmGGWG9cGvxJQZqAYionYEiIoCf2LKgScXZqSBmYbiQVFUBfQ0GkCtojSWJmGVakbTQTtxqwuoEl6F9/DGiAHCReiK0BRcpwyZejkJYWk9btUpGdsGaMX4gtAb8f+gG0OtkCRmJj2VvjS1BNoWMh6RE1/jePQiytSX8St8Ykpuon2j7lFTOXV82j6amN7NDrVY9W24YWPB4N04UB8GSbozO0y/7OPIEIg37MP7PIyaUFG4EAj+m8V1g6sKdQj1CXeKUjQRThvB45jTSYmctQEdqb/Zm24nuG20XxxKkDwQ2VOD4SF2YejRktK2AH+C21ZHaYKrzuomEoGYXTnc44p50p1xhTcLTwT6iUBf3omzRGz3EwVnnPTbvMLdlVsPjTLFGDVYXZMErr5X1180srQpgEBf/rSnAA7j2oWBpTtPKK7Htf9ZeCIw6RCYAnwF5nUOMdIejTT9pBvibHAikAjMPggk3Zl9xjp7OjIE6kRhZDmHU+MKYyxhFJV2zzKi9jS1fwKoT/cqRtT47jjk00QgEZgNEUi6MxsOenZ5dkGAV7LjavgshzvwGLu9zRXb8D10pBs/6FEXZcuVQ2V47ZSPMfVSVHcm1EsJmSYRSARmcwSS7szmEyC73xGBUYjYQdNAOKOPe7Ut5fFho45d7e2BTfU+LVk+s9Vbpiel4vRt+73DbPh9P+lB3iQCiUAiMM4IJN0ZZ4Cz+EmLwEi5yyjoUR+xcSCQ03rio5KlWFvNff+8fKGzxLcN2IjuTD/H2Dgeum0CKhkn3Dj435mBtqpJ6aygSGkXvaMXOSCLjOPs+CPTA/lUlhOQ7ZB3YKCUDon2OSqb5x30V6/CYX1OlLbdXTIfi6g/ynAikAgkAn1BIOlOX2DMQqYsAsS2g20cslcOomUhItedDqzP9hbVtxe1oiCv7UgOq5Xd2bvCNBxunebnkcLFK1ykW+fcKM0Jtp7GsX60KR/84AedTOicHjHSMCf5uIE0tCzOEY7zLZwCbGu3D2Y54F9eHzHYYYcdnD3oYxd+HeUX+71Vp9m+OOGcQAf5OLzHGYO+PGVTvbP77KdwCg524qsXcdRya3fExKG9Ajbh+3SDVoV9So0++OUkoe9+97ueOnlZSo13IrM2OL9HpEodlmi7PlpWjkV2FpFyHNiod3b4S5ZXIpAIJAJ9R2B630vMAhOBKYNAfNqQusJRe3F0L2LBD+YDH/iAw4JxDgoP5/V16q+jjX3S3GcNOLv4EKNkmIrvWlPDCDtzzxGC8UUIFMEXFRwq6HMTyvddAgl8DBLRwVHwGJFoFg5BC0JBwhgkpa9j4ihSYi0ULSiRc4d9Zty5xiJ9qCGUKJFGjG8vSObD4D6tgJfwoaGVcUI0cqNfvtauCpobpxhL3On61a9+Fd9UAkh80lwuRy07VdkBjPGNUnml8a1yn4Pw3Qn1RmnORXQaNYaH3pXyZafXoVLyZQacqcRnIBFIBBKBPiKQdKePYGZRUw0BKhO6EAoV34dyxrHu0b4Q5L6BQKXB7IKXtH7BoKDAaQYvYanxASPaC24rFB4+GOksY7oNmh5ffHTmnvTOF0ZWfFfBIc4luwQUMMgN/oF4sUm59XEJ317wSSkl+0IT1Yj0dDOUOpRGSANqhTdEZHx7oRSImTk9Gf1CenyPwlcg1CgvPic7j+ZQQdHBlCytAXmlRPVwFOooCeiZ/vjHPzpcUdeUE1l8nkKvfb4Kr8KoIqVHqB6eR5FTSkYEQeQAa1+Jx5/0ujzKQCKQCCQC/UIg6U6/kMxypiACPkrlWw1sPfQTYV0irfEDtABdoKfBLZiKOvXcF6NwFB/NpsygEOKzIqVPhLLdYAB4AzEvhgWKXic+RUlP4zY+nEnpguVQnHCXoRTBcjpVNKJ45Ud6rAXzGFFezCb6CxB7vvSIx4+2+SKET1w5NNmnwXBEZfr4uW9uIFgYDDWVj2lERdyDfMKiWAB9XoM9zmcxaKS4MEvjc2CR0pcxDjzwwKKaisj8TQQSgURgdAik787ocMtcUx8BGgjqGfobHjDkui+D6jPtBYpDSEf/ucIcd9xx733ve9vCoQRf8PaBTMyG0QoV8E0ruhMfz6Ji4emCS/mSpTKpYdACbi64lO+KS7/CCivgClgFTxeFqx0nEMC6lMDJRi5tKx/LxI18LYsvMEWRb4bT+lCTKEoWyWhfUCifI6U98gi1QiMwj/jYO1IlsY9g8EnyKW+966SyUgsKcuSRR0rD+kYxg735wpfPpLPHhYmKBsvHTdm8fA6dYkwtfIniA914nmTIon6xW8kIYd8qh4NIcFF6IZEBJiIVJAlfjJj8TQQSgURg1Agk3Rk1dJlxiiPAaebCCy9ESnCUs88+mwELJ2Cj4fbLwMSpllqC3oUTLsWGL0C1wsGO44vlKBFZbis4Rx8+QKxRFCTsU0gJukB1xJ+X6wwKQmNkExMmQV+C7tj4ja/YcsUBiFol3I2ZkOyKUhRyg0j59HfUi0IhOieddJJbzIYKR8N8j5N6SUd8u5QCBlHjI+yrVT/4wQ8UyB5Hy4KH2cCFCUmMbNHQqIJuprU7YjbffHP2KS3HujgG4ToiBZRMV4SxKVMkdujD41RWqpbSFaUxV7ncii+Pgs+1VgeN7ma11iwZkwgkAolAJwTyE6GdkMn42ReB2FL+4N4P4iskN19aTscoC3MS+kItYWcTsY36UHXwPsYh2GLkqu9dd3vfh++zGZvd6qCDDkJ0cAIynuIEn+Aug3AomU4luALdDzUMBYnb8qFyVIlFDAvBUWI81EWVoljcq8k1p78D1tqd/pY/0tLq2I40b6ZPBAKB+NPOuTSu84HmOHaMUu7mF9HHFeosPBEYKwLxThxrKZk/EUgEBhKBpDvjOiwDS3fSVXlcxz0LTwQSgUQgEUgEEoFZj0D67sz6McgWDBoCufgbtBHJ9iQCiUAiMEYEUrszRgAzeyKQCCQCiUAikAgMOgJJdwZ9hLJ9iUAikAgkAolAIjBGBJLujBHAzJ4IJAKJQCKQCCQCg45A0p1BH6FsXyKQCCQCiUAikAiMEYGkO2MEMLMnAolAIpAIJAKJwKAjkHRn0Eco25cIJAKJQCKQCCQCY0Qg6c4YAczsiUAikAgkAolAIjDoCCTdGfQRyvYlAolAIpAIJAKJwBgRSLozRgAzeyKQCCQCiUAikAgMOgJJdwZ9hLJ9iUAikAgkAolAIjBGBJLujBHAzJ4IJAKJQCKQCCQCg45A0p1BH6FsXyKQCCQCiUAikAiMEYGkO2MEMLMnAolAIpAIJAKJwKAjkHRn0Eco25cIJAKJQCKQCCQCY0Qg6c4YAczsiUAikAgkAolAIjDoCCTdGfQRyvYlAolAIpAIJAKJwBgRSLozRgAzeyKQCCQCiUAikAgMOgJJdwZ9hLJ9iUAikAgkAolAIjBGBJLujBHAzJ4IJAKJQCKQCCQCg45A0p1BH6FsXyKQCCQCiUAikAiMEYGkO2MEMLMnAolAIpAIJAKJwKAjkHRn0Eco25cIJAKJQCKQCCQCY0Qg6c4YAczsiUAikAgkAolAIjDoCCTdGfQRyvYlAolAIpAIJAKJwBgRSLozRgAzeyKQCCQCiUAikAgMOgJJdwZ9hLJ9iUAikAj0C4HPf/7z3/3ud/tVWpaTCEwiBOacRG3NpiYCiUAikAiMBYF3vetd06fnKncsEGbeyYpA0p3JOnLZ7kQgEUgERorAggsuONIsmT4RmBoIJM2fGuOYvUgEEoFEIBFIBBKBjggk3ekITT5IBBKBRCARSAQSgamBQNKdqTGO2YtEIBFIBBKBRCAR6IhA0p2O0OSDRCARSAQSgUQgEZgaCCTdmRrjmL1IBBKBRCARSAQSgY4IJN3pCE0+SAQSgUQgEUgEEoGpgUDSnakxjtmLRCARSAQSgUQgEeiIQNKdjtDkg0QgEUgEEoFEIBGYGggk3Zka45i9SAQSgUQgEUgEEoGOCCTd6QhNPkgEEoFEIBFIBBKBqYFA0p2pMY7Zi0QgEUgEEoFEIBHoiEDSnY7Q5INEIBFIBBKBRCARmBoIJN2ZGuOYvUgEEoFEYPZF4DOfafT98surr31t9gUhe94dgaQ73fHJp4lAIpAIJAKDjkDQnZVXrt797kFvarZvViGQdGdWIZ/1JgKJQCLQTwQmo4bjlluqzTev1l232mmnatFFZ6BRAu4jfPvt1Q47VBttVK23XnXJJY1kX/5yteqq1WqrVWeeWX3849U991SvfnUjPtLffHO12WaNxH6FI36ffar1169WWaU6+eRGTF6zGwJJd2a3Ec/+JgKJwNREYDJqOD74wWqbbaoLLqi22KJ64IGO4/KhD1W7716ddVZ17LHVbrs1kh14YHX++dXxxzdiDjigWnDBBu8p1157Vdtt10jgVxWuhx6qnva06rzzGlxnjz1KwgzMRggk3ZmNBju7mggkAgOIwOys4Tj33OrNb26MyeteV80xR5vBeeyxRuTPf1595CPVBhtUb31rde+91aOPNtQ2wtdfXx19dJtcit1660a833POaQSUs/POjcDyy1d33tkI5DW7IZB0Z8wj/sNFx1TEGLOPqe7MnAgkArMegdlZw0HpEhc6MjT0RDhCd9zR0Mq4HnmkOuOMCok5++zqyCMbxOioo6o992w4JgeJmZHz8f+Uoh6PqOae+wlj2bRpJToDsxECSXdmo8HOriYCicAAIjA7azjWXrs65ZTGmLAxFY6yyCKNPVau446rgpqss84Mh5vTT68OOqihnuGFs9Za1THHVKed1kiJLYUeqHFTVRtuWP3oR42A3w02aASmp6xrwDBbX3PO1r3vV+cv3ae69cLqoduqF32iWvaN1UO3V7/bvXrg5uqxh6pVP18t9rLqzsurS95ZPXRH9ZxdqpX2rB64pbp410ayhZ4zowmtWTyg+FHaU1atnve+frU0y0kEEoFBQ2BEGo55523I9QsvnKHh4J7yxS82XFi+853mbhX2UB4MoIbjkEOqt72tOvzwCu+ZZ54ZLT3ssIYRaoklqpe9bEbkoYc2XHa+/vVqzjmrb32rwocYv9ZcswHFvvs2cnF25vJ86qkzSvjc56pddqm+8Y1qgQWqb397RmT+Z3ZHYCivMSJwwrxDVxzSKOOuvw+dvGwj8Jtdhv77m0bgnmuHTlulEbjkXUO3nD/04P+GTlqqcfurHYb+dWwjcP3JQ9+bpxFozSJSyTed0XiaVyKQCExdBLbYYuj7329074QThuadd0Y/l1lm6C9/aYQPP3xG5JZbDh1/fCPm1FOHNt106I47htZbb+ihh4buuWdoiSUa8QstNPToo43AIos0ft/ylqFjh18zfoVdEd8IPTkcMeP0W1VsVKP5N07tyWLHG4FzwluqYn8cLPmV2p0x811rqOV3bpSy0IrVw3c2Av/+eXX3VY2A65F7q6FHq5ccXF17QnXTqdXDdzUi/3NuteYRjcDSr6umz9EItGaZNkfl35IbN57mlQgkAlMXgdRwTN2xzZ4NEAJJd8Y8GHPMXc296OOlTGsEHnuk2vCMao55q6HHGkYurOXCraplt6xW3L36x/CRn4xccUkQGufWLBJMm7OalgbnGVDlfxKByYtAj76x9mO76on/+teGf25EelXwXKlftmf7V66f/WxGkIev6xnPaE4f8ZGoHo6Ycf1ttax1qa6OQJdk+SgRGBECKU1HBFfbxC0YLr5OdcPJjaT/Pr26/KBG4LbfVc/aunr0gerRBxu3T1u7uuGURuB6yah5q6o1SyM2r0QgEUgEpgICr371q7/O9Wb4euc73/n617/+c/xr8koEJhCB1O6MA9irH1pdvFv1j6831DMv/1ajghXeU525drXoKg090GMPVqsdUv3mbdWVhzd4z/Rh97zWLOPQriwyEUgEZiECI9Jw1Ns5BbQdv/vd737xi1+89KUvXX311W+//fZTTz11PWce55UITCAC03gtTWB1k7Cq44ftU5Ow4dnkRGCqIfCWyfqyCr6y0UYbP/DAA1/4whcWWGCB3XfffZ555qHweNaznjXTYYrsk/RVHY3fbLPXnnbaadtvv/2xxx579tlnb7TRRrfddtuiw198uP766xGg+eeff8kll1zQ6ciPm/MmaX9nOppTPsG55567oZMAhl2VN9lkk8Hpb4shZnCali1JBBKBRGAKIfCud71rvvnme9nLXrbyyis/9thjT3/60wvXic0yTX0VKdnUWJHed999bFj333//b3/727ltiG8chDNd5Gc/+9nNN9/8+OOPf+ELXyhBEwJ5mwj0EYE0ZvUG5qRdVvbWvcmTaryVbWWgVVTCgwNPu1a95jWvOX3HM7Tx2nWu4RIh8NrXvvZ1r3vdOo5mm8DrjjvuWGKJJdZYY42LLrqoL9Wecsopu+666/nnn3/55Zdv+eCb+1LmrC1kyy23pM455JBDnv/85999992f/vSnoz0UHt/97neJ/2222ebtb397RIo5+uijn/3sZ9/iGxPVqbO25X2pXQf33HNP5Obzn//8nMPXpZde+tGPfvQnP/mJebvSSisZbvgstNBCfakuC0kEmhBIutMESN4OBAIWtS7vR1dzg8aPhbRwqT/+8Y/WncTSXHPNZZH98Y9//N577/3kJz9pjd7cqll0f/HFFzMKROVkBpazzDLLOO4ilMn1RsFz2vAVigTBRx99lNApaYYhf8xtiXzkkUdOPPHETZ3xMjT0sY997IMf/CBzAyjklQYUEZDFev3II498+OGHP/WpT5UCBe66664Pf/jD4uedd9799tuPPkMky8VHPvIRC/3ttttus802U4vCb731VoLwH//4B8xXXXVVuVZcccVPfOITpOBDjuH7S73USRw2nZDRVVZZ5aSTTnqGrVON04RPPuCAA372s58Blj8vYN/61reCHZJ4gO47xaRsuZrEPW98COKRV7ziFS9+8Yu/+MUv6qb++lPSo6WXXtovq8eaa67ZGOu8EoHxQeCJl934lD9VSm0RhH3r2PgJ79LE8Wt8qaLfARznSTRnAlBq1wWv5ne/+91ksxX5Zz7zmQMPPPDggw8eV67zy1/+kobfqz8U/nQbeMAzn/lMfh6owJY28g0NIRnRWIQDF/nmN79ZPby1mMsuu+z0008nPJZbbrnFF1/86quv/tOf/sQlghC1jEZHXvSiF0n/7W9/mwcJ/vGVr3xF3le96lXhQrHXXnuRQ2SwQnRcgYwLEr/pTW/CqNjjqVuIajKY68nf/vY3j77//e//61//OuGEE1RKYMtS2iaM1uywww7UGHgVlQ9vFXQHFdt2220RGo1/85vf/Ne//pUCY6211pLyuOOO48c6xxxzIFWyU4G4rrvuOo/+/FERU+EyLm94wxt+//vfFzPWJZdcctVVV0EASigguPTToDB4GQX84CAfTZgSlw7qx49//GO8HPVBr3WQQ49Zutpqq5muf/nLX9CgKdHX7MRAIhBLvfztiMBx1dBxldc9qfPf//7XO9of7f/+9z9hMqNjrh4fKLxcwxWpqz//SrEC9Vrq8SMJW6DrtTfUSDI9kdb7feutt+4dMQJgqaWW+r//+79GEfX2D4ctAeHv0ir6A9p+bTMu0j744IP/+c9/brrpJu9Tt1IauHucOzs0dOedd0oZbRBmKfjDH/5AJJO+Rx11lAStFYnDD0hfm0qIXn/B3/nOd0SqSwl77LEHbQptvBjel2uvvTZKgTQQz3vvvbfIuESK2WmnnSziH48bYqoQSXtPwyFLtFbh2Al5j1RFyjBIMRIt7zvOuM5xvgU9fG7u8GNOr7RfiEij5cc1VCwoBaOStnmOSYT+ADg/90Xpqnre857397//XYOFWQ00DDt5y/CBu+gLlQP6gtiRxJiTEpQTDTAQpJRCRKJ9CN+///1v4X333VcuARckySr2mrj1+9Of/hSpgr8xAvIVV1whkiBXvv4aO2KPO0ukR6S0yoiU7ALKfM5znvPlL385Olh/NLnCcaxwtNm83W233Ur7Q2dG2WOz0g9/+ENwmcPm7Q033IBfYgNIaj17yThZAtF4f0dY9Xve8x7NRuIXW2wxs0IYpRb+f//v/6H4oIhOTer+TpZxGb92DuypyjVxO369n9QlDwsS606qV6/j973vffYRCLi+9a1vjbVnLYJ8rAVG/nqxYppuR1UHxQYEGN3JngsuuKCUQRtB6FqCl5gbb7xRGpdARFq/er+T4rJ/6Utf+s1vfiMeczrmmGPcuqgHIiVZzo+BzcjLcdlllyVNG/H19g+Hy5/Teeedp/CnPe1pxPa1114rrbcnxsAb9EMf+pCYs846y0hhFR6hLAjB4c7kH2qwDetpDMzv2972NrkalKilIinRkVB12EMbJhuRRJFi0R0tF/jRj35khUqJIkx+K4qNhlpISot1jaHbQLMWXnhh8kwkPY2UKODNN9+844474tAiTSeRwQlwkR/84AciST5PUYozzzyzwTVrLcTqNthgA7NRskb8cRXdAIGBHygHMqIv9Gklxz8NUxM4420if/WrX4mUXdjYMX4J4Geo2/e+9z3ON54SsSJdW221Fd+gCJdf7qW77LKLxkOmDD1qAh9UpiQTQOCCMG2xxRa0VigOzwyyLdIYo5e85CUR1hduK/W8wiSivjcmzHAHm55Ootsiv40FbQ1m7JUSzBXRwVnNQAYssDPhmT8YMJWePxAXH96SfRJ1uTQ1Gn/YYYeZS0FodNxcjQSIrxmO5Jk/hcpP6v6Wjs+2gfJ+HrSPSCTdmdmcfPw9a1Fr8RrSiEeh1TaVz8wyNz+X5Zprrnkitia9QpKRBxwzr7zySim9BYTV+Oc//1kWCz7KXlYJWl/vhbgNGU8qWI4TPzNKrhcraviWeOMh8YIXvGDjjTcuIgpZEcM/gKpDdWQnHQap46308pe/3OuJXFeAlT0lPClIzUBmKycqIiCREoszniJeWCIpEqjfGTtcr3zlKyMZ+oLrsFlQD5D9+++/v3hkSGnsKYD1Zg8wNeApT3kKrwUuKcRwJ+0OrYNVL4rjV1HaH5KS3mL99deHEqGCA2FXnpLfxitaQhgT8BH+2te+ZtdrgaIRWcft8TB9iUbqOw8eRiLWHwm9o628iWFKEYCEcshYSIb3SBCuGCAVxjywq+BMQXekVLXGYx4777yzNC6OC7Kz76CG2J5XxnD0EJ5U0tRbaMgowKKKRvxxDeORLHxf2IzwPGEwKjPozle/+tVWuoMDsUNJCRbsza4Z9FEJ5T1lDhhlCeqXip773OeaOfhKiW+lO7ggIojlEOSaASuJDZa+U7/RQuFMeholIFXmjKmOIJYyBUw2DDg6WI+fXOEivw2uvxcT3hgZwegFTuPvi/Lj0EMPDf76z3/+098mAGnF0OKSfVb12jSjF0TTu19eXEa2qZGjaPwosjRVmrezEIGBpTtpKPUe7unyfrd4DZuCt5U/foJZTq8kVIPoJdE5eVAhWMojRpT2Vq6cIVATMkOYpYBqgYmBBLWGY0RoW7H3O1HKSdMuBqYByyAB5IZ4RnQ0gM+E9yNTCFUTae0FRPyzBZDrIVdaiyXDtAfV0AzOkpxGLbst/a2z+YdqrcU9mwiJSOroAkXFBz7wAWJGLroc3gZEEfZA3y5xKd/CXVHUHuuuuy5O42UtPR5D5CMEKAj2RieE31i2aqRiXZFdByEm0p8lCeeIVXxin3324b0BAWnAS59R6qoHMAzt5FNiZSzAZMO7UwICVS5OD8LoDmOKVbKnbctRL7mLrtVLbg2T1uxQSrDIDt4jDdUL2mrcxZMERr81oxgON2iE0cQYGG6Ctoo3f8DrDBIjSw9UzwuEFVZYQck8WJ3D1sZTezg1OkLfRuVDlVWyo0oolCFGVeEvPhpm1DBLzAMZNTm1yiMVwcqgm5xu5UJGiVgzzS0exriA7LIuKcS4GOvS1EUWWYTzjcnG8iWxy8w0t011JEZitJJcx5+wWKMJImkA7hd1Nk80FeeTTEdEmsP+LiTjoawB4R4k3lzSzsZ8aAzpVLhMoW/4TvcwGmVa+lt21buHWLvEYOr1+FkV9hJATHup3bvCELem7PAn0powYxKB8ULgCdE1XjVMlXK99L2IiQdqDDKMESR6ZomGN3iLkawWNxgDIfHe976XmKTesEqjtSa3WCWkZKSwqmPmwH/b0h1kgkGBIPfqJ4zVgi4QG7gOTwschejFukga70cUh4pYMyhCSDjEqBPYGIy1I7FH1CEuVvlSitQphglhRAGL0mxdo0vAbETSDWAM3GgsPYlP1dW5DmUSrsAexHpC9hO0Ok5o0e6ghrIT2CW9+CZigeuQvvgKZJA/i35ZRnQBiqaKhgPClDpNeZVPN2YUFE5mGzu4YQ9ca5tSzvRW3yEjmUBkN44wAR2VBqKmd57GL7jYX4TV5UIydBx1QOmIeSt1IwUWPBg5Fm+gf/3rXxto5j8SBUfEDhFZBAWVxAPwDGmMHQvIjxseyQ3eQGRqwLCZoxETF7KCQHhKIYRNisREEVkzR9i4wArliqmLKsWYGnFP6efQsvDmwSCPOOIIkdRC6BT/G0zd/Cl0x7RhekNEYqCl1FrmKifnYkICpq5Ifxf4rsbDgSInlgr8h/yxhJYUE41dxxQeZprJGXO4TBt/LFLSC1YnfVqBs/aiaKEzg0b3ZugywhpmxNaUpWswNEVbEwxmjMnjr8k4dm8eAmcp0j1NPk0EZhUCSXd6Rd7riXhgS/Iqp8wgRyMneW+d6kXvlR22GCoTy1NLHCLHC93LnVTDdSxk6f/RF5oh8Z0q5gdKLlJXsCyQ02iElN6hjA64jrDdm6H/6FRCazwRqFiXR8wxsazUo5IywiRTiRFgG7J8lzcidV/Ar+yoAzHJRiOBhb7FOnGFwGFyTDyRXpnveMc7tJaUZUqzQKTP4KfJUoYUKoF4w7EofgAVAhKHU4IEpC+FATKEme2+WJTX/AtJUMOfJI5niJo2h1bJqxmnJK3REbhhEvRGRo0SgsEOV8CW0AI8Bl2jZWkufRhzzsUUY4isXlBZwYfjBf6EgOoy0omYqo4CX/b4lYBOTljvjBpVBwLEkVkCiCkBA0YOcA5tYOfSQiOiGcqxJYoXJ0qkzcEtTCpjDSuwD+tdTlEOY5PZZUY1tVnXDI1KjQjKFU+RkqZkFDxiEHcNKI8MFsOWq8QIYEvoUT2mhNEaV7nFWjBOQ1xiBAoZqkcKE/NNRO2pw1dTMrfIwSh4cGs5fYmhaKEfLXylU5mGQG/aPq39wbV9PriR1kjeXaNr3+Pvj9HlzlyJQP8QIMzy6obAsFeEBJbpJBNVhHBxsaTpYaTAZsKLxRooirIkNUSEKIYRzjoUM6QyqY8SEflWsY2UjzuINIeHhiz9lUBCx64iS39vHDxJSktMtEAAw6DxJk1J8TBUMSW0FqUW0pH4ty2CSoajCUlMc2M1T/B7RHPAs4T8lpfji16I9NaO7TwUSOIJZiWw3HmqYbRBlBACBL/Fd8gAXJA5AyCENKIjsuww8oh1CUEhCTbYYAMEkeDXC4Kf5AMgfNRCVONMdDZIDEjFE+1dUMIP6E7q7lBaroVEb/jQKNOlWMQFerpvc5ZRcLEDCiNVxaW6qSIIKNlTBAXVoMih7VCCvB75lR3ypkSMpr6LCSckkZEsGtD0a7CK1wtzHkHyhHdOU9Km2+EJY9cuVvekJ4/P0idFdrgJuoPKaGGHJIMXPZIODl7rLRj68G8A+5VNSgRaERhY352GYjyvbgg8/p7FEnCXcN3lYUBEyUXJj4XEkp3ChvcMcUgWusL8YZ8OKSileGKeWsjanSGDwwS1QZN8rTeDtEZKsJyIVC9Ggv3QZ8Q+nYhXJrn1xje+kQ5ZS6hPGvHDQjESlFsMQAK/CAfFQHgWM0lYauMxesT+IjHlBJqCmRHkmAe9AuEqnhRnM1ILZQNKQUhjPCggHQn3W3YrYYRASiIfK+IhRC/ltlyUVRIjKCVGgD4A8arHtAnXu1MPD7v3Ur20yTK6qHrh9fDoSuucCz6UFtyY6Jx4OzHZmBWdk9eeDLfKZjHg12KHR7znBrMh0ksZoCe5aT+puMG70bueOzh4rc8WJQKzEQIDS3emGQRr9Lw6IjB8Rt9Db36QfwyKIBn1PrUKIwVTDvrCowKVodhnwrBu5vlL7YEYYTwSsEkVCz0egFVQ+zNMUN7wV53j+3M+8aUCFdUO07NfSTlxmku0TS46A2oGNIieqUSyyKgrXAo8xWmmfW96vahquGQaDsn8yk7LEtmNvhhhFAfpEUDOXAJhQJGFmaOkV35JGSVMxG8dmeEw8odgcXnRHmQrLHF9aElLRX0os0MR7HTBlW1Do+Iqk6RD8sejh1toJhiFx6OG/yt+drhqfyCzQ3ezj4nAZESAoZw3gpbz36ChH5wuPPmlOTjtGrCWkPe2Fgdj4OrhpBYOpBbo1uWYLKMAtYe9LSwjceqJ5mMPLBT1fkiMANVjuoSZe2y/wqVKGhLOhc2UGAEx4fUSkThK/Wk9HJQF16lHIgpNWcjdInoVXk8s3JS46emE3VJQ8bPG1frJdVpbP54c4k1V9aY3DFd5zndaa+4Wc/y05lGJ1FObCoznWHRDO58lAonAVEEgtTszG8l8z84MoXyeCEwQAlOb0k0QiFlNIjC+CAysdqdhv8grEUgEEoFEIBFIBBKBKYxAe734FO7wiLuWC8oRQ5YZEoFEIBFIBBKBwUIgtTuDNR7ZmkQgEUgEEoFEIBHoOwJJd/oOaRaYCCQCiUAikAgkAoOFQNKdwRqPbE0ikAgkAolAIpAI9B2BpDt9hzQLTAQSgUQgEUgEEoHBQiDpzmCNR7YmEUgEEoFEIBFIBPqOQNKdvkOaBSYCiUAikAgkAonAYCGQdGewxiNbkwgkAolAIpAIJAJ9RyDpTt8hzQITgUQgEUgEEoFEYLAQSLozWOORrUkEEoFEIBFIBBKBviOQdKfvkGaBiUAikAgkAolAIjBYCCTdGazxyNYkAolAIpAIJAKJQN8RSLrTd0izwEQgEUgEEoFEIBEYLASS7gzWeGRr+oLA5bde/opvv+KFX33hob85NApc9DOL7nP2Pusftf4qX1/l5L+dLPLLl3x51W+suto3Vjvz6jOfd/jzrr3zWpGbHLvJHmfsIXDuNedud+J2tz9w+w4n7bDR0Rut9531LrnxklLUzqfsfNjFh8Vt/iYCiUAikAgMPgL5RfTBH6Ns4YgROPySww/a6KCVF18Z49lzzT3lf+jRh542/9PO2+m8f97+zw2O2uCNK73xwPMOvHqPq2+868ZPX/DpTZ+76fnXnr/9i7Z/bOixP938J+ndvua5r/nQmR/a/eW7v3zpl19353Wbf2/zP72r8ejBRx/c9oXbbvKcTYTzSgQSgUQgEZgUCCTdmRTDlI0cGQIHb3zwCX854dQrT73rwbsiJx6z80t2Fl7+Kcvf+eCdAputsNlbT37re176nqPfePTpV51+0hUnrfL0VVZdctVLb7n07ofuRnfeucY7KYSuuu2qKOHeh+99dOjROabN4d/Gy28ckfmbCCQCiUAiMCkQSLozKYYpGzkyBLb6wVZbvmDL3V+2+9d++7XIOfcccy8676IRnlZNEzhqi6Nwmi/+5ovHX3b8V1/71b3P2vui6y96xTNfMd9c87FkUeE8fYGnP/LYI2fscMa8c86LLV143YWIjoxzTp9z+rS0AgeW+ZsIJAKJwORAIN/ak2OcspUjQuB3N/1u65W3fuCRB7CWyNhEUCh4+PGstexax7zpmNP+cdp8c8635IJLUvCs88x1MJ5Dfn3I+s9aX8Z1ll0nHH2ofw668KARtSETJwKJQCKQCAwOAkl3Bmcsqs98ptGYyy+vvjZDJTFAbZtcTWGiWvvItfc7Z7+5H1sU4wHpQw89qQeLzLPI61Z83ZpHrMmjed/19vWM+86Nd9+42HyLrbnMmhdce4FbkYdueujRlx6NGCFAX9nsK08qIm8SgUQgEUgEJg8C04aGhiZPa6d4SxddtLrjjinex351b9oBDYNUXolAIjBZEBj6eMqayTJWY2rnueeeu+GGGyrijDPO2GSTAdrSkdqdMY1rZL7llmrzzat116122qlCWeIqAbcRvv32aocdqo02qtZbr7pkeFPzl79crbpqtdpq1ZlnVh//eHXPPdWrX93IHelvvrnabLNGYr/CEb/PPtX661errFKdfHIjZqpeM4V0qnY8+5UIJAKJQCIwLgjQ7uQ1RgR22GHo2GMbZZx88tA888wobJFFZgT8J8K77DL0m980Iq+9dmiVVRqBxRcfuuuuoSuuGNpxx8ZtyRKBt7xl6OijG/F+t9++EZhvvqFDDmkErr56aNllG4Gpes0U0mr/yr+EdKpOgOzXqBHwd1HPe9ddd91///31mIkM/+c//7ntttvir3Ui6826ZiEC55xzTpAV2p1Z2IzWqtOY1QcSueyy1VVXVfPMUz3ySLXIItW99zbKpKEplqmFF67uuquS7DnPmVHdjTdWf/sbaV3deWf1nvdUGw/vay5ZIrD00tU//9ko9sEHq+WXr2SZd96Gmid0PyqSd6peM4U0jFnLHDGUkE7VOTA79KsvNtkmI5EyI+aBBx744Q9/+NGPfvTFL37xG97whvXXX//5z3/+BKP6zne+85vf/GaD7lRVUzsnuCVZ3YQhMLDGrNyI3oc5UNxgH3vMumpGgcJxIT2RABk644wGZfHowgurOeaojjqqOv/86otfrI4/vvrOd5pbUooqD+aeewbXETNtSvuuzBTSwOSGd0y7oaBji/gnq2q5xv2PL6oq/1x7VtMOqAV2q+Yd9gdvRO02/Gjv6ilfGk7g5wOPJ348oi//nRRv+b7I3b7A1VRIK3oD29Smlne6bepR022nXE3xm2+++U9/+tO//OUvL/zRC5seldsrrrgC3fn+979/7733UvAssMAC5dE4BW699dZHH310ySWXLOV/9atfveqqq86uzi4xGUgEZhUCSXf6gPzaa1ennFJtvXXDn6ZwFNoXG4JWXrk67rgZ1GSddRoJttuuOv306vDDG/43PH7OOqtaffWG8saFBvk3ffqMJnH2+tGPqu23b/xusEEjsjyakWLq/memkEbXt7xsaMstG5D+7GcNSE84YQak2BJIOQDRq6GbcAuFGTA5Qvk1KKed1vgtGjUF1sP9graTbO4U3696Z1pOq5RtjZlpIeOdoBNKs7apv/zlL1ddddWnPvWpo+h+px6NtKgvfvGL6E73XB/60IeWXnrpV7ziFU3JHhteik1//G3y5z//+Xvf+x6X0he96EUHH3zwyiuvvOOOO37+85+fe+6599hjj5tvvvkrX/nKtGnTtt566xe+sEGtzj//fFW/+c1vfvnLX45FHXrooffcc89rX/vaK6+8UvblllvuNH9aVfXd73736quvXnDBBW/xd5hXIjAICLTatzJmpAj8859D667b+PeRjzzhf3PSSUMveMHQBhsMffjDMyKvu25o002H1ltv6JWvbDjfuA4+eGi11YZe8pKhL3+5cbvZZkOvfW0jEL47N97YSK9Yvzfd9ER8I/R4mghPvd+ZQtpQj+9fDT6kGtl2dNrGf+ELX3j605++/PLLv//972+bq1+RrbW3xoy0rkceeeSSSy658847R5qxpP/2t7998cUXl1uBtq1qG1nPNbrw9ddff+GFF9JP1LNfd911vx6+SO6IP/nkk+eZZ57Xv/71F110EcHPMSXir7nmml/84hfaj0xEzAYbbLDSSiv961//Er/MMsscO+zf19T4uL377rvPO++85z3veaussoraZD/ooIPQqc985jPsUKbEBz7wAVoT8ejF9ttvv+2222IbxAftTlOB0oh5+OGH99xzTxmf85znvOMd73jrW9+Kc3gk/TbbbPOWt7xF+z/ibTU0ZNS22247zAYvQVnMPelln3POORmh9O6OO+543/vep66zzz77D3/4w+qrr/7qV7/aRNVUw62ESy+9FFWS/nWve91ll10GMZHHHXfcM5/5zD/+8Y8CDTG3f+Of+LxmBwQG1ncnp2BP04/dOf9NAAJtB6N4cNef1l+gBIwXNJfMhx56qJ5mEMKd3vJt48mP3XbbjXTYcsstx7XxrbW3xsy0AWAPGRwp//3vf2u5df+DDz5IRvqNeMmI8/vuu69eYKSpR5Ksa6211k477USiyx5D2bZVIn/2s5+R+m9/+9vJ5t///vdK/vSnP33iiScKMNyQ9BHpVsoddtjhXe96l8SkdbRBSj4lpDi09957b5H//e9/X/KSl2g/jhK8RCQ3W2xDpEt1kRcRcYvHfOITn3jpS19K+SGejCf+sZM111zziCOOiJQk/XrrradT8847r1zInPimHsUtJqFMahIlCFC3aP/OO+9MASNmv/32E4k6yE7FQvUigEWJ7ER3JHDhH29729uGg40fwLJn/b//9/+EjQhXnssvvzye0sRo5+233x63/pTmmGOOX/3qV2jNBRdcYCygF4+Mr1HTX0RqM+uz4UszbDym44lbv/qr2XGLTulmU8dLygxMPQQGlu6kMctLI6/JioD38sILL8xHYd111/XCpb2nYJ+snakq4tP1v//9j0Sp94Iw5v3HTGBtXY8nv2kdSOjFF1884kloUorpASyvfOUrI9LKXnY6CdK3iwkGLznrrLOoZ6z1n/KUp0gsO0Lz85//XKTlO58MOBN4VALzzTcf44ViP/zhD5PxUnIT8ctXIyQiaR0NoJmQUqeorKglokycQOOJcNnpG0TSJYRigwFF99/97nevzaLZ4eJ++4xnPAPHRRRe85rXaPD++++v/De96U20L3gD4b3aaqvRuNCCICLXXnstWY4bKU9j9tlnnx/96Ef4ykknnfTjH/9YJFaEJ5Hi3Ht33313eo5FF13UI8zjb3/72yKLLKLYaMt73/teKH3uc59jz9JUOKvlVa96lerWWWed+eef//jjj0dKFlpoIUqUM8880wDRGOEZBiVK6PRLswJnT/VLaZyLX/CCF3zwgx8Uo1X4GdWRsWBaEkNGdiqnxGsGFVS5FTBwdDMCdDmqwPYotNzqrD8cv8IuUwVoiM4//vEP5I95KyZYGLZOOeUUE1K/gpxJ/7vf/c4cKL5BWguuXWzEyCsRGCgEph61HI8ehWKjqWTvx/rqtunpLLkdfg02atY2b1uvNi9NL8oJbszXv/71G264oUulRVFU0rRFuDxtDcR6kYj1aNddd/U3RaSVZOQlmVFuvX+tUK1uCR6/Jd7b34u7yf7iViTx7NciOBITlqSa7IoSI8BX1OqZ1PzNb35DuPJaKMXWA20XtcARv8UWWxD/zAqYQWmtR6wACq8XQm7pIAGvp0iJR9pjwc0zQ3xRBema0ojVueaai0aByJHSTNh4442ZMxAUxCKKbW2VmC87BqqqVEHaWbvDUOLPfvazGJiiqDeU/JOf/ISwD37zsY99TPdXWGEF8k9KTZKAX0tUEb9UPioFGpRwiIjESzAPYWISHSkp1d6jMWuppZb65z//afjYiW5k9B0aWmONNRQrAEmy/IQTThAmrZXJSqW6jTbaKCpSaWh09KhAR7UTJWAAgIoNtEcddZSiZIQ/HhljRO+izPr0plgSg3LBnFJEN8u0AXupN2pvQj5uwzKFttIAKSpUUzD/xje+EbkOPPDAFVdcURjxCuWT7ksJrqYCpSkxqtaAKMGv6aGF2FjE4G1HHnlkhPn3NL0l1KJ8+DCxCUR//V3TnMnC9CbSvIrsfHpwRKPsrybmp5IlMApMXYsttpgmlVZFlvydwggMrHZnukmZV48IWJ7V/y2wwPxzzDG9HjOrwk3tJ+GIUtYByzWiKDwHm9KM3y0qYHm911579VIFo4Z3+k033dRL4tY0ltciQwKVp+SxVb4GWJeLpABgzqAPwP8sUr3WkVTxVvlUAk972tO8rC1VI7tdJFa9IqX0y7YiXjkUFZxDl112WW9wMQgBKXvqqacSVKDmmVGWtlFO919SRwIr9eAQTAlUMpGFvKRHqWe3/g6OhdsRb4Sup9QqRDLlhJcmERjaIPLeoJM3uB1lyaabbkruhrhVxemnn84CIn298HqYuuWAAw6QMdQzFveesncQ9vpI/j33uc8lvWgysA286lOf+hRxCEzatXo59bC2bbDBBscccwxVCsbgEcIEyegjZZV9Q/X0PYbRQewEq/vrX/+qv91zqd1YwyGSGSmmFlYqWH3pS1+KSPPQ2uCQQw4xdRllQgXCYkV9iAmhMvxgYN62IhNGPL6LT2BgCmeMa5uyUyT2gEkQEthVSQMivkFulUnvpbPCwPcX/dvf/ja0MihLSd8U8DdluP/+979jHocddhgSb9YBAbc+/PDDKdVMOcMnl3WCi0HK0KO85oxILMckx2Xf+MY3lpLFwAepZQgTiWuahNyc5ZVR+SaGRYJHuDhVKzavwSZPKSEDicAsROBJL9ZZ2I5JUvU0f8D+vL/zne/4e/bKsPbtS8u9KL1wizJZmd7FXhyE37Of/Wy/YtAIby5r5SWWWOIHP/gBtbmweByrfpF83lA0BOwF4kkUngqRgLyh7LHSJaTJITwDFSCqvQq9Z4lDKn0vQS/90BDIRXBaDtJmC1vYWaN773/ta1/zXvOCUwJXAAt6jSFRjj76aGtQsFhVK19FOmXtiyWQ01wlKOe9TIfXi5+KJhEt1PXDfOWbETOiX69dmgZvbaI6MqIgCA2RQDATWnwnQaHN9BB8KTAATxl0vLX1heglLyn8rVOlZ4Dw+qalIE4IGD3yytZguSz6iRaSUneIfynBRRBy0qQqIBVG1OzGereqsAf6IUSKcogiIUSIOQDbIGTSMK+gboZDA0wDOBt67E2DGYk0yWSw0A/+hNJJhqLpi8KNsi7oCPzFIzrPetazFNWpqdAI4qJw4MDNOAp83IHfVWWKYl2RXVExJzsVFfFG3/TQF0OvX6EwCF5YWJcOMpyZLZElKJG6dArb6FQ+zAlR5Rt6rBSRZWhDMlhblKBGZBRTic1H5hgZzwxnGVBYqUGkGzO4lHb+xBinTG/OKOCFmOEwVyGsy7qA6GA8kRdP4glEipP9Wm76semYXXRdckEYDwsWrm0IgS4oCq9lQevUHbXjZEx7pqJWAQqFYkpDiFEQE4BNzV+ov1Z/jGa48qmgtIopbbWfNMhW6+VvygSgIvJ3iooFW9JCRcGN9o4+JmDXNfFGNsY3UuqFv1nlAxYsYcwSwMkCVb9wtpkLG9MSt8ZUIeUlhjpLDyJ2sSMPaCh78koEZjEC5mheM0XgceNLY7C8L6xrBb71rW+VjPsetu8z9n3G0p9a2rckCRsifIFPLrDZ5zdbdr9lF99v8UPPOFTKwy4+bIUvrLDEfkts9dGtlvzUktfccY3IV377lWt9Yi0C7KVbvXSVT6yy76f33e5H273qu6961v7PqpZuVEe/vchBi+z0452evc2z3VJaxGrSayi068WApTRhglyyVtuKcpjnvakJQoQDl4rNIPvuu6+VOhpEyGEqXmcoi1cznTza5LWuRiXjNAQGPmQZSh2CE3iVh5RF/kI9E0p4iTlekDea58Uaym0ZvUZRMTKJVH4czyG3Xt/R8npHxHS/qv0b6nHKc29YXfNrhSoLmQF8pERP4RBKeO4ONBaekoX6jgZF4eijlAiQl7VHIskG5EBAFyyCBZhjrLNDBiiQ1NF38S4sh5Uhwp1+NbLtI/FERTxqMjpw7USw4lHDF3XYfzZugUm6GDtMCx1BTMkkbAkrlcDYaRvMdYqY+b//+z9kTvawIsnLrMObRMrWVkV7sCL6LWUadDJMSjI7stuZrKiYV2aLy1MXjxN/DgKqJjgxDz6q6Ahk/vSnP+ljrAp4AuElRKBZgS5rPxZlmgEWaZadrMUdyVdp8HhzUk9b2ymlSBdPJr4yiCzdm0ichvOWeK311yRA0uNSAuaGSyAsaKHzK5Hl74gSVK+RHqxdgS7Txq3pSm0WZtOIh+QnP/lJdKEYhsRjJ+YM2h1p/MLK7id9xPbCjVpkU4/KLVgggEBIE3/X9V+RMfQCLskipXApYfhJ46c1pjyaVQFNGsBWzSo0pny9XkT+3FxhFB6c/qZ2J8al11+y0EouzENGUTZKl5e97GV3rnvnEjcvcc1vr/lk9ck11l3DjoZqn+pPf/jT4lcvfv091x8494Hv3+T9B5xzwMNfeHjJFZY894Xn3vaX2w5f9vDP7vDZBx9+8Nf/+vXSDyz96LKPXnripdetet3pbz393r/f+96vvXfFvVb8+Rt/rvD7d79/2xdue/CXD9530X2VzBuUOPS+62WFXTpGBDIByE7FTTCgBaQsScnKwKBAohMY3uyWqlxEvc3pQoh2vSN+iDpCi1WC4oE0xSHwG9kpkCgAwuJjKcwrAhXz1rbIVqCr1E4sWRZbRpOFVCbx7XdPrS/Jp5JspAF6Gop6FcVYyE7Jr0nkHAYQQq5epkUqGRl+DwDxZ4nxWFKTuJEMsDrFfwW2ZH9EkrssFCJxOPYF+gDSul5sPUyFQOYR7TM9wZZqAZuxZGd9U75C2NRCq+cRMBVCr4aP0ruEXQOXpeChWZQSK8XbkEXaCIwN52PbIlyZijSeAoneThuQHqJaOYQxbYEO4rX1BpcwmgUNDNIQs2FRrlA4UTwQ9txOjSk1AxnPPoKkqsKUINFNITBqlWSosBgaNXMAt7Csx1rUThHiQoxo3ZSAiYLUwKFHXohmuDZIgBNQw+AQbEy8SbpM77BhKSS6KTvVi4pwU3+hKBTQ4EO7oNcQkJIK0xQVUDutmGmvkZy4kWNTxRTi8uwqaAi8x3nn7S7zCs5NT4IC1iPN8/pt93Djr+Xxv5cI1H/lVWkBJPQrXQrs1+k+XarIR4nApEPgCYE06Zo+8Q229GTCsE61XPPG9+rUBu9ZgvDN27/5S2d96avVV6tHfCt0XXLo59XPj//w8eu/fH3Lvu3+vJ2Umyy/yaXvu3SF21dY/O7Fv/X3b/3+f7//y3/+svJTV/7VI7864KADNj1q06XuW6paufrILz6Cizz20sfmunOuLx32Ja/p6dX0jZffePq06RpA0HqDd+m7JTKaEm2TjCwkRfAVq0OGDzGWxQSVd32XQlofUX5gORRXNDSkZphv6GzCBCM9JhE0gmAm1QhOkTiZishCjIriBAuxtkY4quoJbw/CZlh30tHI0tqYEiMv0aWPYlAEWFmO46NkjzEiszUDwbJQporDz4g38jVsahx3yH7iOXQAbBbCVBooCE0+uCJGv/AA3IhqBN0hoVEHIBCo5kAYv8ghygwCWzOwATPEKHhU2tk2gDZRfiiN8aKxWXeYOmtSbAPmIKxrQCOYoc2+JgHjF65D8lHS0MH4VSklBJA1hsWEMQXhIw51JByZNQxZ4XJEraXAti2JSCoZV1MCs8Vo1iOVo/ASEyaquEVWXOWRAMWPqx4TYS1pbYw/Jbak1sStMW2pJOrjisS4jgDuiBcaaIpMLBCvwiHMDdQQX0GRjTWczc/WKiYspu/UZOjjjWXYQF197+NA9S4bM1kQSLozgpHCIQgn5154mRY+4U1qgf7N+765xH+XqC6upq37uNh+tFporoWidC7OAlvPvfWVf7rykmdeMn2e6dU11T8f+OdF11+0xhJrfPOGb77kjS+Ze8O593vHfodOO/SMHc5Y+7C111p7rc233Xy1xVbb9R27vvTEl0YJvbSVJPBCZ0fwNicXyTnORuiOFz0znBLQEbZ/lEWY8oaehsgkTale0A7SmsMHuU4SsFUFQ5ISzUK2CD8Mgz+BkhEIYo8PAYFBqYMJUZOQrKgehY2FMolCRURFwSpEwKAj1AMKFCgdIZAsxymQquqDJbL3gIU7jqIv1vEYCWMEBqYuvxb6OIfWwkHHMR695nqFYegXyxcaKi/6haxoLaLAPEQxoy+YjVyYDQUJnQF9g3i6AboxGgtIonGkNdZoGtCFKGGYsTUaLjvFBlhm2gusS8NogwAbiTmCoIwKd6sBRQybck2lSelqimSsdDVFujWywwbE1idTPIZZCutlUcKDDXrAuNVWW1m0mOTmhpWJaTMLURhAajIL0ciqE4HxRcBbNa+ZIhC+JmgBVX8kZtYhLIUZhrxGF/vsYv++7d9Pfe5T59h/DpHW6NVHK2xAmBPivAfMe8cDdyy8x8K77LbLPQ/ds9AnGjTo+Z96/sZHb/z7K35fPad65n7P3PV7u9IZvO6Y1x1/2fHWuEutv9Sz/+/ZnDMQrOkfm07ZQDSSvpxkKVTwg2iG37rLS4St9XkpWsvSoxD5CJlkuAi2wSuC7w5G4l1PN4CLKI3XpwBbFTbDNkE3QGFAGLu4WfA9JB5IZbt7CGbKfwwATVEm3QO5zokHmdBmvCoOLmOIQRF03C9JIyVG4qkYEmjYoaTRbP9wBconxpq4lbLHazy8AWiwjAvTTLQBuaHmKSPeY8MwRZyDxijSd3JZEI8kMS/SyvRYch+TtbaqNaaP1Y26qLatahs56iomOOOkbvyosdLr2bPjo0ZsUmccWN+daWAdXz41JUp/fDvLNByCpwUVCB9eRgeeE+EzUW1oA0ZV3VxNe860uw64a5sttzntxaetcvoqtCzUBte95bpdbt3l1hVv/ck/f0LRs9ztyz3vzuddv/T1Q6sN/Wyzny230nK40fTvTn/smsee9pynrfbx1R549IHb/3v78pcvv+jQolxePvHQJ+746B00NDQuKBcCwbOh2AK0rYxhCdMQUHVwx6HDZ9uKQRBJs0JpoRCyNuxZ9BPmgEiUhYrCrV9PESy5BDASupzwSkaS6DaK64A00ss70kF+HM/mfKUjzQ9a7lM93gJJRiQCA41AqrIGenj61zjrfFoA5THoW2/3r+CxlpR0pycEG+J5f//PKxFIBBKBRGA0CCTdGQ1qkzDPwNKd9N2ZhLMpm5wItEMgxUk7VDIuEUgEEoEGAkl3RjgP9k/b3wgR65R8/2ljF8+MazYo+XpRMdh1qq3HeDayplaVGBv47aViyHNSi91JPRY40mT8txwbY4cRT/DIa3s5hydnH3Cx6rRxKU17I8U50ycCicDshkDSndljxEdqiWtidSPN3hbUpjKH03AYio1IXIJcbfN1irRdnz8Tb2gn/9Z3JDmFzyYsbtdODyp5+SepaKRVlOx2ctm9xWdLDHfv+JREedrHAE8pe+XKPi8lczB3OQXYWcN9rCiLSgQSgURgtkJgZAJmtoKm3lkutNMOGI7oi+CvFz0O4Sb9hBo0vjWyU80NfcaTdVhtszvPxpku2EacGdOptIhvW6ZzeG1Zj1NzcAj7tupivnuBnsYZeg61cx6gbfAlPU5ja1i5jYDjYeIIlqb4Xm5tvHc4nt+3ve1tNvlTwPSSq5c02um7Ddzeff4z0js1xz52W+J7yZ5pEoFEIBFIBHpEIOlOj0DNSNY7aRhZub2lpqKwHax8YKhtpi52DXltpHIScduMM420xdoJfhQnkdLnAmzFH4vsd2iefe8+JmDnl7OMbZW3Kz50GHFujZ1lNpEVDqQu27Z1P75eZLOYXW/C5fhjDbNhntXJhjLH5JQe2SrvdD5GKGRCIY4JUKbPSvgaBhLj6B2ns7CL1bVBJa+As4ztj8N1hLU21FHS2xzn3EIFMqXZTu/UAOf9SOlQ4EsuuUSZzv1Tr7OIEDt7+CEPQ4caw1Aux/Y4A8luOxv+FRVfvXDWjiY5hNphAfU2ZDgRSAQSgURgLAhMH0vmzDvBCPhIdQjd0dXrrDlmkdHlZSGiifGVAGcG+rAAbxIfGcA8SH3fF/SpVEyilOycHl9FKN4nJb4pQNJjA3YqEu0ODnboPpaAHNhCLyUC4VgaX4SIXJxXHBLopGAcgsUnIpED3MWJgqVkx8ehHVQmhSR5hGrgT1rrzCEfR0QmlINXxRccUSgBpKd83bCUFgGPHEQUYacIOlZRWIwO0sRgbDqiec46siUhPiSuLpYv3cHGdM3hBfrlUxU2/4uUHT5Op3CWEu0UDlQ+6k7To5FYaVSXv4lAIpAIJAJ9QSC1OyOGkfLA6TWO++MdEpmduUdiUVFY5TvB1rk4TpmrH04jkpMK/4/6ETU0EE5nlgyT8H0GZ9g4648Vw2F34b2hQNKRaUZFqlOXj3E60d/hfh6Jpw8g+H3T0cd9aDW4svp8Qaf++BaBcwW13Ccv5KLqiGMSnTlL7iIBvpZALVGa3VSOxhPq2u/wPdnpRd761rfiEExayATqoDQ+NPG5A59P0jxF+bwX71qRTaXFLergEMUIYycMUqS+oxoiIyrDzqUcCRxqrJ2OTqYFQY/gU8Cn46EO8T3qKIfbMqMYkkF9EjF+efZwLnZYUXw/NeLpljgFx3mJ9C7q1anqxJLpSQE1xj0iIovW6q8vY/gmlAtlcQYj2ocwxXlFqvOpc2dRyqU7bhsnT1YVuBy3GEWFUgoCCJDORmT+JgKJQCKQCIwHAqndGRmq5K6TBn1JwBH+jhCUmeynb2DC8HUCC30OIr4p4ZbsjEvYV658YZHbx+Nxjf9KTDVCKqMpHrF9kMq4FMMHr1gJCEIfSVCRjzepCFOhMKCZEPDxB/xGpOqklJHk5ghCUSGy7UXQ0hxgHnQSBLNPgUpG30NVgwDxvaVHKadhtpaw+uqr85ZlbNJCsh9zkgaHc3CzNiBDEjiAWCQdBtLmS9roBYjogVpLa41RFE4AKEyOzQ4yQGCQCtaCGAnjDU3fb2otJ2J8mCJoR6cE4lEcZ2FBHlVloury1U+JyychQedcaY00oNQwpXw0CMeilyo0ixmu9dNOiG8QOM2Lz4opAc01r0pR3QNMaaVrqCS7GL7bPUs+TQQSgUQgEUi6M7I5YMlOwDPoEGZhlfjVr35FqPuOBA0NHQlNwxvf+Eayn9WJaUPp/DmwAfKbQoJF45e//KVI4o2gFcl7QwnUIfFlH44dpP7JJ58sDUrBRELjYiuylBQ8CASFAU2Gj0iExUckL1cqjQ022MBnsQVk7HQR0i5P8QaXAHmpqFAzsBwVv5xOJTTF4ygsXCJpOyBDySFMTWLDNvONnVMidbMpV7mFD7NXuY2A7hPn0U7UKoxZ7FO0KQgKytWUvtMtC1T9EV2aUQi7FRNSPDJquAIVVPjN1NPXwwicnmot7yKu2YaAFkcuNNHw+bK3z28FWwqdkyH2JSaJQ5EDnKhXv1jZ9AgywYT4HhnHsudLpcioXBgzTWH5YCfzGdOe+WCDOrZdjHc+vqF2aNdbm+FEIBFIBBKBVgTSmNWKSbcYq/OwWVDJ8PyV1O4kRpZYqTMY+ew2j1cLfd4bPnElAbMR8xbWwhJETEYkOUee4RykuF8MhkBllyHmLd/ZlWSkovBLxtN2CLS9pCFcudRwHJag07ksrXkppTA2bcDGqCsYUzAq7WxNWWK0LXxKKJa0mSVLjFyRQPt58GAAeJ6zcJAeagyuzSw+vjxVCqkHONAwjdEYUWhpRnwWAxTMQzyXeeEQ/PgQSqdk/ryUW77/pQTGO7ArNraG8Rfmk4Tq+Uo51xkWK5QCCfCJD2nCzmVrlYZxEvIxVGYsfsrKMTSch4TrRsZ6CyOMDhqCOBYdMdIY8RRRlFi0PnRddGPhFEXPB0kfBWPggwDrXrTNgOJVKCnc9E4C2jiNQWJASrFnPkRdZg7Gg5yxDxaFE0rEazsiKbriU+fSaxgG3DAI/ipy528ikAgkAolAewSS7rTHpVMs/xIqB5KVyAmpQ6gTw0wYndwvCEVyjhKFlG0qlqijtyDM6G/CuZU5iVTrwm+iBL5B1vokH2JBi8CnB20iiRvnwby4qZInbumcCGAf+MRRKCc42+JJ5CX5SgOx5557ktBPpG4JSYln4Ac0HPyU6bR0GUdhINMSxjLmPJkIcu1RIKLGfBb+Ky2FNSJ8/RtfQbn0F28IJROURFIOAUdF6AuE2bAAyH4EHMQC6cRjaMgo2LSEuRBhQuCUiSyioZpEfUKnEpHi7ZbHSvWUV3KYk0SiaByS1l57beHuF5dkW+W1Ex0pKWm2qK/UqAslkm6vhLVNmP0RV4tI2jtXhH0cHmcqiSMQtLUpko92U0zcctVytX2UkYlAIpAIJAJ1BJLu1NGYeZi023///X0nnOCnEiCPaRRIaI44T3nKUziv8AIhkslRj9hlSH0ajnCeJWUFQriSnTQQtAs4ChuQhT4dhoxUGmIokDSFqQUZorDBpeg5KCfoTgh4tIDqAvGi12HdQAWkVDjdzHHHHXfSISd16obsimIPIvjRC9odtIC9jCKBIKfkYCjplFc8Yxnfap5DCAdyJoZ/Lkqh47RW1DN+ReIZYc/So9CIiGx7ARBJot1hZmKUUSxFhVbxWCrpy6E+rWYvHCuUNCWxAGbpqsdEmFpFO+39jlv2IKopQ+BT7cNfaG/N8aQYQxO9e1JsVcWG+abIvE0EEoFEIBEYNASS7oxsRGgdUBOCmaFhq622QjIsrxlNCH4FsVNQ1VB7kMRUKaQp5QcnEjYOxggKCXoIrjZcjy33w4DCTdVWLKoLDrOsYFb8ysF4qCsYqtZdd10WLvohdYnHTjQAO1FvWL74Kdv/HHyFroVQ794fdhNmHZLeFSk5jnTPEk/bHOdz9uP5/lhVpz0e/sXjgfjv+U++bblDB5n/ROs+xPBIfW9J1f8IXi8qQla43Sy//PL9ryBLTAQSgUQgERgkBPKL6L2ORht532vWTJcITAQCs/YMzInoYdaRCCQCA4+AXR2h16fmd27I4LR3JsqAwWlotiQRSAQSgUQgEUgEEoHRIZDGrF5xy6Vzr0hlukQgEUgEEoFEYMAQSO3OgA1INicRSAQSgUQgEUgE+o1A0p1+I5rlJQKJQCKQCCQCicCAIZB0Z8AGJJuTCCQCiUAikAgkAv1GIOlOvxHN8hKBRCARSAQSgURgwBBIujNgA5LNSQQSgUQgEUgEEoF+I5B0p9+IZnmJQCKQCCQCiUAiMGAIJN0ZsAHJ5iQCiUAikAgkAolAvxFIutNvRLO8RCARSAQSgUQgERgwBJLuDNiAZHMSgUQgEUgEEoFEoN8IJN3pN6JZXiKQCCQCiUAikAgMGAJJdwZsQLI5iUAikAgkAolAItBvBJLu9BvRLC8RSAQSgUQgEUgEBgyBpDsDNiDZnEQgEUgEEoFEIBHoNwJJd/qNaJaXCCQCiUAikAgkAgOGQNKdARuQbE4ikAgkAolAIpAI9BuBpDv9RjTLSwQSgUQgEUgEEoEBQyDpzoANSDYnEUgEEoFEIBFIBPqNwJz9LjDLSwQSgUQgEUgEmhF4bPgSO336dMHmx8P3Ht1+++2HHHJI26ejjpw2bZqS22bfa6+9FllkkbaPMnKKIZB0Z4oNaHYnEUgEpjgC//nPf/7+97/PMccc0c9HH330gQceKH2eZ555HnzwwXI7HoF55533iCOOOO2009TVY/ka+exnP3vllVd++OGHr7jiihe+8IVDQ0OtefESjb/ssstaH4065pFHHnnWs5716U9/WhtaC5lvvvlaIzNmSiKQdGdKDmt2KhGYsggQk0TmqLuHGXRSLdTLnHPOOa+77rpPfepTAvX47mFtQwWkGT8hOtdcc/35z3/+xS9+UVryghe84D3vec9DDz0kRte+//3vb7/99r30sZQwisBqq622+uqr957RkK2xxhrrr78+znHOOedstNFGvefNlIlAXxAYwV9yX+rLQhKBRGBKInDxxRdfc801IyIHdRwQhV50ElQat95660c/+tF63t7DZO1rXvOapz/96W0X+vVyQs1wyy23CNTju4d14dWvfrVGbrXVVkX70j3LSJ8CCuNBpwTk9UvFUjfH7LbbbgsttNBIi52w9GBJrjNhaGdFdQSS7tTRyHAiMAIEOBlYs45IHEbpIUqJxlHk7aV9c88990EHHfSXv/yFXIz0HBeWXXZZkkabxbhdeOGFQ172UuBM02A555133tVXXz06ukMVseiiix588MFa2L1VaMpiiy129NFHz7RJbRPITtY+9alPbft0akQOMteZGghnLyYpAkl3JunAZbNnggAdwLHHHjuWFTYZ3EX0kuvE8w033DCTdnR4/LKXvWzdddcdi1GmQ8GNaCzq/vvvf+Yznxl0SkcWXHDBT3ziEwThT3/6U5H0AaR+L9qULrU0PVLmWNDWqkLOmkrO20QgEUgExo5A0p2xYzhlS+ARSYDR51MGWBaToP3qKtnGf/B973vfm9/85pNPPvnuu+8Owdxj+eQ3WY4r+BVuzaXBd95550UXXSTQ+rSXGB4e7373uzfeeOMunOB73/ve6MoHJrdN6pZeWtLfNIwspcDx8y8pVWQgEUgEEoEBQSDpzkQMBNEe1RTZTLqTxxdeeOF6663H7jAiYd+pxUTvWJbXTcXSXpxxxhnzzz//ueee6xFi8Y53vKO/2ggKhrvuumvDDTdsqnqmt5rx2te+9p577vFbsG3KBdI+otFUeN4mAolAIpAITC4Eku6MYLx23nlnqoiRrokt5W1J8ItALLXUUgJRJZlNfXLiiSfysRhBIzokpYRgHHn/+9/fRRvRIWvH6G233TYcIbE0vV5mmWU6Jp11D0bnLDLr2ps1JwKJQCKQCMwCBJLujAD0bbbZxvbLkcpXtOb1r389JYSMyy233Ajqy6SJQCKQCCQCiUAi0A8Eku6MAMVNh68RZMikiUAikAgkAolAIjAACIzSkXMAWp5NSAQSgUQgEUgEEoFEoCcEku70BFMmSgQSgUQgEUgEEoHJi0DSnck7dtnyRCARSAQSgUQgEegJgaQ7PcGUiRKBRCARSAQSgURg8iKQdGfyjl22PBFIBBKBRCARSAR6QiDpTk8wZaJEIBFIBBKBRCARmLwIJN2ZvGOXLU8EEoFEIBFIBBKBnhBIutMTTJkoEUgEEoFEIBFIBCYvAkl3Ju/YZcsTgUQgEUgEEoFEoCcEku70BFMmSgQSgUQgEUgEEoHJi0DSnck7dtnyRCARSAQSgUQgEegJgaQ7PcGUiRKBRCARSAQSgURg8iKQdGfyjl22PBFIBBKBRCARSAR6QiDpTk8wZaJEIBFIBBKBRCARmLwIJN2ZvGOXLU8EEoFEIBFIBBKBnhCYs6dUmSgRSAQSgUQgERgbAkNDQ2MrYOa5p02bdu6555599tlzzz231G5V6rdTzt13333hhRfu9DTjpxICSXem0mhmXxKBRGCKI/Doo49edtlljz32WL/6iQrcd99906dPn3feeR988EG3fpsK9/See+7ZY489dtxxx2OPPfbhhx9uSjDTW81edtlln/e85wnMNPFYEswxxxz/+te/rrnmmkceeWS99dbbeeedd9111wMOOEDVbZs9zzzzjKW6zDuJEEi6M4kGK5uaCMzuCIR6IBbrwnHbIyik+DjJWiLzhBNOOOecc+aaa65QKoyTENXxBx544Bvf+EZbyd0jDq3J3vnOd/7nP/85+eSTN9poI9Rniy22aAvU29/+doAjEK0lzDRGg1/+8pdvvPHGM03Z9wRXX31138vMAicjAkl3JuOoZZsTgUFB4IILLrjzzjut/sfYIHLUcpzSopPegqS/4447TjvtNAm22morBoijjjrq1FNP7ZFYKHzdddelYGgryMfYeN2/+eabb7vtNkJ9k002cbvNNttQM4yx2LbZ4fCRj3wkCF/bBCONhPwSSyyh5f/73/+e8pSngHeRRRYZaSGZPhEYfASS7gz+GGULJzEC1srzzz//3XffTcqSuNETC/S+iCuS/qyzziL411hjDeKK3Np7770J3bGTj2inAhdbbDFNvf3225daaqnWYVDRSSeddOutt45RtBOxT3/609dZZ53ll19+5ZVX1pfWusRoyeabby5w//D1+te/nh6ibcrWSOC/6lWvWmaZZVofZQwEKKUWWGCBhCIRmMIIJN2ZwoM7e3XtmGOOedGLXkRS+hUeXec7CdrRlYYEfPe7391+++0//elP33TTTSussAK5LvI1r3lNXyoi/sl9v3QeqIlGKraPQov15y1veYsGw/MTn/iEilpx+OxnP9sXdqWQOeec0+8YmVNrCzMmEUgEEgEINLzWE4hEIBB46KGHQhtxww03tJVtvQB17733EuoWi6ZW0WfUM5JnH/vYx6699lrirR7fe5jXIcVG09Q988wz6QbU6Fe499IiZejwv/CFL3C/aCp5pEXV08MBqpxARVKQqIVEp8Cop8lwIpAIJAJTBgE74zbccEPdOeOMM9h2B6dfo5Q3g9OBwW8J2Tl28UlGfuUrX1lppZWuvPLKG2+8sayAxYfCYOw4KFPJf//739Xy1a9+ddQFvuc971l88cUvvvhiaobnP//5bRkPRrLccsuNrgpg8l1QRZMTBmIhBkvzKzy6wjNXIpAIJAKJwJREIOnOCIZ1t912O+WUU+abb77e8+AivB9WX331JtncewmREq259NJLORLyoqA+CdULwf+Od7zjyCOPPPjgg5dccskxVqEitdC4ICgoy0hbWNKvuOKKFCTaqaiFFlqoxPc90KocipjCBfteYxaYCCQCiUAiMEkRSLozgoF77Wtf+5znPIcs7z1P2Fbe/OY3955lpCn32muvkWaZgPSY2QTUklUkAolAIpAIJAK9IJB0pxeUZqR5w/A1ggyZNBFIBBKBRCARSAQGAIGxnpYxAF3IJiQCiUAikAgkAolAItANgaQ73dDJZ4lAIpAIJAKJQCIwBRBIujMFBjG7kAgkAolAIpAIJALdEEi60w2dfJYIJAKJQCKQCCQCUwCBpDtTYBCzC4lAIpAIJAKJQCLQDYGkO93QyWeJQCKQCCQCiUAiMAUQSLozBQYxu5AIJAKJQCKQCCQC3RBIutMNnXyWCCQCiUAikAgkAlMAgaQ7U2AQswuJQCKQCCQCiUAi0A2BpDvd0MlniUAikAgkAolAIjAFEEi6MwUGMbuQCCQCiUAikAgkAt0QSLrTDZ18lggkAolAIpAIJAJTAIGkO1NgELMLiUAikAgkAolAItANgaQ73dDJZ4lAIpAIJAKJQCIwBRCYcwr0IbuQCCQCiUAiMDsjcP/990+fPv2xxx674447pk2b1iMUQ0ND88wzz1Of+tQe02eySY1A0p1JPXzZ+EQgEUgEBheBb3/727fddhsiMsYm4iWuToXMPffcF198sd8HHnjghBNO6JSsbfxGG230i1/8ou2jjJxiCCTdmWIDmt1JBBKBWYDAzTffTElA4qr7xhtvXHrppa+66irSt3dNQ2n0fffdR0uxwAILPDR8zTvvvA8++GB5OvbAXHPNte+++1555ZUIxC677HLqqaf+73//C0ai3sUWW2yOOeZ49NFHn//85/sdS3X6/utf/1p3RgFCvV4waPCLX/xigXp8Pbzqqqvqjoo+8IEPdCFG9SzC+rvooos2RebtVEUg6c5UHdnsVyIw2yFAznWRiOAg6b/0pS/985//nHPOUb76lKCWpuz4wWmnnfbyl788zCI//elPN9tssyOOOAKNGMUYvOtd71pmmWU+9alPbbLJJmuvvfb3vve91772teodRVGdsrz0pS9dY401PAUX9UZJ9vDDD7/oRS9Sl8B2222HDZRHowuMXa8zunozVyLQisC03olwa+aMSQQSgamHwA033HDFFVcQ4Z265qVBbzHGVwefCYKc0F1ppZXOP//8Qw89VEynGnuJJ5uxjfXWW6+LkCZ9//GPf9x7772j1jdsv/32dB6vf/3ri8aFRueyyy676aabUBweJJqqI57OP//8oxD2UMV1lHnttddStCy44IL//e9/BUbd4F6gyzSJQB8ROPfcczfccEMFnnHGGSh7H0seY1FJd8YIYGafsgiQWI888siou0duhfBrKgGNYPjYb7/9RiELm4qKWxUxfPglGtsmGFGklf0f/vCHCy64oJN8VdF88833yU9+0q/wiApvSgwK1EQhoOjCrppydbrFQpZccsktttiiU4Jxilevge4L+OPUwiw2EZhIBAaW7oxSozuR2GVdiUAnBM4555zrr78+JCXBSQPfKeVI4y3QGSP83Y7OiECEK2HbbbeVvYkToBHaWXQDI21Ya3pFrbvuuspUXevTkcZoLdWCxjc1u16OLiy88MKd+FA95ewQ/vSnP42/fuUrX5kdOpt9TAQmLwJJdybv2FX33HMPaUoy3XLLLaTd2MUPxkCf4Wo1B6jlm9/85llnnSUwashI0GWXXTZUEaMupGTkP4GOMCKgO1wQXvKSl+y9997dXTdK3l4Ce+6554c+9KFeUramCdLwyle+cuxKi9bCM2agEMAyF1988YFqUjYmEUgEWhFIutOKyZhi0A7rvNHtyOhScetS2xIc+WDmf97znmd9abdnl+w9PlpiiSWe+9znLr/88s94xjOaNmXgUjpl+8NYSBVw3ve+9/HVEOixSd2T4V6FT2jYWNrWvaJ8mgh0QmCFFVbo9CjjE4FEYHAQSLozgrG4++677XLsrkfBEpwA0T3NCKoc3iqJhfD8Qmsuv/xyOozllltOLQjQWmutRQ0j/POf/3zsjiAK5FxpW+YiiywiMKJGjjTxWFREI60r0ycCiUAikAgkAkl3RjAHFlpoIQadmWZIHcNMIcoEiUAikAgkAonARCKQdGdkaCeVGRlemToRSAQSgUQgERgABMZ6tvcAdCGbkAgkAolAIpAIJAKJQDcEku50QyefJQKJQCKQCCQCicAUQCDpzhQYxOxCIpAIJAKJQCKQCHRDIOlON3TyWSKQCCQCiUAikAhMAQSS7kyBQcwuJAKJQCKQCCQCiUA3BJLudEMnnyUCiUAikAgkAonAFEAg6c4UGMTsQiKQCCQCiUAikAh0QyDpTjd08lkikAgkAolAIpAITAEEku5MgUHMLiQCiUAikAgkAolANwSS7nRDJ58lAolAIpAIJAKJwBRAIOnOFBjE7EIikAgkAolAIpAIdEMg6U43dPJZIpAIJAKJQCKQCEwBBJLuTIFBzC4kAolAIpAIJAKJQDcEku50QyefJQKJQCKQCCQCicAUQCDpzhQYxOxCIpAIJAKJwIgRGBoauvfee0ecLTNMTgTmnJzNzlYnAolAIpAITCkEfvnLX15++eVzzTXXWHr12GOPTZ8+HY959NFHZ1rOww8/fPzxx59wwgnPfe5zZ5o4E0x2BJLuTPYRzPYnAonAbITAv//9b+KcUL/nnnumTZtW7/l9990355xzzjPPPA888MBDDz3U9LSecizhOeaYY++997722mvVNaJytPkFL3jBHXfcseiii84333wYST27Yv/4xz9ef/31AvX4EYVVseuuu37zm99caaWV9t9/fyDMNPtBBx00//zzzzRZJpgCCIxsvk6BDmcXEoFEIBEIHcAjjzzSFgqC/IILLvjJT34y99xzt03QS2SQkrEI79ZatOfoo4/GFe6///5//OMfTQl22WWXf/3rX2efffamm2665ppr9iLsm0ro8XbllVdGXHpMXJJBe6+99rrssstkf8YzntGqfQE70Er6UQc++clPjjpvZpzCCCTdmcKDm11LBMYRgQcffPD3v/89K8BVV101TtVQANBYdCqc7NcAq3P6jE5p2saTqVb/V1xxxfrrr6+QJjWDLBLcfPPNFBijlr4y7rTTTkcdddShhx66yCKLYFdtWzLSSE3dYostIleTcsWj5ZZbDlw33XTTMsssQ4My0sInJv3SSy8dFfWXCE5M47OWSY1A0p1JPXzZ+FmJAAHD9t+XFlj4Yg9EryXvGEWjQi688MJvf/vbQQJYNCgDgjSQwQsvvHBfGqyoO++88zvf+c5GG2101lln9aXM1kIQhf3226+LUUYz9t1339aM3WPkeuUrX0kL8o53vGPeeeftnngsT9///vePJfso8urOU5/61FFkzCyJwJRHIOnOlB/i2bqDt9xyy7nnntu0Du4dEeSjE6FR5jXXXEMYj7rw0gxc5/nPf/6666578cUXP/OZz1xsscXGwniQg7vvvvvWW28l1BEyXGfrrbc+8sgj3S611FIf+MAHxlJ4abOAij772c9iaSNVrtQL6R7WZmh0TzPqp6Mwx4y6rsyYCCQCsxyBpDuzfAjGvQFW4WRSlyVy7y2waZME7T19jynJyxNPPPGHP/xhCE5abtr4sTdYOTfccMMvfvGL0TESrg8cIPbYYw/otXYER1l22WVt62h9NNIYRa244oqrrrqqbSlU/eNhhthxxx1H2qpMnwgkAonAVEIg6c5Ej6Zl97HHHtsvu3Ws1LtQEKaNww477Morrxx7P5GGt7/97a1bKsZeMmbD9fLZz362gB4xuBxwwAH2o3bpV4+VwnksugfahdFRpR6b15SMC2dTTN4mAolAIpAI9AWBpDsjgJFuY/vtt7choheyQlTTli+wwAJ1mU180rVcdNFFAiOouENSJVu10z288Y1vbKuBiHxHHHFELw3uUMkT0dq8xhprTKT4f6LuDCUCiUAikAgkAmNAIOnOCMDDXT7ykY+cdNJJVCYzzcZC8d73vpe9Q6CemAKjL+SjXmaGE4FEIBFIBBKBRKALAkl3uoDT5tFaw1ebB52jUh3SGZt8kggkAolAIpAITAQCfTCpTEQzs45EIBFIBBKBRCARSARGi0DSndEil/kSgUQgEUgEEoFEYJIgkHRnkgxUNjMRSAQSgUQgEUgERotA0p3RIpf5EoFEIBFIBBKBRGCSIJB0Z5IMVDYzEUgEEoFEIBFIBEaLQNKd0SKX+RKBRCARSAQSgURgkiCQdGeSDFQ2MxFIBBKBRCARSARGi0DSndEil/kSgUQgEUgEEoFEYJIgkHRnkgxUNjMRSAQSgUQgEUgERotA0p3RIpf5EoFEIBFIBBKBRGCSIJB0Z5IMVDYzEUgEEoFEIBFIBEaLQNKd0SKX+RKBRCARSAQSgURgkiCQdGeSDFQ2MxFIBBKBRCARSARGi0DSndEil/kSgUQgEUgEEoFEYJIgkHRnkgxUNjMRSAQSgUQgEUgERotA0p3RIpf5EoFEIBFIBBKBRGCSIJB0Z5IMVDYzEUgEEoFEIBFIBEaLQNKd0SKX+RKBRCARSAQSgURgkiCQdGeSDFQ2MxFIBBKBRCARSARGi0DSndEil/kSgUQgEUgEEoFEYJIgkHRnkgxUNjMRSAQSgUQgEUgERotA0p3RIpf5EoFEIBFIBBKBRGCSIJB0Z5IMVDYzEUgEEoFEIBFIBEaLQNKd0SKX+RKBRCARSAQSgURgkiCQdGeSDFQ2MxFIBBKBRCARSARGi0DSndEil/kSgUQgEUgEEoFEYJIgkHRnkgxUNjMRSAQSgUQgEUgERotA0p3RIpf5EoFEIBFIBBKBRGCSIJB0Z5IMVDYzEUgEEoFEIBFIBEaLQNKd/9/enUDZURR6GJ9L7sxkJhsBgbAkRBIhEA3KElAQRCAoEAigmAcoiIKyi4IoR/RAwIVF0QiIC8qReEBEJESNJCxKIiAGJGxRAmIQRSQbDjOZ/X1DYVvcmZsMndm6893DmVe3u6q7+teek/+rqu6bVs52CiiggAIKKJARAeNOr9+oNQvXhHOsunRVr5/MEyiggAIKKKBAJwHjTieSnt6QxJ2ePrDHU0ABBRRQQIFuCRS7VctK3RZoq2urv72+vam9UFWonVrbuKiRct2suqHHDuUYDXc3tCxraV/TXrNvTeWESgr1c+tpUtFaUXNgTXGrjtvBIBC7iqOK1ZOru31aKyqggAIKKKBAWQHjTlmadDsa5jVUTayqmlTVtLipYX7DkGlDGh9oDFmHTFOoLQw7fljr8ta6G+pGTBhBherdq4tbF9tWt9XdVDf85OEdJ22t4AiV4yrTdcBWCiiggAIKKFAiYNwpAVnfry1/axly2BCOQmRpuKshPlx7e3v1zh0DNoM2HdTe2E6h+enm1hWtoU57c3sF2wod/1VuZ9aJ5SwroIACCiiwXgLGnfXi66JxR4zp+lMYVCgMJs5En7aKoccMLRQLBJ2W51o6sg4f1lO9vlbUwKICCiiggAIKvGEBlyq/YbK1NyiOLTY90UQd/ha3fTVNEoBCBuoUYoqji81LmqncvLR5zYLXHuBa+/Hdq4ACCiiggAJvVMDRnTcqto76NQfUsFS58aHGQmWh9rBaahfHFFmXM3R6x1Llkk/NlJr6OfUsZ2ZEZ8ihHVNgfhRQQAEFFFCgxwUKLCjp8YPm+4ArZ6zs9wscecHIfu+DHVBAAQUUUKBE4J577tlvv/3YOHfu3IMOOqhkbz9+dTKrH/E9tQIKKKCAAgr0hYCTWSmVuxxfeeqpp/bee+/Kykri7fjx47s8dBgcKmnOxpItXbZl40AYWyrXN7croIACCigwMAUc3enJ+9La2looFE466aRx48b15HE9lgIKKKCAAgqsh4CjOynxXn755auuuurII4+87bbbTjjhhM0333zFihUXXngha6EGDx5M6AnHnTlz5uzZs9nY1NR08cUX77PPPuXON2XKFKpdeeWVr7zyyvnnn7/RRhttvPHGnIVDrVmzpqWlheGiq6++ulxztyuggAIKKKBAOQFHd8rJrGP76NGjb7311l133fW8886bMWMGte+7777a2tpisfjggw+GxosXLz7zzDPnz5/P10GDBrFoa+HCheWOO2/evP3333/ixImTJ0/eZZddXnjhhbPOOovZMQ6y/fbb77jjjjfffPNll11WrrnbFVBAAQUUUKCcgKM75WTWsX2zzTYjoDz//POf/exnTznlFGof8urn6KOPbmh47WXKkyZNOuqoo5588sk5c+a0tbWx65prrpm5w8wuD83eqVOnnnPOOSNGjJg2bRoLgPbaay8S1RVXXHHttdfS5P77729sbKwY3GVrNyqggAIKKKBAWQFHd8rSrH3HlltuSS7ZaaedRo0atc0225SrTLXhw4czvcXAD9NVs2bNKldzk002OfjggwlGt9xyyxFHHBFeEDBmzJiqqqpyTdyugAIKKKCAAt0RMO50R6mLOqxK7mJrp01MTrHyZtWqVey58cYbjzvuuKTKo48++vjjjydfJ0yYsGzZMlLOY4899uKLLzKBxS5W8Lz00kv33nsvs2CrV6/ma1LfggIKKKCAAgp0U8B/PrsJVVqtrq6O6Sc+ixYtCvtYksxXVvCwhSXM119/Pdu32GKLRx55hCmts88+m9xz2mmnJQdiXTOLdZ599tmwhV0MFF1yySWnnnoqWYflz2xnWIigwwJnnm//v1c/obJ/FVBAAQUUUKD7Asad7lu9ruZ1113HmA0PTD3zzDMEF/bxHsmamprddtuNNTc8UdXc3MxGBmZYhcNyZh62uvPOO/fcc8/kKHvssccZZ5wxduzYsIU1zkuWLDn88MMvv/zyZLHzggULiESs++GxLx7sYu4saW5BAQUUUEABBbop4FLlbkKVViPW3HHHHWxl3IVpJgrDhg0LIzpxVUIPC5apwzhNyVTUueeeG9ekzGKgsCVZr8P8F5/p06cTg0oq+1UBBRRQQAEFuing6E43obquxhsFmWziWfHly5d3rkEMevjhh//4xz8yS8XbdDpXWOcWprEY/nnooYe6uVRonQe0ggIKKKCAAhuggKM76W86EeT0009n3opnrxja6Xwg3rXDm3Kqq6sp8GRW5wrr3MJyHRIPz2ets6YVFFBAAQUUUKCcgL+IXk6m7PaB8KtV3fyBrbLX4A4FFFBAAQV6QcBfRO8FVA+pgAIKKKCAAgp0Q8DJrG4gvb6KIyuv9/CbAgoooIACA13ApcoD/Q7ZPwUUUEABBRRYTwHjznoC2lwBBRRQQAEFBrqAcWeg3yH7p4ACCiiggALrKWDcWU9AmyuggAIKKKDAQBcw7gz0O2T/FFCgtwUaGxt7+xQeXwEF+lfAuNO//p5dAQX6X2DWrFnt7e393w97oIACvSbgg+i9RuuBFVAgIwInnnhiRnpqNxVQIKWAozsp4WymgAIKKKCAAlkRMO5k5U7ZTwUUUEABBRRIKWDcSQlnMwUUUEABBRTIioBxJyt3yn4qoIACCiigQEoB405KOJspoIACCiigQFYEjDtZuVP2UwEFFFBAAQVSChh3UsLZTAEFFFBAAQWyImDcycqdsp8KKKCAAgookFLAuJMSzmYKKKCAAgookBUB405W7pT9VEABBRRQQIGUAsadlHA2U0ABBRRQQIGsCBh3snKn7KcCCiiggAIKpBQw7qSEs5kCCiiggAIKZEXAuJOVO2U/FVBAAQUUUCClgHEnJZzNFFBAAQUUUCArAsadrNwp+6mAAgoooIACKQWMOynhbKaAAgoooIACWREw7mTlTtlPBRRQQAEFFEgpYNxJCWczBRRQQAEFFMiKgHEnK3fKfiqggAIKKKBASgHjTko4mymggAIKKKBAVgSMO1m5U/ZTAQUUUEABBVIKGHdSwtlMAQUUUEABBbIiYNzJyp2ynwoooIACCiiQUsC4kxLOZgoooIACCiiQFQHjTlbulP1UQAEFFFBAgZQCxp2UcDZTQAEFFFBAgawIGHeycqfspwIKKKCAAgqkFDDupISzmQIKKKCAAgpkRcC4k5U7ZT8VUEABBRRQIKWAcSclnM0UUEABBRRQICsCxp2s3Cn7qYACCiiggAIpBYw7KeFspoACCiiggAJZETDuZOVO2U8FFFBAAQUUSClg3EkJZzMFFFBAAQUUyIqAcScrd8p+KqCAAgoooEBKAeNOSjibKaCAAgoooEBWBIw7WblT9lMBBRRQQAEFUgoYd1LC2UwBBRRQQAEFsiJg3MnKnbKfCiiggAIKKJBSwLiTEs5mCiiggAIKKJAVAeNOVu6U/VRAAQUUUECBlALGnZRwNlNAAQUUUECBrAgYd7Jyp+ynAgoooIACCqQUMO6khLOZAgoooIACCmRFwLiTlTtlPxVQQAEFFFAgpYBxJyWczRRQQAEFFFAgKwLGnazcKfupgAIKKKCAAikFjDsp4WymgAIKKKCAAlkRMO5k5U7ZTwUUUCAbAmsWrgkdXXXpqmz02F5uAALGnQ3gJnuJCiigQB8KJHGnD8/pqRRYh0BxHfvdrYACCiigQHmBtrq2+tvr25vaC1WF2qm1jYsaKdfNqht67FAaNdzd0LKspX1Ne82+NZUTKinUz62nSUVrRc2BNcWtOv4NYhCIXcVRxerJ1eXP4x4F1kvAuLNefDZWQAEFNnCBhnkNVROrqiZVNS1uapjfMGTakMYHGkPWIdMUagvDjh/Wury17oa6ERNGUKF69+ri1sW21W11N9UNP3l4h15rBUeoHFe5gUt6+b0qYNzpVV4ProACCuRcoOVvLUMOG8JFElka7mqIr7a9vb16544Bm0GbDmpvbKfQ/HRz64rWUKe9ub2CbYWO/yq3M+vEcpZ7XsC40/OmHlEBBRTYgAQ6YkzXn8KgQmEwcSb6tFUMPWZooVgg6LQ819KRdfiwiPT1taIGFhXoGQGXKveMo0dRQAEFNkyB4thi0xNNXDt/i9u++v9CE4BCBuoUYoqji81LmqncvLR5zYLXHuDaMN286j4WcHSnj8E9nQIKKJArgZoDaliq3PhQY6GyUHtYLddWHFNkXc7Q6R1LlUs+NVNq6ufUs5yZEZ0hh3ZMgflRoG8ECsyt9s2ZPIsCCiigQBYFVs5YmcVuZ6XPIy8YmZWudqef99xzz3777UfNuXPnHnTQQd1p0jd1nMzqG2fPooACCiiggAL9JuBkVr/Re2IFFFAgQwI5G4QYCPIOm/XlXXB0py+1PZcCCiiggAIK9IOAcacf0D2lAgoooIACCvSlgJNZfantuRRQQIEMCzQ1Nf3lL395y1veUl39ul97+Pe///2Pf/xj9OjRm2yyCZf38ssv//73v//mN7+51VZb8fX555+fPn36u971LirU1NSw5bnnnuMpmTFjxlBes2bN0qVLw9cRI0awpeSzatWqv//9783NzY2NjYVCoba2trKycocddqAc12xpaaFvra2t9fX11CkWi9tvv/2gQYOSOq+88srTTz9ND7fZZptkIwUOvmLFisGDB1Ofrm699dZs5Dgcra2tjY4l18s1brHFFuGYnIWGf/jDHy677DJ6ctFFF02YMGHs2LFVVVXxwf/1r3+9+OKLG2302sgCR0Ng3LhxcR3LfSSAvh8FFFBAAQXKCay4aAX/sfeZZ57hX6aPf/zjX/jCF84777yvfe1rxJrPf/7z++yzD9uvueYa6hBKDjnkEL5eeOGF4YB//vOft912W7YQDsKWY445Zsstt/zrX//K1wsuuIBdfD74wQ8SMthy1113XXHFFaEmIeaII45g77vf/e6vfvWrX/rSl4YMGUK8uOmmm0KF5O+1115LtTe96U2XXHIJmYY6p556KqdOKtx9991U2HHHHT/3uc/x0BD1zz///EceeYSYwnayF+HmhBNOCPVXrlzJidjOJ7mQo48++oc//GGo8JnPfCbsjf9+5StfSU5HgRS1xx57xBUob7755uhx/I4K/4WNW2W9HJy5UpAH1LVUDKje2BkFFFBAgYEmkPyr/Ktf/Sr+x5tBi6FD//dynRB3Pvaxj4U6DHgkF/LpT3+ajfvuu2/YQqrg66RJk0geoTJ/ORqjQbTaeOON3/72t4eap512Wqjwve99jy2M8YwaNYot73vf+8hVoQ5/r7rqqjCCMnv2bL7+/Oc/D62S2MTGyZMnh438DUNEFIYNGxY20vD73/8+ZYZeuEySTdjOX0aSHnjggW9961uUTzzxRA4Vynw98MADCS4/+tGPwnDXTjvttHz5ciqEz8EHHxwOwoAQcY3xrWREiuEu6iSw/22Rh/87YOOOk1nhf43+VUABBRRYh8Cll15KDYZDGJ8gefCPMyMiYXKHrwcccMCTTz45Z86czkehIRNYt9xyy2233Xb44YeHCk888cTjjz9O8khCwEsvvcRQCmM8yRYmjKj85je/mSElCkxRnXTSSTNmzGDk4BOf+ARjLWwkbZx++ul0hkEmEhVbeO8LH/7dPffcczfbbLMPf/jDbGTGjb+EnrPPPpupqBtuuOEjH/kI56L/jCG9853vfOGFF6jMhBcxhfkyEgzHZP6OIaI999yTMs3Z/p///OcHP/gBZT6kMcLZ8ccfjwNJiCs66qij6Bttef3M7373O+qQgS6++OJDDz2Us5DDnn32WfR+85vfPPjgg+Mrxr96GP/0hUCxL07iORRQQAEF8iIwa9asXXbZpcurIc2wWqXzLoZAmKIiE3zoQx9iBQxphmGh+fPnv+1tbyNPxPUZbiEc/OQnP2HjU089RR5iIGTZsmW0DeM3DP/86U9/uv322xcsWBAaMvQSsgjBYvjw4WwkgvzsZz8bP34852UGLcSdUIej8aEOf0la4QjhLxNkRCIGlmh45plnNjQ0sNyHjazIYcKOlT2swmFpDkNTTIHRhDIDNqHtRz/6UaIe63iIOAQdXq/32GOP1dXVsZfz7r333uQkPsceeyxbIJo5cyZrg4w7Qa9v/m7UN6fxLAoooIAC+RBgcXG5C9lrr73IByygoQJDL0uWLKHAv/dkFGZ5KDMDRaRgWQyjIKxrIXAQTeLP6tWrr7/+ehYOU5k1wuQqhnwYg+Fr8omXAxOJbr311mRXUkgGjULmYDvdYHAoZB2+lmQdtpBdSDYMGt18883MPU2ZMoVlQzfeeCNrhlhDTeKhDl0lA1Ho/Al9JpYx78beZJqPGPTe976XoS/iXWhF/CK6lVxU5wO6pWcFHN3pWU+PpoACCuRcgBGas846i6kZrpMAEUYvmAziK0GHVS8s+2W1MiuR3//+97Okl9EXZo4SlFNOOYWRHlolW5ICAx7MTNEwrOk555xzfvrTn7KXyawwtJPUTAqkqC7Hk5IKHJApp912240j0Ge6xNwTIzeslWZIJqlGgQfKmP8i8cQbkzKTcSQkcluYL0u2lyswCHT11VczY0UFRnr4LFq06Itf/CKpiCktYtPOO+9c8bdyrd3e8wLGnZ439YgKKKBALgW++93vkglIKqx9YXnKN77xjV//+tdsIeWwVoYVLWHlLytdWKYTVhl//etfZxKHaSYGOULECX+T1TkBiqU/n/rUp8gBLKBhwc2Xv/xlqjGy0pmR6a2FCxeynUEmltGUi0Fxw3BGlhzxEDhzZ0wkcTo6ySPu3/nOd+gei354bL5zjqEyo0eM6/BIGiHs29/+Nodl/CY++FrKTIqFuBPqcLqwZJuvDPYQd1bOXrmW5u7qWQHjTs96ejQFFFAgtwLMLsXXRhxh4olhDOabmABiyuaTn/xkqPCe97yHXJJUJsTw0p0wIMQD58n2pHDGGWfwZDgJgKATBl3KpYqJEycyZUacYhUzwWXq1KnJQdZeKHmsjMp33nknByG60dUjjzySCFJyBPJc8uwYo0QMC5VUWPtXHnpfewX39qWAa3f6UttzKaCAArkSYA6LHPOGLonppLg+oz4MDt17771M9/z2t79NJpgYtgkPgsWVQ7mnYsT+++8flhlxWB6qKjkR7+9Jsg5zWEnWufzyy0tqdvmVeMTUFQ/nM6hDc1Y6x9VYx8Oy7niL5d4WMO70trDHV0ABBfIgQCL5wAc+wFLf8HB4uCRWDbN8J5TD/BQZhRW+PLsUD88w8RRmlKhfMv3EDBHrb0gbTPQkb/YLB+TlOqy56WxHeuARJypPmzaNASdGkkKdkoe8kobUJFuwOJp3AjGWk2yPC7yhJ/7KuA6Pi4ctLEU67rjjkr2bbrppUu6yENYs845BXq7IcBfLnHmVIo9r7brrruwKz+3TkKGpLpu7sZcEjDu9BOthFVBAgVwJ8EIappB48IqHp5ILY2Fv+NUFtrAyhukh3rb8i1/8gse5eSo7qcai4/AgEutgwhuWk133339/KN93332sIE62U+DlyF3+3sK8efN4Govfc2BJEAEivBaZ+tddd128ViYc6uSTT6Yay6VZGMTUW/L4enyizmXqJxsJVayVTr6OHDnyrW99a/K1pMCSpi4HpVgZTV5kpCeZ7+MJ+ZK2fu1VAeNOr/J6cAUUUCBvAuGRcq6KlcK8IIcHjsIV8pA5Ay3JXBVrcR5++GGW9fDC4jvuuIM6LM0JbwvsUoRwk4x8JBV47x+BhmXCV155JeuLOQVZh4e/GKRhV6jGOwaTCBWWBzHMw6t6KPM0OA+RJUcjchGJkq9xocsfhQgVCExxTUZ3fvnLXxJfOAsTXryMhzcJgUCWYuCKnnBSchtLhch//AgXFUJzvhKGwqt32ML1xoe13NsCLlXubWGPr4ACCuRB4B3veAcDKjz1zcwOLybmn3YexXr00UfDtRECqEBeYc0yPx31z3/+k2ARv42QNwryKmGOUM6C6ND5XTjM+JCQeGsfZ2ToiLYMAjG8xPIdhprCoVi8TJzi9xyIOGQOBmZ4DzKPXLGXBTcM7cRn5FVAPISVTHvxWFnYW1ItbtK5zPQWU29M6vGKHY6WVOB1ggzh8JWZO1bn8AZnfo50u+22ozKP3zMixRNeSX2ut+KZpKmF3hfgrvhRQAEFFFCgnEDy005MPJFpwtqUkn+dWNMTN2exDstxiD48jM3PPlBmnCOukJQJMSQhjvbjH/842VhS4LyMDBFr+H1Ncgkflu+U1Fm8ePHuu+/O5BqjJgyisJCIZT2Ej1CNQSam4ZJfyCrpPCNSDPzEByQw0fNQjTXU8a64HB5ND9XoG/2M97LUKeyiM0yHxWGOrjIClMDGrbJeHrC/mVVAtuTG+1UBBRRQQIFEYOWMjtfDjLxgZNhCLmGCJp54YlUyT1SxqCVp8kYLDMbw8htyzNob8ugWuYd39JWrxuATM19Lly5lxo33I5ckMwaBWEPNi3bi5syRkbdYFh1vpExEY9KKy2SIqNzyZNYzsSSIA3IQ+l/y++f0IcxwcTSm4agWlmkzy8aQD4++l8CWdCCjX1mUzUuY6Dy/Hcaw3MC5CuPOwLkX9kQBBRQYiALhX+WB2LNc9CnJkbm4mooBG3dcu5OP/4F5FQoooIACCvS/AEN0/IgsE0eMw/V/b6IeOLoTYVhUQAEFFFBAgTwK+CB6Hu+q16SAAgoooIACkYBxJ8KwqIACCiiggAJ5FDDu5PGuek0KKKCAAgooEAkYdyIMiwoooIACCiiQRwHjTh7vqtekgAIKKKCAApGAcSfCsKiAAgoooIACeRQw7uTxrnpNCiiggAIKKBAJGHciDIsKKKCAAgookEcB404e76rXpIACCiiggAKRgHEnwrCogAIKKKCAAnkUMO7k8a56TQoooIACCigQCRh3IgyLCiiggAIKKJBHAeNOHu+q16SAAgoooIACkYBxJ8KwqIACCiiggAJ5FDDu5PGuek0KKKCAAgooEAkYdyIMiwoooIACCiiQRwHjTh7vqtekgAIKKKCAApGAcSfCsKiAAgoooIACeRQw7uTxrnpNCiiggAIKKBAJGHciDIsKKKCAAgookEcB404e76rXpIACCiiggAKRgHEnwrCogAIKKKCAAnkUMO7k8a56TQoooIACCigQCRh3IgyLCiiggAIKKJBHAeNOHu+q16SAAgoooIACkYBxJ8KwqIACCiiggAJ5FDDu5PGuek0KKKCAAgooEAkYdyIMiwoooIACCiiQRwHjTh7vqtekgAIKKKCAApGAcSfCsKiAAgoooIACeRQw7uTxrnpNCiiggAIKKBAJGHciDIsKKKCAAgookEcB404e76rXpIACCiiggAKRgHEnwrCogAIKKKCAAnkUMO7k8a56TQoooIACCigQCRh3IgyLCiiggAIKKJBHAeNOHu+q16SAAgoooIACkYBxJ8KwqIACCiiggAJ5FDDu5PGuek0KKKCAAgooEAkYdyIMiwoooIACCiiQRwHjTh7vqtekgAIKKKCAApGAcSfCsKiAAgoooIACeRQw7uTxrnpNCiiggAIKKBAJGHciDIsKKKCAAgookEcB404e76rXpIACCiiggAKRgHEnwrCogAIKKKCAAnkUMO7k8a56TQoooIACCigQCRh3IgyLCiiggAIKKJBHAeNOHu+q16SAAgoooIACkYBxJ8KwqIACCiiggAJ5FDDu5PGuek0KKKCAAgooEAkYdyIMiwoooIACCiiQRwHjTh7vqtekgAIKKKCAApGAcSfCsKiAAgoooIACeRQw7uTxrnpNCiiggAIKKBAJGHciDIsKKKCAAgookEcB404e76rXpIACCiiggAKRgHEnwrCogAIKKKCAAnkUMO7k8a56TQoooIACCigQCRh3IgyLCiiggAIKKJBHAeNOHu+q16SAAgoooIACkYBxJ8KwqIACCiiggAJ5FDDu5PGuek0KKKCAAgooEAkYdyIMiwoooIACCiiQRwHjTh7vqtekgAIKKKCAApGAcSfCsKiAAgoooIACeRQw7uTxrnpNCiiggAIKKBAJGHciDIsKKKCAAgookEcB404e76rXpIACCiiggAKRgHEnwrCogAIKKKCAAnkUMO7k8a56TQoooIACCigQCRh3IgyLCiiggAIKKJBHgf8H+0r8wwOE6jAAAAAASUVORK5CYII=",
+ "text/plain": [
+ ""
+ ]
+ },
+ "execution_count": 7,
+ "metadata": {},
+ "output_type": "execute_result"
+ }
+ ],
+ "source": [
+ "draw = ImageDraw.Draw(image, \"RGBA\")\n",
+ "\n",
+ "font = ImageFont.load_default()\n",
+ "\n",
+ "label2color = {\"question\": \"blue\", \"answer\": \"green\", \"header\": \"orange\", \"other\": \"violet\"}\n",
+ "\n",
+ "for annotation in data[\"form\"]:\n",
+ " label = annotation[\"label\"]\n",
+ " general_box = annotation[\"box\"]\n",
+ " draw.rectangle(general_box, outline=label2color[label], width=2)\n",
+ " draw.text((general_box[0] + 10, general_box[1] - 10), label, fill=label2color[label], font=font)\n",
+ " words = annotation[\"words\"]\n",
+ " for word in words:\n",
+ " box = word[\"box\"]\n",
+ " draw.rectangle(box, outline=label2color[label], width=1)\n",
+ "\n",
+ "image"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "uyWQNLSCRJN7"
+ },
+ "source": [
+ "## Preprocessing the data\n",
+ "\n",
+ "Next, we need to turn the document images into individual tokens and corresponding labels (BIOES format, see further). We do this both for the training and test datasets. Make sure to run this from the `/content` directory:"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "colab": {
+ "base_uri": "https://localhost:8080/"
+ },
+ "id": "4DWRyOR9RuY6",
+ "outputId": "4215a24b-8049-4b1a-a23f-5aaa48e14083"
+ },
+ "outputs": [],
+ "source": [
+ "! python unilm/layoutlm/deprecated/examples/seq_labeling/preprocess.py --data_dir data/training_data/annotations \\\n",
+ " --data_split train \\\n",
+ " --output_dir data \\\n",
+ " --model_name_or_path microsoft/layoutlm-base-uncased \\\n",
+ " --max_len 510\n",
+ "\n",
+ "! python unilm/layoutlm/deprecated/examples/seq_labeling/preprocess.py --data_dir data/testing_data/annotations \\\n",
+ " --data_split test \\\n",
+ " --output_dir data \\\n",
+ " --model_name_or_path microsoft/layoutlm-base-uncased \\\n",
+ " --max_len 510"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "gc4Cu0ZyO5M_"
+ },
+ "source": [
+ "Next, we create a labels.txt file that contains the unique labels of the FUNSD dataset:"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "id": "8iGOU0s3UR2u"
+ },
+ "outputs": [],
+ "source": [
+ "! cat data/train.txt | cut -d$'\\t' -f 2 | grep -v \"^$\"| sort | uniq > data/labels.txt"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "mC9FhkG9U8yg"
+ },
+ "source": [
+ "## Define a PyTorch dataset\n",
+ "\n",
+ "First, we create a list containing the unique labels based on `data/labels.txt` (run this from the content directory):"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 19,
+ "metadata": {
+ "id": "675rRa0QXnMp"
+ },
+ "outputs": [],
+ "source": [
+ "from torch.nn import CrossEntropyLoss\n",
+ "\n",
+ "\n",
+ "def get_labels(path):\n",
+ " with open(path, \"r\") as f:\n",
+ " labels = f.read().splitlines()\n",
+ " if \"O\" not in labels:\n",
+ " labels = [\"O\"] + labels\n",
+ " return labels\n",
+ "\n",
+ "\n",
+ "labels = get_labels(\"data/labels.txt\")\n",
+ "num_labels = len(labels)\n",
+ "label_map = {i: label for i, label in enumerate(labels)}\n",
+ "# Use cross entropy ignore index as padding label id so that only real label ids contribute to the loss later\n",
+ "pad_token_label_id = CrossEntropyLoss().ignore_index"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "kZ2LGEsez2u2"
+ },
+ "source": [
+ "We can see that the dataset uses the so-called BIOES annotation scheme to annotate the tokens. This means that a given token can be either at the beginning (B), inside (I), outside (O), at the end (E) or start (S) of a given entity. Entities include ANSWER, QUESTION, HEADER and OTHER: "
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 20,
+ "metadata": {
+ "colab": {
+ "base_uri": "https://localhost:8080/"
+ },
+ "id": "_-qXLkP9Yq_L",
+ "outputId": "32ab46a4-4cf0-400c-816b-570f950035ec"
+ },
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "['B-ANSWER', 'B-HEADER', 'B-QUESTION', 'E-ANSWER', 'E-HEADER', 'E-QUESTION', 'I-ANSWER', 'I-HEADER', 'I-QUESTION', 'O', 'S-ANSWER', 'S-HEADER', 'S-QUESTION']\n"
+ ]
+ }
+ ],
+ "source": [
+ "print(labels)"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "9_ck0ZFfZInR"
+ },
+ "source": [
+ "Next, we can create a PyTorch dataset and corresponding dataloader (both for training and evaluation):"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 21,
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "import logging\n",
+ "import os\n",
+ "\n",
+ "import torch\n",
+ "from torch.utils.data import Dataset\n",
+ "\n",
+ "logger = logging.getLogger(__name__)\n",
+ "\n",
+ "\n",
+ "class FunsdDataset(Dataset):\n",
+ " def __init__(self, args, tokenizer, labels, pad_token_label_id, mode):\n",
+ " if args.local_rank not in [-1, 0] and mode == \"train\":\n",
+ " torch.distributed.barrier() # Make sure only the first process in distributed training process the dataset, and the others will use the cache\n",
+ "\n",
+ " # Load data features from cache or dataset file\n",
+ " cached_features_file = os.path.join(\n",
+ " args.data_dir,\n",
+ " \"cached_{}_{}_{}\".format(\n",
+ " mode,\n",
+ " list(filter(None, args.model_name_or_path.split(\"/\"))).pop(),\n",
+ " str(args.max_seq_length),\n",
+ " ),\n",
+ " )\n",
+ " if os.path.exists(cached_features_file) and not args.overwrite_cache:\n",
+ " logger.info(\"Loading features from cached file %s\", cached_features_file)\n",
+ " features = torch.load(cached_features_file)\n",
+ " else:\n",
+ " logger.info(\"Creating features from dataset file at %s\", args.data_dir)\n",
+ " examples = read_examples_from_file(args.data_dir, mode)\n",
+ " features = convert_examples_to_features(\n",
+ " examples,\n",
+ " labels,\n",
+ " args.max_seq_length,\n",
+ " tokenizer,\n",
+ " cls_token_at_end=bool(args.model_type in [\"xlnet\"]),\n",
+ " # xlnet has a cls token at the end\n",
+ " cls_token=tokenizer.cls_token,\n",
+ " cls_token_segment_id=2 if args.model_type in [\"xlnet\"] else 0,\n",
+ " sep_token=tokenizer.sep_token,\n",
+ " sep_token_extra=bool(args.model_type in [\"roberta\"]),\n",
+ " # roberta uses an extra separator b/w pairs of sentences, cf. github.com/pytorch/fairseq/commit/1684e166e3da03f5b600dbb7855cb98ddfcd0805\n",
+ " pad_on_left=bool(args.model_type in [\"xlnet\"]),\n",
+ " # pad on the left for xlnet\n",
+ " pad_token=tokenizer.convert_tokens_to_ids([tokenizer.pad_token])[0],\n",
+ " pad_token_segment_id=4 if args.model_type in [\"xlnet\"] else 0,\n",
+ " pad_token_label_id=pad_token_label_id,\n",
+ " )\n",
+ " # if args.local_rank in [-1, 0]:\n",
+ " # logger.info(\"Saving features into cached file %s\", cached_features_file)\n",
+ " # torch.save(features, cached_features_file)\n",
+ "\n",
+ " if args.local_rank == 0 and mode == \"train\":\n",
+ " torch.distributed.barrier() # Make sure only the first process in distributed training process the dataset, and the others will use the cache\n",
+ "\n",
+ " self.features = features\n",
+ " # Convert to Tensors and build dataset\n",
+ " self.all_input_ids = torch.tensor([f.input_ids for f in features], dtype=torch.long)\n",
+ " self.all_input_mask = torch.tensor([f.input_mask for f in features], dtype=torch.long)\n",
+ " self.all_segment_ids = torch.tensor([f.segment_ids for f in features], dtype=torch.long)\n",
+ " self.all_label_ids = torch.tensor([f.label_ids for f in features], dtype=torch.long)\n",
+ " self.all_bboxes = torch.tensor([f.boxes for f in features], dtype=torch.long)\n",
+ "\n",
+ " def __len__(self):\n",
+ " return len(self.features)\n",
+ "\n",
+ " def __getitem__(self, index):\n",
+ " return (\n",
+ " self.all_input_ids[index],\n",
+ " self.all_input_mask[index],\n",
+ " self.all_segment_ids[index],\n",
+ " self.all_label_ids[index],\n",
+ " self.all_bboxes[index],\n",
+ " )\n",
+ "\n",
+ "\n",
+ "class InputExample(object):\n",
+ " \"\"\"A single training/test example for token classification.\"\"\"\n",
+ "\n",
+ " def __init__(self, guid, words, labels, boxes, actual_bboxes, file_name, page_size):\n",
+ " \"\"\"Constructs a InputExample.\n",
+ "\n",
+ " Args:\n",
+ " guid: Unique id for the example.\n",
+ " words: list. The words of the sequence.\n",
+ " labels: (Optional) list. The labels for each word of the sequence. This should be\n",
+ " specified for train and dev examples, but not for test examples.\n",
+ " \"\"\"\n",
+ " self.guid = guid\n",
+ " self.words = words\n",
+ " self.labels = labels\n",
+ " self.boxes = boxes\n",
+ " self.actual_bboxes = actual_bboxes\n",
+ " self.file_name = file_name\n",
+ " self.page_size = page_size\n",
+ "\n",
+ "\n",
+ "class InputFeatures(object):\n",
+ " \"\"\"A single set of features of data.\"\"\"\n",
+ "\n",
+ " def __init__(\n",
+ " self,\n",
+ " input_ids,\n",
+ " input_mask,\n",
+ " segment_ids,\n",
+ " label_ids,\n",
+ " boxes,\n",
+ " actual_bboxes,\n",
+ " file_name,\n",
+ " page_size,\n",
+ " ):\n",
+ " assert (\n",
+ " 0 <= all(boxes) <= 1000\n",
+ " ), \"Error with input bbox ({}): the coordinate value is not between 0 and 1000\".format(boxes)\n",
+ " self.input_ids = input_ids\n",
+ " self.input_mask = input_mask\n",
+ " self.segment_ids = segment_ids\n",
+ " self.label_ids = label_ids\n",
+ " self.boxes = boxes\n",
+ " self.actual_bboxes = actual_bboxes\n",
+ " self.file_name = file_name\n",
+ " self.page_size = page_size\n",
+ "\n",
+ "\n",
+ "def read_examples_from_file(data_dir, mode):\n",
+ " file_path = os.path.join(data_dir, \"{}.txt\".format(mode))\n",
+ " box_file_path = os.path.join(data_dir, \"{}_box.txt\".format(mode))\n",
+ " image_file_path = os.path.join(data_dir, \"{}_image.txt\".format(mode))\n",
+ " guid_index = 1\n",
+ " examples = []\n",
+ " with open(file_path, encoding=\"utf-8\") as f, open(box_file_path, encoding=\"utf-8\") as fb, open(\n",
+ " image_file_path, encoding=\"utf-8\"\n",
+ " ) as fi:\n",
+ " words = []\n",
+ " boxes = []\n",
+ " actual_bboxes = []\n",
+ " file_name = None\n",
+ " page_size = None\n",
+ " labels = []\n",
+ " for line, bline, iline in zip(f, fb, fi):\n",
+ " if line.startswith(\"-DOCSTART-\") or line == \"\" or line == \"\\n\":\n",
+ " if words:\n",
+ " examples.append(\n",
+ " InputExample(\n",
+ " guid=\"{}-{}\".format(mode, guid_index),\n",
+ " words=words,\n",
+ " labels=labels,\n",
+ " boxes=boxes,\n",
+ " actual_bboxes=actual_bboxes,\n",
+ " file_name=file_name,\n",
+ " page_size=page_size,\n",
+ " )\n",
+ " )\n",
+ " guid_index += 1\n",
+ " words = []\n",
+ " boxes = []\n",
+ " actual_bboxes = []\n",
+ " file_name = None\n",
+ " page_size = None\n",
+ " labels = []\n",
+ " else:\n",
+ " splits = line.split(\"\\t\")\n",
+ " bsplits = bline.split(\"\\t\")\n",
+ " isplits = iline.split(\"\\t\")\n",
+ " assert len(splits) == 2\n",
+ " assert len(bsplits) == 2\n",
+ " assert len(isplits) == 4\n",
+ " assert splits[0] == bsplits[0]\n",
+ " words.append(splits[0])\n",
+ " if len(splits) > 1:\n",
+ " labels.append(splits[-1].replace(\"\\n\", \"\"))\n",
+ " box = bsplits[-1].replace(\"\\n\", \"\")\n",
+ " box = [int(b) for b in box.split()]\n",
+ " boxes.append(box)\n",
+ " actual_bbox = [int(b) for b in isplits[1].split()]\n",
+ " actual_bboxes.append(actual_bbox)\n",
+ " page_size = [int(i) for i in isplits[2].split()]\n",
+ " file_name = isplits[3].strip()\n",
+ " else:\n",
+ " # Examples could have no label for mode = \"test\"\n",
+ " labels.append(\"O\")\n",
+ " if words:\n",
+ " examples.append(\n",
+ " InputExample(\n",
+ " guid=\"%s-%d\".format(mode, guid_index),\n",
+ " words=words,\n",
+ " labels=labels,\n",
+ " boxes=boxes,\n",
+ " actual_bboxes=actual_bboxes,\n",
+ " file_name=file_name,\n",
+ " page_size=page_size,\n",
+ " )\n",
+ " )\n",
+ " return examples\n",
+ "\n",
+ "\n",
+ "def convert_examples_to_features(\n",
+ " examples,\n",
+ " label_list,\n",
+ " max_seq_length,\n",
+ " tokenizer,\n",
+ " cls_token_at_end=False,\n",
+ " cls_token=\"[CLS]\",\n",
+ " cls_token_segment_id=1,\n",
+ " sep_token=\"[SEP]\",\n",
+ " sep_token_extra=False,\n",
+ " pad_on_left=False,\n",
+ " pad_token=0,\n",
+ " cls_token_box=[0, 0, 0, 0],\n",
+ " sep_token_box=[1000, 1000, 1000, 1000],\n",
+ " pad_token_box=[0, 0, 0, 0],\n",
+ " pad_token_segment_id=0,\n",
+ " pad_token_label_id=-1,\n",
+ " sequence_a_segment_id=0,\n",
+ " mask_padding_with_zero=True,\n",
+ "):\n",
+ " \"\"\"Loads a data file into a list of `InputBatch`s\n",
+ " `cls_token_at_end` define the location of the CLS token:\n",
+ " - False (Default, BERT/XLM pattern): [CLS] + A + [SEP] + B + [SEP]\n",
+ " - True (XLNet/GPT pattern): A + [SEP] + B + [SEP] + [CLS]\n",
+ " `cls_token_segment_id` define the segment id associated to the CLS token (0 for BERT, 2 for XLNet)\n",
+ " \"\"\"\n",
+ "\n",
+ " label_map = {label: i for i, label in enumerate(label_list)}\n",
+ "\n",
+ " features = []\n",
+ " for ex_index, example in enumerate(examples):\n",
+ " file_name = example.file_name\n",
+ " page_size = example.page_size\n",
+ " width, height = page_size\n",
+ " if ex_index % 10000 == 0:\n",
+ " logger.info(\"Writing example %d of %d\", ex_index, len(examples))\n",
+ "\n",
+ " tokens = []\n",
+ " token_boxes = []\n",
+ " actual_bboxes = []\n",
+ " label_ids = []\n",
+ " for word, label, box, actual_bbox in zip(example.words, example.labels, example.boxes, example.actual_bboxes):\n",
+ " word_tokens = tokenizer.tokenize(word)\n",
+ " tokens.extend(word_tokens)\n",
+ " token_boxes.extend([box] * len(word_tokens))\n",
+ " actual_bboxes.extend([actual_bbox] * len(word_tokens))\n",
+ " # Use the real label id for the first token of the word, and padding ids for the remaining tokens\n",
+ " label_ids.extend([label_map[label]] + [pad_token_label_id] * (len(word_tokens) - 1))\n",
+ "\n",
+ " # Account for [CLS] and [SEP] with \"- 2\" and with \"- 3\" for RoBERTa.\n",
+ " special_tokens_count = 3 if sep_token_extra else 2\n",
+ " if len(tokens) > max_seq_length - special_tokens_count:\n",
+ " tokens = tokens[: (max_seq_length - special_tokens_count)]\n",
+ " token_boxes = token_boxes[: (max_seq_length - special_tokens_count)]\n",
+ " actual_bboxes = actual_bboxes[: (max_seq_length - special_tokens_count)]\n",
+ " label_ids = label_ids[: (max_seq_length - special_tokens_count)]\n",
+ "\n",
+ " # The convention in BERT is:\n",
+ " # (a) For sequence pairs:\n",
+ " # tokens: [CLS] is this jack ##son ##ville ? [SEP] no it is not . [SEP]\n",
+ " # type_ids: 0 0 0 0 0 0 0 0 1 1 1 1 1 1\n",
+ " # (b) For single sequences:\n",
+ " # tokens: [CLS] the dog is hairy . [SEP]\n",
+ " # type_ids: 0 0 0 0 0 0 0\n",
+ " #\n",
+ " # Where \"type_ids\" are used to indicate whether this is the first\n",
+ " # sequence or the second sequence. The embedding vectors for `type=0` and\n",
+ " # `type=1` were learned during pre-training and are added to the wordpiece\n",
+ " # embedding vector (and position vector). This is not *strictly* necessary\n",
+ " # since the [SEP] token unambiguously separates the sequences, but it makes\n",
+ " # it easier for the model to learn the concept of sequences.\n",
+ " #\n",
+ " # For classification tasks, the first vector (corresponding to [CLS]) is\n",
+ " # used as as the \"sentence vector\". Note that this only makes sense because\n",
+ " # the entire model is fine-tuned.\n",
+ " tokens += [sep_token]\n",
+ " token_boxes += [sep_token_box]\n",
+ " actual_bboxes += [[0, 0, width, height]]\n",
+ " label_ids += [pad_token_label_id]\n",
+ " if sep_token_extra:\n",
+ " # roberta uses an extra separator b/w pairs of sentences\n",
+ " tokens += [sep_token]\n",
+ " token_boxes += [sep_token_box]\n",
+ " actual_bboxes += [[0, 0, width, height]]\n",
+ " label_ids += [pad_token_label_id]\n",
+ " segment_ids = [sequence_a_segment_id] * len(tokens)\n",
+ "\n",
+ " if cls_token_at_end:\n",
+ " tokens += [cls_token]\n",
+ " token_boxes += [cls_token_box]\n",
+ " actual_bboxes += [[0, 0, width, height]]\n",
+ " label_ids += [pad_token_label_id]\n",
+ " segment_ids += [cls_token_segment_id]\n",
+ " else:\n",
+ " tokens = [cls_token] + tokens\n",
+ " token_boxes = [cls_token_box] + token_boxes\n",
+ " actual_bboxes = [[0, 0, width, height]] + actual_bboxes\n",
+ " label_ids = [pad_token_label_id] + label_ids\n",
+ " segment_ids = [cls_token_segment_id] + segment_ids\n",
+ "\n",
+ " input_ids = tokenizer.convert_tokens_to_ids(tokens)\n",
+ "\n",
+ " # The mask has 1 for real tokens and 0 for padding tokens. Only real\n",
+ " # tokens are attended to.\n",
+ " input_mask = [1 if mask_padding_with_zero else 0] * len(input_ids)\n",
+ "\n",
+ " # Zero-pad up to the sequence length.\n",
+ " padding_length = max_seq_length - len(input_ids)\n",
+ " if pad_on_left:\n",
+ " input_ids = ([pad_token] * padding_length) + input_ids\n",
+ " input_mask = ([0 if mask_padding_with_zero else 1] * padding_length) + input_mask\n",
+ " segment_ids = ([pad_token_segment_id] * padding_length) + segment_ids\n",
+ " label_ids = ([pad_token_label_id] * padding_length) + label_ids\n",
+ " token_boxes = ([pad_token_box] * padding_length) + token_boxes\n",
+ " else:\n",
+ " input_ids += [pad_token] * padding_length\n",
+ " input_mask += [0 if mask_padding_with_zero else 1] * padding_length\n",
+ " segment_ids += [pad_token_segment_id] * padding_length\n",
+ " label_ids += [pad_token_label_id] * padding_length\n",
+ " token_boxes += [pad_token_box] * padding_length\n",
+ "\n",
+ " assert len(input_ids) == max_seq_length\n",
+ " assert len(input_mask) == max_seq_length\n",
+ " assert len(segment_ids) == max_seq_length\n",
+ " assert len(label_ids) == max_seq_length\n",
+ " assert len(token_boxes) == max_seq_length\n",
+ "\n",
+ " if ex_index < 5:\n",
+ " logger.info(\"*** Example ***\")\n",
+ " logger.info(\"guid: %s\", example.guid)\n",
+ " logger.info(\"tokens: %s\", \" \".join([str(x) for x in tokens]))\n",
+ " logger.info(\"input_ids: %s\", \" \".join([str(x) for x in input_ids]))\n",
+ " logger.info(\"input_mask: %s\", \" \".join([str(x) for x in input_mask]))\n",
+ " logger.info(\"segment_ids: %s\", \" \".join([str(x) for x in segment_ids]))\n",
+ " logger.info(\"label_ids: %s\", \" \".join([str(x) for x in label_ids]))\n",
+ " logger.info(\"boxes: %s\", \" \".join([str(x) for x in token_boxes]))\n",
+ " logger.info(\"actual_bboxes: %s\", \" \".join([str(x) for x in actual_bboxes]))\n",
+ "\n",
+ " features.append(\n",
+ " InputFeatures(\n",
+ " input_ids=input_ids,\n",
+ " input_mask=input_mask,\n",
+ " segment_ids=segment_ids,\n",
+ " label_ids=label_ids,\n",
+ " boxes=token_boxes,\n",
+ " actual_bboxes=actual_bboxes,\n",
+ " file_name=file_name,\n",
+ " page_size=page_size,\n",
+ " )\n",
+ " )\n",
+ " return features"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 23,
+ "metadata": {
+ "id": "HUJftzeBWh2S"
+ },
+ "outputs": [],
+ "source": [
+ "from transformers import LayoutLMTokenizer\n",
+ "\n",
+ "# from .unilm.layoutlm.data.funsd import FunsdDataset, InputFeatures\n",
+ "from torch.utils.data import DataLoader, RandomSampler, SequentialSampler\n",
+ "\n",
+ "batch_size = 16\n",
+ "args = {\n",
+ " \"local_rank\": -1,\n",
+ " \"overwrite_cache\": True,\n",
+ " \"data_dir\": \"data/\",\n",
+ " \"model_name_or_path\": \"microsoft/layoutlm-base-uncased\",\n",
+ " \"max_seq_length\": 512,\n",
+ " \"model_type\": \"layoutlm\",\n",
+ "}\n",
+ "\n",
+ "\n",
+ "# class to turn the keys of a dict into attributes (thanks Stackoverflow)\n",
+ "class AttrDict(dict):\n",
+ " def __init__(self, *args, **kwargs):\n",
+ " super(AttrDict, self).__init__(*args, **kwargs)\n",
+ " self.__dict__ = self\n",
+ "\n",
+ "\n",
+ "args = AttrDict(args)\n",
+ "\n",
+ "tokenizer = LayoutLMTokenizer.from_pretrained(\"microsoft/layoutlm-base-uncased\")\n",
+ "\n",
+ "# the LayoutLM authors already defined a specific FunsdDataset, so we are going to use this here\n",
+ "train_dataset = FunsdDataset(args, tokenizer, labels, pad_token_label_id, mode=\"train\")\n",
+ "train_sampler = RandomSampler(train_dataset)\n",
+ "train_dataloader = DataLoader(train_dataset, sampler=train_sampler, batch_size=batch_size)\n",
+ "\n",
+ "eval_dataset = FunsdDataset(args, tokenizer, labels, pad_token_label_id, mode=\"test\")\n",
+ "eval_sampler = SequentialSampler(eval_dataset)\n",
+ "eval_dataloader = DataLoader(eval_dataset, sampler=eval_sampler, batch_size=batch_size)"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 24,
+ "metadata": {
+ "colab": {
+ "base_uri": "https://localhost:8080/"
+ },
+ "id": "18NMUBzgOdqu",
+ "outputId": "eef47b70-3a9a-4b19-be6b-95900c58337b"
+ },
+ "outputs": [
+ {
+ "data": {
+ "text/plain": [
+ "10"
+ ]
+ },
+ "execution_count": 24,
+ "metadata": {},
+ "output_type": "execute_result"
+ }
+ ],
+ "source": [
+ "len(train_dataloader)"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 25,
+ "metadata": {
+ "colab": {
+ "base_uri": "https://localhost:8080/"
+ },
+ "id": "toFjxtn71B1U",
+ "outputId": "f4651896-cafc-449a-98b4-c81f41177e6d"
+ },
+ "outputs": [
+ {
+ "data": {
+ "text/plain": [
+ "4"
+ ]
+ },
+ "execution_count": 25,
+ "metadata": {},
+ "output_type": "execute_result"
+ }
+ ],
+ "source": [
+ "len(eval_dataloader)"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 26,
+ "metadata": {
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 137
+ },
+ "id": "RhINSBw9I24G",
+ "outputId": "28738ce2-617c-47d3-b8c9-f949d3066d60"
+ },
+ "outputs": [
+ {
+ "data": {
+ "text/plain": [
+ "'[CLS] account agency ss : date 1 / 31 / 88 insert signed 91581919 4th new albany tribune advertisements. bookkeeper mar 08 reco affidavit of performance from newspaper new albany tribune harley davidson cigarettes lorillard media service state of county of indiana ) floyd ) before me a notary public, personally appeared holly inzer who being duly sworn, says that ( he ) ( she ) is of the abovementioned newspaper and that display ads for the above account were made through the aforesaid newspaper during the month of january, 1988 as follows : column inches exclusive advertising for harley davidson cigarettes we hereby certify charges shown above on dates per attached bill are true and correct as billed to the account in upper right hand corner of the affidavit and are exclusive sworn to and subscribed before me this day of march, 1988 in testimony whereof i have set my hand and seal the day and year aforesaid. my commission expires : 2 - 9 - 90 betty j. murphy ( notary public ) [SEP] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD] [PAD]'"
+ ]
+ },
+ "execution_count": 26,
+ "metadata": {},
+ "output_type": "execute_result"
+ }
+ ],
+ "source": [
+ "batch = next(iter(train_dataloader))\n",
+ "input_ids = batch[0][0]\n",
+ "tokenizer.decode(input_ids)"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "66cEmLDoUFcm"
+ },
+ "source": [
+ "## Define and fine-tune the model\n",
+ "\n",
+ "As this is a sequence labeling task, we are going to load `LayoutLMForTokenClassification` (the base sized model) from the hub. We are going to fine-tune it on a downstream task, namely FUNSD."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 27,
+ "metadata": {},
+ "outputs": [
+ {
+ "data": {
+ "text/plain": [
+ "LoraConfig(task_type=, peft_type=, auto_mapping=None, base_model_name_or_path=None, revision=None, inference_mode=False, r=16, target_modules=None, exclude_modules=None, lora_alpha=16, lora_dropout=0.1, fan_in_fan_out=False, bias='all', use_rslora=False, modules_to_save=None, init_lora_weights=True, layers_to_transform=None, layers_pattern=None, rank_pattern={}, alpha_pattern={}, megatron_config=None, megatron_core='megatron.core', trainable_token_indices=None, loftq_config={}, eva_config=None, corda_config=None, use_dora=False, use_qalora=False, qalora_group_size=16, layer_replication=None, runtime_config=LoraRuntimeConfig(ephemeral_gpu_offload=False), lora_bias=False, target_parameters=None)"
+ ]
+ },
+ "execution_count": 27,
+ "metadata": {},
+ "output_type": "execute_result"
+ }
+ ],
+ "source": [
+ "from peft import get_peft_config, PeftModel, get_peft_model, LoraConfig, TaskType\n",
+ "\n",
+ "peft_config = LoraConfig(\n",
+ " task_type=TaskType.TOKEN_CLS, inference_mode=False, r=16, lora_alpha=16, lora_dropout=0.1, bias=\"all\"\n",
+ ")\n",
+ "peft_config"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 1000,
+ "referenced_widgets": [
+ "da1094982d044ab28eb0effebbfcbb78",
+ "513e00b619924f5693259cd919a927ab",
+ "63e819a04f6e4829838c0e30e65516ed",
+ "d1c3e1a66db04227a74ef8d6481d6daf",
+ "c75f0da13a1e4dbe94800711d55390a6",
+ "31642aacae2a44879960da09f938ecc4",
+ "138a6b922e454ebbaeb315ecd5f476b8",
+ "a8126ba98376402888e9ba344cf1c538"
+ ]
+ },
+ "id": "xIdOsFBiTsuw",
+ "outputId": "95e8811c-025a-41a0-9d03-4285a17f2a9b"
+ },
+ "outputs": [],
+ "source": [
+ "from transformers import LayoutLMForTokenClassification\n",
+ "import torch\n",
+ "from transformers import set_seed\n",
+ "\n",
+ "seed = 100\n",
+ "set_seed(seed)\n",
+ "device = torch.accelerator.current_accelerator().type if hasattr(torch, \"accelerator\") else \"cuda\"\n",
+ "\n",
+ "model = LayoutLMForTokenClassification.from_pretrained(\"microsoft/layoutlm-base-uncased\", num_labels=num_labels)\n",
+ "model = get_peft_model(model, peft_config)\n",
+ "model.to(device)"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "print(model.model.layoutlm.encoder.layer[0].attention.self.query.weight)\n",
+ "print(model.model.layoutlm.encoder.layer[0].attention.self.query.lora_A.default.weight)\n",
+ "print(model.model.classifier.weight)"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "3weFr_pz1mla"
+ },
+ "source": [
+ "Now we can start training:"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "colab": {
+ "base_uri": "https://localhost:8080/"
+ },
+ "id": "Yu0qePs2cRKo",
+ "outputId": "cdbb9a03-eb9b-4740-bbe3-da06b9192bae"
+ },
+ "outputs": [],
+ "source": [
+ "from transformers import get_linear_schedule_with_warmup\n",
+ "from tqdm import tqdm\n",
+ "\n",
+ "num_train_epochs = 100\n",
+ "\n",
+ "optimizer = torch.optim.AdamW(model.parameters(), lr=3e-3)\n",
+ "lr_scheduler = get_linear_schedule_with_warmup(\n",
+ " optimizer=optimizer,\n",
+ " num_warmup_steps=0.06 * (len(train_dataloader) * num_train_epochs),\n",
+ " num_training_steps=(len(train_dataloader) * num_train_epochs),\n",
+ ")\n",
+ "\n",
+ "\n",
+ "global_step = 0\n",
+ "\n",
+ "t_total = len(train_dataloader) * num_train_epochs # total number of training steps\n",
+ "\n",
+ "# put the model in training mode\n",
+ "model.train()\n",
+ "for epoch in range(num_train_epochs):\n",
+ " for batch in tqdm(train_dataloader, desc=\"Training\"):\n",
+ " input_ids = batch[0].to(device)\n",
+ " bbox = batch[4].to(device)\n",
+ " attention_mask = batch[1].to(device)\n",
+ " token_type_ids = batch[2].to(device)\n",
+ " labels = batch[3].to(device)\n",
+ "\n",
+ " # forward pass\n",
+ " outputs = model(\n",
+ " input_ids=input_ids, bbox=bbox, attention_mask=attention_mask, token_type_ids=token_type_ids, labels=labels\n",
+ " )\n",
+ " loss = outputs.loss\n",
+ "\n",
+ " # print loss every 100 steps\n",
+ " if global_step % 10 == 0:\n",
+ " print(f\"Loss after {global_step} steps: {loss.item()}\")\n",
+ "\n",
+ " # backward pass to get the gradients\n",
+ " loss.backward()\n",
+ "\n",
+ " # print(\"Gradients on classification head:\")\n",
+ " # print(model.classifier.weight.grad[6,:].sum())\n",
+ "\n",
+ " # update\n",
+ " optimizer.step()\n",
+ " lr_scheduler.step()\n",
+ " optimizer.zero_grad()\n",
+ " global_step += 1"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 35,
+ "metadata": {
+ "colab": {
+ "base_uri": "https://localhost:8080/"
+ },
+ "id": "u1rNslap5Y3N",
+ "outputId": "877183d4-1d29-4d09-bd3a-0e5f88611dc8"
+ },
+ "outputs": [
+ {
+ "name": "stderr",
+ "output_type": "stream",
+ "text": [
+ "Evaluating: 100%|██████████| 4/4 [00:00<00:00, 10.90it/s]\n"
+ ]
+ },
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "{'loss': 1.467050313949585, 'precision': 0.7295341474445952, 'recall': 0.806903451725863, 'f1': 0.7662707838479811}\n"
+ ]
+ }
+ ],
+ "source": [
+ "import numpy as np\n",
+ "from seqeval.metrics import (\n",
+ " classification_report,\n",
+ " f1_score,\n",
+ " precision_score,\n",
+ " recall_score,\n",
+ ")\n",
+ "\n",
+ "eval_loss = 0.0\n",
+ "nb_eval_steps = 0\n",
+ "preds = None\n",
+ "out_label_ids = None\n",
+ "\n",
+ "# put model in evaluation mode\n",
+ "model.eval()\n",
+ "for batch in tqdm(eval_dataloader, desc=\"Evaluating\"):\n",
+ " with torch.no_grad():\n",
+ " input_ids = batch[0].to(device)\n",
+ " bbox = batch[4].to(device)\n",
+ " attention_mask = batch[1].to(device)\n",
+ " token_type_ids = batch[2].to(device)\n",
+ " labels = batch[3].to(device)\n",
+ "\n",
+ " # forward pass\n",
+ " outputs = model(\n",
+ " input_ids=input_ids, bbox=bbox, attention_mask=attention_mask, token_type_ids=token_type_ids, labels=labels\n",
+ " )\n",
+ " # get the loss and logits\n",
+ " tmp_eval_loss = outputs.loss\n",
+ " logits = outputs.logits\n",
+ "\n",
+ " eval_loss += tmp_eval_loss.item()\n",
+ " nb_eval_steps += 1\n",
+ "\n",
+ " # compute the predictions\n",
+ " if preds is None:\n",
+ " preds = logits.detach().cpu().numpy()\n",
+ " out_label_ids = labels.detach().cpu().numpy()\n",
+ " else:\n",
+ " preds = np.append(preds, logits.detach().cpu().numpy(), axis=0)\n",
+ " out_label_ids = np.append(out_label_ids, labels.detach().cpu().numpy(), axis=0)\n",
+ "\n",
+ "# compute average evaluation loss\n",
+ "eval_loss = eval_loss / nb_eval_steps\n",
+ "preds = np.argmax(preds, axis=2)\n",
+ "\n",
+ "out_label_list = [[] for _ in range(out_label_ids.shape[0])]\n",
+ "preds_list = [[] for _ in range(out_label_ids.shape[0])]\n",
+ "\n",
+ "for i in range(out_label_ids.shape[0]):\n",
+ " for j in range(out_label_ids.shape[1]):\n",
+ " if out_label_ids[i, j] != pad_token_label_id:\n",
+ " out_label_list[i].append(label_map[out_label_ids[i][j]])\n",
+ " preds_list[i].append(label_map[preds[i][j]])\n",
+ "\n",
+ "results = {\n",
+ " \"loss\": eval_loss,\n",
+ " \"precision\": precision_score(out_label_list, preds_list),\n",
+ " \"recall\": recall_score(out_label_list, preds_list),\n",
+ " \"f1\": f1_score(out_label_list, preds_list),\n",
+ "}\n",
+ "print(results)"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 36,
+ "metadata": {},
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "trainable params: 702,733 || all params: 113,237,786 || trainable%: 0.6206\n"
+ ]
+ }
+ ],
+ "source": [
+ "model.print_trainable_parameters()"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 37,
+ "metadata": {},
+ "outputs": [],
+ "source": [
+ "model.save_pretrained(\"peft_layoutlm\")"
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 40,
+ "metadata": {},
+ "outputs": [
+ {
+ "name": "stdout",
+ "output_type": "stream",
+ "text": [
+ "2.8M\t./peft_layoutlm/adapter_model.safetensors\n"
+ ]
+ }
+ ],
+ "source": [
+ "!du -h ./peft_layoutlm/adapter_model.safetensors"
+ ]
+ }
+ ],
+ "metadata": {
+ "accelerator": "GPU",
+ "colab": {
+ "collapsed_sections": [],
+ "include_colab_link": true,
+ "name": "Fine-tuning LayoutLMForTokenClassification on FUNSD.ipynb",
+ "provenance": [],
+ "toc_visible": true
+ },
+ "kernelspec": {
+ "display_name": "Python 3",
+ "language": "python",
+ "name": "python3"
+ },
+ "language_info": {
+ "codemirror_mode": {
+ "name": "ipython",
+ "version": 3
+ },
+ "file_extension": ".py",
+ "mimetype": "text/x-python",
+ "name": "python",
+ "nbconvert_exporter": "python",
+ "pygments_lexer": "ipython3",
+ "version": "3.11.13"
+ },
+ "vscode": {
+ "interpreter": {
+ "hash": "aee8b7b246df8f9039afb4144a1f6fd8d2ca17a180786b69acc140d282b71a49"
+ }
+ },
+ "widgets": {
+ "application/vnd.jupyter.widget-state+json": {
+ "138a6b922e454ebbaeb315ecd5f476b8": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_name": "DescriptionStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "DescriptionStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "description_width": ""
+ }
+ },
+ "31642aacae2a44879960da09f938ecc4": {
+ "model_module": "@jupyter-widgets/base",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "513e00b619924f5693259cd919a927ab": {
+ "model_module": "@jupyter-widgets/base",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "63e819a04f6e4829838c0e30e65516ed": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_name": "FloatProgressModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "FloatProgressModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "ProgressView",
+ "bar_style": "success",
+ "description": "Downloading: 100%",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_31642aacae2a44879960da09f938ecc4",
+ "max": 453093832,
+ "min": 0,
+ "orientation": "horizontal",
+ "style": "IPY_MODEL_c75f0da13a1e4dbe94800711d55390a6",
+ "value": 453093832
+ }
+ },
+ "a8126ba98376402888e9ba344cf1c538": {
+ "model_module": "@jupyter-widgets/base",
+ "model_name": "LayoutModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/base",
+ "_model_module_version": "1.2.0",
+ "_model_name": "LayoutModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "LayoutView",
+ "align_content": null,
+ "align_items": null,
+ "align_self": null,
+ "border": null,
+ "bottom": null,
+ "display": null,
+ "flex": null,
+ "flex_flow": null,
+ "grid_area": null,
+ "grid_auto_columns": null,
+ "grid_auto_flow": null,
+ "grid_auto_rows": null,
+ "grid_column": null,
+ "grid_gap": null,
+ "grid_row": null,
+ "grid_template_areas": null,
+ "grid_template_columns": null,
+ "grid_template_rows": null,
+ "height": null,
+ "justify_content": null,
+ "justify_items": null,
+ "left": null,
+ "margin": null,
+ "max_height": null,
+ "max_width": null,
+ "min_height": null,
+ "min_width": null,
+ "object_fit": null,
+ "object_position": null,
+ "order": null,
+ "overflow": null,
+ "overflow_x": null,
+ "overflow_y": null,
+ "padding": null,
+ "right": null,
+ "top": null,
+ "visibility": null,
+ "width": null
+ }
+ },
+ "c75f0da13a1e4dbe94800711d55390a6": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_name": "ProgressStyleModel",
+ "state": {
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "ProgressStyleModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/base",
+ "_view_module_version": "1.2.0",
+ "_view_name": "StyleView",
+ "bar_color": null,
+ "description_width": "initial"
+ }
+ },
+ "d1c3e1a66db04227a74ef8d6481d6daf": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_name": "HTMLModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HTMLModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HTMLView",
+ "description": "",
+ "description_tooltip": null,
+ "layout": "IPY_MODEL_a8126ba98376402888e9ba344cf1c538",
+ "placeholder": "",
+ "style": "IPY_MODEL_138a6b922e454ebbaeb315ecd5f476b8",
+ "value": " 453M/453M [00:15<00:00, 30.0MB/s]"
+ }
+ },
+ "da1094982d044ab28eb0effebbfcbb78": {
+ "model_module": "@jupyter-widgets/controls",
+ "model_name": "HBoxModel",
+ "state": {
+ "_dom_classes": [],
+ "_model_module": "@jupyter-widgets/controls",
+ "_model_module_version": "1.5.0",
+ "_model_name": "HBoxModel",
+ "_view_count": null,
+ "_view_module": "@jupyter-widgets/controls",
+ "_view_module_version": "1.5.0",
+ "_view_name": "HBoxView",
+ "box_style": "",
+ "children": [
+ "IPY_MODEL_63e819a04f6e4829838c0e30e65516ed",
+ "IPY_MODEL_d1c3e1a66db04227a74ef8d6481d6daf"
+ ],
+ "layout": "IPY_MODEL_513e00b619924f5693259cd919a927ab"
+ }
+ }
+ }
+ }
+ },
+ "nbformat": 4,
+ "nbformat_minor": 1
+}
diff --git a/peft/examples/token_classification/requirements.txt b/peft/examples/token_classification/requirements.txt
new file mode 100644
index 0000000000000000000000000000000000000000..2cde65e15268b67b28864f3fd7e6932fb7949802
--- /dev/null
+++ b/peft/examples/token_classification/requirements.txt
@@ -0,0 +1,7 @@
+transformers
+accelerate
+evaluate
+tqdm
+datasets
+Pillow
+torchvision
\ No newline at end of file
diff --git a/peft/examples/waveft_finetuning/README.md b/peft/examples/waveft_finetuning/README.md
new file mode 100644
index 0000000000000000000000000000000000000000..ad2d231698ad24381e289f18a0fe81029d11930f
--- /dev/null
+++ b/peft/examples/waveft_finetuning/README.md
@@ -0,0 +1,64 @@
+
+
+# WaveFT: Wavelet Fine-Tuning
+
+## Introduction
+[WaveFT](https://arxiv.org/abs/2505.12532) is a novel parameter-efficient fine-tuning (PEFT) method that introduces sparse updates in the **wavelet domain** of residual matrices. Unlike LoRA, which is constrained by discrete low-rank choices, WaveFT enables fine-grained control over the number of trainable parameters by directly learning a sparse set of coefficients in the transformed space. These coefficients are then mapped back to the weight domain via the Inverse Discrete Wavelet Transform (IDWT), producing high-rank updates without incurring inference overhead.
+
+## Quick start
+```python
+import torch
+from peft import WaveFTConfig, get_peft_model
+from transformers import AutoTokenizer, AutoModelForCausalLM
+from trl import SFTConfig, SFTTrainer
+from datasets import load_dataset
+
+model = AutoModelForCausalLM.from_pretrained("facebook/opt-350m", dtype=torch.bfloat16, device_map="auto")
+tokenizer = AutoTokenizer.from_pretrained("facebook/opt-350m")
+dataset = load_dataset("imdb", split="train[:1%]")
+waveft_config = WaveFTConfig(
+ n_frequency=2592,
+)
+peft_model = get_peft_model(model, waveft_config)
+training_args = SFTConfig(dataset_text_field="text", max_seq_length=128)
+trainer = SFTTrainer(
+ model=peft_model,
+ train_dataset=dataset,
+ processing_class=tokenizer,
+)
+trainer.train()
+peft_model.save_pretrained("waveft-opt-350m")
+```
+
+For more options and a more detailed example code, you can refer to waveft finetuning script.
+Run the script simply by running:
+```bash
+python3 examples/waveft_finetuning/waveft_finetuning.py --base_model facebook/opt-350m
+```
+
+If you want to run DDP by [accelerate](https://huggingface.co/docs/accelerate/en/index), please run `accelerate config` to set your ddp config, and run:
+```bash
+accelerate launch examples/waveft_finetuning/waveft_finetuning.py --base_model facebook/opt-350m
+```
+please add `--device_map cpu` if you want to run finetune on CPU.
+
+## Use the model
+You can load and use the model as any other 🤗 PEFT model
+```python
+from peft import PeftModel
+from transformers import AutoTokenizer, AutoModelForCausalLM
+model = AutoModelForCausalLM.from_pretrained("facebook/opt-350m")
+tokenizer = AutoTokenizer.from_pretrained("facebook/opt-350m")
+waveft_model = PeftModel.from_pretrained(model, "waveft-opt-350m")
+```
+
+## Citation
+@misc{bilican2025exploringsparsityparameterefficient,
+ title={Exploring Sparsity for Parameter Efficient Fine Tuning Using Wavelets},
+ author={Ahmet Bilican and M. Akın Yılmaz and A. Murat Tekalp and R. Gökberk Cinbiş},
+ year={2025},
+ eprint={2505.12532},
+ archivePrefix={arXiv},
+ primaryClass={cs.CV},
+ url={https://arxiv.org/abs/2505.12532},
+}
\ No newline at end of file
diff --git a/peft/examples/waveft_finetuning/waveft_finetuning.py b/peft/examples/waveft_finetuning/waveft_finetuning.py
new file mode 100644
index 0000000000000000000000000000000000000000..1855f86a26132da9d914e5d5ac504bdef42d54b1
--- /dev/null
+++ b/peft/examples/waveft_finetuning/waveft_finetuning.py
@@ -0,0 +1,189 @@
+# Copyright 2025-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+
+import os
+from typing import Optional
+
+import torch
+import transformers
+from datasets import load_dataset
+from transformers import AutoModelForCausalLM, AutoTokenizer, set_seed
+
+from peft import (
+ WaveFTConfig,
+ get_peft_model,
+)
+
+
+def train(
+ base_model: str,
+ data_path: str = "yahma/alpaca-cleaned",
+ output_dir: str = "waveft",
+ batch_size: int = 16,
+ num_epochs: int = 1,
+ learning_rate: float = 3e-4,
+ cutoff_len: int = 256,
+ val_set_size: int = 16,
+ eval_step: int = 100,
+ save_step: int = 100,
+ device_map: str = "auto",
+ waveft_n_frequency: int = 2592,
+ waveft_target_modules: list[str] = None,
+ waveft_scaling: float = 25.0,
+ waveft_wavelet_family: str = "db1",
+ waveft_use_idwt: bool = True,
+ torch_dtype: str = "float16",
+ seed: Optional[int] = None,
+):
+ # Set device_map to the right place when enabling DDP.
+ world_size = int(os.environ.get("WORLD_SIZE", 0)) or int(os.environ.get("PMI_SIZE", 0))
+ if world_size > 1 and device_map != "cpu":
+ from accelerate import Accelerator
+
+ device_map = {"": Accelerator().process_index}
+ # Set seed
+ if seed is not None:
+ set_seed(seed)
+ model_kwargs = {"dtype": getattr(torch, torch_dtype), "device_map": device_map}
+ model = AutoModelForCausalLM.from_pretrained(base_model, **model_kwargs)
+
+ tokenizer = AutoTokenizer.from_pretrained(base_model, trust_remote_code=True)
+ # For some tokenizer with no pad token like llama
+ if tokenizer.pad_token is None:
+ tokenizer.pad_token = tokenizer.eos_token
+
+ def tokenize(prompt, add_eos_token=True):
+ result = tokenizer(
+ prompt,
+ truncation=True,
+ max_length=cutoff_len,
+ padding=False,
+ return_tensors=None,
+ )
+ if (
+ result["input_ids"][-1] != tokenizer.eos_token_id
+ and len(result["input_ids"]) < cutoff_len
+ and add_eos_token
+ ):
+ result["input_ids"].append(tokenizer.eos_token_id)
+ result["attention_mask"].append(1)
+
+ result["labels"] = result["input_ids"].copy()
+
+ return result
+
+ def generate_and_tokenize_prompt(example):
+ full_prompt = generate_prompt(example)
+ tokenized_full_prompt = tokenize(full_prompt)
+ return tokenized_full_prompt
+
+ config = WaveFTConfig(
+ n_frequency=waveft_n_frequency,
+ scaling=waveft_scaling,
+ wavelet_family=waveft_wavelet_family,
+ use_idwt=waveft_use_idwt,
+ target_modules=waveft_target_modules,
+ task_type="CAUSAL_LM",
+ )
+
+ model = get_peft_model(model, config)
+
+ data = load_dataset(data_path)
+
+ train_val = data["train"].train_test_split(test_size=val_set_size, shuffle=True, seed=42)
+ train_data = train_val["train"].shuffle().map(generate_and_tokenize_prompt)
+ val_data = train_val["test"].shuffle().map(generate_and_tokenize_prompt)
+
+ trainer = transformers.Trainer(
+ model=model,
+ train_dataset=train_data,
+ eval_dataset=val_data,
+ args=transformers.TrainingArguments(
+ per_device_train_batch_size=batch_size,
+ warmup_steps=100,
+ num_train_epochs=num_epochs,
+ learning_rate=learning_rate,
+ logging_steps=100,
+ optim="adamw_torch",
+ eval_strategy="steps",
+ save_strategy="steps",
+ eval_steps=eval_step,
+ save_steps=save_step,
+ output_dir=output_dir,
+ save_total_limit=3,
+ load_best_model_at_end=True,
+ ddp_find_unused_parameters=False if world_size > 1 else None,
+ ),
+ data_collator=transformers.DataCollatorForSeq2Seq(
+ tokenizer, pad_to_multiple_of=8, return_tensors="pt", padding=True
+ ),
+ )
+ trainer.train()
+ model.save_pretrained(output_dir)
+
+
+def generate_prompt(example):
+ return f"""Below is an instruction that describes a task. Write a response that appropriately completes the request.
+ ### Instruction:
+ {example["instruction"]}
+ ### Response:
+ {example["output"]}"""
+
+
+if __name__ == "__main__":
+ import argparse
+
+ parser = argparse.ArgumentParser()
+ parser.add_argument("--base_model", type=str)
+ parser.add_argument("--data_path", type=str, default="yahma/alpaca-cleaned")
+ parser.add_argument("--output_dir", type=str, default="waveft")
+ parser.add_argument("--batch_size", type=int, default=16)
+ parser.add_argument("--num_epochs", type=int, default=1)
+ parser.add_argument("--learning_rate", type=float, default=3e-4)
+ parser.add_argument("--cutoff_len", type=int, default=256)
+ parser.add_argument("--val_set_size", type=int, default=16)
+ parser.add_argument("--eval_step", type=int, default=100)
+ parser.add_argument("--save_step", type=int, default=100)
+ parser.add_argument("--device_map", type=str, default="auto")
+ parser.add_argument("--waveft_n_frequency", type=int, default=2592)
+ parser.add_argument("--waveft_target_modules", type=str, default=None)
+ parser.add_argument("--waveft_scaling", type=float, default=25.0)
+ parser.add_argument("--waveft_wavelet_family", type=str, default="db1")
+ parser.add_argument("--waveft_use_idwt", action="store_true", default=True)
+ parser.add_argument("--torch_dtype", type=str, default="float16")
+ parser.add_argument("--seed", type=int, default=None)
+
+ args = parser.parse_args()
+
+ train(
+ base_model=args.base_model,
+ data_path=args.data_path,
+ output_dir=args.output_dir,
+ batch_size=args.batch_size,
+ num_epochs=args.num_epochs,
+ learning_rate=args.learning_rate,
+ cutoff_len=args.cutoff_len,
+ val_set_size=args.val_set_size,
+ eval_step=args.eval_step,
+ save_step=args.save_step,
+ device_map=args.device_map,
+ waveft_n_frequency=args.waveft_n_frequency,
+ waveft_target_modules=args.waveft_target_modules,
+ waveft_scaling=args.waveft_scaling,
+ waveft_wavelet_family=args.waveft_wavelet_family,
+ waveft_use_idwt=args.waveft_use_idwt,
+ torch_dtype=args.torch_dtype,
+ seed=args.seed,
+ )
diff --git a/peft/examples/xlora/README.md b/peft/examples/xlora/README.md
new file mode 100644
index 0000000000000000000000000000000000000000..ae81cfcd45e5940262504a95dc4805d45bdf280d
--- /dev/null
+++ b/peft/examples/xlora/README.md
@@ -0,0 +1,15 @@
+# X-LoRA examples
+
+## `xlora_inference_mistralrs.py`
+
+Perform inference of an X-LoRA model using the inference engine mistral.rs.
+
+Mistral.rs supports many base models besides Mistral, and can load models directly from saved LoRA checkpoints. Check out [adapter model docs](https://github.com/EricLBuehler/mistral.rs/blob/master/docs/ADAPTER_MODELS.md) and the [models support matrix](https://github.com/EricLBuehler/mistral.rs?tab=readme-ov-file#support-matrix).
+
+Mistral.rs features X-LoRA support and incorporates techniques such as a dual-KV cache, continuous batching, Paged Attention, and optional non granular scalings, will allow vastly improved throughput.
+
+Links:
+
+- Installation: https://github.com/EricLBuehler/mistral.rs/blob/master/mistralrs-pyo3/README.md
+- Runnable example: https://github.com/EricLBuehler/mistral.rs/blob/master/examples/python/xlora_zephyr.py
+- Adapter model docs and making the ordering file: https://github.com/EricLBuehler/mistral.rs/blob/master/docs/ADAPTER_MODELS.md
\ No newline at end of file
diff --git a/peft/examples/xlora/xlora_inference_mistralrs.py b/peft/examples/xlora/xlora_inference_mistralrs.py
new file mode 100644
index 0000000000000000000000000000000000000000..8a3f4de4261ea5613aa3acbfc12930bc89f1344b
--- /dev/null
+++ b/peft/examples/xlora/xlora_inference_mistralrs.py
@@ -0,0 +1,25 @@
+from mistralrs import ChatCompletionRequest, Runner, Which
+
+
+runner = Runner(
+ which=Which.XLora(
+ tok_model_id=None, # Automatically determine from ordering file
+ model_id=..., # Model ID of the base model (local path of HF model ID)
+ xlora_model_id=..., # X-LoRA Model ID of the base model (local path of HF model ID)
+ order=..., # Ordering file to ensure compatability with PEFT
+ tgt_non_granular_index=3, # Only generate scalings for the first 3 decoding tokens, and then use the last generated one
+ )
+)
+
+res = runner.send_chat_completion_request(
+ ChatCompletionRequest(
+ model="mistral",
+ messages=[{"role": "user", "content": "Tell me a story about 2 low rank matrices."}],
+ max_tokens=256,
+ presence_penalty=1.0,
+ top_p=0.1,
+ temperature=0.5,
+ )
+)
+print(res.choices[0].message.content)
+print(res.usage)
diff --git a/peft/method_comparison/MetaMathQA/Makefile b/peft/method_comparison/MetaMathQA/Makefile
new file mode 100644
index 0000000000000000000000000000000000000000..47ce7ab90d5c75e52b57d73a34b35a9056229d83
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/Makefile
@@ -0,0 +1,90 @@
+# Makefile for running MetaMathQA experiments.
+
+# --- Configuration ---
+PYTHON := python
+RUN_SCRIPT := run.py
+EXPERIMENTS_DIR := experiments
+RESULTS_DIR := results
+
+# --- Automatic Experiment and Result Discovery ---
+
+# 1. Find all experiment directories by looking for adapter_config.json files.
+# This gives us a list like: experiments/lora/llama-3.2-3B-rank32 ...
+EXPERIMENT_PATHS := $(shell find $(EXPERIMENTS_DIR) \
+ -name "adapter_config.json" -or \
+ -name "training_params.json" | xargs dirname | sort -u)
+
+# 2. Define a function to replace all occurrences of a character in a string.
+# This is needed to replicate the result naming logic from run.py (e.g., "lora/foo" -> "lora-foo").
+# Usage: $(call replace-all, string, char_to_replace, replacement_char)
+replace-all = $(if $(findstring $(2),$(1)),$(call replace-all,$(subst $(2),$(3),$(1)),$(2),$(3)),$(1))
+
+# 3. Define a function to convert an experiment path to its flat result file path.
+# e.g., "experiments/lora/llama-3.2-3B-rank32" -> "results/lora-llama-3.2-3B-rank32.json"
+exp_to_res = $(RESULTS_DIR)/$(call replace-all,$(patsubst $(EXPERIMENTS_DIR)/%,%,$(1)),/,--).json
+
+# 4. Generate the list of all target result files we want to build.
+RESULT_FILES := $(foreach exp,$(EXPERIMENT_PATHS),$(call exp_to_res,$(exp)))
+
+
+# --- Main Rules ---
+
+# The default 'all' target depends on all possible result files.
+# Running `make` or `make all` will check and run any outdated or missing experiments.
+all: $(RESULT_FILES)
+
+
+# --- Dynamic Rule Generation ---
+
+# This is the core logic. We dynamically generate a specific Makefile rule for each experiment found.
+# This avoids a complex pattern rule and makes the logic clearer.
+define EXPERIMENT_template
+# Input $1: The full experiment path (e.g., experiments/lora/llama-3.2-3B-rank32)
+
+# Define the rule:
+# The target is the result file (e.g., results/lora-llama-3.2-3B-rank32.json).
+# The dependencies are its config files, code changes need to be audited manually since they can
+# vary in degree of importance. Note that we explicitly ignore when the script fails to run
+# so that the other experiments still have a chance to run.
+$(call exp_to_res,$(1)): $(wildcard $(1)/adapter_config.json) $(wildcard $(1)/training_params.json)
+ @echo "---"
+ @echo "Running experiment: $(1)"
+ -$(PYTHON) $(RUN_SCRIPT) -v $(1)
+ @echo "Finished: $$@"
+ @echo "---"
+
+endef
+
+# This command iterates through every found experiment path and evaluates the template,
+# effectively stamping out a unique, explicit rule for each one.
+$(foreach exp_path,$(EXPERIMENT_PATHS),$(eval $(call EXPERIMENT_template,$(exp_path))))
+
+
+# --- Utility Rules ---
+
+.PHONY: all clean list dump_rules
+
+# The 'clean' rule removes all generated results.
+clean:
+ @echo "Cleaning results directory..."
+ @([ -n "$(wildcard $(RESULTS_DIR)/*.json)" ] && rm $(RESULTS_DIR)/*.json) || exit 0
+
+# The 'list' rule is for debugging. It shows the discovered experiments
+# and the result files the Makefile expects to create for them.
+list:
+ @echo "Discovered experiment configurations:"
+ @$(foreach exp,$(EXPERIMENT_PATHS),echo " - $(exp)/adapter_config.json";)
+ @echo "\nTarget result files:"
+ @$(foreach res,$(RESULT_FILES),echo " - $(res)";)
+
+# The 'dump_rules' rule is for debugging. It dumps all dynamically defined rules.
+define newline
+
+
+endef
+define DUMPED_RULES
+ $(foreach exp_path,$(EXPERIMENT_PATHS),$(call EXPERIMENT_template,$(exp_path)))
+endef
+
+dump_rules:
+ @echo -e "$(subst $(newline),\n,${DUMPED_RULES})"
diff --git a/peft/method_comparison/MetaMathQA/README.md b/peft/method_comparison/MetaMathQA/README.md
new file mode 100644
index 0000000000000000000000000000000000000000..4c762406619c56be43fdc0e93c6b6e4dbef02e58
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/README.md
@@ -0,0 +1,241 @@
+# PEFT method comparison on the MetaMathQA and GSM8K datasets
+
+## Goal
+
+This goal is to provide a benchmarking framework for the different PEFT methods that are implemented. It is important that evaluating different PEFT methods is reproducible, idempotent, and version-controlled. Results for more PEFT methods can be added over time.
+
+## Dataset
+
+This task trains on the [MetaMathQA]((https://huggingface.co/datasets/meta-math/MetaMathQA)) dataset and validates/tests on the [GSM8K](https://huggingface.co/datasets/openai/gsm8k) dataset ("main").
+
+For the model to attain good accuracy, it needs to learn to adhere to the output format and it must express basic chain of thought reasoning capabilities to get to the correct result in the first place. The task is challenging for models in the sub 7B parameter range.
+
+The train set uses the whole of MetaMathQA. The validation set is a random sample from the train set of GSM8K. The test set is the whole of the GSM8K test set.
+
+## Running
+
+Create an experiment in the `experiment/` folder of your choice and give it a name (the name itself does not matter but helps identify the experiment). An example would be `experiments/lora/llama-3.2-3B-rank32/`. Inside that directory, create 2 files:
+
+- `adapter_config.json`
+- Optional: `training_parameters.json`
+
+Once you created these two files, you can either
+
+- run the whole suite using by simply calling `make` (takes >24h)
+- run one specific experiment by calling `make results/-.json`,
+ for example `results/vblora-llama-3.2-3B-default.json`
+
+You can get a list of all runnable experiments by running `make list`, e.g.:
+```
+% make list (git)-[method-comparison-results] ⛓ peft
+Discovered experiment configurations:
+ - experiments/ptuning/llama-3.2-3B-default/adapter_config.json
+ [...]
+ - experiments/vblora/llama-3.2-3B-default/adapter_config.json
+
+Target result files:
+ - results/ptuning-llama-3.2-3B-default.json
+ [...]
+ - results/vblora-llama-3.2-3B-default.json
+```
+
+In case you want to force the execution of an experiment, you can simply `touch` the respective adapter config
+without modifying it. For example:
+
+ touch experiments/vblora/llama-3.2-3B-default/adapter_config.json
+ make
+
+to run the VBLoRA default experiment again.
+
+### `adapter_config.json`
+
+This must be a valid PEFT configuration. It is easiest to create it programmatically, e.g.:
+
+```python
+from peft import LoraConfig
+
+config = LoraConfig(...)
+config.save_pretrained()
+```
+
+### `training_parameters.json`
+
+There is a default file for the non-PEFT parameters: `default_training_params.json`. This contains all the other parameters that are relevant for training, e.g. the base model id, number of steps, batch size, learning rate, etc. If parameters that differ from the defaults are needed for a specific experiment, place a `training_parameters.json` into the experiment directory and adjust the parameters that need changing. The other parametes are taken from the aforementioned default config.
+
+For an overview of all possible arguments, you can also check the `TrainConfig` `dataclass` in `utils.py`.
+
+### Runtime performance
+
+Several factors should be considered to achieve a fast runtime performance. Besides the obvious factors like `max_steps` or the base model size, we found the following factors to have a significant impact:
+
+#### Eval batch size
+
+Regarding the `batch_size_eval` parameter, it is quite critical since evaluation takes up a significant portion of the training time and batching helps with reducing that. It should be possible to choose a value that is multiple times higher than the batch size used for training (`batch_size`). You should also pay attention to the size of the validation set -- e.g. if it's 50, don't choose a `batch_size_eval` of 40, as that results in a large batch of 30 and a small batch of 10. 25 might be a better choice. Also, ensure via a quick train run that the batch size does not lead to out of memory errors -- getting this error at the very end on evaluating the test set would be quite a loss of time.
+
+#### Generation length
+
+During testing, we discovered that the validation time is greatly inflated by just a few very long generations. Those can inflate the validation time by a factor of 3 or more. At the same time, we discovered that these long generations do not help with accuracy -- in fact, if they exceed the maximum configured length, they're just cut off mid sentence and would thus produce an accuracy of 0 anyway.
+
+To remedy this, we now set both `max_length` and `max_new_tokens` for the generation kwargs in the default training parameters. Normally, this is not possible when using transformers, as the latter argument overrides the former. However, we have added special logic inside of `get_generation_config` which takes both and chooses the smaller of the two. This way, we can get rid of these excessively long generations, thus considerably reducing eval times, while still guaranteeing a maximum total generation length to guard against OOM errors. Testing showed that this does not hamper test accuracy. It is therefore recommended not to change these settings.
+
+#### Bucketing
+
+The length of the sequences in the training data can vary a lot. Therefore, if samples are taken randomly from the training dataset, we will end up with batches containing very short and very long sequences. This is bad because the batch will be padded to the longest sequence, slowing down training. The obvious solution would be to sort the whole dataset by sequence length, but this is also bad because it introduces an order bias (e.g. first training on only short and then on only long answers).
+
+The solution is to find a trade off between the two factors. This is achieved by the `BucketIterator`. It first creates buckets that contain multiple batches, e.g. 20x the batch size. The bucket is then sorted by sequence length and then batches are yielded from the bucket. Therefore, we have a small order bias within a bucket but not between buckets, stricking a good balance between training speed and training loss.
+
+From practical experiments, for a batch size of 4, a bucket size of 80 provides a good balance with only slightly lower training loss but cutting training time by 25%. For eval, we don't use the iterator since there, the batch size is relatively big and thus there is little upside.
+
+### Start a run
+
+Once everything is set up properly, start a run by using the `run.py` script. Pass `-v` for verbose output to the console (recommended if observing the progress is desired). As an example, for `experiments/lora/llama-3.2-3B-rank32/` the invocation would be:
+
+```sh
+python run.py -v experiments/lora/llama-3.2-3B-rank32/
+```
+
+By default, the adapter will be saved in a temporary file for further inspection if needed. The prevent this, add the `--clean` flag to the call.
+
+### Run status
+
+The run can be categorized 3 different states:
+
+1. Main run: You are on the `main` branch and the run ended successfully. The results are stored in the `results` folder and are used for further analysis.
+2. Test run: You are not on the `main` branch and the run ended successfully. The results are stored in the `temporary_results` folder and are not used for further analysis.
+3. The run was cancelled (`ctrl + c`). The results are stored in the `cancelled_results` folder and are not used for further analysis.
+
+## Outputs
+
+Results are stored in one of the result directories. An example output could look like so:
+
+```js
+{
+ "run_info": {
+ "created_at": "2025-03-05T13:50:05+00:00",
+ "total_time": 2711.0915009640157,
+ "experiment_name": "ia3/lr_0.001",
+ "peft_branch": "ben-method-comparison",
+ "train_config": {
+ "model_id": "meta-llama/Llama-3.2-3B",
+ "dtype": "bfloat16",
+ "max_seq_length": 768,
+ "batch_size": 4,
+ "batch_size_eval": 51,
+ "max_steps": 5000,
+ "eval_steps": 250,
+ "compile": false,
+ "query_template": "Question: {query} Think step by step.\nAnswer:",
+ "seed": 0,
+ "grad_norm_clip": 1.0,
+ "optimizer_kwargs": {
+ "lr": 0.001
+ },
+ "lr_scheduler": "cosine",
+ "use_amp": false,
+ "generation_kwargs": {
+ "max_length": 800
+ },
+ "attn_implementation": null
+ },
+ "peft_config": {
+ "task_type": null,
+ "peft_type": "IA3",
+ "auto_mapping": null,
+ "base_model_name_or_path": "meta-llama/Llama-3.2-3B",
+ "revision": null,
+ "inference_mode": false,
+ "target_modules": [
+ "v_proj",
+ "k_proj",
+ "down_proj"
+ ],
+ "exclude_modules": null,
+ "feedforward_modules": [
+ "down_proj"
+ ],
+ "fan_in_fan_out": false,
+ "modules_to_save": null,
+ "init_ia3_weights": true
+ }
+ },
+ "train_info": {
+ "accelerator_memory_reserved_avg": 14229219940,
+ "accelerator_memory_max": 24847056896,
+ "accelerator_memory_reserved_99th": 19115624366,
+ "train_time": 2238.65277833899,
+ "file_size": 1157064,
+ "status": "success",
+ "metrics": [
+ {
+ "step": 250,
+ "valid accuracy": 0.0784313725490196,
+ "train loss": 1.1336498007774354,
+ "train samples": 1000
+ },
+ [...]
+ {
+ "step": 5000,
+ "valid accuracy": 0.21568627450980393,
+ "train loss": 0.6345920492410659,
+ "train samples": 20000
+ },
+ {
+ "step": 5000,
+ "test accuracy": 0.35129740518962077,
+ "train loss": 0.6345920492410659,
+ "train samples": 20000,
+ "train total tokens": 4197579
+ }
+ ]
+ },
+ "meta_info": {
+ "model_sha": "13afe5124825b4f3751f836b40dafda64c1ed062",
+ "model_created_at": "2024-09-18T15:23:48+00:00",
+ "dataset_sha": "aa4f34d3d2d3231299b5b03d9b3e5a20da45aa18",
+ "dataset_created_at": "2023-09-21T17:22:46+00:00",
+ "package_info": {
+ "transformers-version": "4.50.0.dev0",
+ "transformers-commit-hash": "752ef3fd4e70869626ec70657a770a85c0ad9219",
+ "peft-version": "0.14.1.dev0",
+ "peft-commit-hash": "a447a4e5ecd87b7d57733f4df9616a328cf130f4",
+ "datasets-version": "3.3.2",
+ "datasets-commit-hash": null,
+ "bitsandbytes-version": "0.45.2",
+ "bitsandbytes-commit-hash": null,
+ "torch-version": "2.6.0+cu124",
+ "torch-commit-hash": null
+ },
+ "system_info": {
+ "system": "Linux",
+ "release": "6.11.0-17-generic",
+ "version": "#17~24.04.2-Ubuntu SMP PREEMPT_DYNAMIC Mon Jan 20 22:48:29 UTC 2",
+ "machine": "x86_64",
+ "processor": "x86_64",
+ "accelerator": "NVIDIA GeForce RTX 4090"
+ },
+ "pytorch_info": "PyTorch built with: [...]"
+ }
+}
+```
+
+## Dependencies
+
+Apart from the normal PEFT dependencies, ensure that the packages in the `requirements.txt` are installed, e.g. via:
+
+```sh
+python -m pip install -r requirements.txt
+```
+
+Python 3.12+ is required.
+
+## Open tasks
+
+- consider using `DataLoader`
+- consider adding https://github.com/huggingface/Math-Verify
+- consider adding `weight` argument to cross entropy calculation to downweight the EOS token, but it would require calculating the loss manually instead of relying on transformers (see https://github.com/huggingface/transformers/blob/6a876462c308bd7cd7d3ca8e93abaa7d5b02e90e/src/transformers/loss/loss_utils.py#L24-L48)
+- do a sanity check against/comparison with transformers Trainer
+- consider using vLLM to potentially speed up generations, at least for the test set
+- using `torch.compile` leads to a huge slowdown, investigate (maybe recompiles), although it does save memory
+- AMP does not appear to help, investigate
+- packing of sequences (but this probably requires adjusting the attention matrix)
+- clean up what gets printed and where (stdout, stderr)
diff --git a/peft/method_comparison/MetaMathQA/cancelled_results/.gitkeep b/peft/method_comparison/MetaMathQA/cancelled_results/.gitkeep
new file mode 100644
index 0000000000000000000000000000000000000000..e69de29bb2d1d6434b8b29ae775ad8c2e48c5391
diff --git a/peft/method_comparison/MetaMathQA/data.py b/peft/method_comparison/MetaMathQA/data.py
new file mode 100644
index 0000000000000000000000000000000000000000..be3ace83cfa83c211f5f41086fee9f36660363f7
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/data.py
@@ -0,0 +1,109 @@
+# Copyright 2025-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""
+All utilities related to data handling.
+"""
+
+from functools import partial
+from typing import Callable
+
+import datasets
+import numpy as np
+from datasets import Dataset, load_dataset
+
+
+# with a token limit of 768 for query + response, we have to exclude all texts with length > 1304; this leaves 93.8% of
+# the dataset
+CHAR_LIMIT = 1300
+# train/valid/test split -- note that evaluation takes quite long, so don't choose too large sizes for the valid set,
+# since it's run multiple times during training; test is only run once at the end and thus can be larger
+VALID_SIZE = 50
+
+
+def get_filtered_dataset(*, ds: datasets.Dataset, print_fn: Callable[..., None]) -> Dataset:
+ """Return the filtered dataset, with long queries removed.
+
+ We determined that 99% of queries have 529 or fewer characters. Characters roughly correspond to tokens, so this is
+ a good proxy. We cannot use tokens directly, as that depends on the tokenizer, which can be different for each
+ model, but we want the same filter for each model.
+
+ """
+ char_lengths = [len(f"{q} {r}") for q, r in zip(ds["query"], ds["response"])]
+ idx_filtered = [i for i, length in enumerate(char_lengths) if length <= CHAR_LIMIT]
+ print_fn(f"Filtered dataset: {100 * len(idx_filtered) / len(ds):.1f}% of the original dataset")
+ return ds.select(idx_filtered)
+
+
+def get_train_valid_test_datasets(
+ *, tokenizer, query_template: str, print_fn: Callable[..., None]
+) -> tuple[Dataset, Dataset, Dataset]:
+ """
+ Return the indices of the train, valid, and test splits of the dataset.
+
+ We cannot use ds.train_test_split(..., stratify_by_column="type") as it gives:
+
+ > ValueError: Stratifying by column is only supported for ClassLabel column, and column type is Value.
+
+ even after calling ds_filtered.class_encode_column("type"). Thus, using sklearn's StratifiedKFold instead.
+ """
+ metamath = load_dataset("meta-math/MetaMathQA")["train"]
+ metamath = get_filtered_dataset(ds=metamath, print_fn=print_fn)
+
+ # gsmk8k does not need to be filtered as query and response are short enough
+ gsm8k = load_dataset("openai/gsm8k", "main")
+ gsm8k = gsm8k.rename_columns({"question": "query", "answer": "response"})
+ gsm8k_train = gsm8k["train"]
+ gsm8k_test = gsm8k["test"]
+
+ np.random.seed(0)
+ indices = np.arange(len(gsm8k_train))
+ np.random.shuffle(indices)
+ idx_valid = indices[:VALID_SIZE]
+
+ ds_train = metamath
+ ds_valid = gsm8k_train.select(idx_valid)
+ ds_test = gsm8k_test
+
+ print_fn(f"Train size: {len(ds_train)}")
+ print_fn(f"Valid size: {len(ds_valid)}")
+ print_fn(f"Test size: {len(ds_test)}")
+
+ tokenize_with_answer_ = partial(tokenize_with_answer, tokenizer=tokenizer, template=query_template)
+ tokenize_wo_answer_ = partial(tokenize_wo_answer, tokenizer=tokenizer, template=query_template)
+ ds_train = ds_train.map(tokenize_with_answer_, batched=True).remove_columns(["type", "query", "original_question"])
+ ds_valid = ds_valid.map(tokenize_wo_answer_, batched=True).remove_columns(["query"])
+ ds_test = ds_test.map(tokenize_wo_answer_, batched=True).remove_columns(["query"])
+
+ return ds_train, ds_valid, ds_test
+
+
+def tokenize_with_answer(samples, tokenizer, template):
+ queries = [template.format(query=sample) + answer for sample, answer in zip(samples["query"], samples["response"])]
+ tokenized = tokenizer(queries)
+ tokenized["input_ids"] = [input_ids[: tokenizer.model_max_length] for input_ids in tokenized["input_ids"]]
+ tokenized["attention_mask"] = [
+ input_ids[: tokenizer.model_max_length] for input_ids in tokenized["attention_mask"]
+ ]
+ return tokenized
+
+
+def tokenize_wo_answer(samples, tokenizer, template):
+ queries = [template.format(query=sample) for sample in samples["query"]]
+ tokenized = tokenizer(queries)
+ tokenized["input_ids"] = [input_ids[: tokenizer.model_max_length] for input_ids in tokenized["input_ids"]]
+ tokenized["attention_mask"] = [
+ input_ids[: tokenizer.model_max_length] for input_ids in tokenized["attention_mask"]
+ ]
+ return tokenized
diff --git a/peft/method_comparison/MetaMathQA/default_training_params.json b/peft/method_comparison/MetaMathQA/default_training_params.json
new file mode 100644
index 0000000000000000000000000000000000000000..a200a41ed96409033011b7e4fc33e05fe9c61162
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/default_training_params.json
@@ -0,0 +1,26 @@
+{
+ "model_id": "meta-llama/Llama-3.2-3B",
+ "dtype": "bfloat16",
+ "max_seq_length": 768,
+ "batch_size": 4,
+ "batch_size_eval": 50,
+ "max_steps": 5000,
+ "eval_steps": 250,
+ "compile": false,
+ "seed": 0,
+ "grad_norm_clip": 1.0,
+ "optimizer_type": "AdamW",
+ "optimizer_kwargs": {
+ "lr": 1e-4,
+ "weight_decay": 0.1
+ },
+ "lr_scheduler": "cosine",
+ "use_amp": false,
+ "autocast_adapter_dtype": true,
+ "attn_implementation": null,
+ "generation_kwargs": {
+ "max_length": 800,
+ "max_new_tokens": 300
+ },
+ "query_template": "Question: {query} Think step by step.\nAnswer:"
+}
diff --git a/peft/method_comparison/MetaMathQA/experiments/adalora/llama-3.2-3B-rank32/adapter_config.json b/peft/method_comparison/MetaMathQA/experiments/adalora/llama-3.2-3B-rank32/adapter_config.json
new file mode 100644
index 0000000000000000000000000000000000000000..d20357b52d92ad65b3af6e932c9dd8d16b47bcb4
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/experiments/adalora/llama-3.2-3B-rank32/adapter_config.json
@@ -0,0 +1,39 @@
+{
+ "alpha_pattern": {},
+ "auto_mapping": null,
+ "base_model_name_or_path": null,
+ "beta1": 0.85,
+ "beta2": 0.85,
+ "bias": "none",
+ "corda_config": null,
+ "deltaT": 1,
+ "eva_config": null,
+ "exclude_modules": null,
+ "fan_in_fan_out": false,
+ "inference_mode": false,
+ "init_lora_weights": true,
+ "init_r": 64,
+ "layer_replication": null,
+ "layers_pattern": null,
+ "layers_to_transform": null,
+ "loftq_config": {},
+ "lora_alpha": 8,
+ "lora_bias": false,
+ "lora_dropout": 0.0,
+ "megatron_config": null,
+ "megatron_core": "megatron.core",
+ "modules_to_save": null,
+ "orth_reg_weight": 0.5,
+ "peft_type": "ADALORA",
+ "r": 8,
+ "rank_pattern": null,
+ "revision": null,
+ "target_modules": null,
+ "target_r": 32,
+ "task_type": null,
+ "tfinal": 500,
+ "tinit": 200,
+ "total_step": 5000,
+ "use_dora": false,
+ "use_rslora": false
+}
\ No newline at end of file
diff --git a/peft/method_comparison/MetaMathQA/experiments/adaptionprompt/llama-3.2-3B-lr_0.0005/adapter_config.json b/peft/method_comparison/MetaMathQA/experiments/adaptionprompt/llama-3.2-3B-lr_0.0005/adapter_config.json
new file mode 100644
index 0000000000000000000000000000000000000000..367bea4cf187d10c96a4d8b53f355bfd269a1e6a
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/experiments/adaptionprompt/llama-3.2-3B-lr_0.0005/adapter_config.json
@@ -0,0 +1,11 @@
+{
+ "adapter_layers": 28,
+ "adapter_len": 100,
+ "auto_mapping": null,
+ "base_model_name_or_path": null,
+ "inference_mode": false,
+ "peft_type": "ADAPTION_PROMPT",
+ "revision": null,
+ "target_modules": null,
+ "task_type": "CAUSAL_LM"
+}
\ No newline at end of file
diff --git a/peft/method_comparison/MetaMathQA/experiments/adaptionprompt/llama-3.2-3B-lr_0.0005/training_params.json b/peft/method_comparison/MetaMathQA/experiments/adaptionprompt/llama-3.2-3B-lr_0.0005/training_params.json
new file mode 100644
index 0000000000000000000000000000000000000000..e8106a88d0de4099e2cbd2648abbe43bdebe6091
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/experiments/adaptionprompt/llama-3.2-3B-lr_0.0005/training_params.json
@@ -0,0 +1,6 @@
+{
+ "optimizer_kwargs": {
+ "lr": 5e-4
+ }
+}
+
diff --git a/peft/method_comparison/MetaMathQA/experiments/boft/llama-3.2-3B-default/adapter_config.json b/peft/method_comparison/MetaMathQA/experiments/boft/llama-3.2-3B-default/adapter_config.json
new file mode 100644
index 0000000000000000000000000000000000000000..44d50893ff7f19c1851a2150e879c444ec134fe1
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/experiments/boft/llama-3.2-3B-default/adapter_config.json
@@ -0,0 +1,20 @@
+{
+ "auto_mapping": null,
+ "base_model_name_or_path": null,
+ "bias": "none",
+ "boft_block_num": 0,
+ "boft_block_size": 4,
+ "boft_dropout": 0.0,
+ "boft_n_butterfly_factor": 1,
+ "exclude_modules": null,
+ "fan_in_fan_out": false,
+ "inference_mode": false,
+ "init_weights": true,
+ "layers_pattern": null,
+ "layers_to_transform": null,
+ "modules_to_save": null,
+ "peft_type": "BOFT",
+ "revision": null,
+ "target_modules": null,
+ "task_type": null
+}
\ No newline at end of file
diff --git a/peft/method_comparison/MetaMathQA/experiments/bone/llama-3.2-3B-bat/adapter_config.json b/peft/method_comparison/MetaMathQA/experiments/bone/llama-3.2-3B-bat/adapter_config.json
new file mode 100644
index 0000000000000000000000000000000000000000..cd69e4389edfe1738ceec6c42be177dd17d924c6
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/experiments/bone/llama-3.2-3B-bat/adapter_config.json
@@ -0,0 +1,19 @@
+{
+ "auto_mapping": null,
+ "base_model_name_or_path": null,
+ "bias": "none",
+ "exclude_modules": null,
+ "inference_mode": false,
+ "init_weights": "bat",
+ "layers_pattern": null,
+ "layers_to_transform": null,
+ "modules_to_save": null,
+ "peft_type": "BONE",
+ "r": 64,
+ "revision": null,
+ "target_modules": [
+ "v_proj",
+ "q_proj"
+ ],
+ "task_type": null
+}
\ No newline at end of file
diff --git a/peft/method_comparison/MetaMathQA/experiments/bone/llama-3.2-3B-default/adapter_config.json b/peft/method_comparison/MetaMathQA/experiments/bone/llama-3.2-3B-default/adapter_config.json
new file mode 100644
index 0000000000000000000000000000000000000000..abc68802718821c659614b5fdeabb45db2df824b
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/experiments/bone/llama-3.2-3B-default/adapter_config.json
@@ -0,0 +1,19 @@
+{
+ "auto_mapping": null,
+ "base_model_name_or_path": null,
+ "bias": "none",
+ "exclude_modules": null,
+ "inference_mode": false,
+ "init_weights": true,
+ "layers_pattern": null,
+ "layers_to_transform": null,
+ "modules_to_save": null,
+ "peft_type": "BONE",
+ "r": 64,
+ "revision": null,
+ "target_modules": [
+ "v_proj",
+ "q_proj"
+ ],
+ "task_type": null
+}
\ No newline at end of file
diff --git a/peft/method_comparison/MetaMathQA/experiments/c3a/llama-3.2-3B-default/adapter_config.json b/peft/method_comparison/MetaMathQA/experiments/c3a/llama-3.2-3B-default/adapter_config.json
new file mode 100644
index 0000000000000000000000000000000000000000..170c4bb33e558339b07da8044fb3cb2093d2e4eb
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/experiments/c3a/llama-3.2-3B-default/adapter_config.json
@@ -0,0 +1,21 @@
+{
+ "auto_mapping": null,
+ "base_model_name_or_path": null,
+ "bias": "none",
+ "exclude_modules": null,
+ "fan_in_fan_out": false,
+ "inference_mode": false,
+ "init_weights": false,
+ "layers_pattern": null,
+ "layers_to_transform": null,
+ "modules_to_save": null,
+ "block_size": 64,
+ "block_size_pattern": {},
+ "peft_type": "C3A",
+ "revision": null,
+ "target_modules": [
+ "v_proj",
+ "q_proj"
+ ],
+ "task_type": null
+}
diff --git a/peft/method_comparison/MetaMathQA/experiments/c3a/llama-3.2-3B-default/training_params.json b/peft/method_comparison/MetaMathQA/experiments/c3a/llama-3.2-3B-default/training_params.json
new file mode 100644
index 0000000000000000000000000000000000000000..a39b9dc8a825e9b79ace91032d0755835548eb44
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/experiments/c3a/llama-3.2-3B-default/training_params.json
@@ -0,0 +1,6 @@
+{
+ "optimizer_kwargs": {
+ "lr": 3e-1,
+ "weight_decay": 1e-5
+ }
+}
diff --git a/peft/method_comparison/MetaMathQA/experiments/fourierft/llama-3.2-3B-default/adapter_config.json b/peft/method_comparison/MetaMathQA/experiments/fourierft/llama-3.2-3B-default/adapter_config.json
new file mode 100644
index 0000000000000000000000000000000000000000..a2a379f07427f4c68eeaf06756004ddaa377f96b
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/experiments/fourierft/llama-3.2-3B-default/adapter_config.json
@@ -0,0 +1,23 @@
+{
+ "auto_mapping": null,
+ "base_model_name_or_path": null,
+ "bias": "none",
+ "exclude_modules": null,
+ "fan_in_fan_out": false,
+ "inference_mode": false,
+ "init_weights": false,
+ "layers_pattern": null,
+ "layers_to_transform": null,
+ "modules_to_save": null,
+ "n_frequency": 1000,
+ "n_frequency_pattern": {},
+ "peft_type": "FOURIERFT",
+ "random_loc_seed": 777,
+ "revision": null,
+ "scaling": 300,
+ "target_modules": [
+ "v_proj",
+ "q_proj"
+ ],
+ "task_type": null
+}
\ No newline at end of file
diff --git a/peft/method_comparison/MetaMathQA/experiments/fourierft/llama-3.2-3B-n_frequency-5000/adapter_config.json b/peft/method_comparison/MetaMathQA/experiments/fourierft/llama-3.2-3B-n_frequency-5000/adapter_config.json
new file mode 100644
index 0000000000000000000000000000000000000000..40d40246c48487419ea0d21eb369bea60c729496
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/experiments/fourierft/llama-3.2-3B-n_frequency-5000/adapter_config.json
@@ -0,0 +1,23 @@
+{
+ "auto_mapping": null,
+ "base_model_name_or_path": null,
+ "bias": "none",
+ "exclude_modules": null,
+ "fan_in_fan_out": false,
+ "inference_mode": false,
+ "init_weights": false,
+ "layers_pattern": null,
+ "layers_to_transform": null,
+ "modules_to_save": null,
+ "n_frequency": 5000,
+ "n_frequency_pattern": {},
+ "peft_type": "FOURIERFT",
+ "random_loc_seed": 777,
+ "revision": null,
+ "scaling": 300,
+ "target_modules": [
+ "v_proj",
+ "q_proj"
+ ],
+ "task_type": null
+}
\ No newline at end of file
diff --git a/peft/method_comparison/MetaMathQA/experiments/full-finetuning/llama-3.2-3B-lr_0.00001/training_params.json b/peft/method_comparison/MetaMathQA/experiments/full-finetuning/llama-3.2-3B-lr_0.00001/training_params.json
new file mode 100644
index 0000000000000000000000000000000000000000..6d6c3b0f9114a63d0739eef0c996f4c1c0c0e36c
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/experiments/full-finetuning/llama-3.2-3B-lr_0.00001/training_params.json
@@ -0,0 +1,6 @@
+{
+ "optimizer_kwargs": {
+ "lr": 1e-5
+ }
+}
+
diff --git a/peft/method_comparison/MetaMathQA/experiments/ia3/llama-3.2-3B-default/adapter_config.json b/peft/method_comparison/MetaMathQA/experiments/ia3/llama-3.2-3B-default/adapter_config.json
new file mode 100644
index 0000000000000000000000000000000000000000..0c8e514faa808ac0874e71f21bad7a576d15349d
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/experiments/ia3/llama-3.2-3B-default/adapter_config.json
@@ -0,0 +1,14 @@
+{
+ "auto_mapping": null,
+ "base_model_name_or_path": null,
+ "exclude_modules": null,
+ "fan_in_fan_out": false,
+ "feedforward_modules": null,
+ "inference_mode": false,
+ "init_ia3_weights": true,
+ "modules_to_save": null,
+ "peft_type": "IA3",
+ "revision": null,
+ "target_modules": null,
+ "task_type": null
+}
\ No newline at end of file
diff --git a/peft/method_comparison/MetaMathQA/experiments/ia3/llama-3.2-3B-lr_0.001/adapter_config.json b/peft/method_comparison/MetaMathQA/experiments/ia3/llama-3.2-3B-lr_0.001/adapter_config.json
new file mode 100644
index 0000000000000000000000000000000000000000..0c8e514faa808ac0874e71f21bad7a576d15349d
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/experiments/ia3/llama-3.2-3B-lr_0.001/adapter_config.json
@@ -0,0 +1,14 @@
+{
+ "auto_mapping": null,
+ "base_model_name_or_path": null,
+ "exclude_modules": null,
+ "fan_in_fan_out": false,
+ "feedforward_modules": null,
+ "inference_mode": false,
+ "init_ia3_weights": true,
+ "modules_to_save": null,
+ "peft_type": "IA3",
+ "revision": null,
+ "target_modules": null,
+ "task_type": null
+}
\ No newline at end of file
diff --git a/peft/method_comparison/MetaMathQA/experiments/ia3/llama-3.2-3B-lr_0.001/training_params.json b/peft/method_comparison/MetaMathQA/experiments/ia3/llama-3.2-3B-lr_0.001/training_params.json
new file mode 100644
index 0000000000000000000000000000000000000000..8a120ad9a80c36dc3666f4da481a5292a7dc8072
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/experiments/ia3/llama-3.2-3B-lr_0.001/training_params.json
@@ -0,0 +1,6 @@
+{
+ "optimizer_kwargs": {
+ "lr": 1e-3
+ }
+}
+
diff --git a/peft/method_comparison/MetaMathQA/experiments/ln_tuning/llama-3.2-3B-default/adapter_config.json b/peft/method_comparison/MetaMathQA/experiments/ln_tuning/llama-3.2-3B-default/adapter_config.json
new file mode 100644
index 0000000000000000000000000000000000000000..70b7363d3ac83e8ff2ee85634baafbee1f42b56a
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/experiments/ln_tuning/llama-3.2-3B-default/adapter_config.json
@@ -0,0 +1,11 @@
+{
+ "auto_mapping": null,
+ "base_model_name_or_path": null,
+ "exclude_modules": null,
+ "inference_mode": false,
+ "modules_to_save": null,
+ "peft_type": "LN_TUNING",
+ "revision": null,
+ "target_modules": null,
+ "task_type": null
+}
\ No newline at end of file
diff --git a/peft/method_comparison/MetaMathQA/experiments/loha/llama-3.2-3B-rank32/adapter_config.json b/peft/method_comparison/MetaMathQA/experiments/loha/llama-3.2-3B-rank32/adapter_config.json
new file mode 100644
index 0000000000000000000000000000000000000000..1137259fa26b3abeac269c7bdda56dbeb29e34f7
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/experiments/loha/llama-3.2-3B-rank32/adapter_config.json
@@ -0,0 +1,24 @@
+{
+ "alpha": 64,
+ "alpha_pattern": {},
+ "auto_mapping": null,
+ "base_model_name_or_path": null,
+ "exclude_modules": null,
+ "inference_mode": false,
+ "init_weights": true,
+ "layers_pattern": null,
+ "layers_to_transform": null,
+ "module_dropout": 0.0,
+ "modules_to_save": null,
+ "peft_type": "LOHA",
+ "r": 32,
+ "rank_dropout": 0.0,
+ "rank_pattern": {},
+ "revision": null,
+ "target_modules": [
+ "q_proj",
+ "v_proj"
+ ],
+ "task_type": null,
+ "use_effective_conv2d": false
+}
\ No newline at end of file
diff --git a/peft/method_comparison/MetaMathQA/experiments/lokr/llama-3.2-3B-rank32/adapter_config.json b/peft/method_comparison/MetaMathQA/experiments/lokr/llama-3.2-3B-rank32/adapter_config.json
new file mode 100644
index 0000000000000000000000000000000000000000..7d30dd77a4c5f185fde99a5d60f381961ac7c522
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/experiments/lokr/llama-3.2-3B-rank32/adapter_config.json
@@ -0,0 +1,27 @@
+{
+ "alpha": 64,
+ "alpha_pattern": {},
+ "auto_mapping": null,
+ "base_model_name_or_path": null,
+ "decompose_both": false,
+ "decompose_factor": -1,
+ "exclude_modules": null,
+ "inference_mode": false,
+ "init_weights": true,
+ "layers_pattern": null,
+ "layers_to_transform": null,
+ "module_dropout": 0.0,
+ "modules_to_save": null,
+ "peft_type": "LOKR",
+ "r": 32,
+ "rank_dropout": 0.0,
+ "rank_dropout_scale": false,
+ "rank_pattern": {},
+ "revision": null,
+ "target_modules": [
+ "q_proj",
+ "v_proj"
+ ],
+ "task_type": null,
+ "use_effective_conv2d": false
+}
\ No newline at end of file
diff --git a/peft/method_comparison/MetaMathQA/experiments/lora/llama-3.2-3B-rank32-dora/adapter_config.json b/peft/method_comparison/MetaMathQA/experiments/lora/llama-3.2-3B-rank32-dora/adapter_config.json
new file mode 100644
index 0000000000000000000000000000000000000000..255d09d2508a603fd8eea98152025c6cd8f0a789
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/experiments/lora/llama-3.2-3B-rank32-dora/adapter_config.json
@@ -0,0 +1,30 @@
+{
+ "alpha_pattern": {},
+ "auto_mapping": null,
+ "base_model_name_or_path": null,
+ "bias": "none",
+ "corda_config": null,
+ "eva_config": null,
+ "exclude_modules": null,
+ "fan_in_fan_out": false,
+ "inference_mode": false,
+ "init_lora_weights": true,
+ "layer_replication": null,
+ "layers_pattern": null,
+ "layers_to_transform": null,
+ "loftq_config": {},
+ "lora_alpha": 64,
+ "lora_bias": false,
+ "lora_dropout": 0.0,
+ "megatron_config": null,
+ "megatron_core": "megatron.core",
+ "modules_to_save": null,
+ "peft_type": "LORA",
+ "r": 32,
+ "rank_pattern": {},
+ "revision": null,
+ "target_modules": null,
+ "task_type": "CAUSAL_LM",
+ "use_dora": true,
+ "use_rslora": false
+}
diff --git a/peft/method_comparison/MetaMathQA/experiments/lora/llama-3.2-3B-rank32-lorafa/adapter_config.json b/peft/method_comparison/MetaMathQA/experiments/lora/llama-3.2-3B-rank32-lorafa/adapter_config.json
new file mode 100644
index 0000000000000000000000000000000000000000..8832c108fac1825c52774517fd3e5bf0fc7d8d64
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/experiments/lora/llama-3.2-3B-rank32-lorafa/adapter_config.json
@@ -0,0 +1,30 @@
+{
+ "alpha_pattern": {},
+ "auto_mapping": null,
+ "base_model_name_or_path": null,
+ "bias": "none",
+ "corda_config": null,
+ "eva_config": null,
+ "exclude_modules": null,
+ "fan_in_fan_out": false,
+ "inference_mode": false,
+ "init_lora_weights": true,
+ "layer_replication": null,
+ "layers_pattern": null,
+ "layers_to_transform": null,
+ "loftq_config": {},
+ "lora_alpha": 64,
+ "lora_bias": false,
+ "lora_dropout": 0.0,
+ "megatron_config": null,
+ "megatron_core": "megatron.core",
+ "modules_to_save": null,
+ "peft_type": "LORA",
+ "r": 32,
+ "rank_pattern": {},
+ "revision": null,
+ "target_modules": null,
+ "task_type": "CAUSAL_LM",
+ "use_dora": false,
+ "use_rslora": false
+}
diff --git a/peft/method_comparison/MetaMathQA/experiments/lora/llama-3.2-3B-rank32-lorafa/training_params.json b/peft/method_comparison/MetaMathQA/experiments/lora/llama-3.2-3B-rank32-lorafa/training_params.json
new file mode 100644
index 0000000000000000000000000000000000000000..985db872405905c31c93a10aa9cd3f77ed223437
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/experiments/lora/llama-3.2-3B-rank32-lorafa/training_params.json
@@ -0,0 +1,9 @@
+{
+ "optimizer_type": "lora-fa",
+ "optimizer_kwargs": {
+ "r": 32,
+ "lora_alpha": 64,
+ "lr": 1e-4,
+ "weight_decay": 0.1
+ }
+}
diff --git a/peft/method_comparison/MetaMathQA/experiments/lora/llama-3.2-3B-rank32/adapter_config.json b/peft/method_comparison/MetaMathQA/experiments/lora/llama-3.2-3B-rank32/adapter_config.json
new file mode 100644
index 0000000000000000000000000000000000000000..8832c108fac1825c52774517fd3e5bf0fc7d8d64
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/experiments/lora/llama-3.2-3B-rank32/adapter_config.json
@@ -0,0 +1,30 @@
+{
+ "alpha_pattern": {},
+ "auto_mapping": null,
+ "base_model_name_or_path": null,
+ "bias": "none",
+ "corda_config": null,
+ "eva_config": null,
+ "exclude_modules": null,
+ "fan_in_fan_out": false,
+ "inference_mode": false,
+ "init_lora_weights": true,
+ "layer_replication": null,
+ "layers_pattern": null,
+ "layers_to_transform": null,
+ "loftq_config": {},
+ "lora_alpha": 64,
+ "lora_bias": false,
+ "lora_dropout": 0.0,
+ "megatron_config": null,
+ "megatron_core": "megatron.core",
+ "modules_to_save": null,
+ "peft_type": "LORA",
+ "r": 32,
+ "rank_pattern": {},
+ "revision": null,
+ "target_modules": null,
+ "task_type": "CAUSAL_LM",
+ "use_dora": false,
+ "use_rslora": false
+}
diff --git a/peft/method_comparison/MetaMathQA/experiments/lora/llama-3.2-3B-rank64-rslora/adapter_config.json b/peft/method_comparison/MetaMathQA/experiments/lora/llama-3.2-3B-rank64-rslora/adapter_config.json
new file mode 100644
index 0000000000000000000000000000000000000000..dc1f8039ab02888675a12a1a1a017ebdd196b9d4
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/experiments/lora/llama-3.2-3B-rank64-rslora/adapter_config.json
@@ -0,0 +1,30 @@
+{
+ "alpha_pattern": {},
+ "auto_mapping": null,
+ "base_model_name_or_path": null,
+ "bias": "none",
+ "corda_config": null,
+ "eva_config": null,
+ "exclude_modules": null,
+ "fan_in_fan_out": false,
+ "inference_mode": false,
+ "init_lora_weights": true,
+ "layer_replication": null,
+ "layers_pattern": null,
+ "layers_to_transform": null,
+ "loftq_config": {},
+ "lora_alpha": 64,
+ "lora_bias": false,
+ "lora_dropout": 0.0,
+ "megatron_config": null,
+ "megatron_core": "megatron.core",
+ "modules_to_save": null,
+ "peft_type": "LORA",
+ "r": 64,
+ "rank_pattern": {},
+ "revision": null,
+ "target_modules": null,
+ "task_type": "CAUSAL_LM",
+ "use_dora": false,
+ "use_rslora": true
+}
diff --git a/peft/method_comparison/MetaMathQA/experiments/lora/llama-3.2-3B-rank64/adapter_config.json b/peft/method_comparison/MetaMathQA/experiments/lora/llama-3.2-3B-rank64/adapter_config.json
new file mode 100644
index 0000000000000000000000000000000000000000..75890c9dce9fef14eee47ce19f3baa86d4d4168a
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/experiments/lora/llama-3.2-3B-rank64/adapter_config.json
@@ -0,0 +1,30 @@
+{
+ "alpha_pattern": {},
+ "auto_mapping": null,
+ "base_model_name_or_path": null,
+ "bias": "none",
+ "corda_config": null,
+ "eva_config": null,
+ "exclude_modules": null,
+ "fan_in_fan_out": false,
+ "inference_mode": false,
+ "init_lora_weights": true,
+ "layer_replication": null,
+ "layers_pattern": null,
+ "layers_to_transform": null,
+ "loftq_config": {},
+ "lora_alpha": 128,
+ "lora_bias": false,
+ "lora_dropout": 0.0,
+ "megatron_config": null,
+ "megatron_core": "megatron.core",
+ "modules_to_save": null,
+ "peft_type": "LORA",
+ "r": 64,
+ "rank_pattern": {},
+ "revision": null,
+ "target_modules": null,
+ "task_type": "CAUSAL_LM",
+ "use_dora": false,
+ "use_rslora": false
+}
diff --git a/peft/method_comparison/MetaMathQA/experiments/miss/llama-3.2-3B-bat/adapter_config.json b/peft/method_comparison/MetaMathQA/experiments/miss/llama-3.2-3B-bat/adapter_config.json
new file mode 100644
index 0000000000000000000000000000000000000000..a3267da039aad22dcc2d70006dccc34c8759d359
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/experiments/miss/llama-3.2-3B-bat/adapter_config.json
@@ -0,0 +1,18 @@
+{
+ "auto_mapping": null,
+ "base_model_name_or_path": null,
+ "bias": "none",
+ "exclude_modules": null,
+ "inference_mode": false,
+ "init_weights": "bat",
+ "layers_pattern": null,
+ "layers_to_transform": null,
+ "mini_r": 1,
+ "miss_dropout": 0.0,
+ "modules_to_save": null,
+ "peft_type": "MISS",
+ "r": 64,
+ "revision": null,
+ "target_modules": null,
+ "task_type": null
+}
\ No newline at end of file
diff --git a/peft/method_comparison/MetaMathQA/experiments/miss/llama-3.2-3B-default/adapter_config.json b/peft/method_comparison/MetaMathQA/experiments/miss/llama-3.2-3B-default/adapter_config.json
new file mode 100644
index 0000000000000000000000000000000000000000..02ee9f74396d7372104f2adf9f462e1ac4653d93
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/experiments/miss/llama-3.2-3B-default/adapter_config.json
@@ -0,0 +1,18 @@
+{
+ "auto_mapping": null,
+ "base_model_name_or_path": null,
+ "bias": "none",
+ "exclude_modules": null,
+ "inference_mode": false,
+ "init_weights": true,
+ "layers_pattern": null,
+ "layers_to_transform": null,
+ "mini_r": 1,
+ "miss_dropout": 0.0,
+ "modules_to_save": null,
+ "peft_type": "MISS",
+ "r": 64,
+ "revision": null,
+ "target_modules": null,
+ "task_type": null
+}
\ No newline at end of file
diff --git a/peft/method_comparison/MetaMathQA/experiments/miss/llama-3.2-3B-mini/adapter_config.json b/peft/method_comparison/MetaMathQA/experiments/miss/llama-3.2-3B-mini/adapter_config.json
new file mode 100644
index 0000000000000000000000000000000000000000..d732e181b21e0961029723bc640c25d5917d217e
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/experiments/miss/llama-3.2-3B-mini/adapter_config.json
@@ -0,0 +1,18 @@
+{
+ "auto_mapping": null,
+ "base_model_name_or_path": null,
+ "bias": "none",
+ "exclude_modules": null,
+ "inference_mode": false,
+ "init_weights": "mini",
+ "layers_pattern": null,
+ "layers_to_transform": null,
+ "mini_r": 64,
+ "miss_dropout": 0.0,
+ "modules_to_save": null,
+ "peft_type": "MISS",
+ "r": 64,
+ "revision": null,
+ "target_modules": null,
+ "task_type": null
+}
\ No newline at end of file
diff --git a/peft/method_comparison/MetaMathQA/experiments/oft/llama-3.2-3B-rank32/adapter_config.json b/peft/method_comparison/MetaMathQA/experiments/oft/llama-3.2-3B-rank32/adapter_config.json
new file mode 100644
index 0000000000000000000000000000000000000000..e8cdb86ecd110a0176dd42b34e25b3c133cbab4a
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/experiments/oft/llama-3.2-3B-rank32/adapter_config.json
@@ -0,0 +1,27 @@
+{
+ "alpha_pattern": {},
+ "auto_mapping": null,
+ "base_model_name_or_path": null,
+ "bias": "none",
+ "block_share": false,
+ "coft": false,
+ "eps": 6e-05,
+ "exclude_modules": null,
+ "fan_in_fan_out": false,
+ "inference_mode": false,
+ "init_weights": true,
+ "layers_pattern": null,
+ "layers_to_transform": null,
+ "module_dropout": 0.0,
+ "modules_to_save": null,
+ "oft_block_size": 0,
+ "peft_type": "OFT",
+ "r": 32,
+ "rank_pattern": {},
+ "revision": null,
+ "target_modules": [
+ "q_proj",
+ "v_proj"
+ ],
+ "task_type": null
+}
\ No newline at end of file
diff --git a/peft/method_comparison/MetaMathQA/experiments/prefixtuning/llama-3.2-3B-lr_0.001/adapter_config.json b/peft/method_comparison/MetaMathQA/experiments/prefixtuning/llama-3.2-3B-lr_0.001/adapter_config.json
new file mode 100644
index 0000000000000000000000000000000000000000..77bff7fd16cd3f675655221218e69a55eaead91f
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/experiments/prefixtuning/llama-3.2-3B-lr_0.001/adapter_config.json
@@ -0,0 +1,15 @@
+{
+ "auto_mapping": null,
+ "base_model_name_or_path": null,
+ "encoder_hidden_size": 3072,
+ "inference_mode": false,
+ "num_attention_heads": 24,
+ "num_layers": 28,
+ "num_transformer_submodules": 1,
+ "num_virtual_tokens": 200,
+ "peft_type": "PREFIX_TUNING",
+ "prefix_projection": false,
+ "revision": null,
+ "task_type": "CAUSAL_LM",
+ "token_dim": 3072
+}
\ No newline at end of file
diff --git a/peft/method_comparison/MetaMathQA/experiments/prefixtuning/llama-3.2-3B-lr_0.001/training_params.json b/peft/method_comparison/MetaMathQA/experiments/prefixtuning/llama-3.2-3B-lr_0.001/training_params.json
new file mode 100644
index 0000000000000000000000000000000000000000..8a120ad9a80c36dc3666f4da481a5292a7dc8072
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/experiments/prefixtuning/llama-3.2-3B-lr_0.001/training_params.json
@@ -0,0 +1,6 @@
+{
+ "optimizer_kwargs": {
+ "lr": 1e-3
+ }
+}
+
diff --git a/peft/method_comparison/MetaMathQA/experiments/prompt_tuning/llama-3.2-3B-default/adapter_config.json b/peft/method_comparison/MetaMathQA/experiments/prompt_tuning/llama-3.2-3B-default/adapter_config.json
new file mode 100644
index 0000000000000000000000000000000000000000..efa055b03d6f3a6c6d0f7df76f11550891919b0a
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/experiments/prompt_tuning/llama-3.2-3B-default/adapter_config.json
@@ -0,0 +1,17 @@
+{
+ "auto_mapping": null,
+ "base_model_name_or_path": null,
+ "inference_mode": false,
+ "num_attention_heads": 24,
+ "num_layers": 28,
+ "num_transformer_submodules": 1,
+ "num_virtual_tokens": 200,
+ "peft_type": "PROMPT_TUNING",
+ "prompt_tuning_init": "RANDOM",
+ "prompt_tuning_init_text": null,
+ "revision": null,
+ "task_type": "CAUSAL_LM",
+ "token_dim": 3072,
+ "tokenizer_kwargs": null,
+ "tokenizer_name_or_path": null
+}
\ No newline at end of file
diff --git a/peft/method_comparison/MetaMathQA/experiments/prompt_tuning/llama-3.2-3B-lr_0.001/adapter_config.json b/peft/method_comparison/MetaMathQA/experiments/prompt_tuning/llama-3.2-3B-lr_0.001/adapter_config.json
new file mode 100644
index 0000000000000000000000000000000000000000..efa055b03d6f3a6c6d0f7df76f11550891919b0a
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/experiments/prompt_tuning/llama-3.2-3B-lr_0.001/adapter_config.json
@@ -0,0 +1,17 @@
+{
+ "auto_mapping": null,
+ "base_model_name_or_path": null,
+ "inference_mode": false,
+ "num_attention_heads": 24,
+ "num_layers": 28,
+ "num_transformer_submodules": 1,
+ "num_virtual_tokens": 200,
+ "peft_type": "PROMPT_TUNING",
+ "prompt_tuning_init": "RANDOM",
+ "prompt_tuning_init_text": null,
+ "revision": null,
+ "task_type": "CAUSAL_LM",
+ "token_dim": 3072,
+ "tokenizer_kwargs": null,
+ "tokenizer_name_or_path": null
+}
\ No newline at end of file
diff --git a/peft/method_comparison/MetaMathQA/experiments/prompt_tuning/llama-3.2-3B-lr_0.001/training_params.json b/peft/method_comparison/MetaMathQA/experiments/prompt_tuning/llama-3.2-3B-lr_0.001/training_params.json
new file mode 100644
index 0000000000000000000000000000000000000000..8a120ad9a80c36dc3666f4da481a5292a7dc8072
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/experiments/prompt_tuning/llama-3.2-3B-lr_0.001/training_params.json
@@ -0,0 +1,6 @@
+{
+ "optimizer_kwargs": {
+ "lr": 1e-3
+ }
+}
+
diff --git a/peft/method_comparison/MetaMathQA/experiments/prompt_tuning/llama-3.2-3B-sample_vocab-lr_0.001/adapter_config.json b/peft/method_comparison/MetaMathQA/experiments/prompt_tuning/llama-3.2-3B-sample_vocab-lr_0.001/adapter_config.json
new file mode 100644
index 0000000000000000000000000000000000000000..8b9f14279798195477b8a188feb12dfcd9605e00
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/experiments/prompt_tuning/llama-3.2-3B-sample_vocab-lr_0.001/adapter_config.json
@@ -0,0 +1,17 @@
+{
+ "auto_mapping": null,
+ "base_model_name_or_path": null,
+ "inference_mode": false,
+ "num_attention_heads": 24,
+ "num_layers": 28,
+ "num_transformer_submodules": 1,
+ "num_virtual_tokens": 200,
+ "peft_type": "PROMPT_TUNING",
+ "prompt_tuning_init": "SAMPLE_VOCAB",
+ "prompt_tuning_init_text": null,
+ "revision": null,
+ "task_type": "CAUSAL_LM",
+ "token_dim": 3072,
+ "tokenizer_kwargs": null,
+ "tokenizer_name_or_path": null
+}
diff --git a/peft/method_comparison/MetaMathQA/experiments/prompt_tuning/llama-3.2-3B-sample_vocab-lr_0.001/training_params.json b/peft/method_comparison/MetaMathQA/experiments/prompt_tuning/llama-3.2-3B-sample_vocab-lr_0.001/training_params.json
new file mode 100644
index 0000000000000000000000000000000000000000..8a120ad9a80c36dc3666f4da481a5292a7dc8072
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/experiments/prompt_tuning/llama-3.2-3B-sample_vocab-lr_0.001/training_params.json
@@ -0,0 +1,6 @@
+{
+ "optimizer_kwargs": {
+ "lr": 1e-3
+ }
+}
+
diff --git a/peft/method_comparison/MetaMathQA/experiments/ptuning/llama-3.2-3B-default/adapter_config.json b/peft/method_comparison/MetaMathQA/experiments/ptuning/llama-3.2-3B-default/adapter_config.json
new file mode 100644
index 0000000000000000000000000000000000000000..54469edf776f3de255d054c317887b1312aa7791
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/experiments/ptuning/llama-3.2-3B-default/adapter_config.json
@@ -0,0 +1,17 @@
+{
+ "auto_mapping": null,
+ "base_model_name_or_path": null,
+ "encoder_dropout": 0.0,
+ "encoder_hidden_size": 3072,
+ "encoder_num_layers": 2,
+ "encoder_reparameterization_type": "MLP",
+ "inference_mode": false,
+ "num_attention_heads": 24,
+ "num_layers": 28,
+ "num_transformer_submodules": 1,
+ "num_virtual_tokens": 20,
+ "peft_type": "P_TUNING",
+ "revision": null,
+ "task_type": "CAUSAL_LM",
+ "token_dim": 3072
+}
\ No newline at end of file
diff --git a/peft/method_comparison/MetaMathQA/experiments/randlora/llama-3.2-3B-default/adapter_config.json b/peft/method_comparison/MetaMathQA/experiments/randlora/llama-3.2-3B-default/adapter_config.json
new file mode 100644
index 0000000000000000000000000000000000000000..3dbdfaa6b123a057774dc5c46d86bfe4d4e35b55
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/experiments/randlora/llama-3.2-3B-default/adapter_config.json
@@ -0,0 +1,22 @@
+{
+ "auto_mapping": null,
+ "base_model_name_or_path": null,
+ "bias": "none",
+ "fan_in_fan_out": false,
+ "inference_mode": false,
+ "init_weights": true,
+ "layers_pattern": null,
+ "layers_to_transform": null,
+ "modules_to_save": null,
+ "peft_type": "RANDLORA",
+ "projection_prng_key": 0,
+ "r": 32,
+ "randlora_alpha": 640,
+ "randlora_dropout": 0.0,
+ "revision": null,
+ "save_projection": true,
+ "sparse": false,
+ "target_modules": null,
+ "task_type": null,
+ "very_sparse": false
+}
\ No newline at end of file
diff --git a/peft/method_comparison/MetaMathQA/experiments/road/llama-3.2-3B-lr_0.001/adapter_config.json b/peft/method_comparison/MetaMathQA/experiments/road/llama-3.2-3B-lr_0.001/adapter_config.json
new file mode 100644
index 0000000000000000000000000000000000000000..d0f74c40761246f57831661e4a86dae1d28399d8
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/experiments/road/llama-3.2-3B-lr_0.001/adapter_config.json
@@ -0,0 +1,12 @@
+{
+ "auto_mapping": null,
+ "base_model_name_or_path": null,
+ "group_size": 64,
+ "inference_mode": false,
+ "init_weights": true,
+ "peft_type": "ROAD",
+ "revision": null,
+ "target_modules": null,
+ "task_type": null,
+ "variant": "road_2"
+}
diff --git a/peft/method_comparison/MetaMathQA/experiments/road/llama-3.2-3B-lr_0.001/training_params.json b/peft/method_comparison/MetaMathQA/experiments/road/llama-3.2-3B-lr_0.001/training_params.json
new file mode 100644
index 0000000000000000000000000000000000000000..52d87e3ef6d143c29d2ba640028909a31befffa6
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/experiments/road/llama-3.2-3B-lr_0.001/training_params.json
@@ -0,0 +1,5 @@
+{
+ "optimizer_kwargs": {
+ "lr": 1e-3
+ }
+}
diff --git a/peft/method_comparison/MetaMathQA/experiments/shira/llama-3.2-3B-lr_0.0003-random_seed_42/adapter_config.json b/peft/method_comparison/MetaMathQA/experiments/shira/llama-3.2-3B-lr_0.0003-random_seed_42/adapter_config.json
new file mode 100644
index 0000000000000000000000000000000000000000..0d4565eef10746dd8c02364f737fb7a7143955d0
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/experiments/shira/llama-3.2-3B-lr_0.0003-random_seed_42/adapter_config.json
@@ -0,0 +1,15 @@
+{
+ "auto_mapping": null,
+ "base_model_name_or_path": null,
+ "fan_in_fan_out": false,
+ "inference_mode": false,
+ "init_weights": true,
+ "mask_type": "random",
+ "modules_to_save": null,
+ "peft_type": "SHIRA",
+ "r": 32,
+ "random_seed": 42,
+ "revision": null,
+ "target_modules": null,
+ "task_type": null
+}
\ No newline at end of file
diff --git a/peft/method_comparison/MetaMathQA/experiments/shira/llama-3.2-3B-lr_0.0003-random_seed_42/training_params.json b/peft/method_comparison/MetaMathQA/experiments/shira/llama-3.2-3B-lr_0.0003-random_seed_42/training_params.json
new file mode 100644
index 0000000000000000000000000000000000000000..92f18b8a3c5adb57d1d25314d50f1c8df85eb570
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/experiments/shira/llama-3.2-3B-lr_0.0003-random_seed_42/training_params.json
@@ -0,0 +1,6 @@
+{
+ "optimizer_kwargs": {
+ "lr": 3e-4
+ }
+}
+
diff --git a/peft/method_comparison/MetaMathQA/experiments/trainable_tokens/llama-3.2-3B-sos+eos/adapter_config.json b/peft/method_comparison/MetaMathQA/experiments/trainable_tokens/llama-3.2-3B-sos+eos/adapter_config.json
new file mode 100644
index 0000000000000000000000000000000000000000..bce0cd5b129fe4281eb46c7d17f05bb0fca3935d
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/experiments/trainable_tokens/llama-3.2-3B-sos+eos/adapter_config.json
@@ -0,0 +1,7 @@
+{
+ "auto_mapping": null,
+ "base_model_name_or_path": null,
+ "peft_type": "TRAINABLE_TOKENS",
+ "token_indices": [128000, 128001],
+ "task_type": "CAUSAL_LM"
+}
diff --git a/peft/method_comparison/MetaMathQA/experiments/trainable_tokens/llama-3.2-3B-sos+eos/training_params.json b/peft/method_comparison/MetaMathQA/experiments/trainable_tokens/llama-3.2-3B-sos+eos/training_params.json
new file mode 100644
index 0000000000000000000000000000000000000000..92e546e6cfeadce2db2ab6dbd124790a4fb0dbf4
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/experiments/trainable_tokens/llama-3.2-3B-sos+eos/training_params.json
@@ -0,0 +1,5 @@
+{
+ "optimizer_kwargs": {
+ "lr": 0.2
+ }
+}
diff --git a/peft/method_comparison/MetaMathQA/experiments/vblora/llama-3.2-3B-default/adapter_config.json b/peft/method_comparison/MetaMathQA/experiments/vblora/llama-3.2-3B-default/adapter_config.json
new file mode 100644
index 0000000000000000000000000000000000000000..b6cbc59e57c07e6b883ff34ed98090d51916d652
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/experiments/vblora/llama-3.2-3B-default/adapter_config.json
@@ -0,0 +1,26 @@
+{
+ "auto_mapping": null,
+ "base_model_name_or_path": null,
+ "bias": "none",
+ "exclude_modules": null,
+ "fan_in_fan_out": false,
+ "inference_mode": false,
+ "init_logits_std": 0.1,
+ "init_vector_bank_bound": 0.02,
+ "layers_pattern": null,
+ "layers_to_transform": null,
+ "modules_to_save": null,
+ "num_vectors": 256,
+ "peft_type": "VBLORA",
+ "r": 4,
+ "revision": null,
+ "save_only_topk_weights": false,
+ "target_modules": [
+ "v_proj",
+ "q_proj"
+ ],
+ "task_type": null,
+ "topk": 2,
+ "vblora_dropout": 0.0,
+ "vector_length": 256
+}
\ No newline at end of file
diff --git a/peft/method_comparison/MetaMathQA/experiments/vera/llama-3.2-3B-default/adapter_config.json b/peft/method_comparison/MetaMathQA/experiments/vera/llama-3.2-3B-default/adapter_config.json
new file mode 100644
index 0000000000000000000000000000000000000000..f4962c1b4fa1266ba29f31559fa3260483d8fac7
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/experiments/vera/llama-3.2-3B-default/adapter_config.json
@@ -0,0 +1,20 @@
+{
+ "auto_mapping": null,
+ "base_model_name_or_path": null,
+ "bias": "none",
+ "d_initial": 0.1,
+ "fan_in_fan_out": false,
+ "inference_mode": false,
+ "init_weights": true,
+ "layers_pattern": null,
+ "layers_to_transform": null,
+ "modules_to_save": null,
+ "peft_type": "VERA",
+ "projection_prng_key": 0,
+ "r": 256,
+ "revision": null,
+ "save_projection": true,
+ "target_modules": null,
+ "task_type": null,
+ "vera_dropout": 0.0
+}
\ No newline at end of file
diff --git a/peft/method_comparison/MetaMathQA/experiments/vera/llama-3.2-3B-default/training_params.json b/peft/method_comparison/MetaMathQA/experiments/vera/llama-3.2-3B-default/training_params.json
new file mode 100644
index 0000000000000000000000000000000000000000..8a120ad9a80c36dc3666f4da481a5292a7dc8072
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/experiments/vera/llama-3.2-3B-default/training_params.json
@@ -0,0 +1,6 @@
+{
+ "optimizer_kwargs": {
+ "lr": 1e-3
+ }
+}
+
diff --git a/peft/method_comparison/MetaMathQA/experiments/waveft/llama-3.2-3B-n_frequency-5000/adapter_config.json b/peft/method_comparison/MetaMathQA/experiments/waveft/llama-3.2-3B-n_frequency-5000/adapter_config.json
new file mode 100644
index 0000000000000000000000000000000000000000..6aad104d0f1dec10bf97eee02c9d22b2b49dbeb2
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/experiments/waveft/llama-3.2-3B-n_frequency-5000/adapter_config.json
@@ -0,0 +1,26 @@
+{
+ "auto_mapping": null,
+ "base_model_name_or_path": null,
+ "bias": "none",
+ "exclude_modules": null,
+ "fan_in_fan_out": false,
+ "inference_mode": false,
+ "init_weights": true,
+ "layers_pattern": null,
+ "layers_to_transform": null,
+ "modules_to_save": null,
+ "n_frequency": 5000,
+ "n_frequency_pattern": {},
+ "peft_type": "WAVEFT",
+ "proportional_parameters": false,
+ "random_loc_seed": 777,
+ "revision": null,
+ "scaling": 25.0,
+ "target_modules": [
+ "q_proj",
+ "v_proj"
+ ],
+ "task_type": "CAUSAL_LM",
+ "use_idwt": true,
+ "wavelet_family": "db1"
+}
diff --git a/peft/method_comparison/MetaMathQA/requirements.txt b/peft/method_comparison/MetaMathQA/requirements.txt
new file mode 100644
index 0000000000000000000000000000000000000000..ee25a1ced129a9c13938c22922aa0514230af60b
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/requirements.txt
@@ -0,0 +1,4 @@
+bitsandbytes
+datasets
+numpy
+tqdm
diff --git a/peft/method_comparison/MetaMathQA/results/.gitkeep b/peft/method_comparison/MetaMathQA/results/.gitkeep
new file mode 100644
index 0000000000000000000000000000000000000000..e69de29bb2d1d6434b8b29ae775ad8c2e48c5391
diff --git a/peft/method_comparison/MetaMathQA/results/adalora--llama-3.2-3B-rank32.json b/peft/method_comparison/MetaMathQA/results/adalora--llama-3.2-3B-rank32.json
new file mode 100644
index 0000000000000000000000000000000000000000..8b38ea15e8a213a05e1872f928958e601ce60370
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/results/adalora--llama-3.2-3B-rank32.json
@@ -0,0 +1,4071 @@
+{
+ "run_info": {
+ "created_at": "2025-06-19T23:12:19+00:00",
+ "total_time": 2209.243281380004,
+ "experiment_name": "adalora/llama-3.2-3B-rank32",
+ "peft_branch": "main",
+ "train_config": {
+ "model_id": "meta-llama/Llama-3.2-3B",
+ "dtype": "bfloat16",
+ "max_seq_length": 768,
+ "batch_size": 4,
+ "batch_size_eval": 50,
+ "max_steps": 5000,
+ "eval_steps": 250,
+ "compile": false,
+ "query_template": "Question: {query} Think step by step.\nAnswer:",
+ "seed": 0,
+ "grad_norm_clip": 1.0,
+ "optimizer_type": "AdamW",
+ "optimizer_kwargs": {
+ "lr": 0.0001,
+ "weight_decay": 0.1
+ },
+ "lr_scheduler": "cosine",
+ "use_amp": false,
+ "autocast_adapter_dtype": true,
+ "generation_kwargs": {
+ "max_length": 800,
+ "max_new_tokens": 300
+ },
+ "attn_implementation": null
+ },
+ "peft_config": {
+ "task_type": null,
+ "peft_type": "ADALORA",
+ "auto_mapping": null,
+ "base_model_name_or_path": "meta-llama/Llama-3.2-3B",
+ "revision": null,
+ "inference_mode": false,
+ "r": 8,
+ "target_modules": [
+ "q_proj",
+ "v_proj"
+ ],
+ "exclude_modules": null,
+ "lora_alpha": 8,
+ "lora_dropout": 0.0,
+ "fan_in_fan_out": false,
+ "bias": "none",
+ "use_rslora": false,
+ "modules_to_save": null,
+ "init_lora_weights": true,
+ "layers_to_transform": null,
+ "layers_pattern": null,
+ "rank_pattern": {
+ "model.layers.0.self_attn.q_proj.lora_E": [
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false
+ ],
+ "model.layers.0.self_attn.v_proj.lora_E": [
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true
+ ],
+ "model.layers.1.self_attn.q_proj.lora_E": [
+ false,
+ false,
+ true,
+ true,
+ false,
+ true,
+ true,
+ false,
+ false,
+ false,
+ false,
+ true,
+ false,
+ false,
+ true,
+ true,
+ true,
+ true,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ true,
+ false,
+ true,
+ true,
+ false,
+ false,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ false,
+ false,
+ true,
+ true,
+ true,
+ false,
+ false,
+ false,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ false,
+ false,
+ true,
+ true,
+ false,
+ false,
+ true,
+ true,
+ false,
+ false
+ ],
+ "model.layers.1.self_attn.v_proj.lora_E": [
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true
+ ],
+ "model.layers.2.self_attn.q_proj.lora_E": [
+ true,
+ false,
+ true,
+ false,
+ false,
+ false,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ false,
+ false,
+ true,
+ false,
+ false,
+ true,
+ false,
+ false,
+ false,
+ false,
+ true,
+ true,
+ false,
+ false,
+ false,
+ false,
+ true,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ true,
+ true,
+ true,
+ false,
+ false,
+ false,
+ true,
+ true,
+ false,
+ false,
+ false,
+ true,
+ false,
+ true,
+ true,
+ false,
+ true,
+ false,
+ false,
+ false,
+ true,
+ true,
+ false,
+ true,
+ true,
+ false,
+ false
+ ],
+ "model.layers.2.self_attn.v_proj.lora_E": [
+ true,
+ false,
+ false,
+ false,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ false,
+ true,
+ false,
+ true,
+ false,
+ true,
+ false,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ false,
+ false,
+ false,
+ false,
+ true,
+ false,
+ false,
+ false,
+ false,
+ false,
+ true,
+ true,
+ false,
+ false,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ false,
+ false,
+ true,
+ false,
+ true,
+ false,
+ false,
+ false,
+ true,
+ true,
+ false,
+ false,
+ false,
+ true,
+ true
+ ],
+ "model.layers.3.self_attn.q_proj.lora_E": [
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false
+ ],
+ "model.layers.3.self_attn.v_proj.lora_E": [
+ false,
+ false,
+ false,
+ false,
+ false,
+ true,
+ false,
+ true,
+ false,
+ false,
+ false,
+ false,
+ true,
+ false,
+ false,
+ false,
+ false,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ true,
+ false,
+ false,
+ true,
+ false,
+ false,
+ true,
+ false,
+ true,
+ false,
+ true,
+ true,
+ false,
+ true,
+ false,
+ false,
+ true,
+ false,
+ false,
+ false,
+ false,
+ false,
+ true,
+ false,
+ true,
+ false,
+ false,
+ false,
+ false,
+ true,
+ true,
+ true
+ ],
+ "model.layers.4.self_attn.q_proj.lora_E": [
+ false,
+ false,
+ false,
+ false,
+ false,
+ true,
+ false,
+ false,
+ true,
+ true,
+ false,
+ true,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ true,
+ false,
+ false,
+ true,
+ false,
+ true,
+ false,
+ false,
+ false,
+ false,
+ false,
+ true,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ true,
+ true,
+ false,
+ false,
+ true,
+ false,
+ false,
+ false,
+ true,
+ true,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ true,
+ true,
+ false,
+ false
+ ],
+ "model.layers.4.self_attn.v_proj.lora_E": [
+ true,
+ false,
+ true,
+ true,
+ false,
+ false,
+ true,
+ false,
+ false,
+ false,
+ true,
+ false,
+ true,
+ true,
+ false,
+ true,
+ false,
+ true,
+ true,
+ false,
+ true,
+ true,
+ false,
+ false,
+ true,
+ true,
+ true,
+ true,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ true,
+ false,
+ true,
+ false,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ false,
+ false,
+ false,
+ false,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true
+ ],
+ "model.layers.5.self_attn.q_proj.lora_E": [
+ false,
+ true,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false
+ ],
+ "model.layers.5.self_attn.v_proj.lora_E": [
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ false,
+ false,
+ true,
+ false,
+ false,
+ true,
+ false,
+ true,
+ false,
+ false,
+ false,
+ false,
+ true,
+ true,
+ false,
+ false,
+ false,
+ false,
+ true,
+ false,
+ true,
+ false,
+ true,
+ true,
+ false,
+ false,
+ true,
+ true,
+ true,
+ true,
+ false,
+ false,
+ true,
+ false,
+ true,
+ false,
+ false,
+ true,
+ true,
+ true,
+ false,
+ true,
+ false,
+ false,
+ false,
+ true,
+ true,
+ true,
+ true,
+ false,
+ false,
+ false,
+ true,
+ true
+ ],
+ "model.layers.6.self_attn.q_proj.lora_E": [
+ false,
+ false,
+ true,
+ true,
+ false,
+ false,
+ true,
+ true,
+ false,
+ false,
+ false,
+ true,
+ false,
+ true,
+ false,
+ true,
+ false,
+ false,
+ false,
+ false,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ false,
+ true,
+ false,
+ true,
+ false,
+ false,
+ false,
+ true,
+ true,
+ false,
+ false,
+ false,
+ false,
+ true,
+ true,
+ true,
+ false,
+ false,
+ true,
+ false,
+ false,
+ false,
+ false,
+ true,
+ true,
+ false,
+ false,
+ false,
+ true,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false
+ ],
+ "model.layers.6.self_attn.v_proj.lora_E": [
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ false,
+ false,
+ false,
+ false,
+ true,
+ true,
+ false,
+ false,
+ false,
+ false,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ false,
+ false,
+ false,
+ true,
+ true,
+ false,
+ false,
+ true,
+ false,
+ true,
+ false,
+ true,
+ true,
+ false,
+ true,
+ false,
+ true,
+ false,
+ true
+ ],
+ "model.layers.7.self_attn.q_proj.lora_E": [
+ false,
+ false,
+ false,
+ false,
+ false,
+ true,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ true,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ true,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ true,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false
+ ],
+ "model.layers.7.self_attn.v_proj.lora_E": [
+ false,
+ false,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ false,
+ false,
+ true,
+ true,
+ true,
+ true,
+ false,
+ false,
+ false,
+ true,
+ false,
+ false,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ false,
+ false,
+ true,
+ true,
+ true,
+ true
+ ],
+ "model.layers.8.self_attn.q_proj.lora_E": [
+ false,
+ true,
+ false,
+ false,
+ false,
+ false,
+ false,
+ true,
+ false,
+ false,
+ false,
+ false,
+ true,
+ true,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ true,
+ false,
+ false,
+ false,
+ false,
+ true,
+ false,
+ false,
+ true,
+ false,
+ false,
+ false,
+ false,
+ true,
+ false,
+ false,
+ false,
+ false,
+ false,
+ true,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ true
+ ],
+ "model.layers.8.self_attn.v_proj.lora_E": [
+ false,
+ true,
+ false,
+ false,
+ false,
+ true,
+ false,
+ false,
+ false,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ false,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ false,
+ false,
+ true,
+ true,
+ false,
+ false,
+ true,
+ false,
+ true,
+ false,
+ true,
+ true,
+ false,
+ true,
+ false,
+ true,
+ true,
+ true,
+ false,
+ true,
+ false,
+ false,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ false,
+ false,
+ false,
+ false,
+ true
+ ],
+ "model.layers.9.self_attn.q_proj.lora_E": [
+ true,
+ false,
+ true,
+ true,
+ false,
+ false,
+ true,
+ true,
+ false,
+ false,
+ true,
+ false,
+ false,
+ false,
+ false,
+ true,
+ false,
+ true,
+ false,
+ true,
+ false,
+ false,
+ false,
+ true,
+ false,
+ true,
+ false,
+ true,
+ false,
+ true,
+ false,
+ true,
+ true,
+ false,
+ false,
+ true,
+ true,
+ false,
+ false,
+ false,
+ false,
+ true,
+ true,
+ true,
+ false,
+ false,
+ false,
+ false,
+ true,
+ true,
+ true,
+ false,
+ false,
+ false,
+ false,
+ false,
+ true,
+ false,
+ true,
+ false,
+ false,
+ true,
+ false,
+ true
+ ],
+ "model.layers.9.self_attn.v_proj.lora_E": [
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ false,
+ true,
+ false,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ false
+ ],
+ "model.layers.10.self_attn.q_proj.lora_E": [
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ true,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ true,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ true,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false
+ ],
+ "model.layers.10.self_attn.v_proj.lora_E": [
+ true,
+ true,
+ false,
+ false,
+ false,
+ true,
+ true,
+ false,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ false,
+ false,
+ false,
+ true,
+ true,
+ true,
+ true,
+ false,
+ false,
+ false,
+ false,
+ true,
+ false,
+ false,
+ false,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ false,
+ true,
+ false,
+ false,
+ true,
+ true,
+ false,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true
+ ],
+ "model.layers.11.self_attn.q_proj.lora_E": [
+ true,
+ false,
+ false,
+ false,
+ false,
+ true,
+ false,
+ false,
+ false,
+ true,
+ true,
+ false,
+ true,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ true,
+ false,
+ false,
+ true,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ true,
+ false,
+ false,
+ false,
+ true,
+ true,
+ true,
+ false,
+ true,
+ false,
+ false,
+ false,
+ true,
+ true,
+ false,
+ false,
+ false,
+ false,
+ true,
+ true,
+ false,
+ true,
+ false,
+ true,
+ true,
+ false,
+ false,
+ false
+ ],
+ "model.layers.11.self_attn.v_proj.lora_E": [
+ false,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ false,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ false,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ false,
+ false,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ false,
+ false,
+ false,
+ false,
+ true,
+ false,
+ false,
+ true,
+ true,
+ false,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ false,
+ false
+ ],
+ "model.layers.12.self_attn.q_proj.lora_E": [
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ true,
+ false,
+ true,
+ false,
+ false,
+ false,
+ false,
+ false,
+ true,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ true,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ true,
+ true,
+ false,
+ true,
+ false,
+ false,
+ false,
+ false,
+ true,
+ false,
+ true,
+ false,
+ false,
+ true,
+ false,
+ true,
+ false,
+ false,
+ true,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false
+ ],
+ "model.layers.12.self_attn.v_proj.lora_E": [
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ false,
+ false,
+ false,
+ true,
+ true,
+ false,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ false,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ false,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ false,
+ true,
+ false,
+ true,
+ false,
+ true,
+ false,
+ true,
+ true,
+ false
+ ],
+ "model.layers.13.self_attn.q_proj.lora_E": [
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ false,
+ false,
+ true,
+ true,
+ false,
+ true,
+ false,
+ true,
+ false,
+ true,
+ false,
+ false,
+ true,
+ true,
+ false,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ false,
+ false,
+ true,
+ true,
+ false,
+ false,
+ true,
+ false,
+ true,
+ false,
+ true,
+ true,
+ true,
+ false,
+ false,
+ false,
+ false,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ false,
+ true,
+ true,
+ true,
+ false,
+ true,
+ false,
+ true,
+ true,
+ false,
+ false,
+ false,
+ true,
+ false
+ ],
+ "model.layers.13.self_attn.v_proj.lora_E": [
+ true,
+ false,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ false,
+ true,
+ false,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ false,
+ false,
+ true,
+ true,
+ false,
+ false,
+ true,
+ false,
+ false,
+ true,
+ false,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ false,
+ false,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true
+ ],
+ "model.layers.14.self_attn.q_proj.lora_E": [
+ false,
+ true,
+ false,
+ true,
+ true,
+ false,
+ false,
+ false,
+ true,
+ false,
+ false,
+ true,
+ false,
+ false,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ false,
+ false,
+ false,
+ true,
+ false,
+ true,
+ false,
+ true,
+ false,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ false,
+ true,
+ true,
+ false,
+ true,
+ true,
+ false,
+ false,
+ true,
+ false,
+ false,
+ false,
+ true,
+ false,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ false,
+ false,
+ true,
+ false,
+ true,
+ true,
+ false
+ ],
+ "model.layers.14.self_attn.v_proj.lora_E": [
+ true,
+ true,
+ true,
+ false,
+ false,
+ false,
+ true,
+ false,
+ false,
+ false,
+ false,
+ true,
+ true,
+ false,
+ false,
+ true,
+ false,
+ true,
+ true,
+ true,
+ false,
+ true,
+ false,
+ false,
+ true,
+ false,
+ true,
+ false,
+ true,
+ true,
+ false,
+ true,
+ false,
+ true,
+ false,
+ false,
+ true,
+ false,
+ false,
+ true,
+ false,
+ true,
+ true,
+ false,
+ true,
+ false,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ false,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ false
+ ],
+ "model.layers.15.self_attn.q_proj.lora_E": [
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ false,
+ true,
+ false,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ false,
+ true,
+ false,
+ true,
+ false,
+ true,
+ true,
+ true,
+ false,
+ true,
+ false,
+ false,
+ false,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ false,
+ true,
+ false,
+ true,
+ false,
+ false,
+ true,
+ true,
+ false,
+ true,
+ false,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true
+ ],
+ "model.layers.15.self_attn.v_proj.lora_E": [
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ false,
+ true,
+ true,
+ false,
+ false,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ false,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ false,
+ false,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true
+ ],
+ "model.layers.16.self_attn.q_proj.lora_E": [
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ false,
+ true,
+ true,
+ true,
+ false,
+ true,
+ false,
+ true,
+ true,
+ true,
+ false,
+ false,
+ false,
+ true,
+ false,
+ false,
+ false,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ false,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ false,
+ true,
+ true,
+ false,
+ true,
+ false,
+ false,
+ true,
+ true,
+ true,
+ false,
+ false,
+ true,
+ true
+ ],
+ "model.layers.16.self_attn.v_proj.lora_E": [
+ true,
+ false,
+ true,
+ false,
+ true,
+ false,
+ true,
+ false,
+ false,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ false,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ false,
+ false,
+ false,
+ true,
+ true,
+ true,
+ false,
+ true,
+ false,
+ false,
+ true,
+ false,
+ false,
+ false,
+ true,
+ false,
+ true,
+ false,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ false,
+ false,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ false,
+ true,
+ false,
+ true,
+ false,
+ false
+ ],
+ "model.layers.17.self_attn.q_proj.lora_E": [
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ false,
+ true,
+ false,
+ false,
+ true,
+ true,
+ true,
+ false,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ false,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ false,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true
+ ],
+ "model.layers.17.self_attn.v_proj.lora_E": [
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ false,
+ false,
+ false,
+ true,
+ true,
+ false,
+ true,
+ true,
+ false,
+ false,
+ true,
+ true,
+ false,
+ false,
+ false,
+ false,
+ true,
+ true,
+ true,
+ false,
+ true,
+ false,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ false,
+ true,
+ true,
+ true,
+ true
+ ],
+ "model.layers.18.self_attn.q_proj.lora_E": [
+ false,
+ true,
+ false,
+ true,
+ false,
+ true,
+ false,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ false,
+ true,
+ false,
+ false,
+ false,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ false,
+ false,
+ false,
+ false,
+ true,
+ false,
+ false,
+ true,
+ false,
+ true,
+ false,
+ true,
+ true
+ ],
+ "model.layers.18.self_attn.v_proj.lora_E": [
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ false,
+ false,
+ false,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ false,
+ true
+ ],
+ "model.layers.19.self_attn.q_proj.lora_E": [
+ false,
+ true,
+ false,
+ true,
+ false,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ false,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ false,
+ true,
+ false,
+ true,
+ false,
+ false,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ false,
+ false,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ false,
+ true,
+ true,
+ false,
+ true,
+ true
+ ],
+ "model.layers.19.self_attn.v_proj.lora_E": [
+ false,
+ true,
+ false,
+ true,
+ true,
+ true,
+ false,
+ true,
+ false,
+ false,
+ false,
+ false,
+ true,
+ true,
+ true,
+ false,
+ true,
+ false,
+ false,
+ false,
+ false,
+ true,
+ false,
+ true,
+ true,
+ false,
+ true,
+ true,
+ false,
+ false,
+ true,
+ true,
+ true,
+ true,
+ false,
+ false,
+ false,
+ false,
+ false,
+ true,
+ false,
+ false,
+ true,
+ false,
+ false,
+ false,
+ true,
+ true,
+ false,
+ false,
+ false,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ false,
+ true,
+ false,
+ true,
+ true,
+ true
+ ],
+ "model.layers.20.self_attn.q_proj.lora_E": [
+ false,
+ true,
+ false,
+ false,
+ false,
+ false,
+ true,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ true,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ true,
+ false,
+ false,
+ false,
+ false,
+ false,
+ true,
+ false,
+ true,
+ true,
+ false,
+ false,
+ false,
+ false,
+ true,
+ false,
+ true,
+ false,
+ true,
+ false,
+ false,
+ false,
+ false,
+ true,
+ true,
+ false,
+ false,
+ true,
+ true,
+ false,
+ false,
+ false,
+ false,
+ false,
+ true,
+ false,
+ false
+ ],
+ "model.layers.20.self_attn.v_proj.lora_E": [
+ true,
+ false,
+ true,
+ true,
+ false,
+ false,
+ false,
+ true,
+ true,
+ false,
+ false,
+ true,
+ true,
+ true,
+ false,
+ true,
+ false,
+ true,
+ false,
+ false,
+ false,
+ false,
+ true,
+ false,
+ false,
+ false,
+ true,
+ false,
+ true,
+ false,
+ true,
+ true,
+ true,
+ false,
+ true,
+ false,
+ true,
+ false,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ true,
+ false,
+ false,
+ false,
+ true,
+ false,
+ false,
+ true,
+ false,
+ false,
+ true,
+ true
+ ],
+ "model.layers.21.self_attn.q_proj.lora_E": [
+ false,
+ false,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ false,
+ false,
+ false,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ true,
+ true,
+ true,
+ false,
+ true,
+ false,
+ true,
+ false,
+ true,
+ false,
+ false,
+ false,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ false,
+ true,
+ true,
+ false,
+ true,
+ true,
+ false,
+ false,
+ true,
+ true
+ ],
+ "model.layers.21.self_attn.v_proj.lora_E": [
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ false,
+ true,
+ true,
+ false,
+ false,
+ true,
+ true,
+ false,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ false,
+ false,
+ false,
+ false,
+ false,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ false,
+ true,
+ true,
+ false,
+ true,
+ true,
+ false,
+ false,
+ false,
+ true,
+ true,
+ false,
+ false,
+ false,
+ true,
+ true,
+ false,
+ true,
+ true,
+ false,
+ false,
+ false,
+ false,
+ true,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false
+ ],
+ "model.layers.22.self_attn.q_proj.lora_E": [
+ false,
+ true,
+ false,
+ true,
+ true,
+ false,
+ true,
+ false,
+ false,
+ true,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ true,
+ false,
+ true,
+ true,
+ false,
+ false,
+ false,
+ false,
+ true,
+ true,
+ true,
+ false,
+ false,
+ true,
+ false,
+ false,
+ false,
+ false,
+ false,
+ true,
+ false,
+ false,
+ false,
+ false,
+ true,
+ false,
+ false,
+ false,
+ true,
+ false,
+ true,
+ false,
+ false,
+ false,
+ true,
+ false,
+ true,
+ true,
+ true,
+ false,
+ false,
+ true,
+ false,
+ false,
+ true,
+ true,
+ false,
+ true
+ ],
+ "model.layers.22.self_attn.v_proj.lora_E": [
+ false,
+ true,
+ true,
+ true,
+ true,
+ false,
+ false,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ false,
+ true,
+ true,
+ false,
+ true,
+ false,
+ false,
+ true,
+ false,
+ false,
+ false,
+ false,
+ true,
+ false,
+ false,
+ false,
+ true,
+ true,
+ false,
+ false,
+ false,
+ true,
+ true,
+ false,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ false,
+ true,
+ false,
+ true,
+ true
+ ],
+ "model.layers.23.self_attn.q_proj.lora_E": [
+ true,
+ false,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ false,
+ true,
+ false,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ false,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true
+ ],
+ "model.layers.23.self_attn.v_proj.lora_E": [
+ false,
+ true,
+ false,
+ true,
+ false,
+ false,
+ true,
+ false,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ false,
+ true,
+ false,
+ true,
+ true,
+ false,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ false,
+ false,
+ false,
+ true,
+ true,
+ false,
+ true,
+ false,
+ true,
+ true
+ ],
+ "model.layers.24.self_attn.q_proj.lora_E": [
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ false,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ false,
+ false,
+ false,
+ true,
+ true,
+ true,
+ true,
+ false,
+ false,
+ true
+ ],
+ "model.layers.24.self_attn.v_proj.lora_E": [
+ true,
+ true,
+ true,
+ false,
+ true,
+ false,
+ false,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ false,
+ false,
+ true,
+ false,
+ false,
+ false,
+ false,
+ true,
+ true,
+ true,
+ false,
+ true,
+ false,
+ false,
+ true,
+ false,
+ true,
+ false,
+ true,
+ true,
+ false,
+ true,
+ true,
+ false,
+ false,
+ false,
+ true,
+ false,
+ false,
+ true,
+ true,
+ false,
+ true,
+ true,
+ false,
+ false,
+ true,
+ true,
+ true,
+ true,
+ false,
+ false,
+ true,
+ true,
+ true,
+ false,
+ true,
+ false,
+ true,
+ true,
+ true
+ ],
+ "model.layers.25.self_attn.q_proj.lora_E": [
+ false,
+ false,
+ false,
+ false,
+ true,
+ true,
+ false,
+ true,
+ true,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ true,
+ false,
+ false,
+ true,
+ false,
+ false,
+ true,
+ false,
+ false,
+ false,
+ true,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ true,
+ false,
+ false,
+ false,
+ false,
+ false,
+ true,
+ false,
+ false,
+ false,
+ true,
+ true,
+ true,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false
+ ],
+ "model.layers.25.self_attn.v_proj.lora_E": [
+ false,
+ false,
+ false,
+ true,
+ false,
+ false,
+ false,
+ true,
+ true,
+ false,
+ false,
+ true,
+ false,
+ true,
+ true,
+ true,
+ false,
+ false,
+ false,
+ false,
+ true,
+ false,
+ false,
+ false,
+ true,
+ true,
+ true,
+ true,
+ false,
+ false,
+ false,
+ false,
+ true,
+ false,
+ false,
+ false,
+ false,
+ true,
+ false,
+ true,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ true,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false
+ ],
+ "model.layers.26.self_attn.q_proj.lora_E": [
+ true,
+ false,
+ false,
+ true,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ true,
+ false,
+ true,
+ false,
+ true,
+ true,
+ true,
+ false,
+ false,
+ true,
+ true,
+ true,
+ false,
+ false,
+ true,
+ true,
+ false,
+ false,
+ true,
+ false,
+ true,
+ true,
+ false,
+ false,
+ false,
+ true,
+ true,
+ false,
+ false,
+ false,
+ true,
+ false,
+ false,
+ false,
+ true,
+ true,
+ false,
+ false,
+ true,
+ false,
+ true,
+ true,
+ false,
+ true,
+ false,
+ false,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true
+ ],
+ "model.layers.26.self_attn.v_proj.lora_E": [
+ false,
+ false,
+ true,
+ false,
+ true,
+ false,
+ false,
+ false,
+ true,
+ false,
+ false,
+ false,
+ false,
+ false,
+ true,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ true,
+ false,
+ false,
+ true,
+ false,
+ true,
+ false,
+ true,
+ true,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ true,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ false,
+ true,
+ true,
+ false,
+ false,
+ false,
+ true,
+ false,
+ true,
+ false,
+ true,
+ false,
+ false,
+ false,
+ true,
+ false,
+ false
+ ],
+ "model.layers.27.self_attn.q_proj.lora_E": [
+ true,
+ false,
+ false,
+ true,
+ true,
+ false,
+ false,
+ true,
+ true,
+ false,
+ false,
+ false,
+ true,
+ true,
+ false,
+ true,
+ false,
+ false,
+ true,
+ false,
+ false,
+ true,
+ true,
+ true,
+ true,
+ false,
+ false,
+ true,
+ true,
+ false,
+ false,
+ false,
+ false,
+ true,
+ true,
+ true,
+ false,
+ true,
+ false,
+ false,
+ false,
+ true,
+ false,
+ true,
+ true,
+ true,
+ false,
+ false,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ false,
+ false,
+ false,
+ true,
+ false,
+ false,
+ false,
+ true,
+ false
+ ],
+ "model.layers.27.self_attn.v_proj.lora_E": [
+ false,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ false,
+ false,
+ true,
+ false,
+ false,
+ false,
+ true,
+ true,
+ false,
+ false,
+ false,
+ true,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true,
+ true,
+ false,
+ true,
+ false,
+ true,
+ true,
+ false,
+ true,
+ true,
+ false,
+ false,
+ true,
+ false,
+ true,
+ true,
+ false,
+ false,
+ true,
+ false,
+ true,
+ true,
+ true,
+ false,
+ false,
+ true,
+ false,
+ false,
+ true,
+ true,
+ true,
+ true,
+ true,
+ false,
+ true
+ ]
+ },
+ "alpha_pattern": {},
+ "megatron_config": null,
+ "megatron_core": "megatron.core",
+ "trainable_token_indices": null,
+ "loftq_config": {},
+ "eva_config": null,
+ "corda_config": null,
+ "use_dora": false,
+ "layer_replication": null,
+ "lora_bias": false,
+ "target_r": 32,
+ "init_r": 64,
+ "tinit": 200,
+ "tfinal": 500,
+ "deltaT": 1,
+ "beta1": 0.85,
+ "beta2": 0.85,
+ "orth_reg_weight": 0.5,
+ "total_step": 5000
+ },
+ "error_msg": ""
+ },
+ "train_info": {
+ "accelerator_memory_reserved_avg": 12361399900,
+ "accelerator_memory_max": 22793945088,
+ "accelerator_memory_reserved_99th": 18203426160,
+ "train_time": 1986.3603882369862,
+ "file_size": 35147440,
+ "num_trainable_params": 18353664,
+ "num_total_params": 3231103544,
+ "status": "success",
+ "metrics": [
+ {
+ "step": 250,
+ "valid accuracy": 0.0,
+ "train loss": 1.3241184422969818,
+ "train samples": 1000,
+ "train time": 35.95594502204767,
+ "eval time": 11.413120707002236,
+ "tokens / sec": 5888.289123542072,
+ "mem allocated avg": 7292959393.792,
+ "mem reserved avg": 12441731727.36,
+ "elapsed time": 100.98083375500573
+ },
+ {
+ "step": 500,
+ "valid accuracy": 0.38,
+ "train loss": 1.0195633232593537,
+ "train samples": 2000,
+ "train time": 37.64258231502754,
+ "eval time": 11.37802824100072,
+ "tokens / sec": 5525.524212428035,
+ "mem allocated avg": 7285510731.776,
+ "mem reserved avg": 12328493907.968,
+ "elapsed time": 197.93603045200143
+ },
+ {
+ "step": 750,
+ "valid accuracy": 0.28,
+ "train loss": 0.7883218789100647,
+ "train samples": 3000,
+ "train time": 37.909325722001086,
+ "eval time": 11.385932488003164,
+ "tokens / sec": 5655.626838954038,
+ "mem allocated avg": 7296095842.304,
+ "mem reserved avg": 12484438130.688,
+ "elapsed time": 295.9188707240028
+ },
+ {
+ "step": 1000,
+ "valid accuracy": 0.3,
+ "train loss": 0.7408825470209122,
+ "train samples": 4000,
+ "train time": 37.79932949803333,
+ "eval time": 11.34964040399791,
+ "tokens / sec": 5511.6321576772825,
+ "mem allocated avg": 7286506670.08,
+ "mem reserved avg": 12351948455.936,
+ "elapsed time": 393.33776786700037
+ },
+ {
+ "step": 1250,
+ "valid accuracy": 0.36,
+ "train loss": 0.7282904219627381,
+ "train samples": 5000,
+ "train time": 37.475317073069164,
+ "eval time": 11.342822429993248,
+ "tokens / sec": 5564.676066473135,
+ "mem allocated avg": 7287005519.872,
+ "mem reserved avg": 12349910024.192,
+ "elapsed time": 490.5430299360014
+ },
+ {
+ "step": 1500,
+ "valid accuracy": 0.38,
+ "train loss": 0.7161256531476975,
+ "train samples": 6000,
+ "train time": 37.660518338059774,
+ "eval time": 11.34013032400253,
+ "tokens / sec": 5558.367469107556,
+ "mem allocated avg": 7287642494.976,
+ "mem reserved avg": 12380570386.432,
+ "elapsed time": 588.017992052999
+ },
+ {
+ "step": 1750,
+ "valid accuracy": 0.34,
+ "train loss": 0.7056601424217224,
+ "train samples": 7000,
+ "train time": 37.636171496975294,
+ "eval time": 11.3171367870018,
+ "tokens / sec": 5562.600861695649,
+ "mem allocated avg": 7289782888.448,
+ "mem reserved avg": 12389051269.12,
+ "elapsed time": 685.2421731229988
+ },
+ {
+ "step": 2000,
+ "valid accuracy": 0.34,
+ "train loss": 0.7058932571411133,
+ "train samples": 8000,
+ "train time": 37.505602380944765,
+ "eval time": 11.37751964799827,
+ "tokens / sec": 5537.732680318789,
+ "mem allocated avg": 7287054886.912,
+ "mem reserved avg": 12336119152.64,
+ "elapsed time": 782.1823508529997
+ },
+ {
+ "step": 2250,
+ "valid accuracy": 0.3,
+ "train loss": 0.700018577337265,
+ "train samples": 9000,
+ "train time": 38.06487834800646,
+ "eval time": 11.33160761000181,
+ "tokens / sec": 5646.885247730137,
+ "mem allocated avg": 7297638139.904,
+ "mem reserved avg": 12521129902.08,
+ "elapsed time": 880.444039299
+ },
+ {
+ "step": 2500,
+ "valid accuracy": 0.34,
+ "train loss": 0.6984639673233032,
+ "train samples": 10000,
+ "train time": 37.400825600088865,
+ "eval time": 7.680036880999978,
+ "tokens / sec": 5507.017470745635,
+ "mem allocated avg": 7283608303.616,
+ "mem reserved avg": 12278598467.584,
+ "elapsed time": 973.4031999860017
+ },
+ {
+ "step": 2750,
+ "valid accuracy": 0.32,
+ "train loss": 0.691307947397232,
+ "train samples": 11000,
+ "train time": 37.97861938195274,
+ "eval time": 11.376824188999308,
+ "tokens / sec": 5578.954776346737,
+ "mem allocated avg": 7293332232.192,
+ "mem reserved avg": 12452821467.136,
+ "elapsed time": 1071.2981272770048
+ },
+ {
+ "step": 3000,
+ "valid accuracy": 0.3,
+ "train loss": 0.6851879090070725,
+ "train samples": 12000,
+ "train time": 37.862704559986014,
+ "eval time": 11.377599911000289,
+ "tokens / sec": 5512.839149387935,
+ "mem allocated avg": 7288929478.656,
+ "mem reserved avg": 12371468746.752,
+ "elapsed time": 1168.7257358770003
+ },
+ {
+ "step": 3250,
+ "valid accuracy": 0.34,
+ "train loss": 0.6939580011367797,
+ "train samples": 13000,
+ "train time": 37.79518606400961,
+ "eval time": 7.2029460159974406,
+ "tokens / sec": 5580.102176050141,
+ "mem allocated avg": 7290687285.248,
+ "mem reserved avg": 12403068633.088,
+ "elapsed time": 1261.9857917680056
+ },
+ {
+ "step": 3500,
+ "valid accuracy": 0.4,
+ "train loss": 0.6825792235136032,
+ "train samples": 14000,
+ "train time": 37.73422463506722,
+ "eval time": 11.28984081800445,
+ "tokens / sec": 5558.614282617983,
+ "mem allocated avg": 7289277476.864,
+ "mem reserved avg": 12381820289.024,
+ "elapsed time": 1359.695578400002
+ },
+ {
+ "step": 3750,
+ "valid accuracy": 0.34,
+ "train loss": 0.6795008780956269,
+ "train samples": 15000,
+ "train time": 38.156728624038806,
+ "eval time": 11.362600938999094,
+ "tokens / sec": 5679.286663570962,
+ "mem allocated avg": 7299185600.512,
+ "mem reserved avg": 12562561236.992,
+ "elapsed time": 1458.6053942910003
+ },
+ {
+ "step": 4000,
+ "valid accuracy": 0.32,
+ "train loss": 0.6967895623445511,
+ "train samples": 16000,
+ "train time": 37.352128309052205,
+ "eval time": 11.363241717001074,
+ "tokens / sec": 5471.522219805362,
+ "mem allocated avg": 7281535514.624,
+ "mem reserved avg": 12256066666.496,
+ "elapsed time": 1555.2909630150025
+ },
+ {
+ "step": 4250,
+ "valid accuracy": 0.34,
+ "train loss": 0.6776066061258316,
+ "train samples": 17000,
+ "train time": 37.65609644694632,
+ "eval time": 11.334564828997827,
+ "tokens / sec": 5613.672683726684,
+ "mem allocated avg": 7291894349.824,
+ "mem reserved avg": 12418562392.064,
+ "elapsed time": 1652.928281804001
+ },
+ {
+ "step": 4500,
+ "valid accuracy": 0.34,
+ "train loss": 0.6868188911676407,
+ "train samples": 18000,
+ "train time": 37.48494880297949,
+ "eval time": 11.33762150000257,
+ "tokens / sec": 5544.038517760537,
+ "mem allocated avg": 7285549684.736,
+ "mem reserved avg": 12333837451.264,
+ "elapsed time": 1749.9311109990012
+ },
+ {
+ "step": 4750,
+ "valid accuracy": 0.34,
+ "train loss": 0.6806062284708023,
+ "train samples": 19000,
+ "train time": 33.62080936400889,
+ "eval time": 11.34113016500487,
+ "tokens / sec": 6244.31725384755,
+ "mem allocated avg": 7068488509.44,
+ "mem reserved avg": 12120833916.928,
+ "elapsed time": 1843.633759463999
+ },
+ {
+ "step": 5000,
+ "valid accuracy": 0.28,
+ "train loss": 0.6862971596717834,
+ "train samples": 20000,
+ "train time": 33.47089828590106,
+ "eval time": 11.363945298006001,
+ "tokens / sec": 6222.7191580255185,
+ "mem allocated avg": 7065409925.12,
+ "mem reserved avg": 12064965787.648,
+ "elapsed time": 1937.0431615920024
+ },
+ {
+ "step": 5000,
+ "test accuracy": 0.3904473085670963,
+ "train loss": 0.6862971596717834,
+ "train samples": 20000,
+ "train total tokens": 4198051
+ }
+ ]
+ },
+ "meta_info": {
+ "model_info": {
+ "sha": "13afe5124825b4f3751f836b40dafda64c1ed062",
+ "created_at": "2024-09-18T15:23:48+00:00"
+ },
+ "dataset_info": {
+ "metamath": {
+ "sha": "aa4f34d3d2d3231299b5b03d9b3e5a20da45aa18",
+ "created_at": "2023-09-21T17:22:46+00:00"
+ },
+ "gsm8k": {
+ "sha": "e53f048856ff4f594e959d75785d2c2d37b678ee",
+ "created_at": "2022-04-12T10:22:10+00:00"
+ }
+ },
+ "package_info": {
+ "transformers-version": "4.52.4",
+ "transformers-commit-hash": null,
+ "peft-version": "0.15.2.dev0",
+ "peft-commit-hash": "5fe7f8f8abe914d313fc3751f2ea92de7718fbaf",
+ "datasets-version": "3.6.0",
+ "datasets-commit-hash": null,
+ "bitsandbytes-version": "0.46.0",
+ "bitsandbytes-commit-hash": null,
+ "torch-version": "2.7.1+cu126",
+ "torch-commit-hash": null
+ },
+ "system_info": {
+ "system": "Linux",
+ "release": "6.8.0-1029-aws",
+ "version": "#31-Ubuntu SMP Wed Apr 23 18:42:41 UTC 2025",
+ "machine": "x86_64",
+ "processor": "x86_64",
+ "accelerator": "NVIDIA L40S"
+ },
+ "pytorch_info": "PyTorch built with:\n - GCC 11.2\n - C++ Version: 201703\n - Intel(R) oneAPI Math Kernel Library Version 2024.2-Product Build 20240605 for Intel(R) 64 architecture applications\n - Intel(R) MKL-DNN v3.7.1 (Git Hash 8d263e693366ef8db40acc569cc7d8edf644556d)\n - OpenMP 201511 (a.k.a. OpenMP 4.5)\n - LAPACK is enabled (usually provided by MKL)\n - NNPACK is enabled\n - CPU capability usage: AVX2\n - CUDA Runtime 12.6\n - NVCC architecture flags: -gencode;arch=compute_50,code=sm_50;-gencode;arch=compute_60,code=sm_60;-gencode;arch=compute_70,code=sm_70;-gencode;arch=compute_75,code=sm_75;-gencode;arch=compute_80,code=sm_80;-gencode;arch=compute_86,code=sm_86;-gencode;arch=compute_90,code=sm_90\n - CuDNN 90.7.1 (built against CUDA 12.8)\n - Built with CuDNN 90.5.1\n - Magma 2.6.1\n - Build settings: BLAS_INFO=mkl, BUILD_TYPE=Release, COMMIT_SHA=e2d141dbde55c2a4370fac5165b0561b6af4798b, CUDA_VERSION=12.6, CUDNN_VERSION=9.5.1, CXX_COMPILER=/opt/rh/gcc-toolset-11/root/usr/bin/c++, CXX_FLAGS= -D_GLIBCXX_USE_CXX11_ABI=1 -fvisibility-inlines-hidden -DUSE_PTHREADPOOL -DNDEBUG -DUSE_KINETO -DLIBKINETO_NOROCTRACER -DLIBKINETO_NOXPUPTI=ON -DUSE_FBGEMM -DUSE_PYTORCH_QNNPACK -DUSE_XNNPACK -DSYMBOLICATE_MOBILE_DEBUG_HANDLE -O2 -fPIC -Wall -Wextra -Werror=return-type -Werror=non-virtual-dtor -Werror=range-loop-construct -Werror=bool-operation -Wnarrowing -Wno-missing-field-initializers -Wno-unknown-pragmas -Wno-unused-parameter -Wno-strict-overflow -Wno-strict-aliasing -Wno-stringop-overflow -Wsuggest-override -Wno-psabi -Wno-error=old-style-cast -fdiagnostics-color=always -faligned-new -Wno-maybe-uninitialized -fno-math-errno -fno-trapping-math -Werror=format -Wno-stringop-overflow, LAPACK_INFO=mkl, PERF_WITH_AVX=1, PERF_WITH_AVX2=1, TORCH_VERSION=2.7.1, USE_CUDA=ON, USE_CUDNN=ON, USE_CUSPARSELT=1, USE_GFLAGS=OFF, USE_GLOG=OFF, USE_GLOO=ON, USE_MKL=ON, USE_MKLDNN=ON, USE_MPI=OFF, USE_NCCL=1, USE_NNPACK=ON, USE_OPENMP=ON, USE_ROCM=OFF, USE_ROCM_KERNEL_ASSERT=OFF, \n"
+ }
+}
diff --git a/peft/method_comparison/MetaMathQA/results/adaptionprompt--llama-3.2-3B-lr_0.0005.json b/peft/method_comparison/MetaMathQA/results/adaptionprompt--llama-3.2-3B-lr_0.0005.json
new file mode 100644
index 0000000000000000000000000000000000000000..c35ccc865b46ea711763fef8f6cabfd1d77d5bd8
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/results/adaptionprompt--llama-3.2-3B-lr_0.0005.json
@@ -0,0 +1,341 @@
+{
+ "run_info": {
+ "created_at": "2025-06-20T04:48:22+00:00",
+ "total_time": 2260.6744696069945,
+ "experiment_name": "adaptionprompt/llama-3.2-3B-lr_0.0005",
+ "peft_branch": "main",
+ "train_config": {
+ "model_id": "meta-llama/Llama-3.2-3B",
+ "dtype": "bfloat16",
+ "max_seq_length": 768,
+ "batch_size": 4,
+ "batch_size_eval": 50,
+ "max_steps": 5000,
+ "eval_steps": 250,
+ "compile": false,
+ "query_template": "Question: {query} Think step by step.\nAnswer:",
+ "seed": 0,
+ "grad_norm_clip": 1.0,
+ "optimizer_type": "AdamW",
+ "optimizer_kwargs": {
+ "lr": 0.0005
+ },
+ "lr_scheduler": "cosine",
+ "use_amp": false,
+ "autocast_adapter_dtype": true,
+ "generation_kwargs": {
+ "max_length": 800,
+ "max_new_tokens": 300
+ },
+ "attn_implementation": null
+ },
+ "peft_config": {
+ "task_type": "CAUSAL_LM",
+ "peft_type": "ADAPTION_PROMPT",
+ "auto_mapping": null,
+ "base_model_name_or_path": "meta-llama/Llama-3.2-3B",
+ "revision": null,
+ "inference_mode": false,
+ "target_modules": "self_attn",
+ "adapter_len": 100,
+ "adapter_layers": 28
+ },
+ "error_msg": ""
+ },
+ "train_info": {
+ "accelerator_memory_reserved_avg": 11893757234,
+ "accelerator_memory_max": 22410166272,
+ "accelerator_memory_reserved_99th": 17907664814,
+ "train_time": 1989.2834085189897,
+ "file_size": 17210384,
+ "num_trainable_params": 8601628,
+ "num_total_params": 3221351452,
+ "status": "success",
+ "metrics": [
+ {
+ "step": 250,
+ "valid accuracy": 0.0,
+ "train loss": 1.3201356165409088,
+ "train samples": 1000,
+ "train time": 36.18721537806414,
+ "eval time": 13.46754032199533,
+ "tokens / sec": 5850.657415556191,
+ "mem allocated avg": 6848060076.032,
+ "mem reserved avg": 11943163199.488,
+ "elapsed time": 99.94861951399798
+ },
+ {
+ "step": 500,
+ "valid accuracy": 0.1,
+ "train loss": 1.153662922859192,
+ "train samples": 2000,
+ "train time": 35.6493088029747,
+ "eval time": 13.314302301005227,
+ "tokens / sec": 5834.474972559473,
+ "mem allocated avg": 6840933136.384,
+ "mem reserved avg": 11833045942.272,
+ "elapsed time": 193.4177081749949
+ },
+ {
+ "step": 750,
+ "valid accuracy": 0.22,
+ "train loss": 0.9016587936878204,
+ "train samples": 3000,
+ "train time": 36.424757257977035,
+ "eval time": 13.392894379001518,
+ "tokens / sec": 5886.133941305707,
+ "mem allocated avg": 6851972698.112,
+ "mem reserved avg": 11989870968.832,
+ "elapsed time": 288.2962625699947
+ },
+ {
+ "step": 1000,
+ "valid accuracy": 0.2,
+ "train loss": 0.8571369113922119,
+ "train samples": 4000,
+ "train time": 35.59983186099271,
+ "eval time": 13.363479856001504,
+ "tokens / sec": 5852.1624712581015,
+ "mem allocated avg": 6842572642.304,
+ "mem reserved avg": 11863001661.44,
+ "elapsed time": 381.66334240599826
+ },
+ {
+ "step": 1250,
+ "valid accuracy": 0.18,
+ "train loss": 0.84929132604599,
+ "train samples": 5000,
+ "train time": 35.52914607799903,
+ "eval time": 13.408120855005109,
+ "tokens / sec": 5869.490911551474,
+ "mem allocated avg": 6843078866.944,
+ "mem reserved avg": 11855409971.2,
+ "elapsed time": 475.2031378399988
+ },
+ {
+ "step": 1500,
+ "valid accuracy": 0.18,
+ "train loss": 0.8379741818904877,
+ "train samples": 6000,
+ "train time": 35.84657208897261,
+ "eval time": 13.451748254003178,
+ "tokens / sec": 5839.637873335062,
+ "mem allocated avg": 6844234328.064,
+ "mem reserved avg": 11880013758.464,
+ "elapsed time": 568.970056428996
+ },
+ {
+ "step": 1750,
+ "valid accuracy": 0.2,
+ "train loss": 0.8320568509101868,
+ "train samples": 7000,
+ "train time": 36.04748217701126,
+ "eval time": 13.354637482996623,
+ "tokens / sec": 5807.756529900249,
+ "mem allocated avg": 6845049858.048,
+ "mem reserved avg": 11894333112.32,
+ "elapsed time": 663.2131869919976
+ },
+ {
+ "step": 2000,
+ "valid accuracy": 0.2,
+ "train loss": 0.83651398563385,
+ "train samples": 8000,
+ "train time": 35.70882848704787,
+ "eval time": 13.407459709997056,
+ "tokens / sec": 5816.376756110452,
+ "mem allocated avg": 6842067818.496,
+ "mem reserved avg": 11843724640.256,
+ "elapsed time": 756.9679808469955
+ },
+ {
+ "step": 2250,
+ "valid accuracy": 0.18,
+ "train loss": 0.8321560187339783,
+ "train samples": 9000,
+ "train time": 36.077689886013104,
+ "eval time": 13.313609958000598,
+ "tokens / sec": 5957.92027369615,
+ "mem allocated avg": 6853360060.416,
+ "mem reserved avg": 12025841319.936,
+ "elapsed time": 851.5264306229947
+ },
+ {
+ "step": 2500,
+ "valid accuracy": 0.22,
+ "train loss": 0.830465945482254,
+ "train samples": 10000,
+ "train time": 35.51607862501987,
+ "eval time": 13.570960901000944,
+ "tokens / sec": 5799.260728488849,
+ "mem allocated avg": 6838232895.488,
+ "mem reserved avg": 11785499312.128,
+ "elapsed time": 945.1205676109967
+ },
+ {
+ "step": 2750,
+ "valid accuracy": 0.2,
+ "train loss": 0.8323929319381714,
+ "train samples": 11000,
+ "train time": 36.33290277811466,
+ "eval time": 13.340032396001334,
+ "tokens / sec": 5831.6562619276265,
+ "mem allocated avg": 6849506107.392,
+ "mem reserved avg": 11957667102.72,
+ "elapsed time": 1039.698461469001
+ },
+ {
+ "step": 3000,
+ "valid accuracy": 0.22,
+ "train loss": 0.8273163681030273,
+ "train samples": 12000,
+ "train time": 36.133581758025684,
+ "eval time": 13.486512909999874,
+ "tokens / sec": 5776.648476140576,
+ "mem allocated avg": 6844330549.248,
+ "mem reserved avg": 11874754101.248,
+ "elapsed time": 1134.0729920019949
+ },
+ {
+ "step": 3250,
+ "valid accuracy": 0.18,
+ "train loss": 0.8321007430553437,
+ "train samples": 13000,
+ "train time": 35.81564853595046,
+ "eval time": 13.383609317002993,
+ "tokens / sec": 5888.515456820645,
+ "mem allocated avg": 6845503963.136,
+ "mem reserved avg": 11903065653.248,
+ "elapsed time": 1228.1345331240009
+ },
+ {
+ "step": 3500,
+ "valid accuracy": 0.18,
+ "train loss": 0.8267617487907409,
+ "train samples": 14000,
+ "train time": 35.759473790014454,
+ "eval time": 13.568141147006827,
+ "tokens / sec": 5865.578482269809,
+ "mem allocated avg": 6844375582.72,
+ "mem reserved avg": 11893385199.616,
+ "elapsed time": 1322.3741278140005
+ },
+ {
+ "step": 3750,
+ "valid accuracy": 0.18,
+ "train loss": 0.822540352344513,
+ "train samples": 15000,
+ "train time": 36.6447854490616,
+ "eval time": 13.383382205000089,
+ "tokens / sec": 5913.610827418539,
+ "mem allocated avg": 6855454945.28,
+ "mem reserved avg": 12064244367.36,
+ "elapsed time": 1417.8726171529997
+ },
+ {
+ "step": 4000,
+ "valid accuracy": 0.22,
+ "train loss": 0.842738341331482,
+ "train samples": 16000,
+ "train time": 35.83419257100468,
+ "eval time": 13.484180120998644,
+ "tokens / sec": 5703.295800373884,
+ "mem allocated avg": 6837201041.408,
+ "mem reserved avg": 11769015697.408,
+ "elapsed time": 1511.8286734409994
+ },
+ {
+ "step": 4250,
+ "valid accuracy": 0.24,
+ "train loss": 0.8195172207355499,
+ "train samples": 17000,
+ "train time": 36.032976000991766,
+ "eval time": 13.43221827600064,
+ "tokens / sec": 5866.542913196561,
+ "mem allocated avg": 6847173238.784,
+ "mem reserved avg": 11924070727.68,
+ "elapsed time": 1606.2413196950001
+ },
+ {
+ "step": 4500,
+ "valid accuracy": 0.22,
+ "train loss": 0.8333091423511505,
+ "train samples": 18000,
+ "train time": 35.92476197002543,
+ "eval time": 13.364069708994066,
+ "tokens / sec": 5784.812163081199,
+ "mem allocated avg": 6842308513.792,
+ "mem reserved avg": 11840637632.512,
+ "elapsed time": 1700.1633438569988
+ },
+ {
+ "step": 4750,
+ "valid accuracy": 0.24,
+ "train loss": 0.8247289218902588,
+ "train samples": 19000,
+ "train time": 36.319470202004595,
+ "eval time": 13.367499373998726,
+ "tokens / sec": 5780.343128144329,
+ "mem allocated avg": 6845010323.456,
+ "mem reserved avg": 11893443919.872,
+ "elapsed time": 1795.0117048679967
+ },
+ {
+ "step": 5000,
+ "valid accuracy": 0.24,
+ "train loss": 0.8317011270523071,
+ "train samples": 20000,
+ "train time": 35.778475134953624,
+ "eval time": 13.382634160996531,
+ "tokens / sec": 5821.377216731123,
+ "mem allocated avg": 6841479706.624,
+ "mem reserved avg": 11840956399.616,
+ "elapsed time": 1888.9356832179983
+ },
+ {
+ "step": 5000,
+ "test accuracy": 0.22062168309325247,
+ "train loss": 0.8317011270523071,
+ "train samples": 20000,
+ "train total tokens": 4198051
+ }
+ ]
+ },
+ "meta_info": {
+ "model_info": {
+ "sha": "13afe5124825b4f3751f836b40dafda64c1ed062",
+ "created_at": "2024-09-18T15:23:48+00:00"
+ },
+ "dataset_info": {
+ "metamath": {
+ "sha": "aa4f34d3d2d3231299b5b03d9b3e5a20da45aa18",
+ "created_at": "2023-09-21T17:22:46+00:00"
+ },
+ "gsm8k": {
+ "sha": "e53f048856ff4f594e959d75785d2c2d37b678ee",
+ "created_at": "2022-04-12T10:22:10+00:00"
+ }
+ },
+ "package_info": {
+ "transformers-version": "4.52.4",
+ "transformers-commit-hash": null,
+ "peft-version": "0.15.2.dev0",
+ "peft-commit-hash": "5fe7f8f8abe914d313fc3751f2ea92de7718fbaf",
+ "datasets-version": "3.6.0",
+ "datasets-commit-hash": null,
+ "bitsandbytes-version": "0.46.0",
+ "bitsandbytes-commit-hash": null,
+ "torch-version": "2.7.1+cu126",
+ "torch-commit-hash": null
+ },
+ "system_info": {
+ "system": "Linux",
+ "release": "6.8.0-1029-aws",
+ "version": "#31-Ubuntu SMP Wed Apr 23 18:42:41 UTC 2025",
+ "machine": "x86_64",
+ "processor": "x86_64",
+ "accelerator": "NVIDIA L40S"
+ },
+ "pytorch_info": "PyTorch built with:\n - GCC 11.2\n - C++ Version: 201703\n - Intel(R) oneAPI Math Kernel Library Version 2024.2-Product Build 20240605 for Intel(R) 64 architecture applications\n - Intel(R) MKL-DNN v3.7.1 (Git Hash 8d263e693366ef8db40acc569cc7d8edf644556d)\n - OpenMP 201511 (a.k.a. OpenMP 4.5)\n - LAPACK is enabled (usually provided by MKL)\n - NNPACK is enabled\n - CPU capability usage: AVX2\n - CUDA Runtime 12.6\n - NVCC architecture flags: -gencode;arch=compute_50,code=sm_50;-gencode;arch=compute_60,code=sm_60;-gencode;arch=compute_70,code=sm_70;-gencode;arch=compute_75,code=sm_75;-gencode;arch=compute_80,code=sm_80;-gencode;arch=compute_86,code=sm_86;-gencode;arch=compute_90,code=sm_90\n - CuDNN 90.7.1 (built against CUDA 12.8)\n - Built with CuDNN 90.5.1\n - Magma 2.6.1\n - Build settings: BLAS_INFO=mkl, BUILD_TYPE=Release, COMMIT_SHA=e2d141dbde55c2a4370fac5165b0561b6af4798b, CUDA_VERSION=12.6, CUDNN_VERSION=9.5.1, CXX_COMPILER=/opt/rh/gcc-toolset-11/root/usr/bin/c++, CXX_FLAGS= -D_GLIBCXX_USE_CXX11_ABI=1 -fvisibility-inlines-hidden -DUSE_PTHREADPOOL -DNDEBUG -DUSE_KINETO -DLIBKINETO_NOROCTRACER -DLIBKINETO_NOXPUPTI=ON -DUSE_FBGEMM -DUSE_PYTORCH_QNNPACK -DUSE_XNNPACK -DSYMBOLICATE_MOBILE_DEBUG_HANDLE -O2 -fPIC -Wall -Wextra -Werror=return-type -Werror=non-virtual-dtor -Werror=range-loop-construct -Werror=bool-operation -Wnarrowing -Wno-missing-field-initializers -Wno-unknown-pragmas -Wno-unused-parameter -Wno-strict-overflow -Wno-strict-aliasing -Wno-stringop-overflow -Wsuggest-override -Wno-psabi -Wno-error=old-style-cast -fdiagnostics-color=always -faligned-new -Wno-maybe-uninitialized -fno-math-errno -fno-trapping-math -Werror=format -Wno-stringop-overflow, LAPACK_INFO=mkl, PERF_WITH_AVX=1, PERF_WITH_AVX2=1, TORCH_VERSION=2.7.1, USE_CUDA=ON, USE_CUDNN=ON, USE_CUSPARSELT=1, USE_GFLAGS=OFF, USE_GLOG=OFF, USE_GLOO=ON, USE_MKL=ON, USE_MKLDNN=ON, USE_MPI=OFF, USE_NCCL=1, USE_NNPACK=ON, USE_OPENMP=ON, USE_ROCM=OFF, USE_ROCM_KERNEL_ASSERT=OFF, \n"
+ }
+}
diff --git a/peft/method_comparison/MetaMathQA/results/boft--llama-3.2-3B-default.json b/peft/method_comparison/MetaMathQA/results/boft--llama-3.2-3B-default.json
new file mode 100644
index 0000000000000000000000000000000000000000..83ddbc7c63224c54a14f3d4eb0efdaabb159fb66
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/results/boft--llama-3.2-3B-default.json
@@ -0,0 +1,354 @@
+{
+ "run_info": {
+ "created_at": "2025-06-20T00:26:06+00:00",
+ "total_time": 11113.556226242006,
+ "experiment_name": "boft/llama-3.2-3B-default",
+ "peft_branch": "main",
+ "train_config": {
+ "model_id": "meta-llama/Llama-3.2-3B",
+ "dtype": "bfloat16",
+ "max_seq_length": 768,
+ "batch_size": 4,
+ "batch_size_eval": 50,
+ "max_steps": 5000,
+ "eval_steps": 250,
+ "compile": false,
+ "query_template": "Question: {query} Think step by step.\nAnswer:",
+ "seed": 0,
+ "grad_norm_clip": 1.0,
+ "optimizer_type": "AdamW",
+ "optimizer_kwargs": {
+ "lr": 0.0001,
+ "weight_decay": 0.1
+ },
+ "lr_scheduler": "cosine",
+ "use_amp": false,
+ "autocast_adapter_dtype": true,
+ "generation_kwargs": {
+ "max_length": 800,
+ "max_new_tokens": 300
+ },
+ "attn_implementation": null
+ },
+ "peft_config": {
+ "task_type": null,
+ "peft_type": "BOFT",
+ "auto_mapping": null,
+ "base_model_name_or_path": "meta-llama/Llama-3.2-3B",
+ "revision": null,
+ "inference_mode": false,
+ "boft_block_size": 4,
+ "boft_block_num": 0,
+ "boft_n_butterfly_factor": 1,
+ "target_modules": [
+ "q_proj",
+ "v_proj"
+ ],
+ "exclude_modules": null,
+ "boft_dropout": 0.0,
+ "fan_in_fan_out": false,
+ "bias": "none",
+ "modules_to_save": null,
+ "init_weights": true,
+ "layers_to_transform": null,
+ "layers_pattern": null
+ },
+ "error_msg": ""
+ },
+ "train_info": {
+ "accelerator_memory_reserved_avg": 14814855089,
+ "accelerator_memory_max": 24427626496,
+ "accelerator_memory_reserved_99th": 20103445872,
+ "train_time": 8291.859631775995,
+ "file_size": 3225360,
+ "num_trainable_params": 802816,
+ "num_total_params": 3213552640,
+ "status": "success",
+ "metrics": [
+ {
+ "step": 250,
+ "valid accuracy": 0.0,
+ "train loss": 1.291453486919403,
+ "train samples": 1000,
+ "train time": 168.6401632970519,
+ "eval time": 140.71104099299555,
+ "tokens / sec": 1255.4482625059293,
+ "mem allocated avg": 6794374191.104,
+ "mem reserved avg": 14862272954.368,
+ "elapsed time": 378.35506656600046
+ },
+ {
+ "step": 500,
+ "valid accuracy": 0.12,
+ "train loss": 1.0658165102005004,
+ "train samples": 2000,
+ "train time": 168.0782826189752,
+ "eval time": 140.55351014900225,
+ "tokens / sec": 1237.4888460248842,
+ "mem allocated avg": 6786098696.192,
+ "mem reserved avg": 14759126630.4,
+ "elapsed time": 750.4153373740046
+ },
+ {
+ "step": 750,
+ "valid accuracy": 0.38,
+ "train loss": 0.8760707340240479,
+ "train samples": 3000,
+ "train time": 168.35559053501493,
+ "eval time": 140.5371915020005,
+ "tokens / sec": 1273.5009233649919,
+ "mem allocated avg": 6796379451.392,
+ "mem reserved avg": 14898109087.744,
+ "elapsed time": 1123.1088362480004
+ },
+ {
+ "step": 1000,
+ "valid accuracy": 0.42,
+ "train loss": 0.8187176239490509,
+ "train samples": 4000,
+ "train time": 168.23626853094902,
+ "eval time": 140.51234973900137,
+ "tokens / sec": 1238.3536666570453,
+ "mem allocated avg": 6788017170.432,
+ "mem reserved avg": 14785978564.608,
+ "elapsed time": 1495.2035204040003
+ },
+ {
+ "step": 1250,
+ "valid accuracy": 0.44,
+ "train loss": 0.7968595073223114,
+ "train samples": 5000,
+ "train time": 168.06973706404096,
+ "eval time": 140.56398986800195,
+ "tokens / sec": 1240.7825682534333,
+ "mem allocated avg": 6786994073.6,
+ "mem reserved avg": 14784728662.016,
+ "elapsed time": 1867.293767313
+ },
+ {
+ "step": 1500,
+ "valid accuracy": 0.3,
+ "train loss": 0.7768308148384094,
+ "train samples": 6000,
+ "train time": 168.12391281103191,
+ "eval time": 140.47015122300218,
+ "tokens / sec": 1245.0995013141533,
+ "mem allocated avg": 6790023022.592,
+ "mem reserved avg": 14800616685.568,
+ "elapsed time": 2239.2391544300044
+ },
+ {
+ "step": 1750,
+ "valid accuracy": 0.34,
+ "train loss": 0.7639130955934524,
+ "train samples": 7000,
+ "train time": 168.4569528100401,
+ "eval time": 140.76006173399946,
+ "tokens / sec": 1242.780404772479,
+ "mem allocated avg": 6790166409.216,
+ "mem reserved avg": 14820103421.952,
+ "elapsed time": 2611.854956449002
+ },
+ {
+ "step": 2000,
+ "valid accuracy": 0.28,
+ "train loss": 0.7575103138685226,
+ "train samples": 8000,
+ "train time": 168.38565446306166,
+ "eval time": 140.82750502999988,
+ "tokens / sec": 1233.4542432506432,
+ "mem allocated avg": 6787659706.368,
+ "mem reserved avg": 14766038843.392,
+ "elapsed time": 2984.338527646003
+ },
+ {
+ "step": 2250,
+ "valid accuracy": 0.36,
+ "train loss": 0.7480558000802994,
+ "train samples": 9000,
+ "train time": 168.98983921804756,
+ "eval time": 140.92262020800263,
+ "tokens / sec": 1271.9581307054364,
+ "mem allocated avg": 6798715979.776,
+ "mem reserved avg": 14937929809.92,
+ "elapsed time": 3357.8442202950027
+ },
+ {
+ "step": 2500,
+ "valid accuracy": 0.36,
+ "train loss": 0.7452825582027436,
+ "train samples": 10000,
+ "train time": 168.30827127001976,
+ "eval time": 140.89225408899802,
+ "tokens / sec": 1223.7485326527044,
+ "mem allocated avg": 6783722676.224,
+ "mem reserved avg": 14710111993.856,
+ "elapsed time": 3730.0927005050034
+ },
+ {
+ "step": 2750,
+ "valid accuracy": 0.4,
+ "train loss": 0.7368131847381592,
+ "train samples": 11000,
+ "train time": 168.8352410539519,
+ "eval time": 140.97951381299936,
+ "tokens / sec": 1254.9571918595636,
+ "mem allocated avg": 6794155292.672,
+ "mem reserved avg": 14876869132.288,
+ "elapsed time": 4103.762088249001
+ },
+ {
+ "step": 3000,
+ "valid accuracy": 0.38,
+ "train loss": 0.7284122853279114,
+ "train samples": 12000,
+ "train time": 168.7332625999261,
+ "eval time": 140.92822863799665,
+ "tokens / sec": 1237.0471404616308,
+ "mem allocated avg": 6789107718.144,
+ "mem reserved avg": 14802571231.232,
+ "elapsed time": 4477.013831755001
+ },
+ {
+ "step": 3250,
+ "valid accuracy": 0.34,
+ "train loss": 0.7360657904148101,
+ "train samples": 13000,
+ "train time": 168.6564349730761,
+ "eval time": 140.91345744199498,
+ "tokens / sec": 1250.4770424779092,
+ "mem allocated avg": 6791307786.24,
+ "mem reserved avg": 14825665069.056,
+ "elapsed time": 4850.336532419002
+ },
+ {
+ "step": 3500,
+ "valid accuracy": 0.34,
+ "train loss": 0.7245372575521469,
+ "train samples": 14000,
+ "train time": 168.69712368501496,
+ "eval time": 141.10813598799723,
+ "tokens / sec": 1243.3525564528145,
+ "mem allocated avg": 6789542191.104,
+ "mem reserved avg": 14803175211.008,
+ "elapsed time": 5223.900597244006
+ },
+ {
+ "step": 3750,
+ "valid accuracy": 0.36,
+ "train loss": 0.7196882257461548,
+ "train samples": 15000,
+ "train time": 169.02741387199057,
+ "eval time": 140.85168583100312,
+ "tokens / sec": 1282.0583066135978,
+ "mem allocated avg": 6800711397.376,
+ "mem reserved avg": 14974772576.256,
+ "elapsed time": 5597.923287113001
+ },
+ {
+ "step": 4000,
+ "valid accuracy": 0.4,
+ "train loss": 0.7386573747396469,
+ "train samples": 16000,
+ "train time": 168.47688378201565,
+ "eval time": 141.17620621900278,
+ "tokens / sec": 1213.062560347618,
+ "mem allocated avg": 6781920968.704,
+ "mem reserved avg": 14703241723.904,
+ "elapsed time": 5970.573302798002
+ },
+ {
+ "step": 4250,
+ "valid accuracy": 0.36,
+ "train loss": 0.7167660998106002,
+ "train samples": 17000,
+ "train time": 168.66243355697225,
+ "eval time": 141.03309625500697,
+ "tokens / sec": 1253.3259217358275,
+ "mem allocated avg": 6792739334.144,
+ "mem reserved avg": 14838457696.256,
+ "elapsed time": 6343.574297415005
+ },
+ {
+ "step": 4500,
+ "valid accuracy": 0.36,
+ "train loss": 0.7278824989795685,
+ "train samples": 18000,
+ "train time": 168.825120675996,
+ "eval time": 141.10180295899772,
+ "tokens / sec": 1230.966097745832,
+ "mem allocated avg": 6787403542.528,
+ "mem reserved avg": 14768026943.488,
+ "elapsed time": 6716.868663600006
+ },
+ {
+ "step": 4750,
+ "valid accuracy": 0.34,
+ "train loss": 0.7206774606704712,
+ "train samples": 19000,
+ "train time": 168.64492384497134,
+ "eval time": 140.88104952100548,
+ "tokens / sec": 1244.8581031290848,
+ "mem allocated avg": 6790186668.032,
+ "mem reserved avg": 14817972715.52,
+ "elapsed time": 7090.485984892002
+ },
+ {
+ "step": 5000,
+ "valid accuracy": 0.34,
+ "train loss": 0.7268091850280761,
+ "train samples": 20000,
+ "train time": 168.56219975605927,
+ "eval time": 140.98389447200316,
+ "tokens / sec": 1235.6269691628356,
+ "mem allocated avg": 6787183779.84,
+ "mem reserved avg": 14761332834.304,
+ "elapsed time": 7463.428281595006
+ },
+ {
+ "step": 5000,
+ "test accuracy": 0.3646702047005307,
+ "train loss": 0.7268091850280761,
+ "train samples": 20000,
+ "train total tokens": 4198051
+ }
+ ]
+ },
+ "meta_info": {
+ "model_info": {
+ "sha": "13afe5124825b4f3751f836b40dafda64c1ed062",
+ "created_at": "2024-09-18T15:23:48+00:00"
+ },
+ "dataset_info": {
+ "metamath": {
+ "sha": "aa4f34d3d2d3231299b5b03d9b3e5a20da45aa18",
+ "created_at": "2023-09-21T17:22:46+00:00"
+ },
+ "gsm8k": {
+ "sha": "e53f048856ff4f594e959d75785d2c2d37b678ee",
+ "created_at": "2022-04-12T10:22:10+00:00"
+ }
+ },
+ "package_info": {
+ "transformers-version": "4.52.4",
+ "transformers-commit-hash": null,
+ "peft-version": "0.15.2.dev0",
+ "peft-commit-hash": "5fe7f8f8abe914d313fc3751f2ea92de7718fbaf",
+ "datasets-version": "3.6.0",
+ "datasets-commit-hash": null,
+ "bitsandbytes-version": "0.46.0",
+ "bitsandbytes-commit-hash": null,
+ "torch-version": "2.7.1+cu126",
+ "torch-commit-hash": null
+ },
+ "system_info": {
+ "system": "Linux",
+ "release": "6.8.0-1029-aws",
+ "version": "#31-Ubuntu SMP Wed Apr 23 18:42:41 UTC 2025",
+ "machine": "x86_64",
+ "processor": "x86_64",
+ "accelerator": "NVIDIA L40S"
+ },
+ "pytorch_info": "PyTorch built with:\n - GCC 11.2\n - C++ Version: 201703\n - Intel(R) oneAPI Math Kernel Library Version 2024.2-Product Build 20240605 for Intel(R) 64 architecture applications\n - Intel(R) MKL-DNN v3.7.1 (Git Hash 8d263e693366ef8db40acc569cc7d8edf644556d)\n - OpenMP 201511 (a.k.a. OpenMP 4.5)\n - LAPACK is enabled (usually provided by MKL)\n - NNPACK is enabled\n - CPU capability usage: AVX2\n - CUDA Runtime 12.6\n - NVCC architecture flags: -gencode;arch=compute_50,code=sm_50;-gencode;arch=compute_60,code=sm_60;-gencode;arch=compute_70,code=sm_70;-gencode;arch=compute_75,code=sm_75;-gencode;arch=compute_80,code=sm_80;-gencode;arch=compute_86,code=sm_86;-gencode;arch=compute_90,code=sm_90\n - CuDNN 90.7.1 (built against CUDA 12.8)\n - Built with CuDNN 90.5.1\n - Magma 2.6.1\n - Build settings: BLAS_INFO=mkl, BUILD_TYPE=Release, COMMIT_SHA=e2d141dbde55c2a4370fac5165b0561b6af4798b, CUDA_VERSION=12.6, CUDNN_VERSION=9.5.1, CXX_COMPILER=/opt/rh/gcc-toolset-11/root/usr/bin/c++, CXX_FLAGS= -D_GLIBCXX_USE_CXX11_ABI=1 -fvisibility-inlines-hidden -DUSE_PTHREADPOOL -DNDEBUG -DUSE_KINETO -DLIBKINETO_NOROCTRACER -DLIBKINETO_NOXPUPTI=ON -DUSE_FBGEMM -DUSE_PYTORCH_QNNPACK -DUSE_XNNPACK -DSYMBOLICATE_MOBILE_DEBUG_HANDLE -O2 -fPIC -Wall -Wextra -Werror=return-type -Werror=non-virtual-dtor -Werror=range-loop-construct -Werror=bool-operation -Wnarrowing -Wno-missing-field-initializers -Wno-unknown-pragmas -Wno-unused-parameter -Wno-strict-overflow -Wno-strict-aliasing -Wno-stringop-overflow -Wsuggest-override -Wno-psabi -Wno-error=old-style-cast -fdiagnostics-color=always -faligned-new -Wno-maybe-uninitialized -fno-math-errno -fno-trapping-math -Werror=format -Wno-stringop-overflow, LAPACK_INFO=mkl, PERF_WITH_AVX=1, PERF_WITH_AVX2=1, TORCH_VERSION=2.7.1, USE_CUDA=ON, USE_CUDNN=ON, USE_CUSPARSELT=1, USE_GFLAGS=OFF, USE_GLOG=OFF, USE_GLOO=ON, USE_MKL=ON, USE_MKLDNN=ON, USE_MPI=OFF, USE_NCCL=1, USE_NNPACK=ON, USE_OPENMP=ON, USE_ROCM=OFF, USE_ROCM_KERNEL_ASSERT=OFF, \n"
+ }
+}
diff --git a/peft/method_comparison/MetaMathQA/results/bone--llama-3.2-3B-bat.json b/peft/method_comparison/MetaMathQA/results/bone--llama-3.2-3B-bat.json
new file mode 100644
index 0000000000000000000000000000000000000000..069bbfe1077efd4cc4ea365424fc6d6d3c554ff7
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/results/bone--llama-3.2-3B-bat.json
@@ -0,0 +1,350 @@
+{
+ "run_info": {
+ "created_at": "2025-06-20T03:31:24+00:00",
+ "total_time": 2742.3845372959986,
+ "experiment_name": "bone/llama-3.2-3B-bat",
+ "peft_branch": "main",
+ "train_config": {
+ "model_id": "meta-llama/Llama-3.2-3B",
+ "dtype": "bfloat16",
+ "max_seq_length": 768,
+ "batch_size": 4,
+ "batch_size_eval": 50,
+ "max_steps": 5000,
+ "eval_steps": 250,
+ "compile": false,
+ "query_template": "Question: {query} Think step by step.\nAnswer:",
+ "seed": 0,
+ "grad_norm_clip": 1.0,
+ "optimizer_type": "AdamW",
+ "optimizer_kwargs": {
+ "lr": 0.0001,
+ "weight_decay": 0.1
+ },
+ "lr_scheduler": "cosine",
+ "use_amp": false,
+ "autocast_adapter_dtype": true,
+ "generation_kwargs": {
+ "max_length": 800,
+ "max_new_tokens": 300
+ },
+ "attn_implementation": null
+ },
+ "peft_config": {
+ "task_type": null,
+ "peft_type": "BONE",
+ "auto_mapping": null,
+ "base_model_name_or_path": "meta-llama/Llama-3.2-3B",
+ "revision": null,
+ "inference_mode": false,
+ "r": 64,
+ "target_modules": [
+ "v_proj",
+ "q_proj"
+ ],
+ "exclude_modules": null,
+ "init_weights": "bat",
+ "layers_to_transform": null,
+ "layers_pattern": null,
+ "bias": "none",
+ "modules_to_save": null
+ },
+ "error_msg": ""
+ },
+ "train_info": {
+ "accelerator_memory_reserved_avg": 14713983755,
+ "accelerator_memory_max": 25251807232,
+ "accelerator_memory_reserved_99th": 20472733368,
+ "train_time": 2430.7548372539895,
+ "file_size": 29367552,
+ "num_trainable_params": 7340032,
+ "num_total_params": 3220089856,
+ "status": "success",
+ "metrics": [
+ {
+ "step": 250,
+ "valid accuracy": 0.34,
+ "train loss": 0.8741071329116822,
+ "train samples": 1000,
+ "train time": 44.769113782072964,
+ "eval time": 16.53786130100343,
+ "tokens / sec": 4729.130914464948,
+ "mem allocated avg": 6898425409.536,
+ "mem reserved avg": 14773294989.312,
+ "elapsed time": 124.73039968500234
+ },
+ {
+ "step": 500,
+ "valid accuracy": 0.42,
+ "train loss": 0.6946564470529556,
+ "train samples": 2000,
+ "train time": 43.747789238033874,
+ "eval time": 16.4541177170031,
+ "tokens / sec": 4754.4116770858745,
+ "mem allocated avg": 6890118709.248,
+ "mem reserved avg": 14662749913.088,
+ "elapsed time": 242.48505929599924
+ },
+ {
+ "step": 750,
+ "valid accuracy": 0.42,
+ "train loss": 0.6668610339164733,
+ "train samples": 3000,
+ "train time": 44.788394879076805,
+ "eval time": 8.99262467600056,
+ "tokens / sec": 4786.9766393472355,
+ "mem allocated avg": 6900886024.192,
+ "mem reserved avg": 14820195696.64,
+ "elapsed time": 354.3122298879971
+ },
+ {
+ "step": 1000,
+ "valid accuracy": 0.42,
+ "train loss": 0.6476555281877517,
+ "train samples": 4000,
+ "train time": 43.08444309095648,
+ "eval time": 14.581032188005338,
+ "tokens / sec": 4835.527282090601,
+ "mem allocated avg": 6892210176.0,
+ "mem reserved avg": 14677799075.84,
+ "elapsed time": 469.41999823199876
+ },
+ {
+ "step": 1250,
+ "valid accuracy": 0.38,
+ "train loss": 0.6442477897405624,
+ "train samples": 5000,
+ "train time": 43.81069704208494,
+ "eval time": 16.504536090003967,
+ "tokens / sec": 4759.979048031958,
+ "mem allocated avg": 6892437598.208,
+ "mem reserved avg": 14675995525.12,
+ "elapsed time": 587.4669312400001
+ },
+ {
+ "step": 1500,
+ "valid accuracy": 0.48,
+ "train loss": 0.6370412122011184,
+ "train samples": 6000,
+ "train time": 44.041188616007275,
+ "eval time": 11.50742915799492,
+ "tokens / sec": 4753.07335197389,
+ "mem allocated avg": 6893869041.664,
+ "mem reserved avg": 14704349020.16,
+ "elapsed time": 700.887209352004
+ },
+ {
+ "step": 1750,
+ "valid accuracy": 0.44,
+ "train loss": 0.6277673766613007,
+ "train samples": 7000,
+ "train time": 44.32280573899334,
+ "eval time": 16.494074002999696,
+ "tokens / sec": 4723.414876595195,
+ "mem allocated avg": 6895170344.96,
+ "mem reserved avg": 14718215389.184,
+ "elapsed time": 819.4313268580008
+ },
+ {
+ "step": 2000,
+ "valid accuracy": 0.48,
+ "train loss": 0.6278820457458496,
+ "train samples": 8000,
+ "train time": 43.325528461049544,
+ "eval time": 16.452074027998606,
+ "tokens / sec": 4793.848047040501,
+ "mem allocated avg": 6891568050.176,
+ "mem reserved avg": 14656710115.328,
+ "elapsed time": 936.9070930559974
+ },
+ {
+ "step": 2250,
+ "valid accuracy": 0.44,
+ "train loss": 0.6160005252361298,
+ "train samples": 9000,
+ "train time": 45.04456213898811,
+ "eval time": 16.52133422600309,
+ "tokens / sec": 4771.896757188206,
+ "mem allocated avg": 6903412344.832,
+ "mem reserved avg": 14851812360.192,
+ "elapsed time": 1056.8185863660037
+ },
+ {
+ "step": 2500,
+ "valid accuracy": 0.5,
+ "train loss": 0.6121727240085602,
+ "train samples": 10000,
+ "train time": 43.16439942702709,
+ "eval time": 16.356938169003115,
+ "tokens / sec": 4771.686916395162,
+ "mem allocated avg": 6888002562.048,
+ "mem reserved avg": 14598350569.472,
+ "elapsed time": 1173.7929829869972
+ },
+ {
+ "step": 2750,
+ "valid accuracy": 0.52,
+ "train loss": 0.6007345867156982,
+ "train samples": 11000,
+ "train time": 44.3066304440581,
+ "eval time": 16.514935120998416,
+ "tokens / sec": 4782.151065798665,
+ "mem allocated avg": 6899352545.28,
+ "mem reserved avg": 14785458470.912,
+ "elapsed time": 1292.7444534430033
+ },
+ {
+ "step": 3000,
+ "valid accuracy": 0.52,
+ "train loss": 0.5899704934358597,
+ "train samples": 12000,
+ "train time": 44.07467572299356,
+ "eval time": 16.412788394998643,
+ "tokens / sec": 4735.848796979486,
+ "mem allocated avg": 6894036676.608,
+ "mem reserved avg": 14687865405.44,
+ "elapsed time": 1411.115336062001
+ },
+ {
+ "step": 3250,
+ "valid accuracy": 0.48,
+ "train loss": 0.5988378477096558,
+ "train samples": 13000,
+ "train time": 44.070030323957326,
+ "eval time": 10.250203846997465,
+ "tokens / sec": 4785.587812163363,
+ "mem allocated avg": 6895260303.36,
+ "mem reserved avg": 14725043716.096,
+ "elapsed time": 1523.332073521
+ },
+ {
+ "step": 3500,
+ "valid accuracy": 0.5,
+ "train loss": 0.5801258901357651,
+ "train samples": 14000,
+ "train time": 43.991991777089424,
+ "eval time": 16.38271237299341,
+ "tokens / sec": 4767.913238909897,
+ "mem allocated avg": 6893688922.112,
+ "mem reserved avg": 14703484993.536,
+ "elapsed time": 1641.7187374700006
+ },
+ {
+ "step": 3750,
+ "valid accuracy": 0.5,
+ "train loss": 0.5768071869611741,
+ "train samples": 15000,
+ "train time": 45.04501243098639,
+ "eval time": 16.454509290000715,
+ "tokens / sec": 4810.810083180938,
+ "mem allocated avg": 6905122422.784,
+ "mem reserved avg": 14891314315.264,
+ "elapsed time": 1761.645320085001
+ },
+ {
+ "step": 4000,
+ "valid accuracy": 0.52,
+ "train loss": 0.5858320169448853,
+ "train samples": 16000,
+ "train time": 42.547905418032315,
+ "eval time": 16.350580427999375,
+ "tokens / sec": 4803.36218650576,
+ "mem allocated avg": 6886491265.024,
+ "mem reserved avg": 14582730981.376,
+ "elapsed time": 1878.0724109930015
+ },
+ {
+ "step": 4250,
+ "valid accuracy": 0.54,
+ "train loss": 0.5723247408866883,
+ "train samples": 17000,
+ "train time": 44.19116178697732,
+ "eval time": 16.508775556001638,
+ "tokens / sec": 4783.513070305705,
+ "mem allocated avg": 6897152284.672,
+ "mem reserved avg": 14738381602.816,
+ "elapsed time": 1996.8971549050038
+ },
+ {
+ "step": 4500,
+ "valid accuracy": 0.48,
+ "train loss": 0.5789256048202515,
+ "train samples": 18000,
+ "train time": 43.87211918797402,
+ "eval time": 16.414912490006827,
+ "tokens / sec": 4736.903615473535,
+ "mem allocated avg": 6893093124.096,
+ "mem reserved avg": 14658832433.152,
+ "elapsed time": 2114.9650602839974
+ },
+ {
+ "step": 4750,
+ "valid accuracy": 0.48,
+ "train loss": 0.568240401506424,
+ "train samples": 19000,
+ "train time": 43.939464293958736,
+ "eval time": 16.460097985000175,
+ "tokens / sec": 4777.914418698651,
+ "mem allocated avg": 6894218592.256,
+ "mem reserved avg": 14710372040.704,
+ "elapsed time": 2233.517725938
+ },
+ {
+ "step": 5000,
+ "valid accuracy": 0.5,
+ "train loss": 0.57634852206707,
+ "train samples": 20000,
+ "train time": 42.787552905057964,
+ "eval time": 16.445046182001533,
+ "tokens / sec": 4867.770785166333,
+ "mem allocated avg": 6890906441.728,
+ "mem reserved avg": 14656718503.936,
+ "elapsed time": 2350.279711092
+ },
+ {
+ "step": 5000,
+ "test accuracy": 0.5170583775587566,
+ "train loss": 0.57634852206707,
+ "train samples": 20000,
+ "train total tokens": 4198051
+ }
+ ]
+ },
+ "meta_info": {
+ "model_info": {
+ "sha": "13afe5124825b4f3751f836b40dafda64c1ed062",
+ "created_at": "2024-09-18T15:23:48+00:00"
+ },
+ "dataset_info": {
+ "metamath": {
+ "sha": "aa4f34d3d2d3231299b5b03d9b3e5a20da45aa18",
+ "created_at": "2023-09-21T17:22:46+00:00"
+ },
+ "gsm8k": {
+ "sha": "e53f048856ff4f594e959d75785d2c2d37b678ee",
+ "created_at": "2022-04-12T10:22:10+00:00"
+ }
+ },
+ "package_info": {
+ "transformers-version": "4.52.4",
+ "transformers-commit-hash": null,
+ "peft-version": "0.15.2.dev0",
+ "peft-commit-hash": "5fe7f8f8abe914d313fc3751f2ea92de7718fbaf",
+ "datasets-version": "3.6.0",
+ "datasets-commit-hash": null,
+ "bitsandbytes-version": "0.46.0",
+ "bitsandbytes-commit-hash": null,
+ "torch-version": "2.7.1+cu126",
+ "torch-commit-hash": null
+ },
+ "system_info": {
+ "system": "Linux",
+ "release": "6.8.0-1029-aws",
+ "version": "#31-Ubuntu SMP Wed Apr 23 18:42:41 UTC 2025",
+ "machine": "x86_64",
+ "processor": "x86_64",
+ "accelerator": "NVIDIA L40S"
+ },
+ "pytorch_info": "PyTorch built with:\n - GCC 11.2\n - C++ Version: 201703\n - Intel(R) oneAPI Math Kernel Library Version 2024.2-Product Build 20240605 for Intel(R) 64 architecture applications\n - Intel(R) MKL-DNN v3.7.1 (Git Hash 8d263e693366ef8db40acc569cc7d8edf644556d)\n - OpenMP 201511 (a.k.a. OpenMP 4.5)\n - LAPACK is enabled (usually provided by MKL)\n - NNPACK is enabled\n - CPU capability usage: AVX2\n - CUDA Runtime 12.6\n - NVCC architecture flags: -gencode;arch=compute_50,code=sm_50;-gencode;arch=compute_60,code=sm_60;-gencode;arch=compute_70,code=sm_70;-gencode;arch=compute_75,code=sm_75;-gencode;arch=compute_80,code=sm_80;-gencode;arch=compute_86,code=sm_86;-gencode;arch=compute_90,code=sm_90\n - CuDNN 90.7.1 (built against CUDA 12.8)\n - Built with CuDNN 90.5.1\n - Magma 2.6.1\n - Build settings: BLAS_INFO=mkl, BUILD_TYPE=Release, COMMIT_SHA=e2d141dbde55c2a4370fac5165b0561b6af4798b, CUDA_VERSION=12.6, CUDNN_VERSION=9.5.1, CXX_COMPILER=/opt/rh/gcc-toolset-11/root/usr/bin/c++, CXX_FLAGS= -D_GLIBCXX_USE_CXX11_ABI=1 -fvisibility-inlines-hidden -DUSE_PTHREADPOOL -DNDEBUG -DUSE_KINETO -DLIBKINETO_NOROCTRACER -DLIBKINETO_NOXPUPTI=ON -DUSE_FBGEMM -DUSE_PYTORCH_QNNPACK -DUSE_XNNPACK -DSYMBOLICATE_MOBILE_DEBUG_HANDLE -O2 -fPIC -Wall -Wextra -Werror=return-type -Werror=non-virtual-dtor -Werror=range-loop-construct -Werror=bool-operation -Wnarrowing -Wno-missing-field-initializers -Wno-unknown-pragmas -Wno-unused-parameter -Wno-strict-overflow -Wno-strict-aliasing -Wno-stringop-overflow -Wsuggest-override -Wno-psabi -Wno-error=old-style-cast -fdiagnostics-color=always -faligned-new -Wno-maybe-uninitialized -fno-math-errno -fno-trapping-math -Werror=format -Wno-stringop-overflow, LAPACK_INFO=mkl, PERF_WITH_AVX=1, PERF_WITH_AVX2=1, TORCH_VERSION=2.7.1, USE_CUDA=ON, USE_CUDNN=ON, USE_CUSPARSELT=1, USE_GFLAGS=OFF, USE_GLOG=OFF, USE_GLOO=ON, USE_MKL=ON, USE_MKLDNN=ON, USE_MPI=OFF, USE_NCCL=1, USE_NNPACK=ON, USE_OPENMP=ON, USE_ROCM=OFF, USE_ROCM_KERNEL_ASSERT=OFF, \n"
+ }
+}
diff --git a/peft/method_comparison/MetaMathQA/results/bone--llama-3.2-3B-default.json b/peft/method_comparison/MetaMathQA/results/bone--llama-3.2-3B-default.json
new file mode 100644
index 0000000000000000000000000000000000000000..a473c5827e1b13156e94be30ac5baee3f7350ff6
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/results/bone--llama-3.2-3B-default.json
@@ -0,0 +1,350 @@
+{
+ "run_info": {
+ "created_at": "2025-06-20T04:17:11+00:00",
+ "total_time": 1867.121674144997,
+ "experiment_name": "bone/llama-3.2-3B-default",
+ "peft_branch": "main",
+ "train_config": {
+ "model_id": "meta-llama/Llama-3.2-3B",
+ "dtype": "bfloat16",
+ "max_seq_length": 768,
+ "batch_size": 4,
+ "batch_size_eval": 50,
+ "max_steps": 5000,
+ "eval_steps": 250,
+ "compile": false,
+ "query_template": "Question: {query} Think step by step.\nAnswer:",
+ "seed": 0,
+ "grad_norm_clip": 1.0,
+ "optimizer_type": "AdamW",
+ "optimizer_kwargs": {
+ "lr": 0.0001,
+ "weight_decay": 0.1
+ },
+ "lr_scheduler": "cosine",
+ "use_amp": false,
+ "autocast_adapter_dtype": true,
+ "generation_kwargs": {
+ "max_length": 800,
+ "max_new_tokens": 300
+ },
+ "attn_implementation": null
+ },
+ "peft_config": {
+ "task_type": null,
+ "peft_type": "BONE",
+ "auto_mapping": null,
+ "base_model_name_or_path": "meta-llama/Llama-3.2-3B",
+ "revision": null,
+ "inference_mode": false,
+ "r": 64,
+ "target_modules": [
+ "v_proj",
+ "q_proj"
+ ],
+ "exclude_modules": null,
+ "init_weights": true,
+ "layers_to_transform": null,
+ "layers_pattern": null,
+ "bias": "none",
+ "modules_to_save": null
+ },
+ "error_msg": ""
+ },
+ "train_info": {
+ "accelerator_memory_reserved_avg": 11170837063,
+ "accelerator_memory_max": 20248002560,
+ "accelerator_memory_reserved_99th": 16303469363,
+ "train_time": 1664.0814183089897,
+ "file_size": 29367496,
+ "num_trainable_params": 7340032,
+ "num_total_params": 3220089856,
+ "status": "success",
+ "metrics": [
+ {
+ "step": 250,
+ "valid accuracy": 0.34,
+ "train loss": 0.8771067566871643,
+ "train samples": 1000,
+ "train time": 29.468342912026856,
+ "eval time": 11.086663477995899,
+ "tokens / sec": 7184.625230948821,
+ "mem allocated avg": 6894354876.416,
+ "mem reserved avg": 11212691603.456,
+ "elapsed time": 88.56553585999791
+ },
+ {
+ "step": 500,
+ "valid accuracy": 0.38,
+ "train loss": 0.6947847135066986,
+ "train samples": 2000,
+ "train time": 29.13603712292388,
+ "eval time": 11.12908834600239,
+ "tokens / sec": 7138.753946615206,
+ "mem allocated avg": 6887297284.096,
+ "mem reserved avg": 11116172279.808,
+ "elapsed time": 169.94219922799675
+ },
+ {
+ "step": 750,
+ "valid accuracy": 0.42,
+ "train loss": 0.6673308206796646,
+ "train samples": 3000,
+ "train time": 29.74789179801155,
+ "eval time": 6.2111000180011615,
+ "tokens / sec": 7207.267037805055,
+ "mem allocated avg": 6897885888.512,
+ "mem reserved avg": 11257109282.816,
+ "elapsed time": 247.40845895299572
+ },
+ {
+ "step": 1000,
+ "valid accuracy": 0.44,
+ "train loss": 0.6480507221221924,
+ "train samples": 4000,
+ "train time": 29.01437903306214,
+ "eval time": 11.063560270995367,
+ "tokens / sec": 7180.439731713689,
+ "mem allocated avg": 6888501639.168,
+ "mem reserved avg": 11141564596.224,
+ "elapsed time": 328.43337820599845
+ },
+ {
+ "step": 1250,
+ "valid accuracy": 0.42,
+ "train loss": 0.6442041766643524,
+ "train samples": 5000,
+ "train time": 28.86099356606428,
+ "eval time": 11.061821620001865,
+ "tokens / sec": 7225.600169399779,
+ "mem allocated avg": 6888334700.544,
+ "mem reserved avg": 11139123511.296,
+ "elapsed time": 409.5306018880001
+ },
+ {
+ "step": 1500,
+ "valid accuracy": 0.52,
+ "train loss": 0.6375475705862045,
+ "train samples": 6000,
+ "train time": 29.36598393299937,
+ "eval time": 6.896059851998871,
+ "tokens / sec": 7128.349606047729,
+ "mem allocated avg": 6890338080.768,
+ "mem reserved avg": 11164893315.072,
+ "elapsed time": 487.1438905899995
+ },
+ {
+ "step": 1750,
+ "valid accuracy": 0.42,
+ "train loss": 0.6282199568748474,
+ "train samples": 7000,
+ "train time": 29.2208460940019,
+ "eval time": 11.139122824002698,
+ "tokens / sec": 7164.576936838726,
+ "mem allocated avg": 6891485964.288,
+ "mem reserved avg": 11174582157.312,
+ "elapsed time": 568.6407176649955
+ },
+ {
+ "step": 2000,
+ "valid accuracy": 0.44,
+ "train loss": 0.628275181055069,
+ "train samples": 8000,
+ "train time": 28.774674860083906,
+ "eval time": 11.096917715003656,
+ "tokens / sec": 7218.013791986054,
+ "mem allocated avg": 6889055956.992,
+ "mem reserved avg": 11126481879.04,
+ "elapsed time": 649.4662010969987
+ },
+ {
+ "step": 2250,
+ "valid accuracy": 0.5,
+ "train loss": 0.6164452042579651,
+ "train samples": 9000,
+ "train time": 29.666104338008154,
+ "eval time": 6.740810982002586,
+ "tokens / sec": 7245.575541396888,
+ "mem allocated avg": 6899385456.64,
+ "mem reserved avg": 11287358603.264,
+ "elapsed time": 727.5584506419982
+ },
+ {
+ "step": 2500,
+ "valid accuracy": 0.52,
+ "train loss": 0.6124898854494095,
+ "train samples": 10000,
+ "train time": 28.952800227045373,
+ "eval time": 11.054138113999215,
+ "tokens / sec": 7113.888756349109,
+ "mem allocated avg": 6884753041.408,
+ "mem reserved avg": 11077492408.32,
+ "elapsed time": 808.6757636719994
+ },
+ {
+ "step": 2750,
+ "valid accuracy": 0.48,
+ "train loss": 0.6010023313760757,
+ "train samples": 11000,
+ "train time": 29.36040201097785,
+ "eval time": 5.933361176998005,
+ "tokens / sec": 7216.556500853691,
+ "mem allocated avg": 6895703631.872,
+ "mem reserved avg": 11229007446.016,
+ "elapsed time": 885.2688505609985
+ },
+ {
+ "step": 3000,
+ "valid accuracy": 0.36,
+ "train loss": 0.590470621585846,
+ "train samples": 12000,
+ "train time": 29.152743853985157,
+ "eval time": 11.051910919995862,
+ "tokens / sec": 7159.909236861306,
+ "mem allocated avg": 6890226739.2,
+ "mem reserved avg": 11156563427.328,
+ "elapsed time": 966.2876440099935
+ },
+ {
+ "step": 3250,
+ "valid accuracy": 0.46,
+ "train loss": 0.5996054347753524,
+ "train samples": 13000,
+ "train time": 29.23224936202314,
+ "eval time": 11.06002619300125,
+ "tokens / sec": 7214.668888053154,
+ "mem allocated avg": 6892138940.416,
+ "mem reserved avg": 11182651998.208,
+ "elapsed time": 1047.7634995759945
+ },
+ {
+ "step": 3500,
+ "valid accuracy": 0.46,
+ "train loss": 0.5810788285732269,
+ "train samples": 14000,
+ "train time": 29.556202010979177,
+ "eval time": 7.767598452002858,
+ "tokens / sec": 7096.649289448104,
+ "mem allocated avg": 6891370110.976,
+ "mem reserved avg": 11166763974.656,
+ "elapsed time": 1126.3068484049945
+ },
+ {
+ "step": 3750,
+ "valid accuracy": 0.5,
+ "train loss": 0.5778432558774949,
+ "train samples": 15000,
+ "train time": 30.077826159038523,
+ "eval time": 11.010653469995304,
+ "tokens / sec": 7204.742751493022,
+ "mem allocated avg": 6901065279.488,
+ "mem reserved avg": 11319788961.792,
+ "elapsed time": 1209.0550349339974
+ },
+ {
+ "step": 4000,
+ "valid accuracy": 0.4,
+ "train loss": 0.5869229323863984,
+ "train samples": 16000,
+ "train time": 29.213863794990175,
+ "eval time": 11.144038623999222,
+ "tokens / sec": 6995.753845988955,
+ "mem allocated avg": 6883645001.728,
+ "mem reserved avg": 11058953584.64,
+ "elapsed time": 1290.3985370609953
+ },
+ {
+ "step": 4250,
+ "valid accuracy": 0.46,
+ "train loss": 0.5733816763162612,
+ "train samples": 17000,
+ "train time": 29.18649683901458,
+ "eval time": 11.153094029003114,
+ "tokens / sec": 7242.698607029438,
+ "mem allocated avg": 6893432758.272,
+ "mem reserved avg": 11193884344.32,
+ "elapsed time": 1372.1237251569983
+ },
+ {
+ "step": 4500,
+ "valid accuracy": 0.48,
+ "train loss": 0.5803762240409851,
+ "train samples": 18000,
+ "train time": 29.077459994943638,
+ "eval time": 11.118935573998897,
+ "tokens / sec": 7147.047920834147,
+ "mem allocated avg": 6888416004.096,
+ "mem reserved avg": 11124485390.336,
+ "elapsed time": 1453.4214935309938
+ },
+ {
+ "step": 4750,
+ "valid accuracy": 0.48,
+ "train loss": 0.5692038584947586,
+ "train samples": 19000,
+ "train time": 29.40723867896304,
+ "eval time": 11.099454375005735,
+ "tokens / sec": 7139.024588193769,
+ "mem allocated avg": 6890813089.792,
+ "mem reserved avg": 11168844349.44,
+ "elapsed time": 1535.6791463129994
+ },
+ {
+ "step": 5000,
+ "valid accuracy": 0.48,
+ "train loss": 0.5775641392469406,
+ "train samples": 20000,
+ "train time": 28.941933833950316,
+ "eval time": 11.18307958800142,
+ "tokens / sec": 7196.47834159849,
+ "mem allocated avg": 6887869800.448,
+ "mem reserved avg": 11118328152.064,
+ "elapsed time": 1617.277517963994
+ },
+ {
+ "step": 5000,
+ "test accuracy": 0.5079605761940864,
+ "train loss": 0.5775641392469406,
+ "train samples": 20000,
+ "train total tokens": 4198051
+ }
+ ]
+ },
+ "meta_info": {
+ "model_info": {
+ "sha": "13afe5124825b4f3751f836b40dafda64c1ed062",
+ "created_at": "2024-09-18T15:23:48+00:00"
+ },
+ "dataset_info": {
+ "metamath": {
+ "sha": "aa4f34d3d2d3231299b5b03d9b3e5a20da45aa18",
+ "created_at": "2023-09-21T17:22:46+00:00"
+ },
+ "gsm8k": {
+ "sha": "e53f048856ff4f594e959d75785d2c2d37b678ee",
+ "created_at": "2022-04-12T10:22:10+00:00"
+ }
+ },
+ "package_info": {
+ "transformers-version": "4.52.4",
+ "transformers-commit-hash": null,
+ "peft-version": "0.15.2.dev0",
+ "peft-commit-hash": "5fe7f8f8abe914d313fc3751f2ea92de7718fbaf",
+ "datasets-version": "3.6.0",
+ "datasets-commit-hash": null,
+ "bitsandbytes-version": "0.46.0",
+ "bitsandbytes-commit-hash": null,
+ "torch-version": "2.7.1+cu126",
+ "torch-commit-hash": null
+ },
+ "system_info": {
+ "system": "Linux",
+ "release": "6.8.0-1029-aws",
+ "version": "#31-Ubuntu SMP Wed Apr 23 18:42:41 UTC 2025",
+ "machine": "x86_64",
+ "processor": "x86_64",
+ "accelerator": "NVIDIA L40S"
+ },
+ "pytorch_info": "PyTorch built with:\n - GCC 11.2\n - C++ Version: 201703\n - Intel(R) oneAPI Math Kernel Library Version 2024.2-Product Build 20240605 for Intel(R) 64 architecture applications\n - Intel(R) MKL-DNN v3.7.1 (Git Hash 8d263e693366ef8db40acc569cc7d8edf644556d)\n - OpenMP 201511 (a.k.a. OpenMP 4.5)\n - LAPACK is enabled (usually provided by MKL)\n - NNPACK is enabled\n - CPU capability usage: AVX2\n - CUDA Runtime 12.6\n - NVCC architecture flags: -gencode;arch=compute_50,code=sm_50;-gencode;arch=compute_60,code=sm_60;-gencode;arch=compute_70,code=sm_70;-gencode;arch=compute_75,code=sm_75;-gencode;arch=compute_80,code=sm_80;-gencode;arch=compute_86,code=sm_86;-gencode;arch=compute_90,code=sm_90\n - CuDNN 90.7.1 (built against CUDA 12.8)\n - Built with CuDNN 90.5.1\n - Magma 2.6.1\n - Build settings: BLAS_INFO=mkl, BUILD_TYPE=Release, COMMIT_SHA=e2d141dbde55c2a4370fac5165b0561b6af4798b, CUDA_VERSION=12.6, CUDNN_VERSION=9.5.1, CXX_COMPILER=/opt/rh/gcc-toolset-11/root/usr/bin/c++, CXX_FLAGS= -D_GLIBCXX_USE_CXX11_ABI=1 -fvisibility-inlines-hidden -DUSE_PTHREADPOOL -DNDEBUG -DUSE_KINETO -DLIBKINETO_NOROCTRACER -DLIBKINETO_NOXPUPTI=ON -DUSE_FBGEMM -DUSE_PYTORCH_QNNPACK -DUSE_XNNPACK -DSYMBOLICATE_MOBILE_DEBUG_HANDLE -O2 -fPIC -Wall -Wextra -Werror=return-type -Werror=non-virtual-dtor -Werror=range-loop-construct -Werror=bool-operation -Wnarrowing -Wno-missing-field-initializers -Wno-unknown-pragmas -Wno-unused-parameter -Wno-strict-overflow -Wno-strict-aliasing -Wno-stringop-overflow -Wsuggest-override -Wno-psabi -Wno-error=old-style-cast -fdiagnostics-color=always -faligned-new -Wno-maybe-uninitialized -fno-math-errno -fno-trapping-math -Werror=format -Wno-stringop-overflow, LAPACK_INFO=mkl, PERF_WITH_AVX=1, PERF_WITH_AVX2=1, TORCH_VERSION=2.7.1, USE_CUDA=ON, USE_CUDNN=ON, USE_CUSPARSELT=1, USE_GFLAGS=OFF, USE_GLOG=OFF, USE_GLOO=ON, USE_MKL=ON, USE_MKLDNN=ON, USE_MPI=OFF, USE_NCCL=1, USE_NNPACK=ON, USE_OPENMP=ON, USE_ROCM=OFF, USE_ROCM_KERNEL_ASSERT=OFF, \n"
+ }
+}
diff --git a/peft/method_comparison/MetaMathQA/results/c3a--llama-3.2-3B-default.json b/peft/method_comparison/MetaMathQA/results/c3a--llama-3.2-3B-default.json
new file mode 100644
index 0000000000000000000000000000000000000000..dedfb5f28850701d45d209484d9fdff0b0bafa89
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/results/c3a--llama-3.2-3B-default.json
@@ -0,0 +1,350 @@
+{
+ "run_info": {
+ "created_at": "2025-07-31T13:35:43+00:00",
+ "total_time": 2124.5942297870006,
+ "experiment_name": "c3a/llama-3.2-3B-default",
+ "peft_branch": "main",
+ "train_config": {
+ "model_id": "meta-llama/Llama-3.2-3B",
+ "dtype": "bfloat16",
+ "max_seq_length": 768,
+ "batch_size": 4,
+ "batch_size_eval": 50,
+ "max_steps": 5000,
+ "eval_steps": 250,
+ "compile": false,
+ "query_template": "Question: {query} Think step by step.\nAnswer:",
+ "seed": 0,
+ "grad_norm_clip": 1.0,
+ "optimizer_type": "AdamW",
+ "optimizer_kwargs": {
+ "lr": 0.3,
+ "weight_decay": 1e-05
+ },
+ "lr_scheduler": "cosine",
+ "use_amp": false,
+ "autocast_adapter_dtype": true,
+ "generation_kwargs": {
+ "max_length": 800,
+ "max_new_tokens": 300
+ },
+ "attn_implementation": null
+ },
+ "peft_config": {
+ "task_type": null,
+ "peft_type": "C3A",
+ "auto_mapping": null,
+ "base_model_name_or_path": "meta-llama/Llama-3.2-3B",
+ "revision": null,
+ "inference_mode": false,
+ "block_size": 64,
+ "target_modules": [
+ "q_proj",
+ "v_proj"
+ ],
+ "bias": "none",
+ "modules_to_save": null,
+ "layers_to_transform": null,
+ "layers_pattern": null,
+ "block_size_pattern": {},
+ "init_weights": false
+ },
+ "error_msg": ""
+ },
+ "train_info": {
+ "accelerator_memory_reserved_avg": 11804454210,
+ "accelerator_memory_max": 22280142848,
+ "accelerator_memory_reserved_99th": 17825917829,
+ "train_time": 1924.4760333429977,
+ "file_size": 22027512,
+ "num_trainable_params": 5505024,
+ "num_total_params": 3218254848,
+ "status": "success",
+ "metrics": [
+ {
+ "step": 250,
+ "valid accuracy": 0.36,
+ "train loss": 0.8909663727283478,
+ "train samples": 1000,
+ "train time": 39.02584077800293,
+ "eval time": 13.030882289000147,
+ "tokens / sec": 5425.097724463024,
+ "mem allocated avg": 6868124932.096,
+ "mem reserved avg": 11851408605.184,
+ "elapsed time": 101.62553732800006
+ },
+ {
+ "step": 500,
+ "valid accuracy": 0.42,
+ "train loss": 0.7016348876953125,
+ "train samples": 2000,
+ "train time": 38.45351204700091,
+ "eval time": 7.171581626000261,
+ "tokens / sec": 5408.9987865288385,
+ "mem allocated avg": 6861684402.176,
+ "mem reserved avg": 11746811052.032,
+ "elapsed time": 190.13871278500028
+ },
+ {
+ "step": 750,
+ "valid accuracy": 0.4,
+ "train loss": 0.6737332336902618,
+ "train samples": 3000,
+ "train time": 38.979470817998845,
+ "eval time": 7.451876584000274,
+ "tokens / sec": 5500.356867364139,
+ "mem allocated avg": 6871526113.28,
+ "mem reserved avg": 11907578724.352,
+ "elapsed time": 279.83808459899956
+ },
+ {
+ "step": 1000,
+ "valid accuracy": 0.42,
+ "train loss": 0.654857279419899,
+ "train samples": 4000,
+ "train time": 38.61999764599932,
+ "eval time": 13.0494962570001,
+ "tokens / sec": 5394.5109450720465,
+ "mem allocated avg": 6862362261.504,
+ "mem reserved avg": 11770039107.584,
+ "elapsed time": 374.5986276450003
+ },
+ {
+ "step": 1250,
+ "valid accuracy": 0.36,
+ "train loss": 0.6510260388851166,
+ "train samples": 5000,
+ "train time": 38.424466599010884,
+ "eval time": 9.087004377000085,
+ "tokens / sec": 5427.2191251541835,
+ "mem allocated avg": 6862755778.56,
+ "mem reserved avg": 11764250968.064,
+ "elapsed time": 465.21620532700035
+ },
+ {
+ "step": 1500,
+ "valid accuracy": 0.44,
+ "train loss": 0.6443832906484603,
+ "train samples": 6000,
+ "train time": 38.60136020600203,
+ "eval time": 8.362256499000068,
+ "tokens / sec": 5422.891806995228,
+ "mem allocated avg": 6864079349.76,
+ "mem reserved avg": 11795154599.936,
+ "elapsed time": 555.3471686519997
+ },
+ {
+ "step": 1750,
+ "valid accuracy": 0.46,
+ "train loss": 0.6348284522294998,
+ "train samples": 7000,
+ "train time": 38.819046561000505,
+ "eval time": 12.987756649999938,
+ "tokens / sec": 5393.09999979052,
+ "mem allocated avg": 6865506678.784,
+ "mem reserved avg": 11806663770.112,
+ "elapsed time": 650.521843128
+ },
+ {
+ "step": 2000,
+ "valid accuracy": 0.42,
+ "train loss": 0.6368349348306656,
+ "train samples": 8000,
+ "train time": 38.522883960999025,
+ "eval time": 7.980172546000176,
+ "tokens / sec": 5391.496654567027,
+ "mem allocated avg": 6861885327.36,
+ "mem reserved avg": 11751290568.704,
+ "elapsed time": 740.3195631050003
+ },
+ {
+ "step": 2250,
+ "valid accuracy": 0.54,
+ "train loss": 0.625629832983017,
+ "train samples": 9000,
+ "train time": 39.25956673700239,
+ "eval time": 12.96675302299991,
+ "tokens / sec": 5475.047685572397,
+ "mem allocated avg": 6873176825.856,
+ "mem reserved avg": 11939161833.472,
+ "elapsed time": 836.2159785140002
+ },
+ {
+ "step": 2500,
+ "valid accuracy": 0.48,
+ "train loss": 0.6208862951993942,
+ "train samples": 10000,
+ "train time": 38.55282327599798,
+ "eval time": 13.027243182000348,
+ "tokens / sec": 5342.4621726271835,
+ "mem allocated avg": 6857644570.624,
+ "mem reserved avg": 11701781004.288,
+ "elapsed time": 930.913046529
+ },
+ {
+ "step": 2750,
+ "valid accuracy": 0.5,
+ "train loss": 0.6103025305271149,
+ "train samples": 11000,
+ "train time": 38.69634664399382,
+ "eval time": 8.820525846999772,
+ "tokens / sec": 5475.478136199886,
+ "mem allocated avg": 6868590700.544,
+ "mem reserved avg": 11873739079.68,
+ "elapsed time": 1021.7124050419998
+ },
+ {
+ "step": 3000,
+ "valid accuracy": 0.48,
+ "train loss": 0.5977142386436463,
+ "train samples": 12000,
+ "train time": 38.552098998990004,
+ "eval time": 8.200822365000022,
+ "tokens / sec": 5414.257729662615,
+ "mem allocated avg": 6864444424.192,
+ "mem reserved avg": 11782135480.32,
+ "elapsed time": 1111.412057769
+ },
+ {
+ "step": 3250,
+ "valid accuracy": 0.54,
+ "train loss": 0.6062814455032348,
+ "train samples": 13000,
+ "train time": 38.8476868979933,
+ "eval time": 9.795037900000352,
+ "tokens / sec": 5428.92040274589,
+ "mem allocated avg": 6865998022.656,
+ "mem reserved avg": 11821754875.904,
+ "elapsed time": 1203.456824805
+ },
+ {
+ "step": 3500,
+ "valid accuracy": 0.54,
+ "train loss": 0.5876059620380402,
+ "train samples": 14000,
+ "train time": 39.031564167995384,
+ "eval time": 12.945379363999564,
+ "tokens / sec": 5373.855864377278,
+ "mem allocated avg": 6864331821.056,
+ "mem reserved avg": 11797008482.304,
+ "elapsed time": 1298.7533704500001
+ },
+ {
+ "step": 3750,
+ "valid accuracy": 0.5,
+ "train loss": 0.5839143842458725,
+ "train samples": 15000,
+ "train time": 39.49590561498735,
+ "eval time": 8.033668121999654,
+ "tokens / sec": 5486.720626498778,
+ "mem allocated avg": 6875409352.704,
+ "mem reserved avg": 11980509282.304,
+ "elapsed time": 1390.233747202
+ },
+ {
+ "step": 4000,
+ "valid accuracy": 0.56,
+ "train loss": 0.591371684551239,
+ "train samples": 16000,
+ "train time": 38.53615990600338,
+ "eval time": 12.963392601999658,
+ "tokens / sec": 5303.408551825156,
+ "mem allocated avg": 6856836122.624,
+ "mem reserved avg": 11673922437.12,
+ "elapsed time": 1484.869673702
+ },
+ {
+ "step": 4250,
+ "valid accuracy": 0.56,
+ "train loss": 0.577637273311615,
+ "train samples": 17000,
+ "train time": 38.46427064899399,
+ "eval time": 7.68621369199991,
+ "tokens / sec": 5495.723600975878,
+ "mem allocated avg": 6867260166.144,
+ "mem reserved avg": 11833297600.512,
+ "elapsed time": 1574.4202131299999
+ },
+ {
+ "step": 4500,
+ "valid accuracy": 0.56,
+ "train loss": 0.584571166396141,
+ "train samples": 18000,
+ "train time": 38.4389222480022,
+ "eval time": 7.678759501000968,
+ "tokens / sec": 5406.447107418601,
+ "mem allocated avg": 6862379522.048,
+ "mem reserved avg": 11747851239.424,
+ "elapsed time": 1663.6057326830005
+ },
+ {
+ "step": 4750,
+ "valid accuracy": 0.58,
+ "train loss": 0.5745555943250656,
+ "train samples": 19000,
+ "train time": 38.87202309699023,
+ "eval time": 7.697188709000329,
+ "tokens / sec": 5400.773699793749,
+ "mem allocated avg": 6863993468.928,
+ "mem reserved avg": 11795691470.848,
+ "elapsed time": 1753.6286738400004
+ },
+ {
+ "step": 5000,
+ "valid accuracy": 0.56,
+ "train loss": 0.5808088963031769,
+ "train samples": 20000,
+ "train time": 38.65712555299615,
+ "eval time": 7.723833553000077,
+ "tokens / sec": 5387.8811996629975,
+ "mem allocated avg": 6861167886.336,
+ "mem reserved avg": 11749034033.152,
+ "elapsed time": 1843.4390854000003
+ },
+ {
+ "step": 5000,
+ "test accuracy": 0.510235026535254,
+ "train loss": 0.5808088963031769,
+ "train samples": 20000,
+ "train total tokens": 4198051
+ }
+ ]
+ },
+ "meta_info": {
+ "model_info": {
+ "sha": "13afe5124825b4f3751f836b40dafda64c1ed062",
+ "created_at": "2024-09-18T15:23:48+00:00"
+ },
+ "dataset_info": {
+ "metamath": {
+ "sha": "aa4f34d3d2d3231299b5b03d9b3e5a20da45aa18",
+ "created_at": "2023-09-21T17:22:46+00:00"
+ },
+ "gsm8k": {
+ "sha": "e53f048856ff4f594e959d75785d2c2d37b678ee",
+ "created_at": "2022-04-12T10:22:10+00:00"
+ }
+ },
+ "package_info": {
+ "transformers-version": "4.52.4",
+ "transformers-commit-hash": null,
+ "peft-version": "0.16.1.dev0",
+ "peft-commit-hash": "25e5c6b25c4589eb2683484ede1ba3d985d8a760",
+ "datasets-version": "3.6.0",
+ "datasets-commit-hash": null,
+ "bitsandbytes-version": "0.46.0",
+ "bitsandbytes-commit-hash": null,
+ "torch-version": "2.7.1+cu126",
+ "torch-commit-hash": null
+ },
+ "system_info": {
+ "system": "Linux",
+ "release": "6.8.0-1031-aws",
+ "version": "#33-Ubuntu SMP Fri Jun 20 18:11:07 UTC 2025",
+ "machine": "x86_64",
+ "processor": "x86_64",
+ "accelerator": "NVIDIA L40S"
+ },
+ "pytorch_info": "PyTorch built with:\n - GCC 11.2\n - C++ Version: 201703\n - Intel(R) oneAPI Math Kernel Library Version 2024.2-Product Build 20240605 for Intel(R) 64 architecture applications\n - Intel(R) MKL-DNN v3.7.1 (Git Hash 8d263e693366ef8db40acc569cc7d8edf644556d)\n - OpenMP 201511 (a.k.a. OpenMP 4.5)\n - LAPACK is enabled (usually provided by MKL)\n - NNPACK is enabled\n - CPU capability usage: AVX2\n - CUDA Runtime 12.6\n - NVCC architecture flags: -gencode;arch=compute_50,code=sm_50;-gencode;arch=compute_60,code=sm_60;-gencode;arch=compute_70,code=sm_70;-gencode;arch=compute_75,code=sm_75;-gencode;arch=compute_80,code=sm_80;-gencode;arch=compute_86,code=sm_86;-gencode;arch=compute_90,code=sm_90\n - CuDNN 90.7.1 (built against CUDA 12.8)\n - Built with CuDNN 90.5.1\n - Magma 2.6.1\n - Build settings: BLAS_INFO=mkl, BUILD_TYPE=Release, COMMIT_SHA=e2d141dbde55c2a4370fac5165b0561b6af4798b, CUDA_VERSION=12.6, CUDNN_VERSION=9.5.1, CXX_COMPILER=/opt/rh/gcc-toolset-11/root/usr/bin/c++, CXX_FLAGS= -D_GLIBCXX_USE_CXX11_ABI=1 -fvisibility-inlines-hidden -DUSE_PTHREADPOOL -DNDEBUG -DUSE_KINETO -DLIBKINETO_NOROCTRACER -DLIBKINETO_NOXPUPTI=ON -DUSE_FBGEMM -DUSE_PYTORCH_QNNPACK -DUSE_XNNPACK -DSYMBOLICATE_MOBILE_DEBUG_HANDLE -O2 -fPIC -Wall -Wextra -Werror=return-type -Werror=non-virtual-dtor -Werror=range-loop-construct -Werror=bool-operation -Wnarrowing -Wno-missing-field-initializers -Wno-unknown-pragmas -Wno-unused-parameter -Wno-strict-overflow -Wno-strict-aliasing -Wno-stringop-overflow -Wsuggest-override -Wno-psabi -Wno-error=old-style-cast -fdiagnostics-color=always -faligned-new -Wno-maybe-uninitialized -fno-math-errno -fno-trapping-math -Werror=format -Wno-stringop-overflow, LAPACK_INFO=mkl, PERF_WITH_AVX=1, PERF_WITH_AVX2=1, TORCH_VERSION=2.7.1, USE_CUDA=ON, USE_CUDNN=ON, USE_CUSPARSELT=1, USE_GFLAGS=OFF, USE_GLOG=OFF, USE_GLOO=ON, USE_MKL=ON, USE_MKLDNN=ON, USE_MPI=OFF, USE_NCCL=1, USE_NNPACK=ON, USE_OPENMP=ON, USE_ROCM=OFF, USE_ROCM_KERNEL_ASSERT=OFF, \n"
+ }
+}
\ No newline at end of file
diff --git a/peft/method_comparison/MetaMathQA/results/fourierft--llama-3.2-3B-default.json b/peft/method_comparison/MetaMathQA/results/fourierft--llama-3.2-3B-default.json
new file mode 100644
index 0000000000000000000000000000000000000000..f3bc26876c01612fe60f472439e877c9c3ab1fe8
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/results/fourierft--llama-3.2-3B-default.json
@@ -0,0 +1,354 @@
+{
+ "run_info": {
+ "created_at": "2025-06-20T10:18:57+00:00",
+ "total_time": 2823.832106703994,
+ "experiment_name": "fourierft/llama-3.2-3B-default",
+ "peft_branch": "main",
+ "train_config": {
+ "model_id": "meta-llama/Llama-3.2-3B",
+ "dtype": "bfloat16",
+ "max_seq_length": 768,
+ "batch_size": 4,
+ "batch_size_eval": 50,
+ "max_steps": 5000,
+ "eval_steps": 250,
+ "compile": false,
+ "query_template": "Question: {query} Think step by step.\nAnswer:",
+ "seed": 0,
+ "grad_norm_clip": 1.0,
+ "optimizer_type": "AdamW",
+ "optimizer_kwargs": {
+ "lr": 0.0001,
+ "weight_decay": 0.1
+ },
+ "lr_scheduler": "cosine",
+ "use_amp": false,
+ "autocast_adapter_dtype": true,
+ "generation_kwargs": {
+ "max_length": 800,
+ "max_new_tokens": 300
+ },
+ "attn_implementation": null
+ },
+ "peft_config": {
+ "task_type": null,
+ "peft_type": "FOURIERFT",
+ "auto_mapping": null,
+ "base_model_name_or_path": "meta-llama/Llama-3.2-3B",
+ "revision": null,
+ "inference_mode": false,
+ "n_frequency": 1000,
+ "scaling": 300,
+ "random_loc_seed": 777,
+ "fan_in_fan_out": false,
+ "target_modules": [
+ "q_proj",
+ "v_proj"
+ ],
+ "exclude_modules": null,
+ "bias": "none",
+ "modules_to_save": null,
+ "layers_to_transform": null,
+ "layers_pattern": null,
+ "n_frequency_pattern": {},
+ "init_weights": false
+ },
+ "error_msg": ""
+ },
+ "train_info": {
+ "accelerator_memory_reserved_avg": 13104129350,
+ "accelerator_memory_max": 23653777408,
+ "accelerator_memory_reserved_99th": 19017267937,
+ "train_time": 2424.3862988609762,
+ "file_size": 231416,
+ "num_trainable_params": 56000,
+ "num_total_params": 3212805824,
+ "status": "success",
+ "metrics": [
+ {
+ "step": 250,
+ "valid accuracy": 0.0,
+ "train loss": 1.3263031902313231,
+ "train samples": 1000,
+ "train time": 53.55340486107161,
+ "eval time": 19.578013352002017,
+ "tokens / sec": 3953.4180982374883,
+ "mem allocated avg": 6781303625.728,
+ "mem reserved avg": 13152850804.736,
+ "elapsed time": 119.84825310099404
+ },
+ {
+ "step": 500,
+ "valid accuracy": 0.0,
+ "train loss": 1.3399862418174744,
+ "train samples": 2000,
+ "train time": 52.85717789203045,
+ "eval time": 19.544192551999004,
+ "tokens / sec": 3935.03793231005,
+ "mem allocated avg": 6774035257.344,
+ "mem reserved avg": 13043463356.416,
+ "elapsed time": 233.5829256769939
+ },
+ {
+ "step": 750,
+ "valid accuracy": 0.0,
+ "train loss": 1.3045952091217041,
+ "train samples": 3000,
+ "train time": 53.35706212905643,
+ "eval time": 19.607110917990212,
+ "tokens / sec": 4018.2309790861696,
+ "mem allocated avg": 6783920330.752,
+ "mem reserved avg": 13205673869.312,
+ "elapsed time": 348.1469791559939
+ },
+ {
+ "step": 1000,
+ "valid accuracy": 0.0,
+ "train loss": 1.3111453976631164,
+ "train samples": 4000,
+ "train time": 52.95546973698947,
+ "eval time": 19.472347582006478,
+ "tokens / sec": 3934.1733919976355,
+ "mem allocated avg": 6776025266.176,
+ "mem reserved avg": 13077269446.656,
+ "elapsed time": 461.81266678999236
+ },
+ {
+ "step": 1250,
+ "valid accuracy": 0.0,
+ "train loss": 1.299716483592987,
+ "train samples": 5000,
+ "train time": 52.12036712520057,
+ "eval time": 19.626158429004136,
+ "tokens / sec": 4001.0846335572023,
+ "mem allocated avg": 6775331573.76,
+ "mem reserved avg": 13063344357.376,
+ "elapsed time": 574.6407375999988
+ },
+ {
+ "step": 1500,
+ "valid accuracy": 0.0,
+ "train loss": 1.2867344057559966,
+ "train samples": 6000,
+ "train time": 52.594848359090975,
+ "eval time": 19.54386943600548,
+ "tokens / sec": 3980.0666135738998,
+ "mem allocated avg": 6776458844.16,
+ "mem reserved avg": 13093568512.0,
+ "elapsed time": 688.0431025519938
+ },
+ {
+ "step": 1750,
+ "valid accuracy": 0.0,
+ "train loss": 1.2803141210079194,
+ "train samples": 7000,
+ "train time": 52.98738884186605,
+ "eval time": 19.568909612993593,
+ "tokens / sec": 3951.0344739725274,
+ "mem allocated avg": 6778496358.4,
+ "mem reserved avg": 13108768669.696,
+ "elapsed time": 801.9154772249894
+ },
+ {
+ "step": 2000,
+ "valid accuracy": 0.0,
+ "train loss": 1.2766506419181824,
+ "train samples": 8000,
+ "train time": 52.03297274692159,
+ "eval time": 19.525613270001486,
+ "tokens / sec": 3991.62279292005,
+ "mem allocated avg": 6774647097.344,
+ "mem reserved avg": 13051189264.384,
+ "elapsed time": 914.5343848449993
+ },
+ {
+ "step": 2250,
+ "valid accuracy": 0.0,
+ "train loss": 1.2596003375053406,
+ "train samples": 9000,
+ "train time": 53.934016149127274,
+ "eval time": 19.535415460006334,
+ "tokens / sec": 3985.388356870549,
+ "mem allocated avg": 6785830477.824,
+ "mem reserved avg": 13237223424.0,
+ "elapsed time": 1029.9007452719961
+ },
+ {
+ "step": 2500,
+ "valid accuracy": 0.0,
+ "train loss": 1.2684449093341827,
+ "train samples": 10000,
+ "train time": 52.006629903029534,
+ "eval time": 19.470633051998448,
+ "tokens / sec": 3960.3989026791724,
+ "mem allocated avg": 6771212331.008,
+ "mem reserved avg": 12996118052.864,
+ "elapsed time": 1142.5889472209965
+ },
+ {
+ "step": 2750,
+ "valid accuracy": 0.0,
+ "train loss": 1.2548872971534728,
+ "train samples": 11000,
+ "train time": 53.403087337108445,
+ "eval time": 19.463876378998975,
+ "tokens / sec": 3967.579601952513,
+ "mem allocated avg": 6781916252.16,
+ "mem reserved avg": 13168084516.864,
+ "elapsed time": 1257.0122518049902
+ },
+ {
+ "step": 3000,
+ "valid accuracy": 0.0,
+ "train loss": 1.253697858095169,
+ "train samples": 12000,
+ "train time": 53.20096563108382,
+ "eval time": 19.472515105997445,
+ "tokens / sec": 3923.443823321214,
+ "mem allocated avg": 6777045135.36,
+ "mem reserved avg": 13084844359.68,
+ "elapsed time": 1370.94780872899
+ },
+ {
+ "step": 3250,
+ "valid accuracy": 0.0,
+ "train loss": 1.248513156414032,
+ "train samples": 13000,
+ "train time": 52.962746563891415,
+ "eval time": 19.54665829600708,
+ "tokens / sec": 3982.06312328573,
+ "mem allocated avg": 6779038627.84,
+ "mem reserved avg": 13110345728.0,
+ "elapsed time": 1484.7621198889974
+ },
+ {
+ "step": 3500,
+ "valid accuracy": 0.0,
+ "train loss": 1.2477959940433503,
+ "train samples": 14000,
+ "train time": 52.93443578510778,
+ "eval time": 19.444701158994576,
+ "tokens / sec": 3962.4489595298505,
+ "mem allocated avg": 6776803573.76,
+ "mem reserved avg": 13097142059.008,
+ "elapsed time": 1598.8772237269877
+ },
+ {
+ "step": 3750,
+ "valid accuracy": 0.0,
+ "train loss": 1.228544222354889,
+ "train samples": 15000,
+ "train time": 53.31031796212483,
+ "eval time": 19.472959079008433,
+ "tokens / sec": 4064.9354249577,
+ "mem allocated avg": 6788200585.216,
+ "mem reserved avg": 13268999471.104,
+ "elapsed time": 1713.6814467679942
+ },
+ {
+ "step": 4000,
+ "valid accuracy": 0.0,
+ "train loss": 1.2609001460075377,
+ "train samples": 16000,
+ "train time": 51.9827769130934,
+ "eval time": 19.473652824002784,
+ "tokens / sec": 3931.552182017475,
+ "mem allocated avg": 6770180233.216,
+ "mem reserved avg": 12983610638.336,
+ "elapsed time": 1826.5604049959948
+ },
+ {
+ "step": 4250,
+ "valid accuracy": 0.0,
+ "train loss": 1.227214762210846,
+ "train samples": 17000,
+ "train time": 53.09942602888623,
+ "eval time": 19.547112297004787,
+ "tokens / sec": 3981.0034836347163,
+ "mem allocated avg": 6779591426.048,
+ "mem reserved avg": 13132760088.576,
+ "elapsed time": 1940.5098487799987
+ },
+ {
+ "step": 4500,
+ "valid accuracy": 0.0,
+ "train loss": 1.2504195840358734,
+ "train samples": 18000,
+ "train time": 52.23909889203787,
+ "eval time": 19.522137050997117,
+ "tokens / sec": 3978.207978462565,
+ "mem allocated avg": 6775933241.344,
+ "mem reserved avg": 13056079822.848,
+ "elapsed time": 2053.2267840139975
+ },
+ {
+ "step": 4750,
+ "valid accuracy": 0.0,
+ "train loss": 1.2349513354301453,
+ "train samples": 19000,
+ "train time": 53.36620609794045,
+ "eval time": 19.541859832999762,
+ "tokens / sec": 3933.931514912433,
+ "mem allocated avg": 6777532579.84,
+ "mem reserved avg": 13101604798.464,
+ "elapsed time": 2167.8329333979927
+ },
+ {
+ "step": 5000,
+ "valid accuracy": 0.0,
+ "train loss": 1.2480293517112733,
+ "train samples": 20000,
+ "train time": 52.46977503092785,
+ "eval time": 19.44991449599911,
+ "tokens / sec": 3969.5234042309344,
+ "mem allocated avg": 6773533165.568,
+ "mem reserved avg": 13049645760.512,
+ "elapsed time": 2281.220151823989
+ },
+ {
+ "step": 5000,
+ "test accuracy": 0.000758150113722517,
+ "train loss": 1.2480293517112733,
+ "train samples": 20000,
+ "train total tokens": 4198051
+ }
+ ]
+ },
+ "meta_info": {
+ "model_info": {
+ "sha": "13afe5124825b4f3751f836b40dafda64c1ed062",
+ "created_at": "2024-09-18T15:23:48+00:00"
+ },
+ "dataset_info": {
+ "metamath": {
+ "sha": "aa4f34d3d2d3231299b5b03d9b3e5a20da45aa18",
+ "created_at": "2023-09-21T17:22:46+00:00"
+ },
+ "gsm8k": {
+ "sha": "e53f048856ff4f594e959d75785d2c2d37b678ee",
+ "created_at": "2022-04-12T10:22:10+00:00"
+ }
+ },
+ "package_info": {
+ "transformers-version": "4.52.4",
+ "transformers-commit-hash": null,
+ "peft-version": "0.15.2.dev0",
+ "peft-commit-hash": "5fe7f8f8abe914d313fc3751f2ea92de7718fbaf",
+ "datasets-version": "3.6.0",
+ "datasets-commit-hash": null,
+ "bitsandbytes-version": "0.46.0",
+ "bitsandbytes-commit-hash": null,
+ "torch-version": "2.7.1+cu126",
+ "torch-commit-hash": null
+ },
+ "system_info": {
+ "system": "Linux",
+ "release": "6.8.0-1029-aws",
+ "version": "#31-Ubuntu SMP Wed Apr 23 18:42:41 UTC 2025",
+ "machine": "x86_64",
+ "processor": "x86_64",
+ "accelerator": "NVIDIA L40S"
+ },
+ "pytorch_info": "PyTorch built with:\n - GCC 11.2\n - C++ Version: 201703\n - Intel(R) oneAPI Math Kernel Library Version 2024.2-Product Build 20240605 for Intel(R) 64 architecture applications\n - Intel(R) MKL-DNN v3.7.1 (Git Hash 8d263e693366ef8db40acc569cc7d8edf644556d)\n - OpenMP 201511 (a.k.a. OpenMP 4.5)\n - LAPACK is enabled (usually provided by MKL)\n - NNPACK is enabled\n - CPU capability usage: AVX2\n - CUDA Runtime 12.6\n - NVCC architecture flags: -gencode;arch=compute_50,code=sm_50;-gencode;arch=compute_60,code=sm_60;-gencode;arch=compute_70,code=sm_70;-gencode;arch=compute_75,code=sm_75;-gencode;arch=compute_80,code=sm_80;-gencode;arch=compute_86,code=sm_86;-gencode;arch=compute_90,code=sm_90\n - CuDNN 90.7.1 (built against CUDA 12.8)\n - Built with CuDNN 90.5.1\n - Magma 2.6.1\n - Build settings: BLAS_INFO=mkl, BUILD_TYPE=Release, COMMIT_SHA=e2d141dbde55c2a4370fac5165b0561b6af4798b, CUDA_VERSION=12.6, CUDNN_VERSION=9.5.1, CXX_COMPILER=/opt/rh/gcc-toolset-11/root/usr/bin/c++, CXX_FLAGS= -D_GLIBCXX_USE_CXX11_ABI=1 -fvisibility-inlines-hidden -DUSE_PTHREADPOOL -DNDEBUG -DUSE_KINETO -DLIBKINETO_NOROCTRACER -DLIBKINETO_NOXPUPTI=ON -DUSE_FBGEMM -DUSE_PYTORCH_QNNPACK -DUSE_XNNPACK -DSYMBOLICATE_MOBILE_DEBUG_HANDLE -O2 -fPIC -Wall -Wextra -Werror=return-type -Werror=non-virtual-dtor -Werror=range-loop-construct -Werror=bool-operation -Wnarrowing -Wno-missing-field-initializers -Wno-unknown-pragmas -Wno-unused-parameter -Wno-strict-overflow -Wno-strict-aliasing -Wno-stringop-overflow -Wsuggest-override -Wno-psabi -Wno-error=old-style-cast -fdiagnostics-color=always -faligned-new -Wno-maybe-uninitialized -fno-math-errno -fno-trapping-math -Werror=format -Wno-stringop-overflow, LAPACK_INFO=mkl, PERF_WITH_AVX=1, PERF_WITH_AVX2=1, TORCH_VERSION=2.7.1, USE_CUDA=ON, USE_CUDNN=ON, USE_CUSPARSELT=1, USE_GFLAGS=OFF, USE_GLOG=OFF, USE_GLOO=ON, USE_MKL=ON, USE_MKLDNN=ON, USE_MPI=OFF, USE_NCCL=1, USE_NNPACK=ON, USE_OPENMP=ON, USE_ROCM=OFF, USE_ROCM_KERNEL_ASSERT=OFF, \n"
+ }
+}
diff --git a/peft/method_comparison/MetaMathQA/results/fourierft--llama-3.2-3B-n_frequency-5000.json b/peft/method_comparison/MetaMathQA/results/fourierft--llama-3.2-3B-n_frequency-5000.json
new file mode 100644
index 0000000000000000000000000000000000000000..3c7241b5f04142fdc9bb7a3702e4d08c1b91730a
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/results/fourierft--llama-3.2-3B-n_frequency-5000.json
@@ -0,0 +1,354 @@
+{
+ "run_info": {
+ "created_at": "2025-06-20T09:31:48+00:00",
+ "total_time": 2824.376998209991,
+ "experiment_name": "fourierft/llama-3.2-3B-n_frequency-5000",
+ "peft_branch": "main",
+ "train_config": {
+ "model_id": "meta-llama/Llama-3.2-3B",
+ "dtype": "bfloat16",
+ "max_seq_length": 768,
+ "batch_size": 4,
+ "batch_size_eval": 50,
+ "max_steps": 5000,
+ "eval_steps": 250,
+ "compile": false,
+ "query_template": "Question: {query} Think step by step.\nAnswer:",
+ "seed": 0,
+ "grad_norm_clip": 1.0,
+ "optimizer_type": "AdamW",
+ "optimizer_kwargs": {
+ "lr": 0.0001,
+ "weight_decay": 0.1
+ },
+ "lr_scheduler": "cosine",
+ "use_amp": false,
+ "autocast_adapter_dtype": true,
+ "generation_kwargs": {
+ "max_length": 800,
+ "max_new_tokens": 300
+ },
+ "attn_implementation": null
+ },
+ "peft_config": {
+ "task_type": null,
+ "peft_type": "FOURIERFT",
+ "auto_mapping": null,
+ "base_model_name_or_path": "meta-llama/Llama-3.2-3B",
+ "revision": null,
+ "inference_mode": false,
+ "n_frequency": 5000,
+ "scaling": 300,
+ "random_loc_seed": 777,
+ "fan_in_fan_out": false,
+ "target_modules": [
+ "v_proj",
+ "q_proj"
+ ],
+ "exclude_modules": null,
+ "bias": "none",
+ "modules_to_save": null,
+ "layers_to_transform": null,
+ "layers_pattern": null,
+ "n_frequency_pattern": {},
+ "init_weights": false
+ },
+ "error_msg": ""
+ },
+ "train_info": {
+ "accelerator_memory_reserved_avg": 13111221498,
+ "accelerator_memory_max": 23681040384,
+ "accelerator_memory_reserved_99th": 19054869872,
+ "train_time": 2421.913372163006,
+ "file_size": 1127472,
+ "num_trainable_params": 280000,
+ "num_total_params": 3213029824,
+ "status": "success",
+ "metrics": [
+ {
+ "step": 250,
+ "valid accuracy": 0.0,
+ "train loss": 1.3800132541656494,
+ "train samples": 1000,
+ "train time": 53.57064967796032,
+ "eval time": 19.631924207002157,
+ "tokens / sec": 3952.1454616053315,
+ "mem allocated avg": 6784830552.064,
+ "mem reserved avg": 13158731218.944,
+ "elapsed time": 119.20255395398999
+ },
+ {
+ "step": 500,
+ "valid accuracy": 0.0,
+ "train loss": 1.3702282276153563,
+ "train samples": 2000,
+ "train time": 53.00863014489005,
+ "eval time": 19.629790833001607,
+ "tokens / sec": 3923.7950392508,
+ "mem allocated avg": 6777176354.816,
+ "mem reserved avg": 13048941117.44,
+ "elapsed time": 232.4386439989903
+ },
+ {
+ "step": 750,
+ "valid accuracy": 0.0,
+ "train loss": 1.3024170677661895,
+ "train samples": 3000,
+ "train time": 53.97298614999454,
+ "eval time": 19.64192995200574,
+ "tokens / sec": 3972.3760957780855,
+ "mem allocated avg": 6787548153.856,
+ "mem reserved avg": 13211654946.816,
+ "elapsed time": 346.9217278779979
+ },
+ {
+ "step": 1000,
+ "valid accuracy": 0.0,
+ "train loss": 1.2704877371788026,
+ "train samples": 4000,
+ "train time": 52.95541349705309,
+ "eval time": 19.62998814698949,
+ "tokens / sec": 3934.1775701854103,
+ "mem allocated avg": 6779591346.176,
+ "mem reserved avg": 13082126450.688,
+ "elapsed time": 460.14450727400254
+ },
+ {
+ "step": 1250,
+ "valid accuracy": 0.0,
+ "train loss": 1.2236453666687013,
+ "train samples": 5000,
+ "train time": 53.36593960013124,
+ "eval time": 19.652927816001466,
+ "tokens / sec": 3907.698460152047,
+ "mem allocated avg": 6779029788.672,
+ "mem reserved avg": 13073486184.448,
+ "elapsed time": 573.5348878969962
+ },
+ {
+ "step": 1500,
+ "valid accuracy": 0.0,
+ "train loss": 1.1792121708393097,
+ "train samples": 6000,
+ "train time": 53.3776921518147,
+ "eval time": 19.616937039012555,
+ "tokens / sec": 3921.69446750581,
+ "mem allocated avg": 6779851802.624,
+ "mem reserved avg": 13098995941.376,
+ "elapsed time": 686.9838123609952
+ },
+ {
+ "step": 1750,
+ "valid accuracy": 0.02,
+ "train loss": 1.1485692322254182,
+ "train samples": 7000,
+ "train time": 53.188338823019876,
+ "eval time": 19.653264298991417,
+ "tokens / sec": 3936.1071361264494,
+ "mem allocated avg": 6782223466.496,
+ "mem reserved avg": 13116058370.048,
+ "elapsed time": 800.3354816049978
+ },
+ {
+ "step": 2000,
+ "valid accuracy": 0.06,
+ "train loss": 1.1230667443275453,
+ "train samples": 8000,
+ "train time": 53.074023688037414,
+ "eval time": 19.656479785000556,
+ "tokens / sec": 3913.3268135239105,
+ "mem allocated avg": 6778141935.616,
+ "mem reserved avg": 13055400345.6,
+ "elapsed time": 913.367253695993
+ },
+ {
+ "step": 2250,
+ "valid accuracy": 0.1,
+ "train loss": 1.094045166015625,
+ "train samples": 9000,
+ "train time": 54.34830153394432,
+ "eval time": 19.628162662993418,
+ "tokens / sec": 3955.008600696563,
+ "mem allocated avg": 6789509545.984,
+ "mem reserved avg": 13248556433.408,
+ "elapsed time": 1028.463336018991
+ },
+ {
+ "step": 2500,
+ "valid accuracy": 0.12,
+ "train loss": 1.077717797279358,
+ "train samples": 10000,
+ "train time": 52.1458756570355,
+ "eval time": 19.611369335994823,
+ "tokens / sec": 3949.823402231256,
+ "mem allocated avg": 6775024920.576,
+ "mem reserved avg": 13002233348.096,
+ "elapsed time": 1140.4990660109906
+ },
+ {
+ "step": 2750,
+ "valid accuracy": 0.12,
+ "train loss": 1.0569540388584138,
+ "train samples": 11000,
+ "train time": 53.227410834049806,
+ "eval time": 19.625236430001678,
+ "tokens / sec": 3980.6745562092756,
+ "mem allocated avg": 6785537161.216,
+ "mem reserved avg": 13177051938.816,
+ "elapsed time": 1254.066401210992
+ },
+ {
+ "step": 3000,
+ "valid accuracy": 0.12,
+ "train loss": 1.0361379137039184,
+ "train samples": 12000,
+ "train time": 53.65395914198598,
+ "eval time": 19.719437510997523,
+ "tokens / sec": 3890.3186892066865,
+ "mem allocated avg": 6780720910.336,
+ "mem reserved avg": 13092201168.896,
+ "elapsed time": 1367.8724600419955
+ },
+ {
+ "step": 3250,
+ "valid accuracy": 0.16,
+ "train loss": 1.0240549674034118,
+ "train samples": 13000,
+ "train time": 52.97706237102102,
+ "eval time": 19.7029277440015,
+ "tokens / sec": 3980.9870642311216,
+ "mem allocated avg": 6782688188.416,
+ "mem reserved avg": 13119816466.432,
+ "elapsed time": 1481.1549517469975
+ },
+ {
+ "step": 3500,
+ "valid accuracy": 0.18,
+ "train loss": 1.0098259932994842,
+ "train samples": 14000,
+ "train time": 52.869576787008555,
+ "eval time": 19.597270865997416,
+ "tokens / sec": 3967.3099870839346,
+ "mem allocated avg": 6780575592.448,
+ "mem reserved avg": 13102678540.288,
+ "elapsed time": 1594.3849144269916
+ },
+ {
+ "step": 3750,
+ "valid accuracy": 0.22,
+ "train loss": 0.9942408270835876,
+ "train samples": 15000,
+ "train time": 54.702630093932385,
+ "eval time": 19.623511597994366,
+ "tokens / sec": 3961.4731435744384,
+ "mem allocated avg": 6792074147.84,
+ "mem reserved avg": 13278612815.872,
+ "elapsed time": 1709.9712875620025
+ },
+ {
+ "step": 4000,
+ "valid accuracy": 0.16,
+ "train loss": 1.0123027296066285,
+ "train samples": 16000,
+ "train time": 52.456372838059906,
+ "eval time": 19.68401901901234,
+ "tokens / sec": 3896.056645603915,
+ "mem allocated avg": 6773958766.592,
+ "mem reserved avg": 12989172285.44,
+ "elapsed time": 1822.6668115109933
+ },
+ {
+ "step": 4250,
+ "valid accuracy": 0.24,
+ "train loss": 0.9849327182769776,
+ "train samples": 17000,
+ "train time": 53.25562528491719,
+ "eval time": 19.648335694990237,
+ "tokens / sec": 3969.3271625123257,
+ "mem allocated avg": 6783509901.312,
+ "mem reserved avg": 13139588415.488,
+ "elapsed time": 1936.0694442329986
+ },
+ {
+ "step": 4500,
+ "valid accuracy": 0.18,
+ "train loss": 0.9994378657341003,
+ "train samples": 18000,
+ "train time": 53.01732904899109,
+ "eval time": 19.688141086997348,
+ "tokens / sec": 3919.8127051621955,
+ "mem allocated avg": 6779470948.352,
+ "mem reserved avg": 13063528906.752,
+ "elapsed time": 2048.985867203999
+ },
+ {
+ "step": 4750,
+ "valid accuracy": 0.16,
+ "train loss": 0.9892346875667573,
+ "train samples": 19000,
+ "train time": 53.11992502908106,
+ "eval time": 19.68838914000662,
+ "tokens / sec": 3952.1704875348883,
+ "mem allocated avg": 6781060145.152,
+ "mem reserved avg": 13109733359.616,
+ "elapsed time": 2162.7099456459982
+ },
+ {
+ "step": 5000,
+ "valid accuracy": 0.2,
+ "train loss": 0.9978675174713135,
+ "train samples": 20000,
+ "train time": 52.76285280592856,
+ "eval time": 19.634052573994268,
+ "tokens / sec": 3947.4741967818154,
+ "mem allocated avg": 6777472888.832,
+ "mem reserved avg": 13055861719.04,
+ "elapsed time": 2275.669019541994
+ },
+ {
+ "step": 5000,
+ "test accuracy": 0.1197877179681577,
+ "train loss": 0.9978675174713135,
+ "train samples": 20000,
+ "train total tokens": 4198051
+ }
+ ]
+ },
+ "meta_info": {
+ "model_info": {
+ "sha": "13afe5124825b4f3751f836b40dafda64c1ed062",
+ "created_at": "2024-09-18T15:23:48+00:00"
+ },
+ "dataset_info": {
+ "metamath": {
+ "sha": "aa4f34d3d2d3231299b5b03d9b3e5a20da45aa18",
+ "created_at": "2023-09-21T17:22:46+00:00"
+ },
+ "gsm8k": {
+ "sha": "e53f048856ff4f594e959d75785d2c2d37b678ee",
+ "created_at": "2022-04-12T10:22:10+00:00"
+ }
+ },
+ "package_info": {
+ "transformers-version": "4.52.4",
+ "transformers-commit-hash": null,
+ "peft-version": "0.15.2.dev0",
+ "peft-commit-hash": "5fe7f8f8abe914d313fc3751f2ea92de7718fbaf",
+ "datasets-version": "3.6.0",
+ "datasets-commit-hash": null,
+ "bitsandbytes-version": "0.46.0",
+ "bitsandbytes-commit-hash": null,
+ "torch-version": "2.7.1+cu126",
+ "torch-commit-hash": null
+ },
+ "system_info": {
+ "system": "Linux",
+ "release": "6.8.0-1029-aws",
+ "version": "#31-Ubuntu SMP Wed Apr 23 18:42:41 UTC 2025",
+ "machine": "x86_64",
+ "processor": "x86_64",
+ "accelerator": "NVIDIA L40S"
+ },
+ "pytorch_info": "PyTorch built with:\n - GCC 11.2\n - C++ Version: 201703\n - Intel(R) oneAPI Math Kernel Library Version 2024.2-Product Build 20240605 for Intel(R) 64 architecture applications\n - Intel(R) MKL-DNN v3.7.1 (Git Hash 8d263e693366ef8db40acc569cc7d8edf644556d)\n - OpenMP 201511 (a.k.a. OpenMP 4.5)\n - LAPACK is enabled (usually provided by MKL)\n - NNPACK is enabled\n - CPU capability usage: AVX2\n - CUDA Runtime 12.6\n - NVCC architecture flags: -gencode;arch=compute_50,code=sm_50;-gencode;arch=compute_60,code=sm_60;-gencode;arch=compute_70,code=sm_70;-gencode;arch=compute_75,code=sm_75;-gencode;arch=compute_80,code=sm_80;-gencode;arch=compute_86,code=sm_86;-gencode;arch=compute_90,code=sm_90\n - CuDNN 90.7.1 (built against CUDA 12.8)\n - Built with CuDNN 90.5.1\n - Magma 2.6.1\n - Build settings: BLAS_INFO=mkl, BUILD_TYPE=Release, COMMIT_SHA=e2d141dbde55c2a4370fac5165b0561b6af4798b, CUDA_VERSION=12.6, CUDNN_VERSION=9.5.1, CXX_COMPILER=/opt/rh/gcc-toolset-11/root/usr/bin/c++, CXX_FLAGS= -D_GLIBCXX_USE_CXX11_ABI=1 -fvisibility-inlines-hidden -DUSE_PTHREADPOOL -DNDEBUG -DUSE_KINETO -DLIBKINETO_NOROCTRACER -DLIBKINETO_NOXPUPTI=ON -DUSE_FBGEMM -DUSE_PYTORCH_QNNPACK -DUSE_XNNPACK -DSYMBOLICATE_MOBILE_DEBUG_HANDLE -O2 -fPIC -Wall -Wextra -Werror=return-type -Werror=non-virtual-dtor -Werror=range-loop-construct -Werror=bool-operation -Wnarrowing -Wno-missing-field-initializers -Wno-unknown-pragmas -Wno-unused-parameter -Wno-strict-overflow -Wno-strict-aliasing -Wno-stringop-overflow -Wsuggest-override -Wno-psabi -Wno-error=old-style-cast -fdiagnostics-color=always -faligned-new -Wno-maybe-uninitialized -fno-math-errno -fno-trapping-math -Werror=format -Wno-stringop-overflow, LAPACK_INFO=mkl, PERF_WITH_AVX=1, PERF_WITH_AVX2=1, TORCH_VERSION=2.7.1, USE_CUDA=ON, USE_CUDNN=ON, USE_CUSPARSELT=1, USE_GFLAGS=OFF, USE_GLOG=OFF, USE_GLOO=ON, USE_MKL=ON, USE_MKLDNN=ON, USE_MPI=OFF, USE_NCCL=1, USE_NNPACK=ON, USE_OPENMP=ON, USE_ROCM=OFF, USE_ROCM_KERNEL_ASSERT=OFF, \n"
+ }
+}
diff --git a/peft/method_comparison/MetaMathQA/results/full-finetuning--llama-3.2-3B-lr_0.00001.json b/peft/method_comparison/MetaMathQA/results/full-finetuning--llama-3.2-3B-lr_0.00001.json
new file mode 100644
index 0000000000000000000000000000000000000000..4f15dc9eb28e5cde17637f1ebcfe00e9c01217ae
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/results/full-finetuning--llama-3.2-3B-lr_0.00001.json
@@ -0,0 +1,331 @@
+{
+ "run_info": {
+ "created_at": "2025-06-20T18:02:43+00:00",
+ "total_time": 3274.9747593409993,
+ "experiment_name": "full-finetuning/llama-3.2-3B-lr_0.00001",
+ "peft_branch": "main",
+ "train_config": {
+ "model_id": "meta-llama/Llama-3.2-3B",
+ "dtype": "bfloat16",
+ "max_seq_length": 768,
+ "batch_size": 4,
+ "batch_size_eval": 50,
+ "max_steps": 5000,
+ "eval_steps": 250,
+ "compile": false,
+ "query_template": "Question: {query} Think step by step.\nAnswer:",
+ "seed": 0,
+ "grad_norm_clip": 1.0,
+ "optimizer_type": "AdamW",
+ "optimizer_kwargs": {
+ "lr": 1e-05
+ },
+ "lr_scheduler": "cosine",
+ "use_amp": false,
+ "autocast_adapter_dtype": true,
+ "generation_kwargs": {
+ "max_length": 800,
+ "max_new_tokens": 300
+ },
+ "attn_implementation": null
+ },
+ "peft_config": null,
+ "error_msg": ""
+ },
+ "train_info": {
+ "accelerator_memory_reserved_avg": 33098872284,
+ "accelerator_memory_max": 37241225216,
+ "accelerator_memory_reserved_99th": 33573390254,
+ "train_time": 3111.3685010060144,
+ "file_size": 6425499648,
+ "num_trainable_params": 3212749824,
+ "num_total_params": 3212749824,
+ "status": "success",
+ "metrics": [
+ {
+ "step": 250,
+ "valid accuracy": 0.3,
+ "train loss": 1.0749022357463838,
+ "train samples": 1000,
+ "train time": 90.81602771116013,
+ "eval time": 10.388541491003707,
+ "tokens / sec": 2331.295535996918,
+ "mem allocated avg": 26069449254.912,
+ "mem reserved avg": 33116739600.384,
+ "elapsed time": 162.0596859770012
+ },
+ {
+ "step": 500,
+ "valid accuracy": 0.4,
+ "train loss": 0.7238605101108551,
+ "train samples": 2000,
+ "train time": 90.41340426202805,
+ "eval time": 10.403155545005575,
+ "tokens / sec": 2300.488535938847,
+ "mem allocated avg": 26062513567.744,
+ "mem reserved avg": 33090961408.0,
+ "elapsed time": 315.86630137299653
+ },
+ {
+ "step": 750,
+ "valid accuracy": 0.42,
+ "train loss": 0.6648618497848511,
+ "train samples": 3000,
+ "train time": 91.4961106939445,
+ "eval time": 5.590419113999815,
+ "tokens / sec": 2343.27993150631,
+ "mem allocated avg": 26071394062.336,
+ "mem reserved avg": 33094367182.848,
+ "elapsed time": 465.79339110500587
+ },
+ {
+ "step": 1000,
+ "valid accuracy": 0.42,
+ "train loss": 0.6407654472589492,
+ "train samples": 4000,
+ "train time": 89.8546926038689,
+ "eval time": 10.434167744999286,
+ "tokens / sec": 2318.5878662838986,
+ "mem allocated avg": 26063373086.72,
+ "mem reserved avg": 33094367182.848,
+ "elapsed time": 618.5050604129938
+ },
+ {
+ "step": 1250,
+ "valid accuracy": 0.46,
+ "train loss": 0.6343449921607971,
+ "train samples": 5000,
+ "train time": 90.3596406209981,
+ "eval time": 5.810965301003307,
+ "tokens / sec": 2307.86663787969,
+ "mem allocated avg": 26063789404.16,
+ "mem reserved avg": 33081876545.536,
+ "elapsed time": 766.6042792719963
+ },
+ {
+ "step": 1500,
+ "valid accuracy": 0.54,
+ "train loss": 0.6249808443784713,
+ "train samples": 6000,
+ "train time": 90.81503154609527,
+ "eval time": 10.435444819988334,
+ "tokens / sec": 2305.025901948283,
+ "mem allocated avg": 26066218485.76,
+ "mem reserved avg": 33089409515.52,
+ "elapsed time": 920.292813491993
+ },
+ {
+ "step": 1750,
+ "valid accuracy": 0.46,
+ "train loss": 0.6174132014513016,
+ "train samples": 7000,
+ "train time": 90.68820026615867,
+ "eval time": 10.286707318999106,
+ "tokens / sec": 2308.5142210956765,
+ "mem allocated avg": 26065828059.136,
+ "mem reserved avg": 33101774323.712,
+ "elapsed time": 1073.8488811849966
+ },
+ {
+ "step": 2000,
+ "valid accuracy": 0.42,
+ "train loss": 0.618268838763237,
+ "train samples": 8000,
+ "train time": 90.44998777209548,
+ "eval time": 10.380125819006935,
+ "tokens / sec": 2296.252383398064,
+ "mem allocated avg": 26062920781.824,
+ "mem reserved avg": 33096330117.12,
+ "elapsed time": 1227.2062568730034
+ },
+ {
+ "step": 2250,
+ "valid accuracy": 0.5,
+ "train loss": 0.6107994567155838,
+ "train samples": 9000,
+ "train time": 91.58726547904371,
+ "eval time": 10.372407121991273,
+ "tokens / sec": 2346.920162707366,
+ "mem allocated avg": 26073357961.216,
+ "mem reserved avg": 33114382401.536,
+ "elapsed time": 1381.3805919409933
+ },
+ {
+ "step": 2500,
+ "valid accuracy": 0.54,
+ "train loss": 0.6089532144069671,
+ "train samples": 10000,
+ "train time": 89.29193754095468,
+ "eval time": 10.391672718993505,
+ "tokens / sec": 2306.6696240691504,
+ "mem allocated avg": 26059719045.12,
+ "mem reserved avg": 33086842601.472,
+ "elapsed time": 1533.778675338006
+ },
+ {
+ "step": 2750,
+ "valid accuracy": 0.52,
+ "train loss": 0.6020698472261429,
+ "train samples": 11000,
+ "train time": 90.41624103189679,
+ "eval time": 10.369720178001444,
+ "tokens / sec": 2343.3953632871467,
+ "mem allocated avg": 26070059464.704,
+ "mem reserved avg": 33107805732.864,
+ "elapsed time": 1686.671367884992
+ },
+ {
+ "step": 3000,
+ "valid accuracy": 0.5,
+ "train loss": 0.5949549045562744,
+ "train samples": 12000,
+ "train time": 90.9437831780233,
+ "eval time": 7.315949440002441,
+ "tokens / sec": 2295.165130654474,
+ "mem allocated avg": 26064854972.416,
+ "mem reserved avg": 33098074947.584,
+ "elapsed time": 1837.2926549609983
+ },
+ {
+ "step": 3250,
+ "valid accuracy": 0.48,
+ "train loss": 0.6066494225263596,
+ "train samples": 13000,
+ "train time": 90.87308476005273,
+ "eval time": 5.963120047992561,
+ "tokens / sec": 2320.8302057410824,
+ "mem allocated avg": 26066388537.344,
+ "mem reserved avg": 33098318217.216,
+ "elapsed time": 1986.6408478410012
+ },
+ {
+ "step": 3500,
+ "valid accuracy": 0.48,
+ "train loss": 0.592242598772049,
+ "train samples": 14000,
+ "train time": 90.65281462905114,
+ "eval time": 7.1309342330059735,
+ "tokens / sec": 2313.7726154261322,
+ "mem allocated avg": 26065652588.544,
+ "mem reserved avg": 33100457312.256,
+ "elapsed time": 2137.073564691993
+ },
+ {
+ "step": 3750,
+ "valid accuracy": 0.48,
+ "train loss": 0.5925718579292297,
+ "train samples": 15000,
+ "train time": 91.80342563094746,
+ "eval time": 5.844810517999576,
+ "tokens / sec": 2360.5110431407275,
+ "mem allocated avg": 26075058659.328,
+ "mem reserved avg": 33131771985.92,
+ "elapsed time": 2287.0305021950044
+ },
+ {
+ "step": 4000,
+ "valid accuracy": 0.5,
+ "train loss": 0.6050453131198883,
+ "train samples": 16000,
+ "train time": 89.85742108603881,
+ "eval time": 5.86809825799719,
+ "tokens / sec": 2274.414261280792,
+ "mem allocated avg": 26058425257.984,
+ "mem reserved avg": 33098662150.144,
+ "elapsed time": 2435.1958582270017
+ },
+ {
+ "step": 4250,
+ "valid accuracy": 0.48,
+ "train loss": 0.5929686036109925,
+ "train samples": 17000,
+ "train time": 90.97368233802263,
+ "eval time": 5.8907580230006715,
+ "tokens / sec": 2323.6280489841133,
+ "mem allocated avg": 26067367372.8,
+ "mem reserved avg": 33099207409.664,
+ "elapsed time": 2584.8373482140014
+ },
+ {
+ "step": 4500,
+ "valid accuracy": 0.48,
+ "train loss": 0.6010294322967529,
+ "train samples": 18000,
+ "train time": 90.13679483698797,
+ "eval time": 6.106882603999111,
+ "tokens / sec": 2305.5845326632484,
+ "mem allocated avg": 26064599832.576,
+ "mem reserved avg": 33092253253.632,
+ "elapsed time": 2733.494644669001
+ },
+ {
+ "step": 4750,
+ "valid accuracy": 0.5,
+ "train loss": 0.5936577550172806,
+ "train samples": 19000,
+ "train time": 90.74229130300228,
+ "eval time": 5.885364143003244,
+ "tokens / sec": 2313.5739354319567,
+ "mem allocated avg": 26065537388.544,
+ "mem reserved avg": 33100717359.104,
+ "elapsed time": 2882.6415541759925
+ },
+ {
+ "step": 5000,
+ "valid accuracy": 0.5,
+ "train loss": 0.5987544150352478,
+ "train samples": 20000,
+ "train time": 90.54863398504676,
+ "eval time": 5.88336711798911,
+ "tokens / sec": 2300.2003545895063,
+ "mem allocated avg": 26062803286.016,
+ "mem reserved avg": 33083126448.128,
+ "elapsed time": 3031.523533478001
+ },
+ {
+ "step": 5000,
+ "test accuracy": 0.5003790750568613,
+ "train loss": 0.5987544150352478,
+ "train samples": 20000,
+ "train total tokens": 4198051
+ }
+ ]
+ },
+ "meta_info": {
+ "model_info": {
+ "sha": "13afe5124825b4f3751f836b40dafda64c1ed062",
+ "created_at": "2024-09-18T15:23:48+00:00"
+ },
+ "dataset_info": {
+ "metamath": {
+ "sha": "aa4f34d3d2d3231299b5b03d9b3e5a20da45aa18",
+ "created_at": "2023-09-21T17:22:46+00:00"
+ },
+ "gsm8k": {
+ "sha": "e53f048856ff4f594e959d75785d2c2d37b678ee",
+ "created_at": "2022-04-12T10:22:10+00:00"
+ }
+ },
+ "package_info": {
+ "transformers-version": "4.52.4",
+ "transformers-commit-hash": null,
+ "peft-version": "0.15.2.dev0",
+ "peft-commit-hash": "5fe7f8f8abe914d313fc3751f2ea92de7718fbaf",
+ "datasets-version": "3.6.0",
+ "datasets-commit-hash": null,
+ "bitsandbytes-version": "0.46.0",
+ "bitsandbytes-commit-hash": null,
+ "torch-version": "2.7.1+cu126",
+ "torch-commit-hash": null
+ },
+ "system_info": {
+ "system": "Linux",
+ "release": "6.8.0-1029-aws",
+ "version": "#31-Ubuntu SMP Wed Apr 23 18:42:41 UTC 2025",
+ "machine": "x86_64",
+ "processor": "x86_64",
+ "accelerator": "NVIDIA L40S"
+ },
+ "pytorch_info": "PyTorch built with:\n - GCC 11.2\n - C++ Version: 201703\n - Intel(R) oneAPI Math Kernel Library Version 2024.2-Product Build 20240605 for Intel(R) 64 architecture applications\n - Intel(R) MKL-DNN v3.7.1 (Git Hash 8d263e693366ef8db40acc569cc7d8edf644556d)\n - OpenMP 201511 (a.k.a. OpenMP 4.5)\n - LAPACK is enabled (usually provided by MKL)\n - NNPACK is enabled\n - CPU capability usage: AVX2\n - CUDA Runtime 12.6\n - NVCC architecture flags: -gencode;arch=compute_50,code=sm_50;-gencode;arch=compute_60,code=sm_60;-gencode;arch=compute_70,code=sm_70;-gencode;arch=compute_75,code=sm_75;-gencode;arch=compute_80,code=sm_80;-gencode;arch=compute_86,code=sm_86;-gencode;arch=compute_90,code=sm_90\n - CuDNN 90.7.1 (built against CUDA 12.8)\n - Built with CuDNN 90.5.1\n - Magma 2.6.1\n - Build settings: BLAS_INFO=mkl, BUILD_TYPE=Release, COMMIT_SHA=e2d141dbde55c2a4370fac5165b0561b6af4798b, CUDA_VERSION=12.6, CUDNN_VERSION=9.5.1, CXX_COMPILER=/opt/rh/gcc-toolset-11/root/usr/bin/c++, CXX_FLAGS= -D_GLIBCXX_USE_CXX11_ABI=1 -fvisibility-inlines-hidden -DUSE_PTHREADPOOL -DNDEBUG -DUSE_KINETO -DLIBKINETO_NOROCTRACER -DLIBKINETO_NOXPUPTI=ON -DUSE_FBGEMM -DUSE_PYTORCH_QNNPACK -DUSE_XNNPACK -DSYMBOLICATE_MOBILE_DEBUG_HANDLE -O2 -fPIC -Wall -Wextra -Werror=return-type -Werror=non-virtual-dtor -Werror=range-loop-construct -Werror=bool-operation -Wnarrowing -Wno-missing-field-initializers -Wno-unknown-pragmas -Wno-unused-parameter -Wno-strict-overflow -Wno-strict-aliasing -Wno-stringop-overflow -Wsuggest-override -Wno-psabi -Wno-error=old-style-cast -fdiagnostics-color=always -faligned-new -Wno-maybe-uninitialized -fno-math-errno -fno-trapping-math -Werror=format -Wno-stringop-overflow, LAPACK_INFO=mkl, PERF_WITH_AVX=1, PERF_WITH_AVX2=1, TORCH_VERSION=2.7.1, USE_CUDA=ON, USE_CUDNN=ON, USE_CUSPARSELT=1, USE_GFLAGS=OFF, USE_GLOG=OFF, USE_GLOO=ON, USE_MKL=ON, USE_MKLDNN=ON, USE_MPI=OFF, USE_NCCL=1, USE_NNPACK=ON, USE_OPENMP=ON, USE_ROCM=OFF, USE_ROCM_KERNEL_ASSERT=OFF, \n"
+ }
+}
diff --git a/peft/method_comparison/MetaMathQA/results/ia3--llama-3.2-3B-default.json b/peft/method_comparison/MetaMathQA/results/ia3--llama-3.2-3B-default.json
new file mode 100644
index 0000000000000000000000000000000000000000..50d2efa1f91faafd63fdf9ab606668fd2c40c3c6
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/results/ia3--llama-3.2-3B-default.json
@@ -0,0 +1,351 @@
+{
+ "run_info": {
+ "created_at": "2025-06-19T21:59:33+00:00",
+ "total_time": 2004.8640038169979,
+ "experiment_name": "ia3/llama-3.2-3B-default",
+ "peft_branch": "main",
+ "train_config": {
+ "model_id": "meta-llama/Llama-3.2-3B",
+ "dtype": "bfloat16",
+ "max_seq_length": 768,
+ "batch_size": 4,
+ "batch_size_eval": 50,
+ "max_steps": 5000,
+ "eval_steps": 250,
+ "compile": false,
+ "query_template": "Question: {query} Think step by step.\nAnswer:",
+ "seed": 0,
+ "grad_norm_clip": 1.0,
+ "optimizer_type": "AdamW",
+ "optimizer_kwargs": {
+ "lr": 0.0001,
+ "weight_decay": 0.1
+ },
+ "lr_scheduler": "cosine",
+ "use_amp": false,
+ "autocast_adapter_dtype": true,
+ "generation_kwargs": {
+ "max_length": 800,
+ "max_new_tokens": 300
+ },
+ "attn_implementation": null
+ },
+ "peft_config": {
+ "task_type": null,
+ "peft_type": "IA3",
+ "auto_mapping": null,
+ "base_model_name_or_path": "meta-llama/Llama-3.2-3B",
+ "revision": null,
+ "inference_mode": false,
+ "target_modules": [
+ "down_proj",
+ "v_proj",
+ "k_proj"
+ ],
+ "exclude_modules": null,
+ "feedforward_modules": [
+ "down_proj"
+ ],
+ "fan_in_fan_out": false,
+ "modules_to_save": null,
+ "init_ia3_weights": true
+ },
+ "error_msg": ""
+ },
+ "train_info": {
+ "accelerator_memory_reserved_avg": 12023227429,
+ "accelerator_memory_max": 23137878016,
+ "accelerator_memory_reserved_99th": 18398566154,
+ "train_time": 1782.9318781230104,
+ "file_size": 1157064,
+ "num_trainable_params": 286720,
+ "num_total_params": 3213036544,
+ "status": "success",
+ "metrics": [
+ {
+ "step": 250,
+ "valid accuracy": 0.0,
+ "train loss": 1.3155810165405273,
+ "train samples": 1000,
+ "train time": 30.56459548201383,
+ "eval time": 10.972947114001727,
+ "tokens / sec": 6926.936105684404,
+ "mem allocated avg": 6780994971.648,
+ "mem reserved avg": 12076433014.784,
+ "elapsed time": 90.53726772200025
+ },
+ {
+ "step": 500,
+ "valid accuracy": 0.0,
+ "train loss": 1.205229633808136,
+ "train samples": 2000,
+ "train time": 30.221456803970796,
+ "eval time": 10.954313254995213,
+ "tokens / sec": 6882.361805029583,
+ "mem allocated avg": 6773721065.472,
+ "mem reserved avg": 11963673346.048,
+ "elapsed time": 175.07058417100052
+ },
+ {
+ "step": 750,
+ "valid accuracy": 0.1,
+ "train loss": 1.0194582087993622,
+ "train samples": 3000,
+ "train time": 30.774312397006724,
+ "eval time": 10.944943730006344,
+ "tokens / sec": 6966.881899231445,
+ "mem allocated avg": 6784231882.752,
+ "mem reserved avg": 12126680776.704,
+ "elapsed time": 260.540154495
+ },
+ {
+ "step": 1000,
+ "valid accuracy": 0.24,
+ "train loss": 0.9196457831859589,
+ "train samples": 4000,
+ "train time": 30.61534244806535,
+ "eval time": 10.960088267995161,
+ "tokens / sec": 6804.95409624808,
+ "mem allocated avg": 6775492155.392,
+ "mem reserved avg": 11986893012.992,
+ "elapsed time": 345.30987053900026
+ },
+ {
+ "step": 1250,
+ "valid accuracy": 0.32,
+ "train loss": 0.8685842225551605,
+ "train samples": 5000,
+ "train time": 29.97266351111466,
+ "eval time": 10.924794500999269,
+ "tokens / sec": 6957.606551138459,
+ "mem allocated avg": 6775089207.296,
+ "mem reserved avg": 11983428517.888,
+ "elapsed time": 429.5542291879974
+ },
+ {
+ "step": 1500,
+ "valid accuracy": 0.32,
+ "train loss": 0.8332846148014068,
+ "train samples": 6000,
+ "train time": 29.98314001694962,
+ "eval time": 10.942266878999362,
+ "tokens / sec": 6981.6236685572,
+ "mem allocated avg": 6776724867.072,
+ "mem reserved avg": 12008594341.888,
+ "elapsed time": 513.8152235820016
+ },
+ {
+ "step": 1750,
+ "valid accuracy": 0.32,
+ "train loss": 0.8169269208908081,
+ "train samples": 7000,
+ "train time": 30.245623568014707,
+ "eval time": 10.940915298000618,
+ "tokens / sec": 6921.8278647558345,
+ "mem allocated avg": 6777912934.4,
+ "mem reserved avg": 12032065667.072,
+ "elapsed time": 598.2868188970024
+ },
+ {
+ "step": 2000,
+ "valid accuracy": 0.32,
+ "train loss": 0.8072074156999588,
+ "train samples": 8000,
+ "train time": 30.292844633964705,
+ "eval time": 10.95617212200159,
+ "tokens / sec": 6856.272578875894,
+ "mem allocated avg": 6775099170.816,
+ "mem reserved avg": 11967473385.472,
+ "elapsed time": 682.7948923380027
+ },
+ {
+ "step": 2250,
+ "valid accuracy": 0.32,
+ "train loss": 0.7952859619855881,
+ "train samples": 9000,
+ "train time": 31.20892413101683,
+ "eval time": 10.942549917002907,
+ "tokens / sec": 6887.388975590319,
+ "mem allocated avg": 6786161477.632,
+ "mem reserved avg": 12167709458.432,
+ "elapsed time": 768.9645714229991
+ },
+ {
+ "step": 2500,
+ "valid accuracy": 0.28,
+ "train loss": 0.7890167078971863,
+ "train samples": 10000,
+ "train time": 30.187670495011844,
+ "eval time": 10.954304017002869,
+ "tokens / sec": 6822.884860692832,
+ "mem allocated avg": 6771082014.72,
+ "mem reserved avg": 11910984499.2,
+ "elapsed time": 853.427360558002
+ },
+ {
+ "step": 2750,
+ "valid accuracy": 0.3,
+ "train loss": 0.7823473591804504,
+ "train samples": 11000,
+ "train time": 30.410061570059042,
+ "eval time": 10.93302121299348,
+ "tokens / sec": 6967.4636965751015,
+ "mem allocated avg": 6782254225.408,
+ "mem reserved avg": 12090903363.584,
+ "elapsed time": 938.3584665200033
+ },
+ {
+ "step": 3000,
+ "valid accuracy": 0.24,
+ "train loss": 0.7709820411205291,
+ "train samples": 12000,
+ "train time": 30.02989622000314,
+ "eval time": 10.940404225999373,
+ "tokens / sec": 6950.773271769175,
+ "mem allocated avg": 6776725577.728,
+ "mem reserved avg": 12003133358.08,
+ "elapsed time": 1022.4627897890023
+ },
+ {
+ "step": 3250,
+ "valid accuracy": 0.3,
+ "train loss": 0.7755767168998718,
+ "train samples": 13000,
+ "train time": 30.172652364024543,
+ "eval time": 10.940153044000908,
+ "tokens / sec": 6989.806446431653,
+ "mem allocated avg": 6778589339.648,
+ "mem reserved avg": 12038298402.816,
+ "elapsed time": 1107.0076802080002
+ },
+ {
+ "step": 3500,
+ "valid accuracy": 0.34,
+ "train loss": 0.7658302361965179,
+ "train samples": 14000,
+ "train time": 30.384311634006735,
+ "eval time": 10.941136569999799,
+ "tokens / sec": 6903.233567590308,
+ "mem allocated avg": 6777534660.608,
+ "mem reserved avg": 12020623605.76,
+ "elapsed time": 1191.893303306002
+ },
+ {
+ "step": 3750,
+ "valid accuracy": 0.34,
+ "train loss": 0.7585167481899261,
+ "train samples": 15000,
+ "train time": 31.250990667955193,
+ "eval time": 10.924158087997057,
+ "tokens / sec": 6934.276173913666,
+ "mem allocated avg": 6788426940.416,
+ "mem reserved avg": 12209652498.432,
+ "elapsed time": 1278.4574160839984
+ },
+ {
+ "step": 4000,
+ "valid accuracy": 0.26,
+ "train loss": 0.7766438691616059,
+ "train samples": 16000,
+ "train time": 30.222231689898763,
+ "eval time": 10.98030305699649,
+ "tokens / sec": 6762.339793335249,
+ "mem allocated avg": 6769563977.728,
+ "mem reserved avg": 11885533462.528,
+ "elapsed time": 1362.9405450319973
+ },
+ {
+ "step": 4250,
+ "valid accuracy": 0.34,
+ "train loss": 0.7542061095237732,
+ "train samples": 17000,
+ "train time": 30.273203028933494,
+ "eval time": 10.948997009996674,
+ "tokens / sec": 6982.710081849145,
+ "mem allocated avg": 6780103426.048,
+ "mem reserved avg": 12047483928.576,
+ "elapsed time": 1447.661586811002
+ },
+ {
+ "step": 4500,
+ "valid accuracy": 0.32,
+ "train loss": 0.7659628703594208,
+ "train samples": 18000,
+ "train time": 29.84466753601737,
+ "eval time": 10.942651322002348,
+ "tokens / sec": 6963.320993581165,
+ "mem allocated avg": 6775043430.4,
+ "mem reserved avg": 11968387743.744,
+ "elapsed time": 1531.5572027719973
+ },
+ {
+ "step": 4750,
+ "valid accuracy": 0.28,
+ "train loss": 0.7580052223205567,
+ "train samples": 19000,
+ "train time": 30.03731635398435,
+ "eval time": 10.927273799999966,
+ "tokens / sec": 6989.272860661278,
+ "mem allocated avg": 6776962899.968,
+ "mem reserved avg": 12017695981.568,
+ "elapsed time": 1615.9832882379997
+ },
+ {
+ "step": 5000,
+ "valid accuracy": 0.36,
+ "train loss": 0.7657463653087616,
+ "train samples": 20000,
+ "train time": 30.07570726004633,
+ "eval time": 10.953207714999735,
+ "tokens / sec": 6925.19042691597,
+ "mem allocated avg": 6774270615.552,
+ "mem reserved avg": 11958900228.096,
+ "elapsed time": 1700.4354192270039
+ },
+ {
+ "step": 5000,
+ "test accuracy": 0.34495830174374525,
+ "train loss": 0.7657463653087616,
+ "train samples": 20000,
+ "train total tokens": 4198051
+ }
+ ]
+ },
+ "meta_info": {
+ "model_info": {
+ "sha": "13afe5124825b4f3751f836b40dafda64c1ed062",
+ "created_at": "2024-09-18T15:23:48+00:00"
+ },
+ "dataset_info": {
+ "metamath": {
+ "sha": "aa4f34d3d2d3231299b5b03d9b3e5a20da45aa18",
+ "created_at": "2023-09-21T17:22:46+00:00"
+ },
+ "gsm8k": {
+ "sha": "e53f048856ff4f594e959d75785d2c2d37b678ee",
+ "created_at": "2022-04-12T10:22:10+00:00"
+ }
+ },
+ "package_info": {
+ "transformers-version": "4.52.4",
+ "transformers-commit-hash": null,
+ "peft-version": "0.15.2.dev0",
+ "peft-commit-hash": "5fe7f8f8abe914d313fc3751f2ea92de7718fbaf",
+ "datasets-version": "3.6.0",
+ "datasets-commit-hash": null,
+ "bitsandbytes-version": "0.46.0",
+ "bitsandbytes-commit-hash": null,
+ "torch-version": "2.7.1+cu126",
+ "torch-commit-hash": null
+ },
+ "system_info": {
+ "system": "Linux",
+ "release": "6.8.0-1029-aws",
+ "version": "#31-Ubuntu SMP Wed Apr 23 18:42:41 UTC 2025",
+ "machine": "x86_64",
+ "processor": "x86_64",
+ "accelerator": "NVIDIA L40S"
+ },
+ "pytorch_info": "PyTorch built with:\n - GCC 11.2\n - C++ Version: 201703\n - Intel(R) oneAPI Math Kernel Library Version 2024.2-Product Build 20240605 for Intel(R) 64 architecture applications\n - Intel(R) MKL-DNN v3.7.1 (Git Hash 8d263e693366ef8db40acc569cc7d8edf644556d)\n - OpenMP 201511 (a.k.a. OpenMP 4.5)\n - LAPACK is enabled (usually provided by MKL)\n - NNPACK is enabled\n - CPU capability usage: AVX2\n - CUDA Runtime 12.6\n - NVCC architecture flags: -gencode;arch=compute_50,code=sm_50;-gencode;arch=compute_60,code=sm_60;-gencode;arch=compute_70,code=sm_70;-gencode;arch=compute_75,code=sm_75;-gencode;arch=compute_80,code=sm_80;-gencode;arch=compute_86,code=sm_86;-gencode;arch=compute_90,code=sm_90\n - CuDNN 90.7.1 (built against CUDA 12.8)\n - Built with CuDNN 90.5.1\n - Magma 2.6.1\n - Build settings: BLAS_INFO=mkl, BUILD_TYPE=Release, COMMIT_SHA=e2d141dbde55c2a4370fac5165b0561b6af4798b, CUDA_VERSION=12.6, CUDNN_VERSION=9.5.1, CXX_COMPILER=/opt/rh/gcc-toolset-11/root/usr/bin/c++, CXX_FLAGS= -D_GLIBCXX_USE_CXX11_ABI=1 -fvisibility-inlines-hidden -DUSE_PTHREADPOOL -DNDEBUG -DUSE_KINETO -DLIBKINETO_NOROCTRACER -DLIBKINETO_NOXPUPTI=ON -DUSE_FBGEMM -DUSE_PYTORCH_QNNPACK -DUSE_XNNPACK -DSYMBOLICATE_MOBILE_DEBUG_HANDLE -O2 -fPIC -Wall -Wextra -Werror=return-type -Werror=non-virtual-dtor -Werror=range-loop-construct -Werror=bool-operation -Wnarrowing -Wno-missing-field-initializers -Wno-unknown-pragmas -Wno-unused-parameter -Wno-strict-overflow -Wno-strict-aliasing -Wno-stringop-overflow -Wsuggest-override -Wno-psabi -Wno-error=old-style-cast -fdiagnostics-color=always -faligned-new -Wno-maybe-uninitialized -fno-math-errno -fno-trapping-math -Werror=format -Wno-stringop-overflow, LAPACK_INFO=mkl, PERF_WITH_AVX=1, PERF_WITH_AVX2=1, TORCH_VERSION=2.7.1, USE_CUDA=ON, USE_CUDNN=ON, USE_CUSPARSELT=1, USE_GFLAGS=OFF, USE_GLOG=OFF, USE_GLOO=ON, USE_MKL=ON, USE_MKLDNN=ON, USE_MPI=OFF, USE_NCCL=1, USE_NNPACK=ON, USE_OPENMP=ON, USE_ROCM=OFF, USE_ROCM_KERNEL_ASSERT=OFF, \n"
+ }
+}
diff --git a/peft/method_comparison/MetaMathQA/results/ia3--llama-3.2-3B-lr_0.001.json b/peft/method_comparison/MetaMathQA/results/ia3--llama-3.2-3B-lr_0.001.json
new file mode 100644
index 0000000000000000000000000000000000000000..f1982e8ef38015c53cc79f7f134677ee584bdfeb
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/results/ia3--llama-3.2-3B-lr_0.001.json
@@ -0,0 +1,350 @@
+{
+ "run_info": {
+ "created_at": "2025-06-19T21:27:27+00:00",
+ "total_time": 1921.5641919770023,
+ "experiment_name": "ia3/llama-3.2-3B-lr_0.001",
+ "peft_branch": "main",
+ "train_config": {
+ "model_id": "meta-llama/Llama-3.2-3B",
+ "dtype": "bfloat16",
+ "max_seq_length": 768,
+ "batch_size": 4,
+ "batch_size_eval": 50,
+ "max_steps": 5000,
+ "eval_steps": 250,
+ "compile": false,
+ "query_template": "Question: {query} Think step by step.\nAnswer:",
+ "seed": 0,
+ "grad_norm_clip": 1.0,
+ "optimizer_type": "AdamW",
+ "optimizer_kwargs": {
+ "lr": 0.001
+ },
+ "lr_scheduler": "cosine",
+ "use_amp": false,
+ "autocast_adapter_dtype": true,
+ "generation_kwargs": {
+ "max_length": 800,
+ "max_new_tokens": 300
+ },
+ "attn_implementation": null
+ },
+ "peft_config": {
+ "task_type": null,
+ "peft_type": "IA3",
+ "auto_mapping": null,
+ "base_model_name_or_path": "meta-llama/Llama-3.2-3B",
+ "revision": null,
+ "inference_mode": false,
+ "target_modules": [
+ "k_proj",
+ "down_proj",
+ "v_proj"
+ ],
+ "exclude_modules": null,
+ "feedforward_modules": [
+ "down_proj"
+ ],
+ "fan_in_fan_out": false,
+ "modules_to_save": null,
+ "init_ia3_weights": true
+ },
+ "error_msg": ""
+ },
+ "train_info": {
+ "accelerator_memory_reserved_avg": 12023331867,
+ "accelerator_memory_max": 23135780864,
+ "accelerator_memory_reserved_99th": 18398356439,
+ "train_time": 1746.0246657649877,
+ "file_size": 1157064,
+ "num_trainable_params": 286720,
+ "num_total_params": 3213036544,
+ "status": "success",
+ "metrics": [
+ {
+ "step": 250,
+ "valid accuracy": 0.18,
+ "train loss": 1.1670710837841034,
+ "train samples": 1000,
+ "train time": 30.829080988976784,
+ "eval time": 10.962777282999014,
+ "tokens / sec": 6867.509286952213,
+ "mem allocated avg": 6781095491.584,
+ "mem reserved avg": 12075594153.984,
+ "elapsed time": 91.04478788100096
+ },
+ {
+ "step": 500,
+ "valid accuracy": 0.34,
+ "train loss": 0.8285422480106354,
+ "train samples": 2000,
+ "train time": 30.237734625952726,
+ "eval time": 10.93798775599862,
+ "tokens / sec": 6878.656836331916,
+ "mem allocated avg": 6773575256.064,
+ "mem reserved avg": 11961039323.136,
+ "elapsed time": 175.57074494799963
+ },
+ {
+ "step": 750,
+ "valid accuracy": 0.34,
+ "train loss": 0.7387537934780121,
+ "train samples": 3000,
+ "train time": 30.784141963005823,
+ "eval time": 10.918857135002327,
+ "tokens / sec": 6964.657330961239,
+ "mem allocated avg": 6784163356.672,
+ "mem reserved avg": 12124793339.904,
+ "elapsed time": 261.120397177001
+ },
+ {
+ "step": 1000,
+ "valid accuracy": 0.36,
+ "train loss": 0.7030822492837906,
+ "train samples": 4000,
+ "train time": 30.625773959025537,
+ "eval time": 6.545184372997028,
+ "tokens / sec": 6802.636246147914,
+ "mem allocated avg": 6775321157.632,
+ "mem reserved avg": 11986549080.064,
+ "elapsed time": 341.78445690100125
+ },
+ {
+ "step": 1250,
+ "valid accuracy": 0.34,
+ "train loss": 0.6953592277765274,
+ "train samples": 5000,
+ "train time": 30.090904191973095,
+ "eval time": 7.180137749001005,
+ "tokens / sec": 6930.266989305977,
+ "mem allocated avg": 6774968741.888,
+ "mem reserved avg": 11983218802.688,
+ "elapsed time": 422.45400445199994
+ },
+ {
+ "step": 1500,
+ "valid accuracy": 0.34,
+ "train loss": 0.6861299908161164,
+ "train samples": 6000,
+ "train time": 30.086008766014857,
+ "eval time": 10.923475695002708,
+ "tokens / sec": 6957.75241003254,
+ "mem allocated avg": 6776914077.696,
+ "mem reserved avg": 12007201832.96,
+ "elapsed time": 506.8615667560007
+ },
+ {
+ "step": 1750,
+ "valid accuracy": 0.34,
+ "train loss": 0.6775313948392868,
+ "train samples": 7000,
+ "train time": 30.329398032976314,
+ "eval time": 7.039293795001868,
+ "tokens / sec": 6902.708710946855,
+ "mem allocated avg": 6778176180.224,
+ "mem reserved avg": 12032417988.608,
+ "elapsed time": 587.730657346001
+ },
+ {
+ "step": 2000,
+ "valid accuracy": 0.36,
+ "train loss": 0.6783386437892914,
+ "train samples": 8000,
+ "train time": 30.340071335995162,
+ "eval time": 8.14293124300093,
+ "tokens / sec": 6845.600252547578,
+ "mem allocated avg": 6775202904.064,
+ "mem reserved avg": 11967733432.32,
+ "elapsed time": 669.6239550099999
+ },
+ {
+ "step": 2250,
+ "valid accuracy": 0.5,
+ "train loss": 0.6720720986127854,
+ "train samples": 9000,
+ "train time": 31.104124111985584,
+ "eval time": 7.4280358140022145,
+ "tokens / sec": 6910.594853149151,
+ "mem allocated avg": 6785809762.304,
+ "mem reserved avg": 12167885619.2,
+ "elapsed time": 752.2532132060005
+ },
+ {
+ "step": 2500,
+ "valid accuracy": 0.46,
+ "train loss": 0.6705386472940444,
+ "train samples": 10000,
+ "train time": 30.09476044199255,
+ "eval time": 7.5499184540021815,
+ "tokens / sec": 6843.948812850663,
+ "mem allocated avg": 6770963554.304,
+ "mem reserved avg": 11912058241.024,
+ "elapsed time": 833.2611769709983
+ },
+ {
+ "step": 2750,
+ "valid accuracy": 0.48,
+ "train loss": 0.6631126835346222,
+ "train samples": 11000,
+ "train time": 30.640666239018174,
+ "eval time": 10.92325482400338,
+ "tokens / sec": 6915.025879241109,
+ "mem allocated avg": 6781913962.496,
+ "mem reserved avg": 12090299383.808,
+ "elapsed time": 918.4276470139994
+ },
+ {
+ "step": 3000,
+ "valid accuracy": 0.38,
+ "train loss": 0.6557366658449173,
+ "train samples": 12000,
+ "train time": 30.612569437977072,
+ "eval time": 10.933225860997482,
+ "tokens / sec": 6818.473712992361,
+ "mem allocated avg": 6776591689.728,
+ "mem reserved avg": 12003032694.784,
+ "elapsed time": 1003.438990486
+ },
+ {
+ "step": 3250,
+ "valid accuracy": 0.44,
+ "train loss": 0.6655691808462143,
+ "train samples": 13000,
+ "train time": 30.508301533980557,
+ "eval time": 7.2082155700009025,
+ "tokens / sec": 6912.905320707402,
+ "mem allocated avg": 6778600480.768,
+ "mem reserved avg": 12040143896.576,
+ "elapsed time": 1084.7670880670012
+ },
+ {
+ "step": 3500,
+ "valid accuracy": 0.46,
+ "train loss": 0.6528272937536239,
+ "train samples": 14000,
+ "train time": 30.571383574966603,
+ "eval time": 7.452295711998886,
+ "tokens / sec": 6860.991406740058,
+ "mem allocated avg": 6777338779.648,
+ "mem reserved avg": 12021227585.536,
+ "elapsed time": 1166.2843480039992
+ },
+ {
+ "step": 3750,
+ "valid accuracy": 0.48,
+ "train loss": 0.6513591132164002,
+ "train samples": 15000,
+ "train time": 31.176262214954477,
+ "eval time": 6.50122426100279,
+ "tokens / sec": 6950.897400909496,
+ "mem allocated avg": 6788519866.368,
+ "mem reserved avg": 12209543446.528,
+ "elapsed time": 1248.1537826940003
+ },
+ {
+ "step": 4000,
+ "valid accuracy": 0.42,
+ "train loss": 0.6660103598833084,
+ "train samples": 16000,
+ "train time": 30.1621740100818,
+ "eval time": 10.007692241000768,
+ "tokens / sec": 6775.804686084222,
+ "mem allocated avg": 6769538811.904,
+ "mem reserved avg": 11886321991.68,
+ "elapsed time": 1331.4140659110017
+ },
+ {
+ "step": 4250,
+ "valid accuracy": 0.4,
+ "train loss": 0.648773505806923,
+ "train samples": 17000,
+ "train time": 30.627343150990782,
+ "eval time": 9.851157391000015,
+ "tokens / sec": 6901.969882201866,
+ "mem allocated avg": 6780366684.16,
+ "mem reserved avg": 12050411552.768,
+ "elapsed time": 1415.4855422520013
+ },
+ {
+ "step": 4500,
+ "valid accuracy": 0.42,
+ "train loss": 0.6574939725399017,
+ "train samples": 18000,
+ "train time": 30.04905582394713,
+ "eval time": 6.792122120001295,
+ "tokens / sec": 6915.957733167199,
+ "mem allocated avg": 6775072815.104,
+ "mem reserved avg": 11969042055.168,
+ "elapsed time": 1495.5897211369993
+ },
+ {
+ "step": 4750,
+ "valid accuracy": 0.4,
+ "train loss": 0.6505398267507553,
+ "train samples": 19000,
+ "train time": 30.326544256924535,
+ "eval time": 7.6139581239986,
+ "tokens / sec": 6922.615324100572,
+ "mem allocated avg": 6777039572.992,
+ "mem reserved avg": 12019256262.656,
+ "elapsed time": 1577.114852814997
+ },
+ {
+ "step": 5000,
+ "valid accuracy": 0.42,
+ "train loss": 0.6568749620914459,
+ "train samples": 20000,
+ "train time": 30.342653310064634,
+ "eval time": 6.5661308569979155,
+ "tokens / sec": 6864.264567492972,
+ "mem allocated avg": 6774530805.76,
+ "mem reserved avg": 11958866673.664,
+ "elapsed time": 1657.5746541439985
+ },
+ {
+ "step": 5000,
+ "test accuracy": 0.41243366186504926,
+ "train loss": 0.6568749620914459,
+ "train samples": 20000,
+ "train total tokens": 4198051
+ }
+ ]
+ },
+ "meta_info": {
+ "model_info": {
+ "sha": "13afe5124825b4f3751f836b40dafda64c1ed062",
+ "created_at": "2024-09-18T15:23:48+00:00"
+ },
+ "dataset_info": {
+ "metamath": {
+ "sha": "aa4f34d3d2d3231299b5b03d9b3e5a20da45aa18",
+ "created_at": "2023-09-21T17:22:46+00:00"
+ },
+ "gsm8k": {
+ "sha": "e53f048856ff4f594e959d75785d2c2d37b678ee",
+ "created_at": "2022-04-12T10:22:10+00:00"
+ }
+ },
+ "package_info": {
+ "transformers-version": "4.52.4",
+ "transformers-commit-hash": null,
+ "peft-version": "0.15.2.dev0",
+ "peft-commit-hash": "5fe7f8f8abe914d313fc3751f2ea92de7718fbaf",
+ "datasets-version": "3.6.0",
+ "datasets-commit-hash": null,
+ "bitsandbytes-version": "0.46.0",
+ "bitsandbytes-commit-hash": null,
+ "torch-version": "2.7.1+cu126",
+ "torch-commit-hash": null
+ },
+ "system_info": {
+ "system": "Linux",
+ "release": "6.8.0-1029-aws",
+ "version": "#31-Ubuntu SMP Wed Apr 23 18:42:41 UTC 2025",
+ "machine": "x86_64",
+ "processor": "x86_64",
+ "accelerator": "NVIDIA L40S"
+ },
+ "pytorch_info": "PyTorch built with:\n - GCC 11.2\n - C++ Version: 201703\n - Intel(R) oneAPI Math Kernel Library Version 2024.2-Product Build 20240605 for Intel(R) 64 architecture applications\n - Intel(R) MKL-DNN v3.7.1 (Git Hash 8d263e693366ef8db40acc569cc7d8edf644556d)\n - OpenMP 201511 (a.k.a. OpenMP 4.5)\n - LAPACK is enabled (usually provided by MKL)\n - NNPACK is enabled\n - CPU capability usage: AVX2\n - CUDA Runtime 12.6\n - NVCC architecture flags: -gencode;arch=compute_50,code=sm_50;-gencode;arch=compute_60,code=sm_60;-gencode;arch=compute_70,code=sm_70;-gencode;arch=compute_75,code=sm_75;-gencode;arch=compute_80,code=sm_80;-gencode;arch=compute_86,code=sm_86;-gencode;arch=compute_90,code=sm_90\n - CuDNN 90.7.1 (built against CUDA 12.8)\n - Built with CuDNN 90.5.1\n - Magma 2.6.1\n - Build settings: BLAS_INFO=mkl, BUILD_TYPE=Release, COMMIT_SHA=e2d141dbde55c2a4370fac5165b0561b6af4798b, CUDA_VERSION=12.6, CUDNN_VERSION=9.5.1, CXX_COMPILER=/opt/rh/gcc-toolset-11/root/usr/bin/c++, CXX_FLAGS= -D_GLIBCXX_USE_CXX11_ABI=1 -fvisibility-inlines-hidden -DUSE_PTHREADPOOL -DNDEBUG -DUSE_KINETO -DLIBKINETO_NOROCTRACER -DLIBKINETO_NOXPUPTI=ON -DUSE_FBGEMM -DUSE_PYTORCH_QNNPACK -DUSE_XNNPACK -DSYMBOLICATE_MOBILE_DEBUG_HANDLE -O2 -fPIC -Wall -Wextra -Werror=return-type -Werror=non-virtual-dtor -Werror=range-loop-construct -Werror=bool-operation -Wnarrowing -Wno-missing-field-initializers -Wno-unknown-pragmas -Wno-unused-parameter -Wno-strict-overflow -Wno-strict-aliasing -Wno-stringop-overflow -Wsuggest-override -Wno-psabi -Wno-error=old-style-cast -fdiagnostics-color=always -faligned-new -Wno-maybe-uninitialized -fno-math-errno -fno-trapping-math -Werror=format -Wno-stringop-overflow, LAPACK_INFO=mkl, PERF_WITH_AVX=1, PERF_WITH_AVX2=1, TORCH_VERSION=2.7.1, USE_CUDA=ON, USE_CUDNN=ON, USE_CUSPARSELT=1, USE_GFLAGS=OFF, USE_GLOG=OFF, USE_GLOO=ON, USE_MKL=ON, USE_MKLDNN=ON, USE_MPI=OFF, USE_NCCL=1, USE_NNPACK=ON, USE_OPENMP=ON, USE_ROCM=OFF, USE_ROCM_KERNEL_ASSERT=OFF, \n"
+ }
+}
diff --git a/peft/method_comparison/MetaMathQA/results/ln_tuning--llama-3.2-3B-default.json b/peft/method_comparison/MetaMathQA/results/ln_tuning--llama-3.2-3B-default.json
new file mode 100644
index 0000000000000000000000000000000000000000..2e8dabe44e54439aad25b203985f6b693c33004a
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/results/ln_tuning--llama-3.2-3B-default.json
@@ -0,0 +1,346 @@
+{
+ "run_info": {
+ "created_at": "2025-06-20T11:06:05+00:00",
+ "total_time": 1870.2496634349955,
+ "experiment_name": "ln_tuning/llama-3.2-3B-default",
+ "peft_branch": "main",
+ "train_config": {
+ "model_id": "meta-llama/Llama-3.2-3B",
+ "dtype": "bfloat16",
+ "max_seq_length": 768,
+ "batch_size": 4,
+ "batch_size_eval": 50,
+ "max_steps": 5000,
+ "eval_steps": 250,
+ "compile": false,
+ "query_template": "Question: {query} Think step by step.\nAnswer:",
+ "seed": 0,
+ "grad_norm_clip": 1.0,
+ "optimizer_type": "AdamW",
+ "optimizer_kwargs": {
+ "lr": 0.0001,
+ "weight_decay": 0.1
+ },
+ "lr_scheduler": "cosine",
+ "use_amp": false,
+ "autocast_adapter_dtype": true,
+ "generation_kwargs": {
+ "max_length": 800,
+ "max_new_tokens": 300
+ },
+ "attn_implementation": null
+ },
+ "peft_config": {
+ "task_type": null,
+ "peft_type": "LN_TUNING",
+ "auto_mapping": null,
+ "base_model_name_or_path": "meta-llama/Llama-3.2-3B",
+ "revision": null,
+ "inference_mode": false,
+ "target_modules": [
+ "input_layernorm",
+ "norm",
+ "post_attention_layernorm"
+ ],
+ "exclude_modules": null,
+ "modules_to_save": null
+ },
+ "error_msg": ""
+ },
+ "train_info": {
+ "accelerator_memory_reserved_avg": 11385589622,
+ "accelerator_memory_max": 21177040896,
+ "accelerator_memory_reserved_99th": 16903066091,
+ "train_time": 1657.2412179829698,
+ "file_size": 358288,
+ "num_trainable_params": 175104,
+ "num_total_params": 3212924928,
+ "status": "success",
+ "metrics": [
+ {
+ "step": 250,
+ "valid accuracy": 0.0,
+ "train loss": 1.3265725662708283,
+ "train samples": 1000,
+ "train time": 27.216289801202947,
+ "eval time": 10.492610957997385,
+ "tokens / sec": 7779.127924726981,
+ "mem allocated avg": 6780187711.488,
+ "mem reserved avg": 11433404268.544,
+ "elapsed time": 87.52968039299594
+ },
+ {
+ "step": 500,
+ "valid accuracy": 0.0,
+ "train loss": 1.3411514971256255,
+ "train samples": 2000,
+ "train time": 26.650248568999814,
+ "eval time": 10.469055254012346,
+ "tokens / sec": 7804.617636547848,
+ "mem allocated avg": 6772587255.808,
+ "mem reserved avg": 11331533012.992,
+ "elapsed time": 165.70980707599665
+ },
+ {
+ "step": 750,
+ "valid accuracy": 0.0,
+ "train loss": 1.2789560747146607,
+ "train samples": 3000,
+ "train time": 27.327283490114496,
+ "eval time": 10.448594682005933,
+ "tokens / sec": 7845.6755526965735,
+ "mem allocated avg": 6783227031.552,
+ "mem reserved avg": 11478560145.408,
+ "elapsed time": 245.043655957008
+ },
+ {
+ "step": 1000,
+ "valid accuracy": 0.0,
+ "train loss": 1.263298665046692,
+ "train samples": 4000,
+ "train time": 26.423721938888775,
+ "eval time": 10.48604148600134,
+ "tokens / sec": 7884.430531089723,
+ "mem allocated avg": 6773840521.216,
+ "mem reserved avg": 11353729269.76,
+ "elapsed time": 322.872066240001
+ },
+ {
+ "step": 1250,
+ "valid accuracy": 0.0,
+ "train loss": 1.2484543447494507,
+ "train samples": 5000,
+ "train time": 26.471019316944876,
+ "eval time": 10.449013539997395,
+ "tokens / sec": 7877.973926999808,
+ "mem allocated avg": 6774061203.456,
+ "mem reserved avg": 11347018383.36,
+ "elapsed time": 400.9208664790058
+ },
+ {
+ "step": 1500,
+ "valid accuracy": 0.0,
+ "train loss": 1.2315508608818053,
+ "train samples": 6000,
+ "train time": 26.742762298934394,
+ "eval time": 10.483759973009,
+ "tokens / sec": 7827.575837531978,
+ "mem allocated avg": 6775242500.096,
+ "mem reserved avg": 11381990490.112,
+ "elapsed time": 479.3449222920026
+ },
+ {
+ "step": 1750,
+ "valid accuracy": 0.0,
+ "train loss": 1.2309930021762847,
+ "train samples": 7000,
+ "train time": 26.920282723149285,
+ "eval time": 10.450218685000436,
+ "tokens / sec": 7776.849974163588,
+ "mem allocated avg": 6777141585.92,
+ "mem reserved avg": 11390496538.624,
+ "elapsed time": 558.0740258180012
+ },
+ {
+ "step": 2000,
+ "valid accuracy": 0.0,
+ "train loss": 1.2312077372074126,
+ "train samples": 8000,
+ "train time": 26.66103798917902,
+ "eval time": 10.460793553007534,
+ "tokens / sec": 7790.244328982917,
+ "mem allocated avg": 6774060457.984,
+ "mem reserved avg": 11331650453.504,
+ "elapsed time": 636.1544087350048
+ },
+ {
+ "step": 2250,
+ "valid accuracy": 0.0,
+ "train loss": 1.2250888612270354,
+ "train samples": 9000,
+ "train time": 27.347798306160257,
+ "eval time": 10.455188547988655,
+ "tokens / sec": 7859.791768011602,
+ "mem allocated avg": 6784883898.368,
+ "mem reserved avg": 11515327414.272,
+ "elapsed time": 715.6408126690076
+ },
+ {
+ "step": 2500,
+ "valid accuracy": 0.0,
+ "train loss": 1.237301394701004,
+ "train samples": 10000,
+ "train time": 26.43946731692995,
+ "eval time": 10.463690039992798,
+ "tokens / sec": 7790.134253881636,
+ "mem allocated avg": 6770695682.048,
+ "mem reserved avg": 11285622161.408,
+ "elapsed time": 793.5970988850022
+ },
+ {
+ "step": 2750,
+ "valid accuracy": 0.0,
+ "train loss": 1.2318837890625,
+ "train samples": 11000,
+ "train time": 27.072892207099358,
+ "eval time": 10.45099154500349,
+ "tokens / sec": 7826.3156510643585,
+ "mem allocated avg": 6780353579.008,
+ "mem reserved avg": 11444477231.104,
+ "elapsed time": 872.6363771199976
+ },
+ {
+ "step": 3000,
+ "valid accuracy": 0.0,
+ "train loss": 1.2326687624454498,
+ "train samples": 12000,
+ "train time": 26.88052615702327,
+ "eval time": 10.466728950996185,
+ "tokens / sec": 7765.138181473555,
+ "mem allocated avg": 6776020297.728,
+ "mem reserved avg": 11370128998.4,
+ "elapsed time": 951.0341247300094
+ },
+ {
+ "step": 3250,
+ "valid accuracy": 0.0,
+ "train loss": 1.2315667741298675,
+ "train samples": 13000,
+ "train time": 26.58970486979524,
+ "eval time": 10.440216451999731,
+ "tokens / sec": 7931.678859646707,
+ "mem allocated avg": 6777846503.424,
+ "mem reserved avg": 11400059551.744,
+ "elapsed time": 1029.1816804429982
+ },
+ {
+ "step": 3500,
+ "valid accuracy": 0.0,
+ "train loss": 1.232551732301712,
+ "train samples": 14000,
+ "train time": 26.459182894948754,
+ "eval time": 10.444537474992103,
+ "tokens / sec": 7927.304514004579,
+ "mem allocated avg": 6776805982.208,
+ "mem reserved avg": 11380858028.032,
+ "elapsed time": 1107.2912037770002
+ },
+ {
+ "step": 3750,
+ "valid accuracy": 0.0,
+ "train loss": 1.2162783181667327,
+ "train samples": 15000,
+ "train time": 27.070398101161118,
+ "eval time": 10.439593077011523,
+ "tokens / sec": 8005.164873829656,
+ "mem allocated avg": 6786829993.984,
+ "mem reserved avg": 11549276110.848,
+ "elapsed time": 1186.5560989549995
+ },
+ {
+ "step": 4000,
+ "valid accuracy": 0.0,
+ "train loss": 1.2475486118793488,
+ "train samples": 16000,
+ "train time": 26.172411711973837,
+ "eval time": 10.464052501003607,
+ "tokens / sec": 7808.71867098513,
+ "mem allocated avg": 6768875591.68,
+ "mem reserved avg": 11260808658.944,
+ "elapsed time": 1263.9761855469987
+ },
+ {
+ "step": 4250,
+ "valid accuracy": 0.0,
+ "train loss": 1.2161538779735566,
+ "train samples": 17000,
+ "train time": 26.80681787095091,
+ "eval time": 10.449379954006872,
+ "tokens / sec": 7885.643160543526,
+ "mem allocated avg": 6779425828.864,
+ "mem reserved avg": 11415653974.016,
+ "elapsed time": 1342.6529225870036
+ },
+ {
+ "step": 4500,
+ "valid accuracy": 0.0,
+ "train loss": 1.2418145356178283,
+ "train samples": 18000,
+ "train time": 26.542597533072694,
+ "eval time": 10.46835913900577,
+ "tokens / sec": 7829.602952049208,
+ "mem allocated avg": 6773693413.376,
+ "mem reserved avg": 11331625287.68,
+ "elapsed time": 1420.7107766840054
+ },
+ {
+ "step": 4750,
+ "valid accuracy": 0.0,
+ "train loss": 1.2255646660327912,
+ "train samples": 19000,
+ "train time": 26.923357297797338,
+ "eval time": 10.45829652599059,
+ "tokens / sec": 7797.653081593045,
+ "mem allocated avg": 6775938277.376,
+ "mem reserved avg": 11381587836.928,
+ "elapsed time": 1499.7020156110084
+ },
+ {
+ "step": 5000,
+ "valid accuracy": 0.0,
+ "train loss": 1.2370348122119903,
+ "train samples": 20000,
+ "train time": 26.415459764844854,
+ "eval time": 10.446229163004318,
+ "tokens / sec": 7884.776636641793,
+ "mem allocated avg": 6773129859.072,
+ "mem reserved avg": 11327984631.808,
+ "elapsed time": 1577.772203030996
+ },
+ {
+ "step": 5000,
+ "test accuracy": 0.0,
+ "train loss": 1.2370348122119903,
+ "train samples": 20000,
+ "train total tokens": 4198051
+ }
+ ]
+ },
+ "meta_info": {
+ "model_info": {
+ "sha": "13afe5124825b4f3751f836b40dafda64c1ed062",
+ "created_at": "2024-09-18T15:23:48+00:00"
+ },
+ "dataset_info": {
+ "metamath": {
+ "sha": "aa4f34d3d2d3231299b5b03d9b3e5a20da45aa18",
+ "created_at": "2023-09-21T17:22:46+00:00"
+ },
+ "gsm8k": {
+ "sha": "e53f048856ff4f594e959d75785d2c2d37b678ee",
+ "created_at": "2022-04-12T10:22:10+00:00"
+ }
+ },
+ "package_info": {
+ "transformers-version": "4.52.4",
+ "transformers-commit-hash": null,
+ "peft-version": "0.15.2.dev0",
+ "peft-commit-hash": "5fe7f8f8abe914d313fc3751f2ea92de7718fbaf",
+ "datasets-version": "3.6.0",
+ "datasets-commit-hash": null,
+ "bitsandbytes-version": "0.46.0",
+ "bitsandbytes-commit-hash": null,
+ "torch-version": "2.7.1+cu126",
+ "torch-commit-hash": null
+ },
+ "system_info": {
+ "system": "Linux",
+ "release": "6.8.0-1029-aws",
+ "version": "#31-Ubuntu SMP Wed Apr 23 18:42:41 UTC 2025",
+ "machine": "x86_64",
+ "processor": "x86_64",
+ "accelerator": "NVIDIA L40S"
+ },
+ "pytorch_info": "PyTorch built with:\n - GCC 11.2\n - C++ Version: 201703\n - Intel(R) oneAPI Math Kernel Library Version 2024.2-Product Build 20240605 for Intel(R) 64 architecture applications\n - Intel(R) MKL-DNN v3.7.1 (Git Hash 8d263e693366ef8db40acc569cc7d8edf644556d)\n - OpenMP 201511 (a.k.a. OpenMP 4.5)\n - LAPACK is enabled (usually provided by MKL)\n - NNPACK is enabled\n - CPU capability usage: AVX2\n - CUDA Runtime 12.6\n - NVCC architecture flags: -gencode;arch=compute_50,code=sm_50;-gencode;arch=compute_60,code=sm_60;-gencode;arch=compute_70,code=sm_70;-gencode;arch=compute_75,code=sm_75;-gencode;arch=compute_80,code=sm_80;-gencode;arch=compute_86,code=sm_86;-gencode;arch=compute_90,code=sm_90\n - CuDNN 90.7.1 (built against CUDA 12.8)\n - Built with CuDNN 90.5.1\n - Magma 2.6.1\n - Build settings: BLAS_INFO=mkl, BUILD_TYPE=Release, COMMIT_SHA=e2d141dbde55c2a4370fac5165b0561b6af4798b, CUDA_VERSION=12.6, CUDNN_VERSION=9.5.1, CXX_COMPILER=/opt/rh/gcc-toolset-11/root/usr/bin/c++, CXX_FLAGS= -D_GLIBCXX_USE_CXX11_ABI=1 -fvisibility-inlines-hidden -DUSE_PTHREADPOOL -DNDEBUG -DUSE_KINETO -DLIBKINETO_NOROCTRACER -DLIBKINETO_NOXPUPTI=ON -DUSE_FBGEMM -DUSE_PYTORCH_QNNPACK -DUSE_XNNPACK -DSYMBOLICATE_MOBILE_DEBUG_HANDLE -O2 -fPIC -Wall -Wextra -Werror=return-type -Werror=non-virtual-dtor -Werror=range-loop-construct -Werror=bool-operation -Wnarrowing -Wno-missing-field-initializers -Wno-unknown-pragmas -Wno-unused-parameter -Wno-strict-overflow -Wno-strict-aliasing -Wno-stringop-overflow -Wsuggest-override -Wno-psabi -Wno-error=old-style-cast -fdiagnostics-color=always -faligned-new -Wno-maybe-uninitialized -fno-math-errno -fno-trapping-math -Werror=format -Wno-stringop-overflow, LAPACK_INFO=mkl, PERF_WITH_AVX=1, PERF_WITH_AVX2=1, TORCH_VERSION=2.7.1, USE_CUDA=ON, USE_CUDNN=ON, USE_CUSPARSELT=1, USE_GFLAGS=OFF, USE_GLOG=OFF, USE_GLOO=ON, USE_MKL=ON, USE_MKLDNN=ON, USE_MPI=OFF, USE_NCCL=1, USE_NNPACK=ON, USE_OPENMP=ON, USE_ROCM=OFF, USE_ROCM_KERNEL_ASSERT=OFF, \n"
+ }
+}
diff --git a/peft/method_comparison/MetaMathQA/results/loha--llama-3.2-3B-rank32.json b/peft/method_comparison/MetaMathQA/results/loha--llama-3.2-3B-rank32.json
new file mode 100644
index 0000000000000000000000000000000000000000..7baa8eb00fbb4baea00d55b0bd56b06f286ec04d
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/results/loha--llama-3.2-3B-rank32.json
@@ -0,0 +1,355 @@
+{
+ "run_info": {
+ "created_at": "2025-06-19T16:12:05+00:00",
+ "total_time": 2590.9341236870005,
+ "experiment_name": "loha/llama-3.2-3B-rank32",
+ "peft_branch": "main",
+ "train_config": {
+ "model_id": "meta-llama/Llama-3.2-3B",
+ "dtype": "bfloat16",
+ "max_seq_length": 768,
+ "batch_size": 4,
+ "batch_size_eval": 50,
+ "max_steps": 5000,
+ "eval_steps": 250,
+ "compile": false,
+ "query_template": "Question: {query} Think step by step.\nAnswer:",
+ "seed": 0,
+ "grad_norm_clip": 1.0,
+ "optimizer_type": "AdamW",
+ "optimizer_kwargs": {
+ "lr": 0.0001,
+ "weight_decay": 0.1
+ },
+ "lr_scheduler": "cosine",
+ "use_amp": false,
+ "autocast_adapter_dtype": true,
+ "generation_kwargs": {
+ "max_length": 800,
+ "max_new_tokens": 300
+ },
+ "attn_implementation": null
+ },
+ "peft_config": {
+ "task_type": null,
+ "peft_type": "LOHA",
+ "auto_mapping": null,
+ "base_model_name_or_path": "meta-llama/Llama-3.2-3B",
+ "revision": null,
+ "inference_mode": false,
+ "rank_pattern": {},
+ "alpha_pattern": {},
+ "r": 32,
+ "alpha": 64,
+ "rank_dropout": 0.0,
+ "module_dropout": 0.0,
+ "use_effective_conv2d": false,
+ "target_modules": [
+ "q_proj",
+ "v_proj"
+ ],
+ "exclude_modules": null,
+ "init_weights": true,
+ "layers_to_transform": null,
+ "layers_pattern": null,
+ "modules_to_save": null
+ },
+ "error_msg": ""
+ },
+ "train_info": {
+ "accelerator_memory_reserved_avg": 13446820344,
+ "accelerator_memory_max": 23886561280,
+ "accelerator_memory_reserved_99th": 19247870771,
+ "train_time": 2340.7451966560056,
+ "file_size": 73429560,
+ "num_trainable_params": 18350080,
+ "num_total_params": 3231099904,
+ "status": "success",
+ "metrics": [
+ {
+ "step": 250,
+ "valid accuracy": 0.0,
+ "train loss": 1.2914833688735963,
+ "train samples": 1000,
+ "train time": 47.4107696449737,
+ "eval time": 14.298813604000316,
+ "tokens / sec": 4465.630943885038,
+ "mem allocated avg": 7073903032.32,
+ "mem reserved avg": 13501707845.632,
+ "elapsed time": 120.40146815400112
+ },
+ {
+ "step": 500,
+ "valid accuracy": 0.36,
+ "train loss": 0.9051123185157776,
+ "train samples": 2000,
+ "train time": 47.1910586300055,
+ "eval time": 14.155041256999539,
+ "tokens / sec": 4407.508668766131,
+ "mem allocated avg": 7065529796.608,
+ "mem reserved avg": 13391154380.8,
+ "elapsed time": 234.63223427900084
+ },
+ {
+ "step": 750,
+ "valid accuracy": 0.34,
+ "train loss": 0.7515897085666656,
+ "train samples": 3000,
+ "train time": 48.203471163995346,
+ "eval time": 14.26281827999992,
+ "tokens / sec": 4447.8332124791605,
+ "mem allocated avg": 7076336949.248,
+ "mem reserved avg": 13550454046.72,
+ "elapsed time": 350.3563782780002
+ },
+ {
+ "step": 1000,
+ "valid accuracy": 0.4,
+ "train loss": 0.7082941273450851,
+ "train samples": 4000,
+ "train time": 47.1758063940124,
+ "eval time": 14.148222272999192,
+ "tokens / sec": 4416.161925457669,
+ "mem allocated avg": 7067704416.256,
+ "mem reserved avg": 13415607173.12,
+ "elapsed time": 464.4216197680016
+ },
+ {
+ "step": 1250,
+ "valid accuracy": 0.32,
+ "train loss": 0.6994056793451309,
+ "train samples": 5000,
+ "train time": 47.32811543400385,
+ "eval time": 14.265782994998517,
+ "tokens / sec": 4406.218123998481,
+ "mem allocated avg": 7067674988.544,
+ "mem reserved avg": 13411052158.976,
+ "elapsed time": 578.864341718001
+ },
+ {
+ "step": 1500,
+ "valid accuracy": 0.38,
+ "train loss": 0.6889224811792374,
+ "train samples": 6000,
+ "train time": 47.48961014100678,
+ "eval time": 9.485757000999001,
+ "tokens / sec": 4407.932585221307,
+ "mem allocated avg": 7068496666.624,
+ "mem reserved avg": 13434196328.448,
+ "elapsed time": 688.8339757740014
+ },
+ {
+ "step": 1750,
+ "valid accuracy": 0.36,
+ "train loss": 0.6795901688337326,
+ "train samples": 7000,
+ "train time": 47.5112849769921,
+ "eval time": 8.524607335999463,
+ "tokens / sec": 4406.426812101222,
+ "mem allocated avg": 7070726457.344,
+ "mem reserved avg": 13451493638.144,
+ "elapsed time": 797.8088079910012
+ },
+ {
+ "step": 2000,
+ "valid accuracy": 0.42,
+ "train loss": 0.680127969622612,
+ "train samples": 8000,
+ "train time": 47.15311444799954,
+ "eval time": 14.09636382700046,
+ "tokens / sec": 4404.714353047605,
+ "mem allocated avg": 7067623004.16,
+ "mem reserved avg": 13389174669.312,
+ "elapsed time": 911.8939753530012
+ },
+ {
+ "step": 2250,
+ "valid accuracy": 0.42,
+ "train loss": 0.6731046036481857,
+ "train samples": 9000,
+ "train time": 48.44002798400652,
+ "eval time": 14.30888277199847,
+ "tokens / sec": 4437.404538060332,
+ "mem allocated avg": 7078766321.664,
+ "mem reserved avg": 13582146207.744,
+ "elapsed time": 1028.5093922580018
+ },
+ {
+ "step": 2500,
+ "valid accuracy": 0.42,
+ "train loss": 0.6711453741788864,
+ "train samples": 10000,
+ "train time": 46.86391301901131,
+ "eval time": 8.751619284999833,
+ "tokens / sec": 4395.002182520381,
+ "mem allocated avg": 7063469082.624,
+ "mem reserved avg": 13336376770.56,
+ "elapsed time": 1137.0856770440005
+ },
+ {
+ "step": 2750,
+ "valid accuracy": 0.44,
+ "train loss": 0.6645345565080643,
+ "train samples": 11000,
+ "train time": 47.92562343400823,
+ "eval time": 7.835686906000774,
+ "tokens / sec": 4421.037950434847,
+ "mem allocated avg": 7074535438.336,
+ "mem reserved avg": 13512352989.184,
+ "elapsed time": 1246.1237790820014
+ },
+ {
+ "step": 3000,
+ "valid accuracy": 0.4,
+ "train loss": 0.6566170369386672,
+ "train samples": 12000,
+ "train time": 47.50991778100797,
+ "eval time": 14.152554526999666,
+ "tokens / sec": 4393.419516365485,
+ "mem allocated avg": 7068629661.696,
+ "mem reserved avg": 13428215250.944,
+ "elapsed time": 1360.8028930970013
+ },
+ {
+ "step": 3250,
+ "valid accuracy": 0.42,
+ "train loss": 0.6667062133550644,
+ "train samples": 13000,
+ "train time": 47.62723316902702,
+ "eval time": 14.332656014001259,
+ "tokens / sec": 4428.1598146069355,
+ "mem allocated avg": 7071043653.632,
+ "mem reserved avg": 13457114005.504,
+ "elapsed time": 1476.0946507730005
+ },
+ {
+ "step": 3500,
+ "valid accuracy": 0.42,
+ "train loss": 0.6537795497179031,
+ "train samples": 14000,
+ "train time": 47.07006615899445,
+ "eval time": 14.135684340000807,
+ "tokens / sec": 4456.12290604184,
+ "mem allocated avg": 7069669969.92,
+ "mem reserved avg": 13439749586.944,
+ "elapsed time": 1590.4238928290015
+ },
+ {
+ "step": 3750,
+ "valid accuracy": 0.46,
+ "train loss": 0.6509792991876602,
+ "train samples": 15000,
+ "train time": 48.58318820000204,
+ "eval time": 14.298812560000442,
+ "tokens / sec": 4460.452432802484,
+ "mem allocated avg": 7081669246.976,
+ "mem reserved avg": 13624240242.688,
+ "elapsed time": 1707.3096692510007
+ },
+ {
+ "step": 4000,
+ "valid accuracy": 0.46,
+ "train loss": 0.6675102390050888,
+ "train samples": 16000,
+ "train time": 46.83876558602242,
+ "eval time": 14.188353157000165,
+ "tokens / sec": 4363.330191199334,
+ "mem allocated avg": 7062227976.192,
+ "mem reserved avg": 13316957143.04,
+ "elapsed time": 1821.413719397
+ },
+ {
+ "step": 4250,
+ "valid accuracy": 0.46,
+ "train loss": 0.6494157313108444,
+ "train samples": 17000,
+ "train time": 46.9989987980116,
+ "eval time": 8.258924301999286,
+ "tokens / sec": 4497.7341093688,
+ "mem allocated avg": 7072862310.4,
+ "mem reserved avg": 13470619664.384,
+ "elapsed time": 1930.0706906220003
+ },
+ {
+ "step": 4500,
+ "valid accuracy": 0.44,
+ "train loss": 0.6580193819999695,
+ "train samples": 18000,
+ "train time": 47.171681194990015,
+ "eval time": 9.717189478000364,
+ "tokens / sec": 4405.566957449713,
+ "mem allocated avg": 7068038127.616,
+ "mem reserved avg": 13393654185.984,
+ "elapsed time": 2040.1967968460012
+ },
+ {
+ "step": 4750,
+ "valid accuracy": 0.48,
+ "train loss": 0.6511869616508484,
+ "train samples": 19000,
+ "train time": 47.517527918005726,
+ "eval time": 14.28858694399969,
+ "tokens / sec": 4418.138089217562,
+ "mem allocated avg": 7069871403.008,
+ "mem reserved avg": 13443927113.728,
+ "elapsed time": 2155.4679406510004
+ },
+ {
+ "step": 5000,
+ "valid accuracy": 0.46,
+ "train loss": 0.6569721374511719,
+ "train samples": 20000,
+ "train time": 46.99870921700858,
+ "eval time": 9.378413720998651,
+ "tokens / sec": 4431.6110691104805,
+ "mem allocated avg": 7066192863.232,
+ "mem reserved avg": 13386213490.688,
+ "elapsed time": 2265.1425104650007
+ },
+ {
+ "step": 5000,
+ "test accuracy": 0.4184988627748294,
+ "train loss": 0.6569721374511719,
+ "train samples": 20000,
+ "train total tokens": 4198051
+ }
+ ]
+ },
+ "meta_info": {
+ "model_info": {
+ "sha": "13afe5124825b4f3751f836b40dafda64c1ed062",
+ "created_at": "2024-09-18T15:23:48+00:00"
+ },
+ "dataset_info": {
+ "metamath": {
+ "sha": "aa4f34d3d2d3231299b5b03d9b3e5a20da45aa18",
+ "created_at": "2023-09-21T17:22:46+00:00"
+ },
+ "gsm8k": {
+ "sha": "e53f048856ff4f594e959d75785d2c2d37b678ee",
+ "created_at": "2022-04-12T10:22:10+00:00"
+ }
+ },
+ "package_info": {
+ "transformers-version": "4.52.4",
+ "transformers-commit-hash": null,
+ "peft-version": "0.15.2.dev0",
+ "peft-commit-hash": "5fe7f8f8abe914d313fc3751f2ea92de7718fbaf",
+ "datasets-version": "3.6.0",
+ "datasets-commit-hash": null,
+ "bitsandbytes-version": "0.46.0",
+ "bitsandbytes-commit-hash": null,
+ "torch-version": "2.7.1+cu126",
+ "torch-commit-hash": null
+ },
+ "system_info": {
+ "system": "Linux",
+ "release": "6.8.0-1029-aws",
+ "version": "#31-Ubuntu SMP Wed Apr 23 18:42:41 UTC 2025",
+ "machine": "x86_64",
+ "processor": "x86_64",
+ "accelerator": "NVIDIA L40S"
+ },
+ "pytorch_info": "PyTorch built with:\n - GCC 11.2\n - C++ Version: 201703\n - Intel(R) oneAPI Math Kernel Library Version 2024.2-Product Build 20240605 for Intel(R) 64 architecture applications\n - Intel(R) MKL-DNN v3.7.1 (Git Hash 8d263e693366ef8db40acc569cc7d8edf644556d)\n - OpenMP 201511 (a.k.a. OpenMP 4.5)\n - LAPACK is enabled (usually provided by MKL)\n - NNPACK is enabled\n - CPU capability usage: AVX2\n - CUDA Runtime 12.6\n - NVCC architecture flags: -gencode;arch=compute_50,code=sm_50;-gencode;arch=compute_60,code=sm_60;-gencode;arch=compute_70,code=sm_70;-gencode;arch=compute_75,code=sm_75;-gencode;arch=compute_80,code=sm_80;-gencode;arch=compute_86,code=sm_86;-gencode;arch=compute_90,code=sm_90\n - CuDNN 90.7.1 (built against CUDA 12.8)\n - Built with CuDNN 90.5.1\n - Magma 2.6.1\n - Build settings: BLAS_INFO=mkl, BUILD_TYPE=Release, COMMIT_SHA=e2d141dbde55c2a4370fac5165b0561b6af4798b, CUDA_VERSION=12.6, CUDNN_VERSION=9.5.1, CXX_COMPILER=/opt/rh/gcc-toolset-11/root/usr/bin/c++, CXX_FLAGS= -D_GLIBCXX_USE_CXX11_ABI=1 -fvisibility-inlines-hidden -DUSE_PTHREADPOOL -DNDEBUG -DUSE_KINETO -DLIBKINETO_NOROCTRACER -DLIBKINETO_NOXPUPTI=ON -DUSE_FBGEMM -DUSE_PYTORCH_QNNPACK -DUSE_XNNPACK -DSYMBOLICATE_MOBILE_DEBUG_HANDLE -O2 -fPIC -Wall -Wextra -Werror=return-type -Werror=non-virtual-dtor -Werror=range-loop-construct -Werror=bool-operation -Wnarrowing -Wno-missing-field-initializers -Wno-unknown-pragmas -Wno-unused-parameter -Wno-strict-overflow -Wno-strict-aliasing -Wno-stringop-overflow -Wsuggest-override -Wno-psabi -Wno-error=old-style-cast -fdiagnostics-color=always -faligned-new -Wno-maybe-uninitialized -fno-math-errno -fno-trapping-math -Werror=format -Wno-stringop-overflow, LAPACK_INFO=mkl, PERF_WITH_AVX=1, PERF_WITH_AVX2=1, TORCH_VERSION=2.7.1, USE_CUDA=ON, USE_CUDNN=ON, USE_CUSPARSELT=1, USE_GFLAGS=OFF, USE_GLOG=OFF, USE_GLOO=ON, USE_MKL=ON, USE_MKLDNN=ON, USE_MPI=OFF, USE_NCCL=1, USE_NNPACK=ON, USE_OPENMP=ON, USE_ROCM=OFF, USE_ROCM_KERNEL_ASSERT=OFF, \n"
+ }
+}
diff --git a/peft/method_comparison/MetaMathQA/results/lokr--llama-3.2-3B-rank32.json b/peft/method_comparison/MetaMathQA/results/lokr--llama-3.2-3B-rank32.json
new file mode 100644
index 0000000000000000000000000000000000000000..07ae5b1b5a95ddd9a199e1bc5e3f5d6c01b2557f
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/results/lokr--llama-3.2-3B-rank32.json
@@ -0,0 +1,358 @@
+{
+ "run_info": {
+ "created_at": "2025-06-19T22:33:02+00:00",
+ "total_time": 2351.995087948999,
+ "experiment_name": "lokr/llama-3.2-3B-rank32",
+ "peft_branch": "main",
+ "train_config": {
+ "model_id": "meta-llama/Llama-3.2-3B",
+ "dtype": "bfloat16",
+ "max_seq_length": 768,
+ "batch_size": 4,
+ "batch_size_eval": 50,
+ "max_steps": 5000,
+ "eval_steps": 250,
+ "compile": false,
+ "query_template": "Question: {query} Think step by step.\nAnswer:",
+ "seed": 0,
+ "grad_norm_clip": 1.0,
+ "optimizer_type": "AdamW",
+ "optimizer_kwargs": {
+ "lr": 0.0001,
+ "weight_decay": 0.1
+ },
+ "lr_scheduler": "cosine",
+ "use_amp": false,
+ "autocast_adapter_dtype": true,
+ "generation_kwargs": {
+ "max_length": 800,
+ "max_new_tokens": 300
+ },
+ "attn_implementation": null
+ },
+ "peft_config": {
+ "task_type": null,
+ "peft_type": "LOKR",
+ "auto_mapping": null,
+ "base_model_name_or_path": "meta-llama/Llama-3.2-3B",
+ "revision": null,
+ "inference_mode": false,
+ "rank_pattern": {},
+ "alpha_pattern": {},
+ "r": 32,
+ "alpha": 64,
+ "rank_dropout": 0.0,
+ "module_dropout": 0.0,
+ "use_effective_conv2d": false,
+ "decompose_both": false,
+ "decompose_factor": -1,
+ "rank_dropout_scale": false,
+ "target_modules": [
+ "q_proj",
+ "v_proj"
+ ],
+ "exclude_modules": null,
+ "init_weights": true,
+ "layers_to_transform": null,
+ "layers_pattern": null,
+ "modules_to_save": null
+ },
+ "error_msg": ""
+ },
+ "train_info": {
+ "accelerator_memory_reserved_avg": 13173683073,
+ "accelerator_memory_max": 23565697024,
+ "accelerator_memory_reserved_99th": 18987698094,
+ "train_time": 2152.0406475960117,
+ "file_size": 1131984,
+ "num_trainable_params": 279552,
+ "num_total_params": 3213029376,
+ "status": "success",
+ "metrics": [
+ {
+ "step": 250,
+ "valid accuracy": 0.0,
+ "train loss": 1.2610720434188842,
+ "train samples": 1000,
+ "train time": 43.70352009194903,
+ "eval time": 12.492729608995432,
+ "tokens / sec": 4844.438149479918,
+ "mem allocated avg": 6786119440.384,
+ "mem reserved avg": 13227744296.96,
+ "elapsed time": 111.06800683099573
+ },
+ {
+ "step": 500,
+ "valid accuracy": 0.32,
+ "train loss": 0.9418708410263061,
+ "train samples": 2000,
+ "train time": 42.27786245904281,
+ "eval time": 12.404362346002017,
+ "tokens / sec": 4919.714193249426,
+ "mem allocated avg": 6777965645.824,
+ "mem reserved avg": 13119581585.408,
+ "elapsed time": 215.0703402069994
+ },
+ {
+ "step": 750,
+ "valid accuracy": 0.38,
+ "train loss": 0.7932645809650422,
+ "train samples": 3000,
+ "train time": 42.92248660406767,
+ "eval time": 12.39727676199982,
+ "tokens / sec": 4995.0740733571965,
+ "mem allocated avg": 6788190218.24,
+ "mem reserved avg": 13280533807.104,
+ "elapsed time": 319.9520932419982
+ },
+ {
+ "step": 1000,
+ "valid accuracy": 0.38,
+ "train loss": 0.7486661098003388,
+ "train samples": 4000,
+ "train time": 42.81222543502372,
+ "eval time": 12.462298920996545,
+ "tokens / sec": 4866.273544135012,
+ "mem allocated avg": 6778714585.088,
+ "mem reserved avg": 13136702734.336,
+ "elapsed time": 424.5020112219936
+ },
+ {
+ "step": 1250,
+ "valid accuracy": 0.3,
+ "train loss": 0.7329869548082352,
+ "train samples": 5000,
+ "train time": 42.917129570938414,
+ "eval time": 12.430814264000219,
+ "tokens / sec": 4859.085453403965,
+ "mem allocated avg": 6779904688.128,
+ "mem reserved avg": 13134379089.92,
+ "elapsed time": 529.3957975729936
+ },
+ {
+ "step": 1500,
+ "valid accuracy": 0.38,
+ "train loss": 0.7207228287458419,
+ "train samples": 6000,
+ "train time": 43.03383123301319,
+ "eval time": 12.441326129999652,
+ "tokens / sec": 4864.335663412017,
+ "mem allocated avg": 6779916724.224,
+ "mem reserved avg": 13160828370.944,
+ "elapsed time": 634.2579850239999
+ },
+ {
+ "step": 1750,
+ "valid accuracy": 0.34,
+ "train loss": 0.7103905143737793,
+ "train samples": 7000,
+ "train time": 42.76188673896104,
+ "eval time": 12.393813144997694,
+ "tokens / sec": 4895.831684836612,
+ "mem allocated avg": 6782196824.064,
+ "mem reserved avg": 13176313741.312,
+ "elapsed time": 738.7873818459993
+ },
+ {
+ "step": 2000,
+ "valid accuracy": 0.34,
+ "train loss": 0.709170572757721,
+ "train samples": 8000,
+ "train time": 42.39193291300762,
+ "eval time": 12.418300639998051,
+ "tokens / sec": 4899.422737486692,
+ "mem allocated avg": 6778828410.88,
+ "mem reserved avg": 13120303005.696,
+ "elapsed time": 842.8626621349977
+ },
+ {
+ "step": 2250,
+ "valid accuracy": 0.38,
+ "train loss": 0.7017016235589981,
+ "train samples": 9000,
+ "train time": 43.90131158899749,
+ "eval time": 12.417865242998232,
+ "tokens / sec": 4896.163513571884,
+ "mem allocated avg": 6790482182.144,
+ "mem reserved avg": 13307486404.608,
+ "elapsed time": 949.0399838449957
+ },
+ {
+ "step": 2500,
+ "valid accuracy": 0.36,
+ "train loss": 0.6999357705116271,
+ "train samples": 10000,
+ "train time": 41.90174934701645,
+ "eval time": 7.302261034004914,
+ "tokens / sec": 4915.474967268057,
+ "mem allocated avg": 6775840593.92,
+ "mem reserved avg": 13059930193.92,
+ "elapsed time": 1047.236226049994
+ },
+ {
+ "step": 2750,
+ "valid accuracy": 0.36,
+ "train loss": 0.694103113770485,
+ "train samples": 11000,
+ "train time": 43.541668150042824,
+ "eval time": 12.415209386999777,
+ "tokens / sec": 4866.166341396629,
+ "mem allocated avg": 6786276190.208,
+ "mem reserved avg": 13245360373.76,
+ "elapsed time": 1152.8413292650002
+ },
+ {
+ "step": 3000,
+ "valid accuracy": 0.4,
+ "train loss": 0.686756227850914,
+ "train samples": 12000,
+ "train time": 43.03442109594471,
+ "eval time": 7.144659414996568,
+ "tokens / sec": 4850.32666140987,
+ "mem allocated avg": 6781073500.16,
+ "mem reserved avg": 13155426107.392,
+ "elapsed time": 1252.4253450399992
+ },
+ {
+ "step": 3250,
+ "valid accuracy": 0.38,
+ "train loss": 0.6960614495277405,
+ "train samples": 13000,
+ "train time": 43.27108911598771,
+ "eval time": 7.294012983998982,
+ "tokens / sec": 4873.947115929577,
+ "mem allocated avg": 6783027929.088,
+ "mem reserved avg": 13189282529.28,
+ "elapsed time": 1352.4968370129936
+ },
+ {
+ "step": 3500,
+ "valid accuracy": 0.4,
+ "train loss": 0.6833453825712203,
+ "train samples": 14000,
+ "train time": 43.27389094301907,
+ "eval time": 7.8778488079988165,
+ "tokens / sec": 4847.03352134867,
+ "mem allocated avg": 6781185138.688,
+ "mem reserved avg": 13163252678.656,
+ "elapsed time": 1453.3269581979985
+ },
+ {
+ "step": 3750,
+ "valid accuracy": 0.38,
+ "train loss": 0.6804633007049561,
+ "train samples": 15000,
+ "train time": 44.034181773953605,
+ "eval time": 7.058443625996006,
+ "tokens / sec": 4921.245070759568,
+ "mem allocated avg": 6792035817.472,
+ "mem reserved avg": 13346417934.336,
+ "elapsed time": 1554.5450010249988
+ },
+ {
+ "step": 4000,
+ "valid accuracy": 0.36,
+ "train loss": 0.6990108703374862,
+ "train samples": 16000,
+ "train time": 42.4217994650171,
+ "eval time": 7.152937473998463,
+ "tokens / sec": 4817.6409906547,
+ "mem allocated avg": 6773882982.4,
+ "mem reserved avg": 13037876543.488,
+ "elapsed time": 1653.5999729619944
+ },
+ {
+ "step": 4250,
+ "valid accuracy": 0.4,
+ "train loss": 0.6789947774410248,
+ "train samples": 17000,
+ "train time": 43.347477565999725,
+ "eval time": 7.062385851000727,
+ "tokens / sec": 4876.615938681662,
+ "mem allocated avg": 6784096524.288,
+ "mem reserved avg": 13200808476.672,
+ "elapsed time": 1754.0244643159967
+ },
+ {
+ "step": 4500,
+ "valid accuracy": 0.36,
+ "train loss": 0.6891120710372924,
+ "train samples": 18000,
+ "train time": 42.82309688109672,
+ "eval time": 7.127946433000034,
+ "tokens / sec": 4852.941873331364,
+ "mem allocated avg": 6779667169.28,
+ "mem reserved avg": 13117727703.04,
+ "elapsed time": 1853.5914762979955
+ },
+ {
+ "step": 4750,
+ "valid accuracy": 0.38,
+ "train loss": 0.6815101335048676,
+ "train samples": 19000,
+ "train time": 43.26974187397718,
+ "eval time": 7.069867040001554,
+ "tokens / sec": 4851.866244347975,
+ "mem allocated avg": 6780809029.632,
+ "mem reserved avg": 13175080615.936,
+ "elapsed time": 1954.106976348994
+ },
+ {
+ "step": 5000,
+ "valid accuracy": 0.36,
+ "train loss": 0.6876721383333206,
+ "train samples": 20000,
+ "train time": 43.18727576800302,
+ "eval time": 7.149106363998726,
+ "tokens / sec": 4822.716790909798,
+ "mem allocated avg": 6778227302.4,
+ "mem reserved avg": 13118625284.096,
+ "elapsed time": 2054.7161079569996
+ },
+ {
+ "step": 5000,
+ "test accuracy": 0.3752843062926459,
+ "train loss": 0.6876721383333206,
+ "train samples": 20000,
+ "train total tokens": 4198051
+ }
+ ]
+ },
+ "meta_info": {
+ "model_info": {
+ "sha": "13afe5124825b4f3751f836b40dafda64c1ed062",
+ "created_at": "2024-09-18T15:23:48+00:00"
+ },
+ "dataset_info": {
+ "metamath": {
+ "sha": "aa4f34d3d2d3231299b5b03d9b3e5a20da45aa18",
+ "created_at": "2023-09-21T17:22:46+00:00"
+ },
+ "gsm8k": {
+ "sha": "e53f048856ff4f594e959d75785d2c2d37b678ee",
+ "created_at": "2022-04-12T10:22:10+00:00"
+ }
+ },
+ "package_info": {
+ "transformers-version": "4.52.4",
+ "transformers-commit-hash": null,
+ "peft-version": "0.15.2.dev0",
+ "peft-commit-hash": "5fe7f8f8abe914d313fc3751f2ea92de7718fbaf",
+ "datasets-version": "3.6.0",
+ "datasets-commit-hash": null,
+ "bitsandbytes-version": "0.46.0",
+ "bitsandbytes-commit-hash": null,
+ "torch-version": "2.7.1+cu126",
+ "torch-commit-hash": null
+ },
+ "system_info": {
+ "system": "Linux",
+ "release": "6.8.0-1029-aws",
+ "version": "#31-Ubuntu SMP Wed Apr 23 18:42:41 UTC 2025",
+ "machine": "x86_64",
+ "processor": "x86_64",
+ "accelerator": "NVIDIA L40S"
+ },
+ "pytorch_info": "PyTorch built with:\n - GCC 11.2\n - C++ Version: 201703\n - Intel(R) oneAPI Math Kernel Library Version 2024.2-Product Build 20240605 for Intel(R) 64 architecture applications\n - Intel(R) MKL-DNN v3.7.1 (Git Hash 8d263e693366ef8db40acc569cc7d8edf644556d)\n - OpenMP 201511 (a.k.a. OpenMP 4.5)\n - LAPACK is enabled (usually provided by MKL)\n - NNPACK is enabled\n - CPU capability usage: AVX2\n - CUDA Runtime 12.6\n - NVCC architecture flags: -gencode;arch=compute_50,code=sm_50;-gencode;arch=compute_60,code=sm_60;-gencode;arch=compute_70,code=sm_70;-gencode;arch=compute_75,code=sm_75;-gencode;arch=compute_80,code=sm_80;-gencode;arch=compute_86,code=sm_86;-gencode;arch=compute_90,code=sm_90\n - CuDNN 90.7.1 (built against CUDA 12.8)\n - Built with CuDNN 90.5.1\n - Magma 2.6.1\n - Build settings: BLAS_INFO=mkl, BUILD_TYPE=Release, COMMIT_SHA=e2d141dbde55c2a4370fac5165b0561b6af4798b, CUDA_VERSION=12.6, CUDNN_VERSION=9.5.1, CXX_COMPILER=/opt/rh/gcc-toolset-11/root/usr/bin/c++, CXX_FLAGS= -D_GLIBCXX_USE_CXX11_ABI=1 -fvisibility-inlines-hidden -DUSE_PTHREADPOOL -DNDEBUG -DUSE_KINETO -DLIBKINETO_NOROCTRACER -DLIBKINETO_NOXPUPTI=ON -DUSE_FBGEMM -DUSE_PYTORCH_QNNPACK -DUSE_XNNPACK -DSYMBOLICATE_MOBILE_DEBUG_HANDLE -O2 -fPIC -Wall -Wextra -Werror=return-type -Werror=non-virtual-dtor -Werror=range-loop-construct -Werror=bool-operation -Wnarrowing -Wno-missing-field-initializers -Wno-unknown-pragmas -Wno-unused-parameter -Wno-strict-overflow -Wno-strict-aliasing -Wno-stringop-overflow -Wsuggest-override -Wno-psabi -Wno-error=old-style-cast -fdiagnostics-color=always -faligned-new -Wno-maybe-uninitialized -fno-math-errno -fno-trapping-math -Werror=format -Wno-stringop-overflow, LAPACK_INFO=mkl, PERF_WITH_AVX=1, PERF_WITH_AVX2=1, TORCH_VERSION=2.7.1, USE_CUDA=ON, USE_CUDNN=ON, USE_CUSPARSELT=1, USE_GFLAGS=OFF, USE_GLOG=OFF, USE_GLOO=ON, USE_MKL=ON, USE_MKLDNN=ON, USE_MPI=OFF, USE_NCCL=1, USE_NNPACK=ON, USE_OPENMP=ON, USE_ROCM=OFF, USE_ROCM_KERNEL_ASSERT=OFF, \n"
+ }
+}
diff --git a/peft/method_comparison/MetaMathQA/results/lora--llama-3.2-3B-rank32-dora.json b/peft/method_comparison/MetaMathQA/results/lora--llama-3.2-3B-rank32-dora.json
new file mode 100644
index 0000000000000000000000000000000000000000..a2b645db9b84e0c51f55b54d3d912b9af5ce63d4
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/results/lora--llama-3.2-3B-rank32-dora.json
@@ -0,0 +1,365 @@
+{
+ "run_info": {
+ "created_at": "2025-06-19T18:37:24+00:00",
+ "total_time": 2286.5437473089987,
+ "experiment_name": "lora/llama-3.2-3B-rank32-dora",
+ "peft_branch": "main",
+ "train_config": {
+ "model_id": "meta-llama/Llama-3.2-3B",
+ "dtype": "bfloat16",
+ "max_seq_length": 768,
+ "batch_size": 4,
+ "batch_size_eval": 50,
+ "max_steps": 5000,
+ "eval_steps": 250,
+ "compile": false,
+ "query_template": "Question: {query} Think step by step.\nAnswer:",
+ "seed": 0,
+ "grad_norm_clip": 1.0,
+ "optimizer_type": "AdamW",
+ "optimizer_kwargs": {
+ "lr": 0.0001,
+ "weight_decay": 0.1
+ },
+ "lr_scheduler": "cosine",
+ "use_amp": false,
+ "autocast_adapter_dtype": true,
+ "generation_kwargs": {
+ "max_length": 800,
+ "max_new_tokens": 300
+ },
+ "attn_implementation": null
+ },
+ "peft_config": {
+ "task_type": "CAUSAL_LM",
+ "peft_type": "LORA",
+ "auto_mapping": null,
+ "base_model_name_or_path": "meta-llama/Llama-3.2-3B",
+ "revision": null,
+ "inference_mode": false,
+ "r": 32,
+ "target_modules": [
+ "q_proj",
+ "v_proj"
+ ],
+ "exclude_modules": null,
+ "lora_alpha": 64,
+ "lora_dropout": 0.0,
+ "fan_in_fan_out": false,
+ "bias": "none",
+ "use_rslora": false,
+ "modules_to_save": null,
+ "init_lora_weights": true,
+ "layers_to_transform": null,
+ "layers_pattern": null,
+ "rank_pattern": {},
+ "alpha_pattern": {},
+ "megatron_config": null,
+ "megatron_core": "megatron.core",
+ "trainable_token_indices": null,
+ "loftq_config": {},
+ "eva_config": null,
+ "corda_config": null,
+ "use_dora": true,
+ "layer_replication": null,
+ "lora_bias": false
+ },
+ "error_msg": ""
+ },
+ "train_info": {
+ "accelerator_memory_reserved_avg": 12490471636,
+ "accelerator_memory_max": 24553455616,
+ "accelerator_memory_reserved_99th": 19189150515,
+ "train_time": 2022.7454924520134,
+ "file_size": 37181760,
+ "num_trainable_params": 9289728,
+ "num_total_params": 3222039552,
+ "status": "success",
+ "metrics": [
+ {
+ "step": 250,
+ "valid accuracy": 0.36,
+ "train loss": 0.9800839998722076,
+ "train samples": 1000,
+ "train time": 35.42731901501611,
+ "eval time": 16.70931195599769,
+ "tokens / sec": 5976.150775345474,
+ "mem allocated avg": 6924859500.544,
+ "mem reserved avg": 12552201306.112,
+ "elapsed time": 105.33911871900273
+ },
+ {
+ "step": 500,
+ "valid accuracy": 0.44,
+ "train loss": 0.7162023800611496,
+ "train samples": 2000,
+ "train time": 35.53461015297944,
+ "eval time": 16.7331051809997,
+ "tokens / sec": 5853.307496678993,
+ "mem allocated avg": 6917484427.264,
+ "mem reserved avg": 12427118772.224,
+ "elapsed time": 204.02196035100133
+ },
+ {
+ "step": 750,
+ "valid accuracy": 0.42,
+ "train loss": 0.6790966511964798,
+ "train samples": 3000,
+ "train time": 35.395415813978616,
+ "eval time": 10.35499690800134,
+ "tokens / sec": 6057.309825848329,
+ "mem allocated avg": 6927996166.144,
+ "mem reserved avg": 12609050902.528,
+ "elapsed time": 296.3724143870022
+ },
+ {
+ "step": 1000,
+ "valid accuracy": 0.42,
+ "train loss": 0.6590274780988693,
+ "train samples": 4000,
+ "train time": 35.01134122798976,
+ "eval time": 16.638093278997985,
+ "tokens / sec": 5950.528962696411,
+ "mem allocated avg": 6919690883.072,
+ "mem reserved avg": 12464313860.096,
+ "elapsed time": 394.33112582000103
+ },
+ {
+ "step": 1250,
+ "valid accuracy": 0.42,
+ "train loss": 0.6542477097511291,
+ "train samples": 5000,
+ "train time": 34.85555366096378,
+ "eval time": 16.627405782997812,
+ "tokens / sec": 5982.920312453697,
+ "mem allocated avg": 6919055253.504,
+ "mem reserved avg": 12449952563.2,
+ "elapsed time": 492.1167898590029
+ },
+ {
+ "step": 1500,
+ "valid accuracy": 0.4,
+ "train loss": 0.6471435966491699,
+ "train samples": 6000,
+ "train time": 35.407848127983016,
+ "eval time": 10.318167828998412,
+ "tokens / sec": 5911.994404273457,
+ "mem allocated avg": 6921185224.704,
+ "mem reserved avg": 12477500751.872,
+ "elapsed time": 584.325913470002
+ },
+ {
+ "step": 1750,
+ "valid accuracy": 0.42,
+ "train loss": 0.6376023133993148,
+ "train samples": 7000,
+ "train time": 35.61810469696138,
+ "eval time": 10.057756549002079,
+ "tokens / sec": 5877.7692350896,
+ "mem allocated avg": 6922196224.0,
+ "mem reserved avg": 12495888580.608,
+ "elapsed time": 676.5556904380028
+ },
+ {
+ "step": 2000,
+ "valid accuracy": 0.36,
+ "train loss": 0.6404745506048203,
+ "train samples": 8000,
+ "train time": 35.01814225999988,
+ "eval time": 10.846777078000741,
+ "tokens / sec": 5931.097042724754,
+ "mem allocated avg": 6919877345.28,
+ "mem reserved avg": 12428771328.0,
+ "elapsed time": 768.7593245980024
+ },
+ {
+ "step": 2250,
+ "valid accuracy": 0.48,
+ "train loss": 0.6327905882596969,
+ "train samples": 9000,
+ "train time": 35.941867801058834,
+ "eval time": 16.654083295998134,
+ "tokens / sec": 5980.434884178939,
+ "mem allocated avg": 6930785019.904,
+ "mem reserved avg": 12637135962.112,
+ "elapsed time": 868.0876048490027
+ },
+ {
+ "step": 2500,
+ "valid accuracy": 0.44,
+ "train loss": 0.6293514591455459,
+ "train samples": 10000,
+ "train time": 35.19044898093853,
+ "eval time": 16.654415837998386,
+ "tokens / sec": 5852.923334725435,
+ "mem allocated avg": 6914962546.688,
+ "mem reserved avg": 12361175924.736,
+ "elapsed time": 965.9673830700012
+ },
+ {
+ "step": 2750,
+ "valid accuracy": 0.34,
+ "train loss": 0.6212090995311738,
+ "train samples": 11000,
+ "train time": 35.78923041201051,
+ "eval time": 12.364532577001228,
+ "tokens / sec": 5920.2446535116005,
+ "mem allocated avg": 6926067247.104,
+ "mem reserved avg": 12561110007.808,
+ "elapsed time": 1060.7434992320013
+ },
+ {
+ "step": 3000,
+ "valid accuracy": 0.48,
+ "train loss": 0.6132309092283249,
+ "train samples": 12000,
+ "train time": 35.434680095979274,
+ "eval time": 10.902270734000922,
+ "tokens / sec": 5890.585139604081,
+ "mem allocated avg": 6921261266.944,
+ "mem reserved avg": 12472811520.0,
+ "elapsed time": 1153.3681941970026
+ },
+ {
+ "step": 3250,
+ "valid accuracy": 0.5,
+ "train loss": 0.6223928620815277,
+ "train samples": 13000,
+ "train time": 35.475069620017166,
+ "eval time": 9.885322058999009,
+ "tokens / sec": 5945.048234126565,
+ "mem allocated avg": 6922737405.952,
+ "mem reserved avg": 12498002509.824,
+ "elapsed time": 1245.241280964001
+ },
+ {
+ "step": 3500,
+ "valid accuracy": 0.5,
+ "train loss": 0.605602259516716,
+ "train samples": 14000,
+ "train time": 35.607162244014035,
+ "eval time": 10.090815307001321,
+ "tokens / sec": 5890.668808780496,
+ "mem allocated avg": 6920974434.304,
+ "mem reserved avg": 12474329858.048,
+ "elapsed time": 1337.4724736530006
+ },
+ {
+ "step": 3750,
+ "valid accuracy": 0.48,
+ "train loss": 0.6031041693687439,
+ "train samples": 15000,
+ "train time": 36.209776319014054,
+ "eval time": 10.371932055000798,
+ "tokens / sec": 5984.6544781390285,
+ "mem allocated avg": 6933558140.928,
+ "mem reserved avg": 12681738190.848,
+ "elapsed time": 1431.2058649130013
+ },
+ {
+ "step": 4000,
+ "valid accuracy": 0.46,
+ "train loss": 0.6162525477409363,
+ "train samples": 16000,
+ "train time": 35.48366187599095,
+ "eval time": 12.394127589999698,
+ "tokens / sec": 5759.636666425441,
+ "mem allocated avg": 6914222096.384,
+ "mem reserved avg": 12349406707.712,
+ "elapsed time": 1525.3134414390006
+ },
+ {
+ "step": 4250,
+ "valid accuracy": 0.5,
+ "train loss": 0.6013483003377914,
+ "train samples": 17000,
+ "train time": 35.15769277801883,
+ "eval time": 16.63699178299794,
+ "tokens / sec": 6012.59591562743,
+ "mem allocated avg": 6924507731.968,
+ "mem reserved avg": 12521616441.344,
+ "elapsed time": 1623.6120678540028
+ },
+ {
+ "step": 4500,
+ "valid accuracy": 0.48,
+ "train loss": 0.6073888168334961,
+ "train samples": 18000,
+ "train time": 34.98748015804085,
+ "eval time": 12.561758541996824,
+ "tokens / sec": 5939.781860861995,
+ "mem allocated avg": 6918951696.384,
+ "mem reserved avg": 12432495869.952,
+ "elapsed time": 1717.352138276001
+ },
+ {
+ "step": 4750,
+ "valid accuracy": 0.5,
+ "train loss": 0.5993685643672944,
+ "train samples": 19000,
+ "train time": 35.57701125005042,
+ "eval time": 13.379837485997996,
+ "tokens / sec": 5900.973483254653,
+ "mem allocated avg": 6921678901.248,
+ "mem reserved avg": 12490880581.632,
+ "elapsed time": 1812.886111721
+ },
+ {
+ "step": 5000,
+ "valid accuracy": 0.48,
+ "train loss": 0.6068210340738297,
+ "train samples": 20000,
+ "train time": 35.678432397002325,
+ "eval time": 10.087769599998865,
+ "tokens / sec": 5837.700425916121,
+ "mem allocated avg": 6918288025.6,
+ "mem reserved avg": 12423931101.184,
+ "elapsed time": 1905.221841073002
+ },
+ {
+ "step": 5000,
+ "test accuracy": 0.4806671721000758,
+ "train loss": 0.6068210340738297,
+ "train samples": 20000,
+ "train total tokens": 4198051
+ }
+ ]
+ },
+ "meta_info": {
+ "model_info": {
+ "sha": "13afe5124825b4f3751f836b40dafda64c1ed062",
+ "created_at": "2024-09-18T15:23:48+00:00"
+ },
+ "dataset_info": {
+ "metamath": {
+ "sha": "aa4f34d3d2d3231299b5b03d9b3e5a20da45aa18",
+ "created_at": "2023-09-21T17:22:46+00:00"
+ },
+ "gsm8k": {
+ "sha": "e53f048856ff4f594e959d75785d2c2d37b678ee",
+ "created_at": "2022-04-12T10:22:10+00:00"
+ }
+ },
+ "package_info": {
+ "transformers-version": "4.52.4",
+ "transformers-commit-hash": null,
+ "peft-version": "0.15.2.dev0",
+ "peft-commit-hash": "5fe7f8f8abe914d313fc3751f2ea92de7718fbaf",
+ "datasets-version": "3.6.0",
+ "datasets-commit-hash": null,
+ "bitsandbytes-version": "0.46.0",
+ "bitsandbytes-commit-hash": null,
+ "torch-version": "2.7.1+cu126",
+ "torch-commit-hash": null
+ },
+ "system_info": {
+ "system": "Linux",
+ "release": "6.8.0-1029-aws",
+ "version": "#31-Ubuntu SMP Wed Apr 23 18:42:41 UTC 2025",
+ "machine": "x86_64",
+ "processor": "x86_64",
+ "accelerator": "NVIDIA L40S"
+ },
+ "pytorch_info": "PyTorch built with:\n - GCC 11.2\n - C++ Version: 201703\n - Intel(R) oneAPI Math Kernel Library Version 2024.2-Product Build 20240605 for Intel(R) 64 architecture applications\n - Intel(R) MKL-DNN v3.7.1 (Git Hash 8d263e693366ef8db40acc569cc7d8edf644556d)\n - OpenMP 201511 (a.k.a. OpenMP 4.5)\n - LAPACK is enabled (usually provided by MKL)\n - NNPACK is enabled\n - CPU capability usage: AVX2\n - CUDA Runtime 12.6\n - NVCC architecture flags: -gencode;arch=compute_50,code=sm_50;-gencode;arch=compute_60,code=sm_60;-gencode;arch=compute_70,code=sm_70;-gencode;arch=compute_75,code=sm_75;-gencode;arch=compute_80,code=sm_80;-gencode;arch=compute_86,code=sm_86;-gencode;arch=compute_90,code=sm_90\n - CuDNN 90.7.1 (built against CUDA 12.8)\n - Built with CuDNN 90.5.1\n - Magma 2.6.1\n - Build settings: BLAS_INFO=mkl, BUILD_TYPE=Release, COMMIT_SHA=e2d141dbde55c2a4370fac5165b0561b6af4798b, CUDA_VERSION=12.6, CUDNN_VERSION=9.5.1, CXX_COMPILER=/opt/rh/gcc-toolset-11/root/usr/bin/c++, CXX_FLAGS= -D_GLIBCXX_USE_CXX11_ABI=1 -fvisibility-inlines-hidden -DUSE_PTHREADPOOL -DNDEBUG -DUSE_KINETO -DLIBKINETO_NOROCTRACER -DLIBKINETO_NOXPUPTI=ON -DUSE_FBGEMM -DUSE_PYTORCH_QNNPACK -DUSE_XNNPACK -DSYMBOLICATE_MOBILE_DEBUG_HANDLE -O2 -fPIC -Wall -Wextra -Werror=return-type -Werror=non-virtual-dtor -Werror=range-loop-construct -Werror=bool-operation -Wnarrowing -Wno-missing-field-initializers -Wno-unknown-pragmas -Wno-unused-parameter -Wno-strict-overflow -Wno-strict-aliasing -Wno-stringop-overflow -Wsuggest-override -Wno-psabi -Wno-error=old-style-cast -fdiagnostics-color=always -faligned-new -Wno-maybe-uninitialized -fno-math-errno -fno-trapping-math -Werror=format -Wno-stringop-overflow, LAPACK_INFO=mkl, PERF_WITH_AVX=1, PERF_WITH_AVX2=1, TORCH_VERSION=2.7.1, USE_CUDA=ON, USE_CUDNN=ON, USE_CUSPARSELT=1, USE_GFLAGS=OFF, USE_GLOG=OFF, USE_GLOO=ON, USE_MKL=ON, USE_MKLDNN=ON, USE_MPI=OFF, USE_NCCL=1, USE_NNPACK=ON, USE_OPENMP=ON, USE_ROCM=OFF, USE_ROCM_KERNEL_ASSERT=OFF, \n"
+ }
+}
diff --git a/peft/method_comparison/MetaMathQA/results/lora--llama-3.2-3B-rank32-lorafa.json b/peft/method_comparison/MetaMathQA/results/lora--llama-3.2-3B-rank32-lorafa.json
new file mode 100644
index 0000000000000000000000000000000000000000..35c7a9981da710c1f025c69644ff65550b1e0edc
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/results/lora--llama-3.2-3B-rank32-lorafa.json
@@ -0,0 +1,367 @@
+{
+ "run_info": {
+ "created_at": "2025-06-19T17:29:01+00:00",
+ "total_time": 2025.9028512089972,
+ "experiment_name": "lora/llama-3.2-3B-rank32-lorafa",
+ "peft_branch": "main",
+ "train_config": {
+ "model_id": "meta-llama/Llama-3.2-3B",
+ "dtype": "bfloat16",
+ "max_seq_length": 768,
+ "batch_size": 4,
+ "batch_size_eval": 50,
+ "max_steps": 5000,
+ "eval_steps": 250,
+ "compile": false,
+ "query_template": "Question: {query} Think step by step.\nAnswer:",
+ "seed": 0,
+ "grad_norm_clip": 1.0,
+ "optimizer_type": "lora-fa",
+ "optimizer_kwargs": {
+ "r": 32,
+ "lora_alpha": 64,
+ "lr": 0.0001,
+ "weight_decay": 0.1
+ },
+ "lr_scheduler": "cosine",
+ "use_amp": false,
+ "autocast_adapter_dtype": true,
+ "generation_kwargs": {
+ "max_length": 800,
+ "max_new_tokens": 300
+ },
+ "attn_implementation": null
+ },
+ "peft_config": {
+ "task_type": "CAUSAL_LM",
+ "peft_type": "LORA",
+ "auto_mapping": null,
+ "base_model_name_or_path": "meta-llama/Llama-3.2-3B",
+ "revision": null,
+ "inference_mode": false,
+ "r": 32,
+ "target_modules": [
+ "q_proj",
+ "v_proj"
+ ],
+ "exclude_modules": null,
+ "lora_alpha": 64,
+ "lora_dropout": 0.0,
+ "fan_in_fan_out": false,
+ "bias": "none",
+ "use_rslora": false,
+ "modules_to_save": null,
+ "init_lora_weights": true,
+ "layers_to_transform": null,
+ "layers_pattern": null,
+ "rank_pattern": {},
+ "alpha_pattern": {},
+ "megatron_config": null,
+ "megatron_core": "megatron.core",
+ "trainable_token_indices": null,
+ "loftq_config": {},
+ "eva_config": null,
+ "corda_config": null,
+ "use_dora": false,
+ "layer_replication": null,
+ "lora_bias": false
+ },
+ "error_msg": ""
+ },
+ "train_info": {
+ "accelerator_memory_reserved_avg": 11106307276,
+ "accelerator_memory_max": 20187185152,
+ "accelerator_memory_reserved_99th": 16257394933,
+ "train_time": 1821.1390361119993,
+ "file_size": 36715216,
+ "num_trainable_params": 3670016,
+ "num_total_params": 3221924864,
+ "status": "success",
+ "metrics": [
+ {
+ "step": 250,
+ "valid accuracy": 0.26,
+ "train loss": 1.13827001953125,
+ "train samples": 1000,
+ "train time": 39.487167649953335,
+ "eval time": 11.352047874999698,
+ "tokens / sec": 5361.716542367662,
+ "mem allocated avg": 6857574733.824,
+ "mem reserved avg": 11147042357.248,
+ "elapsed time": 95.33382818899918
+ },
+ {
+ "step": 500,
+ "valid accuracy": 0.34,
+ "train loss": 0.8058450784683228,
+ "train samples": 2000,
+ "train time": 38.91575912100234,
+ "eval time": 11.306344865999563,
+ "tokens / sec": 5344.749908469542,
+ "mem allocated avg": 6850229934.08,
+ "mem reserved avg": 11051613552.64,
+ "elapsed time": 184.45338391399855
+ },
+ {
+ "step": 750,
+ "valid accuracy": 0.4,
+ "train loss": 0.725865609407425,
+ "train samples": 3000,
+ "train time": 39.53630301699741,
+ "eval time": 9.965407437997783,
+ "tokens / sec": 5422.889436774727,
+ "mem allocated avg": 6861271248.896,
+ "mem reserved avg": 11192013684.736,
+ "elapsed time": 273.0429774479999
+ },
+ {
+ "step": 1000,
+ "valid accuracy": 0.36,
+ "train loss": 0.69585602581501,
+ "train samples": 4000,
+ "train time": 38.42195282199464,
+ "eval time": 11.263002069001232,
+ "tokens / sec": 5422.316792829388,
+ "mem allocated avg": 6851626665.984,
+ "mem reserved avg": 11074279571.456,
+ "elapsed time": 361.40852819099746
+ },
+ {
+ "step": 1250,
+ "valid accuracy": 0.4,
+ "train loss": 0.6884716705083848,
+ "train samples": 5000,
+ "train time": 38.42177955799343,
+ "eval time": 11.356440440998995,
+ "tokens / sec": 5427.598679682052,
+ "mem allocated avg": 6851712622.592,
+ "mem reserved avg": 11075865018.368,
+ "elapsed time": 449.83568274799836
+ },
+ {
+ "step": 1500,
+ "valid accuracy": 0.38,
+ "train loss": 0.6801862429380416,
+ "train samples": 6000,
+ "train time": 38.768619330003276,
+ "eval time": 11.348457601998234,
+ "tokens / sec": 5399.495871084515,
+ "mem allocated avg": 6853521098.752,
+ "mem reserved avg": 11096006066.176,
+ "elapsed time": 538.7312806489972
+ },
+ {
+ "step": 1750,
+ "valid accuracy": 0.38,
+ "train loss": 0.6713097202777862,
+ "train samples": 7000,
+ "train time": 38.99274470796445,
+ "eval time": 8.222045223003079,
+ "tokens / sec": 5369.0757490389815,
+ "mem allocated avg": 6854799144.96,
+ "mem reserved avg": 11113831858.176,
+ "elapsed time": 624.957832287997
+ },
+ {
+ "step": 2000,
+ "valid accuracy": 0.36,
+ "train loss": 0.6733613710403442,
+ "train samples": 8000,
+ "train time": 38.96502619797684,
+ "eval time": 9.028824541001086,
+ "tokens / sec": 5330.318500101101,
+ "mem allocated avg": 6852199981.056,
+ "mem reserved avg": 11058584485.888,
+ "elapsed time": 711.7122244169987
+ },
+ {
+ "step": 2250,
+ "valid accuracy": 0.38,
+ "train loss": 0.6658626307249069,
+ "train samples": 9000,
+ "train time": 39.83998639498168,
+ "eval time": 11.38518134900005,
+ "tokens / sec": 5395.282966940854,
+ "mem allocated avg": 6862685554.688,
+ "mem reserved avg": 11223865229.312,
+ "elapsed time": 802.4390404449987
+ },
+ {
+ "step": 2500,
+ "valid accuracy": 0.38,
+ "train loss": 0.6645791643857956,
+ "train samples": 10000,
+ "train time": 38.493957691986,
+ "eval time": 11.311897349998617,
+ "tokens / sec": 5350.631952372099,
+ "mem allocated avg": 6848127772.672,
+ "mem reserved avg": 11012925292.544,
+ "elapsed time": 890.7464078919984
+ },
+ {
+ "step": 2750,
+ "valid accuracy": 0.44,
+ "train loss": 0.658472005367279,
+ "train samples": 11000,
+ "train time": 38.51331885699619,
+ "eval time": 7.521690310000849,
+ "tokens / sec": 5501.499384842303,
+ "mem allocated avg": 6858912532.48,
+ "mem reserved avg": 11161915359.232,
+ "elapsed time": 975.6010923279973
+ },
+ {
+ "step": 3000,
+ "valid accuracy": 0.4,
+ "train loss": 0.6503657740354538,
+ "train samples": 12000,
+ "train time": 38.378428091957176,
+ "eval time": 9.959380172000238,
+ "tokens / sec": 5438.758447841249,
+ "mem allocated avg": 6853735892.992,
+ "mem reserved avg": 11091962757.12,
+ "elapsed time": 1062.3718837759989
+ },
+ {
+ "step": 3250,
+ "valid accuracy": 0.48,
+ "train loss": 0.6599743469953537,
+ "train samples": 13000,
+ "train time": 38.74303203701493,
+ "eval time": 9.720565422001528,
+ "tokens / sec": 5443.585308411229,
+ "mem allocated avg": 6855708461.056,
+ "mem reserved avg": 11117246021.632,
+ "elapsed time": 1149.5592005079998
+ },
+ {
+ "step": 3500,
+ "valid accuracy": 0.4,
+ "train loss": 0.6468936309814454,
+ "train samples": 14000,
+ "train time": 38.947772975978296,
+ "eval time": 10.49309463499958,
+ "tokens / sec": 5385.417033455723,
+ "mem allocated avg": 6854553325.568,
+ "mem reserved avg": 11102364631.04,
+ "elapsed time": 1237.83959684
+ },
+ {
+ "step": 3750,
+ "valid accuracy": 0.44,
+ "train loss": 0.6447412570714951,
+ "train samples": 15000,
+ "train time": 39.208677324022574,
+ "eval time": 11.265130790001422,
+ "tokens / sec": 5526.914315654032,
+ "mem allocated avg": 6864447199.232,
+ "mem reserved avg": 11258292076.544,
+ "elapsed time": 1327.6204509749987
+ },
+ {
+ "step": 4000,
+ "valid accuracy": 0.48,
+ "train loss": 0.6609537017345428,
+ "train samples": 16000,
+ "train time": 38.373366451996844,
+ "eval time": 8.435534727999766,
+ "tokens / sec": 5325.907495128434,
+ "mem allocated avg": 6846769313.792,
+ "mem reserved avg": 10994319360.0,
+ "elapsed time": 1412.8209538019983
+ },
+ {
+ "step": 4250,
+ "valid accuracy": 0.46,
+ "train loss": 0.6430994077920914,
+ "train samples": 17000,
+ "train time": 38.840016363014,
+ "eval time": 8.356262703997345,
+ "tokens / sec": 5442.556924391474,
+ "mem allocated avg": 6857134465.024,
+ "mem reserved avg": 11130768457.728,
+ "elapsed time": 1498.7970963499974
+ },
+ {
+ "step": 4500,
+ "valid accuracy": 0.5,
+ "train loss": 0.6519971441030502,
+ "train samples": 18000,
+ "train time": 38.99225058195225,
+ "eval time": 9.193580140999984,
+ "tokens / sec": 5329.725699295479,
+ "mem allocated avg": 6851737821.184,
+ "mem reserved avg": 11062996893.696,
+ "elapsed time": 1585.3292836179971
+ },
+ {
+ "step": 4750,
+ "valid accuracy": 0.42,
+ "train loss": 0.6448501836061478,
+ "train samples": 19000,
+ "train time": 39.31173135296194,
+ "eval time": 8.482506923999608,
+ "tokens / sec": 5340.365147366681,
+ "mem allocated avg": 6853984409.6,
+ "mem reserved avg": 11104352731.136,
+ "elapsed time": 1672.2648903240006
+ },
+ {
+ "step": 5000,
+ "valid accuracy": 0.46,
+ "train loss": 0.6509636770486832,
+ "train samples": 20000,
+ "train time": 38.96172000500519,
+ "eval time": 11.401191647000815,
+ "tokens / sec": 5345.759888763726,
+ "mem allocated avg": 6850959237.12,
+ "mem reserved avg": 11055900131.328,
+ "elapsed time": 1761.553419697997
+ },
+ {
+ "step": 5000,
+ "test accuracy": 0.42987111448066717,
+ "train loss": 0.6509636770486832,
+ "train samples": 20000,
+ "train total tokens": 4198051
+ }
+ ]
+ },
+ "meta_info": {
+ "model_info": {
+ "sha": "13afe5124825b4f3751f836b40dafda64c1ed062",
+ "created_at": "2024-09-18T15:23:48+00:00"
+ },
+ "dataset_info": {
+ "metamath": {
+ "sha": "aa4f34d3d2d3231299b5b03d9b3e5a20da45aa18",
+ "created_at": "2023-09-21T17:22:46+00:00"
+ },
+ "gsm8k": {
+ "sha": "e53f048856ff4f594e959d75785d2c2d37b678ee",
+ "created_at": "2022-04-12T10:22:10+00:00"
+ }
+ },
+ "package_info": {
+ "transformers-version": "4.52.4",
+ "transformers-commit-hash": null,
+ "peft-version": "0.15.2.dev0",
+ "peft-commit-hash": "5fe7f8f8abe914d313fc3751f2ea92de7718fbaf",
+ "datasets-version": "3.6.0",
+ "datasets-commit-hash": null,
+ "bitsandbytes-version": "0.46.0",
+ "bitsandbytes-commit-hash": null,
+ "torch-version": "2.7.1+cu126",
+ "torch-commit-hash": null
+ },
+ "system_info": {
+ "system": "Linux",
+ "release": "6.8.0-1029-aws",
+ "version": "#31-Ubuntu SMP Wed Apr 23 18:42:41 UTC 2025",
+ "machine": "x86_64",
+ "processor": "x86_64",
+ "accelerator": "NVIDIA L40S"
+ },
+ "pytorch_info": "PyTorch built with:\n - GCC 11.2\n - C++ Version: 201703\n - Intel(R) oneAPI Math Kernel Library Version 2024.2-Product Build 20240605 for Intel(R) 64 architecture applications\n - Intel(R) MKL-DNN v3.7.1 (Git Hash 8d263e693366ef8db40acc569cc7d8edf644556d)\n - OpenMP 201511 (a.k.a. OpenMP 4.5)\n - LAPACK is enabled (usually provided by MKL)\n - NNPACK is enabled\n - CPU capability usage: AVX2\n - CUDA Runtime 12.6\n - NVCC architecture flags: -gencode;arch=compute_50,code=sm_50;-gencode;arch=compute_60,code=sm_60;-gencode;arch=compute_70,code=sm_70;-gencode;arch=compute_75,code=sm_75;-gencode;arch=compute_80,code=sm_80;-gencode;arch=compute_86,code=sm_86;-gencode;arch=compute_90,code=sm_90\n - CuDNN 90.7.1 (built against CUDA 12.8)\n - Built with CuDNN 90.5.1\n - Magma 2.6.1\n - Build settings: BLAS_INFO=mkl, BUILD_TYPE=Release, COMMIT_SHA=e2d141dbde55c2a4370fac5165b0561b6af4798b, CUDA_VERSION=12.6, CUDNN_VERSION=9.5.1, CXX_COMPILER=/opt/rh/gcc-toolset-11/root/usr/bin/c++, CXX_FLAGS= -D_GLIBCXX_USE_CXX11_ABI=1 -fvisibility-inlines-hidden -DUSE_PTHREADPOOL -DNDEBUG -DUSE_KINETO -DLIBKINETO_NOROCTRACER -DLIBKINETO_NOXPUPTI=ON -DUSE_FBGEMM -DUSE_PYTORCH_QNNPACK -DUSE_XNNPACK -DSYMBOLICATE_MOBILE_DEBUG_HANDLE -O2 -fPIC -Wall -Wextra -Werror=return-type -Werror=non-virtual-dtor -Werror=range-loop-construct -Werror=bool-operation -Wnarrowing -Wno-missing-field-initializers -Wno-unknown-pragmas -Wno-unused-parameter -Wno-strict-overflow -Wno-strict-aliasing -Wno-stringop-overflow -Wsuggest-override -Wno-psabi -Wno-error=old-style-cast -fdiagnostics-color=always -faligned-new -Wno-maybe-uninitialized -fno-math-errno -fno-trapping-math -Werror=format -Wno-stringop-overflow, LAPACK_INFO=mkl, PERF_WITH_AVX=1, PERF_WITH_AVX2=1, TORCH_VERSION=2.7.1, USE_CUDA=ON, USE_CUDNN=ON, USE_CUSPARSELT=1, USE_GFLAGS=OFF, USE_GLOG=OFF, USE_GLOO=ON, USE_MKL=ON, USE_MKLDNN=ON, USE_MPI=OFF, USE_NCCL=1, USE_NNPACK=ON, USE_OPENMP=ON, USE_ROCM=OFF, USE_ROCM_KERNEL_ASSERT=OFF, \n"
+ }
+}
diff --git a/peft/method_comparison/MetaMathQA/results/lora--llama-3.2-3B-rank32.json b/peft/method_comparison/MetaMathQA/results/lora--llama-3.2-3B-rank32.json
new file mode 100644
index 0000000000000000000000000000000000000000..f3d348c07ec5957e5cdaad74b5c6d9071763afb1
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/results/lora--llama-3.2-3B-rank32.json
@@ -0,0 +1,365 @@
+{
+ "run_info": {
+ "created_at": "2025-06-19T19:15:35+00:00",
+ "total_time": 1993.494420946001,
+ "experiment_name": "lora/llama-3.2-3B-rank32",
+ "peft_branch": "main",
+ "train_config": {
+ "model_id": "meta-llama/Llama-3.2-3B",
+ "dtype": "bfloat16",
+ "max_seq_length": 768,
+ "batch_size": 4,
+ "batch_size_eval": 50,
+ "max_steps": 5000,
+ "eval_steps": 250,
+ "compile": false,
+ "query_template": "Question: {query} Think step by step.\nAnswer:",
+ "seed": 0,
+ "grad_norm_clip": 1.0,
+ "optimizer_type": "AdamW",
+ "optimizer_kwargs": {
+ "lr": 0.0001,
+ "weight_decay": 0.1
+ },
+ "lr_scheduler": "cosine",
+ "use_amp": false,
+ "autocast_adapter_dtype": true,
+ "generation_kwargs": {
+ "max_length": 800,
+ "max_new_tokens": 300
+ },
+ "attn_implementation": null
+ },
+ "peft_config": {
+ "task_type": "CAUSAL_LM",
+ "peft_type": "LORA",
+ "auto_mapping": null,
+ "base_model_name_or_path": "meta-llama/Llama-3.2-3B",
+ "revision": null,
+ "inference_mode": false,
+ "r": 32,
+ "target_modules": [
+ "v_proj",
+ "q_proj"
+ ],
+ "exclude_modules": null,
+ "lora_alpha": 64,
+ "lora_dropout": 0.0,
+ "fan_in_fan_out": false,
+ "bias": "none",
+ "use_rslora": false,
+ "modules_to_save": null,
+ "init_lora_weights": true,
+ "layers_to_transform": null,
+ "layers_pattern": null,
+ "rank_pattern": {},
+ "alpha_pattern": {},
+ "megatron_config": null,
+ "megatron_core": "megatron.core",
+ "trainable_token_indices": null,
+ "loftq_config": {},
+ "eva_config": null,
+ "corda_config": null,
+ "use_dora": false,
+ "layer_replication": null,
+ "lora_bias": false
+ },
+ "error_msg": ""
+ },
+ "train_info": {
+ "accelerator_memory_reserved_avg": 11868689976,
+ "accelerator_memory_max": 22273851392,
+ "accelerator_memory_reserved_99th": 17710763212,
+ "train_time": 1796.1857790169925,
+ "file_size": 36715216,
+ "num_trainable_params": 9175040,
+ "num_total_params": 3221924864,
+ "status": "success",
+ "metrics": [
+ {
+ "step": 250,
+ "valid accuracy": 0.34,
+ "train loss": 0.9827028260231018,
+ "train samples": 1000,
+ "train time": 31.395267726013117,
+ "eval time": 11.27943390099972,
+ "tokens / sec": 6743.659644748829,
+ "mem allocated avg": 6925580957.696,
+ "mem reserved avg": 11920245522.432,
+ "elapsed time": 94.68654379600048
+ },
+ {
+ "step": 500,
+ "valid accuracy": 0.44,
+ "train loss": 0.7164744178056717,
+ "train samples": 2000,
+ "train time": 30.728173206967767,
+ "eval time": 11.244831023999723,
+ "tokens / sec": 6768.869681873444,
+ "mem allocated avg": 6918363699.2,
+ "mem reserved avg": 11811654991.872,
+ "elapsed time": 182.6767855429971
+ },
+ {
+ "step": 750,
+ "valid accuracy": 0.38,
+ "train loss": 0.6791989279985428,
+ "train samples": 3000,
+ "train time": 31.248708018982143,
+ "eval time": 6.873092081001232,
+ "tokens / sec": 6861.115661798283,
+ "mem allocated avg": 6929003134.976,
+ "mem reserved avg": 11970174517.248,
+ "elapsed time": 267.2763524209986
+ },
+ {
+ "step": 1000,
+ "valid accuracy": 0.42,
+ "train loss": 0.6590347054004669,
+ "train samples": 4000,
+ "train time": 31.016855426081747,
+ "eval time": 7.663122134003061,
+ "tokens / sec": 6716.864012746194,
+ "mem allocated avg": 6919503566.848,
+ "mem reserved avg": 11835008876.544,
+ "elapsed time": 351.92747904299904
+ },
+ {
+ "step": 1250,
+ "valid accuracy": 0.4,
+ "train loss": 0.6547032891511917,
+ "train samples": 5000,
+ "train time": 30.914218463025463,
+ "eval time": 11.249955232000502,
+ "tokens / sec": 6745.698593332356,
+ "mem allocated avg": 6919763681.28,
+ "mem reserved avg": 11832551014.4,
+ "elapsed time": 440.29597954699784
+ },
+ {
+ "step": 1500,
+ "valid accuracy": 0.42,
+ "train loss": 0.647298491358757,
+ "train samples": 6000,
+ "train time": 31.093457819981268,
+ "eval time": 11.25276822899832,
+ "tokens / sec": 6732.316528188762,
+ "mem allocated avg": 6920362313.728,
+ "mem reserved avg": 11859000295.424,
+ "elapsed time": 529.2981231249978
+ },
+ {
+ "step": 1750,
+ "valid accuracy": 0.46,
+ "train loss": 0.6378061240911483,
+ "train samples": 7000,
+ "train time": 31.079548971014447,
+ "eval time": 11.2527706639994,
+ "tokens / sec": 6736.101614449091,
+ "mem allocated avg": 6922653980.672,
+ "mem reserved avg": 11870048092.16,
+ "elapsed time": 617.7172930779998
+ },
+ {
+ "step": 2000,
+ "valid accuracy": 0.4,
+ "train loss": 0.641120473742485,
+ "train samples": 8000,
+ "train time": 30.851661891996628,
+ "eval time": 7.384566520999215,
+ "tokens / sec": 6732.084667823985,
+ "mem allocated avg": 6919747647.488,
+ "mem reserved avg": 11816562327.552,
+ "elapsed time": 702.0775224069985
+ },
+ {
+ "step": 2250,
+ "valid accuracy": 0.46,
+ "train loss": 0.6332860335111618,
+ "train samples": 9000,
+ "train time": 31.288193090975255,
+ "eval time": 11.258606130999397,
+ "tokens / sec": 6869.939704571801,
+ "mem allocated avg": 6930711803.904,
+ "mem reserved avg": 12003997384.704,
+ "elapsed time": 791.1291831710005
+ },
+ {
+ "step": 2500,
+ "valid accuracy": 0.44,
+ "train loss": 0.6298432033061981,
+ "train samples": 10000,
+ "train time": 30.668521790059458,
+ "eval time": 11.22552015600013,
+ "tokens / sec": 6715.908950876132,
+ "mem allocated avg": 6916224055.296,
+ "mem reserved avg": 11759050031.104,
+ "elapsed time": 878.9048607999976
+ },
+ {
+ "step": 2750,
+ "valid accuracy": 0.4,
+ "train loss": 0.6213459351062774,
+ "train samples": 11000,
+ "train time": 31.198134894020768,
+ "eval time": 7.820672179997928,
+ "tokens / sec": 6791.463679471677,
+ "mem allocated avg": 6926273599.488,
+ "mem reserved avg": 11930135691.264,
+ "elapsed time": 964.4001106439973
+ },
+ {
+ "step": 3000,
+ "valid accuracy": 0.46,
+ "train loss": 0.6136174714565277,
+ "train samples": 12000,
+ "train time": 30.652901480014407,
+ "eval time": 8.59450396900138,
+ "tokens / sec": 6809.502197894445,
+ "mem allocated avg": 6921910312.96,
+ "mem reserved avg": 11851509268.48,
+ "elapsed time": 1049.6233134680006
+ },
+ {
+ "step": 3250,
+ "valid accuracy": 0.46,
+ "train loss": 0.6227310271263122,
+ "train samples": 13000,
+ "train time": 30.898520497004938,
+ "eval time": 11.247846516002028,
+ "tokens / sec": 6825.601893153528,
+ "mem allocated avg": 6923552774.144,
+ "mem reserved avg": 11884266782.72,
+ "elapsed time": 1137.9473550990006
+ },
+ {
+ "step": 3500,
+ "valid accuracy": 0.52,
+ "train loss": 0.6058980323076248,
+ "train samples": 14000,
+ "train time": 31.043968706952,
+ "eval time": 7.071496761000162,
+ "tokens / sec": 6756.545916535101,
+ "mem allocated avg": 6922457063.424,
+ "mem reserved avg": 11865602129.92,
+ "elapsed time": 1222.3722963839973
+ },
+ {
+ "step": 3750,
+ "valid accuracy": 0.5,
+ "train loss": 0.6032638043165207,
+ "train samples": 15000,
+ "train time": 31.41906641800597,
+ "eval time": 6.834270917999675,
+ "tokens / sec": 6897.18138397039,
+ "mem allocated avg": 6932064409.6,
+ "mem reserved avg": 12041553182.72,
+ "elapsed time": 1307.517348808
+ },
+ {
+ "step": 4000,
+ "valid accuracy": 0.48,
+ "train loss": 0.6166473155021668,
+ "train samples": 16000,
+ "train time": 30.82234557695483,
+ "eval time": 6.627715251001064,
+ "tokens / sec": 6630.676419149782,
+ "mem allocated avg": 6914480900.096,
+ "mem reserved avg": 11738338557.952,
+ "elapsed time": 1390.9289551410002
+ },
+ {
+ "step": 4250,
+ "valid accuracy": 0.44,
+ "train loss": 0.601645546555519,
+ "train samples": 17000,
+ "train time": 30.811621871023817,
+ "eval time": 11.241402788000414,
+ "tokens / sec": 6860.690452611215,
+ "mem allocated avg": 6925075550.208,
+ "mem reserved avg": 11899366277.12,
+ "elapsed time": 1479.325017957999
+ },
+ {
+ "step": 4500,
+ "valid accuracy": 0.46,
+ "train loss": 0.6076700875759125,
+ "train samples": 18000,
+ "train time": 30.499847401017178,
+ "eval time": 11.232504903000518,
+ "tokens / sec": 6813.73900884072,
+ "mem allocated avg": 6919328847.872,
+ "mem reserved avg": 11814020579.328,
+ "elapsed time": 1567.0791362639975
+ },
+ {
+ "step": 4750,
+ "valid accuracy": 0.46,
+ "train loss": 0.5997640329599381,
+ "train samples": 19000,
+ "train time": 30.974938084971654,
+ "eval time": 11.246996836001927,
+ "tokens / sec": 6777.705234602477,
+ "mem allocated avg": 6921498724.352,
+ "mem reserved avg": 11864662605.824,
+ "elapsed time": 1655.6881185989987
+ },
+ {
+ "step": 5000,
+ "valid accuracy": 0.5,
+ "train loss": 0.6069052599668503,
+ "train samples": 20000,
+ "train time": 30.736502733019734,
+ "eval time": 11.28520023999954,
+ "tokens / sec": 6776.307695418065,
+ "mem allocated avg": 6918408683.52,
+ "mem reserved avg": 11806051401.728,
+ "elapsed time": 1743.785376189
+ },
+ {
+ "step": 5000,
+ "test accuracy": 0.48218347232752085,
+ "train loss": 0.6069052599668503,
+ "train samples": 20000,
+ "train total tokens": 4198051
+ }
+ ]
+ },
+ "meta_info": {
+ "model_info": {
+ "sha": "13afe5124825b4f3751f836b40dafda64c1ed062",
+ "created_at": "2024-09-18T15:23:48+00:00"
+ },
+ "dataset_info": {
+ "metamath": {
+ "sha": "aa4f34d3d2d3231299b5b03d9b3e5a20da45aa18",
+ "created_at": "2023-09-21T17:22:46+00:00"
+ },
+ "gsm8k": {
+ "sha": "e53f048856ff4f594e959d75785d2c2d37b678ee",
+ "created_at": "2022-04-12T10:22:10+00:00"
+ }
+ },
+ "package_info": {
+ "transformers-version": "4.52.4",
+ "transformers-commit-hash": null,
+ "peft-version": "0.15.2.dev0",
+ "peft-commit-hash": "5fe7f8f8abe914d313fc3751f2ea92de7718fbaf",
+ "datasets-version": "3.6.0",
+ "datasets-commit-hash": null,
+ "bitsandbytes-version": "0.46.0",
+ "bitsandbytes-commit-hash": null,
+ "torch-version": "2.7.1+cu126",
+ "torch-commit-hash": null
+ },
+ "system_info": {
+ "system": "Linux",
+ "release": "6.8.0-1029-aws",
+ "version": "#31-Ubuntu SMP Wed Apr 23 18:42:41 UTC 2025",
+ "machine": "x86_64",
+ "processor": "x86_64",
+ "accelerator": "NVIDIA L40S"
+ },
+ "pytorch_info": "PyTorch built with:\n - GCC 11.2\n - C++ Version: 201703\n - Intel(R) oneAPI Math Kernel Library Version 2024.2-Product Build 20240605 for Intel(R) 64 architecture applications\n - Intel(R) MKL-DNN v3.7.1 (Git Hash 8d263e693366ef8db40acc569cc7d8edf644556d)\n - OpenMP 201511 (a.k.a. OpenMP 4.5)\n - LAPACK is enabled (usually provided by MKL)\n - NNPACK is enabled\n - CPU capability usage: AVX2\n - CUDA Runtime 12.6\n - NVCC architecture flags: -gencode;arch=compute_50,code=sm_50;-gencode;arch=compute_60,code=sm_60;-gencode;arch=compute_70,code=sm_70;-gencode;arch=compute_75,code=sm_75;-gencode;arch=compute_80,code=sm_80;-gencode;arch=compute_86,code=sm_86;-gencode;arch=compute_90,code=sm_90\n - CuDNN 90.7.1 (built against CUDA 12.8)\n - Built with CuDNN 90.5.1\n - Magma 2.6.1\n - Build settings: BLAS_INFO=mkl, BUILD_TYPE=Release, COMMIT_SHA=e2d141dbde55c2a4370fac5165b0561b6af4798b, CUDA_VERSION=12.6, CUDNN_VERSION=9.5.1, CXX_COMPILER=/opt/rh/gcc-toolset-11/root/usr/bin/c++, CXX_FLAGS= -D_GLIBCXX_USE_CXX11_ABI=1 -fvisibility-inlines-hidden -DUSE_PTHREADPOOL -DNDEBUG -DUSE_KINETO -DLIBKINETO_NOROCTRACER -DLIBKINETO_NOXPUPTI=ON -DUSE_FBGEMM -DUSE_PYTORCH_QNNPACK -DUSE_XNNPACK -DSYMBOLICATE_MOBILE_DEBUG_HANDLE -O2 -fPIC -Wall -Wextra -Werror=return-type -Werror=non-virtual-dtor -Werror=range-loop-construct -Werror=bool-operation -Wnarrowing -Wno-missing-field-initializers -Wno-unknown-pragmas -Wno-unused-parameter -Wno-strict-overflow -Wno-strict-aliasing -Wno-stringop-overflow -Wsuggest-override -Wno-psabi -Wno-error=old-style-cast -fdiagnostics-color=always -faligned-new -Wno-maybe-uninitialized -fno-math-errno -fno-trapping-math -Werror=format -Wno-stringop-overflow, LAPACK_INFO=mkl, PERF_WITH_AVX=1, PERF_WITH_AVX2=1, TORCH_VERSION=2.7.1, USE_CUDA=ON, USE_CUDNN=ON, USE_CUSPARSELT=1, USE_GFLAGS=OFF, USE_GLOG=OFF, USE_GLOO=ON, USE_MKL=ON, USE_MKLDNN=ON, USE_MPI=OFF, USE_NCCL=1, USE_NNPACK=ON, USE_OPENMP=ON, USE_ROCM=OFF, USE_ROCM_KERNEL_ASSERT=OFF, \n"
+ }
+}
diff --git a/peft/method_comparison/MetaMathQA/results/lora--llama-3.2-3B-rank64-rslora.json b/peft/method_comparison/MetaMathQA/results/lora--llama-3.2-3B-rank64-rslora.json
new file mode 100644
index 0000000000000000000000000000000000000000..dbeb788d4e2455d909eca39139320edbbf9fd173
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/results/lora--llama-3.2-3B-rank64-rslora.json
@@ -0,0 +1,365 @@
+{
+ "run_info": {
+ "created_at": "2025-06-19T18:02:52+00:00",
+ "total_time": 2068.5078051540004,
+ "experiment_name": "lora/llama-3.2-3B-rank64-rslora",
+ "peft_branch": "main",
+ "train_config": {
+ "model_id": "meta-llama/Llama-3.2-3B",
+ "dtype": "bfloat16",
+ "max_seq_length": 768,
+ "batch_size": 4,
+ "batch_size_eval": 50,
+ "max_steps": 5000,
+ "eval_steps": 250,
+ "compile": false,
+ "query_template": "Question: {query} Think step by step.\nAnswer:",
+ "seed": 0,
+ "grad_norm_clip": 1.0,
+ "optimizer_type": "AdamW",
+ "optimizer_kwargs": {
+ "lr": 0.0001,
+ "weight_decay": 0.1
+ },
+ "lr_scheduler": "cosine",
+ "use_amp": false,
+ "autocast_adapter_dtype": true,
+ "generation_kwargs": {
+ "max_length": 800,
+ "max_new_tokens": 300
+ },
+ "attn_implementation": null
+ },
+ "peft_config": {
+ "task_type": "CAUSAL_LM",
+ "peft_type": "LORA",
+ "auto_mapping": null,
+ "base_model_name_or_path": "meta-llama/Llama-3.2-3B",
+ "revision": null,
+ "inference_mode": false,
+ "r": 64,
+ "target_modules": [
+ "v_proj",
+ "q_proj"
+ ],
+ "exclude_modules": null,
+ "lora_alpha": 64,
+ "lora_dropout": 0.0,
+ "fan_in_fan_out": false,
+ "bias": "none",
+ "use_rslora": true,
+ "modules_to_save": null,
+ "init_lora_weights": true,
+ "layers_to_transform": null,
+ "layers_pattern": null,
+ "rank_pattern": {},
+ "alpha_pattern": {},
+ "megatron_config": null,
+ "megatron_core": "megatron.core",
+ "trainable_token_indices": null,
+ "loftq_config": {},
+ "eva_config": null,
+ "corda_config": null,
+ "use_dora": false,
+ "layer_replication": null,
+ "lora_bias": false
+ },
+ "error_msg": ""
+ },
+ "train_info": {
+ "accelerator_memory_reserved_avg": 12128059444,
+ "accelerator_memory_max": 22538092544,
+ "accelerator_memory_reserved_99th": 17953927987,
+ "train_time": 1871.457509397991,
+ "file_size": 73415408,
+ "num_trainable_params": 18350080,
+ "num_total_params": 3231099904,
+ "status": "success",
+ "metrics": [
+ {
+ "step": 250,
+ "valid accuracy": 0.36,
+ "train loss": 0.8666043817996979,
+ "train samples": 1000,
+ "train time": 31.633613975991466,
+ "eval time": 11.220254406001914,
+ "tokens / sec": 6692.848947347132,
+ "mem allocated avg": 7072427177.984,
+ "mem reserved avg": 12177985503.232,
+ "elapsed time": 97.06891104899842
+ },
+ {
+ "step": 500,
+ "valid accuracy": 0.32,
+ "train loss": 0.697043846487999,
+ "train samples": 2000,
+ "train time": 31.400947067988454,
+ "eval time": 11.24747418500192,
+ "tokens / sec": 6623.844801548661,
+ "mem allocated avg": 7064966957.056,
+ "mem reserved avg": 12070787481.6,
+ "elapsed time": 188.02626212299947
+ },
+ {
+ "step": 750,
+ "valid accuracy": 0.38,
+ "train loss": 0.6723507121801376,
+ "train samples": 3000,
+ "train time": 31.849995732016396,
+ "eval time": 11.249978227999236,
+ "tokens / sec": 6731.586459350098,
+ "mem allocated avg": 7075822055.424,
+ "mem reserved avg": 12225037205.504,
+ "elapsed time": 280.16055655299715
+ },
+ {
+ "step": 1000,
+ "valid accuracy": 0.38,
+ "train loss": 0.6529685587882995,
+ "train samples": 4000,
+ "train time": 31.612207354013663,
+ "eval time": 11.24677863100078,
+ "tokens / sec": 6590.365477074112,
+ "mem allocated avg": 7066256992.256,
+ "mem reserved avg": 12092287483.904,
+ "elapsed time": 371.5183315869981
+ },
+ {
+ "step": 1250,
+ "valid accuracy": 0.38,
+ "train loss": 0.6472815409898758,
+ "train samples": 5000,
+ "train time": 31.26670297003875,
+ "eval time": 8.06907803500144,
+ "tokens / sec": 6669.651104557813,
+ "mem allocated avg": 7066435080.192,
+ "mem reserved avg": 12087824744.448,
+ "elapsed time": 459.33407214199906
+ },
+ {
+ "step": 1500,
+ "valid accuracy": 0.44,
+ "train loss": 0.6395461517572403,
+ "train samples": 6000,
+ "train time": 31.471468601008382,
+ "eval time": 6.4898526670003776,
+ "tokens / sec": 6651.4531830043925,
+ "mem allocated avg": 7067292080.128,
+ "mem reserved avg": 12121664389.12,
+ "elapsed time": 545.9371380269986
+ },
+ {
+ "step": 1750,
+ "valid accuracy": 0.5,
+ "train loss": 0.629749027967453,
+ "train samples": 7000,
+ "train time": 31.650018079009897,
+ "eval time": 11.247470542999508,
+ "tokens / sec": 6614.688164707337,
+ "mem allocated avg": 7069213276.16,
+ "mem reserved avg": 12130329821.184,
+ "elapsed time": 637.2524904149977
+ },
+ {
+ "step": 2000,
+ "valid accuracy": 0.4,
+ "train loss": 0.6293291836977005,
+ "train samples": 8000,
+ "train time": 31.45956211398152,
+ "eval time": 11.187045163998846,
+ "tokens / sec": 6601.999075749819,
+ "mem allocated avg": 7066587928.576,
+ "mem reserved avg": 12076634341.376,
+ "elapsed time": 728.2233991199973
+ },
+ {
+ "step": 2250,
+ "valid accuracy": 0.4,
+ "train loss": 0.6171289530992508,
+ "train samples": 9000,
+ "train time": 31.87981533700804,
+ "eval time": 6.866186073002609,
+ "tokens / sec": 6742.448089104055,
+ "mem allocated avg": 7077788481.536,
+ "mem reserved avg": 12265227026.432,
+ "elapsed time": 815.9717469499992
+ },
+ {
+ "step": 2500,
+ "valid accuracy": 0.44,
+ "train loss": 0.6119417071342468,
+ "train samples": 10000,
+ "train time": 31.067599171023176,
+ "eval time": 10.55572699700133,
+ "tokens / sec": 6629.640058962326,
+ "mem allocated avg": 7062992943.104,
+ "mem reserved avg": 12015850487.808,
+ "elapsed time": 905.6140671029971
+ },
+ {
+ "step": 2750,
+ "valid accuracy": 0.48,
+ "train loss": 0.5985908216238022,
+ "train samples": 11000,
+ "train time": 31.864849751029396,
+ "eval time": 6.1964339680016565,
+ "tokens / sec": 6649.364477017663,
+ "mem allocated avg": 7072847513.6,
+ "mem reserved avg": 12192229359.616,
+ "elapsed time": 992.5055643979977
+ },
+ {
+ "step": 3000,
+ "valid accuracy": 0.48,
+ "train loss": 0.5865949945449829,
+ "train samples": 12000,
+ "train time": 31.337576934987737,
+ "eval time": 7.105518241998652,
+ "tokens / sec": 6660.725570232467,
+ "mem allocated avg": 7068560369.664,
+ "mem reserved avg": 12111589670.912,
+ "elapsed time": 1079.4884613180002
+ },
+ {
+ "step": 3250,
+ "valid accuracy": 0.56,
+ "train loss": 0.5926763614416123,
+ "train samples": 13000,
+ "train time": 31.477448584984813,
+ "eval time": 11.220603736997873,
+ "tokens / sec": 6700.066539084199,
+ "mem allocated avg": 7070318487.552,
+ "mem reserved avg": 12143046950.912,
+ "elapsed time": 1171.2174267509981
+ },
+ {
+ "step": 3500,
+ "valid accuracy": 0.54,
+ "train loss": 0.5736529529094696,
+ "train samples": 14000,
+ "train time": 31.59231336902303,
+ "eval time": 11.215632880001067,
+ "tokens / sec": 6639.273216556042,
+ "mem allocated avg": 7068978995.2,
+ "mem reserved avg": 12124969500.672,
+ "elapsed time": 1263.2709914519983
+ },
+ {
+ "step": 3750,
+ "valid accuracy": 0.54,
+ "train loss": 0.5691816571950913,
+ "train samples": 15000,
+ "train time": 31.92663248500321,
+ "eval time": 6.89942428699942,
+ "tokens / sec": 6787.530758271833,
+ "mem allocated avg": 7079011248.128,
+ "mem reserved avg": 12298890510.336,
+ "elapsed time": 1351.894684084
+ },
+ {
+ "step": 4000,
+ "valid accuracy": 0.56,
+ "train loss": 0.5762648656368256,
+ "train samples": 16000,
+ "train time": 31.08475098094641,
+ "eval time": 6.668889390999539,
+ "tokens / sec": 6574.7028221416895,
+ "mem allocated avg": 7061224237.056,
+ "mem reserved avg": 12000969097.216,
+ "elapsed time": 1437.9300296759975
+ },
+ {
+ "step": 4250,
+ "valid accuracy": 0.52,
+ "train loss": 0.562865238904953,
+ "train samples": 17000,
+ "train time": 31.594970259979164,
+ "eval time": 11.218020562002494,
+ "tokens / sec": 6690.590250935068,
+ "mem allocated avg": 7071853715.456,
+ "mem reserved avg": 12157852844.032,
+ "elapsed time": 1529.7590418299988
+ },
+ {
+ "step": 4500,
+ "valid accuracy": 0.5,
+ "train loss": 0.568256908416748,
+ "train samples": 18000,
+ "train time": 31.334908029966755,
+ "eval time": 11.24515695700029,
+ "tokens / sec": 6632.156054240077,
+ "mem allocated avg": 7066128418.816,
+ "mem reserved avg": 12073245343.744,
+ "elapsed time": 1620.988001589998
+ },
+ {
+ "step": 4750,
+ "valid accuracy": 0.52,
+ "train loss": 0.5585172891616821,
+ "train samples": 19000,
+ "train time": 31.425996138961636,
+ "eval time": 11.202903266999783,
+ "tokens / sec": 6680.4246736261675,
+ "mem allocated avg": 7068498065.408,
+ "mem reserved avg": 12124491350.016,
+ "elapsed time": 1712.544705993998
+ },
+ {
+ "step": 5000,
+ "valid accuracy": 0.52,
+ "train loss": 0.5657225311994553,
+ "train samples": 20000,
+ "train time": 31.088545892969705,
+ "eval time": 11.224285021999094,
+ "tokens / sec": 6699.573557317776,
+ "mem allocated avg": 7064964919.296,
+ "mem reserved avg": 12070275776.512,
+ "elapsed time": 1803.3861051699969
+ },
+ {
+ "step": 5000,
+ "test accuracy": 0.5299469294920395,
+ "train loss": 0.5657225311994553,
+ "train samples": 20000,
+ "train total tokens": 4198051
+ }
+ ]
+ },
+ "meta_info": {
+ "model_info": {
+ "sha": "13afe5124825b4f3751f836b40dafda64c1ed062",
+ "created_at": "2024-09-18T15:23:48+00:00"
+ },
+ "dataset_info": {
+ "metamath": {
+ "sha": "aa4f34d3d2d3231299b5b03d9b3e5a20da45aa18",
+ "created_at": "2023-09-21T17:22:46+00:00"
+ },
+ "gsm8k": {
+ "sha": "e53f048856ff4f594e959d75785d2c2d37b678ee",
+ "created_at": "2022-04-12T10:22:10+00:00"
+ }
+ },
+ "package_info": {
+ "transformers-version": "4.52.4",
+ "transformers-commit-hash": null,
+ "peft-version": "0.15.2.dev0",
+ "peft-commit-hash": "5fe7f8f8abe914d313fc3751f2ea92de7718fbaf",
+ "datasets-version": "3.6.0",
+ "datasets-commit-hash": null,
+ "bitsandbytes-version": "0.46.0",
+ "bitsandbytes-commit-hash": null,
+ "torch-version": "2.7.1+cu126",
+ "torch-commit-hash": null
+ },
+ "system_info": {
+ "system": "Linux",
+ "release": "6.8.0-1029-aws",
+ "version": "#31-Ubuntu SMP Wed Apr 23 18:42:41 UTC 2025",
+ "machine": "x86_64",
+ "processor": "x86_64",
+ "accelerator": "NVIDIA L40S"
+ },
+ "pytorch_info": "PyTorch built with:\n - GCC 11.2\n - C++ Version: 201703\n - Intel(R) oneAPI Math Kernel Library Version 2024.2-Product Build 20240605 for Intel(R) 64 architecture applications\n - Intel(R) MKL-DNN v3.7.1 (Git Hash 8d263e693366ef8db40acc569cc7d8edf644556d)\n - OpenMP 201511 (a.k.a. OpenMP 4.5)\n - LAPACK is enabled (usually provided by MKL)\n - NNPACK is enabled\n - CPU capability usage: AVX2\n - CUDA Runtime 12.6\n - NVCC architecture flags: -gencode;arch=compute_50,code=sm_50;-gencode;arch=compute_60,code=sm_60;-gencode;arch=compute_70,code=sm_70;-gencode;arch=compute_75,code=sm_75;-gencode;arch=compute_80,code=sm_80;-gencode;arch=compute_86,code=sm_86;-gencode;arch=compute_90,code=sm_90\n - CuDNN 90.7.1 (built against CUDA 12.8)\n - Built with CuDNN 90.5.1\n - Magma 2.6.1\n - Build settings: BLAS_INFO=mkl, BUILD_TYPE=Release, COMMIT_SHA=e2d141dbde55c2a4370fac5165b0561b6af4798b, CUDA_VERSION=12.6, CUDNN_VERSION=9.5.1, CXX_COMPILER=/opt/rh/gcc-toolset-11/root/usr/bin/c++, CXX_FLAGS= -D_GLIBCXX_USE_CXX11_ABI=1 -fvisibility-inlines-hidden -DUSE_PTHREADPOOL -DNDEBUG -DUSE_KINETO -DLIBKINETO_NOROCTRACER -DLIBKINETO_NOXPUPTI=ON -DUSE_FBGEMM -DUSE_PYTORCH_QNNPACK -DUSE_XNNPACK -DSYMBOLICATE_MOBILE_DEBUG_HANDLE -O2 -fPIC -Wall -Wextra -Werror=return-type -Werror=non-virtual-dtor -Werror=range-loop-construct -Werror=bool-operation -Wnarrowing -Wno-missing-field-initializers -Wno-unknown-pragmas -Wno-unused-parameter -Wno-strict-overflow -Wno-strict-aliasing -Wno-stringop-overflow -Wsuggest-override -Wno-psabi -Wno-error=old-style-cast -fdiagnostics-color=always -faligned-new -Wno-maybe-uninitialized -fno-math-errno -fno-trapping-math -Werror=format -Wno-stringop-overflow, LAPACK_INFO=mkl, PERF_WITH_AVX=1, PERF_WITH_AVX2=1, TORCH_VERSION=2.7.1, USE_CUDA=ON, USE_CUDNN=ON, USE_CUSPARSELT=1, USE_GFLAGS=OFF, USE_GLOG=OFF, USE_GLOO=ON, USE_MKL=ON, USE_MKLDNN=ON, USE_MPI=OFF, USE_NCCL=1, USE_NNPACK=ON, USE_OPENMP=ON, USE_ROCM=OFF, USE_ROCM_KERNEL_ASSERT=OFF, \n"
+ }
+}
diff --git a/peft/method_comparison/MetaMathQA/results/lora--llama-3.2-3B-rank64.json b/peft/method_comparison/MetaMathQA/results/lora--llama-3.2-3B-rank64.json
new file mode 100644
index 0000000000000000000000000000000000000000..5dd3d50954761111762cc831de93cf4f76995044
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/results/lora--llama-3.2-3B-rank64.json
@@ -0,0 +1,365 @@
+{
+ "run_info": {
+ "created_at": "2025-06-19T16:55:20+00:00",
+ "total_time": 2017.2277705579982,
+ "experiment_name": "lora/llama-3.2-3B-rank64",
+ "peft_branch": "main",
+ "train_config": {
+ "model_id": "meta-llama/Llama-3.2-3B",
+ "dtype": "bfloat16",
+ "max_seq_length": 768,
+ "batch_size": 4,
+ "batch_size_eval": 50,
+ "max_steps": 5000,
+ "eval_steps": 250,
+ "compile": false,
+ "query_template": "Question: {query} Think step by step.\nAnswer:",
+ "seed": 0,
+ "grad_norm_clip": 1.0,
+ "optimizer_type": "AdamW",
+ "optimizer_kwargs": {
+ "lr": 0.0001,
+ "weight_decay": 0.1
+ },
+ "lr_scheduler": "cosine",
+ "use_amp": false,
+ "autocast_adapter_dtype": true,
+ "generation_kwargs": {
+ "max_length": 800,
+ "max_new_tokens": 300
+ },
+ "attn_implementation": null
+ },
+ "peft_config": {
+ "task_type": "CAUSAL_LM",
+ "peft_type": "LORA",
+ "auto_mapping": null,
+ "base_model_name_or_path": "meta-llama/Llama-3.2-3B",
+ "revision": null,
+ "inference_mode": false,
+ "r": 64,
+ "target_modules": [
+ "q_proj",
+ "v_proj"
+ ],
+ "exclude_modules": null,
+ "lora_alpha": 128,
+ "lora_dropout": 0.0,
+ "fan_in_fan_out": false,
+ "bias": "none",
+ "use_rslora": false,
+ "modules_to_save": null,
+ "init_lora_weights": true,
+ "layers_to_transform": null,
+ "layers_pattern": null,
+ "rank_pattern": {},
+ "alpha_pattern": {},
+ "megatron_config": null,
+ "megatron_core": "megatron.core",
+ "trainable_token_indices": null,
+ "loftq_config": {},
+ "eva_config": null,
+ "corda_config": null,
+ "use_dora": false,
+ "layer_replication": null,
+ "lora_bias": false
+ },
+ "error_msg": ""
+ },
+ "train_info": {
+ "accelerator_memory_reserved_avg": 12128055669,
+ "accelerator_memory_max": 22540189696,
+ "accelerator_memory_reserved_99th": 17953927987,
+ "train_time": 1853.4967184819961,
+ "file_size": 73415408,
+ "num_trainable_params": 18350080,
+ "num_total_params": 3231099904,
+ "status": "success",
+ "metrics": [
+ {
+ "step": 250,
+ "valid accuracy": 0.38,
+ "train loss": 0.9425119986534118,
+ "train samples": 1000,
+ "train time": 31.823601707994385,
+ "eval time": 11.233909951999522,
+ "tokens / sec": 6652.892464614218,
+ "mem allocated avg": 7072427177.984,
+ "mem reserved avg": 12177985503.232,
+ "elapsed time": 97.04379223199976
+ },
+ {
+ "step": 500,
+ "valid accuracy": 0.4,
+ "train loss": 0.7080548154115677,
+ "train samples": 2000,
+ "train time": 31.45184341498316,
+ "eval time": 8.232533225000225,
+ "tokens / sec": 6613.125890767804,
+ "mem allocated avg": 7065105152.0,
+ "mem reserved avg": 12072179990.528,
+ "elapsed time": 184.765658884
+ },
+ {
+ "step": 750,
+ "valid accuracy": 0.48,
+ "train loss": 0.6735224899053573,
+ "train samples": 3000,
+ "train time": 31.813968455000577,
+ "eval time": 7.057446101998721,
+ "tokens / sec": 6739.20954888921,
+ "mem allocated avg": 7075631579.136,
+ "mem reserved avg": 12224064126.976,
+ "elapsed time": 272.18349517599927
+ },
+ {
+ "step": 1000,
+ "valid accuracy": 0.38,
+ "train loss": 0.6520720717906952,
+ "train samples": 4000,
+ "train time": 31.539530114994704,
+ "eval time": 6.8677342959999805,
+ "tokens / sec": 6605.551802464924,
+ "mem allocated avg": 7066230261.76,
+ "mem reserved avg": 12094502076.416,
+ "elapsed time": 358.6604399049993
+ },
+ {
+ "step": 1250,
+ "valid accuracy": 0.32,
+ "train loss": 0.6483409875631332,
+ "train samples": 5000,
+ "train time": 31.15382274799049,
+ "eval time": 6.63156994000019,
+ "tokens / sec": 6693.817374737786,
+ "mem allocated avg": 7066402795.52,
+ "mem reserved avg": 12090886586.368,
+ "elapsed time": 444.47985113600043
+ },
+ {
+ "step": 1500,
+ "valid accuracy": 0.44,
+ "train loss": 0.6400664356946946,
+ "train samples": 6000,
+ "train time": 31.237405868998394,
+ "eval time": 6.19883855199987,
+ "tokens / sec": 6701.292702661678,
+ "mem allocated avg": 7067143219.2,
+ "mem reserved avg": 12125288267.776,
+ "elapsed time": 529.970450933999
+ },
+ {
+ "step": 1750,
+ "valid accuracy": 0.42,
+ "train loss": 0.6309183040857315,
+ "train samples": 7000,
+ "train time": 31.58418034899296,
+ "eval time": 11.217398733000664,
+ "tokens / sec": 6628.476588175104,
+ "mem allocated avg": 7069430339.584,
+ "mem reserved avg": 12128735985.664,
+ "elapsed time": 620.7944932609989
+ },
+ {
+ "step": 2000,
+ "valid accuracy": 0.38,
+ "train loss": 0.6333342634439468,
+ "train samples": 8000,
+ "train time": 31.370570010996744,
+ "eval time": 11.2056582969999,
+ "tokens / sec": 6620.727641454827,
+ "mem allocated avg": 7066754975.744,
+ "mem reserved avg": 12075980029.952,
+ "elapsed time": 711.143019907
+ },
+ {
+ "step": 2250,
+ "valid accuracy": 0.42,
+ "train loss": 0.6244297958612443,
+ "train samples": 9000,
+ "train time": 32.090800706988375,
+ "eval time": 6.320641570999214,
+ "tokens / sec": 6698.118939524966,
+ "mem allocated avg": 7077559773.184,
+ "mem reserved avg": 12266535649.28,
+ "elapsed time": 798.2718276069991
+ },
+ {
+ "step": 2500,
+ "valid accuracy": 0.48,
+ "train loss": 0.6205919095277787,
+ "train samples": 10000,
+ "train time": 31.211024427002485,
+ "eval time": 7.8215817759992206,
+ "tokens / sec": 6599.1746115775,
+ "mem allocated avg": 7063100512.256,
+ "mem reserved avg": 12017771479.04,
+ "elapsed time": 885.0132823740005
+ },
+ {
+ "step": 2750,
+ "valid accuracy": 0.38,
+ "train loss": 0.6116842222213745,
+ "train samples": 11000,
+ "train time": 31.752687646014238,
+ "eval time": 11.215984603999459,
+ "tokens / sec": 6672.852464084136,
+ "mem allocated avg": 7072850802.688,
+ "mem reserved avg": 12190207705.088,
+ "elapsed time": 976.3748101059991
+ },
+ {
+ "step": 3000,
+ "valid accuracy": 0.48,
+ "train loss": 0.6028307398557663,
+ "train samples": 12000,
+ "train time": 31.220882691013685,
+ "eval time": 10.851913497001078,
+ "tokens / sec": 6685.621353687066,
+ "mem allocated avg": 7068516059.136,
+ "mem reserved avg": 12110624980.992,
+ "elapsed time": 1066.2028727340003
+ },
+ {
+ "step": 3250,
+ "valid accuracy": 0.54,
+ "train loss": 0.6109937611818314,
+ "train samples": 13000,
+ "train time": 31.23074521200033,
+ "eval time": 6.857214526000462,
+ "tokens / sec": 6752.992878279506,
+ "mem allocated avg": 7070265374.72,
+ "mem reserved avg": 12142795292.672,
+ "elapsed time": 1152.2392765660006
+ },
+ {
+ "step": 3500,
+ "valid accuracy": 0.54,
+ "train loss": 0.5937278937101365,
+ "train samples": 14000,
+ "train time": 31.52822203695905,
+ "eval time": 6.510061502001918,
+ "tokens / sec": 6652.7696916787745,
+ "mem allocated avg": 7069306679.296,
+ "mem reserved avg": 12124390686.72,
+ "elapsed time": 1238.6433643029995
+ },
+ {
+ "step": 3750,
+ "valid accuracy": 0.6,
+ "train loss": 0.5906780579090118,
+ "train samples": 15000,
+ "train time": 32.31397023300451,
+ "eval time": 8.545268227000633,
+ "tokens / sec": 6706.170688325575,
+ "mem allocated avg": 7078981097.472,
+ "mem reserved avg": 12299846811.648,
+ "elapsed time": 1328.641089326
+ },
+ {
+ "step": 4000,
+ "valid accuracy": 0.52,
+ "train loss": 0.6025177363157272,
+ "train samples": 16000,
+ "train time": 31.170676869962335,
+ "eval time": 6.8420828330017684,
+ "tokens / sec": 6556.57882735759,
+ "mem allocated avg": 7061331572.736,
+ "mem reserved avg": 12001287864.32,
+ "elapsed time": 1414.365250592
+ },
+ {
+ "step": 4250,
+ "valid accuracy": 0.54,
+ "train loss": 0.5884622411727906,
+ "train samples": 17000,
+ "train time": 31.543792515007226,
+ "eval time": 6.748535185997753,
+ "tokens / sec": 6701.445297024126,
+ "mem allocated avg": 7071957172.224,
+ "mem reserved avg": 12155780857.856,
+ "elapsed time": 1500.9030026039982
+ },
+ {
+ "step": 4500,
+ "valid accuracy": 0.54,
+ "train loss": 0.5941844927072525,
+ "train samples": 18000,
+ "train time": 31.45958714898734,
+ "eval time": 6.4977734870008135,
+ "tokens / sec": 6605.871813123572,
+ "mem allocated avg": 7066011588.608,
+ "mem reserved avg": 12069847957.504,
+ "elapsed time": 1586.8870083309994
+ },
+ {
+ "step": 4750,
+ "valid accuracy": 0.56,
+ "train loss": 0.5860341912508011,
+ "train samples": 19000,
+ "train time": 31.656771414985997,
+ "eval time": 6.746858504000556,
+ "tokens / sec": 6631.724923806254,
+ "mem allocated avg": 7068472178.688,
+ "mem reserved avg": 12124852060.16,
+ "elapsed time": 1673.7380427649987
+ },
+ {
+ "step": 5000,
+ "valid accuracy": 0.58,
+ "train loss": 0.5928755496740341,
+ "train samples": 20000,
+ "train time": 31.260896800042246,
+ "eval time": 6.4877336810022825,
+ "tokens / sec": 6662.636754545011,
+ "mem allocated avg": 7065262428.16,
+ "mem reserved avg": 12067549478.912,
+ "elapsed time": 1759.6036715839982
+ },
+ {
+ "step": 5000,
+ "test accuracy": 0.4890068233510235,
+ "train loss": 0.5928755496740341,
+ "train samples": 20000,
+ "train total tokens": 4198051
+ }
+ ]
+ },
+ "meta_info": {
+ "model_info": {
+ "sha": "13afe5124825b4f3751f836b40dafda64c1ed062",
+ "created_at": "2024-09-18T15:23:48+00:00"
+ },
+ "dataset_info": {
+ "metamath": {
+ "sha": "aa4f34d3d2d3231299b5b03d9b3e5a20da45aa18",
+ "created_at": "2023-09-21T17:22:46+00:00"
+ },
+ "gsm8k": {
+ "sha": "e53f048856ff4f594e959d75785d2c2d37b678ee",
+ "created_at": "2022-04-12T10:22:10+00:00"
+ }
+ },
+ "package_info": {
+ "transformers-version": "4.52.4",
+ "transformers-commit-hash": null,
+ "peft-version": "0.15.2.dev0",
+ "peft-commit-hash": "5fe7f8f8abe914d313fc3751f2ea92de7718fbaf",
+ "datasets-version": "3.6.0",
+ "datasets-commit-hash": null,
+ "bitsandbytes-version": "0.46.0",
+ "bitsandbytes-commit-hash": null,
+ "torch-version": "2.7.1+cu126",
+ "torch-commit-hash": null
+ },
+ "system_info": {
+ "system": "Linux",
+ "release": "6.8.0-1029-aws",
+ "version": "#31-Ubuntu SMP Wed Apr 23 18:42:41 UTC 2025",
+ "machine": "x86_64",
+ "processor": "x86_64",
+ "accelerator": "NVIDIA L40S"
+ },
+ "pytorch_info": "PyTorch built with:\n - GCC 11.2\n - C++ Version: 201703\n - Intel(R) oneAPI Math Kernel Library Version 2024.2-Product Build 20240605 for Intel(R) 64 architecture applications\n - Intel(R) MKL-DNN v3.7.1 (Git Hash 8d263e693366ef8db40acc569cc7d8edf644556d)\n - OpenMP 201511 (a.k.a. OpenMP 4.5)\n - LAPACK is enabled (usually provided by MKL)\n - NNPACK is enabled\n - CPU capability usage: AVX2\n - CUDA Runtime 12.6\n - NVCC architecture flags: -gencode;arch=compute_50,code=sm_50;-gencode;arch=compute_60,code=sm_60;-gencode;arch=compute_70,code=sm_70;-gencode;arch=compute_75,code=sm_75;-gencode;arch=compute_80,code=sm_80;-gencode;arch=compute_86,code=sm_86;-gencode;arch=compute_90,code=sm_90\n - CuDNN 90.7.1 (built against CUDA 12.8)\n - Built with CuDNN 90.5.1\n - Magma 2.6.1\n - Build settings: BLAS_INFO=mkl, BUILD_TYPE=Release, COMMIT_SHA=e2d141dbde55c2a4370fac5165b0561b6af4798b, CUDA_VERSION=12.6, CUDNN_VERSION=9.5.1, CXX_COMPILER=/opt/rh/gcc-toolset-11/root/usr/bin/c++, CXX_FLAGS= -D_GLIBCXX_USE_CXX11_ABI=1 -fvisibility-inlines-hidden -DUSE_PTHREADPOOL -DNDEBUG -DUSE_KINETO -DLIBKINETO_NOROCTRACER -DLIBKINETO_NOXPUPTI=ON -DUSE_FBGEMM -DUSE_PYTORCH_QNNPACK -DUSE_XNNPACK -DSYMBOLICATE_MOBILE_DEBUG_HANDLE -O2 -fPIC -Wall -Wextra -Werror=return-type -Werror=non-virtual-dtor -Werror=range-loop-construct -Werror=bool-operation -Wnarrowing -Wno-missing-field-initializers -Wno-unknown-pragmas -Wno-unused-parameter -Wno-strict-overflow -Wno-strict-aliasing -Wno-stringop-overflow -Wsuggest-override -Wno-psabi -Wno-error=old-style-cast -fdiagnostics-color=always -faligned-new -Wno-maybe-uninitialized -fno-math-errno -fno-trapping-math -Werror=format -Wno-stringop-overflow, LAPACK_INFO=mkl, PERF_WITH_AVX=1, PERF_WITH_AVX2=1, TORCH_VERSION=2.7.1, USE_CUDA=ON, USE_CUDNN=ON, USE_CUSPARSELT=1, USE_GFLAGS=OFF, USE_GLOG=OFF, USE_GLOO=ON, USE_MKL=ON, USE_MKLDNN=ON, USE_MPI=OFF, USE_NCCL=1, USE_NNPACK=ON, USE_OPENMP=ON, USE_ROCM=OFF, USE_ROCM_KERNEL_ASSERT=OFF, \n"
+ }
+}
diff --git a/peft/method_comparison/MetaMathQA/results/miss--llama-3.2-3B-bat.json b/peft/method_comparison/MetaMathQA/results/miss--llama-3.2-3B-bat.json
new file mode 100644
index 0000000000000000000000000000000000000000..fc788b3e6208118bac0eec843b00fdec8b96288b
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/results/miss--llama-3.2-3B-bat.json
@@ -0,0 +1,352 @@
+{
+ "run_info": {
+ "created_at": "2025-08-14T11:55:49+00:00",
+ "total_time": 2808.721444314,
+ "experiment_name": "miss/llama-3.2-3B-bat",
+ "peft_branch": "main",
+ "train_config": {
+ "model_id": "meta-llama/Llama-3.2-3B",
+ "dtype": "bfloat16",
+ "max_seq_length": 768,
+ "batch_size": 4,
+ "batch_size_eval": 50,
+ "max_steps": 5000,
+ "eval_steps": 250,
+ "compile": false,
+ "query_template": "Question: {query} Think step by step.\nAnswer:",
+ "seed": 0,
+ "grad_norm_clip": 1.0,
+ "optimizer_type": "AdamW",
+ "optimizer_kwargs": {
+ "lr": 0.0001,
+ "weight_decay": 0.1
+ },
+ "lr_scheduler": "cosine",
+ "use_amp": false,
+ "autocast_adapter_dtype": true,
+ "generation_kwargs": {
+ "max_length": 800,
+ "max_new_tokens": 300
+ },
+ "attn_implementation": null
+ },
+ "peft_config": {
+ "task_type": null,
+ "peft_type": "MISS",
+ "auto_mapping": null,
+ "base_model_name_or_path": "meta-llama/Llama-3.2-3B",
+ "revision": null,
+ "inference_mode": false,
+ "r": 64,
+ "miss_dropout": 0.0,
+ "mini_r": 1,
+ "target_modules": [
+ "v_proj",
+ "q_proj"
+ ],
+ "exclude_modules": null,
+ "init_weights": "bat",
+ "layers_to_transform": null,
+ "layers_pattern": null,
+ "bias": "none",
+ "modules_to_save": null
+ },
+ "error_msg": ""
+ },
+ "train_info": {
+ "accelerator_memory_reserved_avg": 14713719934,
+ "accelerator_memory_max": 25251807232,
+ "accelerator_memory_reserved_99th": 20472733368,
+ "train_time": 2466.149786608999,
+ "file_size": 29367552,
+ "num_trainable_params": 7340032,
+ "num_total_params": 3220089856,
+ "status": "success",
+ "metrics": [
+ {
+ "step": 250,
+ "valid accuracy": 0.32,
+ "train loss": 0.8741402707099915,
+ "train samples": 1000,
+ "train time": 44.507981576001725,
+ "eval time": 16.603345405999903,
+ "tokens / sec": 4756.8771376088835,
+ "mem allocated avg": 6898417197.056,
+ "mem reserved avg": 14772422574.08,
+ "elapsed time": 128.87205576299993
+ },
+ {
+ "step": 500,
+ "valid accuracy": 0.42,
+ "train loss": 0.6949697629213333,
+ "train samples": 2000,
+ "train time": 43.6579733309992,
+ "eval time": 12.170993550999924,
+ "tokens / sec": 4764.192749467687,
+ "mem allocated avg": 6890132037.632,
+ "mem reserved avg": 14662515032.064,
+ "elapsed time": 244.05737383899998
+ },
+ {
+ "step": 750,
+ "valid accuracy": 0.38,
+ "train loss": 0.667268633723259,
+ "train samples": 3000,
+ "train time": 44.76929137299828,
+ "eval time": 8.243386759000032,
+ "tokens / sec": 4789.0192903368525,
+ "mem allocated avg": 6900972326.912,
+ "mem reserved avg": 14823525974.016,
+ "elapsed time": 357.2643382499999
+ },
+ {
+ "step": 1000,
+ "valid accuracy": 0.48,
+ "train loss": 0.6478440872430802,
+ "train samples": 4000,
+ "train time": 43.91589877199954,
+ "eval time": 9.950706549000074,
+ "tokens / sec": 4743.976687842116,
+ "mem allocated avg": 6892131758.08,
+ "mem reserved avg": 14678444998.656,
+ "elapsed time": 470.61746281599994
+ },
+ {
+ "step": 1250,
+ "valid accuracy": 0.4,
+ "train loss": 0.6435494017601013,
+ "train samples": 5000,
+ "train time": 44.14956537599949,
+ "eval time": 16.547810228000117,
+ "tokens / sec": 4723.444007296278,
+ "mem allocated avg": 6892566360.064,
+ "mem reserved avg": 14674737233.92,
+ "elapsed time": 591.057877963
+ },
+ {
+ "step": 1500,
+ "valid accuracy": 0.44,
+ "train loss": 0.6368351166248322,
+ "train samples": 6000,
+ "train time": 44.08414804900008,
+ "eval time": 16.39257521799982,
+ "tokens / sec": 4748.441543371237,
+ "mem allocated avg": 6893236697.088,
+ "mem reserved avg": 14706580389.888,
+ "elapsed time": 711.4482007859999
+ },
+ {
+ "step": 1750,
+ "valid accuracy": 0.48,
+ "train loss": 0.6278127529621125,
+ "train samples": 7000,
+ "train time": 44.35628801999951,
+ "eval time": 16.51757288099998,
+ "tokens / sec": 4719.849413584954,
+ "mem allocated avg": 6894834587.648,
+ "mem reserved avg": 14716881600.512,
+ "elapsed time": 832.303061434
+ },
+ {
+ "step": 2000,
+ "valid accuracy": 0.44,
+ "train loss": 0.6281237225532532,
+ "train samples": 8000,
+ "train time": 43.95804043099747,
+ "eval time": 16.465996583000106,
+ "tokens / sec": 4724.869397352412,
+ "mem allocated avg": 6891602710.528,
+ "mem reserved avg": 14655669927.936,
+ "elapsed time": 952.480474365
+ },
+ {
+ "step": 2250,
+ "valid accuracy": 0.42,
+ "train loss": 0.6159191156625747,
+ "train samples": 9000,
+ "train time": 44.99231110500091,
+ "eval time": 16.5404373570002,
+ "tokens / sec": 4777.4385160692145,
+ "mem allocated avg": 6903352731.648,
+ "mem reserved avg": 14850520514.56,
+ "elapsed time": 1074.326083797
+ },
+ {
+ "step": 2500,
+ "valid accuracy": 0.44,
+ "train loss": 0.6119081476926803,
+ "train samples": 10000,
+ "train time": 43.74939265700118,
+ "eval time": 16.33099729599985,
+ "tokens / sec": 4707.882498273705,
+ "mem allocated avg": 6887975004.16,
+ "mem reserved avg": 14597494931.456,
+ "elapsed time": 1194.094911997
+ },
+ {
+ "step": 2750,
+ "valid accuracy": 0.44,
+ "train loss": 0.6010881408452987,
+ "train samples": 11000,
+ "train time": 43.686495668999896,
+ "eval time": 11.229614545000004,
+ "tokens / sec": 4850.0342441142875,
+ "mem allocated avg": 6899207546.88,
+ "mem reserved avg": 14785391362.048,
+ "elapsed time": 1308.783695182
+ },
+ {
+ "step": 3000,
+ "valid accuracy": 0.5,
+ "train loss": 0.5899516706466674,
+ "train samples": 12000,
+ "train time": 43.49030302700089,
+ "eval time": 16.45857661900004,
+ "tokens / sec": 4799.483688821613,
+ "mem allocated avg": 6894123913.216,
+ "mem reserved avg": 14693427052.544,
+ "elapsed time": 1428.4006117669999
+ },
+ {
+ "step": 3250,
+ "valid accuracy": 0.52,
+ "train loss": 0.5989595657587051,
+ "train samples": 13000,
+ "train time": 44.46332806799887,
+ "eval time": 16.496417500999996,
+ "tokens / sec": 4743.257177633304,
+ "mem allocated avg": 6895596777.472,
+ "mem reserved avg": 14723995140.096,
+ "elapsed time": 1549.445265484
+ },
+ {
+ "step": 3500,
+ "valid accuracy": 0.46,
+ "train loss": 0.579978278040886,
+ "train samples": 14000,
+ "train time": 43.63575344299579,
+ "eval time": 10.30441635599982,
+ "tokens / sec": 4806.838050224342,
+ "mem allocated avg": 6893774680.064,
+ "mem reserved avg": 14699450073.088,
+ "elapsed time": 1663.316950223
+ },
+ {
+ "step": 3750,
+ "valid accuracy": 0.44,
+ "train loss": 0.5772325273752212,
+ "train samples": 15000,
+ "train time": 45.25726027099972,
+ "eval time": 16.524598716000128,
+ "tokens / sec": 4788.2483098266675,
+ "mem allocated avg": 6905177583.616,
+ "mem reserved avg": 14889795977.216,
+ "elapsed time": 1785.1977310290001
+ },
+ {
+ "step": 4000,
+ "valid accuracy": 0.4,
+ "train loss": 0.5859311088323593,
+ "train samples": 16000,
+ "train time": 43.383903580999686,
+ "eval time": 16.386461492000308,
+ "tokens / sec": 4710.802466597467,
+ "mem allocated avg": 6886734053.376,
+ "mem reserved avg": 14584660361.216,
+ "elapsed time": 1904.6209389110002
+ },
+ {
+ "step": 4250,
+ "valid accuracy": 0.5,
+ "train loss": 0.5724418247938157,
+ "train samples": 17000,
+ "train time": 44.42285394400233,
+ "eval time": 9.048803244000283,
+ "tokens / sec": 4758.564145078759,
+ "mem allocated avg": 6896789555.2,
+ "mem reserved avg": 14740688470.016,
+ "elapsed time": 2018.321323589
+ },
+ {
+ "step": 4500,
+ "valid accuracy": 0.46,
+ "train loss": 0.5792494393587112,
+ "train samples": 18000,
+ "train time": 43.636566284001674,
+ "eval time": 16.3964514889999,
+ "tokens / sec": 4762.4737163655245,
+ "mem allocated avg": 6892818855.936,
+ "mem reserved avg": 14655921586.176,
+ "elapsed time": 2137.859151554
+ },
+ {
+ "step": 4750,
+ "valid accuracy": 0.46,
+ "train loss": 0.5680228790044785,
+ "train samples": 19000,
+ "train time": 43.96985955700529,
+ "eval time": 16.500367100000403,
+ "tokens / sec": 4774.61156608476,
+ "mem allocated avg": 6894185185.28,
+ "mem reserved avg": 14706722996.224,
+ "elapsed time": 2258.0618387639997
+ },
+ {
+ "step": 5000,
+ "valid accuracy": 0.44,
+ "train loss": 0.5760680929422378,
+ "train samples": 20000,
+ "train time": 43.83249596400128,
+ "eval time": 16.474086973999874,
+ "tokens / sec": 4751.7257555001215,
+ "mem allocated avg": 6891346642.944,
+ "mem reserved avg": 14655552487.424,
+ "elapsed time": 2377.7959423069997
+ },
+ {
+ "step": 5000,
+ "test accuracy": 0.5049279757391963,
+ "train loss": 0.5760680929422378,
+ "train samples": 20000,
+ "train total tokens": 4198051
+ }
+ ]
+ },
+ "meta_info": {
+ "model_info": {
+ "sha": "13afe5124825b4f3751f836b40dafda64c1ed062",
+ "created_at": "2024-09-18T15:23:48+00:00"
+ },
+ "dataset_info": {
+ "metamath": {
+ "sha": "aa4f34d3d2d3231299b5b03d9b3e5a20da45aa18",
+ "created_at": "2023-09-21T17:22:46+00:00"
+ },
+ "gsm8k": {
+ "sha": "e53f048856ff4f594e959d75785d2c2d37b678ee",
+ "created_at": "2022-04-12T10:22:10+00:00"
+ }
+ },
+ "package_info": {
+ "transformers-version": "4.52.4",
+ "transformers-commit-hash": null,
+ "peft-version": "0.17.1.dev0",
+ "peft-commit-hash": "47961bb54706e45fd3b5460baa4921a48bcdce35",
+ "datasets-version": "3.6.0",
+ "datasets-commit-hash": null,
+ "bitsandbytes-version": "0.46.0",
+ "bitsandbytes-commit-hash": null,
+ "torch-version": "2.7.1+cu126",
+ "torch-commit-hash": null
+ },
+ "system_info": {
+ "system": "Linux",
+ "release": "6.14.0-1010-aws",
+ "version": "#10~24.04.1-Ubuntu SMP Fri Jul 18 20:44:30 UTC 2025",
+ "machine": "x86_64",
+ "processor": "x86_64",
+ "accelerator": "NVIDIA L40S"
+ },
+ "pytorch_info": "PyTorch built with:\n - GCC 11.2\n - C++ Version: 201703\n - Intel(R) oneAPI Math Kernel Library Version 2024.2-Product Build 20240605 for Intel(R) 64 architecture applications\n - Intel(R) MKL-DNN v3.7.1 (Git Hash 8d263e693366ef8db40acc569cc7d8edf644556d)\n - OpenMP 201511 (a.k.a. OpenMP 4.5)\n - LAPACK is enabled (usually provided by MKL)\n - NNPACK is enabled\n - CPU capability usage: AVX2\n - CUDA Runtime 12.6\n - NVCC architecture flags: -gencode;arch=compute_50,code=sm_50;-gencode;arch=compute_60,code=sm_60;-gencode;arch=compute_70,code=sm_70;-gencode;arch=compute_75,code=sm_75;-gencode;arch=compute_80,code=sm_80;-gencode;arch=compute_86,code=sm_86;-gencode;arch=compute_90,code=sm_90\n - CuDNN 90.7.1 (built against CUDA 12.8)\n - Built with CuDNN 90.5.1\n - Magma 2.6.1\n - Build settings: BLAS_INFO=mkl, BUILD_TYPE=Release, COMMIT_SHA=e2d141dbde55c2a4370fac5165b0561b6af4798b, CUDA_VERSION=12.6, CUDNN_VERSION=9.5.1, CXX_COMPILER=/opt/rh/gcc-toolset-11/root/usr/bin/c++, CXX_FLAGS= -D_GLIBCXX_USE_CXX11_ABI=1 -fvisibility-inlines-hidden -DUSE_PTHREADPOOL -DNDEBUG -DUSE_KINETO -DLIBKINETO_NOROCTRACER -DLIBKINETO_NOXPUPTI=ON -DUSE_FBGEMM -DUSE_PYTORCH_QNNPACK -DUSE_XNNPACK -DSYMBOLICATE_MOBILE_DEBUG_HANDLE -O2 -fPIC -Wall -Wextra -Werror=return-type -Werror=non-virtual-dtor -Werror=range-loop-construct -Werror=bool-operation -Wnarrowing -Wno-missing-field-initializers -Wno-unknown-pragmas -Wno-unused-parameter -Wno-strict-overflow -Wno-strict-aliasing -Wno-stringop-overflow -Wsuggest-override -Wno-psabi -Wno-error=old-style-cast -fdiagnostics-color=always -faligned-new -Wno-maybe-uninitialized -fno-math-errno -fno-trapping-math -Werror=format -Wno-stringop-overflow, LAPACK_INFO=mkl, PERF_WITH_AVX=1, PERF_WITH_AVX2=1, TORCH_VERSION=2.7.1, USE_CUDA=ON, USE_CUDNN=ON, USE_CUSPARSELT=1, USE_GFLAGS=OFF, USE_GLOG=OFF, USE_GLOO=ON, USE_MKL=ON, USE_MKLDNN=ON, USE_MPI=OFF, USE_NCCL=1, USE_NNPACK=ON, USE_OPENMP=ON, USE_ROCM=OFF, USE_ROCM_KERNEL_ASSERT=OFF, \n"
+ }
+}
\ No newline at end of file
diff --git a/peft/method_comparison/MetaMathQA/results/miss--llama-3.2-3B-default.json b/peft/method_comparison/MetaMathQA/results/miss--llama-3.2-3B-default.json
new file mode 100644
index 0000000000000000000000000000000000000000..89af4592383509c5f08d994cb24616421c056bf7
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/results/miss--llama-3.2-3B-default.json
@@ -0,0 +1,352 @@
+{
+ "run_info": {
+ "created_at": "2025-08-14T12:42:42+00:00",
+ "total_time": 1917.9635583239997,
+ "experiment_name": "miss/llama-3.2-3B-default",
+ "peft_branch": "main",
+ "train_config": {
+ "model_id": "meta-llama/Llama-3.2-3B",
+ "dtype": "bfloat16",
+ "max_seq_length": 768,
+ "batch_size": 4,
+ "batch_size_eval": 50,
+ "max_steps": 5000,
+ "eval_steps": 250,
+ "compile": false,
+ "query_template": "Question: {query} Think step by step.\nAnswer:",
+ "seed": 0,
+ "grad_norm_clip": 1.0,
+ "optimizer_type": "AdamW",
+ "optimizer_kwargs": {
+ "lr": 0.0001,
+ "weight_decay": 0.1
+ },
+ "lr_scheduler": "cosine",
+ "use_amp": false,
+ "autocast_adapter_dtype": true,
+ "generation_kwargs": {
+ "max_length": 800,
+ "max_new_tokens": 300
+ },
+ "attn_implementation": null
+ },
+ "peft_config": {
+ "task_type": null,
+ "peft_type": "MISS",
+ "auto_mapping": null,
+ "base_model_name_or_path": "meta-llama/Llama-3.2-3B",
+ "revision": null,
+ "inference_mode": false,
+ "r": 64,
+ "miss_dropout": 0.0,
+ "mini_r": 1,
+ "target_modules": [
+ "q_proj",
+ "v_proj"
+ ],
+ "exclude_modules": null,
+ "init_weights": true,
+ "layers_to_transform": null,
+ "layers_pattern": null,
+ "bias": "none",
+ "modules_to_save": null
+ },
+ "error_msg": ""
+ },
+ "train_info": {
+ "accelerator_memory_reserved_avg": 11170868939,
+ "accelerator_memory_max": 20248002560,
+ "accelerator_memory_reserved_99th": 16301393182,
+ "train_time": 1713.3205038909991,
+ "file_size": 29367496,
+ "num_trainable_params": 7340032,
+ "num_total_params": 3220089856,
+ "status": "success",
+ "metrics": [
+ {
+ "step": 250,
+ "valid accuracy": 0.36,
+ "train loss": 0.8771686832904816,
+ "train samples": 1000,
+ "train time": 29.625120898993828,
+ "eval time": 11.058316758999808,
+ "tokens / sec": 7146.603746254777,
+ "mem allocated avg": 6894354876.416,
+ "mem reserved avg": 11212691603.456,
+ "elapsed time": 89.49706801999992
+ },
+ {
+ "step": 500,
+ "valid accuracy": 0.42,
+ "train loss": 0.6949640859365463,
+ "train samples": 2000,
+ "train time": 29.06092399400177,
+ "eval time": 5.4939734129998214,
+ "tokens / sec": 7157.205326400859,
+ "mem allocated avg": 6887297284.096,
+ "mem reserved avg": 11116172279.808,
+ "elapsed time": 166.80778670399968
+ },
+ {
+ "step": 750,
+ "valid accuracy": 0.42,
+ "train loss": 0.6677889958620071,
+ "train samples": 3000,
+ "train time": 29.654036860997167,
+ "eval time": 6.225696284000151,
+ "tokens / sec": 7230.078016190556,
+ "mem allocated avg": 6897885888.512,
+ "mem reserved avg": 11257109282.816,
+ "elapsed time": 245.76960384799986
+ },
+ {
+ "step": 1000,
+ "valid accuracy": 0.38,
+ "train loss": 0.6483739440441132,
+ "train samples": 4000,
+ "train time": 28.837856293007462,
+ "eval time": 10.98694702900002,
+ "tokens / sec": 7224.392752470884,
+ "mem allocated avg": 6888501639.168,
+ "mem reserved avg": 11141564596.224,
+ "elapsed time": 328.02559429799976
+ },
+ {
+ "step": 1250,
+ "valid accuracy": 0.46,
+ "train loss": 0.6433384964466095,
+ "train samples": 5000,
+ "train time": 28.81160366599852,
+ "eval time": 7.707165779999741,
+ "tokens / sec": 7237.986556302045,
+ "mem allocated avg": 6888334700.544,
+ "mem reserved avg": 11139123511.296,
+ "elapsed time": 407.06604839199963
+ },
+ {
+ "step": 1500,
+ "valid accuracy": 0.5,
+ "train loss": 0.6369507477283478,
+ "train samples": 6000,
+ "train time": 28.99961056100119,
+ "eval time": 8.123675749000085,
+ "tokens / sec": 7218.407280320836,
+ "mem allocated avg": 6890289985.536,
+ "mem reserved avg": 11163484028.928,
+ "elapsed time": 486.7935630989996
+ },
+ {
+ "step": 1750,
+ "valid accuracy": 0.42,
+ "train loss": 0.6278414962291717,
+ "train samples": 7000,
+ "train time": 29.449354215004405,
+ "eval time": 11.046255440000095,
+ "tokens / sec": 7108.984410032798,
+ "mem allocated avg": 6891426932.736,
+ "mem reserved avg": 11175706230.784,
+ "elapsed time": 570.2098619899998
+ },
+ {
+ "step": 2000,
+ "valid accuracy": 0.42,
+ "train loss": 0.62835728931427,
+ "train samples": 8000,
+ "train time": 28.844003398995028,
+ "eval time": 11.063917559999936,
+ "tokens / sec": 7200.664801170994,
+ "mem allocated avg": 6888937164.8,
+ "mem reserved avg": 11125752070.144,
+ "elapsed time": 652.66749592
+ },
+ {
+ "step": 2250,
+ "valid accuracy": 0.46,
+ "train loss": 0.616273587346077,
+ "train samples": 9000,
+ "train time": 29.490800742004012,
+ "eval time": 8.136742810000214,
+ "tokens / sec": 7288.645767215389,
+ "mem allocated avg": 6899370121.216,
+ "mem reserved avg": 11286914007.04,
+ "elapsed time": 733.5518891469997
+ },
+ {
+ "step": 2500,
+ "valid accuracy": 0.48,
+ "train loss": 0.6127588752508163,
+ "train samples": 10000,
+ "train time": 28.812003271001686,
+ "eval time": 11.006928690999757,
+ "tokens / sec": 7148.652527306175,
+ "mem allocated avg": 6884932614.144,
+ "mem reserved avg": 11077299470.336,
+ "elapsed time": 815.9489541349999
+ },
+ {
+ "step": 2750,
+ "valid accuracy": 0.48,
+ "train loss": 0.6011098005771637,
+ "train samples": 11000,
+ "train time": 29.451534630989954,
+ "eval time": 11.065294603999973,
+ "tokens / sec": 7194.226129630993,
+ "mem allocated avg": 6895703631.872,
+ "mem reserved avg": 11229007446.016,
+ "elapsed time": 899.4794512619997
+ },
+ {
+ "step": 3000,
+ "valid accuracy": 0.5,
+ "train loss": 0.590887265920639,
+ "train samples": 12000,
+ "train time": 29.118879764002486,
+ "eval time": 11.043336514999282,
+ "tokens / sec": 7168.235924310477,
+ "mem allocated avg": 6890226739.2,
+ "mem reserved avg": 11156563427.328,
+ "elapsed time": 982.334967583
+ },
+ {
+ "step": 3250,
+ "valid accuracy": 0.52,
+ "train loss": 0.6000960898399353,
+ "train samples": 13000,
+ "train time": 29.13528394500463,
+ "eval time": 11.077541423999719,
+ "tokens / sec": 7238.680096548703,
+ "mem allocated avg": 6892138940.416,
+ "mem reserved avg": 11182651998.208,
+ "elapsed time": 1065.5038535119998
+ },
+ {
+ "step": 3500,
+ "valid accuracy": 0.46,
+ "train loss": 0.5813224712610244,
+ "train samples": 14000,
+ "train time": 29.210709365002003,
+ "eval time": 11.022432370000388,
+ "tokens / sec": 7180.585633134473,
+ "mem allocated avg": 6891394273.28,
+ "mem reserved avg": 11167116296.192,
+ "elapsed time": 1148.6551861069997
+ },
+ {
+ "step": 3750,
+ "valid accuracy": 0.5,
+ "train loss": 0.5779635999202728,
+ "train samples": 15000,
+ "train time": 29.93350169399855,
+ "eval time": 11.012248770000042,
+ "tokens / sec": 7239.48043951862,
+ "mem allocated avg": 6900874864.64,
+ "mem reserved avg": 11322674642.944,
+ "elapsed time": 1233.146194169
+ },
+ {
+ "step": 4000,
+ "valid accuracy": 0.5,
+ "train loss": 0.5870059201717377,
+ "train samples": 16000,
+ "train time": 28.73894150599881,
+ "eval time": 11.028763495000021,
+ "tokens / sec": 7111.361424266106,
+ "mem allocated avg": 6883623936.0,
+ "mem reserved avg": 11058022449.152,
+ "elapsed time": 1315.630321268
+ },
+ {
+ "step": 4250,
+ "valid accuracy": 0.48,
+ "train loss": 0.5732149496078491,
+ "train samples": 17000,
+ "train time": 29.274482168998475,
+ "eval time": 11.023004681000202,
+ "tokens / sec": 7220.930460175991,
+ "mem allocated avg": 6893432758.272,
+ "mem reserved avg": 11193867567.104,
+ "elapsed time": 1399.0288222240001
+ },
+ {
+ "step": 4500,
+ "valid accuracy": 0.48,
+ "train loss": 0.5802423723936081,
+ "train samples": 18000,
+ "train time": 28.807760504997532,
+ "eval time": 11.07264679400032,
+ "tokens / sec": 7213.958890138232,
+ "mem allocated avg": 6888416004.096,
+ "mem reserved avg": 11124485390.336,
+ "elapsed time": 1481.5334540769995
+ },
+ {
+ "step": 4750,
+ "valid accuracy": 0.52,
+ "train loss": 0.5696245921850205,
+ "train samples": 19000,
+ "train time": 29.20943511798214,
+ "eval time": 11.082792330000302,
+ "tokens / sec": 7187.369394581538,
+ "mem allocated avg": 6890813089.792,
+ "mem reserved avg": 11168844349.44,
+ "elapsed time": 1565.0750862589998
+ },
+ {
+ "step": 5000,
+ "valid accuracy": 0.5,
+ "train loss": 0.5774132673740386,
+ "train samples": 20000,
+ "train time": 29.084354959996745,
+ "eval time": 11.092419973000688,
+ "tokens / sec": 7161.238414483417,
+ "mem allocated avg": 6887869800.448,
+ "mem reserved avg": 11118328152.064,
+ "elapsed time": 1648.4280528519998
+ },
+ {
+ "step": 5000,
+ "test accuracy": 0.5087187263078089,
+ "train loss": 0.5774132673740386,
+ "train samples": 20000,
+ "train total tokens": 4198051
+ }
+ ]
+ },
+ "meta_info": {
+ "model_info": {
+ "sha": "13afe5124825b4f3751f836b40dafda64c1ed062",
+ "created_at": "2024-09-18T15:23:48+00:00"
+ },
+ "dataset_info": {
+ "metamath": {
+ "sha": "aa4f34d3d2d3231299b5b03d9b3e5a20da45aa18",
+ "created_at": "2023-09-21T17:22:46+00:00"
+ },
+ "gsm8k": {
+ "sha": "e53f048856ff4f594e959d75785d2c2d37b678ee",
+ "created_at": "2022-04-12T10:22:10+00:00"
+ }
+ },
+ "package_info": {
+ "transformers-version": "4.52.4",
+ "transformers-commit-hash": null,
+ "peft-version": "0.17.1.dev0",
+ "peft-commit-hash": "47961bb54706e45fd3b5460baa4921a48bcdce35",
+ "datasets-version": "3.6.0",
+ "datasets-commit-hash": null,
+ "bitsandbytes-version": "0.46.0",
+ "bitsandbytes-commit-hash": null,
+ "torch-version": "2.7.1+cu126",
+ "torch-commit-hash": null
+ },
+ "system_info": {
+ "system": "Linux",
+ "release": "6.14.0-1010-aws",
+ "version": "#10~24.04.1-Ubuntu SMP Fri Jul 18 20:44:30 UTC 2025",
+ "machine": "x86_64",
+ "processor": "x86_64",
+ "accelerator": "NVIDIA L40S"
+ },
+ "pytorch_info": "PyTorch built with:\n - GCC 11.2\n - C++ Version: 201703\n - Intel(R) oneAPI Math Kernel Library Version 2024.2-Product Build 20240605 for Intel(R) 64 architecture applications\n - Intel(R) MKL-DNN v3.7.1 (Git Hash 8d263e693366ef8db40acc569cc7d8edf644556d)\n - OpenMP 201511 (a.k.a. OpenMP 4.5)\n - LAPACK is enabled (usually provided by MKL)\n - NNPACK is enabled\n - CPU capability usage: AVX2\n - CUDA Runtime 12.6\n - NVCC architecture flags: -gencode;arch=compute_50,code=sm_50;-gencode;arch=compute_60,code=sm_60;-gencode;arch=compute_70,code=sm_70;-gencode;arch=compute_75,code=sm_75;-gencode;arch=compute_80,code=sm_80;-gencode;arch=compute_86,code=sm_86;-gencode;arch=compute_90,code=sm_90\n - CuDNN 90.7.1 (built against CUDA 12.8)\n - Built with CuDNN 90.5.1\n - Magma 2.6.1\n - Build settings: BLAS_INFO=mkl, BUILD_TYPE=Release, COMMIT_SHA=e2d141dbde55c2a4370fac5165b0561b6af4798b, CUDA_VERSION=12.6, CUDNN_VERSION=9.5.1, CXX_COMPILER=/opt/rh/gcc-toolset-11/root/usr/bin/c++, CXX_FLAGS= -D_GLIBCXX_USE_CXX11_ABI=1 -fvisibility-inlines-hidden -DUSE_PTHREADPOOL -DNDEBUG -DUSE_KINETO -DLIBKINETO_NOROCTRACER -DLIBKINETO_NOXPUPTI=ON -DUSE_FBGEMM -DUSE_PYTORCH_QNNPACK -DUSE_XNNPACK -DSYMBOLICATE_MOBILE_DEBUG_HANDLE -O2 -fPIC -Wall -Wextra -Werror=return-type -Werror=non-virtual-dtor -Werror=range-loop-construct -Werror=bool-operation -Wnarrowing -Wno-missing-field-initializers -Wno-unknown-pragmas -Wno-unused-parameter -Wno-strict-overflow -Wno-strict-aliasing -Wno-stringop-overflow -Wsuggest-override -Wno-psabi -Wno-error=old-style-cast -fdiagnostics-color=always -faligned-new -Wno-maybe-uninitialized -fno-math-errno -fno-trapping-math -Werror=format -Wno-stringop-overflow, LAPACK_INFO=mkl, PERF_WITH_AVX=1, PERF_WITH_AVX2=1, TORCH_VERSION=2.7.1, USE_CUDA=ON, USE_CUDNN=ON, USE_CUSPARSELT=1, USE_GFLAGS=OFF, USE_GLOG=OFF, USE_GLOO=ON, USE_MKL=ON, USE_MKLDNN=ON, USE_MPI=OFF, USE_NCCL=1, USE_NNPACK=ON, USE_OPENMP=ON, USE_ROCM=OFF, USE_ROCM_KERNEL_ASSERT=OFF, \n"
+ }
+}
\ No newline at end of file
diff --git a/peft/method_comparison/MetaMathQA/results/miss--llama-3.2-3B-mini.json b/peft/method_comparison/MetaMathQA/results/miss--llama-3.2-3B-mini.json
new file mode 100644
index 0000000000000000000000000000000000000000..66e5f975921692c2d4349a18e3d5975511344864
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/results/miss--llama-3.2-3B-mini.json
@@ -0,0 +1,352 @@
+{
+ "run_info": {
+ "created_at": "2025-08-14T13:14:44+00:00",
+ "total_time": 1939.2463944070005,
+ "experiment_name": "miss/llama-3.2-3B-mini",
+ "peft_branch": "main",
+ "train_config": {
+ "model_id": "meta-llama/Llama-3.2-3B",
+ "dtype": "bfloat16",
+ "max_seq_length": 768,
+ "batch_size": 4,
+ "batch_size_eval": 50,
+ "max_steps": 5000,
+ "eval_steps": 250,
+ "compile": false,
+ "query_template": "Question: {query} Think step by step.\nAnswer:",
+ "seed": 0,
+ "grad_norm_clip": 1.0,
+ "optimizer_type": "AdamW",
+ "optimizer_kwargs": {
+ "lr": 0.0001,
+ "weight_decay": 0.1
+ },
+ "lr_scheduler": "cosine",
+ "use_amp": false,
+ "autocast_adapter_dtype": true,
+ "generation_kwargs": {
+ "max_length": 800,
+ "max_new_tokens": 300
+ },
+ "attn_implementation": null
+ },
+ "peft_config": {
+ "task_type": null,
+ "peft_type": "MISS",
+ "auto_mapping": null,
+ "base_model_name_or_path": "meta-llama/Llama-3.2-3B",
+ "revision": null,
+ "inference_mode": false,
+ "r": 64,
+ "miss_dropout": 0.0,
+ "mini_r": 64,
+ "target_modules": [
+ "q_proj",
+ "v_proj"
+ ],
+ "exclude_modules": null,
+ "init_weights": "mini",
+ "layers_to_transform": null,
+ "layers_pattern": null,
+ "bias": "none",
+ "modules_to_save": null
+ },
+ "error_msg": ""
+ },
+ "train_info": {
+ "accelerator_memory_reserved_avg": 11076096963,
+ "accelerator_memory_max": 20189282304,
+ "accelerator_memory_reserved_99th": 16251103477,
+ "train_time": 1757.4722608399989,
+ "file_size": 924568,
+ "num_trainable_params": 229376,
+ "num_total_params": 3212979200,
+ "status": "success",
+ "metrics": [
+ {
+ "step": 250,
+ "valid accuracy": 0.34,
+ "train loss": 1.0204485692977905,
+ "train samples": 1000,
+ "train time": 30.37152520300151,
+ "eval time": 11.248587610999493,
+ "tokens / sec": 6970.970294869372,
+ "mem allocated avg": 6780477966.336,
+ "mem reserved avg": 11118412038.144,
+ "elapsed time": 90.66597219600044
+ },
+ {
+ "step": 500,
+ "valid accuracy": 0.34,
+ "train loss": 0.747962894320488,
+ "train samples": 2000,
+ "train time": 29.572977570002877,
+ "eval time": 11.171488900999975,
+ "tokens / sec": 7033.278928631729,
+ "mem allocated avg": 6773512382.464,
+ "mem reserved avg": 11022605746.176,
+ "elapsed time": 174.9062917200008
+ },
+ {
+ "step": 750,
+ "valid accuracy": 0.36,
+ "train loss": 0.7062408643960952,
+ "train samples": 3000,
+ "train time": 30.206997992999277,
+ "eval time": 8.297702855000352,
+ "tokens / sec": 7097.726164304351,
+ "mem allocated avg": 6784103079.936,
+ "mem reserved avg": 11160933892.096,
+ "elapsed time": 257.1565456070002
+ },
+ {
+ "step": 1000,
+ "valid accuracy": 0.42,
+ "train loss": 0.688418450832367,
+ "train samples": 4000,
+ "train time": 29.89673271099673,
+ "eval time": 8.431126997999854,
+ "tokens / sec": 6968.520674614356,
+ "mem allocated avg": 6774552799.232,
+ "mem reserved avg": 11046932709.376,
+ "elapsed time": 338.98425150300045
+ },
+ {
+ "step": 1250,
+ "valid accuracy": 0.26,
+ "train loss": 0.6864906589984894,
+ "train samples": 5000,
+ "train time": 29.511754502003896,
+ "eval time": 11.189089829000295,
+ "tokens / sec": 7066.269136450018,
+ "mem allocated avg": 6774476697.6,
+ "mem reserved avg": 11043107504.128,
+ "elapsed time": 423.2539680640002
+ },
+ {
+ "step": 1500,
+ "valid accuracy": 0.34,
+ "train loss": 0.6819815402030944,
+ "train samples": 6000,
+ "train time": 29.53373699200074,
+ "eval time": 10.82430943000054,
+ "tokens / sec": 7087.860234439605,
+ "mem allocated avg": 6776410671.104,
+ "mem reserved avg": 11066327171.072,
+ "elapsed time": 507.00703521000014
+ },
+ {
+ "step": 1750,
+ "valid accuracy": 0.24,
+ "train loss": 0.6748508417606354,
+ "train samples": 7000,
+ "train time": 29.92787808700814,
+ "eval time": 11.135467017999872,
+ "tokens / sec": 6995.317188587526,
+ "mem allocated avg": 6777799206.912,
+ "mem reserved avg": 11081728655.36,
+ "elapsed time": 591.3889150910009
+ },
+ {
+ "step": 2000,
+ "valid accuracy": 0.32,
+ "train loss": 0.6793494290113449,
+ "train samples": 8000,
+ "train time": 29.828631155996845,
+ "eval time": 7.671241181000369,
+ "tokens / sec": 6962.974563391727,
+ "mem allocated avg": 6775091949.568,
+ "mem reserved avg": 11030155493.376,
+ "elapsed time": 672.1807907450002
+ },
+ {
+ "step": 2250,
+ "valid accuracy": 0.36,
+ "train loss": 0.6712708432674408,
+ "train samples": 9000,
+ "train time": 30.12409129900061,
+ "eval time": 7.389505904999169,
+ "tokens / sec": 7135.418554754249,
+ "mem allocated avg": 6785428178.944,
+ "mem reserved avg": 11193422970.88,
+ "elapsed time": 753.4013944540002
+ },
+ {
+ "step": 2500,
+ "valid accuracy": 0.36,
+ "train loss": 0.670761358499527,
+ "train samples": 10000,
+ "train time": 29.392454811994867,
+ "eval time": 11.273840481000661,
+ "tokens / sec": 7007.478664760802,
+ "mem allocated avg": 6770948311.04,
+ "mem reserved avg": 10981837111.296,
+ "elapsed time": 837.4394236850003
+ },
+ {
+ "step": 2750,
+ "valid accuracy": 0.36,
+ "train loss": 0.6636076529026032,
+ "train samples": 11000,
+ "train time": 30.132865259004575,
+ "eval time": 7.065399131999584,
+ "tokens / sec": 7031.558339334618,
+ "mem allocated avg": 6781682612.224,
+ "mem reserved avg": 11132194521.088,
+ "elapsed time": 918.3523091420002
+ },
+ {
+ "step": 3000,
+ "valid accuracy": 0.3,
+ "train loss": 0.6547267787456512,
+ "train samples": 12000,
+ "train time": 29.80804876098864,
+ "eval time": 6.651864860000387,
+ "tokens / sec": 7002.504648112936,
+ "mem allocated avg": 6776379066.368,
+ "mem reserved avg": 11060597751.808,
+ "elapsed time": 998.1520945420007
+ },
+ {
+ "step": 3250,
+ "valid accuracy": 0.36,
+ "train loss": 0.6653184123039245,
+ "train samples": 13000,
+ "train time": 29.843793005994485,
+ "eval time": 11.134645372000705,
+ "tokens / sec": 7066.829607001965,
+ "mem allocated avg": 6778676955.136,
+ "mem reserved avg": 11088607313.92,
+ "elapsed time": 1082.892349787
+ },
+ {
+ "step": 3500,
+ "valid accuracy": 0.4,
+ "train loss": 0.6504588623046875,
+ "train samples": 14000,
+ "train time": 30.091547277996142,
+ "eval time": 11.186960818999978,
+ "tokens / sec": 6970.395974067295,
+ "mem allocated avg": 6777435619.328,
+ "mem reserved avg": 11074858385.408,
+ "elapsed time": 1168.1813894270008
+ },
+ {
+ "step": 3750,
+ "valid accuracy": 0.38,
+ "train loss": 0.6486766980886459,
+ "train samples": 15000,
+ "train time": 30.235947965997184,
+ "eval time": 6.424060680000366,
+ "tokens / sec": 7167.064854182855,
+ "mem allocated avg": 6787226097.664,
+ "mem reserved avg": 11226214039.552,
+ "elapsed time": 1249.1344440330004
+ },
+ {
+ "step": 4000,
+ "valid accuracy": 0.34,
+ "train loss": 0.6649546232223511,
+ "train samples": 16000,
+ "train time": 29.315789502004918,
+ "eval time": 6.29557701000067,
+ "tokens / sec": 6971.430872977951,
+ "mem allocated avg": 6769964711.936,
+ "mem reserved avg": 10964573356.032,
+ "elapsed time": 1328.0223749040006
+ },
+ {
+ "step": 4250,
+ "valid accuracy": 0.38,
+ "train loss": 0.6468708947896957,
+ "train samples": 17000,
+ "train time": 29.780288893992292,
+ "eval time": 6.263248704000034,
+ "tokens / sec": 7098.2857403591015,
+ "mem allocated avg": 6779703865.344,
+ "mem reserved avg": 11102406574.08,
+ "elapsed time": 1408.0423461730006
+ },
+ {
+ "step": 4500,
+ "valid accuracy": 0.36,
+ "train loss": 0.6554104331731796,
+ "train samples": 18000,
+ "train time": 29.55899746599971,
+ "eval time": 8.381054077999579,
+ "tokens / sec": 7030.617335349179,
+ "mem allocated avg": 6774673686.528,
+ "mem reserved avg": 11030071607.296,
+ "elapsed time": 1489.5959585560004
+ },
+ {
+ "step": 4750,
+ "valid accuracy": 0.3,
+ "train loss": 0.6466003597974778,
+ "train samples": 19000,
+ "train time": 29.626044395983627,
+ "eval time": 8.314826920000087,
+ "tokens / sec": 7086.298703733166,
+ "mem allocated avg": 6776780376.064,
+ "mem reserved avg": 11071855263.744,
+ "elapsed time": 1571.4978439640008
+ },
+ {
+ "step": 5000,
+ "valid accuracy": 0.36,
+ "train loss": 0.6535431078672409,
+ "train samples": 20000,
+ "train time": 29.328363572000853,
+ "eval time": 8.339948383999399,
+ "tokens / sec": 7101.657734454723,
+ "mem allocated avg": 6774118805.504,
+ "mem reserved avg": 11025097162.752,
+ "elapsed time": 1652.8993119440001
+ },
+ {
+ "step": 5000,
+ "test accuracy": 0.3912054586808188,
+ "train loss": 0.6535431078672409,
+ "train samples": 20000,
+ "train total tokens": 4198051
+ }
+ ]
+ },
+ "meta_info": {
+ "model_info": {
+ "sha": "13afe5124825b4f3751f836b40dafda64c1ed062",
+ "created_at": "2024-09-18T15:23:48+00:00"
+ },
+ "dataset_info": {
+ "metamath": {
+ "sha": "aa4f34d3d2d3231299b5b03d9b3e5a20da45aa18",
+ "created_at": "2023-09-21T17:22:46+00:00"
+ },
+ "gsm8k": {
+ "sha": "e53f048856ff4f594e959d75785d2c2d37b678ee",
+ "created_at": "2022-04-12T10:22:10+00:00"
+ }
+ },
+ "package_info": {
+ "transformers-version": "4.52.4",
+ "transformers-commit-hash": null,
+ "peft-version": "0.17.1.dev0",
+ "peft-commit-hash": "47961bb54706e45fd3b5460baa4921a48bcdce35",
+ "datasets-version": "3.6.0",
+ "datasets-commit-hash": null,
+ "bitsandbytes-version": "0.46.0",
+ "bitsandbytes-commit-hash": null,
+ "torch-version": "2.7.1+cu126",
+ "torch-commit-hash": null
+ },
+ "system_info": {
+ "system": "Linux",
+ "release": "6.14.0-1010-aws",
+ "version": "#10~24.04.1-Ubuntu SMP Fri Jul 18 20:44:30 UTC 2025",
+ "machine": "x86_64",
+ "processor": "x86_64",
+ "accelerator": "NVIDIA L40S"
+ },
+ "pytorch_info": "PyTorch built with:\n - GCC 11.2\n - C++ Version: 201703\n - Intel(R) oneAPI Math Kernel Library Version 2024.2-Product Build 20240605 for Intel(R) 64 architecture applications\n - Intel(R) MKL-DNN v3.7.1 (Git Hash 8d263e693366ef8db40acc569cc7d8edf644556d)\n - OpenMP 201511 (a.k.a. OpenMP 4.5)\n - LAPACK is enabled (usually provided by MKL)\n - NNPACK is enabled\n - CPU capability usage: AVX2\n - CUDA Runtime 12.6\n - NVCC architecture flags: -gencode;arch=compute_50,code=sm_50;-gencode;arch=compute_60,code=sm_60;-gencode;arch=compute_70,code=sm_70;-gencode;arch=compute_75,code=sm_75;-gencode;arch=compute_80,code=sm_80;-gencode;arch=compute_86,code=sm_86;-gencode;arch=compute_90,code=sm_90\n - CuDNN 90.7.1 (built against CUDA 12.8)\n - Built with CuDNN 90.5.1\n - Magma 2.6.1\n - Build settings: BLAS_INFO=mkl, BUILD_TYPE=Release, COMMIT_SHA=e2d141dbde55c2a4370fac5165b0561b6af4798b, CUDA_VERSION=12.6, CUDNN_VERSION=9.5.1, CXX_COMPILER=/opt/rh/gcc-toolset-11/root/usr/bin/c++, CXX_FLAGS= -D_GLIBCXX_USE_CXX11_ABI=1 -fvisibility-inlines-hidden -DUSE_PTHREADPOOL -DNDEBUG -DUSE_KINETO -DLIBKINETO_NOROCTRACER -DLIBKINETO_NOXPUPTI=ON -DUSE_FBGEMM -DUSE_PYTORCH_QNNPACK -DUSE_XNNPACK -DSYMBOLICATE_MOBILE_DEBUG_HANDLE -O2 -fPIC -Wall -Wextra -Werror=return-type -Werror=non-virtual-dtor -Werror=range-loop-construct -Werror=bool-operation -Wnarrowing -Wno-missing-field-initializers -Wno-unknown-pragmas -Wno-unused-parameter -Wno-strict-overflow -Wno-strict-aliasing -Wno-stringop-overflow -Wsuggest-override -Wno-psabi -Wno-error=old-style-cast -fdiagnostics-color=always -faligned-new -Wno-maybe-uninitialized -fno-math-errno -fno-trapping-math -Werror=format -Wno-stringop-overflow, LAPACK_INFO=mkl, PERF_WITH_AVX=1, PERF_WITH_AVX2=1, TORCH_VERSION=2.7.1, USE_CUDA=ON, USE_CUDNN=ON, USE_CUSPARSELT=1, USE_GFLAGS=OFF, USE_GLOG=OFF, USE_GLOO=ON, USE_MKL=ON, USE_MKLDNN=ON, USE_MPI=OFF, USE_NCCL=1, USE_NNPACK=ON, USE_OPENMP=ON, USE_ROCM=OFF, USE_ROCM_KERNEL_ASSERT=OFF, \n"
+ }
+}
\ No newline at end of file
diff --git a/peft/method_comparison/MetaMathQA/results/oft--llama-3.2-3B-rank32.json b/peft/method_comparison/MetaMathQA/results/oft--llama-3.2-3B-rank32.json
new file mode 100644
index 0000000000000000000000000000000000000000..b57f300fa300c0d85a3554971d8da372e1baa254
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/results/oft--llama-3.2-3B-rank32.json
@@ -0,0 +1,358 @@
+{
+ "run_info": {
+ "created_at": "2025-07-31T14:11:12+00:00",
+ "total_time": 2493.9155955019996,
+ "experiment_name": "oft/llama-3.2-3B-rank32",
+ "peft_branch": "main",
+ "train_config": {
+ "model_id": "meta-llama/Llama-3.2-3B",
+ "dtype": "bfloat16",
+ "max_seq_length": 768,
+ "batch_size": 4,
+ "batch_size_eval": 50,
+ "max_steps": 5000,
+ "eval_steps": 250,
+ "compile": false,
+ "query_template": "Question: {query} Think step by step.\nAnswer:",
+ "seed": 0,
+ "grad_norm_clip": 1.0,
+ "optimizer_type": "AdamW",
+ "optimizer_kwargs": {
+ "lr": 0.0001,
+ "weight_decay": 0.1
+ },
+ "lr_scheduler": "cosine",
+ "use_amp": false,
+ "autocast_adapter_dtype": true,
+ "generation_kwargs": {
+ "max_length": 800,
+ "max_new_tokens": 300
+ },
+ "attn_implementation": null
+ },
+ "peft_config": {
+ "task_type": null,
+ "peft_type": "OFT",
+ "auto_mapping": null,
+ "base_model_name_or_path": "meta-llama/Llama-3.2-3B",
+ "revision": null,
+ "inference_mode": false,
+ "r": 32,
+ "oft_block_size": 0,
+ "module_dropout": 0.0,
+ "target_modules": [
+ "v_proj",
+ "q_proj"
+ ],
+ "fan_in_fan_out": false,
+ "bias": "none",
+ "exclude_modules": null,
+ "init_weights": true,
+ "layers_to_transform": null,
+ "layers_pattern": null,
+ "modules_to_save": null,
+ "coft": false,
+ "eps": 6e-05,
+ "block_share": false,
+ "use_cayley_neumann": true,
+ "num_cayley_neumann_terms": 5
+ },
+ "error_msg": ""
+ },
+ "train_info": {
+ "accelerator_memory_reserved_avg": 12057354384,
+ "accelerator_memory_max": 22294822912,
+ "accelerator_memory_reserved_99th": 17939310837,
+ "train_time": 2214.446992367006,
+ "file_size": 32693568,
+ "num_trainable_params": 8171520,
+ "num_total_params": 3220921344,
+ "status": "success",
+ "metrics": [
+ {
+ "step": 250,
+ "valid accuracy": 0.36,
+ "train loss": 0.9631057088375091,
+ "train samples": 1000,
+ "train time": 43.418166981995455,
+ "eval time": 16.96007740999994,
+ "tokens / sec": 4876.276791873667,
+ "mem allocated avg": 6903823460.352,
+ "mem reserved avg": 12108561383.424,
+ "elapsed time": 113.91408998500083
+ },
+ {
+ "step": 500,
+ "valid accuracy": 0.36,
+ "train loss": 0.7144306401014328,
+ "train samples": 2000,
+ "train time": 42.455775934988196,
+ "eval time": 16.150497423999695,
+ "tokens / sec": 4899.097835792689,
+ "mem allocated avg": 6896105342.976,
+ "mem reserved avg": 11994249822.208,
+ "elapsed time": 220.49977440600014
+ },
+ {
+ "step": 750,
+ "valid accuracy": 0.52,
+ "train loss": 0.6711842056512832,
+ "train samples": 3000,
+ "train time": 43.15603912099323,
+ "eval time": 10.51256339000065,
+ "tokens / sec": 4968.041654585135,
+ "mem allocated avg": 6906686986.24,
+ "mem reserved avg": 12155101380.608,
+ "elapsed time": 322.5515955810006
+ },
+ {
+ "step": 1000,
+ "valid accuracy": 0.48,
+ "train loss": 0.6508683092594146,
+ "train samples": 4000,
+ "train time": 42.42713372799517,
+ "eval time": 16.934662378998837,
+ "tokens / sec": 4910.442485595753,
+ "mem allocated avg": 6897939019.776,
+ "mem reserved avg": 12025262505.984,
+ "elapsed time": 429.7382754350001
+ },
+ {
+ "step": 1250,
+ "valid accuracy": 0.4,
+ "train loss": 0.6453732433319092,
+ "train samples": 5000,
+ "train time": 42.549762738994104,
+ "eval time": 16.92903551499876,
+ "tokens / sec": 4901.03790423462,
+ "mem allocated avg": 6897900118.016,
+ "mem reserved avg": 12017234608.128,
+ "elapsed time": 537.135011331
+ },
+ {
+ "step": 1500,
+ "valid accuracy": 0.5,
+ "train loss": 0.636857116818428,
+ "train samples": 6000,
+ "train time": 42.7670685170051,
+ "eval time": 16.97714005600028,
+ "tokens / sec": 4894.677312679627,
+ "mem allocated avg": 6899436058.624,
+ "mem reserved avg": 12045822984.192,
+ "elapsed time": 644.8122739440005
+ },
+ {
+ "step": 1750,
+ "valid accuracy": 0.48,
+ "train loss": 0.6280697054862976,
+ "train samples": 7000,
+ "train time": 42.93359049599712,
+ "eval time": 11.770931148001182,
+ "tokens / sec": 4876.251848060996,
+ "mem allocated avg": 6900382935.04,
+ "mem reserved avg": 12059630632.96,
+ "elapsed time": 747.525349122001
+ },
+ {
+ "step": 2000,
+ "valid accuracy": 0.4,
+ "train loss": 0.6299525223970414,
+ "train samples": 8000,
+ "train time": 42.82682755300084,
+ "eval time": 11.5680384089992,
+ "tokens / sec": 4849.670448808364,
+ "mem allocated avg": 6896952041.472,
+ "mem reserved avg": 12003611508.736,
+ "elapsed time": 849.5279627600012
+ },
+ {
+ "step": 2250,
+ "valid accuracy": 0.42,
+ "train loss": 0.6208749743700027,
+ "train samples": 9000,
+ "train time": 43.43083962600576,
+ "eval time": 16.986704689999897,
+ "tokens / sec": 4949.20203825146,
+ "mem allocated avg": 6908628027.392,
+ "mem reserved avg": 12188169273.344,
+ "elapsed time": 958.0240945160003
+ },
+ {
+ "step": 2500,
+ "valid accuracy": 0.42,
+ "train loss": 0.6179436918497085,
+ "train samples": 10000,
+ "train time": 42.63891591101674,
+ "eval time": 17.232789900999705,
+ "tokens / sec": 4830.493355643306,
+ "mem allocated avg": 6893492830.208,
+ "mem reserved avg": 11953867063.296,
+ "elapsed time": 1065.2266578140006
+ },
+ {
+ "step": 2750,
+ "valid accuracy": 0.42,
+ "train loss": 0.6097300077676773,
+ "train samples": 11000,
+ "train time": 43.157022238001446,
+ "eval time": 17.135427543998958,
+ "tokens / sec": 4909.537058222485,
+ "mem allocated avg": 6904392247.296,
+ "mem reserved avg": 12124977889.28,
+ "elapsed time": 1173.5244531360004
+ },
+ {
+ "step": 3000,
+ "valid accuracy": 0.42,
+ "train loss": 0.600518134355545,
+ "train samples": 12000,
+ "train time": 42.90499155000907,
+ "eval time": 17.038416949999373,
+ "tokens / sec": 4864.958422301702,
+ "mem allocated avg": 6898886381.568,
+ "mem reserved avg": 12038994657.28,
+ "elapsed time": 1281.100714346001
+ },
+ {
+ "step": 3250,
+ "valid accuracy": 0.54,
+ "train loss": 0.6095727566480637,
+ "train samples": 13000,
+ "train time": 42.991201876006016,
+ "eval time": 17.145920277998812,
+ "tokens / sec": 4905.678157318666,
+ "mem allocated avg": 6900920473.6,
+ "mem reserved avg": 12070426771.456,
+ "elapsed time": 1389.080374264
+ },
+ {
+ "step": 3500,
+ "valid accuracy": 0.54,
+ "train loss": 0.59402192902565,
+ "train samples": 14000,
+ "train time": 43.139979139998104,
+ "eval time": 10.18719298600081,
+ "tokens / sec": 4862.079309758545,
+ "mem allocated avg": 6899826102.272,
+ "mem reserved avg": 12054404530.176,
+ "elapsed time": 1490.7450829120007
+ },
+ {
+ "step": 3750,
+ "valid accuracy": 0.58,
+ "train loss": 0.5927710949182511,
+ "train samples": 15000,
+ "train time": 43.49427866901169,
+ "eval time": 10.884315328999946,
+ "tokens / sec": 4982.333461582249,
+ "mem allocated avg": 6910839183.36,
+ "mem reserved avg": 12223619530.752,
+ "elapsed time": 1593.6702795590008
+ },
+ {
+ "step": 4000,
+ "valid accuracy": 0.52,
+ "train loss": 0.6036465883255004,
+ "train samples": 16000,
+ "train time": 42.54699739801072,
+ "eval time": 10.508950370000093,
+ "tokens / sec": 4803.464697829781,
+ "mem allocated avg": 6892073494.528,
+ "mem reserved avg": 11931788247.04,
+ "elapsed time": 1694.1543825910012
+ },
+ {
+ "step": 4250,
+ "valid accuracy": 0.5,
+ "train loss": 0.5904108211994171,
+ "train samples": 17000,
+ "train time": 42.904117188016244,
+ "eval time": 10.362485865000053,
+ "tokens / sec": 4927.009663749569,
+ "mem allocated avg": 6902539771.904,
+ "mem reserved avg": 12087044603.904,
+ "elapsed time": 1795.3652429800004
+ },
+ {
+ "step": 4500,
+ "valid accuracy": 0.56,
+ "train loss": 0.5975252593755722,
+ "train samples": 18000,
+ "train time": 42.7045542899923,
+ "eval time": 9.970661539999128,
+ "tokens / sec": 4866.413043179837,
+ "mem allocated avg": 6897064284.16,
+ "mem reserved avg": 12006883065.856,
+ "elapsed time": 1895.7771126360003
+ },
+ {
+ "step": 4750,
+ "valid accuracy": 0.54,
+ "train loss": 0.588557964682579,
+ "train samples": 19000,
+ "train time": 42.698231221012975,
+ "eval time": 10.72399718899942,
+ "tokens / sec": 4916.8078863342525,
+ "mem allocated avg": 6900484192.256,
+ "mem reserved avg": 12052575813.632,
+ "elapsed time": 1997.1282366079995
+ },
+ {
+ "step": 5000,
+ "valid accuracy": 0.56,
+ "train loss": 0.5946548076868057,
+ "train samples": 20000,
+ "train time": 42.98944765599845,
+ "eval time": 10.321189939999385,
+ "tokens / sec": 4844.909887343902,
+ "mem allocated avg": 6896923324.416,
+ "mem reserved avg": 12004861411.328,
+ "elapsed time": 2098.129397994
+ },
+ {
+ "step": 5000,
+ "test accuracy": 0.5056861258529188,
+ "train loss": 0.5946548076868057,
+ "train samples": 20000,
+ "train total tokens": 4198051
+ }
+ ]
+ },
+ "meta_info": {
+ "model_info": {
+ "sha": "13afe5124825b4f3751f836b40dafda64c1ed062",
+ "created_at": "2024-09-18T15:23:48+00:00"
+ },
+ "dataset_info": {
+ "metamath": {
+ "sha": "aa4f34d3d2d3231299b5b03d9b3e5a20da45aa18",
+ "created_at": "2023-09-21T17:22:46+00:00"
+ },
+ "gsm8k": {
+ "sha": "e53f048856ff4f594e959d75785d2c2d37b678ee",
+ "created_at": "2022-04-12T10:22:10+00:00"
+ }
+ },
+ "package_info": {
+ "transformers-version": "4.52.4",
+ "transformers-commit-hash": null,
+ "peft-version": "0.16.1.dev0",
+ "peft-commit-hash": "25e5c6b25c4589eb2683484ede1ba3d985d8a760",
+ "datasets-version": "3.6.0",
+ "datasets-commit-hash": null,
+ "bitsandbytes-version": "0.46.0",
+ "bitsandbytes-commit-hash": null,
+ "torch-version": "2.7.1+cu126",
+ "torch-commit-hash": null
+ },
+ "system_info": {
+ "system": "Linux",
+ "release": "6.8.0-1031-aws",
+ "version": "#33-Ubuntu SMP Fri Jun 20 18:11:07 UTC 2025",
+ "machine": "x86_64",
+ "processor": "x86_64",
+ "accelerator": "NVIDIA L40S"
+ },
+ "pytorch_info": "PyTorch built with:\n - GCC 11.2\n - C++ Version: 201703\n - Intel(R) oneAPI Math Kernel Library Version 2024.2-Product Build 20240605 for Intel(R) 64 architecture applications\n - Intel(R) MKL-DNN v3.7.1 (Git Hash 8d263e693366ef8db40acc569cc7d8edf644556d)\n - OpenMP 201511 (a.k.a. OpenMP 4.5)\n - LAPACK is enabled (usually provided by MKL)\n - NNPACK is enabled\n - CPU capability usage: AVX2\n - CUDA Runtime 12.6\n - NVCC architecture flags: -gencode;arch=compute_50,code=sm_50;-gencode;arch=compute_60,code=sm_60;-gencode;arch=compute_70,code=sm_70;-gencode;arch=compute_75,code=sm_75;-gencode;arch=compute_80,code=sm_80;-gencode;arch=compute_86,code=sm_86;-gencode;arch=compute_90,code=sm_90\n - CuDNN 90.7.1 (built against CUDA 12.8)\n - Built with CuDNN 90.5.1\n - Magma 2.6.1\n - Build settings: BLAS_INFO=mkl, BUILD_TYPE=Release, COMMIT_SHA=e2d141dbde55c2a4370fac5165b0561b6af4798b, CUDA_VERSION=12.6, CUDNN_VERSION=9.5.1, CXX_COMPILER=/opt/rh/gcc-toolset-11/root/usr/bin/c++, CXX_FLAGS= -D_GLIBCXX_USE_CXX11_ABI=1 -fvisibility-inlines-hidden -DUSE_PTHREADPOOL -DNDEBUG -DUSE_KINETO -DLIBKINETO_NOROCTRACER -DLIBKINETO_NOXPUPTI=ON -DUSE_FBGEMM -DUSE_PYTORCH_QNNPACK -DUSE_XNNPACK -DSYMBOLICATE_MOBILE_DEBUG_HANDLE -O2 -fPIC -Wall -Wextra -Werror=return-type -Werror=non-virtual-dtor -Werror=range-loop-construct -Werror=bool-operation -Wnarrowing -Wno-missing-field-initializers -Wno-unknown-pragmas -Wno-unused-parameter -Wno-strict-overflow -Wno-strict-aliasing -Wno-stringop-overflow -Wsuggest-override -Wno-psabi -Wno-error=old-style-cast -fdiagnostics-color=always -faligned-new -Wno-maybe-uninitialized -fno-math-errno -fno-trapping-math -Werror=format -Wno-stringop-overflow, LAPACK_INFO=mkl, PERF_WITH_AVX=1, PERF_WITH_AVX2=1, TORCH_VERSION=2.7.1, USE_CUDA=ON, USE_CUDNN=ON, USE_CUSPARSELT=1, USE_GFLAGS=OFF, USE_GLOG=OFF, USE_GLOO=ON, USE_MKL=ON, USE_MKLDNN=ON, USE_MPI=OFF, USE_NCCL=1, USE_NNPACK=ON, USE_OPENMP=ON, USE_ROCM=OFF, USE_ROCM_KERNEL_ASSERT=OFF, \n"
+ }
+}
\ No newline at end of file
diff --git a/peft/method_comparison/MetaMathQA/results/prefixtuning--llama-3.2-3B-lr_0.001.json b/peft/method_comparison/MetaMathQA/results/prefixtuning--llama-3.2-3B-lr_0.001.json
new file mode 100644
index 0000000000000000000000000000000000000000..9c1717d39a8e3e171f29ff94bad443c9e912c558
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/results/prefixtuning--llama-3.2-3B-lr_0.001.json
@@ -0,0 +1,345 @@
+{
+ "run_info": {
+ "created_at": "2025-06-19T20:20:55+00:00",
+ "total_time": 1959.214138561998,
+ "experiment_name": "prefixtuning/llama-3.2-3B-lr_0.001",
+ "peft_branch": "main",
+ "train_config": {
+ "model_id": "meta-llama/Llama-3.2-3B",
+ "dtype": "bfloat16",
+ "max_seq_length": 768,
+ "batch_size": 4,
+ "batch_size_eval": 50,
+ "max_steps": 5000,
+ "eval_steps": 250,
+ "compile": false,
+ "query_template": "Question: {query} Think step by step.\nAnswer:",
+ "seed": 0,
+ "grad_norm_clip": 1.0,
+ "optimizer_type": "AdamW",
+ "optimizer_kwargs": {
+ "lr": 0.001
+ },
+ "lr_scheduler": "cosine",
+ "use_amp": false,
+ "autocast_adapter_dtype": true,
+ "generation_kwargs": {
+ "max_length": 800,
+ "max_new_tokens": 300
+ },
+ "attn_implementation": null
+ },
+ "peft_config": {
+ "task_type": "CAUSAL_LM",
+ "peft_type": "PREFIX_TUNING",
+ "auto_mapping": null,
+ "base_model_name_or_path": "meta-llama/Llama-3.2-3B",
+ "revision": null,
+ "inference_mode": false,
+ "num_virtual_tokens": 200,
+ "token_dim": 1024,
+ "num_transformer_submodules": 1,
+ "num_attention_heads": 8,
+ "num_layers": 28,
+ "encoder_hidden_size": 3072,
+ "prefix_projection": false
+ },
+ "error_msg": ""
+ },
+ "train_info": {
+ "accelerator_memory_reserved_avg": 11766684083,
+ "accelerator_memory_max": 20912799744,
+ "accelerator_memory_reserved_99th": 16945051074,
+ "train_time": 1661.6597991429953,
+ "file_size": 45875328,
+ "num_trainable_params": 11468800,
+ "num_total_params": 3224218624,
+ "status": "success",
+ "metrics": [
+ {
+ "step": 250,
+ "valid accuracy": 0.0,
+ "train loss": 7.371294965744019,
+ "train samples": 1000,
+ "train time": 27.91846932898261,
+ "eval time": 15.451216622001084,
+ "tokens / sec": 7583.474491569318,
+ "mem allocated avg": 7053410574.336,
+ "mem reserved avg": 11800925962.24,
+ "elapsed time": 86.14553656399949
+ },
+ {
+ "step": 500,
+ "valid accuracy": 0.0,
+ "train loss": 3.853111123085022,
+ "train samples": 2000,
+ "train time": 27.30431010902612,
+ "eval time": 15.427179872000124,
+ "tokens / sec": 7617.661796598262,
+ "mem allocated avg": 7047124914.176,
+ "mem reserved avg": 11721854943.232,
+ "elapsed time": 164.76258564100135
+ },
+ {
+ "step": 750,
+ "valid accuracy": 0.0,
+ "train loss": 1.7293416724205017,
+ "train samples": 3000,
+ "train time": 28.03611285903753,
+ "eval time": 15.425274275999982,
+ "tokens / sec": 7647.31548478152,
+ "mem allocated avg": 7057104787.456,
+ "mem reserved avg": 11848237711.36,
+ "elapsed time": 244.72437485599949
+ },
+ {
+ "step": 1000,
+ "valid accuracy": 0.0,
+ "train loss": 1.1541715533733368,
+ "train samples": 4000,
+ "train time": 27.01217528603229,
+ "eval time": 15.417352960001153,
+ "tokens / sec": 7712.670223479868,
+ "mem allocated avg": 7050079920.128,
+ "mem reserved avg": 11745879916.544,
+ "elapsed time": 322.8701755410002
+ },
+ {
+ "step": 1250,
+ "valid accuracy": 0.08,
+ "train loss": 1.01127068066597,
+ "train samples": 5000,
+ "train time": 27.13179545197636,
+ "eval time": 15.418993674997182,
+ "tokens / sec": 7686.111314273877,
+ "mem allocated avg": 7048705087.488,
+ "mem reserved avg": 11725462044.672,
+ "elapsed time": 401.46412933300235
+ },
+ {
+ "step": 1500,
+ "valid accuracy": 0.08,
+ "train loss": 0.9543052833080292,
+ "train samples": 6000,
+ "train time": 27.5597544680204,
+ "eval time": 15.42255902100078,
+ "tokens / sec": 7595.532109798078,
+ "mem allocated avg": 7050476988.416,
+ "mem reserved avg": 11746567782.4,
+ "elapsed time": 480.1674746890021
+ },
+ {
+ "step": 1750,
+ "valid accuracy": 0.18,
+ "train loss": 0.9019801757335663,
+ "train samples": 7000,
+ "train time": 27.391848403010954,
+ "eval time": 15.41637391599943,
+ "tokens / sec": 7642.967240465137,
+ "mem allocated avg": 7051827261.44,
+ "mem reserved avg": 11769468682.24,
+ "elapsed time": 559.677030461
+ },
+ {
+ "step": 2000,
+ "valid accuracy": 0.12,
+ "train loss": 0.8851136872768403,
+ "train samples": 8000,
+ "train time": 27.14071328902719,
+ "eval time": 15.419172215999424,
+ "tokens / sec": 7652.562325396589,
+ "mem allocated avg": 7048325701.632,
+ "mem reserved avg": 11717526421.504,
+ "elapsed time": 638.8433813260017
+ },
+ {
+ "step": 2250,
+ "valid accuracy": 0.1,
+ "train loss": 0.8607708604335785,
+ "train samples": 9000,
+ "train time": 28.18215358697489,
+ "eval time": 15.430102889000409,
+ "tokens / sec": 7627.096323090928,
+ "mem allocated avg": 7058774517.76,
+ "mem reserved avg": 11887655780.352,
+ "elapsed time": 719.1557081280007
+ },
+ {
+ "step": 2500,
+ "valid accuracy": 0.16,
+ "train loss": 0.8404088478088378,
+ "train samples": 10000,
+ "train time": 26.82789152296391,
+ "eval time": 15.41505262499777,
+ "tokens / sec": 7677.3457885685175,
+ "mem allocated avg": 7045414729.728,
+ "mem reserved avg": 11679693799.424,
+ "elapsed time": 797.9182705759995
+ },
+ {
+ "step": 2750,
+ "valid accuracy": 0.14,
+ "train loss": 0.8259119842052459,
+ "train samples": 11000,
+ "train time": 27.303442178006662,
+ "eval time": 15.412094721999892,
+ "tokens / sec": 7760.230326221408,
+ "mem allocated avg": 7055038418.944,
+ "mem reserved avg": 11819196350.464,
+ "elapsed time": 877.4897030700013
+ },
+ {
+ "step": 3000,
+ "valid accuracy": 0.22,
+ "train loss": 0.8099327564239502,
+ "train samples": 12000,
+ "train time": 27.035110770961182,
+ "eval time": 12.827202022002894,
+ "tokens / sec": 7720.737738726083,
+ "mem allocated avg": 7049757696.0,
+ "mem reserved avg": 11756390842.368,
+ "elapsed time": 953.558885925002
+ },
+ {
+ "step": 3250,
+ "valid accuracy": 0.22,
+ "train loss": 0.8175602672100067,
+ "train samples": 13000,
+ "train time": 27.43706444997588,
+ "eval time": 15.41863539300175,
+ "tokens / sec": 7686.718831911532,
+ "mem allocated avg": 7051605612.544,
+ "mem reserved avg": 11776833880.064,
+ "elapsed time": 1033.2767371779992
+ },
+ {
+ "step": 3500,
+ "valid accuracy": 0.18,
+ "train loss": 0.7965063021183014,
+ "train samples": 14000,
+ "train time": 27.750962379970588,
+ "eval time": 15.41753050600164,
+ "tokens / sec": 7558.296434122523,
+ "mem allocated avg": 7051713462.272,
+ "mem reserved avg": 11763227557.888,
+ "elapsed time": 1113.7006878970024
+ },
+ {
+ "step": 3750,
+ "valid accuracy": 0.26,
+ "train loss": 0.788856605052948,
+ "train samples": 15000,
+ "train time": 27.955327479998232,
+ "eval time": 11.66996129099789,
+ "tokens / sec": 7751.760381095479,
+ "mem allocated avg": 7061477945.344,
+ "mem reserved avg": 11919800926.208,
+ "elapsed time": 1190.2235273900005
+ },
+ {
+ "step": 4000,
+ "valid accuracy": 0.26,
+ "train loss": 0.8037499711513519,
+ "train samples": 16000,
+ "train time": 26.957003097031702,
+ "eval time": 15.42233503099851,
+ "tokens / sec": 7581.443651742726,
+ "mem allocated avg": 7042861262.848,
+ "mem reserved avg": 11658604838.912,
+ "elapsed time": 1268.9300010120023
+ },
+ {
+ "step": 4250,
+ "valid accuracy": 0.28,
+ "train loss": 0.7835113587379455,
+ "train samples": 17000,
+ "train time": 27.92120910200174,
+ "eval time": 10.70234186000016,
+ "tokens / sec": 7570.911389537389,
+ "mem allocated avg": 7053768085.504,
+ "mem reserved avg": 11783242776.576,
+ "elapsed time": 1344.1117449459998
+ },
+ {
+ "step": 4500,
+ "valid accuracy": 0.28,
+ "train loss": 0.7824292014837265,
+ "train samples": 18000,
+ "train time": 26.99022845998479,
+ "eval time": 12.42347607800184,
+ "tokens / sec": 7699.749570779183,
+ "mem allocated avg": 7048212195.328,
+ "mem reserved avg": 11725470433.28,
+ "elapsed time": 1419.3379556770014
+ },
+ {
+ "step": 4750,
+ "valid accuracy": 0.28,
+ "train loss": 0.7803363995552063,
+ "train samples": 19000,
+ "train time": 27.08754148402295,
+ "eval time": 15.42501401300251,
+ "tokens / sec": 7750.389607112494,
+ "mem allocated avg": 7051630567.424,
+ "mem reserved avg": 11771876212.736,
+ "elapsed time": 1498.5280245210015
+ },
+ {
+ "step": 5000,
+ "valid accuracy": 0.26,
+ "train loss": 0.7887116296291351,
+ "train samples": 20000,
+ "train time": 26.98893836600837,
+ "eval time": 15.411349758000142,
+ "tokens / sec": 7717.235749529201,
+ "mem allocated avg": 7048690728.96,
+ "mem reserved avg": 11715764813.824,
+ "elapsed time": 1577.725424725002
+ },
+ {
+ "step": 5000,
+ "test accuracy": 0.1470811220621683,
+ "train loss": 0.7887116296291351,
+ "train samples": 20000,
+ "train total tokens": 4198051
+ }
+ ]
+ },
+ "meta_info": {
+ "model_info": {
+ "sha": "13afe5124825b4f3751f836b40dafda64c1ed062",
+ "created_at": "2024-09-18T15:23:48+00:00"
+ },
+ "dataset_info": {
+ "metamath": {
+ "sha": "aa4f34d3d2d3231299b5b03d9b3e5a20da45aa18",
+ "created_at": "2023-09-21T17:22:46+00:00"
+ },
+ "gsm8k": {
+ "sha": "e53f048856ff4f594e959d75785d2c2d37b678ee",
+ "created_at": "2022-04-12T10:22:10+00:00"
+ }
+ },
+ "package_info": {
+ "transformers-version": "4.52.4",
+ "transformers-commit-hash": null,
+ "peft-version": "0.15.2.dev0",
+ "peft-commit-hash": "5fe7f8f8abe914d313fc3751f2ea92de7718fbaf",
+ "datasets-version": "3.6.0",
+ "datasets-commit-hash": null,
+ "bitsandbytes-version": "0.46.0",
+ "bitsandbytes-commit-hash": null,
+ "torch-version": "2.7.1+cu126",
+ "torch-commit-hash": null
+ },
+ "system_info": {
+ "system": "Linux",
+ "release": "6.8.0-1029-aws",
+ "version": "#31-Ubuntu SMP Wed Apr 23 18:42:41 UTC 2025",
+ "machine": "x86_64",
+ "processor": "x86_64",
+ "accelerator": "NVIDIA L40S"
+ },
+ "pytorch_info": "PyTorch built with:\n - GCC 11.2\n - C++ Version: 201703\n - Intel(R) oneAPI Math Kernel Library Version 2024.2-Product Build 20240605 for Intel(R) 64 architecture applications\n - Intel(R) MKL-DNN v3.7.1 (Git Hash 8d263e693366ef8db40acc569cc7d8edf644556d)\n - OpenMP 201511 (a.k.a. OpenMP 4.5)\n - LAPACK is enabled (usually provided by MKL)\n - NNPACK is enabled\n - CPU capability usage: AVX2\n - CUDA Runtime 12.6\n - NVCC architecture flags: -gencode;arch=compute_50,code=sm_50;-gencode;arch=compute_60,code=sm_60;-gencode;arch=compute_70,code=sm_70;-gencode;arch=compute_75,code=sm_75;-gencode;arch=compute_80,code=sm_80;-gencode;arch=compute_86,code=sm_86;-gencode;arch=compute_90,code=sm_90\n - CuDNN 90.7.1 (built against CUDA 12.8)\n - Built with CuDNN 90.5.1\n - Magma 2.6.1\n - Build settings: BLAS_INFO=mkl, BUILD_TYPE=Release, COMMIT_SHA=e2d141dbde55c2a4370fac5165b0561b6af4798b, CUDA_VERSION=12.6, CUDNN_VERSION=9.5.1, CXX_COMPILER=/opt/rh/gcc-toolset-11/root/usr/bin/c++, CXX_FLAGS= -D_GLIBCXX_USE_CXX11_ABI=1 -fvisibility-inlines-hidden -DUSE_PTHREADPOOL -DNDEBUG -DUSE_KINETO -DLIBKINETO_NOROCTRACER -DLIBKINETO_NOXPUPTI=ON -DUSE_FBGEMM -DUSE_PYTORCH_QNNPACK -DUSE_XNNPACK -DSYMBOLICATE_MOBILE_DEBUG_HANDLE -O2 -fPIC -Wall -Wextra -Werror=return-type -Werror=non-virtual-dtor -Werror=range-loop-construct -Werror=bool-operation -Wnarrowing -Wno-missing-field-initializers -Wno-unknown-pragmas -Wno-unused-parameter -Wno-strict-overflow -Wno-strict-aliasing -Wno-stringop-overflow -Wsuggest-override -Wno-psabi -Wno-error=old-style-cast -fdiagnostics-color=always -faligned-new -Wno-maybe-uninitialized -fno-math-errno -fno-trapping-math -Werror=format -Wno-stringop-overflow, LAPACK_INFO=mkl, PERF_WITH_AVX=1, PERF_WITH_AVX2=1, TORCH_VERSION=2.7.1, USE_CUDA=ON, USE_CUDNN=ON, USE_CUSPARSELT=1, USE_GFLAGS=OFF, USE_GLOG=OFF, USE_GLOO=ON, USE_MKL=ON, USE_MKLDNN=ON, USE_MPI=OFF, USE_NCCL=1, USE_NNPACK=ON, USE_OPENMP=ON, USE_ROCM=OFF, USE_ROCM_KERNEL_ASSERT=OFF, \n"
+ }
+}
diff --git a/peft/method_comparison/MetaMathQA/results/prompt_tuning--llama-3.2-3B-default.json b/peft/method_comparison/MetaMathQA/results/prompt_tuning--llama-3.2-3B-default.json
new file mode 100644
index 0000000000000000000000000000000000000000..013c9ebf413306dd841d2bf777f0c7084b56e13d
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/results/prompt_tuning--llama-3.2-3B-default.json
@@ -0,0 +1,348 @@
+{
+ "run_info": {
+ "created_at": "2025-06-20T08:46:44+00:00",
+ "total_time": 2700.1305744579877,
+ "experiment_name": "prompt_tuning/llama-3.2-3B-default",
+ "peft_branch": "main",
+ "train_config": {
+ "model_id": "meta-llama/Llama-3.2-3B",
+ "dtype": "bfloat16",
+ "max_seq_length": 768,
+ "batch_size": 4,
+ "batch_size_eval": 50,
+ "max_steps": 5000,
+ "eval_steps": 250,
+ "compile": false,
+ "query_template": "Question: {query} Think step by step.\nAnswer:",
+ "seed": 0,
+ "grad_norm_clip": 1.0,
+ "optimizer_type": "AdamW",
+ "optimizer_kwargs": {
+ "lr": 0.0001,
+ "weight_decay": 0.1
+ },
+ "lr_scheduler": "cosine",
+ "use_amp": false,
+ "autocast_adapter_dtype": true,
+ "generation_kwargs": {
+ "max_length": 800,
+ "max_new_tokens": 300
+ },
+ "attn_implementation": null
+ },
+ "peft_config": {
+ "task_type": "CAUSAL_LM",
+ "peft_type": "PROMPT_TUNING",
+ "auto_mapping": null,
+ "base_model_name_or_path": "meta-llama/Llama-3.2-3B",
+ "revision": null,
+ "inference_mode": false,
+ "num_virtual_tokens": 200,
+ "token_dim": 3072,
+ "num_transformer_submodules": 1,
+ "num_attention_heads": 24,
+ "num_layers": 28,
+ "prompt_tuning_init": "RANDOM",
+ "prompt_tuning_init_text": null,
+ "tokenizer_name_or_path": null,
+ "tokenizer_kwargs": null
+ },
+ "error_msg": ""
+ },
+ "train_info": {
+ "accelerator_memory_reserved_avg": 15297773830,
+ "accelerator_memory_max": 24379392000,
+ "accelerator_memory_reserved_99th": 20669781770,
+ "train_time": 2379.557773831024,
+ "file_size": 2457728,
+ "num_trainable_params": 614400,
+ "num_total_params": 3213364224,
+ "status": "success",
+ "metrics": [
+ {
+ "step": 250,
+ "valid accuracy": 0.0,
+ "train loss": 3.462425223350525,
+ "train samples": 1000,
+ "train time": 46.206722402057494,
+ "eval time": 15.901069569998072,
+ "tokens / sec": 4581.9956273412845,
+ "mem allocated avg": 7082871494.656,
+ "mem reserved avg": 15331489742.848,
+ "elapsed time": 119.40567356300016
+ },
+ {
+ "step": 500,
+ "valid accuracy": 0.0,
+ "train loss": 2.259350722312927,
+ "train samples": 2000,
+ "train time": 45.66361523300293,
+ "eval time": 15.856271529002697,
+ "tokens / sec": 4554.939396249854,
+ "mem allocated avg": 7075523266.56,
+ "mem reserved avg": 15240674672.64,
+ "elapsed time": 232.12755202699918
+ },
+ {
+ "step": 750,
+ "valid accuracy": 0.0,
+ "train loss": 1.758247773170471,
+ "train samples": 3000,
+ "train time": 46.58154148896574,
+ "eval time": 15.854417883005226,
+ "tokens / sec": 4602.70298377282,
+ "mem allocated avg": 7085465481.216,
+ "mem reserved avg": 15376771448.832,
+ "elapsed time": 346.0752758900053
+ },
+ {
+ "step": 1000,
+ "valid accuracy": 0.0,
+ "train loss": 1.6028480381965637,
+ "train samples": 4000,
+ "train time": 45.41573346107907,
+ "eval time": 15.861826895998092,
+ "tokens / sec": 4587.30893729906,
+ "mem allocated avg": 7077486481.408,
+ "mem reserved avg": 15288170971.136,
+ "elapsed time": 458.6240012299968
+ },
+ {
+ "step": 1250,
+ "valid accuracy": 0.0,
+ "train loss": 1.5049157681465148,
+ "train samples": 5000,
+ "train time": 46.04039786210342,
+ "eval time": 15.877354786993237,
+ "tokens / sec": 4529.456948321703,
+ "mem allocated avg": 7076584331.264,
+ "mem reserved avg": 15265983102.976,
+ "elapsed time": 571.9228152269934
+ },
+ {
+ "step": 1500,
+ "valid accuracy": 0.0,
+ "train loss": 1.4375499501228333,
+ "train samples": 6000,
+ "train time": 45.70124057796784,
+ "eval time": 15.84707298700232,
+ "tokens / sec": 4580.4227052190045,
+ "mem allocated avg": 7078481408.0,
+ "mem reserved avg": 15279463596.032,
+ "elapsed time": 684.8850296739984
+ },
+ {
+ "step": 1750,
+ "valid accuracy": 0.0,
+ "train loss": 1.3827230257987977,
+ "train samples": 7000,
+ "train time": 44.976750778907444,
+ "eval time": 15.845691901995451,
+ "tokens / sec": 4654.7382008346485,
+ "mem allocated avg": 7079360505.856,
+ "mem reserved avg": 15298052751.36,
+ "elapsed time": 796.8428356289951
+ },
+ {
+ "step": 2000,
+ "valid accuracy": 0.0,
+ "train loss": 1.3338124525547028,
+ "train samples": 8000,
+ "train time": 45.10262611102371,
+ "eval time": 15.857041016992298,
+ "tokens / sec": 4604.964675199615,
+ "mem allocated avg": 7075931449.344,
+ "mem reserved avg": 15257242173.44,
+ "elapsed time": 908.9726742479979
+ },
+ {
+ "step": 2250,
+ "valid accuracy": 0.0,
+ "train loss": 1.2829065501689911,
+ "train samples": 9000,
+ "train time": 46.84363810600189,
+ "eval time": 15.872781344005489,
+ "tokens / sec": 4588.627371631486,
+ "mem allocated avg": 7087554078.72,
+ "mem reserved avg": 15416986435.584,
+ "elapsed time": 1023.331907868007
+ },
+ {
+ "step": 2500,
+ "valid accuracy": 0.0,
+ "train loss": 1.2462495183944702,
+ "train samples": 10000,
+ "train time": 45.55510413390584,
+ "eval time": 15.84976143699896,
+ "tokens / sec": 4521.271631705095,
+ "mem allocated avg": 7072915062.784,
+ "mem reserved avg": 15202909159.424,
+ "elapsed time": 1136.1328145180014
+ },
+ {
+ "step": 2750,
+ "valid accuracy": 0.0,
+ "train loss": 1.2045790712833404,
+ "train samples": 11000,
+ "train time": 45.34144312601711,
+ "eval time": 15.8525270359969,
+ "tokens / sec": 4673.009621928461,
+ "mem allocated avg": 7083153442.816,
+ "mem reserved avg": 15344005545.984,
+ "elapsed time": 1248.7101804669946
+ },
+ {
+ "step": 3000,
+ "valid accuracy": 0.0,
+ "train loss": 1.1678078708648683,
+ "train samples": 12000,
+ "train time": 45.599694666831056,
+ "eval time": 15.870247816987103,
+ "tokens / sec": 4577.464860786221,
+ "mem allocated avg": 7077996111.872,
+ "mem reserved avg": 15283892781.056,
+ "elapsed time": 1361.5449211609957
+ },
+ {
+ "step": 3250,
+ "valid accuracy": 0.04,
+ "train loss": 1.1313301923274994,
+ "train samples": 13000,
+ "train time": 45.95094640579191,
+ "eval time": 15.868188906999421,
+ "tokens / sec": 4589.698722144641,
+ "mem allocated avg": 7079686449.152,
+ "mem reserved avg": 15301248811.008,
+ "elapsed time": 1474.734694629995
+ },
+ {
+ "step": 3500,
+ "valid accuracy": 0.06,
+ "train loss": 1.1092858843803406,
+ "train samples": 14000,
+ "train time": 45.96525488591578,
+ "eval time": 15.86030059499899,
+ "tokens / sec": 4563.229346178814,
+ "mem allocated avg": 7078805225.472,
+ "mem reserved avg": 15302347718.656,
+ "elapsed time": 1588.1363447299955
+ },
+ {
+ "step": 3750,
+ "valid accuracy": 0.06,
+ "train loss": 1.079538120508194,
+ "train samples": 15000,
+ "train time": 46.46510764303093,
+ "eval time": 15.86466599200503,
+ "tokens / sec": 4663.779145091515,
+ "mem allocated avg": 7089610215.424,
+ "mem reserved avg": 15446287843.328,
+ "elapsed time": 1702.2553167559963
+ },
+ {
+ "step": 4000,
+ "valid accuracy": 0.04,
+ "train loss": 1.0899075508117675,
+ "train samples": 16000,
+ "train time": 45.08557640206709,
+ "eval time": 15.860410296008922,
+ "tokens / sec": 4533.001822521445,
+ "mem allocated avg": 7071494891.52,
+ "mem reserved avg": 15189319614.464,
+ "elapsed time": 1814.3939928110049
+ },
+ {
+ "step": 4250,
+ "valid accuracy": 0.04,
+ "train loss": 1.0607522547245025,
+ "train samples": 17000,
+ "train time": 46.2303190480452,
+ "eval time": 15.875090683999588,
+ "tokens / sec": 4572.518735601033,
+ "mem allocated avg": 7082239875.072,
+ "mem reserved avg": 15329283538.944,
+ "elapsed time": 1928.1608909490024
+ },
+ {
+ "step": 4500,
+ "valid accuracy": 0.04,
+ "train loss": 1.068591582775116,
+ "train samples": 18000,
+ "train time": 45.96484722109744,
+ "eval time": 15.854171614992083,
+ "tokens / sec": 4521.237697155087,
+ "mem allocated avg": 7076175783.936,
+ "mem reserved avg": 15251420479.488,
+ "elapsed time": 2041.5032397750037
+ },
+ {
+ "step": 4750,
+ "valid accuracy": 0.06,
+ "train loss": 1.0587167317867279,
+ "train samples": 19000,
+ "train time": 45.48911916205543,
+ "eval time": 15.858397545001935,
+ "tokens / sec": 4615.147619194169,
+ "mem allocated avg": 7079419088.896,
+ "mem reserved avg": 15298539290.624,
+ "elapsed time": 2154.3035376479966
+ },
+ {
+ "step": 5000,
+ "valid accuracy": 0.02,
+ "train loss": 1.0654937489032745,
+ "train samples": 20000,
+ "train time": 45.758550852071494,
+ "eval time": 15.85034008299408,
+ "tokens / sec": 4551.7175723796145,
+ "mem allocated avg": 7075618770.944,
+ "mem reserved avg": 15251386925.056,
+ "elapsed time": 2267.4055672899995
+ },
+ {
+ "step": 5000,
+ "test accuracy": 0.050037907505686124,
+ "train loss": 1.0654937489032745,
+ "train samples": 20000,
+ "train total tokens": 4198051
+ }
+ ]
+ },
+ "meta_info": {
+ "model_info": {
+ "sha": "13afe5124825b4f3751f836b40dafda64c1ed062",
+ "created_at": "2024-09-18T15:23:48+00:00"
+ },
+ "dataset_info": {
+ "metamath": {
+ "sha": "aa4f34d3d2d3231299b5b03d9b3e5a20da45aa18",
+ "created_at": "2023-09-21T17:22:46+00:00"
+ },
+ "gsm8k": {
+ "sha": "e53f048856ff4f594e959d75785d2c2d37b678ee",
+ "created_at": "2022-04-12T10:22:10+00:00"
+ }
+ },
+ "package_info": {
+ "transformers-version": "4.52.4",
+ "transformers-commit-hash": null,
+ "peft-version": "0.15.2.dev0",
+ "peft-commit-hash": "5fe7f8f8abe914d313fc3751f2ea92de7718fbaf",
+ "datasets-version": "3.6.0",
+ "datasets-commit-hash": null,
+ "bitsandbytes-version": "0.46.0",
+ "bitsandbytes-commit-hash": null,
+ "torch-version": "2.7.1+cu126",
+ "torch-commit-hash": null
+ },
+ "system_info": {
+ "system": "Linux",
+ "release": "6.8.0-1029-aws",
+ "version": "#31-Ubuntu SMP Wed Apr 23 18:42:41 UTC 2025",
+ "machine": "x86_64",
+ "processor": "x86_64",
+ "accelerator": "NVIDIA L40S"
+ },
+ "pytorch_info": "PyTorch built with:\n - GCC 11.2\n - C++ Version: 201703\n - Intel(R) oneAPI Math Kernel Library Version 2024.2-Product Build 20240605 for Intel(R) 64 architecture applications\n - Intel(R) MKL-DNN v3.7.1 (Git Hash 8d263e693366ef8db40acc569cc7d8edf644556d)\n - OpenMP 201511 (a.k.a. OpenMP 4.5)\n - LAPACK is enabled (usually provided by MKL)\n - NNPACK is enabled\n - CPU capability usage: AVX2\n - CUDA Runtime 12.6\n - NVCC architecture flags: -gencode;arch=compute_50,code=sm_50;-gencode;arch=compute_60,code=sm_60;-gencode;arch=compute_70,code=sm_70;-gencode;arch=compute_75,code=sm_75;-gencode;arch=compute_80,code=sm_80;-gencode;arch=compute_86,code=sm_86;-gencode;arch=compute_90,code=sm_90\n - CuDNN 90.7.1 (built against CUDA 12.8)\n - Built with CuDNN 90.5.1\n - Magma 2.6.1\n - Build settings: BLAS_INFO=mkl, BUILD_TYPE=Release, COMMIT_SHA=e2d141dbde55c2a4370fac5165b0561b6af4798b, CUDA_VERSION=12.6, CUDNN_VERSION=9.5.1, CXX_COMPILER=/opt/rh/gcc-toolset-11/root/usr/bin/c++, CXX_FLAGS= -D_GLIBCXX_USE_CXX11_ABI=1 -fvisibility-inlines-hidden -DUSE_PTHREADPOOL -DNDEBUG -DUSE_KINETO -DLIBKINETO_NOROCTRACER -DLIBKINETO_NOXPUPTI=ON -DUSE_FBGEMM -DUSE_PYTORCH_QNNPACK -DUSE_XNNPACK -DSYMBOLICATE_MOBILE_DEBUG_HANDLE -O2 -fPIC -Wall -Wextra -Werror=return-type -Werror=non-virtual-dtor -Werror=range-loop-construct -Werror=bool-operation -Wnarrowing -Wno-missing-field-initializers -Wno-unknown-pragmas -Wno-unused-parameter -Wno-strict-overflow -Wno-strict-aliasing -Wno-stringop-overflow -Wsuggest-override -Wno-psabi -Wno-error=old-style-cast -fdiagnostics-color=always -faligned-new -Wno-maybe-uninitialized -fno-math-errno -fno-trapping-math -Werror=format -Wno-stringop-overflow, LAPACK_INFO=mkl, PERF_WITH_AVX=1, PERF_WITH_AVX2=1, TORCH_VERSION=2.7.1, USE_CUDA=ON, USE_CUDNN=ON, USE_CUSPARSELT=1, USE_GFLAGS=OFF, USE_GLOG=OFF, USE_GLOO=ON, USE_MKL=ON, USE_MKLDNN=ON, USE_MPI=OFF, USE_NCCL=1, USE_NNPACK=ON, USE_OPENMP=ON, USE_ROCM=OFF, USE_ROCM_KERNEL_ASSERT=OFF, \n"
+ }
+}
diff --git a/peft/method_comparison/MetaMathQA/results/prompt_tuning--llama-3.2-3B-lr_0.001.json b/peft/method_comparison/MetaMathQA/results/prompt_tuning--llama-3.2-3B-lr_0.001.json
new file mode 100644
index 0000000000000000000000000000000000000000..2ce456649c41cd57278667f453ef1b9e9e8406f5
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/results/prompt_tuning--llama-3.2-3B-lr_0.001.json
@@ -0,0 +1,347 @@
+{
+ "run_info": {
+ "created_at": "2025-06-20T08:01:25+00:00",
+ "total_time": 2714.5956150429993,
+ "experiment_name": "prompt_tuning/llama-3.2-3B-lr_0.001",
+ "peft_branch": "main",
+ "train_config": {
+ "model_id": "meta-llama/Llama-3.2-3B",
+ "dtype": "bfloat16",
+ "max_seq_length": 768,
+ "batch_size": 4,
+ "batch_size_eval": 50,
+ "max_steps": 5000,
+ "eval_steps": 250,
+ "compile": false,
+ "query_template": "Question: {query} Think step by step.\nAnswer:",
+ "seed": 0,
+ "grad_norm_clip": 1.0,
+ "optimizer_type": "AdamW",
+ "optimizer_kwargs": {
+ "lr": 0.001
+ },
+ "lr_scheduler": "cosine",
+ "use_amp": false,
+ "autocast_adapter_dtype": true,
+ "generation_kwargs": {
+ "max_length": 800,
+ "max_new_tokens": 300
+ },
+ "attn_implementation": null
+ },
+ "peft_config": {
+ "task_type": "CAUSAL_LM",
+ "peft_type": "PROMPT_TUNING",
+ "auto_mapping": null,
+ "base_model_name_or_path": "meta-llama/Llama-3.2-3B",
+ "revision": null,
+ "inference_mode": false,
+ "num_virtual_tokens": 200,
+ "token_dim": 3072,
+ "num_transformer_submodules": 1,
+ "num_attention_heads": 24,
+ "num_layers": 28,
+ "prompt_tuning_init": "RANDOM",
+ "prompt_tuning_init_text": null,
+ "tokenizer_name_or_path": null,
+ "tokenizer_kwargs": null
+ },
+ "error_msg": ""
+ },
+ "train_info": {
+ "accelerator_memory_reserved_avg": 15297364466,
+ "accelerator_memory_max": 24408752128,
+ "accelerator_memory_reserved_99th": 20650676715,
+ "train_time": 2394.4007484640024,
+ "file_size": 2457728,
+ "num_trainable_params": 614400,
+ "num_total_params": 3213364224,
+ "status": "success",
+ "metrics": [
+ {
+ "step": 250,
+ "valid accuracy": 0.0,
+ "train loss": 2.454602773666382,
+ "train samples": 1000,
+ "train time": 46.58359175696387,
+ "eval time": 15.906975480989786,
+ "tokens / sec": 4544.926486231061,
+ "mem allocated avg": 7082736850.944,
+ "mem reserved avg": 15330147565.568,
+ "elapsed time": 120.51601758999459
+ },
+ {
+ "step": 500,
+ "valid accuracy": 0.02,
+ "train loss": 1.4034885478019714,
+ "train samples": 2000,
+ "train time": 45.99672341402038,
+ "eval time": 15.859127072995761,
+ "tokens / sec": 4521.952534049426,
+ "mem allocated avg": 7075398952.96,
+ "mem reserved avg": 15237637996.544,
+ "elapsed time": 234.56530582100095
+ },
+ {
+ "step": 750,
+ "valid accuracy": 0.1,
+ "train loss": 1.051814435005188,
+ "train samples": 3000,
+ "train time": 45.34941398198134,
+ "eval time": 15.839738530004979,
+ "tokens / sec": 4727.756792738001,
+ "mem allocated avg": 7085216630.784,
+ "mem reserved avg": 15378130403.328,
+ "elapsed time": 347.9996997119888
+ },
+ {
+ "step": 1000,
+ "valid accuracy": 0.2,
+ "train loss": 0.9425526282787323,
+ "train samples": 4000,
+ "train time": 44.85872337181354,
+ "eval time": 15.849193180998554,
+ "tokens / sec": 4644.269482954245,
+ "mem allocated avg": 7077280739.328,
+ "mem reserved avg": 15280109518.848,
+ "elapsed time": 460.8599872249906
+ },
+ {
+ "step": 1250,
+ "valid accuracy": 0.2,
+ "train loss": 0.9085307500362396,
+ "train samples": 5000,
+ "train time": 45.535731699026655,
+ "eval time": 15.864107311004773,
+ "tokens / sec": 4579.656287909338,
+ "mem allocated avg": 7076838449.152,
+ "mem reserved avg": 15263508463.616,
+ "elapsed time": 574.5614464429964
+ },
+ {
+ "step": 1500,
+ "valid accuracy": 0.18,
+ "train loss": 0.8753413548469543,
+ "train samples": 6000,
+ "train time": 45.47140344994841,
+ "eval time": 15.851111587006017,
+ "tokens / sec": 4603.5746451155,
+ "mem allocated avg": 7078501443.584,
+ "mem reserved avg": 15280914825.216,
+ "elapsed time": 688.3081236659928
+ },
+ {
+ "step": 1750,
+ "valid accuracy": 0.18,
+ "train loss": 0.8501973593235016,
+ "train samples": 7000,
+ "train time": 45.876367467062664,
+ "eval time": 15.86328411300201,
+ "tokens / sec": 4563.460700115549,
+ "mem allocated avg": 7079126001.664,
+ "mem reserved avg": 15302154780.672,
+ "elapsed time": 802.3839824919996
+ },
+ {
+ "step": 2000,
+ "valid accuracy": 0.3,
+ "train loss": 0.8353641645908356,
+ "train samples": 8000,
+ "train time": 45.395122604924836,
+ "eval time": 15.847279680005158,
+ "tokens / sec": 4575.293293237354,
+ "mem allocated avg": 7075813670.912,
+ "mem reserved avg": 15257200230.4,
+ "elapsed time": 915.8055839799927
+ },
+ {
+ "step": 2250,
+ "valid accuracy": 0.26,
+ "train loss": 0.8205823216438294,
+ "train samples": 9000,
+ "train time": 46.531550297062495,
+ "eval time": 15.857669960998464,
+ "tokens / sec": 4619.403364550472,
+ "mem allocated avg": 7087054014.464,
+ "mem reserved avg": 15417707855.872,
+ "elapsed time": 1030.8605109579948
+ },
+ {
+ "step": 2500,
+ "valid accuracy": 0.24,
+ "train loss": 0.8074139108657837,
+ "train samples": 10000,
+ "train time": 45.232053409854416,
+ "eval time": 15.864067172005889,
+ "tokens / sec": 4553.562893413265,
+ "mem allocated avg": 7073174814.72,
+ "mem reserved avg": 15210467295.232,
+ "elapsed time": 1144.3065934619954
+ },
+ {
+ "step": 2750,
+ "valid accuracy": 0.22,
+ "train loss": 0.800323983669281,
+ "train samples": 11000,
+ "train time": 46.27672885800712,
+ "eval time": 15.85089660200174,
+ "tokens / sec": 4578.564760921707,
+ "mem allocated avg": 7083499849.728,
+ "mem reserved avg": 15345020567.552,
+ "elapsed time": 1258.9190711479896
+ },
+ {
+ "step": 3000,
+ "valid accuracy": 0.28,
+ "train loss": 0.7878623747825623,
+ "train samples": 12000,
+ "train time": 45.57083585388318,
+ "eval time": 15.872650785997394,
+ "tokens / sec": 4580.3636490071885,
+ "mem allocated avg": 7078042595.328,
+ "mem reserved avg": 15285402730.496,
+ "elapsed time": 1372.7267461329902
+ },
+ {
+ "step": 3250,
+ "valid accuracy": 0.3,
+ "train loss": 0.7943042907714843,
+ "train samples": 13000,
+ "train time": 45.666222987070796,
+ "eval time": 15.852009978989372,
+ "tokens / sec": 4618.314942746877,
+ "mem allocated avg": 7079504875.52,
+ "mem reserved avg": 15299428483.072,
+ "elapsed time": 1486.5100108069892
+ },
+ {
+ "step": 3500,
+ "valid accuracy": 0.28,
+ "train loss": 0.780832305431366,
+ "train samples": 14000,
+ "train time": 45.84015418085619,
+ "eval time": 15.86955204399419,
+ "tokens / sec": 4575.6826901685245,
+ "mem allocated avg": 7078824071.168,
+ "mem reserved avg": 15300871323.648,
+ "elapsed time": 1600.7413567879994
+ },
+ {
+ "step": 3750,
+ "valid accuracy": 0.32,
+ "train loss": 0.7758122501373291,
+ "train samples": 15000,
+ "train time": 46.99727132692351,
+ "eval time": 15.8490629579901,
+ "tokens / sec": 4610.969826153641,
+ "mem allocated avg": 7089586788.352,
+ "mem reserved avg": 15444173914.112,
+ "elapsed time": 1716.2785189549904
+ },
+ {
+ "step": 4000,
+ "valid accuracy": 0.36,
+ "train loss": 0.7912874612808227,
+ "train samples": 16000,
+ "train time": 45.15887627698248,
+ "eval time": 15.855249352011015,
+ "tokens / sec": 4525.644056031772,
+ "mem allocated avg": 7071318118.4,
+ "mem reserved avg": 15188732411.904,
+ "elapsed time": 1829.5188424160006
+ },
+ {
+ "step": 4250,
+ "valid accuracy": 0.36,
+ "train loss": 0.7664959132671356,
+ "train samples": 17000,
+ "train time": 46.26589757904003,
+ "eval time": 15.853440922001028,
+ "tokens / sec": 4569.002463182864,
+ "mem allocated avg": 7081992153.088,
+ "mem reserved avg": 15327354159.104,
+ "elapsed time": 1944.2481972599926
+ },
+ {
+ "step": 4500,
+ "valid accuracy": 0.34,
+ "train loss": 0.7785169410705567,
+ "train samples": 18000,
+ "train time": 45.61058669183694,
+ "eval time": 15.866839458991308,
+ "tokens / sec": 4556.354457882774,
+ "mem allocated avg": 7075963725.824,
+ "mem reserved avg": 15250623561.728,
+ "elapsed time": 2058.0909812989994
+ },
+ {
+ "step": 4750,
+ "valid accuracy": 0.32,
+ "train loss": 0.7709811532497406,
+ "train samples": 19000,
+ "train time": 45.832340708962874,
+ "eval time": 15.847010081997723,
+ "tokens / sec": 4580.586475674911,
+ "mem allocated avg": 7079141249.024,
+ "mem reserved avg": 15295871713.28,
+ "elapsed time": 2172.3217773149954
+ },
+ {
+ "step": 5000,
+ "valid accuracy": 0.3,
+ "train loss": 0.7790318930149078,
+ "train samples": 20000,
+ "train time": 44.844002045996604,
+ "eval time": 15.846091532002902,
+ "tokens / sec": 4644.545323728393,
+ "mem allocated avg": 7075675734.016,
+ "mem reserved avg": 15251831521.28,
+ "elapsed time": 2285.3788618499966
+ },
+ {
+ "step": 5000,
+ "test accuracy": 0.25246398786959817,
+ "train loss": 0.7790318930149078,
+ "train samples": 20000,
+ "train total tokens": 4198051
+ }
+ ]
+ },
+ "meta_info": {
+ "model_info": {
+ "sha": "13afe5124825b4f3751f836b40dafda64c1ed062",
+ "created_at": "2024-09-18T15:23:48+00:00"
+ },
+ "dataset_info": {
+ "metamath": {
+ "sha": "aa4f34d3d2d3231299b5b03d9b3e5a20da45aa18",
+ "created_at": "2023-09-21T17:22:46+00:00"
+ },
+ "gsm8k": {
+ "sha": "e53f048856ff4f594e959d75785d2c2d37b678ee",
+ "created_at": "2022-04-12T10:22:10+00:00"
+ }
+ },
+ "package_info": {
+ "transformers-version": "4.52.4",
+ "transformers-commit-hash": null,
+ "peft-version": "0.15.2.dev0",
+ "peft-commit-hash": "5fe7f8f8abe914d313fc3751f2ea92de7718fbaf",
+ "datasets-version": "3.6.0",
+ "datasets-commit-hash": null,
+ "bitsandbytes-version": "0.46.0",
+ "bitsandbytes-commit-hash": null,
+ "torch-version": "2.7.1+cu126",
+ "torch-commit-hash": null
+ },
+ "system_info": {
+ "system": "Linux",
+ "release": "6.8.0-1029-aws",
+ "version": "#31-Ubuntu SMP Wed Apr 23 18:42:41 UTC 2025",
+ "machine": "x86_64",
+ "processor": "x86_64",
+ "accelerator": "NVIDIA L40S"
+ },
+ "pytorch_info": "PyTorch built with:\n - GCC 11.2\n - C++ Version: 201703\n - Intel(R) oneAPI Math Kernel Library Version 2024.2-Product Build 20240605 for Intel(R) 64 architecture applications\n - Intel(R) MKL-DNN v3.7.1 (Git Hash 8d263e693366ef8db40acc569cc7d8edf644556d)\n - OpenMP 201511 (a.k.a. OpenMP 4.5)\n - LAPACK is enabled (usually provided by MKL)\n - NNPACK is enabled\n - CPU capability usage: AVX2\n - CUDA Runtime 12.6\n - NVCC architecture flags: -gencode;arch=compute_50,code=sm_50;-gencode;arch=compute_60,code=sm_60;-gencode;arch=compute_70,code=sm_70;-gencode;arch=compute_75,code=sm_75;-gencode;arch=compute_80,code=sm_80;-gencode;arch=compute_86,code=sm_86;-gencode;arch=compute_90,code=sm_90\n - CuDNN 90.7.1 (built against CUDA 12.8)\n - Built with CuDNN 90.5.1\n - Magma 2.6.1\n - Build settings: BLAS_INFO=mkl, BUILD_TYPE=Release, COMMIT_SHA=e2d141dbde55c2a4370fac5165b0561b6af4798b, CUDA_VERSION=12.6, CUDNN_VERSION=9.5.1, CXX_COMPILER=/opt/rh/gcc-toolset-11/root/usr/bin/c++, CXX_FLAGS= -D_GLIBCXX_USE_CXX11_ABI=1 -fvisibility-inlines-hidden -DUSE_PTHREADPOOL -DNDEBUG -DUSE_KINETO -DLIBKINETO_NOROCTRACER -DLIBKINETO_NOXPUPTI=ON -DUSE_FBGEMM -DUSE_PYTORCH_QNNPACK -DUSE_XNNPACK -DSYMBOLICATE_MOBILE_DEBUG_HANDLE -O2 -fPIC -Wall -Wextra -Werror=return-type -Werror=non-virtual-dtor -Werror=range-loop-construct -Werror=bool-operation -Wnarrowing -Wno-missing-field-initializers -Wno-unknown-pragmas -Wno-unused-parameter -Wno-strict-overflow -Wno-strict-aliasing -Wno-stringop-overflow -Wsuggest-override -Wno-psabi -Wno-error=old-style-cast -fdiagnostics-color=always -faligned-new -Wno-maybe-uninitialized -fno-math-errno -fno-trapping-math -Werror=format -Wno-stringop-overflow, LAPACK_INFO=mkl, PERF_WITH_AVX=1, PERF_WITH_AVX2=1, TORCH_VERSION=2.7.1, USE_CUDA=ON, USE_CUDNN=ON, USE_CUSPARSELT=1, USE_GFLAGS=OFF, USE_GLOG=OFF, USE_GLOO=ON, USE_MKL=ON, USE_MKLDNN=ON, USE_MPI=OFF, USE_NCCL=1, USE_NNPACK=ON, USE_OPENMP=ON, USE_ROCM=OFF, USE_ROCM_KERNEL_ASSERT=OFF, \n"
+ }
+}
diff --git a/peft/method_comparison/MetaMathQA/results/ptuning--llama-3.2-3B-default.json b/peft/method_comparison/MetaMathQA/results/ptuning--llama-3.2-3B-default.json
new file mode 100644
index 0000000000000000000000000000000000000000..5ad6db218199541d2a426111594958057bc70943
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/results/ptuning--llama-3.2-3B-default.json
@@ -0,0 +1,348 @@
+{
+ "run_info": {
+ "created_at": "2025-06-19T19:48:53+00:00",
+ "total_time": 1918.2703526590012,
+ "experiment_name": "ptuning/llama-3.2-3B-default",
+ "peft_branch": "main",
+ "train_config": {
+ "model_id": "meta-llama/Llama-3.2-3B",
+ "dtype": "bfloat16",
+ "max_seq_length": 768,
+ "batch_size": 4,
+ "batch_size_eval": 50,
+ "max_steps": 5000,
+ "eval_steps": 250,
+ "compile": false,
+ "query_template": "Question: {query} Think step by step.\nAnswer:",
+ "seed": 0,
+ "grad_norm_clip": 1.0,
+ "optimizer_type": "AdamW",
+ "optimizer_kwargs": {
+ "lr": 0.0001,
+ "weight_decay": 0.1
+ },
+ "lr_scheduler": "cosine",
+ "use_amp": false,
+ "autocast_adapter_dtype": true,
+ "generation_kwargs": {
+ "max_length": 800,
+ "max_new_tokens": 300
+ },
+ "attn_implementation": null
+ },
+ "peft_config": {
+ "task_type": "CAUSAL_LM",
+ "peft_type": "P_TUNING",
+ "auto_mapping": null,
+ "base_model_name_or_path": "meta-llama/Llama-3.2-3B",
+ "revision": null,
+ "inference_mode": false,
+ "num_virtual_tokens": 20,
+ "token_dim": 3072,
+ "num_transformer_submodules": 1,
+ "num_attention_heads": 24,
+ "num_layers": 28,
+ "encoder_reparameterization_type": "MLP",
+ "encoder_hidden_size": 3072,
+ "encoder_num_layers": 2,
+ "encoder_dropout": 0.0
+ },
+ "error_msg": ""
+ },
+ "train_info": {
+ "accelerator_memory_reserved_avg": 11867101593,
+ "accelerator_memory_max": 20937965568,
+ "accelerator_memory_reserved_99th": 17215688540,
+ "train_time": 1707.340225783013,
+ "file_size": 245880,
+ "num_trainable_params": 28382208,
+ "num_total_params": 3241132032,
+ "status": "success",
+ "metrics": [
+ {
+ "step": 250,
+ "valid accuracy": 0.06,
+ "train loss": 0.9461167964935303,
+ "train samples": 1000,
+ "train time": 29.476242057011405,
+ "eval time": 11.075081511000462,
+ "tokens / sec": 7182.699870305862,
+ "mem allocated avg": 7263395393.536,
+ "mem reserved avg": 11910330187.776,
+ "elapsed time": 89.09710205499869
+ },
+ {
+ "step": 500,
+ "valid accuracy": 0.3,
+ "train loss": 0.7913461194038391,
+ "train samples": 2000,
+ "train time": 28.956617519994325,
+ "eval time": 11.047425028998987,
+ "tokens / sec": 7182.986751003671,
+ "mem allocated avg": 7255670497.28,
+ "mem reserved avg": 11810254094.336,
+ "elapsed time": 171.9022758780011
+ },
+ {
+ "step": 750,
+ "valid accuracy": 0.26,
+ "train loss": 0.7562740923166275,
+ "train samples": 3000,
+ "train time": 29.73533859500094,
+ "eval time": 11.056799476999004,
+ "tokens / sec": 7210.309689765724,
+ "mem allocated avg": 7266187038.72,
+ "mem reserved avg": 11954009669.632,
+ "elapsed time": 255.8485612350014
+ },
+ {
+ "step": 1000,
+ "valid accuracy": 0.3,
+ "train loss": 0.7289484927654266,
+ "train samples": 4000,
+ "train time": 29.176458327034197,
+ "eval time": 11.069810884997423,
+ "tokens / sec": 7140.551387861937,
+ "mem allocated avg": 7258589235.2,
+ "mem reserved avg": 11838347542.528,
+ "elapsed time": 338.5030210529985
+ },
+ {
+ "step": 1250,
+ "valid accuracy": 0.4,
+ "train loss": 0.7231850942373276,
+ "train samples": 5000,
+ "train time": 29.15449026899296,
+ "eval time": 11.055301014999714,
+ "tokens / sec": 7152.860436794844,
+ "mem allocated avg": 7257714087.936,
+ "mem reserved avg": 11824925769.728,
+ "elapsed time": 421.85765765199903
+ },
+ {
+ "step": 1500,
+ "valid accuracy": 0.38,
+ "train loss": 0.711922277212143,
+ "train samples": 6000,
+ "train time": 29.099172437985544,
+ "eval time": 11.07098460600173,
+ "tokens / sec": 7193.709733364892,
+ "mem allocated avg": 7259322730.496,
+ "mem reserved avg": 11860233420.8,
+ "elapsed time": 504.97678817400083
+ },
+ {
+ "step": 1750,
+ "valid accuracy": 0.44,
+ "train loss": 0.7051182547807694,
+ "train samples": 7000,
+ "train time": 29.301267419017677,
+ "eval time": 11.044947161997698,
+ "tokens / sec": 7144.912778213831,
+ "mem allocated avg": 7260392302.592,
+ "mem reserved avg": 11872371736.576,
+ "elapsed time": 588.3443257949984
+ },
+ {
+ "step": 2000,
+ "valid accuracy": 0.38,
+ "train loss": 0.7055468891859055,
+ "train samples": 8000,
+ "train time": 29.128185330951965,
+ "eval time": 11.045154800998716,
+ "tokens / sec": 7130.413296955362,
+ "mem allocated avg": 7257253203.968,
+ "mem reserved avg": 11821100564.48,
+ "elapsed time": 671.2971968860002
+ },
+ {
+ "step": 2250,
+ "valid accuracy": 0.3,
+ "train loss": 0.699348534822464,
+ "train samples": 9000,
+ "train time": 29.44214156106318,
+ "eval time": 11.039785496999684,
+ "tokens / sec": 7300.691750095574,
+ "mem allocated avg": 7268387997.696,
+ "mem reserved avg": 11993788448.768,
+ "elapsed time": 755.1838785660002
+ },
+ {
+ "step": 2500,
+ "valid accuracy": 0.4,
+ "train loss": 0.6970288401842117,
+ "train samples": 10000,
+ "train time": 28.56064905500898,
+ "eval time": 11.062792377000733,
+ "tokens / sec": 7211.565801718971,
+ "mem allocated avg": 7253500915.712,
+ "mem reserved avg": 11774535401.472,
+ "elapsed time": 837.4507786270005
+ },
+ {
+ "step": 2750,
+ "valid accuracy": 0.38,
+ "train loss": 0.6885807738304138,
+ "train samples": 11000,
+ "train time": 29.626391561985656,
+ "eval time": 11.040969151999889,
+ "tokens / sec": 7151.765329121947,
+ "mem allocated avg": 7264164755.456,
+ "mem reserved avg": 11929330384.896,
+ "elapsed time": 921.4017121549987
+ },
+ {
+ "step": 3000,
+ "valid accuracy": 0.32,
+ "train loss": 0.6827223267555237,
+ "train samples": 12000,
+ "train time": 29.296160228008375,
+ "eval time": 11.056816091997462,
+ "tokens / sec": 7124.85862909926,
+ "mem allocated avg": 7259324233.728,
+ "mem reserved avg": 11842046918.656,
+ "elapsed time": 1004.5840267519998
+ },
+ {
+ "step": 3250,
+ "valid accuracy": 0.5,
+ "train loss": 0.6894591153860092,
+ "train samples": 13000,
+ "train time": 29.611147850035195,
+ "eval time": 11.049655115999485,
+ "tokens / sec": 7122.351388338677,
+ "mem allocated avg": 7259635709.952,
+ "mem reserved avg": 11876809310.208,
+ "elapsed time": 1088.4846693049985
+ },
+ {
+ "step": 3500,
+ "valid accuracy": 0.42,
+ "train loss": 0.6757243422269821,
+ "train samples": 14000,
+ "train time": 28.982272775025194,
+ "eval time": 8.037888349997957,
+ "tokens / sec": 7237.182591861713,
+ "mem allocated avg": 7260029884.416,
+ "mem reserved avg": 11864100569.088,
+ "elapsed time": 1168.5907526180017
+ },
+ {
+ "step": 3750,
+ "valid accuracy": 0.44,
+ "train loss": 0.6726652181148529,
+ "train samples": 15000,
+ "train time": 29.461453213014465,
+ "eval time": 11.036738884999068,
+ "tokens / sec": 7355.475591552708,
+ "mem allocated avg": 7270358327.296,
+ "mem reserved avg": 12018115411.968,
+ "elapsed time": 1252.6760096750004
+ },
+ {
+ "step": 4000,
+ "valid accuracy": 0.44,
+ "train loss": 0.6872537672519684,
+ "train samples": 16000,
+ "train time": 28.49340438899526,
+ "eval time": 11.04012111100019,
+ "tokens / sec": 7172.642384527876,
+ "mem allocated avg": 7252451676.16,
+ "mem reserved avg": 11753454829.568,
+ "elapsed time": 1334.9961819890013
+ },
+ {
+ "step": 4250,
+ "valid accuracy": 0.46,
+ "train loss": 0.6691881531476974,
+ "train samples": 17000,
+ "train time": 29.36704957404436,
+ "eval time": 11.048986494999554,
+ "tokens / sec": 7198.169481309866,
+ "mem allocated avg": 7262467567.616,
+ "mem reserved avg": 11896405098.496,
+ "elapsed time": 1418.9507249929993
+ },
+ {
+ "step": 4500,
+ "valid accuracy": 0.5,
+ "train loss": 0.6769082483053207,
+ "train samples": 18000,
+ "train time": 29.086171291994106,
+ "eval time": 8.132250926999404,
+ "tokens / sec": 7144.907382746569,
+ "mem allocated avg": 7257195100.16,
+ "mem reserved avg": 11816553938.944,
+ "elapsed time": 1499.0322536989988
+ },
+ {
+ "step": 4750,
+ "valid accuracy": 0.46,
+ "train loss": 0.6686601461172104,
+ "train samples": 19000,
+ "train time": 29.45103387799827,
+ "eval time": 7.564945229998557,
+ "tokens / sec": 7128.408492200246,
+ "mem allocated avg": 7260019183.616,
+ "mem reserved avg": 11863848910.848,
+ "elapsed time": 1579.1494789060016
+ },
+ {
+ "step": 5000,
+ "valid accuracy": 0.48,
+ "train loss": 0.6739867876768112,
+ "train samples": 20000,
+ "train time": 29.24236888399173,
+ "eval time": 6.952750485001161,
+ "tokens / sec": 7122.541980995923,
+ "mem allocated avg": 7256318291.968,
+ "mem reserved avg": 11821469663.232,
+ "elapsed time": 1658.0220765080012
+ },
+ {
+ "step": 5000,
+ "test accuracy": 0.3707354056103108,
+ "train loss": 0.6739867876768112,
+ "train samples": 20000,
+ "train total tokens": 4198051
+ }
+ ]
+ },
+ "meta_info": {
+ "model_info": {
+ "sha": "13afe5124825b4f3751f836b40dafda64c1ed062",
+ "created_at": "2024-09-18T15:23:48+00:00"
+ },
+ "dataset_info": {
+ "metamath": {
+ "sha": "aa4f34d3d2d3231299b5b03d9b3e5a20da45aa18",
+ "created_at": "2023-09-21T17:22:46+00:00"
+ },
+ "gsm8k": {
+ "sha": "e53f048856ff4f594e959d75785d2c2d37b678ee",
+ "created_at": "2022-04-12T10:22:10+00:00"
+ }
+ },
+ "package_info": {
+ "transformers-version": "4.52.4",
+ "transformers-commit-hash": null,
+ "peft-version": "0.15.2.dev0",
+ "peft-commit-hash": "5fe7f8f8abe914d313fc3751f2ea92de7718fbaf",
+ "datasets-version": "3.6.0",
+ "datasets-commit-hash": null,
+ "bitsandbytes-version": "0.46.0",
+ "bitsandbytes-commit-hash": null,
+ "torch-version": "2.7.1+cu126",
+ "torch-commit-hash": null
+ },
+ "system_info": {
+ "system": "Linux",
+ "release": "6.8.0-1029-aws",
+ "version": "#31-Ubuntu SMP Wed Apr 23 18:42:41 UTC 2025",
+ "machine": "x86_64",
+ "processor": "x86_64",
+ "accelerator": "NVIDIA L40S"
+ },
+ "pytorch_info": "PyTorch built with:\n - GCC 11.2\n - C++ Version: 201703\n - Intel(R) oneAPI Math Kernel Library Version 2024.2-Product Build 20240605 for Intel(R) 64 architecture applications\n - Intel(R) MKL-DNN v3.7.1 (Git Hash 8d263e693366ef8db40acc569cc7d8edf644556d)\n - OpenMP 201511 (a.k.a. OpenMP 4.5)\n - LAPACK is enabled (usually provided by MKL)\n - NNPACK is enabled\n - CPU capability usage: AVX2\n - CUDA Runtime 12.6\n - NVCC architecture flags: -gencode;arch=compute_50,code=sm_50;-gencode;arch=compute_60,code=sm_60;-gencode;arch=compute_70,code=sm_70;-gencode;arch=compute_75,code=sm_75;-gencode;arch=compute_80,code=sm_80;-gencode;arch=compute_86,code=sm_86;-gencode;arch=compute_90,code=sm_90\n - CuDNN 90.7.1 (built against CUDA 12.8)\n - Built with CuDNN 90.5.1\n - Magma 2.6.1\n - Build settings: BLAS_INFO=mkl, BUILD_TYPE=Release, COMMIT_SHA=e2d141dbde55c2a4370fac5165b0561b6af4798b, CUDA_VERSION=12.6, CUDNN_VERSION=9.5.1, CXX_COMPILER=/opt/rh/gcc-toolset-11/root/usr/bin/c++, CXX_FLAGS= -D_GLIBCXX_USE_CXX11_ABI=1 -fvisibility-inlines-hidden -DUSE_PTHREADPOOL -DNDEBUG -DUSE_KINETO -DLIBKINETO_NOROCTRACER -DLIBKINETO_NOXPUPTI=ON -DUSE_FBGEMM -DUSE_PYTORCH_QNNPACK -DUSE_XNNPACK -DSYMBOLICATE_MOBILE_DEBUG_HANDLE -O2 -fPIC -Wall -Wextra -Werror=return-type -Werror=non-virtual-dtor -Werror=range-loop-construct -Werror=bool-operation -Wnarrowing -Wno-missing-field-initializers -Wno-unknown-pragmas -Wno-unused-parameter -Wno-strict-overflow -Wno-strict-aliasing -Wno-stringop-overflow -Wsuggest-override -Wno-psabi -Wno-error=old-style-cast -fdiagnostics-color=always -faligned-new -Wno-maybe-uninitialized -fno-math-errno -fno-trapping-math -Werror=format -Wno-stringop-overflow, LAPACK_INFO=mkl, PERF_WITH_AVX=1, PERF_WITH_AVX2=1, TORCH_VERSION=2.7.1, USE_CUDA=ON, USE_CUDNN=ON, USE_CUSPARSELT=1, USE_GFLAGS=OFF, USE_GLOG=OFF, USE_GLOO=ON, USE_MKL=ON, USE_MKLDNN=ON, USE_MPI=OFF, USE_NCCL=1, USE_NNPACK=ON, USE_OPENMP=ON, USE_ROCM=OFF, USE_ROCM_KERNEL_ASSERT=OFF, \n"
+ }
+}
diff --git a/peft/method_comparison/MetaMathQA/results/randlora--llama-3.2-3B-default.json b/peft/method_comparison/MetaMathQA/results/randlora--llama-3.2-3B-default.json
new file mode 100644
index 0000000000000000000000000000000000000000..1025019a88057969667507acf0070f182c663d90
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/results/randlora--llama-3.2-3B-default.json
@@ -0,0 +1,356 @@
+{
+ "run_info": {
+ "created_at": "2025-06-20T07:20:24+00:00",
+ "total_time": 2457.3893872150074,
+ "experiment_name": "randlora/llama-3.2-3B-default",
+ "peft_branch": "main",
+ "train_config": {
+ "model_id": "meta-llama/Llama-3.2-3B",
+ "dtype": "bfloat16",
+ "max_seq_length": 768,
+ "batch_size": 4,
+ "batch_size_eval": 50,
+ "max_steps": 5000,
+ "eval_steps": 250,
+ "compile": false,
+ "query_template": "Question: {query} Think step by step.\nAnswer:",
+ "seed": 0,
+ "grad_norm_clip": 1.0,
+ "optimizer_type": "AdamW",
+ "optimizer_kwargs": {
+ "lr": 0.0001,
+ "weight_decay": 0.1
+ },
+ "lr_scheduler": "cosine",
+ "use_amp": false,
+ "autocast_adapter_dtype": true,
+ "generation_kwargs": {
+ "max_length": 800,
+ "max_new_tokens": 300
+ },
+ "attn_implementation": null
+ },
+ "peft_config": {
+ "task_type": null,
+ "peft_type": "RANDLORA",
+ "auto_mapping": null,
+ "base_model_name_or_path": "meta-llama/Llama-3.2-3B",
+ "revision": null,
+ "inference_mode": false,
+ "r": 32,
+ "target_modules": [
+ "v_proj",
+ "q_proj"
+ ],
+ "projection_prng_key": 0,
+ "save_projection": true,
+ "sparse": false,
+ "very_sparse": false,
+ "randlora_dropout": 0.0,
+ "fan_in_fan_out": false,
+ "randlora_alpha": 640,
+ "bias": "none",
+ "modules_to_save": null,
+ "init_weights": true,
+ "layers_to_transform": null,
+ "layers_pattern": null
+ },
+ "error_msg": ""
+ },
+ "train_info": {
+ "accelerator_memory_reserved_avg": 12743670025,
+ "accelerator_memory_max": 22798139392,
+ "accelerator_memory_reserved_99th": 18436063232,
+ "train_time": 2213.072415724004,
+ "file_size": 2211281240,
+ "num_trainable_params": 9289728,
+ "num_total_params": 3222039552,
+ "status": "success",
+ "metrics": [
+ {
+ "step": 250,
+ "valid accuracy": 0.38,
+ "train loss": 0.9159075767993927,
+ "train samples": 1000,
+ "train time": 50.62416129904159,
+ "eval time": 13.32173753400275,
+ "tokens / sec": 4182.172989481373,
+ "mem allocated avg": 6983776778.24,
+ "mem reserved avg": 12791771561.984,
+ "elapsed time": 114.85611474100733
+ },
+ {
+ "step": 500,
+ "valid accuracy": 0.34,
+ "train loss": 0.7009325810670852,
+ "train samples": 2000,
+ "train time": 49.47734279213182,
+ "eval time": 13.318595108998124,
+ "tokens / sec": 4203.843380875268,
+ "mem allocated avg": 6975756310.528,
+ "mem reserved avg": 12690437177.344,
+ "elapsed time": 222.717683150011
+ },
+ {
+ "step": 750,
+ "valid accuracy": 0.38,
+ "train loss": 0.6809726172685623,
+ "train samples": 3000,
+ "train time": 50.701564677088754,
+ "eval time": 6.592474952994962,
+ "tokens / sec": 4228.6860645325305,
+ "mem allocated avg": 6985956540.416,
+ "mem reserved avg": 12840031223.808,
+ "elapsed time": 325.2694208340108
+ },
+ {
+ "step": 1000,
+ "valid accuracy": 0.32,
+ "train loss": 0.6661903276443482,
+ "train samples": 4000,
+ "train time": 49.452677299879724,
+ "eval time": 13.326040301006287,
+ "tokens / sec": 4212.835611238114,
+ "mem allocated avg": 6977344550.912,
+ "mem reserved avg": 12711484194.816,
+ "elapsed time": 432.82023598300293
+ },
+ {
+ "step": 1250,
+ "valid accuracy": 0.44,
+ "train loss": 0.665697453379631,
+ "train samples": 5000,
+ "train time": 49.56871296803001,
+ "eval time": 6.698036557994783,
+ "tokens / sec": 4207.0489127789,
+ "mem allocated avg": 6977509738.496,
+ "mem reserved avg": 12708397187.072,
+ "elapsed time": 534.2725243740133
+ },
+ {
+ "step": 1500,
+ "valid accuracy": 0.44,
+ "train loss": 0.658678293466568,
+ "train samples": 6000,
+ "train time": 49.71162069692218,
+ "eval time": 13.42559558400535,
+ "tokens / sec": 4210.906767176883,
+ "mem allocated avg": 6978434217.984,
+ "mem reserved avg": 12733680451.584,
+ "elapsed time": 642.8949007330084
+ },
+ {
+ "step": 1750,
+ "valid accuracy": 0.44,
+ "train loss": 0.6513392345905304,
+ "train samples": 7000,
+ "train time": 49.957065908936784,
+ "eval time": 8.692238900999655,
+ "tokens / sec": 4190.698476600257,
+ "mem allocated avg": 6980155148.288,
+ "mem reserved avg": 12746875731.968,
+ "elapsed time": 746.9297674360132
+ },
+ {
+ "step": 2000,
+ "valid accuracy": 0.36,
+ "train loss": 0.6511732361316681,
+ "train samples": 8000,
+ "train time": 49.75638979690848,
+ "eval time": 13.350251003997982,
+ "tokens / sec": 4174.257835983607,
+ "mem allocated avg": 6976487055.36,
+ "mem reserved avg": 12692744044.544,
+ "elapsed time": 855.1831161730079
+ },
+ {
+ "step": 2250,
+ "valid accuracy": 0.38,
+ "train loss": 0.6382467728853226,
+ "train samples": 9000,
+ "train time": 51.20128064297023,
+ "eval time": 13.277926524999202,
+ "tokens / sec": 4198.098119827237,
+ "mem allocated avg": 6988260448.256,
+ "mem reserved avg": 12868644765.696,
+ "elapsed time": 965.4057929810078
+ },
+ {
+ "step": 2500,
+ "valid accuracy": 0.42,
+ "train loss": 0.6324679807424546,
+ "train samples": 10000,
+ "train time": 47.79617171884456,
+ "eval time": 13.268003197008511,
+ "tokens / sec": 4309.278182603765,
+ "mem allocated avg": 6973276801.024,
+ "mem reserved avg": 12640810172.416,
+ "elapsed time": 1071.8066454930085
+ },
+ {
+ "step": 2750,
+ "valid accuracy": 0.42,
+ "train loss": 0.6214727911949157,
+ "train samples": 11000,
+ "train time": 49.63376283789694,
+ "eval time": 8.245235234993743,
+ "tokens / sec": 4268.888512281446,
+ "mem allocated avg": 6983764305.92,
+ "mem reserved avg": 12802987130.88,
+ "elapsed time": 1175.2128759590123
+ },
+ {
+ "step": 3000,
+ "valid accuracy": 0.46,
+ "train loss": 0.6079807863235474,
+ "train samples": 12000,
+ "train time": 49.776777152961586,
+ "eval time": 13.29031453501375,
+ "tokens / sec": 4193.340990289104,
+ "mem allocated avg": 6978680711.168,
+ "mem reserved avg": 12727900700.672,
+ "elapsed time": 1283.6379908250092
+ },
+ {
+ "step": 3250,
+ "valid accuracy": 0.5,
+ "train loss": 0.6133705099821091,
+ "train samples": 13000,
+ "train time": 50.014745363077964,
+ "eval time": 7.092912267995416,
+ "tokens / sec": 4216.77644200688,
+ "mem allocated avg": 6980747913.216,
+ "mem reserved avg": 12754257707.008,
+ "elapsed time": 1386.1836155580095
+ },
+ {
+ "step": 3500,
+ "valid accuracy": 0.52,
+ "train loss": 0.5912622555494308,
+ "train samples": 14000,
+ "train time": 49.560089439110016,
+ "eval time": 13.321606318990234,
+ "tokens / sec": 4232.236107194697,
+ "mem allocated avg": 6979099045.888,
+ "mem reserved avg": 12738579398.656,
+ "elapsed time": 1494.848658177012
+ },
+ {
+ "step": 3750,
+ "valid accuracy": 0.48,
+ "train loss": 0.5849999967813492,
+ "train samples": 15000,
+ "train time": 51.10861245104752,
+ "eval time": 13.350408840997261,
+ "tokens / sec": 4240.048586870968,
+ "mem allocated avg": 6990205292.544,
+ "mem reserved avg": 12906016014.336,
+ "elapsed time": 1605.1250539940083
+ },
+ {
+ "step": 4000,
+ "valid accuracy": 0.52,
+ "train loss": 0.5914600425958634,
+ "train samples": 16000,
+ "train time": 48.92153307204717,
+ "eval time": 13.309209176004515,
+ "tokens / sec": 4177.567364845621,
+ "mem allocated avg": 6971749750.784,
+ "mem reserved avg": 12621868695.552,
+ "elapsed time": 1712.7276146870136
+ },
+ {
+ "step": 4250,
+ "valid accuracy": 0.54,
+ "train loss": 0.575433883190155,
+ "train samples": 17000,
+ "train time": 50.056106529867975,
+ "eval time": 13.322275185011677,
+ "tokens / sec": 4223.041196259767,
+ "mem allocated avg": 6981706383.36,
+ "mem reserved avg": 12772226105.344,
+ "elapsed time": 1821.8377219670074
+ },
+ {
+ "step": 4500,
+ "valid accuracy": 0.48,
+ "train loss": 0.5807004086971282,
+ "train samples": 18000,
+ "train time": 49.559131018977496,
+ "eval time": 13.371259606996318,
+ "tokens / sec": 4193.334219690434,
+ "mem allocated avg": 6976847835.136,
+ "mem reserved avg": 12694061056.0,
+ "elapsed time": 1929.8977656790084
+ },
+ {
+ "step": 4750,
+ "valid accuracy": 0.52,
+ "train loss": 0.5704656873941422,
+ "train samples": 19000,
+ "train time": 49.80019182183605,
+ "eval time": 13.346957685993402,
+ "tokens / sec": 4215.62633234572,
+ "mem allocated avg": 6979789905.92,
+ "mem reserved avg": 12742303940.608,
+ "elapsed time": 2038.7162974260136
+ },
+ {
+ "step": 5000,
+ "valid accuracy": 0.52,
+ "train loss": 0.5784689987897873,
+ "train samples": 20000,
+ "train time": 49.38921916205436,
+ "eval time": 13.307282750000013,
+ "tokens / sec": 4217.114656471855,
+ "mem allocated avg": 6976297842.688,
+ "mem reserved avg": 12688323248.128,
+ "elapsed time": 2146.6737093550037
+ },
+ {
+ "step": 5000,
+ "test accuracy": 0.5072024260803639,
+ "train loss": 0.5784689987897873,
+ "train samples": 20000,
+ "train total tokens": 4198051
+ }
+ ]
+ },
+ "meta_info": {
+ "model_info": {
+ "sha": "13afe5124825b4f3751f836b40dafda64c1ed062",
+ "created_at": "2024-09-18T15:23:48+00:00"
+ },
+ "dataset_info": {
+ "metamath": {
+ "sha": "aa4f34d3d2d3231299b5b03d9b3e5a20da45aa18",
+ "created_at": "2023-09-21T17:22:46+00:00"
+ },
+ "gsm8k": {
+ "sha": "e53f048856ff4f594e959d75785d2c2d37b678ee",
+ "created_at": "2022-04-12T10:22:10+00:00"
+ }
+ },
+ "package_info": {
+ "transformers-version": "4.52.4",
+ "transformers-commit-hash": null,
+ "peft-version": "0.15.2.dev0",
+ "peft-commit-hash": "5fe7f8f8abe914d313fc3751f2ea92de7718fbaf",
+ "datasets-version": "3.6.0",
+ "datasets-commit-hash": null,
+ "bitsandbytes-version": "0.46.0",
+ "bitsandbytes-commit-hash": null,
+ "torch-version": "2.7.1+cu126",
+ "torch-commit-hash": null
+ },
+ "system_info": {
+ "system": "Linux",
+ "release": "6.8.0-1029-aws",
+ "version": "#31-Ubuntu SMP Wed Apr 23 18:42:41 UTC 2025",
+ "machine": "x86_64",
+ "processor": "x86_64",
+ "accelerator": "NVIDIA L40S"
+ },
+ "pytorch_info": "PyTorch built with:\n - GCC 11.2\n - C++ Version: 201703\n - Intel(R) oneAPI Math Kernel Library Version 2024.2-Product Build 20240605 for Intel(R) 64 architecture applications\n - Intel(R) MKL-DNN v3.7.1 (Git Hash 8d263e693366ef8db40acc569cc7d8edf644556d)\n - OpenMP 201511 (a.k.a. OpenMP 4.5)\n - LAPACK is enabled (usually provided by MKL)\n - NNPACK is enabled\n - CPU capability usage: AVX2\n - CUDA Runtime 12.6\n - NVCC architecture flags: -gencode;arch=compute_50,code=sm_50;-gencode;arch=compute_60,code=sm_60;-gencode;arch=compute_70,code=sm_70;-gencode;arch=compute_75,code=sm_75;-gencode;arch=compute_80,code=sm_80;-gencode;arch=compute_86,code=sm_86;-gencode;arch=compute_90,code=sm_90\n - CuDNN 90.7.1 (built against CUDA 12.8)\n - Built with CuDNN 90.5.1\n - Magma 2.6.1\n - Build settings: BLAS_INFO=mkl, BUILD_TYPE=Release, COMMIT_SHA=e2d141dbde55c2a4370fac5165b0561b6af4798b, CUDA_VERSION=12.6, CUDNN_VERSION=9.5.1, CXX_COMPILER=/opt/rh/gcc-toolset-11/root/usr/bin/c++, CXX_FLAGS= -D_GLIBCXX_USE_CXX11_ABI=1 -fvisibility-inlines-hidden -DUSE_PTHREADPOOL -DNDEBUG -DUSE_KINETO -DLIBKINETO_NOROCTRACER -DLIBKINETO_NOXPUPTI=ON -DUSE_FBGEMM -DUSE_PYTORCH_QNNPACK -DUSE_XNNPACK -DSYMBOLICATE_MOBILE_DEBUG_HANDLE -O2 -fPIC -Wall -Wextra -Werror=return-type -Werror=non-virtual-dtor -Werror=range-loop-construct -Werror=bool-operation -Wnarrowing -Wno-missing-field-initializers -Wno-unknown-pragmas -Wno-unused-parameter -Wno-strict-overflow -Wno-strict-aliasing -Wno-stringop-overflow -Wsuggest-override -Wno-psabi -Wno-error=old-style-cast -fdiagnostics-color=always -faligned-new -Wno-maybe-uninitialized -fno-math-errno -fno-trapping-math -Werror=format -Wno-stringop-overflow, LAPACK_INFO=mkl, PERF_WITH_AVX=1, PERF_WITH_AVX2=1, TORCH_VERSION=2.7.1, USE_CUDA=ON, USE_CUDNN=ON, USE_CUSPARSELT=1, USE_GFLAGS=OFF, USE_GLOG=OFF, USE_GLOO=ON, USE_MKL=ON, USE_MKLDNN=ON, USE_MPI=OFF, USE_NCCL=1, USE_NNPACK=ON, USE_OPENMP=ON, USE_ROCM=OFF, USE_ROCM_KERNEL_ASSERT=OFF, \n"
+ }
+}
diff --git a/peft/method_comparison/MetaMathQA/results/shira--llama-3.2-3B-lr_0.0003-random_seed_42.json b/peft/method_comparison/MetaMathQA/results/shira--llama-3.2-3B-lr_0.0003-random_seed_42.json
new file mode 100644
index 0000000000000000000000000000000000000000..1263cd479fe1109dc2001db4d0431c99cfc5b36c
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/results/shira--llama-3.2-3B-lr_0.0003-random_seed_42.json
@@ -0,0 +1,348 @@
+{
+ "run_info": {
+ "created_at": "2025-07-31T14:52:50+00:00",
+ "total_time": 2084.7194732099997,
+ "experiment_name": "shira/llama-3.2-3B-lr_0.0003-random_seed_42",
+ "peft_branch": "main",
+ "train_config": {
+ "model_id": "meta-llama/Llama-3.2-3B",
+ "dtype": "bfloat16",
+ "max_seq_length": 768,
+ "batch_size": 4,
+ "batch_size_eval": 50,
+ "max_steps": 5000,
+ "eval_steps": 250,
+ "compile": false,
+ "query_template": "Question: {query} Think step by step.\nAnswer:",
+ "seed": 0,
+ "grad_norm_clip": 1.0,
+ "optimizer_type": "AdamW",
+ "optimizer_kwargs": {
+ "lr": 0.0003
+ },
+ "lr_scheduler": "cosine",
+ "use_amp": false,
+ "autocast_adapter_dtype": true,
+ "generation_kwargs": {
+ "max_length": 800,
+ "max_new_tokens": 300
+ },
+ "attn_implementation": null
+ },
+ "peft_config": {
+ "task_type": null,
+ "peft_type": "SHIRA",
+ "auto_mapping": null,
+ "base_model_name_or_path": "meta-llama/Llama-3.2-3B",
+ "revision": null,
+ "inference_mode": false,
+ "r": 32,
+ "mask_type": "random",
+ "random_seed": 42,
+ "target_modules": [
+ "v_proj",
+ "q_proj"
+ ],
+ "fan_in_fan_out": false,
+ "init_weights": true,
+ "modules_to_save": null
+ },
+ "error_msg": ""
+ },
+ "train_info": {
+ "accelerator_memory_reserved_avg": 12240924809,
+ "accelerator_memory_max": 21743271936,
+ "accelerator_memory_reserved_99th": 17637383864,
+ "train_time": 1867.0518525470034,
+ "file_size": 110115520,
+ "num_trainable_params": 9175040,
+ "num_total_params": 3221924864,
+ "status": "success",
+ "metrics": [
+ {
+ "step": 250,
+ "valid accuracy": 0.38,
+ "train loss": 0.9357188057899475,
+ "train samples": 1000,
+ "train time": 31.692333374005102,
+ "eval time": 12.883808001000943,
+ "tokens / sec": 6680.448470028325,
+ "mem allocated avg": 6994551982.08,
+ "mem reserved avg": 12283740684.288,
+ "elapsed time": 96.08096698400004
+ },
+ {
+ "step": 500,
+ "valid accuracy": 0.36,
+ "train loss": 0.7029980063438416,
+ "train samples": 2000,
+ "train time": 30.742395647013836,
+ "eval time": 12.860161713999332,
+ "tokens / sec": 6765.73818085656,
+ "mem allocated avg": 6987138160.64,
+ "mem reserved avg": 12187783397.376,
+ "elapsed time": 185.3151257690006
+ },
+ {
+ "step": 750,
+ "valid accuracy": 0.46,
+ "train loss": 0.6642508600950241,
+ "train samples": 3000,
+ "train time": 31.300478177990954,
+ "eval time": 10.545964175000336,
+ "tokens / sec": 6849.767558846972,
+ "mem allocated avg": 6997475934.208,
+ "mem reserved avg": 12327495663.616,
+ "elapsed time": 273.0391829120017
+ },
+ {
+ "step": 1000,
+ "valid accuracy": 0.36,
+ "train loss": 0.6439496507644653,
+ "train samples": 4000,
+ "train time": 31.05783393001184,
+ "eval time": 12.813238828999602,
+ "tokens / sec": 6708.00160981866,
+ "mem allocated avg": 6989375735.808,
+ "mem reserved avg": 12216002674.688,
+ "elapsed time": 362.4678097830001
+ },
+ {
+ "step": 1250,
+ "valid accuracy": 0.32,
+ "train loss": 0.6386180140972137,
+ "train samples": 5000,
+ "train time": 31.162159604989938,
+ "eval time": 9.70755834100055,
+ "tokens / sec": 6692.026568229476,
+ "mem allocated avg": 6988624240.64,
+ "mem reserved avg": 12208931078.144,
+ "elapsed time": 449.31565678900006
+ },
+ {
+ "step": 1500,
+ "valid accuracy": 0.5,
+ "train loss": 0.6296385749578476,
+ "train samples": 6000,
+ "train time": 31.37457448001078,
+ "eval time": 12.791106022999884,
+ "tokens / sec": 6671.994870667266,
+ "mem allocated avg": 6990819698.688,
+ "mem reserved avg": 12231488045.056,
+ "elapsed time": 539.3741775020007
+ },
+ {
+ "step": 1750,
+ "valid accuracy": 0.52,
+ "train loss": 0.6209055181741715,
+ "train samples": 7000,
+ "train time": 31.12063506498089,
+ "eval time": 11.802694226998938,
+ "tokens / sec": 6727.208476397092,
+ "mem allocated avg": 6991199850.496,
+ "mem reserved avg": 12244775600.128,
+ "elapsed time": 628.1649310410012
+ },
+ {
+ "step": 2000,
+ "valid accuracy": 0.42,
+ "train loss": 0.622630435705185,
+ "train samples": 8000,
+ "train time": 30.90304242698403,
+ "eval time": 12.802878865999446,
+ "tokens / sec": 6720.8916562416925,
+ "mem allocated avg": 6988364103.68,
+ "mem reserved avg": 12193303101.44,
+ "elapsed time": 717.7866772650013
+ },
+ {
+ "step": 2250,
+ "valid accuracy": 0.5,
+ "train loss": 0.6117782632112503,
+ "train samples": 9000,
+ "train time": 31.835284770990256,
+ "eval time": 12.896296490000168,
+ "tokens / sec": 6751.8792919945945,
+ "mem allocated avg": 6999611363.328,
+ "mem reserved avg": 12359498203.136,
+ "elapsed time": 808.9164720260014
+ },
+ {
+ "step": 2500,
+ "valid accuracy": 0.48,
+ "train loss": 0.6087703567743301,
+ "train samples": 10000,
+ "train time": 31.106087331994786,
+ "eval time": 8.24222338599975,
+ "tokens / sec": 6621.437077627842,
+ "mem allocated avg": 6984549638.144,
+ "mem reserved avg": 12142711406.592,
+ "elapsed time": 894.0944889150014
+ },
+ {
+ "step": 2750,
+ "valid accuracy": 0.54,
+ "train loss": 0.5988683942556381,
+ "train samples": 11000,
+ "train time": 31.549549333021787,
+ "eval time": 10.239751285998864,
+ "tokens / sec": 6715.817007827485,
+ "mem allocated avg": 6995372679.168,
+ "mem reserved avg": 12298949230.592,
+ "elapsed time": 981.9011422450003
+ },
+ {
+ "step": 3000,
+ "valid accuracy": 0.5,
+ "train loss": 0.5887085427045822,
+ "train samples": 12000,
+ "train time": 30.952114122006606,
+ "eval time": 6.788169478999407,
+ "tokens / sec": 6743.6750580986845,
+ "mem allocated avg": 6990271899.648,
+ "mem reserved avg": 12226782035.968,
+ "elapsed time": 1065.3513825200007
+ },
+ {
+ "step": 3250,
+ "valid accuracy": 0.5,
+ "train loss": 0.5973232421875,
+ "train samples": 13000,
+ "train time": 31.107180875995255,
+ "eval time": 8.763070525999865,
+ "tokens / sec": 6779.81720171717,
+ "mem allocated avg": 6991821465.6,
+ "mem reserved avg": 12247829053.44,
+ "elapsed time": 1151.3527770540004
+ },
+ {
+ "step": 3500,
+ "valid accuracy": 0.58,
+ "train loss": 0.5808243087530136,
+ "train samples": 14000,
+ "train time": 31.351620633020502,
+ "eval time": 12.858672252999895,
+ "tokens / sec": 6690.244260581693,
+ "mem allocated avg": 6991037339.648,
+ "mem reserved avg": 12237720780.8,
+ "elapsed time": 1241.8340592570003
+ },
+ {
+ "step": 3750,
+ "valid accuracy": 0.54,
+ "train loss": 0.5781804740428924,
+ "train samples": 15000,
+ "train time": 31.949568995005393,
+ "eval time": 10.286192837000272,
+ "tokens / sec": 6782.658008121384,
+ "mem allocated avg": 7002176088.064,
+ "mem reserved avg": 12393589506.048,
+ "elapsed time": 1330.699673422001
+ },
+ {
+ "step": 4000,
+ "valid accuracy": 0.52,
+ "train loss": 0.5873791750669479,
+ "train samples": 16000,
+ "train time": 30.883606043998952,
+ "eval time": 12.840774923999561,
+ "tokens / sec": 6617.523863917831,
+ "mem allocated avg": 6983247890.432,
+ "mem reserved avg": 12128861814.784,
+ "elapsed time": 1420.291728133001
+ },
+ {
+ "step": 4250,
+ "valid accuracy": 0.54,
+ "train loss": 0.5750357346534729,
+ "train samples": 17000,
+ "train time": 31.41448626901547,
+ "eval time": 7.603731496999899,
+ "tokens / sec": 6729.029346199935,
+ "mem allocated avg": 6993511036.928,
+ "mem reserved avg": 12266485317.632,
+ "elapsed time": 1505.506280988
+ },
+ {
+ "step": 4500,
+ "valid accuracy": 0.54,
+ "train loss": 0.5816998761892319,
+ "train samples": 18000,
+ "train time": 30.81339496200053,
+ "eval time": 6.927671567998914,
+ "tokens / sec": 6744.404511618528,
+ "mem allocated avg": 6988376672.256,
+ "mem reserved avg": 12194603335.68,
+ "elapsed time": 1588.958452021001
+ },
+ {
+ "step": 4750,
+ "valid accuracy": 0.58,
+ "train loss": 0.5723758825063705,
+ "train samples": 19000,
+ "train time": 31.16517290099182,
+ "eval time": 7.508142915999997,
+ "tokens / sec": 6736.333556272963,
+ "mem allocated avg": 6991473983.488,
+ "mem reserved avg": 12240195420.16,
+ "elapsed time": 1673.9547475400013
+ },
+ {
+ "step": 5000,
+ "valid accuracy": 0.54,
+ "train loss": 0.5789329997301101,
+ "train samples": 20000,
+ "train time": 31.123193277984683,
+ "eval time": 7.151714429001004,
+ "tokens / sec": 6692.115366816459,
+ "mem allocated avg": 6987954006.016,
+ "mem reserved avg": 12187749842.944,
+ "elapsed time": 1758.2295099830008
+ },
+ {
+ "step": 5000,
+ "test accuracy": 0.5072024260803639,
+ "train loss": 0.5789329997301101,
+ "train samples": 20000,
+ "train total tokens": 4198051
+ }
+ ]
+ },
+ "meta_info": {
+ "model_info": {
+ "sha": "13afe5124825b4f3751f836b40dafda64c1ed062",
+ "created_at": "2024-09-18T15:23:48+00:00"
+ },
+ "dataset_info": {
+ "metamath": {
+ "sha": "aa4f34d3d2d3231299b5b03d9b3e5a20da45aa18",
+ "created_at": "2023-09-21T17:22:46+00:00"
+ },
+ "gsm8k": {
+ "sha": "e53f048856ff4f594e959d75785d2c2d37b678ee",
+ "created_at": "2022-04-12T10:22:10+00:00"
+ }
+ },
+ "package_info": {
+ "transformers-version": "4.52.4",
+ "transformers-commit-hash": null,
+ "peft-version": "0.16.1.dev0",
+ "peft-commit-hash": "25e5c6b25c4589eb2683484ede1ba3d985d8a760",
+ "datasets-version": "3.6.0",
+ "datasets-commit-hash": null,
+ "bitsandbytes-version": "0.46.0",
+ "bitsandbytes-commit-hash": null,
+ "torch-version": "2.7.1+cu126",
+ "torch-commit-hash": null
+ },
+ "system_info": {
+ "system": "Linux",
+ "release": "6.8.0-1031-aws",
+ "version": "#33-Ubuntu SMP Fri Jun 20 18:11:07 UTC 2025",
+ "machine": "x86_64",
+ "processor": "x86_64",
+ "accelerator": "NVIDIA L40S"
+ },
+ "pytorch_info": "PyTorch built with:\n - GCC 11.2\n - C++ Version: 201703\n - Intel(R) oneAPI Math Kernel Library Version 2024.2-Product Build 20240605 for Intel(R) 64 architecture applications\n - Intel(R) MKL-DNN v3.7.1 (Git Hash 8d263e693366ef8db40acc569cc7d8edf644556d)\n - OpenMP 201511 (a.k.a. OpenMP 4.5)\n - LAPACK is enabled (usually provided by MKL)\n - NNPACK is enabled\n - CPU capability usage: AVX2\n - CUDA Runtime 12.6\n - NVCC architecture flags: -gencode;arch=compute_50,code=sm_50;-gencode;arch=compute_60,code=sm_60;-gencode;arch=compute_70,code=sm_70;-gencode;arch=compute_75,code=sm_75;-gencode;arch=compute_80,code=sm_80;-gencode;arch=compute_86,code=sm_86;-gencode;arch=compute_90,code=sm_90\n - CuDNN 90.7.1 (built against CUDA 12.8)\n - Built with CuDNN 90.5.1\n - Magma 2.6.1\n - Build settings: BLAS_INFO=mkl, BUILD_TYPE=Release, COMMIT_SHA=e2d141dbde55c2a4370fac5165b0561b6af4798b, CUDA_VERSION=12.6, CUDNN_VERSION=9.5.1, CXX_COMPILER=/opt/rh/gcc-toolset-11/root/usr/bin/c++, CXX_FLAGS= -D_GLIBCXX_USE_CXX11_ABI=1 -fvisibility-inlines-hidden -DUSE_PTHREADPOOL -DNDEBUG -DUSE_KINETO -DLIBKINETO_NOROCTRACER -DLIBKINETO_NOXPUPTI=ON -DUSE_FBGEMM -DUSE_PYTORCH_QNNPACK -DUSE_XNNPACK -DSYMBOLICATE_MOBILE_DEBUG_HANDLE -O2 -fPIC -Wall -Wextra -Werror=return-type -Werror=non-virtual-dtor -Werror=range-loop-construct -Werror=bool-operation -Wnarrowing -Wno-missing-field-initializers -Wno-unknown-pragmas -Wno-unused-parameter -Wno-strict-overflow -Wno-strict-aliasing -Wno-stringop-overflow -Wsuggest-override -Wno-psabi -Wno-error=old-style-cast -fdiagnostics-color=always -faligned-new -Wno-maybe-uninitialized -fno-math-errno -fno-trapping-math -Werror=format -Wno-stringop-overflow, LAPACK_INFO=mkl, PERF_WITH_AVX=1, PERF_WITH_AVX2=1, TORCH_VERSION=2.7.1, USE_CUDA=ON, USE_CUDNN=ON, USE_CUSPARSELT=1, USE_GFLAGS=OFF, USE_GLOG=OFF, USE_GLOO=ON, USE_MKL=ON, USE_MKLDNN=ON, USE_MPI=OFF, USE_NCCL=1, USE_NNPACK=ON, USE_OPENMP=ON, USE_ROCM=OFF, USE_ROCM_KERNEL_ASSERT=OFF, \n"
+ }
+}
\ No newline at end of file
diff --git a/peft/method_comparison/MetaMathQA/results/trainable_tokens--llama-3.2-3B-sos+eos.json b/peft/method_comparison/MetaMathQA/results/trainable_tokens--llama-3.2-3B-sos+eos.json
new file mode 100644
index 0000000000000000000000000000000000000000..eff36db4db861519316e19d0696797c8eb04da97
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/results/trainable_tokens--llama-3.2-3B-sos+eos.json
@@ -0,0 +1,344 @@
+{
+ "run_info": {
+ "created_at": "2025-07-31T11:51:03+00:00",
+ "total_time": 1813.5205606600002,
+ "experiment_name": "trainable_tokens/llama-3.2-3B-sos+eos",
+ "peft_branch": "main",
+ "train_config": {
+ "model_id": "meta-llama/Llama-3.2-3B",
+ "dtype": "bfloat16",
+ "max_seq_length": 768,
+ "batch_size": 4,
+ "batch_size_eval": 50,
+ "max_steps": 5000,
+ "eval_steps": 250,
+ "compile": false,
+ "query_template": "Question: {query} Think step by step.\nAnswer:",
+ "seed": 0,
+ "grad_norm_clip": 1.0,
+ "optimizer_type": "AdamW",
+ "optimizer_kwargs": {
+ "lr": 0.2
+ },
+ "lr_scheduler": "cosine",
+ "use_amp": false,
+ "autocast_adapter_dtype": true,
+ "generation_kwargs": {
+ "max_length": 800,
+ "max_new_tokens": 300
+ },
+ "attn_implementation": null
+ },
+ "peft_config": {
+ "task_type": "CAUSAL_LM",
+ "peft_type": "TRAINABLE_TOKENS",
+ "auto_mapping": null,
+ "base_model_name_or_path": "meta-llama/Llama-3.2-3B",
+ "revision": null,
+ "inference_mode": false,
+ "token_indices": [
+ 128000,
+ 128001
+ ],
+ "target_modules": "model.embed_tokens",
+ "init_weights": true
+ },
+ "error_msg": ""
+ },
+ "train_info": {
+ "accelerator_memory_reserved_avg": 12730137942,
+ "accelerator_memory_max": 20956839936,
+ "accelerator_memory_reserved_99th": 16957675929,
+ "train_time": 1571.9034050299992,
+ "file_size": 49424,
+ "num_trainable_params": 6144,
+ "num_total_params": 3212755968,
+ "status": "success",
+ "metrics": [
+ {
+ "step": 250,
+ "valid accuracy": 0.2,
+ "train loss": 0.9600473783016205,
+ "train samples": 1000,
+ "train time": 28.046887916000458,
+ "eval time": 11.940005464000023,
+ "tokens / sec": 7548.751955443032,
+ "mem allocated avg": 6772620728.32,
+ "mem reserved avg": 12816987717.632,
+ "elapsed time": 79.72835956
+ },
+ {
+ "step": 500,
+ "valid accuracy": 0.1,
+ "train loss": 0.9827968046665192,
+ "train samples": 2000,
+ "train time": 27.568676805000052,
+ "eval time": 11.946740159,
+ "tokens / sec": 7544.613093736749,
+ "mem allocated avg": 6765130303.488,
+ "mem reserved avg": 12640885669.888,
+ "elapsed time": 153.151956972
+ },
+ {
+ "step": 750,
+ "valid accuracy": 0.26,
+ "train loss": 1.078141197681427,
+ "train samples": 3000,
+ "train time": 28.346493393999594,
+ "eval time": 11.913883551000026,
+ "tokens / sec": 7563.581040517151,
+ "mem allocated avg": 6775356669.952,
+ "mem reserved avg": 12829595795.456,
+ "elapsed time": 227.42617082600003
+ },
+ {
+ "step": 1000,
+ "valid accuracy": 0.18,
+ "train loss": 0.9337297527790069,
+ "train samples": 4000,
+ "train time": 27.80469767599925,
+ "eval time": 11.935028867000028,
+ "tokens / sec": 7492.834571613906,
+ "mem allocated avg": 6767140114.432,
+ "mem reserved avg": 12714495705.088,
+ "elapsed time": 301.119469732
+ },
+ {
+ "step": 1250,
+ "valid accuracy": 0.06,
+ "train loss": 1.1530333435535431,
+ "train samples": 5000,
+ "train time": 27.832769999000448,
+ "eval time": 11.899406999999997,
+ "tokens / sec": 7492.534879118722,
+ "mem allocated avg": 6766889218.048,
+ "mem reserved avg": 12706635579.392,
+ "elapsed time": 374.949399381
+ },
+ {
+ "step": 1500,
+ "valid accuracy": 0.16,
+ "train loss": 0.9257006254196167,
+ "train samples": 6000,
+ "train time": 27.848633210000685,
+ "eval time": 11.963534283000058,
+ "tokens / sec": 7516.7423270463205,
+ "mem allocated avg": 6768338049.024,
+ "mem reserved avg": 12713531015.168,
+ "elapsed time": 448.64371043399996
+ },
+ {
+ "step": 1750,
+ "valid accuracy": 0.04,
+ "train loss": 0.9480950233936309,
+ "train samples": 7000,
+ "train time": 28.10500999800047,
+ "eval time": 11.907140037999966,
+ "tokens / sec": 7449.027771735166,
+ "mem allocated avg": 6769886017.536,
+ "mem reserved avg": 12724176158.72,
+ "elapsed time": 523.0294692360001
+ },
+ {
+ "step": 2000,
+ "valid accuracy": 0.22,
+ "train loss": 1.099897492647171,
+ "train samples": 8000,
+ "train time": 27.50086192600054,
+ "eval time": 11.908490246000042,
+ "tokens / sec": 7552.345106814087,
+ "mem allocated avg": 6767001008.128,
+ "mem reserved avg": 12671663472.64,
+ "elapsed time": 596.5166793630001
+ },
+ {
+ "step": 2250,
+ "valid accuracy": 0.2,
+ "train loss": 1.0596771531105043,
+ "train samples": 9000,
+ "train time": 28.679387931000633,
+ "eval time": 11.905819370000017,
+ "tokens / sec": 7494.860089662325,
+ "mem allocated avg": 6777668958.208,
+ "mem reserved avg": 12765641048.064,
+ "elapsed time": 671.4013165209999
+ },
+ {
+ "step": 2500,
+ "valid accuracy": 0.28,
+ "train loss": 0.8838931715488434,
+ "train samples": 10000,
+ "train time": 27.525735084001553,
+ "eval time": 11.918955123999922,
+ "tokens / sec": 7482.70661515273,
+ "mem allocated avg": 6762954442.752,
+ "mem reserved avg": 12636850749.44,
+ "elapsed time": 744.8136404429999
+ },
+ {
+ "step": 2750,
+ "valid accuracy": 0.28,
+ "train loss": 0.8453443908691406,
+ "train samples": 11000,
+ "train time": 28.56140573299922,
+ "eval time": 11.910845225000003,
+ "tokens / sec": 7418.437382975074,
+ "mem allocated avg": 6773394008.064,
+ "mem reserved avg": 12781445185.536,
+ "elapsed time": 819.4217107059999
+ },
+ {
+ "step": 3000,
+ "valid accuracy": 0.28,
+ "train loss": 0.8956673395633697,
+ "train samples": 12000,
+ "train time": 27.520784680998986,
+ "eval time": 11.922119511000119,
+ "tokens / sec": 7584.485777548084,
+ "mem allocated avg": 6768260833.28,
+ "mem reserved avg": 12729855246.336,
+ "elapsed time": 892.9293128969998
+ },
+ {
+ "step": 3250,
+ "valid accuracy": 0.28,
+ "train loss": 0.8384639675617218,
+ "train samples": 13000,
+ "train time": 27.425537425002176,
+ "eval time": 11.90852308500007,
+ "tokens / sec": 7689.9495799026545,
+ "mem allocated avg": 6769824622.592,
+ "mem reserved avg": 12732145336.32,
+ "elapsed time": 966.4361498369999
+ },
+ {
+ "step": 3500,
+ "valid accuracy": 0.28,
+ "train loss": 0.8318528242111206,
+ "train samples": 14000,
+ "train time": 27.599476771002628,
+ "eval time": 11.926854094000191,
+ "tokens / sec": 7599.781754572018,
+ "mem allocated avg": 6769281437.696,
+ "mem reserved avg": 12748083691.52,
+ "elapsed time": 1040.349463558
+ },
+ {
+ "step": 3750,
+ "valid accuracy": 0.3,
+ "train loss": 0.825278183221817,
+ "train samples": 15000,
+ "train time": 28.668002616999956,
+ "eval time": 11.920088525999972,
+ "tokens / sec": 7559.054702733158,
+ "mem allocated avg": 6780301985.792,
+ "mem reserved avg": 12867151593.472,
+ "elapsed time": 1115.464965257
+ },
+ {
+ "step": 4000,
+ "valid accuracy": 0.34,
+ "train loss": 0.8279166626930237,
+ "train samples": 16000,
+ "train time": 27.677960625997912,
+ "eval time": 11.956045786999994,
+ "tokens / sec": 7383.961656771504,
+ "mem allocated avg": 6761672556.544,
+ "mem reserved avg": 12607280906.24,
+ "elapsed time": 1189.311786065
+ },
+ {
+ "step": 4250,
+ "valid accuracy": 0.26,
+ "train loss": 0.7829471210241318,
+ "train samples": 17000,
+ "train time": 27.69402594300027,
+ "eval time": 11.900985279999986,
+ "tokens / sec": 7633.018053607661,
+ "mem allocated avg": 6771771314.176,
+ "mem reserved avg": 12787006832.64,
+ "elapsed time": 1263.137991501
+ },
+ {
+ "step": 4500,
+ "valid accuracy": 0.36,
+ "train loss": 0.788821615934372,
+ "train samples": 18000,
+ "train time": 27.622178668999823,
+ "eval time": 11.941970926000067,
+ "tokens / sec": 7523.591911062131,
+ "mem allocated avg": 6766746431.488,
+ "mem reserved avg": 12679666204.672,
+ "elapsed time": 1336.699760115
+ },
+ {
+ "step": 4750,
+ "valid accuracy": 0.3,
+ "train loss": 0.7817396788597107,
+ "train samples": 19000,
+ "train time": 28.053782109000622,
+ "eval time": 11.908781481000005,
+ "tokens / sec": 7483.447300770342,
+ "mem allocated avg": 6769035872.256,
+ "mem reserved avg": 12704303546.368,
+ "elapsed time": 1411.011856929
+ },
+ {
+ "step": 5000,
+ "valid accuracy": 0.32,
+ "train loss": 0.786205664396286,
+ "train samples": 20000,
+ "train time": 27.865934093999613,
+ "eval time": 11.930896392000022,
+ "tokens / sec": 7474.359169063313,
+ "mem allocated avg": 6766191118.336,
+ "mem reserved avg": 12745357393.92,
+ "elapsed time": 1484.8831304389998
+ },
+ {
+ "step": 5000,
+ "test accuracy": 0.2880970432145565,
+ "train loss": 0.786205664396286,
+ "train samples": 20000,
+ "train total tokens": 4198051
+ }
+ ]
+ },
+ "meta_info": {
+ "model_info": {
+ "sha": "13afe5124825b4f3751f836b40dafda64c1ed062",
+ "created_at": "2024-09-18T15:23:48+00:00"
+ },
+ "dataset_info": {
+ "metamath": {
+ "sha": "aa4f34d3d2d3231299b5b03d9b3e5a20da45aa18",
+ "created_at": "2023-09-21T17:22:46+00:00"
+ },
+ "gsm8k": {
+ "sha": "e53f048856ff4f594e959d75785d2c2d37b678ee",
+ "created_at": "2022-04-12T10:22:10+00:00"
+ }
+ },
+ "package_info": {
+ "transformers-version": "4.52.4",
+ "transformers-commit-hash": null,
+ "peft-version": "0.16.1.dev0",
+ "peft-commit-hash": "25e5c6b25c4589eb2683484ede1ba3d985d8a760",
+ "datasets-version": "3.6.0",
+ "datasets-commit-hash": null,
+ "bitsandbytes-version": "0.46.0",
+ "bitsandbytes-commit-hash": null,
+ "torch-version": "2.7.1+cu126",
+ "torch-commit-hash": null
+ },
+ "system_info": {
+ "system": "Linux",
+ "release": "6.8.0-1031-aws",
+ "version": "#33-Ubuntu SMP Fri Jun 20 18:11:07 UTC 2025",
+ "machine": "x86_64",
+ "processor": "x86_64",
+ "accelerator": "NVIDIA L40S"
+ },
+ "pytorch_info": "PyTorch built with:\n - GCC 11.2\n - C++ Version: 201703\n - Intel(R) oneAPI Math Kernel Library Version 2024.2-Product Build 20240605 for Intel(R) 64 architecture applications\n - Intel(R) MKL-DNN v3.7.1 (Git Hash 8d263e693366ef8db40acc569cc7d8edf644556d)\n - OpenMP 201511 (a.k.a. OpenMP 4.5)\n - LAPACK is enabled (usually provided by MKL)\n - NNPACK is enabled\n - CPU capability usage: AVX2\n - CUDA Runtime 12.6\n - NVCC architecture flags: -gencode;arch=compute_50,code=sm_50;-gencode;arch=compute_60,code=sm_60;-gencode;arch=compute_70,code=sm_70;-gencode;arch=compute_75,code=sm_75;-gencode;arch=compute_80,code=sm_80;-gencode;arch=compute_86,code=sm_86;-gencode;arch=compute_90,code=sm_90\n - CuDNN 90.7.1 (built against CUDA 12.8)\n - Built with CuDNN 90.5.1\n - Magma 2.6.1\n - Build settings: BLAS_INFO=mkl, BUILD_TYPE=Release, COMMIT_SHA=e2d141dbde55c2a4370fac5165b0561b6af4798b, CUDA_VERSION=12.6, CUDNN_VERSION=9.5.1, CXX_COMPILER=/opt/rh/gcc-toolset-11/root/usr/bin/c++, CXX_FLAGS= -D_GLIBCXX_USE_CXX11_ABI=1 -fvisibility-inlines-hidden -DUSE_PTHREADPOOL -DNDEBUG -DUSE_KINETO -DLIBKINETO_NOROCTRACER -DLIBKINETO_NOXPUPTI=ON -DUSE_FBGEMM -DUSE_PYTORCH_QNNPACK -DUSE_XNNPACK -DSYMBOLICATE_MOBILE_DEBUG_HANDLE -O2 -fPIC -Wall -Wextra -Werror=return-type -Werror=non-virtual-dtor -Werror=range-loop-construct -Werror=bool-operation -Wnarrowing -Wno-missing-field-initializers -Wno-unknown-pragmas -Wno-unused-parameter -Wno-strict-overflow -Wno-strict-aliasing -Wno-stringop-overflow -Wsuggest-override -Wno-psabi -Wno-error=old-style-cast -fdiagnostics-color=always -faligned-new -Wno-maybe-uninitialized -fno-math-errno -fno-trapping-math -Werror=format -Wno-stringop-overflow, LAPACK_INFO=mkl, PERF_WITH_AVX=1, PERF_WITH_AVX2=1, TORCH_VERSION=2.7.1, USE_CUDA=ON, USE_CUDNN=ON, USE_CUSPARSELT=1, USE_GFLAGS=OFF, USE_GLOG=OFF, USE_GLOO=ON, USE_MKL=ON, USE_MKLDNN=ON, USE_MPI=OFF, USE_NCCL=1, USE_NNPACK=ON, USE_OPENMP=ON, USE_ROCM=OFF, USE_ROCM_KERNEL_ASSERT=OFF, \n"
+ }
+}
\ No newline at end of file
diff --git a/peft/method_comparison/MetaMathQA/results/vblora--llama-3.2-3B-default.json b/peft/method_comparison/MetaMathQA/results/vblora--llama-3.2-3B-default.json
new file mode 100644
index 0000000000000000000000000000000000000000..ccf041765e8ee3c837eefb23eadba2249638e909
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/results/vblora--llama-3.2-3B-default.json
@@ -0,0 +1,357 @@
+{
+ "run_info": {
+ "created_at": "2025-06-19T23:49:12+00:00",
+ "total_time": 2210.184595478997,
+ "experiment_name": "vblora/llama-3.2-3B-default",
+ "peft_branch": "main",
+ "train_config": {
+ "model_id": "meta-llama/Llama-3.2-3B",
+ "dtype": "bfloat16",
+ "max_seq_length": 768,
+ "batch_size": 4,
+ "batch_size_eval": 50,
+ "max_steps": 5000,
+ "eval_steps": 250,
+ "compile": false,
+ "query_template": "Question: {query} Think step by step.\nAnswer:",
+ "seed": 0,
+ "grad_norm_clip": 1.0,
+ "optimizer_type": "AdamW",
+ "optimizer_kwargs": {
+ "lr": 0.0001,
+ "weight_decay": 0.1
+ },
+ "lr_scheduler": "cosine",
+ "use_amp": false,
+ "autocast_adapter_dtype": true,
+ "generation_kwargs": {
+ "max_length": 800,
+ "max_new_tokens": 300
+ },
+ "attn_implementation": null
+ },
+ "peft_config": {
+ "task_type": null,
+ "peft_type": "VBLORA",
+ "auto_mapping": null,
+ "base_model_name_or_path": "meta-llama/Llama-3.2-3B",
+ "revision": null,
+ "inference_mode": false,
+ "r": 4,
+ "num_vectors": 256,
+ "vector_length": 256,
+ "topk": 2,
+ "target_modules": [
+ "v_proj",
+ "q_proj"
+ ],
+ "exclude_modules": null,
+ "save_only_topk_weights": false,
+ "vblora_dropout": 0.0,
+ "fan_in_fan_out": false,
+ "bias": "none",
+ "modules_to_save": null,
+ "init_vector_bank_bound": 0.02,
+ "init_logits_std": 0.1,
+ "layers_to_transform": null,
+ "layers_pattern": null
+ },
+ "error_msg": ""
+ },
+ "train_info": {
+ "accelerator_memory_reserved_avg": 11735344663,
+ "accelerator_memory_max": 22181576704,
+ "accelerator_memory_reserved_99th": 17635223797,
+ "train_time": 1961.761054087001,
+ "file_size": 4864912,
+ "num_trainable_params": 1212416,
+ "num_total_params": 3213962240,
+ "status": "success",
+ "metrics": [
+ {
+ "step": 250,
+ "valid accuracy": 0.0,
+ "train loss": 1.308416832447052,
+ "train samples": 1000,
+ "train time": 40.12101128498034,
+ "eval time": 12.847303112997906,
+ "tokens / sec": 5277.010554299236,
+ "mem allocated avg": 6798303909.888,
+ "mem reserved avg": 11786547888.128,
+ "elapsed time": 101.0704645309961
+ },
+ {
+ "step": 500,
+ "valid accuracy": 0.38,
+ "train loss": 1.0353211228847503,
+ "train samples": 2000,
+ "train time": 39.44148263899842,
+ "eval time": 12.918682472998626,
+ "tokens / sec": 5273.508653408011,
+ "mem allocated avg": 6790843463.68,
+ "mem reserved avg": 11678368399.36,
+ "elapsed time": 195.96383863499796
+ },
+ {
+ "step": 750,
+ "valid accuracy": 0.3,
+ "train loss": 0.8149400608539581,
+ "train samples": 3000,
+ "train time": 39.73428049797076,
+ "eval time": 12.816220013999555,
+ "tokens / sec": 5395.869695210651,
+ "mem allocated avg": 6801506754.56,
+ "mem reserved avg": 11833448595.456,
+ "elapsed time": 291.3562671039981
+ },
+ {
+ "step": 1000,
+ "valid accuracy": 0.34,
+ "train loss": 0.766725031375885,
+ "train samples": 4000,
+ "train time": 39.66955411599338,
+ "eval time": 12.954798815000686,
+ "tokens / sec": 5251.785774824381,
+ "mem allocated avg": 6791902521.344,
+ "mem reserved avg": 11700715651.072,
+ "elapsed time": 386.48246048299916
+ },
+ {
+ "step": 1250,
+ "valid accuracy": 0.4,
+ "train loss": 0.7548577107191086,
+ "train samples": 5000,
+ "train time": 39.58740361595119,
+ "eval time": 12.921318173001055,
+ "tokens / sec": 5267.786744063522,
+ "mem allocated avg": 6792241373.184,
+ "mem reserved avg": 11698584944.64,
+ "elapsed time": 481.6297270110008
+ },
+ {
+ "step": 1500,
+ "valid accuracy": 0.42,
+ "train loss": 0.744083244919777,
+ "train samples": 6000,
+ "train time": 39.58100679998461,
+ "eval time": 7.990361490003124,
+ "tokens / sec": 5288.672950079719,
+ "mem allocated avg": 6792975718.4,
+ "mem reserved avg": 11729908006.912,
+ "elapsed time": 571.7995823969977
+ },
+ {
+ "step": 1750,
+ "valid accuracy": 0.4,
+ "train loss": 0.7353366105556488,
+ "train samples": 7000,
+ "train time": 39.89848869200068,
+ "eval time": 9.013003496002057,
+ "tokens / sec": 5247.191231129864,
+ "mem allocated avg": 6795538806.784,
+ "mem reserved avg": 11737281593.344,
+ "elapsed time": 663.3418345429964
+ },
+ {
+ "step": 2000,
+ "valid accuracy": 0.36,
+ "train loss": 0.735884799003601,
+ "train samples": 8000,
+ "train time": 39.573877232054656,
+ "eval time": 13.005171182994673,
+ "tokens / sec": 5248.3106161699825,
+ "mem allocated avg": 6792414906.368,
+ "mem reserved avg": 11683577724.928,
+ "elapsed time": 758.2818646219966
+ },
+ {
+ "step": 2250,
+ "valid accuracy": 0.34,
+ "train loss": 0.7294247032403945,
+ "train samples": 9000,
+ "train time": 40.16309046502283,
+ "eval time": 12.827437616993848,
+ "tokens / sec": 5351.878989172747,
+ "mem allocated avg": 6803159742.464,
+ "mem reserved avg": 11872145244.16,
+ "elapsed time": 854.2901024749954
+ },
+ {
+ "step": 2500,
+ "valid accuracy": 0.36,
+ "train loss": 0.7273153622150421,
+ "train samples": 10000,
+ "train time": 39.40831322706072,
+ "eval time": 12.578817460002028,
+ "tokens / sec": 5226.48606686793,
+ "mem allocated avg": 6788682082.304,
+ "mem reserved avg": 11624815525.888,
+ "elapsed time": 948.6046375669976
+ },
+ {
+ "step": 2750,
+ "valid accuracy": 0.3,
+ "train loss": 0.7221734907627105,
+ "train samples": 11000,
+ "train time": 39.99460277392063,
+ "eval time": 12.831681943003787,
+ "tokens / sec": 5297.739827488966,
+ "mem allocated avg": 6798795204.608,
+ "mem reserved avg": 11800045158.4,
+ "elapsed time": 1044.2291650330008
+ },
+ {
+ "step": 3000,
+ "valid accuracy": 0.44,
+ "train loss": 0.7163265677690506,
+ "train samples": 12000,
+ "train time": 39.72457089692762,
+ "eval time": 9.721318816998973,
+ "tokens / sec": 5254.455750864856,
+ "mem allocated avg": 6794274019.328,
+ "mem reserved avg": 11717786468.352,
+ "elapsed time": 1136.276137433997
+ },
+ {
+ "step": 3250,
+ "valid accuracy": 0.24,
+ "train loss": 0.7239821909666061,
+ "train samples": 13000,
+ "train time": 39.57894092098286,
+ "eval time": 12.939295003001462,
+ "tokens / sec": 5328.616559524724,
+ "mem allocated avg": 6796102031.36,
+ "mem reserved avg": 11749923225.6,
+ "elapsed time": 1231.5789504099957
+ },
+ {
+ "step": 3500,
+ "valid accuracy": 0.3,
+ "train loss": 0.7123430745601654,
+ "train samples": 14000,
+ "train time": 39.774808847985696,
+ "eval time": 12.81972120499995,
+ "tokens / sec": 5273.438291096208,
+ "mem allocated avg": 6794877718.528,
+ "mem reserved avg": 11727257206.784,
+ "elapsed time": 1327.2042175199967
+ },
+ {
+ "step": 3750,
+ "valid accuracy": 0.32,
+ "train loss": 0.7080619329214096,
+ "train samples": 15000,
+ "train time": 40.429172475058294,
+ "eval time": 12.810948685997573,
+ "tokens / sec": 5360.065188910042,
+ "mem allocated avg": 6804612114.432,
+ "mem reserved avg": 11907847159.808,
+ "elapsed time": 1424.0900874009967
+ },
+ {
+ "step": 4000,
+ "valid accuracy": 0.42,
+ "train loss": 0.7257569855451584,
+ "train samples": 16000,
+ "train time": 39.64596449997771,
+ "eval time": 12.844434396996803,
+ "tokens / sec": 5154.950890401844,
+ "mem allocated avg": 6787030419.456,
+ "mem reserved avg": 11605689499.648,
+ "elapsed time": 1519.344677588997
+ },
+ {
+ "step": 4250,
+ "valid accuracy": 0.38,
+ "train loss": 0.7041294666528701,
+ "train samples": 17000,
+ "train time": 39.938396073041076,
+ "eval time": 12.83599700799823,
+ "tokens / sec": 5292.876549508964,
+ "mem allocated avg": 6797280624.64,
+ "mem reserved avg": 11765333098.496,
+ "elapsed time": 1614.829351510998
+ },
+ {
+ "step": 4500,
+ "valid accuracy": 0.38,
+ "train loss": 0.7148806138038635,
+ "train samples": 18000,
+ "train time": 39.55479707601626,
+ "eval time": 12.901207727001747,
+ "tokens / sec": 5253.926586972907,
+ "mem allocated avg": 6791958038.528,
+ "mem reserved avg": 11679299534.848,
+ "elapsed time": 1710.0793527279966
+ },
+ {
+ "step": 4750,
+ "valid accuracy": 0.32,
+ "train loss": 0.7083848255872727,
+ "train samples": 19000,
+ "train time": 39.88160159892141,
+ "eval time": 12.8585010780007,
+ "tokens / sec": 5264.056396513368,
+ "mem allocated avg": 6794248144.896,
+ "mem reserved avg": 11730923028.48,
+ "elapsed time": 1806.240128286001
+ },
+ {
+ "step": 5000,
+ "valid accuracy": 0.36,
+ "train loss": 0.7142883945703506,
+ "train samples": 20000,
+ "train time": 39.631631882970396,
+ "eval time": 12.818420095005422,
+ "tokens / sec": 5255.398026885119,
+ "mem allocated avg": 6791235981.312,
+ "mem reserved avg": 11677395320.832,
+ "elapsed time": 1901.3912653839943
+ },
+ {
+ "step": 5000,
+ "test accuracy": 0.36997725549658833,
+ "train loss": 0.7142883945703506,
+ "train samples": 20000,
+ "train total tokens": 4198051
+ }
+ ]
+ },
+ "meta_info": {
+ "model_info": {
+ "sha": "13afe5124825b4f3751f836b40dafda64c1ed062",
+ "created_at": "2024-09-18T15:23:48+00:00"
+ },
+ "dataset_info": {
+ "metamath": {
+ "sha": "aa4f34d3d2d3231299b5b03d9b3e5a20da45aa18",
+ "created_at": "2023-09-21T17:22:46+00:00"
+ },
+ "gsm8k": {
+ "sha": "e53f048856ff4f594e959d75785d2c2d37b678ee",
+ "created_at": "2022-04-12T10:22:10+00:00"
+ }
+ },
+ "package_info": {
+ "transformers-version": "4.52.4",
+ "transformers-commit-hash": null,
+ "peft-version": "0.15.2.dev0",
+ "peft-commit-hash": "5fe7f8f8abe914d313fc3751f2ea92de7718fbaf",
+ "datasets-version": "3.6.0",
+ "datasets-commit-hash": null,
+ "bitsandbytes-version": "0.46.0",
+ "bitsandbytes-commit-hash": null,
+ "torch-version": "2.7.1+cu126",
+ "torch-commit-hash": null
+ },
+ "system_info": {
+ "system": "Linux",
+ "release": "6.8.0-1029-aws",
+ "version": "#31-Ubuntu SMP Wed Apr 23 18:42:41 UTC 2025",
+ "machine": "x86_64",
+ "processor": "x86_64",
+ "accelerator": "NVIDIA L40S"
+ },
+ "pytorch_info": "PyTorch built with:\n - GCC 11.2\n - C++ Version: 201703\n - Intel(R) oneAPI Math Kernel Library Version 2024.2-Product Build 20240605 for Intel(R) 64 architecture applications\n - Intel(R) MKL-DNN v3.7.1 (Git Hash 8d263e693366ef8db40acc569cc7d8edf644556d)\n - OpenMP 201511 (a.k.a. OpenMP 4.5)\n - LAPACK is enabled (usually provided by MKL)\n - NNPACK is enabled\n - CPU capability usage: AVX2\n - CUDA Runtime 12.6\n - NVCC architecture flags: -gencode;arch=compute_50,code=sm_50;-gencode;arch=compute_60,code=sm_60;-gencode;arch=compute_70,code=sm_70;-gencode;arch=compute_75,code=sm_75;-gencode;arch=compute_80,code=sm_80;-gencode;arch=compute_86,code=sm_86;-gencode;arch=compute_90,code=sm_90\n - CuDNN 90.7.1 (built against CUDA 12.8)\n - Built with CuDNN 90.5.1\n - Magma 2.6.1\n - Build settings: BLAS_INFO=mkl, BUILD_TYPE=Release, COMMIT_SHA=e2d141dbde55c2a4370fac5165b0561b6af4798b, CUDA_VERSION=12.6, CUDNN_VERSION=9.5.1, CXX_COMPILER=/opt/rh/gcc-toolset-11/root/usr/bin/c++, CXX_FLAGS= -D_GLIBCXX_USE_CXX11_ABI=1 -fvisibility-inlines-hidden -DUSE_PTHREADPOOL -DNDEBUG -DUSE_KINETO -DLIBKINETO_NOROCTRACER -DLIBKINETO_NOXPUPTI=ON -DUSE_FBGEMM -DUSE_PYTORCH_QNNPACK -DUSE_XNNPACK -DSYMBOLICATE_MOBILE_DEBUG_HANDLE -O2 -fPIC -Wall -Wextra -Werror=return-type -Werror=non-virtual-dtor -Werror=range-loop-construct -Werror=bool-operation -Wnarrowing -Wno-missing-field-initializers -Wno-unknown-pragmas -Wno-unused-parameter -Wno-strict-overflow -Wno-strict-aliasing -Wno-stringop-overflow -Wsuggest-override -Wno-psabi -Wno-error=old-style-cast -fdiagnostics-color=always -faligned-new -Wno-maybe-uninitialized -fno-math-errno -fno-trapping-math -Werror=format -Wno-stringop-overflow, LAPACK_INFO=mkl, PERF_WITH_AVX=1, PERF_WITH_AVX2=1, TORCH_VERSION=2.7.1, USE_CUDA=ON, USE_CUDNN=ON, USE_CUSPARSELT=1, USE_GFLAGS=OFF, USE_GLOG=OFF, USE_GLOO=ON, USE_MKL=ON, USE_MKLDNN=ON, USE_MPI=OFF, USE_NCCL=1, USE_NNPACK=ON, USE_OPENMP=ON, USE_ROCM=OFF, USE_ROCM_KERNEL_ASSERT=OFF, \n"
+ }
+}
diff --git a/peft/method_comparison/MetaMathQA/results/vera--llama-3.2-3B-default.json b/peft/method_comparison/MetaMathQA/results/vera--llama-3.2-3B-default.json
new file mode 100644
index 0000000000000000000000000000000000000000..690c35072932a4de9167712c9a2634f92db6f29d
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/results/vera--llama-3.2-3B-default.json
@@ -0,0 +1,353 @@
+{
+ "run_info": {
+ "created_at": "2025-06-19T20:53:39+00:00",
+ "total_time": 2024.6820476150024,
+ "experiment_name": "vera/llama-3.2-3B-default",
+ "peft_branch": "main",
+ "train_config": {
+ "model_id": "meta-llama/Llama-3.2-3B",
+ "dtype": "bfloat16",
+ "max_seq_length": 768,
+ "batch_size": 4,
+ "batch_size_eval": 50,
+ "max_steps": 5000,
+ "eval_steps": 250,
+ "compile": false,
+ "query_template": "Question: {query} Think step by step.\nAnswer:",
+ "seed": 0,
+ "grad_norm_clip": 1.0,
+ "optimizer_type": "AdamW",
+ "optimizer_kwargs": {
+ "lr": 0.001
+ },
+ "lr_scheduler": "cosine",
+ "use_amp": false,
+ "autocast_adapter_dtype": true,
+ "generation_kwargs": {
+ "max_length": 800,
+ "max_new_tokens": 300
+ },
+ "attn_implementation": null
+ },
+ "peft_config": {
+ "task_type": null,
+ "peft_type": "VERA",
+ "auto_mapping": null,
+ "base_model_name_or_path": "meta-llama/Llama-3.2-3B",
+ "revision": null,
+ "inference_mode": false,
+ "r": 256,
+ "target_modules": [
+ "v_proj",
+ "q_proj"
+ ],
+ "projection_prng_key": 0,
+ "save_projection": true,
+ "vera_dropout": 0.0,
+ "d_initial": 0.1,
+ "fan_in_fan_out": false,
+ "bias": "none",
+ "modules_to_save": null,
+ "init_weights": true,
+ "layers_to_transform": null,
+ "layers_pattern": null
+ },
+ "error_msg": ""
+ },
+ "train_info": {
+ "accelerator_memory_reserved_avg": 11489715316,
+ "accelerator_memory_max": 21596471296,
+ "accelerator_memory_reserved_99th": 17291123097,
+ "train_time": 1819.9693055349999,
+ "file_size": 6821968,
+ "num_trainable_params": 129024,
+ "num_total_params": 3212878848,
+ "status": "success",
+ "metrics": [
+ {
+ "step": 250,
+ "valid accuracy": 0.0,
+ "train loss": 1.3017588877677917,
+ "train samples": 1000,
+ "train time": 32.843521857023006,
+ "eval time": 11.480974874997628,
+ "tokens / sec": 6446.294064372017,
+ "mem allocated avg": 6784826523.648,
+ "mem reserved avg": 11538438029.312,
+ "elapsed time": 95.45296428899746
+ },
+ {
+ "step": 500,
+ "valid accuracy": 0.28,
+ "train loss": 1.0202219936847687,
+ "train samples": 2000,
+ "train time": 32.35236015598639,
+ "eval time": 11.4980273259971,
+ "tokens / sec": 6429.051821788439,
+ "mem allocated avg": 6777359808.512,
+ "mem reserved avg": 11429948162.048,
+ "elapsed time": 183.95939499299857
+ },
+ {
+ "step": 750,
+ "valid accuracy": 0.38,
+ "train loss": 0.8040032889842987,
+ "train samples": 3000,
+ "train time": 32.52055500800634,
+ "eval time": 11.426841341002728,
+ "tokens / sec": 6592.784162115804,
+ "mem allocated avg": 6787965165.568,
+ "mem reserved avg": 11585061912.576,
+ "elapsed time": 272.8589564269969
+ },
+ {
+ "step": 1000,
+ "valid accuracy": 0.3,
+ "train loss": 0.7544035723209381,
+ "train samples": 4000,
+ "train time": 32.27830113501477,
+ "eval time": 11.54098314699877,
+ "tokens / sec": 6454.3669485133405,
+ "mem allocated avg": 6779215933.44,
+ "mem reserved avg": 11460172316.672,
+ "elapsed time": 361.1500098109973
+ },
+ {
+ "step": 1250,
+ "valid accuracy": 0.44,
+ "train loss": 0.7379197257757187,
+ "train samples": 5000,
+ "train time": 32.060909217962035,
+ "eval time": 11.406497389998549,
+ "tokens / sec": 6504.431879404317,
+ "mem allocated avg": 6779128844.288,
+ "mem reserved avg": 11454770053.12,
+ "elapsed time": 449.3482204989996
+ },
+ {
+ "step": 1500,
+ "valid accuracy": 0.4,
+ "train loss": 0.7252234178781509,
+ "train samples": 6000,
+ "train time": 31.98088176901365,
+ "eval time": 11.480169268001191,
+ "tokens / sec": 6545.504326988923,
+ "mem allocated avg": 6780286265.344,
+ "mem reserved avg": 11479667441.664,
+ "elapsed time": 537.3097453219998
+ },
+ {
+ "step": 1750,
+ "valid accuracy": 0.4,
+ "train loss": 0.7148357192277909,
+ "train samples": 7000,
+ "train time": 32.29452324002341,
+ "eval time": 11.44221062500219,
+ "tokens / sec": 6482.678144650271,
+ "mem allocated avg": 6782215264.256,
+ "mem reserved avg": 11493600919.552,
+ "elapsed time": 625.780868398997
+ },
+ {
+ "step": 2000,
+ "valid accuracy": 0.4,
+ "train loss": 0.7139411936998368,
+ "train samples": 8000,
+ "train time": 32.33002986999054,
+ "eval time": 11.472246884000924,
+ "tokens / sec": 6424.243987253105,
+ "mem allocated avg": 6778636718.08,
+ "mem reserved avg": 11439217573.888,
+ "elapsed time": 714.3076436519987
+ },
+ {
+ "step": 2250,
+ "valid accuracy": 0.38,
+ "train loss": 0.7067342863082886,
+ "train samples": 9000,
+ "train time": 32.69249906902769,
+ "eval time": 11.424881449998793,
+ "tokens / sec": 6574.841511692143,
+ "mem allocated avg": 6789716504.576,
+ "mem reserved avg": 11617542602.752,
+ "elapsed time": 803.4051666009982
+ },
+ {
+ "step": 2500,
+ "valid accuracy": 0.4,
+ "train loss": 0.7048580280542374,
+ "train samples": 10000,
+ "train time": 31.796681229010574,
+ "eval time": 11.401134708998143,
+ "tokens / sec": 6477.625715607085,
+ "mem allocated avg": 6775192217.6,
+ "mem reserved avg": 11386755219.456,
+ "elapsed time": 890.7853266579987
+ },
+ {
+ "step": 2750,
+ "valid accuracy": 0.36,
+ "train loss": 0.6994425257444382,
+ "train samples": 11000,
+ "train time": 32.589996781029186,
+ "eval time": 6.453208308001194,
+ "tokens / sec": 6501.412118068606,
+ "mem allocated avg": 6785945655.296,
+ "mem reserved avg": 11552530890.752,
+ "elapsed time": 974.6122346880002
+ },
+ {
+ "step": 3000,
+ "valid accuracy": 0.4,
+ "train loss": 0.6912879683971405,
+ "train samples": 12000,
+ "train time": 32.34826778500428,
+ "eval time": 11.457833226999355,
+ "tokens / sec": 6452.617536966281,
+ "mem allocated avg": 6780318763.008,
+ "mem reserved avg": 11474030297.088,
+ "elapsed time": 1062.897270567999
+ },
+ {
+ "step": 3250,
+ "valid accuracy": 0.4,
+ "train loss": 0.700449936747551,
+ "train samples": 13000,
+ "train time": 32.51472582996939,
+ "eval time": 8.004199169998174,
+ "tokens / sec": 6486.322569744963,
+ "mem allocated avg": 6782387701.76,
+ "mem reserved avg": 11501452656.64,
+ "elapsed time": 1148.3985279560002
+ },
+ {
+ "step": 3500,
+ "valid accuracy": 0.36,
+ "train loss": 0.6886729755401612,
+ "train samples": 14000,
+ "train time": 32.572147220984334,
+ "eval time": 11.456443364000734,
+ "tokens / sec": 6439.550901479111,
+ "mem allocated avg": 6781381988.352,
+ "mem reserved avg": 11484943876.096,
+ "elapsed time": 1237.2252680229976
+ },
+ {
+ "step": 3750,
+ "valid accuracy": 0.38,
+ "train loss": 0.6851948540210724,
+ "train samples": 15000,
+ "train time": 32.8770313250061,
+ "eval time": 8.042231839001033,
+ "tokens / sec": 6591.318962402083,
+ "mem allocated avg": 6791807023.104,
+ "mem reserved avg": 11653781389.312,
+ "elapsed time": 1323.4750151669978
+ },
+ {
+ "step": 4000,
+ "valid accuracy": 0.36,
+ "train loss": 0.7032276903390884,
+ "train samples": 16000,
+ "train time": 31.65130396198947,
+ "eval time": 7.9955749260007,
+ "tokens / sec": 6457.016754994822,
+ "mem allocated avg": 6773653422.08,
+ "mem reserved avg": 11367989903.36,
+ "elapsed time": 1407.2714081800004
+ },
+ {
+ "step": 4250,
+ "valid accuracy": 0.36,
+ "train loss": 0.684476065993309,
+ "train samples": 17000,
+ "train time": 32.02934406197164,
+ "eval time": 8.007123895000404,
+ "tokens / sec": 6599.854170943876,
+ "mem allocated avg": 6784119472.128,
+ "mem reserved avg": 11519949537.28,
+ "elapsed time": 1492.0019941529972
+ },
+ {
+ "step": 4500,
+ "valid accuracy": 0.38,
+ "train loss": 0.6939880999326706,
+ "train samples": 18000,
+ "train time": 31.936327281997364,
+ "eval time": 9.855819755000994,
+ "tokens / sec": 6507.260467522446,
+ "mem allocated avg": 6777879162.88,
+ "mem reserved avg": 11436331892.736,
+ "elapsed time": 1578.2498042659972
+ },
+ {
+ "step": 4750,
+ "valid accuracy": 0.36,
+ "train loss": 0.68637368786335,
+ "train samples": 19000,
+ "train time": 32.33460194401778,
+ "eval time": 6.469711448000453,
+ "tokens / sec": 6492.704019164238,
+ "mem allocated avg": 6781104441.344,
+ "mem reserved avg": 11484004352.0,
+ "elapsed time": 1662.171022565999
+ },
+ {
+ "step": 5000,
+ "valid accuracy": 0.38,
+ "train loss": 0.6926896897554398,
+ "train samples": 20000,
+ "train time": 32.14674746405217,
+ "eval time": 8.441190715999255,
+ "tokens / sec": 6479.038049896257,
+ "mem allocated avg": 6777818853.376,
+ "mem reserved avg": 11434117300.224,
+ "elapsed time": 1747.4833575960001
+ },
+ {
+ "step": 5000,
+ "test accuracy": 0.3684609552691433,
+ "train loss": 0.6926896897554398,
+ "train samples": 20000,
+ "train total tokens": 4198051
+ }
+ ]
+ },
+ "meta_info": {
+ "model_info": {
+ "sha": "13afe5124825b4f3751f836b40dafda64c1ed062",
+ "created_at": "2024-09-18T15:23:48+00:00"
+ },
+ "dataset_info": {
+ "metamath": {
+ "sha": "aa4f34d3d2d3231299b5b03d9b3e5a20da45aa18",
+ "created_at": "2023-09-21T17:22:46+00:00"
+ },
+ "gsm8k": {
+ "sha": "e53f048856ff4f594e959d75785d2c2d37b678ee",
+ "created_at": "2022-04-12T10:22:10+00:00"
+ }
+ },
+ "package_info": {
+ "transformers-version": "4.52.4",
+ "transformers-commit-hash": null,
+ "peft-version": "0.15.2.dev0",
+ "peft-commit-hash": "5fe7f8f8abe914d313fc3751f2ea92de7718fbaf",
+ "datasets-version": "3.6.0",
+ "datasets-commit-hash": null,
+ "bitsandbytes-version": "0.46.0",
+ "bitsandbytes-commit-hash": null,
+ "torch-version": "2.7.1+cu126",
+ "torch-commit-hash": null
+ },
+ "system_info": {
+ "system": "Linux",
+ "release": "6.8.0-1029-aws",
+ "version": "#31-Ubuntu SMP Wed Apr 23 18:42:41 UTC 2025",
+ "machine": "x86_64",
+ "processor": "x86_64",
+ "accelerator": "NVIDIA L40S"
+ },
+ "pytorch_info": "PyTorch built with:\n - GCC 11.2\n - C++ Version: 201703\n - Intel(R) oneAPI Math Kernel Library Version 2024.2-Product Build 20240605 for Intel(R) 64 architecture applications\n - Intel(R) MKL-DNN v3.7.1 (Git Hash 8d263e693366ef8db40acc569cc7d8edf644556d)\n - OpenMP 201511 (a.k.a. OpenMP 4.5)\n - LAPACK is enabled (usually provided by MKL)\n - NNPACK is enabled\n - CPU capability usage: AVX2\n - CUDA Runtime 12.6\n - NVCC architecture flags: -gencode;arch=compute_50,code=sm_50;-gencode;arch=compute_60,code=sm_60;-gencode;arch=compute_70,code=sm_70;-gencode;arch=compute_75,code=sm_75;-gencode;arch=compute_80,code=sm_80;-gencode;arch=compute_86,code=sm_86;-gencode;arch=compute_90,code=sm_90\n - CuDNN 90.7.1 (built against CUDA 12.8)\n - Built with CuDNN 90.5.1\n - Magma 2.6.1\n - Build settings: BLAS_INFO=mkl, BUILD_TYPE=Release, COMMIT_SHA=e2d141dbde55c2a4370fac5165b0561b6af4798b, CUDA_VERSION=12.6, CUDNN_VERSION=9.5.1, CXX_COMPILER=/opt/rh/gcc-toolset-11/root/usr/bin/c++, CXX_FLAGS= -D_GLIBCXX_USE_CXX11_ABI=1 -fvisibility-inlines-hidden -DUSE_PTHREADPOOL -DNDEBUG -DUSE_KINETO -DLIBKINETO_NOROCTRACER -DLIBKINETO_NOXPUPTI=ON -DUSE_FBGEMM -DUSE_PYTORCH_QNNPACK -DUSE_XNNPACK -DSYMBOLICATE_MOBILE_DEBUG_HANDLE -O2 -fPIC -Wall -Wextra -Werror=return-type -Werror=non-virtual-dtor -Werror=range-loop-construct -Werror=bool-operation -Wnarrowing -Wno-missing-field-initializers -Wno-unknown-pragmas -Wno-unused-parameter -Wno-strict-overflow -Wno-strict-aliasing -Wno-stringop-overflow -Wsuggest-override -Wno-psabi -Wno-error=old-style-cast -fdiagnostics-color=always -faligned-new -Wno-maybe-uninitialized -fno-math-errno -fno-trapping-math -Werror=format -Wno-stringop-overflow, LAPACK_INFO=mkl, PERF_WITH_AVX=1, PERF_WITH_AVX2=1, TORCH_VERSION=2.7.1, USE_CUDA=ON, USE_CUDNN=ON, USE_CUSPARSELT=1, USE_GFLAGS=OFF, USE_GLOG=OFF, USE_GLOO=ON, USE_MKL=ON, USE_MKLDNN=ON, USE_MPI=OFF, USE_NCCL=1, USE_NNPACK=ON, USE_OPENMP=ON, USE_ROCM=OFF, USE_ROCM_KERNEL_ASSERT=OFF, \n"
+ }
+}
diff --git a/peft/method_comparison/MetaMathQA/run.py b/peft/method_comparison/MetaMathQA/run.py
new file mode 100644
index 0000000000000000000000000000000000000000..0d159220eb881ade49ff4fb8ad5d12d8cd7e9c69
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/run.py
@@ -0,0 +1,473 @@
+# Copyright 2025-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""
+Main entry point to run the experiments. Contains general setup and the proper training code.
+"""
+
+import argparse
+import datetime as dt
+import gc
+import json
+import os
+import random
+import sys
+import textwrap
+import time
+from contextlib import AbstractContextManager, nullcontext
+from functools import partial
+from typing import Any, Callable, Literal, Optional
+
+import torch
+from torch import nn
+from torch.amp import GradScaler, autocast
+from tqdm import tqdm
+from transformers import GenerationConfig, set_seed
+from utils import (
+ FILE_NAME_TRAIN_PARAMS,
+ BucketIterator,
+ TrainResult,
+ TrainStatus,
+ get_accuracy,
+ get_base_model_info,
+ get_dataset_info,
+ get_file_size,
+ get_model,
+ get_optimizer_and_scheduler,
+ get_peft_branch,
+ get_tokenizer,
+ get_train_config,
+ init_accelerator,
+ log_results,
+ validate_experiment_path,
+)
+
+from data import get_train_valid_test_datasets
+from peft import AdaLoraConfig, PeftConfig
+from peft.utils import infer_device, CONFIG_NAME
+
+
+# # suppress all warnings
+# warnings.filterwarnings("ignore") # FIXME?
+
+dtype_to_bytes_linear = {"float32": 4, "float16": 2, "bfloat16": 2, "int8": 1, "int4": 0.5}
+# if lr scheduler with warmup is used, the ratio of warmup steps to total steps
+BUCKET_FACTOR = 20 # number of batches per bucket, increasing this further has diminishing returns
+
+
+def get_generation_config(*, seq_len, generate_kwargs) -> GenerationConfig:
+ # filter out None values so that we don't depend on setting correct defaults in the config
+ generation_kwargs = {k: v for k, v in generate_kwargs.items() if v is not None}
+ if ("max_length" in generation_kwargs) and ("max_new_tokens" in generation_kwargs):
+ # transformers does not support setting both max_length and max_new_tokens, but what we want in this case is to
+ # take the smaller of the two values
+ new_max_length = min(generation_kwargs["max_new_tokens"] + seq_len, generation_kwargs["max_length"])
+ del generation_kwargs["max_new_tokens"]
+ generation_kwargs["max_length"] = new_max_length
+ generation_config = GenerationConfig(**generate_kwargs)
+ return generation_config
+
+
+def evaluate(model, tokenizer, ds, batch_size, generate_kwargs, use_tqdm: bool = False) -> tuple[list[str], list[str]]:
+ with torch.inference_mode():
+ predictions = []
+ responses = []
+ pbar = range(0, len(ds), batch_size)
+ if use_tqdm:
+ pbar = tqdm(pbar)
+ for j in pbar:
+ sliced = ds[j : j + batch_size]
+ responses += sliced.pop("response")
+ batch = tokenizer.pad(sliced, return_tensors="pt", padding_side="left").to(model.device)
+ seq_len = batch["input_ids"].shape[1]
+ generation_config = get_generation_config(seq_len=seq_len, generate_kwargs=generate_kwargs)
+ outputs = model.generate(**batch, generation_config=generation_config, pad_token_id=tokenizer.eos_token_id)
+ predictions += tokenizer.batch_decode(outputs, skip_special_tokens=True)
+ return predictions, responses
+
+
+class DummyGradScaler:
+ # if no mixed precision is being used
+ def scale(self, loss):
+ return loss
+
+ def unscale_(self, optimizer):
+ pass
+
+ def step(self, optimizer):
+ optimizer.step()
+
+ def update(self):
+ pass
+
+
+def train(
+ *,
+ model: nn.Module,
+ max_steps: int,
+ batch_size: int,
+ batch_size_eval: int,
+ tokenizer: Any,
+ accelerator_memory_init: int,
+ eval_steps: int,
+ generation_kwargs: dict[str, Any],
+ grad_norm_clip: float,
+ optimizer_type: str,
+ optimizer_kwargs: dict[str, Any],
+ query_template: str,
+ lr_scheduler_arg: Optional[Literal["cosine"]],
+ use_amp: bool,
+ is_adalora: bool,
+) -> TrainResult:
+ accelerator_memory_allocated_log = []
+ accelerator_memory_reserved_log = []
+ losses = []
+ durations = []
+ metrics = []
+ sample = 0 # keep count of the current sample
+ total_samples = 0 # total number of samples over all epochs
+ total_tokens = [] # total number of tokens over all epochs
+
+ device_type = infer_device()
+ torch_accelerator_module = getattr(torch, device_type, torch.cuda)
+ if use_amp:
+ grad_scaler: GradScaler | DummyGradScaler = GradScaler(device=device_type)
+ autocast_ctx: Callable[[], ContextManager[Any]] = partial(autocast, device_type=device_type)
+ else:
+ grad_scaler = DummyGradScaler()
+ autocast_ctx = nullcontext
+
+ optimizer, lr_scheduler = get_optimizer_and_scheduler(
+ model,
+ optimizer_type=optimizer_type,
+ max_steps=max_steps,
+ lr_scheduler_arg=lr_scheduler_arg,
+ **optimizer_kwargs,
+ )
+ # print this after getting the optimizer, in case it modifies requires_gard
+ if hasattr(model, "get_nb_trainable_parameters"):
+ num_trainable_params, num_params = model.get_nb_trainable_parameters()
+ else:
+ num_params = model.num_parameters()
+ num_trainable_params = num_params
+ print_verbose(
+ f"trainable params: {num_trainable_params:,d} || all params: {num_params:,d} || "
+ f"trainable: {100 * num_trainable_params / num_params:.4f}%"
+ )
+
+ status = TrainStatus.FAILED
+ tic_train = time.perf_counter()
+ eval_time = 0.0
+ error_msg = ""
+
+ ds_train, ds_valid, ds_test = get_train_valid_test_datasets(
+ tokenizer=tokenizer, query_template=query_template, print_fn=print_verbose
+ )
+ # note: bucketing by length is only really worth it for the train dataset, since it's length is big compared to the
+ # batch size
+ iterator_train = BucketIterator(
+ ds_train,
+ batch_size=batch_size,
+ bucket_factor=BUCKET_FACTOR,
+ delete_cols=["response"],
+ )
+ try:
+ pbar = tqdm(range(1, max_steps + 1))
+ for step, batch in zip(pbar, iterator_train):
+ tic = time.perf_counter()
+
+ # create the batch
+ tokens_per_sample = [len(i) for i in batch["input_ids"]]
+ total_tokens.append(sum(tokens_per_sample) + len(tokens_per_sample)) # add EOS token
+ batch = tokenizer.pad(batch, return_tensors="pt").to(model.device)
+ actual_batch_size = len(batch["input_ids"])
+ total_samples += actual_batch_size
+ sample += batch_size
+ if sample >= len(ds_train): # new epoch
+ sample = 0
+
+ # add labels, they are automatically shifted by transformers
+ labels = batch["input_ids"].clone()
+ # We want to ignore the padding tokens except for the first EOS token; if we don't ignore them, the loss
+ # will be dominated by padding tokens; if we ignore all, the model will not learn to predict the EOS token.
+ # TODO: Note that the longest sequence in the batch won't have any PAD/EOS token at the end, this is fine if
+ # the batch size is > 1 but should still be fixed eventually.
+ for i, num_tokens in enumerate(tokens_per_sample):
+ labels[i, num_tokens + 1 :] = -100
+ batch["labels"] = labels
+ num_items_in_batch = batch["attention_mask"].sum().item()
+
+ # train step
+ optimizer.zero_grad()
+ with autocast_ctx():
+ outputs = model(**batch, num_items_in_batch=num_items_in_batch)
+ loss = outputs.loss
+ grad_scaler.scale(loss).backward()
+ if grad_norm_clip:
+ grad_scaler.unscale_(optimizer)
+ torch.nn.utils.clip_grad_norm_(model.parameters(), grad_norm_clip)
+ grad_scaler.step(optimizer)
+ grad_scaler.update()
+ lr_scheduler.step()
+
+ if is_adalora:
+ model.base_model.update_and_allocate(step)
+
+ losses.append(loss.item())
+ pbar.set_postfix({"loss": loss.item()})
+ accelerator_memory_allocated_log.append(
+ torch_accelerator_module.memory_allocated() - accelerator_memory_init
+ )
+ accelerator_memory_reserved_log.append(
+ torch_accelerator_module.memory_reserved() - accelerator_memory_init
+ )
+ toc = time.perf_counter()
+ durations.append(toc - tic)
+
+ # every couple of steps, evaluate; this can be slow due to generation
+ if step % eval_steps == 0:
+ tic_eval = time.perf_counter()
+ loss_avg = sum(losses[-eval_steps:]) / eval_steps
+ memory_allocated_avg = sum(accelerator_memory_allocated_log[-eval_steps:]) / eval_steps
+ memory_reserved_avg = sum(accelerator_memory_reserved_log[-eval_steps:]) / eval_steps
+ token_sum = sum(total_tokens[-eval_steps:])
+ dur_train = sum(durations[-eval_steps:])
+ tokens_per_sec = token_sum / dur_train
+
+ model.eval()
+ predictions, responses = evaluate(
+ model=model,
+ tokenizer=tokenizer,
+ ds=ds_valid,
+ batch_size=batch_size_eval,
+ generate_kwargs={**generation_kwargs},
+ )
+ model.train()
+
+ example = random.choice(predictions)
+ example = textwrap.shorten(example, width=750)
+ example = textwrap.indent(example, " ")
+ print_verbose(f"\nExample prediction:\n{example}\n")
+ accuracy = get_accuracy(predictions=predictions, responses=responses)
+ num_tokens_generated = sum(sum(mask) for mask in tokenizer(predictions)["attention_mask"])
+
+ toc_eval = time.perf_counter()
+ dur_eval = toc_eval - tic_eval
+ eval_time += toc_eval - tic_eval
+ elapsed = time.perf_counter() - tic_train
+
+ metrics.append(
+ {
+ "step": step,
+ "valid accuracy": accuracy,
+ "train loss": loss_avg,
+ "train samples": total_samples,
+ "train time": dur_train,
+ "eval time": dur_eval,
+ "tokens / sec": tokens_per_sec,
+ "mem allocated avg": memory_allocated_avg,
+ "mem reserved avg": memory_reserved_avg,
+ "elapsed time": elapsed,
+ }
+ )
+
+ log_dict = {
+ "step": f"{step:5d}",
+ "samples": f"{total_samples:7d}",
+ "lr": f"{lr_scheduler.get_last_lr()[0]:.2e}",
+ "loss avg": f"{loss_avg:.4f}",
+ "valid acc": f"{accuracy:.3f}",
+ "gen valid tokens": num_tokens_generated,
+ "train time": f"{dur_train:.1f}s",
+ "eval time": f"{dur_eval:.1f}s",
+ "train tokens / sec": f"{tokens_per_sec:.0f}",
+ "mem allocated": f"{memory_allocated_avg:.0f}",
+ "mem reserved": f"{memory_reserved_avg:.0f}",
+ "elapsed time": f"{elapsed // 60:.0f}min {elapsed % 60:.0f}s",
+ }
+ print_verbose(json.dumps(log_dict))
+
+ # # TODO is this needed?
+ torch_accelerator_module.empty_cache()
+ gc.collect()
+
+ print_verbose(f"Training finished after {max_steps} steps, evaluation on test set follows.")
+ # test set evaluation
+ model.eval()
+ predictions, responses = evaluate(
+ model=model,
+ tokenizer=tokenizer,
+ ds=ds_test,
+ batch_size=batch_size_eval,
+ generate_kwargs={**generation_kwargs, "pad_token_id": tokenizer.eos_token_id},
+ use_tqdm=len(ds_test) > 100,
+ )
+ accuracy = get_accuracy(predictions=predictions, responses=responses)
+ metrics.append(
+ {
+ "step": step,
+ "test accuracy": accuracy,
+ "train loss": sum(losses[-eval_steps:]) / eval_steps,
+ "train samples": total_samples,
+ "train total tokens": sum(total_tokens),
+ }
+ )
+ print_verbose(f"Test accuracy: {accuracy:.3f}")
+
+ except KeyboardInterrupt:
+ print_verbose("canceled training")
+ status = TrainStatus.CANCELED
+ error_msg = "manually canceled"
+ except torch.OutOfMemoryError as exc:
+ # ouch, still let's try to log some results
+ print_verbose("out of memory error encountered")
+ status = TrainStatus.CANCELED
+ error_msg = str(exc)
+ except Exception as exc:
+ print_verbose(f"encountered an error: {exc}")
+ status = TrainStatus.CANCELED
+ error_msg = str(exc)
+
+ toc_train = time.perf_counter()
+ train_time = toc_train - tic_train - eval_time
+
+ if status != TrainStatus.CANCELED:
+ status = TrainStatus.SUCCESS
+ train_result = TrainResult(
+ status=status,
+ train_time=train_time,
+ accelerator_memory_reserved_log=accelerator_memory_reserved_log,
+ losses=losses,
+ metrics=metrics,
+ error_msg=error_msg,
+ num_trainable_params=num_trainable_params,
+ num_total_params=num_params,
+ )
+ return train_result
+
+
+def main(*, path_experiment: str, experiment_name: str, clean: bool) -> None:
+ tic_total = time.perf_counter()
+ start_date = dt.datetime.now(tz=dt.timezone.utc).replace(microsecond=0).isoformat()
+
+ peft_branch = get_peft_branch()
+ if peft_branch == "main":
+ print_verbose("===== This experiment is categorized as a MAIN run because the PEFT branch is 'main' ======")
+ else:
+ print_verbose(
+ f"===== This experiment is categorized as a TEST run because the PEFT branch is '{peft_branch}' ======"
+ )
+
+ # load configs
+ peft_config: Optional[PeftConfig] = None
+ if os.path.exists(os.path.join(path_experiment, CONFIG_NAME)):
+ peft_config = PeftConfig.from_pretrained(path_experiment)
+ else:
+ print_verbose(f"Could not find PEFT config at {path_experiment}, performing FULL FINETUNING")
+ path_train_config = os.path.join(path_experiment, FILE_NAME_TRAIN_PARAMS)
+ train_config = get_train_config(path_train_config)
+ set_seed(train_config.seed)
+
+ # initialize objects
+ accelerator_memory_init = init_accelerator()
+ tokenizer = get_tokenizer(model_id=train_config.model_id, max_seq_length=train_config.max_seq_length)
+
+ model_info = get_base_model_info(train_config.model_id)
+ metamath_info = get_dataset_info("meta-math/MetaMathQA")
+ gsm8k_info = get_dataset_info("openai/gsm8k")
+ model = get_model(
+ model_id=train_config.model_id,
+ dtype=train_config.dtype,
+ compile=train_config.compile,
+ attn_implementation=train_config.attn_implementation,
+ peft_config=peft_config,
+ autocast_adapter_dtype=train_config.autocast_adapter_dtype,
+ )
+ print_verbose(model)
+
+ # train model
+ train_result = train(
+ model=model,
+ max_steps=train_config.max_steps,
+ batch_size=train_config.batch_size,
+ batch_size_eval=train_config.batch_size_eval,
+ tokenizer=tokenizer,
+ accelerator_memory_init=accelerator_memory_init,
+ eval_steps=train_config.eval_steps,
+ generation_kwargs=train_config.generation_kwargs,
+ grad_norm_clip=train_config.grad_norm_clip,
+ optimizer_type=train_config.optimizer_type,
+ optimizer_kwargs=train_config.optimizer_kwargs,
+ query_template=train_config.query_template,
+ lr_scheduler_arg=train_config.lr_scheduler,
+ use_amp=train_config.use_amp,
+ is_adalora=isinstance(peft_config, AdaLoraConfig),
+ )
+
+ if train_result.status == TrainStatus.FAILED:
+ print_verbose("Training failed, not logging results")
+ sys.exit(1)
+
+ file_size = get_file_size(
+ model,
+ peft_config=peft_config,
+ clean=clean,
+ print_fn=print_verbose,
+ )
+
+ time_total = time.perf_counter() - tic_total
+ # log results: print and save to file
+ log_results(
+ experiment_name=experiment_name,
+ train_result=train_result,
+ accelerator_memory_init=accelerator_memory_init,
+ time_total=time_total,
+ file_size=file_size,
+ model_info=model_info,
+ datasets_info={"metamath": metamath_info, "gsm8k": gsm8k_info},
+ start_date=start_date,
+ train_config=train_config,
+ peft_config=peft_config,
+ print_fn=print_verbose,
+ )
+
+
+if __name__ == "__main__":
+ parser = argparse.ArgumentParser()
+ parser.add_argument("-v", "--verbose", action="store_true", help="Enable verbose output")
+ parser.add_argument("path_experiment", type=str, help="Path to the experiment directory")
+ parser.add_argument(
+ "--clean",
+ action="store_true",
+ help="Delete training artifacts after run finishes (logs are still saved)",
+ )
+ args = parser.parse_args()
+
+ experiment_name = validate_experiment_path(args.path_experiment)
+
+ if args.verbose:
+
+ def print_verbose(*args, **kwargs) -> None:
+ kwargs["file"] = sys.stderr
+ print(*args, **kwargs)
+ else:
+
+ def print_verbose(*args, **kwargs) -> None:
+ pass
+
+ main(
+ path_experiment=args.path_experiment,
+ experiment_name=experiment_name,
+ clean=args.clean,
+ )
diff --git a/peft/method_comparison/MetaMathQA/temporary_results/.gitkeep b/peft/method_comparison/MetaMathQA/temporary_results/.gitkeep
new file mode 100644
index 0000000000000000000000000000000000000000..e69de29bb2d1d6434b8b29ae775ad8c2e48c5391
diff --git a/peft/method_comparison/MetaMathQA/utils.py b/peft/method_comparison/MetaMathQA/utils.py
new file mode 100644
index 0000000000000000000000000000000000000000..d48a301b35b7759d947f18a121d906fce55b3fb4
--- /dev/null
+++ b/peft/method_comparison/MetaMathQA/utils.py
@@ -0,0 +1,709 @@
+# Copyright 2025-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""
+All utilities not related to data handling.
+"""
+
+import enum
+import json
+import os
+import platform
+import subprocess
+import tempfile
+import warnings
+from dataclasses import asdict, dataclass
+from decimal import Decimal, DivisionByZero, InvalidOperation
+from typing import Any, Callable, Literal, Optional
+
+import bitsandbytes
+import datasets
+import huggingface_hub
+import numpy as np
+import torch
+import transformers
+from torch import nn
+from transformers import (
+ AutoModelForCausalLM,
+ AutoTokenizer,
+ BitsAndBytesConfig,
+ get_cosine_schedule_with_warmup,
+)
+
+import peft
+from peft import PeftConfig, get_peft_model, prepare_model_for_kbit_training
+from peft.optimizers import create_lorafa_optimizer, create_loraplus_optimizer
+from peft.utils import infer_device, SAFETENSORS_WEIGHTS_NAME
+
+device = infer_device()
+
+if device not in ["cuda", "xpu"]:
+ raise RuntimeError("CUDA or XPU is not available, currently only CUDA or XPU is supported")
+
+ACCELERATOR_MEMORY_INIT_THRESHOLD = 500 * 2**20 # 500MB
+FILE_NAME_DEFAULT_TRAIN_PARAMS = os.path.join(os.path.dirname(__file__), "default_training_params.json")
+FILE_NAME_TRAIN_PARAMS = "training_params.json" # specific params for this experiment
+# main results
+RESULT_PATH = os.path.join(os.path.dirname(__file__), "results")
+# testing results
+RESULT_PATH_TEST = os.path.join(os.path.dirname(__file__), "temporary_results")
+# cancelled results
+RESULT_PATH_CANCELLED = os.path.join(os.path.dirname(__file__), "cancelled_results")
+hf_api = huggingface_hub.HfApi()
+WARMUP_STEP_RATIO = 0.1
+
+
+@dataclass
+class TrainConfig:
+ """All configuration parameters associated with training the model
+
+ Args:
+ model_id: The model identifier
+ dtype: The data type to use for the model
+ max_seq_length: The maximum sequence length
+ batch_size: The batch size for training
+ batch_size_eval: The batch size for eval/test, can be much higher than for training
+ max_steps: The maximum number of steps to train for
+ eval_steps: The number of steps between evaluations
+ compile: Whether to compile the model
+ query_template: The template for the query
+ seed: The random seed
+ grad_norm_clip: The gradient norm clipping value (set to 0 to skip)
+ optimizer_type: The name of a torch optimizer (e.g. AdamW) or a PEFT method ("lora+", "lora-fa")
+ optimizer_kwargs: The optimizer keyword arguments (lr etc.)
+ lr_scheduler: The learning rate scheduler (currently only None or 'cosine' are supported)
+ use_amp: Whether to use automatic mixed precision
+ autocast_adapter_dtype: Whether to cast adapter dtype to float32, same argument as in PEFT
+ generation_kwargs: Arguments passed to transformers GenerationConfig (used in evaluation)
+ attn_implementation: The attention implementation to use (if any), see transformers docs
+ """
+
+ model_id: str
+ dtype: Literal["float32", "float16", "bfloat16", "int8", "int4"]
+ max_seq_length: int
+ batch_size: int
+ batch_size_eval: int
+ max_steps: int
+ eval_steps: int
+ compile: bool
+ query_template: str
+ seed: int
+ grad_norm_clip: float # set to 0 to skip
+ optimizer_type: str
+ optimizer_kwargs: dict[str, Any]
+ lr_scheduler: Optional[Literal["cosine"]]
+ use_amp: bool
+ autocast_adapter_dtype: bool
+ generation_kwargs: dict[str, Any]
+ attn_implementation: Optional[str]
+
+ def __post_init__(self) -> None:
+ if not isinstance(self.model_id, str):
+ raise ValueError(f"Invalid model_id: {self.model_id}")
+ if self.dtype not in ["float32", "float16", "bfloat16", "int8", "int4"]:
+ raise ValueError(f"Invalid dtype: {self.dtype}")
+ if self.max_seq_length < 0:
+ raise ValueError(f"Invalid max_seq_length: {self.max_seq_length}")
+ if self.batch_size <= 0:
+ raise ValueError(f"Invalid batch_size: {self.batch_size}")
+ if self.batch_size_eval <= 0:
+ raise ValueError(f"Invalid eval batch_size: {self.batch_size_eval}")
+ if self.max_steps <= 0:
+ raise ValueError(f"Invalid max_steps: {self.max_steps}")
+ if self.eval_steps <= 0:
+ raise ValueError(f"Invalid eval_steps: {self.eval_steps}")
+ if self.eval_steps > self.max_steps:
+ raise ValueError(f"Invalid eval_steps: {self.eval_steps} > max_steps: {self.max_steps}")
+ if self.grad_norm_clip < 0:
+ raise ValueError(f"Invalid grad_norm_clip: {self.grad_norm_clip}")
+ if self.optimizer_type not in ["lora+", "lora-fa"] and not hasattr(torch.optim, self.optimizer_type):
+ raise ValueError(f"Invalid optimizer_type: {self.optimizer_type}")
+ if self.lr_scheduler not in [None, "cosine"]:
+ raise ValueError(f"Invalid lr_scheduler: {self.lr_scheduler}, must be None or 'cosine'")
+ if "{query}" not in self.query_template:
+ raise ValueError("Invalid query_template, must contain '{query}'")
+
+
+def validate_experiment_path(path: str) -> str:
+ # the experiment path should take the form of ./experiments//
+ # e.g. ./experiments/lora/rank32
+ # it should contain:
+ # - adapter_config.json
+ # - optional: training_params.json
+ if not os.path.exists(FILE_NAME_DEFAULT_TRAIN_PARAMS):
+ raise FileNotFoundError(
+ f"Missing default training params file '{FILE_NAME_DEFAULT_TRAIN_PARAMS}' in the ./experiments directory"
+ )
+ if not os.path.exists(path):
+ raise FileNotFoundError(f"Path {path} does not exist")
+
+ # check path structure
+ path_parts = path.rstrip(os.path.sep).split(os.path.sep)
+ if (len(path_parts) != 3) or (path_parts[-3] != "experiments"):
+ raise ValueError(
+ f"Path {path} does not have the correct structure, should be ./experiments//"
+ )
+
+ experiment_name = os.path.join(*path_parts[-2:])
+ return experiment_name
+
+
+def get_train_config(path: str) -> TrainConfig:
+ # first, load the default params, then update with experiment-specific params
+ with open(FILE_NAME_DEFAULT_TRAIN_PARAMS) as f:
+ default_config_kwargs = json.load(f)
+
+ config_kwargs = {}
+ if os.path.exists(path):
+ with open(path) as f:
+ config_kwargs = json.load(f)
+
+ config_kwargs = {**default_config_kwargs, **config_kwargs}
+ return TrainConfig(**config_kwargs)
+
+
+def init_accelerator() -> int:
+ torch_accelerator_module = getattr(torch, device, torch.cuda)
+ torch.manual_seed(0)
+ torch_accelerator_module.reset_peak_memory_stats()
+ torch_accelerator_module.manual_seed_all(0)
+ # might not be necessary, but just to be sure
+ nn.Linear(1, 1).to(device)
+
+ accelerator_memory_init = torch_accelerator_module.max_memory_reserved()
+ if accelerator_memory_init > ACCELERATOR_MEMORY_INIT_THRESHOLD:
+ raise RuntimeError(
+ f"{device} memory usage at start is too high: {accelerator_memory_init // 2**20}MB, please ensure that no other "
+ f"processes are running on {device}."
+ )
+
+ torch_accelerator_module.reset_peak_memory_stats()
+ accelerator_memory_init = torch_accelerator_module.max_memory_reserved()
+ return accelerator_memory_init
+
+
+def get_tokenizer(*, model_id: str, max_seq_length: int):
+ tokenizer = AutoTokenizer.from_pretrained(model_id)
+ tokenizer.model_max_length = max_seq_length
+ if not tokenizer.pad_token:
+ tokenizer.pad_token = tokenizer.eos_token
+ return tokenizer
+
+
+def get_base_model(
+ *,
+ model_id: str,
+ dtype: Literal["float32", "float16", "bfloat16", "int8", "int4"],
+ compile: bool,
+ attn_implementation: Optional[str],
+) -> nn.Module:
+ kwargs: dict[str, Any] = {
+ "pretrained_model_name_or_path": model_id,
+ "device_map": device,
+ "attn_implementation": attn_implementation,
+ }
+ if dtype == "int4":
+ quant_config = BitsAndBytesConfig(load_in_4bit=True)
+ kwargs["quantization_config"] = quant_config
+ elif dtype == "int8":
+ quant_config = BitsAndBytesConfig(load_in_8bit=True)
+ kwargs["quantization_config"] = quant_config
+ elif dtype == "bfloat16":
+ kwargs["torch_dtype"] = torch.bfloat16
+ elif dtype == "float16":
+ kwargs["torch_dtype"] = torch.float16
+ elif dtype != "float32":
+ raise ValueError(f"Invalid dtype: {dtype}")
+
+ model = AutoModelForCausalLM.from_pretrained(**kwargs)
+
+ if dtype in ["int8", "int4"]:
+ model = prepare_model_for_kbit_training(model)
+
+ if compile:
+ model = torch.compile(model)
+
+ return model
+
+
+def get_model(
+ *,
+ model_id: str,
+ dtype: Literal["float32", "float16", "bfloat16", "int8", "int4"],
+ compile: bool,
+ attn_implementation: Optional[str],
+ peft_config: Optional[PeftConfig],
+ autocast_adapter_dtype: bool,
+) -> nn.Module:
+ base_model = get_base_model(
+ model_id=model_id, dtype=dtype, compile=compile, attn_implementation=attn_implementation
+ )
+ if peft_config is None:
+ model = base_model
+ else:
+ model = get_peft_model(base_model, peft_config, autocast_adapter_dtype=autocast_adapter_dtype)
+ return model
+
+
+class DummyScheduler:
+ # if no lr scheduler is being used
+ def __init__(self, lr):
+ self.lr = lr
+
+ def get_last_lr(self):
+ return [self.lr]
+
+ def step(self):
+ pass
+
+
+def get_optimizer_and_scheduler(
+ model, *, optimizer_type: str, max_steps: int, lr_scheduler_arg: Optional[Literal["cosine"]], **optimizer_kwargs
+) -> tuple[torch.optim.Optimizer, Any]:
+ if optimizer_type == "lora+":
+ optimizer = create_loraplus_optimizer(model, optimizer_cls=torch.optim.AdamW, **optimizer_kwargs)
+ elif optimizer_type == "lora-fa":
+ optimizer = create_lorafa_optimizer(model, **optimizer_kwargs)
+ else:
+ cls = getattr(torch.optim, optimizer_type)
+ optimizer = cls(model.parameters(), **optimizer_kwargs)
+
+ if lr_scheduler_arg == "cosine":
+ warmup_steps = int(WARMUP_STEP_RATIO * max_steps)
+ lr_scheduler = get_cosine_schedule_with_warmup(
+ optimizer, num_warmup_steps=warmup_steps, num_training_steps=max_steps
+ )
+ elif lr_scheduler_arg is None:
+ lr_scheduler = DummyScheduler(optimizer_kwargs["lr"])
+ else:
+ raise ValueError(f"Invalid lr_scheduler argument: {lr_scheduler_arg}")
+
+ return optimizer, lr_scheduler
+
+
+class BucketIterator:
+ """
+ Iterator that yields batches of data from a torch Dataset, grouped in buckets by sequence length
+
+ The iterator will yield batches of size `batch_size`, where the samples in each batch are sorted by sequence length.
+ This is done to minimize the amount of padding required for each batch. To avoid sorting the entire dataset and thus
+ introducing a bias, the dataset is first split into buckets of size `batch_size * bucket_factor`.
+
+ Args:
+ ds: The torch Dataset to iterate over
+ batch_size: The batch size
+ bucket_factor: The factor by which to multiply the batch size to determine the bucket size
+ delete_cols: The columns to delete from the dataset before yielding a batch
+ """
+
+ def __init__(self, ds, *, batch_size: int, bucket_factor: int, delete_cols: list[str]) -> None:
+ self.ds = ds
+ self.batch_size = batch_size
+ self.bucket_factor = bucket_factor
+ self.delete_cols = set(delete_cols)
+
+ assert self.bucket_factor > 0, "bucket_factor must be greater than 0"
+
+ def _batch_iterator(self, bucket):
+ tokens_per_sample_bucket = torch.tensor([len(i) for i in bucket["input_ids"]])
+ # sort long to short instead to encounter possible OOM errors as early as possible
+ sorted = torch.argsort(tokens_per_sample_bucket, descending=True)
+ cls = type(bucket) # conserve the type returned by the ds
+ bucket = {k: [v[i] for i in sorted] for k, v in bucket.items() if k not in self.delete_cols}
+ num_samples = len(bucket["input_ids"])
+ for j in range(0, num_samples, self.batch_size):
+ batch = {k: v[j : j + self.batch_size] for k, v in bucket.items()}
+ yield cls(batch)
+
+ def __iter__(self):
+ bucket_size = self.batch_size * self.bucket_factor
+ for i in range(0, len(self.ds), bucket_size):
+ bucket = self.ds[i : i + bucket_size]
+ yield from self._batch_iterator(bucket)
+
+ # if there is a remainder, we yield the last batch
+ if len(self.ds) % bucket_size != 0:
+ bucket = self.ds[-(len(self.ds) % bucket_size) :]
+ yield from self._batch_iterator(bucket)
+
+
+def get_file_size(
+ model: nn.Module, *, peft_config: Optional[PeftConfig], clean: bool, print_fn: Callable[..., None]
+) -> int:
+ file_size = 99999999 # set a default dummy value
+ if peft_config is not None:
+ try:
+ with tempfile.TemporaryDirectory(ignore_cleanup_errors=True, delete=clean) as tmp_dir:
+ model.save_pretrained(tmp_dir)
+ stat = os.stat(os.path.join(tmp_dir, SAFETENSORS_WEIGHTS_NAME))
+ file_size = stat.st_size
+ if not clean:
+ print_fn(f"Saved PEFT checkpoint to {tmp_dir}")
+ except Exception as exc:
+ print(f"Failed to save PEFT checkpoint due to the following error: {exc}")
+ else:
+ print_fn("Not saving the fully fine-tuned model because it's too big, estimating the size instead")
+ try:
+ num_params = model.num_parameters()
+ dtype_size = next(model.parameters()).element_size()
+ file_size = num_params * dtype_size
+ except Exception as exc:
+ print(f"Failed to determine file size for fully finetuned model because of: {exc}")
+ return file_size
+
+
+##################
+# ANSWER PARSING #
+##################
+
+
+def parse_answer(text: str) -> Optional[str]:
+ """
+ A label/prediction can look like this:
+
+ Question: If the magnitude of vector v is equal to 4, what is the dot product of vector v with itself?. Think step
+ by step
+ Answer: The dot product of a vector with itself is equal to the square of its magnitude. So, the dot product of
+ vector v with itself is equal to $4^2 = \boxed{16}$.The answer is: 16
+
+ We want to extract '16' from this string.
+
+ """
+ # This implementation is based on sampling meta-llama/Llama-3.1-8B-Instruct. It may not work for other models.
+ candidate_delimiters = [
+ # MetaMath:
+ "The answer is: ",
+ "The answer is ",
+ "The final answer is: ",
+ "The final answer is ",
+ # GSM8K:
+ "#### ",
+ ]
+ text = text.strip()
+ text = text.rstrip(".!?")
+ for delimiter in candidate_delimiters:
+ if delimiter in text:
+ break
+ else: # no match
+ return None
+
+ text = text.rpartition(delimiter)[-1].strip()
+ # if a new paragraph follows after the final answer, we want to remove it
+ text = text.split("\n", 1)[0]
+ # note: we can just remove % here since the GSM8K dataset just omits it, i.e. 50% -> 50, no need to divide by 100
+ text = text.strip(" .!?$%")
+ return text
+
+
+def convert_to_decimal(s: Optional[str]) -> Optional[Decimal]:
+ """
+ Converts a string representing a number to a Decimal.
+
+ The string may be:
+ - A simple number (e.g., "13", "65.33")
+ - A fraction (e.g., "20/14")
+ """
+ if s is None:
+ return None
+
+ try:
+ s = s.strip()
+ # Check if the string represents a fraction.
+ if "/" in s:
+ parts = s.split("/")
+ if len(parts) != 2:
+ return None
+ numerator = Decimal(parts[0].strip())
+ denominator = Decimal(parts[1].strip())
+ if denominator == 0:
+ return None
+ value = numerator / denominator
+ else:
+ # Parse as a regular decimal or integer string.
+ value = Decimal(s)
+ return value
+ except (DivisionByZero, InvalidOperation, ValueError):
+ return None
+
+
+def get_accuracy(*, predictions: list[str], responses: list[str]) -> float:
+ if len(predictions) != len(responses):
+ raise ValueError(f"Prediction length mismatch: {len(predictions)} != {len(responses)}")
+
+ y_true: list[str | float | None] = []
+ y_pred: list[str | float | None] = []
+
+ for prediction, response in zip(predictions, responses):
+ parsed_prediction = parse_answer(prediction)
+ parsed_response = parse_answer(response)
+ if parsed_response is None:
+ raise ValueError(f"Error encountered while trying to parse response: {response}")
+
+ decimal_prediction = convert_to_decimal(parsed_prediction)
+ decimal_answer = convert_to_decimal(parsed_response)
+ if decimal_prediction is not None:
+ y_pred.append(float(decimal_prediction))
+ elif parsed_prediction is not None:
+ y_pred.append(parsed_prediction)
+ else:
+ y_pred.append(None)
+
+ # we convert decimals to float so that stuff like this works:
+ # float(convert_to_decimal('20/35')) == float(convert_to_decimal('0.5714285714285714'))
+ if decimal_answer is not None:
+ y_true.append(float(decimal_answer))
+ elif parsed_prediction is not None:
+ y_true.append(parsed_response)
+ else:
+ y_true.append(None)
+
+ correct: list[bool] = []
+ for true, pred in zip(y_true, y_pred):
+ if (true is not None) and (pred is not None):
+ correct.append(true == pred)
+ else:
+ correct.append(False)
+
+ accuracy = sum(correct) / len(correct)
+ return accuracy
+
+
+###########
+# LOGGING #
+###########
+
+
+def get_base_model_info(model_id: str) -> Optional[huggingface_hub.ModelInfo]:
+ try:
+ return hf_api.model_info(model_id)
+ except Exception as exc:
+ warnings.warn(f"Could not retrieve model info, failed with error {exc}")
+ return None
+
+
+def get_dataset_info(dataset_id: str) -> Optional[huggingface_hub.DatasetInfo]:
+ try:
+ return hf_api.dataset_info(dataset_id)
+ except Exception as exc:
+ warnings.warn(f"Could not retrieve dataset info, failed with error {exc}")
+ return None
+
+
+def get_git_hash(module) -> Optional[str]:
+ if "site-packages" in module.__path__[0]:
+ return None
+
+ return subprocess.check_output("git rev-parse HEAD".split(), cwd=os.path.dirname(module.__file__)).decode().strip()
+
+
+def get_package_info() -> dict[str, Optional[str]]:
+ """Get the package versions and commit hashes of transformers, peft, datasets, bnb, and torch"""
+ package_info = {
+ "transformers-version": transformers.__version__,
+ "transformers-commit-hash": get_git_hash(transformers),
+ "peft-version": peft.__version__,
+ "peft-commit-hash": get_git_hash(peft),
+ "datasets-version": datasets.__version__,
+ "datasets-commit-hash": get_git_hash(datasets),
+ "bitsandbytes-version": bitsandbytes.__version__,
+ "bitsandbytes-commit-hash": get_git_hash(bitsandbytes),
+ "torch-version": torch.__version__,
+ "torch-commit-hash": get_git_hash(torch),
+ }
+ return package_info
+
+
+def get_system_info() -> dict[str, str]:
+ device = infer_device()
+ torch_accelerator_module = getattr(torch, device, torch.cuda)
+ system_info = {
+ "system": platform.system(),
+ "release": platform.release(),
+ "version": platform.version(),
+ "machine": platform.machine(),
+ "processor": platform.processor(),
+ "accelerator": torch_accelerator_module.get_device_name(0),
+ }
+ return system_info
+
+
+@dataclass
+class MetaInfo:
+ package_info: dict[str, Optional[str]]
+ system_info: dict[str, str]
+ pytorch_info: str
+
+
+def get_meta_info() -> MetaInfo:
+ meta_info = MetaInfo(
+ package_info=get_package_info(),
+ system_info=get_system_info(),
+ pytorch_info=torch.__config__.show(),
+ )
+ return meta_info
+
+
+def get_peft_branch() -> str:
+ return (
+ subprocess.check_output("git rev-parse --abbrev-ref HEAD".split(), cwd=os.path.dirname(peft.__file__))
+ .decode()
+ .strip()
+ )
+
+
+class TrainStatus(enum.Enum):
+ FAILED = "failed"
+ SUCCESS = "success"
+ CANCELED = "canceled"
+
+
+@dataclass
+class TrainResult:
+ status: TrainStatus
+ train_time: float
+ accelerator_memory_reserved_log: list[int]
+ losses: list[float]
+ metrics: list[Any] # TODO
+ error_msg: str
+ num_trainable_params: int
+ num_total_params: int
+
+
+def log_to_console(log_data: dict[str, Any], print_fn: Callable[..., None]) -> None:
+ accelerator_memory_max = log_data["train_info"]["accelerator_memory_max"]
+ accelerator_memory_avg = log_data["train_info"]["accelerator_memory_reserved_avg"]
+ accelerator_memory_reserved_99th = log_data["train_info"]["accelerator_memory_reserved_99th"]
+ time_train = log_data["train_info"]["train_time"]
+ time_total = log_data["run_info"]["total_time"]
+ file_size = log_data["train_info"]["file_size"]
+
+ print_fn(f"accelerator memory max: {accelerator_memory_max // 2**20}MB")
+ print_fn(f"accelerator memory reserved avg: {accelerator_memory_avg // 2**20}MB")
+ print_fn(f"accelerator memory reserved 99th percentile: {accelerator_memory_reserved_99th // 2**20}MB")
+ print_fn(f"train time: {time_train}s")
+ print_fn(f"total time: {time_total:.2f}s")
+ print_fn(f"file size of checkpoint: {file_size / 2**20:.1f}MB")
+
+
+def log_to_file(
+ *, log_data: dict, save_dir: str, experiment_name: str, timestamp: str, print_fn: Callable[..., None]
+) -> None:
+ if save_dir.endswith(RESULT_PATH):
+ file_name = f"{experiment_name.replace(os.path.sep, '--')}.json"
+ else:
+ # For cancelled and temporary runs, we want to include the timestamp, as these runs are not tracked in git, thus
+ # we need unique names to avoid losing history.
+ file_name = f"{experiment_name.replace(os.path.sep, '--')}--{timestamp.replace(':', '-')}.json"
+ file_name = os.path.join(save_dir, file_name)
+ with open(file_name, "w") as f:
+ json.dump(log_data, f, indent=2)
+ print_fn(f"Saved log to: {file_name}")
+
+
+def log_results(
+ *,
+ experiment_name: str,
+ train_result: TrainResult,
+ accelerator_memory_init: int,
+ time_total: float,
+ file_size: int,
+ model_info: Optional[huggingface_hub.ModelInfo],
+ datasets_info: dict[str, Optional[huggingface_hub.DatasetInfo]],
+ start_date: str,
+ train_config: TrainConfig,
+ peft_config: Optional[PeftConfig],
+ print_fn: Callable[..., None],
+) -> None:
+ # collect results
+ device = infer_device()
+ torch_accelerator_module = getattr(torch, device, torch.cuda)
+ accelerator_memory_final = torch_accelerator_module.max_memory_reserved()
+ accelerator_memory_avg = int(
+ sum(train_result.accelerator_memory_reserved_log) / len(train_result.accelerator_memory_reserved_log)
+ )
+ accelerator_memory_reserved_99th = int(np.percentile(train_result.accelerator_memory_reserved_log, 99))
+
+ meta_info = get_meta_info()
+ if model_info is not None:
+ model_sha = model_info.sha
+ model_created_at = model_info.created_at.isoformat()
+ else:
+ model_sha = None
+ model_created_at = None
+
+ dataset_info_log = {}
+ for key, dataset_info in datasets_info.items():
+ if dataset_info is not None:
+ dataset_sha = dataset_info.sha
+ dataset_created_at = dataset_info.created_at.isoformat()
+ else:
+ dataset_sha = None
+ dataset_created_at = None
+ dataset_info_log[key] = {"sha": dataset_sha, "created_at": dataset_created_at}
+
+ peft_branch = get_peft_branch()
+
+ if train_result.status == TrainStatus.CANCELED:
+ save_dir = RESULT_PATH_CANCELLED
+ print_fn("Experiment run was categorized as canceled")
+ elif peft_branch != "main":
+ save_dir = RESULT_PATH_TEST
+ print_fn(f"Experiment run was categorized as a test run on branch {peft_branch}")
+ elif train_result.status == TrainStatus.SUCCESS:
+ save_dir = RESULT_PATH
+ print_fn("Experiment run was categorized as successful run")
+ else:
+ save_dir = tempfile.mkdtemp()
+ print_fn(f"Experiment could not be categorized, writing results to {save_dir}. Please open an issue on PEFT.")
+
+ if peft_config is None:
+ peft_config_dict: Optional[dict[str, Any]] = None
+ else:
+ peft_config_dict = peft_config.to_dict()
+ for key, value in peft_config_dict.items():
+ if isinstance(value, set):
+ peft_config_dict[key] = list(value)
+
+ log_data = {
+ "run_info": {
+ "created_at": start_date,
+ "total_time": time_total,
+ "experiment_name": experiment_name,
+ "peft_branch": peft_branch,
+ "train_config": asdict(train_config),
+ "peft_config": peft_config_dict,
+ "error_msg": train_result.error_msg,
+ },
+ "train_info": {
+ "accelerator_memory_reserved_avg": accelerator_memory_avg,
+ "accelerator_memory_max": (accelerator_memory_final - accelerator_memory_init),
+ "accelerator_memory_reserved_99th": accelerator_memory_reserved_99th,
+ "train_time": train_result.train_time,
+ "file_size": file_size,
+ "num_trainable_params": train_result.num_trainable_params,
+ "num_total_params": train_result.num_total_params,
+ "status": train_result.status.value,
+ "metrics": train_result.metrics,
+ },
+ "meta_info": {
+ "model_info": {"sha": model_sha, "created_at": model_created_at},
+ "dataset_info": dataset_info_log,
+ **asdict(meta_info),
+ },
+ }
+
+ log_to_console(log_data, print_fn=print) # use normal print to be able to redirect if so desired
+ log_to_file(
+ log_data=log_data, save_dir=save_dir, experiment_name=experiment_name, timestamp=start_date, print_fn=print_fn
+ )
diff --git a/peft/method_comparison/README.md b/peft/method_comparison/README.md
new file mode 100644
index 0000000000000000000000000000000000000000..c34fec0f9d0ef4de9342c539ca1e29642f4f6133
--- /dev/null
+++ b/peft/method_comparison/README.md
@@ -0,0 +1,116 @@
+---
+title: PEFT Method Comparison
+sdk: gradio
+app_file: app.py
+pinned: false
+emoji: ⚖️
+---
+
+# Comparison of PEFT Methods
+
+The goal of this project is to provide replicable experiments that produce outcomes allowing us to compare different PEFT methods with one another. This gives you more information to make an informed decision about which methods best fit your use case and what trade-offs to expect.
+
+Visit our [Gradio Space](https://huggingface.co/spaces/peft-internal-testing/PEFT-method-comparison) to check the results.
+
+## Community Contributions
+
+We envision the PEFT method comparison project as an ongoing endeavor with heavy involvement from the community. As maintainers, it is impossible for us to know all the perfect hyperparameters for each method or to predict all the use cases that PEFT users may have. As a consequence, community contributions are very welcome.
+
+Below, we outline all the ways you can contribute to this project.
+
+### Creating New Experiments
+
+Creating a new experiment requires setting up a new PEFT configuration for us to test. This will result in one more data point being added to the total comparison.
+
+Working on this is especially relevant if:
+
+1. You are the author of a paper whose method is introduced in PEFT, or worked on the PEFT integration, and know what hyperparameters work best.
+2. You have experience with a specific method and want to share your knowledge with the community.
+
+Of course, you can contribute even without meeting these criteria. Please follow the instructions below.
+
+#### How to Add New Experiments
+
+Start by navigating to one of the existing experiment folders, e.g. `peft/method_comparison/MetaMathQA`, if your experiment involves using the [MetaMathQA dataset](https://huggingface.co/datasets/meta-math/MetaMathQA). There, create a new directory inside the `experiments/` folder using a descriptive name. For example, if you want to test LoRA with rank 123 using Llama-3.2 3B as the base model, you could name the folder `experiments/lora/llama-3.2-3B-rank123`.
+
+Inside this directory, you will find a default configuration file called `default_training_params.json`, which contains the default parameters used in the `run.py` training script. Create a new JSON file containing all the parameters you want to modify compared to the defaults, and save it as `training_params.json` in the newly created folder. If you are satisfied with all the default training parameters, you can skip this step.
+
+Finally, you need to create a PEFT configuration file for the PEFT method you want to add. This should be a JSON file called `adapter_config.json`, placed in the same directory. Below is an example of how this could look:
+
+```python
+from peft import LoraConfig
+config = LoraConfig(r=123)
+config.save_pretrained("experiments/lora/llama-3.2-3B-rank123/")
+```
+
+Once you've created the configuration files for your experiment, please [create a PR on PEFT](https://github.com/huggingface/peft/pulls). After it is reviewed and merged, we will run it on our hardware to ensure that the results are comparable. Of course, it is best if you run the experiment at least once on your hardware to verify that the proposed settings work well.
+
+#### Considerations When Adding New Experiments
+
+When adding a new experiment, please consider the following points:
+
+1. Avoid changing too many training parameters at once, as this would make it difficult to compare results with existing ones. For example, if all existing results were created with 5000 training steps but your result uses 10000 steps, it would be unclear whether an improvement in the test score is due to the PEFT method itself or simply due to longer training. Similarly, using a completely different base model, especially if it is significantly more capable, does not contribute to a fair comparison.
+2. Avoid suggesting configurations that are very close to existing ones. For example, if there is already an experiment with LoRA and rank 123, do not add an experiment with LoRA and rank 124.
+3. Experiments for less-tested methods are more valuable than additional experiments for widely tested methods.
+4. Do not edit existing experiments, always create new ones.
+5. If you found hyper parameters that work especially well with a given method but are not trivial to find out, consider updating the PEFT documentation of that method so that other users can benefit from your findings.
+
+### Updating the Training Script
+
+We provide a training script that includes features typically useful for improving training outcomes, such as AMP support, a cosine learning rate schedule, etc. However, there is always room for improvement. For example, at the time of writing, the script does not support gradient accumulation. Therefore, PRs that extend the training script are welcome.
+
+#### How to Update the Training Script
+
+Follow the same process as when contributing to PEFT in general (see the [contribution guidelines](https://huggingface.co/docs/peft/developer_guides/contributing)). If the same training script is used across multiple datasets, please ensure that all relevant scripts are updated accordingly.
+
+#### Considerations When Updating the Training Script
+
+1. Updates should be backward-compatible. By default, any new features should be disabled to ensure that existing results remain valid. For example, if you add gradient accumulation, ensure it is disabled by default so that new experiments must opt in.
+2. Before adding a bug fix that could invalidate existing results, consider whether the trade-off is worthwhile. If we already have many experimental results, rerunning all of them can be expensive. If the bug fix is not critical, it may not be worth invalidating previous results. However, if you discover a significant bug that could meaningfully impact outcomes, it should be addressed.
+3. Avoid unnecessary complexity. While we could add support for DeepSpeed, FSDP, etc., doing so would add significant complexity, exclude users with limited hardware, and is unlikely to alter the relative performance of different PEFT methods.
+4. Minimize reliance on specific training frameworks. For example, we deliberately avoid using the `Trainer` class from transformers or PyTorch Lightning. This ensures transparency, making it easier to understand the training process and replicate results over time. If a training framework were used, we would have to pin the version or risk future incompatibilities.
+
+### Adding a New Dataset
+
+Adding a new dataset increases the breadth and usefulness of the PEFT method comparison. The goal is not necessarily to outperform benchmarks or replicate paper results, but to fairly compare different PEFT methods in a way that is useful for PEFT users. If this involves replicating an experiment from a paper, that is great, but it is not a requirement.
+
+#### How to Add a New Dataset
+
+The easiest way to add support for a new dataset is to copy an existing setup, such as `method_comparison/MetaMathQA`, rename it, and modify `data.py`, as well as any other necessary parts of the code. Ideally, as much existing code as possible should be reused. The general folder structure and experiment logging format should remain consistent.
+
+After adding the dataset, ensure it functions correctly and produces meaningful results by running at least one experimental setup, such as using LoRA with default settings.
+
+#### Considerations When Adding a New Dataset
+
+1. Before beginning, it is best to open an [issue on PEFT](https://github.com/huggingface/peft/issues) to share your plans. This allows for early feedback and prevents wasted effort on impractical ideas.
+2. The most valuable new datasets are those that test different capabilities than those already present. Bonus points if the task is similar to what users may face in the real world. Task ideas that would be great to add:
+ - A task involving both language and image modalities.
+ - An image generation task (like stable diffusion)
+ - A task involving audio (like whisper)
+ - A task that requires knowledge preservation (checked, for instance, via an auxiliary test set)
+ - Learning something completely new (e.g. a new language)
+ - A reinforcement learning task (e.g. using [trl](https://github.com/huggingface/trl))
+3. Training should be reasonably fast. Running dozens of experiments is impractical if each one takes multiple days and incurs high costs. Ideally, training should take a few hours at most on high-end consumer hardware.
+4. The chosen base model should not be too large, to avoid VRAM constraints. Morevoer, if the base model is too powerful, there is little room for improvement through further fine-tuning.
+5. Test scores should be informative and have a broad range:
+ - Besides loss, there should ideally be at least one additional metric, such as accuracy.
+ - Comparisons are not meaningful if all methods score near 0% or near 100%. The dataset should yield a range of scores to facilitate meaningful differentiation between methods.
+6. The dataset should be publicly available and have a track record as a useful dataset. The license should permit the intended usage.
+
+## Result dashboard
+
+For convenience, we included a [Gradio](https://www.gradio.app/) app that shows the results of the experiments. It allows you to filter down the task and base model and show the experiment results for this selection. Give it a try [here](https://huggingface.co/spaces/peft-internal-testing/PEFT-method-comparison).
+
+### Local deployment
+
+This app requires additional packages to be installed, please install the packages listed in `requirements-app.txt`, e.g. via:
+
+```sh
+python -m pip install -r requirements-app.txt
+```
+
+To launch the demo, run:
+
+```sh
+python app.py
+```
diff --git a/peft/method_comparison/__init__.py b/peft/method_comparison/__init__.py
new file mode 100644
index 0000000000000000000000000000000000000000..e69de29bb2d1d6434b8b29ae775ad8c2e48c5391
diff --git a/peft/method_comparison/app.py b/peft/method_comparison/app.py
new file mode 100644
index 0000000000000000000000000000000000000000..96444b6c155091ba2eee0da73cc0b7142cf6f4f7
--- /dev/null
+++ b/peft/method_comparison/app.py
@@ -0,0 +1,379 @@
+# Copyright 2025-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Gradio app to show the results"""
+
+import os
+import tempfile
+
+import gradio as gr
+import plotly.express as px
+import plotly.graph_objects as go
+from processing import load_df
+from sanitizer import parse_and_filter
+
+
+metric_preferences = {
+ "accelerator_memory_reserved_avg": "lower",
+ "accelerator_memory_max": "lower",
+ "accelerator_memory_reserved_99th": "lower",
+ "total_time": "lower",
+ "train_time": "lower",
+ "file_size": "lower",
+ "test_accuracy": "higher",
+ "train_loss": "lower",
+ "num_trainable_params": "lower",
+}
+
+
+def get_model_ids(task_name, df):
+ filtered = df[df["task_name"] == task_name]
+ return sorted(filtered["model_id"].unique())
+
+
+def filter_data(task_name, model_id, df):
+ filtered = df[(df["task_name"] == task_name) & (df["model_id"] == model_id)]
+ return filtered
+
+
+# Compute the Pareto frontier for two selected metrics.
+def compute_pareto_frontier(df, metric_x, metric_y):
+ if df.empty:
+ return df
+
+ df = df.copy()
+ points = df[[metric_x, metric_y]].values
+ selected_indices = []
+
+ def dominates(a, b, metric_x, metric_y):
+ # Check for each metric whether b is as good or better than a
+ if metric_preferences[metric_x] == "higher":
+ cond_x = b[0] >= a[0]
+ better_x = b[0] > a[0]
+ else:
+ cond_x = b[0] <= a[0]
+ better_x = b[0] < a[0]
+ if metric_preferences[metric_y] == "higher":
+ cond_y = b[1] >= a[1]
+ better_y = b[1] > a[1]
+ else:
+ cond_y = b[1] <= a[1]
+ better_y = b[1] < a[1]
+ return cond_x and cond_y and (better_x or better_y)
+
+ for i, point in enumerate(points):
+ dominated = False
+ for j, other_point in enumerate(points):
+ if i == j:
+ continue
+ if dominates(point, other_point, metric_x, metric_y):
+ dominated = True
+ break
+ if not dominated:
+ selected_indices.append(i)
+ pareto_df = df.iloc[selected_indices]
+ return pareto_df
+
+
+def generate_pareto_plot(df, metric_x, metric_y):
+ if df.empty:
+ return {}
+
+ # Compute Pareto frontier and non-frontier points.
+ pareto_df = compute_pareto_frontier(df, metric_x, metric_y)
+ non_pareto_df = df.drop(pareto_df.index)
+
+ # Create an empty figure.
+ fig = go.Figure()
+
+ # Draw the line connecting Pareto frontier points.
+ if not pareto_df.empty:
+ # Sort the Pareto frontier points by metric_x for a meaningful connection.
+ pareto_sorted = pareto_df.sort_values(by=metric_x)
+ line_trace = go.Scatter(
+ x=pareto_sorted[metric_x],
+ y=pareto_sorted[metric_y],
+ mode="lines",
+ line={"color": "rgba(0,0,255,0.3)", "width": 4},
+ name="Pareto Frontier",
+ )
+ fig.add_trace(line_trace)
+
+ # Add non-frontier points in gray with semi-transparency.
+ if not non_pareto_df.empty:
+ non_frontier_trace = go.Scatter(
+ x=non_pareto_df[metric_x],
+ y=non_pareto_df[metric_y],
+ mode="markers",
+ marker={"color": "rgba(128,128,128,0.5)", "size": 12},
+ hoverinfo="text",
+ text=non_pareto_df.apply(
+ lambda row: f"experiment_name: {row['experiment_name']}
"
+ f"peft_type: {row['peft_type']}
"
+ f"{metric_x}: {row[metric_x]}
"
+ f"{metric_y}: {row[metric_y]}",
+ axis=1,
+ ),
+ showlegend=False,
+ )
+ fig.add_trace(non_frontier_trace)
+
+ # Add Pareto frontier points with legend
+ if not pareto_df.empty:
+ pareto_scatter = px.scatter(
+ pareto_df,
+ x=metric_x,
+ y=metric_y,
+ color="experiment_name",
+ hover_data={"experiment_name": True, "peft_type": True, metric_x: True, metric_y: True},
+ )
+ for trace in pareto_scatter.data:
+ trace.marker = {"size": 12}
+ fig.add_trace(trace)
+
+ # Update layout with axes labels.
+ fig.update_layout(
+ title=f"Pareto Frontier for {metric_x} vs {metric_y}",
+ template="seaborn",
+ height=700,
+ autosize=True,
+ xaxis_title=metric_x,
+ yaxis_title=metric_y,
+ )
+
+ return fig
+
+
+def compute_pareto_summary(filtered, pareto_df, metric_x, metric_y):
+ if filtered.empty:
+ return "No data available."
+
+ stats = filtered[[metric_x, metric_y]].agg(["min", "max", "mean"]).to_string()
+ total_points = len(filtered)
+ pareto_points = len(pareto_df)
+ excluded_points = total_points - pareto_points
+ summary_text = (
+ f"{stats}\n\n"
+ f"Total points: {total_points}\n"
+ f"Pareto frontier points: {pareto_points}\n"
+ f"Excluded points: {excluded_points}"
+ )
+ return summary_text
+
+
+def export_csv(df):
+ if df.empty:
+ return None
+ csv_data = df.to_csv(index=False)
+ with tempfile.NamedTemporaryFile(delete=False, suffix=".csv", mode="w", encoding="utf-8") as tmp:
+ tmp.write(csv_data)
+ tmp_path = tmp.name
+ return tmp_path
+
+
+def format_df(df):
+ return df.style.format(precision=3, thousands=",", decimal=".")
+
+
+def build_app(df):
+ with gr.Blocks(theme=gr.themes.Soft()) as demo:
+ gr.Markdown("# PEFT method comparison")
+ gr.Markdown(
+ "Find more information [on the PEFT GitHub repo](https://github.com/huggingface/peft/tree/main/method_comparison)"
+ )
+
+ # Hidden state to store the current filter query.
+ filter_state = gr.State("")
+
+ gr.Markdown("## Choose the task and base model")
+ with gr.Row():
+ task_dropdown = gr.Dropdown(
+ label="Select Task",
+ choices=sorted(df["task_name"].unique()),
+ value=sorted(df["task_name"].unique())[0],
+ )
+ model_dropdown = gr.Dropdown(
+ label="Select Model ID", choices=get_model_ids(sorted(df["task_name"].unique())[0], df)
+ )
+
+ # Make dataframe columns all equal in width so that they are good enough for numbers but don't
+ # get hugely extended by columns like `train_config`.
+ column_widths = ["150px" for _ in df.columns]
+ column2index = dict(zip(df.columns, range(len(df.columns))))
+ column_widths[column2index['experiment_name']] = '300px'
+
+ data_table = gr.DataFrame(
+ label="Results",
+ value=format_df(df),
+ interactive=False,
+ max_chars=100,
+ wrap=False,
+ column_widths=column_widths,
+ )
+
+ with gr.Row():
+ filter_textbox = gr.Textbox(
+ label="Filter DataFrame",
+ placeholder="Enter filter (e.g.: peft_type=='LORA')",
+ interactive=True,
+ )
+ apply_filter_button = gr.Button("Apply Filter")
+ reset_filter_button = gr.Button("Reset Filter")
+
+ gr.Markdown("## Pareto plot")
+ gr.Markdown(
+ "Select 2 criteria to plot the Pareto frontier. This will show the best PEFT methods along this axis and "
+ "the trade-offs with the other axis. The PEFT methods that Pareto-dominate are shown in colors. All other "
+ "methods are inferior with regard to these two metrics. Hover over a point to show details."
+ )
+
+ with gr.Row():
+ x_default = (
+ "accelerator_memory_max"
+ if "accelerator_memory_max" in metric_preferences
+ else list(metric_preferences.keys())[0]
+ )
+ y_default = (
+ "test_accuracy" if "test_accuracy" in metric_preferences else list(metric_preferences.keys())[1]
+ )
+ metric_x_dropdown = gr.Dropdown(
+ label="1st metric for Pareto plot",
+ choices=list(metric_preferences.keys()),
+ value=x_default,
+ )
+ metric_y_dropdown = gr.Dropdown(
+ label="2nd metric for Pareto plot",
+ choices=list(metric_preferences.keys()),
+ value=y_default,
+ )
+
+ pareto_plot = gr.Plot(label="Pareto Frontier Plot")
+ summary_box = gr.Textbox(label="Summary Statistics", lines=6)
+ csv_output = gr.File(label="Export Filtered Data as CSV")
+
+ def update_on_task(task_name, current_filter):
+ new_models = get_model_ids(task_name, df)
+ filtered = filter_data(task_name, new_models[0] if new_models else "", df)
+ if current_filter.strip():
+ try:
+ mask = parse_and_filter(filtered, current_filter)
+ df_queried = filtered[mask]
+ if not df_queried.empty:
+ filtered = df_queried
+ except Exception:
+ # invalid filter query
+ pass
+ return gr.update(choices=new_models, value=new_models[0] if new_models else None), format_df(filtered)
+
+ task_dropdown.change(
+ fn=update_on_task, inputs=[task_dropdown, filter_state], outputs=[model_dropdown, data_table]
+ )
+
+ def update_on_model(task_name, model_id, current_filter):
+ filtered = filter_data(task_name, model_id, df)
+ if current_filter.strip():
+ try:
+ mask = parse_and_filter(filtered, current_filter)
+ filtered = filtered[mask]
+ except Exception:
+ pass
+ return format_df(filtered)
+
+ model_dropdown.change(
+ fn=update_on_model, inputs=[task_dropdown, model_dropdown, filter_state], outputs=data_table
+ )
+
+ def update_pareto_plot_and_summary(task_name, model_id, metric_x, metric_y, current_filter):
+ filtered = filter_data(task_name, model_id, df)
+ if current_filter.strip():
+ try:
+ mask = parse_and_filter(filtered, current_filter)
+ filtered = filtered[mask]
+ except Exception as e:
+ return generate_pareto_plot(filtered, metric_x, metric_y), f"Filter error: {e}"
+
+ pareto_df = compute_pareto_frontier(filtered, metric_x, metric_y)
+ fig = generate_pareto_plot(filtered, metric_x, metric_y)
+ summary = compute_pareto_summary(filtered, pareto_df, metric_x, metric_y)
+ return fig, summary
+
+ for comp in [model_dropdown, metric_x_dropdown, metric_y_dropdown]:
+ comp.change(
+ fn=update_pareto_plot_and_summary,
+ inputs=[task_dropdown, model_dropdown, metric_x_dropdown, metric_y_dropdown, filter_state],
+ outputs=[pareto_plot, summary_box],
+ )
+
+ def apply_filter(filter_query, task_name, model_id, metric_x, metric_y):
+ filtered = filter_data(task_name, model_id, df)
+ if filter_query.strip():
+ try:
+ mask = parse_and_filter(filtered, filter_query)
+ filtered = filtered[mask]
+ except Exception as e:
+ # Update the table, plot, and summary even if there is a filter error.
+ return (
+ filter_query,
+ filtered,
+ generate_pareto_plot(filtered, metric_x, metric_y),
+ f"Filter error: {e}",
+ )
+
+ pareto_df = compute_pareto_frontier(filtered, metric_x, metric_y)
+ fig = generate_pareto_plot(filtered, metric_x, metric_y)
+ summary = compute_pareto_summary(filtered, pareto_df, metric_x, metric_y)
+ return filter_query, format_df(filtered), fig, summary
+
+ apply_filter_button.click(
+ fn=apply_filter,
+ inputs=[filter_textbox, task_dropdown, model_dropdown, metric_x_dropdown, metric_y_dropdown],
+ outputs=[filter_state, data_table, pareto_plot, summary_box],
+ )
+
+ def reset_filter(task_name, model_id, metric_x, metric_y):
+ filtered = filter_data(task_name, model_id, df)
+ pareto_df = compute_pareto_frontier(filtered, metric_x, metric_y)
+ fig = generate_pareto_plot(filtered, metric_x, metric_y)
+ summary = compute_pareto_summary(filtered, pareto_df, metric_x, metric_y)
+ # Return empty strings to clear the filter state and textbox.
+ return "", "", format_df(filtered), fig, summary
+
+ reset_filter_button.click(
+ fn=reset_filter,
+ inputs=[task_dropdown, model_dropdown, metric_x_dropdown, metric_y_dropdown],
+ outputs=[filter_state, filter_textbox, data_table, pareto_plot, summary_box],
+ )
+
+ gr.Markdown("## Export data")
+ # Export button for CSV download.
+ export_button = gr.Button("Export Filtered Data")
+ export_button.click(
+ fn=lambda task, model: export_csv(filter_data(task, model, df)),
+ inputs=[task_dropdown, model_dropdown],
+ outputs=csv_output,
+ )
+
+ demo.load(
+ fn=update_pareto_plot_and_summary,
+ inputs=[task_dropdown, model_dropdown, metric_x_dropdown, metric_y_dropdown, filter_state],
+ outputs=[pareto_plot, summary_box],
+ )
+
+ return demo
+
+
+path = os.path.join(os.path.dirname(__file__), "MetaMathQA", "results")
+df = load_df(path, task_name="MetaMathQA")
+demo = build_app(df)
+demo.launch()
diff --git a/peft/method_comparison/processing.py b/peft/method_comparison/processing.py
new file mode 100644
index 0000000000000000000000000000000000000000..8f7460b9b6b68d0420cc1ea51e6db6abf6b1242a
--- /dev/null
+++ b/peft/method_comparison/processing.py
@@ -0,0 +1,147 @@
+# Copyright 2025-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Data processing used for analyzing and presenting the results"""
+
+import json
+import os
+
+import pandas as pd
+
+
+def preprocess(rows, task_name: str, print_fn=print):
+ results = []
+ skipped = 0
+ for row in rows:
+ run_info = row["run_info"]
+ train_info = row["train_info"]
+ meta_info = row["meta_info"]
+ if run_info["peft_config"]:
+ peft_type = run_info["peft_config"]["peft_type"]
+ else:
+ peft_type = "full-finetuning"
+ if train_info["status"] != "success":
+ skipped += 1
+ continue
+
+ train_metrics = train_info["metrics"][-1]
+
+ # extract the fields that make most sense
+ dct = {
+ "task_name": task_name,
+ "experiment_name": run_info["experiment_name"],
+ "model_id": run_info["train_config"]["model_id"],
+ "train_config": run_info["train_config"],
+ "peft_type": peft_type,
+ "peft_config": run_info["peft_config"],
+ "accelerator_memory_reserved_avg": train_info["accelerator_memory_reserved_avg"],
+ "accelerator_memory_max": train_info["accelerator_memory_max"],
+ "accelerator_memory_reserved_99th": train_info["accelerator_memory_reserved_99th"],
+ "total_time": run_info["total_time"],
+ "train_time": train_info["train_time"],
+ "file_size": train_info["file_size"],
+ "num_trainable_params": train_info["num_trainable_params"],
+ "test_accuracy": train_metrics["test accuracy"],
+ "train_loss": train_metrics["train loss"],
+ "train_samples": train_metrics["train samples"],
+ "train_total_tokens": train_metrics["train total tokens"],
+ "peft_version": meta_info["package_info"]["peft-version"],
+ "peft_branch": run_info["peft_branch"],
+ "transformers_version": meta_info["package_info"]["transformers-version"],
+ "datasets_version": meta_info["package_info"]["datasets-version"],
+ "torch_version": meta_info["package_info"]["torch-version"],
+ "bitsandbytes_version": meta_info["package_info"]["bitsandbytes-version"],
+ "package_info": meta_info["package_info"],
+ "system_info": meta_info["system_info"],
+ "created_at": run_info["created_at"],
+ }
+ results.append(dct)
+
+ if skipped:
+ print_fn(f"Skipped {skipped} of {len(rows)} entries because the train status != success")
+
+ return results
+
+
+def load_jsons(path):
+ results = []
+ for fn in os.listdir(path):
+ if fn.endswith(".json"):
+ with open(os.path.join(path, fn)) as f:
+ row = json.load(f)
+ results.append(row)
+ return results
+
+
+def load_df(path, task_name, print_fn=print):
+ jsons = load_jsons(path)
+ preprocessed = preprocess(jsons, task_name=task_name, print_fn=print_fn)
+ dtype_dict = {
+ "task_name": "string",
+ "experiment_name": "string",
+ "model_id": "string",
+ "train_config": "string",
+ "peft_type": "string",
+ "peft_config": "string",
+ "accelerator_memory_reserved_avg": int,
+ "accelerator_memory_max": int,
+ "accelerator_memory_reserved_99th": int,
+ "total_time": float,
+ "train_time": float,
+ "file_size": int,
+ "test_accuracy": float,
+ "train_loss": float,
+ "train_samples": int,
+ "train_total_tokens": int,
+ "num_trainable_params": int,
+ "peft_version": "string",
+ "peft_branch": "string",
+ "transformers_version": "string",
+ "datasets_version": "string",
+ "torch_version": "string",
+ "bitsandbytes_version": "string",
+ "package_info": "string",
+ "system_info": "string",
+ "created_at": "string",
+ }
+ df = pd.DataFrame(preprocessed)
+ df = df.astype(dtype_dict)
+ df["created_at"] = pd.to_datetime(df["created_at"])
+ # round training time to nearest second
+ df["train_time"] = df["train_time"].round().astype(int)
+ df["total_time"] = df["total_time"].round().astype(int)
+
+ # reorder columns for better viewing, pinned_columns arg in Gradio seems not to work correctly
+ important_columns = [
+ "experiment_name",
+ "peft_type",
+ "total_time",
+ "train_time",
+ "test_accuracy",
+ "train_loss",
+ "accelerator_memory_max",
+ "accelerator_memory_reserved_99th",
+ "accelerator_memory_reserved_avg",
+ "num_trainable_params",
+ "file_size",
+ "created_at",
+ "task_name",
+ ]
+ other_columns = [col for col in df if col not in important_columns]
+ df = df[important_columns + other_columns]
+
+ columns = ["experiment_name", "model_id", "peft_type", "created_at"]
+ # we want to keep only the most recent run for each experiment
+ df = df.sort_values("created_at").drop_duplicates(columns, keep="last")
+ return df
diff --git a/peft/method_comparison/requirements-app.txt b/peft/method_comparison/requirements-app.txt
new file mode 100644
index 0000000000000000000000000000000000000000..5fa065143fd408250351c885e334bba64ab5086e
--- /dev/null
+++ b/peft/method_comparison/requirements-app.txt
@@ -0,0 +1,3 @@
+dash
+gradio>=5.38.0
+pandas
diff --git a/peft/method_comparison/sanitizer.py b/peft/method_comparison/sanitizer.py
new file mode 100644
index 0000000000000000000000000000000000000000..7659d650c0fb293806d314f7334950ebaffbda33
--- /dev/null
+++ b/peft/method_comparison/sanitizer.py
@@ -0,0 +1,100 @@
+import ast
+
+import pandas as pd
+
+
+def _evaluate_node(df, node):
+ """
+ Recursively evaluates an AST node to generate a pandas boolean mask.
+ """
+ # Base Case: A simple comparison like 'price > 100'
+ if isinstance(node, ast.Compare):
+ if not isinstance(node.left, ast.Name):
+ raise ValueError("Left side of comparison must be a column name.")
+ col = node.left.id
+ if col not in df.columns:
+ raise ValueError(f"Column '{col}' not found in DataFrame.")
+
+ if len(node.ops) > 1:
+ raise ValueError("Chained comparisons like '10 < price < 100' are not supported.")
+
+ op_node = node.ops[0]
+ val_node = node.comparators[0]
+ try:
+ value = ast.literal_eval(val_node)
+ except ValueError:
+ raise ValueError("Right side of comparison must be a literal (number, string, list).")
+
+ operator_map = {
+ ast.Gt: lambda c, v: df[c] > v,
+ ast.GtE: lambda c, v: df[c] >= v,
+ ast.Lt: lambda c, v: df[c] < v,
+ ast.LtE: lambda c, v: df[c] <= v,
+ ast.Eq: lambda c, v: df[c] == v,
+ ast.NotEq: lambda c, v: df[c] != v,
+ ast.In: lambda c, v: df[c].isin(v),
+ ast.NotIn: lambda c, v: ~df[c].isin(v)
+ }
+ op_type = type(op_node)
+ if op_type not in operator_map:
+ raise ValueError(f"Unsupported operator '{op_type.__name__}'.")
+ return operator_map[op_type](col, value)
+
+ # Recursive Step: "Bitwise" operation & and | (the same as boolean operations)
+ elif isinstance(node, ast.BinOp):
+ if isinstance(node.op, ast.BitOr):
+ return _evaluate_node(df, node.left) | _evaluate_node(df, node.right)
+ elif isinstance(node.op, ast.BitAnd):
+ return _evaluate_node(df, node.left) & _evaluate_node(df, node.right)
+
+ # Recursive Step: A boolean operation like '... and ...' or '... or ...'
+ elif isinstance(node, ast.BoolOp):
+ op_type = type(node.op)
+ # Evaluate the first value in the boolean expression
+ result = _evaluate_node(df, node.values[0])
+ # Combine it with the rest of the values based on the operator
+ for i in range(1, len(node.values)):
+ if op_type is ast.And or op_type is ast.BitAnd:
+ result &= _evaluate_node(df, node.values[i])
+ elif op_type is ast.Or or op_type is ast.BitOr:
+ result |= _evaluate_node(df, node.values[i])
+ return result
+
+ elif isinstance(node, ast.UnaryOp):
+ if not isinstance(node.op, ast.Not):
+ raise ValueError("Only supported unary op is negation.")
+ return ~_evaluate_node(df, node.operand)
+
+ # If the node is not a comparison or boolean op, it's an unsupported expression type
+ else:
+ raise ValueError(f"Unsupported expression type: {type(node).__name__}")
+
+
+def parse_and_filter(df, filter_str):
+ """
+ Filters a pandas DataFrame using a string expression parsed by AST.
+ This is done to avoid the security vulnerables that `DataFrame.query`
+ brings (arbitrary code execution).
+
+ Args:
+ df (pd.DataFrame): The DataFrame to filter.
+ filter_str (str): A string representing a filter expression.
+ e.g., "price > 100 and stock < 50"
+ Supported operators: >, >=, <, <=, ==, !=, in, not in, and, or.
+
+ Returns:
+ pd.Series: A boolean Series representing the filter mask.
+ """
+ if not filter_str:
+ return pd.Series([True] * len(df), index=df.index)
+
+ try:
+ # 'eval' mode ensures the source is a single expression.
+ tree = ast.parse(filter_str, mode='eval')
+ expression_node = tree.body
+ except (SyntaxError, ValueError) as e:
+ raise ValueError(f"Invalid filter syntax: {e}")
+
+ # The recursive evaluation starts here
+ mask = _evaluate_node(df, expression_node)
+ return mask
diff --git a/peft/method_comparison/test_sanitizer.py b/peft/method_comparison/test_sanitizer.py
new file mode 100644
index 0000000000000000000000000000000000000000..59c0dd191e887aaeebbfce9dff9e88e6be0e2152
--- /dev/null
+++ b/peft/method_comparison/test_sanitizer.py
@@ -0,0 +1,38 @@
+import pandas as pd
+import pytest
+
+from .sanitizer import parse_and_filter
+
+
+@pytest.fixture
+def df_products():
+ data = {
+ 'product_id': [101, 102, 103, 104, 105, 106],
+ 'category': ['Electronics', 'Books', 'Electronics', 'Home Goods', 'Books', 'Electronics'],
+ 'price': [799.99, 19.99, 49.50, 120.00, 24.99, 150.00],
+ 'stock': [15, 300, 50, 25, 150, 0]
+ }
+ return pd.DataFrame(data)
+
+
+def test_exploit_fails(df_products):
+ with pytest.raises(ValueError) as e:
+ mask1 = parse_and_filter(df_products,
+ """price < 50 and @os.system("/bin/echo password")""")
+ assert 'Invalid filter syntax' in str(e)
+
+
+@pytest.mark.parametrize('expression,ids', [
+ ("price < 50", [102, 103, 105]),
+ ("product_id in [101, 102]", [101, 102]),
+ ("price < 50 and category == 'Electronics'", [103]),
+ ("stock < 100 or category == 'Home Goods'", [101, 103, 104, 106]),
+ ("(price > 100 and stock < 20) or category == 'Books'", [101, 102, 105, 106]),
+ ("not (price > 50 or stock > 100)", [103]),
+ ("not price > 50", [102, 103, 105]),
+ ("(price < 50) & (category == 'Electronics')", [103]),
+ ("(stock < 100) | (category == 'Home Goods')", [101, 103, 104, 106]),
+])
+def test_operations(df_products, expression, ids):
+ mask1 = parse_and_filter(df_products, expression)
+ assert sorted(df_products[mask1].product_id) == sorted(ids)
diff --git a/peft/method_comparison/text_generation_benchmark/README.md b/peft/method_comparison/text_generation_benchmark/README.md
new file mode 100644
index 0000000000000000000000000000000000000000..9f727fbf7276fa42501d65fca364b6201d1e0c57
--- /dev/null
+++ b/peft/method_comparison/text_generation_benchmark/README.md
@@ -0,0 +1,179 @@
+## Base Model Inference Caching
+
+The benchmarking suite uses a separate script, `run_base.py`, to measure base model inference times and save results for reuse. This should be run once per model configuration to avoid redundant computations and ensure consistent baseline metrics for all PEFT experiments.
+
+**Usage:**
+```bash
+python run_base.py
+```
+This will cache the base model inference results for the specified configuration. Subsequent runs of `run.py` will automatically load these cached results.
+
+# PEFT Benchmarking Suite
+
+This directory contains a comprehensive benchmarking framework for Parameter-Efficient Fine-Tuning (PEFT) methods. For the task of text generation, the suite measures inference performance, memory usage, and other key metrics across different PEFT configurations.
+
+## Overview
+
+The benchmarking suite provides:
+- **Inference time measurement** across different prompt categories
+- **Memory usage during inference** (RAM and GPU)
+- **Parameter efficiency metrics** (trainable vs total parameters)
+- **Time per token analysis** for fair comparison across different generation lengths
+- **Structured result logging** with detailed metadata
+
+## Architecture
+
+The suite follows a clean separation between:
+1. **Default benchmark configuration** - shared settings for consistent comparison
+2. **Individual adapter configurations** - PEFT-specific parameters for each experiment
+
+This ensures that all experiments are comparable while allowing flexibility in adapter parameters.
+
+## Quick Start
+
+### Running a Single Experiment
+
+```bash
+# From the peft_bench directory
+python run.py experiments/lora/lora_r8 --verbose
+```
+
+## Configuration Structure
+
+The benchmarking suite uses a hierarchical configuration system:
+
+1. **Default benchmark parameters** (`default_benchmark_params.json`) - Base configuration shared by all experiments
+2. **Experiment-specific overrides** (`benchmark_params.json` in each experiment) - Optional overrides for specific experiments
+3. **Adapter configuration** (`adapter_config.json` in each experiment) - PEFT method parameters
+
+This structure ensures consistent comparison while allowing flexibility where needed.
+
+### Default Configuration (`default_benchmark_params.json`)
+
+Contains shared benchmark settings that apply to all experiments. Here are the key configuration fields:
+
+- `model_id`: The Hugging Face model ID to use as the base model (e.g., "facebook/opt-350m")
+- `dtype`: Model precision ("float16", "float32", or "bfloat16")
+- `seed`: Random seed for reproducibility
+- `max_new_tokens`: Maximum number of tokens to generate during inference
+- `num_inference_runs`: Number of inference runs per prompt for statistical reliability
+- `use_4bit`: Whether to use 4-bit quantization (bool)
+- `use_8bit`: Whether to use 8-bit quantization (bool)
+
+Each experiment can override these settings by providing its own `benchmark_params.json` file.
+
+### Experiment Structure
+
+Each experiment directory should contain:
+
+1. `adapter_config.json`: PEFT adapter configuration. For details on available parameters and their meanings, refer to the [PEFT documentation](https://huggingface.co/docs/peft/main/en/developer_guides/adapters).
+
+2. (Optional) `benchmark_params.json`: Override specific benchmark parameters for this experiment.
+
+Example directory structure:
+```
+experiments/
+└── lora/
+ ├── lora_r8/ # LoRA rank 8 experiment
+ │ ├── adapter_config.json # PEFT adapter configuration
+ │ └── benchmark_params.json # Optional benchmark overrides
+ └── lora_r16/ # LoRA rank 16 experiment
+ └── adapter_config.json
+```
+
+### Experiment-Specific Overrides Example
+
+If an experiment needs different benchmark settings, create `benchmark_params.json`:
+```json
+{
+ "_comment": "Override settings for this specific experiment",
+ "max_new_tokens": 50,
+ "num_inference_runs": 15,
+ "num_prompt_samples": 2
+}
+```
+
+These parameters will override the defaults from `default_benchmark_params.json`. However, the defaults should generally not be changed to keep the results from the individual experiments comparable.
+
+### Create a New Experiment Adapter Configuration
+
+To create a new experiment, follow these steps:
+
+1. **Create the experiment directory**
+ ```bash
+ mkdir -p experiments/lora/lora_r8
+ ```
+
+2. **Generate the adapter configuration programmatically**
+ Use the PEFT library to create and save your adapter config:
+
+ ```python
+ from peft import LoraConfig
+
+ config = LoraConfig(
+ lora_alpha=16,
+ lora_dropout=0.1,
+ r=8,
+ target_modules=["q_proj", "v_proj"],
+ task_type="CAUSAL_LM"
+ )
+ config.save_pretrained("experiments/lora/lora_r8")
+ ```
+
+ This will create an `adapter_config.json` in your experiment directory. Adjust parameters as needed for your experiment.
+
+3. **(Optional) Add benchmark overrides**
+ If you need to override default benchmark settings, create a `benchmark_params.json` in the same directory.
+
+4. **Run the benchmark**
+ ```bash
+ python run.py experiments/lora/lora_r8 --verbose
+ ```
+
+## Prompt Categories
+
+The benchmark automatically runs across all prompt categories for consistent comparison:
+- **short** - Brief prompts (1-2 sentences)
+- **medium** - Moderate length prompts (paragraph-level)
+- **long** - Extended prompts (multiple paragraphs)
+
+Results are tracked separately for each category, allowing analysis of how different PEFT methods perform across varying input lengths.
+
+## Results Structure
+
+Results are saved in a structured JSON format with three main sections:
+
+### `run_info`
+- Execution metadata (timestamp, duration, status)
+- Hardware information (GPU type, CUDA version, etc.)
+- Error information (if applicable)
+- PEFT and benchmark configurations
+
+### `generation_info`
+- Memory usage logs at different stages
+- Per-category metrics (inference time, time per token, etc.)
+- Overall aggregated metrics
+- Individual sample results for detailed analysis
+
+### `meta_info`
+- Model information (ID, PEFT method)
+- Parameter counts (adapter, total, ratio)
+- Model size information (base model, adapter)
+- System and package information
+
+## Key Metrics
+
+### Inference Performance
+- **Inference Time**: Total time for generation per category
+- **Time Per Token**: Normalized time accounting for different generation lengths
+- **Inference Overhead**: Percentage increase compared to base model
+
+### Memory Usage
+- **Peak GPU Memory**: Maximum GPU memory during benchmark
+- **Peak RAM Memory**: Maximum RAM usage
+- **Memory Logs**: Detailed tracking at each stage
+
+### Parameter Efficiency
+- **Adapter Parameters**: Number of parameters in the PEFT adapter
+- **Parameter Ratio**: Percentage of total model parameters that are in the adapter
+- **Adapter Size**: Memory footprint of the adapter in MB
diff --git a/peft/method_comparison/text_generation_benchmark/cancelled_results/.gitkeep b/peft/method_comparison/text_generation_benchmark/cancelled_results/.gitkeep
new file mode 100644
index 0000000000000000000000000000000000000000..e69de29bb2d1d6434b8b29ae775ad8c2e48c5391
diff --git a/peft/method_comparison/text_generation_benchmark/configs/prompts.json b/peft/method_comparison/text_generation_benchmark/configs/prompts.json
new file mode 100644
index 0000000000000000000000000000000000000000..7768b420a0ff49511be9e689e659fb2c97022207
--- /dev/null
+++ b/peft/method_comparison/text_generation_benchmark/configs/prompts.json
@@ -0,0 +1,23 @@
+{
+ "short": [
+ "Explain quantum computing in one paragraph.",
+ "Write a haiku about machine learning.",
+ "What's the difference between supervised and unsupervised learning?",
+ "Define parameter-efficient fine-tuning in one sentence.",
+ "List three applications of natural language processing."
+ ],
+ "medium": [
+ "Explain the concept of low-rank adaptation (LoRA) for large language models. Include its benefits and limitations.",
+ "Compare and contrast prompt tuning and prefix tuning approaches for adapting large language models.",
+ "What are the key differences between full fine-tuning and parameter-efficient methods? Explain with examples.",
+ "Describe the process of quantization for neural networks and how it affects model size and inference speed.",
+ "Explain how sparse expert models like Mixture of Experts work and their advantages over dense models."
+ ],
+ "long": [
+ "Analyze the evolution of parameter-efficient fine-tuning methods from 2020 to present. Include a detailed comparison of at least five different approaches, their theoretical foundations, and practical implications for deploying large language models.",
+ "Provide a comprehensive tutorial on implementing LoRA for a transformer-based language model. Include code examples, hyperparameter selection guidance, and best practices for training and deployment.",
+ "Compare the computational efficiency, parameter count, and performance characteristics of different PEFT methods (LoRA, Prefix Tuning, Prompt Tuning, IA3, AdaLoRA) across various downstream tasks. Include a discussion of when each method is most appropriate.",
+ "Explain the mathematical foundations of various parameter-efficient fine-tuning techniques. Discuss how each technique modifies the original neural network architecture and the optimization challenges involved.",
+ "Discuss the ethical implications of parameter-efficient fine-tuning methods in democratizing access to large language models. Include considerations about computational resources, environmental impact, and accessibility for researchers in resource-constrained settings."
+ ]
+}
\ No newline at end of file
diff --git a/peft/method_comparison/text_generation_benchmark/data.py b/peft/method_comparison/text_generation_benchmark/data.py
new file mode 100644
index 0000000000000000000000000000000000000000..ce3343f1ca63a74908395d8789da6d58491efc4f
--- /dev/null
+++ b/peft/method_comparison/text_generation_benchmark/data.py
@@ -0,0 +1,119 @@
+# Copyright 2025-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""
+Data handling utilities for PEFT benchmarking.
+"""
+
+import json
+import os
+from typing import Optional
+
+from transformers import PreTrainedTokenizer
+from utils import BenchmarkConfig
+
+
+DEFAULT_PROMPTS_PATH = os.path.join(os.path.dirname(__file__), "configs", "prompts.json")
+
+
+def load_test_prompts(config: dict) -> dict[str, list[str]]:
+ """
+ Load prompts from JSON file.
+
+ Args:
+ config: Configuration containing prompts file path
+
+ Returns:
+ dictionary with prompts by category
+ """
+ prompts_file = getattr(config, "prompts_file", DEFAULT_PROMPTS_PATH)
+
+ with open(prompts_file) as f:
+ prompts = json.load(f)
+
+ return prompts
+
+
+def truncate_prompt_for_model(
+ prompt: str,
+ tokenizer: PreTrainedTokenizer,
+ max_length: Optional[int] = None,
+ reserve_output_tokens: int = 50,
+) -> str:
+ """
+ Truncate a prompt to fit within the model's context window.
+
+ Args:
+ prompt: Input prompt
+ tokenizer: Model tokenizer
+ max_length: Maximum sequence length (if None, uses model's max_length)
+ reserve_output_tokens: Number of tokens to reserve for response
+
+ Returns:
+ Truncated prompt
+ """
+ if max_length is None:
+ if hasattr(tokenizer, "model_max_length"):
+ max_length = tokenizer.model_max_length
+ else:
+ max_length = 2048
+
+ max_prompt_length = max_length - reserve_output_tokens
+ input_ids = tokenizer.encode(prompt, return_tensors="pt")[0]
+
+ if len(input_ids) <= max_prompt_length:
+ return prompt
+
+ truncated_ids = input_ids[:max_prompt_length]
+ truncated_prompt = tokenizer.decode(truncated_ids, skip_special_tokens=True)
+
+ return truncated_prompt
+
+
+def prepare_benchmark_prompts(
+ config: BenchmarkConfig,
+ tokenizer: PreTrainedTokenizer,
+ max_input_length: Optional[int] = None,
+ seed: int = 42,
+) -> dict[str, list[str]]:
+ """
+ Prepare prompts for benchmarking, ensuring appropriate length and variety.
+ Always returns all prompt categories for consistent benchmarking.
+
+ Args:
+ config: Benchmark configuration
+ tokenizer: Model tokenizer
+ max_input_length: Maximum input length (overrides model default if provided)
+ seed: Random seed (kept for backwards compatibility)
+
+ Returns:
+ Dictionary with processed prompts by category (all categories included)
+ """
+ all_prompts = load_test_prompts(config)
+
+ processed_prompts = {}
+ for category, prompts in all_prompts.items():
+ truncated_prompts = [
+ truncate_prompt_for_model(
+ prompt,
+ tokenizer,
+ max_length=max_input_length,
+ reserve_output_tokens=getattr(config, "reserve_output_tokens", 50),
+ )
+ for prompt in prompts
+ ]
+
+ processed_prompts[category] = truncated_prompts
+
+ return processed_prompts
diff --git a/peft/method_comparison/text_generation_benchmark/default_benchmark_params.json b/peft/method_comparison/text_generation_benchmark/default_benchmark_params.json
new file mode 100644
index 0000000000000000000000000000000000000000..c7d9a148e53d5975b66c641e3f6269519cc7bb82
--- /dev/null
+++ b/peft/method_comparison/text_generation_benchmark/default_benchmark_params.json
@@ -0,0 +1,12 @@
+{
+ "model_id": "meta-llama/Llama-3.2-3B",
+ "dtype": "float16",
+ "seed": 42,
+ "num_inference_runs": 10,
+ "max_new_tokens": 20,
+ "category_generation_params": {
+ "short": {"max_new_tokens": 20},
+ "medium": {"max_new_tokens": 50},
+ "long": {"max_new_tokens": 100}
+ }
+}
diff --git a/peft/method_comparison/text_generation_benchmark/experiments/lora/lora_r8/adapter_config.json b/peft/method_comparison/text_generation_benchmark/experiments/lora/lora_r8/adapter_config.json
new file mode 100644
index 0000000000000000000000000000000000000000..f3fd26121a544399ccc14f9cbb017a7ba3abeac2
--- /dev/null
+++ b/peft/method_comparison/text_generation_benchmark/experiments/lora/lora_r8/adapter_config.json
@@ -0,0 +1,17 @@
+{
+ "base_model_name_or_path": null,
+ "bias": "none",
+ "fan_in_fan_out": false,
+ "inference_mode": false,
+ "init_lora_weights": true,
+ "lora_alpha": 16,
+ "lora_dropout": 0.1,
+ "modules_to_save": null,
+ "peft_type": "LORA",
+ "r": 8,
+ "target_modules": [
+ "q_proj",
+ "v_proj"
+ ],
+ "task_type": "CAUSAL_LM"
+}
diff --git a/peft/method_comparison/text_generation_benchmark/results/.gitkeep b/peft/method_comparison/text_generation_benchmark/results/.gitkeep
new file mode 100644
index 0000000000000000000000000000000000000000..e69de29bb2d1d6434b8b29ae775ad8c2e48c5391
diff --git a/peft/method_comparison/text_generation_benchmark/run.py b/peft/method_comparison/text_generation_benchmark/run.py
new file mode 100644
index 0000000000000000000000000000000000000000..1cfba8931f29cf8571a89253859781a16e2203a8
--- /dev/null
+++ b/peft/method_comparison/text_generation_benchmark/run.py
@@ -0,0 +1,358 @@
+# Copyright 2025-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""
+Main entry point to run the experiments. Contains general setup and the proper inference code.
+"""
+
+import argparse
+import gc
+import json
+import os
+import sys
+import time
+from typing import Optional
+
+import bitsandbytes
+import torch
+import transformers
+from data import prepare_benchmark_prompts
+from transformers import AutoModelForCausalLM, AutoTokenizer, BitsAndBytesConfig, set_seed
+from utils import (
+ BenchmarkConfig,
+ BenchmarkResult,
+ BenchmarkStatus,
+ get_memory_usage,
+ init_accelerator,
+ log_results,
+ validate_experiment_path,
+)
+
+import peft
+from peft import PeftConfig, get_peft_model
+
+
+def load_base_results(model_id: str) -> Optional[dict]:
+ """Load base model results if they exist."""
+ base_results_dir = os.path.join(os.path.dirname(__file__), "base_results")
+ model_name = model_id.replace("/", "_").replace("-", "_")
+ filename = f"base_{model_name}.json"
+ filepath = os.path.join(base_results_dir, filename)
+
+ if os.path.exists(filepath):
+ with open(filepath) as f:
+ return json.load(f)
+ return None
+
+
+def measure_inference_time(model, tokenizer, prompts, max_new_tokens, num_runs, print_fn, category_generation_params):
+ """Measure inference time for each prompt category."""
+ inference_times = {}
+ time_per_token = {}
+ generated_tokens = {}
+ individual_samples = {}
+
+ for category, category_prompts in prompts.items():
+ print_fn(f"\nMeasuring inference time for {category} prompts...")
+ category_times = []
+ category_tokens = []
+ category_time_per_token = []
+ category_samples = []
+
+ for prompt in category_prompts:
+ prompt_times = []
+ prompt_tokens = []
+ prompt_time_per_token = []
+
+ inputs = tokenizer(prompt, return_tensors="pt").to(model.device)
+
+ cat_max_new_tokens = category_generation_params.get(category, {}).get("max_new_tokens", max_new_tokens)
+
+ for _ in range(num_runs):
+ start_time = time.perf_counter()
+ outputs = model.generate(
+ **inputs,
+ max_new_tokens=cat_max_new_tokens,
+ min_new_tokens=cat_max_new_tokens,
+ pad_token_id=tokenizer.pad_token_id,
+ )
+ end_time = time.perf_counter()
+
+ # Calculate metrics
+ inference_time = end_time - start_time
+ num_tokens = len(outputs[0]) - len(inputs["input_ids"][0])
+ time_per_token_val = inference_time / num_tokens if num_tokens > 0 else 0
+
+ prompt_times.append(inference_time)
+ prompt_tokens.append(num_tokens)
+ prompt_time_per_token.append(time_per_token_val)
+
+ # Calculate averages for this prompt
+ avg_time = sum(prompt_times) / len(prompt_times)
+ avg_tokens = sum(prompt_tokens) / len(prompt_tokens)
+ avg_time_per_token = sum(prompt_time_per_token) / len(prompt_time_per_token)
+
+ sample_result = {
+ "inference_time": avg_time,
+ "generated_tokens": avg_tokens,
+ "time_per_token": avg_time_per_token,
+ "individual_runs": [
+ {"inference_time": t, "generated_tokens": tok, "time_per_token": tpt}
+ for t, tok, tpt in zip(prompt_times, prompt_tokens, prompt_time_per_token)
+ ],
+ }
+ category_samples.append(sample_result)
+
+ category_times.append(avg_time)
+ category_tokens.append(avg_tokens)
+ category_time_per_token.append(avg_time_per_token)
+
+ if category_times:
+ avg_category_time = sum(category_times) / len(category_times)
+ avg_category_tokens = sum(category_tokens) / len(category_tokens)
+ avg_category_time_per_token = sum(category_time_per_token) / len(category_time_per_token)
+
+ inference_times[category] = avg_category_time
+ generated_tokens[category] = avg_category_tokens
+ time_per_token[category] = avg_category_time_per_token
+ individual_samples[category] = category_samples
+
+ return {
+ "inference_times": inference_times,
+ "time_per_token": time_per_token,
+ "generated_tokens": generated_tokens,
+ "individual_samples": individual_samples,
+ }
+
+
+def run_benchmark(
+ benchmark_config: BenchmarkConfig, experiment_name: str, experiment_path: str, print_fn=print
+) -> BenchmarkResult:
+ """Run benchmarks for the specified PEFT method configuration."""
+ result = BenchmarkResult(
+ experiment_name=experiment_name,
+ status=BenchmarkStatus.RUNNING,
+ model_id=benchmark_config.model_id,
+ )
+
+ result.save()
+
+ start_time = time.perf_counter()
+ e_main_benchmark: Optional[Exception] = None
+
+ try:
+ print_fn("Initializing accelerator...")
+ accelerator_allocated_init, accelerator_reserved_init = init_accelerator()
+ set_seed(benchmark_config.seed)
+
+ print_fn(f"Loading base model: {benchmark_config.model_id}")
+ tokenizer = AutoTokenizer.from_pretrained(benchmark_config.model_id)
+ if tokenizer.pad_token is None:
+ tokenizer.pad_token = tokenizer.eos_token
+
+ model_kwargs = {
+ "device_map": "auto" if (torch.cuda.is_available() or torch.xpu.is_available()) else None,
+ }
+
+ if benchmark_config.dtype == "float32":
+ model_kwargs["torch_dtype"] = torch.float32
+ elif benchmark_config.dtype == "float16":
+ model_kwargs["torch_dtype"] = torch.float16
+ elif benchmark_config.dtype == "bfloat16":
+ model_kwargs["torch_dtype"] = torch.bfloat16
+ else:
+ raise ValueError(f"Unsupported dtype: {benchmark_config.dtype}")
+
+ if benchmark_config.use_8bit:
+ model_kwargs["quantization_config"] = BitsAndBytesConfig(
+ load_in_8bit=True, llm_int8_enable_fp32_cpu_offload=True
+ )
+ elif benchmark_config.use_4bit:
+ model_kwargs["quantization_config"] = BitsAndBytesConfig(
+ load_in_4bit=True,
+ bnb_4bit_compute_dtype=model_kwargs.get("torch_dtype", torch.float16),
+ bnb_4bit_use_double_quant=True,
+ bnb_4bit_quant_type="nf4",
+ )
+
+ base_model = AutoModelForCausalLM.from_pretrained(benchmark_config.model_id, **model_kwargs)
+
+ base_results = load_base_results(benchmark_config.model_id)
+
+ print_fn("Preparing benchmark prompts...")
+ prompts = prepare_benchmark_prompts(
+ config=benchmark_config,
+ tokenizer=tokenizer,
+ max_input_length=None,
+ seed=benchmark_config.seed,
+ )
+
+ if base_results:
+ print_fn("Using cached base model results...")
+ base_inference_times = base_results["inference_results"]
+ else:
+ raise FileNotFoundError(
+ "No cached base results found. Please run `python run_base.py` first to generate base model results."
+ )
+
+ try:
+ print_fn(f"Loading PEFT config from {experiment_path}")
+ peft_config = PeftConfig.from_pretrained(experiment_path)
+ print_fn(f"Loaded PEFT config: {peft_config.peft_type}, with parameters: {vars(peft_config)}")
+ model = get_peft_model(base_model, peft_config)
+ except Exception as exc:
+ error_msg = f"Error loading PEFT config: {str(exc)}"
+ print_fn(error_msg)
+
+ del base_model
+ gc.collect()
+ if torch.cuda.is_available():
+ torch.cuda.empty_cache()
+ elif torch.xpu.is_available():
+ torch.xpu.empty_cache()
+
+ ram, accelerator_allocated, accelerator_reserved = get_memory_usage()
+ result.add_memory_log("peft_model_loaded", ram, accelerator_allocated, accelerator_reserved)
+
+ # Calculate PEFT model metrics
+ trainable_params = model.get_nb_trainable_parameters()[0]
+ total_params = sum(p.numel() for p in model.parameters())
+ base_params = sum(p.numel() for p in model.base_model.parameters())
+ dtype_bytes = 2 if benchmark_config.dtype in ["float16", "bfloat16"] else 4
+ adapter_size_mb = trainable_params * dtype_bytes / (1024 * 1024)
+ base_model_size_mb = base_params * dtype_bytes / (1024 * 1024)
+ param_ratio = trainable_params / total_params if total_params > 0 else 0
+
+ result.update_meta_info(
+ param_counts={
+ "base_params": base_params,
+ "trainable_params": trainable_params,
+ "total_params": total_params,
+ "param_ratio": param_ratio,
+ },
+ size_info={"base_model_size_mb": base_model_size_mb, "adapter_size_mb": adapter_size_mb},
+ package_info={
+ "transformers-version": transformers.__version__,
+ "peft-version": peft.__version__,
+ "bitsandbytes-version": bitsandbytes.__version__ if hasattr(bitsandbytes, "__version__") else None,
+ },
+ )
+
+ print_fn("Measuring PEFT model inference times...")
+ peft_inference_times = measure_inference_time(
+ model,
+ tokenizer,
+ prompts,
+ max_new_tokens=benchmark_config.max_new_tokens,
+ num_runs=benchmark_config.num_inference_runs,
+ print_fn=print_fn,
+ category_generation_params=benchmark_config.category_generation_params,
+ )
+
+ # Calculate inference overhead for each category
+ inference_overhead = {
+ k: (peft_inference_times["inference_times"][k] - base_inference_times["inference_times"][k])
+ / base_inference_times["inference_times"][k]
+ * 100
+ for k in base_inference_times["inference_times"]
+ }
+
+ for category in prompts:
+ category_metrics = {
+ "inference_time": peft_inference_times["inference_times"][category],
+ "base_inference_time": base_inference_times["inference_times"][category],
+ "inference_overhead_pct": inference_overhead[category],
+ "time_per_token": peft_inference_times["time_per_token"][category],
+ "generated_tokens": peft_inference_times["generated_tokens"][category],
+ }
+ result.add_metrics_for_category(
+ category, category_metrics, individual_samples=peft_inference_times["individual_samples"][category]
+ )
+
+ result.update_generation_info(
+ memory_data={
+ "peak_accelerator_memory_mb": max(
+ (log["accelerator_allocated_mb"] for log in result.generation_info["memory"]["memory_logs"]), default=0
+ ),
+ "peak_ram_memory_mb": max(
+ (log["ram_mb"] for log in result.generation_info["memory"]["memory_logs"]), default=0
+ ),
+ }
+ )
+
+ ram, accelerator_allocated, accelerator_reserved = get_memory_usage()
+ result.add_memory_log("benchmark_complete", ram, accelerator_allocated, accelerator_reserved)
+
+ result.status = BenchmarkStatus.SUCCESS
+
+ except Exception as exc:
+ print_fn(f"Benchmark failed with error: {exc}")
+ result.status = BenchmarkStatus.FAILED
+ e_main_benchmark = exc
+ end_time = time.perf_counter()
+ error_message = str(e_main_benchmark) if e_main_benchmark is not None else None
+
+ peft_config_dict = peft_config.to_dict() if "peft_config" in locals() else None
+ if peft_config_dict:
+ for key, value in peft_config_dict.items():
+ if isinstance(value, set):
+ peft_config_dict[key] = list(value)
+
+ result.update_run_info(
+ duration=end_time - start_time,
+ status=result.status,
+ error=error_message,
+ peft_config=peft_config_dict,
+ benchmark_config=benchmark_config.to_dict(),
+ )
+
+ return result
+
+
+def main() -> None:
+ """Main entry point for the benchmark runner."""
+ parser = argparse.ArgumentParser(description="Run PEFT method benchmarks")
+ parser.add_argument("experiment_path", help="Path to experiment directory")
+ parser.add_argument("--verbose", "-v", action="store_true", help="Enable verbose output")
+ args = parser.parse_args()
+
+ print_fn = print if args.verbose else lambda *args, **kwargs: None
+
+ experiment_path = args.experiment_path
+ allowed_root = os.path.abspath(os.path.join(os.path.dirname(__file__)))
+ abs_experiment_path = os.path.abspath(experiment_path)
+ if not abs_experiment_path.startswith(allowed_root):
+ print(f"Experiment path must be inside {allowed_root}, got: {abs_experiment_path}. Skipping execution.")
+ return 0
+ if not os.path.exists(abs_experiment_path):
+ print(f"Experiment path not found: {abs_experiment_path}. Skipping execution.")
+ return 0
+ experiment_path = abs_experiment_path
+
+ experiment_name, benchmark_config = validate_experiment_path(experiment_path)
+
+ print_fn(f"Running benchmark for experiment: {experiment_name}")
+
+ result = run_benchmark(
+ benchmark_config=benchmark_config,
+ experiment_name=experiment_name,
+ experiment_path=experiment_path,
+ print_fn=print_fn,
+ )
+
+ log_results(experiment_name, result, print_fn=print)
+
+
+if __name__ == "__main__":
+ sys.exit(main())
diff --git a/peft/method_comparison/text_generation_benchmark/run_base.py b/peft/method_comparison/text_generation_benchmark/run_base.py
new file mode 100644
index 0000000000000000000000000000000000000000..1489cff08786e76473bcdcd237afd365594d9a63
--- /dev/null
+++ b/peft/method_comparison/text_generation_benchmark/run_base.py
@@ -0,0 +1,185 @@
+# Copyright 2025-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+# Copyright 2025-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+import argparse
+import json
+import os
+import sys
+import time
+
+import torch
+from data import prepare_benchmark_prompts
+from run import measure_inference_time
+from transformers import AutoModelForCausalLM, AutoTokenizer, BitsAndBytesConfig, set_seed
+from utils import (
+ BenchmarkConfig,
+ get_memory_usage,
+ init_accelerator,
+)
+
+
+def run_base_model_benchmark(benchmark_config: BenchmarkConfig, print_fn=print) -> dict:
+ """Run benchmark for base model only and return results."""
+
+ print_fn(f"Running base model benchmark for: {benchmark_config.model_id}")
+
+ print_fn("Initializing accelerator...")
+ init_accelerator()
+
+ set_seed(benchmark_config.seed)
+
+ print_fn(f"Loading base model: {benchmark_config.model_id}")
+ tokenizer = AutoTokenizer.from_pretrained(benchmark_config.model_id)
+ if tokenizer.pad_token is None:
+ tokenizer.pad_token = tokenizer.eos_token
+
+ model_kwargs = {
+ "device_map": "auto" if (torch.cuda.is_available() or torch.xpu.is_available()) else None,
+ }
+
+ if benchmark_config.dtype == "float32":
+ model_kwargs["torch_dtype"] = torch.float32
+ elif benchmark_config.dtype == "float16":
+ model_kwargs["torch_dtype"] = torch.float16
+ elif benchmark_config.dtype == "bfloat16":
+ model_kwargs["torch_dtype"] = torch.bfloat16
+
+ if benchmark_config.use_8bit:
+ model_kwargs["quantization_config"] = BitsAndBytesConfig(
+ load_in_8bit=True, llm_int8_enable_fp32_cpu_offload=True
+ )
+ elif benchmark_config.use_4bit:
+ model_kwargs["quantization_config"] = BitsAndBytesConfig(
+ load_in_4bit=True,
+ bnb_4bit_compute_dtype=model_kwargs.get("torch_dtype", torch.float16),
+ bnb_4bit_use_double_quant=True,
+ bnb_4bit_quant_type="nf4",
+ )
+
+ model = AutoModelForCausalLM.from_pretrained(benchmark_config.model_id, **model_kwargs)
+
+ ram, accelerator_allocated, accelerator_reserved = get_memory_usage()
+ print_fn(f"Memory after model load - RAM: {ram:.2f}MB, {model.device.type.upper()}: {accelerator_allocated:.2f}MB")
+
+ print_fn("Preparing benchmark prompts...")
+ prompts = prepare_benchmark_prompts(
+ config=benchmark_config.to_dict(),
+ tokenizer=tokenizer,
+ max_input_length=None,
+ seed=benchmark_config.seed,
+ )
+
+ # Measure base model inference for each prompt category
+ print_fn("Measuring base model inference times...")
+ base_inference_results = measure_inference_time(
+ model,
+ tokenizer,
+ prompts,
+ max_new_tokens=benchmark_config.max_new_tokens,
+ num_runs=benchmark_config.num_inference_runs,
+ print_fn=print_fn,
+ category_generation_params=benchmark_config.category_generation_params,
+ )
+
+ result = {
+ "model_id": benchmark_config.model_id,
+ "benchmark_config": benchmark_config.to_dict(),
+ "timestamp": time.strftime("%Y-%m-%d %H:%M:%S"),
+ "inference_results": base_inference_results,
+ "memory_info": {
+ "ram_mb": ram,
+ "accelerator_allocated_mb": accelerator_allocated,
+ "accelerator_reserved_mb": accelerator_reserved,
+ },
+ }
+
+ return result
+
+
+def save_base_results(result: dict, model_id: str) -> str:
+ """Save base model results with a filename based on model and config."""
+ base_results_dir = os.path.join(os.path.dirname(__file__), "base_results")
+ os.makedirs(base_results_dir, exist_ok=True)
+
+ model_name = model_id.replace("/", "_").replace("-", "_")
+ filename = f"base_{model_name}.json"
+ filepath = os.path.join(base_results_dir, filename)
+
+ with open(filepath, "w") as f:
+ json.dump(result, f, indent=2)
+
+ return filepath
+
+
+def main():
+ """Main entry point for the base model benchmark runner."""
+ parser = argparse.ArgumentParser(description="Run base model benchmarks")
+ parser.add_argument("--verbose", "-v", action="store_true", help="Enable verbose output")
+ parser.add_argument("--force", "-f", action="store_true", help="Force re-run even if results exist")
+ args = parser.parse_args()
+
+ print_fn = print if args.verbose else lambda *args, **kwargs: None
+
+ default_config_path = os.path.join(os.path.dirname(__file__), "default_benchmark_params.json")
+ benchmark_config = BenchmarkConfig.from_json(default_config_path)
+
+ model_name = benchmark_config.model_id.replace("/", "_").replace("-", "_")
+ base_results_dir = os.path.join(os.path.dirname(__file__), "base_results")
+ filename = f"base_{model_name}.json"
+ filepath = os.path.join(base_results_dir, filename)
+
+ if os.path.exists(filepath) and not args.force:
+ print(f"Base results already exist at: {filepath}")
+ print("Use --force to re-run the benchmark")
+ return 0
+
+ print_fn(f"Running base model benchmark for: {benchmark_config.model_id}")
+
+ result = run_base_model_benchmark(benchmark_config, print_fn=print_fn)
+
+ saved_path = save_base_results(result, benchmark_config.model_id)
+ device_type = torch.accelerator.current_accelerator().type if hasattr(torch, "accelerator") else "cuda"
+ print(f"Base model results saved to: {saved_path}")
+
+ print("\nBase Model Benchmark Summary:")
+ print(f"Model: {result['model_id']}")
+ print(
+ f"Memory Usage - RAM: {result['memory_info']['ram_mb']:.2f}MB, {device_type.upper()}: {result['memory_info']['accelerator_allocated_mb']:.2f}MB"
+ )
+
+ print("\nInference Times by Category:")
+ for category, time_val in result["inference_results"]["inference_times"].items():
+ time_per_token = result["inference_results"]["time_per_token"][category]
+ tokens = result["inference_results"]["generated_tokens"][category]
+ print(f" {category}: {time_val:.4f}s ({time_per_token:.6f}s/token, {tokens:.1f} tokens)")
+
+ return 0
+
+
+if __name__ == "__main__":
+ sys.exit(main())
diff --git a/peft/method_comparison/text_generation_benchmark/temporary_results/.gitkeep b/peft/method_comparison/text_generation_benchmark/temporary_results/.gitkeep
new file mode 100644
index 0000000000000000000000000000000000000000..e69de29bb2d1d6434b8b29ae775ad8c2e48c5391
diff --git a/peft/method_comparison/text_generation_benchmark/utils.py b/peft/method_comparison/text_generation_benchmark/utils.py
new file mode 100644
index 0000000000000000000000000000000000000000..99533e9ac6ada83c2ccbc1ca356a916b585aa141
--- /dev/null
+++ b/peft/method_comparison/text_generation_benchmark/utils.py
@@ -0,0 +1,456 @@
+# Copyright 2025-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""
+Utilities for PEFT benchmarking.
+"""
+
+import datetime
+import json
+import os
+import platform
+import subprocess
+from dataclasses import asdict, dataclass, field
+from enum import Enum
+from typing import Any, Callable, Optional
+from peft.utils import infer_device
+
+import psutil
+import torch
+
+
+FILE_NAME_BENCHMARK_PARAMS = "benchmark_params.json"
+FILE_NAME_DEFAULT_CONFIG = "default_benchmark_params.json"
+
+RESULT_PATH = os.path.join(os.path.dirname(__file__), "results")
+RESULT_PATH_TEMP = os.path.join(os.path.dirname(__file__), "temporary_results")
+RESULT_PATH_CANCELLED = os.path.join(os.path.dirname(__file__), "cancelled_results")
+
+
+class BenchmarkStatus(Enum):
+ """Status of a benchmark run."""
+
+ SUCCESS = "success"
+ FAILED = "failed"
+ CANCELLED = "cancelled"
+ RUNNING = "running"
+
+
+@dataclass
+class BenchmarkResult:
+ """Container for benchmark results."""
+
+ experiment_name: str
+ status: BenchmarkStatus
+
+ model_id: str
+
+ run_info: dict = field(default_factory=dict)
+ generation_info: dict = field(default_factory=dict)
+ meta_info: dict = field(default_factory=dict)
+
+ def __post_init__(self):
+ """Initialize structured data format."""
+ device = infer_device()
+ torch_accelerator_module = getattr(torch, device, torch.cuda)
+ self.run_info = {
+ "timestamp": datetime.datetime.now(tz=datetime.timezone.utc).isoformat(),
+ "duration": 0.0,
+ "status": self.status.value,
+ "hardware": {
+ "num_accelerators": torch_accelerator_module.device_count() if torch_accelerator_module.is_available() else 0,
+ "accelerator_type": torch_accelerator_module.get_device_name(0) if torch_accelerator_module.is_available() else "N/A",
+ "cuda_version": torch.version.cuda if torch.cuda.is_available() else "N/A",
+ "pytorch_version": torch.__version__,
+ },
+ }
+
+ self.meta_info = {
+ "model_id": self.model_id,
+ "parameters": {
+ "base_params": 0,
+ "trainable_params": 0,
+ "total_params": 0,
+ "param_ratio": 0.0,
+ },
+ "model_size": {
+ "base_model_size_mb": 0.0,
+ "adapter_size_mb": 0.0,
+ },
+ "package_info": {
+ "transformers-version": None,
+ "transformers-commit-hash": None,
+ "peft-version": None,
+ "peft-commit-hash": None,
+ "datasets-version": None,
+ "datasets-commit-hash": None,
+ "bitsandbytes-version": None,
+ "bitsandbytes-commit-hash": None,
+ "torch-version": torch.__version__,
+ "torch-commit-hash": None,
+ },
+ "system_info": {
+ "system": platform.system(),
+ "release": platform.release(),
+ "version": platform.version(),
+ "machine": platform.machine(),
+ "processor": platform.processor(),
+ "accelerator": torch_accelerator_module.get_device_name(0) if torch_accelerator_module.is_available() else "N/A",
+ },
+ }
+
+ self.generation_info = {
+ "memory": {
+ "peak_accelerator_memory_mb": 0.0,
+ "peak_ram_memory_mb": 0.0,
+ "memory_logs": [],
+ },
+ "by_category": {},
+ "overall": {},
+ }
+
+ def update_meta_info(self, param_counts: dict, size_info: dict, package_info: Optional[dict] = None):
+ """Update model metadata information."""
+ self.meta_info["parameters"].update(param_counts)
+ self.meta_info["model_size"].update(size_info)
+ if package_info:
+ self.meta_info["package_info"].update(package_info)
+
+ def update_generation_info(self, memory_data: Optional[dict] = None, performance_metrics: Optional[dict] = None):
+ """Update generation performance information, primarily for memory and high-level performance."""
+ if memory_data:
+ self.generation_info["memory"].update(memory_data)
+ if performance_metrics: # For things like overall tokens/sec if calculated
+ self.generation_info.update(performance_metrics)
+
+ def add_memory_log(self, stage: str, ram_mb: float, accelerator_allocated_mb: float, accelerator_reserved_mb: float):
+ """Add a memory usage log entry to generation_info."""
+ self.generation_info["memory"]["memory_logs"].append(
+ {
+ "stage": stage,
+ "ram_mb": ram_mb,
+ "accelerator_allocated_mb": accelerator_allocated_mb,
+ "accelerator_reserved_mb": accelerator_reserved_mb,
+ }
+ )
+
+ def add_metrics_for_category(self, category: str, metrics: dict, individual_samples: list = None):
+ """Add metrics for a specific prompt category under generation_info."""
+ category_data = {"metrics": metrics, "samples": individual_samples if individual_samples is not None else []}
+ self.generation_info["by_category"][category] = category_data
+
+ def update_run_info(
+ self,
+ duration: float,
+ status: BenchmarkStatus,
+ error: Optional[str] = None,
+ peft_config: Optional[dict] = None,
+ benchmark_config: Optional[dict] = None,
+ ):
+ """Update run information."""
+ self.run_info["duration"] = duration
+ self.run_info["status"] = status.value
+ if error:
+ self.run_info["error"] = error
+ if peft_config:
+ self.run_info["peft_config"] = peft_config
+ if benchmark_config:
+ self.run_info["benchmark_config"] = benchmark_config
+
+ def compute_overall_metrics(self):
+ """Compute overall metrics across all categories within generation_info."""
+ if not self.generation_info["by_category"]:
+ return
+
+ categories = self.generation_info["by_category"]
+ key_metrics = [
+ "inference_time",
+ "base_inference_time",
+ "inference_overhead_pct",
+ "time_per_token",
+ "generated_tokens",
+ ]
+
+ for metric in key_metrics:
+ values = []
+ for category_data in categories.values():
+ if "metrics" in category_data and metric in category_data["metrics"]:
+ values.append(category_data["metrics"][metric])
+
+ if values:
+ self.generation_info["overall"][metric] = sum(values) / len(values)
+
+ def to_dict(self) -> dict[str, Any]:
+ """Convert result to dictionary."""
+ self.compute_overall_metrics()
+ return {
+ "run_info": self.run_info,
+ "generation_info": self.generation_info,
+ "meta_info": self.meta_info,
+ }
+
+ def save(self, path: Optional[str] = None):
+ """Save result to JSON file."""
+ if path is None:
+ peft_branch = get_peft_branch()
+ if self.status == BenchmarkStatus.CANCELLED:
+ base_path = RESULT_PATH_CANCELLED
+ elif peft_branch != "main":
+ base_path = RESULT_PATH_TEMP
+ elif self.status == BenchmarkStatus.SUCCESS:
+ base_path = RESULT_PATH
+ elif self.status == BenchmarkStatus.FAILED:
+ base_path = RESULT_PATH_CANCELLED
+ else:
+ base_path = RESULT_PATH_TEMP
+
+ filename = f"{self.experiment_name}.json"
+ path = os.path.join(base_path, filename)
+
+ os.makedirs(os.path.dirname(path), exist_ok=True)
+
+ with open(path, "w") as f:
+ json.dump(self.to_dict(), f, indent=2)
+
+ return path
+
+
+@dataclass
+class BenchmarkConfig:
+ """Configuration for benchmarking PEFT methods."""
+
+ model_id: str
+
+ seed: int
+ num_inference_runs: int
+ max_new_tokens: int
+
+ dtype: str = "float16"
+ use_4bit: bool = False
+ use_8bit: bool = False
+
+ category_generation_params: Optional[dict] = None
+
+ def __post_init__(self) -> None:
+ """Validate configuration."""
+ if not isinstance(self.model_id, str):
+ raise ValueError(f"Invalid model_id: {self.model_id}")
+
+ if self.seed < 0:
+ raise ValueError(f"Invalid seed: {self.seed}")
+
+ if self.num_inference_runs <= 0:
+ raise ValueError(f"Invalid num_inference_runs: {self.num_inference_runs}")
+
+ if self.max_new_tokens <= 0:
+ raise ValueError(f"Invalid max_new_tokens: {self.max_new_tokens}")
+
+ @classmethod
+ def from_dict(cls, config_dict: dict) -> "BenchmarkConfig":
+ """Create config from dictionary."""
+ valid_keys = set(cls.__dataclass_fields__.keys())
+ filtered_dict = {k: v for k, v in config_dict.items() if k in valid_keys}
+
+ return cls(**filtered_dict)
+
+ @classmethod
+ def from_json(cls, json_path: str) -> "BenchmarkConfig":
+ """Load config from JSON file."""
+ with open(json_path) as f:
+ config_dict = json.load(f)
+ return cls.from_dict(config_dict)
+
+ def to_dict(self) -> dict[str, Any]:
+ """Convert config to dictionary."""
+ result = asdict(self)
+ return result
+
+ def save(self, path: str) -> None:
+ """Save config to JSON file."""
+ with open(path, "w") as f:
+ json.dump(self.to_dict(), f, indent=2)
+
+ def merge_from_dict(self, config_dict: dict) -> None:
+ """Merge settings from a dictionary into this config object.
+ Keys in config_dict will override existing attributes.
+ """
+ for key, value in config_dict.items():
+ if hasattr(self, key):
+ setattr(self, key, value)
+
+
+def validate_experiment_path(path: str) -> tuple[str, "BenchmarkConfig"]:
+ """Validate experiment path, load and merge configs, and return them."""
+ if not os.path.exists(path):
+ raise FileNotFoundError(f"Experiment path not found: {path}")
+
+ path_parts = os.path.normpath(path).split(os.sep)
+
+ try:
+ experiments_idx = path_parts.index("experiments")
+ except ValueError:
+ experiment_name = os.path.basename(path.rstrip(os.sep))
+ else:
+ if experiments_idx + 1 < len(path_parts):
+ method_name = path_parts[experiments_idx + 1]
+ remaining_parts = path_parts[experiments_idx + 2 :]
+ if remaining_parts:
+ remaining_name = "-".join(remaining_parts)
+ experiment_name = f"{method_name}--{remaining_name}"
+ else:
+ experiment_name = method_name
+ else:
+ experiment_name = os.path.basename(path.rstrip(os.sep))
+
+ default_config_path = os.path.join(os.path.dirname(__file__), FILE_NAME_DEFAULT_CONFIG)
+ experiment_benchmark_params_path = os.path.join(path, FILE_NAME_BENCHMARK_PARAMS)
+
+ if not os.path.exists(default_config_path):
+ raise FileNotFoundError(f"Default configuration file not found: {default_config_path}. This is required.")
+ benchmark_config = BenchmarkConfig.from_json(default_config_path)
+ print(f"Loaded default configuration from {default_config_path}")
+
+ if os.path.exists(experiment_benchmark_params_path):
+ with open(experiment_benchmark_params_path) as f:
+ experiment_specific_params = json.load(f)
+
+ benchmark_config.merge_from_dict(experiment_specific_params)
+ print(f"Loaded and merged experiment-specific parameters from {experiment_benchmark_params_path}")
+ else:
+ print(f"No {FILE_NAME_BENCHMARK_PARAMS} found in {path}. Using only default configuration.")
+
+ return experiment_name, benchmark_config
+
+
+def get_memory_usage() -> tuple[float, float, float]:
+ """Get current memory usage (RAM and accelerator)."""
+ process = psutil.Process(os.getpid())
+ ram_usage_bytes = process.memory_info().rss
+ ram_usage_mb = ram_usage_bytes / (1024 * 1024)
+
+ if torch.cuda.is_available():
+ accelerator_allocated = torch.cuda.memory_allocated()
+ accelerator_reserved = torch.cuda.memory_reserved()
+ accelerator_allocated_mb = accelerator_allocated / (1024 * 1024)
+ accelerator_reserved_mb = accelerator_reserved / (1024 * 1024)
+ elif torch.xpu.is_available():
+ accelerator_allocated = torch.xpu.memory_allocated()
+ accelerator_reserved = torch.xpu.memory_reserved()
+ accelerator_allocated_mb = accelerator_allocated / (1024 * 1024)
+ accelerator_reserved_mb = accelerator_reserved / (1024 * 1024)
+ else:
+ accelerator_allocated_mb = 0.0
+ accelerator_reserved_mb = 0.0
+
+ return ram_usage_mb, accelerator_allocated_mb, accelerator_reserved_mb
+
+
+def init_accelerator() -> tuple[float, float]:
+ """Initialize accelerator and return initial memory usage."""
+ if torch.cuda.is_available():
+ torch.cuda.init()
+ torch.cuda.empty_cache()
+ _, accelerator_allocated, accelerator_reserved = get_memory_usage()
+ elif torch.xpu.is_available():
+ torch.xpu.init()
+ torch.xpu.empty_cache()
+ _, accelerator_allocated, accelerator_reserved = get_memory_usage()
+ else:
+ accelerator_allocated = 0.0
+ accelerator_reserved = 0.0
+ return accelerator_allocated, accelerator_reserved
+
+
+def get_model_size_mb(model: torch.nn.Module, dtype_bytes: int = 4) -> float:
+ """Calculate model size in MB."""
+ return sum(p.numel() * dtype_bytes for p in model.parameters()) / (1024 * 1024)
+
+
+def get_peft_branch() -> str:
+ repo_root = os.path.dirname(__file__)
+ return subprocess.check_output("git rev-parse --abbrev-ref HEAD".split(), cwd=repo_root).decode().strip()
+
+
+def log_results(
+ experiment_name: str,
+ benchmark_result: BenchmarkResult,
+ print_fn: Callable = print,
+) -> None:
+ """Log benchmark results to console."""
+ print_fn("\n" + "=" * 50)
+ print_fn(f"Benchmark Results: {experiment_name}")
+ print_fn("=" * 50)
+
+ print_fn(f"Status: {benchmark_result.run_info.get('status', 'N/A')}")
+ print_fn(f"Duration: {benchmark_result.run_info.get('duration', 0):.2f} seconds")
+
+ if benchmark_result.run_info.get("status") != BenchmarkStatus.SUCCESS.value:
+ print_fn(f"Error: {benchmark_result.run_info.get('error', 'Unknown error')}")
+ print_fn("=" * 50)
+ return
+
+ print_fn("\nModel Information:")
+ print_fn(f" Base Model: {benchmark_result.meta_info.get('model_id', 'N/A')}")
+
+ print_fn("\nParameter Counts:")
+ params = benchmark_result.meta_info.get("parameters", {})
+ print_fn(f" Base Parameters: {params.get('base_params', 0):,}")
+ print_fn(f" Trainable Parameters: {params.get('trainable_params', 0):,}")
+ print_fn(f" Parameter Ratio: {params.get('param_ratio', 0):.5%}")
+
+ print_fn("\nModel Size:")
+ size_info = benchmark_result.meta_info.get("model_size", {})
+ print_fn(f" Base Model: {size_info.get('base_model_size_mb', 0):.2f} MB")
+ print_fn(f" Adapter: {size_info.get('adapter_size_mb', 0):.2f} MB")
+
+ print_fn("\nMemory Usage (from generation_info):")
+ memory_data = benchmark_result.generation_info.get("memory", {})
+ print_fn(f" Peak Accelerator Memory: {memory_data.get('peak_accelerator_memory_mb', 0):.2f} MB")
+ print_fn(f" Peak RAM Memory: {memory_data.get('peak_ram_memory_mb', 0):.2f} MB")
+
+ print_fn("\nDetailed Metrics (from generation_info.by_category):")
+ if benchmark_result.generation_info.get("by_category"):
+ for category, cat_data in benchmark_result.generation_info["by_category"].items():
+ print_fn(f" Category: {category}")
+ metrics = cat_data.get("metrics", {})
+ print_fn(f" Inference Time: {metrics.get('inference_time', 0):.4f} seconds")
+ print_fn(f" Base Inference Time: {metrics.get('base_inference_time', 0):.4f} seconds")
+ print_fn(f" Inference Overhead: {metrics.get('inference_overhead_pct', 0):.2f}%")
+ print_fn(f" Time Per Token: {metrics.get('time_per_token', 0):.6f} seconds/token")
+ print_fn(f" Generated Tokens: {metrics.get('generated_tokens', 0):.1f}")
+
+ samples = cat_data.get("samples", [])
+ if samples:
+ print_fn(f" Number of Samples: {len(samples)}")
+ print_fn(
+ f" Average Generated Tokens: {sum(s.get('generated_tokens', 0) for s in samples) / len(samples):.1f}"
+ )
+ else:
+ print_fn(" No per-category metrics available.")
+
+ benchmark_result.compute_overall_metrics()
+
+ print_fn("\nOverall Metrics (from generation_info.overall):")
+ overall = benchmark_result.generation_info.get("overall")
+ if overall:
+ print_fn(f" Inference Time: {overall.get('inference_time', 0):.4f} seconds")
+ print_fn(f" Base Inference Time: {overall.get('base_inference_time', 0):.4f} seconds")
+ print_fn(f" Inference Overhead: {overall.get('inference_overhead_pct', 0):.2f}%")
+ print_fn(f" Time Per Token: {overall.get('time_per_token', 0):.6f} seconds/token")
+ print_fn(f" Generated Tokens: {overall.get('generated_tokens', 0):.1f}")
+ else:
+ print_fn(" No overall metrics computed.")
+
+ print_fn("\nSaved results to:", benchmark_result.save())
+ print_fn("=" * 50)
diff --git a/peft/pyproject.toml b/peft/pyproject.toml
new file mode 100644
index 0000000000000000000000000000000000000000..76c7294107b8c59bd4705ea77b1ea674f2ec012a
--- /dev/null
+++ b/peft/pyproject.toml
@@ -0,0 +1,56 @@
+[tool.black]
+# Only used by `hf-doc-builder´.
+line-length = 119
+target-version = ['py38']
+
+[tool.ruff]
+target-version = "py39"
+line-length = 119
+extend-exclude = ["*.ipynb"]
+
+[tool.ruff.lint]
+preview = true
+explicit-preview-rules = true
+extend-select = [
+ "C", # Complexity
+ "E", # PEP8 errors
+ "F", # PEP8 formatting
+ "I", # Import sorting
+ "UP", # Pyupgrade upgrades
+ "W", # PEP8 warnings
+ "PT009", # Pytest assertions
+ "RUF022", # Sorting of __all__
+]
+ignore = [
+ "C901", # Function too complex
+ "E501", # Line length (handled by ruff-format)
+ "F841", # unused variable
+ "UP007", # X | Y style Unions
+ "C420", # dict.fromkeys
+ "UP045", # don't force replacing Optional[X] with X | None
+]
+
+[tool.ruff.lint.isort]
+lines-after-imports = 2
+known-first-party = ["peft"]
+
+[tool.pytest]
+doctest_optionflags = [
+ "NORMALIZE_WHITESPACE",
+ "ELLIPSIS",
+ "NUMBER",
+]
+
+[tool.pytest.ini_options]
+addopts = "--cov=src/peft --cov-report=term-missing --durations=10"
+markers = [
+ "single_gpu_tests: tests that run on a single GPU",
+ "multi_gpu_tests: tests that run on multiple GPUs",
+ "regression: whether to run regression suite test",
+ "bitsandbytes: select bitsandbytes integration tests"
+]
+
+filterwarnings = [
+ "error::DeprecationWarning:transformers",
+ "error::FutureWarning:transformers",
+]
diff --git a/peft/requirements.txt b/peft/requirements.txt
new file mode 100644
index 0000000000000000000000000000000000000000..dca857de3249b60ea3786b49156d14166cd57ac0
--- /dev/null
+++ b/peft/requirements.txt
@@ -0,0 +1,15 @@
+accelerate
+torch
+safetensors
+bitsandbytes
+scipy
+peft
+transformers
+tqdm
+packaging
+pytest
+numpy
+pyyaml
+datasets
+psutil
+setuptools
\ No newline at end of file
diff --git a/peft/scripts/ci_clean_cache.py b/peft/scripts/ci_clean_cache.py
new file mode 100644
index 0000000000000000000000000000000000000000..8e4bfbaa0abc8fee26098d1b6496d3891ac7bc3f
--- /dev/null
+++ b/peft/scripts/ci_clean_cache.py
@@ -0,0 +1,67 @@
+"""
+Utility to clean cache files that exceed a specific time in days according to their
+last access time recorded in the cache.
+
+Exit code:
+- 1 if no candidates are found
+- 0 if candidates are found
+
+Deletion can be enabled by passing `-d` parameter, otherwise it will only list the candidates.
+"""
+
+import sys
+from datetime import datetime as dt
+
+from huggingface_hub import scan_cache_dir
+
+
+def find_old_revisions(scan_results, max_age_days=30):
+ """Find commit hashes of objects in the cache. These objects need a last access time that
+ is above the passed `max_age_days` parameter. Returns an empty list if no objects are found.
+ Time measurement is based of the current time and the recorded last access tiem in the cache.
+ """
+ now = dt.now()
+ revisions = [(i.revisions, i.last_accessed) for i in scan_results.repos]
+ revisions_ages = [(rev, (now - dt.fromtimestamp(ts_access)).days) for rev, ts_access in revisions]
+ delete_candidates = [rev for rev, age in revisions_ages if age > max_age_days]
+ hashes = [n.commit_hash for rev in delete_candidates for n in rev]
+
+ return hashes
+
+
+def delete_old_revisions(scan_results, delete_candidates, do_delete=False):
+ delete_operation = scan_results.delete_revisions(*delete_candidates)
+ print(f"Would free {delete_operation.expected_freed_size_str}")
+ print(f"Candidates: {delete_candidates}")
+
+ if do_delete:
+ print("Deleting now.")
+ delete_operation.execute()
+ else:
+ print("Not deleting, pass the -d flag.")
+
+
+if __name__ == "__main__":
+ from argparse import ArgumentParser
+
+ parser = ArgumentParser()
+ parser.add_argument("-a", "--max-age", type=int, default=30, help="Max. age in days items in the cache may have.")
+ parser.add_argument(
+ "-d",
+ "--delete",
+ action="store_true",
+ help=(
+ "Delete mode; Really delete items if there are candidates. Exit code = 0 when we found something to delete, 1 "
+ "otherwise."
+ ),
+ )
+ args = parser.parse_args()
+
+ scan_results = scan_cache_dir()
+
+ delete_candidates = find_old_revisions(scan_results, args.max_age)
+ if not delete_candidates:
+ print("No delete candidates found, not deleting anything.")
+ sys.exit(1)
+
+ delete_old_revisions(scan_results, delete_candidates, do_delete=args.delete)
diff --git a/peft/scripts/convert-bone-to-miss.py b/peft/scripts/convert-bone-to-miss.py
new file mode 100644
index 0000000000000000000000000000000000000000..e709410fa806bb0fa35e6f01160084c9dc2d4652
--- /dev/null
+++ b/peft/scripts/convert-bone-to-miss.py
@@ -0,0 +1,70 @@
+#!/usr/bin/env python3
+# Copyright (c) 2025 Your Organization/Project. All rights reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""Convert Bone checkpoint to MiSS format."""
+
+import argparse
+import json
+import os
+from pathlib import Path
+
+from safetensors import safe_open
+from safetensors.torch import save_file
+
+from peft.utils import CONFIG_NAME, SAFETENSORS_WEIGHTS_NAME
+
+
+def convert_bone_to_miss(bone_dir: Path, miss_dir: Path) -> None:
+ """Convert Bone checkpoint files to MiSS format."""
+ bone_config_path = bone_dir / CONFIG_NAME
+ miss_config_path = miss_dir / CONFIG_NAME
+ if not os.path.exists(miss_dir):
+ os.makedirs(miss_dir, exist_ok=True)
+ with open(bone_config_path, encoding="utf-8") as f:
+ config = json.load(f)
+
+ config["peft_type"] = "MISS"
+
+ with open(miss_config_path, "w", encoding="utf-8") as f:
+ json.dump(config, f, indent=2, ensure_ascii=False)
+
+ bone_weight_path = bone_dir / SAFETENSORS_WEIGHTS_NAME
+ miss_weight_path = miss_dir / SAFETENSORS_WEIGHTS_NAME
+
+ new_data = {}
+
+ with safe_open(bone_weight_path, framework="pt") as f:
+ for old_key in f.keys():
+ tensor = f.get_tensor(old_key)
+ new_key = old_key.replace(".bone_", ".miss_")
+ new_data[new_key] = tensor
+
+ save_file(new_data, miss_weight_path)
+
+ print(f"Converted checkpoint saved at {miss_weight_path}")
+
+
+def main() -> None:
+ parser = argparse.ArgumentParser(description="Convert Bone checkpoint to MiSS format.")
+ parser.add_argument("bone_dir", type=Path, help="Directory containing Bone checkpoint files")
+ parser.add_argument("miss_dir", type=Path, help="Directory to save MiSS checkpoint files")
+ args = parser.parse_args()
+
+ args.miss_dir.mkdir(parents=True, exist_ok=True)
+ convert_bone_to_miss(args.bone_dir, args.miss_dir)
+
+
+if __name__ == "__main__":
+ main()
diff --git a/peft/scripts/launch_notebook_mp.py b/peft/scripts/launch_notebook_mp.py
new file mode 100644
index 0000000000000000000000000000000000000000..ce5439afa82a4220cdecbd73e545c58cd14f8442
--- /dev/null
+++ b/peft/scripts/launch_notebook_mp.py
@@ -0,0 +1,47 @@
+# Copyright 2023-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+# This is a minimal example of launching PEFT with Accelerate. This used to cause issues because PEFT would eagerly
+# import bitsandbytes, which initializes CUDA, resulting in:
+# > RuntimeError: Cannot re-initialize CUDA in forked subprocess. To use CUDA with multiprocessing, you must use the
+# > 'spawn' start method
+# This script exists to ensure that this issue does not reoccur.
+
+import torch
+from accelerate import notebook_launcher
+
+import peft
+from peft.utils import infer_device
+
+
+def init():
+ class MyModule(torch.nn.Module):
+ def __init__(self):
+ super().__init__()
+ self.linear = torch.nn.Linear(1, 2)
+
+ def forward(self, x):
+ return self.linear(x)
+
+ device = infer_device()
+ model = MyModule().to(device)
+ peft.get_peft_model(model, peft.LoraConfig(target_modules=["linear"]))
+
+
+def main():
+ notebook_launcher(init, (), num_processes=2)
+
+
+if __name__ == "__main__":
+ main()
diff --git a/peft/scripts/log_reports.py b/peft/scripts/log_reports.py
new file mode 100644
index 0000000000000000000000000000000000000000..c8191ee8f5a2d79c83b266e4a60d2f280fa9d376
--- /dev/null
+++ b/peft/scripts/log_reports.py
@@ -0,0 +1,144 @@
+import argparse
+import json
+import os
+from datetime import date
+from pathlib import Path
+
+from tabulate import tabulate
+
+
+MAX_LEN_MESSAGE = 2900 # slack endpoint has a limit of 3001 characters
+
+parser = argparse.ArgumentParser()
+parser.add_argument(
+ "--slack_channel_name",
+ default="peft-ci-daily",
+)
+
+
+def main(slack_channel_name=None):
+ failed = []
+ passed = []
+
+ group_info = []
+
+ total_num_failed = 0
+ empty_file = False or len(list(Path().glob("*.log"))) == 0
+
+ total_empty_files = []
+
+ for log in Path().glob("*.log"):
+ section_num_failed = 0
+ i = 0
+ with open(log) as f:
+ for line in f:
+ line = json.loads(line)
+ i += 1
+ if line.get("nodeid", "") != "":
+ test = line["nodeid"]
+ if line.get("duration", None) is not None:
+ duration = f"{line['duration']:.4f}"
+ if line.get("outcome", "") == "failed":
+ section_num_failed += 1
+ failed.append([test, duration, log.name.split("_")[0]])
+ total_num_failed += 1
+ else:
+ passed.append([test, duration, log.name.split("_")[0]])
+ empty_file = i == 0
+ group_info.append([str(log), section_num_failed, failed])
+ total_empty_files.append(empty_file)
+ os.remove(log)
+ failed = []
+ text = (
+ "🌞 There were no failures!"
+ if not any(total_empty_files)
+ else "Something went wrong there is at least one empty file - please check GH action results."
+ )
+ no_error_payload = {
+ "type": "section",
+ "text": {
+ "type": "plain_text",
+ "text": text,
+ "emoji": True,
+ },
+ }
+
+ message = ""
+ payload = [
+ {
+ "type": "header",
+ "text": {
+ "type": "plain_text",
+ "text": "🤗 Results of the {} PEFT scheduled tests.".format(os.environ.get("TEST_TYPE", "")),
+ },
+ },
+ ]
+ if total_num_failed > 0:
+ for i, (name, num_failed, failed_tests) in enumerate(group_info):
+ if num_failed > 0:
+ if num_failed == 1:
+ message += f"*{name}: {num_failed} failed test*\n"
+ else:
+ message += f"*{name}: {num_failed} failed tests*\n"
+ failed_table = []
+ for test in failed_tests:
+ failed_table.append(test[0].split("::"))
+ failed_table = tabulate(
+ failed_table,
+ headers=["Test Location", "Test Case", "Test Name"],
+ showindex="always",
+ tablefmt="grid",
+ maxcolwidths=[12, 12, 12],
+ )
+ message += "\n```\n" + failed_table + "\n```"
+
+ if total_empty_files[i]:
+ message += f"\n*{name}: Warning! Empty file - please check the GitHub action job *\n"
+ print(f"### {message}")
+ else:
+ payload.append(no_error_payload)
+
+ if os.environ.get("TEST_TYPE", "") != "":
+ from slack_sdk import WebClient
+
+ if len(message) > MAX_LEN_MESSAGE:
+ print(f"Truncating long message from {len(message)} to {MAX_LEN_MESSAGE}")
+ message = message[:MAX_LEN_MESSAGE] + "..."
+
+ if len(message) != 0:
+ md_report = {
+ "type": "section",
+ "text": {"type": "mrkdwn", "text": message},
+ }
+ payload.append(md_report)
+ action_button = {
+ "type": "section",
+ "text": {"type": "mrkdwn", "text": "*For more details:*"},
+ "accessory": {
+ "type": "button",
+ "text": {"type": "plain_text", "text": "Check Action results", "emoji": True},
+ "url": f"https://github.com/huggingface/peft/actions/runs/{os.environ['GITHUB_RUN_ID']}",
+ },
+ }
+ payload.append(action_button)
+
+ date_report = {
+ "type": "context",
+ "elements": [
+ {
+ "type": "plain_text",
+ "text": f"Nightly {os.environ.get('TEST_TYPE')} test results for {date.today()}",
+ },
+ ],
+ }
+ payload.append(date_report)
+
+ print(payload)
+
+ client = WebClient(token=os.environ.get("SLACK_API_TOKEN"))
+ client.chat_postMessage(channel=f"#{slack_channel_name}", text=message, blocks=payload)
+
+
+if __name__ == "__main__":
+ args = parser.parse_args()
+ main(args.slack_channel_name)
diff --git a/peft/scripts/stale.py b/peft/scripts/stale.py
new file mode 100644
index 0000000000000000000000000000000000000000..794ec8451282c69ae9cff18c15329b14816d707a
--- /dev/null
+++ b/peft/scripts/stale.py
@@ -0,0 +1,65 @@
+# Copyright 2023 The HuggingFace Team, the AllenNLP library authors. All rights reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+"""
+Script to close stale issue. Taken in part from the AllenNLP repository.
+https://github.com/allenai/allennlp.
+"""
+
+import os
+from datetime import datetime as dt
+from datetime import timezone
+
+from github import Github
+
+
+LABELS_TO_EXEMPT = [
+ "good first issue",
+ "good second issue",
+ "good difficult issue",
+ "feature request",
+ "new model",
+ "wip",
+ "PRs welcome to address this",
+]
+
+
+def main():
+ g = Github(os.environ["GITHUB_TOKEN"])
+ repo = g.get_repo("huggingface/peft")
+ open_issues = repo.get_issues(state="open")
+
+ for issue in open_issues:
+ comments = sorted(issue.get_comments(), key=lambda i: i.created_at, reverse=True)
+ last_comment = comments[0] if len(comments) > 0 else None
+ if (
+ (last_comment is not None and last_comment.user.login == "github-actions[bot]")
+ and (dt.now(timezone.utc) - issue.updated_at).days > 7
+ and (dt.now(timezone.utc) - issue.created_at).days >= 30
+ and not any(label.name.lower() in LABELS_TO_EXEMPT for label in issue.get_labels())
+ ):
+ issue.edit(state="closed")
+ elif (
+ (dt.now(timezone.utc) - issue.updated_at).days > 23
+ and (dt.now(timezone.utc) - issue.created_at).days >= 30
+ and not any(label.name.lower() in LABELS_TO_EXEMPT for label in issue.get_labels())
+ ):
+ issue.create_comment(
+ "This issue has been automatically marked as stale because it has not had "
+ "recent activity. If you think this still needs to be addressed "
+ "please comment on this thread.\n\n"
+ )
+
+
+if __name__ == "__main__":
+ main()
diff --git a/peft/scripts/train_memory.py b/peft/scripts/train_memory.py
new file mode 100644
index 0000000000000000000000000000000000000000..c764fe84ae095ee65b923b517fc438b412ad10ed
--- /dev/null
+++ b/peft/scripts/train_memory.py
@@ -0,0 +1,276 @@
+# Copyright 2025-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""This script trains a model on a small text dataset and measures the memory consumption, as well as a few other
+useful metrics.
+
+Example:
+
+Get help:
+
+```bash
+python train_memory.py --help
+```
+
+Train the google/gemma-2-2b model with a LoRA config json at the indicated location.
+
+```bash
+python train_memory.py "google/gemma-2-2b" --max_seq_length 256 --batch_size 1 --rank 32 --dtype bfloat16 --path_config
+```
+
+Fully fine-tune the model (i.e. without LoRA) by setting the rank to 0:
+
+```bash
+python train_memory.py "google/gemma-2-2b" --rank 0
+```
+
+Get an estimate of the size of the hidden states by passing `--monitor_tensors`. This trains just for a single epoch. For realistic estimates, the batch size for this:
+
+```bash
+python train_memory.py "google/gemma-2-2b" --max_seq_length 256 --batch_size 32 --rank 32 --dtype bfloat16 --path_config configs/lora_rank-32_embedding-lora/ --monitor_tensors
+```
+
+"""
+
+import argparse
+import gc
+import os
+import sys
+import tempfile
+import time
+import warnings
+from collections import Counter
+from contextlib import nullcontext
+from functools import partial
+
+import torch
+from datasets import load_dataset
+from torch import nn
+from transformers import (
+ AutoModelForCausalLM,
+ AutoTokenizer,
+ BitsAndBytesConfig,
+)
+
+from peft import LoraConfig, get_peft_model, prepare_model_for_kbit_training
+from peft.utils import CONFIG_NAME, SAFETENSORS_WEIGHTS_NAME
+
+
+# suppress all warnings
+warnings.filterwarnings("ignore")
+
+device = torch.accelerator.current_accelerator().type if hasattr(torch, "accelerator") else "cuda"
+dtype_to_bytes_linear = {"float32": 4, "float16": 2, "bfloat16": 2, "int8": 1, "int4": 0.5}
+
+
+def init_accelerator():
+ torch.manual_seed(0)
+ if device == "cpu":
+ return
+
+ device_module = getattr(torch, device, torch.cuda)
+ device_module.reset_peak_memory_stats()
+ device_module.manual_seed_all(0)
+ # might not be necessary, but just to be sure
+ nn.Linear(1, 1).to(device)
+
+
+def get_data(tokenizer):
+ def tokenize(samples):
+ # For some reason, the max sequence length is not honored by the tokenizer, resulting in IndexErrors. Thus,
+ # manually ensure that sequences are not too long.
+ tokenized = tokenizer(samples["quote"])
+ tokenized["input_ids"] = [input_ids[: tokenizer.model_max_length] for input_ids in tokenized["input_ids"]]
+ tokenized["attention_mask"] = [
+ input_ids[: tokenizer.model_max_length] for input_ids in tokenized["attention_mask"]
+ ]
+ return tokenized
+
+ data = load_dataset("ybelkada/english_quotes_copy")
+ data = data.map(tokenize, batched=True)
+ # We need to manually remove unused columns. This is because we cannot use remove_unused_columns=True in the
+ # Trainer, as this leads to errors with torch.compile. We also cannot just leave them in, as they contain
+ # strings. Therefore, manually remove all unused columns.
+ data = data.remove_columns(["quote", "author", "tags"])
+ return data
+
+
+def train(model_id, rank, dtype, monitor_tensors, max_seq_length, batch_size, max_steps, path_config):
+ init_accelerator()
+ device_module = getattr(torch, device, torch.cuda)
+ accelerator_memory_init = device_module.max_memory_allocated()
+ accelerator_memory_log = []
+
+ tokenizer = AutoTokenizer.from_pretrained(model_id)
+ tokenizer.model_max_length = max_seq_length
+ if not tokenizer.pad_token:
+ tokenizer.pad_token = tokenizer.eos_token
+ data = get_data(tokenizer)
+
+ if dtype == "int4":
+ quant_config = BitsAndBytesConfig(load_in_4bit=True)
+ model = AutoModelForCausalLM.from_pretrained(model_id, device_map=device, quantization_config=quant_config)
+ model = prepare_model_for_kbit_training(model)
+ elif dtype == "int8":
+ quant_config = BitsAndBytesConfig(load_in_8bit=True)
+ model = AutoModelForCausalLM.from_pretrained(model_id, device_map=device, quantization_config=quant_config)
+ model = prepare_model_for_kbit_training(model)
+ elif dtype == "bfloat16":
+ model = AutoModelForCausalLM.from_pretrained(model_id, device_map=device, torch_dtype=torch.bfloat16)
+ elif dtype == "float16":
+ model = AutoModelForCausalLM.from_pretrained(model_id, device_map=device, torch_dtype=torch.float16)
+ elif dtype == "float32":
+ model = AutoModelForCausalLM.from_pretrained(model_id, device_map=device)
+ else:
+ raise ValueError(f"Invalid dtype: {dtype}")
+
+ if rank > 0:
+ if path_config is None:
+ raise RuntimeError("LoRA rank > 0 requires a path to a LoRA config")
+ if path_config.endswith(CONFIG_NAME):
+ path_config = path_config.removesuffix(CONFIG_NAME)
+ config = LoraConfig.from_pretrained(path_config)
+ model = get_peft_model(model, config)
+ model.print_trainable_parameters()
+ else:
+ print("Not using LoRA")
+
+ model.config.use_cache = False
+ storage = []
+
+ def pack(x):
+ storage.append(x)
+ return len(storage) - 1
+
+ def unpack(x):
+ return storage[x]
+
+ train_ctx = partial(torch.autograd.graph.saved_tensors_hooks, pack, unpack) if monitor_tensors else nullcontext
+
+ optimizer = torch.optim.AdamW(model.parameters(), lr=1e-5)
+ losses = []
+ sample = 0
+ tic_total = time.perf_counter()
+ for i in range(0, max_steps):
+ storage.clear()
+ tic = time.perf_counter()
+ try:
+ batch = tokenizer.pad(data["train"][sample : sample + batch_size], return_tensors="pt").to(model.device)
+ sample += batch_size
+
+ # add targets
+ batch["labels"] = batch["input_ids"].clone()
+ optimizer.zero_grad()
+
+ with train_ctx():
+ outputs = model(**batch)
+ loss = outputs.loss
+ loss.backward()
+ optimizer.step()
+ losses.append(loss.item())
+ accelerator_memory_log.append(device_module.memory_allocated() - accelerator_memory_init)
+ device_module.empty_cache()
+ gc.collect()
+ toc = time.perf_counter()
+ print(f"step {i:3d} loss {loss.item():.6f} time {toc - tic:.2f}s", file=sys.stderr)
+ except KeyboardInterrupt:
+ print("canceled training")
+ break
+
+ if monitor_tensors:
+ break
+
+ toc_total = time.perf_counter()
+
+ accelerator_memory_final = device_module.max_memory_allocated()
+ accelerator_memory_avg = int(sum(accelerator_memory_log) / len(accelerator_memory_log))
+ print(f"{model.device.type} memory avg: {accelerator_memory_avg // 2**20}MB")
+ print(f"{model.device.type} memory max: {(accelerator_memory_final - accelerator_memory_init) // 2**20}MB")
+ print(f"total time: {toc_total - tic_total:.2f}s")
+
+ with tempfile.TemporaryDirectory() as tmp_dir:
+ model.save_pretrained(tmp_dir)
+ stat = os.stat(os.path.join(tmp_dir, SAFETENSORS_WEIGHTS_NAME))
+ file_size = stat.st_size
+ print(f"file size: {file_size / 2**20:.1f}MB")
+
+ if monitor_tensors:
+ dtype_counts = Counter(t.dtype for t in storage)
+ shape_counts = Counter(t.shape for t in storage)
+ param_shape_counts = Counter(p.shape for p in model.parameters())
+ param_shape_counts_copy = dict(param_shape_counts).copy()
+
+ # shape counts includes the params, so we need to subtract them; note that they can be transposed
+ # this is an approximation
+ diff_shape_counts = {}
+ for shape, count in shape_counts.items():
+ if shape in param_shape_counts_copy:
+ diff_count = count - param_shape_counts[shape]
+ if diff_count > 0:
+ diff_shape_counts[shape] = diff_count
+ param_shape_counts_copy[shape] = max(0, param_shape_counts_copy[shape] - diff_count)
+ elif shape[::-1] in param_shape_counts:
+ diff_count = count - param_shape_counts[shape[::-1]]
+ if diff_count > 0:
+ diff_shape_counts[shape] = diff_count
+ param_shape_counts_copy[shape[::-1]] = max(0, param_shape_counts_copy[shape[::-1]] - diff_count)
+ else:
+ diff_shape_counts[shape] = count
+
+ total_size = sum(t.numel() * t.element_size() for t in storage)
+ total_size_mb = f"{total_size // 2**20}MB"
+ diff_size = 0
+ for shape, count in diff_shape_counts.items():
+ diff_size += count * torch.zeros(shape).numel() * dtype_to_bytes_linear[dtype]
+ param_size = total_size - diff_size
+
+ diff_size_mb = f"{diff_size // 2**20}MB"
+ param_size_mb = f"{param_size // 2**20}MB"
+
+ print(f"Dtype counts: {dtype_counts.most_common()}")
+ print(f"Total size of tensors: {total_size_mb: >12}")
+ print(f"Total size of activations: {diff_size_mb: >12}")
+ print(f"Total size of parameters: {param_size_mb: >12}")
+
+
+if __name__ == "__main__":
+ parser = argparse.ArgumentParser()
+ parser.add_argument("model_id", type=str, help="Model name on Hugging Face Hub")
+ parser.add_argument("--rank", type=int, default=8, help="Rank of LoRA, 0 => no LoRA, default 8")
+ parser.add_argument(
+ "--dtype",
+ type=str,
+ default="float32",
+ help="Data type, one of float32, float16, bfloat16, int8, int4, default float32",
+ )
+ parser.add_argument(
+ "--monitor_tensors",
+ action="store_true",
+ help="Monitor tensor sizes during training for a single training step, off by default",
+ )
+ parser.add_argument("--max_seq_length", type=int, default=128, help="Maximum sequence length, default 128")
+ parser.add_argument("--batch_size", type=int, default=1, help="Batch size, default 1")
+ parser.add_argument("--max_steps", type=int, default=50, help="Maximum number of training steps, default 50")
+ parser.add_argument("--path_config", type=str, default=None, help="Path to LoRA config")
+ args = parser.parse_args()
+ train(
+ model_id=args.model_id,
+ rank=args.rank,
+ dtype=args.dtype,
+ monitor_tensors=args.monitor_tensors,
+ max_seq_length=args.max_seq_length,
+ batch_size=args.batch_size,
+ max_steps=args.max_steps,
+ path_config=args.path_config,
+ )
diff --git a/peft/setup.py b/peft/setup.py
new file mode 100644
index 0000000000000000000000000000000000000000..a677afe0117b5e831dbadd1319bea69834fe9d83
--- /dev/null
+++ b/peft/setup.py
@@ -0,0 +1,110 @@
+# Copyright 2023 The HuggingFace Team. All rights reserved.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+from setuptools import find_packages, setup
+
+
+VERSION = "0.17.2.dev0"
+
+extras = {}
+extras["quality"] = [
+ "black", # doc-builder has an implicit dependency on Black, see huggingface/doc-builder#434
+ "hf-doc-builder",
+ "ruff~=0.12.8",
+]
+extras["docs_specific"] = [
+ "black", # doc-builder has an implicit dependency on Black, see huggingface/doc-builder#434
+ "hf-doc-builder",
+]
+extras["dev"] = extras["quality"] + extras["docs_specific"]
+extras["test"] = extras["dev"] + [
+ "pytest",
+ "pytest-cov",
+ "pytest-xdist",
+ "parameterized",
+ "datasets",
+ "diffusers",
+ "scipy",
+ "protobuf",
+ "sentencepiece",
+]
+
+setup(
+ name="peft",
+ version=VERSION,
+ description="Parameter-Efficient Fine-Tuning (PEFT)",
+ license_files=["LICENSE"],
+ long_description=open("README.md", encoding="utf-8").read(),
+ long_description_content_type="text/markdown",
+ keywords="deep learning",
+ license="Apache",
+ author="The HuggingFace team",
+ author_email="benjamin@huggingface.co",
+ url="https://github.com/huggingface/peft",
+ package_dir={"": "src"},
+ packages=find_packages("src"),
+ package_data={"peft": ["py.typed", "tuners/boft/fbd/fbd_cuda.cpp", "tuners/boft/fbd/fbd_cuda_kernel.cu"]},
+ entry_points={},
+ python_requires=">=3.10.0",
+ install_requires=[
+ "numpy>=1.17",
+ "packaging>=20.0",
+ "psutil",
+ "pyyaml",
+ "torch>=1.13.0",
+ "transformers",
+ "tqdm",
+ "accelerate>=0.21.0",
+ "safetensors",
+ "huggingface_hub>=0.25.0",
+ ],
+ extras_require=extras,
+ classifiers=[
+ "Development Status :: 5 - Production/Stable",
+ "Intended Audience :: Developers",
+ "Intended Audience :: Education",
+ "Intended Audience :: Science/Research",
+ "License :: OSI Approved :: Apache Software License",
+ "Operating System :: OS Independent",
+ "Programming Language :: Python :: 3",
+ "Programming Language :: Python :: 3.10",
+ "Programming Language :: Python :: 3.11",
+ "Programming Language :: Python :: 3.12",
+ "Programming Language :: Python :: 3.13",
+ "Topic :: Scientific/Engineering :: Artificial Intelligence",
+ ],
+)
+
+# Release checklist
+# 1. Change the version in __init__.py and setup.py to the release version, e.g. from "0.6.1.dev0" to "0.7.0"
+# 2. Check if there are any deprecations that need to be addressed for this release by searching for "# TODO" in the code
+# 3. Commit these changes with the message: "Release: VERSION", create a PR and merge it.
+# 4. Add a tag in git to mark the release: "git tag -a v -m 'Adds tag for pypi' "
+# Push the tag to git:
+# git push --tags origin main
+# It is necessary to work on the original repository, not on a fork.
+# 5. Run the following commands in the top-level directory:
+# python setup.py bdist_wheel
+# python setup.py sdist
+# Ensure that you are on the clean and up-to-date main branch (git status --untracked-files=no should not list any
+# files and show the main branch)
+# 6. Upload the package to the pypi test server first:
+# twine upload dist/* -r pypitest
+# 7. Check that you can install it in a virtualenv by running:
+# pip install -i https://testpypi.python.org/pypi --extra-index-url https://pypi.org/simple peft
+# 8. Upload the final version to actual pypi:
+# twine upload dist/* -r pypi
+# 9. Add release notes to the tag on https://github.com/huggingface/peft/releases once everything is looking hunky-dory.
+# Check the notes here: https://docs.google.com/document/d/1k-sOIfykuKjWcOIALqjhFKz4amFEp-myeJUJEzNgjoU/edit?usp=sharing
+# 10. Update the version in __init__.py, setup.py to the bumped patch version + ".dev0" (e.g. from "0.7.0" to "0.7.1.dev0")
diff --git a/peft/src/peft/__init__.py b/peft/src/peft/__init__.py
new file mode 100644
index 0000000000000000000000000000000000000000..af26f8309b0a2637a484f5bfa73f838de61d8ef3
--- /dev/null
+++ b/peft/src/peft/__init__.py
@@ -0,0 +1,236 @@
+# Copyright 2023-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+__version__ = "0.17.2.dev0"
+
+from .auto import (
+ MODEL_TYPE_TO_PEFT_MODEL_MAPPING,
+ AutoPeftModel,
+ AutoPeftModelForCausalLM,
+ AutoPeftModelForFeatureExtraction,
+ AutoPeftModelForQuestionAnswering,
+ AutoPeftModelForSeq2SeqLM,
+ AutoPeftModelForSequenceClassification,
+ AutoPeftModelForTokenClassification,
+)
+from .config import PeftConfig, PromptLearningConfig
+from .mapping import (
+ PEFT_TYPE_TO_CONFIG_MAPPING,
+ PEFT_TYPE_TO_MIXED_MODEL_MAPPING,
+ PEFT_TYPE_TO_TUNER_MAPPING,
+ get_peft_config,
+ inject_adapter_in_model,
+)
+from .mapping_func import get_peft_model
+from .mixed_model import PeftMixedModel
+from .peft_model import (
+ PeftModel,
+ PeftModelForCausalLM,
+ PeftModelForFeatureExtraction,
+ PeftModelForQuestionAnswering,
+ PeftModelForSeq2SeqLM,
+ PeftModelForSequenceClassification,
+ PeftModelForTokenClassification,
+ get_layer_status,
+ get_model_status,
+)
+from .tuners import (
+ AdaLoraConfig,
+ AdaLoraModel,
+ AdaptionPromptConfig,
+ AdaptionPromptModel,
+ ArrowConfig,
+ BOFTConfig,
+ BOFTModel,
+ BoneConfig,
+ BoneModel,
+ C3AConfig,
+ C3AModel,
+ CPTConfig,
+ CPTEmbedding,
+ EvaConfig,
+ FourierFTConfig,
+ FourierFTModel,
+ HRAConfig,
+ HRAModel,
+ IA3Config,
+ IA3Model,
+ LNTuningConfig,
+ LNTuningModel,
+ LoftQConfig,
+ LoHaConfig,
+ LoHaModel,
+ LoKrConfig,
+ LoKrModel,
+ LoraConfig,
+ LoraModel,
+ LoraRuntimeConfig,
+ MissConfig,
+ MissModel,
+ MultitaskPromptTuningConfig,
+ MultitaskPromptTuningInit,
+ OFTConfig,
+ OFTModel,
+ PolyConfig,
+ PolyModel,
+ PrefixEncoder,
+ PrefixTuningConfig,
+ PromptEmbedding,
+ PromptEncoder,
+ PromptEncoderConfig,
+ PromptEncoderReparameterizationType,
+ PromptTuningConfig,
+ PromptTuningInit,
+ RandLoraConfig,
+ RandLoraModel,
+ RoadConfig,
+ RoadModel,
+ ShiraConfig,
+ ShiraModel,
+ TrainableTokensConfig,
+ TrainableTokensModel,
+ VBLoRAConfig,
+ VBLoRAModel,
+ VeraConfig,
+ VeraModel,
+ WaveFTConfig,
+ WaveFTModel,
+ XLoraConfig,
+ XLoraModel,
+ create_arrow_model,
+ get_eva_state_dict,
+ initialize_lora_eva_weights,
+)
+from .utils import (
+ TRANSFORMERS_MODELS_TO_PREFIX_TUNING_POSTPROCESS_MAPPING,
+ PeftType,
+ PeftWarning,
+ TaskType,
+ bloom_model_postprocess_past_key_value,
+ cast_mixed_precision_params,
+ get_peft_model_state_dict,
+ load_peft_weights,
+ prepare_model_for_kbit_training,
+ replace_lora_weights_loftq,
+ set_peft_model_state_dict,
+ shift_tokens_right,
+)
+
+
+__all__ = [
+ "MODEL_TYPE_TO_PEFT_MODEL_MAPPING",
+ "PEFT_TYPE_TO_CONFIG_MAPPING",
+ "PEFT_TYPE_TO_MIXED_MODEL_MAPPING",
+ "PEFT_TYPE_TO_TUNER_MAPPING",
+ "TRANSFORMERS_MODELS_TO_PREFIX_TUNING_POSTPROCESS_MAPPING",
+ "AdaLoraConfig",
+ "AdaLoraModel",
+ "AdaptionPromptConfig",
+ "AdaptionPromptModel",
+ "ArrowConfig",
+ "AutoPeftModel",
+ "AutoPeftModelForCausalLM",
+ "AutoPeftModelForFeatureExtraction",
+ "AutoPeftModelForQuestionAnswering",
+ "AutoPeftModelForSeq2SeqLM",
+ "AutoPeftModelForSequenceClassification",
+ "AutoPeftModelForTokenClassification",
+ "BOFTConfig",
+ "BOFTModel",
+ "BoneConfig",
+ "BoneModel",
+ "C3AConfig",
+ "C3AModel",
+ "CPTConfig",
+ "CPTEmbedding",
+ "EvaConfig",
+ "FourierFTConfig",
+ "FourierFTModel",
+ "HRAConfig",
+ "HRAModel",
+ "IA3Config",
+ "IA3Model",
+ "LNTuningConfig",
+ "LNTuningModel",
+ "LoHaConfig",
+ "LoHaModel",
+ "LoKrConfig",
+ "LoKrModel",
+ "LoftQConfig",
+ "LoraConfig",
+ "LoraModel",
+ "LoraRuntimeConfig",
+ "MissConfig",
+ "MissModel",
+ "MultitaskPromptTuningConfig",
+ "MultitaskPromptTuningInit",
+ "OFTConfig",
+ "OFTModel",
+ "PeftConfig",
+ "PeftMixedModel",
+ "PeftModel",
+ "PeftModelForCausalLM",
+ "PeftModelForFeatureExtraction",
+ "PeftModelForQuestionAnswering",
+ "PeftModelForSeq2SeqLM",
+ "PeftModelForSequenceClassification",
+ "PeftModelForTokenClassification",
+ "PeftType",
+ "PeftWarning",
+ "PolyConfig",
+ "PolyModel",
+ "PrefixEncoder",
+ "PrefixTuningConfig",
+ "PromptEmbedding",
+ "PromptEncoder",
+ "PromptEncoderConfig",
+ "PromptEncoderReparameterizationType",
+ "PromptLearningConfig",
+ "PromptTuningConfig",
+ "PromptTuningInit",
+ "RandLoraConfig",
+ "RandLoraModel",
+ "RoadConfig",
+ "RoadModel",
+ "ShiraConfig",
+ "ShiraModel",
+ "TaskType",
+ "TrainableTokensConfig",
+ "TrainableTokensModel",
+ "VBLoRAConfig",
+ "VBLoRAConfig",
+ "VBLoRAModel",
+ "VeraConfig",
+ "VeraModel",
+ "WaveFTConfig",
+ "WaveFTModel",
+ "XLoraConfig",
+ "XLoraModel",
+ "bloom_model_postprocess_past_key_value",
+ "cast_mixed_precision_params",
+ "create_arrow_model",
+ "get_eva_state_dict",
+ "get_layer_status",
+ "get_model_status",
+ "get_peft_config",
+ "get_peft_model",
+ "get_peft_model_state_dict",
+ "initialize_lora_eva_weights",
+ "inject_adapter_in_model",
+ "load_peft_weights",
+ "prepare_model_for_kbit_training",
+ "replace_lora_weights_loftq",
+ "set_peft_model_state_dict",
+ "shift_tokens_right",
+]
diff --git a/peft/src/peft/auto.py b/peft/src/peft/auto.py
new file mode 100644
index 0000000000000000000000000000000000000000..613f67c707e344eab1a5281565fb0fdb3d827d01
--- /dev/null
+++ b/peft/src/peft/auto.py
@@ -0,0 +1,184 @@
+# Copyright 2023-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+from __future__ import annotations
+
+import importlib
+import os
+from typing import Optional
+
+from transformers import (
+ AutoModel,
+ AutoModelForCausalLM,
+ AutoModelForQuestionAnswering,
+ AutoModelForSeq2SeqLM,
+ AutoModelForSequenceClassification,
+ AutoModelForTokenClassification,
+ AutoTokenizer,
+)
+
+from .config import PeftConfig
+from .peft_model import (
+ PeftModel,
+ PeftModelForCausalLM,
+ PeftModelForFeatureExtraction,
+ PeftModelForQuestionAnswering,
+ PeftModelForSeq2SeqLM,
+ PeftModelForSequenceClassification,
+ PeftModelForTokenClassification,
+)
+from .utils.constants import TOKENIZER_CONFIG_NAME
+from .utils.other import check_file_exists_on_hf_hub
+
+
+MODEL_TYPE_TO_PEFT_MODEL_MAPPING: dict[str, type[PeftModel]] = {
+ "SEQ_CLS": PeftModelForSequenceClassification,
+ "SEQ_2_SEQ_LM": PeftModelForSeq2SeqLM,
+ "CAUSAL_LM": PeftModelForCausalLM,
+ "TOKEN_CLS": PeftModelForTokenClassification,
+ "QUESTION_ANS": PeftModelForQuestionAnswering,
+ "FEATURE_EXTRACTION": PeftModelForFeatureExtraction,
+}
+
+
+class _BaseAutoPeftModel:
+ _target_class = None
+ _target_peft_class = None
+
+ def __init__(self, *args, **kwargs):
+ # For consistency with transformers: https://github.com/huggingface/transformers/blob/91d7df58b6537d385e90578dac40204cb550f706/src/transformers/models/auto/auto_factory.py#L400
+ raise EnvironmentError( # noqa: UP024
+ f"{self.__class__.__name__} is designed to be instantiated "
+ f"using the `{self.__class__.__name__}.from_pretrained(pretrained_model_name_or_path)` or "
+ f"`{self.__class__.__name__}.from_config(config)` methods."
+ )
+
+ @classmethod
+ def from_pretrained(
+ cls,
+ pretrained_model_name_or_path,
+ adapter_name: str = "default",
+ is_trainable: bool = False,
+ config: Optional[PeftConfig] = None,
+ revision: Optional[str] = None,
+ **kwargs,
+ ):
+ r"""
+ A wrapper around all the preprocessing steps a user needs to perform in order to load a PEFT model. The kwargs
+ are passed along to `PeftConfig` that automatically takes care of filtering the kwargs of the Hub methods and
+ the config object init.
+ """
+ peft_config = PeftConfig.from_pretrained(pretrained_model_name_or_path, revision=revision, **kwargs)
+ base_model_path = peft_config.base_model_name_or_path
+ base_model_revision = peft_config.revision
+
+ task_type = getattr(peft_config, "task_type", None)
+
+ if cls._target_class is not None:
+ target_class = cls._target_class
+ elif cls._target_class is None and task_type is not None:
+ # this is only in the case where we use `AutoPeftModel`
+ raise ValueError(
+ "Cannot use `AutoPeftModel` with a task type, please use a specific class for your task type. (e.g. `AutoPeftModelForCausalLM` for `task_type='CAUSAL_LM'`)"
+ )
+
+ if task_type is not None:
+ expected_target_class = MODEL_TYPE_TO_PEFT_MODEL_MAPPING[task_type]
+ if cls._target_peft_class.__name__ != expected_target_class.__name__:
+ raise ValueError(
+ f"Expected target PEFT class: {expected_target_class.__name__}, but you have asked for: {cls._target_peft_class.__name__}"
+ " make sure that you are loading the correct model for your task type."
+ )
+ elif task_type is None and getattr(peft_config, "auto_mapping", None) is not None:
+ auto_mapping = getattr(peft_config, "auto_mapping", None)
+ base_model_class = auto_mapping["base_model_class"]
+ parent_library_name = auto_mapping["parent_library"]
+
+ parent_library = importlib.import_module(parent_library_name)
+ target_class = getattr(parent_library, base_model_class)
+ else:
+ raise ValueError(
+ "Cannot infer the auto class from the config, please make sure that you are loading the correct model for your task type."
+ )
+
+ base_model = target_class.from_pretrained(base_model_path, revision=base_model_revision, **kwargs)
+
+ tokenizer_exists = False
+ if os.path.exists(os.path.join(pretrained_model_name_or_path, TOKENIZER_CONFIG_NAME)):
+ tokenizer_exists = True
+ else:
+ token = kwargs.get("token", None)
+ if token is None:
+ token = kwargs.get("use_auth_token", None)
+
+ tokenizer_exists = check_file_exists_on_hf_hub(
+ repo_id=pretrained_model_name_or_path,
+ filename=TOKENIZER_CONFIG_NAME,
+ revision=revision,
+ repo_type=kwargs.get("repo_type", None),
+ token=token,
+ )
+
+ if tokenizer_exists and hasattr(base_model, "get_input_embeddings"):
+ tokenizer = AutoTokenizer.from_pretrained(
+ pretrained_model_name_or_path, trust_remote_code=kwargs.get("trust_remote_code", False)
+ )
+ embedding_size = base_model.get_input_embeddings().weight.shape[0]
+ if len(tokenizer) > embedding_size:
+ # only resize if the tokenizer has a larger vocab size than there are embeddings
+ base_model.resize_token_embeddings(len(tokenizer))
+
+ return cls._target_peft_class.from_pretrained(
+ base_model,
+ pretrained_model_name_or_path,
+ adapter_name=adapter_name,
+ is_trainable=is_trainable,
+ config=config,
+ **kwargs,
+ )
+
+
+class AutoPeftModel(_BaseAutoPeftModel):
+ _target_class = None
+ _target_peft_class = PeftModel
+
+
+class AutoPeftModelForCausalLM(_BaseAutoPeftModel):
+ _target_class = AutoModelForCausalLM
+ _target_peft_class = PeftModelForCausalLM
+
+
+class AutoPeftModelForSeq2SeqLM(_BaseAutoPeftModel):
+ _target_class = AutoModelForSeq2SeqLM
+ _target_peft_class = PeftModelForSeq2SeqLM
+
+
+class AutoPeftModelForSequenceClassification(_BaseAutoPeftModel):
+ _target_class = AutoModelForSequenceClassification
+ _target_peft_class = PeftModelForSequenceClassification
+
+
+class AutoPeftModelForTokenClassification(_BaseAutoPeftModel):
+ _target_class = AutoModelForTokenClassification
+ _target_peft_class = PeftModelForTokenClassification
+
+
+class AutoPeftModelForQuestionAnswering(_BaseAutoPeftModel):
+ _target_class = AutoModelForQuestionAnswering
+ _target_peft_class = PeftModelForQuestionAnswering
+
+
+class AutoPeftModelForFeatureExtraction(_BaseAutoPeftModel):
+ _target_class = AutoModel
+ _target_peft_class = PeftModelForFeatureExtraction
diff --git a/peft/src/peft/config.py b/peft/src/peft/config.py
new file mode 100644
index 0000000000000000000000000000000000000000..60a5c20c74bc2b8b97a5e0262e99cc10a79be481
--- /dev/null
+++ b/peft/src/peft/config.py
@@ -0,0 +1,408 @@
+# Copyright 2023-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+from __future__ import annotations
+
+import importlib.metadata
+import inspect
+import json
+import os
+import warnings
+from dataclasses import asdict, dataclass, field
+from typing import Optional, Union
+
+import packaging.version
+from huggingface_hub import hf_hub_download
+from transformers.utils import PushToHubMixin, http_user_agent
+
+from peft import __version__
+
+from .utils import CONFIG_NAME, PeftType, TaskType
+
+
+# we expect at least these keys to be present in a PEFT adapter_config.json
+MIN_EXPECTED_CONFIG_KEYS = {"peft_type"}
+
+
+def _check_and_remove_unused_kwargs(cls, kwargs):
+ """Make PEFT configs forward-compatible by removing unused kwargs that were added in later PEFT versions.
+
+ This assumes that removing the unused kwargs will not affect the default behavior.
+
+ Returns the filtered kwargs and the set of removed keys.
+ """
+ # it's not pretty but eh
+ signature_parameters = inspect.signature(cls.__init__).parameters
+ unexpected_kwargs = set(kwargs.keys()) - set(signature_parameters.keys())
+ for key in unexpected_kwargs:
+ del kwargs[key]
+ return kwargs, unexpected_kwargs
+
+
+def _is_dev_version(version: str) -> bool:
+ # check if the given version is a dev version
+ return packaging.version.Version(version).dev is not None
+
+
+def _get_commit_hash(pkg_name: str) -> str | None:
+ # If PEFT was installed from a specific commit hash, try to get it. This works e.g. when installing PEFT with `pip
+ # install git+https://github.com/huggingface/peft.git@`. This works not for other means, like editable
+ # installs.
+ try:
+ dist = importlib.metadata.distribution(pkg_name)
+ except importlib.metadata.PackageNotFoundError:
+ return None
+
+ # See: https://packaging.python.org/en/latest/specifications/direct-url/
+ for path in dist.files or []:
+ if path.name == "direct_url.json":
+ direct_url = json.loads((dist.locate_file(path)).read_text())
+ vcs_info = direct_url.get("vcs_info")
+ if vcs_info and "commit_id" in vcs_info:
+ return vcs_info["commit_id"]
+ return None
+
+
+@dataclass
+class PeftConfigMixin(PushToHubMixin):
+ r"""
+ This is the base configuration class for PEFT adapter models. It contains all the methods that are common to all
+ PEFT adapter models. This class inherits from [`~transformers.utils.PushToHubMixin`] which contains the methods to
+ push your model to the Hub. The method `save_pretrained` will save the configuration of your adapter model in a
+ directory. The method `from_pretrained` will load the configuration of your adapter model from a directory.
+
+ Args:
+ peft_type (Union[[`~peft.utils.config.PeftType`], `str`]): The type of Peft method to use.
+ """
+
+ task_type: Optional[TaskType] = field(default=None, metadata={"help": "The type of task."})
+ peft_type: Optional[PeftType] = field(default=None, metadata={"help": "The type of PEFT model."})
+ auto_mapping: Optional[dict] = field(
+ default=None, metadata={"help": "An auto mapping dict to help retrieve the base model class if needed."}
+ )
+ peft_version: Optional[str] = field(default=None, metadata={"help": "PEFT version, leave empty to auto-fill."})
+
+ def __post_init__(self):
+ # check for invalid task type
+ if (self.task_type is not None) and (self.task_type not in list(TaskType)):
+ raise ValueError(
+ f"Invalid task type: '{self.task_type}'. Must be one of the following task types: {', '.join(TaskType)}."
+ )
+ if self.peft_version is None:
+ self.peft_version = self._get_peft_version()
+
+ @staticmethod
+ def _get_peft_version() -> str:
+ # gets the current peft version; if it's a dev version, try to get the commit hash too, as the dev version is
+ # ambiguous
+ version = __version__
+ if not _is_dev_version(version):
+ return version
+
+ try:
+ git_hash = _get_commit_hash("peft")
+ if git_hash is None:
+ git_hash = "UNKNOWN"
+ except Exception:
+ # Broad exception: We never want to break user code just because the git_hash could not be determined
+ warnings.warn(
+ "A dev version of PEFT is used but there was an error while trying to determine the commit hash. "
+ "Please open an issue: https://github.com/huggingface/peft/issues"
+ )
+ git_hash = "UNKNOWN"
+ version = version + f"@{git_hash}"
+ return version
+
+ def to_dict(self) -> dict:
+ r"""
+ Returns the configuration for your adapter model as a dictionary.
+ """
+ return asdict(self)
+
+ def save_pretrained(self, save_directory: str, **kwargs) -> None:
+ r"""
+ This method saves the configuration of your adapter model in a directory.
+
+ Args:
+ save_directory (`str`):
+ The directory where the configuration will be saved.
+ kwargs (additional keyword arguments, *optional*):
+ Additional keyword arguments passed along to the [`~transformers.utils.PushToHubMixin.push_to_hub`]
+ method.
+ """
+ if os.path.isfile(save_directory):
+ raise AssertionError(f"Provided path ({save_directory}) should be a directory, not a file")
+
+ os.makedirs(save_directory, exist_ok=True)
+ auto_mapping_dict = kwargs.pop("auto_mapping_dict", None)
+
+ output_dict = self.to_dict()
+ # converting set type to list
+ for key, value in output_dict.items():
+ if isinstance(value, set):
+ output_dict[key] = list(value)
+
+ output_path = os.path.join(save_directory, CONFIG_NAME)
+
+ # Add auto mapping details for custom models.
+ if auto_mapping_dict is not None:
+ output_dict["auto_mapping"] = auto_mapping_dict
+
+ # save it
+ with open(output_path, "w") as writer:
+ writer.write(json.dumps(output_dict, indent=2, sort_keys=True))
+
+ @classmethod
+ def from_peft_type(cls, **kwargs):
+ r"""
+ This method loads the configuration of your adapter model from a set of kwargs.
+
+ The appropriate configuration type is determined by the `peft_type` argument. If `peft_type` is not provided,
+ the calling class type is instantiated.
+
+ Args:
+ kwargs (configuration keyword arguments):
+ Keyword arguments passed along to the configuration initialization.
+ """
+ # Avoid circular dependency .. TODO: fix this with a larger refactor
+ from peft.mapping import PEFT_TYPE_TO_CONFIG_MAPPING
+
+ # TODO: this hack is needed to fix the following issue (on commit 702f937):
+ # if someone saves a default config and loads it back with `PeftConfig` class it yields to
+ # not loading the correct config class.
+ #
+ # from peft import AdaLoraConfig, PeftConfig
+ # peft_config = AdaLoraConfig()
+ # print(peft_config)
+ # >>> AdaLoraConfig(peft_type=, auto_mapping=None, base_model_name_or_path=None,
+ # revision=None, task_type=None, inference_mode=False, r=8, target_modules=None, lora_alpha=8, lora_dropout=0.0, ...
+ #
+ # peft_config.save_pretrained("./test_config")
+ # peft_config = PeftConfig.from_pretrained("./test_config")
+ # print(peft_config)
+ # >>> PeftConfig(peft_type='ADALORA', auto_mapping=None, base_model_name_or_path=None, revision=None, task_type=None, inference_mode=False)
+
+ if "peft_type" in kwargs:
+ peft_type = kwargs["peft_type"]
+ config_cls = PEFT_TYPE_TO_CONFIG_MAPPING[peft_type]
+ else:
+ config_cls = cls
+
+ try:
+ config = config_cls(**kwargs)
+ except TypeError as exc:
+ # Here we potentially handle forward compatibility. Sometimes new keywords are added to configs, which makes
+ # new configs incompatible with older PEFT versions. We catch these and remove them to allow the program to
+ # continue, but warn the user about it.
+
+ # First check if the error is due to unexpected keyword arguments, we don't want to accidentally catch
+ # other TypeErrors.
+ if "got an unexpected keyword argument" not in str(exc):
+ raise exc
+
+ filtered_kwargs, unexpected_kwargs = _check_and_remove_unused_kwargs(config_cls, kwargs)
+ if not MIN_EXPECTED_CONFIG_KEYS.issubset(set(filtered_kwargs.keys())):
+ raise TypeError(
+ f"The {cls.__name__} config that is trying to be loaded is missing required keys: "
+ f"{MIN_EXPECTED_CONFIG_KEYS}."
+ )
+
+ warnings.warn(
+ f"Unexpected keyword arguments {sorted(unexpected_kwargs)} for class {config_cls.__name__}, these are "
+ "ignored. This probably means that you're loading a configuration file that was saved using a "
+ "higher version of the library and additional parameters have been introduced since. It is "
+ "highly recommended to upgrade the PEFT version before continuing (e.g. by running `pip install "
+ "-U peft`)."
+ )
+ config = config_cls.from_peft_type(**filtered_kwargs)
+ return config
+
+ @classmethod
+ def from_pretrained(cls, pretrained_model_name_or_path: str, subfolder: Optional[str] = None, **kwargs):
+ r"""
+ This method loads the configuration of your adapter model from a directory.
+
+ Args:
+ pretrained_model_name_or_path (`str`):
+ The directory or the Hub repository id where the configuration is saved.
+ kwargs (additional keyword arguments, *optional*):
+ Additional keyword arguments passed along to the child class initialization.
+ """
+ path = (
+ os.path.join(pretrained_model_name_or_path, subfolder)
+ if subfolder is not None
+ else pretrained_model_name_or_path
+ )
+
+ hf_hub_download_kwargs, class_kwargs, _ = cls._split_kwargs(kwargs)
+ if "user_agent" not in hf_hub_download_kwargs:
+ hf_hub_download_kwargs["user_agent"] = http_user_agent()
+
+ if os.path.isfile(os.path.join(path, CONFIG_NAME)):
+ config_file = os.path.join(path, CONFIG_NAME)
+ else:
+ try:
+ config_file = hf_hub_download(
+ pretrained_model_name_or_path, CONFIG_NAME, subfolder=subfolder, **hf_hub_download_kwargs
+ )
+ except Exception as exc:
+ raise ValueError(f"Can't find '{CONFIG_NAME}' at '{pretrained_model_name_or_path}'") from exc
+
+ loaded_attributes = cls.from_json_file(config_file)
+ kwargs = {**class_kwargs, **loaded_attributes}
+ kwargs = cls.check_kwargs(**kwargs)
+ return cls.from_peft_type(**kwargs)
+
+ @classmethod
+ def from_json_file(cls, path_json_file: str, **kwargs):
+ r"""
+ Loads a configuration file from a json file.
+
+ Args:
+ path_json_file (`str`):
+ The path to the json file.
+ """
+ with open(path_json_file) as file:
+ json_object = json.load(file)
+
+ # Sanity check that config does not contain a runtime_config
+ if "runtime_config" in json_object:
+ warnings.warn(
+ "The configuration file contains a `runtime_config` key. This is ignored. Runtime configurations are only valid at runtime."
+ )
+ del json_object["runtime_config"]
+
+ return json_object
+
+ @classmethod
+ def _split_kwargs(cls, kwargs):
+ hf_hub_download_kwargs = {}
+ class_kwargs = {}
+ other_kwargs = {}
+
+ for key, value in kwargs.items():
+ if key in inspect.signature(hf_hub_download).parameters:
+ hf_hub_download_kwargs[key] = value
+ elif key in list(cls.__annotations__):
+ class_kwargs[key] = value
+ else:
+ other_kwargs[key] = value
+
+ return hf_hub_download_kwargs, class_kwargs, other_kwargs
+
+ @classmethod
+ def _get_peft_type(
+ cls,
+ model_id: str,
+ **hf_hub_download_kwargs,
+ ):
+ subfolder = hf_hub_download_kwargs.get("subfolder", None)
+
+ path = os.path.join(model_id, subfolder) if subfolder is not None else model_id
+
+ if os.path.isfile(os.path.join(path, CONFIG_NAME)):
+ config_file = os.path.join(path, CONFIG_NAME)
+ else:
+ try:
+ config_file = hf_hub_download(
+ model_id,
+ CONFIG_NAME,
+ **hf_hub_download_kwargs,
+ )
+ except Exception:
+ raise ValueError(f"Can't find '{CONFIG_NAME}' at '{model_id}'")
+
+ loaded_attributes = cls.from_json_file(config_file)
+ return loaded_attributes["peft_type"]
+
+ @classmethod
+ def check_kwargs(cls, **kwargs):
+ """Check kwargs before initializing the config instance.
+
+ Subclasses can override this method to add specific checks.
+
+ """
+ return kwargs
+
+ @property
+ def is_prompt_learning(self) -> bool:
+ r"""
+ Utility method to check if the configuration is for prompt learning.
+ """
+ return False
+
+ @property
+ def is_adaption_prompt(self) -> bool:
+ """Return True if this is an adaption prompt config."""
+ return False
+
+
+@dataclass
+class PeftConfig(PeftConfigMixin):
+ """
+ This is the base configuration class to store the configuration of a [`PeftModel`].
+
+ Args:
+ peft_type (Union[[`~peft.utils.config.PeftType`], `str`]): The type of Peft method to use.
+ task_type (Union[[`~peft.utils.config.TaskType`], `str`]): The type of task to perform.
+ inference_mode (`bool`, defaults to `False`): Whether to use the Peft model in inference mode.
+ """
+
+ base_model_name_or_path: Optional[str] = field(
+ default=None, metadata={"help": "The name of the base model to use."}
+ )
+ revision: Optional[str] = field(default=None, metadata={"help": "The specific base model version to use."})
+ peft_type: Optional[Union[str, PeftType]] = field(default=None, metadata={"help": "Peft type"})
+ task_type: Optional[Union[str, TaskType]] = field(default=None, metadata={"help": "Task type"})
+ inference_mode: bool = field(default=False, metadata={"help": "Whether to use inference mode"})
+
+
+@dataclass
+class PromptLearningConfig(PeftConfig):
+ """
+ This is the base configuration class to store the configuration of [`PrefixTuning`], [`PromptEncoder`], or
+ [`PromptTuning`].
+
+ Args:
+ num_virtual_tokens (`int`): The number of virtual tokens to use.
+ token_dim (`int`): The hidden embedding dimension of the base transformer model.
+ num_transformer_submodules (`int`): The number of transformer submodules in the base transformer model.
+ num_attention_heads (`int`): The number of attention heads in the base transformer model.
+ num_layers (`int`): The number of layers in the base transformer model.
+ """
+
+ num_virtual_tokens: int = field(default=None, metadata={"help": "Number of virtual tokens"})
+ token_dim: int = field(
+ default=None, metadata={"help": "The hidden embedding dimension of the base transformer model"}
+ )
+ num_transformer_submodules: Optional[int] = field(
+ default=None, metadata={"help": "Number of transformer submodules"}
+ )
+ num_attention_heads: Optional[int] = field(default=None, metadata={"help": "Number of attention heads"})
+ num_layers: Optional[int] = field(default=None, metadata={"help": "Number of transformer layers"})
+ modules_to_save: Optional[list[str]] = field(
+ default=None,
+ metadata={
+ "help": "List of extra modules to be set as trainable and saved in the final checkpoint. "
+ "For example, in Sequence Classification or Token Classification tasks, "
+ "the final layer `classifier/score` are randomly initialized and as such need to be trainable and saved. "
+ "The module(s) will be fully fine-tuned."
+ },
+ )
+
+ @property
+ def is_prompt_learning(self) -> bool:
+ r"""
+ Utility method to check if the configuration is for prompt learning.
+ """
+ return True
diff --git a/peft/src/peft/functional.py b/peft/src/peft/functional.py
new file mode 100644
index 0000000000000000000000000000000000000000..60df690cafe1e9a3b5c8ff09d550f82110afe593
--- /dev/null
+++ b/peft/src/peft/functional.py
@@ -0,0 +1,34 @@
+# Copyright 2025-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+"""
+Functions that are useful for integration with non-PeftModel models, e.g. transformers or diffusers.
+
+The functions provided here can be considered "public API" of PEFT and hence are safe to be used by packages that
+provide PEFT integrations.
+"""
+
+from peft.mapping import inject_adapter_in_model
+from peft.tuners.tuners_utils import cast_adapter_dtype, delete_adapter, set_adapter, set_requires_grad
+from peft.utils import get_peft_model_state_dict, set_peft_model_state_dict
+
+
+__all__ = [
+ "cast_adapter_dtype",
+ "delete_adapter",
+ "get_peft_model_state_dict",
+ "inject_adapter_in_model",
+ "set_adapter",
+ "set_peft_model_state_dict",
+ "set_requires_grad",
+]
diff --git a/peft/src/peft/helpers.py b/peft/src/peft/helpers.py
new file mode 100644
index 0000000000000000000000000000000000000000..d748c62e696d57034e4e9fd6458b27febbd9c90c
--- /dev/null
+++ b/peft/src/peft/helpers.py
@@ -0,0 +1,251 @@
+# Copyright 2023-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+import inspect
+from contextlib import contextmanager
+from copy import deepcopy
+from functools import update_wrapper
+from types import MethodType
+
+from torch import nn
+
+from .peft_model import PeftConfig, PeftModel
+from .tuners.lora import LoraLayer
+from .tuners.tuners_utils import BaseTunerLayer
+
+
+def update_forward_signature(model: PeftModel) -> None:
+ """
+ Updates the forward signature of the PeftModel to include parents class signature
+ model (`PeftModel`): Peft model to update the forward signature
+
+ Example:
+
+ ```python
+ >>> from transformers import WhisperForConditionalGeneration
+ >>> from peft import get_peft_model, LoraConfig, update_forward_signature
+
+ >>> model = WhisperForConditionalGeneration.from_pretrained("openai/whisper-tiny.en")
+ >>> peft_config = LoraConfig(r=8, lora_alpha=32, lora_dropout=0.1, target_modules=["q_proj", "v_proj"])
+
+ >>> peft_model = get_peft_model(model, peft_config)
+ >>> update_forward_signature(peft_model)
+ ```
+ """
+
+ # Only update signature when the current forward signature only has *args and **kwargs
+ current_signature = inspect.signature(model.forward)
+ if (
+ len(current_signature.parameters) == 2
+ and "args" in current_signature.parameters
+ and "kwargs" in current_signature.parameters
+ ):
+ forward = deepcopy(model.forward.__func__)
+ update_wrapper(
+ forward, type(model.get_base_model()).forward, assigned=("__doc__", "__name__", "__annotations__")
+ )
+ model.forward = MethodType(forward, model)
+
+
+def update_generate_signature(model: PeftModel) -> None:
+ """
+ Updates the generate signature of a PeftModel with overriding generate to include parents class signature
+ model (`PeftModel`): Peft model to update the generate signature
+
+ Example:
+
+ ```python
+ >>> from transformers import AutoModelForSeq2SeqLM, AutoTokenizer
+ >>> from peft import get_peft_model, LoraConfig, TaskType, update_generate_signature
+
+ >>> model_name_or_path = "bigscience/mt0-large"
+ >>> tokenizer = AutoTokenizer.from_pretrained(model_name_or_path)
+ >>> model = AutoModelForSeq2SeqLM.from_pretrained(model_name_or_path)
+
+ >>> peft_config = LoraConfig(
+ ... task_type=TaskType.SEQ_2_SEQ_LM, inference_mode=False, r=8, lora_alpha=32, lora_dropout=0.1
+ ... )
+ >>> peft_model = get_peft_model(model, peft_config)
+ >>> update_generate_signature(peft_model)
+ >>> help(peft_model.generate)
+ ```
+ """
+ if not hasattr(model, "generate"):
+ return
+ current_signature = inspect.signature(model.generate)
+ if (
+ len(current_signature.parameters) == 2
+ and "args" in current_signature.parameters
+ and "kwargs" in current_signature.parameters
+ ) or (len(current_signature.parameters) == 1 and "kwargs" in current_signature.parameters):
+ generate = deepcopy(model.generate.__func__)
+ update_wrapper(
+ generate,
+ type(model.get_base_model()).generate,
+ assigned=("__doc__", "__name__", "__annotations__"),
+ )
+ model.generate = MethodType(generate, model)
+
+
+def update_signature(model: PeftModel, method: str = "all") -> None:
+ """
+ Updates the signature of a PeftModel include parents class signature for forward or generate method
+ model (`PeftModel`): Peft model to update generate or forward signature method (`str`): method to update
+ signature choose one of "forward", "generate", "all"
+
+ Example:
+ ```python
+ >>> from transformers import AutoModelForSeq2SeqLM, AutoTokenizer
+ >>> from peft import get_peft_model, LoraConfig, TaskType, update_signature
+
+ >>> model_name_or_path = "bigscience/mt0-large"
+ >>> tokenizer = AutoTokenizer.from_pretrained(model_name_or_path)
+ >>> model = AutoModelForSeq2SeqLM.from_pretrained(model_name_or_path)
+
+ >>> peft_config = LoraConfig(
+ ... task_type=TaskType.SEQ_2_SEQ_LM, inference_mode=False, r=8, lora_alpha=32, lora_dropout=0.1
+ ... )
+ >>> peft_model = get_peft_model(model, peft_config)
+ >>> update_signature(peft_model)
+ >>> help(peft_model.generate)
+ ```
+ """
+ if method == "forward":
+ update_forward_signature(model)
+ elif method == "generate":
+ update_generate_signature(model)
+ elif method == "all":
+ update_forward_signature(model)
+ update_generate_signature(model)
+ else:
+ raise ValueError(f"method {method} is not supported please choose one of ['forward', 'generate', 'all']")
+
+
+def check_if_peft_model(model_name_or_path: str) -> bool:
+ """
+ Check if the model is a PEFT model.
+
+ Args:
+ model_name_or_path (`str`):
+ Model id to check, can be local or on the Hugging Face Hub.
+
+ Returns:
+ `bool`: True if the model is a PEFT model, False otherwise.
+ """
+ is_peft_model = True
+ try:
+ PeftConfig.from_pretrained(model_name_or_path)
+ except Exception:
+ # allow broad exceptions so that this works even if new exceptions are added on HF Hub side
+ is_peft_model = False
+
+ return is_peft_model
+
+
+@contextmanager
+def rescale_adapter_scale(model, multiplier):
+ """
+ Context manager to temporarily rescale the scaling of the LoRA adapter in a model.
+
+ The original scaling values are restored when the context manager exits. This context manager works with the
+ transformers and diffusers models that have directly loaded LoRA adapters.
+
+ For LoRA, applying this context manager with multiplier in [0, 1] is strictly equivalent to applying
+ [wise-ft](https://huggingface.co/papers/2109.01903) (see [#1940](https://github.com/huggingface/peft/issues/1940)
+ for details). It can improve the performances of the model if there is a distribution shiftbetween the training
+ data used for fine-tuning, and the test data used during inference.
+
+ Warning: It has been reported that when using Apple's MPS backend for PyTorch, it is necessary to add a short sleep
+ time after exiting the context before the scales are fully restored.
+
+ Args:
+ model: The model containing `LoraLayer` modules whose scaling is to be adjusted.
+ multiplier (float or int):
+ The multiplier that rescales the `scaling` attribute. Must be of type float or int.
+
+ Raises:
+ ValueError: If the model does not contain any `LoraLayer`
+ instances, indicating that the model does not support scaling.
+
+ Example:
+
+ ```python
+ >>> model = ModelWithLoraLayer()
+ >>> multiplier = 0.5
+ >>> with rescale_adapter_scale(model, multiplier):
+ ... outputs = model(**inputs) # Perform operations with the scaled model
+ >>> outputs = model(**inputs) # The original scaling values are restored here
+ ```
+ """
+ # check if multiplier has a valid data type
+ if not isinstance(multiplier, (float, int)):
+ raise TypeError(f"Argument multiplier should be of type float, got {type(multiplier)}")
+
+ # iterate on the model's modules and grab the original scaling attribute
+ # from the lora layers if present
+ original_scaling = {}
+ for module in model.modules():
+ if isinstance(module, LoraLayer):
+ original_scaling[module] = module.scaling.copy()
+ module.scaling = {k: v * multiplier for k, v in module.scaling.items()}
+
+ # check whether scaling is prohibited on model
+ # the original scaling dictionary should be empty
+ # if there were no lora layers
+ if not original_scaling:
+ raise ValueError("scaling is only supported for models with `LoraLayer`s")
+ try:
+ yield
+
+ finally:
+ # restore original scaling values after exiting the context
+ for module, scaling in original_scaling.items():
+ module.scaling = scaling
+
+
+@contextmanager
+def disable_input_dtype_casting(model: nn.Module, active: bool = True):
+ """
+ Context manager disables input dtype casting to the dtype of the weight.
+
+ Parameters:
+ model (nn.Module):
+ The model containing PEFT modules whose input dtype casting is to be adjusted.
+ active (bool):
+ Whether the context manager is active (default) or inactive.
+
+ """
+ # Additional info: Normally, the dtype of the weight and input need to match, which is why the dtype is cast.
+ # However, in certain circumustances, this is handled by forward hooks, e.g. when using layerwise casting in
+ # diffusers. In that case, PEFT casting the dtype interferes with the layerwise casting, which is why the option to
+ # disable it is given.
+ if not active:
+ yield
+ return
+
+ original_values = {}
+ for name, module in model.named_modules():
+ if not isinstance(module, BaseTunerLayer):
+ continue
+ original_values[name] = module.cast_input_dtype_enabled
+ module.cast_input_dtype_enabled = False
+
+ try:
+ yield
+ finally:
+ for name, module in model.named_modules():
+ if not isinstance(module, BaseTunerLayer):
+ continue
+ if name in original_values:
+ module.cast_input_dtype_enabled = original_values[name]
diff --git a/peft/src/peft/import_utils.py b/peft/src/peft/import_utils.py
new file mode 100644
index 0000000000000000000000000000000000000000..6aa69a85190bc91bb8bd0649fa80806d7209c584
--- /dev/null
+++ b/peft/src/peft/import_utils.py
@@ -0,0 +1,172 @@
+# Copyright 2023-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+import importlib
+import importlib.metadata as importlib_metadata
+import platform
+from functools import lru_cache
+
+import packaging.version
+import torch
+
+
+@lru_cache
+def is_bnb_available() -> bool:
+ return importlib.util.find_spec("bitsandbytes") is not None
+
+
+@lru_cache
+def is_bnb_4bit_available() -> bool:
+ if not is_bnb_available():
+ return False
+
+ import bitsandbytes as bnb
+
+ return hasattr(bnb.nn, "Linear4bit")
+
+
+@lru_cache
+def is_auto_gptq_available():
+ if importlib.util.find_spec("auto_gptq") is not None:
+ AUTOGPTQ_MINIMUM_VERSION = packaging.version.parse("0.5.0")
+ version_autogptq = packaging.version.parse(importlib_metadata.version("auto_gptq"))
+ if AUTOGPTQ_MINIMUM_VERSION <= version_autogptq:
+ return True
+ else:
+ raise ImportError(
+ f"Found an incompatible version of auto-gptq. Found version {version_autogptq}, "
+ f"but only versions above {AUTOGPTQ_MINIMUM_VERSION} are supported"
+ )
+
+
+@lru_cache
+def is_gptqmodel_available():
+ if importlib.util.find_spec("gptqmodel") is not None:
+ GPTQMODEL_MINIMUM_VERSION = packaging.version.parse("2.0.0")
+ OPTIMUM_MINIMUM_VERSION = packaging.version.parse("1.24.0")
+ version_gptqmodel = packaging.version.parse(importlib_metadata.version("gptqmodel"))
+ if GPTQMODEL_MINIMUM_VERSION <= version_gptqmodel:
+ if is_optimum_available():
+ version_optimum = packaging.version.parse(importlib_metadata.version("optimum"))
+ if OPTIMUM_MINIMUM_VERSION <= version_optimum:
+ return True
+ else:
+ raise ImportError(
+ f"gptqmodel requires optimum version `{OPTIMUM_MINIMUM_VERSION}` or higher. Found version `{version_optimum}`, "
+ f"but only versions above `{OPTIMUM_MINIMUM_VERSION}` are supported"
+ )
+ else:
+ raise ImportError(
+ f"gptqmodel requires optimum version `{OPTIMUM_MINIMUM_VERSION}` or higher to be installed."
+ )
+ else:
+ raise ImportError(
+ f"Found an incompatible version of gptqmodel. Found version `{version_gptqmodel}`, "
+ f"but only versions above `{GPTQMODEL_MINIMUM_VERSION}` are supported"
+ )
+
+
+@lru_cache
+def is_optimum_available() -> bool:
+ return importlib.util.find_spec("optimum") is not None
+
+
+@lru_cache
+def is_torch_tpu_available(check_device=True):
+ "Checks if `torch_xla` is installed and potentially if a TPU is in the environment"
+ if importlib.util.find_spec("torch_xla") is not None:
+ if check_device:
+ # We need to check if `xla_device` can be found, will raise a RuntimeError if not
+ try:
+ import torch_xla.core.xla_model as xm
+
+ _ = xm.xla_device()
+ return True
+ except RuntimeError:
+ return False
+ return True
+ return False
+
+
+@lru_cache
+def is_aqlm_available():
+ return importlib.util.find_spec("aqlm") is not None
+
+
+@lru_cache
+def is_auto_awq_available():
+ return importlib.util.find_spec("awq") is not None
+
+
+@lru_cache
+def is_eetq_available():
+ return importlib.util.find_spec("eetq") is not None
+
+
+@lru_cache
+def is_hqq_available():
+ return importlib.util.find_spec("hqq") is not None
+
+
+@lru_cache
+def is_inc_available():
+ return importlib.util.find_spec("neural_compressor") is not None
+
+
+@lru_cache
+def is_torchao_available():
+ if importlib.util.find_spec("torchao") is None:
+ return False
+
+ TORCHAO_MINIMUM_VERSION = packaging.version.parse("0.4.0")
+ try:
+ torchao_version = packaging.version.parse(importlib_metadata.version("torchao"))
+ except importlib_metadata.PackageNotFoundError:
+ # Same idea as in diffusers:
+ # https://github.com/huggingface/diffusers/blob/9f06a0d1a4a998ac6a463c5be728c892f95320a8/src/diffusers/utils/import_utils.py#L351-L357
+ # It's not clear under what circumstances `importlib_metadata.version("torchao")` can raise an error even
+ # though `importlib.util.find_spec("torchao") is not None` but it has been observed, so adding this for
+ # precaution.
+ return False
+
+ if torchao_version < TORCHAO_MINIMUM_VERSION:
+ raise ImportError(
+ f"Found an incompatible version of torchao. Found version {torchao_version}, "
+ f"but only versions above {TORCHAO_MINIMUM_VERSION} are supported"
+ )
+ return True
+
+
+@lru_cache
+def is_xpu_available(check_device=False):
+ """
+ Checks if XPU acceleration is available and potentially if a XPU is in the environment
+ """
+
+ system = platform.system()
+ if system == "Darwin":
+ return False
+ else:
+ if check_device:
+ try:
+ # Will raise a RuntimeError if no XPU is found
+ _ = torch.xpu.device_count()
+ return torch.xpu.is_available()
+ except RuntimeError:
+ return False
+ return hasattr(torch, "xpu") and torch.xpu.is_available()
+
+
+@lru_cache
+def is_diffusers_available():
+ return importlib.util.find_spec("diffusers") is not None
diff --git a/peft/src/peft/mapping.py b/peft/src/peft/mapping.py
new file mode 100644
index 0000000000000000000000000000000000000000..82c6ec1e40bb7b06f505b82346245b8bf00d789c
--- /dev/null
+++ b/peft/src/peft/mapping.py
@@ -0,0 +1,92 @@
+# Copyright 2023-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+from __future__ import annotations
+
+from typing import TYPE_CHECKING, Any, Optional
+
+import torch
+
+from .utils import PeftType
+
+
+if TYPE_CHECKING:
+ from .config import PeftConfig
+ from .tuners.tuners_utils import BaseTuner
+
+
+# these will be filled by the register_peft_method function
+PEFT_TYPE_TO_CONFIG_MAPPING: dict[PeftType, type[PeftConfig]] = {}
+PEFT_TYPE_TO_TUNER_MAPPING: dict[PeftType, type[BaseTuner]] = {}
+PEFT_TYPE_TO_MIXED_MODEL_MAPPING: dict[PeftType, type[BaseTuner]] = {}
+PEFT_TYPE_TO_PREFIX_MAPPING: dict[PeftType, str] = {}
+
+
+def get_peft_config(config_dict: dict[str, Any]) -> PeftConfig:
+ """
+ Returns a Peft config object from a dictionary.
+
+ Args:
+ config_dict (`Dict[str, Any]`): Dictionary containing the configuration parameters.
+ """
+
+ return PEFT_TYPE_TO_CONFIG_MAPPING[config_dict["peft_type"]](**config_dict)
+
+
+def inject_adapter_in_model(
+ peft_config: PeftConfig,
+ model: torch.nn.Module,
+ adapter_name: str = "default",
+ low_cpu_mem_usage: bool = False,
+ state_dict: Optional[dict[str, torch.Tensor]] = None,
+) -> torch.nn.Module:
+ r"""
+ Create PEFT layers and inject them into the model in-place.
+
+ Currently the API does not support prompt learning methods and adaption prompt.
+
+ This function is similar to [`get_peft_model`] but it does not return a [`PeftModel`] instance. Instead, it returns
+ the original, mutated instance of the passed model.
+
+ Args:
+ peft_config (`PeftConfig`):
+ Configuration object containing the parameters of the PEFT model.
+ model (`torch.nn.Module`):
+ The input model where the adapter will be injected.
+ adapter_name (`str`, `optional`, defaults to `"default"`):
+ The name of the adapter to be injected, if not provided, the default adapter name is used ("default").
+ low_cpu_mem_usage (`bool`, `optional`, defaults to `False`):
+ Create empty adapter weights on meta device. Useful to speed up the loading process.
+ state_dict (`dict`, *optional*, defaults to `None`)
+ If a `state_dict` is passed here, the adapters will be injected based on the entries of the state_dict.
+ This can be useful when the exact `target_modules` of the PEFT method is unknown, for instance because the
+ checkpoint was created without meta data. Note that the values from the `state_dict` are not used, only the
+ keys are used to determine the correct layers that should be adapted.
+ """
+ if peft_config.is_prompt_learning or peft_config.is_adaption_prompt:
+ raise ValueError("`create_and_replace` does not support prompt learning and adaption prompt yet.")
+
+ if peft_config.peft_type not in PEFT_TYPE_TO_TUNER_MAPPING.keys():
+ raise ValueError(
+ f"`inject_adapter_in_model` does not support {peft_config.peft_type} yet. Please use `get_peft_model`."
+ )
+
+ tuner_cls = PEFT_TYPE_TO_TUNER_MAPPING[peft_config.peft_type]
+
+ # By instantiating a peft model we are injecting randomly initialized LoRA layers into the model's modules.
+ peft_model = tuner_cls(
+ model, peft_config, adapter_name=adapter_name, low_cpu_mem_usage=low_cpu_mem_usage, state_dict=state_dict
+ )
+
+ return peft_model.model
diff --git a/peft/src/peft/mapping_func.py b/peft/src/peft/mapping_func.py
new file mode 100644
index 0000000000000000000000000000000000000000..adcb55a8e5c3ac587f9b6c39482e99804cc981f4
--- /dev/null
+++ b/peft/src/peft/mapping_func.py
@@ -0,0 +1,131 @@
+# Copyright 2024-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+from __future__ import annotations
+
+import warnings
+from typing import Optional
+
+from transformers import PreTrainedModel
+
+from .auto import MODEL_TYPE_TO_PEFT_MODEL_MAPPING
+from .config import PeftConfig
+from .mapping import PEFT_TYPE_TO_CONFIG_MAPPING, PEFT_TYPE_TO_PREFIX_MAPPING
+from .mixed_model import PeftMixedModel
+from .peft_model import PeftModel
+from .tuners.tuners_utils import BaseTuner, BaseTunerLayer
+from .utils import _prepare_prompt_learning_config
+
+
+def get_peft_model(
+ model: PreTrainedModel,
+ peft_config: PeftConfig,
+ adapter_name: str = "default",
+ mixed: bool = False,
+ autocast_adapter_dtype: bool = True,
+ revision: Optional[str] = None,
+ low_cpu_mem_usage: bool = False,
+) -> PeftModel | PeftMixedModel:
+ """
+ Returns a Peft model object from a model and a config, where the model will be modified in-place.
+
+ Args:
+ model ([`transformers.PreTrainedModel`]):
+ Model to be wrapped.
+ peft_config ([`PeftConfig`]):
+ Configuration object containing the parameters of the Peft model.
+ adapter_name (`str`, `optional`, defaults to `"default"`):
+ The name of the adapter to be injected, if not provided, the default adapter name is used ("default").
+ mixed (`bool`, `optional`, defaults to `False`):
+ Whether to allow mixing different (compatible) adapter types.
+ autocast_adapter_dtype (`bool`, *optional*):
+ Whether to autocast the adapter dtype. Defaults to `True`. Right now, this will only cast adapter weights
+ using float16 or bfloat16 to float32, as this is typically required for stable training, and only affect
+ select PEFT tuners.
+ revision (`str`, `optional`, defaults to `main`):
+ The revision of the base model. If this isn't set, the saved peft model will load the `main` revision for
+ the base model
+ low_cpu_mem_usage (`bool`, `optional`, defaults to `False`):
+ Create empty adapter weights on meta device. Useful to speed up the loading process. Leave this setting as
+ False if you intend on training the model, unless the adapter weights will be replaced by different weights
+ before training starts.
+ """
+ model_config = BaseTuner.get_model_config(model)
+ old_name = peft_config.base_model_name_or_path
+ new_name = model.__dict__.get("name_or_path", None)
+ peft_config.base_model_name_or_path = new_name
+
+ # Especially in notebook environments there could be a case that a user wants to experiment with different
+ # configuration values. However, it is likely that there won't be any changes for new configs on an already
+ # initialized PEFT model. The best we can do is warn the user about it.
+ if any(isinstance(module, BaseTunerLayer) for module in model.modules()):
+ warnings.warn(
+ "You are trying to modify a model with PEFT for a second time. If you want to reload the model with a "
+ "different config, make sure to call `.unload()` before."
+ )
+
+ if (old_name is not None) and (old_name != new_name):
+ warnings.warn(
+ f"The PEFT config's `base_model_name_or_path` was renamed from '{old_name}' to '{new_name}'. "
+ "Please ensure that the correct base model is loaded when loading this checkpoint."
+ )
+
+ if revision is not None:
+ if peft_config.revision is not None and peft_config.revision != revision:
+ warnings.warn(
+ f"peft config has already set base model revision to {peft_config.revision}, overwriting with revision {revision}"
+ )
+ peft_config.revision = revision
+
+ if (
+ (isinstance(peft_config, PEFT_TYPE_TO_CONFIG_MAPPING["LORA"]))
+ and (peft_config.init_lora_weights == "eva")
+ and not low_cpu_mem_usage
+ ):
+ warnings.warn(
+ "lora with eva initialization used with low_cpu_mem_usage=False. "
+ "Setting low_cpu_mem_usage=True can improve the maximum batch size possible for eva initialization."
+ )
+
+ prefix = PEFT_TYPE_TO_PREFIX_MAPPING.get(peft_config.peft_type)
+ if prefix and adapter_name in prefix:
+ warnings.warn(
+ f"Adapter name '{adapter_name}' should not be contained in the prefix '{prefix}'. "
+ "This may lead to reinitialization of the adapter weights during loading."
+ )
+
+ if mixed:
+ # note: PeftMixedModel does not support autocast_adapter_dtype, so don't pass it
+ return PeftMixedModel(model, peft_config, adapter_name=adapter_name)
+
+ # We explicitly exclude prompt learning here since prompt learning is specific to the task and needs special
+ # handling in the PEFT model's forward method.
+ if peft_config.task_type not in MODEL_TYPE_TO_PEFT_MODEL_MAPPING.keys() and not peft_config.is_prompt_learning:
+ return PeftModel(
+ model,
+ peft_config,
+ adapter_name=adapter_name,
+ autocast_adapter_dtype=autocast_adapter_dtype,
+ low_cpu_mem_usage=low_cpu_mem_usage,
+ )
+
+ if peft_config.is_prompt_learning:
+ peft_config = _prepare_prompt_learning_config(peft_config, model_config)
+ return MODEL_TYPE_TO_PEFT_MODEL_MAPPING[peft_config.task_type](
+ model,
+ peft_config,
+ adapter_name=adapter_name,
+ autocast_adapter_dtype=autocast_adapter_dtype,
+ low_cpu_mem_usage=low_cpu_mem_usage,
+ )
diff --git a/peft/src/peft/mixed_model.py b/peft/src/peft/mixed_model.py
new file mode 100644
index 0000000000000000000000000000000000000000..c3ad517e7eb65b10b955410eddb2f1962e43e3e1
--- /dev/null
+++ b/peft/src/peft/mixed_model.py
@@ -0,0 +1,460 @@
+# Copyright 2023-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+from __future__ import annotations
+
+import os
+from contextlib import contextmanager
+from typing import Any, Optional, Union
+
+import torch
+from accelerate.hooks import remove_hook_from_submodules
+from torch import nn
+from transformers.utils import PushToHubMixin
+
+from peft.utils.constants import DUMMY_MODEL_CONFIG
+
+from .config import PeftConfig
+from .peft_model import PeftModel
+from .tuners import MixedModel
+from .utils import _set_adapter, _set_trainable
+
+
+def _prepare_model_for_gradient_checkpointing(model: nn.Module) -> None:
+ r"""
+ Prepares the model for gradient checkpointing if necessary
+ """
+ # Note: same as PeftModel._prepare_model_for_gradient_checkpointing
+ if not getattr(model, "is_gradient_checkpointing", True):
+ return model
+
+ if not (
+ getattr(model, "is_loaded_in_8bit", False)
+ or getattr(model, "is_loaded_in_4bit", False)
+ or getattr(model, "is_quantized", False)
+ ):
+ if hasattr(model, "enable_input_require_grads"):
+ model.enable_input_require_grads()
+ elif hasattr(model, "get_input_embeddings"):
+
+ def make_inputs_require_grad(module, input, output):
+ output.requires_grad_(True)
+
+ model.get_input_embeddings().register_forward_hook(make_inputs_require_grad)
+
+
+def _check_config_compatible(peft_config: PeftConfig) -> None:
+ from .tuners.mixed import COMPATIBLE_TUNER_TYPES
+
+ if peft_config.peft_type not in COMPATIBLE_TUNER_TYPES:
+ raise ValueError(
+ f"The provided `peft_type` '{peft_config.peft_type.value}' is not compatible with the `PeftMixedModel`. "
+ f"Compatible types are: {COMPATIBLE_TUNER_TYPES}"
+ )
+
+
+class PeftMixedModel(PushToHubMixin, torch.nn.Module):
+ """
+ PeftMixedModel for loading mixing different types of adapters for inference.
+
+ This class does not support loading/saving, and it shouldn't usually be initialized directly. Instead, use
+ `get_peft_model` with the argument `mixed=True`.
+
+ > [!TIP] > Read the [Mixed adapter types](https://huggingface.co/docs/peft/en/developer_guides/mixed_models) guide
+ to learn > more about using different adapter types.
+
+ Example:
+
+ ```py
+ >>> base_model = ... # load the base model, e.g. from transformers
+ >>> peft_model = PeftMixedModel.from_pretrained(base_model, path_to_adapter1, "adapter1").eval()
+ >>> peft_model.load_adapter(path_to_adapter2, "adapter2")
+ >>> peft_model.set_adapter(["adapter1", "adapter2"]) # activate both adapters
+ >>> peft_model(data) # forward pass using both adapters
+ ```
+
+ Args:
+ model (`torch.nn.Module`):
+ The model to be tuned.
+ config (`PeftConfig`):
+ The config of the model to be tuned. The adapter type must be compatible.
+ adapter_name (`str`, `optional`, defaults to `"default"`):
+ The name of the first adapter.
+ low_cpu_mem_usage (`bool`, `optional`, defaults to `False`):
+ Create empty adapter weights on meta device. Useful to speed up the loading process.
+ """
+
+ def __init__(self, model: nn.Module, peft_config: PeftConfig, adapter_name: str = "default") -> None:
+ super().__init__()
+ _check_config_compatible(peft_config)
+ _prepare_model_for_gradient_checkpointing(model)
+ self.modules_to_save = None
+ self.base_model = MixedModel(model, {adapter_name: peft_config}, adapter_name)
+ self.set_modules_to_save(peft_config, adapter_name)
+
+ self.config = getattr(model, "config", DUMMY_MODEL_CONFIG)
+
+ # the `pretraining_tp` is set for some models to simulate Tensor Parallelism during inference to avoid
+ # numerical differences, https://github.com/pytorch/pytorch/issues/76232 - to avoid any unexpected
+ # behavior we disable that in this line.
+ if hasattr(self.base_model, "config") and hasattr(self.base_model.config, "pretraining_tp"):
+ self.base_model.config.pretraining_tp = 1
+
+ @property
+ def peft_config(self) -> dict[str, PeftConfig]:
+ return self.base_model.peft_config
+
+ @property
+ def active_adapter(self) -> str:
+ return self.base_model.active_adapter
+
+ @property
+ def active_adapters(self) -> list[str]:
+ return self.base_model.active_adapters
+
+ def get_nb_trainable_parameters(self):
+ r"""
+ Returns the number of trainable parameters and number of all parameters in the model.
+ """
+ # note: same as PeftModel.get_nb_trainable_parameters
+ trainable_params = 0
+ all_param = 0
+ for _, param in self.named_parameters():
+ num_params = param.numel()
+ # if using DS Zero 3 and the weights are initialized empty
+ if num_params == 0 and hasattr(param, "ds_numel"):
+ num_params = param.ds_numel
+
+ # Due to the design of 4bit linear layers from bitsandbytes
+ # one needs to multiply the number of parameters by 2 to get
+ # the correct number of parameters
+ if param.__class__.__name__ == "Params4bit":
+ num_params = num_params * 2
+
+ all_param += num_params
+ if param.requires_grad:
+ trainable_params += num_params
+
+ return trainable_params, all_param
+
+ def print_trainable_parameters(self):
+ """
+ Prints the number of trainable parameters in the model.
+
+ Note: print_trainable_parameters() uses get_nb_trainable_parameters() which is different from
+ num_parameters(only_trainable=True) from huggingface/transformers. get_nb_trainable_parameters() returns
+ (trainable parameters, all parameters) of the Peft Model which includes modified backbone transformer model.
+ For techniques like LoRA, the backbone transformer model is modified in place with LoRA modules. However, for
+ prompt tuning, the backbone transformer model is unmodified. num_parameters(only_trainable=True) returns number
+ of trainable parameters of the backbone transformer model which can be different.
+ """
+ # note: same as PeftModel.print_trainable_parameters
+ trainable_params, all_param = self.get_nb_trainable_parameters()
+
+ print(
+ f"trainable params: {trainable_params:,d} || "
+ f"all params: {all_param:,d} || "
+ f"trainable%: {100 * trainable_params / all_param:.4f}"
+ )
+
+ def __getattr__(self, name: str):
+ """Forward missing attributes to the wrapped module."""
+ try:
+ return super().__getattr__(name) # defer to nn.Module's logic
+ except AttributeError:
+ if name == "base_model": # see #1892: prevent infinite recursion if class is not initialized
+ raise
+ return getattr(self.base_model, name)
+
+ def forward(self, *args: Any, **kwargs: Any):
+ """
+ Forward pass of the model.
+ """
+ return self.base_model(*args, **kwargs)
+
+ def generate(self, *args: Any, **kwargs: Any):
+ """
+ Generate output.
+ """
+ return self.base_model.generate(*args, **kwargs)
+
+ @contextmanager
+ def disable_adapter(self):
+ """
+ Disables the adapter module.
+ """
+ try:
+ self.base_model.disable_adapter_layers()
+ yield
+ finally:
+ self.base_model.enable_adapter_layers()
+
+ def add_adapter(self, adapter_name: str, peft_config: PeftConfig, low_cpu_mem_usage: bool = False) -> None:
+ """
+ Add an adapter to the model based on the passed configuration.
+
+ This adapter is not trained. To load a trained adapter, check out [`PeftModel.load_adapter`].
+
+ The name for the new adapter should be unique.
+
+ The new adapter is not automatically set as the active adapter. Use [`PeftModel.set_adapter`] to set the active
+ adapter.
+
+ Args:
+ adapter_name (`str`):
+ The name of the adapter to be added.
+ peft_config ([`PeftConfig`]):
+ The configuration of the adapter to be added.
+ low_cpu_mem_usage (`bool`, `optional`, defaults to `False`):
+ Create empty adapter weights on meta device. Useful to speed up the process when loading saved
+ adapters.
+
+ > [!TIP] > Don't use `low_cpu_mem_usage=True` when creating a new PEFT adapter for training (training
+ is untested > and discouraged for PeftMixedModel in general).
+ """
+ _check_config_compatible(peft_config)
+
+ try:
+ self.peft_config[adapter_name] = peft_config
+ self.base_model.inject_adapter(self, adapter_name, low_cpu_mem_usage=low_cpu_mem_usage)
+ except Exception: # something went wrong, roll back
+ if adapter_name in self.peft_config:
+ del self.peft_config[adapter_name]
+ raise
+
+ self.set_modules_to_save(peft_config, adapter_name)
+
+ def set_modules_to_save(self, peft_config: PeftConfig, adapter_name: str) -> None:
+ if (modules_to_save := getattr(peft_config, "modules_to_save", None)) is None:
+ return
+
+ if self.modules_to_save is None:
+ self.modules_to_save = set(modules_to_save)
+ else:
+ self.modules_to_save.update(modules_to_save)
+ _set_trainable(
+ self,
+ adapter_name,
+ module_names=getattr(peft_config, "modules_to_save", None),
+ inference_mode=peft_config.inference_mode,
+ )
+
+ def set_adapter(self, adapter_name: Union[str, list[str]], inference_mode: bool = False) -> None:
+ """
+ Sets the active adapter(s) for the model.
+
+ Note that the order in which the adapters are applied during the forward pass may not be the same as the order
+ in which they are passed to this function. Instead, the order during the forward pass is determined by the
+ order in which the adapters were loaded into the model. The active adapters only determine which adapters are
+ active during the forward pass, but not the order in which they are applied.
+
+ Additionally, this function will set the specified adapter to trainable (i.e., requires_grad=True) unless
+ inference_mode is True.
+
+ Args:
+ adapter_name (str, list[str]):
+ The name(s) of the adapter(s) to set as active
+ inference_mode (bool, optional):
+ Whether the activated adapter should be frozen (i.e. `requires_grad=False`). Default is False.
+ """
+ if isinstance(adapter_name, str):
+ adapter_name = [adapter_name]
+
+ mismatched = set(adapter_name) - set(self.peft_config.keys())
+ if mismatched:
+ raise ValueError(
+ f"Adapter(s) {sorted(mismatched)} not found, available adapters: {sorted(self.peft_config.keys())}"
+ )
+
+ self.base_model.set_adapter(adapter_name, inference_mode=inference_mode)
+ _set_adapter(self, adapter_name, inference_mode=inference_mode)
+
+ def delete_adapter(self, adapter_name: Union[str, list[str]]) -> None:
+ if isinstance(adapter_name, str):
+ adapter_name = [adapter_name]
+
+ mismatched = set(adapter_name) - set(self.peft_config.keys())
+ if mismatched:
+ raise ValueError(
+ f"Adapter(s) {sorted(mismatched)} not found, available adapters: {sorted(self.peft_config.keys())}"
+ )
+
+ self.base_model.delete_adapter(adapter_name)
+
+ def merge_and_unload(self, *args: Any, **kwargs: Any):
+ r"""
+ This method merges the adapter layers into the base model. This is needed if someone wants to use the base
+ model as a standalone model.
+
+ Args:
+ progressbar (`bool`):
+ whether to show a progressbar indicating the unload and merge process
+ safe_merge (`bool`):
+ whether to activate the safe merging check to check if there is any potential Nan in the adapter
+ weights
+ adapter_names (`List[str]`, *optional*):
+ The list of adapter names that should be merged. If None, all active adapters will be merged. Defaults
+ to `None`.
+ """
+ return self.base_model.merge_and_unload(*args, **kwargs)
+
+ def unload(self, *args: Any, **kwargs: Any):
+ """
+ Gets back the base model by removing all the adapter modules without merging. This gives back the original base
+ model.
+ """
+ return self.base_model.unload(*args, **kwargs)
+
+ def get_layer_status(self):
+ raise TypeError(f"get_layer_status is not supported for {self.__class__.__name__}.")
+
+ def get_model_status(self):
+ raise TypeError(f"get_model_status is not supported for {self.__class__.__name__}.")
+
+ @classmethod
+ def _split_kwargs(cls, kwargs: dict[str, Any]):
+ return PeftModel._split_kwargs(kwargs)
+
+ def _check_new_adapter_config(self, peft_config: PeftConfig, is_trainable: bool) -> None:
+ return PeftModel._check_new_adapter_config(self, peft_config, is_trainable=is_trainable)
+
+ def load_adapter(self, model_id: str, adapter_name: str, *args: Any, **kwargs: Any):
+ """
+ Load a trained adapter into the model.
+
+ The name for the new adapter should be unique.
+
+ The new adapter is not automatically set as the active adapter. Use [`PeftModel.set_adapter`] to set the active
+ adapter.
+
+ Args:
+ adapter_name (`str`):
+ The name of the adapter to be added.
+ peft_config ([`PeftConfig`]):
+ The configuration of the adapter to be added.
+ is_trainable (`bool`, *optional*, defaults to `False`):
+ Whether the adapter should be trainable or not. If `False`, the adapter will be frozen and can only be
+ used for inference.
+ torch_device (`str`, *optional*, defaults to None):
+ The device to load the adapter on. If `None`, the device will be inferred.
+ autocast_adapter_dtype (`bool`, *optional*, defaults to `True`):
+ Whether to autocast the adapter dtype. Defaults to `True`. Right now, this will only cast adapter
+ weights using float16 and bfloat16 to float32, as this is typically required for stable training, and
+ only affect select PEFT tuners.
+ ephemeral_gpu_offload (`bool`, *optional*, defaults to `False`):
+ Whether to use ephemeral GPU offloading for partially loaded modules. Defaults to `False`.
+ low_cpu_mem_usage (`bool`, `optional`, defaults to `False`):
+ Create empty adapter weights on meta device before loading the saved weights. Useful to speed up the
+ process.
+ kwargs: (`optional`):
+ Additional arguments to modify the way the adapter is loaded, e.g. the token for Hugging Face Hub.
+ """
+ # the low_cpu_mem_usage option is handled through kwargs
+ output = PeftModel.load_adapter(self, model_id, adapter_name, *args, **kwargs)
+ # TODO: not quite clear why this is necessary but tests fail without it
+ self.set_adapter(self.active_adapters)
+ return output
+
+ def create_or_update_model_card(self, output_dir: str):
+ raise NotImplementedError(f"Model card creation is not supported for {self.__class__.__name__} (yet).")
+
+ def save_pretrained(
+ self,
+ save_directory: str,
+ safe_serialization: bool = False,
+ selected_adapters: Optional[list[str]] = None,
+ **kwargs: Any,
+ ):
+ raise NotImplementedError(f"Saving is not supported for {self.__class__.__name__} (yet).")
+
+ @classmethod
+ def from_pretrained(
+ cls,
+ model: nn.Module,
+ model_id: str | os.PathLike,
+ adapter_name: str = "default",
+ is_trainable: bool = False,
+ config: Optional[PeftConfig] = None,
+ **kwargs: Any,
+ ):
+ r"""
+ Instantiate a PEFT mixed model from a pretrained model and loaded PEFT weights.
+
+ Note that the passed `model` may be modified inplace.
+
+ Args:
+ model (`nn.Module`):
+ The model to be adapted.
+ model_id (`str` or `os.PathLike`):
+ The name of the PEFT configuration to use. Can be either:
+ - A string, the `model id` of a PEFT configuration hosted inside a model repo on the Hugging Face
+ Hub.
+ - A path to a directory containing a PEFT configuration file saved using the `save_pretrained`
+ method (`./my_peft_config_directory/`).
+ adapter_name (`str`, *optional*, defaults to `"default"`):
+ The name of the adapter to be loaded. This is useful for loading multiple adapters.
+ is_trainable (`bool`, *optional*, defaults to `False`):
+ Whether the adapter should be trainable or not. If `False`, the adapter will be frozen and use for
+ inference
+ config ([`~peft.PeftConfig`], *optional*):
+ The configuration object to use instead of an automatically loaded configuration. This configuration
+ object is mutually exclusive with `model_id` and `kwargs`. This is useful when configuration is already
+ loaded before calling `from_pretrained`.
+ low_cpu_mem_usage (`bool`, `optional`, defaults to `False`):
+ Create empty adapter weights on meta device before loading the saved weights. Useful to speed up the
+ process.
+ kwargs: (`optional`):
+ Additional keyword arguments passed along to the specific PEFT configuration class.
+ """
+ # note: adapted from PeftModel.from_pretrained
+ from .mapping import PEFT_TYPE_TO_CONFIG_MAPPING, PEFT_TYPE_TO_MIXED_MODEL_MAPPING
+
+ # load the config
+ if config is None:
+ hf_kwargs = {
+ "subfolder": kwargs.get("subfolder", None),
+ "revision": kwargs.get("revision", None),
+ "cache_dir": kwargs.get("cache_dir", None),
+ "token": kwargs.get("token", None),
+ }
+ if use_auth_token := kwargs.get("use_auth_token", None):
+ hf_kwargs["use_auth_token"] = use_auth_token
+ config = PEFT_TYPE_TO_CONFIG_MAPPING[PeftConfig._get_peft_type(model_id, **hf_kwargs)].from_pretrained(
+ model_id, **kwargs
+ )
+ elif isinstance(config, PeftConfig):
+ config.inference_mode = not is_trainable
+ else:
+ raise ValueError(f"The input config must be a PeftConfig, got {config.__class__}")
+
+ # note: this is different from PeftModel.from_pretrained
+ if config.peft_type not in PEFT_TYPE_TO_MIXED_MODEL_MAPPING:
+ raise ValueError(f"Adapter of type {config.peft_type} is not supported for mixed models.")
+
+ if (getattr(model, "hf_device_map", None) is not None) and len(
+ set(model.hf_device_map.values()).intersection({"cpu", "disk"})
+ ) > 0:
+ remove_hook_from_submodules(model)
+
+ if config.is_prompt_learning and is_trainable:
+ # note: should not be possible to reach, but just in case
+ raise ValueError("Cannot set a prompt learning adapter to trainable when loading pretrained adapter.")
+ else:
+ config.inference_mode = not is_trainable
+
+ # note: this is different from PeftModel.from_pretrained, we always return a PeftMixedModel
+ model = cls(model, config, adapter_name)
+ # the low_cpu_mem_usage option is handled through kwargs
+ model.load_adapter(model_id, adapter_name, is_trainable=is_trainable, **kwargs)
+ return model
diff --git a/peft/src/peft/optimizers/__init__.py b/peft/src/peft/optimizers/__init__.py
new file mode 100644
index 0000000000000000000000000000000000000000..0e8821f45db8e2dcf8f26fd8b38f8f90a28f5c09
--- /dev/null
+++ b/peft/src/peft/optimizers/__init__.py
@@ -0,0 +1,19 @@
+# Copyright 2025-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+from .lorafa import create_lorafa_optimizer
+from .loraplus import create_loraplus_optimizer
+
+
+__all__ = ["create_lorafa_optimizer", "create_loraplus_optimizer"]
diff --git a/peft/src/peft/optimizers/lorafa.py b/peft/src/peft/optimizers/lorafa.py
new file mode 100644
index 0000000000000000000000000000000000000000..61e331ed100174b4ac645c08a07b1619328f17d5
--- /dev/null
+++ b/peft/src/peft/optimizers/lorafa.py
@@ -0,0 +1,257 @@
+# Copyright 2025-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""
+This module contains the implementation of the LoRA-FA optimizer.
+"""
+
+from __future__ import annotations
+
+import math
+from collections.abc import Iterable
+from typing import Callable
+
+import torch
+import torch.nn as nn
+from accelerate.utils.imports import is_bf16_available
+from torch import autocast
+from torch.optim import Optimizer
+
+from ..peft_model import PeftModel
+from ..utils.other import infer_device
+
+
+class LoraFAOptimizer(Optimizer):
+ """
+ Implements the LoRA-FA optimizer designed specifically for training Low-Rank Adaptation (LoRA) parameters
+ efficiently. Note that LoraFAOptimizer is based on adamw-hf in transformers, with only LoRA part modified. Without
+ LoRA it will fall back to adamw-hf.
+
+ Args:
+ params (Iterable[nn.parameter.Parameter]): Parameters to optimize.
+ lr (float, optional): Learning rate (default: 1e-3).
+ betas (Tuple[float, float], optional):
+ Coefficients for computing running averages of gradient and squared gradient (default: (0.9, 0.999)).
+ eps (float, optional): Term added to denominator to improve numerical stability (default: 1e-6).
+ weight_decay (float, optional): Weight decay (L2 penalty) (default: 0.0).
+ correct_bias (bool, optional): Whether to apply bias correction as in original Adam (default: True).
+
+ Args in sub-function step:
+ closure (Callable, optional): A closure that reevaluates the model and returns the loss.
+
+ Reference:
+ - LoRA-FA: https://huggingface.co/papers/2308.03303
+ """
+
+ def __init__(
+ self,
+ params: Iterable[nn.parameter.Parameter],
+ lr: float = 1e-3,
+ betas: tuple[float, float] = (0.9, 0.999),
+ eps: float = 1e-6,
+ weight_decay: float = 0.0,
+ correct_bias: bool = True,
+ ):
+ if lr < 0.0:
+ raise ValueError(f"Invalid learning rate: {lr} - should be >= 0.0")
+ if not 0.0 <= betas[0] < 1.0:
+ raise ValueError(f"Invalid beta parameter: {betas[0]} - should be in [0.0, 1.0)")
+ if not 0.0 <= betas[1] < 1.0:
+ raise ValueError(f"Invalid beta parameter: {betas[1]} - should be in [0.0, 1.0)")
+ if not 0.0 <= eps:
+ raise ValueError(f"Invalid epsilon value: {eps} - should be >= 0.0")
+ defaults = {
+ "lr": lr,
+ "betas": betas,
+ "eps": eps,
+ "weight_decay": weight_decay,
+ "correct_bias": correct_bias,
+ }
+ super().__init__(params, defaults)
+
+ @torch.no_grad()
+ def step(self, closure: Callable = None):
+ """
+ Performs a single optimization step.
+
+ Arguments:
+ closure (`Callable`, *optional*): A closure that reevaluates the model and returns the loss.
+ """
+ loss = None
+ if closure is not None:
+ loss = closure()
+
+ for group in self.param_groups:
+ scaling_factor = group["scaling_factor"]
+ param_list = []
+ name_list = []
+ for p, n in zip(group["params"], group["names"]):
+ # Skip non-lora no-grad module, since we need lora_A which is no-grad.
+ if "lora" not in n and p.grad is None:
+ continue
+ grad = p.grad
+
+ if "lora" in n:
+ param_list.append(p)
+ name_list.append(n)
+ if len(param_list) == 2:
+ name = n[: n.find("lora")] + "lora"
+ elif len(param_list) == 1:
+ continue
+ else:
+ name = n
+ # param_list contains a pair of A and B adapters
+ # i.e., param_list -> [A,B]
+
+ state = self.state[name]
+ # State initialization
+ if len(state) == 0:
+ if len(param_list) == 2:
+ state["step"] = 0
+ # Exponential moving average of gradient values
+ state["exp_avg_B"] = torch.zeros_like(param_list[1])
+ # Exponential moving average of squared gradient values
+ state["exp_avg_sq_B"] = torch.zeros_like(param_list[1])
+ else:
+ state["step"] = 0
+ # Exponential moving average of gradient values
+ state["exp_avg"] = torch.zeros_like(p)
+ # Exponential moving average of squared gradient values
+ state["exp_avg_sq"] = torch.zeros_like(p)
+
+ # Below is the LoRA-FA part
+ # 1. In this part, we optimize the gradient of B as:
+ # g^B = \left(\frac{r}{\alpha}\right)^2 (A^\top A)^{-1} g_{\text{LoRA-FA}}^B
+ # to min the func as described below:
+ # \min_{g^B} \|\hat{g}_\text{LoRA-FA} - g\|_F^2
+ # 2. After the gradient of B is ready, update the optimizer state
+ if len(param_list) == 2:
+ A = param_list[0]
+ B = param_list[1]
+ grad_B_orin = B.grad
+
+ # projection
+ delta = 1e-8
+
+ # computing the inverse matrix
+ AA_T = A @ A.T
+ AA_T_inv = torch.linalg.pinv(AA_T + delta * torch.eye(A.shape[0]).to(A.device))
+
+ device_type = infer_device()
+
+ if is_bf16_available():
+ with autocast(device_type=device_type, dtype=torch.bfloat16):
+ grad_B = (1 / scaling_factor**2) * (grad_B_orin @ AA_T_inv)
+ else:
+ grad_B = (1 / scaling_factor**2) * (grad_B_orin @ AA_T_inv)
+
+ if grad_B.dtype != B.grad.dtype:
+ grad_B = grad_B.to(B.grad.dtype)
+
+ exp_avg_B, exp_avg_sq_B = state["exp_avg_B"], state["exp_avg_sq_B"]
+ beta1, beta2 = group["betas"]
+ state["step"] += 1
+ exp_avg_B.mul_(beta1).add_(grad_B, alpha=(1.0 - beta1))
+ exp_avg_sq_B.mul_(beta2).addcmul_(grad_B, grad_B, value=1.0 - beta2)
+
+ denom_B = exp_avg_sq_B.sqrt().add_(group["eps"])
+ step_size = group["lr"]
+ if group["correct_bias"]: # No bias correction for Bert
+ bias_correction1 = 1.0 - beta1 ** state["step"]
+ bias_correction2 = 1.0 - beta2 ** state["step"]
+ step_size = step_size * math.sqrt(bias_correction2) / bias_correction1
+ B.addcdiv_(exp_avg_B, denom_B, value=-step_size)
+ if group["weight_decay"] > 0.0:
+ B.add_(B, alpha=(-group["lr"] * group["weight_decay"]))
+ param_list = []
+ name_list = []
+
+ # Below is the original AdamW
+ else:
+ exp_avg, exp_avg_sq = state["exp_avg"], state["exp_avg_sq"]
+ beta1, beta2 = group["betas"]
+
+ state["step"] += 1
+
+ # Decay the first and second moment running average coefficient
+ # In-place operations to update the averages at the same time
+ exp_avg.mul_(beta1).add_(grad, alpha=(1.0 - beta1))
+ exp_avg_sq.mul_(beta2).addcmul_(grad, grad, value=1.0 - beta2)
+ denom = exp_avg_sq.sqrt().add_(group["eps"])
+
+ step_size = group["lr"]
+ if group["correct_bias"]: # No bias correction for Bert
+ bias_correction1 = 1.0 - beta1 ** state["step"]
+ bias_correction2 = 1.0 - beta2 ** state["step"]
+ step_size = step_size * math.sqrt(bias_correction2) / bias_correction1
+
+ p.addcdiv_(exp_avg, denom, value=-step_size)
+
+ # Just adding the square of the weights to the loss function is *not*
+ # the correct way of using L2 regularization/weight decay with Adam,
+ # since that will interact with the m and v parameters in strange ways.
+ #
+ # Instead we want to decay the weights in a manner that doesn't interact
+ # with the m/v parameters. This is equivalent to adding the square
+ # of the weights to the loss with plain (non-momentum) SGD.
+ # Add weight decay at the end (fixed version)
+ if group["weight_decay"] > 0.0:
+ p.add_(p, alpha=(-group["lr"] * group["weight_decay"]))
+
+ return loss
+
+
+def create_lorafa_optimizer(
+ model: PeftModel, r: int, lora_alpha: int, lr: float, weight_decay: float = 0.0, use_rslora: bool = False
+) -> Optimizer:
+ """
+ Helper function to instantiate a lorafa optimizer specifically configured for a given model using the LoRA method.
+
+ This function will:
+ - Disable gradient updates for the "lora_A" parameters (these are typically frozen during LoRA training).
+ - Compute the scaling factor based on provided `lora_alpha` and rank `r` for proper gradient projection.
+ - Create and configure parameter groups for the optimizer including specified learning rate, weight decay, and
+ additional optimizer options.
+
+ For hyper-params, LoRA-FA uses the same hyper-params as AdamW, except for the LoRA hyper-params (r, lora_alpha,
+ use_rslora). One can always use the same hyper-params such as lr and weight_decay, as AdamW in LoRA tuning.
+
+ Args:
+ model (PeftModel): The model containing LoRA-adapted parameters.
+ r (int): Rank of the LoRA decomposition.
+ lora_alpha (int): Scaling factor for LoRA parameterization.
+ lr (float): Learning rate for optimizer updates.
+ weight_decay (float): Weight decay for AdamW.
+ use_rslora (bool):
+ whether to use rslora. In rslora, the lora scaling factor becomes to lora_alpha / math.sqrt(r) instead of
+ lora_alpha / r.
+
+ Returns:
+ Optimizer: Configured lorafa optimizer instance ready for training.
+ """
+ for name, param in model.named_parameters():
+ if "lora_A" in name:
+ param.requires_grad_(False)
+ lora_scaling = lora_alpha / math.sqrt(r) if use_rslora else lora_alpha / r
+ param_groups = [
+ {
+ "params": model.parameters(),
+ "lr": lr,
+ "names": [name for name, _ in model.named_parameters()],
+ "scaling_factor": lora_scaling,
+ "betas": (0.9, 0.999),
+ "weight_decay": weight_decay,
+ }
+ ]
+ return LoraFAOptimizer(param_groups)
diff --git a/peft/src/peft/optimizers/loraplus.py b/peft/src/peft/optimizers/loraplus.py
new file mode 100644
index 0000000000000000000000000000000000000000..e4ecae770d5acab4215479141f2db1d17e42da81
--- /dev/null
+++ b/peft/src/peft/optimizers/loraplus.py
@@ -0,0 +1,121 @@
+# Copyright 2024-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""
+This module contains the implementation of the LoraPlus optimizer.
+"""
+
+from __future__ import annotations
+
+from operator import attrgetter
+
+import torch.nn as nn
+from torch.optim import Optimizer
+from transformers.pytorch_utils import ALL_LAYERNORM_LAYERS
+from transformers.trainer_pt_utils import get_parameter_names
+
+from ..peft_model import PeftModel
+from ..tuners.lora.layer import Embedding
+
+
+def create_loraplus_optimizer(
+ model: PeftModel, optimizer_cls: type[Optimizer], *, lr: float, loraplus_lr_ratio: float, **kwargs
+) -> Optimizer:
+ """
+ Creates a LoraPlus optimizer.
+
+ Efficient Low Rank Adaptation of Large Models: https://huggingface.co/papers/2402.12354
+
+ Reference: https://github.com/nikhil-ghosh-berkeley/loraplus/
+
+ Args:
+ model (`torch.nn.Module`): The model to be optimized.
+ optimizer_cls (`torch.optim.Optimizer`): The optimizer class to be used.
+ lr (`float`): The learning rate to be used for the optimizer.
+ loraplus_lr_ratio (`float`):
+ The ratio of learning ηB/ηA where ηA (lr) is passed in as the optimizer learning rate. Should be ≥1. Should
+ be set in tandem with the optimizer learning rate (lr); should be larger when the task is more difficult
+ and the model needs to update its features to learn well. In this case, it helps to make the learning rate
+ slightly smaller (e.g., by a factor of 2) than typical vanilla LoRA learning rates
+ loraplus_lr_embedding (optional `float`):
+ If LoRA modules are added to embedding layers your can specify a different learning rate for them. Default
+ value 1e-6.
+ kwargs (`dict`): Additional keyword arguments to be passed to the optimizer.
+
+ Returns:
+ `torch.optim.Optimizer`: An instance of the specified optimizer class configured with the model's parameters
+ organized into groups with custom learning rates.
+ """
+
+ decay_parameters = get_parameter_names(model, ALL_LAYERNORM_LAYERS)
+ decay_parameters = [name for name in decay_parameters if "bias" not in name]
+ param_groups = {
+ "groupA": {},
+ "groupB": {},
+ "groupB_no_decay": {},
+ "embedding": {},
+ }
+
+ for name, param in model.named_parameters():
+ if not param.requires_grad:
+ continue
+
+ module = attrgetter(name)(model)
+ if isinstance(module, Embedding):
+ param_groups["embedding"][name] = param
+ elif "lora_B" in name or param.ndim == 1:
+ if name in decay_parameters:
+ param_groups["groupB"][name] = param
+ else:
+ param_groups["groupB_no_decay"][name] = param
+ else:
+ param_groups["groupA"][name] = param
+
+ kwargs["lr"] = lr
+ loraplus_weight_decay = kwargs.pop("loraplus_weight_decay", 0.0)
+ loraplus_lr_embedding = kwargs.pop("loraplus_lr_embedding", 1e-6)
+
+ optimizer_grouped_parameters = [
+ {
+ "params": list(param_groups["groupA"].values()),
+ "weight_decay": loraplus_weight_decay,
+ "lr": lr,
+ },
+ {
+ "params": list(param_groups["embedding"].values()),
+ "weight_decay": loraplus_weight_decay,
+ "lr": loraplus_lr_embedding,
+ },
+ {
+ "params": list(param_groups["groupB"].values()),
+ "weight_decay": loraplus_weight_decay,
+ "lr": lr * loraplus_lr_ratio,
+ },
+ {
+ "params": list(param_groups["groupB_no_decay"].values()),
+ "weight_decay": 0.0,
+ "lr": lr * loraplus_lr_ratio,
+ },
+ ]
+
+ optimizer = optimizer_cls(optimizer_grouped_parameters, **kwargs)
+ eight_bit_names = ["Adam8bit", "AdamW8bit", "PagedAdam8bit", "PagedAdamW8bit"]
+ if optimizer_cls.__name__ in eight_bit_names:
+ import bitsandbytes
+
+ manager = bitsandbytes.optim.GlobalOptimManager.get_instance()
+ for module in model.modules():
+ if isinstance(module, nn.Embedding):
+ manager.register_module_override(module, "weight", {"optim_bits": 32})
+ return optimizer
diff --git a/peft/src/peft/peft_model.py b/peft/src/peft/peft_model.py
new file mode 100644
index 0000000000000000000000000000000000000000..3b7e6364169a86d4fab988b9f2b7739d628dec01
--- /dev/null
+++ b/peft/src/peft/peft_model.py
@@ -0,0 +1,3311 @@
+# Copyright 2023-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+from __future__ import annotations
+
+import collections
+import copy
+import inspect
+import os
+import warnings
+from collections.abc import Sequence
+from contextlib import contextmanager, nullcontext
+from copy import deepcopy
+from dataclasses import dataclass
+from typing import Any, Literal, Optional, Union
+
+import packaging.version
+import torch
+import transformers
+from accelerate import dispatch_model, infer_auto_device_map
+from accelerate.hooks import AlignDevicesHook, add_hook_to_module, remove_hook_from_submodules
+from accelerate.utils import get_balanced_memory, named_module_tensors
+from huggingface_hub import HfFileSystem, ModelCard, ModelCardData, hf_hub_download
+from safetensors import safe_open
+from safetensors.torch import save_file as safe_save_file
+from torch.nn import BCEWithLogitsLoss, CrossEntropyLoss, MSELoss
+from transformers import Cache, DynamicCache, EncoderDecoderCache, PreTrainedModel
+from transformers.modeling_outputs import QuestionAnsweringModelOutput, SequenceClassifierOutput, TokenClassifierOutput
+from transformers.utils import PushToHubMixin
+
+from peft.tuners.lora.variants import get_alora_offsets_for_forward, get_alora_offsets_for_generate
+from peft.tuners.tuners_utils import BaseTuner, BaseTunerLayer
+from peft.utils import AuxiliaryTrainingWrapper
+from peft.utils.constants import DUMMY_MODEL_CONFIG
+from peft.utils.integrations import init_empty_weights
+from peft.utils.other import TrainableTokensWrapper, create_attention_mask, set_additional_trainable_modules
+
+from . import __version__
+from .config import PeftConfig
+from .mapping import PEFT_TYPE_TO_CONFIG_MAPPING, PEFT_TYPE_TO_PREFIX_MAPPING, PEFT_TYPE_TO_TUNER_MAPPING
+from .utils import (
+ SAFETENSORS_WEIGHTS_NAME,
+ TRANSFORMERS_MODELS_TO_PREFIX_TUNING_POSTPROCESS_MAPPING,
+ WEIGHTS_NAME,
+ PeftType,
+ TaskType,
+ _get_batch_size,
+ _prepare_prompt_learning_config,
+ _set_adapter,
+ _set_trainable,
+ get_peft_model_state_dict,
+ id_tensor_storage,
+ infer_device,
+ load_peft_weights,
+ map_cache_to_layer_device_map,
+ set_peft_model_state_dict,
+ shift_tokens_right,
+)
+
+
+class PeftModel(PushToHubMixin, torch.nn.Module):
+ """
+ Base model encompassing various Peft methods.
+
+ Args:
+ model ([`~transformers.PreTrainedModel`]): The base transformer model used for Peft.
+ peft_config ([`PeftConfig`]): The configuration of the Peft model.
+ adapter_name (`str`, *optional*): The name of the adapter, defaults to `"default"`.
+ autocast_adapter_dtype (`bool`, *optional*):
+ Whether to autocast the adapter dtype. Defaults to `True`. Right now, this will only cast adapter weights
+ using float16 and bfloat16 to float32, as this is typically required for stable training, and only affect
+ select PEFT tuners.
+ low_cpu_mem_usage (`bool`, `optional`, defaults to `False`):
+ Create empty adapter weights on meta device. Useful to speed up the loading loading process.
+
+ > [!TIP] > Don't use `low_cpu_mem_usage=True` when creating a new PEFT adapter for training.
+
+ **Attributes**:
+ - **base_model** ([`torch.nn.Module`]) -- The base transformer model used for Peft.
+ - **peft_config** ([`PeftConfig`]) -- The configuration of the Peft model.
+ - **modules_to_save** (`list` of `str`) -- The list of sub-module names to save when
+ saving the model.
+ - **prompt_encoder** ([`PromptEncoder`]) -- The prompt encoder used for Peft if
+ using [`PromptLearningConfig`].
+ - **prompt_tokens** (`torch.Tensor`) -- The virtual prompt tokens used for Peft if
+ using [`PromptLearningConfig`].
+ - **transformer_backbone_name** (`str`) -- The name of the transformer
+ backbone in the base model if using [`PromptLearningConfig`].
+ - **word_embeddings** (`torch.nn.Embedding`) -- The word embeddings of the transformer backbone
+ in the base model if using [`PromptLearningConfig`].
+ """
+
+ def __init__(
+ self,
+ model: PreTrainedModel,
+ peft_config: PeftConfig,
+ adapter_name: str = "default",
+ autocast_adapter_dtype: bool = True,
+ low_cpu_mem_usage: bool = False,
+ ) -> None:
+ super().__init__()
+ self.active_adapter = adapter_name
+ self.peft_type = peft_config.peft_type
+ # These args are special PEFT arguments that users can pass. They need to be removed before passing them to
+ # forward.
+ self.special_peft_forward_args = {"adapter_names", "alora_offsets"}
+
+ self._is_prompt_learning = peft_config.is_prompt_learning
+ if self._is_prompt_learning:
+ self._peft_config = {adapter_name: peft_config}
+ self.base_model = model
+ self.add_adapter(adapter_name, peft_config, low_cpu_mem_usage=low_cpu_mem_usage)
+ else:
+ self._peft_config = None
+ cls = PEFT_TYPE_TO_TUNER_MAPPING[peft_config.peft_type]
+ ctx = init_empty_weights if low_cpu_mem_usage else nullcontext
+ with ctx():
+ self.base_model = cls(model, {adapter_name: peft_config}, adapter_name)
+
+ if hasattr(self.base_model, "_cast_adapter_dtype"):
+ self.base_model._cast_adapter_dtype(
+ adapter_name=adapter_name, autocast_adapter_dtype=autocast_adapter_dtype
+ )
+
+ if getattr(model, "is_gradient_checkpointing", True):
+ model = self.prepare_model_for_gradient_checkpointing(model)
+
+ # the `pretraining_tp` is set for some models to simulate Tensor Parallelism during inference to avoid
+ # numerical differences, https://github.com/pytorch/pytorch/issues/76232 - to avoid any unexpected
+ # behavior we disable that in this line.
+ if hasattr(self.base_model, "config") and hasattr(self.base_model.config, "pretraining_tp"):
+ self.base_model.config.pretraining_tp = 1
+
+ @property
+ def peft_config(self) -> dict[str, PeftConfig]:
+ if self._is_prompt_learning:
+ return self._peft_config
+ return self.base_model.peft_config
+
+ @property
+ def active_adapters(self) -> list[str]:
+ try:
+ adapters = self.base_model.active_adapters
+ if not isinstance(adapters, list):
+ # Base model is probably a transformers model, see:
+ # https://github.com/huggingface/transformers/pull/30790#issuecomment-2253808249
+ # Unfortunately, transformers models also have an active_adapters method but it's 1) not a property and
+ # 2) calling it fails because the base model (usually) has no loaded adapter. The base model can be a
+ # transformers model for prompt learning, where the base model is not wrapped in a LoraModel or similar.
+ adapters = self.active_adapter
+ if isinstance(adapters, str):
+ adapters = [adapters]
+ except AttributeError:
+ adapters = self.active_adapter
+ if isinstance(adapters, str):
+ adapters = [adapters]
+ return adapters
+
+ @peft_config.setter
+ def peft_config(self, value: dict[str, PeftConfig]):
+ if self._is_prompt_learning:
+ self._peft_config = value
+ else:
+ self.base_model.peft_config = value
+
+ def save_pretrained(
+ self,
+ save_directory: str,
+ safe_serialization: bool = True,
+ selected_adapters: Optional[list[str]] = None,
+ save_embedding_layers: Union[str, bool] = "auto",
+ is_main_process: bool = True,
+ path_initial_model_for_weight_conversion: Optional[str] = None,
+ **kwargs: Any,
+ ) -> None:
+ r"""
+ This function saves the adapter model and the adapter configuration files to a directory, so that it can be
+ reloaded using the [`PeftModel.from_pretrained`] class method, and also used by the [`PeftModel.push_to_hub`]
+ method.
+
+ Args:
+ save_directory (`str`):
+ Directory where the adapter model and configuration files will be saved (will be created if it does not
+ exist).
+ safe_serialization (`bool`, *optional*):
+ Whether to save the adapter files in safetensors format, defaults to `True`.
+ selected_adapters (`List[str]`, *optional*):
+ A list of adapters to be saved. If `None`, will default to all adapters.
+ save_embedding_layers (`Union[bool, str]`, *optional*, defaults to `"auto"`):
+ If `True`, save the embedding layers in addition to adapter weights. If `auto`, checks the common
+ embedding layers `peft.utils.other.EMBEDDING_LAYER_NAMES` in config's `target_modules` when available.
+ and automatically sets the boolean flag. This only works for 🤗 transformers models.
+ is_main_process (`bool`, *optional*):
+ Whether the process calling this is the main process or not. Will default to `True`. Will not save the
+ checkpoint if not on the main process, which is important for multi device setups (e.g. DDP).
+ path_initial_model_for_weight_conversion (`str, *optional*`):
+ The path to the initialized adapter, which is obtained after initializing the model with
+ PiSSA/CorDA/OLoRA and before performing any training. When `path_initial_model_for_weight_conversion`
+ is not None, the difference in adapter before and after fine-tuning is calculated. This difference can
+ be represented as the parameters of a standard LoRA adapter. Using this converted adapter does not
+ require changes to the base model, thus conveniently allowing the use of multiple PiSSA/CorDA/OLoRA
+ adapters with LoRA adapters, and the activation or deactivation of any adapters. Note that this
+ conversion is not supported if `rslora` is used in combination with `rank_pattern` or `alpha_pattern`.
+ kwargs (additional keyword arguments, *optional*):
+ Additional keyword arguments passed along to the `push_to_hub` method.
+
+ """
+ if os.path.isfile(save_directory):
+ raise ValueError(f"Provided path ({save_directory}) should be a directory, not a file")
+
+ if selected_adapters is None:
+ selected_adapters = list(self.peft_config.keys())
+ else:
+ if any(
+ selected_adapter_name not in list(self.peft_config.keys())
+ for selected_adapter_name in selected_adapters
+ ):
+ raise ValueError(
+ f"You passed an invalid `selected_adapters` arguments, current supported adapter names are"
+ f" {list(self.peft_config.keys())} - got {selected_adapters}."
+ )
+
+ def save_mutated_as_lora(peft_config, path_initial_model_for_weight_conversion, output_state_dict, kwargs):
+ if peft_config.use_rslora and (peft_config.rank_pattern or peft_config.alpha_pattern):
+ msg = (
+ "Passing `path_initial_model_for_weight_conversion` to `save_pretrained` is not supported when "
+ "using `rank_pattern` or `alpha_pattern` at the same time as `use_rslora=True`."
+ )
+ raise ValueError(msg)
+
+ if not any(
+ str(peft_config.init_lora_weights).lower().startswith(prefix)
+ for prefix in ["pissa", "corda", "olora", "true"]
+ ):
+ warnings.warn(
+ "`path_initial_model_for_weight_conversion` only works for converting a PiSSA/CorDA/OLoRA adapter to "
+ "a LoRA adapter"
+ )
+ initial_adapter_name = os.path.basename(path_initial_model_for_weight_conversion)
+ try:
+ self.load_adapter(
+ os.path.dirname(path_initial_model_for_weight_conversion),
+ subfolder=initial_adapter_name,
+ adapter_name=initial_adapter_name,
+ )
+ is_pissa = str(self.peft_config[initial_adapter_name].init_lora_weights).lower().startswith("pissa")
+ is_corda = str(self.peft_config[initial_adapter_name].init_lora_weights).lower() == "corda"
+ is_olora = str(self.peft_config[initial_adapter_name].init_lora_weights).lower() == "olora"
+ if is_pissa or is_corda or is_olora:
+ raise ValueError(
+ "The `init_lora_weights` parameter of the initial adapter should be set to `True`. "
+ "Otherwise, `self.load_adapter` will subtract the decomposed values again based on the "
+ "residual model."
+ )
+ output_state_dict = self.base_model.subtract_mutated_init(
+ output_state_dict, initial_adapter_name, kwargs
+ )
+ finally:
+ self.delete_adapter(initial_adapter_name)
+ return output_state_dict
+
+ if is_main_process:
+ os.makedirs(save_directory, exist_ok=True)
+ self.create_or_update_model_card(save_directory)
+
+ for adapter_name in selected_adapters:
+ peft_config = self.peft_config[adapter_name]
+ # save only the trainable weights
+ output_state_dict = get_peft_model_state_dict(
+ self,
+ state_dict=kwargs.get("state_dict", None),
+ adapter_name=adapter_name,
+ save_embedding_layers=save_embedding_layers,
+ )
+ output_dir = os.path.join(save_directory, adapter_name) if adapter_name != "default" else save_directory
+ os.makedirs(output_dir, exist_ok=True)
+
+ if is_main_process and safe_serialization:
+ # Section copied from: https://github.com/huggingface/transformers/blob/main/src/transformers/modeling_utils.py#L2111-L2134
+ # Safetensors does not allow tensor aliasing.
+ # We're going to remove aliases before saving
+ ptrs = collections.defaultdict(list)
+ for name, tensor in output_state_dict.items():
+ # Sometimes in the state_dict we have non-tensor objects.
+ # e.g. in bitsandbytes we have some `str` objects in the state_dict
+ if isinstance(tensor, torch.Tensor):
+ ptrs[id_tensor_storage(tensor)].append(name)
+ else:
+ # In the non-tensor case, fall back to the pointer of the object itself
+ ptrs[id(tensor)].append(name)
+
+ # These are all the pointers of shared tensors.
+ shared_ptrs = {ptr: names for ptr, names in ptrs.items() if len(names) > 1}
+
+ for _, names in shared_ptrs.items():
+ # Here we just clone the shared tensors to avoid tensor aliasing which is
+ # not supported in safetensors.
+ for shared_tensor_name in names[1:]:
+ output_state_dict[shared_tensor_name] = output_state_dict[shared_tensor_name].clone()
+ if path_initial_model_for_weight_conversion is not None:
+ peft_config = copy.deepcopy(peft_config)
+ peft_config.init_lora_weights = True
+ peft_config.save_pretrained(path_initial_model_for_weight_conversion)
+ output_state_dict = save_mutated_as_lora(
+ peft_config, path_initial_model_for_weight_conversion, output_state_dict, kwargs
+ )
+ safe_save_file(
+ output_state_dict,
+ os.path.join(output_dir, SAFETENSORS_WEIGHTS_NAME),
+ metadata={"format": "pt"},
+ )
+ elif is_main_process:
+ if path_initial_model_for_weight_conversion is not None:
+ peft_config = copy.deepcopy(peft_config)
+ peft_config.init_lora_weights = True
+ peft_config.save_pretrained(path_initial_model_for_weight_conversion)
+ output_state_dict = save_mutated_as_lora(
+ peft_config, path_initial_model_for_weight_conversion, output_state_dict, kwargs
+ )
+ torch.save(output_state_dict, os.path.join(output_dir, WEIGHTS_NAME))
+
+ # save the config and change the inference mode to `True`
+ if peft_config.base_model_name_or_path is None:
+ peft_config.base_model_name_or_path = (
+ self.base_model.__dict__.get("name_or_path", None)
+ if peft_config.is_prompt_learning
+ else self.base_model.model.__dict__.get("name_or_path", None)
+ )
+ inference_mode = peft_config.inference_mode
+ peft_config.inference_mode = True
+
+ if peft_config.task_type is None:
+ # deal with auto mapping
+ base_model_class = self._get_base_model_class(
+ is_prompt_tuning=peft_config.is_prompt_learning,
+ )
+ parent_library = base_model_class.__module__
+
+ auto_mapping_dict = {
+ "base_model_class": base_model_class.__name__,
+ "parent_library": parent_library,
+ }
+ else:
+ auto_mapping_dict = None
+
+ if is_main_process:
+ if path_initial_model_for_weight_conversion is not None:
+ peft_config.init_lora_weights = True
+ peft_config.r *= 2
+ if not peft_config.use_rslora:
+ peft_config.lora_alpha *= 2
+ else:
+ # with rslora, we have scaling = alpha / sqrt(r), we thus adjust alpha to keep the same scaling
+ peft_config.lora_alpha *= 2**0.5
+
+ if peft_config.rank_pattern:
+ peft_config.rank_pattern = {key: 2 * val for key, val in peft_config.rank_pattern.items()}
+ if peft_config.alpha_pattern:
+ peft_config.alpha_pattern = {key: 2 * val for key, val in peft_config.alpha_pattern.items()}
+
+ peft_config.save_pretrained(output_dir, auto_mapping_dict=auto_mapping_dict)
+ peft_config.inference_mode = inference_mode
+
+ @classmethod
+ def from_pretrained(
+ cls,
+ model: torch.nn.Module,
+ model_id: Union[str, os.PathLike],
+ adapter_name: str = "default",
+ is_trainable: bool = False,
+ config: Optional[PeftConfig] = None,
+ autocast_adapter_dtype: bool = True,
+ ephemeral_gpu_offload: bool = False,
+ low_cpu_mem_usage: bool = False,
+ key_mapping: Optional[dict[str, str]] = None,
+ **kwargs: Any,
+ ) -> PeftModel:
+ r"""
+ Instantiate a PEFT model from a pretrained model and loaded PEFT weights.
+
+ Note that the passed `model` may be modified inplace.
+
+ Args:
+ model ([`torch.nn.Module`]):
+ The model to be adapted. For 🤗 Transformers models, the model should be initialized with the
+ [`~transformers.PreTrainedModel.from_pretrained`].
+ model_id (`str` or `os.PathLike`):
+ The name of the PEFT configuration to use. Can be either:
+ - A string, the `model id` of a PEFT configuration hosted inside a model repo on the Hugging Face
+ Hub.
+ - A path to a directory containing a PEFT configuration file saved using the `save_pretrained`
+ method (`./my_peft_config_directory/`).
+ adapter_name (`str`, *optional*, defaults to `"default"`):
+ The name of the adapter to be loaded. This is useful for loading multiple adapters.
+ is_trainable (`bool`, *optional*, defaults to `False`):
+ Whether the adapter should be trainable or not. If `False`, the adapter will be frozen and can only be
+ used for inference.
+ config ([`~peft.PeftConfig`], *optional*):
+ The configuration object to use instead of an automatically loaded configuration. This configuration
+ object is mutually exclusive with `model_id` and `kwargs`. This is useful when configuration is already
+ loaded before calling `from_pretrained`.
+ autocast_adapter_dtype (`bool`, *optional*):
+ Whether to autocast the adapter dtype. Defaults to `True`. Only relevant for specific adapter types.
+ ephemeral_gpu_offload (`bool`, *optional*):
+ Whether to use ephemeral GPU offloading for partially loaded modules. Defaults to `False`. This is
+ useful when parts of the model and/or components (such as adapters) are kept in CPU memory until they
+ are needed. Rather than perform expensive operations on small data, the data is transferred to the GPU
+ on-demand, the operation(s) performed, and the results moved back to CPU memory. This brings a slight
+ momentary VRAM overhead but gives orders of magnitude speedup in certain cases.
+ low_cpu_mem_usage (`bool`, `optional`, defaults to `False`):
+ Create empty adapter weights on meta device before loading the saved weights. Useful to speed up the
+ process.
+ torch_device (`str`, *optional*, defaults to None):
+ The device to load the adapter on. If `None`, the device will be inferred.
+ key_mapping (dict, *optional*, defaults to None)
+ Extra mapping of PEFT `state_dict` keys applied before loading the `state_dict`. When this mapping is
+ applied, the PEFT-specific `"base_model.model"` prefix is removed beforehand and the adapter name (e.g.
+ `"default"`) is not inserted yet. Only pass this argument if you know what you're doing.
+ kwargs: (`optional`):
+ Additional keyword arguments passed along to the specific PEFT configuration class.
+ """
+ from .auto import MODEL_TYPE_TO_PEFT_MODEL_MAPPING
+ from .tuners import XLoraConfig, XLoraModel
+
+ # load the config
+ if config is None:
+ hf_kwargs = {
+ "subfolder": kwargs.get("subfolder", None),
+ "revision": kwargs.get("revision", None),
+ "cache_dir": kwargs.get("cache_dir", None),
+ "token": kwargs.get("token", None),
+ }
+ if use_auth_token := kwargs.get("use_auth_token", None):
+ hf_kwargs["use_auth_token"] = use_auth_token
+ config = PEFT_TYPE_TO_CONFIG_MAPPING[PeftConfig._get_peft_type(model_id, **hf_kwargs)].from_pretrained(
+ model_id, **kwargs
+ )
+ elif isinstance(config, PeftConfig):
+ config.inference_mode = not is_trainable
+ else:
+ raise ValueError(f"The input config must be a PeftConfig, got {config.__class__}")
+
+ # See discussion in https://github.com/huggingface/transformers/pull/38627
+ # Some transformers models can have a _checkpoint_conversion_mapping dict that is used to map state_dicts
+ # stemming from updated model architectures so that they still correspond to the initial architecture. When
+ # loading a PEFT state_dict created with the initial architecture on a model with the new architecture, we need
+ # to map it too according to the same rules. Note that we skip prompt learning methods. This is because they
+ # don't have the "base_model.model." prefix, which we need to remove before mapping. Instead just using
+ # "base_model.". This could be fine, we could only remove "base_model.", However, the subsequent sub-module
+ # could also be called "model", resulting in what looks like "base_model.model.". To avoid this confusion, we
+ # skip prompt learning. Since it applies itself directly to the pre-trained model (unlike LoRA et al that target
+ # sub-modules), skipping should be fine.
+ if (key_mapping is None) and (not config.is_prompt_learning):
+ key_mapping = getattr(model, "_checkpoint_conversion_mapping", {})
+
+ # Runtime configuration, if supported
+ if hasattr(config, "runtime_config"):
+ config.runtime_config.ephemeral_gpu_offload = ephemeral_gpu_offload
+ else:
+ if ephemeral_gpu_offload:
+ warnings.warn("Ephemeral GPU offloading is not supported for this model. Ignoring.")
+
+ if hasattr(model, "hf_device_map"):
+ weight_map = dict(named_module_tensors(model, recurse=True))
+
+ # recreate the offload_index for disk-offloaded modules: we need to know the location in storage of each weight
+ # before the offload hook is removed from the model
+ disk_modules = set()
+ index = None
+ for name, module in model.named_modules():
+ if hasattr(module, "_hf_hook") and hasattr(module._hf_hook, "original_devices"):
+ if hasattr(module._hf_hook.weights_map, "dataset"):
+ index = module._hf_hook.weights_map.dataset.index
+ for key in module._hf_hook.original_devices.keys():
+ if module._hf_hook.original_devices[key] == torch.device("meta"):
+ disk_modules.add(str(name) + "." + str(key))
+
+ if disk_modules and not kwargs.get("use_safetensors", True):
+ raise ValueError("Disk offloading currently only supported for safetensors")
+
+ if index:
+ offload_index = {
+ p: {
+ "safetensors_file": index[p]["safetensors_file"],
+ "weight_name": p,
+ "dtype": str(weight_map[p].dtype).replace("torch.", ""),
+ }
+ for p in weight_map.keys()
+ if p in disk_modules
+ }
+ kwargs["offload_index"] = offload_index
+
+ if (getattr(model, "hf_device_map", None) is not None) and len(
+ set(model.hf_device_map.values()).intersection({"cpu", "disk"})
+ ) > 0:
+ remove_hook_from_submodules(model)
+
+ if config.is_prompt_learning and is_trainable:
+ raise ValueError("Cannot set a prompt learning adapter to trainable when loading pretrained adapter.")
+ else:
+ config.inference_mode = not is_trainable
+ if isinstance(getattr(model, "base_model", None), XLoraModel):
+ if not isinstance(config, XLoraConfig):
+ raise TypeError(f"Expected 'XLoraConfig', got '{type(config)}' instead.")
+ if "adapters" in kwargs:
+ config.adapters = kwargs["adapters"]
+ else:
+ # If the path is on HF hub, then we get the adapter names to create a subfolders list which tells
+ # `load_adapter` where the adapters are.
+ if not os.path.exists(model_id):
+ s = HfFileSystem()
+
+ # The names of the adapters which must be in folders
+ adapter_names = [
+ file["name"][len(model_id) + 1 :] for file in s.ls(model_id) if file["type"] == "directory"
+ ]
+ # Prepare a dict of adapter paths, which really just point to the hf id; we will use the subfolders
+ adapter_paths = {}
+ for adapter_name in adapter_names:
+ adapter_paths[adapter_name] = os.path.join(model_id, model_id)
+ config.adapters = adapter_paths
+ config._subfolders = adapter_names
+ else:
+ if "adapters" not in kwargs:
+ raise ValueError("If model_id is a local path, then `adapters` must be passed in kwargs.")
+
+ if config.task_type not in MODEL_TYPE_TO_PEFT_MODEL_MAPPING.keys():
+ model = cls(
+ model,
+ config,
+ adapter_name,
+ autocast_adapter_dtype=autocast_adapter_dtype,
+ low_cpu_mem_usage=low_cpu_mem_usage,
+ )
+ else:
+ model = MODEL_TYPE_TO_PEFT_MODEL_MAPPING[config.task_type](
+ model,
+ config,
+ adapter_name,
+ autocast_adapter_dtype=autocast_adapter_dtype,
+ low_cpu_mem_usage=low_cpu_mem_usage,
+ )
+
+ load_result = model.load_adapter(
+ model_id,
+ adapter_name,
+ is_trainable=is_trainable,
+ autocast_adapter_dtype=autocast_adapter_dtype,
+ low_cpu_mem_usage=low_cpu_mem_usage,
+ key_mapping=key_mapping,
+ **kwargs,
+ )
+
+ # 1. Remove VB-LoRA vector bank, since it's a shared parameter set via the VBLoRAModel
+ # 2. Remove the prompt encoder, as it does not need to be part of the checkpoint
+ missing_keys = [
+ k for k in load_result.missing_keys if "vblora_vector_bank" not in k and "prompt_encoder" not in k
+ ]
+ if missing_keys:
+ # Let's warn here since (in contrast to load_adapter) we don't return the load result, so it could be quite
+ # difficult for users to even notice that something might have gone wrong here. As we filter out non PEFT
+ # keys from the missing keys, this gives no false positives.
+
+ # careful: if the wording of the warning is changed, adjust the unit tests accordingly!
+ warn_message = f"Found missing adapter keys while loading the checkpoint: {missing_keys}."
+
+ prefix = PEFT_TYPE_TO_PREFIX_MAPPING.get(config.peft_type)
+ if prefix and adapter_name in prefix:
+ warn_message = (
+ f"Adapter name '{adapter_name}' should not be contained in the prefix '{prefix}'. "
+ "This could be the potential reason for missing adapter keys. "
+ ) + warn_message
+
+ warnings.warn(warn_message)
+
+ return model
+
+ def _setup_prompt_encoder(self, adapter_name: str):
+ config = self.peft_config[adapter_name]
+ if not hasattr(self, "prompt_encoder"):
+ self.prompt_encoder = torch.nn.ModuleDict({})
+ self.prompt_tokens = {}
+ transformer_backbone = None
+ for name, module in self.base_model.named_children():
+ for param in module.parameters():
+ param.requires_grad = False
+ if isinstance(module, PreTrainedModel):
+ # Make sure to freeze Tranformers model
+ if transformer_backbone is None:
+ transformer_backbone = module
+ self.transformer_backbone_name = name
+ if transformer_backbone is None:
+ transformer_backbone = self.base_model
+
+ if config.num_transformer_submodules is None:
+ config.num_transformer_submodules = 2 if config.task_type == TaskType.SEQ_2_SEQ_LM else 1
+
+ # determine the word embeddings
+ word_embeddings = None
+ try:
+ # First try to find the word embeddings based on the module name, this should work for models like Bert,
+ # Roberta, Deberta, etc.
+ word_embeddings = self.base_model.get_submodule("embeddings.word_embeddings")
+ except AttributeError:
+ pass
+
+ if word_embeddings is None:
+ # Word embeddings could not be determined. Next try to guess them by checking which parameter has the size
+ # of the vocab.
+ for named_param, value in list(transformer_backbone.named_parameters()):
+ # for ZeRO-3, the tensor is sharded across accelerators and deepspeed modifies it to a tensor with shape
+ # [0] the actual unsharded shape is stored in "ds_shape" attribute special handling is needed in case
+ # the model is initialized in deepspeed.zero.Init() context or HfDeepSpeedConfig has been called before
+ # For reference refer to issue: https://github.com/huggingface/peft/issues/996
+ deepspeed_distributed_tensor_shape = getattr(value, "ds_shape", None)
+
+ # Handle VLM case with separate text and vision configs
+ if hasattr(self.base_model.config, "get_text_config"):
+ vocab_size = self.base_model.config.get_text_config().vocab_size
+ # below: for older transformers versions before get_text_config was added
+ elif "text_config" in self.base_model.config:
+ vocab_size = self.base_model.config.text_config.vocab_size
+ else:
+ vocab_size = self.base_model.config.vocab_size
+
+ if value.shape[0] == vocab_size or (
+ deepspeed_distributed_tensor_shape is not None
+ and deepspeed_distributed_tensor_shape[0] == vocab_size
+ ):
+ word_embeddings = transformer_backbone.get_submodule(named_param.replace(".weight", ""))
+ break
+
+ self.word_embeddings = word_embeddings
+ model_cls = PEFT_TYPE_TO_TUNER_MAPPING[config.peft_type]
+
+ if config.peft_type in (PeftType.PROMPT_TUNING, PeftType.MULTITASK_PROMPT_TUNING, PeftType.CPT):
+ prompt_encoder = model_cls(config, self.word_embeddings)
+ elif config.peft_type == PeftType.P_TUNING:
+ prompt_encoder = model_cls(config)
+ elif config.peft_type == PeftType.PREFIX_TUNING:
+ # prefix tuning now uses Cache but that won't work with gradient checkpointing
+ if any(getattr(module, "gradient_checkpointing", False) for module in self.get_base_model().modules()):
+ raise ValueError("Prefix tuning does not work with gradient checkpointing.")
+ prompt_encoder = model_cls(config)
+ else:
+ raise ValueError("Not supported")
+
+ prompt_encoder = prompt_encoder.to(self.device)
+ self.prompt_encoder.update(torch.nn.ModuleDict({adapter_name: prompt_encoder}))
+ self.prompt_tokens[adapter_name] = torch.arange(
+ config.num_virtual_tokens * config.num_transformer_submodules
+ ).long()
+
+ def prepare_model_for_gradient_checkpointing(self, model: PreTrainedModel):
+ r"""
+ Prepares the model for gradient checkpointing if necessary
+ """
+ self._prepare_model_for_gradient_checkpointing(model)
+
+ def _prepare_model_for_gradient_checkpointing(self, model: PreTrainedModel):
+ if not (
+ getattr(model, "is_loaded_in_8bit", False)
+ or getattr(model, "is_loaded_in_4bit", False)
+ or getattr(model, "is_quantized", False)
+ ):
+ if hasattr(model, "enable_input_require_grads"):
+ model.enable_input_require_grads()
+ elif hasattr(model, "get_input_embeddings"):
+
+ def make_inputs_require_grad(module, input, output):
+ output.requires_grad_(True)
+
+ model.get_input_embeddings().register_forward_hook(make_inputs_require_grad)
+ return model
+
+ def get_prompt_embedding_to_save(self, adapter_name: str) -> torch.Tensor:
+ """
+ Returns the prompt embedding to save when saving the model. Only applicable when using a prompt learning
+ method.
+ """
+ prompt_encoder = self.prompt_encoder[adapter_name]
+ prompt_tokens = (
+ self.prompt_tokens[adapter_name].unsqueeze(0).expand(1, -1).to(prompt_encoder.embedding.weight.device)
+ )
+ peft_type = self.peft_config[adapter_name].peft_type
+ if self.peft_config[adapter_name].peft_type == PeftType.PREFIX_TUNING:
+ prompt_tokens = prompt_tokens[:, : self.peft_config[adapter_name].num_virtual_tokens]
+
+ if self.peft_config[adapter_name].peft_type == PeftType.MULTITASK_PROMPT_TUNING:
+ prompt_embedding_cls = PEFT_TYPE_TO_TUNER_MAPPING[peft_type]
+ prompt_embeddings = super(prompt_embedding_cls, prompt_encoder).forward(prompt_tokens)
+ else:
+ prompt_embeddings = prompt_encoder(prompt_tokens)
+
+ return prompt_embeddings[0].detach().cpu()
+
+ def get_prompt(
+ self, batch_size: int, task_ids: Optional[torch.Tensor] = None, max_cache_len: Optional[int] = None
+ ) -> torch.Tensor:
+ """
+ Returns the virtual prompts to use for Peft. Only applicable when using a prompt learning method.
+ """
+ peft_config = self.active_peft_config
+ prompt_encoder = self.prompt_encoder[self.active_adapter]
+ prompt_tokens = (
+ self.prompt_tokens[self.active_adapter]
+ .unsqueeze(0)
+ .expand(batch_size, -1)
+ .to(prompt_encoder.embedding.weight.device)
+ )
+ if peft_config.peft_type == PeftType.PREFIX_TUNING:
+ prompt_tokens = prompt_tokens[:, : peft_config.num_virtual_tokens]
+ if peft_config.inference_mode:
+ past_key_values = prompt_encoder.embedding.weight.repeat(batch_size, 1, 1)
+ else:
+ past_key_values = prompt_encoder(prompt_tokens)
+ if self.base_model_torch_dtype is not None:
+ past_key_values = past_key_values.to(self.base_model_torch_dtype)
+ past_key_values = past_key_values.view(
+ batch_size,
+ peft_config.num_virtual_tokens,
+ peft_config.num_layers * 2,
+ peft_config.num_attention_heads,
+ peft_config.token_dim // peft_config.num_attention_heads,
+ )
+ if peft_config.num_transformer_submodules == 2:
+ past_key_values = torch.cat([past_key_values, past_key_values], dim=2)
+
+ # Transpose: 2 x [num_layers, batch_size, num_heads, num_virtual_tokens, head_dim]
+ past_key_values = past_key_values.permute([2, 0, 3, 1, 4]).split(
+ peft_config.num_transformer_submodules * 2
+ )
+
+ base_model = self.get_base_model()
+ model_config = getattr(base_model, "config", None)
+ model_type = getattr(model_config, "model_type", "")
+ if TRANSFORMERS_MODELS_TO_PREFIX_TUNING_POSTPROCESS_MAPPING.get(self.config.model_type, None) is not None:
+ post_process_fn = TRANSFORMERS_MODELS_TO_PREFIX_TUNING_POSTPROCESS_MAPPING[self.config.model_type]
+ past_key_values = post_process_fn(past_key_values)
+ elif ("gemma2" in model_type) or ("gemma3_text" in model_type):
+ # TODO: remove this logic once transformers < 4.56 is dropped
+ transformers_lt_4_56 = packaging.version.parse(transformers.__version__) < packaging.version.parse(
+ "4.56.0.dev0"
+ )
+ # Gemma2 and Gemma3 only support HybridCache (which does not have the from_legacy_cache method)
+ if transformers_lt_4_56 and ((max_cache_len is None) or (max_cache_len == -1)):
+ raise ValueError(
+ "max_cache_len is missing but it should have been passed. Something went wrong, please open an "
+ "issue on GitHub with a reproducer: https://github.com/huggingface/peft/issues"
+ )
+ base_config = base_model.config
+ if hasattr(base_config, "get_text_config"):
+ base_config = base_config.get_text_config()
+ if transformers_lt_4_56:
+ # HybridCache is deprecated, and will be removed in 4.60.0
+ # see https://github.com/huggingface/transformers/pull/40276
+ from transformers import HybridCache
+
+ new_cache = HybridCache(
+ config=base_config,
+ max_batch_size=batch_size,
+ max_cache_len=max_cache_len,
+ dtype=past_key_values[0].dtype,
+ device=past_key_values[0].device,
+ )
+ else:
+ # transformers 4.56+ uses DynamicCache for gemma
+ new_cache = DynamicCache(config=base_config)
+ cache_position = torch.arange(peft_config.num_virtual_tokens, device=past_key_values[0].device)
+ for layer_idx in range(peft_config.num_layers):
+ key_states, value_states = past_key_values[0][layer_idx], past_key_values[1][layer_idx]
+ new_cache.update(
+ key_states, value_states, layer_idx, cache_kwargs={"cache_position": cache_position}
+ )
+ past_key_values = new_cache
+ elif peft_config.num_transformer_submodules == 1:
+ # Dont' apply this to encoder-decoder models and not to models requiring special processing.
+ # TODO: remove from_legacy_cache once transformers < 4.56 is dropped
+ transformers_lt_4_56 = packaging.version.parse(transformers.__version__) < packaging.version.parse(
+ "4.56.0.dev0"
+ )
+ if transformers_lt_4_56:
+ past_key_values = DynamicCache.from_legacy_cache(past_key_values)
+ else:
+ past_key_values = DynamicCache(past_key_values)
+
+ elif (peft_config.num_transformer_submodules == 2) and getattr(
+ self.base_model, "_supports_cache_class", True
+ ):
+ # Dont' apply this to encoder-decoder models that don't support new Cache format yet
+ # If we don't apply this, prefix-tuning fails to update cross-attn cache
+ # TODO: remove check for _supports_cache_class once transformers 4.53 is no longer supported
+ # TODO: remove from_legacy_cache once transformers < 4.56 is dropped
+ transformers_lt_4_56 = packaging.version.parse(transformers.__version__) < packaging.version.parse(
+ "4.56.0.dev0"
+ )
+ if transformers_lt_4_56:
+ past_key_values = EncoderDecoderCache.from_legacy_cache(past_key_values)
+ else:
+ past_key_values = EncoderDecoderCache(past_key_values)
+
+ past_key_values.cross_attention_cache = DynamicCache()
+ # invalidate the cross attention cache, since we add virtual tokens to the encoder
+ for key in past_key_values.is_updated.keys():
+ past_key_values.is_updated[key] = False
+ map_cache_to_layer_device_map(self.get_base_model(), past_key_values) # no-op if not a Cache instance
+ return past_key_values
+ else:
+ if peft_config.peft_type == PeftType.MULTITASK_PROMPT_TUNING:
+ prompts = prompt_encoder(prompt_tokens, task_ids)
+ else:
+ if peft_config.inference_mode:
+ prompts = prompt_encoder.embedding.weight
+ else:
+ # Take only one prompt token sample and expand the output instead of expanding the input, see:
+ # https://github.com/huggingface/peft/issues/2043#issuecomment-2321522577
+ prompt_tokens = prompt_tokens[:1]
+ prompts = prompt_encoder(prompt_tokens)
+ prompts = prompts.repeat(batch_size, 1, 1)
+ return prompts
+
+ def get_nb_trainable_parameters(self) -> tuple[int, int]:
+ r"""
+ Returns the number of trainable parameters and the number of all parameters in the model.
+ """
+ trainable_params = 0
+ all_param = 0
+ for _, param in self.named_parameters():
+ num_params = param.numel()
+ # if using DS Zero 3 and the weights are initialized empty
+ if num_params == 0 and hasattr(param, "ds_numel"):
+ num_params = param.ds_numel
+
+ # Due to the design of 4bit linear layers from bitsandbytes
+ # one needs to multiply the number of parameters by 2 to get
+ # the correct number of parameters
+ if param.__class__.__name__ == "Params4bit":
+ if hasattr(param, "element_size"):
+ num_bytes = param.element_size()
+ elif not hasattr(param, "quant_storage"):
+ num_bytes = 1
+ else:
+ num_bytes = param.quant_storage.itemsize
+ num_params = num_params * 2 * num_bytes
+
+ all_param += num_params
+ if param.requires_grad:
+ trainable_params += num_params
+
+ return trainable_params, all_param
+
+ def print_trainable_parameters(self) -> None:
+ """
+ Prints the number of trainable parameters in the model.
+
+ Note: print_trainable_parameters() uses get_nb_trainable_parameters() which is different from
+ num_parameters(only_trainable=True) from huggingface/transformers. get_nb_trainable_parameters() returns
+ (trainable parameters, all parameters) of the Peft Model which includes modified backbone transformer model.
+ For techniques like LoRA, the backbone transformer model is modified in place with LoRA modules. However, for
+ prompt tuning, the backbone transformer model is unmodified. num_parameters(only_trainable=True) returns number
+ of trainable parameters of the backbone transformer model which can be different.
+ """
+ trainable_params, all_param = self.get_nb_trainable_parameters()
+
+ print(
+ f"trainable params: {trainable_params:,d} || all params: {all_param:,d} || trainable%: {100 * trainable_params / all_param:.4f}"
+ )
+
+ def __getattr__(self, name: str):
+ """Forward missing attributes to the wrapped module."""
+ try:
+ return super().__getattr__(name) # defer to nn.Module's logic
+ except AttributeError:
+ if name == "base_model": # see #1892: prevent infinite recursion if class is not initialized
+ raise
+ return getattr(self.base_model, name)
+
+ @contextmanager
+ def _enable_peft_forward_hooks(self, *args, **kwargs):
+ # If the base model has a method called _enable_peft_forward_hooks, it is invoked as a context. Otherwise, this
+ # runs without any changes
+ if hasattr(self.base_model, "_enable_peft_forward_hooks"):
+ with self.base_model._enable_peft_forward_hooks(*args, **kwargs):
+ yield
+ return
+ else:
+ # nothing to enable
+ yield
+ return
+
+ def forward(self, *args: Any, **kwargs: Any):
+ """
+ Forward pass of the model.
+ """
+ with self._enable_peft_forward_hooks(*args, **kwargs):
+ kwargs = {k: v for k, v in kwargs.items() if k not in self.special_peft_forward_args}
+ return self.get_base_model()(*args, **kwargs)
+
+ def generate(self, *args, **kwargs):
+ with self._enable_peft_forward_hooks(*args, **kwargs):
+ kwargs = {k: v for k, v in kwargs.items() if k not in self.special_peft_forward_args}
+ return self.get_base_model().generate(*args, **kwargs)
+
+ def _get_base_model_class(self, is_prompt_tuning=False):
+ """
+ Returns the base model class.
+ """
+ if not is_prompt_tuning:
+ return self.base_model.model.__class__
+ return self.base_model.__class__
+
+ @contextmanager
+ def disable_adapter(self):
+ """
+ Context manager that disables the adapter module. Use this to run inference on the base model.
+
+ Example:
+
+ ```py
+ >>> with model.disable_adapter():
+ ... model(inputs)
+ ```
+ """
+ if self.peft_config[self.active_adapter].is_prompt_learning:
+ try:
+ # TODO: consider replacing this patching of methods with a more robust mechanism: setting a flag and
+ # letting the underlying methods deal with it, same as how LoRA does it.
+ old_forward = self.forward
+ self.forward = self.base_model.forward
+ old_prepare_inputs_for_generation = self.prepare_inputs_for_generation
+ self.prepare_inputs_for_generation = self.base_model.prepare_inputs_for_generation
+ yield
+ finally:
+ self.forward = old_forward
+ self.prepare_inputs_for_generation = old_prepare_inputs_for_generation
+
+ elif self.peft_config[self.active_adapter].is_adaption_prompt:
+ try:
+ self.base_model.disable_adapter_layers()
+ yield
+ finally:
+ self.base_model.enable_adapter_layers()
+
+ else: # LoRA, LoHa, etc.
+ model_status = self.get_model_status()
+ if model_status.enabled == "irregular":
+ warnings.warn(
+ "The model contains some adapter layers that are enabled and others that are disabled. "
+ "This is most likely unintentional. After exiting the disable_adapter context, all adapters "
+ "will be enabled"
+ )
+ try:
+ self.base_model.disable_adapter_layers()
+ yield
+ finally:
+ if model_status.enabled is not False:
+ # model_status.enabled is `True` or `"irregular"`
+ self.base_model.enable_adapter_layers()
+
+ def get_base_model(self) -> torch.nn.Module:
+ """
+ Returns the base model.
+ """
+ return self.base_model if self.active_peft_config.is_prompt_learning else self.base_model.model
+
+ def add_adapter(self, adapter_name: str, peft_config: PeftConfig, low_cpu_mem_usage: bool = False) -> None:
+ """
+ Add an adapter to the model based on the passed configuration.
+
+ This adapter is not trained. To load a trained adapter, check out [`PeftModel.load_adapter`].
+
+ The name for the new adapter should be unique.
+
+ The new adapter is not automatically set as the active adapter. Use [`PeftModel.set_adapter`] to set the active
+ adapter.
+
+ Args:
+ adapter_name (`str`):
+ The name of the adapter to be added.
+ peft_config ([`PeftConfig`]):
+ The configuration of the adapter to be added.
+ low_cpu_mem_usage (`bool`, `optional`, defaults to `False`):
+ Create empty adapter weights on meta device. Useful to speed up the process when loading saved
+ adapters. Don't use this option when creating a new PEFT adapter for training.
+
+ """
+ prefix = PEFT_TYPE_TO_PREFIX_MAPPING.get(peft_config.peft_type)
+ if prefix and adapter_name in prefix:
+ warnings.warn(
+ f"Adapter name '{adapter_name}' should not be contained in the prefix '{prefix}'. "
+ "This may lead to reinitialization of the adapter weights during loading."
+ )
+
+ if peft_config.peft_type != self.peft_type:
+ raise ValueError(
+ f"Cannot combine adapters with different peft types. "
+ f"Found {self.peft_type} and {peft_config.peft_type}."
+ )
+
+ try:
+ if peft_config.is_prompt_learning:
+ self.peft_config[adapter_name] = peft_config
+ if hasattr(self.config, "to_dict"):
+ dict_config = self.config.to_dict()
+ else:
+ dict_config = self.config
+
+ peft_config = _prepare_prompt_learning_config(peft_config, dict_config)
+ self._setup_prompt_encoder(adapter_name)
+ set_additional_trainable_modules(
+ model=self.base_model,
+ peft_config=peft_config,
+ model_config=BaseTuner.get_model_config(self),
+ adapter_name=adapter_name,
+ )
+ elif peft_config.is_adaption_prompt:
+ self.base_model.add_adapter(adapter_name, peft_config)
+ set_additional_trainable_modules(
+ model=self.base_model,
+ peft_config=peft_config,
+ model_config=BaseTuner.get_model_config(self),
+ adapter_name=adapter_name,
+ )
+ else:
+ self.peft_config[adapter_name] = peft_config
+ self.base_model.inject_adapter(
+ self.base_model.model, adapter_name, low_cpu_mem_usage=low_cpu_mem_usage
+ )
+ except Exception: # something went wrong, roll back
+ if adapter_name in self.peft_config:
+ del self.peft_config[adapter_name]
+ raise
+
+ def delete_adapter(self, adapter_name: str) -> None:
+ """
+ Deletes an existing adapter.
+
+ Args:
+ adapter_name (str): Name of the adapter to be deleted.
+ """
+ if adapter_name not in self.peft_config:
+ raise ValueError(f"Adapter {adapter_name} does not exist")
+
+ self.base_model.delete_adapter(adapter_name=adapter_name)
+ new_active_adapters = self.active_adapters
+ num_adapters = len(new_active_adapters)
+ # Note: PeftModel assumes that there is exactly one active adapter, so we should theoretically raise if
+ # num_adapters != 1. However, we have allowed this in the past (maybe inadvertently), so we let it slip and
+ # don't introduce a backwards incompatibility by raising an error.
+ if num_adapters == 1:
+ self.active_adapter = new_active_adapters[0]
+
+ @property
+ def modules_to_save(self) -> Optional[set[str]]:
+ modules: set[str] = set()
+ for config in self.peft_config.values():
+ if getattr(config, "modules_to_save", None) is not None:
+ # modules_to_save can only be a sequence of str, not a str
+ modules.update(config.modules_to_save)
+
+ if not modules:
+ # for backwards compatibility, as modules_to_save was initialized as None
+ return None
+ return modules
+
+ def get_layer_status(self) -> list[TunerLayerStatus]:
+ """Get the status of each adapter layer in the model.
+
+ This method returns a list of `TunerLayerStatus` dataclass instances, each of which contains the following
+ attributes:
+
+ - `name` (`str`):
+ The name of the adapter layer, e.g. `model.encoder.block.0.layer.0.SelfAttention.q`.
+ - `module_type` (`str`):
+ The type of the adapter layer, e.g. `lora.Linear`.
+ - `enabled` (`bool`):
+ Whether the adapter layer is enabled.
+ - `active_adapters` (`list[str]`):
+ The names of the active adapters, if any, e.g. `["default"]`.
+ - `merged_adapters` (`list[str]`):
+ The names of the merged adapters, if any, e.g. `["default"]`.
+ - `available_adapters` (`list[str]`):
+ The names of the available adapters, e.g. `["default"]`.
+
+ Args:
+ model ([`~PeftModel`]):
+ The model to get the adapter layer status from.
+
+ Returns:
+ list[`peft.peft_model.TunerLayerStatus`]:
+ A list of dataclasses, each containing the status of the corresponding adapter layer.
+
+ """
+ return get_layer_status(self)
+
+ def get_model_status(self) -> TunerModelStatus:
+ """Get the status of tuners of the model.
+
+ This method returns a `TunerModelStatus` dataclass instance, which contains the following attributes:
+
+ - `base_model_type` (`str`):
+ The type of the base model, e.g. `T5Model`.
+ - `adapter_model_type` (`str`):
+ The type of the adapter model, e.g. `LoraModel`.
+ - `peft_types` (`dict[str, str]`):
+ The mapping of adapter name to adapter type, e.g. `{"default": "LORA"}`.
+ - `trainable_params` (`int`):
+ The number of trainable parameters in the model.
+ - `total_params` (`int`):
+ The total number of parameters in the model.
+ - `num_adapter_layers` (`int`):
+ The number of adapter layers in the model.
+ - `enabled` (`bool`, `Literal["irregular"]`):
+ Whether all adapter layers are enabled. If some are enabled and some are not, this will be `"irregular"`.
+ This means that your model is in an inconsistent state and might not work as expected.
+ - `active_adapters` (`list[str]`, `Literal["irregular"]`):
+ The names of the active adapters. If the active adapters are not consistent across all layers, this will be
+ `"irregular"`, which means that your model is in an inconsistent state and might not work as expected.
+ - `merged_adapters` (`list[str]`, `Literal["irregular"]`):
+ The names of the merged adapters. If the merged adapters are not consistent across all layers, this will be
+ `"irregular"`, which means that your model is in an inconsistent state and might not work as expected.
+ - `available_adapters` (`list[str]`):
+ The names of the available adapters, e.g. `["default"]`.
+
+ Args:
+ model ([`~PeftModel`]):
+ The model to get the adapter layer status from.
+
+ Returns:
+ `peft.peft_model.TunerModelStatus`:
+ A dataclass containing the status of the model.
+
+ """
+ return get_model_status(self)
+
+ @classmethod
+ def _split_kwargs(cls, kwargs: dict[str, Any]):
+ _kwargs_not_in_hf_hub_download_signature = ("use_auth_token",)
+ hf_hub_download_kwargs = {}
+ other_kwargs = {}
+
+ for key, value in kwargs.items():
+ if key in inspect.signature(hf_hub_download).parameters or key in _kwargs_not_in_hf_hub_download_signature:
+ hf_hub_download_kwargs[key] = value
+ else:
+ other_kwargs[key] = value
+
+ return hf_hub_download_kwargs, other_kwargs
+
+ def _update_offload(self, offload_index: dict[str, dict[str, str]], adapters_weights: dict[str, torch.tensor]):
+ """
+ Update the offload_index and safetensors files for loading and mergine PeftModels with disk-offloaded modules.
+
+ Args:
+ offload_index (Dict[str: str]):
+ Dictionary of disk-offloaded modules with their metadata and safetensors filenames
+ adapters_weights (Dict[str: torch.tensor]):
+ Dictionary of Peft adapter module names and weights
+ """
+
+ if not offload_index:
+ return offload_index
+
+ prefix = "base_model.model."
+ # rename offload index weight and model names
+ adapter_names = list(self.peft_config.keys())
+ for adapter_name in adapter_names:
+ keys = list(offload_index.keys())
+ block_id = keys[0].split(".")[0] + "." # for writing safetensors key,
+
+ # replace original offload index keys with PeftModel keys
+ for key in keys:
+ suffix_pos = key.rfind(".")
+ extended_prefix = prefix + key[:suffix_pos]
+ module = dict(self.named_modules())[extended_prefix]
+ if isinstance(module, BaseTunerLayer):
+ new_key = prefix + key[:suffix_pos] + ".base_layer" + key[suffix_pos:]
+ else:
+ new_key = prefix + key
+ offload_index[key]["weight_name"] = new_key
+ offload_index[new_key] = offload_index[key]
+ del offload_index[key]
+
+ files_seen = set()
+ # rename safetensors for dispatch
+ for new_key in list(offload_index.keys()):
+ fname = offload_index[new_key]["safetensors_file"]
+
+ # make a new file name
+ new_fname_list = list(fname.split(os.sep))
+ for i, name in enumerate(new_fname_list):
+ if "--" in name:
+ new_fname_list[i] += "-peft"
+ break
+ new_fname = os.path.join(*new_fname_list)
+
+ if fname in files_seen:
+ continue
+ safe_dict = {}
+ with safe_open(fname, framework="pt") as f:
+ for safe_key in f.keys():
+ safe_tensor = f.get_tensor(safe_key)
+ metadata = f.metadata()
+ suffix_pos = safe_key.rfind(".")
+ extended_prefix = prefix + block_id + safe_key[:suffix_pos]
+ safe_module = dict(self.named_modules())[extended_prefix]
+ if isinstance(safe_module, BaseTunerLayer):
+ final_key = extended_prefix + ".base_layer" + safe_key[suffix_pos:]
+ lora_dict = {key: val for key, val in adapters_weights.items() if extended_prefix in key}
+
+ # add LoRA keys and values to disk offload
+ for lora_key, lora_val in lora_dict.items():
+ divide = lora_key.rfind(".")
+ new_key = lora_key[:divide] + f".{adapter_name}" + lora_key[divide:]
+ safe_dict[new_key] = lora_val
+ else:
+ final_key = prefix + block_id + safe_key
+ safe_dict[final_key] = safe_tensor
+ files_seen.add(new_fname)
+
+ # avoid overwriting original safetensors
+ for key in safe_dict.keys():
+ offload_index[key] = {"safetensors_file": new_fname, "weight_name": key}
+
+ base_name = os.path.dirname(new_fname)
+ if not os.path.exists(base_name):
+ os.makedirs(base_name)
+ safe_save_file(safe_dict, new_fname, metadata=metadata)
+
+ def _check_new_adapter_config(self, peft_config: PeftConfig, is_trainable: bool) -> None:
+ """Perform checks on newly added PEFT configs to ensure integrity."""
+ if peft_config.is_prompt_learning and is_trainable:
+ raise ValueError("Cannot set a prompt learning adapter to trainable when loading pretrained adapter.")
+
+ # Since PiSSA/CorDA/OLoRA modifies the base weights, it should not be combined with other adapters.
+ all_configs = [peft_config] + list(self.peft_config.values())
+ if len(all_configs) > 1:
+ if any(getattr(config, "init_lora_weights", None) == "pissa" for config in all_configs):
+ msg = (
+ "PiSSA changes the base weights of the model and should thus not be used with other adapters. "
+ "Consider converting the PiSSA adapter into a normal LoRA adapter: "
+ "https://github.com/huggingface/peft/tree/main/examples/pissa_finetuning#convert-pissa-to-lora"
+ )
+ warnings.warn(msg)
+ elif any(getattr(config, "init_lora_weights", None) == "corda" for config in all_configs):
+ msg = (
+ "CorDA changes the base weights of the model and should thus not be used with other adapters. "
+ "Consider converting the CorDA adapter into a normal LoRA adapter: "
+ "https://github.com/huggingface/peft/tree/main/examples/corda_finetuning#convert-corda-to-lora"
+ )
+ warnings.warn(msg)
+ elif any(getattr(config, "init_lora_weights", None) == "olora" for config in all_configs):
+ msg = (
+ "OLoRA changes the base weights of the model and should thus not be used with other adapters. "
+ "Consider converting the OLoRA adapter into a normal LoRA adapter: "
+ "https://github.com/huggingface/peft/tree/main/examples/olora_finetuning#olora-and-lora"
+ )
+ warnings.warn(msg)
+
+ def load_adapter(
+ self,
+ model_id: Union[str, os.PathLike],
+ adapter_name: str,
+ is_trainable: bool = False,
+ torch_device: Optional[str] = None,
+ autocast_adapter_dtype: bool = True,
+ ephemeral_gpu_offload: bool = False,
+ low_cpu_mem_usage: bool = False,
+ key_mapping: Optional[dict[str, str]] = None,
+ **kwargs: Any,
+ ):
+ """
+ Load a trained adapter into the model.
+
+ The name for the new adapter should be unique.
+
+ The new adapter is not automatically set as the active adapter. Use [`PeftModel.set_adapter`] to set the active
+ adapter.
+
+ Args:
+ model_id (`str` or `os.PathLike`):
+ The name of the PEFT configuration to use. Can be either:
+ - A string, the `model id` of a PEFT configuration hosted inside a model repo on the Hugging Face
+ Hub.
+ - A path to a directory containing a PEFT configuration file saved using the `save_pretrained`
+ method (`./my_peft_config_directory/`).
+ adapter_name (`str`):
+ The name of the adapter to be added.
+ is_trainable (`bool`, *optional*, defaults to `False`):
+ Whether the adapter should be trainable or not. If `False`, the adapter will be frozen and can only be
+ used for inference.
+ torch_device (`str`, *optional*, defaults to None):
+ The device to load the adapter on. If `None`, the device will be inferred.
+ autocast_adapter_dtype (`bool`, *optional*, defaults to `True`):
+ Whether to autocast the adapter dtype. Defaults to `True`. Right now, this will only cast adapter
+ weights using float16 and bfloat16 to float32, as this is typically required for stable training, and
+ only affect select PEFT tuners.
+ ephemeral_gpu_offload (`bool`, *optional*, defaults to `False`):
+ Whether to use ephemeral GPU offloading for partially loaded modules. Defaults to `False`.
+ low_cpu_mem_usage (`bool`, `optional`, defaults to `False`):
+ Create empty adapter weights on meta device before loading the saved weights. Useful to speed up the
+ process.
+ key_mapping (dict, *optional*, defaults to None)
+ Extra mapping of PEFT `state_dict` keys applied before loading the `state_dict`. When this mapping is
+ applied, the PEFT-specific `"base_model.model"` prefix is removed beforehand and the adapter name (e.g.
+ `"default"`) is not inserted yet. Only pass this argument if you know what you're doing.
+ kwargs: (`optional`):
+ Additional arguments to modify the way the adapter is loaded, e.g. the token for Hugging Face Hub.
+ """
+ from .mapping import PEFT_TYPE_TO_CONFIG_MAPPING
+
+ hf_hub_download_kwargs, kwargs = self._split_kwargs(kwargs)
+ if torch_device is None:
+ torch_device = infer_device()
+
+ if adapter_name not in self.peft_config:
+ # load the config
+ peft_config = PEFT_TYPE_TO_CONFIG_MAPPING[
+ PeftConfig._get_peft_type(
+ model_id,
+ **hf_hub_download_kwargs,
+ )
+ ].from_pretrained(
+ model_id,
+ ephemeral_gpu_offload=ephemeral_gpu_offload,
+ **hf_hub_download_kwargs,
+ )
+ self._check_new_adapter_config(peft_config, is_trainable=is_trainable)
+ peft_config.inference_mode = not is_trainable
+ self.add_adapter(adapter_name, peft_config, low_cpu_mem_usage=low_cpu_mem_usage)
+
+ adapters_weights = load_peft_weights(
+ model_id, device=torch_device, key_mapping=key_mapping, **hf_hub_download_kwargs
+ )
+
+ # load the weights into the model
+ ignore_mismatched_sizes = kwargs.get("ignore_mismatched_sizes", False)
+ load_result = set_peft_model_state_dict(
+ self,
+ adapters_weights,
+ adapter_name=adapter_name,
+ ignore_mismatched_sizes=ignore_mismatched_sizes,
+ low_cpu_mem_usage=low_cpu_mem_usage,
+ )
+
+ tuner = self.peft_config[adapter_name].peft_type
+ tuner_prefix = PEFT_TYPE_TO_PREFIX_MAPPING.get(tuner, "")
+ adapter_missing_keys = []
+
+ # Filter missing keys specific to the current adapter and tuner prefix.
+ for key in load_result.missing_keys:
+ if tuner_prefix in key and adapter_name in key:
+ adapter_missing_keys.append(key)
+
+ load_result.missing_keys.clear()
+ load_result.missing_keys.extend(adapter_missing_keys)
+
+ if (
+ (getattr(self, "hf_device_map", None) is not None)
+ and (len(set(self.hf_device_map.values()).intersection({"cpu", "disk"})) > 0)
+ and len(self.peft_config) == 1
+ ):
+ device_map = kwargs.get("device_map", "auto")
+ max_memory = kwargs.get("max_memory", None)
+ offload_folder = kwargs.get("offload_folder", None)
+ offload_dir = kwargs.get("offload_dir", None)
+ offload_index = kwargs.get("offload_index", None)
+
+ if offload_dir is not None and offload_folder is not None:
+ # see https://github.com/huggingface/peft/issues/2541
+ raise ValueError("Cannot use `offload_folder` when `offload_dir` is specified.")
+ elif offload_dir is None:
+ # to keep backwards compatibility
+ offload_dir = offload_folder
+
+ dispatch_model_kwargs = {}
+ # Safety checker for previous `accelerate` versions
+ # `offload_index` was introduced in https://github.com/huggingface/accelerate/pull/873/
+ if "offload_index" in inspect.signature(dispatch_model).parameters:
+ dispatch_model_kwargs["offload_index"] = offload_index
+
+ no_split_module_classes = self._no_split_modules
+
+ if device_map != "sequential":
+ max_memory = get_balanced_memory(
+ self,
+ max_memory=max_memory,
+ no_split_module_classes=no_split_module_classes,
+ low_zero=(device_map == "balanced_low_0"),
+ )
+
+ if isinstance(device_map, str):
+ device_map = infer_auto_device_map(
+ self, max_memory=max_memory, no_split_module_classes=no_split_module_classes
+ )
+
+ self._update_offload(offload_index, adapters_weights)
+ dispatch_model_kwargs["offload_index"] = offload_index
+
+ dispatch_model(
+ self,
+ device_map=device_map,
+ offload_dir=offload_dir,
+ **dispatch_model_kwargs,
+ )
+
+ hook = AlignDevicesHook(io_same_device=True)
+ if self.peft_config[adapter_name].is_prompt_learning:
+ remove_hook_from_submodules(self.prompt_encoder)
+ add_hook_to_module(self.get_base_model(), hook)
+
+ if hasattr(self.base_model, "_cast_adapter_dtype"):
+ self.base_model._cast_adapter_dtype(
+ adapter_name=adapter_name, autocast_adapter_dtype=autocast_adapter_dtype
+ )
+
+ # Set model in evaluation mode to deactivate Dropout modules by default
+ if not is_trainable:
+ self.eval()
+ return load_result
+
+ def set_adapter(self, adapter_name: str) -> None:
+ """
+ Sets the active adapter.
+
+ Only one adapter can be active at a time.
+
+ Additionally, this function will set the specified adapter to trainable (i.e., requires_grad=True). If this is
+ not desired, use the following code.
+
+ ```py
+ >>> for name, param in model_peft.named_parameters():
+ ... if ...: # some check on name (ex. if 'lora' in name)
+ ... param.requires_grad = False
+ ```
+
+ Args:
+ adapter_name (`str`):
+ The name of the adapter to be set as active. The adapter must be loaded first.
+ """
+ if adapter_name not in self.peft_config:
+ raise ValueError(f"Adapter {adapter_name} not found.")
+ self.active_adapter = adapter_name
+ if not self.peft_config[adapter_name].is_prompt_learning:
+ # _set_adapter does not need to be called, since it's called through the BaseTuner class.
+ self.base_model.set_adapter(adapter_name)
+ else:
+ # handle auxiliary modules
+ _set_adapter(self, adapter_name)
+
+ def set_requires_grad(self, adapter_names: str | Sequence[str], requires_grad: bool = True) -> None:
+ """
+ Enable or disable gradients on the given adapter(s).
+
+ Note: Not supported for prompt learning methods like prompt tuning.
+
+ Args:
+ adapter_name (`str` or `Sequence[str]`):
+ The name of the adapter(s) whose gradients should be enabled/disabled.
+ requires_grad (`bool`, *optional*)
+ Whether to enable (`True`, default) or disable (`False`).
+ """
+ if self.active_peft_config.is_prompt_learning:
+ raise TypeError(
+ "Setting `requires_grad` is not supported for prompt learning methods like "
+ f"{self.active_peft_config.peft_type.value}."
+ )
+
+ self.base_model.set_requires_grad(adapter_names=adapter_names, requires_grad=requires_grad)
+
+ @property
+ def base_model_torch_dtype(self):
+ return getattr(self.base_model, "dtype", None)
+
+ @property
+ def active_peft_config(self):
+ return self.peft_config[self.active_adapter]
+
+ def _get_peft_specific_model_tags(self):
+ """Derive tags for the model card from the adapter's config. For example, setting the
+ base model is important for enabling support for HF inference providers but it also makes models more
+ searchable on the HF hub.
+ """
+ peft_method = self.active_peft_config.peft_type
+ if not isinstance(peft_method, str):
+ peft_method = peft_method.value
+
+ tags = []
+
+ if hasattr(self.base_model, "model") and isinstance(self.base_model.model, transformers.PreTrainedModel):
+ tags.append("transformers")
+
+ if peft_method == "LORA":
+ tags.append("lora")
+
+ if hasattr(self.base_model, "name_or_path"):
+ tags.append(f"base_model:adapter:{self.base_model.name_or_path}")
+
+ return tags
+
+ def create_or_update_model_card(self, output_dir: str):
+ """
+ Updates or create model card to include information about peft:
+ 1. Adds `peft` library tag
+ 2. Adds peft version
+ 3. Adds base model info
+ 4. Adds quantization information if it was used
+ """
+
+ filename = os.path.join(output_dir, "README.md")
+
+ card = ModelCard.load(filename) if os.path.exists(filename) else ModelCard.from_template(ModelCardData())
+
+ card.data["library_name"] = "peft"
+
+ tags = set()
+ base_model = self.get_base_model()
+ if hasattr(base_model, "model_tags"):
+ tags = tags.union(base_model.model_tags or [])
+
+ tags = tags.union(self._get_peft_specific_model_tags())
+ if tags:
+ card.data["tags"] = sorted(tags)
+
+ # One of the rare moments where we can select the pipeline tag with certainty, so let's do that.
+ # Makes it easier to deploy an adapter with auto inference since the user doesn't have to add any tags.
+ if not card.data.pipeline_tag and isinstance(self, PeftModelForCausalLM):
+ card.data.pipeline_tag = "text-generation"
+
+ model_config = BaseTuner.get_model_config(self)
+ model_config = None if model_config == DUMMY_MODEL_CONFIG else model_config
+ if model_config is not None and "_name_or_path" in model_config:
+ card.data["base_model"] = model_config["_name_or_path"]
+
+ lines = card.text.splitlines()
+
+ quantization_config = None
+ if hasattr(model_config, "quantization_config"):
+ quantization_config = self.config.quantization_config.to_dict()
+ training_config_text = ""
+ quantization_prefix = "The following `bitsandbytes` quantization config was used during training:"
+ # Adds quantization information if it was used
+ if quantization_config is not None:
+ training_config_text += f"\n{quantization_prefix}\n"
+ training_config_text += "\n".join([f"- {name}: {value}" for name, value in quantization_config.items()])
+ training_config_text += "\n"
+
+ training_procedure_heading = "## Training procedure"
+ if quantization_prefix not in lines and bool(training_config_text):
+ if training_procedure_heading in lines:
+ lines.insert(lines.index(training_procedure_heading) + 2, training_config_text)
+ else:
+ lines.append(f"{training_procedure_heading}\n{training_config_text}")
+
+ # Adds peft version
+ framework_block_heading = "### Framework versions"
+ if f"- PEFT {__version__}" not in lines:
+ if framework_block_heading in lines:
+ lines.insert(lines.index(framework_block_heading) + 2, f"- PEFT {__version__}")
+ else:
+ lines.append(f"{framework_block_heading}\n\n- PEFT {__version__}")
+
+ card.text = "\n".join(lines)
+ card.save(filename)
+
+
+class PeftModelForSequenceClassification(PeftModel):
+ """
+ Peft model for sequence classification tasks.
+
+ Args:
+ model ([`~transformers.PreTrainedModel`]): Base transformer model.
+ peft_config ([`PeftConfig`]): Peft config.
+ adapter_name (`str`, *optional*): The name of the adapter, defaults to `"default"`.
+ autocast_adapter_dtype (`bool`, *optional*):
+ Whether to autocast the adapter dtype. Defaults to `True`. Right now, this will only cast adapter weights
+ using float16 and bfloat16 to float32, as this is typically required for stable training, and only affect
+ select PEFT tuners.
+
+ **Attributes**:
+ - **config** ([`~transformers.PretrainedConfig`]) -- The configuration object of the base model.
+ - **cls_layer_name** (`str`) -- The name of the classification layer.
+
+ Example:
+
+ ```py
+ >>> from transformers import AutoModelForSequenceClassification
+ >>> from peft import PeftModelForSequenceClassification, get_peft_config
+
+ >>> config = {
+ ... "peft_type": "PREFIX_TUNING",
+ ... "task_type": "SEQ_CLS",
+ ... "inference_mode": False,
+ ... "num_virtual_tokens": 20,
+ ... "token_dim": 768,
+ ... "num_transformer_submodules": 1,
+ ... "num_attention_heads": 12,
+ ... "num_layers": 12,
+ ... "encoder_hidden_size": 768,
+ ... "prefix_projection": False,
+ ... "postprocess_past_key_value_function": None,
+ ... }
+
+ >>> peft_config = get_peft_config(config)
+ >>> model = AutoModelForSequenceClassification.from_pretrained("bert-base-cased")
+ >>> peft_model = PeftModelForSequenceClassification(model, peft_config)
+ >>> peft_model.print_trainable_parameters()
+ trainable params: 370178 || all params: 108680450 || trainable%: 0.3406113979101117
+ ```
+ """
+
+ def __init__(
+ self, model: torch.nn.Module, peft_config: PeftConfig, adapter_name: str = "default", **kwargs
+ ) -> None:
+ classifier_module_names = ["classifier", "score"]
+
+ if hasattr(peft_config, "modules_to_save"):
+ if peft_config.modules_to_save is None:
+ peft_config.modules_to_save = classifier_module_names[:]
+ else:
+ peft_config.modules_to_save.extend(classifier_module_names)
+
+ # The modification of peft_config must happen before the init call as the `modules_to_save` information
+ # will be used to guard the target layer matching against matching `modules_to_save` layers. Only the
+ # config is relevant for this, the `modules_to_save` attribute can follow later.
+ super().__init__(model, peft_config, adapter_name, **kwargs)
+
+ if hasattr(peft_config, "modules_to_save"):
+ for name, _ in self.base_model.named_children():
+ if any(module_name in name for module_name in self.modules_to_save):
+ self.cls_layer_name = name
+ break
+
+ # to make sure classifier layer is trainable; this may add a new ModulesToSaveWrapper
+ _set_trainable(
+ self,
+ adapter_name,
+ module_names=getattr(peft_config, "modules_to_save", None),
+ inference_mode=peft_config.inference_mode,
+ )
+
+ def add_adapter(self, adapter_name: str, peft_config: PeftConfig, low_cpu_mem_usage: bool = False) -> None:
+ """
+ Add an adapter to the model based on the passed configuration.
+
+ This adapter is not trained. To load a trained adapter, check out [`PeftModel.load_adapter`].
+
+ The name for the new adapter should be unique.
+
+ The new adapter is not automatically set as the active adapter. Use [`PeftModel.set_adapter`] to set the active
+ adapter.
+
+ Args:
+ adapter_name (`str`):
+ The name of the adapter to be added.
+ peft_config ([`PeftConfig`]):
+ The configuration of the adapter to be added.
+ low_cpu_mem_usage (`bool`, `optional`, defaults to `False`):
+ Create empty adapter weights on meta device. Useful to speed up the process when loading saved
+ adapters. Don't use this option when creating a new PEFT adapter for training.
+
+ """
+ # ensure that additional adapters also add the classifier layer to modules_to_save
+ if hasattr(peft_config, "modules_to_save"):
+ classifier_module_names = ["classifier", "score"]
+ if peft_config.modules_to_save is None:
+ peft_config.modules_to_save = classifier_module_names[:]
+ else:
+ peft_config.modules_to_save.extend(classifier_module_names)
+
+ return super().add_adapter(adapter_name, peft_config, low_cpu_mem_usage=low_cpu_mem_usage)
+
+ def forward(
+ self,
+ input_ids=None,
+ attention_mask=None,
+ inputs_embeds=None,
+ labels=None,
+ output_attentions=None,
+ output_hidden_states=None,
+ return_dict=None,
+ task_ids=None,
+ **kwargs,
+ ):
+ return_dict = return_dict if return_dict is not None else self.config.use_return_dict
+ peft_config = self.active_peft_config
+ if not peft_config.is_prompt_learning:
+ with self._enable_peft_forward_hooks(**kwargs):
+ kwargs = {k: v for k, v in kwargs.items() if k not in self.special_peft_forward_args}
+ if peft_config.peft_type == PeftType.POLY:
+ kwargs["task_ids"] = task_ids
+ return self.base_model(
+ input_ids=input_ids,
+ attention_mask=attention_mask,
+ inputs_embeds=inputs_embeds,
+ labels=labels,
+ output_attentions=output_attentions,
+ output_hidden_states=output_hidden_states,
+ return_dict=return_dict,
+ **kwargs,
+ )
+
+ batch_size = _get_batch_size(input_ids, inputs_embeds)
+ if attention_mask is not None:
+ # concat prompt attention mask
+ prefix_attention_mask = torch.ones(batch_size, peft_config.num_virtual_tokens).to(attention_mask.device)
+ attention_mask = torch.cat((prefix_attention_mask, attention_mask), dim=1)
+ if kwargs.get("position_ids", None) is not None:
+ warnings.warn("Position ids are not supported for parameter efficient tuning. Ignoring position ids.")
+ kwargs["position_ids"] = None
+ kwargs.update(
+ {
+ "attention_mask": attention_mask,
+ "labels": labels,
+ "output_attentions": output_attentions,
+ "output_hidden_states": output_hidden_states,
+ "return_dict": return_dict,
+ }
+ )
+
+ if peft_config.peft_type == PeftType.PREFIX_TUNING:
+ return self._prefix_tuning_forward(input_ids=input_ids, **kwargs)
+ else:
+ if kwargs.get("token_type_ids", None) is not None:
+ kwargs["token_type_ids"] = torch.cat(
+ (
+ torch.zeros(batch_size, peft_config.num_virtual_tokens).to(self.word_embeddings.weight.device),
+ kwargs["token_type_ids"],
+ ),
+ dim=1,
+ ).long()
+ if inputs_embeds is None:
+ inputs_embeds = self.word_embeddings(input_ids)
+ prompts = self.get_prompt(batch_size=batch_size, task_ids=task_ids)
+ prompts = prompts.to(inputs_embeds.dtype)
+ inputs_embeds = torch.cat((prompts, inputs_embeds), dim=1)
+ return self.base_model(inputs_embeds=inputs_embeds, **kwargs)
+
+ def _prefix_tuning_forward(
+ self,
+ input_ids=None,
+ attention_mask=None,
+ inputs_embeds=None,
+ labels=None,
+ output_attentions=None,
+ output_hidden_states=None,
+ return_dict=None,
+ **kwargs,
+ ):
+ batch_size = _get_batch_size(input_ids, inputs_embeds)
+ past_key_values = self.get_prompt(batch_size)
+ fwd_params = list(inspect.signature(self.base_model.forward).parameters.keys())
+ kwargs.update(
+ {
+ "input_ids": input_ids,
+ "attention_mask": attention_mask,
+ "inputs_embeds": inputs_embeds,
+ "output_attentions": output_attentions,
+ "output_hidden_states": output_hidden_states,
+ "return_dict": return_dict,
+ "past_key_values": past_key_values,
+ }
+ )
+ if "past_key_values" in fwd_params:
+ return self.base_model(labels=labels, **kwargs)
+ else:
+ transformer_backbone_name = self.base_model.get_submodule(self.transformer_backbone_name)
+ fwd_params = list(inspect.signature(transformer_backbone_name.forward).parameters.keys())
+ if "past_key_values" not in fwd_params:
+ raise ValueError("Model does not support past key values which are required for prefix tuning.")
+ outputs = transformer_backbone_name(**kwargs)
+ pooled_output = outputs[1] if len(outputs) > 1 else outputs[0]
+ if "dropout" in [name for name, _ in list(self.base_model.named_children())]:
+ pooled_output = self.base_model.dropout(pooled_output)
+ logits = self.base_model.get_submodule(self.cls_layer_name)(pooled_output)
+
+ loss = None
+ if labels is not None:
+ if self.config.problem_type is None:
+ if self.base_model.num_labels == 1:
+ self.config.problem_type = "regression"
+ elif self.base_model.num_labels > 1 and (labels.dtype == torch.long or labels.dtype == torch.int):
+ self.config.problem_type = "single_label_classification"
+ else:
+ self.config.problem_type = "multi_label_classification"
+
+ if self.config.problem_type == "regression":
+ loss_fct = MSELoss()
+ if self.base_model.num_labels == 1:
+ loss = loss_fct(logits.squeeze(), labels.squeeze())
+ else:
+ loss = loss_fct(logits, labels)
+ elif self.config.problem_type == "single_label_classification":
+ loss_fct = CrossEntropyLoss()
+ loss = loss_fct(logits.view(-1, self.base_model.num_labels), labels.view(-1))
+ elif self.config.problem_type == "multi_label_classification":
+ loss_fct = BCEWithLogitsLoss()
+ loss = loss_fct(logits, labels)
+ if not return_dict:
+ output = (logits,) + outputs[2:]
+ return ((loss,) + output) if loss is not None else output
+
+ return SequenceClassifierOutput(
+ loss=loss,
+ logits=logits,
+ hidden_states=outputs.hidden_states,
+ attentions=outputs.attentions,
+ )
+
+
+class PeftModelForCausalLM(PeftModel):
+ """
+ Peft model for causal language modeling.
+
+ Args:
+ model ([`~transformers.PreTrainedModel`]): Base transformer model.
+ peft_config ([`PeftConfig`]): Peft config.
+ adapter_name (`str`, *optional*): The name of the adapter, defaults to `"default"`.
+ autocast_adapter_dtype (`bool`, *optional*):
+ Whether to autocast the adapter dtype. Defaults to `True`. Right now, this will only cast adapter weights
+ using float16 and bfloat16 to float32, as this is typically required for stable training, and only affect
+ select PEFT tuners.
+
+ Example:
+
+ ```py
+ >>> from transformers import AutoModelForCausalLM
+ >>> from peft import PeftModelForCausalLM, get_peft_config
+
+ >>> config = {
+ ... "peft_type": "PREFIX_TUNING",
+ ... "task_type": "CAUSAL_LM",
+ ... "inference_mode": False,
+ ... "num_virtual_tokens": 20,
+ ... "token_dim": 1280,
+ ... "num_transformer_submodules": 1,
+ ... "num_attention_heads": 20,
+ ... "num_layers": 36,
+ ... "encoder_hidden_size": 1280,
+ ... "prefix_projection": False,
+ ... "postprocess_past_key_value_function": None,
+ ... }
+
+ >>> peft_config = get_peft_config(config)
+ >>> model = AutoModelForCausalLM.from_pretrained("gpt2-large")
+ >>> peft_model = PeftModelForCausalLM(model, peft_config)
+ >>> peft_model.print_trainable_parameters()
+ trainable params: 1843200 || all params: 775873280 || trainable%: 0.23756456724479544
+ ```
+ """
+
+ def __init__(
+ self, model: torch.nn.Module, peft_config: PeftConfig, adapter_name: str = "default", **kwargs
+ ) -> None:
+ super().__init__(model, peft_config, adapter_name, **kwargs)
+ self.base_model_prepare_inputs_for_generation = self.base_model.prepare_inputs_for_generation
+
+ def forward(
+ self,
+ input_ids=None,
+ attention_mask=None,
+ inputs_embeds=None,
+ labels=None,
+ output_attentions=None,
+ output_hidden_states=None,
+ return_dict=None,
+ task_ids=None,
+ **kwargs,
+ ):
+ peft_config = self.active_peft_config
+
+ if not peft_config.is_prompt_learning:
+ # Adds alora_offsets to kwargs if relevant. No other modifications.
+ kwargs = get_alora_offsets_for_forward(self, input_ids, inputs_embeds, **kwargs)
+ if self.base_model.config.model_type == "mpt":
+ if inputs_embeds is not None:
+ raise AssertionError("forward in MPTForCausalLM does not support inputs_embeds")
+ return self.base_model(
+ input_ids=input_ids,
+ attention_mask=attention_mask,
+ labels=labels,
+ output_attentions=output_attentions,
+ output_hidden_states=output_hidden_states,
+ return_dict=return_dict,
+ **kwargs,
+ )
+
+ if peft_config.peft_type == PeftType.POLY:
+ kwargs["task_ids"] = task_ids
+
+ with self._enable_peft_forward_hooks(**kwargs):
+ kwargs = {k: v for k, v in kwargs.items() if k not in self.special_peft_forward_args}
+ return self.base_model(
+ input_ids=input_ids,
+ attention_mask=attention_mask,
+ inputs_embeds=inputs_embeds,
+ labels=labels,
+ output_attentions=output_attentions,
+ output_hidden_states=output_hidden_states,
+ return_dict=return_dict,
+ **kwargs,
+ )
+
+ batch_size = _get_batch_size(input_ids, inputs_embeds)
+ if attention_mask is not None:
+ # concat prompt attention mask
+ prefix_attention_mask = torch.ones(batch_size, peft_config.num_virtual_tokens).to(attention_mask.device)
+ attention_mask = torch.cat((prefix_attention_mask, attention_mask), dim=1)
+
+ if kwargs.get("position_ids", None) is not None:
+ warnings.warn("Position ids are not supported for parameter efficient tuning. Ignoring position ids.")
+ kwargs["position_ids"] = None
+ if kwargs.get("token_type_ids", None) is not None:
+ warnings.warn("Token type ids are not supported for parameter efficient tuning. Ignoring token type ids")
+ kwargs["token_type_ids"] = None
+ kwargs.update(
+ {
+ "attention_mask": attention_mask,
+ "labels": labels,
+ "output_attentions": output_attentions,
+ "output_hidden_states": output_hidden_states,
+ "return_dict": return_dict,
+ }
+ )
+
+ if peft_config.peft_type == PeftType.PREFIX_TUNING:
+ # overwrite past_kv in kwargs
+ # some archs require max_cache_len to re-initialize the cache
+ if input_ids is not None:
+ max_cache_len = input_ids.shape[1] + peft_config.num_virtual_tokens
+ else:
+ max_cache_len = inputs_embeds.shape[1] + peft_config.num_virtual_tokens
+ kwargs["past_key_values"] = self.get_prompt(batch_size, max_cache_len=max_cache_len)
+ return self.base_model(input_ids=input_ids, inputs_embeds=inputs_embeds, **kwargs)
+ elif peft_config.peft_type == PeftType.CPT:
+ return self._cpt_forward(input_ids, inputs_embeds, peft_config, task_ids, batch_size, **kwargs)
+ else:
+ if inputs_embeds is None:
+ inputs_embeds = self.word_embeddings(input_ids)
+ # concat prompt labels
+ if labels is not None:
+ prefix_labels = torch.full((batch_size, peft_config.num_virtual_tokens), -100).to(labels.device)
+ kwargs["labels"] = torch.cat((prefix_labels, labels), dim=1)
+ prompts = self.get_prompt(batch_size=batch_size, task_ids=task_ids)
+ prompts = prompts.to(inputs_embeds.dtype)
+ inputs_embeds = torch.cat((prompts, inputs_embeds), dim=1)
+ return self.base_model(inputs_embeds=inputs_embeds, **kwargs)
+
+ def _cpt_forward(self, input_ids, inputs_embeds, peft_config, task_ids, batch_size, **kwargs):
+ # Extract labels from kwargs
+ labels = kwargs.pop("labels")
+ device = [i.device for i in [input_ids, inputs_embeds, labels] if i is not None][0]
+ # Extract input_type_mask from kwargs and move it to the same device as labels
+ if "input_type_mask" in kwargs.keys():
+ input_type_mask = kwargs.pop("input_type_mask").to(device)
+ else:
+ if input_ids is None:
+ N_tokens = inputs_embeds.shape[1]
+ else:
+ N_tokens = input_ids.shape[1]
+ input_type_mask = torch.ones((batch_size, N_tokens)).to(device) * 4
+
+ cpt_token_ids = peft_config.cpt_token_ids
+ cpt_tokens_type_mask = peft_config.cpt_tokens_type_mask
+
+ # Generate embeddings if not provided
+ if inputs_embeds is None:
+ inputs_embeds = self.word_embeddings(input_ids)
+ # Get prompt and concatenate with input embeddings
+ prompts = self.get_prompt(batch_size=batch_size, task_ids=task_ids)
+ prompts = prompts.to(inputs_embeds.dtype)
+ inputs_embeds = torch.cat((prompts, inputs_embeds), dim=1)
+ # If labels are provided, generate prefix labels and type mask
+ cpt_labels = None
+ if labels is not None:
+ # Generate prefix labels and concatenate with the input labels
+ prefix_labels = torch.Tensor(cpt_token_ids).long().view(1, -1)
+ prefix_labels = prefix_labels.repeat(batch_size, 1).to(labels.device)
+ cpt_labels = torch.cat((prefix_labels, labels), dim=1)
+ # Generate prefix type mask and shift input type mask values to avoid conflicts
+ prefix_type_mask = torch.Tensor(cpt_tokens_type_mask).long().view(1, -1)
+ prefix_type_mask = prefix_type_mask.repeat(batch_size, 1).to(labels.device)
+ adjusted_input_type_mask = input_type_mask
+ adjusted_input_type_mask[adjusted_input_type_mask > 0] += prefix_type_mask.max()
+ # Concatenate prefix and shifted input type masks
+ cpt_type_mask = torch.cat((prefix_type_mask, adjusted_input_type_mask), dim=1)
+ # Identify valid label positions and mask invalid ones with -100
+ labels_idx = (cpt_type_mask > 0) & (cpt_type_mask % 4 == 0)
+ cpt_labels[~labels_idx] = -100
+ # Update kwargs with the modified labels
+
+ kwargs["labels"] = cpt_labels
+ # Pass the modified inputs to the base model
+ base_model_output = self.base_model(inputs_embeds=inputs_embeds, **kwargs)
+ if labels is None:
+ return base_model_output
+ else:
+ # Calculate the loss using the custom CPT loss function
+ cpt_embedding = PEFT_TYPE_TO_TUNER_MAPPING[peft_config.peft_type]
+ base_model_output = cpt_embedding.calculate_loss(
+ base_model_output, cpt_labels, cpt_type_mask, self.peft_config["default"]
+ )
+ return base_model_output
+
+ def generate(self, *args, **kwargs):
+ peft_config = self.active_peft_config
+ self.base_model.prepare_inputs_for_generation = self.prepare_inputs_for_generation
+ if hasattr(self.base_model, "model"):
+ self.base_model.model.generation_config = self.generation_config
+ else:
+ self.base_model.generation_config = self.generation_config
+ try:
+ if not peft_config.is_prompt_learning:
+ # Adds alora_offsets to kwargs if relevant. No other changes.
+ kwargs = get_alora_offsets_for_generate(self, *args, **kwargs)
+ with self._enable_peft_forward_hooks(*args, **kwargs):
+ kwargs = {k: v for k, v in kwargs.items() if k not in self.special_peft_forward_args}
+ outputs = self.base_model.generate(*args, **kwargs)
+ else:
+ outputs = self.base_model.generate(**kwargs)
+ except:
+ self.base_model.prepare_inputs_for_generation = self.base_model_prepare_inputs_for_generation
+ raise
+ else:
+ self.base_model.prepare_inputs_for_generation = self.base_model_prepare_inputs_for_generation
+ return outputs
+
+ def prepare_inputs_for_generation(self, *args, task_ids: Optional[torch.Tensor] = None, **kwargs):
+ peft_config = self.active_peft_config
+ model_kwargs = self.base_model_prepare_inputs_for_generation(*args, **kwargs)
+
+ # https://github.com/huggingface/transformers/pull/26681/ introduced new cache format
+ # for some architectures which requires a special fix for prompt tuning etc.
+ # TODO: starting with transformers 4.38, all architectures should support caching.
+ uses_transformers_4_38 = packaging.version.parse(transformers.__version__) >= packaging.version.parse("4.38.0")
+ uses_transformers_4_36 = packaging.version.parse(transformers.__version__) >= packaging.version.parse("4.36.0")
+ transformers_new_cache_archs = ["llama", "mistral", "persimmon", "phi"]
+ if packaging.version.parse(transformers.__version__) > packaging.version.parse("4.43.3"):
+ # https://github.com/huggingface/transformers/pull/31445
+ transformers_new_cache_archs.append("bloom")
+
+ uses_cache = uses_transformers_4_38 or (
+ uses_transformers_4_36 and self.base_model.config.model_type in transformers_new_cache_archs
+ )
+
+ # heuristic to determine if we're in 'prefill stage' (when the KV cache is filled with the values from the
+ # initial input)
+ is_prefill = (model_kwargs.get("cache_position") is not None) and (model_kwargs["cache_position"][0] == 0)
+
+ if peft_config.peft_type == PeftType.POLY:
+ model_kwargs["task_ids"] = task_ids
+ if peft_config.is_prompt_learning:
+ if uses_cache and (model_kwargs.get("past_key_values", None) is not None):
+ # change in the logic of `prepare_inputs_for_generation` makes the below code necessary
+ # In prompt learning methods, past key values are longer when compared to the `input_ids`.
+ # As such only consider the last input ids in the autogressive generation phase.
+ past_key_values = model_kwargs["past_key_values"]
+ if isinstance(past_key_values, (tuple, list)):
+ seq_len = past_key_values[0][0].shape[-2]
+ else: # using transformers kv cache
+ seq_len = past_key_values.get_seq_length()
+ if seq_len >= model_kwargs["input_ids"].shape[1]:
+ model_kwargs["input_ids"] = model_kwargs["input_ids"][:, -1:]
+
+ if (attention_mask := model_kwargs.get("attention_mask", None)) is not None:
+ if isinstance(attention_mask, dict):
+ # see: https://github.com/huggingface/transformers/pull/37866
+ # For now, just deal with the case of a single attention mask
+ if len(attention_mask) != 1:
+ raise ValueError(
+ f"Expected a single attention mask, got {len(attention_mask)} instead, please open an "
+ "issue (https://github.com/huggingface/peft/issues) and report the error."
+ )
+ attention_mask = list(attention_mask.values())[0]
+
+ size = model_kwargs["input_ids"].shape[0], peft_config.num_virtual_tokens
+ prefix_attention_mask = torch.ones(size).to(model_kwargs["input_ids"].device)
+ if attention_mask.dim() == 4:
+ # Transform the 4d attention mask to 2d, leave it up to the model to deal with it instead of trying
+ # to create a 4d attention mask here.
+ # from [batch_size, heads, input_ids_length, total_sequence_length]
+ # to [batch_size, total_sequence_length]
+ bs = attention_mask.shape[0]
+ total_seq_len = prefix_attention_mask.shape[1] + attention_mask.shape[2]
+ attention_mask_2d = torch.ones((bs, total_seq_len), dtype=attention_mask.dtype)
+
+ if is_prefill and (peft_config.peft_type != PeftType.PREFIX_TUNING):
+ # if in prefill stage, for prompt learning methods that are not prefix tuning, new tokens
+ # (embeddings) are inserted, thus set cache_position to correspond to these tokens
+ cache_position_ = torch.arange(total_seq_len, device=model_kwargs["input_ids"].device)
+ else:
+ # prefix tuning acts directly on the cache, no need to upate cache_position
+ cache_position_ = model_kwargs["cache_position"]
+
+ attention_mask_new = create_attention_mask(
+ self.get_base_model(),
+ model_input=None,
+ attention_mask=attention_mask_2d,
+ past_key_values=model_kwargs.get("past_key_values"),
+ cache_position=cache_position_,
+ batch_size=bs,
+ sequence_length=total_seq_len,
+ position_ids=model_kwargs.get("position_ids", None),
+ )
+ model_kwargs["attention_mask"] = attention_mask_new
+ else:
+ # 2d attention mask
+ model_kwargs["attention_mask"] = torch.cat((prefix_attention_mask, attention_mask), dim=1)
+
+ if model_kwargs.get("position_ids", None) is not None:
+ warnings.warn("Position ids are not supported for parameter efficient tuning. Ignoring position ids.")
+ model_kwargs["position_ids"] = None
+
+ if kwargs.get("token_type_ids", None) is not None:
+ warnings.warn(
+ "Token type ids are not supported for parameter efficient tuning. Ignoring token type ids"
+ )
+ kwargs["token_type_ids"] = None
+
+ cache: transformers.Cache | None = model_kwargs.get("past_key_values", None)
+ # no past_key_values or past_key_values empty cache
+ requires_prompt_injection = (cache is None) or (
+ isinstance(cache, transformers.Cache) and not cache.get_seq_length()
+ )
+
+ if requires_prompt_injection and peft_config.peft_type == PeftType.PREFIX_TUNING:
+ # some archs require max_cache_len to re-initialize the cache, but DynamicCache has no max len
+ if isinstance(cache, transformers.Cache) and not isinstance(cache, transformers.DynamicCache):
+ max_cache_len = cache.max_cache_len
+ else:
+ max_cache_len = -1 # -1 means no max length
+ new_past_key_values = self.get_prompt(
+ batch_size=model_kwargs["input_ids"].shape[0],
+ max_cache_len=max_cache_len,
+ )
+ model_kwargs["past_key_values"] = new_past_key_values
+ elif requires_prompt_injection:
+ inputs_embeds = self.word_embeddings(model_kwargs["input_ids"])
+ prompts = self.get_prompt(batch_size=model_kwargs["input_ids"].shape[0], task_ids=task_ids)
+ prompts = prompts.to(inputs_embeds.dtype)
+ model_kwargs["inputs_embeds"] = torch.cat((prompts, inputs_embeds), dim=1)
+ model_kwargs["input_ids"] = None
+
+ # if we're in the prefill stage
+ if is_prefill and (peft_config.peft_type == PeftType.PREFIX_TUNING):
+ # for prefix tuning, the past_key_values have been prefilled
+ model_kwargs["cache_position"] += peft_config.num_virtual_tokens
+ elif peft_config.peft_type != PeftType.PREFIX_TUNING: # prefix tuning needs cache_position
+ # For transformers>=4.38.0 - for some architectures such as Llama, `cache_position` is passed in the forward
+ # pass to keep track of the position ids of the cache. We have to pop that from `model_kwargs` as
+ # `cache_position` is properly created by the model, using the passed `inputs_embeds`:
+ # https://github.com/huggingface/transformers/blob/593230f0a1150ea9c0477b9d859f25daf73c8c33/src/transformers/models/llama/modeling_llama.py#L956
+ _ = model_kwargs.pop("cache_position", None)
+
+ return model_kwargs
+
+
+class PeftModelForSeq2SeqLM(PeftModel):
+ """
+ Peft model for sequence-to-sequence language modeling.
+
+ Args:
+ model ([`~transformers.PreTrainedModel`]): Base transformer model.
+ peft_config ([`PeftConfig`]): Peft config.
+ adapter_name (`str`, *optional*): The name of the adapter, defaults to `"default"`.
+ autocast_adapter_dtype (`bool`, *optional*):
+ Whether to autocast the adapter dtype. Defaults to `True`. Right now, this will only cast adapter weights
+ using float16 and bfloat16 to float32, as this is typically required for stable training, and only affect
+ select PEFT tuners.
+
+ Example:
+
+ ```py
+ >>> from transformers import AutoModelForSeq2SeqLM
+ >>> from peft import PeftModelForSeq2SeqLM, get_peft_config
+
+ >>> config = {
+ ... "peft_type": "LORA",
+ ... "task_type": "SEQ_2_SEQ_LM",
+ ... "inference_mode": False,
+ ... "r": 8,
+ ... "target_modules": ["q", "v"],
+ ... "lora_alpha": 32,
+ ... "lora_dropout": 0.1,
+ ... "fan_in_fan_out": False,
+ ... "enable_lora": None,
+ ... "bias": "none",
+ ... }
+
+ >>> peft_config = get_peft_config(config)
+ >>> model = AutoModelForSeq2SeqLM.from_pretrained("t5-base")
+ >>> peft_model = PeftModelForSeq2SeqLM(model, peft_config)
+ >>> peft_model.print_trainable_parameters()
+ trainable params: 884736 || all params: 223843584 || trainable%: 0.3952474242013566
+ ```
+ """
+
+ def __init__(
+ self, model: torch.nn.Module, peft_config: PeftConfig, adapter_name: str = "default", **kwargs
+ ) -> None:
+ super().__init__(model, peft_config, adapter_name, **kwargs)
+ self.base_model_prepare_inputs_for_generation = self.base_model.prepare_inputs_for_generation
+ self.base_model_prepare_encoder_decoder_kwargs_for_generation = (
+ self.base_model._prepare_encoder_decoder_kwargs_for_generation
+ )
+
+ def forward(
+ self,
+ input_ids=None,
+ attention_mask=None,
+ inputs_embeds=None,
+ decoder_input_ids=None,
+ decoder_attention_mask=None,
+ decoder_inputs_embeds=None,
+ labels=None,
+ output_attentions=None,
+ output_hidden_states=None,
+ return_dict=None,
+ task_ids=None,
+ **kwargs,
+ ):
+ peft_config = self.active_peft_config
+ if not peft_config.is_prompt_learning:
+ if peft_config.peft_type == PeftType.POLY:
+ kwargs["task_ids"] = task_ids
+
+ with self._enable_peft_forward_hooks(**kwargs):
+ kwargs = {k: v for k, v in kwargs.items() if k not in self.special_peft_forward_args}
+ return self.base_model(
+ input_ids=input_ids,
+ attention_mask=attention_mask,
+ inputs_embeds=inputs_embeds,
+ decoder_input_ids=decoder_input_ids,
+ decoder_attention_mask=decoder_attention_mask,
+ decoder_inputs_embeds=decoder_inputs_embeds,
+ labels=labels,
+ output_attentions=output_attentions,
+ output_hidden_states=output_hidden_states,
+ return_dict=return_dict,
+ **kwargs,
+ )
+
+ batch_size = _get_batch_size(input_ids, inputs_embeds)
+ if decoder_attention_mask is not None:
+ # concat prompt attention mask
+ prefix_attention_mask = torch.ones(batch_size, peft_config.num_virtual_tokens).to(
+ decoder_attention_mask.device
+ )
+ if peft_config.peft_type not in [PeftType.PROMPT_TUNING, PeftType.P_TUNING]:
+ decoder_attention_mask = torch.cat((prefix_attention_mask, decoder_attention_mask), dim=1)
+
+ if kwargs.get("position_ids", None) is not None:
+ warnings.warn("Position ids are not supported for parameter efficient tuning. Ignoring position ids.")
+ kwargs["position_ids"] = None
+ if kwargs.get("token_type_ids", None) is not None:
+ warnings.warn("Token type ids are not supported for parameter efficient tuning. Ignoring token type ids")
+ kwargs["token_type_ids"] = None
+ kwargs.update(
+ {
+ "attention_mask": attention_mask,
+ "decoder_attention_mask": decoder_attention_mask,
+ "labels": labels,
+ "output_attentions": output_attentions,
+ "output_hidden_states": output_hidden_states,
+ "return_dict": return_dict,
+ }
+ )
+
+ if peft_config.peft_type == PeftType.PREFIX_TUNING:
+ # overwrite past_kv in kwargs
+ kwargs["past_key_values"] = self.get_prompt(batch_size)
+ return self.base_model(
+ input_ids=input_ids,
+ decoder_input_ids=decoder_input_ids,
+ decoder_inputs_embeds=decoder_inputs_embeds,
+ **kwargs,
+ )
+ elif peft_config.peft_type in [PeftType.PROMPT_TUNING, PeftType.P_TUNING]:
+ if inputs_embeds is None:
+ inputs_embeds = self.word_embeddings(input_ids)
+
+ if attention_mask is not None:
+ # concat prompt attention mask
+ prefix_attention_mask = torch.ones(batch_size, peft_config.num_virtual_tokens).to(
+ attention_mask.device
+ )
+ kwargs["attention_mask"] = torch.cat((prefix_attention_mask, attention_mask), dim=1)
+
+ prompts = self.get_prompt(batch_size=batch_size)
+ prompts = prompts.to(inputs_embeds.dtype)
+ inputs_embeds = torch.cat((prompts[:, : peft_config.num_virtual_tokens], inputs_embeds), dim=1)
+
+ return self.base_model(
+ inputs_embeds=inputs_embeds,
+ decoder_input_ids=decoder_input_ids,
+ decoder_inputs_embeds=decoder_inputs_embeds,
+ **kwargs,
+ )
+ else:
+ if inputs_embeds is None:
+ inputs_embeds = self.word_embeddings(input_ids)
+ if decoder_inputs_embeds is None and decoder_input_ids is None:
+ decoder_input_ids = shift_tokens_right(
+ labels, self.config.pad_token_id, self.config.decoder_start_token_id
+ )
+ decoder_inputs_embeds = self.word_embeddings(decoder_input_ids)
+
+ if attention_mask is not None:
+ # concat prompt attention mask
+ prefix_attention_mask = torch.ones(batch_size, peft_config.num_virtual_tokens).to(
+ attention_mask.device
+ )
+ kwargs["attention_mask"] = torch.cat((prefix_attention_mask, attention_mask), dim=1)
+ # concat prompt labels
+ if labels is not None:
+ if peft_config.num_transformer_submodules == 1:
+ kwargs["labels"] = labels
+ elif peft_config.num_transformer_submodules == 2:
+ prefix_labels = torch.full((batch_size, peft_config.num_virtual_tokens), -100).to(labels.device)
+ kwargs["labels"] = torch.cat((prefix_labels, labels), dim=1)
+ prompts = self.get_prompt(batch_size=batch_size, task_ids=task_ids)
+ prompts = prompts.to(inputs_embeds.dtype)
+ inputs_embeds = torch.cat((prompts[:, : peft_config.num_virtual_tokens], inputs_embeds), dim=1)
+ if peft_config.num_transformer_submodules == 1:
+ return self.base_model(inputs_embeds=inputs_embeds, **kwargs)
+ elif peft_config.num_transformer_submodules == 2:
+ decoder_inputs_embeds = torch.cat(
+ (prompts[:, peft_config.num_virtual_tokens :], decoder_inputs_embeds), dim=1
+ )
+ return self.base_model(
+ inputs_embeds=inputs_embeds, decoder_inputs_embeds=decoder_inputs_embeds, **kwargs
+ )
+
+ def generate(self, **kwargs):
+ peft_config = self.active_peft_config
+ self.base_model.prepare_inputs_for_generation = self.prepare_inputs_for_generation
+ self.base_model._prepare_encoder_decoder_kwargs_for_generation = (
+ self._prepare_encoder_decoder_kwargs_for_generation
+ )
+ try:
+ if not peft_config.is_prompt_learning:
+ with self._enable_peft_forward_hooks(**kwargs):
+ kwargs = {k: v for k, v in kwargs.items() if k not in self.special_peft_forward_args}
+ outputs = self.base_model.generate(**kwargs)
+ else:
+ if "input_ids" not in kwargs:
+ raise ValueError("input_ids must be provided for Peft model generation")
+ if kwargs.get("position_ids", None) is not None:
+ warnings.warn(
+ "Position ids are not supported for parameter efficient tuning. Ignoring position ids."
+ )
+ kwargs["position_ids"] = None
+ if kwargs.get("token_type_ids", None) is not None:
+ warnings.warn(
+ "Token type ids are not supported for parameter efficient tuning. Ignoring token type ids"
+ )
+ kwargs["token_type_ids"] = None
+
+ if peft_config.peft_type == PeftType.PREFIX_TUNING:
+ outputs = self.base_model.generate(**kwargs)
+ elif peft_config.peft_type in [
+ PeftType.PROMPT_TUNING,
+ PeftType.P_TUNING,
+ PeftType.MULTITASK_PROMPT_TUNING,
+ ]:
+ kwargs = deepcopy(kwargs)
+
+ if "encoder_outputs" in kwargs:
+ del kwargs["encoder_outputs"]
+ warnings.warn(
+ "`encoder_outputs` should not be passed to `generate` when using prompt tuning. Ignoring it."
+ )
+
+ input_ids = kwargs.pop("input_ids")
+ inputs_embeds = self.word_embeddings(input_ids)
+ batch_size = inputs_embeds.shape[0]
+ prompts = self.get_prompt(batch_size=batch_size, task_ids=kwargs.pop("task_ids", None))
+ prompts = prompts.to(inputs_embeds.dtype)
+
+ inputs_embeds = torch.cat((prompts[:, : peft_config.num_virtual_tokens], inputs_embeds), dim=1)
+ kwargs["inputs_embeds"] = inputs_embeds
+
+ if "attention_mask" in kwargs:
+ prefix_attention_mask = torch.ones(batch_size, peft_config.num_virtual_tokens).to(
+ kwargs["attention_mask"].device
+ )
+ kwargs["attention_mask"] = torch.cat((prefix_attention_mask, kwargs["attention_mask"]), dim=1)
+
+ return self.base_model.generate(**kwargs)
+ else:
+ raise NotImplementedError
+ except:
+ self.base_model.prepare_inputs_for_generation = self.base_model_prepare_inputs_for_generation
+ self.base_model._prepare_encoder_decoder_kwargs_for_generation = (
+ self.base_model_prepare_encoder_decoder_kwargs_for_generation
+ )
+ raise
+ else:
+ self.base_model.prepare_inputs_for_generation = self.base_model_prepare_inputs_for_generation
+ self.base_model._prepare_encoder_decoder_kwargs_for_generation = (
+ self.base_model_prepare_encoder_decoder_kwargs_for_generation
+ )
+ return outputs
+
+ def prepare_inputs_for_generation(self, *args, task_ids: torch.Tensor = None, **kwargs):
+ peft_config = self.active_peft_config
+ model_kwargs = self.base_model_prepare_inputs_for_generation(*args, **kwargs)
+ if peft_config.peft_type == PeftType.POLY:
+ model_kwargs["task_ids"] = task_ids
+ elif peft_config.peft_type == PeftType.PREFIX_TUNING:
+ past_key_values = model_kwargs.get("past_key_values", None)
+ cache_position = model_kwargs.get("cache_position", [None])
+ # check prefill stage
+ is_prefill_stage = (
+ # old cache implementation
+ (past_key_values is None)
+ # new cache implementation
+ or (isinstance(past_key_values, Cache) and (cache_position[0] == 0))
+ )
+ if is_prefill_stage:
+ batch_size = model_kwargs["decoder_input_ids"].shape[0]
+ new_past_key_values = self.get_prompt(batch_size)
+ model_kwargs["past_key_values"] = new_past_key_values
+
+ return model_kwargs
+
+
+class PeftModelForTokenClassification(PeftModel):
+ """
+ Peft model for token classification tasks.
+
+ Args:
+ model ([`~transformers.PreTrainedModel`]): Base transformer model.
+ peft_config ([`PeftConfig`]): Peft config.
+ adapter_name (`str`, *optional*): The name of the adapter, defaults to `"default"`.
+ autocast_adapter_dtype (`bool`, *optional*):
+ Whether to autocast the adapter dtype. Defaults to `True`. Right now, this will only cast adapter weights
+ using float16 and bfloat16 to float32, as this is typically required for stable training, and only affect
+ select PEFT tuners.
+
+ **Attributes**:
+ - **config** ([`~transformers.PretrainedConfig`]) -- The configuration object of the base model.
+ - **cls_layer_name** (`str`) -- The name of the classification layer.
+
+ Example:
+
+ ```py
+ >>> from transformers import AutoModelForSequenceClassification
+ >>> from peft import PeftModelForTokenClassification, get_peft_config
+
+ >>> config = {
+ ... "peft_type": "PREFIX_TUNING",
+ ... "task_type": "TOKEN_CLS",
+ ... "inference_mode": False,
+ ... "num_virtual_tokens": 20,
+ ... "token_dim": 768,
+ ... "num_transformer_submodules": 1,
+ ... "num_attention_heads": 12,
+ ... "num_layers": 12,
+ ... "encoder_hidden_size": 768,
+ ... "prefix_projection": False,
+ ... "postprocess_past_key_value_function": None,
+ ... }
+
+ >>> peft_config = get_peft_config(config)
+ >>> model = AutoModelForTokenClassification.from_pretrained("bert-base-cased")
+ >>> peft_model = PeftModelForTokenClassification(model, peft_config)
+ >>> peft_model.print_trainable_parameters()
+ trainable params: 370178 || all params: 108680450 || trainable%: 0.3406113979101117
+ ```
+ """
+
+ def __init__(
+ self, model: torch.nn.Module, peft_config: PeftConfig = None, adapter_name: str = "default", **kwargs
+ ) -> None:
+ super().__init__(model, peft_config, adapter_name, **kwargs)
+
+ classifier_module_names = ["classifier", "score"]
+ if hasattr(peft_config, "modules_to_save"):
+ if peft_config.modules_to_save is None:
+ peft_config.modules_to_save = classifier_module_names[:]
+ else:
+ peft_config.modules_to_save.extend(classifier_module_names)
+
+ for name, _ in self.base_model.named_children():
+ if any(module_name in name for module_name in self.modules_to_save):
+ self.cls_layer_name = name
+ break
+
+ # to make sure classifier layer is trainable; this may add a new ModulesToSaveWrapper
+ _set_trainable(
+ self,
+ adapter_name,
+ module_names=getattr(peft_config, "modules_to_save", None),
+ inference_mode=peft_config.inference_mode,
+ )
+
+ def add_adapter(self, adapter_name: str, peft_config: PeftConfig, low_cpu_mem_usage: bool = False) -> None:
+ """
+ Add an adapter to the model based on the passed configuration.
+
+ This adapter is not trained. To load a trained adapter, check out [`PeftModel.load_adapter`].
+
+ The name for the new adapter should be unique.
+
+ The new adapter is not automatically set as the active adapter. Use [`PeftModel.set_adapter`] to set the active
+ adapter.
+
+ Args:
+ adapter_name (`str`):
+ The name of the adapter to be added.
+ peft_config ([`PeftConfig`]):
+ The configuration of the adapter to be added.
+ low_cpu_mem_usage (`bool`, `optional`, defaults to `False`):
+ Create empty adapter weights on meta device. Useful to speed up the process when loading saved
+ adapters. Don't use this option when creating a new PEFT adapter for training.
+
+ """
+ # ensure that additional adapters also add the classifier layer to modules_to_save
+ if hasattr(peft_config, "modules_to_save"):
+ classifier_module_names = ["classifier", "score"]
+ if peft_config.modules_to_save is None:
+ peft_config.modules_to_save = classifier_module_names[:]
+ else:
+ peft_config.modules_to_save.extend(classifier_module_names)
+
+ return super().add_adapter(adapter_name, peft_config, low_cpu_mem_usage=low_cpu_mem_usage)
+
+ def forward(
+ self,
+ input_ids=None,
+ attention_mask=None,
+ inputs_embeds=None,
+ labels=None,
+ output_attentions=None,
+ output_hidden_states=None,
+ return_dict=None,
+ task_ids=None,
+ **kwargs,
+ ):
+ peft_config = self.active_peft_config
+ return_dict = return_dict if return_dict is not None else self.config.use_return_dict
+
+ if not peft_config.is_prompt_learning:
+ with self._enable_peft_forward_hooks(**kwargs):
+ kwargs = {k: v for k, v in kwargs.items() if k not in self.special_peft_forward_args}
+ if peft_config.peft_type == PeftType.POLY:
+ kwargs["task_ids"] = task_ids
+ return self.base_model(
+ input_ids=input_ids,
+ attention_mask=attention_mask,
+ inputs_embeds=inputs_embeds,
+ labels=labels,
+ output_attentions=output_attentions,
+ output_hidden_states=output_hidden_states,
+ return_dict=return_dict,
+ **kwargs,
+ )
+
+ batch_size = _get_batch_size(input_ids, inputs_embeds)
+ if attention_mask is not None:
+ # concat prompt attention mask
+ prefix_attention_mask = torch.ones(batch_size, peft_config.num_virtual_tokens).to(attention_mask.device)
+ attention_mask = torch.cat((prefix_attention_mask, attention_mask), dim=1)
+ if kwargs.get("position_ids", None) is not None:
+ warnings.warn("Position ids are not supported for parameter efficient tuning. Ignoring position ids.")
+ kwargs["position_ids"] = None
+ kwargs.update(
+ {
+ "attention_mask": attention_mask,
+ "labels": labels,
+ "output_attentions": output_attentions,
+ "output_hidden_states": output_hidden_states,
+ "return_dict": return_dict,
+ }
+ )
+
+ if peft_config.peft_type == PeftType.PREFIX_TUNING:
+ return self._prefix_tuning_forward(input_ids=input_ids, **kwargs)
+ else:
+ if kwargs.get("token_type_ids", None) is not None:
+ kwargs["token_type_ids"] = torch.cat(
+ (
+ torch.zeros(batch_size, peft_config.num_virtual_tokens).to(self.word_embeddings.weight.device),
+ kwargs["token_type_ids"],
+ ),
+ dim=1,
+ ).long()
+ if inputs_embeds is None:
+ inputs_embeds = self.word_embeddings(input_ids)
+ prompts = self.get_prompt(batch_size=batch_size, task_ids=task_ids)
+ prompts = prompts.to(inputs_embeds.dtype)
+ inputs_embeds = torch.cat((prompts, inputs_embeds), dim=1)
+ return self.base_model(inputs_embeds=inputs_embeds, **kwargs)
+
+ def _prefix_tuning_forward(
+ self,
+ input_ids=None,
+ attention_mask=None,
+ inputs_embeds=None,
+ labels=None,
+ output_attentions=None,
+ output_hidden_states=None,
+ return_dict=None,
+ **kwargs,
+ ):
+ batch_size = _get_batch_size(input_ids, inputs_embeds)
+ past_key_values = self.get_prompt(batch_size)
+ fwd_params = list(inspect.signature(self.base_model.forward).parameters.keys())
+ kwargs.update(
+ {
+ "input_ids": input_ids,
+ "attention_mask": attention_mask,
+ "inputs_embeds": inputs_embeds,
+ "output_attentions": output_attentions,
+ "output_hidden_states": output_hidden_states,
+ "return_dict": return_dict,
+ "past_key_values": past_key_values,
+ }
+ )
+ if "past_key_values" in fwd_params:
+ return self.base_model(labels=labels, **kwargs)
+ else:
+ transformer_backbone_name = self.base_model.get_submodule(self.transformer_backbone_name)
+ fwd_params = list(inspect.signature(transformer_backbone_name.forward).parameters.keys())
+ if "past_key_values" not in fwd_params:
+ raise ValueError("Model does not support past key values which are required for prefix tuning.")
+ outputs = transformer_backbone_name(**kwargs)
+ sequence_output = outputs[0]
+ if "dropout" in [name for name, _ in list(self.base_model.named_children())]:
+ sequence_output = self.base_model.dropout(sequence_output)
+ logits = self.base_model.get_submodule(self.cls_layer_name)(sequence_output)
+
+ loss = None
+ if labels is not None:
+ loss_fct = CrossEntropyLoss()
+ loss = loss_fct(logits.view(-1, self.num_labels), labels.view(-1))
+
+ if not return_dict:
+ output = (logits,) + outputs[2:]
+ return ((loss,) + output) if loss is not None else output
+
+ return TokenClassifierOutput(
+ loss=loss,
+ logits=logits,
+ hidden_states=outputs.hidden_states,
+ attentions=outputs.attentions,
+ )
+
+
+class PeftModelForQuestionAnswering(PeftModel):
+ """
+ Peft model for extractive question answering.
+
+ Args:
+ model ([`~transformers.PreTrainedModel`]): Base transformer model.
+ peft_config ([`PeftConfig`]): Peft config.
+ adapter_name (`str`, *optional*): The name of the adapter, defaults to `"default"`.
+ autocast_adapter_dtype (`bool`, *optional*):
+ Whether to autocast the adapter dtype. Defaults to `True`. Right now, this will only cast adapter weights
+ using float16 and bfloat16 to float32, as this is typically required for stable training, and only affect
+ select PEFT tuners.
+
+ **Attributes**:
+ - **config** ([`~transformers.PretrainedConfig`]) -- The configuration object of the base model.
+ - **cls_layer_name** (`str`) -- The name of the classification layer.
+
+ Example:
+
+ ```py
+ >>> from transformers import AutoModelForQuestionAnswering
+ >>> from peft import PeftModelForQuestionAnswering, get_peft_config
+
+ >>> config = {
+ ... "peft_type": "LORA",
+ ... "task_type": "QUESTION_ANS",
+ ... "inference_mode": False,
+ ... "r": 16,
+ ... "target_modules": ["query", "value"],
+ ... "lora_alpha": 32,
+ ... "lora_dropout": 0.05,
+ ... "fan_in_fan_out": False,
+ ... "bias": "none",
+ ... }
+
+ >>> peft_config = get_peft_config(config)
+ >>> model = AutoModelForQuestionAnswering.from_pretrained("bert-base-cased")
+ >>> peft_model = PeftModelForQuestionAnswering(model, peft_config)
+ >>> peft_model.print_trainable_parameters()
+ trainable params: 592900 || all params: 108312580 || trainable%: 0.5473971721475013
+ ```
+ """
+
+ def __init__(
+ self, model: torch.nn.Module, peft_config: PeftConfig, adapter_name: str = "default", **kwargs
+ ) -> None:
+ super().__init__(model, peft_config, adapter_name, **kwargs)
+
+ qa_module_names = ["qa_outputs"]
+ if hasattr(peft_config, "modules_to_save"):
+ if peft_config.modules_to_save is None:
+ peft_config.modules_to_save = qa_module_names[:]
+ else:
+ peft_config.modules_to_save.extend(qa_module_names)
+
+ for name, _ in self.base_model.named_children():
+ if any(module_name in name for module_name in self.modules_to_save):
+ self.cls_layer_name = name
+ break
+
+ # to make sure classifier layer is trainable; this may add a new ModulesToSaveWrapper
+ _set_trainable(
+ self,
+ adapter_name,
+ module_names=getattr(peft_config, "modules_to_save", None),
+ inference_mode=peft_config.inference_mode,
+ )
+
+ def add_adapter(self, adapter_name: str, peft_config: PeftConfig, low_cpu_mem_usage: bool = False) -> None:
+ """
+ Add an adapter to the model based on the passed configuration.
+
+ This adapter is not trained. To load a trained adapter, check out [`PeftModel.load_adapter`].
+
+ The name for the new adapter should be unique.
+
+ The new adapter is not automatically set as the active adapter. Use [`PeftModel.set_adapter`] to set the active
+ adapter.
+
+ Args:
+ adapter_name (`str`):
+ The name of the adapter to be added.
+ peft_config ([`PeftConfig`]):
+ The configuration of the adapter to be added.
+ low_cpu_mem_usage (`bool`, `optional`, defaults to `False`):
+ Create empty adapter weights on meta device. Useful to speed up the process when loading saved
+ adapters. Don't use this option when creating a new PEFT adapter for training.
+
+ """
+ # ensure that additional adapters also add the classifier layer to modules_to_save
+ if hasattr(peft_config, "modules_to_save"):
+ qa_module_names = ["qa_outputs"]
+ if peft_config.modules_to_save is None:
+ peft_config.modules_to_save = qa_module_names[:]
+ else:
+ peft_config.modules_to_save.extend(qa_module_names)
+
+ return super().add_adapter(adapter_name, peft_config, low_cpu_mem_usage=low_cpu_mem_usage)
+
+ def forward(
+ self,
+ input_ids=None,
+ attention_mask=None,
+ token_type_ids=None,
+ position_ids=None,
+ inputs_embeds=None,
+ start_positions=None,
+ end_positions=None,
+ output_attentions=None,
+ output_hidden_states=None,
+ return_dict=None,
+ task_ids=None,
+ **kwargs,
+ ):
+ peft_config = self.active_peft_config
+ return_dict = return_dict if return_dict is not None else self.config.use_return_dict
+
+ if not peft_config.is_prompt_learning:
+ if peft_config.peft_type == PeftType.POLY:
+ kwargs["task_ids"] = task_ids
+
+ with self._enable_peft_forward_hooks(**kwargs):
+ kwargs = {k: v for k, v in kwargs.items() if k not in self.special_peft_forward_args}
+ return self.base_model(
+ input_ids=input_ids,
+ attention_mask=attention_mask,
+ inputs_embeds=inputs_embeds,
+ start_positions=start_positions,
+ end_positions=end_positions,
+ output_attentions=output_attentions,
+ output_hidden_states=output_hidden_states,
+ return_dict=return_dict,
+ **kwargs,
+ )
+
+ batch_size = _get_batch_size(input_ids, inputs_embeds)
+ if attention_mask is not None:
+ # concat prompt attention mask
+ prefix_attention_mask = torch.ones(batch_size, peft_config.num_virtual_tokens).to(attention_mask.device)
+ attention_mask = torch.cat((prefix_attention_mask, attention_mask), dim=1)
+ if kwargs.get("position_ids", None) is not None:
+ warnings.warn("Position ids are not supported for parameter efficient tuning. Ignoring position ids.")
+ kwargs["position_ids"] = None
+ kwargs.update(
+ {
+ "attention_mask": attention_mask,
+ "start_positions": start_positions,
+ "end_positions": end_positions,
+ "output_attentions": output_attentions,
+ "output_hidden_states": output_hidden_states,
+ "return_dict": return_dict,
+ }
+ )
+
+ if peft_config.peft_type == PeftType.PREFIX_TUNING:
+ return self._prefix_tuning_forward(input_ids=input_ids, **kwargs)
+ else:
+ if kwargs.get("token_type_ids", None) is not None:
+ kwargs["token_type_ids"] = torch.cat(
+ (
+ torch.zeros(batch_size, peft_config.num_virtual_tokens).to(self.word_embeddings.weight.device),
+ kwargs["token_type_ids"],
+ ),
+ dim=1,
+ ).long()
+ if inputs_embeds is None:
+ inputs_embeds = self.word_embeddings(input_ids)
+ prompts = self.get_prompt(batch_size=batch_size)
+ prompts = prompts.to(inputs_embeds.dtype)
+ inputs_embeds = torch.cat((prompts, inputs_embeds), dim=1)
+ return self.base_model(inputs_embeds=inputs_embeds, **kwargs)
+
+ def _prefix_tuning_forward(
+ self,
+ input_ids=None,
+ attention_mask=None,
+ inputs_embeds=None,
+ start_positions=None,
+ end_positions=None,
+ output_attentions=None,
+ output_hidden_states=None,
+ return_dict=None,
+ **kwargs,
+ ):
+ batch_size = _get_batch_size(input_ids, inputs_embeds)
+ past_key_values = self.get_prompt(batch_size)
+ fwd_params = list(inspect.signature(self.base_model.forward).parameters.keys())
+ kwargs.update(
+ {
+ "input_ids": input_ids,
+ "attention_mask": attention_mask,
+ "inputs_embeds": inputs_embeds,
+ "output_attentions": output_attentions,
+ "output_hidden_states": output_hidden_states,
+ "return_dict": return_dict,
+ "past_key_values": past_key_values,
+ }
+ )
+ if "past_key_values" in fwd_params:
+ return self.base_model(start_positions=start_positions, end_positions=end_positions, **kwargs)
+ else:
+ transformer_backbone_name = self.base_model.get_submodule(self.transformer_backbone_name)
+ fwd_params = list(inspect.signature(transformer_backbone_name.forward).parameters.keys())
+ if "past_key_values" not in fwd_params:
+ raise ValueError("Model does not support past key values which are required for prefix tuning.")
+ outputs = transformer_backbone_name(**kwargs)
+ sequence_output = outputs[0]
+ if "dropout" in [name for name, _ in list(self.base_model.named_children())]:
+ sequence_output = self.base_model.dropout(sequence_output)
+ logits = self.base_model.get_submodule(self.cls_layer_name)(sequence_output)
+ start_logits, end_logits = logits.split(1, dim=-1)
+ start_logits = start_logits.squeeze(-1).contiguous()
+ end_logits = end_logits.squeeze(-1).contiguous()
+
+ total_loss = None
+ if start_positions is not None and end_positions is not None:
+ # If we are on multi-GPU, split add a dimension
+ if len(start_positions.size()) > 1:
+ start_positions = start_positions.squeeze(-1)
+ if len(end_positions.size()) > 1:
+ end_positions = end_positions.squeeze(-1)
+ # sometimes the start/end positions are outside our model inputs, we ignore these terms
+ ignored_index = start_logits.size(1)
+ start_positions = start_positions.clamp(0, ignored_index)
+ end_positions = end_positions.clamp(0, ignored_index)
+
+ loss_fct = CrossEntropyLoss(ignore_index=ignored_index)
+ start_loss = loss_fct(start_logits, start_positions)
+ end_loss = loss_fct(end_logits, end_positions)
+ total_loss = (start_loss + end_loss) / 2
+
+ if not return_dict:
+ output = (start_logits, end_logits) + outputs[2:]
+ return ((total_loss,) + output) if total_loss is not None else output
+
+ return QuestionAnsweringModelOutput(
+ loss=total_loss,
+ start_logits=start_logits,
+ end_logits=end_logits,
+ hidden_states=outputs.hidden_states,
+ attentions=outputs.attentions,
+ )
+
+
+class PeftModelForFeatureExtraction(PeftModel):
+ """
+ Peft model for extracting features/embeddings from transformer models
+
+ Args:
+ model ([`~transformers.PreTrainedModel`]): Base transformer model.
+ peft_config ([`PeftConfig`]): Peft config.
+ adapter_name (`str`, *optional*): The name of the adapter, defaults to `"default"`.
+ autocast_adapter_dtype (`bool`, *optional*):
+ Whether to autocast the adapter dtype. Defaults to `True`. Right now, this will only cast adapter weights
+ using float16 and bfloat16 to float32, as this is typically required for stable training, and only affect
+ select PEFT tuners.
+
+ **Attributes**:
+ - **config** ([`~transformers.PretrainedConfig`]) -- The configuration object of the base model.
+
+ Example:
+
+ ```py
+ >>> from transformers import AutoModel
+ >>> from peft import PeftModelForFeatureExtraction, get_peft_config
+
+ >>> config = {
+ ... "peft_type": "LORA",
+ ... "task_type": "FEATURE_EXTRACTION",
+ ... "inference_mode": False,
+ ... "r": 16,
+ ... "target_modules": ["query", "value"],
+ ... "lora_alpha": 32,
+ ... "lora_dropout": 0.05,
+ ... "fan_in_fan_out": False,
+ ... "bias": "none",
+ ... }
+ >>> peft_config = get_peft_config(config)
+ >>> model = AutoModel.from_pretrained("bert-base-cased")
+ >>> peft_model = PeftModelForFeatureExtraction(model, peft_config)
+ >>> peft_model.print_trainable_parameters()
+ ```
+ """
+
+ def __init__(self, model: torch.nn.Module, peft_config: PeftConfig, adapter_name: str = "default", **kwargs):
+ super().__init__(model, peft_config, adapter_name, **kwargs)
+
+ def forward(
+ self,
+ input_ids=None,
+ attention_mask=None,
+ inputs_embeds=None,
+ output_attentions=None,
+ output_hidden_states=None,
+ return_dict=None,
+ task_ids=None,
+ **kwargs,
+ ):
+ peft_config = self.active_peft_config
+ if not peft_config.is_prompt_learning:
+ if peft_config.peft_type == PeftType.POLY:
+ kwargs["task_ids"] = task_ids
+
+ with self._enable_peft_forward_hooks(**kwargs):
+ kwargs = {k: v for k, v in kwargs.items() if k not in self.special_peft_forward_args}
+ return self.base_model(
+ input_ids=input_ids,
+ attention_mask=attention_mask,
+ inputs_embeds=inputs_embeds,
+ output_attentions=output_attentions,
+ output_hidden_states=output_hidden_states,
+ return_dict=return_dict,
+ **kwargs,
+ )
+
+ batch_size = _get_batch_size(input_ids, inputs_embeds)
+ if attention_mask is not None:
+ # concat prompt attention mask
+ prefix_attention_mask = torch.ones(batch_size, peft_config.num_virtual_tokens).to(attention_mask.device)
+ attention_mask = torch.cat((prefix_attention_mask, attention_mask), dim=1)
+
+ if kwargs.get("position_ids", None) is not None:
+ warnings.warn("Position ids are not supported for parameter efficient tuning. Ignoring position ids.")
+ kwargs["position_ids"] = None
+ if kwargs.get("token_type_ids", None) is not None:
+ warnings.warn("Token type ids are not supported for parameter efficient tuning. Ignoring token type ids")
+ kwargs["token_type_ids"] = None
+ kwargs.update(
+ {
+ "attention_mask": attention_mask,
+ "output_attentions": output_attentions,
+ "output_hidden_states": output_hidden_states,
+ "return_dict": return_dict,
+ }
+ )
+
+ if peft_config.peft_type == PeftType.PREFIX_TUNING:
+ # overwrite past_kv in kwargs
+ kwargs["past_key_values"] = self.get_prompt(batch_size)
+ return self.base_model(input_ids=input_ids, **kwargs)
+ else:
+ if inputs_embeds is None:
+ inputs_embeds = self.word_embeddings(input_ids)
+ prompts = self.get_prompt(batch_size=batch_size)
+ prompts = prompts.to(inputs_embeds.dtype)
+ inputs_embeds = torch.cat((prompts, inputs_embeds), dim=1)
+ return self.base_model(inputs_embeds=inputs_embeds, **kwargs)
+
+
+@dataclass
+class TunerLayerStatus:
+ name: str
+ module_type: str
+ enabled: bool
+ active_adapters: list[str]
+ merged_adapters: list[str]
+ requires_grad: dict[str, bool | Literal["irregular"]]
+ available_adapters: list[str]
+ devices: dict[str, list[str]]
+
+
+def get_layer_status(model: torch.nn.Module) -> list[TunerLayerStatus]:
+ """Get the status of each adapter layer in the model.
+
+ This function returns a list of `TunerLayerStatus` dataclass instances, each of which contains the following
+ attributes:
+
+ - `name` (`str`):
+ The name of the adapter layer, e.g. `model.encoder.block.0.layer.0.SelfAttention.q`.
+ - `module_type` (`str`):
+ The type of the adapter layer, e.g. `lora.Linear`.
+ - `enabled` (`bool`):
+ Whether the adapter layer is enabled.
+ - `active_adapters` (`list[str]`):
+ The names of the active adapters, if any, e.g. `["default"]`.
+ - `merged_adapters` (`list[str]`):
+ The names of the merged adapters, if any, e.g. `["default"]`.
+ - requires_grad : dict[str, bool | Literal["irregular"]]
+ The requires_grad status of the parameters for each adapter module. Ideally, it should be either `True` or
+ `False`. If the requires_grad status is not consistent across all parameters, the value will be set to
+ `"irregular"`.
+ - `available_adapters` (`list[str]`):
+ The names of the available adapters, e.g. `["default"]`.
+ - `devices` (`dict[str, list[str]]`):
+ The devices where the parameters of the given adapter are stored, e.g. `["cuda"]`.
+
+ Args:
+ model ([Union[`~PeftModel`, `~transformers.PreTrainedModel`, `nn.Module`]]):
+ The model to get the adapter layer status from.
+
+ Returns:
+ list[`peft.peft_model.TunerLayerStatus`]:
+ A list of dataclasses, each containing the status of the corresponding adapter layer.
+
+ """
+ if isinstance(model, PeftModel):
+ base_model = model.base_model
+ if not isinstance(base_model, BaseTuner):
+ raise TypeError(
+ "get_layer_status() got an invalid PeftModel instance; prefix tuning and adaption prompt are not "
+ "supported."
+ )
+ else:
+ base_model = model
+
+ layer_status: list[TunerLayerStatus] = []
+ for name, module in base_model.named_modules():
+ if not isinstance(module, (BaseTunerLayer, AuxiliaryTrainingWrapper)):
+ continue
+ if isinstance(module, TrainableTokensWrapper):
+ # Skip TrainableTokensWrapper, since it wraps TrainableTokensLayer, which is the actual PEFT layer we're
+ # interested in.
+ continue
+
+ # determine if all submodules/parameters if this module require grad or not
+ mapping_requires_grad_list: dict[str, list[bool]] = collections.defaultdict(list)
+ for adapter_module_name in module.adapter_layer_names:
+ adapter_module = getattr(module, adapter_module_name)
+ if isinstance(adapter_module, torch.nn.ModuleDict):
+ for key, submodule in adapter_module.items():
+ for param in submodule.parameters():
+ mapping_requires_grad_list[key].append(param.requires_grad)
+ elif isinstance(adapter_module, torch.nn.ParameterDict):
+ for key, param in adapter_module.items():
+ mapping_requires_grad_list[key].append(param.requires_grad)
+ else:
+ # strange, we don't know how to handle this, ignore for now
+ pass
+
+ def check_irrgular(vals: list[bool]) -> bool | Literal["irregular"]:
+ if all(vals):
+ return True
+ if not any(vals):
+ return False
+ return "irregular"
+
+ requires_grad = {key: check_irrgular(vals) for key, vals in mapping_requires_grad_list.items()}
+
+ devices_dd = collections.defaultdict(list)
+ for adapter_module_name in module.adapter_layer_names + module.other_param_names:
+ adapter_module = getattr(module, adapter_module_name)
+ if isinstance(adapter_module, torch.nn.ModuleDict):
+ for key, submodule in adapter_module.items():
+ devices_dd[key].extend([param.device.type for param in submodule.parameters()])
+ elif isinstance(adapter_module, torch.nn.ParameterDict) or (
+ adapter_module.__class__.__name__ == "BufferDict"
+ ): # VeRA
+ for key, param in adapter_module.items():
+ devices_dd[key].append(param.device.type)
+ devices = {key: sorted(set(val)) for key, val in devices_dd.items()}
+
+ status = TunerLayerStatus(
+ name=name,
+ module_type=repr(module).partition("(")[0],
+ enabled=not module.disable_adapters,
+ active_adapters=module.active_adapters,
+ merged_adapters=module.merged_adapters,
+ requires_grad=requires_grad,
+ available_adapters=sorted(module._get_available_adapters()),
+ devices=devices,
+ )
+ layer_status.append(status)
+
+ if not layer_status:
+ raise ValueError(
+ "No adapter layers found in the model, please ensure that it's a PEFT model or that you have PEFT adapters "
+ "injected in the model."
+ )
+
+ return layer_status
+
+
+@dataclass
+class TunerModelStatus:
+ base_model_type: str
+ adapter_model_type: str
+ peft_types: dict[str, str]
+ trainable_params: int
+ total_params: int
+ num_adapter_layers: int
+ enabled: bool | Literal["irregular"]
+ active_adapters: list[str] | Literal["irregular"]
+ merged_adapters: list[str] | Literal["irregular"]
+ requires_grad: dict[str, bool | Literal["irregular"]]
+ available_adapters: list[str]
+ devices: dict[str, list[str]]
+
+
+def get_model_status(model: torch.nn.Module) -> TunerModelStatus:
+ """Get the status of tuners of the model.
+
+ This function returns a `TunerModelStatus` dataclass instance, which contains the following attributes:
+
+ - `base_model_type` (`str`):
+ The type of the base model, e.g. `T5Model`.
+ - `adapter_model_type` (`str`):
+ The type of the adapter model, e.g. `LoraModel`.
+ - `peft_types` (`dict[str, str]`):
+ The mapping of adapter name to adapter type, e.g. `{"default": "LORA"}`.
+ - `trainable_params` (`int`):
+ The number of trainable parameters in the model.
+ - `total_params` (`int`):
+ The total number of parameters in the model.
+ - `num_adapter_layers` (`int`):
+ The number of adapter layers in the model.
+ - `enabled` (`bool`, `Literal["irregular"]`):
+ Whether all adapter layers are enabled. If some are enabled and some are not, this will be `"irregular"`. This
+ means that your model is in an inconsistent state and might not work as expected.
+ - `active_adapters` (`list[str]`, `Literal["irregular"]`):
+ The names of the active adapters. If the active adapters are not consistent across all layers, this will be
+ `"irregular"`, which means that your model is in an inconsistent state and might not work as expected.
+ - `merged_adapters` (`list[str]`, `Literal["irregular"]`):
+ The names of the merged adapters. If the merged adapters are not consistent across all layers, this will be
+ `"irregular"`, which means that your model is in an inconsistent state and might not work as expected.
+ - `requires_grad` (`dict[str, bool | Literal["irregular"]]`):
+ Whether for the given adapter, all adapter layers have `requires_grad` set to `True` or `False`. If there is a
+ mix, this will be set to `"irregular"`, which means that your model is in an inconsistent state and might not
+ work as expected.
+ - `available_adapters` (`list[str]`):
+ The names of the available adapters, e.g. `["default"]`.
+ - `devices` (`dict[str, list[str]]`):
+ The devices where the parameters of the given adapter are stored, e.g. `["cuda"]`.
+
+ Args:
+ model ([Union[`~PeftModel`, `~transformers.PreTrainedModel`, `nn.Module`]]):
+ The model to get the adapter layer status from.
+
+ Returns:
+ `peft.peft_model.TunerModelStatus`:
+ A dataclass containing the status of the model.
+
+ """
+ if isinstance(model, PeftModel):
+ if not isinstance(model.base_model, BaseTuner):
+ raise TypeError(
+ "get_model_status() got an invalid PeftModel instance; prefix tuning and adaption prompt are not "
+ "supported."
+ )
+ base_model_type = model.get_base_model().__class__.__name__
+ trainable_params, total_params = model.get_nb_trainable_parameters()
+ base_model = model.base_model
+ peft_types = {key: str(config.peft_type).partition(".")[-1] for key, config in base_model.peft_config.items()}
+ adapter_model_type = base_model.__class__.__name__
+ elif isinstance(model, PreTrainedModel):
+ base_model_type = model.__class__.__name__
+ trainable_params, total_params = PeftModel.get_nb_trainable_parameters(model)
+ base_model = model
+ peft_types = {}
+ adapter_model_type = "None"
+ else:
+ base_model_type = "other"
+ trainable_params, total_params = PeftModel.get_nb_trainable_parameters(model)
+ base_model = model
+ peft_types = {}
+ adapter_model_type = "None"
+
+ layer_status = get_layer_status(model)
+ num_adapter_layers = len(layer_status)
+
+ enabled_set: set[bool] = {status.enabled for status in layer_status} # must be {True}, {False}, or {True, False}
+ enabled: bool | Literal["irregular"]
+ if len(enabled_set) == 1:
+ enabled = enabled_set.pop()
+ else:
+ enabled = "irregular"
+
+ available_adapters: list[str] = sorted(set().union(*(status.available_adapters for status in layer_status)))
+
+ # ideally, active adapters should be consistent across all layers of the model, but we cannot guarantee it
+ all_active_adapters: set[tuple[str, ...]] = {tuple(status.active_adapters) for status in layer_status}
+ active_adapters: list[str] | Literal["irregular"]
+ if not all_active_adapters:
+ active_adapters = []
+ elif len(all_active_adapters) == 1:
+ active_adapters = list(all_active_adapters.pop())
+ else:
+ active_adapters = "irregular"
+
+ # Here we determine what adapters are merged. This is not trivial because multiple adapters can be merged or not at
+ # the same time. Some layers may only have adapter A, some only adapter B, so it's not as easy as just checking
+ # which adapters are merged on each layer.
+
+ # First, determine all adapters that are merged on at least on module.
+ merged_all: set[str] = set()
+ for status in layer_status:
+ merged_all.update(status.merged_adapters)
+
+ # Next, check if on any layer, on of these adapters is not merged.
+ merged_adapters: list[str] | Literal["irregular"] = sorted(merged_all)
+ for status in layer_status:
+ unmerged = set(status.available_adapters) - set(status.merged_adapters)
+ if unmerged & merged_all:
+ # there is overlap between unmerged adapters and adapters that should be merged
+ merged_adapters = "irregular"
+ break
+
+ # check status of requires_grad
+ # first, merge the values for all layers
+ requires_grad_all: dict[str, list[bool | Literal["irregular"]]] = collections.defaultdict(list)
+ for status in layer_status:
+ for key, val in status.requires_grad.items():
+ requires_grad_all[key].append(val)
+
+ # then, check if the values are consistent
+ def check_irrgular(vals: list[bool | Literal["irregular"]]) -> bool | Literal["irregular"]:
+ if all(val is True for val in vals):
+ return True
+ if all(val is False for val in vals):
+ return False
+ return "irregular"
+
+ requires_grad = {key: check_irrgular(vals) for key, vals in requires_grad_all.items()}
+
+ devices_dd = collections.defaultdict(list)
+ for status in layer_status:
+ for key, val in status.devices.items():
+ devices_dd[key].extend(val)
+ devices = {key: sorted(set(val)) for key, val in devices_dd.items()}
+
+ adapter_model_status = TunerModelStatus(
+ base_model_type=base_model_type,
+ adapter_model_type=adapter_model_type,
+ peft_types=peft_types,
+ trainable_params=trainable_params,
+ total_params=total_params,
+ num_adapter_layers=num_adapter_layers,
+ enabled=enabled,
+ active_adapters=active_adapters,
+ merged_adapters=merged_adapters,
+ requires_grad=requires_grad,
+ available_adapters=available_adapters,
+ devices=devices,
+ )
+ return adapter_model_status
+
+
+def __getattr__(name):
+ if name == "PEFT_TYPE_TO_MODEL_MAPPING":
+ # This is for backwards compatibility: In #2282, PEFT_TYPE_TO_MODEL_MAPPING was removed as it was redundant with
+ # PEFT_TYPE_TO_TUNER_MAPPING. However, third party code could still use this mapping, e.g.:
+ # https://github.com/AutoGPTQ/AutoGPTQ/blob/6689349625de973b9ee3016c28c11f32acf7f02c/auto_gptq/utils/peft_utils.py#L8
+ # TODO: Remove after 2026-01
+ msg = (
+ "PEFT_TYPE_TO_MODEL_MAPPING is deprecated, please use `from peft import PEFT_TYPE_TO_TUNER_MAPPING` instead. "
+ "The deprecated variable will be removed in 2026."
+ )
+ warnings.warn(msg, category=DeprecationWarning)
+ return PEFT_TYPE_TO_TUNER_MAPPING
+
+ raise AttributeError(f"module {__name__!r} has no attribute {name!r}")
diff --git a/peft/src/peft/py.typed b/peft/src/peft/py.typed
new file mode 100644
index 0000000000000000000000000000000000000000..e69de29bb2d1d6434b8b29ae775ad8c2e48c5391
diff --git a/peft/src/peft/tuners/__init__.py b/peft/src/peft/tuners/__init__.py
new file mode 100644
index 0000000000000000000000000000000000000000..c193f89d4958d98c0086ecfeba1260ccc9980e1a
--- /dev/null
+++ b/peft/src/peft/tuners/__init__.py
@@ -0,0 +1,124 @@
+# Copyright 2023-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+from .adalora import AdaLoraConfig, AdaLoraModel
+from .adaption_prompt import AdaptionPromptConfig, AdaptionPromptModel
+from .boft import BOFTConfig, BOFTModel
+from .bone import BoneConfig, BoneModel
+from .c3a import C3AConfig, C3AModel
+from .cpt import CPTConfig, CPTEmbedding
+from .fourierft import FourierFTConfig, FourierFTModel
+from .hra import HRAConfig, HRAModel
+from .ia3 import IA3Config, IA3Model
+from .ln_tuning import LNTuningConfig, LNTuningModel
+from .loha import LoHaConfig, LoHaModel
+from .lokr import LoKrConfig, LoKrModel
+from .lora import (
+ ArrowConfig,
+ EvaConfig,
+ LoftQConfig,
+ LoraConfig,
+ LoraModel,
+ LoraRuntimeConfig,
+ create_arrow_model,
+ get_eva_state_dict,
+ initialize_lora_eva_weights,
+)
+from .miss import MissConfig, MissModel
+from .mixed import MixedModel
+from .multitask_prompt_tuning import MultitaskPromptEmbedding, MultitaskPromptTuningConfig, MultitaskPromptTuningInit
+from .oft import OFTConfig, OFTModel
+from .p_tuning import PromptEncoder, PromptEncoderConfig, PromptEncoderReparameterizationType
+from .poly import PolyConfig, PolyModel
+from .prefix_tuning import PrefixEncoder, PrefixTuningConfig
+from .prompt_tuning import PromptEmbedding, PromptTuningConfig, PromptTuningInit
+from .randlora import RandLoraConfig, RandLoraModel
+from .road import RoadConfig, RoadModel
+from .shira import ShiraConfig, ShiraModel
+from .trainable_tokens import TrainableTokensConfig, TrainableTokensModel
+from .vblora import VBLoRAConfig, VBLoRAModel
+from .vera import VeraConfig, VeraModel
+from .waveft import WaveFTConfig, WaveFTModel
+from .xlora import XLoraConfig, XLoraModel
+
+
+__all__ = [
+ "AdaLoraConfig",
+ "AdaLoraModel",
+ "AdaptionPromptConfig",
+ "AdaptionPromptModel",
+ "ArrowConfig",
+ "BOFTConfig",
+ "BOFTModel",
+ "BoneConfig",
+ "BoneModel",
+ "C3AConfig",
+ "C3AModel",
+ "CPTConfig",
+ "CPTEmbedding",
+ "EvaConfig",
+ "FourierFTConfig",
+ "FourierFTModel",
+ "HRAConfig",
+ "HRAModel",
+ "IA3Config",
+ "IA3Model",
+ "LNTuningConfig",
+ "LNTuningModel",
+ "LoHaConfig",
+ "LoHaModel",
+ "LoKrConfig",
+ "LoKrModel",
+ "LoftQConfig",
+ "LoraConfig",
+ "LoraModel",
+ "LoraRuntimeConfig",
+ "MissConfig",
+ "MissModel",
+ "MixedModel",
+ "MultitaskPromptEmbedding",
+ "MultitaskPromptTuningConfig",
+ "MultitaskPromptTuningInit",
+ "OFTConfig",
+ "OFTModel",
+ "PolyConfig",
+ "PolyModel",
+ "PrefixEncoder",
+ "PrefixTuningConfig",
+ "PromptEmbedding",
+ "PromptEncoder",
+ "PromptEncoderConfig",
+ "PromptEncoderReparameterizationType",
+ "PromptTuningConfig",
+ "PromptTuningInit",
+ "RandLoraConfig",
+ "RandLoraModel",
+ "RoadConfig",
+ "RoadModel",
+ "ShiraConfig",
+ "ShiraModel",
+ "TrainableTokensConfig",
+ "TrainableTokensModel",
+ "VBLoRAConfig",
+ "VBLoRAModel",
+ "VeraConfig",
+ "VeraModel",
+ "WaveFTConfig",
+ "WaveFTModel",
+ "XLoraConfig",
+ "XLoraModel",
+ "create_arrow_model",
+ "get_eva_state_dict",
+ "initialize_lora_eva_weights",
+]
diff --git a/peft/src/peft/tuners/_buffer_dict.py b/peft/src/peft/tuners/_buffer_dict.py
new file mode 100644
index 0000000000000000000000000000000000000000..16e8fae5ac164ee952780fefc1e247f08ff54909
--- /dev/null
+++ b/peft/src/peft/tuners/_buffer_dict.py
@@ -0,0 +1,159 @@
+# Copyright (c) Meta Platforms, Inc. and affiliates.
+#
+# This source code is licensed under the MIT license found in the
+# LICENSE file in the root directory of this source tree.
+
+# Adapted from https://botorch.org/api/_modules/botorch/utils/torch.html
+
+# TODO: To be removed once (if) https://github.com/pytorch/pytorch/pull/37385 lands
+
+from __future__ import annotations
+
+import collections
+from collections import OrderedDict
+
+import torch
+from torch.nn import Module
+
+
+class BufferDict(Module):
+ r"""
+ Holds buffers in a dictionary.
+
+ BufferDict can be indexed like a regular Python dictionary, but buffers it contains are properly registered, and
+ will be visible by all Module methods. `torch.nn.BufferDict` is an **ordered** dictionary that respects
+
+ * the order of insertion, and
+ * in `torch.nn.BufferDict.update`, the order of the merged `OrderedDict` or another `torch.nn.BufferDict` (the
+ argument to `torch.nn.BufferDict.update`).
+
+ Note that `torch.nn.BufferDict.update` with other unordered mapping types (e.g., Python's plain `dict`) does not
+ preserve the order of the merged mapping.
+
+ Args:
+ buffers (iterable, optional):
+ a mapping (dictionary) of (string : `torch.Tensor`) or an iterable of key-value pairs of type (string,
+ `torch.Tensor`)
+
+ ```python
+ class MyModule(nn.Module):
+ def __init__(self):
+ super().__init__()
+ self.buffers = nn.BufferDict({"left": torch.randn(5, 10), "right": torch.randn(5, 10)})
+
+ def forward(self, x, choice):
+ x = self.buffers[choice].mm(x)
+ return x
+ ```
+ """
+
+ def __init__(self, buffers=None, persistent: bool = False):
+ r"""
+ Args:
+ buffers (`dict`):
+ A mapping (dictionary) from string to `torch.Tensor`, or an iterable of key-value pairs of type
+ (string, `torch.Tensor`).
+ """
+ super().__init__()
+ self.persistent = persistent
+
+ if buffers is not None:
+ self.update(buffers)
+
+ def __getitem__(self, key):
+ return self._buffers[key]
+
+ def __setitem__(self, key, buffer):
+ self.register_buffer(key, buffer, persistent=self.persistent)
+
+ def __delitem__(self, key):
+ del self._buffers[key]
+
+ def __len__(self):
+ return len(self._buffers)
+
+ def __iter__(self):
+ return iter(self._buffers.keys())
+
+ def __contains__(self, key):
+ return key in self._buffers
+
+ def clear(self):
+ """Remove all items from the BufferDict."""
+ self._buffers.clear()
+
+ def pop(self, key):
+ r"""Remove key from the BufferDict and return its buffer.
+
+ Args:
+ key (`str`):
+ Key to pop from the BufferDict
+ """
+ v = self[key]
+ del self[key]
+ return v
+
+ def keys(self):
+ r"""Return an iterable of the BufferDict keys."""
+ return self._buffers.keys()
+
+ def items(self):
+ r"""Return an iterable of the BufferDict key/value pairs."""
+ return self._buffers.items()
+
+ def values(self):
+ r"""Return an iterable of the BufferDict values."""
+ return self._buffers.values()
+
+ def update(self, buffers):
+ r"""
+ Update the `torch.nn.BufferDict` with the key-value pairs from a mapping or an iterable, overwriting existing
+ keys.
+
+ Note:
+ If `buffers` is an `OrderedDict`, a `torch.nn.BufferDict`, or an iterable of key-value pairs, the order of
+ new elements in it is preserved.
+
+ Args:
+ buffers (iterable):
+ a mapping (dictionary) from string to `torch.Tensor`, or an iterable of key-value pairs of type
+ (string, `torch.Tensor`).
+ """
+ if not isinstance(buffers, collections.abc.Iterable):
+ raise TypeError(
+ "BuffersDict.update should be called with an "
+ "iterable of key/value pairs, but got " + type(buffers).__name__
+ )
+
+ if isinstance(buffers, (OrderedDict, BufferDict)):
+ for key, buffer in buffers.items():
+ self[key] = buffer
+ elif isinstance(buffers, collections.abc.Mapping):
+ for key, buffer in sorted(buffers.items()):
+ self[key] = buffer
+ else:
+ for j, p in enumerate(buffers):
+ if not isinstance(p, collections.abc.Iterable):
+ raise TypeError(
+ "BufferDict update sequence element #" + str(j) + " should be Iterable; is" + type(p).__name__
+ )
+ if not len(p) == 2:
+ raise ValueError(
+ "BufferDict update sequence element "
+ "#" + str(j) + " has length " + str(len(p)) + "; 2 is required"
+ )
+ self[p[0]] = p[1]
+
+ def extra_repr(self):
+ child_lines = []
+ for k, p in self._buffers.items():
+ size_str = "x".join(str(size) for size in p.size())
+ device_type = p.device.type
+ device_str = "" if device_type == "cpu" else f" ({device_type.upper()} {p.get_device()})"
+ parastr = f"Buffer containing: [{torch.typename(p)} of size {size_str}{device_str}]"
+ child_lines.append(" (" + k + "): " + parastr)
+ tmpstr = "\n".join(child_lines)
+ return tmpstr
+
+ def __call__(self, input):
+ raise RuntimeError("BufferDict should not be called.")
diff --git a/peft/src/peft/tuners/adalora/__init__.py b/peft/src/peft/tuners/adalora/__init__.py
new file mode 100644
index 0000000000000000000000000000000000000000..64d5f3e5ce6ba3c5873f01ee88f4c4766e1fde75
--- /dev/null
+++ b/peft/src/peft/tuners/adalora/__init__.py
@@ -0,0 +1,43 @@
+# Copyright 2023-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+from peft.import_utils import is_bnb_4bit_available, is_bnb_available
+from peft.utils import register_peft_method
+
+from .config import AdaLoraConfig
+from .gptq import SVDQuantLinear
+from .layer import AdaLoraLayer, RankAllocator, SVDLinear
+from .model import AdaLoraModel
+
+
+__all__ = ["AdaLoraConfig", "AdaLoraLayer", "AdaLoraModel", "RankAllocator", "SVDLinear", "SVDQuantLinear"]
+
+
+register_peft_method(
+ name="adalora", config_cls=AdaLoraConfig, model_cls=AdaLoraModel, prefix="lora_", is_mixed_compatible=True
+)
+
+
+def __getattr__(name):
+ if (name == "SVDLinear8bitLt") and is_bnb_available():
+ from .bnb import SVDLinear8bitLt
+
+ return SVDLinear8bitLt
+
+ if (name == "SVDLinear4bit") and is_bnb_4bit_available():
+ from .bnb import SVDLinear4bit
+
+ return SVDLinear4bit
+
+ raise AttributeError(f"module {__name__} has no attribute {name}")
diff --git a/peft/src/peft/tuners/adalora/bnb.py b/peft/src/peft/tuners/adalora/bnb.py
new file mode 100644
index 0000000000000000000000000000000000000000..fef3d25e65c459d20855e49832aabe56881734c0
--- /dev/null
+++ b/peft/src/peft/tuners/adalora/bnb.py
@@ -0,0 +1,143 @@
+# Copyright 2023-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+from typing import Any
+
+import torch
+
+from peft.import_utils import is_bnb_4bit_available, is_bnb_available
+
+from .layer import AdaLoraLayer
+
+
+if is_bnb_available():
+
+ class SVDLinear8bitLt(torch.nn.Module, AdaLoraLayer):
+ # Low-rank matrix for SVD-based adaptation
+ def __init__(
+ self,
+ base_layer: torch.nn.Module,
+ adapter_name: str,
+ r: int = 0,
+ lora_alpha: int = 1,
+ lora_dropout: float = 0.0,
+ init_lora_weights: bool = True,
+ **kwargs,
+ ) -> None:
+ super().__init__()
+ AdaLoraLayer.__init__(self, base_layer)
+ # Freezing the pre-trained weight matrix
+ self.get_base_layer().weight.requires_grad = False
+
+ self._active_adapter = adapter_name
+ self.update_layer(adapter_name, r, lora_alpha, lora_dropout, init_lora_weights)
+
+ def forward(self, x: torch.Tensor) -> torch.Tensor:
+ # note: no check for self.merged because merging is not supported (yet)
+ result = self.base_layer(x)
+
+ if self.disable_adapters:
+ return result
+
+ for active_adapter in self.active_adapters:
+ if active_adapter not in self.lora_A.keys():
+ continue
+ requires_conversion = not torch.is_autocast_enabled()
+ if requires_conversion:
+ expected_dtype = result.dtype
+ if x.dtype != torch.float32:
+ x = x.float()
+
+ lora_A = self.lora_A[active_adapter]
+ lora_B = self.lora_B[active_adapter]
+ lora_E = self.lora_E[active_adapter]
+ dropout = self.lora_dropout[active_adapter]
+ scaling = self.scaling[active_adapter]
+ ranknum = self.ranknum[active_adapter] + 1e-5
+
+ output = dropout(x) @ (lora_A * lora_E).T @ lora_B.T
+ if requires_conversion:
+ output = output.to(expected_dtype)
+ output = output * scaling / ranknum
+ # inplace operation on view is forbidden for MatMul8bitLtBackward, so avoid it
+ result = result + output
+ return result
+
+ def __repr__(self) -> str:
+ rep = super().__repr__()
+ return "adalora." + rep
+
+
+if is_bnb_4bit_available():
+
+ class SVDLinear4bit(torch.nn.Module, AdaLoraLayer):
+ # Low-rank matrix for SVD-based adaptation
+ def __init__(
+ self,
+ base_layer: torch.nn.Module,
+ adapter_name: str,
+ r: int = 0,
+ lora_alpha: int = 1,
+ lora_dropout: float = 0.0,
+ init_lora_weights: bool = True,
+ **kwargs,
+ ) -> None:
+ super().__init__()
+ AdaLoraLayer.__init__(self, base_layer)
+ # Freezing the pre-trained weight matrix
+ self.get_base_layer().weight.requires_grad = False
+
+ self._active_adapter = adapter_name
+ self.update_layer(adapter_name, r, lora_alpha, lora_dropout, init_lora_weights)
+
+ def forward(self, x: torch.Tensor, *args: Any, **kwargs: Any) -> torch.Tensor:
+ # note: no check for self.merged because merging is not supported (yet)
+ result = self.base_layer(x, *args, **kwargs)
+
+ if self.disable_adapters:
+ return result
+
+ # As per Tim Dettmers, for 4bit, we need to defensively clone here.
+ # The reason is that in some cases, an error can occur that backprop
+ # does not work on a manipulated view. This issue may be solved with
+ # newer PyTorch versions but this would need extensive testing to be
+ # sure.
+ result = result.clone()
+
+ for active_adapter in self.active_adapters:
+ if active_adapter not in self.lora_A.keys():
+ continue
+
+ lora_A = self.lora_A[active_adapter]
+ lora_B = self.lora_B[active_adapter]
+ lora_E = self.lora_E[active_adapter]
+ dropout = self.lora_dropout[active_adapter]
+ scaling = self.scaling[active_adapter]
+ ranknum = self.ranknum[active_adapter] + 1e-5
+
+ requires_conversion = not torch.is_autocast_enabled()
+ if requires_conversion:
+ expected_dtype = result.dtype
+ x = self._cast_input_dtype(x, lora_A.dtype)
+
+ output = dropout(x) @ (lora_A * lora_E).T @ lora_B.T
+ if requires_conversion:
+ output = output.to(expected_dtype)
+ output = output * scaling / ranknum
+ result += output
+ return result
+
+ def __repr__(self) -> str:
+ rep = super().__repr__()
+ return "adalora." + rep
diff --git a/peft/src/peft/tuners/adalora/config.py b/peft/src/peft/tuners/adalora/config.py
new file mode 100644
index 0000000000000000000000000000000000000000..004c26b0fe5ecf88212bd11de062baec2f10de83
--- /dev/null
+++ b/peft/src/peft/tuners/adalora/config.py
@@ -0,0 +1,108 @@
+# Copyright 2023-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+import warnings
+from dataclasses import dataclass, field
+from typing import Optional
+
+from peft.tuners.lora import LoraConfig
+from peft.utils import PeftType
+
+
+@dataclass
+class AdaLoraConfig(LoraConfig):
+ """
+ This is the configuration class to store the configuration of a [`~peft.AdaLora`].
+
+ AdaLoRA has three phases defined by `tinit`, `tfinal` and `total_step`.
+
+ The initial phase can be understood as a step for pre-training the adapters so that when reducing their rank, there
+ is already some information encoded that can be reduced instead of random matrices. This phase is defined by
+ supplying `tinit`.
+
+ After the initial phase is over (`tinit` steps have passed) and the final phase has not begun, AdaLoRA reduces the
+ budget of how much rank each layer is allowed to have with each step. This is where the reduction of rank is
+ happening. This goes on until `total_step - tfinal` steps are reached.
+
+ The last phase, beginning once `total_step - tfinal` steps are reached, does not change the layer ranks anymore but
+ fine-tunes the reduced-rank layers that resulted from the previous phase.
+
+ A practical example: `tinit` is 10, `tfinal` is 20, `total_step` is 100. We spend 10 steps doing pre-training
+ without rank reduction because our budget is constant (init phase), then we spend 80 (100-20) steps in the
+ reduction phase where our budget decreases step-wise and, finally, 20 steps in the final fine-tuning stage without
+ reduction.
+
+ Args:
+ target_r (`int`): The target average rank of incremental matrix.
+ init_r (`int`): The initial rank for each incremental matrix.
+ tinit (`int`): The steps of initial fine-tuning warmup.
+ tfinal (`int`): The number of steps of final fine-tuning.
+ deltaT (`int`): The time internval between two budget allocations.
+ beta1 (`float`): The hyperparameter of EMA for sensitivity smoothing.
+ beta2 (`float`): The hyperparameter of EMA for undertainty quantification.
+ orth_reg_weight (`float`): The coefficient of orthogonal regularization.
+ total_step (`int`): The total training steps that should be specified before training.
+ rank_pattern (`list`): The allocated rank for each weight matrix by RankAllocator.
+ """
+
+ target_r: int = field(default=8, metadata={"help": "Target Lora matrix dimension."})
+ init_r: int = field(default=12, metadata={"help": "Initial Lora matrix dimension."})
+ tinit: int = field(default=0, metadata={"help": "The steps of initial warmup."})
+ tfinal: int = field(default=0, metadata={"help": "The steps of final warmup."})
+ deltaT: int = field(default=1, metadata={"help": "Step interval of rank allocation."})
+ beta1: float = field(default=0.85, metadata={"help": "Hyperparameter of EMA."})
+ beta2: float = field(default=0.85, metadata={"help": "Hyperparameter of EMA."})
+ orth_reg_weight: float = field(default=0.5, metadata={"help": "The orthogonal regularization coefficient."})
+ total_step: Optional[int] = field(default=None, metadata={"help": "The total training steps."})
+ rank_pattern: Optional[dict] = field(default=None, metadata={"help": "The saved rank pattern."})
+
+ def __post_init__(self):
+ super().__post_init__()
+ self.peft_type = PeftType.ADALORA
+
+ if self.use_dora:
+ raise ValueError(f"{self.peft_type} does not support DoRA.")
+
+ if self.loftq_config:
+ raise ValueError(f"{self.peft_type} does not support LOFTQ.")
+
+ self.target_modules = (
+ set(self.target_modules) if isinstance(self.target_modules, list) else self.target_modules
+ )
+ self.exclude_modules = (
+ set(self.exclude_modules) if isinstance(self.exclude_modules, list) else self.exclude_modules
+ )
+ # if target_modules is a regex expression, then layers_to_transform should be None
+ if isinstance(self.target_modules, str) and self.layers_to_transform is not None:
+ raise ValueError("`layers_to_transform` cannot be used when `target_modules` is a str.")
+
+ # check for layers_to_transform and layers_pattern
+ if self.layers_pattern and not self.layers_to_transform:
+ raise ValueError("When `layers_pattern` is specified, `layers_to_transform` must also be specified. ")
+
+ # Check if 'r' has been set to a non-default value
+ if self.r != 8: # 8 is the default value for 'r' in LoraConfig
+ warnings.warn(
+ "Note that `r` is not used in AdaLora and will be ignored."
+ "If you intended to set the initial rank, use `init_r` instead."
+ )
+
+ if self.total_step is None or self.total_step <= 0:
+ raise ValueError("AdaLoRA does not work when `total_step` is None, supply a value > 0.")
+
+ if self.tinit >= (self.total_step - self.tfinal):
+ raise ValueError(
+ "The supplied schedule values don't allow for a budgeting phase. Decrease `tfinal`/`tinit` or "
+ "increase `total_step`."
+ )
diff --git a/peft/src/peft/tuners/adalora/gptq.py b/peft/src/peft/tuners/adalora/gptq.py
new file mode 100644
index 0000000000000000000000000000000000000000..bed1a0a7ca8dabb9d068bcf2470a97e34ec348fe
--- /dev/null
+++ b/peft/src/peft/tuners/adalora/gptq.py
@@ -0,0 +1,71 @@
+# Copyright 2023-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+import torch
+
+from .layer import AdaLoraLayer
+
+
+class SVDQuantLinear(torch.nn.Module, AdaLoraLayer):
+ def __init__(
+ self,
+ base_layer,
+ adapter_name,
+ r: int = 0,
+ lora_alpha: int = 1,
+ lora_dropout: float = 0.0,
+ init_lora_weights: bool = True,
+ **kwargs,
+ ) -> None:
+ super().__init__()
+ AdaLoraLayer.__init__(self, base_layer)
+
+ # self.base_layer and self.quant_linear_module are the same; we need the former for consistency and the latter
+ # for backwards compatibility
+ self.quant_linear_module = base_layer
+ self._active_adapter = adapter_name
+ self.update_layer(adapter_name, r, lora_alpha, lora_dropout, init_lora_weights)
+
+ def forward(self, x: torch.Tensor) -> torch.Tensor:
+ result = self.quant_linear_module(x)
+
+ if self.disable_adapters:
+ return result
+
+ for active_adapter in self.active_adapters:
+ if active_adapter not in self.lora_A.keys():
+ continue
+ lora_A = self.lora_A[active_adapter]
+ lora_B = self.lora_B[active_adapter]
+ lora_E = self.lora_E[active_adapter]
+ dropout = self.lora_dropout[active_adapter]
+ scaling = self.scaling[active_adapter]
+ ranknum = self.ranknum[active_adapter] + 1e-5
+
+ requires_conversion = not torch.is_autocast_enabled()
+ if requires_conversion:
+ expected_dtype = result.dtype
+ x = self._cast_input_dtype(x, torch.float32)
+
+ output = (dropout(x) @ (lora_A * lora_E).T @ lora_B.T) * scaling / ranknum
+ # TODO: here, the dtype conversion is applied on the *whole expression*,
+ # not the intermediate result, unlike for SVDLinear8bitLT and
+ # SVDLinear4bit, is that correct?
+ if requires_conversion:
+ output = output.to(expected_dtype)
+ result += output
+ return result
+
+ def __repr__(self) -> str:
+ rep = super().__repr__()
+ return "adalora." + rep
diff --git a/peft/src/peft/tuners/adalora/layer.py b/peft/src/peft/tuners/adalora/layer.py
new file mode 100644
index 0000000000000000000000000000000000000000..635e5105515df70abac2af5b17174be8f1ed8052
--- /dev/null
+++ b/peft/src/peft/tuners/adalora/layer.py
@@ -0,0 +1,360 @@
+# Copyright 2023-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+import warnings
+from typing import Any, Optional
+
+import packaging
+import torch
+import transformers
+from torch import nn
+
+from peft.tuners.lora import LoraLayer
+from peft.tuners.tuners_utils import check_adapters_to_merge
+from peft.utils import transpose
+
+
+if packaging.version.parse(transformers.__version__) >= packaging.version.parse("4.33.0"):
+ from transformers.integrations import deepspeed_config
+else:
+ from transformers.deepspeed import deepspeed_config
+
+
+class AdaLoraLayer(LoraLayer):
+ # List all names of layers that may contain adapter weights
+ # Note: ranknum doesn't need to be included as it is not an nn.Module
+ adapter_layer_names = ("lora_A", "lora_B", "lora_E", "lora_embedding_A", "lora_embedding_B")
+ # All names of other parameters that may contain adapter-related parameters
+ other_param_names = ("r", "lora_alpha", "scaling", "lora_dropout", "ranknum")
+
+ def __init__(self, base_layer: nn.Module) -> None:
+ super().__init__(base_layer)
+ self.lora_E = nn.ParameterDict({})
+ self.lora_A = nn.ParameterDict({})
+ self.lora_B = nn.ParameterDict({})
+ self.ranknum = nn.ParameterDict({})
+
+ def update_layer(
+ self, adapter_name, r, lora_alpha, lora_dropout, init_lora_weights, inference_mode: bool = False, **kwargs
+ ):
+ if r < 0:
+ # note: r == 0 is allowed for AdaLora, see #1539
+ raise ValueError(f"`r` should be a positive integer or 0, but the value passed is {r}")
+
+ self.r[adapter_name] = r
+ self.lora_alpha[adapter_name] = lora_alpha
+ if lora_dropout > 0.0:
+ lora_dropout_layer = nn.Dropout(p=lora_dropout)
+ else:
+ lora_dropout_layer = nn.Identity()
+
+ self.lora_dropout[adapter_name] = lora_dropout_layer
+ # Actual trainable parameters
+ # Right singular vectors
+ self.lora_A[adapter_name] = nn.Parameter(torch.randn(r, self.in_features))
+ # Singular values
+ self.lora_E[adapter_name] = nn.Parameter(torch.randn(r, 1))
+ # Left singular vectors
+ self.lora_B[adapter_name] = nn.Parameter(torch.randn(self.out_features, r))
+ # The current rank
+ self.ranknum[adapter_name] = nn.Parameter(torch.randn(1), requires_grad=False)
+ self.ranknum[adapter_name].data.fill_(float(r))
+ self.ranknum[adapter_name].requires_grad = False
+ self.scaling[adapter_name] = lora_alpha if lora_alpha > 0 else float(r)
+ if init_lora_weights:
+ self.reset_lora_parameters(adapter_name)
+
+ self._move_adapter_to_device_of_base_layer(adapter_name)
+ self.set_adapter(self.active_adapters, inference_mode=inference_mode)
+
+ def reset_lora_parameters(self, adapter_name):
+ if adapter_name in self.lora_A.keys():
+ nn.init.zeros_(self.lora_E[adapter_name])
+ nn.init.normal_(self.lora_A[adapter_name], mean=0.0, std=0.02)
+ nn.init.normal_(self.lora_B[adapter_name], mean=0.0, std=0.02)
+
+
+class SVDLinear(nn.Module, AdaLoraLayer):
+ # SVD-based adaptation by a dense layer
+ def __init__(
+ self,
+ base_layer: nn.Module,
+ adapter_name: str,
+ r: int = 0,
+ lora_alpha: int = 1,
+ lora_dropout: float = 0.0,
+ fan_in_fan_out: bool = False,
+ init_lora_weights: bool = True,
+ **kwargs,
+ ) -> None:
+ super().__init__()
+ AdaLoraLayer.__init__(self, base_layer)
+ # Freezing the pre-trained weight matrix
+ self.get_base_layer().weight.requires_grad = False
+
+ self.fan_in_fan_out = fan_in_fan_out
+ self._active_adapter = adapter_name
+ self.update_layer(adapter_name, r, lora_alpha, lora_dropout, init_lora_weights)
+
+ def merge(self, safe_merge: bool = False, adapter_names: Optional[list[str]] = None) -> None:
+ """
+ Merge the active adapter weights into the base weights
+
+ Args:
+ safe_merge (`bool`, *optional*):
+ If True, the merge operation will be performed in a copy of the original weights and check for NaNs
+ before merging the weights. This is useful if you want to check if the merge operation will produce
+ NaNs. Defaults to `False`.
+ adapter_names (`List[str]`, *optional*):
+ The list of adapter names that should be merged. If None, all active adapters will be merged. Defaults
+ to `None`.
+ """
+ adapter_names = check_adapters_to_merge(self, adapter_names)
+ if not adapter_names:
+ # no adapter to merge
+ return
+
+ for active_adapter in adapter_names:
+ base_layer = self.get_base_layer()
+ if active_adapter in self.lora_A.keys():
+ if safe_merge:
+ # Note that safe_merge will be slower than the normal merge
+ # because of the copy operation.
+ orig_weights = base_layer.weight.data.clone()
+ orig_weights += self.get_delta_weight(active_adapter)
+
+ if not torch.isfinite(orig_weights).all():
+ raise ValueError(
+ f"NaNs detected in the merged weights. The adapter {active_adapter} seems to be broken"
+ )
+
+ base_layer.weight.data = orig_weights
+ else:
+ base_layer.weight.data += self.get_delta_weight(active_adapter)
+ self.merged_adapters.append(active_adapter)
+
+ def unmerge(self) -> None:
+ """
+ This method unmerges all merged adapter layers from the base weights.
+ """
+ if not self.merged:
+ warnings.warn("Already unmerged. Nothing to do.")
+ return
+ while len(self.merged_adapters) > 0:
+ active_adapter = self.merged_adapters.pop()
+ if active_adapter in self.lora_A.keys():
+ self.get_base_layer().weight.data -= self.get_delta_weight(active_adapter)
+
+ def get_delta_weight(self, adapter) -> torch.Tensor:
+ return (
+ transpose(self.lora_B[adapter] @ (self.lora_A[adapter] * self.lora_E[adapter]), self.fan_in_fan_out)
+ * self.scaling[adapter]
+ / (self.ranknum[adapter] + 1e-5)
+ )
+
+ def forward(self, x: torch.Tensor, *args: Any, **kwargs: Any) -> torch.Tensor:
+ if self.disable_adapters:
+ if self.merged:
+ self.unmerge()
+ result = self.base_layer(x, *args, **kwargs)
+ elif self.merged:
+ result = self.base_layer(x, *args, **kwargs)
+ else:
+ result = self.base_layer(x, *args, **kwargs)
+ for active_adapter in self.active_adapters:
+ if active_adapter not in self.lora_A.keys():
+ continue
+ lora_A = self.lora_A[active_adapter]
+ lora_B = self.lora_B[active_adapter]
+ lora_E = self.lora_E[active_adapter]
+ dropout = self.lora_dropout[active_adapter]
+ scaling = self.scaling[active_adapter]
+ ranknum = self.ranknum[active_adapter] + 1e-5
+
+ x = self._cast_input_dtype(x, lora_A.dtype)
+ result += (dropout(x) @ (lora_A * lora_E).T @ lora_B.T) * scaling / ranknum
+
+ return result
+
+ def __repr__(self) -> str:
+ rep = super().__repr__()
+ return "adalora." + rep
+
+
+class RankAllocator:
+ """
+ The RankAllocator for AdaLoraModel. Paper: https://openreview.net/pdf?id=lq62uWRJjiY
+
+ Args:
+ config ([`AdaLoraConfig`]): The configuration of the AdaLora model.
+ model: the model that we apply AdaLoRA to.
+
+ """
+
+ def __init__(self, model, peft_config, adapter_name):
+ self.peft_config = peft_config
+ self.adapter_name = adapter_name
+ self.beta1 = peft_config.beta1
+ self.beta2 = peft_config.beta2
+ assert self.beta1 > 0 and self.beta1 < 1
+ assert self.beta2 > 0 and self.beta2 < 1
+
+ self.reset_ipt()
+ self._set_budget_scheduler(model)
+
+ def set_total_step(self, total_step):
+ self.peft_config.total_step = total_step
+
+ def reset_ipt(self):
+ self.ipt = {}
+ self.exp_avg_ipt = {}
+ self.exp_avg_unc = {}
+
+ def _set_budget_scheduler(self, model):
+ self.init_bgt = 0
+ self.name_set = set()
+ for n, p in model.named_parameters():
+ if f"lora_A.{self.adapter_name}" in n:
+ self.init_bgt += p.size(0)
+ self.name_set.add(n.replace("lora_A", "%s"))
+ self.name_set = sorted(self.name_set)
+ # The total final rank budget
+ self.target_bgt = self.peft_config.target_r * len(self.name_set)
+
+ def budget_schedule(self, step: int):
+ tinit = self.peft_config.tinit
+ tfinal = self.peft_config.tfinal
+ total_step = self.peft_config.total_step
+ # Initial warmup
+ if step <= tinit:
+ budget = self.init_bgt
+ mask_ind = False
+ # Final fine-tuning
+ elif step > total_step - tfinal:
+ budget = self.target_bgt
+ mask_ind = True
+ else:
+ # Budget decreasing with a cubic scheduler
+ mul_coeff = 1 - (step - tinit) / (total_step - tfinal - tinit)
+ budget = int((self.init_bgt - self.target_bgt) * (mul_coeff**3) + self.target_bgt)
+ mask_ind = True if step % self.peft_config.deltaT == 0 else False
+ return budget, mask_ind
+
+ def update_ipt(self, model):
+ # Update the sensitivity and uncertainty for every weight
+ for n, p in model.named_parameters():
+ if "lora_" in n and self.adapter_name in n:
+ if n not in self.ipt:
+ self.ipt[n] = torch.zeros_like(p)
+ self.exp_avg_ipt[n] = torch.zeros_like(p)
+ self.exp_avg_unc[n] = torch.zeros_like(p)
+ with torch.no_grad():
+ if deepspeed_config() is not None:
+ import deepspeed
+
+ grad = deepspeed.utils.safe_get_full_grad(p)
+ self.ipt[n] = (p * grad).abs().detach()
+ else:
+ self.ipt[n] = (p * p.grad).abs().detach()
+ # Sensitivity smoothing
+ self.exp_avg_ipt[n] = self.beta1 * self.exp_avg_ipt[n] + (1 - self.beta1) * self.ipt[n]
+ # Uncertainty quantification
+ self.exp_avg_unc[n] = (
+ self.beta2 * self.exp_avg_unc[n] + (1 - self.beta2) * (self.ipt[n] - self.exp_avg_ipt[n]).abs()
+ )
+
+ def _element_score(self, n):
+ return self.exp_avg_ipt[n] * self.exp_avg_unc[n]
+
+ def _combine_ipt(self, ipt_E, ipt_AB):
+ ipt_AB = ipt_AB.sum(dim=1, keepdim=False)
+ sum_ipt = ipt_E.view(-1) + ipt_AB.view(-1)
+ return sum_ipt
+
+ def mask_to_budget(self, model, budget):
+ value_ipt = {}
+ vector_ipt = {}
+ triplet_ipt = {}
+ # Get the importance score for A, E, B
+ for n, p in model.named_parameters():
+ if f"lora_A.{self.adapter_name}" in n:
+ entry_ipt = self._element_score(n)
+ comb_ipt = torch.mean(entry_ipt, dim=1, keepdim=True)
+ name_m = n.replace("lora_A", "%s")
+ if name_m not in vector_ipt:
+ vector_ipt[name_m] = [comb_ipt]
+ else:
+ vector_ipt[name_m].append(comb_ipt)
+ if f"lora_B.{self.adapter_name}" in n:
+ entry_ipt = self._element_score(n)
+ comb_ipt = torch.mean(entry_ipt, dim=0, keepdim=False).view(-1, 1)
+ name_m = n.replace("lora_B", "%s")
+ if name_m not in vector_ipt:
+ vector_ipt[name_m] = [comb_ipt]
+ else:
+ vector_ipt[name_m].append(comb_ipt)
+ if f"lora_E.{self.adapter_name}" in n:
+ entry_ipt = self._element_score(n)
+ name_m = n.replace("lora_E", "%s")
+ value_ipt[name_m] = entry_ipt
+
+ all_score = []
+ # Calculate the score for each triplet
+ for name_m in vector_ipt:
+ ipt_E = value_ipt[name_m]
+ ipt_AB = torch.cat(vector_ipt[name_m], dim=1)
+ sum_ipt = self._combine_ipt(ipt_E, ipt_AB)
+ name_E = name_m % "lora_E"
+ triplet_ipt[name_E] = sum_ipt.view(-1, 1)
+ all_score.append(sum_ipt.view(-1))
+
+ # Get the threshold by ranking ipt
+ mask_threshold = torch.kthvalue(
+ torch.cat(all_score),
+ k=self.init_bgt - budget,
+ )[0].item()
+
+ rank_pattern = {}
+ # Mask the unimportant triplets
+ with torch.no_grad():
+ for n, p in model.named_parameters():
+ if f"lora_E.{self.adapter_name}" in n:
+ p.masked_fill_(triplet_ipt[n] <= mask_threshold, 0.0)
+ rank_pattern[n] = (~(triplet_ipt[n] <= mask_threshold)).view(-1).tolist()
+ return rank_pattern
+
+ def update_and_allocate(self, model, global_step, force_mask=False):
+ # # Update the importance score and allocate the budget
+ if global_step < self.peft_config.total_step - self.peft_config.tfinal:
+ self.update_ipt(model)
+ budget, mask_ind = self.budget_schedule(global_step)
+ # Allocate the budget according to importance scores
+ if mask_ind or force_mask:
+ rank_pattern = self.mask_to_budget(model, budget)
+ else:
+ rank_pattern = None
+ return budget, rank_pattern
+
+ def mask_using_rank_pattern(self, model, rank_pattern):
+ # Mask the unimportant triplets
+ is_adapter_name_truncated = False
+ if self.adapter_name not in next(iter(rank_pattern.keys())):
+ is_adapter_name_truncated = True
+
+ with torch.no_grad():
+ for n, p in model.named_parameters():
+ if f"lora_E.{self.adapter_name}" in n:
+ key = n if not is_adapter_name_truncated else n.replace(f".{self.adapter_name}", "")
+ mask = torch.Tensor(rank_pattern[key]).unsqueeze(-1).to(p.device)
+ p.masked_fill_(~mask.bool(), 0.0)
diff --git a/peft/src/peft/tuners/adalora/model.py b/peft/src/peft/tuners/adalora/model.py
new file mode 100644
index 0000000000000000000000000000000000000000..c5c345c0ef8f5f99b1bff8a65619ad4f16c9c449
--- /dev/null
+++ b/peft/src/peft/tuners/adalora/model.py
@@ -0,0 +1,346 @@
+# Copyright 2023-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+import warnings
+
+import torch
+from transformers.pytorch_utils import Conv1D
+
+from peft.import_utils import is_bnb_4bit_available, is_bnb_available, is_gptqmodel_available
+from peft.tuners.lora import LoraConfig, LoraModel
+from peft.tuners.tuners_utils import BaseTunerLayer
+from peft.utils import (
+ TRANSFORMERS_MODELS_TO_ADALORA_TARGET_MODULES_MAPPING,
+ _freeze_adapter,
+ _get_submodules,
+ get_auto_gptq_quant_linear,
+ get_gptqmodel_quant_linear,
+ get_quantization_config,
+)
+from peft.utils.integrations import gather_params_ctx
+
+from .gptq import SVDQuantLinear
+from .layer import AdaLoraLayer, RankAllocator, SVDLinear
+
+
+class AdaLoraModel(LoraModel):
+ """
+ Creates AdaLoRA (Adaptive LoRA) model from a pretrained transformers model. Paper:
+ https://openreview.net/forum?id=lq62uWRJjiY
+
+ Args:
+ model ([`transformers.PreTrainedModel`]): The model to be adapted.
+ config ([`AdaLoraConfig`]): The configuration of the AdaLora model.
+ adapter_name (`str`): The name of the adapter, defaults to `"default"`.
+ low_cpu_mem_usage (`bool`, `optional`, defaults to `False`):
+ Create empty adapter weights on meta device. Useful to speed up the loading process.
+
+ Returns:
+ `torch.nn.Module`: The AdaLora model.
+
+ Example::
+
+ >>> from transformers import AutoModelForSeq2SeqLM >>> from peft import LoraConfig, AdaLoraModel, AdaLoraConfig
+ >>> config = AdaLoraConfig(
+ peft_type="ADALORA", task_type="SEQ_2_SEQ_LM", init_r=12, lora_alpha=32, target_modules=["q", "v"],
+ lora_dropout=0.01,
+ )
+ >>> model = AutoModelForSeq2SeqLM.from_pretrained("t5-base") >>> model = AdaLoraModel(model, config, "default")
+
+ **Attributes**:
+ - **model** ([`transformers.PreTrainedModel`]) -- The model to be adapted.
+ - **peft_config** ([`AdaLoraConfig`]): The configuration of the AdaLora model.
+ """
+
+ # Note: don't redefine prefix or tuner_layer_cls here, it should be inherited from LoraModel
+ target_module_mapping = TRANSFORMERS_MODELS_TO_ADALORA_TARGET_MODULES_MAPPING
+
+ def __init__(self, model, config, adapter_name, **kwargs):
+ super().__init__(model, config, adapter_name, **kwargs)
+
+ traininable_mode_counter = 0
+ for config in self.peft_config.values():
+ if not config.inference_mode:
+ traininable_mode_counter += 1
+
+ if traininable_mode_counter > 1:
+ raise ValueError(
+ "AdaLoraModel supports only 1 trainable adapter. "
+ "When using multiple adapters, set inference_mode to True for all adapters except the one you want to train."
+ )
+
+ if self.peft_config[adapter_name].inference_mode:
+ _freeze_adapter(self.model, adapter_name)
+ else:
+ self.trainable_adapter_name = adapter_name
+ self.rankallocator = RankAllocator(self.model, self.peft_config[adapter_name], self.trainable_adapter_name)
+
+ def _check_new_adapter_config(self, config: LoraConfig) -> None:
+ """
+ A helper method to check the config when a new adapter is being added.
+
+ Raise a ValueError if there is something wrong with the config or if it conflicts with existing adapters.
+
+ """
+ super()._check_new_adapter_config(config)
+
+ traininable_mode_counter = 0
+ for config_ in self.peft_config.values():
+ if not config_.inference_mode:
+ traininable_mode_counter += 1
+
+ if traininable_mode_counter > 1:
+ raise ValueError(
+ f"{self.__class__.__name__} supports only 1 trainable adapter. "
+ "When using multiple adapters, set inference_mode to True for all adapters except the one "
+ "you want to train."
+ )
+
+ def _create_and_replace(
+ self,
+ lora_config,
+ adapter_name,
+ target,
+ target_name,
+ parent,
+ current_key,
+ ):
+ kwargs = {
+ "r": lora_config.init_r,
+ "lora_alpha": lora_config.lora_alpha,
+ "lora_dropout": lora_config.lora_dropout,
+ "fan_in_fan_out": lora_config.fan_in_fan_out,
+ "init_lora_weights": lora_config.init_lora_weights,
+ "loaded_in_8bit": getattr(self.model, "is_loaded_in_8bit", False),
+ "loaded_in_4bit": getattr(self.model, "is_loaded_in_4bit", False),
+ }
+ if (kwargs["loaded_in_8bit"] or kwargs["loaded_in_4bit"]) and not is_bnb_available():
+ raise ImportError(
+ "To use AdaLora with 8-bit quantization, please install the `bitsandbytes` package. "
+ "You can install it with `pip install bitsandbytes`."
+ )
+
+ quantization_config = get_quantization_config(self.model, method="gptq")
+ if quantization_config is not None:
+ kwargs["gptq_quantization_config"] = quantization_config
+
+ # If it is not an AdaLoraLayer, create a new module, else update it with new adapters
+ if not isinstance(target, AdaLoraLayer):
+ device_map = self.model.hf_device_map if hasattr(self.model, "hf_device_map") else None
+ new_module = self._create_new_module(lora_config, adapter_name, target, device_map=device_map, **kwargs)
+ if adapter_name not in self.active_adapters:
+ # adding an additional adapter: it is not automatically trainable
+ new_module.requires_grad_(False)
+ self._replace_module(parent, target_name, new_module, target)
+ else:
+ target.update_layer(
+ adapter_name,
+ lora_config.init_r,
+ lora_config.lora_alpha,
+ lora_config.lora_dropout,
+ lora_config.init_lora_weights,
+ )
+
+ @staticmethod
+ def _create_new_module(lora_config, adapter_name, target, device_map=None, **kwargs):
+ # avoid eager bnb import
+ if is_bnb_available():
+ import bitsandbytes as bnb
+
+ from .bnb import SVDLinear8bitLt
+ if is_bnb_4bit_available():
+ from .bnb import SVDLinear4bit
+
+ gptq_quantization_config = kwargs.get("gptq_quantization_config", None)
+
+ if is_gptqmodel_available():
+ QuantLinear = get_gptqmodel_quant_linear(gptq_quantization_config, device_map=device_map)
+ else:
+ QuantLinear = get_auto_gptq_quant_linear(gptq_quantization_config)
+
+ loaded_in_8bit = kwargs.pop("loaded_in_8bit", False)
+ loaded_in_4bit = kwargs.pop("loaded_in_4bit", False)
+
+ if isinstance(target, BaseTunerLayer):
+ target_base_layer = target.get_base_layer()
+ else:
+ target_base_layer = target
+
+ if loaded_in_8bit and isinstance(target_base_layer, bnb.nn.Linear8bitLt):
+ kwargs.update(
+ {
+ "has_fp16_weights": target_base_layer.state.has_fp16_weights,
+ "threshold": target_base_layer.state.threshold,
+ "index": target_base_layer.index,
+ }
+ )
+ new_module = SVDLinear8bitLt(target, adapter_name, **kwargs)
+ elif loaded_in_4bit and is_bnb_4bit_available() and isinstance(target_base_layer, bnb.nn.Linear4bit):
+ fourbit_kwargs = kwargs.copy()
+ fourbit_kwargs.update(
+ {
+ "compute_dtype": target_base_layer.compute_dtype,
+ "compress_statistics": target_base_layer.weight.compress_statistics,
+ "quant_type": target_base_layer.weight.quant_type,
+ }
+ )
+ new_module = SVDLinear4bit(target, adapter_name, **fourbit_kwargs)
+ elif QuantLinear is not None and isinstance(target, QuantLinear):
+ new_module = SVDQuantLinear(target, adapter_name, **kwargs)
+ else:
+ if isinstance(target_base_layer, torch.nn.Linear):
+ if kwargs["fan_in_fan_out"]:
+ warnings.warn(
+ "fan_in_fan_out is set to True but the target module is `torch.nn.Linear`. "
+ "Setting fan_in_fan_out to False."
+ )
+ kwargs["fan_in_fan_out"] = lora_config.fan_in_fan_out = False
+ elif isinstance(target_base_layer, Conv1D):
+ if not kwargs["fan_in_fan_out"]:
+ warnings.warn(
+ "fan_in_fan_out is set to False but the target module is `Conv1D`. "
+ "Setting fan_in_fan_out to True."
+ )
+ kwargs["fan_in_fan_out"] = lora_config.fan_in_fan_out = True
+ else:
+ raise ValueError(
+ f"Target module {target} is not supported. "
+ f"Currently, only `torch.nn.Linear` and `Conv1D` are supported."
+ )
+ new_module = SVDLinear(target, adapter_name, **kwargs)
+
+ return new_module
+
+ def forward(self, *args, **kwargs):
+ outputs = self.model.forward(*args, **kwargs)
+
+ if (getattr(outputs, "loss", None) is not None) and isinstance(outputs.loss, torch.Tensor):
+ # Calculate the orthogonal regularization
+ orth_reg_weight = self.peft_config[self.trainable_adapter_name].orth_reg_weight
+
+ if orth_reg_weight <= 0:
+ raise ValueError("orth_reg_weight should be greater than 0. ")
+
+ regu_loss = 0
+ num_param = 0
+ for n, p in self.model.named_parameters():
+ if ("lora_A" in n or "lora_B" in n) and self.trainable_adapter_name in n:
+ if p.shape == torch.Size([0]):
+ with gather_params_ctx(p, fwd_module=self):
+ para_cov = p @ p.T if "lora_A" in n else p.T @ p
+ else:
+ para_cov = p @ p.T if "lora_A" in n else p.T @ p
+ I = torch.eye(*para_cov.size(), out=torch.empty_like(para_cov)) # noqa: E741
+ I.requires_grad = False
+ num_param += 1
+ regu_loss += torch.norm(para_cov - I, p="fro")
+ if num_param > 0:
+ regu_loss = regu_loss / num_param
+ else:
+ regu_loss = 0
+ outputs.loss += orth_reg_weight * regu_loss
+ return outputs
+
+ def resize_modules_by_rank_pattern(self, rank_pattern, adapter_name):
+ lora_config = self.peft_config[adapter_name]
+ for name, rank_idx in rank_pattern.items():
+ if isinstance(rank_idx, list):
+ rank = sum(rank_idx)
+ elif isinstance(rank_idx, torch.Tensor):
+ rank_idx = rank_idx.view(-1)
+ rank = rank_idx.sum().item()
+ else:
+ raise ValueError("Unexpected type of rank_idx")
+ key = ".".join(name.split(".")[0:-2]) if adapter_name in name else ".".join(name.split(".")[0:-1])
+ _, target, _ = _get_submodules(self.model, key)
+ lora_E_weights = target.lora_E[adapter_name][rank_idx]
+ lora_A_weights = target.lora_A[adapter_name][rank_idx]
+ lora_B_weights = target.lora_B[adapter_name][:, rank_idx]
+ ranknum = target.ranknum[adapter_name]
+ target.update_layer(
+ adapter_name,
+ rank,
+ lora_config.lora_alpha,
+ lora_config.lora_dropout,
+ lora_config.init_lora_weights,
+ )
+ with torch.no_grad():
+ if rank > 0:
+ target.lora_E[adapter_name].copy_(lora_E_weights)
+ target.lora_A[adapter_name].copy_(lora_A_weights)
+ target.lora_B[adapter_name].copy_(lora_B_weights)
+ # The scaling is exactly as the previous
+ target.ranknum[adapter_name].copy_(ranknum)
+
+ def resize_state_dict_by_rank_pattern(self, rank_pattern, state_dict, adapter_name):
+ for name, rank_idx in rank_pattern.items():
+ rank = sum(rank_idx)
+ prefix = ".".join(name.split(".")[0:-2]) if adapter_name in name else ".".join(name.split(".")[0:-1])
+ for layer in ["lora_E", "lora_A", "lora_B"]:
+ key = f"base_model.model.{prefix}.{layer}.{adapter_name}"
+ if layer != "lora_B":
+ state_dict[key] = (
+ state_dict[key][rank_idx] if rank != state_dict[key].shape[0] else state_dict[key]
+ )
+ else:
+ state_dict[key] = (
+ state_dict[key][:, rank_idx] if rank != state_dict[key].shape[1] else state_dict[key]
+ )
+ return state_dict
+
+ def update_and_allocate(self, global_step):
+ """
+ This method updates Adalora budget and mask.
+
+ This should be called in every training step after `loss.backward()` and before `zero_grad()`.
+
+ `tinit`, `tfinal` and `deltaT` are handled with in the method.
+
+ Args:
+ global_step (`int`): The current training step, it is used to calculate adalora budget.
+
+ Example:
+
+ ```python
+ >>> loss = model(**input).loss
+ >>> loss.backward()
+ >>> optimizer.step()
+ >>> model.base_model.update_and_allocate(i_step)
+ >>> optimizer.zero_grad()
+ ```
+ """
+ lora_config = self.peft_config[self.trainable_adapter_name]
+ # Update the importance score and allocate the budget
+ if global_step < lora_config.total_step - lora_config.tfinal:
+ _, rank_pattern = self.rankallocator.update_and_allocate(self.model, global_step)
+ if rank_pattern:
+ lora_config.rank_pattern = rank_pattern
+ # Finalize the budget allocation
+ elif global_step == lora_config.total_step - lora_config.tfinal:
+ _, rank_pattern = self.rankallocator.update_and_allocate(self.model, global_step, force_mask=True)
+ # for some reason, this freezes the trainable parameters and nothing gets updates
+ # self.resize_modules_by_rank_pattern(rank_pattern, self.trainable_adapter_name)
+ lora_config.rank_pattern = rank_pattern
+ self.rankallocator.reset_ipt()
+ # Currently using inefficient way to mask the unimportant weights using the rank pattern
+ # due to problem mentioned above
+ elif global_step > lora_config.total_step - lora_config.tfinal:
+ self.rankallocator.mask_using_rank_pattern(self.model, lora_config.rank_pattern)
+ # Pass the function and do forward propagation
+ else:
+ return None
+
+ def add_weighted_adapter(self, *args, **kwargs):
+ """This method is not supported for AdaLoRA, use LoRA instead."""
+ raise TypeError(f"{self.__class__.__name__} does not support add_weighted_adapter method.")
diff --git a/peft/src/peft/tuners/adaption_prompt/__init__.py b/peft/src/peft/tuners/adaption_prompt/__init__.py
new file mode 100644
index 0000000000000000000000000000000000000000..68882a222625eedc770d28816a3a0646964739bb
--- /dev/null
+++ b/peft/src/peft/tuners/adaption_prompt/__init__.py
@@ -0,0 +1,23 @@
+# Copyright 2023-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+from peft.utils import register_peft_method
+
+from .config import AdaptionPromptConfig
+from .layer import AdaptedAttention
+from .model import AdaptionPromptModel
+
+
+__all__ = ["AdaptedAttention", "AdaptionPromptConfig", "AdaptionPromptModel"]
+
+register_peft_method(name="adaption_prompt", config_cls=AdaptionPromptConfig, model_cls=AdaptionPromptModel)
diff --git a/peft/src/peft/tuners/adaption_prompt/config.py b/peft/src/peft/tuners/adaption_prompt/config.py
new file mode 100644
index 0000000000000000000000000000000000000000..4a9f780383d425fb551e2635017de9eaac3c2b81
--- /dev/null
+++ b/peft/src/peft/tuners/adaption_prompt/config.py
@@ -0,0 +1,88 @@
+# Copyright 2023-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+from collections import namedtuple
+from dataclasses import dataclass, field
+
+from peft.config import PeftConfig
+from peft.utils import PeftType
+
+from .utils import gpt2_compute_query_states, llama_compute_query_states
+
+
+@dataclass
+class AdaptionPromptConfig(PeftConfig):
+ """Stores the configuration of an [`AdaptionPromptModel`]."""
+
+ target_modules: str = field(
+ default=None, metadata={"help": "Name of the attention submodules to insert adaption prompts into."}
+ )
+ adapter_len: int = field(default=None, metadata={"help": "Number of adapter tokens to insert"})
+ adapter_layers: int = field(default=None, metadata={"help": "Number of adapter layers (from the top)"})
+
+ def __post_init__(self):
+ super().__post_init__()
+ self.peft_type = PeftType.ADAPTION_PROMPT
+
+ @property
+ def is_adaption_prompt(self) -> bool:
+ """Return True if this is an adaption prompt config."""
+ return True
+
+
+# Contains the config that is specific to a transformers model type.
+ModelTypeConfig = namedtuple(
+ "ModelTypeConfig", ["compute_query_states", "target_modules", "k_proj_layer", "v_proj_layer", "o_proj_layer"]
+)
+
+# Mapping of transformers model types to their specific configuration.
+TRANSFORMERS_MODEL_CONFIG = {
+ "llama": ModelTypeConfig(
+ compute_query_states=llama_compute_query_states,
+ target_modules="self_attn",
+ k_proj_layer="k_proj",
+ v_proj_layer="v_proj",
+ o_proj_layer="o_proj",
+ ),
+ "mistral": ModelTypeConfig( # same as llama,
+ compute_query_states=llama_compute_query_states,
+ target_modules="self_attn",
+ k_proj_layer="k_proj",
+ v_proj_layer="v_proj",
+ o_proj_layer="o_proj",
+ ),
+ "gpt2": ModelTypeConfig( # piggybacking of off the prior definitions, GPTs attention calculation is different
+ compute_query_states=gpt2_compute_query_states,
+ target_modules="attn",
+ k_proj_layer="c_attn",
+ v_proj_layer=None,
+ o_proj_layer=None,
+ ),
+}
+
+
+def prepare_config(
+ peft_config: AdaptionPromptConfig,
+ model,
+) -> AdaptionPromptConfig:
+ """Prepare the config based on the llama model type."""
+ if model.config.model_type not in TRANSFORMERS_MODEL_CONFIG:
+ raise ValueError(f"Unsupported model type for adaption prompt: '{model.config.model_type}'.")
+
+ model_config = TRANSFORMERS_MODEL_CONFIG[model.config.model_type]
+
+ if peft_config.target_modules is None:
+ peft_config.target_modules = model_config.target_modules
+
+ return peft_config
diff --git a/peft/src/peft/tuners/adaption_prompt/layer.py b/peft/src/peft/tuners/adaption_prompt/layer.py
new file mode 100644
index 0000000000000000000000000000000000000000..4dd877841f176b1688d5c0fc224c79f3b089ceff
--- /dev/null
+++ b/peft/src/peft/tuners/adaption_prompt/layer.py
@@ -0,0 +1,236 @@
+# Copyright 2023-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+import math
+from typing import Optional, Union
+
+import torch
+import torch.nn as nn
+import torch.nn.functional as F
+
+from .config import TRANSFORMERS_MODEL_CONFIG
+
+
+class _BaseAdaptedAttention(nn.Module):
+ """Base module, which defines adaption prompts for multiple model types."""
+
+ def __init__(self, model_type: str, adapter_len: int, model, target_dtype=torch.float32):
+ """
+ Initialize object.
+
+ Args:
+ model_type: The transformer model type. This is used to retrieve the right method to
+ compute query states.
+ adapter_len: The length of the adaption prompt to insert.
+ model: The original transformer attention module that is being wrapped.
+ """
+ if isinstance(model, _BaseAdaptedAttention):
+ raise ValueError("Unable to stack multiple adaption prompts")
+ super().__init__()
+ self.model_type = model_type
+ self.model = model
+ self.adapter_len = adapter_len
+ # Assume all parameters of the attention model we are wrapping are on the same device.
+
+ device = next(model.parameters()).device
+ # Don't think this was specified in the paper, but we follow the official repo which used an Embedding
+ # which initializes the tokens with standard normal values.
+ # https://github.com/ZrrSkywalker/LLaMA-Adapter/blob/41c3546fe1997ab8a65809dc8d8f9252b19d9faf/llama/model.py#L234
+ # (bsz, adapter_len, hidden_size)
+
+ if hasattr(self.model, "hidden_size"):
+ # TODO: remove this clause after 2026-01-01
+ hidden_size = self.model.hidden_size
+ else: # changed in https://github.com/huggingface/transformers/pull/35235
+ hidden_size = self.model.config.hidden_size
+
+ if hasattr(self.model, "num_heads"):
+ # TODO: remove this clause after 2026-01-01
+ self.num_heads = self.model.num_heads
+ else: # changed in https://github.com/huggingface/transformers/pull/35235
+ self.num_heads = self.model.config.num_attention_heads
+
+ self.adaption_prompt = nn.Parameter(
+ torch.empty(1, adapter_len, hidden_size, device=device, dtype=target_dtype).normal_()
+ )
+ # Initialize the gate to 0 as this is "zero-init".
+ self.adaption_gate = nn.Parameter(torch.zeros(1, device=device, dtype=target_dtype))
+
+
+class AdaptedAttentionGPT(_BaseAdaptedAttention):
+ """This module wraps a GPT2Attention module and injects adaption prompts"""
+
+ def __init__(self, model_type, adapter_len, model):
+ target_dtype = (
+ model.c_proj.weight.dtype if model.c_proj.weight.dtype not in [torch.int8, torch.uint8] else torch.float32
+ )
+ super().__init__(model_type, adapter_len, model, target_dtype=target_dtype)
+
+ def forward(
+ self,
+ hidden_states: Optional[tuple[torch.FloatTensor]],
+ layer_past: Optional[tuple[torch.Tensor]] = None,
+ attention_mask: Optional[torch.FloatTensor] = None,
+ head_mask: Optional[torch.FloatTensor] = None,
+ encoder_hidden_states: Optional[torch.Tensor] = None,
+ encoder_attention_mask: Optional[torch.FloatTensor] = None,
+ use_cache: Optional[bool] = False,
+ output_attentions: Optional[bool] = False,
+ **kwargs,
+ ) -> tuple[Union[torch.Tensor, tuple[torch.Tensor]], ...]:
+ attn_outputs = self.model(
+ hidden_states=hidden_states,
+ attention_mask=attention_mask,
+ head_mask=head_mask,
+ encoder_hidden_states=encoder_hidden_states,
+ encoder_attention_mask=encoder_attention_mask,
+ use_cache=use_cache,
+ output_attentions=output_attentions,
+ **kwargs,
+ )
+ """
+ Forward pass for the adapter which wraps the GPT2Attention module
+ """
+
+ attn_output = attn_outputs[0]
+ add_outputs = attn_outputs[1:]
+
+ c_attn_layer = TRANSFORMERS_MODEL_CONFIG[self.model_type].k_proj_layer
+
+ bsz = attn_output.shape[0]
+ q_len = attn_output.shape[1]
+ embed_dim = attn_output.shape[2]
+
+ _, key, value = getattr(self.model, c_attn_layer)(self.adaption_prompt).split(embed_dim, dim=2)
+
+ adapter_k = (
+ key.view(1, self.adapter_len, self.num_heads, self.model.head_dim).repeat(bsz, 1, 1, 1).transpose(1, 2)
+ )
+ adapter_v = (
+ value.view(1, self.adapter_len, self.num_heads, self.model.head_dim).repeat(bsz, 1, 1, 1).transpose(1, 2)
+ )
+ # recompute query state since it is not returned by GPT2 forward
+ compute_query_states = TRANSFORMERS_MODEL_CONFIG[self.model_type].compute_query_states
+ query_states = compute_query_states(
+ self.model, hidden_states=hidden_states, encoder_hidden_states=encoder_hidden_states
+ )
+
+ previous_dtype = query_states.dtype
+
+ scores = torch.matmul(query_states, adapter_k.transpose(2, 3).to(previous_dtype)) / math.sqrt(
+ self.model.head_dim
+ )
+ # Upcast attention to fp32
+ # (bsz, num_heads, q_len, adapter_len)
+ scores = self.adaption_gate * F.softmax(scores, dim=-1, dtype=torch.float32).to(previous_dtype)
+ # (bsz, q_len, num_heads * head_dim)
+ adapter_output = torch.matmul(scores, adapter_v).transpose(1, 2).reshape(bsz, q_len, -1)
+
+ # Add adaption prompt output to original output.
+ hidden_state = attn_output + adapter_output
+
+ # Restore original dtype.
+ hidden_state = hidden_state.to(previous_dtype)
+
+ # add additional attention outputs (attention and cross attention)
+ output = (hidden_state,) + add_outputs
+ return output
+
+
+class AdaptedAttention(_BaseAdaptedAttention):
+ """This module wraps a LLamaAttention module and injects adaption prompts."""
+
+ def __init__(self, model_type, adapter_len, model):
+ target_dtype = (
+ model.q_proj.weight.dtype if model.q_proj.weight.dtype not in [torch.int8, torch.uint8] else torch.float32
+ )
+ super().__init__(model_type, adapter_len, model, target_dtype=target_dtype)
+
+ def forward(self, **kwargs):
+ """
+ Forward pass for the adapter which wraps the original LlamaAttention module.
+
+ "Official" paper implementation:
+ https://github.com/ZrrSkywalker/LLaMA-Adapter/blob/41c3546fe1997ab8a65809dc8d8f9252b19d9faf/llama/model.py#L141
+
+ Args:
+ kwargs: See the original LlamaAttention module.
+ """
+ if kwargs.get("output_attention", False):
+ raise NotImplementedError("output_attention is not currently supported.")
+
+ output, *_ = self.model(**kwargs)
+ bsz = output.shape[0]
+ q_len = output.shape[1]
+ embed_dim = output.shape[2]
+ k_proj_layer = TRANSFORMERS_MODEL_CONFIG[self.model_type].k_proj_layer
+ v_proj_layer = TRANSFORMERS_MODEL_CONFIG[self.model_type].v_proj_layer
+ o_proj_layer = TRANSFORMERS_MODEL_CONFIG[self.model_type].o_proj_layer
+ factor = (
+ self.model.k_proj.in_features // self.model.k_proj.out_features
+ ) # Mistral has different input and output dimension for k_proj and v_proj layers
+
+ if k_proj_layer == v_proj_layer:
+ _, key, value = getattr(self.model, k_proj_layer)(self.adaption_prompt).split(embed_dim, dim=2)
+ else:
+ key = getattr(self.model, k_proj_layer)(self.adaption_prompt)
+ value = getattr(self.model, v_proj_layer)(self.adaption_prompt)
+
+ if hasattr(self.model, "num_heads"):
+ # TODO: remove this clause after 2026-01-01
+ num_heads = self.model.num_heads
+ else: # changed in https://github.com/huggingface/transformers/pull/35235
+ num_heads = self.model.config.num_attention_heads
+ # (bsz, num_key_value_heads, adapter_len, head_dim)
+ adapter_k = (
+ key.view(1, self.adapter_len, (num_heads // factor), self.model.head_dim)
+ .repeat(bsz, 1, 1, 1)
+ .transpose(1, 2)
+ )
+ adapter_v = (
+ value.view(1, self.adapter_len, (num_heads // factor), self.model.head_dim)
+ .repeat(bsz, 1, 1, 1)
+ .transpose(1, 2)
+ )
+ # Below is taken from https://github.com/huggingface/transformers/blob/e547458c43dfdbbb8f6a7757237e234c44e20a8f/src/transformers/models/mistral/modeling_mistral.py#L181
+ # (bsz, num_heads, adapter_len, head_dim)
+ adapter_k = torch.repeat_interleave(adapter_k, repeats=factor, dim=1)
+ adapter_v = torch.repeat_interleave(adapter_v, repeats=factor, dim=1)
+ # Recompute query states.
+ compute_query_states = TRANSFORMERS_MODEL_CONFIG[self.model_type].compute_query_states
+ # (bsz, num_heads, q_len, head_dim)
+ query_states = compute_query_states(model=self.model, **kwargs)
+
+ previous_dtype = query_states.dtype
+
+ # (bsz, num_heads, q_len, adapter_len)
+ scores = torch.matmul(query_states, adapter_k.transpose(2, 3).to(previous_dtype)) / math.sqrt(
+ self.model.head_dim
+ )
+ # Upcast attention to fp32
+ # (bsz, num_heads, q_len, adapter_len)
+ scores = self.adaption_gate * F.softmax(scores, dim=-1, dtype=torch.float32).to(previous_dtype)
+ # (bsz, q_len, num_heads * head_dim)
+ adapter_output = torch.matmul(scores, adapter_v).transpose(1, 2).reshape(bsz, q_len, -1)
+
+ # (bsz, q_len, hidden_size)
+ if o_proj_layer is not None:
+ adapter_output = getattr(self.model, o_proj_layer)(adapter_output)
+
+ # Add adaption prompt output to original output.
+ output = output + adapter_output
+
+ # Restore original dtype.
+ output = output.to(previous_dtype)
+ return output, *_
diff --git a/peft/src/peft/tuners/adaption_prompt/model.py b/peft/src/peft/tuners/adaption_prompt/model.py
new file mode 100644
index 0000000000000000000000000000000000000000..6b91c06fc0d5ad20789c4fdc6f2b76ffb4cb114e
--- /dev/null
+++ b/peft/src/peft/tuners/adaption_prompt/model.py
@@ -0,0 +1,169 @@
+# Copyright 2023-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+
+import torch.nn as nn
+
+from peft.utils import _freeze_adapter, _get_submodules
+
+from .config import AdaptionPromptConfig, prepare_config
+from .layer import AdaptedAttention, AdaptedAttentionGPT
+from .utils import is_adaption_prompt_trainable
+
+
+class AdaptionPromptModel(nn.Module):
+ """
+ Implements adaption prompts as described in https://huggingface.co/papers/2303.16199.
+
+ The top L attention modules are replaced with AdaptedAttention modules that wrap the original ones, but insert
+ trainable prompts with gates (for zero init).
+
+ Notes on the multi-adapter pattern:
+ - We store the states of different adapters by keeping a dictionary of AdaptedAttention modules indexed by adapter
+ name.
+ - Every time we switch adapters, we remove the modules of the currently active adapter from the model, store them
+ in the dictionary, and replace them with the modules of the new adapter.
+ - To avoid duplicated and potentially inconsistent state, the currently active adapter is always removed from the
+ dictionary.
+ - Disabling the adapter would also result in the modules being removed from the model.
+ """
+
+ def __init__(self, model, configs: dict, adapter_name: str):
+ super().__init__()
+ self.model = model
+ # Store adapter configs by name.
+ self.peft_config: dict[str, AdaptionPromptConfig] = {}
+ # Store lists of the parents of the affected attention modules by adapter name.
+ # We keep references to the parents so we can swap the adapters in-and-out of the model.
+ self._parents: dict[str, list[nn.Module]] = {}
+ # Store lists of cached AdaptedAttention modules by name.
+ self._cached_adapters: dict[str, list] = {}
+ # The name of the currently active adapter.
+ self._active_adapter = None
+ # Whether the adapter is enabled.
+ self._enabled = True
+ self.forward = self.model.forward
+ self.add_adapter(adapter_name, configs[adapter_name])
+ self._mark_only_adaption_prompts_as_trainable(self.model)
+
+ def add_adapter(self, adapter_name: str, config: AdaptionPromptConfig) -> None:
+ """Add an adapter with the given name and config."""
+ config = prepare_config(config, self.model)
+ if adapter_name in self.peft_config:
+ raise ValueError(f"Adapter with name '{adapter_name}' already exists.")
+
+ parents = []
+ for name, _ in self.model.named_modules():
+ if name.endswith(f".{config.target_modules}"):
+ par, _, _ = _get_submodules(self.model, name)
+ parents.append(par)
+ if len(parents) < config.adapter_layers:
+ raise ValueError(
+ f"Config specifies more adapter layers '{config.adapter_layers}' than the model has '{len(parents)}'."
+ )
+ # Note that if the target modules are not in Sequential, ModuleList, or
+ # some other PyTorch ordered container, the behavior is undefined as we
+ # assume here that the order of the modules is the same as the order of
+ # the transformer decoder layers.
+ parents = parents[-config.adapter_layers :]
+ self._parents[adapter_name] = parents
+
+ # It is only None during initialization.
+ # If it is disabled, we don't have to remove the modules.
+ if self._active_adapter is not None and self._enabled:
+ self._remove_adapted_attentions(self._active_adapter)
+ self._active_adapter = adapter_name
+ self.peft_config[adapter_name] = config
+ self._create_adapted_attentions(config, parents)
+ if not self._enabled:
+ self._remove_adapted_attentions(self._active_adapter)
+
+ if config.inference_mode:
+ _freeze_adapter(self.model, adapter_name)
+
+ def set_adapter(self, adapter_name: str) -> None:
+ """Set the model to use the adapter with the given name."""
+ if self._active_adapter == adapter_name:
+ return
+ if adapter_name not in self.peft_config:
+ raise ValueError(f"Adapter with name '{adapter_name}' does not exist.")
+
+ if self._enabled:
+ self._remove_adapted_attentions(self._active_adapter)
+ self._set_adapted_attentions(adapter_name)
+
+ self._active_adapter = adapter_name
+
+ def enable_adapter_layers(self):
+ """Enable adapter layers by swapping in cached AdaptedAttention modules."""
+ self._enabled = True
+ self._set_adapted_attentions(self._active_adapter)
+
+ def disable_adapter_layers(self):
+ """Disable adapter layers by swapping out AdaptedAttention modules."""
+ self._enabled = False
+ self._remove_adapted_attentions(self._active_adapter)
+
+ def _create_adapted_attentions(self, config: AdaptionPromptConfig, parents: list[nn.Module]) -> None:
+ """Wrap LlamaAttention modules with newly created AdaptedAttention modules."""
+ for par in parents:
+ if self.model.config.model_type == "gpt2":
+ attn = AdaptedAttentionGPT(
+ model_type=self.model.config.model_type,
+ adapter_len=config.adapter_len,
+ model=getattr(par, config.target_modules),
+ )
+
+ else:
+ attn = AdaptedAttention(
+ model_type=self.model.config.model_type,
+ adapter_len=config.adapter_len,
+ model=getattr(par, config.target_modules),
+ )
+ setattr(par, config.target_modules, attn)
+
+ def _set_adapted_attentions(self, adapter_name: str) -> None:
+ """Replace LlamaAttention modules with cached AdaptedAttention modules."""
+ cached = self._cached_adapters[adapter_name]
+ del self._cached_adapters[adapter_name]
+ config = self.peft_config[adapter_name]
+ for i, par in enumerate(self._parents[adapter_name]):
+ setattr(par, config.target_modules, cached[i])
+
+ def _remove_adapted_attentions(self, adapter_name: str) -> None:
+ """Remove AdaptedAttention modules from the model and store them in the cache."""
+ config = self.peft_config[adapter_name]
+ adapted_attentions = []
+ for par in self._parents[adapter_name]:
+ attn = getattr(par, config.target_modules)
+ adapted_attentions.append(attn)
+ setattr(par, config.target_modules, attn.model)
+ self._cached_adapters[adapter_name] = adapted_attentions
+
+ def _mark_only_adaption_prompts_as_trainable(self, model: nn.Module) -> None:
+ """Freeze all parameters of the model except the adaption prompts."""
+ for n, p in model.named_parameters():
+ if not is_adaption_prompt_trainable(n):
+ p.requires_grad = False
+
+ def __getattr__(self, name: str):
+ """Forward missing attributes to the wrapped module."""
+ try:
+ return super().__getattr__(name) # defer to nn.Module's logic
+ except AttributeError:
+ # This is necessary as e.g. causal models have various methods that we
+ # don't want to re-implement here.
+ if name == "model": # see #1892: prevent infinite recursion if class is not initialized
+ raise
+ return getattr(self.model, name)
diff --git a/peft/src/peft/tuners/adaption_prompt/utils.py b/peft/src/peft/tuners/adaption_prompt/utils.py
new file mode 100644
index 0000000000000000000000000000000000000000..967dabf47c2af6973c4b3c8a0ba67cb957c0fceb
--- /dev/null
+++ b/peft/src/peft/tuners/adaption_prompt/utils.py
@@ -0,0 +1,158 @@
+# Copyright 2023-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+import inspect
+from typing import Optional
+
+import torch
+import torch.nn as nn
+
+
+def llama_rotate_half(x: torch.Tensor) -> torch.Tensor:
+ """
+ Rotate half the hidden dims of the input.
+
+ This function was duplicated verbatim from:
+ https://github.com/huggingface/transformers/blob/1de8ce9ee1191ba761a593ac15d9ccbf5851bfc5/src/transformers/models/llama/modeling_llama.py#L126
+
+ This was done to eliminate the Llama transformers implementation as a dependency of this file. Note that some other
+ functions were also adapted from the transformers implementation but were modified.
+ """
+ x1 = x[..., : x.shape[-1] // 2]
+ x2 = x[..., x.shape[-1] // 2 :]
+ return torch.cat((-x2, x1), dim=-1)
+
+
+def llama_apply_rotary_pos_emb(q, cos, sin, position_ids):
+ """
+ Apply rotary position embedding to query states in the Llama model.
+
+ This function was adapted from:
+ https://github.com/huggingface/transformers/blob/1de8ce9ee1191ba761a593ac15d9ccbf5851bfc5/src/transformers/models/llama/modeling_llama.py#L133
+
+ It was modified to remove unnecessary processing of key states. The method is compatible with transformers <=
+ 4.34.2 and also with the latest version (>=4.35).
+ """
+ # In previous transformers version cos/sin cached had a shape of 4D
+ if len(cos.shape) == 4:
+ gather_indices = position_ids[:, None, :, None] # [bs, 1, seq_len, 1]
+ gather_indices = gather_indices.repeat(1, cos.shape[1], 1, cos.shape[3])
+ cos = torch.gather(cos.repeat(gather_indices.shape[0], 1, 1, 1), 2, gather_indices)
+ sin = torch.gather(sin.repeat(gather_indices.shape[0], 1, 1, 1), 2, gather_indices)
+ # In the new version, it is 2D so we fall back to the new implementation
+ # https://github.com/huggingface/transformers/blame/eef7ea98c31a333bacdc7ae7a2372bde772be8e4/src/transformers/models/llama/modeling_llama.py#L222-L226
+ else:
+ cos = cos[position_ids].unsqueeze(1)
+ sin = sin[position_ids].unsqueeze(1)
+ q_embed = (q * cos) + (llama_rotate_half(q) * sin)
+ return q_embed
+
+
+def llama_compute_query_states(model: nn.Module, **kwargs) -> torch.Tensor:
+ """
+ Compute query states for Llama models specifically. They need to be recomputed as the forward() method of the
+ original LlamaModel in the transformers library does not return them. See the related discussion in the PR:
+ https://github.com/huggingface/peft/pull/268
+ """
+ hidden_states = kwargs.get("hidden_states")
+ position_ids = kwargs.get("position_ids")
+ past_key_value = kwargs.get("past_key_value")
+ bsz, q_len, _ = hidden_states.size()
+ if hasattr(model, "num_heads"):
+ # TODO: remove this clause after 2026-01-01
+ num_heads = model.num_heads
+ else: # changed in https://github.com/huggingface/transformers/pull/35235
+ num_heads = model.config.num_attention_heads
+ query_states = model.q_proj(hidden_states).view(bsz, q_len, num_heads, model.head_dim).transpose(1, 2)
+
+ factor = model.k_proj.in_features // model.k_proj.out_features
+ value_states = model.v_proj(hidden_states).view(bsz, q_len, (num_heads // factor), model.head_dim).transpose(1, 2)
+
+ seq_len = q_len
+
+ if past_key_value is not None:
+ if isinstance(past_key_value, tuple):
+ # for transformers <= 4.35
+ seq_len += past_key_value[0].shape[-2]
+ else:
+ # since transformers 4.36, this is a DynamicCache instance
+ seq_len += past_key_value.get_seq_length(model.layer_idx)
+
+ # model.rotary_emb is deprecated and will be removed in transformers > 4.47.0. Instead, the position embeddings are
+ # passed via the kwargs
+ if "position_embeddings" in kwargs:
+ cos, sin = kwargs["position_embeddings"]
+ cos = cos.unsqueeze(1)
+ sin = sin.unsqueeze(1)
+ return (query_states * cos) + (llama_rotate_half(query_states) * sin)
+
+ # For transformers > 4.37.2 `position_ids` became a required arguments in the rotary embedding's forward pass.
+ if "position_ids" not in inspect.signature(model.rotary_emb.forward).parameters:
+ # TODO we assume that position_ids is not None here, not sure if that is safe but the old code also did that
+ cos, sin = model.rotary_emb(value_states, seq_len=seq_len)
+ return llama_apply_rotary_pos_emb(query_states, cos, sin, position_ids)
+
+ past_seen_tokens = 0
+ if position_ids is None:
+ # Compute position_ids, since they are required for transformers > 4.37.2
+ if past_key_value is None:
+ new_cache_positions = torch.arange(q_len, q_len + q_len, device=value_states.device)
+ else:
+ past_seen_tokens = past_key_value.get_usable_length(q_len, model.layer_idx)
+ new_cache_positions = torch.arange(past_seen_tokens, past_seen_tokens + q_len, device=value_states.device)
+ position_ids = new_cache_positions.unsqueeze(0)
+
+ rotary_emb_kwargs = {"position_ids": position_ids}
+ # The `seq_len` argument has been officially removed in transformers >= 4.39.0
+ if "seq_len" in inspect.signature(model.rotary_emb.forward).parameters:
+ rotary_emb_kwargs["seq_len"] = q_len + past_seen_tokens
+
+ cos, sin = model.rotary_emb(value_states, **rotary_emb_kwargs)
+
+ # For batched inference unsqueeze it on the correct dim
+ # since: https://github.com/huggingface/transformers/pull/29109
+ if len(cos.shape) == 3:
+ cos = cos.unsqueeze(1)
+ sin = sin.unsqueeze(1)
+
+ return (query_states * cos) + (llama_rotate_half(query_states) * sin)
+
+
+def gpt2_compute_query_states(
+ model: nn.Module,
+ hidden_states: Optional[tuple[torch.FloatTensor]],
+ encoder_hidden_states: Optional[torch.Tensor] = None,
+) -> torch.Tensor:
+ """
+ Compute query states for GPT2 models. They need to be recomputed as the forward() method of the GPT@ in the
+ transformers library does not return them. See the related discussion in the PR:
+ """
+ if encoder_hidden_states is not None:
+ if not hasattr(model, "q_attn"):
+ raise ValueError(
+ f"If `{model.__class__.__name__}` is used as cross attention, the weights `q_attn` must be defined. "
+ f"Please make sure to instantiate it with `GPT2Attention(..., is_cross_attention=True)`."
+ )
+ query_states = model.q_attn(hidden_states)
+ else:
+ query_states, _, _ = model.c_attn(hidden_states).split(model.split_size, dim=2)
+
+ shape_q = (*query_states.shape[:-1], -1, model.head_dim)
+ query_states = query_states.view(shape_q).transpose(1, 2)
+
+ return query_states
+
+
+def is_adaption_prompt_trainable(params: str) -> bool:
+ """Return True if module is trainable under adaption prompt fine-tuning."""
+ return params.split(".")[-1].startswith("adaption_")
diff --git a/peft/src/peft/tuners/boft/__init__.py b/peft/src/peft/tuners/boft/__init__.py
new file mode 100644
index 0000000000000000000000000000000000000000..c84b8358da8fc52d3f332c195f22b8b9620c665f
--- /dev/null
+++ b/peft/src/peft/tuners/boft/__init__.py
@@ -0,0 +1,24 @@
+# Copyright 2023-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+from peft.utils import register_peft_method
+
+from .config import BOFTConfig
+from .layer import BOFTLayer
+from .model import BOFTModel
+
+
+__all__ = ["BOFTConfig", "BOFTLayer", "BOFTModel"]
+
+register_peft_method(name="boft", config_cls=BOFTConfig, model_cls=BOFTModel)
diff --git a/peft/src/peft/tuners/boft/config.py b/peft/src/peft/tuners/boft/config.py
new file mode 100644
index 0000000000000000000000000000000000000000..1715cc5bc65c190d3ba4dd160707d3fb0c93307a
--- /dev/null
+++ b/peft/src/peft/tuners/boft/config.py
@@ -0,0 +1,160 @@
+# Copyright 2023-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+# The implementation is based on "Parameter-Efficient Orthogonal Finetuning
+# via Butterfly Factorization" (https://huggingface.co/papers/2311.06243) in ICLR 2024.
+
+from __future__ import annotations
+
+from dataclasses import dataclass, field
+from typing import Optional, Union
+
+from peft.config import PeftConfig
+from peft.utils import PeftType
+
+
+@dataclass
+class BOFTConfig(PeftConfig):
+ """
+ This is the configuration class to store the configuration of a [`BOFTModel`].
+
+ Args:
+ boft_block_size (`int`): BOFT block size across different layers.
+ boft_block_num (`int`): Number of BOFT blocks per injected layer.
+ boft_n_butterfly_factor (`int`): Number of butterfly factors across different layers.
+ target_modules (`Union[List[str],str]`): The names of the modules to apply the adapter to.
+ exclude_modules (`Optional[Union[List[str], str]]`):
+ The names of the modules to not apply the adapter. When passing a string, a regex match will be performed.
+ When passing a list of strings, either an exact match will be performed or it is checked if the name of the
+ module ends with any of the passed strings.
+ boft_dropout (`float`):
+ The multiplicative dropout probability, by setting OFT blocks to identity during training, similar to the
+ dropout layer in LoRA.
+ fan_in_fan_out (`bool`): Set this to True if the layer to replace stores weight like (fan_in, fan_out).
+ For example, gpt-2 uses `Conv1D` which stores weights like (fan_in, fan_out) and hence this should be set
+ to `True`.
+ bias (`str`): Bias type for BOFT. Can be 'none', 'all' or 'boft_only'. If 'all' or 'boft_only', the
+ corresponding biases will be updated during training. Be aware that this means that, even when disabling
+ the adapters, the model will not produce the same output as the base model would have without adaptation.
+ modules_to_save (`List[str]`):List of modules apart from BOFT layers to be set as trainable
+ and saved in the final checkpoint.
+ layers_to_transform (`Union[List[int],int]`):
+ The layer indexes to transform, if this argument is specified, it will apply the BOFT transformations on
+ the layer indexes that are specified in this list. If a single integer is passed, it will apply the BOFT
+ transformations on the layer at this index.
+ layers_pattern (`Optional[Union[List[str], str]]`):
+ The layer pattern name, used only if `layers_to_transform` is different from `None` and if the layer
+ pattern is not in the common layers pattern. This should target the `nn.ModuleList` of the model, which is
+ often called `'layers'` or `'h'`.
+ """
+
+ boft_block_size: int = field(
+ default=4,
+ metadata={
+ "help": "BOFT block size across different layers.",
+ "note": "You can only specify either boft_block_size or boft_block_num, but not both simultaneously, because boft_block_size x boft_block_num = layer dimension.",
+ },
+ )
+ boft_block_num: int = field(
+ default=0,
+ metadata={
+ "help": "Number of BOFT blocks per injected layer.",
+ "note": "You can only specify either boft_block_size or boft_block_num, but not both simultaneously, because boft_block_size x boft_block_num = layer dimension.",
+ },
+ )
+ boft_n_butterfly_factor: int = field(
+ default=1,
+ metadata={
+ "help": "Number of butterfly factors.",
+ "note": (
+ "for example, boft_n_butterfly_factor=2, the effective block size of OFT becomes twice as big and the number of blocks become half.",
+ "note: for boft_n_butterfly_factor=1, BOFT is the same as vanilla OFT.",
+ ),
+ },
+ )
+ target_modules: Optional[Union[list[str], str]] = field(
+ default=None,
+ metadata={
+ "help": "List of module names or regex expression of the module names to replace with BOFT.",
+ "example": "For example, ['q', 'v'] or '.*decoder.*(SelfAttention|EncDecAttention).*(q|v)$' ",
+ },
+ )
+ exclude_modules: Optional[Union[list[str], str]] = field(
+ default=None,
+ metadata={"help": "List of module names or regex expression of the module names to exclude from BOFT."},
+ )
+ boft_dropout: float = field(
+ default=0.0,
+ metadata={
+ "help": "BOFT multiplicative dropout, randomly setting blocks of OFT to be identity matrix, similar to the dropout layer in LoRA."
+ },
+ )
+ fan_in_fan_out: bool = field(
+ default=False,
+ metadata={"help": "Set this to True if the layer to replace stores weight like (fan_in, fan_out)"},
+ )
+ bias: str = field(default="none", metadata={"help": "Bias type for BOFT. Can be 'none', 'all' or 'boft_only'"})
+ modules_to_save: Optional[list[str]] = field(
+ default=None,
+ metadata={
+ "help": "List of modules apart from BOFT layers to be set as trainable and saved in the final checkpoint. ",
+ "note": (
+ "For example, in Sequence Classification or Token Classification tasks, ",
+ "the final layer `classifier/score` are randomly initialized and as such need to be trainable and saved.",
+ ),
+ },
+ )
+ init_weights: bool = field(
+ default=True,
+ metadata={
+ "help": (
+ "Whether to initialize the weights of the BOFT layers with their default initialization. Don't change ",
+ "this setting, except if you know exactly what you're doing.",
+ ),
+ },
+ )
+ layers_to_transform: Optional[Union[list[int], int]] = field(
+ default=None,
+ metadata={
+ "help": "The layer indexes to transform, is this argument is specified, PEFT will transform only the layers indexes that are specified inside this list. If a single integer is passed, PEFT will transform only the layer at this index."
+ },
+ )
+ layers_pattern: Optional[Union[list[str], str]] = field(
+ default=None,
+ metadata={
+ "help": "The layer pattern name, used only if `layers_to_transform` is different to None and if the layer pattern is not in the common layers pattern. "
+ "This should target the `nn.ModuleList` of the model, which is often called `'layers'` or `'h'`."
+ },
+ )
+
+ def __post_init__(self):
+ super().__post_init__()
+ self.peft_type = PeftType.BOFT
+ self.target_modules = (
+ set(self.target_modules) if isinstance(self.target_modules, list) else self.target_modules
+ )
+ self.exclude_modules = (
+ set(self.exclude_modules) if isinstance(self.exclude_modules, list) else self.exclude_modules
+ )
+ # check for layers_to_transform and layers_pattern
+ if self.layers_pattern and not self.layers_to_transform:
+ raise ValueError("When `layers_pattern` is specified, `layers_to_transform` must also be specified. ")
+ if self.boft_block_size == 0 and self.boft_block_num == 0:
+ raise ValueError(
+ f"Either `boft_block_size` or `boft_block_num` must be non-zero. Currently, boft_block_size = {self.boft_block_size} and boft_block_num = {self.boft_block_num}."
+ )
+ if not (self.boft_block_size != 0) ^ (self.boft_block_num != 0):
+ raise ValueError(
+ f"You can only specify either boft_block_size ({self.boft_block_size}) or boft_block_num ({self.boft_block_num}), but not both simultaneously, because boft_block_size x boft_block_num == in_features."
+ )
diff --git a/peft/src/peft/tuners/boft/fbd/__init__.py b/peft/src/peft/tuners/boft/fbd/__init__.py
new file mode 100644
index 0000000000000000000000000000000000000000..e69de29bb2d1d6434b8b29ae775ad8c2e48c5391
diff --git a/peft/src/peft/tuners/boft/fbd/fbd_cuda.cpp b/peft/src/peft/tuners/boft/fbd/fbd_cuda.cpp
new file mode 100644
index 0000000000000000000000000000000000000000..d63111b04083f3b1359aba0a9de9656060a4d515
--- /dev/null
+++ b/peft/src/peft/tuners/boft/fbd/fbd_cuda.cpp
@@ -0,0 +1,28 @@
+#include
+#include
+#include
+#include
+
+std::vector forward_fast_block_diag_cuda(
+ at::Tensor input);
+
+std::vector forward_fast_block_diag(
+ at::Tensor input
+ ) {
+ return forward_fast_block_diag_cuda(input);
+}
+
+std::vector backward_fast_block_diag_cuda(
+ at::Tensor grad_output,
+ at::Tensor input);
+std::vector backward_fast_block_diag(
+ at::Tensor grad_output,
+ at::Tensor input
+ ) {
+ return backward_fast_block_diag_cuda(grad_output, input);
+}
+
+PYBIND11_MODULE(TORCH_EXTENSION_NAME, m) {
+ m.def("forward", &forward_fast_block_diag, "FAST BLOCK DIAG (CUDA)");
+ m.def("backward", &backward_fast_block_diag, "FAST BLOCK DIAG backward (CUDA)");
+}
diff --git a/peft/src/peft/tuners/boft/fbd/fbd_cuda_kernel.cu b/peft/src/peft/tuners/boft/fbd/fbd_cuda_kernel.cu
new file mode 100644
index 0000000000000000000000000000000000000000..9f307455349e6ea8067d47ebf8a39b98ba452d09
--- /dev/null
+++ b/peft/src/peft/tuners/boft/fbd/fbd_cuda_kernel.cu
@@ -0,0 +1,109 @@
+// Author: Yao Feng
+// Date: 2023/08
+// Description: cuda kernel for fast block diag
+
+#include
+
+#include
+#include
+#include
+
+namespace{
+template
+__global__ void forward_fast_block_diag_cuda_kernel(
+ const scalar_t* __restrict__ input, //[z, N, b, b]
+ scalar_t* output, //[z, Nxb, Nxb]
+ int z, int N, int b
+ ) {
+
+ const int i = blockIdx.x * blockDim.x + threadIdx.x;
+ if (i >= z*N*b*b) {
+ return;
+ }
+ const int zi = i/(N*b*b);
+ const int Ni = (i%(N*b*b))/(b*b);
+ const int x = ((i%(N*b*b))%(b*b))/b;
+ const int y = ((i%(N*b*b))%(b*b))%b;
+
+ output[zi*N*b*N*b + (Ni*b+x)*N*b + Ni*b + y] = input[zi*N*b*b + Ni*b*b + x*b + y];
+
+}
+
+template
+__global__ void backward_fast_block_diag_cuda_kernel(
+ const scalar_t* __restrict__ grad_output,
+ scalar_t* grad_input,
+ int z, int N, int b
+ ) {
+
+ const int i = blockIdx.x * blockDim.x + threadIdx.x;
+ if (i >= z*N*b*b) {
+ return;
+ }
+ const int zi = i/(N*b*b);
+ const int Ni = (i%(N*b*b))/(b*b);
+ const int x = ((i%(N*b*b))%(b*b))/b;
+ const int y = ((i%(N*b*b))%(b*b))%b;
+
+ grad_input[zi*N*b*b + Ni*b*b + x*b + y] = grad_output[zi*N*b*N*b + (Ni*b+x)*N*b + Ni*b + y];
+
+} // namespace
+}
+
+std::vector forward_fast_block_diag_cuda(
+ at::Tensor input
+ ){
+ const auto z = input.size(0);
+ const auto N = input.size(1);
+ const auto b = input.size(2);
+
+ // print(channel_size)
+ const int threads = 512;
+ const dim3 blocks_1 ((z*N*b*b - 1) / threads +1);
+ // initlaize output
+ auto output = at::zeros({z, N*b, N*b}, input.options());
+
+ AT_DISPATCH_FLOATING_TYPES_AND_HALF(input.type(), "forward_fast_block_diag1", ([&] {
+ forward_fast_block_diag_cuda_kernel<<>>(
+ input.data_ptr(),
+ output.data_ptr(),
+ z, N, b);
+ }));
+
+
+ cudaError_t err = cudaGetLastError();
+ if (err != cudaSuccess)
+ printf("Error in forward_fast_block_diag_cuda_kernel: %s\n", cudaGetErrorString(err));
+
+ return {output};
+}
+
+std::vector backward_fast_block_diag_cuda(
+ at::Tensor grad_output,
+ at::Tensor input
+ ){
+
+ const auto z = input.size(0);
+ const auto N = input.size(1);
+ const auto b = input.size(2);
+
+ // print(channel_size)
+ const int threads = 512;
+ const dim3 blocks_1 ((z*N*b*b - 1) / threads +1);
+
+ // initialize grad input
+ auto grad_input = at::zeros_like(input);
+
+ AT_DISPATCH_FLOATING_TYPES_AND_HALF(grad_output.type(), "backward_fast_block_diag", ([&] {
+ backward_fast_block_diag_cuda_kernel<<>>(
+ grad_output.data_ptr(),
+ grad_input.data_ptr(),
+ z, N, b);
+ }));
+
+ cudaError_t err = cudaGetLastError();
+ if (err != cudaSuccess)
+ printf("Error in backward_fast_block_diag_cuda_kernel: %s\n", cudaGetErrorString(err));
+
+ return {grad_input};
+}
diff --git a/peft/src/peft/tuners/boft/layer.py b/peft/src/peft/tuners/boft/layer.py
new file mode 100644
index 0000000000000000000000000000000000000000..7232f39d176192ef9819d1395b6cd081c74c1d38
--- /dev/null
+++ b/peft/src/peft/tuners/boft/layer.py
@@ -0,0 +1,1011 @@
+# Copyright 2023-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+# The implementation is based on "Parameter-Efficient Orthogonal Finetuning
+# via Butterfly Factorization" (https://huggingface.co/papers/2311.06243) in ICLR 2024.
+
+from __future__ import annotations
+
+import math
+import os
+import warnings
+from contextlib import contextmanager
+from typing import Any, Optional, Union
+
+import torch
+import torch.nn as nn
+import torch.nn.functional as F
+from torch.autograd import Function
+
+from peft.tuners.tuners_utils import BaseTunerLayer, check_adapters_to_merge
+
+
+_FBD_CUDA = None
+
+
+# this function is a 1:1 copy from accelerate
+@contextmanager
+def patch_environment(**kwargs):
+ """
+ A context manager that will add each keyword argument passed to `os.environ` and remove them when exiting.
+
+ Will convert the values in `kwargs` to strings and upper-case all the keys.
+
+ Example:
+
+ ```python
+ >>> import os
+ >>> from accelerate.utils import patch_environment
+
+ >>> with patch_environment(FOO="bar"):
+ ... print(os.environ["FOO"]) # prints "bar"
+ >>> print(os.environ["FOO"]) # raises KeyError
+ ```
+ """
+ existing_vars = {}
+ for key, value in kwargs.items():
+ key = key.upper()
+ if key in os.environ:
+ existing_vars[key] = os.environ[key]
+ os.environ[key] = str(value)
+
+ yield
+
+ for key in kwargs:
+ key = key.upper()
+ if key in existing_vars:
+ # restore previous value
+ os.environ[key] = existing_vars[key]
+ else:
+ os.environ.pop(key, None)
+
+
+def get_fbd_cuda():
+ global _FBD_CUDA
+
+ if _FBD_CUDA is not None:
+ return _FBD_CUDA
+
+ # This import initializes cuda context and should thus be local, see issue 1877
+ from torch.utils.cpp_extension import load
+
+ curr_dir = os.path.dirname(__file__)
+ # need ninja to build the extension
+ try:
+ with patch_environment(CC="gcc", CXX="gcc"):
+ fbd_cuda = load(
+ name="fbd_cuda",
+ sources=[f"{curr_dir}/fbd/fbd_cuda.cpp", f"{curr_dir}/fbd/fbd_cuda_kernel.cu"],
+ verbose=True,
+ # build_directory='/tmp/' # for debugging
+ )
+ # extra_cuda_cflags = ['-std=c++14', '-ccbin=$$(which gcc-7)']) # cuda10.2 is not compatible with gcc9. Specify gcc 7
+ except Exception as e:
+ warnings.warn(f"Failed to load the CUDA extension: {e}, check if ninja is available.")
+ warnings.warn("Setting boft_n_butterfly_factor to 1 to speed up the finetuning process.")
+ fbd_cuda = None
+
+ _FBD_CUDA = fbd_cuda
+ return _FBD_CUDA
+
+
+class FastBlockDiag(Function):
+ """
+ Implements a custom autograd Function for a fast block diagonal operation using CUDA.
+
+ This function is optimized for 4D tensors where the last two dimensions are equal, representing block diagonal
+ matrices for efficient computation on CUDA devices.
+ """
+
+ @staticmethod
+ def forward(ctx, input):
+ """
+ The forward method for FastBlockDiag.
+
+ Computes the block diagonal operation on the input tensor using a CUDA-optimized function. This method assumes
+ that the input is a 4D tensor where the last two dimensions are equal, which represent the blocks to be
+ diagonalized.
+
+ Parameters:
+ ctx: A context object that can be used to stash information for backward computation.
+ input (Tensor): The input tensor of shape (N, D, H, H), where `N` is the batch size,
+ `D` represents one additional dimension (In BOFT, the number of BOFT blocks), and `H` is the
+ size of the square blocks along the last two dimensions (In BOFT, the block size).
+
+ Returns:
+ Tensor: The resulting tensor after applying the block diagonal operation,
+ will have the shape (N, DxH, DxH).
+ """
+ output = get_fbd_cuda().forward(input)[0]
+ ctx.save_for_backward(input)
+ return output
+
+ @staticmethod
+ def backward(ctx, grad_output):
+ (input,) = ctx.saved_tensors
+ grad_input = get_fbd_cuda().backward(grad_output, input)[0]
+ return grad_input
+
+
+class MultiplicativeDropoutLayer(nn.Module):
+ """
+ Implements the multiplicative dropout layer for BOFT.
+ """
+
+ def __init__(self, p=0.0):
+ """
+ Initializes the multiplicative dropout layer.
+
+ Parameters:
+ p (float): The probability of dropping out a block. Defaults to 0.0.
+ """
+ super().__init__()
+ self.p = p
+
+ def forward(self, x):
+ """
+ Applies multiplicative dropout to the input tensor.
+
+ Parameters:
+ x (Tensor): The input tensor of shape (N, D, H, H), where `N` is the batch size, `D` represents
+ one additional dimension (In BOFT, the number of BOFT blocks), and `H` is the size of the square
+ blocks along the last two dimensions (In BOFT, the block size).
+ """
+ if self.training:
+ # Ensure the last two dimensions are the same
+ if x.shape[-1] != x.shape[-2]:
+ raise ValueError("The last two dimensions of input should be the same!")
+
+ N, D, H, _ = x.shape
+
+ # Randomly select one from N
+ n_random = torch.randint(0, N, (1,)).item()
+
+ # Create a mask with 1s for matrices to be replaced with identity and 0s otherwise
+ num_to_replace = int(self.p * D)
+ num_zeros = D - num_to_replace
+
+ # Generate a flat tensor with desired number of 1s and 0s
+ mask = torch.cat([torch.ones(num_to_replace, device=x.device), torch.zeros(num_zeros, device=x.device)])
+
+ # Shuffle and reshape the mask
+ mask = mask[torch.randperm(D)].view(1, D, 1, 1)
+
+ full_mask = torch.zeros(N, D, 1, 1, device=x.device)
+ full_mask[n_random] = mask
+
+ # Use the mask to combine original matrices and identity matrices
+ eye_matrix = torch.eye(H, device=x.device).repeat(N, D, 1, 1)
+ x = (1 - full_mask) * x + full_mask * eye_matrix
+ return x
+
+
+class BOFTLayer(BaseTunerLayer):
+ """
+ Implements the BOFT layer.
+ """
+
+ # All names of layers that may contain (trainable) adapter weights
+ adapter_layer_names = ("boft_R", "boft_s")
+ # All names of other parameters that may contain adapter-related parameters
+ other_param_names = ("boft_block_size", "boft_block_num", "boft_dropout")
+
+ def __init__(self, base_layer: nn.Module, **kwargs) -> None:
+ """
+ Initializes the BOFT layer.
+
+ Note, currently only support linear layer and convolutional layer, with further support for other layers to be
+ added soon.
+
+ Parameters:
+ base_layer: the pretrained model layer
+ """
+ self.base_layer = base_layer
+ self.boft_block_size = {}
+ self.boft_block_num = {}
+ self.boft_dropout = nn.ModuleDict({})
+ self.boft_R = nn.ParameterDict({})
+ self.boft_s = nn.ParameterDict({})
+ # Mark the weight as unmerged
+ self._disable_adapters = False
+ self.merged_adapters = []
+ # flag to enable/disable casting of input to weight dtype during forward call
+ self.cast_input_dtype_enabled = True
+ self.kwargs = kwargs
+
+ base_layer = self.get_base_layer()
+
+ if isinstance(base_layer, nn.Linear):
+ in_features, out_features = base_layer.in_features, base_layer.out_features
+ elif isinstance(base_layer, nn.Conv2d):
+ in_features, out_features = base_layer.in_channels, base_layer.out_channels
+ else:
+ raise ValueError(f"Unsupported layer type {type(base_layer)}")
+
+ self.in_features = in_features
+ self.out_features = out_features
+
+ def set_scale(self, adapter, scale):
+ if adapter not in self.scaling:
+ # Ignore the case where the adapter is not in the layer
+ return
+
+ warnings.warn("Scaling operation for BOFT not supported! Automatically set scale to 1.")
+
+ def scale_layer(self, scale: float) -> None:
+ if scale == 1:
+ return
+
+ for active_adapter in self.active_adapters:
+ if active_adapter not in self.boft_R.keys():
+ continue
+
+ warnings.warn("Scaling operation for BOFT not supported! Automatically set scale to 1.")
+
+ def unscale_layer(self, scale=None) -> None:
+ for active_adapter in self.active_adapters:
+ if active_adapter not in self.boft_R.keys():
+ continue
+
+ warnings.warn("Unscaling operation for BOFT not supported! Keeping scale to 1.")
+
+ def update_layer(
+ self,
+ adapter_name,
+ boft_block_size,
+ boft_block_num,
+ boft_n_butterfly_factor,
+ boft_dropout,
+ init_weights,
+ inference_mode: bool = False,
+ **kwargs,
+ ):
+ """
+ Update the linear layer with trainable BOFT weights. Override for other layer types.
+ """
+ # Attempt to load the CUDA extension during model initialization
+ if not get_fbd_cuda():
+ self.fbd_cuda_available = False
+ # If the CUDA extension is not available, set the butterfly factor to 1 to speed up the finetuning process
+ boft_n_butterfly_factor = 1
+ else:
+ self.fbd_cuda_available = True
+
+ # to be consistent with the paper notation
+ boft_n_butterfly_factor = boft_n_butterfly_factor - 1
+ if boft_n_butterfly_factor < 0:
+ raise ValueError(
+ f"You can only specify boft_n_butterfly_factor {boft_n_butterfly_factor + 1} to be a positive integer number."
+ )
+
+ # Initialize the MultiplicativeDropoutLayer for boft_dropout > 0.0.
+ if boft_dropout > 0.0:
+ boft_dropout_layer = MultiplicativeDropoutLayer(p=boft_dropout)
+ else:
+ boft_dropout_layer = nn.Identity()
+ self.boft_dropout.update(nn.ModuleDict({adapter_name: boft_dropout_layer}))
+
+ if boft_block_size == 0 and boft_block_num != 0:
+ if self.in_features % boft_block_num != 0:
+ raise ValueError(
+ f"in_features ({self.in_features}) must be divisible by boft_block_num ({boft_block_num})!"
+ )
+
+ if boft_n_butterfly_factor != 0:
+ if boft_n_butterfly_factor > int(math.log2(boft_block_num)):
+ raise ValueError(
+ f"Invalid combination of boft_n_butterfly_factor ({boft_n_butterfly_factor + 1}) and boft_block_num ({boft_block_num})!"
+ )
+ if boft_block_num % (2**boft_n_butterfly_factor) != 0:
+ raise ValueError(
+ f"boft_block_num ({boft_block_num}) must be a multiple of 2 raised to the power of boft_n_butterfly_factor ({boft_n_butterfly_factor + 1})!"
+ )
+
+ boft_block_size = int(self.in_features // boft_block_num)
+
+ elif boft_block_size != 0 and boft_block_num == 0:
+ if self.in_features % boft_block_size != 0:
+ raise ValueError(
+ f"in_features ({self.in_features}) must be divisible by boft_block_size ({boft_block_size})!"
+ )
+
+ if boft_n_butterfly_factor != 0:
+ if self.in_features < (boft_block_size * (2**boft_n_butterfly_factor)):
+ raise ValueError(
+ f"Invalid combination of in_features ({self.in_features}), boft_n_butterfly_factor ({boft_n_butterfly_factor + 1}) and boft_block_size ({boft_block_size})!"
+ )
+ if self.in_features % (boft_block_size * (2**boft_n_butterfly_factor)) != 0:
+ raise ValueError(
+ f"Invalid combination of in_features ({self.in_features}), boft_n_butterfly_factor ({boft_n_butterfly_factor + 1}) and boft_block_size ({boft_block_size})!"
+ )
+
+ boft_block_num = int(self.in_features // boft_block_size)
+
+ else:
+ raise ValueError(
+ "Something went wrong, please report this error: https://github.com/huggingface/peft/issues"
+ )
+
+ # In OFT you can specify the number of blocks to be 1
+ if boft_n_butterfly_factor != 0:
+ if boft_block_num % 2 != 0:
+ raise ValueError(f"boft_block_num ({boft_block_num}) must be an even number!")
+
+ if boft_block_size % 2 != 0:
+ raise ValueError(f"boft_block_size ({boft_block_size}) must be an even number!")
+
+ # If there is no butterfly factor, then permutation matrix P will be an identity matrix.
+ P = torch.empty((boft_n_butterfly_factor + 1, self.in_features, self.in_features))
+ for i in range(boft_n_butterfly_factor + 1):
+ perm = self.block_butterfly_perm(
+ self.in_features, int(boft_block_num / (2 ** (i))), int(boft_block_size / 2), boft_n_butterfly_factor
+ )
+ perm_mat = self.perm2mat(perm)
+ P[i] = perm_mat
+
+ self.register_buffer("boft_P", P, persistent=False)
+
+ self.boft_R[adapter_name] = nn.Parameter(
+ torch.zeros(boft_n_butterfly_factor + 1, boft_block_num, boft_block_size, boft_block_size)
+ )
+ self.boft_s[adapter_name] = nn.Parameter(torch.ones(int(self.out_features), 1))
+
+ self.reset_boft_parameters(adapter_name, init_weights)
+
+ # set the boft block size and number
+ self.boft_block_size[adapter_name] = boft_block_size
+ self.boft_block_num[adapter_name] = boft_block_num
+
+ self._move_adapter_to_device_of_base_layer(adapter_name)
+ self.set_adapter(self.active_adapters, inference_mode=inference_mode)
+
+ def reset_boft_parameters(self, adapter_name, init_weights):
+ """
+ Reset the BOFT parameters.
+ """
+ if init_weights is False:
+ nn.init.normal_(self.boft_R[adapter_name], mean=0.0, std=0.1)
+ nn.init.normal_(self.boft_s[adapter_name], mean=1.0, std=0.1)
+ return
+
+ if adapter_name in self.boft_R.keys():
+ if init_weights is True:
+ # initialize R to zero
+ nn.init.zeros_(self.boft_R[adapter_name])
+ nn.init.ones_(self.boft_s[adapter_name])
+ else:
+ raise ValueError(f"Unknown initialization {init_weights=}")
+
+ def perm2mat(self, indices):
+ """
+ Convert permutation indices to permutation matrix.
+
+ Args:
+ indices: A list of indices representing the permutation.
+ """
+ # Number of indices determines the size of the square matrix
+ n = len(indices)
+
+ # Initialize a matrix of zeros
+ perm_mat = torch.zeros((n, n))
+
+ # Set the 1s according to the indices
+ for i, idx in enumerate(indices):
+ perm_mat[i, idx] = 1
+
+ return perm_mat
+
+ def block_butterfly_perm(self, n, b, r=3, n_butterfly_factor=1):
+ """
+ Define the permutation matrix for the block butterfly permutation.
+
+ Args:
+ n: size of the permutation matrix
+ b: desired number of blocks after multiplying with the permutation matrix
+ r: base block size of the block diagonal matrix, e.g. 2x2, 3x3, 5x5 etc.
+ """
+
+ if n_butterfly_factor == 0:
+ return torch.arange(n)
+
+ if b * r * 2 > n:
+ raise ValueError("Invalid number of blocks!")
+
+ block_size = int(n // b)
+ indices = torch.arange(n)
+
+ def sort_block(b, r):
+ step = b / r
+ initial_order = torch.arange(b)
+ sorted_order = torch.empty(b, dtype=torch.long)
+
+ evens = torch.arange(0, step, 2)
+ odds = torch.arange(1, step, 2)
+ sorted_seq = torch.cat((evens, odds), dim=0)
+ for i, pos in enumerate(sorted_seq):
+ sorted_order[int(i * r) : int(i * r + r)] = initial_order[int(pos * r) : int(pos * r + r)]
+ return sorted_order
+
+ sorted_order = sort_block(block_size, r)
+
+ for i in range(0, n, block_size):
+ block_end = i + block_size
+ tmp_indices = indices[i:block_end]
+ indices[i:block_end] = tmp_indices[sorted_order]
+ return indices
+
+ def cayley_batch(self, data):
+ """
+ Perform the Cayley parametrization on a batch of skew-symmetric matrices.
+
+ Args:
+ data: A batch of skew-symmetric matrices of shape (b, r, c).
+ """
+ b, r, c = data.shape
+ # Ensure the input matrix is skew-symmetric
+ skew_mat = 0.5 * (data - data.transpose(1, 2))
+ id_mat = torch.eye(r, device=data.device).unsqueeze(0).expand(b, r, c)
+
+ # Perform the Cayley parametrization
+ Q = torch.linalg.solve(id_mat + skew_mat, id_mat - skew_mat, left=False)
+
+ return Q
+
+
+class Linear(nn.Module, BOFTLayer):
+ """
+ BOFT implemented in a dense layer.
+ """
+
+ def __init__(
+ self,
+ base_layer,
+ adapter_name: str,
+ boft_block_size: int = 8,
+ boft_block_num: int = 0,
+ boft_n_butterfly_factor: int = 0,
+ boft_dropout: float = 0.1,
+ fan_in_fan_out: bool = False, # Set this to True if the layer to replace stores weight like (fan_in, fan_out)
+ init_weights: Union[bool, str] = True,
+ is_target_conv_1d_layer: bool = False,
+ **kwargs,
+ ) -> None:
+ super().__init__()
+ BOFTLayer.__init__(self, base_layer, **kwargs)
+ self.fan_in_fan_out = fan_in_fan_out
+
+ self._active_adapter = adapter_name
+
+ self.update_layer(
+ adapter_name, boft_block_size, boft_block_num, boft_n_butterfly_factor, boft_dropout, init_weights
+ )
+ self.is_target_conv_1d_layer = is_target_conv_1d_layer
+
+ def merge(self, safe_merge: bool = False, adapter_names: Optional[list[str]] = None) -> None:
+ """
+ Merge the active adapter weights into the base weights
+
+ Args:
+ safe_merge (`bool`, *optional*):
+ If True, the merge operation will be performed in a copy of the original weights and check for NaNs
+ before merging the weights. This is useful if you want to check if the merge operation will produce
+ NaNs. Defaults to `False`.
+ adapter_names (`List[str]`, *optional*):
+ The list of adapter names that should be merged. If None, all active adapters will be merged. Defaults
+ to `None`.
+ """
+ adapter_names = check_adapters_to_merge(self, adapter_names)
+ if not adapter_names:
+ # no adapter to merge
+ return
+
+ for active_adapter in adapter_names:
+ if active_adapter in self.boft_R.keys():
+ base_layer = self.get_base_layer()
+ orig_dtype = base_layer.weight.dtype
+ if safe_merge:
+ # Note that safe_merge will be slower than the normal merge
+ # because of the copy operation.
+ orig_weight = base_layer.weight.data.clone()
+ butterfly_oft_mat, boft_s = self.get_delta_weight(active_adapter)
+ orig_weight = torch.transpose(orig_weight, 0, 1)
+ orig_weight = torch.mm(butterfly_oft_mat, orig_weight.to(butterfly_oft_mat.dtype))
+ orig_weight = torch.transpose(orig_weight, 0, 1)
+ orig_weight = orig_weight * boft_s
+
+ if not torch.isfinite(orig_weight).all():
+ raise ValueError(
+ f"NaNs detected in the merged weights. The adapter {active_adapter} seems to be broken"
+ )
+
+ self.base_layer.weight.data = orig_weight.contiguous().to(orig_dtype)
+ else:
+ butterfly_oft_mat, boft_s = self.get_delta_weight(active_adapter)
+ orig_weight = base_layer.weight.data.clone()
+ orig_weight = torch.transpose(orig_weight, 0, 1)
+ orig_weight = torch.mm(butterfly_oft_mat, orig_weight.to(butterfly_oft_mat.dtype))
+ orig_weight = torch.transpose(orig_weight, 0, 1)
+ orig_weight = orig_weight * boft_s
+
+ self.base_layer.weight.data = orig_weight.contiguous().to(orig_dtype)
+
+ self.merged_adapters.append(active_adapter)
+
+ def unmerge(self) -> None:
+ """
+ This method unmerges all merged adapter layers from the base weights.
+ """
+ if not self.merged:
+ warnings.warn("Already unmerged. Nothing to do.")
+ return
+
+ while len(self.merged_adapters) > 0:
+ active_adapter = self.merged_adapters.pop()
+ base_layer = self.get_base_layer()
+ orig_dtype = base_layer.weight.dtype
+ if active_adapter in self.boft_R.keys():
+ butterfly_oft_mat, boft_s = self.get_delta_weight(active_adapter)
+
+ orig_weight = base_layer.weight.data.clone()
+ orig_weight = torch.transpose(orig_weight, 0, 1)
+ orig_weight = torch.mm(butterfly_oft_mat.t(), orig_weight.to(butterfly_oft_mat.dtype))
+ orig_weight = torch.transpose(orig_weight, 0, 1)
+
+ base_layer.weight.data = (orig_weight * (1 / boft_s)).to(orig_dtype)
+
+ def get_delta_weight(self, adapter) -> tuple[torch.Tensor, torch.Tensor]:
+ """
+ Compute the delta weight for the given adapter.
+
+ Args:
+ adapter (str):
+ The name of the adapter for which the delta weight should be computed.
+ """
+ boft_R = self.boft_R[adapter]
+ boft_s = self.boft_s[adapter]
+
+ N, D, H, _ = boft_R.shape
+ boft_R = boft_R.view(N * D, H, H)
+ orth_rotate_butterfly = self.cayley_batch(boft_R)
+ orth_rotate_butterfly = orth_rotate_butterfly.view(N, D, H, H)
+ if self.fbd_cuda_available:
+ block_diagonal_butterfly = FastBlockDiag.apply(orth_rotate_butterfly)
+ else:
+ orth_rotate_butterfly = orth_rotate_butterfly.squeeze(0)
+ block_diagonal_butterfly = torch.block_diag(*torch.unbind(orth_rotate_butterfly))
+ block_diagonal_butterfly = block_diagonal_butterfly.unsqueeze(0)
+
+ boft_P = self.boft_P.to(block_diagonal_butterfly.device)
+ butterfly_oft_mat_batch = torch.bmm(block_diagonal_butterfly, boft_P.permute(0, 2, 1))
+ butterfly_oft_mat_batch = torch.bmm(boft_P, butterfly_oft_mat_batch)
+ butterfly_oft_mat = butterfly_oft_mat_batch[0]
+
+ for i in range(1, butterfly_oft_mat_batch.shape[0]):
+ butterfly_oft_mat = butterfly_oft_mat_batch[i] @ butterfly_oft_mat
+
+ return butterfly_oft_mat, boft_s
+
+ def forward(self, x: torch.Tensor, *args: Any, **kwargs: Any) -> torch.Tensor:
+ previous_dtype = x.dtype
+
+ if self.disable_adapters:
+ if self.merged:
+ self.unmerge()
+ result = self.base_layer(x, *args, **kwargs)
+ elif self.merged:
+ result = self.base_layer(x, *args, **kwargs)
+ else:
+ boft_rotation = torch.eye(self.in_features, device=x.device, dtype=previous_dtype)
+ boft_scale = torch.ones((int(self.out_features), 1), device=x.device, dtype=previous_dtype)
+
+ for active_adapter in self.active_adapters:
+ if active_adapter not in self.boft_R.keys():
+ continue
+ boft_R = self.boft_R[active_adapter]
+ boft_s = self.boft_s[active_adapter]
+ dropout = self.boft_dropout[active_adapter]
+
+ N, D, H, _ = boft_R.shape
+ boft_R = boft_R.view(N * D, H, H)
+ orth_rotate_butterfly = self.cayley_batch(boft_R)
+ orth_rotate_butterfly = orth_rotate_butterfly.view(N, D, H, H)
+ orth_rotate_butterfly = dropout(orth_rotate_butterfly)
+ if self.fbd_cuda_available:
+ block_diagonal_butterfly = FastBlockDiag.apply(orth_rotate_butterfly)
+ else:
+ orth_rotate_butterfly = orth_rotate_butterfly.squeeze(0)
+ block_diagonal_butterfly = torch.block_diag(*torch.unbind(orth_rotate_butterfly))
+ block_diagonal_butterfly = block_diagonal_butterfly.unsqueeze(0)
+
+ # The BOFT author's cayley_batch, dropout and FastBlockDiag ONLY return fp32 outputs.
+ boft_P = self.boft_P.to(x)
+ block_diagonal_butterfly = block_diagonal_butterfly.to(x)
+ butterfly_oft_mat_batch = torch.bmm(block_diagonal_butterfly, boft_P.permute(0, 2, 1))
+ butterfly_oft_mat_batch = torch.bmm(boft_P, butterfly_oft_mat_batch)
+ butterfly_oft_mat = butterfly_oft_mat_batch[0]
+
+ for i in range(1, butterfly_oft_mat_batch.shape[0]):
+ butterfly_oft_mat = butterfly_oft_mat_batch[i] @ butterfly_oft_mat
+
+ boft_rotation = butterfly_oft_mat @ boft_rotation
+ boft_scale = boft_s * boft_scale
+
+ x = x.to(self.get_base_layer().weight.data.dtype)
+
+ orig_weight = self.get_base_layer().weight.data
+ orig_weight = torch.transpose(orig_weight, 0, 1)
+ boft_rotation = boft_rotation.to(previous_dtype)
+ orig_weight = orig_weight.to(previous_dtype)
+ rotated_weight = torch.mm(boft_rotation, orig_weight)
+ rotated_weight = torch.transpose(rotated_weight, 0, 1)
+
+ scaled_rotated_weight = rotated_weight * boft_scale
+
+ scaled_rotated_weight = scaled_rotated_weight.to(previous_dtype)
+ if self.base_layer.bias is not None:
+ self.base_layer.bias = self.base_layer.bias.to(previous_dtype)
+ result = F.linear(input=x, weight=scaled_rotated_weight, bias=self.base_layer.bias)
+
+ result = result.to(previous_dtype)
+ return result
+
+ def __repr__(self) -> str:
+ rep = super().__repr__()
+ return "boft." + rep
+
+
+class Conv2d(nn.Module, BOFTLayer):
+ """
+ BOFT implemented in a Conv2d layer.
+ """
+
+ def __init__(
+ self,
+ base_layer: nn.Module,
+ adapter_name: str,
+ boft_block_size: int = 8,
+ boft_block_num: int = 0,
+ boft_n_butterfly_factor: int = 0,
+ boft_dropout: float = 0.1,
+ init_weights: Union[bool, str] = True,
+ **kwargs,
+ ) -> None:
+ super().__init__()
+ BOFTLayer.__init__(self, base_layer)
+
+ self._active_adapter = adapter_name
+ self.update_layer(
+ adapter_name, boft_block_size, boft_block_num, boft_n_butterfly_factor, boft_dropout, init_weights
+ )
+
+ def update_layer(
+ self,
+ adapter_name,
+ boft_block_size,
+ boft_block_num,
+ boft_n_butterfly_factor,
+ boft_dropout,
+ init_weights,
+ inference_mode: bool = False,
+ **kwargs,
+ ):
+ """
+ Update the conv2d layer with trainable BOFT weights.
+ """
+
+ # Attempt to load the CUDA extension during model initialization
+ if not get_fbd_cuda():
+ self.fbd_cuda_available = False
+ # If the CUDA extension is not available, set the butterfly factor to 1 to speed up the finetuning process
+ boft_n_butterfly_factor = 1
+ else:
+ self.fbd_cuda_available = True
+
+ # to be consistent with the paper notation
+ boft_n_butterfly_factor = boft_n_butterfly_factor - 1
+ if boft_n_butterfly_factor < 0:
+ raise ValueError(
+ f"You can only specify boft_n_butterfly_factor {boft_n_butterfly_factor + 1} to be a positive integer number."
+ )
+
+ # Initialize the MultiplicativeDropoutLayer for boft_dropout > 0.0.
+ if boft_dropout > 0.0:
+ boft_dropout_layer = MultiplicativeDropoutLayer(p=boft_dropout)
+ else:
+ boft_dropout_layer = nn.Identity()
+ self.boft_dropout.update(nn.ModuleDict({adapter_name: boft_dropout_layer}))
+
+ # layer information from the base layer
+ base_layer = self.get_base_layer()
+ conv_filter_dim = self.in_features * base_layer.kernel_size[0] * base_layer.kernel_size[0]
+
+ # Initialize the BOFT parameters.
+ if boft_block_size == 0 and boft_block_num != 0:
+ if conv_filter_dim % boft_block_num != 0:
+ raise ValueError(
+ f"Convolutional kernel dimension ({conv_filter_dim}) must be divisible by boft_block_num ({boft_block_num})!"
+ )
+
+ if boft_n_butterfly_factor != 0:
+ if boft_n_butterfly_factor > int(math.log2(boft_block_num)):
+ raise ValueError(
+ f"Invalid combination of boft_n_butterfly_factor ({boft_n_butterfly_factor + 1}) and boft_block_num ({boft_block_num})!"
+ )
+ if boft_block_num % (2**boft_n_butterfly_factor) != 0:
+ raise ValueError(
+ f"boft_block_num ({boft_block_num}) must be a multiple of 2 raised to the power of boft_n_butterfly_factor ({boft_n_butterfly_factor + 1})!"
+ )
+
+ boft_block_size = int(conv_filter_dim // boft_block_num)
+
+ elif boft_block_size != 0 and boft_block_num == 0:
+ if conv_filter_dim % boft_block_size != 0:
+ raise ValueError(
+ f"Convolutional kernel dimension ({conv_filter_dim}) must be divisible by boft_block_size ({boft_block_size})!"
+ )
+
+ if boft_n_butterfly_factor != 0:
+ if conv_filter_dim < (boft_block_size * (2**boft_n_butterfly_factor)):
+ raise ValueError(
+ f"Invalid combination of convolutional kernel dimension ({conv_filter_dim}), boft_n_butterfly_factor ({boft_n_butterfly_factor + 1}) and boft_block_size ({boft_block_size})!"
+ )
+ if conv_filter_dim % (boft_block_size * (2**boft_n_butterfly_factor)) != 0:
+ raise ValueError(
+ f"Invalid combination of convolutional kernel dimension ({conv_filter_dim}), boft_n_butterfly_factor ({boft_n_butterfly_factor + 1}) and boft_block_size ({boft_block_size})!"
+ )
+
+ boft_block_num = int(conv_filter_dim // boft_block_size)
+
+ else:
+ raise ValueError(
+ "Something went wrong, please report this error: https://github.com/huggingface/peft/issues"
+ )
+
+ # In OFT you can specify the number of blocks to be 1
+ if boft_n_butterfly_factor != 0:
+ if boft_block_num % 2 != 0:
+ raise ValueError(f"boft_block_num ({boft_block_num}) must be an even number!")
+
+ if boft_block_size % 2 != 0:
+ raise ValueError(f"boft_block_size ({boft_block_size}) must be an even number!")
+
+ # If there is no butterfly factor, then permutation matrix P will be an identity matrix.
+ P = torch.empty((boft_n_butterfly_factor + 1, conv_filter_dim, conv_filter_dim))
+ for i in range(boft_n_butterfly_factor + 1):
+ perm = self.block_butterfly_perm(
+ conv_filter_dim, int(boft_block_num / (2 ** (i))), int(boft_block_size / 2), boft_n_butterfly_factor
+ )
+ perm_mat = self.perm2mat(perm)
+ P[i] = perm_mat
+
+ self.register_buffer("boft_P", P, persistent=False)
+
+ self.boft_R[adapter_name] = nn.Parameter(
+ torch.zeros(boft_n_butterfly_factor + 1, boft_block_num, boft_block_size, boft_block_size)
+ )
+ self.boft_s[adapter_name] = nn.Parameter(torch.ones(1, int(self.out_features)))
+
+ self.reset_boft_parameters(adapter_name, init_weights)
+
+ # set the boft block size and number
+ self.boft_block_size[adapter_name] = boft_block_size
+ self.boft_block_num[adapter_name] = boft_block_num
+
+ self._move_adapter_to_device_of_base_layer(adapter_name)
+ self.set_adapter(self.active_adapters, inference_mode=inference_mode)
+
+ def merge(self, safe_merge: bool = False, adapter_names: Optional[list[str]] = None) -> None:
+ """
+ Merge the active adapter weights into the base weights
+
+ Args:
+ safe_merge (`bool`, *optional*):
+ If True, the merge operation will be performed in a copy of the original weights and check for NaNs
+ before merging the weights. This is useful if you want to check if the merge operation will produce
+ NaNs. Defaults to `False`.
+ adapter_names (`List[str]`, *optional*):
+ The list of adapter names that should be merged. If None, all active adapters will be merged. Defaults
+ to `None`.
+ """
+ adapter_names = check_adapters_to_merge(self, adapter_names)
+ if not adapter_names:
+ # no adapter to merge
+ return
+
+ for active_adapter in adapter_names:
+ if active_adapter in self.boft_R.keys():
+ base_layer = self.get_base_layer()
+ orig_dtype = base_layer.weight.dtype
+ if safe_merge:
+ # Note that safe_merge will be slower than the normal merge
+ # because of the copy operation.
+ orig_weight = base_layer.weight.data.clone()
+ butterfly_oft_mat, boft_s = self.get_delta_weight(active_adapter)
+
+ orig_weight = orig_weight.view(
+ self.out_features, self.in_features * base_layer.kernel_size[0] * base_layer.kernel_size[0]
+ )
+ orig_weight = torch.transpose(orig_weight, 0, 1)
+ orig_weight = torch.mm(butterfly_oft_mat, orig_weight.to(butterfly_oft_mat.dtype))
+ orig_weight = torch.transpose(orig_weight, 0, 1)
+ orig_weight = orig_weight * boft_s
+ orig_weight = orig_weight.view(
+ self.out_features, self.in_features, base_layer.kernel_size[0], base_layer.kernel_size[0]
+ )
+
+ self.base_layer.weight.data = orig_weight.contiguous().to(orig_dtype)
+ else:
+ butterfly_oft_mat, boft_s = self.get_delta_weight(active_adapter)
+
+ orig_weight = base_layer.weight.data.clone()
+ orig_weight = orig_weight.view(
+ self.out_features, self.in_features * base_layer.kernel_size[0] * base_layer.kernel_size[0]
+ )
+ orig_weight = torch.transpose(orig_weight, 0, 1)
+ orig_weight = torch.mm(butterfly_oft_mat, orig_weight.to(butterfly_oft_mat.dtype))
+ orig_weight = torch.transpose(orig_weight, 0, 1)
+ orig_weight = orig_weight * boft_s
+ orig_weight = orig_weight.view(
+ self.out_features, self.in_features, base_layer.kernel_size[0], base_layer.kernel_size[0]
+ )
+
+ self.base_layer.weight.data = orig_weight.contiguous().to(orig_dtype)
+
+ self.merged_adapters.append(active_adapter)
+
+ def unmerge(self) -> None:
+ """
+ This method unmerges all merged adapter layers from the base weights.
+ """
+ if not self.merged:
+ warnings.warn("Already unmerged. Nothing to do.")
+ return
+ while len(self.merged_adapters) > 0:
+ active_adapter = self.merged_adapters.pop()
+ base_layer = self.get_base_layer()
+ orig_dtype = base_layer.weight.dtype
+ if active_adapter in self.boft_R.keys():
+ butterfly_oft_mat, boft_s = self.get_delta_weight(active_adapter)
+
+ orig_weight = base_layer.weight.data.clone()
+ orig_weight = orig_weight.view(
+ self.out_features,
+ self.in_features * base_layer.kernel_size[0] * base_layer.kernel_size[0],
+ )
+ orig_weight = torch.transpose(orig_weight, 0, 1)
+ orig_weight = torch.mm(butterfly_oft_mat.t(), orig_weight.to(butterfly_oft_mat.dtype))
+ orig_weight = torch.transpose(orig_weight, 0, 1)
+ orig_weight = orig_weight * (1 / boft_s)
+ orig_weight = orig_weight.view(
+ self.out_features,
+ self.in_features,
+ base_layer.kernel_size[0],
+ base_layer.kernel_size[0],
+ )
+
+ base_layer.weight.data = orig_weight.to(orig_dtype)
+
+ def get_delta_weight(self, adapter) -> tuple[torch.Tensor, torch.Tensor]:
+ """
+ Compute the delta weight for the given adapter.
+
+ Args:
+ adapter (str):
+ The name of the adapter for which the delta weight should be computed.
+ """
+
+ boft_R = self.boft_R[adapter]
+ boft_s = self.boft_s[adapter].transpose(0, 1)
+
+ N, D, H, _ = boft_R.shape
+ boft_R = boft_R.view(N * D, H, H)
+ orth_rotate_butterfly = self.cayley_batch(boft_R)
+ orth_rotate_butterfly = orth_rotate_butterfly.view(N, D, H, H)
+ if self.fbd_cuda_available:
+ block_diagonal_butterfly = FastBlockDiag.apply(orth_rotate_butterfly)
+ else:
+ orth_rotate_butterfly = orth_rotate_butterfly.squeeze(0)
+ block_diagonal_butterfly = torch.block_diag(*torch.unbind(orth_rotate_butterfly))
+ block_diagonal_butterfly = block_diagonal_butterfly.unsqueeze(0)
+
+ boft_P = self.boft_P.to(block_diagonal_butterfly.device)
+ butterfly_oft_mat_batch = torch.bmm(block_diagonal_butterfly, boft_P.permute(0, 2, 1))
+ butterfly_oft_mat_batch = torch.bmm(boft_P, butterfly_oft_mat_batch)
+ butterfly_oft_mat = butterfly_oft_mat_batch[0]
+
+ for i in range(1, butterfly_oft_mat_batch.shape[0]):
+ butterfly_oft_mat = butterfly_oft_mat_batch[i] @ butterfly_oft_mat
+
+ return butterfly_oft_mat, boft_s
+
+ def forward(self, x: torch.Tensor, *args: Any, **kwargs: Any) -> torch.Tensor:
+ previous_dtype = x.dtype
+
+ if self.disable_adapters:
+ if self.merged:
+ self.unmerge()
+ result = self.base_layer(x, *args, **kwargs)
+ elif self.merged:
+ result = self.base_layer(x, *args, **kwargs)
+ else:
+ boft_rotation = torch.eye(
+ self.in_features * self.base_layer.kernel_size[0] * self.base_layer.kernel_size[0],
+ device=x.device,
+ dtype=x.dtype,
+ )
+ boft_scale = torch.ones((int(self.out_features), 1), device=x.device, dtype=x.dtype)
+
+ for active_adapter in self.active_adapters:
+ if active_adapter not in self.boft_R.keys():
+ continue
+ boft_R = self.boft_R[active_adapter]
+ boft_s = self.boft_s[active_adapter].transpose(0, 1)
+ dropout = self.boft_dropout[active_adapter]
+
+ N, D, H, _ = boft_R.shape
+ boft_R = boft_R.view(N * D, H, H)
+ orth_rotate_butterfly = self.cayley_batch(boft_R)
+ orth_rotate_butterfly = orth_rotate_butterfly.view(N, D, H, H)
+ orth_rotate_butterfly = dropout(orth_rotate_butterfly)
+ if self.fbd_cuda_available:
+ block_diagonal_butterfly = FastBlockDiag.apply(orth_rotate_butterfly)
+ else:
+ orth_rotate_butterfly = orth_rotate_butterfly.squeeze(0)
+ block_diagonal_butterfly = torch.block_diag(*torch.unbind(orth_rotate_butterfly))
+ block_diagonal_butterfly = block_diagonal_butterfly.unsqueeze(0)
+
+ boft_P = self.boft_P.to(x)
+ block_diagonal_butterfly = block_diagonal_butterfly.to(x)
+ butterfly_oft_mat_batch = torch.bmm(block_diagonal_butterfly, boft_P.permute(0, 2, 1))
+ butterfly_oft_mat_batch = torch.bmm(boft_P, butterfly_oft_mat_batch)
+ butterfly_oft_mat = butterfly_oft_mat_batch[0]
+
+ for i in range(1, butterfly_oft_mat_batch.shape[0]):
+ butterfly_oft_mat = butterfly_oft_mat_batch[i] @ butterfly_oft_mat
+
+ boft_rotation = butterfly_oft_mat @ boft_rotation
+ boft_scale = boft_s * boft_scale
+
+ x = x.to(self.base_layer.weight.data.dtype)
+
+ orig_weight = self.base_layer.weight.data
+ orig_weight = orig_weight.view(
+ self.out_features,
+ self.in_features * self.base_layer.kernel_size[0] * self.base_layer.kernel_size[0],
+ )
+ orig_weight = torch.transpose(orig_weight, 0, 1)
+ rotated_weight = torch.mm(boft_rotation, orig_weight)
+ rotated_weight = torch.transpose(rotated_weight, 0, 1)
+
+ scaled_rotated_weight = rotated_weight * boft_scale
+
+ scaled_rotated_weight = scaled_rotated_weight.view(
+ self.out_features, self.in_features, self.base_layer.kernel_size[0], self.base_layer.kernel_size[0]
+ )
+ x = self._cast_input_dtype(x, scaled_rotated_weight.dtype)
+ bias = self._cast_input_dtype(self.base_layer.bias, scaled_rotated_weight.dtype)
+ result = F.conv2d(
+ input=x,
+ weight=scaled_rotated_weight,
+ bias=bias,
+ padding=self.base_layer.padding[0],
+ stride=self.base_layer.stride[0],
+ )
+
+ result = result.to(previous_dtype)
+ return result
+
+ def __repr__(self) -> str:
+ rep = super().__repr__()
+ return "boft." + rep
diff --git a/peft/src/peft/tuners/boft/model.py b/peft/src/peft/tuners/boft/model.py
new file mode 100644
index 0000000000000000000000000000000000000000..11bfa45ccb898fa5df101121892325a2ef54dc71
--- /dev/null
+++ b/peft/src/peft/tuners/boft/model.py
@@ -0,0 +1,131 @@
+# Copyright 2023-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+# The implementation is based on "Parameter-Efficient Orthogonal Finetuning
+# via Butterfly Factorization" (https://huggingface.co/papers/2311.06243) in ICLR 2024.
+
+import warnings
+
+import torch
+
+from peft.tuners.tuners_utils import (
+ BaseTuner,
+ BaseTunerLayer,
+)
+from peft.utils import TRANSFORMERS_MODELS_TO_BOFT_TARGET_MODULES_MAPPING
+
+from .layer import BOFTLayer, Conv2d, Linear
+
+
+class BOFTModel(BaseTuner):
+ """
+ Creates BOFT and OFT model from a pretrained transformers model. Paper: https://huggingface.co/papers/2311.06243
+ https://huggingface.co/papers/2306.07280
+
+ Args:
+ model ([`transformers.PreTrainedModel`]): The model to be adapted.
+ config ([`BOFTConfig`]): The configuration of the BOFT model.
+ adapter_name (`str`): The name of the adapter, defaults to `"default"`.
+ low_cpu_mem_usage (`bool`, `optional`, defaults to `False`):
+ Create empty adapter weights on meta device. Useful to speed up the loading process.
+
+ Returns:
+ `torch.nn.Module`: The BOFT model.
+
+ Example::
+
+ >>> import transformers >>> from transformers import AutoModelForSeq2SeqLM, BOFTConfig >>> from peft import
+ BOFTConfig, get_peft_model
+
+ >>> config = BOFTConfig( ... boft_block_size=8, ... boft_n_butterfly_factor=1, ... target_modules=["query",
+ "value", "key", "output.dense", "mlp.fc1", "mlp.fc2"], ... boft_dropout=0.1, ... bias="boft_only", ...
+ modules_to_save=["classifier"], ... )
+
+ >>> model = transformers.Dinov2ForImageClassification.from_pretrained( ... "facebook/dinov2-large", ...
+ num_labels=100, ... ) >>> boft_model = get_peft_model(model, config)
+
+ **Attributes**:
+ - **model** ([`transformers.PreTrainedModel`]) -- The model to be adapted.
+ - **peft_config** ([`BOFTConfig`]): The configuration of the BOFT model.
+ """
+
+ prefix: str = "boft_"
+ tuner_layer_cls = BOFTLayer
+ target_module_mapping = TRANSFORMERS_MODELS_TO_BOFT_TARGET_MODULES_MAPPING
+
+ def _create_and_replace(
+ self,
+ boft_config,
+ adapter_name,
+ target,
+ target_name,
+ parent,
+ current_key,
+ **optional_kwargs,
+ ):
+ if current_key is None:
+ raise ValueError("Current Key shouldn't be `None`")
+
+ bias = hasattr(target, "bias") and target.bias is not None
+ kwargs = {
+ "boft_block_size": boft_config.boft_block_size,
+ "boft_block_num": boft_config.boft_block_num,
+ "boft_n_butterfly_factor": boft_config.boft_n_butterfly_factor,
+ "boft_dropout": boft_config.boft_dropout,
+ "fan_in_fan_out": boft_config.fan_in_fan_out,
+ "init_weights": boft_config.init_weights,
+ }
+ kwargs["bias"] = bias
+
+ # If it is not a BOFTLayer, create a new module, else update it with new adapters
+ if not isinstance(target, BOFTLayer):
+ new_module = self._create_new_module(boft_config, adapter_name, target, **kwargs)
+ if adapter_name not in self.active_adapters:
+ # adding an additional adapter: it is not automatically trainable
+ new_module.requires_grad_(False)
+ self._replace_module(parent, target_name, new_module, target)
+ else:
+ target.update_layer(
+ adapter_name,
+ boft_block_size=boft_config.boft_block_size,
+ boft_block_num=boft_config.boft_block_num,
+ boft_n_butterfly_factor=boft_config.boft_n_butterfly_factor,
+ boft_dropout=boft_config.boft_dropout,
+ init_weights=boft_config.init_weights,
+ )
+
+ @staticmethod
+ def _create_new_module(boft_config, adapter_name, target, **kwargs):
+ if isinstance(target, BaseTunerLayer):
+ target_base_layer = target.get_base_layer()
+ else:
+ target_base_layer = target
+
+ if isinstance(target_base_layer, torch.nn.Linear):
+ if kwargs["fan_in_fan_out"]:
+ warnings.warn(
+ "fan_in_fan_out is set to True but the target module is `torch.nn.Linear`. "
+ "Setting fan_in_fan_out to False."
+ )
+ kwargs["fan_in_fan_out"] = boft_config.fan_in_fan_out = False
+ new_module = Linear(target, adapter_name, **kwargs)
+ elif isinstance(target_base_layer, torch.nn.Conv2d):
+ new_module = Conv2d(target, adapter_name, **kwargs)
+ else:
+ raise ValueError(
+ f"Target module {target} is not supported. "
+ "Currently, only `torch.nn.Linear` and `torch.nn.Conv2d` are supported."
+ )
+
+ return new_module
diff --git a/peft/src/peft/tuners/bone/__init__.py b/peft/src/peft/tuners/bone/__init__.py
new file mode 100644
index 0000000000000000000000000000000000000000..f131e8c17d3d11fa06c11a473cf2a54075cf443a
--- /dev/null
+++ b/peft/src/peft/tuners/bone/__init__.py
@@ -0,0 +1,24 @@
+# Copyright 2024-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+from peft.utils import register_peft_method
+
+from .config import BoneConfig
+from .layer import BoneLayer, BoneLinear
+from .model import BoneModel
+
+
+__all__ = ["BoneConfig", "BoneLayer", "BoneLinear", "BoneModel"]
+
+register_peft_method(name="bone", config_cls=BoneConfig, model_cls=BoneModel)
diff --git a/peft/src/peft/tuners/bone/config.py b/peft/src/peft/tuners/bone/config.py
new file mode 100644
index 0000000000000000000000000000000000000000..10ca673ddc5dc78a19da5f2712754f939e882fd1
--- /dev/null
+++ b/peft/src/peft/tuners/bone/config.py
@@ -0,0 +1,129 @@
+# Copyright 2024-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+from __future__ import annotations
+
+import warnings
+from dataclasses import dataclass, field
+from typing import Literal, Optional, Union
+
+from peft.config import PeftConfig
+from peft.utils import PeftType
+
+
+@dataclass
+class BoneConfig(PeftConfig):
+ """
+ This is the configuration class to store the configuration of a [`BoneModel`].
+
+ Args:
+ r (`int`):
+ The rank of Bone across different layers. It is best to set 'r' to an even number; otherwise, the default
+ initialization method will not work.
+ target_modules (`Optional[Union[List[str], str]]`):
+ The names of the modules to apply the adapter to. If this is specified, only the modules with the specified
+ names will be replaced. When passing a string, a regex match will be performed. When passing a list of
+ strings, either an exact match will be performed or it is checked if the name of the module ends with any
+ of the passed strings. If this is specified as 'all-linear', then all linear modules are chosen, excluding
+ the output layer. If this is not specified, modules will be chosen according to the model architecture. If
+ the architecture is not known, an error will be raised -- in this case, you should specify the target
+ modules manually.
+ exclude_modules (`Optional[Union[List[str], str]]`):
+ The names of the modules to not apply the adapter. When passing a string, a regex match will be performed.
+ When passing a list of strings, either an exact match will be performed or it is checked if the name of the
+ module ends with any of the passed strings.
+ init_weights (bool | Literal["bat"]):
+ Different initializations correspond to different Bone variants. By default, setting True uses the Bone
+ structure, while "bat" selects the Bat structure.
+ layers_to_transform (`Union[List[int], int]`):
+ The layer indices to transform. If a list of ints is passed, it will apply the adapter to the layer indices
+ that are specified in this list. If a single integer is passed, it will apply the transformations on the
+ layer at this index.
+ layers_pattern (`str`):
+ The layer pattern name, used only if `layers_to_transform` is different from `None`.
+ modules_to_save (`List[str]`):
+ List of modules apart from adapter layers to be set as trainable and saved in the final checkpoint.
+ """
+
+ r: int = field(
+ default=64,
+ metadata={
+ "help": "The rank of Bone across different layers.",
+ "note": "It is best to set 'r' to an even number; otherwise, the default initialization method will not work.",
+ },
+ )
+
+ target_modules: Optional[Union[list[str], str]] = field(
+ default=None,
+ metadata={
+ "help": "List of module names or regex expression of the module names to replace with Bone.",
+ "example": "For example, ['q', 'v'] or '.*decoder.*(SelfAttention|EncDecAttention).*(q|v)$' ",
+ },
+ )
+ exclude_modules: Optional[Union[list[str], str]] = field(
+ default=None,
+ metadata={"help": "List of module names or regex expression of the module names to exclude from Bone."},
+ )
+ init_weights: bool | Literal["bat"] = field(
+ default=True,
+ metadata={
+ "help": (
+ "Whether to initialize the weights of the Bone layers with their default initialization. Don't change "
+ "this setting, except if you know exactly what you're doing."
+ ),
+ },
+ )
+ layers_to_transform: Optional[Union[list[int], int]] = field(
+ default=None,
+ metadata={
+ "help": "The layer indexes to transform, is this argument is specified, PEFT will transform only the layers indexes that are specified inside this list. If a single integer is passed, PEFT will transform only the layer at this index."
+ },
+ )
+ layers_pattern: Optional[str] = field(
+ default=None,
+ metadata={
+ "help": "The layer pattern name, used only if `layers_to_transform` is different to None and if the layer pattern is not in the common layers pattern."
+ },
+ )
+ bias: str = field(default="none", metadata={"help": "Bias type for Bone. Can be 'none', 'all' or 'bone_only'"})
+ modules_to_save: Optional[list[str]] = field(
+ default=None,
+ metadata={
+ "help": "List of modules apart from Bone layers to be set as trainable and saved in the final checkpoint. "
+ "For example, in Sequence Classification or Token Classification tasks, "
+ "the final layer `classifier/score` are randomly initialized and as such need to be trainable and saved."
+ },
+ )
+
+ def __post_init__(self):
+ super().__post_init__()
+ self.peft_type = PeftType.BONE
+ self.target_modules = (
+ set(self.target_modules) if isinstance(self.target_modules, list) else self.target_modules
+ )
+ self.exclude_modules = (
+ set(self.exclude_modules) if isinstance(self.exclude_modules, list) else self.exclude_modules
+ )
+ # if target_modules is a regex expression, then layers_to_transform should be None
+ if isinstance(self.target_modules, str) and self.layers_to_transform is not None:
+ raise ValueError("`layers_to_transform` cannot be used when `target_modules` is a str.")
+
+ # if target_modules is a regex expression, then layers_pattern should be None
+ if isinstance(self.target_modules, str) and self.layers_pattern is not None:
+ raise ValueError("`layers_pattern` cannot be used when `target_modules` is a str.")
+
+ warnings.warn(
+ "Bone will be removed in v0.19.0 of PEFT, use `MissConfig` instead. "
+ "If you already have a Bone checkpoint, you can use `/scripts/convert-bone-to-miss.py` to convert it into "
+ )
diff --git a/peft/src/peft/tuners/bone/layer.py b/peft/src/peft/tuners/bone/layer.py
new file mode 100644
index 0000000000000000000000000000000000000000..2cd04c57c8701a794970705cf05a28a087dbbec2
--- /dev/null
+++ b/peft/src/peft/tuners/bone/layer.py
@@ -0,0 +1,352 @@
+# Copyright 2024-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+import math
+import warnings
+from typing import Any, Optional, Union
+
+import torch
+import torch.nn as nn
+import torch.nn.functional as F
+
+from peft.tuners.tuners_utils import BaseTunerLayer, check_adapters_to_merge
+
+
+class BoneLayer(BaseTunerLayer):
+ # All names of layers that may contain (trainable) adapter weights
+ adapter_layer_names = ("bone_block",)
+ # All names of other parameters that may contain adapter-related parameters
+ other_param_names = ("bone_r",)
+
+ def __init__(self, base_layer: nn.Module, **kwargs) -> None:
+ self.base_layer = base_layer
+ self.bone_r = {}
+ self.bone_block = nn.ParameterDict({})
+ # Mark the weight as unmerged
+ self._disable_adapters = False
+ self.merged_adapters = []
+ # flag to enable/disable casting of input to weight dtype during forward call
+ self.cast_input_dtype_enabled = True
+ self.kwargs = kwargs
+
+ base_layer = self.get_base_layer()
+ if isinstance(base_layer, nn.Linear):
+ self.in_features, self.out_features = base_layer.in_features, base_layer.out_features
+ else:
+ raise ValueError(f"Unsupported layer type {type(base_layer)}")
+
+ def update_layer(
+ self,
+ adapter_name: str,
+ r: int,
+ init_weights: bool,
+ inference_mode: bool = False,
+ **kwargs,
+ ) -> None:
+ """Internal function to create bone adapter
+
+ Args:
+ adapter_name (`str`): Name for the adapter to add.
+ r (`int`): Rank for the added adapter.
+ init_weights (`bool`): Whether to initialize weights.
+ """
+ if r <= 0:
+ raise ValueError(f"`r` should be a positive integer value but the value passed is {r}")
+
+ self.bone_r[adapter_name] = r
+
+ # Determine shape of Bone weights
+ base_layer = self.get_base_layer()
+ if isinstance(base_layer, nn.Linear):
+ self.bone_block[adapter_name] = nn.Parameter(torch.zeros(r, self.out_features), requires_grad=True)
+
+ else:
+ raise TypeError(f"Bone is not implemented for base layers of type {type(base_layer).__name__}")
+
+ # Initialize weights
+ if init_weights == "bat":
+ if self.in_features % r != 0 or self.out_features % r != 0:
+ raise ValueError("The weight matrix must be fully divisible into [r, r] blocks.")
+ self.reset_bat_parameters(adapter_name, r)
+ elif init_weights:
+ self.reset_bone_parameters(adapter_name, r)
+ else:
+ self.reset_bone_parameters_random(adapter_name)
+ # Move new weights to device
+ self._move_adapter_to_device_of_base_layer(adapter_name)
+ self.set_adapter(self.active_adapters, inference_mode=inference_mode)
+
+ def reset_bone_parameters(self, adapter_name: str, r):
+ self.bone_block[adapter_name] = nn.Parameter(torch.zeros(r, self.out_features), requires_grad=True)
+
+ def reset_bat_parameters(self, adapter_name: str, r):
+ self.bone_block[adapter_name] = nn.Parameter(torch.zeros(self.out_features // r, r, r), requires_grad=True)
+
+ def reset_bone_parameters_random(self, adapter_name: str):
+ nn.init.kaiming_uniform_(self.bone_block[adapter_name], a=math.sqrt(5))
+
+ def scale_layer(self, scale: float) -> None:
+ if scale == 1:
+ return
+
+ for active_adapter in self.active_adapters:
+ if active_adapter not in self.bone_block.keys():
+ continue
+
+ warnings.warn("Scaling operation for Bone not supported! Automatically set scale to 1.")
+
+ def unscale_layer(self, scale=None) -> None:
+ for active_adapter in self.active_adapters:
+ if active_adapter not in self.bone_block.keys():
+ continue
+
+ warnings.warn("Unscaling operation for Bone not supported! Keeping scale at 1.")
+
+
+class BoneLinear(nn.Module, BoneLayer):
+ """
+ Bone implemented in a dense layer.
+ """
+
+ def __init__(
+ self,
+ base_layer,
+ adapter_name: str,
+ r: int = 0,
+ init_weights: Union[bool, str] = True,
+ **kwargs,
+ ) -> None:
+ super().__init__()
+ BoneLayer.__init__(self, base_layer, **kwargs)
+ self._active_adapter = adapter_name
+ self.update_layer(adapter_name, r, init_weights, **kwargs)
+ self.bone_fn = init_weights
+
+ def merge(self, safe_merge: bool = False, adapter_names: Optional[list[str]] = None) -> None:
+ """
+ Merge the active adapter weights into the base weights
+
+ Args:
+ safe_merge (`bool`, *optional*):
+ If `True`, the merge operation will be performed in a copy of the original weights and check for NaNs
+ before merging the weights. This is useful if you want to check if the merge operation will produce
+ NaNs. Defaults to `False`.
+ adapter_names (`List[str]`, *optional*):
+ The list of adapter names that should be merged. If `None`, all active adapters will be merged.
+ Defaults to `None`.
+ """
+ adapter_names = check_adapters_to_merge(self, adapter_names)
+ if not adapter_names:
+ # no adapter to merge
+ return
+
+ for active_adapter in adapter_names:
+ if active_adapter in self.bone_block.keys():
+ base_layer = self.get_base_layer()
+ orig_dtype = base_layer.weight.dtype
+ if safe_merge:
+ # Note that safe_merge will be slower than the normal merge
+ # because of the copy operation.
+ orig_weight = base_layer.weight.data.clone()
+ if self.bone_fn == "bat":
+ delta_weight = self.get_delta_weight(active_adapter, orig_weight)
+ orig_weight += delta_weight
+ else:
+ delta_weight = self.get_delta_weight_bone(active_adapter, self.base_layer.weight.data)
+ orig_weight = delta_weight
+
+ if not torch.isfinite(orig_weight).all():
+ raise ValueError(
+ f"NaNs detected in the merged weights. The adapter {active_adapter} seems to be broken"
+ )
+
+ base_layer.weight.data = orig_weight.to(orig_dtype)
+ else:
+ if self.bone_fn == "bat":
+ delta_weight = self.get_delta_weight(active_adapter, self.base_layer.weight.data)
+ base_layer.weight.data += delta_weight.to(orig_dtype)
+ else:
+ delta_weight = self.get_delta_weight_bone(active_adapter, self.base_layer.weight.data)
+ base_layer.weight.data = delta_weight.to(orig_dtype)
+ self.merged_adapters.append(active_adapter)
+
+ def unmerge(self) -> None:
+ """
+ This method unmerges all merged adapter layers from the base weights.
+ """
+ if not self.merged:
+ warnings.warn("Already unmerged. Nothing to do.")
+ return
+
+ while len(self.merged_adapters) > 0:
+ active_adapter = self.merged_adapters.pop()
+ base_layer = self.get_base_layer()
+ orig_dtype = base_layer.weight.dtype
+ if active_adapter in self.bone_block.keys():
+ orig_weight = self.get_base_layer().weight.data.clone()
+ if self.bone_fn == "bat":
+ delta_weight = self.get_delta_weight(active_adapter, orig_weight, re=True)
+ else:
+ delta_weight = self.get_delta_weight_bone(active_adapter, orig_weight, re=True)
+
+ base_layer.weight.data = delta_weight.to(orig_dtype)
+
+ def get_delta_weight(self, adapter, orig_weight, re: bool = False) -> torch.Tensor:
+ """
+ Compute the delta weight for the given adapter.
+
+ Args:
+ adapter (str):
+ The name of the adapter for which the delta weight should be computed.
+ """
+ device = self.bone_block[adapter].device
+ dtype = self.bone_block[adapter].dtype
+ # In case users wants to merge the adapter weights that are in
+ # (b)float16 while being on CPU, we need to cast the weights to float32, perform the merge and then cast back to
+ # (b)float16 because some CPUs have slow bf16/fp16 matmuls.
+ cast_to_fp32 = device.type == "cpu" and (dtype == torch.float16 or dtype == torch.bfloat16)
+
+ weight_bone = self.bone_block[adapter]
+
+ if cast_to_fp32:
+ weight_bone = weight_bone.float()
+ orig_weight = orig_weight.to(weight_bone.dtype)
+
+ r = weight_bone.size(-1)
+ if re:
+ o = orig_weight.reshape(orig_weight.size(0) // r, r, orig_weight.size(1) // r, r).permute(2, 0, 1, 3)
+ one = torch.eye(weight_bone.size(-1)).to(weight_bone.device)
+ # inverse must be in float32, after that the dtype can be adjusted if needed
+ inv_I_plus_b = torch.inverse(one + weight_bone)
+ inv_I_plus_b = inv_I_plus_b.to(weight_bone.dtype)
+ w = (o - weight_bone) @ inv_I_plus_b
+ output_tensor = w.permute(1, 2, 0, 3).reshape(*orig_weight.shape)
+ else:
+ w = (
+ orig_weight.reshape(orig_weight.size(0) // r, r, orig_weight.size(1) // r, r).permute(2, 0, 1, 3)
+ @ weight_bone
+ + weight_bone
+ )
+ output_tensor = w.permute(1, 2, 0, 3).reshape(*orig_weight.shape)
+
+ if cast_to_fp32:
+ output_tensor = output_tensor.to(dtype=dtype)
+
+ # cast back the weights
+ self.bone_block[adapter].data = weight_bone.to(dtype)
+
+ return output_tensor
+
+ def get_delta_weight_bone(self, adapter, orig_weight, re: bool = False) -> torch.Tensor:
+ """
+ Compute the delta weight for the given adapter.
+
+ Args:
+ adapter (str):
+ The name of the adapter for which the delta weight should be computed.
+ """
+ device = self.bone_block[adapter].device
+ dtype = self.bone_block[adapter].dtype
+ # In case users wants to merge the adapter weights that are in
+ # (b)float16 while being on CPU, we need to cast the weights to float32, perform the merge and then cast back to
+ # (b)float16 because some CPUs have slow bf16/fp16 matmuls.
+ cast_to_fp32 = device.type == "cpu" and (dtype == torch.float16 or dtype == torch.bfloat16)
+
+ weight_bone = self.bone_block[adapter]
+
+ if cast_to_fp32:
+ weight_bone = weight_bone.float()
+
+ in_features = orig_weight.size(-1)
+ r = weight_bone.size(0)
+ if in_features % r != 0:
+ last_size = in_features % r
+ n_block = in_features // r
+ n_block_size = n_block * r
+
+ if re:
+ orig_weight[:, :n_block_size] = (
+ (orig_weight[:, :n_block_size].reshape(-1, n_block, r).permute(1, 2, 0) - weight_bone)
+ .permute(2, 0, 1)
+ .reshape(*orig_weight[:, :n_block_size].shape)
+ )
+ orig_weight[:, n_block_size:] = (
+ orig_weight[:, n_block_size:] - (weight_bone.transpose(0, 1))[:, :last_size]
+ )
+ else:
+ orig_weight[:, :n_block_size] = (
+ (orig_weight[:, :n_block_size].reshape(-1, n_block, r).permute(1, 2, 0) + weight_bone)
+ .permute(2, 0, 1)
+ .reshape(*orig_weight[:, :n_block_size].shape)
+ )
+ orig_weight[:, n_block_size:] = (
+ orig_weight[:, n_block_size:] + (weight_bone.transpose(0, 1))[:, :last_size]
+ )
+ output_tensor = orig_weight
+
+ else:
+ if re:
+ w = orig_weight.reshape(-1, orig_weight.size(1) // r, r).permute(1, 2, 0) - weight_bone
+ output_tensor = w.permute(2, 0, 1).reshape(*orig_weight.shape)
+ else:
+ w = orig_weight.reshape(-1, orig_weight.size(1) // r, r).permute(1, 2, 0) + weight_bone
+ output_tensor = w.permute(2, 0, 1).reshape(*orig_weight.shape)
+
+ if cast_to_fp32:
+ output_tensor = output_tensor.to(dtype=dtype)
+
+ # cast back the weights
+ self.bone_block[adapter].data = weight_bone.to(dtype)
+
+ return output_tensor
+
+ def forward(self, x: torch.Tensor, *args: Any, **kwargs: Any) -> torch.Tensor:
+ previous_dtype = x.dtype
+
+ if self.disable_adapters:
+ if self.merged:
+ self.unmerge()
+ result = self.base_layer(x, *args, **kwargs)
+ elif self.merged:
+ result = self.base_layer(x, *args, **kwargs)
+ else:
+ if self.bone_fn == "bat":
+ orig_weight = self.base_layer.weight.data.clone()
+ for active_adapter in self.active_adapters:
+ if active_adapter not in self.bone_block.keys():
+ continue
+ delta_weight = self.get_delta_weight(active_adapter, orig_weight)
+ orig_weight = orig_weight + delta_weight
+
+ x = self._cast_input_dtype(x, orig_weight.dtype)
+ bias = self._cast_input_dtype(self.base_layer.bias, orig_weight.dtype)
+ result = F.linear(input=x, weight=orig_weight, bias=bias)
+ else:
+ result = self.base_layer(x, *args, **kwargs)
+ for active_adapter in self.active_adapters:
+ if active_adapter not in self.bone_block.keys():
+ continue
+ bone = self.bone_block[active_adapter]
+ r = bone.size(0)
+ if x.size(-1) % r != 0:
+ padding_size = (r - x.size(-1) % r) % r
+ x = F.pad(x, (0, padding_size))
+ x = self._cast_input_dtype(x, bone.dtype)
+ result = result + torch.sum(x.reshape(*x.shape[:-1], x.size(-1) // r, r), dim=-2) @ bone
+
+ result = result.to(previous_dtype)
+ return result
+
+ def __repr__(self) -> str:
+ rep = super().__repr__()
+ return "bone." + rep
diff --git a/peft/src/peft/tuners/bone/model.py b/peft/src/peft/tuners/bone/model.py
new file mode 100644
index 0000000000000000000000000000000000000000..412489e75a4296cfa8814be193212c465da91145
--- /dev/null
+++ b/peft/src/peft/tuners/bone/model.py
@@ -0,0 +1,126 @@
+# Copyright 2024-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+
+import torch
+
+from peft.tuners.tuners_utils import BaseTuner, BaseTunerLayer
+from peft.utils import TRANSFORMERS_MODELS_TO_BONE_TARGET_MODULES_MAPPING
+
+from .layer import BoneLayer, BoneLinear
+
+
+class BoneModel(BaseTuner):
+ """
+ Creates Householder reflection adaptation (Bone) model from a pretrained model. The method is described in
+ https://huggingface.co/papers/2409.15371
+
+ Args:
+ model (`torch.nn.Module`): The model to which the adapter tuner layers will be attached.
+ config ([`BoneConfig`]): The configuration of the Bone model.
+ adapter_name (`str`): The name of the adapter, defaults to `"default"`.
+ low_cpu_mem_usage (`bool`, `optional`, defaults to `False`):
+ Create empty adapter weights on meta device. Useful to speed up the loading process.
+
+ Returns:
+ `torch.nn.Module`: The Bone model.
+
+ Example:
+ ```py
+ >>> from diffusers import StableDiffusionPipeline
+ >>> from peft import BoneModel, BoneConfig
+
+ >>> config_te = BoneConfig(
+ ... r=8,
+ ... target_modules=["k_proj", "q_proj", "v_proj", "out_proj", "fc1", "fc2"],
+ ... init_weights=True,
+ ... )
+ >>> config_unet = BoneConfig(
+ ... r=8,
+ ... target_modules=[
+ ... "proj_in",
+ ... "proj_out",
+ ... "to_k",
+ ... "to_q",
+ ... "to_v",
+ ... "to_out.0",
+ ... "ff.net.0.proj",
+ ... "ff.net.2",
+ ... ],
+ ... init_weights=True,
+ ... )
+
+ >>> model = StableDiffusionPipeline.from_pretrained("runwayml/stable-diffusion-v1-5")
+ >>> model.text_encoder = BoneModel(model.text_encoder, config_te, "default")
+ >>> model.unet = BoneModel(model.unet, config_unet, "default")
+ ```
+
+ **Attributes**:
+ - **model** ([`~torch.nn.Module`]) -- The model to be adapted.
+ - **peft_config** ([`BoneConfig`]): The configuration of the Bone model.
+ """
+
+ prefix: str = "bone_"
+ tuner_layer_cls = BoneLayer
+ target_module_mapping = TRANSFORMERS_MODELS_TO_BONE_TARGET_MODULES_MAPPING
+
+ def _create_and_replace(
+ self,
+ bone_config,
+ adapter_name,
+ target,
+ target_name,
+ parent,
+ current_key,
+ **optional_kwargs,
+ ):
+ if current_key is None:
+ raise ValueError("Current Key shouldn't be `None`")
+
+ bias = hasattr(target, "bias") and target.bias is not None
+ kwargs = {
+ "r": bone_config.r,
+ "init_weights": bone_config.init_weights,
+ }
+ kwargs["bias"] = bias
+
+ # If it is not a BoneLayer, create a new module, else update it with new adapters
+ if not isinstance(target, BoneLayer):
+ new_module = self._create_new_module(bone_config, adapter_name, target, **kwargs)
+ if adapter_name not in self.active_adapters:
+ # adding an additional adapter: it is not automatically trainable
+ new_module.requires_grad_(False)
+ self._replace_module(parent, target_name, new_module, target)
+ else:
+ target.update_layer(
+ adapter_name,
+ r=bone_config.r,
+ init_weights=bone_config.init_weights,
+ )
+
+ @staticmethod
+ def _create_new_module(bone_config, adapter_name, target, **kwargs):
+ if isinstance(target, BaseTunerLayer):
+ target_base_layer = target.get_base_layer()
+ else:
+ target_base_layer = target
+
+ if isinstance(target_base_layer, torch.nn.Linear):
+ new_module = BoneLinear(target, adapter_name, **kwargs)
+ else:
+ raise ValueError(
+ f"Target module {target} is not supported. Currently, only `torch.nn.Linear` is supported."
+ )
+
+ return new_module
diff --git a/peft/src/peft/tuners/c3a/__init__.py b/peft/src/peft/tuners/c3a/__init__.py
new file mode 100644
index 0000000000000000000000000000000000000000..ba8a7cbf61845f934737e11be277a7e2f48e7b34
--- /dev/null
+++ b/peft/src/peft/tuners/c3a/__init__.py
@@ -0,0 +1,23 @@
+# Copyright 2025-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+from peft.utils import register_peft_method
+
+from .config import C3AConfig
+from .layer import C3ALayer, C3ALinear
+from .model import C3AModel
+
+
+__all__ = ["C3AConfig", "C3ALayer", "C3ALinear", "C3AModel"]
+
+register_peft_method(name="c3a", model_cls=C3AModel, config_cls=C3AConfig)
diff --git a/peft/src/peft/tuners/c3a/config.py b/peft/src/peft/tuners/c3a/config.py
new file mode 100644
index 0000000000000000000000000000000000000000..2059c77a417f9f4eaa54f9d1f73943836646d328
--- /dev/null
+++ b/peft/src/peft/tuners/c3a/config.py
@@ -0,0 +1,137 @@
+# Copyright 2025-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+from __future__ import annotations
+
+from dataclasses import dataclass, field
+from typing import Literal, Optional, Union
+
+from peft.config import PeftConfig
+from peft.utils import PeftType
+
+
+@dataclass
+class C3AConfig(PeftConfig):
+ """This is the configuration class to store the configuration of a [`C3AModel`].
+
+ Args:
+ block_size (`int`):
+ block size for C3A, must be divisible by both the input size and the output size of the target layer. If
+ you have no idea what block_size you should use, set it to the greatest common divisor of all input &
+ output sizes of your target layers. Increasing this would result in less parameters.
+ target_modules (`Union[list[str],str]`): The names of the modules to apply C3A to.
+ bias (`str`): Bias type for C3A. Can be 'none', 'all' or 'c3a_only'. If 'all' or 'c3a_only', the
+ corresponding biases will be updated during training. Be aware that this means that, even when disabling
+ the adapters, the model will not produce the same output as the base model would have without adaptation.
+ modules_to_save (`list[str]`):list of modules apart from C3A layers to be set as trainable
+ and saved in the final checkpoint.
+ layers_to_transform (`Union[list[int],int]`):
+ The layer indexes to transform, if this argument is specified, it will apply C3A on the layer indexes that
+ are specified in this list. If a single integer is passed, it will apply C3A on the layer at this index.
+ layers_pattern (`str`):
+ The layer pattern name, used only if `layers_to_transform` is different from `None` and if the layer
+ pattern is not in the common layers pattern.
+ block_size_pattern (`dict`):
+ The mapping from layer names or regexp expression to block_size which are different from the default
+ specified. For example, `{"model.decoder.layers.0.encoder_attn.k_proj": 1280`}
+ init_weights (`Union[bool, Literal["gaussian", "kaiming_uniform", "xavier_uniform"]]`):
+ Defaults to 'xavier_uniform'. Setting this to `False` also uses 'xavier_uniform'. To set the weights to
+ zeros (thus making C3A a no-op), set the value to `True`.
+ """
+
+ block_size: int = field(
+ default=256,
+ metadata={
+ "help": (
+ "block size for C3A, must be divisible by both the input size and the output size of the target layer."
+ " If you have no idea what block_size you should use, set it to the greatest common divisor of all"
+ " input & output sizes of your target layers. Increasing this would result in less parameters."
+ )
+ },
+ )
+ target_modules: Optional[Union[list[str], str]] = field(
+ default=None,
+ metadata={
+ "help": (
+ "list of module names or regex expression of the module names to replace with C3A."
+ " For example, ['q', 'v'] or '.*decoder.*(SelfAttention|EncDecAttention).*(q|v)$' "
+ )
+ },
+ )
+ bias: str = field(default="none", metadata={"help": "Bias type for C3A. Can be 'none', 'all' or 'c3a_only'"})
+ modules_to_save: Optional[list[str]] = field(
+ default=None,
+ metadata={
+ "help": (
+ "list of modules apart from C3A layers to be set as trainable and saved in the final checkpoint."
+ " For example, in Sequence Classification or Token Classification tasks,"
+ " the final layer `classifier/score` are randomly initialized"
+ " and as such need to be trainable and saved."
+ )
+ },
+ )
+ layers_to_transform: Optional[Union[list[int], int]] = field(
+ default=None,
+ metadata={
+ "help": (
+ "The layer indexes to transform, is this argument is specified,"
+ " PEFT will transform only the layers indexes that are specified inside this list."
+ " If a single integer is passed, PEFT will transform only the layer at this index."
+ " This only works when target_modules is a list of str."
+ )
+ },
+ )
+ layers_pattern: Optional[Union[list[str], str]] = field(
+ default=None,
+ metadata={
+ "help": (
+ "The layer pattern name, used only if `layers_to_transform` is different to None"
+ " and if the layer pattern is not in the common layers pattern."
+ " This only works when target_modules is a list of str."
+ )
+ },
+ )
+ block_size_pattern: Optional[dict] = field(
+ default_factory=dict,
+ metadata={
+ "help": (
+ "The mapping from layer names or regexp expression to block_size"
+ " which are different from the default specified."
+ " For example, `{model.decoder.layers.0.encoder_attn.k_proj: 1280`}"
+ )
+ },
+ )
+ init_weights: Optional[Union[bool, Literal["gaussian", "kaiming_uniform", "xavier_uniform"]]] = field(
+ default="xavier_uniform",
+ metadata={
+ "help": (
+ "Defaults to 'xavier_uniform'. Setting this to `False` also uses 'xavier_uniform'. To set the weights "
+ "to zeros (thus making C3A a no-op), set the value to `True`."
+ )
+ },
+ )
+
+ def __post_init__(self):
+ super().__post_init__()
+ self.peft_type = PeftType.C3A
+ self.target_modules = (
+ set(self.target_modules) if isinstance(self.target_modules, list) else self.target_modules
+ )
+ # if target_modules is a regex expression, then layers_to_transform should be None
+ if isinstance(self.target_modules, str) and self.layers_to_transform is not None:
+ raise ValueError("`layers_to_transform` cannot be used when `target_modules` is a str.")
+
+ # if target_modules is a regex expression, then layers_pattern should be None
+ if isinstance(self.target_modules, str) and self.layers_pattern is not None:
+ raise ValueError("`layers_pattern` cannot be used when `target_modules` is a str.")
diff --git a/peft/src/peft/tuners/c3a/layer.py b/peft/src/peft/tuners/c3a/layer.py
new file mode 100644
index 0000000000000000000000000000000000000000..0890ba0e2571df384e4a629f4902d963b6181e02
--- /dev/null
+++ b/peft/src/peft/tuners/c3a/layer.py
@@ -0,0 +1,202 @@
+# Copyright 2025-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+from __future__ import annotations
+
+import math
+import warnings
+from typing import Any, Literal, Optional
+
+import torch
+import torch.nn as nn
+
+from peft.tuners.tuners_utils import BaseTunerLayer, check_adapters_to_merge
+
+from .utils import BlockCircularConvolution, get_circulant_fast
+
+
+class C3ALayer(BaseTunerLayer):
+ # All names of layers that may contain (trainable) adapter weights
+ adapter_layer_names = ("c3a_kernel",)
+ # All names of other parameters that may contain adapter-related parameters
+ other_param_names = ("block_size",)
+
+ def __init__(self, base_layer: nn.Module, **kwargs) -> None:
+ self.base_layer = base_layer
+ self.block_size = {}
+ self.c3a_kernel = nn.ParameterDict({})
+ # Mark the weight as unmerged
+ self._disable_adapters = False
+ self.merged_adapters = []
+ self.kwargs = kwargs
+
+ base_layer = self.get_base_layer()
+ if isinstance(base_layer, nn.Linear):
+ self.in_features, self.out_features = base_layer.in_features, base_layer.out_features
+ else:
+ raise ValueError(f"Unsupported layer type {type(base_layer)}")
+
+ def get_delta_weight(self, adapter) -> torch.Tensor:
+ if adapter not in self.c3a_kernel.keys():
+ raise ValueError(f"Adapter {adapter} not found.")
+ base_layer_weight = self.get_base_layer().weight
+ base_layer_weight_dtype = base_layer_weight.dtype
+ c3a_kernel = self.c3a_kernel[adapter]
+
+ delta_weight = get_circulant_fast(c3a_kernel.to(torch.float32)).to(base_layer_weight_dtype)
+ return delta_weight / base_layer_weight.size(-1)
+
+ def update_layer(self, adapter_name, block_size, init_weights, inference_mode: bool = False, **kwargs):
+ if block_size <= 0:
+ raise ValueError(f"`block_size` should be a positive integer value but the value passed is {block_size}")
+ if self.in_features % block_size != 0:
+ raise ValueError(
+ f"The block size should be a factor of the input size. However, the input size is {self.in_features} and the block size is {block_size}"
+ )
+ if self.out_features % block_size != 0:
+ raise ValueError(
+ f"The block size should be a factor of the output size. However, the output size is {self.out_features} and the block size is {block_size}"
+ )
+
+ self.block_size[adapter_name] = block_size
+
+ weight = self.get_base_layer().weight
+ self.c3a_kernel[adapter_name] = nn.Parameter(
+ torch.zeros(
+ self.out_features // block_size,
+ self.in_features // block_size,
+ block_size,
+ # Currently, only fp32 is widely supported for FFT (fp16 is only supported on GPU with shapes of powers
+ # of 2, bf16 lacks FFT support)
+ dtype=torch.float32,
+ device=weight.device,
+ )
+ )
+
+ self.reset_c3a_parameters(adapter_name, init_weights)
+ self._move_adapter_to_device_of_base_layer(adapter_name)
+ self.set_adapter(self.active_adapters, inference_mode=inference_mode)
+
+ @torch.no_grad()
+ def reset_c3a_parameters(self, adapter_name, init_weights):
+ if init_weights is True:
+ return
+
+ if adapter_name in self.c3a_kernel.keys():
+ if init_weights == "gaussian":
+ nn.init.normal_(self.c3a_kernel[adapter_name])
+ elif init_weights in ["xavier_uniform", False]:
+ fan_in, fan_out = self.in_features, self.out_features
+ std = 1.0 * math.sqrt(2.0 / float(fan_in + fan_out))
+ a = math.sqrt(3.0) * std
+ nn.init.uniform_(self.c3a_kernel[adapter_name], -a, a)
+ elif init_weights == "kaiming_uniform":
+ fan_in = self.in_features
+ a = 1.0 * math.sqrt(1.0 / float(fan_in))
+ nn.init.uniform_(self.c3a_kernel[adapter_name], -a, a)
+ else:
+ raise ValueError(f"Unknown init_weights: {init_weights}")
+
+
+class C3ALinear(nn.Module, C3ALayer):
+ # Lora implemented in a dense layer
+ def __init__(
+ self,
+ base_layer,
+ adapter_name: str,
+ block_size: int,
+ init_weights: bool | Literal["gaussian", "kaiming_uniform", "xavier_uniform"],
+ **kwargs,
+ ) -> None:
+ super().__init__()
+ C3ALayer.__init__(self, base_layer, **kwargs)
+ self._active_adapter = adapter_name
+ self.update_layer(adapter_name, block_size, init_weights)
+
+ def merge(self, safe_merge: bool = False, adapter_names: Optional[list[str]] = None) -> None:
+ """
+ Merge the active adapter weights into the base weights
+
+ Args:
+ safe_merge (`bool`, *optional*):
+ If True, the merge operation will be performed in a copy of the original weights and check for NaNs
+ before merging the weights. This is useful if you want to check if the merge operation will produce
+ NaNs. Defaults to `False`.
+ adapter_names (`list[str]`, *optional*):
+ The list of adapter names that should be merged. If None, all active adapters will be merged. Defaults
+ to `None`.
+ """
+ adapter_names = check_adapters_to_merge(self, adapter_names)
+ if not adapter_names:
+ # no adapter to merge
+ return
+
+ for active_adapter in adapter_names:
+ if active_adapter in self.c3a_kernel.keys():
+ base_layer = self.get_base_layer()
+ if safe_merge:
+ # Note that safe_merge will be slower than the normal merge
+ # because of the copy operation.
+ orig_weights = base_layer.weight.data.clone()
+ delta_weight = self.get_delta_weight(active_adapter)
+ orig_weights = orig_weights + delta_weight
+
+ if not torch.isfinite(orig_weights).all():
+ raise ValueError(
+ f"NaNs detected in the merged weights. The adapter {active_adapter} seems to be broken"
+ )
+
+ base_layer.weight.data = orig_weights
+ else:
+ delta_weight = self.get_delta_weight(active_adapter)
+ base_layer.weight.data = base_layer.weight.data + delta_weight
+
+ self.merged_adapters.append(active_adapter)
+
+ def unmerge(self) -> None:
+ """
+ This method unmerges all merged adapter layers from the base weights.
+ """
+ if not self.merged:
+ warnings.warn("Already unmerged. Nothing to do.")
+ return
+ while len(self.merged_adapters) > 0:
+ active_adapter = self.merged_adapters.pop()
+ if active_adapter in self.c3a_kernel.keys():
+ self.get_base_layer().weight.data -= self.get_delta_weight(active_adapter)
+
+ def forward(self, x: torch.Tensor, *args: Any, **kwargs: Any) -> torch.Tensor:
+ previous_dtype = x.dtype
+
+ if self.disable_adapters:
+ if self.merged:
+ self.unmerge()
+ result = self.base_layer(x, *args, **kwargs)
+ elif self.merged:
+ result = self.base_layer(x, *args, **kwargs)
+ else:
+ result = self.base_layer(x, *args, **kwargs)
+ x = x.to(torch.float32)
+ for active_adapter in self.active_adapters:
+ if active_adapter not in self.c3a_kernel.keys():
+ continue
+ c3a_kernel = self.c3a_kernel[active_adapter].to(torch.float32)
+ x = BlockCircularConvolution.apply(x, c3a_kernel) / x.size(-1)
+ result += x.to(result.dtype)
+
+ result = result.to(previous_dtype)
+ return result
+
+ def __repr__(self) -> str:
+ rep = super().__repr__()
+ return "c3a." + rep
diff --git a/peft/src/peft/tuners/c3a/model.py b/peft/src/peft/tuners/c3a/model.py
new file mode 100644
index 0000000000000000000000000000000000000000..6e71973691717551b5bd442873f9a6da378e34aa
--- /dev/null
+++ b/peft/src/peft/tuners/c3a/model.py
@@ -0,0 +1,97 @@
+# Copyright 2025-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+from __future__ import annotations
+
+import re
+from itertools import chain
+
+import torch
+
+from peft.tuners.tuners_utils import BaseTuner, BaseTunerLayer
+from peft.utils import (
+ TRANSFORMERS_MODELS_TO_C3A_TARGET_MODULES_MAPPING,
+)
+
+from .layer import C3ALayer, C3ALinear
+
+
+class C3AModel(BaseTuner):
+ """
+ Creates C3A model from a pretrained transformers model.
+
+ The method is described in detail in [TODO].
+
+ Args:
+ model ([`torch.nn.Module`]): The model to be adapted.
+ config ([`C3AConfig`]): The configuration of the C3A model.
+ adapter_name (`str`): The name of the adapter, defaults to `"default"`.
+
+ Returns:
+ `torch.nn.Module`: The C3A model.
+
+ **Attributes**:
+ - **model** ([`~transformers.PreTrainedModel`]) -- The model to be adapted.
+ - **peft_config** ([`C3AConfig`]): The configuration of the C3A model.
+ """
+
+ prefix: str = "c3a_"
+ tuner_layer_cls = C3ALayer
+ target_module_mapping = TRANSFORMERS_MODELS_TO_C3A_TARGET_MODULES_MAPPING
+
+ def _create_and_replace(
+ self,
+ c3a_config,
+ adapter_name,
+ target,
+ target_name,
+ parent,
+ current_key,
+ **optional_kwargs,
+ ):
+ if current_key is None:
+ raise ValueError("Current Key shouldn't be `None`")
+ # Regexp matching - Find key which matches current target_name in patterns provided
+ pattern_keys = list(chain(c3a_config.block_size_pattern.keys()))
+ target_name_key = next(filter(lambda key: re.match(rf".*\.{key}$", current_key), pattern_keys), current_key)
+
+ block_size = c3a_config.block_size_pattern.get(target_name_key, c3a_config.block_size)
+ kwargs = {
+ "block_size": block_size,
+ "init_weights": c3a_config.init_weights,
+ }
+
+ if isinstance(target, C3ALinear):
+ target.update_layer(
+ adapter_name,
+ block_size,
+ c3a_config.init_weights,
+ )
+ else:
+ new_module = self._create_new_module(c3a_config, adapter_name, target, **kwargs)
+ if adapter_name != self.active_adapter:
+ # adding an additional adapter: it is not automatically trainable
+ new_module.requires_grad_(False)
+ self._replace_module(parent, target_name, new_module, target)
+
+ @staticmethod
+ def _create_new_module(c3a_config, adapter_name, target, **kwargs):
+ if isinstance(target, BaseTunerLayer):
+ target_base_layer = target.get_base_layer()
+ else:
+ target_base_layer = target
+
+ if isinstance(target_base_layer, torch.nn.Linear):
+ new_module = C3ALinear(target, adapter_name, **kwargs)
+
+ return new_module
diff --git a/peft/src/peft/tuners/c3a/utils.py b/peft/src/peft/tuners/c3a/utils.py
new file mode 100644
index 0000000000000000000000000000000000000000..89b80ec5797a514a368c9138405871cb620602d6
--- /dev/null
+++ b/peft/src/peft/tuners/c3a/utils.py
@@ -0,0 +1,48 @@
+# Copyright 2025-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+import torch
+from torch.autograd import Function
+from torch.fft import fft, ifft
+
+
+def get_circulant_fast(w):
+ m, n, b = w.shape
+ x = torch.eye(n * b, dtype=w.dtype, device=w.device)
+ x = x.reshape(*x.shape[:-1], n, b)
+ x = torch.einsum("...nb,mnb->...mb", ifft(x), fft(w))
+ x = fft(x).real.flatten(start_dim=1).T
+ return x
+
+
+class BlockCircularConvolution(Function):
+ @staticmethod
+ def forward(ctx, x, w):
+ m, n, b = w.shape
+ x = x.reshape(*x.shape[:-1], n, b)
+ ctx.save_for_backward(x, w)
+ x = torch.einsum("...nb,mnb->...mb", ifft(x), fft(w))
+ x = fft(x).real
+ x = x.reshape(*x.shape[:-2], -1)
+ return x
+
+ @staticmethod
+ def backward(ctx, grad_output):
+ x, w = ctx.saved_tensors
+ m, n, b = w.shape
+ grad_output = grad_output.reshape(*grad_output.shape[:-1], m, b)
+ grad_output_fft = fft(grad_output)
+ x_grad = fft(torch.einsum("...mb,mnb->...nb", grad_output_fft, ifft(w))).real
+ x_grad = x_grad.reshape(*x_grad.shape[:-2], -1)
+ w_grad = fft(torch.einsum("...mb,...nb->mnb", grad_output_fft, ifft(x))).real
+ return x_grad, w_grad
diff --git a/peft/src/peft/tuners/cpt/__init__.py b/peft/src/peft/tuners/cpt/__init__.py
new file mode 100644
index 0000000000000000000000000000000000000000..fcd4de85989168ad6834712679c805cba39c1df1
--- /dev/null
+++ b/peft/src/peft/tuners/cpt/__init__.py
@@ -0,0 +1,24 @@
+# Copyright 2024-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+
+from peft.utils import register_peft_method
+
+from .config import CPTConfig
+from .model import CPTEmbedding
+
+
+__all__ = ["CPTConfig", "CPTEmbedding"]
+
+register_peft_method(name="cpt", config_cls=CPTConfig, model_cls=CPTEmbedding)
diff --git a/peft/src/peft/tuners/cpt/config.py b/peft/src/peft/tuners/cpt/config.py
new file mode 100644
index 0000000000000000000000000000000000000000..324c22995da217655da841e3a919f92ed6a0794b
--- /dev/null
+++ b/peft/src/peft/tuners/cpt/config.py
@@ -0,0 +1,106 @@
+# Copyright 2024-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+import warnings
+from dataclasses import dataclass, field
+from typing import Literal, Optional
+
+from peft.config import PromptLearningConfig
+from peft.utils import PeftType, TaskType
+
+
+@dataclass
+class CPTConfig(PromptLearningConfig):
+ """
+ CPT Configuration class extending PeftConfig for Context-aware Prompt Tuning (CPT).
+
+ This class introduces additional parameters required for CPT, such as:
+ - Token type masks
+ - Prompt tuning initialization
+ - Loss weighting
+ - Projection settings
+
+ For more details, see the paper: https://huggingface.co/papers/2410.17222
+ """
+
+ # Token-related configurations
+ cpt_token_ids: Optional[list[int]] = field(
+ default=None, metadata={"help": "Tensor of token IDs used for CPT prompts."}
+ )
+ cpt_mask: Optional[list[int]] = field(default=None, metadata={"help": "Tensor mask applied to CPT tokens."})
+ cpt_tokens_type_mask: Optional[list[int]] = field(
+ default=None, metadata={"help": "Mask indicating the type of each CPT token."}
+ )
+
+ # Loss-related configurations
+ opt_weighted_loss_type: Optional[Literal["none", "decay"]] = field(
+ default="none", metadata={"help": "Type of weighted loss: 'none' or 'decay'."}
+ )
+ opt_loss_decay_factor: Optional[float] = field(
+ default=1.0, metadata={"help": "Factor for exponential decay in loss weighting."}
+ )
+
+ # Projection-related configurations
+ opt_projection_epsilon: Optional[float] = field(
+ default=0.1, metadata={"help": "Epsilon value for input projection."}
+ )
+ opt_projection_format_epsilon: Optional[float] = field(
+ default=0.1, metadata={"help": "Epsilon value for format projection."}
+ )
+
+ # Tokenizer configuration
+ tokenizer_name_or_path: Optional[str] = field(
+ default=None,
+ metadata={
+ "help": "The tokenizer to use for prompt tuning initialization. Only used if prompt_tuning_init is `TEXT`"
+ },
+ )
+ # Neet to define CPT-specific static attributes
+ is_prompt_learning = True # Indicates that CPT is a prompt-learning method.
+
+ def __post_init__(self):
+ """
+ Post-initialization hook to set additional attributes after the config is initialized.
+ """
+ # CPT-specific static attributes
+ self.is_prompt_learning = True # Indicates that CPT is a prompt-learning method.
+ self.num_layers = None # Number of layers (optional, not always required).
+ self.token_dim = None # Dimension of token embeddings.
+ self.num_attention_heads = None # Number of attention heads (if applicable).
+ self.num_transformer_submodules = 1 # Number of transformer submodules used.
+ self.peft_type = PeftType.CPT # Specifies that the PEFT type is CPT.
+ if self.task_type != TaskType.CAUSAL_LM:
+ # TODO: adjust this to raise an error with PEFT v0.18.0
+ warnings.warn(
+ f"{self.__class__.__name__} only supports task_type = {TaskType.CAUSAL_LM.value}, "
+ "setting it automatically. This will raise an error starting from PEFT v0.18.0.",
+ FutureWarning,
+ )
+ self.task_type = TaskType.CAUSAL_LM # Ensures task type is causal language modeling.
+
+ if self.cpt_token_ids is None:
+ self.cpt_token_ids = [0]
+
+ self.num_virtual_tokens = len(self.cpt_token_ids)
+
+ if self.cpt_mask is None:
+ self.cpt_mask = [1 for _ in self.cpt_token_ids]
+
+ if self.cpt_tokens_type_mask is None:
+ self.cpt_tokens_type_mask = [1 for _ in self.cpt_token_ids]
+
+ if not (
+ len(self.cpt_token_ids) == len(self.cpt_mask) == len(self.cpt_tokens_type_mask) == self.num_virtual_tokens
+ ):
+ raise ValueError("cpt_token_ids, cpt_mask and cpt_tokens_type_mask must have the same length.")
diff --git a/peft/src/peft/tuners/cpt/model.py b/peft/src/peft/tuners/cpt/model.py
new file mode 100644
index 0000000000000000000000000000000000000000..934a3b7928c125bd433441f36cf4b26de15b535f
--- /dev/null
+++ b/peft/src/peft/tuners/cpt/model.py
@@ -0,0 +1,200 @@
+# Copyright 2024-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+import copy
+
+import torch
+from torch.nn import CrossEntropyLoss
+
+from peft.utils.integrations import gather_params_ctx
+
+
+class CPTEmbedding(torch.nn.Module):
+ """
+ CPTEmbedding is a custom embedding layer designed for Context-aware Prompt Tuning (CPT) in PEFT. It initializes
+ embeddings, applies prompt-specific projections, and computes loss using label masks.
+ """
+
+ def __init__(self, config, word_embeddings):
+ """
+ Initializes the CPTEmbedding module.
+
+ Args:
+ config (Namespace):
+ Configuration object containing model hyperparameters and CPT-specific settings.
+ word_embeddings (torch.nn.Embedding):
+ The base word embedding layer used to initialize CPT embeddings.
+ """
+ super().__init__()
+ self.config = copy.deepcopy(config)
+ num_virtual_tokens = config.num_virtual_tokens
+
+ # Initialize embeddings with virtual token dimensions
+ self.embedding = torch.nn.Embedding(num_virtual_tokens, config.token_dim)
+
+ # Initialize embeddings using text-based prompt tuning, if configured
+ if not config.inference_mode:
+ assert config.num_virtual_tokens == len(config.cpt_token_ids)
+
+ init_token_ids = torch.LongTensor(config.cpt_token_ids).to(word_embeddings.weight.device)
+ with gather_params_ctx(word_embeddings.parameters()):
+ word_embedding_weights = word_embeddings(init_token_ids).detach().clone()
+ word_embedding_weights = word_embedding_weights.to(torch.float32)
+ self.embedding.weight = torch.nn.Parameter(word_embedding_weights)
+
+ # Initialize delta embedding with zero weights
+ self.delta_embedding = torch.nn.Embedding(num_virtual_tokens, config.token_dim)
+ self.delta_embedding.weight.data = torch.zeros_like(self.delta_embedding.weight).to(torch.float32)
+
+ # Apply hook for backward gradient updates
+ self.set_updated_tokens()
+
+ def forward(self, indices):
+ """
+ Computes the prompt embeddings and applies delta adjustments.
+
+ Args:
+ indices (torch.Tensor):
+ Indices of the tokens to be embedded.
+
+ Returns:
+ torch.Tensor:
+ Sum of prompt embeddings and delta embeddings.
+ """
+ with torch.no_grad():
+ prompt_embeddings = self.embedding(indices)
+
+ self.delta_embedding.weight.data = self.get_projection() # Apply epsilon-based projection
+
+ delta_prompt_embeddings = self.delta_embedding(indices)
+
+ return prompt_embeddings + delta_prompt_embeddings
+
+ def set_updated_tokens(self):
+ """
+ Sets up a backward hook to selectively update token gradients based on the CPT token type mask.
+ """
+ tensor_ICL_mask = torch.Tensor(self.config.cpt_tokens_type_mask).long()
+ mask_input_template = torch.remainder(tensor_ICL_mask, 4) == 1
+ mask_input = torch.remainder(tensor_ICL_mask, 4) == 2
+ mask_output_template = torch.remainder(tensor_ICL_mask, 4) == 3
+ mask = mask_input_template | mask_input | mask_output_template
+ mask = mask.view(-1, 1)
+
+ def backward_hook(grad):
+ grad = grad * mask.to(grad.device) # Apply mask to gradients
+ return grad
+
+ self.delta_embedding.weight.register_hook(backward_hook)
+
+ def get_epsilon(self):
+ cpt_tokens_type_mask = self.config.cpt_tokens_type_mask
+
+ MIN_VALUE = 1e-10
+
+ # Calculate normalized epsilon values for input, output, and format tokens
+ normalized_format_eps = self.config.opt_projection_format_epsilon * torch.sqrt(
+ torch.Tensor([self.config.token_dim / 2048])
+ )
+ normalized_input_eps = self.config.opt_projection_epsilon * torch.sqrt(
+ torch.Tensor([self.config.token_dim / 2048])
+ )
+
+ epsilon = torch.ones_like(torch.Tensor(cpt_tokens_type_mask)).to(torch.float32) * MIN_VALUE
+ cpt_tokens_type_mask = torch.Tensor(cpt_tokens_type_mask).long()
+
+ epsilon[(cpt_tokens_type_mask > 0) & (torch.remainder(cpt_tokens_type_mask, 4) == 1)] = normalized_format_eps
+ epsilon[(cpt_tokens_type_mask > 0) & (torch.remainder(cpt_tokens_type_mask, 4) == 3)] = normalized_format_eps
+ epsilon[(cpt_tokens_type_mask > 0) & (torch.remainder(cpt_tokens_type_mask, 4) == 2)] = normalized_input_eps
+
+ return epsilon
+
+ def get_projection(self):
+ """
+ Applies epsilon-based projection to the delta embeddings to control their norm.
+ """
+
+ # Apply projection to control delta embedding norm
+ with torch.no_grad():
+ new_embeddings_weights = self.delta_embedding.weight.clone().to(self.delta_embedding.weight.device)
+ token_norm = torch.norm(new_embeddings_weights, p=2, dim=1)
+
+ projection_mask = token_norm > 0
+ if torch.any(projection_mask):
+ epsilon = self.get_epsilon().to(self.delta_embedding.weight.device)
+ new_embeddings_weights[projection_mask] *= (
+ epsilon[projection_mask] / (token_norm[projection_mask].clamp(min=epsilon[projection_mask]))
+ ).view(-1, 1)
+ return new_embeddings_weights
+
+ @staticmethod
+ def calculate_loss(base_model_output, labels, cpt_type_mask, config):
+ """
+ Computes the loss for CPT models with optional exponential decay.
+
+ Args:
+ base_model_output (ModelOutput):
+ Output from the base model containing logits.
+ labels (torch.Tensor):
+ Ground-truth labels for the input tokens.
+ cpt_type_mask (torch.Tensor):
+ Token type mask used for filtering valid loss terms.
+ config (Namespace):
+ Configuration object containing loss-related hyperparameters.
+
+ Returns:
+ ModelOutput:
+ The base model output with computed loss.
+ """
+
+ device = base_model_output.logits.device
+
+ lm_logits = base_model_output.logits
+ labels = labels.to(device)
+
+ # Shift logits and labels for token prediction
+ shift_logits = lm_logits[..., :-1, :].contiguous()
+ shift_labels = labels[..., 1:].contiguous()
+ shift_cpt_type_mask = cpt_type_mask[..., 1:].contiguous()
+
+ shift_labels_bool = (shift_labels.clone().detach() != -100).bool()
+ batch_size, seq_length, vocab_size = shift_logits.shape
+
+ # Compute cross-entropy loss
+ loss_fct = CrossEntropyLoss(reduction="none", ignore_index=-100)
+ loss = loss_fct(
+ shift_logits.view(batch_size * seq_length, vocab_size), shift_labels.view(batch_size * seq_length)
+ )
+ loss = loss.view(batch_size, seq_length)
+ # Apply exponential decay weights to the loss
+ shift_labels_weights = shift_labels_bool.clone().detach().float()
+
+ for i in range(batch_size):
+ idx_labels = (shift_cpt_type_mask[i] > 0) & (shift_cpt_type_mask[i] % 4 == 0)
+ labels_ids = shift_cpt_type_mask[i][idx_labels].unique()
+
+ exponential_decay = torch.ones_like(shift_cpt_type_mask[i]).to(device=device).float()
+ decay_value = 1
+ for label_mask_idx in torch.flip(labels_ids, [0]):
+ exponential_decay[shift_cpt_type_mask[i] == label_mask_idx] = decay_value
+ decay_value *= config.opt_loss_decay_factor
+ if config.opt_weighted_loss_type == "decay":
+ shift_labels_weights[i] *= exponential_decay
+
+ # Compute the weighted mean loss
+ loss = (loss[shift_labels_bool] * shift_labels_weights[shift_labels_bool]).mean()
+
+ base_model_output.loss = loss
+
+ return base_model_output
diff --git a/peft/src/peft/tuners/fourierft/__init__.py b/peft/src/peft/tuners/fourierft/__init__.py
new file mode 100644
index 0000000000000000000000000000000000000000..dfe3f5d89e36123eefef7fc6e675c6b80bd8d44c
--- /dev/null
+++ b/peft/src/peft/tuners/fourierft/__init__.py
@@ -0,0 +1,24 @@
+# Copyright 2024-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+from peft.utils import register_peft_method
+
+from .config import FourierFTConfig
+from .layer import FourierFTLayer, FourierFTLinear
+from .model import FourierFTModel
+
+
+__all__ = ["FourierFTConfig", "FourierFTLayer", "FourierFTLinear", "FourierFTModel"]
+
+register_peft_method(name="fourierft", model_cls=FourierFTModel, config_cls=FourierFTConfig)
diff --git a/peft/src/peft/tuners/fourierft/config.py b/peft/src/peft/tuners/fourierft/config.py
new file mode 100644
index 0000000000000000000000000000000000000000..dbbb80d8e080e9237b711473b44d55f6ff186239
--- /dev/null
+++ b/peft/src/peft/tuners/fourierft/config.py
@@ -0,0 +1,206 @@
+# Copyright 2024-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+from __future__ import annotations
+
+from dataclasses import dataclass, field
+from typing import Optional, Union
+
+from peft.config import PeftConfig
+from peft.utils import PeftType
+
+
+@dataclass
+class FourierFTConfig(PeftConfig):
+ """
+ This is the configuration class to store the configuration of a [`FourierFTModel`].
+
+ Args:
+ n_frequency (`int`):
+ Num of learnable frequencies for the Discrete Fourier Transform. 'n_frequency' is an integer that is
+ greater than 0 and less than or equal to d^2 (assuming the weight W has dimensions of d by d).
+ Additionally, it is the number of trainable parameters required to update each delta W weight.
+ 'n_frequency' will affect the performance and efficiency for PEFT. Specifically, it has little impact on
+ training speed, but higher values of it (typically) result in larger GPU memory costs and better accuracy.
+ With the same `target_modules`, the number of parameters of LoRA is (2*d*r/n_frequency) times that of
+ FourierFT. The following examples of settings regarding 'n_frequency' can be used as reference for users.
+ For NLU tasks with the RoBERTa-large model, adopting 'n_frequency': 1000 can almost achieve similar results
+ as 'r': 8 in LoRA. At this time, the number of parameters of LoRA is about 16 times that of FourierFT. For
+ image classification tasks with Vit-large models, adopting 'n_frequency': 3000 can almost achieve similar
+ results as 'r': 16 in LoRA, where the number of parameters of LoRA is about 11 times that of FourierFT.
+ scaling (`float`):
+ The scaling value for the delta W matrix. This is an important hyperparameter used for scaling, similar to
+ the 'lora_alpha' parameter in the LoRA method. 'scaling' can be determined during the hyperparameter search
+ process. However, if users want to skip this process, one can refer to the settings in the following
+ scenarios. This parameter can be set to 100.0 or 150.0 for both RoBERTa-base and RoBERTa-large models
+ across all NLU (GLUE) tasks. This parameter can be set to 300.0 for both LLaMA family models for all
+ instruction tuning. This parameter can be set to 300.0 for both ViT-base and ViT-large models across all
+ image classification tasks.
+ random_loc_seed (`int`):
+ Seed for the random location of the frequencies, i.e., the spectral entry matrix.
+ target_modules (`Union[list[str],str]`):
+ List of module names or regex expression of the module names to replace with FourierFT. For example, ['q',
+ 'v'] or '.*decoder.*(SelfAttention|EncDecAttention).*(q|v)$'. Only linear layers are supported.
+ exclude_modules (`Optional[Union[List[str], str]]`):
+ The names of the modules to not apply the adapter. When passing a string, a regex match will be performed.
+ When passing a list of strings, either an exact match will be performed or it is checked if the name of the
+ module ends with any of the passed strings.
+ fan_in_fan_out (`bool`):
+ Set this to True if the layer to replace stores weight like (fan_in, fan_out).
+ bias (`str`):
+ Bias type for FourierFT. Can be 'none', 'all' or 'fourier_only'.
+ modules_to_save (`list[str]`):
+ List of modules apart from FourierFT layers to be set as trainable and saved in the final checkpoint. For
+ example, in Sequence Classification or Token Classification tasks, the final layer `classifier/score` are
+ randomly initialized and as such need to be trainable and saved.
+ layers_to_transform (`Union[list[int],int]`):
+ The layer indexes to transform, is this argument is specified, PEFT will transform only the layers indexes
+ that are specified inside this list. If a single integer is passed, PEFT will transform only the layer at
+ this index.
+ layers_pattern (`Optional[Union[List[str], str]]`):
+ The layer pattern name, used only if `layers_to_transform` is different to None and if the layer pattern is
+ not in the common layers pattern. This should target the `nn.ModuleList` of the model, which is often
+ called `'layers'` or `'h'`.
+ n_frequency_pattern (`dict`):
+ The mapping from layer names or regexp expression to n_frequency which are different from the default
+ specified. For example, `{model.decoder.layers.0.encoder_attn.k_proj: 1000`}.
+ init_weights (`bool`):
+ The initialization of the Fourier weights. Set this to False (the default) if the spectrum are initialized
+ to a standard normal distribution. Set this to True if the spectrum are initialized to zeros.
+ """
+
+ n_frequency: int = field(
+ default=1000,
+ metadata={
+ "help": (
+ "Num of learnable frequencies for the Discrete Fourier Transform. 'n_frequency' is an integer that is"
+ "greater than 0 and less than or equal to d^2 (assuming the weight W has dimensions of d by d)."
+ "Additionally, it is the number of trainable parameters required to update each delta W weight."
+ "'n_frequency' will affect the performance and efficiency for PEFT. Specifically, it has little impact on"
+ "training speed, but higher values of it (typically) result in larger GPU memory costs and better accuracy."
+ "With the same `target_modules`, the number of parameters of LoRA is (2*d*r/n_frequency) times that of FourierFT."
+ "The following examples of settings regarding 'n_frequency' can be used as reference for users. For NLU"
+ "tasks with the RoBERTa-large model, adopting 'n_frequency': 1000 can almost achieve similar results as"
+ "'r': 8 in LoRA. At this time, the number of parameters of LoRA is about 16 times that of FourierFT."
+ "For image classification tasks with Vit-large models, adopting 'n_frequency': 3000 can almost achieve"
+ "similar results as 'r': 16 in LoRA, where the number of parameters of LoRA is about 11 times that of FourierFT."
+ )
+ },
+ )
+ scaling: float = field(
+ default=150.0,
+ metadata={
+ "help": (
+ "The scaling value for the delta W matrix. This is an important hyperparameter used for scaling, similar to the"
+ "'lora_alpha' parameter in the LoRA method. 'scaling' can be determined during the hyperparameter search process."
+ "However, if users want to skip this process, one can refer to the settings in the following scenarios."
+ "This parameter can be set to 100.0 or 150.0 for both RoBERTa-base and RoBERTa-large models across all NLU (GLUE) tasks."
+ "This parameter can be set to 300.0 for both LLaMA family models for all instruction tuning."
+ "This parameter can be set to 300.0 for both ViT-base and ViT-large models across all image classification tasks."
+ )
+ },
+ )
+ random_loc_seed: Optional[int] = field(
+ default=777, metadata={"help": "Seed for the random location of the frequencies."}
+ )
+ fan_in_fan_out: bool = field(
+ default=False,
+ metadata={"help": "Set this to True if the layer to replace stores weight like (fan_in, fan_out)"},
+ )
+ target_modules: Optional[Union[list[str], str]] = field(
+ default=None,
+ metadata={
+ "help": (
+ "List of module names or regex expression of the module names to replace with FourierFT."
+ "For example, ['q', 'v'] or '.*decoder.*(SelfAttention|EncDecAttention).*(q|v)$'. "
+ "Only linear layers are supported."
+ )
+ },
+ )
+ exclude_modules: Optional[Union[list[str], str]] = field(
+ default=None,
+ metadata={"help": "List of module names or regex expression of the module names to exclude from fourierft."},
+ )
+ bias: str = field(
+ default="none", metadata={"help": "Bias type for FourierFT. Can be 'none', 'all' or 'fourier_only'."}
+ )
+ modules_to_save: Optional[list[str]] = field(
+ default=None,
+ metadata={
+ "help": (
+ "List of modules apart from FourierFT layers to be set as trainable and saved in the final checkpoint. For"
+ " example, in Sequence Classification or Token Classification tasks, the final layer"
+ " `classifier/score` are randomly initialized and as such need to be trainable and saved."
+ )
+ },
+ )
+ layers_to_transform: Optional[Union[list[int], int]] = field(
+ default=None,
+ metadata={
+ "help": (
+ "The layer indexes to transform, is this argument is specified, PEFT will transform only the layers"
+ " indexes that are specified inside this list. If a single integer is passed, PEFT will transform only"
+ " the layer at this index."
+ )
+ },
+ )
+ layers_pattern: Optional[Union[list[str], str]] = field(
+ default=None,
+ metadata={
+ "help": (
+ "The layer pattern name, used only if `layers_to_transform` is different to None and if the layer"
+ " pattern is not in the common layers pattern. This should target the `nn.ModuleList` of the "
+ "model, which is often called `'layers'` or `'h'`."
+ )
+ },
+ )
+ n_frequency_pattern: Optional[dict] = field(
+ default_factory=dict,
+ metadata={
+ "help": (
+ "The mapping from layer names or regexp expression to n_frequency which are different from the default specified."
+ "For example, `{model.decoder.layers.0.encoder_attn.k_proj: 500`}."
+ )
+ },
+ )
+ init_weights: bool = field(
+ default=False,
+ metadata={
+ "help": (
+ "The initialization of the Fourier weights. Set this to False (the default) if the spectrum should be "
+ "initialized to a standard normal distribution. Set this to True if the spectrum should be initialized "
+ "to zeros."
+ )
+ },
+ )
+
+ def __post_init__(self):
+ super().__post_init__()
+ self.peft_type = PeftType.FOURIERFT
+ self.target_modules = (
+ set(self.target_modules) if isinstance(self.target_modules, list) else self.target_modules
+ )
+ self.exclude_modules = (
+ set(self.exclude_modules) if isinstance(self.exclude_modules, list) else self.exclude_modules
+ )
+ # if target_modules is a regex expression, then layers_to_transform should be None
+ if isinstance(self.target_modules, str) and self.layers_to_transform is not None:
+ raise ValueError("`layers_to_transform` cannot be used when `target_modules` is a str.")
+
+ # if target_modules is a regex expression, then layers_pattern should be None
+ if isinstance(self.target_modules, str) and self.layers_pattern is not None:
+ raise ValueError("`layers_pattern` cannot be used when `target_modules` is a str.")
+ # check for layers_to_transform and layers_pattern
+ if self.layers_pattern and not self.layers_to_transform:
+ raise ValueError("When `layers_pattern` is specified, `layers_to_transform` must also be specified. ")
diff --git a/peft/src/peft/tuners/fourierft/layer.py b/peft/src/peft/tuners/fourierft/layer.py
new file mode 100644
index 0000000000000000000000000000000000000000..a03a57f118052d15e5f9cc4b53dc5c06cecd139e
--- /dev/null
+++ b/peft/src/peft/tuners/fourierft/layer.py
@@ -0,0 +1,193 @@
+# Copyright 2024-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+import warnings
+from typing import Any, Optional, Union
+
+import torch
+import torch.nn as nn
+import torch.nn.functional as F
+from transformers.pytorch_utils import Conv1D
+
+from peft.tuners.tuners_utils import BaseTunerLayer, check_adapters_to_merge
+
+
+class FourierFTLayer(BaseTunerLayer):
+ # All names of layers that may contain (trainable) adapter weights
+ adapter_layer_names = ("fourierft_spectrum",)
+ # All names of other parameters that may contain adapter-related parameters
+ other_param_names = ("fourierft_n_frequency", "fourierft_scaling", "fourierft_random_loc_seed")
+
+ def __init__(self, base_layer: nn.Module, **kwargs) -> None:
+ self.base_layer = base_layer
+ self.fourierft_n_frequency = {}
+ self.fourierft_scaling = {}
+ self.fourierft_spectrum = nn.ParameterDict({})
+ self.indices = {}
+ self.fourierft_random_loc_seed = {}
+ # Mark the weight as unmerged
+ self._disable_adapters = False
+ self.merged_adapters = []
+ self.kwargs = kwargs
+
+ base_layer = self.get_base_layer()
+ if isinstance(base_layer, nn.Linear):
+ self.in_features, self.out_features = base_layer.in_features, base_layer.out_features
+ elif isinstance(base_layer, Conv1D):
+ self.in_features, self.out_features = (
+ base_layer.weight.ds_shape if hasattr(base_layer.weight, "ds_shape") else base_layer.weight.shape
+ )
+ else:
+ raise ValueError(f"Unsupported layer type {type(base_layer)}")
+
+ def update_layer(
+ self, adapter_name, n_frequency, scaling, init_weights, random_loc_seed, inference_mode: bool = False, **kwargs
+ ):
+ if n_frequency <= 0:
+ raise ValueError(f"`n_frequency` should be a positive integer value but the value passed is {n_frequency}")
+ if n_frequency > self.in_features * self.out_features:
+ raise ValueError(
+ f"`n_frequency` should be less than or equal to the product of the input and output dimensions "
+ f"but the value passed is {n_frequency} and the product is {self.in_features * self.out_features}"
+ )
+ self.fourierft_n_frequency[adapter_name] = n_frequency
+ self.fourierft_random_loc_seed[adapter_name] = random_loc_seed
+ self.indices[adapter_name] = torch.randperm(
+ self.out_features * self.in_features,
+ generator=torch.Generator().manual_seed(self.fourierft_random_loc_seed[adapter_name]),
+ )[:n_frequency]
+ self.indices[adapter_name] = torch.stack(
+ [self.indices[adapter_name] // self.in_features, self.indices[adapter_name] % self.in_features], dim=0
+ )
+ self.fourierft_scaling[adapter_name] = scaling
+ # Actual trainable parameters
+ self.fourierft_spectrum[adapter_name] = nn.Parameter(torch.randn(n_frequency), requires_grad=True)
+
+ if init_weights:
+ self.reset_fourier_parameters(adapter_name)
+
+ self._move_adapter_to_device_of_base_layer(adapter_name)
+ self.set_adapter(self.active_adapters, inference_mode=inference_mode)
+
+ @torch.no_grad()
+ def reset_fourier_parameters(self, adapter_name):
+ if adapter_name in self.fourierft_spectrum.keys():
+ nn.init.zeros_(self.fourierft_spectrum[adapter_name])
+
+ def get_delta_weight(self, adapter) -> torch.Tensor:
+ # careful: ifft2 does not work with float16 or bfloat16
+ spectrum = self.fourierft_spectrum[adapter]
+ indices = self.indices[adapter].to(spectrum.device)
+ dense_spectrum = torch.zeros(self.out_features, self.in_features, device=spectrum.device)
+ dense_spectrum[indices[0, :], indices[1, :]] = spectrum.float()
+ delta_weight = torch.fft.ifft2(dense_spectrum).real * self.fourierft_scaling[adapter]
+ return delta_weight.to(spectrum.dtype)
+
+
+class FourierFTLinear(nn.Module, FourierFTLayer):
+ # FourierFT implemented in a dense layer
+ def __init__(
+ self,
+ base_layer,
+ adapter_name: str,
+ n_frequency: int = 1000,
+ scaling: float = 150.0,
+ fan_in_fan_out: bool = False, # Set this to True if the layer to replace stores weight like (fan_in, fan_out)
+ init_weights: Union[bool, str] = False,
+ random_loc_seed: int = 777,
+ **kwargs,
+ ) -> None:
+ super().__init__()
+ FourierFTLayer.__init__(self, base_layer, **kwargs)
+ self.fan_in_fan_out = fan_in_fan_out
+ self._active_adapter = adapter_name
+ self.update_layer(adapter_name, n_frequency, scaling, init_weights, random_loc_seed)
+
+ def merge(self, safe_merge: bool = False, adapter_names: Optional[list[str]] = None) -> None:
+ """
+ Merge the active adapter weights into the base weights
+
+ Args:
+ safe_merge (`bool`, *optional*):
+ If True, the merge operation will be performed in a copy of the original weights and check for NaNs
+ before merging the weights. This is useful if you want to check if the merge operation will produce
+ NaNs. Defaults to `False`.
+ adapter_names (`List[str]`, *optional*):
+ The list of adapter names that should be merged. If None, all active adapters will be merged. Defaults
+ to `None`.
+ """
+ adapter_names = check_adapters_to_merge(self, adapter_names)
+ if not adapter_names:
+ # no adapter to merge
+ return
+
+ for active_adapter in adapter_names:
+ if active_adapter in self.fourierft_spectrum.keys():
+ base_layer = self.get_base_layer()
+ if safe_merge:
+ # Note that safe_merge will be slower than the normal merge
+ # because of the copy operation.
+ orig_weights = base_layer.weight.data.clone()
+ orig_weights += self.get_delta_weight(active_adapter)
+
+ if not torch.isfinite(orig_weights).all():
+ raise ValueError(
+ f"NaNs detected in the merged weights. The adapter {active_adapter} seems to be broken"
+ )
+
+ base_layer.weight.data = orig_weights
+ else:
+ base_layer.weight.data += self.get_delta_weight(active_adapter)
+ self.merged_adapters.append(active_adapter)
+
+ def unmerge(self) -> None:
+ """
+ This method unmerges all merged adapter layers from the base weights.
+ """
+ if not self.merged:
+ warnings.warn("Already unmerged. Nothing to do.")
+ return
+ while len(self.merged_adapters) > 0:
+ active_adapter = self.merged_adapters.pop()
+ if active_adapter in self.fourierft_spectrum.keys():
+ self.get_base_layer().weight.data -= self.get_delta_weight(active_adapter)
+
+ def get_delta_weight(self, adapter) -> torch.Tensor:
+ return super().get_delta_weight(adapter)
+
+ def forward(self, x: torch.Tensor, *args: Any, **kwargs: Any) -> torch.Tensor:
+ previous_dtype = x.dtype
+
+ if self.disable_adapters:
+ if self.merged:
+ self.unmerge()
+ result = self.base_layer(x, *args, **kwargs)
+ elif self.merged:
+ result = self.base_layer(x, *args, **kwargs)
+ else:
+ result = self.base_layer(x, *args, **kwargs)
+ for active_adapter in self.active_adapters:
+ if active_adapter not in self.fourierft_spectrum.keys():
+ continue
+
+ delta_w = self.get_delta_weight(active_adapter)
+ x = x.to(delta_w.dtype)
+ result = result + F.linear(x, delta_w)
+
+ result = result.to(previous_dtype)
+ return result
+
+ def __repr__(self) -> str:
+ rep = super().__repr__()
+ return "fourierft." + rep
diff --git a/peft/src/peft/tuners/fourierft/model.py b/peft/src/peft/tuners/fourierft/model.py
new file mode 100644
index 0000000000000000000000000000000000000000..5347d90b1777fcef235215c15999d6b39fd09ede
--- /dev/null
+++ b/peft/src/peft/tuners/fourierft/model.py
@@ -0,0 +1,128 @@
+# Copyright 2024-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+from __future__ import annotations
+
+import re
+import warnings
+from itertools import chain
+
+import torch
+from transformers.pytorch_utils import Conv1D
+
+from peft.tuners.tuners_utils import BaseTuner, BaseTunerLayer
+from peft.utils import (
+ TRANSFORMERS_MODELS_TO_FOURIERFT_TARGET_MODULES_MAPPING,
+)
+
+from .layer import FourierFTLayer, FourierFTLinear
+
+
+class FourierFTModel(BaseTuner):
+ """
+ Creates FourierFT model from a pretrained transformers model.
+
+ The method is described in detail in https://huggingface.co/papers/2405.03003.
+
+ Args:
+ model ([`torch.nn.Module`]): The model to be adapted.
+ config ([`FourierFTConfig`]): The configuration of the FourierFT model.
+ adapter_name (`str`): The name of the adapter, defaults to `"default"`.
+ low_cpu_mem_usage (`bool`, `optional`, defaults to `False`):
+ Create empty adapter weights on meta device. Useful to speed up the loading process.
+
+ Returns:
+ `torch.nn.Module`: The FourierFT model.
+
+ **Attributes**:
+ - **model** ([`~transformers.PreTrainedModel`]) -- The model to be adapted.
+ - **peft_config** ([`FourierFTConfig`]): The configuration of the Fourier model.
+ """
+
+ prefix: str = "fourierft_"
+ tuner_layer_cls = FourierFTLayer
+ target_module_mapping = TRANSFORMERS_MODELS_TO_FOURIERFT_TARGET_MODULES_MAPPING
+
+ def _create_and_replace(
+ self,
+ fourierft_config,
+ adapter_name,
+ target,
+ target_name,
+ parent,
+ current_key,
+ **optional_kwargs,
+ ):
+ if current_key is None:
+ raise ValueError("Current Key shouldn't be `None`")
+ # Regexp matching - Find key which matches current target_name in patterns provided
+ pattern_keys = list(chain(fourierft_config.n_frequency_pattern.keys()))
+ target_name_key = next(filter(lambda key: re.match(rf".*\.{key}$", current_key), pattern_keys), current_key)
+
+ n_frequency = fourierft_config.n_frequency_pattern.get(target_name_key, fourierft_config.n_frequency)
+ scaling = fourierft_config.scaling
+ random_loc_seed = fourierft_config.random_loc_seed
+ bias = hasattr(target, "bias") and target.bias is not None
+ kwargs = {
+ "n_frequency": n_frequency,
+ "scaling": scaling,
+ "fan_in_fan_out": fourierft_config.fan_in_fan_out,
+ "init_weights": fourierft_config.init_weights,
+ "random_loc_seed": fourierft_config.random_loc_seed,
+ }
+ kwargs["bias"] = bias
+ if isinstance(target, FourierFTLayer):
+ target.update_layer(
+ adapter_name,
+ n_frequency,
+ scaling,
+ fourierft_config.init_weights,
+ random_loc_seed,
+ )
+ else:
+ new_module = self._create_new_module(fourierft_config, adapter_name, target, **kwargs)
+ if adapter_name != self.active_adapter:
+ # adding an additional adapter: it is not automatically trainable
+ new_module.requires_grad_(False)
+ self._replace_module(parent, target_name, new_module, target)
+
+ @staticmethod
+ def _create_new_module(fourierft_config, adapter_name, target, **kwargs):
+ if isinstance(target, BaseTunerLayer):
+ target_base_layer = target.get_base_layer()
+ else:
+ target_base_layer = target
+
+ if isinstance(target_base_layer, torch.nn.Linear):
+ if kwargs["fan_in_fan_out"]:
+ warnings.warn(
+ "fan_in_fan_out is set to True but the target module is `torch.nn.Linear`. "
+ "Setting fan_in_fan_out to False."
+ )
+ kwargs["fan_in_fan_out"] = fourierft_config.fan_in_fan_out = False
+ elif isinstance(target_base_layer, Conv1D):
+ kwargs["is_target_conv_1d_layer"] = True
+ if not kwargs["fan_in_fan_out"]:
+ warnings.warn(
+ "fan_in_fan_out is set to False but the target module is `Conv1D`. Setting fan_in_fan_out to True."
+ )
+ kwargs["fan_in_fan_out"] = fourierft_config.fan_in_fan_out = True
+ else:
+ raise ValueError(
+ f"Target module {target} is not supported. Currently, only the following modules are supported: "
+ "`torch.nn.Linear`."
+ )
+
+ new_module = FourierFTLinear(target, adapter_name, **kwargs)
+
+ return new_module
diff --git a/peft/src/peft/tuners/hra/__init__.py b/peft/src/peft/tuners/hra/__init__.py
new file mode 100644
index 0000000000000000000000000000000000000000..8f5f6a54435d0fcaa1bd275c623168b5491f2d9e
--- /dev/null
+++ b/peft/src/peft/tuners/hra/__init__.py
@@ -0,0 +1,24 @@
+# Copyright 2024-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+from peft.utils import register_peft_method
+
+from .config import HRAConfig
+from .layer import HRAConv2d, HRALayer, HRALinear
+from .model import HRAModel
+
+
+__all__ = ["HRAConfig", "HRAConv2d", "HRALayer", "HRALinear", "HRAModel"]
+
+register_peft_method(name="hra", config_cls=HRAConfig, model_cls=HRAModel)
diff --git a/peft/src/peft/tuners/hra/config.py b/peft/src/peft/tuners/hra/config.py
new file mode 100644
index 0000000000000000000000000000000000000000..9e6d87cc17c3ba003eac963467bb1253725ebe10
--- /dev/null
+++ b/peft/src/peft/tuners/hra/config.py
@@ -0,0 +1,133 @@
+# Copyright 2024-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+from __future__ import annotations
+
+from dataclasses import dataclass, field
+from typing import Optional, Union
+
+from peft.config import PeftConfig
+from peft.utils import PeftType
+
+
+@dataclass
+class HRAConfig(PeftConfig):
+ """
+ This is the configuration class to store the configuration of a [`HRAModel`].
+
+ Args:
+ r (`int`):
+ The rank of HRA across different layers. It is best to set 'r' to an even number; otherwise, the default
+ initialization method will not work.
+ apply_GS (`bool`):
+ Whether to apply Gram-Schmidt orthogonalization.
+ target_modules (`Optional[Union[List[str], str]]`):
+ The names of the modules to apply the adapter to. If this is specified, only the modules with the specified
+ names will be replaced. When passing a string, a regex match will be performed. When passing a list of
+ strings, either an exact match will be performed or it is checked if the name of the module ends with any
+ of the passed strings. If this is specified as 'all-linear', then all linear modules are chosen, excluding
+ the output layer. If this is not specified, modules will be chosen according to the model architecture. If
+ the architecture is not known, an error will be raised -- in this case, you should specify the target
+ modules manually.
+ exclude_modules (`Optional[Union[List[str], str]]`):
+ The names of the modules to not apply the adapter. When passing a string, a regex match will be performed.
+ When passing a list of strings, either an exact match will be performed or it is checked if the name of the
+ module ends with any of the passed strings.
+ init_weights (`bool`):
+ Whether to perform initialization of HRA weights.
+ layers_to_transform (`Union[List[int], int]`):
+ The layer indices to transform. If a list of ints is passed, it will apply the adapter to the layer indices
+ that are specified in this list. If a single integer is passed, it will apply the transformations on the
+ layer at this index.
+ layers_pattern (`Optional[Union[List[str], str]]`):
+ The layer pattern name, used only if `layers_to_transform` is different from `None`. This should target the
+ `nn.ModuleList` of the model, which is often called `'layers'` or `'h'`.
+ modules_to_save (`List[str]`):
+ List of modules apart from adapter layers to be set as trainable and saved in the final checkpoint.
+ """
+
+ r: int = field(
+ default=8,
+ metadata={
+ "help": "The rank of HRA across different layers.",
+ "note": "It is best to set 'r' to an even number; otherwise, the default initialization method will not work.",
+ },
+ )
+ apply_GS: bool = field(
+ default=False,
+ metadata={"help": "Whether to apply Gram-Schmidt orthogonalization or not."},
+ )
+ target_modules: Optional[Union[list[str], str]] = field(
+ default=None,
+ metadata={
+ "help": "List of module names or regex expression of the module names to replace with HRA.",
+ "example": "For example, ['q', 'v'] or '.*decoder.*(SelfAttention|EncDecAttention).*(q|v)$' ",
+ },
+ )
+ exclude_modules: Optional[Union[list[str], str]] = field(
+ default=None,
+ metadata={"help": "List of module names or regex expression of the module names to exclude from HRA."},
+ )
+ init_weights: bool = field(
+ default=True,
+ metadata={
+ "help": (
+ "Whether to initialize the weights of the HRA layers with their default initialization. Don't change "
+ "this setting, except if you know exactly what you're doing."
+ ),
+ },
+ )
+ layers_to_transform: Optional[Union[list[int], int]] = field(
+ default=None,
+ metadata={
+ "help": "The layer indexes to transform, is this argument is specified, PEFT will transform only the layers indexes that are specified inside this list. If a single integer is passed, PEFT will transform only the layer at this index."
+ },
+ )
+ layers_pattern: Optional[Union[list[str], str]] = field(
+ default=None,
+ metadata={
+ "help": "The layer pattern name, used only if `layers_to_transform` is different to None and if the layer pattern is not in the common layers pattern. "
+ "This should target the `nn.ModuleList` of the model, which is often called `'layers'` or `'h'`."
+ },
+ )
+ bias: str = field(default="none", metadata={"help": "Bias type for HRA. Can be 'none', 'all' or 'hra_only'"})
+ modules_to_save: Optional[list[str]] = field(
+ default=None,
+ metadata={
+ "help": "List of modules apart from HRA layers to be set as trainable and saved in the final checkpoint. "
+ "For example, in Sequence Classification or Token Classification tasks, "
+ "the final layer `classifier/score` are randomly initialized and as such need to be trainable and saved."
+ },
+ )
+
+ def __post_init__(self):
+ super().__post_init__()
+ self.peft_type = PeftType.HRA
+ self.target_modules = (
+ set(self.target_modules) if isinstance(self.target_modules, list) else self.target_modules
+ )
+ self.exclude_modules = (
+ set(self.exclude_modules) if isinstance(self.exclude_modules, list) else self.exclude_modules
+ )
+ # if target_modules is a regex expression, then layers_to_transform should be None
+ if isinstance(self.target_modules, str) and self.layers_to_transform is not None:
+ raise ValueError("`layers_to_transform` cannot be used when `target_modules` is a str.")
+
+ # if target_modules is a regex expression, then layers_pattern should be None
+ if isinstance(self.target_modules, str) and self.layers_pattern is not None:
+ raise ValueError("`layers_pattern` cannot be used when `target_modules` is a str.")
+
+ # check for layers_to_transform and layers_pattern
+ if self.layers_pattern and not self.layers_to_transform:
+ raise ValueError("When `layers_pattern` is specified, `layers_to_transform` must also be specified. ")
diff --git a/peft/src/peft/tuners/hra/layer.py b/peft/src/peft/tuners/hra/layer.py
new file mode 100644
index 0000000000000000000000000000000000000000..55ab6db69a6730f0ef3b4e46ee46071426091269
--- /dev/null
+++ b/peft/src/peft/tuners/hra/layer.py
@@ -0,0 +1,461 @@
+# Copyright 2024-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+import math
+import warnings
+from typing import Any, Optional, Union
+
+import torch
+import torch.nn as nn
+import torch.nn.functional as F
+
+from peft.tuners.tuners_utils import BaseTunerLayer, check_adapters_to_merge
+
+
+class HRALayer(BaseTunerLayer):
+ # All names of layers that may contain (trainable) adapter weights
+ adapter_layer_names = ("hra_u",)
+ # All names of other parameters that may contain adapter-related parameters
+ other_param_names = ("hra_r", "hra_apply_GS")
+
+ def __init__(self, base_layer: nn.Module, **kwargs) -> None:
+ self.base_layer = base_layer
+ self.hra_r = {}
+ self.hra_apply_GS = {}
+ self.hra_u = nn.ParameterDict({})
+ # Mark the weight as unmerged
+ self._disable_adapters = False
+ self.merged_adapters = []
+ # flag to enable/disable casting of input to weight dtype during forward call
+ self.cast_input_dtype_enabled = True
+ self.kwargs = kwargs
+
+ base_layer = self.get_base_layer()
+ if isinstance(base_layer, nn.Linear):
+ self.in_features, self.out_features = base_layer.in_features, base_layer.out_features
+ elif isinstance(base_layer, nn.Conv2d):
+ self.in_features, self.out_features = base_layer.in_channels, base_layer.out_channels
+ else:
+ raise ValueError(f"Unsupported layer type {type(base_layer)}")
+
+ def update_layer(
+ self,
+ adapter_name: str,
+ r: int,
+ apply_GS: bool,
+ init_weights: bool,
+ inference_mode: bool = False,
+ **kwargs,
+ ) -> None:
+ """Internal function to create hra adapter
+
+ Args:
+ adapter_name (`str`): Name for the adapter to add.
+ r (`int`): Rank for the added adapter.
+ init_weights (`bool`): Whether to initialize weights.
+ apply_GS (`bool`): Whether to apply Gram-Schmidt orthogonalization or not.
+ """
+ if r <= 0:
+ raise ValueError(f"`r` should be a positive integer value but the value passed is {r}")
+
+ self.hra_r[adapter_name] = r
+ self.hra_apply_GS[adapter_name] = apply_GS
+
+ # Determine shape of HRA weights
+ base_layer = self.get_base_layer()
+ if isinstance(base_layer, nn.Linear):
+ self.hra_u[adapter_name] = nn.Parameter(torch.empty(self.in_features, r), requires_grad=True)
+ elif isinstance(base_layer, nn.Conv2d):
+ self.hra_u[adapter_name] = nn.Parameter(
+ torch.empty(self.in_features * base_layer.kernel_size[0] * base_layer.kernel_size[0], r),
+ requires_grad=True,
+ )
+ else:
+ raise TypeError(f"HRA is not implemented for base layers of type {type(base_layer).__name__}")
+
+ # Initialize weights
+ if init_weights:
+ self.reset_hra_parameters(adapter_name)
+ else:
+ self.reset_hra_parameters_random(adapter_name)
+
+ # Move new weights to device
+ self._move_adapter_to_device_of_base_layer(adapter_name)
+ self.set_adapter(self.active_adapters, inference_mode=inference_mode)
+
+ def reset_hra_parameters(self, adapter_name: str):
+ if self.hra_r[adapter_name] % 2 != 0:
+ warnings.warn("The symmetric initialization can NOT be performed when r is odd!")
+ nn.init.kaiming_uniform_(self.hra_u[adapter_name], a=math.sqrt(5))
+ else:
+ shape = self.hra_u[adapter_name].shape
+ half_u = torch.zeros(shape[0], shape[1] // 2)
+ nn.init.kaiming_uniform_(half_u, a=math.sqrt(5))
+ self.hra_u[adapter_name] = nn.Parameter(torch.repeat_interleave(half_u, 2, dim=1))
+
+ def reset_hra_parameters_random(self, adapter_name: str):
+ nn.init.kaiming_uniform_(self.hra_u[adapter_name], a=math.sqrt(5))
+
+ def scale_layer(self, scale: float) -> None:
+ if scale == 1:
+ return
+
+ for active_adapter in self.active_adapters:
+ if active_adapter not in self.hra_u.keys():
+ continue
+
+ warnings.warn("Scaling operation for HRA not supported! Automatically set scale to 1.")
+
+ def unscale_layer(self, scale=None) -> None:
+ for active_adapter in self.active_adapters:
+ if active_adapter not in self.hra_u.keys():
+ continue
+
+ warnings.warn("Unscaling operation for HRA not supported! Keeping scale at 1.")
+
+
+class HRALinear(nn.Module, HRALayer):
+ """
+ HRA implemented in a dense layer.
+ """
+
+ def __init__(
+ self,
+ base_layer,
+ adapter_name: str,
+ r: int = 0,
+ apply_GS: bool = False,
+ init_weights: Union[bool, str] = True,
+ **kwargs,
+ ) -> None:
+ super().__init__()
+ HRALayer.__init__(self, base_layer, **kwargs)
+ self._active_adapter = adapter_name
+ self.update_layer(adapter_name, r, apply_GS, init_weights, **kwargs)
+
+ def merge(self, safe_merge: bool = False, adapter_names: Optional[list[str]] = None) -> None:
+ """
+ Merge the active adapter weights into the base weights
+
+ Args:
+ safe_merge (`bool`, *optional*):
+ If `True`, the merge operation will be performed in a copy of the original weights and check for NaNs
+ before merging the weights. This is useful if you want to check if the merge operation will produce
+ NaNs. Defaults to `False`.
+ adapter_names (`List[str]`, *optional*):
+ The list of adapter names that should be merged. If `None`, all active adapters will be merged.
+ Defaults to `None`.
+ """
+ adapter_names = check_adapters_to_merge(self, adapter_names)
+ if not adapter_names:
+ # no adapter to merge
+ return
+
+ for active_adapter in adapter_names:
+ if active_adapter in self.hra_u.keys():
+ base_layer = self.get_base_layer()
+ orig_dtype = base_layer.weight.dtype
+ if safe_merge:
+ # Note that safe_merge will be slower than the normal merge
+ # because of the copy operation.
+ orig_weight = base_layer.weight.data.clone()
+ delta_weight = self.get_delta_weight(active_adapter)
+ orig_weight = torch.mm(orig_weight.to(delta_weight.dtype), delta_weight)
+
+ if not torch.isfinite(orig_weight).all():
+ raise ValueError(
+ f"NaNs detected in the merged weights. The adapter {active_adapter} seems to be broken"
+ )
+
+ base_layer.weight.data = orig_weight.to(orig_dtype)
+ else:
+ delta_weight = self.get_delta_weight(active_adapter)
+ new_weight = torch.mm(base_layer.weight.data.to(delta_weight.dtype), delta_weight)
+ base_layer.weight.data = new_weight.to(orig_dtype)
+ self.merged_adapters.append(active_adapter)
+
+ def unmerge(self) -> None:
+ """
+ This method unmerges all merged adapter layers from the base weights.
+ """
+ if not self.merged:
+ warnings.warn("Already unmerged. Nothing to do.")
+ return
+
+ while len(self.merged_adapters) > 0:
+ active_adapter = self.merged_adapters.pop()
+ base_layer = self.get_base_layer()
+ orig_dtype = base_layer.weight.dtype
+ if active_adapter in self.hra_u.keys():
+ orig_weight = base_layer.weight.data.clone()
+ delta_weight = self.get_delta_weight(active_adapter, reverse=True)
+ new_weight = torch.mm(orig_weight.to(delta_weight.dtype), delta_weight)
+ base_layer.weight.data = new_weight.to(orig_dtype)
+
+ def get_delta_weight(self, adapter_name: str, reverse: bool = False) -> torch.Tensor:
+ rank = self.hra_r[adapter_name]
+ apply_GS = self.hra_apply_GS[adapter_name]
+ opt_u = self.hra_u[adapter_name]
+ shape = opt_u.shape
+
+ if apply_GS:
+ weight = [(opt_u[:, 0] / opt_u[:, 0].norm()).view(-1, 1)]
+ for i in range(1, rank):
+ ui = opt_u[:, i].view(-1, 1)
+ for j in range(i):
+ ui = ui - (weight[j].t() @ ui) * weight[j]
+ weight.append((ui / ui.norm()).view(-1, 1))
+ weight = torch.cat(weight, dim=1)
+ weight = torch.eye(shape[0], device=opt_u.device, dtype=opt_u.dtype) - 2 * weight @ weight.t()
+
+ else:
+ opt_u = opt_u / opt_u.norm(dim=0)
+ weight = torch.eye(shape[0], device=opt_u.device, dtype=opt_u.dtype)
+ if reverse:
+ indices = range(rank - 1, -1, -1)
+ else:
+ indices = range(rank)
+
+ for i in indices:
+ ui = opt_u[:, i].view(-1, 1)
+ weight = weight - 2 * weight @ ui @ ui.t()
+
+ return weight
+
+ def forward(self, x: torch.Tensor, *args: Any, **kwargs: Any) -> torch.Tensor:
+ previous_dtype = x.dtype
+
+ if self.disable_adapters:
+ if self.merged:
+ self.unmerge()
+ result = self.base_layer(x, *args, **kwargs)
+ elif self.merged:
+ result = self.base_layer(x, *args, **kwargs)
+ else:
+ new_weight = torch.eye(self.in_features, device=x.device)
+
+ for active_adapter in self.active_adapters:
+ if active_adapter not in self.hra_u.keys():
+ continue
+ delta_weight = self.get_delta_weight(active_adapter)
+ new_weight = torch.mm(new_weight.to(delta_weight.dtype), delta_weight)
+
+ orig_weight = self.get_base_layer().weight.data
+ orig_weight = self._cast_input_dtype(orig_weight, new_weight.dtype)
+ new_weight = torch.mm(orig_weight, new_weight)
+ bias = self._cast_input_dtype(self.base_layer.bias, new_weight.dtype)
+
+ if self.cast_input_dtype_enabled:
+ x = self._cast_input_dtype(x, new_weight.dtype)
+ else:
+ x = x.to(self.get_base_layer().weight.data.dtype)
+ result = F.linear(input=x, weight=new_weight, bias=bias)
+
+ result = result.to(previous_dtype)
+ return result
+
+ def __repr__(self) -> str:
+ rep = super().__repr__()
+ return "hra." + rep
+
+
+class HRAConv2d(nn.Module, HRALayer):
+ """HRA implemented in Conv2d layer"""
+
+ def __init__(
+ self,
+ base_layer,
+ adapter_name: str,
+ r: int = 0,
+ apply_GS: bool = False,
+ init_weights: Union[bool, str] = True,
+ **kwargs,
+ ):
+ super().__init__()
+ HRALayer.__init__(self, base_layer)
+ self._active_adapter = adapter_name
+ self.update_layer(adapter_name, r, apply_GS, init_weights, **kwargs)
+
+ def merge(self, safe_merge: bool = False, adapter_names: Optional[list[str]] = None) -> None:
+ """
+ Merge the active adapter weights into the base weights
+
+ Args:
+ safe_merge (`bool`, *optional*):
+ If `True`, the merge operation will be performed in a copy of the original weights and check for NaNs
+ before merging the weights. This is useful if you want to check if the merge operation will produce
+ NaNs. Defaults to `False`.
+ adapter_names (`List[str]`, *optional*):
+ The list of adapter names that should be merged. If `None`, all active adapters will be merged.
+ Defaults to `None`.
+ """
+ adapter_names = check_adapters_to_merge(self, adapter_names)
+ if not adapter_names:
+ # no adapter to merge
+ return
+
+ for active_adapter in adapter_names:
+ if active_adapter in self.hra_u.keys():
+ base_layer = self.get_base_layer()
+ orig_dtype = base_layer.weight.dtype
+ if safe_merge:
+ # Note that safe_merge will be slower than the normal merge
+ # because of the copy operation.
+ orig_weight = base_layer.weight.data.clone()
+ orig_weight = orig_weight.view(
+ self.out_features,
+ self.in_features * base_layer.kernel_size[0] * self.base_layer.kernel_size[0],
+ )
+ delta_weight = self.get_delta_weight(active_adapter)
+ orig_weight = torch.mm(orig_weight.to(delta_weight.dtype), delta_weight)
+ orig_weight = orig_weight.view(
+ self.out_features,
+ self.in_features,
+ base_layer.kernel_size[0],
+ base_layer.kernel_size[0],
+ )
+
+ if not torch.isfinite(orig_weight).all():
+ raise ValueError(
+ f"NaNs detected in the merged weights. The adapter {active_adapter} seems to be broken"
+ )
+
+ base_layer.weight.data = orig_weight.to(orig_dtype)
+ else:
+ orig_weight = base_layer.weight.data
+ orig_weight = orig_weight.view(
+ self.out_features,
+ self.in_features * self.base_layer.kernel_size[0] * self.base_layer.kernel_size[0],
+ )
+ delta_weight = self.get_delta_weight(active_adapter)
+ orig_weight = torch.mm(orig_weight.to(delta_weight.dtype), delta_weight)
+ orig_weight = orig_weight.view(
+ self.out_features,
+ self.in_features,
+ base_layer.kernel_size[0],
+ base_layer.kernel_size[0],
+ )
+
+ base_layer.weight.data = orig_weight.to(orig_dtype)
+ self.merged_adapters.append(active_adapter)
+
+ def unmerge(self) -> None:
+ """
+ This method unmerges all merged adapter layers from the base weights.
+ """
+ if not self.merged:
+ warnings.warn("Already unmerged. Nothing to do.")
+ return
+ while len(self.merged_adapters) > 0:
+ active_adapter = self.merged_adapters.pop()
+ base_layer = self.get_base_layer()
+ orig_dtype = base_layer.weight.dtype
+ if active_adapter in self.hra_u.keys():
+ orig_weight = base_layer.weight.data.clone()
+ orig_weight = orig_weight.view(
+ self.out_features,
+ self.in_features * base_layer.kernel_size[0] * base_layer.kernel_size[0],
+ )
+ delta_weight = self.get_delta_weight(active_adapter, reverse=True)
+ orig_weight = torch.mm(orig_weight.to(delta_weight.dtype), delta_weight)
+ orig_weight = orig_weight.view(
+ self.out_features, self.in_features, base_layer.kernel_size[0], base_layer.kernel_size[0]
+ )
+
+ base_layer.weight.data = orig_weight.to(orig_dtype)
+
+ def get_delta_weight(self, adapter_name: str, reverse: bool = False) -> torch.Tensor:
+ rank = self.hra_r[adapter_name]
+ apply_GS = self.hra_apply_GS[adapter_name]
+ opt_u = self.hra_u[adapter_name]
+ shape = opt_u.shape
+
+ if apply_GS:
+ weight = [(opt_u[:, 0] / opt_u[:, 0].norm()).view(-1, 1)]
+ for i in range(1, rank):
+ ui = opt_u[:, i].view(-1, 1)
+ for j in range(i):
+ ui = ui - (weight[j].t() @ ui) * weight[j]
+ weight.append((ui / ui.norm()).view(-1, 1))
+ weight = torch.cat(weight, dim=1)
+ weight = torch.eye(shape[0], device=opt_u.device, dtype=opt_u.dtype) - 2 * weight @ weight.t()
+
+ else:
+ opt_u = opt_u / opt_u.norm(dim=0)
+ weight = torch.eye(shape[0], device=opt_u.device, dtype=opt_u.dtype)
+ if reverse:
+ indices = range(rank - 1, -1, -1)
+ else:
+ indices = range(rank)
+
+ for i in indices:
+ ui = opt_u[:, i].view(-1, 1)
+ weight = weight - 2 * weight @ ui @ ui.t()
+
+ return weight
+
+ def forward(self, x: torch.Tensor, *args: Any, **kwargs: Any) -> torch.Tensor:
+ previous_dtype = x.dtype
+
+ if self.disable_adapters:
+ if self.merged:
+ self.unmerge()
+ result = self.base_layer(x, *args, **kwargs)
+ elif self.merged:
+ result = self.base_layer(x, *args, **kwargs)
+ else:
+ new_weight = torch.eye(
+ self.in_features * self.base_layer.kernel_size[0] * self.base_layer.kernel_size[0],
+ device=x.device,
+ )
+ for active_adapter in self.active_adapters:
+ if active_adapter not in self.hra_u.keys():
+ continue
+ delta_weight = self.get_delta_weight(active_adapter)
+ new_weight = torch.mm(new_weight.to(delta_weight.dtype), delta_weight)
+
+ orig_weight = self.base_layer.weight.data
+ orig_weight = orig_weight.view(
+ self.out_features,
+ self.in_features * self.base_layer.kernel_size[0] * self.base_layer.kernel_size[0],
+ )
+ orig_weight = self._cast_input_dtype(orig_weight, new_weight.dtype)
+ bias = self._cast_input_dtype(self.base_layer.bias, new_weight.dtype)
+
+ new_weight = torch.mm(orig_weight, new_weight)
+ new_weight = new_weight.view(
+ self.out_features,
+ self.in_features,
+ self.base_layer.kernel_size[0],
+ self.base_layer.kernel_size[0],
+ )
+
+ if self.cast_input_dtype_enabled:
+ x = self._cast_input_dtype(x, new_weight.dtype)
+ else:
+ x = x.to(self.get_base_layer().weight.data.dtype)
+ result = F.conv2d(
+ input=x,
+ weight=new_weight,
+ bias=bias,
+ padding=self.base_layer.padding[0],
+ stride=self.base_layer.stride[0],
+ )
+
+ result = result.to(previous_dtype)
+ return result
+
+ def __repr__(self) -> str:
+ rep = super().__repr__()
+ return "hra." + rep
diff --git a/peft/src/peft/tuners/hra/model.py b/peft/src/peft/tuners/hra/model.py
new file mode 100644
index 0000000000000000000000000000000000000000..e210d226b5294053788188b9d3b307b73c7d9457
--- /dev/null
+++ b/peft/src/peft/tuners/hra/model.py
@@ -0,0 +1,131 @@
+# Copyright 2024-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+
+import torch
+
+from peft.tuners.tuners_utils import BaseTuner, BaseTunerLayer
+from peft.utils import TRANSFORMERS_MODELS_TO_HRA_TARGET_MODULES_MAPPING
+
+from .layer import HRAConv2d, HRALayer, HRALinear
+
+
+class HRAModel(BaseTuner):
+ """
+ Creates Householder reflection adaptation (HRA) model from a pretrained model. The method is described in
+ https://huggingface.co/papers/2405.17484
+
+ Args:
+ model (`torch.nn.Module`): The model to which the adapter tuner layers will be attached.
+ config ([`HRAConfig`]): The configuration of the HRA model.
+ adapter_name (`str`): The name of the adapter, defaults to `"default"`.
+ low_cpu_mem_usage (`bool`, `optional`, defaults to `False`):
+ Create empty adapter weights on meta device. Useful to speed up the loading process.
+
+ Returns:
+ `torch.nn.Module`: The HRA model.
+
+ Example:
+ ```py
+ >>> from diffusers import StableDiffusionPipeline
+ >>> from peft import HRAModel, HRAConfig
+
+ >>> config_te = HRAConfig(
+ ... r=8,
+ ... target_modules=["k_proj", "q_proj", "v_proj", "out_proj", "fc1", "fc2"],
+ ... init_weights=True,
+ ... )
+ >>> config_unet = HRAConfig(
+ ... r=8,
+ ... target_modules=[
+ ... "proj_in",
+ ... "proj_out",
+ ... "to_k",
+ ... "to_q",
+ ... "to_v",
+ ... "to_out.0",
+ ... "ff.net.0.proj",
+ ... "ff.net.2",
+ ... ],
+ ... init_weights=True,
+ ... )
+
+ >>> model = StableDiffusionPipeline.from_pretrained("runwayml/stable-diffusion-v1-5")
+ >>> model.text_encoder = HRAModel(model.text_encoder, config_te, "default")
+ >>> model.unet = HRAModel(model.unet, config_unet, "default")
+ ```
+
+ **Attributes**:
+ - **model** ([`~torch.nn.Module`]) -- The model to be adapted.
+ - **peft_config** ([`HRAConfig`]): The configuration of the HRA model.
+ """
+
+ prefix: str = "hra_"
+ tuner_layer_cls = HRALayer
+ target_module_mapping = TRANSFORMERS_MODELS_TO_HRA_TARGET_MODULES_MAPPING
+
+ def _create_and_replace(
+ self,
+ hra_config,
+ adapter_name,
+ target,
+ target_name,
+ parent,
+ current_key,
+ **optional_kwargs,
+ ):
+ if current_key is None:
+ raise ValueError("Current Key shouldn't be `None`")
+
+ bias = hasattr(target, "bias") and target.bias is not None
+ kwargs = {
+ "r": hra_config.r,
+ "apply_GS": hra_config.apply_GS,
+ "init_weights": hra_config.init_weights,
+ }
+ kwargs["bias"] = bias
+
+ # If it is not a HRALayer, create a new module, else update it with new adapters
+ if not isinstance(target, HRALayer):
+ new_module = self._create_new_module(hra_config, adapter_name, target, **kwargs)
+ if adapter_name not in self.active_adapters:
+ # adding an additional adapter: it is not automatically trainable
+ new_module.requires_grad_(False)
+ self._replace_module(parent, target_name, new_module, target)
+ else:
+ target.update_layer(
+ adapter_name,
+ r=hra_config.r,
+ apply_GS=hra_config.apply_GS,
+ init_weights=hra_config.init_weights,
+ )
+
+ @staticmethod
+ def _create_new_module(hra_config, adapter_name, target, **kwargs):
+ if isinstance(target, BaseTunerLayer):
+ target_base_layer = target.get_base_layer()
+ else:
+ target_base_layer = target
+
+ if isinstance(target_base_layer, torch.nn.Linear):
+ new_module = HRALinear(target, adapter_name, **kwargs)
+ elif isinstance(target_base_layer, torch.nn.Conv2d):
+ new_module = HRAConv2d(target, adapter_name, **kwargs)
+ else:
+ raise ValueError(
+ f"Target module {target} is not supported. "
+ "Currently, only `torch.nn.Linear` and `torch.nn.Conv2d` are supported."
+ )
+
+ return new_module
diff --git a/peft/src/peft/tuners/ia3/__init__.py b/peft/src/peft/tuners/ia3/__init__.py
new file mode 100644
index 0000000000000000000000000000000000000000..21cab4d6d8a6437766f395e90079ce6ecd9e4f26
--- /dev/null
+++ b/peft/src/peft/tuners/ia3/__init__.py
@@ -0,0 +1,39 @@
+# Copyright 2023-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+from peft.import_utils import is_bnb_4bit_available, is_bnb_available
+from peft.utils import register_peft_method
+
+from .config import IA3Config
+from .layer import Conv2d, Conv3d, IA3Layer, Linear
+from .model import IA3Model
+
+
+__all__ = ["Conv2d", "Conv3d", "IA3Config", "IA3Layer", "IA3Model", "Linear"]
+
+register_peft_method(name="ia3", config_cls=IA3Config, model_cls=IA3Model, is_mixed_compatible=True)
+
+
+def __getattr__(name):
+ if (name == "Linear8bitLt") and is_bnb_available():
+ from .bnb import Linear8bitLt
+
+ return Linear8bitLt
+
+ if (name == "Linear4bit") and is_bnb_4bit_available():
+ from .bnb import Linear4bit
+
+ return Linear4bit
+
+ raise AttributeError(f"module {__name__} has no attribute {name}")
diff --git a/peft/src/peft/tuners/ia3/bnb.py b/peft/src/peft/tuners/ia3/bnb.py
new file mode 100644
index 0000000000000000000000000000000000000000..628e3ce7229528a0b3157da349b2b34153573c51
--- /dev/null
+++ b/peft/src/peft/tuners/ia3/bnb.py
@@ -0,0 +1,129 @@
+# Copyright 2023-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+from typing import Any
+
+import torch
+
+from peft.import_utils import is_bnb_4bit_available, is_bnb_available
+
+from .layer import IA3Layer
+
+
+if is_bnb_available():
+
+ class Linear8bitLt(torch.nn.Module, IA3Layer):
+ # (IA)^3 implemented in a dense layer
+ def __init__(
+ self,
+ base_layer: torch.nn.Module,
+ adapter_name: str,
+ is_feedforward: bool,
+ init_ia3_weights: bool = True,
+ **kwargs,
+ ) -> None:
+ super().__init__()
+ IA3Layer.__init__(self, base_layer, is_feedforward=is_feedforward)
+
+ # Freezing the pre-trained weight matrix
+ self.get_base_layer().weight.requires_grad = False
+ self._active_adapter = adapter_name
+ self.update_layer(adapter_name, init_ia3_weights)
+
+ def forward(self, x: torch.Tensor, *args: Any, **kwargs: Any) -> torch.Tensor:
+ # note: no check for self.merged because merging is not supported (yet)
+ if self.disable_adapters:
+ return self.base_layer(x)
+
+ ia3_scaling = 1
+ for active_adapter in self.active_adapters:
+ if active_adapter not in self.ia3_l.keys():
+ continue
+ ia3_scaling *= self.ia3_l[active_adapter].flatten()
+
+ requires_conversion = (not torch.is_autocast_enabled()) and (x.dtype != torch.float32)
+ if requires_conversion:
+ x = x.float()
+ if self.is_feedforward:
+ result = self.base_layer(x * ia3_scaling)
+ expected_dtype = result.dtype
+ else:
+ result = self.base_layer(x)
+ expected_dtype = result.dtype
+ result = result * ia3_scaling
+
+ if requires_conversion:
+ result = result.to(expected_dtype)
+
+ return result
+
+ def __repr__(self) -> str:
+ rep = super().__repr__()
+ return "ia3." + rep
+
+
+if is_bnb_4bit_available():
+
+ class Linear4bit(torch.nn.Module, IA3Layer):
+ # IA3 implemented in a dense layer
+ def __init__(
+ self,
+ base_layer: torch.nn.Module,
+ adapter_name: str,
+ is_feedforward: bool,
+ init_ia3_weights: bool = True,
+ **kwargs,
+ ) -> None:
+ super().__init__()
+ IA3Layer.__init__(self, base_layer, is_feedforward=is_feedforward)
+
+ # Freezing the pre-trained weight matrix
+ self.get_base_layer().weight.requires_grad = False
+ self._active_adapter = adapter_name
+ self.update_layer(adapter_name, init_ia3_weights)
+
+ def forward(self, x: torch.Tensor, *args: Any, **kwargs: Any) -> torch.Tensor:
+ # note: no check for self.merged because merging is not supported (yet)
+ if self.disable_adapters:
+ return self.base_layer(x)
+
+ ia3_scaling = 1
+ for active_adapter in self.active_adapters:
+ if active_adapter not in self.ia3_l.keys():
+ continue
+ ia3_scaling *= self.ia3_l[active_adapter].flatten()
+
+ requires_conversion = (not torch.is_autocast_enabled()) and (x.dtype != torch.float32)
+ if requires_conversion:
+ x = x.float()
+ if self.is_feedforward:
+ result = self.base_layer(x * ia3_scaling)
+ expected_dtype = result.dtype
+ else:
+ result = self.base_layer(x)
+ expected_dtype = result.dtype
+ result = result * ia3_scaling
+
+ result = result.clone()
+ # adalora.py and lora.py both suggest that this is necessary for 4-bit training on older versions of Pytorch.
+ # This has been duplicated here.
+
+ if requires_conversion:
+ result = result.to(expected_dtype)
+
+ return result
+
+ def __repr__(self) -> str:
+ rep = super().__repr__()
+ return "ia3." + rep
diff --git a/peft/src/peft/tuners/ia3/config.py b/peft/src/peft/tuners/ia3/config.py
new file mode 100644
index 0000000000000000000000000000000000000000..1c4161e5ed97998017b800535d4315c66c9d14cd
--- /dev/null
+++ b/peft/src/peft/tuners/ia3/config.py
@@ -0,0 +1,112 @@
+# Copyright 2023-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+from __future__ import annotations
+
+from dataclasses import dataclass, field
+from typing import Optional, Union
+
+from peft.config import PeftConfig
+from peft.utils import PeftType
+
+
+@dataclass
+class IA3Config(PeftConfig):
+ """
+ This is the configuration class to store the configuration of a [`IA3Model`].
+
+ Args:
+ target_modules (`Optional[Union[List[str], str]]`):
+ The names of the modules to apply the adapter to. If this is specified, only the modules with the specified
+ names will be replaced. When passing a string, a regex match will be performed. When passing a list of
+ strings, either an exact match will be performed or it is checked if the name of the module ends with any
+ of the passed strings. If this is specified as 'all-linear', then all linear/Conv1D modules are chosen,
+ excluding the output layer. If this is not specified, modules will be chosen according to the model
+ architecture. If the architecture is not known, an error will be raised -- in this case, you should specify
+ the target modules manually.
+ exclude_modules (`Optional[Union[List[str], str]]`):
+ The names of the modules to not apply the adapter. When passing a string, a regex match will be performed.
+ When passing a list of strings, either an exact match will be performed or it is checked if the name of the
+ module ends with any of the passed strings.
+ feedforward_modules (`Optional[Union[List[str], str]]`):
+ The names of the modules to be treated as feedforward modules, as in the original paper. These modules will
+ have (IA)³ vectors multiplied to the input, instead of the output. `feedforward_modules` must be a name or
+ a subset of names present in `target_modules`.
+ fan_in_fan_out (`bool`):
+ Set this to True if the layer to replace stores weight like (fan_in, fan_out). For example, gpt-2 uses
+ `Conv1D` which stores weights like (fan_in, fan_out) and hence this should be set to `True`.
+ modules_to_save (`Optional[List[str]]`):
+ List of modules apart from (IA)³ layers to be set as trainable and saved in the final checkpoint.
+ init_ia3_weights (`bool`):
+ Whether to initialize the vectors in the (IA)³ layers, defaults to `True`. Setting this to `False` is
+ discouraged.
+ """
+
+ target_modules: Optional[Union[list[str], str]] = field(
+ default=None,
+ metadata={
+ "help": (
+ "List of module names or regex expression of the module names to replace with (IA)³."
+ "For example, ['q', 'v'] or '.*decoder.*(SelfAttention|EncDecAttention).*(q|v)$'."
+ "This can also be a wildcard 'all-linear' which matches all linear/Conv1D layers except the output layer."
+ "If not specified, modules will be chosen according to the model architecture, If the architecture is "
+ "not known, an error will be raised -- in this case, you should specify the target modules manually."
+ ),
+ },
+ )
+ exclude_modules: Optional[Union[list[str], str]] = field(
+ default=None,
+ metadata={"help": "List of module names or regex expression of the module names to exclude from (IA)³."},
+ )
+ feedforward_modules: Optional[Union[list[str], str]] = field(
+ default=None,
+ metadata={
+ "help": "List of module names or a regex expression of module names which are feedforward"
+ "For example, ['output.dense']"
+ },
+ )
+ fan_in_fan_out: bool = field(
+ default=False,
+ metadata={"help": "Set this to True if the layer to replace stores weight like (fan_in, fan_out)"},
+ )
+ modules_to_save: Optional[list[str]] = field(
+ default=None,
+ metadata={
+ "help": "List of modules apart from (IA)^3 layers to be set as trainable and saved in the final checkpoint. "
+ "For example, in Sequence Classification or Token Classification tasks, "
+ "the final layer `classifier/score` are randomly initialized and as such need to be trainable and saved."
+ },
+ )
+ init_ia3_weights: bool = field(
+ default=True,
+ metadata={"help": "Whether to initialize the vectors in the (IA)^3 layers."},
+ )
+
+ def __post_init__(self):
+ super().__post_init__()
+ self.peft_type = PeftType.IA3
+ self.target_modules = (
+ set(self.target_modules) if isinstance(self.target_modules, list) else self.target_modules
+ )
+ self.exclude_modules = (
+ set(self.exclude_modules) if isinstance(self.exclude_modules, list) else self.exclude_modules
+ )
+ self.feedforward_modules = (
+ set(self.feedforward_modules) if isinstance(self.feedforward_modules, list) else self.feedforward_modules
+ )
+
+ # check if feedforward_modules is a subset of target_modules. run the check only if both are sets
+ if isinstance(self.feedforward_modules, set) and isinstance(self.target_modules, set):
+ if not self.feedforward_modules.issubset(self.target_modules):
+ raise ValueError("`feedforward_modules` should be a subset of `target_modules`")
diff --git a/peft/src/peft/tuners/ia3/layer.py b/peft/src/peft/tuners/ia3/layer.py
new file mode 100644
index 0000000000000000000000000000000000000000..48cb08ba46aa7af05f1d891507e39ee6300f10dc
--- /dev/null
+++ b/peft/src/peft/tuners/ia3/layer.py
@@ -0,0 +1,330 @@
+# Copyright 2023-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+import warnings
+from typing import Any, Optional
+
+import torch
+import torch.nn as nn
+from transformers.pytorch_utils import Conv1D
+
+from peft.tuners.tuners_utils import BaseTunerLayer, check_adapters_to_merge
+from peft.utils import transpose
+
+
+class IA3Layer(BaseTunerLayer):
+ # All names of layers that may contain adapter weights
+ adapter_layer_names = ("ia3_l",)
+
+ def __init__(self, base_layer: nn.Module, is_feedforward: bool, **kwargs) -> None:
+ self.base_layer = base_layer
+ self.ia3_l = nn.ParameterDict({})
+ # Mark the weight as unmerged
+ self._disable_adapters = False
+ self.merged_adapters = []
+ self.is_feedforward = is_feedforward
+
+ base_layer = self.get_base_layer()
+ if isinstance(base_layer, nn.Linear):
+ in_features, out_features = base_layer.in_features, base_layer.out_features
+ elif isinstance(base_layer, (nn.Conv2d, nn.Conv3d)):
+ in_features, out_features = base_layer.in_channels, base_layer.out_channels
+ elif isinstance(base_layer, nn.Embedding):
+ in_features, out_features = base_layer.num_embeddings, base_layer.embedding_dim
+ elif isinstance(base_layer, Conv1D):
+ in_features, out_features = (
+ base_layer.weight.ds_shape if hasattr(base_layer.weight, "ds_shape") else base_layer.weight.shape
+ )
+ else:
+ raise ValueError(f"Unsupported layer type {type(base_layer)}")
+ self.in_features = in_features
+ self.out_features = out_features
+
+ def update_layer(self, adapter_name, init_ia3_weights, inference_mode: bool = False, **kwargs):
+ # This code works for linear layers, override for other layer types
+ # Actual trainable parameters
+ if self.is_feedforward:
+ weight = torch.randn((1, self.in_features))
+ else:
+ weight = torch.randn((self.out_features, 1))
+ self.ia3_l[adapter_name] = nn.Parameter(weight)
+ if init_ia3_weights:
+ self.reset_ia3_parameters(adapter_name)
+ self._move_adapter_to_device_of_base_layer(adapter_name)
+ self.set_adapter(self.active_adapters, inference_mode=inference_mode)
+
+ def reset_ia3_parameters(self, adapter_name):
+ if adapter_name in self.ia3_l.keys():
+ # initialize learned vector with torch.ones
+ nn.init.constant_(self.ia3_l[adapter_name], 1.0)
+
+
+class Linear(nn.Module, IA3Layer):
+ # (IA)^3 implemented in a dense layer
+ def __init__(
+ self,
+ base_layer: nn.Module,
+ adapter_name: str,
+ fan_in_fan_out: bool = False, # Set this to True if the layer to replace stores weight like (fan_in, fan_out)
+ is_feedforward: bool = False, # Set to True if the layer is treated as a feedforward layer
+ is_target_conv_1d_layer: bool = False, # whether target module is a conv1d layer. useful while unloading later
+ init_ia3_weights: bool = True, # whether to initialize IA3 weights
+ **kwargs,
+ ) -> None:
+ super().__init__()
+ IA3Layer.__init__(self, base_layer, is_feedforward=is_feedforward)
+ self.fan_in_fan_out = fan_in_fan_out
+ self.is_target_conv_1d_layer = is_target_conv_1d_layer
+ self._active_adapter = adapter_name
+ self.update_layer(adapter_name, init_ia3_weights)
+
+ def merge(self, safe_merge: bool = False, adapter_names: Optional[list[str]] = None) -> None:
+ """
+ Merge the active adapter weights into the base weights
+
+ Args:
+ safe_merge (`bool`, *optional*):
+ If True, the merge operation will be performed in a copy of the original weights and check for NaNs
+ before merging the weights. This is useful if you want to check if the merge operation will produce
+ NaNs. Defaults to `False`.
+ adapter_names (`List[str]`, *optional*):
+ The list of adapter names that should be merged. If None, all active adapters will be merged. Defaults
+ to `None`.
+ """
+ adapter_names = check_adapters_to_merge(self, adapter_names)
+ if not adapter_names:
+ # no adapter to merge
+ return
+
+ for active_adapter in adapter_names:
+ if active_adapter in self.ia3_l.keys():
+ base_layer = self.get_base_layer()
+ ia3_l = transpose(self.ia3_l[active_adapter].data, self.fan_in_fan_out)
+ orig_dtype = base_layer.weight.data.dtype
+ if safe_merge:
+ orig_weights = base_layer.weight.data
+ orig_weights = torch.mul(orig_weights, ia3_l)
+
+ if not torch.isfinite(orig_weights).all():
+ raise ValueError(
+ f"NaNs detected in the merged weights. The adapter {active_adapter} seems to be broken"
+ )
+ base_layer.weight.data = orig_weights.to(orig_dtype)
+ else:
+ base_layer.weight.data = torch.mul(base_layer.weight.data, ia3_l).to(orig_dtype)
+
+ if not self.is_feedforward and (base_layer.bias is not None):
+ scaling = self.ia3_l[active_adapter].reshape(base_layer.bias.shape)
+ orig_dtype = base_layer.bias.data.dtype
+ base_layer.bias.data = torch.mul(base_layer.bias.data, scaling.data).to(orig_dtype)
+
+ self.merged_adapters.append(active_adapter)
+
+ def unmerge(self) -> None:
+ """
+ This method unmerges all merged adapter layers from the base weights.
+ """
+ if not self.merged:
+ warnings.warn("Already unmerged. Nothing to do.")
+ return
+
+ warnings.warn("Unmerge result can be inaccurate for (IA)^3.")
+ while len(self.merged_adapters) > 0:
+ active_adapter = self.merged_adapters.pop()
+ if active_adapter in self.ia3_l.keys():
+ base_layer = self.get_base_layer()
+ # Add tolerace to avoid division by zero
+ ia3_l = transpose(self.ia3_l[active_adapter].data, self.fan_in_fan_out) + 1e-8
+ orig_dtype = base_layer.weight.data.dtype
+ base_layer.weight.data = torch.div(base_layer.weight.data, ia3_l).to(orig_dtype)
+
+ if not self.is_feedforward and (base_layer.bias is not None):
+ scaling = self.ia3_l[active_adapter].reshape(base_layer.bias.shape)
+ orig_dtype = base_layer.bias.data.dtype
+ base_layer.bias.data = torch.div(base_layer.bias.data, scaling.data + 1e-8).to(orig_dtype)
+
+ def forward(self, x: torch.Tensor, *args: Any, **kwargs: Any) -> torch.Tensor:
+ dtype = previous_dtype = x.dtype
+ if self.disable_adapters:
+ if self.merged:
+ self.unmerge()
+ result = self.base_layer(x, *args, **kwargs)
+ elif self.merged:
+ result = self.base_layer(x, *args, **kwargs)
+ else:
+ ia3_scaling = 1
+ for active_adapter in self.active_adapters:
+ if active_adapter not in self.ia3_l.keys():
+ continue
+ dtype = self.ia3_l[active_adapter].dtype
+ ia3_scaling *= self.ia3_l[active_adapter].flatten()
+
+ if self.is_feedforward:
+ x = x.to(dtype)
+ # TODO: weight.dtype can be != self.ia3_l[self.active_adapters].dtype
+ # e.g. bf16 vs fp32. Is that okay?
+ interm = (x * ia3_scaling).to(previous_dtype)
+ result = self.base_layer(interm, *args, **kwargs)
+ else:
+ result = self.base_layer(x, *args, **kwargs)
+ result_dtype = result.dtype
+ result = (result * ia3_scaling).to(result_dtype)
+
+ return result
+
+
+class _ConvNd(nn.Module, IA3Layer):
+ def __init__(
+ self,
+ base_layer: nn.Module,
+ adapter_name: str,
+ fan_in_fan_out: bool = False, # Set this to True if the layer to replace stores weight like (fan_in, fan_out)
+ is_feedforward: bool = False, # Set to True if the layer is treated as a feedforward layer
+ init_ia3_weights: bool = True,
+ **kwargs,
+ ) -> None:
+ super().__init__()
+ IA3Layer.__init__(self, base_layer, is_feedforward=is_feedforward)
+ self.fan_in_fan_out = fan_in_fan_out
+ self._active_adapter = adapter_name
+ self._kernel_dim = base_layer.weight.dim()
+
+ self.update_layer(adapter_name, init_ia3_weights)
+
+ def update_layer(self, adapter_name, init_ia3_weights, inference_mode: bool = False, **kwargs):
+ # Actual trainable parameters
+ num_features = self.in_features if self.is_feedforward else self.out_features
+ weights_size = (1, num_features) + (1,) * (self._kernel_dim - 2)
+ weight = torch.randn(weights_size)
+ self.ia3_l[adapter_name] = nn.Parameter(weight)
+ if init_ia3_weights:
+ self.reset_ia3_parameters(adapter_name)
+ self._move_adapter_to_device_of_base_layer(adapter_name)
+ self.set_adapter(self.active_adapters, inference_mode=inference_mode)
+
+ def merge(self, safe_merge: bool = False, adapter_names: Optional[list[str]] = None) -> None:
+ """
+ Merge the active adapter weights into the base weights
+
+ Args:
+ safe_merge (`bool`, *optional*):
+ If True, the merge operation will be performed in a copy of the original weights and check for NaNs
+ before merging the weights. This is useful if you want to check if the merge operation will produce
+ NaNs. Defaults to `False`.
+ adapter_names (`List[str]`, *optional*):
+ The list of adapter names that should be merged. If None, all active adapters will be merged. Defaults
+ to `None`.
+ """
+ adapter_names = check_adapters_to_merge(self, adapter_names)
+ if not adapter_names:
+ # no adapter to merge
+ return
+
+ for active_adapter in adapter_names:
+ if active_adapter in self.ia3_l.keys():
+ base_layer = self.get_base_layer()
+ orig_dtype = base_layer.weight.data.dtype
+ ia3_scaling = self.ia3_l[active_adapter].data
+ if not self.is_feedforward:
+ ia3_scaling = ia3_scaling.transpose(0, 1)
+
+ if safe_merge:
+ output_weight = torch.mul(base_layer.weight.data, ia3_scaling).clone()
+
+ if not torch.isfinite(output_weight).all():
+ raise ValueError(
+ f"NaNs detected in the merged weights. The adapter {active_adapter} seems to be broken"
+ )
+
+ base_layer.weight.data = output_weight.to(orig_dtype)
+ else:
+ base_layer.weight.data = torch.mul(base_layer.weight.data, ia3_scaling).to(orig_dtype)
+
+ if not self.is_feedforward and (base_layer.bias is not None):
+ scaling = self.ia3_l[active_adapter].reshape(base_layer.bias.shape)
+ base_layer.bias.data = torch.mul(base_layer.bias.data, scaling.data).to(orig_dtype)
+
+ self.merged_adapters.append(active_adapter)
+
+ def unmerge(self) -> None:
+ """
+ This method unmerges all merged adapter layers from the base weights.
+ """
+ if not self.merged:
+ warnings.warn("Already unmerged. Nothing to do.")
+ return
+
+ warnings.warn("Unmerge result can be inaccurate for (IA)^3.")
+ while len(self.merged_adapters) > 0:
+ active_adapter = self.merged_adapters.pop()
+ if active_adapter in self.ia3_l.keys():
+ base_layer = self.get_base_layer()
+ orig_dtype = base_layer.weight.data.dtype
+ # divide by (IA)^3 vector. Add tolerace to avoid division by zero
+ ia3_scaling = self.ia3_l[active_adapter].data
+ if not self.is_feedforward:
+ ia3_scaling = ia3_scaling.transpose(0, 1)
+ base_layer.weight.data = torch.div(base_layer.weight.data, ia3_scaling + 1e-8).to(orig_dtype)
+
+ if not self.is_feedforward and (base_layer.bias is not None):
+ scaling = self.ia3_l[active_adapter].reshape(base_layer.bias.shape)
+ orig_dtype = base_layer.bias.data.dtype
+ base_layer.bias.data = torch.mul(base_layer.bias.data, scaling.data).to(orig_dtype)
+
+ def forward(self, x: torch.Tensor, *args: Any, **kwargs: Any) -> torch.Tensor:
+ dtype = previous_dtype = x.dtype
+
+ if self.disable_adapters:
+ if self.merged:
+ self.unmerge()
+ result = self.base_layer(x, *args, **kwargs)
+ elif self.merged:
+ result = self.base_layer(x, *args, **kwargs)
+ else:
+ ia3_scaling = 1
+ for active_adapter in self.active_adapters:
+ if active_adapter not in self.ia3_l.keys():
+ continue
+ dtype = self.ia3_l[active_adapter].dtype
+ ia3_scaling *= self.ia3_l[active_adapter]
+
+ if self.is_feedforward:
+ x = x.to(dtype)
+ # TODO: weight.dtype can be != self.ia3_l[self.active_adapters].dtype
+ # e.g. bf16 vs fp32. Is that okay?
+ interm = (x * ia3_scaling).to(self.get_base_layer().weight.dtype)
+ result = self.base_layer(interm, *args, **kwargs)
+ else:
+ result = self.base_layer(x, *args, **kwargs)
+ result = result.to(dtype) * ia3_scaling
+
+ result = result.to(previous_dtype)
+ return result
+
+
+class Conv2d(_ConvNd):
+ # IA3 implemented in a 2D convolutional layer
+
+ def __init__(self, *args, **kwargs):
+ super().__init__(*args, **kwargs)
+ if not self._kernel_dim == 4:
+ raise ValueError(f"Conv2d layer kernel must have 4 dimensions, not {self._kernel_dim}")
+
+
+class Conv3d(_ConvNd):
+ # IA3 implemented in a 3D convolutional layer
+ def __init__(self, *args, **kwargs):
+ super().__init__(*args, **kwargs)
+ if not self._kernel_dim == 5:
+ raise ValueError(f"Conv2d layer kernel must have 5 dimensions, not {self._kernel_dim}")
diff --git a/peft/src/peft/tuners/ia3/model.py b/peft/src/peft/tuners/ia3/model.py
new file mode 100644
index 0000000000000000000000000000000000000000..e322b167fc53f4dadc8ba068c36a6e65d3e22f37
--- /dev/null
+++ b/peft/src/peft/tuners/ia3/model.py
@@ -0,0 +1,315 @@
+# Copyright 2023-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+from __future__ import annotations
+
+import re
+import warnings
+from dataclasses import replace
+
+import torch
+from transformers.pytorch_utils import Conv1D
+
+from peft.import_utils import is_bnb_4bit_available, is_bnb_available
+from peft.tuners.tuners_utils import BaseTuner, BaseTunerLayer
+from peft.utils import (
+ TRANSFORMERS_MODELS_TO_IA3_FEEDFORWARD_MODULES_MAPPING,
+ TRANSFORMERS_MODELS_TO_IA3_TARGET_MODULES_MAPPING,
+ ModulesToSaveWrapper,
+ _freeze_adapter,
+ _get_submodules,
+)
+
+from .layer import Conv2d, Conv3d, IA3Layer, Linear
+
+
+class IA3Model(BaseTuner):
+ """
+ Creates a Infused Adapter by Inhibiting and Amplifying Inner Activations ((IA)^3) model from a pretrained
+ transformers model. The method is described in detail in https://huggingface.co/papers/2205.05638
+
+ Args:
+ model ([`~transformers.PreTrainedModel`]): The model to be adapted.
+ config ([`IA3Config`]): The configuration of the (IA)^3 model.
+ adapter_name (`str`): The name of the adapter, defaults to `"default"`.
+ low_cpu_mem_usage (`bool`, `optional`, defaults to `False`):
+ Create empty adapter weights on meta device. Useful to speed up the loading process.
+
+ Returns:
+ `torch.nn.Module`: The (IA)^3 model.
+
+ Example:
+
+ ```py
+ >>> from transformers import AutoModelForSeq2SeqLM, ia3Config
+ >>> from peft import IA3Model, IA3Config
+
+ >>> config = IA3Config(
+ ... peft_type="IA3",
+ ... task_type="SEQ_2_SEQ_LM",
+ ... target_modules=["k", "v", "w0"],
+ ... feedforward_modules=["w0"],
+ ... )
+
+ >>> model = AutoModelForSeq2SeqLM.from_pretrained("t5-base")
+ >>> ia3_model = IA3Model(config, model)
+ ```
+
+ **Attributes**:
+ - **model** ([`~transformers.PreTrainedModel`]) -- The model to be adapted.
+ - **peft_config** ([`ia3Config`]): The configuration of the (IA)^3 model.
+ """
+
+ prefix: str = "ia3_"
+ tuner_layer_cls = IA3Layer
+
+ @staticmethod
+ def _create_new_module(ia3_config, adapter_name, target, **kwargs):
+ # avoid eager bnb import
+ if is_bnb_available():
+ import bitsandbytes as bnb
+
+ from .bnb import Linear8bitLt
+
+ if is_bnb_4bit_available():
+ from .bnb import Linear4bit
+
+ loaded_in_8bit = kwargs.pop("loaded_in_8bit", False)
+ loaded_in_4bit = kwargs.pop("loaded_in_4bit", False)
+ is_feedforward = kwargs.pop("is_feedforward", False)
+
+ if isinstance(target, BaseTunerLayer):
+ target_base_layer = target.get_base_layer()
+ else:
+ target_base_layer = target
+
+ if loaded_in_8bit and isinstance(target_base_layer, bnb.nn.Linear8bitLt):
+ eightbit_kwargs = kwargs.copy()
+ eightbit_kwargs.update(
+ {
+ "has_fp16_weights": target_base_layer.state.has_fp16_weights,
+ "threshold": target_base_layer.state.threshold,
+ "index": target_base_layer.index,
+ }
+ )
+ new_module = Linear8bitLt(target, adapter_name, is_feedforward=is_feedforward, **eightbit_kwargs)
+ elif loaded_in_4bit and isinstance(target_base_layer, bnb.nn.Linear4bit):
+ fourbit_kwargs = kwargs.copy()
+ fourbit_kwargs.update(
+ {
+ "compute_dtype": target_base_layer.compute_dtype,
+ "compress_statistics": target_base_layer.weight.compress_statistics,
+ "quant_type": target_base_layer.weight.quant_type,
+ }
+ )
+ new_module = Linear4bit(target, adapter_name, is_feedforward=is_feedforward, **fourbit_kwargs)
+ elif isinstance(target, torch.nn.Conv2d):
+ new_module = Conv2d(target, adapter_name, is_feedforward=is_feedforward, **kwargs)
+ elif isinstance(target, torch.nn.Conv3d):
+ new_module = Conv3d(target, adapter_name, is_feedforward=is_feedforward, **kwargs)
+ elif isinstance(target_base_layer, torch.nn.Linear):
+ if kwargs["fan_in_fan_out"]:
+ warnings.warn(
+ "fan_in_fan_out is set to True but the target module is `torch.nn.Linear`. "
+ "Setting fan_in_fan_out to False."
+ )
+ kwargs["fan_in_fan_out"] = ia3_config.fan_in_fan_out = False
+ new_module = Linear(target, adapter_name, is_feedforward=is_feedforward, **kwargs)
+ elif isinstance(target_base_layer, Conv1D):
+ if not kwargs["fan_in_fan_out"]:
+ warnings.warn(
+ "fan_in_fan_out is set to False but the target module is `Conv1D`. Setting fan_in_fan_out to True."
+ )
+ kwargs["fan_in_fan_out"] = ia3_config.fan_in_fan_out = True
+ new_module = Linear(
+ target, adapter_name, is_feedforward=is_feedforward, is_target_conv_1d_layer=True, **kwargs
+ )
+ else:
+ raise ValueError(
+ f"Target module {target} is not supported. "
+ f"Currently, only `torch.nn.Linear`, `torch.nn.Conv2d`, and `Conv1D` are supported."
+ )
+ return new_module
+
+ def _create_and_replace(
+ self,
+ ia3_config,
+ adapter_name,
+ target,
+ target_name,
+ parent,
+ current_key,
+ ):
+ # check if target module is in feedforward_modules
+ is_feedforward = self._check_target_module_feedforward(ia3_config, current_key)
+
+ kwargs = {
+ "fan_in_fan_out": ia3_config.fan_in_fan_out,
+ "init_ia3_weights": ia3_config.init_ia3_weights,
+ "is_feedforward": is_feedforward,
+ "loaded_in_8bit": getattr(self.model, "is_loaded_in_8bit", False),
+ "loaded_in_4bit": getattr(self.model, "is_loaded_in_4bit", False),
+ }
+
+ if isinstance(target, IA3Layer):
+ target.update_layer(
+ adapter_name,
+ ia3_config.init_ia3_weights,
+ )
+ else:
+ new_module = self._create_new_module(ia3_config, adapter_name, target, **kwargs)
+ if adapter_name not in self.active_adapters:
+ # adding an additional adapter: it is not automatically trainable
+ new_module.requires_grad_(False)
+ self._replace_module(parent, target_name, new_module, target)
+
+ @staticmethod
+ def _check_target_module_feedforward(ia3_config, key) -> bool:
+ """
+ A helper private method that checks if the target module `key` matches with a feedforward module specified in
+ `ia3_config`
+ """
+ if isinstance(ia3_config.feedforward_modules, str):
+ is_feedforward = bool(re.fullmatch(ia3_config.feedforward_modules, key))
+ else:
+ is_feedforward = any(key.endswith(target_key) for target_key in ia3_config.feedforward_modules)
+ return is_feedforward
+
+ @staticmethod
+ def _prepare_adapter_config(peft_config, model_config):
+ if peft_config.target_modules is None:
+ if model_config["model_type"] not in TRANSFORMERS_MODELS_TO_IA3_TARGET_MODULES_MAPPING:
+ raise ValueError("Please specify `target_modules` in `peft_config`")
+ peft_config.target_modules = set(
+ TRANSFORMERS_MODELS_TO_IA3_TARGET_MODULES_MAPPING[model_config["model_type"]]
+ )
+ if peft_config.feedforward_modules is None:
+ if model_config["model_type"] not in TRANSFORMERS_MODELS_TO_IA3_FEEDFORWARD_MODULES_MAPPING:
+ raise ValueError("Please specify `feedforward_modules` in `peft_config`")
+ peft_config.feedforward_modules = set(
+ TRANSFORMERS_MODELS_TO_IA3_FEEDFORWARD_MODULES_MAPPING[model_config["model_type"]]
+ )
+ return peft_config
+
+ def _unload_and_optionally_merge(self, *args, **kwargs):
+ r"""
+ This method merges the (IA)^3 layers into the base model. This is needed if someone wants to use the base model
+ as a standalone model.
+
+ Args:
+ safe_merge (`bool`, `optional`, defaults to `False`):
+ If True, the merge operation will be performed in a copy of the original weights and check for NaNs
+ before merging the weights. This is useful if you want to check if the merge operation will produce
+ NaNs. Defaults to `False`.
+ adapter_names (`List[str]`, *optional*):
+ The list of adapter names that should be merged. If None, all active adapters will be merged. Defaults
+ to `None`.
+ """
+ if getattr(self.model, "is_loaded_in_8bit", False):
+ raise ValueError("Cannot merge ia3 layers when the model is loaded in 8-bit mode")
+
+ if getattr(self.model, "is_loaded_in_4bit", False):
+ raise ValueError("Cannot merge ia3 layers when the model is loaded in 4-bit mode")
+
+ return super()._unload_and_optionally_merge(*args, **kwargs)
+
+ def _check_add_weighted_adapter(self, adapters: list[str]) -> tuple[str, str]:
+ """
+ Helper function to check if the arguments to add_weighted_adapter are valid and compatible with the underlying
+ model.
+ """
+ # Validate existence of adapters
+ for adapter in adapters:
+ if adapter not in self.peft_config:
+ raise ValueError(f"Adapter {adapter} does not exist")
+
+ # Check for conflicting modules_to_save
+ modules_to_save_wrappers = [module for module in self.modules() if isinstance(module, ModulesToSaveWrapper)]
+ if any(
+ sum(adapter in wrapper.modules_to_save for adapter in adapters) > 1 for wrapper in modules_to_save_wrappers
+ ):
+ raise ValueError("Cannot add weighted adapters targeting the same module with modules_to_save.")
+
+ # Ensure all adapters have compatible target and feedforward module types
+ target_module_types = {type(self.peft_config[adapter].target_modules) for adapter in adapters}
+ feedforward_module_types = {type(self.peft_config[adapter].feedforward_modules) for adapter in adapters}
+ if len(target_module_types) > 1 or len(feedforward_module_types) > 1:
+ raise ValueError("All adapter configs should have the same type for target and feedforward modules.")
+
+ # Combine target and feedforward modules
+ if str in target_module_types:
+ new_target_modules = "|".join(f"({self.peft_config[adapter].target_modules})" for adapter in adapters)
+ else:
+ new_target_modules = set.union(*(self.peft_config[adapter].target_modules for adapter in adapters))
+
+ if str in feedforward_module_types:
+ new_feedforward_modules = "|".join(
+ f"({self.peft_config[adapter].feedforward_modules})" for adapter in adapters
+ )
+ else:
+ new_feedforward_modules = set.union(
+ *(self.peft_config[adapter].feedforward_modules for adapter in adapters)
+ )
+
+ return new_target_modules, new_feedforward_modules
+
+ def add_weighted_adapter(
+ self,
+ adapters: list[str],
+ weights: list[float],
+ adapter_name: str,
+ ) -> None:
+ """
+ This method adds a new adapter by merging the given adapters with the given weights.
+
+ Args:
+ adapters (`list`):
+ List of adapter names to be merged.
+ weights (`list`):
+ List of weights for each adapter.
+ adapter_name (`str`):
+ Name of the new adapter.
+ """
+ if adapter_name in list(self.peft_config.keys()):
+ return
+
+ new_target_modules, new_feedforward_modules = self._check_add_weighted_adapter(
+ adapters=adapters,
+ )
+
+ self.peft_config[adapter_name] = replace(
+ self.peft_config[adapters[0]],
+ target_modules=new_target_modules,
+ feedforward_modules=new_feedforward_modules,
+ )
+ self.inject_adapter(self.model, adapter_name)
+
+ # Do we really need that?
+ _freeze_adapter(self.model, adapter_name)
+
+ key_list = [key for key, _ in self.model.named_modules() if self.prefix not in key]
+ for key in key_list:
+ _, target, _ = _get_submodules(self.model, key)
+ if isinstance(target, IA3Layer):
+ if adapter_name in target.ia3_l:
+ target_ia3_l = target.ia3_l[adapter_name]
+ else:
+ continue
+
+ target_ia3_l.data = target_ia3_l.data.zero_()
+ for adapter, weight in zip(adapters, weights):
+ if adapter in target.ia3_l:
+ current_adapter_ia3_l = target.ia3_l[adapter]
+ else:
+ continue
+ target_ia3_l.data += current_adapter_ia3_l.data * weight
diff --git a/peft/src/peft/tuners/ln_tuning/__init__.py b/peft/src/peft/tuners/ln_tuning/__init__.py
new file mode 100644
index 0000000000000000000000000000000000000000..8f90a8fb058cf75450b89166bf2e562f07b835fd
--- /dev/null
+++ b/peft/src/peft/tuners/ln_tuning/__init__.py
@@ -0,0 +1,23 @@
+# Copyright 2024-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+from peft.utils import register_peft_method
+
+from .config import LNTuningConfig
+from .model import LNTuningModel
+
+
+__all__ = ["LNTuningConfig", "LNTuningModel"]
+
+register_peft_method(name="ln_tuning", config_cls=LNTuningConfig, model_cls=LNTuningModel)
diff --git a/peft/src/peft/tuners/ln_tuning/config.py b/peft/src/peft/tuners/ln_tuning/config.py
new file mode 100644
index 0000000000000000000000000000000000000000..127ee9017333bce22706b58b13701049244b1da9
--- /dev/null
+++ b/peft/src/peft/tuners/ln_tuning/config.py
@@ -0,0 +1,70 @@
+# Copyright 2024-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+from __future__ import annotations
+
+from dataclasses import dataclass, field
+from typing import Optional, Union
+
+from peft.config import PeftConfig
+from peft.utils import PeftType
+
+
+@dataclass
+class LNTuningConfig(PeftConfig):
+ """
+ This is the configuration class to store the configuration of a :class:`~peft.tuners.LNTuningModel`.
+
+ Args:
+ target_modules (`Optional[Union[List[str], str]]`):
+ List of module names or regex expression of the module names to replace with LNTuning. For example,
+ '.*decoder.*' or '.*encoder.*'. If this is not specified, modules will be chosen according to the model
+ architecture. If the architecture is not known, an error will be raised -- in this case, you should specify
+ the target modules manually.
+ exclude_modules (`Optional[Union[List[str], str]]`):
+ The names of the modules to not apply the adapter. When passing a string, a regex match will be performed.
+ When passing a list of strings, either an exact match will be performed or it is checked if the name of the
+ module ends with any of the passed strings.
+ modules_to_save (`Optional[Union[List[str], str]]`):
+ List of modules to be set as trainable and saved in the final checkpoint. For example, in Sequence
+ Classification or Token Classification tasks, the final layer `classifier/score` are randomly initialized
+ and as such need to be trainable and saved.
+ """
+
+ target_modules: Optional[Union[list[str], str]] = field(
+ default=None,
+ metadata={
+ "help": (
+ "List of module names or regex expression of the module names to replace with LNTuning."
+ "For example, '.*decoder.*' or '.*encoder.*'. "
+ "If not specified, modules will be chosen according to the model architecture, If the architecture is "
+ "not known, an error will be raised -- in this case, you shoud specify the target modules manually."
+ ),
+ },
+ )
+ exclude_modules: Optional[Union[list[str], str]] = field(
+ default=None,
+ metadata={"help": "List of module names or regex expression of the module names to exclude from LNTuning."},
+ )
+ modules_to_save: Optional[Union[list[str], str]] = field(
+ default=None,
+ metadata={
+ "help": "List of modules to be set as trainable and saved in the final checkpoint. "
+ "For example, in Sequence Classification or Token Classification tasks, "
+ "the final layer `classifier/score` are randomly initialized and as such need to be trainable and saved."
+ },
+ )
+
+ def __post_init__(self):
+ super().__post_init__()
+ self.peft_type = PeftType.LN_TUNING
diff --git a/peft/src/peft/tuners/ln_tuning/layer.py b/peft/src/peft/tuners/ln_tuning/layer.py
new file mode 100644
index 0000000000000000000000000000000000000000..e29149f2cbbc023161873a91772fd642296052e0
--- /dev/null
+++ b/peft/src/peft/tuners/ln_tuning/layer.py
@@ -0,0 +1,123 @@
+# Copyright 2024-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+import warnings
+from copy import deepcopy
+from typing import Optional
+
+import torch
+import torch.nn as nn
+
+from peft.tuners.tuners_utils import BaseTunerLayer, _get_in_out_features, check_adapters_to_merge
+
+
+class LNTuningLayer(nn.Module, BaseTunerLayer):
+ """
+ Selects a layer from the model.
+ """
+
+ adapter_layer_names = ("ln_tuning_layers",)
+
+ def __init__(self, base_layer: nn.Module, adapter_name: str):
+ super().__init__()
+ self.base_layer = base_layer
+ self.ln_tuning_layers = nn.ModuleDict({})
+ self.update_layer(self.base_layer, adapter_name)
+ self._active_adapter = adapter_name
+ self.merged_adapters = []
+
+ in_features, out_features = _get_in_out_features(self.get_base_layer())
+ self.in_features = in_features
+ self.out_features = out_features
+
+ def update_layer(self, layer: nn.Module, adapter_name: str, inference_mode: bool = False, **kwargs):
+ self.ln_tuning_layers[adapter_name] = deepcopy(layer)
+ self.set_adapter(adapter_name, inference_mode=inference_mode)
+
+ def enable_adapters(self, enabled: bool) -> None:
+ """Toggle the enabling and disabling of adapters
+
+ Takes care of setting the requires_grad flag for the adapter weights.
+
+ Args:
+ enabled (bool): True to enable adapters, False to disable adapters
+ """
+ if enabled:
+ self.set_adapter(self.active_adapters)
+ self._disable_adapters = False
+ else:
+ if self.merged:
+ self.unmerge()
+ # disable grads on all adapter layers
+ for layer_name in self.adapter_layer_names:
+ layer = getattr(self, layer_name)
+ layer.requires_grad_(False)
+ self._disable_adapters = True
+
+ def merge(self, adapter_names: Optional[list[str]] = None, safe_merge: bool = False):
+ # note that there is no actual merging, so whether safe_merge is True or False is irrelevant
+ adapter_names = check_adapters_to_merge(self, adapter_names)
+ if not adapter_names:
+ # no adapter to merge
+ return
+
+ if len(adapter_names) > 1:
+ raise ValueError(
+ f"Trying to merge {len(adapter_names)} adapters, but LN "
+ f"tuning does not allow merging more than one adapter at a time"
+ )
+ merged_adapters = set(self.merged_adapters)
+ if merged_adapters:
+ warnings.warn(f"Already merged with {merged_adapters}. Unmerging first.")
+ self.unmerge()
+
+ self.base_layer, self.ln_tuning_layers[adapter_names[0]] = (
+ self.ln_tuning_layers[adapter_names[0]],
+ self.base_layer,
+ )
+ self.merged_adapters.append(adapter_names[0])
+
+ def unmerge(self):
+ if not self.merged:
+ warnings.warn("Already unmerged. Nothing to do.")
+ return
+ # popping one element is sufficient because LN
+ # tuning does not allow merging more than one adapter at a time.
+ merged_name = self.merged_adapters.pop()
+ self.base_layer, self.ln_tuning_layers[merged_name] = (
+ self.ln_tuning_layers[merged_name],
+ self.base_layer,
+ )
+
+ def forward(self, x: torch.Tensor, *args, **kwargs) -> torch.Tensor:
+ if self.disable_adapters:
+ if self.merged:
+ self.unmerge()
+ result = self.base_layer(x, *args, **kwargs)
+ elif self.merged:
+ result = self.base_layer(x, *args, **kwargs)
+ else:
+ if len(self.active_adapters) != 1:
+ raise ValueError(
+ f"Trying to run forward with {len(self.active_adapters)} active "
+ f"adapters, but LN tuning does not allow inference with more than one adapter at a time"
+ )
+ active_adapter = self.active_adapters[0]
+ result = self.ln_tuning_layers[active_adapter](x, *args, **kwargs)
+
+ return result
+
+ def __repr__(self) -> str:
+ rep = super().__repr__()
+ return "ln_tuning." + rep
diff --git a/peft/src/peft/tuners/ln_tuning/model.py b/peft/src/peft/tuners/ln_tuning/model.py
new file mode 100644
index 0000000000000000000000000000000000000000..e193d22da8e08216e0a3800b27dccc4d60298855
--- /dev/null
+++ b/peft/src/peft/tuners/ln_tuning/model.py
@@ -0,0 +1,132 @@
+# Copyright 2024-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+from __future__ import annotations
+
+from typing import Optional
+
+from torch.nn.modules import Module
+from tqdm import tqdm
+
+from peft.config import PeftConfig
+from peft.tuners.tuners_utils import BaseTuner, _get_submodules
+from peft.utils import TRANSFORMERS_MODELS_TO_LNTUNING_TARGET_MODULES_MAPPING
+
+from .layer import LNTuningLayer
+
+
+class LNTuningModel(BaseTuner):
+ """
+ Creates LayerNorm tuning from a pretrained transformer model.
+
+ The method is described in detail in https://huggingface.co/papers/2312.11420.
+
+ Args:
+ model ([`torch.nn.Module`]): The model to be adapted.
+ config ([`LNTuningConfig`]): The configuration of the Lora model.
+ adapter_name (`str`): The name of the adapter, defaults to `"default"`.
+ low_cpu_mem_usage (`bool`, `optional`, defaults to `False`):
+ This option has no effect on LN tuning but exists for consistency with other PEFT methods.
+
+ Returns:
+ 'torch.nn.Module': The adapted model with LayerNorm tuned on.
+
+ Example:
+
+ ```py
+ >>> from transformers import AutoModelForCausalLM
+ >>> from peft import get_peft_model, TaskType, LNTuningConfig
+
+ >>> peft_config = LNTuningConfig(
+ ... task_type=TaskType.CAUSAL_LM,
+ ... )
+
+ >>> model = AutoModelForCausalLM.from_pretrained("meta-llama/Llama-2-7b-hf")
+ >>> model = get_peft_model(model, peft_config)
+ >>> model.print_trainable_parameters()
+ ```
+
+ **Attributes**:
+ - **model** ([`~transformers.PreTrainedModel`]) -- The model to be adapted.
+ - **peft_config** ([`LNTuningConfig`]): The configuration of the Lora model.
+ """
+
+ prefix: str = "ln_tuning_"
+ tuner_layer_cls = LNTuningLayer
+ target_module_mapping = TRANSFORMERS_MODELS_TO_LNTUNING_TARGET_MODULES_MAPPING
+
+ def _create_and_replace(
+ self,
+ peft_config: PeftConfig,
+ adapter_name: str,
+ target: Module,
+ target_name: str,
+ parent: Module,
+ current_key: str,
+ ) -> None:
+ # replace the original module with a same new module
+ new_module = self._create_new_module(peft_config, target, adapter_name)
+ if adapter_name != self.active_adapter:
+ new_module.requires_grad_(False)
+ self._replace_module(parent, target_name, new_module, target)
+
+ def _create_new_module(
+ self,
+ peft_config: PeftConfig,
+ target: Module,
+ adapter_name: str,
+ ) -> Module:
+ if not isinstance(target, LNTuningLayer):
+ new_module = LNTuningLayer(target, adapter_name)
+ else:
+ new_module = target
+ new_module.update_layer(target.base_layer, adapter_name)
+ return new_module
+
+ def _unloading_checks(self, adapter_names: Optional[list[str]]):
+ adapters_to_consider = adapter_names or self.active_adapters
+ is_modules_to_save_available = any(
+ self.peft_config[adapter].modules_to_save for adapter in adapters_to_consider
+ )
+ if is_modules_to_save_available and len(adapters_to_consider) > 1:
+ raise ValueError("Cannot unload multiple adapters that specify `modules_to_save`.")
+
+ def _unload_and_optionally_merge(
+ self,
+ merge=True,
+ progressbar: bool = False,
+ safe_merge: bool = False,
+ adapter_names: Optional[list[str]] = None,
+ ):
+ self._unloading_checks(adapter_names)
+ key_list = [key for key, _ in self.model.named_modules() if self.prefix not in key]
+ desc = "Unloading adapters " + ("and merging " if merge else "") + "model"
+
+ for key in tqdm(key_list, disable=not progressbar, desc=desc):
+ try:
+ parent, target, target_name = _get_submodules(self.model, key)
+ except AttributeError:
+ continue
+
+ if hasattr(target, "base_layer"):
+ if merge:
+ target.merge(adapter_names)
+ self._replace_module(parent, target_name, target.get_base_layer(), target)
+
+ return self.model
+
+ def _cast_adapter_dtype(self, adapter_name: str, autocast_adapter_dtype: bool = True) -> None:
+ # Note: LN Tuning does not add adapter layers, instead it creates copies of the original layer. For this reason,
+ # we need to skip adapter autocasting, otherwise we would change the dtype of copies of the original layer,
+ # resulting in dtype errors down the line.
+ pass
diff --git a/peft/src/peft/tuners/loha/__init__.py b/peft/src/peft/tuners/loha/__init__.py
new file mode 100644
index 0000000000000000000000000000000000000000..70dd1545bbd49b0aaa5eafbde05f82b6a04c3d74
--- /dev/null
+++ b/peft/src/peft/tuners/loha/__init__.py
@@ -0,0 +1,24 @@
+# Copyright 2023-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+from peft.utils import register_peft_method
+
+from .config import LoHaConfig
+from .layer import Conv2d, Linear, LoHaLayer
+from .model import LoHaModel
+
+
+__all__ = ["Conv2d", "Linear", "LoHaConfig", "LoHaLayer", "LoHaModel"]
+
+register_peft_method(name="loha", config_cls=LoHaConfig, model_cls=LoHaModel, prefix="hada_", is_mixed_compatible=True)
diff --git a/peft/src/peft/tuners/loha/config.py b/peft/src/peft/tuners/loha/config.py
new file mode 100644
index 0000000000000000000000000000000000000000..79c1f630130133c393c18e09a2624795f9353157
--- /dev/null
+++ b/peft/src/peft/tuners/loha/config.py
@@ -0,0 +1,143 @@
+# Copyright 2023-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+from __future__ import annotations
+
+from dataclasses import dataclass, field
+from typing import Optional, Union
+
+from peft.tuners.lycoris_utils import LycorisConfig
+from peft.utils import PeftType
+
+
+@dataclass
+class LoHaConfig(LycorisConfig):
+ """
+ This is the configuration class to store the configuration of a [`LoHaModel`].
+
+ Args:
+ r (`int`):
+ LoHa rank.
+ alpha (`int`):
+ The alpha parameter for LoHa scaling.
+ rank_dropout (`float`):
+ The dropout probability for rank dimension during training.
+ module_dropout (`float`):
+ The dropout probability for disabling LoHa modules during training.
+ use_effective_conv2d (`bool`):
+ Use parameter effective decomposition for Conv2d (and Conv1d) with ksize > 1 ("Proposition 3" from FedPara
+ paper).
+ target_modules (`Optional[Union[List[str], str]]`):
+ The names of the modules to apply the adapter to. If this is specified, only the modules with the specified
+ names will be replaced. When passing a string, a regex match will be performed. When passing a list of
+ strings, either an exact match will be performed or it is checked if the name of the module ends with any
+ of the passed strings. If this is specified as 'all-linear', then all linear/Conv1D modules are chosen,
+ excluding the output layer. If this is not specified, modules will be chosen according to the model
+ architecture. If the architecture is not known, an error will be raised -- in this case, you should specify
+ the target modules manually.
+ exclude_modules (`Optional[Union[List[str], str]]`):
+ The names of the modules to not apply the adapter. When passing a string, a regex match will be performed.
+ When passing a list of strings, either an exact match will be performed or it is checked if the name of the
+ module ends with any of the passed strings.
+ init_weights (`bool`):
+ Whether to perform initialization of adapter weights. This defaults to `True`, passing `False` is
+ discouraged.
+ layers_to_transform (`Union[List[int], int]`):
+ The layer indices to transform. If a list of ints is passed, it will apply the adapter to the layer indices
+ that are specified in this list. If a single integer is passed, it will apply the transformations on the
+ layer at this index.
+ layers_pattern (`Optional[Union[List[str], str]]`):
+ The layer pattern name, used only if `layers_to_transform` is different from `None`. This should target the
+ `nn.ModuleList` of the model, which is often called `'layers'` or `'h'`.
+ rank_pattern (`dict`):
+ The mapping from layer names or regexp expression to ranks which are different from the default rank
+ specified by `r`. For example, `{'^model.decoder.layers.0.encoder_attn.k_proj': 16}`.
+ alpha_pattern (`dict`):
+ The mapping from layer names or regexp expression to alphas which are different from the default alpha
+ specified by `alpha`. For example, `{'^model.decoder.layers.0.encoder_attn.k_proj': 16}`.
+ modules_to_save (`Optional[List[str]]`):
+ List of modules apart from adapter layers to be set as trainable and saved in the final checkpoint.
+ """
+
+ r: int = field(default=8, metadata={"help": "LoHa rank"})
+ alpha: int = field(default=8, metadata={"help": "LoHa alpha"})
+ rank_dropout: float = field(
+ default=0.0, metadata={"help": "The dropout probability for rank dimension during training"}
+ )
+ module_dropout: float = field(
+ default=0.0, metadata={"help": "The dropout probability for disabling LoHa modules during training"}
+ )
+ use_effective_conv2d: bool = field(
+ default=False,
+ metadata={
+ "help": (
+ "Use parameter effective decomposition for Conv2d (and Conv1d) with ksize > 1 "
+ '("Proposition 3" from FedPara paper)'
+ )
+ },
+ )
+ target_modules: Optional[Union[list[str], str]] = field(
+ default=None,
+ metadata={
+ "help": "List of module names or regex expression of the module names to replace with LoHa."
+ "For example, ['q', 'v'] or '.*decoder.*(SelfAttention|EncDecAttention).*(q|v)$' "
+ "This can also be a wildcard 'all-linear' which matches all linear/Conv1D layers except the output layer."
+ },
+ )
+ exclude_modules: Optional[Union[list[str], str]] = field(
+ default=None,
+ metadata={"help": "List of module names or regex expression of the module names to exclude from LoHa."},
+ )
+ init_weights: bool = field(
+ default=True,
+ metadata={
+ "help": (
+ "Whether to initialize the weights of the LoHa layers with their default initialization. Don't change "
+ "this setting, except if you know exactly what you're doing."
+ ),
+ },
+ )
+ layers_to_transform: Optional[Union[list[int], int]] = field(
+ default=None,
+ metadata={
+ "help": "The layer indexes to transform, is this argument is specified, PEFT will transform only the layers indexes that are specified inside this list. If a single integer is passed, PEFT will transform only the layer at this index."
+ },
+ )
+ layers_pattern: Optional[Union[list[str], str]] = field(
+ default=None,
+ metadata={
+ "help": "The layer pattern name, used only if `layers_to_transform` is different to None and if the layer pattern is not in the common layers pattern. "
+ "This should target the `nn.ModuleList` of the model, which is often called `'layers'` or `'h'`."
+ },
+ )
+ modules_to_save: Optional[list[str]] = field(
+ default=None,
+ metadata={
+ "help": "List of modules apart from LoHA layers to be set as trainable and saved in the final checkpoint. "
+ "For example, in Sequence Classification or Token Classification tasks, "
+ "the final layer `classifier/score` are randomly initialized and as such need to be trainable and saved."
+ },
+ )
+
+ def __post_init__(self):
+ super().__post_init__()
+ self.peft_type = PeftType.LOHA
+ self.target_modules = (
+ set(self.target_modules) if isinstance(self.target_modules, list) else self.target_modules
+ )
+ self.exclude_modules = (
+ set(self.exclude_modules) if isinstance(self.exclude_modules, list) else self.exclude_modules
+ )
+ # check for layers_to_transform and layers_pattern
+ if self.layers_pattern and not self.layers_to_transform:
+ raise ValueError("When `layers_pattern` is specified, `layers_to_transform` must also be specified. ")
diff --git a/peft/src/peft/tuners/loha/layer.py b/peft/src/peft/tuners/loha/layer.py
new file mode 100644
index 0000000000000000000000000000000000000000..96f9b1e01671a134784f6f0f2c183c7dcbf9f1c2
--- /dev/null
+++ b/peft/src/peft/tuners/loha/layer.py
@@ -0,0 +1,444 @@
+# Copyright 2023-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+import math
+from typing import Any
+
+import torch
+import torch.nn as nn
+import torch.nn.functional as F
+
+from peft.tuners.lycoris_utils import LycorisLayer
+
+
+class LoHaLayer(nn.Module, LycorisLayer):
+ # All names of layers that may contain adapter weights
+ adapter_layer_names = ("hada_w1_a", "hada_w1_b", "hada_w2_a", "hada_w2_b", "hada_t1", "hada_t2")
+ # other_param_names is defined on parent class
+
+ def __init__(self, base_layer: nn.Module):
+ super().__init__()
+ LycorisLayer.__init__(self, base_layer)
+
+ # LoHa info
+ self.hada_w1_a = nn.ParameterDict({})
+ self.hada_w1_b = nn.ParameterDict({})
+ self.hada_w2_a = nn.ParameterDict({})
+ self.hada_w2_b = nn.ParameterDict({})
+ self.hada_t1 = nn.ParameterDict({})
+ self.hada_t2 = nn.ParameterDict({})
+
+ @property
+ def _available_adapters(self) -> set[str]:
+ return {*self.hada_w1_a, *self.hada_w1_b, *self.hada_w2_a, *self.hada_w2_b, *self.hada_t1, *self.hada_t2}
+
+ def create_adapter_parameters(self, adapter_name: str, r: int, shape: tuple[int, ...]):
+ # https://github.com/KohakuBlueleaf/LyCORIS/blob/eb460098187f752a5d66406d3affade6f0a07ece/lycoris/modules/loha.py#L130C9-L143C75
+ if len(shape) == 4: # Conv2d
+ self.hada_t1[adapter_name] = nn.Parameter(torch.empty(r, r, shape[2], shape[3]))
+ self.hada_w1_a[adapter_name] = nn.Parameter(torch.empty(r, shape[0])) # out_dim, 1-mode
+ self.hada_w1_b[adapter_name] = nn.Parameter(torch.empty(r, shape[1])) # in_dim , 2-mode
+
+ self.hada_t2[adapter_name] = nn.Parameter(torch.empty(r, r, shape[2], shape[3]))
+ self.hada_w2_a[adapter_name] = nn.Parameter(torch.empty(r, shape[0])) # out_dim, 1-mode
+ self.hada_w2_b[adapter_name] = nn.Parameter(torch.empty(r, shape[1])) # in_dim , 2-mode
+ elif len(shape) == 3: # Conv1d
+ self.hada_t1[adapter_name] = nn.Parameter(torch.empty(r, r, shape[2], 1))
+ self.hada_w1_a[adapter_name] = nn.Parameter(torch.empty(r, shape[0])) # out_dim, 1-mode
+ self.hada_w1_b[adapter_name] = nn.Parameter(torch.empty(r, shape[1])) # in_dim , 2-mode
+
+ self.hada_t2[adapter_name] = nn.Parameter(torch.empty(r, r, shape[2], 1))
+ self.hada_w2_a[adapter_name] = nn.Parameter(torch.empty(r, shape[0])) # out_dim, 1-mode
+ self.hada_w2_b[adapter_name] = nn.Parameter(torch.empty(r, shape[1])) # in_dim , 2-mode
+ else: # Linear
+ self.hada_w1_a[adapter_name] = nn.Parameter(torch.empty(shape[0], r))
+ self.hada_w1_b[adapter_name] = nn.Parameter(torch.empty(r, shape[1]))
+
+ self.hada_w2_a[adapter_name] = nn.Parameter(torch.empty(shape[0], r))
+ self.hada_w2_b[adapter_name] = nn.Parameter(torch.empty(r, shape[1]))
+
+ def reset_adapter_parameters(self, adapter_name: str):
+ # Original implementation performs initialization with normal distribution
+ # https://github.com/KohakuBlueleaf/LyCORIS/blob/3549fdef8f564761d68b695a08ef88b1122fdedc/lycoris/modules/loha.py#L158
+
+ # FedPara paper proposes to perform He initialization, let's stick with it
+ # It is enough to initialize only single matrix with zeros to make adapter do nothing after initialization
+ if adapter_name in self.hada_w1_a.keys():
+ nn.init.kaiming_uniform_(self.hada_w1_a[adapter_name], a=math.sqrt(5))
+ nn.init.kaiming_uniform_(self.hada_w1_b[adapter_name], a=math.sqrt(5))
+ nn.init.kaiming_uniform_(self.hada_w2_a[adapter_name], a=math.sqrt(5))
+ nn.init.zeros_(self.hada_w2_b[adapter_name])
+ if adapter_name in self.hada_t1.keys():
+ nn.init.kaiming_uniform_(self.hada_t1[adapter_name], a=math.sqrt(5))
+ nn.init.kaiming_uniform_(self.hada_t2[adapter_name], a=math.sqrt(5))
+
+ def reset_adapter_parameters_random(self, adapter_name: str):
+ # Original implementation performs initialization with normal distribution
+ # https://github.com/KohakuBlueleaf/LyCORIS/blob/3549fdef8f564761d68b695a08ef88b1122fdedc/lycoris/modules/loha.py#L158
+
+ # FedPara paper proposes to perform He initialization, let's stick with it
+ # It is enough to initialize only single matrix with zeros to make adapter do nothing after initialization
+ if adapter_name in self.hada_w1_a.keys():
+ nn.init.kaiming_uniform_(self.hada_w1_a[adapter_name], a=math.sqrt(5))
+ nn.init.kaiming_uniform_(self.hada_w1_b[adapter_name], a=math.sqrt(5))
+ nn.init.kaiming_uniform_(self.hada_w2_a[adapter_name], a=math.sqrt(5))
+ nn.init.kaiming_uniform_(self.hada_w2_b[adapter_name], a=math.sqrt(5))
+ if adapter_name in self.hada_t1.keys():
+ nn.init.kaiming_uniform_(self.hada_t1[adapter_name], a=math.sqrt(5))
+ nn.init.kaiming_uniform_(self.hada_t2[adapter_name], a=math.sqrt(5))
+
+ def update_layer(
+ self,
+ adapter_name: str,
+ r: int,
+ alpha: float,
+ rank_dropout: float,
+ module_dropout: float,
+ init_weights: bool,
+ use_effective_conv2d: bool = False,
+ inference_mode: bool = False,
+ **kwargs,
+ ) -> None:
+ """Internal function to create loha adapter
+
+ Args:
+ adapter_name (`str`): Name for the adapter to add.
+ r (`int`): Rank for the added adapter.
+ alpha (`float`): Alpha for the added adapter.
+ rank_dropout (`float`): The dropout probability for rank dimension during training.
+ module_dropout (`float`): The dropout probability for disabling adapter during training.
+ init_weights (`bool`): Whether to initialize weights.
+ use_effective_conv2d (`bool`, *optional*, defaults to `False`):
+ Use parameter effective decomposition for Conv2d with ksize > 1.
+ """
+ if r <= 0:
+ raise ValueError(f"`r` should be a positive integer value but the value passed is {r}")
+
+ self.r[adapter_name] = r
+ self.alpha[adapter_name] = alpha
+ self.scaling[adapter_name] = alpha / r
+ self.rank_dropout[adapter_name] = rank_dropout
+ self.module_dropout[adapter_name] = module_dropout
+
+ # Determine shape of LoHa weights
+ base_layer = self.get_base_layer()
+ if isinstance(base_layer, nn.Linear):
+ shape = tuple(base_layer.weight.shape)
+ elif isinstance(base_layer, nn.Conv2d):
+ # For 1x1 convolutions, disable effective_conv2d to avoid unnecessary tensor reshaping overhead.
+ # Since 1x1 convolutions are essentially pointwise operations (matrix multiplications),
+ # they can be more efficiently handled with the flattened weight representation,
+ # similar to how Linear layers work. This optimization reduces computational cost
+ # without affecting the mathematical equivalence of the operation.
+ use_effective_conv2d = use_effective_conv2d and base_layer.kernel_size != (1, 1)
+ if use_effective_conv2d:
+ shape = (base_layer.out_channels, base_layer.in_channels, *base_layer.kernel_size)
+ else:
+ shape = (
+ base_layer.out_channels,
+ base_layer.in_channels * base_layer.kernel_size[0] * base_layer.kernel_size[1],
+ )
+ elif isinstance(base_layer, nn.Conv1d):
+ # For Conv1d with kernel_size=1, disable effective_conv2d for the same optimization reasons
+ # as 1x1 Conv2d. Kernel size 1 means no spatial/temporal context, making it equivalent
+ # to a Linear layer applied across the channel dimension. Using flattened representation
+ # avoids unnecessary reshaping and improves computational efficiency.
+ use_effective_conv2d = use_effective_conv2d and base_layer.kernel_size[0] != 1
+ if use_effective_conv2d:
+ shape = (base_layer.out_channels, base_layer.in_channels, base_layer.kernel_size[0])
+ else:
+ shape = (
+ base_layer.out_channels,
+ base_layer.in_channels * base_layer.kernel_size[0],
+ )
+ else:
+ raise TypeError(f"LoHa is not implemented for base layers of type {type(base_layer).__name__}")
+
+ # Create weights with provided shape
+ self.create_adapter_parameters(adapter_name, r, shape)
+
+ # Initialize weights
+ if init_weights:
+ self.reset_adapter_parameters(adapter_name)
+ else:
+ self.reset_adapter_parameters_random(adapter_name)
+
+ # Move new weights to device
+ self._move_adapter_to_device_of_base_layer(adapter_name)
+ self.set_adapter(self.active_adapters, inference_mode=inference_mode)
+
+ def get_delta_weight(self, adapter_name: str) -> torch.Tensor:
+ # https://github.com/KohakuBlueleaf/LyCORIS/blob/eb460098187f752a5d66406d3affade6f0a07ece/lycoris/modules/loha.py#L178
+ if adapter_name in self.hada_t1.keys():
+ weight = make_weight_cp(
+ self.hada_t1[adapter_name],
+ self.hada_w1_a[adapter_name],
+ self.hada_w1_b[adapter_name],
+ self.hada_t2[adapter_name],
+ self.hada_w2_a[adapter_name],
+ self.hada_w2_b[adapter_name],
+ scale=torch.tensor(self.scaling[adapter_name]),
+ )
+ else:
+ weight = make_weight(
+ self.hada_w1_a[adapter_name],
+ self.hada_w1_b[adapter_name],
+ self.hada_w2_a[adapter_name],
+ self.hada_w2_b[adapter_name],
+ scale=torch.tensor(self.scaling[adapter_name]),
+ )
+
+ base_layer = self.get_base_layer()
+
+ # Reshape to match base layer shape
+ weight = weight.reshape(base_layer.weight.shape)
+
+ # Perform rank dropout during training - drop rows of addition weights
+ rank_dropout = self.rank_dropout[adapter_name]
+ if self.training and rank_dropout:
+ drop = (torch.rand(weight.size(0)) > rank_dropout).to(weight.dtype)
+ drop = drop.view(-1, *[1] * len(weight.shape[1:])).to(weight.device)
+ # TODO: Investigate if there should be a scaler like in normal dropout during training
+ # Original implementation doesn't have it
+ # https://github.com/KohakuBlueleaf/LyCORIS/blob/eb460098187f752a5d66406d3affade6f0a07ece/lycoris/modules/loha.py#L193
+ drop /= drop.mean()
+ weight *= drop
+
+ return weight
+
+ def forward(self, x: torch.Tensor, *args, **kwargs) -> torch.Tensor:
+ previous_dtype = x.dtype
+
+ if self.disable_adapters:
+ if self.merged:
+ self.unmerge()
+ result = self.base_layer(x, *args, **kwargs)
+ elif self.merged:
+ result = self.base_layer(x, *args, **kwargs)
+ else:
+ result = self.base_layer(x, *args, **kwargs)
+
+ # Execute all the adapters
+ for active_adapter in self.active_adapters:
+ if active_adapter not in self._available_adapters:
+ continue
+
+ module_dropout = self.module_dropout[active_adapter]
+
+ # Modify current execution weights
+ if (not self.training) or (self.training and torch.rand(1) > module_dropout):
+ result = result + self._get_delta_activations(active_adapter, x, *args, **kwargs)
+
+ result = result.to(previous_dtype)
+ return result
+
+
+class Linear(LoHaLayer):
+ """LoHa implemented in Linear layer"""
+
+ def __init__(
+ self,
+ base_layer: nn.Module,
+ adapter_name: str = "default",
+ r: int = 0,
+ alpha: float = 0.0,
+ rank_dropout: float = 0.0,
+ module_dropout: float = 0.0,
+ init_weights: bool = True,
+ **kwargs,
+ ):
+ super().__init__(base_layer)
+
+ # Create adapter and set it active
+ self._active_adapter = adapter_name
+ self.update_layer(adapter_name, r, alpha, rank_dropout, module_dropout, init_weights, **kwargs)
+
+ def _get_delta_activations(
+ self, adapter_name: str, input: torch.Tensor, *args: Any, **kwargs: Any
+ ) -> torch.Tensor:
+ delta_weight = self.get_delta_weight(adapter_name)
+ input = self._cast_input_dtype(input, delta_weight.dtype)
+ # don't add bias here, because the bias is already included in the output of the base_layer
+ return F.linear(input, delta_weight)
+
+ def __repr__(self) -> str:
+ rep = super().__repr__()
+ return "loha." + rep
+
+
+class Conv2d(LoHaLayer):
+ """LoHa implemented in Conv2d layer"""
+
+ def __init__(
+ self,
+ base_layer: nn.Module,
+ adapter_name: str = "default",
+ r: int = 0,
+ alpha: float = 0.0,
+ rank_dropout: float = 0.0,
+ module_dropout: float = 0.0,
+ use_effective_conv2d: bool = False,
+ init_weights: bool = True,
+ **kwargs,
+ ):
+ super().__init__(base_layer)
+
+ # Create adapter and set it active
+ self._active_adapter = adapter_name
+ self.update_layer(
+ adapter_name, r, alpha, rank_dropout, module_dropout, init_weights, use_effective_conv2d, **kwargs
+ )
+
+ def _get_delta_activations(
+ self, adapter_name: str, input: torch.Tensor, *args: Any, **kwargs: Any
+ ) -> torch.Tensor:
+ delta_weight = self.get_delta_weight(adapter_name)
+ input = self._cast_input_dtype(input, delta_weight.dtype)
+ # don't add bias here, because the bias is already included in the output of the base_layer
+ base_layer = self.get_base_layer()
+ return F.conv2d(
+ input,
+ delta_weight,
+ stride=base_layer.stride,
+ padding=base_layer.padding,
+ dilation=base_layer.dilation,
+ groups=base_layer.groups,
+ )
+
+ def __repr__(self) -> str:
+ rep = super().__repr__()
+ return "loha." + rep
+
+
+class Conv1d(LoHaLayer):
+ """LoHa implemented in Conv1d layer"""
+
+ def __init__(
+ self,
+ base_layer: nn.Module,
+ adapter_name: str = "default",
+ r: int = 0,
+ alpha: float = 0.0,
+ rank_dropout: float = 0.0,
+ module_dropout: float = 0.0,
+ use_effective_conv2d: bool = False,
+ init_weights: bool = True,
+ **kwargs,
+ ):
+ super().__init__(base_layer)
+
+ # Create adapter and set it active
+ self._active_adapter = adapter_name
+ self.update_layer(
+ adapter_name, r, alpha, rank_dropout, module_dropout, init_weights, use_effective_conv2d, **kwargs
+ )
+
+ def _get_delta_activations(
+ self, adapter_name: str, input: torch.Tensor, *args: Any, **kwargs: Any
+ ) -> torch.Tensor:
+ delta_weight = self.get_delta_weight(adapter_name)
+ input = self._cast_input_dtype(input, delta_weight.dtype)
+ # don't add bias here, because the bias is already included in the output of the base_layer
+ base_layer = self.get_base_layer()
+ return F.conv1d(
+ input,
+ delta_weight,
+ stride=base_layer.stride,
+ padding=base_layer.padding,
+ dilation=base_layer.dilation,
+ groups=base_layer.groups,
+ )
+
+ def __repr__(self) -> str:
+ rep = super().__repr__()
+ return "loha." + rep
+
+
+# Below code is a direct copy from https://github.com/KohakuBlueleaf/LyCORIS/blob/eb460098187f752a5d66406d3affade6f0a07ece/lycoris/modules/loha.py#L9
+
+
+class HadaWeight(torch.autograd.Function):
+ @staticmethod
+ def forward(ctx, w1a, w1b, w2a, w2b, scale=torch.tensor(1)):
+ ctx.save_for_backward(w1a, w1b, w2a, w2b, scale)
+ diff_weight = ((w1a @ w1b) * (w2a @ w2b)) * scale
+ return diff_weight
+
+ @staticmethod
+ def backward(ctx, grad_out):
+ (w1a, w1b, w2a, w2b, scale) = ctx.saved_tensors
+ grad_out = grad_out * scale
+ temp = grad_out * (w2a @ w2b)
+ grad_w1a = temp @ w1b.T
+ grad_w1b = w1a.T @ temp
+
+ temp = grad_out * (w1a @ w1b)
+ grad_w2a = temp @ w2b.T
+ grad_w2b = w2a.T @ temp
+
+ del temp
+ return grad_w1a, grad_w1b, grad_w2a, grad_w2b, None
+
+
+class HadaWeightCP(torch.autograd.Function):
+ @staticmethod
+ def forward(ctx, t1, w1a, w1b, t2, w2a, w2b, scale=torch.tensor(1)):
+ ctx.save_for_backward(t1, w1a, w1b, t2, w2a, w2b, scale)
+
+ rebuild1 = torch.einsum("i j k l, j r, i p -> p r k l", t1, w1b, w1a)
+ rebuild2 = torch.einsum("i j k l, j r, i p -> p r k l", t2, w2b, w2a)
+
+ return rebuild1 * rebuild2 * scale
+
+ @staticmethod
+ def backward(ctx, grad_out):
+ (t1, w1a, w1b, t2, w2a, w2b, scale) = ctx.saved_tensors
+ grad_out = grad_out * scale
+
+ temp = torch.einsum("i j k l, j r -> i r k l", t2, w2b)
+ rebuild = torch.einsum("i j k l, i r -> r j k l", temp, w2a)
+
+ grad_w = rebuild * grad_out
+ del rebuild
+
+ grad_w1a = torch.einsum("r j k l, i j k l -> r i", temp, grad_w)
+ grad_temp = torch.einsum("i j k l, i r -> r j k l", grad_w, w1a.T)
+ del grad_w, temp
+
+ grad_w1b = torch.einsum("i r k l, i j k l -> r j", t1, grad_temp)
+ grad_t1 = torch.einsum("i j k l, j r -> i r k l", grad_temp, w1b.T)
+ del grad_temp
+
+ temp = torch.einsum("i j k l, j r -> i r k l", t1, w1b)
+ rebuild = torch.einsum("i j k l, i r -> r j k l", temp, w1a)
+
+ grad_w = rebuild * grad_out
+ del rebuild
+
+ grad_w2a = torch.einsum("r j k l, i j k l -> r i", temp, grad_w)
+ grad_temp = torch.einsum("i j k l, i r -> r j k l", grad_w, w2a.T)
+ del grad_w, temp
+
+ grad_w2b = torch.einsum("i r k l, i j k l -> r j", t2, grad_temp)
+ grad_t2 = torch.einsum("i j k l, j r -> i r k l", grad_temp, w2b.T)
+ del grad_temp
+ return grad_t1, grad_w1a, grad_w1b, grad_t2, grad_w2a, grad_w2b, None
+
+
+def make_weight(w1a, w1b, w2a, w2b, scale):
+ return HadaWeight.apply(w1a, w1b, w2a, w2b, scale)
+
+
+def make_weight_cp(t1, w1a, w1b, t2, w2a, w2b, scale):
+ return HadaWeightCP.apply(t1, w1a, w1b, t2, w2a, w2b, scale)
diff --git a/peft/src/peft/tuners/loha/model.py b/peft/src/peft/tuners/loha/model.py
new file mode 100644
index 0000000000000000000000000000000000000000..c39be6434d90fe47a8bdc7aae990d0ca4aaab230
--- /dev/null
+++ b/peft/src/peft/tuners/loha/model.py
@@ -0,0 +1,116 @@
+# Copyright 2023-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+from typing import Union
+
+import torch
+from torch import nn
+
+from peft.tuners.lycoris_utils import LycorisConfig, LycorisTuner
+from peft.utils import TRANSFORMERS_MODELS_TO_LOHA_TARGET_MODULES_MAPPING
+from peft.utils.other import get_pattern_key
+
+from .layer import Conv1d, Conv2d, Linear, LoHaLayer
+
+
+class LoHaModel(LycorisTuner):
+ """
+ Creates Low-Rank Hadamard Product model from a pretrained model. The method is partially described in
+ https://huggingface.co/papers/2108.06098 Current implementation heavily borrows from
+ https://github.com/KohakuBlueleaf/LyCORIS/blob/eb460098187f752a5d66406d3affade6f0a07ece/lycoris/modules/loha.py
+
+ Args:
+ model (`torch.nn.Module`): The model to which the adapter tuner layers will be attached.
+ config ([`LoHaConfig`]): The configuration of the LoHa model.
+ adapter_name (`str`): The name of the adapter, defaults to `"default"`.
+ low_cpu_mem_usage (`bool`, `optional`, defaults to `False`):
+ Create empty adapter weights on meta device. Useful to speed up the loading process.
+
+ Returns:
+ `torch.nn.Module`: The LoHa model.
+
+ Example:
+ ```py
+ >>> from diffusers import StableDiffusionPipeline
+ >>> from peft import LoHaModel, LoHaConfig
+
+ >>> config_te = LoHaConfig(
+ ... r=8,
+ ... lora_alpha=32,
+ ... target_modules=["k_proj", "q_proj", "v_proj", "out_proj", "fc1", "fc2"],
+ ... rank_dropout=0.0,
+ ... module_dropout=0.0,
+ ... init_weights=True,
+ ... )
+ >>> config_unet = LoHaConfig(
+ ... r=8,
+ ... lora_alpha=32,
+ ... target_modules=[
+ ... "proj_in",
+ ... "proj_out",
+ ... "to_k",
+ ... "to_q",
+ ... "to_v",
+ ... "to_out.0",
+ ... "ff.net.0.proj",
+ ... "ff.net.2",
+ ... ],
+ ... rank_dropout=0.0,
+ ... module_dropout=0.0,
+ ... init_weights=True,
+ ... use_effective_conv2d=True,
+ ... )
+
+ >>> model = StableDiffusionPipeline.from_pretrained("runwayml/stable-diffusion-v1-5")
+ >>> model.text_encoder = LoHaModel(model.text_encoder, config_te, "default")
+ >>> model.unet = LoHaModel(model.unet, config_unet, "default")
+ ```
+
+ **Attributes**:
+ - **model** ([`~torch.nn.Module`]) -- The model to be adapted.
+ - **peft_config** ([`LoHaConfig`]): The configuration of the LoHa model.
+ """
+
+ prefix: str = "hada_"
+ tuner_layer_cls = LoHaLayer
+ target_module_mapping = TRANSFORMERS_MODELS_TO_LOHA_TARGET_MODULES_MAPPING
+ layers_mapping: dict[type[torch.nn.Module], type[LoHaLayer]] = {
+ torch.nn.Conv2d: Conv2d,
+ torch.nn.Conv1d: Conv1d,
+ torch.nn.Linear: Linear,
+ }
+
+ def _create_and_replace(
+ self,
+ config: LycorisConfig,
+ adapter_name: str,
+ target: Union[LoHaLayer, nn.Module],
+ target_name: str,
+ parent: nn.Module,
+ current_key: str,
+ ) -> None:
+ """
+ A private method to create and replace the target module with the adapter module.
+ """
+ r_key = get_pattern_key(config.rank_pattern.keys(), current_key)
+ alpha_key = get_pattern_key(config.alpha_pattern.keys(), current_key)
+ kwargs = config.to_dict()
+ kwargs["r"] = config.rank_pattern.get(r_key, config.r)
+ kwargs["alpha"] = config.alpha_pattern.get(alpha_key, config.alpha)
+
+ if isinstance(target, LoHaLayer):
+ target.update_layer(adapter_name, **kwargs)
+ else:
+ new_module = self._create_new_module(config, adapter_name, target, **kwargs)
+ self._replace_module(parent, target_name, new_module, target)
diff --git a/peft/src/peft/tuners/lokr/__init__.py b/peft/src/peft/tuners/lokr/__init__.py
new file mode 100644
index 0000000000000000000000000000000000000000..f4fe0e92c6eacd0cc276ad3584230ea58ee4a8a6
--- /dev/null
+++ b/peft/src/peft/tuners/lokr/__init__.py
@@ -0,0 +1,24 @@
+# Copyright 2023-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+from peft.utils import register_peft_method
+
+from .config import LoKrConfig
+from .layer import Conv2d, Linear, LoKrLayer
+from .model import LoKrModel
+
+
+__all__ = ["Conv2d", "Linear", "LoKrConfig", "LoKrLayer", "LoKrModel"]
+
+register_peft_method(name="lokr", config_cls=LoKrConfig, model_cls=LoKrModel, is_mixed_compatible=True)
diff --git a/peft/src/peft/tuners/lokr/config.py b/peft/src/peft/tuners/lokr/config.py
new file mode 100644
index 0000000000000000000000000000000000000000..6d25dc5c129f711b59e848a38a63fac766d78754
--- /dev/null
+++ b/peft/src/peft/tuners/lokr/config.py
@@ -0,0 +1,155 @@
+# Copyright 2023-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+from __future__ import annotations
+
+from dataclasses import dataclass, field
+from typing import Literal, Optional, Union
+
+from peft.tuners.lycoris_utils import LycorisConfig
+from peft.utils import PeftType
+
+
+@dataclass
+class LoKrConfig(LycorisConfig):
+ """
+ Configuration class of [`LoKrModel`].
+
+ Args:
+ r (`int`):
+ LoKr rank.
+ alpha (`int`):
+ The alpha parameter for LoKr scaling.
+ rank_dropout (`float`):
+ The dropout probability for rank dimension during training.
+ module_dropout (`float`):
+ The dropout probability for disabling LoKr modules during training.
+ use_effective_conv2d (`bool`):
+ Use parameter effective decomposition for Conv2d (and Conv1d) with ksize > 1 ("Proposition 3" from FedPara
+ paper).
+ decompose_both (`bool`):
+ Perform rank decomposition of left kronecker product matrix.
+ decompose_factor (`int`):
+ Kronecker product decomposition factor.
+ rank_dropout_scale ('bool)
+ Whether to scale the rank dropout while training, defaults to `False`.
+ target_modules (`Optional[Union[List[str], str]]`):
+ The names of the modules to apply the adapter to. If this is specified, only the modules with the specified
+ names will be replaced. When passing a string, a regex match will be performed. When passing a list of
+ strings, either an exact match will be performed or it is checked if the name of the module ends with any
+ of the passed strings. If this is specified as 'all-linear', then all linear/Conv1D modules are chosen,
+ excluding the output layer. If this is not specified, modules will be chosen according to the model
+ architecture. If the architecture is not known, an error will be raised -- in this case, you should specify
+ the target modules manually.
+ exclude_modules (`Optional[Union[List[str], str]]`):
+ The names of the modules to not apply the adapter. When passing a string, a regex match will be performed.
+ When passing a list of strings, either an exact match will be performed or it is checked if the name of the
+ module ends with any of the passed strings.
+ init_weights (`bool`):
+ Whether to perform initialization of adapter weights. This defaults to `True`. Use "lycoris" to initialize
+ weights in the style of the LYCORIS repository. Passing `False` is discouraged.
+ layers_to_transform (`Union[List[int], int]`):
+ The layer indices to transform. If a list of ints is passed, it will apply the adapter to the layer indices
+ that are specified in this list. If a single integer is passed, it will apply the transformations on the
+ layer at this index.
+ layers_pattern (`Optional[Union[List[str], str]]`):
+ The layer pattern name, used only if `layers_to_transform` is different from `None`. This should target the
+ `nn.ModuleList` of the model, which is often called `'layers'` or `'h'`.
+ rank_pattern (`dict`):
+ The mapping from layer names or regexp expression to ranks which are different from the default rank
+ specified by `r`. For example, `{'^model.decoder.layers.0.encoder_attn.k_proj': 16}`.
+ alpha_pattern (`dict`):
+ The mapping from layer names or regexp expression to alphas which are different from the default alpha
+ specified by `alpha`. For example, `{'^model.decoder.layers.0.encoder_attn.k_proj': 16}`.
+ modules_to_save (`Optional[List[str]]`):
+ List of modules apart from adapter layers to be set as trainable and saved in the final checkpoint.
+ """
+
+ r: int = field(default=8, metadata={"help": "LoKr rank"})
+ alpha: int = field(default=8, metadata={"help": "LoKr alpha"})
+ rank_dropout: float = field(
+ default=0.0, metadata={"help": "The dropout probability for rank dimension during training"}
+ )
+ module_dropout: float = field(
+ default=0.0, metadata={"help": "The dropout probability for disabling LoKr modules during training"}
+ )
+ use_effective_conv2d: bool = field(
+ default=False,
+ metadata={
+ "help": (
+ "Use parameter effective decomposition for Conv2d (and Conv1d) with ksize > 1 "
+ '("Proposition 3" from FedPara paper)'
+ )
+ },
+ )
+ decompose_both: bool = field(
+ default=False,
+ metadata={"help": "Perform rank decomposition of left kronecker product matrix."},
+ )
+ decompose_factor: int = field(default=-1, metadata={"help": "Kronecker product decomposition factor."})
+ rank_dropout_scale: bool = field(default=False, metadata={"help": "Rank dropout scale"})
+ target_modules: Optional[Union[list[str], str]] = field(
+ default=None,
+ metadata={
+ "help": "List of module names or regex expression of the module names to replace with LoKr."
+ "For example, ['q', 'v'] or '.*decoder.*(SelfAttention|EncDecAttention).*(q|v)$' "
+ "This can also be a wildcard 'all-linear' which matches all linear/Conv1D layers except the output layer."
+ },
+ )
+ exclude_modules: Optional[Union[list[str], str]] = field(
+ default=None,
+ metadata={"help": "List of module names or regex expression of the module names to exclude from LoKr."},
+ )
+ init_weights: Union[bool, Literal["lycoris"]] = field(
+ default=True,
+ metadata={
+ "help": (
+ "Whether to initialize the weights of the LoKr layers with their default initialization. Can be True, False or 'lycoris'."
+ "Default is True. Don't change this setting to False, except if you know exactly what you're doing."
+ ),
+ },
+ )
+ layers_to_transform: Optional[Union[list[int], int]] = field(
+ default=None,
+ metadata={
+ "help": "The layer indexes to transform, is this argument is specified, PEFT will transform only the layers indexes that are specified inside this list. If a single integer is passed, PEFT will transform only the layer at this index."
+ },
+ )
+ layers_pattern: Optional[Union[list[str], str]] = field(
+ default=None,
+ metadata={
+ "help": "The layer pattern name, used only if `layers_to_transform` is different to None and if the layer pattern is not in the common layers pattern. "
+ "This should target the `nn.ModuleList` of the model, which is often called `'layers'` or `'h'`."
+ },
+ )
+ modules_to_save: Optional[list[str]] = field(
+ default=None,
+ metadata={
+ "help": "List of modules apart from LoKr layers to be set as trainable and saved in the final checkpoint. "
+ "For example, in Sequence Classification or Token Classification tasks, "
+ "the final layer `classifier/score` are randomly initialized and as such need to be trainable and saved."
+ },
+ )
+
+ def __post_init__(self):
+ super().__post_init__()
+ self.peft_type = PeftType.LOKR
+ self.target_modules = (
+ set(self.target_modules) if isinstance(self.target_modules, list) else self.target_modules
+ )
+ self.exclude_modules = (
+ set(self.exclude_modules) if isinstance(self.exclude_modules, list) else self.exclude_modules
+ )
+ # check for layers_to_transform and layers_pattern
+ if self.layers_pattern and not self.layers_to_transform:
+ raise ValueError("When `layers_pattern` is specified, `layers_to_transform` must also be specified. ")
diff --git a/peft/src/peft/tuners/lokr/layer.py b/peft/src/peft/tuners/lokr/layer.py
new file mode 100644
index 0000000000000000000000000000000000000000..295193bfac5f4cb2d62df3e465e9633e71ca8ed3
--- /dev/null
+++ b/peft/src/peft/tuners/lokr/layer.py
@@ -0,0 +1,511 @@
+# Copyright 2023-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+import math
+from typing import Any, Optional, Union
+
+import torch
+import torch.nn as nn
+import torch.nn.functional as F
+
+from peft.tuners.lycoris_utils import LycorisLayer
+
+
+class LoKrLayer(nn.Module, LycorisLayer):
+ # All names of layers that may contain adapter weights
+ adapter_layer_names = (
+ "lokr_w1",
+ "lokr_w1_a",
+ "lokr_w1_b",
+ "lokr_w2",
+ "lokr_w2_a",
+ "lokr_w2_b",
+ "lokr_t2",
+ )
+ # other_param_names is defined on parent class
+
+ def __init__(self, base_layer: nn.Module) -> None:
+ super().__init__()
+ LycorisLayer.__init__(self, base_layer)
+
+ # LoKr info
+ self.lokr_w1 = nn.ParameterDict({})
+ self.lokr_w1_a = nn.ParameterDict({})
+ self.lokr_w1_b = nn.ParameterDict({})
+ self.lokr_w2 = nn.ParameterDict({})
+ self.lokr_w2_a = nn.ParameterDict({})
+ self.lokr_w2_b = nn.ParameterDict({})
+ self.lokr_t2 = nn.ParameterDict({})
+
+ @property
+ def _available_adapters(self) -> set[str]:
+ return {
+ *self.lokr_w1,
+ *self.lokr_w1_a,
+ *self.lokr_w1_b,
+ *self.lokr_w2,
+ *self.lokr_w2_a,
+ *self.lokr_w2_b,
+ *self.lokr_t2,
+ }
+
+ def create_adapter_parameters(
+ self,
+ adapter_name: str,
+ r: int,
+ shape,
+ use_w1: bool,
+ use_w2: bool,
+ use_effective_conv2d: bool,
+ ):
+ if use_w1:
+ self.lokr_w1[adapter_name] = nn.Parameter(torch.empty(shape[0][0], shape[1][0]))
+ else:
+ self.lokr_w1_a[adapter_name] = nn.Parameter(torch.empty(shape[0][0], r))
+ self.lokr_w1_b[adapter_name] = nn.Parameter(torch.empty(r, shape[1][0]))
+
+ # Handle both Conv2d and Conv1d
+ if len(shape) == 4: # Conv2d
+ if use_w2:
+ self.lokr_w2[adapter_name] = nn.Parameter(torch.empty(shape[0][1], shape[1][1], *shape[2:]))
+ elif use_effective_conv2d:
+ self.lokr_t2[adapter_name] = nn.Parameter(torch.empty(r, r, shape[2], shape[3]))
+ self.lokr_w2_a[adapter_name] = nn.Parameter(torch.empty(r, shape[0][1])) # b, 1-mode
+ self.lokr_w2_b[adapter_name] = nn.Parameter(torch.empty(r, shape[1][1])) # d, 2-mode
+ else:
+ self.lokr_w2_a[adapter_name] = nn.Parameter(torch.empty(shape[0][1], r))
+ self.lokr_w2_b[adapter_name] = nn.Parameter(torch.empty(r, shape[1][1] * shape[2] * shape[3]))
+ elif len(shape) == 3: # Conv1d
+ if use_w2:
+ self.lokr_w2[adapter_name] = nn.Parameter(torch.empty(shape[0][1], shape[1][1], shape[2]))
+ elif use_effective_conv2d: # Even for Conv1d, use the effective parameter for kernel dimension
+ # We pass (r, r, kernel_size, 1) in order to be compatible with the 2d assumptions made
+ # in make_weight_cp (only relevant for the effective conv2d case).
+ self.lokr_t2[adapter_name] = nn.Parameter(torch.empty(r, r, shape[2], 1))
+ self.lokr_w2_a[adapter_name] = nn.Parameter(torch.empty(r, shape[0][1])) # b, 1-mode
+ self.lokr_w2_b[adapter_name] = nn.Parameter(torch.empty(r, shape[1][1])) # d, 2-mode
+ else:
+ self.lokr_w2_a[adapter_name] = nn.Parameter(torch.empty(shape[0][1], r))
+ self.lokr_w2_b[adapter_name] = nn.Parameter(torch.empty(r, shape[1][1] * shape[2]))
+ else:
+ # Linear
+ if use_w2:
+ self.lokr_w2[adapter_name] = nn.Parameter(torch.empty(shape[0][1], shape[1][1]))
+ else:
+ self.lokr_w2_a[adapter_name] = nn.Parameter(torch.empty(shape[0][1], r))
+ self.lokr_w2_b[adapter_name] = nn.Parameter(torch.empty(r, shape[1][1]))
+
+ def reset_adapter_parameters(self, adapter_name: str):
+ if adapter_name in self.lokr_w1:
+ nn.init.zeros_(self.lokr_w1[adapter_name])
+ else:
+ nn.init.zeros_(self.lokr_w1_a[adapter_name])
+ nn.init.kaiming_uniform_(self.lokr_w1_b[adapter_name], a=math.sqrt(5))
+
+ if adapter_name in self.lokr_w2:
+ nn.init.kaiming_uniform_(self.lokr_w2[adapter_name], a=math.sqrt(5))
+ else:
+ nn.init.kaiming_uniform_(self.lokr_w2_a[adapter_name], a=math.sqrt(5))
+ nn.init.kaiming_uniform_(self.lokr_w2_b[adapter_name], a=math.sqrt(5))
+
+ if adapter_name in self.lokr_t2:
+ nn.init.kaiming_uniform_(self.lokr_t2[adapter_name], a=math.sqrt(5))
+
+ def reset_adapter_parameters_random(self, adapter_name: str):
+ if adapter_name in self.lokr_w1:
+ nn.init.kaiming_uniform_(self.lokr_w1[adapter_name], a=math.sqrt(5))
+ else:
+ nn.init.kaiming_uniform_(self.lokr_w1_a[adapter_name], a=math.sqrt(5))
+ nn.init.kaiming_uniform_(self.lokr_w1_b[adapter_name], a=math.sqrt(5))
+
+ if adapter_name in self.lokr_w2:
+ nn.init.kaiming_uniform_(self.lokr_w2[adapter_name], a=math.sqrt(5))
+ else:
+ nn.init.kaiming_uniform_(self.lokr_w2_a[adapter_name], a=math.sqrt(5))
+ nn.init.kaiming_uniform_(self.lokr_w2_b[adapter_name], a=math.sqrt(5))
+
+ if adapter_name in self.lokr_t2:
+ nn.init.kaiming_uniform_(self.lokr_t2[adapter_name], a=math.sqrt(5))
+
+ # Initializes weight matrices similar to the way initialized in the LyCORIS repository.
+ def reset_adapter_parameters_lycoris_way(self, adapter_name):
+ if adapter_name in self.lokr_w1:
+ nn.init.kaiming_uniform_(self.lokr_w1[adapter_name], a=math.sqrt(5))
+ else:
+ nn.init.kaiming_uniform_(self.lokr_w1_a[adapter_name], a=math.sqrt(5))
+ nn.init.kaiming_uniform_(self.lokr_w1_b[adapter_name], a=math.sqrt(5))
+
+ if adapter_name in self.lokr_w2:
+ nn.init.zeros_(self.lokr_w2[adapter_name])
+ else:
+ nn.init.zeros_(self.lokr_w2_b[adapter_name])
+ nn.init.kaiming_uniform_(self.lokr_w2_a[adapter_name], a=math.sqrt(5))
+
+ if adapter_name in self.lokr_t2:
+ nn.init.kaiming_uniform_(self.lokr_t2[adapter_name], a=math.sqrt(5))
+
+ def update_layer(
+ self,
+ adapter_name: str,
+ r: int,
+ alpha: float,
+ rank_dropout: float,
+ module_dropout: float,
+ init_weights: bool,
+ use_effective_conv2d: bool,
+ decompose_both: bool,
+ decompose_factor: int,
+ inference_mode: bool = False,
+ **kwargs,
+ ) -> None:
+ """Internal function to create lokr adapter
+
+ Args:
+ adapter_name (`str`): Name for the adapter to add.
+ r (`int`): Rank for the added adapter.
+ alpha (`float`): Alpha for the added adapter.
+ rank_dropout (`float`): The dropout probability for rank dimension during training
+ module_dropout (`float`): The dropout probability for disabling adapter during training.
+ init_weights (`bool`): Whether to initialize adapter weights.
+ use_effective_conv2d (`bool`): Use parameter effective decomposition for Conv2d with ksize > 1.
+ decompose_both (`bool`): Perform rank decomposition of left kronecker product matrix.
+ decompose_factor (`int`): Kronecker product decomposition factor.
+ """
+ if r <= 0:
+ raise ValueError(f"`r` should be a positive integer value but the value passed is {r}")
+
+ self.r[adapter_name] = r
+ self.alpha[adapter_name] = alpha
+ self.scaling[adapter_name] = alpha / r
+ self.rank_dropout[adapter_name] = rank_dropout
+ self.module_dropout[adapter_name] = module_dropout
+ self.rank_dropout_scale[adapter_name] = kwargs["rank_dropout_scale"]
+ base_layer = self.get_base_layer()
+
+ # Determine shape of LoKr weights
+ if isinstance(base_layer, nn.Linear):
+ in_dim, out_dim = base_layer.in_features, base_layer.out_features
+
+ in_m, in_n = factorization(in_dim, decompose_factor)
+ out_l, out_k = factorization(out_dim, decompose_factor)
+ shape = ((out_l, out_k), (in_m, in_n)) # ((a, b), (c, d)), out_dim = a*c, in_dim = b*d
+
+ use_w1 = not (decompose_both and r < max(shape[0][0], shape[1][0]) / 2)
+ use_w2 = not (r < max(shape[0][1], shape[1][1]) / 2)
+ use_effective_conv2d = False
+ elif isinstance(base_layer, nn.Conv2d):
+ in_dim, out_dim = base_layer.in_channels, base_layer.out_channels
+ k_size = base_layer.kernel_size
+
+ in_m, in_n = factorization(in_dim, decompose_factor)
+ out_l, out_k = factorization(out_dim, decompose_factor)
+ shape = ((out_l, out_k), (in_m, in_n), *k_size) # ((a, b), (c, d), *k_size)
+
+ use_w1 = not (decompose_both and r < max(shape[0][0], shape[1][0]) / 2)
+ use_w2 = r >= max(shape[0][1], shape[1][1]) / 2
+ # For 1x1 convolutions, disable effective_conv2d to avoid unnecessary tensor reshaping overhead.
+ # Since 1x1 convolutions are essentially pointwise operations (matrix multiplications),
+ # they can be more efficiently handled with the flattened weight representation,
+ # similar to how Linear layers work. This optimization reduces computational cost
+ # without affecting the mathematical equivalence of the operation.
+ use_effective_conv2d = use_effective_conv2d and base_layer.kernel_size != (1, 1)
+ elif isinstance(base_layer, nn.Conv1d):
+ in_dim, out_dim = base_layer.in_channels, base_layer.out_channels
+ k_size = (base_layer.kernel_size[0],) # Convert to a tuple with single element
+
+ in_m, in_n = factorization(in_dim, decompose_factor)
+ out_l, out_k = factorization(out_dim, decompose_factor)
+ shape = ((out_l, out_k), (in_m, in_n), *k_size) # ((a, b), (c, d), k)
+
+ use_w1 = not (decompose_both and r < max(shape[0][0], shape[1][0]) / 2)
+ use_w2 = r >= max(shape[0][1], shape[1][1]) / 2
+ # For Conv1d with kernel_size=1, disable effective_conv2d for the same optimization reasons
+ # as 1x1 Conv2d. Kernel size 1 means no spatial/temporal context, making it equivalent
+ # to a Linear layer applied across the channel dimension. Using flattened representation
+ # avoids unnecessary reshaping and improves computational efficiency.
+ use_effective_conv2d = use_effective_conv2d and base_layer.kernel_size[0] != 1
+ else:
+ raise TypeError(f"LoKr is not implemented for base layers of type {type(base_layer).__name__}")
+
+ # Create weights with provided shape
+ self.create_adapter_parameters(adapter_name, r, shape, use_w1, use_w2, use_effective_conv2d)
+
+ # Initialize weights
+ if init_weights:
+ if init_weights == "lycoris":
+ self.reset_adapter_parameters_lycoris_way(adapter_name)
+ else:
+ self.reset_adapter_parameters(adapter_name)
+ else:
+ self.reset_adapter_parameters_random(adapter_name)
+
+ # Move new weights to device
+ self._move_adapter_to_device_of_base_layer(adapter_name)
+ self.set_adapter(self.active_adapters, inference_mode=inference_mode)
+
+ def get_delta_weight(self, adapter_name: str) -> torch.Tensor:
+ # https://github.com/KohakuBlueleaf/LyCORIS/blob/e4259b870d3354a9615a96be61cb5d07455c58ea/lycoris/modules/lokr.py#L224
+ if adapter_name in self.lokr_w1:
+ w1 = self.lokr_w1[adapter_name]
+ else:
+ w1 = self.lokr_w1_a[adapter_name] @ self.lokr_w1_b[adapter_name]
+
+ if adapter_name in self.lokr_w2:
+ w2 = self.lokr_w2[adapter_name]
+ elif adapter_name in self.lokr_t2:
+ w2 = make_weight_cp(self.lokr_t2[adapter_name], self.lokr_w2_a[adapter_name], self.lokr_w2_b[adapter_name])
+ else:
+ w2 = self.lokr_w2_a[adapter_name] @ self.lokr_w2_b[adapter_name]
+
+ # Make weights with Kronecker product
+ weight = make_kron(w1, w2, self.scaling[adapter_name])
+
+ # Get base layer for reshaping
+ base_layer = self.get_base_layer()
+
+ # Regular reshape to match base layer shape
+ weight = weight.reshape(base_layer.weight.shape)
+
+ # Perform rank dropout during training - drop rows of addition weights
+ rank_dropout = self.rank_dropout[adapter_name]
+ if self.training and rank_dropout:
+ drop = (torch.rand(weight.size(0)) > rank_dropout).float()
+ drop = drop.view(-1, *[1] * len(weight.shape[1:])).to(weight.device)
+ if self.rank_dropout_scale[adapter_name]:
+ drop /= drop.mean()
+ weight *= drop
+
+ return weight
+
+ def forward(self, x: torch.Tensor, *args, **kwargs) -> torch.Tensor:
+ previous_dtype = x.dtype
+
+ if self.disable_adapters:
+ if self.merged:
+ self.unmerge()
+ result = self.base_layer(x, *args, **kwargs)
+ elif self.merged:
+ result = self.base_layer(x, *args, **kwargs)
+ else:
+ result = self.base_layer(x, *args, **kwargs)
+
+ # Execute all the adapters
+ for active_adapter in self.active_adapters:
+ if active_adapter not in self._available_adapters:
+ continue
+
+ module_dropout = self.module_dropout[active_adapter]
+
+ # Modify current execution weights
+ if (not self.training) or (self.training and torch.rand(1) > module_dropout):
+ result = result + self._get_delta_activations(active_adapter, x, *args, **kwargs)
+
+ result = result.to(previous_dtype)
+ return result
+
+
+class Linear(LoKrLayer):
+ """LoKr implemented in Linear layer"""
+
+ def __init__(
+ self,
+ base_layer: nn.Module,
+ device: Optional[Union[str, torch.device]] = None,
+ dtype: Optional[torch.dtype] = None,
+ adapter_name: str = "default",
+ r: int = 0,
+ alpha: float = 0.0,
+ rank_dropout: float = 0.0,
+ module_dropout: float = 0.0,
+ init_weights: bool = True,
+ **kwargs,
+ ):
+ super().__init__(base_layer)
+
+ # Create adapter and set it active
+ self._active_adapter = adapter_name
+ self.update_layer(adapter_name, r, alpha, rank_dropout, module_dropout, init_weights, **kwargs)
+
+ def _get_delta_activations(
+ self, adapter_name: str, input: torch.Tensor, *args: Any, **kwargs: Any
+ ) -> torch.Tensor:
+ delta_weight = self.get_delta_weight(adapter_name)
+ input = self._cast_input_dtype(input, delta_weight.dtype)
+ # don't add bias here, because the bias is already included in the output of the base_layer
+ return F.linear(input, delta_weight)
+
+ def __repr__(self) -> str:
+ rep = super().__repr__()
+ return "lokr." + rep
+
+
+class Conv2d(LoKrLayer):
+ """LoKr implemented in Conv2d layer"""
+
+ def __init__(
+ self,
+ base_layer: nn.Module,
+ device: Optional[Union[str, torch.device]] = None,
+ dtype: Optional[torch.dtype] = None,
+ adapter_name: str = "default",
+ r: int = 0,
+ alpha: float = 0.0,
+ rank_dropout: float = 0.0,
+ module_dropout: float = 0.0,
+ use_effective_conv2d: bool = False,
+ init_weights: bool = True,
+ **kwargs,
+ ):
+ super().__init__(base_layer)
+
+ # Create adapter and set it active
+ self._active_adapter = adapter_name
+ self.update_layer(
+ adapter_name, r, alpha, rank_dropout, module_dropout, init_weights, use_effective_conv2d, **kwargs
+ )
+
+ def _get_delta_activations(
+ self, adapter_name: str, input: torch.Tensor, *args: Any, **kwargs: Any
+ ) -> torch.Tensor:
+ delta_weight = self.get_delta_weight(adapter_name)
+ input = self._cast_input_dtype(input, delta_weight.dtype)
+ # don't add bias here, because the bias is already included in the output of the base_layer
+ base_layer = self.get_base_layer()
+ return F.conv2d(
+ input,
+ delta_weight,
+ stride=base_layer.stride,
+ padding=base_layer.padding,
+ dilation=base_layer.dilation,
+ groups=base_layer.groups,
+ )
+
+ def __repr__(self) -> str:
+ rep = super().__repr__()
+ return "lokr." + rep
+
+
+class Conv1d(LoKrLayer):
+ """LoKr implemented in Conv1d layer"""
+
+ def __init__(
+ self,
+ base_layer: nn.Module,
+ device: Optional[Union[str, torch.device]] = None,
+ dtype: Optional[torch.dtype] = None,
+ adapter_name: str = "default",
+ r: int = 0,
+ alpha: float = 0.0,
+ rank_dropout: float = 0.0,
+ module_dropout: float = 0.0,
+ use_effective_conv2d: bool = False,
+ init_weights: bool = True,
+ **kwargs,
+ ):
+ super().__init__(base_layer)
+
+ # Create adapter and set it active
+ self._active_adapter = adapter_name
+ self.update_layer(
+ adapter_name, r, alpha, rank_dropout, module_dropout, init_weights, use_effective_conv2d, **kwargs
+ )
+
+ def _get_delta_activations(
+ self, adapter_name: str, input: torch.Tensor, *args: Any, **kwargs: Any
+ ) -> torch.Tensor:
+ delta_weight = self.get_delta_weight(adapter_name)
+ input = self._cast_input_dtype(input, delta_weight.dtype)
+ # don't add bias here, because the bias is already included in the output of the base_layer
+ base_layer = self.get_base_layer()
+ return F.conv1d(
+ input,
+ delta_weight,
+ stride=base_layer.stride,
+ padding=base_layer.padding,
+ dilation=base_layer.dilation,
+ groups=base_layer.groups,
+ )
+
+ def __repr__(self) -> str:
+ rep = super().__repr__()
+ return "lokr." + rep
+
+
+# Below code is a direct copy from https://github.com/KohakuBlueleaf/LyCORIS/blob/eb460098187f752a5d66406d3affade6f0a07ece/lycoris/modules/lokr.py#L11
+
+
+def factorization(dimension: int, factor: int = -1) -> tuple[int, int]:
+ """Factorizes the provided number into the product of two numbers
+
+ Args:
+ dimension (`int`): The number that needs to be factorized.
+ factor (`int`, optional):
+ Factorization divider. The algorithm will try to output two numbers, one of each will be as close to the
+ factor as possible. If -1 is provided, the decomposition algorithm would try to search dividers near the
+ square root of the dimension. Defaults to -1.
+
+ Returns:
+ Tuple[`int`, `int`]: A tuple of two numbers, whose product is equal to the provided number. The first number is
+ always less than or equal to the second.
+
+ Example:
+ ```py
+ >>> factorization(256, factor=-1)
+ (16, 16)
+
+ >>> factorization(128, factor=-1)
+ (8, 16)
+
+ >>> factorization(127, factor=-1)
+ (1, 127)
+
+ >>> factorization(128, factor=4)
+ (4, 32)
+ ```
+ """
+
+ if factor > 0 and (dimension % factor) == 0:
+ m = factor
+ n = dimension // factor
+ return m, n
+ if factor == -1:
+ factor = dimension
+ m, n = 1, dimension
+ length = m + n
+ while m < n:
+ new_m = m + 1
+ while dimension % new_m != 0:
+ new_m += 1
+ new_n = dimension // new_m
+ if new_m + new_n > length or new_m > factor:
+ break
+ else:
+ m, n = new_m, new_n
+ if m > n:
+ n, m = m, n
+ return m, n
+
+
+def make_weight_cp(t, wa, wb):
+ rebuild2 = torch.einsum("i j k l, i p, j r -> p r k l", t, wa, wb) # [c, d, k1, k2]
+ return rebuild2
+
+
+def make_kron(w1, w2, scale=1.0):
+ if len(w2.shape) == 4:
+ w1 = w1.unsqueeze(2).unsqueeze(2)
+ w2 = w2.contiguous()
+ rebuild = torch.kron(w1, w2)
+
+ return rebuild * scale
diff --git a/peft/src/peft/tuners/lokr/model.py b/peft/src/peft/tuners/lokr/model.py
new file mode 100644
index 0000000000000000000000000000000000000000..10e187a4bf2272af72481f261d92601ee67112fb
--- /dev/null
+++ b/peft/src/peft/tuners/lokr/model.py
@@ -0,0 +1,118 @@
+# Copyright 2023-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+from typing import Union
+
+import torch
+from torch import nn
+
+from peft.tuners.lycoris_utils import LycorisConfig, LycorisTuner
+from peft.utils import TRANSFORMERS_MODELS_TO_LOKR_TARGET_MODULES_MAPPING
+from peft.utils.other import get_pattern_key
+
+from .layer import Conv1d, Conv2d, Linear, LoKrLayer
+
+
+class LoKrModel(LycorisTuner):
+ """
+ Creates Low-Rank Kronecker Product model from a pretrained model. The original method is partially described in
+ https://huggingface.co/papers/2108.06098 and in https://huggingface.co/papers/2309.14859 Current implementation
+ heavily borrows from
+ https://github.com/KohakuBlueleaf/LyCORIS/blob/eb460098187f752a5d66406d3affade6f0a07ece/lycoris/modules/lokr.py
+
+ Args:
+ model (`torch.nn.Module`): The model to which the adapter tuner layers will be attached.
+ config ([`LoKrConfig`]): The configuration of the LoKr model.
+ adapter_name (`str`): The name of the adapter, defaults to `"default"`.
+ low_cpu_mem_usage (`bool`, `optional`, defaults to `False`):
+ Create empty adapter weights on meta device. Useful to speed up the loading process.
+
+ Returns:
+ `torch.nn.Module`: The LoKr model.
+
+ Example:
+ ```py
+ >>> from diffusers import StableDiffusionPipeline
+ >>> from peft import LoKrModel, LoKrConfig
+
+ >>> config_te = LoKrConfig(
+ ... r=8,
+ ... lora_alpha=32,
+ ... target_modules=["k_proj", "q_proj", "v_proj", "out_proj", "fc1", "fc2"],
+ ... rank_dropout=0.0,
+ ... module_dropout=0.0,
+ ... init_weights=True,
+ ... )
+ >>> config_unet = LoKrConfig(
+ ... r=8,
+ ... lora_alpha=32,
+ ... target_modules=[
+ ... "proj_in",
+ ... "proj_out",
+ ... "to_k",
+ ... "to_q",
+ ... "to_v",
+ ... "to_out.0",
+ ... "ff.net.0.proj",
+ ... "ff.net.2",
+ ... ],
+ ... rank_dropout=0.0,
+ ... module_dropout=0.0,
+ ... init_weights=True,
+ ... use_effective_conv2d=True,
+ ... )
+
+ >>> model = StableDiffusionPipeline.from_pretrained("runwayml/stable-diffusion-v1-5")
+ >>> model.text_encoder = LoKrModel(model.text_encoder, config_te, "default")
+ >>> model.unet = LoKrModel(model.unet, config_unet, "default")
+ ```
+
+ **Attributes**:
+ - **model** ([`~torch.nn.Module`]) -- The model to be adapted.
+ - **peft_config** ([`LoKrConfig`]): The configuration of the LoKr model.
+ """
+
+ prefix: str = "lokr_"
+ tuner_layer_cls = LoKrLayer
+ target_module_mapping = TRANSFORMERS_MODELS_TO_LOKR_TARGET_MODULES_MAPPING
+ layers_mapping: dict[type[torch.nn.Module], type[LoKrLayer]] = {
+ torch.nn.Conv2d: Conv2d,
+ torch.nn.Conv1d: Conv1d,
+ torch.nn.Linear: Linear,
+ }
+
+ def _create_and_replace(
+ self,
+ config: LycorisConfig,
+ adapter_name: str,
+ target: Union[LoKrLayer, nn.Module],
+ target_name: str,
+ parent: nn.Module,
+ current_key: str,
+ ) -> None:
+ """
+ A private method to create and replace the target module with the adapter module.
+ """
+ r_key = get_pattern_key(config.rank_pattern.keys(), current_key)
+ alpha_key = get_pattern_key(config.alpha_pattern.keys(), current_key)
+ kwargs = config.to_dict()
+ kwargs["r"] = config.rank_pattern.get(r_key, config.r)
+ kwargs["alpha"] = config.alpha_pattern.get(alpha_key, config.alpha)
+ kwargs["rank_dropout_scale"] = config.rank_dropout_scale
+
+ if isinstance(target, LoKrLayer):
+ target.update_layer(adapter_name, **kwargs)
+ else:
+ new_module = self._create_new_module(config, adapter_name, target, **kwargs)
+ self._replace_module(parent, target_name, new_module, target)
diff --git a/peft/src/peft/tuners/lora/__init__.py b/peft/src/peft/tuners/lora/__init__.py
new file mode 100644
index 0000000000000000000000000000000000000000..b8f08afdf00eb8cbfc1e827faa465fde6432e2ff
--- /dev/null
+++ b/peft/src/peft/tuners/lora/__init__.py
@@ -0,0 +1,64 @@
+# Copyright 2023-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+from peft.import_utils import is_bnb_4bit_available, is_bnb_available, is_eetq_available
+from peft.utils import register_peft_method
+
+from .arrow import create_arrow_model
+from .config import ArrowConfig, EvaConfig, LoftQConfig, LoraConfig, LoraRuntimeConfig
+from .eva import get_eva_state_dict, initialize_lora_eva_weights
+from .gptq import GPTQLoraLinear
+from .layer import Conv2d, Conv3d, Embedding, Linear, LoraLayer, ParamWrapper
+from .model import LoraModel
+
+
+__all__ = [
+ "ArrowConfig",
+ "Conv2d",
+ "Conv3d",
+ "Embedding",
+ "EvaConfig",
+ "GPTQLoraLinear",
+ "Linear",
+ "LoftQConfig",
+ "LoraConfig",
+ "LoraLayer",
+ "LoraModel",
+ "LoraRuntimeConfig",
+ "ParamWrapper",
+ "create_arrow_model",
+ "get_eva_state_dict",
+ "initialize_lora_eva_weights",
+]
+
+register_peft_method(name="lora", config_cls=LoraConfig, model_cls=LoraModel, is_mixed_compatible=True)
+
+
+def __getattr__(name):
+ if (name == "Linear8bitLt") and is_bnb_available():
+ from .bnb import Linear8bitLt
+
+ return Linear8bitLt
+
+ if (name == "Linear4bit") and is_bnb_4bit_available():
+ from .bnb import Linear4bit
+
+ return Linear4bit
+
+ if (name == "EetqLoraLinear") and is_eetq_available():
+ from .eetq import EetqLoraLinear
+
+ return EetqLoraLinear
+
+ raise AttributeError(f"module {__name__} has no attribute {name}")
diff --git a/peft/src/peft/tuners/lora/aqlm.py b/peft/src/peft/tuners/lora/aqlm.py
new file mode 100644
index 0000000000000000000000000000000000000000..81c7cdbb4ec45ed4d86fd08ab26f4baab64c0cab
--- /dev/null
+++ b/peft/src/peft/tuners/lora/aqlm.py
@@ -0,0 +1,114 @@
+# Copyright 2024-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+from typing import Any, Optional
+
+import torch
+
+from peft.import_utils import is_aqlm_available
+from peft.tuners.lora.layer import LoraLayer
+from peft.tuners.tuners_utils import BaseTunerLayer
+
+
+if is_aqlm_available():
+ from aqlm import QuantizedLinear
+
+
+class AqlmLoraLinear(torch.nn.Module, LoraLayer):
+ def __init__(
+ self,
+ base_layer,
+ adapter_name: str,
+ r: int = 0,
+ lora_alpha: int = 1,
+ lora_dropout: float = 0.0,
+ init_lora_weights: bool = True,
+ use_rslora: bool = False,
+ use_dora: bool = False,
+ lora_bias: bool = False,
+ **kwargs,
+ ):
+ if use_dora:
+ raise ValueError(f"{self.__class__.__name__} does not support DoRA yet, please set it to False")
+
+ super().__init__()
+ LoraLayer.__init__(self, base_layer)
+
+ self._active_adapter = adapter_name
+ self.update_layer(
+ adapter_name,
+ r,
+ lora_alpha=lora_alpha,
+ lora_dropout=lora_dropout,
+ init_lora_weights=init_lora_weights,
+ use_rslora=use_rslora,
+ use_dora=use_dora,
+ lora_bias=lora_bias,
+ )
+
+ def forward(self, x: torch.Tensor):
+ # note: logic differs from default Linear because merging is not supported
+ result = self.base_layer(x)
+
+ if self.disable_adapters:
+ return result
+
+ for active_adapter in self.active_adapters:
+ if active_adapter not in self.lora_A.keys():
+ continue
+ lora_A = self.lora_A[active_adapter]
+ lora_B = self.lora_B[active_adapter]
+ dropout = self.lora_dropout[active_adapter]
+ scaling = self.scaling[active_adapter]
+
+ requires_conversion = not torch.is_autocast_enabled()
+ if requires_conversion:
+ expected_dtype = result.dtype
+ x = self._cast_input_dtype(x, lora_A.weight.dtype)
+
+ output = lora_B(lora_A(dropout(x)))
+ if requires_conversion:
+ output = output.to(expected_dtype)
+ output = output * scaling
+ result += output
+ return result
+
+ def __repr__(self) -> str:
+ rep = super().__repr__()
+ return "lora." + rep
+
+ # TODO: Check if it is better as suggested by users https://github.com/PanQiWei/AutoGPTQ/pull/102
+ # def reset_lora_parameters(self, adapter_name):
+ # if adapter_name in self.lora_A.keys():
+ # torch.nn.init.xavier_uniform_(self.lora_A[adapter_name].weight)
+ # torch.nn.init.zeros_(self.lora_B[adapter_name].weight)
+
+
+def dispatch_aqlm(
+ target: torch.nn.Module,
+ adapter_name: str,
+ **kwargs: Any,
+) -> Optional[torch.nn.Module]:
+ new_module = None
+
+ if isinstance(target, BaseTunerLayer):
+ target_base_layer = target.get_base_layer()
+ else:
+ target_base_layer = target
+
+ if is_aqlm_available() and isinstance(target_base_layer, QuantizedLinear):
+ new_module = AqlmLoraLinear(target, adapter_name, **kwargs)
+ target.qweight = target_base_layer.codes
+
+ return new_module
diff --git a/peft/src/peft/tuners/lora/arrow.py b/peft/src/peft/tuners/lora/arrow.py
new file mode 100644
index 0000000000000000000000000000000000000000..070f295112b9504dbdcc64d78b6ec2e19127a726
--- /dev/null
+++ b/peft/src/peft/tuners/lora/arrow.py
@@ -0,0 +1,476 @@
+# Copyright 2025-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+from __future__ import annotations
+
+import os
+from typing import Any
+
+import torch
+from torch import nn
+from transformers import PreTrainedModel
+
+from .config import ArrowConfig
+
+
+TASK_ADAPTER_PREFIX = "task_"
+GKS_ADAPTER_PREFIX = "gks_"
+
+
+class ArrowLoraLinearLayer(nn.Module):
+ """
+ This class represent the main logic of the arrow routing algorithm for linear layers.
+ """
+
+ def __init__(self, in_features, arrow_config):
+ super().__init__()
+ # extra parameters needed for arrow
+ self.in_features = in_features
+ self._protos_ready = False
+ self.top_k = arrow_config.top_k
+ self.temperature = arrow_config.router_temperature
+ self.rng_seed = arrow_config.rng_seed
+ self.task_adapter_names = (
+ arrow_config.task_adapter_names.copy()
+ ) # Set in create_arrow_model() with this format: task_0, task_1, ...
+ self.gks_adapter_names = (
+ arrow_config.gks_adapter_names
+ ) # Set in create_arrow_model() with this format: gks_0, gks_1, ...
+ self.use_gks = arrow_config.use_gks
+ self.gks_done = False
+ self.gks_added_adapter_names = []
+ self.in_features = in_features
+ self.cast_input_dtype_enabled = True
+
+ @torch.no_grad()
+ def on_adapter_change(self, lora_A, lora_B):
+ """
+ Called when adapters are added/removed/renamed so Arrow can refresh its internal state before the next forward
+ pass.
+ """
+ all_ts_adapter_names = [
+ k
+ for k in lora_A.keys()
+ if k in lora_B and k != "arrow_router" and not (k.startswith("gks_") and k[len("gks_") :].isdigit())
+ ]
+
+ if sorted(self.task_adapter_names) == sorted(all_ts_adapter_names): # No changes in the ts_adapters
+ return
+
+ # Getting the name(s) of added adapter(s)
+ if len(self.task_adapter_names) < len(all_ts_adapter_names): # Adapter(s) are added.
+ self.gks_added_adapter_names = [x for x in all_ts_adapter_names if x not in self.task_adapter_names]
+
+ # Updating the task_adapter_names
+ self.task_adapter_names = all_ts_adapter_names.copy()
+ # Invalidate caches so they’ll be rebuilt lazily on next forward()
+ self._protos_ready = False
+ # GKS will be handled by self.gks_added_adapter_names
+
+ def top_right_singular_vec_from_BA(self, A, B, iters=15, eps=1e-8):
+ """
+ Computes the top *right* singular vector of ΔW = B @ A without forming ΔW.
+
+ Theory:
+ For any matrix M, the right singular vectors are the eigenvectors of Mᵀ M. If ΔW = B @ A (with A ∈
+ ℝ^{r×in}, B ∈ ℝ^{out×r}), then
+ ΔWᵀ ΔW = (B @ A)ᵀ (B @ A) = Aᵀ (Bᵀ B) A ∈ ℝ^{in×in}.
+ Therefore, the dominant right singular vector of ΔW is the dominant eigenvector of M := Aᵀ (Bᵀ B) A. We
+ find it by *power iteration* on the linear operator
+ v ↦ Aᵀ (Bᵀ B) (A v),
+ which avoids materializing ΔW (out×in) or M (in×in). The result lives in the input/token space (size =
+ in_features), which is exactly what Arrow needs. (Right singular vectors ≡ eigenvectors of MᵀM; power
+ iteration converges to the dominant eigenvector under mild conditions.)
+ =============================== Practical notes:
+ - We perform all iteration in float32 for numerical stability, then cast back
+ to the LoRA dtype/device before storing/using the prototype.
+ - Convergence is checked with a simple fixed-iter cap (`iters`) and/or
+ `allclose` tolerance (`tol`).
+ - The returned vector is unique up to sign (±), as with any singular vector.
+ Downstream code should be sign-invariant.
+ """
+
+ # A: (r, in), B: (out, r)
+ A32 = A.to(torch.float32)
+ B32 = B.to(torch.float32)
+ C = B32.T @ B32 # (r, r)
+
+ # Private RNG on A's device
+ gen = None
+ if self.rng_seed is not None:
+ gen = torch.Generator(device=A32.device.type)
+ gen.manual_seed(int(self.rng_seed))
+
+ # init vector in input space
+ v = torch.randn(A32.size(1), dtype=A32.dtype, device=A32.device, generator=gen)
+ v = v / (v.norm() + eps)
+
+ for _ in range(iters):
+ # w = (ΔWᵀΔW) v = Aᵀ (BᵀB) (A v)
+ w = A32.T @ (C @ (A32 @ v))
+ v = w / (w.norm() + eps)
+
+ return v # fp32
+
+ @torch.no_grad()
+ def build_prototypes(self, lora_A, lora_B):
+ """
+ Computes a prototype vector for each LoRA module in every layer by applying Singular Value Decomposition (SVD)
+ to the `lora_A` matrix and extracting the top right singular vector.
+
+ These prototypes are later used to calculate the cosine similarity between each input token and each expert.
+ The resulting similarity scores serve as coefficients to compute a weighted average of the corresponding LoRA
+ modules, effectively routing each token through its most relevant experts.
+
+ ** This prototype computation is done is done once for all experts and is re-done on newly added adapters.**
+
+ Args:
+ lora_A : Matrices A in LoRA layer.
+ lora_B (optional): Matrices B in LoRA layer. Defaults to None.
+ """
+
+ if self._protos_ready:
+ return
+ protos = []
+ for name in self.task_adapter_names:
+ A = lora_A[name].weight # (r, in_features)
+ B = lora_B[name].weight # (out_features, r)
+
+ # Efficiently computing right singular vector of A @ B
+ proto32 = self.top_right_singular_vec_from_BA(A, B)
+
+ proto = proto32.to(dtype=A.dtype, device=A.device)
+ protos.append(proto)
+
+ proto_stack = torch.stack(protos, dim=0) # (E, in_features)
+
+ # Register the prototypes buffer with correct dtype/device consistent with A and B weights
+ self.register_buffer("prototypes", proto_stack, persistent=False)
+ self._protos_ready = True
+
+ @torch.no_grad()
+ def gen_know_sub(self, lora_A, lora_B):
+ """
+ This function performs General Knowledge Subtraction. It takes an average of provided general_adapters, and
+ subtract it from each task_adapter. This subtraction tries to purify the task adapters, based on
+ "forgetting-via-negation" principle. Forgetting-via-negation is a task-arithmetic operation, explained in:
+ https://arxiv.org/abs/2212.04089 The task adapters will be more focused and isolated, enhancing the performance
+ on new tasks.
+
+ Args:
+ lora_A : Matrices A in LoRA layer.
+ lora_B : Matrices A in LoRA layer.
+ """
+ if not self.use_gks:
+ return
+ elif self.gks_done and not self.gks_added_adapter_names:
+ return
+ else:
+ # 1) compute average A/B over gks_adapter_names
+ avg_A = torch.stack([lora_A[n].weight for n in self.gks_adapter_names], dim=0).mean(
+ 0
+ ) # shape (r, in_features)
+ avg_B = torch.stack([lora_B[n].weight for n in self.gks_adapter_names], dim=0).mean(
+ 0
+ ) # shape (out_features, r)
+
+ # 2) Subtract the average from task-specific experts
+ if self.gks_done is False: # GKS is done for all the experts, since it hasn't been done yet.
+ for name in self.task_adapter_names:
+ lora_A[name].weight.data.sub_(avg_A)
+ lora_B[name].weight.data.sub_(avg_B)
+ else: # GKS is only done on new added experts, since GKS has been done previously.
+ for name in self.gks_added_adapter_names:
+ lora_A[name].weight.data.sub_(avg_A)
+ lora_B[name].weight.data.sub_(avg_B)
+
+ # 3) Set gks_done flag as true, so we won't do it again in ArrowLinearVariant.forward().
+ self.gks_done = True
+ # Clearing the self.gks_added_adapter_names
+ self.gks_added_adapter_names = []
+
+ def _cast_input_dtype(self, x, dtype: torch.dtype):
+ """
+ Whether to cast the dtype of the input of the forward method.
+
+ Usually, we want to enable this to align the input dtype with the dtype of the weight, but by setting
+ layer.cast_input_dtype=False, this can be disabled if necessary.
+
+ Enabling or disabling can be managed via the peft.helpers.disable_lora_input_dtype_casting context manager.
+ """
+ if x is None: # useful e.g. if x is the bias, which can be None
+ return None
+
+ cast_input_dtype_enabled = getattr(self, "cast_input_dtype_enabled", True)
+ if (not cast_input_dtype_enabled) or (x.dtype == dtype):
+ return x
+ return x.to(dtype=dtype)
+
+ def forward(self, x, lora_A, lora_B, dropout, scaling):
+ """
+ Applies Arrow routing inside a LoRA layer.
+
+ Steps:
+ 1. Compute cosine similarity between each token representation and all adapter prototypes.
+ 2. Select the top-k experts per token and normalize their scores with a softmax.
+ 3. Project tokens into each selected expert’s low-rank space (A weights).
+ 4. Map back to the output space (B weights).
+ 5. Aggregate expert outputs via the weighted sum of their contributions.
+ 6. Apply dropout, scaling, and return the reshaped delta.
+
+ - Conceptually, this is a Mixture-of-Experts (MoE) over LoRA adapters,
+ where coefficients are derived from prototype similarity.
+
+ Returns:
+ delta: LoRA output adjustment computed by Arrow routing.
+ """
+ x = self._cast_input_dtype(x, lora_A[self.task_adapter_names[0]].weight.dtype)
+ B, *rest, F_in = x.shape
+ tok = x.view(-1, F_in) # (t, F_in)
+ t, E = tok.size(0), self.prototypes.size(0)
+
+ # We now turn scaling, which is a dict, to tensors in order to use them later
+ scales_tens = torch.tensor(
+ [scaling[n] for n in self.task_adapter_names],
+ device=tok.device,
+ dtype=tok.dtype,
+ ) # shape (E,)
+
+ # 1) similarity — sign-agnostic
+ sim = torch.abs(tok @ self.prototypes.T) # (t, E)
+
+ # 2) top-k + softmax over full E (non-top-k = -inf)
+ top_v, idx = torch.topk(sim, self.top_k, dim=1)
+ full_score = tok.new_full((t, E), float("-inf"))
+ full_score.scatter_(1, idx, top_v)
+ coeff = torch.softmax(full_score / self.temperature, dim=1) # (t, E)
+
+ # 3) stack all A and B weights once
+ # A_stack: (E, r, in_features), B_stack: (E, out_features, r)
+ A_stack = torch.stack([lora_A[n].weight for n in self.task_adapter_names], dim=0)
+ B_stack = torch.stack([lora_B[n].weight for n in self.task_adapter_names], dim=0)
+
+ # 4) project tokens into each expert’s low‑rank space:
+ # z[e] = tok @ A_e.T → shape (t, E, r)
+ z = torch.einsum("tf, erf -> ter", tok, A_stack)
+
+ # 5) lift back each expert’s output:
+ # y[e] = z[e] @ B_e.T → shape (t, E, out_features)
+ y = torch.einsum("ter, eor -> teo", z, B_stack)
+
+ # 6) apply per-expert scaling before the weighted sum
+ # y_scaled[t, e, o] = scales[e] * y[t, e, o]
+ y = y * scales_tens.view(1, -1, 1)
+
+ # 6) weighted sum over experts:
+ # delta_flat[t,o] = Σ_e coeff[t,e] * y[t,e,o]
+ delta_flat = torch.einsum("te, teo -> to", coeff, y) # (t, out_features)
+
+ # 7) dropout, scale, and reshape
+ delta = dropout(delta_flat)
+ out_dim = delta_flat.size(-1)
+ return delta.view(B, *rest, out_dim)
+
+
+def check_loaded_lora_compatibility_arrow(model, adapter_names: list[str]):
+ """
+ After loading all adapters into `model`, check they share:
+ - the same LoRA rank (r)
+ - identical weight shapes
+ - identical sets of target_modules
+ Returns (sorted list of target module names, agreed rank r).
+ """
+ reference = None # {'r':…, 'shapes':(Ashape,Bshape), 'modules':set([...])}
+
+ for name in adapter_names:
+ curr_modules = set()
+ curr_r = None
+ curr_shapes = None
+
+ for full_name, module in model.named_modules():
+ if hasattr(module, "lora_A") and name in module.lora_A:
+ A = module.lora_A[name].weight
+ B = module.lora_B[name].weight
+ mod_name = full_name.split(".")[-1]
+ curr_modules.add(mod_name)
+ # A has shape (r, in_features); B has shape (out_features, r)
+ curr_r = A.shape[0]
+ curr_shapes = (A.shape, B.shape)
+
+ if reference is None:
+ reference = {"r": curr_r, "shapes": curr_shapes, "modules": curr_modules}
+ else:
+ if curr_r != reference["r"]:
+ raise ValueError(f"[{name}] rank mismatch: {curr_r} != {reference['r']}")
+ if curr_shapes != reference["shapes"]:
+ raise ValueError(f"[{name}] shape mismatch: {curr_shapes} != {reference['shapes']}")
+ if curr_modules != reference["modules"]:
+ raise ValueError(
+ f"[{name}] target_modules mismatch:\n"
+ f" this adapter -> {sorted(curr_modules)}\n"
+ f" reference -> {sorted(reference['modules'])}"
+ )
+
+ agreed_modules = sorted(reference["modules"])
+ return agreed_modules, int(reference["r"])
+
+
+def ensure_adapters_target_linear_layers_only(model, adapter_names: list[str]):
+ """
+ Validate that every module holding LoRA weights for any of `adapter_names` is Linear-like: nn.Linear,
+ bitsandbytes.nn.Linear4bit, nn.Conv1d, or transformers.models.gpt2.modeling_gpt2.Conv1D. If not, raise.
+ """
+ import torch.nn as nn
+
+ Linear4bit = None
+ try:
+ import bitsandbytes as bnb # type: ignore
+
+ Linear4bit = bnb.nn.Linear4bit
+ except ImportError:
+ pass
+
+ HFConv1D = None
+ try:
+ from transformers.models.gpt2.modeling_gpt2 import Conv1D as HFConv1D # type: ignore
+ except ImportError:
+ pass
+
+ allowed_types = (nn.Linear, nn.Conv1d)
+ if Linear4bit is not None:
+ allowed_types = allowed_types + (Linear4bit,)
+ if HFConv1D is not None:
+ allowed_types = allowed_types + (HFConv1D,)
+
+ offenders = []
+
+ for full_name, module in model.named_modules():
+ if hasattr(module, "lora_A"):
+ for name in adapter_names:
+ if name in getattr(module, "lora_A", {}):
+ base = getattr(module, "base_layer", None) or getattr(module, "original_module", None)
+ layer_to_check = base if base is not None else module
+
+ if not isinstance(layer_to_check, allowed_types):
+ offenders.append((name, full_name, type(layer_to_check).__name__))
+
+ if offenders:
+ lines = [
+ "LoRA adapters must only target Linear-like layers "
+ "(nn.Linear, nn.Conv1d, HF Conv1D, or bitsandbytes.nn.Linear4bit). Found:"
+ ]
+ for name, full_name, tname in offenders:
+ lines.append(f" - adapter '{name}' on module '{full_name}' of type {tname}")
+ raise TypeError("\n".join(lines))
+
+
+def _resolve_adapter_source(path: str) -> tuple[str, str | None]:
+ """
+ Resolve a user-provided adapter `path` into (model_id, subfolder).
+
+ Supports:
+ - Local path to a folder that contains `adapter_config.json`
+ - Hub path with subfolder, e.g. "user/repo/ts_expert_0[/more/...]", which becomes:
+ model_id="user/repo", subfolder="ts_expert_0[/more/...]"
+ - Plain Hub repo id "user/repo" (no subfolder)
+ """
+ if os.path.isdir(path):
+ if not os.path.isfile(os.path.join(path, "adapter_config.json")):
+ raise ValueError(f"Local adapter path '{path}' does not contain 'adapter_config.json'.")
+ return path, None
+
+ parts = path.strip("/").split("/")
+ if len(parts) >= 2:
+ model_id = "/".join(parts[:2])
+ if len(parts) > 2:
+ subfolder = "/".join(parts[2:])
+ return model_id, subfolder
+ return model_id, None
+
+ return path, None
+
+
+def create_arrow_model(
+ base_model: PreTrainedModel,
+ task_specific_adapter_paths: list[str],
+ arrow_config: ArrowConfig,
+ general_adapter_paths: list[str] | None = None,
+ **adapter_kwargs: Any,
+):
+ if task_specific_adapter_paths is None or len(task_specific_adapter_paths) == 0:
+ raise ValueError("`task_specific_adapter_paths` should contain at least one adapter path")
+
+ from peft import LoraConfig, PeftModel
+
+ model_id0, sub0 = _resolve_adapter_source(task_specific_adapter_paths[0])
+ initial_ts_expert_name = f"{TASK_ADAPTER_PREFIX}0"
+
+ first_kwargs = dict(adapter_kwargs)
+ if sub0 is not None and "subfolder" not in first_kwargs:
+ first_kwargs["subfolder"] = sub0
+
+ model = PeftModel.from_pretrained(
+ base_model,
+ model_id=model_id0,
+ adapter_name=initial_ts_expert_name,
+ **first_kwargs,
+ )
+
+ for i in range(1, len(task_specific_adapter_paths)):
+ ts_expert_name = f"{TASK_ADAPTER_PREFIX}{i}"
+ mid, sub = _resolve_adapter_source(task_specific_adapter_paths[i])
+ more_kwargs = dict(adapter_kwargs)
+ if sub is not None and "subfolder" not in more_kwargs:
+ more_kwargs["subfolder"] = sub
+ model.load_adapter(
+ model_id=mid,
+ adapter_name=ts_expert_name,
+ **more_kwargs,
+ )
+ arrow_config.task_adapter_names = [f"{TASK_ADAPTER_PREFIX}{i}" for i in range(len(task_specific_adapter_paths))]
+
+ if arrow_config.use_gks:
+ if general_adapter_paths is None or len(general_adapter_paths) == 0:
+ raise ValueError("You should provide general LoRA paths if you want to use GenKnowSub.")
+ for i in range(len(general_adapter_paths)):
+ gen_expert_name = f"{GKS_ADAPTER_PREFIX}{i}"
+ mid, sub = _resolve_adapter_source(general_adapter_paths[i])
+ gks_kwargs = dict(adapter_kwargs)
+ if sub is not None and "subfolder" not in gks_kwargs:
+ gks_kwargs["subfolder"] = sub
+ model.load_adapter(
+ model_id=mid,
+ adapter_name=gen_expert_name,
+ **gks_kwargs,
+ )
+ arrow_config.gks_adapter_names = [f"{GKS_ADAPTER_PREFIX}{i}" for i in range(len(general_adapter_paths))]
+ else:
+ arrow_config.gks_adapter_names = []
+
+ target_modules, r = check_loaded_lora_compatibility_arrow(
+ model, adapter_names=arrow_config.task_adapter_names + arrow_config.gks_adapter_names
+ )
+
+ ensure_adapters_target_linear_layers_only(
+ model, adapter_names=arrow_config.task_adapter_names + arrow_config.gks_adapter_names
+ )
+
+ router_cfg = LoraConfig(
+ arrow_config=arrow_config,
+ target_modules=target_modules,
+ r=r,
+ )
+ model.add_adapter(adapter_name="arrow_router", peft_config=router_cfg)
+ model.set_adapter("arrow_router")
+
+ return model
diff --git a/peft/src/peft/tuners/lora/awq.py b/peft/src/peft/tuners/lora/awq.py
new file mode 100644
index 0000000000000000000000000000000000000000..61eb487ad6756e1e31b612ec7a8e4649b860e4c5
--- /dev/null
+++ b/peft/src/peft/tuners/lora/awq.py
@@ -0,0 +1,121 @@
+# Copyright 2024-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+import importlib.metadata as importlib_metadata
+from typing import Any, Optional
+
+import packaging.version
+import torch
+
+from peft.import_utils import is_auto_awq_available
+from peft.tuners.lora.layer import LoraLayer
+from peft.tuners.tuners_utils import BaseTunerLayer
+
+
+class AwqLoraLinear(torch.nn.Module, LoraLayer):
+ def __init__(
+ self,
+ base_layer,
+ adapter_name,
+ r: int = 0,
+ lora_alpha: int = 1,
+ lora_dropout: float = 0.0,
+ init_lora_weights: bool = True,
+ use_rslora: bool = False,
+ use_dora: bool = False,
+ lora_bias: bool = False,
+ **kwargs,
+ ):
+ if use_dora:
+ raise ValueError(f"{self.__class__.__name__} does not support DoRA yet, please set it to False")
+
+ super().__init__()
+ LoraLayer.__init__(self, base_layer)
+
+ # self.base_layer and self.quant_linear_module are the same; we need the former for consistency and the latter
+ # for backwards compatibility
+ self.quant_linear_module = base_layer
+
+ self._active_adapter = adapter_name
+ self.update_layer(
+ adapter_name,
+ r,
+ lora_alpha=lora_alpha,
+ lora_dropout=lora_dropout,
+ init_lora_weights=init_lora_weights,
+ use_rslora=use_rslora,
+ use_dora=use_dora,
+ lora_bias=lora_bias,
+ )
+
+ def forward(self, x: torch.Tensor):
+ result = self.quant_linear_module(x)
+
+ if self.disable_adapters:
+ return result
+
+ for active_adapter in self.active_adapters:
+ if active_adapter not in self.lora_A.keys():
+ continue
+ lora_A = self.lora_A[active_adapter]
+ lora_B = self.lora_B[active_adapter]
+ dropout = self.lora_dropout[active_adapter]
+ scaling = self.scaling[active_adapter]
+
+ requires_conversion = not torch.is_autocast_enabled()
+ if requires_conversion:
+ expected_dtype = result.dtype
+ x = self._cast_input_dtype(x, lora_A.weight.dtype)
+
+ output = lora_B(lora_A(dropout(x)))
+ if requires_conversion:
+ output = output.to(expected_dtype)
+ output = output * scaling
+ result = result + output
+ return result
+
+ def __repr__(self) -> str:
+ rep = super().__repr__()
+ return "lora." + rep
+
+
+def dispatch_awq(
+ target: torch.nn.Module,
+ adapter_name: str,
+ **kwargs: Any,
+) -> Optional[torch.nn.Module]:
+ new_module = None
+
+ if isinstance(target, BaseTunerLayer):
+ target_base_layer = target.get_base_layer()
+ else:
+ target_base_layer = target
+
+ if is_auto_awq_available():
+ from awq.modules.linear import WQLinear_GEMM
+
+ if isinstance(target_base_layer, WQLinear_GEMM):
+ # Raise the error only at the dispatch level
+ AUTOAWQ_MINIMUM_VERSION = packaging.version.parse("0.2.0")
+ version_autoawq = packaging.version.parse(importlib_metadata.version("autoawq"))
+
+ if AUTOAWQ_MINIMUM_VERSION > version_autoawq:
+ raise ImportError(
+ f"Found an incompatible version of auto-awq. Found version {version_autoawq}, "
+ f"but only versions above {AUTOAWQ_MINIMUM_VERSION} are supported for PEFT."
+ )
+
+ new_module = AwqLoraLinear(target, adapter_name, **kwargs)
+ target.qweight = target_base_layer.qweight
+
+ return new_module
diff --git a/peft/src/peft/tuners/lora/bnb.py b/peft/src/peft/tuners/lora/bnb.py
new file mode 100644
index 0000000000000000000000000000000000000000..632abf5a66592c9bd5e4a76a3dabeca3c50a0b65
--- /dev/null
+++ b/peft/src/peft/tuners/lora/bnb.py
@@ -0,0 +1,611 @@
+# Copyright 2023-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+from __future__ import annotations
+
+import warnings
+from typing import Any, Optional
+
+import bitsandbytes as bnb
+import torch
+
+from peft.import_utils import is_bnb_4bit_available, is_bnb_available
+from peft.tuners.tuners_utils import BaseTunerLayer, check_adapters_to_merge
+from peft.utils.integrations import dequantize_bnb_weight
+from peft.utils.other import transpose
+
+from .config import ArrowConfig
+from .layer import LoraLayer, LoraVariant
+
+
+VARIANT_KWARG_KEYS = ["alora_offsets"]
+
+if is_bnb_available():
+
+ class Linear8bitLt(torch.nn.Module, LoraLayer):
+ # Lora implemented in a dense layer
+ def __init__(
+ self,
+ base_layer: torch.nn.Module,
+ adapter_name: str,
+ r: int = 0,
+ lora_alpha: int = 1,
+ lora_dropout: float = 0.0,
+ init_lora_weights: bool = True,
+ use_rslora: bool = False,
+ use_alora: bool = False,
+ use_dora: bool = False,
+ arrow_config: ArrowConfig = None,
+ lora_bias: bool = False,
+ **kwargs,
+ ) -> None:
+ super().__init__()
+ LoraLayer.__init__(self, base_layer)
+ self.fan_in_fan_out = False
+
+ self._active_adapter = adapter_name
+ self.update_layer(
+ adapter_name,
+ r,
+ lora_alpha=lora_alpha,
+ lora_dropout=lora_dropout,
+ init_lora_weights=init_lora_weights,
+ use_rslora=use_rslora,
+ use_dora=use_dora,
+ use_alora=use_alora,
+ lora_bias=lora_bias,
+ arrow_config=arrow_config,
+ )
+
+ def resolve_lora_variant(
+ self, *, arrow_config: ArrowConfig, use_dora: bool, use_alora: bool, **kwargs
+ ) -> Optional[LoraVariant]:
+ if arrow_config is not None:
+ from .variants import ArrowLinearVariant
+
+ return ArrowLinearVariant()
+
+ if not use_dora and not use_alora:
+ return None
+
+ from .variants import ALoraLinearVariant, DoraLinearVariant
+
+ if use_alora:
+ return ALoraLinearVariant()
+ else:
+ return DoraLinearVariant()
+
+ def merge(self, safe_merge: bool = False, adapter_names: Optional[list[str]] = None) -> None:
+ """
+ Merge the active adapter weights into the base weights
+
+ Args:
+ safe_merge (`bool`, *optional*):
+ If True, the merge operation will be performed in a copy of the original weights and check for NaNs
+ before merging the weights. This is useful if you want to check if the merge operation will produce
+ NaNs. Defaults to `False`.
+ adapter_names (`list[str]`, *optional*):
+ The list of adapter names that should be merged. If None, all active adapters will be merged.
+ Defaults to `None`.
+ """
+ adapter_names = check_adapters_to_merge(self, adapter_names)
+ if not adapter_names:
+ # no adapter to merge
+ return
+
+ for active_adapter in adapter_names:
+ if active_adapter not in self.lora_A.keys():
+ continue
+
+ warnings.warn(
+ "Merge lora module to 8-bit linear may get different generations due to rounding errors."
+ )
+
+ weight = self.get_base_layer().weight
+ state = self.get_base_layer().state
+ if state.SCB is None:
+ state.SCB = weight.SCB
+
+ # Dequantize the result of identity matrix and int8 weight because bitsandbytes does not support int8
+ # dequantization directly
+ output = dequantize_bnb_weight(weight, state=state)
+ if active_adapter not in self.lora_variant: # vanilla LoRA
+ lora_data = self.get_delta_weight(active_adapter)
+ w_data = output.to(lora_data.dtype).to(lora_data.device) + lora_data
+ else:
+ w_data = self.lora_variant[active_adapter].merge_safe(self, active_adapter, output)
+
+ if safe_merge and not torch.isfinite(w_data).all():
+ raise ValueError(
+ f"NaNs detected in the merged weights. The adapter {active_adapter} seems to be broken"
+ )
+
+ self.get_base_layer().weight = bnb.nn.Int8Params(
+ w_data.to("cpu"), requires_grad=False, has_fp16_weights=weight.has_fp16_weights
+ ).to(weight.device)
+
+ if self.lora_bias[active_adapter]:
+ bias_data = self.get_base_layer().bias.data + self.lora_B[active_adapter].bias
+ if safe_merge and not torch.isfinite(bias_data):
+ raise ValueError(
+ f"NaNs detected in the merged weights. The adapter {active_adapter} seems to be broken"
+ )
+ self.get_base_layer().bias.data = bias_data
+
+ state.reset_grads()
+ self.merged_adapters.append(active_adapter)
+
+ def unmerge(self) -> None:
+ """
+ This method unmerges all merged adapter layers from the base weights.
+ """
+ if not self.merged:
+ warnings.warn("Already unmerged. Nothing to do.")
+ return
+
+ while len(self.merged_adapters) > 0:
+ active_adapter = self.merged_adapters.pop()
+ if active_adapter not in self.lora_A.keys():
+ continue
+ warnings.warn(
+ "Unmerge lora module to 8-bit linear may get different generations due to rounding errors."
+ )
+
+ weight = self.get_base_layer().weight
+ state = self.get_base_layer().state
+ if state.SCB is None:
+ state.SCB = weight.SCB
+ output = dequantize_bnb_weight(weight, state=state)
+
+ if active_adapter not in self.lora_variant: # vanilla LoRA
+ lora_data = self.get_delta_weight(active_adapter)
+ w_data = output.to(lora_data.dtype).to(lora_data.device) - lora_data
+ else:
+ w_data = self.lora_variant[active_adapter].unmerge(self, active_adapter, output)
+
+ self.get_base_layer().weight = bnb.nn.Int8Params(
+ w_data.to("cpu"), requires_grad=False, has_fp16_weights=weight.has_fp16_weights
+ ).to(weight.device)
+
+ if self.lora_bias[active_adapter]:
+ self.get_base_layer().bias.data -= self.lora_B[active_adapter].bias
+ state.reset_grads()
+
+ def get_delta_weight(self, adapter):
+ return (
+ transpose(
+ self.lora_B[adapter].weight @ self.lora_A[adapter].weight,
+ False,
+ )
+ * self.scaling[adapter]
+ )
+
+ def _mixed_batch_forward(
+ self, x: torch.Tensor, *args: Any, adapter_names: list[str], **kwargs: Any
+ ) -> torch.Tensor:
+ # This is a special method that handles the case when users pass the argument `adapter_names`. This is an
+ # extra argument that allows mixing different adapters in the same batch at inference time.
+ variant_kwargs = {k: kwargs.pop(k, None) for k in VARIANT_KWARG_KEYS} # don't pass these to base_layer
+ result = self.base_layer(x, *args, **kwargs)
+
+ unique_adapters = set(adapter_names)
+ sub_batch_indices_list = []
+ for adapter in unique_adapters:
+ sub_batch_indices_list.append([index for index, item in enumerate(adapter_names) if item == adapter])
+
+ for i, active_adapter in enumerate(unique_adapters):
+ if active_adapter == "__base__":
+ continue
+ if active_adapter not in self.lora_A.keys():
+ continue
+
+ lora_A = self.lora_A[active_adapter]
+ lora_B = self.lora_B[active_adapter]
+ dropout = self.lora_dropout[active_adapter]
+ scaling = self.scaling[active_adapter]
+
+ requires_conversion = not torch.is_autocast_enabled()
+ if requires_conversion:
+ expected_dtype = result.dtype
+ x = self._cast_input_dtype(x, lora_A.weight.dtype)
+
+ # getting the sub-batch, passing it to LoRA layers and updating the corresponding indices of the linear
+ # layer output
+ sub_batch = x[sub_batch_indices_list[i]]
+ if active_adapter not in self.lora_variant: # vanilla LoRA:
+ output = lora_B(lora_A(dropout(sub_batch))) * scaling
+ if requires_conversion:
+ output = output.to(expected_dtype)
+ result[sub_batch_indices_list[i]] += output
+ else:
+ alora_offsets = variant_kwargs.get("alora_offsets", None)
+ if alora_offsets is not None:
+ variant_kwargs["alora_offsets"] = [alora_offsets[j] for j in sub_batch_indices_list[i]]
+ output = self.lora_variant[active_adapter].forward(
+ self,
+ active_adapter=active_adapter,
+ x=sub_batch,
+ result=result[sub_batch_indices_list[i]],
+ **variant_kwargs,
+ **kwargs,
+ )
+ if requires_conversion:
+ output = output.to(expected_dtype)
+ result[sub_batch_indices_list[i]] = output
+
+ return result
+
+ def forward(self, x: torch.Tensor, *args, **kwargs) -> torch.Tensor:
+ self._check_forward_args(x, *args, **kwargs)
+ adapter_names = kwargs.pop("adapter_names", None)
+ variant_kwargs = {k: kwargs.pop(k, None) for k in VARIANT_KWARG_KEYS} # don't pass these to base_layer
+
+ if self.disable_adapters:
+ if self.merged:
+ self.unmerge()
+ result = self.base_layer(x, *args, **kwargs)
+ elif adapter_names is not None:
+ result = self._mixed_batch_forward(x, *args, adapter_names=adapter_names, **variant_kwargs, **kwargs)
+ elif self.merged:
+ result = self.base_layer(x, *args, **kwargs)
+ else:
+ result = self.base_layer(x, *args, **kwargs)
+ for active_adapter in self.active_adapters:
+ if active_adapter not in self.lora_A.keys():
+ continue
+ lora_A = self.lora_A[active_adapter]
+ lora_B = self.lora_B[active_adapter]
+ dropout = self.lora_dropout[active_adapter]
+ scaling = self.scaling[active_adapter]
+
+ requires_conversion = not torch.is_autocast_enabled()
+ if requires_conversion:
+ expected_dtype = result.dtype
+ x = self._cast_input_dtype(x, lora_A.weight.dtype)
+
+ if active_adapter not in self.lora_variant: # vanilla LoRA
+ output = lora_B(lora_A(dropout(x))) * scaling
+ if requires_conversion:
+ output = output.to(expected_dtype)
+ result = result + output
+ else:
+ result = self.lora_variant[active_adapter].forward(
+ self,
+ active_adapter=active_adapter,
+ x=x,
+ result=result,
+ **variant_kwargs,
+ **kwargs,
+ )
+ if requires_conversion:
+ result = result.to(expected_dtype)
+
+ return result
+
+ def __repr__(self) -> str:
+ rep = super().__repr__()
+ return "lora." + rep
+
+ def dispatch_bnb_8bit(target: torch.nn.Module, adapter_name: str, **kwargs):
+ new_module = None
+
+ if isinstance(target, BaseTunerLayer):
+ target_base_layer = target.get_base_layer()
+ else:
+ target_base_layer = target
+
+ loaded_in_8bit = kwargs.get("loaded_in_8bit", False)
+ if loaded_in_8bit and isinstance(target_base_layer, bnb.nn.Linear8bitLt):
+ eightbit_kwargs = kwargs.copy()
+ eightbit_kwargs.update(
+ {
+ "has_fp16_weights": target.state.has_fp16_weights,
+ "threshold": target.state.threshold,
+ "index": target.index,
+ }
+ )
+ new_module = Linear8bitLt(target, adapter_name, **eightbit_kwargs)
+
+ return new_module
+
+
+if is_bnb_4bit_available():
+
+ class Linear4bit(torch.nn.Module, LoraLayer):
+ # Lora implemented in a dense layer
+ def __init__(
+ self,
+ base_layer: torch.nn.Module,
+ adapter_name: str,
+ r: int = 0,
+ lora_alpha: int = 1,
+ lora_dropout: float = 0.0,
+ init_lora_weights: bool = True,
+ use_rslora: bool = False,
+ use_dora: bool = False,
+ arrow_config: ArrowConfig = None,
+ lora_bias: bool = False,
+ **kwargs,
+ ) -> None:
+ super().__init__()
+ LoraLayer.__init__(self, base_layer)
+ self.fan_in_fan_out = False
+
+ self._active_adapter = adapter_name
+ self.update_layer(
+ adapter_name,
+ r,
+ lora_alpha=lora_alpha,
+ lora_dropout=lora_dropout,
+ init_lora_weights=init_lora_weights,
+ use_rslora=use_rslora,
+ use_dora=use_dora,
+ lora_bias=lora_bias,
+ arrow_config=arrow_config,
+ )
+
+ def resolve_lora_variant(
+ self, *, arrow_config: ArrowConfig, use_dora: bool, use_alora: bool, **kwargs
+ ) -> Optional[LoraVariant]:
+ if arrow_config is not None:
+ from .variants import ArrowLinearVariant
+
+ return ArrowLinearVariant()
+
+ if not use_dora and not use_alora:
+ return None
+
+ from .variants import ALoraLinearVariant, DoraLinearVariant
+
+ if use_alora:
+ return ALoraLinearVariant()
+ else:
+ return DoraLinearVariant()
+
+ def merge(self, safe_merge: bool = False, adapter_names: Optional[list[str]] = None) -> None:
+ """
+ Merge the active adapter weights into the base weights
+
+ Args:
+ safe_merge (`bool`, *optional*):
+ If True, the merge operation will be performed in a copy of the original weights and check for NaNs
+ before merging the weights. This is useful if you want to check if the merge operation will produce
+ NaNs. Defaults to `False`.
+ adapter_names (`list[str]`, *optional*):
+ The list of adapter names that should be merged. If None, all active adapters will be merged.
+ Defaults to `None`.
+ """
+ adapter_names = check_adapters_to_merge(self, adapter_names)
+ if not adapter_names:
+ # no adapter to merge
+ return
+
+ for active_adapter in adapter_names:
+ if active_adapter not in self.lora_A.keys():
+ continue
+
+ warnings.warn(
+ "Merge lora module to 4-bit linear may get different generations due to rounding errors."
+ )
+ # Refer to https://gist.github.com/ChrisHayduk/1a53463331f52dca205e55982baf9930
+ weight = self.get_base_layer().weight
+ kwargs = weight.__dict__
+
+ output = dequantize_bnb_weight(weight, state=weight.quant_state)
+ if active_adapter not in self.lora_variant: # vanilla LoRA
+ lora_data = self.get_delta_weight(active_adapter)
+ w_data = output + lora_data
+ else:
+ w_data = self.lora_variant[active_adapter].merge_safe(self, active_adapter, output)
+
+ if safe_merge and not torch.isfinite(w_data).all():
+ raise ValueError(
+ f"NaNs detected in the merged weights. The adapter {active_adapter} seems to be broken"
+ )
+
+ if "bnb_quantized" in kwargs:
+ kwargs["bnb_quantized"] = False
+ kwargs["requires_grad"] = False
+ kwargs.pop("data", None)
+ # torch.compile can introduce attributes preceded by '_', remove them
+ kwargs = {k: v for k, v in kwargs.items() if not k.startswith("_")}
+ self.get_base_layer().weight = bnb.nn.Params4bit(w_data.to("cpu"), **kwargs).to(weight.device)
+
+ if self.lora_bias[active_adapter]:
+ bias_data = self.get_base_layer().bias.data + self.lora_B[active_adapter].bias
+ if safe_merge and not torch.isfinite(bias_data):
+ raise ValueError(
+ f"NaNs detected in the merged weights. The adapter {active_adapter} seems to be broken"
+ )
+ self.get_base_layer().bias.data = bias_data
+
+ self.merged_adapters.append(active_adapter)
+
+ def unmerge(self) -> None:
+ """
+ This method unmerges all merged adapter layers from the base weights.
+ """
+ if not self.merged:
+ warnings.warn("Already unmerged. Nothing to do.")
+ return
+
+ while len(self.merged_adapters) > 0:
+ active_adapter = self.merged_adapters.pop()
+ if active_adapter not in self.lora_A.keys():
+ continue
+ warnings.warn(
+ "Unmerge lora module to 4-bit linear may get different generations due to rounding errors."
+ )
+
+ weight = self.get_base_layer().weight
+ kwargs = weight.__dict__
+ output = dequantize_bnb_weight(weight, state=weight.quant_state)
+
+ if active_adapter not in self.lora_variant: # vanilla LoRA
+ lora_data = self.get_delta_weight(active_adapter)
+ w_data = output - lora_data
+ else:
+ w_data = self.lora_variant[active_adapter].unmerge(self, active_adapter, output)
+
+ if "bnb_quantized" in kwargs:
+ kwargs["bnb_quantized"] = False
+ kwargs["requires_grad"] = False
+ kwargs.pop("data", None)
+ self.get_base_layer().weight = bnb.nn.Params4bit(w_data.to("cpu"), **kwargs).to(weight.device)
+
+ if self.lora_bias[active_adapter]:
+ self.get_base_layer().bias.data -= self.lora_B[active_adapter].bias
+
+ def get_delta_weight(self, adapter):
+ return (
+ transpose(
+ self.lora_B[adapter].weight @ self.lora_A[adapter].weight,
+ False,
+ )
+ * self.scaling[adapter]
+ )
+
+ def _mixed_batch_forward(
+ self, x: torch.Tensor, *args: Any, adapter_names: list[str], **kwargs: Any
+ ) -> torch.Tensor:
+ # This is a special method that handles the case when users pass the argument `adapter_names`. This is an
+ # extra argument that allows mixing different adapters in the same batch at inference time.
+ variant_kwargs = {k: kwargs.pop(k, None) for k in VARIANT_KWARG_KEYS} # don't pass these to base_layer
+ result = self.base_layer(x, *args, **kwargs)
+
+ unique_adapters = set(adapter_names)
+ sub_batch_indices_list = []
+ for adapter in unique_adapters:
+ sub_batch_indices_list.append([index for index, item in enumerate(adapter_names) if item == adapter])
+
+ for i, active_adapter in enumerate(unique_adapters):
+ if active_adapter == "__base__":
+ continue
+ if active_adapter not in self.lora_A.keys():
+ continue
+
+ lora_A = self.lora_A[active_adapter]
+ lora_B = self.lora_B[active_adapter]
+ dropout = self.lora_dropout[active_adapter]
+ scaling = self.scaling[active_adapter]
+
+ requires_conversion = not torch.is_autocast_enabled()
+ if requires_conversion:
+ expected_dtype = result.dtype
+ x = self._cast_input_dtype(x, lora_A.weight.dtype)
+
+ # getting the sub-batch, passing it to LoRA layers and updating the corresponding indices of the linear
+ # layer output
+ sub_batch = x[sub_batch_indices_list[i]]
+ if active_adapter not in self.lora_variant: # vanilla LoRA
+ output = lora_B(lora_A(dropout(sub_batch))) * scaling
+ if requires_conversion:
+ output = output.to(expected_dtype)
+ result[sub_batch_indices_list[i]] += output
+ else:
+ alora_offsets = variant_kwargs.get("alora_offsets", None)
+ if alora_offsets is not None:
+ variant_kwargs["alora_offsets"] = [alora_offsets[j] for j in sub_batch_indices_list[i]]
+ output = self.lora_variant[active_adapter].forward(
+ self,
+ active_adapter=active_adapter,
+ x=sub_batch,
+ result=result[sub_batch_indices_list[i]],
+ **variant_kwargs,
+ **kwargs,
+ )
+ if requires_conversion:
+ output = output.to(expected_dtype)
+ result[sub_batch_indices_list[i]] = output
+
+ return result
+
+ def forward(self, x: torch.Tensor, *args, **kwargs) -> torch.Tensor:
+ self._check_forward_args(x, *args, **kwargs)
+ adapter_names = kwargs.pop("adapter_names", None)
+ variant_kwargs = {k: kwargs.pop(k, None) for k in VARIANT_KWARG_KEYS} # don't pass these to base_layer
+
+ if self.disable_adapters:
+ if self.merged:
+ self.unmerge()
+ result = self.base_layer(x, *args, **kwargs)
+ elif adapter_names is not None:
+ result = self._mixed_batch_forward(x, *args, adapter_names=adapter_names, **variant_kwargs, **kwargs)
+ elif self.merged:
+ result = self.base_layer(x, *args, **kwargs)
+ else:
+ result = self.base_layer(x, *args, **kwargs)
+ # As per Tim Dettmers, for 4bit, we need to defensively clone here.
+ # The reason is that in some cases, an error can occur that backprop
+ # does not work on a manipulated view. This issue may be solved with
+ # newer PyTorch versions but this would need extensive testing to be
+ # sure.
+ result = result.clone()
+
+ for active_adapter in self.active_adapters:
+ if active_adapter not in self.lora_A.keys():
+ continue
+ lora_A = self.lora_A[active_adapter]
+ lora_B = self.lora_B[active_adapter]
+ dropout = self.lora_dropout[active_adapter]
+ scaling = self.scaling[active_adapter]
+
+ requires_conversion = not torch.is_autocast_enabled()
+ if requires_conversion:
+ expected_dtype = result.dtype
+ x = self._cast_input_dtype(x, lora_A.weight.dtype)
+
+ if active_adapter not in self.lora_variant: # vanilla LoRA
+ output = lora_B(lora_A(dropout(x))) * scaling
+ if requires_conversion:
+ output = output.to(expected_dtype)
+ result = result + output
+ else:
+ result = self.lora_variant[active_adapter].forward(
+ self,
+ active_adapter=active_adapter,
+ x=x,
+ result=result,
+ **variant_kwargs,
+ **kwargs,
+ )
+ if requires_conversion:
+ result = result.to(expected_dtype)
+
+ return result
+
+ def __repr__(self) -> str:
+ rep = super().__repr__()
+ return "lora." + rep
+
+ def dispatch_bnb_4bit(target: torch.nn.Module, adapter_name: str, **kwargs):
+ new_module = None
+
+ if isinstance(target, BaseTunerLayer):
+ target_base_layer = target.get_base_layer()
+ else:
+ target_base_layer = target
+
+ loaded_in_4bit = kwargs.get("loaded_in_4bit", False)
+ if loaded_in_4bit and is_bnb_4bit_available() and isinstance(target_base_layer, bnb.nn.Linear4bit):
+ fourbit_kwargs = kwargs.copy()
+ fourbit_kwargs.update(
+ {
+ "compute_dtype": target_base_layer.compute_dtype,
+ "compress_statistics": target_base_layer.weight.compress_statistics,
+ "quant_type": target_base_layer.weight.quant_type,
+ }
+ )
+ new_module = Linear4bit(target, adapter_name, **fourbit_kwargs)
+
+ return new_module
diff --git a/peft/src/peft/tuners/lora/config.py b/peft/src/peft/tuners/lora/config.py
new file mode 100644
index 0000000000000000000000000000000000000000..36ad31ceebe4385cf9be21efad8dd5ec854124bd
--- /dev/null
+++ b/peft/src/peft/tuners/lora/config.py
@@ -0,0 +1,783 @@
+# Copyright 2023-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+from __future__ import annotations
+
+import warnings
+from dataclasses import dataclass, field
+from typing import Literal, Optional, Union
+
+from torch import nn
+
+from peft.config import PeftConfig
+from peft.utils import PeftType
+
+
+@dataclass
+class LoraRuntimeConfig:
+ """
+ This is the sub-configuration class to store the runtime configurations for the model.
+
+ Args:
+ ephemeral_gpu_offload (`bool`):
+ Whether to use ephemeral GPU offloading for models partially kept in CPU memory.
+ """
+
+ ephemeral_gpu_offload: bool = field(
+ default=False,
+ metadata={
+ "help": (
+ "Whether to use ephemeral GPU offloading for models partially kept in CPU memory. Ephemeral GPU offloading result in "
+ "the data involved in intense operations being momentarily copied over to the GPU, and the results copied "
+ "back to CPU. There is a momentary VRAM overhead, but operations are generally orders of magnitude faster "
+ "compared to performing them on the CPU. This is useful when parts of the model and/or components (such "
+ "as adapters) are kept in CPU memory until they are needed. Rather than perform expensive operations on "
+ "small data, the data is transferred to the GPU on-demand, the operation(s) performed, and the results "
+ "moved back to CPU memory. Currently only affects DoRA initialization."
+ )
+ },
+ )
+
+
+@dataclass
+class LoftQConfig:
+ """
+ This is the sub-configuration class to store the configuration of a [`LoraModel`].
+
+ Args:
+ bits_pattern (`dict`): The mapping from layer names or regexp expression to bits which are different from the
+ default bits specified by `bits`. For example, `{model.decoder.layers.0.encoder_attn.k_proj: 2`}.
+ bits (`int`): Quantization bits for LoftQ.
+ iter (`int`): Alternating iterations for LoftQ.
+ fake (`bool`): True: use fp16/fp32; used for first time to save weights. False: use bitsandbytes 4bit linear
+ models. weights can't be saved. Recommend to set to True, save the weights and load the saved weights in 4
+ bits.
+ """
+
+ loftq_bits: int = field(default=4, metadata={"help": "Quantization bits for LoftQ"})
+ loftq_iter: int = field(default=1, metadata={"help": "Alternating iterations for LoftQ"})
+
+
+@dataclass
+class ArrowConfig:
+ """
+ This is the sub-configuration class to store the configuration for Arrow and GenKnowSub algorithm. Arrow is a
+ routing algorithm to combine the trained LoRA modules to solve new tasks, proposed in
+ 'https://arxiv.org/pdf/2405.11157'. GenKnowSub is a refinement on the trained modules before being combined via
+ Arrow, introduced in 'https://aclanthology.org/2025.acl-short.54/'
+ """
+
+ top_k: int = field(
+ default=3,
+ metadata={"help": "Number of top LoRA modules to combine in Arrow routing."},
+ )
+
+ router_temperature: float = field(
+ default=1.0,
+ metadata={"help": "Softmax temperature for computing Arrow expert coefficients."},
+ )
+
+ use_gks: bool = field(
+ default=False,
+ metadata={"help": "Enable GenKnowSub."},
+ )
+
+ task_adapter_names: Optional[list[str]] = field(
+ default=None,
+ init=False,
+ metadata={"help": "list of task-specific LoRA adapter names. It will be set in create_arrow_model()."},
+ )
+
+ gks_adapter_names: Optional[list[str]] = field(
+ default=None,
+ init=False,
+ metadata={
+ "help": "list of general LoRA adapter names for GenKnowSub. It will be set in create_arrow_model()."
+ },
+ )
+
+ rng_seed: Optional[int] = field(
+ default=None,
+ metadata={"help": "Optional RNG seed for reproducibility. If None, sampling is non-deterministic."},
+ )
+
+ def __post_init__(self):
+ if self.top_k <= 0:
+ raise ValueError("top_k cannot be negative.")
+ if self.router_temperature <= 0:
+ raise ValueError("router_temperature must be greater than 0.")
+
+
+@dataclass
+class EvaConfig:
+ """
+ This is the sub-configuration class to store the configuration for a data-driven initialization via EVA. EVA was
+ introduced in Explained Variance Adaptation.
+
+ Args:
+ rho (`float`):
+ Rho value for EVA redistribution (>= 1.0). The maximum rank for a layer is lora_r * rho. Default is 2.0,
+ meaning the maximum rank allowed for a layer is 2r. Increasing rho will allow for a higher degree of
+ redistribution of ranks across layers. Some pre-trained models might be more sensitive to a rank
+ redistribution. It can therefore be beneficial to try rho=1.0 (no redistribution) if the performance is
+ lower than expected.
+ tau (`float`):
+ Cosine similarity threshold for early stopping. Compares the cosine similarity of right-singular vectors
+ between two consecutive SVD steps. If the cosine similarity is above this threshold, the SVD iteration is
+ stopped. Default is 0.99.
+ use_label_mask (`bool`):
+ Use label mask for EVA initialization. This means that positions where labels=label_mask_value are ignored
+ for the SVD computation. Setting use_label_mask=True is preferred in most cases and can be especially
+ beneficial for multi-turn conversations. The default value is True. Filtering out items based on the label
+ mask can sometimes lead to a small batch size and as a result instabilities in the SVD computation. For
+ cases where a large share of batch items would be filtered out, set use_label_mask=False.
+ label_mask_value (`int`):
+ If use_label_mask=True the value to look for to mask out ignored tokens. Default is -100.
+ whiten (`bool`): Apply whitening to singular vectors. Default is False.
+ Whitening has been shown to be beneficial for EVA in the vision domain.
+ adjust_scaling_factors (`bool`):
+ Adjust LoRA scaling factors after the rank redistribution. Setting this to True means the scaling factors
+ are adjusted so that all LoRA gradients have the same scale regardless of their rank. Default is True.
+ """
+
+ rho: float = field(default=2.0, metadata={"help": "Rho value for EVA redistribution"})
+ tau: float = field(default=0.99, metadata={"help": "Cosine similarity threshold for early stopping"})
+ use_label_mask: bool = field(default=True, metadata={"help": "Use label mask for EVA initialization"})
+ label_mask_value: int = field(
+ default=-100, metadata={"help": "if use_label_mask=True the value to look for to mask out ignored tokens"}
+ )
+ whiten: bool = field(default=False, metadata={"help": "Apply whitening to singular vectors"})
+ adjust_scaling_factors: bool = field(
+ default=True,
+ metadata={"help": "Adjust LoRA scaling factors after the rank redistribution"},
+ )
+
+ def __post_init__(self):
+ if self.rho < 1.0:
+ raise ValueError("`rho` must be >= 1.0")
+ if self.tau < 0.0 or self.tau > 1.0:
+ raise ValueError("`tau` must be between 0.0 and 1.0.")
+
+
+@dataclass
+class CordaConfig:
+ """
+ This is the sub-configuration class to store the configuration of a [`LoraModel`].
+
+ Args:
+ cache_file (`Optional[str]`):
+ File to store the SVD cache. The SVD cache is much smaller than the residual model (for example, residual
+ model of Llama-3-8b is 15GB, while SVD cache is 1.4GB), but with SVD cache and original model weights,
+ residual model weights can be built quickly. If you need to reuse residual model weights with limited
+ storage, you can store the SVD cache instead.
+ covariance_file (`Optional[str]`):
+ File to store the covariance matrix. If you wish to train multiple models with different ranks, but they
+ sample from the same dataset, you can store the covariance matrix and reuse it for different ranks. Note
+ that covariance file is usually large (comparable to model size), so you will need sufficient storage.
+ corda_method (`Literal["ipm", "kpm"]`):
+ Method to build adapter. The KPM (Knowledge-Preserved Mode) not only achieves better performance than LoRA
+ on fine-tuning tasks, but also mitigates the catastrophic forgetting of pre-trained world knowledge. When
+ preserving pre-trained knowledge is not a concern, the IPM (Instruction-Previewed Mode) is favored because
+ it can further accelerate convergence and enhance the fine-tuning performance. Defaults to `'ipm'`.
+ verbose (`bool`):
+ If true, prints the progress of CorDA initialization. Defaults to `False`.
+ use_float16_for_covariance (`bool`):
+ If true, uses float16 for the covariance matrix. This can reduce the memory usage of the covariance matrix
+ by half, but may lead to numerical instability. Defaults to `False`.
+ prune_temporary_fields (`bool`):
+ If true, temporary fields generated in CorDA preprocessing will be pruned. Defaults to `True`.
+ """
+
+ cache_file: Optional[str] = field(
+ default=None,
+ metadata={
+ "help": (
+ "File to store the SVD cache. The SVD cache is much smaller than the residual model (for example, "
+ "residual model of Llama-3-8b is 15GB, while SVD cache is 1.4GB), but with SVD cache and original model "
+ "weights, residual model weights can be built quickly. If you need to reuse residual model weights with "
+ "limited storage, you can store the SVD cache instead."
+ )
+ },
+ )
+ covariance_file: Optional[str] = field(
+ default=None,
+ metadata={
+ "help": (
+ "File to store the covariance matrix. If you wish to train multiple models with different ranks, but "
+ "they sample from the same dataset, you can store the covariance matrix and reuse it for different ranks. "
+ "Note that covariance file is usually large (comparable to model size), so you will need sufficient storage."
+ )
+ },
+ )
+ corda_method: Literal["ipm", "kpm"] = field(
+ default="ipm",
+ metadata={
+ "help": (
+ "Method to build adapter. The KPM not only achieves better performance than LoRA on fine-tuning tasks, but "
+ "also mitigates the catastrophic forgetting of pre-trained world knowledge. When preserving pre-trained "
+ "knowledge is not a concern, the IPM is favored because it can further accelerate convergence and enhance "
+ "the fine-tuning performance."
+ )
+ },
+ )
+ verbose: bool = field(default=False, metadata={"help": "If true, prints the progress of CorDA initialization."})
+ use_float16_for_covariance: bool = field(
+ default=False,
+ metadata={
+ "help": (
+ "If true, uses float16 for the covariance matrix. This can reduce the memory usage of the covariance matrix "
+ "by half, but may lead to numerical instability."
+ )
+ },
+ )
+ prune_temporary_fields: bool = field(
+ default=True, metadata={"help": "If true, temporary fields generated in CorDA preprocessing will be pruned."}
+ )
+
+
+@dataclass
+class LoraConfig(PeftConfig):
+ """
+ This is the configuration class to store the configuration of a [`LoraModel`].
+
+ Args:
+ r (`int`):
+ Lora attention dimension (the "rank").
+ target_modules (`Optional[Union[List[str], str]]`):
+ The names of the modules to apply the adapter to. If this is specified, only the modules with the specified
+ names will be replaced. When passing a string, a regex match will be performed. When passing a list of
+ strings, either an exact match will be performed or it is checked if the name of the module ends with any
+ of the passed strings. If this is specified as 'all-linear', then all linear/Conv1D modules are chosen (if
+ the model is a PreTrainedModel, the output layer excluded). If this is not specified, modules will be
+ chosen according to the model architecture. If the architecture is not known, an error will be raised -- in
+ this case, you should specify the target modules manually. To avoid targeting any modules (because you want
+ to apply `target_parameters`), set `target_modules=[]`.
+ exclude_modules (`Optional[Union[List[str], str]]`):
+ The names of the modules to not apply the adapter. When passing a string, a regex match will be performed.
+ When passing a list of strings, either an exact match will be performed or it is checked if the name of the
+ module ends with any of the passed strings.
+ lora_alpha (`int`):
+ The alpha parameter for Lora scaling.
+ lora_dropout (`float`):
+ The dropout probability for Lora layers.
+ fan_in_fan_out (`bool`):
+ Set this to True if the layer to replace stores weight like (fan_in, fan_out). For example, gpt-2 uses
+ `Conv1D` which stores weights like (fan_in, fan_out) and hence this should be set to `True`.
+ bias (`str`):
+ Bias type for LoRA. Can be 'none', 'all' or 'lora_only'. If 'all' or 'lora_only', the corresponding biases
+ will be updated during training. Be aware that this means that, even when disabling the adapters, the model
+ will not produce the same output as the base model would have without adaptation.
+ use_rslora (`bool`):
+ When set to True, uses [Rank-Stabilized LoRA](https://huggingface.co/papers/2312.03732) which sets the
+ adapter scaling factor to `lora_alpha/math.sqrt(r)`, since it was proven to work better. Otherwise, it will
+ use the original default value of `lora_alpha/r`.
+ modules_to_save (`List[str]`):
+ List of modules apart from adapter layers to be set as trainable and saved in the final checkpoint.
+ init_lora_weights (`bool` | `Literal["gaussian", "eva", "olora", "pissa", "pissa_niter_[number of iters]", "corda", "loftq", "orthogonal"]`):
+ How to initialize the weights of the adapter layers. Passing True (default) results in the default
+ initialization from the reference implementation from Microsoft, with the LoRA B weight being set to 0.
+ This means that without further training, the LoRA adapter will be a no-op. Setting the initialization to
+ False leads to random initialization of LoRA A and B, meaning that LoRA is not a no-op before training;
+ this setting is intended for debugging purposes. Passing 'gaussian' results in Gaussian initialization
+ scaled by the LoRA rank for linear and layers. Pass `'loftq'` to use LoftQ initialization. Passing `'eva'`
+ results in a data-driven initialization of Explained
+ Variance Adaptation. EVA initializes LoRA based on the SVD of layer input activations and achieves SOTA
+ performance due to its ability to adapt to the finetuning data. Pass `'olora'` to use OLoRA initialization.
+ Passing `'pissa'` results in the initialization of Principal Singular values and Singular vectors Adaptation (PiSSA), which converges more rapidly than
+ LoRA and ultimately achieves superior performance. Moreover, PiSSA reduces the quantization error compared
+ to QLoRA, leading to further enhancements. Passing `'pissa_niter_[number of iters]'` initiates
+ Fast-SVD-based PiSSA initialization, where `[number of iters]` indicates the number of subspace iterations
+ to perform FSVD, and must be a nonnegative integer. When `[number of iters]` is set to 16, it can complete
+ the initialization of a 7B model within seconds, and the training effect is approximately equivalent to
+ using SVD. Passing `'corda'` results in the initialization of Context-Oriented Decomposition Adaptation, which
+ converges even more rapidly than PiSSA in Instruction-Previewed Mode, and preserves world knowledge better
+ than LoRA in Knowledge-Preserved Mode. Passing `"orthogonal"` results in LoRA A and B being intialized
+ orthogonally; in this, it resembles `"olora"`, but the base weights are left untouched (requires `r` to be
+ even, only supported for linear layers for now).
+ layers_to_transform (`Union[List[int], int]`):
+ The layer indices to transform. If a list of ints is passed, it will apply the adapter to the layer indices
+ that are specified in this list. If a single integer is passed, it will apply the transformations on the
+ layer at this index.
+ layers_pattern (`Optional[Union[List[str], str]]`):
+ The layer pattern name, used only if `layers_to_transform` is different from `None`. This should target the
+ `nn.ModuleList` of the model, which is often called `'layers'` or `'h'`.
+ rank_pattern (`dict`):
+ The mapping from layer names or regexp expression to ranks which are different from the default rank
+ specified by `r`. For example, `{'^model.decoder.layers.0.encoder_attn.k_proj': 16}`.
+ alpha_pattern (`dict`):
+ The mapping from layer names or regexp expression to alphas which are different from the default alpha
+ specified by `lora_alpha`. For example, `{'^model.decoder.layers.0.encoder_attn.k_proj': 16}`.
+ megatron_config (`Optional[dict]`):
+ The TransformerConfig arguments for Megatron. It is used to create LoRA's parallel linear layer. You can
+ get it like this, `core_transformer_config_from_args(get_args())`, these two functions being from Megatron.
+ The arguments will be used to initialize the TransformerConfig of Megatron. You need to specify this
+ parameter when you want to apply LoRA to the ColumnParallelLinear and RowParallelLinear layers of megatron.
+ megatron_core (`Optional[str]`):
+ The core module from Megatron to use, defaults to `"megatron.core"`.
+ trainable_token_indices (`Optional[Union[List[int], dict[str, List[int]]]]`)
+ Lets you specify which token indices to selectively fine-tune without requiring to re-train the whole
+ embedding matrix using the `peft.TrainableTokensModel` method. You can specify token indices in two ways.
+ Either you specify a list of indices which will then target the model's input embedding layer (or, if not
+ found, `embed_tokens`). Alternatively, you can specify a dictionary where the key is the name of the
+ embedding module and the values are the list of token indices, e.g. `{'embed_tokens': [0, 1, ...]}`. Note
+ that training with FSDP requires `use_orig_params=True` to avoid issues with non-uniform `requires_grad`.
+ loftq_config (`Optional[LoftQConfig]`):
+ The configuration of LoftQ. If this is not None, then LoftQ will be used to quantize the backbone weights
+ and initialize Lora layers. Also pass `init_lora_weights='loftq'`. Note that you should not pass a
+ quantized model in this case, as LoftQ will quantize the model itself.
+ eva_config (`Optional[EvaConfig]`):
+ The configuration of EVA. At a minimum the dataset argument needs to be set (use the same dataset as for
+ finetuning).
+ corda_config (`Optional[CordaConfig]`):
+ The configuration of CorDA. If this is not None, then CorDA will be used to build the adapter layers. Also
+ pass `init_lora_weights='corda'`.
+ use_dora (`bool`):
+ Enable 'Weight-Decomposed Low-Rank Adaptation' (DoRA). This technique decomposes the updates of the weights
+ into two parts, magnitude and direction. Direction is handled by normal LoRA, whereas the magnitude is
+ handled by a separate learnable parameter. This can improve the performance of LoRA especially at low
+ ranks. Right now, DoRA only supports linear and Conv2D layers. DoRA introduces a bigger overhead than pure
+ LoRA, so it is recommended to merge weights for inference. For more information, see
+ https://huggingface.co/papers/2402.09353.
+ alora_invocation_tokens (`List[int]`):
+ If not None, enable 'Activated LoRA' (aLoRA), with
+ alora_invocation_tokens being the tokenized invocation string for the adapter (must be present in all model
+ input strings). This technique selectively activates the adapter weights only on tokens during and after
+ the alora_invocation_tokens. When used in a CausalLM, this means that the KV cache prior to invocation is
+ interchangeable with that of the base model (and other aLoRA adapters operating this way). As a result, in
+ inference pipelines involving switching between base model inference and adapter inference (e.g. agentic
+ pipelines, see paper for examples), significant savings are realized (relative to LoRA) by saving prefill
+ operations. Overall adapter inference speedups of an order of magnitude or more can occur on vLLM,
+ depending on the length of the shared context. Note that merging is not possible due to the selective
+ application of the weights.
+ layer_replication (`List[Tuple[int, int]]`):
+ Build a new stack of layers by stacking the original model layers according to the ranges specified. This
+ allows expanding (or shrinking) the model without duplicating the base model weights. The new layers will
+ all have separate LoRA adapters attached to them.
+ runtime_config (`LoraRuntimeConfig`):
+ Runtime configurations (which are not saved or restored).
+ lora_bias (`bool`):
+ Defaults to `False`. Whether to enable the bias term for the LoRA B parameter. Typically, this should be
+ disabled. The main use case for this is when the LoRA weights were extracted from fully fine-tuned
+ parameters so the bias of those parameters can be taken into account.
+ target_parameters (`List[str]`, *optional*)
+ List of parameter names or regex expression of the parameter names to replace with LoRA. This argument
+ behaves similarly to `target_modules`, except that the parameter name should be passed. Generally, you
+ should use `target_modules` to target the module (e.g. `nn.Linear`). However, in some circumstances, this
+ is not possible. E.g., in many mixture of expert (MoE) layers in HF Transformers, instead of using
+ `nn.Linear`, an `nn.Parameter` is used. PEFT normally overwrites the `forward` method for LoRA, but for
+ `nn.Parameter`, there is none. Therefore, to apply LoRA to that parameter, it needs to be targeted with
+ `target_parameters`. As an example, for Llama4, you can pass:
+ `target_parameters=['feed_forward.experts.gate_up_proj', 'feed_forward.experts.down_proj]`. Passing a
+ string for regex matching is not implemented yet.
+ """
+
+ r: int = field(default=8, metadata={"help": "Lora attention dimension"})
+ target_modules: Optional[Union[list[str], str]] = field(
+ default=None,
+ metadata={
+ "help": (
+ "List of module names or regex expression of the module names to replace with LoRA. "
+ "For example, ['q', 'v'] or '.*decoder.*(SelfAttention|EncDecAttention).*(q|v)$'. "
+ "This can also be a wildcard 'all-linear' which matches all linear/Conv1D "
+ "(if the model is a PreTrainedModel, the output layer excluded). "
+ "If not specified, modules will be chosen according to the model architecture, If the architecture is "
+ "not known, an error will be raised -- in this case, you should specify the target modules manually. "
+ "To avoid targeting any modules (because you want to apply `target_parameters`), set "
+ "`target_modules=[]`."
+ ),
+ },
+ )
+ exclude_modules: Optional[Union[list[str], str]] = field(
+ default=None,
+ metadata={"help": "List of module names or regex expression of the module names to exclude from Lora."},
+ )
+ lora_alpha: int = field(default=8, metadata={"help": "Lora alpha"})
+ lora_dropout: float = field(default=0.0, metadata={"help": "Lora dropout"})
+ fan_in_fan_out: bool = field(
+ default=False,
+ metadata={"help": "Set this to True if the layer to replace stores weight like (fan_in, fan_out)"},
+ )
+ bias: Literal["none", "all", "lora_only"] = field(
+ default="none", metadata={"help": "Bias type for Lora. Can be 'none', 'all' or 'lora_only'"}
+ )
+ use_rslora: bool = field(
+ default=False,
+ metadata={
+ "help": (
+ "When set to True, uses [Rank-Stabilized LoRA](https://huggingface.co/papers/2312.03732)"
+ " which sets the adapter scaling factor to `lora_alpha/math.sqrt(r)`, since it"
+ " was proven to work better. Otherwise, it will use the original default"
+ " value of `lora_alpha/r`."
+ )
+ },
+ )
+ modules_to_save: Optional[list[str]] = field(
+ default=None,
+ metadata={
+ "help": "List of modules apart from LoRA layers to be set as trainable and saved in the final checkpoint. "
+ "For example, in Sequence Classification or Token Classification tasks, "
+ "the final layer `classifier/score` are randomly initialized and as such need to be trainable and saved."
+ },
+ )
+ init_lora_weights: (
+ bool
+ | Literal["gaussian", "eva", "olora", "pissa", "pissa_niter_[number of iters]", "corda", "loftq", "orthogonal"]
+ ) = field(
+ default=True,
+ metadata={
+ "help": (
+ "How to initialize the weights of the LoRA layers. "
+ "Passing True (default) results in the default initialization from the reference implementation from "
+ "Microsoft, with the LoRA B weight being set to 0. This means that without further training, the LoRA "
+ "adapter will be a no-op. "
+ "Setting the initialization to False leads to random initialization of LoRA A and B, meaning that LoRA "
+ "is not a no-op before training; this setting is intended for debugging purposes. "
+ "Passing `'gaussian'` results in Gaussian initialization scaled by the LoRA rank for linear and layers. "
+ "Passing `'eva'` results in a data-driven initialization of Explained Variance Adaptation. "
+ "Passing `'olora'` results in OLoRA initialization. "
+ "Passing `'pissa'` results in PiSSA initialization. "
+ "Passing `'pissa_niter_[number of iters]'` initiates Fast-SVD-based PiSSA initialization, where "
+ "[number of iters] indicates the number of subspace iterations to perform fsvd, and must be a "
+ "nonnegative integer. "
+ "Passing `'corda'` results in CorDA initialization. "
+ "Pass `'loftq'` to use LoftQ initialization. "
+ "Pass `'orthogonal'` for orthogonal initialization of LoRA A and B."
+ ),
+ },
+ )
+ layers_to_transform: Optional[Union[list[int], int]] = field(
+ default=None,
+ metadata={
+ "help": "The layer indexes to transform, is this argument is specified, PEFT will transform only the layers indexes that are specified inside this list. If a single integer is passed, PEFT will transform only the layer at this index. "
+ "This only works when target_modules is a list of str."
+ },
+ )
+ layers_pattern: Optional[Union[list[str], str]] = field(
+ default=None,
+ metadata={
+ "help": "The layer pattern name, used only if `layers_to_transform` is different to None and if the layer pattern is not in the common layers pattern."
+ "This only works when target_modules is a list of str. This should target the `nn.ModuleList` of the "
+ "model, which is often called `'layers'` or `'h'`."
+ },
+ )
+ rank_pattern: Optional[dict] = field(
+ default_factory=dict,
+ metadata={
+ "help": (
+ "The mapping from layer names or regexp expression to ranks which are different from the default rank specified by `r`. "
+ "For example, `{'^model.decoder.layers.0.encoder_attn.k_proj': 16}`."
+ )
+ },
+ )
+ alpha_pattern: Optional[dict] = field(
+ default_factory=dict,
+ metadata={
+ "help": (
+ "The mapping from layer names or regexp expression to alphas which are different from the default alpha specified by `lora_alpha`. "
+ "For example, `{'^model.decoder.layers.0.encoder_attn.k_proj': 16}`."
+ )
+ },
+ )
+ megatron_config: Optional[dict] = field(
+ default=None,
+ metadata={
+ "help": (
+ "The TransformerConfig from Megatron. It is used to create LoRA's parallel linear layer."
+ "You can get it like this, `core_transformer_config_from_args(get_args())`, "
+ "these two functions being from Megatron."
+ "You need to specify this parameter when you want to apply LoRA to the ColumnParallelLinear and "
+ "RowParallelLinear layers of megatron."
+ "It should be noted that we may not be able to use the `save_pretrained` and `from_pretrained` "
+ "functions, because TransformerConfig may not necessarily be serialized."
+ "But when using megatron, we can use `get_peft_model_state_dict` function and "
+ "megatron's framework, they can also save and load models and configurations."
+ )
+ },
+ )
+ megatron_core: Optional[str] = field(
+ default="megatron.core",
+ metadata={
+ "help": (
+ "The core module from Megatron, it is used to create LoRA's parallel linear layer. "
+ "It only needs to be passed in when you need to use your own modified megatron core module. "
+ "Otherwise, it will use the default value `megatron.core`. "
+ )
+ },
+ )
+ trainable_token_indices: Optional[Union[list[int], dict[str, list[int]]]] = field(
+ default=None,
+ metadata={
+ "help": (
+ "Lets you specify which token indices to selectively fine-tune without requiring to re-train the "
+ "whole embedding matrix using the `peft.TrainableTokensModel` method. You can specify token indices "
+ "in two ways. Either you specify a list of indices which will then target the model's input embedding "
+ "layer (or, if not found, `embed_tokens`). Alternatively, you can specify a dictionary where the key "
+ "is the name of the embedding module and the values are the list of token indices, e.g. "
+ "`{'embed_tokens': [0, 1, ...]}`. Note that training with FSDP requires `use_orig_params=True` to "
+ "avoid issues with non-uniform `requires_grad`."
+ )
+ },
+ )
+ # dict type is used when loading config.json
+ loftq_config: Union[LoftQConfig, dict] = field(
+ default_factory=dict,
+ metadata={
+ "help": (
+ "The configuration of LoftQ. If this is passed, then LoftQ will be used to quantize the backbone "
+ "weights and initialize Lora layers. Also set `init_lora_weights='loftq'` in this case."
+ )
+ },
+ )
+ eva_config: Optional[EvaConfig] = field(
+ default=None,
+ metadata={
+ "help": (
+ "The configuration of EVA. If this is passed, then EVA will be used to initialize the LoRA layers. "
+ "Also set `init_lora_weights='eva'` in this case. "
+ )
+ },
+ )
+ corda_config: Optional[CordaConfig] = field(
+ default=None,
+ metadata={
+ "help": (
+ "The configuration of CorDA. If this is passed, then CorDA will be used to build the adapter layers. "
+ "Also set `init_lora_weights='corda'` in this case."
+ )
+ },
+ )
+ use_dora: bool = field(
+ default=False,
+ metadata={
+ "help": (
+ "Enable 'Weight-Decomposed Low-Rank Adaptation' (DoRA). This technique decomposes the updates of the "
+ "weights into two parts, magnitude and direction. Direction is handled by normal LoRA, whereas the "
+ "magnitude is handled by a separate learnable parameter. This can improve the performance of LoRA, "
+ "especially at low ranks. Right now, DoRA only supports linear and Conv2D layers. DoRA introduces a bigger"
+ "overhead than pure LoRA, so it is recommended to merge weights for inference."
+ )
+ },
+ )
+ alora_invocation_tokens: Optional[list[int]] = field(
+ default=None,
+ metadata={
+ "help": (
+ "If not None, enable 'Activated LoRA' (aLoRA), with "
+ "alora_invocation_tokens being the tokenized invocation string for the adapter (must be present in all model "
+ "input strings). This technique selectively activates the adapter weights only on tokens during and after "
+ "the alora_invocation_tokens. When used in a CausalLM, this means that the KV cache prior to invocation is "
+ "interchangeable with that of the base model (and other aLoRA adapters operating this way). As a result, in "
+ "inference pipelines involving switching between base model inference and adapter inference (e.g. agentic "
+ "pipelines, see paper for examples), significant savings are realized (relative to LoRA) by saving prefill "
+ "operations. Overall adapter inference speedups of an order of magnitude or more can occur on vLLM, "
+ "depending on the length of the shared context. Note that merging is not possible due to the selective "
+ "application of the weights."
+ )
+ },
+ )
+ use_qalora: bool = field(
+ default=False,
+ metadata={
+ "help": (
+ "It is only implemented in GPTQ for now. Enable Quantization-Aware Low-Rank Adaptation (QALoRA)."
+ "This technique combines quantization-aware training "
+ "with LoRA to improve performance for quantized models. This can improve the performance of LoRA, "
+ "especially at low ranks. Right now, QALoRA only supports linear layers."
+ )
+ },
+ )
+ qalora_group_size: int = field(
+ default=16,
+ metadata={
+ "help": (
+ "Group size parameter for QALoRA pooling, controlling the dimension reduction factor. "
+ "Input dimensions are pooled into groups of this size, reducing the computational cost. "
+ "Higher values provide more compression but may reduce model quality. "
+ "This parameter determines how many original features are averaged together to create "
+ "one pooled feature. Only used when `use_qalora=True`."
+ )
+ },
+ )
+ # Enables replicating layers in a model to expand it to a larger model.
+ layer_replication: Optional[list[tuple[int, int]]] = field(
+ default=None,
+ metadata={
+ "help": (
+ "This enables using LoRA to effectively expand a transformer model to a larger size by repeating some layers. "
+ "The transformation handles models (currently Llama, Bert or Falcon compatible architectures) with "
+ "a module list in the model which it modifies to expand the number of modules. "
+ "Base weights are shared so the memory usage is close to the original model. The intended use is these base weights "
+ "remain fixed during finetuning but each layer has a separate LoRA adapter so the layers can be specialed via "
+ "the adapter layers fit during fine tuning."
+ "The format is a list of [start, end) pairs which specify the layer ranges to stack. For example:\n"
+ " Original model has 5 layers labelled by their position in the model: `[0, 1, 2, 3, 4]`\n"
+ " layer_replication: `[[0, 4], [2, 5]]`\n"
+ " Final model will have this arrangement of original layers: `[0, 1, 2, 3, 2, 3, 4]`\n"
+ "This format is based on what is used for pass-through merges in mergekit. It makes it simple to select sequential "
+ "ranges of a model and stack them while reusing layers at either end of each sequence."
+ )
+ },
+ )
+ runtime_config: LoraRuntimeConfig = field(
+ default_factory=LoraRuntimeConfig, metadata={"help": "Runtime configurations"}
+ )
+ lora_bias: bool = field(
+ default=False,
+ metadata={
+ "help": (
+ "Whether to enable the bias term for the LoRA B parameter. Typically, this should be disabled. The "
+ "main use case for this is when the LoRA weights were extracted from fully fine-tuned parameters so "
+ "the bias of those parameters can be taken into account."
+ )
+ },
+ )
+ target_parameters: Optional[list[str]] = field(
+ default=None,
+ metadata={
+ "help": (
+ "List of parameter names or regex expression of the parameter names to replace with LoRA. "
+ "This argument behaves similarly to `target_modules`, except that the parameter name should be passed. "
+ "Generally, you should use `target_modules` to target the module (e.g. `nn.Linear`). However, in some "
+ "circumstances, this is not possible. E.g., in many mixture of expert (MoE) layers in HF Transformers, "
+ "instead of using `nn.Linear`, an `nn.Parameter` is used. PEFT normally overwrites the `forward` "
+ "method for LoRA, but for `nn.Parameter`, there is none. Therefore, to apply LoRA to that parameter, "
+ "it needs to be targeted with `target_parameters`. As an example, for Llama4, you can pass: "
+ "`target_parameters=['feed_forward.experts.gate_up_proj', 'feed_forward.experts.down_proj]`. Passing a "
+ "string for regex matching is not implemented yet."
+ )
+ },
+ )
+ arrow_config: Optional[ArrowConfig] = field(
+ default=None, metadata={"help": "The necessary config to apply arrow routing on the model."}
+ )
+
+ def to_dict(self):
+ """
+ Returns the configuration for your adapter model as a dictionary. Removes runtime configurations.
+ """
+ rv = super().to_dict()
+ rv.pop("runtime_config")
+ return rv
+
+ def __post_init__(self):
+ super().__post_init__()
+ self.peft_type = PeftType.LORA
+ self.target_modules = (
+ set(self.target_modules) if isinstance(self.target_modules, list) else self.target_modules
+ )
+ self.exclude_modules = (
+ set(self.exclude_modules) if isinstance(self.exclude_modules, list) else self.exclude_modules
+ )
+ if isinstance(self.target_parameters, str):
+ raise TypeError("`target_parameters` must be a list of strings or None.")
+
+ # if target_modules is a regex expression, then layers_to_transform should be None
+ if isinstance(self.target_modules, str) and self.layers_to_transform is not None:
+ raise ValueError("`layers_to_transform` cannot be used when `target_modules` is a str.")
+
+ # if target_modules is a regex expression, then layers_pattern should be None
+ if isinstance(self.target_modules, str) and self.layers_pattern is not None:
+ raise ValueError("`layers_pattern` cannot be used when `target_modules` is a str.")
+
+ # check for layers_to_transform and layers_pattern
+ if self.layers_pattern and not self.layers_to_transform:
+ raise ValueError("When `layers_pattern` is specified, `layers_to_transform` must also be specified. ")
+
+ if self.use_dora and self.megatron_config:
+ raise ValueError("DoRA does not support megatron_core, please set `use_dora=False`.")
+
+ # handle init_lora_weights and loftq_config
+ if self.init_lora_weights == "loftq":
+ import importlib
+
+ if not importlib.util.find_spec("scipy"):
+ raise ImportError("The required package 'scipy' is not installed. Please install it to continue.")
+ if not self.loftq_config:
+ raise ValueError("`loftq_config` must be specified when `init_lora_weights` is 'loftq'.")
+ if not isinstance(self.loftq_config, dict):
+ # convert loftq_config to dict
+ self.loftq_config = vars(self.loftq_config)
+ elif self.loftq_config:
+ self.loftq_config = {}
+ warnings.warn("`loftq_config` specified but will be ignored when `init_lora_weights` is not 'loftq'.")
+
+ elif self.init_lora_weights == "eva" and self.eva_config is None:
+ warnings.warn("`init_lora_weights` is 'eva' but `eva_config` is not specified. Using default EVA config.")
+ self.eva_config = EvaConfig()
+ elif self.init_lora_weights != "eva" and self.eva_config is not None:
+ warnings.warn("`eva_config` specified but will be ignored when `init_lora_weights` is not 'eva'.")
+
+ elif self.init_lora_weights == "corda" and self.corda_config is None:
+ warnings.warn(
+ "`init_lora_weights` is 'corda' but `corda_config` is not specified. Using default CorDA config."
+ )
+ self.corda_config = CordaConfig()
+ elif self.init_lora_weights != "corda" and self.corda_config is not None:
+ warnings.warn("`corda_config` specified but will be ignored when `init_lora_weights` is not 'corda'.")
+
+ if self.lora_bias:
+ if self.init_lora_weights not in (True, False):
+ raise ValueError(
+ f"The argument lora_bias=True is only supported with init_lora_weights=True or False, got "
+ f"init_lora_weights={self.init_lora_weights} instead."
+ )
+ if self.use_dora:
+ raise ValueError("The argument lora_bias=True is not supported for DoRA, please pass use_dora=False")
+
+ if self.alora_invocation_tokens is not None and self.task_type != "CAUSAL_LM":
+ warnings.warn("aLoRA is currently only supported for CAUSAL_LM task.")
+
+ # Using post training conversion of modified base weights to restore their initial values PiSSA/CorDA/OLoRA cannot
+ # be correctly done when using rslora + rank_pattern/alpha_pattern. We can't really know if the user intends
+ # this when they'll eventually call save_pretrained (i.e. if they'll pass
+ # path_initial_model_for_weight_conversionl). Therefore, we only warn but don't raise an error here.
+ if (
+ self.use_rslora
+ and (self.rank_pattern or self.alpha_pattern)
+ and (
+ (isinstance(self.init_lora_weights, str) and (self.init_lora_weights.startswith("pissa")))
+ or (self.init_lora_weights == "olora")
+ or (self.init_lora_weights == "corda")
+ )
+ ):
+ msg = (
+ "Using Rank-Stabilized LoRA with rank_pattern/alpha_pattern and post-training conversion of modified "
+ "base weights PiSSA/CorDA/OLoRA means that you won't be able to pass "
+ "`path_initial_model_for_weight_conversion` to `save_pretrained` to restore the initial values of the "
+ "base weights; if you intend to do this, please ensure not to use rslora or rank_pattern/alpha_pattern."
+ )
+ warnings.warn(msg)
+
+ self._custom_modules: Optional[dict[type[nn.Module], type[nn.Module]]] = None
+
+ def _register_custom_module(self, mapping: dict[type[nn.Module], type[nn.Module]]) -> None:
+ """
+ Experimental API to support providing custom LoRA layers.
+
+ This API is subject to change, you should carefully read the docs before deciding to use it:
+
+ https://huggingface.co/docs/peft/developer_guides/custom_models
+
+ To register custom LoRA module types, call this method with a `mapping` argument that is a dict that maps from
+ the target layer type to the custom LoRA layer type. The dict can contain multiple items if you wish to target
+ multiple layer types. The target layer type can be any nn.Module that we currently don't support in PEFT,
+ whether that is an official PyTorch layer type or a custom layer type. The custom LoRA module class has to be
+ implemented by the user and follow the PEFT conventions for LoRA layers.
+
+ """
+ if self._custom_modules is None:
+ self._custom_modules = {}
+ self._custom_modules.update(mapping)
diff --git a/peft/src/peft/tuners/lora/corda.py b/peft/src/peft/tuners/lora/corda.py
new file mode 100644
index 0000000000000000000000000000000000000000..d9eba35eb8a55ee76324c32e4bbfac127506633d
--- /dev/null
+++ b/peft/src/peft/tuners/lora/corda.py
@@ -0,0 +1,360 @@
+# Copyright 2024-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+# Reference code: https://github.com/iboing/CorDA/blob/main/cordalib/decomposition.py
+# Reference paper: https://huggingface.co/papers/2406.05223
+
+import os
+from collections.abc import Iterable
+from typing import Any, Callable, Optional
+
+import torch
+import torch.nn as nn
+from attr import dataclass
+from tqdm import tqdm
+
+from peft.tuners.lora.config import LoraConfig
+from peft.tuners.lora.model import LoraModel
+from peft.utils.other import get_pattern_key
+
+
+@dataclass
+class CordaEigens:
+ S_WC: torch.Tensor
+ U_WC: torch.Tensor
+ V_WC: torch.Tensor
+
+
+def target_modules(model: nn.Module, config: LoraConfig) -> Iterable[nn.Module]:
+ """
+ Iterate over CorDA target name and modules of a model. A module is a target if its name is in
+ `config.target_modules` and is `nn.Linear`.
+ """
+ for name, module in model.named_modules():
+ if LoraModel._check_target_module_exists(config, name) and isinstance(module, nn.Linear):
+ yield name, module
+
+
+def get_model_device(model: nn.Module) -> str:
+ if hasattr(model, "module"): # Handle DeepSpeed/DataParallel
+ model = model.module
+ return next(iter(model.parameters())).device.type
+
+
+@torch.no_grad()
+def preprocess_corda(
+ model: nn.Module,
+ lora_config: LoraConfig,
+ run_model: Optional[Callable[[], None]] = None,
+ hooked_model: Optional[nn.Module] = None,
+):
+ """
+ Build necessary CorDA fields for a model.
+
+ For each `M * N` linear layer, a `M * M` covariance matrix will be built temporarily during the preprocessing
+ process, consuming roughly another `2 * MODEL_SIZE` memory for typical LLMs if model weight is FP16 and covariance
+ is FP32. If that's too much, consider specifying `use_float16_for_covariance` in `lora_config.corda_config`.
+
+ Args:
+ model (`nn.Module`):
+ Model to preprocess.
+ lora_config (`LoraConfig`):
+ Lora configuration of the model. `lora_config.corda_config` should be set.
+ run_model (`Optional[Callable[[], None]]`):
+ Callback to run the model when building covariance. Typically you should run model inference on your sample
+ dataset in this callback. Experiments have shown that when token count per sample is 2048, hidden dimension
+ is 4096, collecting 256 distinct samples is enough. If you collect too few or too repetitive samples, the
+ covariance matrix may be low-ranked and unstabilize preprocessing. You can estimate sample count as
+ `HIDDEN_DIM / TOKEN_PER_SAMPLE * 128`. `run_model` can be `None` only if covariance file in
+ `lora_config.corda_config` is already created.
+ hooked_model (`Optional[nn.Module]`):
+ Model to hook when building covariance. If none, original model will be hooked. This is only useful when
+ you want to hook a different model than the one you are training, typically you should leave this `None`.
+
+ Upon completion, the following fields are set for each target module:
+ eigens.S_WC (`torch.Tensor`):
+ Singular values of the weight matrix.
+ eigens.U_WC (`torch.Tensor`):
+ Left singular vectors of the weight matrix.
+ eigens.V_WC (`torch.Tensor`):
+ Right singular vectors of the weight matrix, multiplied by inverse of covariance matrix.
+ """
+ cache_file = lora_config.corda_config.cache_file
+ covariance_file = lora_config.corda_config.covariance_file
+ corda_method = lora_config.corda_config.corda_method
+ verbose = lora_config.corda_config.verbose
+ prune_temporary_fields = lora_config.corda_config.prune_temporary_fields
+
+ # If cache exists, skip building
+ if cache_file is not None and os.path.exists(cache_file) and os.path.getsize(cache_file) > 0:
+ cache = torch.load(cache_file, map_location=get_model_device(model))
+ for name, module in target_modules(model, lora_config):
+ module.eigens = CordaEigens(
+ S_WC=cache[f"{name}.eigens.S_WC"],
+ U_WC=cache[f"{name}.eigens.U_WC"],
+ V_WC=cache[f"{name}.eigens.V_WC"],
+ )
+ else:
+ # Specify CorDA method for each layer
+ if corda_method is None:
+ raise ValueError("corda_method is required when cache_file is not provided.")
+ for name, module in target_modules(model, lora_config):
+ module.corda_method = corda_method
+
+ # Specify CorDA rank for each layer
+ for name, module in target_modules(model, lora_config):
+ r_key = get_pattern_key(lora_config.rank_pattern.keys(), name)
+ module.rank = lora_config.rank_pattern.get(r_key, lora_config.r)
+
+ # Calculate covariance matrix
+ calib_cov_distribution(model, lora_config, run_model, hooked_model, covariance_file)
+
+ # Calculate eigens
+ collect_eigens(model, lora_config, verbose)
+
+ # Crop CorDA eigens so that there's less to save
+ crop_corda_eigens(model, lora_config)
+
+ # Remove redundant fields if exist
+ if prune_temporary_fields:
+ for name, module in target_modules(model, lora_config):
+ if hasattr(module, "sample_count"):
+ del module.sample_count
+ if hasattr(module, "covariance_matrix"):
+ del module.covariance_matrix
+ if hasattr(module, "corda_method"):
+ del module.corda_method
+ if hasattr(module, "rank"):
+ del module.rank
+
+ # Save cache to disk
+ if cache_file is not None:
+ cache: dict[str, Any] = {}
+ for name, module in target_modules(model, lora_config):
+ cache[f"{name}.eigens.S_WC"] = module.eigens.S_WC
+ cache[f"{name}.eigens.U_WC"] = module.eigens.U_WC
+ cache[f"{name}.eigens.V_WC"] = module.eigens.V_WC
+
+ os.makedirs(os.path.dirname(cache_file), exist_ok=True)
+ torch.save(cache, cache_file)
+
+
+@torch.no_grad()
+def calib_cov_distribution(
+ model: nn.Module,
+ config: LoraConfig,
+ run_model: Optional[Callable[[], None]],
+ hooked_model: Optional[nn.Module],
+ covariance_file: Optional[str],
+):
+ if covariance_file is not None and os.path.exists(covariance_file) and os.path.getsize(covariance_file) > 0:
+ all_covariance_matrix = torch.load(covariance_file, map_location=get_model_device(model))
+ for name, module in target_modules(model, config):
+ module.covariance_matrix = all_covariance_matrix[name]
+ return
+
+ if run_model is None:
+ raise ValueError("run_model must be specified when covariance file and cache file aren't built.")
+ if hooked_model is None:
+ hooked_model = model
+ hooked_model.eval()
+
+ def hook(module, input, output):
+ input = input[0].detach().squeeze(0).data ## (context_length = 2048, dim)
+ if not config.corda_config.use_float16_for_covariance:
+ input = input.float()
+ input = input / torch.max(input).abs()
+
+ # check if input is valid
+ if torch.isnan(input).any() or torch.isinf(input).any():
+ raise ValueError("Invalid value found in input, please check your input data.")
+
+ # calculate covariance and check if it's valid
+ covariance = input.t().matmul(input)
+ if torch.isnan(covariance).any() or torch.isinf(covariance).any():
+ raise ValueError(
+ "Invalid value found in covariance. Please file an issue at https://github.com/huggingface/peft/issues."
+ )
+
+ # add to module
+ module.sample_count += 1
+ module.covariance_matrix += covariance
+
+ # free memory
+ del covariance, input
+
+ handles = []
+ for name, module in target_modules(hooked_model, config):
+ module.sample_count = 0
+ module.covariance_matrix = 0
+ handles.append(module.register_forward_hook(hook))
+
+ run_model()
+
+ # Clear the hooks
+ for handle in handles:
+ handle.remove()
+
+ # In some edge cases you might need to hook a model different from the model to add adapters,
+ # this case you would specify `hooked_model` and set it to a different model from `model`.
+ if hooked_model is not model:
+ targets = {}
+ for name, module in target_modules(model, config):
+ targets[name] = module
+ for name, module in target_modules(hooked_model, config):
+ # There can be modules used only in inference, but not training
+ # Exclude modules not in target model to prevent KeyError in this case
+ if name in targets:
+ targets[name].sample_count = module.sample_count
+ targets[name].covariance_matrix = module.covariance_matrix
+
+ # Divide by sample count
+ for name, module in target_modules(model, config):
+ module.covariance_matrix /= module.sample_count
+
+ # Save covariance to disk
+ if covariance_file is not None:
+ all_covariance_matrix = {}
+ for name, module in target_modules(model, config):
+ all_covariance_matrix[name] = module.covariance_matrix
+ os.makedirs(os.path.dirname(covariance_file), exist_ok=True)
+ torch.save(all_covariance_matrix, covariance_file)
+
+
+@torch.no_grad()
+def collect_eigens(
+ model: nn.Module,
+ config: LoraConfig,
+ verbose: bool,
+):
+ """Call collect_eigens_for_layer and store result in key `eigens` of each layer."""
+ linear_modules = []
+ for name, module in target_modules(model, config):
+ linear_modules.append((name, module))
+ if verbose:
+ linear_modules = tqdm(linear_modules, desc="Collecting eigens")
+ for name, module in linear_modules:
+ module.eigens = collect_eigens_for_layer(module, config)
+
+
+@torch.no_grad()
+def collect_eigens_for_layer(
+ linear: nn.Linear,
+ config: LoraConfig,
+) -> CordaEigens:
+ w = linear.weight.data.float()
+ out_dim = w.size(0)
+ in_dim = w.size(1)
+ min_dim = min(in_dim, out_dim)
+
+ if not hasattr(linear, "covariance_matrix"):
+ raise ValueError(
+ "Covariance matrix not found in linear module. Please do not call this function directly, "
+ "instead call `preprocess_corda`. If your usage is correct but this error still encounters, "
+ "please file an issue at https://github.com/huggingface/peft/issues."
+ )
+ covariance_matrix = linear.covariance_matrix.float()
+
+ damp = 0.01
+ while True:
+ compensate = torch.diag(
+ torch.ones(covariance_matrix.size(0)).to(covariance_matrix.device)
+ * torch.mean(torch.diag(covariance_matrix))
+ * damp
+ )
+ fix_covariance_matrix = covariance_matrix + compensate
+ cov_inv = torch.linalg.inv(fix_covariance_matrix)
+ inv_error = torch.dist(
+ fix_covariance_matrix @ cov_inv, torch.eye(covariance_matrix.size(0)).to(get_model_device(linear))
+ ).item()
+ if inv_error < 0.05:
+ break
+ else:
+ damp = damp * 2
+ w = w @ fix_covariance_matrix ## w: out_dim, in_dim; covariance_matrix: in_dim, in_dim
+
+ U, S, Vh = torch.linalg.svd(w, full_matrices=False)
+ V = (Vh @ cov_inv).transpose(0, 1)
+
+ # Sanity check, temporarily U and V are large, they will be crop after rank search
+ r = min_dim
+ if U.size(0) != out_dim or U.size(1) != r:
+ raise ValueError(
+ f"Matrix U size mismatch: {U.size()} vs. ({out_dim}, {r}), "
+ "please file an issue at https://github.com/huggingface/peft/issues."
+ )
+ if S.size(0) != r:
+ raise ValueError(
+ f"Matrix S size mismatch: {S.size()} vs. ({r},), "
+ "please file an issue at https://github.com/huggingface/peft/issues."
+ )
+ if V.size(0) != in_dim or V.size(1) != r:
+ raise ValueError(
+ f"Matrix V size mismatch: {V.size()} vs. ({in_dim}, {r}), "
+ "please file an issue at https://github.com/huggingface/peft/issues."
+ )
+
+ # Offload U and V to CPU, they consume too much memory
+ U = U.cpu()
+ V = V.cpu()
+ return CordaEigens(
+ S_WC=S,
+ U_WC=U,
+ V_WC=V,
+ )
+
+
+@torch.no_grad()
+def crop_corda_eigens(model: nn.Module, config: LoraConfig):
+ for name, module in target_modules(model, config):
+ # We don't expect saving sliced tensor writes the whole tensor to disk,
+ # so it's necessary to copy the tensors.
+ # Reference: https://github.com/pytorch/pytorch/issues/40157
+ if module.corda_method == "ipm":
+ module.eigens.S_WC = module.eigens.S_WC[: module.rank].clone()
+ module.eigens.U_WC = module.eigens.U_WC[:, : module.rank].clone().to(get_model_device(model))
+ module.eigens.V_WC = module.eigens.V_WC[:, : module.rank].clone().to(get_model_device(model))
+ elif module.corda_method == "kpm":
+ module.eigens.S_WC = module.eigens.S_WC[-module.rank :].clone()
+ module.eigens.U_WC = module.eigens.U_WC[:, -module.rank :].clone().to(get_model_device(model))
+ module.eigens.V_WC = module.eigens.V_WC[:, -module.rank :].clone().to(get_model_device(model))
+ else:
+ raise ValueError(f"Invalid corda_method found: {module.corda_method}, it should be 'ipm' or 'kpm'.")
+
+ # Sanity check
+ if module.eigens.S_WC.size(0) != module.rank:
+ raise ValueError(
+ f"rank mismatch: {module.eigens.S_WC.size(0)} vs. {module.rank},"
+ "please file an issue at https://github.com/huggingface/peft/issues."
+ )
+ if module.eigens.U_WC.size(0) != module.weight.size(0):
+ raise ValueError(
+ f"U size mismatch: {module.eigens.U_WC.size(0)} vs. {module.weight.size(0)},"
+ "please file an issue at https://github.com/huggingface/peft/issues."
+ )
+ if module.eigens.U_WC.size(1) != module.rank:
+ raise ValueError(
+ f"U size mismatch: {module.eigens.U_WC.size(1)} vs. {module.rank},"
+ "please file an issue at https://github.com/huggingface/peft/issues."
+ )
+ if module.eigens.V_WC.size(0) != module.weight.size(1):
+ raise ValueError(
+ f"V size mismatch: {module.eigens.V_WC.size(0)} vs. {module.weight.size(1)},"
+ "please file an issue at https://github.com/huggingface/peft/issues."
+ )
+ if module.eigens.V_WC.size(1) != module.rank:
+ raise ValueError(
+ f"V size mismatch: {module.eigens.V_WC.size(1)} vs. {module.rank},"
+ "please file an issue at https://github.com/huggingface/peft/issues."
+ )
diff --git a/peft/src/peft/tuners/lora/dora.py b/peft/src/peft/tuners/lora/dora.py
new file mode 100644
index 0000000000000000000000000000000000000000..f38a7df125651dca198286cd3bbde0dea148784b
--- /dev/null
+++ b/peft/src/peft/tuners/lora/dora.py
@@ -0,0 +1,203 @@
+# Copyright 2024-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+from copy import deepcopy
+
+import torch
+import torch.nn.functional as F
+from torch import nn
+
+from peft.utils.integrations import dequantize_module_weight, gather_params_ctx
+from peft.utils.other import transpose
+
+
+class DoraLinearLayer(nn.Module):
+ def __init__(self, fan_in_fan_out):
+ super().__init__()
+ self.fan_in_fan_out = fan_in_fan_out
+
+ def get_weight_norm(self, weight, lora_weight, scaling) -> torch.Tensor:
+ # calculate L2 norm of weight matrix, column-wise
+ weight = transpose(weight, self.fan_in_fan_out)
+ weight = weight + scaling * lora_weight
+ weight_norm = torch.linalg.norm(weight, dim=1).to(weight.dtype)
+ return weight_norm
+
+ def update_layer(self, *, base_layer, lora_A, lora_B, scaling, place_on_cpu=False) -> None:
+ # temporarily convert fp16 to fp32, as fp16 can cause trouble on CPU with PyTorch < 2.2
+ dtype_is_fp16 = lora_A.dtype == torch.float16
+ if dtype_is_fp16:
+ lora_A = lora_A.float()
+ lora_B = lora_B.float()
+
+ with gather_params_ctx(base_layer.parameters()):
+ if base_layer.__class__.__name__ == "Linear4bit":
+ # We have to create a copy of the base layer, otherwise, FSDP will throw an error. 8bit does not work
+ # yet because Int8Params cannot be correctly deep-copied (attributes vanish)
+ base_layer = deepcopy(base_layer)
+
+ weight = dequantize_module_weight(base_layer)
+ if weight.data.ndim >= 3: # For handling LoRAs applied to Conv layers.
+ r = lora_A.shape[0]
+ lora_weight = torch.mm(lora_B.view([-1, r]), lora_A.view([r, -1]))
+ lora_weight = lora_weight.reshape(weight.shape)
+ else:
+ lora_weight = lora_B @ lora_A
+
+ if dtype_is_fp16:
+ lora_weight = lora_weight.half()
+ weight_norm = self.get_weight_norm(weight.to(lora_A.device), lora_weight, scaling)
+
+ if place_on_cpu:
+ weight_norm = weight_norm.to("cpu")
+ self.weight = nn.Parameter(weight_norm, requires_grad=True)
+
+ def forward(self, x, *, lora_A, lora_B, scaling, base_layer, base_result=None):
+ """
+ For DoRA, calculate the extra output from LoRA with DoRA applied. This should be added on top of the base layer
+ output.
+ """
+ # Don't use `lora_weight = lora_B.weight @ lora_A.weight` because this causes errors with FSDP. Instead,
+ # calculate the same but using forward.
+ x_eye = torch.eye(lora_A.weight.shape[1], device=lora_A.weight.device, dtype=x.dtype)
+ lora_weight = lora_B(lora_A(x_eye)).T
+
+ magnitude = self.weight
+ weight = dequantize_module_weight(base_layer)
+ weight = weight.to(x.dtype)
+ weight_norm = self.get_weight_norm(weight, lora_weight.detach(), scaling)
+ # see section 4.3 of DoRA (https://huggingface.co/papers/2402.09353)
+ # "[...] we suggest treating ||V +∆V ||_c in
+ # Eq. (5) as a constant, thereby detaching it from the gradient
+ # graph. This means that while ||V + ∆V ||_c dynamically
+ # reflects the updates of ∆V , it won’t receive any gradient
+ # during backpropagation"
+ weight_norm = weight_norm.detach()
+ mag_norm_scale = (magnitude / weight_norm).view(1, -1)
+
+ lora_result = lora_B(lora_A(x))
+
+ bias = None
+ if base_result is not None:
+ bias = base_layer.bias
+ if bias is not None:
+ base_result = base_result - bias
+ else:
+ base_result = F.linear(x, transpose(weight, self.fan_in_fan_out))
+
+ result_dora = (mag_norm_scale - 1) * base_result + mag_norm_scale * lora_result * scaling
+
+ return result_dora
+
+ def __repr__(self) -> str:
+ rep = super().__repr__()
+ return "lora.dora." + rep
+
+
+class DoraEmbeddingLayer(DoraLinearLayer):
+ def forward(self, x, *, lora_A, lora_B, scaling, base_layer, embed_fn):
+ """
+ For DoRA, calculate the extra output from LoRA with DoRA applied. This should be added on top of the base layer
+ output.
+ """
+ lora_weight = (lora_A @ lora_B).T
+ magnitude = self.weight
+ weight = base_layer.weight
+ weight_norm = self.get_weight_norm(weight, lora_weight.detach(), scaling)
+ # see section 4.3 of DoRA (https://huggingface.co/papers/2402.09353)
+ # "[...] we suggest treating ||V +∆V ||_c in
+ # Eq. (5) as a constant, thereby detaching it from the gradient
+ # graph. This means that while ||V + ∆V ||_c dynamically
+ # reflects the updates of ∆V , it won’t receive any gradient
+ # during backpropagation"
+ weight_norm = weight_norm.detach()
+ mag_norm_scale = magnitude / weight_norm
+ result_dora = mag_norm_scale * (embed_fn(x, lora_A) @ lora_B) * scaling
+ return mag_norm_scale, result_dora
+
+ def __repr__(self) -> str:
+ rep = super().__repr__()
+ return "lora.dora." + rep
+
+
+class _DoraConvNdLayer(DoraLinearLayer):
+ def get_weight_norm(self, weight, lora_weight, scaling) -> torch.Tensor:
+ # calculate L2 norm of weight matrix, column-wise
+ weight = weight + scaling * lora_weight
+ # the following is needed to have compatibility with the 4/5D weight tensors of Conv2D/3D
+ dim = tuple(range(1, weight.dim()))
+ weight_norm = weight.norm(p=2, dim=dim, keepdim=True).transpose(1, 0)
+ return weight_norm
+
+ def forward(self, x, *, lora_A, lora_B, scaling, base_layer, base_result=None):
+ """
+ For DoRA, calculate the extra output from LoRA with DoRA applied. This should be added on top of the base layer
+ output.
+ """
+ weight = base_layer.weight
+ r = lora_A.weight.shape[0]
+ lora_weight = torch.mm(lora_B.weight.view([-1, r]), lora_A.weight.view([r, -1]))
+ lora_weight = lora_weight.reshape(weight.shape)
+ magnitude = self.weight
+ weight_norm = self.get_weight_norm(weight, lora_weight.detach(), scaling)
+ # see section 4.3 of DoRA (https://huggingface.co/papers/2402.09353)
+ # "[...] we suggest treating ||V +∆V ||_c in
+ # Eq. (5) as a constant, thereby detaching it from the gradient
+ # graph. This means that while ||V + ∆V ||_c dynamically
+ # reflects the updates of ∆V , it won’t receive any gradient
+ # during backpropagation"
+ weight_norm = weight_norm.detach()
+ mag_norm_scale = magnitude / weight_norm
+
+ if base_result is None:
+ base_result = self.conv_fn(
+ x,
+ weight,
+ bias=None,
+ stride=base_layer.stride,
+ padding=base_layer.padding,
+ dilation=base_layer.dilation,
+ groups=base_layer.groups,
+ )
+ else:
+ bias = base_layer.bias
+ if bias is not None:
+ # reshape bias to (1, -1, 1, ...)
+ bias_shape = (1, -1) + (1,) * (base_result.dim() - 2)
+ base_result = base_result - bias.view(*bias_shape)
+
+ result_dora = (mag_norm_scale - 1) * base_result + mag_norm_scale * lora_B(lora_A(x)) * scaling
+ return result_dora
+
+ def __repr__(self) -> str:
+ rep = super().__repr__()
+ return "lora.dora." + rep
+
+
+class DoraConv1dLayer(_DoraConvNdLayer):
+ def __init__(self, fan_in_fan_out):
+ super().__init__(fan_in_fan_out)
+ self.conv_fn = F.conv1d
+
+
+class DoraConv2dLayer(_DoraConvNdLayer):
+ def __init__(self, fan_in_fan_out):
+ super().__init__(fan_in_fan_out)
+ self.conv_fn = F.conv2d
+
+
+class DoraConv3dLayer(_DoraConvNdLayer):
+ def __init__(self, fan_in_fan_out):
+ super().__init__(fan_in_fan_out)
+ self.conv_fn = F.conv3d
diff --git a/peft/src/peft/tuners/lora/eetq.py b/peft/src/peft/tuners/lora/eetq.py
new file mode 100644
index 0000000000000000000000000000000000000000..b864d9fba2481bd00b238a099689cd6fe9cea57a
--- /dev/null
+++ b/peft/src/peft/tuners/lora/eetq.py
@@ -0,0 +1,118 @@
+# Copyright 2024-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+from typing import Any, Optional
+
+import torch
+
+from peft.import_utils import is_eetq_available
+from peft.tuners.lora.layer import LoraLayer
+from peft.tuners.tuners_utils import BaseTunerLayer
+
+
+if is_eetq_available():
+ from eetq import EetqLinear
+
+ class EetqLoraLinear(torch.nn.Module, LoraLayer):
+ def __init__(
+ self,
+ base_layer,
+ adapter_name,
+ r: int = 0,
+ lora_alpha: int = 1,
+ lora_dropout: float = 0.0,
+ init_lora_weights: bool = True,
+ use_rslora: bool = False,
+ use_dora: bool = False,
+ lora_bias: bool = False,
+ **kwargs,
+ ):
+ if use_dora:
+ raise ValueError(f"{self.__class__.__name__} does not support DoRA yet, please set it to False")
+
+ super().__init__()
+ LoraLayer.__init__(self, base_layer)
+
+ # self.base_layer and self.quant_linear_module are the same; we need the former for consistency and the latter
+ # for backwards compatibility
+ self.quant_linear_module = base_layer
+
+ self._active_adapter = adapter_name
+ self.update_layer(
+ adapter_name,
+ r,
+ lora_alpha=lora_alpha,
+ lora_dropout=lora_dropout,
+ init_lora_weights=init_lora_weights,
+ use_rslora=use_rslora,
+ use_dora=use_dora,
+ lora_bias=lora_bias,
+ )
+
+ def forward(self, x: torch.Tensor):
+ result = self.quant_linear_module(x)
+
+ if self.disable_adapters:
+ return result
+
+ for active_adapter in self.active_adapters:
+ if active_adapter not in self.lora_A.keys():
+ continue
+ lora_A = self.lora_A[active_adapter]
+ lora_B = self.lora_B[active_adapter]
+ dropout = self.lora_dropout[active_adapter]
+ scaling = self.scaling[active_adapter]
+
+ requires_conversion = not torch.is_autocast_enabled()
+ if requires_conversion:
+ expected_dtype = result.dtype
+ x = self._cast_input_dtype(x, lora_A.weight.dtype)
+
+ output = lora_B(lora_A(dropout(x)))
+ if requires_conversion:
+ output = output.to(expected_dtype)
+ output = output * scaling
+ result = result + output
+ return result
+
+ def merge(self, safe_merge: bool = False, adapter_names: Optional[list[str]] = None) -> None:
+ raise AttributeError("Merging LoRA layers is not supported for Eetq layers.")
+
+ def unmerge(self) -> None:
+ raise AttributeError("Unmerging LoRA layers is not supported for Eetq layers.")
+
+ def __repr__(self) -> str:
+ rep = super().__repr__()
+ return "lora." + rep
+
+
+def dispatch_eetq(
+ target: torch.nn.Module,
+ adapter_name: str,
+ **kwargs: Any,
+) -> Optional[torch.nn.Module]:
+ new_module = None
+
+ if isinstance(target, BaseTunerLayer):
+ target_base_layer = target.get_base_layer()
+ else:
+ target_base_layer = target
+
+ if is_eetq_available() and isinstance(target_base_layer, EetqLinear):
+ new_module = EetqLoraLinear(target, adapter_name, **kwargs)
+ target.weight = target_base_layer.weight
+
+ if hasattr(target, "bias"):
+ target.bias = target_base_layer.bias
+
+ return new_module
diff --git a/peft/src/peft/tuners/lora/eva.py b/peft/src/peft/tuners/lora/eva.py
new file mode 100644
index 0000000000000000000000000000000000000000..1bc75453b1f35116ca307a3ea71c59d7d0efbf66
--- /dev/null
+++ b/peft/src/peft/tuners/lora/eva.py
@@ -0,0 +1,739 @@
+# Copyright 2024-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+import warnings
+from collections import Counter, defaultdict
+from collections.abc import Iterable, Mapping
+from contextlib import nullcontext
+from copy import deepcopy
+from functools import partial
+from itertools import cycle
+from typing import Optional, Union
+
+import torch
+import torch.distributed as dist
+from tqdm import tqdm
+from transformers.pytorch_utils import Conv1D
+
+from peft.tuners.tuners_utils import _find_minimal_target_modules, check_target_module_exists
+from peft.utils.constants import MIN_TARGET_MODULES_FOR_OPTIMIZATION
+from peft.utils.incremental_pca import IncrementalPCA
+from peft.utils.other import _get_submodules, get_pattern_key
+
+from .config import LoraConfig
+from .layer import Embedding, LoraLayer, MultiheadAttention, _ConvNd
+
+
+UNSUPPORTED_LORA_MODULES = (Embedding, MultiheadAttention, _ConvNd)
+
+
+class _Hook:
+ """
+ A base class for hooks that prepares layer inputs for EVA.
+ """
+
+ def __init__(
+ self,
+ name: str,
+ prepare_layer_inputs_fn: Optional[callable] = None,
+ gather_distributed_inputs: bool = True,
+ ):
+ self.name = name
+ self.gather_distributed_inputs = gather_distributed_inputs
+ if prepare_layer_inputs_fn is None:
+ self._prepare_layer_inputs_fn = self._prepare_layer_inputs_fn_default
+ else:
+ self._prepare_layer_inputs_fn = prepare_layer_inputs_fn
+ self.model_input = None
+
+ @staticmethod
+ def _prepare_layer_inputs_fn_default(layer_input, model_input, layer_name) -> torch.Tensor:
+ if isinstance(layer_input, torch.Tensor):
+ pass
+ elif isinstance(layer_input, (tuple, list)):
+ layer_input = layer_input[0]
+ else:
+ raise ValueError(
+ f"unsupported input type {type(layer_input)} for prepare_layer_inputs_fn in layer {layer_name}, "
+ "please provide a custom prepare_layer_inputs_fn"
+ )
+ # if the input has more than 2 dimensions, we flatten all but the last dimension
+ if layer_input.ndim > 2:
+ layer_input = layer_input.view(-1, layer_input.size(-1))
+ return layer_input
+
+ @torch.no_grad()
+ def prepare_layer_inputs(self, layer_input):
+ return self._prepare_layer_inputs_fn(layer_input, self.model_input, self.name)
+
+ def gather_layer_inputs(self, layer_input):
+ if dist.is_initialized() and self.gather_distributed_inputs:
+ world_size = dist.get_world_size()
+
+ # First gather sizes from all processes more efficiently
+ local_size = torch.tensor([layer_input.shape[0]], device=layer_input.device)
+ all_sizes = torch.empty(world_size, dtype=local_size.dtype, device=layer_input.device)
+ dist.all_gather_into_tensor(all_sizes, local_size)
+ all_sizes = all_sizes.tolist()
+
+ # Find maximum size and pad tensors
+ padded_input = layer_input.new_zeros((max(all_sizes), *layer_input.shape[1:]))
+ padded_input[: layer_input.shape[0]] = layer_input
+
+ # Gather padded tensors
+ gathered_inputs = [torch.zeros_like(padded_input) for _ in range(world_size)]
+ dist.all_gather(gathered_inputs, padded_input.contiguous())
+
+ # Remove padding for each gathered tensor
+ gathered_inputs = [tensor[:size] for tensor, size in zip(gathered_inputs, all_sizes)]
+
+ # Concatenate along batch dimension
+ return torch.cat(gathered_inputs, dim=0)
+ return layer_input
+
+
+class SVDHook(_Hook):
+ """
+ A forward hook for calculating incremental SVD on layer inputs. The hook is designed to be registered to a PyTorch
+ module using the `register_forward_hook` method.
+
+ This hook performs a step of incremental Singular Value Decomposition (SVD) on the inputs of a specified layer
+ during the forward pass of a neural network. The hook also tracks convergence of the computed components using
+ cosine similarity between the current and previous components.
+
+ Args:
+ name (str): Name of the layer to which this hook is attached.
+ n_components (int): Number of principal components to compute.
+ sim_thresh (Union[float, torch.Tensor]): Similarity threshold for convergence.
+ prepare_layer_inputs_fn (Optional[callable]): Function to prepare layer inputs for SVD.
+ """
+
+ def __init__(
+ self,
+ n_components: int,
+ sim_thresh: Union[float, torch.Tensor],
+ **base_class_kwargs,
+ ):
+ super().__init__(**base_class_kwargs)
+ self.n_components = n_components
+ self.sim_thresh = sim_thresh
+ if isinstance(sim_thresh, torch.Tensor) and len(sim_thresh.shape) > 0:
+ check1 = sim_thresh.size(0) == n_components or sim_thresh.size(0) == 1
+ check2 = len(sim_thresh.shape) == 1
+ if not (check1 and check2):
+ raise ValueError(
+ "if sim_thresh is a tensor with more than 0 dimensions it must have shape (n_components,) or (1,)"
+ )
+ self.svd = IncrementalPCA(
+ n_components=n_components,
+ copy=True,
+ lowrank=True,
+ lowrank_seed=42,
+ )
+ self.model_input = None
+ self.converged = torch.zeros((n_components,), dtype=torch.bool)
+
+ @torch.no_grad()
+ def __call__(self, model, input, output):
+ previous_components = None
+ if hasattr(self.svd, "components_"):
+ previous_components = self.svd.components_.clone().detach()
+ states = self.prepare_layer_inputs(input)
+ states = self.gather_layer_inputs(states)
+ # check if batch sizes is more than the number of components
+ if states.size(0) < self.n_components:
+ print(f"skipping SVD for {self.name} because there are less than {self.n_components} examples")
+ return
+ self.svd.partial_fit(states.to(torch.float32))
+ # add if statement to check if we are in the first step where previous_components is None
+ if previous_components is None:
+ return
+ components = self.svd.components_
+ if len(components.shape) == 1:
+ components = components.reshape(1, -1)
+ previous_components = previous_components.reshape(1, -1)
+ # consider as converged if enough components have converged via cossim
+ sim = torch.nn.functional.cosine_similarity(components, previous_components)
+ self.converged = sim >= self.sim_thresh
+
+
+# This is used to determine if inputs of two different layers are equal. For such cases, SVD
+# needs to be done for only for one of the equal inputs.
+class HashHook(_Hook):
+ """
+ A forward hook for hashing layer inputs. The hook is designed to be registered to a PyTorch module using the
+ `register_forward_hook` method.
+
+ This hook hashes the inputs of a specified layer during the forward pass of a neural network and stores the hash
+ values for later analysis or comparison.
+
+ Args:
+ name (str): Name of the layer to which this hook is attached. hashed_inputs (list): List of hashed inputs.
+ prepare_layer_inputs_fn (Optional[callable]): Function to prepare layer inputs for hashing.
+ """
+
+ def __init__(self, **base_class_kwargs):
+ super().__init__(**base_class_kwargs)
+ self.hashed_inputs = []
+
+ @staticmethod
+ def hash_fn(tensor):
+ return hash(tuple(tensor.view(-1).tolist()))
+
+ @torch.no_grad()
+ def __call__(self, model, input, output):
+ x = self.prepare_layer_inputs(input)
+ x = self.gather_layer_inputs(x)
+ self.hashed_inputs.append(self.hash_fn(x.cpu()))
+
+
+def find_equal_values(dictionary: dict) -> dict:
+ """
+ Find keys in a dictionary that have the same value.
+
+ This function takes a dictionary and returns a new dictionary containing keys that have the same value. The keys in
+ the output dictionary are the values from the input dictionary, and the values are lists of keys that share the
+ same value.
+ """
+ value_dict = defaultdict(list)
+ for k, v in dictionary.items():
+ value_dict[v].append(k)
+ return {k: v for k, v in value_dict.items() if len(v) > 1}
+
+
+def get_device_with_meta_params(model: torch.nn.Module) -> torch.device:
+ """
+ Get the device of the model's parameters. Useful if some parameters are on meta device.
+ """
+ devices = list({p.device for p in model.parameters() if p.device.type != "meta"})
+ if len(devices) > 1:
+ warnings.warn(f"Could not determine device, model has multiple devices: {devices}")
+ return
+ return devices[0]
+
+
+def move_inputs_to_device(inputs, device: Union[str, torch.device]):
+ """
+ Move the inputs to the specified device. Adapted from hf.Trainer.
+ """
+ if hasattr(inputs, "to"):
+ return inputs.to(device)
+ if isinstance(inputs, Mapping):
+ return type(inputs)({k: move_inputs_to_device(v, device) for k, v in inputs.items()})
+ elif isinstance(inputs, (tuple, list)):
+ return type(inputs)(move_inputs_to_device(v, device) for v in inputs)
+ else:
+ warnings.warn(f"input of type {type(inputs)} could not be moved to the correct device")
+ return inputs
+
+
+def prepare_model_inputs_fn_language_modeling(model_input, peft_config: LoraConfig):
+ """
+ Get the indices of the items that should be used for SVD.
+
+ Attributes:
+ model_input (dict): The model inputs.
+ peft_config (LoraConfig): The configuration for the LoRA layers.
+ """
+ if not isinstance(model_input, dict):
+ raise ValueError("When using `prepare_model_inputs_fn_language_modeling` inputs must be a dictionary")
+ mask = model_input.get("attention_mask", torch.ones_like(model_input["input_ids"])).bool()
+ if peft_config.eva_config.use_label_mask and hasattr(model_input, "labels"):
+ mask = torch.logical_and(mask, model_input["labels"] != peft_config.eva_config.label_mask_value)
+ return mask.nonzero()
+
+
+def prepare_layer_inputs_fn_language_modeling(layer_input, model_input, layer_name) -> torch.Tensor:
+ """
+ if not all items in the input should be used for SVD, this function can be used to get the indices of the items
+ that should be used.
+
+ Attributes:
+ layer_input (torch.Tensor): The layer inputs.
+ model_input (torch.Tensor):
+ The model inputs or if `prepare_model_inputs_fn` is not None the output of this function.
+ layer_name (str): The name of the layer.
+
+ Returns:
+ torch.Tensor: The input to the SVD.
+ """
+ # if layer inputs are not a tensor, we simply get the first item
+ if isinstance(layer_input, torch.Tensor):
+ pass
+ elif isinstance(layer_input, (tuple, list)):
+ layer_input = layer_input[0]
+ else:
+ raise ValueError(
+ f"unsupported input type {type(layer_input)} for prepare_layer_inputs_fn in layer {layer_name}, "
+ "please provide a custom prepare_layer_inputs_fn"
+ )
+ # in this case model_input is the output of `prepare_model_inputs_fn_language_modeling`
+ return layer_input[model_input.T.unbind()]
+
+
+def forward_fn_dict(model, inputs):
+ return model(**inputs)
+
+
+def _get_eva_state_dict(
+ model: torch.nn.Module,
+ dataloader: Iterable,
+ peft_config: Optional[LoraConfig],
+ target_module_check_fn: callable,
+ forward_fn: Optional[callable],
+ prepare_model_inputs_fn: Optional[callable],
+ prepare_layer_inputs_fn: Union[callable, dict[str, callable], None],
+ gather_distributed_inputs: bool,
+ show_progress_bar: bool,
+) -> dict:
+ # Computes the rank distribution for each layer based on the explained variance ratio.
+ # when rank_pattern flag is False, all values in max_components are the same
+ def _get_rank_distribution(hooks, layer_hook_map, equal_inputs_map, rank_budget, max_components):
+ exp_vars = {k: h[0].svd.explained_variance_ratio_[: max_components[k]] for k, h in hooks.items()}
+ keys, values = zip(*[(k, c) for k, name in layer_hook_map.items() for c in exp_vars[name]])
+ idx = torch.stack(values).argsort(descending=True)
+ counts = Counter([keys[i] for i in idx[:rank_budget]])
+ counts = {k: counts.get(k, 0) for k in layer_hook_map.keys()} # add layers with 0 rank
+ for k, k_hook in equal_inputs_map.items():
+ # ensure hook layers have the highest rank if they are equal to another layer
+ rank, rank_hook = counts[k], counts[k_hook]
+ if rank_hook >= rank:
+ continue
+ counts[k_hook], counts[k] = rank, rank_hook
+ return counts
+
+ # dataloader is not empty
+ if len(dataloader) == 0:
+ raise ValueError("dataloader is empty")
+
+ # check if dist is initialized
+ if dist.is_initialized() and gather_distributed_inputs:
+ warnings.warn(
+ "torch.distributed is initialized and `gather_distributed_inputs` is True, "
+ "therefore EVA initialization will gather tensors from all ranks. "
+ "Ensure the model does not receive the same inputs on different ranks."
+ )
+
+ # for unusually high rho values, define an upper limit
+ rho_threshold = 1000
+ rho = peft_config.eva_config.rho
+ if rho > rho_threshold:
+ max_dim = max(max(p.shape) for p in model.parameters())
+ rho_ceil = max_dim // peft_config.r
+ rho = min(rho, rho_ceil)
+
+ training = model.training
+ device = get_device_with_meta_params(model)
+ model.eval()
+
+ # get model inputs
+ inputs = next(iter(dataloader))
+ if device is not None:
+ inputs = move_inputs_to_device(inputs, device)
+ if prepare_model_inputs_fn is not None:
+ model_inputs_for_hooks = prepare_model_inputs_fn(inputs, peft_config)
+ else:
+ model_inputs_for_hooks = deepcopy(inputs)
+
+ hooks = {}
+ max_components = {}
+ rank_budget = 0
+ for name, module in model.named_modules():
+ if not target_module_check_fn(name, module):
+ continue
+ if isinstance(prepare_layer_inputs_fn, Mapping):
+ fn = prepare_layer_inputs_fn.pop(name, None)
+ else:
+ fn = prepare_layer_inputs_fn
+ hook = HashHook(name=name, prepare_layer_inputs_fn=fn, gather_distributed_inputs=gather_distributed_inputs)
+ hook.model_input = model_inputs_for_hooks
+ handle = module.register_forward_hook(hook)
+ hooks[name] = (hook, handle)
+ layer_rank = peft_config.rank_pattern.get(
+ get_pattern_key(peft_config.rank_pattern.keys(), name), peft_config.r
+ )
+ max_components[name] = round(layer_rank * rho)
+ rank_budget += layer_rank
+ if isinstance(prepare_layer_inputs_fn, Mapping) and len(prepare_layer_inputs_fn) > 0:
+ raise ValueError(
+ "prepare_layer_inputs_fn is a mapping but the following module names were not found in the model: "
+ f"{prepare_layer_inputs_fn.keys()}"
+ )
+
+ # forward for one batch to check which layer inputs are equal to avoid unneeded svd calculations
+ forward_fn(model, inputs)
+ hash_dict = {k: h[0].hashed_inputs[0] for k, h in hooks.items()}
+ # equal input maps groups layers which receive the same input. One layer is defined as the key and receives an svd
+ # hook. For the remaining layers the svd results can be skipped.
+ equal_inputs = list(find_equal_values(hash_dict).values())
+ equal_inputs_map = {vv: v[0] for v in equal_inputs for vv in v[1:]}
+ # for layers with equal inputs we need to make sure that the max_components are the same
+ for names in equal_inputs:
+ max_value = max(max_components[n] for n in names)
+ for n in names:
+ max_components[n] = max_value
+
+ # initialize svd hooks
+ for name in list(hooks.keys()):
+ hook, handle = hooks.pop(name)
+ handle.remove()
+ if name in equal_inputs_map:
+ continue
+ hook = SVDHook(
+ n_components=max_components[name],
+ sim_thresh=peft_config.eva_config.tau,
+ name=name,
+ prepare_layer_inputs_fn=hook._prepare_layer_inputs_fn,
+ gather_distributed_inputs=gather_distributed_inputs,
+ )
+ module = model.get_submodule(name)
+ handle = module.register_forward_hook(hook)
+ hooks[name] = (hook, handle) # adding the old handle here so we dont get errors in the first forward pass
+ layer_hook_map = {**dict(zip(hooks.keys(), hooks.keys())), **equal_inputs_map}
+
+ # start svd calculation
+ if show_progress_bar and (not dist.is_initialized() or dist.get_rank() == 0):
+ pbar = tqdm(iter(cycle(dataloader)), position=0, leave=False)
+ use_tqdm = True
+ else:
+ pbar = iter(cycle(dataloader))
+ use_tqdm = False
+ convergence_dict = {k: False for k in hooks.keys()}
+ rank_dist = max_components.copy()
+ for inputs in pbar:
+ if device is not None:
+ inputs = move_inputs_to_device(inputs, device)
+ if prepare_model_inputs_fn is not None:
+ model_inputs_for_hooks = prepare_model_inputs_fn(inputs, peft_config)
+ else:
+ model_inputs_for_hooks = deepcopy(inputs)
+
+ for name in list(hooks.keys()):
+ hook, handle = hooks[name]
+ # check if all components that are needed for the rank distribution have converged
+ converged = torch.all(hook.converged[: rank_dist[name]])
+ # if a layer has switched from not converged to converged in the current step
+ if (not convergence_dict[name]) and converged and handle:
+ handle.remove()
+ handle = None
+ convergence_dict[name] = True
+ continue
+ # if a layer has switched from converged to not converged in the current step
+ elif convergence_dict[name] and not converged:
+ module = model.get_submodule(name)
+ handle = module.register_forward_hook(hook)
+ convergence_dict[name] = False
+ hook.model_input = model_inputs_for_hooks
+ hooks[name] = (hook, handle)
+
+ if use_tqdm:
+ layer_converged = list(convergence_dict.values()) + [
+ convergence_dict[v] for v in equal_inputs_map.values()
+ ]
+ pbar.set_description(f"{sum(layer_converged)}/{len(layer_converged)} layers have converged")
+
+ if all(convergence_dict.values()):
+ break
+
+ forward_fn(model, inputs)
+
+ # in case some hooks have to skip the svd calculation because the number of tokens is less than the number of
+ # components
+ if not all(hasattr(h[0].svd, "components_") for h in hooks.values()):
+ continue
+
+ rank_dist = _get_rank_distribution(hooks, layer_hook_map, equal_inputs_map, rank_budget, max_components)
+
+ # check all custom hooks have been removed
+ remaining_hooks = {n for n, m in model.named_modules() for v in m._forward_hooks.values() if isinstance(v, _Hook)}
+ if len(remaining_hooks) > 0:
+ raise ValueError(
+ f"Found active hooks added by EVA that weren't properly removed: {remaining_hooks}. "
+ "Please report this issue at https://github.com/huggingface/peft/issues"
+ )
+
+ eva_state_dict = {}
+ for name, rank in rank_dist.items():
+ hook = hooks[layer_hook_map[name]][0]
+ if not torch.all(hook.converged[:rank]):
+ raise ValueError(
+ f"Layer {name} has not converged but was assigned rank {rank}. "
+ "Please report this issue at https://github.com/huggingface/peft/issues"
+ )
+ u = hook.svd.components_[:rank]
+ if peft_config.eva_config.whiten:
+ u /= hook.svd.singular_values_[:rank].sqrt().reshape(-1, 1)
+ eva_state_dict[name] = u
+
+ # restore model state
+ model.train(training)
+
+ # move tensors to device
+ if device is not None:
+ eva_state_dict = {k: v.to(device) for k, v in eva_state_dict.items()}
+
+ return eva_state_dict
+
+
+def _load_eva_state_dict(
+ model: torch.nn.Module,
+ eva_state_dict: dict,
+ adapter_name: str,
+):
+ peft_config = model.peft_config[adapter_name]
+ update_layer_kwargs = {
+ "adapter_name": adapter_name,
+ "lora_dropout": peft_config.lora_dropout,
+ "use_rslora": peft_config.use_rslora,
+ "use_dora": peft_config.use_dora,
+ "lora_bias": peft_config.lora_bias,
+ }
+ missing_eva_inits = []
+ new_target_modules = []
+ other_module_names = []
+ rank_pattern = {}
+ alpha_pattern = {}
+ for name, module in model.named_modules():
+ name_in_base_model = name.replace("base_model.model.", "")
+ if not isinstance(module, LoraLayer):
+ other_module_names.append(name_in_base_model)
+ continue
+ # Regexp matching - Find key which matches current target_name in patterns provided
+ r = peft_config.rank_pattern.get(get_pattern_key(peft_config.rank_pattern.keys(), name), peft_config.r)
+ alpha = peft_config.alpha_pattern.get(
+ get_pattern_key(peft_config.alpha_pattern.keys(), name), peft_config.lora_alpha
+ )
+ if name in eva_state_dict:
+ w = eva_state_dict.pop(name)
+ new_rank = w.size(0)
+ if new_rank == 0:
+ parent, _, target_name = _get_submodules(model, name)
+ setattr(parent, target_name, module.get_base_layer())
+ continue
+ elif new_rank != r:
+ if peft_config.eva_config.adjust_scaling_factors:
+ alpha *= new_rank / r
+ if new_rank != r or module.lora_A[adapter_name].weight.device.type == "meta":
+ module.update_layer(r=new_rank, lora_alpha=alpha, init_lora_weights="eva", **update_layer_kwargs)
+ module.lora_A[adapter_name].weight.copy_(w)
+ new_target_modules.append(name_in_base_model)
+ else:
+ module.update_layer(r=r, lora_alpha=alpha, init_lora_weights=True, **update_layer_kwargs)
+ missing_eva_inits.append(name_in_base_model)
+ new_rank = r
+ # update rank pattern and alpha pattern
+ if new_rank != peft_config.r:
+ rank_pattern[name_in_base_model] = new_rank
+ if alpha != peft_config.lora_alpha:
+ alpha_pattern[name_in_base_model] = alpha
+
+ # update target modules if some lora layers have been removed due to their EVA rank being 0
+ new_target_modules = new_target_modules + missing_eva_inits
+ if len(new_target_modules) >= MIN_TARGET_MODULES_FOR_OPTIMIZATION:
+ new_target_modules = _find_minimal_target_modules(new_target_modules, other_module_names)
+ model.peft_config[adapter_name].target_modules = new_target_modules
+
+ # set rank pattern obtained from EVA
+ model.peft_config[adapter_name].rank_pattern = rank_pattern
+
+ # when adjust_scaling_factors is True, lora scaling factors have been adjusted after the rank redistribution
+ model.peft_config[adapter_name].alpha_pattern = alpha_pattern
+
+ if missing_eva_inits:
+ warnings.warn(
+ "the following layers were initialized with init_lora_weights=True because they "
+ f"were not found in the eva state_dict: {missing_eva_inits}\ncurrently the "
+ f"following lora modules are not supported by EVA: {UNSUPPORTED_LORA_MODULES}"
+ )
+
+
+@torch.no_grad()
+def get_eva_state_dict(
+ model: torch.nn.Module,
+ dataloader: Iterable,
+ peft_config: Optional[LoraConfig] = None,
+ forward_fn: Optional[callable] = forward_fn_dict,
+ prepare_model_inputs_fn: Optional[callable] = prepare_model_inputs_fn_language_modeling,
+ prepare_layer_inputs_fn: Union[callable, dict[str, callable], None] = prepare_layer_inputs_fn_language_modeling,
+ adapter_name: str = "default",
+ gather_distributed_inputs: bool = True,
+ show_progress_bar: bool = True,
+) -> dict:
+ """
+ Compute the SVD for each layer in the model.
+
+ This function computes the Singular Value Decomposition (SVD) for each layer in the model. It uses the incremental
+ PCA method to compute the SVD components. The function also checks for convergence of the computed components using
+ cosine similarity. The rank distribution for each layer is determined based on the explained variance ratio.
+
+ Args:
+ model (torch.nn.Module): The model to compute the SVD for. Does not need to be a PeftModel.
+ dataloader (Iterable): The dataloader to use for the forward pass.
+ peft_config (Optional[LoraConfig]):
+ The configuration for the LoRA layers. Only required if `model` is not a PeftModel.
+ forward_fn (callable):
+ The forward function to use for the forward pass. Takes two arguments: `model` and `inputs`. Default
+ behavior is `return model(**inputs)`
+ prepare_model_inputs_fn (Optional[callable]):
+ This function receives the model inputs and the peft_config and passes the output to
+ `prepare_layer_inputs_fn`. Can be used to modify the input to the SVD computation based on the original
+ model inputs. For example for language modeling the attention mask is used to determine which indices are
+ padding tokens and should not be used for SVD. Any function defined here expects two arguments:
+ `model_input` and `peft_config`. `peft.tuners.lora.eva.prepare_model_inputs_fn_language_modeling` is used
+ by default.
+ prepare_layer_inputs_fn (Union[callable, Dict[str, callable], None]):
+ This function receives the layer inputs, the model inputs (potentially modified by
+ `prepare_model_inputs_fn`) and the name of the layer and returns the inputs that should be used for SVD for
+ that particular layer. Any custom function defined here expects three arguments: `layer_input`,
+ `model_input`, and `layer_name` and should return a 2d tensor. The default logic can be found in
+ peft.tuners.lora.eva.prepare_layer_inputs_fn_language_modeling and works for language modeling. In this
+ case model_inputs is the mask used to determine which indices should be used for SVD (created by
+ `prepare_model_inputs_fn_language_modeling`).
+ adapter_name (str): The name of the adapter to compute the SVD for.
+ gather_distributed_inputs (bool):
+ Whether to gather the layer inputs from all ranks. Default is True meaning in a distributed setting the
+ layer inputs will be gathered from all ranks for the SVD computation. For non-distributed settings this
+ argument is ignored. Set to False if you are using a non-distributed dataloader in a distributed setting.
+ show_progress_bar (bool): Whether to show a progress bar. Default is True.
+
+ Returns:
+ eva_state_dict (dict): The state dictionary containing the SVD components for each layer.
+ """
+
+ def target_module_check_fn_peft_model(name, module, unsupported_lora_modules):
+ "check if a module is an adapter module via base_layer attribute"
+ return hasattr(module, "base_layer") and not isinstance(module, unsupported_lora_modules)
+
+ def target_module_check_fn_default(name, module, peft_config):
+ "check if a module is an adapter module via target_modules"
+ is_target_module = True
+ if peft_config.target_modules is not None:
+ is_target_module = check_target_module_exists(peft_config, name)
+ # Conv1D for GPT2 support
+ return isinstance(module, (torch.nn.Linear, Conv1D)) and is_target_module
+
+ is_peft_model = hasattr(model, "peft_config")
+
+ # get peft_config
+ if is_peft_model and peft_config is None:
+ peft_config = model.peft_config[adapter_name]
+ elif peft_config is None:
+ raise ValueError("peft_config is required if model is not a PeftModel")
+
+ # setup context and target module check function
+ if is_peft_model:
+ ctx = model.disable_adapter()
+ target_module_check_fn = partial(
+ target_module_check_fn_peft_model, unsupported_lora_modules=UNSUPPORTED_LORA_MODULES
+ )
+ else:
+ ctx = nullcontext()
+ target_module_check_fn = partial(target_module_check_fn_default, peft_config=peft_config)
+
+ with ctx:
+ eva_state_dict = _get_eva_state_dict(
+ model=model,
+ dataloader=dataloader,
+ peft_config=peft_config,
+ target_module_check_fn=target_module_check_fn,
+ forward_fn=forward_fn,
+ prepare_model_inputs_fn=prepare_model_inputs_fn,
+ prepare_layer_inputs_fn=prepare_layer_inputs_fn,
+ gather_distributed_inputs=gather_distributed_inputs,
+ show_progress_bar=show_progress_bar,
+ )
+ return eva_state_dict
+
+
+@torch.no_grad()
+def initialize_lora_eva_weights(
+ model: torch.nn.Module,
+ dataloader: Optional[Iterable] = None,
+ eva_state_dict: Optional[dict] = None,
+ forward_fn: Optional[callable] = forward_fn_dict,
+ prepare_model_inputs_fn: Optional[callable] = prepare_model_inputs_fn_language_modeling,
+ prepare_layer_inputs_fn: Union[callable, dict[str, callable], None] = prepare_layer_inputs_fn_language_modeling,
+ adapter_name: str = "default",
+ gather_distributed_inputs: bool = True,
+ show_progress_bar: bool = True,
+):
+ """
+ Initialize the weights of the LoRA layers using the EVA method.
+
+ This function initializes the weights of the LoRA layers using the EVA method. It computes the SVD for each adapter
+ layer and updates the weights accordingly.
+
+ Args:
+ model (PeftModel): The peft model to compute the SVD for.
+ dataloader (Optional[Iterable]):
+ The dataloader to use for the forward pass. If None, eva_state_dict needs to be provided.
+ eva_state_dict (Optional[dict]):
+ The state_dict to load into the model. If None, a dataloader needs to be provided and the state_dict will
+ be computed using `get_eva_state_dict`.
+ forward_fn (callable):
+ The forward function to use for the forward pass. Takes two arguments: `model` and `inputs`. Default
+ behavior is `return model(**inputs)`
+ prepare_model_inputs_fn (Optional[callable]):
+ This function receives the model inputs and the peft_config and passes the output to
+ `prepare_layer_inputs_fn`. Can be used to modify the input to the SVD computation based on the original
+ model inputs. For example for language modeling the attention mask is used to determine which indices are
+ padding tokens and should not be used for SVD. Any function defined here expects two arguments:
+ `model_input` and `peft_config`. `peft.tuners.lora.eva.prepare_model_inputs_fn_language_modeling` is used
+ by default.
+ prepare_layer_inputs_fn (Union[callable, Dict[str, callable], None]):
+ This function receives the layer inputs, the model inputs (potentially modified by
+ `prepare_model_inputs_fn`) and the name of the layer and returns the inputs that should be used for SVD for
+ that particular layer. Any custom function defined here expects three arguments: `layer_input`,
+ `model_input`, and `layer_name` and should return a 2d tensor. The default logic can be found in
+ peft.tuners.lora.eva.prepare_layer_inputs_fn_language_modeling and works for language modeling. In this
+ case model_inputs is the mask used to determine which indices should be used for SVD (created by
+ `prepare_model_inputs_fn_language_modeling`).
+ adapter_name (str): The name of the adapter to initialize the weights for.
+ gather_distributed_inputs (bool):
+ Whether to gather the layer inputs from all ranks. Default is True meaning in a distributed setting the
+ layer inputs will be gathered from all ranks for the SVD computation. For non-distributed settings this
+ argument is ignored. Set to False if you are using a non-distributed dataloader in a distributed setting.
+ show_progress_bar (bool): Whether to show a progress bar. Default is True.
+
+ Returns:
+ model (torch.nn.Module): The model with the initialized LoRA weights.
+ """
+ if not hasattr(model, "peft_config"):
+ raise ValueError("model must be a PeftModel")
+
+ # eva currently only works with a single active adapter
+ # Important: when removing this requirement, make sure eva init works correctly if the new rank is 0.
+ if len(model.active_adapters) > 1:
+ raise ValueError("`initialize_lora_eva_weights` currently only works with a single active adapter")
+
+ # initialize_lora_eva_weights only works with `init_lora_weights='eva'`
+ if model.peft_config[adapter_name].init_lora_weights != "eva":
+ raise ValueError("`initialize_lora_eva_weights` can only be used with `init_lora_weights='eva'`")
+
+ # compute svd
+ if eva_state_dict is None:
+ if dataloader is None:
+ raise ValueError("dataloader is required if eva_state_dict is not provided")
+ eva_state_dict = get_eva_state_dict(
+ model=model,
+ dataloader=dataloader,
+ forward_fn=forward_fn,
+ prepare_model_inputs_fn=prepare_model_inputs_fn,
+ prepare_layer_inputs_fn=prepare_layer_inputs_fn,
+ adapter_name=adapter_name,
+ gather_distributed_inputs=gather_distributed_inputs,
+ show_progress_bar=show_progress_bar,
+ )
+
+ _load_eva_state_dict(model, eva_state_dict, adapter_name)
diff --git a/peft/src/peft/tuners/lora/gptq.py b/peft/src/peft/tuners/lora/gptq.py
new file mode 100644
index 0000000000000000000000000000000000000000..7ff40bc9efd61f681b50db7aeed09e64815ea60a
--- /dev/null
+++ b/peft/src/peft/tuners/lora/gptq.py
@@ -0,0 +1,154 @@
+# Copyright 2023-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+from typing import Any, Optional
+
+import torch
+
+from peft.import_utils import is_gptqmodel_available
+from peft.tuners.lora.layer import LoraLayer
+from peft.tuners.tuners_utils import BaseTunerLayer
+from peft.utils import get_auto_gptq_quant_linear
+
+from .layer import LoraVariant
+
+
+class GPTQLoraLinear(torch.nn.Module, LoraLayer):
+ def __init__(
+ self,
+ base_layer,
+ adapter_name: str,
+ r: int = 0,
+ lora_alpha: int = 1,
+ lora_dropout: float = 0.0,
+ init_lora_weights: bool = True,
+ use_rslora: bool = False,
+ use_dora: bool = False,
+ use_qalora: bool = False,
+ lora_bias: bool = False,
+ qalora_group_size: int = 32,
+ **kwargs,
+ ):
+ super().__init__()
+ LoraLayer.__init__(self, base_layer)
+
+ if use_dora:
+ raise ValueError(f"{self.__class__.__name__} does not support DoRA yet, please set it to False")
+
+ # self.base_layer and self.quant_linear_module are the same; we need the former for consistency and the latter
+ # for backwards compatibility
+ self.quant_linear_module = base_layer
+ self._active_adapter = adapter_name
+ self.update_layer(
+ adapter_name,
+ r,
+ lora_alpha=lora_alpha,
+ lora_dropout=lora_dropout,
+ init_lora_weights=init_lora_weights,
+ use_rslora=use_rslora,
+ use_dora=use_dora,
+ use_qalora=use_qalora,
+ lora_bias=lora_bias,
+ qalora_group_size=qalora_group_size,
+ )
+
+ def resolve_lora_variant(self, *, use_dora: bool, use_qalora: bool, **kwargs) -> Optional[LoraVariant]:
+ if use_dora and use_qalora:
+ raise NotImplementedError(
+ f"Dora and QA_lora at the same time is not supported for {self.__class__.__name__} (yet)."
+ )
+ elif use_dora:
+ from .variants import DoraLinearVariant
+
+ variant = DoraLinearVariant()
+ elif use_qalora:
+ from .variants import QALoraLinearVariant
+
+ variant = QALoraLinearVariant()
+ else:
+ variant = None
+ return variant
+
+ def forward(self, x: torch.Tensor):
+ # note: logic differs from default Linear because merging is not supported
+ result = self.quant_linear_module(x)
+
+ if self.disable_adapters:
+ return result
+
+ lora_A_keys = self.lora_A.keys()
+
+ for active_adapter in self.active_adapters:
+ if active_adapter not in lora_A_keys:
+ continue
+ torch_result_dtype = result.dtype
+
+ lora_A = self.lora_A[active_adapter]
+ lora_B = self.lora_B[active_adapter]
+ dropout = self.lora_dropout[active_adapter]
+ scaling = self.scaling[active_adapter]
+
+ x = self._cast_input_dtype(x, lora_A.weight.dtype)
+
+ if active_adapter not in self.lora_variant: # vanilla LoRA
+ result = result + lora_B(lora_A(dropout(x))) * scaling
+ else:
+ result = self.lora_variant[active_adapter].forward(
+ self,
+ active_adapter=active_adapter,
+ x=x,
+ result=result,
+ )
+
+ result = result.to(torch_result_dtype)
+ return result
+
+ def __repr__(self) -> str:
+ rep = super().__repr__()
+ return "lora." + rep
+
+ # TODO: Check if it is better as suggested by users https://github.com/PanQiWei/AutoGPTQ/pull/102
+ # def reset_lora_parameters(self, adapter_name):
+ # if adapter_name in self.lora_A.keys():
+ # torch.nn.init.xavier_uniform_(self.lora_A[adapter_name].weight)
+ # torch.nn.init.zeros_(self.lora_B[adapter_name].weight)
+
+
+def dispatch_gptq(
+ target: torch.nn.Module,
+ adapter_name: str,
+ **kwargs: Any,
+) -> Optional[torch.nn.Module]:
+ new_module = None
+
+ if isinstance(target, BaseTunerLayer):
+ target_base_layer = target.get_base_layer()
+ else:
+ target_base_layer = target
+
+ cfg = kwargs.get("gptq_quantization_config", None)
+
+ if is_gptqmodel_available():
+ from gptqmodel.nn_modules.qlinear import BaseQuantLinear
+
+ if isinstance(target_base_layer, BaseQuantLinear):
+ new_module = GPTQLoraLinear(target, adapter_name, **kwargs)
+ target.qweight = target_base_layer.qweight
+ else:
+ quant_linear = get_auto_gptq_quant_linear(cfg)
+
+ if quant_linear is not None and isinstance(target_base_layer, quant_linear):
+ new_module = GPTQLoraLinear(target, adapter_name, **kwargs)
+ target.qweight = target_base_layer.qweight
+
+ return new_module
diff --git a/peft/src/peft/tuners/lora/hqq.py b/peft/src/peft/tuners/lora/hqq.py
new file mode 100644
index 0000000000000000000000000000000000000000..924acb2d4d254e61421de2a1e5efa391458c1ae9
--- /dev/null
+++ b/peft/src/peft/tuners/lora/hqq.py
@@ -0,0 +1,251 @@
+# Copyright 2024-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+from __future__ import annotations
+
+import copy
+import warnings
+from typing import Any, Optional
+
+import torch
+
+from peft.import_utils import is_hqq_available
+from peft.tuners.tuners_utils import BaseTunerLayer, check_adapters_to_merge
+from peft.utils.other import transpose
+
+from .layer import LoraLayer, LoraVariant
+
+
+if is_hqq_available():
+ from hqq.core.quantize import HQQLinear
+
+ class HqqLoraLinear(torch.nn.Module, LoraLayer):
+ # Lora implemented in a dense layer
+ def __init__(
+ self,
+ base_layer: torch.nn.Module,
+ adapter_name: str,
+ r: int = 0,
+ lora_alpha: int = 1,
+ lora_dropout: float = 0.0,
+ init_lora_weights: bool = True,
+ use_rslora: bool = False,
+ use_dora: bool = False,
+ lora_bias: bool = False,
+ **kwargs,
+ ) -> None:
+ if lora_bias:
+ raise ValueError(f"{self.__class__.__name__} does not support lora_bias yet, set it to False")
+
+ super().__init__()
+ LoraLayer.__init__(self, base_layer)
+ self.fan_in_fan_out = False
+
+ self._active_adapter = adapter_name
+ self.update_layer(
+ adapter_name,
+ r,
+ lora_alpha=lora_alpha,
+ lora_dropout=lora_dropout,
+ init_lora_weights=init_lora_weights,
+ use_rslora=use_rslora,
+ use_dora=use_dora,
+ lora_bias=lora_bias,
+ )
+
+ def resolve_lora_variant(self, *, use_dora: bool, **kwargs) -> Optional[LoraVariant]:
+ if not use_dora:
+ return None
+
+ from .variants import DoraLinearVariant
+
+ return DoraLinearVariant()
+
+ def merge(self, safe_merge: bool = False, adapter_names: Optional[list[str]] = None) -> None:
+ """
+ Merge the active adapter weights into the base weights
+
+ Args:
+ safe_merge (`bool`, *optional*):
+ If True, the merge operation will be performed in a copy of the original weights and check for NaNs
+ before merging the weights. This is useful if you want to check if the merge operation will produce
+ NaNs. Defaults to `False`.
+ adapter_names (`list[str]`, *optional*):
+ The list of adapter names that should be merged. If None, all active adapters will be merged.
+ Defaults to `None`.
+ """
+ adapter_names = check_adapters_to_merge(self, adapter_names)
+ if not adapter_names:
+ # no adapter to merge
+ return
+
+ for active_adapter in adapter_names:
+ if active_adapter not in self.lora_A.keys():
+ continue
+
+ layer = self.get_base_layer()
+ quant_config = {**copy.deepcopy(layer.quant_config), "offload_meta": layer.offload_meta}
+
+ output = layer.dequantize()
+ if active_adapter not in self.lora_variant: # vanilla LoRA
+ lora_data = self.get_delta_weight(active_adapter)
+ w_data = output + lora_data
+ else:
+ w_data = self.lora_variant[active_adapter].merge_safe(self, active_adapter, output)
+
+ if safe_merge and not torch.isfinite(w_data).all():
+ raise ValueError(
+ f"NaNs detected in the merged weights. The adapter {active_adapter} seems to be broken"
+ )
+
+ new_hqq_layer = HQQLinear(None, quant_config, compute_dtype=layer.compute_dtype, device=layer.device)
+ quant_config.pop("offload_meta", None)
+ new_hqq_layer.quantize(w_data, **quant_config)
+ self.base_layer = new_hqq_layer
+ self.merged_adapters.append(active_adapter)
+
+ def unmerge(self) -> None:
+ """
+ This method unmerges all merged adapter layers from the base weights.
+ """
+ if not self.merged:
+ warnings.warn("Already unmerged. Nothing to do.")
+ return
+
+ while len(self.merged_adapters) > 0:
+ active_adapter = self.merged_adapters.pop()
+ if active_adapter not in self.lora_A.keys():
+ continue
+
+ layer = self.get_base_layer()
+ quant_config = {**copy.deepcopy(layer.quant_config), "offload_meta": layer.offload_meta}
+ output = layer.dequantize()
+
+ if active_adapter not in self.lora_variant: # vanilla LoRA
+ lora_data = self.get_delta_weight(active_adapter)
+ w_data = output.to(lora_data.dtype).to(lora_data.device) - lora_data
+ else:
+ w_data = self.lora_variant[active_adapter].unmerge(self, active_adapter, output)
+
+ new_hqq_layer = HQQLinear(None, quant_config, compute_dtype=layer.compute_dtype, device=layer.device)
+ quant_config.pop("offload_meta", None)
+ new_hqq_layer.quantize(w_data, **quant_config)
+ self.base_layer = new_hqq_layer
+
+ def get_delta_weight(self, adapter):
+ return (
+ transpose(
+ self.lora_B[adapter].weight @ self.lora_A[adapter].weight,
+ False,
+ )
+ * self.scaling[adapter]
+ )
+
+ def _mixed_batch_forward(
+ self, x: torch.Tensor, *args: Any, adapter_names: list[str], **kwargs: Any
+ ) -> torch.Tensor:
+ # This is a special method that handles the case when users pass the argument `adapter_names`. This is an
+ # extra argument that allows mixing different adapters in the same batch at inference time.
+ result = self.base_layer(x, *args, **kwargs)
+
+ unique_adapters = set(adapter_names)
+ sub_batch_indices_list = []
+ for adapter in unique_adapters:
+ sub_batch_indices_list.append([index for index, item in enumerate(adapter_names) if item == adapter])
+
+ for i, active_adapter in enumerate(unique_adapters):
+ if active_adapter == "__base__":
+ continue
+ if active_adapter not in self.lora_A.keys():
+ continue
+
+ lora_A = self.lora_A[active_adapter]
+ lora_B = self.lora_B[active_adapter]
+ dropout = self.lora_dropout[active_adapter]
+ scaling = self.scaling[active_adapter]
+
+ requires_conversion = not torch.is_autocast_enabled()
+ if requires_conversion:
+ expected_dtype = result.dtype
+ x = self._cast_input_dtype(x, lora_A.weight.dtype)
+
+ # getting the sub-batch, passing it to LoRA layers and updating the corresponding indices of the linear
+ # layer output
+ sub_batch = x[sub_batch_indices_list[i]]
+ output = lora_B(lora_A(dropout(sub_batch))) * scaling
+ if requires_conversion:
+ output = output.to(expected_dtype)
+ result[sub_batch_indices_list[i]] += output
+
+ return result
+
+ def forward(self, x: torch.Tensor, *args, **kwargs) -> torch.Tensor:
+ self._check_forward_args(x, *args, **kwargs)
+ adapter_names = kwargs.pop("adapter_names", None)
+
+ if self.disable_adapters:
+ if self.merged:
+ self.unmerge()
+ result = self.base_layer(x, *args, **kwargs)
+ elif adapter_names is not None:
+ result = self._mixed_batch_forward(x, *args, adapter_names=adapter_names, **kwargs)
+ elif self.merged:
+ result = self.base_layer(x, *args, **kwargs)
+ else:
+ result = self.base_layer(x, *args, **kwargs)
+
+ for active_adapter in self.active_adapters:
+ if active_adapter not in self.lora_A.keys():
+ continue
+ lora_A = self.lora_A[active_adapter]
+ lora_B = self.lora_B[active_adapter]
+ dropout = self.lora_dropout[active_adapter]
+ scaling = self.scaling[active_adapter]
+
+ requires_conversion = not torch.is_autocast_enabled()
+ if requires_conversion:
+ expected_dtype = result.dtype
+ x = self._cast_input_dtype(x, lora_A.weight.dtype)
+
+ if active_adapter not in self.lora_variant: # vanilla LoRA
+ result = result + lora_B(lora_A(dropout(x))) * scaling
+ else:
+ result = self.lora_variant[active_adapter].forward(
+ self,
+ active_adapter=active_adapter,
+ x=x,
+ result=result,
+ )
+
+ if requires_conversion:
+ result = result.to(expected_dtype)
+
+ return result
+
+ def __repr__(self) -> str:
+ rep = super().__repr__()
+ return "lora." + rep
+
+
+def dispatch_hqq(target: torch.nn.Module, adapter_name: str, **kwargs):
+ new_module = None
+
+ if isinstance(target, BaseTunerLayer):
+ target_base_layer = target.get_base_layer()
+ else:
+ target_base_layer = target
+
+ if is_hqq_available() and isinstance(target_base_layer, HQQLinear):
+ new_module = HqqLoraLinear(target_base_layer, adapter_name, **kwargs)
+
+ return new_module
diff --git a/peft/src/peft/tuners/lora/inc.py b/peft/src/peft/tuners/lora/inc.py
new file mode 100644
index 0000000000000000000000000000000000000000..e9fea9dc266a72cdf1368963df5b039691c22bdc
--- /dev/null
+++ b/peft/src/peft/tuners/lora/inc.py
@@ -0,0 +1,78 @@
+# Copyright 2025-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+# NOTE: PEFT tests related to INC are handled under Optimum-Habana repository:
+# - LLMs: https://github.com/huggingface/optimum-habana/blob/main/tests/test_peft_inference.py
+# - Diffusers: https://github.com/huggingface/optimum-habana/blob/main/tests/test_diffusers.py
+
+from typing import Optional
+
+import torch
+
+from peft.import_utils import is_inc_available
+from peft.tuners.tuners_utils import BaseTunerLayer
+
+from .layer import Linear
+
+
+if is_inc_available():
+
+ class IncLoraLinear(Linear):
+ def __init__(
+ self,
+ base_layer: torch.nn.Module,
+ adapter_name: str,
+ **kwargs,
+ ):
+ super().__init__(base_layer, adapter_name, **kwargs)
+
+ def merge(self, safe_merge: bool = False, adapter_names: Optional[list[str]] = None) -> None:
+ """
+ Merge the active adapter weights into the base weights
+
+ Args:
+ safe_merge (`bool`, *optional*):
+ If True, the merge operation will be performed in a copy of the original weights and check for NaNs
+ before merging the weights. This is useful if you want to check if the merge operation will produce
+ NaNs. Defaults to `False`.
+ adapter_names (`list[str]`, *optional*):
+ The list of adapter names that should be merged. If None, all active adapters will be merged.
+ Defaults to `None`.
+ """
+ raise NotImplementedError("Merging LoRA with INC layers is not yet implemented")
+
+ def unmerge(self) -> None:
+ """
+ This method unmerges all merged adapter layers from the base weights.
+ """
+ raise NotImplementedError("Unmerging LoRA from INC layers is not yet implemented")
+
+
+def dispatch_inc(target: torch.nn.Module, adapter_name: str, **kwargs):
+ new_module = None
+
+ if isinstance(target, BaseTunerLayer):
+ target_base_layer = target.get_base_layer()
+ else:
+ target_base_layer = target
+
+ if is_inc_available():
+ from neural_compressor.torch.algorithms.fp8_quant._quant_common.helper_modules import (
+ PatchedLinear,
+ )
+
+ if isinstance(target_base_layer, PatchedLinear):
+ new_module = IncLoraLinear(target, adapter_name, **kwargs)
+
+ return new_module
diff --git a/peft/src/peft/tuners/lora/layer.py b/peft/src/peft/tuners/lora/layer.py
new file mode 100644
index 0000000000000000000000000000000000000000..b01e87e6a5d2a69e123c6198d83946a21871a9fd
--- /dev/null
+++ b/peft/src/peft/tuners/lora/layer.py
@@ -0,0 +1,2271 @@
+# Copyright 2023-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+from __future__ import annotations
+
+import math
+import warnings
+from contextlib import contextmanager
+from typing import Any, Optional, Union
+
+import torch
+import torch.nn as nn
+import torch.nn.functional as F
+from torch import svd_lowrank
+from transformers.pytorch_utils import Conv1D
+
+from peft.tuners._buffer_dict import BufferDict
+from peft.tuners.tuners_utils import BaseTunerLayer, _get_in_out_features, check_adapters_to_merge
+from peft.utils.integrations import (
+ dequantize_module_weight,
+ gather_params_ctx,
+ get_bnb_param_type,
+ skip_init_on_device,
+)
+from peft.utils.other import transpose
+from peft.utils.warning import PeftWarning
+
+from .config import ArrowConfig, LoraConfig
+
+
+VARIANT_KWARG_KEYS = ["alora_offsets"]
+
+
+class LoraVariant:
+ """
+ Base class for LoRA variants, e.g. DoRA.
+
+ This class should be subclassed and the methods below should be implemented accordingly. The methods should be
+ implemented as static methods, this makes it easier to combine variants.
+
+ Note for developers: These methods are prone to change and should thus considered to be "private". Use at your own
+ discretion.
+ """
+
+ @staticmethod
+ def init(module: LoraLayer, adapter_name: str) -> None:
+ """Initialization code for the LoRA variant, it's called within `update_layer`"""
+ raise NotImplementedError
+
+ @staticmethod
+ def merge_safe(module: LoraLayer, active_adapter: str, orig_weight: torch.Tensor) -> torch.Tensor:
+ """Safe merging of the weights from `merge(..., safe_merge=True)`, should return a new tensor"""
+ raise NotImplementedError
+
+ @staticmethod
+ def merge_unsafe(module: LoraLayer, active_adapter: str, orig_weight: torch.Tensor) -> None:
+ """Unsafe merging of the weights from `merge(..., safe_merge=False)`, should modify the weight in-place"""
+
+ @staticmethod
+ def unmerge(module: LoraLayer, active_adapter: str, orig_weight: torch.Tensor) -> torch.Tensor:
+ """Remove the adapter weights from the original weights, then return them"""
+
+ @staticmethod
+ def forward(
+ module: LoraLayer,
+ active_adapter: str,
+ x: torch.Tensor,
+ result: torch.Tensor,
+ **kwargs,
+ ) -> torch.Tensor:
+ """
+ The forward pass of the LoRA variant, should return the overall result (not just the diff)
+
+ Args:
+ module (LoraLayer): The module on which the forward pass is called
+ active_adapter (str): The name of the active adapter
+ x (torch.Tensor): The input to the forward call
+ result (torch.Tensor): The result from the base model
+ **kwargs: Additional arguments passed from [`LoraLayer.forward`].
+ """
+ raise NotImplementedError
+
+
+class LoraLayer(BaseTunerLayer):
+ # All names of layers that may contain (trainable) adapter weights
+ adapter_layer_names: tuple[str, ...] = ("lora_A", "lora_B", "lora_embedding_A", "lora_embedding_B")
+ # All names of other parameters that may contain adapter-related parameters
+ other_param_names: tuple[str, ...] = ("r", "lora_alpha", "scaling", "lora_dropout")
+
+ def __init__(self, base_layer: nn.Module, ephemeral_gpu_offload: bool = False, **kwargs) -> None:
+ self.base_layer = base_layer
+ self.r = {}
+ self.lora_alpha = {}
+ self.scaling = {}
+ self.lora_dropout = nn.ModuleDict({})
+ self.lora_A = nn.ModuleDict({})
+ self.lora_B = nn.ModuleDict({})
+ # For Embedding layer
+ self.lora_embedding_A = nn.ParameterDict({})
+ self.lora_embedding_B = nn.ParameterDict({})
+ # Mark the weight as unmerged
+ self._disable_adapters = False
+ self.merged_adapters = []
+ self.use_dora: dict[str, bool] = {} # not actively used anymore after #2443, keep it for BC
+ self.use_rslora: dict[str, bool] = {}
+ self.lora_bias: dict[str, bool] = {}
+ self.lora_magnitude_vector = torch.nn.ModuleDict() # for DoRA
+ self._caches: dict[str, Any] = {}
+ self.ephemeral_gpu_offload: bool = ephemeral_gpu_offload
+ # flag to enable/disable casting of input to weight dtype during forward call
+ self.cast_input_dtype_enabled: bool = True
+ self.lora_variant: dict[str, LoraVariant] = {}
+ self.kwargs = kwargs
+
+ base_layer = self.get_base_layer()
+ in_features, out_features = _get_in_out_features(base_layer)
+ self.in_features = in_features
+ self.out_features = out_features
+
+ def resolve_lora_variant(self, *, use_dora: bool, **kwargs) -> Optional[LoraVariant]:
+ """Return a matching LoRA variant for this layer type.
+
+ Given the init arguments of this layer, return the correct LoRA variant, if any. E.g., if `use_dora=True`, this
+ method should return the DoRA variant for the given layer. If `use_alora=True`, same for aLoRA.
+
+ If there is no fitting variant, return None.
+
+ Note: If this layer type does not support the LoRA variant at all, please raise an error during __init__ as is
+ convention, and not here.
+
+ """
+ return None
+
+ def update_layer(
+ self,
+ adapter_name,
+ r,
+ lora_alpha,
+ lora_dropout,
+ init_lora_weights,
+ use_rslora,
+ use_dora: bool = False,
+ use_alora: bool = False,
+ use_qalora: bool = False,
+ lora_bias: bool = False,
+ arrow_config: ArrowConfig = None,
+ qalora_group_size: int = 32,
+ inference_mode: bool = False,
+ **kwargs,
+ ):
+ # collect the kwargs
+ kwargs = locals().copy()
+ del kwargs["self"]
+
+ # This code works for linear layers, override for other layer types
+ if r <= 0:
+ raise ValueError(f"`r` should be a positive integer value but the value passed is {r}")
+
+ if lora_bias and (getattr(self.get_base_layer(), "bias", None) is None):
+ warnings.warn(
+ f"`lora_bias=True` was passed but the targeted layer of type {type(self.get_base_layer()).__name__} "
+ "has no bias. This means that merging LoRA weights won't be possible.",
+ PeftWarning,
+ )
+
+ lora_variant = self.resolve_lora_variant(
+ use_dora=use_dora,
+ use_alora=use_alora,
+ use_qalora=use_qalora,
+ qalora_group_size=qalora_group_size,
+ arrow_config=arrow_config,
+ )
+ if lora_variant is not None:
+ self.lora_variant[adapter_name] = lora_variant
+
+ self.r[adapter_name] = r
+ self.lora_alpha[adapter_name] = lora_alpha
+ if lora_dropout > 0.0:
+ lora_dropout_layer = nn.Dropout(p=lora_dropout)
+ else:
+ lora_dropout_layer = nn.Identity()
+
+ self.lora_dropout.update(nn.ModuleDict({adapter_name: lora_dropout_layer}))
+
+ # Actual trainable parameters
+ self.lora_A[adapter_name] = nn.Linear(self.in_features, r, bias=False)
+ self.lora_B[adapter_name] = nn.Linear(r, self.out_features, bias=lora_bias)
+ self.lora_bias[adapter_name] = lora_bias
+
+ if use_rslora:
+ self.scaling[adapter_name] = lora_alpha / math.sqrt(r)
+ else:
+ self.scaling[adapter_name] = lora_alpha / r
+
+ self.use_rslora[adapter_name] = use_rslora
+
+ self.use_dora[adapter_name] = use_dora
+
+ # for inits that require access to the base weight, use gather_param_ctx so that the weight is gathered when using DeepSpeed
+ if isinstance(init_lora_weights, str) and init_lora_weights.startswith("pissa"):
+ with gather_params_ctx(self.get_base_layer().weight):
+ self.pissa_init(adapter_name, init_lora_weights)
+ elif isinstance(init_lora_weights, str) and init_lora_weights.startswith("corda"):
+ with gather_params_ctx(self.get_base_layer().weight):
+ self.corda_init(adapter_name, init_lora_weights)
+ elif isinstance(init_lora_weights, str) and init_lora_weights.lower() == "olora":
+ with gather_params_ctx(self.get_base_layer().weight):
+ self.olora_init(adapter_name)
+ elif init_lora_weights == "loftq":
+ with gather_params_ctx(self.get_base_layer().weight):
+ self.loftq_init(adapter_name)
+ elif init_lora_weights == "eva":
+ nn.init.zeros_(self.lora_B[adapter_name].weight)
+ elif init_lora_weights == "orthogonal":
+ with gather_params_ctx(self.get_base_layer().weight):
+ self.orthogonal_init(adapter_name)
+ elif init_lora_weights:
+ self.reset_lora_parameters(adapter_name, init_lora_weights)
+ # call this before init of the lora variants
+ self._move_adapter_to_device_of_base_layer(adapter_name)
+
+ if adapter_name in self.lora_variant:
+ self.lora_variant[adapter_name].init(self, **kwargs)
+
+ self.set_adapter(self.active_adapters, inference_mode=inference_mode)
+
+ # Check for adapters that were added or removed from the arrow_model.
+ # The arrow model may be modified after creation by adding new experts
+ # (pre-trained or trainable) or by removing existing ones. Whenever such
+ # a change occurs, on_adapter_change() is called to update the set of
+ # active task-specific experts and, if needed, to handle recomputing prototypes
+ # and doing general knowledge subtraction (GKS) again.
+ if hasattr(self, "lora_arrow"):
+ for adapter in self.lora_variant:
+ if adapter in self.lora_arrow:
+ self.lora_arrow[adapter].on_adapter_change(self.lora_A, self.lora_B)
+
+ def reset_lora_parameters(self, adapter_name, init_lora_weights):
+ if init_lora_weights is False:
+ return
+
+ if adapter_name in self.lora_A.keys():
+ if init_lora_weights is True:
+ # initialize A the same way as the default for nn.Linear and B to zero
+ # https://github.com/microsoft/LoRA/blob/a0a92e0f26c067cf94747bdbf1ce73793fa44d19/loralib/layers.py#L124
+ nn.init.kaiming_uniform_(self.lora_A[adapter_name].weight, a=math.sqrt(5))
+ elif init_lora_weights.lower() == "gaussian":
+ nn.init.normal_(self.lora_A[adapter_name].weight, std=1 / self.r[adapter_name])
+ else:
+ raise ValueError(f"Unknown initialization {init_lora_weights=}")
+ nn.init.zeros_(self.lora_B[adapter_name].weight)
+ if self.lora_bias[adapter_name]:
+ nn.init.zeros_(self.lora_B[adapter_name].bias)
+ if adapter_name in self.lora_embedding_A.keys():
+ # Initialize A to zeros and B the same way as the default for nn.Embedding, see:
+ # https://github.com/microsoft/LoRA/blob/4c0333854cb905966f8cc4e9a74068c1e507c7b7/loralib/layers.py#L59-L60
+ nn.init.zeros_(self.lora_embedding_A[adapter_name])
+ nn.init.normal_(self.lora_embedding_B[adapter_name])
+ if self.lora_bias[adapter_name]:
+ # embeddings are not supported at the moment, but still adding this for consistency
+ nn.init.zeros_(self.lora_embedding_B[adapter_name].bias)
+
+ def olora_init(self, adapter_name):
+ base_layer = self.get_base_layer()
+ orig_weight = base_layer.weight
+ bnb_param_type = get_bnb_param_type(orig_weight)
+ dtype = orig_weight.dtype
+
+ if bnb_param_type:
+ # check without importing bitsandbytes and robust to bnb_4bit_quant_storage=float*
+ weight_tensor = dequantize_module_weight(base_layer)
+ elif dtype in [torch.float32, torch.float16, torch.bfloat16]:
+ weight_tensor = orig_weight
+ else:
+ raise TypeError(f"Unsupported data type for the base layer. Got {dtype}.")
+
+ scale_factor = self.scaling[adapter_name]
+ r = self.r[adapter_name]
+ weight_tensor = weight_tensor.to(torch.float32)
+ Q, R = torch.linalg.qr(weight_tensor.data)
+
+ Qr, Rr = Q[:, :r], R[:r]
+
+ self.lora_A[adapter_name].weight.data = Rr.contiguous()
+ self.lora_B[adapter_name].weight.data = Qr.contiguous()
+
+ weight_tensor.data -= scale_factor * self.lora_B[adapter_name].weight @ self.lora_A[adapter_name].weight
+ if bnb_param_type == "4bit":
+ weight_tensor = orig_weight.__class__(
+ weight_tensor,
+ quant_type=orig_weight.quant_type,
+ quant_storage=orig_weight.quant_storage,
+ compress_statistics=orig_weight.compress_statistics,
+ module=orig_weight.module,
+ ).to(orig_weight.device)
+ base_layer.weight = weight_tensor
+ elif bnb_param_type == "8bit":
+ weight_tensor = orig_weight.__class__(
+ weight_tensor,
+ requires_grad=orig_weight.requires_grad,
+ has_fp16_weights=orig_weight.has_fp16_weights,
+ ).to(orig_weight.device)
+ base_layer.weight = weight_tensor
+ else:
+ weight_tensor = weight_tensor.to(dtype)
+ base_layer.weight.data = weight_tensor
+
+ def pissa_init(self, adapter_name, init_lora_weights):
+ weight = self.get_base_layer().weight
+ dtype = weight.dtype
+ if dtype not in [torch.float32, torch.float16, torch.bfloat16]:
+ raise TypeError(
+ "Please initialize PiSSA under float32, float16, or bfloat16. "
+ "Subsequently, re-quantize the residual model to help minimize quantization errors."
+ )
+ weight = transpose(weight.to(torch.float32), self.fan_in_fan_out)
+ if init_lora_weights == "pissa":
+ # USV^T = W <-> VSU^T = W^T, where W^T = weight.data in R^{out_channel, in_channel},
+ V, S, Uh = torch.linalg.svd(weight.data, full_matrices=False)
+ Vr = V[:, : self.r[adapter_name]]
+ Sr = S[: self.r[adapter_name]]
+ Sr /= self.scaling[adapter_name]
+ Uhr = Uh[: self.r[adapter_name]]
+ elif len(init_lora_weights.split("_niter_")) == 2:
+ Vr, Sr, Ur = svd_lowrank(
+ weight.data, self.r[adapter_name], niter=int(init_lora_weights.split("_niter_")[-1])
+ )
+ Sr /= self.scaling[adapter_name]
+ Uhr = Ur.t()
+ else:
+ raise ValueError(
+ f"init_lora_weights should be 'pissa' or 'pissa_niter_[number of iters]', got {init_lora_weights} instead."
+ )
+
+ lora_A = torch.diag(torch.sqrt(Sr)) @ Uhr
+ lora_B = Vr @ torch.diag(torch.sqrt(Sr))
+ self.lora_A[adapter_name].weight.data = lora_A
+ self.lora_B[adapter_name].weight.data = lora_B
+ weight = weight.data - self.scaling[adapter_name] * lora_B @ lora_A
+ weight = transpose(weight.to(dtype), self.fan_in_fan_out)
+ self.get_base_layer().weight.data = weight
+
+ def corda_init(self, adapter_name, init_lora_weights):
+ linear = self.get_base_layer()
+ weight = linear.weight
+ dtype = weight.dtype
+ if dtype not in [torch.float32, torch.float16, torch.bfloat16]:
+ raise TypeError(
+ "Please initialize CorDA under float32, float16, or bfloat16. "
+ "Subsequently, re-quantize the residual model to help minimize quantization errors."
+ )
+ weight = weight.to(torch.float32)
+ out_dim = weight.data.size(0)
+ in_dim = weight.data.size(1)
+
+ # Calculate WC from covariance matrix
+ if not hasattr(linear, "eigens"):
+ raise ValueError(
+ "`eigens` attribute not found for layer, please run `preprocess_corda` first. "
+ "More information can be found at examples/corda_finetuning/README.md."
+ )
+ eigens = linear.eigens
+ U = eigens.U_WC
+ S = eigens.S_WC
+ V = eigens.V_WC
+ r = self.r[adapter_name]
+
+ # nan or inf check
+ if torch.isnan(S).any() or torch.isinf(S).any():
+ raise ValueError(
+ "Invalid value found in matrix S. Please file an issue at https://github.com/huggingface/peft/issues."
+ )
+ if torch.isnan(U).any() or torch.isinf(U).any():
+ raise ValueError(
+ "Invalid value found in matrix U. Please file an issue at https://github.com/huggingface/peft/issues."
+ )
+ if torch.isnan(V).any() or torch.isinf(V).any():
+ raise ValueError(
+ "Invalid value found in matrix V. Please file an issue at https://github.com/huggingface/peft/issues."
+ )
+
+ # Sanity check
+ if U.size(0) != out_dim or U.size(1) != r:
+ raise ValueError(
+ f"Matrix U size mismatch: {U.size()} vs. ({out_dim}, {r}). Please make sure the `lora_config` and "
+ "`model` argument of `preprocess_corda` is consistent with `get_peft_model`. If you're using cache "
+ "in `preprocess_corda`, please make sure the cache is built with the same model and LoRA rank."
+ )
+ if S.size(0) != r:
+ raise ValueError(
+ f"Matrix S size mismatch: {S.size()} vs. ({r},). Please make sure the `lora_config` and `model` argument "
+ "of `preprocess_corda` is consistent with `get_peft_model`. If you're using cache in `preprocess_corda`, "
+ "please make sure the cache is built with the same model and LoRA rank."
+ )
+ if V.size(0) != in_dim or V.size(1) != r:
+ raise ValueError(
+ f"Matrix V size mismatch: {V.size()} vs. ({in_dim}, {r}). Please make sure the `lora_config` and "
+ "`model` argument of `preprocess_corda` is consistent with `get_peft_model`. If you're using cache "
+ "in `preprocess_corda`, please make sure the cache is built with the same model and LoRA rank."
+ )
+
+ # Apply alpha
+ S /= self.scaling[adapter_name]
+
+ # Init lora_A and lora_B weights
+ lora_A = V.t().mul(S.sqrt().view(-1, 1)).contiguous()
+ lora_B = U.mul(S.sqrt()).contiguous()
+ self.lora_A[adapter_name].weight.data = lora_A
+ self.lora_B[adapter_name].weight.data = lora_B
+ weight = weight.data - self.scaling[adapter_name] * lora_B @ lora_A
+ weight = weight.to(dtype)
+ self.get_base_layer().weight.data = weight
+
+ # Remove redundant fields
+ del linear.eigens
+
+ def loftq_init(self, adapter_name):
+ from peft.utils.loftq_utils import loftq_init
+
+ weight = self.get_base_layer().weight
+ kwargs = {
+ "num_bits": self.kwargs.get("loftq_bits", 4),
+ "reduced_rank": self.r[adapter_name],
+ "num_iter": self.kwargs.get("loftq_iter", 1),
+ }
+
+ qweight, lora_A, lora_B = loftq_init(weight, **kwargs)
+ if adapter_name in self.lora_A.keys():
+ # initialize A the same way as the default for nn.Linear and B to zero
+ self.lora_A[adapter_name].weight.data = lora_A
+ self.lora_B[adapter_name].weight.data = lora_B
+ if adapter_name in self.lora_embedding_A.keys():
+ # initialize a the same way as the default for nn.linear and b to zero
+ self.lora_embedding_A[adapter_name].weight.data = lora_A
+ self.lora_embedding_B[adapter_name].weight.data = lora_B
+ self.get_base_layer().weight.data = qweight
+
+ @torch.no_grad()
+ def orthogonal_init(self, adapter_name):
+ # https://datta0.github.io/posts/rethink-lora-init/#orthogonal-initialisation
+ rank = self.r[adapter_name]
+ if rank % 2 != 0:
+ raise ValueError(f"Orthogonal initialization requires the LoRA rank to be even, got {rank} instead.")
+
+ X = torch.randn(rank, rank)
+ Q, _ = torch.linalg.qr(X)
+ q_odd = Q[0::2, :] # Odd rows
+ q_even = Q[1::2, :] # Even rows
+ dtype = self.get_base_layer().weight.dtype
+ lora_A = torch.randn(self.in_features, rank // 2).mm(q_odd).T / 10.0
+ lora_B = torch.randn(rank // 2, self.out_features).T.mm(q_even) / 10.0
+ self.lora_A[adapter_name].weight = nn.Parameter(lora_A.contiguous().to(dtype))
+ self.lora_B[adapter_name].weight = nn.Parameter(lora_B.contiguous().to(dtype))
+
+ def _cache_store(self, key: str, value: Any) -> None:
+ self._caches[key] = value
+
+ def _cache_pop(self, key: str) -> Any:
+ value = self._caches.pop(key)
+ return value
+
+ def set_scale(self, adapter: str, scale: float | int) -> None:
+ """Set the scale of the given adapter to the initial scale multiplied by the provided factor
+
+ The initial scale is determined by the configured `r` (rank) and `lora_alpha`.
+ """
+ if adapter not in self.scaling:
+ # Ignore the case where the adapter is not in the layer
+ return
+ if self.use_rslora.get(adapter, False):
+ self.scaling[adapter] = scale * self.lora_alpha[adapter] / math.sqrt(self.r[adapter])
+ else:
+ self.scaling[adapter] = scale * self.lora_alpha[adapter] / self.r[adapter]
+
+ def scale_layer(self, scale: float | int) -> None:
+ """Multiply the current scale of all active adapters by the provided factor"""
+ if scale == 1:
+ return
+
+ for active_adapter in self.active_adapters:
+ if active_adapter not in self.lora_A.keys():
+ continue
+
+ self.scaling[active_adapter] *= scale
+
+ def unscale_layer(self, scale: Optional[float | int] = None) -> None:
+ """Divide the current scale of all active adapters by the provided factor. If `scale=None` is passed, reset to
+ initial scale
+
+ The initial scale is determined by the configured `r` (rank) and `lora_alpha`.
+
+ """
+ for active_adapter in self.active_adapters:
+ if active_adapter not in self.lora_A.keys():
+ continue
+
+ if scale is None:
+ if self.use_rslora.get(active_adapter, False):
+ self.scaling[active_adapter] = self.lora_alpha[active_adapter] / math.sqrt(self.r[active_adapter])
+ else:
+ self.scaling[active_adapter] = self.lora_alpha[active_adapter] / self.r[active_adapter]
+ else:
+ self.scaling[active_adapter] = self.scaling[active_adapter] / scale
+
+ def _check_forward_args(self, x, *args, **kwargs):
+ """Check if the arguments are compatible with the configs and state of the model"""
+ adapter_names = kwargs.get("adapter_names", None)
+ if adapter_names is None:
+ return
+
+ if len(x) != len(adapter_names):
+ msg = (
+ "Length of `adapter_names` should be the same as the number of inputs, but got "
+ f"{len(adapter_names)} and {len(x)} respectively."
+ )
+ raise ValueError(msg)
+
+ if self.merged:
+ # It is unclear what would be the right thing to do if users pass adapter_names and there are merged
+ # adapters. Therefore, it is better to raise an error in this case.
+ msg = "Cannot pass `adapter_names` when there are merged adapters, please call `unmerge_adapter` first."
+ raise ValueError(msg)
+
+ # DoRA is not supported (yet), check that it's not being used. Don't check "__base__", as this is the
+ # placeholder for the base model.
+ unique_adapters = {name for name in adapter_names if name != "__base__"}
+ for adapter_name in unique_adapters:
+ if self.use_dora.get(adapter_name, False):
+ msg = "Cannot pass `adapter_names` when DoRA is enabled."
+ raise ValueError(msg)
+
+ def _mixed_batch_forward(
+ self, x: torch.Tensor, *args: Any, adapter_names: list[str], **kwargs: Any
+ ) -> torch.Tensor:
+ # This is a special method that handles the case when users pass the argument `adapter_names`. This is an
+ # extra argument that allows mixing different adapters in the same batch at inference time.
+ variant_kwargs = {k: kwargs.pop(k, None) for k in VARIANT_KWARG_KEYS} # don't pass these to base_layer
+ result = self.base_layer(x, *args, **kwargs)
+ torch_result_dtype = result.dtype
+
+ unique_adapters = set(adapter_names)
+ sub_batch_indices_list = []
+ for adapter in unique_adapters:
+ sub_batch_indices_list.append([index for index, item in enumerate(adapter_names) if item == adapter])
+ alora_offsets = variant_kwargs.get("alora_offsets", None)
+ for i, active_adapter in enumerate(unique_adapters):
+ if active_adapter == "__base__":
+ continue
+ if active_adapter not in self.lora_A.keys():
+ continue
+
+ lora_A = self.lora_A[active_adapter]
+ lora_B = self.lora_B[active_adapter]
+ dropout = self.lora_dropout[active_adapter]
+ scaling = self.scaling[active_adapter]
+
+ # getting the sub-batch, passing it to LoRA layers and updating the corresponding indices of the linear
+ # layer output
+ sub_batch = x[sub_batch_indices_list[i]].to(lora_A.weight.dtype)
+ if active_adapter not in self.lora_variant: # vanilla LoRA
+ lora_output = lora_B(lora_A(dropout(sub_batch))) * scaling
+ result[sub_batch_indices_list[i]] += lora_output.to(torch_result_dtype)
+ else:
+ if alora_offsets is not None:
+ variant_kwargs["alora_offsets"] = [alora_offsets[j] for j in sub_batch_indices_list[i]]
+ lora_output = self.lora_variant[active_adapter].forward(
+ self,
+ active_adapter=active_adapter,
+ x=sub_batch,
+ result=result[sub_batch_indices_list[i]],
+ **variant_kwargs,
+ **kwargs,
+ )
+ result[sub_batch_indices_list[i]] = lora_output.to(torch_result_dtype)
+
+ return result
+
+
+# Below code is based on https://github.com/microsoft/LoRA/blob/main/loralib/layers.py
+# and modified to work with PyTorch FSDP
+
+
+# ------------------------------------------------------------------------------------------
+# Copyright (c) Microsoft Corporation. All rights reserved.
+# Licensed under the MIT License (MIT). See LICENSE in the repo root for license information.
+# ------------------------------------------------------------------------------------------
+
+
+class Linear(nn.Module, LoraLayer):
+ # Lora implemented in a dense layer
+ def __init__(
+ self,
+ base_layer,
+ adapter_name: str,
+ r: int = 0,
+ lora_alpha: int = 1,
+ lora_dropout: float = 0.0,
+ fan_in_fan_out: bool = False, # Set this to True if the layer to replace stores weight like (fan_in, fan_out)
+ is_target_conv_1d_layer: bool = False,
+ init_lora_weights: Union[bool, str] = True,
+ use_rslora: bool = False,
+ use_dora: bool = False,
+ use_alora: bool = False,
+ arrow_config: ArrowConfig = None,
+ lora_bias: bool = False,
+ **kwargs,
+ ) -> None:
+ super().__init__()
+ LoraLayer.__init__(self, base_layer, **kwargs)
+ self.fan_in_fan_out = fan_in_fan_out
+
+ self._active_adapter = adapter_name
+ self.update_layer(
+ adapter_name,
+ r,
+ lora_alpha=lora_alpha,
+ lora_dropout=lora_dropout,
+ init_lora_weights=init_lora_weights,
+ use_rslora=use_rslora,
+ use_dora=use_dora,
+ use_alora=use_alora,
+ lora_bias=lora_bias,
+ arrow_config=arrow_config,
+ )
+ self.is_target_conv_1d_layer = is_target_conv_1d_layer
+
+ def resolve_lora_variant(
+ self, *, arrow_config: ArrowConfig, use_dora: bool, use_alora: bool, **kwargs
+ ) -> Optional[LoraVariant]:
+ if arrow_config is not None:
+ from .variants import ArrowLinearVariant
+
+ return ArrowLinearVariant()
+
+ if not use_dora and not use_alora:
+ return None
+
+ from .variants import ALoraLinearVariant, DoraLinearVariant
+
+ if use_alora:
+ return ALoraLinearVariant()
+ else:
+ return DoraLinearVariant()
+
+ def merge(self, safe_merge: bool = False, adapter_names: Optional[list[str]] = None) -> None:
+ """
+ Merge the active adapter weights into the base weights
+
+ Args:
+ safe_merge (`bool`, *optional*):
+ If True, the merge operation will be performed in a copy of the original weights and check for NaNs
+ before merging the weights. This is useful if you want to check if the merge operation will produce
+ NaNs. Defaults to `False`.
+ adapter_names (`list[str]`, *optional*):
+ The list of adapter names that should be merged. If None, all active adapters will be merged. Defaults
+ to `None`.
+ """
+ adapter_names = check_adapters_to_merge(self, adapter_names)
+ if not adapter_names:
+ # no adapter to merge
+ return
+
+ for active_adapter in adapter_names:
+ if active_adapter in self.lora_A.keys():
+ base_layer = self.get_base_layer()
+ if safe_merge:
+ # Note that safe_merge will be slower than the normal merge
+ # because of the copy operation.
+ orig_weight = base_layer.weight.data.clone()
+ orig_dtype = orig_weight.dtype
+ if active_adapter not in self.lora_variant: # vanilla LoRA
+ delta_weight = self.get_delta_weight(active_adapter)
+ orig_weight += delta_weight.to(orig_dtype)
+ else:
+ orig_weight = self.lora_variant[active_adapter].merge_safe(self, active_adapter, orig_weight)
+
+ if not torch.isfinite(orig_weight).all():
+ raise ValueError(
+ f"NaNs detected in the merged weights. The adapter {active_adapter} seems to be broken"
+ )
+
+ base_layer.weight.data = orig_weight
+
+ if self.lora_bias[active_adapter]:
+ if getattr(base_layer, "bias", None) is None:
+ raise RuntimeError(
+ "Impossible to merge LoRA with `lora_bias=True` because the base layer has no bias."
+ )
+ new_bias = base_layer.bias + self.lora_B[active_adapter].bias * self.scaling[active_adapter]
+ if not torch.isfinite(new_bias).all():
+ raise ValueError(
+ f"NaNs detected in the merged weights. The adapter {active_adapter} seems to be broken"
+ )
+ base_layer.bias.data = new_bias.to(orig_dtype)
+
+ else:
+ if active_adapter not in self.lora_variant: # vanilla LoRA
+ delta_weight = self.get_delta_weight(active_adapter)
+ base_layer.weight.data += delta_weight
+ else:
+ self.lora_variant[active_adapter].merge_unsafe(self, active_adapter, base_layer.weight)
+
+ if self.lora_bias[active_adapter]:
+ if getattr(base_layer, "bias", None) is None:
+ raise RuntimeError(
+ "Impossible to merge LoRA with `lora_bias=True` because the base layer has no bias."
+ )
+ base_layer.bias.data += self.lora_B[active_adapter].bias * self.scaling[active_adapter]
+
+ self.merged_adapters.append(active_adapter)
+
+ def unmerge(self) -> None:
+ """
+ This method unmerges all merged adapter layers from the base weights.
+ """
+
+ if not self.merged:
+ warnings.warn("Already unmerged. Nothing to do.")
+ return
+ while len(self.merged_adapters) > 0:
+ active_adapter = self.merged_adapters.pop()
+ if active_adapter in self.lora_A.keys():
+ weight = self.get_base_layer().weight
+ if active_adapter not in self.lora_variant: # vanilla LoRA
+ orig_dtype = weight.dtype
+ delta_weight = self.get_delta_weight(active_adapter)
+ weight.data -= delta_weight.to(orig_dtype)
+ else:
+ unmerged = self.lora_variant[active_adapter].unmerge(self, active_adapter, weight)
+ weight.data = unmerged
+
+ if self.lora_bias[active_adapter]:
+ self.get_base_layer().bias.data -= self.lora_B[active_adapter].bias * self.scaling[active_adapter]
+
+ def get_delta_weight(self, adapter) -> torch.Tensor:
+ """
+ Compute the delta weight for the given adapter.
+
+ Args:
+ adapter (str):
+ The name of the adapter for which the delta weight should be computed.
+ """
+ device = self.lora_B[adapter].weight.device
+ dtype = self.lora_B[adapter].weight.dtype
+
+ # In case users wants to merge the adapter weights that are in
+ # (b)float16 while being on CPU, we need to cast the weights to float32, perform the merge and then cast back to
+ # (b)float16 because some CPUs have slow bf16/fp16 matmuls.
+ cast_to_fp32 = device.type == "cpu" and (dtype == torch.float16 or dtype == torch.bfloat16)
+
+ weight_A = self.lora_A[adapter].weight
+ weight_B = self.lora_B[adapter].weight
+
+ if cast_to_fp32:
+ weight_A = weight_A.float()
+ weight_B = weight_B.float()
+
+ output_tensor = transpose(weight_B @ weight_A, self.fan_in_fan_out) * self.scaling[adapter]
+
+ if cast_to_fp32:
+ output_tensor = output_tensor.to(dtype=dtype)
+
+ # cast back the weights
+ self.lora_A[adapter].weight.data = weight_A.to(dtype)
+ self.lora_B[adapter].weight.data = weight_B.to(dtype)
+
+ return output_tensor
+
+ def forward(self, x: torch.Tensor, *args: Any, **kwargs: Any) -> torch.Tensor:
+ self._check_forward_args(x, *args, **kwargs)
+ adapter_names = kwargs.pop("adapter_names", None)
+ variant_kwargs = {k: kwargs.pop(k, None) for k in VARIANT_KWARG_KEYS} # don't pass these to base_layer
+
+ if self.disable_adapters:
+ if self.merged:
+ self.unmerge()
+ result = self.base_layer(x, *args, **kwargs)
+ elif adapter_names is not None:
+ result = self._mixed_batch_forward(x, *args, adapter_names=adapter_names, **variant_kwargs, **kwargs)
+ elif self.merged:
+ result = self.base_layer(x, *args, **kwargs)
+ else:
+ result = self.base_layer(x, *args, **kwargs)
+ torch_result_dtype = result.dtype
+
+ lora_A_keys = self.lora_A.keys()
+ for active_adapter in self.active_adapters:
+ if active_adapter not in lora_A_keys:
+ continue
+
+ lora_A = self.lora_A[active_adapter]
+ lora_B = self.lora_B[active_adapter]
+ dropout = self.lora_dropout[active_adapter]
+ scaling = self.scaling[active_adapter]
+ x = self._cast_input_dtype(x, lora_A.weight.dtype)
+ if active_adapter not in self.lora_variant: # vanilla LoRA
+ result = result + lora_B(lora_A(dropout(x))) * scaling
+ else:
+ result = self.lora_variant[active_adapter].forward(
+ self,
+ active_adapter=active_adapter,
+ x=x,
+ result=result,
+ **variant_kwargs,
+ **kwargs,
+ )
+
+ result = result.to(torch_result_dtype)
+
+ return result
+
+ def __repr__(self) -> str:
+ rep = super().__repr__()
+ return "lora." + rep
+
+
+class Embedding(nn.Module, LoraLayer):
+ # LoRA implemented in a Embedding layer
+ def __init__(
+ self,
+ base_layer: nn.Module,
+ adapter_name: str,
+ r: int = 0,
+ lora_alpha: int = 1,
+ lora_dropout: float = 0.0,
+ fan_in_fan_out: bool = False, # Set this to True if the layer to replace stores weight like (fan_in, fan_out)
+ init_lora_weights: Union[bool, str] = True,
+ use_rslora: bool = False,
+ use_dora: bool = False,
+ arrow_config: ArrowConfig = None,
+ lora_bias: bool = False,
+ **kwargs,
+ ) -> None:
+ if lora_bias:
+ # lora_bias=True is not supported (yet) for embedding layers, as they use nn.Parameter
+ raise ValueError(f"lora_bias={lora_bias} is not supported for {self.__class__.__name__}.")
+
+ super().__init__()
+ LoraLayer.__init__(self, base_layer)
+ self.fan_in_fan_out = fan_in_fan_out
+
+ self._active_adapter = adapter_name
+ self.update_layer(
+ adapter_name,
+ r,
+ lora_alpha=lora_alpha,
+ lora_dropout=lora_dropout,
+ init_lora_weights=init_lora_weights,
+ use_rslora=use_rslora,
+ use_dora=use_dora,
+ lora_bias=lora_bias,
+ arrow_config=arrow_config,
+ )
+
+ def resolve_lora_variant(self, *, use_dora: bool, **kwargs) -> Optional[LoraVariant]:
+ if not use_dora:
+ return None
+
+ from .variants import DoraEmbeddingVariant
+
+ return DoraEmbeddingVariant()
+
+ def update_layer(
+ self,
+ adapter_name,
+ r,
+ lora_alpha,
+ lora_dropout,
+ init_lora_weights,
+ use_rslora,
+ use_dora,
+ lora_bias,
+ arrow_config: ArrowConfig = None,
+ inference_mode: bool = False,
+ **kwargs,
+ ):
+ # collect the kwargs
+ kwargs = locals().copy()
+ del kwargs["self"]
+
+ if r <= 0:
+ raise ValueError(f"`r` should be a positive integer value but the value passed is {r}")
+
+ lora_variant = self.resolve_lora_variant(use_dora=use_dora, arrow_config=arrow_config)
+ if lora_variant is not None:
+ self.lora_variant[adapter_name] = lora_variant
+
+ self.r[adapter_name] = r
+ self.lora_alpha[adapter_name] = lora_alpha
+ if lora_dropout > 0.0:
+ lora_dropout_layer = nn.Dropout(p=lora_dropout)
+ else:
+ lora_dropout_layer = nn.Identity()
+
+ self.lora_dropout[adapter_name] = lora_dropout_layer
+ # Actual trainable parameters
+ weight_A = torch.randn((r, self.in_features))
+ weight_B = torch.randn((self.out_features, r))
+ self.lora_embedding_A[adapter_name] = nn.Parameter(weight_A)
+ self.lora_embedding_B[adapter_name] = nn.Parameter(weight_B)
+ self.lora_bias[adapter_name] = lora_bias
+
+ if use_rslora:
+ self.scaling[adapter_name] = lora_alpha / math.sqrt(r)
+ else:
+ self.scaling[adapter_name] = lora_alpha / r
+
+ self.use_rslora[adapter_name] = use_rslora
+
+ self.use_dora[adapter_name] = use_dora
+
+ if init_lora_weights == "loftq":
+ self.loftq_init(adapter_name)
+ elif init_lora_weights:
+ self.reset_lora_parameters(adapter_name, init_lora_weights)
+
+ # call this before init of the lora variants
+ self._move_adapter_to_device_of_base_layer(adapter_name)
+
+ if adapter_name in self.lora_variant:
+ self.lora_variant[adapter_name].init(self, **kwargs)
+
+ self.set_adapter(self.active_adapters, inference_mode=inference_mode)
+
+ def merge(self, safe_merge: bool = False, adapter_names: Optional[list[str]] = None) -> None:
+ """
+ Merge the active adapter weights into the base weights
+
+ Args:
+ safe_merge (`bool`, *optional*):
+ If True, the merge operation will be performed in a copy of the original weights and check for NaNs
+ before merging the weights. This is useful if you want to check if the merge operation will produce
+ NaNs. Defaults to `False`.
+ adapter_names (`list[str]`, *optional*):
+ The list of adapter names that should be merged. If None, all active adapters will be merged. Defaults
+ to `None`.
+ """
+ adapter_names = check_adapters_to_merge(self, adapter_names)
+ if not adapter_names:
+ # no adapter to merge
+ return
+
+ for active_adapter in adapter_names:
+ if active_adapter in self.lora_embedding_A.keys():
+ base_layer = self.get_base_layer()
+ orig_dtype = base_layer.weight.dtype
+ if safe_merge:
+ # Note that safe_merge will be slower than the normal merge
+ # because of the copy operation.
+ orig_weight = base_layer.weight.data.clone()
+ if active_adapter not in self.lora_variant: # vanilla LoRA
+ orig_weight += self.get_delta_weight(active_adapter).to(orig_dtype)
+ else:
+ orig_weight = self.lora_variant[active_adapter].merge_safe(self, active_adapter, orig_weight)
+
+ if not torch.isfinite(orig_weight).all():
+ raise ValueError(
+ f"NaNs detected in the merged weights. The adapter {active_adapter} seems to be broken"
+ )
+
+ base_layer.weight.data = orig_weight
+ else:
+ if active_adapter not in self.lora_variant: # vanilla LoRA
+ base_layer.weight.data += self.get_delta_weight(active_adapter).to(orig_dtype)
+ else:
+ self.lora_variant[active_adapter].merge_unsafe(self, active_adapter, base_layer.weight)
+ self.merged_adapters.append(active_adapter)
+
+ def unmerge(self) -> None:
+ """
+ This method unmerges all merged adapter layers from the base weights.
+ """
+ if not self.merged:
+ warnings.warn("Already unmerged. Nothing to do.")
+ return
+ while len(self.merged_adapters) > 0:
+ active_adapter = self.merged_adapters.pop()
+ orig_dtype = self.get_base_layer().weight.dtype
+ if active_adapter in self.lora_embedding_A.keys():
+ weight = self.get_base_layer().weight
+ if active_adapter not in self.lora_variant: # vanilla LoRA
+ weight.data -= self.get_delta_weight(active_adapter).to(orig_dtype)
+ else:
+ unmerged = self.lora_variant[active_adapter].unmerge(self, active_adapter, weight)
+ weight.data = unmerged
+
+ def get_delta_weight(self, adapter) -> torch.Tensor:
+ """
+ Compute the delta weight for the given adapter.
+
+ Args:
+ adapter (str):
+ The name of the adapter for which the delta weight should be computed.
+ """
+ device = self.lora_embedding_B[adapter].device
+ dtype = self.lora_embedding_A[adapter].dtype
+
+ # In case users wants to merge the adapter weights that are in
+ # (b)float16 while being on CPU, we need to cast the weights to float32, perform the merge and then cast back to
+ # (b)float16 because some CPUs have slow bf16/fp16 matmuls.
+ cast_to_fp32 = device.type == "cpu" and (dtype == torch.float16 or dtype == torch.bfloat16)
+
+ weight_A = self.lora_embedding_A[adapter]
+ weight_B = self.lora_embedding_B[adapter]
+
+ if cast_to_fp32:
+ weight_A = weight_A.float()
+ weight_B = weight_B.float()
+
+ output_tensor = transpose(weight_B @ weight_A, True) * self.scaling[adapter]
+
+ if cast_to_fp32:
+ output_tensor = output_tensor.to(dtype=dtype)
+
+ # cast back the weights
+ self.lora_embedding_A[adapter] = weight_A.to(dtype)
+ self.lora_embedding_B[adapter] = weight_B.to(dtype)
+
+ return output_tensor
+
+ def _mixed_batch_forward(
+ self, x: torch.Tensor, *args: Any, adapter_names: list[str], **kwargs: Any
+ ) -> torch.Tensor:
+ # This is a special method that handles the case when users pass the argument `adapter_names`. This is an
+ # extra argument that allows mixing different adapters in the same batch at inference time.
+ result = self.base_layer(x, *args, **kwargs)
+
+ unique_adapters = set(adapter_names)
+ sub_batch_indices_list = []
+ for adapter in unique_adapters:
+ sub_batch_indices_list.append([index for index, item in enumerate(adapter_names) if item == adapter])
+
+ for i, active_adapter in enumerate(unique_adapters):
+ if active_adapter == "__base__":
+ continue
+ if active_adapter not in self.lora_embedding_A.keys():
+ continue
+
+ embedding_A = self.lora_embedding_A[active_adapter].T
+ embedding_B = self.lora_embedding_B[active_adapter].T
+ scaling = self.scaling[active_adapter]
+
+ # getting the sub-batch, passing it to LoRA layers and updating the corresponding indices of the linear
+ # layer output
+ sub_batch = x[sub_batch_indices_list[i]]
+ after_A = self._embed(sub_batch, embedding_A)
+ result[sub_batch_indices_list[i]] += (after_A @ embedding_B) * scaling
+
+ return result
+
+ def _embed(self, input: torch.Tensor, weight: torch.Tensor) -> torch.Tensor:
+ base_layer = self.get_base_layer()
+ return F.embedding(
+ input,
+ weight,
+ padding_idx=base_layer.padding_idx,
+ max_norm=base_layer.max_norm,
+ norm_type=base_layer.norm_type,
+ scale_grad_by_freq=base_layer.scale_grad_by_freq,
+ sparse=base_layer.sparse,
+ )
+
+ def forward(self, x: torch.Tensor, *args: Any, **kwargs: Any) -> torch.Tensor:
+ # TODO: no dtype conversion here, unlike in Linear, is that correct?
+ self._check_forward_args(x, *args, **kwargs)
+ adapter_names = kwargs.pop("adapter_names", None)
+ variant_kwargs = {k: kwargs.pop(k, None) for k in VARIANT_KWARG_KEYS} # don't pass these to base_layer
+ if self.disable_adapters:
+ if self.merged:
+ self.unmerge()
+ result = self.base_layer(x, *args, **kwargs)
+ elif adapter_names is not None:
+ result = self._mixed_batch_forward(x, *args, adapter_names=adapter_names, **kwargs)
+ elif self.merged:
+ result = self.base_layer(x, *args, **kwargs)
+ else:
+ result = self.base_layer(x, *args, **kwargs)
+ torch_result_dtype = result.dtype
+ for active_adapter in self.active_adapters:
+ if active_adapter not in self.lora_embedding_A:
+ continue
+
+ if active_adapter not in self.lora_variant: # vanilla LoRA
+ embedding_A = self.lora_embedding_A[active_adapter].T
+ embedding_B = self.lora_embedding_B[active_adapter].T
+ scaling = self.scaling[active_adapter]
+ after_A = self._embed(x, embedding_A)
+ result = result + (after_A @ embedding_B) * scaling
+ else:
+ result = self.lora_variant[active_adapter].forward(
+ self,
+ active_adapter=active_adapter,
+ x=x,
+ result=result,
+ **variant_kwargs,
+ **kwargs,
+ )
+ result = result.to(torch_result_dtype)
+
+ return result
+
+ def __repr__(self) -> str:
+ rep = super().__repr__()
+ return "lora." + rep
+
+
+class _ConvNd(nn.Module, LoraLayer):
+ # Lora implemented in a conv(2,3)d layer
+ def __init__(
+ self,
+ base_layer: nn.Module,
+ adapter_name: str,
+ r: int = 0,
+ lora_alpha: int = 1,
+ lora_dropout: float = 0.0,
+ init_lora_weights: Union[bool, str] = True,
+ use_rslora: bool = False,
+ use_dora: bool = False,
+ arrow_config: ArrowConfig = None,
+ lora_bias: bool = False,
+ **kwargs,
+ ) -> None:
+ super().__init__()
+ LoraLayer.__init__(self, base_layer)
+ if kwargs.get("use_alora", False):
+ raise ValueError("aLoRA does not support adapting conv layers.")
+ if base_layer.groups > 1:
+ warnings.warn("LoRA adapter added to ConvNd layer with groups > 1. Merging is not supported.")
+
+ if r % base_layer.groups != 0:
+ raise ValueError(
+ f"Targeting a {base_layer.__class__.__name__} with groups={base_layer.groups} and rank {r}. "
+ "Currently, support is limited to conv layers where the rank is divisible by groups. "
+ "Either choose a different rank or do not target this specific layer."
+ )
+
+ self._active_adapter = adapter_name
+ self._kernel_dim = base_layer.weight.dim()
+
+ self.update_layer(
+ adapter_name,
+ r,
+ lora_alpha=lora_alpha,
+ lora_dropout=lora_dropout,
+ init_lora_weights=init_lora_weights,
+ use_rslora=use_rslora,
+ use_dora=use_dora,
+ lora_bias=lora_bias,
+ arrow_config=arrow_config,
+ )
+
+ def update_layer(
+ self,
+ adapter_name,
+ r,
+ lora_alpha,
+ lora_dropout,
+ init_lora_weights,
+ use_rslora,
+ use_dora,
+ lora_bias,
+ arrow_config: ArrowConfig = None,
+ inference_mode: bool = False,
+ **kwargs,
+ ):
+ # collect the kwargs
+ kwargs = locals().copy()
+ del kwargs["self"]
+
+ if r <= 0:
+ raise ValueError(f"`r` should be a positive integer value but the value passed is {r}")
+
+ if lora_bias and (getattr(self.get_base_layer(), "bias", None) is None):
+ warnings.warn(
+ f"`lora_bias=True` was passed but the targeted layer of type {type(self.get_base_layer()).__name__} "
+ "has no bias. This means that merging LoRA weights won't be possible.",
+ PeftWarning,
+ )
+
+ lora_variant = self.resolve_lora_variant(use_dora=use_dora, arrow_config=arrow_config)
+ if lora_variant is not None:
+ self.lora_variant[adapter_name] = lora_variant
+
+ self.r[adapter_name] = r
+ self.lora_alpha[adapter_name] = lora_alpha
+ if lora_dropout > 0.0:
+ lora_dropout_layer = nn.Dropout(p=lora_dropout)
+ else:
+ lora_dropout_layer = nn.Identity()
+
+ self.lora_dropout[adapter_name] = lora_dropout_layer
+ # Actual trainable parameters
+ base_layer = self.get_base_layer()
+ kernel_size = base_layer.kernel_size
+ stride = base_layer.stride
+ padding = base_layer.padding
+ conv_layer = type(base_layer)
+ out_kernel = out_stride = (1,) * (self._kernel_dim - 2)
+ self.lora_A[adapter_name] = conv_layer(self.in_features, r, kernel_size, stride, padding, bias=False)
+ self.lora_B[adapter_name] = conv_layer(
+ r, self.out_features, out_kernel, out_stride, groups=base_layer.groups, bias=lora_bias
+ )
+ self.lora_bias[adapter_name] = lora_bias
+
+ if use_rslora:
+ self.scaling[adapter_name] = lora_alpha / math.sqrt(r)
+ else:
+ self.scaling[adapter_name] = lora_alpha / r
+
+ self.use_rslora[adapter_name] = use_rslora
+
+ self.use_dora[adapter_name] = use_dora
+
+ if init_lora_weights == "loftq":
+ self.loftq_init(adapter_name)
+ elif init_lora_weights:
+ self.reset_lora_parameters(adapter_name, init_lora_weights)
+
+ # call this before init of the lora variants
+ self._move_adapter_to_device_of_base_layer(adapter_name)
+
+ if adapter_name in self.lora_variant:
+ self.lora_variant[adapter_name].init(self, **kwargs)
+
+ self.set_adapter(self.active_adapters, inference_mode=inference_mode)
+
+ def _get_dora_factor_view(self):
+ return (-1,) + (1,) * (self._kernel_dim - 1)
+
+ def merge(self, safe_merge: bool = False, adapter_names: Optional[list[str]] = None) -> None:
+ """
+ Merge the active adapter weights inside the base weights
+
+ Args:
+ safe_merge (`bool`, *optional*):
+ If True, the merge operation will be performed in a copy of the original weights and check for NaNs
+ before merging the weights. This is useful if you want to check if the merge operation will produce
+ NaNs. Defaults to `False`.
+ adapter_names (`list[str]`, *optional*):
+ The list of adapter names that should be merged. If None, all active adapters will be merged. Defaults
+ to `None`.
+ """
+ adapter_names = check_adapters_to_merge(self, adapter_names)
+ if not adapter_names:
+ # no adapter to merge
+ return
+
+ for active_adapter in adapter_names:
+ if active_adapter in self.lora_A.keys():
+ base_layer = self.get_base_layer()
+ orig_dtype = base_layer.weight.dtype
+
+ if base_layer.groups > 1:
+ # https://github.com/huggingface/peft/pull/2403
+ raise NotImplementedError("Merging is not supported for _ConvNd layers with groups > 1!")
+
+ if safe_merge:
+ # Note that safe_merge will be slower than the normal merge
+ # because of the copy operation.
+ orig_weight = base_layer.weight.data.clone()
+ if active_adapter not in self.lora_variant: # vanilla LoRA
+ delta_weight = self.get_delta_weight(active_adapter)
+ orig_weight += delta_weight.to(orig_dtype)
+ else:
+ orig_weight = self.lora_variant[active_adapter].merge_safe(self, active_adapter, orig_weight)
+
+ if not torch.isfinite(orig_weight).all():
+ raise ValueError(
+ f"NaNs detected in the merged weights. The adapter {active_adapter} seems to be broken"
+ )
+
+ base_layer.weight.data = orig_weight
+
+ if self.lora_bias[active_adapter]:
+ if getattr(base_layer, "bias", None) is None:
+ raise RuntimeError(
+ "Impossible to merge LoRA with `lora_bias=True` because the base layer has no bias."
+ )
+ new_bias = base_layer.bias + self.lora_B[active_adapter].bias * self.scaling[active_adapter]
+ if not torch.isfinite(new_bias).all():
+ raise ValueError(
+ f"NaNs detected in the merged weights. The adapter {active_adapter} seems to be broken"
+ )
+ base_layer.bias.data = new_bias.to(orig_dtype)
+
+ else:
+ if active_adapter not in self.lora_variant: # vanilla LoRA
+ delta_weight = self.get_delta_weight(active_adapter)
+ base_layer.weight.data += delta_weight.to(orig_dtype)
+ else:
+ self.lora_variant[active_adapter].merge_unsafe(self, active_adapter, base_layer.weight)
+
+ if self.lora_bias[active_adapter]:
+ if getattr(base_layer, "bias", None) is None:
+ raise RuntimeError(
+ "Impossible to merge LoRA with `lora_bias=True` because the base layer has no bias."
+ )
+ base_layer.bias.data += self.lora_B[active_adapter].bias * self.scaling[active_adapter]
+
+ self.merged_adapters.append(active_adapter)
+
+ def unmerge(self) -> None:
+ """
+ This method unmerges all merged adapter layers from the base weights.
+ """
+ if not self.merged:
+ warnings.warn("Already unmerged. Nothing to do.")
+ return
+ while len(self.merged_adapters) > 0:
+ active_adapter = self.merged_adapters.pop()
+ if active_adapter in self.lora_A.keys():
+ weight = self.get_base_layer().weight
+ if active_adapter not in self.lora_variant: # vanilla LoRA
+ orig_dtype = weight.dtype
+ delta_weight = self.get_delta_weight(active_adapter)
+ weight.data -= delta_weight.to(orig_dtype)
+ else:
+ unmerged = self.lora_variant[active_adapter].unmerge(self, active_adapter, weight)
+ weight.data = unmerged
+
+ if self.lora_bias[active_adapter]:
+ self.get_base_layer().bias.data -= self.lora_B[active_adapter].bias * self.scaling[active_adapter]
+
+ def get_delta_weight(self, adapter) -> torch.Tensor:
+ """
+ Compute the delta weight for the given adapter.
+
+ Args:
+ adapter (str):
+ The name of the adapter for which the delta weight should be computed.
+ """
+ device = self.lora_B[adapter].weight.device
+ dtype = self.lora_A[adapter].weight.dtype
+
+ # In case users wants to merge the adapter weights that are in
+ # (b)float16 while being on CPU, we need to cast the weights to float32, perform the merge and then cast back to
+ # (b)float16 because some CPUs have slow bf16/fp16 matmuls.
+ cast_to_fp32 = device.type == "cpu" and (dtype == torch.float16 or dtype == torch.bfloat16)
+
+ weight_A = self.lora_A[adapter].weight
+ weight_B = self.lora_B[adapter].weight
+
+ if cast_to_fp32:
+ weight_A = weight_A.float()
+ weight_B = weight_B.float()
+
+ # https://github.com/bmaltais/kohya_ss/blob/feb6728762a8f463d15ba936d189d4c3abfaa1ab/networks/lora.py#L117
+ if self.get_base_layer().weight.size()[2:4] == (1, 1):
+ # conv2d 1x1
+ output_tensor = (weight_B.squeeze(3).squeeze(2) @ weight_A.squeeze(3).squeeze(2)).unsqueeze(2).unsqueeze(
+ 3
+ ) * self.scaling[adapter]
+ else:
+ output_tensor = self.conv_fn(weight_A.transpose(0, 1), weight_B)
+
+ if self.get_base_layer().groups > 1:
+ output_tensor = output_tensor * self.scaling[adapter]
+ else:
+ output_tensor = output_tensor.transpose(0, 1) * self.scaling[adapter]
+
+ if cast_to_fp32:
+ output_tensor = output_tensor.to(dtype=dtype)
+
+ # cast back the weights
+ self.lora_A[adapter].weight.data = weight_A.to(dtype)
+ self.lora_B[adapter].weight.data = weight_B.to(dtype)
+
+ return output_tensor
+
+ def forward(self, x: torch.Tensor, *args, **kwargs) -> torch.Tensor:
+ self._check_forward_args(x, *args, **kwargs)
+ adapter_names = kwargs.pop("adapter_names", None)
+ variant_kwargs = {k: kwargs.pop(k, None) for k in VARIANT_KWARG_KEYS} # don't pass these to base_layer
+ if self.disable_adapters:
+ if self.merged:
+ self.unmerge()
+ result = self.base_layer(x, *args, **kwargs)
+ elif adapter_names is not None:
+ result = self._mixed_batch_forward(x, *args, adapter_names=adapter_names, **kwargs)
+ elif self.merged:
+ result = self.base_layer(x, *args, **kwargs)
+
+ else:
+ result = self.base_layer(x, *args, **kwargs)
+ torch_result_dtype = result.dtype
+
+ for active_adapter in self.active_adapters:
+ if active_adapter not in self.lora_A.keys():
+ continue
+ lora_A = self.lora_A[active_adapter]
+ lora_B = self.lora_B[active_adapter]
+ dropout = self.lora_dropout[active_adapter]
+ scaling = self.scaling[active_adapter]
+ x = self._cast_input_dtype(x, lora_A.weight.dtype)
+
+ if active_adapter not in self.lora_variant: # vanilla LoRA
+ result = result + lora_B(lora_A(dropout(x))) * scaling
+ else:
+ result = self.lora_variant[active_adapter].forward(
+ self,
+ active_adapter=active_adapter,
+ x=x,
+ result=result,
+ **variant_kwargs,
+ **kwargs,
+ )
+
+ result = result.to(torch_result_dtype)
+ return result
+
+ def __repr__(self) -> str:
+ rep = super().__repr__()
+ return "lora." + rep
+
+
+class Conv2d(_ConvNd):
+ # Lora implemented in a conv2d layer
+ def __init__(self, *args, **kwargs):
+ super().__init__(*args, **kwargs)
+ if not self._kernel_dim == 4:
+ raise ValueError(f"Conv2d layer kernel must have 4 dimensions, not {self._kernel_dim}")
+ self.conv_fn = F.conv2d
+
+ def resolve_lora_variant(self, *, use_dora: bool, **kwargs) -> Optional[LoraVariant]:
+ if not use_dora:
+ return None
+
+ from .variants import DoraConv2dVariant
+
+ return DoraConv2dVariant()
+
+
+class Conv1d(_ConvNd):
+ # Lora implemented in a conv1d layer
+ def __init__(self, *args, **kwargs):
+ super().__init__(*args, **kwargs)
+ if not self._kernel_dim == 3:
+ raise ValueError(f"Conv1d layer kernel must have 3 dimensions, not {self._kernel_dim}")
+ self.conv_fn = F.conv1d
+
+ def resolve_lora_variant(self, *, use_dora: bool, **kwargs) -> Optional[LoraVariant]:
+ if not use_dora:
+ return None
+
+ from .variants import DoraConv1dVariant
+
+ return DoraConv1dVariant()
+
+
+class Conv3d(_ConvNd):
+ # Lora implemented in a conv3d layer
+ def __init__(self, *args, **kwargs):
+ super().__init__(*args, **kwargs)
+ if not self._kernel_dim == 5:
+ raise ValueError(f"Conv3d layer kernel must have 5 dimensions, not {self._kernel_dim}")
+ self.conv_fn = F.conv3d
+
+ def resolve_lora_variant(self, *, use_dora: bool, **kwargs) -> Optional[LoraVariant]:
+ if not use_dora:
+ return None
+
+ from .variants import DoraConv3dVariant
+
+ return DoraConv3dVariant()
+
+
+class MultiheadAttention(nn.Module, LoraLayer):
+ """LoRA implemented in a multihead attention layer
+
+ This is currently only implemented for the case of `_qkv_same_embed_dim = True`, i.e. query, key, and value having
+ the same dimension.
+
+ Note: LoRA is applied to both the in_proj (query/key/value) and out_proj. There is currently no way to specify only
+ one of them. Don't try to apply LoRA to the out_proj of MultiheadAttention by targeting that layer specifically,
+ since the forward method of that layer is not being used, hence the LoRA adapter would be ignored.
+
+ This is a little bit hacky because of the way that MultiheadAttention is implemented in PyTorch: There are no
+ `nn.Linear` layers which we can hook onto or, in case of output projection, `.forward` is not used. This
+ implementation works around these problems by merging the weights before the forward call and unmerging them after
+ the forward call.
+ """
+
+ def __init__(
+ self,
+ base_layer,
+ adapter_name: str,
+ r: int = 0,
+ lora_alpha: int = 1,
+ lora_dropout: float = 0.0,
+ init_lora_weights: Union[bool, str] = True,
+ use_rslora: bool = False,
+ use_dora: bool = False,
+ **kwargs,
+ ) -> None:
+ # TODO work with separate weights
+ if not getattr(base_layer, "_qkv_same_embed_dim", True):
+ # default for this value appears to be True:
+ # https://github.com/pytorch/pytorch/blob/701ba5203fe68d55d655bd4d6c008be94cf34ea5/torch/nn/modules/activation.py#L1128-L1130
+ raise ValueError(
+ f"Only same embed for query/key/value is supported as of now for {self.__class__.__name__}."
+ )
+ if use_dora:
+ # TODO: probably not so hard to implement
+ raise ValueError(f"{self.__class__.__name__} does not support DoRA (yet), please set use_dora to False")
+ if kwargs.get("use_alora", False):
+ raise ValueError(f"{self.__class__.__name__} does not support aLoRA (yet), please set use_alora to False")
+ super().__init__()
+ LoraLayer.__init__(self, base_layer, **kwargs)
+
+ # Note: LoRA is applied to both in_proj and out_proj. There is currently no way to only specify one of them.
+ if isinstance(base_layer.out_proj, nn.Linear):
+ self.base_layer.out_proj = Linear(
+ base_layer.out_proj,
+ adapter_name,
+ r=r,
+ lora_alpha=lora_alpha,
+ lora_dropout=lora_dropout,
+ init_lora_weights=init_lora_weights,
+ use_rslora=use_rslora,
+ use_dora=use_dora,
+ **kwargs,
+ )
+ else:
+ raise ValueError(f"out_proj must be an instance of nn.Linear for {self.__class__.__name__}.")
+
+ self._active_adapter = adapter_name
+ self.update_layer(adapter_name, r, lora_alpha, lora_dropout, init_lora_weights, use_rslora)
+
+ @property
+ def embed_dim(self) -> int:
+ return self.get_base_layer().embed_dim
+
+ @property
+ def kdim(self) -> Optional[int]:
+ return self.get_base_layer().kdim
+
+ @property
+ def vdim(self) -> Optional[int]:
+ return self.get_base_layer().vdim
+
+ @property
+ def _qkv_same_embed_dim(self) -> bool:
+ return self.get_base_layer()._qkv_same_embed_dim
+
+ @property
+ def num_heads(self) -> int:
+ return self.get_base_layer().num_heads
+
+ @property
+ def dropout(self) -> float:
+ return self.get_base_layer().dropout
+
+ @property
+ def batch_first(self) -> bool:
+ return self.get_base_layer().batch_first
+
+ @property
+ def head_dim(self) -> int:
+ return self.get_base_layer().head_dim
+
+ @property
+ def in_proj_weight(self) -> nn.Parameter:
+ return self.get_base_layer().in_proj_weight
+
+ @property
+ def in_proj_bias(self) -> nn.Parameter:
+ return self.get_base_layer().in_proj_bias
+
+ @property
+ def out_proj(self) -> nn.Module:
+ return self.get_base_layer().out_proj.get_base_layer()
+
+ @property
+ def bias_k(self) -> Optional[nn.Parameter]:
+ return self.get_base_layer().bias_k
+
+ @property
+ def bias_v(self) -> Optional[nn.Parameter]:
+ return self.get_base_layer().bias_v
+
+ def merge_masks(self, *args, **kwargs) -> tuple[Optional[torch.Tensor], Optional[int]]:
+ return self.get_base_layer().merge_masks(*args, **kwargs)
+
+ @property
+ def add_zero_attn(self) -> bool:
+ return self.get_base_layer().add_zero_attn
+
+ def update_layer(self, *args, **kwargs) -> None:
+ super().update_layer(*args, **kwargs)
+ # Note: LoRA is applied to both in_proj and out_proj. There is currently no way to only specify one of them.
+ self.base_layer.out_proj.update_layer(*args, **kwargs)
+
+ def merge(self, safe_merge: bool = False, adapter_names: Optional[list[str]] = None) -> None:
+ """
+ Merge the active adapter weights into the base weights
+
+ Args:
+ safe_merge (`bool`, *optional*):
+ If True, the merge operation will be performed in a copy of the original weights and check for NaNs
+ before merging the weights. This is useful if you want to check if the merge operation will produce
+ NaNs. Defaults to `False`.
+ adapter_names (`List[str]`, *optional*):
+ The list of adapter names that should be merged. If None, all active adapters will be merged. Defaults
+ to `None`.
+ """
+ adapter_names = check_adapters_to_merge(self, adapter_names)
+ if not adapter_names:
+ # no adapter to merge
+ return
+
+ # Implementation follows this:
+ # https://github.com/Baijiong-Lin/LoRA-Torch/blob/4bfed6820b64fcf47064c30f30606a190a4f0d2e/loratorch/layers.py#L73-L79
+ # Notably, instead of mutating the weight, we delete the original weight and replace it by the merged weight
+ # TODO: work with separate weights
+ for active_adapter in adapter_names:
+ if active_adapter in self.lora_A.keys():
+ base_layer = self.get_base_layer()
+ orig_dtype = base_layer.out_proj.weight.dtype
+ if safe_merge:
+ # TODO: work with separate weights
+ # merging in_proj (nn.Parameter)
+ orig_weight_in = base_layer.in_proj_weight.data.detach().clone()
+ orig_weight_in += self.get_delta_weight(active_adapter).to(orig_dtype)
+ if not torch.isfinite(orig_weight_in).all():
+ raise ValueError(
+ f"NaNs detected in the merged weights. The adapter {active_adapter} seems to be broken"
+ )
+
+ # merging out_proj (subclass of nn.Linear)
+ orig_weight_out = base_layer.out_proj.weight.data.detach().clone()
+ orig_weight_out += base_layer.out_proj.get_delta_weight(active_adapter).to(orig_dtype)
+ if not torch.isfinite(orig_weight_out).all():
+ raise ValueError(
+ f"NaNs detected in the merged weights. The adapter {active_adapter} seems to be broken"
+ )
+
+ # unregister parameter implicitly and overwrite using merged weights; gradients are computed after
+ # forward and, thus, after unmerging (see forward()), therefore this is safe to do.
+ del base_layer.in_proj_weight
+ base_layer.in_proj_weight = orig_weight_in
+
+ del base_layer.out_proj.get_base_layer().weight
+ base_layer.out_proj.get_base_layer().weight = orig_weight_out
+ base_layer.out_proj.merge(adapter_names=[active_adapter])
+ else:
+ # merging in_proj (nn.Parameter)
+ # TODO: work with separate weights
+ delta_weight = self.get_delta_weight(active_adapter).to(orig_dtype)
+ weight_merged = base_layer.in_proj_weight.data.detach() + delta_weight
+
+ # unregister parameter implicitly and overwrite using merged weights; gradients are computed after
+ # forward and, thus, after unmerging (see forward()), therefore this is safe to do.
+ del base_layer.in_proj_weight
+ base_layer.in_proj_weight = weight_merged
+
+ # merging out_proj (subclass of nn.Linear)
+ delta_weight = base_layer.out_proj.get_delta_weight(active_adapter).to(orig_dtype)
+ weight_merged = base_layer.out_proj.weight.data.detach() + delta_weight
+ del base_layer.out_proj.get_base_layer().weight
+ base_layer.out_proj.get_base_layer().weight = weight_merged
+ base_layer.out_proj.merge(adapter_names=[active_adapter])
+ self.merged_adapters.append(active_adapter)
+
+ def unmerge(self) -> None:
+ """
+ This method unmerges all merged adapter layers from the base weights.
+ """
+ if not self.merged:
+ warnings.warn("Already unmerged. Nothing to do.")
+ return
+
+ # TODO work with separate weights
+ base_layer = self.get_base_layer()
+ orig_dtype = base_layer.out_proj.base_layer.weight.dtype
+ while len(self.merged_adapters) > 0:
+ active_adapter = self.merged_adapters.pop()
+ if active_adapter in self.lora_A.keys():
+ # Ensure that requires_grad=False for the base weights after unmerging. This may not matter since
+ # requires_grad was False when the optimizer was initialized, but still let's try to be correct here.
+
+ # in_proj
+ delta_weight = self.get_delta_weight(active_adapter).to(orig_dtype)
+ old_weight = base_layer.in_proj_weight.data - delta_weight
+ del base_layer.in_proj_weight
+ base_layer.register_parameter("in_proj_weight", nn.Parameter(old_weight, requires_grad=False))
+
+ # out_proj
+ delta_weight = base_layer.out_proj.get_delta_weight(active_adapter).to(orig_dtype)
+ old_weight = base_layer.out_proj.base_layer.weight.data - delta_weight
+ del base_layer.out_proj.base_layer.weight
+ base_layer.out_proj.base_layer.register_parameter(
+ "weight", nn.Parameter(old_weight, requires_grad=False)
+ )
+
+ self.get_base_layer().out_proj.unmerge()
+
+ def unload_and_optionally_merge_module(
+ self, merge: bool, safe_merge: bool, adapter_names: Optional[list[str]]
+ ) -> nn.MultiheadAttention:
+ """
+ Merging and unloading of the MultiheadAttention module
+
+ This requires an extra step for MultiheadAttention, which is why there is this special method instead of
+ relying on the normal merge_and_unload code path.
+ """
+ if merge:
+ self.merge(safe_merge=safe_merge, adapter_names=adapter_names)
+ base_layer = self.get_base_layer()
+
+ # extra steps: re-register weights, take care of out_proj layer
+ # in_proj
+ weight = base_layer.in_proj_weight
+ del base_layer.in_proj_weight
+ base_layer.register_parameter("in_proj_weight", nn.Parameter(weight.data, requires_grad=weight.requires_grad))
+
+ # out_proj
+ out_proj_layer = base_layer.out_proj.get_base_layer()
+ weight = out_proj_layer.weight
+ del out_proj_layer.weight
+ out_proj_layer.register_parameter("weight", nn.Parameter(weight.data, requires_grad=weight.requires_grad))
+
+ base_layer.out_proj = out_proj_layer
+ return base_layer
+
+ def get_delta_weight(self, adapter) -> torch.Tensor:
+ """
+ Compute the delta weight for the given adapter.
+
+ Args:
+ adapter (str):
+ The name of the adapter for which the delta weight should be computed.
+ """
+ device = self.lora_B[adapter].weight.device
+ dtype = self.lora_B[adapter].weight.dtype
+
+ # In case users wants to merge the adapter weights that are in
+ # float16 while being on CPU, we need to cast the weights to float32, perform the merge and then cast back to
+ # float16 because the `@` and matmul operation in general is not supported in torch + cpu + fp16.
+ cast_to_fp32 = device.type == "cpu" and dtype == torch.float16
+
+ weight_A = self.lora_A[adapter].weight
+ weight_B = self.lora_B[adapter].weight
+
+ if cast_to_fp32:
+ weight_A = weight_A.float()
+ weight_B = weight_B.float()
+
+ output_tensor = (weight_B @ weight_A) * self.scaling[adapter]
+
+ if cast_to_fp32:
+ output_tensor = output_tensor.to(dtype=dtype)
+
+ # cast back the weights
+ self.lora_A[adapter].weight.data = weight_A.to(dtype)
+ self.lora_B[adapter].weight.data = weight_B.to(dtype)
+
+ return output_tensor
+
+ def _check_forward_args(self, x, *args, **kwargs):
+ if "adapter_names" in kwargs:
+ raise TypeError(f"lora.{self.__class__.__name__} does not support mixed adapter batches.")
+ super()._check_forward_args(x, *args, **kwargs)
+
+ def forward(self, query: torch.Tensor, *args: Any, **kwargs: Any) -> torch.Tensor:
+ previous_dtype = query.dtype
+ self._check_forward_args(query, *args, **kwargs)
+
+ if self.disable_adapters:
+ if self.merged:
+ self.unmerge()
+ result = self.base_layer(query, *args, **kwargs)
+ elif self.merged:
+ result = self.base_layer(query, *args, **kwargs)
+ else:
+ out_proj = self.get_base_layer().out_proj
+ if out_proj.active_adapters != self.active_adapters:
+ # We have a case that in_proj and out_proj have diverging merged adapters. We cannot
+ # really deal with this correctly, thus it's better to raise than possibly create a hard to debug mess
+ cls_name = self.get_base_layer().__class__.__name__
+ raise ValueError(
+ f"The out_proj layer of {cls_name} has merged layers but {cls_name} itself doesn't; please ensure "
+ "that either both or none have merged layers"
+ )
+
+ # Merge all adapters that are active for this module, i.e. the LoRA weights for in_proj and out_proj.
+ # in_proj uses nn.Parameters, therefore, there is no forward method to be used and we have to explicitly
+ # merge for the LoRA weights to have an effect:
+ # https://github.com/pytorch/pytorch/blob/6ebb26d572d5fcdc6ac0d1297bdf8d1eb5d20722/torch/nn/modules/activation.py#L1020
+ # For out_proj, we have an nn.Linear (or rather: NonDynamicallyQuantizableLinear), but its forward method
+ # is not used:
+ # https://github.com/pytorch/pytorch/blob/6ebb26d572d5fcdc6ac0d1297bdf8d1eb5d20722/torch/nn/modules/activation.py#L1267-L1271
+ # Therefore, its LoRA weights also need to be merged to have an effect.
+ active_adapters = [a for a in self.active_adapters if a in self.lora_A]
+ try:
+ self.merge(adapter_names=active_adapters)
+ result = self.base_layer(query, *args, **kwargs)
+ finally:
+ # it's safe to call unmerge(), which unmerges all adapters, because we checked that not self.merged,
+ # i.e. there is was no merged layer before
+ self.unmerge()
+
+ result = (result[0].to(previous_dtype), result[1].to(previous_dtype) if result[1] is not None else result[1])
+ return result
+
+ # The decorator is needed in case low_cpu_mem_usage=True is used, as we don't want the base layer weights to be
+ # moved to meta device. This requires the use of PEFT's implementation of init_empty_weight instead of using the one
+ # from accelerate.
+ @skip_init_on_device
+ def _restore_weights(self):
+ # Restore the weights as registered parameters on the base layer.
+ # This is necessary because the way that weights are merged/unmerged (which is necessary for forward to work
+ # correctly), the Module "forgets" these attributes. Therefore, we need to call register_parameter explicitly.
+ # We cannot call register_parameter for merging/unmerging because that cuts them off from the autograd graph.
+ # Note that this is hacky, since we need to ensure that _restore_weights is called by each method that needs it.
+
+ # in_proj
+ # TODO work with separate weights
+ base_layer = self.get_base_layer()
+ weight = base_layer.in_proj_weight
+ del base_layer.in_proj_weight
+ base_layer.register_parameter("in_proj_weight", nn.Parameter(weight.data, requires_grad=weight.requires_grad))
+
+ # out_proj
+ base_layer = base_layer.out_proj.get_base_layer()
+ weight = base_layer.weight
+ del base_layer.weight
+ base_layer.register_parameter("weight", nn.Parameter(weight.data, requires_grad=weight.requires_grad))
+
+ def state_dict(self, *args, **kwargs):
+ self._restore_weights()
+ return super().state_dict(*args, **kwargs)
+
+ def named_modules(self, *args, **kwargs):
+ # Note: no need to also implement modules(), as modules() calls named_modules() under the hood
+ self._restore_weights()
+ return super().named_modules(*args, **kwargs)
+
+ def __repr__(self) -> str:
+ rep = super().__repr__()
+ return "lora." + rep
+
+
+class _LoraParameterProxy(nn.Module):
+ """This proxies an `nn.Parameter` that is targeted with LoRA.
+ Intended to be used in conjunction with `nn.utils.parametrize`, see `ParamWrapper`.
+ """
+
+ def __init__(self, delta_weight):
+ super().__init__()
+ self.delta_weight = delta_weight
+
+ def forward(self, W):
+ with nn.utils.parametrize.cached():
+ return W + self.delta_weight
+
+
+# copied from:
+# https://github.com/pytorch/pytorch/blob/5e386eec9426f174eea130c0c012d9f65ebe65fb/torch/nn/utils/parametrize.py#L75-L79
+def _register_parameter_or_buffer(module, name, X):
+ if isinstance(X, nn.Parameter):
+ module.register_parameter(name, X)
+ else:
+ module.register_buffer(name, X)
+
+
+class ParamWrapper(nn.Module, LoraLayer):
+ """A LoRA wrapper for `nn.Parameter`. This layer is dispatched if users target a parameter directly with
+ `lora_config.target_parameters`
+ Note:
+ - When accessing the wrapped nn.Parameter directly, e.g. via `module.weight`, the LoRA weights are *not*
+ applied.
+ - It is currently not implemented to target multiple parameters on the same module. To achieve this, it is
+ currently required to create a separate LoRA adapter (with another adapter name) and activate both at the
+ same time.
+ """
+
+ def __init__(
+ self,
+ base_layer,
+ adapter_name: str,
+ parameter_name: str,
+ r: int = 0,
+ lora_alpha: int = 1,
+ lora_dropout: float = 0.0,
+ fan_in_fan_out: bool = False, # Set this to True if the layer to replace stores weight like (fan_in, fan_out)
+ is_target_conv_1d_layer: bool = False,
+ init_lora_weights: Union[bool, str] = True,
+ use_rslora: bool = False,
+ use_dora: bool = False,
+ lora_bias: bool = False,
+ **kwargs,
+ ) -> None:
+ super().__init__()
+ LoraLayer.__init__(self, base_layer, **kwargs)
+ self.parameter_name = parameter_name
+ param = self.get_param()
+ if param.ndim == 3:
+ self.num_experts, self.in_features, self.out_features = param.shape
+ else:
+ self.num_experts, self.in_features, self.out_features = 1, param.shape[1], param.shape[0]
+
+ if param.ndim not in (2, 3):
+ raise ValueError(
+ f"lora.{self.__class__.__name__} was initialized with {param.ndim} dimensional Parameter, but only 2d "
+ "and 3d are supported."
+ )
+ if lora_dropout:
+ # It's not possible to factor out x from lora_B(lora_A(dropout(x))), so dropout can't be correctly
+ # implemented
+ raise ValueError(f"lora.{self.__class__.__name__} does not work with lora_dropout != 0.")
+ if fan_in_fan_out:
+ raise ValueError(f"lora.{self.__class__.__name__} does not work with fan_in_fan_out.")
+ if lora_bias:
+ raise ValueError(f"lora.{self.__class__.__name__} does not work with lora_bias=True.")
+ if use_dora:
+ raise ValueError(f"lora.{self.__class__.__name__} does not work with use_dora=True.")
+ if is_target_conv_1d_layer:
+ raise ValueError(f"lora.{self.__class__.__name__} does not work with is_target_conv_1d_layer=True.")
+
+ self.fan_in_fan_out = fan_in_fan_out
+ self._active_adapter = adapter_name
+ self.update_layer(
+ adapter_name,
+ r,
+ lora_alpha=lora_alpha,
+ lora_dropout=lora_dropout,
+ init_lora_weights=init_lora_weights,
+ use_rslora=use_rslora,
+ use_dora=use_dora,
+ lora_bias=lora_bias,
+ )
+
+ def update_layer(
+ self,
+ adapter_name,
+ r,
+ lora_alpha,
+ lora_dropout,
+ init_lora_weights,
+ use_rslora,
+ use_dora: bool = False,
+ use_qalora: bool = False,
+ lora_bias: bool = False,
+ qalora_group_size: int = 32,
+ inference_mode: bool = False,
+ **kwargs,
+ ):
+ # same method as in lora.Linear but taking into account that there can be multiple experts (3d parameter)
+ # collect the kwargs
+ kwargs = locals().copy()
+ del kwargs["self"]
+
+ # This code works for linear layers, override for other layer types
+ if r <= 0:
+ raise ValueError(f"`r` should be a positive integer value but the value passed is {r}")
+
+ lora_variant = self.resolve_lora_variant(
+ use_dora=use_dora, use_qalora=use_qalora, qalora_group_size=qalora_group_size
+ )
+ if lora_variant is not None:
+ raise ValueError(f"lora.{self.__class__.__name__} does not work with LoRA variants like DoRA.")
+
+ self.r[adapter_name] = r
+ self.lora_alpha[adapter_name] = lora_alpha
+ if lora_dropout > 0.0:
+ # It's not possible to factor out x from lora_B(lora_A(dropout(x))), so dropout can't be correctly
+ # implemented
+ raise ValueError(f"lora.{self.__class__.__name__} does not work with lora_dropout != 0.")
+ else:
+ lora_dropout_layer = nn.Identity()
+
+ self.lora_dropout.update(nn.ModuleDict({adapter_name: lora_dropout_layer}))
+ # Actual trainable parameters
+ # Difference to normal update_layer: consider experts. LoRA layers still use nn.Linear for consistency with
+ # lora.Linear.
+ self.lora_A[adapter_name] = nn.Linear(self.in_features, r * self.num_experts, bias=False)
+ self.lora_B[adapter_name] = nn.Linear(r * self.num_experts, self.out_features, bias=lora_bias)
+ self.lora_bias[adapter_name] = lora_bias
+
+ if use_rslora:
+ self.scaling[adapter_name] = lora_alpha / math.sqrt(r)
+ else:
+ self.scaling[adapter_name] = lora_alpha / r
+
+ self.use_rslora[adapter_name] = use_rslora
+
+ self.use_dora[adapter_name] = use_dora
+
+ # for inits that require access to the base weight, use gather_param_ctx so that the weight is gathered when using DeepSpeed
+ if isinstance(init_lora_weights, str) and init_lora_weights.startswith("pissa"):
+ with gather_params_ctx(self.get_base_layer().weight):
+ self.pissa_init(adapter_name, init_lora_weights)
+ elif isinstance(init_lora_weights, str) and init_lora_weights.startswith("corda"):
+ with gather_params_ctx(self.get_base_layer().weight):
+ self.corda_init(adapter_name, init_lora_weights)
+ elif isinstance(init_lora_weights, str) and init_lora_weights.lower() == "olora":
+ with gather_params_ctx(self.get_base_layer().weight):
+ self.olora_init(adapter_name)
+ elif init_lora_weights == "loftq":
+ with gather_params_ctx(self.get_base_layer().weight):
+ self.loftq_init(adapter_name)
+ elif init_lora_weights == "eva":
+ nn.init.zeros_(self.lora_B[adapter_name].weight)
+ elif init_lora_weights == "orthogonal":
+ with gather_params_ctx(self.get_base_layer().weight):
+ self.orthogonal_init(adapter_name)
+ elif init_lora_weights:
+ self.reset_lora_parameters(adapter_name, init_lora_weights)
+ # call this before init of the lora variants
+ self._move_adapter_to_device_of_base_layer(adapter_name)
+
+ if adapter_name in self.lora_variant:
+ self.lora_variant[adapter_name].init(self, **kwargs)
+
+ self.set_adapter(self.active_adapters, inference_mode=inference_mode)
+
+ def _move_adapter_to_device_of_base_layer(self, adapter_name: str, device: Optional[torch.device] = None) -> None:
+ """
+ Move the adapter of the given name to the device of the base layer. Needs special handling for nn.Parameter
+ """
+ device = self.get_param().device
+ meta = torch.device("meta")
+ param = self.get_param()
+
+ for adapter_layer_name in self.adapter_layer_names + self.other_param_names:
+ adapter_layer = getattr(self, adapter_layer_name, None)
+ if not isinstance(adapter_layer, (nn.ModuleDict, nn.ParameterDict, BufferDict)):
+ continue
+ if adapter_name not in adapter_layer:
+ continue
+ if any(p.device == meta for p in adapter_layer.parameters()):
+ continue
+
+ if param.dtype.is_floating_point or param.dtype.is_complex:
+ adapter_layer[adapter_name] = adapter_layer[adapter_name].to(device, dtype=param.dtype)
+ else:
+ adapter_layer[adapter_name] = adapter_layer[adapter_name].to(device)
+
+ def get_param(self):
+ param = getattr(self.get_base_layer(), self.parameter_name)
+ return param
+
+ def get_delta_weight(self, adapter_name, *args, **kwargs):
+ if self.num_experts == 1:
+ delta_weight = Linear.get_delta_weight(self, adapter_name, *args, **kwargs)
+ else:
+ weight_A = self.lora_A[adapter_name].weight
+ weight_B = self.lora_B[adapter_name].weight
+ # shape: experts x rank x in_features
+ weight_A = weight_A.reshape(self.num_experts, -1, weight_A.shape[-1])
+ # shape: out_features x rank x experts
+ weight_B = weight_B.reshape(weight_B.shape[0], -1, self.num_experts)
+ # fan_in_fan_out must be False, so no transpose call here
+ delta_weight = torch.einsum("o r e, e r i -> e i o", weight_B, weight_A) * self.scaling[adapter_name]
+
+ base_layer = self.get_base_layer()
+ param = self.get_param()
+ delta_weight = delta_weight.to(param.device, param.dtype)
+ return delta_weight
+
+ @contextmanager
+ def _activate_lora(self, active_adapters: list[str]):
+ if not active_adapters or not any(adapter in self.lora_A for adapter in active_adapters):
+ # no active adapters for this layer
+ yield
+ return
+
+ delta_weight = None
+ for active_adapter in active_adapters:
+ if active_adapter not in self.lora_A:
+ continue
+ if delta_weight is None:
+ delta_weight = self.get_delta_weight(active_adapter)
+ else:
+ delta_weight = delta_weight + self.get_delta_weight(active_adapter)
+
+ base_layer = self.get_base_layer()
+ requires_grad_before = self.get_param().requires_grad
+ nn.utils.parametrize.register_parametrization(
+ base_layer, self.parameter_name, _LoraParameterProxy(delta_weight)
+ )
+ # set requires_grad, as it defaults to False
+ base_layer.parametrizations[self.parameter_name].original.requires_grad_(requires_grad_before)
+ try:
+ yield
+ finally:
+ self._remove_parametrizations()
+
+ def _remove_parametrizations(self):
+ # Remove the parametrization of this specific parameter
+ base_layer = self.get_base_layer()
+ parameter_name = self.parameter_name
+ if parameter_name not in base_layer.parametrizations:
+ raise ValueError(
+ "Something went wrong, please report this issue on PEFT: https://github.com/huggingface/peft/issues"
+ )
+
+ param_list = base_layer.parametrizations[parameter_name]
+ if len(param_list) == 1:
+ # last parametrization, we can safely remove it completely
+ nn.utils.parametrize.remove_parametrizations(base_layer, parameter_name, leave_parametrized=False)
+ return
+
+ # If there are multiple parametrizations for the same parameter_name, we only want to remove the LoRA proxy.
+ # Unfortunately, PyTorch does not support this directly, so we need to take care of it manually. To achieve
+ # this, we check the ParameterList from the back until we find the _LoraParameterProxy instance and then remove
+ # it.
+ reversed_indices = reversed(range(len(param_list)))
+ for i in reversed_indices:
+ module = param_list[i]
+ if isinstance(module, _LoraParameterProxy):
+ del param_list[i]
+ break
+ else: # no break encountered
+ # this should not happen, but raising an error is probably not necessary
+ warnings.warn(
+ f"Could not find any LoRA parametrization on {self}, please open an issue on "
+ "https://github.com/huggingface/peft/issues and report this warning."
+ )
+
+ def merge(self, safe_merge: bool = False, adapter_names: Optional[list[str]] = None) -> None:
+ # same as lora.Linear.merge but not hard-coding base_layer.weight and without special cases like variants removed
+ adapter_names = check_adapters_to_merge(self, adapter_names)
+ if not adapter_names:
+ # no adapter to merge
+ return
+
+ for active_adapter in adapter_names:
+ if active_adapter in self.lora_A.keys():
+ base_layer = self.get_base_layer()
+ param = getattr(base_layer, self.parameter_name)
+ if safe_merge:
+ # Note that safe_merge will be slower than the normal merge
+ # because of the copy operation.
+ orig_weight = param.data.clone()
+ orig_dtype = orig_weight.dtype
+ delta_weight = self.get_delta_weight(active_adapter)
+ orig_weight += delta_weight.to(orig_dtype)
+
+ if not torch.isfinite(orig_weight).all():
+ raise ValueError(
+ f"NaNs detected in the merged weights. The adapter {active_adapter} seems to be broken"
+ )
+
+ param.data = orig_weight
+
+ else:
+ delta_weight = self.get_delta_weight(active_adapter)
+ param.data += delta_weight
+
+ self.merged_adapters.append(active_adapter)
+
+ def unmerge(self) -> None:
+ # same as lora.Linear.unmerge but not hard-coding base_layer.weight and without special cases like variants removed
+ if not self.merged:
+ warnings.warn("Already unmerged. Nothing to do.")
+ return
+ while len(self.merged_adapters) > 0:
+ active_adapter = self.merged_adapters.pop()
+ if active_adapter in self.lora_A.keys():
+ param = getattr(self.get_base_layer(), self.parameter_name)
+ orig_dtype = param.dtype
+ delta_weight = self.get_delta_weight(active_adapter)
+ param.data -= delta_weight.to(orig_dtype)
+
+ def _check_forward_args(self, x, *args, **kwargs):
+ """Check if the arguments are compatible with the configs and state of the model"""
+ if kwargs.get("adapter_names", None):
+ raise ValueError(f"lora.{self.__class__.__name__} does not support mixed adapter batches yet.")
+ super()._check_forward_args(x, *args, **kwargs)
+
+ def unload_and_optionally_merge_module(self, merge: bool, safe_merge: bool, adapter_names: Optional[list[str]]):
+ base_layer = self.base_layer
+ # ParamWrappers can be nested, so merge and retrieve base layer recursively
+ if merge:
+ self.merge(safe_merge=safe_merge, adapter_names=adapter_names)
+ while isinstance(base_layer, ParamWrapper):
+ base_layer.merge(safe_merge=safe_merge, adapter_names=adapter_names)
+ base_layer = base_layer.base_layer
+ else:
+ base_layer = self.get_base_layer()
+ return base_layer
+
+ def forward(self, x: torch.Tensor, *args: Any, **kwargs: Any) -> torch.Tensor:
+ self._check_forward_args(x, *args, **kwargs)
+ adapter_names = kwargs.pop("adapter_names", None)
+
+ if self.disable_adapters:
+ if self.merged:
+ self.unmerge()
+ result = self.base_layer(x, *args, **kwargs)
+ elif adapter_names is not None:
+ raise ValueError(f"lora.{self.__class__.__name__} does not support mixed batch inference")
+ elif self.merged:
+ result = self.base_layer(x, *args, **kwargs)
+ else:
+ with self._activate_lora(self.active_adapters):
+ result = self.base_layer(x, *args, **kwargs)
+ return result
+
+ def __repr__(self) -> str:
+ rep = super().__repr__()
+ idx = rep.find("(") + 1
+ # insert the name of the parameter to allow the repr to be disambiguous when multiple parameters on the same
+ # module are being targeted
+ rep = f"{rep[:idx]}\n parameter_name='{self.parameter_name}',{rep[idx:]}"
+ return "lora." + rep
+
+
+def dispatch_default(
+ target: torch.nn.Module,
+ adapter_name: str,
+ lora_config: LoraConfig,
+ parameter_name: Optional[str] = None,
+ **kwargs,
+) -> Optional[torch.nn.Module]:
+ new_module = None
+
+ if isinstance(target, BaseTunerLayer):
+ target_base_layer = target.get_base_layer()
+ else:
+ target_base_layer = target
+
+ if parameter_name is not None:
+ new_module = ParamWrapper(target, adapter_name, parameter_name=parameter_name, **kwargs)
+ elif isinstance(target_base_layer, torch.nn.Embedding):
+ embedding_kwargs = kwargs.copy()
+ embedding_kwargs.pop("fan_in_fan_out", None)
+ embedding_kwargs.update(lora_config.loftq_config)
+ new_module = Embedding(target, adapter_name, **embedding_kwargs)
+ elif isinstance(target_base_layer, torch.nn.Conv2d):
+ kwargs.update(lora_config.loftq_config)
+ new_module = Conv2d(target, adapter_name, **kwargs)
+ elif isinstance(target_base_layer, torch.nn.Conv3d):
+ kwargs.update(lora_config.loftq_config)
+ new_module = Conv3d(target, adapter_name, **kwargs)
+ elif isinstance(target_base_layer, nn.Conv1d):
+ kwargs.update(lora_config.loftq_config)
+ new_module = Conv1d(target, adapter_name, **kwargs)
+ elif isinstance(target_base_layer, torch.nn.MultiheadAttention):
+ kwargs.update(lora_config.loftq_config)
+ new_module = MultiheadAttention(target, adapter_name, **kwargs)
+ elif isinstance(target_base_layer, torch.nn.Linear):
+ if kwargs["fan_in_fan_out"]:
+ warnings.warn(
+ "fan_in_fan_out is set to True but the target module is `torch.nn.Linear`. "
+ "Setting fan_in_fan_out to False."
+ )
+ kwargs["fan_in_fan_out"] = lora_config.fan_in_fan_out = False
+ kwargs.update(lora_config.loftq_config)
+ new_module = Linear(target, adapter_name, **kwargs)
+ elif isinstance(target_base_layer, Conv1D):
+ if not kwargs["fan_in_fan_out"]:
+ warnings.warn(
+ "fan_in_fan_out is set to False but the target module is `Conv1D`. Setting fan_in_fan_out to True."
+ )
+ kwargs["fan_in_fan_out"] = lora_config.fan_in_fan_out = True
+ kwargs.update(lora_config.loftq_config)
+ new_module = Linear(target, adapter_name, is_target_conv_1d_layer=True, **kwargs)
+
+ return new_module
diff --git a/peft/src/peft/tuners/lora/model.py b/peft/src/peft/tuners/lora/model.py
new file mode 100644
index 0000000000000000000000000000000000000000..f03b45640d9f93b7e3afca2d4a4ae847b2a9cc96
--- /dev/null
+++ b/peft/src/peft/tuners/lora/model.py
@@ -0,0 +1,807 @@
+# Copyright 2023-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+from __future__ import annotations
+
+import math
+import operator
+import warnings
+from contextlib import contextmanager
+from dataclasses import replace
+from functools import partial, reduce
+from typing import Literal, Optional
+
+import torch
+from torch import nn
+
+from peft.import_utils import is_bnb_4bit_available, is_bnb_available
+from peft.tuners.tuners_utils import (
+ BaseTuner,
+ BaseTunerLayer,
+ replicate_layers,
+)
+from peft.utils import (
+ TRANSFORMERS_MODELS_TO_LORA_TARGET_MODULES_MAPPING,
+ AuxiliaryTrainingWrapper,
+ ModulesToSaveWrapper,
+ _freeze_adapter,
+ _get_submodules,
+ get_peft_model_state_dict,
+ get_quantization_config,
+)
+from peft.utils.merge_utils import dare_linear, dare_ties, magnitude_prune, task_arithmetic, ties
+from peft.utils.other import get_pattern_key
+
+from .aqlm import dispatch_aqlm
+from .awq import dispatch_awq
+from .config import LoraConfig
+from .eetq import dispatch_eetq
+from .gptq import dispatch_gptq
+from .hqq import dispatch_hqq
+from .inc import dispatch_inc
+from .layer import Conv2d, LoraLayer, ParamWrapper, dispatch_default
+from .torchao import dispatch_torchao
+from .tp_layer import dispatch_megatron
+
+
+def _adapter_names_pre_forward_hook(target, args, kwargs, adapter_names):
+ # pre-forward hook to inject the adapter_names argument when using mixed adapter batches inference
+ kwargs["adapter_names"] = adapter_names
+ return args, kwargs
+
+
+def _alora_offsets_pre_forward_hook(target, args, kwargs, alora_offsets):
+ kwargs["alora_offsets"] = alora_offsets
+ return args, kwargs
+
+
+class LoraModel(BaseTuner):
+ """
+ Creates Low Rank Adapter (LoRA) model from a pretrained transformers model.
+
+ The method is described in detail in https://huggingface.co/papers/2106.09685.
+
+ Args:
+ model ([`torch.nn.Module`]): The model to be adapted.
+ config ([`LoraConfig`]): The configuration of the Lora model.
+ adapter_name (`str`): The name of the adapter, defaults to `"default"`.
+ low_cpu_mem_usage (`bool`, `optional`, defaults to `False`):
+ Create empty adapter weights on meta device. Useful to speed up the loading process.
+
+ Returns:
+ `torch.nn.Module`: The Lora model.
+
+ Example:
+
+ ```py
+ >>> from transformers import AutoModelForSeq2SeqLM
+ >>> from peft import LoraModel, LoraConfig
+
+ >>> config = LoraConfig(
+ ... task_type="SEQ_2_SEQ_LM",
+ ... r=8,
+ ... lora_alpha=32,
+ ... target_modules=["q", "v"],
+ ... lora_dropout=0.01,
+ ... )
+
+ >>> model = AutoModelForSeq2SeqLM.from_pretrained("t5-base")
+ >>> lora_model = LoraModel(model, config, "default")
+ ```
+
+ ```py
+ >>> import torch
+ >>> import transformers
+ >>> from peft import LoraConfig, PeftModel, get_peft_model, prepare_model_for_kbit_training
+
+ >>> rank = ...
+ >>> target_modules = ["q_proj", "k_proj", "v_proj", "out_proj", "fc_in", "fc_out", "wte"]
+ >>> config = LoraConfig(
+ ... r=4, lora_alpha=16, target_modules=target_modules, lora_dropout=0.1, bias="none", task_type="CAUSAL_LM"
+ ... )
+ >>> quantization_config = transformers.BitsAndBytesConfig(load_in_8bit=True)
+
+ >>> tokenizer = transformers.AutoTokenizer.from_pretrained(
+ ... "kakaobrain/kogpt",
+ ... revision="KoGPT6B-ryan1.5b-float16", # or float32 version: revision=KoGPT6B-ryan1.5b
+ ... bos_token="[BOS]",
+ ... eos_token="[EOS]",
+ ... unk_token="[UNK]",
+ ... pad_token="[PAD]",
+ ... mask_token="[MASK]",
+ ... )
+ >>> model = transformers.GPTJForCausalLM.from_pretrained(
+ ... "kakaobrain/kogpt",
+ ... revision="KoGPT6B-ryan1.5b-float16", # or float32 version: revision=KoGPT6B-ryan1.5b
+ ... pad_token_id=tokenizer.eos_token_id,
+ ... use_cache=False,
+ ... device_map={"": rank},
+ ... torch_dtype=torch.float16,
+ ... quantization_config=quantization_config,
+ ... )
+ >>> model = prepare_model_for_kbit_training(model)
+ >>> lora_model = get_peft_model(model, config)
+ ```
+
+ **Attributes**:
+ - **model** ([`~transformers.PreTrainedModel`]) -- The model to be adapted.
+ - **peft_config** ([`LoraConfig`]): The configuration of the Lora model.
+ """
+
+ prefix: str = "lora_"
+ tuner_layer_cls = LoraLayer
+ target_module_mapping = TRANSFORMERS_MODELS_TO_LORA_TARGET_MODULES_MAPPING
+
+ def _prepare_model(self, peft_config: LoraConfig, model: nn.Module):
+ r"""
+ A private method to modify the model structure before adapter is applied.
+
+ Args:
+ peft_config (`PeftConfig`):
+ The prepared adapter config.
+ model (`nn.Module`):
+ The model that is going to be adapted.
+ """
+ if peft_config.layer_replication:
+ replicate_layers(model, peft_config.layer_replication)
+
+ def _create_and_replace(
+ self,
+ lora_config,
+ adapter_name,
+ target,
+ target_name,
+ parent,
+ current_key,
+ *,
+ parameter_name: Optional[str] = None,
+ ) -> None:
+ if current_key is None:
+ raise ValueError("Current Key shouldn't be `None`")
+
+ if lora_config.target_parameters:
+ # Right now, unfortunately, we don't support multiple adapters with target_parameters on the same model.
+ other_configs_use_target_params = any(
+ conf.target_parameters for key, conf in self.peft_config.items() if key != adapter_name
+ )
+ if other_configs_use_target_params:
+ raise ValueError(
+ f"Adding a LoRA config with `target_parameters={lora_config.target_parameters}` but there are "
+ "already other LoRA adapters on this model that use `target_parameters`. At the moment, only "
+ "one LoRA adapter per model with `target_parameters` is allowed."
+ )
+
+ # Regexp matching - Find key which matches current target_name in patterns provided
+ r_key = get_pattern_key(lora_config.rank_pattern.keys(), current_key)
+ alpha_key = get_pattern_key(lora_config.alpha_pattern.keys(), current_key)
+ r = lora_config.rank_pattern.get(r_key, lora_config.r)
+ alpha = lora_config.alpha_pattern.get(alpha_key, lora_config.lora_alpha)
+
+ kwargs = {
+ "r": r,
+ "lora_alpha": alpha,
+ "lora_dropout": lora_config.lora_dropout,
+ "fan_in_fan_out": lora_config.fan_in_fan_out,
+ "init_lora_weights": lora_config.init_lora_weights,
+ "use_rslora": lora_config.use_rslora,
+ "use_dora": lora_config.use_dora,
+ "use_alora": lora_config.alora_invocation_tokens is not None,
+ "use_qalora": lora_config.use_qalora,
+ "qalora_group_size": lora_config.qalora_group_size,
+ "ephemeral_gpu_offload": lora_config.runtime_config.ephemeral_gpu_offload,
+ "lora_bias": lora_config.lora_bias,
+ "arrow_config": lora_config.arrow_config,
+ "loaded_in_8bit": getattr(self.model, "is_loaded_in_8bit", False),
+ "loaded_in_4bit": getattr(self.model, "is_loaded_in_4bit", False),
+ "parameter_name": parameter_name,
+ }
+
+ # for torchao merging, we need the get_apply_tensor_subclass from the quantization config
+ try:
+ kwargs["get_apply_tensor_subclass"] = operator.attrgetter(
+ "hf_quantizer.quantization_config.get_apply_tensor_subclass"
+ )(self.model)
+ except AttributeError:
+ pass
+
+ quant_methods = ["gptq", "aqlm", "awq"]
+ for quant_method in quant_methods:
+ quantization_config = get_quantization_config(self.model, method=quant_method)
+ if quantization_config is not None:
+ kwargs[f"{quant_method}_quantization_config"] = quantization_config
+
+ # note: AdaLoraLayer is a subclass of LoraLayer, we need to exclude it
+ from peft.tuners.adalora import AdaLoraLayer
+
+ # if the target is a ParamWrapper, we nest it to allow targeting multiple nn.Parameter on the same module
+ wrap_target_param = isinstance(target, ParamWrapper) and (adapter_name in target.lora_A)
+ if isinstance(target, LoraLayer) and not isinstance(target, AdaLoraLayer) and not wrap_target_param:
+ target.update_layer(
+ adapter_name,
+ r,
+ lora_alpha=alpha,
+ lora_dropout=lora_config.lora_dropout,
+ init_lora_weights=lora_config.init_lora_weights,
+ use_rslora=lora_config.use_rslora,
+ use_dora=lora_config.use_dora,
+ lora_bias=lora_config.lora_bias,
+ arrow_config=lora_config.arrow_config,
+ inference_mode=lora_config.inference_mode,
+ )
+ else:
+ if isinstance(target, ParamWrapper) and (parameter_name == target.parameter_name):
+ raise ValueError(
+ "Trying to target the same nn.Parameter twice, this should not happen. Please open an issue on the "
+ "PEFT repo: https://github.com/huggingface/peft/issues"
+ )
+ device_map = self.model.hf_device_map if hasattr(self.model, "hf_device_map") else None
+ new_module = self._create_new_module(lora_config, adapter_name, target, device_map=device_map, **kwargs)
+ if adapter_name not in self.active_adapters:
+ # adding an additional adapter: it is not automatically trainable
+ new_module.requires_grad_(False)
+ self._replace_module(parent, target_name, new_module, target)
+
+ def _replace_module(self, parent, child_name, new_module, child):
+ # override in LoraModel to handle quantized weights properly
+
+ setattr(parent, child_name, new_module)
+ # It's not necessary to set requires_grad here, as that is handled by
+ # _mark_only_adapters_as_trainable
+
+ # child layer wraps the original module, unpack it
+ if hasattr(child, "base_layer"):
+ child = child.base_layer
+
+ meta = torch.device("meta")
+ # dispatch to correct device
+ for name, module in new_module.named_modules():
+ if (self.prefix in name) or ("ranknum" in name):
+ if hasattr(child, "qweight"):
+ weight = child.qweight
+ elif hasattr(child, "W_q"):
+ weight = child.W_q
+ elif hasattr(child, "weight"):
+ weight = child.weight
+ elif getattr(child, "in_proj_weight", None) is not None: # MHA
+ weight = child.in_proj_weight
+ else:
+ weight = next(child.parameters())
+ if not any(p.device == meta for p in module.parameters()):
+ module.to(weight.device)
+
+ @staticmethod
+ def _create_new_module(lora_config, adapter_name, target, **kwargs):
+ # Collect dispatcher functions to decide what backend to use for the replaced LoRA layer. The order matters,
+ # because the first match is always used. Therefore, the default layers should be checked last.
+ dispatchers = []
+
+ if lora_config._custom_modules:
+ # Experimental custom LoRA module support. Allows users to pass a custom mapping for unsupported layer
+ # types by impelementing their own LoRA layers.
+ def dynamic_dispatch_func(target, adapter_name, lora_config, **kwargs):
+ new_module = None
+
+ if isinstance(target, BaseTunerLayer):
+ target_base_layer = target.get_base_layer()
+ else:
+ target_base_layer = target
+
+ for key, custom_cls in lora_config._custom_modules.items():
+ if isinstance(target_base_layer, key):
+ new_module = custom_cls(target, adapter_name, **kwargs)
+ break
+
+ return new_module
+
+ dispatchers.append(dynamic_dispatch_func)
+
+ # avoid eager bnb import
+ if is_bnb_available():
+ from .bnb import dispatch_bnb_8bit
+
+ dispatchers.append(dispatch_bnb_8bit)
+
+ if is_bnb_4bit_available():
+ from .bnb import dispatch_bnb_4bit
+
+ dispatchers.append(dispatch_bnb_4bit)
+
+ dispatchers.extend(
+ [
+ dispatch_eetq,
+ dispatch_aqlm,
+ dispatch_awq,
+ dispatch_gptq,
+ dispatch_hqq,
+ dispatch_inc,
+ dispatch_torchao,
+ dispatch_megatron,
+ dispatch_default,
+ ]
+ )
+
+ new_module = None
+ for dispatcher in dispatchers:
+ new_module = dispatcher(target, adapter_name, lora_config=lora_config, **kwargs)
+ if new_module is not None: # first match wins
+ break
+
+ if new_module is None:
+ # no module could be matched
+ raise ValueError(
+ f"Target module {target} is not supported. Currently, only the following modules are supported: "
+ "`torch.nn.Linear`, `torch.nn.Embedding`, `torch.nn.Conv1d`, `torch.nn.Conv2d`, `torch.nn.Conv3d`, "
+ "`transformers.pytorch_utils.Conv1D`, `torch.nn.MultiheadAttention.`."
+ )
+
+ return new_module
+
+ @contextmanager
+ def _enable_peft_forward_hooks(self, *args, **kwargs):
+ # If adapter_names is passed as an argument, we inject it into the forward arguments.
+ adapter_names = kwargs.pop("adapter_names", None)
+ alora_offsets = kwargs.pop("alora_offsets", None)
+ if adapter_names is None and alora_offsets is None:
+ # nothing to do
+ yield
+ return
+ hook_handles = []
+ if alora_offsets is not None:
+ for layer in self.modules():
+ if isinstance(layer, LoraLayer):
+ pre_forward = partial(_alora_offsets_pre_forward_hook, alora_offsets=alora_offsets)
+ handle = layer.register_forward_pre_hook(pre_forward, with_kwargs=True)
+ hook_handles.append(handle)
+ num_beams = kwargs.get("num_beams", None)
+ uses_beam_search = isinstance(num_beams, int) and (num_beams > 1)
+ if uses_beam_search:
+ if alora_offsets is not None:
+ raise ValueError("Beam search not yet supported for aLoRA.")
+ if adapter_names is not None:
+ if self.training:
+ raise ValueError("Cannot pass `adapter_names` when the model is in training mode.")
+
+ # Check that users only passed actually existing adapters.
+ # Note: We cannot do this on the layer level, as each individual layer may not have each adapter. Still, we want
+ # to check that there is at least one layer with the given name, or else something like typos can easily slip.
+ expected_adapters = set()
+ for layer in self.modules():
+ if isinstance(layer, LoraLayer):
+ expected_adapters |= layer.lora_A.keys()
+ expected_adapters |= layer.lora_embedding_A.keys()
+ unique_adapters = {name for name in adapter_names if name != "__base__"}
+ unexpected_adapters = unique_adapters - expected_adapters
+ if unexpected_adapters:
+ raise ValueError(
+ f"Trying to infer with non-existing adapter(s): {', '.join(sorted(unexpected_adapters))}"
+ )
+
+ # deal with beam search
+ original_adapter_names = adapter_names[:]
+ if uses_beam_search:
+ if not isinstance(adapter_names, (list, tuple)):
+ raise TypeError(f"Got adapter names of type {type(adapter_names)}, expected a list of str.")
+ # When there is beam search, the inputs are repeated n times, thus we repeat each adapter name n times and
+ # then flatten the nested list. For encoder-decoder models, this extended list should not be applied to the
+ # encoder part. Further below, the original argument is thus restored for the encoder.
+ adapter_names = sum(([n] * kwargs["num_beams"] for n in adapter_names), [])
+
+ for module in self.modules():
+ if isinstance(module, LoraLayer) or isinstance(module, AuxiliaryTrainingWrapper):
+ pre_forward = partial(_adapter_names_pre_forward_hook, adapter_names=adapter_names)
+ handle = module.register_forward_pre_hook(pre_forward, with_kwargs=True)
+ hook_handles.append(handle)
+
+ if uses_beam_search and hasattr(self.model, "get_encoder"):
+ # For encoder-decoder models, even when applying beam search, the encoder part of the model should not use
+ # the extended adapter_names. This is because the encoder still uses the original, non-extended samples.
+ for module in self.model.get_encoder().modules():
+ if isinstance(module, LoraLayer) or isinstance(module, AuxiliaryTrainingWrapper):
+ # Add another hook to overwrite the kwargs with the original adapter names -- this is easier than
+ # trying to exclude the encoder.
+ pre_forward = partial(_adapter_names_pre_forward_hook, adapter_names=original_adapter_names)
+ handle = module.register_forward_pre_hook(pre_forward, with_kwargs=True)
+ hook_handles.append(handle)
+
+ yield
+
+ for handle in hook_handles:
+ handle.remove()
+
+ def _check_merge_allowed(self):
+ """Verify that the configuration supports merging.
+
+ Currently gptq quantization and replicated layers do not support merging.
+ """
+ super()._check_merge_allowed()
+ if getattr(self.model, "quantization_method", None) == "gptq":
+ raise ValueError("Cannot merge LORA layers when the model is gptq quantized")
+ if self.peft_config.get("layer_replication"):
+ raise ValueError("Cannot merge LORA layers when base model layers are replicated")
+
+ def _prepare_adapter_config(self, peft_config, model_config):
+ if peft_config.target_modules is None:
+ if model_config["model_type"] in self.target_module_mapping:
+ peft_config.target_modules = set(self.target_module_mapping[model_config["model_type"]])
+ elif not peft_config.target_parameters:
+ raise ValueError("Please specify `target_modules` or `target_parameters`in `peft_config`")
+ return peft_config
+
+ def _check_add_weighted_adapter(
+ self, adapters: list[str], combination_type: str, svd_rank: int | None
+ ) -> tuple[str, int, str]:
+ """
+ Helper function to check if the arguments to add_weighted_adapter are valid and compatible with the underlying
+ model.
+ """
+ for adapter in adapters:
+ if adapter not in list(self.peft_config.keys()):
+ raise ValueError(f"Adapter {adapter} does not exist")
+
+ for adapter in adapters:
+ if self.peft_config[adapter].target_parameters:
+ raise ValueError(
+ f"add_weighted_adapter does not support targeting nn.Parameter (problematic adapter '{adapter}')"
+ )
+
+ # If more than one of the adapters targets the same module with modules_to_save, raise an error, as these
+ # modules cannot be merged. First, find the ModulesToSaveWrapper instances in the model, then check if they
+ # have modules for the adapters to be merged.
+ modules_to_save_wrappers = [module for module in self.modules() if isinstance(module, ModulesToSaveWrapper)]
+ problematic_wrappers = [
+ wrapper
+ for wrapper in modules_to_save_wrappers
+ if sum(adapter in wrapper.modules_to_save for adapter in adapters) > 1
+ ]
+ if problematic_wrappers:
+ raise ValueError(
+ "Cannot add weighted adapters if they target the same module with modules_to_save, but found "
+ f"{len(problematic_wrappers)} such instance(s)."
+ )
+
+ # if there is only one adapter, we can only use linear merging
+ combination_type = "linear" if len(adapters) == 1 else combination_type
+
+ adapters_ranks: list[int] = [
+ # When allocating tensors for the new adapter, we need the maximum possible rank to not overflow
+ config.r if not config.rank_pattern else max(config.r, *config.rank_pattern.values())
+ for config in (self.peft_config[adapter] for adapter in adapters)
+ ]
+
+ if combination_type in ("linear", "ties", "dare_ties", "dare_linear", "magnitude_prune"):
+ # all adapters ranks should be same, new rank is just this value
+ if len(set(adapters_ranks)) != 1:
+ raise ValueError(
+ "All adapters must have the same r value when using combination_type linear, ties, dare_ties or "
+ "dare_linear."
+ )
+ new_rank = adapters_ranks[0]
+ elif combination_type == "cat":
+ # adapters ranks may be different, new rank is sum of all ranks
+ # be careful, because output adapter rank may be really big if mixing a lot of adapters
+ new_rank = sum(adapters_ranks)
+ elif combination_type.endswith("svd"):
+ # new rank is the max of all ranks of the adapters if not provided
+ new_rank = svd_rank or max(adapters_ranks)
+ else:
+ raise ValueError(f"Invalid combination_type: {combination_type}")
+
+ target_module_types = [type(self.peft_config[adapter].target_modules) for adapter in adapters]
+ if not target_module_types:
+ raise ValueError(f"Found no adapter matching the names in {adapters}")
+ if len(set(target_module_types)) > 1:
+ raise ValueError(
+ "all adapter configs should follow the same target modules type. "
+ "Combining adapters with `target_modules` type being a mix of list/set and string is not supported."
+ )
+
+ if target_module_types[0] is str:
+ new_target_modules = "|".join(f"({self.peft_config[adapter].target_modules})" for adapter in adapters)
+ elif target_module_types[0] is set:
+ new_target_modules = reduce(
+ operator.or_, (self.peft_config[adapter].target_modules for adapter in adapters)
+ )
+ else:
+ raise TypeError(f"Invalid type {target_module_types[0]} found in target_modules")
+
+ return combination_type, new_rank, new_target_modules
+
+ def add_weighted_adapter(
+ self,
+ adapters: list[str],
+ weights: list[float],
+ adapter_name: str,
+ combination_type: str = "svd",
+ svd_rank: int | None = None,
+ svd_clamp: int | None = None,
+ svd_full_matrices: bool = True,
+ svd_driver: str | None = None,
+ density: float | None = None,
+ majority_sign_method: Literal["total", "frequency"] = "total",
+ ) -> None:
+ """
+ This method adds a new adapter by merging the given adapters with the given weights.
+
+ When using the `cat` combination_type you should be aware that rank of the resulting adapter will be equal to
+ the sum of all adapters ranks. So it's possible that the mixed adapter may become too big and result in OOM
+ errors.
+
+ Args:
+ adapters (`list`):
+ List of adapter names to be merged.
+ weights (`list`):
+ List of weights for each adapter. Weights can be positive or negative, allowing for both addition and
+ subtraction of adapter effects.
+ adapter_name (`str`):
+ Name of the new adapter.
+ combination_type (`str`):
+ The merging type can be one of [`svd`, `linear`, `cat`, `ties`, `ties_svd`, `dare_ties`, `dare_linear`,
+ `dare_ties_svd`, `dare_linear_svd`, `magnitude_prune`, `magnitude_prune_svd`]. When using the `cat`
+ combination_type, the rank of the resulting adapter is equal to the sum of all adapters ranks (the
+ mixed adapter may be too big and result in OOM errors).
+ svd_rank (`int`, *optional*):
+ Rank of output adapter for svd. If None provided, will use max rank of merging adapters.
+ svd_clamp (`float`, *optional*):
+ A quantile threshold for clamping SVD decomposition output. If None is provided, do not perform
+ clamping. Defaults to None.
+ svd_full_matrices (`bool`, *optional*):
+ Controls whether to compute the full or reduced SVD, and consequently, the shape of the returned
+ tensors U and Vh. Defaults to True.
+ svd_driver (`str`, *optional*):
+ Name of the cuSOLVER method to be used. This keyword argument only works when merging on CUDA. Can be
+ one of [None, `gesvd`, `gesvdj`, `gesvda`]. For more info please refer to `torch.linalg.svd`
+ documentation. Defaults to None.
+ density (`float`, *optional*):
+ Value between 0 and 1. 0 means all values are pruned and 1 means no values are pruned. Should be used
+ with [`ties`, `ties_svd`, `dare_ties`, `dare_linear`, `dare_ties_svd`, `dare_linear_svd`,
+ `magnintude_prune`, `magnitude_prune_svd`]
+ majority_sign_method (`str`):
+ The method, should be one of ["total", "frequency"], to use to get the magnitude of the sign values.
+ Should be used with [`ties`, `ties_svd`, `dare_ties`, `dare_ties_svd`]
+ """
+
+ if adapter_name in list(self.peft_config.keys()):
+ return
+
+ combination_type, new_rank, new_target_modules = self._check_add_weighted_adapter(
+ adapters=adapters,
+ combination_type=combination_type,
+ svd_rank=svd_rank,
+ )
+
+ self.peft_config[adapter_name] = replace(
+ self.peft_config[adapters[0]],
+ r=new_rank,
+ lora_alpha=new_rank,
+ target_modules=new_target_modules,
+ alpha_pattern={},
+ rank_pattern={},
+ )
+ self.inject_adapter(self.model, adapter_name)
+
+ # Do we really need that?
+ _freeze_adapter(self.model, adapter_name)
+
+ key_list = [key for key, _ in self.model.named_modules() if self.prefix not in key]
+ for key in key_list:
+ _, target, _ = _get_submodules(self.model, key)
+ if isinstance(target, LoraLayer):
+ if adapter_name in target.lora_A:
+ target_lora_A = target.lora_A[adapter_name].weight
+ target_lora_B = target.lora_B[adapter_name].weight
+ elif adapter_name in target.lora_embedding_A:
+ target_lora_A = target.lora_embedding_A[adapter_name]
+ target_lora_B = target.lora_embedding_B[adapter_name]
+ else:
+ continue
+
+ target_lora_A.data = target_lora_A.data * 0.0
+ target_lora_B.data = target_lora_B.data * 0.0
+ if combination_type == "cat":
+ loras_A, loras_B = [], []
+ for adapter, weight in zip(adapters, weights):
+ if adapter in target.lora_A:
+ current_adapter_lora_A = target.lora_A[adapter].weight
+ current_adapter_lora_B = target.lora_B[adapter].weight
+ elif adapter in target.lora_embedding_A:
+ current_adapter_lora_A = target.lora_embedding_A[adapter]
+ current_adapter_lora_B = target.lora_embedding_B[adapter]
+ else:
+ continue
+ loras_A.append(current_adapter_lora_A.data * weight * target.scaling[adapter])
+ loras_B.append(current_adapter_lora_B.data)
+
+ if len(loras_A) == 0:
+ raise ValueError("No matching LoRAs found. Please raise an issue on GitHub.")
+ loras_A = torch.cat(loras_A, dim=0)
+ loras_B = torch.cat(loras_B, dim=1)
+ target_lora_A.data[: loras_A.shape[0], :] = loras_A
+ target_lora_B.data[:, : loras_B.shape[1]] = loras_B
+ elif combination_type in [
+ "svd",
+ "ties_svd",
+ "dare_linear_svd",
+ "dare_ties_svd",
+ "magnitude_prune_svd",
+ ]:
+ target_lora_A.data, target_lora_B.data = self._svd_generalized_task_arithmetic_weighted_adapter(
+ combination_type,
+ adapters,
+ weights,
+ new_rank,
+ target,
+ target_lora_A,
+ target_lora_B,
+ density,
+ majority_sign_method,
+ svd_clamp,
+ full_matrices=svd_full_matrices,
+ driver=svd_driver,
+ )
+ elif combination_type in ["linear", "ties", "dare_linear", "dare_ties", "magnitude_prune"]:
+ target_lora_A.data, target_lora_B.data = self._generalized_task_arithmetic_weighted_adapter(
+ combination_type, adapters, weights, target, density, majority_sign_method
+ )
+
+ def _svd_generalized_task_arithmetic_weighted_adapter(
+ self,
+ combination_type,
+ adapters,
+ weights,
+ new_rank,
+ target,
+ target_lora_A,
+ target_lora_B,
+ density,
+ majority_sign_method,
+ clamp=None,
+ full_matrices=True,
+ driver=None,
+ ):
+ valid_adapters = []
+ valid_weights = []
+ is_embedding = any(adapter in target.lora_embedding_A for adapter in adapters)
+ for adapter, weight in zip(adapters, weights):
+ if adapter in target.lora_A or adapter in target.lora_embedding_A:
+ valid_adapters.append(adapter)
+ valid_weights.append(weight * target.scaling[adapter])
+
+ # if no valid adapter, nothing to do
+ if len(valid_adapters) == 0:
+ raise ValueError("No matching LoRAs found. Please raise an issue on Github.")
+ delta_weight = [target.get_delta_weight(adapter) for adapter in valid_adapters]
+ valid_weights = torch.tensor(valid_weights).to(delta_weight[0].device)
+ if combination_type == "svd":
+ delta_weight = task_arithmetic(delta_weight, valid_weights)
+ elif combination_type == "ties_svd":
+ delta_weight = ties(delta_weight, valid_weights, density, majority_sign_method)
+ elif combination_type == "dare_linear_svd":
+ delta_weight = dare_linear(delta_weight, valid_weights, density)
+ elif combination_type == "dare_ties_svd":
+ delta_weight = dare_ties(delta_weight, valid_weights, density, majority_sign_method)
+ elif combination_type == "magnitude_prune_svd":
+ delta_weight = magnitude_prune(delta_weight, valid_weights, density)
+ else:
+ raise ValueError(f"Invalid value passed to combination type: {combination_type}")
+
+ conv2d = isinstance(target, Conv2d)
+ if conv2d:
+ conv2d_1x1 = target.weight.size()[2:4] == (1, 1)
+ if not conv2d_1x1:
+ delta_weight = delta_weight.flatten(start_dim=1)
+ else:
+ delta_weight = delta_weight.squeeze()
+ if (hasattr(target, "fan_in_fan_out") and target.fan_in_fan_out) or is_embedding:
+ delta_weight = delta_weight.T
+
+ # based on https://github.com/kohya-ss/sd-scripts/blob/main/networks/svd_merge_lora.py#L114-L131
+ U, S, Vh = torch.linalg.svd(delta_weight, full_matrices=full_matrices, driver=driver)
+ U = U[:, :new_rank]
+ S = S[:new_rank]
+ U = U @ torch.diag(S)
+ Vh = Vh[:new_rank, :]
+ if clamp is not None:
+ dist = torch.cat([U.flatten(), Vh.flatten()])
+ hi_val = torch.quantile(dist, clamp)
+ low_val = -hi_val
+ U = U.clamp(low_val, hi_val)
+ Vh = Vh.clamp(low_val, hi_val)
+ if conv2d:
+ U = U.reshape(target_lora_B.data.shape)
+ Vh = Vh.reshape(target_lora_A.data.shape)
+ return Vh, U
+
+ def _generalized_task_arithmetic_weighted_adapter(
+ self,
+ combination_type,
+ adapters,
+ weights,
+ target,
+ density,
+ majority_sign_method,
+ ):
+ # account weights for LoRA A and B layers.
+ valid_weights = []
+ lora_A_deltas = []
+ lora_B_deltas = []
+ for adapter, weight in zip(adapters, weights):
+ if adapter in target.lora_A:
+ current_adapter_lora_A = target.lora_A[adapter].weight
+ current_adapter_lora_B = target.lora_B[adapter].weight
+ elif adapter in target.lora_embedding_A:
+ current_adapter_lora_A = target.lora_embedding_A[adapter]
+ current_adapter_lora_B = target.lora_embedding_B[adapter]
+ else:
+ continue
+ # Support negative weights: take absolute value for sqrt, then apply sign
+ weight_with_scaling = weight * target.scaling[adapter]
+ sign = 1 if weight_with_scaling >= 0 else -1
+ valid_weights.append(sign * math.sqrt(abs(weight_with_scaling)))
+ lora_A_deltas.append(current_adapter_lora_A.data)
+ lora_B_deltas.append(current_adapter_lora_B.data)
+ valid_weights = torch.tensor(valid_weights).to(lora_A_deltas[0].device)
+ lora_deltas = [lora_A_deltas, lora_B_deltas]
+ dtype = lora_A_deltas[0].dtype
+ for i, task_tensors in enumerate(lora_deltas):
+ if combination_type == "linear":
+ lora_deltas[i] = task_arithmetic(task_tensors, valid_weights)
+ elif combination_type == "ties":
+ lora_deltas[i] = ties(task_tensors, valid_weights, density, majority_sign_method)
+ elif combination_type == "dare_linear":
+ lora_deltas[i] = dare_linear(task_tensors, valid_weights, density)
+ elif combination_type == "dare_ties":
+ lora_deltas[i] = dare_ties(task_tensors, valid_weights, density, majority_sign_method)
+ elif combination_type == "magnitude_prune":
+ lora_deltas[i] = magnitude_prune(task_tensors, valid_weights, density)
+ else:
+ raise ValueError("Invalid combination type")
+ lora_deltas = [delta.to(dtype) for delta in lora_deltas]
+ return lora_deltas
+
+ def subtract_mutated_init(self, output_state_dict: dict[str, torch.Tensor], adapter_name: str, kwargs=None):
+ """
+ This function can calculate the updates of the PiSSA/CorDA/OLoRA by comparing the parameters of the
+ PiSSA/CorDA/OLoRA adapter in `output_state_dict` with the initial values of PiSSA/CorDA/OLoRA in
+ `adapter_name`, thus converting PiSSA/CorDA/OLoRA to LoRA.
+ """
+ for name, param in self.model.named_parameters():
+ if (
+ param.data.dtype != torch.float32
+ and param.data.dtype != torch.float16
+ and param.data.dtype != torch.bfloat16
+ ) and adapter_name.startswith("pissa"):
+ warnings.warn(
+ r"Note that Quant(W_res) + AB != Quant(W) + \Delta(AB); "
+ "the converted LoRA, when combined with W or Quant(W), may introduce a certain gap in the fine-tuned model. "
+ "Therefore, we recommend directly using the Quant(W_res) in conjunction with the PiSSA adapter. "
+ )
+ mutated_init_state_dict = get_peft_model_state_dict(
+ self,
+ state_dict=kwargs.get("state_dict", None),
+ adapter_name=adapter_name,
+ )
+ tensors_lora = {}
+ for name in output_state_dict.keys():
+ ## W = W^{res} + A_0 \times B_0,
+ ## W + \Delta W = W^{res} + A \times B,
+ ## \Delta W = A \times B - A_0 \times B_0 = [A | A_0] \times [B | -B_0]^T = A'B'.
+ if "lora_A" in name:
+ tensors_lora[name] = torch.cat(
+ [output_state_dict[name], mutated_init_state_dict[".".join(name.split(".")[1:])]], dim=0
+ )
+ elif "lora_B" in name:
+ tensors_lora[name] = torch.cat(
+ [output_state_dict[name], -mutated_init_state_dict[".".join(name.split(".")[1:])]], dim=1
+ )
+
+ return tensors_lora
diff --git a/peft/src/peft/tuners/lora/torchao.py b/peft/src/peft/tuners/lora/torchao.py
new file mode 100644
index 0000000000000000000000000000000000000000..5e7240a053502bd2be450fd87187c756eeb0c17c
--- /dev/null
+++ b/peft/src/peft/tuners/lora/torchao.py
@@ -0,0 +1,156 @@
+# Copyright 2024-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+from __future__ import annotations
+
+import warnings
+from typing import Any, Optional
+
+import torch
+
+# from torch import nn
+from peft.import_utils import is_torchao_available
+from peft.tuners.tuners_utils import BaseTunerLayer, check_adapters_to_merge
+
+from .config import LoraConfig
+from .layer import Linear
+
+
+class TorchaoLoraLinear(Linear):
+ """LoRA layer implementation for Linear layers using torchao data"""
+
+ def __init__(self, *args, get_apply_tensor_subclass, **kwargs):
+ # this is not strictly necessary, as kwargs are stored either way, but we want to error early if
+ # get_apply_tensor_subclass is missing.
+ if kwargs.get("lora_bias", False):
+ raise ValueError(f"{self.__class__.__name__} does not support lora_bias yet, set it to False")
+
+ super().__init__(*args, **kwargs)
+ self.get_apply_tensor_subclass = get_apply_tensor_subclass
+ self._check_dtype_supported()
+
+ def _check_dtype_supported(self):
+ # TODO: Not required once int4_weight_only is properly supported by torchao
+ base_layer = self.get_base_layer()
+ weight = base_layer.weight
+ # pytest tests/test_gpu_examples.py::PeftTorchaoGPUTests::test_causal_lm_training_single_gpu_torchao_0_int8_weight_only
+ if (
+ # torchao 0.7.0+
+ (hasattr(weight, "tensor_impl") and (weight.tensor_impl.data.dtype != torch.int8))
+ or
+ # torchao < 0.7.0
+ (hasattr(weight, "layout_tensor") and (weight.layout_tensor.data.dtype != torch.int8))
+ ):
+ raise ValueError(f"{type(self).__name__} only supports int8 weights for now.")
+
+ def merge(self, safe_merge: bool = False, adapter_names: Optional[list[str]] = None) -> None:
+ from torchao import quantize_
+
+ adapter_names = check_adapters_to_merge(self, adapter_names)
+ if not adapter_names:
+ # no adapter to merge
+ return
+
+ self._check_dtype_supported()
+
+ base_layer = self.get_base_layer()
+ weight = base_layer.weight
+
+ for active_adapter in adapter_names:
+ try:
+ weight = weight.dequantize()
+ except NotImplementedError as exc:
+ msg = (
+ f"Weights of type {type(weight).__name__} do not support dequantization (yet), which is needed to "
+ "support merging."
+ )
+ raise NotImplementedError(msg) from exc
+
+ if safe_merge and not torch.isfinite(weight).all():
+ raise ValueError(
+ f"NaNs detected in the merged weights. The adapter {active_adapter} seems to be broken"
+ )
+
+ weight += self.get_delta_weight(active_adapter)
+ # TODO: once (if) torchao supports directly mutating the data, use that instead.
+ del base_layer.weight
+ base_layer.weight = weight
+ quantize_(base_layer, self.get_apply_tensor_subclass())
+ del weight
+
+ self.merged_adapters.append(active_adapter)
+
+ def unmerge(self) -> None:
+ from torchao import quantize_
+
+ if not self.merged:
+ warnings.warn("Already unmerged. Nothing to do.")
+ return
+
+ while len(self.merged_adapters) > 0:
+ active_adapter = self.merged_adapters.pop()
+ if active_adapter not in self.lora_A.keys():
+ continue
+
+ base_layer = self.get_base_layer()
+ weight = base_layer.weight
+ try:
+ weight = weight.dequantize()
+ except NotImplementedError as exc:
+ msg = (
+ f"Weights of type {type(weight).__name__} do not support dequantization (yet), which is needed to "
+ "support unmerging."
+ )
+ raise NotImplementedError(msg) from exc
+
+ weight -= self.get_delta_weight(active_adapter)
+ # We go through a dummy module because overriding the weight.data does not work, the tensor retains the old
+ # data. Therefore, we need to go through quantize_, which takes a module as input, and we need to delete and
+ # re-assign the weight.
+ # TODO: once (if) torchao supports directly mutating the data, use that instead.
+ del base_layer.weight
+ base_layer.weight = weight
+ quantize_(base_layer, self.get_apply_tensor_subclass())
+ del weight
+
+ def __repr__(self) -> str:
+ rep = super().__repr__()
+ return rep.replace("lora.Linear", f"lora.{self.__class__.__name__}")
+
+
+def dispatch_torchao(
+ target: torch.nn.Module,
+ adapter_name: str,
+ lora_config: LoraConfig,
+ **kwargs: Any,
+) -> Optional[torch.nn.Module]:
+ new_module = None
+
+ if isinstance(target, BaseTunerLayer):
+ target_base_layer = target.get_base_layer()
+ else:
+ target_base_layer = target
+
+ if not hasattr(target_base_layer, "weight"):
+ return new_module
+
+ if not is_torchao_available():
+ return new_module
+
+ from torchao.dtypes import AffineQuantizedTensor
+ from torchao.quantization import LinearActivationQuantizedTensor
+
+ if isinstance(target_base_layer.weight, (AffineQuantizedTensor, LinearActivationQuantizedTensor)):
+ new_module = TorchaoLoraLinear(target, adapter_name, **kwargs)
+
+ return new_module
diff --git a/peft/src/peft/tuners/lora/tp_layer.py b/peft/src/peft/tuners/lora/tp_layer.py
new file mode 100644
index 0000000000000000000000000000000000000000..7edd4d3a6ff1f4b7dda6ea62a46bb3c743c3ee12
--- /dev/null
+++ b/peft/src/peft/tuners/lora/tp_layer.py
@@ -0,0 +1,350 @@
+# Copyright 2023-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+from __future__ import annotations
+
+import importlib
+import math
+import warnings
+from typing import Any, Optional, Union
+
+import torch
+import torch.nn as nn
+import torch.nn.init as init
+
+from peft.tuners.tuners_utils import BaseTunerLayer, check_adapters_to_merge
+from peft.utils import transpose
+from peft.utils.integrations import gather_params_ctx
+
+from .layer import LoraLayer
+
+
+class LoraParallelLinear(nn.Module, LoraLayer):
+ """
+ When the target layer parallel_linear is RowParallelLinear, in order to keep the input and output shapes
+ consistent, we need to split the lora matrix A into rows, and the lora_B at this time should be a complete linear
+ layer; In the same way, when the target layer is ColumnParallelLinear, we perform column segmentation on lora_B,
+ while lora_A is still a complete linear layer.
+ """
+
+ def __init__(
+ self,
+ base_layer,
+ adapter_name: str,
+ backend,
+ r: int = 0,
+ lora_alpha: int = 1,
+ lora_dropout: float = 0.0,
+ fan_in_fan_out: bool = False,
+ is_target_conv_1d_layer: bool = False,
+ init_lora_weights: Union[bool, str] = True,
+ use_rslora: bool = False,
+ use_dora: bool = False,
+ lora_bias: bool = False,
+ **kwargs,
+ ):
+ if lora_bias:
+ raise ValueError(f"{self.__class__.__name__} does not support lora_bias yet, set it to False")
+
+ super().__init__()
+ LoraLayer.__init__(self, base_layer=base_layer, **kwargs)
+
+ if use_dora:
+ raise ValueError(f"{self.__class__.__name__} does not support DoRA yet, please set it to False")
+
+ self.backend = backend
+ self.is_parallel_a = isinstance(base_layer, backend.RowParallelLinear)
+ self.fan_in_fan_out = fan_in_fan_out
+ self._active_adapter = adapter_name
+
+ megatron_config = kwargs["megatron_config"]
+ parallel_linear_kwargs = {"megatron_config": megatron_config}
+ init_method = init.xavier_normal_
+ if hasattr(megatron_config, "init_method"):
+ init_method = megatron_config.init_method
+ input_is_parallel = True
+ gather_output = False
+ if self.is_parallel_a:
+ input_is_parallel = base_layer.input_is_parallel
+ else:
+ gather_output = base_layer.gather_output
+ self.update_layer(
+ adapter_name,
+ r,
+ lora_alpha=lora_alpha,
+ lora_dropout=lora_dropout,
+ init_lora_weights=init_lora_weights,
+ use_rslora=use_rslora,
+ use_dora=use_dora,
+ init_method=init_method,
+ input_is_parallel=input_is_parallel,
+ gather_output=gather_output,
+ **parallel_linear_kwargs,
+ )
+
+ if is_target_conv_1d_layer:
+ raise ValueError(
+ f"{self.__class__.__name__} does not support target_conv_1d_layer yet, please set it to False"
+ )
+ self.is_target_conv_1d_layer = False
+
+ def update_layer(
+ self,
+ adapter_name,
+ r,
+ lora_alpha,
+ lora_dropout,
+ init_lora_weights,
+ use_rslora,
+ use_dora=False,
+ init_method=init.xavier_normal_,
+ input_is_parallel=True,
+ gather_output=False,
+ inference_mode: bool = False,
+ **parallel_linear_kwargs,
+ ):
+ # collect the kwargs
+ kwargs = locals().copy()
+ del kwargs["self"]
+
+ if r <= 0:
+ raise ValueError(f"`r` should be a positive integer value but the value passed is {r}")
+ self.r[adapter_name] = r
+ self.lora_alpha[adapter_name] = lora_alpha
+ if lora_dropout > 0.0:
+ lora_dropout_layer = nn.Dropout(p=lora_dropout)
+ else:
+ lora_dropout_layer = nn.Identity()
+
+ self.lora_dropout[adapter_name] = lora_dropout_layer
+
+ megatron_config = parallel_linear_kwargs["megatron_config"]
+ # lora needs to be forced to upgrade to 32-bit precision, otherwise it will overflow
+ megatron_config.params_dtype = torch.float32
+ if self.is_parallel_a:
+ lora_a = self.backend.RowParallelLinear(
+ input_size=self.in_features,
+ output_size=r,
+ bias=False,
+ input_is_parallel=input_is_parallel,
+ skip_bias_add=True,
+ init_method=init_method,
+ config=megatron_config,
+ )
+ lora_b = nn.Linear(in_features=r, out_features=self.out_features, bias=False, dtype=torch.float32)
+ else:
+ lora_a = nn.Linear(in_features=self.in_features, out_features=r, bias=False, dtype=torch.float32)
+ lora_b = self.backend.ColumnParallelLinear(
+ input_size=r,
+ output_size=self.out_features,
+ bias=False,
+ gather_output=gather_output,
+ init_method=init_method,
+ config=megatron_config,
+ )
+ self.lora_A[adapter_name] = lora_a
+ self.lora_B[adapter_name] = lora_b
+ if use_rslora:
+ self.scaling[adapter_name] = lora_alpha / math.sqrt(r)
+ else:
+ self.scaling[adapter_name] = lora_alpha / r
+
+ self.use_dora[adapter_name] = use_dora
+
+ # for inits that require access to the base weight, use gather_param_ctx so that the weight is gathered when using DeepSpeed
+ if isinstance(init_lora_weights, str) and init_lora_weights.startswith("pissa"):
+ with gather_params_ctx(self.get_base_layer().weight):
+ self.pissa_init(adapter_name, init_lora_weights)
+ elif isinstance(init_lora_weights, str) and init_lora_weights.startswith("corda"):
+ with gather_params_ctx(self.get_base_layer().weight):
+ self.corda_init(adapter_name, init_lora_weights)
+ elif isinstance(init_lora_weights, str) and init_lora_weights.lower() == "olora":
+ with gather_params_ctx(self.get_base_layer().weight):
+ self.olora_init(adapter_name)
+ elif init_lora_weights == "loftq":
+ with gather_params_ctx(self.get_base_layer().weight):
+ self.loftq_init(adapter_name)
+ elif init_lora_weights:
+ self.reset_lora_parameters(adapter_name, init_lora_weights)
+
+ # call this before dora_init
+ self._move_adapter_to_device_of_base_layer(adapter_name)
+
+ if adapter_name in self.lora_variant:
+ self.lora_variant[adapter_name].init(self, **kwargs)
+
+ self.set_adapter(self.active_adapters, inference_mode=inference_mode)
+
+ def forward(self, x: torch.Tensor, *args: Any, **kwargs: Any):
+ self._check_forward_args(x, *args, **kwargs)
+ adapter_names = kwargs.pop("adapter_names", None)
+ # If weight is used for matrix multiplication here, the final aggregation operation of the original
+ # parallel_linear layer will be missing, so we need to directly call its forward function to obtain the
+ # output of the original parallel_linear layer.
+ if self.disable_adapters:
+ if self.merged:
+ self.unmerge()
+ result, bias = self.base_layer(x, *args, **kwargs)
+ elif adapter_names is not None:
+ raise ValueError(f"{self.__class__.__name__} does not support mixed_batch_forward yet.")
+ elif self.merged:
+ result, bias = self.base_layer(x, *args, **kwargs)
+ else:
+ result, bias = self.base_layer(x, *args, **kwargs)
+ torch_result_dtype = result.dtype
+ for active_adapter in self.active_adapters:
+ if active_adapter not in self.lora_A.keys():
+ continue
+ lora_A = self.lora_A[active_adapter]
+ lora_B = self.lora_B[active_adapter]
+ dropout = self.lora_dropout[active_adapter]
+ scaling = self.scaling[active_adapter]
+ x = self._cast_input_dtype(x, lora_A.weight.dtype)
+ result = result + lora_B(lora_A(dropout(x))) * scaling
+
+ result = result.to(torch_result_dtype)
+ return result, bias
+
+ def merge(self, safe_merge: bool = False, adapter_names: Optional[list[str]] = None) -> None:
+ """
+ Merge the active adapter weights into the base weights
+
+ Args:
+ safe_merge (`bool`, *optional*):
+ If True, the merge operation will be performed in a copy of the original weights and check for NaNs
+ before merging the weights. This is useful if you want to check if the merge operation will produce
+ NaNs. Defaults to `False`.
+ adapter_names (`list[str]`, *optional*):
+ The list of adapter names that should be merged. If None, all active adapters will be merged. Defaults
+ to `None`.
+ """
+ adapter_names = check_adapters_to_merge(self, adapter_names)
+ if not adapter_names:
+ # no adapter to merge
+ return
+
+ for active_adapter in adapter_names:
+ if active_adapter in self.lora_A.keys():
+ base_layer = self.get_base_layer()
+ if safe_merge:
+ # Note that safe_merge will be slower than the normal merge
+ # because of the copy operation.
+ orig_weights = base_layer.weight.data.clone()
+ delta_weight = self.get_delta_weight(active_adapter)
+ orig_weights = orig_weights + delta_weight
+
+ if not torch.isfinite(orig_weights).all():
+ raise ValueError(
+ f"NaNs detected in the merged weights. The adapter {active_adapter} seems to be broken"
+ )
+
+ base_layer.weight.data = orig_weights
+ else:
+ delta_weight = self.get_delta_weight(active_adapter)
+ base_layer.weight.data = base_layer.weight.data + delta_weight
+
+ self.merged_adapters.append(active_adapter)
+
+ def unmerge(self) -> None:
+ """
+ This method unmerges all merged adapter layers from the base weights.
+ """
+ if not self.merged:
+ warnings.warn("Already unmerged. Nothing to do.")
+ return
+ while len(self.merged_adapters) > 0:
+ active_adapter = self.merged_adapters.pop()
+ if active_adapter in self.lora_A.keys():
+ weight = self.get_base_layer().weight
+ delta_weight = self.get_delta_weight(active_adapter)
+ weight.data -= delta_weight
+
+ def get_delta_weight(self, adapter) -> torch.Tensor:
+ """
+ Compute the delta weight for the given adapter.
+
+ Args:
+ adapter (str):
+ The name of the adapter for which the delta weight should be computed.
+ """
+ device = self.lora_B[adapter].weight.device
+ dtype = self.lora_B[adapter].weight.dtype
+
+ # In case users wants to merge the adapter weights that are in
+ # (b)float16 while being on CPU, we need to cast the weights to float32, perform the merge and then cast back to
+ # (b)float16 because some CPUs have slow bf16/fp16 matmuls.
+ cast_to_fp32 = device.type == "cpu" and (dtype == torch.float16 or dtype == torch.bfloat16)
+
+ weight_A = self.lora_A[adapter].weight
+ weight_B = self.lora_B[adapter].weight
+
+ if cast_to_fp32:
+ weight_A = weight_A.float()
+ weight_B = weight_B.float()
+
+ output_tensor = transpose(weight_B @ weight_A, self.fan_in_fan_out) * self.scaling[adapter]
+
+ if cast_to_fp32:
+ output_tensor = output_tensor.to(dtype=dtype)
+
+ # cast back the weights
+ self.lora_A[adapter].weight.data = weight_A.to(dtype)
+ self.lora_B[adapter].weight.data = weight_B.to(dtype)
+
+ return output_tensor
+
+ def __repr__(self) -> str:
+ rep = super().__repr__()
+ return "lora." + rep
+
+
+def dispatch_megatron(
+ target: torch.nn.Module,
+ adapter_name: str,
+ lora_config,
+ **kwargs: Any,
+) -> Optional[torch.nn.Module]:
+ new_module = None
+
+ if isinstance(target, BaseTunerLayer):
+ target_base_layer = target.get_base_layer()
+ else:
+ target_base_layer = target
+
+ if lora_config.megatron_config:
+ megatron_core = importlib.import_module(lora_config.megatron_core)
+ else:
+ megatron_core = None
+
+ if megatron_core and isinstance(
+ target_base_layer,
+ (megatron_core.tensor_parallel.ColumnParallelLinear, megatron_core.tensor_parallel.RowParallelLinear),
+ ):
+ megatron_kwargs = kwargs.copy()
+ megatron_config = lora_config.megatron_config
+ if isinstance(megatron_config, dict):
+ transformer_config_class = megatron_core.transformer.transformer_config.TransformerConfig
+ megatron_config = transformer_config_class(**lora_config.megatron_config)
+ megatron_kwargs["megatron_config"] = megatron_config
+ if megatron_kwargs["fan_in_fan_out"]:
+ warnings.warn(
+ "fan_in_fan_out is set to True but the target module is `ColumnParallelLinear` "
+ "or `RowParallelLinear`. "
+ "Setting fan_in_fan_out to False."
+ )
+ megatron_kwargs["fan_in_fan_out"] = lora_config.fan_in_fan_out = False
+ new_module = LoraParallelLinear(
+ base_layer=target, adapter_name=adapter_name, backend=megatron_core.tensor_parallel, **megatron_kwargs
+ )
+
+ return new_module
diff --git a/peft/src/peft/tuners/lora/variants.py b/peft/src/peft/tuners/lora/variants.py
new file mode 100644
index 0000000000000000000000000000000000000000..54cdfae30c586a92b365d522a3182dc1a10bb137
--- /dev/null
+++ b/peft/src/peft/tuners/lora/variants.py
@@ -0,0 +1,765 @@
+# Copyright 2023-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+from __future__ import annotations
+
+import collections
+import warnings
+from typing import Any, Optional
+
+import torch
+from accelerate.utils.imports import is_xpu_available
+from torch import nn
+
+from peft.utils.other import transpose
+
+from .arrow import ArrowLoraLinearLayer
+from .config import PeftConfig
+from .dora import DoraConv1dLayer, DoraConv2dLayer, DoraConv3dLayer, DoraEmbeddingLayer, DoraLinearLayer
+from .layer import Conv1d, Conv2d, Conv3d, Embedding, Linear, LoraVariant, _ConvNd
+
+
+class ArrowLinearVariant(LoraVariant):
+ @staticmethod
+ def init(module: Linear, adapter_name: str, **kwargs):
+ """
+ Initialise the ArrowLoraLinearLayer() inside lora_arrow. lora_arrow is nn.ModuleDict(), serving as a container
+ for ArrowLoraLinearLayer(). A layer of the base model with LoRA adapter loaded on it will be like:
+ ----------------------------------------------------
+ (qkv_proj): lora.Linear4bit or lora.Linear(
+ (base_layer): Linear4bit or Linear (lora_dropout): ModuleDict( ... ) (lora_A): ModuleDict( ... )
+ (lora_B): ModuleDict( ... ) (lora_embedding_A): ParameterDict( ... ) (lora_embedding_B): ParameterDict(
+ ... ) (lora_magnitude_vector): ModuleDict( ... ) (lora_arrow): ModuleDict(
+ (arrow_router): ArrowLoraLinearLayer() )
+ )
+ ----------------------------------------------------
+
+ Args:
+ module (Linear): LoRA Layer of the model, containing base_layer, lora_A, lora_B, etc.
+ adapter_name (str): name of the adapter that will be put in lora_arrow.
+ The adapter_name is "arrow_router" by default, set in create_arrow_model() in ./arrow.py
+ """
+ # Checking for arrow necessary config
+ arrow_config = kwargs.get("arrow_config")
+ if arrow_config is None:
+ raise ValueError("ArrowLinearVariant.init() did not receive an arrow_config")
+
+ # 1-a) build the ArrowLoRALayer
+ arrow_layer = ArrowLoraLinearLayer(
+ in_features=module.in_features,
+ arrow_config=arrow_config,
+ ).to(module.weight.device)
+
+ # 1-b) register a container if it doesn’t exist yet
+ if not hasattr(module, "lora_arrow"):
+ module.lora_arrow = nn.ModuleDict()
+
+ module.lora_arrow[adapter_name] = arrow_layer
+
+ @staticmethod
+ def forward(
+ module: Linear,
+ *,
+ active_adapter: str,
+ x: torch.Tensor,
+ result: torch.Tensor,
+ **kwargs,
+ ) -> torch.Tensor:
+ """
+ Parameters mirror those in PEFT’s `LoraVariant.forward`. Called every time the host Linear does a fwd pass.
+
+ build_prototypes() and gen_know_sub() should run only once before routing. Both are implemented in
+ ArrowLoraLinearLayer (see ./arrow.py). They are lazily invoked in the forward pass below. Attributes of
+ ArrowLoraLinearLayer() class ensure they execute only a single time.
+
+ Args:
+ module (Linear): LoRA Layer of the model
+ active_adapter (str): name of the arrow route, which should be active to perform arrow.
+ x (torch.Tensor): input to the layer
+ result (torch.Tensor): output of the base layer.
+
+ Return value:
+ output of the base model + delta weight computed by arrow layer.
+ """
+ arrow = module.lora_arrow[active_adapter] # ArrowLoraLinearLayer
+ # Apply GenKnowSub the 1st time if applcable. By calling arrow/on_adapter_change(),
+ # gen_know_sub() is redone for newly added adapters after arrow.create_arrow_model().
+ arrow.gen_know_sub(module.lora_A, module.lora_B)
+ # lazily build prototypes the 1st time after GenKnowSub. By calling arrow/on_adapter_change(),
+ # build_prototypes() is redone for newly added adapters after arrow.create_arrow_model().
+ arrow.build_prototypes(module.lora_A, module.lora_B)
+
+ # A forward path of ArrowLoraLinearLayer is called so routing performs.
+ # Accept and ignore extra variant kwargs (e.g., 'alora_offsets') for compatibility
+ delta = arrow(
+ x,
+ lora_A=module.lora_A,
+ lora_B=module.lora_B,
+ dropout=module.lora_dropout[active_adapter],
+ scaling=module.scaling,
+ )
+ return result + delta
+
+ """
+ Since Arrow is a Mixture-of-Experts (MoE) approach, merging adapters is not meaningful or even possible: for each
+ token, the top-k LoRA experts are dynamically selected and routed. Because of this per-token routing, there is no
+ single set of weights that can represent a merged adapter.
+ """
+
+ @staticmethod
+ def merge_safe(module: Linear, active_adapter: str, orig_weight: torch.Tensor) -> torch.Tensor:
+ raise RuntimeError("Cannot merge an active Arrow router adapter. Remove it first.")
+
+ @staticmethod
+ def merge_unsafe(module: Linear, active_adapter: str, orig_weight: torch.Tensor) -> None:
+ raise RuntimeError("Cannot merge an active Arrow router adapter. Remove it first.")
+
+ @staticmethod
+ def unmerge(module: Linear, active_adapter: str, orig_weight: torch.Tensor) -> torch.Tensor:
+ raise RuntimeError("Cannot unmerge an active Arrow router adapter. Remove it first.")
+
+
+class DoraLinearVariant(LoraVariant):
+ @staticmethod
+ def init(module: Linear, adapter_name: str, **kwargs: Any) -> None:
+ if not module.lora_magnitude_vector:
+ # first dora layer being added, add lora_magnitude_vector to the list of learnable parameters
+ module.adapter_layer_names = module.adapter_layer_names[:] + ("lora_magnitude_vector",)
+
+ dora_layer = DoraLinearLayer(fan_in_fan_out=getattr(module, "fan_in_fan_out", False))
+ lora_A = module.lora_A[adapter_name].weight
+ lora_B = module.lora_B[adapter_name].weight
+ place_on_cpu = module.ephemeral_gpu_offload and (lora_A.device.type == "cpu" or lora_B.device.type == "cpu")
+ if module.ephemeral_gpu_offload:
+ if lora_A.device.type in ["cuda", "xpu"]:
+ lora_B = lora_B.to(lora_A.device)
+ else:
+ if lora_B.device.type not in ["cuda", "xpu"]:
+ if is_xpu_available():
+ lora_B = lora_B.to("xpu")
+ else:
+ lora_B = lora_B.to("cuda")
+ lora_A = lora_A.to(lora_B.device)
+ scaling = module.scaling[adapter_name]
+ dora_layer.update_layer(
+ base_layer=module.get_base_layer(),
+ lora_A=lora_A,
+ lora_B=lora_B,
+ scaling=scaling,
+ place_on_cpu=place_on_cpu,
+ )
+ module.lora_magnitude_vector[adapter_name] = dora_layer
+
+ @staticmethod
+ def merge_safe(module: Linear, active_adapter: str, orig_weight: torch.Tensor) -> torch.Tensor:
+ orig_dtype = orig_weight.dtype
+ delta_weight = module.get_delta_weight(active_adapter)
+
+ # since delta_weight already includes scaling, set it to 1 here
+ weight_norm = (
+ module.lora_magnitude_vector[active_adapter]
+ .get_weight_norm(orig_weight, transpose(delta_weight, module.fan_in_fan_out), scaling=1)
+ .detach()
+ )
+ # We need to cache weight_norm because it has to be based on the original weights. We
+ # cannot calculate it on the fly based on the merged weights when unmerging because its a
+ # different value
+ module._cache_store(f"{active_adapter}-weight_norm", weight_norm)
+ dora_factor = module.lora_magnitude_vector[active_adapter].weight / weight_norm
+ dora_factor = transpose(dora_factor.view(-1, 1), module.fan_in_fan_out)
+ new_weight = dora_factor * (orig_weight + delta_weight)
+ new_weight = new_weight.to(orig_dtype)
+ return new_weight
+
+ @staticmethod
+ def merge_unsafe(module: Linear, active_adapter: str, orig_weight: torch.Tensor) -> None:
+ orig_dtype = orig_weight.dtype
+ delta_weight = module.get_delta_weight(active_adapter)
+ weight_norm = (
+ module.lora_magnitude_vector[active_adapter]
+ .get_weight_norm(orig_weight, transpose(delta_weight, module.fan_in_fan_out), scaling=1)
+ .detach()
+ )
+ # We need to cache weight_norm because it has to be based on the original weights. We
+ # cannot calculate it on the fly based on the merged weights when unmerging because its a
+ # different value
+ module._cache_store(f"{active_adapter}-weight_norm", weight_norm)
+ dora_factor = module.lora_magnitude_vector[active_adapter].weight / weight_norm
+ dora_factor = transpose(dora_factor.view(-1, 1), module.fan_in_fan_out)
+ new_weight = dora_factor * (orig_weight.data + delta_weight)
+ new_weight = new_weight.to(orig_dtype)
+ orig_weight.data = new_weight
+
+ @staticmethod
+ def unmerge(module: Linear, active_adapter: str, orig_weight: torch.Tensor) -> torch.Tensor:
+ orig_dtype = orig_weight.dtype
+ delta_weight = module.get_delta_weight(active_adapter)
+ weight_norm = module._cache_pop(f"{active_adapter}-weight_norm")
+ dora_factor = module.lora_magnitude_vector[active_adapter].weight / weight_norm
+ new_weight = orig_weight.data / dora_factor.view(-1, 1) - delta_weight
+ new_weight = new_weight.to(orig_dtype)
+ return new_weight
+
+ @staticmethod
+ def forward(
+ module: Linear,
+ active_adapter: str,
+ x: torch.Tensor,
+ result: torch.Tensor,
+ **kwargs,
+ ) -> torch.Tensor:
+ lora_A = module.lora_A[active_adapter]
+ lora_B = module.lora_B[active_adapter]
+ dropout = module.lora_dropout[active_adapter]
+ scaling = module.scaling[active_adapter]
+
+ if isinstance(dropout, nn.Identity) or not module.training:
+ base_result = result
+ else:
+ x = dropout(x)
+ base_result = None
+
+ result = result + module.lora_magnitude_vector[active_adapter](
+ x,
+ lora_A=lora_A,
+ lora_B=lora_B,
+ scaling=scaling,
+ base_layer=module.get_base_layer(),
+ base_result=base_result,
+ )
+ return result
+
+
+class DoraEmbeddingVariant(DoraLinearVariant):
+ @staticmethod
+ def init(module: Embedding, adapter_name: str, **kwargs: Any) -> None:
+ if module.lora_magnitude_vector is None:
+ # first dora layer being added, add lora_magnitude_vector to the list of learnable parameters
+ module.adapter_layer_names = module.adapter_layer_names[:] + ("lora_magnitude_vector",)
+
+ dora_layer = DoraEmbeddingLayer(fan_in_fan_out=True)
+ lora_embedding_A = module.lora_embedding_A[adapter_name]
+ lora_embedding_B = module.lora_embedding_B[adapter_name]
+ scaling = module.scaling[adapter_name]
+ dora_layer.update_layer(
+ base_layer=module.get_base_layer(), lora_A=lora_embedding_A, lora_B=lora_embedding_B, scaling=scaling
+ )
+ module.lora_magnitude_vector[adapter_name] = dora_layer
+
+ @staticmethod
+ def merge_safe(module: Embedding, active_adapter: str, orig_weight: torch.Tensor) -> torch.Tensor:
+ orig_dtype = orig_weight.dtype
+ delta_weight = module.get_delta_weight(active_adapter)
+
+ # since delta_weight already includes scaling, set it to 1 here
+ weight_norm = (
+ module.lora_magnitude_vector[active_adapter]
+ .get_weight_norm(orig_weight, delta_weight.T, scaling=1)
+ .detach()
+ )
+ # We need to cache weight_norm because it has to be based on the original weights. We
+ # cannot calculate it on the fly based on the merged weights when unmerging because its a
+ # different value
+ module._cache_store(f"{active_adapter}-weight_norm", weight_norm)
+ dora_factor = module.lora_magnitude_vector[active_adapter].weight / weight_norm
+ dora_factor = dora_factor.view(1, -1)
+ new_weight = dora_factor * (orig_weight + delta_weight)
+ new_weight = new_weight.to(orig_dtype)
+ return new_weight
+
+ @staticmethod
+ def merge_unsafe(module: Embedding, active_adapter: str, orig_weight: torch.Tensor) -> None:
+ orig_dtype = orig_weight.dtype
+ delta_weight = module.get_delta_weight(active_adapter)
+ weight_norm = (
+ module.lora_magnitude_vector[active_adapter]
+ .get_weight_norm(orig_weight, delta_weight.T, scaling=1)
+ .detach()
+ )
+ # We need to cache weight_norm because it has to be based on the original weights. We
+ # cannot calculate it on the fly based on the merged weights when unmerging because its a
+ # different value
+ module._cache_store(f"{active_adapter}-weight_norm", weight_norm)
+ dora_factor = module.lora_magnitude_vector[active_adapter].weight / weight_norm
+ dora_factor = dora_factor.view(1, -1)
+ new_weight = dora_factor * (orig_weight.data + delta_weight)
+ new_weight = new_weight.to(orig_dtype)
+ orig_weight.data = new_weight
+
+ @staticmethod
+ def unmerge(module: Embedding, active_adapter: str, orig_weight: torch.Tensor) -> torch.Tensor:
+ orig_dtype = orig_weight.dtype
+ delta_weight = module.get_delta_weight(active_adapter)
+ weight_norm = module._cache_pop(f"{active_adapter}-weight_norm")
+ dora_factor = module.lora_magnitude_vector[active_adapter].weight / weight_norm
+ new_weight = orig_weight.data / dora_factor.view(1, -1) - delta_weight
+ new_weight = new_weight.to(orig_dtype)
+ return new_weight
+
+ @staticmethod
+ def forward(
+ module: Embedding,
+ active_adapter: str,
+ x: torch.Tensor,
+ result: torch.Tensor,
+ **kwargs,
+ ) -> torch.Tensor:
+ embedding_A = module.lora_embedding_A[active_adapter].T
+ embedding_B = module.lora_embedding_B[active_adapter].T
+ scaling = module.scaling[active_adapter]
+
+ mag_norm_scale, dora_result = module.lora_magnitude_vector[active_adapter](
+ x,
+ lora_A=embedding_A,
+ lora_B=embedding_B,
+ scaling=scaling,
+ base_layer=module.get_base_layer(),
+ embed_fn=module._embed,
+ )
+ result = mag_norm_scale * result + dora_result
+ return result
+
+
+class _DoraConvNdVariant(LoraVariant):
+ @staticmethod
+ def init_convd_variant(module: _ConvNd, adapter_name: str, dora_layer: nn.Module) -> None:
+ if module.lora_magnitude_vector is None:
+ # first dora layer being added, add lora_magnitude_vector to the list of learnable parameters
+ module.adapter_layer_names = module.adapter_layer_names[:] + ("lora_magnitude_vector",)
+
+ lora_A = module.lora_A[adapter_name].weight
+ lora_B = module.lora_B[adapter_name].weight
+ scaling = module.scaling[adapter_name]
+ dora_layer.update_layer(base_layer=module.get_base_layer(), lora_A=lora_A, lora_B=lora_B, scaling=scaling)
+ module.lora_magnitude_vector[adapter_name] = dora_layer
+
+ @staticmethod
+ def merge_safe(module: _ConvNd, active_adapter: str, orig_weight: torch.Tensor) -> torch.Tensor:
+ orig_dtype = orig_weight.dtype
+ delta_weight = module.get_delta_weight(active_adapter)
+
+ # since delta_weight already includes scaling, set it to 1 here
+ weight_norm = (
+ module.lora_magnitude_vector[active_adapter].get_weight_norm(orig_weight, delta_weight, scaling=1).detach()
+ )
+ # We need to cache weight_norm because it has to be based on the original weights. We
+ # cannot calculate it on the fly based on the merged weights when unmerging because its a
+ # different value
+ module._cache_store(f"{active_adapter}-weight_norm", weight_norm)
+ dora_factor = module.lora_magnitude_vector[active_adapter].weight / weight_norm
+ new_weight = dora_factor.view(*module._get_dora_factor_view()) * (orig_weight + delta_weight)
+ new_weight = new_weight.to(orig_dtype)
+ return new_weight
+
+ @staticmethod
+ def merge_unsafe(module: _ConvNd, active_adapter: str, orig_weight: torch.Tensor) -> None:
+ orig_dtype = orig_weight.dtype
+ delta_weight = module.get_delta_weight(active_adapter)
+ # since delta_weight already includes scaling, set it to 1 here
+ weight_norm = (
+ module.lora_magnitude_vector[active_adapter].get_weight_norm(orig_weight, delta_weight, scaling=1).detach()
+ )
+ # We need to cache weight_norm because it has to be based on the original weights. We
+ # cannot calculate it on the fly based on the merged weights when unmerging because its a
+ # different value
+ module._cache_store(f"{active_adapter}-weight_norm", weight_norm)
+ dora_factor = module.lora_magnitude_vector[active_adapter].weight / weight_norm
+ new_weight = dora_factor.view(*module._get_dora_factor_view()) * (orig_weight.data + delta_weight)
+ new_weight = new_weight.to(orig_dtype)
+ orig_weight.data = new_weight
+
+ @staticmethod
+ def unmerge(module: _ConvNd, active_adapter: str, orig_weight: torch.Tensor) -> torch.Tensor:
+ orig_dtype = orig_weight.dtype
+ delta_weight = module.get_delta_weight(active_adapter)
+ weight_norm = module._cache_pop(f"{active_adapter}-weight_norm")
+ dora_factor = module.lora_magnitude_vector[active_adapter].weight / weight_norm
+ new_weight = orig_weight.data / dora_factor.view(*module._get_dora_factor_view()) - delta_weight
+ new_weight = new_weight.to(orig_dtype)
+ return new_weight
+
+ @staticmethod
+ def forward(
+ module: _ConvNd,
+ active_adapter: str,
+ x: torch.Tensor,
+ result: torch.Tensor,
+ **kwargs,
+ ) -> torch.Tensor:
+ lora_A = module.lora_A[active_adapter]
+ lora_B = module.lora_B[active_adapter]
+ dropout = module.lora_dropout[active_adapter]
+ scaling = module.scaling[active_adapter]
+
+ if isinstance(dropout, nn.Identity) or not module.training:
+ base_result = result
+ else:
+ x = dropout(x)
+ base_result = None
+
+ result = result + module.lora_magnitude_vector[active_adapter](
+ x,
+ lora_A=lora_A,
+ lora_B=lora_B,
+ scaling=scaling,
+ base_layer=module.get_base_layer(),
+ base_result=base_result,
+ )
+ return result
+
+
+class DoraConv1dVariant(_DoraConvNdVariant):
+ @staticmethod
+ def init(module: Conv1d, adapter_name: str, **kwargs: Any) -> None:
+ dora_layer = DoraConv1dLayer(fan_in_fan_out=False)
+ _DoraConvNdVariant.init_convd_variant(module, adapter_name, dora_layer=dora_layer)
+
+
+class DoraConv2dVariant(_DoraConvNdVariant):
+ @staticmethod
+ def init(module: Conv2d, adapter_name: str, **kwargs: Any) -> None:
+ dora_layer = DoraConv2dLayer(fan_in_fan_out=False)
+ _DoraConvNdVariant.init_convd_variant(module, adapter_name, dora_layer=dora_layer)
+
+
+class DoraConv3dVariant(_DoraConvNdVariant):
+ @staticmethod
+ def init(module: Conv3d, adapter_name: str, **kwargs: Any) -> None:
+ dora_layer = DoraConv3dLayer(fan_in_fan_out=False)
+ _DoraConvNdVariant.init_convd_variant(module, adapter_name, dora_layer=dora_layer)
+
+
+class QALoraLinearVariant(LoraVariant):
+ @staticmethod
+ def init(module: Linear, adapter_name: str, **kwargs: Any) -> None:
+ """
+ Initializes QALoRA specific parameters for a given adapter.
+
+ Args:
+ module (Linear): The linear module to be adapted.
+ adapter_name (str): The name of the adapter.
+ **kwargs: Additional keyword arguments.
+ qalora_group_size (int): The size of groups for pooling. This is expected to be passed.
+ """
+ if "qalora_group_size" not in kwargs:
+ raise ValueError(
+ "`use_qalora=True` requires 'qalora_group_size' to be provided in kwargs."
+ " Please ensure it is passed from the LoraConfig."
+ )
+
+ if module.in_features is not None and module.in_features % kwargs["qalora_group_size"] != 0:
+ raise ValueError(
+ f"`use_qalora=True` requires `module.in_features` ({module.in_features}) to be"
+ f"divisible by 'qalora_group_size' ({kwargs['qalora_group_size']})"
+ )
+ qalora_group_size = kwargs["qalora_group_size"]
+
+ if "qalora_group_size" not in module.other_param_names:
+ module.other_param_names = module.other_param_names + ("qalora_group_size",)
+
+ if not hasattr(module, "qalora_group_size"):
+ module.qalora_group_size = {}
+ module.qalora_group_size[adapter_name] = qalora_group_size
+
+ old_lora_A_layer = module.lora_A[adapter_name]
+ r = old_lora_A_layer.out_features
+ device = old_lora_A_layer.weight.device
+ dtype = old_lora_A_layer.weight.dtype
+
+ new_lora_A_layer = nn.Linear(
+ old_lora_A_layer.in_features // module.qalora_group_size[adapter_name],
+ r,
+ bias=False,
+ device=device,
+ dtype=dtype,
+ )
+ module.lora_A[adapter_name] = new_lora_A_layer
+
+ @staticmethod
+ def get_delta_weight(module: Linear, active_adapter: str) -> torch.Tensor:
+ raise NotImplementedError("QALoRA for GPTQ layers does not support 'get_delta_weight'.")
+
+ @staticmethod
+ def merge_safe(module: Linear, active_adapter: str, orig_weight: torch.Tensor) -> torch.Tensor:
+ raise NotImplementedError("QALoRA for GPTQ layers does not support 'safe_merge'.")
+
+ @staticmethod
+ def merge_unsafe(module: Linear, active_adapter: str, orig_weight: torch.Tensor) -> None:
+ raise NotImplementedError("QALoRA for GPTQ layers does not support 'merge_unsafe'.")
+
+ @staticmethod
+ def unmerge(module: Linear, active_adapter: str, orig_weight: torch.Tensor) -> torch.Tensor:
+ raise NotImplementedError("QALoRA for GPTQ layers does not support 'unmerge'.")
+
+ @staticmethod
+ def forward(
+ module: Linear,
+ active_adapter: str,
+ x: torch.Tensor,
+ result: torch.Tensor,
+ **kwargs,
+ ) -> torch.Tensor:
+ lora_A_weight = module.lora_A[active_adapter].weight
+ lora_B_weight = module.lora_B[active_adapter].weight
+ dropout = module.lora_dropout[active_adapter]
+ scaling = module.scaling[active_adapter]
+ group_size = module.qalora_group_size[active_adapter]
+
+ x_dropped = dropout(x) if module.training and not isinstance(dropout, nn.Identity) else x
+ orig_shape = x_dropped.shape
+
+ # Reshape to 2D
+ if len(orig_shape) > 2:
+ x_flat = x_dropped.view(-1, module.in_features)
+ else:
+ x_flat = x_dropped
+
+ batch_size, in_features = x_flat.shape
+ pooled_features = in_features // group_size
+
+ x_pooled = x_flat.view(batch_size, pooled_features, group_size).mean(dim=2)
+
+ x_pooled_scaled = x_pooled * pooled_features
+
+ # LoRA computation
+ delta = x_pooled_scaled @ lora_A_weight.t() @ lora_B_weight.t() * scaling
+
+ # Reshape back
+ if len(orig_shape) > 2:
+ delta = delta.view(orig_shape[:-1] + (delta.size(-1),))
+
+ return result + delta
+
+
+class ALoraLinearVariant(LoraVariant):
+ @staticmethod
+ def init(module: Linear, adapter_name: str, **kwargs: Any) -> None:
+ pass
+
+ @staticmethod
+ def merge_safe(module: Linear, active_adapter: str, orig_weight: torch.Tensor) -> torch.Tensor:
+ raise NotImplementedError("aLoRA does not support safe merging.")
+
+ @staticmethod
+ def merge_unsafe(module: Linear, active_adapter: str, orig_weight: torch.Tensor) -> None:
+ raise NotImplementedError("aLoRA does not support merging.")
+
+ @staticmethod
+ def unmerge(module: Linear, active_adapter: str, orig_weight: torch.Tensor) -> torch.Tensor:
+ raise NotImplementedError("aLoRA does not support unmerging.")
+
+ @staticmethod
+ def forward(
+ module: Linear,
+ active_adapter: str,
+ x: torch.Tensor,
+ result: torch.Tensor,
+ **kwargs,
+ ) -> torch.Tensor:
+ alora_offsets = kwargs.get("alora_offsets", None)
+ lora_A = module.lora_A[active_adapter]
+ lora_B = module.lora_B[active_adapter]
+ dropout = module.lora_dropout[active_adapter]
+ scaling = module.scaling[active_adapter]
+ x = x.to(lora_A.weight.dtype)
+ result_shape = result.shape
+ B = result_shape[0] # batch
+ if len(result_shape) == 3:
+ T = result_shape[1] # tokens
+ else:
+ T = 1
+ D = result_shape[-1] # dimensions
+ Dx = x.shape[-1]
+ device = result.device
+ if alora_offsets is None: # use base model only, but ensure 0 gradient
+ mask = torch.zeros((B, T), dtype=torch.bool)
+ else:
+ # If alora_offsets[i] is None, this means that the invocation sequence was not found in the
+ # input. As a result, the weights should not be activated anywhere (equivalent to base model).
+ # Convert None -> 0 and clip to T
+ offsets = torch.tensor(
+ [0 if o is None else min(int(o), T) for o in alora_offsets],
+ device=device,
+ dtype=torch.long,
+ )
+ # Mask True on the last `offsets[i]` positions for each row i
+ pos = torch.arange(T, device=device).unsqueeze(0) # [1, T]
+ mask = pos >= (T - offsets).unsqueeze(1)
+
+ # Flatten for vectorization
+ x_flat = x.view(-1, Dx)
+ res_flat = result.view(-1, D)
+ mask_flat = mask.view(-1)
+
+ # Compute adapter on the selected tokens only
+ res_flat[mask_flat] += lora_B(lora_A(dropout(x_flat[mask_flat]))) * scaling
+ return result
+
+
+def calculate_alora_offsets(
+ peft_config: PeftConfig, active_adapter: str, input_ids: torch.Tensor, adapter_names: Optional[list[str]] = None
+) -> list[int]:
+ """
+ This is a helper function for Activated LoRA (aLoRA) that searches each input token sequence for the last occurence
+ of the appropriate "alora_invocation_tokens" invocation sequence. The calculated alora_offset is the location of
+ the *start* of the invocation tokens, counting backward from the end (will therefore always be >=
+ len(alora_invocation_tokens). If adapter_names is passed, then each input uses the appropriate invocation sequence
+ for the specified adapter for that row. Logic is provided to handle mixed collections of adapters for which not all
+ are aLoRAs (e.g. some base model, some LoRA).
+ """
+ if input_ids is None:
+ return []
+
+ batch_size = input_ids.shape[0]
+ alora_offsets = [None] * batch_size
+
+ cached_invocation_tensors = {}
+ adapters_to_process_indices = collections.defaultdict(list)
+
+ for i in range(batch_size):
+ current_adapter_name = adapter_names[i] if adapter_names and i < len(adapter_names) else active_adapter
+
+ if current_adapter_name == "__base__":
+ alora_offsets[i] = None
+ continue
+
+ if current_adapter_name not in peft_config:
+ warnings.warn(f"Adapter '{current_adapter_name}' not found in peft_config. Using base model for row {i}.")
+ alora_offsets[i] = None
+ continue
+
+ current_peft_config = peft_config[current_adapter_name]
+
+ invocation_tokens = getattr(current_peft_config, "alora_invocation_tokens", None)
+ if invocation_tokens is None:
+ alora_offsets[i] = None # Not an aLoRA adapter or wrong type
+ continue
+
+ if current_adapter_name not in cached_invocation_tensors:
+ cached_invocation_tensors[current_adapter_name] = torch.tensor(
+ invocation_tokens, dtype=torch.long, device=input_ids.device
+ )
+
+ adapters_to_process_indices[current_adapter_name].append(i)
+
+ for adapter_name_to_process, indices in adapters_to_process_indices.items():
+ current_invocation_ids_tensor = cached_invocation_tensors[adapter_name_to_process]
+ invocation_len = len(current_invocation_ids_tensor)
+
+ for i in indices:
+ sequence = input_ids[i]
+ seq_len = len(sequence)
+ best_match_start_idx = -1
+
+ possible_starts = (sequence == current_invocation_ids_tensor[0]).nonzero(as_tuple=True)[0]
+
+ for start_idx_tensor in possible_starts:
+ idx = start_idx_tensor.item()
+ if idx + invocation_len <= seq_len:
+ if torch.equal(sequence[idx : idx + invocation_len], current_invocation_ids_tensor):
+ if idx > best_match_start_idx:
+ best_match_start_idx = idx
+
+ if best_match_start_idx != -1:
+ offset_val = seq_len - best_match_start_idx
+ alora_offsets[i] = offset_val if offset_val > 0 else None
+ else: # Invocation sequence not found in input
+ alora_offsets[i] = None
+ return alora_offsets
+
+
+def is_alora_relevant_in_batch(model: nn.Module, adapter_names: Optional[list[str]] = None):
+ """
+ Helper function to determine if the current batch has any aLoRA adapters.
+ """
+ is_alora_relevant = False
+ if getattr(model.active_peft_config, "alora_invocation_tokens", None):
+ is_alora_relevant = True
+ elif adapter_names:
+ for name in adapter_names:
+ if name == "__base__":
+ continue
+ config_ = model.peft_config.get(name)
+ if config_ and getattr(config_, "alora_invocation_tokens", None):
+ is_alora_relevant = True
+ break
+
+ return is_alora_relevant
+
+
+def get_alora_offsets_for_forward(
+ model: nn.Module, input_ids: torch.Tensor = None, inputs_embeds: torch.Tensor = None, **kwargs
+):
+ """
+ Wrapper around calculate_alora_offsets, for the .forward of the model. It only calculates alora_offsets if the
+ batch contains aLoRA adapters.
+ """
+ adapter_names_for_offset_calc = kwargs.get("adapter_names", None)
+ if not is_alora_relevant_in_batch(model, adapter_names_for_offset_calc):
+ # Nothing to compute
+ return kwargs
+ alora_offsets = kwargs.get("alora_offsets")
+ if alora_offsets is None:
+ if input_ids is None and inputs_embeds is not None:
+ warnings.warn(
+ "Cannot calculate aLoRA offsets when only inputs_embeds are provided. Disabling aLoRA for this forward pass."
+ )
+ kwargs["alora_offsets"] = None
+ elif input_ids is not None:
+ kwargs["alora_offsets"] = calculate_alora_offsets(
+ model.peft_config,
+ model.active_adapter,
+ input_ids,
+ adapter_names=adapter_names_for_offset_calc,
+ )
+ else:
+ kwargs["alora_offsets"] = None
+ return kwargs
+
+
+def get_alora_offsets_for_generate(model: nn.module, *args, **kwargs):
+ """
+ Wrapper around calculate_alora_offsets, for the .generate of the model. It only calculates alora_offsets if the
+ batch contains aLoRA adapters.
+ """
+ adapter_names_for_offset_calc = kwargs.get("adapter_names")
+ if not is_alora_relevant_in_batch(model, adapter_names_for_offset_calc):
+ # Nothing to compute
+ return kwargs
+ alora_offsets_from_kwargs = kwargs.get("alora_offsets")
+ if alora_offsets_from_kwargs is None:
+ current_input_ids = kwargs.get("input_ids")
+ if current_input_ids is None: # args[0] is usually input_ids
+ if args and isinstance(args[0], torch.Tensor):
+ current_input_ids = args[0]
+ else:
+ current_input_ids = None
+
+ if current_input_ids is not None:
+ if current_input_ids.ndim == 1:
+ current_input_ids = current_input_ids.unsqueeze(0)
+ calculated_offsets = calculate_alora_offsets(
+ model.peft_config,
+ model.active_adapter,
+ current_input_ids,
+ adapter_names=adapter_names_for_offset_calc,
+ )
+ kwargs["alora_offsets"] = calculated_offsets
+
+ else:
+ warnings.warn(
+ "Cannot calculate aLoRA offsets during generate as input_ids are not available. Disabling aLoRA."
+ )
+
+ kwargs["alora_offsets"] = None
+ return kwargs
diff --git a/peft/src/peft/tuners/lycoris_utils.py b/peft/src/peft/tuners/lycoris_utils.py
new file mode 100644
index 0000000000000000000000000000000000000000..7ea7a260569cb1f16ed868b55b529e02d4a0c11a
--- /dev/null
+++ b/peft/src/peft/tuners/lycoris_utils.py
@@ -0,0 +1,263 @@
+# Copyright 2023-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+from __future__ import annotations
+
+import warnings
+from abc import abstractmethod
+from dataclasses import dataclass, field
+from typing import Any, Optional, Union
+
+import torch
+import torch.nn as nn
+
+from peft.config import PeftConfig
+
+from .tuners_utils import (
+ BaseTuner,
+ BaseTunerLayer,
+ _get_in_out_features,
+ check_adapters_to_merge,
+)
+
+
+@dataclass
+class LycorisConfig(PeftConfig):
+ r"""
+ A base config for LyCORIS like adapters
+ """
+
+ rank_pattern: Optional[dict] = field(
+ default_factory=dict,
+ metadata={
+ "help": (
+ "The mapping from layer names or regexp expression to ranks which are different from the default rank specified by `r`. "
+ "For example, `{'^model.decoder.layers.0.encoder_attn.k_proj': 16}`."
+ )
+ },
+ )
+ alpha_pattern: Optional[dict] = field(
+ default_factory=dict,
+ metadata={
+ "help": (
+ "The mapping from layer names or regexp expression to alphas which are different from the default alpha specified by `alpha`. "
+ "For example, `{'^model.decoder.layers.0.encoder_attn.k_proj': 16}`."
+ )
+ },
+ )
+
+
+class LycorisLayer(BaseTunerLayer):
+ r"""
+ A base layer for LyCORIS like adapters
+ """
+
+ # adapter_layer_names needs to be defined on the child class
+ other_param_names = ("r", "alpha", "scaling", "rank_dropout", "module_dropout")
+
+ def __init__(self, base_layer: nn.Module) -> None:
+ self.base_layer = base_layer
+ self.r = {}
+ self.alpha = {}
+ self.scaling = {}
+ self.rank_dropout = {}
+ self.rank_dropout_scale = {}
+ self.module_dropout = {}
+
+ # Tuner info
+ self._disable_adapters = False
+ self.merged_adapters = []
+ # flag to enable/disable casting of input to weight dtype during forward call
+ self.cast_input_dtype_enabled = True
+
+ in_features, out_features = _get_in_out_features(self.get_base_layer())
+ self.in_features = in_features
+ self.out_features = out_features
+
+ @property
+ @abstractmethod
+ def _available_adapters(self) -> set[str]: ...
+
+ def _init_empty_weights(self, cls, *args, **kwargs) -> None:
+ # A helper method that allows to initialize the layer of the given class without spending time to initialize the
+ # model weights. The implementation is inspired by
+ # https://pytorch.org/docs/stable/generated/torch.nn.utils.skip_init.html but this function cannot be used
+ # directly.
+ # Instead of this approach, it would be possible to bypass the __init__ of the class but that runs the risk of
+ # omitting important logic inside that __init__.
+ kwargs = kwargs.copy()
+ final_device = kwargs.pop("device", "cpu")
+ cls.__init__(self, *args, device="meta", **kwargs)
+ self.to_empty(device=final_device)
+
+ @abstractmethod
+ def create_adapter_parameters(self, adapter_name: str, r: int, **kwargs): ...
+
+ # TODO: refactor LoRA to use the same approach
+ @abstractmethod
+ def _get_delta_activations(self, adapter_name: str, x: torch.Tensor, *args: Any, **kwargs: Any) -> torch.Tensor:
+ """Activations added on top of the base layer output (i.e. after the base layer forward pass)"""
+
+ @abstractmethod
+ def get_delta_weight(self, adapter_name: str) -> torch.Tensor: ...
+
+ def merge(self, safe_merge: bool = False, adapter_names: Optional[list[str]] = None) -> None:
+ """
+ Merge the active adapter weights into the base weights
+
+ Args:
+ safe_merge (`bool`, *optional*):
+ If `True`, the merge operation will be performed in a copy of the original weights and check for NaNs
+ before merging the weights. This is useful if you want to check if the merge operation will produce
+ NaNs. Defaults to `False`.
+ adapter_names (`List[str]`, *optional*):
+ The list of adapter names that should be merged. If `None`, all active adapters will be merged.
+ Defaults to `None`.
+ """
+ adapter_names = check_adapters_to_merge(self, adapter_names)
+ if not adapter_names:
+ # no adapter to merge
+ return
+
+ for active_adapter in adapter_names:
+ if active_adapter in self._available_adapters:
+ base_layer = self.get_base_layer()
+ if safe_merge:
+ orig_weights = base_layer.weight.data.clone()
+ orig_weights += self.get_delta_weight(active_adapter)
+
+ if not torch.isfinite(orig_weights).all():
+ raise ValueError(
+ f"NaNs detected in the merged weights. The adapter {active_adapter} seems to be broken"
+ )
+
+ base_layer.weight.data = orig_weights
+ else:
+ base_layer.weight.data += self.get_delta_weight(active_adapter)
+ self.merged_adapters.append(active_adapter)
+
+ @abstractmethod
+ def reset_adapter_parameters(self, adapter_name: str): ...
+
+ def set_scale(self, adapter, scale):
+ if adapter not in self._available_adapters:
+ # Ignore the case where the adapter is not in the layer
+ return
+ self.scaling[adapter] = scale * self.alpha[adapter] / self.r[adapter]
+
+ def scale_layer(self, scale: float) -> None:
+ if scale == 1:
+ return
+
+ for active_adapter in self.active_adapters:
+ if active_adapter not in self._available_adapters:
+ continue
+
+ self.scaling[active_adapter] *= scale
+
+ def unmerge(self) -> None:
+ """
+ This method unmerges all merged adapter layers from the base weights.
+ """
+ if not self.merged:
+ warnings.warn("Already unmerged. Nothing to do.")
+ return
+ while len(self.merged_adapters) > 0:
+ active_adapter = self.merged_adapters.pop()
+ if active_adapter in self._available_adapters:
+ self.get_base_layer().weight.data -= self.get_delta_weight(active_adapter)
+
+ def unscale_layer(self, scale=None) -> None:
+ for active_adapter in self.active_adapters:
+ if active_adapter not in self._available_adapters:
+ continue
+
+ if scale is None:
+ self.scaling[active_adapter] = self.alpha[active_adapter] / self.r[active_adapter]
+ else:
+ self.scaling[active_adapter] /= scale
+
+ @abstractmethod
+ def update_layer(self, adapter_name: str, r: int, alpha: float, **kwargs): ...
+
+
+class LycorisTuner(BaseTuner):
+ r"""
+ A base tuner for LyCORIS like adapters
+
+ Args:
+ model ([`torch.nn.Module`]): The model to be adapted.
+ config ([`LoraConfig`]): The configuration of the Lora model.
+ adapter_name (`str`): The name of the adapter, defaults to `"default"`.
+ low_cpu_mem_usage (`bool`, `optional`, defaults to `False`):
+ Create empty adapter weights on meta device. Useful to speed up the loading process.
+
+ """
+
+ prefix: str
+ tuner_layer_cls = LycorisLayer
+ layers_mapping: dict[type[torch.nn.Module], type[LycorisLayer]]
+
+ @abstractmethod
+ def _create_and_replace(
+ self,
+ config: LycorisConfig,
+ adapter_name: str,
+ target: Union[LycorisLayer, nn.Module],
+ target_name,
+ parent,
+ current_key,
+ ): ...
+
+ @classmethod
+ def _create_new_module(cls, config: LycorisConfig, adapter_name: str, target: nn.Module, **kwargs) -> LycorisLayer:
+ # Find corresponding subtype of provided target module
+ new_module_cls = None
+ for subtype, target_cls in cls.layers_mapping.items():
+ if (
+ hasattr(target, "base_layer")
+ and isinstance(target.get_base_layer(), subtype)
+ and isinstance(target, BaseTunerLayer)
+ ):
+ # nested tuner layers are allowed
+ new_module_cls = target_cls
+ break
+ elif isinstance(target, subtype):
+ new_module_cls = target_cls
+ break
+
+ # We didn't find corresponding type, so adapter for this layer is not supported
+ if new_module_cls is None:
+ supported_modules = ", ".join(layer.__name__ for layer in cls.layers_mapping.keys())
+ raise ValueError(
+ f"Target module of type {type(target)} not supported, "
+ f"currently only adapters for {supported_modules} are supported"
+ )
+
+ if isinstance(target, BaseTunerLayer):
+ target_base_layer = target.get_base_layer()
+ else:
+ target_base_layer = target
+
+ if isinstance(target_base_layer, (torch.nn.Conv2d, torch.nn.Conv1d)):
+ new_module = new_module_cls(target, adapter_name=adapter_name, **kwargs)
+ elif isinstance(target_base_layer, torch.nn.Linear):
+ new_module = new_module_cls(target, adapter_name=adapter_name, **kwargs)
+ else:
+ supported_modules = ", ".join(layer.__name__ for layer in cls.layers_mapping.keys())
+ raise ValueError(
+ f"Target module of type {type(target)} not supported, "
+ f"currently only adapters for {supported_modules} are supported"
+ )
+
+ return new_module
diff --git a/peft/src/peft/tuners/miss/__init__.py b/peft/src/peft/tuners/miss/__init__.py
new file mode 100644
index 0000000000000000000000000000000000000000..ca8aceeb0dc772c6db6157834de40ab2c43fe291
--- /dev/null
+++ b/peft/src/peft/tuners/miss/__init__.py
@@ -0,0 +1,24 @@
+# Copyright 2025-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+from peft.utils import register_peft_method
+
+from .config import MissConfig
+from .layer import MissLayer, MissLinear
+from .model import MissModel
+
+
+__all__ = ["MissConfig", "MissLayer", "MissLinear", "MissModel"]
+
+register_peft_method(name="miss", config_cls=MissConfig, model_cls=MissModel)
diff --git a/peft/src/peft/tuners/miss/config.py b/peft/src/peft/tuners/miss/config.py
new file mode 100644
index 0000000000000000000000000000000000000000..a0cef7ab34b3b35a4806c58a2e74acfbd3980b36
--- /dev/null
+++ b/peft/src/peft/tuners/miss/config.py
@@ -0,0 +1,140 @@
+# Copyright 2025-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+from __future__ import annotations
+
+from dataclasses import dataclass, field
+from typing import Literal, Optional, Union
+
+from peft.config import PeftConfig
+from peft.utils import PeftType
+
+
+@dataclass
+class MissConfig(PeftConfig):
+ """
+ This is the configuration class to store the configuration of a [`MiSSModel`].
+
+ Args:
+ r (`int`):
+ The rank of MiSS across different layers. It is best to set 'r' to an even number; otherwise, the default
+ initialization method will not work. The rank of MiSS corresponds to a low-rank decomposition along the
+ in_features dimension.
+ miss_dropout (`float`):
+ The dropout probability for MiSS layers.
+ mini_r (`int`):
+ The rank of MiSS corresponds to a low-rank decomposition along the out_features dimension. When you set
+ `init_weights=mini`, you need to set `mini_r`. Please make sure that `out_features` is divisible by
+ `mini_r`.
+ target_modules (`Optional[Union[List[str], str]]`):
+ The names of the modules to apply the adapter to. If this is specified, only the modules with the specified
+ names will be replaced. When passing a string, a regex match will be performed. When passing a list of
+ strings, either an exact match will be performed or it is checked if the name of the module ends with any
+ of the passed strings. If this is specified as 'all-linear', then all linear modules are chosen, excluding
+ the output layer. If this is not specified, modules will be chosen according to the model architecture. If
+ the architecture is not known, an error will be raised -- in this case, you should specify the target
+ modules manually.
+ exclude_modules (`Optional[Union[List[str], str]]`):
+ The names of the modules to not apply the adapter. When passing a string, a regex match will be performed.
+ When passing a list of strings, either an exact match will be performed or it is checked if the name of the
+ module ends with any of the passed strings.
+ init_weights (bool | Literal["bat", "mini"]):
+ Different initializations correspond to different MiSS variants. By default(balance), the most efficient
+ and general method in MiSS will be used. 'bat': In this mode, you can enable nonlinear updates across
+ different shards. 'mini': In this mode, you can set a smaller rank to use fewer trainable parameters, but
+ it is recommended to keep `out_features % mini_r == 0`.
+ layers_to_transform (`Union[List[int], int]`):
+ The layer indices to transform. If a list of ints is passed, it will apply the adapter to the layer indices
+ that are specified in this list. If a single integer is passed, it will apply the transformations on the
+ layer at this index.
+ layers_pattern (`str`):
+ The layer pattern name, used only if `layers_to_transform` is different from `None`.
+ modules_to_save (`List[str]`):
+ List of modules apart from adapter layers to be set as trainable and saved in the final checkpoint.
+ """
+
+ r: int = field(
+ default=64,
+ metadata={
+ "help": "The rank of MiSS corresponds to a low-rank decomposition along the in_features dimension.",
+ "note": "It is best to set 'r' to an even number; otherwise, the default initialization method will not work.",
+ },
+ )
+ miss_dropout: float = field(default=0.0, metadata={"help": "MiSS dropout"})
+ mini_r: int = field(
+ default=1,
+ metadata={
+ "help": "The rank of MiSS corresponds to a low-rank decomposition along the out_features dimension.",
+ "note": "It is recommended that mini_r be divisible by out_features. When mini_r == out_features, the mini method is equivalent to the default efficient MiSS.",
+ },
+ )
+ target_modules: Optional[Union[list[str], str]] = field(
+ default=None,
+ metadata={
+ "help": "List of module names or regex expression of the module names to replace with MiSS.",
+ "example": "For example, ['q', 'v'] or '.*decoder.*(SelfAttention|EncDecAttention).*(q|v)$' ",
+ },
+ )
+ exclude_modules: Optional[Union[list[str], str]] = field(
+ default=None,
+ metadata={"help": "List of module names or regex expression of the module names to exclude from MiSS."},
+ )
+ init_weights: bool | Literal["bat", "mini"] = field(
+ default=True,
+ metadata={
+ "help": (
+ "True -> MiSS balance; `bat` -> Bat; `mini` -> smaller rank and efficiency"
+ "Whether to initialize the weights of the MiSS layers with their default initialization. Don't change "
+ "this setting, except if you know exactly what you're doing."
+ ),
+ },
+ )
+ layers_to_transform: Optional[Union[list[int], int]] = field(
+ default=None,
+ metadata={
+ "help": "The layer indexes to transform, is this argument is specified, PEFT will transform only the layers indexes that are specified inside this list. If a single integer is passed, PEFT will transform only the layer at this index."
+ },
+ )
+ layers_pattern: Optional[str] = field(
+ default=None,
+ metadata={
+ "help": "The layer pattern name, used only if `layers_to_transform` is different to None and if the layer pattern is not in the common layers pattern."
+ },
+ )
+ bias: str = field(default="none", metadata={"help": "Bias type for MiSS. Can be 'none', 'all' or 'MiSS_only'"})
+ modules_to_save: Optional[list[str]] = field(
+ default=None,
+ metadata={
+ "help": "List of modules apart from MiSS layers to be set as trainable and saved in the final checkpoint. "
+ "For example, in Sequence Classification or Token Classification tasks, "
+ "the final layer `classifier/score` are randomly initialized and as such need to be trainable and saved."
+ },
+ )
+
+ def __post_init__(self):
+ super().__post_init__()
+ self.peft_type = PeftType.MISS
+ self.target_modules = (
+ set(self.target_modules) if isinstance(self.target_modules, list) else self.target_modules
+ )
+ self.exclude_modules = (
+ set(self.exclude_modules) if isinstance(self.exclude_modules, list) else self.exclude_modules
+ )
+ # if target_modules is a regex expression, then layers_to_transform should be None
+ if isinstance(self.target_modules, str) and self.layers_to_transform is not None:
+ raise ValueError("`layers_to_transform` cannot be used when `target_modules` is a str.")
+
+ # if target_modules is a regex expression, then layers_pattern should be None
+ if isinstance(self.target_modules, str) and self.layers_pattern is not None:
+ raise ValueError("`layers_pattern` cannot be used when `target_modules` is a str.")
diff --git a/peft/src/peft/tuners/miss/layer.py b/peft/src/peft/tuners/miss/layer.py
new file mode 100644
index 0000000000000000000000000000000000000000..dc238a036e987f699d8609543cce965dc5ca0506
--- /dev/null
+++ b/peft/src/peft/tuners/miss/layer.py
@@ -0,0 +1,393 @@
+# Copyright 2024-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+from __future__ import annotations
+
+import math
+import warnings
+from typing import Any, Optional, Union
+
+import torch
+import torch.nn as nn
+import torch.nn.functional as F
+
+from peft.tuners.tuners_utils import BaseTunerLayer, check_adapters_to_merge
+
+
+class MissLayer(BaseTunerLayer):
+ # All names of layers that may contain (trainable) adapter weights
+ adapter_layer_names = ("miss_block",)
+ # All names of other parameters that may contain adapter-related parameters
+ other_param_names = ("miss_r", "miss_dropout", "miss_mini_r")
+
+ def __init__(self, base_layer: nn.Module, **kwargs) -> None:
+ self.base_layer = base_layer
+ self.miss_r = {}
+ self.miss_dropout = nn.ModuleDict({})
+ self.miss_mini_r = {}
+ self.miss_block = nn.ParameterDict({})
+ # Mark the weight as unmerged
+ self._disable_adapters = False
+ self.merged_adapters = []
+ # flag to enable/disable casting of input to weight dtype during forward call
+ self.cast_input_dtype_enabled = True
+ self.kwargs = kwargs
+
+ base_layer = self.get_base_layer()
+ if isinstance(base_layer, nn.Linear):
+ self.in_features, self.out_features = base_layer.in_features, base_layer.out_features
+ else:
+ raise ValueError(f"Unsupported layer type {type(base_layer)}")
+
+ def update_layer(
+ self,
+ adapter_name: str,
+ r: int,
+ mini_r: int,
+ miss_dropout,
+ init_weights: bool | str,
+ inference_mode: bool = False,
+ **kwargs,
+ ) -> None:
+ """Internal function to create miss adapter
+
+ Args:
+ adapter_name (`str`): Name for the adapter to add.
+ r (`int`): Rank for the added adapter.
+ init_weights (`bool`): Whether to initialize weights.
+ """
+ if r <= 0:
+ raise ValueError(f"`r` should be a positive integer value but the value passed is {r}")
+
+ self.miss_r[adapter_name] = r
+ self.miss_mini_r[adapter_name] = mini_r
+ if miss_dropout > 0.0:
+ miss_dropout_layer = nn.Dropout(p=miss_dropout)
+ else:
+ miss_dropout_layer = nn.Identity()
+
+ self.miss_dropout[adapter_name] = miss_dropout_layer
+
+ # Determine shape of MiSS weights
+ base_layer = self.get_base_layer()
+ if isinstance(base_layer, nn.Linear):
+ self.miss_block[adapter_name] = nn.Parameter(torch.zeros(r, self.out_features), requires_grad=True)
+ else:
+ raise TypeError(f"MiSS is not implemented for base layers of type {type(base_layer).__name__}")
+
+ # Initialize weights
+ if init_weights == "bat":
+ if self.in_features % r != 0 or self.out_features % r != 0:
+ raise ValueError("The weight matrix must be fully divisible into [r, r] blocks.")
+ self.reset_bat_parameters(adapter_name, r)
+ elif init_weights == "mini":
+ if self.out_features % mini_r != 0:
+ raise ValueError(
+ "mini_r is divided along the out_features dimension. For optimal performance and implementation simplicity,"
+ "it is recommended that out_features be divisible by mini_r."
+ "Error: {self.out_features} % mini_r != 0"
+ )
+ self.reset_mini_parameters(adapter_name, r, mini_r)
+ elif init_weights:
+ self.reset_miss_parameters(adapter_name, r)
+ else:
+ self.reset_miss_parameters_random(adapter_name)
+ # Move new weights to device
+ self._move_adapter_to_device_of_base_layer(adapter_name)
+ self.set_adapter(self.active_adapters, inference_mode=inference_mode)
+
+ def reset_miss_parameters(self, adapter_name: str, r):
+ self.miss_block[adapter_name] = nn.Parameter(torch.zeros(r, self.out_features), requires_grad=True)
+
+ def reset_bat_parameters(self, adapter_name: str, r):
+ self.miss_block[adapter_name] = nn.Parameter(torch.zeros(self.out_features // r, r, r), requires_grad=True)
+
+ def reset_mini_parameters(self, adapter_name: str, r, mini_r):
+ self.miss_block[adapter_name] = nn.Parameter(torch.zeros(r, mini_r), requires_grad=True)
+
+ def reset_miss_parameters_random(self, adapter_name: str):
+ nn.init.kaiming_uniform_(self.miss_block[adapter_name], a=math.sqrt(5))
+
+ def scale_layer(self, scale: float) -> None:
+ if scale == 1:
+ return
+
+ for active_adapter in self.active_adapters:
+ if active_adapter not in self.miss_block.keys():
+ continue
+
+ warnings.warn("Scaling operation for MiSS not supported! Automatically set scale to 1.")
+
+ def unscale_layer(self, scale=None) -> None:
+ for active_adapter in self.active_adapters:
+ if active_adapter not in self.miss_block.keys():
+ continue
+
+ warnings.warn("Unscaling operation for MiSS not supported! Keeping scale at 1.")
+
+
+class MissLinear(nn.Module, MissLayer):
+ """
+ MiSS implemented in a dense layer.
+ """
+
+ def __init__(
+ self,
+ base_layer,
+ adapter_name: str,
+ r: int = 0,
+ mini_r: int = 0,
+ miss_dropout: float = 0.0,
+ init_weights: Union[bool, str] = True,
+ **kwargs,
+ ) -> None:
+ super().__init__()
+ MissLayer.__init__(self, base_layer, **kwargs)
+ self._active_adapter = adapter_name
+ self.update_layer(adapter_name, r, mini_r, miss_dropout, init_weights, **kwargs)
+ self.miss_fn = init_weights
+
+ def merge(self, safe_merge: bool = False, adapter_names: Optional[list[str]] = None) -> None:
+ """
+ Merge the active adapter weights into the base weights
+
+ Args:
+ safe_merge (`bool`, *optional*):
+ If `True`, the merge operation will be performed in a copy of the original weights and check for NaNs
+ before merging the weights. This is useful if you want to check if the merge operation will produce
+ NaNs. Defaults to `False`.
+ adapter_names (`List[str]`, *optional*):
+ The list of adapter names that should be merged. If `None`, all active adapters will be merged.
+ Defaults to `None`.
+ """
+ adapter_names = check_adapters_to_merge(self, adapter_names)
+ if not adapter_names:
+ # no adapter to merge
+ return
+
+ for active_adapter in adapter_names:
+ if active_adapter in self.miss_block.keys():
+ base_layer = self.get_base_layer()
+ orig_dtype = base_layer.weight.dtype
+ if safe_merge:
+ # Note that safe_merge will be slower than the normal merge
+ # because of the copy operation.
+ orig_weight = base_layer.weight.data.clone()
+ if self.miss_fn == "bat":
+ delta_weight = self.get_delta_weight(active_adapter, orig_weight)
+ orig_weight += delta_weight
+ elif self.miss_fn == "mini":
+ delta_weight = self.get_delta_weight_miss(active_adapter, self.base_layer.weight.data)
+ orig_weight = delta_weight
+ else:
+ delta_weight = self.get_delta_weight_miss(active_adapter, self.base_layer.weight.data)
+ orig_weight = delta_weight
+
+ if not torch.isfinite(orig_weight).all():
+ raise ValueError(
+ f"NaNs detected in the merged weights. The adapter {active_adapter} seems to be broken"
+ )
+
+ base_layer.weight.data = orig_weight.to(orig_dtype)
+ else:
+ if self.miss_fn == "bat":
+ delta_weight = self.get_delta_weight(active_adapter, self.base_layer.weight.data)
+ base_layer.weight.data += delta_weight.to(orig_dtype)
+ elif self.miss_fn == "mini":
+ delta_weight = self.get_delta_weight_miss(active_adapter, self.base_layer.weight.data)
+ base_layer.weight.data = delta_weight.to(orig_dtype)
+ else:
+ delta_weight = self.get_delta_weight_miss(active_adapter, self.base_layer.weight.data)
+ base_layer.weight.data = delta_weight.to(orig_dtype)
+ self.merged_adapters.append(active_adapter)
+
+ def unmerge(self) -> None:
+ """
+ This method unmerges all merged adapter layers from the base weights.
+ """
+ if not self.merged:
+ warnings.warn("Already unmerged. Nothing to do.")
+ return
+
+ while len(self.merged_adapters) > 0:
+ active_adapter = self.merged_adapters.pop()
+ base_layer = self.get_base_layer()
+ orig_dtype = base_layer.weight.dtype
+ if active_adapter in self.miss_block.keys():
+ orig_weight = self.get_base_layer().weight.data.clone()
+ if self.miss_fn == "bat":
+ delta_weight = self.get_delta_weight(active_adapter, orig_weight, re=True)
+ elif self.miss_fn == "mini":
+ delta_weight = self.get_delta_weight_miss(active_adapter, orig_weight, re=True)
+ else:
+ delta_weight = self.get_delta_weight_miss(active_adapter, orig_weight, re=True)
+
+ base_layer.weight.data = delta_weight.to(orig_dtype)
+
+ def get_delta_weight(self, adapter, orig_weight, re: bool = False) -> torch.Tensor:
+ """
+ Compute the delta weight for the given adapter.
+
+ Args:
+ adapter (str):
+ The name of the adapter for which the delta weight should be computed.
+ """
+ device = self.miss_block[adapter].device
+ dtype = self.miss_block[adapter].dtype
+ # In case users wants to merge the adapter weights that are in
+ # (b)float16 while being on CPU, we need to cast the weights to float32, perform the merge and then cast back to
+ # (b)float16 because some CPUs have slow bf16/fp16 matmuls.
+ cast_to_fp32 = device.type == "cpu" and (dtype == torch.float16 or dtype == torch.bfloat16)
+
+ weight_miss = self.miss_block[adapter]
+
+ if cast_to_fp32:
+ weight_miss = weight_miss.float()
+ orig_weight = orig_weight.to(weight_miss.dtype)
+
+ r = weight_miss.size(-1)
+ if re:
+ o = orig_weight.reshape(orig_weight.size(0) // r, r, orig_weight.size(1) // r, r).permute(2, 0, 1, 3)
+ one = torch.eye(weight_miss.size(-1)).to(weight_miss.device)
+ # inverse must be in float32, after that the dtype can be adjusted if needed
+ inv_I_plus_b = torch.inverse(one + weight_miss)
+ inv_I_plus_b = inv_I_plus_b.to(weight_miss.dtype)
+ w = (o - weight_miss) @ inv_I_plus_b
+ output_tensor = w.permute(1, 2, 0, 3).reshape(*orig_weight.shape)
+ else:
+ w = (
+ orig_weight.reshape(orig_weight.size(0) // r, r, orig_weight.size(1) // r, r).permute(2, 0, 1, 3)
+ @ weight_miss
+ + weight_miss
+ )
+ output_tensor = w.permute(1, 2, 0, 3).reshape(*orig_weight.shape)
+
+ if cast_to_fp32:
+ output_tensor = output_tensor.to(dtype=dtype)
+
+ # cast back the weights
+ self.miss_block[adapter].data = weight_miss.to(dtype)
+
+ return output_tensor
+
+ def get_delta_weight_miss(self, adapter, orig_weight, re: bool = False) -> torch.Tensor:
+ """
+ Compute the delta weight for the given adapter.
+
+ Args:
+ adapter (str):
+ The name of the adapter for which the delta weight should be computed.
+ """
+ device = self.miss_block[adapter].device
+ dtype = self.miss_block[adapter].dtype
+ # In case users wants to merge the adapter weights that are in
+ # (b)float16 while being on CPU, we need to cast the weights to float32, perform the merge and then cast back to
+ # (b)float16 because some CPUs have slow bf16/fp16 matmuls.
+ cast_to_fp32 = device.type == "cpu" and (dtype == torch.float16 or dtype == torch.bfloat16)
+
+ weight_miss = self.miss_block[adapter]
+
+ if cast_to_fp32:
+ weight_miss = weight_miss.float()
+
+ in_features = orig_weight.size(-1)
+ out_features = orig_weight.size(0)
+ r = weight_miss.size(0)
+ if self.miss_fn == "mini":
+ weight_miss = weight_miss.repeat(1, out_features // self.miss_mini_r[adapter])
+
+ if in_features % r != 0:
+ last_size = in_features % r
+ n_block = in_features // r
+ n_block_size = n_block * r
+
+ if re:
+ orig_weight[:, :n_block_size] = (
+ (orig_weight[:, :n_block_size].reshape(-1, n_block, r).permute(1, 2, 0) - weight_miss)
+ .permute(2, 0, 1)
+ .reshape(*orig_weight[:, :n_block_size].shape)
+ )
+ orig_weight[:, n_block_size:] = (
+ orig_weight[:, n_block_size:] - (weight_miss.transpose(0, 1))[:, :last_size]
+ )
+ else:
+ orig_weight[:, :n_block_size] = (
+ (orig_weight[:, :n_block_size].reshape(-1, n_block, r).permute(1, 2, 0) + weight_miss)
+ .permute(2, 0, 1)
+ .reshape(*orig_weight[:, :n_block_size].shape)
+ )
+ orig_weight[:, n_block_size:] = (
+ orig_weight[:, n_block_size:] + (weight_miss.transpose(0, 1))[:, :last_size]
+ )
+ output_tensor = orig_weight
+
+ else:
+ if re:
+ w = orig_weight.reshape(-1, orig_weight.size(1) // r, r).permute(1, 2, 0) - weight_miss
+ output_tensor = w.permute(2, 0, 1).reshape(*orig_weight.shape)
+ else:
+ w = orig_weight.reshape(-1, orig_weight.size(1) // r, r).permute(1, 2, 0) + weight_miss
+ output_tensor = w.permute(2, 0, 1).reshape(*orig_weight.shape)
+
+ if cast_to_fp32:
+ output_tensor = output_tensor.to(dtype=dtype)
+
+ # cast back the weights
+ self.miss_block[adapter].data = weight_miss.to(dtype)
+
+ return output_tensor
+
+ def forward(self, x: torch.Tensor, *args: Any, **kwargs: Any) -> torch.Tensor:
+ previous_dtype = x.dtype
+
+ if self.disable_adapters:
+ if self.merged:
+ self.unmerge()
+ result = self.base_layer(x, *args, **kwargs)
+ elif self.merged:
+ result = self.base_layer(x, *args, **kwargs)
+ else:
+ if self.miss_fn == "bat":
+ orig_weight = self.base_layer.weight.data.clone()
+ for active_adapter in self.active_adapters:
+ if active_adapter not in self.miss_block.keys():
+ continue
+ delta_weight = self.get_delta_weight(active_adapter, orig_weight)
+ orig_weight = orig_weight + delta_weight
+
+ x = self._cast_input_dtype(x, orig_weight.dtype)
+ bias = self._cast_input_dtype(self.base_layer.bias, orig_weight.dtype)
+ result = F.linear(input=x, weight=orig_weight, bias=bias)
+ else:
+ result = self.base_layer(x, *args, **kwargs)
+ for active_adapter in self.active_adapters:
+ if active_adapter not in self.miss_block.keys():
+ continue
+ miss = self.miss_block[active_adapter]
+ if self.miss_fn == "mini":
+ miss = miss.repeat(1, self.base_layer.out_features // self.miss_mini_r[active_adapter])
+
+ dropout = self.miss_dropout[active_adapter]
+ r = miss.size(0)
+ if x.size(-1) % r != 0:
+ padding_size = (r - x.size(-1) % r) % r
+ x = F.pad(x, (0, padding_size))
+ x = self._cast_input_dtype(x, miss.dtype)
+ result = result + torch.sum(dropout(x).reshape(*x.shape[:-1], x.size(-1) // r, r), dim=-2) @ miss
+
+ result = result.to(previous_dtype)
+ return result
+
+ def __repr__(self) -> str:
+ rep = super().__repr__()
+ return "miss." + rep
diff --git a/peft/src/peft/tuners/miss/model.py b/peft/src/peft/tuners/miss/model.py
new file mode 100644
index 0000000000000000000000000000000000000000..7dd6e655e181a0a3e495e1d38edf0d06c48d1e57
--- /dev/null
+++ b/peft/src/peft/tuners/miss/model.py
@@ -0,0 +1,130 @@
+# Copyright 2024-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+
+import torch
+
+from peft.tuners.tuners_utils import BaseTuner, BaseTunerLayer
+from peft.utils import TRANSFORMERS_MODELS_TO_MISS_TARGET_MODULES_MAPPING
+
+from .layer import MissLayer, MissLinear
+
+
+class MissModel(BaseTuner):
+ """
+ Creates Householder reflection adaptation (MiSS) model from a pretrained model. The method is described in
+ https://huggingface.co/papers/2409.15371
+
+ Args:
+ model (`torch.nn.Module`): The model to which the adapter tuner layers will be attached.
+ config ([`MissConfig`]): The configuration of the MiSS model.
+ adapter_name (`str`): The name of the adapter, defaults to `"default"`.
+ low_cpu_mem_usage (`bool`, `optional`, defaults to `False`):
+ Create empty adapter weights on meta device. Useful to speed up the loading process.
+
+ Returns:
+ `torch.nn.Module`: The MiSS model.
+
+ Example:
+ ```py
+ >>> from diffusers import StableDiffusionPipeline
+ >>> from peft import MissModel, MissConfig
+
+ >>> config_te = MissConfig(
+ ... r=8,
+ ... target_modules=["k_proj", "q_proj", "v_proj", "out_proj", "fc1", "fc2"],
+ ... init_weights=True,
+ ... )
+ >>> config_unet = MissConfig(
+ ... r=8,
+ ... target_modules=[
+ ... "proj_in",
+ ... "proj_out",
+ ... "to_k",
+ ... "to_q",
+ ... "to_v",
+ ... "to_out.0",
+ ... "ff.net.0.proj",
+ ... "ff.net.2",
+ ... ],
+ ... init_weights=True,
+ ... )
+
+ >>> model = StableDiffusionPipeline.from_pretrained("runwayml/stable-diffusion-v1-5")
+ >>> model.text_encoder = MissModel(model.text_encoder, config_te, "default")
+ >>> model.unet = MissModel(model.unet, config_unet, "default")
+ ```
+
+ **Attributes**:
+ - **model** ([`~torch.nn.Module`]) -- The model to be adapted.
+ - **peft_config** ([`MissConfig`]): The configuration of the MiSS model.
+ """
+
+ prefix: str = "miss_"
+ tuner_layer_cls = MissLayer
+ target_module_mapping = TRANSFORMERS_MODELS_TO_MISS_TARGET_MODULES_MAPPING
+
+ def _create_and_replace(
+ self,
+ miss_config,
+ adapter_name,
+ target,
+ target_name,
+ parent,
+ current_key,
+ **optional_kwargs,
+ ):
+ if current_key is None:
+ raise ValueError("Current Key shouldn't be `None`")
+
+ bias = hasattr(target, "bias") and target.bias is not None
+ kwargs = {
+ "r": miss_config.r,
+ "mini_r": miss_config.mini_r,
+ "miss_dropout": miss_config.miss_dropout,
+ "init_weights": miss_config.init_weights,
+ }
+ kwargs["bias"] = bias
+
+ # If it is not a MissLayer, create a new module, else update it with new adapters
+ if not isinstance(target, MissLayer):
+ new_module = self._create_new_module(miss_config, adapter_name, target, **kwargs)
+ if adapter_name not in self.active_adapters:
+ # adding an additional adapter: it is not automatically trainable
+ new_module.requires_grad_(False)
+ self._replace_module(parent, target_name, new_module, target)
+ else:
+ target.update_layer(
+ adapter_name,
+ r=miss_config.r,
+ init_weights=miss_config.init_weights,
+ miss_dropout=miss_config.miss_dropout,
+ mini_r=miss_config.mini_r,
+ )
+
+ @staticmethod
+ def _create_new_module(miss_config, adapter_name, target, **kwargs):
+ if isinstance(target, BaseTunerLayer):
+ target_base_layer = target.get_base_layer()
+ else:
+ target_base_layer = target
+
+ if isinstance(target_base_layer, torch.nn.Linear):
+ new_module = MissLinear(target, adapter_name, **kwargs)
+ else:
+ raise ValueError(
+ f"Target module {target} is not supported. Currently, only `torch.nn.Linear` is supported."
+ )
+
+ return new_module
diff --git a/peft/src/peft/tuners/mixed/__init__.py b/peft/src/peft/tuners/mixed/__init__.py
new file mode 100644
index 0000000000000000000000000000000000000000..2955d7258ddcf76b47b38fd6fd5ebeb3d1d6110c
--- /dev/null
+++ b/peft/src/peft/tuners/mixed/__init__.py
@@ -0,0 +1,18 @@
+# Copyright 2023-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+from .model import COMPATIBLE_TUNER_TYPES, MixedModel
+
+
+__all__ = ["COMPATIBLE_TUNER_TYPES", "MixedModel"]
diff --git a/peft/src/peft/tuners/mixed/model.py b/peft/src/peft/tuners/mixed/model.py
new file mode 100644
index 0000000000000000000000000000000000000000..8b009c4a960a1a75244e7f53b24daff75ac64dfd
--- /dev/null
+++ b/peft/src/peft/tuners/mixed/model.py
@@ -0,0 +1,296 @@
+# Copyright 2023-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+from __future__ import annotations
+
+import warnings
+from typing import Any, Optional, Union
+
+from torch import nn
+from tqdm import tqdm
+
+from peft.tuners import adalora, loha, lokr, lora, oft, shira
+from peft.tuners.tuners_utils import BaseTuner, BaseTunerLayer, _delete_auxiliary_adapter
+from peft.utils import (
+ TRANSFORMERS_MODELS_TO_LORA_TARGET_MODULES_MAPPING,
+ ModulesToSaveWrapper,
+ PeftType,
+ _get_submodules,
+ get_auto_gptq_quant_linear,
+)
+
+
+# Collection of constants used for all tuners
+COMPATIBLE_TUNER_TYPES = (PeftType.LORA, PeftType.LOHA, PeftType.LOKR, PeftType.ADALORA, PeftType.OFT, PeftType.SHIRA)
+PREFIXES = [
+ lora.LoraModel.prefix,
+ lokr.LoKrModel.prefix,
+ loha.LoHaModel.prefix,
+ oft.OFTModel.prefix,
+ shira.ShiraModel.prefix,
+]
+Configs = Union[
+ lora.LoraConfig, loha.LoHaConfig, lokr.LoKrConfig, adalora.AdaLoraConfig, oft.OFTConfig, shira.ShiraConfig
+]
+Layers = (
+ lora.layer.LoraLayer,
+ loha.layer.LoHaLayer,
+ lokr.layer.LoKrLayer,
+ adalora.layer.AdaLoraLayer,
+ oft.OFTLayer,
+ shira.ShiraLayer,
+)
+
+
+class MixedModel(BaseTuner):
+ """
+ A class that allows to mix different types of adapters in a single model.
+
+ Note: This class should usually not be initialized directly. Instead, use `get_peft_model` with the argument
+ `mixed=True`.
+
+ Args:
+ model (:obj:`nn.Module`):
+ The model to be tuned.
+ config (:obj:`PeftConfig`):
+ The config of the model to be tuned. The adapter type must be compatible.
+ adapter_name (:obj:`str`):
+ The name of the first adapter.
+ """
+
+ def __init__(self, model: nn.Module, config: Configs, adapter_name: str) -> None:
+ super().__init__(model, config, adapter_name)
+
+ def _check_new_adapter_config(self, config: Configs) -> None:
+ """
+ A helper method to check the config when a new adapter is being added.
+
+ Raise a ValueError if there is something wrong with the config or if it conflicts with existing adapters.
+
+ """
+ if not isinstance(config, Configs.__args__):
+ raise ValueError(
+ f"{self.__class__.__name__} only supports {COMPATIBLE_TUNER_TYPES} configs, but got {type(config)}."
+ )
+
+ super()._check_new_adapter_config(config)
+
+ def _create_and_replace(
+ self,
+ config: Configs,
+ *args: Any,
+ **kwargs: Any,
+ ) -> None:
+ if isinstance(config, adalora.AdaLoraConfig):
+ adalora.AdaLoraModel._create_and_replace(self, config, *args, **kwargs)
+ elif isinstance(config, lora.LoraConfig):
+ lora.LoraModel._create_and_replace(self, config, *args, **kwargs)
+ elif isinstance(config, loha.LoHaConfig):
+ loha.LoHaModel._create_and_replace(self, config, *args, **kwargs)
+ elif isinstance(config, lokr.LoKrConfig):
+ lokr.LoKrModel._create_and_replace(self, config, *args, **kwargs)
+ elif isinstance(config, oft.OFTConfig):
+ oft.OFTModel._create_and_replace(self, config, *args, **kwargs)
+ elif isinstance(config, shira.ShiraConfig):
+ shira.ShiraModel._create_and_replace(self, config, *args, **kwargs)
+ else:
+ raise ValueError(f"Unsupported config type {type(config)}, should be one of {COMPATIBLE_TUNER_TYPES}.")
+
+ def _replace_module(self, parent, child_name, new_module, child) -> None:
+ setattr(parent, child_name, new_module)
+ # It's not necessary to set requires_grad here, as that is handled by
+ # _mark_only_adapters_as_trainable
+
+ # child layer wraps the original module, unpack it
+ if hasattr(child, "base_layer"):
+ child = child.get_base_layer()
+ elif hasattr(child, "quant_linear_module"):
+ # TODO maybe not necessary to have special treatment?
+ child = child.quant_linear_module
+
+ if not hasattr(new_module, "base_layer"):
+ new_module.weight = child.weight
+ if hasattr(child, "bias"):
+ new_module.bias = child.bias
+
+ if getattr(child, "state", None) is not None:
+ if hasattr(new_module, "base_layer"):
+ new_module.base_layer.state = child.state
+ else:
+ new_module.state = child.state
+ new_module.to(child.weight.device)
+
+ # dispatch to correct device
+ for name, module in new_module.named_modules():
+ if any(prefix in name for prefix in PREFIXES):
+ module.to(child.weight.device)
+ if "ranknum" in name:
+ module.to(child.weight.device)
+
+ def _mark_only_adapters_as_trainable(self, model: nn.Module) -> None:
+ for n, p in model.named_parameters():
+ if not any(prefix in n for prefix in PREFIXES):
+ p.requires_grad = False
+
+ for active_adapter in self.active_adapters:
+ bias = getattr(self.peft_config[active_adapter], "bias", "none")
+ if bias == "none":
+ continue
+
+ if bias == "all":
+ for n, p in model.named_parameters():
+ if "bias" in n:
+ p.requires_grad = True
+ elif bias == "lora_only":
+ # TODO: check if this is needed for other supported types
+ for m in model.modules():
+ if isinstance(m, Layers) and hasattr(m, "bias") and m.bias is not None:
+ m.bias.requires_grad = True
+ else:
+ raise ValueError(f"Requested bias: {bias}, is not implemented.")
+
+ @staticmethod
+ def _create_new_module(config, adapter_name, target, **kwargs):
+ gptq_quantization_config = kwargs.get("gptq_quantization_config", None)
+ AutoGPTQQuantLinear = get_auto_gptq_quant_linear(gptq_quantization_config)
+ if (gptq_quantization_config is not None) or (AutoGPTQQuantLinear is not None):
+ raise ValueError(f"GPTQ quantization not supported for {config.peft_type.value} (yet).")
+
+ loaded_in_8bit = kwargs.pop("loaded_in_8bit", False)
+ loaded_in_4bit = kwargs.pop("loaded_in_4bit", False)
+ if loaded_in_8bit or loaded_in_4bit:
+ raise ValueError(f"8bit and 4bit quantization not supported for {config.peft_type.value} (yet).")
+
+ if isinstance(config, adalora.AdaLoraConfig):
+ new_module = adalora.AdaLoraModel._create_new_module(config, adapter_name, target, **kwargs)
+ elif isinstance(config, lora.LoraConfig):
+ new_module = lora.LoraModel._create_new_module(config, adapter_name, target, **kwargs)
+ elif isinstance(config, loha.LoHaConfig):
+ new_module = loha.LoHaModel._create_new_module(config, adapter_name, target, **kwargs)
+ elif isinstance(config, lokr.LoKrConfig):
+ new_module = lokr.LoKrModel._create_new_module(config, adapter_name, target, **kwargs)
+ elif isinstance(config, oft.OFTConfig):
+ new_module = oft.OFTModel._create_new_module(config, adapter_name, target, **kwargs)
+ elif isinstance(config, shira.ShiraConfig):
+ new_module = shira.ShiraModel._create_new_module(config, adapter_name, target, **kwargs)
+ else:
+ raise ValueError(f"Unknown config type {type(config)}, should be one of {COMPATIBLE_TUNER_TYPES}.")
+ return new_module
+
+ def set_adapter(self, adapter_name: Union[str, list[str]], inference_mode: bool = False) -> None:
+ self.set_auxiliary_adapters(adapter_name, inference_mode=inference_mode)
+ for module in self.model.modules():
+ if isinstance(module, Layers):
+ if module.merged:
+ warnings.warn("Adapter cannot be set when the model is merged. Unmerging the model first.")
+ module.unmerge()
+ module.set_adapter(adapter_name, inference_mode=inference_mode)
+ self.active_adapter = adapter_name
+
+ @staticmethod
+ def _prepare_adapter_config(peft_config, model_config):
+ if peft_config.target_modules is None:
+ if model_config["model_type"] not in TRANSFORMERS_MODELS_TO_LORA_TARGET_MODULES_MAPPING:
+ raise ValueError("Please specify `target_modules` in `peft_config`")
+
+ peft_config.target_modules = set(
+ TRANSFORMERS_MODELS_TO_LORA_TARGET_MODULES_MAPPING[model_config["model_type"]]
+ )
+ return peft_config
+
+ def _unload_and_optionally_merge(
+ self,
+ merge=True,
+ progressbar: bool = False,
+ safe_merge: bool = False,
+ adapter_names: Optional[list[str]] = None,
+ ):
+ if merge:
+ if getattr(self.model, "quantization_method", None) == "gptq":
+ raise ValueError("Cannot merge layers when the model is gptq quantized")
+
+ def merge_recursively(module):
+ # helper function to recursively merge the base_layer of the target
+ path = []
+ layer = module
+ while hasattr(layer, "base_layer"):
+ path.append(layer)
+ layer = layer.base_layer
+ for layer_before, layer_after in zip(path[:-1], path[1:]):
+ layer_after.merge(safe_merge=safe_merge, adapter_names=adapter_names)
+ layer_before.base_layer = layer_after.base_layer
+ module.merge(safe_merge=safe_merge, adapter_names=adapter_names)
+
+ key_list = [key for key, _ in self.model.named_modules() if not any(prefix in key for prefix in PREFIXES)]
+ desc = "Unloading " + ("and merging " if merge else "") + "model"
+
+ for key in tqdm(key_list, disable=not progressbar, desc=desc):
+ try:
+ parent, target, target_name = _get_submodules(self.model, key)
+ except AttributeError:
+ continue
+
+ if hasattr(target, "base_layer"):
+ if merge:
+ merge_recursively(target)
+ self._replace_module(parent, target_name, target.get_base_layer(), target)
+ elif isinstance(target, ModulesToSaveWrapper):
+ # save any additional trainable modules part of `modules_to_save`
+ new_module = target.modules_to_save[target.active_adapter]
+ if hasattr(new_module, "base_layer"):
+ # check if the module is itself a tuner layer
+ if merge:
+ new_module.merge(safe_merge=safe_merge, adapter_names=adapter_names)
+ new_module = new_module.get_base_layer()
+ setattr(parent, target_name, new_module)
+
+ return self.model
+
+ def add_weighted_adapter(self, *args: Any, **kwargs: Any) -> None:
+ raise NotImplementedError(f"Weighted adapters are not supported for {self.__class__.__name__} (yet).")
+
+ def delete_adapter(self, adapter_name: Union[str, list[str]]) -> None:
+ """
+ Deletes an existing adapter.
+
+ Args:
+ adapter_name (Union[str, list[str]]): Name of the adapter(s) to delete.
+ """
+ if isinstance(adapter_name, str):
+ adapter_names = [adapter_name]
+ else:
+ adapter_names = adapter_name
+
+ mismatched = set(adapter_names) - set(self.peft_config.keys())
+ if mismatched:
+ raise ValueError(
+ f"Adapter(s) {sorted(mismatched)} not found, available adapters: {sorted(self.peft_config.keys())}"
+ )
+
+ for adapter_name in adapter_names:
+ del self.peft_config[adapter_name]
+
+ key_list = [key for key, _ in self.model.named_modules() if not any(prefix in key for prefix in PREFIXES)]
+ new_adapter = None
+ for key in key_list:
+ _, target, _ = _get_submodules(self.model, key)
+ if isinstance(target, BaseTunerLayer):
+ target.delete_adapter(adapter_name)
+ if new_adapter is None:
+ new_adapter = target.active_adapters[:]
+
+ self.active_adapter = new_adapter or []
+ _delete_auxiliary_adapter(self.model, adapter_name, new_active_adapters=new_adapter)
+
+ def generate(self, *args: Any, **kwargs: Any):
+ return self.model.generate(*args, **kwargs)
diff --git a/peft/src/peft/tuners/multitask_prompt_tuning/__init__.py b/peft/src/peft/tuners/multitask_prompt_tuning/__init__.py
new file mode 100644
index 0000000000000000000000000000000000000000..fe692a93378254601753cc9b17218fdd5a92b8de
--- /dev/null
+++ b/peft/src/peft/tuners/multitask_prompt_tuning/__init__.py
@@ -0,0 +1,25 @@
+# Copyright 2023-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+from peft.utils import register_peft_method
+
+from .config import MultitaskPromptTuningConfig, MultitaskPromptTuningInit
+from .model import MultitaskPromptEmbedding
+
+
+__all__ = ["MultitaskPromptEmbedding", "MultitaskPromptTuningConfig", "MultitaskPromptTuningInit"]
+
+register_peft_method(
+ name="multitask_prompt_tuning", config_cls=MultitaskPromptTuningConfig, model_cls=MultitaskPromptEmbedding
+)
diff --git a/peft/src/peft/tuners/multitask_prompt_tuning/config.py b/peft/src/peft/tuners/multitask_prompt_tuning/config.py
new file mode 100644
index 0000000000000000000000000000000000000000..6cb279573559e4fa33a973aa35e052647a6ab8f9
--- /dev/null
+++ b/peft/src/peft/tuners/multitask_prompt_tuning/config.py
@@ -0,0 +1,62 @@
+# Copyright 2023-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+import enum
+from dataclasses import dataclass, field
+from typing import Optional, Union
+
+from peft.tuners.prompt_tuning import PromptTuningConfig
+from peft.utils import PeftType
+
+
+class MultitaskPromptTuningInit(str, enum.Enum):
+ # initialize prompt with text
+ TEXT = "TEXT"
+ # initialize prompt with random matrix
+ RANDOM = "RANDOM"
+ # average the prefix and column matrices obtained during source training
+ AVERAGE_SOURCE_TASKS = "AVERAGE_SOURCE_TASKS"
+ # pick prefix and column matrices for a particular task obtained during source training
+ EXACT_SOURCE_TASK = "EXACT_SOURCE_TASK"
+ # only use the prompt embeddings trained during source training
+ ONLY_SOURCE_SHARED = "ONLY_SOURCE_SHARED"
+
+
+@dataclass
+class MultitaskPromptTuningConfig(PromptTuningConfig):
+ prompt_tuning_init: Union[MultitaskPromptTuningInit, str] = field(
+ default=MultitaskPromptTuningInit.RANDOM,
+ metadata={
+ "help": (
+ "How to initialize the prompt tuning parameters. Can be one of TEXT, RANDOM, AVERAGE_SOURCE_TASKS, "
+ "EXACT_SOURCE_TASK, ONLY_SOURCE_SHARED."
+ ),
+ },
+ )
+ prompt_tuning_init_state_dict_path: Optional[str] = field(
+ default=None,
+ metadata={
+ "help": (
+ "The path of source state dict. This is required when training the downstream target prompt from "
+ "the pretrained source prompt"
+ ),
+ },
+ )
+ prompt_tuning_init_task: Optional[int] = field(default=0, metadata={"help": "source task id for initialization"})
+ num_ranks: Optional[int] = field(default=1, metadata={"help": "ranks"})
+ num_tasks: Optional[int] = field(default=1, metadata={"help": "number of tasks"})
+
+ def __post_init__(self):
+ super().__post_init__()
+ self.peft_type = PeftType.MULTITASK_PROMPT_TUNING
diff --git a/peft/src/peft/tuners/multitask_prompt_tuning/model.py b/peft/src/peft/tuners/multitask_prompt_tuning/model.py
new file mode 100644
index 0000000000000000000000000000000000000000..20d9d498f48c4f3bc7087c38b4f8072d8de66637
--- /dev/null
+++ b/peft/src/peft/tuners/multitask_prompt_tuning/model.py
@@ -0,0 +1,120 @@
+# Copyright 2023-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+import torch
+
+from peft.tuners.prompt_tuning import PromptEmbedding
+from peft.utils import TaskType
+from peft.utils.save_and_load import torch_load
+
+from .config import MultitaskPromptTuningConfig, MultitaskPromptTuningInit
+
+
+# This code is adapted for the paper: https://huggingface.co/papers/2303.02861 and
+# constitutes the work done at MIT-IBM Watson Research Lab.
+
+
+class MultitaskPromptEmbedding(PromptEmbedding):
+ def __init__(self, config: MultitaskPromptTuningConfig, word_embeddings):
+ super().__init__(config, word_embeddings)
+
+ self.num_tasks = config.num_tasks
+ self.num_ranks = config.num_ranks
+ self.num_virtual_tokens = config.num_virtual_tokens
+
+ self.num_transformer_submodules = config.num_transformer_submodules
+ if self.num_transformer_submodules is None:
+ self.num_transformer_submodules = 2 if config.task_type == TaskType.SEQ_2_SEQ_LM else 1
+
+ self.token_dim = config.token_dim
+
+ total_virtual_tokens = self.num_virtual_tokens * self.num_transformer_submodules
+
+ self.prefix_task_cols = torch.nn.Parameter(
+ torch.normal(
+ mean=0,
+ std=0.02,
+ size=(self.num_tasks, total_virtual_tokens, self.num_ranks),
+ )
+ )
+ self.prefix_task_rows = torch.nn.Parameter(
+ torch.normal(
+ mean=0,
+ std=0.02,
+ size=(self.num_tasks, self.num_ranks, self.token_dim),
+ )
+ )
+
+ if config.prompt_tuning_init in [
+ MultitaskPromptTuningInit.AVERAGE_SOURCE_TASKS,
+ MultitaskPromptTuningInit.EXACT_SOURCE_TASK,
+ MultitaskPromptTuningInit.ONLY_SOURCE_SHARED,
+ ]:
+ if config.prompt_tuning_init_state_dict_path is None:
+ raise ValueError(
+ f"prompt_tuning_init_state_dict_path needs to be specified with {config.prompt_tuning_init} "
+ "init method"
+ )
+
+ if config.prompt_tuning_init_state_dict_path.endswith(".safetensors"):
+ from safetensors.torch import load_file
+
+ state_dict: dict = load_file(config.prompt_tuning_init_state_dict_path)
+ else:
+ state_dict: dict = torch_load(
+ config.prompt_tuning_init_state_dict_path,
+ map_location=word_embeddings.weight.device,
+ )
+
+ if config.prompt_tuning_init in [
+ MultitaskPromptTuningInit.AVERAGE_SOURCE_TASKS,
+ MultitaskPromptTuningInit.EXACT_SOURCE_TASK,
+ ]:
+ prefix_task_cols_: torch.Tensor = state_dict["prefix_task_cols"]
+ prefix_task_rows_: torch.Tensor = state_dict["prefix_task_rows"]
+
+ if config.prompt_tuning_init == MultitaskPromptTuningInit.AVERAGE_SOURCE_TASKS:
+ prefix_task_cols_ = prefix_task_cols_.mean(0, keepdim=True)
+ prefix_task_rows_ = prefix_task_rows_.mean(0, keepdim=True)
+ elif config.prompt_tuning_init == MultitaskPromptTuningInit.EXACT_SOURCE_TASK:
+ prefix_task_cols_ = prefix_task_cols_[config.prompt_tuning_init_task, ...].unsqueeze(0)
+ prefix_task_rows_ = prefix_task_rows_[config.prompt_tuning_init_task, ...].unsqueeze(0)
+
+ state_dict = {
+ "embedding.weight": state_dict["prompt_embeddings"],
+ "prefix_task_cols": prefix_task_cols_,
+ "prefix_task_rows": prefix_task_rows_,
+ }
+
+ self.load_state_dict(state_dict, strict=True)
+ elif config.prompt_tuning_init == MultitaskPromptTuningInit.ONLY_SOURCE_SHARED:
+ state_dict = {
+ "embedding.weight": state_dict["prompt_embeddings"],
+ }
+
+ self.load_state_dict(state_dict, strict=False)
+
+ def forward(self, indices, task_ids):
+ if task_ids is None:
+ raise ValueError("task_ids cannot be None")
+
+ prompt_embeddings = self.embedding(indices)
+
+ task_cols = torch.index_select(self.prefix_task_cols, 0, task_ids)
+ task_rows = torch.index_select(self.prefix_task_rows, 0, task_ids)
+ task_prompts = torch.matmul(task_cols, task_rows)
+
+ prompt_embeddings *= task_prompts
+
+ return prompt_embeddings
diff --git a/peft/src/peft/tuners/oft/__init__.py b/peft/src/peft/tuners/oft/__init__.py
new file mode 100644
index 0000000000000000000000000000000000000000..32e21e32f64b02315731642542cf0bf31227d7a4
--- /dev/null
+++ b/peft/src/peft/tuners/oft/__init__.py
@@ -0,0 +1,52 @@
+# Copyright 2023-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+from peft.import_utils import is_bnb_4bit_available, is_bnb_available, is_eetq_available
+from peft.utils import register_peft_method
+
+from .config import OFTConfig
+from .gptq import GPTQOFTLinear
+from .layer import Conv2d, Linear, OFTLayer
+from .model import OFTModel
+
+
+__all__ = [
+ "Conv2d",
+ "GPTQOFTLinear",
+ "Linear",
+ "OFTConfig",
+ "OFTLayer",
+ "OFTModel",
+]
+
+register_peft_method(name="oft", config_cls=OFTConfig, model_cls=OFTModel)
+
+
+def __getattr__(name):
+ if (name == "Linear8bitLt") and is_bnb_available():
+ from .bnb import Linear8bitLt
+
+ return Linear8bitLt
+
+ if (name == "Linear4bit") and is_bnb_4bit_available():
+ from .bnb import Linear4bit
+
+ return Linear4bit
+
+ if (name == "EetqOFTLinear") and is_eetq_available():
+ from .eetq import EetqOFTLinear
+
+ return EetqOFTLinear
+
+ raise AttributeError(f"module {__name__} has no attribute {name}")
diff --git a/peft/src/peft/tuners/oft/aqlm.py b/peft/src/peft/tuners/oft/aqlm.py
new file mode 100644
index 0000000000000000000000000000000000000000..d455d2fe4149be2d78e8386c1aee668de4a74829
--- /dev/null
+++ b/peft/src/peft/tuners/oft/aqlm.py
@@ -0,0 +1,105 @@
+# Copyright 2025-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+from typing import Any, Optional
+
+import torch
+
+from peft.import_utils import is_aqlm_available
+from peft.tuners.oft.layer import OFTLayer
+from peft.tuners.tuners_utils import BaseTunerLayer
+
+
+if is_aqlm_available():
+ from aqlm import QuantizedLinear
+
+
+class AqlmOFTLinear(torch.nn.Module, OFTLayer):
+ def __init__(
+ self,
+ base_layer,
+ adapter_name: str,
+ r: int = 0,
+ oft_block_size: int = 32,
+ module_dropout: float = 0.0,
+ init_weights: bool = True,
+ coft: bool = False,
+ eps: float = 6e-5,
+ block_share: bool = False,
+ fan_in_fan_out: bool = False, # Set this to True if the layer to replace stores weight like (fan_in, fan_out)
+ use_cayley_neumann: bool = False,
+ num_cayley_neumann_terms: int = 5,
+ **kwargs,
+ ):
+ super().__init__()
+ OFTLayer.__init__(self, base_layer)
+
+ self._active_adapter = adapter_name
+ self.update_layer(
+ adapter_name,
+ r,
+ oft_block_size=oft_block_size,
+ module_dropout=module_dropout,
+ init_weights=init_weights,
+ coft=coft,
+ eps=eps,
+ block_share=block_share,
+ use_cayley_neumann=use_cayley_neumann,
+ num_cayley_neumann_terms=num_cayley_neumann_terms,
+ )
+
+ def forward(self, x: torch.Tensor):
+ # note: logic differs from default Linear because merging is not supported
+ if self.disable_adapters:
+ return self.base_layer(x)
+
+ for active_adapter in self.active_adapters:
+ if active_adapter not in self.oft_R.keys():
+ continue
+ oft_R = self.oft_R[active_adapter]
+
+ requires_conversion = not torch.is_autocast_enabled()
+ if requires_conversion:
+ expected_dtype = x.dtype
+ x = self._cast_input_dtype(x, oft_R.weight.dtype)
+
+ x = oft_R(x)
+
+ result = self.base_layer(x)
+ if requires_conversion:
+ result = result.to(expected_dtype)
+ return result
+
+ def __repr__(self) -> str:
+ rep = super().__repr__()
+ return "oft." + rep
+
+
+def dispatch_aqlm(
+ target: torch.nn.Module,
+ adapter_name: str,
+ **kwargs: Any,
+) -> Optional[torch.nn.Module]:
+ new_module = None
+
+ if isinstance(target, BaseTunerLayer):
+ target_base_layer = target.get_base_layer()
+ else:
+ target_base_layer = target
+
+ if is_aqlm_available() and isinstance(target_base_layer, QuantizedLinear):
+ new_module = AqlmOFTLinear(target, adapter_name, **kwargs)
+ target.qweight = target_base_layer.codes
+
+ return new_module
diff --git a/peft/src/peft/tuners/oft/awq.py b/peft/src/peft/tuners/oft/awq.py
new file mode 100644
index 0000000000000000000000000000000000000000..4af5addaede9e098e6a87b5212436936f9426c80
--- /dev/null
+++ b/peft/src/peft/tuners/oft/awq.py
@@ -0,0 +1,119 @@
+# Copyright 2025-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+import importlib.metadata as importlib_metadata
+from typing import Any, Optional
+
+import packaging.version
+import torch
+
+from peft.import_utils import is_auto_awq_available
+from peft.tuners.oft.layer import OFTLayer
+from peft.tuners.tuners_utils import BaseTunerLayer
+
+
+class AwqOFTLinear(torch.nn.Module, OFTLayer):
+ def __init__(
+ self,
+ base_layer,
+ adapter_name,
+ r: int = 0,
+ oft_block_size: int = 32,
+ module_dropout: float = 0.0,
+ coft: bool = False,
+ eps: float = 6e-5,
+ block_share: bool = False,
+ fan_in_fan_out: bool = False, # Set this to True if the layer to replace stores weight like (fan_in, fan_out)
+ init_weights: bool = True,
+ use_cayley_neumann: bool = False,
+ num_cayley_neumann_terms: int = 5,
+ **kwargs,
+ ):
+ super().__init__()
+ OFTLayer.__init__(self, base_layer)
+
+ # self.base_layer and self.quant_linear_module are the same; we need the former for consistency and the latter
+ # for backwards compatibility
+ self.quant_linear_module = base_layer
+
+ self._active_adapter = adapter_name
+ self.update_layer(
+ adapter_name,
+ r,
+ oft_block_size=oft_block_size,
+ module_dropout=module_dropout,
+ coft=coft,
+ eps=eps,
+ block_share=block_share,
+ init_weights=init_weights,
+ use_cayley_neumann=use_cayley_neumann,
+ num_cayley_neumann_terms=num_cayley_neumann_terms,
+ )
+
+ def forward(self, x: torch.Tensor):
+ if self.disable_adapters:
+ result = self.quant_linear_module(x)
+ return result
+
+ for active_adapter in self.active_adapters:
+ if active_adapter not in self.oft_R.keys():
+ continue
+ oft_R = self.oft_R[active_adapter]
+
+ requires_conversion = not torch.is_autocast_enabled()
+ if requires_conversion:
+ expected_dtype = x.dtype
+ x = self._cast_input_dtype(x, oft_R.weight.dtype)
+
+ x = oft_R(x)
+ if requires_conversion:
+ x = x.to(expected_dtype)
+
+ result = self.quant_linear_module(x)
+ return result
+
+ def __repr__(self) -> str:
+ rep = super().__repr__()
+ return "oft." + rep
+
+
+def dispatch_awq(
+ target: torch.nn.Module,
+ adapter_name: str,
+ **kwargs: Any,
+) -> Optional[torch.nn.Module]:
+ new_module = None
+
+ if isinstance(target, BaseTunerLayer):
+ target_base_layer = target.get_base_layer()
+ else:
+ target_base_layer = target
+
+ if is_auto_awq_available():
+ from awq.modules.linear import WQLinear_GEMM
+
+ if isinstance(target_base_layer, WQLinear_GEMM):
+ # Raise the error only at the dispatch level
+ AUTOAWQ_MINIMUM_VERSION = packaging.version.parse("0.2.0")
+ version_autoawq = packaging.version.parse(importlib_metadata.version("autoawq"))
+
+ if AUTOAWQ_MINIMUM_VERSION > version_autoawq:
+ raise ImportError(
+ f"Found an incompatible version of auto-awq. Found version {version_autoawq}, "
+ f"but only versions above {AUTOAWQ_MINIMUM_VERSION} are supported for PEFT."
+ )
+
+ new_module = AwqOFTLinear(target, adapter_name, **kwargs)
+ target.qweight = target_base_layer.qweight
+
+ return new_module
diff --git a/peft/src/peft/tuners/oft/bnb.py b/peft/src/peft/tuners/oft/bnb.py
new file mode 100644
index 0000000000000000000000000000000000000000..a5da56279bac877da807faacbb74121fb10e3875
--- /dev/null
+++ b/peft/src/peft/tuners/oft/bnb.py
@@ -0,0 +1,388 @@
+# Copyright 2025-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+from __future__ import annotations
+
+import warnings
+from typing import Optional
+
+import bitsandbytes as bnb
+import torch
+
+from peft.import_utils import is_bnb_4bit_available, is_bnb_available
+from peft.tuners.tuners_utils import BaseTunerLayer, check_adapters_to_merge
+from peft.utils.integrations import dequantize_bnb_weight
+
+from .layer import OFTLayer
+
+
+if is_bnb_available():
+
+ class Linear8bitLt(torch.nn.Module, OFTLayer):
+ # OFT implemented in a dense layer
+ def __init__(
+ self,
+ base_layer: torch.nn.Module,
+ adapter_name: str,
+ r: int = 8,
+ oft_block_size: int = 0,
+ module_dropout: float = 0.0,
+ init_weights: bool = True,
+ coft: bool = False,
+ eps: float = 6e-5,
+ block_share: bool = False,
+ use_cayley_neumann: bool = False,
+ num_cayley_neumann_terms: int = 5,
+ **kwargs,
+ ) -> None:
+ super().__init__()
+ OFTLayer.__init__(self, base_layer)
+ self.fan_in_fan_out = False
+
+ self._active_adapter = adapter_name
+ self.update_layer(
+ adapter_name,
+ r,
+ oft_block_size=oft_block_size,
+ module_dropout=module_dropout,
+ coft=coft,
+ eps=eps,
+ block_share=block_share,
+ init_weights=init_weights,
+ use_cayley_neumann=use_cayley_neumann,
+ num_cayley_neumann_terms=num_cayley_neumann_terms,
+ )
+
+ def merge(self, safe_merge: bool = False, adapter_names: Optional[list[str]] = None) -> None:
+ """
+ Merge the active adapter weights into the base weights
+
+ Args:
+ safe_merge (`bool`, *optional*):
+ If True, the merge operation will be performed in a copy of the original weights and check for NaNs
+ before merging the weights. This is useful if you want to check if the merge operation will produce
+ NaNs. Defaults to `False`.
+ adapter_names (`list[str]`, *optional*):
+ The list of adapter names that should be merged. If None, all active adapters will be merged.
+ Defaults to `None`.
+ """
+ adapter_names = check_adapters_to_merge(self, adapter_names)
+ if not adapter_names:
+ # no adapter to merge
+ return
+
+ for active_adapter in adapter_names:
+ if active_adapter not in self.oft_R.keys():
+ continue
+
+ warnings.warn("Merge oft module to 8-bit linear may get different generations due to rounding errors.")
+
+ weight = self.get_base_layer().weight
+ state = self.get_base_layer().state
+ if state.SCB is None:
+ state.SCB = weight.SCB
+
+ # Dequantize the result of identity matrix and int8 weight because bitsandbytes does not support int8
+ # dequantization directly
+ output = dequantize_bnb_weight(weight, state=state)
+ oft_data = self.get_delta_weight(active_adapter)
+
+ output = torch.transpose(output, 0, 1)
+ w_data = torch.mm(oft_data, output.to(oft_data.dtype))
+ w_data = torch.transpose(w_data, 0, 1)
+ w_data = output.to(oft_data.dtype).to(oft_data.device)
+
+ if safe_merge and not torch.isfinite(w_data).all():
+ raise ValueError(
+ f"NaNs detected in the merged weights. The adapter {active_adapter} seems to be broken"
+ )
+
+ self.get_base_layer().weight = bnb.nn.Int8Params(
+ w_data.to("cpu"), requires_grad=False, has_fp16_weights=weight.has_fp16_weights
+ ).to(weight.device)
+
+ state.reset_grads()
+ self.merged_adapters.append(active_adapter)
+
+ def unmerge(self) -> None:
+ """
+ This method unmerges all merged adapter layers from the base weights.
+ """
+ if not self.merged:
+ warnings.warn("Already unmerged. Nothing to do.")
+ return
+
+ while len(self.merged_adapters) > 0:
+ active_adapter = self.merged_adapters.pop()
+ if active_adapter not in self.oft_R.keys():
+ continue
+ warnings.warn(
+ "Unmerge oft module to 8-bit linear may get different generations due to rounding errors."
+ )
+
+ weight = self.get_base_layer().weight
+ state = self.get_base_layer().state
+ if state.SCB is None:
+ state.SCB = weight.SCB
+ output = dequantize_bnb_weight(weight, state=state)
+
+ oft_data = self.get_delta_weight(active_adapter)
+
+ output = torch.transpose(output, 0, 1)
+ w_data = torch.mm(oft_data.t(), output.to(oft_data.dtype))
+ w_data = torch.transpose(w_data, 0, 1)
+ w_data = w_data.to(oft_data.dtype).to(oft_data.device)
+
+ self.get_base_layer().weight = bnb.nn.Int8Params(
+ w_data.to("cpu"), requires_grad=False, has_fp16_weights=weight.has_fp16_weights
+ ).to(weight.device)
+
+ state.reset_grads()
+
+ def get_delta_weight(self, adapter):
+ return self.oft_R[adapter].get_weight()
+
+ def forward(self, x: torch.Tensor, *args, **kwargs) -> torch.Tensor:
+ if self.disable_adapters:
+ if self.merged:
+ self.unmerge()
+ result = self.base_layer(x, *args, **kwargs)
+ elif self.merged:
+ result = self.base_layer(x, *args, **kwargs)
+ else:
+ for active_adapter in self.active_adapters:
+ if active_adapter not in self.oft_R.keys():
+ continue
+ oft_R = self.oft_R[active_adapter]
+
+ requires_conversion = not torch.is_autocast_enabled()
+ if requires_conversion:
+ expected_dtype = x.dtype
+ x = self._cast_input_dtype(x, oft_R.weight.dtype)
+
+ x = oft_R(x)
+ if requires_conversion:
+ x = x.to(expected_dtype)
+
+ result = self.base_layer(x, *args, **kwargs)
+
+ return result
+
+ def __repr__(self) -> str:
+ rep = super().__repr__()
+ return "oft." + rep
+
+ def dispatch_bnb_8bit(target: torch.nn.Module, adapter_name: str, **kwargs):
+ new_module = None
+
+ if isinstance(target, BaseTunerLayer):
+ target_base_layer = target.get_base_layer()
+ else:
+ target_base_layer = target
+
+ loaded_in_8bit = kwargs.get("loaded_in_8bit", False)
+ if loaded_in_8bit and isinstance(target_base_layer, bnb.nn.Linear8bitLt):
+ eightbit_kwargs = kwargs.copy()
+ eightbit_kwargs.update(
+ {
+ "has_fp16_weights": target.state.has_fp16_weights,
+ "threshold": target.state.threshold,
+ "index": target.index,
+ }
+ )
+ new_module = Linear8bitLt(target, adapter_name, **eightbit_kwargs)
+
+ return new_module
+
+
+if is_bnb_4bit_available():
+
+ class Linear4bit(torch.nn.Module, OFTLayer):
+ # OFT implemented in a dense layer
+ def __init__(
+ self,
+ base_layer: torch.nn.Module,
+ adapter_name: str,
+ r: int = 8,
+ oft_block_size: int = 0,
+ module_dropout: float = 0.0,
+ coft: bool = False,
+ eps: float = 6e-5,
+ block_share: bool = False,
+ init_weights: bool = True,
+ use_cayley_neumann: bool = False,
+ num_cayley_neumann_terms: int = 5,
+ **kwargs,
+ ) -> None:
+ super().__init__()
+ OFTLayer.__init__(self, base_layer)
+ self.fan_in_fan_out = False
+
+ self._active_adapter = adapter_name
+ self.update_layer(
+ adapter_name,
+ r,
+ oft_block_size=oft_block_size,
+ module_dropout=module_dropout,
+ coft=coft,
+ eps=eps,
+ block_share=block_share,
+ init_weights=init_weights,
+ use_cayley_neumann=use_cayley_neumann,
+ num_cayley_neumann_terms=num_cayley_neumann_terms,
+ )
+
+ def merge(self, safe_merge: bool = False, adapter_names: Optional[list[str]] = None) -> None:
+ """
+ Merge the active adapter weights into the base weights
+
+ Args:
+ safe_merge (`bool`, *optional*):
+ If True, the merge operation will be performed in a copy of the original weights and check for NaNs
+ before merging the weights. This is useful if you want to check if the merge operation will produce
+ NaNs. Defaults to `False`.
+ adapter_names (`list[str]`, *optional*):
+ The list of adapter names that should be merged. If None, all active adapters will be merged.
+ Defaults to `None`.
+ """
+ adapter_names = check_adapters_to_merge(self, adapter_names)
+ if not adapter_names:
+ # no adapter to merge
+ return
+
+ for active_adapter in adapter_names:
+ if active_adapter not in self.oft_R.keys():
+ continue
+
+ warnings.warn("Merge oft module to 4-bit linear may get different generations due to rounding errors.")
+ # Refer to https://gist.github.com/ChrisHayduk/1a53463331f52dca205e55982baf9930
+ weight = self.get_base_layer().weight
+ kwargs = weight.__dict__
+
+ output = dequantize_bnb_weight(weight, state=weight.quant_state)
+
+ oft_data = self.get_delta_weight(active_adapter)
+ output = torch.transpose(output, 0, 1)
+ w_data = torch.mm(oft_data, output.to(oft_data.dtype))
+ w_data = torch.transpose(w_data, 0, 1)
+ w_data = output.to(oft_data.dtype).to(oft_data.device)
+
+ if safe_merge and not torch.isfinite(w_data).all():
+ raise ValueError(
+ f"NaNs detected in the merged weights. The adapter {active_adapter} seems to be broken"
+ )
+
+ if "bnb_quantized" in kwargs:
+ kwargs["bnb_quantized"] = False
+ kwargs["requires_grad"] = False
+ kwargs.pop("data", None)
+ # torch.compile can introduce attributes preceded by '_', remove them
+ kwargs = {k: v for k, v in kwargs.items() if not k.startswith("_")}
+ self.get_base_layer().weight = bnb.nn.Params4bit(w_data.to("cpu"), **kwargs).to(weight.device)
+
+ self.merged_adapters.append(active_adapter)
+
+ def unmerge(self) -> None:
+ """
+ This method unmerges all merged adapter layers from the base weights.
+ """
+ if not self.merged:
+ warnings.warn("Already unmerged. Nothing to do.")
+ return
+
+ while len(self.merged_adapters) > 0:
+ active_adapter = self.merged_adapters.pop()
+ if active_adapter not in self.oft_R.keys():
+ continue
+ warnings.warn(
+ "Unmerge oft module to 4-bit linear may get different generations due to rounding errors."
+ )
+
+ weight = self.get_base_layer().weight
+ kwargs = weight.__dict__
+ output = dequantize_bnb_weight(weight, state=weight.quant_state)
+
+ oft_data = self.get_delta_weight(active_adapter)
+
+ output = torch.transpose(output, 0, 1)
+ w_data = torch.mm(oft_data.t(), output.to(oft_data.dtype))
+ w_data = torch.transpose(w_data, 0, 1)
+ w_data = output.to(oft_data.dtype).to(oft_data.device)
+
+ if "bnb_quantized" in kwargs:
+ kwargs["bnb_quantized"] = False
+ kwargs["requires_grad"] = False
+ kwargs.pop("data", None)
+ self.get_base_layer().weight = bnb.nn.Params4bit(w_data.to("cpu"), **kwargs).to(weight.device)
+
+ def get_delta_weight(self, adapter):
+ return self.oft_R[adapter].get_weight()
+
+ def forward(self, x: torch.Tensor, *args, **kwargs) -> torch.Tensor:
+ if self.disable_adapters:
+ if self.merged:
+ self.unmerge()
+ result = self.base_layer(x, *args, **kwargs)
+ elif self.merged:
+ result = self.base_layer(x, *args, **kwargs)
+ else:
+ # As per Tim Dettmers, for 4bit, we need to defensively clone here.
+ # The reason is that in some cases, an error can occur that backprop
+ # does not work on a manipulated view. This issue may be solved with
+ # newer PyTorch versions but this would need extensive testing to be
+ # sure.
+ # result = result.clone()
+
+ for active_adapter in self.active_adapters:
+ if active_adapter not in self.oft_R.keys():
+ continue
+ oft_R = self.oft_R[active_adapter]
+
+ requires_conversion = not torch.is_autocast_enabled()
+ if requires_conversion:
+ expected_dtype = x.dtype
+ x = self._cast_input_dtype(x, oft_R.weight.dtype)
+
+ x = oft_R(x)
+ if requires_conversion:
+ x = x.to(expected_dtype)
+
+ result = self.base_layer(x, *args, **kwargs)
+
+ return result
+
+ def __repr__(self) -> str:
+ rep = super().__repr__()
+ return "oft." + rep
+
+ def dispatch_bnb_4bit(target: torch.nn.Module, adapter_name: str, **kwargs):
+ new_module = None
+
+ if isinstance(target, BaseTunerLayer):
+ target_base_layer = target.get_base_layer()
+ else:
+ target_base_layer = target
+
+ loaded_in_4bit = kwargs.get("loaded_in_4bit", False)
+ if loaded_in_4bit and is_bnb_4bit_available() and isinstance(target_base_layer, bnb.nn.Linear4bit):
+ fourbit_kwargs = kwargs.copy()
+ fourbit_kwargs.update(
+ {
+ "compute_dtype": target_base_layer.compute_dtype,
+ "compress_statistics": target_base_layer.weight.compress_statistics,
+ "quant_type": target_base_layer.weight.quant_type,
+ }
+ )
+ new_module = Linear4bit(target, adapter_name, **fourbit_kwargs)
+
+ return new_module
diff --git a/peft/src/peft/tuners/oft/config.py b/peft/src/peft/tuners/oft/config.py
new file mode 100644
index 0000000000000000000000000000000000000000..4b33f13cb362a8eec851c5750e16bd50f109ddc6
--- /dev/null
+++ b/peft/src/peft/tuners/oft/config.py
@@ -0,0 +1,196 @@
+# Copyright 2023-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+from __future__ import annotations
+
+from dataclasses import dataclass, field
+from typing import Literal, Optional, Union
+
+from peft.config import PeftConfig
+from peft.utils import PeftType
+
+
+@dataclass
+class OFTConfig(PeftConfig):
+ """
+ This is the configuration class to store the configuration of a [`OFTModel`].
+
+ Args:
+ r (`int`): OFT rank, number of OFT blocks per injected layer.
+ oft_block_size (`int`): OFT block size across different layers.
+ module_dropout (`float`):
+ The multiplicative dropout probability, by setting OFT blocks to identity during training, similar to the
+ dropout layer in LoRA.
+ target_modules (`Optional[Union[list[str], str]]`):
+ The names of the modules to apply the adapter to. If this is specified, only the modules with the specified
+ names will be replaced. When passing a string, a regex match will be performed. When passing a list of
+ strings, either an exact match will be performed or it is checked if the name of the module ends with any
+ of the passed strings. If this is specified as 'all-linear', then all linear modules are chosen, excluding
+ the output layer. If this is not specified, modules will be chosen according to the model architecture. If
+ the architecture is not known, an error will be raised -- in this case, you should specify the target
+ modules manually.
+ fan_in_fan_out (`bool`): Set this to True if the layer to replace stores weight like (fan_in, fan_out).
+ bias (`str`): Bias type for OFT. Can be 'none', 'all' or 'oft_only'. If 'all' or 'oft_only', the
+ corresponding biases will be updated during training. Be aware that this means that, even when disabling
+ the adapters, the model will not produce the same output as the base model would have without adaptation.
+ exclude_modules (`Optional[Union[List[str], str]]`):
+ The names of the modules to not apply the adapter. When passing a string, a regex match will be performed.
+ When passing a list of strings, either an exact match will be performed or it is checked if the name of the
+ module ends with any of the passed strings.
+ init_weights (`bool`):
+ Whether to perform initialization of OFT weights.
+ layers_to_transform (`Union[List[int], int]`):
+ The layer indices to transform. If a list of ints is passed, it will apply the adapter to the layer indices
+ that are specified in this list. If a single integer is passed, it will apply the transformations on the
+ layer at this index.
+ layers_pattern (`Optional[Union[List[str], str]]`):
+ The layer pattern name, used only if `layers_to_transform` is different from `None`. This should target the
+ `nn.ModuleList` of the model, which is often called `'layers'` or `'h'`.
+ modules_to_save (`List[str]`):
+ List of modules apart from adapter layers to be set as trainable and saved in the final checkpoint.
+ coft (`bool`):
+ Whether to use the constrained variant of OFT or not, off by default.
+ eps (`float`):
+ The control strength of COFT. The freedom of rotation. Only has an effect if `coft` is set to True.
+ block_share (`bool`):
+ Whether to share the OFT parameters between blocks or not. This is `False` by default.
+ """
+
+ r: int = field(default=0, metadata={"help": "OFT rank, number of OFT blocks per injected layer."})
+ oft_block_size: int = field(
+ default=32,
+ metadata={
+ "help": "OFT block size across different layers.",
+ "note": "You can only specify either r or oft_block_size, but not both simultaneously, because r x oft_block_size = layer dimension.",
+ },
+ )
+ module_dropout: float = field(
+ default=0.0,
+ metadata={
+ "help": "OFT multiplicative dropout, randomly setting blocks of OFT to be identity matrix, similar to the dropout layer in LoRA."
+ },
+ )
+ target_modules: Optional[Union[list[str], str]] = field(
+ default=None,
+ metadata={
+ "help": "List of module names or regex expression of the module names to replace with OFT."
+ "For example, ['q', 'v'] or '.*decoder.*(SelfAttention|EncDecAttention).*(q|v)$' "
+ "This can also be a wildcard 'all-linear' which matches all linear/Conv1D layers except the output layer."
+ },
+ )
+ fan_in_fan_out: bool = field(
+ default=False,
+ metadata={"help": "Set this to True if the layer to replace stores weight like (fan_in, fan_out)"},
+ )
+ bias: Literal["none", "all", "oft_only"] = field(
+ default="none", metadata={"help": "Bias type for OFT. Can be 'none', 'all' or 'oft_only'"}
+ )
+ exclude_modules: Optional[Union[list[str], str]] = field(
+ default=None,
+ metadata={"help": "List of module names or regex expression of the module names to exclude from OFT."},
+ )
+ init_weights: bool = field(
+ default=True,
+ metadata={
+ "help": (
+ "Whether to initialize the weights of the OFT layers with their default initialization. Don't change "
+ "this setting, except if you know exactly what you're doing."
+ ),
+ },
+ )
+ layers_to_transform: Optional[Union[list[int], int]] = field(
+ default=None,
+ metadata={
+ "help": "The layer indexes to transform, is this argument is specified, PEFT will transform only the layers indexes that are specified inside this list. If a single integer is passed, PEFT will transform only the layer at this index."
+ },
+ )
+ layers_pattern: Optional[Union[list[str], str]] = field(
+ default=None,
+ metadata={
+ "help": "The layer pattern name, used only if `layers_to_transform` is different to None and if the layer pattern is not in the common layers pattern. "
+ "This should target the `nn.ModuleList` of the model, which is often called `'layers'` or `'h'`."
+ },
+ )
+ modules_to_save: Optional[list[str]] = field(
+ default=None,
+ metadata={
+ "help": "List of modules apart from OFT layers to be set as trainable and saved in the final checkpoint. "
+ "For example, in Sequence Classification or Token Classification tasks, "
+ "the final layer `classifier/score` are randomly initialized and as such need to be trainable and saved."
+ },
+ )
+ coft: bool = field(
+ default=False,
+ metadata={"help": "Whether to use the constrained variant of OFT or not."},
+ )
+ eps: float = field(
+ default=6e-5,
+ metadata={
+ "help": "The control strength of COFT. The freedom of rotation. Only has an effect if `coft` is set to True."
+ },
+ )
+ block_share: bool = field(
+ default=False,
+ metadata={"help": "Whether to share the OFT parameters between blocks or not."},
+ )
+ use_cayley_neumann: bool = field(
+ default=True,
+ metadata={
+ "help": "Whether to use the Cayley-Neumann Formulation of OFT or not. Set to True to improve computational efficiency but comes at costs of bigger approximation error for orthogonality."
+ },
+ )
+ num_cayley_neumann_terms: int = field(
+ default=5,
+ metadata={
+ "help": "Number of Cayley-Neumann terms to use. Higher number results in less approximation error for orthogonality."
+ },
+ )
+
+ def __post_init__(self):
+ super().__post_init__()
+ self.peft_type = PeftType.OFT
+ self.target_modules = (
+ set(self.target_modules) if isinstance(self.target_modules, list) else self.target_modules
+ )
+ self.exclude_modules = (
+ set(self.exclude_modules) if isinstance(self.exclude_modules, list) else self.exclude_modules
+ )
+ # check for layers_to_transform and layers_pattern
+ if self.layers_pattern and not self.layers_to_transform:
+ raise ValueError("When `layers_pattern` is specified, `layers_to_transform` must also be specified. ")
+ if self.r == 0 and self.oft_block_size == 0:
+ raise ValueError(
+ f"Either `r` or `oft_block_size` must be non-zero. Currently, r = {self.r} and oft_block_size = {self.oft_block_size}."
+ )
+ if not (self.r != 0) ^ (self.oft_block_size != 0):
+ raise ValueError(
+ f"You can only specify either r ({self.r}) or oft_block_size ({self.oft_block_size}), but not both simultaneously, because r x oft_block_size == in_features."
+ )
+
+ @classmethod
+ def check_kwargs(cls, **kwargs):
+ r"""
+ Check if the kwargs are valid for the configuration.
+
+ Args:
+ kwargs (additional keyword arguments, *optional*):
+ Additional keyword arguments passed along to the child class initialization.
+ """
+ if "oft_block_size" not in kwargs:
+ raise ValueError(
+ "OFT has been updated since PEFT 0.14.0. Your trained adapter weights are incompatible "
+ "with the latest version of OFT. Please retrain your adapter weights with newer PEFT versions. "
+ "Alternatively, downgrade PEFT to version 0.13.0 to use the old adapter weights."
+ )
+ return super().check_kwargs(**kwargs)
diff --git a/peft/src/peft/tuners/oft/eetq.py b/peft/src/peft/tuners/oft/eetq.py
new file mode 100644
index 0000000000000000000000000000000000000000..2d6538165a4f040617e68ff1bceca494f112c3e5
--- /dev/null
+++ b/peft/src/peft/tuners/oft/eetq.py
@@ -0,0 +1,116 @@
+# Copyright 2024-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+from typing import Any, Optional
+
+import torch
+
+from peft.import_utils import is_eetq_available
+from peft.tuners.oft.layer import OFTLayer
+from peft.tuners.tuners_utils import BaseTunerLayer
+
+
+if is_eetq_available():
+ from eetq import EetqLinear
+
+ class EetqOFTLinear(torch.nn.Module, OFTLayer):
+ def __init__(
+ self,
+ base_layer,
+ adapter_name,
+ r: int = 0,
+ oft_block_size: int = 0,
+ module_dropout: float = 0.0,
+ init_weights: bool = True,
+ coft: bool = False,
+ eps: float = 6e-5,
+ block_share: bool = False,
+ use_cayley_neumann: bool = False,
+ num_cayley_neumann_terms: int = 5,
+ fan_in_fan_out: bool = False,
+ **kwargs,
+ ):
+ super().__init__()
+ OFTLayer.__init__(self, base_layer)
+
+ # self.base_layer and self.quant_linear_module are the same; we need the former for consistency and the latter
+ # for backwards compatibility
+ self.quant_linear_module = base_layer
+
+ self._active_adapter = adapter_name
+ self.update_layer(
+ adapter_name,
+ r,
+ oft_block_size=oft_block_size,
+ module_dropout=module_dropout,
+ init_weights=init_weights,
+ coft=coft,
+ eps=eps,
+ block_share=block_share,
+ fan_in_fan_out=fan_in_fan_out,
+ use_cayley_neumann=use_cayley_neumann,
+ num_cayley_neumann_terms=num_cayley_neumann_terms,
+ )
+
+ def forward(self, x: torch.Tensor):
+ if self.disable_adapters:
+ return self.quant_linear_module(x)
+
+ for active_adapter in self.active_adapters:
+ if active_adapter not in self.oft_R.keys():
+ continue
+ oft_R = self.oft_R[active_adapter]
+
+ requires_conversion = not torch.is_autocast_enabled()
+ if requires_conversion:
+ expected_dtype = x.dtype
+ x = self._cast_input_dtype(x, oft_R.weight.dtype)
+
+ x = oft_R(x)
+
+ result = self.quant_linear_module(x)
+ if requires_conversion:
+ result = result.to(expected_dtype)
+ return result
+
+ def merge(self, safe_merge: bool = False, adapter_names: Optional[list[str]] = None) -> None:
+ raise AttributeError("Merging LoRA layers is not supported for Eetq layers.")
+
+ def unmerge(self) -> None:
+ raise AttributeError("Unmerging LoRA layers is not supported for Eetq layers.")
+
+ def __repr__(self) -> str:
+ rep = super().__repr__()
+ return "oft." + rep
+
+
+def dispatch_eetq(
+ target: torch.nn.Module,
+ adapter_name: str,
+ **kwargs: Any,
+) -> Optional[torch.nn.Module]:
+ new_module = None
+
+ if isinstance(target, BaseTunerLayer):
+ target_base_layer = target.get_base_layer()
+ else:
+ target_base_layer = target
+
+ if is_eetq_available() and isinstance(target_base_layer, EetqLinear):
+ new_module = EetqOFTLinear(target, adapter_name, **kwargs)
+ target.weight = target_base_layer.weight
+
+ if hasattr(target, "bias"):
+ target.bias = target_base_layer.bias
+
+ return new_module
diff --git a/peft/src/peft/tuners/oft/gptq.py b/peft/src/peft/tuners/oft/gptq.py
new file mode 100644
index 0000000000000000000000000000000000000000..e64c1319522a94f366149ca4cb028cfc918bd124
--- /dev/null
+++ b/peft/src/peft/tuners/oft/gptq.py
@@ -0,0 +1,118 @@
+# Copyright 2023-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+from typing import Any, Optional
+
+import torch
+
+from peft.import_utils import is_gptqmodel_available
+from peft.tuners.oft.layer import OFTLayer
+from peft.tuners.tuners_utils import BaseTunerLayer
+from peft.utils import get_auto_gptq_quant_linear
+
+
+class GPTQOFTLinear(torch.nn.Module, OFTLayer):
+ def __init__(
+ self,
+ base_layer,
+ adapter_name: str,
+ r: int = 8,
+ oft_block_size: int = 0,
+ module_dropout: float = 0.0,
+ coft: bool = False,
+ eps: float = 6e-5,
+ block_share: bool = False,
+ use_cayley_neumann: bool = False,
+ num_cayley_neumann_terms: int = 5,
+ fan_in_fan_out: bool = False, # Set this to True if the layer to replace stores weight like (fan_in, fan_out)
+ init_weights: bool = True,
+ **kwargs,
+ ):
+ super().__init__()
+ OFTLayer.__init__(self, base_layer)
+
+ # self.base_layer and self.quant_linear_module are the same; we need the former for consistency and the latter
+ # for backwards compatibility
+ self.quant_linear_module = base_layer
+ self._active_adapter = adapter_name
+ self.update_layer(
+ adapter_name,
+ r,
+ oft_block_size=oft_block_size,
+ module_dropout=module_dropout,
+ coft=coft,
+ eps=eps,
+ block_share=block_share,
+ init_weights=init_weights,
+ use_cayley_neumann=use_cayley_neumann,
+ num_cayley_neumann_terms=num_cayley_neumann_terms,
+ )
+
+ def forward(self, x: torch.Tensor):
+ # note: logic differs from default Linear because merging is not supported
+ result = self.quant_linear_module(x)
+
+ if self.disable_adapters:
+ return self.quant_linear_module(x)
+
+ for active_adapter in self.active_adapters:
+ if active_adapter not in self.oft_R.keys():
+ continue
+
+ oft_R = self.oft_R[active_adapter]
+
+ requires_conversion = not torch.is_autocast_enabled()
+ if requires_conversion:
+ expected_dtype = x.dtype
+ x = self._cast_input_dtype(x, oft_R.weight.dtype)
+
+ x = oft_R(x)
+
+ result = self.quant_linear_module(x)
+ if requires_conversion:
+ result = result.to(expected_dtype)
+ return result
+
+ def __repr__(self) -> str:
+ rep = super().__repr__()
+ return "oft." + rep
+
+
+def dispatch_gptq(
+ target: torch.nn.Module,
+ adapter_name: str,
+ **kwargs: Any,
+) -> Optional[torch.nn.Module]:
+ new_module = None
+
+ if isinstance(target, BaseTunerLayer):
+ target_base_layer = target.get_base_layer()
+ else:
+ target_base_layer = target
+
+ cfg = kwargs.get("gptq_quantization_config", None)
+
+ if is_gptqmodel_available():
+ from gptqmodel.nn_modules.qlinear import BaseQuantLinear
+
+ if isinstance(target_base_layer, BaseQuantLinear):
+ new_module = GPTQOFTLinear(target, adapter_name, **kwargs)
+ target.qweight = target_base_layer.qweight
+ else:
+ quant_linear = get_auto_gptq_quant_linear(cfg)
+
+ if quant_linear is not None and isinstance(target_base_layer, quant_linear):
+ new_module = GPTQOFTLinear(target, adapter_name, **kwargs)
+ target.qweight = target_base_layer.qweight
+
+ return new_module
diff --git a/peft/src/peft/tuners/oft/hqq.py b/peft/src/peft/tuners/oft/hqq.py
new file mode 100644
index 0000000000000000000000000000000000000000..5f83dd11b0bb4f4c349dd1beb95733b5e617c158
--- /dev/null
+++ b/peft/src/peft/tuners/oft/hqq.py
@@ -0,0 +1,186 @@
+# Copyright 2024-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+from __future__ import annotations
+
+import copy
+import warnings
+from typing import Optional
+
+import torch
+
+from peft.import_utils import is_hqq_available
+from peft.tuners.tuners_utils import BaseTunerLayer, check_adapters_to_merge
+
+from .layer import OFTLayer
+
+
+if is_hqq_available():
+ from hqq.core.quantize import HQQLinear
+
+ class HqqOFTLinear(torch.nn.Module, OFTLayer):
+ # Lora implemented in a dense layer
+ def __init__(
+ self,
+ base_layer: torch.nn.Module,
+ adapter_name: str,
+ r: int = 8,
+ oft_block_size: int = 0,
+ module_dropout: float = 0.0,
+ init_weights: bool = True,
+ coft: bool = False,
+ eps: float = 6e-5,
+ block_share: bool = False,
+ use_cayley_neumann: bool = False,
+ num_cayley_neumann_terms: int = 5,
+ **kwargs,
+ ) -> None:
+ super().__init__()
+ OFTLayer.__init__(self, base_layer)
+ self.fan_in_fan_out = False
+
+ self._active_adapter = adapter_name
+ self.update_layer(
+ adapter_name,
+ r,
+ oft_block_size=oft_block_size,
+ module_dropout=module_dropout,
+ init_weights=init_weights,
+ coft=coft,
+ eps=eps,
+ block_share=block_share,
+ use_cayley_neumann=use_cayley_neumann,
+ num_cayley_neumann_terms=num_cayley_neumann_terms,
+ )
+
+ def merge(self, safe_merge: bool = False, adapter_names: Optional[list[str]] = None) -> None:
+ """
+ Merge the active adapter weights into the base weights
+
+ Args:
+ safe_merge (`bool`, *optional*):
+ If True, the merge operation will be performed in a copy of the original weights and check for NaNs
+ before merging the weights. This is useful if you want to check if the merge operation will produce
+ NaNs. Defaults to `False`.
+ adapter_names (`list[str]`, *optional*):
+ The list of adapter names that should be merged. If None, all active adapters will be merged.
+ Defaults to `None`.
+ """
+ adapter_names = check_adapters_to_merge(self, adapter_names)
+ if not adapter_names:
+ # no adapter to merge
+ return
+
+ for active_adapter in adapter_names:
+ if active_adapter not in self.lora_A.keys():
+ continue
+
+ layer = self.get_base_layer()
+ quant_config = {**copy.deepcopy(layer.quant_config), "offload_meta": layer.offload_meta}
+
+ output = layer.dequantize()
+ oft_data = self.get_delta_weight(active_adapter)
+
+ output = torch.transpose(output, 0, 1)
+ w_data = torch.mm(oft_data, output.to(oft_data.dtype))
+ w_data = torch.transpose(w_data, 0, 1)
+ w_data = output.to(oft_data.dtype).to(oft_data.device)
+
+ if safe_merge and not torch.isfinite(w_data).all():
+ raise ValueError(
+ f"NaNs detected in the merged weights. The adapter {active_adapter} seems to be broken"
+ )
+
+ new_hqq_layer = HQQLinear(None, quant_config, compute_dtype=layer.compute_dtype, device=layer.device)
+ quant_config.pop("offload_meta", None)
+ new_hqq_layer.quantize(w_data, **quant_config)
+ self.base_layer = new_hqq_layer
+ self.merged_adapters.append(active_adapter)
+
+ def unmerge(self) -> None:
+ """
+ This method unmerges all merged adapter layers from the base weights.
+ """
+ if not self.merged:
+ warnings.warn("Already unmerged. Nothing to do.")
+ return
+
+ while len(self.merged_adapters) > 0:
+ active_adapter = self.merged_adapters.pop()
+ if active_adapter not in self.oft_R.keys():
+ continue
+
+ layer = self.get_base_layer()
+ quant_config = {**copy.deepcopy(layer.quant_config), "offload_meta": layer.offload_meta}
+ output = layer.dequantize()
+
+ oft_data = self.get_delta_weight(active_adapter)
+
+ output = torch.transpose(output, 0, 1)
+ w_data = torch.mm(oft_data.t(), output.to(oft_data.dtype))
+ w_data = torch.transpose(w_data, 0, 1)
+ w_data = w_data.to(oft_data.dtype).to(oft_data.device)
+
+ new_hqq_layer = HQQLinear(None, quant_config, compute_dtype=layer.compute_dtype, device=layer.device)
+ quant_config.pop("offload_meta", None)
+ new_hqq_layer.quantize(w_data, **quant_config)
+ self.base_layer = new_hqq_layer
+
+ def get_delta_weight(self, adapter):
+ return self.oft_R[adapter].get_weight()
+
+ def forward(self, x: torch.Tensor, *args, **kwargs) -> torch.Tensor:
+ self._check_forward_args(x, *args, **kwargs)
+ adapter_names = kwargs.pop("adapter_names", None)
+
+ if self.disable_adapters:
+ if self.merged:
+ self.unmerge()
+ result = self.base_layer(x, *args, **kwargs)
+ elif self.merged:
+ result = self.base_layer(x, *args, **kwargs)
+ else:
+ for active_adapter in self.active_adapters:
+ if active_adapter not in self.oft_R.keys():
+ continue
+ oft_R = self.oft_R[active_adapter]
+
+ requires_conversion = not torch.is_autocast_enabled()
+ if requires_conversion:
+ expected_dtype = x.dtype
+ x = self._cast_input_dtype(x, oft_R.weight.dtype)
+
+ x = oft_R(x)
+
+ result = self.base_layer(x, *args, **kwargs)
+ if requires_conversion:
+ result = result.to(expected_dtype)
+ return result
+
+ def __repr__(self) -> str:
+ rep = super().__repr__()
+ return "oft." + rep
+
+
+def dispatch_hqq(target: torch.nn.Module, adapter_name: str, **kwargs):
+ new_module = None
+
+ if isinstance(target, BaseTunerLayer):
+ target_base_layer = target.get_base_layer()
+ else:
+ target_base_layer = target
+
+ if is_hqq_available() and isinstance(target_base_layer, HQQLinear):
+ new_module = HqqOFTLinear(target_base_layer, adapter_name, **kwargs)
+
+ return new_module
diff --git a/peft/src/peft/tuners/oft/inc.py b/peft/src/peft/tuners/oft/inc.py
new file mode 100644
index 0000000000000000000000000000000000000000..6ed855bc7dc65af10d77a2f486abb8fc27c12dd5
--- /dev/null
+++ b/peft/src/peft/tuners/oft/inc.py
@@ -0,0 +1,78 @@
+# Copyright 2025-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+# NOTE: PEFT tests related to INC are handled under Optimum-Habana repository:
+# - LLMs: https://github.com/huggingface/optimum-habana/blob/main/tests/test_peft_inference.py
+# - Diffusers: https://github.com/huggingface/optimum-habana/blob/main/tests/test_diffusers.py
+
+from typing import Optional
+
+import torch
+
+from peft.import_utils import is_inc_available
+from peft.tuners.tuners_utils import BaseTunerLayer
+
+from .layer import Linear
+
+
+if is_inc_available():
+
+ class IncOFTLinear(Linear):
+ def __init__(
+ self,
+ base_layer: torch.nn.Module,
+ adapter_name: str,
+ **kwargs,
+ ):
+ super().__init__(base_layer, adapter_name, **kwargs)
+
+ def merge(self, safe_merge: bool = False, adapter_names: Optional[list[str]] = None) -> None:
+ """
+ Merge the active adapter weights into the base weights
+
+ Args:
+ safe_merge (`bool`, *optional*):
+ If True, the merge operation will be performed in a copy of the original weights and check for NaNs
+ before merging the weights. This is useful if you want to check if the merge operation will produce
+ NaNs. Defaults to `False`.
+ adapter_names (`list[str]`, *optional*):
+ The list of adapter names that should be merged. If None, all active adapters will be merged.
+ Defaults to `None`.
+ """
+ raise NotImplementedError("Merging OFT with INC layers is not yet implemented")
+
+ def unmerge(self) -> None:
+ """
+ This method unmerges all merged adapter layers from the base weights.
+ """
+ raise NotImplementedError("Unmerging OFT from INC layers is not yet implemented")
+
+
+def dispatch_inc(target: torch.nn.Module, adapter_name: str, **kwargs):
+ new_module = None
+
+ if isinstance(target, BaseTunerLayer):
+ target_base_layer = target.get_base_layer()
+ else:
+ target_base_layer = target
+
+ if is_inc_available():
+ from neural_compressor.torch.algorithms.fp8_quant._quant_common.helper_modules import (
+ PatchedLinear,
+ )
+
+ if isinstance(target_base_layer, PatchedLinear):
+ new_module = IncOFTLinear(target, adapter_name, **kwargs)
+
+ return new_module
diff --git a/peft/src/peft/tuners/oft/layer.py b/peft/src/peft/tuners/oft/layer.py
new file mode 100644
index 0000000000000000000000000000000000000000..6b14d015ae9b98f5baf34f5d4ba343a4900c32b4
--- /dev/null
+++ b/peft/src/peft/tuners/oft/layer.py
@@ -0,0 +1,938 @@
+# Copyright 2023-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+from __future__ import annotations
+
+import warnings
+from typing import Any, Optional, Union
+
+import torch
+import torch.nn as nn
+import torch.nn.functional as F
+
+from peft.tuners.tuners_utils import BaseTunerLayer, check_adapters_to_merge
+
+from .config import OFTConfig
+
+
+class MultiplicativeDropoutLayer(nn.Module):
+ """
+ Implements the multiplicative dropout layer for OFT.
+ """
+
+ def __init__(self, p=0.0):
+ """
+ Initializes the multiplicative dropout layer.
+
+ Parameters:
+ p (float): The probability of dropping out a block. Defaults to 0.0.
+ """
+ super().__init__()
+ self.p = p
+
+ def forward(self, x):
+ """
+ Applies multiplicative dropout to the input tensor.
+
+ Parameters:
+ x (Tensor): The input tensor of shape (D, H, H), where `D` represents
+ the number of OFT blocks, and `H` is the size of the square blocks along the last two dimensions,
+ the block size in OFT.
+ """
+ if self.training and self.p > 0:
+ # Ensure the last two dimensions are the same
+ if x.shape[-1] != x.shape[-2]:
+ raise ValueError("The last two dimensions of input should be the same!")
+
+ D, H, _ = x.shape
+
+ # If block share, skip the multiplicative dropout
+ if D == 1:
+ return x
+
+ num_to_replace = int(self.p * D)
+ num_zeros = D - num_to_replace
+ mask = torch.cat([torch.ones(num_to_replace, device=x.device), torch.zeros(num_zeros, device=x.device)])
+ mask = mask[torch.randperm(D)].view(D, 1, 1)
+ eye_matrix = torch.eye(H, device=x.device).repeat(D, 1, 1)
+ x = (1 - mask) * x + mask * eye_matrix
+ return x
+
+
+class OFTRotationModule(nn.Module):
+ def __init__(
+ self,
+ r,
+ n_elements,
+ block_size,
+ in_features,
+ coft=False,
+ eps=6e-5,
+ block_share=False,
+ kernel_size=(0, 0),
+ use_cayley_neumann=True,
+ num_cayley_neumann_terms=5,
+ ):
+ super().__init__()
+ self.r = r
+ self.n_elements = n_elements
+ self.block_size = block_size
+ self.in_features = in_features
+ self.weight = nn.Parameter(torch.empty(r, n_elements))
+ self.coft = coft
+ self.eps = eps
+ self.block_share = block_share
+ # Conv2d specific parameters
+ self.kernel_size = kernel_size
+ self.use_cayley_neumann = use_cayley_neumann
+ self.num_cayley_neumann_terms = num_cayley_neumann_terms
+ # Create indices for upper triangle (excluding diagonal)
+ self.rows, self.cols = torch.triu_indices(block_size, block_size, 1)
+
+ def _pytorch_skew_symmetric(self, vec, block_size):
+ batch_size = vec.shape[0]
+ matrix = torch.zeros(batch_size, block_size, block_size, device=vec.device, dtype=vec.dtype)
+
+ matrix[:, self.rows, self.cols] = vec
+ matrix = matrix - matrix.transpose(-2, -1)
+ return matrix
+
+ def _pytorch_skew_symmetric_inv(self, matrix, block_size):
+ batch_size = matrix.shape[0]
+
+ # Extract the upper triangular elements
+ vec = matrix[:, self.rows, self.cols]
+ return vec
+
+ def _cayley_batch(
+ self, Q: torch.Tensor, block_size: int, use_cayley_neumann: bool = True, num_neumann_terms: int = 5
+ ) -> torch.Tensor:
+ """
+ Perform the Cayley parametrization on a batch of skew-symmetric matrices.
+
+ Args:
+ data: A batch of skew-symmetric matrices of shape (b, r, c).
+ """
+
+ b, _ = Q.shape
+ previous_dtype = Q.dtype
+
+ # Q_skew = SkewSymmetric.apply(Q, block_size)
+ Q_skew = self._pytorch_skew_symmetric(Q, block_size)
+
+ if use_cayley_neumann:
+ R = torch.eye(block_size, device=Q.device, dtype=Q.dtype).repeat(b, 1, 1)
+ if num_neumann_terms > 1:
+ R.add_(Q_skew, alpha=2.0)
+ if num_neumann_terms > 2:
+ Q_squared = torch.bmm(Q_skew, Q_skew)
+ R.add_(Q_squared, alpha=2.0)
+
+ Q_power = Q_squared
+ for i in range(3, num_neumann_terms):
+ Q_power = torch.bmm(Q_power, Q_skew)
+ R.add_(Q_power, alpha=2.0)
+ else:
+ id_mat = (
+ torch.eye(Q_skew.shape[-1], device=Q_skew.device)
+ .unsqueeze(0)
+ .expand(b, Q_skew.shape[-1], Q_skew.shape[-1])
+ )
+ R = torch.linalg.solve(id_mat + Q_skew, id_mat - Q_skew, left=False)
+
+ return R.to(previous_dtype)
+
+ # Copied from https://github.com/Zeju1997/oft/blob/84cebb965df69781e3d9c3c875f5980b421eaf24/oft-control/oft.py#L52
+ def _project_batch(self, Q, eps=1e-5):
+ oft_R = self._pytorch_skew_symmetric(Q, self.block_size)
+ # scaling factor for each of the smaller block matrix
+ eps = eps * 1 / torch.sqrt(torch.tensor(oft_R.shape[0]))
+ I = ( # noqa: E741
+ torch.zeros((oft_R.size(1), oft_R.size(1)), device=oft_R.device, dtype=oft_R.dtype)
+ .unsqueeze(0)
+ .expand_as(oft_R)
+ )
+ diff = oft_R - I
+ norm_diff = torch.norm(oft_R - I, dim=(1, 2), keepdim=True)
+ mask = (norm_diff <= eps).bool()
+ out = torch.where(mask, oft_R, I + eps * (diff / norm_diff))
+
+ return self._pytorch_skew_symmetric_inv(out, self.block_size)
+
+ # Copied from https://github.com/Zeju1997/oft/blob/84cebb965df69781e3d9c3c875f5980b421eaf24/oft-control/oft.py#L155
+ def _block_diagonal(self, oft_R: torch.Tensor, rank: int) -> torch.Tensor:
+ if oft_R.shape[0] == 1:
+ # block share
+ blocks = [oft_R[0, ...] for i in range(rank)]
+ else:
+ blocks = [oft_R[i, ...] for i in range(rank)]
+
+ # Use torch.block_diag to create the block diagonal matrix
+ A = torch.block_diag(*blocks)
+
+ return A
+
+ def _unfold(self, x):
+ """
+ Unfold with stride=1, padding=0 to preserve spatial dimensions. Only use kernel_size from base layer to define
+ patch size.
+ """
+ batch_size, in_channels, in_height, in_width = x.shape
+
+ if isinstance(self.kernel_size, int):
+ kernel_height, kernel_width = self.kernel_size, self.kernel_size
+ else:
+ kernel_height, kernel_width = self.kernel_size
+
+ stride_h = stride_w = 1
+ pad_h = pad_w = 0
+
+ # output dimensions
+ out_height = (in_height + 2 * pad_h - kernel_height) // stride_h + 1
+ out_width = (in_width + 2 * pad_w - kernel_width) // stride_w + 1
+
+ # Reshape input from [B, C, H, W] to [B, C, H_out, W_out, K_H, K_W]
+ x_unfolded = x.unfold(2, kernel_height, stride_h).unfold(3, kernel_width, stride_w)
+ x_unfolded = x_unfolded.permute(0, 2, 3, 1, 4, 5).contiguous()
+ x_unfolded = x_unfolded.view(batch_size * out_height * out_width, -1)
+
+ return x_unfolded
+
+ def _fold(self, x_unfolded, orig_shape):
+ """
+ Fold back to preserve spatial dimensions.
+ """
+ batch_size, in_channels, in_height, in_width = orig_shape
+
+ if isinstance(self.kernel_size, int):
+ kernel_height, kernel_width = self.kernel_size, self.kernel_size
+ else:
+ kernel_height, kernel_width = self.kernel_size
+
+ # With stride=1, padding=0:
+ out_height = in_height - kernel_height + 1
+ out_width = in_width - kernel_width + 1
+
+ # Reshape: [B*H_out*W_out, C*K_H*K_W] -> [B, H_out, W_out, C, K_H, K_W]
+ x_reshaped = x_unfolded.view(batch_size, out_height, out_width, in_channels, kernel_height, kernel_width)
+
+ # Permute to: [B, C, H_out, W_out, K_H, K_W]
+ x_reshaped = x_reshaped.permute(0, 3, 1, 2, 4, 5).contiguous()
+
+ # Use F.fold to reconstruct 4D tensor
+ x_folded = F.fold(
+ x_reshaped.view(batch_size, in_channels * kernel_height * kernel_width, out_height * out_width),
+ output_size=(in_height, in_width),
+ kernel_size=(kernel_height, kernel_width),
+ stride=(1, 1),
+ )
+
+ return x_folded
+
+ def forward(self, x):
+ # This module doesn't need to implement the orthogonal transform
+ # It's primarily a container for the parameter
+ # The actual transformation logic stays in your OFTLayer
+
+ required_dtype = x.dtype
+ if required_dtype != self.weight.dtype:
+ x = x.to(self.weight.dtype)
+
+ orig_shape = x.shape
+
+ if self.coft:
+ with torch.no_grad():
+ self.weight.copy_(self._project_batch(self.weight, eps=self.eps))
+
+ orth_rotate = self._cayley_batch(
+ self.weight, self.block_size, self.use_cayley_neumann, self.num_cayley_neumann_terms
+ )
+
+ # Unfold the input for Conv2d layer
+ if len(orig_shape) == 4:
+ x = self._unfold(x)
+
+ folded_shape = x.shape
+ rank = self.in_features // self.block_size if self.block_share else self.r
+ batch_dims = x.shape[:-1]
+ x_reshaped = x.reshape(*batch_dims, rank, self.block_size)
+
+ if self.block_share:
+ orth_rotate = orth_rotate.repeat(rank, 1, 1)
+ x_rotated_reshaped = torch.einsum("...rk,rkc->...rc", x_reshaped, orth_rotate)
+ else:
+ x_rotated_reshaped = torch.einsum("...rk,rkc->...rc", x_reshaped, orth_rotate)
+
+ x_rotated = x_rotated_reshaped.reshape(*folded_shape)
+
+ if len(orig_shape) == 4:
+ x_rotated = self._fold(x_rotated, orig_shape)
+
+ return x_rotated.to(required_dtype)
+
+ def get_weight(self):
+ """
+ Compute the delta weight for the given adapter.
+
+ Args:
+ adapter (str):
+ The name of the adapter for which the delta weight should be computed.
+ """
+ weight = self.weight
+
+ if self.coft:
+ with torch.no_grad():
+ weight = self._project_batch(weight, eps=self.eps)
+ self.weight.copy_(weight)
+
+ orth_rotate = self._cayley_batch(
+ weight, self.block_size, self.use_cayley_neumann, self.num_cayley_neumann_terms
+ )
+
+ rank = self.r if not self.block_share else self.in_features // self.block_size
+ return self._block_diagonal(orth_rotate, rank)
+
+
+class OFTLayer(BaseTunerLayer):
+ """
+ Implements the OFT layer.
+ """
+
+ # All names of layers that may contain (trainable) adapter weights
+ adapter_layer_names: tuple[str, ...] = ("oft_R",)
+ # All names of other parameters that may contain adapter-related parameters
+ other_param_names: tuple[str, ...] = ("r", "oft_block_size", "oft_dropout")
+
+ def __init__(self, base_layer: nn.Module, **kwargs) -> None:
+ """
+ Initializes the OFT layer.
+
+ Note, currently only support linear layer and convolutional layer, with further support for other layers to be
+ added soon.
+
+ Parameters:
+ base_layer: the pretrained model layer
+ """
+ self.base_layer = base_layer
+ self.oft_R = nn.ModuleDict({})
+ self.oft_block_size = {}
+ self.r = {}
+ self.oft_block_size = {}
+ self.oft_dropout = nn.ModuleDict({})
+ # Mark the weight as unmerged
+ self._disable_adapters = False
+ self.merged_adapters = []
+ # flag to enable/disable casting of input to weight dtype during forward call
+ self.cast_input_dtype_enabled = True
+ self.kwargs = kwargs
+
+ base_layer = self.get_base_layer()
+ if isinstance(base_layer, nn.Linear):
+ in_features, out_features = base_layer.in_features, base_layer.out_features
+ elif isinstance(base_layer, nn.Conv2d):
+ in_features, out_features = base_layer.in_channels, base_layer.out_channels
+ elif hasattr(base_layer, "infeatures") and hasattr(base_layer, "outfeatures"):
+ # QuantLinear
+ in_features, out_features = base_layer.infeatures, base_layer.outfeatures
+ elif hasattr(base_layer, "input_size") and hasattr(base_layer, "output_size"):
+ # Megatron ColumnParallelLinear,RowParallelLinear
+ in_features, out_features = base_layer.input_size, base_layer.output_size
+ elif hasattr(base_layer, "codebooks") and base_layer.__class__.__name__ == "QuantizedLinear":
+ # AQLM QuantLinear
+ in_features, out_features = base_layer.in_features, base_layer.out_features
+ elif hasattr(base_layer, "w_bit") and base_layer.__class__.__name__ == "WQLinear_GEMM":
+ # Awq layers
+ in_features, out_features = base_layer.in_features, base_layer.out_features
+ elif base_layer.__class__.__name__ == "EetqLinear":
+ # Eetq layers
+ in_features, out_features = base_layer.in_features, base_layer.out_features
+ elif hasattr(base_layer, "W_q") and base_layer.__class__.__name__ == "HQQLinear":
+ # HQQ layers
+ in_features, out_features = base_layer.in_features, base_layer.out_features
+ else:
+ # possibly support user provided custom layer types using dynamic dispatch
+ if hasattr(base_layer, "in_features") and hasattr(base_layer, "out_features"):
+ in_features, out_features = base_layer.in_features, base_layer.out_features
+ else:
+ in_features, out_features = None, None
+ warnings.warn(
+ f"Unsupported layer type '{type(base_layer)}' encountered, proceed at your own risk.", UserWarning
+ )
+
+ self.in_features = in_features
+ self.out_features = out_features
+
+ @property
+ def _available_adapters(self) -> set[str]:
+ return {*self.oft_R}
+
+ def set_scale(self, adapter, scale):
+ if adapter not in self.scaling:
+ # Ignore the case where the adapter is not in the layer
+ return
+
+ warnings.warn("Scaling operation for OFT not supported! Automatically set scale to 1.")
+
+ def scale_layer(self, scale: float) -> None:
+ if scale == 1:
+ return
+
+ for active_adapter in self.active_adapters:
+ if active_adapter not in self.oft_R.keys():
+ continue
+
+ warnings.warn("Scaling operation for OFT not supported! Automatically set scale to 1.")
+
+ def unscale_layer(self, scale=None) -> None:
+ for active_adapter in self.active_adapters:
+ if active_adapter not in self.oft_R.keys():
+ continue
+
+ warnings.warn("Unscaling operation for OFT not supported! Keeping scale to 1.")
+
+ def update_layer(
+ self,
+ adapter_name,
+ r,
+ oft_block_size,
+ module_dropout,
+ coft,
+ eps,
+ block_share,
+ init_weights,
+ use_cayley_neumann,
+ num_cayley_neumann_terms,
+ inference_mode: bool = False,
+ **kwargs,
+ ):
+ """
+ Update the linear layer with trainable OFT weights. Override for other layer types.
+ """
+ """Internal function to create oft adapter
+
+ Args:
+ adapter_name (`str`): Name for the adapter to add.
+ r (`int`): Rank for the added adapter.
+ oft_block_size (`int`): The block size for added adapter.
+ module_dropout (`float`):
+ The multiplicative dropout probability for disabling adapter blocks during training.
+ coft (`bool`): Whether to use the constrained variant of OFT or not.
+ eps (`float`):
+ The control strength of COFT. The freedom of rotation. Only has an effect if `coft` is set to True.
+ block_share (`bool`): Whether to share the OFT parameters between blocks or not.
+ init_weights (`bool`): Whether to initialize weights.
+ """
+ # Initialize the MultiplicativeDropoutLayer for module_dropout > 0.0.
+ if module_dropout > 0.0:
+ oft_dropout_layer = MultiplicativeDropoutLayer(p=module_dropout)
+ else:
+ oft_dropout_layer = nn.Identity()
+ self.oft_dropout.update(nn.ModuleDict({adapter_name: oft_dropout_layer}))
+
+ if r == 0 and oft_block_size != 0:
+ if self.in_features % oft_block_size != 0 or oft_block_size > self.in_features:
+ old_oft_block_size = oft_block_size
+ oft_block_size = self.adjust_oft_parameters(self.in_features, oft_block_size)
+ warnings.warn(
+ f"Invalid `oft_block_size` ({old_oft_block_size})! Adjusted `oft_block_size` to ({oft_block_size})."
+ )
+ r = int(self.in_features // oft_block_size)
+ elif r != 0 and oft_block_size == 0:
+ if self.in_features % r != 0 or r > self.in_features:
+ old_r = r
+ r = self.adjust_oft_parameters(self.in_features, r)
+ warnings.warn(f"Invalid `r` ({old_r})! Adjusted `r` to ({r}).")
+ oft_block_size = int(self.in_features // r)
+ else:
+ raise ValueError(
+ "Something went wrong, please report this error: https://github.com/huggingface/peft/issues"
+ )
+
+ # Create weights with provided shape
+ n_elements = oft_block_size * (oft_block_size - 1) // 2
+ self.oft_R[adapter_name] = OFTRotationModule(
+ r if not block_share else 1,
+ n_elements,
+ oft_block_size,
+ self.in_features,
+ coft=coft,
+ eps=eps,
+ block_share=block_share,
+ use_cayley_neumann=use_cayley_neumann,
+ num_cayley_neumann_terms=num_cayley_neumann_terms,
+ )
+
+ # Initialize weights
+ self.reset_oft_parameters(adapter_name, init_weights)
+
+ # set oft r and block size
+ self.r[adapter_name] = r
+ self.oft_block_size[adapter_name] = oft_block_size
+
+ # Move new weights to device
+ self._move_adapter_to_device_of_base_layer(adapter_name)
+ self.set_adapter(self.active_adapters, inference_mode=inference_mode)
+
+ def reset_oft_parameters(self, adapter_name, init_weights):
+ """
+ Reset the OFT parameters.
+ """
+ if init_weights is False:
+ nn.init.normal_(self.oft_R[adapter_name].weight, mean=0.0, std=0.1)
+ return
+
+ if adapter_name in self.oft_R.keys():
+ if init_weights is True:
+ # initialize oft_R to zero
+ nn.init.zeros_(self.oft_R[adapter_name].weight)
+ else:
+ raise ValueError(f"Unknown initialization {init_weights=}")
+
+ def adjust_oft_parameters(self, in_features, params):
+ """
+ Adjust the OFT parameters to be divisible by the in_features dimension.
+ """
+ if params < in_features:
+ higher_params = params
+ while higher_params <= in_features and in_features % higher_params != 0:
+ higher_params += 1
+ else:
+ return in_features
+
+ lower_params = params
+ while lower_params > 1 and in_features % lower_params != 0:
+ lower_params -= 1
+
+ if (params - lower_params) <= (higher_params - params):
+ return lower_params
+ else:
+ return higher_params
+
+
+class Linear(nn.Module, OFTLayer):
+ """OFT implemented in Linear layer"""
+
+ def __init__(
+ self,
+ base_layer,
+ adapter_name: str,
+ r: int = 8,
+ oft_block_size: int = 0,
+ module_dropout: float = 0.0,
+ coft: bool = False,
+ eps: float = 6e-5,
+ block_share: bool = False,
+ use_cayley_neumann: bool = False,
+ num_cayley_neumann_terms: int = 5,
+ fan_in_fan_out: bool = False, # Set this to True if the layer to replace stores weight like (fan_in, fan_out)
+ init_weights: Union[bool, str] = True,
+ is_target_conv_1d_layer: bool = False,
+ **kwargs,
+ ) -> None:
+ super().__init__()
+ OFTLayer.__init__(self, base_layer, **kwargs)
+ self.fan_in_fan_out = fan_in_fan_out
+
+ self._active_adapter = adapter_name
+
+ self.update_layer(
+ adapter_name,
+ r,
+ oft_block_size=oft_block_size,
+ module_dropout=module_dropout,
+ coft=coft,
+ eps=eps,
+ block_share=block_share,
+ init_weights=init_weights,
+ use_cayley_neumann=use_cayley_neumann,
+ num_cayley_neumann_terms=num_cayley_neumann_terms,
+ )
+ self.is_target_conv_1d_layer = is_target_conv_1d_layer
+
+ def merge(self, safe_merge: bool = False, adapter_names: Optional[list[str]] = None) -> None:
+ """
+ Merge the active adapter weights into the base weights
+
+ Args:
+ safe_merge (`bool`, *optional*):
+ If `True`, the merge operation will be performed in a copy of the original weights and check for NaNs
+ before merging the weights. This is useful if you want to check if the merge operation will produce
+ NaNs. Defaults to `False`.
+ adapter_names (`List[str]`, *optional*):
+ The list of adapter names that should be merged. If `None`, all active adapters will be merged.
+ Defaults to `None`.
+ """
+ adapter_names = check_adapters_to_merge(self, adapter_names)
+ if not adapter_names:
+ # no adapter to merge
+ return
+
+ for active_adapter in adapter_names:
+ if active_adapter in self._available_adapters:
+ base_layer = self.get_base_layer()
+ orig_dtype = base_layer.weight.dtype
+ if safe_merge:
+ # Note that safe_merge will be slower than the normal merge
+ orig_weights = base_layer.weight.data
+ oft_mat = self.get_delta_weight(active_adapter)
+ orig_weights = torch.transpose(orig_weights, 0, 1)
+ orig_weights = torch.mm(oft_mat, orig_weights.to(oft_mat.dtype))
+ orig_weights = torch.transpose(orig_weights, 0, 1)
+
+ if not torch.isfinite(orig_weights).all():
+ raise ValueError(
+ f"NaNs detected in the merged weights. The adapter {active_adapter} seems to be broken"
+ )
+
+ base_layer.weight.data = orig_weights.contiguous().to(orig_dtype)
+ else:
+ orig_weights = base_layer.weight.data
+ oft_mat = self.get_delta_weight(active_adapter)
+ orig_weights = torch.transpose(orig_weights, 0, 1)
+ orig_weights = torch.mm(oft_mat, orig_weights.to(oft_mat.dtype))
+ orig_weights = torch.transpose(orig_weights, 0, 1)
+
+ base_layer.weight.data = orig_weights.contiguous().to(orig_dtype)
+
+ self.merged_adapters.append(active_adapter)
+
+ def unmerge(self) -> None:
+ """
+ This method unmerges all merged adapter layers from the base weights.
+ """
+ if not self.merged:
+ warnings.warn("Already unmerged. Nothing to do.")
+ return
+
+ base_layer = self.get_base_layer()
+ orig_dtype = base_layer.weight.dtype
+ while len(self.merged_adapters) > 0:
+ active_adapter = self.merged_adapters.pop()
+ if active_adapter in self.oft_R.keys():
+ oft_mat = self.get_delta_weight(active_adapter)
+
+ orig_weights = self.get_base_layer().weight.data
+ orig_weights = torch.transpose(orig_weights, 0, 1)
+ orig_weights = torch.mm(oft_mat.t(), orig_weights.to(oft_mat.dtype))
+ orig_weights = torch.transpose(orig_weights, 0, 1)
+
+ base_layer.weight.data = orig_weights.to(orig_dtype)
+
+ def get_delta_weight(self, adapter_name) -> tuple[torch.Tensor, torch.Tensor]:
+ """
+ Compute the delta weight for the given adapter.
+
+ Args:
+ adapter (str):
+ The name of the adapter for which the delta weight should be computed.
+ """
+
+ return self.oft_R[adapter_name].get_weight()
+
+ def forward(self, x: torch.Tensor, *args, **kwargs) -> torch.Tensor:
+ previous_dtype = x.dtype
+
+ if self.disable_adapters:
+ if self.merged:
+ self.unmerge()
+ result = self.base_layer(x, *args, **kwargs)
+ elif self.merged:
+ result = self.base_layer(x, *args, **kwargs)
+ else:
+ for active_adapter in self.active_adapters:
+ if active_adapter not in self.oft_R.keys():
+ continue
+ oft_R = self.oft_R[active_adapter]
+
+ x = self._cast_input_dtype(x, oft_R.weight.dtype)
+ x = oft_R(x)
+
+ result = self.base_layer(x.to(previous_dtype), *args, **kwargs)
+
+ result = result.to(previous_dtype)
+ return result
+
+ def __repr__(self) -> str:
+ rep = super().__repr__()
+ return "oft." + rep
+
+
+class Conv2d(nn.Module, OFTLayer):
+ """OFT implemented in Conv2d layer"""
+
+ def __init__(
+ self,
+ base_layer: nn.Module,
+ adapter_name: str,
+ r: int = 8,
+ oft_block_size: int = 0,
+ fan_in_fan_out: bool = False, # Set this to True if the layer to replace stores weight like (fan_in, fan_out)
+ module_dropout: float = 0.0,
+ coft: bool = False,
+ eps: float = 6e-5,
+ block_share: bool = False,
+ init_weights: Union[bool, str] = True,
+ use_cayley_neumann: bool = False,
+ num_cayley_neumann_terms: int = 5,
+ **kwargs,
+ ) -> None:
+ super().__init__()
+ OFTLayer.__init__(self, base_layer)
+ self.fan_in_fan_out = fan_in_fan_out
+
+ self._active_adapter = adapter_name
+
+ # Create adapter and set it active
+ self.update_layer(
+ adapter_name,
+ r,
+ oft_block_size=oft_block_size,
+ module_dropout=module_dropout,
+ coft=coft,
+ eps=eps,
+ block_share=block_share,
+ init_weights=init_weights,
+ use_cayley_neumann=use_cayley_neumann,
+ num_cayley_neumann_terms=num_cayley_neumann_terms,
+ )
+
+ def update_layer(
+ self,
+ adapter_name,
+ r,
+ oft_block_size,
+ module_dropout,
+ coft,
+ eps,
+ block_share,
+ init_weights,
+ use_cayley_neumann,
+ num_cayley_neumann_terms,
+ inference_mode: bool = False,
+ **kwargs,
+ ):
+ """
+ Update the conv2d layer with trainable OFT weights.
+ """
+ # Initialize the MultiplicativeDropoutLayer for module_dropout > 0.0.
+ if module_dropout > 0.0:
+ oft_dropout_layer = MultiplicativeDropoutLayer(p=module_dropout)
+ else:
+ oft_dropout_layer = nn.Identity()
+ self.oft_dropout.update(nn.ModuleDict({adapter_name: oft_dropout_layer}))
+
+ # layer information from the base layer
+ base_layer = self.get_base_layer()
+ if base_layer.dilation[0] > 1:
+ raise ValueError("Conv2d with dilation > 1 is not supported by OFT.")
+
+ conv_filter_dim = self.in_features * base_layer.kernel_size[0] * base_layer.kernel_size[0]
+
+ if r == 0 and oft_block_size != 0:
+ if conv_filter_dim % oft_block_size != 0 or oft_block_size > conv_filter_dim:
+ old_oft_block_size = oft_block_size
+ oft_block_size = self.adjust_oft_parameters(conv_filter_dim, oft_block_size)
+ warnings.warn(
+ f"Invalid `oft_block_size` ({old_oft_block_size})! Adjusted `oft_block_size` to ({oft_block_size})."
+ )
+ r = int(conv_filter_dim // oft_block_size)
+ elif r != 0 and oft_block_size == 0:
+ if conv_filter_dim % r != 0 or r > conv_filter_dim:
+ old_r = r
+ r = self.adjust_oft_parameters(conv_filter_dim, r)
+ warnings.warn(f"Invalid `r` ({old_r})! Adjusted `r` to ({r}).")
+ oft_block_size = int(conv_filter_dim // r)
+ else:
+ raise ValueError(
+ "Something went wrong, please report this error: https://github.com/huggingface/peft/issues"
+ )
+
+ # Create weights with provided shape
+ n_elements = oft_block_size * (oft_block_size - 1) // 2
+ self.oft_R[adapter_name] = OFTRotationModule(
+ r if not block_share else 1,
+ n_elements,
+ oft_block_size,
+ conv_filter_dim,
+ coft=coft,
+ eps=eps,
+ block_share=block_share,
+ kernel_size=base_layer.kernel_size,
+ use_cayley_neumann=use_cayley_neumann,
+ num_cayley_neumann_terms=num_cayley_neumann_terms,
+ )
+
+ # Initialize weights
+ self.reset_oft_parameters(adapter_name, init_weights)
+
+ # set oft r and block size
+ self.r[adapter_name] = r
+ self.oft_block_size[adapter_name] = oft_block_size
+
+ # Move new weights to device
+ self._move_adapter_to_device_of_base_layer(adapter_name)
+ self.set_adapter(self.active_adapters, inference_mode=inference_mode)
+
+ def merge(self, safe_merge: bool = False, adapter_names: Optional[list[str]] = None) -> None:
+ """
+ Merge the active adapter weights into the base weights
+
+ Args:
+ safe_merge (`bool`, *optional*):
+ If True, the merge operation will be performed in a copy of the original weights and check for NaNs
+ before merging the weights. This is useful if you want to check if the merge operation will produce
+ NaNs. Defaults to `False`.
+ adapter_names (`List[str]`, *optional*):
+ The list of adapter names that should be merged. If None, all active adapters will be merged. Defaults
+ to `None`.
+ """
+ adapter_names = check_adapters_to_merge(self, adapter_names)
+ if not adapter_names:
+ # no adapter to merge
+ return
+
+ for active_adapter in adapter_names:
+ if active_adapter in self.oft_R.keys():
+ base_layer = self.get_base_layer()
+ orig_dtype = base_layer.weight.dtype
+ if safe_merge:
+ # Note that safe_merge will be slower than the normal merge
+ # because of the copy operation.
+ orig_weights = base_layer.weight.data.clone()
+ oft_mat = self.get_delta_weight(active_adapter)
+
+ orig_weights = orig_weights.view(
+ self.out_features, self.in_features * base_layer.kernel_size[0] * base_layer.kernel_size[0]
+ )
+ orig_weights = torch.transpose(orig_weights, 0, 1)
+ orig_weights = torch.mm(oft_mat, orig_weights.to(oft_mat.dtype))
+ orig_weights = torch.transpose(orig_weights, 0, 1)
+ orig_weights = orig_weights.view(
+ self.out_features, self.in_features, base_layer.kernel_size[0], base_layer.kernel_size[0]
+ )
+
+ base_layer.weight.data = orig_weights.contiguous().to(orig_dtype)
+ else:
+ oft_mat = self.get_delta_weight(active_adapter)
+
+ orig_weights = base_layer.weight.data.clone()
+ orig_weights = orig_weights.view(
+ self.out_features, self.in_features * base_layer.kernel_size[0] * base_layer.kernel_size[0]
+ )
+ orig_weights = torch.transpose(orig_weights, 0, 1)
+ orig_weights = torch.mm(oft_mat, orig_weights.to(oft_mat.dtype))
+ orig_weights = torch.transpose(orig_weights, 0, 1)
+ orig_weights = orig_weights.view(
+ self.out_features, self.in_features, base_layer.kernel_size[0], base_layer.kernel_size[0]
+ )
+
+ base_layer.weight.data = orig_weights.contiguous().to(orig_dtype)
+
+ self.merged_adapters.append(active_adapter)
+
+ def unmerge(self) -> None:
+ """
+ This method unmerges all merged adapter layers from the base weights.
+ """
+ if not self.merged:
+ warnings.warn("Already unmerged. Nothing to do.")
+ return
+
+ base_layer = self.get_base_layer()
+ orig_dtype = base_layer.weight.dtype
+ while len(self.merged_adapters) > 0:
+ active_adapter = self.merged_adapters.pop()
+ if active_adapter in self.oft_R.keys():
+ oft_mat = self.get_delta_weight(active_adapter)
+
+ orig_weights = self.get_base_layer().weight.data.clone()
+ orig_weights = orig_weights.view(
+ self.out_features,
+ self.in_features * self.get_base_layer().kernel_size[0] * self.get_base_layer().kernel_size[0],
+ )
+ orig_weights = torch.transpose(orig_weights, 0, 1)
+ orig_weights = torch.mm(oft_mat.t(), orig_weights.to(oft_mat.dtype))
+ orig_weights = torch.transpose(orig_weights, 0, 1)
+ orig_weights = orig_weights.view(
+ self.out_features,
+ self.in_features,
+ self.get_base_layer().kernel_size[0],
+ self.get_base_layer().kernel_size[0],
+ )
+
+ base_layer.weight.data = orig_weights.to(orig_dtype)
+
+ def get_delta_weight(self, adapter_name) -> tuple[torch.Tensor, torch.Tensor]:
+ """
+ Compute the delta weight for the given adapter.
+
+ Args:
+ adapter (str):
+ The name of the adapter for which the delta weight should be computed.
+ """
+
+ return self.oft_R[adapter_name].get_weight()
+
+ def forward(self, x: torch.Tensor, *args: Any, **kwargs: Any) -> torch.Tensor:
+ previous_dtype = x.dtype
+
+ if self.disable_adapters:
+ if self.merged:
+ self.unmerge()
+ result = self.base_layer(x, *args, **kwargs)
+ elif self.merged:
+ result = self.base_layer(x, *args, **kwargs)
+ else:
+ for active_adapter in self.active_adapters:
+ if active_adapter not in self.oft_R.keys():
+ continue
+
+ oft_R = self.oft_R[active_adapter]
+ x = self._cast_input_dtype(x, oft_R.weight.dtype)
+ x = oft_R(x)
+
+ result = self.base_layer(x.to(previous_dtype), *args, **kwargs)
+
+ result = result.to(previous_dtype)
+ return result
+
+ def __repr__(self) -> str:
+ rep = super().__repr__()
+ return "oft." + rep
+
+
+def dispatch_default(
+ target: torch.nn.Module,
+ adapter_name: str,
+ oft_config: OFTConfig,
+ **kwargs,
+) -> Optional[torch.nn.Module]:
+ new_module = None
+
+ if isinstance(target, BaseTunerLayer):
+ target_base_layer = target.get_base_layer()
+ else:
+ target_base_layer = target
+
+ if isinstance(target_base_layer, torch.nn.Conv2d):
+ new_module = Conv2d(target, adapter_name, **kwargs)
+ elif isinstance(target_base_layer, torch.nn.Linear):
+ if kwargs["fan_in_fan_out"]:
+ warnings.warn(
+ "fan_in_fan_out is set to True but the target module is `torch.nn.Linear`. "
+ "Setting fan_in_fan_out to False."
+ )
+ kwargs["fan_in_fan_out"] = oft_config.fan_in_fan_out = False
+ new_module = Linear(target, adapter_name, **kwargs)
+
+ return new_module
diff --git a/peft/src/peft/tuners/oft/model.py b/peft/src/peft/tuners/oft/model.py
new file mode 100644
index 0000000000000000000000000000000000000000..8c3dc4336b4271c7002a9e2722e65c1988454832
--- /dev/null
+++ b/peft/src/peft/tuners/oft/model.py
@@ -0,0 +1,199 @@
+# Copyright 2023-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+
+from peft.import_utils import is_bnb_4bit_available, is_bnb_available
+from peft.tuners.tuners_utils import (
+ BaseTuner,
+)
+from peft.utils import (
+ TRANSFORMERS_MODELS_TO_OFT_TARGET_MODULES_MAPPING,
+ get_quantization_config,
+)
+
+from .aqlm import dispatch_aqlm
+from .awq import dispatch_awq
+from .eetq import dispatch_eetq
+from .gptq import dispatch_gptq
+from .hqq import dispatch_hqq
+from .inc import dispatch_inc
+from .layer import OFTLayer, dispatch_default
+
+
+class OFTModel(BaseTuner):
+ """
+ Creates Orthogonal Finetuning model from a pretrained model. The method is described in
+ https://huggingface.co/papers/2306.07280
+
+ Args:
+ model (`torch.nn.Module`): The model to which the adapter tuner layers will be attached.
+ config ([`OFTConfig`]): The configuration of the OFT model.
+ adapter_name (`str`): The name of the adapter, defaults to `"default"`.
+ low_cpu_mem_usage (`bool`, `optional`, defaults to `False`):
+ Create empty adapter weights on meta device. Useful to speed up the loading process.
+
+ Returns:
+ `torch.nn.Module`: The OFT model.
+
+ Example:
+ ```py
+ >>> from diffusers import StableDiffusionPipeline
+ >>> from peft import OFTModel, OFTConfig
+
+ >>> config_te = OFTConfig(
+ ... r=8,
+ ... target_modules=["k_proj", "q_proj", "v_proj", "out_proj", "fc1", "fc2"],
+ ... module_dropout=0.0,
+ ... init_weights=True,
+ ... )
+ >>> config_unet = OFTConfig(
+ ... r=8,
+ ... target_modules=[
+ ... "proj_in",
+ ... "proj_out",
+ ... "to_k",
+ ... "to_q",
+ ... "to_v",
+ ... "to_out.0",
+ ... "ff.net.0.proj",
+ ... "ff.net.2",
+ ... ],
+ ... module_dropout=0.0,
+ ... init_weights=True,
+ ... )
+
+ >>> model = StableDiffusionPipeline.from_pretrained("runwayml/stable-diffusion-v1-5")
+ >>> model.text_encoder = OFTModel(model.text_encoder, config_te, "default")
+ >>> model.unet = OFTModel(model.unet, config_unet, "default")
+ ```
+
+ **Attributes**:
+ - **model** ([`~torch.nn.Module`]) -- The model to be adapted.
+ - **peft_config** ([`OFTConfig`]): The configuration of the OFT model.
+ """
+
+ prefix: str = "oft_"
+ tuner_layer_cls = OFTLayer
+ target_module_mapping = TRANSFORMERS_MODELS_TO_OFT_TARGET_MODULES_MAPPING
+
+ def _create_and_replace(
+ self,
+ oft_config,
+ adapter_name,
+ target,
+ target_name,
+ parent,
+ current_key,
+ **optional_kwargs,
+ ):
+ if current_key is None:
+ raise ValueError("Current Key shouldn't be `None`")
+
+ kwargs = {
+ "r": oft_config.r,
+ "oft_block_size": oft_config.oft_block_size,
+ "module_dropout": oft_config.module_dropout,
+ "coft": oft_config.coft,
+ "eps": oft_config.eps,
+ "block_share": oft_config.block_share,
+ "use_cayley_neumann": oft_config.use_cayley_neumann,
+ "num_cayley_neumann_terms": oft_config.num_cayley_neumann_terms,
+ "fan_in_fan_out": oft_config.fan_in_fan_out,
+ "init_weights": oft_config.init_weights,
+ "loaded_in_8bit": getattr(self.model, "is_loaded_in_8bit", False),
+ "loaded_in_4bit": getattr(self.model, "is_loaded_in_4bit", False),
+ }
+
+ quant_methods = ["gptq", "aqlm", "awq"]
+ for quant_method in quant_methods:
+ quantization_config = get_quantization_config(self.model, method=quant_method)
+ if quantization_config is not None:
+ kwargs[f"{quant_method}_quantization_config"] = quantization_config
+
+ # If it is not a OFTLayer, create a new module, else update it with new adapters
+ if not isinstance(target, OFTLayer):
+ device_map = self.model.hf_device_map if hasattr(self.model, "hf_device_map") else None
+ new_module = self._create_new_module(oft_config, adapter_name, target, device_map=device_map, **kwargs)
+ if adapter_name not in self.active_adapters:
+ # adding an additional adapter: it is not automatically trainable
+ new_module.requires_grad_(False)
+ self._replace_module(parent, target_name, new_module, target)
+ else:
+ target.update_layer(
+ adapter_name,
+ r=oft_config.r,
+ oft_block_size=oft_config.oft_block_size,
+ module_dropout=oft_config.module_dropout,
+ coft=oft_config.coft,
+ eps=oft_config.eps,
+ block_share=oft_config.block_share,
+ use_cayley_neumann=oft_config.use_cayley_neumann,
+ num_cayley_neumann_terms=oft_config.num_cayley_neumann_terms,
+ init_weights=oft_config.init_weights,
+ )
+
+ @staticmethod
+ def _create_new_module(oft_config, adapter_name, target, **kwargs):
+ # Collect dispatcher functions to decide what backend to use for the replaced OFT layer. The order matters,
+ # because the first match is always used. Therefore, the default layers should be checked last.
+ dispatchers = []
+
+ # avoid eager bnb import
+ if is_bnb_available():
+ from .bnb import dispatch_bnb_8bit
+
+ dispatchers.append(dispatch_bnb_8bit)
+
+ if is_bnb_4bit_available():
+ from .bnb import dispatch_bnb_4bit
+
+ dispatchers.append(dispatch_bnb_4bit)
+
+ dispatchers.extend(
+ [
+ dispatch_eetq,
+ dispatch_aqlm,
+ dispatch_awq,
+ dispatch_gptq,
+ dispatch_hqq,
+ dispatch_inc,
+ dispatch_default,
+ ]
+ )
+
+ new_module = None
+ for dispatcher in dispatchers:
+ new_module = dispatcher(target, adapter_name, oft_config=oft_config, **kwargs)
+ if new_module is not None: # first match wins
+ break
+
+ if new_module is None:
+ # no module could be matched
+ raise ValueError(
+ f"Target module {target} is not supported. Currently, only the following modules are supported: "
+ "`torch.nn.Linear`, `torch.nn.Conv2d`."
+ )
+
+ return new_module
+
+ def _check_merge_allowed(self):
+ """Verify that the configuration supports merging.
+
+ Currently gptq quantization and replicated layers do not support merging.
+ """
+ super()._check_merge_allowed()
+ if getattr(self.model, "quantization_method", None) == "gptq":
+ raise ValueError("Cannot merge OFT layers when the model is gptq quantized")
+ if self.peft_config.get("layer_replication"):
+ raise ValueError("Cannot merge OFT layers when base model layers are replicated")
diff --git a/peft/src/peft/tuners/p_tuning/__init__.py b/peft/src/peft/tuners/p_tuning/__init__.py
new file mode 100644
index 0000000000000000000000000000000000000000..9195c0d75d3d11e752d0477b64edd79599bdaa01
--- /dev/null
+++ b/peft/src/peft/tuners/p_tuning/__init__.py
@@ -0,0 +1,23 @@
+# Copyright 2023-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+from peft.utils import register_peft_method
+
+from .config import PromptEncoderConfig, PromptEncoderReparameterizationType
+from .model import PromptEncoder
+
+
+__all__ = ["PromptEncoder", "PromptEncoderConfig", "PromptEncoderReparameterizationType"]
+
+register_peft_method(name="p_tuning", config_cls=PromptEncoderConfig, model_cls=PromptEncoder)
diff --git a/peft/src/peft/tuners/p_tuning/config.py b/peft/src/peft/tuners/p_tuning/config.py
new file mode 100644
index 0000000000000000000000000000000000000000..a69c13db9c8a0f57a7daa7d312472625251fb6c8
--- /dev/null
+++ b/peft/src/peft/tuners/p_tuning/config.py
@@ -0,0 +1,60 @@
+# Copyright 2023-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+import enum
+from dataclasses import dataclass, field
+from typing import Union
+
+from peft.config import PromptLearningConfig
+from peft.utils import PeftType
+
+
+class PromptEncoderReparameterizationType(str, enum.Enum):
+ MLP = "MLP"
+ LSTM = "LSTM"
+
+
+@dataclass
+class PromptEncoderConfig(PromptLearningConfig):
+ """
+ This is the configuration class to store the configuration of a [`PromptEncoder`].
+
+ Args:
+ encoder_reparameterization_type (Union[[`PromptEncoderReparameterizationType`], `str`]):
+ The type of reparameterization to use.
+ encoder_hidden_size (`int`): The hidden size of the prompt encoder.
+ encoder_num_layers (`int`): The number of layers of the prompt encoder.
+ encoder_dropout (`float`): The dropout probability of the prompt encoder.
+ """
+
+ encoder_reparameterization_type: Union[str, PromptEncoderReparameterizationType] = field(
+ default=PromptEncoderReparameterizationType.MLP,
+ metadata={"help": "How to reparameterize the prompt encoder"},
+ )
+ encoder_hidden_size: int = field(
+ default=None,
+ metadata={"help": "The hidden size of the prompt encoder"},
+ )
+ encoder_num_layers: int = field(
+ default=2,
+ metadata={"help": "The number of layers of the prompt encoder"},
+ )
+ encoder_dropout: float = field(
+ default=0.0,
+ metadata={"help": "The dropout of the prompt encoder"},
+ )
+
+ def __post_init__(self):
+ super().__post_init__()
+ self.peft_type = PeftType.P_TUNING
diff --git a/peft/src/peft/tuners/p_tuning/model.py b/peft/src/peft/tuners/p_tuning/model.py
new file mode 100644
index 0000000000000000000000000000000000000000..ade2b1128158376c134441687803b85d444cfb96
--- /dev/null
+++ b/peft/src/peft/tuners/p_tuning/model.py
@@ -0,0 +1,130 @@
+# Copyright 2023-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+# Based on https://github.com/NVIDIA/NeMo/blob/main/nemo/collections/nlp/modules/common/prompt_encoder.py
+# with some refactor
+import warnings
+
+import torch
+
+from .config import PromptEncoderConfig, PromptEncoderReparameterizationType
+
+
+class PromptEncoder(torch.nn.Module):
+ """
+ The prompt encoder network that is used to generate the virtual token embeddings for p-tuning.
+
+ Args:
+ config ([`PromptEncoderConfig`]): The configuration of the prompt encoder.
+
+ Example:
+
+ ```py
+ >>> from peft import PromptEncoder, PromptEncoderConfig
+
+ >>> config = PromptEncoderConfig(
+ ... peft_type="P_TUNING",
+ ... task_type="SEQ_2_SEQ_LM",
+ ... num_virtual_tokens=20,
+ ... token_dim=768,
+ ... num_transformer_submodules=1,
+ ... num_attention_heads=12,
+ ... num_layers=12,
+ ... encoder_reparameterization_type="MLP",
+ ... encoder_hidden_size=768,
+ ... )
+
+ >>> prompt_encoder = PromptEncoder(config)
+ ```
+
+ **Attributes**:
+ - **embedding** (`torch.nn.Embedding`) -- The embedding layer of the prompt encoder.
+ - **mlp_head** (`torch.nn.Sequential`) -- The MLP head of the prompt encoder if `inference_mode=False`.
+ - **lstm_head** (`torch.nn.LSTM`) -- The LSTM head of the prompt encoder if `inference_mode=False` and
+ `encoder_reparameterization_type="LSTM"`.
+ - **token_dim** (`int`) -- The hidden embedding dimension of the base transformer model.
+ - **input_size** (`int`) -- The input size of the prompt encoder.
+ - **output_size** (`int`) -- The output size of the prompt encoder.
+ - **hidden_size** (`int`) -- The hidden size of the prompt encoder.
+ - **total_virtual_tokens** (`int`): The total number of virtual tokens of the
+ prompt encoder.
+ - **encoder_type** (Union[[`PromptEncoderReparameterizationType`], `str`]): The encoder type of the prompt
+ encoder.
+
+
+ Input shape: (`batch_size`, `total_virtual_tokens`)
+
+ Output shape: (`batch_size`, `total_virtual_tokens`, `token_dim`)
+ """
+
+ def __init__(self, config):
+ super().__init__()
+ self.token_dim = config.token_dim
+ self.input_size = self.token_dim
+ self.output_size = self.token_dim
+ self.hidden_size = config.encoder_hidden_size
+ self.total_virtual_tokens = config.num_virtual_tokens * config.num_transformer_submodules
+ self.encoder_type = config.encoder_reparameterization_type
+
+ # embedding
+ self.embedding = torch.nn.Embedding(self.total_virtual_tokens, self.token_dim)
+ if not config.inference_mode:
+ if self.encoder_type == PromptEncoderReparameterizationType.LSTM:
+ lstm_dropout = config.encoder_dropout
+ num_layers = config.encoder_num_layers
+ # LSTM
+ self.lstm_head = torch.nn.LSTM(
+ input_size=self.input_size,
+ hidden_size=self.hidden_size,
+ num_layers=num_layers,
+ dropout=lstm_dropout,
+ bidirectional=True,
+ batch_first=True,
+ )
+
+ self.mlp_head = torch.nn.Sequential(
+ torch.nn.Linear(self.hidden_size * 2, self.hidden_size * 2),
+ torch.nn.ReLU(),
+ torch.nn.Linear(self.hidden_size * 2, self.output_size),
+ )
+
+ elif self.encoder_type == PromptEncoderReparameterizationType.MLP:
+ encoder_num_layers_default = PromptEncoderConfig.encoder_num_layers
+ if config.encoder_num_layers != encoder_num_layers_default:
+ warnings.warn(
+ f"for {self.encoder_type.value}, the argument `encoder_num_layers` is ignored. "
+ f"Exactly {encoder_num_layers_default} MLP layers are used."
+ )
+ layers = [
+ torch.nn.Linear(self.input_size, self.hidden_size),
+ torch.nn.ReLU(),
+ torch.nn.Linear(self.hidden_size, self.hidden_size),
+ torch.nn.ReLU(),
+ torch.nn.Linear(self.hidden_size, self.output_size),
+ ]
+ self.mlp_head = torch.nn.Sequential(*layers)
+
+ else:
+ raise ValueError("Prompt encoder type not recognized. Please use one of MLP (recommended) or LSTM.")
+
+ def forward(self, indices):
+ input_embeds = self.embedding(indices)
+ if self.encoder_type == PromptEncoderReparameterizationType.LSTM:
+ output_embeds = self.mlp_head(self.lstm_head(input_embeds)[0])
+ elif self.encoder_type == PromptEncoderReparameterizationType.MLP:
+ output_embeds = self.mlp_head(input_embeds)
+ else:
+ raise ValueError("Prompt encoder type not recognized. Please use one of MLP (recommended) or LSTM.")
+
+ return output_embeds
diff --git a/peft/src/peft/tuners/poly/__init__.py b/peft/src/peft/tuners/poly/__init__.py
new file mode 100644
index 0000000000000000000000000000000000000000..1c18933eba3fa44106ba9fa89ba34ecd12a2bed4
--- /dev/null
+++ b/peft/src/peft/tuners/poly/__init__.py
@@ -0,0 +1,24 @@
+# Copyright 2023-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+from peft.utils import register_peft_method
+
+from .config import PolyConfig
+from .layer import Linear, PolyLayer
+from .model import PolyModel
+
+
+__all__ = ["Linear", "PolyConfig", "PolyLayer", "PolyModel"]
+
+register_peft_method(name="poly", config_cls=PolyConfig, model_cls=PolyModel)
diff --git a/peft/src/peft/tuners/poly/config.py b/peft/src/peft/tuners/poly/config.py
new file mode 100644
index 0000000000000000000000000000000000000000..c4a77bc5db447edd4ba97c1b1c407f3cfc620cb4
--- /dev/null
+++ b/peft/src/peft/tuners/poly/config.py
@@ -0,0 +1,103 @@
+# Copyright 2023-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+from __future__ import annotations
+
+from dataclasses import dataclass, field
+from typing import Literal, Optional, Union
+
+from peft.config import PeftConfig
+from peft.utils import PeftType
+
+
+@dataclass
+class PolyConfig(PeftConfig):
+ """
+ This is the configuration class to store the configuration of a [`PolyModel`].
+ - [Polytropon (Poly)](https://huggingface.co/papers/2202.13914)
+ - [Multi-Head Routing (MHR)](https://huggingface.co/papers/2211.03831)
+
+ Args:
+ r (`int`): Attention dimension of each Lora in Poly.
+ target_modules (`Union[List[str],str]`): The names of the modules to apply Poly to.
+ exclude_modules (`Optional[Union[List[str], str]]`):
+ The names of the modules to not apply the adapter. When passing a string, a regex match will be performed.
+ When passing a list of strings, either an exact match will be performed or it is checked if the name of the
+ module ends with any of the passed strings.
+ modules_to_save (`List[str]`): List of modules apart from Poly layers to be set as trainable
+ and saved in the final checkpoint.
+ init_weights (bool): Whether to perform initialization of Poly weights.
+ poly_type (`Literal["poly"]`): The variant of the Poly module to use. Currently, only "poly"
+ is supported.
+ n_tasks (`int`): The number of tasks in a multitasking scenario.
+ n_skills (`int`): The number of skills (LoRA) in each Poly layer.
+ n_splits (`int`): The number of splits within each LoRA of a Poly layer. A value greater
+ than 1 indicates the use of Multi-Head Routing (MHR).
+ """
+
+ r: int = field(default=8, metadata={"help": "Lora attention dimension"})
+ target_modules: Optional[Union[list[str], str]] = field(
+ default=None,
+ metadata={
+ "help": "List of module names or regex expression of the module names to replace with Poly."
+ "For example, ['q', 'v'] or '.*decoder.*(SelfAttention|EncDecAttention).*(q|v)$' "
+ },
+ )
+ exclude_modules: Optional[Union[list[str], str]] = field(
+ default=None,
+ metadata={"help": "List of module names or regex expression of the module names to exclude from Poly."},
+ )
+ modules_to_save: Optional[list[str]] = field(
+ default=None,
+ metadata={
+ "help": "List of modules apart from Poly layers to be set as trainable and saved in the final checkpoint. "
+ "For example, in Sequence Classification or Token Classification tasks, "
+ "the final layer `classifier/score` are randomly initialized and as such need to be trainable and saved."
+ },
+ )
+ init_weights: bool = field(
+ default=True,
+ metadata={
+ "help": (
+ "Whether to initialize the weights of the Poly layers with their default initialization. Don't change "
+ "this setting, except if you know exactly what you're doing."
+ ),
+ },
+ )
+ poly_type: Literal["poly"] = field(
+ default="poly",
+ metadata={"help": 'Type of Poly modules to be used. Currently only "poly" is supported.'},
+ )
+ n_tasks: int = field(
+ default=1,
+ metadata={"help": "Number of tasks in multitasking scenario."},
+ )
+ n_skills: int = field(
+ default=4,
+ metadata={"help": "Number of skills (LoRA) in each Poly layer."},
+ )
+ n_splits: int = field(
+ default=1,
+ metadata={"help": "Number of splits within each LoRA of a Poly layer."},
+ )
+
+ def __post_init__(self):
+ super().__post_init__()
+ self.peft_type = PeftType.POLY
+ self.target_modules = (
+ set(self.target_modules) if isinstance(self.target_modules, list) else self.target_modules
+ )
+ self.exclude_modules = (
+ set(self.exclude_modules) if isinstance(self.exclude_modules, list) else self.exclude_modules
+ )
diff --git a/peft/src/peft/tuners/poly/layer.py b/peft/src/peft/tuners/poly/layer.py
new file mode 100644
index 0000000000000000000000000000000000000000..2f700997a54f247f4cf77172700d40b54e6c2600
--- /dev/null
+++ b/peft/src/peft/tuners/poly/layer.py
@@ -0,0 +1,165 @@
+# Copyright 2023-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+import math
+from typing import Any
+
+import torch
+import torch.nn as nn
+
+from peft.tuners.tuners_utils import BaseTunerLayer
+
+from .config import PolyConfig
+from .router import get_router
+
+
+class PolyLayer(BaseTunerLayer):
+ # All names of layers that may contain (trainable) adapter weights
+ adapter_layer_names = ("poly_lora_A", "poly_lora_B", "poly_router")
+ # All names of other parameters that may contain adapter-related parameters
+ other_param_names = ("r", "n_tasks", "n_skills", "n_splits")
+
+ def __init__(self, base_layer: nn.Module, **kwargs):
+ self.base_layer = base_layer
+ self.r = {}
+ self.n_tasks = {}
+ self.n_skills = {}
+ self.n_splits = {}
+ self.poly_type = {}
+ self.poly_router = nn.ModuleDict()
+ self.poly_lora_A = nn.ParameterDict()
+ self.poly_lora_B = nn.ParameterDict()
+ self.kwargs = kwargs
+
+ base_layer = self.get_base_layer()
+ if isinstance(base_layer, nn.Linear):
+ in_features, out_features = base_layer.in_features, base_layer.out_features
+ else:
+ raise ValueError(f"Unsupported layer type {type(base_layer)}")
+
+ self.in_features = in_features
+ self.out_features = out_features
+
+ def update_layer(self, adapter_name, poly_config, inference_mode: bool = False, **kwargs):
+ if poly_config.r <= 0:
+ raise ValueError(f"`r` should be a positive integer value but the value passed is {poly_config.r}")
+
+ self.r[adapter_name] = poly_config.r
+ self.n_tasks[adapter_name] = poly_config.n_tasks
+ self.n_skills[adapter_name] = poly_config.n_skills
+ self.n_splits[adapter_name] = poly_config.n_splits
+ self.poly_type[adapter_name] = poly_config.poly_type
+
+ self.poly_lora_A[adapter_name] = nn.Parameter(
+ torch.empty(
+ poly_config.n_splits,
+ poly_config.n_skills,
+ self.in_features // poly_config.n_splits,
+ poly_config.r,
+ )
+ )
+ self.poly_lora_B[adapter_name] = nn.Parameter(
+ torch.empty(
+ poly_config.n_splits,
+ poly_config.n_skills,
+ poly_config.r,
+ self.out_features // poly_config.n_splits,
+ )
+ )
+ self.poly_router[adapter_name] = get_router(poly_config)
+
+ self.reset_poly_parameters(adapter_name, init_weights=poly_config.init_weights)
+
+ self._move_adapter_to_device_of_base_layer(adapter_name)
+ self.set_adapter(self.active_adapters, inference_mode=inference_mode)
+
+ def reset_poly_parameters(self, adapter_name, init_weights):
+ if adapter_name in self.poly_lora_A.keys():
+ # initialize A the same way as the default for nn.Linear
+ # https://github.com/microsoft/mttl/blob/ce4ca51dbca73be656feb9b3e5233633e3c5dec7/mttl/models/poly.py#L269
+ n_splits, n_skills, d, r = self.poly_lora_A[adapter_name].shape
+ for skill in range(n_skills):
+ for split in range(n_splits):
+ param = torch.empty((r, d))
+ torch.nn.init.kaiming_uniform_(param, a=math.sqrt(5))
+ self.poly_lora_A[adapter_name].data[split, skill, :, :] = param.T
+
+ if init_weights:
+ # initialize B to zero
+ torch.nn.init.zeros_(self.poly_lora_B[adapter_name])
+ else:
+ # initialize B the same way as the default for nn.Linear
+ n_splits, n_skills, r, d = self.poly_lora_B[adapter_name].shape
+ for skill in range(n_skills):
+ for split in range(n_splits):
+ param = torch.empty((d, r))
+ torch.nn.init.kaiming_uniform_(param, a=math.sqrt(5))
+ self.poly_lora_B[adapter_name].data[split, skill, :, :] = param.T
+
+ # initialized router
+ self.poly_router[adapter_name].reset()
+
+
+class Linear(nn.Module, PolyLayer):
+ # Lora implemented in a dense layer
+ def __init__(
+ self,
+ base_layer,
+ adapter_name: str,
+ poly_config: PolyConfig,
+ **kwargs,
+ ) -> None:
+ super().__init__()
+ PolyLayer.__init__(self, base_layer, **kwargs)
+
+ self._active_adapter = adapter_name
+ self.update_layer(adapter_name, poly_config)
+
+ def forward(self, x: torch.Tensor, *args: Any, task_ids: torch.Tensor = None, **kwargs: Any) -> torch.Tensor:
+ previous_dtype = x.dtype
+ if self.disable_adapters:
+ result = self.base_layer(x, *args, **kwargs)
+ else:
+ result = self.base_layer(x, *args, **kwargs)
+ for active_adapter in self.active_adapters:
+ if active_adapter not in self.poly_lora_A.keys():
+ continue
+
+ r = self.r[active_adapter]
+ poly_router = self.poly_router[active_adapter]
+ poly_lora_A = self.poly_lora_A[active_adapter]
+ poly_lora_B = self.poly_lora_B[active_adapter]
+
+ # Combine the output of LoRAs
+ # https://github.com/microsoft/mttl/blob/ce4ca51dbca73be656feb9b3e5233633e3c5dec7/mttl/models/poly.py#L293
+ mixing_weights = poly_router(task_ids=task_ids, input_ids=x)
+ bs, n_splits, n_skills = mixing_weights.size()
+
+ # A is n_splits, n_skills, D // n_splits, rank
+ # we want bs, n_splits, D // n_splits, rank
+ A = torch.einsum("bqs,qsdr->bqdr", (mixing_weights, poly_lora_A))
+ B = torch.einsum("bqs,qsrd->bqrd", (mixing_weights, poly_lora_B))
+
+ A = A.reshape(bs, self.in_features, r)
+ B = B.transpose(1, 2).reshape(bs, r, self.out_features)
+
+ x = x.to(A.dtype)
+ result += x.bmm(A).bmm(B) / r
+
+ result = result.to(previous_dtype)
+ return result
+
+ def __repr__(self) -> str:
+ rep = super().__repr__()
+ return "poly." + rep
diff --git a/peft/src/peft/tuners/poly/model.py b/peft/src/peft/tuners/poly/model.py
new file mode 100644
index 0000000000000000000000000000000000000000..bf7060026310a1f489512293b3afa216105a16cc
--- /dev/null
+++ b/peft/src/peft/tuners/poly/model.py
@@ -0,0 +1,104 @@
+# Copyright 2023-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+from contextlib import contextmanager
+from typing import Any
+
+import torch
+from torch import nn
+
+from peft.tuners.tuners_utils import BaseTuner, BaseTunerLayer
+from peft.utils import TRANSFORMERS_MODELS_TO_POLY_TARGET_MODULES_MAPPING
+
+from .config import PolyConfig
+from .layer import Linear, PolyLayer
+
+
+class PolyModel(BaseTuner):
+ prefix: str = "poly_"
+ tuner_layer_cls = PolyLayer
+ target_module_mapping = TRANSFORMERS_MODELS_TO_POLY_TARGET_MODULES_MAPPING
+
+ def _create_and_replace(
+ self,
+ poly_config: PolyConfig,
+ adapter_name: str,
+ target: nn.Module,
+ target_name: str,
+ parent: nn.Module,
+ **optional_kwargs: Any,
+ ):
+ if isinstance(target, PolyLayer):
+ target.update_layer(adapter_name, poly_config)
+ else:
+ new_module = self._create_new_module(
+ poly_config,
+ adapter_name,
+ target,
+ )
+ if adapter_name not in self.active_adapters:
+ # adding an additional adapter: it is not automatically trainable
+ new_module.requires_grad_(False)
+ self._replace_module(parent, target_name, new_module, target)
+
+ @staticmethod
+ def _create_new_module(poly_config, adapter_name, target, **kwargs):
+ if isinstance(target, BaseTunerLayer):
+ target_base_layer = target.get_base_layer()
+ else:
+ target_base_layer = target
+
+ if isinstance(target_base_layer, torch.nn.Linear):
+ return Linear(target, adapter_name, poly_config, **kwargs)
+ else:
+ raise ValueError(
+ f"Target module {target} is not supported. Currently, only the following modules are supported: "
+ "`torch.nn.Linear`."
+ )
+
+ def _register_pre_hooks(self, task_ids):
+ """Helper method to register pre hooks."""
+ if task_ids is None:
+ return []
+
+ def pre_hook(_, args, kwargs):
+ kwargs["task_ids"] = task_ids
+ return args, kwargs
+
+ handles = []
+
+ for module in self.model.modules():
+ if isinstance(module, Linear):
+ handle = module.register_forward_pre_hook(pre_hook, with_kwargs=True)
+ handles.append(handle)
+
+ return handles
+
+ @contextmanager
+ def _manage_pre_hooks(self, task_ids):
+ """Context manager to handle the lifecycle of pre hooks."""
+ handles = self._register_pre_hooks(task_ids)
+ try:
+ yield
+ finally:
+ for handle in handles:
+ handle.remove()
+
+ def forward(self, *args, task_ids=None, **kwargs):
+ with self._manage_pre_hooks(task_ids):
+ return self.model(*args, **kwargs)
+
+ def generate(self, *args, task_ids=None, **kwargs):
+ with self._manage_pre_hooks(task_ids):
+ return self.model.generate(*args, **kwargs)
diff --git a/peft/src/peft/tuners/poly/router.py b/peft/src/peft/tuners/poly/router.py
new file mode 100644
index 0000000000000000000000000000000000000000..3dda3e75e35b6a9fbd5a2412815a0f05421f2ef4
--- /dev/null
+++ b/peft/src/peft/tuners/poly/router.py
@@ -0,0 +1,81 @@
+# Copyright 2023-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+from abc import ABC, abstractmethod
+
+import torch
+from torch import nn
+from torch.distributions.relaxed_bernoulli import RelaxedBernoulli
+
+from .config import PolyConfig
+
+
+EPS = 1e-12
+
+
+def get_router(poly_config: PolyConfig) -> nn.Module:
+ if poly_config.poly_type == "poly":
+ return PolyRouter(poly_config)
+ else:
+ raise ValueError(
+ f"Unsupported poly_type: {poly_config.poly_type}. "
+ "Currently, only the following types are supported: "
+ "`poly`."
+ )
+
+
+class Router(nn.Module, ABC):
+ @abstractmethod
+ def reset(self): ...
+
+ @abstractmethod
+ def forward(self, task_ids: torch.Tensor, input_ids: torch.Tensor): ...
+
+
+class PolyRouter(Router):
+ # It's a simplified implementation of
+ # https://github.com/microsoft/mttl/blob/ce4ca51dbca73be656feb9b3e5233633e3c5dec7/mttl/models/poly.py#L138
+ def __init__(self, poly_config: PolyConfig):
+ super().__init__()
+
+ self.poly_type = poly_config.poly_type
+ self.n_tasks = poly_config.n_tasks
+ self.n_skills = poly_config.n_skills
+ self.n_splits = poly_config.n_splits
+
+ self.module_logits = nn.Parameter(torch.empty((self.n_tasks, self.n_splits * self.n_skills)))
+
+ def reset(self):
+ torch.nn.init.uniform_(self.module_logits, -1e-3, 1e-3)
+
+ def forward(self, task_ids: torch.Tensor, input_ids: torch.Tensor):
+ if task_ids is None:
+ raise ValueError("task_ids should not be None.")
+ if task_ids.max().item() >= self.n_tasks:
+ raise ValueError(f"Only {self.n_tasks} tasks available. Found task id = {task_ids.max().item()}")
+
+ # move task id to input's device
+ task_ids = task_ids.to(self.module_logits.device)
+
+ module_logits = self.module_logits[task_ids]
+ module_logits = module_logits.view(-1, self.n_splits, self.n_skills)
+
+ if self.training:
+ module_logits = RelaxedBernoulli(temperature=1.0, logits=module_logits).rsample()
+ else:
+ module_logits = torch.sigmoid(module_logits)
+
+ module_weights = module_logits / (module_logits.sum(dim=-1, keepdim=True) + EPS)
+
+ return module_weights
diff --git a/peft/src/peft/tuners/prefix_tuning/__init__.py b/peft/src/peft/tuners/prefix_tuning/__init__.py
new file mode 100644
index 0000000000000000000000000000000000000000..939f74d3f689f400dfdcb0139f4a2cf04cce52fc
--- /dev/null
+++ b/peft/src/peft/tuners/prefix_tuning/__init__.py
@@ -0,0 +1,23 @@
+# Copyright 2023-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+from peft.utils import register_peft_method
+
+from .config import PrefixTuningConfig
+from .model import PrefixEncoder
+
+
+__all__ = ["PrefixEncoder", "PrefixTuningConfig"]
+
+register_peft_method(name="prefix_tuning", config_cls=PrefixTuningConfig, model_cls=PrefixEncoder)
diff --git a/peft/src/peft/tuners/prefix_tuning/config.py b/peft/src/peft/tuners/prefix_tuning/config.py
new file mode 100644
index 0000000000000000000000000000000000000000..6eed77167a6e0b928e59e7e07fbf842c2d7a2d83
--- /dev/null
+++ b/peft/src/peft/tuners/prefix_tuning/config.py
@@ -0,0 +1,42 @@
+# Copyright 2023-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+from dataclasses import dataclass, field
+
+from peft.config import PromptLearningConfig
+from peft.utils import PeftType
+
+
+@dataclass
+class PrefixTuningConfig(PromptLearningConfig):
+ """
+ This is the configuration class to store the configuration of a [`PrefixEncoder`].
+
+ Args:
+ encoder_hidden_size (`int`): The hidden size of the prompt encoder.
+ prefix_projection (`bool`): Whether to project the prefix embeddings.
+ """
+
+ encoder_hidden_size: int = field(
+ default=None,
+ metadata={"help": "The hidden size of the encoder"},
+ )
+ prefix_projection: bool = field(
+ default=False,
+ metadata={"help": "Whether to project the prefix tokens"},
+ )
+
+ def __post_init__(self):
+ super().__post_init__()
+ self.peft_type = PeftType.PREFIX_TUNING
diff --git a/peft/src/peft/tuners/prefix_tuning/model.py b/peft/src/peft/tuners/prefix_tuning/model.py
new file mode 100644
index 0000000000000000000000000000000000000000..ffd51892a3cc074406791f6bc7d1b088d25148e3
--- /dev/null
+++ b/peft/src/peft/tuners/prefix_tuning/model.py
@@ -0,0 +1,80 @@
+# Copyright 2023-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+# Based on https://github.com/THUDM/P-tuning-v2/blob/main/model/prefix_encoder.py
+# with some refactor
+import torch
+
+
+class PrefixEncoder(torch.nn.Module):
+ r"""
+ The `torch.nn` model to encode the prefix.
+
+ Args:
+ config ([`PrefixTuningConfig`]): The configuration of the prefix encoder.
+
+ Example:
+
+ ```py
+ >>> from peft import PrefixEncoder, PrefixTuningConfig
+
+ >>> config = PrefixTuningConfig(
+ ... peft_type="PREFIX_TUNING",
+ ... task_type="SEQ_2_SEQ_LM",
+ ... num_virtual_tokens=20,
+ ... token_dim=768,
+ ... num_transformer_submodules=1,
+ ... num_attention_heads=12,
+ ... num_layers=12,
+ ... encoder_hidden_size=768,
+ ... )
+ >>> prefix_encoder = PrefixEncoder(config)
+ ```
+
+ **Attributes**:
+ - **embedding** (`torch.nn.Embedding`) -- The embedding layer of the prefix encoder.
+ - **transform** (`torch.nn.Sequential`) -- The two-layer MLP to transform the prefix embeddings if
+ `prefix_projection` is `True`.
+ - **prefix_projection** (`bool`) -- Whether to project the prefix embeddings.
+
+ Input shape: (`batch_size`, `num_virtual_tokens`)
+
+ Output shape: (`batch_size`, `num_virtual_tokens`, `2*layers*hidden`)
+ """
+
+ def __init__(self, config):
+ super().__init__()
+ self.prefix_projection = config.prefix_projection
+ token_dim = config.token_dim
+ num_layers = config.num_layers
+ encoder_hidden_size = config.encoder_hidden_size
+ num_virtual_tokens = config.num_virtual_tokens
+ if self.prefix_projection and not config.inference_mode:
+ # Use a two-layer MLP to encode the prefix
+ self.embedding = torch.nn.Embedding(num_virtual_tokens, token_dim)
+ self.transform = torch.nn.Sequential(
+ torch.nn.Linear(token_dim, encoder_hidden_size),
+ torch.nn.Tanh(),
+ torch.nn.Linear(encoder_hidden_size, num_layers * 2 * token_dim),
+ )
+ else:
+ self.embedding = torch.nn.Embedding(num_virtual_tokens, num_layers * 2 * token_dim)
+
+ def forward(self, prefix: torch.Tensor):
+ if self.prefix_projection:
+ prefix_tokens = self.embedding(prefix)
+ past_key_values = self.transform(prefix_tokens)
+ else:
+ past_key_values = self.embedding(prefix)
+ return past_key_values
diff --git a/peft/src/peft/tuners/prompt_tuning/__init__.py b/peft/src/peft/tuners/prompt_tuning/__init__.py
new file mode 100644
index 0000000000000000000000000000000000000000..c99ca6a26fea22e3d829c16eec378e82633e1b7b
--- /dev/null
+++ b/peft/src/peft/tuners/prompt_tuning/__init__.py
@@ -0,0 +1,23 @@
+# Copyright 2023-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+from peft.utils import register_peft_method
+
+from .config import PromptTuningConfig, PromptTuningInit
+from .model import PromptEmbedding
+
+
+__all__ = ["PromptEmbedding", "PromptTuningConfig", "PromptTuningInit"]
+
+register_peft_method(name="prompt_tuning", config_cls=PromptTuningConfig, model_cls=PromptEmbedding)
diff --git a/peft/src/peft/tuners/prompt_tuning/config.py b/peft/src/peft/tuners/prompt_tuning/config.py
new file mode 100644
index 0000000000000000000000000000000000000000..b41669efe898e88dfd015042e0c78258fb9b3a14
--- /dev/null
+++ b/peft/src/peft/tuners/prompt_tuning/config.py
@@ -0,0 +1,91 @@
+# Copyright 2023-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+import enum
+from dataclasses import dataclass, field
+from typing import Optional, Union
+
+from peft.config import PromptLearningConfig
+from peft.utils import PeftType
+
+
+class PromptTuningInit(str, enum.Enum):
+ TEXT = "TEXT"
+ SAMPLE_VOCAB = "SAMPLE_VOCAB"
+ RANDOM = "RANDOM"
+
+
+@dataclass
+class PromptTuningConfig(PromptLearningConfig):
+ """
+ This is the configuration class to store the configuration of a [`PromptEmbedding`].
+
+ Args:
+ prompt_tuning_init (Union[[`PromptTuningInit`], `str`]):
+ The initialization of the prompt embedding. `TEXT` will initialize with your text. `SAMPLE_VOCAB` will
+ initialize with randomly sampled tokens from the model's vocabulary. `RANDOM` will initialize with randomly
+ sampled continuous, soft tokens (warning: sampled soft tokens may fall outside of embedding manifold)
+ prompt_tuning_init_text (`str`, *optional*):
+ The text to initialize the prompt embedding. Only used if `prompt_tuning_init` is `TEXT`.
+ tokenizer_name_or_path (`str`, *optional*):
+ The name or path of the tokenizer. Only used if `prompt_tuning_init` is `TEXT`.
+ tokenizer_kwargs (`dict`, *optional*):
+ The keyword arguments to pass to `AutoTokenizer.from_pretrained`. Only used if `prompt_tuning_init` is
+ `TEXT`.
+ """
+
+ prompt_tuning_init: Union[PromptTuningInit, str] = field(
+ default=PromptTuningInit.RANDOM,
+ metadata={"help": "How to initialize the prompt tuning parameters"},
+ )
+ prompt_tuning_init_text: Optional[str] = field(
+ default=None,
+ metadata={
+ "help": "The text to use for prompt tuning initialization. Only used if prompt_tuning_init is `TEXT`"
+ },
+ )
+ tokenizer_name_or_path: Optional[str] = field(
+ default=None,
+ metadata={
+ "help": "The tokenizer to use for prompt tuning initialization. Only used if prompt_tuning_init is `TEXT`"
+ },
+ )
+
+ tokenizer_kwargs: Optional[dict] = field(
+ default=None,
+ metadata={
+ "help": (
+ "The keyword arguments to pass to `AutoTokenizer.from_pretrained`. Only used if prompt_tuning_init is "
+ "`TEXT`"
+ ),
+ },
+ )
+
+ def __post_init__(self):
+ super().__post_init__()
+ self.peft_type = PeftType.PROMPT_TUNING
+ if (self.prompt_tuning_init == PromptTuningInit.TEXT) and not self.tokenizer_name_or_path:
+ raise ValueError(
+ f"When prompt_tuning_init='{PromptTuningInit.TEXT.value}', "
+ f"tokenizer_name_or_path can't be {self.tokenizer_name_or_path}."
+ )
+ if (self.prompt_tuning_init == PromptTuningInit.TEXT) and self.prompt_tuning_init_text is None:
+ raise ValueError(
+ f"When prompt_tuning_init='{PromptTuningInit.TEXT.value}', "
+ f"prompt_tuning_init_text can't be {self.prompt_tuning_init_text}."
+ )
+ if self.tokenizer_kwargs and (self.prompt_tuning_init != PromptTuningInit.TEXT):
+ raise ValueError(
+ f"tokenizer_kwargs only valid when using prompt_tuning_init='{PromptTuningInit.TEXT.value}'."
+ )
diff --git a/peft/src/peft/tuners/prompt_tuning/model.py b/peft/src/peft/tuners/prompt_tuning/model.py
new file mode 100644
index 0000000000000000000000000000000000000000..9852ea28b4583b273729799e5b2b3fcad9c72ee7
--- /dev/null
+++ b/peft/src/peft/tuners/prompt_tuning/model.py
@@ -0,0 +1,102 @@
+# Copyright 2023-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+import math
+
+import torch
+
+from peft.utils.integrations import gather_params_ctx
+
+from .config import PromptTuningInit
+
+
+class PromptEmbedding(torch.nn.Module):
+ """
+ The model to encode virtual tokens into prompt embeddings.
+
+ Args:
+ config ([`PromptTuningConfig`]): The configuration of the prompt embedding.
+ word_embeddings (`torch.nn.Module`): The word embeddings of the base transformer model.
+
+ **Attributes**:
+ - **embedding** (`torch.nn.Embedding`) -- The embedding layer of the prompt embedding.
+
+ Example:
+
+ ```py
+ >>> from peft import PromptEmbedding, PromptTuningConfig
+
+ >>> config = PromptTuningConfig(
+ ... peft_type="PROMPT_TUNING",
+ ... task_type="SEQ_2_SEQ_LM",
+ ... num_virtual_tokens=20,
+ ... token_dim=768,
+ ... num_transformer_submodules=1,
+ ... num_attention_heads=12,
+ ... num_layers=12,
+ ... prompt_tuning_init="TEXT",
+ ... prompt_tuning_init_text="Predict if sentiment of this review is positive, negative or neutral",
+ ... tokenizer_name_or_path="t5-base",
+ ... )
+
+ >>> # t5_model.shared is the word embeddings of the base model
+ >>> prompt_embedding = PromptEmbedding(config, t5_model.shared)
+ ```
+
+ Input Shape: (`batch_size`, `total_virtual_tokens`)
+
+ Output Shape: (`batch_size`, `total_virtual_tokens`, `token_dim`)
+ """
+
+ def __init__(self, config, word_embeddings):
+ super().__init__()
+
+ total_virtual_tokens = config.num_virtual_tokens * config.num_transformer_submodules
+ self.embedding = torch.nn.Embedding(total_virtual_tokens, config.token_dim)
+ if config.prompt_tuning_init == PromptTuningInit.SAMPLE_VOCAB and not config.inference_mode:
+ # Randomly sample tokens from the tokenizer's vocab
+ vocab_size = word_embeddings.num_embeddings
+ init_token_ids = torch.randint(0, vocab_size, (total_virtual_tokens,), dtype=torch.long).to(
+ word_embeddings.weight.device
+ )
+ with gather_params_ctx(word_embeddings.parameters()):
+ word_embedding_weights = word_embeddings(init_token_ids).detach().clone()
+ word_embedding_weights = word_embedding_weights.to(torch.float32)
+ self.embedding.weight = torch.nn.Parameter(word_embedding_weights)
+
+ elif config.prompt_tuning_init == PromptTuningInit.TEXT and not config.inference_mode:
+ from transformers import AutoTokenizer
+
+ tokenizer_kwargs = config.tokenizer_kwargs or {}
+ tokenizer = AutoTokenizer.from_pretrained(config.tokenizer_name_or_path, **tokenizer_kwargs)
+ init_text = config.prompt_tuning_init_text
+ init_token_ids = tokenizer(init_text)["input_ids"]
+ # Trim or iterate until num_text_tokens matches total_virtual_tokens
+ num_text_tokens = len(init_token_ids)
+ if num_text_tokens > total_virtual_tokens:
+ init_token_ids = init_token_ids[:total_virtual_tokens]
+ elif num_text_tokens < total_virtual_tokens:
+ num_reps = math.ceil(total_virtual_tokens / num_text_tokens)
+ init_token_ids = init_token_ids * num_reps
+ init_token_ids = init_token_ids[:total_virtual_tokens]
+ init_token_ids = torch.LongTensor(init_token_ids).to(word_embeddings.weight.device)
+ with gather_params_ctx(word_embeddings.parameters()):
+ word_embedding_weights = word_embeddings(init_token_ids).detach().clone()
+ word_embedding_weights = word_embedding_weights.to(torch.float32)
+ self.embedding.weight = torch.nn.Parameter(word_embedding_weights)
+
+ def forward(self, indices):
+ # Just get embeddings
+ prompt_embeddings = self.embedding(indices)
+ return prompt_embeddings
diff --git a/peft/src/peft/tuners/randlora/__init__.py b/peft/src/peft/tuners/randlora/__init__.py
new file mode 100644
index 0000000000000000000000000000000000000000..fbad681aeb0231254f5caae6b9bf9aa3a2c76ef0
--- /dev/null
+++ b/peft/src/peft/tuners/randlora/__init__.py
@@ -0,0 +1,40 @@
+# Copyright 2025-present the HuggingFace Inc. team.
+
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+from peft.import_utils import is_bnb_4bit_available, is_bnb_available
+from peft.utils import register_peft_method
+
+from .config import RandLoraConfig
+from .layer import Linear, RandLoraLayer
+from .model import RandLoraModel
+
+
+__all__ = ["Linear", "RandLoraConfig", "RandLoraLayer", "RandLoraModel"]
+
+register_peft_method(name="randlora", config_cls=RandLoraConfig, model_cls=RandLoraModel, prefix="randlora_")
+
+
+def __getattr__(name):
+ if (name == "Linear8bitLt") and is_bnb_available():
+ from .bnb import Linear8bitLt
+
+ return Linear8bitLt
+
+ if (name == "Linear4bit") and is_bnb_4bit_available():
+ from .bnb import Linear4bit
+
+ return Linear4bit
+
+ raise AttributeError(f"module {__name__} has no attribute {name}")
diff --git a/peft/src/peft/tuners/randlora/bnb.py b/peft/src/peft/tuners/randlora/bnb.py
new file mode 100644
index 0000000000000000000000000000000000000000..353295e88aab41f4ca59669ec51e4dc479ad1e3e
--- /dev/null
+++ b/peft/src/peft/tuners/randlora/bnb.py
@@ -0,0 +1,456 @@
+# Copyright 2025-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+from __future__ import annotations
+
+import warnings
+from typing import Optional
+
+import bitsandbytes as bnb
+import torch
+
+from peft.import_utils import is_bnb_4bit_available, is_bnb_available
+from peft.tuners.tuners_utils import check_adapters_to_merge
+from peft.utils.integrations import dequantize_bnb_weight
+from peft.utils.other import transpose
+
+from .layer import RandLoraLayer, UniqueBaseGrad
+
+
+if is_bnb_available():
+
+ class Linear8bitLt(torch.nn.Module, RandLoraLayer):
+ def __init__(
+ self,
+ base_layer: torch.nn.Module,
+ adapter_name: str,
+ randlora_A,
+ randlora_B,
+ r: int = 0,
+ randlora_alpha: int = 0,
+ randlora_dropout: float = 0.0,
+ fan_in_fan_out: bool = False,
+ init_weights: bool = True,
+ **kwargs,
+ ) -> None:
+ super().__init__()
+ RandLoraLayer.__init__(self, base_layer)
+ self.fan_in_fan_out = fan_in_fan_out
+
+ self._active_adapter = adapter_name
+ self.update_layer(
+ adapter_name,
+ randlora_A,
+ randlora_B,
+ r,
+ randlora_alpha=randlora_alpha,
+ randlora_dropout=randlora_dropout,
+ init_weights=init_weights,
+ )
+
+ def merge(self, safe_merge: bool = False, adapter_names: Optional[list[str]] = None) -> None:
+ """
+ Merge the active adapter weights into the base weights
+
+ Args:
+ safe_merge (`bool`, *optional*):
+ If True, the merge operation will be performed in a copy of the original weights and check for NaNs
+ before merging the weights. This is useful if you want to check if the merge operation will produce
+ NaNs. Defaults to `False`.
+ adapter_names (`list[str]`, *optional*):
+ The list of adapter names that should be merged. If None, all active adapters will be merged.
+ Defaults to `None`.
+ """
+
+ adapter_names = check_adapters_to_merge(self, adapter_names)
+ if not adapter_names:
+ return
+
+ for active_adapter in adapter_names:
+ if active_adapter not in self.randlora_lambda.keys():
+ continue
+
+ warnings.warn(
+ "Merge RandLora module to 8-bit linear may get different generations due to rounding errors."
+ )
+ randlora_data = self.get_delta_weight(active_adapter)
+
+ weight = self.get_base_layer().weight
+ state = self.get_base_layer().state
+ if state.SCB is None:
+ state.SCB = weight.SCB
+
+ output = dequantize_bnb_weight(weight, state)
+ w_data = output.to(randlora_data.dtype).to(randlora_data.device) + randlora_data
+
+ if safe_merge and not torch.isfinite(w_data).all():
+ raise ValueError(
+ f"NaNs detected in the merged weights. The adapter {active_adapter} seems to be broken"
+ )
+
+ self.get_base_layer().weight = bnb.nn.Int8Params(
+ w_data.to("cpu"), requires_grad=False, has_fp16_weights=weight.has_fp16_weights
+ ).to(weight.device)
+ state.reset_grads()
+ self.merged_adapters.append(active_adapter)
+
+ def unmerge(self) -> None:
+ """
+ This method unmerges all merged adapter layers from the base weights.
+ """
+ if not self.merged:
+ warnings.warn("Already unmerged. Nothing to do")
+ return
+
+ while len(self.merged_adapters) > 0:
+ active_adapter = self.merged_adapters.pop()
+ if active_adapter not in self.randlora_lambda.keys():
+ continue
+ warnings.warn(
+ "Unmerge randlora module to 8-bit linear may get different generations due to rounding errors."
+ )
+ randlora_data = self.get_delta_weight(active_adapter)
+
+ weight = self.get_base_layer().weight
+ state = self.get_base_layer().state
+ if state.SCB is None:
+ state.SCB = weight.SCB
+ output = dequantize_bnb_weight(weight, state=state)
+
+ w_data = output.to(randlora_data.dtype).to(randlora_data.device) - randlora_data
+
+ self.get_base_layer().weight = bnb.nn.Int8Params(
+ w_data.to("cpu"), requires_grad=False, has_fp16_weights=weight.has_fp16_weights
+ ).to(weight.device)
+ state.reset_grads()
+
+ def get_scaled_bases(self, adapter, device=None) -> list[torch.Tensor, torch.Tensor]:
+ """
+ Performs scaling on the smallest random base (randlora_A) and returns randlora_A and randlora_B in the
+ correct order to fit the target layers' dimensions
+
+ Args:
+ adapter (str):
+ The name of the adapter for which the delta weight should be computed.
+ """
+
+ randlora_A = self.randlora_A[adapter]
+ randlora_B = self.randlora_B[adapter]
+
+ if device is None:
+ device = randlora_B.device
+ dtype = randlora_B.dtype
+
+ # In case users wants to merge the adapter weights that are in
+ # (b)float16 while being on CPU, we need to cast the weights to float32, perform the merge and then cast back to
+ # (b)float16 because some CPUs have slow bf16/fp16 matmuls.
+ cast_to_fp32 = device.type == "cpu" and (dtype == torch.float16 or dtype == torch.bfloat16)
+
+ randlora_lambda = self.randlora_lambda[adapter].to(device)
+ randlora_gamma = self.randlora_gamma[adapter].to(device)
+
+ if cast_to_fp32:
+ randlora_A = randlora_A.float()
+ randlora_B = randlora_B.float()
+ randlora_lambda = randlora_lambda.float()
+ randlora_gamma = randlora_gamma.float()
+
+ # The trainable parameters are always applied to randlora_A, the smallest basis.
+ min_dim, max_dim = min(self.out_features, self.in_features), max(self.out_features, self.in_features)
+
+ # As adapted layers may have different shapes and RandLora contains a single shared pair of A and B matrices,
+ # we initialize these matrices with the largest required size for each dimension.
+ # During the forward pass, required submatrices are sliced out from the shared randlora_A and randlora_B.
+ sliced_A = randlora_A[:, : self.num_bases, :min_dim].to(device)
+ sliced_B = randlora_B[:max_dim, : self.num_bases, :].to(device)
+
+ # Flattening the matrices over the rank and number of bases dimensions is more memory efficient
+ update_B = sliced_B.flatten(start_dim=1)
+ update_A = UniqueBaseGrad.apply(sliced_A, randlora_lambda, randlora_gamma).flatten(end_dim=1)
+ if min_dim == self.in_features:
+ return update_A, update_B
+
+ return update_B.T, update_A.T
+
+ def get_delta_weight(self, adapter) -> torch.Tensor:
+ """
+ Compute the delta weight for the given adapter.
+
+ Args:
+ adapter (str):
+ The name of the adapter for which the delta weight should be computed.
+ """
+
+ update_B, update_A = self.get_scaled_bases(adapter)
+
+ update = update_B @ update_A
+ output_tensor = transpose(update, self.fan_in_fan_out)
+
+ scaling = self.scaling[adapter]
+
+ return output_tensor * scaling
+
+ def forward(self, x: torch.Tensor, *args, **kwargs) -> torch.Tensor:
+ """
+ Perform the forward pass using the RandLora adapter.
+
+ Args:
+ x (torch.Tensor): Input tensor.
+
+ Returns:
+ torch.Tensor: Output tensor after applying the RandLora adaptation.
+
+ Note:
+ This method implements the RandLora-specific forward pass. It applies the shared projections
+ (randlora_A and randlora_B) along with the per-layer trainable parameters (lambda and gamma) to compute
+ the adapter output.
+ """
+ if self.disable_adapters:
+ if self.merged:
+ self.unmerge()
+ result = self.base_layer(x, *args, **kwargs)
+ elif self.merged:
+ result = self.base_layer(x, *args, **kwargs)
+ else:
+ result = self.base_layer(x, *args, **kwargs)
+ for active_adapter in self.active_adapters:
+ if active_adapter not in self.randlora_lambda.keys():
+ continue
+
+ update_B, update_A = self.get_scaled_bases(active_adapter, device=x.device)
+
+ requires_conversion = not torch.is_autocast_enabled()
+ if requires_conversion:
+ expected_dtype = result.dtype
+ compute_dtype = update_A.dtype
+ if x.dtype != compute_dtype:
+ x = x.to(compute_dtype)
+
+ dropout = self.randlora_dropout[active_adapter]
+ x_temp = dropout(x.to(update_A.dtype))
+
+ adapter_output = torch.nn.functional.linear(torch.nn.functional.linear(x_temp, update_B), update_A)
+
+ if requires_conversion:
+ adapter_output = adapter_output.to(expected_dtype)
+
+ scaling = self.scaling[active_adapter]
+ result = result + adapter_output * scaling
+
+ # Ensure the output tensor has the same dtype as the input tensor
+ return result.to(x.dtype)
+
+ def __repr__(self) -> str:
+ rep = super().__repr__()
+ return "randlora." + rep
+
+
+if is_bnb_4bit_available():
+
+ class Linear4bit(torch.nn.Module, RandLoraLayer):
+ def __init__(
+ self,
+ base_layer: torch.nn.Module,
+ adapter_name: str,
+ randlora_A,
+ randlora_B,
+ r: int = 0,
+ randlora_alpha: int = 0,
+ randlora_dropout: float = 0.0,
+ fan_in_fan_out: bool = False,
+ init_weights: bool = True,
+ **kwargs,
+ ) -> None:
+ super().__init__()
+ RandLoraLayer.__init__(self, base_layer)
+ self.fan_in_fan_out = fan_in_fan_out
+ self._active_adapter = adapter_name
+ self.update_layer(
+ adapter_name,
+ randlora_A,
+ randlora_B,
+ r,
+ randlora_alpha=randlora_alpha,
+ randlora_dropout=randlora_dropout,
+ init_weights=init_weights,
+ )
+
+ def merge(self, safe_merge: bool = False, adapter_names: Optional[list[str]] = None) -> None:
+ """
+ Merge the active adapter weights into the base weights
+
+ Args:
+ safe_merge (`bool`, *optional*):
+ If True, the merge operation will be performed in a copy of the original weights and check for NaNs
+ before merging the weights. This is useful if you want to check if the merge operation will produce
+ NaNs. Defaults to `False`.
+ adapter_names (`list[str]`, *optional*):
+ The list of adapter names that should be merged. If None, all active adapters will be merged.
+ Defaults to `None`.
+ """
+
+ adapter_names = check_adapters_to_merge(self, adapter_names)
+ if not adapter_names:
+ return
+
+ for active_adapter in adapter_names:
+ if active_adapter not in self.randlora_lambda.keys():
+ continue
+
+ warnings.warn(
+ "Merge RandLora module to 4-bit linear may get different generations due to rounding errors."
+ )
+ randlora_data = self.get_delta_weight(active_adapter)
+
+ weight = self.get_base_layer().weight
+ kwargs = weight.__dict__
+ w_data = bnb.functional.dequantize_4bit(weight.data, weight.quant_state) + randlora_data
+
+ if safe_merge and not torch.isfinite(w_data).all():
+ raise ValueError(
+ f"NaNs detected in the merged weights. The adapter {active_adapter} seems to be broken"
+ )
+
+ self.get_base_layer().weight = bnb.nn.Params4bit(w_data.to("cpu"), requires_grad=False, **kwargs).to(
+ weight.device
+ )
+ self.merged_adapters.append(active_adapter)
+
+ def unmerge(self) -> None:
+ """
+ This method unmerges all merged adapter layers from the base weights.
+ """
+ if not self.merged:
+ warnings.warn("Already unmerged. Nothing to do")
+ return
+
+ while len(self.merged_adapters) > 0:
+ active_adapter = self.merged_adapters.pop()
+ if active_adapter not in self.randlora_lambda.keys():
+ continue
+ warnings.warn(
+ "Unmerge RandLora module to 4-bit linear may get different generations due to rounding errors."
+ )
+ randlora_data = self.get_delta_weight(active_adapter)
+
+ weight = self.get_base_layer().weight
+ kwargs = weight.__dict__
+ w_data = bnb.functional.dequantize_4bit(weight.data, weight.quant_state) - randlora_data
+
+ self.get_base_layer().weight = bnb.nn.Params4bit(w_data.to("cpu"), requires_grad=False, **kwargs).to(
+ weight.device
+ )
+
+ def get_scaled_bases(self, adapter, device=None) -> list[torch.Tensor, torch.Tensor]:
+ """
+ Performs scaling on the smallest random base (randlora_A) and returns randlora_A and randlora_B in the
+ correct order to fit the target layers' dimensions
+
+ Args:
+ adapter (str):
+ The name of the adapter for which the delta weight should be computed.
+ """
+
+ randlora_A = self.randlora_A[adapter]
+ randlora_B = self.randlora_B[adapter]
+ if device is None:
+ device = randlora_B.device
+ dtype = randlora_B.dtype
+
+ # In case users wants to merge the adapter weights that are in
+ # (b)float16 while being on CPU, we need to cast the weights to float32, perform the merge and then cast back to
+ # (b)float16 because some CPUs have slow bf16/fp16 matmuls.
+ cast_to_fp32 = device.type == "cpu" and (dtype == torch.float16 or dtype == torch.bfloat16)
+
+ randlora_lambda = self.randlora_lambda[adapter].to(device)
+ randlora_gamma = self.randlora_gamma[adapter].to(device)
+
+ if cast_to_fp32:
+ randlora_A = randlora_A.float()
+ randlora_B = randlora_B.float()
+ randlora_lambda = randlora_lambda.float()
+ randlora_gamma = randlora_gamma.float()
+
+ # The trainable parameters are always applied to randlora_A, the smallest basis.
+ min_dim, max_dim = min(self.out_features, self.in_features), max(self.out_features, self.in_features)
+
+ # As adapted layers may have different shapes and RandLora contains a single shared pair of A and B matrices,
+ # we initialize these matrices with the largest required size for each dimension.
+ # During the forward pass, required submatrices are sliced out from the shared randlora_A and randlora_B.
+ sliced_A = randlora_A[:, : self.num_bases, :min_dim].to(device)
+ sliced_B = randlora_B[:max_dim, : self.num_bases, :].to(device)
+ # Flattening the matrices over the rank and number of bases dimensions is more memory efficient
+ update_B = sliced_B.flatten(start_dim=1)
+ update_A = UniqueBaseGrad.apply(sliced_A, randlora_lambda, randlora_gamma).flatten(end_dim=1)
+ if min_dim == self.in_features:
+ return update_A, update_B
+
+ return update_B.T, update_A.T
+
+ def get_delta_weight(self, adapter) -> torch.Tensor:
+ """
+ Compute the delta weight for the given adapter.
+
+ Args:
+ adapter (str):
+ The name of the adapter for which the delta weight should be computed.
+ """
+ update_B, update_A = self.get_scaled_bases(adapter)
+
+ update = update_B @ update_A
+ output_tensor = transpose(update, self.fan_in_fan_out)
+
+ scaling = self.scaling[adapter]
+
+ return output_tensor * scaling
+
+ def forward(self, x: torch.Tensor, *args, **kwargs) -> torch.Tensor:
+ if self.disable_adapters:
+ if self.merged:
+ self.unmerge()
+ result = self.base_layer(x, *args, **kwargs)
+ elif self.merged:
+ result = self.base_layer(x, *args, **kwargs)
+ else:
+ result = self.base_layer(x, *args, **kwargs)
+ result = result.clone()
+ for active_adapter in self.active_adapters:
+ if active_adapter not in self.randlora_lambda.keys():
+ continue
+
+ update_B, update_A = self.get_scaled_bases(active_adapter, device=x.device)
+
+ requires_conversion = not torch.is_autocast_enabled()
+ if requires_conversion:
+ expected_dtype = result.dtype
+ compute_dtype = update_A.dtype
+ if x.dtype != compute_dtype:
+ x = x.to(compute_dtype)
+
+ dropout = self.randlora_dropout[active_adapter]
+ x_temp = dropout(x.to(update_A.dtype))
+
+ adapter_output = torch.nn.functional.linear(torch.nn.functional.linear(x_temp, update_B), update_A)
+
+ if requires_conversion:
+ adapter_output = adapter_output.to(expected_dtype)
+
+ scaling = self.scaling[active_adapter]
+ result = result + adapter_output * scaling
+
+ # Ensure the output tensor has the same dtype as the input tensor
+ return result.to(x.dtype)
+
+ def __repr__(self) -> str:
+ rep = super().__repr__()
+ return "randlora." + rep
diff --git a/peft/src/peft/tuners/randlora/config.py b/peft/src/peft/tuners/randlora/config.py
new file mode 100644
index 0000000000000000000000000000000000000000..b194b974331dd9abcb5777295ae4e79d8b81da56
--- /dev/null
+++ b/peft/src/peft/tuners/randlora/config.py
@@ -0,0 +1,199 @@
+# Copyright 2025-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+import warnings
+from dataclasses import dataclass, field
+from typing import Optional, Union
+
+from peft.config import PeftConfig
+from peft.utils import PeftType
+
+
+@dataclass
+class RandLoraConfig(PeftConfig):
+ """
+ This is the configuration class to store the configuration of a [`RandLoraModel`].
+
+ Paper: https://huggingface.co/papers/2502.00987.
+
+ Args:
+ r (`int`, *optional*, defaults to `32`):
+ RandLora's random basis rank dimension. Contrary to Lora, this parameter is inversely proportional to the
+ amount of trainable parameters as reducing it increases trainable parameters.
+ target_modules (`Union[list[str], str]`):
+ The names of the modules to apply RandLora to. Only linear layers are supported.
+ projection_prng_key (`int`):
+ RandLora PRNG init key. Used for initialising basis_A and basis_B for new models or when loading a
+ checkpoint that did not include these projections. Defaults to `0`.
+ save_projection (`bool`):
+ Whether to save the global basis_A / basis_B random basis in the state dict alongside per layer lambda /
+ gamma diagonal matrices. This will increase the size of the checkpoint, but guarantee that we can reload
+ the checkpoint on all system configurations. Defaults to `True`.
+ sparse (`bool`):
+ Whether to use sparse random bases as described in the RandLora paper. The bases are ternary sparse bases
+ (only containing -1, 0 and 1) where the attribution probability is 1/6 for -1 and 1 and 2/3 for 0. These
+ sparse matrices aim to be used for matmul free computation in the future, see
+ https://huggingface.co/papers/2406.02528v1 The current implementation is a proof of concept however where
+ the sparseness is not used to improve speed or memory usage. Using sparse matrices typically does not
+ reduce performance and can even help reduce overfitting. Defaults to `False`.
+ very_sparse (`bool`):
+ Whether to use highly sparse random bases as described in the RandLora paper. The very sparse bases are
+ ternary sparse bases (only containing -1, 0 and 1) given a matrix with smallest dimension d, the
+ attribution probability is 1/√D for -1 and 1 and 1- 2/√D for 0. Using these sparse matrices can further
+ reduce overfitting over the `sparse` alternatives but will most likely decrease performance as a results.
+ Use carefully. Defaults to `False`.
+ randlora_dropout (`float`):
+ The dropout probability for RandLora layers.
+ randlora_alpha (`float`):
+ The scaling coefficient for RandLora layers, this would typically be 20 times the rank. Because the
+ `randlora_alpha` coefficient is large by default, it can lead to numerical instabilities especially when
+ learning rates are high. If training is unstable, consider reducing the learning rate or the
+ `randlora_alpha` coefficient.
+ fan_in_fan_out (`bool`):
+ Set this to True if the layer to replace stores weight like (fan_in, fan_out). For example, gpt-2 uses
+ `Conv1D` which stores weights like (fan_in, fan_out) and hence this should be set to `True`.
+ bias (`str`):
+ Bias type. Can be 'none', 'all' or 'randlora_only'. If 'all' or 'randlora_only', the corresponding biases
+ will be updated during training. Be aware that this means that, even when disabling the adapters, the model
+ will not produce the same output as the base model would have without adaptation.
+ modules_to_save (`list[str]`):
+ list of modules apart from RandLora layers to be set as trainable and saved in the final checkpoint.
+ init_weights (`bool`):
+ Whether to initialize the weights of the RandLora layers with their default initialization. Don't change
+ this setting, except if you know exactly what you're doing.
+ layers_to_transform (`Union[list[int],int]`):
+ The layer indexes to transform, if this argument is specified, it will apply the RandLora transformations
+ on the layer indexes that are specified in this list. If a single integer is passed, it will apply the
+ RandLora transformations on the layer at this index.
+ layers_pattern (`str`):
+ The layer pattern name, used only if `layers_to_transform` is different from `None` and if the layer
+ pattern is not in the common layers pattern.
+ """
+
+ r: int = field(default=32, metadata={"help": "RandLora random basis rank"})
+
+ target_modules: Optional[Union[list[str], str]] = field(
+ default=None,
+ metadata={
+ "help": (
+ "list of module names or regex expression of the module names to replace with RandLora."
+ "For example, ['q', 'v'] or '.*decoder.*(SelfAttention|EncDecAttention).*(q|v)$'. "
+ "Only linear layers are supported."
+ )
+ },
+ )
+ projection_prng_key: int = field(
+ default=0,
+ metadata={
+ "help": (
+ "RandLora PRNG init key. Used for initialising basis_A and basis_B for new models or when loading a "
+ "checkpoint that did not include these projections."
+ )
+ },
+ )
+ save_projection: bool = field(
+ default=True,
+ metadata={
+ "help": (
+ "Whether to save the basis_A / basis_B projections in the state dict alongside per layer lambda / "
+ "gamma weights. This will increase the size of the checkpoint, but guarantee that we can reload "
+ "the checkpoint on all system configurations."
+ )
+ },
+ )
+ sparse: bool = field(
+ default=False,
+ metadata={
+ "help": (
+ "Whether to use sparse random bases as described in the RandLora paper."
+ "The current implementation is a proof of concept where the sparseness"
+ "is not used to improve speed or memory usage."
+ )
+ },
+ )
+ very_sparse: bool = field(
+ default=False,
+ metadata={
+ "help": (
+ "Whether to use very sparse random bases."
+ "The current implementation is a proof of concept where the sparseness"
+ "is not used to improve speed or memory usage."
+ )
+ },
+ )
+ randlora_dropout: float = field(default=0.0, metadata={"help": "Dropout in the adapter layers"})
+ fan_in_fan_out: bool = field(
+ default=False,
+ metadata={"help": "Set this to True if the layer to replace stores weight like (fan_in, fan_out)"},
+ )
+ randlora_alpha: int = field(
+ default=640,
+ metadata={
+ "help": "Scaling coefficient in the adapter layers, typically 20 times the rank of the random bases."
+ },
+ )
+ bias: str = field(
+ default="none", metadata={"help": "Bias type for RandLora. Can be 'none', 'all' or 'randlora_only'"}
+ )
+ modules_to_save: Optional[list[str]] = field(
+ default=None,
+ metadata={
+ "help": (
+ "list of modules apart from RandLora layers to be set as trainable and saved in the final checkpoint. For"
+ " example, in Sequence Classification or Token Classification tasks, the final layer"
+ " `classifier/score` are randomly initialized and as such need to be trainable and saved."
+ )
+ },
+ )
+ init_weights: bool = field(
+ default=True,
+ metadata={
+ "help": (
+ "Whether to initialize the weights of the RandLora layers with their default initialization. Don't change "
+ "this setting, except if you know exactly what you're doing."
+ ),
+ },
+ )
+ layers_to_transform: Optional[Union[list[int], int]] = field(
+ default=None,
+ metadata={
+ "help": (
+ "The layer indexes to transform, is this argument is specified, PEFT will transform only the layers"
+ " indexes that are specified inside this list. If a single integer is passed, PEFT will transform only"
+ " the layer at this index."
+ )
+ },
+ )
+ layers_pattern: Optional[str] = field(
+ default=None,
+ metadata={
+ "help": (
+ "The layer pattern name, used only if `layers_to_transform` is different to None and if the layer"
+ " pattern is not in the common layers pattern."
+ )
+ },
+ )
+
+ def __post_init__(self):
+ self.peft_type = PeftType.RANDLORA
+ self.target_modules = (
+ set(self.target_modules) if isinstance(self.target_modules, list) else self.target_modules
+ )
+
+ if not self.save_projection:
+ warnings.warn(
+ "Specified to not save basis_A and basis_B within the state dictionary, instead they will be restored "
+ "using the PRNG key store in `config.projection_prng_key`. Consider setting `config.save_projection` "
+ "to `True` to guarantee restoring the checkpoint correctly on all system configurations."
+ )
diff --git a/peft/src/peft/tuners/randlora/layer.py b/peft/src/peft/tuners/randlora/layer.py
new file mode 100644
index 0000000000000000000000000000000000000000..77ecbdafac05ee4b3cfa0472f7fe0af54603bc5d
--- /dev/null
+++ b/peft/src/peft/tuners/randlora/layer.py
@@ -0,0 +1,350 @@
+# Copyright 2025-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+import warnings
+from typing import Optional
+
+import torch
+import torch.nn as nn
+import torch.nn.functional as F
+from transformers.pytorch_utils import Conv1D
+
+from peft.tuners.tuners_utils import BaseTunerLayer, check_adapters_to_merge
+from peft.utils.other import transpose
+
+from .._buffer_dict import BufferDict
+
+
+class UniqueBaseGrad(torch.autograd.Function):
+ # Memory efficent for a unique base
+ @staticmethod
+ def forward(ctx, randlora_A, randlora_lambda, randlora_gamma):
+ out = randlora_lambda[:, :, None] * randlora_A * randlora_gamma[None,]
+ ctx.save_for_backward(randlora_A, randlora_lambda, randlora_gamma)
+ return out
+
+ @staticmethod
+ def backward(ctx, grad_output):
+ randlora_A, randlora_lambda, randlora_gamma = ctx.saved_tensors
+ randlora_A, randlora_lambda, randlora_gamma = (
+ randlora_A.to(grad_output.dtype),
+ randlora_lambda.to(grad_output.dtype),
+ randlora_gamma.to(grad_output.dtype),
+ )
+ grad_randlora_lambda = torch.einsum("kbj,kvj,bj->kb", grad_output, randlora_A, randlora_gamma)
+ grad_randlora_gamma = torch.einsum("kbj,kvj,kb->bj", grad_output, randlora_A, randlora_lambda)
+ return None, grad_randlora_lambda, grad_randlora_gamma
+
+
+class RandLoraLayer(BaseTunerLayer):
+ # List all names of layers that may contain adapter weights
+ adapter_layer_names = ("randlora_lambda", "randlora_gamma")
+ other_param_names = ("randlora_A", "randlora_B")
+
+ def __init__(self, base_layer: nn.Module, **kwargs):
+ self.base_layer = base_layer
+ self.r = {}
+ self.scaling = {}
+ self.randlora_dropout = nn.ModuleDict({})
+
+ # For storing vector scale
+ self.randlora_lambda = nn.ParameterDict({})
+ self.randlora_gamma = nn.ParameterDict({})
+
+ # Stores a reference to the randlora_A/B BufferDict.
+ # Set to `None` otherwise to avoid computation with random weights
+ self.randlora_A: Optional[BufferDict] = None
+ self.randlora_B: Optional[BufferDict] = None
+
+ # Mark the weight as unmerged
+ self._disable_adapters = False
+ self.merged_adapters = []
+
+ # flag to enable/disable casting of input to weight dtype during forward call
+ self.cast_input_dtype_enabled = True
+
+ base_layer = self.get_base_layer()
+ if isinstance(base_layer, nn.Linear):
+ in_features, out_features = base_layer.in_features, base_layer.out_features
+ elif isinstance(base_layer, Conv1D):
+ in_features, out_features = (
+ base_layer.weight.ds_shape if hasattr(base_layer.weight, "ds_shape") else base_layer.weight.shape
+ )
+
+ self.in_features = in_features
+ self.out_features = out_features
+ self.kwargs = kwargs
+
+ @property
+ def merged(self) -> bool:
+ return bool(self.merged_adapters)
+
+ def update_layer(
+ self,
+ adapter_name,
+ randlora_A: BufferDict,
+ randlora_B: BufferDict,
+ r,
+ randlora_alpha,
+ randlora_dropout,
+ init_weights,
+ inference_mode: bool = False,
+ **kwargs,
+ ):
+ if r <= 0:
+ raise ValueError(f"`r` should be a positive integer value but the value passed is {r}")
+ self.r[adapter_name] = r
+ if randlora_dropout > 0.0:
+ randlora_dropout_layer = nn.Dropout(p=randlora_dropout)
+ else:
+ randlora_dropout_layer = nn.Identity()
+
+ self.randlora_dropout.update(nn.ModuleDict({adapter_name: randlora_dropout_layer}))
+
+ # Actual trainable parameters
+ num_bases = min(self.in_features, self.out_features) / r
+ self.num_bases = int(num_bases) if num_bases.is_integer() else int(num_bases) + 1 # Full rank
+ self.randlora_lambda[adapter_name] = nn.Parameter(torch.randn(r, self.num_bases), requires_grad=True)
+ self.randlora_gamma[adapter_name] = nn.Parameter(
+ torch.ones(self.num_bases, min(self.out_features, self.in_features))
+ / max(self.out_features, self.in_features),
+ requires_grad=True,
+ )
+
+ self.scaling[adapter_name] = randlora_alpha / r
+
+ # non trainable references to randlora_A/B buffers
+ self.randlora_A = randlora_A
+ self.randlora_B = randlora_B
+ if adapter_name not in randlora_A:
+ # This means that this is not the first RandLora adapter. We have to add an entry in the dict for this adapter.
+ if len(self.randlora_A) < 1:
+ raise ValueError(
+ "The `randlora_A` and `randlora_B` buffers are empty. This should not happen. Please report this issue."
+ )
+ # we can take any of the existing adapter's parameters, as they should all be identical
+ randlora_A_param = list(self.randlora_A.values())[0]
+ randlora_B_param = list(self.randlora_B.values())[0]
+
+ error_tmpl = (
+ "{} has a size of {} but {} or greater is required; this probably happened because an additional RandLora "
+ "adapter was added after the first one with incompatible shapes."
+ )
+ max_dim, min_dim = max(self.in_features, self.out_features), min(self.in_features, self.out_features)
+ # check input size
+ if randlora_B_param.shape[0] < max_dim:
+ raise ValueError(error_tmpl.format("randlora_B", randlora_B_param.shape[0], max_dim))
+ # check output size
+ if randlora_A_param.shape[-1] < min_dim:
+ raise ValueError(error_tmpl.format("randlora_A", randlora_A_param.shape[1], min_dim))
+
+ # check r
+ error_tmpl = (
+ "{} has a size of {} but {} or greater is required; this probably happened because an additional RandLora "
+ "adapter with a lower rank was added after the first one; loading the adapters "
+ "in reverse order may solve this."
+ )
+ if randlora_A_param.shape[0] < self.r[adapter_name]:
+ raise ValueError(error_tmpl.format("randlora_A", randlora_A_param.shape[0], self.r[adapter_name]))
+
+ if randlora_B_param.shape[-1] < self.r[adapter_name]:
+ raise ValueError(error_tmpl.format("randlora_B", randlora_B_param.shape[-1], self.r[adapter_name]))
+
+ self.randlora_A[adapter_name] = randlora_A_param
+ self.randlora_B[adapter_name] = randlora_B_param
+
+ if init_weights:
+ self.reset_randlora_parameters(adapter_name)
+
+ self._move_adapter_to_device_of_base_layer(adapter_name)
+ self.set_adapter(self.active_adapters, inference_mode=inference_mode)
+
+ def reset_randlora_parameters(self, adapter_name):
+ if adapter_name in self.randlora_lambda.keys():
+ with torch.no_grad():
+ nn.init.zeros_(self.randlora_lambda[adapter_name])
+ nn.init.constant_(self.randlora_gamma[adapter_name], 1 / max(self.randlora_gamma[adapter_name].shape))
+
+
+class Linear(nn.Linear, RandLoraLayer):
+ # RandLora implemented in a dense layer
+ def __init__(
+ self,
+ base_layer,
+ randlora_A: BufferDict,
+ randlora_B: BufferDict,
+ adapter_name: str,
+ r: int = 0,
+ randlora_alpha: int = 0,
+ randlora_dropout: float = 0.0,
+ fan_in_fan_out: bool = False, # Set this to True if the layer to replace stores weight like (fan_in, fan_out)
+ is_target_conv_1d_layer: bool = False,
+ init_weights: bool = True,
+ **kwargs,
+ ) -> None:
+ # this gets the init from nn.Linear's super perspective, i.e. nn.Module.__init__, which should always be called
+ super(nn.Linear, self).__init__()
+ RandLoraLayer.__init__(self, base_layer, **kwargs)
+ self.fan_in_fan_out = fan_in_fan_out
+ self._active_adapter = adapter_name
+ self.update_layer(adapter_name, randlora_A, randlora_B, r, randlora_alpha, randlora_dropout, init_weights)
+ self.is_target_conv_1d_layer = is_target_conv_1d_layer
+
+ def merge(self, safe_merge: bool = False, adapter_names: Optional[list[str]] = None) -> None:
+ """
+ Merge the active adapter weights into the base weights
+
+ Args:
+ safe_merge (`bool`, *optional*):
+ If True, the merge operation will be performed in a copy of the original weights and check for NaNs
+ before merging the weights. This is useful if you want to check if the merge operation will produce
+ NaNs. Defaults to `False`.
+ adapter_names (`list[str]`, *optional*):
+ The list of adapter names that should be merged. If None, all active adapters will be merged. Defaults
+ to `None`.
+ """
+ adapter_names = check_adapters_to_merge(self, adapter_names)
+ if not adapter_names:
+ # no adapter to merge
+ return
+
+ for active_adapter in adapter_names:
+ if active_adapter in self.randlora_lambda.keys():
+ base_layer = self.get_base_layer()
+ orig_dtype = base_layer.weight.dtype
+
+ if safe_merge:
+ # Note that safe_merge will be slower than the normal merge
+ # because of the copy operation.
+ orig_weights = base_layer.weight.data.clone()
+
+ orig_weights += self.get_delta_weight(active_adapter)
+
+ if not torch.isfinite(orig_weights).all():
+ raise ValueError(
+ f"NaNs detected in the merged weights. The adapter {active_adapter} seems to be broken"
+ )
+
+ base_layer.weight.data = orig_weights.to(orig_dtype)
+ else:
+ delta_weight = self.get_delta_weight(active_adapter)
+ base_layer.weight.data += delta_weight.to(orig_dtype)
+
+ self.merged_adapters.append(active_adapter)
+
+ def unmerge(self) -> None:
+ """
+ This method unmerges all merged adapter layers from the base weights.
+ """
+ if not self.merged:
+ warnings.warn("Already unmerged. Nothing to do.")
+ return
+
+ while len(self.merged_adapters) > 0:
+ base_layer = self.get_base_layer()
+ orig_dtype = base_layer.weight.dtype
+ active_adapter = self.merged_adapters.pop()
+ if active_adapter in self.randlora_lambda.keys():
+ delta_weight = self.get_delta_weight(active_adapter)
+ base_layer.weight.data -= delta_weight.to(orig_dtype)
+
+ def get_scaled_bases(self, adapter, device=None) -> tuple[torch.Tensor, torch.Tensor]:
+ """
+ Performs scaling on the smallest random base (randlora_A) and returns randlora_A and randlora_B in the correct
+ order to fit the target layers' dimensions
+
+ Args:
+ adapter (str):
+ The name of the adapter for which the delta weight should be computed.
+ """
+
+ randlora_A = self.randlora_A[adapter]
+ randlora_B = self.randlora_B[adapter]
+ if device is None:
+ device = randlora_B.device
+ dtype = randlora_B.dtype
+
+ # In case users wants to merge the adapter weights that are in
+ # (b)float16 while being on CPU, we need to cast the weights to float32, perform the merge and then cast back to
+ # (b)float16 because some CPUs have slow bf16/fp16 matmuls.
+ cast_to_fp32 = device.type == "cpu" and (dtype == torch.float16 or dtype == torch.bfloat16)
+
+ randlora_lambda = self.randlora_lambda[adapter].to(device)
+ randlora_gamma = self.randlora_gamma[adapter].to(device)
+
+ if cast_to_fp32:
+ randlora_A = randlora_A.float()
+ randlora_B = randlora_B.float()
+ randlora_lambda = randlora_lambda.float()
+ randlora_gamma = randlora_gamma.float()
+
+ # The trainable parameters are always applied to randlora_A, the smallest basis.
+ min_dim, max_dim = min(self.out_features, self.in_features), max(self.out_features, self.in_features)
+
+ # As adapted layers may have different shapes and RandLora contains a single shared pair of A and B matrices,
+ # we initialize these matrices with the largest required size for each dimension.
+ # During the forward pass, required submatrices are sliced out from the shared randlora_A and randlora_B.
+ sliced_A = randlora_A[:, : self.num_bases, :min_dim].to(device)
+ sliced_B = randlora_B[:max_dim, : self.num_bases, :].to(device)
+
+ # Flattening the matrices over the rank and number of bases dimensions is more memory efficient
+ update_B = sliced_B.flatten(start_dim=1)
+ update_A = UniqueBaseGrad.apply(sliced_A, randlora_lambda, randlora_gamma).flatten(end_dim=1)
+
+ # Since update_A is applied on the smallest dimension, test whether update_A or update_B should be applied first. This is done to reduce trainable parameters.
+ if min_dim == self.in_features:
+ return update_A, update_B
+ return update_B.T, update_A.T
+
+ def get_delta_weight(self, adapter) -> torch.Tensor:
+ """
+ Compute the delta weight for the given adapter.
+
+ Args:
+ adapter (str):
+ The name of the adapter for which the delta weight should be computed.
+ """
+
+ update_B, update_A = self.get_scaled_bases(adapter)
+
+ update = (update_B.T @ update_A.T).T
+ output_tensor = transpose(update, self.fan_in_fan_out)
+
+ scaling = self.scaling[adapter]
+ return output_tensor * scaling
+
+ def forward(self, x: torch.Tensor, *args, **kwargs) -> torch.Tensor:
+ previous_dtype = x.dtype
+ if self.disable_adapters:
+ if self.merged:
+ self.unmerge()
+ result = self.base_layer(x, *args, **kwargs)
+ elif self.merged:
+ result = self.base_layer(x, *args, **kwargs)
+ else:
+ result = self.base_layer(x, *args, **kwargs)
+ for active_adapter in self.active_adapters:
+ if active_adapter not in self.randlora_lambda.keys():
+ continue
+ dropout = self.randlora_dropout[active_adapter]
+ update_B, update_A = self.get_scaled_bases(active_adapter, device=x.device)
+ x = x.to(update_A.dtype)
+ scaling = self.scaling[active_adapter]
+ result = result + F.linear(F.linear(dropout(x), update_B), update_A) * scaling
+ result = result.to(previous_dtype)
+ return result
+
+ def __repr__(self) -> str:
+ rep = super().__repr__()
+ return "randlora." + rep
diff --git a/peft/src/peft/tuners/randlora/model.py b/peft/src/peft/tuners/randlora/model.py
new file mode 100644
index 0000000000000000000000000000000000000000..3146438f3821aba61ac94c8e31243b00eb748011
--- /dev/null
+++ b/peft/src/peft/tuners/randlora/model.py
@@ -0,0 +1,356 @@
+# Copyright 2025-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+from __future__ import annotations
+
+import math
+import warnings
+from typing import Union
+
+import torch
+import torch.nn as nn
+from accelerate.utils.imports import is_bf16_available
+from transformers.pytorch_utils import Conv1D
+
+from peft.import_utils import is_bnb_4bit_available, is_bnb_available
+from peft.tuners.tuners_utils import BaseTuner, BaseTunerLayer
+from peft.utils import (
+ TRANSFORMERS_MODELS_TO_RANDLORA_TARGET_MODULES_MAPPING,
+)
+
+from .._buffer_dict import BufferDict
+from ..tuners_utils import _maybe_include_all_linear_layers
+from .config import RandLoraConfig
+from .layer import Linear, RandLoraLayer
+
+
+def _kaiming_init(
+ tensor_or_shape: Union[torch.Tensor, tuple[int, ...]],
+ generator: torch.Generator,
+) -> torch.Tensor:
+ """
+ Kaiming Uniform Initialisation adapted to accept a `torch.Generator` object for PRNG.
+
+ Args:
+ tensor_or_shape (`Union[torch.Tensor, tuple[int, ...]]`):
+ Tensor to initialise, or shape of new tensor to create and then initialise.
+ generator: (`torch.Generator`):
+ Generator object that manages the state of the PRNG algorithm in use.
+
+ Returns:
+ `torch.Tensor`: The initialised tensor.
+ """
+ if isinstance(tensor_or_shape, tuple):
+ tensor = torch.empty(
+ tensor_or_shape,
+ dtype=torch.bfloat16 if is_bf16_available() else torch.float16,
+ )
+ else:
+ tensor = tensor_or_shape
+
+ with torch.no_grad():
+ basis = torch.nn.init.kaiming_uniform_(tensor, a=math.sqrt(5), generator=generator)
+ return basis
+
+
+class RandLoraModel(BaseTuner):
+ """
+ Creates a RandLoRA model from a pretrained transformers model.
+
+ Args:
+ model ([`~transformers.PreTrainedModel`]): The model to be adapted.
+ config ([`RandLoraConfig`]): The configuration of the RandLora model.
+ adapter_name (`str`): The name of the adapter, defaults to `"default"`.
+ low_cpu_mem_usage (`bool`, `optional`, defaults to `False`):
+ Create empty adapter weights on meta device. Useful to speed up the loading process.
+
+ Returns:
+ `torch.nn.Module`: The RandLora model.
+
+ Example:
+
+ ```py
+ >>> from transformers import AutoModelForCausalLM
+ >>> from peft import RandLoraConfig, get_peft_model
+
+ >>> base_model = AutoModelForCausalLM.from_pretrained("facebook/opt-125m")
+ >>> config = RandLoraConfig(r=32)
+ >>> model = get_peft_model(base_model, config)
+ ```
+
+ **Attributes**:
+ - **model** ([`~transformers.PreTrainedModel`]) -- The model to be adapted.
+ - **peft_config** ([`RandLoraConfig`]): The configuration of the RandLora model.
+ """
+
+ prefix: str = "randlora_"
+ tuner_layer_cls = RandLoraLayer
+ target_module_mapping = TRANSFORMERS_MODELS_TO_RANDLORA_TARGET_MODULES_MAPPING
+
+ def _find_dim(self, config) -> tuple[int, int]:
+ """
+ Finds the largest input and output dimensions across linear layers that have been wrapped with RandLora.
+
+ This will be used for determining the size of the shared randlora_A and randlora_B matrices.
+ """
+ model_config = self.get_model_config(self.model)
+
+ peft_config = self._prepare_adapter_config(config, model_config)
+ peft_config = _maybe_include_all_linear_layers(peft_config, self.model)
+
+ largest_shape = None
+ for key, module in self.model.named_modules():
+ if not self._check_target_module_exists(peft_config, key):
+ continue
+
+ if isinstance(module, nn.Linear):
+ module_shape = module.out_features, module.in_features
+ elif isinstance(module, Conv1D):
+ module_shape = module.weight.ds_shape if hasattr(module.weight, "ds_shape") else module.weight.shape
+ module_shape = module_shape[::-1]
+ else:
+ continue
+
+ if largest_shape is None:
+ largest_shape = module_shape
+ continue
+
+ if module_shape != largest_shape:
+ largest_shape = tuple(max(a, b) for a, b in zip(largest_shape, module_shape))
+
+ if largest_shape is None:
+ msg = "No layers types compatible with RandLora were found. Please check `peft_config.target_modules`."
+ raise ValueError(msg)
+
+ return largest_shape
+
+ def _init_randlora_A_randlora_B_sparse(self, config: RandLoraConfig, adapter_name: str, sparsity: int = 3) -> None:
+ """
+ Sparse random projections as described in https://cs-people.bu.edu/evimaria/cs565/kdd-rp.pdf
+ """
+
+ linear_out_dim, linear_in_dim = self._find_dim(config)
+ max_dim, min_dim = max(linear_out_dim, linear_in_dim), min(linear_out_dim, linear_in_dim)
+
+ # use of persistent to exclude randlora_A and randlora_B from the state dict if we choose not to save them.
+ self.randlora_A = BufferDict({}, persistent=config.save_projection)
+ self.randlora_B = BufferDict({}, persistent=config.save_projection)
+
+ # deterministic init of randlora_A and randlora_B if we know the key
+ generator = torch.Generator(device="cpu").manual_seed(config.projection_prng_key)
+
+ # The gamma matrix is applied on A meaning it can be unique (shared) across the n scaling matrices.
+ # We also set randlora_A as the smallest matrix to reduce trainable parameters.
+ randlora_A = torch.rand((config.r, 1, min_dim), generator=generator)
+
+ # Number of bases to ensure full rank
+ num_bases = min_dim / config.r
+ num_bases = int(num_bases) if num_bases.is_integer() else int(num_bases) + 1 # Ensure full rank
+ randlora_B = torch.rand((max_dim, num_bases, config.r), generator=generator)
+
+ # The current implementation is a proof of concept and does take into consideration
+ # the sparsity to reduce memory usage or speed up compute
+ randlora_B_sparse = torch.zeros(randlora_B.shape)
+ randlora_A_sparse = torch.zeros(randlora_A.shape)
+ randlora_B_sparse[randlora_B < 1 / (2 * sparsity)] = -1
+ randlora_B_sparse[randlora_B > 1 - 1 / (2 * sparsity)] = 1
+ randlora_A_sparse[randlora_A < 1 / (2 * sparsity)] = -1
+ randlora_A_sparse[randlora_A > 1 - 1 / (2 * sparsity)] = 1
+
+ # Std normalization is empirically found to be the best
+ randlora_A, randlora_B = (
+ randlora_A_sparse / randlora_A_sparse.std(),
+ randlora_B_sparse / randlora_B_sparse.std(),
+ )
+ self.randlora_A[adapter_name] = randlora_A
+ self.randlora_B[adapter_name] = randlora_B
+
+ def _init_randlora_A_randlora_B(self, config: RandLoraConfig, adapter_name: str) -> None:
+ linear_out_dim, linear_in_dim = self._find_dim(config)
+ max_dim, min_dim = max(linear_out_dim, linear_in_dim), min(linear_out_dim, linear_in_dim)
+
+ # use of persistent to exclude randlora_A and randlora_B from the state dict if we choose not to save them.
+ self.randlora_A = BufferDict({}, persistent=config.save_projection)
+ self.randlora_B = BufferDict({}, persistent=config.save_projection)
+
+ # deterministic init of randlora_A and randlora_B if we know the key
+ generator = torch.Generator(device="cpu").manual_seed(config.projection_prng_key)
+
+ # The gamma matrix is applied on A meaning it can be unique (shared) across the n scaling matrices.
+ # We also set randlora_A as the smallest matrix to reduce trainable parameters.
+ randlora_A = _kaiming_init((config.r, 1, min_dim), generator=generator)
+
+ # Ensure full rank
+ num_bases = min(linear_out_dim, linear_in_dim) / config.r
+ num_bases = int(num_bases) if num_bases.is_integer() else int(num_bases) + 1
+ randlora_B = torch.cat(
+ [_kaiming_init((max_dim, 1, config.r), generator=generator) for _ in range(num_bases)], dim=1
+ )
+
+ # Std normalization is empirically found to be the best
+ randlora_A, randlora_B = randlora_A / randlora_A.std(), randlora_B / randlora_B.std()
+ self.randlora_A[adapter_name] = randlora_A
+ self.randlora_B[adapter_name] = randlora_B
+
+ def _pre_injection_hook(self, model: nn.Module, config: RandLoraConfig, adapter_name: str) -> None:
+ if config.very_sparse:
+ linear_out_dim, linear_in_dim = self._find_dim(config)
+ self._init_randlora_A_randlora_B_sparse(
+ config, adapter_name, sparsity=math.sqrt(min(linear_out_dim, linear_in_dim))
+ )
+ elif config.sparse:
+ self._init_randlora_A_randlora_B_sparse(config, adapter_name, sparsity=3)
+ else:
+ self._init_randlora_A_randlora_B(config, adapter_name)
+
+ def _check_new_adapter_config(self, config: RandLoraConfig) -> None:
+ """
+ A helper method to check the config when a new adapter is being added.
+
+ Raise a ValueError if there is something wrong with the config or if it conflicts with existing adapters.
+
+ """
+ super()._check_new_adapter_config(config)
+
+ for existing_config in self.peft_config.values():
+ if existing_config is config:
+ # skip the current config
+ continue
+
+ if existing_config.projection_prng_key != config.projection_prng_key:
+ raise ValueError(
+ f"RandLora PRNG initialisation key must be the same for all adapters. Got {config.projection_prng_key=} but "
+ f"previous config had {existing_config.projection_prng_key}."
+ )
+
+ save_project_unique_values = sorted({config.save_projection for config in self.peft_config.values()})
+ if len(save_project_unique_values) > 1:
+ raise ValueError(
+ "RandLora projection weights must be saved for all adapters or none, but got multiple different values: "
+ f"{save_project_unique_values}"
+ )
+
+ def _create_and_replace(
+ self,
+ randlora_config,
+ adapter_name,
+ target,
+ target_name,
+ parent,
+ current_key,
+ **optional_kwargs,
+ ):
+ if current_key is None:
+ raise ValueError("Current Key shouldn't be `None`")
+
+ r = randlora_config.r
+ bias = hasattr(target, "bias") and target.bias is not None
+ kwargs = {
+ "r": r,
+ "randlora_alpha": randlora_config.randlora_alpha,
+ "randlora_dropout": randlora_config.randlora_dropout,
+ "fan_in_fan_out": randlora_config.fan_in_fan_out,
+ "init_weights": randlora_config.init_weights,
+ "loaded_in_8bit": getattr(self.model, "is_loaded_in_8bit", False),
+ "loaded_in_4bit": getattr(self.model, "is_loaded_in_4bit", False),
+ }
+ kwargs["bias"] = bias
+ if isinstance(target, Linear):
+ target.update_layer(
+ adapter_name,
+ self.randlora_A,
+ self.randlora_B,
+ r,
+ randlora_config.randlora_alpha,
+ randlora_config.randlora_dropout,
+ randlora_config.init_weights,
+ )
+ else:
+ new_module = self._create_new_module(
+ randlora_config, self.randlora_A, self.randlora_B, adapter_name, target, **kwargs
+ )
+ if adapter_name not in self.active_adapter:
+ # adding an additional adapter: it is not automatically trainable
+ new_module.requires_grad_(False)
+ self._replace_module(parent, target_name, new_module, target)
+
+ @staticmethod
+ def _create_new_module(randlora_config, randlora_A, randlora_B, adapter_name, target, **kwargs):
+ # avoid eager bnb import
+ if is_bnb_available():
+ import bitsandbytes as bnb
+
+ from .bnb import Linear8bitLt
+
+ if is_bnb_4bit_available():
+ from .bnb import Linear4bit
+
+ bias = kwargs.pop("bias", False)
+ loaded_in_8bit = kwargs.get("loaded_in_8bit", False)
+ loaded_in_4bit = kwargs.get("loaded_in_4bit", False)
+
+ if isinstance(target, BaseTunerLayer):
+ target_base_layer = target.get_base_layer()
+ else:
+ target_base_layer = target
+
+ if loaded_in_8bit and isinstance(target_base_layer, bnb.nn.Linear8bitLt):
+ eightbit_kwargs = kwargs.copy()
+ eightbit_kwargs.update(
+ {
+ "has_fp16_weights": target_base_layer.state.has_fp16_weights,
+ "threshold": target_base_layer.state.threshold,
+ "index": target_base_layer.index,
+ }
+ )
+ return Linear8bitLt(target, adapter_name, randlora_A, randlora_B, **eightbit_kwargs)
+ elif loaded_in_4bit and isinstance(target_base_layer, bnb.nn.Linear4bit):
+ fourbit_kwargs = kwargs.copy()
+ fourbit_kwargs.update(
+ {
+ "compute_dtype": target_base_layer.compute_dtype,
+ "compress_statistics": target_base_layer.weight.compress_statistics,
+ "quant_type": target_base_layer.weight.quant_type,
+ }
+ )
+ return Linear4bit(target, adapter_name, randlora_A, randlora_B, **fourbit_kwargs)
+ elif isinstance(target_base_layer, torch.nn.Linear):
+ if kwargs["fan_in_fan_out"]:
+ warnings.warn(
+ "fan_in_fan_out is set to True but the target module is `torch.nn.Linear`. "
+ "Setting fan_in_fan_out to False."
+ )
+ kwargs["fan_in_fan_out"] = randlora_config.fan_in_fan_out = False
+ elif isinstance(target_base_layer, Conv1D):
+ kwargs["is_target_conv_1d_layer"] = True
+ if not kwargs["fan_in_fan_out"]:
+ warnings.warn(
+ "fan_in_fan_out is set to False but the target module is `Conv1D`. Setting fan_in_fan_out to True."
+ )
+ kwargs["fan_in_fan_out"] = randlora_config.fan_in_fan_out = True
+ else:
+ raise ValueError(
+ f"Target module {target} is not supported. Currently, only the following modules are supported: "
+ "`torch.nn.Linear`, `transformers.pytorch_utils.Conv1D`."
+ )
+ new_module = Linear(
+ target,
+ randlora_A,
+ randlora_B,
+ adapter_name,
+ bias=bias,
+ **kwargs,
+ )
+
+ return new_module
diff --git a/peft/src/peft/tuners/road/__init__.py b/peft/src/peft/tuners/road/__init__.py
new file mode 100644
index 0000000000000000000000000000000000000000..97b2f0f54fc113f3470c5c7835b0b2cec133319e
--- /dev/null
+++ b/peft/src/peft/tuners/road/__init__.py
@@ -0,0 +1,47 @@
+# Copyright 2025-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+
+# Based on implementation made available in https://github.com/ppetrushkov/peft/tree/road (not from paper authors)
+
+from peft.import_utils import is_bnb_4bit_available, is_bnb_available
+from peft.utils import register_peft_method
+
+from .config import RoadConfig
+from .layer import Linear, RoadLayer
+from .model import RoadModel
+
+
+__all__ = [
+ "Linear",
+ "RoadConfig",
+ "RoadLayer",
+ "RoadModel",
+]
+
+register_peft_method(name="road", config_cls=RoadConfig, model_cls=RoadModel, is_mixed_compatible=True)
+
+
+def __getattr__(name):
+ if (name == "Linear8bitLt") and is_bnb_available():
+ from .bnb import Linear8bitLt
+
+ return Linear8bitLt
+
+ if (name == "Linear4bit") and is_bnb_4bit_available():
+ from .bnb import Linear4bit
+
+ return Linear4bit
+
+ raise AttributeError(f"module {__name__} has no attribute {name}")
diff --git a/peft/src/peft/tuners/road/bnb.py b/peft/src/peft/tuners/road/bnb.py
new file mode 100644
index 0000000000000000000000000000000000000000..95e9b82b0ca7cee95b179762f6820467731a76d9
--- /dev/null
+++ b/peft/src/peft/tuners/road/bnb.py
@@ -0,0 +1,407 @@
+# Copyright 2025-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+from __future__ import annotations
+
+import warnings
+from typing import Any, Optional
+
+import bitsandbytes as bnb
+import torch
+
+from peft.import_utils import is_bnb_4bit_available, is_bnb_available
+from peft.tuners.tuners_utils import BaseTunerLayer, check_adapters_to_merge
+from peft.utils.integrations import dequantize_bnb_weight
+
+from .config import RoadVariant
+from .layer import RoadLayer, _apply_road, _get_delta_weight
+
+
+if is_bnb_available():
+
+ class Linear8bitLt(torch.nn.Module, RoadLayer):
+ # Road implemented in a dense layer
+ def __init__(
+ self,
+ base_layer: torch.nn.Module,
+ adapter_name: str,
+ variant: RoadVariant = "road_1",
+ group_size: int = 64,
+ init_weights: bool = True,
+ **kwargs,
+ ) -> None:
+ super().__init__()
+ RoadLayer.__init__(self, base_layer)
+
+ self._active_adapter = adapter_name
+ self.update_layer(
+ adapter_name,
+ variant=variant,
+ group_size=group_size,
+ init_weights=init_weights,
+ )
+
+ def merge(self, safe_merge: bool = False, adapter_names: Optional[list[str]] = None) -> None:
+ """
+ Merge the active adapter weights into the base weights
+
+ Args:
+ safe_merge (`bool`, *optional*):
+ If True, the merge operation will be performed in a copy of the original weights and check for NaNs
+ before merging the weights. This is useful if you want to check if the merge operation will produce
+ NaNs. Defaults to `False`.
+ adapter_names (`list[str]`, *optional*):
+ The list of adapter names that should be merged. If None, all active adapters will be merged.
+ Defaults to `None`.
+ """
+ adapter_names = check_adapters_to_merge(self, adapter_names)
+ if not adapter_names:
+ # no adapter to merge
+ return
+
+ for active_adapter in adapter_names:
+ if active_adapter in self._available_adapters:
+ warnings.warn(
+ "Merge road module to 8-bit linear may get different generations due to rounding errors."
+ )
+
+ weight = self.get_base_layer().weight
+ state = self.get_base_layer().state
+ if state.SCB is None:
+ state.SCB = weight.SCB
+
+ # Dequantize the result of identity matrix and int8 weight because bitsandbytes does not support int8
+ # dequantization directly
+ output = dequantize_bnb_weight(weight, state=state)
+ road_R = _get_delta_weight(
+ self.variant[active_adapter],
+ self.group_size[active_adapter],
+ self.road_theta[active_adapter].data,
+ self.road_alpha[active_adapter].data,
+ )
+
+ w_data = torch.matmul(road_R, output.to(road_R.dtype))
+ w_data = w_data.to(road_R.dtype).to(road_R.device).contiguous()
+
+ if safe_merge and not torch.isfinite(w_data).all():
+ raise ValueError(
+ f"NaNs detected in the merged weights. The adapter {active_adapter} seems to be broken"
+ )
+
+ self.get_base_layer().weight = bnb.nn.Int8Params(
+ w_data.to("cpu"), requires_grad=False, has_fp16_weights=weight.has_fp16_weights
+ ).to(weight.device)
+
+ if self.get_base_layer().bias is not None:
+ bias = self.get_base_layer().bias
+ orig_dtype = bias.dtype
+ bias_data = bias.data
+ new_bias = torch.matmul(road_R, bias_data.to(road_R.dtype))
+ bias.data = new_bias.to(orig_dtype)
+
+ state.reset_grads()
+ self.merged_adapters.append(active_adapter)
+
+ def unmerge(self) -> None:
+ """
+ This method unmerges all merged adapter layers from the base weights.
+ """
+ if not self.merged:
+ warnings.warn("Already unmerged. Nothing to do.")
+ return
+
+ while len(self.merged_adapters) > 0:
+ active_adapter = self.merged_adapters.pop()
+ if active_adapter in self._available_adapters:
+ warnings.warn(
+ "Unmerge road module to 8-bit linear may get different generations due to rounding errors."
+ )
+
+ weight = self.get_base_layer().weight
+ state = self.get_base_layer().state
+ if state.SCB is None:
+ state.SCB = weight.SCB
+ output = dequantize_bnb_weight(weight, state=state)
+
+ road_R = _get_delta_weight(
+ self.variant[active_adapter],
+ self.group_size[active_adapter],
+ self.road_theta[active_adapter].data,
+ self.road_alpha[active_adapter].data,
+ )
+ inv_road_R = torch.linalg.inv(road_R.to(torch.float32)).to(road_R.dtype)
+
+ w_data = torch.matmul(inv_road_R, output.to(road_R.dtype))
+ w_data = w_data.to(road_R.dtype).to(road_R.device).contiguous()
+
+ self.get_base_layer().weight = bnb.nn.Int8Params(
+ w_data.to("cpu"), requires_grad=False, has_fp16_weights=weight.has_fp16_weights
+ ).to(weight.device)
+
+ if self.get_base_layer().bias is not None:
+ bias = self.get_base_layer().bias
+ orig_dtype = bias.dtype
+ bias_data = bias.data
+ new_bias = torch.matmul(inv_road_R, bias_data)
+ bias.data = new_bias.to(orig_dtype)
+
+ state.reset_grads()
+
+ def forward(self, x: torch.Tensor, *args: Any, **kwargs: Any) -> torch.Tensor:
+ if self.disable_adapters:
+ if self.merged:
+ self.unmerge()
+ result = self.base_layer(x, *args, **kwargs)
+ elif self.merged:
+ result = self.base_layer(x, *args, **kwargs)
+ else:
+ result = self.base_layer(x, *args, **kwargs)
+
+ for active_adapter in self.active_adapters:
+ if active_adapter not in self._available_adapters:
+ continue
+
+ requires_conversion = not torch.is_autocast_enabled()
+ if requires_conversion:
+ expected_dtype = result.dtype
+ result = self._cast_input_dtype(result, self.road_theta[active_adapter].dtype)
+
+ result = _apply_road(
+ self.variant[active_adapter],
+ self.group_size[active_adapter],
+ self.road_theta[active_adapter],
+ self.road_alpha[active_adapter],
+ result,
+ )
+
+ if requires_conversion:
+ x = x.to(expected_dtype)
+
+ return result
+
+ def __repr__(self) -> str:
+ rep = super().__repr__()
+ return "road." + rep
+
+ def dispatch_bnb_8bit(target: torch.nn.Module, adapter_name: str, **kwargs):
+ new_module = None
+
+ if isinstance(target, BaseTunerLayer):
+ target_base_layer = target.get_base_layer()
+ else:
+ target_base_layer = target
+
+ loaded_in_8bit = kwargs.get("loaded_in_8bit", False)
+ if loaded_in_8bit and isinstance(target_base_layer, bnb.nn.Linear8bitLt):
+ eightbit_kwargs = kwargs.copy()
+ eightbit_kwargs.update(
+ {
+ "has_fp16_weights": target.state.has_fp16_weights,
+ "threshold": target.state.threshold,
+ "index": target.index,
+ }
+ )
+ new_module = Linear8bitLt(target, adapter_name, **eightbit_kwargs)
+
+ return new_module
+
+
+if is_bnb_4bit_available():
+
+ class Linear4bit(torch.nn.Module, RoadLayer):
+ # OFT implemented in a dense layer
+ def __init__(
+ self,
+ base_layer: torch.nn.Module,
+ adapter_name: str,
+ variant: RoadVariant = "road_1",
+ group_size: int = 64,
+ init_weights: bool = True,
+ **kwargs,
+ ) -> None:
+ super().__init__()
+ RoadLayer.__init__(self, base_layer)
+
+ self._active_adapter = adapter_name
+ self.update_layer(
+ adapter_name,
+ variant=variant,
+ group_size=group_size,
+ init_weights=init_weights,
+ )
+
+ def merge(self, safe_merge: bool = False, adapter_names: Optional[list[str]] = None) -> None:
+ """
+ Merge the active adapter weights into the base weights
+
+ Args:
+ safe_merge (`bool`, *optional*):
+ If True, the merge operation will be performed in a copy of the original weights and check for NaNs
+ before merging the weights. This is useful if you want to check if the merge operation will produce
+ NaNs. Defaults to `False`.
+ adapter_names (`list[str]`, *optional*):
+ The list of adapter names that should be merged. If None, all active adapters will be merged.
+ Defaults to `None`.
+ """
+ adapter_names = check_adapters_to_merge(self, adapter_names)
+ if not adapter_names:
+ # no adapter to merge
+ return
+
+ for active_adapter in adapter_names:
+ if active_adapter in self._available_adapters:
+ warnings.warn(
+ "Merge oft module to 4-bit linear may get different generations due to rounding errors."
+ )
+ # Refer to https://gist.github.com/ChrisHayduk/1a53463331f52dca205e55982baf9930
+ weight = self.get_base_layer().weight
+ kwargs = weight.__dict__
+
+ output = dequantize_bnb_weight(weight, state=weight.quant_state)
+
+ road_R = _get_delta_weight(
+ self.variant[active_adapter],
+ self.group_size[active_adapter],
+ self.road_theta[active_adapter].data,
+ self.road_alpha[active_adapter].data,
+ )
+ w_data = torch.matmul(road_R, output.to(road_R.dtype))
+ w_data = w_data.to(road_R.dtype).to(road_R.device)
+
+ if safe_merge and not torch.isfinite(w_data).all():
+ raise ValueError(
+ f"NaNs detected in the merged weights. The adapter {active_adapter} seems to be broken"
+ )
+
+ if "bnb_quantized" in kwargs:
+ kwargs["bnb_quantized"] = False
+ kwargs["requires_grad"] = False
+ kwargs.pop("data", None)
+ # torch.compile can introduce attributes preceded by '_', remove them
+ kwargs = {k: v for k, v in kwargs.items() if not k.startswith("_")}
+ self.get_base_layer().weight = bnb.nn.Params4bit(w_data.to("cpu"), **kwargs).to(weight.device)
+
+ if self.get_base_layer().bias is not None:
+ bias = self.get_base_layer().bias
+ orig_dtype = bias.dtype
+ bias_data = bias.data
+ new_bias = torch.matmul(road_R, bias_data.to(road_R.dtype))
+ bias.data = new_bias.to(orig_dtype)
+
+ self.merged_adapters.append(active_adapter)
+
+ def unmerge(self) -> None:
+ """
+ This method unmerges all merged adapter layers from the base weights.
+ """
+ if not self.merged:
+ warnings.warn("Already unmerged. Nothing to do.")
+ return
+
+ while len(self.merged_adapters) > 0:
+ active_adapter = self.merged_adapters.pop()
+ if active_adapter in self._available_adapters:
+ warnings.warn(
+ "Unmerge oft module to 4-bit linear may get different generations due to rounding errors."
+ )
+
+ weight = self.get_base_layer().weight
+ kwargs = weight.__dict__
+ output = dequantize_bnb_weight(weight, state=weight.quant_state)
+
+ road_R = _get_delta_weight(
+ self.variant[active_adapter],
+ self.group_size[active_adapter],
+ self.road_theta[active_adapter].data,
+ self.road_alpha[active_adapter].data,
+ )
+ inv_road_R = torch.linalg.inv(road_R.to(torch.float32)).to(road_R.dtype)
+
+ w_data = torch.matmul(inv_road_R, output.to(road_R.dtype))
+ w_data = w_data.to(road_R.dtype).to(road_R.device)
+
+ if "bnb_quantized" in kwargs:
+ kwargs["bnb_quantized"] = False
+ kwargs["requires_grad"] = False
+ kwargs.pop("data", None)
+ self.get_base_layer().weight = bnb.nn.Params4bit(w_data.to("cpu"), **kwargs).to(weight.device)
+
+ if self.get_base_layer().bias is not None:
+ bias = self.get_base_layer().bias
+ orig_dtype = bias.dtype
+ bias_data = bias.data
+ new_bias = torch.matmul(inv_road_R, bias_data)
+ bias.data = new_bias.to(orig_dtype)
+
+ def forward(self, x: torch.Tensor, *args, **kwargs) -> torch.Tensor:
+ if self.disable_adapters:
+ if self.merged:
+ self.unmerge()
+ result = self.base_layer(x, *args, **kwargs)
+ elif self.merged:
+ result = self.base_layer(x, *args, **kwargs)
+ else:
+ result = self.base_layer(x, *args, **kwargs)
+ # As per Tim Dettmers, for 4bit, we need to defensively clone here.
+ # The reason is that in some cases, an error can occur that backprop
+ # does not work on a manipulated view. This issue may be solved with
+ # newer PyTorch versions but this would need extensive testing to be
+ # sure.
+ # result = result.clone()
+
+ for active_adapter in self.active_adapters:
+ if active_adapter not in self._available_adapters:
+ continue
+
+ requires_conversion = not torch.is_autocast_enabled()
+ if requires_conversion:
+ expected_dtype = result.dtype
+ result = self._cast_input_dtype(result, self.road_theta[active_adapter].dtype)
+
+ result = _apply_road(
+ self.variant[active_adapter],
+ self.group_size[active_adapter],
+ self.road_theta[active_adapter],
+ self.road_alpha[active_adapter],
+ result,
+ )
+ if requires_conversion:
+ x = x.to(expected_dtype)
+
+ return result
+
+ def __repr__(self) -> str:
+ rep = super().__repr__()
+ return "oft." + rep
+
+ def dispatch_bnb_4bit(target: torch.nn.Module, adapter_name: str, **kwargs):
+ new_module = None
+
+ if isinstance(target, BaseTunerLayer):
+ target_base_layer = target.get_base_layer()
+ else:
+ target_base_layer = target
+
+ loaded_in_4bit = kwargs.get("loaded_in_4bit", False)
+ if loaded_in_4bit and is_bnb_4bit_available() and isinstance(target_base_layer, bnb.nn.Linear4bit):
+ fourbit_kwargs = kwargs.copy()
+ fourbit_kwargs.update(
+ {
+ "compute_dtype": target_base_layer.compute_dtype,
+ "compress_statistics": target_base_layer.weight.compress_statistics,
+ "quant_type": target_base_layer.weight.quant_type,
+ }
+ )
+ new_module = Linear4bit(target, adapter_name, **fourbit_kwargs)
+
+ return new_module
diff --git a/peft/src/peft/tuners/road/config.py b/peft/src/peft/tuners/road/config.py
new file mode 100644
index 0000000000000000000000000000000000000000..50125786c5ce10ca1546f949be30d8dd52a56422
--- /dev/null
+++ b/peft/src/peft/tuners/road/config.py
@@ -0,0 +1,126 @@
+# Copyright 2025-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+from __future__ import annotations
+
+from dataclasses import dataclass, field
+from typing import Literal, Optional, Union
+
+from peft.config import PeftConfig
+from peft.utils import PeftType
+
+
+RoadVariant = Literal["road_1", "road_2", "road_4"]
+
+
+@dataclass
+class RoadConfig(PeftConfig):
+ """
+ This is the configuration class to store the configuration of a [`RoadModel`]. RoAd adapter is proposed in
+ https://arxiv.org/pdf/2409.00119.
+
+ Args:
+ variant (Union[`RoadVariant`, `str`]):
+ The variant of the Road model to use. It can be one of road_1, road_2, or road_4. Refer to the paper for
+ more details.
+ - road_1: Uses the same scale and angle for all pairs of elements.
+ This variant has lowest number of parameters, it stores a number equal to the output hidden size of
+ parameters for each layer that RoAd is applied to.
+ - road_2: Uses the same scale and angle for each element.
+ This variant has 2x the number of parameters compared to road_1.
+ - road_4: Uses two different scales and angles for each ellement.
+ This variant has 4x the number of parameters compared to road_1.
+ group_size (`int`):
+ Group size defines how elements are grouped together into 2D vectors for rotation. Within each group
+ element 0 is paired with element group_size/2, then element 1 is paired with element group_size/2+1 and so
+ on. This has no effect on the model performance, since elements are unordered, however it has some effect
+ on inference speed when used in e.g. VLLM. For best speed group size of at least 32 or 64 (the default) is
+ recommended. Note that model hidden size (or hidden size per partition when used with tensor parallelism)
+ must be divisible by group_size, so for very small models you might need to reduce this parameter.
+ init_weights (`bool`):
+ Whether to perform initialization of RoAd weights.
+ target_modules (`Optional[Union[List[str], str]]`):
+ The names of the modules to apply the adapter to. If this is specified, only the modules with the specified
+ names will be replaced. When passing a string, a regex match will be performed. When passing a list of
+ strings, either an exact match will be performed or it is checked if the name of the module ends with any
+ of the passed strings. If this is specified as 'all-linear', then all linear/Conv1D modules are chosen (if
+ the model is a PreTrainedModel, the output layer excluded). If this is not specified, modules will be
+ chosen according to the model architecture. If the architecture is not known, an error will be raised -- in
+ this case, you should specify the target modules manually.
+ modules_to_save (`List[str]`):
+ List of modules apart from Road layers to be set as trainable and saved in the final checkpoint.
+ """
+
+ variant: Union[str, RoadVariant] = field(
+ default="road_1",
+ metadata={"help": ("Variant of the Road model to use.")},
+ )
+ group_size: int = field(
+ default=64,
+ metadata={
+ "help": (
+ "Group size defines how elements are grouped together into 2D vectors for rotation. "
+ "Within each group element 0 is paired with element group_size/2, "
+ "then element 1 is paired with element group_size/2+1 and so on. "
+ "This has no effect on the model performance, since elements are unordered, "
+ "however it has some effect on inference speed when used in e.g. VLLM. "
+ "For best speed group size of at least 64 is recommended. "
+ "Note that model hidden size (or hidden size per partition when used with tensor parallelism) "
+ "must be divisible by group_size, so for very small models you might need to reduce this parameter."
+ )
+ },
+ )
+ init_weights: bool = field(
+ default=True,
+ metadata={
+ "help": (
+ "Whether to initialize the weights of the RoAd layers with their default initialization. Don't change "
+ "this setting, except if you know exactly what you're doing."
+ ),
+ },
+ )
+ target_modules: Optional[Union[list[str], str]] = field(
+ default=None,
+ metadata={
+ "help": (
+ "List of module names or regex expression of the module names to replace with Road."
+ "For example, ['q', 'v'] or '.*decoder.*(SelfAttention|EncDecAttention).*(q|v)$'."
+ "This can also be a wildcard 'all-linear' which matches all linear/Conv1D "
+ "(if the model is a PreTrainedModel, the output layer excluded)."
+ "If not specified, modules will be chosen according to the model architecture, If the architecture is "
+ "not known, an error will be raised -- in this case, you should specify the target modules manually."
+ ),
+ },
+ )
+ modules_to_save: Optional[list[str]] = field(
+ default=None,
+ metadata={
+ "help": (
+ "List of modules apart from RoAd layers to be set as trainable and saved in the final checkpoint. For"
+ " example, in Sequence Classification or Token Classification tasks, the final layer"
+ " `classifier/score` are randomly initialized and as such need to be trainable and saved."
+ )
+ },
+ )
+
+ def __post_init__(self):
+ super().__post_init__()
+ self.peft_type = PeftType.ROAD
+ self.target_modules = (
+ set(self.target_modules) if isinstance(self.target_modules, list) else self.target_modules
+ )
+ if self.variant not in ["road_1", "road_2", "road_4"]:
+ raise ValueError(f"Invalid variant {self.variant} specified. Please choose from road_1, road_2 or road_4")
+ if self.group_size <= 0 or self.group_size % 2 != 0:
+ raise ValueError(f"The group_size must be divisible by 2 when using RoadLayer, but got {self.group_size}.")
diff --git a/peft/src/peft/tuners/road/layer.py b/peft/src/peft/tuners/road/layer.py
new file mode 100644
index 0000000000000000000000000000000000000000..d59dc056d5d293315aec29e089cca99a4d9a3279
--- /dev/null
+++ b/peft/src/peft/tuners/road/layer.py
@@ -0,0 +1,418 @@
+# Copyright 2025-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+import warnings
+from typing import Any, Optional, Union
+
+import torch
+import torch.nn as nn
+
+from peft.tuners.tuners_utils import BaseTunerLayer, check_adapters_to_merge
+
+from .config import RoadConfig, RoadVariant
+
+
+class RoadLayer(BaseTunerLayer):
+ """
+ Road layer.
+
+ Generally the idea of RoAD is to split the input vector into many 2D vectors and rotate each 2D vector with its own
+ 2D rotation matrix. For additional flexibility, each rotation matrix is multiplied by a trainable scale.
+
+ when applied to vector R @ x each pair of elements of x is transformed like this: `y₀ = x₀ * α * cosθ - xₙ * α *
+ sinθ` and `yₙ = x₀ * α * sinθ + xₙ * α * cosθ`
+
+ The scales α and angles θ are learned for each pair of elements and, moreover, each of the 4 instances in the
+ rotation matrix may actually be different (when using variant 2 or 4).
+
+ Note that instead of using two consecutive elements x₀ x₁ we first split the whole vector into groups and pair
+ elements from the first with the second half of the same group, which allows for more efficient inference
+ implementation.
+
+ The adapter needs to only store the angles θ and scales α, rather than the full matrix R and the inference
+ implementation only needs to do elementwise vector multiplications.
+
+ For merging the weights, we make use of the following formula: R @ (W @ x + b) = (R @ W) @ x + R @ b. The lhs part
+ is how it is used in unmerged state (using efficient elementwise implementation instead of matrix multiplication)
+ and the rhs part is how it is used in merged state where (R @ W) becomes the new weight matrix and R @ b becomes
+ the new bias.
+
+ """
+
+ adapter_layer_names: tuple[str, ...] = ("road_theta", "road_alpha")
+ other_param_names: tuple[str, ...] = ("variant", "group_size")
+
+ def __init__(self, base_layer: nn.Module, ephemeral_gpu_offload: bool = False, **kwargs) -> None:
+ self.base_layer = base_layer
+ self.variant = {}
+ self.group_size = {}
+ self.road_theta = nn.ParameterDict({})
+ self.road_alpha = nn.ParameterDict({})
+
+ self._disable_adapters = False
+ self.merged_adapters = []
+
+ base_layer = self.get_base_layer()
+ if isinstance(base_layer, nn.Linear):
+ in_features, out_features = base_layer.in_features, base_layer.out_features
+ else:
+ raise ValueError(f"Unsupported layer type '{type(base_layer)}' encountered, cannot apply RoAd adapter.")
+ self.in_features = in_features
+ self.out_features = out_features
+
+ @property
+ def _available_adapters(self) -> set[str]:
+ return {*self.road_theta}
+
+ def update_layer(
+ self,
+ adapter_name,
+ variant,
+ group_size,
+ init_weights,
+ inference_mode: bool = False,
+ ):
+ self.variant[adapter_name] = variant
+ self.group_size[adapter_name] = group_size
+
+ if self.out_features % group_size != 0:
+ raise ValueError(
+ f"The out_features of the base layer must be divisible by group_size ({group_size}) when using RoadLayer."
+ )
+
+ # Actual trainable parameters
+ if variant == "road_1":
+ size = self.out_features // 2
+ elif variant == "road_2":
+ size = self.out_features
+ elif variant == "road_4":
+ size = self.out_features * 2
+ else:
+ raise ValueError(
+ f"Unsupported variant {variant} for RoadLayer. Supported variants are road_1, road_2, and road_4."
+ )
+ self.road_theta[adapter_name] = nn.Parameter(torch.empty(size))
+ self.road_alpha[adapter_name] = nn.Parameter(torch.empty(size))
+
+ self.reset_parameters(adapter_name, init_weights)
+ self._move_adapter_to_device_of_base_layer(adapter_name)
+
+ self.set_adapter(self.active_adapters, inference_mode=inference_mode)
+
+ def reset_parameters(self, adapter_name, init_weights):
+ if init_weights is False:
+ nn.init.normal_(self.road_theta[adapter_name].data, mean=0.0, std=0.5)
+ nn.init.normal_(self.road_alpha[adapter_name].data, mean=1.0, std=0.5)
+ return
+ nn.init.zeros_(self.road_theta[adapter_name].data)
+ nn.init.ones_(self.road_alpha[adapter_name].data)
+
+
+class Linear(nn.Module, RoadLayer):
+ # Road implemented in a dense layer
+ def __init__(
+ self,
+ base_layer,
+ adapter_name: str,
+ variant: RoadVariant = "road_1",
+ group_size: int = 64,
+ init_weights: Union[bool, str] = True,
+ **kwargs,
+ ) -> None:
+ super().__init__()
+ RoadLayer.__init__(self, base_layer, **kwargs)
+
+ self._active_adapter = adapter_name
+
+ self.update_layer(
+ adapter_name,
+ variant,
+ group_size,
+ init_weights=init_weights,
+ )
+
+ def _check_forward_args(self, x, *args, **kwargs):
+ """Check if the arguments are compatible with the configs and state of the model"""
+ adapter_names = kwargs.get("adapter_names", None)
+ if adapter_names is None:
+ return
+
+ if len(x) != len(adapter_names):
+ msg = (
+ "Length of `adapter_names` should be the same as the number of inputs, but got "
+ f"{len(adapter_names)} and {len(x)} respectively."
+ )
+ raise ValueError(msg)
+
+ if self.merged:
+ # It is unclear what would be the right thing to do if users pass adapter_names and there are merged
+ # adapters. Therefore, it is better to raise an error in this case.
+ msg = "Cannot pass `adapter_names` when there are merged adapters, please call `unmerge_adapter` first."
+ raise ValueError(msg)
+
+ def forward(self, x: torch.Tensor, *args: Any, **kwargs: Any) -> torch.Tensor:
+ self._check_forward_args(x, *args, **kwargs)
+ adapter_names = kwargs.pop("adapter_names", None)
+
+ if self.disable_adapters:
+ if self.merged:
+ self.unmerge()
+ result = self.base_layer(x, *args, **kwargs)
+ elif self.merged:
+ result = self.base_layer(x, *args, **kwargs)
+ elif adapter_names is not None:
+ result = self._mixed_batch_forward(x, *args, adapter_names=adapter_names, **kwargs)
+ else:
+ result = self.base_layer(x, *args, **kwargs)
+ torch_result_dtype = result.dtype
+
+ for active_adapter in self.active_adapters:
+ if active_adapter not in self._available_adapters:
+ continue
+
+ result = self._cast_input_dtype(result, self.road_theta[active_adapter].dtype)
+ result = _apply_road(
+ self.variant[active_adapter],
+ self.group_size[active_adapter],
+ self.road_theta[active_adapter],
+ self.road_alpha[active_adapter],
+ result,
+ )
+
+ result = result.to(torch_result_dtype)
+
+ return result
+
+ def _mixed_batch_forward(
+ self, x: torch.Tensor, *args: Any, adapter_names: list[str], **kwargs: Any
+ ) -> torch.Tensor:
+ # This is a special method that handles the case when users pass the argument `adapter_names`. This is an
+ # extra argument that allows mixing different adapters in the same batch at inference time.
+ result = self.base_layer(x, *args, **kwargs)
+
+ unique_adapters = set(adapter_names)
+ sub_batch_indices_list = []
+ for adapter in unique_adapters:
+ sub_batch_indices_list.append([index for index, item in enumerate(adapter_names) if item == adapter])
+
+ for i, active_adapter in enumerate(unique_adapters):
+ if active_adapter == "__base__":
+ continue
+ if active_adapter not in self._available_adapters:
+ continue
+
+ dtype = self.road_theta[active_adapter].data.dtype
+
+ # getting the sub-batch, passing it to Road layers and updating the corresponding indices of the linear
+ # layer output
+ sub_batch = result[sub_batch_indices_list[i]].to(dtype)
+ result[sub_batch_indices_list[i]] = _apply_road(
+ self.variant[active_adapter],
+ self.group_size[active_adapter],
+ self.road_theta[active_adapter],
+ self.road_alpha[active_adapter],
+ sub_batch,
+ )
+
+ return result
+
+ def merge(self, safe_merge: bool = False, adapter_names: Optional[list[str]] = None) -> None:
+ """
+ Merge the active adapter weights into the base weights
+
+ Args:
+ safe_merge (`bool`, *optional*):
+ If `True`, the merge operation will be performed in a copy of the original weights and check for NaNs
+ before merging the weights. This is useful if you want to check if the merge operation will produce
+ NaNs. Defaults to `False`.
+ adapter_names (`List[str]`, *optional*):
+ The list of adapter names that should be merged. If `None`, all active adapters will be merged.
+ Defaults to `None`.
+ """
+ adapter_names = check_adapters_to_merge(self, adapter_names)
+ if not adapter_names:
+ # no adapter to merge
+ return
+
+ for active_adapter in adapter_names:
+ if active_adapter in self._available_adapters:
+ base_layer = self.get_base_layer()
+ orig_dtype = base_layer.weight.dtype
+ road_R = _get_delta_weight(
+ self.variant[active_adapter],
+ self.group_size[active_adapter],
+ self.road_theta[active_adapter].data,
+ self.road_alpha[active_adapter].data,
+ )
+ if safe_merge:
+ # Note that safe_merge will be slower than the normal merge
+ # because of the copy operation.
+ orig_weight = base_layer.weight.data.clone()
+ orig_weight = torch.matmul(road_R.to(orig_dtype), orig_weight)
+
+ if not torch.isfinite(orig_weight).all():
+ raise ValueError(
+ f"NaNs detected in the merged weights. The adapter {active_adapter} seems to be broken"
+ )
+
+ base_layer.weight.data = orig_weight.contiguous().to(orig_dtype)
+
+ if base_layer.bias is not None:
+ orig_bias = base_layer.bias.clone()
+ orig_bias = torch.matmul(road_R.to(orig_dtype), orig_bias)
+
+ if not torch.isfinite(orig_bias).all():
+ raise ValueError(
+ f"NaNs detected in the merged bias. The adapter {active_adapter} seems to be broken"
+ )
+
+ base_layer.bias.data = orig_bias.contiguous().to(orig_dtype)
+ else:
+ orig_weight = base_layer.weight.data
+ orig_weight = torch.matmul(road_R.to(orig_dtype), orig_weight)
+ base_layer.weight.data = orig_weight.contiguous().to(orig_dtype)
+
+ if base_layer.bias is not None:
+ orig_bias = base_layer.bias.data
+ orig_bias = torch.matmul(road_R.to(orig_dtype), orig_bias)
+ base_layer.bias.data = orig_bias.contiguous().to(orig_dtype)
+
+ self.merged_adapters.append(active_adapter)
+
+ def unmerge(self) -> None:
+ """
+ This method unmerges all merged adapter layers from the base weights.
+ """
+ if not self.merged:
+ warnings.warn("Already unmerged. Nothing to do.")
+ return
+ while len(self.merged_adapters) > 0:
+ # Going in reverse order
+ active_adapter = self.merged_adapters.pop()
+ if active_adapter in self._available_adapters:
+ weight = self.get_base_layer().weight
+ orig_dtype = weight.dtype
+ road_R = _get_delta_weight(
+ self.variant[active_adapter],
+ self.group_size[active_adapter],
+ self.road_theta[active_adapter].data,
+ self.road_alpha[active_adapter].data,
+ )
+ # Since our matrix are not necessarily orthogonal we need inverse instead of transpose.
+ # In practice we expect this to basically always work since we start from block diagonal rotation matrix.
+ inv_road_R = torch.linalg.inv(road_R.to(torch.float32)).to(orig_dtype)
+ orig_weight = torch.matmul(inv_road_R, weight.data)
+ weight.data = orig_weight.contiguous()
+
+ if self.get_base_layer().bias is not None:
+ orig_bias = torch.matmul(inv_road_R, self.get_base_layer().bias.data)
+ self.get_base_layer().bias.data = orig_bias.contiguous()
+
+ def __repr__(self) -> str:
+ rep = super().__repr__()
+ return "road." + rep
+
+
+def _get_delta_weight(variant: RoadVariant, group_size: int, road_theta: torch.Tensor, road_alpha: torch.Tensor):
+ first_col, second_col = _prepare_cols(variant, group_size, road_theta, road_alpha)
+
+ # To help understand the logic below consider how rope embeddings work
+ # here it is similar, but done in groups.
+ # https://discuss.huggingface.co/t/is-llama-rotary-embedding-implementation-correct/44509/3
+
+ # First column is simply put on the main diagonal
+ output_tensor = torch.diag(first_col)
+ # For second column we need to swap each half groups and add minus sign
+ size = second_col.shape[0]
+ swapped_second_col = second_col.reshape(-1, 2, group_size // 2)[:, [1, 0], :].flatten()
+ rotated_diag_second_col = torch.diag(swapped_second_col).reshape(-1, 2, group_size // 2, size)[:, [1, 0], :, :]
+ rotated_diag_second_col[:, 0, :, :] *= -1
+ rotated_diag_second_col = rotated_diag_second_col.reshape(size, size)
+ output_tensor += rotated_diag_second_col
+
+ return output_tensor
+
+
+def _prepare_cols(
+ variant: RoadVariant, group_size: int, road_theta: torch.Tensor, road_alpha: torch.Tensor
+) -> tuple[torch.Tensor, torch.Tensor]:
+ # In inference mode, this can be cached
+ if variant == "road_1":
+ # In each group there are only group_size // 2 parameters that are reused
+ road_theta = road_theta.reshape(-1, group_size // 2).repeat_interleave(2, dim=0).flatten()
+ road_alpha = road_alpha.reshape(-1, group_size // 2).repeat_interleave(2, dim=0).flatten()
+
+ theta_cos = road_theta.cos()
+ theta_sin = road_theta.sin()
+
+ first_col = road_alpha * theta_cos
+ second_col = road_alpha * theta_sin
+ elif variant == "road_2":
+ # Each group has exactly group_size parameters
+ theta_cos = road_theta.cos()
+ theta_sin = road_theta.sin()
+
+ first_col = road_alpha * theta_cos
+ second_col = road_alpha * theta_sin
+ elif variant == "road_4":
+ # Each group has 2*group_size parameters, first half used for first column, second half for second column
+ road_theta = road_theta.reshape(-1, 2, group_size)
+ theta_cos = road_theta[:, 0, :].cos().flatten()
+ theta_sin = road_theta[:, 1, :].sin().flatten()
+ road_alpha = road_alpha.reshape(-1, 2, group_size)
+ alpha_1 = road_alpha[:, 0, :].flatten()
+ alpha_2 = road_alpha[:, 1, :].flatten()
+
+ first_col = alpha_1 * theta_cos
+ second_col = alpha_2 * theta_sin
+ else:
+ raise ValueError(
+ f"Unsupported variant {variant} for RoadLayer. Supported variants are road_1, road_2, and road_4."
+ )
+
+ return first_col, second_col
+
+
+def _apply_road(
+ variant: RoadVariant, group_size: int, road_theta: torch.Tensor, road_alpha: torch.Tensor, x: torch.Tensor
+):
+ first_col, second_col = _prepare_cols(variant, group_size, road_theta, road_alpha)
+
+ # Split in half groups and join back
+ # See equation 4 in the RoAD paper
+ x_grouped = x.reshape(-1, 2, group_size // 2)
+ x1 = x_grouped[:, 0, :]
+ x2 = x_grouped[:, 1, :]
+ rotate_half_x = torch.stack((-x2, x1), dim=1).reshape(x.shape)
+ result = x * first_col + rotate_half_x * second_col
+ return result
+
+
+def dispatch_default(
+ target: torch.nn.Module,
+ adapter_name: str,
+ road_config: RoadConfig,
+ **kwargs,
+) -> Optional[torch.nn.Module]:
+ new_module = None
+
+ if isinstance(target, BaseTunerLayer):
+ target_base_layer = target.get_base_layer()
+ else:
+ target_base_layer = target
+
+ if isinstance(target_base_layer, torch.nn.Linear):
+ new_module = Linear(target, adapter_name, **kwargs)
+
+ return new_module
diff --git a/peft/src/peft/tuners/road/model.py b/peft/src/peft/tuners/road/model.py
new file mode 100644
index 0000000000000000000000000000000000000000..e2285c4451822baf990ab57cdf6af702d969dacf
--- /dev/null
+++ b/peft/src/peft/tuners/road/model.py
@@ -0,0 +1,163 @@
+# Copyright 2025-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+from __future__ import annotations
+
+import operator
+from contextlib import contextmanager
+from functools import partial
+
+from torch import nn
+
+from peft.import_utils import is_bnb_4bit_available, is_bnb_available
+from peft.tuners.road.config import RoadConfig
+from peft.tuners.tuners_utils import (
+ BaseTuner,
+)
+from peft.utils import TRANSFORMERS_MODELS_TO_ROAD_TARGET_MODULES_MAPPING
+
+from .layer import RoadLayer, dispatch_default
+
+
+def _adapter_names_pre_forward_hook(target, args, kwargs, adapter_names):
+ # pre-forward hook to inject the adapter_names argument when using mixed adapter batches inference
+ kwargs["adapter_names"] = adapter_names
+ return args, kwargs
+
+
+class RoadModel(BaseTuner):
+ """ """
+
+ prefix: str = "road_"
+ tuner_layer_cls = RoadLayer
+ target_module_mapping = TRANSFORMERS_MODELS_TO_ROAD_TARGET_MODULES_MAPPING
+
+ def _create_and_replace(
+ self,
+ road_config: RoadConfig,
+ adapter_name: str,
+ target: nn.Module,
+ target_name: str,
+ parent: nn.Module,
+ current_key,
+ ) -> None:
+ if current_key is None:
+ raise ValueError("Current Key shouldn't be `None`")
+
+ # Regexp matching - Find key which matches current target_name in patterns provided
+ variant = road_config.variant
+ group_size = road_config.group_size
+
+ kwargs = {
+ "variant": variant,
+ "group_size": group_size,
+ "init_weights": road_config.init_weights,
+ "loaded_in_8bit": getattr(self.model, "is_loaded_in_8bit", False),
+ "loaded_in_4bit": getattr(self.model, "is_loaded_in_4bit", False),
+ }
+ # for torchao merging, we need the get_apply_tensor_subclass from the quantization config
+ try:
+ kwargs["get_apply_tensor_subclass"] = operator.attrgetter(
+ "hf_quantizer.quantization_config.get_apply_tensor_subclass"
+ )(self.model)
+ except AttributeError:
+ pass
+
+ if isinstance(target, RoadLayer):
+ target.update_layer(
+ adapter_name,
+ variant,
+ group_size,
+ init_weights=road_config.init_weights,
+ )
+ else:
+ device_map = self.model.hf_device_map if hasattr(self.model, "hf_device_map") else None
+ new_module = self._create_new_module(road_config, adapter_name, target, device_map=device_map, **kwargs)
+ if adapter_name not in self.active_adapters:
+ # adding an additional adapter: it is not automatically trainable
+ new_module.requires_grad_(False)
+ self._replace_module(parent, target_name, new_module, target)
+
+ @staticmethod
+ def _create_new_module(road_config: RoadConfig, adapter_name, target, **kwargs):
+ dispatchers = []
+
+ # avoid eager bnb import
+ if is_bnb_available():
+ from .bnb import dispatch_bnb_8bit
+
+ dispatchers.append(dispatch_bnb_8bit)
+
+ if is_bnb_4bit_available():
+ from .bnb import dispatch_bnb_4bit
+
+ dispatchers.append(dispatch_bnb_4bit)
+
+ dispatchers.extend(
+ [
+ dispatch_default,
+ ]
+ )
+
+ new_module = None
+ for dispatcher in dispatchers:
+ new_module = dispatcher(target, adapter_name, road_config=road_config, **kwargs)
+ if new_module is not None: # first match wins
+ break
+
+ if new_module is None:
+ # no module could be matched
+ raise ValueError(
+ f"Target module {target} is not supported. Currently, only the following modules are supported: "
+ "`torch.nn.Linear`."
+ )
+
+ return new_module
+
+ @contextmanager
+ def _enable_peft_forward_hooks(self, *args, **kwargs):
+ # If adapter_names is passed as an argument, we inject it into the forward arguments.
+ adapter_names = kwargs.pop("adapter_names", None)
+ if adapter_names is None:
+ # nothing to do
+ yield
+ return
+
+ if self.training:
+ raise ValueError("Cannot pass `adapter_names` when the model is in training mode.")
+
+ # Check that users only passed actually existing adapters.
+ # Note: We cannot do this on the layer level, as each individual layer may not have each adapter. Still, we want
+ # to check that there is at least one layer with the given name, or else something like typos can easily slip.
+ expected_adapters = set()
+ for layer in self.modules():
+ if isinstance(layer, RoadLayer):
+ expected_adapters |= layer.road_theta.keys()
+ unique_adapters = {name for name in adapter_names if name != "__base__"}
+ unexpected_adapters = unique_adapters - expected_adapters
+ if unexpected_adapters:
+ raise ValueError(f"Trying to infer with non-existing adapter(s): {', '.join(sorted(unexpected_adapters))}")
+
+ hook_handles = []
+ for module in self.modules():
+ if isinstance(module, RoadLayer):
+ pre_forward = partial(_adapter_names_pre_forward_hook, adapter_names=adapter_names)
+ handle = module.register_forward_pre_hook(pre_forward, with_kwargs=True)
+ hook_handles.append(handle)
+
+ # TODO LoRA also has hooks for beam search, ignore this for now
+
+ yield
+
+ for handle in hook_handles:
+ handle.remove()
diff --git a/peft/src/peft/tuners/shira/__init__.py b/peft/src/peft/tuners/shira/__init__.py
new file mode 100644
index 0000000000000000000000000000000000000000..d5391b96059fc08580a12adb8b216b3a8bfd8024
--- /dev/null
+++ b/peft/src/peft/tuners/shira/__init__.py
@@ -0,0 +1,27 @@
+# Copyright 2025-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+from peft.utils import register_peft_method
+
+from .config import ShiraConfig
+from .layer import Linear, ShiraLayer
+from .model import ShiraModel
+
+
+__all__ = ["Linear", "ShiraConfig", "ShiraLayer", "ShiraModel"]
+
+
+register_peft_method(
+ name="shira", config_cls=ShiraConfig, model_cls=ShiraModel, prefix="shira_", is_mixed_compatible=True
+)
diff --git a/peft/src/peft/tuners/shira/config.py b/peft/src/peft/tuners/shira/config.py
new file mode 100644
index 0000000000000000000000000000000000000000..d868e51490637c47c13b3c0ae2cb1f5c88cb7ebc
--- /dev/null
+++ b/peft/src/peft/tuners/shira/config.py
@@ -0,0 +1,129 @@
+# Copyright 2025-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+from __future__ import annotations
+
+import warnings
+from dataclasses import dataclass, field
+from typing import Literal, Optional, Union
+
+from peft.config import PeftConfig
+from peft.utils import PeftType
+
+from .mask_functions import random_mask
+
+
+@dataclass
+class ShiraConfig(PeftConfig):
+ """
+ This is the configuration class to store the configuration of a [`ShiraModel`].
+
+ Args:
+ r (`int`, *optional*, defaults to `32`):
+ For a given target module, the number of SHiRA parameters is computed as r(m+n), where the original tensor
+ dimensions are m x n. This means the number of SHiRA parameters is the same as that for a LoRA adapter.
+ SHiRA is a high rank adapter. Setting this r parameter does not restrict the rank to this value.
+ mask_type (`str`, defaults to `random`):
+ Type of mask function. Defaults to a random sparse mask. An optional user-defined mask_fn to compute the
+ mask value can also be supplied by instantiating `config = ShiraConfig(...)` and then setting
+ `config.mask_fn = `. For a pretrained weight with shape m x n, the custom mask
+ function must return only one mask (shape: m x n) which must be binary 0 or 1 with num_shira_parameters =
+ r(m + n) for linear layers. Device and dtype of mask must be same as base layer's weight's device and
+ dtype. Please see mask_functions.py for more details and to see the default random sparse mask
+ implementation.
+ random_seed (`int`, *optional*, defaults to `None`):
+ random seed for the torch generator for random_mask.
+ target_modules (`Union[List[str], str]`):
+ List of module names or regex expression of the module names to replace with SHiRA. For example, ['q', 'v']
+ or '.*decoder.*(SelfAttention|EncDecAttention).*(q|v)$'. Only linear layers are supported.
+ fan_in_fan_out (`bool`):
+ Set this to True if the layer to replace stores weight like (fan_in, fan_out). For example, gpt-2 uses
+ `Conv1D` which stores weights like (fan_in, fan_out) and hence this should be set to `True`.
+ init_weights (`bool`, defaults to `True`):
+ Initialize SHiRA weight to have zero values. If set to False, SHiRA weights are initialized to randn values
+ instead of zeros and this is used only for testing.
+ modules_to_save (`List[str]`):
+ List of modules apart from SHiRA layers to be set as trainable and saved in the final checkpoint.
+ """
+
+ r: int = field(
+ default=32,
+ metadata={
+ "help": (
+ "For a given target module, the number of SHiRA parameters is computed as r(m+n), where the original "
+ "tensor dimensions are m x n. This means the number of SHiRA parameters is the same as that for a LoRA adapter. "
+ "SHiRA is a high rank adapter. Setting this r parameter does not restrict the rank to this value."
+ )
+ },
+ )
+ mask_type: Literal["random"] = field(
+ default="random",
+ metadata={
+ "help": (
+ "Type of mask function. Defaults to a random sparse mask. "
+ "An optional user-defined mask_fn to compute the mask value can also be supplied by instantiating `config = ShiraConfig(...)` and then setting "
+ "`config.mask_fn = `. For a pretrained weight with shape m x n, the custom mask function must return only one mask (shape: m x n) "
+ "which must be binary 0 or 1 with num_shira_parameters = r(m + n) for linear layers. Device and dtype of mask must be same as base layer's weight's device and dtype. "
+ "Please see mask_functions.py for more details and to see the default random sparse mask implementation."
+ )
+ },
+ )
+ random_seed: Optional[int] = field(
+ default=None, metadata={"help": "random seed for the torch generator for random_mask"}
+ )
+ target_modules: Optional[Union[list[str], str]] = field(
+ default=None,
+ metadata={
+ "help": (
+ "List of module names or regex expression of the module names to replace with SHiRA."
+ "For example, ['q', 'v'] or '.*decoder.*(SelfAttention|EncDecAttention).*(q|v)$'. "
+ "Only linear layers are supported."
+ )
+ },
+ )
+ fan_in_fan_out: bool = field(
+ default=False,
+ metadata={"help": "Set this to True if the layer to replace stores weight like (fan_in, fan_out)"},
+ )
+ init_weights: bool = field(
+ default=True,
+ metadata={
+ "help": "Initialize SHiRA weight to have zero values. If set to False, SHiRA weights are initialized to randn values instead of zeros and this is used only for testing."
+ },
+ )
+ modules_to_save: Optional[list[str]] = field(
+ default=None,
+ metadata={
+ "help": (
+ "List of modules apart from SHiRA layers to be set as trainable and saved in the final checkpoint. For"
+ " example, in Sequence Classification or Token Classification tasks, the final layer"
+ " `classifier/score` are randomly initialized and as such need to be trainable and saved."
+ )
+ },
+ )
+
+ def __post_init__(self):
+ super().__post_init__()
+ self.peft_type = PeftType.SHIRA
+ self.target_modules = (
+ set(self.target_modules) if isinstance(self.target_modules, list) else self.target_modules
+ )
+ if self.mask_type == "random":
+ self.mask_fn = random_mask
+ else:
+ if not self.inference_mode:
+ warnings.warn(
+ f"Argument {self.mask_type=} is not recognized, please supply your own masking function by calling `config.mask_fn = my_mask_fn`."
+ )
+ self.mask_fn = None
diff --git a/peft/src/peft/tuners/shira/layer.py b/peft/src/peft/tuners/shira/layer.py
new file mode 100644
index 0000000000000000000000000000000000000000..15fb4f3c32b41396ca44d9b78b7d0dc6157fd545
--- /dev/null
+++ b/peft/src/peft/tuners/shira/layer.py
@@ -0,0 +1,217 @@
+# Copyright 2025-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+import copy
+import warnings
+from typing import Optional
+
+import torch
+import torch.nn as nn
+import torch.nn.functional as F
+
+from peft.tuners.tuners_utils import BaseTunerLayer, check_adapters_to_merge
+
+
+class ShiraLayer(BaseTunerLayer):
+ # List all names of layers that may contain trainable adapter weights
+ adapter_layer_names = ("shira_weight",)
+ # All names of other adapter-related parameters
+ other_param_names = ("r", "scaling", "shira_indices")
+
+ def __init__(self, base_layer: nn.Module, **kwargs):
+ self.base_layer = base_layer
+ self.r = {}
+ self.scaling = {}
+ self.shira_weight = nn.ParameterDict({})
+ self.shira_indices = {}
+ self.weight_shape = base_layer.weight.shape # Assumes SHiRA is on some layer with "weight" parameter
+
+ # Mark the weight as unmerged
+ self._disable_adapters = False
+ self.merged_adapters = []
+
+ base_layer = self.get_base_layer()
+ if isinstance(base_layer, nn.Linear):
+ in_features, out_features = base_layer.in_features, base_layer.out_features
+ else:
+ raise NotImplementedError("Only nn.Linear layers supported currently")
+
+ self.in_features = in_features
+ self.out_features = out_features
+ self.kwargs = kwargs
+
+ def update_layer(
+ self,
+ adapter_name,
+ mask,
+ r,
+ init_weights: bool = True,
+ inference_mode: bool = False,
+ **kwargs,
+ ):
+ if r <= 0:
+ raise ValueError(f"`r` should be a positive integer value but the value passed is {r}")
+ self.r[adapter_name] = r
+ self.scaling[adapter_name] = (
+ 1.0 # Default scale during training. Can be set to any (non-negative) value during inference.
+ )
+ # The number of shira weights in this layer is determined by r such that the total number of weights is the same as a LoRA Layer (for direct comparisons)
+ num_shira_weight = r * (self.in_features + self.out_features)
+ if num_shira_weight > self.in_features * self.out_features:
+ raise ValueError(
+ f"The set rank {r} results in more shira params than the total number of params in the base layer {self.in_features * self.out_features} and this is not allowed."
+ )
+
+ # Actual trainable parameters
+ # We have used a vector parameter with fixed indices that we use inside a torch.sparse_coo_tensor in get_delta_weight function.
+ # Directly using a torch.sparse_coo_tensor as a parameter could have been possible but we ran into some issues similar to:
+ # https://github.com/pytorch/pytorch/issues/79542.
+ shira_init_weight = torch.zeros(num_shira_weight) if init_weights else torch.randn(num_shira_weight)
+ self.shira_weight[adapter_name] = nn.Parameter(
+ shira_init_weight.to(self.base_layer.weight.dtype).to(self.base_layer.weight.device),
+ requires_grad=True,
+ )
+
+ if mask is not None:
+ # Compute the shira_indices from the mask. Make sure the mask is formed using r*(self.in_features + self.out_features) and not some other K.
+ mask_indices = torch.where(mask == 1.0)
+ self.shira_indices[adapter_name] = torch.cat(
+ [mask_indices[0].unsqueeze(0), mask_indices[1].unsqueeze(0)], 0
+ ).to(torch.int)
+ self.shira_indices[adapter_name] = self.shira_indices[adapter_name].to(self.base_layer.weight.device)
+
+ if self.shira_indices[adapter_name].shape[1] != self.shira_weight[adapter_name].shape[0]:
+ raise ValueError(
+ f"The SHiRA indices and weights are not the same dimensions for adapter {adapter_name} in layer {self.base_layer}"
+ )
+
+ self._move_adapter_to_device_of_base_layer(adapter_name)
+ self.set_adapter(self.active_adapters, inference_mode=inference_mode)
+
+ def reset_shira_parameters(self, adapter_name):
+ nn.init.zeros_(self.shira_weight[adapter_name])
+
+ def set_scale(self, adapter, scale):
+ if adapter not in self.scaling:
+ # Ignore the case where the adapter is not in the layer
+ return
+ self.scaling[adapter] = scale
+
+
+class Linear(nn.Module, ShiraLayer):
+ # SHiRA implemented in a dense layer
+ def __init__(
+ self,
+ base_layer,
+ mask,
+ adapter_name: str,
+ r: int = 0,
+ fan_in_fan_out: bool = False, # Set this to True if the layer to replace stored weight like (fan_in, fan_out)
+ init_weights: bool = True,
+ **kwargs,
+ ) -> None:
+ super().__init__()
+ ShiraLayer.__init__(self, base_layer, **kwargs)
+ self.fan_in_fan_out = fan_in_fan_out
+ if self.base_layer is not self.get_base_layer():
+ raise ValueError("SHiRA does not support nested base layers")
+
+ self._active_adapter = adapter_name
+ self.update_layer(adapter_name, mask, r, init_weights=init_weights)
+
+ def merge(self, safe_merge: bool = False, adapter_names: Optional[list[str]] = None) -> None:
+ """
+ Merge the active adapter weights into the base weights
+
+ Args:
+ safe_merge (`bool`, *optional*):
+ If True, the merge operation will be performed in a copy of the original weights and check for NaNs
+ before merging the weights. This is useful if you want to check if the merge operation will produce
+ NaNs. Defaults to `False`.
+ adapter_names (`List[str]`, *optional*):
+ The list of adapter names that should be merged. If None, all active adapters will be merged. Defaults
+ to `None`.
+ """
+
+ adapter_names = check_adapters_to_merge(self, adapter_names)
+ if not adapter_names:
+ # no adapter to merge
+ return
+
+ for active_adapter in adapter_names:
+ if active_adapter in self.shira_weight.keys():
+ base_layer = self.get_base_layer()
+ if safe_merge:
+ # Note that safe_merge will be slower than the normal merge
+ # because of the copy operation.
+ orig_weights = base_layer.weight.data.clone()
+
+ orig_weights += self.get_delta_weight(active_adapter)
+
+ if not torch.isfinite(orig_weights).all():
+ raise ValueError(
+ f"NaNs detected in the merged weights. The adapter {active_adapter} seems to be broken"
+ )
+
+ base_layer.weight.data = orig_weights
+ else:
+ base_layer.weight.data += self.get_delta_weight(active_adapter)
+ self.merged_adapters.append(active_adapter)
+
+ def unmerge(self) -> None:
+ if not self.merged:
+ warnings.warn("Already unmerged. Nothing to do.")
+ return
+
+ while len(self.merged_adapters) > 0:
+ active_adapter = self.merged_adapters.pop()
+ if active_adapter in self.shira_weight.keys():
+ self.get_base_layer().weight.data -= self.get_delta_weight(active_adapter)
+
+ def get_delta_weight(self, adapter) -> torch.Tensor:
+ """
+ Compute the delta weight for the given adapter.
+
+ Args:
+ adapter (str):
+ The name of the adapter for which the delta weight should be computed.
+ """
+
+ # In multi-gpu environment, the indices are at the wrong gpu. This is needed to correct this.
+ self.shira_indices[adapter] = self.shira_indices[adapter].to(self.shira_weight[adapter].device)
+ return torch.sparse_coo_tensor(
+ self.shira_indices[adapter], self.shira_weight[adapter] * self.scaling[adapter], self.weight_shape
+ )
+
+ def forward(self, x: torch.Tensor, *args, **kwargs) -> torch.Tensor:
+ if self.disable_adapters:
+ if self.merged:
+ self.unmerge()
+ result = self.base_layer(x, *args, **kwargs)
+ elif self.merged:
+ result = self.base_layer(x, *args, **kwargs)
+ else:
+ new_weight = copy.deepcopy(self.base_layer.weight.data)
+ for active_adapter in self.active_adapters:
+ if active_adapter not in self.shira_weight.keys():
+ continue
+ new_weight += self.get_delta_weight(active_adapter)
+
+ result = F.linear(x, new_weight, bias=self.base_layer.bias)
+
+ return result
+
+ def __repr__(self) -> str:
+ rep = super().__repr__()
+ return "shira." + rep
diff --git a/peft/src/peft/tuners/shira/mask_functions.py b/peft/src/peft/tuners/shira/mask_functions.py
new file mode 100644
index 0000000000000000000000000000000000000000..d8afbfa8ed23589c74306b0d6e2da071e2f64a11
--- /dev/null
+++ b/peft/src/peft/tuners/shira/mask_functions.py
@@ -0,0 +1,72 @@
+# Copyright 2025-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""
+This module is intended to store mask functions for use inside SHiRA construction. The mask functions are required to
+have a specific signature as shown below.
+
+Required positional arguments:
+ base_layer - This is the linear layer where the shira adapter will be attached. r - This parameter is used to
+ determine the number of parameters in the
+ shira adapter in a way that is consistent with LoRA sizing. SHiRA is a high rank adapter. Setting this
+ parameter does not restrict the adapter rank.
+Keyword arguments can be provided as needed by the particular mask function implementation.
+
+Return:
+ mask - this is a torch.tensor of the same shape as base_layer.weight that contains 0s and 1s with the same
+ dtype and device as base_layer.weight
+
+If you would like to attach SHiRA adapters to a model using PEFT methods (such as get_peft_model()), using more
+arguments than the provided positional arguments, you can create the mask function reference like the following:
+
+```
+ def create_mask_function_reference(**my_kwargs):
+ def mask_fn(base_layer, r):
+ ... your implementation here that might use my_kwargs ...
+ return mask
+ return mask_fn
+```
+Then, you can create your peft model with custom SHiRA mask as follows:
+```
+ model = ...
+ my_kwargs = ...
+ mask_fn = create_mask_function_reference(**my_kwargs)
+ peft_config = ShiraConfig(r=4, mask_type='my_custom_mask')
+ peft_config.mask_fn = mask_fn
+ peft_model = get_peft_model(model, peft_config)
+```
+
+Complete training examples are provided in the examples/shira/ directory.
+"""
+
+from typing import Optional
+
+import torch
+import torch.nn as nn
+
+
+def random_mask(base_layer: nn.Module, r: int, random_seed: Optional[int] = None, **kwargs) -> torch.tensor:
+ shape = base_layer.weight.shape
+ num_shira_weights = r * (shape[0] + shape[1])
+ random_generator = torch.Generator()
+ if random_seed is not None:
+ random_generator.manual_seed(random_seed)
+ idx = (torch.randperm(base_layer.weight.numel(), generator=random_generator)[:num_shira_weights]).to(
+ base_layer.weight.device
+ )
+ val = torch.ones_like(idx.type(base_layer.weight.dtype))
+ mask = torch.zeros_like(base_layer.weight.view(1, -1))
+ mask = mask.scatter_(1, idx.unsqueeze(0), val.unsqueeze(0)).view(shape)
+
+ return mask
diff --git a/peft/src/peft/tuners/shira/model.py b/peft/src/peft/tuners/shira/model.py
new file mode 100644
index 0000000000000000000000000000000000000000..c212a9bf2c110bba5a180eaf2cac0bda9a93ee6e
--- /dev/null
+++ b/peft/src/peft/tuners/shira/model.py
@@ -0,0 +1,142 @@
+# Copyright 2025-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+from __future__ import annotations
+
+import warnings
+
+import torch
+
+from peft.tuners.tuners_utils import BaseTuner, BaseTunerLayer
+from peft.utils import (
+ TRANSFORMERS_MODELS_TO_SHIRA_TARGET_MODULES_MAPPING,
+)
+
+from .layer import Linear, ShiraLayer
+
+
+class ShiraModel(BaseTuner):
+ """
+ Creates a Sparse High Rank Adapter (SHiRA) Model from a pretrained model.
+
+ Args:
+ model ([`~transformers.PreTrainedModel`]): The model to be adapted.
+ config ([`ShiraConfig`]): The configuration of the SHiRA model.
+ adapter_name (`str`): The name of the adapter, defaults to `"default"`.
+
+ Returns:
+ `torch.nn.Module`: The SHiRA model.
+
+ Example:
+
+ ```py
+ >>> from transformers import AutoModelForCausalLM
+ >>> from peft import ShiraConfig, get_peft_model
+
+ >>> base_model = AutoModelForCausalLM.from_pretrained("facebook/opt-125m")
+ >>> config = ShiraConfig(r=32)
+ >>> model = get_peft_model(base_model, config)
+ ```
+
+ **Attributes**:
+ - **model** ([`~transformers.PreTrainedModel`]) -- The model to be adapted.
+ - **peft_config** ([`ShiraConfig`]): The configuration of the SHiRA model.
+ """
+
+ prefix: str = "shira_"
+ tuner_layer_cls = ShiraLayer
+ target_module_mapping = TRANSFORMERS_MODELS_TO_SHIRA_TARGET_MODULES_MAPPING
+
+ def _create_and_replace(
+ self,
+ shira_config,
+ adapter_name,
+ target,
+ target_name,
+ parent,
+ current_key,
+ **optional_kwargs,
+ ):
+ if current_key is None:
+ raise ValueError("Current Key shouldn't be `None`")
+
+ bias = hasattr(target, "bias") and target.bias is not None
+ kwargs = {}
+ kwargs["bias"] = bias
+ if shira_config.mask_type == "random":
+ kwargs["random_seed"] = shira_config.random_seed
+
+ for k, v in optional_kwargs.items():
+ kwargs[k] = v
+
+ if isinstance(target, Linear):
+ mask = (
+ shira_config.mask_fn(target.base_layer, shira_config.r, **kwargs)
+ if shira_config.mask_fn is not None
+ else None
+ )
+ target.update_layer(
+ adapter_name,
+ mask,
+ shira_config.r,
+ init_weights=shira_config.init_weights,
+ )
+ else:
+ new_module = self._create_new_module(shira_config, adapter_name, target, **kwargs)
+ if adapter_name not in self.active_adapter:
+ # adding an additional adapter: it is not automatically trainable
+ new_module.requires_grad_(False)
+ self._replace_module(parent, target_name, new_module, target)
+
+ @staticmethod
+ def _create_new_module(shira_config, adapter_name, target, **kwargs):
+ fan_in_fan_out = shira_config.fan_in_fan_out
+
+ _ = kwargs.pop("bias", False)
+
+ if isinstance(target, BaseTunerLayer):
+ target_base_layer = target.get_base_layer()
+ else:
+ target_base_layer = target
+
+ if isinstance(target_base_layer, torch.nn.Linear):
+ if fan_in_fan_out:
+ warnings.warn(
+ "fan_in_fan_out is set to True but the target module is `torch.nn.Linear`. "
+ "Setting fan_in_fan_out to False."
+ )
+ fan_in_fan_out = shira_config.fan_in_fan_out = False
+ else:
+ raise ValueError(
+ f"Target module {target} is not supported. Currently, only the following modules are supported: "
+ "`torch.nn.Linear`."
+ )
+
+ mask = (
+ shira_config.mask_fn(target_base_layer, shira_config.r, **kwargs)
+ if shira_config.mask_fn is not None
+ else None
+ )
+
+ new_module = Linear(
+ target,
+ mask,
+ adapter_name,
+ shira_config.r,
+ fan_in_fan_out,
+ init_weights=shira_config.init_weights,
+ **kwargs,
+ )
+
+ return new_module
diff --git a/peft/src/peft/tuners/trainable_tokens/__init__.py b/peft/src/peft/tuners/trainable_tokens/__init__.py
new file mode 100644
index 0000000000000000000000000000000000000000..4aa7bf8e5fc4705cb7b190cee0de53ac8db89573
--- /dev/null
+++ b/peft/src/peft/tuners/trainable_tokens/__init__.py
@@ -0,0 +1,33 @@
+# Copyright 2025-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+from peft.utils import register_peft_method
+
+from .config import TrainableTokensConfig
+from .layer import TrainableTokensLayer
+from .model import TrainableTokensModel
+
+
+__all__ = [
+ "TrainableTokensConfig",
+ "TrainableTokensLayer",
+ "TrainableTokensModel",
+]
+
+register_peft_method(
+ name="trainable_tokens",
+ config_cls=TrainableTokensConfig,
+ model_cls=TrainableTokensModel,
+ is_mixed_compatible=False,
+)
diff --git a/peft/src/peft/tuners/trainable_tokens/config.py b/peft/src/peft/tuners/trainable_tokens/config.py
new file mode 100644
index 0000000000000000000000000000000000000000..7412d7f06474c510679e0f3004ae10c20910b00f
--- /dev/null
+++ b/peft/src/peft/tuners/trainable_tokens/config.py
@@ -0,0 +1,89 @@
+# Copyright 2025-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+from __future__ import annotations
+
+from dataclasses import dataclass, field
+from typing import Optional, Union
+
+from peft.config import PeftConfig
+from peft.utils import PeftType
+
+
+@dataclass
+class TrainableTokensConfig(PeftConfig):
+ """
+ Configuration for the `TrainableTokens` method.
+
+ Allows for training new tokens (and re-training existing ones) without training the full embedding matrix. By
+ marking a few select tokens (identified by their indices) trainable and leaving the rest untouched, this method can
+ be used to add new tokens or changing the embedding of existing tokens while saving on memory. Both storage as well
+ as working memory usage are reduced in contrast to training the embedding matrix fully.
+
+ Note that training with FSDP/DeepSpeed might not yet be fully supported.
+
+ Args:
+ token_indices (`list[int]`):
+ List of integers, signifying the indices of the tokens you want to be trainable. To find the index of a
+ token with a tokenizer, you can tokenize the string and look at the returned `input_ids`. The closer the
+ amount of indices is to the total amount of tokens, the less efficient this method gets.
+ target_modules (`Optional[Union[list[str], str]]`):
+ List of module names or regex expression of the module names to replace with our `TrainableTokensLayer`. If
+ not defined, it will attempt to get the model's input embedding layer if the model has a
+ `get_input_embeddings` method (transformer models usually do), if that fails the default is 'embed_tokens'.
+ Other example targets are `embedding`, `encoder.embeddings` or `decoder.embeddings`.
+ init_weights (`bool`):
+ By default the new token weights are initialized to be the same as the respective token embeddings. This
+ makes TrainableTokens a no-op when not trained. If set to `False` the weights will be random values. Do not
+ change this setting unless you know exactly what you're doing.
+ """
+
+ token_indices: list[int] = field(
+ default_factory=list,
+ metadata={
+ "help": (
+ "List of integers, signifying the indices of the tokens you want to be trainable. "
+ "To find the index of a token with a tokenizer, you can tokenize the string and "
+ "look at the returned `input_ids`. The closer the amount of indices is to the total amount of "
+ "tokens, the less efficient this method gets."
+ )
+ },
+ )
+ target_modules: Optional[Union[list[str], str]] = field(
+ default=None,
+ metadata={
+ "help": (
+ "List of module names or regex expression of the module names to replace with our "
+ "`TrainableTokensLayer`. If not defined, it will default to the model's input embedding layer if "
+ "the model has a `get_input_embeddings` method (transformer models usually do), if that fails the "
+ "default is 'embed_tokens'. Other example targets could be `embedding`, `encoder.embeddings` or "
+ "`decoder.embeddings`."
+ ),
+ },
+ )
+
+ init_weights: bool = field(
+ default=True,
+ metadata={
+ "help": (
+ "By default the new token weights are initialized to be the same as the respective token embeddings. "
+ "This makes TrainableTokens a no-op when not trained. If set to `False` the weights will be random "
+ "values. Do not change this setting unless you know exactly what you're doing. "
+ )
+ },
+ )
+
+ def __post_init__(self):
+ super().__post_init__()
+ self.peft_type = PeftType.TRAINABLE_TOKENS
diff --git a/peft/src/peft/tuners/trainable_tokens/layer.py b/peft/src/peft/tuners/trainable_tokens/layer.py
new file mode 100644
index 0000000000000000000000000000000000000000..0f35462224e178f340d23309f6a8420914d24b31
--- /dev/null
+++ b/peft/src/peft/tuners/trainable_tokens/layer.py
@@ -0,0 +1,249 @@
+# Copyright 2025-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+from __future__ import annotations
+
+import warnings
+from typing import Optional
+
+import torch
+import torch.distributed as dist
+import torch.nn as nn
+import torch.nn.functional as F
+
+from peft.tuners._buffer_dict import BufferDict
+from peft.tuners.tuners_utils import BaseTunerLayer, _get_in_out_features, check_adapters_to_merge
+from peft.utils.integrations import check_deepspeed_zero3_enabled, gather_params_ctx
+
+
+class TrainableTokensLayer(nn.Module, BaseTunerLayer):
+ # All names of layers that may contain (trainable) adapter weights
+ adapter_layer_names = ("trainable_tokens_delta",)
+
+ # All names of other parameters that may contain adapter-related parameters
+ other_param_names = ("token_indices", "trainable_tokens_original")
+
+ def __init__(
+ self,
+ base_layer: nn.Module,
+ adapter_name: str,
+ token_indices: list[int],
+ tied_adapter: Optional[TrainableTokensLayer] = None,
+ **kwargs,
+ ) -> None:
+ super().__init__()
+
+ self.base_layer = base_layer
+ self._active_adapter = adapter_name
+ self.kwargs = kwargs
+
+ # wrap the tied adapter in a list so that it is excluded from .(named_)modules() and, therefore,
+ # not included in the state dict since it would be a copy of the tied adapter anyway.
+ self._tied_adapter = [tied_adapter] if tied_adapter else []
+
+ # we store the updated weights of particular tokens and their originals. we assume
+ # that the count of new tokens is far smaller than the number of total tokens.
+ #
+ # In case we have weight tying with another token adapter, we'll have no actual
+ # references on our own but use everything from the tied adapter.
+ if not self.tied_adapter:
+ self.trainable_tokens_delta = nn.ParameterDict({})
+ self.trainable_tokens_original = BufferDict({})
+ self.token_indices = {}
+ else:
+ self.trainable_tokens_delta = self.tied_adapter.trainable_tokens_delta
+ self.trainable_tokens_original = self.tied_adapter.trainable_tokens_original
+ self.token_indices = self.tied_adapter.token_indices
+
+ # Mark the weight as unmerged
+ self.merged_adapters = []
+
+ in_features, out_features = _get_in_out_features(self.get_base_layer())
+ self.in_features = in_features
+ self.out_features = out_features
+
+ @property
+ def tied_adapter(self):
+ if self._tied_adapter:
+ return self._tied_adapter[0]
+ return None
+
+ def _collect_token_weights(self, weight: torch.Tensor, rows: torch.Tensor, embed_dim: int) -> torch.Tensor:
+ """DeepSpeed zero3 specific code to initialize trainable tokens.
+
+ Ensures that only the necessary weights are collected to a single rank, initialized, and then shared with all
+ ranks.
+ """
+ src_rank = 0
+ # right now, only CUDA is implemented
+ device = torch.device("cuda", torch.cuda.current_device())
+
+ with gather_params_ctx([weight], modifier_rank=None):
+ if dist.get_rank() == src_rank:
+ token_weights = weight[rows].clone()
+ else:
+ # build an empty tensor with correct shape/type/device
+ token_weights = torch.empty(
+ (len(rows), embed_dim),
+ dtype=weight.dtype,
+ device=device,
+ )
+
+ # share the weights with all ranks
+ dist.broadcast(token_weights, src=src_rank)
+ return token_weights
+
+ def update_layer(self, adapter_name, **kwargs):
+ if kwargs.get("tied_adapter", None):
+ # as a tied adapter, we're just following whatever the adpater we're tied to does, we don't update anything.
+ return
+
+ self.token_indices[adapter_name] = kwargs["token_indices"]
+ init_weights = kwargs.get("init_weights", True)
+
+ # we initialize the delta embedding weights from the base embedding matrix and replace values instead of
+ # adding/subtracting deltas. we do it this way and use `embedding.weight.index_copy()` to write the updated
+ # values during `forward()` to avoid that the user resizing the embedding matrix, effectively filling the new
+ # token space with random values, training the model with TrainableTokensLayer, initializing the model anew -
+ # thus re-initializing the new embeddings again with new random variables. If we would add/subtract deltas
+ # onto the new values, we would get undefined behavior. By replacing the specific token values we always
+ # get defined behavior.
+ weight = self.get_base_layer().weight
+ embed_dim = self.get_base_layer().embedding_dim
+
+ if init_weights:
+ if check_deepspeed_zero3_enabled():
+ values = self._collect_token_weights(weight, self.token_indices[adapter_name], embed_dim)
+ else:
+ values = self.weight[self.token_indices[adapter_name]]
+ else:
+ # random init with matching dtype/device
+ values = torch.randn(
+ (len(self.token_indices[adapter_name]), embed_dim),
+ dtype=weight.dtype,
+ device=weight.device,
+ )
+
+ self.trainable_tokens_delta[adapter_name] = nn.Parameter(values.clone(), requires_grad=True)
+ self.trainable_tokens_original[adapter_name] = values.clone()
+
+ self._move_adapter_to_device_of_base_layer(adapter_name)
+
+ def _check_overlapping_tokens(self, adapter_names):
+ """Raises an error if the token indices of the given adapter names are overlapping.
+ This is currently not supported and can lead to undefined behavior of the model if no specific merging between
+ the overlapping indices' values is applied.
+ """
+ if len(adapter_names) <= 1:
+ return
+
+ indices = set()
+
+ # we take already merged adapters into account as well since they can be overridden by new adapters as well.
+ for adapter_name in set(adapter_names + self.merged_adapters):
+ index_set = set(self.token_indices[adapter_name])
+ if len(indices.intersection(index_set)):
+ raise ValueError(
+ f"Token indices of adapter {adapter_name} are already defined and would result in "
+ "undefined merging behavior. Only disjunct token indices are currently supported."
+ )
+ indices.update(index_set)
+
+ def merge(self, safe_merge: bool = False, adapter_names: Optional[list[str]] = None) -> None:
+ adapter_names = check_adapters_to_merge(self, adapter_names)
+
+ if not adapter_names:
+ # no adapter to merge
+ return
+
+ self._check_overlapping_tokens(adapter_names)
+
+ merged = self.base_layer.weight.data
+
+ for adapter_name in adapter_names:
+ index = torch.tensor(self.token_indices[adapter_name]).to(merged.device)
+ deltas = self.trainable_tokens_delta[adapter_name].to(merged)
+ merged = merged.index_copy(dim=0, index=index, source=deltas)
+
+ if safe_merge and not torch.isfinite(merged).all():
+ raise ValueError(f"NaNs detected in the merged weights. The adapter {adapter_name} seems to be broken")
+
+ self.base_layer.weight.data = merged
+ self.merged_adapters.extend(adapter_names)
+
+ def unmerge(self) -> None:
+ if not self.merged:
+ warnings.warn("Already unmerged. Nothing to do.")
+ return
+
+ while len(self.merged_adapters) > 0:
+ adapter_name = self.merged_adapters.pop()
+
+ index = torch.tensor(self.token_indices[adapter_name]).to(self.base_layer.weight.device)
+ originals = self.trainable_tokens_original[adapter_name].to(self.base_layer.weight)
+ self.base_layer.weight.data.index_copy_(dim=0, index=index, source=originals)
+
+ def get_merged_weights(self, active_adapters):
+ W = self.base_layer.weight
+
+ for adapter_name in active_adapters:
+ index = torch.tensor(self.token_indices[adapter_name]).to(W.device)
+ deltas = self.trainable_tokens_delta[adapter_name].to(W)
+ W = W.index_copy(dim=0, index=index, source=deltas)
+
+ return W
+
+ def forward_adapters(self, x: torch.Tensor, active_adapters, *args, **kwargs) -> torch.Tensor:
+ if self.disable_adapters or not active_adapters:
+ if self.merged:
+ self.unmerge()
+ result = self.base_layer(x, *args, **kwargs)
+ elif self.merged:
+ result = self.base_layer(x, *args, **kwargs)
+ else:
+ self._check_overlapping_tokens(active_adapters)
+
+ W = self.get_merged_weights(active_adapters)
+
+ # Normally it should be very clear that we're wrapping Embedding layers but there are cases, such as
+ # tying weights with an LM head where the layer we wrap is a Linear layer. Therefore we must choose
+ # accordingly.
+ #
+ # TODO: the isinstance checks, especially the one for nn.Linear, may not hold for quantized layers;
+ # TODO: we may need to find a better way to detect quantized layers.
+ if isinstance(self.base_layer, torch.nn.Embedding):
+ result = F.embedding(
+ input=x,
+ weight=W,
+ padding_idx=self.base_layer.padding_idx,
+ max_norm=self.base_layer.max_norm,
+ norm_type=self.base_layer.norm_type,
+ scale_grad_by_freq=self.base_layer.scale_grad_by_freq,
+ sparse=self.base_layer.sparse,
+ )
+ elif isinstance(self.base_layer, torch.nn.Linear):
+ # Probably a tied adapter that wraps an LM head.
+ result = F.linear(
+ input=x,
+ weight=W,
+ )
+ else:
+ raise ValueError(
+ "TrainableTokensLayer wraps an unknown layer type, maybe you are targeting the wrong layer?"
+ )
+
+ return result
+
+ def forward(self, x: torch.Tensor, *args, **kwargs) -> torch.Tensor:
+ return self.forward_adapters(x, self.active_adapters, *args, **kwargs)
diff --git a/peft/src/peft/tuners/trainable_tokens/model.py b/peft/src/peft/tuners/trainable_tokens/model.py
new file mode 100644
index 0000000000000000000000000000000000000000..50abef90f5120712a65160eb70b091e6854c64e9
--- /dev/null
+++ b/peft/src/peft/tuners/trainable_tokens/model.py
@@ -0,0 +1,139 @@
+# Copyright 2025-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+from __future__ import annotations
+
+import torch.nn as nn
+
+from peft.config import PeftConfig
+from peft.tuners.tuners_utils import BaseTuner
+from peft.utils import _get_input_embeddings_name, _get_submodules
+
+from .layer import TrainableTokensLayer
+
+
+class TrainableTokensModel(BaseTuner):
+ prefix: str = "trainable_tokens_"
+ tuner_layer_cls = TrainableTokensLayer
+
+ def _prepare_adapter_config(self, peft_config, model_config):
+ # target_modules can be none which prompts us to infer the embedding layer name ourselves.
+ if peft_config.target_modules is None:
+ peft_config.target_modules = _get_input_embeddings_name(self.model, "embed_tokens")
+
+ return peft_config
+
+ def inject_adapter(
+ self,
+ model: nn.Module,
+ adapter_name: str,
+ autocast_adapter_dtype: bool = True,
+ low_cpu_mem_usage: bool = False,
+ **kwargs,
+ ) -> None:
+ super().inject_adapter(
+ model=model,
+ adapter_name=adapter_name,
+ autocast_adapter_dtype=autocast_adapter_dtype,
+ low_cpu_mem_usage=low_cpu_mem_usage,
+ **kwargs,
+ )
+
+ model_config = self.get_model_config(self)
+
+ # In case of weight-tying we need to adapt the tied weights as well and use tie the embedding adapter.
+ #
+ # The TrainableTokensLayer supports being tied to another TrainableTokensLayer meaning that the layer will
+ # not do any changes on its own but solely rely on the weights from the tied adapter. We will search for the
+ # tied weights and put tied TrainableTokensLayer adapters on them, all tied to the adapter of the embedding
+ # matrix.
+ if (
+ model_config.get("tie_word_embeddings", False)
+ # some models may be misconfigured to have weight tying enabled but don't define tied weights keys
+ and self.model._tied_weights_keys is not None
+ and isinstance(self.model.get_input_embeddings(), TrainableTokensLayer)
+ ):
+ module_keys = [".".join(n.split(".")[:-1]) for n in self.model._tied_weights_keys]
+ # disable removing of duplicates since we're essentially only dealing with duplicates (i.e. tied weights)
+ for name, module in self.model.named_modules(remove_duplicate=False):
+ matched_keys = [target_key for target_key in module_keys if name.endswith(target_key)]
+ if matched_keys:
+ parent, target, target_name = _get_submodules(model, name)
+
+ peft_config = self.peft_config[adapter_name].to_dict()
+ peft_config["tied_adapter"] = self.model.get_input_embeddings()
+
+ self._create_and_replace_dict(
+ peft_config,
+ adapter_name,
+ target,
+ target_name,
+ parent,
+ matched_keys[0],
+ )
+
+ def _get_tied_target_modules(self, *args, **kwargs):
+ # Normally this method would return the layers that target tied layers.
+ #
+ # We override this method since we explicitly support tied weights tied to the embedding layer.
+ # Therefore, we don't need the warning issued by returning the modules here.
+ return []
+
+ def _create_and_replace_dict(
+ self,
+ peft_config: dict,
+ adapter_name: str,
+ target: nn.Module,
+ target_name: str,
+ parent: nn.Module,
+ current_key: str,
+ ) -> None:
+ """
+ The same as `_create_and_replace` but takes a dictionary instead of a peft config so that we can add keys that
+ are not present in the config, such as `tied_adapter`.
+ """
+ kwargs = peft_config
+
+ if isinstance(target, TrainableTokensLayer):
+ target.update_layer(adapter_name, **kwargs)
+ else:
+ new_module = self._create_new_module(peft_config, adapter_name, target, **kwargs)
+ self._replace_module(parent, target_name, new_module, target)
+
+ def _create_and_replace(
+ self,
+ peft_config: PeftConfig,
+ adapter_name: str,
+ target: nn.Module,
+ target_name: str,
+ parent: nn.Module,
+ current_key: str,
+ ) -> None:
+ """
+ A private method to create and replace the target module with the adapter module.
+ """
+ kwargs = peft_config.to_dict()
+ self._create_and_replace_dict(kwargs, adapter_name, target, target_name, parent, current_key)
+
+ @staticmethod
+ def _create_new_module(peft_config, adapter_name, target, **kwargs):
+ new_module = TrainableTokensLayer(target, adapter_name, **kwargs)
+ new_module.update_layer(
+ adapter_name,
+ init_weights=kwargs["init_weights"],
+ token_indices=kwargs["token_indices"],
+ tied_adapter=kwargs.get("tied_adapter", None),
+ )
+
+ return new_module
diff --git a/peft/src/peft/tuners/tuners_utils.py b/peft/src/peft/tuners/tuners_utils.py
new file mode 100644
index 0000000000000000000000000000000000000000..66903296a8f834010dd443491cc38128f2560eb8
--- /dev/null
+++ b/peft/src/peft/tuners/tuners_utils.py
@@ -0,0 +1,1930 @@
+# Copyright 2023-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+from __future__ import annotations
+
+import copy
+import dataclasses
+import os
+import re
+import textwrap
+import warnings
+from abc import ABC, abstractmethod
+from collections.abc import Sequence
+from contextlib import contextmanager, nullcontext
+from typing import Any, Optional, Union, overload
+
+import torch
+from accelerate.hooks import AlignDevicesHook
+from accelerate.utils import named_module_tensors, offload_state_dict
+from packaging import version
+from torch import nn
+from tqdm import tqdm
+from transformers import PreTrainedModel
+from transformers.pytorch_utils import Conv1D
+
+from peft.mapping import PEFT_TYPE_TO_PREFIX_MAPPING
+from peft.utils import INCLUDE_LINEAR_LAYERS_SHORTHAND
+from peft.utils.constants import (
+ DUMMY_MODEL_CONFIG,
+ DUMMY_TARGET_MODULES,
+ EMBEDDING_LAYER_NAMES,
+ MIN_TARGET_MODULES_FOR_OPTIMIZATION,
+ SEQ_CLS_HEAD_NAMES,
+)
+from peft.utils.integrations import init_empty_weights
+from peft.utils.other import (
+ AuxiliaryTrainingWrapper,
+ _set_adapter,
+ match_target_against_key,
+ set_additional_trainable_modules,
+)
+from peft.utils.peft_types import PeftType, TaskType
+
+from ..config import PeftConfig
+from ..utils import _get_submodules
+from ._buffer_dict import BufferDict
+
+
+@contextmanager
+def onload_layer(layer):
+ r"""
+ A utility for modifying a module containing one or more tuners and a base layer, any of which are offloaded to the
+ CPU or disk. Moves a module's sub-modules to the execution device before some action is performed, after that the
+ base layer state dictionary is re-assigned (if that layer was offloaded to the disk) and finally the parameters are
+ offloaded.
+
+ If the module has no offloaded sub-modules, this function does nothing.
+
+ Args:
+ layer ('torch.nn.Module'):
+ layer with tuners to be merged
+ """
+
+ offloaded_modules = []
+ for name, module in layer.named_modules():
+ if name in ["", "base_layer"]:
+ continue
+ if hasattr(module, "_hf_hook") and isinstance(module._hf_hook, AlignDevicesHook) and module._hf_hook.offload:
+ module._hf_hook.pre_forward(module)
+ offloaded_modules.append(module)
+
+ base_layer_offload = False
+ if hasattr(layer, "base_layer") and (
+ hasattr(layer.base_layer, "_hf_hook")
+ and isinstance(layer.base_layer._hf_hook, AlignDevicesHook)
+ and layer.base_layer._hf_hook.offload
+ ):
+ # check if the base layer is disk-offloaded (must contain a 'dataset' and an offload index)
+ if torch.device("meta") in layer.base_layer._hf_hook.original_devices.values() and hasattr(
+ layer.base_layer._hf_hook.weights_map, "dataset"
+ ):
+ # find the disk-offload index (maps modules to safetensors) from the `dataset` (OffloadedWeightsLoader object)
+ index = layer.base_layer._hf_hook.weights_map.dataset.index
+ module_name = list(dict(layer.base_layer._hf_hook.weights_map.dataset).keys())[0] # any module will do
+ file_name = index[module_name]["safetensors_file"]
+ base_name_arr = []
+ # get effective dir name
+ for i in os.path.split(file_name):
+ if "--" in i:
+ base_name_arr.append(i)
+ break
+ base_name_arr.append(i)
+ base_name = os.path.join(*base_name_arr)
+ safetensors_filename = base_name + "-merged"
+ layer.base_layer._hf_hook.pre_forward(layer.base_layer)
+ base_layer_offload = True
+
+ yield
+
+ for module in offloaded_modules:
+ module._hf_hook.post_forward(module, torch.tensor([]))
+
+ if base_layer_offload:
+ # re-make weights map (must be on cpu to send params to the disk via memmap if disk offload)
+ layer.base_layer._hf_hook.weights_map = {
+ name: param.to("cpu") for name, param in named_module_tensors(layer.base_layer)
+ }
+ # offload weights map to disk if original device is the disk
+ if torch.device("meta") in layer.base_layer._hf_hook.original_devices.values() and hasattr(
+ layer.base_layer._hf_hook.weights_map, "dataset"
+ ):
+ # rewrite directory with merged weights
+ offload_state_dict(safetensors_filename, layer.base_layer._hf_hook.weights_map)
+ layer.base_layer._hf_hook.post_forward(layer.base_layer, torch.tensor([]))
+
+
+def _check_lora_target_modules_mamba(peft_config: PeftConfig, model: nn.Module, target_name: str):
+ """
+ Prevent applying LoRA to incompatible modules in specific architectures (e.g., Mamba).
+ """
+
+ lora_like_types = {"LORA", "ADALORA", "XLORA", "RANDLORA"}
+ incompatible_modules = {"out_proj", "conv1d"}
+ mamba_model_types = {"falcon_h1", "mamba", "mamba2", "falcon_mamba"}
+
+ if (
+ peft_config.peft_type in lora_like_types
+ and hasattr(model, "config")
+ and getattr(model.config, "model_type", None) in mamba_model_types
+ ):
+ if target_name in incompatible_modules:
+ raise ValueError(
+ f"[PEFT:{peft_config.peft_type}] Module '{target_name}' is incompatible with Mamba-based models "
+ f"(model_type='{model.config.model_type}'). Incompatible modules: {incompatible_modules}. "
+ "Please remove it from `target_modules` to avoid compatibility issues."
+ )
+
+
+def _get_in_out_features(module: nn.Module) -> tuple[int, int] | tuple[None, None]:
+ """
+ Get the in_features and out_features of the layer.
+
+ Returns in_features and out_features as a tuple. If they cannot be determined, return a tuple of None and None.
+ This function covers a broad range of layers, some of which the caller might not support. Therefore, just because
+ this function returns a valid result does not imply that the layer type is supported.
+ """
+ if isinstance(module, nn.Linear):
+ torch_supports_dtensor = version.parse(torch.__version__) >= version.parse("2.5.0")
+ if torch_supports_dtensor and isinstance(module.weight, torch.distributed.tensor.DTensor):
+ # If Tensor Parallel is used, the weight is sharded, so we need to get the local shape
+ out_features, in_features = module.weight.to_local().shape
+ else:
+ in_features, out_features = module.in_features, module.out_features
+ elif isinstance(module, nn.Conv1d):
+ in_features, out_features = module.in_channels, module.out_channels
+ elif isinstance(module, nn.Conv2d):
+ in_features, out_features = module.in_channels, module.out_channels
+ elif isinstance(module, nn.Conv3d):
+ in_features, out_features = module.in_channels, module.out_channels
+ elif isinstance(module, nn.Embedding):
+ in_features, out_features = module.num_embeddings, module.embedding_dim
+ elif isinstance(module, Conv1D):
+ in_features, out_features = (
+ module.weight.ds_shape if hasattr(module.weight, "ds_shape") else module.weight.shape
+ )
+ elif isinstance(module, nn.MultiheadAttention):
+ if not module._qkv_same_embed_dim:
+ raise ValueError("Only same dim for query/key/value is supported as of now for MultiheadAttention.")
+ in_features, out_features = module.embed_dim, 3 * module.embed_dim
+ elif hasattr(module, "infeatures") and hasattr(module, "outfeatures"):
+ # QuantLinear
+ in_features, out_features = module.infeatures, module.outfeatures
+ elif hasattr(module, "input_size") and hasattr(module, "output_size"):
+ # Megatron ColumnParallelLinear,RowParallelLinear
+ in_features, out_features = module.input_size, module.output_size
+ elif hasattr(module, "codebooks") and module.__class__.__name__ == "QuantizedLinear":
+ # AQLM QuantLinear
+ in_features, out_features = module.in_features, module.out_features
+ elif hasattr(module, "w_bit") and module.__class__.__name__ == "WQLinear_GEMM":
+ # Awq layers
+ in_features, out_features = module.in_features, module.out_features
+ elif module.__class__.__name__ == "EetqLinear":
+ # Eetq layers
+ in_features, out_features = module.in_features, module.out_features
+ elif hasattr(module, "W_q") and module.__class__.__name__ == "HQQLinear":
+ # HQQ layers
+ in_features, out_features = module.in_features, module.out_features
+ elif module.__class__.__name__ == "PatchedLinear":
+ # INC layers
+ in_features, out_features = module.in_features, module.out_features
+ else:
+ # possibly support user provided custom layer types using dynamic dispatch
+ if hasattr(module, "in_features") and hasattr(module, "out_features"):
+ in_features, out_features = module.in_features, module.out_features
+ else:
+ in_features, out_features = None, None
+ warnings.warn(f"Unsupported layer type '{type(module)}' encountered, proceed at your own risk.", UserWarning)
+ return in_features, out_features
+
+
+class BaseTuner(nn.Module, ABC):
+ r"""
+ A base tuner model that provides the common methods and attributes for all tuners that are injectable into a
+ torch.nn.Module
+
+ For adding a new Tuner class, one needs to overwrite the following methods:
+
+ - **_prepare_adapter_config**:
+ A private method to eventually prepare the adapter config, for example in case the field `target_modules` is
+ missing.
+ - **_create_and_replace**:
+ A private method to create and replace the target module with the adapter module.
+ - **_check_target_module_exists**:
+ A private helper method to check if the passed module's key name matches any of the target modules in the
+ adapter_config.
+
+ The easiest is to check what is done in the `peft.tuners.lora.LoraModel` class.
+
+ Attributes:
+ model (`torch.nn.Module`):
+ The model to which the adapter tuner layers will be attached.
+ forward (`Callable`):
+ The forward method of the model.
+ peft_config (`Union[`PeftConfig`, dict[str, PeftConfig]]`):
+ The adapter configuration object, it should be a dictionary of `str` to `PeftConfig` objects. One can also
+ pass a PeftConfig object and a new adapter will be created with the default name `adapter` or create a new
+ dictionary with a key `adapter_name` and a value of that peft config.
+ config (`dict[str, Any]`):
+ The model configuration object, it should be a dictionary of `str` to `Any` objects.
+ targeted_module_names (`list[str]`):
+ The list of module names that were actually adapted. Can be useful to inspect if you want to quickly
+ double-check that the `config.target_modules` were specified correctly.
+ targeted_parameter_names (`list[str]`):
+ The list of parameter names that were actually adapted. Can be useful to inspect if you want to quickly
+ double-check that the `config.target_parameters` were specified correctly.
+ prefix (`str`)
+ The PEFT-method specific unique prefix. E.g. `"lora_"` for LoRA.
+ """
+
+ # Required attributes for child classes:
+
+ # The unique prefix for this PEFT method, e.g. 'lora_' for LoRA.
+ prefix: str
+ # The class of the tuner layer, e.g. `LoraLayer` for LoRA.
+ tuner_layer_cls: type[BaseTunerLayer]
+ # The default target modules for various transformers model architectures, like Llama. This is useful to allow users
+ # to skip specifying the `target_modules` in the config of the PEFT method. The default is often something like
+ # `{'llama': ['q_proj', 'v_proj'], ...}`.
+ target_module_mapping: dict[str, list[str]]
+
+ def __init__(
+ self,
+ model,
+ peft_config: Union[PeftConfig, dict[str, PeftConfig]],
+ adapter_name: str,
+ low_cpu_mem_usage: bool = False,
+ state_dict: Optional[dict[str, torch.Tensor]] = None,
+ ) -> None:
+ super().__init__()
+
+ self.model = model
+ self.targeted_module_names: list[str] = []
+ self.targeted_parameter_names: list[str] = []
+
+ # For advanced developers, if you want to attach multiple adapters to your
+ # model, just add a `peft_config` dict attribute to your model.
+ if not hasattr(self, "peft_config"):
+ self.peft_config = {adapter_name: peft_config} if isinstance(peft_config, PeftConfig) else peft_config
+ else:
+ warnings.warn(
+ "Already found a `peft_config` attribute in the model. This will lead to having multiple adapters"
+ " in the model. Make sure to know what you are doing!"
+ )
+ if isinstance(peft_config, PeftConfig):
+ self.peft_config[adapter_name] = peft_config
+ else:
+ # user is adding a dict of PeftConfigs
+ self.peft_config.update(peft_config)
+
+ self.active_adapter: str | list[str] = adapter_name
+ self._pre_injection_hook(self.model, self.peft_config[adapter_name], adapter_name)
+ if peft_config != PeftType.XLORA or peft_config[adapter_name] != PeftType.XLORA:
+ self.inject_adapter(self.model, adapter_name, low_cpu_mem_usage=low_cpu_mem_usage, state_dict=state_dict)
+
+ # Copy the peft_config in the injected model.
+ self.model.peft_config = self.peft_config
+
+ @property
+ def active_adapters(self) -> list[str]:
+ if isinstance(self.active_adapter, str):
+ return [self.active_adapter]
+ # is already a list of str
+ return self.active_adapter
+
+ def forward(self, *args: Any, **kwargs: Any):
+ return self.model.forward(*args, **kwargs)
+
+ def _pre_injection_hook(self, model: nn.Module, config: PeftConfig, adapter_name: str) -> None:
+ r"""
+ A hook to be called before the adapter is injected into the model. This method can be overridden by child
+ classes to perform any pre-injection operations.
+
+ Args:
+ model (`nn.Module`):
+ The model to be adapted.
+ config (`PeftConfig`):
+ The adapter config.
+ adapter_name (`str`):
+ The adapter name.
+ """
+ pass
+
+ def _prepare_adapter_config(self, peft_config: PeftConfig, model_config: dict) -> PeftConfig:
+ r"""
+ A private method to prepare the adapter config.
+
+ For transformers based models, if `peft_config.target_modules` is None, for some model architectures, we can
+ automatically infer the target modules from the `TRANSFORMERS_MODELS_TO_XXX_TARGET_MODULES_MAPPING`.
+
+ Args:
+ peft_config (`PeftConfig`):
+ The adapter config.
+ model_config (`dict`):
+ The transformers model config, that config should contain the `model_type` key.
+
+ Returns:
+ peft_config (`PeftConfig`):
+ The PEFT config with updated `target_modules`.
+
+ Raises:
+ ValueError:
+ Raises an error if the model type was not recognized.
+ """
+ if peft_config.target_modules is None:
+ target_modules = self.target_module_mapping.get(model_config["model_type"])
+ if target_modules is None:
+ raise ValueError("Please specify `target_modules` in `peft_config`")
+ peft_config.target_modules = set(target_modules)
+ return peft_config
+
+ def _prepare_model(self, peft_config: PeftConfig, model: nn.Module):
+ r"""
+ A private method to modify the model structure before adapter is applied.
+
+ See `peft.tuner.lora.LoraModel._prepare_model` for an example.
+
+ Args:
+ peft_config (`PeftConfig`):
+ The prepared adapter config.
+ model (`nn.Module`):
+ The model that is going to be adapted.
+ """
+ pass
+
+ @staticmethod
+ def _check_target_module_exists(peft_config: PeftConfig, key: str) -> bool | re.Match[str] | None:
+ """
+ A helper method to check if the passed module's key name matches any of the target modules in the
+ adapter_config.
+
+ Args:
+ config (`PeftConfig`):
+ A config to match target modules from.
+ key (`str`):
+ A key to search any matches in config.
+
+ Returns:
+ `bool` | `re.Match[str]` | `None`:
+ True or re.Match object if key matches any target modules from config, False or None if no match found.
+ """
+ return check_target_module_exists(peft_config, key)
+
+ @abstractmethod
+ def _create_and_replace(
+ self,
+ peft_config: PeftConfig,
+ adapter_name: str,
+ target: nn.Module,
+ target_name: str,
+ parent: nn.Module,
+ current_key: str,
+ parameter_name: Optional[str] = None,
+ ) -> None:
+ r"""
+ Inplace replacement of the target module with the adapter layer. This method needs to be overridden by all the
+ tuner classes.
+
+ Check `peft.tuners.lora.LoraModel._create_and_replace` for an example.
+
+ Args:
+ peft_config (`PeftConfig`):
+ The adapter config.
+ adapter_name (`str`):
+ The adapter name.
+ target (`nn.Module`):
+ The target module.
+ target_name (`str`):
+ The target module's name.
+ parent (`nn.Module`):
+ The parent module.
+ current_key (`str`):
+ The key of the current target being adapted.
+ parameter_name (`str`, *optional*)
+ If, and only if, an `nn.Parameter` is being targeted, this is the name of the parameter.
+ """
+ ...
+
+ def _mark_only_adapters_as_trainable(self, model: nn.Module) -> None:
+ """
+ A helper method to mark only the adapter layers as trainable (i.e. module.requires_grad = False).
+ """
+ for n, p in model.named_parameters():
+ if self.prefix not in n:
+ p.requires_grad = False
+
+ for active_adapter in self.active_adapters:
+ bias = getattr(self.peft_config[active_adapter], "bias", "none")
+ if bias == "none":
+ continue
+
+ if bias == "all":
+ for n, p in model.named_parameters():
+ if "bias" in n:
+ p.requires_grad = True
+ elif bias.endswith("_only"): # e.g. "lora_only" or "boft_only"
+ for m in model.modules():
+ if isinstance(m, self.tuner_layer_cls) and hasattr(m, "bias") and m.bias is not None:
+ m.bias.requires_grad = True
+ else:
+ raise NotImplementedError(f"Requested bias: {bias}, is not implemented.")
+
+ def _set_adapter_layers(self, enabled: bool = True) -> None:
+ for module in self.model.modules():
+ if isinstance(module, (BaseTunerLayer, AuxiliaryTrainingWrapper)):
+ module.enable_adapters(enabled)
+
+ def disable_adapter_layers(self) -> None:
+ """
+ Disable all adapters in-place.
+
+ When disabling all adapters, the model output corresponds to the output of the base model.
+ """
+ # TODO: deprecate in favor of enable_adapters
+ for active_adapter in self.active_adapters:
+ bias_val = getattr(self.peft_config[active_adapter], "bias", "none")
+ if bias_val != "none":
+ msg = (
+ f"Careful, disabling adapter layers with bias configured to be '{bias_val}' does not produce the "
+ "same output as the base model would without adaption."
+ )
+ warnings.warn(msg)
+ self._set_adapter_layers(enabled=False)
+
+ def enable_adapter_layers(self) -> None:
+ """
+ Enable all adapters in-place
+ """
+ # TODO: deprecate in favor of enable_adapters
+ self._set_adapter_layers(enabled=True)
+
+ def delete_adapter(self, adapter_name: str) -> None:
+ """
+ Deletes an existing adapter.
+
+ Args:
+ adapter_name (str): Name of the adapter to be deleted.
+ """
+ if adapter_name not in list(self.peft_config.keys()):
+ raise ValueError(f"Adapter {adapter_name} does not exist")
+ del self.peft_config[adapter_name]
+
+ new_adapter = delete_adapter(
+ model=self.model, adapter_name=adapter_name, prefix=self.prefix, layer_cls=self.tuner_layer_cls
+ )
+ self.active_adapter = new_adapter or []
+
+ def set_requires_grad(self, adapter_names: str | Sequence[str], requires_grad: bool = True) -> None:
+ """
+ Enable or disable gradients on the given adapter(s).
+
+ Args:
+ adapter_name (`str` or `Sequence[str]`):
+ The name of the adapter(s) whose gradients should be enabled/disabled.
+ requires_grad (`bool`, *optional*)
+ Whether to enable (`True`, default) or disable (`False`).
+ """
+ set_requires_grad(self.model, adapter_names=adapter_names, requires_grad=requires_grad)
+
+ def _check_new_adapter_config(self, config: PeftConfig) -> None:
+ """
+ A helper method to check the config of a new adapter being added.
+
+ Raise a ValueError if there is something wrong with the config or if it conflicts with existing adapters.
+
+ """
+ if len(self.peft_config) <= 1:
+ return
+
+ # It is assumed that the config was added to self.peft_config *before* calling this check. We should thus never
+ # encounter the error below. Still, it is better to verify this, or else subsequent checks could be incorrect.
+ if not any(conf is config for conf in self.peft_config.values()):
+ raise ValueError(
+ "_check_new_peft_config was called incorrectly, this should not happen. Please open an issue and "
+ "report the error: https://github.com/huggingface/peft/issues"
+ )
+
+ bias_values = [getattr(conf, "bias", "none") for conf in self.peft_config.values()]
+ if sum(bias_value != "none" for bias_value in bias_values) > 1:
+ raise ValueError(
+ f"{self.__class__.__name__} supports only 1 adapter with bias. When using multiple adapters, "
+ "set bias to 'none' for all adapters."
+ )
+
+ def _cast_adapter_dtype(self, adapter_name: str, autocast_adapter_dtype: bool = True) -> None:
+ """
+ A helper method to cast the adapter weights to the correct dtype.
+
+ Currently, this only upcasts float16 and bfloat16 to float32.
+
+ Args:
+ adapter_name (`str`):
+ The adapter name.
+ autocast_adapter_dtype (`bool`, *optional*):
+ Whether to autocast the adapter dtype. Defaults to `True`.
+
+ """
+ cast_adapter_dtype(self.model, adapter_name=adapter_name, autocast_adapter_dtype=autocast_adapter_dtype)
+
+ def _check_merge_allowed(self):
+ """Helper method to check whether the adapter can be merged.
+
+ Raise a ValueError if it is not possible to merge the adapter with the given configuration.
+ """
+ example_code = textwrap.dedent(
+ """
+ ```python
+ from transformers import AutoModelForCausalLM
+
+ # Load original tied model
+ model = AutoModelForCausalLM.from_pretrained("google/gemma-2-2b-it", tie_word_embeddings=False)
+
+ # Set the randomly initialized lm_head to the previously tied embeddings
+ model.lm_head.weight.data = model.model.embed_tokens.weight.data.clone()
+
+ # Save the untied model
+ untied_model_dir = "dir/for/untied/model"
+ model.save_pretrained(untied_model_dir)
+ model.config.save_pretrained(untied_model_dir)
+
+ # Now use the original model but in untied format
+ model = AutoModelForCausalLM.from_pretrained(untied_model_dir)
+ ```
+ """
+ )
+ tied_target_modules = self._get_tied_target_modules(self.model)
+ if tied_target_modules:
+ warnings.warn(
+ f"Model with `tie_word_embeddings=True` and the {tied_target_modules=} are part of the adapter. "
+ "This can lead to complications. "
+ "You can opt to merge the adapter after cloning the weights (to untie the embeddings). "
+ "You can untie the embeddings by loading the model with `tie_word_embeddings=False`. For example:"
+ + example_code
+ )
+
+ def _unload_and_optionally_merge(
+ self,
+ merge: bool = True,
+ progressbar: bool = False,
+ safe_merge: bool = False,
+ adapter_names: Optional[list[str]] = None,
+ ) -> None:
+ if merge:
+ self._check_merge_allowed()
+
+ key_list = [key for key, _ in self.model.named_modules() if self.prefix not in key]
+ desc = "Unloading " + ("and merging " if merge else "") + "model"
+ for key in tqdm(key_list, disable=not progressbar, desc=desc):
+ try:
+ parent, target, target_name = _get_submodules(self.model, key)
+ except AttributeError:
+ continue
+ with onload_layer(target):
+ if hasattr(target, "unload_and_optionally_merge_module"):
+ # if layers have special unloading method, like MultiheadAttention, use that
+ unloaded_module = target.unload_and_optionally_merge_module(
+ merge=merge, safe_merge=safe_merge, adapter_names=adapter_names
+ )
+ self._replace_module(parent, target_name, unloaded_module, target)
+ elif hasattr(target, "base_layer"):
+ if merge:
+ target.merge(safe_merge=safe_merge, adapter_names=adapter_names)
+ self._replace_module(parent, target_name, target.get_base_layer(), target)
+
+ return self.model
+
+ def merge_and_unload(
+ self, progressbar: bool = False, safe_merge: bool = False, adapter_names: Optional[list[str]] = None
+ ) -> torch.nn.Module:
+ r"""
+ This method merges the adapter layers into the base model.
+
+ This is needed if someone wants to use the base model as a standalone model. The returned model has the same
+ architecture as the original base model.
+
+ It is important to assign the returned model to a variable and use it, this is not an in-place operation!
+
+ Args:
+ progressbar (`bool`):
+ whether to show a progressbar indicating the unload and merge process (default: False).
+ safe_merge (`bool`):
+ whether to activate the safe merging check to check if there is any potential Nan in the adapter
+ weights.
+ adapter_names (`List[str]`, *optional*):
+ The list of adapter names that should be merged. If None, all active adapters will be merged. Defaults
+ to `None`.
+
+ Example:
+
+ ```py
+ >>> from transformers import AutoModelForCausalLM
+ >>> from peft import PeftModel
+
+ >>> model_id = ...
+ >>> base_model = AutoModelForCausalLM.from_pretrained(model_id)
+ >>> peft_model_id = ...
+ >>> model = PeftModel.from_pretrained(base_model, peft_model_id)
+ >>> merged_model = model.merge_and_unload()
+ ```
+ """
+ return self._unload_and_optionally_merge(
+ progressbar=progressbar, safe_merge=safe_merge, adapter_names=adapter_names
+ )
+
+ def unload(self) -> torch.nn.Module:
+ """
+ Return the base model by removing all the PEFT modules.
+
+ It is important to assign the returned model to a variable and use it, this is not an in-place operation!
+ """
+ return self._unload_and_optionally_merge(merge=False)
+
+ def _check_target_module_compatiblity(self, peft_config: PeftConfig, model: nn.Module, target_name: str):
+ """
+ Prevent applying LoRA to incompatible modules in specific architectures (e.g., Mamba).
+ """
+ _check_lora_target_modules_mamba(peft_config, model, target_name)
+
+ def _create_and_replace_parameter(
+ self, peft_config, adapter_name, target, target_name, parent, current_key
+ ) -> None:
+ raise NotImplementedError(f"{self.__class__.__name__} does not support targeting nn.Parameter.")
+
+ def inject_adapter(
+ self,
+ model: nn.Module,
+ adapter_name: str,
+ autocast_adapter_dtype: bool = True,
+ low_cpu_mem_usage: bool = False,
+ state_dict: Optional[dict[str, torch.Tensor]] = None,
+ ) -> None:
+ r"""
+ Creates adapter layers and replaces the target modules with the adapter layers. This method is called under the
+ hood by `peft.mapping.get_peft_model` if a non-prompt tuning adapter class is passed.
+
+ The corresponding PEFT config is directly retrieved from the `peft_config` attribute of the BaseTuner class.
+
+ Args:
+ model (`nn.Module`):
+ The model to be tuned.
+ adapter_name (`str`):
+ The adapter name.
+ autocast_adapter_dtype (`bool`, *optional*):
+ Whether to autocast the adapter dtype. Defaults to `True`.
+ low_cpu_mem_usage (`bool`, `optional`, defaults to `False`):
+ Create empty adapter weights on meta device. Useful to speed up the loading process.
+ state_dict (`dict`, *optional*, defaults to `None`)
+ If a state_dict is passed here, the adapters will be injected based on the entries of the state_dict.
+ This can be useful when the exact `target_modules` of the PEFT method is unknown, for instance because
+ the checkpoint was created without meta data. Note that the values from the state_dict are not used,
+ only the keys are used to determine the correct layers that should be adapted.
+
+ """
+ ###################################
+ # PREPARATION OF MODEL AND CONFIG #
+ ###################################
+
+ peft_config = self.peft_config[adapter_name]
+ excluded_modules = []
+ unmatched_modules = []
+ targeted_modules_from_peft_config: list[str] = [] # only relevant if state_dict is passed
+ # Note: If possible, all checks should be performed *at the start of this method*.
+ # This way, we can raise early if something goes wrong, without leaving the model
+ # in a bad (half-initialized) state.
+ self._check_new_adapter_config(peft_config)
+
+ model_config = self.get_model_config(model)
+
+ peft_config = self._prepare_adapter_config(peft_config, model_config)
+
+ self._prepare_model(peft_config, model)
+
+ if getattr(peft_config, "target_parameters", []) and state_dict:
+ raise ValueError(
+ "Trying to inject a PEFT adapter from a state_dict but the PEFT config uses `target_parameters`. This "
+ "is not supported -- when using `target_parameters`, please inject the adapter without the state_dict."
+ )
+
+ named_modules = list(model.named_modules())
+ key_list = [key for key, _ in named_modules]
+
+ uses_dummy_target_modules = getattr(peft_config, "target_modules", None) == DUMMY_TARGET_MODULES
+ if uses_dummy_target_modules:
+ # dummy adapter, we allow not matching any module
+ named_modules = []
+ key_list = []
+
+ # update peft_config.target_modules if required
+ peft_config = _maybe_include_all_linear_layers(peft_config, model)
+
+ # This is an optimization to reduce the number of entries in the target_modules list. The reason is that in some
+ # circumstances, target_modules can contain hundreds of entries. Since each target module is checked against
+ # each module of the net (which can be thousands), this can become quite expensive when many adapters are being
+ # added. Often, the target_modules can be condensed in such a case, which speeds up the process.
+ # A context in which this can happen is when diffusers loads non-PEFT LoRAs. As there is no meta info on
+ # target_modules in that case, they are just inferred by listing all keys from the state_dict, which can be
+ # quite a lot. See: https://github.com/huggingface/diffusers/issues/9297
+ # As there is a small chance for undiscovered bugs, we apply this optimization only if the list of
+ # target_modules is sufficiently big.
+ # We also exclude IA³ from this optimization. This is because IA³ has both target_modules and
+ # feedforward_modules, which are coupled (the latter must be a subset). It would be possible to change the logic
+ # to keep both in sync, but it's not quite trivial and probably not worth the effort. See #2429.
+ if (
+ isinstance(peft_config.target_modules, (list, set))
+ and (len(peft_config.target_modules) >= MIN_TARGET_MODULES_FOR_OPTIMIZATION)
+ and (peft_config.peft_type != PeftType.IA3)
+ ):
+ suffixes = tuple("." + suffix for suffix in peft_config.target_modules)
+ names_no_target = [
+ name for name in key_list if (name not in peft_config.target_modules) and not name.endswith(suffixes)
+ ]
+ new_target_modules = _find_minimal_target_modules(peft_config.target_modules, names_no_target)
+ if len(new_target_modules) < len(peft_config.target_modules):
+ peft_config.target_modules = new_target_modules
+
+ ###############################
+ # MATCHING & CREATING MODULES #
+ ###############################
+
+ existing_adapter_prefixes = []
+ for key, module in named_modules:
+ if isinstance(module, BaseTunerLayer):
+ existing_adapter_prefixes.append(key + ".")
+
+ # TODO: check if this the most robust way
+ module_names: set[str] = set()
+ if state_dict is not None:
+ prefix = PEFT_TYPE_TO_PREFIX_MAPPING[peft_config.peft_type]
+ module_names = {k.rsplit("." + prefix, 1)[0] for k in state_dict}
+
+ for key, module in named_modules:
+ if not key:
+ continue
+
+ # It is possible that we're adding an additional adapter, so if we encounter a key that clearly belongs to a
+ # previous adapter we can skip here since we don't want to interfere with adapter internals.
+ for adapter_key in existing_adapter_prefixes:
+ if key.startswith(adapter_key):
+ excluded_modules.append(key)
+ break
+
+ if excluded_modules and excluded_modules[-1] == key:
+ continue
+
+ if state_dict is None:
+ # normal mechanism: match the modules using the peft_config
+ result = self._check_target_module_exists(peft_config, key)
+ if isinstance(result, _ExcludedModule):
+ excluded_modules.append(key)
+ elif not result:
+ unmatched_modules.append(key)
+ else:
+ self.targeted_module_names.append(key)
+ parent, target, target_name = _get_submodules(model, key)
+ self._check_target_module_compatiblity(peft_config, model, target_name)
+ ctx = init_empty_weights if low_cpu_mem_usage else nullcontext
+ with ctx():
+ self._create_and_replace(
+ peft_config, adapter_name, target, target_name, parent, current_key=key
+ )
+ else:
+ # use the state_dict to match modules instead
+ if key not in module_names:
+ unmatched_modules.append(key)
+ else:
+ self.targeted_module_names.append(key)
+ parent, target, target_name = _get_submodules(model, key)
+ self._check_target_module_compatiblity(peft_config, model, target_name)
+ ctx = init_empty_weights if low_cpu_mem_usage else nullcontext
+ with ctx():
+ self._create_and_replace(
+ peft_config, adapter_name, target, target_name, parent, current_key=key
+ )
+
+ # still record what would have been matched via the config so that the two results can be compared
+ if self._check_target_module_exists(peft_config, key):
+ targeted_modules_from_peft_config.append(key)
+
+ if getattr(peft_config, "target_parameters", []):
+ # Note: We don't need to check for no state_dict being passed, since we already checked this earlier.
+ self._inject_parameters(
+ peft_config=peft_config, model=model, adapter_name=adapter_name, low_cpu_mem_usage=low_cpu_mem_usage
+ )
+
+ ####################
+ # CHECK FOR ERRORS #
+ ####################
+
+ if state_dict is not None:
+ # in case that the state_dict was used as source of truth and it resulted in different outcomes than what
+ # would have been matched with the PEFT config, warn the user about that.
+ targeted_set_from_peft_config = set(targeted_modules_from_peft_config)
+ targeted_set_from_state_dict = set(self.targeted_module_names)
+ diff_peft_config = targeted_set_from_peft_config - targeted_set_from_state_dict
+ diff_state_dict = targeted_set_from_state_dict - targeted_set_from_peft_config
+ warning_msg = ""
+ if diff_peft_config or diff_state_dict:
+ warning_msg = (
+ "While injecting the PEFT adapters, an inconsistency was discovered between the PEFT config and "
+ "the provided state_dict. This is not necessarily an issue and can be ignored if this was the "
+ "intent. "
+ )
+ if diff_peft_config:
+ warning_msg += (
+ f"The PEFT config contained these additional target modules: {sorted(diff_peft_config)}. "
+ )
+ if diff_state_dict:
+ warning_msg += f"The state_dict contained these additional target modules: {sorted(diff_state_dict)}. "
+ if warning_msg:
+ warnings.warn(warning_msg, RuntimeWarning)
+
+ if not self.targeted_module_names and not self.targeted_parameter_names and not uses_dummy_target_modules:
+ if excluded_modules and not unmatched_modules:
+ # All targeted modules were excluded
+ raise ValueError(
+ "All modules were excluded. This is likely unintended. "
+ "Check your `target_modules`, `exclude_modules` and `modules_to_save` configuration."
+ )
+ elif not excluded_modules and unmatched_modules and not peft_config.target_modules:
+ raise ValueError(
+ "No `target_modules` passed but also no `target_parameters` found. Please check the values for "
+ "these arguments."
+ )
+ elif not excluded_modules and unmatched_modules:
+ # None of the targeted modules matched
+ error_msg = (
+ f"Target modules {peft_config.target_modules} not found in the base model. "
+ f"Please check the target modules and try again."
+ )
+ if getattr(peft_config, "layers_to_transform", None) is not None:
+ error_msg += f" Note: You specified 'layers_to_transform': {peft_config.layers_to_transform}."
+ if getattr(peft_config, "layers_pattern", None) is not None:
+ error_msg += f" You also specified 'layers_pattern': {peft_config.layers_pattern}."
+ raise ValueError(error_msg)
+ else:
+ # Some modules did not match and some matched but were excluded
+ error_msg = (
+ "No modules were targeted for adaptation. "
+ "This might be caused by a combination of mismatched target modules and excluded modules. "
+ "Please check your `target_modules` and `exclude_modules` configuration. You may also have "
+ "only targeted modules that are marked to be saved (`modules_to_save`)."
+ )
+ if getattr(peft_config, "layers_to_transform", None) is not None:
+ error_msg += f" Note: You specified 'layers_to_transform': {peft_config.layers_to_transform}."
+ if getattr(peft_config, "layers_pattern", None) is not None:
+ error_msg += f" You also specified 'layers_pattern': {peft_config.layers_pattern}."
+ raise ValueError(error_msg)
+
+ elif hasattr(peft_config, "exclude_modules") and peft_config.exclude_modules and not excluded_modules:
+ # exclude_modules was passed but was not used
+ warnings.warn(
+ f"You have passed exclude_modules={peft_config.exclude_modules} but no modules were excluded. "
+ "Please check that exclude_modules was set correctly."
+ )
+
+ elif not uses_dummy_target_modules:
+ # If we landed here, it means that at least one module or parameter was adapted, so let's not raise an
+ # error. However, let's warn the user if it seems like
+ # - they wanted to match a module but there was no match
+ # - they wanted to match a parameter but there was no match
+ if peft_config.target_modules and not self.targeted_module_names:
+ warnings.warn(
+ f"target_modules={peft_config.target_modules} were set but no module was matched.", RuntimeWarning
+ )
+ elif getattr(peft_config, "target_parameters", []) and not self.targeted_parameter_names:
+ warnings.warn(
+ f"target_parameters={peft_config.target_parameters} were set but no parameter was matched.",
+ RuntimeWarning,
+ )
+
+ tied_target_modules = self._get_tied_target_modules(model=model)
+ if tied_target_modules:
+ warnings.warn(
+ f"Model with `tie_word_embeddings=True` and the {tied_target_modules=} are part of the adapter. "
+ "This can lead to complications, for example when merging the adapter "
+ "or converting your model to formats other than safetensors. "
+ "See for example https://github.com/huggingface/peft/issues/2018."
+ )
+
+ ################
+ # HOUSEKEEPING #
+ ################
+
+ # It's important to set the adapter here (again), because otherwise it can happen that if a 2nd adapter is
+ # added, and it targets different layer(s) than the first adapter (which is active), then those different
+ # layers will be activated, which we don't want.
+ self.set_adapter(self.active_adapters, inference_mode=peft_config.inference_mode)
+ self._mark_only_adapters_as_trainable(model)
+
+ if self.peft_config[adapter_name].inference_mode:
+ for n, p in model.named_parameters():
+ if adapter_name in n:
+ p.requires_grad = False
+
+ set_additional_trainable_modules(
+ model=model,
+ peft_config=peft_config,
+ model_config=BaseTuner.get_model_config(self),
+ adapter_name=adapter_name,
+ activate_adapter=adapter_name in self.active_adapters,
+ )
+
+ def _inject_parameters(
+ self, peft_config: PeftConfig, model: nn.Module, adapter_name: str, low_cpu_mem_usage: bool
+ ) -> None:
+ """Inject layers based on peft_config.target_modules"""
+
+ def strip_base_layer_from_name(module_name):
+ # It is possible that the layer is already a PEFT layer and needs updating with a new adapter. In this case,
+ # the name of parameter would be something like `model.layers.0.experts.base_layer.weight`, i.e. there is a
+ # "base_layer" inserted in the name. We need to remove that, otherwise we won't be able to match correctly
+ # (in this case, "experts.weight" would not match).
+ name = ".base_layer"
+ while name in module_name:
+ prefix, _, suffix = module_name.rpartition(name)
+ module_name = prefix + suffix
+ return module_name
+
+ def create_and_replace_param(module_name, key, param_name):
+ # helper function to avoid duplication
+ parent, target, target_name = _get_submodules(model, module_name)
+ unwrapped_module_name = strip_base_layer_from_name(module_name)
+ unwrapped_module = model.get_submodule(unwrapped_module_name)
+ # use the class name for checking to avoid circular import
+ if isinstance(unwrapped_module, BaseTunerLayer) and unwrapped_module.__class__.__name__ != "ParamWrapper":
+ raise ValueError(
+ f"Trying to wrap an `nn.Parameter` of layer '{unwrapped_module_name}' of type "
+ f"{type(target).__name__}, which is not a valid target. Make sure that this layer is not "
+ "also targeted with `target_modules`. For some models, PEFT will do this automatically, "
+ "try setting `target_modules=[]` to prevent it."
+ )
+
+ self._check_target_module_compatiblity(peft_config, model, target_name)
+ ctx = init_empty_weights if low_cpu_mem_usage else nullcontext
+ with ctx():
+ self._create_and_replace(
+ peft_config,
+ adapter_name,
+ target,
+ target_name,
+ parent,
+ current_key=key,
+ parameter_name=param_name.rpartition(".")[-1],
+ )
+
+ # TODO very simple matching, might not cover all use cases
+ unsorted_target_names = set(peft_config.target_parameters)
+ # As the order of matching can influence the nesting of multiple params on the same module, ensure determinism
+ # by sorting.
+ target_names = sorted(unsorted_target_names)
+ for module_name, module in model.named_modules():
+ if hasattr(module, "parametrizations"):
+ # Deal with the case that the parameter is already parametrized. The issue is that we would not be able
+ # to match `f"{module_name}.{param_name}"`, as the parameter is now something like
+ # `module.parametrization.weight`.
+ for key in target_names:
+ target_module_name, _, param_name = key.rpartition(".")
+ if target_module_name != module_name:
+ continue
+ if getattr(module, param_name, None) is None:
+ continue
+ create_and_replace_param(module_name, key, param_name)
+ self.targeted_parameter_names.append(key)
+ else:
+ # Standard case: the parameter is not already parametrized. Note, however, that the model could already
+ # be nested with lora.ParamWrapper, as this is how we allow targeting multiple Parameters on the same
+ # module.
+ unwrapped_module_name = strip_base_layer_from_name(module_name)
+ # we're interested in finding the "lowest" module that contains the parameter, hence recurse=False
+ for param_name, param in module.named_parameters(recurse=False):
+ key = f"{unwrapped_module_name}.{param_name}"
+ if (key in target_names) or any(key.endswith(f".{target_key}") for target_key in target_names):
+ # Note: We use the unwrapped_module_name to check if the key matches, but we use the module_name for
+ # replacement, since we want to replace the wrapped module.
+ create_and_replace_param(module_name, key, param_name)
+ self.targeted_parameter_names.append(key)
+
+ def _replace_module(self, parent, child_name, new_module, child) -> None:
+ """
+ Replace the sub-module of a given moduel with a new PEFT module.
+
+ This also deals with device placement of the new module to be in line with the child module.
+
+ Args:
+ parent (`nn.Module`):
+ The parent module on which the replacement should take place.
+ child_name (`str`):
+ The name of the child module to be replaced.
+ new_module (`nn.Module`):
+ The new PEFT module.
+ child (`nn.Module`):
+ The original child module that is being replaced.
+
+ """
+ setattr(parent, child_name, new_module)
+ # It's not necessary to set requires_grad here, as that is handled by
+ # _mark_only_adapters_as_trainable
+
+ # child layer wraps the original module, unpack it
+ if hasattr(child, "base_layer"):
+ child = child.base_layer
+
+ if not hasattr(new_module, "base_layer"):
+ new_module.weight = child.weight
+ if hasattr(child, "bias"):
+ new_module.bias = child.bias
+
+ if getattr(child, "state", None) is not None:
+ if hasattr(new_module, "base_layer"):
+ new_module.base_layer.state = child.state
+ else:
+ new_module.state = child.state
+ new_module.to(child.weight.device)
+
+ meta = torch.device("meta")
+ # dispatch to correct device
+ for name, module in new_module.named_modules():
+ if self.prefix in name:
+ if hasattr(child, "qweight"):
+ weight = child.qweight
+ elif hasattr(child, "W_q"):
+ weight = child.W_q
+ elif hasattr(child, "weight"):
+ weight = child.weight
+ elif getattr(child, "in_proj_weight", None) is not None: # MHA
+ weight = child.in_proj_weight
+ else:
+ weight = next(child.parameters())
+
+ if not any(p.device == meta for p in module.parameters()):
+ module.to(weight.device)
+
+ def merge_adapter(self, adapter_names: Optional[list[str]] = None, safe_merge: bool = False) -> None:
+ """
+ This method merges the adapter layers into the base model.
+
+ Merging adapters can lead to a speed up of the forward pass. A copy of the adapter weights is still kept in
+ memory, which is required to unmerge the adapters. In order to merge the adapter weights without keeping them
+ in memory, please call `merge_and_unload`.
+
+ Args:
+ adapter_names (`list[str]`, *optional*):
+ The list of adapter names that should be merged. If `None`, all active adapters will be merged.
+ Defaults to `None`.
+ safe_merge (`bool`, *optional*):
+ If `True`, the merge operation will be performed in a copy of the original weights and check for NaNs
+ before merging the weights. This is useful if you want to check if the merge operation will produce
+ NaNs. Defaults to `False`.
+ """
+ # Note: The order of arguments here is:
+ # adapter_names, safe_merge
+ # For layer.merge, the order is:
+ # safe_merge, adapter_names
+ # This is not so nice but this method here started with only adapter_names, thus putting safe_merge first would
+ # be a backwards incompatible change.
+ self._check_merge_allowed()
+ for module in self.model.modules():
+ if isinstance(module, BaseTunerLayer):
+ with onload_layer(module):
+ module.merge(adapter_names=adapter_names, safe_merge=safe_merge)
+
+ def unmerge_adapter(self):
+ """
+ This method unmerges all merged adapter layers from the base model.
+ """
+ for module in self.model.modules():
+ if isinstance(module, BaseTunerLayer):
+ with onload_layer(module):
+ module.unmerge()
+
+ def set_auxiliary_adapters(self, adapter_name: str | list[str], inference_mode: bool) -> None:
+ """
+ Sets the active adapter(s) on auxiliary modules.
+
+ If the subclass (e.g. `LoraModel`) supports auxiliary modules like `modules_to_save`, it should call this
+ method in `set_adapter` to ensure that those auxiliary modules are being set correctly.
+
+ Args:
+ adapter_name (`str` or `list[str]`):
+ The name(s) of the adapter(s) to be set as active. The adapters must be loaded first.
+ inference_mode (bool, optional):
+ Whether the activated adapter should be frozen (i.e. `requires_grad=False`). Default is False.
+ """
+ _set_adapter(self, adapter_name, inference_mode=inference_mode)
+
+ def set_adapter(self, adapter_name: str | list[str], inference_mode: bool = False) -> None:
+ """Set the active adapter(s).
+
+ Args:
+ adapter_name (str, list[str]):
+ The name(s) of the adapter(s) to set as active
+ inference_mode (bool, optional):
+ Whether the activated adapter should be frozen (i.e. `requires_grad=False`). Default is False.
+ """
+ set_adapter(
+ self.model, adapter_name=adapter_name, inference_mode=inference_mode, layer_cls=self.tuner_layer_cls
+ )
+ self.active_adapter = adapter_name
+
+ @staticmethod
+ def get_model_config(model: nn.Module) -> dict:
+ """
+ This method gets the config from a model in dictionary form. If model has not attribute config, then this
+ method returns a default config.
+
+ Args:
+ model (`nn.Module`):
+ Model to get the config from.
+ default (`dict|None`, *optional*)::
+ What to return if model does not have a config attribute.
+ """
+ model_config = getattr(model, "config", DUMMY_MODEL_CONFIG)
+ if hasattr(model_config, "to_dict"):
+ model_config = model_config.to_dict()
+ elif dataclasses.is_dataclass(model_config):
+ model_config = dataclasses.asdict(model_config)
+ return model_config
+
+ def _get_tied_target_modules(self, model: nn.Module) -> list[str]:
+ tied_target_modules = []
+ model_config = self.get_model_config(model)
+ if model_config.get("tie_word_embeddings"):
+ for target_module in self.targeted_module_names:
+ # This potentially yields false positives since we're just looking at the layer names. So if we use a
+ # model that uses weight-tying of lm_head and embed_tokens, a third, unrelated, layer which is
+ # unfortunately named so that it is in EMBEDDING_LAYER_NAMES will be falsely reported here as well.
+ if target_module.split(".")[-1] in EMBEDDING_LAYER_NAMES:
+ tied_target_modules.append(target_module)
+ return tied_target_modules
+
+ def __getattr__(self, name: str):
+ """Forward missing attributes to the wrapped module."""
+ try:
+ return super().__getattr__(name) # defer to nn.Module's logic
+ except AttributeError:
+ if name == "model": # see #1892: prevent infinite recursion if class is not initialized
+ raise
+ return getattr(self.model, name)
+
+
+class BaseTunerLayer(ABC):
+ r"""
+ A tuner layer mixin that provides the common methods and attributes for all tuners.
+
+ Args:
+ is_pluggable (`bool`, *optional*):
+ Whether the adapter layer can be plugged to any pytorch module
+ active_adapters (Union[List[`str`], `str`], *optional*):
+ The name of the active adapter.
+ """
+
+ # All names of layers that may contain adapter (trainable) weights
+ adapter_layer_names: tuple[str, ...] = ()
+ # All names of other parameters that may contain adapter-related parameters
+ other_param_names: tuple[str, ...] = ()
+
+ # indicates whether all adapters should be disabled
+ _disable_adapters: bool = False
+
+ # the currently active adapter(s)
+ _active_adapter: str | list[str] = "default"
+
+ # List all merged adapters
+ merged_adapters: list[str] = []
+
+ def get_base_layer(self) -> nn.Module:
+ """
+ (Recursively) get the base_layer.
+
+ This is necessary for the case that the tuner layer wraps another tuner layer.
+
+ """
+ base_layer = self
+ while hasattr(base_layer, "base_layer"):
+ base_layer = base_layer.base_layer
+ return base_layer
+
+ @property
+ def weight(self) -> torch.Tensor:
+ # This is required for some transformers code, e.g. for T5, weight is accessed as:
+ # self.wo.weight
+ # where "wo" is the adapter layer.
+ # https://github.com/huggingface/transformers/blob/78f6ed6c70b29c1560780e3869a7ad4c6b3d2710/src/transformers
+ # /models/t5/modeling_t5.py#L292
+ base_layer = self.get_base_layer()
+ if hasattr(base_layer, "qweight"):
+ # QuantLinear
+ weight = base_layer.qweight
+ else:
+ # Other layers
+ weight = base_layer.weight
+ return weight
+
+ @property
+ def bias(self) -> torch.Tensor:
+ base_layer = self.get_base_layer()
+ return base_layer.bias
+
+ def merge(self, safe_merge: bool = False, adapter_names: Optional[list[str]] = None) -> None:
+ raise NotImplementedError
+
+ def unmerge(self) -> None:
+ raise NotImplementedError
+
+ @property
+ def merged(self) -> bool:
+ return bool(self.merged_adapters)
+
+ @property
+ def disable_adapters(self) -> bool:
+ # use a property to ensure that disable_adapters is not set directly, instead use the enable_adapters method
+ return self._disable_adapters
+
+ @property
+ def active_adapter(self) -> str | list[str]:
+ # use a property to ensure that active_adapter is not set directly, instead use the set_adapter method
+ return self._active_adapter
+
+ def _get_available_adapters(self) -> set[str]:
+ """Return all adapter names that can be found on this module."""
+ adapters = set()
+ for layer_name in self.adapter_layer_names:
+ module = getattr(self, layer_name)
+ if not isinstance(module, (nn.ModuleDict, nn.ParameterDict)):
+ continue
+ adapters.update(set(module.keys()))
+ return adapters
+
+ @property
+ def active_adapters(self):
+ if isinstance(self.active_adapter, str):
+ return [self.active_adapter]
+ # is already a list of str
+ return self.active_adapter
+
+ def enable_adapters(self, enabled: bool) -> None:
+ """Toggle the enabling and disabling of adapters
+
+ Takes care of setting the requires_grad flag for the adapter weights.
+
+ Args:
+ enabled (bool): True to enable adapters, False to disable adapters
+ """
+ if enabled:
+ self.set_adapter(self.active_adapters)
+ self._disable_adapters = False
+ else:
+ # disable grads on all adapter layers
+ for layer_name in self.adapter_layer_names:
+ layer = getattr(self, layer_name)
+ layer.requires_grad_(False)
+ self._disable_adapters = True
+
+ def set_adapter(self, adapter_names: str | list[str], inference_mode: bool = False) -> None:
+ """Set the active adapter(s).
+
+ Additionally, this function will set the specified adapter to trainable (i.e., requires_grad=True) unless
+ inference_mode is True.
+
+ Args:
+ adapter_name (`str` or `list[str]`):
+ The name(s) of the adapter(s) to set as active.
+ inference_mode (bool, optional):
+ Whether the activated adapter should be frozen (i.e. `requires_grad=False`). Default is False.
+ """
+ if isinstance(adapter_names, str):
+ adapter_names = [adapter_names]
+
+ # Deactivate grads on the inactive adapter and activate grads on the active adapter (if not in inference mode)
+ for layer_name in self.adapter_layer_names:
+ module_dict = getattr(self, layer_name)
+ for key, layer in module_dict.items():
+ if (key in adapter_names) and (not inference_mode):
+ # Note: It is possible that not a single layer is called with requires_grad_(True) here. This may
+ # happen if a completely different adapter layer is being activated.
+ layer.requires_grad_(True)
+ else:
+ layer.requires_grad_(False)
+
+ self._active_adapter = adapter_names
+
+ def _all_available_adapter_names(self) -> list[str]:
+ """Return a sorted list of all available adapter names"""
+ adapter_names = set()
+ for name in self.adapter_layer_names + self.other_param_names:
+ # we check each possible attribute and if it's a dict or ModuleDict, we assume that the keys are the adapter
+ # names
+ attr = getattr(self, name)
+ if hasattr(attr, "keys"):
+ adapter_names.update(attr.keys())
+ return sorted(adapter_names)
+
+ def delete_adapter(self, adapter_name: str) -> None:
+ """
+ Delete an adapter from the layer
+
+ This should be called on all adapter layers, or else we will get an inconsistent state.
+
+ This method will also set a new active adapter if the deleted adapter was an active adapter. It is important
+ that the new adapter is chosen in a deterministic way, so that the same adapter is chosen on all layers.
+
+ Args:
+ adapter_name (`str`): The name of the adapter to delete
+
+ """
+ for attr in self.adapter_layer_names + self.other_param_names:
+ if adapter_name in getattr(self, attr):
+ del getattr(self, attr)[adapter_name]
+
+ if adapter_name in self.active_adapters:
+ # choose a new active adapter
+ active_adapters = self.active_adapters[:]
+ active_adapters.remove(adapter_name)
+ if active_adapters:
+ self.set_adapter(active_adapters)
+ else:
+ # no active adapters left, set a new default adapter
+ # here we get the list of all adapters existing adapter names and choose the first one
+ remaining_adapters = self._all_available_adapter_names()
+ if not remaining_adapters:
+ self.set_adapter([])
+ else:
+ new_active_adapter = remaining_adapters[0]
+ warnings.warn(
+ f"Adapter {adapter_name} was active which is now deleted. Setting active adapter to "
+ f"{new_active_adapter}."
+ )
+ self.set_adapter(remaining_adapters[0])
+
+ def set_requires_grad(self, adapter_names: str | Sequence[str], requires_grad: bool = True) -> None:
+ """
+ Enable or disable gradients on the given adapter(s).
+
+ Args:
+ adapter_name (`str` or `Sequence[str]`):
+ The name of the adapter(s) whose gradients should be enabled/disabled.
+ requires_grad (`bool`, *optional*)
+ Whether to enable (`True`, default) or disable (`False`).
+ """
+ if isinstance(adapter_names, str):
+ adapter_names_set = {adapter_names}
+ else:
+ adapter_names_set = set(adapter_names)
+
+ for layer_name in self.adapter_layer_names:
+ module_dict = getattr(self, layer_name)
+ for key, layer in module_dict.items():
+ if key in adapter_names_set:
+ layer.requires_grad_(requires_grad)
+
+ def _move_adapter_to_device_of_base_layer(self, adapter_name: str, device: Optional[torch.device] = None) -> None:
+ """
+ Move the adapter of the given name to the device of the base layer.
+ """
+ if device is None:
+ base_layer = self.get_base_layer()
+ if isinstance(base_layer, nn.MultiheadAttention):
+ base_layer = base_layer.out_proj
+ # check weight and qweight (for GPTQ)
+ for weight_name in ("weight", "qweight"):
+ weight = getattr(base_layer, weight_name, None)
+ if weight is not None:
+ device = weight.device
+ dtype = weight.dtype
+ break
+ else:
+ # no break encountered: could not determine the device
+ return
+
+ meta = torch.device("meta")
+
+ # loop through all potential adapter layers and move them to the device of the base layer; be careful to only
+ # move this specific adapter to the device, as the other adapters could be on different devices
+ # see #1639
+ for adapter_layer_name in self.adapter_layer_names + self.other_param_names:
+ adapter_layer = getattr(self, adapter_layer_name, None)
+ if not isinstance(adapter_layer, (nn.ModuleDict, nn.ParameterDict, BufferDict)):
+ continue
+ if adapter_name not in adapter_layer:
+ continue
+ if any(p.device == meta for p in adapter_layer.parameters()):
+ continue
+
+ # TODO: weight is not necessarily defined here, leading to a NameError, fix that
+ if weight.dtype.is_floating_point or weight.dtype.is_complex:
+ adapter_layer[adapter_name] = adapter_layer[adapter_name].to(device, dtype=dtype)
+ else:
+ adapter_layer[adapter_name] = adapter_layer[adapter_name].to(device)
+
+ @overload
+ def _cast_input_dtype(self, x: None, dtype: torch.dtype) -> None: ...
+
+ @overload
+ def _cast_input_dtype(self, x: torch.Tensor, dtype: torch.dtype) -> torch.Tensor: ...
+
+ def _cast_input_dtype(self, x, dtype: torch.dtype):
+ """
+ Whether to cast the dtype of the input of the forward method.
+
+ Usually, we want to enable this to align the input dtype with the dtype of the weight, but by setting
+ layer.cast_input_dtype=False, this can be disabled if necessary.
+
+ Enabling or disabling can be managed via the peft.helpers.disable_lora_input_dtype_casting context manager.
+ """
+ if x is None: # useful e.g. if x is the bias, which can be None
+ return None
+
+ cast_input_dtype_enabled = getattr(self, "cast_input_dtype_enabled", True)
+ if (not cast_input_dtype_enabled) or (x.dtype == dtype):
+ return x
+ return x.to(dtype=dtype)
+
+
+def _find_minimal_target_modules(
+ target_modules: list[str] | set[str], other_module_names: list[str] | set[str]
+) -> set[str]:
+ """Find the minimal set of target modules that is sufficient to separate them from the other modules.
+
+ Sometimes, a very large list of target_modules could be passed, which can slow down loading of adapters (e.g. when
+ loaded from diffusers). It may be possible to condense this list from hundreds of items to just a handful of
+ suffixes that are sufficient to distinguish the target modules from the other modules.
+
+ Example:
+ ```py
+ >>> from peft.tuners.tuners_utils import _find_minimal_target_modules
+
+ >>> target_modules = [f"model.decoder.layers.{i}.self_attn.q_proj" for i in range(100)]
+ >>> target_modules += [f"model.decoder.layers.{i}.self_attn.v_proj" for i in range(100)]
+ >>> other_module_names = [f"model.encoder.layers.{i}.self_attn.k_proj" for i in range(100)]
+ >>> _find_minimal_target_modules(target_modules, other_module_names)
+ {"q_proj", "v_proj"}
+ ```
+
+ Args:
+ target_modules (`list[str]` | `set[str]`):
+ The list of target modules.
+ other_module_names (`list[str]` | `set[str]`):
+ The list of other module names. They must not overlap with the target modules.
+
+ Returns:
+ `set[str]`:
+ The minimal set of target modules that is sufficient to separate them from the other modules.
+
+ Raises:
+ ValueError:
+ If `target_modules` is not a list or set of strings or if it contains an empty string. Also raises an error
+ if `target_modules` and `other_module_names` contain common elements.
+ """
+ if isinstance(target_modules, str) or not target_modules:
+ raise ValueError("target_modules should be a list or set of strings.")
+
+ target_modules = set(target_modules)
+ if "" in target_modules:
+ raise ValueError("target_modules should not contain an empty string.")
+
+ other_module_names = set(other_module_names)
+ if not target_modules.isdisjoint(other_module_names):
+ msg = (
+ "target_modules and other_module_names contain common elements, this should not happen, please "
+ "open a GitHub issue at https://github.com/huggingface/peft/issues with the code to reproduce this issue"
+ )
+ raise ValueError(msg)
+
+ # it is assumed that module name parts are separated by a "."
+ def generate_suffixes(s):
+ parts = s.split(".")
+ return [".".join(parts[i:]) for i in range(len(parts))][::-1]
+
+ # Create a reverse lookup for other_module_names to quickly check suffix matches
+ other_module_suffixes = {suffix for item in other_module_names for suffix in generate_suffixes(item)}
+
+ # Find all potential suffixes from target_modules
+ target_modules_suffix_map = {item: generate_suffixes(item) for item in target_modules}
+
+ # Initialize a set for required suffixes
+ required_suffixes = set()
+
+ # We sort the target_modules_suffix_map simply to get deterministic behavior, since sets have no order. In theory
+ # the order should not matter but in case there is a bug, it's better for the bug to be deterministic.
+ for item, suffixes in sorted(target_modules_suffix_map.items(), key=lambda tup: tup[1]):
+ # Go through target_modules items, shortest suffixes first
+ for suffix in suffixes:
+ # If the suffix is already in required_suffixes or matches other_module_names, skip it
+ if suffix in required_suffixes or suffix in other_module_suffixes:
+ continue
+ # Check if adding this suffix covers the item
+ if not any(item.endswith("." + req_suffix) for req_suffix in required_suffixes):
+ required_suffixes.add(suffix)
+ break
+
+ if not required_suffixes:
+ return set(target_modules)
+ return required_suffixes
+
+
+class _ExcludedModule:
+ """
+ A private helper method used to represent excluded modules in the check_target_module_exists function.
+ """
+
+ def __bool__(self):
+ return False
+
+
+def check_target_module_exists(config, key: str) -> bool | re.Match[str] | None:
+ """A helper method to check if the passed module's key name matches any of the target modules in the adapter_config.
+
+ Args:
+ config (`PeftConfig`):
+ A config to match target modules from.
+ key (`str`):
+ A key to search any matches in config
+
+ Returns:
+ `bool` | `re.Match[str]` | `None`:
+ True or re.Match object if key matches any target modules from config, False or None if no match found.
+ """
+ if hasattr(config, "exclude_modules") and config.exclude_modules:
+ if isinstance(config.exclude_modules, str):
+ if re.fullmatch(config.exclude_modules, key):
+ return _ExcludedModule()
+ elif key in config.exclude_modules:
+ return _ExcludedModule()
+ elif any(key.endswith(f".{exclude_key}") for exclude_key in config.exclude_modules):
+ return _ExcludedModule()
+
+ # Adapters should never match on modules to save modules as it is a guarantee for conflicts of behavior
+ # between `ModulesToSaveWrapper` internals and the potential adapter.
+ modules_to_save = getattr(config, "modules_to_save", None)
+ if modules_to_save:
+ if any(re.match(rf"(^|.*\.){m}($|\..*)", key) for m in modules_to_save):
+ return _ExcludedModule()
+
+ if (config.target_modules is None) and (config.target_parameters is not None):
+ # this is allowed if config.target_parameters are specified
+ return False
+
+ if isinstance(config.target_modules, str):
+ target_module_found = match_target_against_key(config.target_modules, key)
+ elif key in config.target_modules:
+ # this module is specified directly in target_modules
+ target_module_found = True
+ else:
+ target_module_found = any(key.endswith(f".{target_key}") for target_key in config.target_modules)
+
+ layer_indexes = getattr(config, "layers_to_transform", None)
+ layers_pattern = getattr(config, "layers_pattern", None)
+
+ is_using_layer_indexes = layer_indexes is not None and (
+ len(layer_indexes) != 0 if isinstance(layer_indexes, list) else True
+ )
+ if is_using_layer_indexes and target_module_found:
+ layer_index = None
+ # TODO: It's still unclear how empty layers_pattern (None, [], or "") should behave
+ # For now, empty layers_pattern means any layer pattern is ok
+ if layers_pattern is None or len(layers_pattern) == 0:
+ layer_index = re.match(r".*\.[^.]*\.(\d+)\.", key)
+ else:
+ layers_pattern = [layers_pattern] if isinstance(layers_pattern, str) else layers_pattern
+ for pattern in layers_pattern:
+ layer_index = re.match(rf".*\.{pattern}\.(\d+)\.", key)
+ if layer_index is not None:
+ break
+
+ if layer_index is None:
+ target_module_found = False
+ else:
+ layer_index = int(layer_index.group(1))
+ if isinstance(layer_indexes, int):
+ target_module_found = layer_index == layer_indexes
+ else:
+ target_module_found = layer_index in layer_indexes
+
+ return target_module_found
+
+
+def inspect_matched_modules(tuner: BaseTuner, adapter_name: str = "default") -> dict:
+ """
+ A helper function to inspect the set of matched and unmatched modules for a PEFT model and the given adapter.
+ """
+ config = tuner.peft_config[adapter_name]
+ key_list = [key for key, _ in tuner.model.named_modules()]
+ module_dict = {"matched": [], "unmatched": []}
+ for key in key_list:
+ if tuner._check_target_module_exists(config, key):
+ module_dict["matched"].append(key)
+ else:
+ module_dict["unmatched"].append(key)
+ return module_dict
+
+
+def _maybe_include_all_linear_layers(peft_config: PeftConfig, model: nn.Module) -> PeftConfig:
+ """
+ Helper function to update `target_modules` to all linear/Conv1D layers if provided as 'all-linear'. Adapted from
+ the QLoRA repository: https://github.com/artidoro/qlora/blob/main/qlora.py
+ """
+ if not hasattr(peft_config, "target_modules"):
+ return peft_config
+
+ # if `target_modules` is a string, convert to lower case and check if it matches "all-linear"
+ if not (
+ isinstance(peft_config.target_modules, str)
+ and peft_config.target_modules.lower() == INCLUDE_LINEAR_LAYERS_SHORTHAND
+ ):
+ return peft_config
+
+ linear_classes = (torch.nn.Linear, Conv1D)
+ linear_names = ("Linear",)
+ linear_module_names = set()
+ for name, module in model.named_modules():
+ # match with all linear classes.
+ if isinstance(module, linear_classes):
+ linear_module_names.add(name)
+ elif isinstance(module, BaseTunerLayer) and any(n in type(module).__name__ for n in linear_names):
+ # If the model already has adapter layers applied, then the "linear" layer is actually an adapter layer,
+ # e.g. lora.Linear, and not nn.Linear. To target this layer, we don't want to check the layer type, as there
+ # are many possible layer types (one for each PEFT method) and the list would quickly get out of date. Thus
+ # we rely on the name of the layer class, which by convention is something like "Linear", "Linear4bit",
+ # "HqqLoraLinear", ... in PEFT. It's not pretty but should generally work.
+ # See 2390
+ linear_module_names.add(name)
+
+ # Try to remove linear layers that should not be targeted as best as possible. We have to rely on convention as
+ # there are no hard rules to detect these modules.
+ module_names_to_exclude = set()
+ if isinstance(model, PreTrainedModel):
+ output_emb = model.get_output_embeddings()
+ if output_emb is not None:
+ # ignore the last classification head for text generation models
+ last_module_name = [name for name, module in model.named_modules() if module is output_emb][0]
+ module_names_to_exclude.add(last_module_name)
+ elif peft_config.task_type == TaskType.SEQ_CLS:
+ # ignore classifier head for classification models (issue 2027)
+ # there is no fix name for the classifier head, so check the common ones
+ for name in SEQ_CLS_HEAD_NAMES:
+ cls_head = getattr(model, name, None)
+ if cls_head is not None:
+ last_module_name = [name for name, module in model.named_modules() if module is cls_head][0]
+ module_names_to_exclude.add(last_module_name)
+ break
+
+ # we don't want nested LoRA layers, i.e. LoRA being applied to possibly existing lora_A, lora_B, etc.
+ # see 2390
+ for prefix, module in model.named_modules():
+ if isinstance(module, BaseTunerLayer):
+ for suffix, child in module.named_modules():
+ if suffix:
+ module_names_to_exclude.add(f"{prefix}.{suffix}")
+
+ linear_module_names -= module_names_to_exclude
+ peft_config.target_modules = linear_module_names
+ return peft_config
+
+
+def check_adapters_to_merge(module: BaseTunerLayer, adapter_names: Optional[list[str]] = None) -> list[str]:
+ """
+ Helper function to check which adapters should be merged.
+
+ Only return those adapters that are not already merged. Give a warning if some or all of the adapters are already
+ merged.
+
+ """
+ if adapter_names is None:
+ adapter_names = module.active_adapters
+ if isinstance(adapter_names, str):
+ raise ValueError(f"adapter_names should be a list of strings, got {adapter_names!r}.")
+
+ if module.merged:
+ merged_adapters = set(module.merged_adapters)
+ adapter_names = [name for name in adapter_names if name not in merged_adapters]
+
+ if adapter_names:
+ warnings.warn(
+ f"Already following adapters were merged {','.join(module.merged_adapters)}. "
+ f"You are now additionally merging {','.join(adapter_names)}."
+ )
+ else:
+ warnings.warn("All adapters are already merged, nothing to do.")
+
+ return adapter_names
+
+
+def clone_module(module: nn.Module, share_weights=False):
+ """Clone a module in a pytorch model.
+
+ Clones a module of a model, optionally sharing all the parameters between the original and the clone. Simplifies
+ reusing a module when manipulating the architecture of a model.
+ """
+ clone = copy.deepcopy(module)
+
+ def _share_weights(src: nn.Module, dst: nn.Module):
+ for name, param in src.named_parameters(recurse=False):
+ dst.register_parameter(name, param)
+
+ if share_weights:
+ for name, submodule in module.named_modules():
+ _share_weights(submodule, clone.get_submodule(name))
+
+ return clone
+
+
+def replicate_layers(model: nn.Module, layer_map: list[tuple[int, int]]):
+ """Replicate layers in a transfomer model with weight sharing.
+
+ This function looks for a module list attribute at model[(.model)*].layers and replicates the layers in the module
+ list according to the layer map. For example the map `[[0, 4], [2, 5]]` will take the set of layers `[0, 1, 2, 3,
+ 4]` and replace them with a module list containing `[0, 1, 2, 3, 2, 3, 4]`.
+ """
+ while hasattr(model, "model"):
+ model = model.model
+ # Some variants of the bert model nest the main model under the bert attribute.
+ if hasattr(model, "bert"):
+ model = model.bert
+
+ model_type = None
+ layers: nn.ModuleList = None
+ if hasattr(model, "layers"):
+ model_type = "llama"
+ layers = model.layers
+ elif hasattr(model, "encoder") and hasattr(model.encoder, "layer"):
+ model_type = "bert"
+ layers = model.encoder.layer
+ elif hasattr(model, "h"):
+ model_type = "falcon"
+ layers = model.h
+ if not model_type or not isinstance(layers, nn.ModuleList):
+ raise ValueError(
+ "Could not locate the layers attribute in the model. "
+ "Expected Llama, Bert or Falcon compatible architectures."
+ )
+
+ new_layers = []
+ for start, end in layer_map:
+ for i in range(start, end):
+ current_idx = len(new_layers)
+ new_layers.append(clone_module(layers[i], share_weights=True))
+ # This is a hack needed to work around the layer_idx introduced in HF transformers.
+ for submodule in new_layers[-1].modules():
+ if hasattr(submodule, "layer_idx"):
+ submodule.layer_idx = current_idx
+ layers = nn.ModuleList(new_layers)
+ if model_type == "llama":
+ model.layers = layers
+ elif model_type == "bert":
+ model.encoder.layer = layers
+ elif model_type == "falcon":
+ model.h = layers
+ else:
+ raise ValueError("Unexpected model type, need to handle post-processing of layers.")
+ if hasattr(model.config, "num_hidden_layers"): # Common to Llama, Bert, Falcon.
+ model.config.num_hidden_layers = len(new_layers)
+
+
+###############################
+# FUNCTIONS FOR functional.py #
+###############################
+
+
+def set_adapter(
+ model,
+ adapter_name: str | list[str],
+ inference_mode: bool = False,
+ layer_cls: type[BaseTunerLayer] = BaseTunerLayer,
+) -> None:
+ """Set the active PEFT adapter(s) of the model.
+
+ Active adapters are those adapters that participate in the forward pass. Use this function if you want to switch
+ between multiple PEFT adapters.
+
+ Args:
+ model (`nn.Module`):
+ The model on which the adapter(s) should be set.
+ adapter_name (str, list[str]):
+ The name(s) of the adapter(s) to set as active
+ inference_mode (bool, optional):
+ Whether the activated adapter should be frozen (i.e. `requires_grad=False`). Default is False.
+ layer_cls (type, optional):
+ The class of the adapter layer. Defaults to `BaseTunerLayer`.
+ """
+ _set_adapter(model, adapter_name, inference_mode=inference_mode) # auxiliary modules
+ for module in model.modules():
+ if isinstance(module, layer_cls):
+ if module.merged:
+ warnings.warn("Adapter cannot be set when the model is merged. Unmerging the model first.")
+ module.unmerge()
+ module.set_adapter(adapter_name, inference_mode=inference_mode)
+
+
+def _delete_auxiliary_adapter(model, adapter_name: str, new_active_adapters: Optional[list[str]]) -> None:
+ for module in model.modules():
+ if isinstance(module, AuxiliaryTrainingWrapper):
+ module.delete_adapter(adapter_name, new_active_adapters=new_active_adapters)
+
+
+def delete_adapter(
+ model: nn.Module, adapter_name: str, prefix: str, layer_cls: type[BaseTunerLayer] = BaseTunerLayer
+) -> list[str] | None:
+ """
+ Delete an existing PEFT adapter.
+
+ Note: This function does not delete the PEFT config on the model, if there is one. It will also not completely
+ purge the PEFT layers if the last PEFT adapter is deleted. For this, consider using `model.unload()` if using a
+ PEFT model instance, or just reloading the base model.
+
+ Args:
+ model (`nn.Module`):
+ The model from which the adapter should be deleted.
+ adapter_name (str):
+ The name of the adapter to be deleted.
+ prefix (str):
+ The prefix of the PEFT method, e.g. "lora_" for LoRA.
+ layer_cls (type, optional):
+ The class of the adapter layer. Defaults to `BaseTunerLayer`.
+
+ Returns:
+ new_adapter (list[str] | None):
+ The name of remaining adapter(s) after deletion, or `None` if there are no active adapters left. Use this
+ to set the new active adapter of the model if necessary.
+ """
+ key_list = [key for key, _ in model.named_modules() if prefix not in key]
+ new_adapter = None
+
+ for key in key_list:
+ _, target, _ = _get_submodules(model, key)
+ if isinstance(target, layer_cls):
+ target.delete_adapter(adapter_name)
+ if new_adapter is None:
+ new_adapter = target.active_adapters[:]
+
+ _delete_auxiliary_adapter(model, adapter_name=adapter_name, new_active_adapters=new_adapter)
+ return new_adapter
+
+
+def cast_adapter_dtype(model: nn.Module, adapter_name: str, autocast_adapter_dtype: bool = True) -> None:
+ """
+ A helper method to cast the adapter weights to the correct dtype.
+
+ Currently, this only upcasts float16 and bfloat16 to float32.
+
+ Args:
+ adapter_name (`str`):
+ The adapter name.
+ autocast_adapter_dtype (`bool`, *optional*):
+ Whether to autocast the adapter dtype. Defaults to `True`.
+ """
+ if not autocast_adapter_dtype:
+ return
+
+ dtypes_to_convert_to_fp32 = {torch.float16, torch.bfloat16}
+
+ for module in model.modules():
+ if not isinstance(module, BaseTunerLayer):
+ continue
+
+ for submodule in module.modules():
+ if not isinstance(submodule, (nn.ModuleDict, nn.ParameterDict, BufferDict)):
+ continue
+
+ if adapter_name not in submodule:
+ continue
+
+ if isinstance(submodule[adapter_name], nn.Parameter):
+ if submodule[adapter_name].dtype in dtypes_to_convert_to_fp32:
+ submodule[adapter_name].data = submodule[adapter_name].data.to(torch.float32)
+ continue
+
+ if isinstance(submodule[adapter_name], torch.Tensor): # e.g. from a BufferDict
+ if submodule[adapter_name].dtype in dtypes_to_convert_to_fp32:
+ submodule[adapter_name] = submodule[adapter_name].to(torch.float32)
+ continue
+
+ for param in submodule[adapter_name].parameters():
+ if param.dtype in dtypes_to_convert_to_fp32:
+ param.data = param.data.to(torch.float32)
+
+
+def set_requires_grad(model, adapter_names: str | Sequence[str], requires_grad: bool = True) -> None:
+ """
+ Enable or disable gradients on the given adapter(s).
+
+ Args:
+ model (`nn.Module`):
+ The model from which the adapter should be deleted.
+ adapter_name (`str` or `Sequence[str]`):
+ The name of the adapter(s) whose gradients should be enabled/disabled.
+ requires_grad (`bool`, *optional*)
+ Whether to enable (`True`, default) or disable (`False`).
+ """
+ for module in model.modules():
+ if isinstance(module, (BaseTunerLayer, AuxiliaryTrainingWrapper)):
+ module.set_requires_grad(adapter_names=adapter_names, requires_grad=requires_grad)
diff --git a/peft/src/peft/tuners/vblora/__init__.py b/peft/src/peft/tuners/vblora/__init__.py
new file mode 100644
index 0000000000000000000000000000000000000000..8e71a08461e8b7cb2fb5513a3bf908a4a98c0747
--- /dev/null
+++ b/peft/src/peft/tuners/vblora/__init__.py
@@ -0,0 +1,24 @@
+# Copyright 2024-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+from peft.utils import register_peft_method
+
+from .config import VBLoRAConfig
+from .layer import Linear, VBLoRALayer
+from .model import VBLoRAModel
+
+
+__all__ = ["Linear", "VBLoRAConfig", "VBLoRALayer", "VBLoRAModel"]
+
+register_peft_method(name="vblora", config_cls=VBLoRAConfig, model_cls=VBLoRAModel)
diff --git a/peft/src/peft/tuners/vblora/config.py b/peft/src/peft/tuners/vblora/config.py
new file mode 100644
index 0000000000000000000000000000000000000000..0a969b0875d883cf8967d5601f72ee3bb3684ee3
--- /dev/null
+++ b/peft/src/peft/tuners/vblora/config.py
@@ -0,0 +1,196 @@
+# Copyright 2024-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+from __future__ import annotations
+
+from dataclasses import dataclass, field
+from typing import Optional, Union
+
+from peft.config import PeftConfig
+from peft.utils import PeftType
+
+
+@dataclass
+class VBLoRAConfig(PeftConfig):
+ """
+ This is the configuration class to store the configuration of a [`VBLoRAConfig`].
+
+ Paper: https://huggingface.co/papers/2405.15179
+
+ Args:
+ r (`int`):
+ The rank of incremental matrices.
+ num_vectors (`int`):
+ Number of vectors in the vector bank. Use higher values when the model size increases.
+ vector_length (`int`):
+ The length of the vectors in the vector bank. The length of the vectors should be divisible by the hidden
+ dimension of the model.
+ topk (`int`):
+ The K value for top-K selection. A larger value of K increases the size of the saved model. In practice,
+ setting K=2 typically provides the best performance and parameter efficiency. For more details, refer to
+ the discussion in the paper.
+ target_modules (`Union[List[str], str]`):
+ The names of the modules to apply the adapter to. If this is specified, only the modules with the specified
+ names will be replaced. When passing a string, a regex match will be performed. When passing a list of
+ strings, either an exact match will be performed or it is checked if the name of the module ends with any
+ of the passed strings. If this is specified as 'all-linear', then all linear/Conv1D modules are chosen,
+ excluding the output layer. If this is not specified, modules will be chosen according to the model
+ architecture. If the architecture is not known, an error will be raised -- in this case, you should specify
+ the target modules manually.
+ exclude_modules (`Optional[Union[List[str], str]]`):
+ The names of the modules to not apply the adapter. When passing a string, a regex match will be performed.
+ When passing a list of strings, either an exact match will be performed or it is checked if the name of the
+ module ends with any of the passed strings.
+ save_only_topk_weights (`bool`):
+ Whether to only save the topk weights. Setting `save_only_topk_weights = True` significantly reduces
+ storage space. However, models saved in this mode can be used for merging or inference only, not for
+ resuming training.
+ vblora_dropout (`float`):
+ The dropout probability for VBLoRA layers.
+ fan_in_fan_out (`bool`):
+ Set this to True if the layer to replace stores weight like (fan_in, fan_out). For example, gpt-2 uses
+ `Conv1D` which stores weights like (fan_in, fan_out) and hence this should be set to `True`.
+ bias (`str`):
+ Bias type for VBLoRA. Can be 'none', 'all' or 'vblora_only'. If 'all' or 'vblora_only', the corresponding
+ biases will be updated during training. Be aware that this means that, even when disabling the adapters,
+ the model will not produce the same output as the base model would have without adaptation.
+ modules_to_save (`List[str]`):
+ List of modules apart from VBLoRA layers to be set as trainable and saved in the final checkpoint.
+ init_vector_bank_bound (`float`):
+ The vector bank is initialized with a uniform distribution between -init_vector_bank_bound and
+ init_vector_bank_bound. Avoid initializing the vector bank with all zeros to prevent zero gradients. A
+ small value, such as 0.02, is typically effective. Initializing with a large value may cause training
+ instability.
+ init_logits_std (`float`):
+ The logits are initialized with a normal distribution with a standard deviation of init_logits_std. Default
+ is 0.1.
+ layers_to_transform (`Union[List[int],int]`):
+ The layer indices to transform. If a list of ints is passed, it will apply the adapter to the layer indices
+ that are specified in this list. If a single integer is passed, it will apply the transformations on the
+ layer at this index.
+ layers_pattern (`Optional[Union[List[str], str]]`):
+ The layer pattern name, used only if `layers_to_transform` is different from `None`. This should target the
+ `nn.ModuleList` of the model, which is often called `'layers'` or `'h'`.
+ """
+
+ r: int = field(default=4, metadata={"help": "The rank of incremental matrices."})
+ num_vectors: int = field(
+ default=256,
+ metadata={"help": "Number of vectors in the vector bank. Use higher values when the model size increases."},
+ )
+ vector_length: int = field(
+ default=256,
+ metadata={
+ "help": "The length of the vectors in the vector bank. The length of the vectors should be divisible by "
+ "the hidden dimension of the model."
+ },
+ )
+ topk: int = field(
+ default=2,
+ metadata={
+ "help": "The K value for top-K selection. A larger value of K increases the size of the saved model. "
+ "In practice, setting K=2 typically provides the best performance and parameter efficiency. "
+ "For more details, refer to the discussion in the paper."
+ },
+ )
+ target_modules: Optional[Union[list[str], str]] = field(
+ default=None,
+ metadata={
+ "help": (
+ "List of module names or regex expression of the module names to replace with LoRA."
+ "For example, ['q', 'v'] or '.*decoder.*(SelfAttention|EncDecAttention).*(q|v)$'."
+ "This can also be a wildcard 'all-linear' which matches all linear/Conv1D layers except the output layer."
+ "If not specified, modules will be chosen according to the model architecture, If the architecture is "
+ "not known, an error will be raised -- in this case, you should specify the target modules manually."
+ )
+ },
+ )
+ exclude_modules: Optional[Union[list[str], str]] = field(
+ default=None,
+ metadata={"help": "List of module names or regex expression of the module names to exclude from VBLoRA."},
+ )
+ save_only_topk_weights: bool = field(
+ default=False,
+ metadata={
+ "help": (
+ "Whether to only save the topk weights. Setting `save_only_topk_weights = True` significantly reduces "
+ "storage space. However, models saved in this mode can be used for merging or inference only, not for "
+ "resuming training."
+ )
+ },
+ )
+ vblora_dropout: float = field(default=0.0, metadata={"help": "VBLoRA dropout"})
+ fan_in_fan_out: bool = field(
+ default=False,
+ metadata={"help": "Set this to True if the layer to replace stores weight like (fan_in, fan_out)"},
+ )
+ bias: str = field(default="none", metadata={"help": "Bias type for VBLoRA. Can be 'none', 'all' or 'vblora_only'"})
+ modules_to_save: Optional[list[str]] = field(
+ default=None,
+ metadata={
+ "help": (
+ "List of modules apart from VBLoRA layers to be set as trainable and saved in the final checkpoint. For"
+ " example, in Sequence Classification or Token Classification tasks, the final layer"
+ " `classifier/score` are randomly initialized and as such need to be trainable and saved."
+ )
+ },
+ )
+ init_vector_bank_bound: float = field(
+ default=0.02,
+ metadata={
+ "help": (
+ "The vector bank is initialized with a uniform distribution between -init_vector_bank_bound and"
+ " init_vector_bank_bound. Avoid initializing the vector bank with all zeros to prevent zero gradients."
+ " A small value, such as 0.02, is typically effective. Initializing with a large value may cause"
+ " training instability."
+ ),
+ },
+ )
+ init_logits_std: float = field(
+ default=0.1,
+ metadata={
+ "help": (
+ "The logits are initialized with a normal distribution with a standard deviation of init_logits_std. "
+ "Default value 0.1 typically works well."
+ ),
+ },
+ )
+ layers_to_transform: Optional[Union[list[int], int]] = field(
+ default=None,
+ metadata={
+ "help": "The layer indexes to transform, is this argument is specified, PEFT will transform only the layers indexes that are specified inside this list. If a single integer is passed, PEFT will transform only the layer at this index. "
+ "This only works when target_modules is a list of str. This should target the `nn.ModuleList` of the "
+ "model, which is often called `'layers'` or `'h'`."
+ },
+ )
+ layers_pattern: Optional[Union[list[str], str]] = field(
+ default=None,
+ metadata={
+ "help": "The layer pattern name, used only if `layers_to_transform` is different to None and if the layer pattern is not in the common layers pattern."
+ "This only works when target_modules is a list of str."
+ },
+ )
+
+ def __post_init__(self):
+ super().__post_init__()
+ self.peft_type = PeftType.VBLORA
+ self.target_modules = (
+ set(self.target_modules) if isinstance(self.target_modules, list) else self.target_modules
+ )
+ self.exclude_modules = (
+ set(self.exclude_modules) if isinstance(self.exclude_modules, list) else self.exclude_modules
+ )
+ # check for layers_to_transform and layers_pattern
+ if self.layers_pattern and not self.layers_to_transform:
+ raise ValueError("When `layers_pattern` is specified, `layers_to_transform` must also be specified. ")
diff --git a/peft/src/peft/tuners/vblora/layer.py b/peft/src/peft/tuners/vblora/layer.py
new file mode 100644
index 0000000000000000000000000000000000000000..ea2f0cca77b78e59fe840adc08b3c3f1a2444d3b
--- /dev/null
+++ b/peft/src/peft/tuners/vblora/layer.py
@@ -0,0 +1,251 @@
+# Copyright 2024-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+import warnings
+from typing import Optional
+
+import torch
+import torch.nn as nn
+import torch.nn.functional as F
+from transformers.pytorch_utils import Conv1D
+
+from peft.tuners.tuners_utils import BaseTunerLayer, check_adapters_to_merge
+from peft.utils.other import transpose
+
+
+class VBLoRALayer(BaseTunerLayer):
+ # List all names of layers that may contain adapter weights
+ adapter_layer_names = ("vblora_logits_A", "vblora_logits_B", "vblora_vector_bank")
+
+ def __init__(self, base_layer: nn.Module, **kwargs):
+ self.base_layer = base_layer
+ self.r = {}
+ self.topk = {}
+ self.vblora_dropout = nn.ModuleDict({})
+
+ # For storing vector scale
+ self.vblora_logits_A = nn.ParameterDict({})
+ self.vblora_logits_B = nn.ParameterDict({})
+
+ # Mark the weight as unmerged
+ self._disable_adapters = False
+ self.merged_adapters = []
+
+ base_layer = self.get_base_layer()
+ if isinstance(base_layer, nn.Linear):
+ in_features, out_features = base_layer.in_features, base_layer.out_features
+ elif isinstance(base_layer, Conv1D):
+ in_features, out_features = (
+ base_layer.weight.ds_shape if hasattr(base_layer.weight, "ds_shape") else base_layer.weight.shape
+ )
+
+ self.in_features = in_features
+ self.out_features = out_features
+ self.kwargs = kwargs
+
+ @property
+ def merged(self) -> bool:
+ return bool(self.merged_adapters)
+
+ def update_layer(
+ self,
+ adapter_name: str,
+ vblora_vector_bank,
+ r: int,
+ topk: int,
+ num_vectors: int,
+ vector_length: float,
+ vblora_dropout: float = 0.0,
+ init_logits_std: float = 0.01,
+ inference_mode: bool = False,
+ **kwargs,
+ ):
+ if r <= 0:
+ raise ValueError(f"`r` {r} should be a positive integer value")
+ if topk <= 0:
+ raise ValueError(f"`topk` {topk} should be a positive integer value")
+
+ if self.in_features % vector_length != 0:
+ raise ValueError(f"`in_features` {self.in_features} must be divisible by `vector_length` {vector_length}")
+ if self.out_features % vector_length != 0:
+ raise ValueError(
+ f"`out_features` {self.out_features} must be divisible by `vector_length` {vector_length}"
+ )
+
+ self.r[adapter_name] = r
+ self.topk[adapter_name] = topk
+ if vblora_dropout > 0.0:
+ vblora_dropout_layer = nn.Dropout(p=vblora_dropout)
+ else:
+ vblora_dropout_layer = nn.Identity()
+ self.vblora_dropout.update(nn.ModuleDict({adapter_name: vblora_dropout_layer}))
+ self.vblora_logits_A[adapter_name] = nn.Parameter(
+ torch.zeros(r, self.in_features // vector_length, num_vectors), requires_grad=True
+ )
+ self.vblora_logits_B[adapter_name] = nn.Parameter(
+ torch.zeros(self.out_features // vector_length, r, num_vectors), requires_grad=True
+ )
+ self.vblora_vector_bank = vblora_vector_bank
+ self.reset_vblora_logits(adapter_name, init_logits_std)
+ self._move_adapter_to_device_of_base_layer(adapter_name)
+ self.set_adapter(self.active_adapters, inference_mode=inference_mode)
+
+ def reset_vblora_logits(self, adapter_name, init_logits_std):
+ if adapter_name in self.vblora_logits_A.keys():
+ with torch.no_grad():
+ nn.init.normal_(self.vblora_logits_A[adapter_name], 0, init_logits_std)
+ nn.init.normal_(self.vblora_logits_B[adapter_name], 0, init_logits_std)
+
+
+class Linear(nn.Linear, VBLoRALayer):
+ # VBLoRA implemented in a dense layer
+ def __init__(
+ self,
+ base_layer,
+ vblora_vector_bank,
+ adapter_name: str,
+ r: int,
+ num_vectors: int,
+ vector_length: int,
+ topk: int = 2,
+ vblora_dropout: float = 0.0,
+ init_logits_std: float = 0.01,
+ fan_in_fan_out: bool = False, # Set this to True if the layer to replace stores weight like (fan_in, fan_out)
+ is_target_conv_1d_layer: bool = False,
+ **kwargs,
+ ) -> None:
+ # this gets the init from nn.Linear's super perspective, i.e. nn.Module.__init__, which should always be called
+ super(nn.Linear, self).__init__()
+ VBLoRALayer.__init__(self, base_layer, **kwargs)
+ self.fan_in_fan_out = fan_in_fan_out
+ self._active_adapter = adapter_name
+ self.update_layer(
+ adapter_name, vblora_vector_bank, r, topk, num_vectors, vector_length, vblora_dropout, init_logits_std
+ )
+ self.is_target_conv_1d_layer = is_target_conv_1d_layer
+
+ def merge(self, safe_merge: bool = False, adapter_names: Optional[list[str]] = None) -> None:
+ """
+ Merge the active adapter weights into the base weights
+
+ Args:
+ safe_merge (`bool`, *optional*):
+ If True, the merge operation will be performed in a copy of the original weights and check for NaNs
+ before merging the weights. This is useful if you want to check if the merge operation will produce
+ NaNs. Defaults to `False`.
+ adapter_names (`List[str]`, *optional*):
+ The list of adapter names that should be merged. If None, all active adapters will be merged. Defaults
+ to `None`.
+ """
+ adapter_names = check_adapters_to_merge(self, adapter_names)
+ if not adapter_names:
+ # no adapter to merge
+ return
+
+ for active_adapter in adapter_names:
+ if active_adapter in self.vblora_logits_A.keys():
+ base_layer = self.get_base_layer()
+ if safe_merge:
+ # Note that safe_merge will be slower than the normal merge
+ # because of the copy operation.
+ orig_weights = base_layer.weight.data.clone()
+ orig_weights += self.get_delta_weight(active_adapter)
+ if not torch.isfinite(orig_weights).all():
+ raise ValueError(
+ f"NaNs detected in the merged weights. The adapter {active_adapter} seems to be broken"
+ )
+ base_layer.weight.data = orig_weights
+ else:
+ base_layer.weight.data += self.get_delta_weight(active_adapter)
+ self.merged_adapters.append(active_adapter)
+
+ def unmerge(self) -> None:
+ if not self.merged:
+ warnings.warn("Already unmerged. Nothing to do.")
+ return
+
+ while len(self.merged_adapters) > 0:
+ active_adapter = self.merged_adapters.pop()
+ if active_adapter in self.vblora_logits_A.keys():
+ self.get_base_layer().weight.data -= self.get_delta_weight(active_adapter)
+
+ def _get_low_rank_matrix(self, logits: torch.tensor, vblora_vector_bank, topk) -> torch.Tensor:
+ top_k_logits, indices = logits.topk(topk, dim=-1)
+ topk_weights = F.softmax(top_k_logits, dim=-1)
+ return (topk_weights.unsqueeze(-1) * vblora_vector_bank[indices]).sum(-2)
+
+ def _get_lora_matrices(self, adapter, cast_to_fp32=False) -> tuple[torch.Tensor, torch.Tensor]:
+ vblora_logits_A = self.vblora_logits_A[adapter]
+ vblora_logits_B = self.vblora_logits_B[adapter]
+
+ # Check for infinity values when training. If found, training was likely resumed from a `save_only_topk_weights` model.
+ if self.training and vblora_logits_A[0, 0].isinf().any():
+ raise RuntimeError(
+ "Found infinity values in VB-LoRA logits. Ensure training was not resumed from a `save_only_topk_weights` model."
+ )
+
+ vblora_vector_bank = self.vblora_vector_bank[adapter].to(vblora_logits_A.device)
+ topk = self.topk[adapter]
+ # In case users wants to merge the adapter weights that are in
+ # float16 while being on CPU, we need to cast the weights to float32, perform the merge and then cast back to
+ # float16 because the `@` and matmul operation in general is not supported in torch + cpu + fp16.
+ if cast_to_fp32:
+ vblora_logits_A = vblora_logits_A.float()
+ vblora_logits_B = vblora_logits_B.float()
+ vblora_vector_bank = vblora_vector_bank.float()
+
+ # A: (rank, in_tile, vector_length) -> (rank, in_tile x vector_length)
+ A = self._get_low_rank_matrix(vblora_logits_A, vblora_vector_bank, topk).reshape(vblora_logits_A.shape[0], -1)
+ # B: (out_tile, rank, vector_length) -> (out_tile, vector_length, rank) -> (out_tile x vector_length, rank)
+ B = (
+ self._get_low_rank_matrix(vblora_logits_B, vblora_vector_bank, topk)
+ .transpose(1, 2)
+ .reshape(-1, vblora_logits_B.shape[1])
+ )
+ return A, B
+
+ def get_delta_weight(self, adapter) -> torch.Tensor:
+ """
+ Compute the delta weight for the given adapter.
+
+ Args:
+ adapter (str):
+ The name of the adapter for which the delta weight should be computed.
+ """
+ device = self.vblora_logits_A[adapter].device
+ dtype = self.vblora_logits_A[adapter].dtype
+ cast_to_fp32 = device.type == "cpu" and dtype == torch.float16
+ A, B = self._get_lora_matrices(adapter, cast_to_fp32)
+ output_tensor = transpose(B @ A, self.fan_in_fan_out)
+ return output_tensor
+
+ def forward(self, x: torch.Tensor, *args, **kwargs) -> torch.Tensor:
+ previous_dtype = x.dtype
+ if self.disable_adapters:
+ if self.merged:
+ self.unmerge()
+ result = self.base_layer(x, *args, **kwargs)
+ elif self.merged:
+ result = self.base_layer(x, *args, **kwargs)
+ else:
+ result = self.base_layer(x, *args, **kwargs)
+ for active_adapter in self.active_adapters:
+ if active_adapter not in self.vblora_logits_A.keys():
+ continue
+ A, B = self._get_lora_matrices(active_adapter)
+ x = x.to(self.vblora_vector_bank[active_adapter].dtype)
+ dropout = self.vblora_dropout[active_adapter]
+ result = result + F.linear(F.linear(dropout(x), A), B)
+ result = result.to(previous_dtype)
+ return result
diff --git a/peft/src/peft/tuners/vblora/model.py b/peft/src/peft/tuners/vblora/model.py
new file mode 100644
index 0000000000000000000000000000000000000000..745ce61ffedbd58e9c87a80ee887f403dc9a1941
--- /dev/null
+++ b/peft/src/peft/tuners/vblora/model.py
@@ -0,0 +1,209 @@
+# Copyright 2024-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+from __future__ import annotations
+
+import warnings
+
+import torch
+import torch.nn as nn
+from transformers.pytorch_utils import Conv1D
+
+from peft.tuners.tuners_utils import BaseTuner, BaseTunerLayer
+from peft.utils import TRANSFORMERS_MODELS_TO_VBLORA_TARGET_MODULES_MAPPING
+
+from .config import VBLoRAConfig
+from .layer import Linear, VBLoRALayer
+
+
+class VBLoRAModel(BaseTuner):
+ """
+ Creates VBLoRA model from a pretrained transformers model.
+
+ The method is described in detail in https://huggingface.co/papers/2405.15179.
+
+ Args:
+ model ([`~transformers.PreTrainedModel`]): The model to be adapted.
+ config ([`VBLoRAConfig`]): The configuration of the VBLoRA model.
+ adapter_name (`str`): The name of the adapter, defaults to `"default"`.
+ low_cpu_mem_usage (`bool`, `optional`, defaults to `False`):
+ Create empty adapter weights on meta device. Useful to speed up the loading process.
+
+ Returns:
+ `torch.nn.Module`: The VBLoRA model.
+
+ Example:
+
+ ```py
+ >>> from transformers import AutoModelForCausalLM
+ >>> from peft import VBLoRAConfig, get_peft_model
+
+ >>> base_model = AutoModelForCausalLM.from_pretrained("facebook/opt-125m")
+ >>> config = VBLoRAConfig(
+ ... task_type="SEQ_CLS",
+ ... r=4,
+ ... target_modules=["fc1", "fc2", "k_proj", "out_proj", "q_proj", "v_proj"],
+ ... num_vectors=60,
+ ... vector_length=256,
+ ... save_only_topk_weights=True,
+ ... )
+ >>> model = get_peft_model(base_model, config)
+ ```
+
+ **Attributes**:
+ - **model** ([`~transformers.PreTrainedModel`]) -- The model to be adapted.
+ - **peft_config** ([`VBLoRAConfig`]): The configuration of the VBLoRAConfig model.
+ """
+
+ prefix: str = "vblora_"
+ tuner_layer_cls = VBLoRALayer
+ target_module_mapping = TRANSFORMERS_MODELS_TO_VBLORA_TARGET_MODULES_MAPPING
+
+ def _init_vblora_vector_bank(self, config: VBLoRAConfig, adapter_name: str) -> None:
+ vblora_vector_bank = torch.zeros(config.num_vectors, config.vector_length)
+ torch.nn.init.uniform_(vblora_vector_bank, -config.init_vector_bank_bound, config.init_vector_bank_bound)
+ self.vblora_vector_bank[adapter_name] = vblora_vector_bank
+
+ def _pre_injection_hook(self, model: nn.Module, config: VBLoRAConfig, adapter_name: str) -> None:
+ self.vblora_vector_bank = nn.ParameterDict({})
+
+ def _create_and_replace(
+ self,
+ vblora_config,
+ adapter_name,
+ target,
+ target_name,
+ parent,
+ current_key,
+ ):
+ if current_key is None:
+ raise ValueError("Current Key shouldn't be `None`")
+
+ bias = hasattr(target, "bias") and target.bias is not None
+ kwargs = {
+ "fan_in_fan_out": vblora_config.fan_in_fan_out,
+ "bias": bias,
+ }
+ self._init_vblora_vector_bank(vblora_config, adapter_name)
+ # TODO: add quantization support
+
+ if isinstance(target, Linear):
+ target.update_layer(
+ adapter_name=adapter_name,
+ vblora_vector_bank=self.vblora_vector_bank,
+ r=vblora_config.r,
+ topk=vblora_config.topk,
+ num_vectors=vblora_config.num_vectors,
+ vector_length=vblora_config.vector_length,
+ vblora_dropout=vblora_config.vblora_dropout,
+ init_logits_std=vblora_config.init_logits_std,
+ )
+ else:
+ new_module = self._create_new_module(
+ vblora_config=vblora_config,
+ vblora_vector_bank=self.vblora_vector_bank,
+ adapter_name=adapter_name,
+ target=target,
+ **kwargs,
+ )
+ if adapter_name not in self.active_adapter:
+ # adding an additional adapter: it is not automatically trainable
+ new_module.requires_grad_(False)
+ self._replace_module(parent, target_name, new_module, target)
+
+ @staticmethod
+ def _create_new_module(vblora_config, vblora_vector_bank, adapter_name, target, **kwargs):
+ if isinstance(target, BaseTunerLayer):
+ target_base_layer = target.get_base_layer()
+ else:
+ target_base_layer = target
+
+ if isinstance(target_base_layer, torch.nn.Linear):
+ if kwargs["fan_in_fan_out"]:
+ warnings.warn(
+ "fan_in_fan_out is set to True but the target module is `torch.nn.Linear`. "
+ "Setting fan_in_fan_out to False."
+ )
+ kwargs["fan_in_fan_out"] = vblora_config.fan_in_fan_out = False
+ elif isinstance(target_base_layer, Conv1D):
+ kwargs["is_target_conv_1d_layer"] = True
+ if not kwargs["fan_in_fan_out"]:
+ warnings.warn(
+ "fan_in_fan_out is set to False but the target module is `Conv1D`. Setting fan_in_fan_out to True."
+ )
+ kwargs["fan_in_fan_out"] = vblora_config.fan_in_fan_out = True
+ else:
+ raise ValueError(
+ f"Target module {target} is not supported. Currently, only the following modules are supported: "
+ "`torch.nn.Linear`, `transformers.pytorch_utils.Conv1D`."
+ )
+ new_module = Linear(
+ base_layer=target,
+ vblora_vector_bank=vblora_vector_bank,
+ adapter_name=adapter_name,
+ r=vblora_config.r,
+ num_vectors=vblora_config.num_vectors,
+ vector_length=vblora_config.vector_length,
+ topk=vblora_config.topk,
+ vblora_dropout=vblora_config.vblora_dropout,
+ init_logits_std=vblora_config.init_logits_std,
+ **kwargs,
+ )
+
+ return new_module
+
+ def get_nb_savable_parameters(self, adapter="default") -> tuple[int, int]:
+ r"""
+ Returns the number of savable VB-LoRA parameters and other savable parameters.
+ """
+ logits_params = 0
+ vector_bank_params = 0
+ other_params = 0
+ for name, param in self.named_parameters():
+ if "vblora_logits" in name:
+ logits_params += param.numel()
+ elif "vblora_vector_bank" in name:
+ vector_bank_params += param.numel()
+ elif param.requires_grad:
+ other_params += param.numel()
+ if self.peft_config[adapter].save_only_topk_weights:
+ num_vectors = self.peft_config[adapter].num_vectors
+ factor = 1 # factor to count float32-equivalent parameters
+ if num_vectors < 2**8:
+ factor = 0.25
+ elif num_vectors < 2**15:
+ factor = 0.5
+ elif num_vectors < 2**31:
+ factor = 1
+ else:
+ factor = 2
+ topk_weight_params = (
+ logits_params / self.peft_config[adapter].num_vectors * (self.peft_config[adapter].topk - 1)
+ )
+ topk_indices_params = (
+ logits_params / self.peft_config[adapter].num_vectors * self.peft_config[adapter].topk * factor
+ )
+ vblora_params = int(vector_bank_params + topk_weight_params + topk_indices_params)
+ else:
+ vblora_params = vector_bank_params + logits_params
+ return vblora_params, other_params
+
+ def print_savable_parameters(self) -> None:
+ r"""
+ Prints the number of savable VB-LoRA parameters and total savable parameters.
+ """
+ vblora_params, other_params = self.get_nb_savable_parameters()
+ print(
+ f"VB-LoRA params to-be-saved (float32-equivalent): {vblora_params:,d} "
+ f"|| total params to-be-saved: {(vblora_params + other_params):,d}"
+ )
diff --git a/peft/src/peft/tuners/vera/__init__.py b/peft/src/peft/tuners/vera/__init__.py
new file mode 100644
index 0000000000000000000000000000000000000000..25c4a96619524bfdcd41a8f7df331533ba370782
--- /dev/null
+++ b/peft/src/peft/tuners/vera/__init__.py
@@ -0,0 +1,40 @@
+# Copyright 2023-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+from peft.import_utils import is_bnb_4bit_available, is_bnb_available
+from peft.utils import register_peft_method
+
+from .config import VeraConfig
+from .layer import Linear, VeraLayer
+from .model import VeraModel
+
+
+__all__ = ["Linear", "VeraConfig", "VeraLayer", "VeraModel"]
+
+
+register_peft_method(name="vera", config_cls=VeraConfig, model_cls=VeraModel, prefix="vera_lambda_")
+
+
+def __getattr__(name):
+ if (name == "Linear8bitLt") and is_bnb_available():
+ from .bnb import Linear8bitLt
+
+ return Linear8bitLt
+
+ if (name == "Linear4bit") and is_bnb_4bit_available():
+ from .bnb import Linear4bit
+
+ return Linear4bit
+
+ raise AttributeError(f"module {__name__} has no attribute {name}")
diff --git a/peft/src/peft/tuners/vera/bnb.py b/peft/src/peft/tuners/vera/bnb.py
new file mode 100644
index 0000000000000000000000000000000000000000..71d20e4b1163ab9cc93b7b33c2aa022ddd3eb11f
--- /dev/null
+++ b/peft/src/peft/tuners/vera/bnb.py
@@ -0,0 +1,411 @@
+# Copyright 2024-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+from __future__ import annotations
+
+import warnings
+from typing import Optional
+
+import bitsandbytes as bnb
+import torch
+
+from peft.import_utils import is_bnb_4bit_available, is_bnb_available
+from peft.tuners.tuners_utils import check_adapters_to_merge
+from peft.utils.integrations import dequantize_bnb_weight
+from peft.utils.other import transpose
+
+from .layer import VeraLayer
+
+
+if is_bnb_available():
+
+ class Linear8bitLt(torch.nn.Module, VeraLayer):
+ def __init__(
+ self,
+ base_layer: torch.nn.Module,
+ adapter_name: str,
+ vera_A,
+ vera_B,
+ r: int = 0,
+ vera_dropout: float = 0.0,
+ fan_in_fan_out: bool = False,
+ init_weights: bool = True,
+ d_initial: float = 0.1,
+ **kwargs,
+ ) -> None:
+ super().__init__()
+ VeraLayer.__init__(self, base_layer)
+ self.fan_in_fan_out = fan_in_fan_out
+
+ self._active_adapter = adapter_name
+ self.update_layer(
+ adapter_name,
+ vera_A,
+ vera_B,
+ r,
+ vera_dropout=vera_dropout,
+ init_weights=init_weights,
+ d_initial=d_initial,
+ )
+
+ def merge(self, safe_merge: bool = False, adapter_names: Optional[list[str]] = None) -> None:
+ if self.merged:
+ warnings.warn(
+ f"Already following adapters were merged {','.join(self.merged_adapters)}. "
+ f"You are now additionally merging {','.join(self.active_adapters)}."
+ )
+
+ adapter_names = check_adapters_to_merge(self, adapter_names)
+ if not adapter_names:
+ return
+
+ for active_adapter in adapter_names:
+ if active_adapter not in self.vera_lambda_d.keys():
+ continue
+
+ warnings.warn(
+ "Merge vera module to 8-bit linear may get different generations due to rounding errors."
+ )
+ vera_data = self.get_delta_weight(active_adapter)
+
+ weight = self.get_base_layer().weight
+ state = self.get_base_layer().state
+ if state.SCB is None:
+ state.SCB = weight.SCB
+
+ output = dequantize_bnb_weight(weight, state)
+ w_data = output.to(vera_data.dtype).to(vera_data.device) + vera_data
+
+ if safe_merge and not torch.isfinite(w_data).all():
+ raise ValueError(
+ f"NaNs detected in the merged weights. The adapter {active_adapter} seems to be broken"
+ )
+
+ self.get_base_layer().weight = bnb.nn.Int8Params(
+ w_data.to("cpu"), requires_grad=False, has_fp16_weights=weight.has_fp16_weights
+ ).to(weight.device)
+ state.reset_grads()
+ self.merged_adapters.append(active_adapter)
+
+ def unmerge(self) -> None:
+ if not self.merged:
+ warnings.warn("Already unmerged. Nothing to do")
+ return
+
+ while len(self.merged_adapters) > 0:
+ active_adapter = self.merged_adapters.pop()
+ if active_adapter not in self.vera_lambda_d.keys():
+ continue
+ warnings.warn(
+ "Unmerge vera module to 8-bit linear may get different generations due to rounding errors."
+ )
+ vera_data = self.get_delta_weight(active_adapter)
+
+ weight = self.get_base_layer().weight
+ state = self.get_base_layer().state
+ if state.SCB is None:
+ state.SCB = weight.SCB
+ output = dequantize_bnb_weight(weight, state=state)
+
+ w_data = output.to(vera_data.dtype).to(vera_data.device) - vera_data
+
+ self.get_base_layer().weight = bnb.nn.Int8Params(
+ w_data.to("cpu"), requires_grad=False, has_fp16_weights=weight.has_fp16_weights
+ ).to(weight.device)
+ state.reset_grads()
+
+ def get_delta_weight(self, adapter) -> torch.Tensor:
+ """
+ Compute the delta weight for the given adapter.
+
+ Args:
+ adapter (str): The name of the adapter for which the delta weight should be computed.
+
+ Returns:
+ torch.Tensor: The computed delta weight for the VeRA adapter.
+
+ Note:
+ This method implements the VeRA-specific weight update. Unlike LoRA, VeRA uses shared projection
+ matrices (vera_A and vera_B) across all layers, along with per-layer trainable parameters (lambda_d and
+ lambda_b).
+ """
+ # Retrieve shared projection matrices
+ vera_A = self.vera_A[adapter]
+ vera_B = self.vera_B[adapter]
+
+ # Retrieve per-layer trainable parameters
+ device = vera_B.device
+ dtype = vera_B.dtype
+
+ # In case users wants to merge the adapter weights that are in
+ # (b)float16 while being on CPU, we need to cast the weights to float32, perform the merge and then cast back to
+ # (b)float16 because some CPUs have slow bf16/fp16 matmuls.
+ cast_to_fp32 = device.type == "cpu" and (dtype == torch.float16 or dtype == torch.bfloat16)
+
+ lambda_d = self.vera_lambda_d[adapter]
+ lambda_b = self.vera_lambda_b[adapter]
+
+ if cast_to_fp32:
+ vera_A = vera_A.float()
+ vera_B = vera_B.float()
+ lambda_d = lambda_d.float()
+ lambda_b = lambda_b.float()
+
+ sliced_A = vera_A[:, : self.in_features].to(lambda_d.device)
+ sliced_B = vera_B[: self.out_features, :].to(lambda_d.device)
+ lambda_b = lambda_b.unsqueeze(-1)
+ lambda_d = lambda_d.unsqueeze(-1)
+
+ # VeRA-specific computation:
+ # 1. Apply lambda_d to the input projection (vera_A)
+ # 2. Apply lambda_b to the output projection (vera_B)
+ # 3. Compute the outer product of the scaled projections
+ output_tensor = transpose((lambda_b * sliced_B) @ (lambda_d * sliced_A), self.fan_in_fan_out)
+
+ if cast_to_fp32:
+ output_tensor = output_tensor.to(dtype=dtype)
+
+ return output_tensor
+
+ def forward(self, x: torch.Tensor, *args, **kwargs) -> torch.Tensor:
+ """
+ Perform the forward pass using the VeRA adapter.
+
+ Args:
+ x (torch.Tensor): Input tensor.
+
+ Returns:
+ torch.Tensor: Output tensor after applying the VeRA adaptation.
+
+ Note:
+ This method implements the VeRA-specific forward pass. It applies the shared projections (vera_A and
+ vera_B) along with the per-layer trainable parameters (lambda_d and lambda_b) to compute the adapter
+ output.
+ """
+ if self.disable_adapters:
+ if self.merged:
+ self.unmerge()
+ result = self.base_layer(x, *args, **kwargs)
+ elif self.merged:
+ result = self.base_layer(x, *args, **kwargs)
+ else:
+ result = self.base_layer(x, *args, **kwargs)
+ for active_adapter in self.active_adapters:
+ if active_adapter not in self.vera_lambda_d.keys():
+ continue
+
+ lambda_d = self.vera_lambda_d[active_adapter]
+ lambda_b = self.vera_lambda_b[active_adapter]
+
+ vera_A = self.vera_A[active_adapter]
+ vera_B = self.vera_B[active_adapter]
+
+ dropout = self.vera_dropout[active_adapter]
+
+ requires_conversion = not torch.is_autocast_enabled()
+ if requires_conversion:
+ expected_dtype = result.dtype
+ compute_dtype = lambda_d.dtype
+ if x.dtype != compute_dtype:
+ x = x.to(compute_dtype)
+
+ sliced_A = vera_A[:, : self.in_features].to(x.device)
+ sliced_B = vera_B[: self.out_features, :].to(x.device)
+
+ x_temp = dropout(x.to(lambda_d.dtype))
+
+ adapter_output = lambda_b * torch.nn.functional.linear(
+ lambda_d * torch.nn.functional.linear(x_temp, sliced_A), sliced_B
+ )
+
+ if requires_conversion:
+ adapter_output = adapter_output.to(expected_dtype)
+
+ result = result + adapter_output
+
+ # Ensure the output tensor has the same dtype as the input tensor
+ return result.to(x.dtype)
+
+ def __repr__(self) -> str:
+ rep = super().__repr__()
+ return "vera." + rep
+
+
+if is_bnb_4bit_available():
+
+ class Linear4bit(torch.nn.Module, VeraLayer):
+ def __init__(
+ self,
+ base_layer: torch.nn.Module,
+ adapter_name: str,
+ vera_A,
+ vera_B,
+ r: int = 0,
+ vera_dropout: float = 0.0,
+ fan_in_fan_out: bool = False,
+ init_weights: bool = True,
+ d_initial: float = 0.1,
+ **kwargs,
+ ) -> None:
+ super().__init__()
+ VeraLayer.__init__(self, base_layer)
+ self.fan_in_fan_out = fan_in_fan_out
+
+ self._active_adapter = adapter_name
+ self.update_layer(
+ adapter_name,
+ vera_A,
+ vera_B,
+ r,
+ vera_dropout=vera_dropout,
+ init_weights=init_weights,
+ d_initial=d_initial,
+ )
+
+ def merge(self, safe_merge: bool = False, adapter_names: Optional[list[str]] = None) -> None:
+ if self.merged:
+ warnings.warn(
+ f"Already following adapters were merged {','.join(self.merged_adapters)}. "
+ f"You are now additionally merging {','.join(self.active_adapters)}."
+ )
+
+ adapter_names = check_adapters_to_merge(self, adapter_names)
+ if not adapter_names:
+ return
+
+ for active_adapter in adapter_names:
+ if active_adapter not in self.vera_lambda_d.keys():
+ continue
+
+ warnings.warn(
+ "Merge vera module to 4-bit linear may get different generations due to rounding errors."
+ )
+ vera_data = self.get_delta_weight(active_adapter)
+
+ weight = self.get_base_layer().weight
+ kwargs = weight.__dict__
+ # torch.compile can introduce attributes preceded by '_', remove them
+ kwargs = {k: v for k, v in kwargs.items() if not k.startswith("_")}
+ w_data = bnb.functional.dequantize_4bit(weight.data, weight.quant_state) + vera_data
+
+ if safe_merge and not torch.isfinite(w_data).all():
+ raise ValueError(
+ f"NaNs detected in the merged weights. The adapter {active_adapter} seems to be broken"
+ )
+
+ self.get_base_layer().weight = bnb.nn.Params4bit(w_data.to("cpu"), requires_grad=False, **kwargs).to(
+ weight.device
+ )
+ self.merged_adapters.append(active_adapter)
+
+ def unmerge(self) -> None:
+ if not self.merged:
+ warnings.warn("Already unmerged. Nothing to do")
+ return
+
+ while len(self.merged_adapters) > 0:
+ active_adapter = self.merged_adapters.pop()
+ if active_adapter not in self.vera_lambda_d.keys():
+ continue
+ warnings.warn(
+ "Unmerge vera module to 4-bit linear may get different generations due to rounding errors."
+ )
+ vera_data = self.get_delta_weight(active_adapter)
+
+ weight = self.get_base_layer().weight
+ kwargs = weight.__dict__
+ w_data = bnb.functional.dequantize_4bit(weight.data, weight.quant_state) - vera_data
+
+ self.get_base_layer().weight = bnb.nn.Params4bit(w_data.to("cpu"), requires_grad=False, **kwargs).to(
+ weight.device
+ )
+
+ def get_delta_weight(self, adapter) -> torch.Tensor:
+ vera_A = self.vera_A[adapter]
+ vera_B = self.vera_B[adapter]
+
+ device = vera_B.device
+ dtype = vera_B.dtype
+
+ cast_to_fp32 = device.type == "cpu" and (dtype == torch.float16 or dtype == torch.bfloat16)
+
+ lambda_d = self.vera_lambda_d[adapter]
+ lambda_b = self.vera_lambda_b[adapter]
+
+ if cast_to_fp32:
+ vera_A = vera_A.float()
+ vera_B = vera_B.float()
+ lambda_d = lambda_d.float()
+ lambda_b = lambda_b.float()
+
+ sliced_A = vera_A[:, : self.in_features].to(lambda_d.device)
+ sliced_B = vera_B[: self.out_features, :].to(lambda_d.device)
+ lambda_b = lambda_b.unsqueeze(-1)
+ lambda_d = lambda_d.unsqueeze(-1)
+
+ output_tensor = transpose((lambda_b * sliced_B) @ (lambda_d * sliced_A), self.fan_in_fan_out)
+
+ if cast_to_fp32:
+ output_tensor = output_tensor.to(dtype=dtype)
+
+ return output_tensor
+
+ def forward(self, x: torch.Tensor, *args, **kwargs) -> torch.Tensor:
+ if self.disable_adapters:
+ if self.merged:
+ self.unmerge()
+ result = self.base_layer(x, *args, **kwargs)
+ elif self.merged:
+ result = self.base_layer(x, *args, **kwargs)
+ else:
+ result = self.base_layer(x, *args, **kwargs)
+ result = result.clone()
+ for active_adapter in self.active_adapters:
+ if active_adapter not in self.vera_lambda_d.keys():
+ continue
+
+ lambda_d = self.vera_lambda_d[active_adapter]
+ lambda_b = self.vera_lambda_b[active_adapter]
+
+ vera_A = self.vera_A[active_adapter]
+ vera_B = self.vera_B[active_adapter]
+
+ dropout = self.vera_dropout[active_adapter]
+
+ requires_conversion = not torch.is_autocast_enabled()
+ if requires_conversion:
+ expected_dtype = result.dtype
+ compute_dtype = lambda_d.dtype
+ if x.dtype != compute_dtype:
+ x = x.to(compute_dtype)
+
+ sliced_A = vera_A[:, : self.in_features].to(x.device)
+ sliced_B = vera_B[: self.out_features, :].to(x.device)
+
+ x_temp = dropout(x.to(lambda_d.dtype))
+
+ adapter_output = lambda_b * torch.nn.functional.linear(
+ lambda_d * torch.nn.functional.linear(x_temp, sliced_A), sliced_B
+ )
+
+ if requires_conversion:
+ adapter_output = adapter_output.to(expected_dtype)
+
+ result = result + adapter_output
+
+ # Ensure the output tensor has the same dtype as the input tensor
+ return result.to(x.dtype)
+
+ def __repr__(self) -> str:
+ rep = super().__repr__()
+ return "vera." + rep
diff --git a/peft/src/peft/tuners/vera/config.py b/peft/src/peft/tuners/vera/config.py
new file mode 100644
index 0000000000000000000000000000000000000000..df880b7af0df6b92717e339f131474340e2ade3c
--- /dev/null
+++ b/peft/src/peft/tuners/vera/config.py
@@ -0,0 +1,162 @@
+# Copyright 2023-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+from __future__ import annotations
+
+import warnings
+from dataclasses import dataclass, field
+from typing import Optional, Union
+
+from peft.config import PeftConfig
+from peft.utils import PeftType
+
+
+@dataclass
+class VeraConfig(PeftConfig):
+ """
+ This is the configuration class to store the configuration of a [`VeraModel`].
+
+ Paper: https://huggingface.co/papers/2310.11454.
+
+ Args:
+ r (`int`, *optional*, defaults to `256`):
+ VeRA parameter dimension ("rank"). Choose higher values than LoRA ranks here, since VeRA uses far fewer
+ parameters than LoRA (see Table 1).
+ target_modules (`Union[List[str], str]`):
+ The names of the modules to apply Vera to. Only linear layers are supported.
+ projection_prng_key (`int`):
+ Vera PRNG init key. Used for initialising vera_A and vera_B for new models or when loading a checkpoint
+ that did not include these projections. Defaults to `0`.
+ save_projection (`bool`):
+ Whether to save the vera_A / vera_B projections in the state dict alongside per layer lambda_b / lambda_d
+ weights. This will increase the size of the checkpoint, but guarantee that we can reload the checkpoint on
+ all system configurations. Defaults to `True`.
+ vera_dropout (`float`):
+ The dropout probability for Vera layers.
+ d_initial (`float`, *optional*, defaults to `0.1`):
+ Initial init value for `vera_lambda_d` vector used when initializing the VeRA parameters. Small values
+ (<=0.1) are recommended (see Table 6c in the paper).
+ fan_in_fan_out (`bool`):
+ Set this to True if the layer to replace stores weight like (fan_in, fan_out). For example, gpt-2 uses
+ `Conv1D` which stores weights like (fan_in, fan_out) and hence this should be set to `True`.
+ bias (`str`):
+ Bias type for Vera. Can be 'none', 'all' or 'vera_only'. If 'all' or 'vera_only', the corresponding biases
+ will be updated during training. Be aware that this means that, even when disabling the adapters, the model
+ will not produce the same output as the base model would have without adaptation.
+ modules_to_save (`List[str]`):
+ List of modules apart from Vera layers to be set as trainable and saved in the final checkpoint.
+ init_weights (`bool`):
+ Whether to initialize the weights of the Vera layers with their default initialization. Don't change this
+ setting, except if you know exactly what you're doing.
+ layers_to_transform (`Union[List[int],int]`):
+ The layer indexes to transform, if this argument is specified, it will apply the Vera transformations on
+ the layer indexes that are specified in this list. If a single integer is passed, it will apply the Vera
+ transformations on the layer at this index.
+ layers_pattern (`Optional[Union[List[str], str]]`):
+ The layer pattern name, used only if `layers_to_transform` is different from `None`. This should target the
+ `nn.ModuleList` of the model, which is often called `'layers'` or `'h'`.
+ """
+
+ r: int = field(default=256, metadata={"help": "Vera attention dimension"})
+
+ target_modules: Optional[Union[list[str], str]] = field(
+ default=None,
+ metadata={
+ "help": (
+ "List of module names or regex expression of the module names to replace with Vera."
+ "For example, ['q', 'v'] or '.*decoder.*(SelfAttention|EncDecAttention).*(q|v)$'. "
+ "Only linear layers are supported."
+ )
+ },
+ )
+ projection_prng_key: int = field(
+ default=0,
+ metadata={
+ "help": (
+ "Vera PRNG init key. Used for initialising vera_A and vera_B for new models or when loading a "
+ "checkpoint that did not include these projections."
+ )
+ },
+ )
+ save_projection: bool = field(
+ default=True,
+ metadata={
+ "help": (
+ "Whether to save the vera_A / vera_B projections in the state dict alongside per layer lambda_b / "
+ "lambda_d weights. This will increase the size of the checkpoint, but guarantee that we can reload "
+ "the checkpoint on all system configurations."
+ )
+ },
+ )
+ vera_dropout: float = field(default=0.0, metadata={"help": "Vera dropout"})
+ d_initial: float = field(default=0.1, metadata={"help": "Initial init value for d vector."})
+ fan_in_fan_out: bool = field(
+ default=False,
+ metadata={"help": "Set this to True if the layer to replace stores weight like (fan_in, fan_out)"},
+ )
+ bias: str = field(default="none", metadata={"help": "Bias type for Vera. Can be 'none', 'all' or 'vera_only'"})
+ modules_to_save: Optional[list[str]] = field(
+ default=None,
+ metadata={
+ "help": (
+ "List of modules apart from Vera layers to be set as trainable and saved in the final checkpoint. For"
+ " example, in Sequence Classification or Token Classification tasks, the final layer"
+ " `classifier/score` are randomly initialized and as such need to be trainable and saved."
+ )
+ },
+ )
+ init_weights: bool = field(
+ default=True,
+ metadata={
+ "help": (
+ "Whether to initialize the weights of the Vera layers with their default initialization. Don't change "
+ "this setting, except if you know exactly what you're doing."
+ ),
+ },
+ )
+ layers_to_transform: Optional[Union[list[int], int]] = field(
+ default=None,
+ metadata={
+ "help": (
+ "The layer indexes to transform, is this argument is specified, PEFT will transform only the layers"
+ " indexes that are specified inside this list. If a single integer is passed, PEFT will transform only"
+ " the layer at this index."
+ )
+ },
+ )
+ layers_pattern: Optional[Union[list[str], str]] = field(
+ default=None,
+ metadata={
+ "help": (
+ "The layer pattern name, used only if `layers_to_transform` is different to None and if the layer "
+ "pattern is not in the common layers pattern. This should target the `nn.ModuleList` of the "
+ "model, which is often called `'layers'` or `'h'`."
+ )
+ },
+ )
+
+ def __post_init__(self):
+ super().__post_init__()
+ self.peft_type = PeftType.VERA
+ self.target_modules = (
+ set(self.target_modules) if isinstance(self.target_modules, list) else self.target_modules
+ )
+ # check for layers_to_transform and layers_pattern
+ if self.layers_pattern and not self.layers_to_transform:
+ raise ValueError("When `layers_pattern` is specified, `layers_to_transform` must also be specified. ")
+ if not self.save_projection:
+ warnings.warn(
+ "Specified to not save vera_A and vera_B within the state dictionary, instead they will be restored "
+ "using the PRNG key store in `config.projection_prng_key`. Consider setting `config.save_projection` "
+ "to `True` to guarantee restoring the checkpoint correctly on all system configurations."
+ )
diff --git a/peft/src/peft/tuners/vera/layer.py b/peft/src/peft/tuners/vera/layer.py
new file mode 100644
index 0000000000000000000000000000000000000000..7559eea49597c6a222beb8ec65c220ed39fe3f58
--- /dev/null
+++ b/peft/src/peft/tuners/vera/layer.py
@@ -0,0 +1,291 @@
+# Copyright 2023-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+import warnings
+from typing import Optional
+
+import torch
+import torch.nn as nn
+import torch.nn.functional as F
+from transformers.pytorch_utils import Conv1D
+
+from peft.tuners.tuners_utils import BaseTunerLayer, check_adapters_to_merge
+from peft.utils.other import transpose
+
+from .._buffer_dict import BufferDict
+
+
+class VeraLayer(BaseTunerLayer):
+ # List all names of layers that may contain adapter weights
+ adapter_layer_names = ("vera_lambda_b", "vera_lambda_d")
+ other_param_names = ("vera_A", "vera_B")
+
+ def __init__(self, base_layer: nn.Module, **kwargs):
+ self.base_layer = base_layer
+ self.r = {}
+ self.vera_dropout = nn.ModuleDict({})
+
+ # For storing vector scale
+ self.vera_lambda_b = nn.ParameterDict({})
+ self.vera_lambda_d = nn.ParameterDict({})
+
+ # Stores a reference to the vera_A/B BufferDict.
+ # Set to `None` otherwise to avoid computation with random weights
+ self.vera_A: Optional[BufferDict] = None
+ self.vera_B: Optional[BufferDict] = None
+
+ # Mark the weight as unmerged
+ self._disable_adapters = False
+ self.merged_adapters = []
+
+ base_layer = self.get_base_layer()
+ if isinstance(base_layer, nn.Linear):
+ in_features, out_features = base_layer.in_features, base_layer.out_features
+ elif isinstance(base_layer, Conv1D):
+ in_features, out_features = (
+ base_layer.weight.ds_shape if hasattr(base_layer.weight, "ds_shape") else base_layer.weight.shape
+ )
+
+ self.in_features = in_features
+ self.out_features = out_features
+ self.kwargs = kwargs
+
+ @property
+ def merged(self) -> bool:
+ return bool(self.merged_adapters)
+
+ def update_layer(
+ self,
+ adapter_name,
+ vera_A: BufferDict,
+ vera_B: BufferDict,
+ r,
+ vera_dropout,
+ init_weights,
+ d_initial: float = 0.1,
+ inference_mode: bool = False,
+ **kwargs,
+ ):
+ if r <= 0:
+ raise ValueError(f"`r` should be a positive integer value but the value passed is {r}")
+ self.r[adapter_name] = r
+ if vera_dropout > 0.0:
+ vera_dropout_layer = nn.Dropout(p=vera_dropout)
+ else:
+ vera_dropout_layer = nn.Identity()
+
+ self.vera_dropout.update(nn.ModuleDict({adapter_name: vera_dropout_layer}))
+ # Actual trainable parameters
+ self.vera_lambda_b[adapter_name] = nn.Parameter(torch.ones(self.out_features), requires_grad=True)
+ self.vera_lambda_d[adapter_name] = nn.Parameter(torch.randn(r), requires_grad=True)
+
+ # non trainable references to vera_A/B buffers
+ self.vera_A = vera_A
+ self.vera_B = vera_B
+ if adapter_name not in vera_A:
+ # This means that this is not the first VeRA adapter. We have to add an entry in the dict for this adapter.
+ if len(self.vera_A) < 1:
+ raise ValueError(
+ "The `vera_A` and `vera_B` buffers are empty. This should not happen. Please report this issue."
+ )
+ # we can take any of the existing adapter's parameters, as they should all be identical
+ vera_A_param = list(self.vera_A.values())[0]
+ vera_B_param = list(self.vera_B.values())[0]
+
+ error_tmpl = (
+ "{} has a size of {} but {} or greater is required; this probably happened because an additional VeRA "
+ "adapter was added after the first one with incompatible shapes."
+ )
+ # check input size
+ if vera_A_param.shape[1] < self.in_features:
+ raise ValueError(error_tmpl.format("vera_A", vera_A_param.shape[1], self.in_features))
+ # check output size
+ if vera_B_param.shape[0] < self.out_features:
+ raise ValueError(error_tmpl.format("vera_B", vera_B_param.shape[0], self.out_features))
+ # check r
+ error_tmpl = (
+ "{} has a size of {} but {} or greater is required; this probably happened because an additional VeRA "
+ "adapter with a lower rank was added after the first one; loading the adapters "
+ "in reverse order may solve this."
+ )
+ if vera_A_param.shape[0] < self.r[adapter_name]:
+ raise ValueError(error_tmpl.format("vera_A", vera_A_param.shape[0], self.r[adapter_name]))
+ if vera_B_param.shape[1] < self.r[adapter_name]:
+ raise ValueError(error_tmpl.format("vera_B", vera_B_param.shape[1], self.r[adapter_name]))
+
+ self.vera_A[adapter_name] = vera_A_param
+ self.vera_B[adapter_name] = vera_B_param
+
+ if init_weights:
+ self.reset_vera_parameters(adapter_name, d_initial=d_initial)
+
+ self._move_adapter_to_device_of_base_layer(adapter_name)
+ self.set_adapter(self.active_adapters, inference_mode=inference_mode)
+
+ def reset_vera_parameters(self, adapter_name, d_initial: float = 0.1):
+ if adapter_name in self.vera_lambda_d.keys():
+ with torch.no_grad():
+ nn.init.zeros_(self.vera_lambda_d[adapter_name]).fill_(d_initial)
+ nn.init.zeros_(self.vera_lambda_b[adapter_name])
+
+
+class Linear(nn.Linear, VeraLayer):
+ # Vera implemented in a dense layer
+ def __init__(
+ self,
+ base_layer,
+ vera_A: BufferDict,
+ vera_B: BufferDict,
+ adapter_name: str,
+ r: int = 0,
+ vera_dropout: float = 0.0,
+ fan_in_fan_out: bool = False, # Set this to True if the layer to replace stores weight like (fan_in, fan_out)
+ is_target_conv_1d_layer: bool = False,
+ init_weights: bool = True,
+ d_initial: float = 0.1,
+ **kwargs,
+ ) -> None:
+ # this gets the init from nn.Linear's super perspective, i.e. nn.Module.__init__, which should always be called
+ super(nn.Linear, self).__init__()
+ VeraLayer.__init__(self, base_layer, **kwargs)
+ self.fan_in_fan_out = fan_in_fan_out
+
+ self._active_adapter = adapter_name
+ self.update_layer(adapter_name, vera_A, vera_B, r, vera_dropout, init_weights, d_initial=d_initial)
+ self.is_target_conv_1d_layer = is_target_conv_1d_layer
+
+ def merge(self, safe_merge: bool = False, adapter_names: Optional[list[str]] = None) -> None:
+ """
+ Merge the active adapter weights into the base weights
+
+ Args:
+ safe_merge (`bool`, *optional*):
+ If True, the merge operation will be performed in a copy of the original weights and check for NaNs
+ before merging the weights. This is useful if you want to check if the merge operation will produce
+ NaNs. Defaults to `False`.
+ adapter_names (`List[str]`, *optional*):
+ The list of adapter names that should be merged. If None, all active adapters will be merged. Defaults
+ to `None`.
+ """
+ adapter_names = check_adapters_to_merge(self, adapter_names)
+ if not adapter_names:
+ # no adapter to merge
+ return
+
+ for active_adapter in adapter_names:
+ if active_adapter in self.vera_lambda_d.keys():
+ base_layer = self.get_base_layer()
+ if safe_merge:
+ # Note that safe_merge will be slower than the normal merge
+ # because of the copy operation.
+ orig_weights = base_layer.weight.data.clone()
+
+ orig_weights += self.get_delta_weight(active_adapter)
+
+ if not torch.isfinite(orig_weights).all():
+ raise ValueError(
+ f"NaNs detected in the merged weights. The adapter {active_adapter} seems to be broken"
+ )
+
+ base_layer.weight.data = orig_weights
+ else:
+ base_layer.weight.data += self.get_delta_weight(active_adapter)
+ self.merged_adapters.append(active_adapter)
+
+ def unmerge(self) -> None:
+ if not self.merged:
+ warnings.warn("Already unmerged. Nothing to do.")
+ return
+
+ while len(self.merged_adapters) > 0:
+ active_adapter = self.merged_adapters.pop()
+ if active_adapter in self.vera_lambda_d.keys():
+ self.get_base_layer().weight.data -= self.get_delta_weight(active_adapter)
+
+ def get_delta_weight(self, adapter) -> torch.Tensor:
+ """
+ Compute the delta weight for the given adapter.
+
+ Args:
+ adapter (str):
+ The name of the adapter for which the delta weight should be computed.
+ """
+ vera_A = self.vera_A[adapter]
+ vera_B = self.vera_B[adapter]
+
+ device = vera_B.device
+ dtype = vera_B.dtype
+
+ # In case users wants to merge the adapter weights that are in
+ # (b)float16 while being on CPU, we need to cast the weights to float32, perform the merge and then cast back to
+ # (b)float16 because some CPUs have slow bf16/fp16 matmuls.
+ cast_to_fp32 = device.type == "cpu" and (dtype == torch.float16 or dtype == torch.bfloat16)
+
+ lambda_d = self.vera_lambda_d[adapter]
+ lambda_b = self.vera_lambda_b[adapter]
+
+ if cast_to_fp32:
+ vera_A = vera_A.float()
+ vera_B = vera_B.float()
+ lambda_d = lambda_d.float()
+ lambda_b = lambda_b.float()
+
+ sliced_A = vera_A[:, : self.in_features].to(lambda_d.device)
+ sliced_B = vera_B[: self.out_features, :].to(lambda_d.device)
+ lambda_b = lambda_b.unsqueeze(-1)
+ lambda_d = lambda_d.unsqueeze(-1)
+ output_tensor = transpose((lambda_b * sliced_B) @ (lambda_d * sliced_A), self.fan_in_fan_out)
+
+ if cast_to_fp32:
+ output_tensor = output_tensor.to(dtype=dtype)
+
+ return output_tensor
+
+ def forward(self, x: torch.Tensor, *args, **kwargs) -> torch.Tensor:
+ previous_dtype = x.dtype
+
+ if self.disable_adapters:
+ if self.merged:
+ self.unmerge()
+ result = self.base_layer(x, *args, **kwargs)
+ elif self.merged:
+ result = self.base_layer(x, *args, **kwargs)
+ else:
+ result = self.base_layer(x, *args, **kwargs)
+ for active_adapter in self.active_adapters:
+ if active_adapter not in self.vera_lambda_d.keys():
+ continue
+
+ lambda_d = self.vera_lambda_d[active_adapter]
+ lambda_b = self.vera_lambda_b[active_adapter]
+
+ vera_A = self.vera_A[active_adapter]
+ vera_B = self.vera_B[active_adapter]
+
+ # As adapted layers may have different shapes and VeRA contains a single shared pair of A and B matrices,
+ # we initialize these matrices with the largest required size for each dimension.
+ # During the forward pass, required submatrices are sliced out from the shared vera_A and vera_B.
+ sliced_A = vera_A[:, : self.in_features].to(x.device)
+ sliced_B = vera_B[: self.out_features, :].to(x.device)
+
+ dropout = self.vera_dropout[active_adapter]
+ x = x.to(lambda_d.dtype)
+ result = result + lambda_b * F.linear(lambda_d * F.linear(dropout(x), sliced_A), sliced_B)
+
+ result = result.to(previous_dtype)
+ return result
+
+ def __repr__(self) -> str:
+ rep = super().__repr__()
+ return "vera." + rep
diff --git a/peft/src/peft/tuners/vera/model.py b/peft/src/peft/tuners/vera/model.py
new file mode 100644
index 0000000000000000000000000000000000000000..f85d84e259a008bdc9dd709e810f881815450e7d
--- /dev/null
+++ b/peft/src/peft/tuners/vera/model.py
@@ -0,0 +1,294 @@
+# Copyright 2023-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+from __future__ import annotations
+
+import math
+import warnings
+from typing import Union
+
+import torch
+import torch.nn as nn
+from torch.nn.init import _calculate_correct_fan
+from transformers.pytorch_utils import Conv1D
+
+from peft.import_utils import is_bnb_4bit_available, is_bnb_available
+from peft.tuners.tuners_utils import BaseTuner, BaseTunerLayer
+from peft.utils import (
+ TRANSFORMERS_MODELS_TO_VERA_TARGET_MODULES_MAPPING,
+)
+
+from .._buffer_dict import BufferDict
+from ..tuners_utils import _maybe_include_all_linear_layers
+from .config import VeraConfig
+from .layer import Linear, VeraLayer
+
+
+def _kaiming_init(
+ tensor_or_shape: Union[torch.Tensor, tuple[int, ...]],
+ generator: torch.Generator,
+) -> torch.Tensor:
+ """
+ Kaiming Uniform Initialisation adapted to accept a `torch.Generator` object for PRNG.
+
+ Args:
+ tensor_or_shape (`Union[torch.Tensor, tuple[int, ...]]`):
+ Tensor to initialise, or shape of new tensor to create and then initialise.
+ generator: (`torch.Generator`):
+ Generator object that manages the state of the PRNG algorithm in use.
+
+ Returns:
+ `torch.Tensor`: The initialised tensor.
+ """
+ if isinstance(tensor_or_shape, tuple):
+ tensor = torch.empty(tensor_or_shape)
+ else:
+ tensor = tensor_or_shape
+ fan = _calculate_correct_fan(tensor, "fan_in")
+ gain = math.sqrt(2)
+ std = gain / math.sqrt(fan)
+ bound = math.sqrt(3.0) * std
+
+ with torch.no_grad():
+ return tensor.uniform_(-bound, bound, generator=generator)
+
+
+class VeraModel(BaseTuner):
+ """
+ Creates Vector-based Random Matrix Adaptation (Vera) model from a pretrained transformers model.
+
+ Args:
+ model ([`~transformers.PreTrainedModel`]): The model to be adapted.
+ config ([`VeraConfig`]): The configuration of the Vera model.
+ adapter_name (`str`): The name of the adapter, defaults to `"default"`.
+ low_cpu_mem_usage (`bool`, `optional`, defaults to `False`):
+ Create empty adapter weights on meta device. Useful to speed up the loading process.
+
+ Returns:
+ `torch.nn.Module`: The Vera model.
+
+ Example:
+
+ ```py
+ >>> from transformers import AutoModelForCausalLM
+ >>> from peft import VeraConfig, get_peft_model
+
+ >>> base_model = AutoModelForCausalLM.from_pretrained("facebook/opt-125m")
+ >>> config = VeraConfig(r=128)
+ >>> model = get_peft_model(base_model, config)
+ ```
+
+ **Attributes**:
+ - **model** ([`~transformers.PreTrainedModel`]) -- The model to be adapted.
+ - **peft_config** ([`VeraConfig`]): The configuration of the Vera model.
+ """
+
+ prefix: str = "vera_lambda_"
+ tuner_layer_cls = VeraLayer
+ target_module_mapping = TRANSFORMERS_MODELS_TO_VERA_TARGET_MODULES_MAPPING
+
+ def _find_dim(self, config) -> tuple[int, int]:
+ """
+ Finds the largest input and output dimensions across linear layers that have been wrapped with VeRA.
+
+ This will be used for determining the size of the shared vera_A and vera_B matrices.
+ """
+ model_config = self.get_model_config(self.model)
+
+ peft_config = self._prepare_adapter_config(config, model_config)
+ peft_config = _maybe_include_all_linear_layers(peft_config, self.model)
+
+ largest_shape = None
+ for key, module in self.model.named_modules():
+ if not self._check_target_module_exists(peft_config, key):
+ continue
+
+ if isinstance(module, nn.Linear):
+ module_shape = module.out_features, module.in_features
+ elif isinstance(module, Conv1D):
+ module_shape = module.weight.ds_shape if hasattr(module.weight, "ds_shape") else module.weight.shape
+ module_shape = module_shape[::-1]
+ else:
+ continue
+
+ if largest_shape is None:
+ largest_shape = module_shape
+ continue
+
+ if module_shape != largest_shape:
+ largest_shape = tuple(max(a, b) for a, b in zip(largest_shape, module_shape))
+
+ if largest_shape is None:
+ msg = "No layers types compatible with VeRA were found. Please check `peft_config.target_modules`."
+ raise ValueError(msg)
+
+ return largest_shape
+
+ def _init_vera_A_vera_B(self, config: VeraConfig, adapter_name: str) -> None:
+ linear_out_dim, linear_in_dim = self._find_dim(config)
+
+ # use of persistent to exclude vera_A and vera_B from the state dict if we choose not to save them.
+ self.vera_A = BufferDict({}, persistent=config.save_projection)
+ self.vera_B = BufferDict({}, persistent=config.save_projection)
+
+ # deterministic init of vera_A and vera_B if we know the key
+ generator = torch.Generator(device="cpu").manual_seed(config.projection_prng_key)
+ vera_A = _kaiming_init((config.r, linear_in_dim), generator=generator)
+ vera_B = _kaiming_init((linear_out_dim, config.r), generator=generator)
+
+ self.vera_A[adapter_name] = vera_A
+ self.vera_B[adapter_name] = vera_B
+
+ def _pre_injection_hook(self, model: nn.Module, config: VeraConfig, adapter_name: str) -> None:
+ self._init_vera_A_vera_B(config, adapter_name)
+
+ def _check_new_adapter_config(self, config: VeraConfig) -> None:
+ """
+ A helper method to check the config when a new adapter is being added.
+
+ Raise a ValueError if there is something wrong with the config or if it conflicts with existing adapters.
+
+ """
+ super()._check_new_adapter_config(config)
+
+ for existing_config in self.peft_config.values():
+ if existing_config is config:
+ # skip the current config
+ continue
+
+ if existing_config.projection_prng_key != config.projection_prng_key:
+ raise ValueError(
+ f"Vera PRNG initialisation key must be the same for all adapters. Got {config.projection_prng_key=} but "
+ f"previous config had {existing_config.projection_prng_key}."
+ )
+
+ save_project_unique_values = sorted({config.save_projection for config in self.peft_config.values()})
+ if len(save_project_unique_values) > 1:
+ raise ValueError(
+ "VeRA projection weights must be saved for all adapters or none, but got multiple different values: "
+ f"{save_project_unique_values}"
+ )
+
+ def _create_and_replace(
+ self,
+ vera_config,
+ adapter_name,
+ target,
+ target_name,
+ parent,
+ current_key,
+ **optional_kwargs,
+ ):
+ if current_key is None:
+ raise ValueError("Current Key shouldn't be `None`")
+
+ r = vera_config.r
+ bias = hasattr(target, "bias") and target.bias is not None
+ kwargs = {
+ "r": r,
+ "vera_dropout": vera_config.vera_dropout,
+ "fan_in_fan_out": vera_config.fan_in_fan_out,
+ "init_weights": vera_config.init_weights,
+ "loaded_in_8bit": getattr(self.model, "is_loaded_in_8bit", False),
+ "loaded_in_4bit": getattr(self.model, "is_loaded_in_4bit", False),
+ }
+ kwargs["bias"] = bias
+
+ if isinstance(target, Linear):
+ target.update_layer(
+ adapter_name,
+ self.vera_A,
+ self.vera_B,
+ r,
+ vera_config.vera_dropout,
+ vera_config.init_weights,
+ d_initial=vera_config.d_initial,
+ )
+ else:
+ new_module = self._create_new_module(vera_config, self.vera_A, self.vera_B, adapter_name, target, **kwargs)
+ if adapter_name not in self.active_adapter:
+ # adding an additional adapter: it is not automatically trainable
+ new_module.requires_grad_(False)
+ self._replace_module(parent, target_name, new_module, target)
+
+ @staticmethod
+ def _create_new_module(vera_config, vera_A, vera_B, adapter_name, target, **kwargs):
+ # avoid eager bnb import
+ if is_bnb_available():
+ import bitsandbytes as bnb
+
+ from .bnb import Linear8bitLt
+
+ if is_bnb_4bit_available():
+ from .bnb import Linear4bit
+
+ bias = kwargs.pop("bias", False)
+ loaded_in_8bit = kwargs.get("loaded_in_8bit", False)
+ loaded_in_4bit = kwargs.get("loaded_in_4bit", False)
+
+ if isinstance(target, BaseTunerLayer):
+ target_base_layer = target.get_base_layer()
+ else:
+ target_base_layer = target
+
+ if loaded_in_8bit and isinstance(target_base_layer, bnb.nn.Linear8bitLt):
+ eightbit_kwargs = kwargs.copy()
+ eightbit_kwargs.update(
+ {
+ "has_fp16_weights": target_base_layer.state.has_fp16_weights,
+ "threshold": target_base_layer.state.threshold,
+ "index": target_base_layer.index,
+ }
+ )
+ return Linear8bitLt(target, adapter_name, vera_A, vera_B, **eightbit_kwargs)
+ elif loaded_in_4bit and isinstance(target_base_layer, bnb.nn.Linear4bit):
+ fourbit_kwargs = kwargs.copy()
+ fourbit_kwargs.update(
+ {
+ "compute_dtype": target_base_layer.compute_dtype,
+ "compress_statistics": target_base_layer.weight.compress_statistics,
+ "quant_type": target_base_layer.weight.quant_type,
+ }
+ )
+ return Linear4bit(target, adapter_name, vera_A, vera_B, **fourbit_kwargs)
+ elif isinstance(target_base_layer, torch.nn.Linear):
+ if kwargs["fan_in_fan_out"]:
+ warnings.warn(
+ "fan_in_fan_out is set to True but the target module is `torch.nn.Linear`. "
+ "Setting fan_in_fan_out to False."
+ )
+ kwargs["fan_in_fan_out"] = vera_config.fan_in_fan_out = False
+ elif isinstance(target_base_layer, Conv1D):
+ kwargs["is_target_conv_1d_layer"] = True
+ if not kwargs["fan_in_fan_out"]:
+ warnings.warn(
+ "fan_in_fan_out is set to False but the target module is `Conv1D`. Setting fan_in_fan_out to True."
+ )
+ kwargs["fan_in_fan_out"] = vera_config.fan_in_fan_out = True
+ else:
+ raise ValueError(
+ f"Target module {target} is not supported. Currently, only the following modules are supported: "
+ "`torch.nn.Linear`, `transformers.pytorch_utils.Conv1D`."
+ )
+ new_module = Linear(
+ target,
+ vera_A,
+ vera_B,
+ adapter_name,
+ bias=bias,
+ d_initial=vera_config.d_initial,
+ **kwargs,
+ )
+
+ return new_module
diff --git a/peft/src/peft/tuners/waveft/__init__.py b/peft/src/peft/tuners/waveft/__init__.py
new file mode 100644
index 0000000000000000000000000000000000000000..f0e6fbc7e40eeccc393c662c09c81c032760dbfe
--- /dev/null
+++ b/peft/src/peft/tuners/waveft/__init__.py
@@ -0,0 +1,24 @@
+# Copyright 2025-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+from peft.utils import register_peft_method
+
+from .config import WaveFTConfig
+from .layer import WaveFTLayer, WaveFTLinear
+from .model import WaveFTModel
+
+
+__all__ = ["WaveFTConfig", "WaveFTLayer", "WaveFTLinear", "WaveFTModel"]
+
+register_peft_method(name="waveft", model_cls=WaveFTModel, config_cls=WaveFTConfig)
diff --git a/peft/src/peft/tuners/waveft/config.py b/peft/src/peft/tuners/waveft/config.py
new file mode 100644
index 0000000000000000000000000000000000000000..f2233c94e4ec583f52cb3cd4193e93de25f8ea3f
--- /dev/null
+++ b/peft/src/peft/tuners/waveft/config.py
@@ -0,0 +1,265 @@
+# Copyright 2025-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+from __future__ import annotations
+
+from dataclasses import dataclass, field
+from typing import Optional, Union
+
+from peft.config import PeftConfig
+from peft.utils import PeftType
+
+from .constants import WAVELET_REDUCTIONS
+
+
+@dataclass
+class WaveFTConfig(PeftConfig):
+ """
+ This is the configuration class to store the configuration of a [`WaveFTModel`]. It is used to define the
+ parameters for Wavelet-based Fine-Tuning (WaveFT), an approach that leverages the sparsity of wavelet transforms
+ for parameter-efficient fine-tuning of pretrained models.
+
+ Args:
+ n_frequency (`int`):
+ Number of learnable wavelet coefficients for the Discrete Wavelet Transform (DWT). 'n_frequency' is an
+ integer that is greater than 0 and less than or equal to the total number of elements in the original
+ weight matrix (d_out * d_in). This parameter directly controls the number of trainable parameters for each
+ adapted layer. A higher 'n_frequency' generally leads to better performance but also increases GPU memory
+ usage, with a minor impact on training speed.
+ scaling (`float`):
+ The scaling factor applied to the reconstructed delta W matrix. This is a crucial hyperparameter, analogous
+ to `lora_alpha` in LoRA. It can be tuned during hyperparameter search. Our default value for SDXL
+ personalization is 25.
+ wavelet_family (`str`):
+ The wavelet family (e.g., 'db1', 'sym2', 'coif1') to use for the DWT and Inverse DWT (IDWT). Defaults to
+ 'db1' (Haar wavelet). Different wavelet families have varying filter lengths which affect the training time
+ substantially
+ use_idwt (`bool`):
+ Set to False for efficient adaptation. Whether to use the Inverse Discrete Wavelet Transform (IDWT) to
+ reconstruct the delta weights from the learned wavelet coefficients. If `True` (default), the IDWT is
+ applied. If `False`, the learned coefficients are directly used to form a sparse delta weight matrix, which
+ is faster but performs worse for the SDXL personalization task.
+ random_loc_seed (`int`):
+ Seed for determining the random locations of the `n_frequency` learnable wavelet coefficients within the
+ full wavelet coefficient matrix.
+ target_modules (`Union[list[str],str]`):
+ List of module names or a regex expression identifying the modules to be adapted with WaveFT. For example,
+ `['q_proj', 'v_proj']` or `'.*decoder.*(SelfAttention|EncDecAttention).*(q|v)$'`. Currently, only linear
+ layers (`torch.nn.Linear`) are supported.
+ exclude_modules (`Optional[Union[List[str], str]]`):
+ List of module names or a regex expression for modules to exclude from WaveFT adaptation.
+ fan_in_fan_out (`bool`):
+ Set to `True` if the weights of the layer to be replaced are stored in `(fan_in, fan_out)` format. Default
+ is `False`.
+ bias (`str`):
+ Bias type for WaveFT. Can be 'none', 'all', or 'waveft_only'. ('fourier_only' was likely a typo and has
+ been corrected to 'waveft_only' if it implies bias only on adapted parameters) If 'waveft_only', biases are
+ added only to the WaveFT components. If 'all', biases are added to both base and WaveFT components. If
+ 'none', no new biases are added.
+ modules_to_save (`list[str]`):
+ List of modules, in addition to WaveFT layers, that should be marked as trainable and saved in the final
+ checkpoint. Useful for layers like classifiers in sequence or token classification tasks that are randomly
+ initialized and need training.
+ layers_to_transform (`Union[list[int],int]`):
+ Specific layer indices to transform. If provided, PEFT will only adapt layers at these indices. If a single
+ integer is given, only that layer is transformed.
+ layers_pattern (`Optional[Union[List[str], str]]`):
+ Pattern for layer names, used if `layers_to_transform` is specified and the layer pattern is not standard
+ (e.g., not 'layers' or 'h'). This should target the `nn.ModuleList` attribute in the model.
+ n_frequency_pattern (`dict`):
+ A dictionary mapping layer names (or regex) to specific `n_frequency` values, overriding the global
+ `n_frequency`. Example: `{"model.decoder.layers.0.encoder_attn.k_proj": 1000}`.
+ init_weights (`bool`):
+ Initialization strategy for the learnable wavelet coefficients (spectrum). If `True` (default),
+ coefficients are initialized to zeros. If `False`, coefficients are initialized from a standard normal
+ distribution scaled by a small factor.
+ proportional_parameters (`bool`):
+ If `True`, `n_frequency` is allocated proportionally to each layer's `input_dim * output_dim`. Default is
+ `False`. Note: This option is included for experimental thoroughness to allow researchers to reproduce
+ paper results, rather than for practical utility, as no beneficial scenarios have been identified.
+ """
+
+ n_frequency: int = field(
+ default=2592, # Default value might need adjustment based on common use cases or paper findings
+ metadata={
+ "help": (
+ "Number of learnable wavelet coefficients for the Discrete Wavelet Transform (DWT). "
+ "'n_frequency' is an integer that is greater than 0 and less than or equal to the "
+ "total number of elements in the original weight matrix (d_out * d_in). "
+ "This parameter directly controls the number of trainable parameters for each adapted layer. "
+ "A higher 'n_frequency' generally leads to better performance but also increases "
+ "GPU memory usage, with a minor impact on training speed."
+ )
+ },
+ )
+ scaling: float = field(
+ default=25.0, # Default value seems low based on typical examples, might need adjustment
+ metadata={
+ "help": (
+ "The scaling factor applied to the reconstructed delta W matrix. This is a crucial "
+ "hyperparameter, analogous to 'lora_alpha' in LoRA. It can be tuned during hyperparameter "
+ "search. Default value for SDXL personalization is 25. "
+ )
+ },
+ )
+ wavelet_family: str = field(
+ default="db1",
+ metadata={
+ "help": (
+ "The wavelet family (e.g., 'db1', 'sym2', 'coif1') to use for the DWT and Inverse DWT (IDWT). "
+ "Defaults to 'db1' (Haar wavelet). Different wavelet families have varying filter lengths "
+ "which affect the training time substantially. Size differences are handled automatically "
+ "if use_idwt is True."
+ )
+ },
+ )
+ use_idwt: bool = field(
+ default=True,
+ metadata={
+ "help": (
+ "Set to False for efficient adaptation. "
+ "Whether to use the Inverse Discrete Wavelet Transform (IDWT) to reconstruct the delta "
+ "weights from the learned wavelet coefficients. If True (default), the IDWT is applied. "
+ "If False, the learned coefficients are directly used to form a sparse delta weight matrix, "
+ "which is faster but performs worse for the SDXL personalization task."
+ )
+ },
+ )
+ random_loc_seed: int = field(
+ default=777,
+ metadata={
+ "help": (
+ "Seed for determining the random locations of the 'n_frequency' learnable wavelet "
+ "coefficients within the full wavelet coefficient matrix."
+ )
+ },
+ )
+ fan_in_fan_out: bool = field(
+ default=False,
+ metadata={
+ "help": (
+ "Set to True if the weights of the layer to be replaced are stored in (fan_in, fan_out) "
+ "format. Default is False."
+ )
+ },
+ )
+ target_modules: Optional[Union[list[str], str]] = field(
+ default=None,
+ metadata={
+ "help": (
+ "List of module names or a regex expression identifying the modules to be adapted with WaveFT. "
+ "For example, ['q_proj', 'v_proj'] or '.*decoder.*(SelfAttention|EncDecAttention).*(q|v)$'. "
+ "Currently, only linear layers (torch.nn.Linear) are supported."
+ )
+ },
+ )
+ exclude_modules: Optional[Union[list[str], str]] = field(
+ default=None,
+ metadata={"help": "List of module names or regex for modules to exclude from WaveFT adaptation."},
+ )
+ bias: str = field(
+ default="none",
+ metadata={
+ "help": (
+ "Bias type for WaveFT. Can be 'none', 'all', or 'waveft_only'. "
+ "If 'waveft_only', biases are added only to the WaveFT components. "
+ "If 'all', biases are added to both base and WaveFT components. "
+ "If 'none', no new biases are added."
+ )
+ },
+ )
+ modules_to_save: Optional[list[str]] = field(
+ default=None,
+ metadata={
+ "help": (
+ "List of modules, in addition to WaveFT layers, that should be marked as trainable "
+ "and saved in the final checkpoint. Useful for layers like classifiers in sequence "
+ "or token classification tasks that are randomly initialized and need training."
+ )
+ },
+ )
+ layers_to_transform: Optional[Union[list[int], int]] = field(
+ default=None,
+ metadata={
+ "help": (
+ "Specific layer indices to transform. If provided, PEFT will only adapt layers at these "
+ "indices. If a single integer is given, only that layer is transformed."
+ )
+ },
+ )
+ layers_pattern: Optional[Union[list[str], str]] = field(
+ default=None,
+ metadata={
+ "help": (
+ "Pattern for layer names, used if `layers_to_transform` is specified and the layer "
+ "pattern is not standard (e.g., not 'layers' or 'h'). This should target the "
+ "`nn.ModuleList` attribute in the model."
+ )
+ },
+ )
+ n_frequency_pattern: Optional[dict] = field(
+ default_factory=dict,
+ metadata={
+ "help": (
+ "A dictionary mapping layer names (or regex) to specific `n_frequency` values, "
+ 'overriding the global `n_frequency`. Example: {"model.decoder.layers.0.encoder_attn.k_proj": 1000}.'
+ )
+ },
+ )
+ proportional_parameters: bool = field(
+ default=False,
+ metadata={
+ "help": (
+ "If True, 'n_frequency' is allocated proportionally to each layer's "
+ "input_dim * output_dim. Default is False. Note: This option is included "
+ "for experimental thoroughness to allow researchers to reproduce paper results, "
+ "rather than for practical utility, as no beneficial scenarios have been identified."
+ )
+ },
+ )
+ init_weights: bool = field(
+ default=True,
+ metadata={
+ "help": (
+ "Initialization strategy for the learnable wavelet coefficients (spectrum). "
+ "If True (default), coefficients are initialized to zeros. "
+ "If False, coefficients are initialized from a standard normal distribution scaled by a small factor."
+ )
+ },
+ )
+
+ def __post_init__(self):
+ super().__post_init__()
+ self.peft_type = PeftType.WAVEFT
+ self.target_modules = (
+ set(self.target_modules) if isinstance(self.target_modules, list) else self.target_modules
+ )
+ self.exclude_modules = (
+ set(self.exclude_modules) if isinstance(self.exclude_modules, list) else self.exclude_modules
+ )
+ # if target_modules is a regex expression, then layers_to_transform should be None
+ if isinstance(self.target_modules, str) and self.layers_to_transform is not None:
+ raise ValueError("`layers_to_transform` cannot be used when `target_modules` is a str.")
+
+ # if target_modules is a regex expression, then layers_pattern should be None
+ if isinstance(self.target_modules, str) and self.layers_pattern is not None:
+ raise ValueError("`layers_pattern` cannot be used when `target_modules` is a str.")
+ # check for layers_to_transform and layers_pattern
+ if self.layers_pattern and not self.layers_to_transform:
+ raise ValueError("When `layers_pattern` is specified, `layers_to_transform` must also be specified. ")
+
+ if self.wavelet_family not in WAVELET_REDUCTIONS:
+ raise ValueError(
+ f"Wavelet family {self.wavelet_family} not supported. Supported wavelet families are: {list(WAVELET_REDUCTIONS.keys())}"
+ )
diff --git a/peft/src/peft/tuners/waveft/constants.py b/peft/src/peft/tuners/waveft/constants.py
new file mode 100644
index 0000000000000000000000000000000000000000..b1559f4fa5bb13039ab9687b643690d988513eb9
--- /dev/null
+++ b/peft/src/peft/tuners/waveft/constants.py
@@ -0,0 +1,96 @@
+# Copyright 2025-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+"""
+Dimensional reduction amounts for different wavelet families during wavelet transforms Each tuple (rows, cols)
+represents the reduction in matrix dimensions that occurs when applying wavelet decomposition/reconstruction due to
+boundary effects and filter sizes. These values are used to pre-pad matrices before wavelet processing to ensure the
+reconstructed matrix maintains the original target dimensions.
+"""
+
+WAVELET_REDUCTIONS = {
+ "db1": (0, 0),
+ "db2": (2, 2),
+ "db3": (4, 4),
+ "db4": (6, 6),
+ "db5": (8, 8),
+ "db6": (10, 10),
+ "db7": (12, 12),
+ "db8": (14, 14),
+ "db9": (16, 16),
+ "db10": (18, 18),
+ "db11": (20, 20),
+ "db12": (22, 22),
+ "db13": (24, 24),
+ "db14": (26, 26),
+ "db15": (28, 28),
+ "db16": (30, 30),
+ "db17": (32, 32),
+ "db18": (34, 34),
+ "db19": (36, 36),
+ "db20": (38, 38),
+ "db21": (40, 40),
+ "db22": (42, 42),
+ "db23": (44, 44),
+ "db24": (46, 46),
+ "db25": (48, 48),
+ "db26": (50, 50),
+ "db27": (52, 52),
+ "db28": (54, 54),
+ "db29": (56, 56),
+ "db30": (58, 58),
+ "db31": (60, 60),
+ "db32": (62, 62),
+ "db33": (64, 64),
+ "db34": (66, 66),
+ "db35": (68, 68),
+ "db36": (70, 70),
+ "db37": (72, 72),
+ "db38": (74, 74),
+ "sym2": (2, 2),
+ "sym3": (4, 4),
+ "sym4": (6, 6),
+ "sym5": (8, 8),
+ "sym6": (10, 10),
+ "sym7": (12, 12),
+ "sym8": (14, 14),
+ "sym9": (16, 16),
+ "sym10": (18, 18),
+ "sym11": (20, 20),
+ "sym12": (22, 22),
+ "sym13": (24, 24),
+ "sym14": (26, 26),
+ "sym15": (28, 28),
+ "sym16": (30, 30),
+ "sym17": (32, 32),
+ "sym18": (34, 34),
+ "sym19": (36, 36),
+ "sym20": (38, 38),
+ "coif1": (4, 4),
+ "coif2": (10, 10),
+ "coif3": (16, 16),
+ "coif4": (22, 22),
+ "coif5": (28, 28),
+ "coif6": (34, 34),
+ "coif7": (40, 40),
+ "coif8": (46, 46),
+ "coif9": (52, 52),
+ "coif10": (58, 58),
+ "coif11": (64, 64),
+ "coif12": (70, 70),
+ "coif13": (76, 76),
+ "coif14": (82, 82),
+ "coif15": (88, 88),
+ "coif16": (94, 94),
+ "coif17": (100, 100),
+}
diff --git a/peft/src/peft/tuners/waveft/layer.py b/peft/src/peft/tuners/waveft/layer.py
new file mode 100644
index 0000000000000000000000000000000000000000..a17f3ffba365384664c2df04888a0e83f9305af8
--- /dev/null
+++ b/peft/src/peft/tuners/waveft/layer.py
@@ -0,0 +1,291 @@
+# Copyright 2025-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+import warnings
+from typing import Any, Optional, Union
+
+import torch
+import torch.nn as nn
+import torch.nn.functional as F
+from transformers.pytorch_utils import Conv1D
+
+from peft.tuners.tuners_utils import BaseTunerLayer, check_adapters_to_merge
+
+from .constants import WAVELET_REDUCTIONS
+from .waverec2d import waverec2d
+
+
+class WaveFTLayer(BaseTunerLayer):
+ # All names of layers that may contain (trainable) adapter weights
+ adapter_layer_names = ("waveft_spectrum",)
+ # All names of other parameters that may contain adapter-related parameters
+ other_param_names = (
+ "waveft_n_frequency",
+ "waveft_scaling",
+ "waveft_random_loc_seed",
+ "waveft_wavelet_family",
+ "waveft_indices",
+ "waveft_use_idwt",
+ )
+
+ def __init__(self, base_layer: nn.Module, **kwargs) -> None:
+ self.base_layer = base_layer
+ self.waveft_n_frequency = {}
+ self.waveft_scaling = {}
+ self.waveft_spectrum = nn.ParameterDict({})
+ self.waveft_wavelet_family = {}
+ self.waveft_indices = {}
+ self.waveft_random_loc_seed = {}
+ self.waveft_use_idwt = {}
+ # Mark the weight as unmerged
+ self._disable_adapters = False
+ self.merged_adapters = []
+ self.kwargs = kwargs
+
+ base_layer = self.get_base_layer()
+ if isinstance(base_layer, nn.Linear):
+ self.in_features, self.out_features = base_layer.in_features, base_layer.out_features
+ elif isinstance(base_layer, Conv1D):
+ self.in_features, self.out_features = (
+ base_layer.weight.ds_shape if hasattr(base_layer.weight, "ds_shape") else base_layer.weight.shape
+ )
+ else:
+ raise ValueError(f"Unsupported layer type {type(base_layer)}")
+
+ def update_layer(
+ self, adapter_name, n_frequency, scaling, init_weights, random_loc_seed, wavelet_family="db1", use_idwt=True
+ ):
+ if n_frequency <= 0:
+ raise ValueError(f"`n_frequency` should be a positive integer value but the value passed is {n_frequency}")
+ if n_frequency > self.in_features * self.out_features:
+ raise ValueError(
+ f"`n_frequency` should be less than or equal to the product of the input and output dimensions "
+ f"but the value passed is {n_frequency} and the product is {self.in_features * self.out_features}"
+ )
+
+ self.waveft_n_frequency[adapter_name] = n_frequency
+ self.waveft_random_loc_seed[adapter_name] = random_loc_seed
+ self.waveft_wavelet_family[adapter_name] = wavelet_family
+ self.waveft_use_idwt[adapter_name] = use_idwt
+
+ # Get the expanded dimensions based on wavelet family
+ reduction_rows, reduction_cols = WAVELET_REDUCTIONS[wavelet_family]
+
+ # Generate random indices within the original dimensions
+ # We handle padding separately in get_delta_weight
+ generator = torch.Generator().manual_seed(self.waveft_random_loc_seed[adapter_name])
+ indices = torch.randperm(self.out_features * self.in_features, generator=generator)[:n_frequency]
+
+ # Convert to row, col format for the original dimensions
+ self.waveft_indices[adapter_name] = torch.stack(
+ [indices // self.in_features, indices % self.in_features], dim=0
+ )
+
+ self.waveft_scaling[adapter_name] = scaling
+
+ # Actual trainable parameters
+ # Initialize based on init_weights
+ if init_weights:
+ # Initialize with zeros later using reset_wave_parameters
+ self.waveft_spectrum[adapter_name] = nn.Parameter(torch.empty(n_frequency), requires_grad=True)
+ self.reset_wave_parameters(adapter_name) # Initialize to zeros now
+ else:
+ # Initialize with randn scaled by a small std dev to prevent explosion
+ std_dev = 0.01 # Using a small std dev for initial random weights
+ self.waveft_spectrum[adapter_name] = nn.Parameter(torch.randn(n_frequency) * std_dev, requires_grad=True)
+
+ self._move_adapter_to_device_of_base_layer(adapter_name)
+ self.set_adapter(self.active_adapters)
+
+ @torch.no_grad()
+ def reset_wave_parameters(self, adapter_name):
+ if adapter_name in self.waveft_spectrum.keys():
+ nn.init.zeros_(self.waveft_spectrum[adapter_name])
+
+ def get_delta_weight(self, adapter) -> torch.Tensor:
+ spectrum = self.waveft_spectrum[adapter]
+ indices = self.waveft_indices[adapter].to(spectrum.device)
+ wavelet_family = self.waveft_wavelet_family[adapter]
+
+ # Choose whether to use IDWT or direct spectrum based on adapter setting
+ if self.waveft_use_idwt[adapter]:
+ reduction_rows, reduction_cols = WAVELET_REDUCTIONS[wavelet_family]
+
+ # Create a padded spectrum matrix with additional rows and columns
+ # to account for the reduction during wavelet reconstruction
+ padded_out_features = self.out_features + reduction_rows
+ padded_in_features = self.in_features + reduction_cols
+
+ # Make dimensions even if needed for wavelet processing
+ if padded_out_features % 2 != 0:
+ padded_out_features += 1
+ if padded_in_features % 2 != 0:
+ padded_in_features += 1
+
+ # Create the padded dense spectrum matrix
+ dense_spectrum = torch.zeros(
+ padded_out_features, padded_in_features, device=spectrum.device, dtype=spectrum.dtype
+ )
+
+ # Calculate padding offsets to center the original data in the padded matrix
+ row_offset = (padded_out_features - self.out_features) // 2
+ col_offset = (padded_in_features - self.in_features) // 2
+
+ # Adjust indices to account for padding offsets
+ padded_indices = indices.clone()
+ padded_indices[0, :] += row_offset
+ padded_indices[1, :] += col_offset
+
+ # Place spectrum values in the padded matrix
+ # Filter out any indices that would be out of bounds
+ valid_mask = (padded_indices[0, :] < padded_out_features) & (padded_indices[1, :] < padded_in_features)
+ valid_indices = padded_indices[:, valid_mask]
+ valid_spectrum = spectrum[valid_mask]
+
+ # Set the spectrum values in the padded matrix
+ dense_spectrum[valid_indices[0, :], valid_indices[1, :]] = valid_spectrum
+
+ # Split into four sub-bands
+ H, W = dense_spectrum.shape
+ H2, W2 = H // 2, W // 2
+ cA = dense_spectrum[:H2, :W2] # top-left
+ cH = dense_spectrum[:H2, W2:] # top-right
+ cV = dense_spectrum[H2:, :W2] # bottom-left
+ cD = dense_spectrum[H2:, W2:] # bottom-right
+
+ # Construct wavelet-coefficient tuple
+ coeffs = (cA, (cH, cV, cD))
+
+ # Reconstruct with the specified wavelet family
+ delta_weight = waverec2d(coeffs, wavelet_family) * self.waveft_scaling[adapter]
+
+ # Ensure the delta weight has exactly the correct dimensions
+ if delta_weight.shape[0] != self.out_features or delta_weight.shape[1] != self.in_features:
+ # Calculate where to start slicing to get a centered crop
+ start_row = (delta_weight.shape[0] - self.out_features) // 2
+ start_col = (delta_weight.shape[1] - self.in_features) // 2
+
+ # Slice to the exact output size needed
+ delta_weight = delta_weight[
+ start_row : start_row + self.out_features, start_col : start_col + self.in_features
+ ]
+ else:
+ # Simple direct use of spectrum without IDWT
+ dense_spectrum = torch.zeros(
+ self.out_features, self.in_features, device=spectrum.device, dtype=spectrum.dtype
+ )
+ dense_spectrum[indices[0, :], indices[1, :]] = spectrum
+ delta_weight = dense_spectrum * self.waveft_scaling[adapter]
+
+ return delta_weight
+
+
+class WaveFTLinear(nn.Module, WaveFTLayer):
+ # WaveFT implemented in a dense layer
+ def __init__(
+ self,
+ base_layer,
+ adapter_name: str,
+ n_frequency: int = 1000,
+ scaling: float = 150.0,
+ fan_in_fan_out: bool = False, # Set this to True if the layer to replace stores weight like (fan_in, fan_out)
+ init_weights: Union[bool, str] = False,
+ random_loc_seed: int = 777,
+ wavelet_family: str = "db1",
+ use_idwt: bool = True,
+ **kwargs,
+ ) -> None:
+ super().__init__()
+ WaveFTLayer.__init__(self, base_layer, **kwargs)
+ self.fan_in_fan_out = fan_in_fan_out
+ self._active_adapter = adapter_name
+ self.update_layer(adapter_name, n_frequency, scaling, init_weights, random_loc_seed, wavelet_family, use_idwt)
+
+ def merge(self, safe_merge: bool = False, adapter_names: Optional[list[str]] = None) -> None:
+ """
+ Merge the active adapter weights into the base weights
+
+ Args:
+ safe_merge (`bool`, *optional*):
+ If True, the merge operation will be performed in a copy of the original weights and check for NaNs
+ before merging the weights. This is useful if you want to check if the merge operation will produce
+ NaNs. Defaults to `False`.
+ adapter_names (`List[str]`, *optional*):
+ The list of adapter names that should be merged. If None, all active adapters will be merged. Defaults
+ to `None`.
+ """
+ adapter_names = check_adapters_to_merge(self, adapter_names)
+ if not adapter_names:
+ # no adapter to merge
+ return
+
+ for active_adapter in adapter_names:
+ if active_adapter in self.waveft_spectrum.keys():
+ base_layer = self.get_base_layer()
+ if safe_merge:
+ # Note that safe_merge will be slower than the normal merge
+ # because of the copy operation.
+ orig_weights = base_layer.weight.data.clone()
+ orig_weights += self.get_delta_weight(active_adapter)
+
+ if not torch.isfinite(orig_weights).all():
+ raise ValueError(
+ f"NaNs detected in the merged weights. The adapter {active_adapter} seems to be broken"
+ )
+
+ base_layer.weight.data = orig_weights
+ else:
+ base_layer.weight.data += self.get_delta_weight(active_adapter)
+ self.merged_adapters.append(active_adapter)
+
+ def unmerge(self) -> None:
+ """
+ This method unmerges all merged adapter layers from the base weights.
+ """
+ if not self.merged:
+ warnings.warn("Already unmerged. Nothing to do.")
+ return
+ while len(self.merged_adapters) > 0:
+ active_adapter = self.merged_adapters.pop()
+ if active_adapter in self.waveft_spectrum.keys():
+ self.get_base_layer().weight.data -= self.get_delta_weight(active_adapter)
+
+ def get_delta_weight(self, adapter) -> torch.Tensor:
+ return super().get_delta_weight(adapter)
+
+ def forward(self, x: torch.Tensor, *args: Any, **kwargs: Any) -> torch.Tensor:
+ previous_dtype = x.dtype
+
+ if self.disable_adapters:
+ if self.merged:
+ self.unmerge()
+ result = self.base_layer(x, *args, **kwargs)
+ elif self.merged:
+ result = self.base_layer(x, *args, **kwargs)
+ else:
+ result = self.base_layer(x, *args, **kwargs)
+ for active_adapter in self.active_adapters:
+ if active_adapter not in self.waveft_spectrum.keys():
+ continue
+
+ delta_w = self.get_delta_weight(active_adapter)
+ x = self._cast_input_dtype(x, delta_w.dtype)
+ result = result + F.linear(x, delta_w)
+
+ result = result.to(previous_dtype)
+ return result
+
+ def __repr__(self) -> str:
+ rep = super().__repr__()
+ return "waveft." + rep
diff --git a/peft/src/peft/tuners/waveft/model.py b/peft/src/peft/tuners/waveft/model.py
new file mode 100644
index 0000000000000000000000000000000000000000..3ecc8ac6b0d8407ed378517e91de9c35f05b9be9
--- /dev/null
+++ b/peft/src/peft/tuners/waveft/model.py
@@ -0,0 +1,195 @@
+# Copyright 2025-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+from __future__ import annotations
+
+import warnings
+
+import torch
+from transformers.pytorch_utils import Conv1D
+
+from peft.tuners.tuners_utils import BaseTuner, BaseTunerLayer, check_target_module_exists
+from peft.utils import (
+ TRANSFORMERS_MODELS_TO_WAVEFT_TARGET_MODULES_MAPPING,
+)
+from peft.utils.other import get_pattern_key
+
+from .layer import WaveFTLayer, WaveFTLinear
+
+
+class WaveFTModel(BaseTuner):
+ prefix: str = "waveft_"
+ tuner_layer_cls: type[BaseTunerLayer] = WaveFTLayer
+ target_module_mapping = TRANSFORMERS_MODELS_TO_WAVEFT_TARGET_MODULES_MAPPING
+
+ def _calculate_proportional_parameters(self, model: torch.nn.Module, waveft_config):
+ """Calculate proportional parameter allocation for all target modules."""
+ target_modules_info = []
+ for name, module in model.named_modules():
+ if check_target_module_exists(waveft_config, name):
+ # Handle case where module is already wrapped with WaveFT
+ if isinstance(module, WaveFTLayer):
+ # Use the base layer for dimension calculations
+ base_module = module.base_layer
+ if isinstance(base_module, torch.nn.Linear):
+ input_dim, output_dim = base_module.in_features, base_module.out_features
+ elif isinstance(base_module, Conv1D):
+ input_dim, output_dim = base_module.weight.shape[1], base_module.weight.shape[0]
+ else:
+ continue
+ elif isinstance(module, torch.nn.Linear):
+ input_dim, output_dim = module.in_features, module.out_features
+ elif isinstance(module, Conv1D):
+ input_dim, output_dim = module.weight.shape[1], module.weight.shape[0]
+ else:
+ continue
+ target_modules_info.append((name, input_dim, output_dim))
+
+ if not target_modules_info:
+ raise ValueError("No target modules found for proportional parameter allocation.")
+
+ total_sum = sum(input_dim * output_dim for (_, input_dim, output_dim) in target_modules_info)
+ num_layers = len(target_modules_info)
+ total_budget = waveft_config.n_frequency * num_layers
+
+ n_frequency_dict = {}
+ for name, input_dim, output_dim in target_modules_info:
+ layer_ratio = (input_dim * output_dim) / total_sum
+ n_freq = round(layer_ratio * total_budget)
+ n_frequency_dict[name] = n_freq
+
+ return n_frequency_dict
+
+ def _create_and_replace(
+ self,
+ waveft_config,
+ adapter_name,
+ target,
+ target_name,
+ parent,
+ current_key,
+ **optional_kwargs,
+ ):
+ if current_key is None:
+ raise ValueError("Current Key shouldn't be `None`")
+
+ # Calculate proportional parameters if needed (only once per adapter)
+ if waveft_config.proportional_parameters:
+ if not hasattr(self, "_proportional_params_cache"):
+ self._proportional_params_cache = {}
+ if adapter_name not in self._proportional_params_cache:
+ n_frequency_dict = self._calculate_proportional_parameters(self.model, waveft_config)
+ self._proportional_params_cache[adapter_name] = n_frequency_dict
+
+ # Determine n_frequency: Priority order:
+ # 1. From proportional parameter cache (if proportional_parameters=True)
+ # 2. From optional_kwargs (if passed directly)
+ # 3. From n_frequency_pattern in config
+ # 4. From default n_frequency in config
+ n_frequency = None
+ if (
+ waveft_config.proportional_parameters
+ and hasattr(self, "_proportional_params_cache")
+ and adapter_name in self._proportional_params_cache
+ ):
+ n_frequency = self._proportional_params_cache[adapter_name].get(current_key)
+
+ if n_frequency is None and "n_frequency" in optional_kwargs:
+ n_frequency = optional_kwargs["n_frequency"]
+
+ if n_frequency is None:
+ pattern_keys = list(waveft_config.n_frequency_pattern.keys())
+ target_name_key = get_pattern_key(pattern_keys, current_key)
+ n_frequency = waveft_config.n_frequency_pattern.get(target_name_key, waveft_config.n_frequency)
+
+ # Determine wavelet_family
+ wavelet_family = None
+ if "wavelet_family" in optional_kwargs:
+ wavelet_family = optional_kwargs["wavelet_family"]
+ if wavelet_family is None:
+ wavelet_family = waveft_config.wavelet_family
+
+ scaling = waveft_config.scaling
+ random_loc_seed = waveft_config.random_loc_seed
+ bias = hasattr(target, "bias") and target.bias is not None
+ # Prepare kwargs for module creation/update
+ kwargs = {
+ "n_frequency": n_frequency,
+ "scaling": scaling,
+ "fan_in_fan_out": waveft_config.fan_in_fan_out,
+ "init_weights": waveft_config.init_weights,
+ "random_loc_seed": waveft_config.random_loc_seed,
+ "wavelet_family": wavelet_family, # Use determined wavelet family
+ }
+ kwargs["bias"] = bias
+
+ if isinstance(target, WaveFTLayer):
+ target.update_layer(
+ adapter_name,
+ n_frequency,
+ scaling,
+ waveft_config.init_weights,
+ random_loc_seed,
+ wavelet_family=wavelet_family, # Pass determined wavelet family
+ use_idwt=waveft_config.use_idwt,
+ )
+ else:
+ new_module = self._create_new_module(waveft_config, adapter_name, target, **kwargs)
+ if adapter_name != self.active_adapter:
+ new_module.requires_grad_(False)
+ self._replace_module(parent, target_name, new_module, target)
+
+ @staticmethod
+ def _create_new_module(waveft_config, adapter_name, target, **kwargs):
+ if isinstance(target, BaseTunerLayer):
+ target_base_layer = target.get_base_layer()
+ else:
+ target_base_layer = target
+
+ if isinstance(target_base_layer, torch.nn.Linear):
+ if kwargs["fan_in_fan_out"]:
+ warnings.warn(
+ "fan_in_fan_out is set to True but the target module is `torch.nn.Linear`. "
+ "Setting fan_in_fan_out to False."
+ )
+ kwargs["fan_in_fan_out"] = waveft_config.fan_in_fan_out = False
+ elif isinstance(target_base_layer, Conv1D):
+ kwargs["is_target_conv_1d_layer"] = True
+ if not kwargs["fan_in_fan_out"]:
+ warnings.warn(
+ "fan_in_fan_out is set to False but the target module is `Conv1D`. Setting fan_in_fan_out to True."
+ )
+ kwargs["fan_in_fan_out"] = waveft_config.fan_in_fan_out = True
+ else:
+ raise ValueError(
+ f"Target module {target} is not supported. Currently, only the following modules are supported: "
+ "`torch.nn.Linear`."
+ )
+
+ kwargs["wavelet_family"] = waveft_config.wavelet_family
+ kwargs["use_idwt"] = waveft_config.use_idwt
+ new_module = WaveFTLinear(target, adapter_name, **kwargs)
+
+ return new_module
+
+ def delete_adapter(self, adapter_name: str) -> None:
+ """
+ Deletes an existing adapter.
+
+ Args:
+ adapter_name (str): Name of the adapter to be deleted.
+ """
+ super().delete_adapter(adapter_name)
+ # Clean up proportional parameters cache
+ if hasattr(self, "_proportional_params_cache") and adapter_name in self._proportional_params_cache:
+ del self._proportional_params_cache[adapter_name]
diff --git a/peft/src/peft/tuners/waveft/wavelet.py b/peft/src/peft/tuners/waveft/wavelet.py
new file mode 100644
index 0000000000000000000000000000000000000000..c66acd85f65570652f18d47d5bed12eb3a174ea5
--- /dev/null
+++ b/peft/src/peft/tuners/waveft/wavelet.py
@@ -0,0 +1,513 @@
+# Copyright 2025-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+"""
+Minimal wavelet implementation extracted from PyWavelets
+
+This code contains portions derived from PyWavelets: Copyright (c) 2006-2012 Filip Wasilewski
+Copyright (c) 2012- The PyWavelets Developers
+
+Permission is hereby granted, free of charge, to any person obtaining a copy of this software and associated
+documentation files (the "Software"), to deal in the Software without restriction, including without limitation the
+rights to use, copy, modify, merge, publish, distribute, sublicense, and/or sell copies of the Software, and to permit
+persons to whom the Software is furnished to do so, subject to the following conditions:
+
+The above copyright notice and this permission notice shall be included in all copies or substantial portions of the
+Software.
+
+THE SOFTWARE IS PROVIDED "AS IS", WITHOUT WARRANTY OF ANY KIND, EXPRESS OR IMPLIED, INCLUDING BUT NOT LIMITED TO THE
+WARRANTIES OF MERCHANTABILITY, FITNESS FOR A PARTICULAR PURPOSE AND NONINFRINGEMENT. IN NO EVENT SHALL THE AUTHORS OR
+COPYRIGHT HOLDERS BE LIABLE FOR ANY CLAIM, DAMAGES OR OTHER LIABILITY, WHETHER IN AN ACTION OF CONTRACT, TORT OR
+OTHERWISE, ARISING FROM, OUT OF OR IN CONNECTION WITH THE SOFTWARE OR THE USE OR OTHER DEALINGS IN THE SOFTWARE.
+
+Original source: https://github.com/PyWavelets/pywt
+"""
+
+import math
+from collections.abc import Sequence
+
+
+class Wavelet:
+ """
+ Minimal wavelet class that implements the most commonly used wavelets.
+
+ Supports:
+ - Daubechies wavelets: db1-db10, haar
+ - Symlets: sym2-sym10
+ - Coiflets: coif1-coif5
+ """
+
+ def __init__(self, name: str):
+ """
+ Initialize a wavelet by name.
+
+ Args:
+ name: Wavelet name (e.g., 'db4', 'haar', 'sym5', 'coif2')
+ """
+ self.name = name.lower()
+ self._compute_filters()
+
+ def _compute_filters(self):
+ """Compute the four filter banks from the base coefficients."""
+ if self.name == "haar":
+ # Haar is the same as db1
+ base_coeffs = _WAVELET_COEFFS["db1"]
+ elif self.name in _WAVELET_COEFFS:
+ base_coeffs = _WAVELET_COEFFS[self.name]
+ else:
+ raise ValueError(f"Unknown wavelet name '{self.name}'. Available wavelets: {list(_WAVELET_COEFFS.keys())}")
+
+ # Determine if this is a coiflet (needs sqrt(2) scaling)
+ scale_factor = math.sqrt(2) if self.name.startswith("coif") else 1.0
+
+ # Apply scaling to base coefficients
+ scaled_coeffs = [c * scale_factor for c in base_coeffs]
+
+ # Compute the four filter banks following PyWavelets convention
+ # rec_lo = scaled base coefficients
+ self._rec_lo = scaled_coeffs[:]
+
+ # dec_lo = rec_lo reversed
+ self._dec_lo = scaled_coeffs[::-1]
+
+ # rec_hi = alternating signs of dec_lo
+ self._rec_hi = [(-1) ** i * scaled_coeffs[len(scaled_coeffs) - 1 - i] for i in range(len(scaled_coeffs))]
+
+ # dec_hi = alternating signs of rec_lo
+ self._dec_hi = [(-1) ** (len(scaled_coeffs) - 1 - i) * scaled_coeffs[i] for i in range(len(scaled_coeffs))]
+
+ @property
+ def dec_lo(self) -> Sequence[float]:
+ """Lowpass decomposition filter."""
+ return self._dec_lo
+
+ @property
+ def dec_hi(self) -> Sequence[float]:
+ """Highpass decomposition filter."""
+ return self._dec_hi
+
+ @property
+ def rec_lo(self) -> Sequence[float]:
+ """Lowpass reconstruction filter."""
+ return self._rec_lo
+
+ @property
+ def rec_hi(self) -> Sequence[float]:
+ """Highpass reconstruction filter."""
+ return self._rec_hi
+
+ @property
+ def dec_len(self) -> int:
+ """Decomposition filters length."""
+ return len(self._dec_lo)
+
+ @property
+ def rec_len(self) -> int:
+ """Reconstruction filters length."""
+ return len(self._rec_lo)
+
+ @property
+ def filter_bank(self) -> tuple[Sequence[float], Sequence[float], Sequence[float], Sequence[float]]:
+ """Tuple of all four filter banks (dec_lo, dec_hi, rec_lo, rec_hi)."""
+ return (self.dec_lo, self.dec_hi, self.rec_lo, self.rec_hi)
+
+ def __len__(self) -> int:
+ """Return the length of the decomposition filters."""
+ return self.dec_len
+
+ def __repr__(self) -> str:
+ return f"Wavelet(name='{self.name}')"
+
+
+# Wavelet coefficients extracted from PyWavelets
+# These are the reconstruction lowpass filter coefficients
+_WAVELET_COEFFS = {
+ # Daubechies wavelets
+ "db1": [
+ 0.7071067811865475244008443621048490392848359376884740365883398,
+ 0.7071067811865475244008443621048490392848359376884740365883398,
+ ],
+ "db2": [
+ 0.4829629131445341433748715998644486838169524195042022752011715,
+ 0.8365163037378079055752937809168732034593703883484392934953414,
+ 0.2241438680420133810259727622404003554678835181842717613871683,
+ -0.1294095225512603811744494188120241641745344506599652569070016,
+ ],
+ "db3": [
+ 0.3326705529500826159985115891390056300129233992450683597084705,
+ 0.80689150931333875,
+ 0.45987750211933132,
+ -0.13501102001039084,
+ -0.085441273882241486,
+ 0.035226291882100656,
+ ],
+ "db4": [
+ 0.2303778133088965008632911830440708500016152482483092977910968,
+ 0.7148465705529156470899219552739926037076084010993081758450110,
+ 0.6308807679298589078817163383006152202032229226771951174057473,
+ -0.02798376941685985421141374718007538541198732022449175284003358,
+ -0.1870348117190930840795706727890814195845441743745800912057770,
+ 0.03084138183556076362721936253495905017031482172003403341821219,
+ 0.03288301166688519973540751354924438866454194113754971259727278,
+ -0.01059740178506903210488320852402722918109996490637641983484974,
+ ],
+ "db5": [
+ 0.1601023979741929144807237480204207336505441246250578327725699,
+ 0.6038292697971896705401193065250621075074221631016986987969283,
+ 0.7243085284377729277280712441022186407687562182320073725767335,
+ 0.1384281459013207315053971463390246973141057911739561022694652,
+ -0.2422948870663820318625713794746163619914908080626185983913726,
+ -0.03224486958463837464847975506213492831356498416379847225434268,
+ 0.07757149384004571352313048938860181980623099452012527983210146,
+ -0.006241490212798274274190519112920192970763557165687607323417435,
+ -0.01258075199908199946850973993177579294920459162609785020169232,
+ 0.003335725285473771277998183415817355747636524742305315099706428,
+ ],
+ "db6": [
+ 0.1115407433501094636213239172409234390425395919844216759082360,
+ 0.4946238903984530856772041768778555886377863828962743623531834,
+ 0.7511339080210953506789344984397316855802547833382612009730420,
+ 0.3152503517091976290859896548109263966495199235172945244404163,
+ -0.2262646939654398200763145006609034656705401539728969940143487,
+ -0.1297668675672619355622896058765854608452337492235814701599310,
+ 0.09750160558732304910234355253812534233983074749525514279893193,
+ 0.02752286553030572862554083950419321365738758783043454321494202,
+ -0.03158203931748602956507908069984866905747953237314842337511464,
+ 0.0005538422011614961392519183980465012206110262773864964295476524,
+ 0.004777257510945510639635975246820707050230501216581434297593254,
+ -0.001077301085308479564852621609587200035235233609334419689818580,
+ ],
+ "db7": [
+ 0.07785205408500917901996352195789374837918305292795568438702937,
+ 0.3965393194819173065390003909368428563587151149333287401110499,
+ 0.7291320908462351199169430703392820517179660611901363782697715,
+ 0.4697822874051931224715911609744517386817913056787359532392529,
+ -0.1439060039285649754050683622130460017952735705499084834401753,
+ -0.2240361849938749826381404202332509644757830896773246552665095,
+ 0.07130921926683026475087657050112904822711327451412314659575113,
+ 0.08061260915108307191292248035938190585823820965629489058139218,
+ -0.03802993693501441357959206160185803585446196938467869898283122,
+ -0.01657454163066688065410767489170265479204504394820713705239272,
+ 0.01255099855609984061298988603418777957289474046048710038411818,
+ 0.0004295779729213665211321291228197322228235350396942409742946366,
+ -0.001801640704047490915268262912739550962585651469641090625323864,
+ 0.0003537137999745202484462958363064254310959060059520040012524275,
+ ],
+ "db8": [
+ 0.05441584224310400995500940520299935503599554294733050397729280,
+ 0.3128715909142999706591623755057177219497319740370229185698712,
+ 0.6756307362972898068078007670471831499869115906336364227766759,
+ 0.5853546836542067127712655200450981944303266678053369055707175,
+ -0.01582910525634930566738054787646630415774471154502826559735335,
+ -0.2840155429615469265162031323741647324684350124871451793599204,
+ 0.0004724845739132827703605900098258949861948011288770074644084096,
+ 0.1287474266204784588570292875097083843022601575556488795577000,
+ -0.01736930100180754616961614886809598311413086529488394316977315,
+ -0.04408825393079475150676372323896350189751839190110996472750391,
+ 0.01398102791739828164872293057263345144239559532934347169146368,
+ 0.008746094047405776716382743246475640180402147081140676742686747,
+ -0.004870352993451574310422181557109824016634978512157003764736208,
+ -0.0003917403733769470462980803573237762675229350073890493724492694,
+ 0.0006754494064505693663695475738792991218489630013558432103617077,
+ -0.0001174767841247695337306282316988909444086693950311503927620013,
+ ],
+ "db9": [
+ 0.03807794736387834658869765887955118448771714496278417476647192,
+ 0.2438346746125903537320415816492844155263611085609231361429088,
+ 0.6048231236901111119030768674342361708959562711896117565333713,
+ 0.6572880780513005380782126390451732140305858669245918854436034,
+ 0.1331973858250075761909549458997955536921780768433661136154346,
+ -0.2932737832791749088064031952421987310438961628589906825725112,
+ -0.09684078322297646051350813353769660224825458104599099679471267,
+ 0.1485407493381063801350727175060423024791258577280603060771649,
+ 0.03072568147933337921231740072037882714105805024670744781503060,
+ -0.06763282906132997367564227482971901592578790871353739900748331,
+ 0.0002509471148314519575871897499885543315176271993709633321834164,
+ 0.02236166212367909720537378270269095241855646688308853754721816,
+ -0.004723204757751397277925707848242465405729514912627938018758526,
+ -0.004281503682463429834496795002314531876481181811463288374860455,
+ 0.001847646883056226476619129491125677051121081359600318160732515,
+ 0.0002303857635231959672052163928245421692940662052463711972260006,
+ -0.0002519631889427101369749886842878606607282181543478028214134265,
+ 0.00003934732031627159948068988306589150707782477055517013507359938,
+ ],
+ "db10": [
+ 0.02667005790055555358661744877130858277192498290851289932779975,
+ 0.1881768000776914890208929736790939942702546758640393484348595,
+ 0.5272011889317255864817448279595081924981402680840223445318549,
+ 0.6884590394536035657418717825492358539771364042407339537279681,
+ 0.2811723436605774607487269984455892876243888859026150413831543,
+ -0.2498464243273153794161018979207791000564669737132073715013121,
+ -0.1959462743773770435042992543190981318766776476382778474396781,
+ 0.1273693403357932600826772332014009770786177480422245995563097,
+ 0.09305736460357235116035228983545273226942917998946925868063974,
+ -0.07139414716639708714533609307605064767292611983702150917523756,
+ -0.02945753682187581285828323760141839199388200516064948779769654,
+ 0.03321267405934100173976365318215912897978337413267096043323351,
+ 0.003606553566956169655423291417133403299517350518618994762730612,
+ -0.01073317548333057504431811410651364448111548781143923213370333,
+ 0.001395351747052901165789318447957707567660542855688552426721117,
+ 0.001992405295185056117158742242640643211762555365514105280067936,
+ -0.0006858566949597116265613709819265714196625043336786920516211903,
+ -0.0001164668551292854509514809710258991891527461854347597362819235,
+ 0.00009358867032006959133405013034222854399688456215297276443521873,
+ -0.00001326420289452124481243667531226683305749240960605829756400674,
+ ],
+ # Symlets
+ "sym2": [0.48296291314469025, 0.83651630373746899, 0.22414386804185735, -0.12940952255092145],
+ "sym3": [
+ 0.33267055295095688,
+ 0.80689150931333875,
+ 0.45987750211933132,
+ -0.13501102001039084,
+ -0.085441273882241486,
+ 0.035226291882100656,
+ ],
+ "sym4": [
+ 0.032223100604042702,
+ -0.012603967262037833,
+ -0.099219543576847216,
+ 0.29785779560527736,
+ 0.80373875180591614,
+ 0.49761866763201545,
+ -0.02963552764599851,
+ -0.075765714789273325,
+ ],
+ "sym5": [
+ 0.019538882735286728,
+ -0.021101834024758855,
+ -0.17532808990845047,
+ 0.016602105764522319,
+ 0.63397896345821192,
+ 0.72340769040242059,
+ 0.1993975339773936,
+ -0.039134249302383094,
+ 0.029519490925774643,
+ 0.027333068345077982,
+ ],
+ "sym6": [
+ -0.007800708325034148,
+ 0.0017677118642428036,
+ 0.044724901770665779,
+ -0.021060292512300564,
+ -0.072637522786462516,
+ 0.3379294217276218,
+ 0.787641141030194,
+ 0.49105594192674662,
+ -0.048311742585632998,
+ -0.11799011114819057,
+ 0.0034907120842174702,
+ 0.015404109327027373,
+ ],
+ "sym7": [
+ 0.010268176708511255,
+ 0.0040102448715336634,
+ -0.10780823770381774,
+ -0.14004724044296152,
+ 0.28862963175151463,
+ 0.76776431700316405,
+ 0.5361019170917628,
+ 0.017441255086855827,
+ -0.049552834937127255,
+ 0.067892693501372697,
+ 0.03051551316596357,
+ -0.01263630340325193,
+ -0.0010473848886829163,
+ 0.0026818145682578781,
+ ],
+ "sym8": [
+ 0.0018899503327594609,
+ -0.0003029205147213668,
+ -0.014952258337048231,
+ 0.0038087520138906151,
+ 0.049137179673607506,
+ -0.027219029917056003,
+ -0.051945838107709037,
+ 0.3644418948353314,
+ 0.77718575170052351,
+ 0.48135965125837221,
+ -0.061273359067658524,
+ -0.14329423835080971,
+ 0.0076074873249176054,
+ 0.031695087811492981,
+ -0.00054213233179114812,
+ -0.0033824159510061256,
+ ],
+ "sym9": [
+ 0.0010694900329086053,
+ -0.00047315449868008311,
+ -0.010264064027633142,
+ 0.0088592674934004842,
+ 0.06207778930288603,
+ -0.018233770779395985,
+ -0.19155083129728512,
+ 0.035272488035271894,
+ 0.61733844914093583,
+ 0.717897082764412,
+ 0.238760914607303,
+ -0.054568958430834071,
+ 0.00058346274612580684,
+ 0.03022487885827568,
+ -0.01152821020767923,
+ -0.013271967781817119,
+ 0.00061978088898558676,
+ 0.0014009155259146807,
+ ],
+ "sym10": [
+ -0.00045932942100465878,
+ 0.000057036083618494284,
+ 0.0045931735853118284,
+ -0.00080435893201654491,
+ -0.02035493981231129,
+ 0.0057649120335819086,
+ 0.049994972077376687,
+ -0.0319900568824278,
+ -0.035536740473817552,
+ 0.38382676106708546,
+ 0.7695100370211071,
+ 0.47169066693843925,
+ -0.070880535783243853,
+ -0.15949427888491757,
+ 0.011609893903711381,
+ 0.045927239231092203,
+ -0.0014653825813050513,
+ -0.0086412992770224222,
+ 0.000095632670722894754,
+ 0.00077015980911449011,
+ ],
+ # Coiflets (note: these will be multiplied by sqrt(2) in the class)
+ "coif1": [
+ -0.05142972847076845595317549230122688830344559947132656813651045,
+ 0.2389297284707684559531754923012268883034455994713265681365104,
+ 0.6028594569415369119063509846024537766068911989426531362730209,
+ 0.2721405430584630880936490153975462233931088010573468637269790,
+ -0.05142972847076845595317549230122688830344559947132656813651045,
+ -0.01107027152923154404682450769877311169655440052867343186348954,
+ ],
+ "coif2": [
+ 0.01158759673871686817889714882853120395708315073355502818875931,
+ -0.02932013798346856448679594524397843054053420947418409889774786,
+ -0.04763959031100813225872995081511549408622753909592460525840745,
+ 0.2730210465347666137982239328923516270034828327990699588033501,
+ 0.5746823938568638472459483149751499367740786490481481391460366,
+ 0.2948671936956191896750637208703777973914107635455611537640778,
+ -0.05408560709171142997443672832006888537570221990444706777525838,
+ -0.04202648046077160694657530752545884878978719268926222513485613,
+ 0.01674441016327950635146257083249391698866289538037299820224006,
+ 0.003967883612962012109043447090269950094081810916481648252817197,
+ -0.001289203356140659543141355500990678257894936161704492503370186,
+ -0.0005095053991076441489598480835620951586540050976664367876412655,
+ ],
+ "coif3": [
+ -0.002682418670922068664584689955153722375535836177157637134187840,
+ 0.005503126707831385107969640263617469178794666057252906037981936,
+ 0.01658356047917034608134280439996549525220639437145367606178002,
+ -0.04650776447872697640390293095170192691113917841041002855534619,
+ -0.04322076356021191118175840907244577856782537221435748296465882,
+ 0.2865033352736474630249006862976158896891076238443844211133873,
+ 0.5612852568703300445990941995240077241406247774064453800050914,
+ 0.3029835717728241602862575774374668529867757043461413348549577,
+ -0.05077014075488886159516471867138370972545857441670871832472707,
+ -0.05819625076158553022607041679522801089624825903982541419721721,
+ 0.02443409432116695639462954438418928805487699080947974989338820,
+ 0.01122924096203786563399489540091488781245346096838814728167341,
+ -0.006369601011048822977293753932627342482077585617391852852955559,
+ -0.001820458915566242322836631665832145136570132777862391313328351,
+ 0.0007902051009575939937150950543290226440287715441826917281929124,
+ 0.0003296651737931830308416338897758022998655744276957481989605186,
+ -0.00005019277455327664998007173088097694083956570594580641192332170,
+ -0.00002446573425530813115445387662881902303945941576472342106918209,
+ ],
+ "coif4": [
+ 0.0006309612114309468490753696608619526520153127603444406835368201,
+ -0.001152225143769973488683007937016166047881572156705066038094891,
+ -0.005194525163470323267558201363327294331811309729430512113592118,
+ 0.011360930899781950641704454327495718441159520023894304805142070,
+ 0.018945061045616642675204041814669158097013442370604397885045773,
+ -0.051719843705815280952009072709014825996085808127950893370164031,
+ -0.034486140470944806827159094088779177962124655341862998060866093,
+ 0.30227251053656843537076103037201073987915654650542997843779746,
+ 0.55454790624088107896085831311334062609863843227892842936901802,
+ 0.30791766802517503548651698686002846493302655084140026096325632,
+ -0.04352500928126570063143077306027663648139777048547894956715080,
+ -0.06488795097143100103160862688937301504802507374726020928892066,
+ 0.01988077364815951966984001670075537628468542316950829728327598,
+ 0.01763894787126169746077061344050946967036166456074020965866088,
+ -0.007366054847173363935072651649653007115003169492027095040477055,
+ -0.002312432307658842282830374733100847689924654369899030169556169,
+ 0.0014260063442333715226509754100697734398974715092509045804651032,
+ 0.0004666984635537353670445650012678936080062341977092967649055398,
+ -0.0001270007842387334077388950072420113055088253899932456267893098,
+ -0.0001130536369789104919020013936507623832962772709844179610938550,
+ 0.00003048364879677801030096883509693508426509710688913073244616617,
+ 0.00001266744808933008194725929652978169473830765616675686100903086,
+ -0.000001584926580756893754069651095690142946796090146306140001598,
+ -0.000001123948088281542889088159169056968300680087779667334879506,
+ ],
+ "coif5": [
+ -0.0001444992186438190986841213894961515720877049723502928655308158,
+ 0.0002541649492011946935899015644804259825374993423205648946709984,
+ 0.0015016192805175522217354963668928299350735326077949346507003370,
+ -0.0029411108712655515426850089360913424188662278991737055486839309,
+ -0.0071777671514877191801104649507158618871157411936681659380839993,
+ 0.016680426640070654149267486742006854522334094142598667043628439,
+ 0.019433238433489604119639447772308536988043628308900006988094899,
+ -0.064934946567212502582522008002547701764467194128935170823607736,
+ -0.036249793089132571825087765037251085892962369926089901862924065,
+ 0.29804266217809436069693444260411251439893892734398765007426945,
+ 0.55749162970920071628061190166750547398568080072951806509736879,
+ 0.30731644529206781686031633026138686170779831068030092889493625,
+ -0.047088034719761145117688715152051398948700623993077406913889346,
+ -0.068890522508050074805015336128652797797076949077503388892816063,
+ 0.020697343297747766068568936830651656003659188170019885439659031,
+ 0.021640668655956855043817421090949779825140639715020046717736369,
+ -0.0081089373078953680936950024508066654697766705721301481097854397,
+ -0.0049881737671041853808073796089816945023009226058734090095808033,
+ 0.0024486914321021269742893936892468103370072825113159100554056433,
+ 0.0014095103899593442621166984842002926701899968616244946547893994,
+ -0.0005637801876093825733169550088901318936072015721509885859509815,
+ -0.0002859004477225750899655442618734663056802618537327806113618985,
+ 0.00012739637513815208006169426577159456832051015616166327985688948,
+ 0.00005416263410701044073894700796327336007788688985721449717765655,
+ -0.00001736867944346280636144226913926838103159698473080996002509476,
+ -0.00001392656190060010871169838885327726938969652863554900825705905,
+ 0.000003582065515946048838215026334503092089635988710863959063568069,
+ 0.000001914022895847318655772885654240700542388103264097264264779554,
+ -0.00000031262488377016899432194683906058825900951892071223097080609,
+ -0.00000034030635502511647536690616071863203084936306302829968850306,
+ 0.000000059816065238516936893488966688516710847096926983547983503726,
+ 0.000000047001427849456491830476615736016736014244615701046223529866,
+ -0.000000006158615709678364180659098549671046676203853020063205641804,
+ -0.000000009225635096344935080070901936862847863830913641424076095562,
+ 0.000000001028486074518821265015830073593127726988903862842106883701,
+ 0.000000001168734175186263778695686067593866982925127816327529890618,
+ -0.00000000009468626176069127302554946536142654377756003084491946024,
+ -0.00000000016230233142152041788509334089966065953985768924968863072,
+ 0.000000000015076656859346950325398899897135970089618140503825462985,
+ 0.000000000015770990416421915106306877550025550097686639869166742016,
+ -0.000000000001084900468648598127623517893686893316653633996513097476,
+ -0.000000000001968659779411804788815966829825641065085077654946686012,
+ 0.000000000000098745634639726633264577838416327095717894829823436076,
+ 0.000000000000196734781460508097097473336847436635654948853090962606,
+ -0.000000000000008021080145299890797556481653726965016924825037889883,
+ -0.000000000000021030408801651651406095853493993966926736862877194669,
+ 0.000000000000000723888697830915633925166893301949334507697669655816,
+ 0.000000000000001943208515072761516084547140065815027641765976721267,
+ ],
+}
+
+
+def wavelist() -> list[str]:
+ """Return a list of available wavelet names."""
+ return list(_WAVELET_COEFFS.keys()) + ["haar"]
diff --git a/peft/src/peft/tuners/waveft/waverec2d.py b/peft/src/peft/tuners/waveft/waverec2d.py
new file mode 100644
index 0000000000000000000000000000000000000000..e05f5dc5471d07bb2a7b3c98272d0f30965fb0c3
--- /dev/null
+++ b/peft/src/peft/tuners/waveft/waverec2d.py
@@ -0,0 +1,316 @@
+# Copyright 2021 Moritz Wolter
+# Copyright 2025-present the HuggingFace Inc. team.
+#
+# Licensed under the EUPL v1.2
+#
+# This file contains code derived from PyTorch-Wavelet-Toolbox:
+# https://github.com/v0lta/PyTorch-Wavelet-Toolbox
+#
+# Original work by Moritz Wolter, licensed under EUPL v1.2
+# Modifications and integration by HuggingFace Inc. team
+
+from collections.abc import Callable, Sequence
+from functools import partial
+from typing import Any, NamedTuple, Protocol, Union, cast, overload
+
+import numpy as np
+import torch
+from typing_extensions import TypeAlias, Unpack
+
+from .wavelet import Wavelet as minimal_wavelet
+
+
+class WaveletDetailTuple2d(NamedTuple):
+ horizontal: torch.Tensor
+ vertical: torch.Tensor
+ diagonal: torch.Tensor
+
+
+WaveletCoeff2d: TypeAlias = tuple[torch.Tensor, Unpack[tuple[WaveletDetailTuple2d, ...]]]
+WaveletDetailDict: TypeAlias = dict[str, torch.Tensor]
+WaveletCoeffNd: TypeAlias = tuple[torch.Tensor, Unpack[tuple[WaveletDetailDict, ...]]]
+
+
+class Wavelet(Protocol):
+ name: str
+ dec_lo: Sequence[float]
+ dec_hi: Sequence[float]
+ rec_lo: Sequence[float]
+ rec_hi: Sequence[float]
+ dec_len: int
+ rec_len: int
+ filter_bank: tuple[Sequence[float], Sequence[float], Sequence[float], Sequence[float]]
+
+ def __len__(self) -> int:
+ return len(self.dec_lo)
+
+
+class WaveletTensorTuple(NamedTuple):
+ dec_lo: torch.Tensor
+ dec_hi: torch.Tensor
+ rec_lo: torch.Tensor
+ rec_hi: torch.Tensor
+
+ @classmethod
+ def from_wavelet(cls, wavelet: Wavelet, dtype: torch.dtype) -> "WaveletTensorTuple":
+ return cls(
+ torch.tensor(wavelet.dec_lo, dtype=dtype),
+ torch.tensor(wavelet.dec_hi, dtype=dtype),
+ torch.tensor(wavelet.rec_lo, dtype=dtype),
+ torch.tensor(wavelet.rec_hi, dtype=dtype),
+ )
+
+
+def _as_wavelet(wavelet: Union[Wavelet, str]) -> Wavelet:
+ if isinstance(wavelet, str):
+ return minimal_wavelet(wavelet)
+ else:
+ return wavelet
+
+
+def _is_dtype_supported(dtype: torch.dtype) -> bool:
+ return dtype in [torch.float16, torch.bfloat16, torch.float32, torch.float64]
+
+
+def _outer(a: torch.Tensor, b: torch.Tensor) -> torch.Tensor:
+ a_flat = torch.reshape(a, [-1])
+ b_flat = torch.reshape(b, [-1])
+ a_mul = torch.unsqueeze(a_flat, dim=-1)
+ b_mul = torch.unsqueeze(b_flat, dim=0)
+ return a_mul * b_mul
+
+
+def _check_if_tensor(array: Any) -> torch.Tensor:
+ if not isinstance(array, torch.Tensor):
+ raise ValueError("First element of coeffs must be the approximation coefficient tensor.")
+ return array
+
+
+def _check_axes_argument(axes: Sequence[int]) -> None:
+ if len(set(axes)) != len(axes):
+ raise ValueError("Cant transform the same axis twice.")
+
+
+def _check_same_device(tensor: torch.Tensor, torch_device: torch.device) -> torch.Tensor:
+ if torch_device != tensor.device:
+ raise ValueError("coefficients must be on the same device")
+ return tensor
+
+
+def _check_same_dtype(tensor: torch.Tensor, torch_dtype: torch.dtype) -> torch.Tensor:
+ if torch_dtype != tensor.dtype:
+ raise ValueError("coefficients must have the same dtype")
+ return tensor
+
+
+@overload
+def _coeff_tree_map(
+ coeffs: list[torch.Tensor], function: Callable[[torch.Tensor], torch.Tensor]
+) -> list[torch.Tensor]: ...
+@overload
+def _coeff_tree_map(coeffs: WaveletCoeff2d, function: Callable[[torch.Tensor], torch.Tensor]) -> WaveletCoeff2d: ...
+@overload
+def _coeff_tree_map(coeffs: WaveletCoeffNd, function: Callable[[torch.Tensor], torch.Tensor]) -> WaveletCoeffNd: ...
+def _coeff_tree_map(coeffs, function):
+ approx = function(coeffs[0])
+ result_lst: list[Any] = []
+ for element in coeffs[1:]:
+ if isinstance(element, tuple):
+ result_lst.append(WaveletDetailTuple2d(function(element[0]), function(element[1]), function(element[2])))
+ elif isinstance(element, dict):
+ new_dict = {key: function(value) for key, value in element.items()}
+ result_lst.append(new_dict)
+ elif isinstance(element, torch.Tensor):
+ result_lst.append(function(element))
+ else:
+ raise ValueError(f"Unexpected input type {type(element)}")
+ if not result_lst:
+ return [approx] if isinstance(coeffs, list) else (approx,)
+ elif isinstance(result_lst[0], torch.Tensor):
+ return [approx] + cast(list[torch.Tensor], result_lst)
+ else:
+ cast_result_lst = cast(Union[list[WaveletDetailDict], list[WaveletDetailTuple2d]], result_lst)
+ return (approx, *cast_result_lst)
+
+
+def _check_same_device_dtype(
+ coeffs: Union[list[torch.Tensor], WaveletCoeff2d, WaveletCoeffNd],
+) -> tuple[torch.device, torch.dtype]:
+ c = _check_if_tensor(coeffs[0])
+ torch_device, torch_dtype = c.device, c.dtype
+ _coeff_tree_map(coeffs, partial(_check_same_device, torch_device=torch_device))
+ _coeff_tree_map(coeffs, partial(_check_same_dtype, torch_dtype=torch_dtype))
+ return torch_device, torch_dtype
+
+
+def _get_transpose_order(axes: Sequence[int], data_shape: Sequence[int]) -> tuple[list[int], list[int]]:
+ axes = [a + len(data_shape) if a < 0 else a for a in axes]
+ all_axes = list(range(len(data_shape)))
+ remove_transformed = list(filter(lambda a: a not in axes, all_axes))
+ return remove_transformed, axes
+
+
+def _swap_axes(data: torch.Tensor, axes: Sequence[int]) -> torch.Tensor:
+ _check_axes_argument(axes)
+ front, back = _get_transpose_order(axes, list(data.shape))
+ return torch.permute(data, front + back)
+
+
+def _undo_swap_axes(data: torch.Tensor, axes: Sequence[int]) -> torch.Tensor:
+ _check_axes_argument(axes)
+ front, back = _get_transpose_order(axes, list(data.shape))
+ restore_sorted = torch.argsort(torch.tensor(front + back)).tolist()
+ return torch.permute(data, restore_sorted)
+
+
+def _fold_axes(data: torch.Tensor, keep_no: int) -> tuple[torch.Tensor, list[int]]:
+ dshape = list(data.shape)
+ return (torch.reshape(data, [int(np.prod(dshape[:-keep_no]))] + dshape[-keep_no:]), dshape)
+
+
+def _unfold_axes(data: torch.Tensor, ds: list[int], keep_no: int) -> torch.Tensor:
+ return torch.reshape(data, ds[:-keep_no] + list(data.shape[-keep_no:]))
+
+
+def _preprocess_coeffs(coeffs, ndim: int, axes, add_channel_dim: bool = False):
+ if isinstance(axes, int):
+ axes = (axes,)
+ torch_dtype = _check_if_tensor(coeffs[0]).dtype
+ if not _is_dtype_supported(torch_dtype):
+ raise ValueError(f"Input dtype {torch_dtype} not supported")
+ if ndim <= 0:
+ raise ValueError("Number of dimensions must be positive")
+ if tuple(axes) != tuple(range(-ndim, 0)):
+ if len(axes) != ndim:
+ raise ValueError(f"{ndim}D transforms work with {ndim} axes.")
+ else:
+ swap_fn = partial(_swap_axes, axes=axes)
+ coeffs = _coeff_tree_map(coeffs, swap_fn)
+ ds = list(coeffs[0].shape)
+ if len(ds) < ndim:
+ raise ValueError(f"At least {ndim} input dimensions required.")
+ elif len(ds) == ndim:
+ coeffs = _coeff_tree_map(coeffs, lambda x: x.unsqueeze(0))
+ elif len(ds) > ndim + 1:
+ coeffs = _coeff_tree_map(coeffs, lambda t: _fold_axes(t, ndim)[0])
+ if add_channel_dim:
+ coeffs = _coeff_tree_map(coeffs, lambda x: x.unsqueeze(1))
+ return coeffs, ds
+
+
+def _postprocess_coeffs(coeffs, ndim: int, ds: list[int], axes):
+ if isinstance(axes, int):
+ axes = (axes,)
+ if ndim <= 0:
+ raise ValueError("Number of dimensions must be positive")
+ if len(ds) < ndim:
+ raise ValueError(f"At least {ndim} input dimensions required.")
+ elif len(ds) == ndim:
+ coeffs = _coeff_tree_map(coeffs, lambda x: x.squeeze(0))
+ elif len(ds) > ndim + 1:
+ unfold_axes_fn = partial(_unfold_axes, ds=ds, keep_no=ndim)
+ coeffs = _coeff_tree_map(coeffs, unfold_axes_fn)
+ if tuple(axes) != tuple(range(-ndim, 0)):
+ if len(axes) != ndim:
+ raise ValueError(f"{ndim}D transforms work with {ndim} axes.")
+ else:
+ undo_swap_fn = partial(_undo_swap_axes, axes=axes)
+ coeffs = _coeff_tree_map(coeffs, undo_swap_fn)
+ return coeffs
+
+
+def _postprocess_tensor(
+ data: torch.Tensor, ndim: int, ds: list[int], axes: Union[tuple[int, ...], int]
+) -> torch.Tensor:
+ return _postprocess_coeffs(coeffs=[data], ndim=ndim, ds=ds, axes=axes)[0]
+
+
+def _get_filter_tensors(
+ wavelet: Union[Wavelet, str], flip: bool, device: torch.device, dtype: torch.dtype
+) -> WaveletTensorTuple:
+ wavelet = _as_wavelet(wavelet)
+ if flip:
+ filters = WaveletTensorTuple(
+ torch.tensor(wavelet.rec_lo, device=device, dtype=dtype),
+ torch.tensor(wavelet.rec_hi, device=device, dtype=dtype),
+ torch.tensor(wavelet.dec_lo, device=device, dtype=dtype),
+ torch.tensor(wavelet.dec_hi, device=device, dtype=dtype),
+ )
+ else:
+ filters = WaveletTensorTuple.from_wavelet(wavelet, dtype=dtype)
+ filters = WaveletTensorTuple(
+ filters.dec_lo.to(device),
+ filters.dec_hi.to(device),
+ filters.rec_lo.to(device),
+ filters.rec_hi.to(device),
+ )
+ return filters
+
+
+def _adjust_padding_at_reconstruction(tensor_len: int, coeff_len: int, padr: int, padl: int) -> tuple[int, int]:
+ if 2 * coeff_len - tensor_len == 1:
+ padr += 1
+ elif 2 * coeff_len - tensor_len != 0:
+ raise ValueError("incorrect padding")
+ return padr, padl
+
+
+def _construct_2d_filt(lo: torch.Tensor, hi: torch.Tensor) -> torch.Tensor:
+ ll = _outer(lo, lo)
+ lh = _outer(hi, lo)
+ hl = _outer(lo, hi)
+ hh = _outer(hi, hi)
+ filt = torch.stack([ll, lh, hl, hh], 0)
+ filt = filt.unsqueeze(1)
+ return filt
+
+
+def waverec2d(
+ coeffs: WaveletCoeff2d,
+ wavelet: Union[Wavelet, str],
+ axes: tuple[int, int] = (-2, -1),
+) -> torch.Tensor:
+ coeffs, ds = _preprocess_coeffs(coeffs, ndim=2, axes=axes)
+ torch_device, torch_dtype = _check_same_device_dtype(coeffs)
+
+ _, _, rec_lo, rec_hi = _get_filter_tensors(wavelet, flip=False, device=torch_device, dtype=torch_dtype)
+ filt_len = rec_lo.shape[-1]
+ rec_filt = _construct_2d_filt(lo=rec_lo, hi=rec_hi)
+
+ res_ll = coeffs[0]
+ for c_pos, coeff_tuple in enumerate(coeffs[1:]):
+ if not isinstance(coeff_tuple, tuple) or len(coeff_tuple) != 3:
+ raise ValueError(f"Unexpected detail coefficient type: {type(coeff_tuple)}. Must be a 3-tuple.")
+
+ curr_shape = res_ll.shape
+ for coeff in coeff_tuple:
+ if coeff.shape != curr_shape:
+ raise ValueError("All coefficients on each level must have the same shape")
+
+ res_lh, res_hl, res_hh = coeff_tuple
+ res_ll = torch.stack([res_ll, res_lh, res_hl, res_hh], 1)
+ res_ll = torch.nn.functional.conv_transpose2d(res_ll, rec_filt, stride=2).squeeze(1)
+
+ padl = (2 * filt_len - 3) // 2
+ padr = (2 * filt_len - 3) // 2
+ padt = (2 * filt_len - 3) // 2
+ padb = (2 * filt_len - 3) // 2
+ if c_pos < len(coeffs) - 2:
+ padr, padl = _adjust_padding_at_reconstruction(
+ res_ll.shape[-1], coeffs[c_pos + 2][0].shape[-1], padr, padl
+ )
+ padb, padt = _adjust_padding_at_reconstruction(
+ res_ll.shape[-2], coeffs[c_pos + 2][0].shape[-2], padb, padt
+ )
+
+ if padt > 0:
+ res_ll = res_ll[..., padt:, :]
+ if padb > 0:
+ res_ll = res_ll[..., :-padb, :]
+ if padl > 0:
+ res_ll = res_ll[..., padl:]
+ if padr > 0:
+ res_ll = res_ll[..., :-padr]
+
+ res_ll = _postprocess_tensor(res_ll, ndim=2, ds=ds, axes=axes)
+ return res_ll
diff --git a/peft/src/peft/tuners/xlora/__init__.py b/peft/src/peft/tuners/xlora/__init__.py
new file mode 100644
index 0000000000000000000000000000000000000000..6eae1f779b81e883f1dd64e3a4fca859391836c5
--- /dev/null
+++ b/peft/src/peft/tuners/xlora/__init__.py
@@ -0,0 +1,23 @@
+# Copyright 2023-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+from peft.utils import register_peft_method
+
+from .config import XLoraConfig
+from .model import XLoraModel
+
+
+__all__ = ["XLoraConfig", "XLoraModel"]
+
+register_peft_method(name="xlora", config_cls=XLoraConfig, model_cls=XLoraModel)
diff --git a/peft/src/peft/tuners/xlora/classifier.py b/peft/src/peft/tuners/xlora/classifier.py
new file mode 100644
index 0000000000000000000000000000000000000000..1ccf9edf9db3178ba9dc4dd3e07989251a676cb8
--- /dev/null
+++ b/peft/src/peft/tuners/xlora/classifier.py
@@ -0,0 +1,195 @@
+# Copyright 2023-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+from __future__ import annotations
+
+import builtins
+from typing import Optional, Union
+
+import torch
+import torch.nn as nn
+
+from .config import XLoraConfig
+
+
+Number = Union[builtins.int, builtins.float, builtins.bool]
+
+
+class TemperatureScaledSoftmax(nn.Module):
+ def __init__(self, temperature=1.0):
+ super().__init__()
+ self.temperature = temperature
+ self.softmax = nn.Softmax(dim=-1)
+
+ def forward(self, logits):
+ # Scale logits by the temperature
+ scaled_logits = logits / self.temperature
+ # Apply softmax to the scaled logits
+ return self.softmax(scaled_logits)
+
+
+class XLoraClassifier(nn.Module):
+ """
+ A classifier to select LoRA layers for XLora.
+ """
+
+ def __init__(
+ self,
+ model: nn.Module, # PeftModel
+ config: XLoraConfig,
+ n_classes: int,
+ n_layers: int,
+ device: torch.device,
+ ):
+ """
+ Construct an X-LoRA classifier from a model, config and some metadata. Note that n_layers is the number of LoRA
+ adapter layers, not the number of model layers.
+ """
+ super().__init__()
+
+ self.n_classes = n_classes
+ self.n_layers = n_layers
+ self.config = config
+ self.log_scalings = []
+ self.softmax = TemperatureScaledSoftmax(temperature=self.config.softmax_temperature)
+ self.override_scaling_pass_value: Number = config.scaling_pass_value
+
+ self.scalings_logging = False
+
+ self.dtype = next(model.parameters()).dtype
+ add_dropout = config.xlora_dropout_p > 0.0
+
+ layers = []
+ if self.config.xlora_depth == 1:
+ if config.layerwise_scalings: # bias=False if we have just one layer
+ last = nn.Linear(config.hidden_size, n_classes * n_layers, bias=True).to(device).to(self.dtype)
+ else:
+ last = nn.Linear(config.hidden_size, n_classes, bias=True).to(device).to(self.dtype)
+ else:
+ if self.config.xlora_depth <= 0:
+ raise ValueError("X-LoRA depth must be strictly positive.")
+
+ layers.append(nn.Linear(config.hidden_size, config.xlora_size, bias=True).to(device).to(self.dtype))
+
+ layers.append(nn.ReLU())
+ if add_dropout:
+ layers.append(nn.Dropout(p=config.xlora_dropout_p))
+
+ for _ in range(config.xlora_depth - 2):
+ layers.append(nn.Linear(config.xlora_size, config.xlora_size, bias=True).to(device).to(self.dtype))
+
+ layers.append(nn.ReLU())
+ if add_dropout:
+ layers.append(nn.Dropout(p=config.xlora_dropout_p))
+
+ if config.layerwise_scalings:
+ last = nn.Linear(config.xlora_size, n_classes * n_layers, bias=True).to(device).to(self.dtype)
+ else:
+ last = nn.Linear(config.xlora_size, n_classes, bias=True).to(device).to(self.dtype)
+ self.layers = nn.Sequential(*layers, last)
+
+ def make_dummy_scalings(
+ self,
+ input_ids: Optional[torch.LongTensor] = None,
+ inputs_embeds: Optional[torch.FloatTensor] = None,
+ *args,
+ **kwargs,
+ ) -> torch.Tensor:
+ """
+ Make some dummy scalings for the scalings pass (the one to get the logits for the X-LoRA classifier). These are
+ of shape (batch_size, seq_len, n_layers, n_classes) and filled with the override scalings pass value. Note that
+ n_layers is the number of LoRA adapter layers, not the number of model layers.
+ """
+ if input_ids is not None:
+ batch_size = input_ids.shape[0]
+ device = input_ids.device
+ seq_len = input_ids.shape[1]
+ else:
+ batch_size = inputs_embeds.shape[0]
+ device = inputs_embeds.device
+ seq_len = inputs_embeds.shape[1]
+
+ return torch.full( # type: ignore
+ (batch_size, seq_len, self.n_layers, self.n_classes),
+ self.override_scaling_pass_value,
+ ).to(device=device, dtype=self.dtype)
+
+ def forward(
+ self,
+ result,
+ input_ids: Optional[torch.LongTensor] = None,
+ inputs_embeds: Optional[torch.FloatTensor] = None,
+ *args,
+ **kwargs,
+ ) -> torch.Tensor:
+ """
+ Using the hidden states of the model, predict `n_classes` LoRA alpha values. Returns the scalings.
+ """
+ if input_ids is not None:
+ batch_size = input_ids.shape[0]
+ seq_len = input_ids.shape[1]
+ else:
+ batch_size = inputs_embeds.shape[0]
+ seq_len = inputs_embeds.shape[1]
+
+ hidden_states = result.hidden_states # type: ignore
+
+ hidden_state = hidden_states[-1] # Get the last hidden state
+
+ ### Classifier run
+ # hidden_state=[batch_size, seq_len, hidden_size]
+ logits = self.layers.forward(hidden_state)
+
+ ### Repeat to make layerwise scalings
+ ### If layerwise_scalings=False, then the classifier only outputs logits which are not layer-wise.
+ ### So, we expand them to the correct shape.
+ if not self.config.layerwise_scalings:
+ logits = logits.unsqueeze(2)
+ logits = logits.expand(-1, -1, self.n_layers, -1)
+
+ ### Classifier run
+
+ scalings = logits.reshape(batch_size, seq_len, self.n_layers, self.n_classes)
+ # scalings = [batch_size, seq_len, n_layers, n_classes]
+
+ if self.config.enable_softmax:
+ scalings = self.softmax(scalings)
+
+ if self.scalings_logging:
+ self.log_scalings.append(scalings)
+
+ return scalings
+
+ def _get_bucketed_scalings(self) -> dict[int, tuple[list[int], list[torch.Tensor]]]:
+ """
+ Returns bucketed scalings, bucketed by seq_len. Each value consists of the positions (the first) and the
+ associated tensors. The positions are paired with the associated tensors and give the position in the scaling
+ log. Each scaling is a tensor of shape (batch_size, seq_len, n_layers, n_classes)).
+ """
+ seqlens_map: dict[int, tuple[list[int], list[torch.Tensor]]] = {}
+ for i, scaling in enumerate(self.log_scalings):
+ seq_len = scaling.shape[1]
+ if seq_len not in seqlens_map:
+ seqlens_map[seq_len] = ([i], [scaling])
+ else:
+ seqlens_map[seq_len][0].append(i)
+ seqlens_map[seq_len][1].append(scaling)
+
+ return seqlens_map
+
+ def _set_override_scaling_pass_value(self, value: Union[Number, None]):
+ if value is None:
+ self.override_scaling_pass_value = 1 / self.n_classes
+ else:
+ self.override_scaling_pass_value = value
+ self.config.scaling_pass_value = self.override_scaling_pass_value
diff --git a/peft/src/peft/tuners/xlora/config.py b/peft/src/peft/tuners/xlora/config.py
new file mode 100644
index 0000000000000000000000000000000000000000..9cdb0f6e49f367c640ef4abf14e29b3b60f22fa6
--- /dev/null
+++ b/peft/src/peft/tuners/xlora/config.py
@@ -0,0 +1,102 @@
+# Copyright 2023-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+from __future__ import annotations
+
+import warnings
+from dataclasses import dataclass
+from typing import Optional
+
+from peft.config import PeftConfig
+from peft.utils.peft_types import PeftType
+
+
+@dataclass
+class XLoraConfig(PeftConfig):
+ r"""
+ This is the configuration class to store the configuration of a `XLoraModel`. When the config is reloaded, the
+ paths of the `adapters` field is disregarded in favor of the saved adapters. As such, only the keys matter during
+ loading.
+
+ Args:
+ hidden_size (`int`):
+ Hidden size of the base model.
+ adapters (`dict`):
+ Mapping of adapter names to the LoRA adapter id, as per PeftModel.load_adapter. *They will be automatically
+ loaded*, to use as LoRA experts. When using from_pretrained, pass the new adapters dict as a keyword
+ argument.
+ enable_softmax (`bool`, *optional*, defaults to `True`):
+ Enable softmax application for the X-LoRA classifier.
+ enable_softmax_topk (`bool`, *optional*, defaults to `False`):
+ Enable softmax application for the top-k LoRA adapters. Mutually exclusive to `enable_softmax` and must
+ only be set if `top_k_lora` is.
+ softmax_temperature (`float`, *optional*, defaults to 1.0):
+ Softmax temperature, lower yields sharper predictions
+ layerwise_scalings (`bool`, *optional*, defaults to `False`):
+ If True, generate scalings for each LoRA adapter (each layer). If this is False, then scalings will be
+ broadcasted, the same, to each layer.
+ top_k_lora (`int`, *optional*, defaults to None):
+ Sparsely select the top_k LoRA experts instead of the default dense method.
+ xlora_depth (`int`, *optional*, defaults to 1):
+ Depth of the X-LoRA classifier.
+ xlora_size (`int`, *optional*, defaults to 2048):
+ Hidden size of the X-LoRA classifier, irrelevant if `xlora_depth=1`.
+ xlora_dropout_p (`float`, *optional*, defaults to 0.2):
+ Dropout probability of the X-LoRA classifier, irrelevant if `xlora_depth=1`.
+ use_trainable_adapters (`bool`, *optional*, defaults to False):
+ Make the adapters trainable.
+ scaling_pass_value (`float`, *optional*, defaults to 0):
+ Scaling pass value.
+ global_scaling_weight (`float`, *optional*, defaults to 1):
+ Weight to multiply output of each LoRA adapter by.
+ """
+
+ hidden_size: int = None # type: ignore
+ adapters: dict[str, str] = None # type: ignore
+ enable_softmax: bool = True
+ enable_softmax_topk: bool = False
+ layerwise_scalings: bool = False
+ xlora_depth: int = 1
+ xlora_size: int = 2048
+ xlora_dropout_p: float = 0.2
+ use_trainable_adapters: bool = False
+ softmax_temperature: float = 1.0
+ top_k_lora: Optional[int] = None
+ scaling_pass_value: float = 0.0
+ global_scaling_weight: float = 1.0
+
+ def __post_init__(self):
+ super().__post_init__()
+ self.peft_type = PeftType.XLORA
+
+ if self.hidden_size is None:
+ warnings.warn(
+ "No value was provided for `hidden_size`. This will be set to 4096 by default, please ensure that this is correct."
+ )
+ self.hidden_size = 4096
+ if self.adapters is None:
+ warnings.warn(
+ "No value was provided for for `adapters`. This will be set to empty, please ensure that this is correct."
+ )
+ self.adapters = {}
+
+ if self.enable_softmax_topk and self.top_k_lora is None:
+ warnings.warn("`enable_softmax_topk` enabled `top_k_lora` is not set")
+
+ if self.enable_softmax_topk and self.enable_softmax:
+ warnings.warn(
+ "`enable_softmax_topk` and `enable_softmax` are both enabled. This will result in worse performance."
+ )
+
+ if self.top_k_lora is not None and self.top_k_lora < 1:
+ warnings.warn("`top_k_lora` value must be at least 1.")
diff --git a/peft/src/peft/tuners/xlora/layer.py b/peft/src/peft/tuners/xlora/layer.py
new file mode 100644
index 0000000000000000000000000000000000000000..bf2afcd58939815e59eacef0e10d0c5757d523e6
--- /dev/null
+++ b/peft/src/peft/tuners/xlora/layer.py
@@ -0,0 +1,225 @@
+# Copyright 2024-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+from __future__ import annotations
+
+from typing import Any, Callable, Optional
+
+import torch
+import torch.nn as nn
+from torch import Tensor
+
+from peft.tuners import lora
+
+from .config import XLoraConfig
+
+
+class XLoraLayer:
+ """
+ A XLoraLayer wraps any LoraLayer and performs the XLora operation on the LoRA adaptors specified. Its primary API
+ is the forward method, which uses the scalings to execute the XLora algorithm.
+ """
+
+ def __init__(
+ self,
+ model: nn.Module, # XLoraModel
+ target: lora.LoraLayer,
+ target_forward: Callable[..., Any],
+ layer_number: int,
+ config: XLoraConfig,
+ ) -> None:
+ self.model = model
+ self.target_forward = target_forward
+ self.target = target
+ self.layer_number = layer_number
+ self.config = config
+
+ """
+ Apply the scalings for the adapter.
+ """
+
+ @staticmethod
+ def apply_scalings_to_x(x: torch.Tensor, scalings_layer: torch.Tensor, adapter: int) -> torch.Tensor:
+ # scalings_layer = [batch_size, seq_len, n_classes]
+ scalings = scalings_layer[:, :, adapter].unsqueeze(-1)
+ # scalings_layer = [batch_size, seq_len, 1]
+ return x * scalings
+
+ """
+ Get the scalings for this layer, potentially applying topk and topk+softmax. This is called before
+ `apply_scalings_to_x`
+ """
+
+ def get_maybe_topk_scalings(self, scalings) -> torch.Tensor:
+ # xlora_scalings = [batch_size, seq_len, n_classes]
+ xlora_scalings: Tensor = scalings[:, :, self.layer_number, :] # type: ignore
+
+ if self.config.top_k_lora is not None:
+ _, topk_indices = torch.topk(xlora_scalings, k=self.config.top_k_lora, dim=-1)
+
+ # Mask the topk to True, the rest to False
+ mask = torch.zeros_like(xlora_scalings, dtype=torch.bool)
+ mask.scatter_(-1, topk_indices, True)
+
+ xlora_scalings = xlora_scalings * mask.to(xlora_scalings.dtype)
+
+ # Apply per-token normalization to the xLoRA scaling factors using a softmax
+ if self.config.enable_softmax_topk:
+ nonzero_mask = xlora_scalings != 0
+ full = xlora_scalings.masked_fill(~nonzero_mask, float("-inf"))
+ new_scalings = torch.softmax(full, dim=-1)
+ xlora_scalings = new_scalings.masked_fill(~nonzero_mask, 0.0)
+
+ return xlora_scalings
+
+
+class XLoraLinearLayer(XLoraLayer):
+ def __init__(
+ self,
+ model: nn.Module,
+ target: lora.Linear,
+ target_forward: Callable[..., Any],
+ layer_number: int,
+ config: XLoraConfig,
+ ) -> None:
+ super().__init__(model, target, target_forward, layer_number, config)
+
+ def forward(self, x: Tensor, *args: Any, scalings: Optional[Tensor] = None, **kwargs: Any) -> Tensor:
+ """
+ This method is designed to be a drop-in-replacement for the LoRA layers' .forward method. To use it, a bound
+ method must be created (bound to an instance of the XLoraLayer class).
+ """
+
+ previous_dtype = x.dtype
+ if scalings is not None:
+ xlora_scalings = self.get_maybe_topk_scalings(scalings)
+
+ result = self.target.base_layer(x, *args, **kwargs)
+
+ # Ignore if disabled. We want to make sure this is always run.
+ if not self.target.merged:
+ for adapter_n, active_adapter in enumerate(self.target.active_adapters):
+ if active_adapter not in self.target.lora_A.keys():
+ continue
+ # TODO: implement X-LoRA with Lora+Dora layers
+ if self.target.use_dora[active_adapter]:
+ raise ValueError("X-LoRA currently does not support LoRA layers with DoRA")
+ lora_A = self.target.lora_A[active_adapter]
+ lora_B = self.target.lora_B[active_adapter]
+ dropout = self.target.lora_dropout[active_adapter]
+ scaling = self.target.scaling[active_adapter]
+ x = x.to(lora_A.weight.dtype) # type: ignore
+ if scalings is not None:
+ x_mod = self.apply_scalings_to_x(x, xlora_scalings, adapter_n)
+ scaling_weight = self.config.global_scaling_weight
+ else:
+ x_mod = x
+ scaling_weight = 1
+ result += lora_B(lora_A(dropout(x_mod))) * scaling * scaling_weight
+
+ result = result.to(previous_dtype)
+ return result
+
+
+class XLoraEmbeddingLayer(XLoraLayer):
+ def __init__(
+ self,
+ model: nn.Module,
+ target: lora.Embedding,
+ target_forward: Callable[..., Any],
+ layer_number: int,
+ config: XLoraConfig,
+ ) -> None:
+ super().__init__(model, target, target_forward, layer_number, config)
+
+ def forward(self, x: Tensor, *args: Any, scalings: Optional[Tensor] = None, **kwargs: Any) -> Tensor:
+ """
+ This method is designed to be a drop-in-replacement for the LoRA layers' .forward method. To use it, a bound
+ method must be created (bound to an instance of the XLoraLayer class).
+ """
+
+ if scalings is not None:
+ xlora_scalings = self.get_maybe_topk_scalings(scalings)
+
+ result = self.target.base_layer(x, *args, **kwargs)
+
+ # Ignore if disabled. We want to make sure this is always run.
+ if not self.target.merged:
+ for adapter_n, active_adapter in enumerate(self.target.active_adapters):
+ if active_adapter not in self.target.lora_embedding_A:
+ continue
+ # TODO: implement X-LoRA with Lora+Dora layers
+ if self.target.use_dora.get(active_adapter, False):
+ raise ValueError("X-LoRA currently does not support LoRA layers with DoRA")
+ embedding_A = self.target.lora_embedding_A[active_adapter].T
+ embedding_B = self.target.lora_embedding_B[active_adapter].T
+ scaling = self.target.scaling[active_adapter]
+ after_A = self.target._embed(x, embedding_A) # type: ignore
+ if scalings is not None:
+ after_A_mod = self.apply_scalings_to_x(after_A, xlora_scalings, adapter_n)
+ scaling_weight = self.config.global_scaling_weight
+ else:
+ after_A_mod = after_A
+ scaling_weight = 1
+ result += (after_A_mod @ embedding_B) * scaling * scaling_weight
+
+ return result
+
+
+class XLoraConv2dLayer(XLoraLayer):
+ def __init__(
+ self,
+ model: nn.Module,
+ target: lora.Conv2d,
+ target_forward: Callable[..., Any],
+ layer_number: int,
+ config: XLoraConfig,
+ ) -> None:
+ super().__init__(model, target, target_forward, layer_number, config)
+
+ def forward(self, x: Tensor, *args: Any, scalings: Optional[Tensor] = None, **kwargs: Any) -> Tensor:
+ """
+ This method is designed to be a drop-in-replacement for the LoRA layers' .forward method. To use it, a bound
+ method must be created (bound to an instance of the XLoraLayer class).
+ """
+
+ previous_dtype = x.dtype
+
+ if scalings is not None:
+ xlora_scalings = self.get_maybe_topk_scalings(scalings)
+
+ result = self.target.base_layer(x, *args, **kwargs)
+
+ # Ignore if disabled. We want to make sure this is always run.
+ if not self.target.merged:
+ for adapter_n, active_adapter in enumerate(self.target.active_adapters):
+ if active_adapter not in self.target.lora_A.keys():
+ continue
+ # TODO: implement X-LoRA with Lora+Dora layers
+ if self.target.use_dora[active_adapter]:
+ raise ValueError("X-LoRA currently does not support LoRA layers with DoRA")
+ lora_A = self.target.lora_A[active_adapter]
+ lora_B = self.target.lora_B[active_adapter]
+ dropout = self.target.lora_dropout[active_adapter]
+ scaling = self.target.scaling[active_adapter]
+ x = x.to(lora_A.weight.dtype) # type: ignore
+ if scalings is not None:
+ x_mod = self.apply_scalings_to_x(x, xlora_scalings, adapter_n)
+ scaling_weight = self.config.global_scaling_weight
+ else:
+ x_mod = x
+ scaling_weight = 1
+ result += lora_B(lora_A(dropout(x_mod))) * scaling * scaling_weight
+
+ result = result.to(previous_dtype)
+ return result
diff --git a/peft/src/peft/tuners/xlora/model.py b/peft/src/peft/tuners/xlora/model.py
new file mode 100644
index 0000000000000000000000000000000000000000..25e0902bfd0ea2580ee790116f2e5ffb1c1abd32
--- /dev/null
+++ b/peft/src/peft/tuners/xlora/model.py
@@ -0,0 +1,524 @@
+# Copyright 2023-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+from __future__ import annotations
+
+import copy
+from contextlib import contextmanager
+from functools import partial
+from typing import Optional, Union
+
+import torch
+import torch.nn as nn
+
+from peft.tuners.lora.layer import LoraLayer
+from peft.tuners.lora.model import LoraModel
+from peft.tuners.tuners_utils import BaseTuner
+from peft.utils.constants import DUMMY_TARGET_MODULES
+from peft.utils.save_and_load import set_peft_model_state_dict
+
+from .. import lora
+from .classifier import XLoraClassifier
+from .config import XLoraConfig
+from .layer import XLoraConv2dLayer, XLoraEmbeddingLayer, XLoraLinearLayer
+
+
+def convert_layers_to_xlora(
+ base: nn.Module, # PeftModel
+ xloramodel: nn.Module, # XLoraModel
+ config: XLoraConfig,
+) -> tuple[int, torch.device | None]:
+ """
+ Returns the number of swapped layers.
+ """
+ total_swapped = 0
+ all_layers = []
+
+ device = None
+ for module in base.modules():
+ # Check the exact type because classes like OPTLearnedPositionalEmbedding inherit from nn.Embedding
+ if isinstance(module, lora.Linear):
+ device = module.lora_A[next(iter(module.lora_A))].weight.device
+ new_layer = XLoraLinearLayer(
+ model=xloramodel,
+ target=module,
+ target_forward=module.forward,
+ layer_number=total_swapped,
+ config=config,
+ )
+ all_layers.append(new_layer)
+ module.forward = new_layer.forward # type: ignore[method-assign]
+ total_swapped += 1
+ elif isinstance(module, lora.Embedding):
+ device = module.lora_embedding_A[next(iter(module.lora_embedding_A))].device
+ new_layer = XLoraEmbeddingLayer(
+ model=xloramodel,
+ target=module,
+ target_forward=module.forward,
+ layer_number=total_swapped,
+ config=config,
+ )
+ all_layers.append(new_layer)
+ module.forward = new_layer.forward # type: ignore[method-assign]
+ total_swapped += 1
+ elif isinstance(module, lora.Conv2d):
+ device = module.lora_A[next(iter(module.lora_A))].weight.device
+ new_layer = XLoraConv2dLayer(
+ model=xloramodel,
+ target=module,
+ target_forward=module.forward,
+ layer_number=total_swapped,
+ config=config,
+ )
+ all_layers.append(new_layer)
+ module.forward = new_layer.forward # type: ignore[method-assign]
+ total_swapped += 1
+
+ return (total_swapped, device)
+
+
+def _load_adapter_into_lora_model(
+ lora_model: LoraModel,
+ adapter_name: str,
+ model_id: str,
+ torch_device: Optional[str] = None,
+ ephemeral_gpu_offload: bool = False,
+ autocast_adapter_dtype: bool = True,
+ subfolder: Optional[str] = None,
+ **kwargs,
+):
+ """
+ This method emulates the behavior of `PeftModel.from_pretrained`. Updates to `PeftModel.from_pretrained` may need
+ to be reflected here.
+
+ All params pertain to the adapter (adapter name, model id, `i` is the adapter number in 0 indexing).
+ """
+ from peft.peft_model import PeftModel
+ from peft.tuners.lora.config import LoraConfig
+ from peft.utils.other import infer_device
+ from peft.utils.save_and_load import load_peft_weights
+
+ hf_hub_download_kwargs, kwargs = PeftModel._split_kwargs(kwargs)
+ if torch_device is None:
+ torch_device = infer_device()
+
+ if adapter_name not in lora_model.peft_config:
+ # load the config
+ lora_peft_config = LoraConfig.from_pretrained(
+ model_id,
+ ephemeral_gpu_offload=ephemeral_gpu_offload,
+ subfolder=subfolder,
+ **hf_hub_download_kwargs,
+ )
+ lora_peft_config.inference_mode = False
+ lora_model.peft_config[adapter_name] = lora_peft_config
+ lora_model.inject_adapter(lora_model.model, adapter_name)
+
+ adapter_weights = load_peft_weights(model_id, device=torch_device, subfolder=subfolder, **hf_hub_download_kwargs)
+ new_adapter_weights = {}
+ # Rework the keys to contain the adapter numbers
+ for old_key in adapter_weights.keys():
+ key: str = old_key
+ # Remove all the prefixes until we have model.<...>
+ while not (key.startswith("model.") and not key.startswith("model.model.")):
+ key = key[key.find(".") + 1 :]
+ # We always want model.model
+ key = "model." + key
+ new_adapter_weights[key] = adapter_weights[old_key]
+
+ # load the weights into the model
+ ignore_mismatched_sizes = kwargs.get("ignore_mismatched_sizes", False)
+ load_result = set_peft_model_state_dict(
+ lora_model,
+ new_adapter_weights,
+ adapter_name=adapter_name,
+ ignore_mismatched_sizes=ignore_mismatched_sizes,
+ )
+ if len(load_result.unexpected_keys) > 0:
+ raise ValueError(
+ f"Got unexpected keys! Please raise an issue and tag @EricLBuehler.\n\nunexpected_keys={load_result.unexpected_keys}"
+ )
+
+ if hasattr(lora_model, "_cast_adapter_dtype"):
+ lora_model._cast_adapter_dtype(adapter_name=adapter_name, autocast_adapter_dtype=autocast_adapter_dtype)
+
+
+class XLoraModel(BaseTuner):
+ """
+ Creates an X-LoRA (Mixture of LoRA experts), model from a pretrained transformers model. Currently, this X-LoRA
+ implementation only works with models with a transformer architecture.
+
+ The method is described in detail in https://huggingface.co/papers/2402.07148.
+
+ Args:
+ model ([`torch.nn.Module`]): The model to be adapted.
+ config ([`XLoraConfig`]): The configuration of the Lora model.
+ adapter_name (`str`): The name of the adapter, does not affect the LoRA adapter names.
+
+ Returns:
+ `torch.nn.Module`: The X-LoRA model.
+
+ Example:
+ ```py
+ >>> from transformers import AutoModelForCausalLM, AutoConfig, BitsAndBytesConfig
+ >>> from peft import LoraConfig, PeftModel, get_peft_model, prepare_model_for_kbit_training
+
+ >>> model_config = AutoConfig.from_pretrained("mistralai/Mistral-7B-Instruct-v0.1")
+ >>> config = XLoraConfig(
+ ... task_type="CAUSAL_LM",
+ ... hidden_size=model_config.hidden_size,
+ ... xlora_depth=4,
+ ... adapters={
+ ... "adapter_1": "./path/to/the/checkpoint/",
+ ... "adapter_2": "./path/to/the/checkpoint/",
+ ... "adapter_n": "./path/to/the/checkpoint/",
+ ... },
+ ... )
+ >>> int8_config = BitsAndBytesConfig(load_in_8bit=True)
+ >>> model = AutoModelForCausalLM.from_pretrained(
+ ... "mistralai/Mistral-7B-Instruct-v0.1",
+ ... trust_remote_code=True,
+ ... attn_implementation="flash_attention_2",
+ ... device_map="cuda:0",
+ ... torch_dtype=torch.bfloat16,
+ ... quantization_config=int8_config,
+ ... )
+ >>> model = prepare_model_for_kbit_training(4)
+ >>> xlora_model = get_peft_model(model, config)
+ ```
+ """
+
+ def __init__(
+ self,
+ model: nn.Module,
+ config: Union[dict[str, XLoraConfig], XLoraConfig],
+ adapter_name: str,
+ torch_device: Optional[str] = None,
+ ephemeral_gpu_offload: bool = False,
+ autocast_adapter_dtype: bool = True,
+ **kwargs,
+ ) -> None:
+ """
+ Create a new X-LoRA model
+
+ Args:
+ model (`nn.Module`):
+ Base model to apply X-LoRA to.
+ config: ([`XLoraConfig`]):
+ X-LoRA configuration object.
+ adapter_name: (`str`):
+ Adapter name for the X-LoRA adapter.
+ torch_device (`str`, *optional*, defaults to None):
+ (For loading the LoRA adapters) The device to load the adapter on. If `None`, the device will be
+ inferred.
+ ephemeral_gpu_offload (`bool`, *optional*, defaults to `False`):
+ (For loading the LoRA adapters) Whether to use ephemeral GPU offloading for partially loaded modules.
+ Defaults to `False`.
+ autocast_adapter_dtype (`bool`, *optional*, defaults to `True`):
+ (For loading the LoRA adapters) Whether to autocast the adapter dtype. Defaults to `True`. Right now,
+ this will only cast adapter weights using float16 and bfloat16 to float32, as this is typically
+ required for stable training, and only affect select PEFT tuners.
+ kwargs: (`optional`):
+ (For loading the LoRA adapters) Additional arguments to modify the way the adapter is loaded, e.g. the
+ token for Hugging Face Hub.
+ """
+
+ nn.Module.__init__(self)
+
+ if isinstance(config, dict):
+ conf = config[adapter_name]
+ else:
+ conf = config
+
+ # Create an empty LoraModel
+ base_lora_config = copy.copy(conf)
+ base_lora_config.target_modules = DUMMY_TARGET_MODULES
+ # Imitate a LoraConfig, fields might need to be updated if LoraConfig is updated
+ base_lora_config.layer_replication = None
+ base_lora_config.bias = "none"
+ lora_model = LoraModel(model, base_lora_config, adapter_name)
+
+ self.xlora_config = conf
+ self.lora_model = lora_model
+
+ peft_config = conf
+
+ if hasattr(model.config, "use_cache") and model.config.use_cache:
+ raise ValueError("`use_cache` must be False")
+
+ adapters_items = peft_config.adapters.items()
+ if hasattr(self.xlora_config, "_subfolders"):
+ adapters_items = zip(peft_config.adapters.items(), self.xlora_config._subfolders)
+ else:
+ adapters_items = peft_config.adapters.items()
+
+ if hasattr(self.xlora_config, "_subfolders"):
+ for i, (_adapter_name, model_id), subfolder in enumerate(adapters_items):
+ _load_adapter_into_lora_model(
+ lora_model=self.lora_model,
+ adapter_name=str(i),
+ model_id=model_id,
+ torch_device=torch_device,
+ ephemeral_gpu_offload=ephemeral_gpu_offload,
+ autocast_adapter_dtype=autocast_adapter_dtype,
+ subfolder=subfolder,
+ **kwargs,
+ )
+ else:
+ for i, (_adapter_name, model_id) in enumerate(adapters_items):
+ _load_adapter_into_lora_model(
+ lora_model=self.lora_model,
+ adapter_name=str(i),
+ model_id=model_id,
+ torch_device=torch_device,
+ ephemeral_gpu_offload=ephemeral_gpu_offload,
+ autocast_adapter_dtype=autocast_adapter_dtype,
+ subfolder=None,
+ **kwargs,
+ )
+
+ self.lora_model.set_adapter(list(peft_config.adapters.keys()))
+
+ self._maybe_freeze_all_adapters()
+
+ total_swapped, device = convert_layers_to_xlora(
+ model,
+ self,
+ peft_config,
+ )
+
+ n_classes = len(peft_config.adapters)
+ xlora_classifier = XLoraClassifier(model, peft_config, n_classes, total_swapped, device)
+
+ # Setup the model internal state
+ self.internal_xlora_classifier = xlora_classifier
+ self.internal_xlora_scalings = None # type: ignore
+ # Controlled by enable_adapter_layers or disable_adapter_layers
+ self.disabled = False
+
+ def _maybe_freeze_all_adapters(self):
+ self.eval()
+ if not self.xlora_config.use_trainable_adapters:
+ for name, param in self.named_parameters():
+ if "lora_" in name:
+ param.requires_grad = False
+
+ def generate(self, *args, **kwargs):
+ kwargs["use_cache"] = False
+ res = self.lora_model.generate(*args, **kwargs) # type: ignore
+ # This is necessary because we use PeftModel.disable_adapter() which reenables the adapters
+ self._maybe_freeze_all_adapters()
+ return res
+
+ @contextmanager
+ def _enable_peft_forward_hooks(self, *generate_args, **generate_kwargs):
+ def scalings_injection_hook(target, args, kwargs, scalings):
+ # pre-forward hook to inject the adapter_names argument when using mixed adapter batches inference
+ kwargs["scalings"] = scalings
+ return args, kwargs
+
+ hook_handles = []
+
+ def _pre_forward(module, *args, **kwargs):
+ # =========================== Forward pass with "dummy" scalings ==================
+ nonlocal hook_handles
+
+ args_real = args[0]
+ kwargs_real = args[1]
+ kwargs_real.update(kwargs)
+
+ dummy_scalings = self.internal_xlora_classifier.make_dummy_scalings(*args_real, **kwargs_real)
+
+ for module in self.modules():
+ if isinstance(module, LoraLayer):
+ pre_forward = partial(scalings_injection_hook, scalings=dummy_scalings)
+ existing_hooks = getattr(module, "_forward_pre_hooks", {})
+ if any(val is scalings_injection_hook for val in existing_hooks.values()):
+ # When calling generate, module.forward is called multiple times inside the forward hook
+ # context, resulting in multiple hooks being registered. Therefore, we check if the hooks is
+ # already present and skip it in that case.
+ continue
+ handle = module.register_forward_pre_hook(pre_forward, with_kwargs=True)
+ hook_handles.append(handle)
+
+ with torch.no_grad():
+ self.lora_model.disable_adapter_layers()
+
+ try:
+ scaling_pass_kwargs = kwargs_real.copy()
+ scaling_pass_kwargs["output_hidden_states"] = True
+ scaling_pass_kwargs["return_dict"] = True
+ try:
+ base_output = self.lora_model.model.forward(*args_real, **scaling_pass_kwargs)
+ finally:
+ # Clean everything up
+ for handle in hook_handles:
+ handle.remove()
+ finally:
+ self.lora_model.enable_adapter_layers()
+
+ xlora_scalings = self.internal_xlora_classifier(result=base_output, *args_real, **kwargs_real)
+ # Store computed scalings to fix get_latest_scalings() returning None
+ self.internal_xlora_scalings = xlora_scalings
+
+ # =========================== Real forward pass with calculated scalings ==================
+
+ hook_handles = []
+ for module in self.modules():
+ if isinstance(module, LoraLayer):
+ pre_forward = partial(scalings_injection_hook, scalings=xlora_scalings)
+ handle = module.register_forward_pre_hook(pre_forward, with_kwargs=True)
+ hook_handles.append(handle)
+
+ if not self.disabled:
+ forward_handle = self.lora_model.model.register_forward_pre_hook(_pre_forward, with_kwargs=True)
+
+ # Run the forward pass: first the scaling pass in the hook, and then with the base model
+ try:
+ yield
+ finally:
+ if not self.disabled:
+ for handle in hook_handles:
+ handle.remove()
+ forward_handle.remove()
+
+ def __getattr__(self, name: str):
+ """Forward missing attributes to the wrapped module."""
+ try:
+ return super().__getattr__(name) # defer to nn.Module's logic
+ except AttributeError:
+ if name == "lora_model": # see #1892: prevent infinite recursion if class is not initialized
+ raise
+ return getattr(self.lora_model, name)
+
+ @staticmethod
+ def _prepare_adapter_config(peft_config, _model_config):
+ # Handle X-LoRA case
+ return peft_config
+
+ """
+ Does nothing. X-LoRA needs adapters to be frozen.
+ """
+
+ def _mark_only_adapters_as_trainable(self) -> None: ...
+
+ """
+ This enables the X-LoRA adapter.
+ """
+
+ def enable_adapter_layers(self) -> None:
+ self.disabled = False
+
+ """
+ This diasables the X-LoRA adapter.
+ """
+
+ def disable_adapter_layers(self) -> None:
+ self.disabled = True
+
+ def _create_and_replace(
+ self,
+ lora_config,
+ adapter_name,
+ target,
+ target_name,
+ parent,
+ current_key,
+ ):
+ # Does nothing because XLoraModel has no target modules
+ pass
+
+ @staticmethod
+ def _check_target_module_exists(lora_config, key):
+ # Does nothing because XLoraModel has no target modules
+ return False
+
+ def forward(self, *args, **kwargs):
+ return self.lora_model.model(*args, **kwargs)
+
+ def set_topk_lora(self, value: Optional[int]):
+ """
+ Sparsely select the specified top_k LoRA experts instead of the default dense method. Set to None to use dense.
+ This is reflected in the config.
+ """
+ classifier: XLoraClassifier = self.internal_xlora_classifier # type: ignore
+ classifier.config.top_k_lora = value
+
+ def set_global_scaling_weight(self, weight: float):
+ """
+ Set the global LoRA weight, a scalar to multiply the output of each LoRA adapter by. This is by default 1. This
+ is reflected in the config.
+ """
+ classifier: XLoraClassifier = self.internal_xlora_classifier # type: ignore
+ classifier.config.global_scaling_weight = weight
+
+ def set_scaling_pass_value(self, value: float | None):
+ """
+ Set the scaling pass value, the value to set the scalings to during the scaling pass. If the value is None, the
+ scaling pass value will be 1/n where n is the number of adapters.
+ """
+ classifier: XLoraClassifier = self.internal_xlora_classifier # type: ignore
+ classifier._set_override_scaling_pass_value(value)
+
+ def get_global_scaling_weight(self) -> float:
+ """
+ Get the global LoRA weight.
+ """
+ classifier: XLoraClassifier = self.internal_xlora_classifier # type: ignore
+ return classifier.config.global_scaling_weight
+
+ def get_latest_scalings(self) -> Optional[torch.Tensor]:
+ """
+ Returns the latest scalings prediction, or None if no scalings have been predicted. The tensor is of shape
+ (batch_size, seq_len, n_layers, n_classes).
+ """
+ return self.internal_xlora_scalings
+
+ def get_scalings_log(self) -> list[torch.Tensor]:
+ """
+ Returns a shallow (only copying the list itself not the tensors) copy of the list containing the scalings log.
+ Editing the list does not change the underlying log. The tensors are of shape (batch_size, seq_len, n_layers,
+ n_classes). The seq_len dim may vary with input dimension.
+ """
+ classifier: XLoraClassifier = self.internal_xlora_classifier # type: ignore
+ return classifier.log_scalings.copy()
+
+ def enable_scalings_logging(self):
+ """
+ Enable scalings logging.
+ """
+ classifier: XLoraClassifier = self.internal_xlora_classifier # type: ignore
+ classifier.scalings_logging = True
+
+ def disable_scalings_logging(self):
+ """
+ Disable scalings logging, without clearing the log.
+ """
+ classifier: XLoraClassifier = self.internal_xlora_classifier # type: ignore
+ classifier.scalings_logging = False
+
+ def clear_scalings_log(self):
+ """
+ Clear the scalings log.
+ """
+ classifier: XLoraClassifier = self.internal_xlora_classifier # type: ignore
+ classifier.log_scalings.clear()
+
+ def get_bucketed_scalings_log(self) -> dict[int, tuple[list[int], list[torch.Tensor]]]:
+ """
+ Returns bucketed scalings, bucketed by seq_len. Each value consists of the positions (the first) and the
+ associated tensors. The positions are paired with the associated tensors and give the position in the scaling
+ log.
+ """
+ classifier: XLoraClassifier = self.internal_xlora_classifier # type: ignore
+ return classifier._get_bucketed_scalings()
diff --git a/peft/src/peft/utils/__init__.py b/peft/src/peft/utils/__init__.py
new file mode 100644
index 0000000000000000000000000000000000000000..781495465ec4dda4aa2d20fe6d12c8af9f9d3198
--- /dev/null
+++ b/peft/src/peft/utils/__init__.py
@@ -0,0 +1,130 @@
+# Copyright 2023-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+from .integrations import map_cache_to_layer_device_map
+from .loftq_utils import replace_lora_weights_loftq
+from .other import (
+ CONFIG_NAME,
+ INCLUDE_LINEAR_LAYERS_SHORTHAND,
+ SAFETENSORS_WEIGHTS_NAME,
+ TRANSFORMERS_MODELS_TO_ADALORA_TARGET_MODULES_MAPPING,
+ TRANSFORMERS_MODELS_TO_BOFT_TARGET_MODULES_MAPPING,
+ TRANSFORMERS_MODELS_TO_BONE_TARGET_MODULES_MAPPING,
+ TRANSFORMERS_MODELS_TO_C3A_TARGET_MODULES_MAPPING,
+ TRANSFORMERS_MODELS_TO_FOURIERFT_TARGET_MODULES_MAPPING,
+ TRANSFORMERS_MODELS_TO_HRA_TARGET_MODULES_MAPPING,
+ TRANSFORMERS_MODELS_TO_IA3_FEEDFORWARD_MODULES_MAPPING,
+ TRANSFORMERS_MODELS_TO_IA3_TARGET_MODULES_MAPPING,
+ TRANSFORMERS_MODELS_TO_LNTUNING_TARGET_MODULES_MAPPING,
+ TRANSFORMERS_MODELS_TO_LOHA_TARGET_MODULES_MAPPING,
+ TRANSFORMERS_MODELS_TO_LOKR_TARGET_MODULES_MAPPING,
+ TRANSFORMERS_MODELS_TO_LORA_TARGET_MODULES_MAPPING,
+ TRANSFORMERS_MODELS_TO_MISS_TARGET_MODULES_MAPPING,
+ TRANSFORMERS_MODELS_TO_OFT_TARGET_MODULES_MAPPING,
+ TRANSFORMERS_MODELS_TO_POLY_TARGET_MODULES_MAPPING,
+ TRANSFORMERS_MODELS_TO_PREFIX_TUNING_POSTPROCESS_MAPPING,
+ TRANSFORMERS_MODELS_TO_RANDLORA_TARGET_MODULES_MAPPING,
+ TRANSFORMERS_MODELS_TO_ROAD_TARGET_MODULES_MAPPING,
+ TRANSFORMERS_MODELS_TO_SHIRA_TARGET_MODULES_MAPPING,
+ TRANSFORMERS_MODELS_TO_VBLORA_TARGET_MODULES_MAPPING,
+ TRANSFORMERS_MODELS_TO_VERA_TARGET_MODULES_MAPPING,
+ TRANSFORMERS_MODELS_TO_WAVEFT_TARGET_MODULES_MAPPING,
+ WEIGHTS_NAME,
+ AuxiliaryTrainingWrapper,
+ ModulesToSaveWrapper,
+ TrainableTokensWrapper,
+ _freeze_adapter,
+ _get_batch_size,
+ _get_input_embeddings_name,
+ _get_submodules,
+ _is_valid_match,
+ _prepare_prompt_learning_config,
+ _set_adapter,
+ _set_trainable,
+ bloom_model_postprocess_past_key_value,
+ cast_mixed_precision_params,
+ get_auto_gptq_quant_linear,
+ get_gptqmodel_quant_linear,
+ get_quantization_config,
+ id_tensor_storage,
+ infer_device,
+ prepare_model_for_kbit_training,
+ set_additional_trainable_modules,
+ shift_tokens_right,
+ transpose,
+)
+from .peft_types import PeftType, TaskType, register_peft_method
+from .save_and_load import get_peft_model_state_dict, load_peft_weights, set_peft_model_state_dict
+from .warning import PeftWarning
+
+
+__all__ = [
+ "CONFIG_NAME",
+ "INCLUDE_LINEAR_LAYERS_SHORTHAND",
+ "SAFETENSORS_WEIGHTS_NAME",
+ "TRANSFORMERS_MODELS_TO_ADALORA_TARGET_MODULES_MAPPING",
+ "TRANSFORMERS_MODELS_TO_BOFT_TARGET_MODULES_MAPPING",
+ "TRANSFORMERS_MODELS_TO_BONE_TARGET_MODULES_MAPPING",
+ "TRANSFORMERS_MODELS_TO_C3A_TARGET_MODULES_MAPPING",
+ "TRANSFORMERS_MODELS_TO_FOURIERFT_TARGET_MODULES_MAPPING",
+ "TRANSFORMERS_MODELS_TO_HRA_TARGET_MODULES_MAPPING",
+ "TRANSFORMERS_MODELS_TO_IA3_FEEDFORWARD_MODULES_MAPPING",
+ "TRANSFORMERS_MODELS_TO_IA3_TARGET_MODULES_MAPPING",
+ "TRANSFORMERS_MODELS_TO_LNTUNING_TARGET_MODULES_MAPPING",
+ "TRANSFORMERS_MODELS_TO_LOHA_TARGET_MODULES_MAPPING",
+ "TRANSFORMERS_MODELS_TO_LOKR_TARGET_MODULES_MAPPING",
+ "TRANSFORMERS_MODELS_TO_LORA_TARGET_MODULES_MAPPING",
+ "TRANSFORMERS_MODELS_TO_MISS_TARGET_MODULES_MAPPING",
+ "TRANSFORMERS_MODELS_TO_OFT_TARGET_MODULES_MAPPING",
+ "TRANSFORMERS_MODELS_TO_POLY_TARGET_MODULES_MAPPING",
+ "TRANSFORMERS_MODELS_TO_PREFIX_TUNING_POSTPROCESS_MAPPING",
+ "TRANSFORMERS_MODELS_TO_RANDLORA_TARGET_MODULES_MAPPING",
+ "TRANSFORMERS_MODELS_TO_ROAD_TARGET_MODULES_MAPPING",
+ "TRANSFORMERS_MODELS_TO_SHIRA_TARGET_MODULES_MAPPING",
+ "TRANSFORMERS_MODELS_TO_VBLORA_TARGET_MODULES_MAPPING",
+ "TRANSFORMERS_MODELS_TO_VERA_TARGET_MODULES_MAPPING",
+ "TRANSFORMERS_MODELS_TO_WAVEFT_TARGET_MODULES_MAPPING",
+ "WEIGHTS_NAME",
+ "AuxiliaryTrainingWrapper",
+ "ModulesToSaveWrapper",
+ "PeftType",
+ "PeftWarning",
+ "TaskType",
+ "TrainableTokensWrapper",
+ "_freeze_adapter",
+ "_get_batch_size",
+ "_get_input_embeddings_name",
+ "_get_submodules",
+ "_is_valid_match",
+ "_prepare_prompt_learning_config",
+ "_set_adapter",
+ "_set_trainable",
+ "bloom_model_postprocess_past_key_value",
+ "cast_mixed_precision_params",
+ "get_auto_gptq_quant_linear",
+ "get_gptqmodel_quant_linear",
+ "get_peft_model_state_dict",
+ "get_quantization_config",
+ "id_tensor_storage",
+ "infer_device",
+ "load_peft_weights",
+ "map_cache_to_layer_device_map",
+ "prepare_model_for_kbit_training",
+ "register_peft_method",
+ "replace_lora_weights_loftq",
+ "set_additional_trainable_modules",
+ "set_peft_model_state_dict",
+ "shift_tokens_right",
+ "transpose",
+]
diff --git a/peft/src/peft/utils/constants.py b/peft/src/peft/utils/constants.py
new file mode 100644
index 0000000000000000000000000000000000000000..79c7d92b00f66cad731fa853e4abc182829f0f5a
--- /dev/null
+++ b/peft/src/peft/utils/constants.py
@@ -0,0 +1,340 @@
+# Copyright 2023-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+import packaging.version
+import torch
+import transformers
+from transformers import BloomPreTrainedModel
+
+
+# needed for prefix-tuning of bloom model
+def bloom_model_postprocess_past_key_value(past_key_values):
+ past_key_values = torch.cat(past_key_values)
+ total_layers, batch_size, num_attention_heads, num_virtual_tokens, head_dim = past_key_values.shape
+ keys = past_key_values[: total_layers // 2]
+ keys = keys.transpose(2, 3).reshape(
+ total_layers // 2, batch_size * num_attention_heads, head_dim, num_virtual_tokens
+ )
+ values = past_key_values[total_layers // 2 :]
+ values = values.reshape(total_layers // 2, batch_size * num_attention_heads, num_virtual_tokens, head_dim)
+
+ return tuple(zip(keys, values))
+
+
+# needed for prefix-tuning of StarCoder models
+def starcoder_model_postprocess_past_key_value(past_key_values):
+ result = []
+ for k in past_key_values:
+ k = k[:, :, 0]
+ k = k.permute([1, 2, 0, 3])
+ k = k.reshape(*k.shape[:-2], -1)
+ result.append(k)
+ return tuple(result)
+
+
+# TODO: remove this once transformers 4.53 is no longer supported
+TRANSFORMERS_MODELS_TO_PREFIX_TUNING_POSTPROCESS_MAPPING = {}
+transformers_le_4_53 = packaging.version.parse(transformers.__version__) < packaging.version.parse("4.54.0.dev0")
+if transformers_le_4_53:
+ TRANSFORMERS_MODELS_TO_PREFIX_TUNING_POSTPROCESS_MAPPING["gpt_bigcode"] = (
+ starcoder_model_postprocess_past_key_value
+ )
+
+
+if hasattr(BloomPreTrainedModel, "_convert_to_standard_cache"):
+ # special handling for bloom architecture was fixed in:
+ # https://github.com/huggingface/transformers/pull/31445
+ # the _convert_to_standard_cache method is removed in the PR and thus serves as an indicator
+ TRANSFORMERS_MODELS_TO_PREFIX_TUNING_POSTPROCESS_MAPPING["bloom"] = bloom_model_postprocess_past_key_value
+
+
+#######################################
+# DEFAULT MAPPINGS FOR TARGET_MODULES #
+#######################################
+
+TRANSFORMERS_MODELS_TO_LORA_TARGET_MODULES_MAPPING = {
+ "t5": ["q", "v"],
+ "mt5": ["q", "v"],
+ "bart": ["q_proj", "v_proj"],
+ "gpt2": ["c_attn"],
+ "bloom": ["query_key_value"],
+ "blip-2": ["q", "v", "q_proj", "v_proj"],
+ "opt": ["q_proj", "v_proj"],
+ "gptj": ["q_proj", "v_proj"],
+ "gpt_neox": ["query_key_value"],
+ "gpt_neo": ["q_proj", "v_proj"],
+ "bert": ["query", "value"],
+ "roberta": ["query", "value"],
+ "xlm-roberta": ["query", "value"],
+ "electra": ["query", "value"],
+ "deberta-v2": ["query_proj", "value_proj"],
+ "deberta": ["in_proj"],
+ "layoutlm": ["query", "value"],
+ "llama": ["q_proj", "v_proj"],
+ "llama4": ["q_proj", "v_proj"],
+ "chatglm": ["query_key_value"],
+ "gpt_bigcode": ["c_attn"],
+ "mpt": ["Wqkv"],
+ "RefinedWebModel": ["query_key_value"],
+ "RefinedWeb": ["query_key_value"],
+ "falcon": ["query_key_value"],
+ "btlm": ["c_proj", "c_attn"],
+ "codegen": ["qkv_proj"],
+ "mistral": ["q_proj", "v_proj"],
+ "mixtral": ["q_proj", "v_proj"],
+ "stablelm": ["q_proj", "v_proj"],
+ "phi": ["q_proj", "v_proj", "fc1", "fc2"],
+ "gemma": ["q_proj", "v_proj"],
+ "gemma2": ["q_proj", "v_proj"],
+ "gemma3_text": ["q_proj", "v_proj"],
+ "qwen2": ["q_proj", "v_proj"],
+ "qwen3": ["q_proj", "v_proj"],
+}
+
+# target module mappings that are identical to LORA
+TRANSFORMERS_MODELS_TO_BOFT_TARGET_MODULES_MAPPING = TRANSFORMERS_MODELS_TO_LORA_TARGET_MODULES_MAPPING.copy()
+TRANSFORMERS_MODELS_TO_BONE_TARGET_MODULES_MAPPING = TRANSFORMERS_MODELS_TO_LORA_TARGET_MODULES_MAPPING.copy()
+TRANSFORMERS_MODELS_TO_C3A_TARGET_MODULES_MAPPING = TRANSFORMERS_MODELS_TO_LORA_TARGET_MODULES_MAPPING.copy()
+TRANSFORMERS_MODELS_TO_HRA_TARGET_MODULES_MAPPING = TRANSFORMERS_MODELS_TO_LORA_TARGET_MODULES_MAPPING.copy()
+TRANSFORMERS_MODELS_TO_LOHA_TARGET_MODULES_MAPPING = TRANSFORMERS_MODELS_TO_LORA_TARGET_MODULES_MAPPING.copy()
+TRANSFORMERS_MODELS_TO_LOKR_TARGET_MODULES_MAPPING = TRANSFORMERS_MODELS_TO_LORA_TARGET_MODULES_MAPPING.copy()
+TRANSFORMERS_MODELS_TO_MISS_TARGET_MODULES_MAPPING = TRANSFORMERS_MODELS_TO_LORA_TARGET_MODULES_MAPPING.copy()
+TRANSFORMERS_MODELS_TO_OFT_TARGET_MODULES_MAPPING = TRANSFORMERS_MODELS_TO_LORA_TARGET_MODULES_MAPPING.copy()
+TRANSFORMERS_MODELS_TO_POLY_TARGET_MODULES_MAPPING = TRANSFORMERS_MODELS_TO_LORA_TARGET_MODULES_MAPPING.copy()
+TRANSFORMERS_MODELS_TO_RANDLORA_TARGET_MODULES_MAPPING = TRANSFORMERS_MODELS_TO_LORA_TARGET_MODULES_MAPPING.copy()
+TRANSFORMERS_MODELS_TO_ROAD_TARGET_MODULES_MAPPING = TRANSFORMERS_MODELS_TO_LORA_TARGET_MODULES_MAPPING.copy()
+
+# mappings that are similar to LORA with small changes
+TRANSFORMERS_MODELS_TO_FOURIERFT_TARGET_MODULES_MAPPING = TRANSFORMERS_MODELS_TO_LORA_TARGET_MODULES_MAPPING.copy()
+TRANSFORMERS_MODELS_TO_FOURIERFT_TARGET_MODULES_MAPPING["gpt_bigcode"] = ["mlp.c_proj"]
+TRANSFORMERS_MODELS_TO_FOURIERFT_TARGET_MODULES_MAPPING["gpt2"] = ["mlp.c_proj"]
+
+TRANSFORMERS_MODELS_TO_SHIRA_TARGET_MODULES_MAPPING = TRANSFORMERS_MODELS_TO_LORA_TARGET_MODULES_MAPPING.copy()
+TRANSFORMERS_MODELS_TO_SHIRA_TARGET_MODULES_MAPPING["phi"] = ["q_proj", "v_proj"]
+
+TRANSFORMERS_MODELS_TO_VERA_TARGET_MODULES_MAPPING = TRANSFORMERS_MODELS_TO_LORA_TARGET_MODULES_MAPPING.copy()
+TRANSFORMERS_MODELS_TO_VERA_TARGET_MODULES_MAPPING["phi"] = ["q_proj", "v_proj"]
+
+TRANSFORMERS_MODELS_TO_C3A_TARGET_MODULES_MAPPING = TRANSFORMERS_MODELS_TO_LORA_TARGET_MODULES_MAPPING.copy()
+TRANSFORMERS_MODELS_TO_C3A_TARGET_MODULES_MAPPING["gpt_bigcode"] = ["mlp.c_proj"]
+TRANSFORMERS_MODELS_TO_C3A_TARGET_MODULES_MAPPING["gpt2"] = ["mlp.c_proj"]
+
+# target module mappings that differ from LORA
+TRANSFORMERS_MODELS_TO_LNTUNING_TARGET_MODULES_MAPPING = {
+ "llama": ["input_layernorm", "post_attention_layernorm", "norm"],
+ "bloom": ["input_layernorm", "post_attention_layernorm", "ln_f"],
+ "llava": [
+ "multi_modal_projector",
+ "input_layernorm",
+ "post_attention_layernorm",
+ "norm",
+ "embed_tokens",
+ "lm_head",
+ ],
+ "t5": ["layer_norm", "final_layer_norm"],
+ "mt5": ["layer_norm", "final_layer_norm"],
+ "bart": ["self_attn_layer_norm", "encoder_attn_layer_norm", "final_layer_norm"],
+ "gpt2": ["ln_1", "ln_2", "ln_f"],
+ "blip-2": ["layernorm", "LayerNorm", "final_layer_norm", "self_attn_layer_norm"],
+ "gptj": ["ln_1", "ln_f"],
+ "falcon": ["input_layernorm", "post_attention_layernorm", "ln_f"],
+ "mistral": ["input_layernorm", "post_attention_layernorm", "norm"],
+ "phi": ["input_layernorm", "final_layernorm"],
+ "gemma": ["input_layernorm", "post_attention_layernorm", "norm"],
+ "gemma2": [
+ "input_layernorm",
+ "post_attention_layernorm",
+ "pre_feedforward_layernorm",
+ "post_feedforward_layernorm",
+ "norm",
+ ],
+ "gemma3_text": [
+ "input_layernorm",
+ "post_attention_layernorm",
+ "pre_feedforward_layernorm",
+ "post_feedforward_layernorm",
+ "norm",
+ ],
+ "qwen2": ["post_attention_layernorm"],
+ "qwen3": ["post_attention_layernorm"],
+}
+
+TRANSFORMERS_MODELS_TO_IA3_TARGET_MODULES_MAPPING = {
+ "t5": ["k", "v", "wo"],
+ "mt5": ["k", "v", "wi_1"],
+ "gpt2": ["c_attn", "mlp.c_proj"],
+ "bloom": ["query_key_value", "mlp.dense_4h_to_h"],
+ "roberta": ["key", "value", "output.dense"],
+ "opt": ["q_proj", "k_proj", "fc2"],
+ "gptj": ["q_proj", "v_proj", "fc_out"],
+ "gpt_neox": ["query_key_value", "dense_4h_to_h"],
+ "gpt_neo": ["q_proj", "v_proj", "c_proj"],
+ "bart": ["q_proj", "v_proj", "fc2"],
+ "gpt_bigcode": ["c_attn", "mlp.c_proj"],
+ "llama": ["k_proj", "v_proj", "down_proj"],
+ "llama4": ["q_proj", "v_proj", "down_proj"],
+ "mistral": ["k_proj", "v_proj", "down_proj"],
+ "mixtral": ["k_proj", "v_proj", "w2"],
+ "bert": ["key", "value", "output.dense"],
+ "deberta-v2": ["key_proj", "value_proj", "output.dense"],
+ "deberta": ["in_proj", "output.dense"],
+ "RefinedWebModel": ["query_key_value", "dense_4h_to_h"],
+ "RefinedWeb": ["query_key_value", "dense_4h_to_h"],
+ "falcon": ["query_key_value", "dense_4h_to_h"],
+ "phi": ["q_proj", "v_proj", "fc2"],
+ "gemma": ["q_proj", "v_proj", "down_proj"],
+ "gemma2": ["q_proj", "v_proj", "down_proj"],
+ "gemma3_text": ["q_proj", "v_proj", "down_proj"],
+ "qwen2": ["q_proj", "v_proj", "down_proj"],
+ "qwen3": ["q_proj", "v_proj", "down_proj"],
+}
+
+TRANSFORMERS_MODELS_TO_IA3_FEEDFORWARD_MODULES_MAPPING = {
+ "t5": ["wo"],
+ "mt5": [],
+ "gpt2": ["mlp.c_proj"],
+ "bloom": ["mlp.dense_4h_to_h"],
+ "roberta": ["output.dense"],
+ "opt": ["fc2"],
+ "gptj": ["fc_out"],
+ "gpt_neox": ["dense_4h_to_h"],
+ "gpt_neo": ["c_proj"],
+ "bart": ["fc2"],
+ "gpt_bigcode": ["mlp.c_proj"],
+ "llama": ["down_proj"],
+ "llama4": ["down_proj"],
+ "mistral": ["down_proj"],
+ "mixtral": ["w2"],
+ "bert": ["output.dense"],
+ "deberta-v2": ["output.dense"],
+ "deberta": ["output.dense"],
+ "RefinedWeb": ["dense_4h_to_h"],
+ "RefinedWebModel": ["dense_4h_to_h"],
+ "falcon": ["dense_4h_to_h"],
+ "phi": ["fc2"],
+ "gemma": ["down_proj"],
+ "gemma2": ["down_proj"],
+ "gemma3_text": ["down_proj"],
+ "qwen2": ["down_proj"],
+ "qwen3": ["down_proj"],
+}
+
+TRANSFORMERS_MODELS_TO_ADALORA_TARGET_MODULES_MAPPING = {
+ "t5": ["q", "k", "v", "o", "wi", "wo"],
+ "mt5": ["q", "k", "v", "o", "wi_0", "wi_1", "wo"],
+ "bart": ["q_proj", "k_proj", "v_proj", "out_proj", "fc1", "fc2"],
+ "gpt2": ["c_attn"],
+ "bloom": ["query_key_value"],
+ "opt": ["q_proj", "k_proj", "v_proj", "out_proj", "fc1", "fc2"],
+ "gptj": ["q_proj", "v_proj"],
+ "gpt_neox": ["query_key_value"],
+ "gpt_neo": ["q_proj", "v_proj"],
+ "llama": ["q_proj", "v_proj"],
+ "llama4": ["q_proj", "v_proj"],
+ "bert": ["query", "value"],
+ "roberta": ["query", "key", "value", "dense"],
+ # "xlm-roberta": ["query", "value"],
+ # "electra": ["query", "value"],
+ "deberta-v2": ["query_proj", "key_proj", "value_proj", "dense"],
+ "gpt_bigcode": ["c_attn"],
+ "deberta": ["in_proj"],
+ # "layoutlm": ["query", "value"],
+ "gemma": ["q_proj", "v_proj"],
+ "gemma2": ["q_proj", "v_proj"],
+ "gemma3_text": ["q_proj", "v_proj"],
+ "qwen2": ["q_proj", "v_proj"],
+ "qwen3": ["q_proj", "v_proj"],
+}
+
+TRANSFORMERS_MODELS_TO_VBLORA_TARGET_MODULES_MAPPING = {
+ "t5": ["q", "k", "v", "o", "wi", "wo"],
+ "mt5": ["q", "k", "v", "o", "wi_0", "wi_1", "wo"],
+ "bart": ["q_proj", "k_proj", "v_proj", "out_proj", "fc1", "fc2"],
+ "gpt2": ["c_attn"],
+ "bloom": ["query_key_value"],
+ "opt": ["q_proj", "k_proj", "v_proj", "out_proj", "fc1", "fc2"],
+ "gptj": ["q_proj", "v_proj"],
+ "gpt_neox": ["query_key_value"],
+ "gpt_neo": ["q_proj", "v_proj"],
+ "llama": ["q_proj", "v_proj"],
+ "llama4": ["q_proj", "v_proj"],
+ "bert": ["query", "value"],
+ "roberta": ["query", "value"],
+ "deberta-v2": ["query_proj", "key_proj", "value_proj", "dense"],
+ "gpt_bigcode": ["c_attn"],
+ "deberta": ["in_proj"],
+ "gemma": ["q_proj", "v_proj"],
+ "gemma2": ["q_proj", "v_proj"],
+ "gemma3_text": ["q_proj", "v_proj"],
+ "qwen2": ["q_proj", "v_proj"],
+ "qwen3": ["q_proj", "v_proj"],
+}
+
+##################
+# MISC CONSTANTS #
+##################
+
+TRANSFORMERS_MODELS_TO_WAVEFT_TARGET_MODULES_MAPPING = {
+ "t5": ["q", "v"],
+ "mt5": ["q", "v"],
+ "bart": ["q_proj", "v_proj"],
+ "gpt2": ["mlp.c_proj"],
+ "bloom": ["query_key_value"],
+ "blip-2": ["q", "v", "q_proj", "v_proj"],
+ "opt": ["q_proj", "v_proj"],
+ "gptj": ["q_proj", "v_proj"],
+ "gpt_neox": ["query_key_value"],
+ "gpt_neo": ["q_proj", "v_proj"],
+ "bert": ["query", "value"],
+ "roberta": ["query", "value"],
+ "xlm-roberta": ["query", "value"],
+ "electra": ["query", "value"],
+ "deberta-v2": ["query_proj", "value_proj"],
+ "deberta": ["in_proj"],
+ "layoutlm": ["query", "value"],
+ "llama": ["q_proj", "v_proj"],
+ "llama4": ["q_proj", "v_proj"],
+ "chatglm": ["query_key_value"],
+ "gpt_bigcode": ["mlp.c_proj"],
+ "mpt": ["Wqkv"],
+ "RefinedWebModel": ["query_key_value"],
+ "RefinedWeb": ["query_key_value"],
+ "falcon": ["query_key_value"],
+ "codegen": ["qkv_proj"],
+ "mistral": ["q_proj", "v_proj"],
+ "mixtral": ["q_proj", "v_proj"],
+ "stablelm": ["q_proj", "v_proj"],
+ "phi": ["q_proj", "v_proj", "fc1", "fc2"],
+ "gemma": ["q_proj", "v_proj"],
+ "gemma2": ["q_proj", "v_proj"],
+ "gemma3_text": ["q_proj", "v_proj"],
+ "qwen2": ["q_proj", "v_proj"],
+ "qwen3": ["q_proj", "v_proj"],
+}
+
+WEIGHTS_NAME = "adapter_model.bin"
+SAFETENSORS_WEIGHTS_NAME = "adapter_model.safetensors"
+CONFIG_NAME = "adapter_config.json"
+EMBEDDING_LAYER_NAMES = ["embed_tokens", "lm_head"]
+SEQ_CLS_HEAD_NAMES = ["score", "classifier"]
+INCLUDE_LINEAR_LAYERS_SHORTHAND = "all-linear"
+TOKENIZER_CONFIG_NAME = "tokenizer_config.json"
+DUMMY_TARGET_MODULES = "dummy-target-modules"
+DUMMY_MODEL_CONFIG = {"model_type": "custom"}
+
+# If users specify more than this number of target modules, we apply an optimization to try to reduce the target modules
+# to a minimal set of suffixes, which makes loading faster. We only apply this when exceeding a certain size since
+# otherwise there is no point in optimizing and there is a small chance of bugs in the optimization algorithm, so no
+# point in taking unnecessary risks. See #2045 for more context.
+MIN_TARGET_MODULES_FOR_OPTIMIZATION = 20
diff --git a/peft/src/peft/utils/hotswap.py b/peft/src/peft/utils/hotswap.py
new file mode 100644
index 0000000000000000000000000000000000000000..2b08c372e132b1084c10df79ab35a42f2cdf19ef
--- /dev/null
+++ b/peft/src/peft/utils/hotswap.py
@@ -0,0 +1,630 @@
+# Copyright 2024-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+from __future__ import annotations
+
+import math
+import warnings
+from operator import attrgetter
+from typing import Literal, Optional
+
+import torch
+
+from peft.config import PeftConfig
+from peft.mapping import PEFT_TYPE_TO_CONFIG_MAPPING, PEFT_TYPE_TO_PREFIX_MAPPING
+from peft.tuners.lora import Conv2d, Linear, LoraConfig, LoraLayer
+
+from .other import get_pattern_key, infer_device
+from .peft_types import PeftType
+from .save_and_load import _insert_adapter_name_into_state_dict, load_peft_weights
+
+
+# so far only LoRA is supported
+CONFIG_KEYS_TO_CHECK = {PeftType.LORA: ["use_rslora", "lora_dropout", "alpha_pattern", "use_dora"]}
+
+
+def _update_scaling(lora_module, adapter_name, scaling=None):
+ """
+ Update the value of the scalings of the LoRA module.
+
+ Takes into consideration that scalings can be tensors from prepare_model_for_compiled_hotswap.
+ """
+ if lora_module.scaling[adapter_name] == scaling:
+ return
+
+ if isinstance(lora_module.scaling[adapter_name], torch.Tensor):
+ lora_module.scaling[adapter_name].fill_(scaling)
+ elif isinstance(lora_module.scaling[adapter_name], (float, int)):
+ lora_module.scaling[adapter_name] = scaling
+ else:
+ raise ValueError(
+ "Something went wrong when trying to set the new scale value, expected to find the old value to be of type "
+ f"float or torch.Tensor, got {type(lora_module.scaling[adapter_name])} instead."
+ )
+
+
+def _convert_scalings_to_tensor(model) -> bool:
+ """
+ Convert the LoRA scaling values into torch.tensors to prevent recompilation if they change.
+
+ Returns:
+ bool:
+ Returns `True` if an appropriate adapter was found, else `False`.
+ """
+ found_adapter = False
+ for module in model.modules():
+ if not isinstance(module, LoraLayer):
+ continue
+
+ found_adapter = True
+ scaling = module.scaling
+ for key, val in scaling.items():
+ if isinstance(val, float):
+ # no need to deal with dtype as scalars are coerced
+ scaling[key] = torch.tensor(val, device=module.weight.device)
+ elif not isinstance(val, torch.Tensor):
+ raise ValueError(
+ "Something went wrong while trying to convert the scalings, expected to find values of type float "
+ f"but found {type(val)} instead."
+ )
+ return found_adapter
+
+
+def _get_padded_linear(lora_module: torch.nn.Module, target_rank: int, is_lora_A: bool) -> torch.nn.Linear:
+ """
+ Get a new Linear layer for LoRA with padded weights according to the target rank.
+
+ Args:
+ lora_module (nn.Module):
+ The LoRA sub-module (e.g. module.lora_A[adapter_name]).
+ target_rank (int):
+ The desired rank to pad to.
+ is_lora_A (bool):
+ True if this is the LoRA A matrix, False if LoRA B.
+
+ Returns:
+ nn.Linear:
+ A newly created and padded Linear layer. If the rank already fit, the original layer is returned.
+ """
+ weight = lora_module.weight
+ # For LoRA A, the "rank dimension" is weight.size(0) (out_features).
+ # For LoRA B, it is weight.size(1) (in_features).
+ original_rank = weight.size(0) if is_lora_A else weight.size(1)
+
+ # If no padding needed
+ if original_rank == target_rank:
+ return lora_module
+
+ if original_rank > target_rank:
+ raise ValueError(
+ f"Trying to pad the adapter to the target rank {target_rank}, but the original rank is larger "
+ f"({original_rank}). This is not possible."
+ )
+
+ out_features, in_features = weight.shape
+
+ # lora_A and lora_B are always nn.Linear
+ if is_lora_A:
+ # LoRA A affects out_features
+ padded = torch.zeros(target_rank, in_features, device=weight.device, dtype=weight.dtype)
+ padded[:original_rank, :] = weight
+ new_layer = torch.nn.Linear(in_features, target_rank, bias=lora_module.bias is not None)
+ else:
+ # LoRA B affects in_features
+ padded = torch.zeros(out_features, target_rank, device=weight.device, dtype=weight.dtype)
+ padded[:, :original_rank] = weight
+ new_layer = torch.nn.Linear(target_rank, out_features, bias=lora_module.bias is not None)
+
+ # Sanity check
+ if new_layer.weight.shape != padded.shape:
+ raise ValueError(
+ "Something went wrong when trying to pad the LoRA Linear weights, the new shape should be "
+ f"{padded.shape} but {new_layer.weight.shape} was found. Please open an issue on PEFT "
+ "(https://github.com/huggingface/peft/issues) and report this error."
+ )
+ if (lora_module.bias is not None) and (new_layer.bias.shape != lora_module.bias.shape):
+ raise ValueError(
+ "Something went wrong when trying to pad the LoRA Linear bias, the new shape should be "
+ f"{lora_module.bias.shape} but {new_layer.bias.shape} was found. Please open an issue on PEFT "
+ "(https://github.com/huggingface/peft/issues) and report this error."
+ )
+
+ new_layer.weight.data = padded
+ # Copy bias if present
+ if lora_module.bias is not None:
+ new_layer.bias.data = lora_module.bias.data
+
+ return new_layer
+
+
+def _get_padded_conv2d(lora_module: torch.nn.Module, target_rank: int, is_lora_A: bool) -> torch.nn.Conv2d:
+ """
+ Get a new Conv2d layer for LoRA with padded weights according to the target rank.
+
+ Args:
+ lora_module (nn.Module):
+ The LoRA sub-module (e.g. module.lora_A[adapter_name]).
+ target_rank (int):
+ The desired rank to pad to.
+ is_lora_A (bool):
+ True if this is the LoRA A matrix, False if LoRA B.
+
+ Returns:
+ nn.Conv2d:
+ A newly created and padded Conv2d layer. If the rank already fit, the original layer is returned.
+ """
+ weight = lora_module.weight
+ # For Conv2d: [out_channels, in_channels, kernel_height, kernel_width]
+ out_channels, in_channels, kh, kw = weight.shape
+ original_rank = out_channels if is_lora_A else in_channels
+
+ if original_rank == target_rank:
+ return lora_module
+
+ if original_rank > target_rank:
+ raise ValueError(
+ f"Trying to pad the adapter to the target rank {target_rank}, but the original rank is larger "
+ f"({original_rank}). This is not possible."
+ )
+
+ # lora_A and lora_B are always nn.Conv2d
+ if is_lora_A:
+ # LoRA A affects out_channels
+ padded = torch.zeros(target_rank, in_channels, kh, kw, device=weight.device, dtype=weight.dtype)
+ padded[:out_channels, :, :, :] = weight
+ new_layer = torch.nn.Conv2d(
+ in_channels,
+ target_rank,
+ kernel_size=lora_module.kernel_size,
+ stride=lora_module.stride,
+ padding=lora_module.padding,
+ bias=lora_module.bias is not None,
+ groups=lora_module.groups,
+ )
+ else:
+ # LoRA B affects in_channels
+ padded = torch.zeros(out_channels, target_rank, kh, kw, device=weight.device, dtype=weight.dtype)
+ padded[:, :in_channels, :, :] = weight
+ new_layer = torch.nn.Conv2d(
+ target_rank,
+ out_channels,
+ kernel_size=lora_module.kernel_size,
+ stride=lora_module.stride,
+ padding=lora_module.padding,
+ bias=lora_module.bias is not None,
+ groups=lora_module.groups,
+ )
+
+ # Sanity check
+ if new_layer.weight.shape != padded.shape:
+ raise ValueError(
+ "Something went wrong when trying to pad the LoRA weights, the new shape should be "
+ f"{padded.shape} but {new_layer.weight.shape} was found. Please open an issue on PEFT "
+ "(https://github.com/huggingface/peft/issues) and report this error."
+ )
+ if (lora_module.bias is not None) and (new_layer.bias.shape != lora_module.bias.shape):
+ raise ValueError(
+ "Something went wrong when trying to pad the LoRA Conv2d bias, the new shape should be "
+ f"{lora_module.bias.shape} but {new_layer.bias.shape} was found. Please open an issue on PEFT "
+ "(https://github.com/huggingface/peft/issues) and report this error."
+ )
+
+ new_layer.weight.data = padded
+ # Copy bias if present
+ if lora_module.bias is not None:
+ new_layer.bias.data = lora_module.bias.data
+
+ return new_layer
+
+
+def _pad_lora_weights(model: torch.nn.Module, target_rank: int) -> bool:
+ """
+ Pad LoRA weights in a model to a target rank while preserving the original behavior.
+
+ Args:
+ model (nn.Module): The model containing LoRA modules (with lora_A and lora_B).
+ target_rank (int): The target rank to pad to.
+
+ Returns:
+ bool:
+ Returns `True` if an appropriate adapter was found, else `False`.
+ """
+ found_adapter = False
+
+ for module in model.modules():
+ # Decide which pad function to call based on module type
+ if isinstance(module, Linear):
+ pad_fn = _get_padded_linear
+ elif isinstance(module, Conv2d):
+ pad_fn = _get_padded_conv2d
+ else:
+ # Skip any other module types
+ continue
+
+ # Pad LoRA A
+ for adapter_name, lora_A_module in module.lora_A.items():
+ new_layer = pad_fn(lora_A_module, target_rank=target_rank, is_lora_A=True)
+ module.lora_A[adapter_name] = new_layer
+
+ # Pad LoRA B
+ for adapter_name, lora_B_module in module.lora_B.items():
+ new_layer = pad_fn(lora_B_module, target_rank=target_rank, is_lora_A=False)
+ module.lora_B[adapter_name] = new_layer
+
+ found_adapter = True
+ return found_adapter
+
+
+def prepare_model_for_compiled_hotswap(
+ model: torch.nn.Module,
+ *,
+ target_rank: Optional[int] = None,
+ config: Optional[LoraConfig | dict[str, LoraConfig]] = None,
+ check_compiled: Literal["error", "warn", "ignore"] = "error",
+) -> None:
+ """
+ Helper function that prepares the model so that it can later be compiled and then used with hot-swapping.
+
+ It is necessary to call this function on the model for hot-swapping to work if both of these are true:
+
+ - the different LoRA adapters have different ranks and/or different alpha values (i.e. scalings)
+ - you plan to torch.compile the model and want to avoid re-compilation
+
+ It is important to call this function *after* the first LoRA adapter has been loaded (i.e. the one that will be
+ swapped out) but *before* the model is compiled.
+
+ Even with this function, hot-swapping LoRA adapters that target different layers is still not supported.
+
+ Note: This function modifies the model in-place. If you want to restore the model to its initial state, you will
+ have to reload it.
+
+ Args:
+ model (`nn.Module`):
+ The model with the loaded adapter, before compilation.
+ target_rank (`int`, *optional*):
+ The target rank to pad the LoRA weights to. Should be the maximum rank among all LoRA adapters that will be
+ hot-swapped. If not specified, the target ranks will not be changed.
+ config (`LoraConfig` or `dict[str, LoraConfig]`, *optional*):
+ Optionally pass the `LoraConfig`s of the LoRA adapters. If passed, the rank in the configs will be updated
+ to `target_rank`.
+ check_compiled (`str`, *optional*, defaults to `"error"`):
+ How to handle the case when the model is already compiled, which should generally be avoided. The options
+ are:
+ - "error" (default): raise an error
+ - "warn": issue a warning
+ - "ignore": do nothing
+
+ Raises:
+ ValueError
+ If the model is already compiled or if no adpater layer was found, raise an error.
+
+ Example:
+
+ ```py
+ base_model = ...
+ model = PeftModel.from_pretrained(base_model, path_adapter_0)
+ # Prepare the model to allow hotswapping even if ranks/scalings of 2nd adapter differ.
+ # You can skip this step if all ranks and scalings are identical.
+ prepare_model_for_compiled_hotswap(model, target_rank=highest_lora_rank)
+ model = torch.compile(model)
+ # do inference with adapter 0
+ # replace the "default" lora adapter with the new one
+ hotswap_adapter(model, path_adapter_1, adapter_name="default", torch_device=device)
+ # do inference with adapter 1
+ ```
+
+ """
+ is_compiled = hasattr(model, "_orig_mod") or getattr(model, "_compiled_call_impl", False)
+ if is_compiled:
+ if check_compiled == "error":
+ raise ValueError("Call prepare_model_for_compiled_hotswap *before* compiling the model")
+ elif check_compiled == "warn":
+ warnings.warn(
+ "prepare_model_for_compiled_hotswap was called with a model that is already compiled. This will likely "
+ "result in re-compilation, hurting performance. Call the function before compiling the model."
+ )
+ elif check_compiled != "ignore":
+ raise ValueError(
+ f"check_compiles should be one of 'error', 'warn', or 'ignore', got '{check_compiled}' instead."
+ )
+
+ conversion_found_adapter = _convert_scalings_to_tensor(model)
+ if target_rank is not None:
+ padding_found_adapter = _pad_lora_weights(model, target_rank=target_rank)
+ else:
+ padding_found_adapter = False
+
+ if not (conversion_found_adapter or padding_found_adapter):
+ raise ValueError(
+ "No adapter layers found on the model, make sure call `prepare_model_for_compiled_hotswap` after loading "
+ "the first adapter and before loading the second adapter."
+ )
+
+ if not config:
+ return
+ if target_rank is None:
+ return
+
+ if not isinstance(config, dict):
+ # config can be either a PeftConfig, or a dict of PeftConfigs like PeftModel.peft_config
+ config = {"dummy": config}
+
+ for lora_config in config.values():
+ lora_config.r = target_rank
+ if lora_config.rank_pattern:
+ for key in lora_config.rank_pattern:
+ lora_config.rank_pattern[key] = target_rank
+
+
+def hotswap_adapter_from_state_dict(
+ model: torch.nn.Module,
+ state_dict: dict[str, torch.Tensor],
+ adapter_name: str,
+ config: LoraConfig,
+ parameter_prefix: str = "lora_",
+):
+ """
+ Swap out the adapter weights from the model with the weights from state_dict.
+
+ As of now, only LoRA is supported.
+
+ This is a low-level function that assumes that the adapters have been checked for compatibility and that the
+ state_dict has been correctly mapped to work with PEFT. For a high level function that performs this work for you,
+ use `hotswap_adapter` instead.
+
+ Args:
+ model (`nn.Module`):
+ The model with the loaded adapter.
+ state_dict (`dict[str, torch.Tensor]`):
+ The state dict of the new adapter, which needs to be compatible (targeting same modules etc.).
+ adapter_name (`str`):
+ The name of the adapter that should be hot-swapped, e.g. `"default"`. The name will remain the same after
+ swapping.
+ config (`LoraConfig`):
+ The config of the LoRA adapter. This is used to determine the scaling and rank of the adapter.
+ parameter_prefix (`str`, *optional*, defaults to `"lora_"`)
+ The prefix used to identify the adapter's keys in the state dict. For LoRA, this would be `"lora_"` (the
+ default).
+
+ Raises:
+ RuntimeError
+ If the old and the new adapter are not compatible, a RuntimeError is raised.
+
+ """
+ # Ensure that all the keys of the new adapter correspond exactly to the keys of the old adapter, otherwise
+ # hot-swapping is not possible
+
+ # _orig_mod is for torch.compile(model) and _compiled_call_impl is for model.compile() (not wrapped)
+ is_compiled = hasattr(model, "_orig_mod")
+ is_compiled_inplace = bool(getattr(model, "_compiled_call_impl", None))
+ # TODO: there is probably a more precise way to identify the adapter keys
+ missing_keys = {k for k in model.state_dict() if (parameter_prefix in k) and (adapter_name in k)}
+ unexpected_keys = []
+
+ # first: dry run, not swapping anything
+ for key, new_val in state_dict.items():
+ try:
+ old_val = attrgetter(key)(model)
+ except AttributeError:
+ unexpected_keys.append(key)
+ continue
+
+ if is_compiled:
+ missing_keys.remove("_orig_mod." + key)
+ else:
+ missing_keys.remove(key)
+
+ # Right now, we don't deal with unexpected keys, i.e. if the adapter being swapped in targeting new layers. We could
+ # probably add LoRA to these layers ad hoc, but that would not work with compiled models.
+ if unexpected_keys:
+ msg = f"Hot swapping the adapter did not succeed, unexpected keys found: {', '.join(unexpected_keys)}."
+ raise RuntimeError(msg)
+
+ # If the adapter that is being swapped in is missing some keys, this is fine. We just need to ensure that those LoRA
+ # weights from the previous adapter are set to 0 so that they don't influence the output. We don't need to worry
+ # about ranks are alphas.
+ for key in missing_keys:
+ # in case it's a compiled model
+ key = key.removeprefix("_orig_mod.")
+ # get LoRA parent module name by removing the 'lora_*..weight' part
+ module_name = ".".join(key.split(".")[:-3])
+ module = model.get_submodule(module_name)
+ old_val = attrgetter(key)(model)
+ old_val.data.fill_(0.0)
+
+ # actual swapping
+ for key, new_val in state_dict.items():
+ # get LoRA parent module name by removing the 'lora_*..weight' part
+ module_name = ".".join(key.split(".")[:-3])
+ module = model.get_submodule(module_name)
+
+ # swap alpha/scaling
+ r_key = get_pattern_key(config.rank_pattern.keys(), key)
+ alpha_key = get_pattern_key(config.alpha_pattern.keys(), key)
+ rank = config.rank_pattern.get(r_key, config.r)
+ alpha = config.alpha_pattern.get(alpha_key, config.lora_alpha)
+ if config.use_rslora:
+ scaling = alpha / math.sqrt(rank)
+ else:
+ scaling = alpha / rank
+ _update_scaling(module, adapter_name=adapter_name, scaling=scaling)
+
+ # swap actual weights
+ # no need to account for potential _orig_mod in key here, as torch handles that
+ old_val = attrgetter(key)(model)
+ new_val = new_val.to(old_val.data.device)
+
+ # We try to detect if the model is compiled but it does not always work, e.g. if hotswapping is called from
+ # within the model itself. In this case, swap_tensors raises RuntimeError and should continue without
+ # swap_tensors.
+ if not is_compiled and not is_compiled_inplace:
+ try:
+ torch.utils.swap_tensors(old_val, new_val)
+ continue
+ except RuntimeError:
+ is_compiled = True
+
+ # Compiled models don't work with swap_tensors because there are weakrefs for the tensor. It is unclear if
+ # this workaround could not cause trouble but the tests indicate that it works.
+ if old_val.shape == new_val.shape:
+ # either
+ # - adapters had the same rank
+ # - adapters were padded with prepare_model_for_compiled_hotswap and 2nd adapter was larger
+ old_val.data.copy_(new_val.data)
+ else:
+ # if 2nd adapter was smaller, ensure to fill up to adapter dimension and set the rest to zeros
+ if old_val.dim() not in (2, 4):
+ raise NotImplementedError(
+ f"Trying to hotswap an adapter whose weight has {old_val.dim()} dimensions, but only Conv2d and "
+ "Linear are supported"
+ )
+
+ # Linear or Conv2d: the check for dim 0 or 1 works for both of these layer types
+ if old_val.shape[0] > new_val.shape[0]:
+ old_val.data.fill_(0)
+ old_val.data[: new_val.shape[0]].copy_(new_val.data)
+ elif old_val.shape[1] > new_val.shape[1]:
+ old_val.data.fill_(0)
+ old_val.data[:, : new_val.shape[1]].copy_(new_val.data)
+ else:
+ raise ValueError(
+ f"Incompatible shapes found for LoRA weights {key}: {old_val.shape} vs {new_val.shape}. Please "
+ "ensure that all ranks are padded to the largest rank among all LoRA adapters by using "
+ "peft.utils.hotswap.prepare_model_for_compiled_hotswap."
+ )
+
+
+def check_hotswap_configs_compatible(config0: PeftConfig, config1: PeftConfig) -> None:
+ """
+ Check if two configs are compatible for hot-swapping.
+
+ Only LoRA parameters are checked for now.
+
+ To hot-swap two adapters, their configs must be compatible. Otherwise, the results could be false. E.g. if they use
+ different alpha values, after hot-swapping, the alphas from the first adapter would still be used with the weights
+ from the 2nd adapter, which would result in incorrect behavior. There is probably a way to swap these values as
+ well, but that's not implemented yet, and we need to be careful not to trigger re-compilation if the model is
+ compiled (so no modification of the dict).
+
+ """
+
+ if config0.peft_type != config1.peft_type:
+ msg = f"Incompatible PEFT types found: {config0.peft_type.value} and {config1.peft_type.value}"
+ raise ValueError(msg)
+
+ if config0.peft_type not in CONFIG_KEYS_TO_CHECK:
+ msg = (
+ f"Hotswapping only supports {', '.join(CONFIG_KEYS_TO_CHECK.keys())} but "
+ f"{config0.peft_type.value} was passed."
+ )
+ raise ValueError(msg)
+ config_keys_to_check = CONFIG_KEYS_TO_CHECK[config0.peft_type]
+
+ # TODO: This is a very rough check only for LoRA at the moment. Also, there might be some options that don't
+ # necessarily require an error.
+ config0 = config0.to_dict()
+ config1 = config1.to_dict()
+ sentinel = object()
+ for key in config_keys_to_check:
+ val0 = config0.get(key, sentinel)
+ val1 = config1.get(key, sentinel)
+ if val0 != val1:
+ raise ValueError(f"Configs are incompatible: for {key}, {val0} != {val1}")
+
+
+def hotswap_adapter(model, model_name_or_path, adapter_name, torch_device=None, **kwargs):
+ """Substitute old adapter data with new adapter data, keeping the rest the same.
+
+ As of now, only LoRA is supported.
+
+ This function is useful when you want to replace the loaded adapter with a new adapter. The adapter name will
+ remain the same, but the weights and other parameters will be swapped out.
+
+ If the adapters are incomptabile, e.g. targeting different layers or having different alpha values, an error will
+ be raised.
+
+ Example:
+
+ ```py
+ >>> import torch
+ >>> from transformers import AutoModelForCausalLM
+ >>> from peft import PeftModel
+ >>> from peft.utils.hotswap import hotswap_adapter
+
+ >>> model_id = ...
+ >>> inputs = ...
+ >>> device = ...
+ >>> model = AutoModelForCausalLM.from_pretrained(model_id).to(device)
+
+ >>> # load lora 0
+ >>> model = PeftModel.from_pretrained(model, "path-adapter-0")
+ >>> model = torch.compile(model) # optionally compile the model
+ >>> with torch.inference_mode():
+ ... output_adapter_0 = model(inputs)
+
+ >>> # replace the "default" lora adapter with the new one
+ >>> hotswap_adapter(model, "path-adapter-1", adapter_name="default", torch_device=device)
+ >>> with torch.inference_mode():
+ ... output_adapter_1 = model(inputs).logits
+ ```
+
+ Args:
+ model ([`~PeftModel`]):
+ The PEFT model with the loaded adapter.
+ model_name_or_path (`str`):
+ The name or path of the model to load the new adapter from.
+ adapter_name (`str`):
+ The name of the adapter to swap, e.g. `"default"`. The name will stay the same after swapping.
+ torch_device: (`str`, *optional*, defaults to None):
+ The device to load the new adapter onto.
+ **kwargs (`optional`):
+ Additional keyword arguments used for loading the config and weights.
+
+ """
+ if torch_device is None:
+ torch_device = infer_device()
+
+ ############################
+ # LOAD CONFIG AND VALIDATE #
+ ############################
+ hf_kwargs = {
+ "subfolder": kwargs.get("subfolder", None),
+ "revision": kwargs.get("revision", None),
+ "cache_dir": kwargs.get("cache_dir", None),
+ "token": kwargs.get("token", None),
+ }
+ if use_auth_token := kwargs.get("use_auth_token", None):
+ hf_kwargs["use_auth_token"] = use_auth_token
+ config_cls = PEFT_TYPE_TO_CONFIG_MAPPING[PeftConfig._get_peft_type(model_name_or_path, **hf_kwargs)]
+ config = config_cls.from_pretrained(model_name_or_path, **kwargs)
+ # config keys that could affect the model output besides what is determined by the state_dict
+ check_hotswap_configs_compatible(model.active_peft_config, config)
+
+ state_dict = load_peft_weights(model_name_or_path, device=torch_device, **kwargs)
+
+ ###########################
+ # LOAD & REMAP STATE_DICT #
+ ###########################
+
+ parameter_prefix = PEFT_TYPE_TO_PREFIX_MAPPING[config.peft_type]
+ peft_model_state_dict = _insert_adapter_name_into_state_dict(
+ state_dict, adapter_name=adapter_name, parameter_prefix=parameter_prefix
+ )
+
+ hotswap_adapter_from_state_dict(
+ model=model,
+ state_dict=peft_model_state_dict,
+ adapter_name=adapter_name,
+ parameter_prefix=parameter_prefix,
+ config=config,
+ )
diff --git a/peft/src/peft/utils/incremental_pca.py b/peft/src/peft/utils/incremental_pca.py
new file mode 100644
index 0000000000000000000000000000000000000000..de4a7c05174dc436f4c75965ef9585afb480183c
--- /dev/null
+++ b/peft/src/peft/utils/incremental_pca.py
@@ -0,0 +1,338 @@
+# Copyright 2024-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+from typing import Optional
+
+import torch
+
+
+class IncrementalPCA:
+ """
+ An implementation of Incremental Principal Components Analysis (IPCA) that leverages PyTorch for GPU acceleration.
+ Adapted from https://github.com/scikit-learn/scikit-learn/blob/main/sklearn/decomposition/_incremental_pca.py
+
+ This class provides methods to fit the model on data incrementally in batches, and to transform new data based on
+ the principal components learned during the fitting process.
+
+ Args:
+ n_components (int, optional): Number of components to keep. If `None`, it's set to the minimum of the
+ number of samples and features. Defaults to None.
+ copy (bool): If False, input data will be overwritten. Defaults to True.
+ batch_size (int, optional): The number of samples to use for each batch. Only needed if self.fit is called.
+ If `None`, it's inferred from the data and set to `5 * n_features`. Defaults to None.
+ svd_driver (str, optional): name of the cuSOLVER method to be used for torch.linalg.svd. This keyword
+ argument only works on CUDA inputs. Available options are: None, gesvd, gesvdj, and gesvda. Defaults to
+ None.
+ lowrank (bool, optional): Whether to use torch.svd_lowrank instead of torch.linalg.svd which can be faster.
+ Defaults to False.
+ lowrank_q (int, optional): For an adequate approximation of n_components, this parameter defaults to
+ n_components * 2.
+ lowrank_niter (int, optional): Number of subspace iterations to conduct for torch.svd_lowrank.
+ Defaults to 4.
+ lowrank_seed (int, optional): Seed for making results of torch.svd_lowrank reproducible.
+ """
+
+ def __init__(
+ self,
+ n_components: Optional[int] = None,
+ copy: Optional[bool] = True,
+ batch_size: Optional[int] = None,
+ svd_driver: Optional[str] = None,
+ lowrank: bool = False,
+ lowrank_q: Optional[int] = None,
+ lowrank_niter: int = 4,
+ lowrank_seed: Optional[int] = None,
+ ):
+ self.n_components = n_components
+ self.copy = copy
+ self.batch_size = batch_size
+ self.svd_driver = svd_driver
+ self.lowrank = lowrank
+ self.lowrank_q = lowrank_q
+ self.lowrank_niter = lowrank_niter
+ self.lowrank_seed = lowrank_seed
+
+ self.n_features_ = None
+
+ if self.lowrank:
+ self._validate_lowrank_params()
+
+ def _validate_lowrank_params(self):
+ if self.lowrank_q is None:
+ if self.n_components is None:
+ raise ValueError("n_components must be specified when using lowrank mode with lowrank_q=None.")
+ self.lowrank_q = self.n_components * 2
+ elif self.lowrank_q < self.n_components:
+ raise ValueError("lowrank_q must be greater than or equal to n_components.")
+
+ def _svd_fn_full(self, X):
+ return torch.linalg.svd(X, full_matrices=False, driver=self.svd_driver)
+
+ def _svd_fn_lowrank(self, X):
+ seed_enabled = self.lowrank_seed is not None
+ with torch.random.fork_rng(enabled=seed_enabled):
+ if seed_enabled:
+ torch.manual_seed(self.lowrank_seed)
+ U, S, V = torch.svd_lowrank(X, q=self.lowrank_q, niter=self.lowrank_niter)
+ return U, S, V.mH
+
+ def _validate_data(self, X) -> torch.Tensor:
+ """
+ Validates and converts the input data `X` to the appropriate tensor format.
+
+ Args:
+ X (torch.Tensor): Input data.
+
+ Returns:
+ torch.Tensor: Converted to appropriate format.
+ """
+ valid_dtypes = [torch.float32, torch.float64]
+
+ if not isinstance(X, torch.Tensor):
+ X = torch.tensor(X, dtype=torch.float32)
+ elif self.copy:
+ X = X.clone()
+
+ n_samples, n_features = X.shape
+ if self.n_components is None:
+ pass
+ elif self.n_components > n_features:
+ raise ValueError(
+ f"n_components={self.n_components} invalid for n_features={n_features}, "
+ "need more rows than columns for IncrementalPCA processing."
+ )
+ elif self.n_components > n_samples:
+ raise ValueError(
+ f"n_components={self.n_components} must be less or equal to the batch number of samples {n_samples}"
+ )
+
+ if X.dtype not in valid_dtypes:
+ X = X.to(torch.float32)
+
+ return X
+
+ @staticmethod
+ def _incremental_mean_and_var(
+ X, last_mean, last_variance, last_sample_count
+ ) -> tuple[torch.Tensor, torch.Tensor, torch.Tensor]:
+ """
+ Computes the incremental mean and variance for the data `X`.
+
+ Args:
+ X (torch.Tensor): The batch input data tensor with shape (n_samples, n_features).
+ last_mean (torch.Tensor): The previous mean tensor with shape (n_features,).
+ last_variance (torch.Tensor): The previous variance tensor with shape (n_features,).
+ last_sample_count (torch.Tensor): The count tensor of samples processed before the current batch.
+
+ Returns:
+ Tuple[torch.Tensor, torch.Tensor, torch.Tensor]: Updated mean, variance tensors, and total sample count.
+ """
+ if X.shape[0] == 0:
+ return last_mean, last_variance, last_sample_count
+
+ if last_sample_count > 0:
+ if last_mean is None:
+ raise ValueError("last_mean should not be None if last_sample_count > 0.")
+ if last_variance is None:
+ raise ValueError("last_variance should not be None if last_sample_count > 0.")
+
+ new_sample_count = torch.tensor([X.shape[0]], device=X.device)
+ updated_sample_count = last_sample_count + new_sample_count
+
+ if last_mean is None:
+ last_sum = torch.zeros(X.shape[1], dtype=torch.float64, device=X.device)
+ else:
+ last_sum = last_mean * last_sample_count
+
+ new_sum = X.sum(dim=0, dtype=torch.float64)
+
+ updated_mean = (last_sum + new_sum) / updated_sample_count
+
+ T = new_sum / new_sample_count
+ temp = X - T
+ correction = temp.sum(dim=0, dtype=torch.float64).square()
+ temp.square_()
+ new_unnormalized_variance = temp.sum(dim=0, dtype=torch.float64)
+ new_unnormalized_variance -= correction / new_sample_count
+ if last_variance is None:
+ updated_variance = new_unnormalized_variance / updated_sample_count
+ else:
+ last_unnormalized_variance = last_variance * last_sample_count
+ last_over_new_count = last_sample_count.double() / new_sample_count
+ updated_unnormalized_variance = (
+ last_unnormalized_variance
+ + new_unnormalized_variance
+ + last_over_new_count / updated_sample_count * (last_sum / last_over_new_count - new_sum).square()
+ )
+ updated_variance = updated_unnormalized_variance / updated_sample_count
+
+ return updated_mean, updated_variance, updated_sample_count
+
+ @staticmethod
+ def _svd_flip(u, v, u_based_decision=True) -> tuple[torch.Tensor, torch.Tensor]:
+ """
+ Adjusts the signs of the singular vectors from the SVD decomposition for deterministic output.
+
+ This method ensures that the output remains consistent across different runs.
+
+ Args:
+ u (torch.Tensor): Left singular vectors tensor.
+ v (torch.Tensor): Right singular vectors tensor.
+ u_based_decision (bool, optional): If True, uses the left singular vectors to determine the sign flipping.
+ Defaults to True.
+
+ Returns:
+ Tuple[torch.Tensor, torch.Tensor]: Adjusted left and right singular vectors tensors.
+ """
+ if u_based_decision:
+ max_abs_cols = torch.argmax(torch.abs(u), dim=0)
+ signs = torch.sign(u[max_abs_cols, range(u.shape[1])])
+ else:
+ max_abs_rows = torch.argmax(torch.abs(v), dim=1)
+ signs = torch.sign(v[range(v.shape[0]), max_abs_rows])
+ u *= signs[: u.shape[1]].view(1, -1)
+ v *= signs.view(-1, 1)
+ return u, v
+
+ def fit(self, X, check_input=True):
+ """
+ Fits the model with data `X` using minibatches of size `batch_size`.
+
+ Args:
+ X (torch.Tensor): The input data tensor with shape (n_samples, n_features).
+ check_input (bool, optional): If True, validates the input. Defaults to True.
+
+ Returns:
+ IncrementalPCA: The fitted IPCA model.
+ """
+ if check_input:
+ X = self._validate_data(X)
+ n_samples, n_features = X.shape
+ if self.batch_size is None:
+ self.batch_size = 5 * n_features
+
+ for batch in self.gen_batches(n_samples, self.batch_size, min_batch_size=self.n_components or 0):
+ self.partial_fit(X[batch], check_input=False)
+
+ return self
+
+ def partial_fit(self, X, check_input=True):
+ """
+ Incrementally fits the model with batch data `X`.
+
+ Args:
+ X (torch.Tensor): The batch input data tensor with shape (n_samples, n_features).
+ check_input (bool, optional): If True, validates the input. Defaults to True.
+
+ Returns:
+ IncrementalPCA: The updated IPCA model after processing the batch.
+ """
+ first_pass = not hasattr(self, "components_")
+
+ if check_input:
+ X = self._validate_data(X)
+ n_samples, n_features = X.shape
+
+ # Initialize attributes to avoid errors during the first call to partial_fit
+ if first_pass:
+ self.mean_ = None # Will be initialized properly in _incremental_mean_and_var based on data dimensions
+ self.var_ = None # Will be initialized properly in _incremental_mean_and_var based on data dimensions
+ self.n_samples_seen_ = torch.tensor([0], device=X.device)
+ self.n_features_ = n_features
+ if not self.n_components:
+ self.n_components = min(n_samples, n_features)
+
+ if n_features != self.n_features_:
+ raise ValueError(
+ "Number of features of the new batch does not match the number of features of the first batch."
+ )
+
+ col_mean, col_var, n_total_samples = self._incremental_mean_and_var(
+ X, self.mean_, self.var_, self.n_samples_seen_
+ )
+
+ if first_pass:
+ X -= col_mean
+ else:
+ col_batch_mean = torch.mean(X, dim=0)
+ X -= col_batch_mean
+ mean_correction_factor = torch.sqrt((self.n_samples_seen_.double() / n_total_samples) * n_samples)
+ mean_correction = mean_correction_factor * (self.mean_ - col_batch_mean)
+ X = torch.vstack(
+ (
+ self.singular_values_.view((-1, 1)) * self.components_,
+ X,
+ mean_correction,
+ )
+ )
+
+ if self.lowrank:
+ U, S, Vt = self._svd_fn_lowrank(X)
+ else:
+ U, S, Vt = self._svd_fn_full(X)
+ U, Vt = self._svd_flip(U, Vt, u_based_decision=False)
+ explained_variance = S**2 / (n_total_samples - 1)
+ explained_variance_ratio = S**2 / torch.sum(col_var * n_total_samples)
+
+ self.n_samples_seen_ = n_total_samples
+ self.components_ = Vt[: self.n_components]
+ self.singular_values_ = S[: self.n_components]
+ self.mean_ = col_mean
+ self.var_ = col_var
+ self.explained_variance_ = explained_variance[: self.n_components]
+ self.explained_variance_ratio_ = explained_variance_ratio[: self.n_components]
+ if self.n_components not in (n_samples, n_features):
+ self.noise_variance_ = explained_variance[self.n_components :].mean()
+ else:
+ self.noise_variance_ = torch.tensor(0.0, device=X.device)
+ return self
+
+ def transform(self, X) -> torch.Tensor:
+ """
+ Applies dimensionality reduction to `X`.
+
+ The input data `X` is projected on the first principal components previously extracted from a training set.
+
+ Args:
+ X (torch.Tensor): New data tensor with shape (n_samples, n_features) to be transformed.
+
+ Returns:
+ torch.Tensor: Transformed data tensor with shape (n_samples, n_components).
+ """
+ X = X - self.mean_
+ return torch.mm(X.double(), self.components_.T).to(X.dtype)
+
+ @staticmethod
+ def gen_batches(n: int, batch_size: int, min_batch_size: int = 0):
+ """Generator to create slices containing `batch_size` elements from 0 to `n`.
+
+ The last slice may contain less than `batch_size` elements, when `batch_size` does not divide `n`.
+
+ Args:
+ n (int): Size of the sequence.
+ batch_size (int): Number of elements in each batch.
+ min_batch_size (int, optional): Minimum number of elements in each batch. Defaults to 0.
+
+ Yields:
+ slice: A slice of `batch_size` elements.
+ """
+ start = 0
+ for _ in range(int(n // batch_size)):
+ end = start + batch_size
+ if end + min_batch_size > n:
+ continue
+ yield slice(start, end)
+ start = end
+ if start < n:
+ yield slice(start, n)
diff --git a/peft/src/peft/utils/integrations.py b/peft/src/peft/utils/integrations.py
new file mode 100644
index 0000000000000000000000000000000000000000..dc5ae465dbe89afaadde6aa9a7a05a0db3132694
--- /dev/null
+++ b/peft/src/peft/utils/integrations.py
@@ -0,0 +1,281 @@
+# Copyright 2023-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+from __future__ import annotations
+
+import functools
+from contextlib import contextmanager
+from typing import Literal, Optional
+
+import packaging.version
+import torch
+import transformers
+from torch import nn
+
+
+def check_deepspeed_zero3_enabled() -> bool:
+ if packaging.version.parse(transformers.__version__) >= packaging.version.parse("4.33.0"):
+ from transformers.integrations import is_deepspeed_zero3_enabled
+ else:
+ from transformers.deepspeed import is_deepspeed_zero3_enabled
+ return is_deepspeed_zero3_enabled()
+
+
+@contextmanager
+def gather_params_ctx(param, modifier_rank: Optional[int] = 0, fwd_module: torch.nn.Module = None):
+ """Call DeepSpeed GatheredParameters context manager if DeepSpeed is enabled, otherwise do nothing."""
+
+ if not check_deepspeed_zero3_enabled():
+ yield
+ return
+
+ import deepspeed
+
+ with deepspeed.zero.GatheredParameters(param, modifier_rank=modifier_rank, fwd_module=fwd_module):
+ yield
+ return
+
+
+def dequantize_module_weight(module: torch.nn.Module) -> torch.nn.Parameter:
+ """
+ Helper function to dequantize a quantized weight.
+
+ This function should be extended if more quantization schemes are added to the library.
+
+ If the weight is not quantized, it will be returned as is.
+ """
+ if hasattr(module, "W_q"): # For handling HQQ quantized weight
+ weight = module.dequantize()
+ return weight
+ elif type(module.weight).__module__.startswith("torchao."):
+ # check for torchao without requiring any torchao imports
+ weight = module.weight.dequantize()
+ return weight
+
+ weight = module.weight
+ if not isinstance(weight, torch.nn.Parameter):
+ if isinstance(weight, torch.Tensor):
+ # this is an FSDP-specific edge case
+ return weight # type: ignore
+ raise TypeError(f"Input weight should be of type nn.Parameter, got {type(weight)} instead")
+
+ cls_name = weight.__class__.__name__
+ if cls_name not in ("Params4bit", "Int8Params"):
+ return weight
+
+ quant_state = getattr(module, "state", None)
+ device = weight.device
+ is_cpu = device.type == torch.device("cpu").type
+ weight = dequantize_bnb_weight(weight, state=quant_state) # no-op if not bnb
+ if is_cpu:
+ # dequantize_bnb_weight for 8bit moves the device in-place, thus we need to move it back to CPU if necessary
+ module.weight = module.weight.to(device)
+ return weight
+
+
+def dequantize_bnb_weight(weight: torch.nn.Parameter, state=None):
+ """Helper function to dequantize 4bit or 8bit bnb weights."""
+ import bitsandbytes as bnb
+
+ if state.SCB is None:
+ state.SCB = weight.SCB
+
+ device = weight.device
+
+ cls_name = weight.__class__.__name__
+ if cls_name == "Params4bit":
+ dequantized = bnb.functional.dequantize_4bit(weight.data, weight.quant_state)
+ return dequantized
+
+ if hasattr(bnb.functional, "int8_vectorwise_dequant"):
+ # Use bitsandbytes API if available (requires v0.45.0+)
+ dequantized = bnb.functional.int8_vectorwise_dequant(weight.data, state.SCB)
+ else:
+ # Multiply by (scale/127) to dequantize.
+ dequantized = weight.data * state.SCB.view(-1, 1) * 7.874015718698502e-3
+
+ return dequantized
+
+
+def get_bnb_param_type(param: torch.nn.Parameter) -> Literal[False, "4bit", "8bit"]:
+ """Returns '4bit' or '8bit' if bitsandbytes parameter, else False"""
+ if param.__class__.__name__ == "Params4bit":
+ return "4bit"
+ if param.__class__.__name__ == "Int8Params":
+ return "8bit"
+ return False
+
+
+# adapted from:
+# https://github.com/huggingface/transformers/blob/eab6c491d439e83d5e31c660df6f7e36592eb0a2/src/transformers/generation/utils.py#L1617-L1643
+def get_layer_device_map(model):
+ """
+ Derive the device map for the layers of the model.
+ """
+ main_device = [d for d in model.hf_device_map.values() if d not in ["cpu", "disk"]][0]
+
+ execution_device_map = {
+ name: main_device if device in ["cpu", "disk"] else device for name, device in model.hf_device_map.items()
+ }
+
+ if execution_device_map is None:
+ return None
+
+ if len(execution_device_map) == 1 and "" in execution_device_map:
+ return {idx: execution_device_map[""] for idx in range(model.config.num_hidden_layers)}
+
+ layer_device_map = {}
+ for layer in execution_device_map:
+ for idx in range(model.config.num_hidden_layers):
+ if f".{idx}." in f"{layer}.":
+ layer_device_map[idx] = execution_device_map[layer]
+ break
+ for idx in range(model.config.num_hidden_layers):
+ if idx not in layer_device_map:
+ raise RuntimeError(f"layer {idx} has not been mapped to a device.")
+ return layer_device_map
+
+
+# adapted from:
+# https://github.com/huggingface/transformers/blob/eab6c491d439e83d5e31c660df6f7e36592eb0a2/src/transformers/cache_utils.py#L1159-L1179
+def map_cache_to_layer_device_map(model, cache) -> None:
+ """
+ Ensure that the key and value cache of the model are on the same device as their corresponding layers.
+ """
+ if not (isinstance(cache, transformers.Cache) and hasattr(model, "hf_device_map")):
+ return
+
+ if isinstance(cache, transformers.EncoderDecoderCache):
+ map_cache_to_layer_device_map(model, cache.self_attention_cache)
+ return
+
+ layer_device_map = get_layer_device_map(model)
+ for idx in range(model.config.num_hidden_layers):
+ layer_device = layer_device_map[idx]
+ if hasattr(cache, "layers"):
+ # new transformers uses cache.layers (>v4.55)
+ layer = cache.layers[idx]
+ layer.keys = layer.keys.to(layer_device)
+ layer.values = layer.values.to(layer_device)
+ else:
+ # old transformers uses cache.{key,value}_cache (<=v4.55)
+ # TODO: remove if we drop support for transformers <= 4.55
+ cache.key_cache[idx] = cache.key_cache[idx].to(layer_device)
+ cache.value_cache[idx] = cache.value_cache[idx].to(layer_device)
+
+
+##################################
+# START: ADAPTED FROM ACCELERATE #
+##################################
+#
+# Modified to support explicitly skipping layer initialization for faster switching between layer states
+# (necessary for supporting `nn.MultiHeadAttention` adapters)
+
+
+@contextmanager
+def init_empty_weights(include_buffers: bool = None):
+ # adapted from accelerate.big_modeling.py
+ with _init_on_device(torch.device("meta"), include_buffers=include_buffers) as f:
+ yield f
+
+
+@contextmanager
+def _init_on_device(device: torch.device, include_buffers: bool = None):
+ # adapted from accelerate.big_modeling.py
+ old_register_parameter = nn.Module.register_parameter
+ if include_buffers:
+ old_register_buffer = nn.Module.register_buffer
+
+ def register_empty_parameter(module, name, param):
+ # This works because torch first initializes the parameters with torch.empty, thus not assigning any new memory.
+ # Then the parameter is moved to meta device before reset_parameters() is called, which then operates on the
+ # meta device, making any subsequent calls to initialization methods no-ops.
+ old_register_parameter(module, name, param)
+ if (param is not None) and (getattr(_init_on_device, "_skip", False) is not True):
+ param_cls = type(module._parameters[name])
+ kwargs = module._parameters[name].__dict__
+ kwargs["requires_grad"] = param.requires_grad
+ module._parameters[name] = param_cls(module._parameters[name].to(device), **kwargs)
+
+ def register_empty_buffer(module, name, buffer, persistent=True):
+ old_register_buffer(module, name, buffer, persistent=persistent)
+ if buffer is not None:
+ module._buffers[name] = module._buffers[name].to(device)
+
+ # Patch tensor creation
+ if include_buffers:
+ tensor_constructors_to_patch = {
+ torch_function_name: getattr(torch, torch_function_name)
+ for torch_function_name in ["empty", "zeros", "ones", "full"]
+ }
+ else:
+ tensor_constructors_to_patch = {}
+
+ def patch_tensor_constructor(fn):
+ def wrapper(*args, **kwargs):
+ kwargs["device"] = device
+ return fn(*args, **kwargs)
+
+ return wrapper
+
+ try:
+ nn.Module.register_parameter = register_empty_parameter
+ if include_buffers:
+ nn.Module.register_buffer = register_empty_buffer
+ for torch_function_name in tensor_constructors_to_patch.keys():
+ setattr(torch, torch_function_name, patch_tensor_constructor(getattr(torch, torch_function_name)))
+ yield
+ finally:
+ nn.Module.register_parameter = old_register_parameter
+ if include_buffers:
+ nn.Module.register_buffer = old_register_buffer
+ for torch_function_name, old_torch_function in tensor_constructors_to_patch.items():
+ setattr(torch, torch_function_name, old_torch_function)
+
+
+@contextmanager
+def _skip_init_on_device():
+ # context manager to skip the _init_on_device context manager
+ old_val = getattr(_init_on_device, "_skip", False)
+ try:
+ _init_on_device._skip = True
+ yield
+ finally:
+ _init_on_device._skip = old_val
+
+
+def skip_init_on_device(func):
+ """
+ Ignore the init_on_device context manager when calling the decorated function.
+
+ This is a narrow use decorator that allows us to avoid initializing on meta device even when we're inside the
+ init_empty_weights context.
+
+ """
+
+ # The need for this functionality arose when working on MultiheadAttention, where we have to call _restore_weights
+ # repeatedly as parametes are overwritten and need to be re-registered. When using low_cpu_mem_usage=True, as
+ # register_parameter is patched inside of the init_empty_weights context, this would result in those parameters
+ # suddenly being moved to meta device. Using this decorator allows us to avoid this.
+ @functools.wraps(func)
+ def wrapper(*args, **kwargs):
+ with _skip_init_on_device():
+ return func(*args, **kwargs)
+
+ return wrapper
+
+
+#######
+# END #
+#######
diff --git a/peft/src/peft/utils/loftq_utils.py b/peft/src/peft/utils/loftq_utils.py
new file mode 100644
index 0000000000000000000000000000000000000000..a5b19b44673c3d1bbf7cb97189e79a8bfc9806af
--- /dev/null
+++ b/peft/src/peft/utils/loftq_utils.py
@@ -0,0 +1,409 @@
+# Copyright 2023-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+# Reference code: https://github.com/yxli2123/LoftQ/blob/main/utils.py
+# Reference paper: https://huggingface.co/papers/2310.08659
+
+from __future__ import annotations
+
+import logging
+import os
+from typing import Callable, Optional, Union
+
+import torch
+from accelerate.utils.memory import clear_device_cache
+from huggingface_hub import snapshot_download
+from huggingface_hub.errors import HFValidationError, LocalEntryNotFoundError
+from safetensors import SafetensorError, safe_open
+from transformers.utils import cached_file
+from transformers.utils.hub import get_checkpoint_shard_files
+
+from peft.import_utils import is_bnb_4bit_available, is_bnb_available, is_xpu_available
+
+
+class NFQuantizer:
+ def __init__(self, num_bits=2, device="cuda", method="normal", block_size=64, *args, **kwargs):
+ super().__init__(*args, **kwargs)
+ self.num_bits = num_bits
+ self.device = device
+ self.method = method
+ self.block_size = block_size
+ if self.method == "normal":
+ self.norm_lookup_table = self.create_normal_map(num_bits=self.num_bits)
+ self.norm_lookup_table = self.norm_lookup_table.to(device)
+ elif self.method == "uniform":
+ self.norm_lookup_table = self.create_uniform_map(num_bits=self.num_bits)
+ self.norm_lookup_table = self.norm_lookup_table.to(device)
+ else:
+ raise NotImplementedError("Other quantization methods not supported yet.")
+
+ @staticmethod
+ def create_uniform_map(symmetric=False, num_bits=4):
+ if symmetric:
+ # print("symmetric uniform quantization")
+ negative = torch.linspace(-1, 0, 2 ** (num_bits - 1))
+ positive = torch.linspace(0, 1, 2 ** (num_bits - 1))
+ table = torch.cat([negative, positive[1:]])
+ else:
+ # print("asymmetric uniform quantization")
+ table = torch.linspace(-1, 1, 2**num_bits)
+ return table
+
+ @staticmethod
+ def create_normal_map(offset=0.9677083, symmetric=False, num_bits=2):
+ try:
+ from scipy.stats import norm
+ except ImportError:
+ raise ImportError("The required package 'scipy' is not installed. Please install it to continue.")
+
+ variations = 2**num_bits
+ if symmetric:
+ v = norm.ppf(torch.linspace(1 - offset, offset, variations + 1)).tolist()
+ values = []
+ for index in range(len(v) - 1):
+ values.append(0.5 * v[index] + 0.5 * v[index + 1])
+ v = values
+ else:
+ # one more positive value, this is an asymmetric type
+ v1 = norm.ppf(torch.linspace(offset, 0.5, variations // 2 + 1)[:-1]).tolist()
+ v2 = [0]
+ v3 = (-norm.ppf(torch.linspace(offset, 0.5, variations // 2)[:-1])).tolist()
+ v = v1 + v2 + v3
+
+ values = torch.Tensor(v)
+ values = values.sort().values
+ values /= values.max()
+ return values
+
+ def quantize_tensor(self, weight):
+ max_abs = torch.abs(weight).max()
+ weight_normed = weight / max_abs
+
+ weight_normed_expanded = weight_normed.unsqueeze(-1)
+
+ # Reshape L to have the same number of dimensions as X_expanded
+ L_reshaped = torch.tensor(self.norm_lookup_table).reshape(1, -1)
+
+ # Calculate the absolute difference between X_expanded and L_reshaped
+ abs_diff = torch.abs(weight_normed_expanded - L_reshaped)
+
+ # Find the index of the minimum absolute difference for each element
+ qweight = torch.argmin(abs_diff, dim=-1)
+ return qweight, max_abs
+
+ def dequantize_tensor(self, qweight, max_abs):
+ qweight_flatten = qweight.flatten()
+
+ weight_normed = self.norm_lookup_table[qweight_flatten]
+ weight = weight_normed * max_abs
+
+ weight = weight.reshape(qweight.shape)
+
+ return weight
+
+ def quantize_block(self, weight):
+ if len(weight.shape) != 2:
+ raise ValueError(f"Only support 2D matrix, but your input has {len(weight.shape)} dimensions.")
+ if weight.shape[0] * weight.shape[1] % self.block_size != 0:
+ raise ValueError(
+ f"Weight with shape ({weight.shape[0]} x {weight.shape[1]}) "
+ f"is not dividable by block size {self.block_size}."
+ )
+
+ M, N = weight.shape
+ device = weight.device
+
+ # Quantization
+ weight_flatten = weight.flatten() # (M*N, )
+ weight_block = weight_flatten.reshape(-1, self.block_size) # (L, B), L = M * N / B
+ if self.method == "normal":
+ weight_max = weight_block.abs().max(dim=-1)[0] # (L, 1)
+ elif self.method == "uniform":
+ weight_max = weight_block.mean(dim=-1) + 2.5 * weight_block.std(dim=-1)
+ else:
+ raise NotImplementedError("Method not supported yet.")
+ weight_max = weight_max.unsqueeze(-1)
+ weight_divabs = weight_block / weight_max # (L, B)
+ weight_divabs = weight_divabs.unsqueeze(-1) # (L, B, 1)
+ L_reshaped = self.norm_lookup_table.reshape(1, -1) # (1, 2**K)
+
+ abs_diff = torch.abs(weight_divabs - L_reshaped) # (L, B, 2**K)
+ qweight = torch.argmin(abs_diff, dim=-1) # (L, B)
+
+ # Pack multiple k-bit into uint8
+ qweight = qweight.reshape(-1, 8 // self.num_bits)
+ qweight_pack = torch.zeros((M * N // 8 * self.num_bits, 1), dtype=torch.uint8, device=device)
+
+ # data format example:
+ # [1, 0, 3, 2] or [01, 00, 11, 10] -> [10110001], LIFO
+ for i in range(8 // self.num_bits):
+ qweight[:, i] = qweight[:, i] << i * self.num_bits
+ qweight_pack[:, 0] |= qweight[:, i]
+
+ return qweight_pack, weight_max, weight.shape
+
+ def dequantize_block(self, qweight, weight_max, weight_shape):
+ # unpack weight
+ device = qweight.device
+ weight = torch.zeros((qweight.shape[0], 8 // self.num_bits), dtype=torch.float32, device=device)
+ for i in range(8 // self.num_bits):
+ lookup_table_idx = qweight.to(torch.long) % 2**self.num_bits # get the most right 2 bits
+ lookup_table_idx = lookup_table_idx.to(torch.long)
+ weight[:, i] = self.norm_lookup_table[lookup_table_idx].squeeze()
+ qweight = qweight >> self.num_bits # right shift 2 bits of the original data
+
+ weight_block = weight.reshape(-1, self.block_size)
+ weight = weight_block * weight_max
+ weight = weight.reshape(weight_shape)
+
+ return weight
+
+
+def _low_rank_decomposition(weight, reduced_rank=32):
+ """
+ :param weight: The matrix to decompose, of shape (H, W) :param reduced_rank: the final rank :return:
+ """
+ matrix_dimension = len(weight.size())
+ if matrix_dimension != 2:
+ raise ValueError(f"Only support 2D matrix, but your input has {matrix_dimension} dimensions.")
+
+ # Use SVD to decompose a matrix, default full_matrices is False to save parameters
+ U, S, Vh = torch.linalg.svd(weight, full_matrices=False)
+
+ L = U @ (torch.sqrt(torch.diag(S)[:, 0:reduced_rank]))
+ R = torch.sqrt(torch.diag(S)[0:reduced_rank, :]) @ Vh
+
+ return {"L": L, "R": R, "U": U, "S": S, "Vh": Vh, "reduced_rank": reduced_rank}
+
+
+@torch.no_grad()
+def loftq_init(weight: Union[torch.Tensor, torch.nn.Parameter], num_bits: int, reduced_rank: int, num_iter=1):
+ if is_bnb_available():
+ import bitsandbytes as bnb
+ else:
+ raise ValueError("bitsandbytes is not available, please install it to use LoftQ.")
+
+ if num_bits not in [2, 4, 8]:
+ raise ValueError("Only support 2, 4, 8 bits quantization")
+ if num_iter <= 0:
+ raise ValueError("Number of iterations must be greater than 0")
+
+ out_feature, in_feature = weight.size()
+ device = weight.device
+ dtype = weight.dtype
+ logging.info(
+ f"Weight: ({out_feature}, {in_feature}) | Rank: {reduced_rank} | Num Iter: {num_iter} | Num Bits: {num_bits}"
+ )
+ if not is_bnb_4bit_available() or num_bits in [2, 8]:
+ quantizer = NFQuantizer(num_bits=num_bits, device=device, method="normal", block_size=64)
+ compute_device = device
+ else:
+ compute_device = "xpu" if is_xpu_available() else "cuda"
+
+ weight = weight.to(device=compute_device, dtype=torch.float32)
+ res = weight.clone()
+ for i in range(num_iter):
+ clear_device_cache()
+ # Quantization
+ if num_bits == 4 and is_bnb_4bit_available():
+ qweight = bnb.nn.Params4bit(
+ res.to("cpu"), requires_grad=False, compress_statistics=False, quant_type="nf4"
+ ).to(compute_device)
+ dequantized_weight = bnb.functional.dequantize_4bit(qweight.data, qweight.quant_state)
+ else:
+ quantized_weight, max_abs, shape = quantizer.quantize_block(res)
+ dequantized_weight = quantizer.dequantize_block(quantized_weight, max_abs, shape)
+
+ res = weight - dequantized_weight
+
+ # Decompose the residual by SVD
+ output = _low_rank_decomposition(res, reduced_rank=reduced_rank)
+ L, R, reduced_rank = output["L"], output["R"], output["reduced_rank"]
+ res = weight - torch.mm(L, R)
+
+ lora_A, lora_B = R, L
+
+ return dequantized_weight.to(device=device, dtype=dtype), lora_A, lora_B
+
+
+@torch.no_grad()
+def _loftq_init_new(qweight, weight, num_bits: int, reduced_rank: int):
+ import bitsandbytes as bnb
+
+ if num_bits != 4:
+ raise ValueError("Only 4 bit quantization supported at the moment.")
+ if not is_bnb_4bit_available():
+ raise ValueError("bitsandbytes 4bit quantization is not available.")
+
+ compute_device = "xpu" if is_xpu_available() else "cuda"
+ dequantized_weight = bnb.functional.dequantize_4bit(qweight.data, qweight.quant_state)
+
+ weight = weight.to(device=compute_device, dtype=torch.float32)
+ residual = weight - dequantized_weight
+ clear_device_cache()
+ # Decompose the residualidual by SVD
+ output = _low_rank_decomposition(residual, reduced_rank=reduced_rank)
+ L, R, reduced_rank = output["L"], output["R"], output["reduced_rank"]
+ return R, L
+
+
+class _SafetensorLoader:
+ """
+ Simple utility class that loads tensors with safetensors from a single file or sharded files.
+
+ Takes care of file name normalization etc.
+
+ """
+
+ def __init__(self, peft_model, model_path):
+ if model_path is None:
+ try:
+ model_path = snapshot_download(peft_model.base_model.config._name_or_path, local_files_only=True)
+ except (AttributeError, HFValidationError) as exc:
+ raise ValueError(
+ "The provided model does not appear to be a transformers model or is a local model. In this case, "
+ "you must pass the model_path argument that points to the safetensors file."
+ ) from exc
+ except LocalEntryNotFoundError as exc:
+ raise ValueError(
+ "The model.safetensors file must be present on disk, but it could not be found."
+ ) from exc
+
+ suffix = "model.safetensors"
+ if not model_path.endswith(suffix):
+ model_path = os.path.join(model_path, suffix)
+
+ self.model_path = model_path
+ self.base_model_prefix = getattr(peft_model.get_base_model(), "base_model_prefix", None)
+ self.prefix = "base_model.model."
+ self.is_sharded = False
+ self.weight_map = None
+
+ if not os.path.exists(model_path):
+ # check if the file is sharded
+ par_dir = model_path.rpartition(os.path.sep)[0]
+ try:
+ resolved_archive_file, sharded_metadata = get_checkpoint_shard_files(
+ par_dir, cached_file(par_dir, "model.safetensors.index.json")
+ )
+ except OSError as exc:
+ raise FileNotFoundError(
+ f"Could not find file for {model_path}, ensure that there is a (sharded) safetensors file of the model."
+ ) from exc
+
+ self.is_sharded = True
+ # maps from 'model-X-of-Y.safetensors' to full file path
+ file_map = {k.rpartition(os.path.sep)[-1]: k for k in resolved_archive_file}
+ self.weight_map = {k: file_map[v] for k, v in sharded_metadata["weight_map"].items()}
+
+ def get_tensor(self, name):
+ if not self.is_sharded:
+ file_path = self.model_path
+ else:
+ file_path = self.weight_map[name]
+
+ with safe_open(file_path, framework="pt", device="cpu") as f:
+ try:
+ tensor = f.get_tensor(name)
+ except SafetensorError as exc:
+ # no matching key found, we probably need to remove the base model prefix
+ if self.base_model_prefix:
+ # remove 1 extra character for "."
+ name = name[len(self.base_model_prefix) + 1 :]
+ tensor = f.get_tensor(name)
+ else:
+ raise exc
+ return tensor
+
+
+@torch.no_grad()
+def replace_lora_weights_loftq(
+ peft_model,
+ model_path: Optional[str] = None,
+ adapter_name: str = "default",
+ callback: Optional[Callable[[torch.nn.Module, str], bool]] = None,
+):
+ """
+ Replace the LoRA weights of a model quantized with bitsandbytes, using the LoftQ technique.
+
+ The replacement is done on the fly by loading in the non-quantized weights from a locally stored safetensors model
+ file and initializing the LoRA weights such that the quantization error between the original and quantized weights
+ is minimized.
+
+ As lazy loading is not possible with pickle, normal PyTorch checkpoint files cannot be supported.
+
+ Depending on the model size, calling this function may take some time to finish.
+
+ Args:
+ peft_model (`PeftModel`):
+ The model to replace the weights of. Must be a quantized PEFT model with LoRA layers.
+ model_path (`Optional[str]`):
+ The path to the model safetensors file. If the model is a Hugging Face model, this will be inferred from
+ the model's config. Otherwise, it must be provided.
+ adapter_name (`str`):
+ The name of the adapter to replace the weights of. The default adapter name is "default".
+ callback (`Optional[Callable[[PeftModel, str], bool]]`):
+ A callback function that will be called after each module is replaced. The callback function should take
+ the model and the name of the current module as input and return a boolean indicating whether the
+ replacement should be kept. If the callback returns False, the replacement will be rolled back. This can be
+ very useful to confirm that the LoftQ initialization actually decreases the quantization error of the
+ model. As an example, this callback could generate logits for given input and compare it with the logits
+ from the original, non-quanitzed model with the same input, and only return `True` if there is an
+ improvement. As this is a greedy optimization, it's possible that calling this function multiple times
+ yields incremental improvements.
+ """
+ if not is_bnb_4bit_available():
+ raise ValueError("bitsandbytes must be installed and the model must be quantized in 4bits.")
+
+ from peft.tuners.lora import Linear4bit
+
+ # model_path = _check_model_path_loftq(model_path, peft_model)
+ prefix = "base_model.model."
+ any_match = False
+ safetensor_loader = _SafetensorLoader(peft_model, model_path)
+
+ # if too slow, consider adding tqdm as an option
+ for name, module in peft_model.named_modules():
+ if not isinstance(module, Linear4bit):
+ continue
+
+ if not name.startswith(prefix):
+ raise TypeError("The passed model does not appear to be a valid PeftModel")
+
+ any_match = True
+ name = name[len(prefix) :]
+ tensor = safetensor_loader.get_tensor(name + ".weight")
+
+ reduced_rank = module.r[adapter_name]
+ lora_A, lora_B = _loftq_init_new(module.weight, tensor, num_bits=4, reduced_rank=reduced_rank)
+ if not callback:
+ module.lora_A[adapter_name].weight.data = lora_A
+ module.lora_B[adapter_name].weight.data = lora_B
+ continue
+
+ lora_A_before = module.lora_A[adapter_name].weight.data
+ lora_B_before = module.lora_B[adapter_name].weight.data
+
+ module.lora_A[adapter_name].weight.data = lora_A
+ module.lora_B[adapter_name].weight.data = lora_B
+ should_replace = callback(peft_model, name)
+ if not should_replace:
+ # roll back
+ module.lora_A[adapter_name].weight.data = lora_A_before
+ module.lora_B[adapter_name].weight.data = lora_B_before
+
+ del lora_A_before, lora_B_before
+
+ if not any_match:
+ raise ValueError("No bnb LoRA module found on the model")
diff --git a/peft/src/peft/utils/merge_utils.py b/peft/src/peft/utils/merge_utils.py
new file mode 100644
index 0000000000000000000000000000000000000000..b62a1abf1eefe17d596461c529925e47e378c563
--- /dev/null
+++ b/peft/src/peft/utils/merge_utils.py
@@ -0,0 +1,268 @@
+# Copyright 2024-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+import warnings
+from typing import Literal
+
+import torch
+
+
+def reshape_weight_task_tensors(task_tensors, weights):
+ """
+ Reshapes `weights` to match the shape of `task_tensors` by unsqeezing in the remaining dimenions.
+
+ Args:
+ task_tensors (`torch.Tensor`): The tensors that will be used to reshape `weights`.
+ weights (`torch.Tensor`): The tensor to be reshaped.
+
+ Returns:
+ `torch.Tensor`: The reshaped tensor.
+ """
+ new_shape = weights.shape + (1,) * (task_tensors.dim() - weights.dim())
+ weights = weights.view(new_shape)
+ return weights
+
+
+def magnitude_based_pruning(tensor: torch.Tensor, density: float) -> torch.Tensor:
+ """
+ Prune the smallest values of the task tensors and retain the top-k values based on the specified fraction
+ `density`.
+
+ Args:
+ tensor (`torch.Tensor`):The tensor to prune.
+ density (`float`):The fraction of values to preserve. Should be in [0,1].
+
+ Returns:
+ `torch.Tensor`: The tensor with the pruned weights.
+ """
+ mask = torch.zeros_like(tensor).reshape(-1)
+ k = int(density * tensor.numel())
+ top_k = torch.topk(tensor.abs().reshape(-1), k=k, largest=True)
+ mask[top_k[1]] = 1
+ return tensor * mask.reshape(tensor.shape)
+
+
+def random_pruning(tensor: torch.Tensor, density: float, rescale: bool) -> torch.Tensor:
+ """
+ Prune random values based on the specified fraction `density`.
+
+ Args:
+ tensor (`torch.Tensor`):The tensor to prune.
+ density (`float`):The fraction of values to preserve. Should be in [0,1].
+ rescale (`bool`):Whether to rescale the result to preserve the expected value of the original tensor.
+
+ Returns:
+ `torch.Tensor`: The pruned tensor.
+ """
+ mask = torch.bernoulli(torch.full_like(input=tensor, fill_value=density))
+ pruned_tensor = tensor * mask
+ if rescale:
+ torch.div(input=pruned_tensor, other=density)
+ return pruned_tensor
+
+
+def prune(
+ tensor: torch.Tensor, density: float, method: Literal["magnitude", "random"], rescale: bool = False
+) -> torch.Tensor:
+ """
+ Prune the values of task tensors based on the `method`.
+
+ Args:
+ tensor (`torch.Tensor`):The tensor to prune.
+ density (`float`):The fraction of values to preserve. Should be in [0,1].
+ method (`str`):The method to use to prune. Should be one of ["magnitude", "random"].
+ rescale (`bool`):Whether to rescale the result to preserve the expected value of the original tensor.
+
+ Returns:
+ `torch.Tensor`: The pruned tensor.
+ """
+ if density >= 1:
+ warnings.warn(f"The density {density} is greater than or equal to 1, no pruning will be performed.")
+ return tensor
+ elif density < 0:
+ raise ValueError(f"Density should be >= 0, got {density}")
+ if method == "magnitude":
+ return magnitude_based_pruning(tensor, density)
+ elif method == "random":
+ return random_pruning(tensor, density, rescale=rescale)
+ else:
+ raise ValueError(f"Unknown method {method}")
+
+
+def calculate_majority_sign_mask(
+ tensor: torch.Tensor, method: Literal["total", "frequency"] = "total"
+) -> torch.Tensor:
+ """
+ Get the mask of the majority sign across the task tensors. Task tensors are stacked on dimension 0.
+
+ Args:
+ tensor (`torch.Tensor`):The tensor to get the mask from.
+ method (`str`):The method to use to get the mask. Should be one of ["total", "frequency"].
+
+ Returns:
+ `torch.Tensor`: The majority sign mask.
+ """
+
+ sign = tensor.sign()
+ if method == "total":
+ sign_magnitude = tensor.sum(dim=0)
+ elif method == "frequency":
+ sign_magnitude = sign.sum(dim=0)
+ else:
+ raise RuntimeError(f'Unimplemented mask method "{method}"')
+ majority_sign = torch.where(sign_magnitude >= 0, 1, -1)
+ return sign == majority_sign
+
+
+def disjoint_merge(task_tensors: torch.Tensor, majority_sign_mask: torch.Tensor) -> torch.Tensor:
+ """
+ Merge the task tensors using disjoint merge.
+
+ Args:
+ task_tensors (`torch.Tensor`):The task tensors to merge.
+ majority_sign_mask (`torch.Tensor`):The mask of the majority sign across the task tensors.
+
+ Returns:
+ `torch.Tensor`: The merged tensor.
+ """
+ mixed_task_tensors = (task_tensors * majority_sign_mask).sum(dim=0)
+ num_params_preserved = majority_sign_mask.sum(dim=0)
+ return mixed_task_tensors / torch.clamp(num_params_preserved, min=1.0)
+
+
+def task_arithmetic(task_tensors: list[torch.Tensor], weights: torch.Tensor) -> torch.Tensor:
+ """
+ Merge the task tensors using `task arithmetic`.
+
+ Args:
+ task_tensors(`List[torch.Tensor]`):The task tensors to merge.
+ weights (`torch.Tensor`):The weights of the task tensors.
+
+ Returns:
+ `torch.Tensor`: The merged tensor.
+ """
+ task_tensors = torch.stack(task_tensors, dim=0)
+ # weighted task tensors
+ weights = reshape_weight_task_tensors(task_tensors, weights)
+ weighted_task_tensors = task_tensors * weights
+ mixed_task_tensors = weighted_task_tensors.sum(dim=0)
+ return mixed_task_tensors
+
+
+def magnitude_prune(task_tensors: list[torch.Tensor], weights: torch.Tensor, density: float) -> torch.Tensor:
+ """
+ Merge the task tensors using `task arithmetic`.
+
+ Args:
+ task_tensors(`List[torch.Tensor]`):The task tensors to merge.
+ weights (`torch.Tensor`):The weights of the task tensors.
+ density (`float`): The fraction of values to preserve. Should be in [0,1].
+
+ Returns:
+ `torch.Tensor`: The merged tensor.
+ """
+ # sparsify
+ task_tensors = [prune(tensor, density, method="magnitude") for tensor in task_tensors]
+ task_tensors = torch.stack(task_tensors, dim=0)
+ # weighted task tensors
+ weights = reshape_weight_task_tensors(task_tensors, weights)
+ weighted_task_tensors = task_tensors * weights
+ mixed_task_tensors = weighted_task_tensors.sum(dim=0)
+ return mixed_task_tensors
+
+
+def ties(
+ task_tensors: list[torch.Tensor],
+ weights: torch.Tensor,
+ density: float,
+ majority_sign_method: Literal["total", "frequency"] = "total",
+) -> torch.Tensor:
+ """
+ Merge the task tensors using `ties`.
+
+ Args:
+ task_tensors(`List[torch.Tensor]`):The task tensors to merge.
+ weights (`torch.Tensor`):The weights of the task tensors.
+ density (`float`):The fraction of values to preserve. Should be in [0,1].
+ majority_sign_method (`str`):
+ The method to use to get the majority sign mask. Should be one of ["total", "frequency"].
+
+ Returns:
+ `torch.Tensor`: The merged tensor.
+ """
+ # sparsify
+ task_tensors = [prune(tensor, density, method="magnitude") for tensor in task_tensors]
+ task_tensors = torch.stack(task_tensors, dim=0)
+ # Elect Sign
+ majority_sign_mask = calculate_majority_sign_mask(task_tensors, method=majority_sign_method)
+ # weighted task tensors
+ weights = reshape_weight_task_tensors(task_tensors, weights)
+ weighted_task_tensors = task_tensors * weights
+ # Disjoint Merge
+ mixed_task_tensors = disjoint_merge(weighted_task_tensors, majority_sign_mask)
+ return mixed_task_tensors
+
+
+def dare_linear(task_tensors: list[torch.Tensor], weights: torch.Tensor, density: float) -> torch.Tensor:
+ """
+ Merge the task tensors using `dare linear`.
+
+ Args:
+ task_tensors(`List[torch.Tensor]`):The task tensors to merge.
+ weights (`torch.Tensor`):The weights of the task tensors.
+ density (`float`):The fraction of values to preserve. Should be in [0,1].
+
+ Returns:
+ `torch.Tensor`: The merged tensor.
+ """
+ # sparsify
+ task_tensors = [prune(tensor, density, method="random", rescale=True) for tensor in task_tensors]
+ task_tensors = torch.stack(task_tensors, dim=0)
+ # weighted task tensors
+ weights = reshape_weight_task_tensors(task_tensors, weights)
+ weighted_task_tensors = task_tensors * weights
+ mixed_task_tensors = weighted_task_tensors.sum(dim=0)
+ return mixed_task_tensors
+
+
+def dare_ties(
+ task_tensors: list[torch.Tensor],
+ weights: torch.Tensor,
+ density: float,
+ majority_sign_method: Literal["total", "frequency"] = "total",
+) -> torch.Tensor:
+ """
+ Merge the task tensors using `dare ties`.
+
+ Args:
+ task_tensors(`List[torch.Tensor]`):The task tensors to merge.
+ weights (`torch.Tensor`):The weights of the task tensors.
+ density (`float`):The fraction of values to preserve. Should be in [0,1].
+ majority_sign_method (`str`):
+ The method to use to get the majority sign mask. Should be one of ["total", "frequency"].
+
+ Returns:
+ `torch.Tensor`: The merged tensor.
+ """
+ # sparsify
+ task_tensors = [prune(tensor, density, method="random", rescale=True) for tensor in task_tensors]
+ task_tensors = torch.stack(task_tensors, dim=0)
+ # Elect Sign
+ majority_sign_mask = calculate_majority_sign_mask(task_tensors, method=majority_sign_method)
+ # weighted task tensors
+ weights = reshape_weight_task_tensors(task_tensors, weights)
+ weighted_task_tensors = task_tensors * weights
+ # Disjoint Merge
+ mixed_task_tensors = disjoint_merge(weighted_task_tensors, majority_sign_mask)
+ return mixed_task_tensors
diff --git a/peft/src/peft/utils/other.py b/peft/src/peft/utils/other.py
new file mode 100644
index 0000000000000000000000000000000000000000..6f8437152efdabc642099277d6d969062e058c64
--- /dev/null
+++ b/peft/src/peft/utils/other.py
@@ -0,0 +1,1532 @@
+# Copyright 2023-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+from __future__ import annotations
+
+import copy
+import functools
+import inspect
+import os
+import re
+import warnings
+from collections.abc import Sequence
+from contextlib import nullcontext
+from operator import attrgetter
+from typing import Any, Optional, Union
+
+import accelerate
+import torch
+import transformers
+from accelerate import FullyShardedDataParallelPlugin
+from accelerate.hooks import add_hook_to_module, remove_hook_from_module
+from accelerate.utils import is_npu_available, is_xpu_available
+from huggingface_hub import file_exists
+from huggingface_hub.errors import EntryNotFoundError, HFValidationError
+from packaging import version
+from safetensors.torch import storage_ptr, storage_size
+from transformers import PreTrainedModel
+
+from ..import_utils import is_auto_gptq_available, is_gptqmodel_available, is_torch_tpu_available
+from .constants import (
+ CONFIG_NAME,
+ EMBEDDING_LAYER_NAMES,
+ INCLUDE_LINEAR_LAYERS_SHORTHAND,
+ SAFETENSORS_WEIGHTS_NAME,
+ TRANSFORMERS_MODELS_TO_ADALORA_TARGET_MODULES_MAPPING,
+ TRANSFORMERS_MODELS_TO_BOFT_TARGET_MODULES_MAPPING,
+ TRANSFORMERS_MODELS_TO_BONE_TARGET_MODULES_MAPPING,
+ TRANSFORMERS_MODELS_TO_C3A_TARGET_MODULES_MAPPING,
+ TRANSFORMERS_MODELS_TO_FOURIERFT_TARGET_MODULES_MAPPING,
+ TRANSFORMERS_MODELS_TO_HRA_TARGET_MODULES_MAPPING,
+ TRANSFORMERS_MODELS_TO_IA3_FEEDFORWARD_MODULES_MAPPING,
+ TRANSFORMERS_MODELS_TO_IA3_TARGET_MODULES_MAPPING,
+ TRANSFORMERS_MODELS_TO_LNTUNING_TARGET_MODULES_MAPPING,
+ TRANSFORMERS_MODELS_TO_LOHA_TARGET_MODULES_MAPPING,
+ TRANSFORMERS_MODELS_TO_LOKR_TARGET_MODULES_MAPPING,
+ TRANSFORMERS_MODELS_TO_LORA_TARGET_MODULES_MAPPING,
+ TRANSFORMERS_MODELS_TO_MISS_TARGET_MODULES_MAPPING,
+ TRANSFORMERS_MODELS_TO_OFT_TARGET_MODULES_MAPPING,
+ TRANSFORMERS_MODELS_TO_POLY_TARGET_MODULES_MAPPING,
+ TRANSFORMERS_MODELS_TO_PREFIX_TUNING_POSTPROCESS_MAPPING,
+ TRANSFORMERS_MODELS_TO_RANDLORA_TARGET_MODULES_MAPPING,
+ TRANSFORMERS_MODELS_TO_ROAD_TARGET_MODULES_MAPPING,
+ TRANSFORMERS_MODELS_TO_SHIRA_TARGET_MODULES_MAPPING,
+ TRANSFORMERS_MODELS_TO_VBLORA_TARGET_MODULES_MAPPING,
+ TRANSFORMERS_MODELS_TO_VERA_TARGET_MODULES_MAPPING,
+ TRANSFORMERS_MODELS_TO_WAVEFT_TARGET_MODULES_MAPPING,
+ WEIGHTS_NAME,
+ bloom_model_postprocess_past_key_value,
+ starcoder_model_postprocess_past_key_value,
+)
+
+
+mlu_available = False
+if version.parse(accelerate.__version__) >= version.parse("0.29.0"):
+ from accelerate.utils import is_mlu_available
+
+ mlu_available = is_mlu_available()
+
+
+__all__ = [
+ "CONFIG_NAME",
+ "EMBEDDING_LAYER_NAMES",
+ "INCLUDE_LINEAR_LAYERS_SHORTHAND",
+ "SAFETENSORS_WEIGHTS_NAME",
+ "TRANSFORMERS_MODELS_TO_ADALORA_TARGET_MODULES_MAPPING",
+ "TRANSFORMERS_MODELS_TO_BOFT_TARGET_MODULES_MAPPING",
+ "TRANSFORMERS_MODELS_TO_BONE_TARGET_MODULES_MAPPING",
+ "TRANSFORMERS_MODELS_TO_C3A_TARGET_MODULES_MAPPING",
+ "TRANSFORMERS_MODELS_TO_FOURIERFT_TARGET_MODULES_MAPPING",
+ "TRANSFORMERS_MODELS_TO_HRA_TARGET_MODULES_MAPPING",
+ "TRANSFORMERS_MODELS_TO_IA3_FEEDFORWARD_MODULES_MAPPING",
+ "TRANSFORMERS_MODELS_TO_IA3_TARGET_MODULES_MAPPING",
+ "TRANSFORMERS_MODELS_TO_LNTUNING_TARGET_MODULES_MAPPING",
+ "TRANSFORMERS_MODELS_TO_LOHA_TARGET_MODULES_MAPPING",
+ "TRANSFORMERS_MODELS_TO_LOKR_TARGET_MODULES_MAPPING",
+ "TRANSFORMERS_MODELS_TO_LORA_TARGET_MODULES_MAPPING",
+ "TRANSFORMERS_MODELS_TO_MISS_TARGET_MODULES_MAPPING",
+ "TRANSFORMERS_MODELS_TO_OFT_TARGET_MODULES_MAPPING",
+ "TRANSFORMERS_MODELS_TO_POLY_TARGET_MODULES_MAPPING",
+ "TRANSFORMERS_MODELS_TO_PREFIX_TUNING_POSTPROCESS_MAPPING",
+ "TRANSFORMERS_MODELS_TO_RANDLORA_TARGET_MODULES_MAPPING",
+ "TRANSFORMERS_MODELS_TO_ROAD_TARGET_MODULES_MAPPING",
+ "TRANSFORMERS_MODELS_TO_SHIRA_TARGET_MODULES_MAPPING",
+ "TRANSFORMERS_MODELS_TO_VBLORA_TARGET_MODULES_MAPPING",
+ "TRANSFORMERS_MODELS_TO_VERA_TARGET_MODULES_MAPPING",
+ "TRANSFORMERS_MODELS_TO_WAVEFT_TARGET_MODULES_MAPPING",
+ "WEIGHTS_NAME",
+ "bloom_model_postprocess_past_key_value",
+ "starcoder_model_postprocess_past_key_value",
+]
+
+
+# Get current device name based on available devices
+def infer_device() -> str:
+ if torch.cuda.is_available():
+ return "cuda"
+ elif hasattr(torch.backends, "mps") and torch.backends.mps.is_available():
+ return "mps"
+ elif mlu_available:
+ return "mlu"
+ elif is_xpu_available():
+ return "xpu"
+ elif is_npu_available():
+ return "npu"
+ return "cpu"
+
+
+def prepare_model_for_kbit_training(model, use_gradient_checkpointing=True, gradient_checkpointing_kwargs=None):
+ r"""
+ Note this method only works for `transformers` models.
+
+ This method wraps the entire protocol for preparing a model before running a training. This includes:
+ 1- Cast the layernorm in fp32 2- making output embedding layer require grads 3- Add the upcasting of the lm
+ head to fp32 4- Freezing the base model layers to ensure they are not updated during training
+
+
+ Args:
+ model (`transformers.PreTrainedModel`):
+ The loaded model from `transformers`
+ use_gradient_checkpointing (`bool`, *optional*, defaults to `True`):
+ If True, use gradient checkpointing to save memory at the expense of slower backward pass.
+ gradient_checkpointing_kwargs (`dict`, *optional*, defaults to `None`):
+ Keyword arguments to pass to the gradient checkpointing function, please refer to the documentation of
+ `torch.utils.checkpoint.checkpoint` for more details about the arguments that you can pass to that method.
+ Note this is only available in the latest transformers versions (> 4.34.1).
+ """
+ loaded_in_kbit = getattr(model, "is_loaded_in_8bit", False) or getattr(model, "is_loaded_in_4bit", False)
+ is_gptq_quantized = getattr(model, "quantization_method", None) == "gptq"
+ is_aqlm_quantized = getattr(model, "quantization_method", None) == "aqlm"
+ is_eetq_quantized = getattr(model, "quantization_method", None) == "eetq"
+ is_torchao_quantized = getattr(model, "quantization_method", None) == "torchao"
+ is_hqq_quantized = getattr(model, "quantization_method", None) == "hqq" or getattr(model, "hqq_quantized", False)
+
+ if gradient_checkpointing_kwargs is None:
+ gradient_checkpointing_kwargs = {}
+
+ for name, param in model.named_parameters():
+ # freeze base model's layers
+ param.requires_grad = False
+
+ if (
+ not is_gptq_quantized
+ and not is_aqlm_quantized
+ and not is_eetq_quantized
+ and not is_hqq_quantized
+ and not is_torchao_quantized
+ ):
+ # cast all non INT8 parameters to fp32
+ for param in model.parameters():
+ if (
+ (param.dtype == torch.float16) or (param.dtype == torch.bfloat16)
+ ) and param.__class__.__name__ != "Params4bit":
+ param.data = param.data.to(torch.float32)
+
+ if (
+ loaded_in_kbit
+ or is_gptq_quantized
+ or is_aqlm_quantized
+ or is_eetq_quantized
+ or is_hqq_quantized
+ or is_torchao_quantized
+ ) and use_gradient_checkpointing:
+ # When having `use_reentrant=False` + gradient_checkpointing, there is no need for this hack
+ if "use_reentrant" not in gradient_checkpointing_kwargs or gradient_checkpointing_kwargs["use_reentrant"]:
+ # For backward compatibility
+ if hasattr(model, "enable_input_require_grads"):
+ model.enable_input_require_grads()
+ else:
+
+ def make_inputs_require_grad(module, input, output):
+ output.requires_grad_(True)
+
+ model.get_input_embeddings().register_forward_hook(make_inputs_require_grad)
+
+ # To support older transformers versions, check if the model supports gradient_checkpointing_kwargs
+ _supports_gc_kwargs = "gradient_checkpointing_kwargs" in list(
+ inspect.signature(model.gradient_checkpointing_enable).parameters
+ )
+
+ if not _supports_gc_kwargs and len(gradient_checkpointing_kwargs) > 0:
+ warnings.warn(
+ "gradient_checkpointing_kwargs is not supported in this version of transformers. The passed kwargs will be ignored."
+ " if you want to use that feature, please upgrade to the latest version of transformers.",
+ FutureWarning,
+ )
+
+ gc_enable_kwargs = (
+ {} if not _supports_gc_kwargs else {"gradient_checkpointing_kwargs": gradient_checkpointing_kwargs}
+ )
+
+ # enable gradient checkpointing for memory efficiency
+ model.gradient_checkpointing_enable(**gc_enable_kwargs)
+ return model
+
+
+# copied from transformers.models.bart.modeling_bart
+def shift_tokens_right(input_ids: torch.Tensor, pad_token_id: int, decoder_start_token_id: int):
+ """
+ Shift input ids one token to the right.
+
+ Args:
+ input_ids (`torch.LongTensor` of shape `(batch_size, sequence_length)`): input ids
+ pad_token_id (`int`): The id of the `padding` token.
+ decoder_start_token_id (`int`): The id of the `start` token.
+ """
+ shifted_input_ids = input_ids.new_zeros(input_ids.shape)
+ shifted_input_ids[:, 1:] = input_ids[:, :-1].clone()
+ shifted_input_ids[:, 0] = decoder_start_token_id
+
+ if pad_token_id is None:
+ raise ValueError("self.model.config.pad_token_id has to be defined.")
+ # replace possible -100 values in labels by `pad_token_id`
+ shifted_input_ids.masked_fill_(shifted_input_ids == -100, pad_token_id)
+
+ return shifted_input_ids
+
+
+class AuxiliaryTrainingWrapper(torch.nn.Module):
+ """Wrap a specific module so that it can be trained and saved in a way that is tangential to how
+ PEFT normally works, e.g. fully training a classification layer instead of using an adapter.
+
+ """
+
+ # All names of layers that may contain adapter (trainable) weights
+ adapter_layer_names: tuple[str, ...] = ()
+ # All names of other parameters that may contain adapter-related parameters
+ other_param_names: tuple[str, ...] = ()
+ # List all merged adapters
+ merged_adapters: list[str] = []
+
+ def __init__(self, module_to_save, adapter_name, **kwargs):
+ """Extra kwargs will be passed to `self.init_modules` and `self.update`."""
+ super().__init__()
+ self.original_module = module_to_save
+ self._active_adapter = [adapter_name]
+ self._disable_adapters = False
+ self._adapters = set()
+
+ self.init_modules(adapter_name, **kwargs)
+
+ self.update(adapter_name, **kwargs)
+ self.check_module()
+
+ def init_modules(self, adapter_name, **kwargs):
+ """A place to initialize PyTorch modules in `__init__` before the call to `self.update()`."""
+ raise NotImplementedError
+
+ def _get_available_adapters(self) -> set[str]:
+ """Return all adapter names that can be found on this module."""
+ raise NotImplementedError
+
+ def _error_message_name(self):
+ """Returns a user friendly identifier for error messages, e.g. for type compatibility error messages from
+ `check_module()` so that the user can backtrack where the error comes from. A generic "training wrapper" is
+ less helpful than "modules_to_save", for example.
+ """
+ return "training wrapper"
+
+ def check_module(self):
+ """Perform some sanity checks on the module to ensure that it works"""
+ # Try to anticipate some modules that users could try to target that would not work.
+ # Note: It's not possible to check hasattr(module, "forward"), since that returns True for ModuleDict and
+ # ModuleList, even though their forward methods cannot be called
+ forbidden_classes = (torch.nn.ModuleDict, torch.nn.ModuleList, torch.nn.ParameterDict, torch.nn.ParameterList)
+ if isinstance(self.original_module, forbidden_classes):
+ cls_name = self.original_module.__class__
+ raise TypeError(f"{self._error_message_name()} cannot be applied to modules of type {cls_name}")
+
+ # local import to avoid circular import
+ from peft.tuners.tuners_utils import BaseTunerLayer
+
+ if isinstance(self.original_module, BaseTunerLayer):
+ # e.g. applying a training wrapper to a lora layer makes no sense
+ cls_name = self.original_module.__class__
+ raise TypeError(f"{self._error_message_name()} cannot be applied to modules of type {cls_name}")
+
+ @property
+ def disable_adapters(self) -> bool:
+ # use a property to ensure that disable_adapters is not set directly, instead use the enable_adapters method
+ return self._disable_adapters
+
+ @property
+ def active_adapter(self) -> Union[list[str], str]:
+ # use a property to ensure that active_adapter is not set directly, instead use the set_adapter method
+ return self._active_adapter
+
+ @property
+ def active_adapters(self) -> list[str]:
+ if isinstance(self._active_adapter, str):
+ return [self._active_adapter]
+ return self._active_adapter
+
+ def _hasattr_wrapped(self, name, modules):
+ """Infrastructure to enable the implementing class to delegate attributes to other modules.
+ Returns True if the implementing class knows how to handle attribute `name`.
+
+ Gets passed `modules` which is PyTorch's internal list of assigned modules from `nn.Module`.
+ """
+ return False
+
+ def _getattr_wrapped(self, name, modules):
+ """If `_hasattr_wrapped` returns True for `name`, then this function should return the corresponding
+ value associated with `name`.
+ """
+ return None
+
+ def __getattr__(self, name: str):
+ # Note: This whole method may seem overly complex at first but PyTorch messes with __getattr__ in a way that
+ # requires very careful handling to avoid infinite recursion.
+ try:
+ return super().__getattr__(name)
+ except AttributeError:
+ pass
+
+ if "_modules" not in self.__dict__:
+ raise AttributeError(f"'{type(self).__name__}' object has no attribute '{name}'")
+
+ # Could not find the attribute the PyTorch way. So let's check if it's an attribute on the
+ # original_module or the module further down (e.g., `modules_to_save[active_adapter]`).
+ modules = self.__dict__["_modules"]
+ if self.disable_adapters:
+ return getattr(self.original_module, name)
+ elif self._hasattr_wrapped(name, modules):
+ return self._getattr_wrapped(name, modules)
+
+ # For some reason, there is no module corresponding to the active adapter; this should normally not be
+ # reached and exists as a failsafe (otherwise, a KeyError would be raised)
+ raise AttributeError(f"'{type(self).__name__}' object has no attribute '{name}'")
+
+ def update(self, adapter_name, **kwargs):
+ """Called when this instance should be part of an adapter's training.
+ Adds the given adapter to the list of adapters that this instance is training along with.
+
+ Additional kwargs are expected to be the same kwargs that are also passed for initializing this class.
+ """
+ if adapter_name not in self._adapters:
+ self._adapters.add(adapter_name)
+
+ def _create_new_hook(self, old_hook):
+ r"""
+ Creates a new hook based on the old hook. Use it only if you know what you are doing !
+ """
+ old_hook_cls = getattr(accelerate.hooks, old_hook.__class__.__name__)
+ old_hook_attr = old_hook.__dict__
+ filtered_old_hook_attr = {}
+ old_hook_init_signature = inspect.signature(old_hook_cls.__init__)
+ for k in old_hook_attr.keys():
+ if k in old_hook_init_signature.parameters:
+ filtered_old_hook_attr[k] = old_hook_attr[k]
+ new_hook = old_hook_cls(**filtered_old_hook_attr)
+ return new_hook
+
+ def _check_forward_args(self, x, *args, **kwargs):
+ """Check if the arguments are compatible with the configs and state of the model"""
+ adapter_names = kwargs.get("adapter_names", None)
+ if adapter_names is None:
+ return
+
+ if len(x) != len(adapter_names):
+ msg = (
+ "Length of `adapter_names` should be the same as the number of inputs, but got "
+ f"{len(adapter_names)} and {len(x)} respectively."
+ )
+ raise ValueError(msg)
+
+ def _forward_wrapped(self, x: torch.Tensor, *args: Any, **kwargs: Any) -> torch.Tensor:
+ raise NotImplementedError
+
+ def _forward_wrapped_mixed_batch(
+ self, x: torch.Tensor, active_adapter: str, *args: Any, **kwargs: Any
+ ) -> torch.Tensor:
+ raise NotImplementedError
+
+ def _forward_wrapped_passthrough(self, x: torch.Tensor, *args: Any, **kwargs: Any) -> torch.Tensor:
+ """The forward call when no adapter is involved in the forward computation, only the base model"""
+ raise NotImplementedError
+
+ def _mixed_batch_forward(
+ self, input: torch.Tensor, *args: Any, adapter_names: list[str], **kwargs: Any
+ ) -> torch.Tensor:
+ # This is a special method that handles the case when users pass the argument `adapter_names`. This is an
+ # extra argument that allows mixing different adapters in the same batch at inference time.
+
+ SUPPORTED_MODULES = (torch.nn.Linear, torch.nn.Embedding, torch.nn.Conv1d, torch.nn.Conv2d, torch.nn.Conv3d)
+
+ module_names = ", ".join([module.__name__ for module in SUPPORTED_MODULES])
+
+ if not isinstance(self.original_module, SUPPORTED_MODULES):
+ raise TypeError(f"Mixed batching is only supported for the following modules: {module_names}.")
+
+ unique_adapters = set(adapter_names)
+ sub_batch_indices_list = []
+
+ for adapter in unique_adapters:
+ sub_batch_indices_list.append([index for index, item in enumerate(adapter_names) if item == adapter])
+
+ results = [0 for _ in range(len(input))]
+
+ for i, active_adapter in enumerate(unique_adapters):
+ sub_batch = input[sub_batch_indices_list[i]]
+
+ if active_adapter == "__base__":
+ output = self.original_module(sub_batch, *args, **kwargs)
+ else:
+ output = self._forward_wrapped_mixed_batch(sub_batch, active_adapter, *args, **kwargs)
+
+ for index, j in enumerate(sub_batch_indices_list[i]):
+ results[j] = output[index]
+
+ return torch.stack(results)
+
+ def forward(self, x: torch.Tensor, *args, **kwargs):
+ self._check_forward_args(x, *args, **kwargs)
+ adapter_names = kwargs.pop("adapter_names", None)
+
+ if self.disable_adapters or any(adapter not in self._adapters for adapter in self.active_adapters):
+ return self._forward_wrapped_passthrough(x, *args, **kwargs)
+
+ if adapter_names is None:
+ return self._forward_wrapped(x, *args, **kwargs)
+ return self._mixed_batch_forward(x, *args, adapter_names=adapter_names, **kwargs)
+
+ def enable_adapters(self, enabled: bool):
+ """Toggle the enabling and disabling of adapters
+
+ Args:
+ enabled (bool): True to enable adapters, False to disable adapters
+ """
+ if enabled:
+ self._disable_adapters = False
+ else:
+ self._disable_adapters = True
+
+ def check_set_adapter(self, adapter_name: str | list[str]) -> str | None:
+ """Helper function to check if the given adapter(s) can be set.
+
+ Return the name of the adapter to be set or None if no adapter should be set.
+ """
+ raise NotImplementedError
+
+ def set_adapter(self, adapter_names: Union[str, list[str]], inference_mode: bool = False) -> None:
+ """Set the active adapter
+
+ Args:
+ adapter_names (str or list[str]):
+ The name(s) of the adapter(s) to set as active
+ inference_mode (bool, optional):
+ Whether the activated adapter should be frozen (i.e. `requires_grad=False`). Default is False.
+ """
+ if isinstance(adapter_names, str):
+ self._active_adapter = adapter_names
+ else:
+ self._active_adapter = []
+ for adapter_name in adapter_names:
+ if adapter_name not in self._adapters:
+ raise ValueError(f"Adapter {adapter_name} not found in {self._adapters}")
+
+ self._active_adapter.append(adapter_name)
+
+ def delete_adapter(self, adapter_name: str, new_active_adapters: Optional[list[str]]) -> None:
+ """Delete an adapter from the layer, set a new active adapter if necessary"""
+ raise NotImplementedError
+
+ def set_requires_grad(self, adapter_names: str | Sequence[str], requires_grad: bool = True) -> None:
+ """
+ Enable or disable gradients on the given adapter(s).
+
+ Args:
+ adapter_name (`str` or `Sequence[str]`):
+ The name of the adapter(s) whose gradients should be enabled/disabled.
+ requires_grad (`bool`, *optional*)
+ Whether to enable (`True`, default) or disable (`False`).
+ """
+ if isinstance(adapter_names, str):
+ adapter_names_set = {adapter_names}
+ else:
+ adapter_names_set = set(adapter_names)
+
+ for layer_name in self.adapter_layer_names:
+ # use attrgetter, as it resolves `.` in the attribute name
+ module_dict = attrgetter(layer_name)(self)
+ for key, layer in module_dict.items():
+ if key in adapter_names_set:
+ layer.requires_grad_(requires_grad)
+
+ def adapter_state_dict(self, adapter_name):
+ """Return the state dict of this module for a given adapter."""
+ raise NotImplementedError
+
+ def adapter_state_dict_load_map(self, adapter_name):
+ """Return a mapping from the key present in disk-loaded state dict
+ and how it should be represented in the loaded model's state dict.
+
+ The default should be a 1:1 mapping but it is important to define a mapping as it also serves as the
+ ground-truth for which keys are supposed to be loaded from a saved state dict.
+ """
+ raise NotImplementedError
+
+ def unload_and_optionally_merge_module(
+ self, merge: bool, safe_merge: bool, adapter_names: Optional[list[str]]
+ ) -> torch.nn.Module:
+ """Handles unloading when called from PEFT models. Returns the wrapped module
+ and handles merging onto the wrapped module if requested.
+ """
+ raise NotImplementedError
+
+
+class ModulesToSaveWrapper(AuxiliaryTrainingWrapper):
+ """Wraps a module that is supposed to be trained (i.e. `requires_grad_(True)`) and saved after training."""
+
+ # All names of layers that may contain adapter (trainable) weights
+ adapter_layer_names: tuple[str, ...] = ("modules_to_save",)
+
+ def __init__(self, module_to_save, adapter_name):
+ super().__init__(module_to_save, adapter_name)
+
+ def init_modules(self, adapter_name):
+ # we treat each adapter separately, so we have multiple adapters, same (copied) module for each
+ self.modules_to_save = torch.nn.ModuleDict({})
+
+ def _error_message_name(self):
+ return "modules_to_save"
+
+ def _forward_wrapped(self, x, *args, **kwargs):
+ if not self.active_adapters:
+ return self._forward_wrapped_passthrough(x, *args, **kwargs)
+ return self.modules_to_save[self.active_adapters[0]](x, *args, **kwargs)
+
+ def _forward_wrapped_mixed_batch(self, x, active_adapter, *args, **kwargs):
+ return self.modules_to_save[active_adapter](x, *args, **kwargs)
+
+ def _forward_wrapped_passthrough(self, x, *args, **kwargs):
+ return self.original_module(x, *args, **kwargs)
+
+ def _hasattr_wrapped(self, name, modules):
+ return self.active_adapters[0] in modules["modules_to_save"]
+
+ def _getattr_wrapped(self, name, modules):
+ return getattr(modules["modules_to_save"][self.active_adapters[0]], name)
+
+ def update(self, adapter_name, **kwargs):
+ super().update(adapter_name)
+
+ context_manager = nullcontext()
+ for _, param in self.original_module.named_parameters():
+ num_params = param.numel()
+ # if using DS Zero 3 and the weights are initialized empty
+ if num_params == 0 and hasattr(param, "ds_numel"):
+ import deepspeed
+
+ context_manager = deepspeed.zero.GatheredParameters(self.original_module.parameters(), modifier_rank=0)
+ break
+
+ if adapter_name not in self.modules_to_save:
+ with context_manager:
+ self.modules_to_save[adapter_name] = copy.deepcopy(self.original_module)
+
+ if hasattr(self.modules_to_save[adapter_name], "_hf_hook"):
+ old_hook = self.modules_to_save[adapter_name]._hf_hook
+ new_hook = self._create_new_hook(old_hook)
+ remove_hook_from_module(self.modules_to_save[adapter_name])
+ add_hook_to_module(self.modules_to_save[adapter_name], new_hook)
+
+ self.original_module.requires_grad_(False)
+
+ # note that there currently cannot be more than one active adapter for the same layer with modules to save
+ # since there would be no clear way to decide which adapter's weights are the correct ones. therefore we
+ # assume that there is only one active adapter. this precondition is enforced by _set_adapter.
+ if adapter_name == self.active_adapter:
+ self.modules_to_save[adapter_name].requires_grad_(True)
+
+ def enable_adapters(self, enabled: bool):
+ """Takes care of setting the required_grad flag on the wrapped module.
+ If adapters are enabled, gradients for the module are required as well.
+ """
+ super().enable_adapters(enabled)
+
+ if enabled:
+ self.original_module.requires_grad_(False)
+ for adapter_name in self.active_adapters:
+ self.modules_to_save[adapter_name].requires_grad_(True)
+ else:
+ self.original_module.requires_grad_(True)
+ self.modules_to_save.requires_grad_(False)
+
+ def check_set_adapter(self, adapter_name: str | list[str]) -> str | None:
+ """Helper function to check if the given adapter(s) can be set.
+
+ Return the name of the adapter to be set or None if no adapter should be set.
+ """
+ if isinstance(adapter_name, str):
+ return adapter_name
+
+ # adapter_name is a list of str
+ if len(adapter_name) == 0:
+ raise ValueError("Please specify at least one adapter to set")
+
+ adapter_names_in_module = [n for n in adapter_name if n in self.modules_to_save]
+
+ if len(adapter_names_in_module) > 1:
+ raise ValueError(f"Only one adapter can be set at a time for {self}, got {len(adapter_names_in_module)}")
+
+ adapter_name_to_set: str | None
+ if not adapter_names_in_module:
+ adapter_name_to_set = None
+ else:
+ adapter_name_to_set = adapter_names_in_module[0]
+
+ return adapter_name_to_set
+
+ def set_adapter(self, adapter_names: Union[str, list[str]], inference_mode: bool = False) -> None:
+ """Set the active adapter
+
+ Additionally, this function will set the specified adapter to trainable (i.e., requires_grad=True) unless
+ inference_mode is True.
+
+ Args:
+ adapter_names (list[str], str):
+ The name(s) of the adapter(s) to set as active.
+ inference_mode (bool, optional):
+ Whether the activated adapter should be frozen (i.e. `requires_grad=False`). Default is False.
+ """
+ if isinstance(adapter_names, str):
+ adapter_names = [adapter_names]
+
+ if len(adapter_names) > 1:
+ raise ValueError(f"Attempted to set multiple ({adapter_names}) adapters at once for modules_to_save.")
+
+ if len(adapter_names) == 0:
+ # when calling model.add_adapter, the new adapter is not automatically active
+ self._active_adapter = []
+ return
+
+ adapter_name = adapter_names[0]
+
+ if adapter_name not in self._adapters:
+ raise ValueError(f"Adapter {adapter_name} not found in {self._adapters}")
+
+ for currently_active_adapter_name in self.active_adapters:
+ self.modules_to_save[currently_active_adapter_name].requires_grad_(False)
+ self.modules_to_save[adapter_name].requires_grad_(not inference_mode)
+ self._active_adapter = adapter_name
+
+ def delete_adapter(self, adapter_name: str, new_active_adapters: Optional[list[str]]) -> None:
+ """
+ Delete the adapter if present.
+
+ This method will also set a new active adapter if the deleted adapter was the active adapter. It is important
+ that the new adapter is chosen by the caller in a deterministic way, so that the same adapter is chosen on all
+ layers.
+ """
+ if adapter_name not in self.modules_to_save:
+ return
+
+ # set new active adapter, if necessary
+ # note: there can only ever be one active adapter, unlike for LoRA etc.
+ if isinstance(new_active_adapters, (list, tuple)) and len(new_active_adapters) > 1:
+ name = self.__class__.__name__
+ raise ValueError(
+ f"Attempted to set multiple ({new_active_adapters}) adapters at once for {name}, which is not allowed."
+ )
+
+ if adapter_name in self._adapters:
+ self._adapters.remove(adapter_name)
+
+ if not new_active_adapters:
+ # no active adapter now
+ del self.modules_to_save[adapter_name]
+ self._active_adapter = []
+ return
+
+ new_active_adapter = new_active_adapters[0]
+ if new_active_adapter not in self.modules_to_save:
+ # a new active adapter was chosen but it seems like it has no modules_to_save
+ del self.modules_to_save[adapter_name]
+ self._active_adapter = []
+ return
+
+ if new_active_adapter != self.active_adapters[0]:
+ self.set_adapter(new_active_adapter)
+ del self.modules_to_save[adapter_name]
+
+ def adapter_state_dict_load_map(self, adapter_name):
+ # Maps the module keys as they are in the saved state dict to the in-memory state dict.
+ # Must contain all keys that are supposed to be loaded.
+ if adapter_name not in self._adapters:
+ # In caes of multiple adapters, each bringing their own modules to save, each
+ # ModulesToSaveWrapper will be queried but not every wrapper is obliged to serve the same adapters.
+ return {}
+ return {k: f"modules_to_save.{adapter_name}.{k}" for k in self.modules_to_save[adapter_name].state_dict()}
+
+ def adapter_state_dict(self, adapter_name, state_dict):
+ if adapter_name not in self._adapters:
+ # In caes of multiple adapters, each bringing their own modules to save, each
+ # ModulesToSaveWrapper will be queried but not every wrapper is obliged to serve the same adapters.
+ return {}
+
+ return {
+ k: state_dict[f"modules_to_save.{adapter_name}.{k}"]
+ for k in self.modules_to_save[adapter_name].state_dict()
+ }
+
+ def unload_and_optionally_merge_module(
+ self, merge: bool, safe_merge: bool, adapter_names: Optional[list[str]]
+ ) -> torch.nn.Module:
+ """Unloading in case of `ModulesToSave` means to simply return the wrapped module.
+
+ However, if the wrapped module is itself a tuner, we'll call merge on it before.
+ """
+ new_module = self.modules_to_save[self.active_adapter]
+
+ # TODO: not sure if this is still a sensible thing to do. We would basically have to
+ # do the same checks as `_unload_and_optionally_merge` to support MHA, for example.
+ if hasattr(new_module, "base_layer"):
+ # check if the module is itself a tuner layer
+ if merge:
+ new_module.merge(safe_merge=safe_merge, adapter_names=adapter_names)
+ new_module = new_module.get_base_layer()
+
+ return new_module
+
+ def _get_available_adapters(self) -> set[str]:
+ """Return all adapter names that can be found on this module."""
+ return set(self.modules_to_save.keys())
+
+
+class TrainableTokensWrapper(AuxiliaryTrainingWrapper):
+ """Wraps a module (typically an embedding layer) that is supposed to be re-trained selectively (i.e.
+ solely updating a few columns) using the `TrainableTokensLayer` PEFT method.
+
+ Supports weight-tying to another adapter when passed a `tied_adapter` which is expected to be a
+ `TrainableTokensLayer`.
+ """
+
+ # All names of layers that may contain adapter (trainable) weights
+ adapter_layer_names: tuple[str, ...] = ("token_adapter.trainable_tokens_delta",)
+ other_param_names: tuple[str, ...] = ("token_adapter.token_indices", "token_adapter.trainable_tokens_original")
+
+ def __init__(
+ self,
+ module_to_save: torch.nn.Module,
+ adapter_name: str,
+ token_indices: list[int],
+ tied_adapter=None,
+ ) -> None:
+ super().__init__(module_to_save, adapter_name, token_indices=token_indices, tied_adapter=tied_adapter)
+
+ # unset the original_module attribute since we're using a property to remove this from the state dict.
+ self.original_module = None
+
+ @property
+ def original_module(self):
+ # use a property instead of an attribute to exclude this pointer from the state dict
+ # to make sure that it will not be saved.
+ return self.token_adapter.base_layer
+
+ def init_modules(self, adapter_name, token_indices, tied_adapter):
+ # use a local import to avoid potential circular imports
+ from peft.tuners.trainable_tokens import TrainableTokensLayer
+
+ # since super().__init__() calls update before we have a chance to initialise the adapter we would
+ # need here, we do the initialization here.
+ self.token_adapter = TrainableTokensLayer(self.original_module, adapter_name, token_indices, tied_adapter)
+
+ def _error_message_name(self):
+ return "trainable_token_indices"
+
+ def _hasattr_wrapped(self, name, modules):
+ return name == "weight"
+
+ def _getattr_wrapped(self, name, modules):
+ # some models query self.wte.weight.dtype, some may query the weights directly. for the first case it is not
+ # necessary to do anything special but we don't know if is going to be `.dtype`. so we need to get the merged
+ # weights from the adapter.
+ if name == "weight":
+ return modules["token_adapter"].get_merged_weights(self.token_adapter.active_adapters)
+
+ raise RuntimeError(
+ f"This code should've never been reached, probably a bad check in `_hasattr_wrapped` for {name}. "
+ "Please file an issue under https://github.com/huggingface/peft/issues."
+ )
+
+ def _forward_wrapped(self, x, *args, **kwargs):
+ if not self.active_adapters:
+ return self._forward_wrapped_passthrough(x, *args, **kwargs)
+ return self.token_adapter(x)
+
+ def _forward_wrapped_mixed_batch(self, x, active_adapter, *args, **kwargs):
+ return self.token_adapter.forward_adapters(x, [active_adapter])
+
+ def _forward_wrapped_passthrough(self, x, *args, **kwargs):
+ # the token adapter knows how to deal with disabled adapter / no active adapter, don't call original_module
+ # directly
+ return self.token_adapter(x, *args, **kwargs)
+
+ def update(self, active_adapter, **kwargs):
+ # TODO this does not support deepspeed/fsdp since it is missing a context manager
+ # see ModulesToSaveWrapper implementation
+ if active_adapter not in self._adapters:
+ self.token_adapter.update_layer(active_adapter, **kwargs)
+
+ super().update(active_adapter)
+
+ def adapter_state_dict_load_map(self, adapter_name):
+ if self.token_adapter.tied_adapter:
+ return {}
+ return {"token_adapter.trainable_tokens_delta": f"token_adapter.trainable_tokens_delta.{adapter_name}"}
+
+ def adapter_state_dict(self, adapter_name, state_dict):
+ if self.token_adapter.tied_adapter:
+ # storing of weight-tied layers is not up to us and will be handled by
+ # transformers. we're just here to keep those layers in sync during training.
+ # therefore we return an empty state dict.
+ return {}
+
+ return {
+ f"token_adapter.{k}": state_dict[f"token_adapter.{k}.{adapter_name}"] for k in ["trainable_tokens_delta"]
+ }
+
+ def enable_adapters(self, enabled: bool):
+ """Enables/disables the underlying `TrainableTokens` adapter.
+ Also handles the internal adapter disable flag.
+ """
+ super().enable_adapters(enabled)
+
+ self.token_adapter.enable_adapters(enabled)
+
+ def check_set_adapter(self, adapter_name: str | list[str]) -> str | None:
+ """Helper function to check if the given adapter(s) can be set.
+
+ Return the name of the adapter to be set or None if no adapter should be set.
+ """
+ if isinstance(adapter_name, str):
+ return adapter_name
+
+ # adapter_name is a list of str
+ if len(adapter_name) == 0:
+ raise ValueError("Please specify at least one adapter to set")
+
+ # TODO In theory, multiple active trainable tokens is fine when the indices don't overlap
+ adapter_names_in_module = [n for n in adapter_name if n in self.token_adapter.trainable_tokens_delta]
+
+ if len(adapter_names_in_module) > 1:
+ raise ValueError(f"Only one adapter can be set at a time for {self}, got {len(adapter_names_in_module)}")
+
+ adapter_name_to_set: str | None
+ if not adapter_names_in_module:
+ adapter_name_to_set = None
+ else:
+ adapter_name_to_set = adapter_names_in_module[0]
+
+ return adapter_name_to_set
+
+ def set_adapter(self, adapter_names: Union[str, list[str]], inference_mode: bool = False) -> None:
+ super().set_adapter(adapter_names, inference_mode=inference_mode)
+ self.token_adapter.set_adapter(adapter_names, inference_mode=inference_mode)
+
+ def delete_adapter(self, adapter_name: str, new_active_adapters: Optional[list[str]]) -> None:
+ """
+ Delete the adapter if present.
+
+ This method will also set a new active adapter if the deleted adapter was the active adapter. It is important
+ that the new adapter is chosen by the caller in a deterministic way, so that the same adapter is chosen on all
+ layers.
+ """
+ self.token_adapter.delete_adapter(adapter_name)
+
+ # set new active adapter, if necessary
+ # note: there can only ever be one active adapter, unlike for LoRA etc.
+ if isinstance(new_active_adapters, (list, tuple)) and len(new_active_adapters) > 1:
+ name = self.__class__.__name__
+ raise ValueError(
+ f"Attempted to set multiple ({new_active_adapters}) adapters at once for {name}, which is not allowed."
+ )
+
+ if adapter_name in self._adapters:
+ self._adapters.remove(adapter_name)
+
+ if not new_active_adapters:
+ self._active_adapter = []
+ return
+
+ if new_active_adapters[0] not in self.token_adapter.trainable_tokens_delta:
+ # a new active adapter was chosen but it seems like it has no trainable_tokens
+ self._active_adapter = []
+ return
+
+ new_active_adapter = new_active_adapters[0]
+ self.set_adapter(new_active_adapter)
+
+ def unload_and_optionally_merge_module(
+ self, merge: bool, safe_merge: bool, adapter_names: Optional[list[str]]
+ ) -> torch.nn.Module:
+ """Unloading for `TrainableTokensWrapper` means to return the wrapped module, e.g. the embedding layer and,
+ if requested, merging the `TrainableTokens` adapter onto the wrapped module.
+ """
+ if merge:
+ self.token_adapter.merge(safe_merge=safe_merge, adapter_names=adapter_names)
+ return self.token_adapter.get_base_layer()
+
+ def _get_available_adapters(self) -> set[str]:
+ """Return all adapter names that can be found on this module."""
+ return set(self.token_adapter.trainable_tokens_delta.keys())
+
+
+def _get_input_embeddings_name(model, default=None):
+ if not hasattr(model, "get_input_embeddings"):
+ return default
+
+ input_embeddings = model.get_input_embeddings()
+ for name, module in model.named_modules():
+ if module is input_embeddings:
+ return name
+
+ return default
+
+
+def _get_submodules(model, key):
+ parent = model.get_submodule(".".join(key.split(".")[:-1]))
+ target_name = key.split(".")[-1]
+ target = model.get_submodule(key)
+ return parent, target, target_name
+
+
+def _get_submodules_with_grandparent(model, key):
+ parent = model.get_submodule(".".join(key.split(".")[:-1]))
+ try:
+ grandparent = model.get_submodule(".".join(key.split(".")[:-2]))
+ except AttributeError:
+ # no grand parent
+ grandparent = None
+ target_name = key.split(".")[-1]
+ target = model.get_submodule(key)
+ return parent, grandparent, target, target_name
+
+
+def _freeze_adapter(model, adapter_name):
+ for n, p in model.named_parameters():
+ if adapter_name in n:
+ p.requires_grad = False
+
+
+def _set_trainable(
+ model,
+ adapter_name,
+ module_names,
+ inference_mode: bool,
+ strict_module_check: bool = False,
+ wrapper_cls: Optional[AuxiliaryTrainingWrapper] = None,
+ activate_adapter: bool = True,
+ **wrapper_kwargs,
+):
+ """Wraps modules that are supposed to be re-trained either normally, i.e. marking them to require gradients and
+ saving them alongside other modules, or with certain methods that go alongside PEFT methods, such as retraining
+ specific token indices using selective read/write.
+
+ Note that you need to validate beforehand if there are layers targeted by multiple wrappers, e.g. if the
+ 'embedding' layer is configured for both `ModulesToSaveWrapper` and `TrainableTokensWrapper` there would be
+ conflicts down the line.
+
+ The default is to wrap the module in a `ModulesToSaveWrapper` wrapper.
+
+ If `strict_module_check` is set, this method raises an ValueError, similar to BaseTuner.inject_adapter when none of
+ the requested modules in `module_names` is not found in the model.
+
+ The `active_adapter` flag indicates if this new adapter should be activated.
+ """
+ from peft.tuners.tuners_utils import BaseTunerLayer
+
+ if wrapper_cls is None:
+ wrapper_cls = ModulesToSaveWrapper
+
+ if not module_names:
+ # This is useful for the case that the PEFT config does not have `modules_to_save`, e.g.
+ # in the case of prompt tuning and friends.
+ return
+
+ trainable_modules = []
+ found_modules = set()
+ # disable removal of duplicates to support targeting tied weights
+ key_list = [key for key, _ in model.named_modules(remove_duplicate=False)]
+
+ for key in key_list:
+ target_module_found = any(key.endswith(target_key) for target_key in module_names)
+ if target_module_found:
+ parent, grandparent, target, target_name = _get_submodules_with_grandparent(model, key)
+ if isinstance(grandparent, BaseTunerLayer):
+ # This is an extreme edge case: Let's assume that there is a PEFT config with
+ # modules_to_save=["default"], which is the same name as the adapter name. The PEFT method's adapter
+ # (e.g. LoRA) is applied first. Then, when the modules_to_save matching is performed, the LoRA layer
+ # would be considered a valid target. Assuming that the name is "foo.bar.lora_A.default", it would
+ # match, with "default" being an nn.Linear and the parent, "lora_A", being an nn.ModuleDict. This by
+ # itself is not enough to prove that this is an unintended match. Thererfore, we also need to check the
+ # grandparent, "bar", that would be a lora.LoraLayer. When we see this, we should raise an error.
+ raise ValueError(
+ f"You are trying to target a module with {wrapper_cls} that is a child of {type(grandparent)}. "
+ "This is almost certainly not the intended behavior. Please ensure that the adapter name, "
+ f"'{adapter_name}', does not conflict with any of the targeted modules."
+ )
+
+ if isinstance(target, wrapper_cls):
+ target.update(adapter_name, **wrapper_kwargs)
+ target.set_adapter(target.active_adapter, inference_mode=inference_mode)
+ else:
+ new_module = wrapper_cls(target, adapter_name, **wrapper_kwargs)
+ if activate_adapter:
+ new_module.set_adapter(adapter_name, inference_mode=inference_mode)
+ else:
+ new_module.set_adapter([], inference_mode=inference_mode)
+ setattr(parent, target_name, new_module)
+ trainable_modules.append(new_module)
+ found_modules.add(target_name)
+
+ not_found = set(module_names).difference(found_modules)
+ if strict_module_check and not found_modules:
+ raise ValueError(
+ f"Target modules {not_found} not found in the base model. Please check the target modules and try again."
+ )
+
+ return trainable_modules
+
+
+def _set_adapter(model, adapter_name: str | list[str], inference_mode: bool = False):
+ for module in model.modules():
+ if isinstance(module, AuxiliaryTrainingWrapper):
+ # only check the adapter_name if we actually encounter a AuxiliaryTrainingWrapper, otherwise we don't care
+ adapter_name_to_set = module.check_set_adapter(adapter_name)
+
+ # if the adapter is found in this module, set it as the active adapter, else disable the adapters of this
+ # module
+ if adapter_name_to_set in module._adapters:
+ module.enable_adapters(True)
+ module.set_adapter(adapter_name_to_set, inference_mode=inference_mode)
+ else:
+ module.enable_adapters(False)
+ module.set_adapter([], inference_mode=inference_mode)
+
+
+def _prepare_prompt_learning_config(peft_config, model_config):
+ # In case of VLM we focus on the language model portion of the model.
+ if "text_config" in model_config:
+ model_config = model_config["text_config"]
+
+ if peft_config.num_layers is None:
+ if "num_hidden_layers" in model_config:
+ num_layers = model_config["num_hidden_layers"]
+ elif "num_layers" in model_config:
+ num_layers = model_config["num_layers"]
+ elif "n_layer" in model_config:
+ num_layers = model_config["n_layer"]
+ else:
+ raise ValueError("Please specify `num_layers` in `peft_config`")
+ peft_config.num_layers = num_layers
+
+ if peft_config.token_dim is None:
+ if "hidden_size" in model_config:
+ token_dim = model_config["hidden_size"]
+ elif "n_embd" in model_config:
+ token_dim = model_config["n_embd"]
+ elif "d_model" in model_config:
+ token_dim = model_config["d_model"]
+ else:
+ raise ValueError("Please specify `token_dim` in `peft_config`")
+ peft_config.token_dim = token_dim
+
+ if peft_config.num_attention_heads is None:
+ if "num_attention_heads" in model_config:
+ num_attention_heads = model_config["num_attention_heads"]
+ elif "n_head" in model_config:
+ num_attention_heads = model_config["n_head"]
+ elif "num_heads" in model_config:
+ num_attention_heads = model_config["num_heads"]
+ elif "encoder_attention_heads" in model_config:
+ num_attention_heads = model_config["encoder_attention_heads"]
+ else:
+ raise ValueError("Please specify `num_attention_heads` in `peft_config`")
+ peft_config.num_attention_heads = num_attention_heads
+
+ # For grouped-query attention, see #1901.
+ if peft_config.peft_type == "PREFIX_TUNING" and "num_key_value_heads" in model_config:
+ num_key_value_heads = model_config["num_key_value_heads"]
+ peft_config.token_dim = peft_config.token_dim // peft_config.num_attention_heads * num_key_value_heads
+ peft_config.num_attention_heads = num_key_value_heads
+
+ if getattr(peft_config, "encoder_hidden_size", None) is None:
+ setattr(peft_config, "encoder_hidden_size", peft_config.token_dim)
+
+ return peft_config
+
+
+def _get_no_split_modules(model) -> set[str]:
+ """
+ Get the modules of the model that should not be split when using device_map. We iterate through the modules to get
+ the underlying `_no_split_modules`.
+
+ Returns:
+ `List[str]`: List of modules that should not be split
+ """
+ # After discussion in https://github.com/huggingface/transformers/pull/38141, based on:
+ # https://github.com/huggingface/transformers/blob/1e921a3a9cea92b383ca4b0484ee45596bbdadc3/src/transformers/modeling_utils.py#L2677-L2704
+ _no_split_modules: set[str] = set()
+ if not hasattr(model, "_no_split_modules"):
+ return _no_split_modules
+
+ modules_to_check = [model]
+ while len(modules_to_check) > 0:
+ module = modules_to_check.pop(-1)
+ # if the module does not appear in _no_split_modules, we also check the children
+ if module.__class__.__name__ not in _no_split_modules:
+ if isinstance(module, PreTrainedModel):
+ if module._no_split_modules is not None:
+ _no_split_modules = _no_split_modules | set(module._no_split_modules)
+ modules_to_check += list(module.children())
+ return _no_split_modules
+
+
+def fsdp_auto_wrap_policy(model):
+ if hasattr(FullyShardedDataParallelPlugin, "get_module_class_from_name"):
+ get_module_class_from_name = FullyShardedDataParallelPlugin.get_module_class_from_name
+ else:
+ from accelerate.utils.dataclasses import get_module_class_from_name
+ from torch.distributed.fsdp.wrap import _or_policy, lambda_auto_wrap_policy, transformer_auto_wrap_policy
+
+ from ..tuners import PrefixEncoder, PromptEmbedding, PromptEncoder
+
+ default_transformer_cls_names_to_wrap = ",".join(_get_no_split_modules(model))
+ transformer_cls_names_to_wrap = os.environ.get(
+ "FSDP_TRANSFORMER_CLS_TO_WRAP", default_transformer_cls_names_to_wrap
+ ).split(",")
+ transformer_cls_to_wrap = {PrefixEncoder, PromptEncoder, PromptEmbedding}
+ for layer_class in transformer_cls_names_to_wrap:
+ if len(layer_class) == 0:
+ continue
+ transformer_cls = get_module_class_from_name(model, layer_class)
+ if transformer_cls is None:
+ raise Exception("Could not find the transformer layer class to wrap in the model.")
+ else:
+ transformer_cls_to_wrap.add(transformer_cls)
+
+ def lambda_policy_fn(module):
+ if (
+ len(list(module.named_children())) == 0
+ and getattr(module, "weight", None) is not None
+ and module.weight.requires_grad
+ ):
+ return True
+ return False
+
+ lambda_policy = functools.partial(lambda_auto_wrap_policy, lambda_fn=lambda_policy_fn)
+ transformer_wrap_policy = functools.partial(
+ transformer_auto_wrap_policy,
+ transformer_layer_cls=transformer_cls_to_wrap,
+ )
+
+ auto_wrap_policy = functools.partial(_or_policy, policies=[lambda_policy, transformer_wrap_policy])
+ return auto_wrap_policy
+
+
+def transpose(weight, fan_in_fan_out):
+ if not fan_in_fan_out:
+ return weight
+
+ if isinstance(weight, torch.nn.Parameter):
+ return torch.nn.Parameter(weight.T)
+ return weight.T
+
+
+def _is_valid_match(key: str, target_key: str):
+ """
+ Helper function to match module names target_key and key. Makes sure that either the key is exactly the target_key
+ or the target_key is a submodule of key
+ """
+ if key.endswith(target_key):
+ if len(key) > len(target_key):
+ return key.endswith("." + target_key) # must be a sub module
+ return True
+ return False
+
+
+def _get_batch_size(input_ids: Optional[torch.Tensor], inputs_embeds: Optional[torch.Tensor]) -> int:
+ """Get the batch size based on either input_ids or input_embeds
+
+ Raises an ValueError if both are None.
+
+ """
+ if (input_ids is None) and (inputs_embeds is None):
+ raise ValueError("You have to provide either input_ids or inputs_embeds")
+
+ if input_ids is not None:
+ batch_size = input_ids.shape[0]
+ else:
+ batch_size = inputs_embeds.shape[0]
+ return batch_size
+
+
+def get_quantization_config(model: torch.nn.Module, method: str):
+ """
+ Get the quantization config of the related quantization method
+ """
+ if (
+ hasattr(model, "config")
+ and hasattr(model.config, "quantization_config")
+ and (getattr(model, "quantization_method", None) == method)
+ ):
+ return model.config.quantization_config
+ return None
+
+
+def get_auto_gptq_quant_linear(gptq_quantization_config):
+ """
+ Get the right AutoGPTQQuantLinear class based on the quantization config file
+ """
+ if gptq_quantization_config is None:
+ return None
+
+ if is_auto_gptq_available():
+ from auto_gptq.utils.import_utils import dynamically_import_QuantLinear
+ else:
+ return None
+
+ desc_act = gptq_quantization_config.desc_act
+ group_size = gptq_quantization_config.group_size
+ bits = gptq_quantization_config.bits
+ if hasattr(gptq_quantization_config, "use_exllama"):
+ use_exllama = gptq_quantization_config.use_exllama
+ else:
+ use_exllama = not gptq_quantization_config.disable_exllama
+ if hasattr(gptq_quantization_config, "exllama_config"):
+ exllama_version = gptq_quantization_config.exllama_config["version"]
+ else:
+ exllama_version = 1
+
+ QuantLinear = dynamically_import_QuantLinear(
+ use_triton=False,
+ desc_act=desc_act,
+ group_size=group_size,
+ bits=bits,
+ disable_exllama=not (use_exllama and exllama_version == 1),
+ disable_exllamav2=not (use_exllama and exllama_version == 2),
+ )
+
+ return QuantLinear
+
+
+def get_gptqmodel_quant_linear(gptq_quantization_config, device_map=None):
+ """
+ Get the right GPTQQuantLinear class based on the quantization config file
+ """
+ if gptq_quantization_config is None:
+ return None
+
+ if not is_gptqmodel_available():
+ return None
+
+ from gptqmodel.utils.importer import hf_select_quant_linear
+
+ desc_act = gptq_quantization_config.desc_act
+ group_size = gptq_quantization_config.group_size
+ bits = gptq_quantization_config.bits
+ checkpoint_format = (
+ gptq_quantization_config.checkpoint_format
+ if hasattr(gptq_quantization_config, "checkpoint_format")
+ else "gptq"
+ )
+ sym = gptq_quantization_config.sym
+ meta = gptq_quantization_config.meta if hasattr(gptq_quantization_config, "meta") else None
+
+ QuantLinear = hf_select_quant_linear(
+ bits=bits,
+ group_size=group_size,
+ desc_act=desc_act,
+ sym=sym,
+ device_map=device_map,
+ checkpoint_format=checkpoint_format,
+ meta=meta,
+ backend="auto_trainable",
+ )
+
+ return QuantLinear
+
+
+def id_tensor_storage(tensor: torch.Tensor) -> tuple[torch.device, int, int]:
+ """
+ Unique identifier to a tensor storage. Multiple different tensors can share the same underlying storage. For
+ example, "meta" tensors all share the same storage, and thus their identifier will all be equal. This identifier is
+ guaranteed to be unique and constant for this tensor's storage during its lifetime. Two tensor storages with
+ non-overlapping lifetimes may have the same id.
+
+ This method is the exact same copy of
+ https://github.com/huggingface/transformers/blob/main/src/transformers/pytorch_utils.py#L282C1-L300C58 but we added
+ it here manually to avoid import issue with old versions of transformers.
+ """
+ if tensor.device.type == "xla" and is_torch_tpu_available():
+ # NOTE: xla tensors dont have storage
+ # use some other unique id to distinguish.
+ # this is a XLA tensor, it must be created using torch_xla's
+ # device. So the following import is safe:
+ import torch_xla
+
+ unique_id = torch_xla._XLAC._xla_get_tensor_id(tensor)
+ else:
+ unique_id = storage_ptr(tensor)
+
+ return tensor.device, unique_id, storage_size(tensor)
+
+
+def cast_mixed_precision_params(model, dtype):
+ """
+ Cast all non-trainable parameters of the model to the given `dtype`. The `dtype` can be `torch.float16` or
+ `torch.bfloat16` as per the mixed-precision training you are performing. The trainable parameters are cast to full
+ precision. This is meant to reduce the GPU memory usage when using PEFT methods by using half-precision dtype for
+ non-trainable parameters. Having the trainable parameters in full-precision preserves training stability when using
+ automatic mixed-precision training.
+
+ Args:
+ model (`torch.nn.Module`):
+ The model to cast the non-trainable parameters of.
+ dtype (`torch.dtype`):
+ The dtype to cast the non-trainable parameters to. The `dtype` can be `torch.float16` or
+ `torch.bfloat16` as per the mixed-precision training you are performing.
+ """
+ for p in model.parameters():
+ if not p.requires_grad:
+ p.data = p.to(dtype)
+ else:
+ p.data = p.to(torch.float32)
+
+
+def str_to_bool(value: str) -> int:
+ """
+ Converts a string representation of truth to `True` (1) or `False` (0).
+
+ True values are `y`, `yes`, `t`, `true`, `on`, and `1`; False value are `n`, `no`, `f`, `false`, `off`, and `0`;
+ """
+ # same as function as in accelerate.utils, which replaces the deprecated distutils.util.strtobool
+ value = value.lower()
+ if value in ("y", "yes", "t", "true", "on", "1"):
+ return 1
+ elif value in ("n", "no", "f", "false", "off", "0"):
+ return 0
+ else:
+ raise ValueError(f"invalid truth value {value}")
+
+
+def check_file_exists_on_hf_hub(repo_id: str, filename: str, **kwargs) -> Optional[bool]:
+ """Check if a file exists on HF Hub, if check was not successful returns None instead of erroring.
+
+ Respect offline mode if set.
+
+ """
+ exists: Optional[bool] = None
+ if str_to_bool(os.environ.get("HF_HUB_OFFLINE", "0")):
+ # user set offline mode, cannot check
+ return exists
+
+ try:
+ exists = file_exists(repo_id, filename, **kwargs)
+ except (HFValidationError, EntryNotFoundError):
+ # error, exists stays None
+ pass
+ except Exception as e:
+ warnings.warn(
+ f"Unable to fetch remote file due to the following error {e} - silently ignoring the lookup"
+ f" for the file {filename} in {repo_id}."
+ )
+
+ return exists
+
+
+def match_target_against_key(target_pattern: str, key: str):
+ """Backing function for `target_modules` config parameter.
+
+ Having this as its own function ensures that target key matching can be implemented in the same way everywhere.
+ """
+ return re.fullmatch(target_pattern, key)
+
+
+def get_pattern_key(pattern_keys: Sequence[str], key_to_match: str) -> str:
+ """Match a substring of key_to_match in pattern keys"""
+ for key in pattern_keys:
+ match = re.match(rf"(.*\.)?({key})$", key_to_match)
+ if not match:
+ continue
+ return key
+
+ return key_to_match
+
+
+def set_additional_trainable_modules(model, peft_config, model_config, adapter_name, activate_adapter: bool = True):
+ """Handle the resolution of additional trainable modules (also called AuxiliaryTrainingWrapper)
+ by checking the config if such modules are requested and adding them to the model.
+
+ Currently trainable tokens and modules to save are considered additional trainable modules.
+
+ If `activate_adapter` is set to `False`, the adapter won't be activated. This is typically the case when
+ `model.add_adapter` or `model.load_adapter` are being called.
+ """
+ if getattr(peft_config, "modules_to_save", None) is not None:
+ # this may add a new ModulesToSaveWrapper
+ _set_trainable(
+ model,
+ adapter_name,
+ inference_mode=peft_config.inference_mode,
+ module_names=getattr(peft_config, "modules_to_save", None),
+ activate_adapter=activate_adapter,
+ )
+
+ if getattr(peft_config, "trainable_token_indices", None) is not None:
+ if isinstance(peft_config.trainable_token_indices, dict):
+ target_layers = peft_config.trainable_token_indices
+ else:
+ layer_name = _get_input_embeddings_name(model, "embed_tokens")
+ target_layers = {layer_name: peft_config.trainable_token_indices}
+
+ modules_to_save = getattr(peft_config, "modules_to_save", None)
+ if modules_to_save is not None:
+ for target_layer in target_layers:
+ if target_layer in modules_to_save:
+ raise ValueError(
+ "The embedding layer is already marked to be trained fully, either specify "
+ f'`modules_to_save=[..., "{target_layer}", ...]` or '
+ f"`trainable_tokens={{'{target_layer}': x}}` but not both."
+ )
+
+ for target_layer, token_indices in target_layers.items():
+ _set_trainable(
+ model,
+ adapter_name,
+ inference_mode=peft_config.inference_mode,
+ module_names=[target_layer],
+ strict_module_check=True,
+ wrapper_cls=TrainableTokensWrapper,
+ token_indices=token_indices,
+ activate_adapter=activate_adapter,
+ )
+
+ # There might be the possibility that we have output weights that are tied to the input weights.
+ # In that case we will tie any module that wants tied weights to the token adapter to make sure that
+ # any modification is reflected in the tied layers as well.
+ if (
+ model_config.get("tie_word_embeddings", False)
+ # some models may be misconfigured to have weight tying enabled but don't define tied weights keys
+ and model._tied_weights_keys is not None
+ and isinstance(model.get_input_embeddings(), TrainableTokensWrapper)
+ ):
+ # the embedding layer is modified and we want weight tying.
+ module_keys = [".".join(n.split(".")[:-1]) for n in model._tied_weights_keys]
+
+ token_adapter = model.get_input_embeddings().token_adapter
+ _set_trainable(
+ model,
+ adapter_name,
+ inference_mode=peft_config.inference_mode,
+ module_names=module_keys,
+ strict_module_check=True,
+ wrapper_cls=TrainableTokensWrapper,
+ token_indices=token_adapter.token_indices[adapter_name],
+ tied_adapter=model.get_input_embeddings().token_adapter,
+ )
+
+
+def create_attention_mask(
+ model, *, model_input, attention_mask, past_key_values, cache_position, batch_size, sequence_length, position_ids
+):
+ # adapted from:
+ # https://github.com/huggingface/transformers/blob/cb4c56ce0dfa1350267ed28e57760986a58a9ba4/src/transformers/generation/utils.py#L644-L680
+ # In PEFT, we sometimes need to re-create the attention mask. This is because some prompt learning methods insert
+ # new items into the sequence, which results in the attention mask needing an update. We re-use transformers code
+ # for this as much as possible.
+ transformers_ge_4_53_1 = version.parse(transformers.__version__) >= version.parse("4.53.1")
+ if transformers_ge_4_53_1:
+ # the function already exists in v4.53.0 but has a different signature, so we check for 4.53.1
+ from transformers.masking_utils import create_masks_for_generate
+ else:
+ raise ImportError("Your transformers version is too old, please upgrade it to >= 4.53.1")
+
+ # Create the causal mask with fixed shape in advance, to reduce recompilations. If the function to create
+ # the 4D causal mask exists, it should be present in the base model (XXXModel class) or in its decoder.
+ base_model = getattr(model, model.base_model_prefix, model)
+ decoder = base_model.get_decoder() if hasattr(base_model, "get_decoder") else None
+ causal_mask_creation_function = getattr(base_model, "_prepare_4d_causal_attention_mask_with_cache_position", None)
+ if causal_mask_creation_function is None and decoder is not None: # it may be in the decoder
+ causal_mask_creation_function = getattr(decoder, "_prepare_4d_causal_attention_mask_with_cache_position", None)
+
+ # If it's not defined, it means the model uses the new general mask API
+ if causal_mask_creation_function is None: # can't be found
+ token_type_ids = getattr(model_input, "token_type_ids", None)
+ # Some models may overwrite the general one
+ causal_mask_creation_function = getattr(model, "create_masks_for_generate", create_masks_for_generate)
+ attention_mask = causal_mask_creation_function(
+ config=model.config,
+ # we only need batch size, seq_length and dtype here - we don't care about the values of the embeddings
+ input_embeds=torch.empty((batch_size, sequence_length), dtype=model.dtype),
+ attention_mask=attention_mask,
+ cache_position=cache_position,
+ past_key_values=past_key_values,
+ token_type_ids=token_type_ids,
+ position_ids=position_ids,
+ )
+ else:
+ attention_mask = causal_mask_creation_function(
+ attention_mask,
+ sequence_length=sequence_length,
+ target_length=past_key_values.get_max_cache_shape(),
+ dtype=model.dtype,
+ cache_position=cache_position,
+ batch_size=batch_size,
+ config=model.config,
+ past_key_values=past_key_values,
+ position_ids=position_ids,
+ )
+ return attention_mask
diff --git a/peft/src/peft/utils/peft_types.py b/peft/src/peft/utils/peft_types.py
new file mode 100644
index 0000000000000000000000000000000000000000..8815aa4684a331fcb53f199beffa9fa96e153e60
--- /dev/null
+++ b/peft/src/peft/utils/peft_types.py
@@ -0,0 +1,177 @@
+# Copyright 2023-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+import enum
+from typing import Optional
+
+
+class PeftType(str, enum.Enum):
+ """
+ Enum class for the different types of adapters in PEFT.
+
+ Supported PEFT types:
+ - PROMPT_TUNING
+ - MULTITASK_PROMPT_TUNING
+ - P_TUNING
+ - PREFIX_TUNING
+ - LORA
+ - ADALORA
+ - BOFT
+ - ADAPTION_PROMPT
+ - IA3
+ - LOHA
+ - LOKR
+ - OFT
+ - XLORA
+ - POLY
+ - LN_TUNING
+ - VERA
+ - FOURIERFT
+ - HRA
+ - BONE
+ - MISS
+ - RANDLORA
+ - SHIRA
+ - C3A
+ - ROAD
+ - WAVEFT
+ """
+
+ PROMPT_TUNING = "PROMPT_TUNING"
+ MULTITASK_PROMPT_TUNING = "MULTITASK_PROMPT_TUNING"
+ P_TUNING = "P_TUNING"
+ PREFIX_TUNING = "PREFIX_TUNING"
+ LORA = "LORA"
+ ADALORA = "ADALORA"
+ BOFT = "BOFT"
+ ADAPTION_PROMPT = "ADAPTION_PROMPT"
+ IA3 = "IA3"
+ LOHA = "LOHA"
+ LOKR = "LOKR"
+ OFT = "OFT"
+ POLY = "POLY"
+ LN_TUNING = "LN_TUNING"
+ VERA = "VERA"
+ FOURIERFT = "FOURIERFT"
+ XLORA = "XLORA"
+ HRA = "HRA"
+ VBLORA = "VBLORA"
+ CPT = "CPT"
+ BONE = "BONE"
+ MISS = "MISS"
+ RANDLORA = "RANDLORA"
+ ROAD = "ROAD"
+ TRAINABLE_TOKENS = "TRAINABLE_TOKENS"
+ SHIRA = "SHIRA"
+ C3A = "C3A"
+ WAVEFT = "WAVEFT"
+
+
+class TaskType(str, enum.Enum):
+ """
+ Enum class for the different types of tasks supported by PEFT.
+
+ Overview of the supported task types:
+ - SEQ_CLS: Text classification.
+ - SEQ_2_SEQ_LM: Sequence-to-sequence language modeling.
+ - CAUSAL_LM: Causal language modeling.
+ - TOKEN_CLS: Token classification.
+ - QUESTION_ANS: Question answering.
+ - FEATURE_EXTRACTION: Feature extraction. Provides the hidden states which can be used as embeddings or features
+ for downstream tasks.
+ """
+
+ SEQ_CLS = "SEQ_CLS"
+ SEQ_2_SEQ_LM = "SEQ_2_SEQ_LM"
+ CAUSAL_LM = "CAUSAL_LM"
+ TOKEN_CLS = "TOKEN_CLS"
+ QUESTION_ANS = "QUESTION_ANS"
+ FEATURE_EXTRACTION = "FEATURE_EXTRACTION"
+
+
+def register_peft_method(
+ *, name: str, config_cls, model_cls, prefix: Optional[str] = None, is_mixed_compatible=False
+) -> None:
+ """
+ Function to register a finetuning method like LoRA to be available in PEFT.
+
+ This method takes care of registering the PEFT method's configuration class, the model class, and optionally the
+ prefix.
+
+ Args:
+ name (str):
+ The name of the PEFT method. It must be unique.
+ config_cls:
+ The configuration class of the PEFT method.
+ model_cls:
+ The model class of the PEFT method.
+ prefix (Optional[str], optional):
+ The prefix of the PEFT method. It should be unique. If not provided, the name of the PEFT method is used as
+ the prefix.
+ is_mixed_compatible (bool, optional):
+ Whether the PEFT method is compatible with `PeftMixedModel`. If you're not sure, leave it as False
+ (default).
+
+ Example:
+
+ ```py
+ # inside of peft/tuners/my_peft_method/__init__.py
+ from peft.utils import register_peft_method
+
+ register_peft_method(name="my_peft_method", config_cls=MyConfig, model_cls=MyModel)
+ ```
+ """
+ from peft.mapping import (
+ PEFT_TYPE_TO_CONFIG_MAPPING,
+ PEFT_TYPE_TO_MIXED_MODEL_MAPPING,
+ PEFT_TYPE_TO_PREFIX_MAPPING,
+ PEFT_TYPE_TO_TUNER_MAPPING,
+ )
+
+ if name.endswith("_"):
+ raise ValueError(f"Please pass the name of the PEFT method without '_' suffix, got {name}.")
+
+ if not name.islower():
+ raise ValueError(f"The name of the PEFT method should be in lower case letters, got {name}.")
+
+ if name.upper() not in list(PeftType):
+ raise ValueError(f"Unknown PEFT type {name.upper()}, please add an entry to peft.utils.peft_types.PeftType.")
+
+ peft_type = getattr(PeftType, name.upper())
+
+ # model_cls can be None for prompt learning methods, which don't have dedicated model classes
+ if prefix is None:
+ prefix = name + "_"
+
+ if (
+ (peft_type in PEFT_TYPE_TO_CONFIG_MAPPING)
+ or (peft_type in PEFT_TYPE_TO_TUNER_MAPPING)
+ or (peft_type in PEFT_TYPE_TO_MIXED_MODEL_MAPPING)
+ ):
+ raise KeyError(f"There is already PEFT method called '{name}', please choose a unique name.")
+
+ if prefix in PEFT_TYPE_TO_PREFIX_MAPPING:
+ raise KeyError(f"There is already a prefix called '{prefix}', please choose a unique prefix.")
+
+ model_cls_prefix = getattr(model_cls, "prefix", None)
+ if (model_cls_prefix is not None) and (model_cls_prefix != prefix):
+ raise ValueError(
+ f"Inconsistent prefixes found: '{prefix}' and '{model_cls_prefix}' (they should be the same)."
+ )
+
+ PEFT_TYPE_TO_PREFIX_MAPPING[peft_type] = prefix
+ PEFT_TYPE_TO_CONFIG_MAPPING[peft_type] = config_cls
+ PEFT_TYPE_TO_TUNER_MAPPING[peft_type] = model_cls
+ if is_mixed_compatible:
+ PEFT_TYPE_TO_MIXED_MODEL_MAPPING[peft_type] = model_cls
diff --git a/peft/src/peft/utils/save_and_load.py b/peft/src/peft/utils/save_and_load.py
new file mode 100644
index 0000000000000000000000000000000000000000..778e6964103c44215abc0c39fd57e93d7065eacc
--- /dev/null
+++ b/peft/src/peft/utils/save_and_load.py
@@ -0,0 +1,724 @@
+# Copyright 2023-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+from __future__ import annotations
+
+import os
+import platform
+import re
+import warnings
+from typing import Optional
+
+import huggingface_hub
+import torch
+from huggingface_hub import file_exists, hf_hub_download
+from huggingface_hub.errors import EntryNotFoundError, LocalEntryNotFoundError
+from safetensors.torch import load_file as safe_load_file
+from transformers.utils import http_user_agent
+
+from peft.mapping import PEFT_TYPE_TO_PREFIX_MAPPING
+
+from .constants import INCLUDE_LINEAR_LAYERS_SHORTHAND
+from .other import (
+ EMBEDDING_LAYER_NAMES,
+ SAFETENSORS_WEIGHTS_NAME,
+ WEIGHTS_NAME,
+ AuxiliaryTrainingWrapper,
+ check_file_exists_on_hf_hub,
+ infer_device,
+ match_target_against_key,
+)
+from .peft_types import PeftType
+
+
+def has_valid_embedding_base_layer(layer):
+ """Check if the layer has an embedding base layer"""
+ return hasattr(layer, "base_layer") and isinstance(layer.base_layer, (torch.nn.Linear, torch.nn.Embedding))
+
+
+def get_embedding_layer_name(model, layer, is_embedding_in_target_modules):
+ """Get the name of the embedding module for a given layer."""
+ for name, module in model.named_modules():
+ if (not is_embedding_in_target_modules and module == layer) or module == getattr(layer, "base_layer", None):
+ return name
+ return None
+
+
+def get_peft_model_state_dict(
+ model, state_dict=None, adapter_name="default", unwrap_compiled=False, save_embedding_layers="auto"
+):
+ """
+ Get the state dict of the given adapter of the PEFT model.
+
+ This only includes the PEFT parameters, not the parameters of the base model. Thus the returned `state_dict` is
+ generally small compared to the full model size. To retrieve the full `state_dict`, just call `model.state_dict()`.
+
+ Note that the adapter name is removed from the `state_dict`, as this is just an arbitrary name that can be changed
+ when loading the adapter. So e.g. if the adapter name is `'default'` and the original key is
+ `'model.q_proj.lora_A.default.weight'`, the returned key will be `'model.q_proj.lora_A.weight'`. Use this function
+ in conjunction with [`set_peft_model_state_dict`] to take care of the adapter name when loading weights.
+
+ Args:
+ model ([`PeftModel`]): The Peft model. When using torch.nn.DistributedDataParallel, DeepSpeed or FSDP,
+ the model should be the underlying model/unwrapped model (i.e. model.module).
+ state_dict (`dict`, *optional*, defaults to `None`):
+ The state dict of the model. If not provided, the state dict of the passed model will be used.
+ adapter_name (`str`, *optional*, defaults to `"default"`):
+ The name of the adapter whose state dict should be returned.
+ unwrap_compiled (`bool`, *optional*, defaults to `False`):
+ Whether to unwrap the model if torch.compile was used.
+ save_embedding_layers (`Union[bool, str]`, , *optional*, defaults to `auto`):
+ If `True`, save the embedding layers in addition to adapter weights. If `auto`, checks the common embedding
+ layers `peft.utils.other.EMBEDDING_LAYER_NAMES` in config's `target_modules` when available. Based on it
+ sets the boolean flag. This only works for 🤗 transformers models.
+
+ """
+ if unwrap_compiled:
+ model = getattr(model, "_orig_mod", model)
+
+ config = model.peft_config[adapter_name]
+ if state_dict is None:
+ state_dict = model.state_dict()
+
+ # TUNER SPECIFIC CODE
+ if config.peft_type in (PeftType.LORA, PeftType.ADALORA):
+ # to_return = lora_state_dict(model, bias=model.peft_config.bias)
+ # adapted from `https://github.com/microsoft/LoRA/blob/main/loralib/utils.py`
+ # to be used directly with the state dict which is necessary when using DeepSpeed or FSDP
+ bias = config.bias
+ if bias == "none":
+ to_return = {k: state_dict[k] for k in state_dict if "lora_" in k}
+ elif bias == "all":
+ to_return = {k: state_dict[k] for k in state_dict if "lora_" in k or "bias" in k}
+ elif bias == "lora_only":
+ to_return = {}
+ for k in state_dict:
+ if "lora_" in k:
+ to_return[k] = state_dict[k]
+ bias_name = k.split("lora_")[0] + "bias"
+ if bias_name in state_dict:
+ to_return[bias_name] = state_dict[bias_name]
+ else:
+ raise NotImplementedError
+ to_return = {k: v for k, v in to_return.items() if (("lora_" in k and adapter_name in k) or ("bias" in k))}
+ if config.peft_type == PeftType.ADALORA:
+ rank_pattern = config.rank_pattern
+ if rank_pattern is not None:
+ rank_pattern = {k.replace(f".{adapter_name}", ""): v for k, v in rank_pattern.items()}
+ config.rank_pattern = rank_pattern
+ to_return = model.resize_state_dict_by_rank_pattern(rank_pattern, to_return, adapter_name)
+
+ if config.use_dora:
+ # Here we take care of a refactor of DoRA which changed lora_magnitude_vector from a ParameterDict to a
+ # ModuleDict with a DoraLayer instance. The old parameter is now the "weight" attribute of that layer. Since
+ # we want the state_dict format not to change, we remove the "weight" part.
+ new_dora_suffix = f"lora_magnitude_vector.{adapter_name}.weight"
+
+ def renamed_dora_weights(k):
+ if k.endswith(new_dora_suffix):
+ k = k[:-7] # remove ".weight"
+ return k
+
+ to_return = {renamed_dora_weights(k): v for k, v in to_return.items()}
+
+ elif config.peft_type == PeftType.BOFT:
+ bias = config.bias
+ if bias == "none":
+ to_return = {k: state_dict[k] for k in state_dict if "boft_" in k}
+ elif bias == "all":
+ to_return = {k: state_dict[k] for k in state_dict if "boft_" in k or "bias" in k}
+ elif bias == "boft_only":
+ to_return = {}
+ for k in state_dict:
+ if "boft_" in k:
+ to_return[k] = state_dict[k]
+ bias_name = k.split("boft_")[0] + "bias"
+ if bias_name in state_dict:
+ to_return[bias_name] = state_dict[bias_name]
+ else:
+ raise NotImplementedError
+
+ elif config.peft_type == PeftType.ADAPTION_PROMPT:
+ to_return = {k: state_dict[k] for k in state_dict if k.split(".")[-1].startswith("adaption_")}
+
+ elif config.is_prompt_learning:
+ to_return = {}
+ if config.peft_type == PeftType.MULTITASK_PROMPT_TUNING:
+ to_return["prefix_task_cols"] = model.prompt_encoder[adapter_name].prefix_task_cols
+ to_return["prefix_task_rows"] = model.prompt_encoder[adapter_name].prefix_task_rows
+ prompt_embeddings = model.prompt_encoder[adapter_name].embedding.weight
+ else:
+ if config.inference_mode:
+ prompt_embeddings = model.prompt_encoder[adapter_name].embedding.weight
+ else:
+ prompt_embeddings = model.get_prompt_embedding_to_save(adapter_name)
+ to_return["prompt_embeddings"] = prompt_embeddings
+
+ elif config.peft_type == PeftType.SHIRA:
+ shira_prefix = PEFT_TYPE_TO_PREFIX_MAPPING[config.peft_type]
+ to_return = {k: state_dict[k] for k in state_dict if shira_prefix in k}
+ if platform.system() == "Windows":
+ warnings.warn(
+ "Windows has issues saving integers into safetensors. Hence, we convert shira_indices to float32 "
+ "before saving on Windows OS. The shira_indices will always be converted to integers when loading."
+ )
+ for name, module in model.named_modules():
+ if hasattr(module, "shira_indices"):
+ for k, v in module.shira_indices.items():
+ # Windows has some issues with saving integers into safetensors. Tests fail with some kind of
+ # PermissionError. This results in failed tests, so we are converting indices to float32 before
+ # saving and then converting them back to int when loading. This is happening only for Windows,
+ # not for Linux and Mac-OS.
+ to_return[f"{name}.shira_indices.{k}"] = (
+ v.to(torch.float32) if platform.system() == "Windows" else v
+ )
+
+ elif config.peft_type == PeftType.VERA:
+ vera_prefix = PEFT_TYPE_TO_PREFIX_MAPPING[config.peft_type]
+ to_return = {k: state_dict[k] for k in state_dict if vera_prefix in k}
+ if config.save_projection:
+ # TODO: adding vera_A and vera_B to `self.get_base_layer` would
+ # make name to match here difficult to predict.
+ if f"base_model.vera_A.{adapter_name}" not in state_dict:
+ raise ValueError(
+ "Model was initialised to not save vera_A and vera_B but config now specifies to save projection!"
+ " Set `config.save_projection` to `False`."
+ )
+ to_return["base_model.vera_A." + adapter_name] = state_dict["base_model.vera_A." + adapter_name]
+ to_return["base_model.vera_B." + adapter_name] = state_dict["base_model.vera_B." + adapter_name]
+ elif config.peft_type == PeftType.XLORA:
+ to_return = {k: state_dict[k] for k in state_dict if "internal_xlora_classifier" in k}
+ elif config.peft_type == PeftType.VBLORA:
+ to_return = {}
+ # choose the most efficient dtype for indices
+ if config.num_vectors < 2**8:
+ indices_dtype = torch.uint8
+ elif config.num_vectors < 2**15:
+ indices_dtype = torch.int16
+ elif config.num_vectors < 2**31:
+ indices_dtype = torch.int32
+ else:
+ indices_dtype = torch.int64
+ if config.save_only_topk_weights:
+ # in save_only_topk_weights mode, we save topk_indices and topk_weights for parameter efficiency
+ for k in state_dict:
+ if "vblora_logits" in k:
+ logits, indices = state_dict[k].topk(config.topk)
+ to_return.update({k + "_topk_indices": indices.to(dtype=indices_dtype)})
+ to_return.update({k + "_topk_weights": torch.softmax(logits, dim=-1)[:, :, :-1].contiguous()})
+ else:
+ to_return = {k: state_dict[k] for k in state_dict if "vblora_logits" in k}
+ to_return["base_model.vblora_vector_bank." + adapter_name] = state_dict[
+ "base_model.vblora_vector_bank." + adapter_name
+ ]
+ elif config.peft_type in list(PeftType):
+ prefix = PEFT_TYPE_TO_PREFIX_MAPPING[config.peft_type]
+ to_return = {k: state_dict[k] for k in state_dict if prefix in k}
+ else:
+ raise ValueError(f"Unknown PEFT type passed: {config.peft_type}")
+
+ # ADDITIONAL TRAINING MODULES / MODULES_TO_SAVE
+ for name, module in model.named_modules():
+ if isinstance(module, AuxiliaryTrainingWrapper):
+ if name.startswith("_fsdp_wrapped_module."):
+ # If FSDP is used, the state_dict is from the unwrapped model, which will result in a key mismatch if we
+ # don't remove the FSDP-specific prefix
+ name = name.removeprefix("_fsdp_wrapped_module.")
+ # Compute the module-relative state dict to make it easier for the adapter to fetch the appropriate
+ # keys that the module thinks need to be saved. We cannot rely on `.state_dict()` internally of the
+ # module since accelerators like DeepSpeed require special handling which is done for the model
+ # state dict from above but most likely not in the module itself. See #2450.
+ module_state_dict = {
+ k.removeprefix(f"{name}."): v for k, v in state_dict.items() if k.startswith(f"{name}.")
+ }
+ to_return.update(
+ {f"{name}.{k}": v for k, v in module.adapter_state_dict(adapter_name, module_state_dict).items()}
+ )
+
+ # DEAL WITH EMBEDDINGS
+ #
+ # save_embedding_layer="auto" needs to check the following logic:
+ #
+ # - when vocab size was NOT changed, embeddings should be saved only when targeted
+ # but not when
+ # - using PeftType.TRAINABLE_TOKENS
+ # - LoRA using trainable_token_indices (since their goal is to space-efficient)
+ # but
+ # - when vocab size was changed, embeddings should be saved automatically regardless to cover this
+ # scenario: 1) fine-tune embedding, 2) resize embedding, 3) train with trainable tokens
+ #
+ embedding_is_targeted = False
+ if hasattr(config, "target_modules"):
+ if isinstance(config.target_modules, str) and (config.target_modules != INCLUDE_LINEAR_LAYERS_SHORTHAND):
+ # `model` could be a PeftModel or something else like transformers/diffusers/..., in which case unwrapping is
+ # not needed.
+ _model = model.get_base_model() if hasattr(model, "get_base_model") else model
+ embedding_is_targeted = any(
+ match_target_against_key(config.target_modules, k)
+ for k, _ in _model.named_modules()
+ if any(re.match(rf"(.*\.)?{e}$", k) for e in EMBEDDING_LAYER_NAMES)
+ )
+ elif config.target_modules:
+ embedding_is_targeted = any(k in config.target_modules for k in EMBEDDING_LAYER_NAMES)
+
+ using_trainable_tokens = (
+ config.peft_type == PeftType.TRAINABLE_TOKENS or getattr(config, "trainable_token_indices", None) is not None
+ )
+
+ if save_embedding_layers == "auto" and embedding_is_targeted and not using_trainable_tokens:
+ warnings.warn("Setting `save_embedding_layers` to `True` as embedding layers found in `target_modules`.")
+ save_embedding_layers = True
+ elif save_embedding_layers == "auto":
+ vocab_size = getattr(getattr(model, "config", None), "vocab_size", None)
+ model_id = getattr(config, "base_model_name_or_path", None)
+
+ # For some models e.g. diffusers the text config file is stored in a subfolder
+ # we need to make sure we can download that config.
+ has_base_config = False
+
+ # ensure that this check is not performed in HF offline mode, see #1452
+ if model_id is not None:
+ local_config_exists = os.path.exists(os.path.join(model_id, "config.json"))
+ exists = local_config_exists or check_file_exists_on_hf_hub(model_id, "config.json")
+ if exists is None:
+ # check failed, could not determine if it exists or not
+ warnings.warn(
+ f"Could not find a config file in {model_id} - will assume that the vocabulary was not modified."
+ )
+ has_base_config = False
+ else:
+ has_base_config = exists
+
+ # check if the vocab size of the base model is different from the vocab size of the finetuned model
+ if (
+ vocab_size
+ and model_id
+ and has_base_config
+ and (vocab_size != model.config.__class__.from_pretrained(model_id).vocab_size)
+ ):
+ warnings.warn(
+ "Setting `save_embedding_layers` to `True` as the embedding layer has been resized during finetuning."
+ )
+ save_embedding_layers = True
+ else:
+ save_embedding_layers = False
+
+ if save_embedding_layers and hasattr(model, "get_input_embeddings"):
+ for layer in [model.get_input_embeddings(), model.get_output_embeddings()]:
+ # Either the layer is not targeted, then it must have been resized and needs saving. Or it is targeted and
+ # therefore has a valid base layer, then we'll save it as well.
+ if not embedding_is_targeted or has_valid_embedding_base_layer(layer):
+ embedding_module_name = get_embedding_layer_name(model, layer, embedding_is_targeted)
+ if embedding_module_name:
+ to_return.update({k: v for k, v in state_dict.items() if embedding_module_name in k})
+ elif save_embedding_layers:
+ warnings.warn("Could not identify embedding layer(s) because the model is not a 🤗 transformers model.")
+
+ # REMOVE ADAPTER NAME
+ # Ensure not to replace in the middle of the key because a module happens to have the same name as the adapter.
+ pattern = re.compile(re.escape(f".{adapter_name}") + r"$")
+
+ def remove_adapter_name(key):
+ if "." not in key:
+ # nothing to do
+ return key
+
+ if key.endswith(f".{adapter_name}"):
+ # comes from an nn.Parameter, so no .weight suffix, the adapter name is directly at the end
+ return key.removesuffix(f".{adapter_name}")
+
+ # comes from an nn.Module, i.e. the adapter name is the 2nd to last element, e.g. v_proj.lora_A.default.weight
+ key, _, suffix = key.rpartition(".") # split, e.g. v_proj.lora_A.default + weight
+
+ if (config.peft_type == PeftType.VBLORA) and suffix.startswith(f"{adapter_name}_"):
+ # special case: VBLoRA creates keys that require this replacement:
+ # base_model.model.lin0.vblora_logits_A.default_topk_indices =>
+ # base_model.model.lin0.vblora_logits_A_topk_indices
+ return key + "_" + suffix.removeprefix(f"{adapter_name}_")
+
+ key = pattern.sub("", key) # remove adapter name, e.g. v_proj.lora_A
+ return f"{key}.{suffix}" # stitch the suffix back, e.g, v_proj.lora_A.weight
+
+ to_return = {remove_adapter_name(k): v for k, v in to_return.items()}
+ return to_return
+
+
+def _find_mismatched_keys(
+ model: torch.nn.Module, peft_model_state_dict: dict[str, torch.Tensor], ignore_mismatched_sizes: bool = False
+) -> tuple[dict[str, torch.Tensor], list[tuple[str, tuple[int, ...], tuple[int, ...]]]]:
+ if not ignore_mismatched_sizes:
+ return peft_model_state_dict, []
+
+ mismatched = []
+ state_dict = model.state_dict()
+ for key, tensor in peft_model_state_dict.items():
+ if key not in state_dict:
+ continue
+
+ # see https://github.com/huggingface/transformers/blob/09f9f566de83eef1f13ee83b5a1bbeebde5c80c1/src/transformers/modeling_utils.py#L3858-L3864
+ if (state_dict[key].shape[-1] == 1) and (state_dict[key].numel() * 2 == tensor.numel()):
+ # This skips size mismatches for 4-bit weights. Two 4-bit values share an 8-bit container, causing size
+ # differences. Without matching with module type or parameter type it seems like a practical way to detect
+ # valid 4bit weights.
+ continue
+
+ if state_dict[key].shape != tensor.shape:
+ mismatched.append((key, tensor.shape, state_dict[key].shape))
+
+ for key, _, _ in mismatched:
+ del peft_model_state_dict[key]
+
+ return peft_model_state_dict, mismatched
+
+
+def _insert_adapter_name_into_state_dict(
+ state_dict: dict[str, torch.Tensor], adapter_name: str, parameter_prefix: str
+) -> dict[str, torch.Tensor]:
+ """Utility function to remap the state_dict keys to fit the PEFT model by inserting the adapter name."""
+ peft_model_state_dict = {}
+ for key, val in state_dict.items():
+ if parameter_prefix in key:
+ _, _, suffix = key.rpartition(parameter_prefix)
+ if "." in suffix:
+ suffix_to_replace = ".".join(suffix.split(".")[1:])
+ # only replace the substring if the key ends on the substring to avoid accidental replacement inside of
+ # the key if a module happens to have a name that contains the substring
+ key = re.sub(re.escape(suffix_to_replace) + r"$", f"{adapter_name}.{suffix_to_replace}", key)
+ else:
+ key = f"{key}.{adapter_name}"
+ peft_model_state_dict[key] = val
+ else:
+ peft_model_state_dict[key] = val
+ return peft_model_state_dict
+
+
+def set_peft_model_state_dict(
+ model,
+ peft_model_state_dict,
+ adapter_name="default",
+ ignore_mismatched_sizes: bool = False,
+ low_cpu_mem_usage: bool = False,
+) -> None:
+ """
+ Set the state dict of the PEFT model.
+
+ Given a PEFT `state_dict` (as returned by [`get_peft_model_state_dict`]), insert the weights into the model. The
+ model needs to have the PEFT adapters already in place (e.g. via [`inject_adapter_in_model`]).
+
+ Setting the adapter weights also takes care of re-inserting the adapter name. This name may be a different name
+ than the one originally used to train the adapter.
+
+ Args:
+ model ([`PeftModel`]):
+ The Peft model.
+ peft_model_state_dict (`dict`):
+ The state dict of the Peft model.
+ adapter_name (`str`, *optional*, defaults to `"default"`):
+ The name of the adapter whose state dict should be set.
+ ignore_mismatched_sizes (`bool`, *optional*, defaults to `False`):
+ Whether to ignore mismatched in the state dict.
+ low_cpu_mem_usage (`bool`, `optional`, defaults to `False`):
+ This argument must be `True` if the `model` was loaded with adapter weights on the meta device, e.g. after
+ calling `inject_adapter_in_model` with `low_cpu_mem_usage=True`. Otherwise, leave it as `False`.
+
+ """
+ config = model.peft_config[adapter_name]
+ state_dict = peft_model_state_dict
+
+ # handle auxiliary training wrappers such as ModulesToSaveWrapper and TrainableTokensWrapper by getting each of
+ # them and translating saved state dict key (which does not include the adapter name) to loaded state dict key
+ # (which includes the adapter name).
+ for name, module in model.named_modules():
+ if isinstance(module, AuxiliaryTrainingWrapper):
+ # Not every module has a 1:1 mapping. ModulesToSaveWrapper, for example, removes the
+ # `modules_to_save.{adapter_name}.` prefix. This prefix must be restored when loading the model from the
+ # saved state dict which is why we fetch a load key map from the wrapper.
+ key_map = module.adapter_state_dict_load_map(adapter_name)
+ if name.startswith("_fsdp_wrapped_module."):
+ # If FSDP is used, the state_dict is from the unwrapped model, which will result in a key mismatch if we
+ # don't remove the FSDP-specific prefix
+ name = name.removeprefix("_fsdp_wrapped_module.")
+ for k in key_map:
+ lookup_key = f"{name}.{k}"
+ store_key = f"{name}.{key_map[k]}"
+
+ state_dict[store_key] = peft_model_state_dict[lookup_key]
+
+ # delete the old key from the previous `state_dict = peft_model_state_dict` statement.
+ del state_dict[lookup_key]
+
+ if config.is_prompt_learning or config.peft_type == PeftType.ADAPTION_PROMPT:
+ peft_model_state_dict = state_dict
+ elif config.peft_type == PeftType.XLORA:
+ peft_model_state_dict = state_dict
+ elif config.peft_type in PEFT_TYPE_TO_PREFIX_MAPPING:
+ peft_model_state_dict = {}
+ parameter_prefix = PEFT_TYPE_TO_PREFIX_MAPPING[config.peft_type]
+ if config.peft_type == PeftType.VBLORA and config.save_only_topk_weights:
+ num_vectors, _ = model.vblora_vector_bank[adapter_name].shape
+ state_dict_keys = list(state_dict.keys())
+ for k in state_dict_keys:
+ # in save_only_topk_weights mode, only topk_indices and topk_weights are saved
+ # note that topk_indices and topk_weights serve as an efficient representation of the logits
+ # so we need to recover the logits from the topk_indices and topk_weights
+ if "_topk_indices" in k:
+ v = state_dict[k].to(torch.long)
+ original_key = k.replace("_topk_indices", "")
+ # find the corresponding topk_weights from the state_dict
+ topk_weights = state_dict[k.replace("_topk_indices", "_topk_weights")]
+ # as we only save the first k-1 topk_weights, here we recover the last one
+ topk_weights = torch.cat([topk_weights, 1 - topk_weights.sum(-1, keepdim=True)], dim=-1)
+ # convert the weights to logits
+ topk_logits = torch.log(topk_weights)
+ matrix = (
+ torch.zeros([*(topk_logits.shape[:-1]), num_vectors])
+ .fill_(float("-inf"))
+ .to(topk_logits.device)
+ .scatter(-1, v, topk_logits)
+ )
+ # add logits to the state_dict
+ state_dict[original_key] = matrix
+ # delete the topk_indices and topk_weights from the state_dict
+ del state_dict[k]
+ del state_dict[k.replace("_topk_indices", "_topk_weights")]
+
+ peft_model_state_dict = _insert_adapter_name_into_state_dict(
+ state_dict, adapter_name=adapter_name, parameter_prefix=parameter_prefix
+ )
+
+ if config.peft_type == PeftType.ADALORA:
+ rank_pattern = config.rank_pattern
+ if rank_pattern is not None:
+ model.resize_modules_by_rank_pattern(rank_pattern, adapter_name)
+ elif config.peft_type == PeftType.SHIRA:
+ if platform.system() == "Windows":
+ warnings.warn(
+ "Windows has issues saving integers into safetensors. Hence, we had converted shira_indices "
+ "to float32 before saving on Windows OS. The shira_indices will always be converted to integers "
+ "when loading."
+ )
+ for name, module in model.named_modules():
+ if hasattr(module, "shira_indices"):
+ # for k, v in module.shira_indices.items():
+ if f"{name}.shira_indices.{adapter_name}" in peft_model_state_dict:
+ shira_indices_values = peft_model_state_dict.pop(f"{name}.shira_indices.{adapter_name}")
+ # Convert shira_indices to int in case they were saved on a Windows OS and are being loaded
+ # on a Linux or a Mac-OS system. If they were saved in Linux or Mac-OS, they are already
+ # integers and the following will not affect anything.
+ module.shira_indices[adapter_name] = shira_indices_values.to(torch.int)
+ elif config.peft_type == PeftType.VERA:
+ if config.save_projection and "base_model.vera_A" not in peft_model_state_dict:
+ raise ValueError(
+ "Specified to load vera_A and vera_B from state dictionary however they were not present!"
+ )
+ elif not config.save_projection and "base_model.vera_A" in peft_model_state_dict:
+ warnings.warn(
+ "Specified to not load vera_A and vera_B from state dictionary however they are present in state"
+ " dictionary! Consider using them to ensure checkpoint loading is correct on all platforms using"
+ " `peft_config.save_projection = True`"
+ )
+ elif not config.save_projection: # and no vera_A in state dictionary
+ warnings.warn(
+ "Specified to not load vera_A and vera_B from state dictionary. This means we will be relying on"
+ " PRNG initialisation to restore these projections using `config.projection_prng_key`, which may"
+ " not be accurate on all system configurations."
+ )
+ elif config.peft_type == PeftType.LORA:
+ # Here we take care of a refactor of DoRA which changed lora_magnitude_vector from a ParameterDict to a
+ # ModuleDict with a DoraLayer instance. The old parameter is now the "weight" attribute of that layer.
+ old_dora_suffix = f"lora_magnitude_vector.{adapter_name}"
+
+ def renamed_dora_weights(k):
+ if k.endswith(old_dora_suffix):
+ k = k + ".weight"
+ return k
+
+ peft_model_state_dict = {renamed_dora_weights(k): v for k, v in peft_model_state_dict.items()}
+ elif config.peft_type == PeftType.OFT:
+ if any(".oft_r." in key for key in peft_model_state_dict):
+ raise ValueError(
+ "Trying to load old OFT checkpoint, which is no longer supported. Please install PEFT <= v0.15.2 to load it or train a new OFT adapter."
+ )
+ else:
+ raise NotImplementedError
+
+ peft_model_state_dict, mismatched_keys = _find_mismatched_keys(
+ model, peft_model_state_dict, ignore_mismatched_sizes=ignore_mismatched_sizes
+ )
+ if low_cpu_mem_usage:
+ load_result = model.load_state_dict(peft_model_state_dict, strict=False, assign=True)
+ # ensure that the correct device is set
+ for module in model.modules():
+ if hasattr(module, "_move_adapter_to_device_of_base_layer"):
+ module._move_adapter_to_device_of_base_layer(adapter_name)
+ else:
+ load_result = model.load_state_dict(peft_model_state_dict, strict=False)
+
+ if config.is_prompt_learning:
+ model.prompt_encoder[adapter_name].embedding.load_state_dict(
+ {"weight": peft_model_state_dict["prompt_embeddings"]}, strict=True
+ )
+
+ if config.peft_type == PeftType.MULTITASK_PROMPT_TUNING:
+ model.prompt_encoder[adapter_name].load_state_dict(peft_model_state_dict, strict=False)
+
+ if mismatched_keys:
+ # see https://github.com/huggingface/transformers/blob/09f9f566de83eef1f13ee83b5a1bbeebde5c80c1/src/transformers/modeling_utils.py#L4039
+ mismatched_warning = "\n".join(
+ [
+ f"- {key}: found shape {shape1} in the checkpoint and {shape2} in the model instantiated"
+ for key, shape1, shape2 in mismatched_keys
+ ]
+ )
+ msg = (
+ f"Some weights of {model.__class__.__name__} were not initialized from the model checkpoint "
+ f"and are being ignored because you passed `ignore_mismatched_sizes=True`: {mismatched_warning}."
+ )
+ warnings.warn(msg)
+ return load_result
+
+
+# TODO: remove this function, use vanilla torch.load as soon as torch < 2.6.0 is no longer supported
+def torch_load(*args, weights_only=True, **kwargs):
+ """Call torch.load and handle weights_only.
+
+ Defaults to weights_only=True to anticipate upcoming switch on the PyTorch side.
+
+ """
+ return torch.load(*args, weights_only=weights_only, **kwargs)
+
+
+def load_peft_weights(
+ model_id: str, device: Optional[str] = None, key_mapping: Optional[dict[str, str]] = None, **hf_hub_download_kwargs
+) -> dict:
+ r"""
+ A helper method to load the PEFT weights from the HuggingFace Hub or locally
+
+ Args:
+ model_id (`str`):
+ The local path to the adapter weights or the name of the adapter to load from the HuggingFace Hub.
+ device (`str`):
+ The device to load the weights onto.
+ key_mapping (dict, *optional*, defaults to None)
+ Extra mapping of PEFT `state_dict` keys applied before loading the `state_dict`. When this mapping is
+ applied, the PEFT-specific `"base_model.model"` prefix is removed beforehand and the adapter name (e.g.
+ `"default"`) is not inserted yet. Only pass this argument if you know what you're doing.
+ hf_hub_download_kwargs (`dict`):
+ Additional arguments to pass to the `hf_hub_download` method when loading from the HuggingFace Hub.
+ """
+ path = (
+ os.path.join(model_id, hf_hub_download_kwargs["subfolder"])
+ if hf_hub_download_kwargs.get("subfolder", None) is not None
+ else model_id
+ )
+
+ if device is None:
+ device = infer_device()
+
+ def get_hub_filename(use_safetensors=True):
+ weights_name = SAFETENSORS_WEIGHTS_NAME if use_safetensors else WEIGHTS_NAME
+ return (
+ os.path.join(hf_hub_download_kwargs["subfolder"], weights_name)
+ if hf_hub_download_kwargs.get("subfolder", None) is not None
+ else weights_name
+ )
+
+ if "user_agent" not in hf_hub_download_kwargs:
+ hf_hub_download_kwargs["user_agent"] = http_user_agent()
+
+ if os.path.exists(os.path.join(path, SAFETENSORS_WEIGHTS_NAME)):
+ filename = os.path.join(path, SAFETENSORS_WEIGHTS_NAME)
+ use_safetensors = True
+ elif os.path.exists(os.path.join(path, WEIGHTS_NAME)):
+ filename = os.path.join(path, WEIGHTS_NAME)
+ use_safetensors = False
+ elif huggingface_hub.constants.HF_HUB_OFFLINE:
+ # if in offline mode, check if we can find the adapter file locally
+ hub_filename = get_hub_filename(use_safetensors=True)
+ hf_hub_download_kwargs.pop("local_files_only", None)
+ try:
+ filename = hf_hub_download(model_id, hub_filename, local_files_only=True, **hf_hub_download_kwargs)
+ use_safetensors = True
+ except LocalEntryNotFoundError:
+ # Could not find safetensors, try pickle. If this also fails, it's fine to let the error be raised here, as
+ # it means that the user tried to load a non-cached model in offline mode.
+ hub_filename = get_hub_filename(use_safetensors=False)
+ filename = hf_hub_download(model_id, hub_filename, local_files_only=True, **hf_hub_download_kwargs)
+ use_safetensors = False
+ else:
+ token = hf_hub_download_kwargs.get("token", None)
+ if token is None:
+ token = hf_hub_download_kwargs.get("use_auth_token", None)
+
+ hub_filename = get_hub_filename(use_safetensors=True)
+ has_remote_safetensors_file = file_exists(
+ repo_id=model_id,
+ filename=hub_filename,
+ revision=hf_hub_download_kwargs.get("revision", None),
+ repo_type=hf_hub_download_kwargs.get("repo_type", None),
+ token=token,
+ )
+ use_safetensors = has_remote_safetensors_file
+
+ if has_remote_safetensors_file:
+ # Priority 1: load safetensors weights
+ filename = hf_hub_download(
+ model_id,
+ SAFETENSORS_WEIGHTS_NAME,
+ **hf_hub_download_kwargs,
+ )
+ else:
+ try:
+ filename = hf_hub_download(model_id, WEIGHTS_NAME, **hf_hub_download_kwargs)
+ except EntryNotFoundError:
+ raise ValueError(
+ f"Can't find weights for {model_id} in {model_id} or in the Hugging Face Hub. "
+ f"Please check that the file {WEIGHTS_NAME} or {SAFETENSORS_WEIGHTS_NAME} is present at {model_id}."
+ )
+
+ if use_safetensors:
+ if hasattr(torch.backends, "mps") and (device == torch.device("mps")):
+ adapters_weights = safe_load_file(filename, device="cpu")
+ else:
+ adapters_weights = safe_load_file(filename, device=device)
+ else:
+ adapters_weights = torch_load(filename, map_location=torch.device(device))
+
+ if not key_mapping:
+ remapped_adapters_weights = adapters_weights
+ else:
+ # See discussion in https://github.com/huggingface/transformers/pull/38627
+ # Remap adapter weight names according to the provided key_mapping.
+ remapped_adapters_weights = {}
+ for key, val in adapters_weights.items():
+ if key.startswith("base_model.model."):
+ prefix = "base_model.model."
+ elif key.startswith("base_model."):
+ prefix = "base_model."
+ else:
+ raise ValueError(
+ "An error occurred while trying to load a PEFT state_dict with key_mapping. This should not "
+ "happen. Please open an issue on https://github.com/huggingface/peft/issues and report the error."
+ )
+
+ key = key.removeprefix(prefix) # the key map assumes that there is no prefix
+ for pattern, replacement in key_mapping.items():
+ key_new, n_replace = re.subn(pattern, replacement, key)
+ # Early exit of the loop
+ if n_replace > 0:
+ key = key_new
+ break
+ key_with_prefix = f"{prefix}{key}"
+ remapped_adapters_weights[key_with_prefix] = val
+
+ return remapped_adapters_weights
diff --git a/peft/src/peft/utils/warning.py b/peft/src/peft/utils/warning.py
new file mode 100644
index 0000000000000000000000000000000000000000..3e2afeb85abf836273c3f7534eea80aebc82d256
--- /dev/null
+++ b/peft/src/peft/utils/warning.py
@@ -0,0 +1,17 @@
+# Copyright 2025-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+
+class PeftWarning(UserWarning):
+ """Base PEFT warning"""
diff --git a/peft/tests/__init__.py b/peft/tests/__init__.py
new file mode 100644
index 0000000000000000000000000000000000000000..e69de29bb2d1d6434b8b29ae775ad8c2e48c5391
diff --git a/peft/tests/bnb/test_bnb_regression.py b/peft/tests/bnb/test_bnb_regression.py
new file mode 100644
index 0000000000000000000000000000000000000000..26570fe43004de87462b92d7b012939ba639ce02
--- /dev/null
+++ b/peft/tests/bnb/test_bnb_regression.py
@@ -0,0 +1,258 @@
+# Copyright 2024-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+# This file contains very basic regression tests for bitsandbytes
+# It currently lives in the PEFT code base but should be moved to bnb eventually.
+# These tests are very simplifistic and crude on purpose. If useful, they can be cleaned up and refactored later.
+
+# Note that we make no assumptions about the correctness of the output, we only check that they didn't change
+# unexpectedly.
+
+# The expected values are generated by running the test until we have the `output`, then pass it to `bytes_from_tensor`
+
+import io
+
+import pytest
+import torch
+from transformers import AutoModelForCausalLM, AutoModelForSeq2SeqLM, BitsAndBytesConfig
+
+from peft.import_utils import is_xpu_available
+
+
+bnb = pytest.importorskip("bitsandbytes")
+
+device = torch.device("xpu") if is_xpu_available() else torch.device("cuda")
+
+
+def bytes_from_tensor(x):
+ # helper function to create the expected output for regression testing
+ f = io.BytesIO()
+ torch.save(x, f)
+ x_bytes = f.getvalue()
+ f.close()
+ return x_bytes
+
+
+############
+# OPT-125M #
+############
+
+
+@pytest.mark.skipif(not torch.cuda.is_available(), reason="No CUDA device available.")
+def test_opt_350m_4bit():
+ torch.manual_seed(0)
+ bnb_config = BitsAndBytesConfig(
+ load_in_4bit=True,
+ bnb_4bit_use_double_quant=False,
+ bnb_4bit_compute_dtype=torch.float32,
+ )
+ model = AutoModelForCausalLM.from_pretrained(
+ "facebook/opt-350m",
+ quantization_config=bnb_config,
+ torch_dtype=torch.float32,
+ )
+
+ input = torch.LongTensor([[1, 0, 1, 0, 1, 2]]).to(device)
+ with torch.no_grad():
+ output = model(input).logits[0, :3, :3].detach().cpu()
+
+ expected_bytes = b"PK\x03\x04\x00\x00\x08\x08\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x10\x00\x12\x00archive/data.pklFB\x0e\x00ZZZZZZZZZZZZZZ\x80\x02ctorch._utils\n_rebuild_tensor_v2\nq\x00((X\x07\x00\x00\x00storageq\x01ctorch\nFloatStorage\nq\x02X\x01\x00\x00\x000q\x03X\x03\x00\x00\x00cpuq\x04K\ttq\x05QK\x00K\x03K\x03\x86q\x06K\x03K\x01\x86q\x07\x89ccollections\nOrderedDict\nq\x08)Rq\ttq\nRq\x0b.PK\x07\x08\x99G\x1f\xb7\x9a\x00\x00\x00\x9a\x00\x00\x00PK\x03\x04\x00\x00\x08\x08\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x11\x00'\x00archive/byteorderFB#\x00ZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZlittlePK\x07\x08\x85=\xe3\x19\x06\x00\x00\x00\x06\x00\x00\x00PK\x03\x04\x00\x00\x08\x08\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x0e\x00>\x00archive/data/0FB:\x00ZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZ\xfc\xd3\xff\xc00\xfe\xfe\xc0&eR@\x19j\x8d@,O\x1e?\xe9\xfb\x0bA\xcc\xb5OA\xc6?\xd6@\xd3\xc2\xe0@PK\x07\x08\xdb\xad]I$\x00\x00\x00$\x00\x00\x00PK\x03\x04\x00\x00\x08\x08\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x0f\x00\x1f\x00archive/versionFB\x1b\x00ZZZZZZZZZZZZZZZZZZZZZZZZZZZ3\nPK\x07\x08\xd1\x9egU\x02\x00\x00\x00\x02\x00\x00\x00PK\x03\x04\x00\x00\x08\x08\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x1e\x002\x00archive/.data/serialization_idFB.\x00ZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZ0576858857385996278200001521679285581783PK\x07\x08\x93\x10\xf6E(\x00\x00\x00(\x00\x00\x00PK\x01\x02\x00\x00\x00\x00\x08\x08\x00\x00\x00\x00\x00\x00\x99G\x1f\xb7\x9a\x00\x00\x00\x9a\x00\x00\x00\x10\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00archive/data.pklPK\x01\x02\x00\x00\x00\x00\x08\x08\x00\x00\x00\x00\x00\x00\x85=\xe3\x19\x06\x00\x00\x00\x06\x00\x00\x00\x11\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\xea\x00\x00\x00archive/byteorderPK\x01\x02\x00\x00\x00\x00\x08\x08\x00\x00\x00\x00\x00\x00\xdb\xad]I$\x00\x00\x00$\x00\x00\x00\x0e\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00V\x01\x00\x00archive/data/0PK\x01\x02\x00\x00\x00\x00\x08\x08\x00\x00\x00\x00\x00\x00\xd1\x9egU\x02\x00\x00\x00\x02\x00\x00\x00\x0f\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\xf4\x01\x00\x00archive/versionPK\x01\x02\x00\x00\x00\x00\x08\x08\x00\x00\x00\x00\x00\x00\x93\x10\xf6E(\x00\x00\x00(\x00\x00\x00\x1e\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00R\x02\x00\x00archive/.data/serialization_idPK\x06\x06,\x00\x00\x00\x00\x00\x00\x00\x1e\x03-\x00\x00\x00\x00\x00\x00\x00\x00\x00\x05\x00\x00\x00\x00\x00\x00\x00\x05\x00\x00\x00\x00\x00\x00\x00B\x01\x00\x00\x00\x00\x00\x00\xf8\x02\x00\x00\x00\x00\x00\x00PK\x06\x07\x00\x00\x00\x00:\x04\x00\x00\x00\x00\x00\x00\x01\x00\x00\x00PK\x05\x06\x00\x00\x00\x00\x05\x00\x05\x00B\x01\x00\x00\xf8\x02\x00\x00\x00\x00"
+ expected = torch.load(io.BytesIO(expected_bytes))
+ torch.testing.assert_allclose(output, expected)
+
+
+@pytest.mark.skipif(not (torch.cuda.is_available() or is_xpu_available()), reason="No CUDA or XPU device available.")
+def test_opt_350m_8bit():
+ torch.manual_seed(0)
+ bnb_config = BitsAndBytesConfig(load_in_8bit=True)
+ model = AutoModelForCausalLM.from_pretrained(
+ "facebook/opt-350m",
+ quantization_config=bnb_config,
+ torch_dtype=torch.float32,
+ )
+
+ input = torch.LongTensor([[1, 0, 1, 0, 1, 2]]).to(device)
+ with torch.no_grad():
+ output = model(input).logits[0, :3, :3].detach().cpu()
+
+ expected_bytes = b"PK\x03\x04\x00\x00\x08\x08\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x10\x00\x12\x00archive/data.pklFB\x0e\x00ZZZZZZZZZZZZZZ\x80\x02ctorch._utils\n_rebuild_tensor_v2\nq\x00((X\x07\x00\x00\x00storageq\x01ctorch\nFloatStorage\nq\x02X\x01\x00\x00\x000q\x03X\x03\x00\x00\x00cpuq\x04K\ttq\x05QK\x00K\x03K\x03\x86q\x06K\x03K\x01\x86q\x07\x89ccollections\nOrderedDict\nq\x08)Rq\ttq\nRq\x0b.PK\x07\x08\x99G\x1f\xb7\x9a\x00\x00\x00\x9a\x00\x00\x00PK\x03\x04\x00\x00\x08\x08\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x11\x00'\x00archive/byteorderFB#\x00ZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZlittlePK\x07\x08\x85=\xe3\x19\x06\x00\x00\x00\x06\x00\x00\x00PK\x03\x04\x00\x00\x08\x08\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x0e\x00>\x00archive/data/0FB:\x00ZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZN\t\xae\xbfR.\x8d\xbf\x88\xae\x01A@\x11\xb1@v\xae\x00@o\xc2\x14AJpNA-\x08\x0cACI\xf6@PK\x07\x08\xfe\xdb\xb9o$\x00\x00\x00$\x00\x00\x00PK\x03\x04\x00\x00\x08\x08\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x0f\x00\x1f\x00archive/versionFB\x1b\x00ZZZZZZZZZZZZZZZZZZZZZZZZZZZ3\nPK\x07\x08\xd1\x9egU\x02\x00\x00\x00\x02\x00\x00\x00PK\x03\x04\x00\x00\x08\x08\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x1e\x002\x00archive/.data/serialization_idFB.\x00ZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZ0576858857385996278200001521667500867612PK\x07\x08\xb0\xb5\xcf\xfe(\x00\x00\x00(\x00\x00\x00PK\x01\x02\x00\x00\x00\x00\x08\x08\x00\x00\x00\x00\x00\x00\x99G\x1f\xb7\x9a\x00\x00\x00\x9a\x00\x00\x00\x10\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00archive/data.pklPK\x01\x02\x00\x00\x00\x00\x08\x08\x00\x00\x00\x00\x00\x00\x85=\xe3\x19\x06\x00\x00\x00\x06\x00\x00\x00\x11\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\xea\x00\x00\x00archive/byteorderPK\x01\x02\x00\x00\x00\x00\x08\x08\x00\x00\x00\x00\x00\x00\xfe\xdb\xb9o$\x00\x00\x00$\x00\x00\x00\x0e\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00V\x01\x00\x00archive/data/0PK\x01\x02\x00\x00\x00\x00\x08\x08\x00\x00\x00\x00\x00\x00\xd1\x9egU\x02\x00\x00\x00\x02\x00\x00\x00\x0f\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\xf4\x01\x00\x00archive/versionPK\x01\x02\x00\x00\x00\x00\x08\x08\x00\x00\x00\x00\x00\x00\xb0\xb5\xcf\xfe(\x00\x00\x00(\x00\x00\x00\x1e\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00R\x02\x00\x00archive/.data/serialization_idPK\x06\x06,\x00\x00\x00\x00\x00\x00\x00\x1e\x03-\x00\x00\x00\x00\x00\x00\x00\x00\x00\x05\x00\x00\x00\x00\x00\x00\x00\x05\x00\x00\x00\x00\x00\x00\x00B\x01\x00\x00\x00\x00\x00\x00\xf8\x02\x00\x00\x00\x00\x00\x00PK\x06\x07\x00\x00\x00\x00:\x04\x00\x00\x00\x00\x00\x00\x01\x00\x00\x00PK\x05\x06\x00\x00\x00\x00\x05\x00\x05\x00B\x01\x00\x00\xf8\x02\x00\x00\x00\x00"
+ expected = torch.load(io.BytesIO(expected_bytes))
+ torch.testing.assert_allclose(output, expected)
+
+
+@pytest.mark.skipif(not torch.cuda.is_available(), reason="No CUDA device available.")
+def test_opt_350m_4bit_double_quant():
+ torch.manual_seed(0)
+ bnb_config = BitsAndBytesConfig(
+ load_in_4bit=True,
+ bnb_4bit_use_double_quant=True,
+ bnb_4bit_compute_dtype=torch.float32,
+ )
+ model = AutoModelForCausalLM.from_pretrained(
+ "facebook/opt-350m",
+ quantization_config=bnb_config,
+ torch_dtype=torch.float32,
+ )
+
+ input = torch.LongTensor([[1, 0, 1, 0, 1, 2]]).to(device)
+ with torch.no_grad():
+ output = model(input).logits[0, :3, :3].detach().cpu()
+
+ expected_bytes = b"PK\x03\x04\x00\x00\x08\x08\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x10\x00\x12\x00archive/data.pklFB\x0e\x00ZZZZZZZZZZZZZZ\x80\x02ctorch._utils\n_rebuild_tensor_v2\nq\x00((X\x07\x00\x00\x00storageq\x01ctorch\nFloatStorage\nq\x02X\x01\x00\x00\x000q\x03X\x03\x00\x00\x00cpuq\x04K\ttq\x05QK\x00K\x03K\x03\x86q\x06K\x03K\x01\x86q\x07\x89ccollections\nOrderedDict\nq\x08)Rq\ttq\nRq\x0b.PK\x07\x08\x99G\x1f\xb7\x9a\x00\x00\x00\x9a\x00\x00\x00PK\x03\x04\x00\x00\x08\x08\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x11\x00'\x00archive/byteorderFB#\x00ZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZlittlePK\x07\x08\x85=\xe3\x19\x06\x00\x00\x00\x06\x00\x00\x00PK\x03\x04\x00\x00\x08\x08\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x0e\x00>\x00archive/data/0FB:\x00ZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZ.\xe3\xfe\xc0H\xaa\xfe\xc0\xf6\x9aS@\xbe\x9c\x8b@\x06\x93\x1a?\xe8&\x0cA\x9f\x0cPA\xd4\xf4\xd6@V\xa3\xe1@PK\x07\x08J\x98\xbfQ$\x00\x00\x00$\x00\x00\x00PK\x03\x04\x00\x00\x08\x08\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x0f\x00\x1f\x00archive/versionFB\x1b\x00ZZZZZZZZZZZZZZZZZZZZZZZZZZZ3\nPK\x07\x08\xd1\x9egU\x02\x00\x00\x00\x02\x00\x00\x00PK\x03\x04\x00\x00\x08\x08\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x1e\x002\x00archive/.data/serialization_idFB.\x00ZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZ0576858857385996278200001521700249059421PK\x07\x08\x9cW<\xe0(\x00\x00\x00(\x00\x00\x00PK\x01\x02\x00\x00\x00\x00\x08\x08\x00\x00\x00\x00\x00\x00\x99G\x1f\xb7\x9a\x00\x00\x00\x9a\x00\x00\x00\x10\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00archive/data.pklPK\x01\x02\x00\x00\x00\x00\x08\x08\x00\x00\x00\x00\x00\x00\x85=\xe3\x19\x06\x00\x00\x00\x06\x00\x00\x00\x11\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\xea\x00\x00\x00archive/byteorderPK\x01\x02\x00\x00\x00\x00\x08\x08\x00\x00\x00\x00\x00\x00J\x98\xbfQ$\x00\x00\x00$\x00\x00\x00\x0e\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00V\x01\x00\x00archive/data/0PK\x01\x02\x00\x00\x00\x00\x08\x08\x00\x00\x00\x00\x00\x00\xd1\x9egU\x02\x00\x00\x00\x02\x00\x00\x00\x0f\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\xf4\x01\x00\x00archive/versionPK\x01\x02\x00\x00\x00\x00\x08\x08\x00\x00\x00\x00\x00\x00\x9cW<\xe0(\x00\x00\x00(\x00\x00\x00\x1e\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00R\x02\x00\x00archive/.data/serialization_idPK\x06\x06,\x00\x00\x00\x00\x00\x00\x00\x1e\x03-\x00\x00\x00\x00\x00\x00\x00\x00\x00\x05\x00\x00\x00\x00\x00\x00\x00\x05\x00\x00\x00\x00\x00\x00\x00B\x01\x00\x00\x00\x00\x00\x00\xf8\x02\x00\x00\x00\x00\x00\x00PK\x06\x07\x00\x00\x00\x00:\x04\x00\x00\x00\x00\x00\x00\x01\x00\x00\x00PK\x05\x06\x00\x00\x00\x00\x05\x00\x05\x00B\x01\x00\x00\xf8\x02\x00\x00\x00\x00"
+ expected = torch.load(io.BytesIO(expected_bytes))
+ torch.testing.assert_allclose(output, expected)
+
+
+@pytest.mark.skipif(not torch.cuda.is_available(), reason="No CUDA device available.")
+def test_opt_350m_4bit_compute_dtype_float16():
+ torch.manual_seed(0)
+ bnb_config = BitsAndBytesConfig(
+ load_in_4bit=True,
+ bnb_4bit_use_double_quant=False,
+ bnb_4bit_compute_dtype=torch.float16,
+ )
+ model = AutoModelForCausalLM.from_pretrained(
+ "facebook/opt-350m",
+ quantization_config=bnb_config,
+ torch_dtype=torch.float32,
+ )
+
+ input = torch.LongTensor([[1, 0, 1, 0, 1, 2]]).to(device)
+ with torch.no_grad():
+ output = model(input).logits[0, :3, :3].detach().cpu()
+
+ expected_bytes = b"PK\x03\x04\x00\x00\x08\x08\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x10\x00\x12\x00archive/data.pklFB\x0e\x00ZZZZZZZZZZZZZZ\x80\x02ctorch._utils\n_rebuild_tensor_v2\nq\x00((X\x07\x00\x00\x00storageq\x01ctorch\nFloatStorage\nq\x02X\x01\x00\x00\x000q\x03X\x03\x00\x00\x00cpuq\x04K\ttq\x05QK\x00K\x03K\x03\x86q\x06K\x03K\x01\x86q\x07\x89ccollections\nOrderedDict\nq\x08)Rq\ttq\nRq\x0b.PK\x07\x08\x99G\x1f\xb7\x9a\x00\x00\x00\x9a\x00\x00\x00PK\x03\x04\x00\x00\x08\x08\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x11\x00'\x00archive/byteorderFB#\x00ZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZlittlePK\x07\x08\x85=\xe3\x19\x06\x00\x00\x00\x06\x00\x00\x00PK\x03\x04\x00\x00\x08\x08\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x0e\x00>\x00archive/data/0FB:\x00ZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZ\xfc\xd3\xff\xc00\xfe\xfe\xc0&eR@\x19j\x8d@,O\x1e?\xe9\xfb\x0bA\xcc\xb5OA\xc6?\xd6@\xd3\xc2\xe0@PK\x07\x08\xdb\xad]I$\x00\x00\x00$\x00\x00\x00PK\x03\x04\x00\x00\x08\x08\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x0f\x00\x1f\x00archive/versionFB\x1b\x00ZZZZZZZZZZZZZZZZZZZZZZZZZZZ3\nPK\x07\x08\xd1\x9egU\x02\x00\x00\x00\x02\x00\x00\x00PK\x03\x04\x00\x00\x08\x08\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x1e\x002\x00archive/.data/serialization_idFB.\x00ZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZ0576858857385996278200001521679285581783PK\x07\x08\x93\x10\xf6E(\x00\x00\x00(\x00\x00\x00PK\x01\x02\x00\x00\x00\x00\x08\x08\x00\x00\x00\x00\x00\x00\x99G\x1f\xb7\x9a\x00\x00\x00\x9a\x00\x00\x00\x10\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00archive/data.pklPK\x01\x02\x00\x00\x00\x00\x08\x08\x00\x00\x00\x00\x00\x00\x85=\xe3\x19\x06\x00\x00\x00\x06\x00\x00\x00\x11\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\xea\x00\x00\x00archive/byteorderPK\x01\x02\x00\x00\x00\x00\x08\x08\x00\x00\x00\x00\x00\x00\xdb\xad]I$\x00\x00\x00$\x00\x00\x00\x0e\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00V\x01\x00\x00archive/data/0PK\x01\x02\x00\x00\x00\x00\x08\x08\x00\x00\x00\x00\x00\x00\xd1\x9egU\x02\x00\x00\x00\x02\x00\x00\x00\x0f\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\xf4\x01\x00\x00archive/versionPK\x01\x02\x00\x00\x00\x00\x08\x08\x00\x00\x00\x00\x00\x00\x93\x10\xf6E(\x00\x00\x00(\x00\x00\x00\x1e\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00R\x02\x00\x00archive/.data/serialization_idPK\x06\x06,\x00\x00\x00\x00\x00\x00\x00\x1e\x03-\x00\x00\x00\x00\x00\x00\x00\x00\x00\x05\x00\x00\x00\x00\x00\x00\x00\x05\x00\x00\x00\x00\x00\x00\x00B\x01\x00\x00\x00\x00\x00\x00\xf8\x02\x00\x00\x00\x00\x00\x00PK\x06\x07\x00\x00\x00\x00:\x04\x00\x00\x00\x00\x00\x00\x01\x00\x00\x00PK\x05\x06\x00\x00\x00\x00\x05\x00\x05\x00B\x01\x00\x00\xf8\x02\x00\x00\x00\x00"
+ expected = torch.load(io.BytesIO(expected_bytes))
+ torch.testing.assert_allclose(output, expected)
+
+
+@pytest.mark.skipif(not (torch.cuda.is_available() or is_xpu_available()), reason="No CUDA or XPU device available.")
+def test_opt_350m_4bit_quant_type_nf4():
+ torch.manual_seed(0)
+ bnb_config = BitsAndBytesConfig(
+ load_in_4bit=True,
+ bnb_4bit_use_double_quant=False,
+ bnb_4bit_compute_dtype=torch.float32,
+ bnb_4bit_quant_type="nf4",
+ )
+ model = AutoModelForCausalLM.from_pretrained(
+ "facebook/opt-350m",
+ quantization_config=bnb_config,
+ torch_dtype=torch.float32,
+ )
+
+ input = torch.LongTensor([[1, 0, 1, 0, 1, 2]]).to(device)
+ with torch.no_grad():
+ output = model(input).logits[0, :3, :3].detach().cpu()
+
+ expected_bytes = b"PK\x03\x04\x00\x00\x08\x08\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x10\x00\x12\x00archive/data.pklFB\x0e\x00ZZZZZZZZZZZZZZ\x80\x02ctorch._utils\n_rebuild_tensor_v2\nq\x00((X\x07\x00\x00\x00storageq\x01ctorch\nFloatStorage\nq\x02X\x01\x00\x00\x000q\x03X\x03\x00\x00\x00cpuq\x04K\ttq\x05QK\x00K\x03K\x03\x86q\x06K\x03K\x01\x86q\x07\x89ccollections\nOrderedDict\nq\x08)Rq\ttq\nRq\x0b.PK\x07\x08\x99G\x1f\xb7\x9a\x00\x00\x00\x9a\x00\x00\x00PK\x03\x04\x00\x00\x08\x08\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x11\x00'\x00archive/byteorderFB#\x00ZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZlittlePK\x07\x08\x85=\xe3\x19\x06\x00\x00\x00\x06\x00\x00\x00PK\x03\x04\x00\x00\x08\x08\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x0e\x00>\x00archive/data/0FB:\x00ZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZ8\x18\xeb>\xd4\x82\x14\xbej\xbe\xff@:\xb9|@\x19\xb8\xb4?\xac\xae\x07A\x94iXA\xc8\x12\x13AHu\xdd@PK\x07\x08\xe1\xec\x0f\xf2$\x00\x00\x00$\x00\x00\x00PK\x03\x04\x00\x00\x08\x08\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x0f\x00\x1f\x00archive/versionFB\x1b\x00ZZZZZZZZZZZZZZZZZZZZZZZZZZZ3\nPK\x07\x08\xd1\x9egU\x02\x00\x00\x00\x02\x00\x00\x00PK\x03\x04\x00\x00\x08\x08\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x1e\x002\x00archive/.data/serialization_idFB.\x00ZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZ0576858857385996278200001521529449342366PK\x07\x08\xbf\xb8\xd6H(\x00\x00\x00(\x00\x00\x00PK\x01\x02\x00\x00\x00\x00\x08\x08\x00\x00\x00\x00\x00\x00\x99G\x1f\xb7\x9a\x00\x00\x00\x9a\x00\x00\x00\x10\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00archive/data.pklPK\x01\x02\x00\x00\x00\x00\x08\x08\x00\x00\x00\x00\x00\x00\x85=\xe3\x19\x06\x00\x00\x00\x06\x00\x00\x00\x11\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\xea\x00\x00\x00archive/byteorderPK\x01\x02\x00\x00\x00\x00\x08\x08\x00\x00\x00\x00\x00\x00\xe1\xec\x0f\xf2$\x00\x00\x00$\x00\x00\x00\x0e\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00V\x01\x00\x00archive/data/0PK\x01\x02\x00\x00\x00\x00\x08\x08\x00\x00\x00\x00\x00\x00\xd1\x9egU\x02\x00\x00\x00\x02\x00\x00\x00\x0f\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\xf4\x01\x00\x00archive/versionPK\x01\x02\x00\x00\x00\x00\x08\x08\x00\x00\x00\x00\x00\x00\xbf\xb8\xd6H(\x00\x00\x00(\x00\x00\x00\x1e\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00R\x02\x00\x00archive/.data/serialization_idPK\x06\x06,\x00\x00\x00\x00\x00\x00\x00\x1e\x03-\x00\x00\x00\x00\x00\x00\x00\x00\x00\x05\x00\x00\x00\x00\x00\x00\x00\x05\x00\x00\x00\x00\x00\x00\x00B\x01\x00\x00\x00\x00\x00\x00\xf8\x02\x00\x00\x00\x00\x00\x00PK\x06\x07\x00\x00\x00\x00:\x04\x00\x00\x00\x00\x00\x00\x01\x00\x00\x00PK\x05\x06\x00\x00\x00\x00\x05\x00\x05\x00B\x01\x00\x00\xf8\x02\x00\x00\x00\x00"
+ expected = torch.load(io.BytesIO(expected_bytes))
+ torch.testing.assert_allclose(output, expected)
+
+
+@pytest.mark.skipif(not (torch.cuda.is_available() or is_xpu_available()), reason="No CUDA or XPU device available.")
+def test_opt_350m_4bit_quant_storage():
+ # note: using torch.float32 instead of the default torch.uint8 does not seem to affect the result
+ torch.manual_seed(0)
+ bnb_config = BitsAndBytesConfig(
+ load_in_4bit=True,
+ bnb_4bit_use_double_quant=False,
+ bnb_4bit_compute_dtype=torch.float32,
+ bnb_4bit_quant_storage=torch.float32,
+ )
+ model = AutoModelForCausalLM.from_pretrained(
+ "facebook/opt-350m",
+ quantization_config=bnb_config,
+ torch_dtype=torch.float32,
+ )
+
+ input = torch.LongTensor([[1, 0, 1, 0, 1, 2]]).to(device)
+ with torch.no_grad():
+ output = model(input).logits[0, :3, :3].detach().cpu()
+
+ expected_bytes = b"PK\x03\x04\x00\x00\x08\x08\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x10\x00\x12\x00archive/data.pklFB\x0e\x00ZZZZZZZZZZZZZZ\x80\x02ctorch._utils\n_rebuild_tensor_v2\nq\x00((X\x07\x00\x00\x00storageq\x01ctorch\nFloatStorage\nq\x02X\x01\x00\x00\x000q\x03X\x03\x00\x00\x00cpuq\x04K\ttq\x05QK\x00K\x03K\x03\x86q\x06K\x03K\x01\x86q\x07\x89ccollections\nOrderedDict\nq\x08)Rq\ttq\nRq\x0b.PK\x07\x08\x99G\x1f\xb7\x9a\x00\x00\x00\x9a\x00\x00\x00PK\x03\x04\x00\x00\x08\x08\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x11\x00'\x00archive/byteorderFB#\x00ZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZlittlePK\x07\x08\x85=\xe3\x19\x06\x00\x00\x00\x06\x00\x00\x00PK\x03\x04\x00\x00\x08\x08\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x0e\x00>\x00archive/data/0FB:\x00ZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZ\xfc\xd3\xff\xc00\xfe\xfe\xc0&eR@\x19j\x8d@,O\x1e?\xe9\xfb\x0bA\xcc\xb5OA\xc6?\xd6@\xd3\xc2\xe0@PK\x07\x08\xdb\xad]I$\x00\x00\x00$\x00\x00\x00PK\x03\x04\x00\x00\x08\x08\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x0f\x00\x1f\x00archive/versionFB\x1b\x00ZZZZZZZZZZZZZZZZZZZZZZZZZZZ3\nPK\x07\x08\xd1\x9egU\x02\x00\x00\x00\x02\x00\x00\x00PK\x03\x04\x00\x00\x08\x08\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x1e\x002\x00archive/.data/serialization_idFB.\x00ZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZ0576858857385996278200001521679285581783PK\x07\x08\x93\x10\xf6E(\x00\x00\x00(\x00\x00\x00PK\x01\x02\x00\x00\x00\x00\x08\x08\x00\x00\x00\x00\x00\x00\x99G\x1f\xb7\x9a\x00\x00\x00\x9a\x00\x00\x00\x10\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00archive/data.pklPK\x01\x02\x00\x00\x00\x00\x08\x08\x00\x00\x00\x00\x00\x00\x85=\xe3\x19\x06\x00\x00\x00\x06\x00\x00\x00\x11\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\xea\x00\x00\x00archive/byteorderPK\x01\x02\x00\x00\x00\x00\x08\x08\x00\x00\x00\x00\x00\x00\xdb\xad]I$\x00\x00\x00$\x00\x00\x00\x0e\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00V\x01\x00\x00archive/data/0PK\x01\x02\x00\x00\x00\x00\x08\x08\x00\x00\x00\x00\x00\x00\xd1\x9egU\x02\x00\x00\x00\x02\x00\x00\x00\x0f\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\xf4\x01\x00\x00archive/versionPK\x01\x02\x00\x00\x00\x00\x08\x08\x00\x00\x00\x00\x00\x00\x93\x10\xf6E(\x00\x00\x00(\x00\x00\x00\x1e\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00R\x02\x00\x00archive/.data/serialization_idPK\x06\x06,\x00\x00\x00\x00\x00\x00\x00\x1e\x03-\x00\x00\x00\x00\x00\x00\x00\x00\x00\x05\x00\x00\x00\x00\x00\x00\x00\x05\x00\x00\x00\x00\x00\x00\x00B\x01\x00\x00\x00\x00\x00\x00\xf8\x02\x00\x00\x00\x00\x00\x00PK\x06\x07\x00\x00\x00\x00:\x04\x00\x00\x00\x00\x00\x00\x01\x00\x00\x00PK\x05\x06\x00\x00\x00\x00\x05\x00\x05\x00B\x01\x00\x00\xf8\x02\x00\x00\x00\x00"
+ expected = torch.load(io.BytesIO(expected_bytes))
+ torch.testing.assert_allclose(output, expected)
+
+
+@pytest.mark.skipif(not (torch.cuda.is_available() or is_xpu_available()), reason="No CUDA or XPU device available.")
+def test_opt_350m_8bit_threshold():
+ torch.manual_seed(0)
+ bnb_config = BitsAndBytesConfig(
+ load_in_8bit=True,
+ llm_int8_threshold=3.0, # default is 6.0
+ )
+ model = AutoModelForCausalLM.from_pretrained(
+ "facebook/opt-350m",
+ quantization_config=bnb_config,
+ torch_dtype=torch.float32,
+ )
+
+ input = torch.LongTensor([[1, 0, 1, 0, 1, 2]]).to(device)
+ with torch.no_grad():
+ output = model(input).logits[0, :3, :3].detach().cpu()
+
+ expected_bytes = b"PK\x03\x04\x00\x00\x08\x08\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x10\x00\x12\x00archive/data.pklFB\x0e\x00ZZZZZZZZZZZZZZ\x80\x02ctorch._utils\n_rebuild_tensor_v2\nq\x00((X\x07\x00\x00\x00storageq\x01ctorch\nFloatStorage\nq\x02X\x01\x00\x00\x000q\x03X\x03\x00\x00\x00cpuq\x04K\ttq\x05QK\x00K\x03K\x03\x86q\x06K\x03K\x01\x86q\x07\x89ccollections\nOrderedDict\nq\x08)Rq\ttq\nRq\x0b.PK\x07\x08\x99G\x1f\xb7\x9a\x00\x00\x00\x9a\x00\x00\x00PK\x03\x04\x00\x00\x08\x08\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x11\x00'\x00archive/byteorderFB#\x00ZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZlittlePK\x07\x08\x85=\xe3\x19\x06\x00\x00\x00\x06\x00\x00\x00PK\x03\x04\x00\x00\x08\x08\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x0e\x00>\x00archive/data/0FB:\x00ZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZR\xd5\x14\xc0\xc3\x9b\xf1\xbf \x9d\xde@D\x17\xc4@\t\xd1\x16@(\x97\x16A#TXA>\xdd\x12A\x08\x03\xfb@PK\x07\x08F\xd1\x87\xa3$\x00\x00\x00$\x00\x00\x00PK\x03\x04\x00\x00\x08\x08\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x0f\x00\x1f\x00archive/versionFB\x1b\x00ZZZZZZZZZZZZZZZZZZZZZZZZZZZ3\nPK\x07\x08\xd1\x9egU\x02\x00\x00\x00\x02\x00\x00\x00PK\x03\x04\x00\x00\x08\x08\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x1e\x002\x00archive/.data/serialization_idFB.\x00ZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZ0576858857385996278200001521620583262466PK\x07\x08\x87\x89*\x93(\x00\x00\x00(\x00\x00\x00PK\x01\x02\x00\x00\x00\x00\x08\x08\x00\x00\x00\x00\x00\x00\x99G\x1f\xb7\x9a\x00\x00\x00\x9a\x00\x00\x00\x10\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00archive/data.pklPK\x01\x02\x00\x00\x00\x00\x08\x08\x00\x00\x00\x00\x00\x00\x85=\xe3\x19\x06\x00\x00\x00\x06\x00\x00\x00\x11\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\xea\x00\x00\x00archive/byteorderPK\x01\x02\x00\x00\x00\x00\x08\x08\x00\x00\x00\x00\x00\x00F\xd1\x87\xa3$\x00\x00\x00$\x00\x00\x00\x0e\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00V\x01\x00\x00archive/data/0PK\x01\x02\x00\x00\x00\x00\x08\x08\x00\x00\x00\x00\x00\x00\xd1\x9egU\x02\x00\x00\x00\x02\x00\x00\x00\x0f\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\xf4\x01\x00\x00archive/versionPK\x01\x02\x00\x00\x00\x00\x08\x08\x00\x00\x00\x00\x00\x00\x87\x89*\x93(\x00\x00\x00(\x00\x00\x00\x1e\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00R\x02\x00\x00archive/.data/serialization_idPK\x06\x06,\x00\x00\x00\x00\x00\x00\x00\x1e\x03-\x00\x00\x00\x00\x00\x00\x00\x00\x00\x05\x00\x00\x00\x00\x00\x00\x00\x05\x00\x00\x00\x00\x00\x00\x00B\x01\x00\x00\x00\x00\x00\x00\xf8\x02\x00\x00\x00\x00\x00\x00PK\x06\x07\x00\x00\x00\x00:\x04\x00\x00\x00\x00\x00\x00\x01\x00\x00\x00PK\x05\x06\x00\x00\x00\x00\x05\x00\x05\x00B\x01\x00\x00\xf8\x02\x00\x00\x00\x00"
+ expected = torch.load(io.BytesIO(expected_bytes))
+ torch.testing.assert_allclose(output, expected)
+
+
+###########
+# FLAN-T5 #
+###########
+
+
+@pytest.mark.skipif(not (torch.cuda.is_available() or is_xpu_available()), reason="No CUDA or XPU device available.")
+def test_flan_t5_4bit():
+ torch.manual_seed(0)
+ bnb_config = BitsAndBytesConfig(
+ load_in_4bit=True,
+ bnb_4bit_use_double_quant=False,
+ bnb_4bit_compute_dtype=torch.float32,
+ )
+ model = AutoModelForSeq2SeqLM.from_pretrained(
+ "google/flan-t5-base",
+ quantization_config=bnb_config,
+ torch_dtype=torch.float32,
+ )
+
+ input = torch.LongTensor([[1, 0, 1, 0, 1, 2]]).to(device)
+ with torch.no_grad():
+ output = model.generate(input_ids=input, return_dict_in_generate=True, output_scores=True)
+ output = output.scores[0][0, :10].detach().cpu()
+
+ expected_bytes = b"PK\x03\x04\x00\x00\x08\x08\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x10\x00\x12\x00archive/data.pklFB\x0e\x00ZZZZZZZZZZZZZZ\x80\x02ctorch._utils\n_rebuild_tensor_v2\nq\x00((X\x07\x00\x00\x00storageq\x01ctorch\nFloatStorage\nq\x02X\x01\x00\x00\x000q\x03X\x03\x00\x00\x00cpuq\x04K\ntq\x05QK\x00K\n\x85q\x06K\x01\x85q\x07\x89ccollections\nOrderedDict\nq\x08)Rq\ttq\nRq\x0b.PK\x07\x08\x19\xea\x16n\x96\x00\x00\x00\x96\x00\x00\x00PK\x03\x04\x00\x00\x08\x08\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x11\x00+\x00archive/byteorderFB'\x00ZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZlittlePK\x07\x08\x85=\xe3\x19\x06\x00\x00\x00\x06\x00\x00\x00PK\x03\x04\x00\x00\x08\x08\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x0e\x00>\x00archive/data/0FB:\x00ZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZpb\x0f\xc2\x91\xa3\x85\xc0\x86\xee\x83\xc0\xae\xea\xdc?F\xad-\xc1\xe4*k\xc0\x12\x84\x86\xc09\xf9\xc8\xc0|\x861\xc0m\xf7\x0c\xc1PK\x07\x08\xf1y:\xda(\x00\x00\x00(\x00\x00\x00PK\x03\x04\x00\x00\x08\x08\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x0f\x00\x1b\x00archive/versionFB\x17\x00ZZZZZZZZZZZZZZZZZZZZZZZ3\nPK\x07\x08\xd1\x9egU\x02\x00\x00\x00\x02\x00\x00\x00PK\x03\x04\x00\x00\x08\x08\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x1e\x002\x00archive/.data/serialization_idFB.\x00ZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZ0576858857385996278200001223527302082336PK\x07\x08~n}q(\x00\x00\x00(\x00\x00\x00PK\x01\x02\x00\x00\x00\x00\x08\x08\x00\x00\x00\x00\x00\x00\x19\xea\x16n\x96\x00\x00\x00\x96\x00\x00\x00\x10\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00archive/data.pklPK\x01\x02\x00\x00\x00\x00\x08\x08\x00\x00\x00\x00\x00\x00\x85=\xe3\x19\x06\x00\x00\x00\x06\x00\x00\x00\x11\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\xe6\x00\x00\x00archive/byteorderPK\x01\x02\x00\x00\x00\x00\x08\x08\x00\x00\x00\x00\x00\x00\xf1y:\xda(\x00\x00\x00(\x00\x00\x00\x0e\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00V\x01\x00\x00archive/data/0PK\x01\x02\x00\x00\x00\x00\x08\x08\x00\x00\x00\x00\x00\x00\xd1\x9egU\x02\x00\x00\x00\x02\x00\x00\x00\x0f\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\xf8\x01\x00\x00archive/versionPK\x01\x02\x00\x00\x00\x00\x08\x08\x00\x00\x00\x00\x00\x00~n}q(\x00\x00\x00(\x00\x00\x00\x1e\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00R\x02\x00\x00archive/.data/serialization_idPK\x06\x06,\x00\x00\x00\x00\x00\x00\x00\x1e\x03-\x00\x00\x00\x00\x00\x00\x00\x00\x00\x05\x00\x00\x00\x00\x00\x00\x00\x05\x00\x00\x00\x00\x00\x00\x00B\x01\x00\x00\x00\x00\x00\x00\xf8\x02\x00\x00\x00\x00\x00\x00PK\x06\x07\x00\x00\x00\x00:\x04\x00\x00\x00\x00\x00\x00\x01\x00\x00\x00PK\x05\x06\x00\x00\x00\x00\x05\x00\x05\x00B\x01\x00\x00\xf8\x02\x00\x00\x00\x00"
+ expected = torch.load(io.BytesIO(expected_bytes))
+ torch.testing.assert_allclose(output, expected)
+
+
+@pytest.mark.skipif(not (torch.cuda.is_available() or is_xpu_available()), reason="No CUDA or XPU device available.")
+@pytest.mark.xfail # might not be reproducible depending on hardware
+def test_flan_t5_8bit():
+ torch.manual_seed(0)
+ bnb_config = BitsAndBytesConfig(load_in_8bit=True)
+ model = AutoModelForSeq2SeqLM.from_pretrained(
+ "google/flan-t5-base",
+ quantization_config=bnb_config,
+ torch_dtype=torch.float32,
+ )
+
+ input = torch.LongTensor([[1, 0, 1, 0, 1, 2]]).to(device)
+ with torch.no_grad():
+ output = model.generate(input_ids=input, return_dict_in_generate=True, output_scores=True)
+ output = output.scores[0][0, :10].detach().cpu()
+
+ expected_bytes = b"PK\x03\x04\x00\x00\x08\x08\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x10\x00\x12\x00archive/data.pklFB\x0e\x00ZZZZZZZZZZZZZZ\x80\x02ctorch._utils\n_rebuild_tensor_v2\nq\x00((X\x07\x00\x00\x00storageq\x01ctorch\nFloatStorage\nq\x02X\x01\x00\x00\x000q\x03X\x03\x00\x00\x00cpuq\x04K\ntq\x05QK\x00K\n\x85q\x06K\x01\x85q\x07\x89ccollections\nOrderedDict\nq\x08)Rq\ttq\nRq\x0b.PK\x07\x08\x19\xea\x16n\x96\x00\x00\x00\x96\x00\x00\x00PK\x03\x04\x00\x00\x08\x08\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x11\x00+\x00archive/byteorderFB'\x00ZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZlittlePK\x07\x08\x85=\xe3\x19\x06\x00\x00\x00\x06\x00\x00\x00PK\x03\x04\x00\x00\x08\x08\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x0e\x00>\x00archive/data/0FB:\x00ZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZ\xebd)\xc2\xac\x1c\xba\xc0F\x0c\xbf\xc0v\\\x88?\x9f\x7fW\xc1H\xbd\xa0\xc0\xf4\xaf\xaf\xc0@:\x02\xc1\xbcjr\xc0\xf7\x95$\xc1PK\x07\x08\x12\xcc\x86\x12(\x00\x00\x00(\x00\x00\x00PK\x03\x04\x00\x00\x08\x08\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x0f\x00\x1b\x00archive/versionFB\x17\x00ZZZZZZZZZZZZZZZZZZZZZZZ3\nPK\x07\x08\xd1\x9egU\x02\x00\x00\x00\x02\x00\x00\x00PK\x03\x04\x00\x00\x08\x08\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x1e\x002\x00archive/.data/serialization_idFB.\x00ZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZZ0576858857385996278200001226216142756281PK\x07\x08\xa0Z\xf3\xd2(\x00\x00\x00(\x00\x00\x00PK\x01\x02\x00\x00\x00\x00\x08\x08\x00\x00\x00\x00\x00\x00\x19\xea\x16n\x96\x00\x00\x00\x96\x00\x00\x00\x10\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00archive/data.pklPK\x01\x02\x00\x00\x00\x00\x08\x08\x00\x00\x00\x00\x00\x00\x85=\xe3\x19\x06\x00\x00\x00\x06\x00\x00\x00\x11\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\xe6\x00\x00\x00archive/byteorderPK\x01\x02\x00\x00\x00\x00\x08\x08\x00\x00\x00\x00\x00\x00\x12\xcc\x86\x12(\x00\x00\x00(\x00\x00\x00\x0e\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00V\x01\x00\x00archive/data/0PK\x01\x02\x00\x00\x00\x00\x08\x08\x00\x00\x00\x00\x00\x00\xd1\x9egU\x02\x00\x00\x00\x02\x00\x00\x00\x0f\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\xf8\x01\x00\x00archive/versionPK\x01\x02\x00\x00\x00\x00\x08\x08\x00\x00\x00\x00\x00\x00\xa0Z\xf3\xd2(\x00\x00\x00(\x00\x00\x00\x1e\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00\x00R\x02\x00\x00archive/.data/serialization_idPK\x06\x06,\x00\x00\x00\x00\x00\x00\x00\x1e\x03-\x00\x00\x00\x00\x00\x00\x00\x00\x00\x05\x00\x00\x00\x00\x00\x00\x00\x05\x00\x00\x00\x00\x00\x00\x00B\x01\x00\x00\x00\x00\x00\x00\xf8\x02\x00\x00\x00\x00\x00\x00PK\x06\x07\x00\x00\x00\x00:\x04\x00\x00\x00\x00\x00\x00\x01\x00\x00\x00PK\x05\x06\x00\x00\x00\x00\x05\x00\x05\x00B\x01\x00\x00\xf8\x02\x00\x00\x00\x00"
+ expected = torch.load(io.BytesIO(expected_bytes))
+ torch.testing.assert_allclose(output, expected)
diff --git a/peft/tests/conftest.py b/peft/tests/conftest.py
new file mode 100644
index 0000000000000000000000000000000000000000..866ae8853675eefcb995222970a720b9bd5c7ba1
--- /dev/null
+++ b/peft/tests/conftest.py
@@ -0,0 +1,86 @@
+# Copyright 2023-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+import logging
+import platform
+import re
+
+import pytest
+
+
+def pytest_addoption(parser):
+ parser.addoption("--regression", action="store_true", default=False, help="run regression tests")
+
+
+def pytest_configure(config):
+ config.addinivalue_line("markers", "regression: mark regression tests")
+
+ # Errors from transformers deprecations
+ logger = logging.getLogger("transformers")
+
+ class ErrorOnDeprecation(logging.Handler):
+ def emit(self, record):
+ msg = record.getMessage().lower()
+ if "deprecat" in msg or "future" in msg:
+ if "torch_dtype" not in msg:
+ # let's ignore the torch_dtype => dtype deprecation for now
+ raise AssertionError(f"**Transformers Deprecation**: {msg}")
+
+ # Add our handler
+ handler = ErrorOnDeprecation()
+ logger.addHandler(handler)
+ logger.setLevel(logging.WARNING)
+
+
+def pytest_collection_modifyitems(config, items):
+ if config.getoption("--regression"):
+ return
+
+ skip_regression = pytest.mark.skip(reason="need --regression option to run regression tests")
+ for item in items:
+ if "regression" in item.keywords:
+ item.add_marker(skip_regression)
+
+
+# TODO: remove this once support for PyTorch 2.2 (the latest one still supported by GitHub MacOS x86_64 runners) is
+# dropped, or if MacOS is removed from the test matrix, see https://github.com/huggingface/peft/issues/2431.
+# Note: the function name is fixed by the pytest plugin system, don't change it
+@pytest.hookimpl(hookwrapper=True)
+def pytest_runtest_makereport(item, call):
+ """
+ Plug into the pytest test report generation to skip a specific MacOS failure caused by transformers.
+
+ The error was introduced by https://github.com/huggingface/transformers/pull/37785, which results in torch.load
+ failing when using torch < 2.6.
+
+ Since the MacOS x86 runners need to use an older torch version, those steps are necessary to get the CI green.
+ """
+ outcome = yield
+ rep = outcome.get_result()
+ # ref:
+ # https://github.com/huggingface/transformers/blob/858ce6879a4aa7fa76a7c4e2ac20388e087ace26/src/transformers/utils/import_utils.py#L1418
+ error_msg = re.compile(r"Due to a serious vulnerability issue in `torch.load`")
+
+ # notes:
+ # - pytest uses hard-coded strings, we cannot import and use constants
+ # https://docs.pytest.org/en/stable/reference/reference.html#pytest.TestReport
+ # - errors can happen during call (running the test) but also setup (e.g. in fixtures)
+ if rep.failed and (rep.when in ("setup", "call")) and (platform.system() == "Darwin"):
+ exc_msg = str(call.excinfo.value)
+ if error_msg.search(exc_msg):
+ # turn this failure into an xfail:
+ rep.outcome = "skipped"
+ # for this attribute, see:
+ # https://github.com/pytest-dev/pytest/blob/bd6877e5874b50ee57d0f63b342a67298ee9a1c3/src/_pytest/reports.py#L266C5-L266C13
+ rep.wasxfail = "Error known to occur on MacOS with older torch versions, won't be fixed"
diff --git a/peft/tests/regression/__init__.py b/peft/tests/regression/__init__.py
new file mode 100644
index 0000000000000000000000000000000000000000..e69de29bb2d1d6434b8b29ae775ad8c2e48c5391
diff --git a/peft/tests/regression/test_regression.py b/peft/tests/regression/test_regression.py
new file mode 100644
index 0000000000000000000000000000000000000000..0e999971056118282455f5b82e98f95701fd8d17
--- /dev/null
+++ b/peft/tests/regression/test_regression.py
@@ -0,0 +1,665 @@
+# Copyright 2023-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+# Regression testing: check that checkpoints from previous PEFT versions still return the same values.
+#
+# For normal regression testing, just run:
+#
+# `pytest tests/regression/test_regression.py -s --regression`
+#
+# Add `-s` to show potentially useful debugging information. `--regression` is a custom marker that is required for
+# regression tests not to be skipped.
+#
+# To create new regression tests, run:
+# `HF_TOKEN= REGRESSION_CREATION_MODE=True pytest tests/regression/test_regression.py -s --regression`
+#
+# This will *fail* if:
+#
+# 1. the git worktree is dirty
+# 2. the git commit is not tagged
+#
+# Note: A Hugging Face Hub token is required to upload the regression artifacts to our
+# https://huggingface.co/peft-internal-testing repo. This can be done by anyone with write access to the repo but
+# apparently it is not possible to create a technical token with write access.
+#
+# This is important to ensure that the regression artifacts correspond to a specific released version of PEFT.
+# Therefore, it is recommended to checkout the tag before running the regression tests, e.g. by running:
+#
+# `git checkout v0.1.0`
+#
+# To override these checks, run:
+# ``HF_TOKEN= REGRESSION_CREATION_MODE=True REGRESSION_FORCE_MODE=True pytest tests/regression/test_regression.py -s --regression`
+#
+# In REGRESSION_CREATION_MODE, one directory will be created in tests/regression/// for each
+# test. This will contain the saved adapter, as well as the output of the test of the model for that version.
+#
+# In normal testing mode, the saved adapter and output for each version found in the directory
+# tests/regression// will be loaded and compared to the current output.
+#
+# When implementing new tests, check the existing ones as well as the description in the docstring of RegressionTester.
+
+import os
+import shutil
+import subprocess
+import sys
+import tempfile
+import unittest
+
+import pytest
+import torch
+from huggingface_hub import snapshot_download, upload_folder
+from torch import nn
+from transformers import AutoModelForCausalLM, BitsAndBytesConfig
+from transformers.pytorch_utils import Conv1D
+
+import peft
+from peft import (
+ AdaLoraConfig,
+ BOFTConfig,
+ IA3Config,
+ LNTuningConfig,
+ LoHaConfig,
+ LoKrConfig,
+ LoraConfig,
+ PeftModel,
+ VBLoRAConfig,
+ VeraConfig,
+ get_peft_model,
+)
+from peft.utils import infer_device
+
+from ..testing_utils import require_bitsandbytes, require_deterministic_for_xpu, require_non_cpu
+
+
+PEFT_VERSION = peft.__version__
+REGRESSION_DIR = tempfile.mkdtemp(prefix="peft_regression_")
+HF_TOKEN = os.environ.get("HF_TOKEN")
+# the repo has to be created manually once, it is not automatically created
+HF_REPO = "peft-internal-testing/regression-tests"
+
+
+@pytest.fixture(scope="session", autouse=True)
+def setup_tearndown():
+ # Use a pytest session-scoped fixture to setup and teardown exactly once per session. AFAICT, unittest does not
+ # provide such a feature
+
+ # download regression artifacts from Hugging Face Hub at the start
+ snapshot_download(repo_id=HF_REPO, local_dir=REGRESSION_DIR)
+ yield
+
+ # delete regression artifacts at the end of the test session; optionally, upload them first if in creation mode
+ creation_mode = strtobool(os.environ.get("REGRESSION_CREATION_MODE", "False"))
+ if creation_mode:
+ # upload the regression directory to Hugging Face Hub, will overwrite by default
+ upload_folder(
+ repo_id=HF_REPO,
+ folder_path=REGRESSION_DIR,
+ token=HF_TOKEN,
+ )
+
+ shutil.rmtree(REGRESSION_DIR)
+
+
+def strtobool(val):
+ """Copied from distutils.util"""
+ val = val.lower()
+ if val in ("y", "yes", "t", "true", "on", "1"):
+ return 1
+ elif val in ("n", "no", "f", "false", "off", "0"):
+ return 0
+ else:
+ raise ValueError(f"invalid truth value {val!r}")
+
+
+def save_output(output, name, force=False):
+ path = os.path.join(REGRESSION_DIR, name, PEFT_VERSION)
+ filename = os.path.join(path, "output.pt")
+ if os.path.exists(filename) and not force:
+ return
+
+ if not os.path.exists(path):
+ os.makedirs(path)
+
+ if os.path.exists(filename) and force:
+ print(f"Overriding existing output in {filename}", file=sys.stderr)
+
+ torch.save(output, filename)
+
+
+def save_model(model, name, force=False):
+ path = os.path.join(REGRESSION_DIR, name, PEFT_VERSION)
+ filename = os.path.join(path, peft.utils.SAFETENSORS_WEIGHTS_NAME)
+ if os.path.exists(filename) and not force:
+ return
+
+ if not os.path.exists(path):
+ os.makedirs(path)
+
+ if os.path.exists(filename) and force:
+ print(f"Overriding existing model in {path}", file=sys.stderr)
+
+ model.save_pretrained(path)
+
+
+def load_output(name):
+ filename = os.path.join(REGRESSION_DIR, name, "output.pt")
+ return torch.load(filename, map_location=infer_device())
+
+
+@pytest.mark.regression
+class RegressionTester(unittest.TestCase):
+ """Base class for regression testing
+
+ Child classes must call assert_results_equal_or_store and pass the model outtput, as well as a unique name that
+ describes the setting (e.g. "lora_opt-350m_bnb_4bit"). They also need to implement get_output(model) to get the
+ model output, and load_base_model(name) to load the base model. Don't forget to fix the seed in load_base_model.
+ """
+
+ torch_device = infer_device()
+
+ def setUp(self):
+ self.tol = 1e-4
+ self.creation_mode = strtobool(os.environ.get("REGRESSION_CREATION_MODE", "False"))
+ self.force_mode = strtobool(os.environ.get("REGRESSION_FORCE_MODE", "False"))
+ if self.force_mode and not self.creation_mode:
+ raise RuntimeError("REGRESSION_FORCE_MODE can only be used together with REGRESSION_CREATION_MODE")
+ if self.creation_mode:
+ self.check_clean_git_status(self.force_mode)
+ if HF_TOKEN is None:
+ raise RuntimeError("HF_TOKEN environment variable must be set in creation mode")
+
+ def fix_seed(self):
+ torch.manual_seed(0)
+
+ def check_clean_git_status(self, force):
+ """Ensure that worktree is not dirty and version tag is checked out"""
+ # check that the worktree is clean
+ try:
+ subprocess.check_output(["git", "diff", "--quiet", "HEAD"])
+ except subprocess.CalledProcessError as exc:
+ if force:
+ print("Overriding despite dirty git worktree", file=sys.stderr)
+ else:
+ raise RuntimeError("Git worktree is dirty") from exc
+
+ # check that the commit is tagged
+ try:
+ subprocess.check_output(["git", "describe", "--exact-match", "HEAD"])
+ except subprocess.CalledProcessError as exc:
+ if force:
+ print("Overriding despite non-tagged commit", file=sys.stderr)
+ else:
+ raise RuntimeError("Git commit is not tagged") from exc
+
+ @require_deterministic_for_xpu
+ def assert_results_equal_or_store(self, model, name):
+ """Check if the outputs are the same or save the outputs if in creation mode."""
+ if not self.creation_mode: # normal regression testing mode
+ self._assert_results_equal(name)
+ else:
+ output = self.get_output(model)
+ if not torch.isfinite(output).all():
+ raise RuntimeError(f"Model output for {name} is not finite")
+
+ output2 = self.get_output(model)
+ if not torch.allclose(output, output2):
+ raise RuntimeError(f"Model output for {name} is not deterministic")
+
+ save_output(output, name, force=self.force_mode)
+ save_model(model, name, force=self.force_mode)
+
+ def _assert_results_equal(self, name):
+ path = os.path.join(REGRESSION_DIR, name)
+ versions = os.listdir(path)
+ for version in versions: # each directory corresponds to a version
+ output_loaded = load_output(os.path.join(name, version))
+ base_model = self.load_base_model()
+ model = PeftModel.from_pretrained(base_model, os.path.join(path, version))
+ output = self.get_output(model)
+ assert torch.allclose(output_loaded, output, atol=self.tol, rtol=self.tol)
+
+ def get_output(self, model):
+ raise NotImplementedError
+
+ def load_base_model(self):
+ raise NotImplementedError
+
+
+##############
+# TEST CASES #
+##############
+
+
+class TestMlp(RegressionTester):
+ def get_output(self, model):
+ input = torch.arange(90).reshape(9, 10).to(self.torch_device)
+ with torch.inference_mode():
+ output = model(input)
+ return output
+
+ def load_base_model(self):
+ class MLP(nn.Module):
+ def __init__(self, bias=True):
+ super().__init__()
+ self.lin0 = nn.Linear(10, 20, bias=bias)
+ self.relu = nn.ReLU()
+ self.lin1 = nn.Linear(20, 2, bias=bias)
+ self.sm = nn.LogSoftmax(dim=-1)
+
+ def forward(self, X):
+ X = X.float()
+ X = self.lin0(X)
+ X = self.relu(X)
+ X = self.lin1(X)
+ X = self.sm(X)
+ return X
+
+ self.fix_seed()
+ return MLP().to(self.torch_device)
+
+ def test_lora(self):
+ base_model = self.load_base_model()
+ config = LoraConfig(
+ r=8,
+ init_lora_weights=False,
+ target_modules=["lin0"],
+ )
+ model = get_peft_model(base_model, config)
+ self.assert_results_equal_or_store(model, "lora_mlp")
+
+ def test_lora_dora(self):
+ base_model = self.load_base_model()
+ config = LoraConfig(
+ r=8,
+ init_lora_weights=False,
+ target_modules=["lin0"],
+ use_dora=True,
+ )
+ model = get_peft_model(base_model, config)
+ self.assert_results_equal_or_store(model, "lora_dora_mlp")
+
+ def test_adalora(self):
+ base_model = self.load_base_model()
+ config = AdaLoraConfig(
+ r=8,
+ init_lora_weights=False,
+ target_modules=["lin0"],
+ total_step=1,
+ )
+ model = get_peft_model(base_model, config)
+ self.assert_results_equal_or_store(model, "adalora_mlp")
+
+ def test_ia3(self):
+ base_model = self.load_base_model()
+ config = IA3Config(
+ init_ia3_weights=False,
+ target_modules=["lin0"],
+ feedforward_modules=["lin0"],
+ )
+ model = get_peft_model(base_model, config)
+ self.assert_results_equal_or_store(model, "ia3_mlp")
+
+ def test_ia3_no_ff(self):
+ base_model = self.load_base_model()
+ config = IA3Config(
+ init_ia3_weights=False,
+ target_modules=["lin0"],
+ feedforward_modules=[],
+ )
+ model = get_peft_model(base_model, config)
+ self.assert_results_equal_or_store(model, "ia3_no_ff_mlp")
+
+ def test_loha(self):
+ # TODO
+ self.skipTest("Skipping LoHa for now because init is not seedable")
+ base_model = self.load_base_model()
+ config = LoHaConfig(
+ r=8,
+ init_weights=False,
+ target_modules=["lin0"],
+ )
+ model = get_peft_model(base_model, config)
+ self.assert_results_equal_or_store(model, "loha_mlp")
+
+ def test_lokr(self):
+ # TODO
+ self.skipTest("Skipping LoKr for now because init is not seedable")
+ base_model = self.load_base_model()
+ config = LoKrConfig(
+ r=8,
+ target_modules=["lin0"],
+ )
+ model = get_peft_model(base_model, config)
+ self.assert_results_equal_or_store(model, "lokr_mlp")
+
+ def test_lora_modules_to_save(self):
+ base_model = self.load_base_model()
+ config = LoraConfig(
+ r=8,
+ init_lora_weights=False,
+ target_modules=["lin0"],
+ modules_to_save=["lin1"],
+ )
+ model = get_peft_model(base_model, config)
+ self.assert_results_equal_or_store(model, "lora_mlp_modules_to_save")
+
+ def test_boft(self):
+ base_model = self.load_base_model()
+ config = BOFTConfig(
+ boft_block_size=2,
+ target_modules=["lin0"],
+ )
+ model = get_peft_model(base_model, config)
+ self.assert_results_equal_or_store(model, "boft_mlp")
+
+ def test_ln_tuning(self):
+ base_model = self.load_base_model()
+ config = LNTuningConfig(target_modules=["lin0"])
+ model = get_peft_model(base_model, config)
+ self.assert_results_equal_or_store(model, "ln_tuning_mlp")
+
+ def test_vera_tuning(self):
+ base_model = self.load_base_model()
+ config = VeraConfig(target_modules=["lin0"])
+ model = get_peft_model(base_model, config)
+ self.assert_results_equal_or_store(model, "vera_tuning_mlp")
+
+ def test_vblora_tuning(self):
+ base_model = self.load_base_model()
+ config = VBLoRAConfig(
+ vector_length=1,
+ num_vectors=2,
+ target_modules=["lin0"],
+ )
+ model = get_peft_model(base_model, config)
+ self.assert_results_equal_or_store(model, "vblora_tuning_mlp")
+
+
+class TestLoraEmbConv1D(RegressionTester):
+ def get_output(self, model):
+ input = torch.arange(90).reshape(9, 10).to(self.torch_device)
+ with torch.inference_mode():
+ output = model(input)
+ return output
+
+ def load_base_model(self):
+ class ModelEmbConv1D(nn.Module):
+ def __init__(self):
+ super().__init__()
+ self.emb = nn.Embedding(100, 5)
+ self.conv1d = Conv1D(1, 5)
+ self.relu = nn.ReLU()
+ self.flat = nn.Flatten()
+ self.lin0 = nn.Linear(10, 2)
+ self.sm = nn.LogSoftmax(dim=-1)
+
+ def forward(self, X):
+ X = self.emb(X)
+ X = self.conv1d(X)
+ X = self.relu(X)
+ X = self.flat(X)
+ X = self.lin0(X)
+ X = self.sm(X)
+ return X
+
+ self.fix_seed()
+ return ModelEmbConv1D().to(self.torch_device)
+
+ def test_lora(self):
+ base_model = self.load_base_model()
+ config = LoraConfig(
+ r=8,
+ init_lora_weights=False,
+ target_modules=["emb", "conv1d"],
+ )
+ model = get_peft_model(base_model, config)
+ self.assert_results_equal_or_store(model, "lora_emb_conv1d")
+
+
+class TestLoraConv2D(RegressionTester):
+ def get_output(self, model):
+ input = torch.arange(90).reshape(9, 10).to(self.torch_device)
+ with torch.inference_mode():
+ output = model(input)
+ return output
+
+ def load_base_model(self):
+ class ModelConv2D(nn.Module):
+ def __init__(self):
+ super().__init__()
+ self.conv2d = nn.Conv2d(5, 10, 3)
+ self.relu = nn.ReLU()
+ self.flat = nn.Flatten()
+ self.lin0 = nn.Linear(10, 2)
+ self.sm = nn.LogSoftmax(dim=-1)
+
+ def forward(self, X):
+ X = X.float().reshape(2, 5, 3, 3)
+ X = self.conv2d(X)
+ X = self.relu(X)
+ X = self.flat(X)
+ X = self.lin0(X)
+ X = self.sm(X)
+ return X
+
+ self.fix_seed()
+ return ModelConv2D().to(self.torch_device)
+
+ def test_lora(self):
+ base_model = self.load_base_model()
+ config = LoraConfig(
+ r=8,
+ init_lora_weights=False,
+ target_modules=["conv2d"],
+ )
+ model = get_peft_model(base_model, config)
+ self.assert_results_equal_or_store(model, "lora_conv2d")
+
+ def test_ia3(self):
+ base_model = self.load_base_model()
+ config = IA3Config(
+ init_ia3_weights=False,
+ target_modules=["conv2d"],
+ feedforward_modules=["conv2d"],
+ )
+ model = get_peft_model(base_model, config)
+ self.assert_results_equal_or_store(model, "ia3_conv2d")
+
+ def test_loha(self):
+ # TODO
+ self.skipTest("Skipping LoHa for now because init is not seedable")
+ base_model = self.load_base_model()
+ config = LoHaConfig(
+ r=8,
+ init_weights=False,
+ target_modules=["conv2d"],
+ )
+ model = get_peft_model(base_model, config)
+ self.assert_results_equal_or_store(model, "loha_conv2d")
+
+ def test_lokr(self):
+ # TODO
+ self.skipTest("Skipping LoKr for now because init is not seedable")
+ base_model = self.load_base_model()
+ config = LoKrConfig(
+ r=8,
+ init_weights=False,
+ target_modules=["conv2d"],
+ )
+ model = get_peft_model(base_model, config)
+ self.assert_results_equal_or_store(model, "lokr_conv2d")
+
+ def test_boft(self):
+ base_model = self.load_base_model()
+ config = BOFTConfig(
+ boft_block_size=3,
+ target_modules=["conv2d"],
+ )
+ model = get_peft_model(base_model, config)
+ self.assert_results_equal_or_store(model, "boft_conv2d")
+
+
+class TestOpt(RegressionTester):
+ def get_output(self, model):
+ input = torch.LongTensor([[1, 0, 1, 0, 1, 2]]).to(self.torch_device)
+ with torch.inference_mode():
+ output = model(input).logits
+ return output
+
+ def load_base_model(self):
+ self.fix_seed()
+ return AutoModelForCausalLM.from_pretrained("facebook/opt-350m").to(self.torch_device)
+
+ def test_lora(self):
+ base_model = self.load_base_model()
+ config = LoraConfig(
+ r=8,
+ init_lora_weights=False,
+ )
+ model = get_peft_model(base_model, config)
+ self.assert_results_equal_or_store(model, "lora_opt-350m")
+
+ def test_adalora(self):
+ base_model = self.load_base_model()
+ config = AdaLoraConfig(
+ r=8,
+ init_lora_weights=False,
+ total_step=1,
+ )
+ model = get_peft_model(base_model, config)
+ self.assert_results_equal_or_store(model, "adalora_opt-350m")
+
+ def test_ia3(self):
+ base_model = self.load_base_model()
+ config = IA3Config(init_ia3_weights=False)
+ model = get_peft_model(base_model, config)
+ self.assert_results_equal_or_store(model, "ia3_opt-350m")
+
+
+@require_non_cpu
+@require_bitsandbytes
+class TestOpt8bitBnb(RegressionTester):
+ def get_output(self, model):
+ input = torch.LongTensor([[1, 0, 1, 0, 1, 2]]).to(self.torch_device)
+ with torch.inference_mode():
+ output = model(input).logits
+ return output
+
+ def load_base_model(self):
+ self.fix_seed()
+ model = AutoModelForCausalLM.from_pretrained(
+ "facebook/opt-350m",
+ quantization_config=BitsAndBytesConfig(load_in_8bit=True),
+ )
+ return model
+
+ def test_lora_8bit(self):
+ # Warning: bnb results can vary significantly depending on the GPU. Therefore, if there is a change in GPU used
+ # in the CI, the test can fail without any code change. In that case, delete the regression artifact and create
+ # a new one using the new GPU.
+ base_model = self.load_base_model()
+ config = LoraConfig(
+ r=8,
+ init_lora_weights=False,
+ )
+ model = get_peft_model(base_model, config)
+ self.assert_results_equal_or_store(model, "lora_opt-350m_bnb_8bit")
+
+ def test_adalora(self):
+ # TODO
+ self.skipTest(
+ "Skipping AdaLora for now, getting TypeError: unsupported operand type(s) for +=: 'dict' and 'Tensor'"
+ )
+ # Warning: bnb results can vary significantly depending on the GPU. Therefore, if there is a change in GPU used
+ # in the CI, the test can fail without any code change. In that case, delete the regression artifact and create
+ # a new one using the new GPU.
+ base_model = self.load_base_model()
+ config = AdaLoraConfig(
+ init_r=6,
+ target_r=4,
+ tinit=50,
+ tfinal=100,
+ total_step=200,
+ deltaT=5,
+ beta1=0.3,
+ beta2=0.3,
+ orth_reg_weight=0.2,
+ lora_alpha=32,
+ lora_dropout=0.05,
+ bias="none",
+ task_type="CAUSAL_LM",
+ )
+ model = get_peft_model(base_model, config)
+ self.assert_results_equal_or_store(model, "adalora_opt-350m_8bit")
+
+
+@require_non_cpu
+@require_bitsandbytes
+class TestOpt4bitBnb(RegressionTester):
+ def get_output(self, model):
+ input = torch.LongTensor([[1, 0, 1, 0, 1, 2]]).to(self.torch_device)
+ with torch.inference_mode():
+ output = model(input).logits
+ return output
+
+ def load_base_model(self):
+ self.fix_seed()
+ bnb_config = BitsAndBytesConfig(
+ load_in_4bit=True,
+ bnb_4bit_use_double_quant=False,
+ bnb_4bit_compute_dtype=torch.float32,
+ )
+ model = AutoModelForCausalLM.from_pretrained(
+ "facebook/opt-350m",
+ quantization_config=bnb_config,
+ torch_dtype=torch.float32,
+ )
+ return model
+
+ def test_lora_4bit(self):
+ # Warning: bnb results can vary significantly depending on the GPU. Therefore, if there is a change in GPU used
+ # in the CI, the test can fail without any code change. In that case, delete the regression artifact and create
+ # a new one using the new GPU.
+ base_model = self.load_base_model()
+ config = LoraConfig(
+ r=8,
+ init_lora_weights=False,
+ )
+ model = get_peft_model(base_model, config)
+ self.assert_results_equal_or_store(model, "lora_opt-350m_bnb_4bit")
+
+ def test_adalora(self):
+ # TODO
+ self.skipTest("Skipping AdaLora for now because of a bug, see #1113")
+ # Warning: bnb results can vary significantly depending on the GPU. Therefore, if there is a change in GPU used
+ # in the CI, the test can fail without any code change. In that case, delete the regression artifact and create
+ # a new one using the new GPU.
+ base_model = self.load_base_model()
+ config = AdaLoraConfig(
+ init_r=6,
+ target_r=4,
+ tinit=50,
+ tfinal=100,
+ total_step=200,
+ deltaT=5,
+ beta1=0.3,
+ beta2=0.3,
+ orth_reg_weight=0.2,
+ lora_alpha=32,
+ lora_dropout=0.05,
+ bias="none",
+ task_type="CAUSAL_LM",
+ )
+ model = get_peft_model(base_model, config)
+ self.assert_results_equal_or_store(model, "adalora_opt-350m_4bit")
diff --git a/peft/tests/test_adaption_prompt.py b/peft/tests/test_adaption_prompt.py
new file mode 100644
index 0000000000000000000000000000000000000000..09e020e0f3918a26e832f0d8ce9cc84cb8ec1469
--- /dev/null
+++ b/peft/tests/test_adaption_prompt.py
@@ -0,0 +1,416 @@
+# Copyright 2023-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+import os
+import tempfile
+
+import pytest
+import torch
+from torch.testing import assert_close
+from transformers import AutoModelForCausalLM
+
+from peft import get_peft_model
+from peft.peft_model import PeftModel
+from peft.tuners.adaption_prompt import AdaptionPromptConfig
+from peft.utils import infer_device
+from peft.utils.other import prepare_model_for_kbit_training
+from peft.utils.save_and_load import get_peft_model_state_dict
+
+
+MODELS_TO_TEST = [
+ "hf-internal-testing/tiny-random-gpt2",
+ "trl-internal-testing/tiny-random-LlamaForCausalLM",
+ "hf-internal-testing/tiny-random-MistralForCausalLM",
+]
+
+
+class TestAdaptionPrompt:
+ """
+ Tests for the AdaptionPrompt model.
+
+ Some of these tests were adapted from `test_peft_model.py` (which has been refactored since), but since we haven't
+ checked in the test checkpoints for Llama into `hf-internal-testing`, we separate them for now.
+ """
+
+ transformers_class = AutoModelForCausalLM
+ torch_device = infer_device()
+
+ @pytest.mark.parametrize("model_id", MODELS_TO_TEST)
+ def test_attributes(self, model_id):
+ model = self.transformers_class.from_pretrained(model_id)
+ config = AdaptionPromptConfig(adapter_layers=1, adapter_len=4)
+ model = get_peft_model(model, config)
+
+ assert hasattr(model, "save_pretrained")
+ assert hasattr(model, "from_pretrained")
+ assert hasattr(model, "push_to_hub")
+
+ @pytest.mark.parametrize("model_id", MODELS_TO_TEST)
+ def test_prepare_for_training(self, model_id):
+ model = self.transformers_class.from_pretrained(model_id)
+ config = AdaptionPromptConfig(adapter_layers=1, adapter_len=4, task_type="CAUSAL_LM")
+ model = get_peft_model(model, config)
+ model = model.to(self.torch_device)
+
+ dummy_input = torch.LongTensor([[1, 1, 1]]).to(self.torch_device)
+ dummy_output = model.get_input_embeddings()(dummy_input)
+
+ assert not dummy_output.requires_grad
+
+ @pytest.mark.parametrize("model_id", MODELS_TO_TEST)
+ def test_prepare_for_int8_training(self, model_id):
+ model = self.transformers_class.from_pretrained(model_id)
+ model = prepare_model_for_kbit_training(model)
+ model = model.to(self.torch_device)
+
+ for param in model.parameters():
+ assert not param.requires_grad
+
+ config = AdaptionPromptConfig(adapter_layers=1, adapter_len=4, task_type="CAUSAL_LM")
+ model = get_peft_model(model, config)
+
+ # For backward compatibility
+ if hasattr(model, "enable_input_require_grads"):
+ model.enable_input_require_grads()
+ else:
+
+ def make_inputs_require_grad(module, input, output):
+ output.requires_grad_(True)
+
+ model.get_input_embeddings().register_forward_hook(make_inputs_require_grad)
+
+ dummy_input = torch.LongTensor([[1, 1, 1]]).to(self.torch_device)
+ dummy_output = model.get_input_embeddings()(dummy_input)
+
+ assert dummy_output.requires_grad
+
+ @pytest.mark.parametrize("model_id", MODELS_TO_TEST)
+ def test_save_pretrained_regression(self, model_id):
+ seed = 420
+ torch.manual_seed(seed)
+ model = self.transformers_class.from_pretrained(model_id)
+ config = AdaptionPromptConfig(adapter_layers=2, adapter_len=4, task_type="CAUSAL_LM")
+ model = get_peft_model(model, config)
+ model = model.to(self.torch_device)
+
+ with tempfile.TemporaryDirectory() as tmp_dirname:
+ model.save_pretrained(tmp_dirname, safe_serialization=False)
+
+ torch.manual_seed(seed)
+ model_from_pretrained = self.transformers_class.from_pretrained(model_id)
+ model_from_pretrained = PeftModel.from_pretrained(model_from_pretrained, tmp_dirname)
+
+ # check if the state dicts are equal
+ state_dict = get_peft_model_state_dict(model)
+ state_dict_from_pretrained = get_peft_model_state_dict(model_from_pretrained)
+
+ # check if same keys
+ assert state_dict.keys() == state_dict_from_pretrained.keys()
+
+ # Check that the number of saved parameters is 4 -- 2 layers of (tokens and gate).
+ assert len(state_dict) == 4
+
+ # check if tensors equal
+ for key in state_dict.keys():
+ assert torch.allclose(
+ state_dict[key].to(self.torch_device), state_dict_from_pretrained[key].to(self.torch_device)
+ )
+
+ # check if `adapter_model.bin` is present
+ assert os.path.exists(os.path.join(tmp_dirname, "adapter_model.bin"))
+
+ # check if `adapter_config.json` is present
+ assert os.path.exists(os.path.join(tmp_dirname, "adapter_config.json"))
+
+ # check if `model.safetensors` is not present
+ assert not os.path.exists(os.path.join(tmp_dirname, "model.safetensors"))
+
+ # check if `config.json` is not present
+ assert not os.path.exists(os.path.join(tmp_dirname, "config.json"))
+
+ @pytest.mark.parametrize("model_id", MODELS_TO_TEST)
+ def test_save_pretrained(self, model_id):
+ seed = 420
+ torch.manual_seed(seed)
+ model = self.transformers_class.from_pretrained(model_id)
+ config = AdaptionPromptConfig(adapter_layers=2, adapter_len=4, task_type="CAUSAL_LM")
+ model = get_peft_model(model, config)
+ model = model.to(self.torch_device)
+
+ with tempfile.TemporaryDirectory() as tmp_dirname:
+ model.save_pretrained(tmp_dirname)
+
+ torch.manual_seed(seed)
+ model_from_pretrained = self.transformers_class.from_pretrained(model_id)
+ model_from_pretrained = PeftModel.from_pretrained(model_from_pretrained, tmp_dirname)
+
+ # check if the state dicts are equal
+ state_dict = get_peft_model_state_dict(model)
+ state_dict_from_pretrained = get_peft_model_state_dict(model_from_pretrained)
+
+ # check if same keys
+ assert state_dict.keys() == state_dict_from_pretrained.keys()
+
+ # Check that the number of saved parameters is 4 -- 2 layers of (tokens and gate).
+ assert len(state_dict) == 4
+
+ # check if tensors equal
+ for key in state_dict.keys():
+ assert torch.allclose(
+ state_dict[key].to(self.torch_device), state_dict_from_pretrained[key].to(self.torch_device)
+ )
+
+ # check if `adapter_model.bin` is present
+ assert os.path.exists(os.path.join(tmp_dirname, "adapter_model.safetensors"))
+
+ # check if `adapter_config.json` is present
+ assert os.path.exists(os.path.join(tmp_dirname, "adapter_config.json"))
+
+ # check if `model.safetensors` is not present
+ assert not os.path.exists(os.path.join(tmp_dirname, "model.safetensors"))
+
+ # check if `config.json` is not present
+ assert not os.path.exists(os.path.join(tmp_dirname, "config.json"))
+
+ @pytest.mark.parametrize("model_id", MODELS_TO_TEST)
+ def test_save_pretrained_selected_adapters(self, model_id):
+ seed = 420
+ torch.manual_seed(seed)
+ model = self.transformers_class.from_pretrained(model_id)
+ config = AdaptionPromptConfig(adapter_layers=2, adapter_len=4, task_type="CAUSAL_LM")
+ model = get_peft_model(model, config)
+ model = model.to(self.torch_device)
+
+ new_adapter_config = AdaptionPromptConfig(adapter_layers=2, adapter_len=4, task_type="CAUSAL_LM")
+ model.add_adapter("new_adapter", new_adapter_config)
+
+ with tempfile.TemporaryDirectory() as tmp_dirname:
+ model.save_pretrained(tmp_dirname)
+
+ torch.manual_seed(seed)
+ model_from_pretrained = self.transformers_class.from_pretrained(model_id)
+ model_from_pretrained = PeftModel.from_pretrained(model_from_pretrained, tmp_dirname)
+
+ model_from_pretrained.load_adapter(tmp_dirname, "new_adapter")
+
+ # check if the state dicts are equal
+ state_dict = get_peft_model_state_dict(model)
+ state_dict_from_pretrained = get_peft_model_state_dict(model_from_pretrained)
+
+ # check if same keys
+ assert state_dict.keys() == state_dict_from_pretrained.keys()
+
+ # Check that the number of saved parameters is 4 -- 2 layers of (tokens and gate).
+ assert len(state_dict) == 4
+
+ # check if tensors equal
+ for key in state_dict.keys():
+ assert torch.allclose(
+ state_dict[key].to(self.torch_device), state_dict_from_pretrained[key].to(self.torch_device)
+ )
+
+ # check if `adapter_model.bin` is present
+ assert os.path.exists(os.path.join(tmp_dirname, "adapter_model.safetensors"))
+
+ # check if `adapter_config.json` is present
+ assert os.path.exists(os.path.join(tmp_dirname, "adapter_config.json"))
+
+ # check if `model.safetensors` is not present
+ assert not os.path.exists(os.path.join(tmp_dirname, "model.safetensors"))
+
+ # check if `config.json` is not present
+ assert not os.path.exists(os.path.join(tmp_dirname, "config.json"))
+
+ @pytest.mark.parametrize("model_id", MODELS_TO_TEST)
+ def test_generate(self, model_id):
+ model = self.transformers_class.from_pretrained(model_id)
+ config = AdaptionPromptConfig(adapter_layers=2, adapter_len=4, task_type="CAUSAL_LM")
+ model = get_peft_model(model, config)
+ model = model.to(self.torch_device)
+
+ input_ids = torch.LongTensor([[1, 1, 1], [2, 1, 2]]).to(self.torch_device)
+ attention_mask = torch.LongTensor([[1, 1, 1], [1, 0, 1]]).to(self.torch_device)
+
+ # check if `generate` works
+ _ = model.generate(input_ids=input_ids, attention_mask=attention_mask)
+
+ # check if `generate` works if positional arguments are passed
+ _ = model.generate(input_ids, attention_mask=attention_mask)
+
+ @pytest.mark.parametrize("model_id", MODELS_TO_TEST)
+ def test_sequence_adapter_ops(self, model_id):
+ """Test sequence of adapter operations."""
+ # Test input data.
+ input_ids = torch.LongTensor([[1, 1, 1], [2, 1, 2]]).to(self.torch_device)
+ target_ids = torch.LongTensor([[0, 0, 0], [0, 0, 0]]).to(self.torch_device)
+ attention_mask = torch.LongTensor([[1, 1, 1], [1, 0, 1]]).to(self.torch_device)
+
+ # Create original llama model.
+ original = self.transformers_class.from_pretrained(model_id)
+ original = original.to(self.torch_device)
+ original_before = original(input_ids=input_ids, attention_mask=attention_mask)
+
+ # Get AdaptionPrompt model.
+ adapted = get_peft_model(
+ original, AdaptionPromptConfig(adapter_layers=2, adapter_len=4, task_type="CAUSAL_LM")
+ )
+ adapted = adapted.to(self.torch_device)
+ default_before = adapted(input_ids=input_ids, attention_mask=attention_mask, labels=target_ids)
+
+ # Test zero-init: The logits should be exactly the same.
+ assert_close(original_before.logits, default_before.logits, rtol=0, atol=0)
+
+ # Single fine-tuning step on "default" adapter.
+ optimizer = torch.optim.SGD(adapted.parameters(), lr=1)
+ optimizer.zero_grad()
+ default_before.loss.backward()
+ optimizer.step()
+
+ # Test that the output changed.
+ default_after = adapted(input_ids=input_ids, attention_mask=attention_mask, labels=target_ids)
+ assert not torch.allclose(default_before.logits, default_after.logits)
+
+ with adapted.disable_adapter():
+ # Test that the output is the same as the original output.
+ default_disabled = adapted(input_ids=input_ids, attention_mask=attention_mask, labels=target_ids)
+ assert_close(original_before.logits, default_disabled.logits, rtol=0, atol=0)
+
+ # Add new adapter 1.
+ adapted.add_adapter("adapter 1", AdaptionPromptConfig(adapter_layers=2, adapter_len=8, task_type="CAUSAL_LM"))
+ # Test zero-init
+ adapter_1_before = adapted(input_ids=input_ids, attention_mask=attention_mask, labels=target_ids)
+ assert_close(original_before.logits, adapter_1_before.logits, rtol=0, atol=0)
+
+ # Single fine-tuning step on adapter 1.
+ optimizer = torch.optim.SGD(adapted.parameters(), lr=1)
+ optimizer.zero_grad()
+ adapter_1_before.loss.backward()
+ optimizer.step()
+
+ # Test that adapter 1 output changed.
+ adapter_1_after = adapted(input_ids=input_ids, attention_mask=attention_mask, labels=target_ids)
+ assert not torch.allclose(adapter_1_before.logits, adapter_1_after.logits)
+ assert not torch.allclose(original_before.logits, adapter_1_after.logits)
+ assert not torch.allclose(default_after.logits, adapter_1_after.logits)
+
+ with adapted.disable_adapter():
+ # Test that the output is the same as the original output.
+ adapter_1_disabled = adapted(input_ids=input_ids, attention_mask=attention_mask, labels=target_ids)
+ assert_close(original_before.logits, adapter_1_disabled.logits, rtol=0, atol=0)
+
+ # Set adapter back to default.
+ adapted.set_adapter("default")
+
+ # Test that the output is the same as the default output after training.
+ default_after_set = adapted(input_ids=input_ids, attention_mask=attention_mask, labels=target_ids)
+ assert_close(default_after.logits, default_after_set.logits, rtol=0, atol=0)
+ assert not torch.allclose(original_before.logits, default_after_set.logits)
+ assert not torch.allclose(adapter_1_after.logits, default_after_set.logits)
+
+ @pytest.mark.parametrize("model_id", MODELS_TO_TEST)
+ def test_add_and_set_while_disabled(self, model_id):
+ """Test that adding and setting adapters while disabled works as intended."""
+ # Test input data.
+ input_ids = torch.LongTensor([[1, 1, 1], [2, 1, 2]]).to(self.torch_device)
+ target_ids = torch.LongTensor([[0, 0, 0], [0, 0, 0]]).to(self.torch_device)
+ attention_mask = torch.LongTensor([[1, 1, 1], [1, 0, 1]]).to(self.torch_device)
+
+ # Create original llama model.
+ original = self.transformers_class.from_pretrained(model_id)
+ original = original.to(self.torch_device)
+ original_before = original(input_ids=input_ids, attention_mask=attention_mask)
+
+ # Get AdaptionPrompt model.
+ adapted = get_peft_model(
+ original, AdaptionPromptConfig(adapter_layers=2, adapter_len=4, task_type="CAUSAL_LM")
+ )
+ adapted = adapted.to(self.torch_device)
+
+ with adapted.disable_adapter():
+ adapted.add_adapter(
+ "adapter 1", AdaptionPromptConfig(adapter_layers=2, adapter_len=8, task_type="CAUSAL_LM")
+ )
+
+ # Test that the output is the same as the original output.
+ adapter_1_before = adapted(input_ids=input_ids, attention_mask=attention_mask, labels=target_ids)
+ assert_close(original_before.logits, adapter_1_before.logits, rtol=0, atol=0)
+
+ # Single fine-tuning step on adapter 1.
+ optimizer = torch.optim.SGD(adapted.parameters(), lr=1)
+ optimizer.zero_grad()
+ adapter_1_before.loss.backward()
+ optimizer.step()
+
+ # Test that adapter 1 output changed.
+ adapter_1_after = adapted(input_ids=input_ids, attention_mask=attention_mask, labels=target_ids)
+ assert not torch.allclose(original_before.logits, adapter_1_after.logits)
+
+ adapted.set_adapter("default")
+ with adapted.disable_adapter():
+ adapted.set_adapter("adapter 1")
+
+ # Test that adapter 1 is active again.
+ adapter_1_after_set = adapted(input_ids=input_ids, attention_mask=attention_mask, labels=target_ids)
+ assert_close(adapter_1_after.logits, adapter_1_after_set.logits, rtol=0, atol=0)
+
+ @pytest.mark.parametrize("model_id", MODELS_TO_TEST)
+ def test_use_cache(self, model_id):
+ """Test that AdaptionPrompt works when Llama config use_cache=True."""
+ torch.manual_seed(0)
+ input_ids = torch.LongTensor([[1, 1, 1], [2, 1, 2]]).to(self.torch_device)
+ original = self.transformers_class.from_pretrained(model_id, use_cache=False)
+ adapted = get_peft_model(
+ original, AdaptionPromptConfig(adapter_layers=2, adapter_len=4, task_type="CAUSAL_LM")
+ )
+ adapted = adapted.to(self.torch_device)
+ expected = adapted.generate(input_ids=input_ids, max_length=8)
+
+ # Set use_cache = True and generate output again.
+ adapted.base_model.config.use_cache = True
+ actual = adapted.generate(input_ids=input_ids, max_length=8)
+ assert_close(expected, actual, rtol=0, atol=0)
+
+ @pytest.mark.parametrize("model_id", MODELS_TO_TEST)
+ def test_bf16_inference(self, model_id):
+ if self.torch_device == "mps":
+ return pytest.skip("Skipping bf16 test on MPS")
+
+ """Test that AdaptionPrompt works when Llama using a half-precision model."""
+ input_ids = torch.LongTensor([[1, 1, 1], [2, 1, 2]]).to(self.torch_device)
+ original = self.transformers_class.from_pretrained(model_id, torch_dtype=torch.bfloat16)
+ adapted = get_peft_model(
+ original, AdaptionPromptConfig(adapter_layers=2, adapter_len=4, task_type="CAUSAL_LM")
+ )
+ adapted = adapted.to(self.torch_device)
+ adapted.generate(input_ids=input_ids) # does not raise
+
+ @pytest.mark.xfail(reason="currently this fails because scores are zeroed out", raises=AssertionError)
+ @pytest.mark.parametrize("model_id", MODELS_TO_TEST)
+ def test_disable_adapter(self, model_id):
+ model = self.transformers_class.from_pretrained(model_id).to(self.torch_device)
+ dummy_input = torch.LongTensor([[1, 1, 1]]).to(self.torch_device)
+ output_before = model(dummy_input).logits
+
+ config = AdaptionPromptConfig(adapter_layers=1, adapter_len=4, task_type="CAUSAL_LM")
+ model = get_peft_model(model, config).to(self.torch_device)
+ output_peft = model(dummy_input).logits
+ # TODO currently this fails because scores are zeroed out:
+ # https://github.com/huggingface/peft/blob/062d95a09eb5d1de35c0e5e23d4387daba99e2db/src/peft/tuners/adaption_prompt.py#L303
+ # This is fine for users but makes it difficult to test if anything happens. In the future, we will have a clean
+ # way to control initialization. Until then, this test is expected to fail.
+ assert not torch.allclose(output_before, output_peft)
+
+ with model.disable_adapter():
+ output_peft_disabled = model(dummy_input).logits
+ assert torch.allclose(output_before, output_peft_disabled)
diff --git a/peft/tests/test_arrow.py b/peft/tests/test_arrow.py
new file mode 100644
index 0000000000000000000000000000000000000000..a6fab059ff528fa5e7ab283dea08ac06b9c0f269
--- /dev/null
+++ b/peft/tests/test_arrow.py
@@ -0,0 +1,509 @@
+# Copyright 2025-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+import copy
+import os
+from pathlib import Path
+from unittest.mock import patch
+
+import pytest
+import torch
+from transformers import AutoModelForCausalLM, AutoModelForImageClassification
+
+from peft import LoraConfig, get_peft_model
+from peft.tuners.lora import ArrowConfig, create_arrow_model
+from peft.tuners.lora.arrow import _resolve_adapter_source
+from tests.testing_utils import hub_online_once
+
+
+# ─── Fixtures ──────────────────────────────────────────────────────────
+
+
+@pytest.fixture(scope="module")
+def workdir(tmp_path_factory):
+ """
+ Create a temp directory and chdir into it for the duration of the module.
+ """
+ wd = tmp_path_factory.mktemp("arrow_workdir")
+ old_cwd = os.getcwd()
+ os.chdir(wd)
+ yield Path(wd)
+ os.chdir(old_cwd)
+ # (pytest will auto-delete wd)
+
+
+def _create_and_save_adapter(out_dir: Path, rank: int = 4):
+ """Helper: build a LoRA adapter around `model` and save into `out_dir`."""
+ # fan_in_fan_out is set to True because of GPT2 model that we use to avoid warning
+ cfg = LoraConfig(r=rank, target_modules=["c_attn"], fan_in_fan_out=True, init_lora_weights=False)
+ model_id = "hf-internal-testing/tiny-random-gpt2"
+ with hub_online_once(model_id):
+ model = AutoModelForCausalLM.from_pretrained(model_id)
+ peft_model = get_peft_model(model, cfg)
+ peft_model.save_pretrained(out_dir)
+
+
+@pytest.fixture(scope="module")
+def ts_adapters(workdir: Path):
+ """
+ Build 3 task-specific adapters and return their absolute paths
+ """
+ abs_paths = []
+ for i in range(3):
+ sub = f"{workdir}/ts{i}"
+ _create_and_save_adapter(sub)
+ abs_paths.append(sub)
+ return abs_paths
+
+
+@pytest.fixture(scope="module")
+def gen_adapter(workdir: Path):
+ """Build 1 general-knowledge adapter and return its absolute path list."""
+ sub = f"{workdir}/gen0"
+ _create_and_save_adapter(sub)
+ return [sub] # list because create_arrow_model expects list
+
+
+class TestArrowRouting:
+ def test_incompatible_rank_raises(self, workdir: Path):
+ """
+ Adding adapters with different ranks must raise a ValueError.
+ """
+ # Create two adapters with different ranks targeting the same modules
+ sub_r4 = workdir / "rank4"
+ sub_r8 = workdir / "rank8"
+ _create_and_save_adapter(sub_r4, rank=4)
+ _create_and_save_adapter(sub_r8, rank=8)
+
+ model_id = "hf-internal-testing/tiny-random-gpt2"
+ with hub_online_once(model_id):
+ base = AutoModelForCausalLM.from_pretrained(model_id)
+
+ # Expect create_arrow_model to raise due to rank mismatch
+ with pytest.raises(ValueError, match=r"rank mismatch"):
+ _ = create_arrow_model(
+ base_model=base,
+ task_specific_adapter_paths=[str(sub_r4), str(sub_r8)],
+ arrow_config=ArrowConfig(top_k=1),
+ )
+
+ def test_arrow_differs_with_extra_expert(self, ts_adapters):
+ """
+ Arrow with 2 experts vs Arrow with 3 experts must produce different logits.
+ """
+ # Arrow over first 2 experts
+ model_id = "hf-internal-testing/tiny-random-gpt2"
+ with hub_online_once(model_id):
+ base_model_1 = AutoModelForCausalLM.from_pretrained(model_id)
+ base_model_2 = copy.deepcopy(base_model_1)
+ cfg_small = ArrowConfig(top_k=2)
+ m_small = create_arrow_model(
+ base_model=base_model_1,
+ task_specific_adapter_paths=ts_adapters[:2],
+ arrow_config=cfg_small,
+ ).eval()
+
+ # Arrow over all 3 experts
+ cfg_big = ArrowConfig(top_k=2)
+ m_big = create_arrow_model(
+ base_model=base_model_2,
+ task_specific_adapter_paths=ts_adapters,
+ arrow_config=cfg_big,
+ ).eval()
+
+ x = torch.ones(1, 4, dtype=torch.long)
+ assert not torch.allclose(m_small(x).logits, m_big(x).logits)
+
+ def test_arrow_gks_with_load_adapter_later_with_forward(self, ts_adapters, gen_adapter):
+ """
+ Loading the last expert after creating the arrow model should produce the same result as loading all the
+ experts at once in create_arrow_model(), when forward path is called before adding the new adapter.
+ """
+ # Arrow over all three experts
+ model_id = "hf-internal-testing/tiny-random-gpt2"
+ with hub_online_once(model_id):
+ base_model_1 = AutoModelForCausalLM.from_pretrained(model_id)
+ base_model_2 = copy.deepcopy(base_model_1)
+ cfg_big = ArrowConfig(top_k=2, use_gks=True, rng_seed=42)
+ m_big = create_arrow_model(
+ base_model=base_model_1,
+ task_specific_adapter_paths=ts_adapters,
+ general_adapter_paths=gen_adapter,
+ arrow_config=cfg_big,
+ ).eval()
+
+ # Arrow over all 2 experts + loading the third expert later
+ cfg_small_later_big = ArrowConfig(top_k=2, use_gks=True, rng_seed=42)
+ m_small_later_big = create_arrow_model(
+ base_model=base_model_2,
+ task_specific_adapter_paths=ts_adapters[:2],
+ general_adapter_paths=gen_adapter,
+ arrow_config=cfg_small_later_big,
+ )
+
+ # Ensuring that the prototypes and gks are done one time by running a forward path
+ x = torch.ones(1, 4, dtype=torch.long)
+ m_small_later_big(x)
+
+ # Now loading the third expert
+ m_small_later_big.load_adapter(
+ model_id=ts_adapters[-1],
+ adapter_name="new_added_ts_expert",
+ )
+ # Activating the new adapter and run forward path on it
+ m_small_later_big.set_adapter("new_added_ts_expert")
+ x = torch.ones(3, 5, dtype=torch.long)
+ m_small_later_big(x)
+
+ # Now we switch back to the arrow_router
+ m_small_later_big.set_adapter("arrow_router")
+ m_small_later_big.eval()
+
+ x = torch.ones(1, 4, dtype=torch.long)
+ assert torch.allclose(m_big(x).logits, m_small_later_big(x).logits)
+
+ def test_arrow_with_load_adapter_later_with_forward_activate_new(self, ts_adapters, gen_adapter):
+ """
+ Loading the last expert after creating the arrow model and activate it should produce different result compared
+ to the case where arrow_router is activate, and the model's using arrow.
+ """
+ # Arrow over all three experts
+ model_id = "hf-internal-testing/tiny-random-gpt2"
+ with hub_online_once(model_id):
+ base_model_1 = AutoModelForCausalLM.from_pretrained(model_id)
+ base_model_2 = copy.deepcopy(base_model_1)
+ cfg_big = ArrowConfig(top_k=2, use_gks=True, rng_seed=42)
+ m_big = create_arrow_model(
+ base_model=base_model_1,
+ task_specific_adapter_paths=ts_adapters,
+ general_adapter_paths=gen_adapter,
+ arrow_config=cfg_big,
+ ).eval()
+
+ # Arrow over all 2 experts + loading the third expert later
+ cfg_small_later_big = ArrowConfig(top_k=2, use_gks=True, rng_seed=42)
+ m_small_later_big = create_arrow_model(
+ base_model=base_model_2,
+ task_specific_adapter_paths=ts_adapters[:2],
+ general_adapter_paths=gen_adapter,
+ arrow_config=cfg_small_later_big,
+ )
+
+ # Ensuring that the prototypes and gks are done one time by running a forward path
+ x = torch.ones(1, 4, dtype=torch.long)
+ m_small_later_big(x)
+
+ # Now loading the third expert
+ m_small_later_big.load_adapter(
+ model_id=ts_adapters[-1],
+ adapter_name="new_added_ts_expert",
+ )
+ # The new adapter is activated
+ m_small_later_big.set_adapter("new_added_ts_expert")
+ m_small_later_big.eval()
+
+ x = torch.ones(1, 4, dtype=torch.long)
+ assert not torch.allclose(m_big(x).logits, m_small_later_big(x).logits)
+
+ def test_arrow_gks_with_load_adapter_later_without_forward(self, ts_adapters, gen_adapter):
+ """
+ Loading the last expert after creating the arrow model should produce the same result as loading all the
+ experts at once in create_arrow_model()
+ """
+ # Arrow over all three experts
+ model_id = "hf-internal-testing/tiny-random-gpt2"
+ with hub_online_once(model_id):
+ base_model_1 = AutoModelForCausalLM.from_pretrained(model_id)
+ base_model_2 = copy.deepcopy(base_model_1)
+ cfg_big = ArrowConfig(top_k=2, use_gks=True, rng_seed=42)
+ m_big = create_arrow_model(
+ base_model=base_model_1,
+ task_specific_adapter_paths=ts_adapters,
+ general_adapter_paths=gen_adapter,
+ arrow_config=cfg_big,
+ ).eval()
+
+ # Arrow over all 2 experts + loading the third expert later
+ cfg_small_later_big = ArrowConfig(top_k=2, use_gks=True, rng_seed=42)
+ m_small_later_big = create_arrow_model(
+ base_model=base_model_2,
+ task_specific_adapter_paths=ts_adapters[:2],
+ general_adapter_paths=gen_adapter,
+ arrow_config=cfg_small_later_big,
+ )
+
+ # Now loading the third expert
+ m_small_later_big.load_adapter(
+ model_id=ts_adapters[-1],
+ adapter_name="new_added_ts_expert",
+ )
+ m_small_later_big.eval()
+
+ x = torch.ones(1, 4, dtype=torch.long)
+ assert torch.allclose(m_big(x).logits, m_small_later_big(x).logits)
+
+ def test_genknowsub_changes_output(self, ts_adapters, gen_adapter):
+ """
+ Arrow+GenKnowSub vs plain Arrow must change logits.
+ """
+ # Plain Arrow
+ model_id = "hf-internal-testing/tiny-random-gpt2"
+ with hub_online_once(model_id):
+ base_model_1 = AutoModelForCausalLM.from_pretrained(model_id)
+ base_model_2 = copy.deepcopy(base_model_1)
+ cfg_plain = ArrowConfig(top_k=2)
+ m_plain = create_arrow_model(
+ base_model=base_model_1,
+ task_specific_adapter_paths=ts_adapters,
+ arrow_config=cfg_plain,
+ ).eval()
+
+ # Arrow + GenKnowSub
+ cfg_gks = ArrowConfig(top_k=2, use_gks=True)
+ m_gks = create_arrow_model(
+ base_model=base_model_2,
+ task_specific_adapter_paths=ts_adapters,
+ general_adapter_paths=gen_adapter,
+ arrow_config=cfg_gks,
+ ).eval()
+
+ x = torch.ones(1, 4, dtype=torch.long)
+ assert not torch.allclose(m_plain(x).logits, m_gks(x).logits)
+
+ def test_merging_adapters_raise_error_in_arrow(self, ts_adapters):
+ """
+ Merging/unmerging is not allowed while an ArrowLinearLayer is loaded on the model and active.
+ """
+ # Arrow over first 2 experts
+ model_id = "hf-internal-testing/tiny-random-gpt2"
+ with hub_online_once(model_id):
+ base_model = AutoModelForCausalLM.from_pretrained(model_id)
+ cfg_small = ArrowConfig(top_k=2)
+ m_small = create_arrow_model(
+ base_model=base_model,
+ task_specific_adapter_paths=ts_adapters[:2],
+ arrow_config=cfg_small,
+ ).eval()
+
+ with pytest.raises(RuntimeError, match=r"Cannot merge an active Arrow router adapter"):
+ m_small.merge_and_unload()
+
+ def test_conv2d_targets_raise_typeerror_in_arrow(self, workdir):
+ """
+ Adapters applied to Conv2d must be rejected by create_arrow_model() which enforces Linear/Linear4bit-only
+ targets.
+ """
+
+ model_id = "hf-internal-testing/tiny-random-ResNetForImageClassification"
+ with hub_online_once(model_id):
+ base = AutoModelForImageClassification.from_pretrained(model_id)
+
+ # Build a LoRA adapter targeting a Conv2d
+ cfg = LoraConfig(r=4, target_modules=["convolution"], init_lora_weights=False)
+ peft_model = get_peft_model(copy.deepcopy(base), cfg)
+
+ conv_dir = workdir / "cv0"
+ peft_model.save_pretrained(conv_dir)
+
+ # Expect create_arrow_model to raise TypeError
+ with pytest.raises(TypeError, match=r"LoRA adapters must only target Linear"):
+ _ = create_arrow_model(
+ base_model=base,
+ task_specific_adapter_paths=[str(conv_dir)],
+ arrow_config=ArrowConfig(top_k=1),
+ )
+
+ def test_arrow_forward_float16_no_autocast_with_merging(self, ts_adapters):
+ """
+ Run Arrow in float16 with autocast disabled; forward should work, while merge/unmerge operations must raise for
+ Arrow models.
+ """
+ import platform
+
+ try:
+ _ = torch.zeros(1, dtype=torch.float16)
+ except Exception:
+ pytest.skip(reason="Test requires float16 support")
+
+ if platform.system() == "Darwin":
+ pytest.skip(reason="MacOS does not support multiple ops in float16")
+
+ model_id = "hf-internal-testing/tiny-random-gpt2"
+
+ # Create base in fp16 (no manual assignment to .dtype)
+ with hub_online_once(model_id):
+ base = AutoModelForCausalLM.from_pretrained(model_id, torch_dtype=torch.float16)
+
+ cfg = ArrowConfig(top_k=2)
+
+ # Build Arrow model and disable adapter dtype autocast
+ model = create_arrow_model(
+ base_model=base,
+ task_specific_adapter_paths=ts_adapters,
+ arrow_config=cfg,
+ autocast_adapter_dtype=False,
+ torch_dtype=torch.float16,
+ ).eval()
+
+ X = {
+ "input_ids": torch.ones(1, 4, dtype=torch.long),
+ "attention_mask": torch.ones(1, 4, dtype=torch.long),
+ }
+
+ # Forward should work in fp16
+ _ = model(**X)
+
+ # Merge must fail on Arrow models
+ with pytest.raises(RuntimeError, match=r"Cannot merge an active Arrow router adapter"):
+ model.merge_adapter(safe_merge=False)
+
+ with pytest.raises(RuntimeError, match=r"Cannot merge an active Arrow router adapter"):
+ _ = model.merge_and_unload()
+
+ def test_prototypes_not_recomputed_on_repeated_forward(self, ts_adapters):
+ """
+ Repeated calls to forward should not recompute prototypes. We verify by spying on
+ ArrowLoraLinearLayer.top_right_singular_vec_from_BA(), which is only called when prototypes are (re)built.
+ """
+ model_id = "hf-internal-testing/tiny-random-gpt2"
+ with hub_online_once(model_id):
+ base = AutoModelForCausalLM.from_pretrained(model_id)
+
+ cfg = ArrowConfig(top_k=2)
+ model = create_arrow_model(
+ base_model=base,
+ task_specific_adapter_paths=ts_adapters,
+ arrow_config=cfg,
+ ).eval()
+
+ # Find one Arrow layer instance on the model
+ arrow_layer = None
+ for _, module in model.named_modules():
+ if hasattr(module, "lora_arrow") and "arrow_router" in module.lora_arrow:
+ arrow_layer = module.lora_arrow["arrow_router"]
+ break
+ assert arrow_layer is not None, "Arrow router layer not found on model"
+
+ x = torch.ones(1, 4, dtype=torch.long)
+
+ # Spy on the internal proto computation; should run once (E calls for E experts)
+ with patch.object(
+ arrow_layer,
+ "top_right_singular_vec_from_BA",
+ wraps=arrow_layer.top_right_singular_vec_from_BA,
+ ) as spy:
+ _ = model(x)
+ first_calls = spy.call_count
+ assert first_calls == len(arrow_layer.task_adapter_names)
+
+ # Call forward again; prototypes should be cached, so no extra calls
+ _ = model(x)
+ assert spy.call_count == first_calls
+
+
+def test_training_updates_when_task_adapter_active(ts_adapters):
+ """
+ Ensure a simple training step works: compute a dummy loss, backward, and take an optimizer step. Verify that
+ task-adapter parameters update.
+ """
+ model_id = "hf-internal-testing/tiny-random-gpt2"
+ with hub_online_once(model_id):
+ base = AutoModelForCausalLM.from_pretrained(model_id)
+
+ # Build Arrow model over two experts
+ cfg = ArrowConfig(top_k=2)
+ model = create_arrow_model(
+ base_model=base,
+ task_specific_adapter_paths=ts_adapters[:2],
+ arrow_config=cfg,
+ )
+ model.train()
+
+ # Switch to a specific task adapter for training (vanilla LoRA)
+ model.set_adapter("task_0")
+
+ # Choose a representative parameter to check updates (task_0 A weight)
+ rep_name = None
+ for n, _ in model.named_parameters():
+ if ".lora_A.task_0.weight" in n:
+ rep_name = n
+ break
+ assert rep_name is not None, "task_0 LoRA A weight not found"
+ rep_param = dict(model.named_parameters())[rep_name]
+ before = rep_param.detach().clone()
+
+ # Optimizer over trainable params (task_0 now active and trainable)
+ opt = torch.optim.SGD([p for p in model.parameters() if p.requires_grad], lr=1e-2)
+
+ # Dummy batch
+ vocab = model.config.vocab_size
+ input_ids = torch.randint(0, vocab, (2, 8))
+ attention_mask = torch.ones_like(input_ids)
+
+ # Compute loss and update
+ opt.zero_grad()
+ out = model(input_ids=input_ids, attention_mask=attention_mask, labels=input_ids)
+ assert hasattr(out, "loss") and out.loss is not None
+ out.loss.backward()
+ opt.step()
+
+ after = rep_param.detach().clone()
+ assert not torch.allclose(before, after), "Active task adapter parameters did not update after optimizer step"
+
+
+@pytest.mark.parametrize(
+ "case",
+ [
+ "local_root",
+ "local_nested",
+ "hub_repo",
+ "hub_with_sub",
+ ],
+)
+def test_resolve_adapter_source_variants(tmp_path: Path, case: str):
+ """
+ Ensure `_resolve_adapter_source` correctly handles:
+ - Local dir (containing adapter_config.json)
+ - Local nested subfolder
+ - Hub repo id "user/repo"
+ - Hub repo with subfolder "user/repo/sub/folder"
+ """
+ if case == "local_root":
+ d = tmp_path / "adapter_local_root"
+ d.mkdir(parents=True, exist_ok=True)
+ (d / "adapter_config.json").write_text("{}")
+ model_id, sub = _resolve_adapter_source(str(d))
+ assert model_id == str(d)
+ assert sub is None
+
+ elif case == "local_nested":
+ d = tmp_path / "repo_like" / "sub" / "folder"
+ d.mkdir(parents=True, exist_ok=True)
+ (d / "adapter_config.json").write_text("{}")
+ model_id, sub = _resolve_adapter_source(str(d))
+ assert model_id == str(d)
+ assert sub is None
+
+ elif case == "hub_repo":
+ model_id, sub = _resolve_adapter_source("user/repo")
+ assert model_id == "user/repo"
+ assert sub is None
+
+ elif case == "hub_with_sub":
+ model_id, sub = _resolve_adapter_source("user/repo/sub/folder")
+ assert model_id == "user/repo"
+ assert sub == "sub/folder"
+
+ else:
+ raise AssertionError(f"unknown case: {case}")
diff --git a/peft/tests/test_auto.py b/peft/tests/test_auto.py
new file mode 100644
index 0000000000000000000000000000000000000000..105d13f455a9f80a74b43127f1a7b009ca5259aa
--- /dev/null
+++ b/peft/tests/test_auto.py
@@ -0,0 +1,231 @@
+# Copyright 2023-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+import tempfile
+
+import torch
+from transformers import AutoModelForCausalLM, AutoTokenizer
+
+from peft import (
+ AutoPeftModel,
+ AutoPeftModelForCausalLM,
+ AutoPeftModelForFeatureExtraction,
+ AutoPeftModelForQuestionAnswering,
+ AutoPeftModelForSeq2SeqLM,
+ AutoPeftModelForSequenceClassification,
+ AutoPeftModelForTokenClassification,
+ LoraConfig,
+ PeftModel,
+ PeftModelForCausalLM,
+ PeftModelForFeatureExtraction,
+ PeftModelForQuestionAnswering,
+ PeftModelForSeq2SeqLM,
+ PeftModelForSequenceClassification,
+ PeftModelForTokenClassification,
+ get_peft_model,
+)
+from peft.utils import infer_device
+
+
+class TestPeftAutoModel:
+ dtype = torch.float16 if infer_device() == "mps" else torch.bfloat16
+
+ def test_peft_causal_lm(self):
+ model_id = "peft-internal-testing/tiny-OPTForCausalLM-lora"
+ model = AutoPeftModelForCausalLM.from_pretrained(model_id)
+ assert isinstance(model, PeftModelForCausalLM)
+
+ with tempfile.TemporaryDirectory() as tmp_dirname:
+ model.save_pretrained(tmp_dirname)
+
+ model = AutoPeftModelForCausalLM.from_pretrained(tmp_dirname)
+ assert isinstance(model, PeftModelForCausalLM)
+
+ # check if kwargs are passed correctly
+ model = AutoPeftModelForCausalLM.from_pretrained(model_id, torch_dtype=self.dtype)
+ assert isinstance(model, PeftModelForCausalLM)
+ assert model.base_model.lm_head.weight.dtype == self.dtype
+
+ adapter_name = "default"
+ is_trainable = False
+ # This should work
+ _ = AutoPeftModelForCausalLM.from_pretrained(model_id, adapter_name, is_trainable, torch_dtype=self.dtype)
+
+ def test_peft_causal_lm_extended_vocab(self):
+ model_id = "peft-internal-testing/tiny-random-OPTForCausalLM-extended-vocab"
+ model = AutoPeftModelForCausalLM.from_pretrained(model_id)
+ assert isinstance(model, PeftModelForCausalLM)
+
+ # check if kwargs are passed correctly
+ model = AutoPeftModelForCausalLM.from_pretrained(model_id, torch_dtype=self.dtype)
+ assert isinstance(model, PeftModelForCausalLM)
+ assert model.base_model.lm_head.weight.dtype == self.dtype
+
+ adapter_name = "default"
+ is_trainable = False
+ # This should work
+ _ = AutoPeftModelForCausalLM.from_pretrained(model_id, adapter_name, is_trainable, torch_dtype=self.dtype)
+
+ def test_peft_seq2seq_lm(self):
+ model_id = "peft-internal-testing/tiny_T5ForSeq2SeqLM-lora"
+ model = AutoPeftModelForSeq2SeqLM.from_pretrained(model_id)
+ assert isinstance(model, PeftModelForSeq2SeqLM)
+
+ with tempfile.TemporaryDirectory() as tmp_dirname:
+ model.save_pretrained(tmp_dirname)
+
+ model = AutoPeftModelForSeq2SeqLM.from_pretrained(tmp_dirname)
+ assert isinstance(model, PeftModelForSeq2SeqLM)
+
+ # check if kwargs are passed correctly
+ model = AutoPeftModelForSeq2SeqLM.from_pretrained(model_id, torch_dtype=self.dtype)
+ assert isinstance(model, PeftModelForSeq2SeqLM)
+ assert model.base_model.lm_head.weight.dtype == self.dtype
+
+ adapter_name = "default"
+ is_trainable = False
+ # This should work
+ _ = AutoPeftModelForSeq2SeqLM.from_pretrained(model_id, adapter_name, is_trainable, torch_dtype=self.dtype)
+
+ def test_peft_sequence_cls(self):
+ model_id = "peft-internal-testing/tiny_OPTForSequenceClassification-lora"
+ model = AutoPeftModelForSequenceClassification.from_pretrained(model_id)
+ assert isinstance(model, PeftModelForSequenceClassification)
+
+ with tempfile.TemporaryDirectory() as tmp_dirname:
+ model.save_pretrained(tmp_dirname)
+
+ model = AutoPeftModelForSequenceClassification.from_pretrained(tmp_dirname)
+ assert isinstance(model, PeftModelForSequenceClassification)
+
+ # check if kwargs are passed correctly
+ model = AutoPeftModelForSequenceClassification.from_pretrained(model_id, torch_dtype=self.dtype)
+ assert isinstance(model, PeftModelForSequenceClassification)
+ assert model.score.original_module.weight.dtype == self.dtype
+
+ adapter_name = "default"
+ is_trainable = False
+ # This should work
+ _ = AutoPeftModelForSequenceClassification.from_pretrained(
+ model_id, adapter_name, is_trainable, torch_dtype=self.dtype
+ )
+
+ def test_peft_token_classification(self):
+ model_id = "peft-internal-testing/tiny_GPT2ForTokenClassification-lora"
+ model = AutoPeftModelForTokenClassification.from_pretrained(model_id)
+ assert isinstance(model, PeftModelForTokenClassification)
+
+ with tempfile.TemporaryDirectory() as tmp_dirname:
+ model.save_pretrained(tmp_dirname)
+
+ model = AutoPeftModelForTokenClassification.from_pretrained(tmp_dirname)
+ assert isinstance(model, PeftModelForTokenClassification)
+
+ # check if kwargs are passed correctly
+ model = AutoPeftModelForTokenClassification.from_pretrained(model_id, torch_dtype=self.dtype)
+ assert isinstance(model, PeftModelForTokenClassification)
+ assert model.base_model.classifier.original_module.weight.dtype == self.dtype
+
+ adapter_name = "default"
+ is_trainable = False
+ # This should work
+ _ = AutoPeftModelForTokenClassification.from_pretrained(
+ model_id, adapter_name, is_trainable, torch_dtype=self.dtype
+ )
+
+ def test_peft_question_answering(self):
+ model_id = "peft-internal-testing/tiny_OPTForQuestionAnswering-lora"
+ model = AutoPeftModelForQuestionAnswering.from_pretrained(model_id)
+ assert isinstance(model, PeftModelForQuestionAnswering)
+
+ with tempfile.TemporaryDirectory() as tmp_dirname:
+ model.save_pretrained(tmp_dirname)
+
+ model = AutoPeftModelForQuestionAnswering.from_pretrained(tmp_dirname)
+ assert isinstance(model, PeftModelForQuestionAnswering)
+
+ # check if kwargs are passed correctly
+ model = AutoPeftModelForQuestionAnswering.from_pretrained(model_id, torch_dtype=self.dtype)
+ assert isinstance(model, PeftModelForQuestionAnswering)
+ assert model.base_model.qa_outputs.original_module.weight.dtype == self.dtype
+
+ adapter_name = "default"
+ is_trainable = False
+ # This should work
+ _ = AutoPeftModelForQuestionAnswering.from_pretrained(
+ model_id, adapter_name, is_trainable, torch_dtype=self.dtype
+ )
+
+ def test_peft_feature_extraction(self):
+ model_id = "peft-internal-testing/tiny_OPTForFeatureExtraction-lora"
+ model = AutoPeftModelForFeatureExtraction.from_pretrained(model_id)
+ assert isinstance(model, PeftModelForFeatureExtraction)
+
+ with tempfile.TemporaryDirectory() as tmp_dirname:
+ model.save_pretrained(tmp_dirname)
+
+ model = AutoPeftModelForFeatureExtraction.from_pretrained(tmp_dirname)
+ assert isinstance(model, PeftModelForFeatureExtraction)
+
+ # check if kwargs are passed correctly
+ model = AutoPeftModelForFeatureExtraction.from_pretrained(model_id, torch_dtype=self.dtype)
+ assert isinstance(model, PeftModelForFeatureExtraction)
+ assert model.base_model.model.decoder.embed_tokens.weight.dtype == self.dtype
+
+ adapter_name = "default"
+ is_trainable = False
+ # This should work
+ _ = AutoPeftModelForFeatureExtraction.from_pretrained(
+ model_id, adapter_name, is_trainable, torch_dtype=self.dtype
+ )
+
+ def test_peft_whisper(self):
+ model_id = "peft-internal-testing/tiny_WhisperForConditionalGeneration-lora"
+ model = AutoPeftModel.from_pretrained(model_id)
+ assert isinstance(model, PeftModel)
+
+ with tempfile.TemporaryDirectory() as tmp_dirname:
+ model.save_pretrained(tmp_dirname)
+
+ model = AutoPeftModel.from_pretrained(tmp_dirname)
+ assert isinstance(model, PeftModel)
+
+ # check if kwargs are passed correctly
+ model = AutoPeftModel.from_pretrained(model_id, torch_dtype=self.dtype)
+ assert isinstance(model, PeftModel)
+ assert model.base_model.model.model.encoder.embed_positions.weight.dtype == self.dtype
+
+ adapter_name = "default"
+ is_trainable = False
+ # This should work
+ _ = AutoPeftModel.from_pretrained(model_id, adapter_name, is_trainable, torch_dtype=self.dtype)
+
+ def test_embedding_size_not_reduced_if_greater_vocab_size(self, tmp_path):
+ # See 2415
+ # There was a bug in AutoPeftModels where the embedding was always resized to the vocab size of the tokenizer
+ # when the tokenizer was found. This makes sense if the vocabulary was extended, but some models like Qwen
+ # already start out with "spare" embeddings, i.e. the embedding size is larger than the vocab size. This could
+ # result in the embedding being shrunk, which in turn resulted in an error when loading the weights.
+
+ # first create a checkpoint; it is important that the tokenizer is also saved in the same location
+ model_id = "Qwen/Qwen2-0.5B"
+ model = AutoModelForCausalLM.from_pretrained(model_id)
+ tokenizer = AutoTokenizer.from_pretrained(model_id)
+ model = get_peft_model(model, LoraConfig(modules_to_save=["lm_head", "embed_token"]))
+ model.save_pretrained(tmp_path)
+ tokenizer.save_pretrained(tmp_path)
+
+ # does not raise; without the fix, it raises:
+ # > size mismatch for base_model.model.lm_head.modules_to_save.default.weight: copying a param with shape
+ # torch.Size([151936, 896]) from checkpoint, the shape in current model is torch.Size([151646, 896]).
+ AutoPeftModelForCausalLM.from_pretrained(tmp_path)
diff --git a/peft/tests/test_boft.py b/peft/tests/test_boft.py
new file mode 100644
index 0000000000000000000000000000000000000000..d0cf74e3edea2a5836068afe2b74df3b8ae6a20f
--- /dev/null
+++ b/peft/tests/test_boft.py
@@ -0,0 +1,84 @@
+# Copyright 2024-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+import torch
+from safetensors.torch import load_file
+from transformers import AutoModelForCausalLM
+
+from peft import BOFTConfig, PeftModel, get_peft_model
+from peft.utils import infer_device
+
+
+class TestBoft:
+ device = infer_device()
+
+ def test_boft_state_dict(self, tmp_path):
+ # see #2050
+ # ensure that the boft_P buffer is not stored in the checkpoint file and is not necessary to load the model
+ # correctly
+ torch.manual_seed(0)
+
+ inputs = torch.arange(10).view(-1, 1).to(self.device)
+ model_id = "hf-internal-testing/tiny-random-OPTForCausalLM"
+ model = AutoModelForCausalLM.from_pretrained(model_id).to(self.device)
+ model.eval()
+ output_base = model(inputs).logits
+
+ config = BOFTConfig(init_weights=False)
+ model = get_peft_model(model, config)
+ model.eval()
+ output_peft = model(inputs).logits
+
+ atol, rtol = 1e-5, 1e-8
+ # sanity check: loading boft changed the output
+ assert not torch.allclose(output_base, output_peft, atol=atol, rtol=rtol)
+
+ model.save_pretrained(tmp_path)
+ del model
+
+ # check that the boft_P buffer is not present
+ state_dict = load_file(tmp_path / "adapter_model.safetensors")
+ assert not any("boft_P" in key for key in state_dict)
+
+ # sanity check: the model still produces the same output after loading
+ model = AutoModelForCausalLM.from_pretrained(model_id).to(self.device)
+ model = PeftModel.from_pretrained(model, tmp_path)
+ output_loaded = model(inputs).logits
+ assert torch.allclose(output_peft, output_loaded, atol=atol, rtol=rtol)
+
+ def test_boft_old_checkpoint_including_boft_P(self, tmp_path):
+ # see #2050
+ # This test exists to ensure that after the boft_P buffer was made non-persistent, old checkpoints can still be
+ # loaded successfully.
+ torch.manual_seed(0)
+
+ inputs = torch.arange(10).view(-1, 1).to(self.device)
+ model_id = "hf-internal-testing/tiny-random-OPTForCausalLM"
+ model = AutoModelForCausalLM.from_pretrained(model_id).to(self.device)
+
+ # first create the expected output
+ config = BOFTConfig(init_weights=False)
+ model = get_peft_model(model, config)
+ model.eval()
+ output_peft = model(inputs).logits
+ del model
+
+ model = AutoModelForCausalLM.from_pretrained(model_id).to(self.device)
+ # checkpoint from before the PR whose state_dict still contains boft_P
+ hub_id = "peft-internal-testing/boft-tiny-opt-peft-v0.12"
+ model = PeftModel.from_pretrained(model, hub_id)
+ output_old = model(inputs).logits
+
+ atol, rtol = 1e-5, 1e-8
+ assert torch.allclose(output_peft, output_old, atol=atol, rtol=rtol)
diff --git a/peft/tests/test_bufferdict.py b/peft/tests/test_bufferdict.py
new file mode 100644
index 0000000000000000000000000000000000000000..eda25e652b4e3f799113c56c36a66330d5c415cd
--- /dev/null
+++ b/peft/tests/test_bufferdict.py
@@ -0,0 +1,48 @@
+import torch
+
+from peft.tuners._buffer_dict import BufferDict
+
+
+class TestBufferDict:
+ def test_init_from_dict_works(self):
+ bd = BufferDict(
+ {
+ "default": torch.randn(10, 2),
+ }
+ )
+
+ def test_update_from_other_bufferdict(self):
+ default_tensor = torch.randn(10, 2)
+ non_default_tensor = torch.randn(10, 2)
+ bd1 = BufferDict({"default": default_tensor})
+ bd2 = BufferDict({"non_default": non_default_tensor})
+
+ bd1.update(bd2)
+
+ assert set(bd1.keys()) == {"default", "non_default"}
+ assert torch.allclose(bd1["default"], default_tensor)
+ assert torch.allclose(bd1["non_default"], non_default_tensor)
+
+ def test_update_from_dict(self):
+ default_tensor = torch.randn(10, 2)
+ non_default_tensor = torch.randn(10, 2)
+ bd1 = BufferDict({"default": default_tensor})
+ d1 = {"non_default": non_default_tensor}
+
+ bd1.update(d1)
+
+ assert set(bd1.keys()) == {"default", "non_default"}
+ assert torch.allclose(bd1["default"], default_tensor)
+ assert torch.allclose(bd1["non_default"], non_default_tensor)
+
+ def test_update_from_dict_items(self):
+ default_tensor = torch.randn(10, 2)
+ non_default_tensor = torch.randn(10, 2)
+ bd1 = BufferDict({"default": default_tensor})
+ d1 = {"non_default": non_default_tensor}
+
+ bd1.update(d1.items())
+
+ assert set(bd1.keys()) == {"default", "non_default"}
+ assert torch.allclose(bd1["default"], default_tensor)
+ assert torch.allclose(bd1["non_default"], non_default_tensor)
diff --git a/peft/tests/test_common_gpu.py b/peft/tests/test_common_gpu.py
new file mode 100644
index 0000000000000000000000000000000000000000..958126ad1b644fca4ab5f7351935333ab27c0a3c
--- /dev/null
+++ b/peft/tests/test_common_gpu.py
@@ -0,0 +1,2185 @@
+# Copyright 2023-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+import gc
+import tempfile
+import unittest
+
+import pytest
+import torch
+import torch.nn.functional as F
+from accelerate.utils.memory import clear_device_cache
+from parameterized import parameterized
+from torch import nn
+from transformers import (
+ AutoImageProcessor,
+ AutoModelForCausalLM,
+ AutoModelForImageClassification,
+ AutoModelForSeq2SeqLM,
+ AutoModelForSequenceClassification,
+ AutoModelForTokenClassification,
+ AutoTokenizer,
+ BitsAndBytesConfig,
+ LlamaForCausalLM,
+ WhisperForConditionalGeneration,
+)
+from transformers.pytorch_utils import Conv1D
+
+from peft import (
+ AdaLoraConfig,
+ AdaptionPromptConfig,
+ BOFTConfig,
+ HRAConfig,
+ IA3Config,
+ LNTuningConfig,
+ LoHaConfig,
+ LoKrConfig,
+ LoraConfig,
+ OFTConfig,
+ PeftModel,
+ RandLoraConfig,
+ RoadConfig,
+ TaskType,
+ VBLoRAConfig,
+ VeraConfig,
+ get_peft_model,
+ prepare_model_for_kbit_training,
+)
+from peft.import_utils import is_bnb_4bit_available, is_bnb_available, is_xpu_available
+from peft.tuners.lora.config import LoraRuntimeConfig
+from peft.utils import infer_device
+
+from .testing_utils import (
+ device_count,
+ load_cat_image,
+ require_bitsandbytes,
+ require_deterministic_for_xpu,
+ require_non_cpu,
+ require_torch_multi_accelerator,
+)
+
+
+if is_bnb_available():
+ import bitsandbytes as bnb
+
+ from peft.tuners.ia3 import Linear8bitLt as IA3Linear8bitLt
+ from peft.tuners.lora import Linear8bitLt as LoraLinear8bitLt
+ from peft.tuners.randlora import Linear8bitLt as RandLoraLinear8bitLt
+ from peft.tuners.road import Linear8bitLt as RoadLinear8bitLt
+ from peft.tuners.vera import Linear8bitLt as VeraLinear8bitLt
+
+ if is_bnb_4bit_available():
+ from peft.tuners.ia3 import Linear4bit as IA3Linear4bit
+ from peft.tuners.lora import Linear4bit as LoraLinear4bit
+ from peft.tuners.randlora import Linear4bit as RandLoraLinear4bit
+ from peft.tuners.road import Linear4bit as RoadLinear4bit
+ from peft.tuners.vera import Linear4bit as VeraLinear4bit
+
+
+@require_non_cpu
+class PeftGPUCommonTests(unittest.TestCase):
+ r"""
+ A common tester to run common operations that are performed on GPU such as generation, loading in 8bit, etc.
+ """
+
+ def setUp(self):
+ self.seq2seq_model_id = "google/flan-t5-base"
+ self.causal_lm_model_id = "facebook/opt-350m"
+ self.audio_model_id = "openai/whisper-large"
+ self.device = infer_device()
+
+ def tearDown(self):
+ r"""
+ Efficient mechanism to free GPU memory after each test. Based on
+ https://github.com/huggingface/transformers/issues/21094
+ """
+ clear_device_cache(garbage_collection=True)
+ gc.collect()
+
+ @require_bitsandbytes
+ @pytest.mark.multi_gpu_tests
+ @pytest.mark.single_gpu_tests
+ def test_lora_bnb_8bit_quantization(self):
+ r"""
+ Test that tests if the 8bit quantization using LoRA works as expected
+ """
+ whisper_8bit = WhisperForConditionalGeneration.from_pretrained(
+ self.audio_model_id,
+ device_map="auto",
+ quantization_config=BitsAndBytesConfig(load_in_8bit=True),
+ )
+
+ opt_8bit = AutoModelForCausalLM.from_pretrained(
+ self.causal_lm_model_id,
+ device_map="auto",
+ quantization_config=BitsAndBytesConfig(load_in_8bit=True),
+ )
+
+ flan_8bit = AutoModelForSeq2SeqLM.from_pretrained(
+ self.seq2seq_model_id,
+ device_map="auto",
+ quantization_config=BitsAndBytesConfig(load_in_8bit=True),
+ )
+
+ flan_lora_config = LoraConfig(
+ r=16, lora_alpha=32, target_modules=["q", "v"], lora_dropout=0.05, bias="none", task_type="SEQ_2_SEQ_LM"
+ )
+
+ opt_lora_config = LoraConfig(
+ r=16,
+ lora_alpha=32,
+ target_modules=["q_proj", "v_proj"],
+ lora_dropout=0.05,
+ bias="none",
+ task_type="CAUSAL_LM",
+ )
+
+ config = LoraConfig(r=32, lora_alpha=64, target_modules=["q_proj", "v_proj"], lora_dropout=0.05, bias="none")
+
+ flan_8bit = get_peft_model(flan_8bit, flan_lora_config)
+ assert isinstance(flan_8bit.base_model.model.encoder.block[0].layer[0].SelfAttention.q, LoraLinear8bitLt)
+
+ opt_8bit = get_peft_model(opt_8bit, opt_lora_config)
+ assert isinstance(opt_8bit.base_model.model.model.decoder.layers[0].self_attn.v_proj, LoraLinear8bitLt)
+
+ whisper_8bit = get_peft_model(whisper_8bit, config)
+ assert isinstance(whisper_8bit.base_model.model.model.decoder.layers[0].self_attn.v_proj, LoraLinear8bitLt)
+
+ @require_bitsandbytes
+ @pytest.mark.multi_gpu_tests
+ @pytest.mark.single_gpu_tests
+ def test_vera_bnb_8bit_quantization(self):
+ r"""
+ Test that tests if the 8bit quantization using VeRA works as expected
+ """
+ whisper_8bit = WhisperForConditionalGeneration.from_pretrained(
+ self.audio_model_id,
+ device_map="auto",
+ quantization_config=BitsAndBytesConfig(load_in_8bit=True),
+ )
+
+ opt_8bit = AutoModelForCausalLM.from_pretrained(
+ self.causal_lm_model_id,
+ device_map="auto",
+ quantization_config=BitsAndBytesConfig(load_in_8bit=True),
+ )
+
+ flan_8bit = AutoModelForSeq2SeqLM.from_pretrained(
+ self.seq2seq_model_id,
+ device_map="auto",
+ quantization_config=BitsAndBytesConfig(load_in_8bit=True),
+ )
+
+ flan_vera_config = VeraConfig(
+ r=16, target_modules=["q", "v"], vera_dropout=0.05, bias="none", task_type="SEQ_2_SEQ_LM"
+ )
+
+ opt_vera_config = VeraConfig(
+ r=16,
+ target_modules=["q_proj", "v_proj"],
+ vera_dropout=0.05,
+ bias="none",
+ task_type="CAUSAL_LM",
+ )
+
+ config = VeraConfig(r=32, target_modules=["q_proj", "v_proj"], vera_dropout=0.05, bias="none")
+
+ flan_8bit = get_peft_model(flan_8bit, flan_vera_config)
+ assert isinstance(flan_8bit.base_model.model.encoder.block[0].layer[0].SelfAttention.q, VeraLinear8bitLt)
+
+ opt_8bit = get_peft_model(opt_8bit, opt_vera_config)
+ assert isinstance(opt_8bit.base_model.model.model.decoder.layers[0].self_attn.v_proj, VeraLinear8bitLt)
+
+ whisper_8bit = get_peft_model(whisper_8bit, config)
+ assert isinstance(whisper_8bit.base_model.model.model.decoder.layers[0].self_attn.v_proj, VeraLinear8bitLt)
+
+ @require_bitsandbytes
+ @pytest.mark.multi_gpu_tests
+ @pytest.mark.single_gpu_tests
+ def test_randlora_bnb_8bit_quantization(self):
+ r"""
+ Test that tests if the 8bit quantization using RandLora works as expected
+ """
+ whisper_8bit = WhisperForConditionalGeneration.from_pretrained(
+ self.audio_model_id,
+ device_map="auto",
+ quantization_config=BitsAndBytesConfig(load_in_8bit=True),
+ )
+
+ opt_8bit = AutoModelForCausalLM.from_pretrained(
+ self.causal_lm_model_id,
+ device_map="auto",
+ quantization_config=BitsAndBytesConfig(load_in_8bit=True),
+ )
+
+ flan_8bit = AutoModelForSeq2SeqLM.from_pretrained(
+ self.seq2seq_model_id,
+ device_map="auto",
+ quantization_config=BitsAndBytesConfig(load_in_8bit=True),
+ )
+
+ flan_randlora_config = RandLoraConfig(
+ r=16, target_modules=["q", "v"], randlora_dropout=0.05, bias="none", task_type="SEQ_2_SEQ_LM"
+ )
+
+ opt_randlora_config = RandLoraConfig(
+ r=10,
+ target_modules=["q_proj", "v_proj"],
+ randlora_dropout=0.05,
+ bias="none",
+ task_type="CAUSAL_LM",
+ )
+
+ config = RandLoraConfig(r=5, target_modules=["q_proj", "v_proj"], randlora_dropout=0.05, bias="none")
+
+ flan_8bit = get_peft_model(flan_8bit, flan_randlora_config)
+ assert isinstance(flan_8bit.base_model.model.encoder.block[0].layer[0].SelfAttention.q, RandLoraLinear8bitLt)
+
+ opt_8bit = get_peft_model(opt_8bit, opt_randlora_config)
+ assert isinstance(opt_8bit.base_model.model.model.decoder.layers[0].self_attn.v_proj, RandLoraLinear8bitLt)
+
+ whisper_8bit = get_peft_model(whisper_8bit, config)
+ assert isinstance(whisper_8bit.base_model.model.model.decoder.layers[0].self_attn.v_proj, RandLoraLinear8bitLt)
+
+ @require_bitsandbytes
+ @pytest.mark.multi_gpu_tests
+ @pytest.mark.single_gpu_tests
+ def test_ia3_bnb_8bit_quantization(self):
+ r"""
+ Test that tests if the 8bit quantization using IA3 works as expected
+ """
+ whisper_8bit = WhisperForConditionalGeneration.from_pretrained(
+ self.audio_model_id,
+ device_map="auto",
+ quantization_config=BitsAndBytesConfig(load_in_8bit=True),
+ )
+
+ opt_8bit = AutoModelForCausalLM.from_pretrained(
+ self.causal_lm_model_id,
+ device_map="auto",
+ quantization_config=BitsAndBytesConfig(load_in_8bit=True),
+ )
+
+ flan_8bit = AutoModelForSeq2SeqLM.from_pretrained(
+ self.seq2seq_model_id,
+ device_map="auto",
+ quantization_config=BitsAndBytesConfig(load_in_8bit=True),
+ )
+
+ flan_ia3_config = IA3Config(target_modules=["q", "v"], task_type="SEQ_2_SEQ_LM")
+
+ opt_ia3_config = IA3Config(
+ target_modules=["q_proj", "v_proj", "fc2"],
+ feedforward_modules=["fc2"],
+ task_type="CAUSAL_LM",
+ )
+
+ config = IA3Config(target_modules=["q_proj", "v_proj", "fc2"], feedforward_modules=["fc2"])
+
+ flan_8bit = get_peft_model(flan_8bit, flan_ia3_config)
+ assert isinstance(flan_8bit.base_model.model.encoder.block[0].layer[0].SelfAttention.q, IA3Linear8bitLt)
+
+ opt_8bit = get_peft_model(opt_8bit, opt_ia3_config)
+ assert isinstance(opt_8bit.base_model.model.model.decoder.layers[0].self_attn.v_proj, IA3Linear8bitLt)
+
+ whisper_8bit = get_peft_model(whisper_8bit, config)
+ assert isinstance(whisper_8bit.base_model.model.model.decoder.layers[0].self_attn.v_proj, IA3Linear8bitLt)
+
+ @require_bitsandbytes
+ @pytest.mark.multi_gpu_tests
+ @pytest.mark.single_gpu_tests
+ def test_road_bnb_8bit_quantization(self):
+ r"""
+ Test that tests if the 8bit quantization using Road works as expected
+ """
+ whisper_8bit = WhisperForConditionalGeneration.from_pretrained(
+ self.audio_model_id,
+ device_map="auto",
+ quantization_config=BitsAndBytesConfig(load_in_8bit=True),
+ )
+
+ opt_8bit = AutoModelForCausalLM.from_pretrained(
+ self.causal_lm_model_id,
+ device_map="auto",
+ quantization_config=BitsAndBytesConfig(load_in_8bit=True),
+ )
+
+ flan_8bit = AutoModelForSeq2SeqLM.from_pretrained(
+ self.seq2seq_model_id,
+ device_map="auto",
+ quantization_config=BitsAndBytesConfig(load_in_8bit=True),
+ )
+
+ flan_road_config = RoadConfig(target_modules=["q", "v"], task_type="SEQ_2_SEQ_LM")
+
+ opt_road_config = RoadConfig(
+ target_modules=["q_proj", "v_proj", "fc2"],
+ task_type="CAUSAL_LM",
+ )
+
+ config = RoadConfig(target_modules=["q_proj", "v_proj", "fc2"])
+
+ flan_8bit = get_peft_model(flan_8bit, flan_road_config)
+ assert isinstance(flan_8bit.base_model.model.encoder.block[0].layer[0].SelfAttention.q, RoadLinear8bitLt)
+
+ opt_8bit = get_peft_model(opt_8bit, opt_road_config)
+ assert isinstance(opt_8bit.base_model.model.model.decoder.layers[0].self_attn.v_proj, RoadLinear8bitLt)
+
+ whisper_8bit = get_peft_model(whisper_8bit, config)
+ assert isinstance(whisper_8bit.base_model.model.model.decoder.layers[0].self_attn.v_proj, RoadLinear8bitLt)
+
+ @require_bitsandbytes
+ @pytest.mark.multi_gpu_tests
+ @pytest.mark.single_gpu_tests
+ @parameterized.expand(["4bit", "8bit"])
+ def test_lora_bnb_quantization_from_pretrained_safetensors(self, quantization):
+ r"""
+ Tests that the bnb quantization using LoRA works as expected with safetensors weights.
+ """
+ model_id = "facebook/opt-350m"
+ peft_model_id = "ybelkada/test-st-lora"
+ kwargs = {"device_map": "auto"}
+ if quantization == "4bit":
+ kwargs["quantization_config"] = BitsAndBytesConfig(load_in_4bit=True)
+ else:
+ kwargs["quantization_config"] = BitsAndBytesConfig(load_in_8bit=True)
+
+ model = AutoModelForCausalLM.from_pretrained(model_id, **kwargs)
+ model = PeftModel.from_pretrained(model, peft_model_id)
+
+ model.generate(input_ids=torch.LongTensor([[0, 2, 3, 1]]).to(0))
+
+ # loading a 2nd adapter works, #1239
+ model.load_adapter(peft_model_id, "adapter2")
+ model.set_adapter("adapter2")
+ model.generate(input_ids=torch.LongTensor([[0, 2, 3, 1]]).to(0))
+
+ # check that both adapters are in the same layer
+ assert "default" in model.base_model.model.model.decoder.layers[0].self_attn.q_proj.lora_A
+ assert "adapter2" in model.base_model.model.model.decoder.layers[0].self_attn.q_proj.lora_A
+
+ @require_bitsandbytes
+ @pytest.mark.multi_gpu_tests
+ @pytest.mark.single_gpu_tests
+ @parameterized.expand(["4bit", "8bit"])
+ def test_adalora_bnb_quantization_from_pretrained_safetensors(self, quantization):
+ r"""
+ Tests that the bnb quantization using AdaLora works as expected with safetensors weights.
+ """
+ model_id = "facebook/opt-350m"
+ kwargs = {"device_map": "auto"}
+ if quantization == "4bit":
+ kwargs["quantization_config"] = BitsAndBytesConfig(load_in_4bit=True)
+ else:
+ kwargs["quantization_config"] = BitsAndBytesConfig(load_in_8bit=True)
+
+ model = AutoModelForCausalLM.from_pretrained(model_id, **kwargs)
+ config = AdaLoraConfig(task_type=TaskType.CAUSAL_LM, total_step=1)
+ peft_model = get_peft_model(model, config)
+ peft_model = prepare_model_for_kbit_training(peft_model)
+ peft_model.generate(input_ids=torch.LongTensor([[0, 2, 3, 1]]).to(0))
+
+ with tempfile.TemporaryDirectory() as tmp_dir:
+ peft_model.save_pretrained(tmp_dir)
+ model = AutoModelForCausalLM.from_pretrained(model_id, **kwargs)
+ model = PeftModel.from_pretrained(model, tmp_dir)
+ model = prepare_model_for_kbit_training(peft_model)
+ model.generate(input_ids=torch.LongTensor([[0, 2, 3, 1]]).to(0))
+
+ # loading a 2nd adapter works, #1239
+ model.load_adapter(tmp_dir, "adapter2")
+ model.set_adapter("adapter2")
+ model.generate(input_ids=torch.LongTensor([[0, 2, 3, 1]]).to(0))
+
+ # check that both adapters are in the same layer
+ assert "default" in model.base_model.model.model.decoder.layers[0].self_attn.q_proj.lora_A
+ assert "adapter2" in model.base_model.model.model.decoder.layers[0].self_attn.q_proj.lora_A
+
+ @require_bitsandbytes
+ @pytest.mark.multi_gpu_tests
+ @pytest.mark.single_gpu_tests
+ @parameterized.expand(["4bit", "8bit"])
+ def test_vera_bnb_quantization_from_pretrained_safetensors(self, quantization):
+ r"""
+ Tests that the bnb quantization using VeRA works as expected with safetensors weights.
+ """
+ model_id = "facebook/opt-350m"
+ kwargs = {"device_map": "auto"}
+ if quantization == "4bit":
+ kwargs["quantization_config"] = BitsAndBytesConfig(load_in_4bit=True)
+ else:
+ kwargs["quantization_config"] = BitsAndBytesConfig(load_in_8bit=True)
+
+ model = AutoModelForCausalLM.from_pretrained(model_id, **kwargs)
+ config = VeraConfig(task_type=TaskType.CAUSAL_LM)
+ peft_model = get_peft_model(model, config)
+ peft_model = prepare_model_for_kbit_training(peft_model)
+ peft_model.generate(input_ids=torch.LongTensor([[0, 2, 3, 1]]).to(0))
+
+ with tempfile.TemporaryDirectory() as tmp_dir:
+ peft_model.save_pretrained(tmp_dir)
+ model = AutoModelForCausalLM.from_pretrained(model_id, **kwargs)
+ model = PeftModel.from_pretrained(model, tmp_dir)
+ model = prepare_model_for_kbit_training(model)
+ model.generate(input_ids=torch.LongTensor([[0, 2, 3, 1]]).to(0))
+
+ # loading a 2nd adapter works, #1239
+ model.load_adapter(tmp_dir, "adapter2")
+ model.set_adapter("adapter2")
+ model.generate(input_ids=torch.LongTensor([[0, 2, 3, 1]]).to(0))
+
+ # check that both adapters are in the same layer
+ assert "default" in model.base_model.model.model.decoder.layers[0].self_attn.q_proj.vera_A
+ assert "adapter2" in model.base_model.model.model.decoder.layers[0].self_attn.q_proj.vera_A
+
+ @require_bitsandbytes
+ @pytest.mark.multi_gpu_tests
+ @pytest.mark.single_gpu_tests
+ @parameterized.expand(["4bit", "8bit"])
+ def test_randlora_bnb_quantization_from_pretrained_safetensors(self, quantization):
+ r"""
+ Tests that the bnb quantization using RandLora works as expected with safetensors weights.
+ """
+ model_id = "facebook/opt-350m"
+ kwargs = {"device_map": "auto"}
+ if quantization == "4bit":
+ kwargs["quantization_config"] = BitsAndBytesConfig(load_in_4bit=True)
+ else:
+ kwargs["quantization_config"] = BitsAndBytesConfig(load_in_8bit=True)
+
+ model = AutoModelForCausalLM.from_pretrained(model_id, **kwargs)
+ config = RandLoraConfig(task_type=TaskType.CAUSAL_LM)
+ peft_model = get_peft_model(model, config)
+ peft_model = prepare_model_for_kbit_training(peft_model)
+ peft_model.generate(input_ids=torch.LongTensor([[0, 2, 3, 1]]).to(0))
+
+ with tempfile.TemporaryDirectory() as tmp_dir:
+ peft_model.save_pretrained(tmp_dir)
+ model = AutoModelForCausalLM.from_pretrained(model_id, **kwargs)
+ model = PeftModel.from_pretrained(model, tmp_dir)
+ model = prepare_model_for_kbit_training(model)
+ model.generate(input_ids=torch.LongTensor([[0, 2, 3, 1]]).to(0))
+
+ # loading a 2nd adapter works, #1239
+ model.load_adapter(tmp_dir, "adapter2")
+ model.set_adapter("adapter2")
+ model.generate(input_ids=torch.LongTensor([[0, 2, 3, 1]]).to(0))
+
+ # check that both adapters are in the same layer
+ assert "default" in model.base_model.model.model.decoder.layers[0].self_attn.q_proj.randlora_A
+ assert "adapter2" in model.base_model.model.model.decoder.layers[0].self_attn.q_proj.randlora_A
+
+ @require_bitsandbytes
+ @pytest.mark.multi_gpu_tests
+ @pytest.mark.single_gpu_tests
+ @parameterized.expand(["4bit", "8bit"])
+ def test_ia3_bnb_quantization_from_pretrained_safetensors(self, quantization):
+ r"""
+ Tests that the bnb quantization using IA³ works as expected with safetensors weights.
+ """
+ model_id = "facebook/opt-350m"
+ kwargs = {"device_map": "auto"}
+ if quantization == "4bit":
+ kwargs["quantization_config"] = BitsAndBytesConfig(load_in_4bit=True)
+ else:
+ kwargs["quantization_config"] = BitsAndBytesConfig(load_in_8bit=True)
+
+ model = AutoModelForCausalLM.from_pretrained(model_id, **kwargs)
+ config = IA3Config(task_type=TaskType.CAUSAL_LM)
+ peft_model = get_peft_model(model, config)
+ peft_model = prepare_model_for_kbit_training(peft_model)
+ peft_model.generate(input_ids=torch.LongTensor([[0, 2, 3, 1]]).to(0))
+
+ with tempfile.TemporaryDirectory() as tmp_dir:
+ peft_model.save_pretrained(tmp_dir)
+ model = AutoModelForCausalLM.from_pretrained(model_id, **kwargs)
+ model = PeftModel.from_pretrained(model, tmp_dir)
+ model = prepare_model_for_kbit_training(model)
+ model.generate(input_ids=torch.LongTensor([[0, 2, 3, 1]]).to(0))
+
+ # loading a 2nd adapter works, #1239
+ model.load_adapter(tmp_dir, "adapter2")
+ model.set_adapter("adapter2")
+ model.generate(input_ids=torch.LongTensor([[0, 2, 3, 1]]).to(0))
+
+ # check that both adapters are in the same layer
+ assert "default" in model.base_model.model.model.decoder.layers[0].self_attn.q_proj.ia3_l
+ assert "adapter2" in model.base_model.model.model.decoder.layers[0].self_attn.q_proj.ia3_l
+
+ @pytest.mark.single_gpu_tests
+ def test_lora_gptq_quantization_from_pretrained_safetensors(self):
+ r"""
+ Tests that the autogptq quantization using LoRA works as expected with safetensors weights.
+ """
+ from transformers import GPTQConfig
+
+ model_id = "marcsun13/opt-350m-gptq-4bit"
+ quantization_config = GPTQConfig(bits=4, use_exllama=False)
+ kwargs = {
+ "pretrained_model_name_or_path": model_id,
+ "torch_dtype": torch.float16,
+ "device_map": "auto",
+ "quantization_config": quantization_config,
+ }
+ model = AutoModelForCausalLM.from_pretrained(**kwargs)
+ model = prepare_model_for_kbit_training(model)
+
+ config = LoraConfig(task_type="CAUSAL_LM")
+ peft_model = get_peft_model(model, config)
+ peft_model.generate(input_ids=torch.LongTensor([[0, 2, 3, 1]]).to(peft_model.device))
+
+ with tempfile.TemporaryDirectory() as tmp_dir:
+ peft_model.save_pretrained(tmp_dir)
+ model = AutoModelForCausalLM.from_pretrained(**kwargs)
+ model = PeftModel.from_pretrained(model, tmp_dir)
+ model = prepare_model_for_kbit_training(model)
+ model.generate(input_ids=torch.LongTensor([[0, 2, 3, 1]]).to(peft_model.device))
+
+ # loading a 2nd adapter works, #1239
+ model.load_adapter(tmp_dir, "adapter2")
+ model.set_adapter("adapter2")
+ model.generate(input_ids=torch.LongTensor([[0, 2, 3, 1]]).to(peft_model.device))
+
+ # check that both adapters are in the same layer
+ assert "default" in model.base_model.model.model.decoder.layers[0].self_attn.q_proj.lora_A
+ assert "adapter2" in model.base_model.model.model.decoder.layers[0].self_attn.q_proj.lora_A
+
+ @require_bitsandbytes
+ @pytest.mark.multi_gpu_tests
+ @pytest.mark.single_gpu_tests
+ def test_lora_bnb_4bit_quantization(self):
+ r"""
+ Test that tests if the 4bit quantization using LoRA works as expected
+ """
+ whisper_4bit = WhisperForConditionalGeneration.from_pretrained(
+ self.audio_model_id,
+ device_map="auto",
+ quantization_config=BitsAndBytesConfig(load_in_4bit=True),
+ )
+
+ opt_4bit = AutoModelForCausalLM.from_pretrained(
+ self.causal_lm_model_id,
+ device_map="auto",
+ quantization_config=BitsAndBytesConfig(load_in_4bit=True),
+ )
+
+ flan_4bit = AutoModelForSeq2SeqLM.from_pretrained(
+ self.seq2seq_model_id,
+ device_map="auto",
+ quantization_config=BitsAndBytesConfig(load_in_4bit=True),
+ )
+
+ flan_lora_config = LoraConfig(
+ r=16, lora_alpha=32, target_modules=["q", "v"], lora_dropout=0.05, bias="none", task_type="SEQ_2_SEQ_LM"
+ )
+
+ opt_lora_config = LoraConfig(
+ r=16,
+ lora_alpha=32,
+ target_modules=["q_proj", "v_proj"],
+ lora_dropout=0.05,
+ bias="none",
+ task_type="CAUSAL_LM",
+ )
+
+ config = LoraConfig(r=32, lora_alpha=64, target_modules=["q_proj", "v_proj"], lora_dropout=0.05, bias="none")
+
+ flan_4bit = get_peft_model(flan_4bit, flan_lora_config)
+ assert isinstance(flan_4bit.base_model.model.encoder.block[0].layer[0].SelfAttention.q, LoraLinear4bit)
+
+ opt_4bit = get_peft_model(opt_4bit, opt_lora_config)
+ assert isinstance(opt_4bit.base_model.model.model.decoder.layers[0].self_attn.v_proj, LoraLinear4bit)
+
+ whisper_4bit = get_peft_model(whisper_4bit, config)
+ assert isinstance(whisper_4bit.base_model.model.model.decoder.layers[0].self_attn.v_proj, LoraLinear4bit)
+
+ @require_bitsandbytes
+ @pytest.mark.multi_gpu_tests
+ @pytest.mark.single_gpu_tests
+ def test_vera_bnb_4bit_quantization(self):
+ r"""
+ Test that tests if the 4bit quantization using VeRA works as expected
+ """
+ whisper_4bit = WhisperForConditionalGeneration.from_pretrained(
+ self.audio_model_id,
+ device_map="auto",
+ quantization_config=BitsAndBytesConfig(load_in_4bit=True),
+ )
+
+ opt_4bit = AutoModelForCausalLM.from_pretrained(
+ self.causal_lm_model_id,
+ device_map="auto",
+ quantization_config=BitsAndBytesConfig(load_in_4bit=True),
+ )
+
+ flan_4bit = AutoModelForSeq2SeqLM.from_pretrained(
+ self.seq2seq_model_id,
+ device_map="auto",
+ quantization_config=BitsAndBytesConfig(load_in_4bit=True),
+ )
+
+ flan_vera_config = VeraConfig(
+ r=16, target_modules=["q", "v"], vera_dropout=0.05, bias="none", task_type="SEQ_2_SEQ_LM"
+ )
+
+ opt_vera_config = VeraConfig(
+ r=16,
+ target_modules=["q_proj", "v_proj"],
+ vera_dropout=0.05,
+ bias="none",
+ task_type="CAUSAL_LM",
+ )
+
+ config = VeraConfig(r=32, target_modules=["q_proj", "v_proj"], vera_dropout=0.05, bias="none")
+
+ flan_4bit = get_peft_model(flan_4bit, flan_vera_config)
+ assert isinstance(flan_4bit.base_model.model.encoder.block[0].layer[0].SelfAttention.q, VeraLinear4bit)
+
+ opt_4bit = get_peft_model(opt_4bit, opt_vera_config)
+ assert isinstance(opt_4bit.base_model.model.model.decoder.layers[0].self_attn.v_proj, VeraLinear4bit)
+
+ whisper_4bit = get_peft_model(whisper_4bit, config)
+ assert isinstance(whisper_4bit.base_model.model.model.decoder.layers[0].self_attn.v_proj, VeraLinear4bit)
+
+ @require_bitsandbytes
+ @pytest.mark.multi_gpu_tests
+ @pytest.mark.single_gpu_tests
+ def test_randlora_bnb_4bit_quantization(self):
+ r"""
+ Test that tests if the 4bit quantization using RandLoRA works as expected
+ """
+ whisper_4bit = WhisperForConditionalGeneration.from_pretrained(
+ self.audio_model_id,
+ device_map="auto",
+ quantization_config=BitsAndBytesConfig(load_in_4bit=True),
+ )
+
+ opt_4bit = AutoModelForCausalLM.from_pretrained(
+ self.causal_lm_model_id,
+ device_map="auto",
+ quantization_config=BitsAndBytesConfig(load_in_4bit=True),
+ )
+
+ flan_4bit = AutoModelForSeq2SeqLM.from_pretrained(
+ self.seq2seq_model_id,
+ device_map="auto",
+ quantization_config=BitsAndBytesConfig(load_in_4bit=True),
+ )
+
+ flan_randlora_config = RandLoraConfig(
+ r=16, target_modules=["q", "v"], randlora_dropout=0.05, bias="none", task_type="SEQ_2_SEQ_LM"
+ )
+
+ opt_randlora_config = RandLoraConfig(
+ r=16,
+ target_modules=["q_proj", "v_proj"],
+ randlora_dropout=0.05,
+ bias="none",
+ task_type="CAUSAL_LM",
+ )
+
+ config = RandLoraConfig(r=32, target_modules=["q_proj", "v_proj"], randlora_dropout=0.05, bias="none")
+
+ flan_4bit = get_peft_model(flan_4bit, flan_randlora_config)
+ assert isinstance(flan_4bit.base_model.model.encoder.block[0].layer[0].SelfAttention.q, RandLoraLinear4bit)
+
+ opt_4bit = get_peft_model(opt_4bit, opt_randlora_config)
+ assert isinstance(opt_4bit.base_model.model.model.decoder.layers[0].self_attn.v_proj, RandLoraLinear4bit)
+
+ whisper_4bit = get_peft_model(whisper_4bit, config)
+ assert isinstance(whisper_4bit.base_model.model.model.decoder.layers[0].self_attn.v_proj, RandLoraLinear4bit)
+
+ @require_bitsandbytes
+ @pytest.mark.multi_gpu_tests
+ @pytest.mark.single_gpu_tests
+ def test_ia3_bnb_4bit_quantization(self):
+ r"""
+ Test that tests if the 4bit quantization using IA3 works as expected
+ """
+ whisper_4bit = WhisperForConditionalGeneration.from_pretrained(
+ self.audio_model_id,
+ device_map="auto",
+ quantization_config=BitsAndBytesConfig(load_in_4bit=True),
+ )
+
+ opt_4bit = AutoModelForCausalLM.from_pretrained(
+ self.causal_lm_model_id,
+ device_map="auto",
+ quantization_config=BitsAndBytesConfig(load_in_4bit=True),
+ )
+
+ flan_4bit = AutoModelForSeq2SeqLM.from_pretrained(
+ self.seq2seq_model_id,
+ device_map="auto",
+ quantization_config=BitsAndBytesConfig(load_in_4bit=True),
+ )
+
+ flan_ia3_config = IA3Config(target_modules=["q", "v"], task_type="SEQ_2_SEQ_LM")
+
+ opt_ia3_config = IA3Config(
+ target_modules=["q_proj", "v_proj", "fc2"],
+ feedforward_modules=["fc2"],
+ task_type="CAUSAL_LM",
+ )
+
+ config = IA3Config(target_modules=["q_proj", "v_proj", "fc2"], feedforward_modules=["fc2"])
+
+ flan_4bit = get_peft_model(flan_4bit, flan_ia3_config)
+ assert isinstance(flan_4bit.base_model.model.encoder.block[0].layer[0].SelfAttention.q, IA3Linear4bit)
+
+ opt_4bit = get_peft_model(opt_4bit, opt_ia3_config)
+ assert isinstance(opt_4bit.base_model.model.model.decoder.layers[0].self_attn.v_proj, IA3Linear4bit)
+
+ whisper_4bit = get_peft_model(whisper_4bit, config)
+ assert isinstance(whisper_4bit.base_model.model.model.decoder.layers[0].self_attn.v_proj, IA3Linear4bit)
+
+ @require_bitsandbytes
+ @pytest.mark.multi_gpu_tests
+ @pytest.mark.single_gpu_tests
+ def test_road_bnb_4bit_quantization(self):
+ r"""
+ Test that tests if the 4bit quantization using IA3 works as expected
+ """
+ whisper_4bit = WhisperForConditionalGeneration.from_pretrained(
+ self.audio_model_id,
+ device_map="auto",
+ quantization_config=BitsAndBytesConfig(load_in_4bit=True),
+ )
+
+ opt_4bit = AutoModelForCausalLM.from_pretrained(
+ self.causal_lm_model_id,
+ device_map="auto",
+ quantization_config=BitsAndBytesConfig(load_in_4bit=True),
+ )
+
+ flan_4bit = AutoModelForSeq2SeqLM.from_pretrained(
+ self.seq2seq_model_id,
+ device_map="auto",
+ quantization_config=BitsAndBytesConfig(load_in_4bit=True),
+ )
+
+ flan_road_config = RoadConfig(target_modules=["q", "v"], task_type="SEQ_2_SEQ_LM")
+
+ opt_road_config = RoadConfig(
+ target_modules=["q_proj", "v_proj", "fc2"],
+ task_type="CAUSAL_LM",
+ )
+
+ config = RoadConfig(target_modules=["q_proj", "v_proj", "fc2"])
+
+ flan_4bit = get_peft_model(flan_4bit, flan_road_config)
+ assert isinstance(flan_4bit.base_model.model.encoder.block[0].layer[0].SelfAttention.q, RoadLinear4bit)
+
+ opt_4bit = get_peft_model(opt_4bit, opt_road_config)
+ assert isinstance(opt_4bit.base_model.model.model.decoder.layers[0].self_attn.v_proj, RoadLinear4bit)
+
+ whisper_4bit = get_peft_model(whisper_4bit, config)
+ assert isinstance(whisper_4bit.base_model.model.model.decoder.layers[0].self_attn.v_proj, RoadLinear4bit)
+
+ @pytest.mark.multi_gpu_tests
+ @require_torch_multi_accelerator
+ def test_lora_causal_lm_multi_gpu_inference(self):
+ r"""
+ Test if LORA can be used for inference on multiple GPUs.
+ """
+ lora_config = LoraConfig(
+ r=16,
+ lora_alpha=32,
+ target_modules=["q_proj", "v_proj"],
+ lora_dropout=0.05,
+ bias="none",
+ task_type="CAUSAL_LM",
+ )
+
+ model = AutoModelForCausalLM.from_pretrained(self.causal_lm_model_id, device_map="balanced")
+ tokenizer = AutoTokenizer.from_pretrained(self.seq2seq_model_id)
+
+ assert set(model.hf_device_map.values()) == set(range(device_count))
+
+ model = get_peft_model(model, lora_config)
+ assert isinstance(model, PeftModel)
+
+ dummy_input = "This is a dummy input:"
+ input_ids = tokenizer(dummy_input, return_tensors="pt").input_ids.to(self.device)
+
+ # this should work without any problem
+ _ = model.generate(input_ids=input_ids)
+
+ @require_torch_multi_accelerator
+ @pytest.mark.multi_gpu_tests
+ @require_bitsandbytes
+ def test_lora_seq2seq_lm_multi_gpu_inference(self):
+ r"""
+ Test if LORA can be used for inference on multiple GPUs - 8bit version.
+ """
+ lora_config = LoraConfig(
+ r=16, lora_alpha=32, target_modules=["q", "v"], lora_dropout=0.05, bias="none", task_type="SEQ_2_SEQ_LM"
+ )
+
+ model = AutoModelForSeq2SeqLM.from_pretrained(
+ self.seq2seq_model_id, device_map="balanced", quantization_config=BitsAndBytesConfig(load_in_8bit=True)
+ )
+ tokenizer = AutoTokenizer.from_pretrained(self.seq2seq_model_id)
+
+ assert set(model.hf_device_map.values()) == set(range(device_count))
+
+ model = get_peft_model(model, lora_config)
+ assert isinstance(model, PeftModel)
+ assert isinstance(model.base_model.model.encoder.block[0].layer[0].SelfAttention.q, LoraLinear8bitLt)
+
+ dummy_input = "This is a dummy input:"
+ input_ids = tokenizer(dummy_input, return_tensors="pt").input_ids.to(self.device)
+
+ # this should work without any problem
+ _ = model.generate(input_ids=input_ids)
+
+ @require_torch_multi_accelerator
+ @pytest.mark.multi_gpu_tests
+ @require_bitsandbytes
+ def test_adaption_prompt_8bit(self):
+ model = LlamaForCausalLM.from_pretrained(
+ "trl-internal-testing/tiny-random-LlamaForCausalLM",
+ quantization_config=BitsAndBytesConfig(load_in_8bit=True),
+ torch_dtype=torch.float16,
+ device_map="auto",
+ )
+
+ model = prepare_model_for_kbit_training(model)
+
+ config = AdaptionPromptConfig(
+ adapter_len=10,
+ adapter_layers=2,
+ task_type="CAUSAL_LM",
+ )
+ model = get_peft_model(model, config)
+
+ random_input = torch.LongTensor([[1, 0, 1, 0, 1, 0]]).to(model.device)
+ _ = model(random_input)
+
+ @require_torch_multi_accelerator
+ @pytest.mark.multi_gpu_tests
+ @require_bitsandbytes
+ def test_adaption_prompt_4bit(self):
+ model = LlamaForCausalLM.from_pretrained(
+ "trl-internal-testing/tiny-random-LlamaForCausalLM",
+ quantization_config=BitsAndBytesConfig(load_in_4bit=True),
+ torch_dtype=torch.float16,
+ device_map="auto",
+ )
+
+ model = prepare_model_for_kbit_training(model)
+
+ config = AdaptionPromptConfig(
+ adapter_len=10,
+ adapter_layers=2,
+ task_type="CAUSAL_LM",
+ )
+ model = get_peft_model(model, config)
+
+ random_input = torch.LongTensor([[1, 0, 1, 0, 1, 0]]).to(model.device)
+ _ = model(random_input)
+
+ @require_non_cpu
+ @pytest.mark.single_gpu_tests
+ @require_bitsandbytes
+ def test_print_4bit_expected(self):
+ EXPECTED_TRAINABLE_PARAMS = 294912
+ EXPECTED_ALL_PARAMS = 125534208
+
+ model = AutoModelForCausalLM.from_pretrained(
+ "facebook/opt-125m",
+ quantization_config=BitsAndBytesConfig(load_in_4bit=True),
+ )
+
+ config = LoraConfig(
+ r=8,
+ )
+ model = get_peft_model(model, config)
+ trainable_params, all_params = model.get_nb_trainable_parameters()
+
+ assert trainable_params == EXPECTED_TRAINABLE_PARAMS
+ assert all_params == EXPECTED_ALL_PARAMS
+
+ # test with double quant
+ bnb_config = BitsAndBytesConfig(
+ load_in_4bit=True,
+ bnb_4bit_use_double_quant=True,
+ )
+
+ model = AutoModelForCausalLM.from_pretrained(
+ "facebook/opt-125m",
+ quantization_config=bnb_config,
+ )
+
+ config = LoraConfig(
+ r=8,
+ )
+ model = get_peft_model(model, config)
+ trainable_params, all_params = model.get_nb_trainable_parameters()
+
+ assert trainable_params == EXPECTED_TRAINABLE_PARAMS
+ assert all_params == EXPECTED_ALL_PARAMS
+
+ @require_non_cpu
+ @pytest.mark.single_gpu_tests
+ @require_bitsandbytes
+ def test_modules_to_save_grad(self):
+ model_id = "bigscience/bloomz-560m"
+
+ model = AutoModelForSequenceClassification.from_pretrained(
+ model_id,
+ quantization_config=BitsAndBytesConfig(load_in_4bit=True),
+ torch_dtype=torch.float32,
+ )
+
+ model = prepare_model_for_kbit_training(model)
+
+ config = LoraConfig(
+ r=16,
+ lora_alpha=16,
+ lora_dropout=0.05,
+ bias="none",
+ task_type="SEQ_CLS",
+ )
+
+ peft_model = get_peft_model(model, config)
+
+ lm_head = peft_model.base_model.model.score
+ original_module = lm_head.original_module
+ modules_to_save = lm_head.modules_to_save.default
+
+ inputs = torch.randn(1024).to(model.device)
+ o1 = lm_head(inputs)
+ o1.mean().backward()
+
+ assert modules_to_save.weight.requires_grad is True
+ assert original_module.weight.grad is None
+ assert modules_to_save.weight.grad is not None
+
+ @require_non_cpu
+ @pytest.mark.single_gpu_tests
+ @require_bitsandbytes
+ def test_8bit_merge_lora(self):
+ torch.manual_seed(1000)
+ model = AutoModelForCausalLM.from_pretrained(
+ "facebook/opt-125m",
+ quantization_config=BitsAndBytesConfig(load_in_8bit=True),
+ )
+ random_input = torch.LongTensor([[1, 0, 1, 0, 1, 0]]).to(model.device)
+ out_base = F.softmax(model(random_input).logits, dim=-1)
+
+ config = LoraConfig(
+ r=8,
+ init_lora_weights=False,
+ )
+ model = get_peft_model(model, config)
+
+ with torch.inference_mode():
+ out_before_merge = F.softmax(model(random_input).logits, dim=-1)
+
+ model.merge_and_unload()
+ with torch.inference_mode():
+ out_after_merge = F.softmax(model(random_input).logits, dim=-1)
+
+ atol = 1e-3
+ rtol = 1
+ assert not torch.allclose(out_base, out_before_merge, atol=atol, rtol=rtol)
+ assert torch.allclose(out_before_merge, out_after_merge, atol=atol, rtol=rtol)
+ assert isinstance(model, PeftModel)
+ assert isinstance(model.base_model.model.model.decoder.layers[0].self_attn.q_proj, bnb.nn.Linear8bitLt)
+ assert isinstance(model.base_model.model.model.decoder.layers[0].self_attn.v_proj, bnb.nn.Linear8bitLt)
+
+ @require_non_cpu
+ @pytest.mark.single_gpu_tests
+ @require_bitsandbytes
+ def test_8bit_merge_and_disable_lora(self):
+ torch.manual_seed(1000)
+ model = AutoModelForCausalLM.from_pretrained(
+ "facebook/opt-125m",
+ quantization_config=BitsAndBytesConfig(load_in_8bit=True),
+ )
+ random_input = torch.LongTensor([[1, 0, 1, 0, 1, 0]]).to(model.device)
+ # compare outputs in probability space, because logits can have outliers
+ # and token ids are not precise enough
+ out_base = F.softmax(model(random_input).logits, dim=-1)
+
+ config = LoraConfig(
+ r=8,
+ init_lora_weights=False,
+ )
+ model = get_peft_model(model, config)
+
+ with torch.inference_mode():
+ out_before = F.softmax(model(random_input).logits, dim=-1)
+
+ model.merge_adapter()
+ with model.disable_adapter():
+ with torch.inference_mode():
+ out_after = F.softmax(model(random_input).logits, dim=-1)
+
+ atol = 1e-3
+ rtol = 1
+ assert not torch.allclose(out_base, out_before, atol=atol, rtol=rtol)
+ assert torch.allclose(out_base, out_after, atol=atol, rtol=rtol)
+ assert isinstance(model, PeftModel)
+ assert isinstance(model.base_model.model.model.decoder.layers[0].self_attn.q_proj, LoraLinear8bitLt)
+ assert isinstance(model.base_model.model.model.decoder.layers[0].self_attn.v_proj, LoraLinear8bitLt)
+
+ @require_non_cpu
+ @pytest.mark.single_gpu_tests
+ @require_bitsandbytes
+ def test_8bit_merge_lora_with_bias(self):
+ # same as test_8bit_merge_lora but with lora_bias=True
+ torch.manual_seed(0)
+ model = AutoModelForCausalLM.from_pretrained(
+ "facebook/opt-125m",
+ quantization_config=BitsAndBytesConfig(load_in_8bit=True),
+ )
+ random_input = torch.LongTensor([[1, 0, 1, 0, 1, 0]]).to(model.device)
+ out_base = F.softmax(model(random_input).logits, dim=-1)
+
+ config = LoraConfig(
+ r=8,
+ init_lora_weights=False,
+ lora_bias=True,
+ )
+ model = get_peft_model(model, config)
+
+ with torch.inference_mode():
+ out_before_merge = F.softmax(model(random_input).logits, dim=-1)
+
+ model.merge_and_unload()
+ with torch.inference_mode():
+ out_after_merge = F.softmax(model(random_input).logits, dim=-1)
+
+ atol = 1e-3
+ rtol = 1
+ assert not torch.allclose(out_base, out_before_merge, atol=atol, rtol=rtol)
+ assert torch.allclose(out_before_merge, out_after_merge, atol=atol, rtol=rtol)
+
+ @require_non_cpu
+ @pytest.mark.single_gpu_tests
+ @require_bitsandbytes
+ def test_4bit_merge_lora(self):
+ torch.manual_seed(3000)
+ bnb_config = BitsAndBytesConfig(
+ load_in_4bit=True,
+ bnb_4bit_use_double_quant=False,
+ bnb_4bit_compute_dtype=torch.float32,
+ )
+ model = AutoModelForCausalLM.from_pretrained(
+ "facebook/opt-125m",
+ quantization_config=bnb_config,
+ torch_dtype=torch.float32,
+ )
+ random_input = torch.LongTensor([[1, 0, 1, 0, 1, 0]]).to(model.device)
+ # compare outputs in probability space, because logits can have outliers
+ # and token ids are not precise enough
+ out_base = F.softmax(model(random_input).logits, dim=-1)
+
+ config = LoraConfig(
+ r=8,
+ init_lora_weights=False,
+ )
+ model = get_peft_model(model, config)
+
+ with torch.inference_mode():
+ out_before_merge = F.softmax(model(random_input).logits, dim=-1)
+
+ model.merge_and_unload()
+ with torch.inference_mode():
+ out_after_merge = F.softmax(model(random_input).logits, dim=-1)
+
+ # tolerances are pretty high because some deviations are expected with quantization
+ atol = 0.01
+ rtol = 10
+ assert not torch.allclose(out_base, out_before_merge, atol=atol, rtol=rtol)
+ assert torch.allclose(out_before_merge, out_after_merge, atol=atol, rtol=rtol)
+ assert isinstance(model, PeftModel)
+ assert isinstance(model.base_model.model.model.decoder.layers[0].self_attn.q_proj, bnb.nn.Linear4bit)
+ assert isinstance(model.base_model.model.model.decoder.layers[0].self_attn.v_proj, bnb.nn.Linear4bit)
+
+ @require_non_cpu
+ @pytest.mark.single_gpu_tests
+ @require_bitsandbytes
+ def test_4bit_merge_and_disable_lora(self):
+ torch.manual_seed(3000)
+ bnb_config = BitsAndBytesConfig(
+ load_in_4bit=True,
+ bnb_4bit_use_double_quant=False,
+ bnb_4bit_compute_dtype=torch.float32,
+ )
+ model = AutoModelForCausalLM.from_pretrained(
+ "facebook/opt-125m",
+ quantization_config=bnb_config,
+ torch_dtype=torch.float32,
+ )
+ random_input = torch.LongTensor([[1, 0, 1, 0, 1, 0]]).to(model.device)
+ # compare outputs in probability space, because logits can have outliers
+ # and token ids are not precise enough
+ out_base = F.softmax(model(random_input).logits, dim=-1)
+
+ config = LoraConfig(
+ r=8,
+ init_lora_weights=False,
+ )
+ model = get_peft_model(model, config)
+
+ with torch.inference_mode():
+ out_before = F.softmax(model(random_input).logits, dim=-1)
+
+ model.merge_adapter()
+ with model.disable_adapter():
+ with torch.inference_mode():
+ out_after = F.softmax(model(random_input).logits, dim=-1)
+
+ atol = 0.01
+ rtol = 10
+ assert not torch.allclose(out_base, out_before, atol=atol, rtol=rtol)
+ assert torch.allclose(out_base, out_after, atol=atol, rtol=rtol)
+ assert isinstance(model, PeftModel)
+ assert isinstance(model.base_model.model.model.decoder.layers[0].self_attn.q_proj, LoraLinear4bit)
+ assert isinstance(model.base_model.model.model.decoder.layers[0].self_attn.v_proj, LoraLinear4bit)
+
+ @require_non_cpu
+ @pytest.mark.single_gpu_tests
+ @require_bitsandbytes
+ def test_4bit_merge_lora_with_bias(self):
+ # same as test_4bit_merge_lora but with lora_bias=True
+ torch.manual_seed(3000)
+ bnb_config = BitsAndBytesConfig(
+ load_in_4bit=True,
+ bnb_4bit_use_double_quant=False,
+ bnb_4bit_compute_dtype=torch.float32,
+ )
+ model = AutoModelForCausalLM.from_pretrained(
+ "facebook/opt-125m",
+ quantization_config=bnb_config,
+ torch_dtype=torch.float32,
+ )
+ random_input = torch.LongTensor([[1, 0, 1, 0, 1, 0]]).to(model.device)
+ # compare outputs in probability space, because logits can have outliers
+ # and token ids are not precise enough
+ out_base = F.softmax(model(random_input).logits, dim=-1)
+
+ config = LoraConfig(
+ r=8,
+ init_lora_weights=False,
+ lora_bias=True,
+ )
+ model = get_peft_model(model, config)
+
+ with torch.inference_mode():
+ out_before_merge = F.softmax(model(random_input).logits, dim=-1)
+
+ model.merge_and_unload()
+ with torch.inference_mode():
+ out_after_merge = F.softmax(model(random_input).logits, dim=-1)
+
+ # tolerances are pretty high because some deviations are expected with quantization
+ atol = 0.01
+ rtol = 10
+ assert not torch.allclose(out_base, out_before_merge, atol=atol, rtol=rtol)
+ assert torch.allclose(out_before_merge, out_after_merge, atol=atol, rtol=rtol)
+
+ @require_non_cpu
+ @pytest.mark.single_gpu_tests
+ @require_bitsandbytes
+ def test_4bit_lora_mixed_adapter_batches_lora(self):
+ # check that we can pass mixed adapter names to the model
+ torch.manual_seed(3000)
+ bnb_config = BitsAndBytesConfig(
+ load_in_4bit=True,
+ bnb_4bit_use_double_quant=False,
+ bnb_4bit_compute_dtype=torch.float32,
+ )
+ model = AutoModelForCausalLM.from_pretrained(
+ "facebook/opt-125m",
+ quantization_config=bnb_config,
+ torch_dtype=torch.float32,
+ ).eval()
+ tokenizer = AutoTokenizer.from_pretrained("facebook/opt-125m")
+ # input with 9 samples
+ inputs = tokenizer(
+ [
+ "Hello, my dog is cute",
+ "Hello, my cat is awesome",
+ "Hello, my fish is great",
+ "Salut, mon chien est mignon",
+ "Salut, mon chat est génial",
+ "Salut, mon poisson est super",
+ "Hallo, mein Hund ist süß",
+ "Hallo, meine Katze ist toll",
+ "Hallo, mein Fisch ist großartig",
+ ],
+ return_tensors="pt",
+ padding=True,
+ ).to(model.device)
+ with torch.inference_mode():
+ out_base = model(**inputs).logits
+
+ config0 = LoraConfig(
+ r=8,
+ init_lora_weights=False,
+ )
+ model = get_peft_model(model, config0).eval()
+ with torch.inference_mode():
+ out_adapter0 = model(**inputs).logits
+
+ config1 = LoraConfig(
+ r=16,
+ init_lora_weights=False,
+ )
+ model.add_adapter("adapter1", config1)
+ model.set_adapter("adapter1")
+ with torch.inference_mode():
+ out_adapter1 = model(**inputs).logits
+
+ atol, rtol = 3e-5, 1e-5
+ # sanity check, outputs have the right shape and are not the same
+ assert len(out_base) >= 3
+ assert len(out_base) == len(out_adapter0) == len(out_adapter1)
+ assert not torch.allclose(out_base, out_adapter0, atol=atol, rtol=rtol)
+ assert not torch.allclose(out_base, out_adapter1, atol=atol, rtol=rtol)
+ assert not torch.allclose(out_adapter0, out_adapter1, atol=atol, rtol=rtol)
+
+ # mixed adapter batch
+ adapters = ["__base__", "default", "adapter1"]
+ adapter_names = [adapters[i % 3] for i in (range(9))]
+ with torch.inference_mode():
+ out_mixed = model(**inputs, adapter_names=adapter_names).logits
+
+ assert torch.allclose(out_base[::3], out_mixed[::3], atol=atol, rtol=rtol)
+ assert torch.allclose(out_adapter0[1::3], out_mixed[1::3], atol=atol, rtol=rtol)
+ assert torch.allclose(out_adapter1[2::3], out_mixed[2::3], atol=atol, rtol=rtol)
+
+ @require_non_cpu
+ @pytest.mark.single_gpu_tests
+ @require_bitsandbytes
+ def test_8bit_lora_mixed_adapter_batches_lora(self):
+ # check that we can pass mixed adapter names to the model
+ # note that with 8bit, we have quite a bit of imprecision, therefore we use softmax and higher tolerances
+ torch.manual_seed(3000)
+ bnb_config = BitsAndBytesConfig(load_in_8bit=True)
+ model = AutoModelForCausalLM.from_pretrained(
+ "facebook/opt-125m",
+ quantization_config=bnb_config,
+ torch_dtype=torch.float32,
+ ).eval()
+ tokenizer = AutoTokenizer.from_pretrained("facebook/opt-125m")
+ # input with 9 samples
+ inputs = tokenizer(
+ [
+ "Hello, my dog is cute",
+ "Hello, my cat is awesome",
+ "Hello, my fish is great",
+ "Salut, mon chien est mignon",
+ "Salut, mon chat est génial",
+ "Salut, mon poisson est super",
+ "Hallo, mein Hund ist süß",
+ "Hallo, meine Katze ist toll",
+ "Hallo, mein Fisch ist großartig",
+ ],
+ return_tensors="pt",
+ padding=True,
+ ).to(model.device)
+ with torch.inference_mode():
+ out_base = F.softmax(model(**inputs).logits, dim=-1)
+
+ config0 = LoraConfig(
+ r=8,
+ init_lora_weights=False,
+ )
+ model = get_peft_model(model, config0).eval()
+ with torch.inference_mode():
+ out_adapter0 = F.softmax(model(**inputs).logits, dim=-1)
+
+ config1 = LoraConfig(
+ r=16,
+ init_lora_weights=False,
+ )
+ model.add_adapter("adapter1", config1)
+ model.set_adapter("adapter1")
+ with torch.inference_mode():
+ out_adapter1 = F.softmax(model(**inputs).logits, dim=-1)
+
+ atol = 0.01
+ rtol = 0.5
+ # sanity check, outputs have the right shape and are not the same
+ assert len(out_base) >= 3
+ assert len(out_base) == len(out_adapter0) == len(out_adapter1)
+ assert not torch.allclose(out_base, out_adapter0, atol=atol, rtol=rtol)
+ assert not torch.allclose(out_base, out_adapter1, atol=atol, rtol=rtol)
+ assert not torch.allclose(out_adapter0, out_adapter1, atol=atol, rtol=rtol)
+
+ # mixed adapter batch
+ adapters = ["__base__", "default", "adapter1"]
+ adapter_names = [adapters[i % 3] for i in (range(9))]
+ with torch.inference_mode():
+ out_mixed = F.softmax(model(**inputs, adapter_names=adapter_names).logits, dim=-1)
+
+ assert torch.allclose(out_base[::3], out_mixed[::3], atol=atol, rtol=rtol)
+ assert torch.allclose(out_adapter0[1::3], out_mixed[1::3], atol=atol, rtol=rtol)
+ assert torch.allclose(out_adapter1[2::3], out_mixed[2::3], atol=atol, rtol=rtol)
+
+ @require_non_cpu
+ @pytest.mark.single_gpu_tests
+ def test_serialization_shared_tensors(self):
+ model_checkpoint = "roberta-base"
+ peft_config = LoraConfig(
+ task_type=TaskType.TOKEN_CLS, inference_mode=False, r=16, lora_alpha=16, lora_dropout=0.1, bias="all"
+ )
+ model = AutoModelForTokenClassification.from_pretrained(model_checkpoint, num_labels=11).to(self.device)
+ model = get_peft_model(model, peft_config)
+
+ with tempfile.TemporaryDirectory() as tmp_dir:
+ model.save_pretrained(tmp_dir, safe_serialization=True)
+
+ @require_non_cpu
+ @pytest.mark.single_gpu_tests
+ @require_deterministic_for_xpu
+ @require_bitsandbytes
+ def test_4bit_dora_inference(self):
+ # check for same result with and without DoRA when initializing with init_lora_weights=False
+ bnb_config = BitsAndBytesConfig(
+ load_in_4bit=True,
+ bnb_4bit_use_double_quant=False,
+ bnb_4bit_compute_dtype=torch.float32,
+ )
+ model = AutoModelForCausalLM.from_pretrained(
+ "facebook/opt-125m",
+ quantization_config=bnb_config,
+ torch_dtype=torch.float32,
+ )
+
+ torch.manual_seed(0)
+ config_lora = LoraConfig(r=8, init_lora_weights=False, use_dora=False)
+ model = get_peft_model(model, config_lora).eval()
+
+ random_input = torch.LongTensor([[1, 0, 1, 0, 1, 0]]).to(model.device)
+ logits_lora = model(random_input).logits
+
+ model = AutoModelForCausalLM.from_pretrained(
+ "facebook/opt-125m",
+ quantization_config=bnb_config,
+ torch_dtype=torch.float32,
+ )
+ torch.manual_seed(0)
+ config_dora = LoraConfig(r=8, init_lora_weights=False, use_dora=True)
+ model = get_peft_model(model, config_dora).eval()
+
+ logits_dora = model(random_input).logits
+
+ assert torch.allclose(logits_lora, logits_dora)
+ # sanity check
+ assert isinstance(model.base_model.model.model.decoder.layers[0].self_attn.q_proj, LoraLinear4bit)
+ assert isinstance(model.base_model.model.model.decoder.layers[0].self_attn.v_proj, LoraLinear4bit)
+
+ @require_non_cpu
+ @pytest.mark.single_gpu_tests
+ @require_deterministic_for_xpu
+ @require_bitsandbytes
+ def test_8bit_dora_inference(self):
+ # check for same result with and without DoRA when initializing with init_lora_weights=False
+ model = AutoModelForCausalLM.from_pretrained(
+ "facebook/opt-125m",
+ quantization_config=BitsAndBytesConfig(load_in_8bit=True),
+ torch_dtype=torch.float32,
+ ).eval()
+
+ torch.manual_seed(0)
+ config_lora = LoraConfig(r=8, init_lora_weights=False, use_dora=False)
+ model = get_peft_model(model, config_lora).eval()
+
+ random_input = torch.LongTensor([[1, 0, 1, 0, 1, 0]]).to(model.device)
+ logits_lora = model(random_input).logits
+
+ model = AutoModelForCausalLM.from_pretrained(
+ "facebook/opt-125m",
+ quantization_config=BitsAndBytesConfig(load_in_8bit=True),
+ torch_dtype=torch.float32,
+ )
+ torch.manual_seed(0)
+ config_dora = LoraConfig(r=8, init_lora_weights=False, use_dora=True)
+ model = get_peft_model(model, config_dora).eval()
+
+ logits_dora = model(random_input).logits
+
+ assert torch.allclose(logits_lora, logits_dora)
+ # sanity check
+ assert isinstance(model.base_model.model.model.decoder.layers[0].self_attn.q_proj, LoraLinear8bitLt)
+ assert isinstance(model.base_model.model.model.decoder.layers[0].self_attn.v_proj, LoraLinear8bitLt)
+
+ @require_non_cpu
+ @pytest.mark.single_gpu_tests
+ @require_bitsandbytes
+ def test_4bit_dora_merging(self):
+ # Check results for merging, unmerging, unloading
+ torch.manual_seed(0)
+ bnb_config = BitsAndBytesConfig(
+ load_in_4bit=True,
+ bnb_4bit_use_double_quant=False,
+ bnb_4bit_compute_dtype=torch.float32,
+ )
+ model = AutoModelForCausalLM.from_pretrained(
+ "trl-internal-testing/tiny-random-LlamaForCausalLM",
+ quantization_config=bnb_config,
+ torch_dtype=torch.float32,
+ ).eval()
+ random_input = torch.LongTensor([[1, 0, 1, 0, 1, 0]]).to(model.device)
+ # compare outputs in probability space, because logits can have outliers
+ # and token ids are not precise enough
+ out_base = F.softmax(model(random_input).logits, dim=-1)
+
+ config = LoraConfig(
+ r=8,
+ init_lora_weights=False,
+ use_dora=True,
+ )
+ model = get_peft_model(model, config).eval()
+
+ # Note: By default, DoRA is a no-op before training, even if we set init_lora_weights=False. In order to
+ # measure any differences, we need to change the magnitude vector.
+ for name, module in model.named_modules():
+ if isinstance(module, LoraLinear4bit):
+ module.lora_magnitude_vector["default"].weight = torch.nn.Parameter(
+ 10 * torch.rand_like(module.lora_magnitude_vector["default"].weight)
+ )
+
+ with torch.inference_mode():
+ out_dora = F.softmax(model(random_input).logits, dim=-1)
+
+ model.merge_adapter()
+ out_merged = F.softmax(model(random_input).logits, dim=-1)
+
+ model.unmerge_adapter()
+ out_unmerged = F.softmax(model(random_input).logits, dim=-1)
+
+ model = model.merge_and_unload()
+ out_unloaded = F.softmax(model(random_input).logits, dim=-1)
+
+ atol = 1e-5
+ rtol = 1e-3
+ # sanity check that using DoRA changes the results
+ assert not torch.allclose(out_base, out_dora, atol=atol, rtol=rtol)
+ assert torch.allclose(out_dora, out_merged, atol=atol, rtol=rtol)
+ assert torch.allclose(out_dora, out_unmerged, atol=atol, rtol=rtol)
+ assert torch.allclose(out_dora, out_unloaded, atol=atol, rtol=rtol)
+
+ @require_non_cpu
+ @pytest.mark.single_gpu_tests
+ @require_bitsandbytes
+ def test_8bit_dora_merging(self):
+ # Check results for merging, unmerging, unloading
+ torch.manual_seed(0)
+ model = AutoModelForCausalLM.from_pretrained(
+ "facebook/opt-125m",
+ quantization_config=BitsAndBytesConfig(load_in_8bit=True),
+ torch_dtype=torch.float32,
+ ).eval()
+
+ random_input = torch.LongTensor([[1, 0, 1, 0, 1, 0]]).to(model.device)
+ # compare outputs in probability space, because logits can have outliers
+ # and token ids are not precise enough
+ out_base = F.softmax(model(random_input).logits, dim=-1)
+
+ config = LoraConfig(
+ r=8,
+ init_lora_weights=False,
+ use_dora=True,
+ )
+ model = get_peft_model(model, config).eval()
+
+ # Note: By default, DoRA is a no-op before training, even if we set init_lora_weights=False. In order to
+ # measure any differences, we need to change the magnitude vector.
+ for name, module in model.named_modules():
+ if isinstance(module, LoraLinear8bitLt):
+ module.lora_magnitude_vector["default"].weight = torch.nn.Parameter(
+ 10 * torch.rand_like(module.lora_magnitude_vector["default"].weight)
+ )
+
+ with torch.inference_mode():
+ out_dora = F.softmax(model(random_input).logits, dim=-1)
+
+ model.merge_adapter()
+ out_merged = F.softmax(model(random_input).logits, dim=-1)
+
+ model.unmerge_adapter()
+ out_unmerged = F.softmax(model(random_input).logits, dim=-1)
+
+ model = model.merge_and_unload()
+ out_unloaded = F.softmax(model(random_input).logits, dim=-1)
+
+ atol = 1e-3
+ rtol = 1
+ # sanity check that using DoRA changes the results
+ assert not torch.allclose(out_base, out_dora, atol=atol, rtol=rtol)
+ assert torch.allclose(out_dora, out_merged, atol=atol, rtol=rtol)
+ assert torch.allclose(out_dora, out_unmerged, atol=atol, rtol=rtol)
+ assert torch.allclose(out_dora, out_unloaded, atol=atol, rtol=rtol)
+
+ @pytest.mark.single_gpu_tests
+ def test_dora_ephemeral_gpu_offload(self):
+ torch.manual_seed(0)
+
+ model = AutoModelForCausalLM.from_pretrained(
+ "facebook/opt-125m",
+ torch_dtype=torch.float32,
+ ).eval()
+
+ config = LoraConfig(
+ r=128,
+ init_lora_weights=False,
+ use_dora=True,
+ runtime_config=LoraRuntimeConfig(
+ ephemeral_gpu_offload=True
+ ), # we enable this, but only to verify that it's gone later
+ )
+ peft_model = get_peft_model(model, config).eval()
+ # Check that ephemeral GPU offloading is present
+ assert peft_model.peft_config["default"].runtime_config.ephemeral_gpu_offload
+
+ # Save to disk
+ with tempfile.TemporaryDirectory() as tmp_dir:
+ peft_model.save_pretrained(tmp_dir)
+
+ # Load from disk 100% on CPU without ephemeral GPU offloading
+ peft_model_cpu = PeftModel.from_pretrained(
+ model,
+ tmp_dir,
+ device_map={"": "cpu"},
+ ).eval()
+
+ # Check that ephemeral GPU offloading is absent
+ assert not peft_model_cpu.peft_config["default"].runtime_config.ephemeral_gpu_offload
+
+ # Load again, with ephemeral GPU offloading enabled
+ peft_model_ego = PeftModel.from_pretrained(
+ model,
+ tmp_dir,
+ device_map={"": "cpu"},
+ ephemeral_gpu_offload=True,
+ ).eval()
+
+ random_input = torch.LongTensor([[1, 0, 1, 0, 1, 0]]).to(model.device)
+ with torch.inference_mode():
+ out_peft_model_cpu = F.softmax(peft_model_cpu(random_input).logits, dim=-1)
+ out_peft_model_ego = F.softmax(peft_model_ego(random_input).logits, dim=-1)
+
+ # The results should be the same
+ assert torch.allclose(out_peft_model_cpu, out_peft_model_ego)
+
+ @require_torch_multi_accelerator
+ @pytest.mark.multi_gpu_tests
+ def test_dora_ephemeral_gpu_offload_multigpu(self):
+ torch.manual_seed(0)
+
+ model = AutoModelForCausalLM.from_pretrained(
+ "facebook/opt-125m",
+ torch_dtype=torch.float32,
+ ).eval()
+
+ config = LoraConfig(
+ r=16, # too small and the time difference is too small
+ init_lora_weights=False,
+ use_dora=True,
+ runtime_config=LoraRuntimeConfig(ephemeral_gpu_offload=True),
+ )
+ peft_model = get_peft_model(model, config).eval()
+
+ layer = peft_model.base_model.model.model.decoder.layers[0].self_attn.v_proj
+ lora_A, lora_B = layer.lora_A, layer.lora_B
+
+ possible_combinations = ["cpu", self.device, f"{self.device}:0", f"{self.device}:1"]
+ adapter_name = layer.active_adapter[0]
+ for device_A in possible_combinations:
+ la = lora_A.to(device_A)
+ for device_B in possible_combinations:
+ lb = lora_B.to(device_B)
+ layer.lora_A, layer.lora_B = la, lb
+ layer.lora_variant[adapter_name].init(layer, adapter_name=adapter_name) # should not raise an error
+
+ @require_non_cpu
+ @pytest.mark.single_gpu_tests
+ @require_bitsandbytes
+ def test_8bit_road_merging(self):
+ # Check results for merging, unmerging, unloading
+ torch.manual_seed(0)
+ model = AutoModelForCausalLM.from_pretrained(
+ "facebook/opt-125m",
+ quantization_config=BitsAndBytesConfig(load_in_8bit=True),
+ torch_dtype=torch.float32,
+ ).eval()
+
+ random_input = torch.LongTensor([[1, 0, 1, 0, 1, 0]]).to(model.device)
+ # compare outputs in probability space, because logits can have outliers
+ # and token ids are not precise enough
+ out_base = F.softmax(model(random_input).logits, dim=-1)
+
+ config = RoadConfig(
+ init_weights=False,
+ )
+ model = get_peft_model(model, config).eval()
+
+ with torch.inference_mode():
+ out_road = F.softmax(model(random_input).logits, dim=-1)
+
+ model.merge_adapter()
+ out_merged = F.softmax(model(random_input).logits, dim=-1)
+
+ model.unmerge_adapter()
+ out_unmerged = F.softmax(model(random_input).logits, dim=-1)
+
+ model = model.merge_and_unload()
+ out_unloaded = F.softmax(model(random_input).logits, dim=-1)
+
+ atol = 1e-3
+ rtol = 1
+ # sanity check that using DoRA changes the results
+ assert not torch.allclose(out_base, out_road, atol=atol, rtol=rtol)
+ assert torch.allclose(out_road, out_merged, atol=atol, rtol=rtol)
+ assert torch.allclose(out_road, out_unmerged, atol=atol, rtol=rtol)
+ assert torch.allclose(out_road, out_unloaded, atol=atol, rtol=rtol)
+
+ @require_non_cpu
+ @pytest.mark.single_gpu_tests
+ @require_bitsandbytes
+ def test_4bit_road_merging(self):
+ # Check results for merging, unmerging, unloading
+ torch.manual_seed(0)
+ bnb_config = BitsAndBytesConfig(
+ load_in_4bit=True,
+ bnb_4bit_use_double_quant=False,
+ bnb_4bit_compute_dtype=torch.float32,
+ )
+ model = AutoModelForCausalLM.from_pretrained(
+ "trl-internal-testing/tiny-random-LlamaForCausalLM",
+ quantization_config=bnb_config,
+ torch_dtype=torch.float32,
+ ).eval()
+ random_input = torch.LongTensor([[1, 0, 1, 0, 1, 0]]).to(model.device)
+ # compare outputs in probability space, because logits can have outliers
+ # and token ids are not precise enough
+ out_base = model(random_input).logits
+ probs_base = F.softmax(out_base, dim=-1)
+
+ config = RoadConfig(
+ init_weights=False,
+ group_size=4,
+ )
+ model = get_peft_model(model, config).eval()
+
+ with torch.inference_mode():
+ out_road = model(random_input).logits
+ probs_road = F.softmax(out_road, dim=-1)
+
+ model.merge_adapter()
+ probs_merged = F.softmax(model(random_input).logits, dim=-1)
+
+ model.unmerge_adapter()
+ probs_unmerged = F.softmax(model(random_input).logits, dim=-1)
+
+ model = model.merge_and_unload()
+ probs_unloaded = F.softmax(model(random_input).logits, dim=-1)
+
+ atol = 1e-5
+ rtol = 1e-3
+ # sanity check that using DoRA changes the results
+ # we compare outputs instead of logits because they may not be sensitive enough
+ assert not torch.allclose(out_base, out_road, atol=atol, rtol=rtol)
+ assert torch.allclose(probs_road, probs_merged, atol=atol, rtol=rtol)
+ assert torch.allclose(probs_road, probs_unmerged, atol=atol, rtol=rtol)
+ assert torch.allclose(probs_road, probs_unloaded, atol=atol, rtol=rtol)
+
+ def test_apply_GS_hra_inference(self):
+ # check for different result with and without apply_GS
+ model = AutoModelForCausalLM.from_pretrained(
+ "facebook/opt-125m",
+ torch_dtype=torch.float32,
+ ).eval()
+
+ torch.manual_seed(0)
+ config_hra = HRAConfig(r=8, init_weights=True, apply_GS=False)
+ model = get_peft_model(model, config_hra).eval()
+
+ random_input = torch.LongTensor([[1, 0, 1, 0, 1, 0]]).to(model.device)
+ logits_hra = model(random_input).logits
+
+ model = AutoModelForCausalLM.from_pretrained(
+ "facebook/opt-125m",
+ torch_dtype=torch.float32,
+ )
+ torch.manual_seed(0)
+ config_hra_GS = HRAConfig(r=8, init_weights=True, apply_GS=True)
+ model = get_peft_model(model, config_hra_GS)
+
+ logits_hra_GS = model(random_input).logits
+
+ assert not torch.allclose(logits_hra, logits_hra_GS)
+
+ @require_non_cpu
+ @pytest.mark.single_gpu_tests
+ def test_apply_GS_hra_conv2d_inference(self):
+ # check for different result with and without apply_GS
+ model_id = "microsoft/resnet-18"
+ image_processor = AutoImageProcessor.from_pretrained(model_id)
+ image = load_cat_image()
+ data = image_processor(image, return_tensors="pt")
+
+ model = AutoModelForImageClassification.from_pretrained(model_id).eval()
+ torch.manual_seed(0)
+ config_hra = HRAConfig(r=8, init_weights=True, target_modules=["convolution"], apply_GS=False)
+ model = get_peft_model(model, config_hra).eval()
+
+ logits_hra = model(**data).logits
+
+ model = AutoModelForImageClassification.from_pretrained(model_id).eval()
+ torch.manual_seed(0)
+ config_hra_GS = HRAConfig(r=8, init_weights=True, target_modules=["convolution"], apply_GS=True)
+ model = get_peft_model(model, config_hra_GS)
+
+ logits_hra_GS = model(**data).logits
+
+ assert not torch.allclose(logits_hra, logits_hra_GS)
+
+ @require_non_cpu
+ @pytest.mark.single_gpu_tests
+ def test_r_odd_hra_inference(self):
+ # check that an untrained HRA adapter can't be initialized as an identity tranformation
+ # when r is an odd number
+ model = AutoModelForCausalLM.from_pretrained(
+ "facebook/opt-125m",
+ torch_dtype=torch.float32,
+ ).eval()
+
+ random_input = torch.LongTensor([[1, 0, 1, 0, 1, 0]]).to(model.device)
+
+ torch.manual_seed(0)
+ logits = model(random_input).logits
+
+ config_hra = HRAConfig(r=7, init_weights=True, apply_GS=False)
+ model = get_peft_model(model, config_hra).eval()
+ logits_hra = model(random_input).logits
+
+ assert not torch.allclose(logits, logits_hra)
+
+
+@pytest.mark.skipif(not (torch.cuda.is_available() or is_xpu_available()), reason="test requires a GPU or XPU")
+@pytest.mark.single_gpu_tests
+class TestSameAdapterDifferentDevices:
+ device = infer_device()
+
+ # 1639
+ # The original issue comes down to the following problem: If the user has a base layer on CUDA, moves the adapter to
+ # CPU, then adds another adapter (which will automatically be moved to CUDA), then the first adapter will also be
+ # moved to CUDA.
+ @pytest.fixture
+ def mlp(self):
+ class MLP(nn.Module):
+ def __init__(self, bias=True):
+ super().__init__()
+ self.lin0 = nn.Linear(8, 32, bias=bias)
+ self.lin1 = nn.Linear(32, 2, bias=bias)
+
+ return MLP()
+
+ @pytest.fixture
+ def emb_conv1d(self):
+ class ModelEmbConv1D(nn.Module):
+ def __init__(self, emb_size=100):
+ super().__init__()
+ self.emb = nn.Embedding(emb_size, 5)
+ self.conv1d = Conv1D(1, 5)
+
+ return ModelEmbConv1D()
+
+ @pytest.fixture
+ def conv2d(self):
+ class ModelConv2D(nn.Module):
+ def __init__(self):
+ super().__init__()
+ self.conv2d = nn.Conv2d(5, 10, 3)
+
+ return ModelConv2D()
+
+ def test_lora_one_target_add_new_adapter_does_not_change_device(self, mlp):
+ config = LoraConfig(target_modules=["lin0"])
+ model = get_peft_model(mlp, config)
+ model = model.to(self.device)
+ model.lin0.lora_A.cpu()
+ model.lin0.lora_B.cpu()
+
+ # check that the adapter is indeed on CPU and the base model on GPU
+ assert model.lin0.lora_A.default.weight.device.type == "cpu"
+ assert model.lin0.lora_B.default.weight.device.type == "cpu"
+ assert model.lin0.base_layer.weight.device.type == self.device
+
+ model.add_adapter("other", config)
+ # check that after adding a new adapter, the old adapter is still on CPU
+ assert model.lin0.lora_A.default.weight.device.type == "cpu"
+ assert model.lin0.lora_B.default.weight.device.type == "cpu"
+ # the rest should be on GPU
+ assert model.lin0.base_layer.weight.device.type == self.device
+ assert model.lin0.lora_A.other.weight.device.type == self.device
+ assert model.lin0.lora_B.other.weight.device.type == self.device
+
+ def test_lora_multiple_targets_add_new_adapater_does_not_change_device(self, mlp):
+ # same as the previous test, but targeting multiple layers
+ config = LoraConfig(target_modules=["lin0", "lin1"])
+ model = get_peft_model(mlp, config)
+ model = model.to(self.device)
+ # move lin1 to CPU but leave lin0 on GPU
+ model.lin1.lora_A.cpu()
+ model.lin1.lora_B.cpu()
+
+ # check that the adapter is indeed on CPU and the base model on GPU
+ assert model.lin1.lora_A.default.weight.device.type == "cpu"
+ assert model.lin1.lora_B.default.weight.device.type == "cpu"
+ assert model.lin1.base_layer.weight.device.type == self.device
+ assert model.lin0.lora_A.default.weight.device.type == self.device
+ assert model.lin0.lora_B.default.weight.device.type == self.device
+ assert model.lin0.base_layer.weight.device.type == self.device
+
+ model.add_adapter("other", config)
+ # check that after adding a new adapter, the old adapter is still on CPU
+ assert model.lin1.lora_A.default.weight.device.type == "cpu"
+ assert model.lin1.lora_B.default.weight.device.type == "cpu"
+ assert model.lin1.base_layer.weight.device.type == self.device
+ # the rest should be on GPU
+ assert model.lin0.lora_A.default.weight.device.type == self.device
+ assert model.lin0.lora_B.default.weight.device.type == self.device
+ assert model.lin0.base_layer.weight.device.type == self.device
+ assert model.lin0.lora_A.other.weight.device.type == self.device
+ assert model.lin0.lora_B.other.weight.device.type == self.device
+ assert model.lin1.lora_A.other.weight.device.type == self.device
+ assert model.lin1.lora_B.other.weight.device.type == self.device
+
+ def test_lora_embedding_target_add_new_adapter_does_not_change_device(self, emb_conv1d):
+ # same as first test, but targeting the embedding layer
+ config = LoraConfig(target_modules=["emb"])
+ model = get_peft_model(emb_conv1d, config)
+ model = model.to(self.device)
+ model.emb.lora_embedding_A.cpu()
+ model.emb.lora_embedding_B.cpu()
+
+ # check that the adapter is indeed on CPU and the base model on GPU
+ assert model.emb.lora_embedding_A.default.device.type == "cpu"
+ assert model.emb.lora_embedding_B.default.device.type == "cpu"
+ assert model.emb.weight.device.type == self.device
+
+ model.add_adapter("other", config)
+ # check that after adding a new adapter, the old adapter is still on CPU
+ assert model.emb.lora_embedding_A.default.device.type == "cpu"
+ assert model.emb.lora_embedding_B.default.device.type == "cpu"
+ # the rest should be on GPU
+ assert model.emb.weight.device.type == self.device
+ assert model.emb.lora_embedding_A.other.device.type == self.device
+ assert model.emb.lora_embedding_B.other.device.type == self.device
+
+ def test_lora_conv1d_target_add_new_adapter_does_not_change_device(self, emb_conv1d):
+ # same as first test, but targeting the Conv1D layer
+ config = LoraConfig(target_modules=["conv1d"])
+ model = get_peft_model(emb_conv1d, config)
+ model = model.to(self.device)
+ model.conv1d.lora_A.cpu()
+ model.conv1d.lora_B.cpu()
+
+ # check that the adapter is indeed on CPU and the base model on GPU
+ assert model.conv1d.lora_A.default.weight.device.type == "cpu"
+ assert model.conv1d.lora_B.default.weight.device.type == "cpu"
+ assert model.conv1d.weight.device.type == self.device
+
+ model.add_adapter("other", config)
+ # check that after adding a new adapter, the old adapter is still on CPU
+ assert model.conv1d.lora_A.default.weight.device.type == "cpu"
+ assert model.conv1d.lora_B.default.weight.device.type == "cpu"
+ # the rest should be on GPU
+ assert model.conv1d.weight.device.type == self.device
+ assert model.conv1d.lora_A.other.weight.device.type == self.device
+ assert model.conv1d.lora_B.other.weight.device.type == self.device
+
+ def test_lora_dora_add_new_adapter_does_not_change_device(self, mlp):
+ # same as first test, but also using DoRA
+ config = LoraConfig(target_modules=["lin0"], use_dora=True)
+ model = get_peft_model(mlp, config)
+ model = model.to(self.device)
+ model.lin0.lora_A.cpu()
+ model.lin0.lora_B.cpu()
+ model.lin0.lora_magnitude_vector.cpu()
+
+ # check that the adapter is indeed on CPU and the base model on GPU
+ assert model.lin0.lora_A.default.weight.device.type == "cpu"
+ assert model.lin0.lora_B.default.weight.device.type == "cpu"
+ assert model.lin0.lora_magnitude_vector.default.weight.device.type == "cpu"
+ assert model.lin0.base_layer.weight.device.type == self.device
+
+ model.add_adapter("other", config)
+ # check that after adding a new adapter, the old adapter is still on CPU
+ assert model.lin0.lora_A.default.weight.device.type == "cpu"
+ assert model.lin0.lora_B.default.weight.device.type == "cpu"
+ assert model.lin0.lora_magnitude_vector.default.weight.device.type == "cpu"
+ # the rest should be on GPU
+ assert model.lin0.base_layer.weight.device.type == self.device
+ assert model.lin0.lora_A.other.weight.device.type == self.device
+ assert model.lin0.lora_B.other.weight.device.type == self.device
+ assert model.lin0.lora_magnitude_vector.other.weight.device.type == self.device
+
+ def test_adalora_add_new_adapter_does_not_change_device(self, mlp):
+ # same as first test, but using AdaLORA
+ # AdaLora does not like multiple trainable adapters, hence inference_mode=True
+ config = AdaLoraConfig(target_modules=["lin0"], inference_mode=True, total_step=1)
+ model = get_peft_model(mlp, config)
+ model = model.to(self.device)
+ model.lin0.lora_A.cpu()
+ model.lin0.lora_E.cpu()
+
+ # check that the adapter is indeed on CPU and the base model on GPU
+ assert model.lin0.lora_A.default.device.type == "cpu"
+ assert model.lin0.lora_E.default.device.type == "cpu"
+ assert model.lin0.base_layer.weight.device.type == self.device
+
+ model.add_adapter("other", config)
+ # check that after adding a new adapter, the old adapter is still on CPU
+ assert model.lin0.lora_A.default.device.type == "cpu"
+ assert model.lin0.lora_E.default.device.type == "cpu"
+ # the rest should be on GPU
+ assert model.lin0.base_layer.weight.device.type == self.device
+ assert model.lin0.lora_A.other.device.type == self.device
+ assert model.lin0.lora_E.other.device.type == self.device
+
+ def test_boft_add_new_adapter_does_not_change_device(self, mlp):
+ # same as first test, but using BoFT
+ config = BOFTConfig(target_modules=["lin0"])
+ model = get_peft_model(mlp, config)
+ model = model.to(self.device)
+ model.lin0.boft_R.cpu()
+ model.lin0.boft_s.cpu()
+
+ # check that the adapter is indeed on CPU and the base model on GPU
+ assert model.lin0.boft_R.default.device.type == "cpu"
+ assert model.lin0.boft_s.default.device.type == "cpu"
+ assert model.lin0.base_layer.weight.device.type == self.device
+
+ model.add_adapter("other", config)
+ # check that after adding a new adapter, the old adapter is still on CPU
+ assert model.lin0.boft_R.default.device.type == "cpu"
+ assert model.lin0.boft_s.default.device.type == "cpu"
+ # the rest should be on GPU
+ assert model.lin0.base_layer.weight.device.type == self.device
+ assert model.lin0.boft_R.other.device.type == self.device
+ assert model.lin0.boft_s.other.device.type == self.device
+
+ def test_ia3_add_new_adapter_does_not_change_device(self, mlp):
+ # same as first test, but using IA3
+ config = IA3Config(target_modules=["lin0"], feedforward_modules=["lin0"])
+ model = get_peft_model(mlp, config)
+ model = model.to(self.device)
+ model.lin0.ia3_l.cpu()
+
+ # check that the adapter is indeed on CPU and the base model on GPU
+ assert model.lin0.ia3_l.default.device.type == "cpu"
+ assert model.lin0.base_layer.weight.device.type == self.device
+
+ model.add_adapter("other", config)
+ # check that after adding a new adapter, the old adapter is still on CPU
+ assert model.lin0.ia3_l.default.device.type == "cpu"
+ # the rest should be on GPU
+ assert model.lin0.base_layer.weight.device.type == self.device
+ assert model.lin0.ia3_l.other.device.type == self.device
+
+ @pytest.mark.xfail(reason="LN Tuning handling of multiple adapters may not be correct", strict=True)
+ def test_ln_tuning_add_new_adapter_does_not_change_device(self, mlp):
+ # same as first test, but using LN tuning
+ config = LNTuningConfig(target_modules=["lin0"])
+ model = get_peft_model(mlp, config)
+ model = model.to(self.device)
+ model.lin0.ln_tuning_layers.cpu()
+
+ # check that the adapter is indeed on CPU and the base model on GPU
+ assert model.lin0.ln_tuning_layers.default.weight.device.type == "cpu"
+ assert model.lin0.base_layer.weight.device.type == self.device
+
+ model.add_adapter("other", config)
+ # check that after adding a new adapter, the old adapter is still on CPU
+ assert model.lin0.ln_tuning_layers.default.weight.device.type == "cpu"
+ # the rest should be on GPU
+ assert model.lin0.base_layer.weight.device.type == self.device
+ assert model.lin0.ln_tuning_layers.other.weight.device.type == self.device
+
+ def test_loha_add_new_adapter_does_not_change_device(self, mlp):
+ # same as first test, but using LoHa
+ config = LoHaConfig(target_modules=["lin0"])
+ model = get_peft_model(mlp, config)
+ model = model.to(self.device)
+ model.lin0.hada_w1_a.cpu()
+ model.lin0.hada_w2_b.cpu()
+
+ # check that the adapter is indeed on CPU and the base model on GPU
+ assert model.lin0.hada_w1_a.default.device.type == "cpu"
+ assert model.lin0.hada_w2_b.default.device.type == "cpu"
+ assert model.lin0.base_layer.weight.device.type == self.device
+
+ model.add_adapter("other", config)
+ # check that after adding a new adapter, the old adapter is still on CPU
+ assert model.lin0.hada_w1_a.default.device.type == "cpu"
+ assert model.lin0.hada_w2_b.default.device.type == "cpu"
+ # the rest should be on GPU
+ assert model.lin0.base_layer.weight.device.type == self.device
+ assert model.lin0.hada_w1_a.other.device.type == self.device
+ assert model.lin0.hada_w2_b.other.device.type == self.device
+
+ def test_lokr_add_new_adapter_does_not_change_device(self, mlp):
+ # same as first test, but using LoKr
+ config = LoKrConfig(target_modules=["lin0"])
+ model = get_peft_model(mlp, config)
+ model = model.to(self.device)
+ model.lin0.lokr_w1.cpu()
+ model.lin0.lokr_w2.cpu()
+
+ # check that the adapter is indeed on CPU and the base model on GPU
+ assert model.lin0.lokr_w1.default.device.type == "cpu"
+ assert model.lin0.lokr_w2.default.device.type == "cpu"
+ assert model.lin0.base_layer.weight.device.type == self.device
+
+ model.add_adapter("other", config)
+ # check that after adding a new adapter, the old adapter is still on CPU
+ assert model.lin0.lokr_w1.default.device.type == "cpu"
+ assert model.lin0.lokr_w2.default.device.type == "cpu"
+ # the rest should be on GPU
+ assert model.lin0.base_layer.weight.device.type == self.device
+ assert model.lin0.lokr_w1.other.device.type == self.device
+ assert model.lin0.lokr_w2.other.device.type == self.device
+
+ def test_oft_add_new_adapter_does_not_change_device(self, mlp):
+ # same as first test, but using OFT
+ config = OFTConfig(target_modules=["lin0"])
+ model = get_peft_model(mlp, config)
+ model = model.to(self.device)
+ model.lin0.oft_R.default.cpu()
+
+ # check that the adapter is indeed on CPU and the base model on GPU
+ assert model.lin0.oft_R.default.weight.device.type == "cpu"
+ assert model.lin0.base_layer.weight.device.type == self.device
+
+ model.add_adapter("other", config)
+ # check that after adding a new adapter, the old adapter is still on CPU
+ assert model.lin0.oft_R.default.weight.device.type == "cpu"
+ # the rest should be on GPU
+ assert model.lin0.base_layer.weight.device.type == self.device
+ assert model.lin0.oft_R.other.weight.device.type == self.device
+
+ def test_vera_add_new_adapter_does_not_change_device(self, mlp):
+ # same as first test, but using VERA
+ config = VeraConfig(target_modules=["lin0"])
+ model = get_peft_model(mlp, config)
+ model = model.to(self.device)
+ model.lin0.vera_A.cpu()
+ model.lin0.vera_lambda_d.cpu()
+
+ # check that the adapter is indeed on CPU and the base model on GPU
+ assert model.lin0.vera_A.default.device.type == "cpu"
+ assert model.lin0.vera_lambda_d.default.device.type == "cpu"
+ assert model.lin0.base_layer.weight.device.type == self.device
+
+ model.add_adapter("other", config)
+ # check that after adding a new adapter, the old adapter is still on CPU
+ assert model.lin0.vera_A.default.device.type == "cpu"
+ assert model.lin0.vera_lambda_d.default.device.type == "cpu"
+ # the rest should be on GPU
+ assert model.lin0.base_layer.weight.device.type == self.device
+ assert model.lin0.vera_A.other.device.type == self.device
+ assert model.lin0.vera_lambda_d.other.device.type == self.device
+
+ def test_randlora_add_new_adapter_does_not_change_device(self, mlp):
+ # same as first test, but using RandLora
+ config = RandLoraConfig(target_modules=["lin0"])
+ model = get_peft_model(mlp, config)
+ model = model.to(self.device)
+ model.lin0.randlora_A.cpu()
+ model.lin0.randlora_lambda.cpu()
+
+ # check that the adapter is indeed on CPU and the base model on GPU
+ assert model.lin0.randlora_A.default.device.type == "cpu"
+ assert model.lin0.randlora_lambda.default.device.type == "cpu"
+ assert model.lin0.base_layer.weight.device.type == self.device
+
+ model.add_adapter("other", config)
+ # check that after adding a new adapter, the old adapter is still on CPU
+ assert model.lin0.randlora_A.default.device.type == "cpu"
+ assert model.lin0.randlora_lambda.default.device.type == "cpu"
+ # the rest should be on GPU
+ assert model.lin0.base_layer.weight.device.type == self.device
+ assert model.lin0.randlora_A.other.device.type == self.device
+ assert model.lin0.randlora_lambda.other.device.type == self.device
+
+ def test_vblora_add_new_adapter_does_not_change_device(self, mlp):
+ # same as first test, but using VBLoRA
+ config = VBLoRAConfig(target_modules=["lin0"], vector_length=2)
+ model = get_peft_model(mlp, config)
+ model = model.to(self.device)
+ model.lin0.vblora_logits_A.cpu()
+ model.lin0.vblora_logits_B.cpu()
+ model.lin0.vblora_vector_bank.cpu()
+
+ # check that the adapter is indeed on CPU and the base model on GPU
+ assert model.lin0.vblora_logits_A.default.device.type == "cpu"
+ assert model.lin0.vblora_logits_B.default.device.type == "cpu"
+ assert model.lin0.vblora_vector_bank.default.device.type == "cpu"
+ assert model.lin0.base_layer.weight.device.type == self.device
+
+ model.add_adapter("other", config)
+ # check that after adding a new adapter, the old adapter is still on CPU
+ assert model.lin0.vblora_logits_A.default.device.type == "cpu"
+ assert model.lin0.vblora_logits_B.default.device.type == "cpu"
+ assert model.lin0.vblora_vector_bank.default.device.type == "cpu"
+ # the rest should be on GPU
+ assert model.lin0.base_layer.weight.device.type == self.device
+ assert model.lin0.vblora_logits_A.other.device.type == self.device
+ assert model.lin0.vblora_logits_B.other.device.type == self.device
+ assert model.lin0.vblora_vector_bank.other.device.type == self.device
+
+ def test_hra_add_new_adapter_does_not_change_device(self, mlp):
+ # same as first test, but using HRA
+ config = HRAConfig(target_modules=["lin0"])
+ model = get_peft_model(mlp, config)
+ model = model.to(self.device)
+ model.lin0.hra_u.cpu()
+
+ # check that the adapter is indeed on CPU and the base model on GPU
+ assert model.lin0.hra_u.default.device.type == "cpu"
+ assert model.lin0.base_layer.weight.device.type == self.device
+
+ model.add_adapter("other", config)
+ # check that after adding a new adapter, the old adapter is still on CPU
+ assert model.lin0.hra_u.default.device.type == "cpu"
+ # the rest should be on GPU
+ assert model.lin0.base_layer.weight.device.type == self.device
+ assert model.lin0.hra_u.other.device.type == self.device
+
+ def test_road_add_new_adapter_does_not_change_device(self, mlp):
+ # same as first test, but using HRA
+ config = RoadConfig(target_modules=["lin0"], group_size=2)
+ model = get_peft_model(mlp, config)
+ model = model.to(self.device)
+ model.lin0.road_theta.cpu()
+
+ # check that the adapter is indeed on CPU and the base model on GPU
+ assert model.lin0.road_theta.default.device.type == "cpu"
+ assert model.lin0.base_layer.weight.device.type == self.device
+
+ model.add_adapter("other", config)
+ # check that after adding a new adapter, the old adapter is still on CPU
+ assert model.lin0.road_theta.default.device.type == "cpu"
+ # the rest should be on GPU
+ assert model.lin0.base_layer.weight.device.type == self.device
+ assert model.lin0.road_theta.other.device.type == self.device
diff --git a/peft/tests/test_config.py b/peft/tests/test_config.py
new file mode 100644
index 0000000000000000000000000000000000000000..4a6d8cffbd5c37e12c31095f33bb0d22f8af07e2
--- /dev/null
+++ b/peft/tests/test_config.py
@@ -0,0 +1,592 @@
+# Copyright 2023-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+import copy
+import json
+import os
+import pickle
+import tempfile
+import warnings
+
+import pytest
+
+from peft import (
+ AdaLoraConfig,
+ AdaptionPromptConfig,
+ BOFTConfig,
+ BoneConfig,
+ C3AConfig,
+ FourierFTConfig,
+ HRAConfig,
+ IA3Config,
+ LNTuningConfig,
+ LoHaConfig,
+ LoKrConfig,
+ LoraConfig,
+ MissConfig,
+ MultitaskPromptTuningConfig,
+ OFTConfig,
+ PeftConfig,
+ PeftType,
+ PolyConfig,
+ PrefixTuningConfig,
+ PromptEncoder,
+ PromptEncoderConfig,
+ PromptTuningConfig,
+ RoadConfig,
+ ShiraConfig,
+ TaskType,
+ TrainableTokensConfig,
+ VBLoRAConfig,
+ VeraConfig,
+ XLoraConfig,
+)
+
+
+PEFT_MODELS_TO_TEST = [("peft-internal-testing/tiny-opt-lora-revision", "test")]
+
+# Config classes and their mandatory parameters
+ALL_CONFIG_CLASSES = (
+ (AdaLoraConfig, {"total_step": 1}),
+ (AdaptionPromptConfig, {}),
+ (BOFTConfig, {}),
+ (BoneConfig, {}),
+ (C3AConfig, {}),
+ (FourierFTConfig, {}),
+ (HRAConfig, {}),
+ (IA3Config, {}),
+ (LNTuningConfig, {}),
+ (LoHaConfig, {}),
+ (LoKrConfig, {}),
+ (LoraConfig, {}),
+ (MissConfig, {}),
+ (MultitaskPromptTuningConfig, {}),
+ (PolyConfig, {}),
+ (PrefixTuningConfig, {}),
+ (PromptEncoderConfig, {}),
+ (PromptTuningConfig, {}),
+ (RoadConfig, {}),
+ (ShiraConfig, {}),
+ (TrainableTokensConfig, {}),
+ (VeraConfig, {}),
+ (VBLoRAConfig, {}),
+ (XLoraConfig, {"hidden_size": 32, "adapters": {}}),
+)
+
+
+class TestPeftConfig:
+ @pytest.mark.parametrize("config_class, mandatory_kwargs", ALL_CONFIG_CLASSES)
+ def test_methods(self, config_class, mandatory_kwargs):
+ r"""
+ Test if all configs have the expected methods. Here we test
+ - to_dict
+ - save_pretrained
+ - from_pretrained
+ - from_json_file
+ """
+ # test if all configs have the expected methods
+ config = config_class(**mandatory_kwargs)
+ assert hasattr(config, "to_dict")
+ assert hasattr(config, "save_pretrained")
+ assert hasattr(config, "from_pretrained")
+ assert hasattr(config, "from_json_file")
+
+ @pytest.mark.parametrize("config_class, mandatory_kwargs", ALL_CONFIG_CLASSES)
+ @pytest.mark.parametrize("valid_task_type", list(TaskType) + [None])
+ def test_valid_task_type(self, config_class, mandatory_kwargs, valid_task_type):
+ r"""
+ Test if all configs work correctly for all valid task types
+ """
+ config_class(task_type=valid_task_type, **mandatory_kwargs)
+
+ @pytest.mark.parametrize("config_class, mandatory_kwargs", ALL_CONFIG_CLASSES)
+ def test_invalid_task_type(self, config_class, mandatory_kwargs):
+ r"""
+ Test if all configs correctly raise the defined error message for invalid task types.
+ """
+ invalid_task_type = "invalid-task-type"
+ with pytest.raises(
+ ValueError,
+ match=f"Invalid task type: '{invalid_task_type}'. Must be one of the following task types: {', '.join(TaskType)}.",
+ ):
+ config_class(task_type=invalid_task_type, **mandatory_kwargs)
+
+ def test_from_peft_type(self):
+ r"""
+ Test if the config is correctly loaded using:
+ - from_peft_type
+ """
+ from peft.mapping import PEFT_TYPE_TO_CONFIG_MAPPING
+
+ for peft_type in PeftType:
+ expected_cls = PEFT_TYPE_TO_CONFIG_MAPPING[peft_type]
+ mandatory_config_kwargs = {}
+
+ if expected_cls == AdaLoraConfig:
+ mandatory_config_kwargs = {"total_step": 1}
+
+ config = PeftConfig.from_peft_type(peft_type=peft_type, **mandatory_config_kwargs)
+ assert type(config) is expected_cls
+
+ @pytest.mark.parametrize("config_class, mandatory_kwargs", ALL_CONFIG_CLASSES)
+ def test_from_pretrained(self, config_class, mandatory_kwargs):
+ r"""
+ Test if the config is correctly loaded using:
+ - from_pretrained
+ """
+ for model_name, revision in PEFT_MODELS_TO_TEST:
+ # Test we can load config from delta
+ config_class.from_pretrained(model_name, revision=revision)
+
+ @pytest.mark.parametrize("config_class, mandatory_kwargs", ALL_CONFIG_CLASSES)
+ def test_save_pretrained(self, config_class, mandatory_kwargs):
+ r"""
+ Test if the config is correctly saved and loaded using
+ - save_pretrained
+ """
+ config = config_class(**mandatory_kwargs)
+ with tempfile.TemporaryDirectory() as tmp_dirname:
+ config.save_pretrained(tmp_dirname)
+
+ config_from_pretrained = config_class.from_pretrained(tmp_dirname)
+ assert config.to_dict() == config_from_pretrained.to_dict()
+
+ @pytest.mark.parametrize("config_class, mandatory_kwargs", ALL_CONFIG_CLASSES)
+ def test_from_json_file(self, config_class, mandatory_kwargs):
+ config = config_class(**mandatory_kwargs)
+ with tempfile.TemporaryDirectory() as tmp_dirname:
+ config.save_pretrained(tmp_dirname)
+
+ config_path = os.path.join(tmp_dirname, "adapter_config.json")
+ config_from_json = config_class.from_json_file(config_path)
+ assert config.to_dict() == config_from_json
+
+ # Also test with a runtime_config entry -- they should be ignored, even if they
+ # were accidentally saved to disk
+ config_from_json["runtime_config"] = {"ephemeral_gpu_offload": True}
+ json.dump(config_from_json, open(config_path, "w"))
+
+ config_from_json = config_class.from_json_file(config_path)
+ assert config.to_dict() == config_from_json
+
+ @pytest.mark.parametrize("config_class, mandatory_kwargs", ALL_CONFIG_CLASSES)
+ def test_to_dict(self, config_class, mandatory_kwargs):
+ r"""
+ Test if the config can be correctly converted to a dict using:
+ - to_dict
+ """
+ config = config_class(**mandatory_kwargs)
+ assert isinstance(config.to_dict(), dict)
+
+ @pytest.mark.parametrize("config_class, mandatory_kwargs", ALL_CONFIG_CLASSES)
+ def test_from_pretrained_cache_dir(self, config_class, mandatory_kwargs):
+ r"""
+ Test if the config is correctly loaded with extra kwargs
+ """
+ with tempfile.TemporaryDirectory() as tmp_dirname:
+ for model_name, revision in PEFT_MODELS_TO_TEST:
+ # Test we can load config from delta
+ config_class.from_pretrained(model_name, revision=revision, cache_dir=tmp_dirname)
+
+ def test_from_pretrained_cache_dir_remote(self):
+ r"""
+ Test if the config is correctly loaded with a checkpoint from the hub
+ """
+ with tempfile.TemporaryDirectory() as tmp_dirname:
+ PeftConfig.from_pretrained("ybelkada/test-st-lora", cache_dir=tmp_dirname)
+ assert "models--ybelkada--test-st-lora" in os.listdir(tmp_dirname)
+
+ @pytest.mark.parametrize("config_class, mandatory_kwargs", ALL_CONFIG_CLASSES)
+ def test_save_pretrained_with_runtime_config(self, config_class, mandatory_kwargs):
+ r"""
+ Test if the config correctly removes runtime config when saving
+ """
+ with tempfile.TemporaryDirectory() as tmp_dirname:
+ for model_name, revision in PEFT_MODELS_TO_TEST:
+ cfg = config_class.from_pretrained(model_name, revision=revision)
+ # NOTE: cfg is always a LoraConfig here, because the configuration of the loaded model was a LoRA.
+ # Hence we can expect a runtime_config to exist regardless of config_class.
+ cfg.runtime_config.ephemeral_gpu_offload = True
+ cfg.save_pretrained(tmp_dirname)
+ cfg = config_class.from_pretrained(tmp_dirname)
+ assert not cfg.runtime_config.ephemeral_gpu_offload
+
+ @pytest.mark.parametrize("config_class, mandatory_kwargs", ALL_CONFIG_CLASSES)
+ def test_set_attributes(self, config_class, mandatory_kwargs):
+ # manually set attributes and check if they are correctly written
+ config = config_class(peft_type="test", **mandatory_kwargs)
+
+ # save pretrained
+ with tempfile.TemporaryDirectory() as tmp_dirname:
+ config.save_pretrained(tmp_dirname)
+
+ config_from_pretrained = config_class.from_pretrained(tmp_dirname)
+ assert config.to_dict() == config_from_pretrained.to_dict()
+
+ @pytest.mark.parametrize("config_class, mandatory_kwargs", ALL_CONFIG_CLASSES)
+ def test_config_copy(self, config_class, mandatory_kwargs):
+ # see https://github.com/huggingface/peft/issues/424
+ config = config_class(**mandatory_kwargs)
+ copied = copy.copy(config)
+ assert config.to_dict() == copied.to_dict()
+
+ @pytest.mark.parametrize("config_class, mandatory_kwargs", ALL_CONFIG_CLASSES)
+ def test_config_deepcopy(self, config_class, mandatory_kwargs):
+ # see https://github.com/huggingface/peft/issues/424
+ config = config_class(**mandatory_kwargs)
+ copied = copy.deepcopy(config)
+ assert config.to_dict() == copied.to_dict()
+
+ @pytest.mark.parametrize("config_class, mandatory_kwargs", ALL_CONFIG_CLASSES)
+ def test_config_pickle_roundtrip(self, config_class, mandatory_kwargs):
+ # see https://github.com/huggingface/peft/issues/424
+ config = config_class(**mandatory_kwargs)
+ copied = pickle.loads(pickle.dumps(config))
+ assert config.to_dict() == copied.to_dict()
+
+ def test_prompt_encoder_warning_num_layers(self):
+ # This test checks that if a prompt encoder config is created with an argument that is ignored, there should be
+ # warning. However, there should be no warning if the default value is used.
+ kwargs = {
+ "num_virtual_tokens": 20,
+ "num_transformer_submodules": 1,
+ "token_dim": 768,
+ "encoder_hidden_size": 768,
+ }
+
+ # there should be no warning with just default argument for encoder_num_layer
+ config = PromptEncoderConfig(**kwargs)
+ with warnings.catch_warnings():
+ PromptEncoder(config)
+
+ # when changing encoder_num_layer, there should be a warning for MLP since that value is not used
+ config = PromptEncoderConfig(encoder_num_layers=123, **kwargs)
+ with pytest.warns(UserWarning) as record:
+ PromptEncoder(config)
+ expected_msg = "for MLP, the argument `encoder_num_layers` is ignored. Exactly 2 MLP layers are used."
+ assert str(record.list[0].message) == expected_msg
+
+ @pytest.mark.parametrize(
+ "config_class", [LoHaConfig, LoraConfig, IA3Config, OFTConfig, BOFTConfig, HRAConfig, VBLoRAConfig]
+ )
+ def test_save_pretrained_with_target_modules(self, config_class):
+ # See #1041, #1045
+ config = config_class(target_modules=["a", "list"])
+ with tempfile.TemporaryDirectory() as tmp_dirname:
+ config.save_pretrained(tmp_dirname)
+
+ config_from_pretrained = config_class.from_pretrained(tmp_dirname)
+ assert config.to_dict() == config_from_pretrained.to_dict()
+ # explicit test that target_modules should be converted to set
+ assert isinstance(config_from_pretrained.target_modules, set)
+
+ def test_regex_with_layer_indexing_lora(self):
+ # This test checks that an error is raised if `target_modules` is a regex expression and `layers_to_transform` or
+ # `layers_pattern` are not None
+
+ invalid_config1 = {"target_modules": ".*foo", "layers_to_transform": [0]}
+ invalid_config2 = {"target_modules": ".*foo", "layers_pattern": ["bar"]}
+
+ valid_config = {"target_modules": ["foo"], "layers_pattern": ["bar"], "layers_to_transform": [0]}
+
+ with pytest.raises(ValueError, match="`layers_to_transform` cannot be used when `target_modules` is a str."):
+ LoraConfig(**invalid_config1)
+
+ with pytest.raises(ValueError, match="`layers_pattern` cannot be used when `target_modules` is a str."):
+ LoraConfig(**invalid_config2)
+
+ # should run without errors
+ LoraConfig(**valid_config)
+
+ def test_ia3_is_feedforward_subset_invalid_config(self):
+ # This test checks that the IA3 config raises a value error if the feedforward_modules argument
+ # is not a subset of the target_modules argument
+
+ # an example invalid config
+ invalid_config = {"target_modules": ["k", "v"], "feedforward_modules": ["q"]}
+
+ with pytest.raises(ValueError, match="^`feedforward_modules` should be a subset of `target_modules`$"):
+ IA3Config(**invalid_config)
+
+ def test_ia3_is_feedforward_subset_valid_config(self):
+ # This test checks that the IA3 config is created without errors with valid arguments.
+ # feedforward_modules should be a subset of target_modules if both are lists
+
+ # an example valid config with regex expressions.
+ valid_config_regex_exp = {
+ "target_modules": ".*.(SelfAttention|EncDecAttention|DenseReluDense).*(q|v|wo)$",
+ "feedforward_modules": ".*.DenseReluDense.wo$",
+ }
+ # an example valid config with module lists.
+ valid_config_list = {"target_modules": ["k", "v", "wo"], "feedforward_modules": ["wo"]}
+
+ # should run without errors
+ IA3Config(**valid_config_regex_exp)
+ IA3Config(**valid_config_list)
+
+ def test_adalora_config_r_warning(self):
+ # This test checks that a warning is raised when r is set other than default in AdaLoraConfig
+ # No warning should be raised when initializing AdaLoraConfig with default values.
+ kwargs = {"peft_type": "ADALORA", "task_type": "SEQ_2_SEQ_LM", "init_r": 12, "lora_alpha": 32, "total_step": 1}
+ # Test that no warning is raised with default initialization
+ with warnings.catch_warnings():
+ warnings.simplefilter("error")
+ try:
+ AdaLoraConfig(**kwargs)
+ except Warning:
+ pytest.fail("AdaLoraConfig raised a warning with default initialization.")
+ # Test that a warning is raised when r != 8 in AdaLoraConfig
+ with pytest.warns(UserWarning, match="Note that `r` is not used in AdaLora and will be ignored."):
+ AdaLoraConfig(r=10, total_step=1)
+
+ def test_adalora_config_correct_timing_still_works(self):
+ pass
+
+ @pytest.mark.parametrize(
+ "timing_kwargs",
+ [
+ {"total_step": 100, "tinit": 0, "tfinal": 0},
+ {"total_step": 100, "tinit": 10, "tfinal": 10},
+ {"total_step": 100, "tinit": 79, "tfinal": 20},
+ {"total_step": 100, "tinit": 80, "tfinal": 19},
+ ],
+ )
+ def test_adalora_config_valid_timing_works(self, timing_kwargs):
+ # Make sure that passing correct timing values is not prevented by faulty config checks.
+ AdaLoraConfig(**timing_kwargs) # does not raise
+
+ def test_adalora_config_invalid_total_step_raises(self):
+ with pytest.raises(ValueError) as e:
+ AdaLoraConfig(total_step=None)
+ assert "AdaLoRA does not work when `total_step` is None, supply a value > 0." in str(e)
+
+ @pytest.mark.parametrize(
+ "timing_kwargs",
+ [
+ {"total_step": 100, "tinit": 20, "tfinal": 80},
+ {"total_step": 100, "tinit": 80, "tfinal": 20},
+ {"total_step": 10, "tinit": 20, "tfinal": 0},
+ {"total_step": 10, "tinit": 0, "tfinal": 10},
+ {"total_step": 10, "tinit": 10, "tfinal": 0},
+ {"total_step": 10, "tinit": 20, "tfinal": 0},
+ {"total_step": 10, "tinit": 20, "tfinal": 20},
+ {"total_step": 10, "tinit": 0, "tfinal": 20},
+ ],
+ )
+ def test_adalora_config_timing_bounds_error(self, timing_kwargs):
+ # Check if the user supplied timing values that will certainly fail because it breaks
+ # AdaLoRA assumptions.
+ with pytest.raises(ValueError) as e:
+ AdaLoraConfig(**timing_kwargs)
+
+ assert "The supplied schedule values don't allow for a budgeting phase" in str(e)
+
+ @pytest.mark.parametrize("config_class, mandatory_kwargs", ALL_CONFIG_CLASSES)
+ def test_from_pretrained_forward_compatible(self, config_class, mandatory_kwargs, tmp_path, recwarn):
+ """
+ Make it possible to load configs that contain unknown keys by ignoring them.
+
+ The idea is to make PEFT configs forward-compatible with future versions of the library.
+ """
+ config = config_class(**mandatory_kwargs)
+ config.save_pretrained(tmp_path)
+ # add a spurious key to the config
+ with open(tmp_path / "adapter_config.json") as f:
+ config_dict = json.load(f)
+ config_dict["foobar"] = "baz"
+ config_dict["spam"] = 123
+ with open(tmp_path / "adapter_config.json", "w") as f:
+ json.dump(config_dict, f)
+
+ msg = f"Unexpected keyword arguments ['foobar', 'spam'] for class {config_class.__name__}, these are ignored."
+ config_from_pretrained = config_class.from_pretrained(tmp_path)
+
+ expected_num_warnings = 1
+ # TODO: remove once Bone is removed in v0.19.0
+ if config_class == BoneConfig:
+ expected_num_warnings = 2 # Bone has 1 more warning about it being deprecated
+
+ assert len(recwarn) == expected_num_warnings
+ assert recwarn.list[-1].message.args[0].startswith(msg)
+ assert "foo" not in config_from_pretrained.to_dict()
+ assert "spam" not in config_from_pretrained.to_dict()
+ assert config.to_dict() == config_from_pretrained.to_dict()
+ assert isinstance(config_from_pretrained, config_class)
+
+ @pytest.mark.parametrize("config_class, mandatory_kwargs", ALL_CONFIG_CLASSES)
+ def test_from_pretrained_forward_compatible_load_from_peft_config(
+ self, config_class, mandatory_kwargs, tmp_path, recwarn
+ ):
+ """Exact same test as before, but instead of using LoraConfig.from_pretrained, AdaLoraconfig.from_pretrained,
+ etc. use PeftConfig.from_pretrained. This covers a previously existing bug where only the known arguments from
+ PeftConfig would be used instead of the more specific config (which is known thanks to the peft_type
+ attribute).
+
+ """
+ config = config_class(**mandatory_kwargs)
+ config.save_pretrained(tmp_path)
+ # add a spurious key to the config
+ with open(tmp_path / "adapter_config.json") as f:
+ config_dict = json.load(f)
+ config_dict["foobar"] = "baz"
+ config_dict["spam"] = 123
+ with open(tmp_path / "adapter_config.json", "w") as f:
+ json.dump(config_dict, f)
+
+ msg = f"Unexpected keyword arguments ['foobar', 'spam'] for class {config_class.__name__}, these are ignored."
+ config_from_pretrained = PeftConfig.from_pretrained(tmp_path) # <== use PeftConfig here
+
+ expected_num_warnings = 1
+ # TODO: remove once Bone is removed in v0.19.0
+ if config_class == BoneConfig:
+ expected_num_warnings = 2 # Bone has 1 more warning about it being deprecated
+
+ assert len(recwarn) == expected_num_warnings
+ assert recwarn.list[-1].message.args[0].startswith(msg)
+ assert "foo" not in config_from_pretrained.to_dict()
+ assert "spam" not in config_from_pretrained.to_dict()
+ assert config.to_dict() == config_from_pretrained.to_dict()
+ assert isinstance(config_from_pretrained, config_class)
+
+ @pytest.mark.parametrize("config_class, mandatory_kwargs", ALL_CONFIG_CLASSES)
+ def test_from_pretrained_sanity_check(self, config_class, mandatory_kwargs, tmp_path):
+ """Following up on the previous test about forward compatibility, we *don't* want any random json to be accepted as
+ a PEFT config. There should be a minimum set of required keys.
+ """
+ non_peft_json = {"foo": "bar", "baz": 123}
+ with open(tmp_path / "adapter_config.json", "w") as f:
+ json.dump(non_peft_json, f)
+
+ msg = f"The {config_class.__name__} config that is trying to be loaded is missing required keys: {{'peft_type'}}."
+ with pytest.raises(TypeError, match=msg):
+ config_class.from_pretrained(tmp_path)
+
+ def test_lora_config_layers_to_transform_validation(self):
+ """Test that specifying layers_pattern without layers_to_transform raises an error"""
+ with pytest.raises(
+ ValueError, match="When `layers_pattern` is specified, `layers_to_transform` must also be specified."
+ ):
+ LoraConfig(r=8, lora_alpha=16, target_modules=["query", "value"], layers_pattern="model.layers")
+
+ # Test that specifying both layers_to_transform and layers_pattern works fine
+ config = LoraConfig(
+ r=8,
+ lora_alpha=16,
+ target_modules=["query", "value"],
+ layers_to_transform=[0, 1, 2],
+ layers_pattern="model.layers",
+ )
+ assert config.layers_to_transform == [0, 1, 2]
+ assert config.layers_pattern == "model.layers"
+
+ # Test that not specifying either works fine
+ config = LoraConfig(
+ r=8,
+ lora_alpha=16,
+ target_modules=["query", "value"],
+ )
+ assert config.layers_to_transform is None
+ assert config.layers_pattern is None
+
+ @pytest.mark.parametrize("version", ["0.10", "0.17.0", "1"])
+ @pytest.mark.parametrize("config_class, mandatory_kwargs", ALL_CONFIG_CLASSES)
+ def test_peft_version_is_stored(self, version, config_class, mandatory_kwargs, monkeypatch, tmp_path):
+ # Check that the PEFT version is automatically stored in/restored from the config file.
+ from peft import config
+
+ monkeypatch.setattr(config, "__version__", version)
+
+ peft_config = config_class(**mandatory_kwargs)
+ assert peft_config.peft_version == version
+
+ peft_config.save_pretrained(tmp_path)
+ with open(tmp_path / "adapter_config.json") as f:
+ config_dict = json.load(f)
+ assert config_dict["peft_version"] == version
+
+ # ensure that the version from the config is being loaded, not just the current version
+ monkeypatch.setattr(config, "__version__", "0.1.another-version")
+
+ # load from config
+ config_loaded = PeftConfig.from_pretrained(tmp_path)
+ assert config_loaded.peft_version == version
+
+ # load from json
+ config_path = tmp_path / "adapter_config.json"
+ config_json = PeftConfig.from_json_file(str(config_path))
+ assert config_json["peft_version"] == version
+
+ @pytest.mark.parametrize("config_class, mandatory_kwargs", ALL_CONFIG_CLASSES)
+ def test_peft_version_is_dev_version(self, config_class, mandatory_kwargs, monkeypatch, tmp_path):
+ # When a dev version of PEFT is installed, the actual state of PEFT is ambiguous. Therefore, try to determine
+ # the commit hash too and store it as part of the version string.
+ from peft import config
+
+ version = "0.15.0.dev7"
+ monkeypatch.setattr(config, "__version__", version)
+
+ def fake_commit_hash(pkg_name):
+ return "abcdef012345"
+
+ monkeypatch.setattr(config, "_get_commit_hash", fake_commit_hash)
+
+ peft_config = config_class(**mandatory_kwargs)
+ expected_version = f"{version}@{fake_commit_hash('peft')}"
+ assert peft_config.peft_version == expected_version
+
+ peft_config.save_pretrained(tmp_path)
+ config_loaded = PeftConfig.from_pretrained(tmp_path)
+ assert config_loaded.peft_version == expected_version
+
+ @pytest.mark.parametrize("config_class, mandatory_kwargs", ALL_CONFIG_CLASSES)
+ def test_peft_version_is_dev_version_but_commit_hash_cannot_be_determined(
+ self, config_class, mandatory_kwargs, monkeypatch, tmp_path
+ ):
+ # There can be cases where PEFT is using a dev version but the commit hash cannot be determined. In this case,
+ # just store the dev version string.
+ from peft import config
+
+ version = "0.15.0.dev7"
+ monkeypatch.setattr(config, "__version__", version)
+
+ def fake_commit_hash(pkg_name):
+ return None
+
+ monkeypatch.setattr(config, "_get_commit_hash", fake_commit_hash)
+
+ peft_config = config_class(**mandatory_kwargs)
+ assert peft_config.peft_version == version + "@UNKNOWN"
+
+ peft_config.save_pretrained(tmp_path)
+ config_loaded = PeftConfig.from_pretrained(tmp_path)
+ assert config_loaded.peft_version == version + "@UNKNOWN"
+
+ @pytest.mark.parametrize("config_class, mandatory_kwargs", ALL_CONFIG_CLASSES)
+ def test_peft_version_warn_when_commit_hash_errors(self, config_class, mandatory_kwargs, monkeypatch, tmp_path):
+ # We try to get the PEFT commit hash if a dev version is installed. But in case there is any kind of error
+ # there, we don't want user code to break. Instead, the code should run and a version without commit hash should
+ # be recorded. In addition, there should be a warning.
+ from peft import config
+
+ version = "0.15.0.dev7"
+ monkeypatch.setattr(config, "__version__", version)
+
+ def fake_commit_hash_raises(pkg_name):
+ raise Exception("Error for testing purpose")
+
+ monkeypatch.setattr(config, "_get_commit_hash", fake_commit_hash_raises)
+
+ msg = "A dev version of PEFT is used but there was an error while trying to determine the commit hash"
+ with pytest.warns(UserWarning, match=msg):
+ peft_config = config_class(**mandatory_kwargs)
+ assert peft_config.peft_version == version + "@UNKNOWN"
diff --git a/peft/tests/test_cpt.py b/peft/tests/test_cpt.py
new file mode 100644
index 0000000000000000000000000000000000000000..6b747f8f41c7fd6416905f76f7bef67d8fdc7bb1
--- /dev/null
+++ b/peft/tests/test_cpt.py
@@ -0,0 +1,301 @@
+# Copyright 2024-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+from typing import Any, Union
+
+import pytest
+import torch
+from datasets import load_dataset
+from torch.utils.data import Dataset
+from tqdm import tqdm
+from transformers import (
+ AutoModelForCausalLM,
+ AutoTokenizer,
+ DataCollatorForLanguageModeling,
+ Trainer,
+ TrainingArguments,
+)
+
+from peft import CPTConfig, TaskType, get_peft_model
+
+
+TEMPLATE = {"input": "input: {}", "intra_seperator": " ", "output": "output: {}", "inter_seperator": "\n"}
+
+MODEL_NAME = "hf-internal-testing/tiny-random-OPTForCausalLM"
+MAX_INPUT_LENGTH = 1024
+
+
+@pytest.fixture(scope="module")
+def global_tokenizer():
+ """Load the tokenizer fixture for the model."""
+
+ return AutoTokenizer.from_pretrained(MODEL_NAME, padding_side="right")
+
+
+@pytest.fixture(scope="module")
+def config_text():
+ """Load the SST2 dataset and prepare it for testing."""
+ config = CPTConfig(
+ cpt_token_ids=[0, 1, 2, 3, 4, 5, 6, 7], # Example token IDs for testing
+ cpt_mask=[1, 1, 1, 1, 1, 1, 1, 1],
+ cpt_tokens_type_mask=[1, 2, 2, 2, 3, 3, 3, 4],
+ opt_weighted_loss_type="decay",
+ opt_loss_decay_factor=0.95,
+ opt_projection_epsilon=0.2,
+ opt_projection_format_epsilon=0.1,
+ tokenizer_name_or_path=MODEL_NAME,
+ )
+ return config
+
+
+@pytest.fixture(scope="module")
+def config_random():
+ """Load the SST2 dataset and prepare it for testing."""
+ config = CPTConfig(
+ opt_weighted_loss_type="decay",
+ opt_loss_decay_factor=0.95,
+ opt_projection_epsilon=0.2,
+ opt_projection_format_epsilon=0.1,
+ tokenizer_name_or_path=MODEL_NAME,
+ )
+ return config
+
+
+@pytest.fixture(scope="module")
+def sst_data():
+ """Load the SST2 dataset and prepare it for testing."""
+ data = load_dataset("glue", "sst2")
+
+ def add_string_labels(example):
+ if example["label"] == 0:
+ example["label_text"] = "negative"
+ elif example["label"] == 1:
+ example["label_text"] = "positive"
+ return example
+
+ train_dataset = data["train"].select(range(4)).map(add_string_labels)
+ test_dataset = data["validation"].select(range(10)).map(add_string_labels)
+
+ return {"train": train_dataset, "test": test_dataset}
+
+
+@pytest.fixture(scope="module")
+def collator(global_tokenizer):
+ class CPTDataCollatorForLanguageModeling(DataCollatorForLanguageModeling):
+ def __init__(self, tokenizer, training=True, mlm=False):
+ super().__init__(tokenizer, mlm=mlm)
+ self.training = training
+ self.tokenizer.add_special_tokens({"pad_token": "[PAD]"}) # mk check why needed
+
+ def torch_call(self, examples: list[Union[list[int], Any, dict[str, Any]]]) -> dict[str, Any]:
+ # Handle dict or lists with proper padding and conversion to tensor.
+ list_sample_mask = []
+ for i in range(len(examples)):
+ if "sample_mask" in examples[i].keys():
+ list_sample_mask.append(examples[i].pop("sample_mask"))
+
+ max_len = max(len(ex["input_ids"]) for ex in examples)
+
+ def pad_sequence(sequence, max_len, pad_value=0):
+ return sequence + [pad_value] * (max_len - len(sequence))
+
+ input_ids = torch.tensor([pad_sequence(ex["input_ids"], max_len) for ex in examples])
+ attention_mask = torch.tensor([pad_sequence(ex["attention_mask"], max_len) for ex in examples])
+ input_type_mask = torch.tensor([pad_sequence(ex["input_type_mask"], max_len) for ex in examples])
+
+ batch = {"input_ids": input_ids, "attention_mask": attention_mask, "input_type_mask": input_type_mask}
+
+ tensor_sample_mask = batch["input_ids"].clone().long()
+ tensor_sample_mask[:, :] = 0
+ for i in range(len(list_sample_mask)):
+ tensor_sample_mask[i, : len(list_sample_mask[i])] = list_sample_mask[i]
+
+ batch["labels"] = batch["input_ids"].clone()
+ if not self.training:
+ batch["sample_mask"] = tensor_sample_mask
+
+ return batch
+
+ collator = CPTDataCollatorForLanguageModeling(global_tokenizer, training=True, mlm=False)
+ return collator
+
+
+def dataset(data, tokenizer):
+ class CPTDataset(Dataset):
+ def __init__(self, samples, tokenizer, template, max_length=MAX_INPUT_LENGTH):
+ self.template = template
+ self.tokenizer = tokenizer
+ self.max_length = max_length
+
+ self.attention_mask = []
+ self.input_ids = []
+ self.input_type_mask = []
+ self.inter_seperator_ids = self._get_input_ids(template["inter_seperator"])
+
+ for sample_i in tqdm(samples):
+ input_text, label = sample_i["sentence"], sample_i["label_text"]
+ input_ids, attention_mask, input_type_mask = self.preprocess_sentence(input_text, label)
+
+ self.input_ids.append(input_ids)
+ self.attention_mask.append(attention_mask)
+ self.input_type_mask.append(input_type_mask)
+
+ def _get_input_ids(self, text):
+ return self.tokenizer(text, add_special_tokens=False)["input_ids"]
+
+ def preprocess_sentence(self, input_text, label):
+ input_template_part_1_text, input_template_part_2_text = self.template["input"].split("{}")
+ input_template_tokenized_part1 = self._get_input_ids(input_template_part_1_text)
+ input_tokenized = self._get_input_ids(input_text)
+ input_template_tokenized_part2 = self._get_input_ids(input_template_part_2_text)
+
+ sep_tokenized = self._get_input_ids(self.template["intra_seperator"])
+
+ label_template_part_1, label_template_part_2 = self.template["output"].split("{}")
+ label_template_part1_tokenized = self._get_input_ids(label_template_part_1)
+ label_tokenized = self._get_input_ids(label)
+ label_template_part2_tokenized = self._get_input_ids(label_template_part_2)
+
+ eos = [self.tokenizer.eos_token_id] if self.tokenizer.eos_token_id is not None else []
+ input_ids = (
+ input_template_tokenized_part1
+ + input_tokenized
+ + input_template_tokenized_part2
+ + sep_tokenized
+ + label_template_part1_tokenized
+ + label_tokenized
+ + label_template_part2_tokenized
+ + eos
+ )
+
+ # determine label tokens, to calculate loss only over them when labels_loss == True
+ attention_mask = [1] * len(input_ids)
+ input_type_mask = (
+ [1] * len(input_template_tokenized_part1)
+ + [2] * len(input_tokenized)
+ + [1] * len(input_template_tokenized_part2)
+ + [0] * len(sep_tokenized)
+ + [3] * len(label_template_part1_tokenized)
+ + [4] * len(label_tokenized)
+ + [3] * len(label_template_part2_tokenized)
+ + [0] * len(eos)
+ )
+
+ assert len(input_type_mask) == len(input_ids) == len(attention_mask)
+
+ return input_ids, attention_mask, input_type_mask
+
+ def __len__(self):
+ return len(self.input_ids)
+
+ def __getitem__(self, idx):
+ return {
+ "input_ids": self.input_ids[idx],
+ "attention_mask": self.attention_mask[idx],
+ "input_type_mask": self.input_type_mask[idx],
+ }
+
+ dataset = CPTDataset(data, tokenizer, TEMPLATE)
+
+ return dataset
+
+
+def test_model_initialization_text(global_tokenizer, config_text):
+ """Test model loading and PEFT model initialization."""
+ base_model = AutoModelForCausalLM.from_pretrained(MODEL_NAME)
+
+ model = get_peft_model(base_model, config_text)
+ assert model is not None, "PEFT model initialization failed"
+
+
+def test_model_initialization_random(global_tokenizer, config_random):
+ """Test model loading and PEFT model initialization."""
+ base_model = AutoModelForCausalLM.from_pretrained(MODEL_NAME)
+
+ model = get_peft_model(base_model, config_random)
+ assert model is not None, "PEFT model initialization failed"
+
+
+def test_model_initialization_wrong_task_type_warns():
+ # TODO: adjust this test to check for an error with PEFT v0.18.0
+ msg = "CPTConfig only supports task_type = CAUSAL_LM, setting it automatically"
+ with pytest.warns(FutureWarning, match=msg):
+ config = CPTConfig(task_type=TaskType.SEQ_CLS)
+ assert config.task_type == TaskType.CAUSAL_LM
+
+
+def test_model_training_random(sst_data, global_tokenizer, collator, config_random):
+ """Perform a short training run to verify the model and data integration."""
+
+ base_model = AutoModelForCausalLM.from_pretrained(MODEL_NAME)
+ model = get_peft_model(base_model, config_random)
+ emb = model.prompt_encoder.default.embedding.weight.data.clone().detach()
+ training_args = TrainingArguments(
+ output_dir="./results",
+ per_device_train_batch_size=1,
+ num_train_epochs=2,
+ remove_unused_columns=False,
+ save_strategy="no",
+ logging_steps=1,
+ )
+
+ train_dataset = dataset(sst_data["train"], global_tokenizer)
+
+ trainer = Trainer(model=model, args=training_args, train_dataset=train_dataset, data_collator=collator)
+
+ trainer.train()
+ # Verify that the embedding tensor remains unchanged (frozen)
+ assert torch.all(model.prompt_encoder.default.embedding.weight.data.clone().detach().cpu() == emb.cpu())
+
+ delta_emb = model.prompt_encoder.default.get_projection().clone().detach()
+ norm_delta = delta_emb.norm(dim=1).cpu()
+ epsilon = model.prompt_encoder.default.get_epsilon().cpu()
+ # Verify that the change in tokens is constrained to epsilon
+ assert torch.all(norm_delta <= epsilon)
+
+
+def test_model_batch_training_text(sst_data, global_tokenizer, collator, config_text):
+ """Perform a short training run to verify the model and data integration."""
+
+ base_model = AutoModelForCausalLM.from_pretrained(MODEL_NAME)
+ model = get_peft_model(base_model, config_text)
+ emb = model.prompt_encoder.default.embedding.weight.data.clone().detach()
+
+ training_args = TrainingArguments(
+ output_dir="./results",
+ per_device_train_batch_size=2,
+ num_train_epochs=2,
+ remove_unused_columns=False,
+ save_strategy="no",
+ logging_steps=1,
+ )
+
+ train_dataset = dataset(sst_data["train"], global_tokenizer)
+
+ trainer = Trainer(model=model, args=training_args, train_dataset=train_dataset, data_collator=collator)
+
+ trainer.train()
+ # Verify that the embedding tensor remains unchanged (frozen)
+ assert torch.all(model.prompt_encoder.default.embedding.weight.data.clone().detach().cpu() == emb.cpu())
+
+ cpt_tokens_type_mask = torch.Tensor(config_text.cpt_tokens_type_mask).long()
+ non_label_idx = (cpt_tokens_type_mask == 1) | (cpt_tokens_type_mask == 2) | (cpt_tokens_type_mask == 3)
+
+ delta_emb = model.prompt_encoder.default.get_projection().clone().detach()
+ norm_delta = delta_emb.norm(dim=1).cpu()
+ epsilon = model.prompt_encoder.default.get_epsilon().cpu()
+ # Verify that the change in tokens is constrained to epsilon
+ assert torch.all(norm_delta <= epsilon)
+ # Ensure that label tokens remain unchanged
+ assert torch.all((norm_delta == 0) == (~non_label_idx))
diff --git a/peft/tests/test_custom_models.py b/peft/tests/test_custom_models.py
new file mode 100644
index 0000000000000000000000000000000000000000..5116919978ae3c45183fe7063b15147d3f744851
--- /dev/null
+++ b/peft/tests/test_custom_models.py
@@ -0,0 +1,6226 @@
+#!/usr/bin/env python3
+
+# coding=utf-8
+# Copyright 2023-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+import copy
+import os
+import platform
+import re
+import shutil
+import tempfile
+import time
+from contextlib import contextmanager
+from functools import partial
+
+import pytest
+import torch
+from safetensors.torch import load_file as safe_load_file
+from torch import nn
+from transformers import AutoModelForCausalLM, AutoModelForSequenceClassification
+from transformers.pytorch_utils import Conv1D
+
+from peft import (
+ AdaLoraConfig,
+ BOFTConfig,
+ BoneConfig,
+ C3AConfig,
+ FourierFTConfig,
+ HRAConfig,
+ IA3Config,
+ LNTuningConfig,
+ LoHaConfig,
+ LoKrConfig,
+ LoraConfig,
+ MissConfig,
+ OFTConfig,
+ PeftModel,
+ PeftWarning,
+ RandLoraConfig,
+ RoadConfig,
+ ShiraConfig,
+ TaskType,
+ TrainableTokensConfig,
+ VBLoRAConfig,
+ VeraConfig,
+ WaveFTConfig,
+ get_peft_model,
+)
+from peft.tuners.tuners_utils import BaseTunerLayer
+from peft.utils import AuxiliaryTrainingWrapper, infer_device
+
+from .testing_common import PeftCommonTester
+from .testing_utils import get_state_dict, require_non_cpu, set_init_weights_false
+
+
+# MLP is a vanilla FF network with only linear layers
+# EmbConv1D has an embedding and a Conv1D layer
+# Conv2D has a Conv2D layer
+TEST_CASES = [
+ ########
+ # LoRA #
+ ########
+ ("Vanilla MLP 1 LoRA", "MLP", LoraConfig, {"target_modules": "lin0"}),
+ ("Vanilla MLP 2 LoRA", "MLP", LoraConfig, {"target_modules": ["lin0"]}),
+ ("Vanilla MLP 3 LoRA", "MLP", LoraConfig, {"target_modules": ["lin1"]}),
+ ("Vanilla MLP 4 LoRA", "MLP", LoraConfig, {"target_modules": ["lin0", "lin1"]}),
+ ("Vanilla MLP 5 LoRA", "MLP", LoraConfig, {"target_modules": ["lin0"], "modules_to_save": ["lin1"]}),
+ (
+ "Vanilla MLP 6 LoRA",
+ "MLP",
+ LoraConfig,
+ {
+ "target_modules": ["lin0"],
+ "lora_alpha": 4,
+ "lora_dropout": 0.1,
+ },
+ ),
+ ("Vanilla MLP 7 LoRA with DoRA", "MLP", LoraConfig, {"target_modules": ["lin0"], "use_dora": True}),
+ ("Vanilla MLP 8 LoRA with DoRA", "MLP", LoraConfig, {"target_modules": ["lin0", "lin1"], "use_dora": True}),
+ (
+ "Vanilla MLP 9 LoRA with DoRA",
+ "MLP",
+ LoraConfig,
+ {"target_modules": "lin1", "use_dora": True, "lora_alpha": 32},
+ ),
+ ("Embedding + transformers Conv1D 1 LoRA", "EmbConv1D", LoraConfig, {"target_modules": ["conv1d"]}),
+ ("Embedding + transformers Conv1D 2 LoRA", "EmbConv1D", LoraConfig, {"target_modules": ["emb"]}),
+ ("Embedding + transformers Conv1D 3 LoRA", "EmbConv1D", LoraConfig, {"target_modules": ["emb", "conv1d"]}),
+ (
+ "Embedding + transformers Conv1D 1 DoRA",
+ "EmbConv1D",
+ LoraConfig,
+ {"target_modules": ["conv1d"], "use_dora": True},
+ ),
+ ("Embedding + transformers Conv1D 2 DoRA", "EmbConv1D", LoraConfig, {"target_modules": ["emb"], "use_dora": True}),
+ (
+ "Embedding + transformers Conv1D 3 DoRA",
+ "EmbConv1D",
+ LoraConfig,
+ {"target_modules": ["emb", "conv1d"], "use_dora": True},
+ ),
+ (
+ "Embedding + transformers Conv1D 1 LoRA trainable_tokens",
+ "EmbConv1D",
+ LoraConfig,
+ {"target_modules": ["conv1d"], "trainable_token_indices": {"emb": [0, 10]}},
+ ),
+ ("Conv1d LoRA", "Conv1d", LoraConfig, {"target_modules": ["conv1d"]}),
+ ("Conv1d LoRA with DoRA", "Conv1d", LoraConfig, {"target_modules": ["conv1d"], "use_dora": True}),
+ ("Conv2d 1 LoRA", "Conv2d", LoraConfig, {"target_modules": ["conv2d"]}),
+ ("Conv2d 2 LoRA", "Conv2d", LoraConfig, {"target_modules": ["conv2d", "lin0"]}),
+ ("Conv2d 1 LoRA with DoRA", "Conv2d", LoraConfig, {"target_modules": ["conv2d"], "use_dora": True}),
+ ("Conv2d 2 LoRA with DoRA", "Conv2d", LoraConfig, {"target_modules": ["conv2d", "lin0"], "use_dora": True}),
+ ("Conv2d Groups LoRA", "Conv2dGroups", LoraConfig, {"target_modules": ["conv2d"]}),
+ ("Conv2d Groups2 LoRA", "Conv2dGroups2", LoraConfig, {"target_modules": ["conv2d"]}),
+ ("Conv2d Groups LoRA with DoRA", "Conv2dGroups", LoraConfig, {"target_modules": ["conv2d"], "use_dora": True}),
+ ("Conv2d Groups2 LoRA with DoRA", "Conv2dGroups2", LoraConfig, {"target_modules": ["conv2d"], "use_dora": True}),
+ ("Conv3d 1 LoRA", "Conv3d", LoraConfig, {"target_modules": ["conv3d"]}),
+ ("Conv3d 2 LoRA", "Conv3d", LoraConfig, {"target_modules": ["conv3d", "lin0"]}),
+ ("Conv3d 1 LoRA with DoRA", "Conv3d", LoraConfig, {"target_modules": ["conv3d"], "use_dora": True}),
+ ("Conv3d 2 LoRA with DoRA", "Conv3d", LoraConfig, {"target_modules": ["conv3d", "lin0"], "use_dora": True}),
+ # LoRA with lora_B bias enabled (note: embedding is not supported)
+ # It's important to set lora_alpha != r to ensure that scaling is taken into account correctly
+ (
+ "Vanilla MLP 1 LoRA with lora_b bias",
+ "MLP",
+ LoraConfig,
+ {"target_modules": ["lin0", "lin1"], "lora_bias": True, "lora_alpha": 32},
+ ),
+ (
+ "Conv2d 1 LoRA with lora_b bias",
+ "Conv2d",
+ LoraConfig,
+ {"target_modules": ["conv2d"], "lora_bias": True, "lora_alpha": 32},
+ ),
+ (
+ "Conv3d 1 LoRA with lora_b bias",
+ "Conv3d",
+ LoraConfig,
+ {"target_modules": ["conv3d"], "lora_bias": True, "lora_alpha": 32},
+ ),
+ ("MHA 1 LoRA", "MHA", LoraConfig, {"target_modules": ["mha"]}),
+ ("MHA 2 LoRA", "MHA", LoraConfig, {"target_modules": ["mha", "lin0"]}),
+ # targeting parameters directly
+ ("MLP 1 using nn.Parameter LoRA", "MlpUsingParameters", LoraConfig, {"target_parameters": ["lin0.weight"]}),
+ (
+ "MLP 2 using nn.Parameter LoRA",
+ "MLP",
+ LoraConfig,
+ {"target_modules": ["lin0"], "target_parameters": ["lin1.weight"]},
+ ),
+ #######
+ # IA³ #
+ #######
+ ("Vanilla MLP 1 IA3", "MLP", IA3Config, {"target_modules": "lin0", "feedforward_modules": []}),
+ ("Vanilla MLP 2 IA3", "MLP", IA3Config, {"target_modules": "lin0", "feedforward_modules": "lin0"}),
+ ("Vanilla MLP 3 IA3", "MLP", IA3Config, {"target_modules": ["lin0"], "feedforward_modules": []}),
+ ("Vanilla MLP 4 IA3", "MLP", IA3Config, {"target_modules": ["lin0"], "feedforward_modules": ["lin0"]}),
+ ("Vanilla MLP 5 IA3", "MLP", IA3Config, {"target_modules": ["lin1"], "feedforward_modules": []}),
+ ("Vanilla MLP 6 IA3", "MLP", IA3Config, {"target_modules": ["lin1"], "feedforward_modules": ["lin1"]}),
+ (
+ "Vanilla MLP 7 IA3",
+ "MLP",
+ IA3Config,
+ {"target_modules": ["lin0", "lin1"], "feedforward_modules": []},
+ ),
+ (
+ "Vanilla MLP 8 IA3",
+ "MLP",
+ IA3Config,
+ {"target_modules": ["lin0", "lin1"], "feedforward_modules": ["lin0", "lin1"]},
+ ),
+ (
+ "Vanilla MLP 9 IA3",
+ "MLP",
+ IA3Config,
+ {"target_modules": ["lin0"], "modules_to_save": ["lin1"], "feedforward_modules": ["lin0"]},
+ ),
+ (
+ "transformers Conv1D 1 IA3",
+ "EmbConv1D",
+ IA3Config,
+ {"target_modules": ["conv1d"], "feedforward_modules": ["conv1d"]},
+ ),
+ (
+ "transformers Conv1D 2 IA3",
+ "EmbConv1D",
+ IA3Config,
+ {"target_modules": ["conv1d", "lin0"], "feedforward_modules": ["conv1d", "lin0"]},
+ ),
+ (
+ "transformers Conv1D 1 IA3",
+ "EmbConv1D",
+ IA3Config,
+ {"target_modules": ["conv1d"], "feedforward_modules": ["conv1d"], "modules_to_save": ["lin0"]},
+ ),
+ ("Conv2d 1 IA3", "Conv2d", IA3Config, {"target_modules": ["conv2d"], "feedforward_modules": []}),
+ ("Conv2d 2 IA3", "Conv2d", IA3Config, {"target_modules": ["conv2d"], "feedforward_modules": ["conv2d"]}),
+ (
+ "Conv2d 3 IA3",
+ "Conv2d",
+ IA3Config,
+ {"target_modules": ["conv2d", "lin0"], "feedforward_modules": []},
+ ),
+ (
+ "Conv2d 4 IA3",
+ "Conv2d",
+ IA3Config,
+ {"target_modules": ["conv2d", "lin0"], "feedforward_modules": ["conv2d"]},
+ ),
+ (
+ "Conv2d 5 IA3",
+ "Conv2d",
+ IA3Config,
+ {"target_modules": ["conv2d", "lin0"], "feedforward_modules": ["conv2d", "lin0"]},
+ ),
+ ("Conv3d 1 IA3", "Conv3d", IA3Config, {"target_modules": ["conv3d"], "feedforward_modules": []}),
+ ("Conv3d 2 IA3", "Conv3d", IA3Config, {"target_modules": ["conv3d"], "feedforward_modules": ["conv3d"]}),
+ (
+ "Conv3d 3 IA3",
+ "Conv3d",
+ IA3Config,
+ {"target_modules": ["conv3d", "lin0"], "feedforward_modules": []},
+ ),
+ (
+ "Conv3d 4 IA3",
+ "Conv3d",
+ IA3Config,
+ {"target_modules": ["conv3d", "lin0"], "feedforward_modules": ["conv3d"]},
+ ),
+ (
+ "Conv3d 5 IA3",
+ "Conv3d",
+ IA3Config,
+ {"target_modules": ["conv3d", "lin0"], "feedforward_modules": ["conv3d", "lin0"]},
+ ),
+ ########
+ # LoHa #
+ ########
+ ("Vanilla MLP 1 LOHA", "MLP", LoHaConfig, {"target_modules": "lin0"}),
+ ("Vanilla MLP 2 LOHA", "MLP", LoHaConfig, {"target_modules": ["lin0"]}),
+ ("Vanilla MLP 3 LOHA", "MLP", LoHaConfig, {"target_modules": ["lin1"]}),
+ ("Vanilla MLP 4 LOHA", "MLP", LoHaConfig, {"target_modules": ["lin0", "lin1"]}),
+ ("Vanilla MLP 5 LOHA", "MLP", LoHaConfig, {"target_modules": ["lin0"], "modules_to_save": ["lin1"]}),
+ (
+ "Vanilla MLP 6 LOHA",
+ "MLP",
+ LoHaConfig,
+ {
+ "target_modules": ["lin0"],
+ "alpha": 4,
+ "module_dropout": 0.1,
+ },
+ ),
+ ("Vanilla MLP 7 LOHA", "MLP", LoHaConfig, {"target_modules": "lin0", "rank_dropout": 0.5}),
+ ("Conv2d 1 LOHA", "Conv2d", LoHaConfig, {"target_modules": ["conv2d"]}),
+ ("Conv2d 2 LOHA", "Conv2d", LoHaConfig, {"target_modules": ["conv2d", "lin0"]}),
+ ("Conv2d 3 LOHA", "Conv2d", LoHaConfig, {"target_modules": ["conv2d"], "use_effective_conv2d": True}),
+ ("Conv2d 4 LOHA", "Conv2d", LoHaConfig, {"target_modules": ["conv2d", "lin0"], "use_effective_conv2d": True}),
+ ("Conv1d LOHA", "Conv1d", LoHaConfig, {"target_modules": ["conv1d"]}),
+ ("Conv1d LOHA 1", "Conv1d", LoHaConfig, {"target_modules": ["conv1d"]}),
+ ("Conv1d LOHA 2", "Conv1d", LoHaConfig, {"target_modules": ["conv1d"], "r": 2}),
+ (
+ "Conv1d LOHA 3",
+ "Conv1dBigger",
+ LoHaConfig,
+ {"target_modules": ["conv1d"], "r": 2, "use_effective_conv2d": True},
+ ),
+ (
+ "Conv1d LOHA 4",
+ "Conv1dBigger",
+ LoHaConfig,
+ {"target_modules": ["conv1d"], "r": 2, "use_effective_conv2d": False},
+ ),
+ ("Conv2d 1x1 LOHA", "Conv2d1x1", LoHaConfig, {"target_modules": ["conv2d"]}),
+ # LoKr
+ ("Vanilla MLP 1 LOKR", "MLP", LoKrConfig, {"target_modules": "lin0"}),
+ ("Vanilla MLP 2 LOKR", "MLP", LoKrConfig, {"target_modules": ["lin0"]}),
+ ("Vanilla MLP 3 LOKR", "MLP", LoKrConfig, {"target_modules": ["lin1"]}),
+ ("Vanilla MLP 4 LOKR", "MLP", LoKrConfig, {"target_modules": ["lin0", "lin1"]}),
+ ("Vanilla MLP 5 LOKR", "MLP", LoKrConfig, {"target_modules": ["lin0"], "modules_to_save": ["lin1"]}),
+ (
+ "Vanilla MLP 6 LOKR",
+ "MLP",
+ LoKrConfig,
+ {
+ "target_modules": ["lin0"],
+ "alpha": 4,
+ "module_dropout": 0.1,
+ },
+ ),
+ ("Vanilla MLP 7 LOKR", "MLP", LoKrConfig, {"target_modules": "lin0", "rank_dropout": 0.5}),
+ ("Vanilla MLP 8 LOKR", "MLP", LoKrConfig, {"target_modules": "lin0", "decompose_both": True, "r": 1, "alpha": 1}),
+ ("Conv1d LOKR 1", "Conv1d", LoKrConfig, {"target_modules": ["conv1d"]}),
+ ("Conv1d LOKR 2", "Conv1d", LoKrConfig, {"target_modules": ["conv1d"], "r": 2}),
+ (
+ "Conv1d LOKR 3",
+ "Conv1dBigger",
+ LoKrConfig,
+ {"target_modules": ["conv1d"], "r": 2, "use_effective_conv2d": True},
+ ),
+ (
+ "Conv1d LOKR 4",
+ "Conv1dBigger",
+ LoKrConfig,
+ {"target_modules": ["conv1d"], "r": 2, "use_effective_conv2d": False},
+ ),
+ ("Conv2d 1 LOKR", "Conv2d", LoKrConfig, {"target_modules": ["conv2d"]}),
+ ("Conv2d 2 LOKR", "Conv2d", LoKrConfig, {"target_modules": ["conv2d", "lin0"]}),
+ ("Conv2d 3 LOKR", "Conv2d", LoKrConfig, {"target_modules": ["conv2d"], "use_effective_conv2d": True}),
+ ("Conv2d 4 LOKR", "Conv2d", LoKrConfig, {"target_modules": ["conv2d", "lin0"], "use_effective_conv2d": True}),
+ ("Conv2d 1x1 LOKR", "Conv2d1x1", LoKrConfig, {"target_modules": ["conv2d"]}),
+ (
+ "Conv2d 5 LOKR",
+ "Conv2d",
+ LoKrConfig,
+ {"target_modules": ["conv2d", "lin0"], "use_effective_conv2d": True, "decompose_both": True},
+ ),
+ (
+ "Conv2d 6 LOKR",
+ "Conv2d",
+ LoKrConfig,
+ {"target_modules": ["conv2d", "lin0"], "use_effective_conv2d": True, "decompose_factor": 4},
+ ),
+ (
+ "Conv2d 7 LOKR",
+ "Conv2d",
+ LoKrConfig,
+ {
+ "target_modules": ["conv2d", "lin0"],
+ "use_effective_conv2d": True,
+ "decompose_both": True,
+ "decompose_factor": 4,
+ },
+ ),
+ ########
+ # OFT #
+ ########
+ (
+ "Vanilla MLP 1 OFT",
+ "MLP",
+ OFTConfig,
+ {"r": 2, "oft_block_size": 0, "target_modules": "lin0", "use_cayley_neumann": False},
+ ),
+ (
+ "Vanilla MLP 2 OFT",
+ "MLP",
+ OFTConfig,
+ {"r": 2, "oft_block_size": 0, "target_modules": ["lin0"], "use_cayley_neumann": False},
+ ),
+ (
+ "Vanilla MLP 5 OFT",
+ "MLP",
+ OFTConfig,
+ {
+ "r": 2,
+ "oft_block_size": 0,
+ "target_modules": ["lin0"],
+ "modules_to_save": ["lin1"],
+ "use_cayley_neumann": False,
+ },
+ ),
+ (
+ "Vanilla MLP 6 OFT",
+ "MLP",
+ OFTConfig,
+ {
+ "r": 2,
+ "oft_block_size": 0,
+ "target_modules": ["lin0"],
+ "module_dropout": 0.1,
+ "use_cayley_neumann": False,
+ },
+ ),
+ (
+ "Vanilla MLP 7 OFT",
+ "MLP",
+ OFTConfig,
+ {"r": 2, "oft_block_size": 0, "target_modules": ["lin0"], "coft": True, "eps": 1e-2},
+ ),
+ (
+ "Vanilla MLP 8 OFT",
+ "MLP",
+ OFTConfig,
+ {"r": 2, "oft_block_size": 0, "target_modules": ["lin0"], "block_share": True, "use_cayley_neumann": False},
+ ),
+ (
+ "Vanilla MLP 9 OFT",
+ "MLP",
+ OFTConfig,
+ {"r": 2, "oft_block_size": 0, "target_modules": ["lin0"], "coft": True, "eps": 1e-2, "block_share": True},
+ ),
+ (
+ "Vanilla MLP 10 OFT",
+ "MLP",
+ OFTConfig,
+ {"r": 0, "oft_block_size": 2, "target_modules": ["lin0"], "use_cayley_neumann": True},
+ ),
+ (
+ "Vanilla MLP 11 OFT",
+ "MLP",
+ OFTConfig,
+ {"r": 0, "oft_block_size": 2, "target_modules": ["lin0"], "use_cayley_neumann": False},
+ ),
+ (
+ "Vanilla MLP 12 OFT",
+ "MLP",
+ OFTConfig,
+ {
+ "r": 0,
+ "oft_block_size": 2,
+ "target_modules": ["lin0"],
+ "coft": True,
+ "eps": 1e-2,
+ "block_share": True,
+ "use_cayley_neumann": True,
+ },
+ ),
+ (
+ "Vanilla MLP 13 OFT",
+ "MLP",
+ OFTConfig,
+ {
+ "r": 0,
+ "oft_block_size": 2,
+ "target_modules": ["lin0"],
+ "coft": True,
+ "eps": 1e-2,
+ "block_share": True,
+ "use_cayley_neumann": False,
+ },
+ ),
+ ("Conv2d 1 OFT", "Conv2d", OFTConfig, {"r": 5, "oft_block_size": 0, "target_modules": ["conv2d"]}),
+ ("Conv2d 3 OFT", "Conv2d", OFTConfig, {"r": 5, "oft_block_size": 0, "target_modules": ["conv2d"], "coft": True}),
+ (
+ "Conv2d 4 OFT",
+ "Conv2d",
+ OFTConfig,
+ {"r": 5, "oft_block_size": 0, "target_modules": ["conv2d"], "block_share": True},
+ ),
+ (
+ "Conv2d 5 OFT",
+ "Conv2d",
+ OFTConfig,
+ {"r": 5, "oft_block_size": 0, "target_modules": ["conv2d"], "coft": True, "block_share": True},
+ ),
+ ########
+ # HRA #
+ ########
+ ("Vanilla MLP 1 HRA", "MLP", HRAConfig, {"target_modules": "lin0"}),
+ ("Vanilla MLP 2 HRA", "MLP", HRAConfig, {"target_modules": ["lin0"]}),
+ ("Vanilla MLP 3 HRA", "MLP", HRAConfig, {"target_modules": ["lin0", "lin1"]}),
+ ("Vanilla MLP 5 HRA", "MLP", HRAConfig, {"target_modules": ["lin0"], "modules_to_save": ["lin1"]}),
+ ("Conv2d 1 HRA", "Conv2d", HRAConfig, {"target_modules": ["conv2d"]}),
+ ########
+ # Bone #
+ ########
+ ("Vanilla MLP 1 Bone", "MLP", BoneConfig, {"target_modules": "lin0", "r": 2}),
+ ("Vanilla MLP 2 Bone", "MLP", BoneConfig, {"target_modules": ["lin0"], "r": 2}),
+ ("Vanilla MLP 3 Bone", "MLP", BoneConfig, {"target_modules": ["lin0", "lin1"], "r": 2}),
+ ("Vanilla MLP 5 Bone", "MLP", BoneConfig, {"target_modules": ["lin0"], "modules_to_save": ["lin1"], "r": 2}),
+ ("Vanilla MLP 1 Bone", "MLP", BoneConfig, {"target_modules": "lin0", "r": 2, "init_weights": "bat"}),
+ ("Vanilla MLP 2 Bone", "MLP", BoneConfig, {"target_modules": ["lin0"], "r": 2, "init_weights": "bat"}),
+ ("Vanilla MLP 3 Bone", "MLP", BoneConfig, {"target_modules": ["lin0", "lin1"], "r": 2, "init_weights": "bat"}),
+ (
+ "Vanilla MLP 5 Bone",
+ "MLP",
+ BoneConfig,
+ {"target_modules": ["lin0"], "modules_to_save": ["lin1"], "r": 2, "init_weights": "bat"},
+ ),
+ ########
+ # MiSS #
+ ########
+ ("Vanilla MLP 1 MiSS", "MLP", MissConfig, {"target_modules": "lin0", "r": 2}),
+ ("Vanilla MLP 2 MiSS", "MLP", MissConfig, {"target_modules": ["lin0"], "r": 2}),
+ ("Vanilla MLP 3 MiSS", "MLP", MissConfig, {"target_modules": ["lin0", "lin1"], "r": 2}),
+ ("Vanilla MLP 5 MiSS", "MLP", MissConfig, {"target_modules": ["lin0"], "modules_to_save": ["lin1"], "r": 2}),
+ ("Vanilla MLP 1 MiSS", "MLP", MissConfig, {"target_modules": "lin0", "r": 2, "init_weights": "bat"}),
+ ("Vanilla MLP 2 MiSS", "MLP", MissConfig, {"target_modules": ["lin0"], "r": 2, "init_weights": "bat"}),
+ ("Vanilla MLP 3 MiSS", "MLP", MissConfig, {"target_modules": ["lin0", "lin1"], "r": 2, "init_weights": "bat"}),
+ (
+ "Vanilla MLP 5 MiSS",
+ "MLP",
+ MissConfig,
+ {"target_modules": ["lin0"], "modules_to_save": ["lin1"], "r": 2, "init_weights": "bat"},
+ ),
+ #############
+ # LN Tuning #
+ #############
+ ("LayerNorm 1 LNTuning", "MLP_LayerNorm", LNTuningConfig, {"target_modules": "layernorm0"}),
+ ("LayerNorm 2 LNTuning", "MLP_LayerNorm", LNTuningConfig, {"target_modules": ["layernorm0"]}),
+ (
+ "LayerNorm 3 LNTuning",
+ "MLP_LayerNorm",
+ LNTuningConfig,
+ {"target_modules": ["layernorm0"], "modules_to_save": ["layernorm1"]},
+ ),
+ ("Linear 4 LNTuning", "MLP_LayerNorm", LNTuningConfig, {"target_modules": "lin0"}),
+ ("Linear 5 LNTuning", "MLP_LayerNorm", LNTuningConfig, {"target_modules": ["lin0"]}),
+ ########
+ # BOFT #
+ ########
+ ("Vanilla MLP 1 BOFT", "MLP", BOFTConfig, {"target_modules": ["lin1"], "boft_block_size": 2}),
+ (
+ "Vanilla MLP 2 BOFT",
+ "MLP",
+ BOFTConfig,
+ {"target_modules": ["lin1"], "modules_to_save": ["lin0"], "boft_block_size": 2},
+ ),
+ (
+ "Vanilla MLP 3 BOFT",
+ "MLP",
+ BOFTConfig,
+ {
+ "target_modules": ["lin1"],
+ "boft_block_size": 2,
+ "boft_dropout": 0.1,
+ },
+ ),
+ (
+ "Vanilla MLP 4 BOFT",
+ "MLP",
+ BOFTConfig,
+ {"target_modules": ["lin1"], "boft_block_size": 2, "boft_block_num": 0, "boft_n_butterfly_factor": 1},
+ ),
+ (
+ "Vanilla MLP 5 BOFT",
+ "MLP",
+ BOFTConfig,
+ {"target_modules": ["lin1"], "boft_block_size": 0, "boft_block_num": 2, "boft_n_butterfly_factor": 1},
+ ),
+ (
+ "Vanilla MLP 6 BOFT",
+ "MLP",
+ BOFTConfig,
+ {"target_modules": ["lin1"], "boft_block_size": 10, "boft_block_num": 0, "boft_n_butterfly_factor": 2},
+ ),
+ (
+ "Conv2d 1 BOFT",
+ "Conv2d",
+ BOFTConfig,
+ {"target_modules": ["conv2d"], "boft_block_size": 45, "boft_block_num": 0, "boft_n_butterfly_factor": 1},
+ ),
+ (
+ "Conv2d 2 BOFT",
+ "Conv2d",
+ BOFTConfig,
+ {"target_modules": ["conv2d"], "boft_block_size": 0, "boft_block_num": 1, "boft_n_butterfly_factor": 1},
+ ),
+ (
+ "MLP2 1 BOFT",
+ "MLP2",
+ BOFTConfig,
+ {"target_modules": ["lin1"], "boft_block_size": 2, "boft_block_num": 0, "boft_n_butterfly_factor": 3},
+ ),
+ (
+ "MLP2 2 BOFT",
+ "MLP2",
+ BOFTConfig,
+ {"target_modules": ["lin1"], "boft_block_size": 0, "boft_block_num": 8, "boft_n_butterfly_factor": 3},
+ ),
+ (
+ "Conv2d2 1 BOFT",
+ "Conv2d2",
+ BOFTConfig,
+ {"target_modules": ["conv2d"], "boft_block_size": 2, "boft_block_num": 0, "boft_n_butterfly_factor": 2},
+ ),
+ (
+ "Conv2d2 1 BOFT",
+ "Conv2d2",
+ BOFTConfig,
+ {"target_modules": ["conv2d"], "boft_block_size": 2, "boft_block_num": 0, "boft_n_butterfly_factor": 3},
+ ),
+ #########
+ # SHiRA #
+ #########
+ ("Vanilla MLP 1 SHiRA", "MLP", ShiraConfig, {"r": 1, "target_modules": "lin0"}),
+ ("Vanilla MLP 2 SHiRA", "MLP", ShiraConfig, {"r": 1, "target_modules": ["lin0"]}),
+ ("Vanilla MLP 3 SHiRA", "MLP", ShiraConfig, {"r": 1, "target_modules": ["lin1"]}),
+ (
+ "Vanilla MLP 4 SHiRA",
+ "MLP",
+ ShiraConfig,
+ {"r": 1, "target_modules": ["lin0", "lin1"], "random_seed": 56},
+ ),
+ (
+ "Vanilla MLP 5 SHiRA",
+ "MLP",
+ ShiraConfig,
+ {"r": 1, "target_modules": ["lin0"]},
+ ),
+ ########
+ # VeRA #
+ ########
+ ("Vanilla MLP 1 VeRA", "MLP", VeraConfig, {"target_modules": "lin0"}),
+ ("Vanilla MLP 2 VeRA", "MLP", VeraConfig, {"target_modules": ["lin0"]}),
+ ("Vanilla MLP 3 VeRA", "MLP", VeraConfig, {"target_modules": ["lin1"]}),
+ ("Vanilla MLP 4 VeRA", "MLP", VeraConfig, {"target_modules": ["lin0", "lin1"]}),
+ (
+ "Vanilla MLP 5 VeRA",
+ "MLP",
+ VeraConfig,
+ {"target_modules": ["lin0"], "modules_to_save": ["lin1"]},
+ ),
+ (
+ "Embedding + transformers Conv1D 1 VeRA",
+ "EmbConv1D",
+ VeraConfig,
+ {"target_modules": ["conv1d"]},
+ ),
+ #############
+ # FourierFT #
+ #############
+ # FourierFT is not initialized as an identity transform by default, hence set init_weights=True
+ (
+ "Vanilla MLP 1 FourierFT",
+ "MLP",
+ FourierFTConfig,
+ {"n_frequency": 10, "target_modules": "lin0", "init_weights": True},
+ ),
+ (
+ "Vanilla MLP 2 FourierFT",
+ "MLP",
+ FourierFTConfig,
+ {"n_frequency": 10, "target_modules": ["lin0"], "init_weights": True},
+ ),
+ (
+ "Vanilla MLP 3 FourierFT",
+ "MLP",
+ FourierFTConfig,
+ {"n_frequency": 10, "target_modules": ["lin1"], "init_weights": True},
+ ),
+ (
+ "Vanilla MLP 5 FourierFT",
+ "MLP",
+ FourierFTConfig,
+ {"n_frequency": 10, "target_modules": ["lin0"], "modules_to_save": ["lin1"], "init_weights": True},
+ ),
+ (
+ "Vanilla MLP 6 FourierFT",
+ "MLP",
+ FourierFTConfig,
+ {"n_frequency": 10, "target_modules": ["lin0", "lin1"], "modules_to_save": ["lin1"], "init_weights": True},
+ ),
+ (
+ "Vanilla MLP 7 FourierFT",
+ "MLP",
+ FourierFTConfig,
+ {
+ "n_frequency_pattern": {"lin0": 5, "lin1": 10},
+ "target_modules": ["lin0", "lin1"],
+ "modules_to_save": ["lin1"],
+ "init_weights": True,
+ },
+ ),
+ ##########
+ # VBLoRA #
+ ##########
+ ("Vanilla MLP 1 VBLoRA", "MLP", VBLoRAConfig, {"target_modules": "lin0", "vector_length": 1, "num_vectors": 5}),
+ ("Vanilla MLP 2 VBLoRA", "MLP", VBLoRAConfig, {"target_modules": ["lin0"], "vector_length": 1, "num_vectors": 5}),
+ ("Vanilla MLP 3 VBLoRA", "MLP", VBLoRAConfig, {"target_modules": ["lin1"], "vector_length": 2, "num_vectors": 5}),
+ (
+ "Vanilla MLP 4 VBLoRA",
+ "MLP",
+ VBLoRAConfig,
+ {"target_modules": ["lin0", "lin1"], "vector_length": 1, "num_vectors": 5},
+ ),
+ (
+ "Vanilla MLP 5 VBLoRA",
+ "MLP",
+ VBLoRAConfig,
+ {"target_modules": ["lin0"], "modules_to_save": ["lin1"], "vector_length": 1, "num_vectors": 5},
+ ),
+ (
+ "Embedding + transformers Conv1D 1 VBLoRA",
+ "EmbConv1D",
+ VBLoRAConfig,
+ {"target_modules": ["conv1d"], "vector_length": 1, "num_vectors": 2},
+ ),
+ ###################
+ # TrainableTokens #
+ ###################
+ (
+ "Embedding + transformers Conv1D 1 trainable_tokens",
+ "EmbConv1D",
+ TrainableTokensConfig,
+ {"target_modules": ["emb"], "token_indices": [0, 1, 3], "init_weights": False},
+ ),
+ ############
+ # RandLora #
+ ############
+ # We have to reduce the default scaling parameter to avoid nans when using large learning rates
+ ("Vanilla MLP 1 RandLora", "MLP", RandLoraConfig, {"target_modules": "lin0", "randlora_alpha": 1}),
+ ("Vanilla MLP 2 RandLora", "MLP", RandLoraConfig, {"target_modules": ["lin0"], "randlora_alpha": 1}),
+ ("Vanilla MLP 3 RandLora", "MLP", RandLoraConfig, {"target_modules": ["lin1"], "randlora_alpha": 1}),
+ ("Vanilla MLP 4 RandLora", "MLP", RandLoraConfig, {"target_modules": ["lin0", "lin1"], "randlora_alpha": 1}),
+ (
+ "Vanilla MLP 5 RandLora",
+ "MLP",
+ RandLoraConfig,
+ {"target_modules": ["lin0", "lin1"], "sparse": True, "randlora_alpha": 1},
+ ),
+ (
+ "Vanilla MLP 6 RandLora",
+ "MLP",
+ RandLoraConfig,
+ {"target_modules": ["lin0", "lin1"], "very_sparse": True, "randlora_alpha": 1},
+ ),
+ (
+ "Vanilla MLP 7 RandLora",
+ "MLP",
+ RandLoraConfig,
+ {"target_modules": ["lin0"], "modules_to_save": ["lin1"], "randlora_alpha": 1},
+ ),
+ #######
+ # C3A #
+ #######
+ # note: C3A is not initialized as an identity transform by default, hence set init_weights=True
+ ("Vanilla MLP 1 C3A", "MLP", C3AConfig, {"block_size": 2, "target_modules": "lin0", "init_weights": True}),
+ ("Vanilla MLP 2 C3A", "MLP", C3AConfig, {"block_size": 2, "target_modules": ["lin0"], "init_weights": True}),
+ ("Vanilla MLP 3 C3A", "MLP", C3AConfig, {"block_size": 2, "target_modules": ["lin1"], "init_weights": True}),
+ (
+ "Vanilla MLP 5 C3A",
+ "MLP",
+ C3AConfig,
+ {"block_size": 10, "target_modules": ["lin0"], "modules_to_save": ["lin1"], "init_weights": True},
+ ),
+ (
+ "Vanilla MLP 6 C3A",
+ "MLP",
+ C3AConfig,
+ {"block_size": 10, "target_modules": ["lin0", "lin1"], "modules_to_save": ["lin1"], "init_weights": True},
+ ),
+ (
+ "Vanilla MLP 7 C3A",
+ "MLP",
+ C3AConfig,
+ {
+ "block_size_pattern": {"lin0": 5, "lin1": 10},
+ "target_modules": ["lin0", "lin1"],
+ "modules_to_save": ["lin1"],
+ "init_weights": True,
+ },
+ ),
+ ##########
+ # WaveFT #
+ ##########
+ ("Vanilla MLP 1 WaveFT", "MLP", WaveFTConfig, {"target_modules": "lin0", "n_frequency": 8}),
+ ("Vanilla MLP 2 WaveFT", "MLP", WaveFTConfig, {"target_modules": ["lin0"], "n_frequency": 8}),
+ ("Vanilla MLP 3 WaveFT", "MLP", WaveFTConfig, {"target_modules": ["lin1"], "n_frequency": 8}),
+ ("Vanilla MLP 4 WaveFT", "MLP", WaveFTConfig, {"target_modules": ["lin0", "lin1"], "n_frequency": 8}),
+ (
+ "Vanilla MLP 5 WaveFT",
+ "MLP",
+ WaveFTConfig,
+ {"target_modules": ["lin0"], "modules_to_save": ["lin1"], "n_frequency": 8},
+ ),
+ (
+ "Vanilla MLP 6 WaveFT",
+ "MLP",
+ WaveFTConfig,
+ {
+ "target_modules": ["lin0"],
+ "n_frequency": 8,
+ "scaling": 25.0,
+ "wavelet_family": "db1",
+ },
+ ),
+ ("Vanilla MLP 7 WaveFT", "MLP", WaveFTConfig, {"target_modules": "lin1", "n_frequency": 8, "use_idwt": False}),
+ (
+ "Vanilla MLP 8 WaveFT",
+ "MLP",
+ WaveFTConfig,
+ {"target_modules": "lin0", "n_frequency": 16, "wavelet_family": "sym2"},
+ ),
+ (
+ "Vanilla MLP 9 WaveFT",
+ "MLP",
+ WaveFTConfig,
+ {"target_modules": "lin0", "n_frequency": 16, "wavelet_family": "sym2", "use_idwt": False},
+ ),
+ (
+ "Vanilla MLP 10 WaveFT",
+ "MLP",
+ WaveFTConfig,
+ {"target_modules": "lin0", "n_frequency": 16, "wavelet_family": "db1", "proportional_parameters": True},
+ ),
+ ########
+ # RoAd #
+ ########
+ ("Vanilla MLP 1 RoAd", "MLP", RoadConfig, {"target_modules": "lin0", "group_size": 2}),
+ ("Vanilla MLP 2 RoAd", "MLP", RoadConfig, {"target_modules": ["lin0"], "group_size": 2}),
+ ("Vanilla MLP 3 RoAd", "MLP", RoadConfig, {"target_modules": ["lin1"], "group_size": 2}),
+ ("Vanilla MLP 4 RoAd", "MLP", RoadConfig, {"target_modules": ["lin0", "lin1"], "group_size": 2}),
+ ("Vanilla MLP 5 RoAd", "MLP", RoadConfig, {"target_modules": ["lin0"], "variant": "road_2", "group_size": 2}),
+ ("Vanilla MLP 6 RoAd", "MLP", RoadConfig, {"target_modules": ["lin0"], "variant": "road_4", "group_size": 2}),
+ ##########
+ # WaveFT #
+ ##########
+ ("Vanilla MLP 1 WaveFT", "MLP", WaveFTConfig, {"target_modules": "lin0", "n_frequency": 8}),
+ ("Vanilla MLP 2 WaveFT", "MLP", WaveFTConfig, {"target_modules": ["lin0"], "n_frequency": 8}),
+ ("Vanilla MLP 3 WaveFT", "MLP", WaveFTConfig, {"target_modules": ["lin1"], "n_frequency": 8}),
+ ("Vanilla MLP 4 WaveFT", "MLP", WaveFTConfig, {"target_modules": ["lin0", "lin1"], "n_frequency": 8}),
+ (
+ "Vanilla MLP 5 WaveFT",
+ "MLP",
+ WaveFTConfig,
+ {"target_modules": ["lin0"], "modules_to_save": ["lin1"], "n_frequency": 8},
+ ),
+ (
+ "Vanilla MLP 6 WaveFT",
+ "MLP",
+ WaveFTConfig,
+ {
+ "target_modules": ["lin0"],
+ "n_frequency": 8,
+ "scaling": 25.0,
+ "wavelet_family": "db1",
+ },
+ ),
+ ("Vanilla MLP 7 WaveFT", "MLP", WaveFTConfig, {"target_modules": "lin1", "n_frequency": 8, "use_idwt": False}),
+ (
+ "Vanilla MLP 8 WaveFT",
+ "MLP",
+ WaveFTConfig,
+ {"target_modules": "lin0", "n_frequency": 16, "wavelet_family": "sym2"},
+ ),
+ (
+ "Vanilla MLP 9 WaveFT",
+ "MLP",
+ WaveFTConfig,
+ {"target_modules": "lin0", "n_frequency": 16, "wavelet_family": "sym2", "use_idwt": False},
+ ),
+ (
+ "Vanilla MLP 10 WaveFT",
+ "MLP",
+ WaveFTConfig,
+ {"target_modules": "lin0", "n_frequency": 16, "wavelet_family": "db1", "proportional_parameters": True},
+ ),
+]
+ALL_PEFT_CONFIG_CLASSES = sorted({row[2] for row in TEST_CASES}, key=lambda cls: cls.__name__)
+
+# For this test matrix, each tuple consists of:
+# - test name
+# - tuner method
+# - config_cls
+# - 1st config kwargs
+# - 2nd config kwargs
+# The model used for this test is `MLP`, which uses linear layers `lin0` and `lin1`
+MULTIPLE_ACTIVE_ADAPTERS_TEST_CASES = [
+ (
+ "LoRA Same",
+ "lora",
+ LoraConfig,
+ {"target_modules": ["lin0"], "init_lora_weights": False},
+ {"target_modules": ["lin0"], "init_lora_weights": False},
+ ),
+ (
+ "LoRA Different",
+ "lora",
+ LoraConfig,
+ {"target_modules": ["lin0"], "init_lora_weights": False},
+ {"target_modules": ["lin1"], "init_lora_weights": False},
+ ),
+ (
+ "LoRA + trainable tokens Same",
+ "lora+trainable_tokens",
+ LoraConfig,
+ {"target_modules": ["lin0"], "init_lora_weights": False, "trainable_token_indices": {"emb": [0, 1, 2]}},
+ {"target_modules": ["lin0"], "init_lora_weights": False, "trainable_token_indices": {"emb": [3, 4, 5, 6]}},
+ ),
+ (
+ "LoRA + trainable tokens Different",
+ "lora+trainable_tokens",
+ LoraConfig,
+ {"target_modules": ["lin0"], "init_lora_weights": False, "trainable_token_indices": {"emb": [0, 1, 2]}},
+ {"target_modules": ["lin1"], "init_lora_weights": False, "trainable_token_indices": {"emb": [3, 4, 5, 6]}},
+ ),
+ (
+ "LoRA targeting nn.Parameter Same",
+ "lora",
+ LoraConfig,
+ {"target_parameters": ["lin0.weight"], "init_lora_weights": False},
+ {"target_parameters": ["lin0.weight"], "init_lora_weights": False},
+ ),
+ (
+ "LoRA targeting nn.Parameter Different",
+ "lora",
+ LoraConfig,
+ {"target_parameters": ["lin0.weight"], "init_lora_weights": False},
+ {"target_parameters": ["lin1.weight"], "init_lora_weights": False},
+ ),
+ (
+ "IA3 Same",
+ "ia3",
+ IA3Config,
+ {
+ "target_modules": ["lin0"],
+ "feedforward_modules": ["lin0"],
+ "init_ia3_weights": False,
+ },
+ {
+ "target_modules": ["lin0"],
+ "feedforward_modules": ["lin0"],
+ "init_ia3_weights": False,
+ },
+ ),
+ (
+ "IA3 Different",
+ "ia3",
+ IA3Config,
+ {
+ "target_modules": ["lin0"],
+ "feedforward_modules": ["lin0"],
+ "init_ia3_weights": False,
+ },
+ {
+ "target_modules": ["lin1"],
+ "feedforward_modules": ["lin1"],
+ "init_ia3_weights": False,
+ },
+ ),
+ (
+ "AdaLora Same",
+ "adalora",
+ AdaLoraConfig,
+ {"target_modules": ["lin0"], "init_lora_weights": False, "inference_mode": True, "total_step": 1},
+ {"target_modules": ["lin0"], "init_lora_weights": False, "inference_mode": True, "total_step": 1},
+ ),
+ (
+ "AdaLora Different",
+ "adalora",
+ AdaLoraConfig,
+ {"target_modules": ["lin0"], "init_lora_weights": False, "inference_mode": True, "total_step": 1},
+ {"target_modules": ["lin1"], "init_lora_weights": False, "inference_mode": True, "total_step": 1},
+ ),
+ (
+ "FourierFT Same",
+ "fourierft",
+ FourierFTConfig,
+ {"n_frequency": 10, "target_modules": ["lin0"]},
+ {"n_frequency": 10, "target_modules": ["lin0"]},
+ ),
+ (
+ "FourierFT Different",
+ "fourierft",
+ FourierFTConfig,
+ {"n_frequency": 10, "target_modules": ["lin0"]},
+ {"n_frequency": 10, "target_modules": ["lin1"]},
+ ),
+ (
+ "SHiRA Same",
+ "shira",
+ ShiraConfig,
+ {"r": 1, "target_modules": ["lin0"], "init_weights": False},
+ {"r": 1, "target_modules": ["lin0"], "init_weights": False},
+ ),
+ (
+ "SHiRA Different",
+ "shira",
+ ShiraConfig,
+ {"r": 1, "target_modules": ["lin0"], "init_weights": False},
+ {"r": 1, "target_modules": ["lin1"], "init_weights": False},
+ ),
+ # Note: Currently, we cannot target lin0 and lin1 with different adapters when using VeRA. The reason is that the
+ # first adapter being created will result in a vera_A or vera_B shape that is too small for the next adapter
+ # (remember that VeRA shares these parameters across all layers), which results in an error.
+ (
+ "VeRA Same",
+ "vera",
+ VeraConfig,
+ {"target_modules": ["lin0"], "init_weights": False},
+ {"target_modules": ["lin0"], "init_weights": False},
+ ),
+ # Note: RandLora may present the same problem mentioned above for Vera.
+ (
+ "RandLora Same",
+ "randlora",
+ RandLoraConfig,
+ {"target_modules": ["lin0"], "init_weights": False},
+ {"target_modules": ["lin0"], "init_weights": False},
+ ),
+ (
+ "HRA Same",
+ "hra",
+ HRAConfig,
+ {"target_modules": ["lin0"], "init_weights": False},
+ {"target_modules": ["lin0"], "init_weights": False},
+ ),
+ (
+ "HRA Different",
+ "hra",
+ HRAConfig,
+ {"target_modules": ["lin0"], "init_weights": False},
+ {"target_modules": ["lin1"], "init_weights": False},
+ ),
+ (
+ "Bone Same",
+ "bone",
+ BoneConfig,
+ {"target_modules": ["lin0"], "init_weights": False, "r": 2},
+ {"target_modules": ["lin0"], "init_weights": False, "r": 2},
+ ),
+ (
+ "Bone Different",
+ "bone",
+ BoneConfig,
+ {"target_modules": ["lin0"], "init_weights": False, "r": 2},
+ {"target_modules": ["lin1"], "init_weights": False, "r": 2},
+ ),
+ (
+ "MiSS Same",
+ "miss",
+ MissConfig,
+ {"target_modules": ["lin0"], "init_weights": False, "r": 2},
+ {"target_modules": ["lin0"], "init_weights": False, "r": 2},
+ ),
+ (
+ "MiSS Different",
+ "miss",
+ MissConfig,
+ {"target_modules": ["lin0"], "init_weights": False, "r": 2},
+ {"target_modules": ["lin1"], "init_weights": False, "r": 2},
+ ),
+ # Not testing "mini" initialization targeting the same layer, because The matrix is initialized to all zeros in MiSS-mini mode.
+ (
+ "VBLoRA Same",
+ "vblora",
+ VBLoRAConfig,
+ {"target_modules": ["lin0"], "vector_length": 2, "init_vector_bank_bound": 0.1},
+ {"target_modules": ["lin0"], "vector_length": 2, "init_vector_bank_bound": 0.1},
+ ),
+ (
+ "VBLoRA Different",
+ "vblora",
+ VBLoRAConfig,
+ {"target_modules": ["lin0"], "vector_length": 2, "init_vector_bank_bound": 0.1},
+ {"target_modules": ["lin1"], "vector_length": 2, "init_vector_bank_bound": 0.1},
+ ),
+ (
+ "BOFT Same",
+ "boft",
+ BOFTConfig,
+ {"target_modules": ["lin0"], "init_weights": False, "boft_block_size": 2},
+ {"target_modules": ["lin0"], "init_weights": False, "boft_block_size": 2},
+ ),
+ (
+ "BOFT Different",
+ "boft",
+ BOFTConfig,
+ {"target_modules": ["lin0"], "init_weights": False, "boft_block_size": 2},
+ {"target_modules": ["lin1"], "init_weights": False, "boft_block_size": 2},
+ ),
+ (
+ "WaveFT Same",
+ "waveft",
+ WaveFTConfig,
+ {"target_modules": ["lin0"], "init_weights": False, "n_frequency": 8},
+ {"target_modules": ["lin0"], "init_weights": False, "n_frequency": 8},
+ ),
+ (
+ "WaveFT Different",
+ "waveft",
+ WaveFTConfig,
+ {"target_modules": ["lin0"], "init_weights": False, "n_frequency": 8},
+ {"target_modules": ["lin1"], "init_weights": False, "n_frequency": 8},
+ ),
+ (
+ "RoAd Same",
+ "road",
+ RoadConfig,
+ {"target_modules": ["lin0"], "init_weights": False, "group_size": 2},
+ {"target_modules": ["lin0"], "init_weights": False, "group_size": 2},
+ ),
+ (
+ "RoAd Different",
+ "road",
+ RoadConfig,
+ {"target_modules": ["lin0"], "init_weights": False, "group_size": 2},
+ {"target_modules": ["lin1"], "init_weights": False, "group_size": 2},
+ ),
+ (
+ "RoAd 2 Different",
+ "road",
+ RoadConfig,
+ {"target_modules": ["lin0"], "init_weights": False, "variant": "road_1", "group_size": 2},
+ {"target_modules": ["lin1"], "init_weights": False, "variant": "road_2", "group_size": 2},
+ ),
+ (
+ "RoAd 4 Different",
+ "road",
+ RoadConfig,
+ {"target_modules": ["lin0"], "init_weights": False, "variant": "road_1", "group_size": 2},
+ {"target_modules": ["lin1"], "init_weights": False, "variant": "road_4", "group_size": 2},
+ ),
+ (
+ "WaveFT Same",
+ "waveft",
+ WaveFTConfig,
+ {"target_modules": ["lin0"], "init_weights": False, "n_frequency": 8},
+ {"target_modules": ["lin0"], "init_weights": False, "n_frequency": 8},
+ ),
+ (
+ "WaveFT Different",
+ "waveft",
+ WaveFTConfig,
+ {"target_modules": ["lin0"], "init_weights": False, "n_frequency": 8},
+ {"target_modules": ["lin1"], "init_weights": False, "n_frequency": 8},
+ ),
+]
+
+PREFIXES = {
+ IA3Config: "ia3_",
+ LoraConfig: "lora_",
+ LoHaConfig: "hada_",
+ LoKrConfig: "lokr_",
+ OFTConfig: "oft_",
+ BOFTConfig: "boft_",
+ LNTuningConfig: "ln_tuning_",
+ VeraConfig: "vera_lambda_",
+ RandLoraConfig: "randlora_",
+ FourierFTConfig: "fourierft_",
+ C3AConfig: "c3a_",
+ HRAConfig: "hra_",
+ ShiraConfig: "shira_",
+ VBLoRAConfig: "vblora_",
+ BoneConfig: "bone_",
+ RoadConfig: "road_",
+ MissConfig: "miss_",
+ TrainableTokensConfig: "trainable_tokens_",
+ WaveFTConfig: "waveft_",
+}
+
+
+def _skip_tests_with_multiple_adapters_with_target_parameters(config_cls, config_kwargs):
+ if (config_cls == LoraConfig) and config_kwargs.get("target_parameters"):
+ pytest.skip("LoRA with multiple adapters with target_parameters is not supported")
+
+
+class MLP(nn.Module):
+ def __init__(self, bias=True):
+ super().__init__()
+ self.lin0 = nn.Linear(10, 20, bias=bias)
+ self.relu = nn.ReLU()
+ self.drop = nn.Dropout(0.5)
+ self.lin1 = nn.Linear(20, 2, bias=bias)
+ self.sm = nn.LogSoftmax(dim=-1)
+ self.dtype = torch.float
+
+ def forward(self, X):
+ X = X.to(self.dtype)
+ X = self.lin0(X)
+ X = self.relu(X)
+ X = self.drop(X)
+ X = self.lin1(X)
+ X = self.sm(X)
+ return X
+
+
+class MLPWithGRU(nn.Module):
+ def __init__(self, bias=True):
+ super().__init__()
+ self.lin0 = nn.Linear(10, 20, bias=bias)
+ self.relu = nn.ReLU()
+ self.drop = nn.Dropout(0.5)
+ self.gru = nn.GRU(input_size=20, hidden_size=20, num_layers=1, batch_first=True, bias=bias)
+ self.fc = nn.Linear(20, 2, bias=bias)
+ self.sm = nn.LogSoftmax(dim=-1)
+ self.dtype = torch.float
+
+ def forward(self, X):
+ X = X.to(self.dtype)
+ X = self.lin0(X)
+ X = self.relu(X)
+ X = self.drop(X)
+ X = X.unsqueeze(1)
+ X, _ = self.gru(X)
+ X = X.squeeze(1)
+ X = self.fc(X)
+ X = self.sm(X)
+ return X
+
+
+class MLP_LayerNorm(nn.Module):
+ def __init__(self, bias=True):
+ super().__init__()
+ self.layernorm0 = nn.LayerNorm(10, 10)
+ self.lin0 = nn.Linear(10, 20, bias=bias)
+ self.relu = nn.ReLU()
+ self.drop = nn.Dropout(0.5)
+ self.layernorm1 = nn.LayerNorm(20, 20)
+ self.lin1 = nn.Linear(20, 2, bias=bias)
+ self.sm = nn.LogSoftmax(dim=-1)
+ self.dtype = torch.float
+
+ def forward(self, X):
+ X = X.to(self.dtype)
+ X = self.layernorm0(X)
+ X = self.lin0(X)
+ X = self.relu(X)
+ X = self.drop(X)
+ X = self.layernorm1(X)
+ X = self.lin1(X)
+ X = self.sm(X)
+ return X
+
+
+class MLP2(nn.Module):
+ def __init__(self, bias=True):
+ super().__init__()
+ self.lin0 = nn.Linear(10, 32, bias=bias)
+ self.relu = nn.ReLU()
+ self.drop = nn.Dropout(0.5)
+ self.lin1 = nn.Linear(32, 2, bias=bias)
+ self.sm = nn.LogSoftmax(dim=-1)
+ self.dtype = torch.float
+
+ def forward(self, X):
+ X = X.to(self.dtype)
+ X = self.lin0(X)
+ X = self.relu(X)
+ X = self.drop(X)
+ X = self.lin1(X)
+ X = self.sm(X)
+ return X
+
+
+class Block(nn.Module):
+ def __init__(self, bias=True, size=10):
+ super().__init__()
+ self.lin0 = nn.Linear(size, size, bias=bias)
+ self.relu = nn.ReLU()
+ self.drop = nn.Dropout(0.5)
+ self.lin1 = nn.Linear(size, size, bias=bias)
+
+ def forward(self, X):
+ X = X.float()
+ X = self.lin0(X)
+ X = self.relu(X)
+ X = self.drop(X)
+ X = self.lin1(X)
+ return X
+
+
+class DeepMLP(nn.Module):
+ def __init__(self, bias=True, num_hidden_layers=12, size=10):
+ super().__init__()
+ self.layers = nn.ModuleList([Block(bias=bias, size=size) for _ in range(num_hidden_layers)])
+ self.out = nn.Linear(10, 2, bias=bias)
+ self.sm = nn.LogSoftmax(dim=-1)
+
+ def forward(self, X):
+ X = X.float(X)
+ for layer in self.layers:
+ X = layer(X)
+ X = self.out(X)
+ X = self.sm(X)
+ return X
+
+
+class ModelEmbConv1D(nn.Module):
+ def __init__(self, emb_size=100):
+ super().__init__()
+ self.emb = nn.Embedding(emb_size, 5)
+ self.conv1d = Conv1D(1, 5)
+ self.relu = nn.ReLU()
+ self.flat = nn.Flatten()
+ self.lin0 = nn.Linear(10, 2)
+ self.sm = nn.LogSoftmax(dim=-1)
+
+ def forward(self, X):
+ X = self.emb(X)
+ X = self.conv1d(X)
+ X = self.relu(X)
+ X = self.flat(X)
+ X = self.lin0(X)
+ X = self.sm(X)
+ return X
+
+
+class ModelEmbWithEmbeddingUtils(nn.Module):
+ # Adds `get_input_embeddings` and `get_output_embeddings` methods to mimic 🤗 transformers models
+ def __init__(self):
+ super().__init__()
+ self.embed_tokens = nn.Embedding(100, 5)
+ self.conv1d = Conv1D(1, 5)
+ self.relu = nn.ReLU()
+ self.flat = nn.Flatten()
+ self.lin0 = nn.Linear(10, 2)
+ self.sm = nn.LogSoftmax(dim=-1)
+
+ def forward(self, X):
+ X = self.embed_tokens(X)
+ X = self.conv1d(X)
+ X = self.relu(X)
+ X = self.flat(X)
+ X = self.lin0(X)
+ X = self.sm(X)
+ return X
+
+ def get_input_embeddings(self):
+ return self.embed_tokens
+
+ def get_output_embeddings(self):
+ return None
+
+
+class ModelConv1D(nn.Module):
+ def __init__(self):
+ super().__init__()
+ self.conv1d = nn.Conv1d(1, 1, 2)
+ self.relu = nn.ReLU()
+ self.flat = nn.Flatten()
+ self.lin0 = nn.Linear(9, 2)
+ self.sm = nn.LogSoftmax(dim=-1)
+ self.dtype = torch.float
+
+ def forward(self, X):
+ X = X.to(self.dtype)
+ X = X.reshape(-1, 1, 10)
+ X = self.conv1d(X)
+ X = self.relu(X)
+ X = self.flat(X)
+ X = self.lin0(X)
+ X = self.sm(X)
+ return X
+
+
+class ModelConv1DBigger(nn.Module):
+ def __init__(self):
+ super().__init__()
+ self.conv1d = nn.Conv1d(64, 16, 2)
+ self.relu = nn.ReLU()
+ self.flat = nn.Flatten()
+ self.lin0 = nn.Linear(144, 2)
+ self.sm = nn.LogSoftmax(dim=-1)
+ self.dtype = torch.float
+
+ def forward(self, X):
+ X = X.to(self.dtype)
+ X = X.reshape(-1, 1, 10)
+ X = torch.concat([X] * 64, dim=1)
+ X = self.conv1d(X)
+ X = self.relu(X)
+ X = self.flat(X)
+ X = self.lin0(X)
+ X = self.sm(X)
+ return X
+
+
+class ModelConv2D(nn.Module):
+ def __init__(self, bias=True):
+ super().__init__()
+ self.conv2d = nn.Conv2d(5, 10, 3, bias=bias)
+ self.relu = nn.ReLU()
+ self.flat = nn.Flatten()
+ self.lin0 = nn.Linear(10, 2)
+ self.sm = nn.LogSoftmax(dim=-1)
+ self.dtype = torch.float
+
+ def forward(self, X):
+ X = X.to(self.dtype)
+ X = X.reshape(-1, 5, 3, 3)
+ X = self.conv2d(X)
+ X = self.relu(X)
+ X = self.flat(X)
+ X = self.lin0(X)
+ X = self.sm(X)
+ return X
+
+
+class ModelConv2D2(nn.Module):
+ def __init__(self):
+ super().__init__()
+ self.lin0 = nn.Linear(10, 40)
+ self.conv2d = nn.Conv2d(8, 32, 3)
+ self.relu = nn.ReLU()
+ self.flat = nn.Flatten()
+ self.lin1 = nn.Linear(32, 2)
+ self.sm = nn.LogSoftmax(dim=-1)
+ self.dtype = torch.float
+
+ def forward(self, X):
+ X = X.to(self.dtype)
+ X = self.lin0(X)
+ X = self.relu(X)
+ X = X.reshape(-1, 8, 3, 3)
+ X = self.conv2d(X)
+ X = self.relu(X)
+ X = self.flat(X)
+ X = self.lin1(X)
+ X = self.sm(X)
+ return X
+
+
+class ModelConv2D1x1(nn.Module):
+ def __init__(self):
+ super().__init__()
+ self.conv2d = nn.Conv2d(1, 10, kernel_size=(1, 1), padding=0)
+ self.relu = nn.ReLU()
+ self.flat = nn.Flatten()
+ self.lin0 = nn.Linear(10 * 3 * 3, 2)
+ self.sm = nn.LogSoftmax(dim=-1)
+ self.dtype = torch.float
+
+ def forward(self, X):
+ X = X.to(self.dtype)
+ X = X.reshape(-1, 1, 3, 3)
+ X = self.conv2d(X)
+ X = self.relu(X)
+ X = self.flat(X)
+ X = self.lin0(X)
+ X = self.sm(X)
+ return X
+
+
+class ModelConv2DGroups(nn.Module):
+ def __init__(self):
+ super().__init__()
+ self.lin0 = nn.Linear(90, 288)
+ # groups is set as 8 since default r=8
+ # hence to make r divisible by groups
+ self.conv2d = nn.Conv2d(16, 16, 3, groups=8)
+ self.relu = nn.ReLU()
+ self.flat = nn.Flatten()
+ self.lin1 = nn.Linear(16, 2)
+ self.sm = nn.LogSoftmax(dim=-1)
+ self.dtype = torch.float
+
+ def forward(self, X):
+ X = X.to(self.dtype)
+ X = X.flatten()
+ X = self.lin0(X)
+ X = X.reshape(2, 16, 3, 3)
+ X = self.conv2d(X)
+ X = self.relu(X)
+ X = self.flat(X)
+ X = self.lin1(X)
+ X = self.sm(X)
+ return X
+
+
+class ModelConv2DGroups2(nn.Module):
+ def __init__(self):
+ super().__init__()
+ self.conv2d = nn.Conv2d(16, 32, 3, padding=1, groups=2)
+ self.relu = nn.ReLU()
+ self.flat = nn.Flatten()
+ self.lin0 = nn.Linear(12800, 2)
+ self.sm = nn.LogSoftmax(dim=-1)
+ self.dtype = torch.float
+
+ def forward(self, X):
+ # Note: needs a different input shape, thus ignore original input
+ X = torch.arange(9 * 16 * 20 * 20).view([9, 16, 20, 20]).to(self.conv2d.weight.device)
+ X = X.to(self.dtype)
+ X = self.conv2d(X)
+ X = self.relu(X)
+ X = self.flat(X)
+ X = self.lin0(X)
+ X = self.sm(X)
+ return X
+
+
+class ModelConv1DKernel1(nn.Module):
+ def __init__(self):
+ super().__init__()
+ self.conv1d = nn.Conv1d(in_channels=3, out_channels=10, kernel_size=1)
+ self.relu = nn.ReLU()
+ self.flat = nn.Flatten()
+ self.lin0 = nn.Linear(10 * 10, 2)
+ self.dtype = torch.float
+
+ def forward(self, x):
+ x = x.to(self.dtype)
+ x = x.reshape(-1, 3, 10) # batch, channels, seq_len
+ x = self.conv1d(x)
+ x = self.relu(x)
+ x = self.flat(x)
+ x = self.lin0(x)
+ return x
+
+
+class ModelConv3D(nn.Module):
+ def __init__(self):
+ super().__init__()
+ self.conv3d = nn.Conv3d(5, 10, 3)
+ self.relu = nn.ReLU()
+ self.flat = nn.Flatten()
+ self.lin0 = nn.Linear(10, 2)
+ self.sm = nn.LogSoftmax(dim=-1)
+ self.dtype = torch.float
+
+ def forward(self, X):
+ X = X.to(self.dtype)
+ # If necessary, convert from 2D image to 3D volume
+ if X.dim() == 2:
+ X = torch.stack([X] * 3, dim=-1)
+ X = X.reshape(-1, 5, 3, 3, 3)
+ X = self.conv3d(X)
+ X = self.relu(X)
+ X = self.flat(X)
+ X = self.lin0(X)
+ X = self.sm(X)
+ return X
+
+
+class ModelMha(nn.Module):
+ def __init__(self):
+ super().__init__()
+ self.mha = nn.MultiheadAttention(10, 2)
+ self.lin0 = nn.Linear(10, 2)
+ self.sm = nn.LogSoftmax(dim=-1)
+ self.dtype = torch.float
+
+ def forward(self, X):
+ X = X.to(self.dtype)
+ X, _ = self.mha(X, X, X)
+ X = self.lin0(X)
+ X = self.sm(X)
+ return X
+
+
+class _LinearUsingParameter(nn.Module):
+ # Linear layer equivalent
+ def __init__(self, in_features, out_features, bias=None):
+ super().__init__()
+ self.in_features = in_features
+ self.out_features = out_features
+ self.weight = nn.Parameter(torch.randn(in_features, out_features))
+ if bias:
+ self.bias = nn.Parameter(torch.ones(out_features))
+
+ def forward(self, x):
+ return x @ self.weight + self.bias
+
+
+class MlpUsingParameters(nn.Module):
+ # MLP that uses layers whose parameters need to be targeted with target_parameters
+ def __init__(self, bias=True):
+ super().__init__()
+
+ self.lin0 = _LinearUsingParameter(10, 20, bias=bias)
+ self.relu = nn.ReLU()
+ self.drop = nn.Dropout(0.5)
+ self.lin1 = _LinearUsingParameter(20, 2, bias=bias)
+ self.sm = nn.LogSoftmax(dim=-1)
+ self.dtype = torch.float
+
+ def forward(self, X):
+ X = X.to(self.dtype)
+ X = self.lin0(X)
+ X = self.relu(X)
+ X = self.drop(X)
+ X = self.lin1(X)
+ X = self.sm(X)
+ return X
+
+
+class MockTransformerWrapper:
+ """Mock class to behave like a transformers model.
+
+ This is needed because the tests initialize the model by calling transformers_class.from_pretrained.
+
+ """
+
+ @classmethod
+ def from_pretrained(cls, model_id, torch_dtype=None):
+ # set the seed so that from_pretrained always returns the same model
+ torch.manual_seed(0)
+
+ if torch_dtype is None:
+ torch_dtype = torch.float32
+
+ if model_id == "MLP":
+ return MLP().to(torch_dtype)
+
+ if model_id == "EmbConv1D":
+ return ModelEmbConv1D().to(torch_dtype)
+
+ if model_id == "Conv1d":
+ return ModelConv1D().to(torch_dtype)
+
+ if model_id == "Conv1dBigger":
+ return ModelConv1DBigger().to(torch_dtype)
+
+ if model_id == "Conv2d":
+ return ModelConv2D().to(torch_dtype)
+
+ if model_id == "Conv2d1x1":
+ return ModelConv2D1x1().to(torch_dtype)
+
+ if model_id == "Conv1dKernel1":
+ return ModelConv1DKernel1().to(torch_dtype)
+
+ if model_id == "Conv2dGroups":
+ return ModelConv2DGroups().to(torch_dtype)
+
+ if model_id == "Conv2dGroups2":
+ return ModelConv2DGroups2().to(torch_dtype)
+
+ if model_id == "Conv3d":
+ return ModelConv3D().to(torch_dtype)
+
+ if model_id == "MLP_LayerNorm":
+ return MLP_LayerNorm().to(torch_dtype)
+
+ if model_id == "MLP2":
+ return MLP2().to(torch_dtype)
+
+ if model_id == "Conv2d2":
+ return ModelConv2D2().to(torch_dtype)
+
+ if model_id == "MHA":
+ return ModelMha().to(torch_dtype)
+
+ if model_id == "MlpUsingParameters":
+ return MlpUsingParameters().to(torch_dtype)
+
+ raise ValueError(f"model_id {model_id} not implemented")
+
+
+class TestPeftCustomModel(PeftCommonTester):
+ """
+ Implements the tests for custom models.
+
+ Most tests should just call the parent class, e.g. test_save_pretrained calls self._test_save_pretrained. Override
+ this if custom models don't work with the parent test method.
+
+ """
+
+ transformers_class = MockTransformerWrapper
+
+ def prepare_inputs_for_testing(self):
+ X = torch.arange(90).view(9, 10).to(self.torch_device)
+ return {"X": X}
+
+ @pytest.mark.parametrize("test_name, model_id, config_cls, config_kwargs", TEST_CASES)
+ def test_attributes_parametrized(self, test_name, model_id, config_cls, config_kwargs):
+ self._test_model_attr(model_id, config_cls, config_kwargs)
+
+ @pytest.mark.parametrize("test_name, model_id, config_cls, config_kwargs", TEST_CASES)
+ def test_adapter_name(self, test_name, model_id, config_cls, config_kwargs):
+ self._test_adapter_name(model_id, config_cls, config_kwargs)
+
+ @pytest.mark.parametrize("test_name, model_id, config_cls, config_kwargs", TEST_CASES)
+ def test_prepare_for_training_parametrized(self, test_name, model_id, config_cls, config_kwargs):
+ # This test does not work with custom models because it assumes that
+ # there is always a method get_input_embeddings that returns a layer
+ # which does not need updates. Instead, a new test is added below that
+ # checks that LoRA works as expected.
+ pass
+
+ @pytest.mark.parametrize("test_name, model_id, config_cls, config_kwargs", TEST_CASES)
+ def test_save_pretrained(self, test_name, model_id, config_cls, config_kwargs):
+ self._test_save_pretrained(model_id, config_cls, config_kwargs)
+
+ @pytest.mark.parametrize("test_name, model_id, config_cls, config_kwargs", TEST_CASES)
+ def test_save_pretrained_pickle(self, test_name, model_id, config_cls, config_kwargs):
+ self._test_save_pretrained(model_id, config_cls, config_kwargs, safe_serialization=False)
+
+ @pytest.mark.parametrize("test_name, model_id, config_cls, config_kwargs", TEST_CASES)
+ def test_load_model_low_cpu_mem_usage(self, test_name, model_id, config_cls, config_kwargs):
+ _skip_tests_with_multiple_adapters_with_target_parameters(config_cls, config_kwargs)
+ self._test_load_model_low_cpu_mem_usage(model_id, config_cls, config_kwargs)
+
+ @pytest.mark.parametrize("test_name, model_id, config_cls, config_kwargs", TEST_CASES)
+ def test_from_pretrained_config_construction(self, test_name, model_id, config_cls, config_kwargs):
+ self._test_from_pretrained_config_construction(model_id, config_cls, config_kwargs)
+
+ @pytest.mark.parametrize("test_name, model_id, config_cls, config_kwargs", TEST_CASES)
+ def test_load_multiple_adapters(self, test_name, model_id, config_cls, config_kwargs):
+ _skip_tests_with_multiple_adapters_with_target_parameters(config_cls, config_kwargs)
+ self._test_load_multiple_adapters(model_id, config_cls, config_kwargs)
+
+ @pytest.mark.parametrize("test_name, model_id, config_cls, config_kwargs", TEST_CASES)
+ def test_merge_layers(self, test_name, model_id, config_cls, config_kwargs):
+ # https://github.com/huggingface/peft/pull/2403
+ if model_id in ["Conv2dGroups", "Conv2dGroups2"]:
+ pytest.skip(
+ f"Skipping test for {model_id} as merging is not supported. (See https://github.com/huggingface/peft/pull/2403 for details)"
+ )
+
+ config_kwargs = set_init_weights_false(config_cls, config_kwargs)
+ self._test_merge_layers(model_id, config_cls, config_kwargs)
+
+ @pytest.mark.parametrize("test_name, model_id, config_cls, config_kwargs", TEST_CASES)
+ def test_merge_layers_fp16(self, test_name, model_id, config_cls, config_kwargs):
+ # https://github.com/huggingface/peft/pull/2403
+ if model_id in ["Conv2dGroups", "Conv2dGroups2"]:
+ pytest.skip(
+ f"Skipping test for {model_id} as merging is not supported. (See https://github.com/huggingface/peft/pull/2403 for details)"
+ )
+
+ config_kwargs = set_init_weights_false(config_cls, config_kwargs)
+ self._test_merge_layers_fp16(model_id, config_cls, config_kwargs)
+
+ @pytest.mark.parametrize("test_name, model_id, config_cls, config_kwargs", TEST_CASES)
+ def test_merge_layers_is_idempotent(self, test_name, model_id, config_cls, config_kwargs):
+ # calling merge twice with the same arguments should not change the output
+
+ # https://github.com/huggingface/peft/pull/2403
+ if model_id in ["Conv2dGroups", "Conv2dGroups2"]:
+ pytest.skip(
+ f"Skipping test for {model_id} as merging is not supported. (See https://github.com/huggingface/peft/pull/2403 for details)"
+ )
+
+ config_kwargs = set_init_weights_false(config_cls, config_kwargs)
+ self._test_merge_layers_is_idempotent(model_id, config_cls, config_kwargs)
+
+ @pytest.mark.parametrize("test_name, model_id, config_cls, config_kwargs", TEST_CASES)
+ def test_safe_merge(self, test_name, model_id, config_cls, config_kwargs):
+ # https://github.com/huggingface/peft/pull/2403
+ if model_id in ["Conv2dGroups", "Conv2dGroups2"]:
+ pytest.skip(
+ f"Skipping test for {model_id} as merging is not supported. (See https://github.com/huggingface/peft/pull/2403 for details)"
+ )
+
+ config_kwargs = set_init_weights_false(config_cls, config_kwargs)
+ self._test_safe_merge(model_id, config_cls, config_kwargs)
+
+ @pytest.mark.parametrize("safe_merge", [False, True])
+ @pytest.mark.parametrize("module_type", ["linear", "conv2d"])
+ def test_merge_with_lora_bias_when_base_layer_has_no_bias_warns_and_raises(self, safe_merge, module_type):
+ # It is not possible to merge the lora_B bias if the base layer doesn't have a bias itself.
+ if module_type == "linear":
+ model = MLP(bias=False)
+ config = LoraConfig(target_modules=["lin0", "lin1"], lora_bias=True)
+ warn_msg = re.escape("`lora_bias=True` was passed but the targeted layer of type Linear has no bias")
+ elif module_type == "conv2d":
+ model = ModelConv2D(bias=False)
+ config = LoraConfig(target_modules=["conv2d"], lora_bias=True)
+ warn_msg = re.escape("`lora_bias=True` was passed but the targeted layer of type Conv2d has no bias")
+ else:
+ raise ValueError(f"Wrong module_type passed, expected 'linear' or 'conv2d', got {module_type}")
+
+ with pytest.warns(PeftWarning, match=warn_msg):
+ model = get_peft_model(model, config)
+
+ err_msg = "Impossible to merge LoRA with `lora_bias=True` because the base layer has no bias"
+ with pytest.raises(RuntimeError, match=err_msg):
+ model.merge_adapter(safe_merge=safe_merge)
+
+ @pytest.mark.parametrize("test_name, model_id, config_cls, config_kwargs", TEST_CASES)
+ def test_generate(self, test_name, model_id, config_cls, config_kwargs):
+ # Custom models do not (necessarily) have a generate method, so this test is not performed
+ pass
+
+ @pytest.mark.parametrize("test_name, model_id, config_cls, config_kwargs", TEST_CASES)
+ def test_generate_half_prec(self, test_name, model_id, config_cls, config_kwargs):
+ # Custom models do not (necessarily) have a generate method, so this test is not performed
+ pass
+
+ @pytest.mark.parametrize("test_name, model_id, config_cls, config_kwargs", TEST_CASES)
+ def test_training_custom_models(self, test_name, model_id, config_cls, config_kwargs):
+ self._test_training(model_id, config_cls, config_kwargs)
+
+ @pytest.mark.parametrize("test_name, model_id, config_cls, config_kwargs", TEST_CASES)
+ def test_training_custom_models_layer_indexing(self, test_name, model_id, config_cls, config_kwargs):
+ # At the moment, layer indexing only works when layer names conform to a specific pattern, which is not
+ # guaranteed here. Therefore, this test is not performed.
+ pass
+
+ @pytest.mark.parametrize("test_name, model_id, config_cls, config_kwargs", TEST_CASES)
+ def test_training_custom_models_gradient_checkpointing(self, test_name, model_id, config_cls, config_kwargs):
+ self._test_training_gradient_checkpointing(model_id, config_cls, config_kwargs)
+
+ @pytest.mark.parametrize("test_name, model_id, config_cls, config_kwargs", TEST_CASES)
+ def test_inference_safetensors(self, test_name, model_id, config_cls, config_kwargs):
+ self._test_inference_safetensors(model_id, config_cls, config_kwargs)
+
+ @pytest.mark.parametrize("test_name, model_id, config_cls, config_kwargs", TEST_CASES)
+ def test_peft_model_device_map(self, test_name, model_id, config_cls, config_kwargs):
+ self._test_peft_model_device_map(model_id, config_cls, config_kwargs)
+
+ @pytest.mark.parametrize("test_name, model_id, config_cls, config_kwargs", TEST_CASES)
+ def test_in_features_out_features_exposed(self, test_name, model_id, config_cls, config_kwargs):
+ # the PEFT layer should expose the .in_features and .out_features attributes
+ model = self.transformers_class.from_pretrained(model_id).to(self.torch_device)
+ config = config_cls(
+ base_model_name_or_path=model_id,
+ **config_kwargs,
+ )
+ model = get_peft_model(model, config)
+ for module in model.modules():
+ if isinstance(module, BaseTunerLayer):
+ assert hasattr(module, "in_features")
+ assert hasattr(module, "out_features")
+
+ @pytest.mark.parametrize("test_name, model_id, config_cls, config_kwargs", TEST_CASES)
+ def test_forward_output_finite(self, test_name, model_id, config_cls, config_kwargs):
+ X = self.prepare_inputs_for_testing()
+ model = self.transformers_class.from_pretrained(model_id).to(self.torch_device)
+ config = config_cls(
+ base_model_name_or_path=model_id,
+ **config_kwargs,
+ )
+ model = get_peft_model(model, config)
+ model.eval()
+ with torch.no_grad():
+ output = model(**X)
+ assert torch.isfinite(output).all()
+
+ @pytest.mark.parametrize("test_name, model_id, config_cls, config_kwargs", TEST_CASES)
+ def test_forward_float16(self, test_name, model_id, config_cls, config_kwargs):
+ # The user manually sets the dtype of the base model to fp16 precision. This should not cause an error for the
+ # different PEFT methods.
+ try:
+ torch.zeros(1, dtype=torch.float16)
+ except Exception:
+ # skip this test if float16 is not supported on this machine
+ pytest.skip(reason="Test requires float16 support")
+
+ # skip on MacOS
+ if platform.system() == "Darwin":
+ pytest.skip(reason="MacOS does not support multiple ops in float16")
+
+ X = self.prepare_inputs_for_testing()
+ model = self.transformers_class.from_pretrained(model_id, torch_dtype=torch.float16).to(self.torch_device)
+ model.dtype = torch.float16
+ config = config_cls(
+ base_model_name_or_path=model_id,
+ **config_kwargs,
+ )
+ model = get_peft_model(model, config)
+ model.eval()
+
+ # check that none of this raises an error
+ model(**X)
+
+ if model_id in ["Conv2dGroups", "Conv2dGroups2"]:
+ # this model does not support merging
+ return
+
+ model.merge_adapter(safe_merge=False)
+ model(**X)
+ model.unmerge_adapter()
+ model(**X)
+ model.merge_adapter(safe_merge=True)
+ model(**X)
+ model.unmerge_adapter()
+ model(**X)
+ model = model.merge_and_unload()
+ model(**X)
+
+ @pytest.mark.parametrize("test_name, model_id, config_cls, config_kwargs", TEST_CASES)
+ def test_forward_bfloat16(self, test_name, model_id, config_cls, config_kwargs):
+ # The user manually sets the dtype of the base model to bf16 precision. This should not cause an error for the
+ # different PEFT methods.
+ try:
+ torch.zeros(1, dtype=torch.bfloat16)
+ except Exception:
+ # skip this test if float16 is not supported on this machine
+ pytest.skip(reason="Test requires bfloat16 support")
+
+ # skip on MacOS
+ if platform.system() == "Darwin":
+ pytest.skip(reason="MacOS does not support multiple ops in bfloat16")
+
+ X = self.prepare_inputs_for_testing()
+ model = self.transformers_class.from_pretrained(model_id, torch_dtype=torch.bfloat16).to(self.torch_device)
+ model.dtype = torch.bfloat16
+ config = config_cls(
+ base_model_name_or_path=model_id,
+ **config_kwargs,
+ )
+ model = get_peft_model(model, config)
+ model.eval()
+
+ # check that none of this raises an error
+ model(**X)
+
+ if model_id in ["Conv2dGroups", "Conv2dGroups2"]:
+ # this model does not support merging
+ return
+
+ model.merge_adapter(safe_merge=False)
+ model(**X)
+ model.unmerge_adapter()
+ model(**X)
+ model.merge_adapter(safe_merge=True)
+ model(**X)
+ model.unmerge_adapter()
+ model(**X)
+ model = model.merge_and_unload()
+ model(**X)
+
+ @pytest.mark.parametrize("test_name, model_id, config_cls, config_kwargs", TEST_CASES)
+ def test_forward_float16_no_autocast(self, test_name, model_id, config_cls, config_kwargs):
+ # Same as above but don't autocast adapter weights to float32 automatically
+ try:
+ torch.zeros(1, dtype=torch.float16)
+ except Exception:
+ # skip this test if float16 is not supported on this machine
+ pytest.skip(reason="Test requires float16 support")
+
+ # skip on MacOS
+ if platform.system() == "Darwin":
+ pytest.skip(reason="MacOS does not support multiple ops in float16")
+
+ X = self.prepare_inputs_for_testing()
+ model = self.transformers_class.from_pretrained(model_id, torch_dtype=torch.float16).to(self.torch_device)
+ model.dtype = torch.float16
+ config = config_cls(
+ base_model_name_or_path=model_id,
+ **config_kwargs,
+ )
+ model = get_peft_model(model, config, autocast_adapter_dtype=False)
+ model.eval()
+
+ # check that none of this raises an error
+ model(**X)
+
+ if model_id in ["Conv2dGroups", "Conv2dGroups2"]:
+ # this model does not support merging
+ return
+
+ model.merge_adapter(safe_merge=False)
+ model(**X)
+ model.unmerge_adapter()
+ model(**X)
+ model.merge_adapter(safe_merge=True)
+ model(**X)
+ model.unmerge_adapter()
+ model(**X)
+ model = model.merge_and_unload()
+ model(**X)
+
+ @pytest.mark.parametrize("test_name, model_id, config_cls, config_kwargs", TEST_CASES)
+ def test_forward_bfloat16_no_autocast(self, test_name, model_id, config_cls, config_kwargs):
+ # Same as above but don't autocast adapter weights to float32 automatically
+ try:
+ torch.zeros(1, dtype=torch.bfloat16)
+ except Exception:
+ # skip this test if float16 is not supported on this machine
+ pytest.skip(reason="Test requires bfloat16 support")
+
+ # skip on MacOS
+ if platform.system() == "Darwin":
+ pytest.skip(reason="MacOS does not support multiple ops in bfloat16")
+
+ X = self.prepare_inputs_for_testing()
+ model = self.transformers_class.from_pretrained(model_id, torch_dtype=torch.bfloat16).to(self.torch_device)
+ model.dtype = torch.bfloat16
+ config = config_cls(
+ base_model_name_or_path=model_id,
+ **config_kwargs,
+ )
+ model = get_peft_model(model, config, autocast_adapter_dtype=False)
+ model.eval()
+
+ # check that none of this raises an error
+ model(**X)
+
+ if model_id in ["Conv2dGroups", "Conv2dGroups2"]:
+ # this model does not support merging
+ return
+
+ model.merge_adapter(safe_merge=False)
+ model(**X)
+ model.unmerge_adapter()
+ model(**X)
+ model.merge_adapter(safe_merge=True)
+ model(**X)
+ model.unmerge_adapter()
+ model(**X)
+ model = model.merge_and_unload()
+ model(**X)
+
+ @pytest.mark.parametrize("test_name, model_id, config_cls, config_kwargs", TEST_CASES)
+ def test_only_params_are_updated(self, test_name, model_id, config_cls, config_kwargs):
+ # An explicit test that when using an adapter on a custom model, only the adapter parameters are updated during
+ # training
+ X = self.prepare_inputs_for_testing()
+ model = self.transformers_class.from_pretrained(model_id).to(self.torch_device)
+ config = config_cls(
+ base_model_name_or_path=model_id,
+ **config_kwargs,
+ )
+ model = get_peft_model(model, config)
+ model_before = copy.deepcopy(model)
+
+ model.train()
+ lr = 0.5
+ if (config_kwargs.get("use_dora") and model_id == "EmbConv1D") or issubclass(config_cls, VBLoRAConfig):
+ # this high learning rate was found through testing to be necessary to avoid flakiness
+ lr = 100
+ elif "mha" in model_id.lower():
+ # we get exploding gradients with MHA when learning rate is too high
+ lr = 1e-3
+ optimizer = torch.optim.SGD(model.parameters(), lr=lr)
+
+ # train at least 3 steps for all parameters to be updated (probably this is required because of symmetry
+ # breaking of some LoRA layers that are initialized with constants)
+ for _ in range(3):
+ optimizer.zero_grad()
+ y_pred = model(**X)
+ loss = y_pred.sum()
+ loss.backward()
+ optimizer.step()
+
+ tol = 1e-4
+ params_before = dict(model_before.named_parameters())
+ params_after = dict(model.named_parameters())
+ assert params_before.keys() == params_after.keys()
+
+ prefix = PREFIXES[config_cls]
+ for name, param_before in params_before.items():
+ param_after = params_after[name]
+ if (prefix in name) or ("modules_to_save" in name) or ("token_adapter.trainable_tokens" in name):
+ # target_modules, modules_to_save and modules of `NewTokensWrapper` _are_ updated
+ assert not torch.allclose(param_before, param_after, atol=tol, rtol=tol)
+ else:
+ assert torch.allclose(param_before, param_after, atol=tol, rtol=tol)
+
+ @pytest.mark.parametrize("test_name, model_id, config_cls, config_kwargs", TEST_CASES)
+ def test_parameters_after_loading_model(self, test_name, model_id, config_cls, config_kwargs):
+ # An explicit test that when loading a trained model, the parameters are loaded correctly
+ # see issue #808
+ X = self.prepare_inputs_for_testing()
+ model = self.transformers_class.from_pretrained(model_id).to(self.torch_device)
+ config = config_cls(
+ base_model_name_or_path=model_id,
+ **config_kwargs,
+ )
+ model = get_peft_model(model, config)
+ model.train()
+
+ lr = 0.5
+ if config_kwargs.get("use_dora"):
+ lr = 0.1 # otherwise we get nan
+ elif "mha" in model_id.lower():
+ lr = 1e-3 # we get exploding gradients with MHA when learning rate is too high
+ elif issubclass(config_cls, VBLoRAConfig) or issubclass(config_cls, RandLoraConfig):
+ lr = 0.01 # otherwise we get nan
+ optimizer = torch.optim.SGD(model.parameters(), lr=lr)
+
+ # train at least 3 steps for all parameters to be updated (probably this is required because of symmetry
+ # breaking of some LoRA layers that are initialized with constants)
+ for _ in range(3):
+ optimizer.zero_grad()
+ y_pred = model(**X)
+ loss = y_pred.sum()
+ loss.backward()
+ optimizer.step()
+
+ tol = 1e-4
+ params_before = get_state_dict(model)
+ # note: no need to sanity check if parameters were updated at all, this
+ # is already covered in the previous test
+
+ with tempfile.TemporaryDirectory() as tmp_dirname:
+ model.save_pretrained(tmp_dirname)
+ model_from_pretrained = self.transformers_class.from_pretrained(model_id).to(self.torch_device)
+ model_from_pretrained = PeftModel.from_pretrained(model_from_pretrained, tmp_dirname)
+ params_after = get_state_dict(model_from_pretrained)
+
+ assert params_before.keys() == params_after.keys()
+ for name, param_before in params_before.items():
+ param_after = params_after[name]
+ assert torch.allclose(param_before, param_after, atol=tol, rtol=tol)
+
+ @pytest.mark.parametrize("test_name, model_id, config_cls, config_kwargs", TEST_CASES)
+ def test_disable_adapters(self, test_name, model_id, config_cls, config_kwargs):
+ # Test that it's possible to disable the adapter, in which case the model output should be identical to that of
+ # the base model.
+ X = self.prepare_inputs_for_testing()
+ model = self.transformers_class.from_pretrained(model_id).to(self.torch_device).eval()
+ outputs_base = model(**X)
+
+ if issubclass(config_cls, (TrainableTokensConfig,)):
+ config_kwargs = config_kwargs.copy()
+ # override the default value and make PEFT operation a no-op
+ config_kwargs["init_weights"] = True
+ config = config_cls(
+ base_model_name_or_path=model_id,
+ **config_kwargs,
+ )
+ model = get_peft_model(model, config)
+ if issubclass(config_cls, VBLoRAConfig):
+ # Manually set the `vblora_vector_bank` to zero so that VB-LoRA functions as an identity operation.
+ torch.nn.init.zeros_(model.vblora_vector_bank["default"])
+ model.eval()
+ outputs_before = model(**X)
+ assert torch.allclose(outputs_base, outputs_before)
+
+ if issubclass(config_cls, VBLoRAConfig):
+ # initialize `vblora_vector_bank` so it can be trained
+ model._init_vblora_vector_bank(config, "default")
+ model.train()
+ # EmbConv1D is slow to learn for some reason
+ lr = 0.01 if model_id != "EmbConv1D" else 1.0
+ if isinstance(config, TrainableTokensConfig):
+ # TrainableTokens is only changing a small subset, so we need a higher lr to see the difference
+ lr = 2.0
+ optimizer = torch.optim.SGD(model.parameters(), lr=lr)
+
+ # train at least 3 steps for all parameters to be updated (probably this is required because of symmetry
+ # breaking of some LoRA layers that are initialized with constants)
+ for _ in range(3):
+ optimizer.zero_grad()
+ y_pred = model(**X)
+ y = torch.arange(len(y_pred)).to(self.torch_device) % 2
+ loss = nn.functional.nll_loss(y_pred, y)
+ loss.backward()
+ optimizer.step()
+
+ model.eval()
+ outputs_after = model(**X)
+
+ with model.disable_adapter():
+ outputs_disabled = model(**X)
+
+ # check that after leaving the disable_adapter context, everything is enabled again
+ outputs_enabled_after_disable = model(**X)
+
+ if self.torch_device == "cpu":
+ # LayerNorm is running float32 on cpu, so difference in outputs are smaller
+ rtol, atol = 1e-8, 1e-8
+ else:
+ rtol, atol = 1e-5, 1e-8
+ assert not torch.allclose(outputs_before, outputs_after, rtol=rtol, atol=atol)
+ assert torch.allclose(outputs_before, outputs_disabled)
+ assert torch.allclose(outputs_after, outputs_enabled_after_disable)
+
+ @pytest.mark.parametrize("test_name, model_id, config_cls, config_kwargs", TEST_CASES)
+ def test_disable_adapters_with_merging(self, test_name, model_id, config_cls, config_kwargs):
+ # Same test as test_disable_adapters, but additionally merge the trained adapter.
+
+ # https://github.com/huggingface/peft/pull/2403
+ if model_id in ["Conv2dGroups", "Conv2dGroups2"]:
+ pytest.skip(
+ f"Skipping test for {model_id} as merging is not supported. (See https://github.com/huggingface/peft/pull/2403 for details)"
+ )
+
+ # same as test_disable_adapters, but with merging
+ X = self.prepare_inputs_for_testing()
+ model = self.transformers_class.from_pretrained(model_id).to(self.torch_device)
+ config = config_cls(
+ base_model_name_or_path=model_id,
+ **config_kwargs,
+ )
+ model = get_peft_model(model, config)
+ if issubclass(config_cls, VBLoRAConfig):
+ # Manually set the `vblora_vector_bank` to zero so that VB-LoRA functions as an identity operation.
+ torch.nn.init.zeros_(model.vblora_vector_bank["default"])
+ model.eval()
+ outputs_before = model(**X)
+
+ if issubclass(config_cls, VBLoRAConfig):
+ # initialize `vblora_vector_bank` so it can be trained
+ model._init_vblora_vector_bank(config, "default")
+ model.train()
+ if isinstance(config_cls, LNTuningConfig):
+ # LayerNorm tuning is slow to learn
+ lr = 1.0
+ optimizer = torch.optim.SGD(model.parameters(), lr=lr)
+ else:
+ # Adam optimizer since SGD isn't great for small models with IA3 + Conv1D
+ lr = 0.01
+ optimizer = torch.optim.Adam(model.parameters(), lr=lr)
+
+ # train at least 3 steps for all parameters to be updated (probably this is required because of symmetry
+ # breaking of some LoRA layers that are initialized with constants)
+ for _ in range(3):
+ optimizer.zero_grad()
+ y_pred = model(**X)
+ y = torch.arange(len(y_pred)).to(self.torch_device) % 2
+ loss = nn.functional.nll_loss(y_pred, y)
+ loss.backward()
+ optimizer.step()
+
+ model.eval()
+ outputs_unmerged = model(**X)
+ model.merge_adapter()
+ outputs_after = model(**X)
+
+ with model.disable_adapter():
+ outputs_disabled = model(**X)
+
+ # check that after leaving the disable_adapter context, everything is enabled again
+ outputs_enabled_after_disable = model(**X)
+
+ atol, rtol = 1e-5, 1e-5 # tolerances higher than defaults since merging introduces some numerical instability
+
+ conv_ids = ["Conv2d", "Conv3d", "Conv2d2"]
+ if issubclass(config_cls, (IA3Config, LoraConfig)) and model_id in conv_ids: # more instability with Conv
+ atol, rtol = 1e-3, 1e-3
+
+ if issubclass(config_cls, OFTConfig):
+ atol, rtol = 1e-4, 1e-4
+
+ if config_kwargs.get("use_dora") and model_id == "EmbConv1D":
+ atol, rtol = 1e-4, 1e-4
+
+ # check that there is a difference in results after training
+ assert not torch.allclose(outputs_before, outputs_after, atol=atol, rtol=rtol)
+
+ if self.torch_device in ["mlu"] and model_id in conv_ids:
+ atol, rtol = 1e-3, 1e-2 # MLU
+
+ # unmerged or merged should make no difference
+ assert torch.allclose(outputs_after, outputs_unmerged, atol=atol, rtol=rtol)
+
+ # check that disabling adapters gives the same results as before training
+ assert torch.allclose(outputs_before, outputs_disabled, atol=atol, rtol=rtol)
+
+ # check that enabling + disabling adapters does not change the results
+ assert torch.allclose(outputs_after, outputs_enabled_after_disable, atol=atol, rtol=rtol)
+
+ @pytest.mark.parametrize("test_name, model_id, config_cls, config_kwargs", TEST_CASES)
+ def test_disable_adapter_with_bias_warns(self, test_name, model_id, config_cls, config_kwargs):
+ # When training biases in lora, disabling adapters does not reset the biases, so the output is not what users
+ # might expect. Therefore, a warning should be given.
+
+ # Note: We test only with custom models since they run really fast. There is really no point in testing the same
+ # thing with decoder, encoder_decoder, etc.
+ if config_cls != LoraConfig or config_cls != BOFTConfig:
+ # skip this test for other configs as bias is specific to Lora
+ pytest.skip("Testing bias warnings only for LoraConfig or BOFTConfig")
+ if not issubclass(config_cls, (LoraConfig, BOFTConfig)):
+ pytest.skip("Bias argument is only supported for LoRA or BOFT models")
+
+ def run_with_disable(config_kwargs, bias):
+ config_kwargs = config_kwargs.copy()
+ config_kwargs["bias"] = bias
+ model = self.transformers_class.from_pretrained(model_id).to(self.torch_device)
+ config = config_cls(
+ base_model_name_or_path=model_id,
+ **config_kwargs,
+ )
+ peft_model = get_peft_model(model, config)
+ with peft_model.disable_adapter():
+ pass # there is nothing to be done
+
+ if config_cls == LoraConfig:
+ # check that bias=all and bias=lora_only give a warning with the correct message
+ msg_start = "Careful, disabling adapter layers with bias configured to be"
+ with pytest.warns(UserWarning, match=msg_start):
+ run_with_disable(config_kwargs, bias="lora_only")
+ with pytest.warns(UserWarning, match=msg_start):
+ run_with_disable(config_kwargs, bias="all")
+
+ if config_cls == BOFTConfig:
+ # check that bias=all and bias=boft_only give a warning with the correct message
+ msg_start = "Careful, disabling adapter layers with bias configured to be"
+ with pytest.warns(UserWarning, match=msg_start):
+ run_with_disable(config_kwargs, bias="boft_only")
+ with pytest.warns(UserWarning, match=msg_start):
+ run_with_disable(config_kwargs, bias="all")
+
+ # For bias=none, there is no warning. Unfortunately, AFAIK unittest has no option to assert that no warning is
+ # given, therefore, we check that the unittest gives us an AssertionError if we check for a warning
+ bias_warning_was_given = False
+ try:
+ with pytest.warns(UserWarning) as cm:
+ run_with_disable(config_kwargs, bias="none")
+ # if we get here, it means there was no AssertionError, i.e. there are warnings -- let's check that they
+ # are not related to the bias setting
+ if any(warning.message.args[0].startswith(msg_start) for warning in cm.warnings):
+ bias_warning_was_given = True
+ except AssertionError:
+ # This is good, there was an AssertionError, i.e. there was no warning
+ pass
+ if bias_warning_was_given:
+ # This is bad, there was a warning about the bias when there should not have been any.
+ self.fail("There should be no warning when bias is set to 'none'")
+
+ @pytest.mark.parametrize("test_name, model_id, config_cls, config_kwargs", TEST_CASES)
+ def test_active_adapter(self, test_name, model_id, config_cls, config_kwargs):
+ _skip_tests_with_multiple_adapters_with_target_parameters(config_cls, config_kwargs)
+ if config_kwargs.get("modules_to_save", []) or config_kwargs.get("trainable_token_indices", []):
+ pytest.skip("Multiple active adapters with modules_to_save/trainable_token_indices is not supported.")
+
+ model = self.transformers_class.from_pretrained(model_id).to(self.torch_device)
+ config = config_cls(
+ base_model_name_or_path=model_id,
+ **config_kwargs,
+ )
+ model = get_peft_model(model, config)
+ assert model.active_adapters == ["default"]
+ assert model.active_adapter == "default"
+
+ # at this stage, "default" is still the activate adapter, "other" is disabled
+ model.add_adapter("other", config)
+ assert model.active_adapters == ["default"]
+ assert model.active_adapter == "default"
+
+ # set "other" as the active adapter
+ model.set_adapter("other")
+ assert model.active_adapters == ["other"]
+ assert model.active_adapter == "other"
+
+ # set both adapters as active
+ # Note: On the PeftModel, there cannot be multiple active adapters, so we have to go through model.base_model
+ # instead.
+ model.base_model.set_adapter(["default", "other"])
+ # model.active_adapters works, as it delegates to the base_model
+ assert model.active_adapters == ["default", "other"]
+ # model.active_adapter would not work, thus we have to check the base_model directly
+ assert model.base_model.active_adapter == ["default", "other"]
+
+ @pytest.mark.parametrize("config_cls", ALL_PEFT_CONFIG_CLASSES)
+ def test_set_adapter_non_overlapping_modules(self, config_cls):
+ # Ensure that when setting multiple adapters, the active adapters are correctly being set, even if
+ # target_modules that only overlap partially. Apart from checking model.set_adapter, also check
+ # model.base_model.set_adapter. Normally, users wouldn't call this, but there are situations where this is
+ # required, e.g. activating multiple adapters at once cannot be done on the PeftModel but works on LoraModel
+ # etc.
+ if config_cls == TrainableTokensConfig:
+ pytest.skip(reason="Model has no embedding layer, skipping TrainableTokensConfig.")
+
+ model = DeepMLP(size=256) # a size that works with all adapters
+ extra_kwargs = {}
+ if config_cls == IA3Config:
+ extra_kwargs["feedforward_modules"] = []
+ # target_modules overlap partially
+ config0 = config_cls(target_modules=["layers.0.lin0", "layers.1.lin0"], **extra_kwargs)
+ config1 = config_cls(target_modules=["layers.1.lin0", "layers.2.lin0"], **extra_kwargs)
+ model = get_peft_model(model, config0, adapter_name="default")
+ model.add_adapter("other", config1)
+
+ # at this point, 'default' is active
+ assert model.base_model.active_adapters == ["default"]
+ # general note: for adapter layers like LoRA, the active_adapters can be "default" even if that layer has no
+ # adapter called "default", it will be simply ignored in that case
+ assert model.base_model.layers[0].lin0.active_adapters == ["default"]
+ assert model.base_model.layers[1].lin0.active_adapters == ["default"]
+ assert model.base_model.layers[2].lin0.active_adapters == ["default"]
+
+ # activate 'other'
+ model.set_adapter("other")
+ assert model.base_model.active_adapters == ["other"]
+ assert model.base_model.layers[0].lin0.active_adapters == ["other"]
+ assert model.base_model.layers[1].lin0.active_adapters == ["other"]
+ assert model.base_model.layers[2].lin0.active_adapters == ["other"]
+
+ # go back to 'default'
+ model.set_adapter("default")
+ assert model.base_model.active_adapters == ["default"]
+ assert model.base_model.layers[0].lin0.active_adapters == ["default"]
+ assert model.base_model.layers[1].lin0.active_adapters == ["default"]
+ assert model.base_model.layers[2].lin0.active_adapters == ["default"]
+
+ # also ensure that model.base_model.set_adapter works as expected
+ # activate 'other'
+ model.base_model.set_adapter(["other"])
+ assert model.base_model.active_adapters == ["other"]
+ assert model.base_model.layers[0].lin0.active_adapters == ["other"]
+ assert model.base_model.layers[1].lin0.active_adapters == ["other"]
+ assert model.base_model.layers[2].lin0.active_adapters == ["other"]
+
+ # go back to 'default'
+ model.base_model.set_adapter(["default"])
+ assert model.base_model.active_adapters == ["default"]
+ assert model.base_model.layers[0].lin0.active_adapters == ["default"]
+ assert model.base_model.layers[1].lin0.active_adapters == ["default"]
+ assert model.base_model.layers[2].lin0.active_adapters == ["default"]
+
+ @pytest.mark.parametrize("config_cls", ALL_PEFT_CONFIG_CLASSES)
+ def test_set_adapter_non_overlapping_modules_to_save(self, config_cls):
+ # This is similar to the previous test, but includes modules_to_save. Specifically, there was a bug where adding
+ # config1 would automatically activate the modules_to_save for 'other'
+ if config_cls == TrainableTokensConfig:
+ pytest.skip(reason="Trainable tokens does not support modules_to_save")
+
+ model = DeepMLP(size=256) # a size that works with all adapters
+ extra_kwargs = {}
+ if config_cls == IA3Config:
+ extra_kwargs["feedforward_modules"] = []
+ # targeting the same modules with modules_to_save:
+ config0 = config_cls(target_modules=["layers.0.lin0"], **extra_kwargs)
+ config1 = config_cls(target_modules=["layers.0.lin0"], modules_to_save=["layers.0.lin1"], **extra_kwargs)
+ model = get_peft_model(model, config0, adapter_name="default")
+ model.add_adapter("other", config1)
+
+ # at this point, 'default' is active
+ assert model.base_model.active_adapters == ["default"]
+ assert model.base_model.layers[0].lin0.active_adapters == ["default"]
+ assert model.base_model.layers[0].lin1.active_adapters == []
+ assert model.base_model.layers[0].lin1.modules_to_save.other.weight.requires_grad is False
+
+ # activate 'other'
+ model.set_adapter("other")
+ assert model.base_model.active_adapters == ["other"]
+ assert model.base_model.layers[0].lin0.active_adapters == ["other"]
+ assert model.base_model.layers[0].lin1.active_adapters == ["other"]
+ assert model.base_model.layers[0].lin1.modules_to_save.other.weight.requires_grad is True
+
+ # go back to 'default'
+ model.set_adapter("default")
+ assert model.base_model.active_adapters == ["default"]
+ assert model.base_model.layers[0].lin0.active_adapters == ["default"]
+ assert model.base_model.layers[0].lin1.active_adapters == []
+ assert model.base_model.layers[0].lin1.modules_to_save.other.weight.requires_grad is False
+
+ # also ensure that model.base_model.set_adapter works as expected
+ # activate 'other'
+ model.base_model.set_adapter(["other"])
+ assert model.base_model.active_adapters == ["other"]
+ assert model.base_model.layers[0].lin0.active_adapters == ["other"]
+ assert model.base_model.layers[0].lin1.active_adapters == ["other"]
+ assert model.base_model.layers[0].lin1.modules_to_save.other.weight.requires_grad is True
+
+ # go back to 'default'
+ model.base_model.set_adapter(["default"])
+ assert model.base_model.active_adapters == ["default"]
+ assert model.base_model.layers[0].lin0.active_adapters == ["default"]
+ assert model.base_model.layers[0].lin1.active_adapters == []
+ assert model.base_model.layers[0].lin1.modules_to_save.other.weight.requires_grad is False
+
+ def test_set_adapter_non_overlapping_trainable_token_indices(self):
+ # Same test as the previous one, but using trainable_token_indices instead of modules_to_save
+ model = ModelEmbConv1D()
+ # targeting the same modules with modules_to_save:
+ config0 = LoraConfig(target_modules=["lin0"])
+ config1 = LoraConfig(target_modules=["lin0"], trainable_token_indices={"emb": [0]})
+
+ model = get_peft_model(model, config0, adapter_name="default")
+ model.add_adapter("other", config1)
+
+ # at this point, 'default' is active
+ assert model.base_model.active_adapters == ["default"]
+ assert model.base_model.lin0.active_adapters == ["default"]
+ assert model.base_model.emb.active_adapters == []
+ assert model.base_model.model.emb.token_adapter.trainable_tokens_delta.other.requires_grad is False
+
+ # activate 'other'
+ model.set_adapter("other")
+ assert model.base_model.active_adapters == ["other"]
+ assert model.base_model.lin0.active_adapters == ["other"]
+ assert model.base_model.emb.active_adapters == ["other"]
+ assert model.base_model.model.emb.token_adapter.trainable_tokens_delta.other.requires_grad is True
+
+ # go back to 'default'
+ model.set_adapter("default")
+ assert model.base_model.active_adapters == ["default"]
+ assert model.base_model.lin0.active_adapters == ["default"]
+ assert model.base_model.emb.active_adapters == []
+ assert model.base_model.model.emb.token_adapter.trainable_tokens_delta.other.requires_grad is False
+
+ # also ensure that model.base_model.set_adapter works as expected
+ # activate 'other'
+ model.base_model.set_adapter(["other"])
+ assert model.base_model.active_adapters == ["other"]
+ assert model.base_model.lin0.active_adapters == ["other"]
+ assert model.base_model.emb.active_adapters == ["other"]
+ assert model.base_model.model.emb.token_adapter.trainable_tokens_delta.other.requires_grad is True
+
+ # go back to 'default'
+ model.base_model.set_adapter(["default"])
+ assert model.base_model.active_adapters == ["default"]
+ assert model.base_model.lin0.active_adapters == ["default"]
+ assert model.base_model.emb.active_adapters == []
+ assert model.base_model.model.emb.token_adapter.trainable_tokens_delta.other.requires_grad is False
+
+ @pytest.mark.parametrize("config_cls", ALL_PEFT_CONFIG_CLASSES)
+ def test_multiple_active_adapters_with_same_modules_to_save_raises(self, config_cls):
+ # When we have multiple adapters each with modules_to_save, we don't allow those to target the same layer, as
+ # module_to_save (unlike LoRA etc) is not additive.
+ if config_cls == TrainableTokensConfig:
+ pytest.skip(reason="Trainable tokens does not support modules_to_save")
+
+ model = DeepMLP(size=256) # a size that works with all adapters
+ extra_kwargs = {}
+ if config_cls == IA3Config:
+ extra_kwargs["feedforward_modules"] = []
+ # targeting the same modules with modules_to_save:
+ config0 = config_cls(target_modules=["layers.0.lin0"], modules_to_save=["layers.0.lin1"], **extra_kwargs)
+ config1 = config_cls(target_modules=["layers.0.lin0"], modules_to_save=["layers.0.lin1"], **extra_kwargs)
+ model = get_peft_model(model, config0, adapter_name="default")
+ # adding the adapter is fine
+ model.add_adapter("other", config1)
+
+ msg = "Only one adapter can be set at a time for ModulesToSaveWrapper"
+ with pytest.raises(ValueError, match=msg):
+ model.base_model.set_adapter(["default", "other"])
+
+ @pytest.mark.parametrize("config_cls", ALL_PEFT_CONFIG_CLASSES)
+ def test_multiple_active_adapters_with_overlapping_modules_to_save_raises(self, config_cls):
+ # same test as the previous one, but targeting multiple modules_to_save, some of which overlap
+ if config_cls == TrainableTokensConfig:
+ pytest.skip(reason="Trainable tokens does not support modules_to_save")
+
+ model = DeepMLP(size=256) # a size that works with all adapters
+ extra_kwargs = {}
+ if config_cls == IA3Config:
+ extra_kwargs["feedforward_modules"] = []
+ # targeting the overlapping modules with modules_to_save:
+ config0 = config_cls(
+ target_modules=["layers.0.lin0"], modules_to_save=["layers.0.lin1", "layers.1.lin1"], **extra_kwargs
+ )
+ config1 = config_cls(
+ target_modules=["0layers..lin0"], modules_to_save=["layers.2.lin1", "layers.1.lin1"], **extra_kwargs
+ )
+ model = get_peft_model(model, config0, adapter_name="default")
+ # adding the adapter is fine
+ model.add_adapter("other", config1)
+
+ msg = "Only one adapter can be set at a time for ModulesToSaveWrapper"
+ with pytest.raises(ValueError, match=msg):
+ model.base_model.set_adapter(["default", "other"])
+
+ @pytest.mark.parametrize("config_cls", ALL_PEFT_CONFIG_CLASSES)
+ def test_multiple_active_adapters_with_different_modules_to_save_works(self, config_cls):
+ # same test as the previous one but targeting distinct modules_to_save; this is fine
+ if config_cls == TrainableTokensConfig:
+ pytest.skip(reason="Trainable tokens does not support modules_to_save")
+
+ model = DeepMLP(size=256) # a size that works with all adapters
+ extra_kwargs = {}
+ if config_cls == IA3Config:
+ extra_kwargs["feedforward_modules"] = []
+ # targeting the different modules with modules_to_save:
+ config0 = config_cls(target_modules=["layers.0.lin0"], modules_to_save=["layers.0.lin1"], **extra_kwargs)
+ config1 = config_cls(target_modules=["layers.0.lin0"], modules_to_save=["layers.1.lin1"], **extra_kwargs)
+ model = get_peft_model(model, config0, adapter_name="default")
+ # adding the adapter is fine
+ model.add_adapter("other", config1)
+ model.base_model.set_adapter(["default", "other"]) # does not raise
+
+ assert model.base_model.model.layers[0].lin1.active_adapters == ["default"]
+ assert model.base_model.model.layers[1].lin1.active_adapters == ["other"]
+
+ def test_multiple_active_adapters_with_same_trainable_token_indices_raises(self):
+ # Same test as test_multiple_active_adapters_with_same_modules_to_save_raises but with trainable_token_indices
+ # instead of modules_to_save.
+ model = ModelEmbConv1D()
+ # targeting the same modules with modules_to_save:
+ config0 = LoraConfig(target_modules=["lin0"], trainable_token_indices={"emb": [0]})
+ config1 = LoraConfig(target_modules=["lin0"], trainable_token_indices={"emb": [0]})
+ model = get_peft_model(model, config0, adapter_name="default")
+ # adding the adapter is fine
+ model.add_adapter("other", config1)
+
+ msg = "Only one adapter can be set at a time for TrainableTokensWrapper"
+ with pytest.raises(ValueError, match=msg):
+ model.base_model.set_adapter(["default", "other"])
+
+ def test_multiple_active_adapters_with_different_trainable_token_indices_works(self):
+ # Same test as the previous one but targeting different embedding layers should work
+ class MyModel(nn.Module):
+ def __init__(self):
+ super().__init__()
+ self.emb0 = nn.Embedding(10, 10)
+ self.emb1 = nn.Embedding(10, 10)
+ self.lin0 = nn.Linear(10, 10)
+
+ model = MyModel()
+ # targeting the same modules with modules_to_save:
+ config0 = LoraConfig(target_modules=["lin0"], trainable_token_indices={"emb0": [0]})
+ config1 = LoraConfig(target_modules=["lin0"], trainable_token_indices={"emb1": [0]})
+ model = get_peft_model(model, config0, adapter_name="default")
+ # adding the adapter is fine
+ model.add_adapter("other", config1)
+ model.base_model.set_adapter(["default", "other"]) # does not raise
+
+ @pytest.mark.parametrize("test_name, model_id, config_cls, config_kwargs", TEST_CASES)
+ def test_disable_adapters_exiting_context_restores_previous_state(
+ self, test_name, model_id, config_cls, config_kwargs
+ ):
+ # Test that when we exit the disable_adapter context, we correctly restore the enabled state of the modules as
+ # they were before the context.
+ model = self.transformers_class.from_pretrained(model_id).to(self.torch_device)
+ config = config_cls(
+ base_model_name_or_path=model_id,
+ **config_kwargs,
+ )
+ model = get_peft_model(model, config)
+ tuner_modules = [module for module in model.modules() if isinstance(module, BaseTunerLayer)]
+
+ # all layers should be enabled
+ assert all(not module.disable_adapters for module in tuner_modules)
+ with model.disable_adapter():
+ pass
+ # this should not change after exiting the context
+ assert all(not module.disable_adapters for module in tuner_modules)
+
+ # now disable all layers
+ model.disable_adapter_layers()
+ assert all(module.disable_adapters for module in tuner_modules)
+ with model.disable_adapter():
+ pass
+ assert all(module.disable_adapters for module in tuner_modules)
+
+ @pytest.mark.parametrize("test_name, model_id, config_cls, config_kwargs", TEST_CASES)
+ def test_disable_adapters_exiting_context_irregular_state(self, test_name, model_id, config_cls, config_kwargs):
+ # When we have a model where some adapters are enabled and others are disabled, we should get a warning when
+ # entering the disable_adapter context because we cannot correctly restore the state of the adapters from
+ # before the context. After exiting the context, all adapters will be enabled, which is the status quo of how
+ # we deal with this.
+ model = self.transformers_class.from_pretrained(model_id).to(self.torch_device)
+ config = config_cls(
+ base_model_name_or_path=model_id,
+ **config_kwargs,
+ )
+ model = get_peft_model(model, config)
+ tuner_modules = [module for module in model.modules() if isinstance(module, BaseTunerLayer)]
+
+ # now we mix the states, some enabled some not
+ if len(tuner_modules) < 2:
+ # next check only works with more than 1 tuner module
+ return
+
+ # disable a single layer
+ tuner_modules[0].enable_adapters(False)
+ # sanity check that we have both enabled and disabled layers
+ assert {module.disable_adapters for module in tuner_modules} == {True, False}
+ # check that we get a warning with irregular states
+ msg = "The model contains some adapter layers that are enabled and others that are disabled"
+ with pytest.warns(UserWarning, match=msg):
+ with model.disable_adapter():
+ pass
+
+ # when encountering irregular adapters, we enable all adapters at the end of the context
+ assert all(not module.disable_adapters for module in tuner_modules)
+
+ @pytest.mark.parametrize("test_name, model_id, config_cls, config_kwargs", TEST_CASES)
+ def test_delete_adapter(self, test_name, model_id, config_cls, config_kwargs):
+ _skip_tests_with_multiple_adapters_with_target_parameters(config_cls, config_kwargs)
+ self._test_delete_adapter(model_id, config_cls, config_kwargs)
+
+ @pytest.mark.parametrize("test_name, model_id, config_cls, config_kwargs", TEST_CASES)
+ def test_delete_inactive_adapter(self, test_name, model_id, config_cls, config_kwargs):
+ _skip_tests_with_multiple_adapters_with_target_parameters(config_cls, config_kwargs)
+ self._test_delete_inactive_adapter(model_id, config_cls, config_kwargs)
+
+ @pytest.mark.parametrize("test_name, model_id, config_cls, config_kwargs", TEST_CASES)
+ def test_delete_unknown_adapter_raises(self, test_name, model_id, config_cls, config_kwargs):
+ self._test_delete_unknown_adapter_raises(model_id, config_cls, config_kwargs)
+
+ def test_delete_adapter_with_multiple_adapters_works(self):
+ # Add 3 adapters, delete the active one, the next one should be active, delete the inactive one, the active one
+ # should stay the same.
+ config0 = LoraConfig(target_modules=["lin0"])
+ config1 = LoraConfig(target_modules=["lin0"])
+ config2 = LoraConfig(target_modules=["lin0"])
+ model = get_peft_model(MLP(), config0, adapter_name="adapter0").to(self.torch_device)
+ model.add_adapter("adapter1", config1)
+ model.add_adapter("adapter2", config2)
+
+ inputs = self.prepare_inputs_for_testing()
+ assert model.active_adapters == ["adapter0"]
+ model(**inputs) # does not raise
+
+ # delete the active adapter, next one should become active
+ model.delete_adapter("adapter0")
+ assert model.active_adapters == ["adapter1"]
+ model(**inputs) # does not raise
+
+ # delete an inactive adapter, should not affect the active adapter
+ model.delete_adapter("adapter2")
+ assert model.active_adapters == ["adapter1"]
+ model(**inputs) # does not raise
+
+ def test_delete_adapter_multiple_adapters_with_modules_to_save(self):
+ # There are 3 adapters. Adapter 0 has modules_to_save. Delete it, we should switch to adapter 1, which does not
+ # have modules_to_save. Then, we delete it too, switching to adapter 2, which has modules_to_save. Finally, we
+ # delete the last adapter (state is updated but forward is no longer possible).
+ model = MLP()
+ inputs = self.prepare_inputs_for_testing()
+
+ config0 = LoraConfig(target_modules=["lin0"], modules_to_save=["lin1"])
+ config1 = LoraConfig(target_modules=["lin0"])
+ config2 = LoraConfig(target_modules=["lin0"], modules_to_save=["lin1"])
+ model = get_peft_model(model, config0, adapter_name="adapter0").to(self.torch_device)
+ model.add_adapter("adapter1", config1)
+ model.add_adapter("adapter2", config2)
+
+ assert model.active_adapters == ["adapter0"]
+ assert model.modules_to_save == {"lin1"}
+ assert set(model.base_model.model.lin1.modules_to_save) == {"adapter0", "adapter2"}
+ model(**inputs) # does not raise
+
+ # delete active adapter, should switch to the next adapter (which does not have modules_to_save)
+ model.delete_adapter("adapter0")
+ assert model.active_adapters == ["adapter1"]
+ assert model.modules_to_save == {"lin1"}
+ assert set(model.base_model.model.lin1.modules_to_save) == {"adapter2"}
+ model(**inputs) # does not raise
+
+ # delete active adapter, should switch to the next adapter (which *does* have modules_to_save)
+ model.delete_adapter("adapter1")
+ assert model.active_adapters == ["adapter2"]
+ assert model.modules_to_save == {"lin1"}
+ assert set(model.base_model.model.lin1.modules_to_save) == {"adapter2"}
+ model(**inputs) # does not raise
+
+ # delete last adapter
+ model.delete_adapter("adapter2")
+ assert model.active_adapters == []
+ assert model.modules_to_save is None
+ assert set(model.base_model.model.lin1.modules_to_save) == set()
+
+ def test_delete_adapter_multiple_adapters_with_trainable_token_indices(self):
+ # Same as the previous test, just using trainable_token_indices instead of modules_to_save
+ # Note that we need to use a transformers model for trainable_token_indices
+ model = AutoModelForCausalLM.from_pretrained("hf-internal-testing/tiny-random-OPTForCausalLM")
+ inputs = {"input_ids": torch.arange(10).view(-1, 1).to(self.torch_device)}
+
+ config0 = LoraConfig(target_modules=["q_proj"], trainable_token_indices=[0, 1])
+ config1 = LoraConfig(target_modules=["q_proj"])
+ config2 = LoraConfig(target_modules=["q_proj"], trainable_token_indices=[1, 3])
+ model = get_peft_model(model, config0, adapter_name="adapter0").to(self.torch_device)
+ model.add_adapter("adapter1", config1)
+ model.add_adapter("adapter2", config2)
+
+ embed_tokens = model.base_model.model.model.decoder.embed_tokens
+ lm_head = model.base_model.model.lm_head
+
+ assert model.active_adapters == ["adapter0"]
+ assert set(embed_tokens.token_adapter.trainable_tokens_delta) == {"adapter0", "adapter2"}
+ assert set(embed_tokens.token_adapter.trainable_tokens_original) == {"adapter0", "adapter2"}
+ assert set(lm_head.token_adapter.trainable_tokens_delta) == {"adapter0", "adapter2"}
+ assert set(lm_head.token_adapter.trainable_tokens_original) == {"adapter0", "adapter2"}
+ model(**inputs) # does not raise
+
+ # delete active adapter, should switch to the next adapter (which does not have modules_to_save)
+ model.delete_adapter("adapter0")
+ assert model.active_adapters == ["adapter1"]
+ assert set(embed_tokens.token_adapter.trainable_tokens_delta) == {"adapter2"}
+ assert set(embed_tokens.token_adapter.trainable_tokens_original) == {"adapter2"}
+ assert set(lm_head.token_adapter.trainable_tokens_delta) == {"adapter2"}
+ assert set(lm_head.token_adapter.trainable_tokens_original) == {"adapter2"}
+ model(**inputs) # does not raise
+
+ # delete active adapter, should switch to the next adapter (which *does* have modules_to_save)
+ model.delete_adapter("adapter1")
+ assert model.active_adapters == ["adapter2"]
+ assert set(embed_tokens.token_adapter.trainable_tokens_delta) == {"adapter2"}
+ assert set(embed_tokens.token_adapter.trainable_tokens_original) == {"adapter2"}
+ assert set(lm_head.token_adapter.trainable_tokens_delta) == {"adapter2"}
+ assert set(lm_head.token_adapter.trainable_tokens_original) == {"adapter2"}
+ model(**inputs) # does not raise
+
+ # delete last adapter
+ model.delete_adapter("adapter2")
+ assert model.active_adapters == []
+ assert set(embed_tokens.token_adapter.trainable_tokens_delta) == set()
+ assert set(embed_tokens.token_adapter.trainable_tokens_original) == set()
+ assert set(lm_head.token_adapter.trainable_tokens_delta) == set()
+ assert set(lm_head.token_adapter.trainable_tokens_original) == set()
+
+ @pytest.mark.parametrize("test_name, model_id, config_cls, config_kwargs", TEST_CASES)
+ def test_adding_multiple_adapters_with_bias_raises(self, test_name, model_id, config_cls, config_kwargs):
+ self._test_adding_multiple_adapters_with_bias_raises(model_id, config_cls, config_kwargs)
+
+ @staticmethod
+ def _check_requires_grad(module, adapter_name, requires_grad):
+ # a bit of a clumsy way to test requires_grad on the PEFT parameters
+ for name in module.adapter_layer_names:
+ module_dict = getattr(module, name)
+ if adapter_name not in module_dict:
+ continue
+ attr = module_dict[adapter_name]
+ if isinstance(attr, nn.Module):
+ for param in attr.parameters():
+ assert param.requires_grad == requires_grad
+ else: # it's an nn.Parameter
+ assert attr.requires_grad == requires_grad
+
+ @pytest.mark.parametrize("config_cls", ALL_PEFT_CONFIG_CLASSES)
+ def test_set_requires_grad(self, config_cls):
+ # checks that the model.set_requires_grad method works as expected
+ if config_cls == TrainableTokensConfig:
+ pytest.skip(
+ "TrainableTokensConfig has a separate test for set_requires_grad, as it needs a different model."
+ )
+
+ config_kwargs = {"target_modules": ["layers.0.lin0"]}
+ if config_cls == IA3Config:
+ config_kwargs["feedforward_modules"] = []
+ config0 = config_cls(**config_kwargs)
+ model = DeepMLP(size=256) # a size that works with all adapters
+ model = get_peft_model(model, config0, adapter_name="adapter0").eval()
+
+ # check that it works with a single adapter
+ self._check_requires_grad(model.base_model.model.layers[0].lin0, adapter_name="adapter0", requires_grad=True)
+
+ # add another adapter with two target modules and with modules_to_save
+ config_kwargs["target_modules"] = ["layers.0.lin0", "layers.1.lin0"]
+ config_kwargs["modules_to_save"] = ["layers.2.lin0"]
+ config1 = config_cls(**config_kwargs)
+ model.add_adapter("adapter1", config1)
+
+ # adapter0 still has requires_grad=True, adapter1 has requires_grad=False
+ self._check_requires_grad(model.base_model.model.layers[0].lin0, adapter_name="adapter0", requires_grad=True)
+ self._check_requires_grad(model.base_model.model.layers[0].lin0, adapter_name="adapter1", requires_grad=False)
+ self._check_requires_grad(model.base_model.model.layers[1].lin0, adapter_name="adapter1", requires_grad=False)
+ self._check_requires_grad(model.base_model.model.layers[2].lin0, adapter_name="adapter1", requires_grad=False)
+
+ # enable grad for adapter1; adapter0 is unaffected
+ model.set_requires_grad(adapter_names="adapter1")
+ self._check_requires_grad(model.base_model.model.layers[0].lin0, adapter_name="adapter0", requires_grad=True)
+ self._check_requires_grad(model.base_model.model.layers[0].lin0, adapter_name="adapter1", requires_grad=True)
+ self._check_requires_grad(model.base_model.model.layers[1].lin0, adapter_name="adapter1", requires_grad=True)
+ self._check_requires_grad(model.base_model.model.layers[2].lin0, adapter_name="adapter1", requires_grad=True)
+
+ # disable adapter for both
+ model.set_requires_grad(adapter_names=["adapter0", "adapter1"], requires_grad=False)
+ self._check_requires_grad(model.base_model.model.layers[0].lin0, adapter_name="adapter0", requires_grad=False)
+ self._check_requires_grad(model.base_model.model.layers[0].lin0, adapter_name="adapter1", requires_grad=False)
+ self._check_requires_grad(model.base_model.model.layers[1].lin0, adapter_name="adapter1", requires_grad=False)
+
+ def test_set_requires_grad_trainable_tokens(self):
+ # same as test_set_requires_grad for trainable tokens
+ class EmbModel(nn.Module):
+ def __init__(self):
+ super().__init__()
+ self.emb0 = nn.Embedding(10, 10)
+ self.emb1 = nn.Embedding(10, 10)
+
+ config_kwargs = {"target_modules": ["emb0"], "token_indices": [0, 2, 4]}
+ config0 = TrainableTokensConfig(**config_kwargs)
+ model = EmbModel()
+ model = get_peft_model(model, config0, adapter_name="adapter0").eval()
+
+ # check that it works with a single adapter
+ self._check_requires_grad(model.base_model.model.emb0, adapter_name="adapter0", requires_grad=True)
+
+ # add another adapter which targets 2 embedding layers
+ config_kwargs["target_modules"] = ["emb0", "emb1"]
+ config1 = TrainableTokensConfig(**config_kwargs)
+ model.add_adapter("adapter1", config1)
+
+ # adapter0 still has requires_grad=True, adapter1 has requires_grad=False
+ self._check_requires_grad(model.base_model.model.emb0, adapter_name="adapter0", requires_grad=True)
+ self._check_requires_grad(model.base_model.model.emb0, adapter_name="adapter1", requires_grad=False)
+ self._check_requires_grad(model.base_model.model.emb1, adapter_name="adapter1", requires_grad=False)
+
+ # enable grad for adapter1; adapter0 is unaffected
+ model.set_requires_grad(adapter_names="adapter1")
+ self._check_requires_grad(model.base_model.model.emb0, adapter_name="adapter0", requires_grad=True)
+ self._check_requires_grad(model.base_model.model.emb0, adapter_name="adapter1", requires_grad=True)
+ self._check_requires_grad(model.base_model.model.emb1, adapter_name="adapter1", requires_grad=True)
+
+ # disable adapter for both
+ model.set_requires_grad(adapter_names=["adapter0", "adapter1"], requires_grad=False)
+ self._check_requires_grad(model.base_model.model.emb0, adapter_name="adapter0", requires_grad=False)
+ self._check_requires_grad(model.base_model.model.emb0, adapter_name="adapter1", requires_grad=False)
+ self._check_requires_grad(model.base_model.model.emb1, adapter_name="adapter1", requires_grad=False)
+
+ def test_weight_bias_attributes(self):
+ model = MLP()
+ config = LoraConfig(target_modules=["lin0"])
+ model = get_peft_model(model, config)
+ assert hasattr(model.base_model.model.lin0, "weight")
+ assert hasattr(model.base_model.model.lin0, "bias")
+
+ def test_multiple_adapters_automatic_modules_to_save(self):
+ # See issue 1574
+ # When we use certain task types, PeftModel.modules_to_save is automatically updated to include some extra
+ # layers not specified in the PeftConfig. This attribute should be honored for all adapters, not just for
+ # the default adapter.
+ config0 = LoraConfig(task_type=TaskType.SEQ_CLS)
+ config1 = LoraConfig(task_type=TaskType.SEQ_CLS)
+ model = AutoModelForSequenceClassification.from_pretrained("bert-base-uncased")
+ model = get_peft_model(model, config0)
+ # sanity check
+ assert model.modules_to_save
+
+ model.add_adapter("other", config1)
+ assert "default" in model.base_model.classifier.modules_to_save
+ assert "other" in model.base_model.classifier.modules_to_save
+
+ @pytest.mark.parametrize(
+ "config_cls", [IA3Config, LoHaConfig, LoKrConfig, LoraConfig, HRAConfig, BoneConfig, ShiraConfig, MissConfig]
+ )
+ def test_multiple_adapters_mixed_modules_to_save(self, config_cls):
+ # See issue 1574
+ # Check that we can have a model where one adapter has modules_to_save and the other doesn't. It should be
+ # possible to switch between those adapters and to use them.
+ if hasattr(config_cls, "feedforward_modules"): # IA³
+ config_cls = partial(config_cls, feedforward_modules=["lin0"])
+
+ if config_cls == BoneConfig or config_cls == MissConfig:
+ config_cls = partial(config_cls, r=2)
+ if config_cls == ShiraConfig:
+ config_cls = partial(config_cls, r=1)
+
+ config0 = config_cls(target_modules=["lin0"], modules_to_save=["lin1"])
+ config1 = config_cls(target_modules=["lin0"])
+ model = MLP()
+ model = get_peft_model(model, config0).to(self.torch_device)
+ model.add_adapter("other", config1)
+
+ assert "default" in model.base_model.lin1.modules_to_save
+ assert "other" not in model.base_model.lin1.modules_to_save
+
+ # check that switching adapters and predicting does not raise
+ inputs = self.prepare_inputs_for_testing()
+ # "default" adapter is active
+ model(**inputs)
+ # switch to "other" adapter
+ model.set_adapter("other")
+ model(**inputs)
+
+ @pytest.mark.parametrize(
+ "config_cls", [IA3Config, LoHaConfig, LoKrConfig, LoraConfig, HRAConfig, BoneConfig, ShiraConfig]
+ )
+ def test_multiple_adapters_mixed_modules_to_save_order_switched(self, config_cls):
+ # See issue 1574
+ # Same test as test_multiple_adapters_mixed_modules_to_save, but this time the 2nd adapter has modules_to_save.
+ if hasattr(config_cls, "feedforward_modules"): # IA³
+ config_cls = partial(config_cls, feedforward_modules=["lin0"])
+
+ if config_cls == BoneConfig or config_cls == MissConfig:
+ config_cls = partial(config_cls, r=2)
+ if config_cls == ShiraConfig:
+ config_cls = partial(config_cls, r=1)
+
+ config0 = config_cls(target_modules=["lin0"])
+ config1 = config_cls(target_modules=["lin0"], modules_to_save=["lin1"])
+ model = MLP()
+ model = get_peft_model(model, config0).to(self.torch_device)
+ model.add_adapter("other", config1)
+
+ assert "default" not in model.base_model.lin1.modules_to_save
+ assert "other" in model.base_model.lin1.modules_to_save
+
+ # check that switching adapters and predicting does not raise
+ inputs = self.prepare_inputs_for_testing()
+ # "default" adapter is active
+ model(**inputs)
+ # switch to "other" adapter
+ model.set_adapter("other")
+ model(**inputs)
+
+ def test_multiple_adapters_mixed_modules_to_save_merging_adapters(self):
+ # See issue 1574
+ # This test is similar to test_multiple_adapters_mixed_modules_to_save, but it also checks that merging adapter
+ # weights works when one adapter has a modules_to_save and the other hasn't
+ config0 = LoraConfig(target_modules=["lin0"], modules_to_save=["lin1"])
+ config1 = LoraConfig(target_modules=["lin0"])
+ model = MLP()
+ model = get_peft_model(model, config0).to(self.torch_device)
+ model.add_adapter("other", config1)
+
+ # check that this does not raise
+ model.add_weighted_adapter(["default", "other"], weights=[1.0, 1.0], adapter_name="merged")
+
+ # since one of the adapters that was merged has a modules_to_save, that one should be used for the merged
+ # adapter
+ assert "default" in model.base_model.model.lin1.modules_to_save
+ assert "other" not in model.base_model.model.lin1.modules_to_save
+ assert "merged" in model.base_model.model.lin1.modules_to_save
+
+ # check that using the merged adapter does not raise
+ model.set_adapter("merged")
+ inputs = self.prepare_inputs_for_testing()
+ model(**inputs)
+
+ def test_multiple_adapters_same_modules_to_save_merging_adapters_raises(self):
+ # See issue 1574
+ # This test is similar to test_multiple_adapters_mixed_modules_to_save_merging_adapters but here the two
+ # adapters target the same module with modules_to_save. In this case, trying to merge the adapter weights
+ # should raise an error.
+ config0 = LoraConfig(target_modules=["lin0"], modules_to_save=["lin1"])
+ config1 = LoraConfig(target_modules=["lin0"], modules_to_save=["lin1"])
+ model = MLP()
+ model = get_peft_model(model, config0).to(self.torch_device)
+ model.add_adapter("other", config1)
+
+ msg = re.escape(
+ "Cannot add weighted adapters if they target the same module with modules_to_save, but found 1 such "
+ "instance(s)."
+ )
+ with pytest.raises(ValueError, match=msg):
+ model.add_weighted_adapter(["default", "other"], weights=[1.0, 1.0], adapter_name="merged")
+
+ def test_multiple_adapters_seq_cls_mixed_modules_to_save_merging_adapters(self):
+ # See issue 1574
+ # This test is similar to test_multiple_adapters_mixed_modules_to_save_merging_adapters but uses a SEQ_CLS
+ # model like in test_multiple_adapters_automatic_modules_to_save. This should raise an error because the same
+ # module is implicitly targeted by modules_to_save twice.
+ config0 = LoraConfig(task_type=TaskType.SEQ_CLS)
+ config1 = LoraConfig(task_type=TaskType.SEQ_CLS)
+ model = AutoModelForSequenceClassification.from_pretrained("bert-base-uncased")
+ model = get_peft_model(model, config0)
+ model.add_adapter("other", config1)
+
+ msg = re.escape(
+ "Cannot add weighted adapters if they target the same module with modules_to_save, but found 1 such "
+ "instance(s)."
+ )
+ with pytest.raises(ValueError, match=msg):
+ model.add_weighted_adapter(["default", "other"], weights=[1.0, 1.0], adapter_name="merged")
+
+ @pytest.mark.parametrize(
+ "config_cls", [IA3Config, LoHaConfig, LoKrConfig, LoraConfig, HRAConfig, BoneConfig, MissConfig]
+ )
+ def test_add_weighted_adapter_cat_with_rank_pattern(self, config_cls):
+ # Fixes a bug described in #2512, which resulted from the rank_pattern not being taken into account
+ config0 = LoraConfig(target_modules=["lin0", "lin1"], r=8, rank_pattern={"lin0": 2})
+ config1 = LoraConfig(target_modules=["lin0", "lin1"], r=8, rank_pattern={"lin0": 16})
+ model = MLP()
+ model = get_peft_model(model, config0).to(self.torch_device)
+ model.add_adapter("other", config1)
+ model.add_weighted_adapter(
+ ["default", "other"], weights=[1.0, 1.0], adapter_name="merged", combination_type="cat"
+ )
+
+ def test_add_weighted_adapter_negative_weight_negates_adapter(self):
+ # Test that weight=-1.0 properly negates an adapter
+ torch.manual_seed(42)
+ model = MLP()
+ config = LoraConfig(target_modules=["lin0"], init_lora_weights=False)
+ model = get_peft_model(model, config, adapter_name="adapter1")
+
+ # Create merged adapter with weight=1.0
+ model.add_weighted_adapter(
+ adapters=["adapter1"],
+ weights=[1.0],
+ adapter_name="merged_positive",
+ combination_type="linear",
+ )
+
+ # Create merged adapter with weight=-1.0
+ model.add_weighted_adapter(
+ adapters=["adapter1"],
+ weights=[-1.0],
+ adapter_name="merged_negative",
+ combination_type="linear",
+ )
+
+ # Get the LoRA weights for comparison
+ for name, module in model.named_modules():
+ if hasattr(module, "lora_A") and "merged_positive" in module.lora_A:
+ pos_A = module.lora_A["merged_positive"].weight.data
+ neg_A = module.lora_A["merged_negative"].weight.data
+ pos_B = module.lora_B["merged_positive"].weight.data
+ neg_B = module.lora_B["merged_negative"].weight.data
+
+ # Check that negative adapter is negation of positive
+ # Since we apply sign to both A and B: sign * sqrt(|w|)
+ # For w=1: sqrt(1) = 1, for w=-1: -sqrt(1) = -1
+ assert torch.allclose(neg_A, -pos_A, atol=1e-6), "A matrices should be negated"
+ assert torch.allclose(neg_B, -pos_B, atol=1e-6), "B matrices should be negated"
+
+ def test_add_weighted_adapter_subtraction_with_negative_weights(self):
+ # Test that merging two identical adapters with weights [1.0, -1.0] results in approximately zero weights
+ model = MLP()
+ config = LoraConfig(target_modules=["lin0"], init_lora_weights=False)
+
+ # Create two identical adapters by using the same seed
+ torch.manual_seed(42)
+ model = get_peft_model(model, config, adapter_name="adapter1")
+
+ torch.manual_seed(42)
+ model.add_adapter("adapter2", config)
+
+ # Merge with weights [1.0, -1.0] - should cancel out exactly
+ model.add_weighted_adapter(
+ adapters=["adapter1", "adapter2"],
+ weights=[1.0, -1.0],
+ adapter_name="cancelled",
+ combination_type="linear",
+ )
+
+ # Verify the merged adapter has weights of approximately 0
+ for name, module in model.named_modules():
+ if hasattr(module, "lora_A") and "cancelled" in module.lora_A:
+ cancelled_A = module.lora_A["cancelled"].weight.data
+ cancelled_B = module.lora_B["cancelled"].weight.data
+
+ # The weights should be approximately zero (they cancel out)
+ assert torch.allclose(cancelled_A, torch.zeros_like(cancelled_A), atol=1e-5), (
+ f"Cancelled A should be ~0, got max abs value {cancelled_A.abs().max()}"
+ )
+ assert torch.allclose(cancelled_B, torch.zeros_like(cancelled_B), atol=1e-5), (
+ f"Cancelled B should be ~0, got max abs value {cancelled_B.abs().max()}"
+ )
+
+ def test_add_weighted_adapter_negative_weight_with_different_scaling(self):
+ # Test negative weights with different scaling factors (lora_alpha)
+ # This edge case ensures negative weights work correctly with different scaling values
+ torch.manual_seed(42)
+ model = MLP()
+
+ # Create two configs with different lora_alpha (different scaling factors)
+ config1 = LoraConfig(
+ r=8,
+ lora_alpha=16, # scaling = 16/8 = 2
+ target_modules=["lin0"],
+ lora_dropout=0.0,
+ bias="none",
+ init_lora_weights=False,
+ )
+ config2 = LoraConfig(
+ r=8,
+ lora_alpha=32, # scaling = 32/8 = 4
+ target_modules=["lin0"],
+ lora_dropout=0.0,
+ bias="none",
+ init_lora_weights=False,
+ )
+
+ model = get_peft_model(model, config1, adapter_name="adapter1")
+ model.add_adapter("adapter2", config2)
+
+ # Merge with negative weight - should handle different scalings correctly
+ model.add_weighted_adapter(
+ adapters=["adapter1", "adapter2"],
+ weights=[0.5, -0.3],
+ adapter_name="merged_diff_scaling",
+ combination_type="linear",
+ )
+
+ # Verify the merged adapter can run forward pass
+ model.set_adapter("merged_diff_scaling")
+ dummy_input = torch.randn(2, 10)
+ output = model(dummy_input)
+ assert output is not None
+
+ def test_multiple_adapters_no_needless_copy_modules_to_save(self):
+ # See 2206
+ # The problem was that we keep a "global" modules_to_save on the model which contains all possible
+ # modules_to_save for each adapter. When the first adapter targets embed_tokens with modules_to_save and the
+ # second adapter targets lm_head, then embed_tokens will create a copy of the original module for the second
+ # adapter, even though it's not needed. The copy still acts as expected but uses unnecessary memory.
+ model_id = "hf-internal-testing/tiny-random-OPTForCausalLM"
+ model = AutoModelForCausalLM.from_pretrained(model_id).to(self.torch_device)
+ config0 = LoraConfig(modules_to_save=["embed_tokens"])
+ config1 = LoraConfig(modules_to_save=["lm_head"])
+ model = get_peft_model(model, config0)
+ model.add_adapter("other", config1)
+
+ lm_head_keys = list(model.base_model.model.lm_head.modules_to_save.keys())
+ assert lm_head_keys == ["other"]
+
+ embed_token_keys = list(model.base_model.model.model.decoder.embed_tokens.modules_to_save.keys())
+ # before the fix, this would be: ['default', 'other']
+ assert embed_token_keys == ["default"]
+
+ def test_existing_model_card(self):
+ # ensure that if there is already a model card, it is not overwritten
+ model = MLP()
+ config = LoraConfig(target_modules=["lin0"])
+ model = get_peft_model(model, config)
+
+ with tempfile.TemporaryDirectory() as tmp_dirname:
+ # create a model card
+ text = "---\nmeta: hello\n---\nThis is a model card\n"
+ with open(os.path.join(tmp_dirname, "README.md"), "w") as f:
+ f.write(text)
+
+ model.save_pretrained(tmp_dirname)
+ with open(os.path.join(tmp_dirname, "README.md")) as f:
+ model_card = f.read()
+
+ assert "library_name: peft" in model_card
+ assert "meta: hello" in model_card
+ assert "This is a model card" in model_card
+
+ def test_non_existing_model_card(self):
+ # ensure that if there is already a model card, it is not overwritten
+ model = MLP()
+ config = LoraConfig(target_modules=["lin0"])
+ model = get_peft_model(model, config)
+
+ with tempfile.TemporaryDirectory() as tmp_dirname:
+ model.save_pretrained(tmp_dirname)
+ with open(os.path.join(tmp_dirname, "README.md")) as f:
+ model_card = f.read()
+
+ assert "library_name: peft" in model_card
+ # rough check that the model card is pre-filled
+ assert len(model_card) > 1000
+
+ @pytest.mark.parametrize("save_embedding_layers", ["auto", True, False])
+ @pytest.mark.parametrize(
+ "peft_config",
+ [
+ (LoraConfig(target_modules=["lin0", "embed_tokens"], init_lora_weights=False)),
+ (LoraConfig(target_modules=r"^embed_tokens", init_lora_weights=False)),
+ ],
+ )
+ def test_save_pretrained_targeting_lora_to_embedding_layer(self, save_embedding_layers, tmp_path, peft_config):
+ model = ModelEmbWithEmbeddingUtils()
+ model = get_peft_model(model, peft_config)
+
+ if save_embedding_layers == "auto":
+ # assert warning
+ msg_start = "Setting `save_embedding_layers` to `True` as embedding layers found in `target_modules`."
+ with pytest.warns(UserWarning, match=msg_start):
+ model.save_pretrained(tmp_path, save_embedding_layers=save_embedding_layers)
+ else:
+ model.save_pretrained(tmp_path, save_embedding_layers=save_embedding_layers)
+
+ state_dict = safe_load_file(tmp_path / "adapter_model.safetensors")
+ contains_embedding = "base_model.model.embed_tokens.base_layer.weight" in state_dict
+
+ if save_embedding_layers in ["auto", True]:
+ assert contains_embedding
+ assert torch.allclose(
+ model.base_model.model.embed_tokens.base_layer.weight,
+ state_dict["base_model.model.embed_tokens.base_layer.weight"],
+ )
+ else:
+ assert not contains_embedding
+
+ @pytest.mark.parametrize("save_embedding_layers", ["auto", True, False])
+ @pytest.mark.parametrize(
+ "peft_config",
+ [
+ (LoraConfig(target_modules=["lin0", "emb"], init_lora_weights=False)),
+ (LoraConfig(target_modules=r"^emb", init_lora_weights=False)),
+ ],
+ )
+ def test_save_pretrained_targeting_lora_to_embedding_layer_non_transformers(
+ self, save_embedding_layers, tmp_path, peft_config
+ ):
+ model = ModelEmbConv1D()
+ model = get_peft_model(model, peft_config)
+
+ if save_embedding_layers is True:
+ with pytest.warns(
+ UserWarning,
+ match=r"Could not identify embedding layer\(s\) because the model is not a 🤗 transformers model\.",
+ ):
+ model.save_pretrained(tmp_path, save_embedding_layers=save_embedding_layers)
+ else:
+ model.save_pretrained(tmp_path, save_embedding_layers=save_embedding_layers)
+
+ state_dict = safe_load_file(tmp_path / "adapter_model.safetensors")
+ assert "base_model.model.emb.base_layer.weight" not in state_dict
+
+ def test_load_resized_embedding_ignore_mismatched_sizes(self):
+ # issue #1605
+ # Make it possible to load a LoRA layer that targets an embedding layer even if the sizes mismatch by passing
+ # ignore_mismatched_sizes=True
+ model = ModelEmbConv1D(emb_size=100)
+ config = LoraConfig(target_modules=["emb", "lin0"], init_lora_weights=False)
+ model = get_peft_model(model, config)
+
+ # note: not using the context manager here because it fails on Windows CI for some reason
+ tmp_dirname = tempfile.mkdtemp()
+ try:
+ model.save_pretrained(tmp_dirname)
+ model = ModelEmbConv1D(emb_size=105)
+
+ # first check that this raises
+ with pytest.raises(RuntimeError) as exc:
+ PeftModel.from_pretrained(model, tmp_dirname)
+ msg = exc.value.args[0]
+ assert "size mismatch" in msg and "100" in msg and "105" in msg
+
+ # does not raise
+ PeftModel.from_pretrained(model, tmp_dirname, ignore_mismatched_sizes=True)
+ finally:
+ try:
+ shutil.rmtree(tmp_dirname)
+ except PermissionError:
+ # windows error
+ pass
+
+ @pytest.mark.parametrize(
+ "config0",
+ [
+ LoraConfig(target_modules=["lin0"], init_lora_weights=False),
+ LoKrConfig(target_modules=["lin0"], init_weights=False),
+ LoHaConfig(target_modules=["lin0"], init_weights=False),
+ AdaLoraConfig(target_modules=["lin0"], init_lora_weights=False, total_step=1),
+ IA3Config(target_modules=["lin0"], feedforward_modules=["lin0"], init_ia3_weights=False),
+ OFTConfig(target_modules=["lin0"], init_weights=False, r=2, oft_block_size=0),
+ BOFTConfig(target_modules=["lin0"], init_weights=False, boft_block_size=2),
+ HRAConfig(target_modules=["lin0"], init_weights=False),
+ BoneConfig(target_modules=["lin0"], init_weights=False, r=2),
+ MissConfig(target_modules=["lin0"], init_weights=False, r=2),
+ ],
+ )
+ def test_adapter_name_makes_no_difference(self, config0):
+ # It should not matter whether we use the default adapter name or a custom one
+ model_cls = MLP
+ input = torch.arange(90).reshape(9, 10).to(self.torch_device)
+
+ # base model
+ torch.manual_seed(0)
+ base_model = model_cls().eval().to(self.torch_device)
+ output_base = base_model(input)
+
+ # default name
+ torch.manual_seed(0)
+ base_model = model_cls().eval().to(self.torch_device)
+ torch.manual_seed(0)
+ peft_model_default = get_peft_model(base_model, config0, adapter_name="default").eval().to(self.torch_device)
+ output_default = peft_model_default(input)
+ sd_default = peft_model_default.state_dict()
+
+ # custom name 1
+ torch.manual_seed(0)
+ base_model = model_cls().eval().to(self.torch_device)
+ torch.manual_seed(0)
+ peft_model_custom1 = get_peft_model(base_model, config0, adapter_name="adapter").eval().to(self.torch_device)
+ output_custom1 = peft_model_custom1(input)
+ sd_custom1 = peft_model_custom1.state_dict()
+
+ # custom name 2
+ torch.manual_seed(0)
+ base_model = model_cls().eval().to(self.torch_device)
+ torch.manual_seed(0)
+ peft_model_custom2 = (
+ get_peft_model(base_model, config0, adapter_name="other-name").eval().to(self.torch_device)
+ )
+ output_custom2 = peft_model_custom2(input)
+ sd_custom2 = peft_model_custom2.state_dict()
+
+ assert len(sd_default) == len(sd_custom1) == len(sd_custom2)
+ for key in sd_default:
+ key1 = key.replace("default", "adapter")
+ key2 = key.replace("default", "other-name")
+ assert key1 in sd_custom1
+ assert key2 in sd_custom2
+ for k0, k1, k2 in zip(sd_default, sd_custom1, sd_custom2):
+ assert torch.allclose(sd_default[k0], sd_custom1[k1])
+ assert torch.allclose(sd_default[k0], sd_custom2[k2])
+
+ assert not torch.allclose(output_base, output_default)
+ assert not torch.allclose(output_base, output_custom1)
+ assert not torch.allclose(output_base, output_custom2)
+ assert torch.allclose(output_custom1, output_custom2)
+ assert torch.allclose(output_default, output_custom1)
+
+ def test_gpt2_dora_merge_and_unload(self):
+ # see https://github.com/huggingface/peft/pull/1588#discussion_r1537914207
+ model = AutoModelForCausalLM.from_pretrained("gpt2")
+ config = LoraConfig(task_type="CAUSAL_LM", use_dora=True)
+ model = get_peft_model(model, config)
+ # should not raise an error
+ model.merge_and_unload()
+
+ def test_gpt2_dora_merge_and_unload_safe_merge(self):
+ # see https://github.com/huggingface/peft/pull/1588#discussion_r1537914207
+ model = AutoModelForCausalLM.from_pretrained("gpt2")
+ config = LoraConfig(task_type="CAUSAL_LM", use_dora=True)
+ model = get_peft_model(model, config)
+ # should not raise an error
+ model.merge_and_unload(safe_merge=True)
+
+ def test_unload_adapter_multihead_attention(self):
+ # MultiheadAttention has special logic for unloading, that logic is covered by this test
+ self._test_unload_adapter(
+ model_id="MHA",
+ config_cls=LoraConfig,
+ config_kwargs={"target_modules": ["mha"], "init_lora_weights": False},
+ )
+
+ def test_dora_save_and_load_remapping(self):
+ # Here we test the refactor of DoRA which changed lora_magnitude_vector from a ParameterDict to a ModuleDict
+ # with a DoraLayer instance. The old parameter is now the "weight" attribute of that layer. Since we want the
+ # state_dict format not to change, we ensure that the ".weight" part of the key is removed.
+ model = AutoModelForCausalLM.from_pretrained("facebook/opt-125m")
+ config = LoraConfig(task_type="CAUSAL_LM", use_dora=True)
+ model = get_peft_model(model, config)
+ state_dict = model.state_dict()
+
+ # sanity check: state dict contains "lora_magnitude_vector.default.weight" keys
+ assert any("lora_magnitude_vector.default.weight" in k for k in state_dict)
+
+ # save the model, check the state dict
+ # note: not using the context manager here because it fails on Windows CI for some reason
+ tmp_dirname = tempfile.mkdtemp()
+ try:
+ model.save_pretrained(tmp_dirname)
+ state_dict_adapter = safe_load_file(os.path.join(tmp_dirname, "adapter_model.safetensors"))
+ # note that in the state dict, the "default" part of the key is removed
+ assert not any("lora_magnitude_vector.weight" in k for k in state_dict_adapter)
+
+ del model
+ loaded = PeftModel.from_pretrained(AutoModelForCausalLM.from_pretrained("facebook/opt-125m"), tmp_dirname)
+ finally:
+ try:
+ shutil.rmtree(tmp_dirname)
+ except PermissionError:
+ # windows error
+ pass
+
+ state_dict_loaded = loaded.state_dict()
+ assert state_dict.keys() == state_dict_loaded.keys()
+ for k in state_dict:
+ assert torch.allclose(state_dict[k], state_dict_loaded[k])
+
+ @pytest.mark.parametrize("with_forward_call", [False, True])
+ def test_mha_gradients_set_correctly(self, with_forward_call):
+ # check for this bug: https://github.com/huggingface/peft/issues/761#issuecomment-1893804738
+ base_model = ModelMha()
+ config = LoraConfig(target_modules=["mha"])
+ model = get_peft_model(base_model, config)
+ model = model.to(self.torch_device)
+
+ if with_forward_call:
+ # after the merge-unmerge roundtrip happening in forward of lora MHA, the base weights should be set to
+ # requires_grad=False
+ inputs = self.prepare_inputs_for_testing()
+ model(**inputs)
+
+ assert model.base_model.model.mha.base_layer.out_proj.base_layer.weight.requires_grad is False
+ assert model.base_model.model.mha.base_layer.in_proj_weight.requires_grad is False
+
+ # _restore_weights used to ignore the gradient, this checks that it is indeed considered
+ model.base_model.model.mha._restore_weights()
+ assert model.base_model.model.mha.base_layer.out_proj.base_layer.weight.requires_grad is False
+ assert model.base_model.model.mha.base_layer.in_proj_weight.requires_grad is False
+
+ model.base_model.model.mha.base_layer.out_proj.base_layer.weight.requires_grad = True
+ model.base_model.model.mha.base_layer.in_proj_weight.requires_grad = True
+ assert model.base_model.model.mha.base_layer.out_proj.base_layer.weight.requires_grad is True
+ assert model.base_model.model.mha.base_layer.in_proj_weight.requires_grad is True
+
+ model.base_model.model.mha._restore_weights()
+ assert model.base_model.model.mha.base_layer.out_proj.base_layer.weight.requires_grad is True
+ assert model.base_model.model.mha.base_layer.in_proj_weight.requires_grad is True
+
+
+class TestMultiRankAdapter:
+ """Tests related to multirank LoRA adapters"""
+
+ def test_multirank(self):
+ config_1 = LoraConfig(
+ r=8,
+ lora_alpha=8,
+ init_lora_weights=False,
+ target_modules=["lin0", "lin1"],
+ )
+ config_2 = LoraConfig(
+ r=8,
+ lora_alpha=8,
+ init_lora_weights=False,
+ target_modules=["lin0", "lin1"],
+ rank_pattern={"lin0": 4},
+ alpha_pattern={"lin0": 4},
+ )
+
+ # Add first adapter
+ model = get_peft_model(MLP(), config_1, adapter_name="first")
+
+ # Add second adapter
+ model.add_adapter("second", config_2)
+
+ # Extract current and expected ranks
+ rank_current = model.lin0.lora_A["second"].weight.shape[0]
+ rank_expected = config_2.rank_pattern["lin0"]
+
+ assert rank_current == rank_expected, f"Rank {rank_current} is not equal to expected {rank_expected}"
+
+ def test_multirank_2(self):
+ rank_pattern = {}
+ alpha_pattern = {}
+ r = 4
+ lora_alpha = 8
+
+ for i in range(10):
+ rank = 64 // (i + 1)
+ for j in range(2):
+ rank_pattern[f"layers.{i}.lin{j}"] = rank
+ alpha_pattern[f"layers.{i}.lin{j}"] = 2 * rank
+
+ config = LoraConfig(
+ r=r,
+ lora_alpha=lora_alpha,
+ init_lora_weights=False,
+ target_modules=["lin0", "lin1"],
+ rank_pattern=rank_pattern,
+ alpha_pattern=alpha_pattern,
+ )
+
+ # Add first adapter
+ model = get_peft_model(DeepMLP(), config, adapter_name="first")
+
+ # Add second adapter
+ model.add_adapter("second", config)
+
+ for adapter in ["first", "second"]:
+ for key, module in model.base_model.model.named_modules():
+ if isinstance(module, BaseTunerLayer):
+ rank_expected = rank_pattern.get(key, r)
+ rank_current = module.lora_A[adapter].weight.shape[0]
+ assert rank_current == rank_expected, (
+ f"Rank {rank_current} is not equal to expected {rank_expected}"
+ )
+
+
+class TestLayerRepr:
+ """Tests related to the repr of adapted models"""
+
+ def test_repr_lora_linear(self):
+ config = LoraConfig(target_modules=["lin0"])
+ model = get_peft_model(MLP(), config)
+ print_output = repr(model.model.lin0)
+ assert print_output.startswith("lora.Linear")
+ assert "in_features=10" in print_output
+ assert "out_features=20" in print_output
+ assert "lora_A" in print_output
+ assert "lora_B" in print_output
+ assert "default" in print_output
+
+ def test_repr_lora_embedding(self):
+ config = LoraConfig(target_modules=["emb"])
+ model = get_peft_model(ModelEmbConv1D(), config)
+ print_output = repr(model.model.emb)
+ assert print_output.startswith("lora.Embedding")
+ assert "100, 5" in print_output
+ assert "lora_embedding_A" in print_output
+ assert "lora_embedding_B" in print_output
+ assert "default" in print_output
+
+ def test_repr_lora_conv1d(self):
+ config = LoraConfig(target_modules=["conv1d"])
+ model = get_peft_model(ModelEmbConv1D(), config)
+ print_output = repr(model.model.conv1d)
+ assert print_output.startswith("lora.Linear")
+ assert "in_features=5" in print_output
+ assert "out_features=1" in print_output
+ assert "lora_A" in print_output
+ assert "lora_B" in print_output
+ assert "default" in print_output
+
+ def test_repr_lora_conv2d(self):
+ config = LoraConfig(target_modules=["conv2d"])
+ model = get_peft_model(ModelConv2D(), config)
+ print_output = repr(model.model.conv2d)
+ assert print_output.startswith("lora.Conv2d")
+ assert "5, 10" in print_output
+ assert "kernel_size=(3, 3)" in print_output
+ assert "stride=(1, 1)" in print_output
+ assert "lora_A" in print_output
+ assert "lora_B" in print_output
+ assert "default" in print_output
+
+ def test_repr_lora_paramwrapper(self):
+ config = LoraConfig(target_parameters=["lin0.weight"])
+ model = get_peft_model(MLP(), config)
+ print_output = repr(model.model.lin0)
+ assert print_output.startswith("lora.ParamWrapper")
+ # important: targeted parameter should be contained:
+ assert "parameter_name='weight'" in print_output
+ assert "in_features=10" in print_output
+ assert "out_features=20" in print_output
+ assert "lora_A" in print_output
+ assert "lora_B" in print_output
+ assert "default" in print_output
+
+
+class TestMultipleActiveAdapters:
+ """
+ A test class to test the functionality of multiple active adapters.
+
+ This is not specifically tied to custom models, it's just easy to test here and testing it on all types of models
+ would be overkill.
+ """
+
+ torch_device = infer_device()
+
+ def prepare_inputs_for_testing(self):
+ X = torch.arange(90).view(9, 10).to(self.torch_device)
+ return {"X": X}
+
+ def set_multiple_active_adapters(self, model, adapter_names):
+ for module in model.modules():
+ if isinstance(module, (BaseTunerLayer, AuxiliaryTrainingWrapper)):
+ module.set_adapter(adapter_names)
+
+ def resolve_model_cls(self, tuner_method):
+ if tuner_method == "lora+trainable_tokens":
+ # for this method we need an Embedding layer to target
+ return ModelEmbConv1D()
+ if tuner_method == "ia3":
+ return MLP(bias=False)
+ return MLP(bias=True)
+
+ @pytest.mark.parametrize(
+ "test_name, tuner_method, config_cls, config_kwargs_1, config_kwargs_2", MULTIPLE_ACTIVE_ADAPTERS_TEST_CASES
+ )
+ def test_multiple_active_adapters_forward(
+ self, test_name, tuner_method, config_cls, config_kwargs_1, config_kwargs_2
+ ):
+ _skip_tests_with_multiple_adapters_with_target_parameters(config_cls, config_kwargs_2)
+
+ torch.manual_seed(0)
+
+ model = self.resolve_model_cls(tuner_method)
+ model = model.to(self.torch_device).eval()
+
+ X = self.prepare_inputs_for_testing()
+
+ config_1 = config_cls(**config_kwargs_1)
+ config_2 = config_cls(**config_kwargs_2)
+
+ peft_model = get_peft_model(model, config_1, adapter_name="adapter_1")
+ peft_model.add_adapter("adapter_2", config_2)
+
+ # the assumption that the output of the combined output of two adapters is != to the output of one
+ # adapter is not true for unmodified trainable tokens as they just mimic the existing embedding matrix.
+ # therefore, we modify the weights so that the adapter weights differs from the embedding weights.
+ #
+ # We do it this way because we have no way to pass something like `init_weights=False` to the token adapter.
+ if "trainable_tokens" in tuner_method:
+ peft_model.emb.token_adapter.trainable_tokens_delta["adapter_1"].data = torch.rand_like(
+ peft_model.emb.token_adapter.trainable_tokens_delta["adapter_1"].data
+ )
+ peft_model.emb.token_adapter.trainable_tokens_delta["adapter_2"].data = torch.rand_like(
+ peft_model.emb.token_adapter.trainable_tokens_delta["adapter_2"].data
+ )
+
+ # set adapter_1
+ peft_model.set_adapter("adapter_1")
+ adapter_1_output = peft_model(**X)
+
+ # set adapter_2
+ peft_model.set_adapter("adapter_2")
+ adapter_2_output = peft_model(**X)
+
+ # set ["adapter_1", "adapter_2"]
+ self.set_multiple_active_adapters(peft_model, ["adapter_1", "adapter_2"])
+ combined_output = peft_model(**X)
+
+ assert not torch.allclose(adapter_1_output, adapter_2_output, atol=1e-5)
+ assert not torch.allclose(adapter_1_output, combined_output, atol=1e-5)
+ assert not torch.allclose(adapter_2_output, combined_output, atol=1e-5)
+
+ if (tuner_method == "lora") and not (config_1.target_parameters or config_2.target_parameters):
+ # Create a weighted adapter combining both adapters and check that its output is same as setting multiple
+ # active adapters. `target_parameters` is not supported.
+ peft_model.add_weighted_adapter(
+ ["adapter_1", "adapter_2"], [1.0, 1.0], "new_combined_adapter", combination_type="cat"
+ )
+ peft_model.set_adapter("new_combined_adapter")
+ new_combined_output = peft_model(**X)
+ assert torch.allclose(new_combined_output, combined_output, atol=1e-5)
+
+ @pytest.mark.parametrize(
+ "test_name, tuner_method, config_cls, config_kwargs_1, config_kwargs_2", MULTIPLE_ACTIVE_ADAPTERS_TEST_CASES
+ )
+ def test_multiple_active_adapters_merge_and_unmerge(
+ self, test_name, tuner_method, config_cls, config_kwargs_1, config_kwargs_2
+ ):
+ _skip_tests_with_multiple_adapters_with_target_parameters(config_cls, config_kwargs_2)
+
+ torch.manual_seed(0)
+
+ model = self.resolve_model_cls(tuner_method)
+ model = model.to(self.torch_device).eval()
+
+ X = self.prepare_inputs_for_testing()
+ base_output = model(**X)
+
+ config_1 = config_cls(**config_kwargs_1)
+ config_2 = config_cls(**config_kwargs_2)
+
+ peft_model = get_peft_model(model, config_1, adapter_name="adapter_1")
+ peft_model.add_adapter("adapter_2", config_2)
+
+ # set ["adapter_1", "adapter_2"]
+ self.set_multiple_active_adapters(peft_model, ["adapter_1", "adapter_2"])
+ combined_output = peft_model(**X)
+
+ peft_model.merge_adapter()
+ merged_combined_output = peft_model(**X)
+ assert torch.allclose(merged_combined_output, combined_output, atol=1e-4)
+
+ peft_model.unmerge_adapter()
+
+ with peft_model.disable_adapter():
+ disabled_adapter_output = peft_model(**X)
+
+ assert torch.allclose(disabled_adapter_output, base_output, atol=1e-4)
+
+ @pytest.mark.parametrize(
+ "test_name, tuner_method, config_cls, config_kwargs_1, config_kwargs_2", MULTIPLE_ACTIVE_ADAPTERS_TEST_CASES
+ )
+ def test_merge_layers_multi(self, test_name, tuner_method, config_cls, config_kwargs_1, config_kwargs_2):
+ _skip_tests_with_multiple_adapters_with_target_parameters(config_cls, config_kwargs_2)
+
+ torch.manual_seed(0)
+
+ model = self.resolve_model_cls(tuner_method)
+ model = model.to(self.torch_device).eval()
+
+ config_1 = config_cls(**config_kwargs_1)
+ config_2 = config_cls(**config_kwargs_2)
+
+ model = get_peft_model(model, config_1)
+
+ # the assumption that the output of the combined output of two adapters is != to the output of one
+ # adapter is not true for unmodified trainable tokens as they just mimic the existing embedding matrix.
+ # therefore, we modify the weights so that the adapter weights differs from the embedding weights. in this
+ # case we even use 20*rand to be very distinct to adapter 2 since we're comparing outputs and not embeddings
+ # with rather high tolerance values. this is also the reason why `init_weights` is not sufficient here and
+ # when using `.trainable_token_indices` we do not have the utility of `init_weights` anyway.
+ if "trainable_tokens" in tuner_method:
+ model.emb.token_adapter.trainable_tokens_delta["default"].data = 20 * torch.rand_like(
+ model.emb.token_adapter.trainable_tokens_delta["default"].data
+ )
+
+ dummy_input = self.prepare_inputs_for_testing()
+ model.eval()
+
+ with torch.inference_mode():
+ logits_adapter_1 = model(**dummy_input)[0]
+
+ model.add_adapter("adapter-2", config_2)
+ model.set_adapter("adapter-2")
+
+ # same as above but for adapter 2
+ if "trainable_tokens" in tuner_method:
+ model.emb.token_adapter.trainable_tokens_delta["adapter-2"].data = 2 * torch.rand_like(
+ model.emb.token_adapter.trainable_tokens_delta["adapter-2"].data
+ )
+
+ model.eval()
+
+ with torch.inference_mode():
+ logits_adapter_2 = model(**dummy_input)[0]
+
+ assert not torch.allclose(logits_adapter_1, logits_adapter_2, atol=1e-3, rtol=1e-3)
+
+ model.set_adapter("default")
+
+ with torch.inference_mode():
+ logits_adapter_1_after_set = model(**dummy_input)[0]
+
+ assert torch.allclose(logits_adapter_1_after_set, logits_adapter_1, atol=1e-3, rtol=1e-3)
+
+ model_copy = copy.deepcopy(model)
+ model_copy_2 = copy.deepcopy(model)
+ model_merged_all = model.merge_and_unload(adapter_names=["adapter-2", "default"])
+
+ with torch.inference_mode():
+ logits_merged_all = model_merged_all(**dummy_input)[0]
+
+ assert not torch.allclose(logits_merged_all, logits_adapter_2, atol=1e-3, rtol=1e-3)
+ assert not torch.allclose(logits_merged_all, logits_adapter_1, atol=1e-3, rtol=1e-3)
+
+ model_merged_adapter_2 = model_copy.merge_and_unload(adapter_names=["adapter-2"])
+
+ with torch.inference_mode():
+ logits_merged_adapter_2 = model_merged_adapter_2(**dummy_input)[0]
+
+ assert torch.allclose(logits_merged_adapter_2, logits_adapter_2, atol=1e-3, rtol=1e-3)
+
+ model_merged_adapter_default = model_copy_2.merge_and_unload(adapter_names=["default"])
+
+ with torch.inference_mode():
+ logits_merged_adapter_default = model_merged_adapter_default(**dummy_input)[0]
+
+ assert torch.allclose(logits_merged_adapter_default, logits_adapter_1, atol=1e-3, rtol=1e-3)
+
+
+class TestRequiresGrad:
+ """Test that requires_grad is set correctly in specific circumstances
+
+ # See issue #899.
+
+ This is not specifically tied to custom models, it's just easy to test here and testing it on all types of models
+ would be overkill.
+
+ """
+
+ def check_requires_grad(self, model, *params_expected: str):
+ # Check that only the given parameters have requires_grad=True, and all others have requires_grad=False.
+ # Calling without arguments besides the model means that all parameters should have requires_grad=False.
+ params_with_requires_grad = [name for name, param in model.named_parameters() if param.requires_grad]
+ diff = set(params_expected).symmetric_difference(set(params_with_requires_grad))
+ msg = f"Expected {params_expected} to require gradients, got {params_with_requires_grad}"
+ assert len(diff) == 0, msg
+
+ def test_requires_grad_modules_to_save_default(self):
+ config = LoraConfig(target_modules=["lin0"], modules_to_save=["lin1"])
+ peft_model = get_peft_model(MLP(), config)
+
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.lin1.modules_to_save.default.weight",
+ "base_model.model.lin1.modules_to_save.default.bias",
+ "base_model.model.lin0.lora_A.default.weight",
+ "base_model.model.lin0.lora_B.default.weight",
+ )
+
+ def test_requires_grad_modules_to_save_disabling(self):
+ config = LoraConfig(target_modules=["lin0"], modules_to_save=["lin1"])
+ peft_model = get_peft_model(MLP(), config)
+
+ # when disabling the adapter, the original module's grad should be enabled and vice versa
+ peft_model.disable_adapter_layers()
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.lin1.original_module.weight",
+ "base_model.model.lin1.original_module.bias",
+ )
+
+ # when re-enabling the adapter, the original module's grad should be disabled and vice versa
+ peft_model.enable_adapter_layers()
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.lin1.modules_to_save.default.weight",
+ "base_model.model.lin1.modules_to_save.default.bias",
+ "base_model.model.lin0.lora_A.default.weight",
+ "base_model.model.lin0.lora_B.default.weight",
+ )
+
+ # when using the disable_adapter context, the original module's grad should be enabled and vice versa
+ with peft_model.disable_adapter():
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.lin1.original_module.weight",
+ "base_model.model.lin1.original_module.bias",
+ )
+
+ # after context is exited, return to the previous state
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.lin1.modules_to_save.default.weight",
+ "base_model.model.lin1.modules_to_save.default.bias",
+ "base_model.model.lin0.lora_A.default.weight",
+ "base_model.model.lin0.lora_B.default.weight",
+ )
+
+ def test_requires_grad_modules_to_save_multiple_adapters(self):
+ config0 = LoraConfig(target_modules=["lin0"], modules_to_save=["lin1"])
+ peft_model = get_peft_model(MLP(), config0)
+
+ config1 = LoraConfig(target_modules=["lin0"], modules_to_save=["lin1"])
+ peft_model.add_adapter("adapter1", config1)
+
+ # active adapter is still "default"
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.lin1.modules_to_save.default.weight",
+ "base_model.model.lin1.modules_to_save.default.bias",
+ "base_model.model.lin0.lora_A.default.weight",
+ "base_model.model.lin0.lora_B.default.weight",
+ )
+
+ # set config0 as active, should not change anything
+ peft_model.set_adapter("default")
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.lin1.modules_to_save.default.weight",
+ "base_model.model.lin1.modules_to_save.default.bias",
+ "base_model.model.lin0.lora_A.default.weight",
+ "base_model.model.lin0.lora_B.default.weight",
+ )
+
+ # set config1 as active, should lead to adapter1 requiring grad
+ peft_model.set_adapter("adapter1")
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.lin1.modules_to_save.adapter1.weight",
+ "base_model.model.lin1.modules_to_save.adapter1.bias",
+ "base_model.model.lin0.lora_A.adapter1.weight",
+ "base_model.model.lin0.lora_B.adapter1.weight",
+ )
+
+ def test_requires_grad_lora_different_targets(self):
+ # test two different LoRA adapters that target different modules
+ config0 = LoraConfig(target_modules=["lin0"])
+ peft_model = get_peft_model(MLP(), config0)
+
+ config1 = LoraConfig(target_modules=["lin1"])
+ peft_model.add_adapter("adapter1", config1)
+
+ # active adapter is still "default"
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.lin0.lora_A.default.weight",
+ "base_model.model.lin0.lora_B.default.weight",
+ )
+
+ # set config0 as active, should not change anything
+ peft_model.set_adapter("default")
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.lin0.lora_A.default.weight",
+ "base_model.model.lin0.lora_B.default.weight",
+ )
+
+ # change activate adapter to adapter1
+ peft_model.set_adapter("adapter1")
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.lin1.lora_A.adapter1.weight",
+ "base_model.model.lin1.lora_B.adapter1.weight",
+ )
+
+ # disable all adapters
+ with peft_model.disable_adapter():
+ self.check_requires_grad(peft_model)
+
+ # after context is exited, return to the previous state
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.lin1.lora_A.adapter1.weight",
+ "base_model.model.lin1.lora_B.adapter1.weight",
+ )
+
+ def test_requires_grad_lora_same_targets(self):
+ # same as previous test, except that LoRA adapters target the same layer
+ config0 = LoraConfig(target_modules=["lin0"])
+ peft_model = get_peft_model(MLP(), config0)
+
+ config1 = LoraConfig(target_modules=["lin0"])
+ peft_model.add_adapter("adapter1", config1)
+
+ # active adapter is still "default"
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.lin0.lora_A.default.weight",
+ "base_model.model.lin0.lora_B.default.weight",
+ )
+
+ # set config0 as active, should not change anything
+ peft_model.set_adapter("default")
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.lin0.lora_A.default.weight",
+ "base_model.model.lin0.lora_B.default.weight",
+ )
+
+ # change activate adapter to adapter1
+ peft_model.set_adapter("adapter1")
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.lin0.lora_A.adapter1.weight",
+ "base_model.model.lin0.lora_B.adapter1.weight",
+ )
+
+ # disable all adapters
+ with peft_model.disable_adapter():
+ self.check_requires_grad(peft_model)
+
+ # after context is exited, return to the previous state
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.lin0.lora_A.adapter1.weight",
+ "base_model.model.lin0.lora_B.adapter1.weight",
+ )
+
+ def test_requires_grad_ia3_different_targets(self):
+ # test two different IA3 adapters that target different modules
+ config0 = IA3Config(target_modules=["lin0"], feedforward_modules=["lin0"])
+ peft_model = get_peft_model(MLP(), config0)
+
+ config1 = IA3Config(target_modules=["lin1"], feedforward_modules=["lin1"])
+ peft_model.add_adapter("adapter1", config1)
+
+ # active adapter is still "default"
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.lin0.ia3_l.default",
+ )
+
+ # set config0 as active, should not change anything
+ peft_model.set_adapter("default")
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.lin0.ia3_l.default",
+ )
+
+ # change activate adapter to adapter1
+ peft_model.set_adapter("adapter1")
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.lin1.ia3_l.adapter1",
+ )
+
+ # disable all adapters
+ with peft_model.disable_adapter():
+ self.check_requires_grad(peft_model)
+
+ # after context is exited, return to the previous state
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.lin1.ia3_l.adapter1",
+ )
+
+ def test_requires_grad_ia3_same_targets(self):
+ # same as previous test, except that IA3 adapters target the same layer
+ config0 = IA3Config(target_modules=["lin0"], feedforward_modules=["lin0"])
+ peft_model = get_peft_model(MLP(), config0)
+
+ config1 = IA3Config(target_modules=["lin0"], feedforward_modules=["lin0"])
+ peft_model.add_adapter("adapter1", config1)
+
+ # active adapter is still "default"
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.lin0.ia3_l.default",
+ )
+
+ # set config0 as active, should not change anything
+ peft_model.set_adapter("default")
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.lin0.ia3_l.default",
+ )
+
+ # change activate adapter to adapter1
+ peft_model.set_adapter("adapter1")
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.lin0.ia3_l.adapter1",
+ )
+
+ # disable all adapters
+ with peft_model.disable_adapter():
+ self.check_requires_grad(peft_model)
+
+ # after context is exited, return to the previous state
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.lin0.ia3_l.adapter1",
+ )
+
+ @pytest.mark.xfail(strict=True)
+ def test_requires_grad_adalora_different_targets(self):
+ # test two different AdaLora adapters that target different modules
+
+ # Note: This test is expected to fail because first loading one adapter, then the next adapter with
+ # inference_mode=True incorrectly leads to the requires_grad of the first adapter being turned to False. This is
+ # of course not desired but has yet to be fixed. In practice, it's unlikely that a user would pass
+ # inference_mode=True for add_adapter, this flag is mostly being used when calling PeftModel.from_pretrained, so
+ # we accept this issue for now. Note that only for AdaLoRA do we even need to pass inference_mode=True here,
+ # other PEFT methods don't require this.
+ config0 = AdaLoraConfig(target_modules=["lin0"], total_step=1)
+ peft_model = get_peft_model(MLP(), config0)
+
+ # note: AdaLoRA cannot have more than 1 trainable active adapter, hence enable inference_mode
+ config1 = AdaLoraConfig(target_modules=["lin1"], total_step=1, inference_mode=True)
+ peft_model.add_adapter("adapter1", config1)
+
+ # active adapter is still "default"
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.lin0.lora_A.default",
+ "base_model.model.lin0.lora_B.default",
+ "base_model.model.lin0.lora_E.default",
+ )
+
+ # set config0 as active, should not change anything
+ peft_model.set_adapter("default")
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.lin0.lora_A.default",
+ "base_model.model.lin0.lora_B.default",
+ "base_model.model.lin0.lora_E.default",
+ )
+
+ # change activate adapter to adapter1
+ peft_model.set_adapter("adapter1")
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.lin1.lora_A.adapter1",
+ "base_model.model.lin1.lora_B.adapter1",
+ "base_model.model.lin1.lora_E.adapter1",
+ )
+
+ # disable all adapters
+ with peft_model.disable_adapter():
+ self.check_requires_grad(peft_model)
+
+ # after context is exited, return to the previous state
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.lin1.lora_A.adapter1",
+ "base_model.model.lin1.lora_B.adapter1",
+ "base_model.model.lin1.lora_E.adapter1",
+ )
+
+ @pytest.mark.xfail(strict=True)
+ def test_requires_grad_adalora_same_targets(self):
+ # same as previous test, except that AdaLora adapters target the same layer
+
+ # Note: This test is expected to fail because first loading one adapter, then the next adapter with
+ # inference_mode=True incorrectly leads to the requires_grad of the first adapter being turned to False. This is
+ # of course not desired but has yet to be fixed. In practice, it's unlikely that a user would pass
+ # inference_mode=True for add_adapter, this flag is mostly being used when calling PeftModel.from_pretrained, so
+ # we accept this issue for now. Note that only for AdaLoRA do we even need to pass inference_mode=True here,
+ # other PEFT methods don't require this.
+ config0 = AdaLoraConfig(target_modules=["lin0"], total_step=1)
+ peft_model = get_peft_model(MLP(), config0)
+
+ # note: AdaLoRA cannot have more than 1 trainable active adapter, hence enable inference_mode
+ config1 = AdaLoraConfig(target_modules=["lin0"], total_step=1, inference_mode=True)
+ peft_model.add_adapter("adapter1", config1)
+
+ # active adapter is still "default"
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.lin0.lora_A.default",
+ "base_model.model.lin0.lora_B.default",
+ "base_model.model.lin0.lora_E.default",
+ )
+
+ # set config0 as active, should not change anything
+ peft_model.set_adapter("default")
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.lin0.lora_A.default",
+ "base_model.model.lin0.lora_B.default",
+ "base_model.model.lin0.lora_E.default",
+ )
+
+ # change activate adapter to adapter1
+ peft_model.set_adapter("adapter1")
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.lin0.lora_A.adapter1",
+ "base_model.model.lin0.lora_B.adapter1",
+ "base_model.model.lin0.lora_E.adapter1",
+ )
+
+ # disable all adapters
+ with peft_model.disable_adapter():
+ self.check_requires_grad(peft_model)
+
+ # after context is exited, return to the previous state
+ peft_model.set_adapter("adapter1")
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.lin0.lora_A.adapter1",
+ "base_model.model.lin0.lora_B.adapter1",
+ "base_model.model.lin0.lora_E.adapter1",
+ )
+
+ def test_requires_grad_lora_conv2d(self):
+ # test two different LoRA adapters that target different modules
+ config0 = LoraConfig(target_modules=["conv2d"])
+ peft_model = get_peft_model(ModelConv2D(), config0)
+
+ config1 = LoraConfig(target_modules=["lin0"])
+ peft_model.add_adapter("adapter1", config1)
+
+ # active adapter is still "default"
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.conv2d.lora_A.default.weight",
+ "base_model.model.conv2d.lora_B.default.weight",
+ )
+
+ # set config0 as active, should not change anything
+ peft_model.set_adapter("default")
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.conv2d.lora_A.default.weight",
+ "base_model.model.conv2d.lora_B.default.weight",
+ )
+
+ # change activate adapter to adapter1
+ peft_model.set_adapter("adapter1")
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.lin0.lora_A.adapter1.weight",
+ "base_model.model.lin0.lora_B.adapter1.weight",
+ )
+
+ # disable all adapters
+ with peft_model.disable_adapter():
+ self.check_requires_grad(peft_model)
+
+ # after context is exited, return to the previous state
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.lin0.lora_A.adapter1.weight",
+ "base_model.model.lin0.lora_B.adapter1.weight",
+ )
+
+ def test_requires_grad_lora_emb_conv1d(self):
+ # test two different LoRA adapters that target different modules
+ config0 = LoraConfig(target_modules=["conv1d"])
+ peft_model = get_peft_model(ModelEmbConv1D(), config0)
+
+ config1 = LoraConfig(target_modules=["emb"])
+ peft_model.add_adapter("adapter1", config1)
+
+ # active adapter is still "default"
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.conv1d.lora_A.default.weight",
+ "base_model.model.conv1d.lora_B.default.weight",
+ )
+
+ # set config0 as active, should not change anything
+ peft_model.set_adapter("default")
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.conv1d.lora_A.default.weight",
+ "base_model.model.conv1d.lora_B.default.weight",
+ )
+
+ # change activate adapter to adapter1
+ peft_model.set_adapter("adapter1")
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.emb.lora_embedding_A.adapter1",
+ "base_model.model.emb.lora_embedding_B.adapter1",
+ )
+
+ # disable all adapters
+ with peft_model.disable_adapter():
+ self.check_requires_grad(peft_model)
+
+ # after context is exited, return to the previous state
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.emb.lora_embedding_A.adapter1",
+ "base_model.model.emb.lora_embedding_B.adapter1",
+ )
+
+ def test_requires_grad_ia3_conv1d(self):
+ # test two different LoRA adapters that target different modules
+ config0 = IA3Config(target_modules=["conv1d"], feedforward_modules=[])
+ peft_model = get_peft_model(ModelEmbConv1D(), config0)
+
+ config1 = IA3Config(target_modules=["lin0"], feedforward_modules=["lin0"])
+ peft_model.add_adapter("adapter1", config1)
+
+ # active adapter is still "default"
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.conv1d.ia3_l.default",
+ )
+
+ # set config0 as active, should not change anything
+ peft_model.set_adapter("default")
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.conv1d.ia3_l.default",
+ )
+
+ # change activate adapter to adapter1
+ peft_model.set_adapter("adapter1")
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.lin0.ia3_l.adapter1",
+ )
+
+ # disable all adapters
+ with peft_model.disable_adapter():
+ self.check_requires_grad(peft_model)
+
+ # after context is exited, return to the previous state
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.lin0.ia3_l.adapter1",
+ )
+
+ def test_requires_grad_ia3_conv2d(self):
+ # test two different LoRA adapters that target different modules
+ config0 = IA3Config(target_modules=["conv2d"], feedforward_modules=["conv2d"])
+ peft_model = get_peft_model(ModelConv2D(), config0)
+
+ config1 = IA3Config(target_modules=["lin0"], feedforward_modules=[])
+ peft_model.add_adapter("adapter1", config1)
+
+ # active adapter is still "default"
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.conv2d.ia3_l.default",
+ )
+
+ # set config0 as active, should not change anything
+ peft_model.set_adapter("default")
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.conv2d.ia3_l.default",
+ )
+
+ # change activate adapter to adapter1
+ peft_model.set_adapter("adapter1")
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.lin0.ia3_l.adapter1",
+ )
+
+ # disable all adapters
+ with peft_model.disable_adapter():
+ self.check_requires_grad(peft_model)
+
+ # after context is exited, return to the previous state
+ peft_model.set_adapter("adapter1")
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.lin0.ia3_l.adapter1",
+ )
+
+ def test_requires_grad_loha_different_targets(self):
+ # test two different LoHa adapters that target different modules
+ config0 = LoHaConfig(target_modules=["lin0"])
+ peft_model = get_peft_model(MLP(), config0)
+
+ config1 = LoHaConfig(target_modules=["lin1"])
+ peft_model.add_adapter("adapter1", config1)
+
+ # active adapter is still "default"
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.lin0.hada_w1_a.default",
+ "base_model.model.lin0.hada_w1_b.default",
+ "base_model.model.lin0.hada_w2_a.default",
+ "base_model.model.lin0.hada_w2_b.default",
+ )
+
+ # set config0 as active, should not change anything
+ peft_model.set_adapter("default")
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.lin0.hada_w1_a.default",
+ "base_model.model.lin0.hada_w1_b.default",
+ "base_model.model.lin0.hada_w2_a.default",
+ "base_model.model.lin0.hada_w2_b.default",
+ )
+
+ # change activate pter to pter1
+ peft_model.set_adapter("adapter1")
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.lin1.hada_w1_a.adapter1",
+ "base_model.model.lin1.hada_w1_b.adapter1",
+ "base_model.model.lin1.hada_w2_a.adapter1",
+ "base_model.model.lin1.hada_w2_b.adapter1",
+ )
+
+ # disable all pters
+ with peft_model.disable_adapter():
+ self.check_requires_grad(peft_model)
+
+ # after context is exited, return to the previous state
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.lin1.hada_w1_a.adapter1",
+ "base_model.model.lin1.hada_w1_b.adapter1",
+ "base_model.model.lin1.hada_w2_a.adapter1",
+ "base_model.model.lin1.hada_w2_b.adapter1",
+ )
+
+ def test_requires_grad_loha_same_targets(self):
+ # same as previous test, except that LoHa adapters target the same layer
+ config0 = LoHaConfig(target_modules=["lin0"])
+ peft_model = get_peft_model(MLP(), config0)
+
+ config1 = LoHaConfig(target_modules=["lin0"])
+ peft_model.add_adapter("adapter1", config1)
+
+ # active adapter is still "default"
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.lin0.hada_w1_a.default",
+ "base_model.model.lin0.hada_w1_b.default",
+ "base_model.model.lin0.hada_w2_a.default",
+ "base_model.model.lin0.hada_w2_b.default",
+ )
+
+ # set config0 as active, should not change anything
+ peft_model.set_adapter("default")
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.lin0.hada_w1_a.default",
+ "base_model.model.lin0.hada_w1_b.default",
+ "base_model.model.lin0.hada_w2_a.default",
+ "base_model.model.lin0.hada_w2_b.default",
+ )
+
+ # change activate adapter to adapter1
+ peft_model.set_adapter("adapter1")
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.lin0.hada_w1_a.adapter1",
+ "base_model.model.lin0.hada_w1_b.adapter1",
+ "base_model.model.lin0.hada_w2_a.adapter1",
+ "base_model.model.lin0.hada_w2_b.adapter1",
+ )
+
+ # disable all adapters
+ with peft_model.disable_adapter():
+ self.check_requires_grad(peft_model)
+
+ # after context is exited, return to the previous state
+ peft_model.set_adapter("adapter1")
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.lin0.hada_w1_a.adapter1",
+ "base_model.model.lin0.hada_w1_b.adapter1",
+ "base_model.model.lin0.hada_w2_a.adapter1",
+ "base_model.model.lin0.hada_w2_b.adapter1",
+ )
+
+ def test_requires_grad_lokr_different_targets(self):
+ # test two different LoKr adapters that target different modules
+ config0 = LoKrConfig(target_modules=["lin0"])
+ peft_model = get_peft_model(MLP(), config0)
+
+ config1 = LoKrConfig(target_modules=["lin1"])
+ peft_model.add_adapter("adapter1", config1)
+
+ # active adapter is still "default"
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.lin0.lokr_w1.default",
+ "base_model.model.lin0.lokr_w2.default",
+ )
+
+ # set config0 as active, should not change anything
+ peft_model.set_adapter("default")
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.lin0.lokr_w1.default",
+ "base_model.model.lin0.lokr_w2.default",
+ )
+
+ # change activate pter to pter1
+ peft_model.set_adapter("adapter1")
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.lin1.lokr_w1.adapter1",
+ "base_model.model.lin1.lokr_w2.adapter1",
+ )
+
+ # disable all pters
+ with peft_model.disable_adapter():
+ self.check_requires_grad(peft_model)
+
+ # after context is exited, return to the previous state
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.lin1.lokr_w1.adapter1",
+ "base_model.model.lin1.lokr_w2.adapter1",
+ )
+
+ def test_requires_grad_lokr_same_targets(self):
+ # same as previous test, except that LoKr adapters target the same layer
+ config0 = LoKrConfig(target_modules=["lin0"])
+ peft_model = get_peft_model(MLP(), config0)
+
+ config1 = LoKrConfig(target_modules=["lin0"])
+ peft_model.add_adapter("adapter1", config1)
+
+ # active adapter is still "default"
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.lin0.lokr_w1.default",
+ "base_model.model.lin0.lokr_w2.default",
+ )
+
+ # set config0 as active, should not change anything
+ peft_model.set_adapter("default")
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.lin0.lokr_w1.default",
+ "base_model.model.lin0.lokr_w2.default",
+ )
+
+ # change activate adapter to adapter1
+ peft_model.set_adapter("adapter1")
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.lin0.lokr_w1.adapter1",
+ "base_model.model.lin0.lokr_w2.adapter1",
+ )
+
+ # disable all adapters
+ with peft_model.disable_adapter():
+ self.check_requires_grad(peft_model)
+
+ # after context is exited, return to the previous state
+ peft_model.set_adapter("adapter1")
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.lin0.lokr_w1.adapter1",
+ "base_model.model.lin0.lokr_w2.adapter1",
+ )
+
+ def test_requires_grad_oft_different_targets(self):
+ # test two different OFT adapters that target different modules
+ config0 = OFTConfig(target_modules=["lin0"], r=2, oft_block_size=0)
+ peft_model = get_peft_model(MLP(), config0)
+
+ config1 = OFTConfig(target_modules=["lin1"], r=2, oft_block_size=0)
+ peft_model.add_adapter("adapter1", config1)
+
+ # active adapter is still "default"
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.lin0.oft_R.default.weight",
+ )
+
+ # set config0 as active, should not change anything
+ peft_model.set_adapter("default")
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.lin0.oft_R.default.weight",
+ )
+
+ # change activate pter to pter1
+ peft_model.set_adapter("adapter1")
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.lin1.oft_R.adapter1.weight",
+ )
+
+ # disable all pters
+ with peft_model.disable_adapter():
+ self.check_requires_grad(peft_model)
+
+ # after context is exited, return to the previous state
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.lin1.oft_R.adapter1.weight",
+ )
+
+ def test_requires_grad_oft_same_targets(self):
+ # same as previous test, except that OFT adapters target the same layer
+ config0 = OFTConfig(target_modules=["lin0"], r=2, oft_block_size=0)
+ peft_model = get_peft_model(MLP(), config0)
+
+ config1 = OFTConfig(target_modules=["lin0"], r=2, oft_block_size=0)
+ peft_model.add_adapter("adapter1", config1)
+
+ # active adapter is still "default"
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.lin0.oft_R.default.weight",
+ )
+
+ # set config0 as active, should not change anything
+ peft_model.set_adapter("default")
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.lin0.oft_R.default.weight",
+ )
+
+ # change activate adapter to adapter1
+ peft_model.set_adapter("adapter1")
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.lin0.oft_R.adapter1.weight",
+ )
+
+ # disable all adapters
+ with peft_model.disable_adapter():
+ self.check_requires_grad(peft_model)
+
+ # after context is exited, return to the previous state
+ peft_model.set_adapter("adapter1")
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.lin0.oft_R.adapter1.weight",
+ )
+
+ def test_requires_grad_hra_different_targets(self):
+ # test two different HRA adapters that target different modules
+ config0 = HRAConfig(target_modules=["lin0"])
+ peft_model = get_peft_model(MLP(), config0)
+
+ config1 = HRAConfig(target_modules=["lin1"])
+ peft_model.add_adapter("adapter1", config1)
+
+ # active adapter is still "default"
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.lin0.hra_u.default",
+ )
+
+ # set config0 as active, should not change anything
+ peft_model.set_adapter("default")
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.lin0.hra_u.default",
+ )
+
+ # change activate pter to pter1
+ peft_model.set_adapter("adapter1")
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.lin1.hra_u.adapter1",
+ )
+
+ # disable all pters
+ with peft_model.disable_adapter():
+ self.check_requires_grad(peft_model)
+
+ # after context is exited, return to the previous state
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.lin1.hra_u.adapter1",
+ )
+
+ def test_requires_grad_hra_same_targets(self):
+ # same as previous test, except that HRA adapters target the same layer
+ config0 = HRAConfig(target_modules=["lin0"])
+ peft_model = get_peft_model(MLP(), config0)
+
+ config1 = HRAConfig(target_modules=["lin0"])
+ peft_model.add_adapter("adapter1", config1)
+
+ # active adapter is still "default"
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.lin0.hra_u.default",
+ )
+
+ # set config0 as active, should not change anything
+ peft_model.set_adapter("default")
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.lin0.hra_u.default",
+ )
+
+ # change activate adapter to adapter1
+ peft_model.set_adapter("adapter1")
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.lin0.hra_u.adapter1",
+ )
+
+ # disable all adapters
+ with peft_model.disable_adapter():
+ self.check_requires_grad(peft_model)
+
+ # after context is exited, return to the previous state
+ peft_model.set_adapter("adapter1")
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.lin0.hra_u.adapter1",
+ )
+
+ def test_requires_grad_bone_different_targets(self):
+ # test two different HRA adapters that target different modules
+ config0 = BoneConfig(target_modules=["lin0"], r=2)
+ peft_model = get_peft_model(MLP(), config0)
+
+ config1 = BoneConfig(target_modules=["lin1"], r=2)
+ peft_model.add_adapter("adapter1", config1)
+
+ # active adapter is still "default"
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.lin0.bone_block.default",
+ )
+
+ # set config0 as active, should not change anything
+ peft_model.set_adapter("default")
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.lin0.bone_block.default",
+ )
+
+ # change activate pter to pter1
+ peft_model.set_adapter("adapter1")
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.lin1.bone_block.adapter1",
+ )
+
+ # disable all pters
+ with peft_model.disable_adapter():
+ self.check_requires_grad(peft_model)
+
+ # after context is exited, return to the previous state
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.lin1.bone_block.adapter1",
+ )
+
+ def test_requires_grad_bone_same_targets(self):
+ # same as previous test, except that HRA adapters target the same layer
+ config0 = BoneConfig(target_modules=["lin0"], r=2)
+ peft_model = get_peft_model(MLP(), config0)
+
+ config1 = BoneConfig(target_modules=["lin0"], r=2)
+ peft_model.add_adapter("adapter1", config1)
+
+ # active adapter is still "default"
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.lin0.bone_block.default",
+ )
+
+ # set config0 as active, should not change anything
+ peft_model.set_adapter("default")
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.lin0.bone_block.default",
+ )
+
+ # change activate adapter to adapter1
+ peft_model.set_adapter("adapter1")
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.lin0.bone_block.adapter1",
+ )
+
+ # disable all adapters
+ with peft_model.disable_adapter():
+ self.check_requires_grad(peft_model)
+
+ # after context is exited, return to the previous state
+ peft_model.set_adapter("adapter1")
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.lin0.bone_block.adapter1",
+ )
+
+ def test_requires_grad_miss_different_targets(self):
+ # test two different HRA adapters that target different modules
+ config0 = MissConfig(target_modules=["lin0"], r=2)
+ peft_model = get_peft_model(MLP(), config0)
+
+ config1 = MissConfig(target_modules=["lin1"], r=2)
+ peft_model.add_adapter("adapter1", config1)
+
+ # active adapter is still "default"
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.lin0.miss_block.default",
+ )
+
+ # set config0 as active, should not change anything
+ peft_model.set_adapter("default")
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.lin0.miss_block.default",
+ )
+
+ # change activate pter to pter1
+ peft_model.set_adapter("adapter1")
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.lin1.miss_block.adapter1",
+ )
+
+ # disable all pters
+ with peft_model.disable_adapter():
+ self.check_requires_grad(peft_model)
+
+ # after context is exited, return to the previous state
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.lin1.miss_block.adapter1",
+ )
+
+ def test_requires_grad_miss_same_targets(self):
+ # same as previous test, except that HRA adapters target the same layer
+ config0 = MissConfig(target_modules=["lin0"], r=2)
+ peft_model = get_peft_model(MLP(), config0)
+
+ config1 = MissConfig(target_modules=["lin0"], r=2)
+ peft_model.add_adapter("adapter1", config1)
+
+ # active adapter is still "default"
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.lin0.miss_block.default",
+ )
+
+ # set config0 as active, should not change anything
+ peft_model.set_adapter("default")
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.lin0.miss_block.default",
+ )
+
+ # change activate adapter to adapter1
+ peft_model.set_adapter("adapter1")
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.lin0.miss_block.adapter1",
+ )
+
+ # disable all adapters
+ with peft_model.disable_adapter():
+ self.check_requires_grad(peft_model)
+
+ # after context is exited, return to the previous state
+ peft_model.set_adapter("adapter1")
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.lin0.miss_block.adapter1",
+ )
+
+ def test_requires_grad_boft_different_targets(self):
+ # test two different OFT adapters that target different modules
+ config0 = BOFTConfig(target_modules=["lin0"], boft_block_size=2)
+ peft_model = get_peft_model(MLP2(), config0)
+
+ config1 = BOFTConfig(target_modules=["lin1"], boft_block_size=2)
+ peft_model.add_adapter("adapter1", config1)
+
+ # active pter is still "default"
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.lin0.boft_R.default",
+ "base_model.model.lin0.boft_s.default",
+ )
+
+ # set config0 as active, should not change anything
+ peft_model.set_adapter("default")
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.lin0.boft_R.default",
+ "base_model.model.lin0.boft_s.default",
+ )
+
+ # change activate pter to pter1
+ peft_model.set_adapter("adapter1")
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.lin1.boft_R.adapter1",
+ "base_model.model.lin1.boft_s.adapter1",
+ )
+
+ # disable all pters
+ with peft_model.disable_adapter():
+ self.check_requires_grad(peft_model)
+
+ # after context is exited, return to the previous state
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.lin1.boft_R.adapter1",
+ "base_model.model.lin1.boft_s.adapter1",
+ )
+
+ def test_requires_grad_boft_same_targets(self):
+ # same as previous test, except that BOFT adapters target the same layer
+ config0 = BOFTConfig(target_modules=["lin1"], boft_block_size=2)
+ peft_model = get_peft_model(MLP(), config0)
+
+ config1 = BOFTConfig(target_modules=["lin1"], boft_block_size=2)
+ peft_model.add_adapter("adapter1", config1)
+
+ # active adapter is still "default"
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.lin1.boft_R.default",
+ "base_model.model.lin1.boft_s.default",
+ )
+
+ # set config0 as active, should not change anything
+ peft_model.set_adapter("default")
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.lin1.boft_R.default",
+ "base_model.model.lin1.boft_s.default",
+ )
+
+ # change activate adapter to adapter1
+ peft_model.set_adapter("adapter1")
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.lin1.boft_R.adapter1",
+ "base_model.model.lin1.boft_s.adapter1",
+ )
+
+ # disable all adapters
+ with peft_model.disable_adapter():
+ self.check_requires_grad(peft_model)
+
+ # after context is exited, return to the previous state
+ peft_model.set_adapter("adapter1")
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.lin1.boft_R.adapter1",
+ "base_model.model.lin1.boft_s.adapter1",
+ )
+
+ def test_requires_grad_lntuning_different_targets(self):
+ config0 = LNTuningConfig(
+ target_modules=["layernorm0"],
+ )
+ peft_model = get_peft_model(MLP_LayerNorm(), config0)
+
+ config1 = LNTuningConfig(target_modules=["layernorm1"])
+ peft_model.add_adapter("adapter1", config1)
+
+ # active adapter is still "default"
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.layernorm0.ln_tuning_layers.default.weight",
+ "base_model.model.layernorm0.ln_tuning_layers.default.bias",
+ )
+
+ # set config0 as active, should not change anything
+ peft_model.set_adapter("default")
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.layernorm0.ln_tuning_layers.default.weight",
+ "base_model.model.layernorm0.ln_tuning_layers.default.bias",
+ )
+
+ # change activate adapter to adapter1
+ peft_model.set_adapter("adapter1")
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.layernorm1.ln_tuning_layers.adapter1.weight",
+ "base_model.model.layernorm1.ln_tuning_layers.adapter1.bias",
+ )
+
+ # disable all adapters
+ with peft_model.disable_adapter():
+ self.check_requires_grad(peft_model)
+
+ # after context is exited, return to the previous state
+ peft_model.set_adapter("adapter1")
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.layernorm1.ln_tuning_layers.adapter1.weight",
+ "base_model.model.layernorm1.ln_tuning_layers.adapter1.bias",
+ )
+
+ def test_requires_grad_lntuning_same_targets(self):
+ config0 = LNTuningConfig(
+ target_modules=["layernorm0"],
+ )
+ peft_model = get_peft_model(MLP_LayerNorm(), config0)
+
+ config1 = LNTuningConfig(target_modules=["layernorm0"])
+ peft_model.add_adapter("adapter1", config1)
+
+ # active adapter is still "default"
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.layernorm0.ln_tuning_layers.default.weight",
+ "base_model.model.layernorm0.ln_tuning_layers.default.bias",
+ )
+
+ # set config0 as active, should not change anything
+ peft_model.set_adapter("default")
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.layernorm0.ln_tuning_layers.default.weight",
+ "base_model.model.layernorm0.ln_tuning_layers.default.bias",
+ )
+
+ # change activate adapter to adapter1
+ peft_model.set_adapter("adapter1")
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.layernorm0.ln_tuning_layers.adapter1.weight",
+ "base_model.model.layernorm0.ln_tuning_layers.adapter1.bias",
+ )
+
+ # disable all adapters
+ with peft_model.disable_adapter():
+ self.check_requires_grad(peft_model)
+
+ # after context is exited, return to the previous state
+ peft_model.set_adapter("adapter1")
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.layernorm0.ln_tuning_layers.adapter1.weight",
+ "base_model.model.layernorm0.ln_tuning_layers.adapter1.bias",
+ )
+
+ def test_requires_grad_vera_different_targets(self):
+ # Test two different VeRA adapters that target different modules. Most notably, ensure that vera_A and vera_B
+ # don't require grads.
+
+ # requires a model with at least 2 layers with the same shapes
+ class MLP2(nn.Module):
+ def __init__(self, bias=True):
+ super().__init__()
+ self.relu = nn.ReLU()
+ self.lin0 = nn.Linear(10, 20, bias=bias)
+ self.lin1 = nn.Linear(20, 20, bias=bias) # lin1 and lin2 have same shape
+ self.lin2 = nn.Linear(20, 20, bias=bias)
+ self.lin3 = nn.Linear(20, 2, bias=bias)
+ self.sm = nn.LogSoftmax(dim=-1)
+
+ def forward(self, X):
+ X = X.float()
+ X = self.lin0(X)
+ X = self.relu(X)
+ X = self.lin1(X)
+ X = self.relu(X)
+ X = self.lin2(X)
+ X = self.relu(X)
+ X = self.lin3(X)
+ X = self.sm(X)
+ return X
+
+ config0 = VeraConfig(target_modules=["lin1"])
+ peft_model = get_peft_model(MLP2(), config0)
+
+ config1 = VeraConfig(target_modules=["lin2"])
+ peft_model.add_adapter("adapter1", config1)
+
+ # active adapter is still "default"
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.lin1.vera_lambda_b.default",
+ "base_model.model.lin1.vera_lambda_d.default",
+ )
+
+ # set config0 as active, should not change anything
+ peft_model.set_adapter("default")
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.lin1.vera_lambda_b.default",
+ "base_model.model.lin1.vera_lambda_d.default",
+ )
+
+ # change activate adapter to adapter1
+ peft_model.set_adapter("adapter1")
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.lin2.vera_lambda_b.adapter1",
+ "base_model.model.lin2.vera_lambda_d.adapter1",
+ )
+
+ # disable all adapters
+ with peft_model.disable_adapter():
+ self.check_requires_grad(peft_model)
+
+ # after context is exited, return to the previous state
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.lin2.vera_lambda_b.adapter1",
+ "base_model.model.lin2.vera_lambda_d.adapter1",
+ )
+
+ def test_requires_grad_vera_same_targets(self):
+ # Test two different VeRA adapters that target the same module. Most notably, ensure that vera_A and vera_B
+ # don't require grads.
+
+ # requires a model with at least 2 layers with the same shapes
+ class MLP2(nn.Module):
+ def __init__(self, bias=True):
+ super().__init__()
+ self.relu = nn.ReLU()
+ self.lin0 = nn.Linear(10, 20, bias=bias)
+ self.lin1 = nn.Linear(20, 20, bias=bias) # lin1 and lin2 have same shape
+ self.lin2 = nn.Linear(20, 20, bias=bias)
+ self.lin3 = nn.Linear(20, 2, bias=bias)
+ self.sm = nn.LogSoftmax(dim=-1)
+
+ def forward(self, X):
+ X = X.float()
+ X = self.lin0(X)
+ X = self.relu(X)
+ X = self.lin1(X)
+ X = self.relu(X)
+ X = self.lin2(X)
+ X = self.relu(X)
+ X = self.lin3(X)
+ X = self.sm(X)
+ return X
+
+ config0 = VeraConfig(target_modules=["lin1", "lin2"])
+ peft_model = get_peft_model(MLP2(), config0)
+
+ config1 = VeraConfig(target_modules=["lin1", "lin2"])
+ peft_model.add_adapter("adapter1", config1)
+
+ # active adapter is still "default"
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.lin1.vera_lambda_b.default",
+ "base_model.model.lin1.vera_lambda_d.default",
+ "base_model.model.lin2.vera_lambda_b.default",
+ "base_model.model.lin2.vera_lambda_d.default",
+ )
+
+ # set config0 as active, should not change anything
+ peft_model.set_adapter("default")
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.lin1.vera_lambda_b.default",
+ "base_model.model.lin1.vera_lambda_d.default",
+ "base_model.model.lin2.vera_lambda_b.default",
+ "base_model.model.lin2.vera_lambda_d.default",
+ )
+
+ # change activate adapter to adapter1
+ peft_model.set_adapter("adapter1")
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.lin1.vera_lambda_b.adapter1",
+ "base_model.model.lin1.vera_lambda_d.adapter1",
+ "base_model.model.lin2.vera_lambda_b.adapter1",
+ "base_model.model.lin2.vera_lambda_d.adapter1",
+ )
+
+ # disable all adapters
+ with peft_model.disable_adapter():
+ self.check_requires_grad(peft_model)
+
+ # after context is exited, return to the previous state
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.lin1.vera_lambda_b.adapter1",
+ "base_model.model.lin1.vera_lambda_d.adapter1",
+ "base_model.model.lin2.vera_lambda_b.adapter1",
+ "base_model.model.lin2.vera_lambda_d.adapter1",
+ )
+
+ def test_requires_grad_randlora_different_targets(self):
+ # Test two different RandLora adapters that target different modules. Most notably, ensure that randbasis_A and randbasis_B
+ # don't require grads.
+
+ # requires a model with at least 2 layers with the same shapes
+ class MLP2(nn.Module):
+ def __init__(self, bias=True):
+ super().__init__()
+ self.relu = nn.ReLU()
+ self.lin0 = nn.Linear(10, 20, bias=bias)
+ self.lin1 = nn.Linear(20, 20, bias=bias) # lin1 and lin2 have same shape
+ self.lin2 = nn.Linear(20, 20, bias=bias)
+ self.lin3 = nn.Linear(20, 2, bias=bias)
+ self.sm = nn.LogSoftmax(dim=-1)
+
+ def forward(self, X):
+ X = X.float()
+ X = self.lin0(X)
+ X = self.relu(X)
+ X = self.lin1(X)
+ X = self.relu(X)
+ X = self.lin2(X)
+ X = self.relu(X)
+ X = self.lin3(X)
+ X = self.sm(X)
+ return X
+
+ config0 = RandLoraConfig(target_modules=["lin1"])
+ peft_model = get_peft_model(MLP2(), config0)
+
+ config1 = RandLoraConfig(target_modules=["lin2"])
+ peft_model.add_adapter("adapter1", config1)
+
+ # active adapter is still "default"
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.lin1.randlora_lambda.default",
+ "base_model.model.lin1.randlora_gamma.default",
+ )
+
+ # set config0 as active, should not change anything
+ peft_model.set_adapter("default")
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.lin1.randlora_lambda.default",
+ "base_model.model.lin1.randlora_gamma.default",
+ )
+
+ # change activate adapter to adapter1
+ peft_model.set_adapter("adapter1")
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.lin2.randlora_lambda.adapter1",
+ "base_model.model.lin2.randlora_gamma.adapter1",
+ )
+
+ # disable all adapters
+ with peft_model.disable_adapter():
+ self.check_requires_grad(peft_model)
+
+ # after context is exited, return to the previous state
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.lin2.randlora_lambda.adapter1",
+ "base_model.model.lin2.randlora_gamma.adapter1",
+ )
+
+ def test_requires_grad_randlora_same_targets(self):
+ # Test two different RandLora adapters that target the same module. Most notably, ensure that randbasis_A and randbasis_B
+ # don't require grads.
+
+ # requires a model with at least 2 layers with the same shapes
+ class MLP2(nn.Module):
+ def __init__(self, bias=True):
+ super().__init__()
+ self.relu = nn.ReLU()
+ self.lin0 = nn.Linear(10, 20, bias=bias)
+ self.lin1 = nn.Linear(20, 20, bias=bias) # lin1 and lin2 have same shape
+ self.lin2 = nn.Linear(20, 20, bias=bias)
+ self.lin3 = nn.Linear(20, 2, bias=bias)
+ self.sm = nn.LogSoftmax(dim=-1)
+
+ def forward(self, X):
+ X = X.float()
+ X = self.lin0(X)
+ X = self.relu(X)
+ X = self.lin1(X)
+ X = self.relu(X)
+ X = self.lin2(X)
+ X = self.relu(X)
+ X = self.lin3(X)
+ X = self.sm(X)
+ return X
+
+ config0 = RandLoraConfig(target_modules=["lin1", "lin2"])
+ peft_model = get_peft_model(MLP2(), config0)
+
+ config1 = RandLoraConfig(target_modules=["lin1", "lin2"])
+ peft_model.add_adapter("adapter1", config1)
+
+ # active adapter is still "default"
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.lin1.randlora_lambda.default",
+ "base_model.model.lin1.randlora_gamma.default",
+ "base_model.model.lin2.randlora_lambda.default",
+ "base_model.model.lin2.randlora_gamma.default",
+ )
+
+ # set config0 as active, should not change anything
+ peft_model.set_adapter("default")
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.lin1.randlora_lambda.default",
+ "base_model.model.lin1.randlora_gamma.default",
+ "base_model.model.lin2.randlora_lambda.default",
+ "base_model.model.lin2.randlora_gamma.default",
+ )
+
+ # change activate adapter to adapter1
+ peft_model.set_adapter("adapter1")
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.lin1.randlora_lambda.adapter1",
+ "base_model.model.lin1.randlora_gamma.adapter1",
+ "base_model.model.lin2.randlora_lambda.adapter1",
+ "base_model.model.lin2.randlora_gamma.adapter1",
+ )
+
+ # disable all adapters
+ with peft_model.disable_adapter():
+ self.check_requires_grad(peft_model)
+
+ # after context is exited, return to the previous state
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.lin1.randlora_lambda.adapter1",
+ "base_model.model.lin1.randlora_gamma.adapter1",
+ "base_model.model.lin2.randlora_lambda.adapter1",
+ "base_model.model.lin2.randlora_gamma.adapter1",
+ )
+
+ def test_requires_grad_vblora_different_targets(self):
+ # test two different VBLoRA adapters that target different modules
+ config0 = VBLoRAConfig(target_modules=["lin0"], vector_length=1, num_vectors=2)
+ peft_model = get_peft_model(MLP(), config0)
+
+ config1 = VBLoRAConfig(target_modules=["lin1"], vector_length=1, num_vectors=2)
+ peft_model.add_adapter("adapter1", config1)
+
+ # active adapter is still "default"
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.lin0.vblora_logits_A.default",
+ "base_model.model.lin0.vblora_logits_B.default",
+ "base_model.model.lin0.vblora_vector_bank.default",
+ )
+
+ # set config0 as active, should not change anything
+ peft_model.set_adapter("default")
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.lin0.vblora_logits_A.default",
+ "base_model.model.lin0.vblora_logits_B.default",
+ "base_model.model.lin0.vblora_vector_bank.default",
+ )
+
+ # change activate adapter to adapter1
+ peft_model.set_adapter("adapter1")
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.lin1.vblora_logits_A.adapter1",
+ "base_model.model.lin1.vblora_logits_B.adapter1",
+ "base_model.model.lin0.vblora_vector_bank.adapter1", # vblora_vector_bank is shared
+ )
+
+ # disable all adapters
+ with peft_model.disable_adapter():
+ self.check_requires_grad(peft_model)
+
+ # after context is exited, return to the previous state
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.lin1.vblora_logits_A.adapter1",
+ "base_model.model.lin1.vblora_logits_B.adapter1",
+ "base_model.model.lin0.vblora_vector_bank.adapter1", # vblora_vector_bank is shared
+ )
+
+ def test_requires_grad_vblora_same_targets(self):
+ # same as previous test, except that VBLoRA adapters target the same layer
+ config0 = VBLoRAConfig(target_modules=["lin0"], vector_length=1, num_vectors=2)
+ peft_model = get_peft_model(MLP(), config0)
+
+ config1 = VBLoRAConfig(target_modules=["lin0"], vector_length=1, num_vectors=2)
+ peft_model.add_adapter("adapter1", config1)
+
+ # active adapter is still "default"
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.lin0.vblora_logits_A.default",
+ "base_model.model.lin0.vblora_logits_B.default",
+ "base_model.model.lin0.vblora_vector_bank.default",
+ )
+
+ # set config0 as active, should not change anything
+ peft_model.set_adapter("default")
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.lin0.vblora_logits_A.default",
+ "base_model.model.lin0.vblora_logits_B.default",
+ "base_model.model.lin0.vblora_vector_bank.default",
+ )
+
+ # change activate adapter to adapter1
+ peft_model.set_adapter("adapter1")
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.lin0.vblora_logits_A.adapter1",
+ "base_model.model.lin0.vblora_logits_B.adapter1",
+ "base_model.model.lin0.vblora_vector_bank.adapter1",
+ )
+
+ # disable all adapters
+ with peft_model.disable_adapter():
+ self.check_requires_grad(peft_model)
+
+ # after context is exited, return to the previous state
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.lin0.vblora_logits_A.adapter1",
+ "base_model.model.lin0.vblora_logits_B.adapter1",
+ "base_model.model.lin0.vblora_vector_bank.adapter1",
+ )
+
+ def test_requires_grad_fourierft_different_targets(self):
+ # test two different fourierft adapters that target different modules
+ config0 = FourierFTConfig(n_frequency=10, target_modules=["lin0"])
+ peft_model = get_peft_model(MLP(), config0)
+
+ config1 = FourierFTConfig(n_frequency=10, target_modules=["lin1"])
+ peft_model.add_adapter("adapter1", config1)
+
+ # active adapter is still "default"
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.lin0.fourierft_spectrum.default",
+ )
+
+ # set config0 as active, should not change anything
+ peft_model.set_adapter("default")
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.lin0.fourierft_spectrum.default",
+ )
+
+ # change activate adapter to adapter1
+ peft_model.set_adapter("adapter1")
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.lin1.fourierft_spectrum.adapter1",
+ )
+
+ # disable all adapters
+ with peft_model.disable_adapter():
+ self.check_requires_grad(peft_model)
+
+ # after context is exited, return to the previous state
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.lin1.fourierft_spectrum.adapter1",
+ )
+
+ def test_requires_grad_fourierft_same_targets(self):
+ # same as previous test, except that AdaLora adapters target the same layer
+ config0 = FourierFTConfig(n_frequency=10, target_modules=["lin0"])
+ peft_model = get_peft_model(MLP(), config0)
+
+ config1 = FourierFTConfig(n_frequency=10, target_modules=["lin0"])
+ peft_model.add_adapter("adapter1", config1)
+
+ # active adapter is still "default"
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.lin0.fourierft_spectrum.default",
+ )
+
+ # set config0 as active, should not change anything
+ peft_model.set_adapter("default")
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.lin0.fourierft_spectrum.default",
+ )
+
+ # change activate adapter to adapter1
+ peft_model.set_adapter("adapter1")
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.lin0.fourierft_spectrum.adapter1",
+ )
+
+ # disable all adapters
+ with peft_model.disable_adapter():
+ self.check_requires_grad(peft_model)
+
+ # after context is exited, return to the previous state
+ peft_model.set_adapter("adapter1")
+ self.check_requires_grad(
+ peft_model,
+ "base_model.model.lin0.fourierft_spectrum.adapter1",
+ )
+
+ @pytest.mark.parametrize("config_cls", ALL_PEFT_CONFIG_CLASSES)
+ @pytest.mark.parametrize("is_trainable", [False, True]) # note: default is False
+ def test_loading_model_requires_grad_set_correctly(self, config_cls, is_trainable, tmp_path):
+ # Test that when loading PeftModel and then loading another adapter, the requires_grad is set correctly and
+ # is_trainable is respected.
+ # See #2759
+ model = DeepMLP(size=256) # a size that works with all adapters
+ extra_kwargs = {}
+ if config_cls == IA3Config:
+ extra_kwargs["feedforward_modules"] = []
+ config = config_cls(target_modules=["layers.0.lin0"], **extra_kwargs)
+
+ if config_cls == TrainableTokensConfig: # TrainbleTokens requires a different base model and config
+ model = ModelEmbConv1D()
+ config = config_cls(target_modules=["emb"], token_indices=[0, 2, 4])
+
+ model = get_peft_model(model, config)
+ model.save_pretrained(tmp_path)
+ del model
+
+ model = DeepMLP(size=256)
+ if config_cls == TrainableTokensConfig: # TrainbleTokens requires a different base
+ model = ModelEmbConv1D()
+ model = PeftModel.from_pretrained(model, tmp_path, is_trainable=is_trainable)
+
+ if is_trainable:
+ for name, param in model.named_parameters():
+ if ".default" in name:
+ assert param.requires_grad
+ else:
+ assert not param.requires_grad
+ else:
+ assert all(not p.requires_grad for p in model.parameters())
+
+ # load one more adapter; this adapter is not automatically activated
+ model.load_adapter(tmp_path, adapter_name="other", is_trainable=is_trainable)
+ if is_trainable:
+ for name, param in model.named_parameters():
+ if ".default" in name:
+ assert param.requires_grad
+ else:
+ assert not param.requires_grad
+ else:
+ assert all(not p.requires_grad for p in model.parameters())
+
+ @pytest.mark.parametrize("config_cls", ALL_PEFT_CONFIG_CLASSES)
+ @pytest.mark.parametrize("is_trainable", [False, True]) # note: default is False
+ def test_loading_model_with_modules_to_save_requires_grad_set_correctly(self, config_cls, is_trainable, tmp_path):
+ # Same test as above, but with modules_to_save
+ if config_cls == TrainableTokensConfig:
+ pytest.skip(reason="Trainable tokens does not support modules_to_save")
+
+ model = DeepMLP(size=256) # a size that works with all adapters
+ extra_kwargs = {}
+ if config_cls == IA3Config:
+ extra_kwargs["feedforward_modules"] = []
+ # targeting the different modules with modules_to_save:
+ config = config_cls(target_modules=["layers.0.lin0"], modules_to_save=["layers.0.lin1"], **extra_kwargs)
+ model = get_peft_model(model, config)
+ model.save_pretrained(tmp_path)
+ del model
+
+ model = DeepMLP(size=256)
+ model = PeftModel.from_pretrained(model, tmp_path, is_trainable=is_trainable)
+
+ if is_trainable:
+ for name, param in model.named_parameters():
+ if ".default" in name:
+ assert param.requires_grad
+ else:
+ assert not param.requires_grad
+ else:
+ assert all(not p.requires_grad for p in model.parameters())
+
+ # load one more adapter
+ model.load_adapter(tmp_path, adapter_name="other", is_trainable=is_trainable)
+ if is_trainable:
+ for name, param in model.named_parameters():
+ if ".default" in name:
+ assert param.requires_grad
+ else:
+ assert not param.requires_grad
+ else:
+ assert all(not p.requires_grad for p in model.parameters())
+
+ @pytest.mark.parametrize("is_trainable", [False, True]) # note: default is False
+ def test_loading_model_with_trainble_tokens_requires_grad_set_correctly(self, is_trainable, tmp_path):
+ model = ModelEmbConv1D()
+ # targeting the same modules with modules_to_save:
+ config = LoraConfig(target_modules=["lin0"], trainable_token_indices={"emb": [0]})
+ model = get_peft_model(model, config)
+ model.save_pretrained(tmp_path)
+ del model
+
+ model = ModelEmbConv1D()
+ model = PeftModel.from_pretrained(model, tmp_path, is_trainable=is_trainable)
+
+ if is_trainable:
+ for name, param in model.named_parameters():
+ if ".default" in name:
+ assert param.requires_grad
+ else:
+ assert not param.requires_grad
+ else:
+ assert all(not p.requires_grad for p in model.parameters())
+
+ # load one more adapter
+ model.load_adapter(tmp_path, adapter_name="other", is_trainable=is_trainable)
+ if is_trainable:
+ for name, param in model.named_parameters():
+ if ".default" in name:
+ assert param.requires_grad
+ else:
+ assert not param.requires_grad
+ else:
+ assert all(not p.requires_grad for p in model.parameters())
+
+ @pytest.mark.xfail(strict=True)
+ @pytest.mark.parametrize("config_cls", [LoraConfig]) # no need to check each method, they all fail
+ def test_loading_model_requires_grad_set_correctly_switch_inference_mode(self, config_cls, tmp_path):
+ # Same as test_loading_model_requires_grad_set_correctly but this time we first load with is_trainable=False and
+ # then with is_trainable=True. Loading the second adapter should not affect the requires_grad of the first
+ # adapter, but it does. The reason is that is_training/inference_mode is taken from the current PEFT config, but
+ # that config does not necessarily belong to the active adapter, creating a mismatch.
+ # When/If this is fixed, the check can be integrated into test_loading_model_requires_grad_set_correctly and
+ # this test can be deleted.
+ model = DeepMLP(size=256) # a size that works with all adapters
+ extra_kwargs = {}
+ config = config_cls(target_modules=["layers.0.lin0"])
+ model = get_peft_model(model, config)
+ model.save_pretrained(tmp_path)
+ del model
+
+ model = DeepMLP(size=256)
+ model = PeftModel.from_pretrained(model, tmp_path, is_trainable=False)
+ assert all(not p.requires_grad for p in model.parameters())
+
+ # load one more adapter; this adapter is not automatically activated
+ model.load_adapter(tmp_path, adapter_name="other", is_trainable=True)
+ params_with_grad = [n for n, p in model.named_parameters() if p.requires_grad]
+ expected = [
+ "base_model.model.layers.0.lin0.lora_A.other.weight",
+ "base_model.model.layers.0.lin0.lora_B.other.weight",
+ ]
+ # this fails, instead with get ...lora_A.default.weight and ...lora_B.default.weight
+ assert params_with_grad == expected
+
+ @pytest.mark.xfail(strict=True)
+ @pytest.mark.parametrize("config_cls", [LoraConfig]) # no need to check each method, they all fail
+ def test_loading_model_requires_grad_load_adapter_then_add_adapter(self, config_cls, tmp_path):
+ # When adding a new adapter with model.add_adapter, through the set_adapter call in update_layer, we activate
+ # the gradients of the first adapter, even if it's not desired. Since there is no is_trainable argument on
+ # add_adapter, there is no way to disable that at the moment.
+ # When/If this is fixed, the check can be integrated into test_loading_model_requires_grad_set_correctly and
+ # this test can be deleted.
+ model = DeepMLP(size=256) # a size that works with all adapters
+ extra_kwargs = {}
+ config = config_cls(target_modules=["layers.0.lin0"])
+ model = get_peft_model(model, config)
+ model.save_pretrained(tmp_path)
+ del model
+
+ model = DeepMLP(size=256)
+ model = PeftModel.from_pretrained(model, tmp_path, is_trainable=False)
+ assert all(not p.requires_grad for p in model.parameters())
+
+ # add a new adapter
+ model.add_adapter(adapter_name="other", peft_config=config)
+ params_with_grad = [n for n, p in model.named_parameters() if p.requires_grad]
+ assert all(not p.requires_grad for p in model.parameters())
+
+
+# this is for PEFT methods that support mixed adapter batches.
+MIXED_ADAPTER_TEST_CASES = [
+ (
+ "LoRA mixed adapter",
+ LoraConfig(target_modules=["lin0"], init_lora_weights=False),
+ LoraConfig(target_modules=["lin0"], r=16, init_lora_weights=False),
+ ),
+ (
+ "RoAd mixed adapter",
+ RoadConfig(target_modules=["lin0"], group_size=2, init_weights=False),
+ RoadConfig(target_modules=["lin0"], group_size=2, variant="road_2", init_weights=False),
+ ),
+]
+
+
+class TestMixedAdapterBatches:
+ torch_device = infer_device()
+
+ def get_mlp_peft(self, config0, config1):
+ """A simple MLP with 2 LoRA adapters"""
+ torch.manual_seed(0)
+
+ base_model = MLP().to(self.torch_device).eval()
+ peft_model = get_peft_model(base_model, config0, "adapter0").eval()
+ peft_model.add_adapter("adapter1", config1)
+ return peft_model
+
+ def run_checks(self, model, inputs):
+ # This checks that we can have mixed adapters in a single batch. The test works by creating the outputs for the
+ # base model, adapter 0, and adapter 1 separately. Then, we create an output with mixed adapters, where the
+ # sample [0, 3, 6] are for the base model, [1, 4, 7] for adapter 0, and [2, 5, 8] for adapter 1. Finally, we
+ # check that the outputs of the mixed batch are correct for the corresponding indices.
+ adapter_name0, adapter_name1 = model.peft_config.keys()
+
+ with model.disable_adapter():
+ output_base = model(**inputs)
+
+ model.set_adapter(adapter_name0)
+ output0 = model(**inputs)
+
+ # sanity check, outputs are not the same
+ assert not torch.allclose(output_base, output0)
+
+ model.set_adapter(adapter_name1)
+ output1 = model(**inputs)
+
+ # sanity check, outputs have the right shape and are not the same
+ assert len(output_base) >= 3
+ assert len(output_base) == len(output0) == len(output1)
+ assert not torch.allclose(output_base, output0)
+ assert not torch.allclose(output_base, output1)
+
+ # set adapter_indices so that it alternates between base, adapter 0, and adapter 1
+ adapters = ["__base__", adapter_name0, adapter_name1]
+ inputs["adapter_names"] = [adapters[i % 3] for i in (range(len(inputs["X"])))]
+ output_mixed = model.forward(**inputs)
+
+ assert torch.allclose(output_base[::3], output_mixed[::3])
+ assert torch.allclose(output0[1::3], output_mixed[1::3])
+ assert torch.allclose(output1[2::3], output_mixed[2::3])
+
+ @pytest.mark.parametrize("test_name, config0, config1", MIXED_ADAPTER_TEST_CASES)
+ def test_mixed_adapter_batches_mlp(self, test_name, config0, config1):
+ mlp_peft = self.get_mlp_peft(config0, config1)
+ inputs = {"X": torch.arange(90).view(-1, 10).to(self.torch_device)}
+ self.run_checks(mlp_peft, inputs)
+
+ @pytest.mark.parametrize(
+ "test_name, config0, config1",
+ [
+ (
+ "LoRA mixed adapter with different target layers",
+ LoraConfig(target_modules=["lin0"], init_lora_weights=False),
+ LoraConfig(target_modules=["lin1"], init_lora_weights=False),
+ ),
+ (
+ "RoAd mixed adapter with different target layers",
+ RoadConfig(target_modules=["lin0"], group_size=2, init_weights=False),
+ RoadConfig(target_modules=["lin1"], group_size=2, init_weights=False),
+ ),
+ ],
+ )
+ def test_mixed_adapter_batches_different_target_layers(self, test_name, config0, config1):
+ base_model = MLP().to(self.torch_device).eval()
+ peft_model = get_peft_model(base_model, config0, "adapter0").eval()
+ peft_model.add_adapter("adapter1", config1)
+ inputs = {"X": torch.arange(90).view(-1, 10).to(self.torch_device)}
+ self.run_checks(peft_model, inputs)
+
+ @pytest.mark.parametrize(
+ "test_name, config0, config1",
+ [
+ (
+ "LoRA mixed adapter with modules to save",
+ LoraConfig(target_modules=["lin0"], modules_to_save=["lin1"], init_lora_weights=False),
+ LoraConfig(target_modules=["lin0"], modules_to_save=["lin1"], init_lora_weights=False),
+ ),
+ (
+ "RoAd mixed adapter with modules to save",
+ RoadConfig(target_modules=["lin0"], modules_to_save=["lin1"], group_size=2, init_weights=False),
+ RoadConfig(target_modules=["lin0"], modules_to_save=["lin1"], group_size=2, init_weights=False),
+ ),
+ ],
+ )
+ def test_mixed_adapter_batches_multiple_modules_to_save(self, test_name, config0, config1):
+ base_model = MLP().to(self.torch_device).eval()
+ peft_model = get_peft_model(base_model, config0, "adapter0").eval()
+ peft_model.add_adapter("adapter1", config1)
+ inputs = {"X": torch.arange(90).view(-1, 10).to(self.torch_device)}
+ self.run_checks(peft_model, inputs)
+
+ @pytest.mark.parametrize(
+ "test_name, config0, config1",
+ [
+ (
+ "LoRA mixed adapter with unsupported layer",
+ LoraConfig(target_modules=["lin0"], modules_to_save=["gru"], init_lora_weights=False),
+ LoraConfig(target_modules=["lin0"], modules_to_save=["gru"], init_lora_weights=False),
+ ),
+ ],
+ )
+ def test_mixed_adapter_batches_unsupported_layer_raises(self, test_name, config0, config1):
+ base_model = MLPWithGRU().to(self.torch_device).eval()
+ peft_model = get_peft_model(base_model, config0, "adapter0").eval()
+ peft_model.add_adapter("adapter1", config1)
+ inputs = {"X": torch.arange(90).view(-1, 10).to(self.torch_device)}
+ SUPPORTED_MODULES = (torch.nn.Linear, torch.nn.Embedding, torch.nn.Conv1d, torch.nn.Conv2d, torch.nn.Conv3d)
+ module_names = ", ".join([module.__name__ for module in SUPPORTED_MODULES])
+ with pytest.raises(
+ TypeError, match=f"Mixed batching is only supported for the following modules: {module_names}."
+ ):
+ self.run_checks(peft_model, inputs)
+
+ @pytest.mark.parametrize(
+ "test_name, config0, config1",
+ [
+ (
+ "LoRA mixed adapter with overlapping layers",
+ LoraConfig(target_modules=["lin0"], init_lora_weights=False),
+ LoraConfig(target_modules=["lin0", "lin1"], init_lora_weights=False),
+ ),
+ (
+ "RoAd mixed adapter with overlapping layers",
+ RoadConfig(target_modules=["lin0"], group_size=2, init_weights=False),
+ RoadConfig(target_modules=["lin0", "lin1"], group_size=2, init_weights=False),
+ ),
+ ],
+ )
+ def test_mixed_adapter_batches_partly_overlapping_target_layers(self, test_name, config0, config1):
+ base_model = MLP().to(self.torch_device).eval()
+ # target different lora layers
+ peft_model = get_peft_model(base_model, config0, "adapter0").eval()
+ peft_model.add_adapter("adapter1", config1)
+
+ inputs = {"X": torch.arange(90).view(-1, 10).to(self.torch_device)}
+ self.run_checks(peft_model, inputs)
+
+ @pytest.mark.parametrize(
+ "test_name, config0, config1",
+ [
+ (
+ "LoRA mixed adapter with conv1d",
+ LoraConfig(target_modules=["emb", "conv1d"], init_lora_weights=False),
+ LoraConfig(target_modules=["emb", "conv1d"], r=16, init_lora_weights=False),
+ ),
+ ],
+ )
+ def test_mixed_adapter_batches_lora_conv1d_emb(self, test_name, config0, config1):
+ base_model = ModelEmbConv1D().to(self.torch_device).eval()
+ peft_model = get_peft_model(base_model, config0, "adapter0").eval()
+ peft_model.add_adapter("adapter1", config1)
+
+ inputs = {"X": torch.arange(90).view(-1, 10).to(self.torch_device)}
+ self.run_checks(peft_model, inputs)
+
+ @pytest.mark.parametrize(
+ "test_name, config0, config1",
+ [
+ (
+ "LoRA mixed adapter with conv1d and emb and modules to save",
+ LoraConfig(target_modules=["emb", "conv1d"], modules_to_save=["lin0"], init_lora_weights=False),
+ LoraConfig(target_modules=["emb", "conv1d"], modules_to_save=["lin0"], init_lora_weights=False),
+ ),
+ ],
+ )
+ def test_mixed_adapter_batches_lora_conv1d_emb_multiple_modules_to_save(self, test_name, config0, config1):
+ base_model = ModelEmbConv1D().to(self.torch_device).eval()
+ peft_model = get_peft_model(base_model, config0, "adapter0").eval()
+ peft_model.add_adapter("adapter1", config1)
+ inputs = {"X": torch.arange(90).view(-1, 10).to(self.torch_device)}
+ self.run_checks(peft_model, inputs)
+
+ @pytest.mark.parametrize(
+ "test_name, config0, config1",
+ [
+ (
+ "LoRA mixed adapter with conv2d",
+ LoraConfig(target_modules=["conv2d"], init_lora_weights=False),
+ LoraConfig(target_modules=["conv2d"], r=16, init_lora_weights=False),
+ ),
+ ],
+ )
+ def test_mixed_adapter_batches_lora_conv2d(self, test_name, config0, config1):
+ base_model = ModelConv2D().to(self.torch_device).eval()
+ peft_model = get_peft_model(base_model, config0, "adapter0").eval()
+ peft_model.add_adapter("adapter1", config1)
+
+ inputs = {"X": torch.arange(270).view(6, 5, 3, 3).to(self.torch_device)}
+ self.run_checks(peft_model, inputs)
+
+ @pytest.mark.parametrize(
+ "test_name, config0, config1",
+ [
+ (
+ "LoRA mixed adapter with mha",
+ LoraConfig(target_modules=["mha"], init_lora_weights=False),
+ LoraConfig(target_modules=["mha"], r=16, init_lora_weights=False),
+ ),
+ ],
+ )
+ def test_mixed_adapter_batches_mha_raises(self, test_name, config0, config1):
+ base_model = ModelMha().to(self.torch_device).eval()
+ peft_model = get_peft_model(base_model, config0, "adapter0").eval()
+ peft_model.add_adapter("adapter1", config1)
+
+ inputs = {"X": torch.arange(90).view(-1, 10).to(self.torch_device)}
+ msg = "lora.MultiheadAttention does not support mixed adapter batches"
+ with pytest.raises(TypeError, match=msg):
+ self.run_checks(peft_model, inputs)
+
+ @pytest.mark.parametrize("test_name, config0, config1", MIXED_ADAPTER_TEST_CASES)
+ def test_mixed_adapter_batches_length_mismatch_raises(self, test_name, config0, config1):
+ mlp_peft = self.get_mlp_peft(config0, config1)
+ inputs = {
+ "X": torch.arange(90).view(-1, 10).to(self.torch_device),
+ "adapter_names": ["__base__"] * 5, # wrong length!
+ }
+ msg = r"Length of `adapter_names` should be the same as the number of inputs, but got "
+ with pytest.raises(ValueError, match=msg):
+ mlp_peft.forward(**inputs)
+
+ @pytest.mark.parametrize("test_name, config0, config1", MIXED_ADAPTER_TEST_CASES)
+ def test_mixed_adapter_batches_training_mode_raises(self, test_name, config0, config1):
+ mlp_peft = self.get_mlp_peft(config0, config1)
+ inputs = {
+ "X": torch.arange(90).view(-1, 10).to(self.torch_device),
+ "adapter_names": ["__base__"] * 9,
+ }
+ mlp_peft = mlp_peft.train()
+ msg = r"Cannot pass `adapter_names` when the model is in training mode."
+ with pytest.raises(ValueError, match=msg):
+ mlp_peft.forward(**inputs)
+
+ @pytest.mark.parametrize("test_name, config0, config1", MIXED_ADAPTER_TEST_CASES)
+ def test_mixed_adapter_batches_disabled(self, test_name, config0, config1):
+ # Disabling adapters should have precedence over passing adapter names
+ mlp_peft = self.get_mlp_peft(config0, config1)
+ inputs = {"X": torch.arange(90).view(-1, 10).to(self.torch_device)}
+ with mlp_peft.disable_adapter():
+ output_disabled = mlp_peft(**inputs)
+
+ adapters = ["__base__", "adapter0", "adapter1"]
+ inputs["adapter_names"] = [adapters[i % 3] for i in (range(len(inputs["X"])))]
+ with mlp_peft.disable_adapter():
+ output_mixed = mlp_peft.forward(**inputs)
+
+ assert torch.allclose(output_disabled, output_mixed)
+
+ @pytest.mark.parametrize("test_name, config0, config1", MIXED_ADAPTER_TEST_CASES)
+ def test_mixed_adapter_batches_merged_raises(self, test_name, config0, config1):
+ # When there are merged adapters, passing adapter names should raise an error
+ mlp_peft = self.get_mlp_peft(config0, config1)
+ inputs = {
+ "X": torch.arange(90).view(-1, 10).to(self.torch_device),
+ "adapter_names": ["adapter0"] * 9,
+ }
+ mlp_peft.merge_adapter(["adapter0"])
+ msg = r"Cannot pass `adapter_names` when there are merged adapters, please call `unmerge_adapter` first."
+ with pytest.raises(ValueError, match=msg):
+ mlp_peft.forward(**inputs)
+
+ @pytest.mark.parametrize(
+ "test_name, config",
+ [
+ (
+ "LoRA mixed batch wrong adapter name",
+ LoraConfig(target_modules=["lin0"], init_lora_weights=False),
+ ),
+ (
+ "RoAD mixed batch wrong adapter name",
+ RoadConfig(target_modules=["lin0"], group_size=2, init_weights=False),
+ ),
+ ],
+ )
+ def test_mixed_adapter_batches_lora_wrong_adapter_name_raises(self, test_name, config):
+ # Ensure that all of the adapter names that are being passed actually exist
+ torch.manual_seed(0)
+ x = torch.arange(90).view(-1, 10).to(self.torch_device)
+
+ base_model = MLP().to(self.torch_device).eval()
+ peft_model = get_peft_model(base_model, config).eval()
+ peft_model.add_adapter(adapter_name="other", peft_config=config)
+
+ # sanity check: this works
+ peft_model.forward(x, adapter_names=["default"] * 5 + ["other"] * 4)
+
+ # check one correct and one incorrect adapter
+ msg = re.escape("Trying to infer with non-existing adapter(s): does-not-exist")
+ with pytest.raises(ValueError, match=msg):
+ peft_model.forward(x, adapter_names=["default"] * 5 + ["does-not-exist"] * 4)
+
+ # check two correct adapters and one incorrect adapter
+ with pytest.raises(ValueError, match=msg):
+ peft_model.forward(x, adapter_names=["default"] * 3 + ["does-not-exist"] * 4 + ["other"] * 2)
+
+ # check only incorrect adapters
+ msg = re.escape("Trying to infer with non-existing adapter(s): does-not-exist, other-does-not-exist")
+ with pytest.raises(ValueError, match=msg):
+ peft_model.forward(x, adapter_names=["does-not-exist"] * 5 + ["other-does-not-exist"] * 4)
+
+ def test_mixed_adapter_batches_lora_with_dora_raises(self):
+ # When there are DoRA adapters, passing adapter names should raise an error
+ torch.manual_seed(0)
+ inputs = {
+ "X": torch.arange(90).view(-1, 10).to(self.torch_device),
+ "adapter_names": ["default"] * 9,
+ }
+
+ base_model = MLP().to(self.torch_device).eval()
+ config = LoraConfig(target_modules=["lin0"], init_lora_weights=False, use_dora=True)
+ peft_model = get_peft_model(base_model, config).eval()
+ msg = r"Cannot pass `adapter_names` when DoRA is enabled."
+ with pytest.raises(ValueError, match=msg):
+ peft_model.forward(**inputs)
+
+ def test_mixed_adapter_batches_lora_with_dora_but_dora_not_included_works(self):
+ # When there are DoRA adapters, passing adapter names should raise an error, see previous test. However, when
+ # the adapter that uses DoRA is not included in adapter_names, it's actually fine.
+ torch.manual_seed(0)
+ base_model = MLP().to(self.torch_device).eval()
+ config_dora = LoraConfig(target_modules=["lin0"], init_lora_weights=False, use_dora=True)
+ peft_model = get_peft_model(base_model, config_dora)
+ config_no_dora = LoraConfig(target_modules=["lin0"], init_lora_weights=False, use_dora=False)
+ peft_model.add_adapter(adapter_name="other", peft_config=config_no_dora)
+ peft_model.eval()
+
+ # The "default" adapter uses DoRA but "other" is not using it, so using "other" is fine. Also, "__base__" is
+ # fine since it uses the base model and thus DoRA is not involved either.
+ inputs = {
+ "X": torch.arange(90).view(-1, 10).to(self.torch_device),
+ "adapter_names": ["other"] * 4 + ["__base__"] * 5,
+ }
+ peft_model.forward(**inputs)
+
+ @pytest.mark.parametrize(
+ "test_name, config0, config1, factor",
+ [
+ (
+ "LoRA mixed adapter timing",
+ LoraConfig(task_type="CAUSAL_LM", init_lora_weights=False),
+ LoraConfig(task_type="CAUSAL_LM", r=16, init_lora_weights=False),
+ 2.0,
+ ),
+ (
+ "RoAd mixed adapter timing",
+ RoadConfig(task_type="CAUSAL_LM", init_weights=False),
+ RoadConfig(task_type="CAUSAL_LM", variant="road_2", init_weights=False),
+ 3.0,
+ ),
+ ],
+ )
+ @require_non_cpu
+ def test_mixed_adapter_batches_lora_opt_timing(self, test_name, config0, config1, factor):
+ # Use a more realistic model (opt-125m) and do a simple runtime check to ensure that mixed adapter batches
+ # don't add too much overhead. These types of tests are inherently flaky, so we try to add in some robustness.
+ logs = [] # store the time it takes to run each forward pass here
+
+ @contextmanager
+ def timed():
+ tic = time.perf_counter()
+ yield
+ toc = time.perf_counter()
+ logs.append(toc - tic)
+
+ base_model = AutoModelForCausalLM.from_pretrained("facebook/opt-125m").to(self.torch_device).eval()
+ inputs = {"input_ids": torch.randint(0, 1000, (16, 64)).to(self.torch_device)}
+ with timed():
+ output_base = base_model(**inputs).logits
+
+ peft_model = get_peft_model(base_model, config0, "adapter1").eval()
+ with timed():
+ output0 = peft_model(**inputs).logits
+
+ # sanity check, outputs are not the same
+ assert not torch.allclose(output_base, output0)
+
+ peft_model.add_adapter("adapter2", config1)
+ peft_model.set_adapter("adapter2")
+ with timed():
+ output1 = peft_model(**inputs).logits
+
+ # sanity check, outputs are not the same
+ assert not torch.allclose(output_base, output1)
+
+ # set adapter_indices so that it alternates between 0 (base), lora 1, and lora 2
+ adapters = ["__base__", "adapter1", "adapter2"]
+ inputs["adapter_names"] = [adapters[i % 3] for i in (range(len(inputs["input_ids"])))]
+ with timed():
+ output_mixed = peft_model.forward(**inputs).logits
+
+ atol, rtol = 1e-4, 1e-4
+ assert torch.allclose(output_base[::3], output_mixed[::3], atol=atol, rtol=rtol)
+ assert torch.allclose(output0[1::3], output_mixed[1::3], atol=atol, rtol=rtol)
+ assert torch.allclose(output1[2::3], output_mixed[2::3], atol=atol, rtol=rtol)
+
+ # Check that the overhead in time added by mixed batches is not too high.
+ # To prevent flakiness, we measure mixed inference 3 times and take the lowest value, then compare it to the mean
+ # of the non-mixed inference times. We also grant a generous margin of 2x the mean time.
+ with timed():
+ output_mixed = peft_model.forward(**inputs).logits
+ with timed():
+ output_mixed = peft_model.forward(**inputs).logits
+
+ time_base, time0, time1, *time_mixed = logs
+ time_non_mixed = (time_base + time0 + time1) / 3
+ time_mixed = min(time_mixed)
+
+ assert time_mixed < factor * time_non_mixed
+
+ # Measure timing of running base and adapter separately vs using a mixed batch. Note that on CPU, the
+ # differences are quite small, so this test requires GPU to avoid flakiness.
+ for _ in range(3):
+ with timed():
+ with peft_model.disable_adapter():
+ peft_model(**{k: v[::3] for k, v in inputs.items()})
+ peft_model.set_adapter("adapter1")
+ peft_model(**{k: v[1::3] for k, v in inputs.items()})
+ peft_model.set_adapter("adapter2")
+ peft_model(**{k: v[2::3] for k, v in inputs.items()})
+
+ times_separate = logs[-3:]
+ time_separate = sum(times_separate) / 3
+ assert time_separate > time_mixed
+
+
+class TestDynamicDispatch:
+ # These are tests for the dynamic dispatch feature for LoRA. We create a custom module and a custom LoRA layer
+ # that targets it.
+
+ @pytest.fixture(scope="class")
+ def custom_module_cls(self):
+ class MyModule(nn.Module):
+ # A custom layer that just behaves like an nn.Linear layer but is not an instance of nn.Linear. Therefore,
+ # it would normally fail to be targeted.
+ def __init__(self):
+ super().__init__()
+ self.in_features = 10
+ self.out_features = 20
+ self.weight = nn.Parameter(torch.randn(20, 10))
+
+ def forward(self, x):
+ return nn.functional.linear(x, self.weight)
+
+ return MyModule
+
+ @pytest.fixture(scope="class")
+ def custom_lora_cls(self):
+ from peft.tuners import lora
+
+ class MyLora(lora.Linear):
+ # just re-use the lora.Linear code here
+ pass
+
+ return MyLora
+
+ @pytest.fixture(scope="class")
+ def model_cls(self, custom_module_cls):
+ class MyModel(nn.Module):
+ def __init__(self):
+ super().__init__()
+ self.lin0 = nn.Linear(10, 10)
+ self.relu = nn.ReLU()
+ self.my_module = custom_module_cls()
+ self.lin1 = nn.Linear(20, 2)
+
+ def forward(self, x):
+ x = self.relu(self.lin0(x))
+ x = self.relu(self.my_module(x))
+ x = self.lin1(x)
+ return x
+
+ return MyModel
+
+ def test_custom_lora_layer_used(self, custom_module_cls, custom_lora_cls, model_cls):
+ # check that when we register custom lora layers, they are indeed being used for the intended module
+ model = model_cls()
+ config = LoraConfig(target_modules=["lin0", "my_module", "lin1"])
+ config._register_custom_module({custom_module_cls: custom_lora_cls})
+
+ peft_model = get_peft_model(model, config)
+ assert isinstance(peft_model.base_model.model.my_module, custom_lora_cls)
+ assert isinstance(peft_model.base_model.model.my_module.base_layer, custom_module_cls)
+ # sanity check that the other lora layer types are still the default ones
+ assert not isinstance(peft_model.base_model.model.lin0.base_layer, custom_module_cls)
+ assert not isinstance(peft_model.base_model.model.lin1.base_layer, custom_module_cls)
+
+ def test_training_works(self, model_cls, custom_module_cls, custom_lora_cls):
+ # check that when we train with custom lora layers, they are indeed updated
+ model = model_cls()
+ config = LoraConfig(target_modules=["lin0", "my_module", "lin1"])
+ config._register_custom_module({custom_module_cls: custom_lora_cls})
+
+ peft_model = get_peft_model(model, config)
+ sd_before = copy.deepcopy(peft_model.state_dict())
+ inputs = torch.randn(16, 10)
+ optimizer = torch.optim.SGD(peft_model.parameters(), lr=1e-4)
+
+ for _ in range(5):
+ optimizer.zero_grad()
+ output = peft_model(inputs)
+ loss = output.sum() ** 2
+ loss.backward()
+ optimizer.step()
+
+ sd_after = peft_model.state_dict()
+
+ # sanity check that for finite results, since nan != nan, which would make the test pass trivially
+ for val in sd_before.values():
+ assert torch.isfinite(val).all()
+ for val in sd_after.values():
+ assert torch.isfinite(val).all()
+
+ assert not torch.allclose(
+ sd_before["base_model.model.my_module.lora_A.default.weight"],
+ sd_after["base_model.model.my_module.lora_A.default.weight"],
+ )
+ assert not torch.allclose(
+ sd_before["base_model.model.my_module.lora_B.default.weight"],
+ sd_after["base_model.model.my_module.lora_B.default.weight"],
+ )
+
+ def test_saving_and_loading(self, custom_module_cls, custom_lora_cls, model_cls, tmp_path):
+ # check that we can successfully save and load the custom lora cls
+ torch.manual_seed(0)
+ model = model_cls()
+ config = LoraConfig(target_modules=["lin0", "my_module", "lin1"])
+ config._register_custom_module({custom_module_cls: custom_lora_cls})
+
+ torch.manual_seed(1)
+ peft_model = get_peft_model(model, config)
+
+ inputs = torch.randn(5, 10)
+ outputs_before = peft_model(inputs) # does not raise
+
+ sd_before = peft_model.state_dict()
+ peft_model.save_pretrained(tmp_path / "lora-custom-module")
+ del model, peft_model
+
+ torch.manual_seed(0) # same seed for base model
+ model = model_cls()
+
+ # custom lora mapping is not persisted at the moment, so as a workaround this is needed
+ config = LoraConfig.from_pretrained(tmp_path / "lora-custom-module")
+ config._register_custom_module({custom_module_cls: custom_lora_cls})
+
+ # different seed for adapter to ensure it is not identical just because of seed
+ torch.manual_seed(123)
+ peft_model = PeftModel.from_pretrained(model, tmp_path / "lora-custom-module", config=config)
+ assert isinstance(peft_model.base_model.model.my_module, custom_lora_cls)
+ assert isinstance(peft_model.base_model.model.my_module.base_layer, custom_module_cls)
+
+ outputs_after = peft_model(inputs) # does not raise
+ assert torch.allclose(outputs_before, outputs_after)
+
+ sd_after = peft_model.state_dict()
+ assert sd_before.keys() == sd_after.keys()
+ for key in sd_before.keys():
+ assert torch.allclose(sd_before[key], sd_after[key])
+
+ def test_override_lora_linear(self, custom_lora_cls):
+ # in this test, we check if users can override default PEFT behavior by supplying a custom lora class that is
+ # being used instead of lora.Linear
+ model = AutoModelForCausalLM.from_pretrained("facebook/opt-125m")
+ config = LoraConfig(task_type=TaskType.CAUSAL_LM)
+ config._register_custom_module({nn.Linear: custom_lora_cls})
+ peft_model = get_peft_model(model, config)
+ layers = peft_model.base_model.model.model.decoder.layers
+ for layer in layers:
+ assert isinstance(layer.self_attn.v_proj, custom_lora_cls)
+ assert isinstance(layer.self_attn.q_proj, custom_lora_cls)
+
+ def test_custom_lora_layer_issues_warning(self, custom_module_cls, custom_lora_cls, model_cls, recwarn):
+ # users will get a warning if they target a layer type that is not officially supported
+ model = model_cls()
+ config = LoraConfig(target_modules=["lin0", "my_module", "lin1"])
+ config._register_custom_module({custom_module_cls: custom_lora_cls})
+
+ get_peft_model(model, config)
+ # check warning message
+ msg = (
+ "Unsupported layer type '.MyModule'>' encountered, proceed at your own risk."
+ )
+ assert str(recwarn.list[-1].message) == msg
+
+ def test_target_layer_without_in_features_out_features(self, recwarn):
+ # It should be possible for users to target layers even if we cannot determine in_features and out_features.
+ # Those are only needed to initialize the LoRA layer via update_layer, so as long as users take care of that,
+ # they should be good and not require those attributes to exist
+ from peft.tuners import lora
+
+ class MyModel(nn.Module):
+ def __init__(self):
+ super().__init__()
+ self.lstm = nn.LSTM(10, 20)
+
+ class MyLora(nn.Module, lora.LoraLayer):
+ def __init__(self, base_layer, adapter_name, **kwargs):
+ super().__init__()
+ lora.LoraLayer.__init__(self, base_layer, **kwargs)
+ self._active_adapter = adapter_name
+
+ model = MyModel()
+ # check that in_features and out_features attributes don't exist on LSTM
+ assert not hasattr(model.lstm, "in_features")
+ assert not hasattr(model.lstm, "out_features")
+
+ config = LoraConfig(target_modules=["lstm"])
+ config._register_custom_module({nn.LSTM: MyLora})
+ peft_model = get_peft_model(model, config)
+
+ # check that custom LoRA layer is correctly applied
+ assert isinstance(peft_model.base_model.lstm, MyLora)
+ assert isinstance(peft_model.base_model.lstm.base_layer, nn.LSTM)
+
+ # we should still get a warning message
+ msg = "Unsupported layer type '' encountered, proceed at your own risk."
+ assert str(recwarn.list[-1].message) == msg
diff --git a/peft/tests/test_decoder_models.py b/peft/tests/test_decoder_models.py
new file mode 100644
index 0000000000000000000000000000000000000000..c0e3710194e0868000698462c3390fd8c37cd0d4
--- /dev/null
+++ b/peft/tests/test_decoder_models.py
@@ -0,0 +1,817 @@
+# Copyright 2023-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+import platform
+import tempfile
+from unittest.mock import Mock, call, patch
+
+import pytest
+import torch
+from safetensors.torch import load_file as safe_load_file
+from transformers import (
+ AutoModelForCausalLM,
+ AutoTokenizer,
+ DataCollatorForLanguageModeling,
+ Trainer,
+ TrainingArguments,
+)
+
+from peft import (
+ AdaLoraConfig,
+ BOFTConfig,
+ BoneConfig,
+ C3AConfig,
+ CPTConfig,
+ FourierFTConfig,
+ HRAConfig,
+ IA3Config,
+ LoraConfig,
+ MissConfig,
+ OFTConfig,
+ PrefixTuningConfig,
+ PromptEncoderConfig,
+ PromptTuningConfig,
+ PromptTuningInit,
+ RoadConfig,
+ ShiraConfig,
+ VBLoRAConfig,
+ VeraConfig,
+ WaveFTConfig,
+ get_peft_model,
+)
+
+from .testing_common import PeftCommonTester
+from .testing_utils import device_count, hub_online_once, load_dataset_english_quotes, set_init_weights_false
+
+
+PEFT_DECODER_MODELS_TO_TEST = [
+ "hf-internal-testing/tiny-random-OPTForCausalLM",
+ "hf-internal-testing/tiny-random-GPT2LMHeadModel",
+ "hf-internal-testing/tiny-random-BloomForCausalLM",
+ "hf-internal-testing/tiny-random-gpt_neo",
+ "hf-internal-testing/tiny-random-GPTJForCausalLM",
+ "hf-internal-testing/tiny-random-GPTBigCodeForCausalLM",
+ "trl-internal-testing/tiny-random-LlamaForCausalLM",
+ "peft-internal-testing/tiny-dummy-qwen2",
+ "hf-internal-testing/tiny-random-Gemma3ForCausalLM",
+]
+
+SMALL_GRID_MODELS = [
+ "hf-internal-testing/tiny-random-gpt2",
+ "hf-internal-testing/tiny-random-OPTForCausalLM",
+ "hf-internal-testing/tiny-random-MistralForCausalLM",
+ "peft-internal-testing/tiny-dummy-qwen2",
+ "trl-internal-testing/tiny-random-LlamaForCausalLM",
+]
+
+
+# TODO Missing from this list are LoKr, LoHa, LN Tuning, add them
+# Note: If the PEFT method offers an initialization option to make it an identity transform (typically via the
+# init_weights argument), then this option should be set here, if it's not already the default.
+ALL_CONFIGS = [
+ (
+ AdaLoraConfig,
+ {
+ "task_type": "CAUSAL_LM",
+ "target_modules": None,
+ "total_step": 1,
+ },
+ ),
+ (
+ BOFTConfig,
+ {
+ "task_type": "CAUSAL_LM",
+ "target_modules": None,
+ },
+ ),
+ (
+ BoneConfig,
+ {
+ "task_type": "CAUSAL_LM",
+ "target_modules": None,
+ "r": 2,
+ },
+ ),
+ (
+ MissConfig,
+ {
+ "task_type": "CAUSAL_LM",
+ "target_modules": None,
+ "r": 2,
+ },
+ ),
+ (
+ CPTConfig,
+ {
+ "task_type": "CAUSAL_LM",
+ "cpt_token_ids": [0, 1, 2, 3, 4, 5, 6, 7], # Example token IDs for testing
+ "cpt_mask": [1, 1, 1, 1, 1, 1, 1, 1],
+ "cpt_tokens_type_mask": [1, 2, 2, 2, 3, 3, 4, 4],
+ },
+ ),
+ (
+ FourierFTConfig,
+ {
+ "task_type": "CAUSAL_LM",
+ "n_frequency": 10,
+ "target_modules": None,
+ },
+ ),
+ (
+ HRAConfig,
+ {
+ "task_type": "CAUSAL_LM",
+ "target_modules": None,
+ },
+ ),
+ (
+ IA3Config,
+ {
+ "task_type": "CAUSAL_LM",
+ "target_modules": None,
+ "feedforward_modules": None,
+ },
+ ),
+ (
+ LoraConfig,
+ {
+ "task_type": "CAUSAL_LM",
+ "r": 8,
+ "lora_alpha": 32,
+ "target_modules": None,
+ "lora_dropout": 0.05,
+ "bias": "none",
+ },
+ ),
+ # Activated LoRA (aLoRA)
+ (
+ LoraConfig,
+ {
+ "task_type": "CAUSAL_LM",
+ "r": 8,
+ "lora_alpha": 32,
+ "target_modules": None,
+ "lora_dropout": 0.05,
+ "bias": "none",
+ "alora_invocation_tokens": [1],
+ },
+ ),
+ (
+ LoraConfig,
+ {
+ "task_type": "CAUSAL_LM",
+ "r": 8,
+ "lora_alpha": 32,
+ "target_modules": None,
+ "lora_dropout": 0.05,
+ "bias": "none",
+ # not one test input sequence will ever have this token, this should do nothing at all
+ "alora_invocation_tokens": [1000],
+ },
+ ),
+ # LoRA + trainable tokens
+ (
+ LoraConfig,
+ {
+ "task_type": "CAUSAL_LM",
+ "r": 8,
+ "lora_alpha": 32,
+ "target_modules": None,
+ "lora_dropout": 0.05,
+ "bias": "none",
+ "trainable_token_indices": [0, 1, 3],
+ },
+ ),
+ (
+ OFTConfig,
+ {
+ "task_type": "CAUSAL_LM",
+ "target_modules": None,
+ },
+ ),
+ (
+ PrefixTuningConfig,
+ {
+ "task_type": "CAUSAL_LM",
+ "num_virtual_tokens": 10,
+ },
+ ),
+ (
+ PromptEncoderConfig,
+ {
+ "task_type": "CAUSAL_LM",
+ "num_virtual_tokens": 10,
+ "encoder_hidden_size": 32,
+ },
+ ),
+ (
+ PromptTuningConfig,
+ {
+ "task_type": "CAUSAL_LM",
+ "num_virtual_tokens": 10,
+ },
+ ),
+ (
+ RoadConfig,
+ {
+ "task_type": "CAUSAL_LM",
+ "variant": "road_1",
+ "group_size": 2,
+ },
+ ),
+ (
+ ShiraConfig,
+ {
+ "r": 1,
+ "task_type": "CAUSAL_LM",
+ "target_modules": None,
+ "init_weights": False,
+ },
+ ),
+ (
+ VBLoRAConfig,
+ {
+ "task_type": "CAUSAL_LM",
+ "target_modules": None,
+ "vblora_dropout": 0.05,
+ "vector_length": 1,
+ "num_vectors": 2,
+ },
+ ),
+ (
+ VeraConfig,
+ {
+ "task_type": "CAUSAL_LM",
+ "r": 8,
+ "target_modules": None,
+ "vera_dropout": 0.05,
+ "projection_prng_key": 0xFF,
+ "d_initial": 0.1,
+ "save_projection": True,
+ "bias": "none",
+ },
+ ),
+ (
+ C3AConfig,
+ {
+ "task_type": "CAUSAL_LM",
+ "block_size": 1, # Some test cases contain shapes of prime numbers where `block_size` must be 1
+ "target_modules": None,
+ },
+ ),
+ (
+ WaveFTConfig,
+ {
+ "task_type": "CAUSAL_LM",
+ "n_frequency": 8,
+ "target_modules": None,
+ },
+ ),
+]
+
+
+def _skip_if_not_conv1d_supported(model_id, config_cls):
+ if "GPT2LMHeadModel" in model_id and config_cls in [
+ BOFTConfig,
+ BoneConfig,
+ HRAConfig,
+ OFTConfig,
+ RoadConfig,
+ ShiraConfig,
+ C3AConfig,
+ MissConfig,
+ ]:
+ pytest.skip("Skipping BOFT/HRA/OFT/Bone/Road/SHiRA/C3A/MiSS for GPT2LMHeadModel")
+
+
+def _skip_adalora_oft_hra_bone_for_gpt2(model_id, config_cls):
+ if "GPT2LMHeadModel" in model_id and config_cls in [
+ AdaLoraConfig,
+ BOFTConfig,
+ HRAConfig,
+ OFTConfig,
+ BoneConfig,
+ C3AConfig,
+ RoadConfig,
+ MissConfig,
+ ]:
+ pytest.skip("Skipping AdaLora/BOFT/HRA/OFT/Bone/MiSS for GPT2LMHeadModel")
+
+
+def _skip_alora_no_activation(config_cls, config_kwargs):
+ if config_cls is LoraConfig and config_kwargs.get("alora_invocation_tokens") == [1000]:
+ pytest.skip("Skipping aLoRA no-activation-case because the test expects changed output which there won't be.")
+
+
+class TestDecoderModels(PeftCommonTester):
+ transformers_class = AutoModelForCausalLM
+
+ def skipTest(self, reason=""):
+ # for backwards compatibility with unittest style test classes
+ pytest.skip(reason)
+
+ def prepare_inputs_for_testing(self):
+ input_ids = torch.tensor([[1, 1, 1], [1, 2, 1]]).to(self.torch_device)
+ attention_mask = torch.tensor([[1, 1, 1], [1, 0, 1]]).to(self.torch_device)
+ return {"input_ids": input_ids, "attention_mask": attention_mask}
+
+ @pytest.mark.parametrize("model_id", PEFT_DECODER_MODELS_TO_TEST)
+ @pytest.mark.parametrize("config_cls,config_kwargs", ALL_CONFIGS)
+ def test_attributes_parametrized(self, model_id, config_cls, config_kwargs):
+ _skip_if_not_conv1d_supported(model_id, config_cls)
+ self._test_model_attr(model_id, config_cls, config_kwargs.copy())
+
+ @pytest.mark.parametrize("model_id", PEFT_DECODER_MODELS_TO_TEST)
+ @pytest.mark.parametrize("config_cls,config_kwargs", ALL_CONFIGS)
+ def test_adapter_name(self, model_id, config_cls, config_kwargs):
+ _skip_if_not_conv1d_supported(model_id, config_cls)
+ self._test_adapter_name(model_id, config_cls, config_kwargs.copy())
+
+ @pytest.mark.parametrize("model_id", PEFT_DECODER_MODELS_TO_TEST)
+ @pytest.mark.parametrize("config_cls,config_kwargs", ALL_CONFIGS)
+ def test_prepare_for_training_parametrized(self, model_id, config_cls, config_kwargs):
+ _skip_if_not_conv1d_supported(model_id, config_cls)
+ self._test_prepare_for_training(model_id, config_cls, config_kwargs.copy())
+
+ @pytest.mark.parametrize("model_id", PEFT_DECODER_MODELS_TO_TEST)
+ @pytest.mark.parametrize("config_cls,config_kwargs", ALL_CONFIGS)
+ def test_prompt_tuning_text_prepare_for_training(self, model_id, config_cls, config_kwargs):
+ if config_cls != PromptTuningConfig:
+ pytest.skip(f"This test does not apply to {config_cls}")
+ config_kwargs = config_kwargs.copy()
+ config_kwargs["prompt_tuning_init"] = PromptTuningInit.TEXT
+ config_kwargs["prompt_tuning_init_text"] = "This is a test prompt."
+ config_kwargs["tokenizer_name_or_path"] = model_id
+ self._test_prepare_for_training(model_id, config_cls, config_kwargs.copy())
+
+ def test_prompt_tuning_text_tokenizer_kwargs(self):
+ # Allow users to pass additional arguments to Tokenizer.from_pretrained
+ # Fix for #1032
+ mock = Mock()
+ orig_from_pretrained = AutoTokenizer.from_pretrained
+
+ def mock_autotokenizer_from_pretrained(*args, **kwargs):
+ mock(*args, **kwargs)
+ return orig_from_pretrained(config.tokenizer_name_or_path)
+
+ model_id = "hf-internal-testing/tiny-random-OPTForCausalLM"
+ config = PromptTuningConfig(
+ base_model_name_or_path=model_id,
+ tokenizer_name_or_path=model_id,
+ num_virtual_tokens=10,
+ prompt_tuning_init=PromptTuningInit.TEXT,
+ task_type="CAUSAL_LM",
+ prompt_tuning_init_text="This is a test prompt.",
+ tokenizer_kwargs={"trust_remote_code": True, "foo": "bar"},
+ )
+ model = self.transformers_class.from_pretrained(model_id).to(self.torch_device)
+ with patch("transformers.AutoTokenizer.from_pretrained", mock_autotokenizer_from_pretrained):
+ _ = get_peft_model(model, config)
+ expected_call = call(model_id, trust_remote_code=True, foo="bar")
+ assert mock.call_args == expected_call
+
+ @pytest.mark.parametrize("model_id", PEFT_DECODER_MODELS_TO_TEST)
+ @pytest.mark.parametrize("config_cls,config_kwargs", ALL_CONFIGS)
+ def test_prompt_tuning_sample_vocab_prepare_for_training(self, model_id, config_cls, config_kwargs):
+ if config_cls != PromptTuningConfig:
+ pytest.skip(f"This test does not apply to {config_cls}")
+
+ config_kwargs = config_kwargs.copy()
+ config_kwargs["prompt_tuning_init"] = PromptTuningInit.SAMPLE_VOCAB
+ config_kwargs["tokenizer_name_or_path"] = model_id
+
+ self._test_prepare_for_training(model_id, config_cls, config_kwargs.copy())
+
+ def test_prompt_tuning_config_invalid_args(self):
+ # Raise an error when tokenizer_kwargs is used with prompt_tuning_init!='TEXT', because this argument has no
+ # function in that case
+ model_id = "hf-internal-testing/tiny-random-OPTForCausalLM"
+ with pytest.raises(ValueError, match="tokenizer_kwargs only valid when using prompt_tuning_init='TEXT'."):
+ PromptTuningConfig(
+ base_model_name_or_path=model_id,
+ tokenizer_name_or_path=model_id,
+ num_virtual_tokens=10,
+ task_type="CAUSAL_LM",
+ prompt_tuning_init_text="This is a test prompt.",
+ prompt_tuning_init=PromptTuningInit.RANDOM, # <= should not be used together with tokenizer_kwargs
+ tokenizer_kwargs={"trust_remote_code": True, "foo": "bar"},
+ )
+
+ @pytest.mark.parametrize("model_id", PEFT_DECODER_MODELS_TO_TEST)
+ @pytest.mark.parametrize("config_cls,config_kwargs", ALL_CONFIGS)
+ def test_save_pretrained(self, model_id, config_cls, config_kwargs):
+ _skip_if_not_conv1d_supported(model_id, config_cls)
+ self._test_save_pretrained(model_id, config_cls, config_kwargs.copy())
+
+ @pytest.mark.parametrize("model_id", PEFT_DECODER_MODELS_TO_TEST)
+ @pytest.mark.parametrize("config_cls,config_kwargs", ALL_CONFIGS)
+ def test_save_pretrained_pickle(self, model_id, config_cls, config_kwargs):
+ _skip_if_not_conv1d_supported(model_id, config_cls)
+ self._test_save_pretrained(model_id, config_cls, config_kwargs.copy(), safe_serialization=False)
+
+ @pytest.mark.parametrize("model_id", PEFT_DECODER_MODELS_TO_TEST)
+ @pytest.mark.parametrize("config_cls,config_kwargs", ALL_CONFIGS)
+ def test_save_pretrained_selected_adapters(self, model_id, config_cls, config_kwargs):
+ _skip_if_not_conv1d_supported(model_id, config_cls)
+ self._test_save_pretrained_selected_adapters(model_id, config_cls, config_kwargs.copy())
+
+ @pytest.mark.parametrize("model_id", PEFT_DECODER_MODELS_TO_TEST)
+ @pytest.mark.parametrize("config_cls,config_kwargs", ALL_CONFIGS)
+ def test_save_pretrained_selected_adapters_pickle(self, model_id, config_cls, config_kwargs):
+ _skip_if_not_conv1d_supported(model_id, config_cls)
+ self._test_save_pretrained_selected_adapters(
+ model_id, config_cls, config_kwargs.copy(), safe_serialization=False
+ )
+
+ @pytest.mark.parametrize("model_id", PEFT_DECODER_MODELS_TO_TEST)
+ @pytest.mark.parametrize("config_cls,config_kwargs", ALL_CONFIGS)
+ def test_from_pretrained_config_construction(self, model_id, config_cls, config_kwargs):
+ _skip_if_not_conv1d_supported(model_id, config_cls)
+ self._test_from_pretrained_config_construction(model_id, config_cls, config_kwargs.copy())
+
+ @pytest.mark.parametrize("model_id", PEFT_DECODER_MODELS_TO_TEST)
+ @pytest.mark.parametrize("config_cls,config_kwargs", ALL_CONFIGS)
+ def test_merge_layers(self, model_id, config_cls, config_kwargs):
+ config_kwargs = set_init_weights_false(config_cls, config_kwargs)
+ self._test_merge_layers(model_id, config_cls, config_kwargs.copy())
+
+ @pytest.mark.parametrize("model_id", PEFT_DECODER_MODELS_TO_TEST)
+ @pytest.mark.parametrize("config_cls,config_kwargs", ALL_CONFIGS)
+ def test_merge_layers_multi(self, model_id, config_cls, config_kwargs):
+ _skip_if_not_conv1d_supported(model_id, config_cls)
+ config_kwargs = set_init_weights_false(config_cls, config_kwargs)
+ self._test_merge_layers_multi(model_id, config_cls, config_kwargs.copy())
+
+ @pytest.mark.parametrize("model_id", PEFT_DECODER_MODELS_TO_TEST)
+ @pytest.mark.parametrize("config_cls,config_kwargs", ALL_CONFIGS)
+ def test_merge_layers_nan(self, model_id, config_cls, config_kwargs):
+ config_kwargs = set_init_weights_false(config_cls, config_kwargs)
+ self._test_merge_layers_nan(model_id, config_cls, config_kwargs.copy())
+
+ @pytest.mark.parametrize("model_id", PEFT_DECODER_MODELS_TO_TEST)
+ @pytest.mark.parametrize("config_cls,config_kwargs", ALL_CONFIGS)
+ def test_mixed_adapter_batches(self, model_id, config_cls, config_kwargs):
+ if config_cls != LoraConfig:
+ pytest.skip("Mixed adapter batches not supported for this config.")
+ _skip_alora_no_activation(config_cls, config_kwargs)
+ config_kwargs = set_init_weights_false(config_cls, config_kwargs)
+ self._test_mixed_adapter_batches(model_id, config_cls, config_kwargs.copy())
+
+ @pytest.mark.parametrize("model_id", PEFT_DECODER_MODELS_TO_TEST)
+ @pytest.mark.parametrize("config_cls,config_kwargs", ALL_CONFIGS)
+ def test_generate_with_mixed_adapter_batches(self, model_id, config_cls, config_kwargs):
+ if config_cls != LoraConfig:
+ pytest.skip("Mixed adapter batches not supported for this config.")
+ config_kwargs = set_init_weights_false(config_cls, config_kwargs)
+ self._test_generate_with_mixed_adapter_batches_and_beam_search(model_id, config_cls, config_kwargs.copy())
+
+ @pytest.mark.parametrize("model_id", PEFT_DECODER_MODELS_TO_TEST)
+ @pytest.mark.parametrize("config_cls,config_kwargs", ALL_CONFIGS)
+ def test_generate(self, model_id, config_cls, config_kwargs):
+ _skip_if_not_conv1d_supported(model_id, config_cls)
+ self._test_generate(model_id, config_cls, config_kwargs.copy())
+
+ @pytest.mark.parametrize("model_id", PEFT_DECODER_MODELS_TO_TEST)
+ @pytest.mark.parametrize("config_cls,config_kwargs", ALL_CONFIGS)
+ def test_generate_pos_args(self, model_id, config_cls, config_kwargs):
+ _skip_if_not_conv1d_supported(model_id, config_cls)
+ self._test_generate_pos_args(model_id, config_cls, config_kwargs.copy(), raises_err=False)
+
+ @pytest.mark.parametrize("model_id", PEFT_DECODER_MODELS_TO_TEST)
+ @pytest.mark.parametrize("config_cls,config_kwargs", ALL_CONFIGS)
+ def test_merge_layers_fp16(self, model_id, config_cls, config_kwargs):
+ self._test_merge_layers_fp16(model_id, config_cls, config_kwargs.copy())
+
+ @pytest.mark.parametrize("model_id", PEFT_DECODER_MODELS_TO_TEST)
+ @pytest.mark.parametrize("config_cls,config_kwargs", ALL_CONFIGS)
+ def test_generate_half_prec(self, model_id, config_cls, config_kwargs):
+ self._test_generate_half_prec(model_id, config_cls, config_kwargs.copy())
+
+ @pytest.mark.parametrize("model_id", PEFT_DECODER_MODELS_TO_TEST)
+ @pytest.mark.parametrize("config_cls,config_kwargs", ALL_CONFIGS)
+ def test_prefix_tuning_half_prec_conversion(self, model_id, config_cls, config_kwargs):
+ self._test_prefix_tuning_half_prec_conversion(model_id, config_cls, config_kwargs.copy())
+
+ @pytest.mark.parametrize("model_id", PEFT_DECODER_MODELS_TO_TEST)
+ @pytest.mark.parametrize("config_cls,config_kwargs", ALL_CONFIGS)
+ def test_training_decoders(self, model_id, config_cls, config_kwargs):
+ _skip_if_not_conv1d_supported(model_id, config_cls)
+ self._test_training(model_id, config_cls, config_kwargs.copy())
+
+ @pytest.mark.parametrize("model_id", PEFT_DECODER_MODELS_TO_TEST)
+ @pytest.mark.parametrize("config_cls,config_kwargs", ALL_CONFIGS)
+ def test_training_decoders_layer_indexing(self, model_id, config_cls, config_kwargs):
+ self._test_training_layer_indexing(model_id, config_cls, config_kwargs.copy())
+
+ @pytest.mark.parametrize("model_id", PEFT_DECODER_MODELS_TO_TEST)
+ @pytest.mark.parametrize("config_cls,config_kwargs", ALL_CONFIGS)
+ def test_training_decoders_gradient_checkpointing(self, model_id, config_cls, config_kwargs):
+ _skip_if_not_conv1d_supported(model_id, config_cls)
+ self._test_training_gradient_checkpointing(model_id, config_cls, config_kwargs.copy())
+
+ @pytest.mark.parametrize("model_id", PEFT_DECODER_MODELS_TO_TEST)
+ @pytest.mark.parametrize("config_cls,config_kwargs", ALL_CONFIGS)
+ def test_inference_safetensors(self, model_id, config_cls, config_kwargs):
+ _skip_if_not_conv1d_supported(model_id, config_cls)
+ self._test_inference_safetensors(model_id, config_cls, config_kwargs.copy())
+
+ @pytest.mark.parametrize("model_id", PEFT_DECODER_MODELS_TO_TEST)
+ @pytest.mark.parametrize("config_cls,config_kwargs", ALL_CONFIGS)
+ def test_peft_model_device_map(self, model_id, config_cls, config_kwargs):
+ self._test_peft_model_device_map(model_id, config_cls, config_kwargs.copy())
+
+ @pytest.mark.parametrize("model_id", PEFT_DECODER_MODELS_TO_TEST)
+ @pytest.mark.parametrize("config_cls,config_kwargs", ALL_CONFIGS)
+ def test_delete_adapter(self, model_id, config_cls, config_kwargs):
+ _skip_if_not_conv1d_supported(model_id, config_cls)
+ self._test_delete_adapter(model_id, config_cls, config_kwargs.copy())
+
+ @pytest.mark.parametrize("model_id", PEFT_DECODER_MODELS_TO_TEST)
+ @pytest.mark.parametrize("config_cls,config_kwargs", ALL_CONFIGS)
+ def test_delete_inactive_adapter(self, model_id, config_cls, config_kwargs):
+ _skip_if_not_conv1d_supported(model_id, config_cls)
+ self._test_delete_inactive_adapter(model_id, config_cls, config_kwargs.copy())
+
+ @pytest.mark.parametrize("model_id", PEFT_DECODER_MODELS_TO_TEST)
+ @pytest.mark.parametrize("config_cls,config_kwargs", ALL_CONFIGS)
+ def test_adding_multiple_adapters_with_bias_raises(self, model_id, config_cls, config_kwargs):
+ _skip_if_not_conv1d_supported(model_id, config_cls)
+ self._test_adding_multiple_adapters_with_bias_raises(model_id, config_cls, config_kwargs.copy())
+
+ @pytest.mark.parametrize("model_id", PEFT_DECODER_MODELS_TO_TEST)
+ @pytest.mark.parametrize("config_cls,config_kwargs", ALL_CONFIGS)
+ def test_unload_adapter(self, model_id, config_cls, config_kwargs):
+ _skip_adalora_oft_hra_bone_for_gpt2(model_id, config_cls)
+ _skip_if_not_conv1d_supported(model_id, config_cls)
+ _skip_alora_no_activation(config_cls, config_kwargs)
+ config_kwargs = set_init_weights_false(config_cls, config_kwargs)
+ self._test_unload_adapter(model_id, config_cls, config_kwargs.copy())
+
+ @pytest.mark.parametrize("model_id", PEFT_DECODER_MODELS_TO_TEST)
+ @pytest.mark.parametrize("config_cls,config_kwargs", ALL_CONFIGS)
+ def test_weighted_combination_of_adapters(self, model_id, config_cls, config_kwargs):
+ config_kwargs = set_init_weights_false(config_cls, config_kwargs)
+ self._test_weighted_combination_of_adapters(model_id, config_cls, config_kwargs.copy())
+
+ @pytest.mark.parametrize("model_id", PEFT_DECODER_MODELS_TO_TEST)
+ @pytest.mark.parametrize("config_cls,config_kwargs", ALL_CONFIGS)
+ def test_training_prompt_learning_tasks(self, model_id, config_cls, config_kwargs):
+ self._test_training_prompt_learning_tasks(model_id, config_cls, config_kwargs.copy())
+
+ @pytest.mark.parametrize("model_id", PEFT_DECODER_MODELS_TO_TEST)
+ @pytest.mark.parametrize("config_cls,config_kwargs", ALL_CONFIGS)
+ def test_disable_adapter(self, model_id, config_cls, config_kwargs):
+ _skip_if_not_conv1d_supported(model_id, config_cls)
+ _skip_alora_no_activation(config_cls, config_kwargs)
+ config_kwargs = set_init_weights_false(config_cls, config_kwargs)
+ self._test_disable_adapter(model_id, config_cls, config_kwargs.copy())
+
+ def test_generate_adalora_no_dropout(self):
+ # test for issue #730
+ model_id = "hf-internal-testing/tiny-random-OPTForCausalLM"
+ config_kwargs = {
+ "target_modules": None,
+ "task_type": "CAUSAL_LM",
+ "lora_dropout": 0.0,
+ "total_step": 1,
+ }
+ self._test_generate(model_id, AdaLoraConfig, config_kwargs.copy())
+
+ @pytest.mark.parametrize("model_id", PEFT_DECODER_MODELS_TO_TEST)
+ @pytest.mark.parametrize("config_cls,config_kwargs", ALL_CONFIGS)
+ def test_passing_input_embeds_works(self, model_id, config_cls, config_kwargs):
+ _skip_if_not_conv1d_supported(model_id, config_cls)
+ if (platform.system() == "Darwin") and (config_cls == PrefixTuningConfig):
+ # the error is:
+ # > RuntimeError: unsupported operation: more than one element of the written-to tensor refers to a single
+ # > memory location. Please clone() the tensor before performing the operation.
+ # in transformers sdpa_mask_older_torch. As we (currently) cannot upgrade PyTorch on MacOS GH runners, we're
+ # stuck with this error.
+ # TODO: remove if torch can be upgraded on MacOS or if MacOS CI is removed
+ pytest.skip("Prefix tuning fails on MacOS in this case, not worth fixing")
+ self._test_passing_input_embeds_works("", model_id, config_cls, config_kwargs.copy())
+
+ def test_lora_layer_replication(self):
+ model_id = "trl-internal-testing/tiny-random-LlamaForCausalLM"
+ config_kwargs = {
+ "target_modules": ["down_proj", "up_proj"],
+ "task_type": "CAUSAL_LM",
+ "lora_dropout": 0.0,
+ "layer_replication": [[0, 1], [0, 2], [1, 2]],
+ }
+ model = self.transformers_class.from_pretrained(model_id).to(self.torch_device)
+ config = LoraConfig(base_model_name_or_path=model_id, **config_kwargs)
+
+ assert len(model.model.layers), "Expected 2 layers in original model." == 2
+ model = get_peft_model(model, config)
+ layers = model.base_model.model.model.layers
+ assert len(layers) == 4, "Expected 4 layers in adapted model."
+ assert (
+ layers[0].mlp.up_proj.base_layer.weight.data.storage().data_ptr()
+ == layers[1].mlp.up_proj.base_layer.weight.data.storage().data_ptr()
+ and layers[2].mlp.up_proj.base_layer.weight.data.storage().data_ptr()
+ == layers[3].mlp.up_proj.base_layer.weight.data.storage().data_ptr()
+ ), "Expected layers 0-1 and 2-3 to share weights"
+ assert (
+ layers[0].mlp.up_proj.base_layer.weight.data.storage().data_ptr()
+ != layers[2].mlp.up_proj.base_layer.weight.data.storage().data_ptr()
+ ), "Expected layers 0 and 2 to have different weights"
+ assert (
+ layers[0].mlp.up_proj.lora_A.default.weight.data.storage().data_ptr()
+ != layers[1].mlp.up_proj.lora_A.default.weight.data.storage().data_ptr()
+ and layers[2].mlp.up_proj.lora_A.default.weight.data.storage().data_ptr()
+ != layers[3].mlp.up_proj.lora_A.default.weight.data.storage().data_ptr()
+ ), "Expected all LoRA adapters to have distinct weights"
+ assert len([n for n, _ in model.named_parameters() if ".lora_A." in n]) == 8, (
+ "Expected 8 LoRA adapters since we are adding one each for up and down."
+ )
+ self._test_prepare_for_training(model_id, LoraConfig, config_kwargs.copy())
+ self._test_generate(model_id, LoraConfig, config_kwargs.copy())
+
+ def test_prompt_learning_with_grouped_query_attention(self):
+ # See 1901, fixes a bug with handling GQA
+ model_id = "peft-internal-testing/tiny-dummy-qwen2"
+ base_model = AutoModelForCausalLM.from_pretrained(model_id)
+ peft_config = PrefixTuningConfig(num_virtual_tokens=10, task_type="CAUSAL_LM")
+ model = get_peft_model(base_model, peft_config)
+ x = torch.tensor([[1, 2, 3]])
+ # does not raise
+ model(x)
+
+ def test_prefix_tuning_mistral(self):
+ # See issue 869, 1962
+ model_id = "hf-internal-testing/tiny-random-MistralForCausalLM"
+ base_model = AutoModelForCausalLM.from_pretrained(model_id)
+ peft_config = PrefixTuningConfig(num_virtual_tokens=10, task_type="CAUSAL_LM")
+ model = get_peft_model(base_model, peft_config)
+
+ tokenizer = AutoTokenizer.from_pretrained(model_id)
+ tokenizer.pad_token = tokenizer.eos_token
+
+ def process(samples):
+ tokenized = tokenizer(samples["quote"], truncation=True, max_length=128)
+ return tokenized
+
+ data = load_dataset_english_quotes()
+ data = data.map(process, batched=True)
+
+ with tempfile.TemporaryDirectory() as tmp_dirname:
+ trainer = Trainer(
+ model=model,
+ train_dataset=data["train"],
+ args=TrainingArguments(
+ num_train_epochs=1,
+ max_steps=5,
+ per_device_train_batch_size=4,
+ output_dir=tmp_dirname,
+ ),
+ data_collator=DataCollatorForLanguageModeling(tokenizer, mlm=False),
+ )
+ trainer.train()
+
+ @pytest.mark.parametrize("model_id", SMALL_GRID_MODELS)
+ @pytest.mark.parametrize(
+ "config_cls,config_kwargs",
+ [
+ (
+ PromptTuningConfig,
+ {
+ "num_virtual_tokens": 10,
+ "task_type": "CAUSAL_LM",
+ },
+ ),
+ (
+ PrefixTuningConfig,
+ {
+ "num_virtual_tokens": 10,
+ "task_type": "CAUSAL_LM",
+ },
+ ),
+ (
+ PromptEncoderConfig,
+ {
+ "num_virtual_tokens": 10,
+ "encoder_hidden_size": 32,
+ "task_type": "CAUSAL_LM",
+ },
+ ),
+ (
+ CPTConfig,
+ {
+ "cpt_token_ids": [0, 1, 2, 3, 4, 5, 6, 7], # Example token IDs for testing
+ "cpt_mask": [1, 1, 1, 1, 1, 1, 1, 1],
+ "cpt_tokens_type_mask": [1, 2, 2, 2, 3, 3, 4, 4],
+ },
+ ),
+ ],
+ )
+ def test_prompt_learning_with_gradient_checkpointing(self, model_id, config_cls, config_kwargs):
+ # See issue 869
+ # Test prompt learning methods with gradient checkpointing in a semi realistic setting.
+ # Prefix tuning does not work if the model uses the new caching implementation. In that case, a helpful error
+ # should be raised.
+
+ # skip if multi GPU, since this results in DataParallel usage by Trainer, which fails with "CUDA device
+ # assertion", breaking subsequent tests
+ if device_count > 1:
+ pytest.skip("Skip on multi-GPU setups")
+ peft_config = config_cls(base_model_name_or_path=model_id, **config_kwargs)
+ base_model = self.transformers_class.from_pretrained(model_id)
+ base_model.gradient_checkpointing_enable()
+
+ try:
+ model = get_peft_model(base_model, peft_config)
+ except ValueError as exc:
+ # Some methods will raise a helpful error. After this, exit the test, as training would fail.
+ assert config_cls == PrefixTuningConfig
+ assert "Prefix tuning does not work with gradient checkpointing" in str(exc)
+ return
+
+ tokenizer = AutoTokenizer.from_pretrained(model_id)
+ tokenizer.pad_token = tokenizer.eos_token
+
+ def process(samples):
+ tokenized = tokenizer(samples["quote"], truncation=True, max_length=128)
+ return tokenized
+
+ data = load_dataset_english_quotes()
+ data = data.map(process, batched=True)
+
+ with tempfile.TemporaryDirectory() as tmp_dirname:
+ trainer = Trainer(
+ model=model,
+ train_dataset=data["train"],
+ args=TrainingArguments(
+ num_train_epochs=1,
+ max_steps=3,
+ per_device_train_batch_size=4,
+ output_dir=tmp_dirname,
+ ),
+ data_collator=DataCollatorForLanguageModeling(tokenizer, mlm=False),
+ )
+ trainer.train()
+
+ @pytest.mark.parametrize("save_embedding_layers", ["auto", True, False])
+ @pytest.mark.parametrize(
+ "peft_config",
+ [
+ (LoraConfig(target_modules=["lin0", "embed_tokens"], init_lora_weights=False)),
+ (LoraConfig(target_modules=r".*\.embed_tokens", init_lora_weights=False)),
+ ],
+ )
+ def test_save_pretrained_targeting_lora_to_embedding_layer(self, save_embedding_layers, tmp_path, peft_config):
+ model_id = "trl-internal-testing/tiny-random-LlamaForCausalLM"
+
+ with hub_online_once(model_id):
+ model = AutoModelForCausalLM.from_pretrained(model_id)
+ model = get_peft_model(model, peft_config)
+
+ if save_embedding_layers == "auto":
+ # assert warning
+ msg_start = "Setting `save_embedding_layers` to `True` as embedding layers found in `target_modules`."
+ with pytest.warns(UserWarning, match=msg_start):
+ model.save_pretrained(tmp_path, save_embedding_layers=save_embedding_layers)
+ else:
+ model.save_pretrained(tmp_path, save_embedding_layers=save_embedding_layers)
+
+ state_dict = safe_load_file(tmp_path / "adapter_model.safetensors")
+ contains_embedding = "base_model.model.model.embed_tokens.base_layer.weight" in state_dict
+
+ if save_embedding_layers in ["auto", True]:
+ assert contains_embedding
+ assert torch.allclose(
+ model.base_model.model.model.embed_tokens.base_layer.weight,
+ state_dict["base_model.model.model.embed_tokens.base_layer.weight"],
+ )
+ else:
+ assert not contains_embedding
+
+ @pytest.mark.parametrize("config_cls,config_kwargs", ALL_CONFIGS)
+ def test_set_requires_grad_prompt_learning_raises(self, config_cls, config_kwargs):
+ # Test that for prompt learning, calling set_requires_grad raises an error with an appropriate error message.
+ # Note that for non-prompt learning methods, set_requires_grad is being tested for custom models, so there is no
+ # specific test here.
+ model_id = PEFT_DECODER_MODELS_TO_TEST[0] # it's enough to test this with one model
+ config = config_cls(
+ base_model_name_or_path=model_id,
+ **config_kwargs,
+ )
+ if not config.is_prompt_learning:
+ pytest.skip("This test is only for prompt learning methods.")
+
+ with hub_online_once(model_id + config_kwargs.get("tokenizer_name_or_path", "")):
+ model = self.transformers_class.from_pretrained(model_id).to(self.torch_device)
+ model = get_peft_model(model, config)
+ msg = "Setting `requires_grad` is not supported for prompt learning methods like"
+ with pytest.raises(TypeError, match=msg):
+ model.set_requires_grad(adapter_names="adpater0")
diff --git a/peft/tests/test_encoder_decoder_models.py b/peft/tests/test_encoder_decoder_models.py
new file mode 100644
index 0000000000000000000000000000000000000000..d940d0f9a1d4e1b711f8f181030b1ab3559dfeec
--- /dev/null
+++ b/peft/tests/test_encoder_decoder_models.py
@@ -0,0 +1,407 @@
+# Copyright 2023-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+import tempfile
+
+import pytest
+import torch
+from transformers import AutoModelForSeq2SeqLM, AutoModelForTokenClassification
+
+from peft import (
+ AdaLoraConfig,
+ BOFTConfig,
+ BoneConfig,
+ C3AConfig,
+ FourierFTConfig,
+ HRAConfig,
+ IA3Config,
+ LoraConfig,
+ MissConfig,
+ OFTConfig,
+ PrefixTuningConfig,
+ PromptEncoderConfig,
+ PromptTuningConfig,
+ RoadConfig,
+ ShiraConfig,
+ TaskType,
+ VBLoRAConfig,
+ VeraConfig,
+ WaveFTConfig,
+ get_peft_model,
+)
+
+from .testing_common import PeftCommonTester
+from .testing_utils import set_init_weights_false
+
+
+PEFT_ENCODER_DECODER_MODELS_TO_TEST = [
+ "ybelkada/tiny-random-T5ForConditionalGeneration-calibrated",
+ "hf-internal-testing/tiny-random-BartForConditionalGeneration",
+]
+
+# TODO Missing from this list are LoKr, LoHa, LN Tuning, add them
+ALL_CONFIGS = [
+ (
+ AdaLoraConfig,
+ {
+ "target_modules": None,
+ "total_step": 1,
+ "task_type": "SEQ_2_SEQ_LM",
+ },
+ ),
+ (
+ BOFTConfig,
+ {
+ "target_modules": None,
+ "task_type": "SEQ_2_SEQ_LM",
+ },
+ ),
+ (
+ BoneConfig,
+ {
+ "target_modules": None,
+ "r": 2,
+ "task_type": "SEQ_2_SEQ_LM",
+ },
+ ),
+ (
+ MissConfig,
+ {
+ "target_modules": None,
+ "r": 2,
+ "task_type": "SEQ_2_SEQ_LM",
+ },
+ ),
+ (
+ FourierFTConfig,
+ {
+ "n_frequency": 10,
+ "target_modules": None,
+ "task_type": "SEQ_2_SEQ_LM",
+ },
+ ),
+ (
+ HRAConfig,
+ {
+ "target_modules": None,
+ "task_type": "SEQ_2_SEQ_LM",
+ },
+ ),
+ (
+ IA3Config,
+ {
+ "target_modules": None,
+ "feedforward_modules": None,
+ "task_type": "SEQ_2_SEQ_LM",
+ },
+ ),
+ (
+ LoraConfig,
+ {
+ "r": 8,
+ "lora_alpha": 32,
+ "target_modules": None,
+ "lora_dropout": 0.05,
+ "bias": "none",
+ "task_type": "SEQ_2_SEQ_LM",
+ },
+ ),
+ (
+ LoraConfig,
+ {
+ "r": 8,
+ "lora_alpha": 32,
+ "target_modules": None,
+ "lora_dropout": 0.05,
+ "bias": "none",
+ "trainable_token_indices": [0, 1, 3],
+ "task_type": "SEQ_2_SEQ_LM",
+ },
+ ),
+ (
+ OFTConfig,
+ {
+ "target_modules": None,
+ "task_type": "SEQ_2_SEQ_LM",
+ },
+ ),
+ (
+ PrefixTuningConfig,
+ {
+ "num_virtual_tokens": 10,
+ "task_type": "SEQ_2_SEQ_LM",
+ },
+ ),
+ (
+ PromptEncoderConfig,
+ {
+ "num_virtual_tokens": 10,
+ "encoder_hidden_size": 32,
+ "task_type": "SEQ_2_SEQ_LM",
+ },
+ ),
+ (
+ PromptTuningConfig,
+ {
+ "num_virtual_tokens": 10,
+ "task_type": "SEQ_2_SEQ_LM",
+ },
+ ),
+ (
+ RoadConfig,
+ {
+ "task_type": "SEQ_2_SEQ_LM",
+ "variant": "road_1",
+ "group_size": 2,
+ },
+ ),
+ (
+ ShiraConfig,
+ {
+ "r": 1,
+ "task_type": "SEQ_2_SEQ_LM",
+ "target_modules": None,
+ "init_weights": False,
+ },
+ ),
+ (
+ VBLoRAConfig,
+ {
+ "target_modules": None,
+ "vblora_dropout": 0.05,
+ "vector_length": 1,
+ "num_vectors": 2,
+ "task_type": "SEQ_2_SEQ_LM",
+ },
+ ),
+ (
+ VeraConfig,
+ {
+ "r": 8,
+ "target_modules": None,
+ "vera_dropout": 0.05,
+ "projection_prng_key": 0xFF,
+ "d_initial": 0.1,
+ "save_projection": True,
+ "bias": "none",
+ "task_type": "SEQ_2_SEQ_LM",
+ },
+ ),
+ (
+ C3AConfig,
+ {
+ "task_type": "SEQ_2_SEQ_LM",
+ "block_size": 1,
+ "target_modules": None,
+ },
+ ),
+ (
+ WaveFTConfig,
+ {
+ "task_type": "SEQ_2_SEQ_LM",
+ "n_frequency": 8,
+ "target_modules": None,
+ },
+ ),
+]
+
+
+class TestEncoderDecoderModels(PeftCommonTester):
+ transformers_class = AutoModelForSeq2SeqLM
+
+ def skipTest(self, reason=""):
+ # for backwards compatibility with unittest style test classes
+ pytest.skip(reason)
+
+ def prepare_inputs_for_testing(self):
+ input_ids = torch.tensor([[1, 1, 1], [1, 2, 1]]).to(self.torch_device)
+ decoder_input_ids = torch.tensor([[1, 1, 1], [1, 2, 1]]).to(self.torch_device)
+ attention_mask = torch.tensor([[1, 1, 1], [1, 0, 1]]).to(self.torch_device)
+
+ input_dict = {
+ "input_ids": input_ids,
+ "decoder_input_ids": decoder_input_ids,
+ "attention_mask": attention_mask,
+ }
+
+ return input_dict
+
+ @pytest.mark.parametrize("model_id", PEFT_ENCODER_DECODER_MODELS_TO_TEST)
+ @pytest.mark.parametrize("config_cls,config_kwargs", ALL_CONFIGS)
+ def test_attributes_parametrized(self, model_id, config_cls, config_kwargs):
+ self._test_model_attr(model_id, config_cls, config_kwargs)
+
+ @pytest.mark.parametrize("model_id", PEFT_ENCODER_DECODER_MODELS_TO_TEST)
+ @pytest.mark.parametrize("config_cls,config_kwargs", ALL_CONFIGS)
+ def test_adapter_name(self, model_id, config_cls, config_kwargs):
+ self._test_adapter_name(model_id, config_cls, config_kwargs)
+
+ @pytest.mark.parametrize("model_id", PEFT_ENCODER_DECODER_MODELS_TO_TEST)
+ @pytest.mark.parametrize("config_cls,config_kwargs", ALL_CONFIGS)
+ def test_prepare_for_training_parametrized(self, model_id, config_cls, config_kwargs):
+ self._test_prepare_for_training(model_id, config_cls, config_kwargs)
+
+ @pytest.mark.parametrize("model_id", PEFT_ENCODER_DECODER_MODELS_TO_TEST)
+ @pytest.mark.parametrize("config_cls,config_kwargs", ALL_CONFIGS)
+ def test_save_pretrained(self, model_id, config_cls, config_kwargs):
+ self._test_save_pretrained(model_id, config_cls, config_kwargs)
+
+ @pytest.mark.parametrize("model_id", PEFT_ENCODER_DECODER_MODELS_TO_TEST)
+ @pytest.mark.parametrize("config_cls,config_kwargs", ALL_CONFIGS)
+ def test_save_pretrained_pickle(self, model_id, config_cls, config_kwargs):
+ self._test_save_pretrained(model_id, config_cls, config_kwargs, safe_serialization=False)
+
+ @pytest.mark.parametrize("model_id", PEFT_ENCODER_DECODER_MODELS_TO_TEST)
+ @pytest.mark.parametrize("config_cls,config_kwargs", ALL_CONFIGS)
+ def test_save_pretrained_selected_adapters(self, model_id, config_cls, config_kwargs):
+ self._test_save_pretrained_selected_adapters(model_id, config_cls, config_kwargs)
+
+ @pytest.mark.parametrize("model_id", PEFT_ENCODER_DECODER_MODELS_TO_TEST)
+ @pytest.mark.parametrize("config_cls,config_kwargs", ALL_CONFIGS)
+ def test_save_pretrained_selected_adapters_pickle(self, model_id, config_cls, config_kwargs):
+ self._test_save_pretrained_selected_adapters(model_id, config_cls, config_kwargs, safe_serialization=False)
+
+ def test_load_model_low_cpu_mem_usage(self):
+ # Using the first model with LoraConfig and an empty config_kwargs.
+ self._test_load_model_low_cpu_mem_usage(PEFT_ENCODER_DECODER_MODELS_TO_TEST[0], LoraConfig, {})
+
+ @pytest.mark.parametrize("model_id", PEFT_ENCODER_DECODER_MODELS_TO_TEST)
+ @pytest.mark.parametrize("config_cls,config_kwargs", ALL_CONFIGS)
+ def test_from_pretrained_config_construction(self, model_id, config_cls, config_kwargs):
+ self._test_from_pretrained_config_construction(model_id, config_cls, config_kwargs)
+
+ @pytest.mark.parametrize("model_id", PEFT_ENCODER_DECODER_MODELS_TO_TEST)
+ @pytest.mark.parametrize("config_cls,config_kwargs", ALL_CONFIGS)
+ def test_merge_layers(self, model_id, config_cls, config_kwargs):
+ config_kwargs = set_init_weights_false(config_cls, config_kwargs)
+ self._test_merge_layers(model_id, config_cls, config_kwargs)
+
+ @pytest.mark.parametrize("model_id", PEFT_ENCODER_DECODER_MODELS_TO_TEST)
+ @pytest.mark.parametrize("config_cls,config_kwargs", ALL_CONFIGS)
+ def test_mixed_adapter_batches(self, model_id, config_cls, config_kwargs):
+ config_kwargs = set_init_weights_false(config_cls, config_kwargs)
+ self._test_mixed_adapter_batches(model_id, config_cls, config_kwargs)
+
+ @pytest.mark.parametrize("model_id", PEFT_ENCODER_DECODER_MODELS_TO_TEST)
+ @pytest.mark.parametrize("config_cls,config_kwargs", ALL_CONFIGS)
+ def test_generate_with_mixed_adapter_batches(self, model_id, config_cls, config_kwargs):
+ config_kwargs = set_init_weights_false(config_cls, config_kwargs)
+ self._test_generate_with_mixed_adapter_batches_and_beam_search(model_id, config_cls, config_kwargs)
+
+ @pytest.mark.parametrize("model_id", PEFT_ENCODER_DECODER_MODELS_TO_TEST)
+ @pytest.mark.parametrize("config_cls,config_kwargs", ALL_CONFIGS)
+ def test_generate(self, model_id, config_cls, config_kwargs):
+ self._test_generate(model_id, config_cls, config_kwargs)
+
+ @pytest.mark.parametrize("model_id", PEFT_ENCODER_DECODER_MODELS_TO_TEST)
+ @pytest.mark.parametrize("config_cls,config_kwargs", ALL_CONFIGS)
+ def test_generate_pos_args(self, model_id, config_cls, config_kwargs):
+ self._test_generate_pos_args(model_id, config_cls, config_kwargs, raises_err=True)
+
+ @pytest.mark.parametrize("model_id", PEFT_ENCODER_DECODER_MODELS_TO_TEST)
+ @pytest.mark.parametrize("config_cls,config_kwargs", ALL_CONFIGS)
+ def test_generate_half_prec(self, model_id, config_cls, config_kwargs):
+ self._test_generate_half_prec(model_id, config_cls, config_kwargs)
+
+ @pytest.mark.parametrize("model_id", PEFT_ENCODER_DECODER_MODELS_TO_TEST)
+ @pytest.mark.parametrize("config_cls,config_kwargs", ALL_CONFIGS)
+ def test_prefix_tuning_half_prec_conversion(self, model_id, config_cls, config_kwargs):
+ self._test_prefix_tuning_half_prec_conversion(model_id, config_cls, config_kwargs)
+
+ @pytest.mark.parametrize("model_id", PEFT_ENCODER_DECODER_MODELS_TO_TEST)
+ @pytest.mark.parametrize("config_cls,config_kwargs", ALL_CONFIGS)
+ def test_training_encoder_decoders(self, model_id, config_cls, config_kwargs):
+ self._test_training(model_id, config_cls, config_kwargs)
+
+ @pytest.mark.parametrize("model_id", PEFT_ENCODER_DECODER_MODELS_TO_TEST)
+ @pytest.mark.parametrize("config_cls,config_kwargs", ALL_CONFIGS)
+ def test_training_encoder_decoders_layer_indexing(self, model_id, config_cls, config_kwargs):
+ self._test_training_layer_indexing(model_id, config_cls, config_kwargs)
+
+ @pytest.mark.parametrize("model_id", PEFT_ENCODER_DECODER_MODELS_TO_TEST)
+ @pytest.mark.parametrize("config_cls,config_kwargs", ALL_CONFIGS)
+ def test_training_encoder_decoders_gradient_checkpointing(self, model_id, config_cls, config_kwargs):
+ self._test_training_gradient_checkpointing(model_id, config_cls, config_kwargs)
+
+ @pytest.mark.parametrize("model_id", PEFT_ENCODER_DECODER_MODELS_TO_TEST)
+ @pytest.mark.parametrize("config_cls,config_kwargs", ALL_CONFIGS)
+ def test_inference_safetensors(self, model_id, config_cls, config_kwargs):
+ self._test_inference_safetensors(model_id, config_cls, config_kwargs)
+
+ @pytest.mark.parametrize("model_id", PEFT_ENCODER_DECODER_MODELS_TO_TEST)
+ @pytest.mark.parametrize("config_cls,config_kwargs", ALL_CONFIGS)
+ def test_peft_model_device_map(self, model_id, config_cls, config_kwargs):
+ self._test_peft_model_device_map(model_id, config_cls, config_kwargs)
+
+ @pytest.mark.parametrize("model_id", PEFT_ENCODER_DECODER_MODELS_TO_TEST)
+ @pytest.mark.parametrize("config_cls,config_kwargs", ALL_CONFIGS)
+ def test_delete_adapter(self, model_id, config_cls, config_kwargs):
+ self._test_delete_adapter(model_id, config_cls, config_kwargs)
+
+ @pytest.mark.parametrize("model_id", PEFT_ENCODER_DECODER_MODELS_TO_TEST)
+ @pytest.mark.parametrize("config_cls,config_kwargs", ALL_CONFIGS)
+ def test_delete_inactive_adapter(self, model_id, config_cls, config_kwargs):
+ self._test_delete_inactive_adapter(model_id, config_cls, config_kwargs)
+
+ @pytest.mark.parametrize("model_id", PEFT_ENCODER_DECODER_MODELS_TO_TEST)
+ @pytest.mark.parametrize("config_cls,config_kwargs", ALL_CONFIGS)
+ def test_adding_multiple_adapters_with_bias_raises(self, model_id, config_cls, config_kwargs):
+ self._test_adding_multiple_adapters_with_bias_raises(model_id, config_cls, config_kwargs)
+
+ @pytest.mark.parametrize("model_id", PEFT_ENCODER_DECODER_MODELS_TO_TEST)
+ @pytest.mark.parametrize("config_cls,config_kwargs", ALL_CONFIGS)
+ def test_unload_adapter(self, model_id, config_cls, config_kwargs):
+ config_kwargs = set_init_weights_false(config_cls, config_kwargs)
+ self._test_unload_adapter(model_id, config_cls, config_kwargs)
+
+ @pytest.mark.parametrize("model_id", PEFT_ENCODER_DECODER_MODELS_TO_TEST)
+ @pytest.mark.parametrize("config_cls,config_kwargs", ALL_CONFIGS)
+ def test_weighted_combination_of_adapters(self, model_id, config_cls, config_kwargs):
+ config_kwargs = set_init_weights_false(config_cls, config_kwargs)
+ self._test_weighted_combination_of_adapters(model_id, config_cls, config_kwargs)
+
+ @pytest.mark.parametrize("model_id", PEFT_ENCODER_DECODER_MODELS_TO_TEST)
+ @pytest.mark.parametrize("config_cls,config_kwargs", ALL_CONFIGS)
+ def test_training_prompt_learning_tasks(self, model_id, config_cls, config_kwargs):
+ self._test_training_prompt_learning_tasks(model_id, config_cls, config_kwargs)
+
+ @pytest.mark.parametrize("model_id", PEFT_ENCODER_DECODER_MODELS_TO_TEST)
+ @pytest.mark.parametrize("config_cls,config_kwargs", ALL_CONFIGS)
+ def test_disable_adapter(self, model_id, config_cls, config_kwargs):
+ config_kwargs = set_init_weights_false(config_cls, config_kwargs)
+ self._test_disable_adapter(model_id, config_cls, config_kwargs)
+
+ def test_active_adapters_prompt_learning(self):
+ model = AutoModelForSeq2SeqLM.from_pretrained(
+ "hf-internal-testing/tiny-random-BartForConditionalGeneration"
+ ).to(self.torch_device)
+ # any prompt learning method would work here
+ config = PromptEncoderConfig(task_type=TaskType.SEQ_2_SEQ_LM, num_virtual_tokens=10)
+ model = get_peft_model(model, config)
+ assert model.active_adapters == ["default"]
+
+ def test_save_shared_tensors(self):
+ model_id = "hf-internal-testing/tiny-random-RobertaModel"
+ peft_config = LoraConfig(
+ task_type=TaskType.TOKEN_CLS,
+ inference_mode=False,
+ r=16,
+ lora_alpha=16,
+ lora_dropout=0.1,
+ bias="all",
+ )
+ model = AutoModelForTokenClassification.from_pretrained(model_id, num_labels=11)
+ model = get_peft_model(model, peft_config)
+ with tempfile.TemporaryDirectory() as tmp_dir:
+ # This should work fine
+ model.save_pretrained(tmp_dir, safe_serialization=True)
diff --git a/peft/tests/test_feature_extraction_models.py b/peft/tests/test_feature_extraction_models.py
new file mode 100644
index 0000000000000000000000000000000000000000..d7dd604c979ba861655498169483327cc4e10100
--- /dev/null
+++ b/peft/tests/test_feature_extraction_models.py
@@ -0,0 +1,364 @@
+# Copyright 2023-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+import pytest
+import torch
+from transformers import AutoModel
+
+from peft import (
+ AdaLoraConfig,
+ BOFTConfig,
+ BoneConfig,
+ C3AConfig,
+ FourierFTConfig,
+ HRAConfig,
+ IA3Config,
+ LoraConfig,
+ MissConfig,
+ OFTConfig,
+ PrefixTuningConfig,
+ PromptEncoderConfig,
+ PromptLearningConfig,
+ PromptTuningConfig,
+ RoadConfig,
+ ShiraConfig,
+ VBLoRAConfig,
+ VeraConfig,
+ WaveFTConfig,
+)
+
+from .testing_common import PeftCommonTester
+from .testing_utils import set_init_weights_false
+
+
+PEFT_FEATURE_EXTRACTION_MODELS_TO_TEST = [
+ "hf-internal-testing/tiny-random-BertModel",
+ "hf-internal-testing/tiny-random-RobertaModel",
+ "hf-internal-testing/tiny-random-DebertaModel",
+ "hf-internal-testing/tiny-random-DebertaV2Model",
+]
+
+# TODO Missing from this list are LoKr, LoHa, LN Tuning, add them
+ALL_CONFIGS = [
+ (
+ AdaLoraConfig,
+ {
+ "task_type": "FEATURE_EXTRACTION",
+ "target_modules": None,
+ "total_step": 1,
+ },
+ ),
+ (
+ BOFTConfig,
+ {
+ "task_type": "FEATURE_EXTRACTION",
+ "target_modules": None,
+ },
+ ),
+ (
+ BoneConfig,
+ {
+ "task_type": "FEATURE_EXTRACTION",
+ "target_modules": None,
+ "r": 2,
+ },
+ ),
+ (
+ MissConfig,
+ {
+ "task_type": "FEATURE_EXTRACTION",
+ "target_modules": None,
+ "r": 2,
+ },
+ ),
+ (
+ FourierFTConfig,
+ {
+ "task_type": "FEATURE_EXTRACTION",
+ "n_frequency": 10,
+ "target_modules": None,
+ },
+ ),
+ (
+ HRAConfig,
+ {
+ "task_type": "FEATURE_EXTRACTION",
+ "target_modules": None,
+ },
+ ),
+ (
+ IA3Config,
+ {
+ "task_type": "FEATURE_EXTRACTION",
+ "target_modules": None,
+ "feedforward_modules": None,
+ },
+ ),
+ (
+ LoraConfig,
+ {
+ "task_type": "FEATURE_EXTRACTION",
+ "r": 8,
+ "lora_alpha": 32,
+ "target_modules": None,
+ "lora_dropout": 0.05,
+ "bias": "none",
+ },
+ ),
+ # LoRA + trainable tokens
+ (
+ LoraConfig,
+ {
+ "task_type": "FEATURE_EXTRACTION",
+ "r": 8,
+ "lora_alpha": 32,
+ "target_modules": None,
+ "lora_dropout": 0.05,
+ "bias": "none",
+ "trainable_token_indices": [0, 1, 3],
+ },
+ ),
+ (
+ OFTConfig,
+ {
+ "task_type": "FEATURE_EXTRACTION",
+ "target_modules": None,
+ },
+ ),
+ (
+ PrefixTuningConfig,
+ {
+ "task_type": "FEATURE_EXTRACTION",
+ "num_virtual_tokens": 10,
+ },
+ ),
+ (
+ PromptEncoderConfig,
+ {
+ "task_type": "FEATURE_EXTRACTION",
+ "num_virtual_tokens": 10,
+ "encoder_hidden_size": 32,
+ },
+ ),
+ (
+ PromptTuningConfig,
+ {
+ "task_type": "FEATURE_EXTRACTION",
+ "num_virtual_tokens": 10,
+ },
+ ),
+ (
+ RoadConfig,
+ {
+ "task_type": "FEATURE_EXTRACTION",
+ "variant": "road_1",
+ "group_size": 2,
+ },
+ ),
+ (
+ ShiraConfig,
+ {
+ "r": 1,
+ "task_type": "FEATURE_EXTRACTION",
+ "target_modules": None,
+ "init_weights": False,
+ },
+ ),
+ (
+ VBLoRAConfig,
+ {
+ "task_type": "FEATURE_EXTRACTION",
+ "target_modules": None,
+ "vblora_dropout": 0.05,
+ "vector_length": 1,
+ "num_vectors": 2,
+ },
+ ),
+ (
+ VeraConfig,
+ {
+ "task_type": "FEATURE_EXTRACTION",
+ "r": 8,
+ "target_modules": None,
+ "vera_dropout": 0.05,
+ "projection_prng_key": 0xFF,
+ "d_initial": 0.1,
+ "save_projection": True,
+ "bias": "none",
+ },
+ ),
+ (
+ C3AConfig,
+ {
+ "task_type": "FEATURE_EXTRACTION",
+ "block_size": 1,
+ "target_modules": None,
+ },
+ ),
+ (
+ WaveFTConfig,
+ {
+ "task_type": "FEATURE_EXTRACTION",
+ "n_frequency": 8,
+ "target_modules": None,
+ },
+ ),
+]
+
+
+def skip_non_prompt_learning(config_cls):
+ if not issubclass(config_cls, PromptLearningConfig) or (config_cls == PrefixTuningConfig):
+ pytest.skip("Skip tests that are not prompt learning or that are prefix tuning")
+
+
+def skip_deberta_lora_tests(config_cls, model_id):
+ if "deberta" not in model_id.lower():
+ return
+
+ to_skip = ["lora", "ia3", "boft", "vera", "fourierft", "hra", "bone", "randlora"]
+ config_name = config_cls.__name__.lower()
+ if any(k in config_name for k in to_skip):
+ pytest.skip(f"Skip tests that use {config_name} for Deberta models")
+
+
+def skip_deberta_pt_tests(config_cls, model_id):
+ if "deberta" not in model_id.lower():
+ return
+
+ to_skip = ["prefix"]
+ config_name = config_cls.__name__.lower()
+ if any(k in config_name for k in to_skip):
+ pytest.skip(f"Skip tests that use {config_name} for Deberta models")
+
+
+class TestPeftFeatureExtractionModel(PeftCommonTester):
+ """
+ Test if the PeftModel behaves as expected. This includes:
+ - test if the model has the expected methods
+ """
+
+ transformers_class = AutoModel
+
+ def skipTest(self, reason=""):
+ # for backwards compatibility with unittest style test classes
+ pytest.skip(reason)
+
+ def prepare_inputs_for_testing(self):
+ input_ids = torch.tensor([[1, 1, 1], [1, 2, 1]]).to(self.torch_device)
+ attention_mask = torch.tensor([[1, 1, 1], [1, 0, 1]]).to(self.torch_device)
+
+ input_dict = {
+ "input_ids": input_ids,
+ "attention_mask": attention_mask,
+ }
+
+ return input_dict
+
+ @pytest.mark.parametrize("model_id", PEFT_FEATURE_EXTRACTION_MODELS_TO_TEST)
+ @pytest.mark.parametrize("config_cls,config_kwargs", ALL_CONFIGS)
+ def test_attributes_parametrized(self, model_id, config_cls, config_kwargs):
+ self._test_model_attr(model_id, config_cls, config_kwargs)
+
+ @pytest.mark.parametrize("model_id", PEFT_FEATURE_EXTRACTION_MODELS_TO_TEST)
+ @pytest.mark.parametrize("config_cls,config_kwargs", ALL_CONFIGS)
+ def test_adapter_name(self, model_id, config_cls, config_kwargs):
+ self._test_adapter_name(model_id, config_cls, config_kwargs)
+
+ @pytest.mark.parametrize("model_id", PEFT_FEATURE_EXTRACTION_MODELS_TO_TEST)
+ @pytest.mark.parametrize("config_cls,config_kwargs", ALL_CONFIGS)
+ def test_prepare_for_training_parametrized(self, model_id, config_cls, config_kwargs):
+ self._test_prepare_for_training(model_id, config_cls, config_kwargs)
+
+ @pytest.mark.parametrize("model_id", PEFT_FEATURE_EXTRACTION_MODELS_TO_TEST)
+ @pytest.mark.parametrize("config_cls,config_kwargs", ALL_CONFIGS)
+ def test_save_pretrained(self, model_id, config_cls, config_kwargs):
+ self._test_save_pretrained(model_id, config_cls, config_kwargs)
+
+ @pytest.mark.parametrize("model_id", PEFT_FEATURE_EXTRACTION_MODELS_TO_TEST)
+ @pytest.mark.parametrize("config_cls,config_kwargs", ALL_CONFIGS)
+ def test_save_pretrained_selected_adapters(self, model_id, config_cls, config_kwargs):
+ self._test_save_pretrained_selected_adapters(model_id, config_cls, config_kwargs)
+
+ def test_load_model_low_cpu_mem_usage(self):
+ self._test_load_model_low_cpu_mem_usage(PEFT_FEATURE_EXTRACTION_MODELS_TO_TEST[0], LoraConfig, {})
+
+ @pytest.mark.parametrize("model_id", PEFT_FEATURE_EXTRACTION_MODELS_TO_TEST)
+ @pytest.mark.parametrize("config_cls,config_kwargs", ALL_CONFIGS)
+ def test_from_pretrained_config_construction(self, model_id, config_cls, config_kwargs):
+ self._test_from_pretrained_config_construction(model_id, config_cls, config_kwargs)
+
+ @pytest.mark.parametrize("model_id", PEFT_FEATURE_EXTRACTION_MODELS_TO_TEST)
+ @pytest.mark.parametrize("config_cls,config_kwargs", ALL_CONFIGS)
+ def test_merge_layers(self, model_id, config_cls, config_kwargs):
+ config_kwargs = set_init_weights_false(config_cls, config_kwargs)
+ self._test_merge_layers(model_id, config_cls, config_kwargs)
+
+ @pytest.mark.parametrize("model_id", PEFT_FEATURE_EXTRACTION_MODELS_TO_TEST)
+ @pytest.mark.parametrize("config_cls,config_kwargs", ALL_CONFIGS)
+ def test_training(self, model_id, config_cls, config_kwargs):
+ self._test_training(model_id, config_cls, config_kwargs)
+
+ @pytest.mark.parametrize("model_id", PEFT_FEATURE_EXTRACTION_MODELS_TO_TEST)
+ @pytest.mark.parametrize("config_cls,config_kwargs", ALL_CONFIGS)
+ def test_training_prompt_learning_tasks(self, model_id, config_cls, config_kwargs):
+ skip_deberta_pt_tests(config_cls, model_id)
+ self._test_training_prompt_learning_tasks(model_id, config_cls, config_kwargs)
+
+ @pytest.mark.parametrize("model_id", PEFT_FEATURE_EXTRACTION_MODELS_TO_TEST)
+ @pytest.mark.parametrize("config_cls,config_kwargs", ALL_CONFIGS)
+ def test_training_layer_indexing(self, model_id, config_cls, config_kwargs):
+ self._test_training_layer_indexing(model_id, config_cls, config_kwargs)
+
+ @pytest.mark.parametrize("model_id", PEFT_FEATURE_EXTRACTION_MODELS_TO_TEST)
+ @pytest.mark.parametrize("config_cls,config_kwargs", ALL_CONFIGS)
+ def test_training_gradient_checkpointing(self, model_id, config_cls, config_kwargs):
+ skip_deberta_lora_tests(config_cls, model_id)
+ self._test_training_gradient_checkpointing(model_id, config_cls, config_kwargs)
+
+ @pytest.mark.parametrize("model_id", PEFT_FEATURE_EXTRACTION_MODELS_TO_TEST)
+ @pytest.mark.parametrize("config_cls,config_kwargs", ALL_CONFIGS)
+ def test_inference_safetensors(self, model_id, config_cls, config_kwargs):
+ self._test_inference_safetensors(model_id, config_cls, config_kwargs)
+
+ @pytest.mark.parametrize("model_id", PEFT_FEATURE_EXTRACTION_MODELS_TO_TEST)
+ @pytest.mark.parametrize("config_cls,config_kwargs", ALL_CONFIGS)
+ def test_peft_model_device_map(self, model_id, config_cls, config_kwargs):
+ self._test_peft_model_device_map(model_id, config_cls, config_kwargs)
+
+ @pytest.mark.parametrize("model_id", PEFT_FEATURE_EXTRACTION_MODELS_TO_TEST)
+ @pytest.mark.parametrize("config_cls,config_kwargs", ALL_CONFIGS)
+ def test_delete_adapter(self, model_id, config_cls, config_kwargs):
+ self._test_delete_adapter(model_id, config_cls, config_kwargs)
+
+ @pytest.mark.parametrize("model_id", PEFT_FEATURE_EXTRACTION_MODELS_TO_TEST)
+ @pytest.mark.parametrize("config_cls,config_kwargs", ALL_CONFIGS)
+ def test_delete_inactive_adapter(self, model_id, config_cls, config_kwargs):
+ self._test_delete_inactive_adapter(model_id, config_cls, config_kwargs)
+
+ @pytest.mark.parametrize("model_id", PEFT_FEATURE_EXTRACTION_MODELS_TO_TEST)
+ @pytest.mark.parametrize("config_cls,config_kwargs", ALL_CONFIGS)
+ def test_unload_adapter(self, model_id, config_cls, config_kwargs):
+ config_kwargs = set_init_weights_false(config_cls, config_kwargs)
+ self._test_unload_adapter(model_id, config_cls, config_kwargs)
+
+ @pytest.mark.parametrize("model_id", PEFT_FEATURE_EXTRACTION_MODELS_TO_TEST)
+ @pytest.mark.parametrize("config_cls,config_kwargs", ALL_CONFIGS)
+ def test_weighted_combination_of_adapters(self, model_id, config_cls, config_kwargs):
+ config_kwargs = set_init_weights_false(config_cls, config_kwargs)
+ self._test_weighted_combination_of_adapters(model_id, config_cls, config_kwargs)
+
+ @pytest.mark.parametrize("model_id", PEFT_FEATURE_EXTRACTION_MODELS_TO_TEST)
+ @pytest.mark.parametrize("config_cls,config_kwargs", ALL_CONFIGS)
+ def test_passing_input_embeds_works(self, model_id, config_cls, config_kwargs):
+ skip_non_prompt_learning(config_cls)
+ self._test_passing_input_embeds_works("test input embeds work", model_id, config_cls, config_kwargs)
diff --git a/peft/tests/test_gptqmodel.py b/peft/tests/test_gptqmodel.py
new file mode 100644
index 0000000000000000000000000000000000000000..3d16b60d2dd89f851c717bc09ca11589e9e56ada
--- /dev/null
+++ b/peft/tests/test_gptqmodel.py
@@ -0,0 +1,563 @@
+# Note: These tests were copied from test_common_gpu.py and test_gpu_examples.py as they can run on CPU too.
+#
+# Copyright 2025-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+import gc
+import os
+import tempfile
+import unittest
+
+import pytest
+import torch
+from accelerate.utils.memory import clear_device_cache
+from transformers import (
+ AutoModelForCausalLM,
+ AutoTokenizer,
+ DataCollatorForLanguageModeling,
+ Trainer,
+ TrainingArguments,
+)
+
+from peft import (
+ AdaLoraConfig,
+ LoraConfig,
+ OFTConfig,
+ PeftModel,
+ get_peft_model,
+ prepare_model_for_kbit_training,
+)
+from peft.tuners.lora import GPTQLoraLinear
+from peft.utils import SAFETENSORS_WEIGHTS_NAME, infer_device
+
+from .testing_utils import (
+ device_count,
+ load_dataset_english_quotes,
+ require_gptqmodel,
+ require_optimum,
+ require_torch_multi_accelerator,
+)
+
+
+@require_gptqmodel
+class PeftGPTQModelCommonTests(unittest.TestCase):
+ r"""
+ A common tester to run common operations that are performed on GPU/CPU such as generation, loading in 8bit, etc.
+ """
+
+ def setUp(self):
+ self.causal_lm_model_id = "facebook/opt-350m"
+ self.device = infer_device()
+
+ def tearDown(self):
+ r"""
+ Efficient mechanism to free GPU memory after each test. Based on
+ https://github.com/huggingface/transformers/issues/21094
+ """
+ clear_device_cache(garbage_collection=True)
+ gc.collect()
+
+ def test_lora_gptq_quantization_from_pretrained_safetensors(self):
+ r"""
+ Tests that the gptqmodel quantization using LoRA works as expected with safetensors weights.
+ """
+ from transformers import GPTQConfig
+
+ model_id = "marcsun13/opt-350m-gptq-4bit"
+ quantization_config = GPTQConfig(bits=4, use_exllama=False)
+ kwargs = {
+ "pretrained_model_name_or_path": model_id,
+ "torch_dtype": torch.float16,
+ "device_map": "auto",
+ "quantization_config": quantization_config,
+ }
+ model = AutoModelForCausalLM.from_pretrained(**kwargs)
+ model = prepare_model_for_kbit_training(model)
+
+ config = LoraConfig(task_type="CAUSAL_LM")
+ peft_model = get_peft_model(model, config)
+ peft_model.generate(input_ids=torch.LongTensor([[0, 2, 3, 1]]).to(peft_model.device))
+
+ with tempfile.TemporaryDirectory() as tmp_dir:
+ peft_model.save_pretrained(tmp_dir)
+ model = AutoModelForCausalLM.from_pretrained(**kwargs)
+ model = PeftModel.from_pretrained(model, tmp_dir)
+ model = prepare_model_for_kbit_training(model)
+ model.generate(input_ids=torch.LongTensor([[0, 2, 3, 1]]).to(peft_model.device))
+
+ # loading a 2nd adapter works, #1239
+ model.load_adapter(tmp_dir, "adapter2")
+ model.set_adapter("adapter2")
+ model.generate(input_ids=torch.LongTensor([[0, 2, 3, 1]]).to(peft_model.device))
+
+ # check that both adapters are in the same layer
+ assert "default" in model.base_model.model.model.decoder.layers[0].self_attn.q_proj.lora_A
+ assert "adapter2" in model.base_model.model.model.decoder.layers[0].self_attn.q_proj.lora_A
+
+ def test_oft_gptq_quantization_from_pretrained_safetensors(self):
+ r"""
+ Tests that the gptqmodel quantization using OFT works as expected with safetensors weights.
+ """
+ from transformers import GPTQConfig
+
+ model_id = "marcsun13/opt-350m-gptq-4bit"
+ quantization_config = GPTQConfig(bits=4, use_exllama=False)
+ kwargs = {
+ "pretrained_model_name_or_path": model_id,
+ "torch_dtype": torch.float16,
+ "device_map": "auto",
+ "quantization_config": quantization_config,
+ }
+ model = AutoModelForCausalLM.from_pretrained(**kwargs)
+ model = prepare_model_for_kbit_training(model)
+
+ config = OFTConfig(task_type="CAUSAL_LM")
+ peft_model = get_peft_model(model, config)
+ peft_model.generate(input_ids=torch.LongTensor([[0, 2, 3, 1]]).to(peft_model.device))
+
+ with tempfile.TemporaryDirectory() as tmp_dir:
+ peft_model.save_pretrained(tmp_dir)
+ model = AutoModelForCausalLM.from_pretrained(**kwargs)
+ model = PeftModel.from_pretrained(model, tmp_dir)
+ model = prepare_model_for_kbit_training(model)
+ model.generate(input_ids=torch.LongTensor([[0, 2, 3, 1]]).to(peft_model.device))
+
+ # loading a 2nd adapter works, #1239
+ model.load_adapter(tmp_dir, "adapter2")
+ model.set_adapter("adapter2")
+ model.generate(input_ids=torch.LongTensor([[0, 2, 3, 1]]).to(peft_model.device))
+
+ # check that both adapters are in the same layer
+ assert "default" in model.base_model.model.model.decoder.layers[0].self_attn.q_proj.oft_R
+ assert "adapter2" in model.base_model.model.model.decoder.layers[0].self_attn.q_proj.oft_R
+
+
+@require_gptqmodel
+@require_optimum
+class PeftGPTQModelTests(unittest.TestCase):
+ r"""
+ GPTQ + peft tests
+ """
+
+ def setUp(self):
+ from transformers import GPTQConfig
+
+ self.causal_lm_model_id = "marcsun13/opt-350m-gptq-4bit"
+ self.quantization_config = GPTQConfig(bits=4, backend="auto_trainable")
+ self.tokenizer = AutoTokenizer.from_pretrained(self.causal_lm_model_id)
+
+ def tearDown(self):
+ r"""
+ Efficient mechanism to free GPU memory after each test. Based on
+ https://github.com/huggingface/transformers/issues/21094
+ """
+ clear_device_cache(garbage_collection=True)
+
+ def _check_inference_finite(self, model, batch):
+ # try inference without Trainer class
+ training = model.training
+ model.eval()
+ output = model(**batch.to(model.device))
+ assert torch.isfinite(output.logits).all()
+ model.train(training)
+
+ def test_causal_lm_training(self):
+ r"""
+ Test the CausalLM training on a single GPU device. The test would simply fail if the adapters are not set
+ correctly.
+ """
+ with tempfile.TemporaryDirectory() as tmp_dir:
+ model = AutoModelForCausalLM.from_pretrained(
+ self.causal_lm_model_id,
+ torch_dtype=torch.float16,
+ device_map="auto",
+ quantization_config=self.quantization_config,
+ )
+
+ model = prepare_model_for_kbit_training(model)
+ config = LoraConfig(
+ r=16,
+ lora_alpha=32,
+ target_modules=["q_proj", "v_proj"],
+ lora_dropout=0.05,
+ bias="none",
+ task_type="CAUSAL_LM",
+ )
+ model = get_peft_model(model, config)
+
+ data = load_dataset_english_quotes()
+ data = data.map(lambda samples: self.tokenizer(samples["quote"]), batched=True)
+
+ trainer = Trainer(
+ model=model,
+ train_dataset=data["train"],
+ args=TrainingArguments(
+ per_device_train_batch_size=4,
+ gradient_accumulation_steps=4,
+ warmup_steps=2,
+ max_steps=3,
+ learning_rate=2e-4,
+ fp16=True,
+ logging_steps=1,
+ output_dir=tmp_dir,
+ ),
+ data_collator=DataCollatorForLanguageModeling(self.tokenizer, mlm=False),
+ )
+ model.config.use_cache = False
+ trainer.train()
+
+ model.cpu().save_pretrained(tmp_dir)
+
+ assert "adapter_config.json" in os.listdir(tmp_dir)
+ assert SAFETENSORS_WEIGHTS_NAME in os.listdir(tmp_dir)
+
+ # assert loss is not None
+ assert trainer.state.log_history[-1]["train_loss"] is not None
+
+ def test_oft_causal_lm_training(self):
+ r"""
+ Test the CausalLM training on a single GPU device. The test would simply fail if the adapters are not set
+ correctly.
+ """
+ with tempfile.TemporaryDirectory() as tmp_dir:
+ model = AutoModelForCausalLM.from_pretrained(
+ self.causal_lm_model_id,
+ torch_dtype=torch.float16,
+ device_map="auto",
+ quantization_config=self.quantization_config,
+ )
+
+ model = prepare_model_for_kbit_training(model)
+ config = OFTConfig(
+ r=0,
+ oft_block_size=8,
+ target_modules=["q_proj", "v_proj"],
+ bias="none",
+ task_type="CAUSAL_LM",
+ )
+ model = get_peft_model(model, config)
+
+ data = load_dataset_english_quotes()
+ data = data.map(lambda samples: self.tokenizer(samples["quote"]), batched=True)
+
+ trainer = Trainer(
+ model=model,
+ train_dataset=data["train"],
+ args=TrainingArguments(
+ per_device_train_batch_size=4,
+ gradient_accumulation_steps=4,
+ warmup_steps=2,
+ max_steps=3,
+ learning_rate=2e-4,
+ fp16=True,
+ logging_steps=1,
+ output_dir=tmp_dir,
+ ),
+ data_collator=DataCollatorForLanguageModeling(self.tokenizer, mlm=False),
+ )
+ model.config.use_cache = False
+ trainer.train()
+
+ model.cpu().save_pretrained(tmp_dir)
+
+ assert "adapter_config.json" in os.listdir(tmp_dir)
+ assert SAFETENSORS_WEIGHTS_NAME in os.listdir(tmp_dir)
+
+ # assert loss is not None
+ assert trainer.state.log_history[-1]["train_loss"] is not None
+
+ @pytest.mark.single_gpu_tests
+ def test_adalora_causalLM(self):
+ r"""
+ Tests the gptq training with adalora
+ """
+
+ model = AutoModelForCausalLM.from_pretrained(
+ self.causal_lm_model_id,
+ torch_dtype=torch.float16,
+ device_map="auto",
+ quantization_config=self.quantization_config,
+ )
+
+ tokenizer = AutoTokenizer.from_pretrained(self.causal_lm_model_id)
+ model = prepare_model_for_kbit_training(model)
+
+ peft_config = AdaLoraConfig(
+ total_step=40,
+ init_r=6,
+ target_r=4,
+ tinit=10,
+ tfinal=20,
+ deltaT=5,
+ beta1=0.3,
+ beta2=0.3,
+ orth_reg_weight=0.2,
+ lora_alpha=32,
+ lora_dropout=0.05,
+ bias="none",
+ task_type="CAUSAL_LM",
+ )
+
+ model = get_peft_model(model, peft_config)
+
+ data = load_dataset_english_quotes()
+ data = data.map(lambda samples: self.tokenizer(samples["quote"]), batched=True)
+ batch = tokenizer(data["train"][:3]["quote"], return_tensors="pt", padding=True)
+ self._check_inference_finite(model, batch)
+
+ with tempfile.TemporaryDirectory() as tmp_dir:
+ trainer = Trainer(
+ model=model,
+ train_dataset=data["train"],
+ args=TrainingArguments(
+ per_device_train_batch_size=4,
+ gradient_accumulation_steps=4,
+ warmup_steps=2,
+ max_steps=3,
+ learning_rate=2e-4,
+ fp16=True,
+ logging_steps=1,
+ output_dir=tmp_dir,
+ ),
+ data_collator=DataCollatorForLanguageModeling(self.tokenizer, mlm=False),
+ )
+ model.config.use_cache = False
+ trainer.train()
+
+ model.cpu().save_pretrained(tmp_dir)
+
+ assert "adapter_config.json" in os.listdir(tmp_dir)
+ assert SAFETENSORS_WEIGHTS_NAME in os.listdir(tmp_dir)
+
+ # assert loss is not None
+ assert trainer.state.log_history[-1]["train_loss"] is not None
+
+ @pytest.mark.multi_gpu_tests
+ @require_torch_multi_accelerator
+ def test_causal_lm_training_multi_accelerator(self):
+ r"""
+ Test the CausalLM training on a multi-accelerator device. The test would simply fail if the adapters are not
+ set correctly.
+ """
+
+ with tempfile.TemporaryDirectory() as tmp_dir:
+ model = AutoModelForCausalLM.from_pretrained(
+ self.causal_lm_model_id,
+ torch_dtype=torch.float16,
+ device_map="auto",
+ quantization_config=self.quantization_config,
+ )
+
+ assert set(model.hf_device_map.values()) == set(range(device_count))
+
+ model = prepare_model_for_kbit_training(model)
+
+ setattr(model, "model_parallel", True)
+ setattr(model, "is_parallelizable", True)
+
+ config = LoraConfig(
+ r=16,
+ lora_alpha=32,
+ target_modules=["q_proj", "v_proj"],
+ lora_dropout=0.05,
+ bias="none",
+ task_type="CAUSAL_LM",
+ )
+
+ model = get_peft_model(model, config)
+
+ data = load_dataset_english_quotes()
+ data = data.map(lambda samples: self.tokenizer(samples["quote"]), batched=True)
+
+ trainer = Trainer(
+ model=model,
+ train_dataset=data["train"],
+ args=TrainingArguments(
+ per_device_train_batch_size=4,
+ gradient_accumulation_steps=4,
+ warmup_steps=2,
+ max_steps=3,
+ learning_rate=2e-4,
+ fp16=True,
+ logging_steps=1,
+ output_dir=tmp_dir,
+ ),
+ data_collator=DataCollatorForLanguageModeling(self.tokenizer, mlm=False),
+ )
+ model.config.use_cache = False
+ trainer.train()
+
+ model.cpu().save_pretrained(tmp_dir)
+
+ assert "adapter_config.json" in os.listdir(tmp_dir)
+ assert SAFETENSORS_WEIGHTS_NAME in os.listdir(tmp_dir)
+
+ # assert loss is not None
+ assert trainer.state.log_history[-1]["train_loss"] is not None
+
+ @pytest.mark.multi_gpu_tests
+ @require_torch_multi_accelerator
+ def test_oft_causal_lm_training_multi_accelerator(self):
+ r"""
+ Test the CausalLM training on a multi-accelerator device. The test would simply fail if the adapters are not
+ set correctly.
+ """
+
+ with tempfile.TemporaryDirectory() as tmp_dir:
+ model = AutoModelForCausalLM.from_pretrained(
+ self.causal_lm_model_id,
+ torch_dtype=torch.float16,
+ device_map="auto",
+ quantization_config=self.quantization_config,
+ )
+
+ assert set(model.hf_device_map.values()) == set(range(device_count))
+
+ model = prepare_model_for_kbit_training(model)
+
+ setattr(model, "model_parallel", True)
+ setattr(model, "is_parallelizable", True)
+
+ config = OFTConfig(
+ r=0,
+ oft_block_size=8,
+ target_modules=["q_proj", "v_proj"],
+ bias="none",
+ task_type="CAUSAL_LM",
+ )
+
+ model = get_peft_model(model, config)
+
+ data = load_dataset_english_quotes()
+ data = data.map(lambda samples: self.tokenizer(samples["quote"]), batched=True)
+
+ trainer = Trainer(
+ model=model,
+ train_dataset=data["train"],
+ args=TrainingArguments(
+ per_device_train_batch_size=4,
+ gradient_accumulation_steps=4,
+ warmup_steps=2,
+ max_steps=3,
+ learning_rate=2e-4,
+ fp16=True,
+ logging_steps=1,
+ output_dir=tmp_dir,
+ ),
+ data_collator=DataCollatorForLanguageModeling(self.tokenizer, mlm=False),
+ )
+ model.config.use_cache = False
+ trainer.train()
+
+ model.cpu().save_pretrained(tmp_dir)
+
+ assert "adapter_config.json" in os.listdir(tmp_dir)
+ assert SAFETENSORS_WEIGHTS_NAME in os.listdir(tmp_dir)
+
+ # assert loss is not None
+ assert trainer.state.log_history[-1]["train_loss"] is not None
+
+ def test_non_default_adapter_name(self):
+ # See issue 1346
+ config = LoraConfig(
+ r=16,
+ target_modules=["q_proj", "v_proj"],
+ task_type="CAUSAL_LM",
+ )
+
+ # default adapter name
+ model = AutoModelForCausalLM.from_pretrained(
+ self.causal_lm_model_id,
+ torch_dtype=torch.float16,
+ device_map="auto",
+ quantization_config=self.quantization_config,
+ )
+ model = prepare_model_for_kbit_training(model)
+ model = get_peft_model(model, config)
+ n_trainable_default, n_total_default = model.get_nb_trainable_parameters()
+
+ # other adapter name
+ model = AutoModelForCausalLM.from_pretrained(
+ self.causal_lm_model_id,
+ torch_dtype=torch.float16,
+ device_map="auto",
+ quantization_config=self.quantization_config,
+ )
+ model = prepare_model_for_kbit_training(model)
+ model = get_peft_model(model, config, adapter_name="other")
+ n_trainable_other, n_total_other = model.get_nb_trainable_parameters()
+
+ assert n_trainable_other > 0
+ # sanity check
+ assert n_trainable_default == n_trainable_other
+ assert n_total_default == n_total_other
+
+ def test_oft_non_default_adapter_name(self):
+ # See issue 1346
+ config = OFTConfig(
+ r=0,
+ oft_block_size=8,
+ target_modules=["q_proj", "v_proj"],
+ task_type="CAUSAL_LM",
+ )
+
+ # default adapter name
+ model = AutoModelForCausalLM.from_pretrained(
+ self.causal_lm_model_id,
+ torch_dtype=torch.float16,
+ device_map="auto",
+ quantization_config=self.quantization_config,
+ )
+ model = prepare_model_for_kbit_training(model)
+ model = get_peft_model(model, config)
+ n_trainable_default, n_total_default = model.get_nb_trainable_parameters()
+
+ # other adapter name
+ model = AutoModelForCausalLM.from_pretrained(
+ self.causal_lm_model_id,
+ torch_dtype=torch.float16,
+ device_map="auto",
+ quantization_config=self.quantization_config,
+ )
+ model = prepare_model_for_kbit_training(model)
+ model = get_peft_model(model, config, adapter_name="other")
+ n_trainable_other, n_total_other = model.get_nb_trainable_parameters()
+
+ assert n_trainable_other > 0
+ # sanity check
+ assert n_trainable_default == n_trainable_other
+ assert n_total_default == n_total_other
+
+ def test_load_lora(self):
+ model_id = "ModelCloud/Llama-3.2-1B-gptqmodel-ci-4bit"
+ adapter_id = "ModelCloud/Llama-3.2-1B-gptqmodel-ci-4bit-lora"
+
+ model = AutoModelForCausalLM.from_pretrained(model_id, device_map="auto")
+ model.load_adapter(adapter_id)
+
+ # assert dynamic rank
+ v_proj_module = model.model.layers[5].self_attn.v_proj
+ assert isinstance(v_proj_module, GPTQLoraLinear)
+ assert v_proj_module.lora_A["default"].weight.data.shape[0] == 128
+ assert v_proj_module.lora_B["default"].weight.data.shape[1] == 128
+ gate_proj_module = model.model.layers[5].mlp.gate_proj
+ assert isinstance(gate_proj_module, GPTQLoraLinear)
+ assert gate_proj_module.lora_A["default"].weight.data.shape[0] == 256
+ assert gate_proj_module.lora_B["default"].weight.data.shape[1] == 256
+
+ tokenizer = AutoTokenizer.from_pretrained(model_id)
+ inp = tokenizer("Capital of France is", return_tensors="pt").to(model.device)
+ tokens = model.generate(**inp)[0]
+ result = tokenizer.decode(tokens)
+
+ assert "paris" in result.lower()
diff --git a/peft/tests/test_gpu_examples.py b/peft/tests/test_gpu_examples.py
new file mode 100644
index 0000000000000000000000000000000000000000..e37d78d49e7c4445273bc76b822f1a917ed59f69
--- /dev/null
+++ b/peft/tests/test_gpu_examples.py
@@ -0,0 +1,5369 @@
+# Copyright 2023-present the HuggingFace Inc. team.
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+import gc
+import importlib
+import itertools
+import os
+import re
+import tempfile
+import unittest
+from collections import Counter, defaultdict
+from copy import deepcopy
+from dataclasses import dataclass
+from pathlib import Path
+from typing import Any, Union
+
+import numpy as np
+import pytest
+import torch
+from accelerate import infer_auto_device_map
+from accelerate.test_utils.testing import run_command
+from accelerate.utils import patch_environment
+from accelerate.utils.imports import is_bf16_available
+from accelerate.utils.memory import clear_device_cache
+from accelerate.utils.versions import is_torch_version
+from datasets import Audio, Dataset, DatasetDict, load_dataset
+from packaging import version
+from parameterized import parameterized
+from torch.distributed import init_process_group
+from torch.distributed.fsdp import FullyShardedDataParallel as FSDP
+from torch.utils.data import DataLoader
+from transformers import (
+ AutoModelForCausalLM,
+ AutoModelForSeq2SeqLM,
+ AutoTokenizer,
+ BitsAndBytesConfig,
+ DataCollatorForLanguageModeling,
+ Seq2SeqTrainer,
+ Seq2SeqTrainingArguments,
+ Trainer,
+ TrainerCallback,
+ TrainingArguments,
+ WhisperFeatureExtractor,
+ WhisperForConditionalGeneration,
+ WhisperProcessor,
+ WhisperTokenizer,
+)
+from transformers.pytorch_utils import Conv1D
+
+from peft import (
+ AdaLoraConfig,
+ ArrowConfig,
+ EvaConfig,
+ LoftQConfig,
+ LoraConfig,
+ PeftModel,
+ PrefixTuningConfig,
+ PromptEncoderConfig,
+ RandLoraConfig,
+ RoadConfig,
+ TaskType,
+ VeraConfig,
+ create_arrow_model,
+ get_peft_model,
+ get_peft_model_state_dict,
+ initialize_lora_eva_weights,
+ inject_adapter_in_model,
+ prepare_model_for_kbit_training,
+ replace_lora_weights_loftq,
+ set_peft_model_state_dict,
+)
+from peft.import_utils import is_diffusers_available, is_xpu_available
+from peft.tuners import boft
+from peft.tuners.tuners_utils import BaseTunerLayer
+from peft.utils import SAFETENSORS_WEIGHTS_NAME, infer_device
+from peft.utils.hotswap import hotswap_adapter, prepare_model_for_compiled_hotswap
+from peft.utils.loftq_utils import NFQuantizer
+from peft.utils.other import fsdp_auto_wrap_policy
+from tests.testing_utils import hub_online_once
+
+from .testing_utils import (
+ device_count,
+ load_dataset_english_quotes,
+ require_aqlm,
+ require_auto_awq,
+ require_auto_gptq,
+ require_bitsandbytes,
+ require_deterministic_for_xpu,
+ require_eetq,
+ require_hqq,
+ require_non_cpu,
+ require_non_xpu,
+ require_optimum,
+ require_torch_gpu,
+ require_torch_multi_accelerator,
+ require_torch_multi_gpu,
+ require_torchao,
+ torch_device,
+)
+
+
+# Some tests with multi GPU require specific device maps to ensure that the models are loaded in two devices
+DEVICE_MAP_MAP: dict[str, dict[str, int]] = {
+ "facebook/opt-6.7b": {
+ "model.decoder.embed_tokens": 0,
+ "model.decoder.embed_positions": 0,
+ "model.decoder.final_layer_norm": 0,
+ "model.decoder.layers.0": 0,
+ "model.decoder.layers.1": 0,
+ "model.decoder.layers.2": 0,
+ "model.decoder.layers.3": 0,
+ "model.decoder.layers.4": 0,
+ "model.decoder.layers.5": 0,
+ "model.decoder.layers.6": 0,
+ "model.decoder.layers.7": 0,
+ "model.decoder.layers.8": 0,
+ "model.decoder.layers.9": 0,
+ "model.decoder.layers.10": 0,
+ "model.decoder.layers.11": 0,
+ "model.decoder.layers.12": 0,
+ "model.decoder.layers.13": 0,
+ "model.decoder.layers.14": 0,
+ "model.decoder.layers.15": 0,
+ "model.decoder.layers.16": 1,
+ "model.decoder.layers.17": 1,
+ "model.decoder.layers.18": 1,
+ "model.decoder.layers.19": 1,
+ "model.decoder.layers.20": 1,
+ "model.decoder.layers.21": 1,
+ "model.decoder.layers.22": 1,
+ "model.decoder.layers.23": 1,
+ "model.decoder.layers.24": 1,
+ "model.decoder.layers.25": 1,
+ "model.decoder.layers.26": 1,
+ "model.decoder.layers.27": 1,
+ "model.decoder.layers.28": 1,
+ "model.decoder.layers.29": 1,
+ "model.decoder.layers.30": 1,
+ "model.decoder.layers.31": 1,
+ "lm_head": 0, # tied with embed_tokens
+ },
+ "facebook/opt-125m": {
+ "model.decoder.embed_tokens": 0,
+ "model.decoder.embed_positions": 0,
+ "model.decoder.final_layer_norm": 1,
+ "model.decoder.layers.0": 0,
+ "model.decoder.layers.1": 0,
+ "model.decoder.layers.2": 0,
+ "model.decoder.layers.3": 0,
+ "model.decoder.layers.4": 0,
+ "model.decoder.layers.5": 0,
+ "model.decoder.layers.6": 1,
+ "model.decoder.layers.7": 1,
+ "model.decoder.layers.8": 1,
+ "model.decoder.layers.9": 1,
+ "model.decoder.layers.10": 1,
+ "model.decoder.layers.11": 1,
+ "lm_head": 0,
+ },
+ "marcsun13/opt-350m-gptq-4bit": {
+ "model.decoder.embed_tokens": 0,
+ "model.decoder.embed_positions": 0,
+ "model.decoder.layers.0": 0,
+ "model.decoder.layers.1": 0,
+ "model.decoder.layers.2": 0,
+ "model.decoder.layers.3": 0,
+ "model.decoder.layers.4": 0,
+ "model.decoder.layers.5": 0,
+ "model.decoder.layers.6": 1,
+ "model.decoder.layers.7": 1,
+ "model.decoder.layers.8": 1,
+ "model.decoder.layers.9": 1,
+ "model.decoder.layers.10": 1,
+ "model.decoder.layers.11": 1,
+ "model.decoder.final_layer_norm": 1,
+ "lm_head": 0, # tied with embed_tokens
+ },
+ "google/flan-t5-base": {
+ "shared": 0,
+ "encoder": 0,
+ "decoder": 1,
+ "final_layer_norm": 1,
+ "decoder.embed_tokens": 0, # tied with encoder.embed_tokens
+ "lm_head": 0, # tied with encoder.embed_tokens
+ },
+}
+
+
+# A full testing suite that tests all the necessary features on GPU. The tests should
+# rely on the example scripts to test the features.
+
+
+@dataclass
+class DataCollatorSpeechSeq2SeqWithPadding:
+ r"""
+ Directly copied from:
+ https://github.com/huggingface/peft/blob/main/examples/int8_training/peft_bnb_whisper_large_v2_training.ipynb
+ """
+
+ processor: Any
+
+ def __call__(self, features: list[dict[str, Union[list[int], torch.Tensor]]]) -> dict[str, torch.Tensor]:
+ # split inputs and labels since they have to be of different lengths and need different padding methods
+ # first treat the audio inputs by simply returning torch tensors
+ input_features = [{"input_features": feature["input_features"]} for feature in features]
+ batch = self.processor.feature_extractor.pad(input_features, return_tensors="pt")
+
+ # get the tokenized label sequences
+ label_features = [{"input_ids": feature["labels"]} for feature in features]
+ # pad the labels to max length
+ labels_batch = self.processor.tokenizer.pad(label_features, return_tensors="pt")
+
+ # replace padding with -100 to ignore loss correctly
+ labels = labels_batch["input_ids"].masked_fill(labels_batch.attention_mask.ne(1), -100)
+
+ # if bos token is appended in previous tokenization step,
+ # cut bos token here as it's append later anyways
+ if (labels[:, 0] == self.processor.tokenizer.bos_token_id).all().cpu().item():
+ labels = labels[:, 1:]
+
+ batch["labels"] = labels
+
+ return batch
+
+
+@require_non_cpu
+@require_bitsandbytes
+class PeftBnbGPUExampleTests(unittest.TestCase):
+ r"""
+ A single GPU int8 + fp4 test suite, this will test if training fits correctly on a single GPU device (1x NVIDIA T4
+ 16GB) using bitsandbytes.
+
+ The tests are the following:
+
+ - Seq2Seq model training based on:
+ https://github.com/huggingface/peft/blob/main/examples/int8_training/Finetune_flan_t5_large_bnb_peft.ipynb
+ - Causal LM model training based on:
+ https://github.com/huggingface/peft/blob/main/examples/int8_training/Finetune_opt_bnb_peft.ipynb
+ - Audio model training based on:
+ https://github.com/huggingface/peft/blob/main/examples/int8_training/peft_bnb_whisper_large_v2_training.ipynb
+
+ """
+
+ def setUp(self):
+ self.seq2seq_model_id = "google/flan-t5-base"
+ self.causal_lm_model_id = "facebook/opt-6.7b"
+ self.tokenizer = AutoTokenizer.from_pretrained(self.causal_lm_model_id)
+ self.audio_model_id = "openai/whisper-large"
+
+ def tearDown(self):
+ r"""
+ Efficient mechanism to free GPU memory after each test. Based on
+ https://github.com/huggingface/transformers/issues/21094
+ """
+ clear_device_cache(garbage_collection=True)
+
+ def _check_inference_finite(self, model, batch):
+ # try inference without Trainer class
+ training = model.training
+ model.eval()
+ output = model(**batch.to(model.device))
+ assert torch.isfinite(output.logits).all()
+ model.train(training)
+
+ @pytest.mark.single_gpu_tests
+ def test_causal_lm_training(self):
+ r"""
+ Test the CausalLM training on a single GPU device. This test is a converted version of
+ https://github.com/huggingface/peft/blob/main/examples/int8_training/Finetune_opt_bnb_peft.ipynb where we train
+ `opt-6.7b` on `english_quotes` dataset in few steps. The test would simply fail if the adapters are not set
+ correctly.
+ """
+ with tempfile.TemporaryDirectory() as tmp_dir:
+ model = AutoModelForCausalLM.from_pretrained(
+ self.causal_lm_model_id,
+ quantization_config=BitsAndBytesConfig(load_in_8bit=True),
+ device_map="auto",
+ )
+
+ tokenizer = AutoTokenizer.from_pretrained(self.causal_lm_model_id)
+ model = prepare_model_for_kbit_training(model)
+
+ config = LoraConfig(
+ r=16,
+ lora_alpha=32,
+ target_modules=["q_proj", "v_proj"],
+ lora_dropout=0.05,
+ bias="none",
+ task_type="CAUSAL_LM",
+ )
+
+ model = get_peft_model(model, config)
+
+ data = load_dataset_english_quotes()
+ data = data.map(lambda samples: tokenizer(samples["quote"]), batched=True)
+
+ trainer = Trainer(
+ model=model,
+ train_dataset=data["train"],
+ args=TrainingArguments(
+ per_device_train_batch_size=4,
+ gradient_accumulation_steps=4,
+ warmup_steps=2,
+ max_steps=3,
+ learning_rate=2e-4,
+ fp16=True,
+ logging_steps=1,
+ output_dir=tmp_dir,
+ ),
+ data_collator=DataCollatorForLanguageModeling(tokenizer, mlm=False),
+ )
+ model.config.use_cache = False
+ trainer.train()
+
+ model.cpu().save_pretrained(tmp_dir)
+
+ assert "adapter_config.json" in os.listdir(tmp_dir)
+ assert SAFETENSORS_WEIGHTS_NAME in os.listdir(tmp_dir)
+
+ # assert loss is not None
+ assert trainer.state.log_history[-1]["train_loss"] is not None
+
+ @pytest.mark.single_gpu_tests
+ def test_causal_lm_training_4bit(self):
+ r"""
+ Test the CausalLM training on a single GPU device. This test is a converted version of
+ https://github.com/huggingface/peft/blob/main/examples/int8_training/Finetune_opt_bnb_peft.ipynb where we train
+ `opt-6.7b` on `english_quotes` dataset in few steps using 4bit base model. The test would simply fail if the
+ adapters are not set correctly.
+ """
+ with tempfile.TemporaryDirectory() as tmp_dir:
+ model = AutoModelForCausalLM.from_pretrained(
+ self.causal_lm_model_id,
+ quantization_config=BitsAndBytesConfig(load_in_4bit=True),
+ device_map="auto",
+ )
+
+ tokenizer = AutoTokenizer.from_pretrained(self.causal_lm_model_id)
+ model = prepare_model_for_kbit_training(model)
+
+ config = LoraConfig(
+ r=16,
+ lora_alpha=32,
+ target_modules=["q_proj", "v_proj"],
+ lora_dropout=0.05,
+ bias="none",
+ task_type="CAUSAL_LM",
+ )
+
+ model = get_peft_model(model, config)
+
+ data = load_dataset_english_quotes()
+ data = data.map(lambda samples: tokenizer(samples["quote"]), batched=True)
+
+ trainer = Trainer(
+ model=model,
+ train_dataset=data["train"],
+ args=TrainingArguments(
+ per_device_train_batch_size=4,
+ gradient_accumulation_steps=4,
+ warmup_steps=2,
+ max_steps=3,
+ learning_rate=2e-4,
+ fp16=True,
+ logging_steps=1,
+ output_dir=tmp_dir,
+ ),
+ data_collator=DataCollatorForLanguageModeling(tokenizer, mlm=False),
+ )
+ model.config.use_cache = False
+ trainer.train()
+
+ model.cpu().save_pretrained(tmp_dir)
+
+ assert "adapter_config.json" in os.listdir(tmp_dir)
+ assert SAFETENSORS_WEIGHTS_NAME in os.listdir(tmp_dir)
+
+ # assert loss is not None
+ assert trainer.state.log_history[-1]["train_loss"] is not None
+
+ @pytest.mark.multi_gpu_tests
+ def test_causal_lm_training_multi_gpu_4bit(self):
+ r"""
+ Test the CausalLM training on a multi-GPU device with 4bit base model. The test would simply fail if the
+ adapters are not set correctly.
+ """
+
+ with tempfile.TemporaryDirectory() as tmp_dir:
+ model = AutoModelForCausalLM.from_pretrained(
+ self.causal_lm_model_id,
+ device_map=DEVICE_MAP_MAP[self.causal_lm_model_id],
+ quantization_config=BitsAndBytesConfig(load_in_4bit=True),
+ )
+
+ assert set(model.hf_device_map.values()) == set(range(device_count))
+ assert {p.device.index for p in model.parameters()} == set(range(device_count))
+
+ model = prepare_model_for_kbit_training(model)
+
+ setattr(model, "model_parallel", True)
+ setattr(model, "is_parallelizable", True)
+
+ config = LoraConfig(
+ r=16,
+ lora_alpha=32,
+ target_modules=["q_proj", "v_proj"],
+ lora_dropout=0.05,
+ bias="none",
+ task_type="CAUSAL_LM",
+ )
+
+ model = get_peft_model(model, config)
+
+ data = load_dataset_english_quotes()
+ data = data.map(lambda samples: self.tokenizer(samples["quote"]), batched=True)
+
+ trainer = Trainer(
+ model=model,
+ train_dataset=data["train"],
+ args=TrainingArguments(
+ per_device_train_batch_size=4,
+ gradient_accumulation_steps=4,
+ warmup_steps=2,
+ max_steps=3,
+ learning_rate=2e-4,
+ fp16=True,
+ logging_steps=1,
+ output_dir=tmp_dir,
+ ),
+ data_collator=DataCollatorForLanguageModeling(self.tokenizer, mlm=False),
+ )
+ model.config.use_cache = False
+ trainer.train()
+
+ model.cpu().save_pretrained(tmp_dir)
+
+ assert "adapter_config.json" in os.listdir(tmp_dir)
+ assert SAFETENSORS_WEIGHTS_NAME in os.listdir(tmp_dir)
+
+ # assert loss is not None
+ assert trainer.state.log_history[-1]["train_loss"] is not None
+
+ @pytest.mark.single_gpu_tests
+ @require_non_cpu
+ def test_4bit_adalora_causalLM(self):
+ r"""
+ Tests the 4bit training with adalora
+ """
+ model_id = "facebook/opt-350m"
+
+ # for >3 GPUs, might need: device_map={"": "cuda:0"}
+ model = AutoModelForCausalLM.from_pretrained(
+ model_id, quantization_config=BitsAndBytesConfig(load_in_4bit=True)
+ )
+ tokenizer = AutoTokenizer.from_pretrained(model_id)
+
+ model.gradient_checkpointing_enable()
+ model = prepare_model_for_kbit_training(model)
+
+ peft_config = AdaLoraConfig(
+ init_r=6,
+ target_r=4,
+ tinit=2,
+ tfinal=2,
+ total_step=6,
+ deltaT=5,
+ beta1=0.3,
+ beta2=0.3,
+ orth_reg_weight=0.2,
+ lora_alpha=32,
+ lora_dropout=0.05,
+ bias="none",
+ task_type="CAUSAL_LM",
+ )
+
+ model = get_peft_model(model, peft_config)
+
+ data = load_dataset_english_quotes()
+ data = data.map(lambda samples: tokenizer(samples["quote"]), batched=True)
+ batch = tokenizer(data["train"][:3]["quote"], return_tensors="pt", padding=True)
+ self._check_inference_finite(model, batch)
+
+ class OptimizerStepCallback(TrainerCallback):
+ def on_optimizer_step(self, args, state, control, **kwargs):
+ model.update_and_allocate(state.global_step)
+
+ step_callback = OptimizerStepCallback()
+
+ with tempfile.TemporaryDirectory() as tmp_dir:
+ trainer = Trainer(
+ model=model,
+ train_dataset=data["train"],
+ args=TrainingArguments(
+ per_device_train_batch_size=4,
+ gradient_accumulation_steps=4,
+ warmup_steps=2,
+ max_steps=6,
+ learning_rate=2e-4,
+ fp16=True,
+ logging_steps=1,
+ output_dir=tmp_dir,
+ ),
+ data_collator=DataCollatorForLanguageModeling(tokenizer, mlm=False),
+ )
+ model.config.use_cache = False
+ trainer.add_callback(step_callback)
+ trainer.train()
+
+ model.cpu().save_pretrained(tmp_dir)
+
+ assert "adapter_config.json" in os.listdir(tmp_dir)
+ assert SAFETENSORS_WEIGHTS_NAME in os.listdir(tmp_dir)
+
+ # assert loss is not None
+ assert trainer.state.log_history[-1]["train_loss"] is not None
+
+ @pytest.mark.single_gpu_tests
+ @require_non_cpu
+ def test_8bit_adalora_causalLM(self):
+ r"""
+ Tests the 8bit training with adalora
+ """
+ model_id = "facebook/opt-350m"
+
+ model = AutoModelForCausalLM.from_pretrained(
+ model_id, quantization_config=BitsAndBytesConfig(load_in_8bit=True)
+ )
+ tokenizer = AutoTokenizer.from_pretrained(model_id)
+
+ model.gradient_checkpointing_enable()
+ model = prepare_model_for_kbit_training(model)
+
+ peft_config = AdaLoraConfig(
+ init_r=6,
+ target_r=4,
+ tinit=2,
+ tfinal=2,
+ total_step=6,
+ deltaT=5,
+ beta1=0.3,
+ beta2=0.3,
+ orth_reg_weight=0.2,
+ lora_alpha=32,
+ lora_dropout=0.05,
+ bias="none",
+ task_type="CAUSAL_LM",
+ )
+
+ model = get_peft_model(model, peft_config)
+
+ data = load_dataset_english_quotes()
+ data = data.map(lambda samples: tokenizer(samples["quote"]), batched=True)
+ batch = tokenizer(data["train"][:3]["quote"], return_tensors="pt", padding=True)
+ self._check_inference_finite(model, batch)
+
+ class OptimizerStepCallback(TrainerCallback):
+ def on_optimizer_step(self, args, state, control, **kwargs):
+ model.update_and_allocate(state.global_step)
+
+ step_callback = OptimizerStepCallback()
+
+ with tempfile.TemporaryDirectory() as tmp_dir:
+ trainer = Trainer(
+ model=model,
+ train_dataset=data["train"],
+ args=TrainingArguments(
+ per_device_train_batch_size=4,
+ gradient_accumulation_steps=4,
+ warmup_steps=2,
+ max_steps=6,
+ learning_rate=2e-4,
+ fp16=True,
+ logging_steps=1,
+ output_dir=tmp_dir,
+ ),
+ data_collator=DataCollatorForLanguageModeling(tokenizer, mlm=False),
+ )
+ model.config.use_cache = False
+ trainer.add_callback(step_callback)
+ trainer.train()
+
+ model.cpu().save_pretrained(tmp_dir)
+
+ assert "adapter_config.json" in os.listdir(tmp_dir)
+ assert SAFETENSORS_WEIGHTS_NAME in os.listdir(tmp_dir)
+
+ # assert loss is not None
+ assert trainer.state.log_history[-1]["train_loss"] is not None
+
+ @pytest.mark.multi_gpu_tests
+ @require_torch_multi_accelerator
+ def test_causal_lm_training_multi_gpu(self):
+ r"""
+ Test the CausalLM training on a multi-GPU device. This test is a converted version of
+ https://github.com/huggingface/peft/blob/main/examples/int8_training/Finetune_opt_bnb_peft.ipynb where we train
+ `opt-6.7b` on `english_quotes` dataset in few steps. The test would simply fail if the adapters are not set
+ correctly.
+ """
+ with tempfile.TemporaryDirectory() as tmp_dir:
+ model = AutoModelForCausalLM.from_pretrained(
+ self.causal_lm_model_id,
+ quantization_config=BitsAndBytesConfig(load_in_8bit=True),
+ device_map="auto",
+ )
+ print(f"device map: {model.hf_device_map}")
+ assert set(model.hf_device_map.values()) == set(range(device_count))
+
+ tokenizer = AutoTokenizer.from_pretrained(self.causal_lm_model_id)
+ model = prepare_model_for_kbit_training(model)
+
+ setattr(model, "model_parallel", True)
+ setattr(model, "is_parallelizable", True)
+
+ config = LoraConfig(
+ r=16,
+ lora_alpha=32,
+ target_modules=["q_proj", "v_proj"],
+ lora_dropout=0.05,
+ bias="none",
+ task_type="CAUSAL_LM",
+ )
+
+ model = get_peft_model(model, config)
+
+ data = load_dataset_english_quotes()
+ data = data.map(lambda samples: tokenizer(samples["quote"]), batched=True)
+
+ trainer = Trainer(
+ model=model,
+ train_dataset=data["train"],
+ args=TrainingArguments(
+ per_device_train_batch_size=4,
+ gradient_accumulation_steps=4,
+ warmup_steps=2,
+ max_steps=3,
+ learning_rate=2e-4,
+ fp16=True,
+ logging_steps=1,
+ output_dir=tmp_dir,
+ ),
+ data_collator=DataCollatorForLanguageModeling(tokenizer, mlm=False),
+ )
+ model.config.use_cache = False
+ trainer.train()
+
+ model.cpu().save_pretrained(tmp_dir)
+
+ assert "adapter_config.json" in os.listdir(tmp_dir)
+ assert SAFETENSORS_WEIGHTS_NAME in os.listdir(tmp_dir)
+
+ # assert loss is not None
+ assert trainer.state.log_history[-1]["train_loss"] is not None
+
+ @pytest.mark.single_gpu_tests
+ def test_seq2seq_lm_training_single_gpu(self):
+ r"""
+ Test the Seq2SeqLM training on a single GPU device. This test is a converted version of
+ https://github.com/huggingface/peft/blob/main/examples/int8_training/Finetune_opt_bnb_peft.ipynb where we train
+ `flan-large` on `english_quotes` dataset in few steps. The test would simply fail if the adapters are not set
+ correctly.
+ """
+ with tempfile.TemporaryDirectory() as tmp_dir:
+ model = AutoModelForSeq2SeqLM.from_pretrained(
+ self.seq2seq_model_id,
+ quantization_config=BitsAndBytesConfig(load_in_8bit=True),
+ device_map={"": 0},
+ )
+
+ assert set(model.hf_device_map.values()) == {0}
+
+ tokenizer = AutoTokenizer.from_pretrained(self.seq2seq_model_id)
+ model = prepare_model_for_kbit_training(model)
+
+ config = LoraConfig(
+ r=16,
+ lora_alpha=32,
+ target_modules=["q", "v"],
+ lora_dropout=0.05,
+ bias="none",
+ task_type="CAUSAL_LM",
+ )
+
+ model = get_peft_model(model, config)
+
+ data = load_dataset_english_quotes()
+ data = data.map(lambda samples: tokenizer(samples["quote"]), batched=True)
+
+ trainer = Trainer(
+ model=model,
+ train_dataset=data["train"],
+ args=TrainingArguments(
+ per_device_train_batch_size=4,
+ gradient_accumulation_steps=4,
+ warmup_steps=2,
+ max_steps=3,
+ learning_rate=2e-4,
+ fp16=True,
+ logging_steps=1,
+ output_dir=tmp_dir,
+ ),
+ data_collator=DataCollatorForLanguageModeling(tokenizer, mlm=False),
+ )
+ model.config.use_cache = False
+ trainer.train()
+
+ model.cpu().save_pretrained(tmp_dir)
+
+ assert "adapter_config.json" in os.listdir(tmp_dir)
+ assert SAFETENSORS_WEIGHTS_NAME in os.listdir(tmp_dir)
+
+ # assert loss is not None
+ assert trainer.state.log_history[-1]["train_loss"] is not None
+
+ @pytest.mark.multi_gpu_tests
+ @require_torch_multi_accelerator
+ def test_seq2seq_lm_training_multi_gpu(self):
+ r"""
+ Test the Seq2SeqLM training on a multi-GPU device. This test is a converted version of
+ https://github.com/huggingface/peft/blob/main/examples/int8_training/Finetune_opt_bnb_peft.ipynb where we train
+ `flan-large` on `english_quotes` dataset in few steps. The test would simply fail if the adapters are not set
+ correctly.
+ """
+ with tempfile.TemporaryDirectory() as tmp_dir:
+ model = AutoModelForSeq2SeqLM.from_pretrained(
+ self.seq2seq_model_id,
+ quantization_config=BitsAndBytesConfig(load_in_8bit=True),
+ device_map=DEVICE_MAP_MAP[self.seq2seq_model_id],
+ )
+
+ assert set(model.hf_device_map.values()) == set(range(device_count))
+ assert {p.device.index for p in model.parameters()} == set(range(device_count))
+
+ tokenizer = AutoTokenizer.from_pretrained(self.seq2seq_model_id)
+ model = prepare_model_for_kbit_training(model)
+
+ config = LoraConfig(
+ r=16,
+ lora_alpha=32,
+ target_modules=["q", "v"],
+ lora_dropout=0.05,
+ bias="none",
+ task_type="CAUSAL_LM",
+ )
+
+ model = get_peft_model(model, config)
+
+ data = load_dataset_english_quotes()
+ data = data.map(lambda samples: tokenizer(samples["quote"]), batched=True)
+
+ trainer = Trainer(
+ model=model,
+ train_dataset=data["train"],
+ args=TrainingArguments(
+ per_device_train_batch_size=4,
+ gradient_accumulation_steps=4,
+ warmup_steps=2,
+ max_steps=3,
+ learning_rate=2e-4,
+ fp16=True,
+ logging_steps=1,
+ output_dir="outputs",
+ ),
+ data_collator=DataCollatorForLanguageModeling(tokenizer, mlm=False),
+ )
+ model.config.use_cache = False
+ trainer.train()
+
+ model.cpu().save_pretrained(tmp_dir)
+
+ assert "adapter_config.json" in os.listdir(tmp_dir)
+ assert SAFETENSORS_WEIGHTS_NAME in os.listdir(tmp_dir)
+
+ # assert loss is not None
+ assert trainer.state.log_history[-1]["train_loss"] is not None
+
+ # TODO skipping to see if this leads to single GPU tests passing
+ @pytest.mark.skip
+ @pytest.mark.single_gpu_tests
+ def test_audio_model_training(self):
+ r"""
+ Test the audio model training on a single GPU device. This test is a converted version of
+ https://github.com/huggingface/peft/blob/main/examples/int8_training/peft_bnb_whisper_large_v2_training.ipynb
+ """
+ with tempfile.TemporaryDirectory() as tmp_dir:
+ dataset_name = "ybelkada/common_voice_mr_11_0_copy"
+ task = "transcribe"
+ language = "Marathi"
+ common_voice = DatasetDict()
+
+ common_voice["train"] = load_dataset(dataset_name, split="train+validation")
+
+ common_voice = common_voice.remove_columns(
+ ["accent", "age", "client_id", "down_votes", "gender", "locale", "path", "segment", "up_votes"]
+ )
+
+ feature_extractor = WhisperFeatureExtractor.from_pretrained(self.audio_model_id)
+ tokenizer = WhisperTokenizer.from_pretrained(self.audio_model_id, language=language, task=task)
+ processor = WhisperProcessor.from_pretrained(self.audio_model_id, language=language, task=task)
+
+ common_voice = common_voice.cast_column("audio", Audio(sampling_rate=16000))
+
+ def prepare_dataset(batch):
+ # load and resample audio data from 48 to 16kHz
+ audio = batch["audio"]
+
+ # compute log-Mel input features from input audio array
+ batch["input_features"] = feature_extractor(
+ audio["array"], sampling_rate=audio["sampling_rate"]
+ ).input_features[0]
+
+ # encode target text to label ids
+ batch["labels"] = tokenizer(batch["sentence"]).input_ids
+ return batch
+
+ common_voice = common_voice.map(
+ prepare_dataset, remove_columns=common_voice.column_names["train"], num_proc=2
+ )
+ data_collator = DataCollatorSpeechSeq2SeqWithPadding(processor=processor)
+
+ model = WhisperForConditionalGeneration.from_pretrained(
+ self.audio_model_id, quantization_config=BitsAndBytesConfig(load_in_8bit=True), device_map="auto"
+ )
+
+ model.config.forced_decoder_ids = None
+ model.config.suppress_tokens = []
+
+ model = prepare_model_for_kbit_training(model)
+
+ # as Whisper model uses Conv layer in encoder, checkpointing disables grad computation
+ # to avoid this, make the inputs trainable
+ def make_inputs_require_grad(module, input, output):
+ output.requires_grad_(True)
+
+ model.model.encoder.conv1.register_forward_hook(make_inputs_require_grad)
+
+ config = LoraConfig(
+ r=32, lora_alpha=64, target_modules=["q_proj", "v_proj"], lora_dropout=0.05, bias="none"
+ )
+
+ model = get_peft_model(model, config)
+ model.print_trainable_parameters()
+
+ training_args = Seq2SeqTrainingArguments(
+ output_dir=tmp_dir, # change to a repo name of your choice
+ per_device_train_batch_size=8,
+ gradient_accumulation_steps=1, # increase by 2x for every 2x decrease in batch size
+ learning_rate=1e-3,
+ warmup_steps=2,
+ max_steps=3,
+ fp16=True,
+ per_device_eval_batch_size=8,
+ generation_max_length=128,
+ logging_steps=25,
+ remove_unused_columns=False, # required as the PeftModel forward doesn't have the signature of the wrapped model's forward
+ label_names=["labels"], # same reason as above
+ )
+
+ trainer = Seq2SeqTrainer(
+ args=training_args,
+ model=model,
+ train_dataset=common_voice["train"],
+ data_collator=data_collator,
+ tokenizer=processor.feature_extractor,
+ )
+
+ trainer.train()
+
+ model.cpu().save_pretrained(tmp_dir)
+
+ assert "adapter_config.json" in os.listdir(tmp_dir)
+ assert SAFETENSORS_WEIGHTS_NAME in os.listdir(tmp_dir)
+
+ # assert loss is not None
+ assert trainer.state.log_history[-1]["train_loss"] is not None
+
+ @pytest.mark.single_gpu_tests
+ def test_4bit_non_default_adapter_name(self):
+ # See PR 1294
+ config = LoraConfig(
+ r=16,
+ target_modules=["q_proj", "v_proj"],
+ bias="none",
+ task_type="CAUSAL_LM",
+ )
+
+ # default adapter name
+ model = AutoModelForCausalLM.from_pretrained(
+ "facebook/opt-125m",
+ device_map="auto",
+ quantization_config=BitsAndBytesConfig(load_in_4bit=True),
+ )
+ model = prepare_model_for_kbit_training(model)
+ model = get_peft_model(model, config)
+ n_trainable_default, n_total_default = model.get_nb_trainable_parameters()
+
+ # other adapter name
+ model = AutoModelForCausalLM.from_pretrained(
+ "facebook/opt-125m",
+ device_map="auto",
+ quantization_config=BitsAndBytesConfig(load_in_4bit=True),
+ )
+ model = prepare_model_for_kbit_training(model)
+ model = get_peft_model(model, config, adapter_name="other")
+ n_trainable_other, n_total_other = model.get_nb_trainable_parameters()
+
+ assert n_trainable_other > 0
+ # sanity check
+ assert n_trainable_default == n_trainable_other
+ assert n_total_default == n_total_other
+
+ @pytest.mark.single_gpu_tests
+ def test_8bit_non_default_adapter_name(self):
+ # See PR 1294
+ config = LoraConfig(
+ r=16,
+ target_modules=["q_proj", "v_proj"],
+ bias="none",
+ task_type="CAUSAL_LM",
+ )
+
+ # default adapter name
+ model = AutoModelForCausalLM.from_pretrained(
+ "facebook/opt-125m",
+ device_map="auto",
+ quantization_config=BitsAndBytesConfig(load_in_8bit=True),
+ )
+ model = prepare_model_for_kbit_training(model)
+ model = get_peft_model(model, config)
+ n_trainable_default, n_total_default = model.get_nb_trainable_parameters()
+
+ # other adapter name
+ model = AutoModelForCausalLM.from_pretrained(
+ "facebook/opt-125m",
+ device_map="auto",
+ quantization_config=BitsAndBytesConfig(load_in_8bit=True),
+ )
+ model = prepare_model_for_kbit_training(model)
+ model = get_peft_model(model, config, adapter_name="other")
+ n_trainable_other, n_total_other = model.get_nb_trainable_parameters()
+
+ assert n_trainable_other > 0
+ # sanity check
+ assert n_trainable_default == n_trainable_other
+ assert n_total_default == n_total_other
+
+ @pytest.mark.single_gpu_tests
+ def test_causal_lm_training_4bit_dora(self):
+ r"""
+ Same as test_causal_lm_training_4bit but with DoRA
+ """
+ with tempfile.TemporaryDirectory() as tmp_dir:
+ model = AutoModelForCausalLM.from_pretrained(
+ self.causal_lm_model_id,
+ quantization_config=BitsAndBytesConfig(load_in_4bit=True),
+ device_map="auto",
+ )
+
+ tokenizer = AutoTokenizer.from_pretrained(self.causal_lm_model_id)
+ model = prepare_model_for_kbit_training(model)
+
+ config = LoraConfig(
+ r=16,
+ lora_alpha=32,
+ target_modules=["q_proj", "v_proj"],
+ lora_dropout=0.05,
+ bias="none",
+ task_type="CAUSAL_LM",
+ use_dora=True,
+ )
+
+ model = get_peft_model(model, config)
+
+ data = load_dataset_english_quotes()
+ data = data.map(lambda samples: tokenizer(samples["quote"]), batched=True)
+
+ trainer = Trainer(
+ model=model,
+ train_dataset=data["train"],
+ args=TrainingArguments(
+ per_device_train_batch_size=4,
+ gradient_accumulation_steps=4,
+ warmup_steps=2,
+ max_steps=3,
+ learning_rate=2e-4,
+ fp16=True,
+ logging_steps=1,
+ output_dir=tmp_dir,
+ ),
+ data_collator=DataCollatorForLanguageModeling(tokenizer, mlm=False),
+ )
+ model.config.use_cache = False
+ trainer.train()
+
+ model.cpu().save_pretrained(tmp_dir)
+
+ assert "adapter_config.json" in os.listdir(tmp_dir)
+ assert SAFETENSORS_WEIGHTS_NAME in os.listdir(tmp_dir)
+
+ # assert loss is not None
+ assert trainer.state.log_history[-1]["train_loss"] is not None
+
+ @pytest.mark.multi_gpu_tests
+ def test_causal_lm_training_multi_gpu_4bit_dora(self):
+ r"""
+ Same as test_causal_lm_training_multi_gpu_4bit but with DoRA
+ """
+
+ with tempfile.TemporaryDirectory() as tmp_dir:
+ model = AutoModelForCausalLM.from_pretrained(
+ self.causal_lm_model_id,
+ device_map=DEVICE_MAP_MAP[self.causal_lm_model_id],
+ quantization_config=BitsAndBytesConfig(load_in_4bit=True),
+ )
+
+ assert set(model.hf_device_map.values()) == set(range(device_count))
+ assert {p.device.index for p in model.parameters()} == set(range(device_count))
+
+ model = prepare_model_for_kbit_training(model)
+
+ setattr(model, "model_parallel", True)
+ setattr(model, "is_parallelizable", True)
+
+ config = LoraConfig(
+ r=16,
+ lora_alpha=32,
+ target_modules=["q_proj", "v_proj"],
+ lora_dropout=0.05,
+ bias="none",
+ task_type="CAUSAL_LM",
+ use_dora=True,
+ )
+
+ model = get_peft_model(model, config)
+
+ data = load_dataset_english_quotes()
+ data = data.map(lambda samples: self.tokenizer(samples["quote"]), batched=True)
+
+ trainer = Trainer(
+ model=model,
+ train_dataset=data["train"],
+ args=TrainingArguments(
+ per_device_train_batch_size=4,
+ gradient_accumulation_steps=4,
+ warmup_steps=2,
+ max_steps=3,
+ learning_rate=2e-4,
+ fp16=True,
+ logging_steps=1,
+ output_dir=tmp_dir,
+ ),
+ data_collator=DataCollatorForLanguageModeling(self.tokenizer, mlm=False),
+ )
+ model.config.use_cache = False
+ trainer.train()
+
+ model.cpu().save_pretrained(tmp_dir)
+
+ assert "adapter_config.json" in os.listdir(tmp_dir)
+ assert SAFETENSORS_WEIGHTS_NAME in os.listdir(tmp_dir)
+
+ # assert loss is not None
+ assert trainer.state.log_history[-1]["train_loss"] is not None
+
+ @pytest.mark.single_gpu_tests
+ def test_causal_lm_training_8bit_dora(self):
+ r"""
+ Same as test_causal_lm_training_4bit_dora but with 8bit
+ """
+ with tempfile.TemporaryDirectory() as tmp_dir:
+ model = AutoModelForCausalLM.from_pretrained(
+ self.causal_lm_model_id,
+ quantization_config=BitsAndBytesConfig(load_in_8bit=True),
+ device_map="auto",
+ )
+
+ tokenizer = AutoTokenizer.from_pretrained(self.causal_lm_model_id)
+ model = prepare_model_for_kbit_training(model)
+
+ config = LoraConfig(
+ r=16,
+ lora_alpha=32,
+ target_modules=["q_proj", "v_proj"],
+ lora_dropout=0.05,
+ bias="none",
+ task_type="CAUSAL_LM",
+ use_dora=True,
+ )
+
+ model = get_peft_model(model, config)
+
+ data = load_dataset_english_quotes()
+ data = data.map(lambda samples: tokenizer(samples["quote"]), batched=True)
+
+ trainer = Trainer(
+ model=model,
+ train_dataset=data["train"],
+ args=TrainingArguments(
+ per_device_train_batch_size=4,
+ gradient_accumulation_steps=4,
+ warmup_steps=2,
+ max_steps=3,
+ learning_rate=2e-4,
+ fp16=True,
+ logging_steps=1,
+ output_dir=tmp_dir,
+ ),
+ data_collator=DataCollatorForLanguageModeling(tokenizer, mlm=False),
+ )
+ model.config.use_cache = False
+ trainer.train()
+
+ model.cpu().save_pretrained(tmp_dir)
+
+ assert "adapter_config.json" in os.listdir(tmp_dir)
+ assert SAFETENSORS_WEIGHTS_NAME in os.listdir(tmp_dir)
+
+ # assert loss is not None
+ assert trainer.state.log_history[-1]["train_loss"] is not None
+
+ @pytest.mark.multi_gpu_tests
+ def test_causal_lm_training_multi_gpu_8bit_dora(self):
+ r"""
+ Same as test_causal_lm_training_multi_gpu_4bit_dora but with 8bit
+ """
+
+ with tempfile.TemporaryDirectory() as tmp_dir:
+ model = AutoModelForCausalLM.from_pretrained(
+ self.causal_lm_model_id,
+ device_map=DEVICE_MAP_MAP[self.causal_lm_model_id],
+ quantization_config=BitsAndBytesConfig(load_in_8bit=True),
+ )
+
+ assert set(model.hf_device_map.values()) == set(range(device_count))
+ assert {p.device.index for p in model.parameters()} == set(range(device_count))
+
+ model = prepare_model_for_kbit_training(model)
+
+ setattr(model, "model_parallel", True)
+ setattr(model, "is_parallelizable", True)
+
+ config = LoraConfig(
+ r=16,
+ lora_alpha=32,
+ target_modules=["q_proj", "v_proj"],
+ lora_dropout=0.05,
+ bias="none",
+ task_type="CAUSAL_LM",
+ use_dora=True,
+ )
+
+ model = get_peft_model(model, config)
+
+ data = load_dataset_english_quotes()
+ data = data.map(lambda samples: self.tokenizer(samples["quote"]), batched=True)
+
+ trainer = Trainer(
+ model=model,
+ train_dataset=data["train"],
+ args=TrainingArguments(
+ per_device_train_batch_size=4,
+ gradient_accumulation_steps=4,
+ warmup_steps=2,
+ max_steps=3,
+ learning_rate=2e-4,
+ fp16=True,
+ logging_steps=1,
+ output_dir=tmp_dir,
+ ),
+ data_collator=DataCollatorForLanguageModeling(self.tokenizer, mlm=False),
+ )
+ model.config.use_cache = False
+ trainer.train()
+
+ model.cpu().save_pretrained(tmp_dir)
+
+ assert "adapter_config.json" in os.listdir(tmp_dir)
+ assert SAFETENSORS_WEIGHTS_NAME in os.listdir(tmp_dir)
+
+ # assert loss is not None
+ assert trainer.state.log_history[-1]["train_loss"] is not None
+
+ @pytest.mark.single_gpu_tests
+ def test_causal_lm_training_gpt2_dora(self):
+ r"""
+ Same as test_causal_lm_training_4bit but with DoRA
+ """
+ with tempfile.TemporaryDirectory() as tmp_dir:
+ model = AutoModelForCausalLM.from_pretrained("gpt2", device_map="auto")
+
+ tokenizer = AutoTokenizer.from_pretrained(self.causal_lm_model_id)
+ model = prepare_model_for_kbit_training(model)
+
+ config = LoraConfig(
+ r=16,
+ lora_alpha=32,
+ lora_dropout=0.05,
+ bias="none",
+ task_type="CAUSAL_LM",
+ use_dora=True,
+ )
+
+ model = get_peft_model(model, config)
+
+ data = load_dataset_english_quotes()
+ data = data.map(lambda samples: tokenizer(samples["quote"]), batched=True)
+
+ trainer = Trainer(
+ model=model,
+ train_dataset=data["train"],
+ args=TrainingArguments(
+ per_device_train_batch_size=4,
+ gradient_accumulation_steps=4,
+ warmup_steps=2,
+ max_steps=3,
+ learning_rate=2e-4,
+ fp16=True,
+ logging_steps=1,
+ output_dir=tmp_dir,
+ ),
+ data_collator=DataCollatorForLanguageModeling(tokenizer, mlm=False),
+ )
+ model.config.use_cache = False
+ trainer.train()
+
+ model.cpu().save_pretrained(tmp_dir)
+
+ assert "adapter_config.json" in os.listdir(tmp_dir)
+ assert SAFETENSORS_WEIGHTS_NAME in os.listdir(tmp_dir)
+
+ # assert loss is not None
+ assert trainer.state.log_history[-1]["train_loss"] is not None
+
+ @parameterized.expand(["4bit", "8bit"])
+ def test_initialize_dora_with_bnb_on_cpu(self, kbit):
+ # 1674
+ # The issue is that to initialize DoRA, we need to dequantize the weights. That only works on GPU for bnb.
+ # Therefore, initializing DoRA with bnb on CPU used to fail.
+ model_id = "facebook/opt-125m"
+ if kbit == "4bit":
+ bnb_config = BitsAndBytesConfig(load_in_4bit=True, bnb_4bit_quant_type="nf4")
+ elif kbit == "8bit":
+ bnb_config = BitsAndBytesConfig(load_in_8bit=True)
+ else:
+ raise ValueError("Only 4bit and 8bit bnb allowed")
+
+ model = AutoModelForCausalLM.from_pretrained(model_id, quantization_config=bnb_config)
+ model = model.cpu() # ensure that we're on CPU
+ # sanity check that all weights are on CPU
+ weights_not_cpu = [name for name, p in model.named_parameters() if p.device != torch.device("cpu")]
+ assert not weights_not_cpu
+
+ lora_config = LoraConfig(use_dora=True)
+
+ # should not raise
+ peft_model = get_peft_model(model, lora_config)
+ # check that the weights are still on CPU
+ weights_not_cpu = [name for name, p in peft_model.named_parameters() if p.device != torch.device("cpu")]
+ assert not weights_not_cpu
+
+ @pytest.mark.single_gpu_tests
+ def test_causal_lm_training_vera(self):
+ r"""
+ Same as test_causal_lm_training but with VeRA
+ """
+ with tempfile.TemporaryDirectory() as tmp_dir:
+ model = AutoModelForCausalLM.from_pretrained(
+ self.causal_lm_model_id,
+ quantization_config=BitsAndBytesConfig(load_in_8bit=True),
+ device_map="auto",
+ )
+
+ tokenizer = AutoTokenizer.from_pretrained(self.causal_lm_model_id)
+ model = prepare_model_for_kbit_training(model)
+
+ config = VeraConfig(
+ r=16,
+ target_modules=["q_proj", "v_proj"],
+ vera_dropout=0.05,
+ bias="none",
+ task_type="CAUSAL_LM",
+ )
+
+ model = get_peft_model(model, config)
+
+ data = load_dataset_english_quotes()
+ data = data.map(lambda samples: tokenizer(samples["quote"]), batched=True)
+
+ trainer = Trainer(
+ model=model,
+ train_dataset=data["train"],
+ args=TrainingArguments(
+ per_device_train_batch_size=4,
+ gradient_accumulation_steps=4,
+ warmup_steps=2,
+ max_steps=3,
+ learning_rate=2e-4,
+ fp16=True,
+ logging_steps=1,
+ output_dir=tmp_dir,
+ ),
+ data_collator=DataCollatorForLanguageModeling(tokenizer, mlm=False),
+ )
+ model.config.use_cache = False
+ trainer.train()
+
+ model.cpu().save_pretrained(tmp_dir)
+
+ assert "adapter_config.json" in os.listdir(tmp_dir)
+ assert SAFETENSORS_WEIGHTS_NAME in os.listdir(tmp_dir)
+
+ # assert loss is not None
+ assert trainer.state.log_history[-1]["train_loss"] is not None
+
+ @pytest.mark.single_gpu_tests
+ def test_causal_lm_training_4bit_vera(self):
+ r"""
+ Same as test_causal_lm_training_4bit but with VeRA
+ """
+ with tempfile.TemporaryDirectory() as tmp_dir:
+ model = AutoModelForCausalLM.from_pretrained(
+ self.causal_lm_model_id,
+ quantization_config=BitsAndBytesConfig(load_in_4bit=True),
+ device_map="auto",
+ )
+
+ tokenizer = AutoTokenizer.from_pretrained(self.causal_lm_model_id)
+ model = prepare_model_for_kbit_training(model)
+
+ config = VeraConfig(
+ r=16,
+ target_modules=["q_proj", "v_proj"],
+ vera_dropout=0.05,
+ bias="none",
+ task_type="CAUSAL_LM",
+ )
+
+ model = get_peft_model(model, config)
+
+ data = load_dataset_english_quotes()
+ data = data.map(lambda samples: tokenizer(samples["quote"]), batched=True)
+
+ trainer = Trainer(
+ model=model,
+ train_dataset=data["train"],
+ args=TrainingArguments(
+ per_device_train_batch_size=4,
+ gradient_accumulation_steps=4,
+ warmup_steps=2,
+ max_steps=3,
+ learning_rate=2e-4,
+ fp16=True,
+ logging_steps=1,
+ output_dir=tmp_dir,
+ ),
+ data_collator=DataCollatorForLanguageModeling(tokenizer, mlm=False),
+ )
+ model.config.use_cache = False
+ trainer.train()
+
+ model.cpu().save_pretrained(tmp_dir)
+
+ assert "adapter_config.json" in os.listdir(tmp_dir)
+ assert SAFETENSORS_WEIGHTS_NAME in os.listdir(tmp_dir)
+
+ # assert loss is not None
+ assert trainer.state.log_history[-1]["train_loss"] is not None
+
+ @pytest.mark.multi_gpu_tests
+ def test_causal_lm_training_multi_gpu_vera(self):
+ r"""
+ Same as test_causal_lm_training_multi_gpu but with VeRA
+ """
+
+ with tempfile.TemporaryDirectory() as tmp_dir:
+ model = AutoModelForCausalLM.from_pretrained(
+ self.causal_lm_model_id,
+ device_map=DEVICE_MAP_MAP[self.causal_lm_model_id],
+ quantization_config=BitsAndBytesConfig(load_in_8bit=True),
+ )
+
+ assert set(model.hf_device_map.values()) == set(range(device_count))
+ assert {p.device.index for p in model.parameters()} == set(range(device_count))
+
+ model = prepare_model_for_kbit_training(model)
+
+ setattr(model, "model_parallel", True)
+ setattr(model, "is_parallelizable", True)
+
+ config = VeraConfig(
+ r=16,
+ target_modules=["q_proj", "v_proj"],
+ vera_dropout=0.05,
+ bias="none",
+ task_type="CAUSAL_LM",
+ )
+
+ model = get_peft_model(model, config)
+
+ data = load_dataset_english_quotes()
+ data = data.map(lambda samples: self.tokenizer(samples["quote"]), batched=True)
+
+ trainer = Trainer(
+ model=model,
+ train_dataset=data["train"],
+ args=TrainingArguments(
+ per_device_train_batch_size=4,
+ gradient_accumulation_steps=4,
+ warmup_steps=2,
+ max_steps=3,
+ learning_rate=2e-4,
+ fp16=True,
+ logging_steps=1,
+ output_dir=tmp_dir,
+ ),
+ data_collator=DataCollatorForLanguageModeling(self.tokenizer, mlm=False),
+ )
+ model.config.use_cache = False
+ trainer.train()
+
+ model.cpu().save_pretrained(tmp_dir)
+
+ assert "adapter_config.json" in os.listdir(tmp_dir)
+ assert SAFETENSORS_WEIGHTS_NAME in os.listdir(tmp_dir)
+
+ # assert loss is not None
+ assert trainer.state.log_history[-1]["train_loss"] is not None
+
+ @pytest.mark.multi_gpu_tests
+ def test_causal_lm_training_multi_gpu_4bit_vera(self):
+ r"""
+ Same as test_causal_lm_training_multi_gpu_4bit but with VeRA
+ """
+
+ with tempfile.TemporaryDirectory() as tmp_dir:
+ model = AutoModelForCausalLM.from_pretrained(
+ self.causal_lm_model_id,
+ device_map=DEVICE_MAP_MAP[self.causal_lm_model_id],
+ quantization_config=BitsAndBytesConfig(load_in_4bit=True),
+ )
+
+ assert set(model.hf_device_map.values()) == set(range(device_count))
+ assert {p.device.index for p in model.parameters()} == set(range(device_count))
+
+ model = prepare_model_for_kbit_training(model)
+
+ setattr(model, "model_parallel", True)
+ setattr(model, "is_parallelizable", True)
+
+ config = VeraConfig(
+ r=16,
+ target_modules=["q_proj", "v_proj"],
+ vera_dropout=0.05,
+ bias="none",
+ task_type="CAUSAL_LM",
+ )
+
+ model = get_peft_model(model, config)
+
+ data = load_dataset_english_quotes()
+ data = data.map(lambda samples: self.tokenizer(samples["quote"]), batched=True)
+
+ trainer = Trainer(
+ model=model,
+ train_dataset=data["train"],
+ args=TrainingArguments(
+ per_device_train_batch_size=4,
+ gradient_accumulation_steps=4,
+ warmup_steps=2,
+ max_steps=3,
+ learning_rate=2e-4,
+ fp16=True,
+ logging_steps=1,
+ output_dir=tmp_dir,
+ ),
+ data_collator=DataCollatorForLanguageModeling(self.tokenizer, mlm=False),
+ )
+ model.config.use_cache = False
+ trainer.train()
+
+ model.cpu().save_pretrained(tmp_dir)
+
+ assert "adapter_config.json" in os.listdir(tmp_dir)
+ assert SAFETENSORS_WEIGHTS_NAME in os.listdir(tmp_dir)
+
+ # assert loss is not None
+ assert trainer.state.log_history[-1]["train_loss"] is not None
+
+ @pytest.mark.single_gpu_tests
+ def test_causal_lm_training_8bit_randlora(self):
+ r"""
+ Same as test_causal_lm_training but with RandLora
+ """
+ with tempfile.TemporaryDirectory() as tmp_dir:
+ model = AutoModelForCausalLM.from_pretrained(
+ self.causal_lm_model_id,
+ quantization_config=BitsAndBytesConfig(load_in_8bit=True),
+ device_map="auto",
+ )
+
+ tokenizer = AutoTokenizer.from_pretrained(self.causal_lm_model_id)
+ model = prepare_model_for_kbit_training(model)
+
+ config = RandLoraConfig(
+ r=16,
+ target_modules=["q_proj", "v_proj"],
+ randlora_dropout=0.05,
+ bias="none",
+ task_type="CAUSAL_LM",
+ )
+
+ model = get_peft_model(model, config)
+
+ data = load_dataset("ybelkada/english_quotes_copy")
+ data = data.map(lambda samples: tokenizer(samples["quote"]), batched=True)
+
+ trainer = Trainer(
+ model=model,
+ train_dataset=data["train"],
+ args=TrainingArguments(
+ per_device_train_batch_size=4,
+ gradient_accumulation_steps=4,
+ warmup_steps=2,
+ max_steps=3,
+ learning_rate=2e-4,
+ fp16=True,
+ logging_steps=1,
+ output_dir=tmp_dir,
+ ),
+ data_collator=DataCollatorForLanguageModeling(tokenizer, mlm=False),
+ )
+ model.config.use_cache = False
+ trainer.train()
+
+ model.cpu().save_pretrained(tmp_dir)
+
+ assert "adapter_config.json" in os.listdir(tmp_dir)
+ assert SAFETENSORS_WEIGHTS_NAME in os.listdir(tmp_dir)
+
+ # assert loss is not None
+ assert trainer.state.log_history[-1]["train_loss"] is not None
+
+ @pytest.mark.single_gpu_tests
+ def test_causal_lm_training_4bit_randlora(self):
+ r"""
+ Same as test_causal_lm_training_4bit but with RandLora
+ """
+ with tempfile.TemporaryDirectory() as tmp_dir:
+ model = AutoModelForCausalLM.from_pretrained(
+ self.causal_lm_model_id,
+ quantization_config=BitsAndBytesConfig(load_in_4bit=True),
+ device_map="auto",
+ )
+
+ tokenizer = AutoTokenizer.from_pretrained(self.causal_lm_model_id)
+ model = prepare_model_for_kbit_training(model)
+
+ config = RandLoraConfig(
+ r=16,
+ target_modules=["q_proj", "v_proj"],
+ randlora_dropout=0.05,
+ bias="none",
+ task_type="CAUSAL_LM",
+ )
+
+ model = get_peft_model(model, config)
+
+ data = load_dataset("ybelkada/english_quotes_copy")
+ data = data.map(lambda samples: tokenizer(samples["quote"]), batched=True)
+
+ trainer = Trainer(
+ model=model,
+ train_dataset=data["train"],
+ args=TrainingArguments(
+ per_device_train_batch_size=4,
+ gradient_accumulation_steps=4,
+ warmup_steps=2,
+ max_steps=3,
+ learning_rate=2e-4,
+ fp16=True,
+ logging_steps=1,
+ output_dir=tmp_dir,
+ ),
+ data_collator=DataCollatorForLanguageModeling(tokenizer, mlm=False),
+ )
+ model.config.use_cache = False
+ trainer.train()
+
+ model.cpu().save_pretrained(tmp_dir)
+
+ assert "adapter_config.json" in os.listdir(tmp_dir)
+ assert SAFETENSORS_WEIGHTS_NAME in os.listdir(tmp_dir)
+
+ # assert loss is not None
+ assert trainer.state.log_history[-1]["train_loss"] is not None
+
+ @pytest.mark.multi_gpu_tests
+ def test_causal_lm_training_multi_gpu_8bit_randlora(self):
+ r"""
+ Same as test_causal_lm_training_multi_gpu but with RandLoRA
+ """
+
+ with tempfile.TemporaryDirectory() as tmp_dir:
+ model = AutoModelForCausalLM.from_pretrained(
+ self.causal_lm_model_id,
+ device_map=DEVICE_MAP_MAP[self.causal_lm_model_id],
+ quantization_config=BitsAndBytesConfig(load_in_8bit=True),
+ )
+
+ assert set(model.hf_device_map.values()) == set(range(device_count))
+ assert {p.device.index for p in model.parameters()} == set(range(device_count))
+
+ model = prepare_model_for_kbit_training(model)
+
+ setattr(model, "model_parallel", True)
+ setattr(model, "is_parallelizable", True)
+
+ config = RandLoraConfig(
+ r=16,
+ target_modules=["q_proj", "v_proj"],
+ randlora_dropout=0.05,
+ bias="none",
+ task_type="CAUSAL_LM",
+ )
+
+ model = get_peft_model(model, config)
+
+ data = load_dataset("Abirate/english_quotes")
+ data = data.map(lambda samples: self.tokenizer(samples["quote"]), batched=True)
+
+ trainer = Trainer(
+ model=model,
+ train_dataset=data["train"],
+ args=TrainingArguments(
+ per_device_train_batch_size=4,
+ gradient_accumulation_steps=4,
+ warmup_steps=2,
+ max_steps=3,
+ learning_rate=2e-4,
+ fp16=True,
+ logging_steps=1,
+ output_dir=tmp_dir,
+ ),
+ data_collator=DataCollatorForLanguageModeling(self.tokenizer, mlm=False),
+ )
+ model.config.use_cache = False
+ trainer.train()
+
+ model.cpu().save_pretrained(tmp_dir)
+
+ assert "adapter_config.json" in os.listdir(tmp_dir)
+ assert SAFETENSORS_WEIGHTS_NAME in os.listdir(tmp_dir)
+
+ # assert loss is not None
+ assert trainer.state.log_history[-1]["train_loss"] is not None
+
+ @pytest.mark.multi_gpu_tests
+ def test_causal_lm_training_multi_gpu_4bit_randlora(self):
+ r"""
+ Same as test_causal_lm_training_multi_gpu_4bit but with RandLora
+ """
+
+ with tempfile.TemporaryDirectory() as tmp_dir:
+ model = AutoModelForCausalLM.from_pretrained(
+ self.causal_lm_model_id,
+ device_map=DEVICE_MAP_MAP[self.causal_lm_model_id],
+ quantization_config=BitsAndBytesConfig(load_in_4bit=True),
+ )
+
+ assert set(model.hf_device_map.values()) == set(range(device_count))
+ assert {p.device.index for p in model.parameters()} == set(range(device_count))
+
+ model = prepare_model_for_kbit_training(model)
+
+ setattr(model, "model_parallel", True)
+ setattr(model, "is_parallelizable", True)
+
+ config = RandLoraConfig(
+ r=16,
+ target_modules=["q_proj", "v_proj"],
+ randlora_dropout=0.05,
+ bias="none",
+ task_type="CAUSAL_LM",
+ )
+
+ model = get_peft_model(model, config)
+
+ data = load_dataset("Abirate/english_quotes")
+ data = data.map(lambda samples: self.tokenizer(samples["quote"]), batched=True)
+
+ trainer = Trainer(
+ model=model,
+ train_dataset=data["train"],
+ args=TrainingArguments(
+ per_device_train_batch_size=4,
+ gradient_accumulation_steps=4,
+ warmup_steps=2,
+ max_steps=3,
+ learning_rate=2e-4,
+ fp16=True,
+ logging_steps=1,
+ output_dir=tmp_dir,
+ ),
+ data_collator=DataCollatorForLanguageModeling(self.tokenizer, mlm=False),
+ )
+ model.config.use_cache = False
+ trainer.train()
+
+ model.cpu().save_pretrained(tmp_dir)
+
+ assert "adapter_config.json" in os.listdir(tmp_dir)
+ assert SAFETENSORS_WEIGHTS_NAME in os.listdir(tmp_dir)
+
+ # assert loss is not None
+ assert trainer.state.log_history[-1]["train_loss"] is not None
+
+ @pytest.mark.single_gpu_tests
+ def test_causal_lm_training_8bit_road(self):
+ r"""
+ Same as test_causal_lm_training but with RoAd
+ """
+ with tempfile.TemporaryDirectory() as tmp_dir:
+ model = AutoModelForCausalLM.from_pretrained(
+ self.causal_lm_model_id,
+ quantization_config=BitsAndBytesConfig(load_in_8bit=True),
+ device_map="auto",
+ )
+
+ tokenizer = AutoTokenizer.from_pretrained(self.causal_lm_model_id)
+ model = prepare_model_for_kbit_training(model)
+
+ config = RoadConfig(
+ variant="road_1",
+ target_modules=["q_proj", "v_proj"],
+ task_type="CAUSAL_LM",
+ )
+
+ model = get_peft_model(model, config)
+
+ data = load_dataset("ybelkada/english_quotes_copy")
+ data = data.map(lambda samples: tokenizer(samples["quote"]), batched=True)
+
+ trainer = Trainer(
+ model=model,
+ train_dataset=data["train"],
+ args=TrainingArguments(
+ per_device_train_batch_size=4,
+ gradient_accumulation_steps=4,
+ warmup_steps=2,
+ max_steps=3,
+ learning_rate=1e-3,
+ fp16=True,
+ logging_steps=1,
+ output_dir=tmp_dir,
+ ),
+ data_collator=DataCollatorForLanguageModeling(tokenizer, mlm=False),
+ )
+ model.config.use_cache = False
+ trainer.train()
+
+ model.cpu().save_pretrained(tmp_dir)
+
+ assert "adapter_config.json" in os.listdir(tmp_dir)
+ assert SAFETENSORS_WEIGHTS_NAME in os.listdir(tmp_dir)
+
+ # assert loss is not None
+ assert trainer.state.log_history[-1]["train_loss"] is not None
+
+ @pytest.mark.single_gpu_tests
+ def test_causal_lm_training_4bit_road(self):
+ r"""
+ Same as test_causal_lm_training_4bit but with RoAd
+ """
+ with tempfile.TemporaryDirectory() as tmp_dir:
+ model = AutoModelForCausalLM.from_pretrained(
+ self.causal_lm_model_id,
+ quantization_config=BitsAndBytesConfig(load_in_4bit=True),
+ device_map="auto",
+ )
+
+ tokenizer = AutoTokenizer.from_pretrained(self.causal_lm_model_id)
+ model = prepare_model_for_kbit_training(model)
+
+ config = RoadConfig(
+ variant="road_1",
+ target_modules=["q_proj", "v_proj"],
+ task_type="CAUSAL_LM",
+ )
+
+ model = get_peft_model(model, config)
+
+ data = load_dataset("ybelkada/english_quotes_copy")
+ data = data.map(lambda samples: tokenizer(samples["quote"]), batched=True)
+
+ trainer = Trainer(
+ model=model,
+ train_dataset=data["train"],
+ args=TrainingArguments(
+ per_device_train_batch_size=4,
+ gradient_accumulation_steps=4,
+ warmup_steps=2,
+ max_steps=3,
+ learning_rate=1e-3,
+ fp16=True,
+ logging_steps=1,
+ output_dir=tmp_dir,
+ ),
+ data_collator=DataCollatorForLanguageModeling(tokenizer, mlm=False),
+ )
+ model.config.use_cache = False
+ trainer.train()
+
+ model.cpu().save_pretrained(tmp_dir)
+
+ assert "adapter_config.json" in os.listdir(tmp_dir)
+ assert SAFETENSORS_WEIGHTS_NAME in os.listdir(tmp_dir)
+
+ # assert loss is not None
+ assert trainer.state.log_history[-1]["train_loss"] is not None
+
+ @pytest.mark.multi_gpu_tests
+ def test_causal_lm_training_multi_gpu_8bit_road(self):
+ r"""
+ Same as test_causal_lm_training_multi_gpu but with RoAd
+ """
+
+ with tempfile.TemporaryDirectory() as tmp_dir:
+ model = AutoModelForCausalLM.from_pretrained(
+ self.causal_lm_model_id,
+ device_map=DEVICE_MAP_MAP[self.causal_lm_model_id],
+ quantization_config=BitsAndBytesConfig(load_in_8bit=True),
+ )
+
+ assert set(model.hf_device_map.values()) == set(range(device_count))
+ assert {p.device.index for p in model.parameters()} == set(range(device_count))
+
+ model = prepare_model_for_kbit_training(model)
+
+ setattr(model, "model_parallel", True)
+ setattr(model, "is_parallelizable", True)
+
+ config = RoadConfig(
+ variant="road_1",
+ target_modules=["q_proj", "v_proj"],
+ task_type="CAUSAL_LM",
+ )
+
+ model = get_peft_model(model, config)
+
+ data = load_dataset("Abirate/english_quotes")
+ data = data.map(lambda samples: self.tokenizer(samples["quote"]), batched=True)
+
+ trainer = Trainer(
+ model=model,
+ train_dataset=data["train"],
+ args=TrainingArguments(
+ per_device_train_batch_size=4,
+ gradient_accumulation_steps=4,
+ warmup_steps=2,
+ max_steps=3,
+ learning_rate=1e-3,
+ fp16=True,
+ logging_steps=1,
+ output_dir=tmp_dir,
+ ),
+ data_collator=DataCollatorForLanguageModeling(self.tokenizer, mlm=False),
+ )
+ model.config.use_cache = False
+ trainer.train()
+
+ model.cpu().save_pretrained(tmp_dir)
+
+ assert "adapter_config.json" in os.listdir(tmp_dir)
+ assert SAFETENSORS_WEIGHTS_NAME in os.listdir(tmp_dir)
+
+ # assert loss is not None
+ assert trainer.state.log_history[-1]["train_loss"] is not None
+
+ @pytest.mark.multi_gpu_tests
+ def test_causal_lm_training_multi_gpu_4bit_road(self):
+ r"""
+ Same as test_causal_lm_training_multi_gpu_4bit but with RoAd
+ """
+
+ with tempfile.TemporaryDirectory() as tmp_dir:
+ model = AutoModelForCausalLM.from_pretrained(
+ self.causal_lm_model_id,
+ device_map=DEVICE_MAP_MAP[self.causal_lm_model_id],
+ quantization_config=BitsAndBytesConfig(load_in_4bit=True),
+ )
+
+ assert set(model.hf_device_map.values()) == set(range(device_count))
+ assert {p.device.index for p in model.parameters()} == set(range(device_count))
+
+ model = prepare_model_for_kbit_training(model)
+
+ setattr(model, "model_parallel", True)
+ setattr(model, "is_parallelizable", True)
+
+ config = RoadConfig(
+ variant="road_1",
+ target_modules=["q_proj", "v_proj"],
+ task_type="CAUSAL_LM",
+ )
+
+ model = get_peft_model(model, config)
+
+ data = load_dataset("Abirate/english_quotes")
+ data = data.map(lambda samples: self.tokenizer(samples["quote"]), batched=True)
+
+ trainer = Trainer(
+ model=model,
+ train_dataset=data["train"],
+ args=TrainingArguments(
+ per_device_train_batch_size=4,
+ gradient_accumulation_steps=4,
+ warmup_steps=2,
+ max_steps=3,
+ learning_rate=1e-3,
+ fp16=True,
+ logging_steps=1,
+ output_dir=tmp_dir,
+ ),
+ data_collator=DataCollatorForLanguageModeling(self.tokenizer, mlm=False),
+ )
+ model.config.use_cache = False
+ trainer.train()
+
+ model.cpu().save_pretrained(tmp_dir)
+
+ assert "adapter_config.json" in os.listdir(tmp_dir)
+ assert SAFETENSORS_WEIGHTS_NAME in os.listdir(tmp_dir)
+
+ # assert loss is not None
+ assert trainer.state.log_history[-1]["train_loss"] is not None
+
+ @pytest.mark.single_gpu_tests
+ def test_causal_lm_training_lora_resize_embeddings_trainable_tokens(self):
+ r"""
+ Test LoRA with trainable tokens on a resized embedding matrix
+ """
+ with tempfile.TemporaryDirectory() as tmp_dir:
+ bnb_config = BitsAndBytesConfig(
+ load_in_4bit=True,
+ bnb_4bit_quant_type="nf4",
+ bnb_4bit_compute_dtype=torch.float16,
+ bnb_4bit_quant_storage=torch.float16,
+ bnb_4bit_use_double_quant=True,
+ )
+
+ model = AutoModelForCausalLM.from_pretrained(
+ self.causal_lm_model_id,
+ quantization_config=bnb_config,
+ device_map="auto",
+ )
+
+ # add 2 new tokens
+ tokenizer = AutoTokenizer.from_pretrained(self.causal_lm_model_id)
+ new_tokens = ["", ""]
+ tokenizer.add_special_tokens({"additional_special_tokens": new_tokens})
+ trainable_token_indices = [tokenizer.vocab[token] for token in new_tokens]
+
+ cur_emb_size = model.model.decoder.embed_tokens.weight.shape[0]
+ model.resize_token_embeddings(max(tokenizer.vocab_size, cur_emb_size))
+ model = prepare_model_for_kbit_training(model)
+
+ config = LoraConfig(
+ r=16,
+ lora_alpha=32,
+ target_modules=["q_proj", "v_proj"],
+ lora_dropout=0.05,
+ bias="none",
+ task_type="CAUSAL_LM",
+ trainable_token_indices={"embed_tokens": trainable_token_indices},
+ )
+
+ model = get_peft_model(model, config)
+
+ data = load_dataset_english_quotes()
+
+ def tokenize(samples):
+ # add new tokens to samples
+ samples = [f"{row}" for row in samples["quote"]]
+ return tokenizer(samples)
+
+ data = data.map(tokenize, batched=True)
+
+ trainer = Trainer(
+ model=model,
+ train_dataset=data["train"],
+ args=TrainingArguments(
+ per_device_train_batch_size=4,
+ gradient_accumulation_steps=4,
+ warmup_steps=2,
+ max_steps=3,
+ # higher learning rate, as embeddings are a bit slow to update
+ learning_rate=1e-3,
+ fp16=True,
+ logging_steps=1,
+ output_dir=tmp_dir,
+ ),
+ data_collator=DataCollatorForLanguageModeling(tokenizer, mlm=False),
+ )
+ model.config.use_cache = False
+ trainer.train()
+
+ model.cpu().save_pretrained(tmp_dir)
+
+ # ensure that the new trainable tokens have been updated
+ embedding = model.base_model.model.model.decoder.embed_tokens
+ tol = 1e-4
+ assert not torch.allclose(
+ embedding.token_adapter.trainable_tokens_delta["default"],
+ embedding.original_module.weight[trainable_token_indices],
+ atol=tol,
+ rtol=tol,
+ )
+
+ # check size of the checkpoint, should be small since the embedding matrix does not need to be stored
+ stat = os.stat(os.path.join(tmp_dir, SAFETENSORS_WEIGHTS_NAME))
+ embed_params = model.base_model.model.model.decoder.embed_tokens.original_module.weight.numel()
+ # fp32 -> 4x
+ emb_file_size = 4 * embed_params
+ assert stat.st_size < emb_file_size
+
+ # sanity check: assert loss is not None
+ assert trainer.state.log_history[-1]["train_loss"] is not None
+
+
+@require_torch_gpu
+@require_auto_gptq
+@require_optimum
+class PeftGPTQGPUTests(unittest.TestCase):
+ r"""
+ GPTQ + peft tests
+ """
+
+ def setUp(self):
+ from transformers import GPTQConfig
+
+ self.causal_lm_model_id = "marcsun13/opt-350m-gptq-4bit"
+ # TODO : check if it works for Exllamav2 kernels
+ self.quantization_config = GPTQConfig(bits=4, use_exllama=False)
+ self.tokenizer = AutoTokenizer.from_pretrained(self.causal_lm_model_id)
+
+ def tearDown(self):
+ r"""
+ Efficient mechanism to free GPU memory after each test. Based on
+ https://github.com/huggingface/transformers/issues/21094
+ """
+ clear_device_cache(garbage_collection=True)
+
+ def _check_inference_finite(self, model, batch):
+ # try inference without Trainer class
+ training = model.training
+ model.eval()
+ output = model(**batch.to(model.device))
+ assert torch.isfinite(output.logits).all()
+ model.train(training)
+
+ @pytest.mark.single_gpu_tests
+ def test_causal_lm_training(self):
+ r"""
+ Test the CausalLM training on a single GPU device. The test would simply fail if the adapters are not set
+ correctly.
+ """
+ with tempfile.TemporaryDirectory() as tmp_dir:
+ model = AutoModelForCausalLM.from_pretrained(
+ self.causal_lm_model_id,
+ torch_dtype=torch.float16,
+ device_map="auto",
+ quantization_config=self.quantization_config,
+ )
+
+ model = prepare_model_for_kbit_training(model)
+ config = LoraConfig(
+ r=16,
+ lora_alpha=32,
+ target_modules=["q_proj", "v_proj"],
+ lora_dropout=0.05,
+ bias="none",
+ task_type="CAUSAL_LM",
+ )
+ model = get_peft_model(model, config)
+
+ data = load_dataset_english_quotes()
+ data = data.map(lambda samples: self.tokenizer(samples["quote"]), batched=True)
+
+ trainer = Trainer(
+ model=model,
+ train_dataset=data["train"],
+ args=TrainingArguments(
+ per_device_train_batch_size=4,
+ gradient_accumulation_steps=4,
+ warmup_steps=2,
+ max_steps=3,
+ learning_rate=2e-4,
+ fp16=True,
+ logging_steps=1,
+ output_dir=tmp_dir,
+ ),
+ data_collator=DataCollatorForLanguageModeling(self.tokenizer, mlm=False),
+ )
+ model.config.use_cache = False
+ trainer.train()
+
+ model.cpu().save_pretrained(tmp_dir)
+
+ assert "adapter_config.json" in os.listdir(tmp_dir)
+ assert SAFETENSORS_WEIGHTS_NAME in os.listdir(tmp_dir)
+
+ # assert loss is not None
+ assert trainer.state.log_history[-1]["train_loss"] is not None
+
+ @pytest.mark.single_gpu_tests
+ def test_adalora_causalLM(self):
+ r"""
+ Tests the gptq training with adalora
+ """
+
+ model = AutoModelForCausalLM.from_pretrained(
+ self.causal_lm_model_id,
+ torch_dtype=torch.float16,
+ device_map="auto",
+ quantization_config=self.quantization_config,
+ )
+
+ tokenizer = AutoTokenizer.from_pretrained(self.causal_lm_model_id)
+ model = prepare_model_for_kbit_training(model)
+
+ peft_config = AdaLoraConfig(
+ init_r=6,
+ target_r=4,
+ tinit=2,
+ tfinal=2,
+ total_step=6,
+ deltaT=5,
+ beta1=0.3,
+ beta2=0.3,
+ orth_reg_weight=0.2,
+ lora_alpha=32,
+ lora_dropout=0.05,
+ bias="none",
+ task_type="CAUSAL_LM",
+ )
+
+ model = get_peft_model(model, peft_config)
+
+ data = load_dataset_english_quotes()
+ data = data.map(lambda samples: self.tokenizer(samples["quote"]), batched=True)
+ batch = tokenizer(data["train"][:3]["quote"], return_tensors="pt", padding=True)
+ self._check_inference_finite(model, batch)
+
+ class OptimizerStepCallback(TrainerCallback):
+ def on_optimizer_step(self, args, state, control, **kwargs):
+ model.update_and_allocate(state.global_step)
+
+ step_callback = OptimizerStepCallback()
+
+ with tempfile.TemporaryDirectory() as tmp_dir:
+ trainer = Trainer(
+ model=model,
+ train_dataset=data["train"],
+ args=TrainingArguments(
+ per_device_train_batch_size=4,
+ gradient_accumulation_steps=4,
+ warmup_steps=2,
+ max_steps=6,
+ learning_rate=2e-4,
+ fp16=True,
+ logging_steps=1,
+ output_dir=tmp_dir,
+ ),
+ data_collator=DataCollatorForLanguageModeling(self.tokenizer, mlm=False),
+ )
+ trainer.add_callback(step_callback)
+ model.config.use_cache = False
+ trainer.train()
+
+ model.cpu().save_pretrained(tmp_dir)
+
+ assert "adapter_config.json" in os.listdir(tmp_dir)
+ assert SAFETENSORS_WEIGHTS_NAME in os.listdir(tmp_dir)
+
+ # assert loss is not None
+ assert trainer.state.log_history[-1]["train_loss"] is not None
+
+ @pytest.mark.single_gpu_tests
+ def test_causal_lm_training_gptq_qalora(self):
+ """
+ Test QALoRA with GPTQ quantization. The test would simply fail if the adapters are not set correctly.
+ """
+ with tempfile.TemporaryDirectory() as tmp_dir:
+ model = AutoModelForCausalLM.from_pretrained(
+ self.causal_lm_model_id,
+ torch_dtype=torch.float16,
+ device_map="auto",
+ quantization_config=self.quantization_config,
+ )
+
+ model = prepare_model_for_kbit_training(model)
+ config = LoraConfig(
+ r=16,
+ lora_alpha=32,
+ target_modules=["q_proj", "v_proj"],
+ lora_dropout=0.05,
+ bias="none",
+ task_type="CAUSAL_LM",
+ use_qalora=True,
+ qalora_group_size=32,
+ )
+ model = get_peft_model(model, config)
+
+ data = load_dataset_english_quotes()
+ data = data.map(lambda samples: self.tokenizer(samples["quote"]), batched=True)
+
+ trainer = Trainer(
+ model=model,
+ train_dataset=data["train"],
+ args=TrainingArguments(
+ per_device_train_batch_size=4,
+ gradient_accumulation_steps=4,
+ warmup_steps=2,
+ max_steps=3,
+ learning_rate=2e-4,
+ fp16=True,
+ logging_steps=1,
+ output_dir=tmp_dir,
+ ),
+ data_collator=DataCollatorForLanguageModeling(self.tokenizer, mlm=False),
+ )
+ model.config.use_cache = False
+ trainer.train()
+
+ model.cpu().save_pretrained(tmp_dir)
+
+ assert "adapter_config.json" in os.listdir(tmp_dir)
+ assert SAFETENSORS_WEIGHTS_NAME in os.listdir(tmp_dir)
+
+ # assert loss is not None
+ assert trainer.state.log_history[-1]["train_loss"] is not None
+
+ @pytest.mark.multi_gpu_tests
+ @require_torch_multi_gpu
+ def test_causal_lm_training_multi_gpu(self):
+ r"""
+ Test the CausalLM training on a multi-GPU device. The test would simply fail if the adapters are not set
+ correctly.
+ """
+ device_map = {
+ "model.decoder.embed_tokens": 0,
+ "lm_head": 0,
+ "model.decoder.embed_positions": 0,
+ "model.decoder.project_out": 0,
+ "model.decoder.project_in": 0,
+ "model.decoder.layers.0": 0,
+ "model.decoder.layers.1": 0,
+ "model.decoder.layers.2": 0,
+ "model.decoder.layers.3": 0,
+ "model.decoder.layers.4": 0,
+ "model.decoder.layers.5": 0,
+ "model.decoder.layers.6": 1,
+ "model.decoder.layers.7": 1,
+ "model.decoder.layers.8": 1,
+ "model.decoder.layers.9": 1,
+ "model.decoder.layers.10": 1,
+ "model.decoder.layers.11": 1,
+ "model.decoder.final_layer_norm": 1,
+ }
+
+ with tempfile.TemporaryDirectory() as tmp_dir:
+ model = AutoModelForCausalLM.from_pretrained(
+ self.causal_lm_model_id,
+ torch_dtype=torch.float16,
+ device_map=device_map,
+ quantization_config=self.quantization_config,
+ )
+
+ assert set(model.hf_device_map.values()) == set(range(device_count))
+ assert {p.device.index for p in model.parameters()} == set(range(device_count))
+
+ model = prepare_model_for_kbit_training(model)
+
+ setattr(model, "model_parallel", True)
+ setattr(model, "is_parallelizable", True)
+
+ config = LoraConfig(
+ r=16,
+ lora_alpha=32,
+ target_modules=["q_proj", "v_proj"],
+ lora_dropout=0.05,
+ bias="none",
+ task_type="CAUSAL_LM",
+ )
+
+ model = get_peft_model(model, config)
+
+ data = load_dataset_english_quotes()
+ data = data.map(lambda samples: self.tokenizer(samples["quote"]), batched=True)
+
+ trainer = Trainer(
+ model=model,
+ train_dataset=data["train"],
+ args=TrainingArguments(
+ per_device_train_batch_size=4,
+ gradient_accumulation_steps=4,
+ warmup_steps=2,
+ max_steps=3,
+ learning_rate=2e-4,
+ fp16=True,
+ logging_steps=1,
+ output_dir=tmp_dir,
+ ),
+ data_collator=DataCollatorForLanguageModeling(self.tokenizer, mlm=False),
+ )
+ model.config.use_cache = False
+ trainer.train()
+
+ model.cpu().save_pretrained(tmp_dir)
+
+ assert "adapter_config.json" in os.listdir(tmp_dir)
+ assert SAFETENSORS_WEIGHTS_NAME in os.listdir(tmp_dir)
+
+ # assert loss is not None
+ assert trainer.state.log_history[-1]["train_loss"] is not None
+
+ @pytest.mark.single_gpu_tests
+ def test_non_default_adapter_name(self):
+ # See issue 1346
+ config = LoraConfig(
+ r=16,
+ target_modules=["q_proj", "v_proj"],
+ task_type="CAUSAL_LM",
+ )
+
+ # default adapter name
+ model = AutoModelForCausalLM.from_pretrained(
+ self.causal_lm_model_id,
+ torch_dtype=torch.float16,
+ device_map="auto",
+ quantization_config=self.quantization_config,
+ )
+ model = prepare_model_for_kbit_training(model)
+ model = get_peft_model(model, config)
+ n_trainable_default, n_total_default = model.get_nb_trainable_parameters()
+
+ # other adapter name
+ model = AutoModelForCausalLM.from_pretrained(
+ self.causal_lm_model_id,
+ torch_dtype=torch.float16,
+ device_map="auto",
+ quantization_config=self.quantization_config,
+ )
+ model = prepare_model_for_kbit_training(model)
+ model = get_peft_model(model, config, adapter_name="other")
+ n_trainable_other, n_total_other = model.get_nb_trainable_parameters()
+
+ assert n_trainable_other > 0
+ # sanity check
+ assert n_trainable_default == n_trainable_other
+ assert n_total_default == n_total_other
+
+
+@require_non_cpu
+class OffloadSaveTests(unittest.TestCase):
+ def setUp(self):
+ self.causal_lm_model_id = "gpt2"
+
+ def tearDown(self):
+ r"""
+ Efficient mechanism to free GPU memory after each test. Based on
+ https://github.com/huggingface/transformers/issues/21094
+ """
+ clear_device_cache(garbage_collection=True)
+
+ def test_offload_load(self):
+ r"""
+ Test the loading of a LoRA model with CPU- and disk-offloaded modules
+ """
+ torch.manual_seed(0)
+ model = AutoModelForCausalLM.from_pretrained(self.causal_lm_model_id)
+ tokenizer = AutoTokenizer.from_pretrained(self.causal_lm_model_id)
+ memory_limits = {"cpu": "0.4GIB"} # no "disk" for PeftModel.from_pretrained() compatibility
+
+ # offload around half of all transformer modules to the disk
+ device_map = infer_auto_device_map(model, max_memory=memory_limits)
+ assert "cpu" in device_map.values()
+ assert "disk" in device_map.values()
+
+ config = LoraConfig(task_type="CAUSAL_LM", init_lora_weights=False, target_modules=["c_attn"])
+
+ model = get_peft_model(model, config)
+ with tempfile.TemporaryDirectory() as tmp_dir:
+ model.save_pretrained(tmp_dir)
+ model = AutoModelForCausalLM.from_pretrained(self.causal_lm_model_id, device_map="cpu")
+ lora_model = PeftModel.from_pretrained(model, tmp_dir).eval()
+ input_tokens = tokenizer.encode("Four score and seven years ago", return_tensors="pt")
+ output = lora_model(input_tokens)[0]
+
+ # load the model with device_map
+ offloaded_model = AutoModelForCausalLM.from_pretrained(self.causal_lm_model_id, device_map=device_map)
+ assert len({p.device for p in offloaded_model.parameters()}) == 2 # 'cpu' and 'meta'
+ offloaded_lora_model = PeftModel.from_pretrained(offloaded_model, tmp_dir, max_memory=memory_limits).eval()
+ offloaded_output = offloaded_lora_model(input_tokens)[0]
+ assert torch.allclose(output, offloaded_output, atol=1e-5)
+
+ @pytest.mark.single_gpu_tests
+ def test_offload_merge(self):
+ r"""
+ Test merging, unmerging, and unloading of a model with CPU- and disk- offloaded modules.
+ """
+ torch.manual_seed(0)
+ model = AutoModelForCausalLM.from_pretrained(self.causal_lm_model_id)
+ tokenizer = AutoTokenizer.from_pretrained(self.causal_lm_model_id)
+ memory_limits = {0: "0.2GIB", "cpu": "0.2GIB"} # no "disk" for PeftModel.from_pretrained() compatibility
+ # offloads around half of all transformer modules
+ device_map = infer_auto_device_map(model, max_memory=memory_limits)
+ assert 0 in device_map.values()
+ assert "cpu" in device_map.values()
+ assert "disk" in device_map.values()
+
+ config = LoraConfig(task_type="CAUSAL_LM", init_lora_weights=False, target_modules=["c_attn"])
+
+ model = get_peft_model(model, config)
+ with tempfile.TemporaryDirectory() as tmp_dir:
+ model.save_pretrained(tmp_dir)
+ # load the model with device_map
+ model = AutoModelForCausalLM.from_pretrained(self.causal_lm_model_id, device_map=device_map).eval()
+ assert len({p.device for p in model.parameters()}) == 2
+
+ model = PeftModel.from_pretrained(model, tmp_dir, max_memory=memory_limits)
+
+ input_tokens = tokenizer.encode("Four score and seven years ago", return_tensors="pt")
+ model.eval()
+
+ # test peft model adapter merge
+ pre_merge_olayer = model(input_tokens)[0]
+ model.merge_adapter()
+ post_merge_olayer = model(input_tokens)[0]
+ assert torch.allclose(post_merge_olayer, pre_merge_olayer)
+
+ # test peft model adapter unmerge
+ model.unmerge_adapter()
+ post_unmerge_olayer = model(input_tokens)[0]
+ assert torch.allclose(post_unmerge_olayer, pre_merge_olayer)
+
+ # test LoRA merge and unload
+ model = model.merge_and_unload()
+ post_unload_merge_olayer = model(input_tokens)[0]
+ assert torch.allclose(post_unload_merge_olayer, pre_merge_olayer)
+
+
+@pytest.mark.skipif(not (torch.cuda.is_available() or is_xpu_available()), reason="test requires a GPU or XPU")
+@pytest.mark.single_gpu_tests
+class TestPiSSA:
+ r"""
+ Tests for PiSSA to ensure that it reduces the quantization error compared to normal LoRA quantization.
+ """
+
+ # The error factor indicates by how much the quantization error should be decreased when using PiSSA compared to
+ # quantization without PiSSA. Thus 1.03 means that the error should be decreased by 3% at least. This is a very
+ # conservative value to prevent flakiness, in practice most gains are > 1.5
+ error_factor = 1.03
+
+ def quantize_model(self, model, num_bits=4, device="cuda"):
+ # Quantize the `weight.data` of the linear layer in the model to `num_bits` and store it with full precision.
+ quantizer = NFQuantizer(num_bits=num_bits, device=device, method="normal", block_size=64)
+ for name, module in model.named_modules():
+ if isinstance(module, (torch.nn.Linear, Conv1D)) and "lm_head" not in name:
+ quantized_weight, max_abs, shape = quantizer.quantize_block(module.weight.data.to(device))
+ module.weight.data = quantizer.dequantize_block(quantized_weight, max_abs, shape)
+ return model
+
+ def nuclear_norm(self, base_model, quantized_model):
+ # Calculate the nuclear norm (sum of singular values) of the error matrices between the `quantized_model` and the `base_model`.
+ error_list = []
+ for name, module in base_model.named_modules():
+ if isinstance(module, (torch.nn.Linear, Conv1D)) and "lm_head" not in name:
+ quant_module = quantized_model.get_submodule(name)
+ error_list.append(torch.linalg.svdvals(module.weight.data - quant_module.weight.data).sum())
+ return torch.Tensor(error_list).sum()
+
+ def get_errors(
+ self,
+ tmp_path,
+ bits=4,
+ device="cuda",
+ model_id="hf-internal-testing/tiny-random-BloomForCausalLM",
+ ):
+ # Comparing the quantized LoRA model to the base model, vs the PiSSA quantized model to the base model.
+ # We expect the PiSSA quantized model to have less error than the normal LoRA quantized model.
+
+ cls = AutoModelForSeq2SeqLM if "t5" in str(model_id) else AutoModelForCausalLM
+ base_model = cls.from_pretrained(model_id).eval().to(device)
+ task_type = TaskType.SEQ_2_SEQ_LM if base_model.config.is_encoder_decoder else TaskType.CAUSAL_LM
+
+ # logits from the normal quantized LoRA model
+ target_modules = "all-linear" if task_type != TaskType.SEQ_2_SEQ_LM else ["o", "k", "wi", "q", "v"]
+ lora_config = LoraConfig(task_type=task_type, target_modules=target_modules)
+
+ qlora_model = self.quantize_model(cls.from_pretrained(model_id).eval().to(device), bits, device)
+ qlora_model = get_peft_model(
+ qlora_model,
+ lora_config,
+ )
+ qlora_model = qlora_model.merge_and_unload()
+ qlora_error = self.nuclear_norm(base_model, qlora_model)
+ del qlora_model
+ clear_device_cache(garbage_collection=True)
+
+ # logits from quantized LoRA model using PiSSA
+ lora_config = LoraConfig(
+ task_type=task_type,
+ init_lora_weights="pissa",
+ target_modules=target_modules,
+ )
+ pissa_model = cls.from_pretrained(model_id).eval().to(device)
+ pissa_model = get_peft_model(pissa_model, lora_config)
+
+ # save LoRA weights, they should be initialized such that they minimize the quantization error
+ pissa_model.base_model.peft_config["default"].init_lora_weights = True
+ pissa_model.save_pretrained(tmp_path / "pissa_model")
+
+ pissa_model = pissa_model.unload()
+ pissa_model.save_pretrained(tmp_path / "residual_model")
+
+ del pissa_model
+ clear_device_cache(garbage_collection=True)
+
+ # now load quantized model and apply PiSSA-initialized weights on top
+ qpissa_model = self.quantize_model(
+ cls.from_pretrained(tmp_path / "residual_model").eval().to(device), bits, device
+ )
+ qpissa_model = PeftModel.from_pretrained(qpissa_model, tmp_path / "pissa_model")
+ qpissa_model = qpissa_model.merge_and_unload()
+ qpissa_error = self.nuclear_norm(base_model, qpissa_model)
+ del qpissa_model
+ clear_device_cache(garbage_collection=True)
+
+ assert qlora_error > 0.0
+ assert qpissa_error > 0.0
+
+ # next, check that PiSSA quantization errors are smaller than LoRA errors by a certain margin
+ assert qpissa_error < (qlora_error / self.error_factor)
+
+ @pytest.mark.parametrize("device", [torch_device, "cpu"])
+ def test_bloomz_pissa_4bit(self, device, tmp_path):
+ # In this test, we compare the logits of the base model, the quantized LoRA model, and the quantized model
+ # using PiSSA. When quantizing, we expect a certain level of error. However, we expect the PiSSA quantized
+ # model to have less error than the normal LoRA quantized model. Note that when using normal LoRA, the
+ # quantization error is simply the error from quantization without LoRA, as LoRA is a no-op before training.
+ # We still apply LoRA for the test for consistency.
+
+ self.get_errors(bits=4, device=device, tmp_path=tmp_path)
+
+ @pytest.mark.parametrize("device", [torch_device, "cpu"])
+ def test_bloomz_pissa_8bit(self, device, tmp_path):
+ # Same test as test_bloomz_pissa_4bit but with 8 bits.
+ self.get_errors(bits=8, device=device, tmp_path=tmp_path)
+
+ @pytest.mark.parametrize("device", [torch_device, "cpu"])
+ def test_t5_pissa_4bit(self, device, tmp_path):
+ self.get_errors(bits=4, device=device, model_id="t5-small", tmp_path=tmp_path)
+
+ @pytest.mark.parametrize("device", [torch_device, "cpu"])
+ def test_t5_pissa_8bit(self, device, tmp_path):
+ self.get_errors(bits=8, device=device, model_id="t5-small", tmp_path=tmp_path)
+
+ @pytest.mark.parametrize("device", [torch_device, "cpu"])
+ def test_gpt2_pissa_4bit(self, device, tmp_path):
+ # see 2104
+ self.get_errors(bits=4, device=device, model_id="gpt2", tmp_path=tmp_path)
+
+ @pytest.mark.parametrize("device", [torch_device, "cpu"])
+ def test_gpt2_pissa_8bit(self, device, tmp_path):
+ # see 2104
+ self.get_errors(bits=8, device=device, model_id="gpt2", tmp_path=tmp_path)
+
+ @require_bitsandbytes
+ def test_lora_pissa_conversion_same_output_after_loading_with_quantization(self, tmp_path):
+ # A copy of the test `test_lora_pissa_conversion_same_output_after_loading` in peft/tests/test_initialization.py,
+ # that would fail if bitsandbytes quantization is used because Quant(W_res) + AB !=Quant(W) + \Delta(AB).
+ import bitsandbytes as bnb
+
+ torch.manual_seed(0)
+ data = torch.rand(10, 1000).to(torch_device)
+
+ class MyModule(torch.nn.Module):
+ def __init__(self):
+ super().__init__()
+ # choose a large weight so that averages are close to expected values
+ self.linear = torch.nn.Linear(1000, 1000)
+ self.embed = torch.nn.Embedding(1000, 1000)
+ self.conv2d = torch.nn.Conv2d(100, 100, 3)
+
+ def forward(self, x):
+ x_int = (100 * x).int()
+ x_4d = x.flatten().reshape(1, 100, 10, 10)
+ return self.linear(x), self.embed(x_int), self.conv2d(x_4d)
+
+ model = MyModule().to(torch_device)
+ output_base = model(data)[0]
+
+ config = LoraConfig(init_lora_weights="pissa", target_modules=["linear"], r=8)
+ peft_model = get_peft_model(deepcopy(model), config)
+ # save the initial model
+ peft_model.peft_config["default"].init_lora_weights = True
+ peft_model.save_pretrained(tmp_path / "init-model")
+ peft_model = peft_model.unload()
+ torch.save(peft_model.state_dict(), tmp_path / "residual-model")
+ del peft_model
+
+ # create 4bit base model
+ base_model = deepcopy(model)
+ base_model.load_state_dict(torch.load(tmp_path / "residual-model"))
+ # sanity check: the base model weights were indeed changed
+ tol = 1e-06
+ assert not torch.allclose(model.linear.weight, base_model.linear.weight, atol=tol, rtol=tol)
+ # quantize the linear layer
+ linear4bit = bnb.nn.Linear4bit(base_model.linear.in_features, base_model.linear.out_features)
+ linear4bit.load_state_dict(base_model.linear.state_dict())
+ linear4bit.to(0)
+ base_model.linear = linear4bit
+ peft_model = PeftModel.from_pretrained(deepcopy(base_model), tmp_path / "init-model")
+ output_quantized_pissa = peft_model(data)[0]
+ # sanity check
+ tol = 1e-06
+ assert not torch.allclose(output_base, output_quantized_pissa, atol=tol, rtol=tol)
+
+ # modify the weights, or else the adapter performs an identity transformation
+ peft_model.base_model.linear.lora_B["default"].weight.data *= 2.0
+ output_finetuned_pissa = peft_model(data)[0]
+ # sanity check
+ tol = 1e-06
+ assert not torch.allclose(output_quantized_pissa, output_finetuned_pissa, atol=tol, rtol=tol)
+
+ # save the model normally
+ peft_model.save_pretrained(tmp_path / "pissa-model")
+ model_loaded = PeftModel.from_pretrained(deepcopy(base_model), tmp_path / "pissa-model")
+ output_loaded = model_loaded(data)[0]
+
+ assert torch.allclose(output_finetuned_pissa, output_loaded, atol=tol, rtol=tol)
+ # sanity check: ranks should still be 8 as initially
+ assert model_loaded.peft_config["default"].r == 8
+ assert model_loaded.base_model.model.linear.lora_A["default"].weight.shape[0] == 8
+
+ # save the model with conversion
+ peft_model.save_pretrained(
+ tmp_path / "pissa-model-converted", path_initial_model_for_weight_conversion=tmp_path / "init-model"
+ )
+ model_converted = PeftModel.from_pretrained(deepcopy(model), tmp_path / "pissa-model-converted")
+ output_converted = model_converted(data)[0]
+
+ # rank should be double of what it was initially
+ assert model_converted.peft_config["default"].r == 16
+ assert model_converted.base_model.model.linear.lora_A["default"].weight.shape[0] == 16
+ # base model weights should be the same as the initial model
+ assert torch.allclose(
+ model.linear.weight, model_converted.base_model.model.linear.base_layer.weight, atol=tol, rtol=tol
+ )
+ # This check is expected to fail when using bnb
+ assert not torch.allclose(output_finetuned_pissa, output_converted, atol=tol, rtol=tol)
+
+
+@pytest.mark.skipif(not (torch.cuda.is_available() or is_xpu_available()), reason="test requires a GPU or XPU")
+@pytest.mark.single_gpu_tests
+class TestOLoRA:
+ r"""
+ Tests for OLoRA to ensure that it reduces the quantization error compared to normal LoRA quantization.
+ """
+
+ # The error factor indicates by how much the quantization error should be decreased when using OLoRA compared to
+ # quantization without OLoRA. Thus 1.03 means that the error should be decreased by 3% at least. This is a very
+ # conservative value to prevent flakiness, in practice most gains are > 1.5
+ error_factor = 1.2
+
+ def quantize_model(self, model, num_bits=4, device="cuda"):
+ # Quantize the `weight.data` of the linear layer in the model to `num_bits` and store it with full precision.
+ quantizer = NFQuantizer(num_bits=num_bits, device=device, method="normal", block_size=64)
+ for name, module in model.named_modules():
+ if isinstance(module, torch.nn.Linear) and "lm_head" not in name:
+ quantized_weight, max_abs, shape = quantizer.quantize_block(module.weight.data.to(device))
+ module.weight.data = quantizer.dequantize_block(quantized_weight, max_abs, shape)
+ return model
+
+ def nuclear_norm(self, base_model, quantized_model):
+ # Calculate the nuclear norm (sum of singular values) of the error matrices between the `quantized_model` and the `base_model`.
+ error_list = []
+ for name, module in base_model.named_modules():
+ if isinstance(module, torch.nn.Linear) and "lm_head" not in name:
+ quant_module = quantized_model.get_submodule(name)
+ error_list.append(torch.linalg.svdvals(module.weight.data - quant_module.weight.data).sum())
+ return torch.Tensor(error_list).sum()
+
+ def get_errors(
+ self,
+ tmp_path,
+ bits=4,
+ device="cuda",
+ model_id="hf-internal-testing/tiny-random-BloomForCausalLM",
+ ):
+ # Comparing the quantized LoRA model to the base model, vs the OLoRA quantized model to the base model.
+ # We expect the OLoRA quantized model to have less error than the normal LoRA quantized model.
+
+ cls = AutoModelForSeq2SeqLM if "t5" in str(model_id) else AutoModelForCausalLM
+ base_model = cls.from_pretrained(model_id).eval().to(device)
+ task_type = TaskType.SEQ_2_SEQ_LM if base_model.config.is_encoder_decoder else TaskType.CAUSAL_LM
+
+ # logits from the normal quantized LoRA model
+ target_modules = "all-linear" if task_type != TaskType.SEQ_2_SEQ_LM else ["o", "k", "wi", "q", "v"]
+ lora_config = LoraConfig(task_type=task_type, target_modules=target_modules)
+
+ qlora_model = self.quantize_model(cls.from_pretrained(model_id).eval().to(device), bits, device)
+ qlora_model = get_peft_model(
+ qlora_model,
+ lora_config,
+ )
+ qlora_model = qlora_model.merge_and_unload()
+ qlora_error = self.nuclear_norm(base_model, qlora_model)
+ del qlora_model
+ clear_device_cache(garbage_collection=True)
+
+ # logits from quantized LoRA model using OLoRA
+ lora_config = LoraConfig(
+ task_type=task_type,
+ init_lora_weights="olora",
+ target_modules=target_modules,
+ )
+ olora_model = cls.from_pretrained(model_id).eval().to(device)
+ olora_model = get_peft_model(olora_model, lora_config)
+
+ # save LoRA weights, they should be initialized such that they minimize the quantization error
+ olora_model.base_model.peft_config["default"].init_lora_weights = True
+ olora_model.save_pretrained(tmp_path / "olora_model")
+
+ olora_model = olora_model.unload()
+ olora_model.save_pretrained(tmp_path / "residual_model")
+
+ del olora_model
+ clear_device_cache(garbage_collection=True)
+
+ # now load quantized model and apply OLoRA-initialized weights on top
+ qolora_model = self.quantize_model(
+ cls.from_pretrained(tmp_path / "residual_model").eval().to(device), bits, device
+ )
+ qolora_model = PeftModel.from_pretrained(qolora_model, tmp_path / "olora_model")
+ qolora_model = qolora_model.merge_and_unload()
+ qolora_error = self.nuclear_norm(base_model, qolora_model)
+ del qolora_model
+ clear_device_cache(garbage_collection=True)
+
+ assert qlora_error > 0.0
+ assert qolora_error > 0.0
+
+ # next, check that OLoRA quantization errors are smaller than LoRA errors by a certain margin
+ assert qolora_error < (qlora_error / self.error_factor)
+
+ @pytest.mark.parametrize("device", [torch_device, "cpu"])
+ def test_bloomz_olora_4bit(self, device, tmp_path):
+ # In this test, we compare the logits of the base model, the quantized LoRA model, and the quantized model
+ # using OLoRA. When quantizing, we expect a certain level of error. However, we expect the OLoRA quantized
+ # model to have less error than the normal LoRA quantized model. Note that when using normal LoRA, the
+ # quantization error is simply the error from quantization without LoRA, as LoRA is a no-op before training.
+ # We still apply LoRA for the test for consistency.
+
+ self.get_errors(bits=4, device=device, tmp_path=tmp_path)
+
+ @pytest.mark.parametrize("device", [torch_device, "cpu"])
+ def test_bloomz_olora_8bit(self, device, tmp_path):
+ # Same test as test_bloomz_olora_4bit but with 8 bits.
+ self.get_errors(bits=8, device=device, tmp_path=tmp_path)
+
+ @pytest.mark.parametrize("bits", [4, 8])
+ def test_olora_with_quantized_model(self, bits):
+ import bitsandbytes as bnb
+
+ # issue 1999
+ model_id = "hf-internal-testing/tiny-random-OPTForCausalLM"
+ if bits == 4:
+ bnb_config = BitsAndBytesConfig(
+ load_in_4bit=True,
+ bnb_4bit_quant_type="nf4",
+ bnb_4bit_compute_dtype=torch.float16,
+ bnb_4bit_quant_storage=torch.float16,
+ bnb_4bit_use_double_quant=True,
+ )
+ elif bits == 8:
+ bnb_config = BitsAndBytesConfig(load_in_8bit=True)
+ else:
+ raise ValueError("bits must be 4 or 8")
+
+ model = AutoModelForCausalLM.from_pretrained(model_id, quantization_config=bnb_config)
+ model = prepare_model_for_kbit_training(model)
+ config = LoraConfig(init_lora_weights="olora")
+ model = get_peft_model(model, config)
+
+ # check that the correct type is used for the weights
+ base_layer = model.base_model.model.model.decoder.layers[0].self_attn.v_proj.base_layer.weight
+ if bits == 4:
+ assert isinstance(base_layer, bnb.nn.modules.Params4bit)
+ else:
+ assert isinstance(base_layer, bnb.nn.modules.Int8Params)
+
+ inputs = torch.arange(10).unsqueeze(0).to(model.device)
+ logits = model(inputs).logits # does not raise
+ assert torch.isfinite(logits).all()
+
+
+@pytest.mark.skipif(
+ not (torch.cuda.is_available() or is_xpu_available()), reason="test requires a hardware accelerator"
+)
+@pytest.mark.single_gpu_tests
+@require_bitsandbytes
+class TestLoftQ:
+ r"""
+ Tests for LoftQ to ensure that it reduces the quantization error compared to normal LoRA quantization.
+ """
+
+ def get_error_factor(self, device):
+ # The error factor indicates by how much the quantization error should be decreased when using LoftQ compared to
+ # quantization without LoftQ. Thus 1.03 means that the error should be decreased by 3% at least. This is a very
+ # conservative value to prevent flakiness, in practice most gains are > 1.5
+ error_factor = 1.005 if device in ("xpu", "cpu") else 1.03
+ return error_factor
+
+ def get_input(self, model_id, device):
+ tokenizer = AutoTokenizer.from_pretrained(model_id)
+ inputs = tokenizer("All I want is", padding=True, return_tensors="pt")
+ inputs = inputs.to(device)
+ return inputs
+
+ def get_base_model(self, model_id, device, **kwargs):
+ cls = AutoModelForSeq2SeqLM if "t5" in str(model_id) else AutoModelForCausalLM
+ model = cls.from_pretrained(model_id, device_map=device, **kwargs).eval()
+ return model
+
+ def get_logits(self, model, inputs):
+ if model.config.is_encoder_decoder:
+ input_ids = inputs["input_ids"]
+ return model(input_ids=input_ids, decoder_input_ids=input_ids).logits
+ return model(**inputs).logits
+
+ def get_errors(
+ self,
+ tmp_path,
+ bits=4,
+ loftq_iter=1,
+ device="cuda",
+ model_id="hf-internal-testing/tiny-random-BloomForCausalLM",
+ use_dora=False,
+ ):
+ # Helper function that returns the quantization errors (MAE and MSE) when comparing the quantized LoRA model
+ # to the base model, vs the LoftQ quantized model to the base model. We expect the LoftQ quantized model to
+ # have less error than the normal LoRA quantized model. Since we compare logits, the observed error is
+ # already somewhat dampened because of the softmax.
+ torch.manual_seed(0)
+ model = self.get_base_model(model_id, device)
+ task_type = TaskType.SEQ_2_SEQ_LM if model.config.is_encoder_decoder else TaskType.CAUSAL_LM
+ inputs = self.get_input(model_id, device)
+ # the base logits are the reference, we try to match those as closely as possible
+ logits_base = self.get_logits(model, inputs)
+ # clean up
+ del model
+ clear_device_cache(garbage_collection=True)
+
+ # logits from the normal quantized LoRA model
+ target_modules = "all-linear" if task_type != TaskType.SEQ_2_SEQ_LM else ["o", "k", "wi", "q", "v"]
+ lora_config = LoraConfig(task_type=task_type, use_dora=use_dora, target_modules=target_modules)
+ kwargs = {}
+ if bits == 4:
+ kwargs["quantization_config"] = BitsAndBytesConfig(load_in_4bit=True, bnb_4bit_quant_type="nf4")
+ elif bits == 8:
+ kwargs["quantization_config"] = BitsAndBytesConfig(load_in_8bit=True)
+ else:
+ raise ValueError("bits must be 4 or 8")
+
+ quantized_model = get_peft_model(
+ self.get_base_model(model_id, device, **kwargs),
+ lora_config,
+ )
+ torch.manual_seed(0)
+ logits_quantized = self.get_logits(quantized_model, inputs)
+ del quantized_model
+ clear_device_cache(garbage_collection=True)
+
+ # logits from quantized LoRA model using LoftQ
+ loftq_config = LoftQConfig(loftq_bits=bits, loftq_iter=loftq_iter)
+ lora_config = LoraConfig(
+ task_type=task_type,
+ init_lora_weights="loftq",
+ loftq_config=loftq_config,
+ use_dora=use_dora,
+ target_modules=target_modules,
+ )
+ model = self.get_base_model(model_id, device)
+ if device != "cpu":
+ model = model.to(device)
+ loftq_model = get_peft_model(model, lora_config)
+ if device != "cpu":
+ loftq_model = loftq_model.to(device)
+
+ # save LoRA weights, they should be initialized such that they minimize the quantization error
+ loftq_model.base_model.peft_config["default"].init_lora_weights = True
+ loftq_model.save_pretrained(tmp_path / "loftq_model")
+
+ loftq_model = loftq_model.unload()
+ loftq_model.save_pretrained(tmp_path / "base_model")
+
+ del loftq_model
+ clear_device_cache(garbage_collection=True)
+
+ # now load quantized model and apply LoftQ-initialized weights on top
+ base_model = self.get_base_model(tmp_path / "base_model", device=device, **kwargs, torch_dtype=torch.float32)
+ loftq_model = PeftModel.from_pretrained(base_model, tmp_path / "loftq_model", is_trainable=True)
+
+ # TODO sanity check: model is quantized
+
+ torch.manual_seed(0)
+ logits_loftq = self.get_logits(loftq_model, inputs)
+ del loftq_model
+ clear_device_cache(garbage_collection=True)
+
+ mae_quantized = torch.abs(logits_base - logits_quantized).mean()
+ mse_quantized = torch.pow(logits_base - logits_quantized, 2).mean()
+ mae_loftq = torch.abs(logits_base - logits_loftq).mean()
+ mse_loftq = torch.pow(logits_base - logits_loftq, 2).mean()
+ return mae_quantized, mse_quantized, mae_loftq, mse_loftq
+
+ @pytest.mark.parametrize("device", [torch_device, "cpu"])
+ def test_bloomz_loftq_4bit(self, device, tmp_path):
+ # In this test, we compare the logits of the base model, the quantized LoRA model, and the quantized model
+ # using LoftQ. When quantizing, we expect a certain level of error. However, we expect the LoftQ quantized
+ # model to have less error than the normal LoRA quantized model. Note that when using normal LoRA, the
+ # quantization error is simply the error from quantization without LoRA, as LoRA is a no-op before training.
+ # We still apply LoRA for the test for consistency.
+
+ mae_quantized, mse_quantized, mae_loftq, mse_loftq = self.get_errors(bits=4, device=device, tmp_path=tmp_path)
+ # first, sanity check that all errors are > 0.0
+ assert mae_quantized > 0.0
+ assert mse_quantized > 0.0
+ assert mae_loftq > 0.0
+ assert mse_loftq > 0.0
+
+ # next, check that LoftQ quantization errors are smaller than LoRA errors by a certain margin
+ assert mse_loftq < (mse_quantized / self.error_factor)
+ assert mae_loftq < (mae_quantized / self.error_factor)
+
+ @pytest.mark.parametrize("device", [torch_device, "cpu"])
+ def test_bloomz_loftq_4bit_iter_5(self, device, tmp_path):
+ # Same test as the previous one but with 5 iterations. We should expect the error to be even smaller with more
+ # iterations, but in practice the difference is not that large, at least not for this small base model.
+ mae_quantized, mse_quantized, mae_loftq, mse_loftq = self.get_errors(
+ bits=4, loftq_iter=5, device=device, tmp_path=tmp_path
+ )
+ # first, sanity check that all errors are > 0.0
+ assert mae_quantized > 0.0
+ assert mse_quantized > 0.0
+ assert mae_loftq > 0.0
+ assert mse_loftq > 0.0
+
+ # next, check that LoftQ quantization errors are smaller than LoRA errors by a certain margin
+ error_factor = self.get_error_factor(device)
+ assert mse_loftq < (mse_quantized / error_factor)
+ assert mae_loftq < (mae_quantized / error_factor)
+
+ @pytest.mark.parametrize("device", [torch_device, "cpu"])
+ def test_bloomz_loftq_8bit(self, device, tmp_path):
+ # Same test as test_bloomz_loftq_4bit but with 8 bits.
+ mae_quantized, mse_quantized, mae_loftq, mse_loftq = self.get_errors(bits=8, device=device, tmp_path=tmp_path)
+
+ # first, sanity check that all errors are > 0.0
+ assert mae_quantized > 0.0
+ assert mse_quantized > 0.0
+ assert mae_loftq > 0.0
+ assert mse_loftq > 0.0
+
+ # next, check that LoftQ quantization errors are smaller than LoRA errors by a certain margin
+ error_factor = self.get_error_factor(device)
+ assert mse_loftq < (mse_quantized / error_factor)
+ assert mae_loftq < (mae_quantized / error_factor)
+
+ @pytest.mark.parametrize("device", [torch_device, "cpu"])
+ def test_bloomz_loftq_8bit_iter_5(self, device, tmp_path):
+ # Same test as test_bloomz_loftq_4bit_iter_5 but with 8 bits.
+ mae_quantized, mse_quantized, mae_loftq, mse_loftq = self.get_errors(
+ bits=8, loftq_iter=5, device=device, tmp_path=tmp_path
+ )
+
+ # first, sanity check that all errors are > 0.0
+ assert mae_quantized > 0.0
+ assert mse_quantized > 0.0
+ assert mae_loftq > 0.0
+ assert mse_loftq > 0.0
+
+ # next, check that LoftQ quantization errors are smaller than LoRA errors by a certain margin
+ error_factor = self.get_error_factor(device)
+ assert mse_loftq < (mse_quantized / error_factor)
+ assert mae_loftq < (mae_quantized / error_factor)
+
+ @pytest.mark.parametrize("device", [torch_device, "cpu"])
+ def test_t5_loftq_4bit(self, device, tmp_path):
+ mae_quantized, mse_quantized, mae_loftq, mse_loftq = self.get_errors(
+ bits=4, device=device, model_id="t5-small", tmp_path=tmp_path
+ )
+ # first, sanity check that all errors are > 0.0
+ assert mae_quantized > 0.0
+ assert mse_quantized > 0.0
+ assert mae_loftq > 0.0
+ assert mse_loftq > 0.0
+
+ # next, check that LoftQ quantization errors are smaller than LoRA errors by a certain margin
+ error_factor = self.get_error_factor(device)
+ assert mse_loftq < (mse_quantized / error_factor)
+ assert mae_loftq < (mae_quantized / error_factor)
+
+ @pytest.mark.parametrize("device", [torch_device, "cpu"])
+ def test_t5_loftq_8bit(self, device, tmp_path):
+ mae_quantized, mse_quantized, mae_loftq, mse_loftq = self.get_errors(
+ bits=8, device=device, model_id="t5-small", tmp_path=tmp_path
+ )
+ # first, sanity check that all errors are > 0.0
+ assert mae_quantized > 0.0
+ assert mse_quantized > 0.0
+ assert mae_loftq > 0.0
+ assert mse_loftq > 0.0
+
+ # next, check that LoftQ quantization errors are smaller than LoRA errors by a certain margin
+ error_factor = self.get_error_factor(device)
+ assert mse_loftq < (mse_quantized / error_factor)
+ assert mae_loftq < (mae_quantized / error_factor)
+
+ @pytest.mark.xfail # failing for now, but having DoRA pass is only a nice-to-have, not a must, so we're good
+ @pytest.mark.parametrize("device", [torch_device, "cpu"])
+ def test_bloomz_loftq_4bit_dora(self, device, tmp_path):
+ # same as test_bloomz_loftq_4bit but with DoRA
+ mae_quantized, mse_quantized, mae_loftq, mse_loftq = self.get_errors(
+ bits=4, device=device, use_dora=True, tmp_path=tmp_path
+ )
+ # first, sanity check that all errors are > 0.0
+ assert mae_quantized > 0.0
+ assert mse_quantized > 0.0
+ assert mae_loftq > 0.0
+ assert mse_loftq > 0.0
+
+ # next, check that LoftQ quantization errors are smaller than LoRA errors by a certain margin
+ factor = 3
+ assert mae_loftq < (mae_quantized / factor)
+ assert mse_loftq < (mse_quantized / factor)
+
+ @pytest.mark.parametrize("device", [torch_device, "cpu"])
+ def test_bloomz_loftq_8bit_dora(self, device, tmp_path):
+ # same as test_bloomz_loftq_8bit but with DoRA
+ mae_quantized, mse_quantized, mae_loftq, mse_loftq = self.get_errors(
+ bits=8, device=device, use_dora=True, tmp_path=tmp_path
+ )
+
+ # first, sanity check that all errors are > 0.0
+ assert mae_quantized > 0.0
+ assert mse_quantized > 0.0
+ assert mae_loftq > 0.0
+ assert mse_loftq > 0.0
+
+ # next, check that LoftQ quantization errors are smaller than LoRA errors by a certain margin
+ error_factor = self.get_error_factor(device)
+ assert mae_loftq < (mae_quantized / error_factor)
+ assert mse_loftq < (mse_quantized / error_factor)
+
+ def test_replace_lora_weights_with_loftq_using_callable(self):
+ """
+ Test replacing LoRa weights with LoFTQ using a callable.
+
+ Using the replace_lora_weights_loftq function, we replace the LoRa weights of a bnb-quantized model with LoRA
+ weights initialized by LoftQ on the fly. We use a callable to decide whether to replace the weights or not.
+ This callable checks, for each weight, if replacing it would actually result in logits that are closer to the
+ original logits of the non-quantized model.
+
+ """
+ torch.manual_seed(0)
+ model_id = "bigscience/bloomz-560m"
+ device = torch_device
+ tokenizer = AutoTokenizer.from_pretrained(model_id)
+ inputs = tokenizer("The dog was", padding=True, return_tensors="pt").to(device)
+
+ with tempfile.TemporaryDirectory() as tmp_dir:
+ model = AutoModelForCausalLM.from_pretrained(model_id).to(device)
+ logits_base = model(**inputs).logits
+ model.save_pretrained(tmp_dir)
+
+ # load in 4bit
+ bnb_config = BitsAndBytesConfig(
+ load_in_4bit=True,
+ bnb_4bit_use_double_quant=True,
+ )
+ model = AutoModelForCausalLM.from_pretrained(model_id, quantization_config=bnb_config)
+ model = get_peft_model(model, LoraConfig(task_type="CAUSAL_LM", target_modules="all-linear"))
+ logits_lora = model(**inputs).logits
+
+ current_mse = float("inf")
+ logs = []
+
+ def my_callback(model, module_name):
+ """Callable to replace weights with LoFTQ if the mse is lower than the current best one."""
+ nonlocal current_mse
+
+ logits = model(**inputs).logits
+ mse = ((logits_base - logits) ** 2).mean()
+ if mse < current_mse:
+ current_mse = mse
+ logs.append(True)
+ return True
+ logs.append(False)
+ return False
+
+ replace_lora_weights_loftq(model, model_path=tmp_dir, callback=my_callback)
+ logits_loftq = model(**inputs).logits
+
+ mae_lora = (logits_base - logits_lora).abs().mean()
+ mae_loftq = (logits_base - logits_loftq).abs().mean()
+ mse_lora = ((logits_base - logits_lora) ** 2).mean()
+ mse_loftq = ((logits_base - logits_loftq) ** 2).mean()
+
+ # check that the error was reduced by a certain margin
+ assert mae_loftq * 1.5 < mae_lora
+ assert mse_loftq * 2.5 < mse_lora
+
+ # check that the callback has returned some True and some False values
+ assert any(logs)
+ assert not all(logs)
+
+ del model
+ clear_device_cache(garbage_collection=True)
+
+ def test_replace_lora_weights_with_local_model(self):
+ # see issue 2020
+ torch.manual_seed(0)
+ model_id = "hf-internal-testing/tiny-random-OPTForCausalLM"
+ device = torch_device
+
+ with tempfile.TemporaryDirectory() as tmp_dir:
+ # save base model locally
+ model = AutoModelForCausalLM.from_pretrained(model_id).to(device)
+ model.save_pretrained(tmp_dir)
+ del model
+
+ # load in 4bit
+ bnb_config = BitsAndBytesConfig(
+ load_in_4bit=True,
+ bnb_4bit_use_double_quant=True,
+ )
+
+ # load the base model from local directory
+ model = AutoModelForCausalLM.from_pretrained(tmp_dir, quantization_config=bnb_config)
+ model = get_peft_model(model, LoraConfig())
+
+ # passing the local path directly works
+ replace_lora_weights_loftq(model, model_path=tmp_dir)
+ del model
+
+ # load the base model from local directory
+ model = AutoModelForCausalLM.from_pretrained(tmp_dir, quantization_config=bnb_config)
+ model = get_peft_model(model, LoraConfig())
+
+ # when not passing, ensure that users are made aware of the `model_path` argument
+ with pytest.raises(ValueError, match="model_path"):
+ replace_lora_weights_loftq(model)
+
+ del model
+ clear_device_cache(garbage_collection=True)
+
+ def test_config_no_loftq_init(self):
+ with pytest.warns(
+ UserWarning,
+ match="`loftq_config` specified but will be ignored when `init_lora_weights` is not 'loftq'.",
+ ):
+ LoraConfig(loftq_config=LoftQConfig())
+
+ def test_config_no_loftq_config(self):
+ with pytest.raises(ValueError, match="`loftq_config` must be specified when `init_lora_weights` is 'loftq'."):
+ LoraConfig(init_lora_weights="loftq")
+
+
+@require_bitsandbytes
+@require_non_cpu
+class MultiprocessTester(unittest.TestCase):
+ def test_notebook_launcher(self):
+ script_path = os.path.join("scripts", "launch_notebook_mp.py")
+ cmd = ["python", script_path]
+ with patch_environment(omp_num_threads=1):
+ run_command(cmd, env=os.environ.copy())
+
+
+@require_non_cpu
+class MixedPrecisionTests(unittest.TestCase):
+ def setUp(self):
+ self.causal_lm_model_id = "facebook/opt-125m"
+ self.tokenizer = AutoTokenizer.from_pretrained(self.causal_lm_model_id)
+ self.config = LoraConfig(
+ r=16,
+ lora_alpha=32,
+ task_type="CAUSAL_LM",
+ )
+
+ data = load_dataset_english_quotes()
+ self.data = data.map(lambda samples: self.tokenizer(samples["quote"]), batched=True)
+
+ def tearDown(self):
+ r"""
+ Efficient mechanism to free GPU memory after each test. Based on
+ https://github.com/huggingface/transformers/issues/21094
+ """
+ clear_device_cache(garbage_collection=True)
+ gc.collect()
+
+ @pytest.mark.single_gpu_tests
+ def test_model_using_float16_with_amp_raises(self):
+ # This test shows the issue with using a model in fp16 and then trying to use it with mixed precision training,
+ # which should not use fp16.
+ model = AutoModelForCausalLM.from_pretrained(
+ self.causal_lm_model_id,
+ torch_dtype=torch.float16,
+ )
+ model = get_peft_model(model, self.config, autocast_adapter_dtype=False)
+
+ with tempfile.TemporaryDirectory() as tmp_dir:
+ trainer = Trainer(
+ model=model,
+ train_dataset=self.data["train"],
+ args=TrainingArguments(
+ fp16=True, # <= this is required for the error to be raised
+ output_dir=tmp_dir,
+ max_steps=3,
+ ),
+ data_collator=DataCollatorForLanguageModeling(self.tokenizer, mlm=False),
+ )
+ with pytest.raises(ValueError, match="Attempting to unscale FP16 gradients."):
+ trainer.train()
+
+ @pytest.mark.single_gpu_tests
+ def test_model_using_float16_autocast_dtype(self):
+ # Here we use autocast_adapter_dtype=True (the default) to automatically promote the adapter weights to float32.
+ # No exception should be raised.
+ model = AutoModelForCausalLM.from_pretrained(
+ self.causal_lm_model_id,
+ torch_dtype=torch.float16,
+ )
+ model = get_peft_model(model, self.config, autocast_adapter_dtype=True)
+
+ with tempfile.TemporaryDirectory() as tmp_dir:
+ trainer = Trainer(
+ model=model,
+ train_dataset=self.data["train"],
+ args=TrainingArguments(
+ fp16=True, # <= this is required for the error to be raised
+ output_dir=tmp_dir,
+ max_steps=3,
+ ),
+ data_collator=DataCollatorForLanguageModeling(self.tokenizer, mlm=False),
+ )
+ trainer.train() # does not raise
+
+ @pytest.mark.single_gpu_tests
+ def test_model_using_float16_explicit_cast(self):
+ # Same test as above but containing the fix to make it work
+ model = AutoModelForCausalLM.from_pretrained(
+ self.causal_lm_model_id,
+ torch_dtype=torch.float16,
+ )
+ model = get_peft_model(model, self.config, autocast_adapter_dtype=False)
+
+ # here we manually promote the adapter weights to float32
+ for param in model.parameters():
+ if param.requires_grad:
+ param.data = param.data.float()
+
+ dtype_counts_before = Counter(p.dtype for p in model.parameters())
+ model = AutoModelForCausalLM.from_pretrained(
+ self.causal_lm_model_id,
+ torch_dtype=torch.float16,
+ )
+
+ model = get_peft_model(model, self.config, autocast_adapter_dtype=True)
+ dtype_counts_after = Counter(p.dtype for p in model.parameters())
+ assert dtype_counts_before == dtype_counts_after
+
+ with tempfile.TemporaryDirectory() as tmp_dir:
+ trainer = Trainer(
+ model=model,
+ train_dataset=self.data["train"],
+ args=TrainingArguments(
+ fp16=True, # <= this is required for the error to be raised
+ max_steps=3,
+ output_dir=tmp_dir,
+ ),
+ data_collator=DataCollatorForLanguageModeling(self.tokenizer, mlm=False),
+ )
+ trainer.train() # does not raise
+
+ @pytest.mark.single_gpu_tests
+ def test_load_model_using_float16_with_amp_raises(self):
+ # Same as previous tests, but loading the adapter with PeftModel.from_pretrained instead
+ model = AutoModelForCausalLM.from_pretrained(
+ self.causal_lm_model_id,
+ torch_dtype=torch.float16,
+ )
+ model = get_peft_model(model, self.config, autocast_adapter_dtype=False)
+
+ with tempfile.TemporaryDirectory() as tmp_dir:
+ model.save_pretrained(tmp_dir)
+ model = AutoModelForCausalLM.from_pretrained(self.causal_lm_model_id, torch_dtype=torch.float16)
+ model = PeftModel.from_pretrained(model, tmp_dir, autocast_adapter_dtype=False, is_trainable=True)
+
+ trainer = Trainer(
+ model=model,
+ train_dataset=self.data["train"],
+ args=TrainingArguments(
+ fp16=True, # <= this is required for the error to be raised
+ output_dir=tmp_dir,
+ max_steps=3,
+ ),
+ data_collator=DataCollatorForLanguageModeling(self.tokenizer, mlm=False),
+ )
+ with pytest.raises(ValueError, match="Attempting to unscale FP16 gradients."):
+ trainer.train()
+
+ @pytest.mark.single_gpu_tests
+ def test_load_model_using_float16_autocast_dtype(self):
+ # Same as previous tests, but loading the adapter with PeftModel.from_pretrained instead
+ model = AutoModelForCausalLM.from_pretrained(
+ self.causal_lm_model_id,
+ torch_dtype=torch.float16,
+ )
+ # Below, we purposefully set autocast_adapter_dtype=False so that the saved adapter uses float16. We still want
+ # the loaded adapter to use float32 when we load it with autocast_adapter_dtype=True.
+ model = get_peft_model(model, self.config, autocast_adapter_dtype=False)
+ # sanity check: this should have float16 adapter weights:
+ assert (
+ model.base_model.model.model.decoder.layers[0].self_attn.v_proj.lora_A["default"].weight.dtype
+ == torch.float16
+ )
+
+ with tempfile.TemporaryDirectory() as tmp_dir:
+ model.save_pretrained(tmp_dir)
+ model = AutoModelForCausalLM.from_pretrained(self.causal_lm_model_id, torch_dtype=torch.float16)
+ model = PeftModel.from_pretrained(model, tmp_dir, autocast_adapter_dtype=True, is_trainable=True)
+ # sanity check: this should NOT have float16 adapter weights:
+ assert (
+ model.base_model.model.model.decoder.layers[0].self_attn.v_proj.lora_A["default"].weight.dtype
+ == torch.float32
+ )
+
+ trainer = Trainer(
+ model=model,
+ train_dataset=self.data["train"],
+ args=TrainingArguments(
+ fp16=True, # <= this is required for the error to be raised
+ output_dir=tmp_dir,
+ max_steps=3,
+ ),
+ data_collator=DataCollatorForLanguageModeling(self.tokenizer, mlm=False),
+ )
+ trainer.train() # does not raise
+
+ @pytest.mark.single_gpu_tests
+ def test_load_adapter_using_float16_autocast_dtype(self):
+ # Here we test the load_adapter method with autocast_adapter_dtype. We show that autocasting is prevented when
+ # calling load_model(..., autocast_adapter_dtype=False) and that it is enabled when calling
+ # load_model(..., autocast_adapter_dtype=True) (the default).
+ model = AutoModelForCausalLM.from_pretrained(
+ self.causal_lm_model_id,
+ torch_dtype=torch.float16,
+ )
+ # Below, we purposefully set autocast_adapter_dtype=False so that the saved adapter uses float16. We still want
+ # the loaded adapter to use float32 when we load it with autocast_adapter_dtype=True.
+ model = get_peft_model(model, self.config, autocast_adapter_dtype=False)
+ # sanity check: this should have float16 adapter weights:
+ assert (
+ model.base_model.model.model.decoder.layers[0].self_attn.v_proj.lora_A["default"].weight.dtype
+ == torch.float16
+ )
+
+ with tempfile.TemporaryDirectory() as tmp_dir:
+ model.save_pretrained(tmp_dir)
+ model = AutoModelForCausalLM.from_pretrained(self.causal_lm_model_id, torch_dtype=torch.float16)
+ # the default adapter is now in float16
+ model = get_peft_model(model, self.config, autocast_adapter_dtype=False)
+ # sanity check: this should NOT have float16 adapter weights:
+ assert (
+ model.base_model.model.model.decoder.layers[0].self_attn.v_proj.lora_A["default"].weight.dtype
+ == torch.float16
+ )
+
+ # now load the first adapter in float16 using the adapter name "loaded16"
+ model.load_adapter(tmp_dir, "loaded16", autocast_adapter_dtype=False)
+ assert (
+ model.base_model.model.model.decoder.layers[0].self_attn.v_proj.lora_A["loaded16"].weight.dtype
+ == torch.float16
+ )
+
+ # now load the first adapter in float32 using the adapter name "loaded32"
+ model.load_adapter(tmp_dir, "loaded32", autocast_adapter_dtype=True)
+ assert (
+ model.base_model.model.model.decoder.layers[0].self_attn.v_proj.lora_A["loaded32"].weight.dtype
+ == torch.float32
+ )
+
+ # training with the default adapter, which is in float16, should raise
+ model.set_adapter("default")
+ trainer = Trainer(
+ model=model,
+ train_dataset=self.data["train"],
+ args=TrainingArguments(
+ fp16=True, # <= this is required for the error to be raised
+ output_dir=tmp_dir,
+ max_steps=3,
+ ),
+ data_collator=DataCollatorForLanguageModeling(self.tokenizer, mlm=False),
+ )
+ with pytest.raises(ValueError, match="Attempting to unscale FP16 gradients."):
+ trainer.train()
+
+ # training the model with the adapter "loaded16", which is in float16, should also raise
+ model.set_adapter("loaded16")
+ trainer = Trainer(
+ model=model,
+ train_dataset=self.data["train"],
+ args=TrainingArguments(
+ fp16=True, # <= this is required for the error to be raised
+ output_dir=tmp_dir,
+ max_steps=3,
+ ),
+ data_collator=DataCollatorForLanguageModeling(self.tokenizer, mlm=False),
+ )
+ with pytest.raises(ValueError, match="Attempting to unscale FP16 gradients."):
+ trainer.train()
+
+ # training the model with the adapter "loaded32", which is in float32, should not raise
+ model.set_adapter("loaded32")
+ trainer = Trainer(
+ model=model,
+ train_dataset=self.data["train"],
+ args=TrainingArguments(
+ fp16=True, # <= this is required for the error to be raised
+ output_dir=tmp_dir,
+ max_steps=3,
+ ),
+ data_collator=DataCollatorForLanguageModeling(self.tokenizer, mlm=False),
+ )
+ trainer.train() # does not raise
+
+
+@require_non_xpu
+@require_torch_gpu
+@require_aqlm
+@unittest.skipUnless(
+ version.parse(importlib.metadata.version("transformers")) >= version.parse("4.38.0"),
+ "test requires `transformers>=4.38.0`",
+)
+class PeftAqlmGPUTests(unittest.TestCase):
+ r"""
+ AQLM + peft tests
+ """
+
+ def setUp(self):
+ self.causal_lm_model_id = "BlackSamorez/TinyLlama-1_1B-Chat-v1_0-AQLM-2Bit-1x16-hf"
+ self.tokenizer = AutoTokenizer.from_pretrained(self.causal_lm_model_id)
+
+ def tearDown(self):
+ r"""
+ Efficient mechanism to free GPU memory after each test. Based on
+ https://github.com/huggingface/transformers/issues/21094
+ """
+ clear_device_cache(garbage_collection=True)
+
+ def _check_inference_finite(self, model, batch):
+ # try inference without Trainer class
+ training = model.training
+ model.eval()
+ output = model(**batch.to(model.device))
+ assert torch.isfinite(output.logits).all()
+ model.train(training)
+
+ @pytest.mark.single_gpu_tests
+ def test_causal_lm_training_aqlm(self):
+ r"""
+ Test the CausalLM training on a single GPU device. The test would simply fail if the adapters are not set
+ correctly.
+ """
+ with tempfile.TemporaryDirectory() as tmp_dir:
+ model = AutoModelForCausalLM.from_pretrained(
+ self.causal_lm_model_id,
+ device_map="cuda",
+ torch_dtype="auto",
+ )
+
+ model = prepare_model_for_kbit_training(model)
+ config = LoraConfig(
+ r=16,
+ lora_alpha=32,
+ target_modules=["q_proj", "v_proj"],
+ lora_dropout=0.05,
+ bias="none",
+ task_type="CAUSAL_LM",
+ )
+ model = get_peft_model(model, config)
+
+ data = load_dataset_english_quotes()
+ data = data.map(lambda samples: self.tokenizer(samples["quote"]), batched=True)
+
+ trainer = Trainer(
+ model=model,
+ train_dataset=data["train"],
+ args=TrainingArguments(
+ per_device_train_batch_size=4,
+ gradient_accumulation_steps=4,
+ warmup_steps=2,
+ max_steps=3,
+ learning_rate=2e-4,
+ logging_steps=1,
+ output_dir=tmp_dir,
+ fp16=True,
+ ),
+ data_collator=DataCollatorForLanguageModeling(self.tokenizer, mlm=False),
+ )
+ model.config.use_cache = False
+ trainer.train()
+
+ model.cpu().save_pretrained(tmp_dir)
+
+ assert "adapter_config.json" in os.listdir(tmp_dir)
+ assert SAFETENSORS_WEIGHTS_NAME in os.listdir(tmp_dir)
+
+ # assert loss is not None
+ assert trainer.state.log_history[-1]["train_loss"] is not None
+
+
+@require_non_xpu
+@require_torch_gpu
+@require_hqq
+@unittest.skipUnless(
+ version.parse(importlib.metadata.version("transformers")) >= version.parse("4.36.1"),
+ "test requires `transformers>=4.36.1`",
+)
+class PeftHqqGPUTests(unittest.TestCase):
+ r"""
+ HQQ + peft tests
+ """
+
+ def setUp(self):
+ self.causal_lm_model_id = "TinyLlama/TinyLlama-1.1B-Chat-v1.0"
+ self.tokenizer = AutoTokenizer.from_pretrained(self.causal_lm_model_id)
+
+ def tearDown(self):
+ r"""
+ Efficient mechanism to free GPU memory after each test. Based on
+ https://github.com/huggingface/transformers/issues/21094
+ """
+ clear_device_cache(garbage_collection=True)
+
+ @pytest.mark.single_gpu_tests
+ @parameterized.expand([False, True])
+ def test_causal_lm_training_hqq(self, use_dora):
+ r"""
+ Test the CausalLM training on a single GPU device. The test would simply fail if the adapters are not set
+ correctly.
+ """
+
+ from transformers import HqqConfig
+
+ with tempfile.TemporaryDirectory() as tmp_dir:
+ device = "cuda"
+ compute_dtype = torch.float16
+
+ quant_config = HqqConfig(nbits=4, group_size=64)
+
+ model = AutoModelForCausalLM.from_pretrained(
+ self.causal_lm_model_id,
+ device_map=device,
+ torch_dtype=compute_dtype,
+ quantization_config=quant_config,
+ )
+
+ model = prepare_model_for_kbit_training(model)
+ config = LoraConfig(
+ r=16,
+ lora_alpha=32,
+ target_modules=["q_proj", "v_proj"],
+ lora_dropout=0.05,
+ bias="none",
+ task_type="CAUSAL_LM",
+ use_dora=use_dora,
+ )
+ model = get_peft_model(model, config)
+
+ data = load_dataset_english_quotes()
+ data = data.map(lambda samples: self.tokenizer(samples["quote"]), batched=True)
+
+ trainer = Trainer(
+ model=model,
+ train_dataset=data["train"],
+ args=TrainingArguments(
+ per_device_train_batch_size=4,
+ gradient_accumulation_steps=4,
+ warmup_steps=2,
+ max_steps=3,
+ learning_rate=2e-4,
+ logging_steps=1,
+ output_dir=tmp_dir,
+ fp16=True,
+ ),
+ data_collator=DataCollatorForLanguageModeling(self.tokenizer, mlm=False),
+ )
+ model.config.use_cache = False
+ trainer.train()
+
+ model.save_pretrained(tmp_dir)
+
+ assert "adapter_config.json" in os.listdir(tmp_dir)
+ assert SAFETENSORS_WEIGHTS_NAME in os.listdir(tmp_dir)
+
+ # assert loss is not None
+ assert trainer.state.log_history[-1]["train_loss"] is not None
+
+ @pytest.mark.single_gpu_tests
+ def test_hqq_lora_model_outputs(self):
+ # check that the outputs generated by HQQ with LoRA are similar to those without HQQ
+ from transformers import HqqConfig
+
+ device = "cuda"
+ compute_dtype = torch.float16
+ min_correlation = 0.96
+
+ # first load the model without HQQ
+ model = AutoModelForCausalLM.from_pretrained(
+ self.causal_lm_model_id,
+ device_map=device,
+ torch_dtype=compute_dtype,
+ )
+ config = LoraConfig(
+ target_modules=["q_proj", "v_proj"],
+ task_type="CAUSAL_LM",
+ init_lora_weights=False,
+ )
+ torch.manual_seed(0)
+ model = get_peft_model(model, config).eval()
+ inputs = self.tokenizer("The meaning of unit tests is", return_tensors="pt").to(model.device)
+
+ with torch.inference_mode():
+ output_normal = model(**inputs).logits
+ assert torch.isfinite(output_normal).all()
+
+ del model
+ clear_device_cache(garbage_collection=True)
+
+ # now load with HQQ
+ quant_config = HqqConfig(nbits=4, group_size=64)
+ model = AutoModelForCausalLM.from_pretrained(
+ self.causal_lm_model_id,
+ device_map=device,
+ torch_dtype=compute_dtype,
+ quantization_config=quant_config,
+ )
+ torch.manual_seed(0)
+ model = get_peft_model(model, config).eval()
+ with torch.inference_mode():
+ output_hqq = model(**inputs).logits
+
+ # check that outputs of HQQ are highly correlated; there are outliers, so don't check for equality
+ cc_matrix = torch.corrcoef(torch.stack((output_normal.float().flatten(), output_hqq.float().flatten())))
+ assert cc_matrix.min() > min_correlation
+
+ # check that outputs are the same after merging
+ cc_matrix = torch.corrcoef(torch.stack((output_normal.float().flatten(), output_hqq.float().flatten())))
+ assert cc_matrix.min() > min_correlation
+
+ # check outputs are the same after unmerging
+ model.unmerge_adapter()
+ with torch.inference_mode():
+ output_unmerged = model(**inputs).logits
+ cc_matrix = torch.corrcoef(torch.stack((output_normal.float().flatten(), output_unmerged.float().flatten())))
+ assert cc_matrix.min() > min_correlation
+
+ # check that the results are the same after saving and loading
+ with tempfile.TemporaryDirectory() as tmp_dir:
+ model.save_pretrained(tmp_dir)
+ del model
+ clear_device_cache(garbage_collection=True)
+
+ quant_config = HqqConfig(nbits=4, group_size=64)
+ model = AutoModelForCausalLM.from_pretrained(
+ self.causal_lm_model_id,
+ device_map=device,
+ torch_dtype=compute_dtype,
+ quantization_config=quant_config,
+ )
+ model = PeftModel.from_pretrained(model, tmp_dir)
+ with torch.inference_mode():
+ output_loaded = model(**inputs).logits
+
+ # for loading, we expect high precision, so check for equality and not just correlation
+ atol, rtol = 1e-6, 1e-6
+ assert torch.allclose(output_hqq, output_loaded, atol=atol, rtol=rtol)
+
+ # check that outputs are the same after merge_and_unload
+ model = model.merge_and_unload()
+ with torch.inference_mode():
+ output_merged_unloaded = model(**inputs).logits
+ cc_matrix = torch.corrcoef(
+ torch.stack((output_normal.float().flatten(), output_merged_unloaded.float().flatten()))
+ )
+ assert cc_matrix.min() > min_correlation
+
+
+@require_non_cpu
+@require_auto_awq
+class PeftAwqGPUTests(unittest.TestCase):
+ r"""
+ Awq + peft tests
+
+ Note that AWQ is no longer being maintained:
+
+ https://github.com/casper-hansen/AutoAWQ/blob/88e4c76b20755db275574e6a03c83c84ba3bece5/README.md
+
+ It is therefore expected that more tests will start failing in the future. If this happens, remove AWQ support from
+ PEFT.
+ """
+
+ def setUp(self):
+ self.causal_lm_model_id = "peft-internal-testing/opt-125m-awq"
+ self.tokenizer = AutoTokenizer.from_pretrained(self.causal_lm_model_id)
+
+ def tearDown(self):
+ r"""
+ Efficient mechanism to free accelerator memory after each test. Based on
+ https://github.com/huggingface/transformers/issues/21094
+ """
+ clear_device_cache(garbage_collection=True)
+
+ def _check_inference_finite(self, model, batch):
+ # try inference without Trainer class
+ training = model.training
+ model.eval()
+ output = model(**batch.to(model.device))
+ assert torch.isfinite(output.logits).all()
+ model.train(training)
+
+ @pytest.mark.single_gpu_tests
+ def test_causal_lm_training_awq(self):
+ r"""
+ Test the CausalLM training on a single accelerator. The test would simply fail if the adapters are not set
+ correctly.
+ """
+ with tempfile.TemporaryDirectory() as tmp_dir:
+ model = AutoModelForCausalLM.from_pretrained(
+ self.causal_lm_model_id,
+ device_map="auto",
+ )
+
+ model = prepare_model_for_kbit_training(model)
+ config = LoraConfig(
+ r=16,
+ lora_alpha=32,
+ target_modules=["q_proj", "v_proj"],
+ lora_dropout=0.05,
+ bias="none",
+ task_type="CAUSAL_LM",
+ )
+ model = get_peft_model(model, config)
+
+ data = load_dataset_english_quotes()
+ data = data.map(lambda samples: self.tokenizer(samples["quote"]), batched=True)
+
+ # TODO: deal correctly with this case in transformers
+ model._is_quantized_training_enabled = True
+
+ trainer = Trainer(
+ model=model,
+ train_dataset=data["train"],
+ args=TrainingArguments(
+ per_device_train_batch_size=4,
+ gradient_accumulation_steps=4,
+ warmup_steps=2,
+ max_steps=3,
+ learning_rate=2e-4,
+ logging_steps=1,
+ output_dir=tmp_dir,
+ fp16=True,
+ ),
+ data_collator=DataCollatorForLanguageModeling(self.tokenizer, mlm=False),
+ )
+ model.config.use_cache = False
+ trainer.train()
+
+ model.cpu().save_pretrained(tmp_dir)
+
+ assert "adapter_config.json" in os.listdir(tmp_dir)
+ assert SAFETENSORS_WEIGHTS_NAME in os.listdir(tmp_dir)
+
+ # assert loss is not None
+ assert trainer.state.log_history[-1]["train_loss"] is not None
+
+ @pytest.mark.multi_gpu_tests
+ # TODO remove marker if/once issue is resolved, most likely requiring a fix in AutoAWQ:
+ # https://github.com/casper-hansen/AutoAWQ/issues/754
+ @pytest.mark.xfail(
+ condition=is_torch_version(">=", "2.7.0"),
+ reason="Multi-GPU test currently not working with AutoAWQ and PyTorch 2.7+",
+ strict=True,
+ )
+ @require_torch_multi_accelerator
+ def test_causal_lm_training_multi_accelerator(self):
+ r"""
+ Test the CausalLM training on a multi-accelerator device. The test would simply fail if the adapters are not
+ set correctly.
+ """
+ device_map = {
+ "model.decoder.embed_tokens": 0,
+ "lm_head": 0,
+ "model.decoder.embed_positions": 0,
+ "model.decoder.project_out": 0,
+ "model.decoder.project_in": 0,
+ "model.decoder.layers.0": 0,
+ "model.decoder.layers.1": 0,
+ "model.decoder.layers.2": 0,
+ "model.decoder.layers.3": 0,
+ "model.decoder.layers.4": 0,
+ "model.decoder.layers.5": 0,
+ "model.decoder.layers.6": 1,
+ "model.decoder.layers.7": 1,
+ "model.decoder.layers.8": 1,
+ "model.decoder.layers.9": 1,
+ "model.decoder.layers.10": 1,
+ "model.decoder.layers.11": 1,
+ "model.decoder.final_layer_norm": 1,
+ }
+
+ with tempfile.TemporaryDirectory() as tmp_dir:
+ model = AutoModelForCausalLM.from_pretrained(
+ self.causal_lm_model_id,
+ device_map=device_map,
+ )
+
+ assert set(model.hf_device_map.values()) == set(range(device_count))
+ assert {p.device.index for p in model.parameters()} == set(range(device_count))
+
+ model = prepare_model_for_kbit_training(model)
+
+ setattr(model, "model_parallel", True)
+ setattr(model, "is_parallelizable", True)
+
+ config = LoraConfig(
+ r=16,
+ lora_alpha=32,
+ target_modules=["q_proj", "v_proj"],
+ lora_dropout=0.05,
+ bias="none",
+ task_type="CAUSAL_LM",
+ )
+
+ model = get_peft_model(model, config)
+
+ data = load_dataset_english_quotes()
+ data = data.map(lambda samples: self.tokenizer(samples["quote"]), batched=True)
+
+ trainer = Trainer(
+ model=model,
+ train_dataset=data["train"],
+ args=TrainingArguments(
+ per_device_train_batch_size=4,
+ gradient_accumulation_steps=4,
+ warmup_steps=2,
+ max_steps=3,
+ learning_rate=2e-4,
+ logging_steps=1,
+ output_dir=tmp_dir,
+ ),
+ data_collator=DataCollatorForLanguageModeling(self.tokenizer, mlm=False),
+ )
+ model.config.use_cache = False
+ trainer.train()
+
+ model.cpu().save_pretrained(tmp_dir)
+
+ assert "adapter_config.json" in os.listdir(tmp_dir)
+ assert SAFETENSORS_WEIGHTS_NAME in os.listdir(tmp_dir)
+
+ # assert loss is not None
+ assert trainer.state.log_history[-1]["train_loss"] is not None
+
+
+@require_non_xpu
+@require_torch_gpu
+@require_eetq
+class PeftEetqGPUTests(unittest.TestCase):
+ r"""
+ EETQ + peft tests
+ """
+
+ def setUp(self):
+ self.causal_lm_model_id = "facebook/opt-125m"
+ self.tokenizer = AutoTokenizer.from_pretrained(self.causal_lm_model_id)
+
+ def tearDown(self):
+ r"""
+ Efficient mechanism to free GPU memory after each test. Based on
+ https://github.com/huggingface/transformers/issues/21094
+ """
+ clear_device_cache(garbage_collection=True)
+
+ def _check_inference_finite(self, model, batch):
+ # try inference without Trainer class
+ training = model.training
+ model.eval()
+ output = model(**batch.to(model.device))
+ assert torch.isfinite(output.logits).all()
+ model.train(training)
+
+ @pytest.mark.single_gpu_tests
+ def test_causal_lm_training_eetq(self):
+ r"""
+ Test the CausalLM training on a single GPU device. The test would simply fail if the adapters are not set
+ correctly.
+ """
+ from transformers import EetqConfig
+
+ with tempfile.TemporaryDirectory() as tmp_dir:
+ quantization_config = EetqConfig("int8")
+
+ model = AutoModelForCausalLM.from_pretrained(
+ self.causal_lm_model_id, device_map="auto", quantization_config=quantization_config
+ )
+
+ model = prepare_model_for_kbit_training(model)
+
+ config = LoraConfig(
+ r=16,
+ lora_alpha=32,
+ target_modules=["q_proj", "v_proj"],
+ lora_dropout=0.05,
+ bias="none",
+ task_type="CAUSAL_LM",
+ )
+ model = get_peft_model(model, config)
+
+ data = load_dataset_english_quotes()
+ data = data.map(lambda samples: self.tokenizer(samples["quote"]), batched=True)
+
+ trainer = Trainer(
+ model=model,
+ train_dataset=data["train"],
+ args=TrainingArguments(
+ per_device_train_batch_size=4,
+ gradient_accumulation_steps=4,
+ warmup_steps=2,
+ max_steps=3,
+ learning_rate=2e-4,
+ logging_steps=1,
+ output_dir=tmp_dir,
+ ),
+ data_collator=DataCollatorForLanguageModeling(self.tokenizer, mlm=False),
+ )
+ model.config.use_cache = False
+ trainer.train()
+
+ model.cpu().save_pretrained(tmp_dir)
+
+ assert "adapter_config.json" in os.listdir(tmp_dir)
+ assert SAFETENSORS_WEIGHTS_NAME in os.listdir(tmp_dir)
+
+ # assert loss is not None
+ assert trainer.state.log_history[-1]["train_loss"] is not None
+
+ @pytest.mark.multi_gpu_tests
+ @require_torch_multi_gpu
+ def test_causal_lm_training_multi_gpu_eetq(self):
+ r"""
+ Test the CausalLM training on a multi-GPU device. The test would simply fail if the adapters are not set
+ correctly.
+ """
+ from transformers import EetqConfig
+
+ with tempfile.TemporaryDirectory() as tmp_dir:
+ quantization_config = EetqConfig("int8")
+
+ model = AutoModelForCausalLM.from_pretrained(
+ self.causal_lm_model_id,
+ device_map=DEVICE_MAP_MAP[self.causal_lm_model_id],
+ quantization_config=quantization_config,
+ )
+
+ assert set(model.hf_device_map.values()) == set(range(device_count))
+ assert {p.device.index for p in model.parameters()} == set(range(device_count))
+
+ model = prepare_model_for_kbit_training(model)
+
+ setattr(model, "model_parallel", True)
+ setattr(model, "is_parallelizable", True)
+
+ config = LoraConfig(
+ r=16,
+ lora_alpha=32,
+ target_modules=["q_proj", "v_proj"],
+ lora_dropout=0.05,
+ bias="none",
+ task_type="CAUSAL_LM",
+ )
+
+ model = get_peft_model(model, config)
+
+ data = load_dataset_english_quotes()
+ data = data.map(lambda samples: self.tokenizer(samples["quote"]), batched=True)
+
+ trainer = Trainer(
+ model=model,
+ train_dataset=data["train"],
+ args=TrainingArguments(
+ per_device_train_batch_size=4,
+ gradient_accumulation_steps=4,
+ warmup_steps=2,
+ max_steps=3,
+ learning_rate=2e-4,
+ logging_steps=1,
+ output_dir=tmp_dir,
+ ),
+ data_collator=DataCollatorForLanguageModeling(self.tokenizer, mlm=False),
+ )
+ model.config.use_cache = False
+ trainer.train()
+
+ model.cpu().save_pretrained(tmp_dir)
+
+ assert "adapter_config.json" in os.listdir(tmp_dir)
+ assert SAFETENSORS_WEIGHTS_NAME in os.listdir(tmp_dir)
+
+ # assert loss is not None
+ assert trainer.state.log_history[-1]["train_loss"] is not None
+
+
+@require_non_cpu
+@require_torchao
+class PeftTorchaoGPUTests(unittest.TestCase):
+ r"""
+ torchao + peft tests
+ """
+
+ supported_quant_types = [
+ "int8_weight_only",
+ "int8_dynamic_activation_int8_weight",
+ # int4_weight_only raises an error:
+ # RuntimeError: derivative for aten::_weight_int4pack_mm is not implemented
+ # "int4_weight_only",
+ ]
+
+ def setUp(self):
+ self.causal_lm_model_id = "facebook/opt-125m"
+ self.tokenizer = AutoTokenizer.from_pretrained(self.causal_lm_model_id)
+ # torchao breaks with fp16 and if a previous test uses fp16, transformers will set this env var, which affects
+ # subsequent tests, therefore the env var needs to be cleared explicitly
+ #
+ # TODO: remove this once https://github.com/huggingface/transformers/pull/39483 is merged
+ os.environ.pop("ACCELERATE_MIXED_PRECISION", None)
+
+ def tearDown(self):
+ r"""
+ Efficient mechanism to free GPU memory after each test. Based on
+ https://github.com/huggingface/transformers/issues/21094
+ """
+ clear_device_cache(garbage_collection=True)
+
+ @parameterized.expand(supported_quant_types)
+ @pytest.mark.single_gpu_tests
+ def test_causal_lm_training_single_gpu_torchao(self, quant_type):
+ from transformers import TorchAoConfig
+
+ device = 0
+
+ with tempfile.TemporaryDirectory() as tmp_dir:
+ quantization_config = TorchAoConfig(quant_type=quant_type)
+ model = AutoModelForCausalLM.from_pretrained(
+ self.causal_lm_model_id, device_map=device, quantization_config=quantization_config
+ )
+ model = prepare_model_for_kbit_training(model)
+
+ config = LoraConfig(
+ r=16,
+ lora_alpha=32,
+ target_modules=["q_proj", "v_proj"],
+ lora_dropout=0.05,
+ bias="none",
+ task_type="CAUSAL_LM",
+ )
+ model = get_peft_model(model, config)
+
+ data = load_dataset_english_quotes()
+ data = data.map(lambda samples: self.tokenizer(samples["quote"]), batched=True)
+
+ trainer = Trainer(
+ model=model,
+ train_dataset=data["train"],
+ args=TrainingArguments(
+ per_device_train_batch_size=4,
+ gradient_accumulation_steps=4,
+ warmup_steps=2,
+ max_steps=3,
+ learning_rate=2e-4,
+ logging_steps=1,
+ output_dir=tmp_dir,
+ ),
+ data_collator=DataCollatorForLanguageModeling(self.tokenizer, mlm=False),
+ )
+ trainer.model.config.use_cache = False
+ trainer.train()
+
+ model.save_pretrained(tmp_dir)
+
+ assert "adapter_config.json" in os.listdir(tmp_dir)
+ assert SAFETENSORS_WEIGHTS_NAME in os.listdir(tmp_dir)
+
+ # assert loss is not None
+ assert trainer.state.log_history[-1]["train_loss"] is not None
+
+ @pytest.mark.single_gpu_tests
+ def test_causal_lm_training_single_gpu_torchao_dora_int8_weight_only(self):
+ from transformers import TorchAoConfig
+
+ device = 0
+
+ with tempfile.TemporaryDirectory() as tmp_dir:
+ quantization_config = TorchAoConfig(quant_type="int8_weight_only")
+ model = AutoModelForCausalLM.from_pretrained(
+ self.causal_lm_model_id, device_map=device, quantization_config=quantization_config
+ )
+ model = prepare_model_for_kbit_training(model)
+
+ config = LoraConfig(
+ r=16,
+ lora_alpha=32,
+ target_modules=["q_proj", "v_proj"],
+ lora_dropout=0.05,
+ bias="none",
+ task_type="CAUSAL_LM",
+ use_dora=True,
+ )
+ model = get_peft_model(model, config)
+
+ data = load_dataset_english_quotes()
+ data = data.map(lambda samples: self.tokenizer(samples["quote"]), batched=True)
+
+ trainer = Trainer(
+ model=model,
+ train_dataset=data["train"],
+ args=TrainingArguments(
+ per_device_train_batch_size=4,
+ gradient_accumulation_steps=4,
+ warmup_steps=2,
+ max_steps=3,
+ learning_rate=2e-4,
+ logging_steps=1,
+ output_dir=tmp_dir,
+ ),
+ data_collator=DataCollatorForLanguageModeling(self.tokenizer, mlm=False),
+ )
+ trainer.model.config.use_cache = False
+ trainer.train()
+
+ model.save_pretrained(tmp_dir)
+
+ assert "adapter_config.json" in os.listdir(tmp_dir)
+ assert SAFETENSORS_WEIGHTS_NAME in os.listdir(tmp_dir)
+
+ # assert loss is not None
+ assert trainer.state.log_history[-1]["train_loss"] is not None
+
+ @pytest.mark.single_gpu_tests
+ def test_causal_lm_training_single_gpu_torchao_dora_int8_dynamic_activation_int8_weight_raises(self):
+ from transformers import TorchAoConfig
+
+ device = 0
+
+ quantization_config = TorchAoConfig(quant_type="int8_dynamic_activation_int8_weight")
+ model = AutoModelForCausalLM.from_pretrained(
+ self.causal_lm_model_id, device_map=device, quantization_config=quantization_config
+ )
+ model = prepare_model_for_kbit_training(model)
+
+ config = LoraConfig(
+ r=16,
+ lora_alpha=32,
+ target_modules=["q_proj", "v_proj"],
+ lora_dropout=0.05,
+ bias="none",
+ task_type="CAUSAL_LM",
+ use_dora=True,
+ )
+ with pytest.raises(NotImplementedError):
+ get_peft_model(model, config)
+
+ @pytest.mark.single_gpu_tests
+ def test_causal_lm_training_single_gpu_torchao_int4_raises(self):
+ # int4_weight_only raises an error:
+ # RuntimeError: derivative for aten::_weight_int4pack_mm is not implemented
+ # TODO: Once proper torchao support for int4 is added, remove this test and add int4 to supported_quant_types
+ from transformers import TorchAoConfig
+
+ device = 0
+
+ quantization_config = TorchAoConfig(quant_type="int4_weight_only")
+ model = AutoModelForCausalLM.from_pretrained(
+ self.causal_lm_model_id, device_map=device, quantization_config=quantization_config
+ )
+ model = prepare_model_for_kbit_training(model)
+
+ config = LoraConfig(
+ r=16,
+ lora_alpha=32,
+ target_modules=["q_proj", "v_proj"],
+ lora_dropout=0.05,
+ bias="none",
+ task_type="CAUSAL_LM",
+ )
+
+ msg = re.escape("TorchaoLoraLinear only supports int8 weights for now")
+ with pytest.raises(ValueError, match=msg):
+ get_peft_model(model, config)
+
+ @parameterized.expand(supported_quant_types)
+ @pytest.mark.multi_gpu_tests
+ @require_torch_multi_accelerator
+ def test_causal_lm_training_multi_accelerator_torchao(self, quant_type):
+ from transformers import TorchAoConfig
+
+ device_map = {
+ "model.decoder.embed_tokens": 0,
+ "lm_head": 0,
+ "model.decoder.embed_positions": 0,
+ "model.decoder.project_out": 0,
+ "model.decoder.project_in": 0,
+ "model.decoder.layers.0": 0,
+ "model.decoder.layers.1": 0,
+ "model.decoder.layers.2": 0,
+ "model.decoder.layers.3": 0,
+ "model.decoder.layers.4": 0,
+ "model.decoder.layers.5": 0,
+ "model.decoder.layers.6": 1,
+ "model.decoder.layers.7": 1,
+ "model.decoder.layers.8": 1,
+ "model.decoder.layers.9": 1,
+ "model.decoder.layers.10": 1,
+ "model.decoder.layers.11": 1,
+ "model.decoder.final_layer_norm": 1,
+ }
+
+ with tempfile.TemporaryDirectory() as tmp_dir:
+ quantization_config = TorchAoConfig(quant_type=quant_type)
+ model = AutoModelForCausalLM.from_pretrained(
+ self.causal_lm_model_id,
+ device_map=device_map,
+ quantization_config=quantization_config,
+ torch_dtype=torch.bfloat16,
+ )
+
+ assert set(model.hf_device_map.values()) == set(range(device_count))
+ assert {p.device.index for p in model.parameters()} == set(range(device_count))
+
+ model = prepare_model_for_kbit_training(model)
+ model.model_parallel = True
+ model.is_parallelizable = True
+
+ config = LoraConfig(
+ r=16,
+ lora_alpha=32,
+ target_modules=["q_proj", "v_proj"],
+ lora_dropout=0.05,
+ bias="none",
+ task_type="CAUSAL_LM",
+ )
+ model = get_peft_model(model, config)
+
+ data = load_dataset_english_quotes()
+ data = data.map(lambda samples: self.tokenizer(samples["quote"]), batched=True)
+
+ trainer = Trainer(
+ model=model,
+ train_dataset=data["train"],
+ args=TrainingArguments(
+ per_device_train_batch_size=4,
+ gradient_accumulation_steps=4,
+ warmup_steps=2,
+ max_steps=3,
+ learning_rate=2e-4,
+ logging_steps=1,
+ output_dir=tmp_dir,
+ ),
+ data_collator=DataCollatorForLanguageModeling(self.tokenizer, mlm=False),
+ )
+ trainer.model.config.use_cache = False
+ trainer.train()
+
+ model.save_pretrained(tmp_dir)
+
+ assert "adapter_config.json" in os.listdir(tmp_dir)
+ assert SAFETENSORS_WEIGHTS_NAME in os.listdir(tmp_dir)
+
+ # assert loss is not None
+ assert trainer.state.log_history[-1]["train_loss"] is not None
+
+ @pytest.mark.multi_gpu_tests
+ @require_torch_multi_accelerator
+ def test_causal_lm_training_multi_accelerator_torchao_int4_raises(self):
+ # int4_weight_only raises an error:
+ # RuntimeError: derivative for aten::_weight_int4pack_mm is not implemented
+ # TODO: Once proper torchao support for int4 is added, remove this test and add int4 to supported_quant_types
+ from transformers import TorchAoConfig
+
+ device_map = {
+ "model.decoder.embed_tokens": 0,
+ "lm_head": 0,
+ "model.decoder.embed_positions": 0,
+ "model.decoder.project_out": 0,
+ "model.decoder.project_in": 0,
+ "model.decoder.layers.0": 0,
+ "model.decoder.layers.1": 0,
+ "model.decoder.layers.2": 0,
+ "model.decoder.layers.3": 0,
+ "model.decoder.layers.4": 0,
+ "model.decoder.layers.5": 0,
+ "model.decoder.layers.6": 1,
+ "model.decoder.layers.7": 1,
+ "model.decoder.layers.8": 1,
+ "model.decoder.layers.9": 1,
+ "model.decoder.layers.10": 1,
+ "model.decoder.layers.11": 1,
+ "model.decoder.final_layer_norm": 1,
+ }
+ quantization_config = TorchAoConfig(quant_type="int4_weight_only")
+ model = AutoModelForCausalLM.from_pretrained(
+ self.causal_lm_model_id,
+ device_map=device_map,
+ quantization_config=quantization_config,
+ torch_dtype=torch.bfloat16,
+ )
+
+ assert set(model.hf_device_map.values()) == set(range(device_count))
+ assert {p.device.index for p in model.parameters()} == set(range(device_count))
+
+ model = prepare_model_for_kbit_training(model)
+ model.model_parallel = True
+ model.is_parallelizable = True
+
+ config = LoraConfig(
+ r=16,
+ lora_alpha=32,
+ target_modules=["q_proj", "v_proj"],
+ lora_dropout=0.05,
+ bias="none",
+ task_type="CAUSAL_LM",
+ )
+
+ msg = re.escape("TorchaoLoraLinear only supports int8 weights for now")
+ with pytest.raises(ValueError, match=msg):
+ get_peft_model(model, config)
+
+ @pytest.mark.single_gpu_tests
+ def test_torchao_merge_layers_int8_weight_only(self):
+ from torchao.dtypes import AffineQuantizedTensor
+ from transformers import TorchAoConfig
+
+ quant_type = "int8_weight_only"
+ torch.manual_seed(0)
+ device = 0
+ dummy_input = torch.arange(10).view(-1, 1).to(device)
+
+ quantization_config = TorchAoConfig(quant_type=quant_type)
+ model = AutoModelForCausalLM.from_pretrained(
+ self.causal_lm_model_id, device_map=device, quantization_config=quantization_config
+ ).eval()
+ logits_base = model(dummy_input)[0]
+
+ config = LoraConfig(
+ r=16,
+ lora_alpha=32,
+ target_modules=["q_proj", "v_proj"],
+ lora_dropout=0.05,
+ bias="none",
+ task_type="CAUSAL_LM",
+ init_lora_weights=False,
+ )
+ model = get_peft_model(model, config)
+
+ model.eval()
+ logits = model(dummy_input)[0]
+
+ # sanity check: outputs changed
+ # precision is quite low, so we need to use high atol and rtol
+ atol, rtol = 1e-1, 1e-1
+ assert not torch.allclose(logits, logits_base, atol=atol, rtol=rtol)
+
+ model.merge_adapter()
+ logits_merged = model(dummy_input)[0]
+ for name, module in model.named_modules():
+ if "base_layer" in name:
+ assert isinstance(module.weight, AffineQuantizedTensor)
+
+ model.unmerge_adapter()
+ logits_unmerged = model(dummy_input)[0]
+ for name, module in model.named_modules():
+ if "base_layer" in name:
+ assert isinstance(module.weight, AffineQuantizedTensor)
+
+ model = model.merge_and_unload()
+ logits_merged_unloaded = model(dummy_input)[0]
+
+ assert torch.allclose(logits, logits_merged, atol=atol, rtol=rtol)
+ assert torch.allclose(logits, logits_unmerged, atol=atol, rtol=rtol)
+ assert torch.allclose(logits, logits_merged_unloaded, atol=atol, rtol=rtol)
+
+ @pytest.mark.single_gpu_tests
+ def test_torchao_merge_layers_int8_dynamic_activation_int8_weight_raises(self):
+ # int8_dynamic_activation_int8_weight does not support dequantize, thus merging does not work
+ from transformers import TorchAoConfig
+
+ quant_type = "int8_dynamic_activation_int8_weight"
+ torch.manual_seed(0)
+ device = 0
+
+ quantization_config = TorchAoConfig(quant_type=quant_type)
+ model = AutoModelForCausalLM.from_pretrained(
+ self.causal_lm_model_id, device_map=device, quantization_config=quantization_config
+ ).eval()
+
+ config = LoraConfig(
+ r=16,
+ lora_alpha=32,
+ target_modules=["q_proj", "v_proj"],
+ lora_dropout=0.05,
+ bias="none",
+ task_type="CAUSAL_LM",
+ init_lora_weights=False,
+ )
+ model = get_peft_model(model, config)
+
+ msg = re.escape(
+ "Weights of type LinearActivationQuantizedTensor do not support dequantization (yet), which is needed to "
+ "support merging."
+ )
+ with pytest.raises(NotImplementedError, match=msg):
+ model.merge_adapter()
+
+
+PRECISIONS = [(torch.float32), (torch.float16), (torch.bfloat16)]
+
+LORA_PARAMS = {
+ "r": 8,
+ "lora_alpha": 16,
+ "lora_dropout": 0.05,
+}
+
+
+class SimpleModel(torch.nn.Module):
+ def __init__(self):
+ super().__init__()
+
+ self.embedding_layer = torch.nn.Embedding(1000, 768)
+ self.layer_norm = torch.nn.LayerNorm(768)
+ self.linear_transform = torch.nn.Linear(768, 256)
+
+ def forward(self, input_ids):
+ embedded_output = self.embedding_layer(input_ids)
+ norm_output = self.layer_norm(embedded_output)
+ linear_output = self.linear_transform(norm_output)
+
+ return linear_output
+
+
+class SimpleConv2DModel(torch.nn.Module):
+ def __init__(self):
+ super().__init__()
+
+ self.embedding_layer = torch.nn.Embedding(1000, 768)
+ self.layer_norm = torch.nn.LayerNorm(768)
+ self.conv2d_transform = torch.nn.Conv2d(1, 256, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1))
+
+ def forward(self, input_ids):
+ # Additional layers for your custom model
+ embedded_output = self.embedding_layer(input_ids)
+ norm_output = self.layer_norm(embedded_output)
+
+ # Reshape for Conv2d input (add batch size dimension)
+ norm_output = norm_output.unsqueeze(1)
+ conv_output = self.conv2d_transform(norm_output)
+
+ # Remove batch size dimension
+ conv_output = conv_output.squeeze(1)
+
+ return conv_output
+
+
+@require_non_cpu
+class TestAutoCast(unittest.TestCase):
+ device = infer_device()
+
+ # This test makes sure, that Lora dtypes are consistent with the types
+ # infered by torch.autocast under tested PRECISIONS
+ @parameterized.expand(PRECISIONS)
+ def test_simple_model(self, *args, **kwargs):
+ self._test_model(SimpleModel(), *args, **kwargs)
+
+ @parameterized.expand(PRECISIONS)
+ def test_simple_lora_linear_model(self, *args, **kwargs):
+ simple_model = SimpleModel()
+ config = LoraConfig(
+ **LORA_PARAMS,
+ target_modules=["linear_transform"],
+ )
+
+ lora_model = get_peft_model(simple_model, config)
+
+ self._test_model(lora_model, *args, **kwargs)
+
+ @parameterized.expand(PRECISIONS)
+ def test_simple_lora_embedding_model(self, *args, **kwargs):
+ simple_model = SimpleModel()
+ config = LoraConfig(
+ **LORA_PARAMS,
+ target_modules=["embedding_layer"],
+ )
+ lora_model = get_peft_model(simple_model, config)
+
+ self._test_model(lora_model, *args, **kwargs)
+
+ @parameterized.expand(PRECISIONS)
+ def test_simple_conv2d_model(self, *args, **kwargs):
+ self._test_model(SimpleConv2DModel(), *args, **kwargs)
+
+ @parameterized.expand(PRECISIONS)
+ def test_simple_lora_conv2d_model(self, *args, **kwargs):
+ simple_model = SimpleConv2DModel()
+ config = LoraConfig(
+ **LORA_PARAMS,
+ target_modules=["conv2d_transform"],
+ )
+ lora_model = get_peft_model(simple_model, config)
+ self._test_model(lora_model, *args, **kwargs)
+
+ def _test_model(self, model, precision):
+ # Move model to GPU
+ model = model.to(self.device)
+
+ # Prepare dummy inputs
+ input_ids = torch.randint(0, 1000, (2, 10)).to(self.device)
+ if precision == torch.bfloat16:
+ if not is_bf16_available():
+ self.skipTest("Bfloat16 not supported on this device")
+
+ # Forward pass with test precision
+ with torch.autocast(enabled=True, dtype=precision, device_type=self.device):
+ outputs = model(input_ids)
+ assert outputs.dtype == precision
+
+
+class TestFSDPWrap:
+ """
+ Test that we can successfully initialize an FSDP instance of the module.
+
+ This is a very simple test, as it does not perform actual FSDP training. Here we just ensure that the FSDP instance
+ can be created. This can fail for several reasons, e.g. int dtype from BNB or inconsistent requires_grad settings
+ due to the auto wrap policy.
+
+ """
+
+ @pytest.mark.single_gpu_tests
+ @require_bitsandbytes
+ def test_bnb_4bit_wrap_fsdp(self):
+ quant_config = BitsAndBytesConfig(
+ load_in_4bit=True,
+ # float32 must be used, or else FSDP will complain about mixed int and float dtypes
+ bnb_4bit_compute_dtype=torch.float32,
+ bnb_4bit_quant_storage=torch.float32,
+ bnb_4bit_use_double_quant=True,
+ )
+ model = AutoModelForCausalLM.from_pretrained(
+ "facebook/opt-125m",
+ quantization_config=quant_config,
+ torch_dtype=torch.float32,
+ )
+ # model = prepare_model_for_kbit_training(model)
+ config = LoraConfig(
+ target_modules=["q_proj", "v_proj"],
+ task_type="CAUSAL_LM",
+ use_dora=True,
+ )
+ model = get_peft_model(model, config)
+
+ os.environ["MASTER_ADDR"] = "localhost"
+ os.environ["MASTER_PORT"] = "29501"
+
+ init_process_group(world_size=1, rank=0)
+ # check that this does not raise:
+ FSDP(model, auto_wrap_policy=fsdp_auto_wrap_policy(model), use_orig_params=False, sync_module_states=True)
+
+ def test_fsdp_auto_wrap_policy_does_not_raise_on_custom_model(self):
+ # See #2167
+ # Avoid raising on custom models since Trainer uses fsdp_auto_wrap_policy automatically for PEFT + FSDP
+ fsdp_auto_wrap_policy(SimpleModel()) # does not raise
+
+
+class TestBOFT:
+ """
+ Test that we can correctly use half-precision models with BOFT.
+ """
+
+ device = infer_device()
+
+ @require_non_cpu
+ @pytest.mark.single_gpu_tests
+ def test_boft_half_linear(self):
+ # Check that we can use BoFT with model loaded in half precision
+ layer = torch.nn.Linear(160, 160).to(self.device)
+ layer = boft.layer.Linear(layer, "layer", boft_n_butterfly_factor=2).to(dtype=torch.bfloat16)
+ x = torch.randn(160, 160, device=self.device, dtype=torch.bfloat16)
+ layer(x) # does not raise
+
+ @require_non_cpu
+ @pytest.mark.single_gpu_tests
+ def test_boft_half_conv(self):
+ conv = torch.nn.Conv2d(1, 1, 4).to(self.device)
+ conv = boft.layer.Conv2d(conv, "conv", boft_n_butterfly_factor=2).to(dtype=torch.bfloat16)
+ x = torch.randn(1, 160, 160, device=self.device, dtype=torch.bfloat16)
+ conv(x) # does not raise
+
+
+class TestPTuningReproducibility:
+ device = infer_device()
+
+ @require_non_cpu
+ @require_deterministic_for_xpu
+ def test_p_tuning_exactly_reproducible_after_loading(self, tmp_path):
+ # See: https://github.com/huggingface/peft/issues/2043#issuecomment-2321522577
+ # Ensure that after loading a p-tuning checkpoint, results are exactly reproducible (before the patch, they were
+ # only _almost_ identical).
+
+ # The model must be sufficiently large for the effect to be measurable, which is why this test requires is not
+ # run on CPU.
+ model_id = "facebook/opt-125m"
+ inputs = torch.arange(10).view(-1, 1).to(self.device)
+
+ torch.manual_seed(0)
+ model = AutoModelForCausalLM.from_pretrained(model_id).to(self.device)
+ peft_config = PromptEncoderConfig(task_type="CAUSAL_LM", num_virtual_tokens=20, encoder_hidden_size=128)
+ model = get_peft_model(model, peft_config).eval()
+
+ with torch.inference_mode():
+ output_peft = model(inputs).logits
+ gen_peft = model.generate(inputs, min_new_tokens=10, max_new_tokens=10)
+
+ model.save_pretrained(tmp_path)
+ del model
+ clear_device_cache(garbage_collection=True)
+
+ model = AutoModelForCausalLM.from_pretrained(model_id).to(self.device)
+ model = PeftModel.from_pretrained(model, tmp_path)
+
+ with torch.inference_mode():
+ output_loaded = model(inputs).logits
+ gen_loaded = model.generate(inputs, min_new_tokens=10, max_new_tokens=10)
+
+ torch.testing.assert_close(output_loaded, output_peft)
+ torch.testing.assert_close(gen_loaded, gen_peft)
+
+
+@pytest.mark.single_gpu_tests
+class TestLowCpuMemUsageDifferentDevices:
+ """Test for the low CPU memory usage option for loading PEFT models.
+
+ There are already tests for low_cpu_mem_usage=True in test_initialization.py but here we want to run tests that
+ require a GPU.
+
+ """
+
+ model_id = "hf-internal-testing/tiny-random-OPTForCausalLM"
+ device = infer_device()
+
+ @require_non_cpu
+ @pytest.mark.parametrize("device_model, device_sd", [("cpu", infer_device()), (infer_device(), "cpu")])
+ def test_low_cpu_mem_usage_model_model_on_gpu_state_dict_on_cpu_works(self, device_model, device_sd):
+ # specifically test diverging devices for the model and state_dict
+ inputs = {"input_ids": torch.randint(0, 100, (1, 10)), "attention_mask": torch.ones(1, 10)}
+ inputs = {k: v.to(device_model) for k, v in inputs.items()}
+
+ model = AutoModelForCausalLM.from_pretrained(self.model_id).to(device_model)
+ lora_config = LoraConfig(init_lora_weights=False, target_modules="all-linear")
+ model = get_peft_model(model, lora_config)
+ model.eval()
+ logits_not_low_cpu_mem = model(**inputs).logits
+
+ state_dict = get_peft_model_state_dict(model)
+ peft_model_state_dict = {}
+ # remap the state dict so that it can be correctly loaded, and move weights to the other device
+ prefix = "base_model.model."
+ for k, v in state_dict.items():
+ k = k[len(prefix) :]
+ peft_model_state_dict[k] = v.to(device_sd)
+
+ del model
+
+ model = AutoModelForCausalLM.from_pretrained(self.model_id).to(device_model)
+ model.eval()
+ inject_adapter_in_model(lora_config, model, low_cpu_mem_usage=True)
+ load_result = set_peft_model_state_dict(model, peft_model_state_dict, low_cpu_mem_usage=True)
+
+ # sanity check: all lora keys are matched
+ assert not any("lora" in k for k in load_result.missing_keys)
+ assert not any("lora" in k for k in load_result.unexpected_keys)
+
+ logits_low_cpu_mem = model(**inputs).logits
+
+ assert torch.allclose(logits_low_cpu_mem, logits_not_low_cpu_mem)
+ assert {p.device.type for p in model.parameters()} == {device_model}
+
+ @require_bitsandbytes
+ @pytest.mark.parametrize("quantization_method", ["bnb-4bit", "bnb-8bit"])
+ def test_low_cpu_mem_usage_with_quantization(self, quantization_method):
+ # Ensure that low_cpu_mem_usage works with quantization
+ # See also https://github.com/huggingface/diffusers/issues/10550
+ if quantization_method == "bnb-4bit":
+ quantization_config = BitsAndBytesConfig(
+ load_in_4bit=True,
+ bnb_4bit_compute_dtype=torch.float32,
+ bnb_4bit_quant_storage=torch.float32,
+ bnb_4bit_use_double_quant=True,
+ )
+ elif quantization_method == "bnb-8bit":
+ quantization_config = BitsAndBytesConfig(load_in_8bit=True)
+ else:
+ raise ValueError(f"Unknown quantization method {quantization_method}")
+
+ model = AutoModelForCausalLM.from_pretrained(self.model_id, quantization_config=quantization_config)
+ if model.device.type != self.device:
+ # calling model.to("cuda") with 8 bit bnb raises an error, thus guard against it
+ model = model.to(self.device)
+
+ lora_config = LoraConfig(init_lora_weights=False, target_modules="all-linear")
+
+ # We use get_peft_model with low_cpu_mem_usage=True here. This is not typically done in practice (the option is
+ # mostly interesting for loading trained adapters), but it does the job for testing purposes.
+ model = get_peft_model(model, lora_config, low_cpu_mem_usage=True) # this should not raise
+ assert {p.device.type for p in model.parameters()} == {self.device, "meta"}
+
+
+class TestEvaInitializationGPU:
+ """GPU tests for the Eva initialization method."""
+
+ # Constants for test configuration
+ COSINE_SIMILARITY_THRESHOLD = 0.75
+ NUM_SEEDS = 3
+ BATCH_SIZE = 4
+ MAX_LENGTH = 256
+ LORA_DIM = 8
+ LORA_ALPHA = 1
+ DEVICE = infer_device()
+
+ @pytest.fixture
+ def tokenizer(self):
+ tokenizer = AutoTokenizer.from_pretrained("openai-community/gpt2")
+ tokenizer.pad_token = tokenizer.eos_token
+ return tokenizer
+
+ @pytest.fixture
+ def dataset(self, tokenizer):
+ dataset = load_dataset_english_quotes()["train"]
+ # concatenate examples
+ examples = []
+ example = ""
+ for data in dataset:
+ if len(example) >= self.MAX_LENGTH:
+ examples.append(example)
+ example = ""
+ example = example + " " + data["quote"]
+ dataset = Dataset.from_dict({"text": examples})
+ # tokenize
+ dataset = dataset.map(
+ lambda x: tokenizer(x["text"], padding="max_length", truncation=True, max_length=self.MAX_LENGTH),
+ batched=True,
+ remove_columns=dataset.column_names,
+ )
+ dataset.set_format(type="torch")
+ return dataset
+
+ @pytest.fixture
+ def model(self):
+ model = AutoModelForCausalLM.from_pretrained("openai-community/gpt2")
+ model.transformer.h = model.transformer.h[:2] # truncate to 2 layers
+ return model.to(self.DEVICE)
+
+ @pytest.fixture
+ def model_bnb(self):
+ bnb_config = BitsAndBytesConfig(load_in_4bit=True)
+ model = AutoModelForCausalLM.from_pretrained(
+ "openai-community/gpt2",
+ quantization_config=bnb_config,
+ attn_implementation="eager", # gpt2 doesnt support flash attention
+ )
+ model.transformer.h = model.transformer.h[:2] # truncate to 2 layers
+ model = prepare_model_for_kbit_training(model)
+ return model
+
+ @pytest.fixture
+ def model_fixture(self, request):
+ return request.getfixturevalue(request.param)
+
+ @pytest.fixture
+ def peft_config(self):
+ return LoraConfig(
+ r=self.LORA_DIM,
+ lora_alpha=self.LORA_ALPHA,
+ target_modules=["c_attn"],
+ init_lora_weights="eva",
+ eva_config=EvaConfig(rho=2),
+ )
+
+ def is_bnb_model(self, model):
+ return hasattr(model.config, "quantization_config")
+
+ @staticmethod
+ def collate_fn(examples):
+ return {k: torch.stack([v[k] for v in examples], dim=0) for k in examples[0].keys()}
+
+ @require_non_cpu
+ @require_bitsandbytes
+ @pytest.mark.single_gpu_tests
+ @pytest.mark.parametrize("model_fixture", ["model", "model_bnb"], indirect=True)
+ def test_eva_initialization_consistency(self, model_fixture, dataset, peft_config):
+ """Test that the state dict returned by get_eva_state_dict loaded correctly and is consistent across different seeds based
+ on the cosine similarity of the svd components."""
+ state_dicts = []
+ for seed in range(self.NUM_SEEDS):
+ shuffled_dataset = dataset.shuffle(seed=seed)
+ dataloader = DataLoader(
+ shuffled_dataset,
+ batch_size=self.BATCH_SIZE,
+ collate_fn=lambda examples: {
+ k: torch.stack([v[k] for v in examples], dim=0) for k in examples[0].keys()
+ },
+ shuffle=False,
+ )
+ peft_model = get_peft_model(deepcopy(model_fixture), peft_config)
+ initialize_lora_eva_weights(peft_model, dataloader)
+ state_dicts.append(
+ {k: v.cpu() for k, v in peft_model.state_dict().items() if "lora_A.default.weight" in k}
+ )
+
+ cos_sims = defaultdict(list)
+ for i, j in itertools.combinations(range(self.NUM_SEEDS), 2):
+ for k, v1 in state_dicts[i].items():
+ v2 = state_dicts[j][k]
+ min_size = min(v1.size(0), v2.size(0))
+ cos_sims[k].extend(torch.cosine_similarity(v1[:min_size], v2[:min_size], dim=1).abs().tolist())
+
+ mean_cosine_similarities = {k: torch.tensor(v).mean() for k, v in cos_sims.items()}
+ for layer_name, mean_cosine_similarity in mean_cosine_similarities.items():
+ assert mean_cosine_similarity > self.COSINE_SIMILARITY_THRESHOLD, (
+ f"Mean absolute cosine similarity {mean_cosine_similarity:.4f} "
+ f"is not greater than {self.COSINE_SIMILARITY_THRESHOLD}"
+ )
+
+
+class TestALoRAInferenceGPU:
+ """GPU inference for Activated LoRA."""
+
+ # Constants for test configuration
+ NUM_SEEDS = 3
+ LORA_DIM = 8
+ LORA_ALPHA = 1
+ DEVICE = infer_device()
+
+ @pytest.fixture
+ def tokenizer(self):
+ tokenizer = AutoTokenizer.from_pretrained("facebook/opt-125m")
+ tokenizer.pad_token = tokenizer.eos_token
+ return tokenizer
+
+ @pytest.fixture
+ def model(self):
+ model = AutoModelForCausalLM.from_pretrained("facebook/opt-125m")
+ model.model.decoder.layers = model.model.decoder.layers[:2] # truncate to 2 layers
+ return model.to(self.DEVICE)
+
+ @pytest.fixture
+ def model_bnb(self):
+ bnb_config = BitsAndBytesConfig(load_in_4bit=True)
+ model = AutoModelForCausalLM.from_pretrained(
+ "facebook/opt-125m",
+ quantization_config=bnb_config,
+ )
+ model.model.decoder.layers = model.model.decoder.layers[:2] # truncate to 2 layers
+ model = prepare_model_for_kbit_training(model)
+ return model
+
+ @pytest.fixture
+ def peft_config(self):
+ return LoraConfig(
+ r=self.LORA_DIM,
+ task_type="CAUSAL_LM",
+ lora_alpha=self.LORA_ALPHA,
+ target_modules=["q_proj"],
+ alora_invocation_tokens=[2], # id for
+ init_lora_weights=False,
+ )
+
+ @require_non_cpu
+ @require_bitsandbytes
+ @pytest.mark.single_gpu_tests
+ def test_alora_forward_consistency(self, model, model_bnb, peft_config):
+ """Test that the forwards of the model with adapter are similar across quantizations."""
+ for seed in range(self.NUM_SEEDS):
+ torch.manual_seed(seed)
+ # random.seed(seed)
+ np.random.seed(seed)
+ peft_model = get_peft_model(deepcopy(model), peft_config)
+ torch.manual_seed(seed)
+ # random.seed(seed)
+ np.random.seed(seed)
+ peft_model_bnb = get_peft_model(deepcopy(model_bnb), peft_config)
+ peft_model.eval()
+ peft_model_bnb.eval()
+ input_ids = torch.tensor([[0, 1, 2, 3]]).to(self.DEVICE)
+ with torch.no_grad():
+ peft_out = peft_model(input_ids=input_ids, return_dict=True, output_hidden_states=True)
+ peft_out_bnb = peft_model_bnb(input_ids=input_ids, return_dict=True, output_hidden_states=True)
+ h_fp = peft_out.hidden_states[-1]
+ h_4b = peft_out_bnb.hidden_states[-1]
+ a = h_fp.detach().to(torch.float32).cpu()
+ b = h_4b.detach().to(torch.float32).cpu()
+ import torch.nn.functional as F
+
+ cos = F.cosine_similarity(a.flatten(), b.flatten(), dim=0).item()
+ assert cos > 0.9
+
+
+@pytest.mark.multi_gpu_tests
+class TestPrefixTuning:
+ device = infer_device()
+
+ @require_torch_multi_accelerator
+ def test_prefix_tuning_multiple_devices_decoder_model(self):
+ # See issue 2134
+ model_id = "hf-internal-testing/tiny-random-MistralForCausalLM"
+ tokenizer = AutoTokenizer.from_pretrained(model_id, padding="left")
+ inputs = tokenizer(["A list of colors: red, blue"], return_tensors="pt").to(self.device)
+
+ device_map = {
+ "model.embed_tokens": 0,
+ "model.layers.0": 0,
+ "model.layers.1": 1,
+ "model.norm": 1,
+ "model.rotary_emb": 1,
+ "lm_head": 1,
+ }
+ model = AutoModelForCausalLM.from_pretrained(model_id, device_map=device_map)
+ # sanity check, as the test passes trivially for a single device
+ assert len({p.device for p in model.parameters()}) > 1
+ # sanity check: this should work without peft
+ model.generate(**inputs) # does not raise
+
+ peft_config = PrefixTuningConfig(num_virtual_tokens=10, task_type="CAUSAL_LM")
+ model = get_peft_model(model, peft_config)
+ model.generate(**inputs) # does not raise
+
+ @require_torch_multi_accelerator
+ def test_prefix_tuning_multiple_devices_encoder_decoder_model(self):
+ # See issue 2134
+ model_id = "hf-internal-testing/tiny-random-T5Model"
+ tokenizer = AutoTokenizer.from_pretrained(model_id, padding="left")
+ inputs = tokenizer(["A list of colors: red, blue"], return_tensors="pt").to(self.device)
+ device_map = {
+ "shared": 0,
+ "encoder.embed_tokens": 0,
+ "encoder.block.0": 0,
+ "encoder.block.1": 0,
+ "encoder.block.2": 1,
+ "encoder.block.3": 1,
+ "encoder.block.4": 1,
+ "encoder.final_layer_norm": 1,
+ "decoder.embed_tokens": 0,
+ "decoder.block.0": 0,
+ "decoder.block.1": 0,
+ "decoder.block.2": 1,
+ "decoder.block.3": 1,
+ "decoder.block.4": 1,
+ "decoder.final_layer_norm": 1,
+ "lm_head": 0,
+ }
+ model = AutoModelForSeq2SeqLM.from_pretrained(model_id, device_map=device_map)
+ # sanity check, as the test passes trivially for a single device
+ assert len({p.device for p in model.parameters()}) > 1
+ # sanity check: this should work without peft
+ model.generate(**inputs) # does not raise
+
+ peft_config = PrefixTuningConfig(num_virtual_tokens=10, task_type="SEQ_2_SEQ_LM")
+ model = get_peft_model(model, peft_config)
+ model.generate(**inputs) # does not raise
+
+
+@pytest.mark.skipif(not (torch.cuda.is_available() or is_xpu_available()), reason="test requires a GPU or XPU")
+@pytest.mark.single_gpu_tests
+class TestHotSwapping:
+ """
+ Test hotswapping on compiled models.
+
+ This test suite is only run on GPU as it is quite slow.
+ """
+
+ torch_device = infer_device()
+
+ @pytest.fixture(scope="class", autouse=True)
+ def reset_float32_matmul_precision(self):
+ # Earlier tests may run torchao, which, at the time this was added, sets the float32 matmul precision to 'high'.
+ # This in turn results in some models producing different outputs when compiled (but only for some seeds).
+ # Therefore, we need to ensure that the precision is reset to "highest", which is the default.
+ # TODO: if torchao removes the side effect, this fixture can be deleted.
+ # https://github.com/pytorch/ao/blob/ffb4350640e76c7e7f449dd1e36d33f19fe384c8/torchao/quantization/utils.py#L589
+ torch.set_float32_matmul_precision("highest")
+
+ @pytest.fixture(autouse=True)
+ def reset_dynamo_cache(self):
+ # It is critical that the dynamo cache is reset for each test. Otherwise, if the test re-uses the same model,
+ # there will be recompilation errors, as torch caches the model when run in the same process.
+ yield
+ torch._dynamo.reset()
+
+ #######
+ # LLM #
+ #######
+
+ def check_hotswap(self, do_hotswap, ranks, alpha_scalings):
+ """
+ Test hotswapping with a compiled model.
+
+ Passing do_hotswap=False should trigger recompilation. Use the raise_error_on_recompile context manager to
+ raise an error when recompilation occurs.
+
+ """
+ torch.manual_seed(0)
+ inputs = torch.arange(10).view(-1, 1).to(self.torch_device)
+ model_id = "hf-internal-testing/tiny-random-OPTForCausalLM"
+ model = AutoModelForCausalLM.from_pretrained(model_id).to(self.torch_device)
+ rank0, rank1 = ranks
+ alpha0, alpha1 = alpha_scalings
+
+ # note that the 2nd adapter targeting a subset of the 1st adapter is okay, but not the other way round
+ config0 = LoraConfig(init_lora_weights=False, r=rank0, lora_alpha=alpha0, target_modules=["q_proj", "v_proj"])
+ config1 = LoraConfig(init_lora_weights=False, r=rank1, lora_alpha=alpha1, target_modules=["q_proj"])
+ model = get_peft_model(model, config0, adapter_name="adapter0").eval()
+ with torch.inference_mode():
+ output0 = model(inputs).logits
+
+ model.add_adapter("adapter1", config1)
+ model.set_adapter("adapter1")
+ with torch.inference_mode():
+ output1 = model(inputs).logits
+
+ # sanity check:
+ tol = 1e-4
+ assert not torch.allclose(output0, output1, atol=tol, rtol=tol)
+
+ with tempfile.TemporaryDirectory() as tmp_dirname:
+ model.save_pretrained(tmp_dirname)
+ del model
+
+ model = AutoModelForCausalLM.from_pretrained(model_id).to(self.torch_device)
+ model = PeftModel.from_pretrained(model, os.path.join(tmp_dirname, "adapter0")).eval()
+ if do_hotswap:
+ prepare_model_for_compiled_hotswap(model, config=model.peft_config, target_rank=max(ranks))
+ model = torch.compile(model, mode="reduce-overhead")
+ output_after0 = model(inputs).logits
+ assert torch.allclose(output0, output_after0, atol=tol, rtol=tol)
+
+ # swap and check that we get the output from adapter1
+ if do_hotswap:
+ hotswap_adapter(model, os.path.join(tmp_dirname, "adapter1"), adapter_name="default")
+ else:
+ model.load_adapter(os.path.join(tmp_dirname, "adapter1"), adapter_name="other")
+ model.set_adapter("other")
+
+ # we need to call forward to potentially trigger recompilation
+ output_after1 = model(inputs).logits
+ assert torch.allclose(output1, output_after1, atol=tol, rtol=tol)
+
+ # we need to call forward third time since cudagraphs are not recorded in first call.
+ if do_hotswap:
+ hotswap_adapter(model, os.path.join(tmp_dirname, "adapter0"), adapter_name="default")
+ output_after2 = model(inputs).logits
+ assert torch.allclose(output0, output_after2, atol=tol, rtol=tol)
+
+ # it is important to check hotswapping small to large ranks and large to small ranks
+ @pytest.mark.parametrize("ranks", [(11, 11), (7, 13), (13, 7)])
+ def test_hotswapping_compiled_model_does_not_trigger_recompilation(self, ranks):
+ # here we set three configs to ensure no recompilation or cudagraph re-record occurs:
+ # 1. error_on_recompile: raise an error on recompilation
+ # 2. inline_inbuilt_nn_modules: needed to raise an error on static input address changes instead of re-recording
+ # 3. triton.cudagraph_support_input_mutation: same as above
+ dynamo_config_ctx = torch._dynamo.config.patch(error_on_recompile=True, inline_inbuilt_nn_modules=False)
+ inductor_config_ctx = torch._inductor.config.patch("triton.cudagraph_support_input_mutation", False)
+ with dynamo_config_ctx, inductor_config_ctx:
+ self.check_hotswap(do_hotswap=True, ranks=ranks, alpha_scalings=ranks)
+
+ def test_no_hotswapping_compiled_model_triggers_recompilation(self):
+ # contingency test to ensure that hotswapping is actually needed to prevent recompilation
+ ranks = 7, 13
+ with torch._dynamo.config.patch(error_on_recompile=True):
+ with pytest.raises(torch._dynamo.exc.RecompileError): # raise an error on recompilation
+ self.check_hotswap(do_hotswap=False, ranks=ranks, alpha_scalings=ranks)
+
+ ###################
+ # DIFFUSION MODEL #
+ ###################
+
+ def get_small_unet(self):
+ # from diffusers UNet2DConditionModelTests
+ from diffusers import UNet2DConditionModel
+
+ torch.manual_seed(0)
+ init_dict = {
+ "block_out_channels": (4, 8),
+ "norm_num_groups": 4,
+ "down_block_types": ("CrossAttnDownBlock2D", "DownBlock2D"),
+ "up_block_types": ("UpBlock2D", "CrossAttnUpBlock2D"),
+ "cross_attention_dim": 8,
+ "attention_head_dim": 2,
+ "out_channels": 4,
+ "in_channels": 4,
+ "layers_per_block": 1,
+ "sample_size": 16,
+ }
+ model = UNet2DConditionModel(**init_dict)
+ return model.to(self.torch_device)
+
+ def get_unet_lora_config(self, lora_rank, lora_alpha, target_modules):
+ # from diffusers test_models_unet_2d_condition.py
+ # note that this only targets linear layers by default
+ unet_lora_config = LoraConfig(
+ r=lora_rank,
+ lora_alpha=lora_alpha,
+ target_modules=target_modules,
+ init_lora_weights=False,
+ use_dora=False,
+ )
+ return unet_lora_config
+
+ def get_dummy_input(self):
+ pipeline_inputs = {
+ "prompt": "A painting of a squirrel eating a burger",
+ "num_inference_steps": 5,
+ "guidance_scale": 6.0,
+ "output_type": "np",
+ "return_dict": False,
+ }
+ return pipeline_inputs
+
+ def set_lora_device(self, model, adapter_names, device):
+ # copied from diffusers LoraBaseMixin.set_lora_device
+ for module in model.modules():
+ if isinstance(module, BaseTunerLayer):
+ for adapter_name in adapter_names:
+ module.lora_A[adapter_name].to(device)
+ module.lora_B[adapter_name].to(device)
+ # this is a param, not a module, so device placement is not in-place -> re-assign
+ if hasattr(module, "lora_magnitude_vector") and module.lora_magnitude_vector is not None:
+ if adapter_name in module.lora_magnitude_vector:
+ module.lora_magnitude_vector[adapter_name] = module.lora_magnitude_vector[adapter_name].to(
+ device
+ )
+
+ def check_hotswap_diffusion(self, ranks, alpha_scalings, target_modules):
+ """
+ Check that hotswapping works on a pipeline.
+
+ This is essentially the same test as:
+ https://github.com/huggingface/diffusers/blob/d7dd924ece56cddf261cd8b9dd901cbfa594c62c/tests/pipelines/test_pipelines.py#L2264
+
+ Steps:
+ - create 2 LoRA adapters and save them
+ - load the first adapter
+ - hotswap the second adapter
+ - check that the outputs are correct
+ - optionally compile the model
+
+ Note: We set rank == alpha here because save_lora_adapter does not save the alpha scalings, thus the test would
+ fail if the values are different. Since rank != alpha does not matter for the purpose of this test, this is
+ fine.
+ """
+ from diffusers import StableDiffusionPipeline
+
+ # create 2 adapters with different ranks and alphas
+ dummy_input = self.get_dummy_input()
+ pipeline = StableDiffusionPipeline.from_pretrained("hf-internal-testing/tiny-sd-pipe").to(torch_device)
+ rank0, rank1 = ranks
+ alpha0, alpha1 = alpha_scalings
+ max_rank = max([rank0, rank1])
+ lora_config0 = self.get_unet_lora_config(rank0, alpha0, target_modules)
+ lora_config1 = self.get_unet_lora_config(rank1, alpha1, target_modules)
+
+ torch.manual_seed(0)
+ pipeline.unet.add_adapter(lora_config0, adapter_name="adapter0")
+ output0_before = pipeline(**dummy_input, generator=torch.manual_seed(0))[0]
+
+ torch.manual_seed(1)
+ pipeline.unet.add_adapter(lora_config1, adapter_name="adapter1")
+ pipeline.unet.set_adapter("adapter1")
+ output1_before = pipeline(**dummy_input, generator=torch.manual_seed(0))[0]
+
+ # sanity check
+ tol = 1e-3
+ assert not np.allclose(output0_before, output1_before, atol=tol, rtol=tol)
+ assert not (output0_before == 0).all()
+ assert not (output1_before == 0).all()
+
+ with tempfile.TemporaryDirectory() as tmp_dirname:
+ # save the adapter checkpoints
+ sd0 = get_peft_model_state_dict(pipeline.unet, adapter_name="adapter0")
+ StableDiffusionPipeline.save_lora_weights(
+ save_directory=os.path.join(tmp_dirname, "adapter0"), safe_serialization=True, unet_lora_layers=sd0
+ )
+ sd1 = get_peft_model_state_dict(pipeline.unet, adapter_name="adapter1")
+ StableDiffusionPipeline.save_lora_weights(
+ save_directory=os.path.join(tmp_dirname, "adapter1"), safe_serialization=True, unet_lora_layers=sd1
+ )
+ del pipeline
+
+ # load the first adapter
+ pipeline = StableDiffusionPipeline.from_pretrained("hf-internal-testing/tiny-sd-pipe").to(torch_device)
+ # no need to prepare if the model is not compiled or if the ranks are identical
+ pipeline.enable_lora_hotswap(target_rank=max_rank)
+
+ file_name0 = os.path.join(tmp_dirname, "adapter0", "pytorch_lora_weights.safetensors")
+ file_name1 = os.path.join(tmp_dirname, "adapter1", "pytorch_lora_weights.safetensors")
+
+ pipeline.load_lora_weights(file_name0)
+ pipeline.unet = torch.compile(pipeline.unet, mode="reduce-overhead")
+
+ output0_after = pipeline(**dummy_input, generator=torch.manual_seed(0))[0]
+
+ # sanity check: still same result
+ assert np.allclose(output0_before, output0_after, atol=tol, rtol=tol)
+
+ # hotswap the 2nd adapter
+ pipeline.load_lora_weights(file_name1, hotswap=True, adapter_name="default_0")
+ output1_after = pipeline(**dummy_input, generator=torch.manual_seed(0))[0]
+
+ # sanity check: since it's the same LoRA, the results should be identical
+ assert np.allclose(output1_before, output1_after, atol=tol, rtol=tol)
+
+ # we need to call forward third time since cudagraphs are not recorded in first call.
+ pipeline.load_lora_weights(file_name0, hotswap=True, adapter_name="default_0")
+ output2_after = pipeline(**dummy_input, generator=torch.manual_seed(0))[0]
+ assert np.allclose(output0_before, output2_after, atol=tol, rtol=tol)
+
+ @pytest.mark.skipif(not is_diffusers_available(), reason="Test requires diffusers to be installed")
+ # it is important to check hotswapping small to large ranks and large to small ranks
+ @pytest.mark.parametrize("ranks", [(11, 11), (7, 13), (13, 7)])
+ @pytest.mark.parametrize(
+ "target_modules",
+ [
+ ["to_q", "to_k", "to_v", "to_out.0"], # Linear layers
+ ["conv", "conv1", "conv2"], # Conv2d layers
+ ["to_q", "conv"], # mix of Linear and Conv2d
+ ],
+ )
+ def test_hotswapping_compiled_diffusers_model_does_not_trigger_recompilation(self, ranks, target_modules):
+ # here we set three configs to ensure no recompilation or cudagraph re-record occurs:
+ # 1. error_on_recompile: raise an error on recompilation
+ # 2. inline_inbuilt_nn_modules: needed to raise an error on static input address changes instead of re-recording
+ # 3. triton.cudagraph_support_input_mutation: same as above
+ dynamo_config_ctx = torch._dynamo.config.patch(error_on_recompile=True, inline_inbuilt_nn_modules=False)
+ inductor_config_ctx = torch._inductor.config.patch("triton.cudagraph_support_input_mutation", False)
+ with dynamo_config_ctx, inductor_config_ctx:
+ self.check_hotswap_diffusion(ranks=ranks, alpha_scalings=ranks, target_modules=target_modules)
+
+
+# Test: 4-bit load + Arrow + generate
+class TestArrowQuantized:
+ @pytest.fixture(scope="class")
+ def workdir(self, tmp_path_factory):
+ """Create and return a temp directory path for this class (no chdir)."""
+ wd = tmp_path_factory.mktemp("arrow_workdir")
+ return Path(wd)
+
+ def _create_and_save_adapter_opt(self, out_dir: Path, rank: int = 4):
+ """
+ Build a randomly initialized LoRA adapter for OPT-125M and save into `out_dir`. We construct a model from
+ CONFIG (no pretrained weights) to avoid slow downloads here.
+ """
+ model_id = "facebook/opt-125m"
+ # Target all linear layers so the adapter matches whatever we later quantize/load.
+ lora_cfg = LoraConfig(
+ r=rank,
+ target_modules="all-linear",
+ task_type="CAUSAL_LM",
+ init_lora_weights=False,
+ )
+ # Load the adapter on the model and save it
+ with hub_online_once(model_id):
+ model = AutoModelForCausalLM.from_pretrained(model_id)
+ peft_model = get_peft_model(model, lora_cfg)
+ peft_model.save_pretrained(out_dir)
+
+ @pytest.fixture(scope="class")
+ def ts_adapters_opt(self, workdir: Path):
+ """
+ Build 3 locally-saved task-specific adapters for OPT-125M and return their absolute paths.
+ """
+ paths = []
+ for i in range(3):
+ sub = workdir / f"ts_expert_{i}"
+ self._create_and_save_adapter_opt(sub)
+ paths.append(str(sub))
+ return paths
+
+ @require_bitsandbytes
+ @pytest.mark.single_gpu_tests
+ def test_arrow_4bit_opt125m_load_and_generate_with_local_adapters(self, ts_adapters_opt):
+ # Skip if CUDA or bitsandbytes isn’t available
+ if not torch.cuda.is_available():
+ pytest.skip("CUDA required for 4-bit bitsandbytes test.")
+
+ model_id = "facebook/opt-125m"
+
+ # Quantization config (nf4, bf16 compute)
+ bnb_config = BitsAndBytesConfig(
+ load_in_4bit=True,
+ bnb_4bit_quant_type="nf4",
+ bnb_4bit_compute_dtype=torch.bfloat16,
+ bnb_4bit_use_double_quant=False,
+ )
+
+ with hub_online_once(model_id):
+ # Load quantized base model
+ base_model = AutoModelForCausalLM.from_pretrained(
+ model_id,
+ torch_dtype=torch.bfloat16,
+ device_map="auto",
+ quantization_config=bnb_config,
+ )
+ with hub_online_once(model_id + "tokenizer"):
+ tok = AutoTokenizer.from_pretrained(model_id, use_fast=True)
+
+ # Build Arrow model from the locally created adapters
+ arrow_cfg = ArrowConfig(top_k=2, router_temperature=1.0, rng_seed=42)
+ model = create_arrow_model(
+ base_model=base_model,
+ task_specific_adapter_paths=ts_adapters_opt, # local dirs (each has adapter_config.json)
+ arrow_config=arrow_cfg,
+ ).eval()
+
+ # Quick generate smoke test
+ inputs = tok("Hello world", return_tensors="pt")
+ inputs = {k: v.to(model.device) for k, v in inputs.items()}
+ with torch.no_grad():
+ out = model.generate(**inputs, max_new_tokens=8)
+
+ assert out is not None
+ assert out.shape[0] == 1 # batch size 1
diff --git a/peft/tests/test_helpers.py b/peft/tests/test_helpers.py
new file mode 100644
index 0000000000000000000000000000000000000000..501bd146a2900cd3266cd5bed1cfe747da308811
--- /dev/null
+++ b/peft/tests/test_helpers.py
@@ -0,0 +1,473 @@
+# Copyright 2024-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+
+import pytest
+import torch
+from diffusers import StableDiffusionPipeline
+from torch import nn
+from transformers import AutoModelForCausalLM, AutoTokenizer
+
+from peft import LoraConfig, get_peft_model
+from peft.helpers import check_if_peft_model, disable_input_dtype_casting, rescale_adapter_scale
+from peft.tuners.lora.layer import LoraLayer
+from peft.utils import infer_device
+
+
+class TestCheckIsPeftModel:
+ def test_valid_hub_model(self):
+ result = check_if_peft_model("peft-internal-testing/gpt2-lora-random")
+ assert result is True
+
+ def test_invalid_hub_model(self):
+ result = check_if_peft_model("gpt2")
+ assert result is False
+
+ def test_nonexisting_hub_model(self):
+ result = check_if_peft_model("peft-internal-testing/non-existing-model")
+ assert result is False
+
+ def test_local_model_valid(self, tmp_path):
+ model = AutoModelForCausalLM.from_pretrained("gpt2")
+ config = LoraConfig()
+ model = get_peft_model(model, config)
+ model.save_pretrained(tmp_path / "peft-gpt2-valid")
+ result = check_if_peft_model(tmp_path / "peft-gpt2-valid")
+ assert result is True
+
+ def test_local_model_invalid(self, tmp_path):
+ model = AutoModelForCausalLM.from_pretrained("gpt2")
+ model.save_pretrained(tmp_path / "peft-gpt2-invalid")
+ result = check_if_peft_model(tmp_path / "peft-gpt2-invalid")
+ assert result is False
+
+ def test_local_model_broken_config(self, tmp_path):
+ with open(tmp_path / "adapter_config.json", "w") as f:
+ f.write('{"foo": "bar"}')
+
+ result = check_if_peft_model(tmp_path)
+ assert result is False
+
+ def test_local_model_non_default_name(self, tmp_path):
+ model = AutoModelForCausalLM.from_pretrained("gpt2")
+ config = LoraConfig()
+ model = get_peft_model(model, config, adapter_name="other")
+ model.save_pretrained(tmp_path / "peft-gpt2-other")
+
+ # no default adapter here
+ result = check_if_peft_model(tmp_path / "peft-gpt2-other")
+ assert result is False
+
+ # with adapter name
+ result = check_if_peft_model(tmp_path / "peft-gpt2-other" / "other")
+ assert result is True
+
+
+class TestScalingAdapters:
+ @pytest.fixture(scope="class")
+ def tokenizer(self):
+ return AutoTokenizer.from_pretrained("facebook/opt-125m")
+
+ def get_scale_from_modules(self, model):
+ layer_to_scale_map = {}
+ for name, module in model.named_modules():
+ if isinstance(module, LoraLayer):
+ layer_to_scale_map[name] = module.scaling
+
+ return layer_to_scale_map
+
+ def test_rescale_adapter_scale(self, tokenizer):
+ model = AutoModelForCausalLM.from_pretrained("facebook/opt-125m")
+ lora_config = LoraConfig(
+ r=4,
+ lora_alpha=4,
+ target_modules=["k_proj", "v_proj"],
+ lora_dropout=0.1,
+ bias="none",
+ init_lora_weights=False,
+ )
+
+ model = get_peft_model(model, lora_config)
+ model.eval()
+ inputs = tokenizer("hello world", return_tensors="pt")
+
+ with torch.no_grad():
+ logits_before_scaling = model(**inputs).logits
+
+ scales_before_scaling = self.get_scale_from_modules(model)
+
+ with rescale_adapter_scale(model=model, multiplier=0.5):
+ scales_during_scaling = self.get_scale_from_modules(model)
+ for key in scales_before_scaling.keys():
+ assert scales_before_scaling[key] != scales_during_scaling[key]
+
+ with torch.no_grad():
+ logits_during_scaling = model(**inputs).logits
+
+ assert not torch.allclose(logits_before_scaling, logits_during_scaling)
+
+ scales_after_scaling = self.get_scale_from_modules(model)
+ for key in scales_before_scaling.keys():
+ assert scales_before_scaling[key] == scales_after_scaling[key]
+
+ with torch.no_grad():
+ logits_after_scaling = model(**inputs).logits
+
+ assert torch.allclose(logits_before_scaling, logits_after_scaling)
+
+ def test_wrong_scaling_datatype(self):
+ model = AutoModelForCausalLM.from_pretrained("facebook/opt-125m")
+ lora_config = LoraConfig(
+ r=4,
+ lora_alpha=4,
+ target_modules=["k_proj", "v_proj"],
+ lora_dropout=0.1,
+ bias="none",
+ init_lora_weights=False,
+ )
+
+ model = get_peft_model(model, lora_config)
+
+ # we expect a type error here becuase of wrong datatpye of multiplier
+ multiplier = "a"
+ with pytest.raises(TypeError, match=f"Argument multiplier should be of type float, got {type(multiplier)}"):
+ with rescale_adapter_scale(model=model, multiplier=multiplier):
+ pass
+
+ def test_not_lora_model(self):
+ model = AutoModelForCausalLM.from_pretrained("facebook/opt-125m")
+
+ # we expect a value error here because the model
+ # does not have lora layers
+ with pytest.raises(ValueError, match="scaling is only supported for models with `LoraLayer`s"):
+ with rescale_adapter_scale(model=model, multiplier=0.5):
+ pass
+
+ def test_scaling_set_to_zero(self, tokenizer):
+ base_model = AutoModelForCausalLM.from_pretrained("facebook/opt-125m")
+ inputs = tokenizer("hello world", return_tensors="pt")
+
+ base_model.eval()
+
+ with torch.no_grad():
+ logits_base_model = base_model(**inputs).logits
+
+ lora_config = LoraConfig(
+ r=4,
+ lora_alpha=4,
+ target_modules=["k_proj", "v_proj"],
+ lora_dropout=0.1,
+ bias="none",
+ init_lora_weights=False,
+ )
+ lora_model = get_peft_model(base_model, lora_config)
+ lora_model.eval()
+
+ with rescale_adapter_scale(model=lora_model, multiplier=0.0):
+ with torch.no_grad():
+ logits_lora_model = lora_model(**inputs).logits
+
+ assert torch.allclose(logits_base_model, logits_lora_model)
+
+ def test_diffusers_pipeline(self):
+ model_id = "hf-internal-testing/tiny-sd-pipe"
+ pipeline = StableDiffusionPipeline.from_pretrained(model_id)
+
+ text_encoder_kwargs = {
+ "r": 8,
+ "lora_alpha": 32,
+ "target_modules": ["k_proj", "q_proj", "v_proj", "out_proj", "fc1", "fc2"],
+ "lora_dropout": 0.0,
+ "bias": "none",
+ }
+ unet_kwargs = {
+ "r": 8,
+ "lora_alpha": 32,
+ "target_modules": ["proj_in", "proj_out", "to_k", "to_q", "to_v", "to_out.0", "ff.net.0.proj", "ff.net.2"],
+ "lora_dropout": 0.0,
+ "bias": "none",
+ }
+
+ # Instantiate text_encoder adapter
+ config_text_encoder = LoraConfig(**text_encoder_kwargs)
+ pipeline.text_encoder = get_peft_model(pipeline.text_encoder, config_text_encoder)
+
+ # Instantiate unet adapter
+ config_unet = LoraConfig(**unet_kwargs)
+ pipeline.unet = get_peft_model(pipeline.unet, config_unet)
+
+ text_scales_before_scaling = self.get_scale_from_modules(pipeline.text_encoder)
+ unet_scales_before_scaling = self.get_scale_from_modules(pipeline.unet)
+
+ with (
+ rescale_adapter_scale(model=pipeline.text_encoder, multiplier=0.5),
+ rescale_adapter_scale(model=pipeline.unet, multiplier=0.5),
+ ):
+ text_scales_during_scaling = self.get_scale_from_modules(pipeline.text_encoder)
+ unet_scales_during_scaling = self.get_scale_from_modules(pipeline.unet)
+ for key in text_scales_before_scaling.keys():
+ assert text_scales_before_scaling[key] != text_scales_during_scaling[key]
+ for key in unet_scales_before_scaling.keys():
+ assert unet_scales_before_scaling[key] != unet_scales_during_scaling[key]
+
+ text_scales_fter_scaling = self.get_scale_from_modules(pipeline.text_encoder)
+ unet_scales_after_scaling = self.get_scale_from_modules(pipeline.unet)
+ for key in text_scales_before_scaling.keys():
+ assert text_scales_before_scaling[key] == text_scales_fter_scaling[key]
+ for key in unet_scales_before_scaling.keys():
+ assert unet_scales_before_scaling[key] == unet_scales_after_scaling[key]
+
+ def test_transformers_pipeline(self, tmp_path, tokenizer):
+ # this uses a transformers model that loads the adapter directly
+ model_id = "facebook/opt-125m"
+ model = AutoModelForCausalLM.from_pretrained(model_id)
+ config = LoraConfig(init_lora_weights=False)
+ model = get_peft_model(model, config)
+ model.save_pretrained(tmp_path / "opt-lora")
+ del model
+
+ # load directly into transformers model
+ model = AutoModelForCausalLM.from_pretrained(model_id)
+ model.load_adapter(tmp_path / "opt-lora")
+
+ inputs = tokenizer("hello world", return_tensors="pt")
+
+ model = model.eval()
+
+ with torch.no_grad():
+ logits_before_scaling = model(**inputs).logits
+ scales_before_scaling = self.get_scale_from_modules(model)
+
+ with rescale_adapter_scale(model=model, multiplier=0.5):
+ scales_during_scaling = self.get_scale_from_modules(model)
+ for key in scales_before_scaling.keys():
+ assert scales_before_scaling[key] != scales_during_scaling[key]
+ with torch.no_grad():
+ logits_during_scaling = model(**inputs).logits
+ assert not torch.allclose(logits_before_scaling, logits_during_scaling)
+ scales_after_scaling = self.get_scale_from_modules(model)
+
+ for key in scales_before_scaling.keys():
+ assert scales_before_scaling[key] == scales_after_scaling[key]
+
+ with torch.no_grad():
+ logits_after_scaling = model(**inputs).logits
+
+ assert torch.allclose(logits_before_scaling, logits_after_scaling)
+
+ def test_multi_adapters(self, tokenizer):
+ model = AutoModelForCausalLM.from_pretrained("facebook/opt-125m")
+ lora_config = LoraConfig(
+ r=4,
+ lora_alpha=4,
+ target_modules=["k_proj", "v_proj"],
+ lora_dropout=0.1,
+ bias="none",
+ init_lora_weights=False,
+ )
+ model = get_peft_model(model, lora_config)
+ inputs = tokenizer("hello world", return_tensors="pt")
+
+ # add another adaper and activate it
+ model.add_adapter("other", lora_config)
+ model.set_adapter("other")
+
+ scales_before_scaling = self.get_scale_from_modules(model)
+ model.eval()
+ with torch.no_grad():
+ logits_before = model(**inputs).logits
+
+ with rescale_adapter_scale(model=model, multiplier=0.5):
+ scales_during_scaling = self.get_scale_from_modules(model)
+ for key in scales_before_scaling.keys():
+ assert scales_before_scaling[key] != scales_during_scaling[key]
+
+ with torch.no_grad():
+ logits_during = model(**inputs).logits
+
+ assert not torch.allclose(logits_before, logits_during)
+
+ scales_after_scaling = self.get_scale_from_modules(model)
+ for key in scales_before_scaling.keys():
+ assert scales_before_scaling[key] == scales_after_scaling[key]
+
+ with torch.no_grad():
+ logits_after = model(**inputs).logits
+
+ assert torch.allclose(logits_before, logits_after)
+
+ def test_rank_alpha_pattern(self, tokenizer):
+ model = AutoModelForCausalLM.from_pretrained("facebook/opt-125m")
+ lora_config = LoraConfig(
+ r=4,
+ lora_alpha=4,
+ target_modules=["k_proj", "v_proj"],
+ lora_dropout=0.1,
+ bias="none",
+ init_lora_weights=False,
+ rank_pattern={"k_proj": 2},
+ alpha_pattern={"k_proj": 8},
+ )
+
+ model = get_peft_model(model, lora_config)
+ model.eval()
+ inputs = tokenizer("hello world", return_tensors="pt")
+
+ with torch.no_grad():
+ logits_before_scaling = model(**inputs).logits
+
+ scales_before_scaling = self.get_scale_from_modules(model)
+
+ with rescale_adapter_scale(model=model, multiplier=0.5):
+ scales_during_scaling = self.get_scale_from_modules(model)
+ for key in scales_before_scaling.keys():
+ assert scales_before_scaling[key] != scales_during_scaling[key]
+
+ with torch.no_grad():
+ logits_during_scaling = model(**inputs).logits
+
+ assert not torch.allclose(logits_before_scaling, logits_during_scaling)
+
+ scales_after_scaling = self.get_scale_from_modules(model)
+ for key in scales_before_scaling.keys():
+ assert scales_before_scaling[key] == scales_after_scaling[key]
+
+ with torch.no_grad():
+ logits_after_scaling = model(**inputs).logits
+
+ assert torch.allclose(logits_before_scaling, logits_after_scaling)
+
+ def test_merging_adapter(self, tokenizer):
+ model = AutoModelForCausalLM.from_pretrained("facebook/opt-125m")
+ lora_config = LoraConfig(
+ r=4,
+ lora_alpha=4,
+ target_modules=["k_proj", "v_proj"],
+ lora_dropout=0.1,
+ bias="none",
+ init_lora_weights=False,
+ )
+
+ model = get_peft_model(model, lora_config)
+ model.eval()
+ inputs = tokenizer("hello world", return_tensors="pt")
+
+ with rescale_adapter_scale(model=model, multiplier=0.5):
+ with torch.no_grad():
+ logits_unmerged_scaling = model(**inputs).logits
+ model = model.merge_and_unload()
+
+ with torch.no_grad():
+ logits_merged_scaling = model(**inputs).logits
+
+ assert torch.allclose(logits_merged_scaling, logits_unmerged_scaling, atol=1e-4, rtol=1e-4)
+
+
+class TestDisableInputDtypeCasting:
+ """Test the context manager `disable_input_dtype_casting` that temporarily disables input dtype casting
+ in the model.
+
+ The test works as follows:
+
+ We create a simple MLP and convert it to a PeftModel. The model dtype is set to float16. Then a pre-foward hook is
+ added that casts the model parameters to float32. Moreover, a post-forward hook is added that casts the weights
+ back to float16. The input dtype is float32.
+
+ Without the disable_input_dtype_casting context, what would happen is that PEFT detects that the input dtype is
+ float32 but the weight dtype is float16, so it casts the input to float16. Then the pre-forward hook casts the
+ weight to float32, which results in a RuntimeError.
+
+ With the disable_input_dtype_casting context, the input dtype is left as float32 and there is no error. We also add
+ a hook to record the dtype of the result from the LoraLayer to ensure that it is indeed float32.
+
+ """
+
+ device = infer_device()
+ dtype_record = []
+
+ @torch.no_grad()
+ def cast_params_to_fp32_pre_hook(self, module, input):
+ for param in module.parameters(recurse=False):
+ param.data = param.data.float()
+ return input
+
+ @torch.no_grad()
+ def cast_params_to_fp16_hook(self, module, input, output):
+ for param in module.parameters(recurse=False):
+ param.data = param.data.half()
+ return output
+
+ def record_dtype_hook(self, module, input, output):
+ self.dtype_record.append(output[0].dtype)
+
+ @pytest.fixture
+ def inputs(self):
+ return torch.randn(4, 10, device=self.device, dtype=torch.float32)
+
+ @pytest.fixture
+ def base_model(self):
+ class MLP(nn.Module):
+ def __init__(self, bias=True):
+ super().__init__()
+ self.lin0 = nn.Linear(10, 20, bias=bias)
+ self.lin1 = nn.Linear(20, 2, bias=bias)
+ self.sm = nn.LogSoftmax(dim=-1)
+
+ def forward(self, X):
+ X = self.lin0(X)
+ X = self.lin1(X)
+ X = self.sm(X)
+ return X
+
+ return MLP()
+
+ @pytest.fixture
+ def model(self, base_model):
+ config = LoraConfig(target_modules=["lin0"], modules_to_save=["lin1"])
+ model = get_peft_model(base_model, config).to(device=self.device, dtype=torch.float16)
+ # Register hooks on the submodule that holds parameters
+ for module in model.modules():
+ if sum(p.numel() for p in module.parameters()) > 0:
+ module.register_forward_pre_hook(self.cast_params_to_fp32_pre_hook)
+ module.register_forward_hook(self.cast_params_to_fp16_hook)
+ if isinstance(module, LoraLayer):
+ module.register_forward_hook(self.record_dtype_hook)
+ return model
+
+ def test_disable_input_dtype_casting_active(self, model, inputs):
+ self.dtype_record.clear()
+ with disable_input_dtype_casting(model, active=True):
+ model(inputs)
+ assert self.dtype_record == [torch.float32]
+
+ def test_no_disable_input_dtype_casting(self, model, inputs):
+ msg = r"expected m.*1 and m.*2 to have the same dtype"
+ with pytest.raises(RuntimeError, match=msg):
+ model(inputs)
+
+ def test_disable_input_dtype_casting_inactive(self, model, inputs):
+ msg = r"expected m.*1 and m.*2 to have the same dtype"
+ with pytest.raises(RuntimeError, match=msg):
+ with disable_input_dtype_casting(model, active=False):
+ model(inputs)
+
+ def test_disable_input_dtype_casting_inactive_after_existing_context(self, model, inputs):
+ # this is to ensure that when the context is left, we return to the previous behavior
+ with disable_input_dtype_casting(model, active=True):
+ model(inputs)
+
+ # after the context exited, we're back to the error
+ msg = r"expected m.*1 and m.*2 to have the same dtype"
+ with pytest.raises(RuntimeError, match=msg):
+ model(inputs)
diff --git a/peft/tests/test_hub_features.py b/peft/tests/test_hub_features.py
new file mode 100644
index 0000000000000000000000000000000000000000..f705167c08f26d0ec7df854b6e4b06d0e4a5c085
--- /dev/null
+++ b/peft/tests/test_hub_features.py
@@ -0,0 +1,236 @@
+# Copyright 2023-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+import copy
+
+import pytest
+import torch
+from huggingface_hub import ModelCard
+from transformers import AutoModelForCausalLM
+
+from peft import AutoPeftModelForCausalLM, BoneConfig, LoraConfig, PeftConfig, PeftModel, TaskType, get_peft_model
+
+from .testing_utils import hub_online_once
+
+
+PEFT_MODELS_TO_TEST = [("peft-internal-testing/test-lora-subfolder", "test")]
+
+
+class PeftHubFeaturesTester:
+ # TODO remove when/if Hub is more stable
+ @pytest.mark.xfail(reason="Test is flaky on CI", raises=ValueError)
+ def test_subfolder(self):
+ r"""
+ Test if subfolder argument works as expected
+ """
+ for model_id, subfolder in PEFT_MODELS_TO_TEST:
+ config = PeftConfig.from_pretrained(model_id, subfolder=subfolder)
+
+ model = AutoModelForCausalLM.from_pretrained(
+ config.base_model_name_or_path,
+ )
+ model = PeftModel.from_pretrained(model, model_id, subfolder=subfolder)
+
+ assert isinstance(model, PeftModel)
+
+
+class TestLocalModel:
+ def test_local_model_saving_no_warning(self, recwarn, tmp_path):
+ # When the model is saved, the library checks for vocab changes by
+ # examining `config.json` in the model path.
+ # However, previously, those checks only covered huggingface hub models.
+ # This test makes sure that the local `config.json` is checked as well.
+ # If `save_pretrained` could not find the file, it will issue a warning.
+ model_id = "facebook/opt-125m"
+ model = AutoModelForCausalLM.from_pretrained(model_id)
+ local_dir = tmp_path / model_id
+ model.save_pretrained(local_dir)
+ del model
+
+ base_model = AutoModelForCausalLM.from_pretrained(local_dir)
+ peft_config = LoraConfig()
+ peft_model = get_peft_model(base_model, peft_config)
+ peft_model.save_pretrained(local_dir)
+
+ for warning in recwarn.list:
+ assert "Could not find a config file" not in warning.message.args[0]
+
+
+class TestBaseModelRevision:
+ def test_save_and_load_base_model_revision(self, tmp_path):
+ r"""
+ Test saving a PeftModel with a base model revision and loading with AutoPeftModel to recover the same base
+ model
+ """
+ lora_config = LoraConfig(r=8, lora_alpha=16, lora_dropout=0.0)
+ test_inputs = torch.arange(10).reshape(-1, 1)
+
+ base_model_id = "peft-internal-testing/tiny-random-BertModel"
+ revision = "v2.0.0"
+
+ base_model_revision = AutoModelForCausalLM.from_pretrained(base_model_id, revision=revision).eval()
+ peft_model_revision = get_peft_model(base_model_revision, lora_config, revision=revision)
+ output_revision = peft_model_revision(test_inputs).logits
+
+ # sanity check: the model without revision should be different
+ base_model_no_revision = AutoModelForCausalLM.from_pretrained(base_model_id, revision="main").eval()
+ # we need a copy of the config because otherwise, we are changing in-place the `revision` of the previous config and model
+ lora_config_no_revision = copy.deepcopy(lora_config)
+ lora_config_no_revision.revision = "main"
+ peft_model_no_revision = get_peft_model(base_model_no_revision, lora_config_no_revision, revision="main")
+ output_no_revision = peft_model_no_revision(test_inputs).logits
+ assert not torch.allclose(output_no_revision, output_revision)
+
+ # check that if we save and load the model, the output corresponds to the one with revision
+ peft_model_revision.save_pretrained(tmp_path / "peft_model_revision")
+ peft_model_revision_loaded = AutoPeftModelForCausalLM.from_pretrained(tmp_path / "peft_model_revision").eval()
+
+ assert peft_model_revision_loaded.peft_config["default"].revision == revision
+
+ output_revision_loaded = peft_model_revision_loaded(test_inputs).logits
+ assert torch.allclose(output_revision, output_revision_loaded)
+
+ # TODO remove when/if Hub is more stable
+ @pytest.mark.xfail(reason="Test is flaky on CI", raises=ValueError)
+ def test_load_different_peft_and_base_model_revision(self, tmp_path):
+ r"""
+ Test loading an AutoPeftModel from the hub where the base model revision and peft revision differ
+ """
+ base_model_id = "hf-internal-testing/tiny-random-BertModel"
+ base_model_revision = None
+ peft_model_id = "peft-internal-testing/tiny-random-BertModel-lora"
+ peft_model_revision = "v1.2.3"
+
+ peft_model = AutoPeftModelForCausalLM.from_pretrained(peft_model_id, revision=peft_model_revision).eval()
+
+ assert peft_model.peft_config["default"].base_model_name_or_path == base_model_id
+ assert peft_model.peft_config["default"].revision == base_model_revision
+
+
+class TestModelCard:
+ @pytest.mark.parametrize(
+ "model_id, peft_config, tags, excluded_tags, pipeline_tag",
+ [
+ (
+ "hf-internal-testing/tiny-random-Gemma3ForCausalLM",
+ LoraConfig(),
+ ["transformers", "base_model:adapter:hf-internal-testing/tiny-random-Gemma3ForCausalLM", "lora"],
+ [],
+ None,
+ ),
+ (
+ "hf-internal-testing/tiny-random-Gemma3ForCausalLM",
+ BoneConfig(),
+ ["transformers", "base_model:adapter:hf-internal-testing/tiny-random-Gemma3ForCausalLM"],
+ ["lora"],
+ None,
+ ),
+ (
+ "hf-internal-testing/tiny-random-BartForConditionalGeneration",
+ LoraConfig(),
+ [
+ "transformers",
+ "base_model:adapter:hf-internal-testing/tiny-random-BartForConditionalGeneration",
+ "lora",
+ ],
+ [],
+ None,
+ ),
+ (
+ "hf-internal-testing/tiny-random-Gemma3ForCausalLM",
+ LoraConfig(task_type=TaskType.CAUSAL_LM),
+ ["transformers", "base_model:adapter:hf-internal-testing/tiny-random-Gemma3ForCausalLM", "lora"],
+ [],
+ "text-generation",
+ ),
+ ],
+ )
+ @pytest.mark.parametrize(
+ "pre_tags",
+ [
+ ["tag1", "tag2"],
+ [],
+ ],
+ )
+ def test_model_card_has_expected_tags(
+ self, model_id, peft_config, tags, excluded_tags, pipeline_tag, pre_tags, tmp_path
+ ):
+ """Make sure that PEFT sets the tags in the model card automatically and correctly.
+ This is important so that a) the models are searchable on the Hub and also 2) some features depend on it to
+ decide how to deal with them (e.g., inference).
+
+ Makes sure that the base model tags are still present (if there are any).
+ """
+ with hub_online_once(model_id):
+ base_model = AutoModelForCausalLM.from_pretrained(model_id)
+
+ if pre_tags:
+ base_model.add_model_tags(pre_tags)
+
+ peft_model = get_peft_model(base_model, peft_config)
+ save_path = tmp_path / "adapter"
+
+ peft_model.save_pretrained(save_path)
+
+ model_card = ModelCard.load(save_path / "README.md")
+ assert set(tags).issubset(set(model_card.data.tags))
+
+ if excluded_tags:
+ assert set(excluded_tags).isdisjoint(set(model_card.data.tags))
+
+ if pre_tags:
+ assert set(pre_tags).issubset(set(model_card.data.tags))
+
+ if pipeline_tag:
+ assert model_card.data.pipeline_tag == pipeline_tag
+
+ @pytest.fixture
+ def custom_model_cls(self):
+ class MyNet(torch.nn.Module):
+ def __init__(self):
+ super().__init__()
+ self.l1 = torch.nn.Linear(10, 20)
+ self.l2 = torch.nn.Linear(20, 1)
+
+ def forward(self, X):
+ return self.l2(self.l1(X))
+
+ return MyNet
+
+ def test_custom_models_dont_have_transformers_tag(self, custom_model_cls, tmp_path):
+ base_model = custom_model_cls()
+ peft_config = LoraConfig(target_modules="all-linear")
+ peft_model = get_peft_model(base_model, peft_config)
+
+ peft_model.save_pretrained(tmp_path)
+
+ model_card = ModelCard.load(tmp_path / "README.md")
+
+ assert model_card.data.tags is not None
+ assert "transformers" not in model_card.data.tags
+
+ def test_custom_peft_type_does_not_raise(self, tmp_path):
+ # Passing a string value as peft_type value in the config is valid, so it should work.
+ # See https://github.com/huggingface/peft/issues/2634
+ model_id = "hf-internal-testing/tiny-random-Gemma3ForCausalLM"
+ with hub_online_once(model_id):
+ base_model = AutoModelForCausalLM.from_pretrained(model_id)
+ peft_config = LoraConfig()
+
+ # We simulate a custom PEFT type by using a string value of an existing method. This skips the need for
+ # registering a new method but tests the case where we pass a string value instead of an enum.
+ peft_type = "LORA"
+ peft_config.peft_type = peft_type
+
+ peft_model = get_peft_model(base_model, peft_config)
+ peft_model.save_pretrained(tmp_path)
diff --git a/peft/tests/test_incremental_pca.py b/peft/tests/test_incremental_pca.py
new file mode 100644
index 0000000000000000000000000000000000000000..8240899d1b9310ade41495febb3c65242e6d9957
--- /dev/null
+++ b/peft/tests/test_incremental_pca.py
@@ -0,0 +1,188 @@
+# Copyright 2024-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+# Adapted from https://github.com/scikit-learn/scikit-learn/blob/main/sklearn/decomposition/tests/test_incremental_pca.py
+
+import pytest
+import torch
+from datasets import load_dataset
+from torch.testing import assert_close
+
+from peft.utils.incremental_pca import IncrementalPCA
+
+
+torch.manual_seed(1999)
+
+
+@pytest.fixture(scope="module")
+def iris():
+ return load_dataset("scikit-learn/iris", split="train")
+
+
+def test_incremental_pca(iris):
+ # Incremental PCA on dense arrays.
+ n_components = 2
+ X = torch.tensor([iris["SepalLengthCm"], iris["SepalWidthCm"], iris["PetalLengthCm"], iris["PetalWidthCm"]]).T
+ batch_size = X.shape[0] // 3
+ ipca = IncrementalPCA(n_components=n_components, batch_size=batch_size)
+ ipca.fit(X)
+ X_transformed = ipca.transform(X)
+
+ # PCA
+ U, S, Vh = torch.linalg.svd(X - torch.mean(X, dim=0))
+ max_abs_rows = torch.argmax(torch.abs(Vh), dim=1)
+ signs = torch.sign(Vh[range(Vh.shape[0]), max_abs_rows])
+ Vh *= signs.view(-1, 1)
+ explained_variance = S**2 / (X.size(0) - 1)
+ explained_variance_ratio = explained_variance / explained_variance.sum()
+
+ assert X_transformed.shape == (X.shape[0], 2)
+ assert_close(
+ ipca.explained_variance_ratio_.sum().item(),
+ explained_variance_ratio[:n_components].sum().item(),
+ rtol=1e-3,
+ atol=1e-3,
+ )
+
+
+def test_incremental_pca_check_projection():
+ # Test that the projection of data is correct.
+ n, p = 100, 3
+ X = torch.randn(n, p, dtype=torch.float64) * 0.1
+ X[:10] += torch.tensor([3, 4, 5])
+ Xt = 0.1 * torch.randn(1, p, dtype=torch.float64) + torch.tensor([3, 4, 5])
+
+ # Get the reconstruction of the generated data X
+ # Note that Xt has the same "components" as X, just separated
+ # This is what we want to ensure is recreated correctly
+ Yt = IncrementalPCA(n_components=2).fit(X).transform(Xt)
+
+ # Normalize
+ Yt /= torch.sqrt((Yt**2).sum())
+
+ # Make sure that the first element of Yt is ~1, this means
+ # the reconstruction worked as expected
+ assert_close(torch.abs(Yt[0][0]).item(), 1.0, atol=1e-1, rtol=1e-1)
+
+
+def test_incremental_pca_validation():
+ # Test that n_components is <= n_features.
+ X = torch.tensor([[0, 1, 0], [1, 0, 0]])
+ n_samples, n_features = X.shape
+ n_components = 4
+ with pytest.raises(
+ ValueError,
+ match=(
+ f"n_components={n_components} invalid"
+ f" for n_features={n_features}, need more rows than"
+ " columns for IncrementalPCA"
+ " processing"
+ ),
+ ):
+ IncrementalPCA(n_components, batch_size=10).fit(X)
+
+ # Tests that n_components is also <= n_samples.
+ n_components = 3
+ with pytest.raises(
+ ValueError,
+ match=(f"n_components={n_components} must be less or equal to the batch number of samples {n_samples}"),
+ ):
+ IncrementalPCA(n_components=n_components).partial_fit(X)
+
+
+def test_n_components_none():
+ # Ensures that n_components == None is handled correctly
+ for n_samples, n_features in [(50, 10), (10, 50)]:
+ X = torch.rand(n_samples, n_features)
+ ipca = IncrementalPCA(n_components=None)
+
+ # First partial_fit call, ipca.n_components_ is inferred from
+ # min(X.shape)
+ ipca.partial_fit(X)
+ assert ipca.n_components == min(X.shape)
+
+
+def test_incremental_pca_num_features_change():
+ # Test that changing n_components will raise an error.
+ n_samples = 100
+ X = torch.randn(n_samples, 20)
+ X2 = torch.randn(n_samples, 50)
+ ipca = IncrementalPCA(n_components=None)
+ ipca.fit(X)
+ with pytest.raises(ValueError):
+ ipca.partial_fit(X2)
+
+
+def test_incremental_pca_batch_signs():
+ # Test that components_ sign is stable over batch sizes.
+ n_samples = 100
+ n_features = 3
+ X = torch.randn(n_samples, n_features)
+ all_components = []
+ batch_sizes = torch.arange(10, 20)
+ for batch_size in batch_sizes:
+ ipca = IncrementalPCA(n_components=None, batch_size=batch_size).fit(X)
+ all_components.append(ipca.components_)
+
+ for i, j in zip(all_components[:-1], all_components[1:]):
+ assert_close(torch.sign(i), torch.sign(j), rtol=1e-6, atol=1e-6)
+
+
+def test_incremental_pca_batch_values():
+ # Test that components_ values are stable over batch sizes.
+ n_samples = 100
+ n_features = 3
+ X = torch.randn(n_samples, n_features)
+ all_components = []
+ batch_sizes = torch.arange(20, 40, 3)
+ for batch_size in batch_sizes:
+ ipca = IncrementalPCA(n_components=None, batch_size=batch_size).fit(X)
+ all_components.append(ipca.components_)
+
+ for i, j in zip(all_components[:-1], all_components[1:]):
+ assert_close(i, j, rtol=1e-1, atol=1e-1)
+
+
+def test_incremental_pca_partial_fit():
+ # Test that fit and partial_fit get equivalent results.
+ n, p = 50, 3
+ X = torch.randn(n, p) # spherical data
+ X[:, 1] *= 0.00001 # make middle component relatively small
+ X += torch.tensor([5, 4, 3]) # make a large mean
+
+ # same check that we can find the original data from the transformed
+ # signal (since the data is almost of rank n_components)
+ batch_size = 10
+ ipca = IncrementalPCA(n_components=2, batch_size=batch_size).fit(X)
+ pipca = IncrementalPCA(n_components=2, batch_size=batch_size)
+ # Add one to make sure endpoint is included
+ batch_itr = torch.arange(0, n + 1, batch_size)
+ for i, j in zip(batch_itr[:-1], batch_itr[1:]):
+ pipca.partial_fit(X[i:j, :])
+ assert_close(ipca.components_, pipca.components_, rtol=1e-3, atol=1e-3)
+
+
+def test_incremental_pca_lowrank(iris):
+ # Test that lowrank mode is equivalent to non-lowrank mode.
+ n_components = 2
+ X = torch.tensor([iris["SepalLengthCm"], iris["SepalWidthCm"], iris["PetalLengthCm"], iris["PetalWidthCm"]]).T
+ batch_size = X.shape[0] // 3
+
+ ipca = IncrementalPCA(n_components=n_components, batch_size=batch_size)
+ ipca.fit(X)
+
+ ipcalr = IncrementalPCA(n_components=n_components, batch_size=batch_size, lowrank=True)
+ ipcalr.fit(X)
+
+ assert_close(ipca.components_, ipcalr.components_, rtol=1e-7, atol=1e-7)
diff --git a/peft/tests/test_initialization.py b/peft/tests/test_initialization.py
new file mode 100644
index 0000000000000000000000000000000000000000..8937f4b0c1ccdec26d2f441adcbd4cd6f9990fcf
--- /dev/null
+++ b/peft/tests/test_initialization.py
@@ -0,0 +1,4731 @@
+# Copyright 2023-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+import copy
+import itertools
+import math
+import platform
+import re
+import warnings
+from collections import defaultdict
+from contextlib import contextmanager
+from copy import deepcopy
+from unittest.mock import patch
+
+import pytest
+import torch
+from datasets import Dataset
+from huggingface_hub import snapshot_download
+from safetensors.torch import load_file
+from scipy import stats
+from torch import nn
+from torch.utils.data import DataLoader
+from transformers import AutoModelForCausalLM, AutoTokenizer
+
+from peft import (
+ AdaLoraConfig,
+ C3AConfig,
+ EvaConfig,
+ IA3Config,
+ LoftQConfig,
+ LoKrConfig,
+ LoraConfig,
+ PeftMixedModel,
+ PeftModel,
+ PeftModelForCausalLM,
+ PeftModelForFeatureExtraction,
+ PeftModelForQuestionAnswering,
+ PeftModelForSeq2SeqLM,
+ PeftModelForSequenceClassification,
+ PeftModelForTokenClassification,
+ PeftWarning,
+ PrefixTuningConfig,
+ PromptTuningConfig,
+ RoadConfig,
+ VBLoRAConfig,
+ VeraConfig,
+ WaveFTConfig,
+ get_eva_state_dict,
+ get_peft_model,
+ initialize_lora_eva_weights,
+ inject_adapter_in_model,
+ set_peft_model_state_dict,
+)
+from peft.mapping import PEFT_TYPE_TO_PREFIX_MAPPING
+from peft.tuners.lora.config import CordaConfig
+from peft.tuners.lora.corda import preprocess_corda
+from peft.tuners.lora.layer import LoraLayer
+from peft.utils import infer_device
+from peft.utils.hotswap import hotswap_adapter, prepare_model_for_compiled_hotswap
+
+from .testing_utils import load_dataset_english_quotes, require_deterministic_for_xpu
+
+
+try:
+ from huggingface_hub.utils import reset_sessions
+except ImportError:
+ # this function was removed in hfh v1.0.0
+ reset_sessions = None
+
+
+class TestLoraInitialization:
+ """Test class to check the initialization of LoRA adapters."""
+
+ torch_device = infer_device()
+
+ def get_uniform(self, amin, amax, size=(10000,)):
+ unif = torch.distributions.uniform.Uniform(amin, amax)
+ samples = unif.sample(size)
+ return samples
+
+ def get_normal(self, mean, std, size=(10000,)):
+ normal = torch.distributions.normal.Normal(mean, std)
+ samples = normal.sample(size)
+ return samples
+
+ def get_model(self, bias=True):
+ class MyModule(nn.Module):
+ def __init__(self):
+ super().__init__()
+ # choose a large weight so that averages are close to expected values
+ self.linear = nn.Linear(1000, 1000, bias=bias)
+ self.embed = nn.Embedding(1000, 1000)
+ self.conv2d = nn.Conv2d(100, 100, 3, bias=bias)
+
+ def forward(self, x):
+ x_int = (100 * x).int()
+ x_4d = x.flatten().reshape(1, 100, 10, 10)
+ return self.linear(x), self.embed(x_int), self.conv2d(x_4d)
+
+ return MyModule().eval().to(self.torch_device)
+
+ @pytest.fixture
+ def data(self):
+ return torch.rand(10, 1000).to(self.torch_device)
+
+ def test_lora_linear_init_default(self):
+ # default is True
+ torch.manual_seed(0)
+
+ model = self.get_model()
+ config = LoraConfig(target_modules=["linear"])
+ model = get_peft_model(model, config)
+ weight_A = model.linear.lora_A["default"].weight
+ weight_B = model.linear.lora_B["default"].weight
+
+ # use statistical test to check if weight A is from a uniform distribution
+ unif = self.get_uniform(weight_A.min().item(), weight_A.max().item())
+ _, p_value = stats.kstest(weight_A.detach().flatten().cpu().numpy(), unif.flatten().cpu().numpy())
+ assert p_value > 0.5
+
+ # check that weight A is *not* from a normal distribution
+ normal = self.get_normal(weight_A.mean().item(), weight_A.std().item())
+ _, p_value = stats.kstest(weight_A.detach().flatten().cpu().numpy(), normal.flatten().cpu().numpy())
+ assert p_value < 0.05
+
+ # check that weight B is zero
+ assert (weight_B == 0.0).all()
+
+ def test_lora_linear_init_gaussian(self):
+ # use gaussian init
+ torch.manual_seed(0)
+
+ model = self.get_model()
+ config = LoraConfig(target_modules=["linear"], init_lora_weights="gaussian")
+ model = get_peft_model(model, config)
+ weight_A = model.linear.lora_A["default"].weight
+ weight_B = model.linear.lora_B["default"].weight
+
+ # use statistical test to check if weight A is from a normal distribution
+ normal = self.get_normal(0.0, 1 / config.r)
+ _, p_value = stats.kstest(weight_A.detach().flatten().cpu().numpy(), normal.flatten().cpu().numpy())
+
+ assert p_value > 0.5
+
+ # check that weight A is *not* from a uniform distribution
+ unif = self.get_uniform(weight_A.min().item(), weight_A.max().item())
+ _, p_value = stats.kstest(weight_A.detach().flatten().cpu().numpy(), unif.flatten().cpu().numpy())
+ assert p_value < 0.05
+
+ # check that weight B is zero
+ assert (weight_B == 0.0).all()
+
+ def test_lora_linear_false(self):
+ torch.manual_seed(0)
+
+ model = self.get_model()
+ config = LoraConfig(target_modules=["linear"], init_lora_weights=False)
+ model = get_peft_model(model, config)
+ weight_B = model.linear.lora_B["default"].weight
+
+ # with init_lora_weights=False, weight B should *not* be zero. We don't care so much about the actual values
+ # as long as they are not zero, in order to avoid identity transformation.
+ assert not torch.allclose(weight_B, torch.zeros_like(weight_B))
+
+ def test_lora_embedding_default(self):
+ # embedding is initialized as a normal distribution, not kaiming uniform
+ torch.manual_seed(0)
+
+ model = self.get_model()
+ config = LoraConfig(target_modules=["embed"])
+ model = get_peft_model(model, config)
+ weight_A = model.embed.lora_embedding_A["default"]
+ weight_B = model.embed.lora_embedding_B["default"]
+
+ # use statistical test to check if weight B is from a normal distribution
+ normal = self.get_normal(0.0, 1.0)
+ _, p_value = stats.kstest(weight_B.detach().flatten().cpu().numpy(), normal.flatten().cpu().numpy())
+ assert p_value > 0.5
+
+ # check that weight B is *not* from a uniform distribution
+ unif = self.get_uniform(weight_B.min().item(), weight_B.max().item())
+ _, p_value = stats.kstest(weight_B.detach().flatten().cpu().numpy(), unif.flatten().cpu().numpy())
+ assert p_value < 0.05
+
+ # check that weight A is zero
+ assert (weight_A == 0.0).all()
+
+ def test_lora_embedding_gaussian(self):
+ # embedding does not change with init_lora_weights="gaussian" vs True
+ torch.manual_seed(0)
+
+ model = self.get_model()
+ config = LoraConfig(target_modules=["embed"], init_lora_weights="gaussian")
+ model = get_peft_model(model, config)
+ weight_A = model.embed.lora_embedding_A["default"]
+ weight_B = model.embed.lora_embedding_B["default"]
+
+ # use statistical test to check if weight B is from a normal distribution
+ normal = self.get_normal(0.0, 1.0)
+ _, p_value = stats.kstest(weight_B.detach().flatten().cpu().numpy(), normal.flatten().cpu().numpy())
+ assert p_value > 0.5
+
+ # check that weight B is *not* from a uniform distribution
+ unif = self.get_uniform(weight_B.min().item(), weight_B.max().item())
+ _, p_value = stats.kstest(weight_B.detach().flatten().cpu().numpy(), unif.flatten().cpu().numpy())
+ assert p_value < 0.05
+
+ # check that weight A is zero
+ assert (weight_A == 0.0).all()
+
+ def test_lora_embedding_false(self):
+ torch.manual_seed(0)
+
+ model = self.get_model()
+ config = LoraConfig(target_modules=["embed"], init_lora_weights=False)
+ model = get_peft_model(model, config)
+ weight_A = model.embed.lora_embedding_B["default"]
+
+ # with init_lora_weights=False, weight A should *not* be zero. We don't care so much about the actual values
+ # as long as they are not zero, in order to avoid identity transformation.
+ assert not torch.allclose(weight_A, torch.zeros_like(weight_A))
+
+ def test_lora_conv2d_default(self):
+ # default is True
+ torch.manual_seed(0)
+
+ model = self.get_model()
+ config = LoraConfig(target_modules=["conv2d"])
+ model = get_peft_model(model, config)
+ weight_A = model.conv2d.lora_A["default"].weight
+ weight_B = model.conv2d.lora_B["default"].weight
+
+ # use statistical test to check if weight A is from a uniform distribution
+ unif = self.get_uniform(weight_A.min().item(), weight_A.max().item())
+ _, p_value = stats.kstest(weight_A.detach().flatten().cpu().numpy(), unif.flatten().cpu().numpy())
+ assert p_value > 0.5
+
+ # check that weight A is *not* from a normal distribution
+ normal = self.get_normal(weight_A.mean().item(), weight_A.std().item())
+ _, p_value = stats.kstest(weight_A.detach().flatten().cpu().numpy(), normal.flatten().cpu().numpy())
+ assert p_value < 0.05
+
+ # check that weight B is zero
+ assert (weight_B == 0.0).all()
+
+ def test_lora_conv2d_init_gaussian(self):
+ # use gaussian init
+ torch.manual_seed(0)
+
+ model = self.get_model()
+ config = LoraConfig(target_modules=["conv2d"], init_lora_weights="gaussian")
+ model = get_peft_model(model, config)
+ weight_A = model.conv2d.lora_A["default"].weight
+ weight_B = model.conv2d.lora_B["default"].weight
+
+ # use statistical test to check if weight A is from a normal distribution
+ normal = self.get_normal(0.0, 1 / config.r)
+ _, p_value = stats.kstest(weight_A.detach().flatten().cpu().numpy(), normal.flatten().cpu().numpy())
+ assert p_value > 0.5
+
+ # check that weight A is *not* from a uniform distribution
+ unif = self.get_uniform(weight_A.min().item(), weight_A.max().item())
+ _, p_value = stats.kstest(weight_A.detach().flatten().cpu().numpy(), unif.flatten().cpu().numpy())
+ assert p_value < 0.05
+
+ # check that weight B is zero
+ assert (weight_B == 0.0).all()
+
+ def test_lora_conv2d_false(self):
+ torch.manual_seed(0)
+
+ model = self.get_model()
+ config = LoraConfig(target_modules=["conv2d"], init_lora_weights=False)
+ model = get_peft_model(model, config)
+ weight_B = model.conv2d.lora_B["default"].weight
+
+ # with init_lora_weights=False, weight B should *not* be zero. We don't care so much about the actual values
+ # as long as they are not zero, in order to avoid identity transformation.
+ assert not torch.allclose(weight_B, torch.zeros_like(weight_B))
+
+ def test_lora_init_orthogonal(self):
+ torch.manual_seed(0)
+
+ model = self.get_model()
+ config = LoraConfig(target_modules=["linear"], init_lora_weights="orthogonal")
+ model = get_peft_model(model, config)
+
+ weight_A = model.linear.lora_A["default"].weight
+ weight_B = model.linear.lora_B["default"].weight
+
+ assert not torch.allclose(weight_A, torch.zeros_like(weight_A))
+ assert not torch.allclose(weight_B, torch.zeros_like(weight_B))
+ assert (weight_B @ weight_A).abs().max() < 1e-6
+
+ @pytest.mark.parametrize("dtype", [torch.float16, torch.bfloat16])
+ def test_lora_init_orthogonal_half_precision_dtype(self, dtype):
+ try:
+ torch.zeros(1, dtype=dtype)
+ except Exception:
+ pytest.skip(f"dtype {dtype} not supported on this system, skipping test")
+
+ torch.manual_seed(0)
+
+ model = self.get_model()
+ config = LoraConfig(target_modules=["linear"], init_lora_weights="orthogonal")
+ model = get_peft_model(model, config).to(dtype)
+
+ weight_A = model.linear.lora_A["default"].weight
+ weight_B = model.linear.lora_B["default"].weight
+
+ assert weight_A.dtype == dtype
+ assert weight_B.dtype == dtype
+
+ def test_lora_init_orthogonal_odd_rank_raises(self):
+ torch.manual_seed(0)
+
+ model = self.get_model()
+ config = LoraConfig(target_modules=["linear"], init_lora_weights="orthogonal", r=7)
+ msg = "Orthogonal initialization requires the LoRA rank to be even, got 7 instead."
+ with pytest.raises(ValueError, match=msg):
+ get_peft_model(model, config)
+
+ def test_lora_scaling_default(self):
+ # default is True
+ torch.manual_seed(0)
+
+ model = self.get_model()
+
+ # check scaling factor use_rslora=False
+ config = LoraConfig(target_modules=["linear", "embed", "conv2d"], lora_alpha=3, r=16, use_rslora=False)
+ model = get_peft_model(model, config)
+
+ expected_scaling = config.lora_alpha / config.r
+
+ assert model.linear.scaling["default"] == expected_scaling
+ assert model.embed.scaling["default"] == expected_scaling
+ assert model.conv2d.scaling["default"] == expected_scaling
+
+ # testcase for bugfix for issue 2194
+ def test_rank_alpha_pattern_override(self):
+ torch.manual_seed(0)
+
+ layer = self.get_model()
+ model = nn.Sequential(layer, layer)
+ config = LoraConfig(
+ target_modules=["linear"],
+ lora_alpha=1,
+ r=8,
+ use_rslora=False,
+ rank_pattern={"linear": 8},
+ alpha_pattern={"0.linear": 2},
+ )
+ model = get_peft_model(model, config)
+ scaling_with_rank_pattern = model.model[0].linear.scaling
+
+ layer = self.get_model()
+ model = nn.Sequential(layer, layer)
+ config = LoraConfig(
+ target_modules=["linear"], lora_alpha=1, r=8, use_rslora=False, alpha_pattern={"0.linear": 2}
+ )
+ model = get_peft_model(model, config)
+ scaling_without_rank_pattern = model.model[0].linear.scaling
+
+ assert scaling_with_rank_pattern == scaling_without_rank_pattern
+
+ def test_lora_pissa_linear_init_default(self, data):
+ model = self.get_model()
+ output = model(data)[0]
+
+ config = LoraConfig(init_lora_weights="pissa", target_modules=["linear"])
+ peft_model = get_peft_model(deepcopy(model), config)
+ assert torch.allclose(output, peft_model(data)[0], atol=1e-06)
+
+ config = LoraConfig(init_lora_weights="pissa_niter_16", target_modules=["linear"])
+ peft_model = get_peft_model(deepcopy(model), config)
+ assert torch.allclose(output, peft_model(data)[0], atol=1e-06)
+
+ def test_lora_olora_linear_init_default(self, data):
+ model = self.get_model()
+ output = model(data)[0]
+
+ # Both OLoRA and olora should work
+ config = LoraConfig(init_lora_weights="OLoRA", target_modules=["linear"])
+ peft_model = get_peft_model(deepcopy(model), config)
+ assert torch.allclose(output, peft_model(data)[0], atol=1e-06)
+
+ def test_lora_pissa_conversion_same_output_after_loading(self, data, tmp_path):
+ model = self.get_model()
+ output_base = model(data)[0]
+
+ config = LoraConfig(init_lora_weights="pissa", target_modules=["linear"], r=8)
+ peft_model = get_peft_model(deepcopy(model), config)
+ # save the initial model
+ peft_model.peft_config["default"].init_lora_weights = True
+ peft_model.save_pretrained(tmp_path / "init-model")
+ peft_model.peft_config["default"].init_lora_weights = "pissa"
+
+ # modify the weights, or else the adapter performs an identity transformation
+ peft_model.base_model.linear.lora_B["default"].weight.data *= 2.0
+ output_pissa = peft_model(data)[0]
+
+ # sanity check
+ tol = 1e-06
+ assert not torch.allclose(output_base, output_pissa, atol=tol, rtol=tol)
+
+ # save the model normally
+ peft_model.save_pretrained(tmp_path / "pissa-model")
+ model_loaded = PeftModel.from_pretrained(deepcopy(model), tmp_path / "pissa-model")
+ output_loaded = model_loaded(data)[0]
+
+ assert torch.allclose(output_pissa, output_loaded, atol=tol, rtol=tol)
+ # sanity check: ranks should still be 8 as initially
+ assert model_loaded.peft_config["default"].r == 8
+ assert model_loaded.base_model.model.linear.lora_A["default"].weight.shape[0] == 8
+ # sanity check: the base model weights were indeed changed
+ assert not torch.allclose(
+ model.linear.weight, model_loaded.base_model.model.linear.base_layer.weight, atol=tol, rtol=tol
+ )
+
+ # save the model with conversion
+ peft_config_keys_before = list(peft_model.peft_config.keys())
+ peft_config_dict_before = peft_model.peft_config["default"].to_dict()
+ peft_model.save_pretrained(
+ tmp_path / "pissa-model-converted", path_initial_model_for_weight_conversion=tmp_path / "init-model"
+ )
+ peft_config_keys_after = list(peft_model.peft_config.keys())
+ peft_config_dict_after = peft_model.peft_config["default"].to_dict()
+ assert peft_config_keys_before == peft_config_keys_after
+ assert peft_config_dict_before == peft_config_dict_after
+
+ model_converted = PeftModel.from_pretrained(deepcopy(model), tmp_path / "pissa-model-converted")
+ output_converted = model_converted(data)[0]
+
+ assert torch.allclose(output_pissa, output_converted, atol=tol, rtol=tol)
+ # rank should be double of what it was initially
+ assert model_converted.peft_config["default"].r == 16
+ assert model_converted.base_model.model.linear.lora_A["default"].weight.shape[0] == 16
+ # base model weights should be the same as the initial model
+ assert torch.allclose(
+ model.linear.weight, model_converted.base_model.model.linear.base_layer.weight, atol=tol, rtol=tol
+ )
+
+ def test_lora_pissa_conversion_same_output_after_loading_with_rank_pattern(self, data, tmp_path):
+ # same as above, but using rank_pattern
+ model = self.get_model()
+ output_base = model(data)[0]
+
+ # use rank_pattern here; note that since there is only a single linear layer, r is completely overridden
+ config = LoraConfig(init_lora_weights="pissa", target_modules=["linear"], r=8, rank_pattern={"linear": 32})
+ peft_model = get_peft_model(deepcopy(model), config)
+ # save the initial model
+ peft_model.peft_config["default"].init_lora_weights = True
+ peft_model.save_pretrained(tmp_path / "init-model")
+ peft_model.peft_config["default"].init_lora_weights = "pissa"
+
+ # modify the weights, or else the adapter performs an identity transformation
+ peft_model.base_model.linear.lora_B["default"].weight.data *= 2.0
+ output_pissa = peft_model(data)[0]
+
+ # sanity check
+ tol = 1e-06
+ assert not torch.allclose(output_base, output_pissa, atol=tol, rtol=tol)
+
+ # save the model normally
+ peft_model.save_pretrained(tmp_path / "pissa-model")
+ model_loaded = PeftModel.from_pretrained(deepcopy(model), tmp_path / "pissa-model")
+ output_loaded = model_loaded(data)[0]
+
+ assert torch.allclose(output_pissa, output_loaded, atol=tol, rtol=tol)
+ # sanity check: ranks should still be 8 as initially
+ assert model_loaded.peft_config["default"].r == 8
+ assert model_loaded.base_model.model.linear.lora_A["default"].weight.shape[0] == 32
+ # sanity check: the base model weights were indeed changed
+ assert not torch.allclose(
+ model.linear.weight, model_loaded.base_model.model.linear.base_layer.weight, atol=tol, rtol=tol
+ )
+
+ # save the model with conversion
+ peft_model.save_pretrained(
+ tmp_path / "pissa-model-converted", path_initial_model_for_weight_conversion=tmp_path / "init-model"
+ )
+ model_converted = PeftModel.from_pretrained(deepcopy(model), tmp_path / "pissa-model-converted")
+ output_converted = model_converted(data)[0]
+
+ assert torch.allclose(output_pissa, output_converted, atol=tol, rtol=tol)
+ # rank should be double of what it was initially
+ assert model_converted.peft_config["default"].r == 16
+ assert model_converted.base_model.model.linear.lora_A["default"].weight.shape[0] == 64
+ # base model weights should be the same as the initial model
+ assert torch.allclose(
+ model.linear.weight, model_converted.base_model.model.linear.base_layer.weight, atol=tol, rtol=tol
+ )
+
+ def test_lora_pissa_conversion_same_output_after_loading_with_alpha_pattern(self, data, tmp_path):
+ # same as above, but using alpha_pattern
+ model = self.get_model()
+ output_base = model(data)[0]
+
+ # use alpha_pattern here; note that since there is only a single linear layer, lora_alpha is completely
+ # overridden
+ config = LoraConfig(init_lora_weights="pissa", target_modules=["linear"], alpha_pattern={"linear": 5})
+ peft_model = get_peft_model(deepcopy(model), config)
+ # save the initial model
+ peft_model.peft_config["default"].init_lora_weights = True
+ peft_model.save_pretrained(tmp_path / "init-model")
+ peft_model.peft_config["default"].init_lora_weights = "pissa"
+
+ # modify the weights, or else the adapter performs an identity transformation
+ peft_model.base_model.linear.lora_B["default"].weight.data *= 2.0
+ output_pissa = peft_model(data)[0]
+
+ # sanity check
+ tol = 1e-06
+ assert not torch.allclose(output_base, output_pissa, atol=tol, rtol=tol)
+
+ # save the model normally
+ peft_model.save_pretrained(tmp_path / "pissa-model")
+ model_loaded = PeftModel.from_pretrained(deepcopy(model), tmp_path / "pissa-model")
+ output_loaded = model_loaded(data)[0]
+
+ assert torch.allclose(output_pissa, output_loaded, atol=tol, rtol=tol)
+ # sanity check: ranks should still be 8 as initially
+ assert model_loaded.peft_config["default"].r == 8
+ assert model_loaded.base_model.model.linear.lora_A["default"].weight.shape[0] == 8
+ assert model_loaded.base_model.model.linear.scaling["default"] == 5 / 8
+ # sanity check: the base model weights were indeed changed
+ assert not torch.allclose(
+ model.linear.weight, model_loaded.base_model.model.linear.base_layer.weight, atol=tol, rtol=tol
+ )
+
+ # save the model with conversion
+ peft_model.save_pretrained(
+ tmp_path / "pissa-model-converted", path_initial_model_for_weight_conversion=tmp_path / "init-model"
+ )
+ model_converted = PeftModel.from_pretrained(deepcopy(model), tmp_path / "pissa-model-converted")
+ output_converted = model_converted(data)[0]
+
+ assert torch.allclose(output_pissa, output_converted, atol=tol, rtol=tol)
+ # rank should be double of what it was initially
+ assert model_converted.peft_config["default"].r == 16
+ assert model_converted.base_model.model.linear.lora_A["default"].weight.shape[0] == 16
+ assert model_converted.base_model.model.linear.scaling["default"] == 10 / 16
+ # base model weights should be the same as the initial model
+ assert torch.allclose(
+ model.linear.weight, model_converted.base_model.model.linear.base_layer.weight, atol=tol, rtol=tol
+ )
+
+ def test_lora_pissa_conversion_same_output_after_loading_with_rslora(self, data, tmp_path):
+ model = self.get_model()
+ output_base = model(data)[0]
+
+ config = LoraConfig(init_lora_weights="pissa", target_modules=["linear"], r=8, use_rslora=True)
+ peft_model = get_peft_model(deepcopy(model), config)
+ # save the initial model
+ peft_model.peft_config["default"].init_lora_weights = True
+ peft_model.save_pretrained(tmp_path / "init-model")
+ peft_model.peft_config["default"].init_lora_weights = "pissa"
+
+ # modify the weights, or else the adapter performs an identity transformation
+ peft_model.base_model.linear.lora_B["default"].weight.data *= 2.0
+ output_pissa = peft_model(data)[0]
+
+ # sanity check
+ tol = 1e-06
+ assert not torch.allclose(output_base, output_pissa, atol=tol, rtol=tol)
+
+ # save the model normally
+ peft_model.save_pretrained(tmp_path / "pissa-model")
+ model_loaded = PeftModel.from_pretrained(deepcopy(model), tmp_path / "pissa-model")
+ output_loaded = model_loaded(data)[0]
+
+ assert torch.allclose(output_pissa, output_loaded, atol=tol, rtol=tol)
+ # sanity check: ranks should still be 8 as initially
+ assert model_loaded.peft_config["default"].r == 8
+ assert model_loaded.base_model.model.linear.lora_A["default"].weight.shape[0] == 8
+ assert model_loaded.base_model.model.linear.scaling["default"] == 8 / (8**0.5)
+ # sanity check: the base model weights were indeed changed
+ assert not torch.allclose(
+ model.linear.weight, model_loaded.base_model.model.linear.base_layer.weight, atol=tol, rtol=tol
+ )
+
+ # save the model with conversion
+ peft_model.save_pretrained(
+ tmp_path / "pissa-model-converted", path_initial_model_for_weight_conversion=tmp_path / "init-model"
+ )
+ model_converted = PeftModel.from_pretrained(deepcopy(model), tmp_path / "pissa-model-converted")
+ output_converted = model_converted(data)[0]
+
+ assert torch.allclose(output_pissa, output_converted, atol=tol, rtol=tol)
+ # rank should be double of what it was initially
+ assert model_converted.peft_config["default"].r == 16
+ assert model_converted.base_model.model.linear.lora_A["default"].weight.shape[0] == 16
+ # same scale as before with a little bit of floating point imprecision
+ assert model_converted.base_model.model.linear.scaling["default"] == pytest.approx(8 / (8**0.5))
+ # base model weights should be the same as the initial model
+ assert torch.allclose(
+ model.linear.weight, model_converted.base_model.model.linear.base_layer.weight, atol=tol, rtol=tol
+ )
+
+ def test_pissa_rank_pattern_and_rslora_raises(self, tmp_path):
+ # it's not possible to determine the correct scale when using rslora with rank or alpha pattern, because the
+ # scale is not stored in the state_dict
+ model = self.get_model()
+ config = LoraConfig(
+ init_lora_weights="pissa", target_modules=["linear"], r=8, rank_pattern={"linear": 2}, use_rslora=True
+ )
+ peft_model = get_peft_model(model, config)
+ peft_model.save_pretrained(tmp_path / "init-model")
+
+ msg = re.escape("Passing `path_initial_model_for_weight_conversion` to `save_pretrained`")
+ with pytest.raises(ValueError, match=msg):
+ peft_model.save_pretrained(
+ tmp_path / "pissa-model", path_initial_model_for_weight_conversion=tmp_path / "init-model"
+ )
+
+ def test_pissa_alpha_pattern_and_rslora_raises(self, tmp_path):
+ # it's not possible to determine the correct scale when using rslora with rank or alpha pattern, because the
+ # scale is not stored in the state_dict
+ model = self.get_model()
+ config = LoraConfig(
+ init_lora_weights="pissa", target_modules=["linear"], r=8, alpha_pattern={"linear": 2}, use_rslora=True
+ )
+ peft_model = get_peft_model(model, config)
+ peft_model.save_pretrained(tmp_path / "init-model")
+
+ msg = re.escape("Passing `path_initial_model_for_weight_conversion` to `save_pretrained`")
+ with pytest.raises(ValueError, match=msg):
+ peft_model.save_pretrained(
+ tmp_path / "pissa-model", path_initial_model_for_weight_conversion=tmp_path / "init-model"
+ )
+
+ def test_olora_conversion_same_output_after_loading(self, data, tmp_path):
+ model = self.get_model()
+ output_base = model(data)[0]
+
+ config = LoraConfig(init_lora_weights="olora", target_modules=["linear"], r=8)
+ peft_model = get_peft_model(deepcopy(model), config)
+ # save the initial model
+ peft_model.save_pretrained(tmp_path / "init-model")
+
+ # modify the weights, or else the adapter performs an identity transformation
+ peft_model.base_model.linear.lora_B["default"].weight.data *= 2.0
+ output_olora = peft_model(data)[0]
+
+ # sanity check
+ tol = 1e-06
+ assert not torch.allclose(output_base, output_olora, atol=tol, rtol=tol)
+
+ # save the model normally
+ peft_model.save_pretrained(tmp_path / "olora-model")
+ model_loaded = PeftModel.from_pretrained(deepcopy(model), tmp_path / "olora-model")
+ output_loaded = model_loaded(data)[0]
+
+ assert torch.allclose(output_olora, output_loaded, atol=tol, rtol=tol)
+ # sanity check: ranks should still be 8 as initially
+ assert model_loaded.peft_config["default"].r == 8
+ assert model_loaded.base_model.model.linear.lora_A["default"].weight.shape[0] == 8
+ # sanity check: the base model weights were indeed changed
+ assert not torch.allclose(
+ model.linear.weight, model_loaded.base_model.model.linear.base_layer.weight, atol=tol, rtol=tol
+ )
+
+ # save the model with conversion
+ peft_config_keys_before = list(peft_model.peft_config.keys())
+ peft_config_dict_before = peft_model.peft_config["default"].to_dict()
+ peft_model.save_pretrained(
+ tmp_path / "olora-model-converted", path_initial_model_for_weight_conversion=tmp_path / "init-model"
+ )
+ peft_config_keys_after = list(peft_model.peft_config.keys())
+ peft_config_dict_after = peft_model.peft_config["default"].to_dict()
+ assert peft_config_keys_before == peft_config_keys_after
+ assert peft_config_dict_before == peft_config_dict_after
+
+ model_converted = PeftModel.from_pretrained(deepcopy(model), tmp_path / "olora-model-converted")
+ output_converted = model_converted(data)[0]
+
+ assert torch.allclose(output_olora, output_converted, atol=tol, rtol=tol)
+ # rank should be double of what it was initially
+ assert model_converted.peft_config["default"].r == 16
+ assert model_converted.base_model.model.linear.lora_A["default"].weight.shape[0] == 16
+ # base model weights should be the same as the initial model
+ assert torch.allclose(
+ model.linear.weight, model_converted.base_model.model.linear.base_layer.weight, atol=tol, rtol=tol
+ )
+
+ def test_olora_conversion_same_output_after_loading_with_rank_pattern(self, data, tmp_path):
+ # same as above, but using rank_pattern
+ model = self.get_model()
+ output_base = model(data)[0]
+
+ # use rank_pattern here; note that since there is only a single linear layer, r is completely overridden
+ config = LoraConfig(init_lora_weights="olora", target_modules=["linear"], r=8, rank_pattern={"linear": 32})
+ peft_model = get_peft_model(deepcopy(model), config)
+ # save the initial model
+ peft_model.save_pretrained(tmp_path / "init-model")
+
+ # modify the weights, or else the adapter performs an identity transformation
+ peft_model.base_model.linear.lora_B["default"].weight.data *= 2.0
+ output_olora = peft_model(data)[0]
+
+ # sanity check
+ tol = 1e-06
+ assert not torch.allclose(output_base, output_olora, atol=tol, rtol=tol)
+
+ # save the model normally
+ peft_model.save_pretrained(tmp_path / "olora-model")
+ model_loaded = PeftModel.from_pretrained(deepcopy(model), tmp_path / "olora-model")
+ output_loaded = model_loaded(data)[0]
+
+ assert torch.allclose(output_olora, output_loaded, atol=tol, rtol=tol)
+ # sanity check: ranks should still be 8 as initially
+ assert model_loaded.peft_config["default"].r == 8
+ assert model_loaded.base_model.model.linear.lora_A["default"].weight.shape[0] == 32
+ # sanity check: the base model weights were indeed changed
+ assert not torch.allclose(
+ model.linear.weight, model_loaded.base_model.model.linear.base_layer.weight, atol=tol, rtol=tol
+ )
+
+ # save the model with conversion
+ peft_model.save_pretrained(
+ tmp_path / "olora-model-converted", path_initial_model_for_weight_conversion=tmp_path / "init-model"
+ )
+ model_converted = PeftModel.from_pretrained(deepcopy(model), tmp_path / "olora-model-converted")
+ output_converted = model_converted(data)[0]
+
+ assert torch.allclose(output_olora, output_converted, atol=tol, rtol=tol)
+ # rank should be double of what it was initially
+ assert model_converted.peft_config["default"].r == 16
+ assert model_converted.base_model.model.linear.lora_A["default"].weight.shape[0] == 64
+ # base model weights should be the same as the initial model
+ assert torch.allclose(
+ model.linear.weight, model_converted.base_model.model.linear.base_layer.weight, atol=tol, rtol=tol
+ )
+
+ def test_olora_conversion_same_output_after_loading_with_alpha_pattern(self, data, tmp_path):
+ # same as above, but using alpha_pattern
+ model = self.get_model()
+ output_base = model(data)[0]
+
+ # use alpha_pattern here; note that since there is only a single linear layer, lora_alpha is completely
+ # overridden
+ config = LoraConfig(init_lora_weights="olora", target_modules=["linear"], alpha_pattern={"linear": 5})
+ peft_model = get_peft_model(deepcopy(model), config)
+ # save the initial model
+ peft_model.save_pretrained(tmp_path / "init-model")
+
+ # modify the weights, or else the adapter performs an identity transformation
+ peft_model.base_model.linear.lora_B["default"].weight.data *= 2.0
+ output_olora = peft_model(data)[0]
+
+ # sanity check
+ tol = 1e-06
+ assert not torch.allclose(output_base, output_olora, atol=tol, rtol=tol)
+
+ # save the model normally
+ peft_model.save_pretrained(tmp_path / "olora-model")
+ model_loaded = PeftModel.from_pretrained(deepcopy(model), tmp_path / "olora-model")
+ output_loaded = model_loaded(data)[0]
+
+ assert torch.allclose(output_olora, output_loaded, atol=tol, rtol=tol)
+ # sanity check: ranks should still be 8 as initially
+ assert model_loaded.peft_config["default"].r == 8
+ assert model_loaded.base_model.model.linear.lora_A["default"].weight.shape[0] == 8
+ assert model_loaded.base_model.model.linear.scaling["default"] == 5 / 8
+ # sanity check: the base model weights were indeed changed
+ assert not torch.allclose(
+ model.linear.weight, model_loaded.base_model.model.linear.base_layer.weight, atol=tol, rtol=tol
+ )
+
+ # save the model with conversion
+ peft_model.save_pretrained(
+ tmp_path / "olora-model-converted", path_initial_model_for_weight_conversion=tmp_path / "init-model"
+ )
+ model_converted = PeftModel.from_pretrained(deepcopy(model), tmp_path / "olora-model-converted")
+ output_converted = model_converted(data)[0]
+
+ assert torch.allclose(output_olora, output_converted, atol=tol, rtol=tol)
+ # rank should be double of what it was initially
+ assert model_converted.peft_config["default"].r == 16
+ assert model_converted.base_model.model.linear.lora_A["default"].weight.shape[0] == 16
+ assert model_converted.base_model.model.linear.scaling["default"] == 10 / 16
+ # base model weights should be the same as the initial model
+ assert torch.allclose(
+ model.linear.weight, model_converted.base_model.model.linear.base_layer.weight, atol=tol, rtol=tol
+ )
+
+ def test_olora_conversion_same_output_after_loading_with_rslora(self, data, tmp_path):
+ # same as above, but using alpha_pattern
+ model = self.get_model()
+ output_base = model(data)[0]
+
+ config = LoraConfig(init_lora_weights="olora", target_modules=["linear"], r=8, use_rslora=True)
+ peft_model = get_peft_model(deepcopy(model), config)
+ # save the initial model
+ peft_model.save_pretrained(tmp_path / "init-model")
+
+ # modify the weights, or else the adapter performs an identity transformation
+ peft_model.base_model.linear.lora_B["default"].weight.data *= 2.0
+ output_olora = peft_model(data)[0]
+
+ # sanity check
+ tol = 1e-06
+ assert not torch.allclose(output_base, output_olora, atol=tol, rtol=tol)
+
+ # save the model normally
+ peft_model.save_pretrained(tmp_path / "olora-model")
+ model_loaded = PeftModel.from_pretrained(deepcopy(model), tmp_path / "olora-model")
+ output_loaded = model_loaded(data)[0]
+
+ assert torch.allclose(output_olora, output_loaded, atol=tol, rtol=tol)
+ # sanity check: ranks should still be 8 as initially
+ assert model_loaded.peft_config["default"].r == 8
+ assert model_loaded.base_model.model.linear.lora_A["default"].weight.shape[0] == 8
+ assert model_loaded.base_model.model.linear.scaling["default"] == 8 / (8**0.5)
+ # sanity check: the base model weights were indeed changed
+ assert not torch.allclose(
+ model.linear.weight, model_loaded.base_model.model.linear.base_layer.weight, atol=tol, rtol=tol
+ )
+
+ # save the model with conversion
+ peft_model.save_pretrained(
+ tmp_path / "olora-model-converted", path_initial_model_for_weight_conversion=tmp_path / "init-model"
+ )
+ model_converted = PeftModel.from_pretrained(deepcopy(model), tmp_path / "olora-model-converted")
+ output_converted = model_converted(data)[0]
+
+ assert torch.allclose(output_olora, output_converted, atol=tol, rtol=tol)
+ # rank should be double of what it was initially
+ assert model_converted.peft_config["default"].r == 16
+ assert model_converted.base_model.model.linear.lora_A["default"].weight.shape[0] == 16
+ # same scale as before with a little bit of floating point imprecision
+ assert model_converted.base_model.model.linear.scaling["default"] == pytest.approx(8 / (8**0.5))
+ # base model weights should be the same as the initial model
+ assert torch.allclose(
+ model.linear.weight, model_converted.base_model.model.linear.base_layer.weight, atol=tol, rtol=tol
+ )
+
+ def test_olora_rank_pattern_and_rslora_raises(self, tmp_path):
+ # it's not possible to determine the correct scale when using rslora with rank or alpha pattern, because the
+ # scale is not stored in the state_dict
+ model = self.get_model()
+ config = LoraConfig(
+ init_lora_weights="olora", target_modules=["linear"], r=8, rank_pattern={"linear": 2}, use_rslora=True
+ )
+ peft_model = get_peft_model(model, config)
+ peft_model.save_pretrained(tmp_path / "init-model")
+
+ msg = re.escape("Passing `path_initial_model_for_weight_conversion` to `save_pretrained`")
+ with pytest.raises(ValueError, match=msg):
+ peft_model.save_pretrained(
+ tmp_path / "olora-model", path_initial_model_for_weight_conversion=tmp_path / "init-model"
+ )
+
+ def test_olora_alpha_pattern_and_rslora_raises(self, tmp_path):
+ # it's not possible to determine the correct scale when using rslora with rank or alpha pattern, because the
+ # scale is not stored in the state_dict
+ model = self.get_model()
+ config = LoraConfig(
+ init_lora_weights="olora", target_modules=["linear"], r=8, alpha_pattern={"linear": 2}, use_rslora=True
+ )
+ peft_model = get_peft_model(model, config)
+ peft_model.save_pretrained(tmp_path / "init-model")
+
+ msg = re.escape("Passing `path_initial_model_for_weight_conversion` to `save_pretrained`")
+ with pytest.raises(ValueError, match=msg):
+ peft_model.save_pretrained(
+ tmp_path / "olora-model", path_initial_model_for_weight_conversion=tmp_path / "init-model"
+ )
+
+ @pytest.mark.parametrize(
+ "config_kwargs, should_warn",
+ [
+ # no warning
+ ({"init_lora_weights": "pissa", "target_modules": ["linear"]}, False),
+ ({"init_lora_weights": "pissa_niter_3", "target_modules": ["linear"]}, False),
+ ({"init_lora_weights": "olora", "target_modules": ["linear"]}, False),
+ ({"init_lora_weights": "pissa", "target_modules": ["linear"], "use_rslora": True}, False),
+ ({"init_lora_weights": "pissa_niter_3", "target_modules": ["linear"], "use_rslora": True}, False),
+ ({"init_lora_weights": "olora", "target_modules": ["linear"], "use_rslora": True}, False),
+ ({"init_lora_weights": "pissa", "target_modules": ["linear"], "rank_pattern": {"linear": 8}}, False),
+ (
+ {"init_lora_weights": "pissa_niter_3", "target_modules": ["linear"], "rank_pattern": {"linear": 8}},
+ False,
+ ),
+ ({"init_lora_weights": "olora", "target_modules": ["linear"], "rank_pattern": {"linear": 8}}, False),
+ ({"init_lora_weights": "pissa", "target_modules": ["linear"], "alpha_pattern": {"linear": 8}}, False),
+ (
+ {"init_lora_weights": "pissa_niter_3", "target_modules": ["linear"], "alpha_pattern": {"linear": 8}},
+ False,
+ ),
+ ({"init_lora_weights": "olora", "target_modules": ["linear"], "alpha_pattern": {"linear": 8}}, False),
+ # warning
+ (
+ {
+ "init_lora_weights": "pissa",
+ "target_modules": ["linear"],
+ "use_rslora": True,
+ "rank_pattern": {"linear": 8},
+ },
+ True,
+ ),
+ (
+ {
+ "init_lora_weights": "pissa_niter_3",
+ "target_modules": ["linear"],
+ "use_rslora": True,
+ "rank_pattern": {"linear": 8},
+ },
+ True,
+ ),
+ (
+ {
+ "init_lora_weights": "olora",
+ "target_modules": ["linear"],
+ "use_rslora": True,
+ "rank_pattern": {"linear": 8},
+ },
+ True,
+ ),
+ (
+ {
+ "init_lora_weights": "pissa",
+ "target_modules": ["linear"],
+ "use_rslora": True,
+ "alpha_pattern": {"linear": 8},
+ },
+ True,
+ ),
+ (
+ {
+ "init_lora_weights": "pissa_niter_3",
+ "target_modules": ["linear"],
+ "use_rslora": True,
+ "alpha_pattern": {"linear": 8},
+ },
+ True,
+ ),
+ (
+ {
+ "init_lora_weights": "olora",
+ "target_modules": ["linear"],
+ "use_rslora": True,
+ "alpha_pattern": {"linear": 8},
+ },
+ True,
+ ),
+ (
+ {
+ "init_lora_weights": "pissa",
+ "target_modules": ["linear"],
+ "use_rslora": True,
+ "rank_pattern": {"linear": 8},
+ "alpha_pattern": {"linear": 8},
+ },
+ True,
+ ),
+ (
+ {
+ "init_lora_weights": "pissa_niter_3",
+ "target_modules": ["linear"],
+ "use_rslora": True,
+ "rank_pattern": {"linear": 8},
+ "alpha_pattern": {"linear": 8},
+ },
+ True,
+ ),
+ (
+ {
+ "init_lora_weights": "olora",
+ "target_modules": ["linear"],
+ "use_rslora": True,
+ "rank_pattern": {"linear": 8},
+ "alpha_pattern": {"linear": 8},
+ },
+ True,
+ ),
+ ],
+ )
+ def test_lora_config_pissa_olora_warns(self, config_kwargs, should_warn, recwarn):
+ # Using post training conversion of modified base weights to restore their initial values (PiSSA, OLoRA) cannot
+ # be correctly done when using rslora + rank_pattern/alpha_pattern. We can't really know if the user intends
+ # this when they'll eventually call save_pretrained (i.e. if they'll pass
+ # path_initial_model_for_weight_conversionl). Therefore, we only warn but don't raise an error here.
+ msg = re.escape("Using Rank-Stabilized LoRA with rank_pattern/alpha_pattern and post-training conversion")
+ if should_warn:
+ LoraConfig(**config_kwargs)
+ assert len(recwarn.list) == 1
+ with pytest.warns(UserWarning, match=msg):
+ LoraConfig(**config_kwargs)
+ else:
+ LoraConfig(**config_kwargs)
+ assert not recwarn.list
+
+ @pytest.mark.parametrize("init_method", ["pissa", "olora"])
+ @pytest.mark.parametrize("pissa_olora_loaded_first", [False, True])
+ def test_load_pissa_olora_with_other_adapter_warns(self, init_method, pissa_olora_loaded_first, recwarn, tmp_path):
+ # Since PiSSA/OLoRA modifies the base weights, it should not be combined with other adapters. Check for a
+ # warning. See #2184.
+
+ # create an adapter without PiSSA/OloRA
+ model_id = "hf-internal-testing/tiny-random-OPTForCausalLM"
+ model = AutoModelForCausalLM.from_pretrained(model_id)
+ model = get_peft_model(model, LoraConfig(init_lora_weights=True))
+ model.save_pretrained(tmp_path / "adapter0")
+ del model
+
+ # create a model with PiSSA/OLoRA
+ model = AutoModelForCausalLM.from_pretrained(model_id)
+ model = get_peft_model(model, LoraConfig(init_lora_weights=init_method))
+ model.save_pretrained(tmp_path / "adapter1")
+ del model
+
+ # load the model
+ if pissa_olora_loaded_first:
+ path0, path1 = tmp_path / "adapter1", tmp_path / "adapter0"
+ else:
+ path0, path1 = tmp_path / "adapter0", tmp_path / "adapter1"
+
+ model = AutoModelForCausalLM.from_pretrained(model_id)
+ model = PeftModel.from_pretrained(model, path0)
+ model = model.load_adapter(path1, adapter_name="other")
+
+ if init_method == "pissa":
+ msg = "PiSSA changes the base weights of the model and should thus not be used with other adapters"
+ else:
+ msg = "OLoRA changes the base weights of the model and should thus not be used with other adapters"
+ assert any(str(w.message).startswith(msg) for w in recwarn.list)
+
+ def test_lora_rslora_scaling(self):
+ # default is True
+ torch.manual_seed(0)
+
+ model = self.get_model()
+
+ # check scaling factor use_rslora=True
+ config = LoraConfig(target_modules=["linear", "embed", "conv2d"], lora_alpha=3, r=16, use_rslora=True)
+ model = get_peft_model(model, config)
+
+ expected_scaling = config.lora_alpha / (config.r**0.5)
+
+ assert model.linear.scaling["default"] == expected_scaling
+ assert model.embed.scaling["default"] == expected_scaling
+ assert model.conv2d.scaling["default"] == expected_scaling
+
+ def test_lora_default_scaling_pattern(self):
+ # default is True
+ torch.manual_seed(0)
+
+ model = self.get_model()
+
+ # check scaling factor use_rslora=False with rank and alpha pattern
+ config = LoraConfig(
+ target_modules=["linear", "embed", "conv2d"],
+ rank_pattern={"embed": 9, "conv2d": 16},
+ alpha_pattern={"linear": 11, "conv2d": 13},
+ lora_alpha=17,
+ r=25,
+ use_rslora=False,
+ )
+ model = get_peft_model(model, config)
+
+ expected_scaling = {
+ "linear": config.alpha_pattern["linear"] / config.r,
+ "embed": config.lora_alpha / config.rank_pattern["embed"],
+ "conv2d": config.alpha_pattern["conv2d"] / config.rank_pattern["conv2d"],
+ }
+
+ assert model.linear.scaling["default"] == expected_scaling["linear"]
+ assert model.embed.scaling["default"] == expected_scaling["embed"]
+ assert model.conv2d.scaling["default"] == expected_scaling["conv2d"]
+
+ def test_lora_rslora_scaling_pattern(self):
+ # default is True
+ torch.manual_seed(0)
+
+ model = self.get_model()
+
+ # check scaling factor use_rslora=True with rank and alpha pattern
+ config = LoraConfig(
+ target_modules=["linear", "embed", "conv2d"],
+ rank_pattern={"embed": 9, "conv2d": 16},
+ alpha_pattern={"linear": 11, "conv2d": 13},
+ lora_alpha=17,
+ r=25,
+ use_rslora=True,
+ )
+ model = get_peft_model(model, config)
+
+ expected_scaling = {
+ "linear": config.alpha_pattern["linear"] / (config.r**0.5),
+ "embed": config.lora_alpha / (config.rank_pattern["embed"] ** 0.5),
+ "conv2d": config.alpha_pattern["conv2d"] / (config.rank_pattern["conv2d"] ** 0.5),
+ }
+
+ assert model.linear.scaling["default"] == expected_scaling["linear"]
+ assert model.embed.scaling["default"] == expected_scaling["embed"]
+ assert model.conv2d.scaling["default"] == expected_scaling["conv2d"]
+
+ def test_modules_to_save_targets_lora_layer_raises(self):
+ # There is no good reason to have auxiliary modules to target a LoRA layer. As auxiliary modules are applied
+ # *after* BaseTunerLayers, a possible way for this to happen accidentally is if the
+ # modules_to_save/trainable_token_indices coincide with the adapter name, e.g. if the adapter name is "foobar",
+ # we can have a module named model.base_model.model.self_attn.lora_A.foobar. If
+ # modules_to_save/trainable_token_indices is also "foobar", there would be a match.
+ # Note: Theoretically, a lot more PEFT methods support modules_to_save, so would have to be tested, but the code
+ # path is the same for all of them, so only testing LoRA.
+ model = self.get_model()
+
+ config = LoraConfig(
+ target_modules=["linear"],
+ modules_to_save=["foobar"],
+ )
+ msg = (
+ "You are trying to target a module with that is a child of "
+ ". This is almost certainly not the intended behavior. Please "
+ "ensure that the adapter name, 'foobar', does not conflict with any of the targeted modules."
+ )
+ with pytest.raises(ValueError, match=msg):
+ get_peft_model(model, config, adapter_name="foobar")
+
+ def test_trainable_token_indices_targets_lora_layer_raises(self):
+ # Same test as test_modules_to_save_targets_lora_layer_raises, but using trainable_token_indices
+ model = self.get_model()
+
+ # check scaling factor use_rslora=True with rank and alpha pattern
+ config = LoraConfig(target_modules=["embed"], trainable_token_indices={"foobar": [1, 2, 3]})
+ msg = (
+ "You are trying to target a module with that is a child "
+ "of . This is almost certainly not the intended behavior. Please "
+ "ensure that the adapter name, 'foobar', does not conflict with any of the targeted modules."
+ )
+ with pytest.raises(ValueError, match=msg):
+ get_peft_model(model, config, adapter_name="foobar")
+
+ @require_deterministic_for_xpu
+ def test_lora_use_dora_linear(self, data):
+ # check that dora is a no-op when initialized
+ torch.manual_seed(0)
+ model = self.get_model()
+ output_base, _, _ = model(data)
+
+ # check scaling factor use_rslora=True
+ config = LoraConfig(target_modules=["linear"], use_dora=True)
+ model = get_peft_model(model, config)
+
+ with model.disable_adapter():
+ output_disabled, _, _ = model(data)
+ output_dora, _, _ = model(data)
+
+ assert torch.allclose(output_base, output_disabled)
+ assert torch.allclose(output_base, output_dora)
+
+ @require_deterministic_for_xpu
+ def test_lora_use_dora_linear_init_false(self, data):
+ # with init_lora_weights=False, dora should not be a no-op
+ torch.manual_seed(0)
+ model = self.get_model()
+ output_base, _, _ = model(data)
+
+ # check scaling factor use_rslora=True
+ config = LoraConfig(target_modules=["linear"], use_dora=True, init_lora_weights=False)
+ model = get_peft_model(model, config)
+
+ with model.disable_adapter():
+ output_disabled, _, _ = model(data)
+ output_dora, _, _ = model(data)
+
+ assert torch.allclose(output_base, output_disabled)
+ assert not torch.allclose(output_base, output_dora)
+
+ def test_lora_use_dora_with_megatron_core_raises(self):
+ megatron_config = {"does-not": "matter-here"}
+ with pytest.raises(ValueError, match="DoRA does not support megatron_core"):
+ LoraConfig(target_modules=["linear"], use_dora=True, megatron_config=megatron_config)
+
+ @pytest.fixture
+ def mha_cls(self):
+ class ModelMha(nn.Module):
+ def __init__(self, kdim=None, vdim=None):
+ super().__init__()
+ self.mha = nn.MultiheadAttention(10, 2, kdim=kdim, vdim=vdim)
+ self.lin0 = nn.Linear(10, 2)
+ self.sm = nn.LogSoftmax(dim=-1)
+
+ def forward(self, X):
+ X = X.float()
+ X, _ = self.mha(X, X, X)
+ X = self.lin0(X)
+ X = self.sm(X)
+ return X
+
+ return ModelMha
+
+ def test_mha_load_init_model_first(self, mha_cls):
+ # This test used to fail and require a workaround, for more context, see:
+ # https://github.com/huggingface/peft/pull/1324#issuecomment-2252473980
+ # The workaround was that _restore_weights had to be called manually on lora.MHA layers in order to make loading
+ # the state dict work. With recent changes, this workaround is no longer required, so that test has been
+ # deleted.
+ inputs = torch.rand(10, 10, 10)
+ model = mha_cls()
+ config = LoraConfig(target_modules=["mha"], init_lora_weights=False)
+ model = get_peft_model(model, config).eval()
+ restore_state_dict = {k: v.detach().cpu() for k, v in model.state_dict().items()}
+
+ del model
+
+ model = mha_cls()
+ model = get_peft_model(model, config)
+ # the workaround used to be:
+ # for module in model.modules():
+ # if isinstance(module, peft.tuners.lora.layer.MultiheadAttention):
+ # module._restore_weights()
+ model(inputs)
+ model.load_state_dict(restore_state_dict)
+
+ def test_mha_with_separate_qkv_embed_raises(self, mha_cls):
+ # passing different kdim and vdim results in separate parameters for q, k, v, which is not supported (yet)
+ model = mha_cls(kdim=20, vdim=30)
+ config = LoraConfig(target_modules=["mha"])
+ msg = "Only same embed for query/key/value is supported as of now for MultiheadAttention"
+ with pytest.raises(ValueError, match=msg):
+ get_peft_model(model, config)
+
+ def test_mha_with_dora_raises(self, mha_cls):
+ model = mha_cls()
+ config = LoraConfig(target_modules=["mha"], use_dora=True)
+ msg = re.escape("MultiheadAttention does not support DoRA (yet), please set use_dora to False")
+ with pytest.raises(ValueError, match=msg):
+ get_peft_model(model, config)
+
+ def test_mha_exposes_attributes(self, mha_cls):
+ # MHA requires a bunch of attributes to be exposed, try to check them exhaustively here
+ model = mha_cls()
+ embed_dim = model.mha.embed_dim
+ kdim = model.mha.kdim
+ vdim = model.mha.vdim
+ qkv_same_embed_dim = model.mha._qkv_same_embed_dim
+ num_heads = model.mha.num_heads
+ dropout = model.mha.dropout
+ batch_first = model.mha.batch_first
+ head_dim = model.mha.head_dim
+ in_proj_weight = model.mha.in_proj_weight
+ in_proj_bias = model.mha.in_proj_bias
+ out_proj = model.mha.out_proj
+ bias_k = model.mha.bias_k
+ bias_v = model.mha.bias_v
+ add_zero_attn = model.mha.add_zero_attn
+
+ config = LoraConfig(target_modules=["mha"])
+ peft_model = get_peft_model(model, config)
+ assert peft_model.base_model.mha.embed_dim == embed_dim
+ assert peft_model.base_model.mha.kdim == kdim
+ assert peft_model.base_model.mha.vdim == vdim
+ assert peft_model.base_model.mha._qkv_same_embed_dim == qkv_same_embed_dim
+ assert peft_model.base_model.mha.num_heads == num_heads
+ assert peft_model.base_model.mha.dropout == dropout
+ assert peft_model.base_model.mha.batch_first == batch_first
+ assert peft_model.base_model.mha.head_dim == head_dim
+ if in_proj_weight is not None:
+ assert torch.allclose(peft_model.base_model.mha.in_proj_weight, in_proj_weight)
+ else:
+ assert peft_model.base_model.mha.in_proj_weight is None
+ if in_proj_bias is not None:
+ assert torch.allclose(peft_model.base_model.mha.in_proj_bias, in_proj_bias)
+ else:
+ assert peft_model.base_model.mha.in_proj_bias is None
+ assert peft_model.base_model.mha.out_proj is out_proj
+ if bias_k is not None:
+ assert torch.allclose(peft_model.base_model.mha.bias_k, bias_k)
+ else:
+ assert peft_model.base_model.mha.bias_k is None
+ if bias_v is not None:
+ assert torch.allclose(peft_model.base_model.mha.bias_v, bias_v)
+ else:
+ assert peft_model.base_model.mha.bias_v is None
+ assert peft_model.base_model.mha.add_zero_attn == add_zero_attn
+
+ def test_mha_merge_masks_method(self, mha_cls):
+ # MHA requires a merge_masks method to be exposed, check that it works
+ model = mha_cls()
+ config = LoraConfig(target_modules=["mha"])
+ peft_model = get_peft_model(model, config)
+
+ attn_mask = torch.randint(0, 2, (10, 10))
+ key_padding_mask = torch.randint(0, 2, (10, 10))
+ query = torch.rand(10, 10, 10)
+ merged_mask0, mask_type0 = model.mha.merge_masks(attn_mask, key_padding_mask, query)
+ merged_mask1, mask_type1 = peft_model.base_model.mha.merge_masks(attn_mask, key_padding_mask, query)
+
+ assert torch.allclose(merged_mask0, merged_mask1)
+ assert mask_type0 == mask_type1
+
+ @pytest.mark.parametrize("bias", ["none", "all", "lora_only", "invalid"])
+ def test_lora_with_bias_argument(self, bias):
+ model = self.get_model()
+ config = LoraConfig(target_modules=["linear", "conv2d"], bias=bias)
+
+ if bias == "invalid":
+ with pytest.raises(NotImplementedError):
+ get_peft_model(model, config)
+ return
+
+ model = get_peft_model(model, config) # does not raise
+ for name, param in model.named_parameters():
+ if not name.endswith("bias"):
+ continue
+ if bias == "none":
+ assert param.requires_grad is False
+ elif bias == "all":
+ assert param.requires_grad is True
+ elif bias == "lora_only":
+ # only layers targeted with target_modules
+ assert param.requires_grad is ("linear" in name) or ("conv2d" in name)
+
+ def test_lora_with_bias_extra_params(self):
+ # lora with lora_bias=True
+ model = self.get_model()
+ config = LoraConfig(target_modules=["linear", "conv2d"], lora_bias=False)
+ model_no_bias = get_peft_model(model, config)
+
+ model = self.get_model()
+ config = LoraConfig(target_modules=["linear", "conv2d"], lora_bias=True)
+ model_bias = get_peft_model(model, config)
+
+ # check that bias for LoRA B is set
+ assert model_no_bias.base_model.model.linear.lora_B["default"].bias is None
+ assert model_bias.base_model.model.linear.lora_B["default"].bias.shape == (1000,)
+ assert model_no_bias.base_model.model.conv2d.lora_B["default"].bias is None
+ assert model_bias.base_model.model.conv2d.lora_B["default"].bias.shape == (100,)
+
+ # check that the same params are present except for the extra bias term
+ params_no_bias = {name for name, _ in model_no_bias.named_parameters()}
+ params_bias = {name for name, _ in model_bias.named_parameters()}
+ extra_params = {
+ "base_model.model.linear.lora_B.default.bias",
+ "base_model.model.conv2d.lora_B.default.bias",
+ }
+ assert params_bias - params_no_bias == extra_params
+ assert params_no_bias.issubset(params_bias)
+
+ def test_lora_with_bias_embedding_raises(self):
+ # lora with lora_bias=True is not supported for embedding layers
+ model = self.get_model()
+ config = LoraConfig(target_modules=["embed"], lora_bias=True)
+ msg = "lora_bias=True is not supported for Embedding"
+ with pytest.raises(ValueError, match=msg):
+ get_peft_model(model, config)
+
+ @pytest.mark.parametrize(
+ "extra_kwargs",
+ [
+ {"use_dora": True},
+ {"init_lora_weights": "eva"},
+ {"init_lora_weights": "gaussian"},
+ {"init_lora_weights": "loftq", "loftq_config": LoftQConfig()},
+ {"init_lora_weights": "olora"},
+ {"init_lora_weights": "pissa"},
+ {"init_lora_weights": "pissa_niter_3"},
+ {"init_lora_weights": "orthogonal"},
+ ],
+ )
+ def test_lora_with_bias_incompatible_arguments(self, extra_kwargs):
+ # some arguments don't work in conjunction with lora_bias and should raise
+ # just check the common chunk of the error message
+ msg = "The argument lora_bias=True is"
+ with pytest.raises(ValueError, match=msg):
+ LoraConfig(target_modules=["linear"], lora_bias=True, **extra_kwargs)
+
+ def test_lora_linear_with_bias_when_base_layer_has_no_bias_warns(self):
+ model = self.get_model(bias=False)
+ config = LoraConfig(target_modules=["linear"], lora_bias=True)
+ msg = re.escape("`lora_bias=True` was passed but the targeted layer of type Linear has no bias")
+ with pytest.warns(PeftWarning, match=msg):
+ get_peft_model(model, config)
+
+ def test_lora_conv2d_with_bias_when_base_layer_has_no_bias_warns(self):
+ model = self.get_model(bias=False)
+ config = LoraConfig(target_modules=["conv2d"], lora_bias=True)
+ msg = re.escape("`lora_bias=True` was passed but the targeted layer of type Conv2d has no bias")
+ with pytest.warns(PeftWarning, match=msg):
+ get_peft_model(model, config)
+
+ def test_lora_incompatible_mamba_modules(self):
+ # Ensure LoRA raises an error when applying to forbidden modules
+ # ('out_proj', 'conv1d') in Mamba-based architectures like Falcon-Mamba tiny.
+ model = AutoModelForCausalLM.from_pretrained("tiiuae/falcon-mamba-tiny-dev")
+
+ config = LoraConfig(
+ task_type="CAUSAL_LM",
+ target_modules=["out_proj", "conv1d"], # Forbidden modules for Mamba-based models
+ )
+ msg = "is incompatible with Mamba-based models"
+ with pytest.raises(ValueError, match=msg):
+ get_peft_model(model, config)
+
+ def get_model_conv2d_groups(self):
+ class ModelConv2DGroups(nn.Module):
+ """For testing when groups argument is used in conv layer"""
+
+ def __init__(self):
+ super().__init__()
+ self.conv2d = nn.Conv2d(16, 32, 3, padding=1, groups=2)
+ self.relu = nn.ReLU()
+ self.flat = nn.Flatten()
+ self.lin0 = nn.Linear(12800, 2)
+ self.sm = nn.LogSoftmax(dim=-1)
+ self.dtype = torch.float
+
+ def forward(self, X):
+ # This is ignoring input since main usage is for checking raising of error when peft is applied
+ X = torch.arange(9 * 16 * 20 * 20).view([9, 16, 20, 20]).to(self.conv2d.weight.device)
+ X = X.to(self.dtype)
+ X = self.conv2d(X)
+ X = self.relu(X)
+ X = self.flat(X)
+ X = self.lin0(X)
+ X = self.sm(X)
+ return X
+
+ return ModelConv2DGroups().eval().to(self.torch_device)
+
+ @pytest.mark.parametrize(
+ "config_cls, config_kwargs",
+ [
+ pytest.param(LoraConfig, {"r": 8, "target_modules": ["conv2d"]}, id="lora with rank divisible by groups"),
+ pytest.param(LoraConfig, {"r": 2, "target_modules": ["conv2d"]}, id="lora with rank equal to groups"),
+ pytest.param(
+ LoraConfig, {"r": 1, "target_modules": ["conv2d"]}, id="lora with rank not divisible by groups"
+ ),
+ pytest.param(
+ LoraConfig,
+ {"r": 8, "target_modules": ["conv2d"], "use_dora": True},
+ id="dora with rank divisible by groups",
+ ),
+ pytest.param(
+ LoraConfig,
+ {"r": 2, "target_modules": ["conv2d"], "use_dora": True},
+ id="dora with rank equal to groups",
+ ),
+ pytest.param(
+ LoraConfig,
+ {"r": 1, "target_modules": ["conv2d"], "use_dora": True},
+ id="dora with rank not divisible by groups",
+ ),
+ ],
+ )
+ def test_error_raised_if_rank_not_divisible_by_groups(self, config_cls, config_kwargs):
+ # This test checks if error is raised when rank is not divisible by groups for conv layer since
+ # currently, support is limited to conv layers where the rank is divisible by groups in lora and dora
+ base_model = self.get_model_conv2d_groups()
+ peft_config = config_cls(**config_kwargs)
+ r = config_kwargs["r"]
+ base_layer = base_model.conv2d
+ groups = base_layer.groups
+ if r % groups != 0:
+ with pytest.raises(
+ ValueError,
+ match=(
+ f"Targeting a {base_layer.__class__.__name__} with groups={base_layer.groups} and rank {r}. "
+ "Currently, support is limited to conv layers where the rank is divisible by groups. "
+ "Either choose a different rank or do not target this specific layer."
+ ),
+ ):
+ peft_model = get_peft_model(base_model, peft_config)
+ else:
+ # No error should be raised
+ peft_model = get_peft_model(base_model, peft_config)
+
+ def test_target_module_and_target_parameter_on_same_layer(self):
+ # When targeting an nn.Parameter with LoRA using target_parameters, ensure that this is not already another LoRA
+ # layer (i.e. avoid double wrapping).
+ class MyModule(nn.Module):
+ def __init__(self):
+ super().__init__()
+ self.linear = nn.Linear(10, 10)
+
+ base_model = MyModule()
+ config = LoraConfig(target_modules=["linear"], target_parameters=["linear.weight"])
+ msg = "Trying to wrap an `nn.Parameter` of layer 'linear' of type Linear, which is not a valid target."
+ with pytest.raises(ValueError, match=msg):
+ get_peft_model(base_model, config)
+
+ @pytest.mark.parametrize("target_parameters", [["linear"], ["foobar"], ["foobar.weight"], ["foo", "bar"]])
+ @pytest.mark.parametrize("target_modules", [None, [], ""])
+ def test_valid_no_target_module_nor_target_parameter_match_raises(self, target_parameters, target_modules):
+ model = self.get_model()
+ config = LoraConfig(target_modules=target_modules, target_parameters=target_parameters)
+ msg = re.escape(
+ "No `target_modules` passed but also no `target_parameters` found. Please check the values for "
+ "these arguments."
+ )
+ with pytest.raises(ValueError, match=msg):
+ get_peft_model(model, config)
+
+ def test_target_parameters_wrong_type_raises(self):
+ # Check that target_parameters being a string raises a useful error message -- this is an easy mistake to make
+ # because strings are allowed for target_modules
+ model = self.get_model()
+ msg = "`target_parameters` must be a list of strings or None."
+ with pytest.raises(TypeError, match=msg):
+ LoraConfig(target_parameters="linear.weight")
+
+ def test_valid_target_parameters_invalid_target_modules_warns(self):
+ model = self.get_model()
+ config = LoraConfig(target_modules=["foobar"], target_parameters=["linear.weight"])
+ msg = re.escape("target_modules={'foobar'} were set but no module was matched.")
+ with pytest.warns(RuntimeWarning, match=msg):
+ get_peft_model(model, config)
+
+ def test_valid_target_modules_invalid_target_parameters_warns(self):
+ model = self.get_model()
+ config = LoraConfig(target_modules=["linear"], target_parameters=["foobar.weight"])
+ msg = re.escape("target_parameters=['foobar.weight'] were set but no parameter was matched.")
+ with pytest.warns(RuntimeWarning, match=msg):
+ get_peft_model(model, config)
+
+ def test_adding_multiple_adapters_with_target_parameters_raises(self):
+ model = self.get_model()
+ config = LoraConfig(target_modules=[], target_parameters=["linear.weight"])
+ model = get_peft_model(model, config)
+ msg = re.escape("only one LoRA adapter per model with `target_parameters` is allowed")
+ with pytest.raises(ValueError, match=msg):
+ model.add_adapter(adapter_name="other", peft_config=config)
+
+ def test_loading_loading_adapters_with_target_parameters_raises(self, tmp_path):
+ model = self.get_model()
+ config = LoraConfig(target_modules=[], target_parameters=["linear.weight"])
+ model = get_peft_model(model, config)
+ model.save_pretrained(tmp_path)
+
+ model = self.get_model()
+ model = PeftModel.from_pretrained(model, tmp_path)
+ msg = re.escape("only one LoRA adapter per model with `target_parameters` is allowed")
+ with pytest.raises(ValueError, match=msg):
+ model.load_adapter(tmp_path, adapter_name="other")
+
+ def test_multiple_configs_with_bias_raises(self, tmp_path):
+ # There cannot be more than one config with bias != "none".
+ # Note: This would need to be tested for all PEFT methods that support the bias parameter, but as this method
+ # comes from BaseTuner, it's fine to only check LoRA.
+ model = self.get_model()
+ config0 = LoraConfig(target_modules=["linear"], bias="all")
+ model = get_peft_model(model, config0)
+
+ config1 = LoraConfig(target_modules=["linear"], bias="lora_only")
+ msg = "supports only 1 adapter with bias. When using multiple adapters"
+ with pytest.raises(ValueError, match=msg):
+ model.add_adapter("other", config1)
+
+ # the invalid peft config was not added
+ assert len(model.peft_config) == 1
+
+ # it's okay to add a config with bias="none" (the default)
+ config2 = LoraConfig(target_modules=["linear"], bias="none")
+ model.add_adapter("other", config2) # does not raise
+
+
+class TestLokrInitialization:
+ torch_device = infer_device()
+
+ def get_model(self):
+ class MyModule(nn.Module):
+ def __init__(self):
+ super().__init__()
+ # Choose a large weight so that averages are close to expected values.
+ self.linear = nn.Linear(1000, 1000)
+ self.conv2d = nn.Conv2d(100, 100, 3)
+
+ def forward(self, x):
+ x_4d = x.flatten().reshape(1, 100, 10, 10)
+ return self.linear(x), self.conv2d(x_4d)
+
+ return MyModule().eval().to(self.torch_device)
+
+ @pytest.fixture
+ def data(self):
+ return torch.rand(10, 1000).to(self.torch_device)
+
+ @require_deterministic_for_xpu
+ def test_lokr_linear_init_default(self, data):
+ torch.manual_seed(0)
+
+ model = self.get_model()
+ output_before = model(data)[0]
+ config = LoKrConfig(target_modules=["linear"])
+ model = get_peft_model(model, config)
+ output_after = model(data)[0]
+
+ assert torch.allclose(output_before, output_after)
+
+ def test_lokr_linear_init_false(self, data):
+ torch.manual_seed(0)
+
+ model = self.get_model()
+ output_before = model(data)[0]
+ config = LoKrConfig(target_modules=["linear"], init_weights=False)
+ model = get_peft_model(model, config)
+ output_after = model(data)[0]
+
+ assert not torch.allclose(output_before, output_after)
+
+ @require_deterministic_for_xpu
+ def test_lokr_linear_init_lycoris(self, data):
+ torch.manual_seed(0)
+
+ model = self.get_model()
+ output_before = model(data)[0]
+ config = LoKrConfig(target_modules=["linear"], init_weights="lycoris")
+ model = get_peft_model(model, config)
+ output_after = model(data)[0]
+
+ assert torch.allclose(output_before, output_after)
+
+ def test_lokr_conv2d_init_default(self, data):
+ torch.manual_seed(0)
+
+ model = self.get_model()
+ output_before = model(data)[1]
+ config = LoKrConfig(target_modules=["conv2d"])
+ model = get_peft_model(model, config)
+ output_after = model(data)[1]
+
+ assert torch.allclose(output_before, output_after)
+
+ def test_lokr_conv2d_init_false(self, data):
+ torch.manual_seed(0)
+
+ model = self.get_model()
+ output_before = model(data)[1]
+ config = LoKrConfig(target_modules=["conv2d"], init_weights=False)
+ model = get_peft_model(model, config)
+ output_after = model(data)[1]
+
+ assert not torch.allclose(output_before, output_after)
+
+ def test_lokr_conv2d_init_lycoris(self, data):
+ torch.manual_seed(0)
+
+ model = self.get_model()
+ output_before = model(data)[1]
+ config = LoKrConfig(target_modules=["conv2d"], init_weights="lycoris")
+ model = get_peft_model(model, config)
+ output_after = model(data)[1]
+
+ assert torch.allclose(output_before, output_after)
+
+
+class TestAdaLoraInitialization:
+ torch_device = infer_device()
+
+ def test_adalora_target_modules_set(self):
+ config = AdaLoraConfig(target_modules=["linear", "embed", "conv2d"], total_step=1)
+ assert config.target_modules == {"linear", "embed", "conv2d"}
+
+ def test_adalora_use_dora_raises(self):
+ with pytest.raises(ValueError, match="ADALORA does not support DoRA"):
+ AdaLoraConfig(use_dora=True, total_step=1)
+
+ def test_adalora_loftq_config_raises(self):
+ with pytest.raises(ValueError, match="ADALORA does not support LOFTQ"):
+ AdaLoraConfig(init_lora_weights="loftq", loftq_config={"loftq": "config"}, total_step=1)
+
+ def get_model(self):
+ class MyModule(nn.Module):
+ def __init__(self):
+ super().__init__()
+ # choose a large weight so that averages are close to expected values
+ self.linear = nn.Linear(1000, 1000)
+
+ def forward(self, x):
+ return self.linear(x)
+
+ return MyModule().eval().to(self.torch_device)
+
+ @pytest.fixture
+ def data(self):
+ return torch.rand(10, 1000).to(self.torch_device)
+
+ @require_deterministic_for_xpu
+ def test_adalora_default_init_identity(self, data):
+ # default is True
+ torch.manual_seed(0)
+
+ model = self.get_model()
+ output_before = model(data)
+ config = AdaLoraConfig(target_modules=["linear"], total_step=1)
+ model = get_peft_model(model, config)
+ output_after = model(data)
+ assert torch.allclose(output_before, output_after)
+
+
+class TestPromptTuningInitialization:
+ torch_device = infer_device()
+
+ def get_model(self):
+ class MyModule(nn.Module):
+ def __init__(self):
+ super().__init__()
+ # choose a large weight so that averages are close to expected values
+ self.linear = nn.Linear(1000, 1000)
+ self.embed = nn.Embedding(1000, 1000)
+ self.conv2d = nn.Conv2d(100, 100, 3)
+
+ def forward(self, x):
+ x_int = (100 * x).int()
+ x_4d = x.flatten().reshape(1, 100, 10, 10)
+ return self.linear(x), self.embed(x_int), self.conv2d(x_4d)
+
+ return MyModule().eval().to(self.torch_device)
+
+ def test_use_prompt_tuning_init_text_raises(self):
+ with pytest.raises(ValueError, match="When prompt_tuning_init='TEXT', tokenizer_name_or_path can't be None"):
+ PromptTuningConfig(prompt_tuning_init="TEXT", prompt_tuning_init_text="prompt tuning init text")
+ with pytest.raises(ValueError, match="When prompt_tuning_init='TEXT', prompt_tuning_init_text can't be None"):
+ PromptTuningConfig(prompt_tuning_init="TEXT", tokenizer_name_or_path="t5-base")
+
+
+class TestVeraInitialization:
+ torch_device = infer_device()
+
+ def get_model(self):
+ class MLP(nn.Module):
+ def __init__(self, bias=True):
+ super().__init__()
+ self.lin0 = nn.Linear(10, 20, bias=bias)
+ self.lin1 = nn.Linear(20, 2, bias=bias)
+
+ def forward(self, X):
+ X = self.lin0(X)
+ X = self.lin1(X)
+ return X
+
+ return MLP().to(self.torch_device)
+
+ def test_vera_mixing_save_projection_raises(self):
+ # it is unclear what the right thing to do would be if some adapters save the projection weights and some don't
+ # so we better raise an error
+
+ config0 = VeraConfig(target_modules=["lin0"], init_weights=False, save_projection=True)
+ model = self.get_model()
+ model = get_peft_model(model, config0)
+ config1 = VeraConfig(target_modules=["lin0"], init_weights=False, save_projection=False)
+ msg = re.escape(
+ "VeRA projection weights must be saved for all adapters or none, but got multiple different values: "
+ "[False, True]"
+ )
+ with pytest.raises(ValueError, match=msg):
+ model.add_adapter("other", config1)
+
+ def test_vera_add_second_adapter_with_incompatible_input_shape(self):
+ config0 = VeraConfig(target_modules=["lin0"], r=8)
+ config1 = VeraConfig(target_modules=["lin1"])
+
+ base_model = self.get_model()
+ lin0_in_feat = base_model.lin0.in_features
+ lin1_in_feat = base_model.lin1.in_features
+ model = get_peft_model(base_model, config0)
+ # not full message but enough to identify the error
+ msg = f"vera_A has a size of {lin0_in_feat} but {lin1_in_feat} or greater is required"
+ with pytest.raises(ValueError, match=msg):
+ model.add_adapter("other", config1)
+
+ def test_vera_add_second_adapter_with_higher_rank(self):
+ rank0 = 123
+ rank1 = 456
+ config0 = VeraConfig(target_modules=["lin0"], r=rank0)
+ # second adapter has higher rank
+ config1 = VeraConfig(target_modules=["lin0"], r=rank1)
+
+ model = get_peft_model(self.get_model(), config0)
+ # not full message but enough to identify the error
+ msg = f"vera_A has a size of {rank0} but {rank1} or greater is required"
+ with pytest.raises(ValueError, match=msg):
+ model.add_adapter("other", config1)
+
+
+class TestVBLoraInitialization:
+ torch_device = infer_device()
+
+ def get_model(self):
+ class MLP(nn.Module):
+ def __init__(self, bias=True):
+ super().__init__()
+ self.lin0 = nn.Linear(10, 30, bias=bias)
+ self.lin1 = nn.Linear(30, 2, bias=bias)
+
+ def forward(self, X):
+ X = self.lin0(X)
+ X = self.lin1(X)
+ return X
+
+ return MLP().to(self.torch_device)
+
+ def test_vblora_with_incompatible_vector_length_with_in_features(self):
+ vector_length = 3
+ model = self.get_model()
+ config = VBLoRAConfig(target_modules=["lin0"], vector_length=vector_length)
+ msg = f"`in_features` {model.lin0.in_features} must be divisible by `vector_length` {vector_length}"
+ with pytest.raises(ValueError, match=msg):
+ get_peft_model(model, config)
+
+ def test_vblora_with_incompatible_vector_length_with_out_features(self):
+ vector_length = 3
+ model = self.get_model()
+ config = VBLoRAConfig(target_modules=["lin1"], vector_length=vector_length)
+ msg = f"`out_features` {model.lin1.out_features} must be divisible by `vector_length` {vector_length}"
+ with pytest.raises(ValueError, match=msg):
+ get_peft_model(model, config)
+
+
+class TestC3AInitialization:
+ torch_device = infer_device()
+
+ def get_model(self):
+ class MLP(nn.Module):
+ def __init__(self, bias=True):
+ super().__init__()
+ self.lin0 = nn.Linear(10, 30, bias=bias)
+ self.lin1 = nn.Linear(30, 2, bias=bias)
+
+ def forward(self, X):
+ X = self.lin0(X)
+ X = self.lin1(X)
+ return X
+
+ return MLP().to(self.torch_device)
+
+ def test_c3a_with_incompatible_block_size_with_in_features(self):
+ block_size = 3
+ model = self.get_model()
+ config = C3AConfig(target_modules=["lin0"], block_size=block_size)
+ msg = f"The block size should be a factor of the input size. However, the input size is {model.lin0.in_features} and the block size is {block_size}"
+ with pytest.raises(ValueError, match=msg):
+ get_peft_model(model, config)
+
+ def test_c3a_with_incompatible_block_size_with_out_features(self):
+ block_size = 3
+ model = self.get_model()
+ config = C3AConfig(target_modules=["lin1"], block_size=block_size)
+ msg = f"The block size should be a factor of the output size. However, the output size is {model.lin1.out_features} and the block size is {block_size}"
+ with pytest.raises(ValueError, match=msg):
+ get_peft_model(model, config)
+
+
+class TestWaveFTInitialization:
+ """Test class to check the initialization of WaveFT adapters."""
+
+ torch_device = infer_device()
+
+ def get_model(self):
+ class MyModule(nn.Module):
+ def __init__(self):
+ super().__init__()
+ # Choose a large weight so that averages are close to expected values.
+ self.linear = nn.Linear(1000, 1000)
+ self.conv2d = nn.Conv2d(100, 100, 3)
+
+ def forward(self, x):
+ x_4d = x.flatten().reshape(1, 100, 10, 10)
+ return self.linear(x), self.conv2d(x_4d)
+
+ return MyModule().eval().to(self.torch_device)
+
+ @pytest.fixture
+ def data(self):
+ return torch.rand(10, 1000).to(self.torch_device)
+
+ @require_deterministic_for_xpu
+ def test_waveft_linear_init_default(self, data):
+ # Default initialization should result in no change to output (zeros initialization)
+ torch.manual_seed(0)
+
+ model = self.get_model()
+ output_before = model(data)[0]
+ config = WaveFTConfig(target_modules=["linear"], n_frequency=100, init_weights=True)
+ model = get_peft_model(model, config)
+ output_after = model(data)[0]
+
+ assert torch.allclose(output_before, output_after, atol=1e-6)
+
+ def test_waveft_linear_init_false(self, data):
+ # With init_weights=False, output should change (random initialization)
+ torch.manual_seed(0)
+
+ model = self.get_model()
+ output_before = model(data)[0]
+ config = WaveFTConfig(target_modules=["linear"], n_frequency=100, init_weights=False)
+ model = get_peft_model(model, config)
+ output_after = model(data)[0]
+
+ assert not torch.allclose(output_before, output_after, atol=1e-6)
+
+ @require_deterministic_for_xpu
+ def test_waveft_linear_with_scaling(self, data):
+ # Test that scaling parameter affects output correctly
+ torch.manual_seed(0)
+
+ model = self.get_model()
+ output_before = model(data)[0]
+ config = WaveFTConfig(target_modules=["linear"], n_frequency=100, init_weights=False, scaling=10.0)
+ model = get_peft_model(model, config)
+ output_after = model(data)[0]
+
+ assert not torch.allclose(output_before, output_after, atol=1e-6)
+
+ @require_deterministic_for_xpu
+ def test_waveft_different_wavelet_families(self, data):
+ # Test different wavelet families
+ torch.manual_seed(0)
+
+ model1 = self.get_model()
+ config1 = WaveFTConfig(target_modules=["linear"], n_frequency=100, wavelet_family="db1", init_weights=False)
+ model1 = get_peft_model(model1, config1)
+ output1 = model1(data)[0]
+
+ torch.manual_seed(0)
+ model2 = self.get_model()
+ config2 = WaveFTConfig(target_modules=["linear"], n_frequency=100, wavelet_family="sym2", init_weights=False)
+ model2 = get_peft_model(model2, config2)
+ output2 = model2(data)[0]
+
+ # Different wavelet families should produce different results
+ assert not torch.allclose(output1, output2, atol=1e-6)
+
+ @require_deterministic_for_xpu
+ def test_waveft_use_idwt_flag(self, data):
+ # Test use_idwt flag
+ torch.manual_seed(0)
+
+ model1 = self.get_model()
+ config1 = WaveFTConfig(target_modules=["linear"], n_frequency=100, use_idwt=True, init_weights=False)
+ model1 = get_peft_model(model1, config1)
+ output1 = model1(data)[0]
+
+ torch.manual_seed(0)
+ model2 = self.get_model()
+ config2 = WaveFTConfig(target_modules=["linear"], n_frequency=100, use_idwt=False, init_weights=False)
+ model2 = get_peft_model(model2, config2)
+ output2 = model2(data)[0]
+
+ # Different use_idwt settings should produce different results
+ assert not torch.allclose(output1, output2, atol=1e-6)
+
+ def test_waveft_non_positive_n_frequency_raises(self):
+ # Test that n_frequency <= 0 raises appropriate error
+ model = self.get_model()
+
+ # Test with n_frequency = 0
+ n_frequency = 0
+ msg = f"`n_frequency` should be a positive integer value but the value passed is {n_frequency}"
+ with pytest.raises(ValueError, match=re.escape(msg)):
+ config = WaveFTConfig(target_modules=["linear"], n_frequency=n_frequency)
+ get_peft_model(model, config)
+
+ # Test with negative n_frequency
+ n_frequency = -1
+ msg = f"`n_frequency` should be a positive integer value but the value passed is {n_frequency}"
+ with pytest.raises(ValueError, match=re.escape(msg)):
+ config = WaveFTConfig(target_modules=["linear"], n_frequency=n_frequency)
+ get_peft_model(model, config)
+
+ def test_waveft_excessive_n_frequency_raises(self):
+ # Test that n_frequency > in_features * out_features raises appropriate error
+ model = self.get_model()
+
+ # The model has a linear layer with 1000 in_features and 1000 out_features
+ # So the maximum n_frequency should be 1000 * 1000 = 1,000,000
+ max_allowed = 1000 * 1000
+ n_frequency = max_allowed + 1
+ msg = (
+ f"`n_frequency` should be less than or equal to the product of the input and output dimensions "
+ f"but the value passed is {n_frequency} and the product is {max_allowed}"
+ )
+ with pytest.raises(ValueError, match=re.escape(msg)):
+ config = WaveFTConfig(target_modules=["linear"], n_frequency=n_frequency)
+ get_peft_model(model, config)
+
+ def test_waveft_n_frequency_pattern(self, data):
+ # Test n_frequency_pattern functionality
+ torch.manual_seed(0)
+
+ model = self.get_model()
+ config = WaveFTConfig(
+ target_modules=["linear"], n_frequency=50, n_frequency_pattern={"linear": 100}, init_weights=True
+ )
+ model = get_peft_model(model, config)
+
+ # Check that the pattern was applied
+ waveft_layer = model.base_model.model.linear
+ assert hasattr(waveft_layer, "waveft_n_frequency")
+ assert waveft_layer.waveft_n_frequency["default"] == 100
+
+ def test_waveft_layers_pattern_without_layers_to_transform_raises(self):
+ # Test that when layers_pattern is specified, layers_to_transform must also be specified
+ msg = "When `layers_pattern` is specified, `layers_to_transform` must also be specified."
+ with pytest.raises(ValueError, match=re.escape(msg)):
+ WaveFTConfig(target_modules=["linear"], layers_pattern=["layers"], layers_to_transform=None)
+
+ def test_waveft_invalid_wavelet_family_raises(self):
+ # Test that invalid wavelet families raise appropriate errors
+ invalid_family = "invalid_wavelet"
+ msg = f"Wavelet family {invalid_family} not supported. Supported wavelet families are:"
+ with pytest.raises(ValueError, match=re.escape(msg)):
+ WaveFTConfig(target_modules=["linear"], wavelet_family=invalid_family)
+
+
+class TestRoadInitialization:
+ torch_device = infer_device()
+
+ def get_model(self):
+ class MLP(nn.Module):
+ def __init__(self, bias=True):
+ super().__init__()
+ self.lin0 = nn.Linear(10, 30, bias=bias)
+ self.lin1 = nn.Linear(30, 2, bias=bias)
+
+ def forward(self, X):
+ X = self.lin0(X)
+ X = self.lin1(X)
+ return X
+
+ return MLP().to(self.torch_device)
+
+ def get_conv2d_model(self):
+ class MyModule(nn.Module):
+ def __init__(self):
+ super().__init__()
+ # choose a large weight so that averages are close to expected values
+ self.linear = nn.Linear(1000, 1000)
+ self.embed = nn.Embedding(1000, 1000)
+ self.conv2d = nn.Conv2d(100, 100, 3)
+
+ def forward(self, x):
+ x_int = (100 * x).int()
+ x_4d = x.flatten().reshape(1, 100, 10, 10)
+ return self.linear(x), self.embed(x_int), self.conv2d(x_4d)
+
+ return MyModule().eval().to(self.torch_device)
+
+ def test_road_default_initialization(self):
+ torch.manual_seed(0)
+ model = self.get_model()
+ config = RoadConfig(target_modules=["lin0"], group_size=2)
+ model = get_peft_model(model, config)
+ weight_alpha = model.lin0.road_alpha["default"].data
+ weight_theta = model.lin0.road_theta["default"].data
+ torch.allclose(weight_alpha, torch.ones_like(weight_alpha))
+ torch.allclose(weight_theta, torch.zeros_like(weight_theta))
+
+ def test_road_with_odd_group_size(self):
+ group_size = 3 # odd values are not allowed
+ msg = f"The group_size must be divisible by 2 when using RoadLayer, but got {group_size}."
+ with pytest.raises(ValueError, match=re.escape(msg)):
+ RoadConfig(group_size=group_size)
+
+ def test_road_with_too_large_group_size(self):
+ group_size = 64 # larger than out_features
+ msg = (
+ f"The out_features of the base layer must be divisible by group_size ({group_size}) when using RoadLayer."
+ )
+ model = self.get_model()
+ config = RoadConfig(target_modules=["lin0"], group_size=group_size)
+ with pytest.raises(ValueError, match=re.escape(msg)):
+ get_peft_model(model, config)
+
+ def test_road_with_incompatible_group_size_with_out_features(self):
+ group_size = 4 # even, but 30 does not divide by 4
+ model = self.get_model()
+ config = RoadConfig(target_modules=["lin0"], group_size=group_size)
+ msg = (
+ f"The out_features of the base layer must be divisible by group_size ({group_size}) when using RoadLayer."
+ )
+ with pytest.raises(ValueError, match=re.escape(msg)):
+ get_peft_model(model, config)
+
+ def test_road_with_conv2d_layer(self):
+ model = self.get_conv2d_model()
+ config = RoadConfig(target_modules=["conv2d"], group_size=2)
+ msg = "Target module Conv2d(100, 100, kernel_size=(3, 3), stride=(1, 1)) is not supported. Currently, only the following modules are supported: `torch.nn.Linear`."
+ with pytest.raises(ValueError, match=re.escape(msg)):
+ get_peft_model(model, config)
+
+
+class TestNoInfiniteRecursionDeepspeed:
+ # see #1892 for details
+ classes = [
+ PeftModel,
+ PeftMixedModel,
+ PeftModelForSequenceClassification,
+ PeftModelForQuestionAnswering,
+ PeftModelForTokenClassification,
+ PeftModelForCausalLM,
+ PeftModelForSeq2SeqLM,
+ PeftModelForFeatureExtraction,
+ ]
+
+ @pytest.fixture
+ def wrap_init(self):
+ # emulates the wrapper from DeepSpeed
+ import functools
+
+ def decorator(f):
+ @functools.wraps(f)
+ def wrapper(self, *args, **kwargs):
+ hasattr(self, "abc") # any hasattr will do
+ f(self, *args, **kwargs)
+
+ return wrapper
+
+ return decorator
+
+ @pytest.fixture
+ def model(self):
+ class MyModule(nn.Module):
+ def __init__(self):
+ super().__init__()
+ self.linear = nn.Linear(10, 10)
+ # to emulate LMs:
+ self.prepare_inputs_for_generation = None
+ self._prepare_encoder_decoder_kwargs_for_generation = None
+
+ return MyModule()
+
+ @pytest.mark.parametrize("cls", classes)
+ def test_no_infinite_recursion(self, cls, model, wrap_init):
+ original_init = cls.__init__
+ try:
+ cls.__init__ = wrap_init(cls.__init__)
+ # this would trigger an infinite loop before the fix in 1892
+ cls(model, LoraConfig(target_modules=["linear"]))
+ finally:
+ # ensure there are no side effects of this test
+ cls.__init__ = original_init
+
+
+class TestLoadAdapterOfflineMode:
+ base_model = "hf-internal-testing/tiny-random-OPTForCausalLM"
+ peft_model_id = "peft-internal-testing/tiny-OPTForCausalLM-lora"
+
+ # make sure that PEFT honors offline mode
+ @contextmanager
+ def hub_offline_ctx(self):
+ # this is required to simulate offline mode, setting the env var dynamically inside the test does not work
+ # because the value is checked only once at the start of the session
+
+ if reset_sessions is None:
+ # this means we're using huggingface_hub >= 1.0.0, there is no need to call reset_sessions() anymore
+ with patch("huggingface_hub.constants.HF_HUB_OFFLINE", True):
+ yield
+ else:
+ # in huggingface_hub < 1.0.0, it's necessary to reset the session
+ # TODO: remove once huggingface_hub < 1.0.0 is no longer supported
+ with patch("huggingface_hub.constants.HF_HUB_OFFLINE", True):
+ reset_sessions()
+ yield
+ reset_sessions()
+
+ def test_load_from_hub_then_offline_model(self):
+ # this uses LoRA but it's the same mechanism for other methods
+ base_model = AutoModelForCausalLM.from_pretrained(self.base_model)
+
+ # first ensure that the adapter model has been downloaded
+ PeftModel.from_pretrained(base_model, self.peft_model_id)
+
+ del base_model
+
+ base_model = AutoModelForCausalLM.from_pretrained(self.base_model)
+ with self.hub_offline_ctx():
+ # does not raise
+ PeftModel.from_pretrained(base_model, self.peft_model_id)
+
+ @pytest.fixture
+ def changed_default_cache_dir(self, tmp_path, monkeypatch):
+ # ensure that this test does not interact with other tests that may use the HF cache
+ monkeypatch.setattr("huggingface_hub.constants.HF_HOME", tmp_path)
+ monkeypatch.setattr("huggingface_hub.constants.HF_HUB_CACHE", tmp_path / "hub")
+ monkeypatch.setattr("huggingface_hub.constants.HF_TOKEN_PATH", tmp_path / "token")
+
+ def load_checkpoints(self, cache_dir):
+ # download model and lora checkpoint to a specific cache dir
+ snapshot_download(self.base_model, cache_dir=cache_dir)
+ snapshot_download(self.peft_model_id, cache_dir=cache_dir)
+
+ def test_load_checkpoint_offline_non_default_cache_dir(self, changed_default_cache_dir, tmp_path):
+ # See #2373 for context
+ self.load_checkpoints(tmp_path)
+ with self.hub_offline_ctx():
+ base_model = AutoModelForCausalLM.from_pretrained(self.base_model, cache_dir=tmp_path)
+ PeftModel.from_pretrained(base_model, self.peft_model_id, cache_dir=tmp_path)
+
+
+class TestCustomModelConfigWarning:
+ # Check potential warnings when the user provided base_model_name_or_path is overridden by PEFT. See #2001 for
+ # context. We use LoRA for this test but the same applies to other methods
+ @pytest.fixture
+ def custom_module(self):
+ class MyModule(nn.Module):
+ def __init__(self):
+ super().__init__()
+ self.lin = nn.Linear(10, 10)
+
+ return MyModule()
+
+ def test_no_warning_by_default_transformers_model(self, recwarn):
+ # first a sanity test that there is no warning by default when using a model from transformers
+ model = AutoModelForCausalLM.from_pretrained("hf-internal-testing/tiny-random-OPTForCausalLM")
+ get_peft_model(model, LoraConfig())
+ for warning in recwarn.list:
+ assert "renamed" not in str(warning.message)
+
+ def test_no_warning_by_default_custom_model(self, custom_module, recwarn):
+ # same as above but with a custom model
+ get_peft_model(custom_module, LoraConfig(target_modules=["lin"]))
+ for warning in recwarn.list:
+ assert "renamed" not in str(warning.message)
+
+ def test_warning_name_transformers_model(self, recwarn):
+ # The base_model_name_or_path provided by the user is overridden.
+ model = AutoModelForCausalLM.from_pretrained("hf-internal-testing/tiny-random-OPTForCausalLM")
+ custom_name = "custom_name"
+ get_peft_model(model, LoraConfig(base_model_name_or_path=custom_name))
+ msg = f"was renamed from '{custom_name}' to 'hf-internal-testing/tiny-random-OPTForCausalLM'"
+ assert any(msg in str(warning.message) for warning in recwarn.list)
+
+ def test_warning_name_custom_model(self, custom_module, recwarn):
+ custom_name = "custom_name"
+ get_peft_model(custom_module, LoraConfig(target_modules=["lin"], base_model_name_or_path=custom_name))
+ msg = f"was renamed from '{custom_name}' to 'None'"
+ assert any(msg in str(warning.message) for warning in recwarn.list)
+
+ def test_warning_name_custom_model_with_custom_name(self, custom_module, recwarn):
+ custom_name = "custom_name"
+ custom_module.name_or_path = "foobar"
+ get_peft_model(custom_module, LoraConfig(target_modules=["lin"], base_model_name_or_path=custom_name))
+ msg = f"was renamed from '{custom_name}' to 'foobar'"
+ assert any(msg in str(warning.message) for warning in recwarn.list)
+
+
+class TestLowCpuMemUsage:
+ """Test for the low CPU memory usage option for loading PEFT models.
+
+ Note that we have `test_load_model_low_cpu_mem_usage` in the custom model and stable diffusion tests. Those are
+ broad tests (i.e. testing all the supported PEFT methods) but not very deep (only testing if loading works and the
+ device is correctly set). The test class here goes deeper but only tests LoRA, as checking all PEFT methods would
+ be too much.
+
+ """
+
+ # test on CPU and optionally on accelerator device
+ devices = ["cpu"]
+ _device = infer_device()
+ if _device != "cpu":
+ devices.append(_device)
+
+ model_id = "hf-internal-testing/tiny-random-OPTForCausalLM"
+
+ def get_model(self):
+ return AutoModelForCausalLM.from_pretrained(self.model_id)
+
+ @pytest.fixture(scope="class")
+ def lora_config(self):
+ return LoraConfig(init_lora_weights=False, target_modules="all-linear")
+
+ @pytest.fixture(scope="class")
+ def lora_path(self, tmp_path_factory, lora_config):
+ torch.manual_seed(0)
+ tmp_path = tmp_path_factory.mktemp("lora")
+ model = self.get_model()
+ model = get_peft_model(model, lora_config)
+ model.save_pretrained(tmp_path)
+ return tmp_path
+
+ @pytest.fixture(scope="class")
+ def inputs(self):
+ return {"input_ids": torch.randint(0, 100, (1, 10)), "attention_mask": torch.ones(1, 10)}
+
+ @pytest.mark.parametrize("device", devices)
+ def test_from_pretrained_low_cpu_mem_usage_works(self, device, inputs, lora_path):
+ model = self.get_model().to(device)
+ inputs = {k: v.to(device) for k, v in inputs.items()}
+ model = PeftModel.from_pretrained(model, lora_path, torch_device=device).eval()
+ device_set_not_low_cpu_mem = {p.device.type for p in model.parameters()}
+ logits_not_low_cpu_mem = model(**inputs).logits
+
+ del model
+
+ model = self.get_model().to(device)
+ model = PeftModel.from_pretrained(model, lora_path, low_cpu_mem_usage=True, torch_device=device).eval()
+ device_set_low_cpu_mem = {p.device.type for p in model.parameters()}
+ logits_low_cpu_mem = model(**inputs).logits
+
+ assert device_set_low_cpu_mem == device_set_not_low_cpu_mem
+ assert torch.allclose(logits_low_cpu_mem, logits_not_low_cpu_mem, atol=1e-6, rtol=1e-6)
+
+ @pytest.mark.parametrize("device", devices)
+ def test_load_adapter_low_cpu_mem_usage_works(self, device, inputs, lora_path, lora_config):
+ model = self.get_model().to(device)
+ inputs = {k: v.to(device) for k, v in inputs.items()}
+
+ torch.manual_seed(0)
+ model = get_peft_model(model, lora_config)
+ model.load_adapter(lora_path, adapter_name="other", torch_device=device)
+ model.set_adapter("other")
+ model.eval()
+ device_set_not_low_cpu_mem = {p.device.type for p in model.parameters()}
+ logits_not_low_cpu_mem = model(**inputs).logits
+
+ del model
+
+ model = self.get_model().to(device)
+ torch.manual_seed(0)
+ model = get_peft_model(model, lora_config)
+ model.load_adapter(lora_path, adapter_name="other", low_cpu_mem_usage=True, torch_device=device)
+ model.set_adapter("other")
+ model.eval()
+ device_set_low_cpu_mem = {p.device.type for p in model.parameters()}
+ logits_low_cpu_mem = model(**inputs).logits
+
+ assert device_set_low_cpu_mem == device_set_not_low_cpu_mem
+ assert torch.allclose(logits_low_cpu_mem, logits_not_low_cpu_mem, atol=1e-6, rtol=1e-6)
+
+ @pytest.mark.parametrize("device", devices)
+ def test_get_peft_model_low_cpu_mem_usage_works(self, device, inputs):
+ # when calling get_peft_model, the PEFT weights will not be initialized on device but remain on meta
+ model = self.get_model().to(device)
+ model = get_peft_model(model, LoraConfig(target_modules="all-linear"), low_cpu_mem_usage=True)
+
+ devices_lora_weights = {p.device for n, p in model.named_parameters() if "lora_" in n}
+ expected = {torch.device("meta")}
+ assert devices_lora_weights == expected
+
+ @pytest.mark.parametrize("device", devices)
+ def test_get_peft_model_with_task_type_low_cpu_mem_usage_works(self, device, inputs):
+ # same as the previous test, but pass the task_type argument
+ model = self.get_model().to(device)
+ model = get_peft_model(
+ model, LoraConfig(target_modules="all-linear", task_type="CAUSAL_LM"), low_cpu_mem_usage=True
+ )
+
+ devices_lora_weights = {p.device for n, p in model.named_parameters() if "lora_" in n}
+ expected = {torch.device("meta")}
+ assert devices_lora_weights == expected
+
+ @pytest.mark.parametrize("device", devices)
+ def test_inject_adapter_low_cpu_mem_usage_works(self, device, inputs, lora_path, lora_config):
+ # external libs like transformers and diffusers use inject_adapter_in_model, let's check that this also works
+ model = self.get_model().to(device)
+ inputs = {k: v.to(device) for k, v in inputs.items()}
+
+ torch.manual_seed(0)
+ model = get_peft_model(model, lora_config)
+ model.load_adapter(lora_path, adapter_name="other", torch_device=device)
+ model.set_adapter("other")
+ model.eval()
+ device_set_not_low_cpu_mem = {p.device.type for p in model.parameters()}
+ logits_not_low_cpu_mem = model(**inputs).logits
+
+ del model
+
+ torch.manual_seed(0)
+ model = self.get_model().to(device)
+ inject_adapter_in_model(lora_config, model, low_cpu_mem_usage=True)
+ device_set_before_loading = {p.device.type for p in model.parameters()}
+ # at this stage, lora weights are still on meta device
+ assert device_set_before_loading == {"meta", device}
+
+ state_dict = load_file(lora_path / "adapter_model.safetensors")
+ remapped_dict = {}
+ prefix = "base_model.model."
+ for key, val in state_dict.items():
+ new_key = key[len(prefix) :]
+ remapped_dict[new_key] = val.to(device)
+ errors = set_peft_model_state_dict(model, remapped_dict, low_cpu_mem_usage=True)
+ # sanity check: no unexpected keys
+ assert not errors.unexpected_keys
+
+ model.eval()
+ device_set_low_cpu_mem = {p.device.type for p in model.parameters()}
+ logits_low_cpu_mem = model(**inputs).logits
+
+ assert device_set_low_cpu_mem == device_set_not_low_cpu_mem
+ assert torch.allclose(logits_low_cpu_mem, logits_not_low_cpu_mem, atol=1e-6, rtol=1e-6)
+
+ ############################
+ # tests for PeftMixedModel #
+ ############################
+
+ @pytest.mark.parametrize("device", devices)
+ def test_mixed_model_from_pretrained_low_cpu_mem_usage_works(self, device, inputs, lora_path):
+ model = self.get_model().to(device)
+ inputs = {k: v.to(device) for k, v in inputs.items()}
+ model = PeftMixedModel.from_pretrained(model, lora_path, torch_device=device).eval()
+ device_set_not_low_cpu_mem = {p.device.type for p in model.parameters()}
+ logits_not_low_cpu_mem = model(**inputs).logits
+
+ del model
+
+ model = self.get_model().to(device)
+ model = PeftMixedModel.from_pretrained(model, lora_path, low_cpu_mem_usage=True, torch_device=device).eval()
+ device_set_low_cpu_mem = {p.device.type for p in model.parameters()}
+ logits_low_cpu_mem = model(**inputs).logits
+
+ assert device_set_low_cpu_mem == device_set_not_low_cpu_mem
+ assert torch.allclose(logits_low_cpu_mem, logits_not_low_cpu_mem, atol=1e-6, rtol=1e-6)
+
+ @pytest.mark.parametrize("device", devices)
+ def test_mixed_model_load_adapter_low_cpu_mem_usage_works(self, device, inputs, lora_path, lora_config):
+ model = self.get_model().to(device)
+ inputs = {k: v.to(device) for k, v in inputs.items()}
+
+ torch.manual_seed(0)
+ model = PeftModel.from_pretrained(model, lora_path)
+ model.load_adapter(lora_path, adapter_name="other", torch_device=device)
+ model.set_adapter("other")
+ model.eval()
+ device_set_not_low_cpu_mem = {p.device.type for p in model.parameters()}
+ logits_not_low_cpu_mem = model(**inputs).logits
+
+ del model
+
+ model = self.get_model().to(device)
+ torch.manual_seed(0)
+ model = PeftModel.from_pretrained(model, lora_path)
+ model.load_adapter(lora_path, adapter_name="other", low_cpu_mem_usage=True, torch_device=device)
+ model.set_adapter("other")
+ model.eval()
+ device_set_low_cpu_mem = {p.device.type for p in model.parameters()}
+ logits_low_cpu_mem = model(**inputs).logits
+
+ assert device_set_low_cpu_mem == device_set_not_low_cpu_mem
+ assert torch.allclose(logits_low_cpu_mem, logits_not_low_cpu_mem, atol=1e-6, rtol=1e-6)
+
+
+def test_from_pretrained_missing_keys_warning(recwarn, tmp_path):
+ # For more context, see issue 2115
+ # When loading a PEFT adapter and we're missing a PEFT-specific weight, there should be a warning.
+ model = AutoModelForCausalLM.from_pretrained("hf-internal-testing/tiny-random-OPTForCausalLM")
+ config = LoraConfig()
+ model = get_peft_model(model, config)
+ state_dict = model.state_dict()
+
+ # first, sanity check that there are no warnings if no key is missing
+ model.save_pretrained(tmp_path)
+ del model
+ model = AutoModelForCausalLM.from_pretrained("hf-internal-testing/tiny-random-OPTForCausalLM")
+ model = PeftModel.from_pretrained(model, tmp_path)
+ msg = "Found missing adapter keys"
+ assert not any(msg in str(w.message) for w in recwarn.list)
+
+ # remove a key from the state_dict
+ missing_key = "base_model.model.model.decoder.layers.0.self_attn.v_proj.lora_A.default.weight"
+
+ def new_state_dict():
+ return {k: v for k, v in state_dict.items() if k != missing_key}
+
+ model.state_dict = new_state_dict
+ model.save_pretrained(tmp_path)
+ del model
+
+ model = AutoModelForCausalLM.from_pretrained("hf-internal-testing/tiny-random-OPTForCausalLM")
+ model = PeftModel.from_pretrained(model, tmp_path)
+ assert any(msg in str(w.message) for w in recwarn.list)
+ assert any(missing_key in str(w.message) for w in recwarn.list)
+
+
+class TestNamingConflictWarning:
+ """
+ Tests for warnings related to naming conflicts between adapter names and tuner prefixes. References: Issue 2252
+ """
+
+ @pytest.fixture(autouse=True)
+ def setup(self):
+ self.peft_config = LoraConfig()
+ self.prefix = PEFT_TYPE_TO_PREFIX_MAPPING[self.peft_config.peft_type]
+ self.base_model = AutoModelForCausalLM.from_pretrained("hf-internal-testing/tiny-random-OPTForCausalLM")
+
+ def _save_and_reload_model(self, model, adapter_name, tmp_path):
+ # Helper method to save and reload the PEFT model
+ model.save_pretrained(tmp_path, selected_adapters=[adapter_name])
+ del model
+ reloaded_base_model = AutoModelForCausalLM.from_pretrained(tmp_path / adapter_name)
+ return PeftModel.from_pretrained(reloaded_base_model, tmp_path / adapter_name)
+
+ def test_no_warning_without_naming_conflict_get_peft_model(self, recwarn):
+ # No warning should be raised when there is no naming conflict during get_peft_model.
+ non_conflict_adapter = "adapter"
+ _ = get_peft_model(self.base_model, self.peft_config, adapter_name=non_conflict_adapter)
+ expected_msg = f"Adapter name '{non_conflict_adapter}' should not be contained in the prefix '{self.prefix}'."
+ assert not any(expected_msg in str(w.message) for w in recwarn.list)
+
+ def test_no_warning_without_naming_conflict_add_adapter(self, recwarn):
+ # No warning should be raised when adding an adapter without naming conflict.
+ non_conflict_adapter = "adapter"
+ other_non_conflict_adapter = "other_adapter"
+ model = get_peft_model(self.base_model, self.peft_config, adapter_name=non_conflict_adapter)
+ _ = model.add_adapter(other_non_conflict_adapter, self.peft_config)
+ expected_msg = (
+ f"Adapter name '{other_non_conflict_adapter}' should not be contained in the prefix '{self.prefix}'."
+ )
+ assert not any(expected_msg in str(w.message) for w in recwarn.list)
+
+ def test_no_warning_without_naming_conflict_save_and_load(self, recwarn, tmp_path):
+ # No warning should be raised when saving and loading the model without naming conflict.
+ non_conflict_adapter = "adapter"
+ model = get_peft_model(self.base_model, self.peft_config, adapter_name=non_conflict_adapter)
+ _ = self._save_and_reload_model(model, non_conflict_adapter, tmp_path)
+ expected_msg = f"Adapter name '{non_conflict_adapter}' should not be contained in the prefix '{self.prefix}'."
+ assert not any(expected_msg in str(w.message) for w in recwarn.list)
+
+ def test_warning_naming_conflict_get_peft_model(self, recwarn):
+ # Warning is raised when the adapter name conflicts with the prefix in get_peft_model.
+ conflicting_adapter_name = self.prefix[:-1]
+ _ = get_peft_model(self.base_model, self.peft_config, adapter_name=conflicting_adapter_name)
+ expected_msg = (
+ f"Adapter name '{conflicting_adapter_name}' should not be contained in the prefix '{self.prefix}'."
+ )
+ assert any(expected_msg in str(w.message) for w in recwarn.list)
+
+ def test_warning_naming_conflict_add_adapter(self, recwarn):
+ # Warning is raised when adding an adapter with a name that conflicts with the prefix.
+ conflicting_adapter = self.prefix[1:]
+ non_conflict_adapter = "adapter"
+ model = get_peft_model(self.base_model, self.peft_config, adapter_name=non_conflict_adapter)
+ _ = model.add_adapter(conflicting_adapter, self.peft_config)
+ expected_msg = f"Adapter name '{conflicting_adapter}' should not be contained in the prefix '{self.prefix}'."
+ assert any(expected_msg in str(w.message) for w in recwarn.list)
+
+ def test_warning_naming_conflict_save_and_load(self, recwarn, tmp_path):
+ # Warning is raised when saving and loading the model with a naming conflict.
+ conflicting_adapter = self.prefix[:-1]
+ model = get_peft_model(self.base_model, self.peft_config, adapter_name=conflicting_adapter)
+ _ = self._save_and_reload_model(model, conflicting_adapter, tmp_path)
+ expected_msg = f"Adapter name '{conflicting_adapter}' should not be contained in the prefix '{self.prefix}'."
+ assert any(expected_msg in str(w.message) for w in recwarn.list)
+
+
+class TestCordaInitialization:
+ """Test class to check the initialization of CorDA adapters."""
+
+ torch_device = infer_device()
+
+ def get_model(self):
+ class MyModule(nn.Module):
+ def __init__(self):
+ super().__init__()
+ # choose a large weight so that averages are close to expected values
+ self.linear = nn.Linear(1000, 1000)
+
+ def forward(self, x):
+ return self.linear(x)
+
+ return MyModule().eval().to(self.torch_device)
+
+ @pytest.fixture
+ def data(self):
+ # larger data is required to pass KPM test
+ torch.manual_seed(233)
+ return torch.rand(1000, 1000).to(self.torch_device)
+
+ @pytest.mark.parametrize("corda_method", ("ipm", "kpm"))
+ def test_lora_corda_no_redundant_fields(self, data, corda_method):
+ original_model = self.get_model()
+ model = deepcopy(original_model)
+
+ corda_config = CordaConfig(
+ corda_method=corda_method,
+ )
+ config = LoraConfig(
+ init_lora_weights="corda",
+ target_modules=["linear"],
+ corda_config=corda_config,
+ )
+ preprocess_corda(
+ model,
+ config,
+ run_model=lambda: model(data),
+ hooked_model=model,
+ )
+ peft_model = get_peft_model(model, config)
+
+ # check if the redundant fields are removed
+ assert not hasattr(peft_model.base_model.linear, "sample_count")
+ assert not hasattr(peft_model.base_model.linear, "covariance_matrix")
+ assert not hasattr(peft_model.base_model.linear, "corda_method")
+ assert not hasattr(peft_model.base_model.linear, "rank")
+ assert not hasattr(peft_model.base_model.linear, "eigens")
+
+ # legacy debug fields
+ assert not hasattr(peft_model.base_model.linear, "mean")
+ assert not hasattr(peft_model.base_model.linear, "std")
+
+ @pytest.mark.parametrize("corda_method", ("ipm", "kpm"))
+ def test_lora_corda_sample_count(self, data, corda_method):
+ original_model = self.get_model()
+ model = deepcopy(original_model)
+
+ corda_config = CordaConfig(
+ corda_method=corda_method,
+ prune_temporary_fields=False,
+ )
+ config = LoraConfig(
+ init_lora_weights="corda",
+ target_modules=["linear"],
+ corda_config=corda_config,
+ )
+ preprocess_corda(
+ model,
+ config,
+ run_model=lambda: [model(data), model(data)], # running model twice to test `sample_count`
+ hooked_model=model,
+ )
+
+ # covariance of linear should be data.T @ data
+ layer = model.linear
+ assert hasattr(layer, "covariance_matrix")
+ assert torch.allclose(layer.covariance_matrix, data.T @ data, atol=1e-06)
+
+ # sample count of linear should be 2
+ assert hasattr(layer, "sample_count")
+ assert layer.sample_count == 2
+
+ @pytest.mark.parametrize("corda_method", ("ipm", "kpm"))
+ def test_lora_corda_hook_unregister(self, data, corda_method):
+ original_model = self.get_model()
+ model = deepcopy(original_model)
+
+ hook_call_count = 0
+
+ def hook(*args):
+ nonlocal hook_call_count
+ hook_call_count += 1
+
+ model.linear.register_forward_hook(hook)
+
+ corda_config = CordaConfig(
+ corda_method=corda_method,
+ prune_temporary_fields=False,
+ )
+ config = LoraConfig(
+ init_lora_weights="corda",
+ target_modules=["linear"],
+ corda_config=corda_config,
+ )
+ preprocess_corda(
+ model,
+ config,
+ run_model=lambda: model(data),
+ hooked_model=model,
+ )
+
+ # after preprocessing, external and internal hook should be run once
+ assert hook_call_count == 1
+ assert model.linear.sample_count == 1
+
+ # run preprocessed model once
+ model(data)[0]
+
+ # the external hook should be kept, but the internal hook should be gone
+ assert hook_call_count == 2
+ assert model.linear.sample_count == 1
+
+ @pytest.mark.parametrize("corda_method", ("ipm", "kpm"))
+ def test_lora_corda_linear_init_default(self, data, tmp_path, corda_method):
+ original_model = self.get_model()
+ model = deepcopy(original_model)
+ output_base = model(data)[0]
+
+ corda_config = CordaConfig(
+ cache_file=tmp_path / "corda_cache.pt",
+ covariance_file=tmp_path / "covariance_cache.pt",
+ corda_method=corda_method,
+ )
+ config = LoraConfig(
+ init_lora_weights="corda",
+ target_modules=["linear"],
+ corda_config=corda_config,
+ )
+ preprocess_corda(
+ model,
+ config,
+ run_model=lambda: model(data),
+ hooked_model=model,
+ )
+ peft_model = get_peft_model(model, config)
+
+ # check if adapter performs an identity transformantion
+ assert torch.allclose(output_base, peft_model(data)[0], atol=1e-06)
+
+ # modify the weights, or else the adapter performs an identity transformation
+ peft_model.base_model.linear.lora_B["default"].weight.data *= 2.0
+ output_corda = peft_model(data)[0]
+
+ # sanity check
+ tol = 1e-06
+ assert not torch.allclose(output_base, output_corda, atol=tol, rtol=tol)
+
+ # if load SVD result from cache, the output should be the same
+ model = deepcopy(original_model)
+ config = LoraConfig(
+ init_lora_weights="corda",
+ target_modules=["linear"],
+ corda_config=CordaConfig(cache_file=tmp_path / "corda_cache.pt", corda_method=corda_method),
+ )
+ preprocess_corda(model, config)
+ peft_model = get_peft_model(model, config)
+ peft_model.base_model.linear.lora_B["default"].weight.data *= 2.0
+ assert torch.allclose(output_corda, peft_model(data)[0], atol=1e-06)
+
+ # if load covariance from cache, the output should be the same
+ model = deepcopy(original_model)
+ config = LoraConfig(
+ init_lora_weights="corda",
+ target_modules=["linear"],
+ corda_config=CordaConfig(covariance_file=tmp_path / "covariance_cache.pt", corda_method=corda_method),
+ )
+ preprocess_corda(model, config)
+ peft_model = get_peft_model(model, config)
+ peft_model.base_model.linear.lora_B["default"].weight.data *= 2.0
+ assert torch.allclose(output_corda, peft_model(data)[0], atol=1e-06)
+
+ @pytest.mark.parametrize("corda_method", ("ipm", "kpm"))
+ def test_lora_corda_hooked_model_linear_init_default(self, data, tmp_path, corda_method):
+ original_model = self.get_model()
+ model = deepcopy(original_model)
+ hooked_model = deepcopy(model)
+ output_base = model(data)[0]
+
+ corda_config = CordaConfig(
+ cache_file=tmp_path / "corda_cache.pt",
+ covariance_file=tmp_path / "covariance_cache.pt",
+ corda_method=corda_method,
+ )
+ config = LoraConfig(
+ init_lora_weights="corda",
+ target_modules=["linear"],
+ corda_config=corda_config,
+ )
+
+ # difference from the above test: this test uses a copied model as hooked model
+ preprocess_corda(
+ model,
+ config,
+ run_model=lambda: hooked_model(data),
+ hooked_model=hooked_model,
+ )
+ peft_model = get_peft_model(model, config)
+
+ # check if adapter performs an identity transformantion
+ assert torch.allclose(output_base, peft_model(data)[0], atol=1e-06)
+
+ # modify the weights, or else the adapter performs an identity transformation
+ peft_model.base_model.linear.lora_B["default"].weight.data *= 2.0
+ output_corda = peft_model(data)[0]
+
+ # sanity check
+ tol = 1e-06
+ assert not torch.allclose(output_base, output_corda, atol=tol, rtol=tol)
+
+ # if load SVD result from cache, the output should be the same
+ model = deepcopy(original_model)
+ config = LoraConfig(
+ init_lora_weights="corda",
+ target_modules=["linear"],
+ corda_config=CordaConfig(cache_file=tmp_path / "corda_cache.pt", corda_method=corda_method),
+ )
+ preprocess_corda(model, config)
+ peft_model = get_peft_model(model, config)
+ peft_model.base_model.linear.lora_B["default"].weight.data *= 2.0
+ assert torch.allclose(output_corda, peft_model(data)[0], atol=1e-06)
+
+ # if load covariance from cache, the output should be the same
+ model = deepcopy(original_model)
+ config = LoraConfig(
+ init_lora_weights="corda",
+ target_modules=["linear"],
+ corda_config=CordaConfig(covariance_file=tmp_path / "covariance_cache.pt", corda_method=corda_method),
+ )
+ preprocess_corda(model, config)
+ peft_model = get_peft_model(model, config)
+ peft_model.base_model.linear.lora_B["default"].weight.data *= 2.0
+ assert torch.allclose(output_corda, peft_model(data)[0], atol=1e-06)
+
+ @pytest.mark.parametrize("corda_method", ("ipm", "kpm"))
+ def test_lora_corda_linear_init_default_with_rank_pattern(self, data, tmp_path, corda_method):
+ original_model = self.get_model()
+ model = deepcopy(original_model)
+ output_base = model(data)[0]
+
+ corda_config = CordaConfig(
+ cache_file=tmp_path / "corda_cache.pt",
+ covariance_file=tmp_path / "covariance_cache.pt",
+ corda_method=corda_method,
+ )
+ config = LoraConfig(
+ rank_pattern={"linear": 8, "embed": 16, "conv2d": 32},
+ init_lora_weights="corda",
+ target_modules=["linear"],
+ corda_config=corda_config,
+ )
+ preprocess_corda(
+ model,
+ config,
+ run_model=lambda: model(data),
+ )
+ peft_model = get_peft_model(model, config)
+
+ # check if adapter performs an identity transformantion
+ assert torch.allclose(output_base, peft_model(data)[0], atol=1e-06)
+
+ # modify the weights, or else the adapter performs an identity transformation
+ peft_model.base_model.linear.lora_B["default"].weight.data *= 2.0
+ output_corda = peft_model(data)[0]
+
+ # sanity check
+ tol = 1e-06
+ assert not torch.allclose(output_base, output_corda, atol=tol, rtol=tol)
+
+ # if load SVD result from cache, the output should be the same
+ model = deepcopy(original_model)
+ config = LoraConfig(
+ rank_pattern={"linear": 8, "embed": 16, "conv2d": 32},
+ init_lora_weights="corda",
+ target_modules=["linear"],
+ corda_config=CordaConfig(cache_file=tmp_path / "corda_cache.pt", corda_method=corda_method),
+ )
+ preprocess_corda(model, config)
+ peft_model = get_peft_model(model, config)
+ peft_model.base_model.linear.lora_B["default"].weight.data *= 2.0
+ assert torch.allclose(output_corda, peft_model(data)[0], atol=1e-06)
+
+ # if load covariance from cache, the output should be the same
+ model = deepcopy(original_model)
+ config = LoraConfig(
+ rank_pattern={"linear": 8, "embed": 16, "conv2d": 32},
+ init_lora_weights="corda",
+ target_modules=["linear"],
+ corda_config=CordaConfig(covariance_file=tmp_path / "covariance_cache.pt", corda_method=corda_method),
+ )
+ preprocess_corda(model, config)
+ peft_model = get_peft_model(model, config)
+ peft_model.base_model.linear.lora_B["default"].weight.data *= 2.0
+ assert torch.allclose(output_corda, peft_model(data)[0], atol=1e-06)
+
+ @pytest.mark.parametrize("corda_method", ("ipm", "kpm"))
+ def test_lora_corda_conversion_same_output_after_loading(self, data, tmp_path, corda_method):
+ model = self.get_model()
+ output_base = model(data)[0]
+
+ corda_config = CordaConfig(corda_method=corda_method)
+ config = LoraConfig(init_lora_weights="corda", target_modules=["linear"], r=8, corda_config=corda_config)
+ preprocess_corda(model, config, run_model=lambda: model(data), hooked_model=model)
+ peft_model = get_peft_model(deepcopy(model), config)
+ # save the initial model
+ peft_model.peft_config["default"].init_lora_weights = True
+ peft_model.save_pretrained(tmp_path / "init-model")
+ peft_model.peft_config["default"].init_lora_weights = "corda"
+
+ # modify the weights, or else the adapter performs an identity transformation
+ peft_model.base_model.linear.lora_B["default"].weight.data *= 2.0
+ output_corda = peft_model(data)[0]
+
+ # sanity check
+ tol = 1e-06
+ assert not torch.allclose(output_base, output_corda, atol=tol, rtol=tol)
+
+ # save the model normally
+ peft_model.save_pretrained(tmp_path / "corda-model")
+ model_loaded = PeftModel.from_pretrained(deepcopy(model), tmp_path / "corda-model")
+ output_loaded = model_loaded(data)[0]
+
+ assert torch.allclose(output_corda, output_loaded, atol=tol, rtol=tol)
+ # sanity check: ranks should still be 8 as initially
+ assert model_loaded.peft_config["default"].r == 8
+ assert model_loaded.base_model.model.linear.lora_A["default"].weight.shape[0] == 8
+ # sanity check: the base model weights were indeed changed
+ assert not torch.allclose(
+ model.linear.weight, model_loaded.base_model.model.linear.base_layer.weight, atol=tol, rtol=tol
+ )
+
+ # save the model with conversion
+ peft_config_keys_before = list(peft_model.peft_config.keys())
+ peft_config_dict_before = peft_model.peft_config["default"].to_dict()
+ peft_model.save_pretrained(
+ tmp_path / "corda-model-converted", path_initial_model_for_weight_conversion=tmp_path / "init-model"
+ )
+ peft_config_keys_after = list(peft_model.peft_config.keys())
+ peft_config_dict_after = peft_model.peft_config["default"].to_dict()
+ assert peft_config_keys_before == peft_config_keys_after
+ assert peft_config_dict_before == peft_config_dict_after
+
+ model_converted = PeftModel.from_pretrained(deepcopy(model), tmp_path / "corda-model-converted")
+ output_converted = model_converted(data)[0]
+
+ assert torch.allclose(output_corda, output_converted, atol=tol, rtol=tol)
+ # rank should be double of what it was initially
+ assert model_converted.peft_config["default"].r == 16
+ assert model_converted.base_model.model.linear.lora_A["default"].weight.shape[0] == 16
+ # base model weights should be the same as the initial model
+ assert torch.allclose(
+ model.linear.weight, model_converted.base_model.model.linear.base_layer.weight, atol=tol, rtol=tol
+ )
+
+ @pytest.mark.parametrize("corda_method", ("ipm", "kpm"))
+ def test_lora_corda_conversion_same_output_after_loading_with_rank_pattern(self, data, tmp_path, corda_method):
+ # same as above, but using rank_pattern
+ model = self.get_model()
+ output_base = model(data)[0]
+
+ # use rank_pattern here; note that since there is only a single linear layer, r is completely overridden
+ corda_config = CordaConfig(corda_method=corda_method)
+ config = LoraConfig(
+ init_lora_weights="corda",
+ target_modules=["linear"],
+ r=8,
+ rank_pattern={"linear": 32},
+ corda_config=corda_config,
+ )
+ preprocess_corda(model, config, run_model=lambda: model(data), hooked_model=model)
+ peft_model = get_peft_model(deepcopy(model), config)
+ # save the initial model
+ peft_model.peft_config["default"].init_lora_weights = True
+ peft_model.save_pretrained(tmp_path / "init-model")
+ peft_model.peft_config["default"].init_lora_weights = "corda"
+
+ # modify the weights, or else the adapter performs an identity transformation
+ peft_model.base_model.linear.lora_B["default"].weight.data *= 2.0
+ output_corda = peft_model(data)[0]
+
+ # sanity check
+ tol = 1e-06
+ assert not torch.allclose(output_base, output_corda, atol=tol, rtol=tol)
+
+ # save the model normally
+ peft_model.save_pretrained(tmp_path / "corda-model")
+ model_loaded = PeftModel.from_pretrained(deepcopy(model), tmp_path / "corda-model")
+ output_loaded = model_loaded(data)[0]
+
+ assert torch.allclose(output_corda, output_loaded, atol=tol, rtol=tol)
+ # sanity check: ranks should still be 8 as initially
+ assert model_loaded.peft_config["default"].r == 8
+ assert model_loaded.base_model.model.linear.lora_A["default"].weight.shape[0] == 32
+ # sanity check: the base model weights were indeed changed
+ assert not torch.allclose(
+ model.linear.weight, model_loaded.base_model.model.linear.base_layer.weight, atol=tol, rtol=tol
+ )
+
+ # save the model with conversion
+ peft_model.save_pretrained(
+ tmp_path / "corda-model-converted", path_initial_model_for_weight_conversion=tmp_path / "init-model"
+ )
+ model_converted = PeftModel.from_pretrained(deepcopy(model), tmp_path / "corda-model-converted")
+ output_converted = model_converted(data)[0]
+
+ assert torch.allclose(output_corda, output_converted, atol=tol, rtol=tol)
+ # rank should be double of what it was initially
+ assert model_converted.peft_config["default"].r == 16
+ assert model_converted.base_model.model.linear.lora_A["default"].weight.shape[0] == 64
+ # base model weights should be the same as the initial model
+ assert torch.allclose(
+ model.linear.weight, model_converted.base_model.model.linear.base_layer.weight, atol=tol, rtol=tol
+ )
+
+ @pytest.mark.parametrize("corda_method", ("ipm", "kpm"))
+ def test_lora_corda_conversion_same_output_after_loading_with_alpha_pattern(self, data, tmp_path, corda_method):
+ # same as above, but using alpha_pattern
+ model = self.get_model()
+ output_base = model(data)[0]
+
+ # use alpha_pattern here; note that since there is only a single linear layer, lora_alpha is completely
+ # overridden
+ corda_config = CordaConfig(corda_method=corda_method)
+ config = LoraConfig(
+ init_lora_weights="corda",
+ target_modules=["linear"],
+ alpha_pattern={"linear": 5},
+ corda_config=corda_config,
+ )
+ preprocess_corda(model, config, run_model=lambda: model(data), hooked_model=model)
+ peft_model = get_peft_model(deepcopy(model), config)
+ # save the initial model
+ peft_model.peft_config["default"].init_lora_weights = True
+ peft_model.save_pretrained(tmp_path / "init-model")
+ peft_model.peft_config["default"].init_lora_weights = "corda"
+
+ # modify the weights, or else the adapter performs an identity transformation
+ peft_model.base_model.linear.lora_B["default"].weight.data *= 2.0
+ output_corda = peft_model(data)[0]
+
+ # sanity check
+ tol = 1e-06
+ assert not torch.allclose(output_base, output_corda, atol=tol, rtol=tol)
+
+ # save the model normally
+ peft_model.save_pretrained(tmp_path / "corda-model")
+ model_loaded = PeftModel.from_pretrained(deepcopy(model), tmp_path / "corda-model")
+ output_loaded = model_loaded(data)[0]
+
+ assert torch.allclose(output_corda, output_loaded, atol=tol, rtol=tol)
+ # sanity check: ranks should still be 8 as initially
+ assert model_loaded.peft_config["default"].r == 8
+ assert model_loaded.base_model.model.linear.lora_A["default"].weight.shape[0] == 8
+ assert model_loaded.base_model.model.linear.scaling["default"] == 5 / 8
+ # sanity check: the base model weights were indeed changed
+ assert not torch.allclose(
+ model.linear.weight, model_loaded.base_model.model.linear.base_layer.weight, atol=tol, rtol=tol
+ )
+
+ # save the model with conversion
+ peft_model.save_pretrained(
+ tmp_path / "corda-model-converted", path_initial_model_for_weight_conversion=tmp_path / "init-model"
+ )
+ model_converted = PeftModel.from_pretrained(deepcopy(model), tmp_path / "corda-model-converted")
+ output_converted = model_converted(data)[0]
+
+ assert torch.allclose(output_corda, output_converted, atol=tol, rtol=tol)
+ # rank should be double of what it was initially
+ assert model_converted.peft_config["default"].r == 16
+ assert model_converted.base_model.model.linear.lora_A["default"].weight.shape[0] == 16
+ assert model_converted.base_model.model.linear.scaling["default"] == 10 / 16
+ # base model weights should be the same as the initial model
+ assert torch.allclose(
+ model.linear.weight, model_converted.base_model.model.linear.base_layer.weight, atol=tol, rtol=tol
+ )
+
+ @pytest.mark.parametrize("corda_method", ("ipm", "kpm"))
+ def test_lora_corda_conversion_same_output_after_loading_with_rslora(self, data, tmp_path, corda_method):
+ model = self.get_model()
+ output_base = model(data)[0]
+
+ corda_config = CordaConfig(corda_method=corda_method)
+ config = LoraConfig(
+ init_lora_weights="corda", target_modules=["linear"], r=8, use_rslora=True, corda_config=corda_config
+ )
+ preprocess_corda(model, config, run_model=lambda: model(data), hooked_model=model)
+ peft_model = get_peft_model(deepcopy(model), config)
+ # save the initial model
+ peft_model.peft_config["default"].init_lora_weights = True
+ peft_model.save_pretrained(tmp_path / "init-model")
+ peft_model.peft_config["default"].init_lora_weights = "corda"
+
+ # modify the weights, or else the adapter performs an identity transformation
+ peft_model.base_model.linear.lora_B["default"].weight.data *= 2.0
+ output_corda = peft_model(data)[0]
+
+ # sanity check
+ tol = 1e-06
+ assert not torch.allclose(output_base, output_corda, atol=tol, rtol=tol)
+
+ # save the model normally
+ peft_model.save_pretrained(tmp_path / "corda-model")
+ model_loaded = PeftModel.from_pretrained(deepcopy(model), tmp_path / "corda-model")
+ output_loaded = model_loaded(data)[0]
+
+ assert torch.allclose(output_corda, output_loaded, atol=tol, rtol=tol)
+ # sanity check: ranks should still be 8 as initially
+ assert model_loaded.peft_config["default"].r == 8
+ assert model_loaded.base_model.model.linear.lora_A["default"].weight.shape[0] == 8
+ assert model_loaded.base_model.model.linear.scaling["default"] == 8 / (8**0.5)
+ # sanity check: the base model weights were indeed changed
+ assert not torch.allclose(
+ model.linear.weight, model_loaded.base_model.model.linear.base_layer.weight, atol=tol, rtol=tol
+ )
+
+ # save the model with conversion
+ peft_model.save_pretrained(
+ tmp_path / "corda-model-converted", path_initial_model_for_weight_conversion=tmp_path / "init-model"
+ )
+ model_converted = PeftModel.from_pretrained(deepcopy(model), tmp_path / "corda-model-converted")
+ output_converted = model_converted(data)[0]
+
+ assert torch.allclose(output_corda, output_converted, atol=tol, rtol=tol)
+ # rank should be double of what it was initially
+ assert model_converted.peft_config["default"].r == 16
+ assert model_converted.base_model.model.linear.lora_A["default"].weight.shape[0] == 16
+ # same scale as before with a little bit of floating point imprecision
+ assert model_converted.base_model.model.linear.scaling["default"] == pytest.approx(8 / (8**0.5))
+ # base model weights should be the same as the initial model
+ assert torch.allclose(
+ model.linear.weight, model_converted.base_model.model.linear.base_layer.weight, atol=tol, rtol=tol
+ )
+
+ @pytest.mark.parametrize("corda_method", ("ipm", "kpm"))
+ def test_lora_corda_rank_pattern_and_rslora_raises(self, data, tmp_path, corda_method):
+ # it's not possible to determine the correct scale when using rslora with rank or alpha pattern, because the
+ # scale is not stored in the state_dict
+ model = self.get_model()
+ corda_config = CordaConfig(corda_method=corda_method)
+ config = LoraConfig(
+ init_lora_weights="corda",
+ target_modules=["linear"],
+ r=8,
+ rank_pattern={"linear": 2},
+ use_rslora=True,
+ corda_config=corda_config,
+ )
+ preprocess_corda(model, config, run_model=lambda: model(data), hooked_model=model)
+ peft_model = get_peft_model(model, config)
+ peft_model.save_pretrained(tmp_path / "init-model")
+
+ msg = re.escape("Passing `path_initial_model_for_weight_conversion` to `save_pretrained`")
+ with pytest.raises(ValueError, match=msg):
+ peft_model.save_pretrained(
+ tmp_path / "corda-model", path_initial_model_for_weight_conversion=tmp_path / "init-model"
+ )
+
+ @pytest.mark.parametrize("corda_method", ("ipm", "kpm"))
+ def test_lora_corda_alpha_pattern_and_rslora_raises(self, data, tmp_path, corda_method):
+ # it's not possible to determine the correct scale when using rslora with rank or alpha pattern, because the
+ # scale is not stored in the state_dict
+ model = self.get_model()
+ corda_config = CordaConfig(corda_method=corda_method)
+ config = LoraConfig(
+ init_lora_weights="corda",
+ target_modules=["linear"],
+ r=8,
+ alpha_pattern={"linear": 2},
+ use_rslora=True,
+ corda_config=corda_config,
+ )
+ preprocess_corda(model, config, run_model=lambda: model(data), hooked_model=model)
+ peft_model = get_peft_model(model, config)
+ peft_model.save_pretrained(tmp_path / "init-model")
+
+ msg = re.escape("Passing `path_initial_model_for_weight_conversion` to `save_pretrained`")
+ with pytest.raises(ValueError, match=msg):
+ peft_model.save_pretrained(
+ tmp_path / "corda-model", path_initial_model_for_weight_conversion=tmp_path / "init-model"
+ )
+
+
+class TestEvaInitialization:
+ """Tests for the EVA (Explained Variance Adaptation) initialization method.
+
+ This test suite verifies:
+ 1. Consistency of initialization across different seeds
+ 2. Proper error handling for invalid inputs
+ 3. Compatibility with different model architectures
+ 4. Reproducibility of results
+ 5. Proper handling of edge cases
+ """
+
+ # Constants for test configuration
+ COSINE_SIMILARITY_THRESHOLD = 0.75
+ NUM_SEEDS = 2
+ BATCH_SIZE = 4
+ MAX_LENGTH = 256
+ LORA_DIM = 8
+ LORA_ALPHA = 1
+ DEVICE = infer_device()
+ # for caching purposes:
+ _dataset = load_dataset_english_quotes()["train"]
+
+ @pytest.fixture
+ def tokenizer(self):
+ tokenizer = AutoTokenizer.from_pretrained("openai-community/gpt2")
+ tokenizer.pad_token = tokenizer.eos_token
+ return tokenizer
+
+ @pytest.fixture
+ def dataset(self, tokenizer):
+ # concatenate examples
+ examples = []
+ example = ""
+ for data in self._dataset:
+ if len(example) >= self.MAX_LENGTH:
+ examples.append(example)
+ example = ""
+ example = example + " " + data["quote"]
+ dataset = Dataset.from_dict({"text": examples})
+ # tokenize
+ dataset = dataset.map(
+ lambda x: tokenizer(x["text"], padding="max_length", truncation=True, max_length=self.MAX_LENGTH),
+ batched=True,
+ remove_columns=dataset.column_names,
+ )
+ dataset.set_format(type="torch")
+ return dataset
+
+ @pytest.fixture
+ def model(self):
+ model = AutoModelForCausalLM.from_pretrained("openai-community/gpt2")
+ model.transformer.h = model.transformer.h[:2] # truncate to 2 layers
+ return model.to(self.DEVICE)
+
+ @pytest.fixture
+ def peft_config(self):
+ return LoraConfig(
+ r=self.LORA_DIM,
+ lora_alpha=self.LORA_ALPHA,
+ target_modules=["c_attn"],
+ init_lora_weights="eva",
+ eva_config=EvaConfig(rho=2),
+ )
+
+ @staticmethod
+ def collate_fn(examples):
+ return {k: torch.stack([v[k] for v in examples], dim=0) for k in examples[0].keys()}
+
+ @staticmethod
+ def prepare_layer_inputs_fn(layer_input, model_input, layer_name):
+ return layer_input[0].view(-1, layer_input[0].size(-1))
+
+ def get_dataloader(self, dataset):
+ return DataLoader(
+ dataset,
+ batch_size=self.BATCH_SIZE,
+ collate_fn=self.collate_fn,
+ shuffle=False,
+ )
+
+ @pytest.mark.parametrize(
+ "prepare_layer_inputs_keys, expected_outcome",
+ [
+ (None, "success"),
+ (["transformer.h.0.attn.c_attn"], "success"),
+ (
+ ["transformer.h.0.attn.c_attn", "transformer.h.1.attn.c_attn", "transformer.h.2.attn.c_attn"],
+ "value_error",
+ ),
+ ],
+ )
+ def test_eva_state_dict_prepare_inputs_mapping(
+ self, model, dataset, peft_config, prepare_layer_inputs_keys, expected_outcome
+ ):
+ """
+ Tests for cases where prepare_layer_inputs_fn is a mapping. Checks that if not all target modules are present,
+ the prepare_layer_inputs_fn for the remaining modules is set to None. Also checks that if more keys than target
+ modules are present, a ValueError is raised.
+ """
+
+ def fn(x, *args):
+ return x[0].view(-1, x[0].size(-1))
+
+ if prepare_layer_inputs_keys is None:
+ prepare_layer_inputs_fn = fn
+ else:
+ prepare_layer_inputs_fn = {k: fn for k in prepare_layer_inputs_keys}
+
+ shuffled_dataset = dataset.shuffle(seed=0)
+ dataloader = self.get_dataloader(shuffled_dataset)
+ modified_peft_config = deepcopy(peft_config)
+ modified_peft_config.eva_config.tau = 0 # converge immediately
+ if expected_outcome == "success":
+ sd = get_eva_state_dict(
+ model,
+ dataloader,
+ modified_peft_config,
+ prepare_model_inputs_fn=None,
+ prepare_layer_inputs_fn=prepare_layer_inputs_fn,
+ )
+ assert len(sd) == 2
+ assert "transformer.h.0.attn.c_attn" in sd
+ assert "transformer.h.1.attn.c_attn" in sd
+ else:
+ with pytest.raises(
+ ValueError, match="prepare_layer_inputs_fn is a mapping but the following module names were not found"
+ ):
+ get_eva_state_dict(
+ model,
+ dataloader,
+ modified_peft_config,
+ prepare_model_inputs_fn=None,
+ prepare_layer_inputs_fn=prepare_layer_inputs_fn,
+ )
+
+ @pytest.mark.parametrize(
+ "eva_config",
+ [EvaConfig(rho=2, adjust_scaling_factors=True)],
+ )
+ def test_eva_state_dict_adjust_scaling_factors(self, model, dataset, peft_config, eva_config):
+ """
+ Tests that the scaling factors are adjusted so that all LoRA gradients have the same scale regardless of their
+ rank.
+ """
+ modified_peft_config = deepcopy(peft_config)
+ modified_peft_config.eva_config = eva_config
+ dataloader = self.get_dataloader(dataset)
+ peft_model = get_peft_model(deepcopy(model), modified_peft_config)
+ scaling_factors_before = {}
+ for n, m in peft_model.named_modules():
+ if isinstance(m, LoraLayer):
+ scaling_factors_before[n] = m.scaling["default"]
+ initialize_lora_eva_weights(peft_model, dataloader)
+ for n, m in peft_model.named_modules():
+ if isinstance(m, LoraLayer):
+ assert m.scaling["default"] == scaling_factors_before[n]
+
+ @pytest.mark.parametrize(
+ "eva_config",
+ [
+ # note: lower tau to decrease number of iterations until convergence, as tests are slow on CPU
+ EvaConfig(rho=2, tau=0.9),
+ EvaConfig(rho=1, tau=0.9),
+ EvaConfig(rho=1, whiten=True, tau=0.9),
+ EvaConfig(rho=1.0001, tau=0.9),
+ ],
+ )
+ def test_eva_initialization_consistency(self, model, dataset, peft_config, eva_config):
+ """
+ Tests that the state dict returned by `get_eva_state_dict` is consistent across different seeds based on the
+ cosine similarity of the svd components.
+ """
+ modified_peft_config = deepcopy(peft_config)
+ modified_peft_config.eva_config = eva_config
+ state_dicts = []
+ for seed in range(self.NUM_SEEDS):
+ shuffled_dataset = dataset.shuffle(seed=seed)
+ dataloader = self.get_dataloader(shuffled_dataset)
+ sd = get_eva_state_dict(model, dataloader, modified_peft_config, show_progress_bar=False)
+ state_dicts.append(sd)
+
+ cos_sims = defaultdict(list)
+ for i, j in itertools.combinations(range(self.NUM_SEEDS), 2):
+ for k, v1 in state_dicts[i].items():
+ v2 = state_dicts[j][k]
+ min_size = min(v1.size(0), v2.size(0))
+ cos_sims[k].extend(torch.cosine_similarity(v1[:min_size].abs(), v2[:min_size].abs(), dim=1).tolist())
+
+ mean_cosine_similarities = {k: torch.tensor(v).mean() for k, v in cos_sims.items()}
+ for layer_name, mean_cosine_similarity in mean_cosine_similarities.items():
+ assert mean_cosine_similarity > self.COSINE_SIMILARITY_THRESHOLD, (
+ f"Mean absolute cosine similarity {mean_cosine_similarity:.4f} "
+ f"is not greater than {self.COSINE_SIMILARITY_THRESHOLD}"
+ )
+
+ @pytest.mark.parametrize("has_rank_zero", [True, False])
+ def test_load_eva_state_dict(self, model, dataset, peft_config, tmp_path, has_rank_zero):
+ """
+ Tests that the `eva_state_dict` argument in `initialize_lora_eva_weights` can be used to initialize a model
+ with EVA weights and that the initialized model can be saved and loaded correctly.
+ """
+ dataloader = self.get_dataloader(dataset)
+ peft_model = get_peft_model(deepcopy(model), peft_config)
+ sd = get_eva_state_dict(peft_model, dataloader)
+ if has_rank_zero:
+ k = "base_model.model.transformer.h.0.attn.c_attn"
+ sd[k] = sd[k][:0]
+ initialize_lora_eva_weights(peft_model, eva_state_dict=sd)
+ if has_rank_zero:
+ assert not isinstance(peft_model.model.transformer.h[0].attn.c_attn, LoraLayer)
+ else:
+ assert isinstance(peft_model.model.transformer.h[0].attn.c_attn, LoraLayer)
+ peft_model.save_pretrained(tmp_path)
+ peft_model = PeftModel.from_pretrained(model, tmp_path, torch_device=self.DEVICE, low_cpu_mem_usage=True)
+ peft_model(**{k: v.to(self.DEVICE) for k, v in next(iter(dataloader)).items()})
+
+ def test_missing_eva_inits(self, model, dataset, peft_config):
+ """
+ Tests that a warning is raised when some adapter modules were not initialized with EVA weights.
+ """
+ modified_peft_config = deepcopy(peft_config)
+ modified_peft_config.target_modules = ["wte"]
+ dataloader = self.get_dataloader(dataset)
+ peft_model = get_peft_model(deepcopy(model), modified_peft_config)
+ with pytest.warns(
+ UserWarning,
+ match="the following layers were initialized with init_lora_weights=True because they were not found in the eva state_dict:*",
+ ):
+ initialize_lora_eva_weights(peft_model, dataloader)
+
+ def test_load_eva_model(self, model, dataset, peft_config, tmp_path):
+ """
+ Tests that a model initialized with EVA weights can be loaded correctly.
+ """
+ dataloader = self.get_dataloader(dataset)
+ peft_model = get_peft_model(deepcopy(model), peft_config)
+ initialize_lora_eva_weights(peft_model, dataloader)
+ peft_model.save_pretrained(tmp_path)
+ peft_model = PeftModel.from_pretrained(model, tmp_path, torch_device=self.DEVICE, low_cpu_mem_usage=True)
+ peft_model(**{k: v.to(self.DEVICE) for k, v in next(iter(dataloader)).items()})
+
+ def test_eva_initialization_with_invalid_dataloader(self, model, peft_config):
+ """Test that appropriate error is raised when dataloader is empty."""
+ empty_dataset = Dataset.from_dict({"text": []})
+ dataloader = self.get_dataloader(empty_dataset)
+
+ with pytest.raises(ValueError, match="dataloader is empty"):
+ get_eva_state_dict(model, dataloader, peft_config)
+
+ def test_eva_config_rho(self):
+ """
+ Tests that EvaConfig.__init__ raises a ValueError when rho is negative.
+ """
+ with pytest.raises(ValueError, match="`rho` must be >= 1.0"):
+ EvaConfig(rho=-1)
+
+ def test_eva_config_tau(self):
+ """
+ Tests that EvaConfig.__init__ raises a ValueError when tau is not between 0.0 and 1.0.
+ """
+ with pytest.raises(ValueError, match="`tau` must be between 0.0 and 1.0."):
+ EvaConfig(tau=-0.1)
+ with pytest.raises(ValueError, match="`tau` must be between 0.0 and 1.0."):
+ EvaConfig(tau=1.1)
+
+ def test_lora_config_raises_warning_with_eva_init_but_not_eva_config(self):
+ """
+ Tests that LoraConfig.__init__ raises a warning when init_lora_weights='eva' but eva_config is not set.
+ """
+ with pytest.warns(
+ UserWarning,
+ match="`init_lora_weights` is 'eva' but `eva_config` is not specified. Using default EVA config.",
+ ):
+ LoraConfig(init_lora_weights="eva")
+
+ def test_lora_config_raises_warning_with_eva_config_but_not_eva_init(self):
+ """
+ Tests that LoraConfig.__init__ raises a warning when init_lora_weights is not 'eva' but eva_config is set.
+ """
+ with pytest.warns(
+ UserWarning, match="`eva_config` specified but will be ignored when `init_lora_weights` is not 'eva'."
+ ):
+ LoraConfig(init_lora_weights=True, eva_config=EvaConfig())
+
+
+@pytest.mark.skipif(
+ platform.system() != "Linux", reason="Out of the box, torch.compile does not work on Windows or MacOS"
+)
+class TestHotSwapping:
+ """Tests for the hotswapping function"""
+
+ torch_device = infer_device()
+
+ def compile(self, model, do_compile):
+ if not do_compile:
+ return model
+ return torch.compile(model)
+
+ def get_model(self):
+ class MLP(nn.Module):
+ def __init__(self, bias=True):
+ super().__init__()
+ self.lin0 = nn.Linear(10, 20, bias=True)
+ self.relu = nn.ReLU()
+ self.lin1 = nn.Linear(20, 5, bias=False)
+
+ def forward(self, X):
+ X = X.float()
+ X = self.lin0(X)
+ X = self.relu(X)
+ X = self.lin1(X)
+ return X
+
+ torch.manual_seed(0)
+ return MLP().to(self.torch_device)
+
+ def get_model_conv2d(self):
+ class ConvModel(nn.Module):
+ def __init__(self):
+ super().__init__()
+ self.conv = nn.Conv2d(3, 10, kernel_size=3)
+
+ def forward(self, X):
+ return self.conv(X)
+
+ torch.manual_seed(0)
+ return ConvModel().to(self.torch_device)
+
+ # this works with all adapters except prompt learning, but we don't test all
+ # as it is unnecessary and would be slow
+ @pytest.mark.parametrize(
+ "config",
+ [
+ LoraConfig(init_lora_weights=0, target_modules=["lin0"]),
+ LoraConfig(init_lora_weights=0, target_modules=["lin0", "lin1"]),
+ ],
+ )
+ @pytest.mark.parametrize("do_compile", [False, True])
+ def test_hotswap_works(self, config, do_compile, tmp_path):
+ # Load 2 different adapters and check that we can hotswap between them, with the model optionally being
+ # compiled.
+ atol, rtol = 1e-4, 1e-4
+ inputs = torch.rand(3, 10).to(self.torch_device)
+
+ # create adapter 0
+ model = self.get_model()
+ torch.manual_seed(0)
+ model = get_peft_model(model, config)
+ model = self.compile(model, do_compile=do_compile)
+ model.eval()
+ with torch.inference_mode():
+ output0 = model(inputs)
+ model.save_pretrained(tmp_path / "adapter0")
+
+ del model
+
+ # create adapter 1
+ model = self.get_model()
+ torch.manual_seed(1)
+ model = get_peft_model(model, config)
+ model = self.compile(model, do_compile=do_compile)
+ model.eval()
+ with torch.inference_mode():
+ output1 = model(inputs)
+ model.save_pretrained(tmp_path / "adapter1")
+
+ # sanity check: they're not the same
+ assert not torch.allclose(output0, output1, atol=atol, rtol=rtol)
+
+ del model
+
+ # load adapter 0
+ model = self.get_model()
+ model = PeftModel.from_pretrained(model, tmp_path / "adapter0")
+ model = self.compile(model, do_compile=do_compile)
+ with torch.inference_mode():
+ output_loaded0 = model(inputs)
+
+ # sanity check: same output after loading for adapter 0
+ assert torch.allclose(output0, output_loaded0, atol=atol, rtol=rtol)
+
+ # hotswap with adapter 1
+ hotswap_adapter(model, tmp_path / "adapter1", adapter_name="default")
+ with torch.inference_mode():
+ output_loaded1 = model(inputs)
+
+ # real check: model now behaves like adapter 1
+ assert torch.allclose(output1, output_loaded1, atol=atol, rtol=rtol)
+
+ # hotswap back to adapter 0
+ hotswap_adapter(model, tmp_path / "adapter0", adapter_name="default")
+ with torch.inference_mode():
+ output_loaded_back0 = model(inputs)
+
+ # real check: model now behaves again like adapter 0
+ assert torch.allclose(output0, output_loaded_back0, atol=atol, rtol=rtol)
+
+ def test_hotswap_different_peft_types_raises(self, tmp_path):
+ # When the configs of the two adapters are different PEFT methods, raise
+ config0 = LoraConfig(target_modules=["lin0"])
+ config1 = IA3Config(target_modules=["lin0"], feedforward_modules=[])
+
+ model = self.get_model()
+ model = get_peft_model(model, config0)
+ model.save_pretrained(tmp_path / "adapter0")
+ del model
+
+ model = self.get_model()
+ model = get_peft_model(model, config1)
+ model.save_pretrained(tmp_path / "adapter1")
+ del model
+
+ # load adapter 0
+ model = self.get_model()
+ model = PeftModel.from_pretrained(model, tmp_path / "adapter0")
+
+ msg = r"Incompatible PEFT types found: LORA and IA3"
+ with pytest.raises(ValueError, match=msg):
+ hotswap_adapter(model, tmp_path / "adapter1", adapter_name="default")
+
+ def test_hotswap_wrong_peft_types_raises(self, tmp_path):
+ # Only LoRA is supported at the moment
+ config0 = IA3Config(target_modules=["lin0"], feedforward_modules=[])
+ config1 = IA3Config(target_modules=["lin0"], feedforward_modules=[])
+
+ model = self.get_model()
+ model = get_peft_model(model, config0)
+ model.save_pretrained(tmp_path / "adapter0")
+ del model
+
+ model = self.get_model()
+ model = get_peft_model(model, config1)
+ model.save_pretrained(tmp_path / "adapter1")
+ del model
+
+ # load adapter 0
+ model = self.get_model()
+ model = PeftModel.from_pretrained(model, tmp_path / "adapter0")
+
+ msg = r"Hotswapping only supports LORA but IA3 was passed"
+ with pytest.raises(ValueError, match=msg):
+ hotswap_adapter(model, tmp_path / "adapter1", adapter_name="default")
+
+ def test_hotswap_missing_key_works(self, tmp_path):
+ # When a key is missing, it is fine, the extra weight is zeroed out
+ config = LoraConfig(target_modules=["lin0", "lin1"])
+
+ model = self.get_model()
+ model = get_peft_model(model, config)
+ model.save_pretrained(tmp_path / "adapter0")
+ del model
+
+ model = self.get_model()
+ model = get_peft_model(model, config)
+
+ # remove one key from the state_dict
+ key = "base_model.model.lin1.lora_A.default.weight"
+ state_dict = model.state_dict()
+ del state_dict[key]
+ model.state_dict = lambda: state_dict
+ model.save_pretrained(tmp_path / "adapter1")
+ del model
+
+ # load adapter 0
+ model = self.get_model()
+ model = PeftModel.from_pretrained(model, tmp_path / "adapter0")
+
+ # sanity check: the missing weight is not already all zeros
+ assert not (model.base_model.model.lin1.lora_A["default"].weight == 0).all()
+ hotswap_adapter(model, tmp_path / "adapter1", adapter_name="default")
+ # after hotswapping, it is zeroed out
+ assert (model.base_model.model.lin1.lora_A["default"].weight == 0).all()
+
+ def test_hotswap_extra_key_raises(self, tmp_path):
+ # When there is an extra key, raise
+ config = LoraConfig(target_modules=["lin0"])
+
+ model = self.get_model()
+ model = get_peft_model(model, config)
+ model.save_pretrained(tmp_path / "adapter0")
+ del model
+
+ model = self.get_model()
+ model = get_peft_model(model, config)
+
+ # add an unexpected key
+ state_dict = model.state_dict()
+ new_key = "base_model.model.lin1.lora_A.default.weight"
+ state_dict[new_key] = torch.zeros(8, 20)
+ model.state_dict = lambda: state_dict
+ model.save_pretrained(tmp_path / "adapter1")
+ del model
+
+ # load adapter 0
+ model = self.get_model()
+ model = PeftModel.from_pretrained(model, tmp_path / "adapter0")
+
+ msg = f"Hot swapping the adapter did not succeed, unexpected keys found: {new_key}"
+ with pytest.raises(RuntimeError, match=msg):
+ hotswap_adapter(model, tmp_path / "adapter1", adapter_name="default")
+
+ @pytest.mark.parametrize("ranks", [(7, 13), (13, 7)])
+ def test_hotswap_works_different_ranks_alphas(self, ranks, tmp_path):
+ # same as test_hotswap_works but different rank and alpha
+ # Load 2 different adapters and check that we can hotswap between them, with the model optionally being
+ # compiled.
+ atol, rtol = 1e-4, 1e-4
+ inputs = torch.rand(3, 10).to(self.torch_device)
+
+ # create adapter 0
+ config0 = LoraConfig(target_modules=["lin0", "lin1"], r=ranks[0], lora_alpha=ranks[0], init_lora_weights=False)
+ model = self.get_model()
+ torch.manual_seed(0)
+ model = get_peft_model(model, config0)
+ model.eval()
+ with torch.inference_mode():
+ output0 = model(inputs)
+ model.save_pretrained(tmp_path / "adapter0")
+
+ del model
+
+ # create adapter 1
+ config1 = LoraConfig(target_modules=["lin0"], r=ranks[1], lora_alpha=ranks[1], init_lora_weights=False)
+ model = self.get_model()
+ torch.manual_seed(1)
+ model = get_peft_model(model, config1)
+ model.eval()
+ with torch.inference_mode():
+ output1 = model(inputs)
+ model.save_pretrained(tmp_path / "adapter1")
+
+ # sanity check: they're not the same
+ assert not torch.allclose(output0, output1, atol=atol, rtol=rtol)
+
+ del model
+
+ # load adapter 0
+ model = self.get_model()
+ model = PeftModel.from_pretrained(model, tmp_path / "adapter0")
+ with torch.inference_mode():
+ output_loaded0 = model(inputs)
+
+ # sanity check: same output after loading for adapter 0
+ assert torch.allclose(output0, output_loaded0, atol=atol, rtol=rtol)
+
+ # hotswap with adapter 1
+ hotswap_adapter(model, tmp_path / "adapter1", adapter_name="default")
+ with torch.inference_mode():
+ output_loaded1 = model(inputs)
+
+ # real check: model now behaves like adapter 1
+ assert torch.allclose(output1, output_loaded1, atol=atol, rtol=rtol)
+
+ # hotswap back to adapter 0
+ hotswap_adapter(model, tmp_path / "adapter0", adapter_name="default")
+ with torch.inference_mode():
+ output_loaded_back0 = model(inputs)
+
+ # real check: model now behaves again like adapter 0
+ assert torch.allclose(output0, output_loaded_back0, atol=atol, rtol=rtol)
+
+ @pytest.mark.parametrize("ranks", [(7, 13), (13, 7)])
+ def test_hotswap_works_different_ranks_alphas_conv2d(self, ranks, tmp_path):
+ # same as previous test, but for a Conv2d model
+ atol, rtol = 1e-4, 1e-4
+ inputs = torch.rand(3, 3, 10, 10).to(self.torch_device)
+
+ # create adapter 0
+ config0 = LoraConfig(target_modules=["conv"], r=ranks[0], init_lora_weights=False)
+ model = self.get_model_conv2d()
+ torch.manual_seed(0)
+ model = get_peft_model(model, config0)
+ model.eval()
+ with torch.inference_mode():
+ output0 = model(inputs)
+ model.save_pretrained(tmp_path / "adapter0")
+
+ del model
+
+ # create adapter 1
+ config1 = LoraConfig(target_modules=["conv"], r=ranks[1], init_lora_weights=False)
+ model = self.get_model_conv2d()
+ torch.manual_seed(1)
+ model = get_peft_model(model, config1)
+ model.eval()
+ with torch.inference_mode():
+ output1 = model(inputs)
+ model.save_pretrained(tmp_path / "adapter1")
+
+ # sanity check: they're not the same
+ assert not torch.allclose(output0, output1, atol=atol, rtol=rtol)
+
+ del model
+
+ # load adapter 0
+ model = self.get_model_conv2d()
+ model = PeftModel.from_pretrained(model, tmp_path / "adapter0")
+ with torch.inference_mode():
+ output_loaded0 = model(inputs)
+
+ # sanity check: same output after loading for adapter 0
+ assert torch.allclose(output0, output_loaded0, atol=atol, rtol=rtol)
+
+ # hotswap with adapter 1
+ hotswap_adapter(model, tmp_path / "adapter1", adapter_name="default")
+ with torch.inference_mode():
+ output_loaded1 = model(inputs)
+
+ # real check: model now behaves like adapter 1
+ assert torch.allclose(output1, output_loaded1, atol=atol, rtol=rtol)
+
+ # hotswap back to adapter 0
+ hotswap_adapter(model, tmp_path / "adapter0", adapter_name="default")
+ with torch.inference_mode():
+ output_loaded_back0 = model(inputs)
+
+ # real check: model now behaves again like adapter 0
+ assert torch.allclose(output0, output_loaded_back0, atol=atol, rtol=rtol)
+
+ def test_prepare_model_for_compiled_hotswap_scalings_are_tensors(self):
+ config = LoraConfig(target_modules=["lin0", "lin1"])
+ model = self.get_model()
+ model = get_peft_model(model, config)
+
+ # sanity check: all scalings are floats
+ scalings_before = {}
+ for name, module in model.named_modules():
+ if hasattr(module, "scaling"):
+ for key, val in module.scaling.items():
+ assert isinstance(val, float)
+ scalings_before[f"{name}.{key}"] = val
+
+ prepare_model_for_compiled_hotswap(model)
+
+ scalings_after = {}
+ for name, module in model.named_modules():
+ if hasattr(module, "scaling"):
+ for key, val in module.scaling.items():
+ assert isinstance(val, torch.Tensor)
+ scalings_after[f"{name}.{key}"] = val.item()
+
+ assert scalings_before == scalings_after
+
+ def test_prepare_model_for_compiled_hotswap_rank_padding_works(self):
+ old_rank = 8
+ config = LoraConfig(target_modules=["lin0", "lin1"], r=old_rank)
+ model = self.get_model()
+ model = get_peft_model(model, config)
+
+ # sanity check
+ for name, param in model.named_parameters():
+ if "lora_A" in name:
+ assert param.shape[0] == old_rank
+ elif "lora_B" in name:
+ assert param.shape[1] == old_rank
+
+ new_rank = 13
+ prepare_model_for_compiled_hotswap(model, target_rank=new_rank)
+
+ for name, param in model.named_parameters():
+ if "lora_A" in name:
+ assert param.shape[0] == new_rank
+ elif "lora_B" in name:
+ assert param.shape[1] == new_rank
+
+ def test_prepare_model_for_compiled_hotswap_same_rank_padding_works(self):
+ # same as previous test, but ensure there is no error if the rank to pad to is the same
+ old_rank = 8
+ config = LoraConfig(target_modules=["lin0", "lin1"], r=old_rank)
+ model = self.get_model()
+ model = get_peft_model(model, config)
+ prepare_model_for_compiled_hotswap(model, target_rank=old_rank)
+
+ for name, param in model.named_parameters():
+ if "lora_A" in name:
+ assert param.shape[0] == old_rank
+ elif "lora_B" in name:
+ assert param.shape[1] == old_rank
+
+ def test_prepare_model_for_compiled_hotswap_conv2d_rank_padding_works(self):
+ # same as previous test, but for a Conv2d model
+ old_rank = 8
+ config = LoraConfig(target_modules=["conv"], r=old_rank)
+ model = self.get_model_conv2d()
+ model = get_peft_model(model, config)
+
+ # sanity check
+ for name, param in model.named_parameters():
+ if "lora_A" in name:
+ assert param.shape[0] == old_rank
+ elif "lora_B" in name:
+ assert param.shape[1] == old_rank
+
+ new_rank = 13
+ prepare_model_for_compiled_hotswap(model, target_rank=new_rank)
+
+ for name, param in model.named_parameters():
+ if "lora_A" in name:
+ assert param.shape[0] == new_rank
+ elif "lora_B" in name:
+ assert param.shape[1] == new_rank
+
+ def test_prepare_model_for_compiled_hotswap_lower_rank_padding_raises(self):
+ # when trying to pad to a lower rank, raise an error
+ old_rank0 = 8
+ old_rank1 = 10
+ new_rank = 9
+ config = LoraConfig(target_modules=["lin0", "lin1"], r=old_rank0, rank_pattern={"lin1": old_rank1})
+ model = self.get_model()
+ model = get_peft_model(model, config)
+
+ msg = re.escape("Trying to pad the adapter to the target rank 9, but the original rank is larger (10)")
+ with pytest.raises(ValueError, match=msg):
+ prepare_model_for_compiled_hotswap(model, target_rank=new_rank)
+
+ def test_prepare_model_for_compiled_hotswap_with_rank_pattern(self):
+ old_rank0 = 8
+ old_rank1 = 9
+ config = LoraConfig(target_modules=["lin0", "lin1"], r=old_rank0, rank_pattern={"lin1": old_rank1})
+ model = self.get_model()
+ model = get_peft_model(model, config)
+
+ # sanity check
+ for name, param in model.named_parameters():
+ if "lora_A" in name:
+ if "lin0" in name:
+ assert param.shape[0] == old_rank0
+ else:
+ assert param.shape[0] == old_rank1
+ elif "lora_B" in name:
+ if "lin0" in name:
+ assert param.shape[1] == old_rank0
+ else:
+ assert param.shape[1] == old_rank1
+
+ new_rank = 13
+ prepare_model_for_compiled_hotswap(model, target_rank=new_rank)
+
+ for name, param in model.named_parameters():
+ if "lora_A" in name:
+ assert param.shape[0] == new_rank
+ elif "lora_B" in name:
+ assert param.shape[1] == new_rank
+
+ def test_prepare_model_for_compiled_hotswap_model_already_compiled_raises(self):
+ config = LoraConfig(target_modules=["lin0"])
+ model = self.get_model()
+ model = get_peft_model(model, config)
+ model = torch.compile(model, mode="reduce-overhead")
+
+ msg = re.escape("Call prepare_model_for_compiled_hotswap *before* compiling the model")
+ with pytest.raises(ValueError, match=msg):
+ prepare_model_for_compiled_hotswap(model)
+
+ def test_prepare_model_for_compiled_hotswap_model_already_compiled_warns(self, recwarn):
+ config = LoraConfig(target_modules=["lin0"])
+ model = self.get_model()
+ model = get_peft_model(model, config)
+ model = torch.compile(model, mode="reduce-overhead")
+
+ msg = "prepare_model_for_compiled_hotswap was called with a model that is already compiled"
+ prepare_model_for_compiled_hotswap(model, check_compiled="warn")
+ assert any(msg in str(w.message) for w in recwarn)
+
+ def test_prepare_model_for_compiled_hotswap_model_already_compiled_ignore(self, recwarn):
+ config = LoraConfig(target_modules=["lin0"])
+ model = self.get_model()
+ model = get_peft_model(model, config)
+ model = torch.compile(model, mode="reduce-overhead")
+
+ msg = "prepare_model_for_compiled_hotswap was called with a model that is already compiled"
+ prepare_model_for_compiled_hotswap(model, check_compiled="ignore")
+ # no error, no warning
+ assert not any(msg in str(w.message) for w in recwarn)
+
+ def test_prepare_model_for_compiled_hotswap_model_already_compiled_wrong_argument(self, recwarn):
+ config = LoraConfig(target_modules=["lin0"])
+ model = self.get_model()
+ model = get_peft_model(model, config)
+ model = torch.compile(model, mode="reduce-overhead")
+
+ msg = re.escape("check_compiles should be one of 'error', 'warn', or 'ignore', got 'wrong-option' instead.")
+ with pytest.raises(ValueError, match=msg):
+ prepare_model_for_compiled_hotswap(model, check_compiled="wrong-option")
+
+ def test_prepare_model_for_compiled_hotswap_model_no_adapter_raises(self):
+ model = self.get_model()
+ msg = re.escape("No adapter layers found on the model")
+ with pytest.raises(ValueError, match=msg):
+ prepare_model_for_compiled_hotswap(model)
+
+ def test_prepare_model_for_compiled_hotswap_does_not_change_output(self):
+ # preparing the model for hotswapping should not change the model output
+ inputs = torch.rand(3, 10).to(self.torch_device)
+ model = self.get_model().eval()
+ with torch.inference_mode():
+ output_base = model(inputs)
+
+ old_rank = 8
+ config = LoraConfig(target_modules=["lin0", "lin1"], r=old_rank, init_lora_weights=False)
+ model = get_peft_model(model, config).eval()
+ with torch.inference_mode():
+ output_before = model(inputs)
+
+ # sanity check: LoRA changed output
+ assert not torch.allclose(output_base, output_before)
+
+ new_rank = 13
+ prepare_model_for_compiled_hotswap(model, target_rank=new_rank)
+ with torch.inference_mode():
+ output_after = model(inputs)
+
+ assert torch.allclose(output_before, output_after)
+
+ def test_prepare_model_for_compiled_hotswap_does_not_change_output_conv2d(self):
+ # preparing the model for hotswapping should not change the model output
+ inputs = torch.rand(3, 3, 10, 10).to(self.torch_device)
+ model = self.get_model_conv2d().eval()
+ with torch.inference_mode():
+ output_base = model(inputs)
+
+ old_rank = 8
+ config = LoraConfig(target_modules=["conv"], r=old_rank, init_lora_weights=False)
+ model = get_peft_model(model, config).eval()
+ with torch.inference_mode():
+ output_before = model(inputs)
+
+ # sanity check: LoRA changed output
+ assert not torch.allclose(output_base, output_before)
+
+ new_rank = 13
+ prepare_model_for_compiled_hotswap(model, target_rank=new_rank)
+ with torch.inference_mode():
+ output_after = model(inputs)
+
+ assert torch.allclose(output_before, output_after)
+
+ def test_prepare_model_for_compiled_hotswap_scalings_update_config(self):
+ old_rank0 = 11
+ old_rank1 = 13
+ config = LoraConfig(target_modules=["lin0", "lin1"], r=old_rank0, rank_pattern={"lin1": old_rank1})
+ model = self.get_model()
+ model = get_peft_model(model, config)
+
+ new_rank = 15
+ prepare_model_for_compiled_hotswap(model, target_rank=new_rank, config=model.peft_config)
+
+ assert model.peft_config["default"].r == new_rank
+ assert model.peft_config["default"].rank_pattern == {"lin1": new_rank}
+
+ def test_prepare_model_for_compiled_hotswap_lora_bias(self):
+ # When setting lora_bias=True in the LoraConfig, the LoRA B parameter will have a bias term. Check that padding
+ # still works correctly. Note that the LoRA A parameter still won't have a bias term.
+ old_rank = 8
+ config = LoraConfig(target_modules=["lin0", "lin1"], r=old_rank, lora_bias=True)
+ model = self.get_model()
+ model = get_peft_model(model, config)
+
+ # sanity check
+ for name, param in model.named_parameters():
+ if "lora_A" in name and name.endswith(".weight"):
+ assert param.shape[0] == old_rank
+ elif "lora_B" in name and name.endswith(".weight"):
+ assert param.shape[1] == old_rank
+ elif "lora_A" in name and name.endswith(".bias"):
+ assert False, "LoRA A should not have a bias term"
+ elif "lora_B" in name and name.endswith(".bias"):
+ assert param.shape[0] in (5, 20) # output shapes of the 2 layers
+
+ new_rank = 13
+ prepare_model_for_compiled_hotswap(model, target_rank=new_rank)
+
+ for name, param in model.named_parameters():
+ if "lora_A" in name and name.endswith(".weight"):
+ assert param.shape[0] == new_rank
+ elif "lora_B" in name and name.endswith(".weight"):
+ assert param.shape[1] == new_rank
+ elif "lora_A" in name and name.endswith(".bias"):
+ assert False, "LoRA A should not have a bias term"
+ elif "lora_B" in name and name.endswith(".bias"):
+ assert param.shape[0] in (5, 20) # output shapes of the 2 layers
+
+ def test_prepare_model_for_compiled_hotswap_conv2d_lora_bias(self):
+ # same as previous test, but for a Conv2d model
+ old_rank = 8
+ config = LoraConfig(target_modules=["conv"], r=old_rank, lora_bias=True)
+ model = self.get_model_conv2d()
+ model = get_peft_model(model, config)
+
+ # sanity check
+ for name, param in model.named_parameters():
+ if "lora_A" in name and name.endswith(".weight"):
+ assert param.shape[0] == old_rank
+ elif "lora_B" in name and name.endswith(".weight"):
+ assert param.shape[1] == old_rank
+ elif "lora_A" in name and name.endswith(".bias"):
+ assert False, "LoRA A should not have a bias term"
+ elif "lora_B" in name and name.endswith(".bias"):
+ assert param.shape[0] == 10 # output shape of conv layer
+
+ new_rank = 13
+ prepare_model_for_compiled_hotswap(model, target_rank=new_rank)
+
+ for name, param in model.named_parameters():
+ if "lora_A" in name and name.endswith(".weight"):
+ assert param.shape[0] == new_rank
+ elif "lora_B" in name and name.endswith(".weight"):
+ assert param.shape[1] == new_rank
+ elif "lora_A" in name and name.endswith(".bias"):
+ assert False, "LoRA A should not have a bias term"
+ elif "lora_B" in name and name.endswith(".bias"):
+ assert param.shape[0] == 10 # output shape of conv layer
+
+
+def test_import_peft_type_to_model_mapping_deprecation_warning(recwarn):
+ # This is for backwards compatibility: In #2282, PEFT_TYPE_TO_MODEL_MAPPING was removed as it was redundant with
+ # PEFT_TYPE_TO_TUNER_MAPPING. However, third party code could still use this mapping, e.g.:
+ # https://github.com/AutoGPTQ/AutoGPTQ/blob/6689349625de973b9ee3016c28c11f32acf7f02c/auto_gptq/utils/peft_utils.py#L8
+ # TODO: Remove after 2026-01
+
+ # first check that there is no warning under normal circumstances
+ from peft.peft_model import PeftModel # noqa
+
+ expected = (
+ "PEFT_TYPE_TO_MODEL_MAPPING is deprecated, please use `from peft import PEFT_TYPE_TO_TUNER_MAPPING` instead"
+ )
+ warnings = (w.message.args[0] for w in recwarn.list)
+ assert not any(w.startswith(expected) for w in warnings)
+
+ from peft.peft_model import PEFT_TYPE_TO_MODEL_MAPPING # noqa
+
+ # check that there is a warning with this message after importing the variable
+ warnings = (w.message.args[0] for w in recwarn.list)
+ assert any(w.startswith(expected) for w in warnings)
+
+
+class TestScaling:
+ """Tests for scaling and unscaling
+
+ Those methods are currently only implemented for LoRA and were added for use in diffusers.
+ """
+
+ @pytest.fixture
+ def model(self):
+ # tiny opt with 5 attention layers
+ model_id = "hf-internal-testing/tiny-random-OPTForCausalLM"
+ return AutoModelForCausalLM.from_pretrained(model_id)
+
+ def get_scalings(self, model, adapter_name="default"):
+ # helper function, returns the scalings of the 5 attention layers
+ return [m.scaling[adapter_name] for m in model.modules() if isinstance(m, LoraLayer)]
+
+ def set_scale(self, model, adapter_name, scale):
+ for module in model.modules():
+ if isinstance(module, LoraLayer):
+ module.set_scale(adapter_name, scale)
+
+ def scale_layer(self, model, scale):
+ for module in model.modules():
+ if isinstance(module, LoraLayer):
+ module.scale_layer(scale)
+
+ def unscale_layer(self, model, scale):
+ for module in model.modules():
+ if isinstance(module, LoraLayer):
+ module.unscale_layer(scale)
+
+ def test_scaling_simple(self, model):
+ n_layers = 5
+ rank, lora_alpha = 8, 16
+ config = LoraConfig(
+ r=rank,
+ lora_alpha=lora_alpha,
+ target_modules=["k_proj"],
+ )
+ model = get_peft_model(model, config)
+ scalings = self.get_scalings(model)
+ expected = [lora_alpha / rank] * n_layers
+ assert scalings == expected
+
+ # double
+ self.scale_layer(model, 2)
+ scalings = self.get_scalings(model)
+ expected = [4.0] * n_layers
+ assert scalings == expected
+
+ # back to original
+ self.unscale_layer(model, None)
+ scalings = self.get_scalings(model)
+ expected = [2.0] * n_layers
+ assert scalings == expected
+
+ # triple
+ self.set_scale(model, "default", 3)
+ scalings = self.get_scalings(model)
+ expected = [6.0] * n_layers
+ assert scalings == expected
+
+ # back to original
+ self.unscale_layer(model, 3)
+ scalings = self.get_scalings(model)
+ expected = [2.0] * n_layers
+ assert scalings == expected
+
+ def test_scaling_with_rslora(self, model):
+ n_layers = 5
+ rank, lora_alpha = 8, 16
+ config = LoraConfig(
+ r=rank,
+ lora_alpha=lora_alpha,
+ use_rslora=True,
+ target_modules=["k_proj"],
+ )
+ model = get_peft_model(model, config)
+ scalings = self.get_scalings(model)
+ expected = [lora_alpha / math.sqrt(rank)] * n_layers
+ assert scalings == expected
+
+ # double
+ self.scale_layer(model, 2)
+ scalings = self.get_scalings(model)
+ expected = [2 * lora_alpha / math.sqrt(rank)] * n_layers
+ assert scalings == expected
+
+ # back to original
+ self.unscale_layer(model, None)
+ scalings = self.get_scalings(model)
+ expected = [lora_alpha / math.sqrt(rank)] * n_layers
+ assert scalings == expected
+
+ # triple
+ self.set_scale(model, "default", 3)
+ scalings = self.get_scalings(model)
+ expected = [3 * lora_alpha / math.sqrt(rank)] * n_layers
+ assert scalings == expected
+
+ # back to original
+ self.unscale_layer(model, 3)
+ scalings = self.get_scalings(model)
+ expected = [lora_alpha / math.sqrt(rank)] * n_layers
+ assert scalings == expected
+
+ def test_scaling_rank_pattern_alpha_pattern(self, model):
+ # layer 0: 8 / 8
+ # layer 1: 8 / 16
+ # layer 2: 4 / 32
+ # layer 3: 16 / 8
+ # layer 4: 8 / 8
+ config = LoraConfig(
+ r=8,
+ lora_alpha=8,
+ target_modules=["k_proj"],
+ rank_pattern={"layers.1.self_attn.k_proj": 16, "layers.2.self_attn.k_proj": 32},
+ alpha_pattern={"layers.2.self_attn.k_proj": 4, "layers.3.self_attn.k_proj": 16},
+ )
+ model = get_peft_model(model, config)
+ scalings = self.get_scalings(model)
+ expected = [1.0, 0.5, 0.125, 2.0, 1.0]
+ assert scalings == expected
+
+ # double
+ self.scale_layer(model, 2)
+ scalings = self.get_scalings(model)
+ expected = [2.0, 1.0, 0.25, 4.0, 2.0]
+ assert scalings == expected
+
+ # back to original
+ self.unscale_layer(model, None)
+ scalings = self.get_scalings(model)
+ expected = [1.0, 0.5, 0.125, 2.0, 1.0]
+ assert scalings == expected
+
+ # triple
+ self.set_scale(model, "default", 3)
+ scalings = self.get_scalings(model)
+ expected = [3.0, 1.5, 0.375, 6.0, 3.0]
+ assert scalings == expected
+
+ # back to original
+ self.unscale_layer(model, 3)
+ scalings = self.get_scalings(model)
+ expected = [1.0, 0.5, 0.125, 2.0, 1.0]
+ assert scalings == expected
+
+ def test_scaling_multiple_times(self, model):
+ # same as previous test, but scale and unscale multiple times in a row
+ # layer 0: 8 / 8
+ # layer 1: 8 / 16
+ # layer 2: 4 / 32
+ # layer 3: 16 / 8
+ # layer 4: 8 / 8
+ config = LoraConfig(
+ r=8,
+ lora_alpha=8,
+ target_modules=["k_proj"],
+ rank_pattern={"layers.1.self_attn.k_proj": 16, "layers.2.self_attn.k_proj": 32},
+ alpha_pattern={"layers.2.self_attn.k_proj": 4, "layers.3.self_attn.k_proj": 16},
+ )
+ model = get_peft_model(model, config)
+ scalings = self.get_scalings(model)
+ expected = [1.0, 0.5, 0.125, 2.0, 1.0]
+ assert scalings == expected
+
+ # scale of 1 makes no difference
+ self.scale_layer(model, 1)
+ scalings = self.get_scalings(model)
+ expected = [1.0, 0.5, 0.125, 2.0, 1.0]
+
+ # double
+ self.scale_layer(model, 2)
+ scalings = self.get_scalings(model)
+ expected = [2.0, 1.0, 0.25, 4.0, 2.0]
+ assert scalings == expected
+
+ # triple, on top of previous double
+ self.scale_layer(model, 3)
+ scalings = self.get_scalings(model)
+ expected = [6.0, 3.0, 0.75, 12.0, 6.0]
+ assert scalings == expected
+
+ # half
+ self.unscale_layer(model, 2)
+ scalings = self.get_scalings(model)
+ expected = [3.0, 1.5, 0.375, 6.0, 3.0]
+ assert scalings == expected
+
+ # divide by 3, on top of previous half
+ self.unscale_layer(model, 3)
+ scalings = self.get_scalings(model)
+ expected = [1.0, 0.5, 0.125, 2.0, 1.0]
+ assert scalings == expected
+
+ # set scale to 2
+ self.set_scale(model, "default", 2)
+ scalings = self.get_scalings(model)
+ expected = [2.0, 1.0, 0.25, 4.0, 2.0]
+ assert scalings == expected
+
+ # set scale to 3, it is cumulative but based on the initial scaling, so factor 3, not 6
+ self.set_scale(model, "default", 3)
+ scalings = self.get_scalings(model)
+ expected = [3.0, 1.5, 0.375, 6.0, 3.0]
+ assert scalings == expected
+
+ # back to original
+ self.unscale_layer(model, None)
+ scalings = self.get_scalings(model)
+ expected = [1.0, 0.5, 0.125, 2.0, 1.0]
+ assert scalings == expected
+
+ # back to original again
+ self.unscale_layer(model, None)
+ scalings = self.get_scalings(model)
+ expected = [1.0, 0.5, 0.125, 2.0, 1.0]
+ assert scalings == expected
+
+ def test_scaling_multiple_adapters(self, model):
+ # ensure that scaling works with multiple adapters
+ n_layers = 5
+ rank0, lora_alpha0 = 8, 16
+ config0 = LoraConfig(
+ r=rank0,
+ lora_alpha=lora_alpha0,
+ target_modules=["k_proj"],
+ )
+ rank1, lora_alpha1 = 16, 8
+ config1 = LoraConfig(
+ r=rank1,
+ lora_alpha=lora_alpha1,
+ target_modules=["k_proj"],
+ )
+ model = get_peft_model(model, config0)
+ model.add_adapter("other", config1)
+
+ scalings_default = self.get_scalings(model, "default")
+ scalings_other = self.get_scalings(model, "other")
+ expected_default = [lora_alpha0 / rank0] * n_layers
+ expected_other = [lora_alpha1 / rank1] * n_layers
+ assert scalings_default == expected_default
+ assert scalings_other == expected_other
+
+ # double the scale for other
+ self.set_scale(model, "other", 2)
+ scalings_default = self.get_scalings(model, "default")
+ scalings_other = self.get_scalings(model, "other")
+ expected_default = [lora_alpha0 / rank0] * n_layers
+ expected_other = [2 * lora_alpha1 / rank1] * n_layers
+ assert scalings_default == expected_default
+ assert scalings_other == expected_other
+
+ # quarter the scale for default
+ self.set_scale(model, "default", 0.25)
+ scalings_default = self.get_scalings(model, "default")
+ scalings_other = self.get_scalings(model, "other")
+ expected_default = [lora_alpha0 / rank0 / 4] * n_layers
+ expected_other = [2 * lora_alpha1 / rank1] * n_layers
+ assert scalings_default == expected_default
+ assert scalings_other == expected_other
+
+ # unscale resets for all *active* adapters
+ self.unscale_layer(model, None)
+ scalings_default = self.get_scalings(model, "default")
+ scalings_other = self.get_scalings(model, "other")
+ expected_default = [lora_alpha0 / rank0] * n_layers
+ expected_other = [2 * lora_alpha1 / rank1] * n_layers # stays the same as 'other' is not active
+ assert scalings_default == expected_default
+ assert scalings_other == expected_other
+
+ # scale all *active* adapters by 2
+ self.scale_layer(model, 2)
+ scalings_default = self.get_scalings(model, "default")
+ scalings_other = self.get_scalings(model, "other")
+ expected_default = [2 * lora_alpha0 / rank0] * n_layers
+ expected_other = [2 * lora_alpha1 / rank1] * n_layers # stays the same as 'other' is not active
+ assert scalings_default == expected_default
+ assert scalings_other == expected_other
+
+ # switch to 'other'
+ model.set_adapter("other")
+
+ # unscale, this time 'other'
+ self.unscale_layer(model, None)
+ scalings_default = self.get_scalings(model, "default")
+ scalings_other = self.get_scalings(model, "other")
+ expected_default = [2 * lora_alpha0 / rank0] * n_layers # stays the same as 'other' is not active
+ expected_other = [lora_alpha1 / rank1] * n_layers
+ assert scalings_default == expected_default
+ assert scalings_other == expected_other
+
+ # scale all *active* adapters by 3
+ self.scale_layer(model, 3)
+ scalings_default = self.get_scalings(model, "default")
+ scalings_other = self.get_scalings(model, "other")
+ expected_default = [2 * lora_alpha0 / rank0] * n_layers # stays the same as 'other' is not active
+ expected_other = [3 * lora_alpha1 / rank1] * n_layers
+ assert scalings_default == expected_default
+ assert scalings_other == expected_other
+
+
+class TestLoadPeftKeyMapping:
+ # See discussion in https://github.com/huggingface/transformers/pull/38627
+
+ # transformers PR #37033 re-arranges the way visual language models are built by moving the LM head from the
+ # language model to the top-level VLM (among other things). A consequence of this is that the keys in the PEFT
+ # state_dict now also follow the new architecture. This test class serves to ensure that old checkpoints can be
+ # loaded with the changed architecture. Unfortunately, new checkpoints cannot be loaded with the old architecture,
+ # the corresponding test is marked as xfail.
+
+ # Note: We only test prefix tuning (prompt learning method), LoRA (non-prompt learning method), and VBLoRA (shared
+ # parameters) as the other PEFT methods should work the same way. It would be excessive to test all of them here.
+
+ @pytest.fixture
+ def fake_model_config(self):
+ # mimics a transformers model config
+ class FakeConfig(dict):
+ def __init__(self):
+ self.vocab_size = 10
+
+ def __getattr__(self, item):
+ if item in self:
+ return self[item]
+ raise AttributeError(f"'{self.__class__.__name__}' object has no attribute '{item}'")
+
+ return FakeConfig()
+
+ @pytest.fixture
+ def old_model(self, fake_model_config):
+ # create a small model that mimics the old architecture of, for instance, Qwen/Qwen2-VL-2B-Instruct
+ # Qwen2VLForConditionalGeneration(
+ # (visual): Qwen2VisionTransformerPretrainedModel(
+ # (patch_embed): PatchEmbed(
+ # (proj): Conv3d(3, 1280, kernel_size=(2, 14, 14), stride=(2, 14, 14), bias=False)
+ # )
+ # (rotary_pos_emb): VisionRotaryEmbedding()
+ # (blocks): ModuleList(
+ # (0-31): 32 x Qwen2VLVisionBlock(
+ # (norm1): LayerNorm((1280,), eps=1e-06, elementwise_affine=True)
+ # (norm2): LayerNorm((1280,), eps=1e-06, elementwise_affine=True)
+ # (attn): VisionSdpaAttention(
+ # (qkv): Linear(in_features=1280, out_features=3840, bias=True)
+ # (proj): Linear(in_features=1280, out_features=1280, bias=True)
+ # )
+ # (mlp): VisionMlp(
+ # (fc1): Linear(in_features=1280, out_features=5120, bias=True)
+ # (act): QuickGELUActivation()
+ # (fc2): Linear(in_features=5120, out_features=1280, bias=True)
+ # )
+ # )
+ # )
+ # (merger): PatchMerger(
+ # (ln_q): LayerNorm((1280,), eps=1e-06, elementwise_affine=True)
+ # (mlp): Sequential(
+ # (0): Linear(in_features=5120, out_features=5120, bias=True)
+ # (1): GELU(approximate='none')
+ # (2): Linear(in_features=5120, out_features=1536, bias=True)
+ # )
+ # )
+ # )
+ # (model): Qwen2VLModel(
+ # (embed_tokens): Embedding(151936, 1536)
+ # (layers): ModuleList(
+ # (0-27): 28 x Qwen2VLDecoderLayer(
+ # (self_attn): Qwen2VLSdpaAttention(
+ # (q_proj): Linear(in_features=1536, out_features=1536, bias=True)
+ # (k_proj): Linear(in_features=1536, out_features=256, bias=True)
+ # (v_proj): Linear(in_features=1536, out_features=256, bias=True)
+ # (o_proj): Linear(in_features=1536, out_features=1536, bias=False)
+ # (rotary_emb): Qwen2VLRotaryEmbedding()
+ # )
+ # (mlp): Qwen2MLP(
+ # (gate_proj): Linear(in_features=1536, out_features=8960, bias=False)
+ # (up_proj): Linear(in_features=1536, out_features=8960, bias=False)
+ # (down_proj): Linear(in_features=8960, out_features=1536, bias=False)
+ # (act_fn): SiLU()
+ # )
+ # (input_layernorm): Qwen2RMSNorm((1536,), eps=1e-06)
+ # (post_attention_layernorm): Qwen2RMSNorm((1536,), eps=1e-06)
+ # )
+ # )
+ # (norm): Qwen2RMSNorm((1536,), eps=1e-06)
+ # (rotary_emb): Qwen2VLRotaryEmbedding()
+ # )
+ # (lm_head): Linear(in_features=1536, out_features=151936, bias=False)
+ # )
+ class Block(nn.Module):
+ def __init__(self):
+ super().__init__()
+ self.attn = nn.Linear(10, 10)
+
+ class OldModel(nn.Module):
+ def __init__(self):
+ super().__init__()
+ self.config = fake_model_config
+ self.device = "cpu"
+ self.proj = nn.Conv3d(3, 10, 3)
+ self.visual = nn.ModuleDict(
+ {
+ "blocks": nn.ModuleList([Block() for _ in range(2)]),
+ }
+ )
+ self.model = nn.ModuleDict(
+ {
+ "layers": nn.ModuleList([Block() for _ in range(2)]),
+ }
+ )
+ self.lm_head = nn.Linear(10, 10)
+
+ def prepare_inputs_for_generation(self):
+ return
+
+ model = OldModel()
+ return model
+
+ @pytest.fixture
+ def new_model(self, fake_model_config):
+ # create a small model that mimics the new architecture of, for instance, Qwen/Qwen2-VL-2B-Instruct
+ # Qwen2VLForConditionalGeneration(
+ # (model): Qwen2VLModel(
+ # (visual): Qwen2VisionTransformerPretrainedModel(
+ # (patch_embed): PatchEmbed(
+ # (proj): Conv3d(3, 1280, kernel_size=(2, 14, 14), stride=(2, 14, 14), bias=False)
+ # )
+ # (rotary_pos_emb): VisionRotaryEmbedding()
+ # (blocks): ModuleList(
+ # (0-31): 32 x Qwen2VLVisionBlock(
+ # (norm1): LayerNorm((1280,), eps=1e-06, elementwise_affine=True)
+ # (norm2): LayerNorm((1280,), eps=1e-06, elementwise_affine=True)
+ # (attn): VisionSdpaAttention(
+ # (qkv): Linear(in_features=1280, out_features=3840, bias=True)
+ # (proj): Linear(in_features=1280, out_features=1280, bias=True)
+ # )
+ # (mlp): VisionMlp(
+ # (fc1): Linear(in_features=1280, out_features=5120, bias=True)
+ # (act): QuickGELUActivation()
+ # (fc2): Linear(in_features=5120, out_features=1280, bias=True)
+ # )
+ # )
+ # )
+ # (merger): PatchMerger(
+ # (ln_q): LayerNorm((1280,), eps=1e-06, elementwise_affine=True)
+ # (mlp): Sequential(
+ # (0): Linear(in_features=5120, out_features=5120, bias=True)
+ # (1): GELU(approximate='none')
+ # (2): Linear(in_features=5120, out_features=1536, bias=True)
+ # )
+ # )
+ # )
+ # (language_model): Qwen2VLTextModel(
+ # (embed_tokens): Embedding(151936, 1536)
+ # (layers): ModuleList(
+ # (0-27): 28 x Qwen2VLDecoderLayer(
+ # (self_attn): Qwen2VLAttention(
+ # (q_proj): Linear(in_features=1536, out_features=1536, bias=True)
+ # (k_proj): Linear(in_features=1536, out_features=256, bias=True)
+ # (v_proj): Linear(in_features=1536, out_features=256, bias=True)
+ # (o_proj): Linear(in_features=1536, out_features=1536, bias=False)
+ # (rotary_emb): Qwen2VLRotaryEmbedding()
+ # )
+ # (mlp): Qwen2MLP(
+ # (gate_proj): Linear(in_features=1536, out_features=8960, bias=False)
+ # (up_proj): Linear(in_features=1536, out_features=8960, bias=False)
+ # (down_proj): Linear(in_features=8960, out_features=1536, bias=False)
+ # (act_fn): SiLU()
+ # )
+ # (input_layernorm): Qwen2RMSNorm((1536,), eps=1e-06)
+ # (post_attention_layernorm): Qwen2RMSNorm((1536,), eps=1e-06)
+ # )
+ # )
+ # (norm): Qwen2RMSNorm((1536,), eps=1e-06)
+ # (rotary_emb): Qwen2VLRotaryEmbedding()
+ # )
+ # )
+ # (lm_head): Linear(in_features=1536, out_features=151936, bias=False)
+ # )
+ class Block(nn.Module):
+ def __init__(self):
+ super().__init__()
+ self.attn = nn.Linear(10, 10)
+
+ class InnerModel(nn.Module):
+ def __init__(self):
+ super().__init__()
+ self.visual = nn.ModuleDict(
+ {
+ "blocks": nn.ModuleList([Block() for _ in range(2)]),
+ }
+ )
+ self.language_model = nn.ModuleDict(
+ {
+ "layers": nn.ModuleList([Block() for _ in range(2)]),
+ }
+ )
+
+ class NewModel(nn.Module):
+ def __init__(self):
+ super().__init__()
+ self.config = fake_model_config
+ self.device = "cpu"
+ self.model = InnerModel()
+ self.lm_head = nn.Linear(10, 10)
+ # new transformers models have this attribute to map old checkpoints to new ones:
+ self._checkpoint_conversion_mapping = {
+ "^visual": "model.visual",
+ "^model(?!\\.(language_model|visual))": "model.language_model",
+ }
+
+ def prepare_inputs_for_generation(self):
+ return
+
+ model = NewModel()
+ return model
+
+ def check_lora_load_no_warning(self, model1, model2, path):
+ # helper method: save with model1, load with model2, ensure that there is no warning about missing keys and that
+ # the parameters are loaded correctly
+ model1 = copy.deepcopy(model1)
+ model2 = copy.deepcopy(model2)
+ config = LoraConfig(target_modules=["attn"])
+ peft_model = get_peft_model(copy.deepcopy(model1), config)
+
+ # set all values to 1.0 or 2.0 so we can check that they are loaded correctly
+ for name, param in peft_model.named_parameters():
+ if name.endswith("lora_A.default.weight"):
+ param.data.fill_(1.0)
+ elif name.endswith("lora_B.default.weight"):
+ param.data.fill_(2.0)
+
+ peft_model.save_pretrained(path)
+ del peft_model
+
+ # ensure that there is no warning: UserWarning: Found missing adapter keys while loading the checkpoint
+ with warnings.catch_warnings(record=True) as w:
+ warnings.simplefilter("always")
+ loaded = PeftModel.from_pretrained(copy.deepcopy(model2), path)
+ assert not any("Found missing adapter keys" in str(warning.message) for warning in w)
+
+ # sanity check on parameter values to not only rely on the absence of warnings
+ for name, param in loaded.named_parameters():
+ if name.endswith("lora_A.default.weight"):
+ assert torch.allclose(param, torch.full_like(param, 1.0))
+ elif name.endswith("lora_B.default.weight"):
+ assert torch.allclose(param, torch.full_like(param, 2.0))
+
+ def check_prefix_tuning_load_no_warning(self, model1, model2, path):
+ # helper method: save with model1, load with model2, ensure that there is no warning about missing keys and that
+ # the parameters are loaded correctly.
+ model1 = copy.deepcopy(model1)
+ model2 = copy.deepcopy(model2)
+ config = PrefixTuningConfig(
+ task_type="CAUSAL_LM", num_virtual_tokens=5, num_layers=2, token_dim=10, num_attention_heads=2
+ )
+ peft_model = get_peft_model(copy.deepcopy(model1), config)
+
+ # set all values to 1.0 so we can check that they are loaded correctly
+ peft_model.prompt_encoder.default.embedding.weight.data.fill_(1.0)
+
+ peft_model.save_pretrained(path)
+ del peft_model
+
+ # ensure that there is no warning: UserWarning: Found missing adapter keys while loading the checkpoint
+ with warnings.catch_warnings(record=True) as w:
+ warnings.simplefilter("always")
+ loaded = PeftModel.from_pretrained(copy.deepcopy(model2), path)
+ assert not any("Found missing adapter keys" in str(warning.message) for warning in w)
+
+ # sanity check on parameter values to not only rely on the absence of warnings
+ weight = loaded.prompt_encoder.default.embedding.weight
+ assert torch.allclose(weight, torch.full_like(weight, 1.0))
+
+ def check_vblora_load_no_warning(self, model1, model2, path):
+ # helper method: save with model1, load with model2, ensure that there is no warning about missing keys and that
+ # the parameters are loaded correctly
+ model1 = copy.deepcopy(model1)
+ model2 = copy.deepcopy(model2)
+
+ config = VBLoRAConfig(target_modules=["attn"], vector_length=2, num_vectors=4)
+ peft_model = get_peft_model(copy.deepcopy(model1), config)
+
+ # set all values to 1.0 or 2.0 so we can check that they are loaded correctly
+ peft_model.base_model.vblora_vector_bank["default"].data.fill_(1.0)
+ for name, param in peft_model.named_parameters():
+ if "logits" in name:
+ param.data.fill_(2.0)
+
+ peft_model.save_pretrained(path)
+ del peft_model
+
+ # ensure that there is no warning: UserWarning: Found missing adapter keys while loading the checkpoint
+ with warnings.catch_warnings(record=True) as w:
+ warnings.simplefilter("always")
+ loaded = PeftModel.from_pretrained(copy.deepcopy(model2), path)
+ assert not any("Found missing adapter keys" in str(warning.message) for warning in w)
+
+ # sanity check on parameter values to not only rely on the absence of warnings
+ param = loaded.base_model.vblora_vector_bank["default"]
+ assert torch.allclose(param, torch.full_like(param, 1.0))
+ for name, param in loaded.named_parameters():
+ if "logits" in name:
+ assert torch.allclose(param, torch.full_like(param, 2.0))
+
+ def test_key_mapping_save_new_load_new_lora(self, new_model, tmp_path):
+ # save and load the new model, should work without issues
+ self.check_lora_load_no_warning(new_model, new_model, tmp_path)
+
+ def test_key_mapping_save_old_load_old_lora(self, old_model, tmp_path):
+ # save and load the old model, should work without issues
+ self.check_lora_load_no_warning(old_model, old_model, tmp_path)
+
+ def test_key_mapping_save_old_load_new_lora(self, old_model, new_model, tmp_path):
+ # save the old model, load it into the new model, should work without issues (backwards compatibility)
+ self.check_lora_load_no_warning(old_model, new_model, tmp_path)
+
+ @pytest.mark.xfail(reason="Loading new checkpoints with old transformers is not supported.", strict=True)
+ def test_key_mapping_save_new_load_old_lora(self, old_model, new_model, tmp_path):
+ # save the new model, load it into the old model, should work without issues (forwards compatibility)
+ self.check_lora_load_no_warning(new_model, old_model, tmp_path)
+
+ def test_key_mapping_save_new_load_new_prefix_tuning(self, new_model, tmp_path):
+ # save and load the new model, should work without issues
+ self.check_prefix_tuning_load_no_warning(new_model, new_model, tmp_path)
+
+ def test_key_mapping_save_old_load_old_prefix_tuning(self, old_model, tmp_path):
+ # save and load the old model, should work without issues
+ self.check_prefix_tuning_load_no_warning(old_model, old_model, tmp_path)
+
+ def test_key_mapping_save_old_load_new_prefix_tuning(self, old_model, new_model, tmp_path):
+ # save the old model, load it into the new model, should work without issues (backwards compatibility)
+ self.check_prefix_tuning_load_no_warning(old_model, new_model, tmp_path)
+
+ def test_key_mapping_save_new_load_old_prefix_tuning(self, old_model, new_model, tmp_path):
+ # save the new model, load it into the old model, should work without issues (forwards compatibility)
+ self.check_prefix_tuning_load_no_warning(new_model, old_model, tmp_path)
+
+ def test_key_mapping_save_new_load_new_vblora(self, new_model, tmp_path):
+ # save and load the new model, should work without issues
+ self.check_vblora_load_no_warning(new_model, new_model, tmp_path)
+
+ def test_key_mapping_save_old_load_old_vblora(self, old_model, tmp_path):
+ # save and load the old model, should work without issues
+ self.check_vblora_load_no_warning(old_model, old_model, tmp_path)
+
+ def test_key_mapping_save_old_load_new_vblora(self, old_model, new_model, tmp_path):
+ # save the old model, load it into the new model, should work without issues (backwards compatibility)
+ self.check_vblora_load_no_warning(old_model, new_model, tmp_path)
+
+ @pytest.mark.xfail(reason="Loading new checkpoints with old transformers is not supported.", strict=True)
+ def test_key_mapping_save_new_load_old_vblora(self, old_model, new_model, tmp_path):
+ # save the new model, load it into the old model, should work without issues (forwards compatibility)
+ self.check_vblora_load_no_warning(new_model, old_model, tmp_path)
diff --git a/peft/tests/test_integrations.py b/peft/tests/test_integrations.py
new file mode 100644
index 0000000000000000000000000000000000000000..18ce4b2f0625424f566b93de1d6accaf4b87ced1
--- /dev/null
+++ b/peft/tests/test_integrations.py
@@ -0,0 +1,97 @@
+# Copyright 2024-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+import torch
+from torch import nn
+
+from peft.utils.integrations import init_empty_weights, skip_init_on_device
+
+
+class MLP(nn.Module):
+ def __init__(self, bias=True):
+ super().__init__()
+ self.lin0 = nn.Linear(10, 20, bias=bias)
+ self.relu = nn.ReLU()
+ self.drop = nn.Dropout(0.5)
+ self.lin1 = nn.Linear(20, 2, bias=bias)
+
+
+def get_mlp():
+ return MLP()
+
+
+class TestInitEmptyWeights:
+ def test_init_empty_weights_works(self):
+ # this is a very rudimentary test, as init_empty_weights is copied almost 1:1 from accelerate and is tested
+ # there
+ with init_empty_weights():
+ mlp = get_mlp()
+
+ expected = torch.device("meta")
+ assert all(p.device == expected for p in mlp.parameters())
+
+ def test_skip_init_on_device_works(self):
+ # when a function is decorated with skip_init_on_device, the parameters are not moved to meta device, even when
+ # inside the context
+ decorated_fn = skip_init_on_device(get_mlp)
+ with init_empty_weights():
+ mlp = decorated_fn()
+
+ expected = torch.device("cpu")
+ assert all(p.device == expected for p in mlp.parameters())
+
+ def test_skip_init_on_device_works_outside_context(self):
+ # same as before, but ensure that skip_init_on_device does not break when no init_empty_weights context is used
+ decorated_fn = skip_init_on_device(get_mlp)
+ mlp = decorated_fn()
+ expected = torch.device("cpu")
+ assert all(p.device == expected for p in mlp.parameters())
+
+ def test_skip_init_on_device_not_permanent(self):
+ # ensure that after skip_init_on_device has been used, init_empty_weights reverts to its original functionality
+
+ # with decorator => cpu
+ decorated_fn = skip_init_on_device(get_mlp)
+ with init_empty_weights():
+ mlp = decorated_fn()
+
+ expected = torch.device("cpu")
+ assert all(p.device == expected for p in mlp.parameters())
+
+ # without decorator => meta
+ with init_empty_weights():
+ mlp = get_mlp()
+
+ expected = torch.device("meta")
+ assert all(p.device == expected for p in mlp.parameters())
+
+ def test_skip_init_on_device_nested(self):
+ # ensure that skip_init_on_device works even if the decorated function is nested inside another decorated
+ # function
+ @skip_init_on_device
+ def outer_fn():
+ @skip_init_on_device
+ def inner_fn():
+ return get_mlp()
+
+ mlp0 = inner_fn()
+ mlp1 = get_mlp()
+ return mlp0, mlp1
+
+ with init_empty_weights():
+ mlp0, mlp1 = outer_fn()
+
+ expected = torch.device("cpu")
+ assert all(p.device == expected for p in mlp0.parameters())
+ assert all(p.device == expected for p in mlp1.parameters())
diff --git a/peft/tests/test_lora_megatron.py b/peft/tests/test_lora_megatron.py
new file mode 100644
index 0000000000000000000000000000000000000000..ff91a41387d768d8741e2568b98ae405aff47778
--- /dev/null
+++ b/peft/tests/test_lora_megatron.py
@@ -0,0 +1,171 @@
+#!/usr/bin/env python3
+
+# coding=utf-8
+# Copyright 2023-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+import copy
+import importlib
+import os
+import unittest
+
+import torch
+import torch.nn.init as init
+
+from peft import LoraConfig, PeftModel, get_peft_model, get_peft_model_state_dict
+
+from .testing_utils import require_torch_gpu
+
+
+def is_megatron_available() -> bool:
+ return importlib.util.find_spec("megatron") is not None
+
+
+if is_megatron_available():
+ from megatron.core import parallel_state, tensor_parallel
+ from megatron.core.tensor_parallel.random import model_parallel_cuda_manual_seed
+ from megatron.core.transformer.module import MegatronModule
+ from megatron.core.transformer.transformer_config import TransformerConfig
+
+ world_size = 1
+ rank = 0
+
+ def initialize_distributed():
+ print(f"Initializing torch.distributed with rank: {rank}, world_size: {world_size}")
+ torch.cuda.set_device(0)
+ init_method = "tcp://"
+ master_ip = os.getenv("MASTER_ADDR", "localhost")
+ master_port = os.getenv("MASTER_PORT", "6001")
+ init_method += master_ip + ":" + master_port
+ torch.distributed.init_process_group(backend="nccl", world_size=world_size, rank=rank, init_method=init_method)
+
+ def destroy_model_parallel():
+ parallel_state.destroy_model_parallel()
+ torch.distributed.barrier()
+
+ def initialize_model_parallel(
+ tensor_model_parallel_size=1,
+ pipeline_model_parallel_size=1,
+ virtual_pipeline_model_parallel_size=None,
+ pipeline_model_parallel_split_rank=None,
+ ):
+ parallel_state.destroy_model_parallel()
+ if not torch.distributed.is_initialized():
+ initialize_distributed()
+ parallel_state.initialize_model_parallel(
+ tensor_model_parallel_size,
+ pipeline_model_parallel_size,
+ virtual_pipeline_model_parallel_size,
+ pipeline_model_parallel_split_rank,
+ )
+
+ class DummyModule(MegatronModule):
+ def __init__(self, config: TransformerConfig):
+ super().__init__(config)
+ self.linear = tensor_parallel.ColumnParallelLinear(
+ input_size=10,
+ output_size=10,
+ config=config,
+ init_method=init.xavier_normal_,
+ bias=False,
+ gather_output=False,
+ )
+ self.lm_head = tensor_parallel.RowParallelLinear(
+ input_size=10,
+ output_size=10,
+ config=config,
+ init_method=init.xavier_normal_,
+ bias=False,
+ input_is_parallel=True,
+ skip_bias_add=True,
+ )
+
+ def forward(self, input):
+ x = self.linear(input)[0]
+ x = self.lm_head(x)[0]
+ return x
+
+ @require_torch_gpu
+ class TestMegatronLora(unittest.TestCase):
+ def setUp(self):
+ initialize_model_parallel(1, 1)
+ model_parallel_cuda_manual_seed(123)
+ transformer_config = {
+ "num_layers": 2,
+ "hidden_size": 12,
+ "num_attention_heads": 4,
+ "use_cpu_initialization": True,
+ }
+ config = TransformerConfig(**transformer_config)
+ self.megatron_module = DummyModule(config=config).cuda()
+ self.dummy_module = copy.deepcopy(self.megatron_module).cuda()
+
+ lora_config = LoraConfig(
+ lora_alpha=16,
+ lora_dropout=0.1,
+ r=64,
+ bias="none",
+ target_modules=["linear", "lm_head"],
+ megatron_config=config,
+ megatron_core="megatron.core",
+ )
+ self.megatron_module = get_peft_model(self.megatron_module, lora_config)
+
+ def tearDown(self):
+ destroy_model_parallel()
+
+ def test_megatron_lora_module(self):
+ megatron_module = self.megatron_module
+ assert isinstance(megatron_module, PeftModel)
+
+ for name, module in megatron_module.named_modules():
+ if name.endswith("linear"):
+ assert hasattr(module, "lora_A")
+ assert hasattr(module, "lora_B")
+ if name.endswith("linear.lora_A.default"):
+ assert isinstance(module, torch.nn.Linear)
+ if name.endswith("linear.lora_B.default"):
+ assert isinstance(module, tensor_parallel.ColumnParallelLinear)
+
+ if name.endswith("lm_head.lora_A.default"):
+ assert isinstance(module, tensor_parallel.RowParallelLinear)
+ if name.endswith("lm_head.lora_B.default"):
+ assert isinstance(module, torch.nn.Linear)
+
+ def test_forward(self):
+ x = torch.ones((2, 4, 10)).cuda()
+ megatron_module_result = self.megatron_module(x)
+ dummt_module_result = self.dummy_module(x)
+
+ # Because lora_B is initialized with 0, the forward results of two models should be equal before backward.
+ assert megatron_module_result.equal(dummt_module_result)
+
+ def test_backward(self):
+ optimizer = torch.optim.AdamW(self.megatron_module.parameters())
+ loss_fn = torch.nn.CrossEntropyLoss()
+
+ x = torch.randn(2, 4, 10, requires_grad=True).cuda()
+ label = torch.randint(10, (2 * 4,)).cuda()
+
+ output = self.megatron_module(x)
+ output = output.reshape(2 * 4, 10)
+ loss = loss_fn(output, label)
+
+ loss.backward()
+ optimizer.step()
+
+ def test_get_peft_model_state_dict(self):
+ peft_state_dict = get_peft_model_state_dict(self.megatron_module)
+
+ for key in peft_state_dict.keys():
+ assert "lora" in key
diff --git a/peft/tests/test_lora_variants.py b/peft/tests/test_lora_variants.py
new file mode 100644
index 0000000000000000000000000000000000000000..1c2a3c20a29264b83cea3fe22d9f630b6b190f2a
--- /dev/null
+++ b/peft/tests/test_lora_variants.py
@@ -0,0 +1,267 @@
+# Copyright 2025-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+import pytest
+import torch
+from torch import nn
+
+from peft import LoraConfig, get_peft_model
+from peft.tuners.lora.layer import Conv1d as LoraConv1d
+from peft.tuners.lora.layer import Conv2d as LoraConv2d
+from peft.tuners.lora.layer import Embedding as LoraEmbedding
+from peft.tuners.lora.layer import Linear as LoraLinear
+from peft.tuners.lora.variants import (
+ ALoraLinearVariant,
+ DoraConv1dVariant,
+ DoraConv2dVariant,
+ DoraEmbeddingVariant,
+ DoraLinearVariant,
+ calculate_alora_offsets,
+ get_alora_offsets_for_forward,
+ get_alora_offsets_for_generate,
+)
+
+
+# Custom model featuring embeddings and a 'visual stack'
+class CustomModel(nn.Module):
+ """pytorch module that contains common targetable layers (linear, embedding, conv, ...)"""
+
+ def __init__(self, num_embeddings=100, embedding_dim=16, num_classes=10):
+ super().__init__()
+ self.embedding = nn.Embedding(num_embeddings, embedding_dim)
+ self.conv1d = nn.Conv1d(in_channels=embedding_dim, out_channels=32, kernel_size=3, padding=1)
+ self.conv2d = nn.Conv2d(in_channels=1, out_channels=16, kernel_size=3, stride=1, padding=1)
+ self.flatten = nn.Flatten()
+ self.dummy_conv1d_output_dim = 32 * 10
+ self.dummy_conv2d_output_dim = 16 * 10 * 10
+ self.linear1 = nn.Linear(self.dummy_conv1d_output_dim + self.dummy_conv2d_output_dim, 64)
+ self.linear2 = nn.Linear(64, num_classes)
+ self.relu = nn.ReLU()
+
+ def forward(self, input_ids, dummy_image_input):
+ # Path 1: Embedding -> Conv1d
+ x1 = self.embedding(input_ids) # (batch_size, seq_len, embedding_dim)
+ x1 = x1.transpose(1, 2) # (batch_size, embedding_dim, seq_len)
+ x1 = self.relu(self.conv1d(x1)) # (batch_size, 32, seq_len)
+ x1_flat = self.flatten(x1)
+ # Path 2: Conv2d -> Linear
+ x2 = self.relu(self.conv2d(dummy_image_input)) # (batch_size, 16, H, W)
+ x2_flat = self.flatten(x2) # (batch_size, 16*H*W)
+ # Combine or select paths if making a functional model.
+ # For this test, we mainly care about layer types, so forward might not be fully executed.
+ # Let's use x2_flat for subsequent linear layers.
+ output = self.relu(self.linear1(torch.concat([x1_flat, x2_flat], dim=1)))
+ output = self.linear2(output)
+ return output
+
+
+# Used for testing alora_offsets for aLoRA
+class DummyLM(nn.Module):
+ def __init__(self, vocab_size: int = 10, hidden_dim: int = 8):
+ super().__init__()
+ self.embed = nn.Embedding(vocab_size, hidden_dim)
+ self.linear = nn.Linear(hidden_dim, vocab_size)
+
+ def forward(self, X=None, embeds=None, num_beams=None, alora_offsets=None):
+ if X is not None:
+ embeds = self.embed(X)
+ return self.linear(embeds)
+
+
+class MockTransformerWrapper:
+ """Mock class to behave like a transformers model.
+
+ This is needed because the tests initialize the model by calling transformers_class.from_pretrained.
+
+ """
+
+ @classmethod
+ def from_pretrained(cls):
+ # set the seed so that from_pretrained always returns the same model
+ torch.manual_seed(0)
+
+ torch_dtype = torch.float32
+
+ return DummyLM().to(torch_dtype)
+
+
+VARIANT_MAP = {
+ "dora": {
+ LoraLinear: DoraLinearVariant,
+ LoraEmbedding: DoraEmbeddingVariant,
+ LoraConv1d: DoraConv1dVariant,
+ LoraConv2d: DoraConv2dVariant,
+ },
+ "alora": {
+ LoraLinear: ALoraLinearVariant,
+ },
+}
+
+
+TEST_CASES = [
+ (
+ "dora",
+ LoraConfig,
+ {"target_modules": ["linear1", "linear2", "conv1d", "conv2d", "embedding"], "use_dora": True},
+ ),
+ (
+ "alora",
+ LoraConfig,
+ {"target_modules": ["linear1", "linear2"], "alora_invocation_tokens": [1]},
+ ),
+]
+
+
+class TestLoraVariants:
+ @pytest.mark.parametrize("variant_name, config_cls, config_kwargs", TEST_CASES)
+ def test_variant_is_applied_to_layers(self, variant_name, config_cls, config_kwargs):
+ # This test assumes that targeting and replacing layers works and that after `get_peft_model` we
+ # have a model with LoRA layers. We just make sure that each LoRA layer has its variant set and
+ # it is also the correct variant for that layer.
+ base_model = CustomModel()
+ peft_config = config_cls(**config_kwargs)
+ peft_model = get_peft_model(base_model, peft_config)
+
+ layer_type_map = VARIANT_MAP[variant_name]
+
+ for _, module in peft_model.named_modules():
+ if not hasattr(module, "lora_variant"):
+ continue
+
+ # Note that not every variant supports every layer. If it is not mapped it is deemed unsupported and
+ # will not be tested.
+ expected_variant_type = layer_type_map.get(type(module), None)
+ if not expected_variant_type:
+ continue
+
+ assert isinstance(module.lora_variant["default"], expected_variant_type)
+
+ def custom_model_with_loss_backpropagated(self, peft_config):
+ """Returns the CustomModel + PEFT model instance with a dummy loss that was backpropagated once."""
+ base_model = CustomModel()
+ peft_model = get_peft_model(base_model, peft_config)
+
+ x, y = torch.ones(10, 10).long(), torch.ones(10, 1, 10, 10)
+ out = peft_model(x, y)
+ loss = out.sum()
+ loss.backward()
+
+ return base_model, peft_model
+
+ def test_dora_params_have_gradients(self):
+ """Ensure that the parameters added by the DoRA variant are participating in the output computation."""
+ layer_names = ["linear1", "linear2", "conv1d", "conv2d", "embedding"]
+ peft_config = LoraConfig(target_modules=layer_names, use_dora=True)
+ base_model, peft_model = self.custom_model_with_loss_backpropagated(peft_config)
+
+ for layer in layer_names:
+ assert getattr(peft_model.base_model.model, layer).lora_magnitude_vector["default"].weight.grad is not None
+
+
+class TestActivatedLora:
+ @pytest.mark.parametrize(
+ "input_ids, alora_invocation_tokens, expected_offsets",
+ [
+ ([[0, 1, 2, 3], [0, 4, 5, 6]], [1, 2], [3, None]),
+ ([[1, 2, 1, 2], [0, 4, 1, 2]], [1, 2], [2, 2]),
+ ([[1, 2, 3, 4], [0, 4, 1, 4]], [1, 2], [4, None]),
+ ([[1, 2, 3, 4]], None, [None]),
+ ],
+ )
+ # Verify alora_offsets are calculated correctly
+ def test_calculate_alora_offsets(self, input_ids, alora_invocation_tokens, expected_offsets):
+ config = LoraConfig(alora_invocation_tokens=alora_invocation_tokens)
+ peft_config = {"default": config}
+
+ # compute offsets
+ offsets = calculate_alora_offsets(peft_config, "default", torch.tensor(input_ids))
+
+ assert offsets == expected_offsets
+
+ @pytest.mark.parametrize(
+ "input_ids, alora_invocations, expected_offsets",
+ [
+ ([[0, 1, 1], [0, 2, 2]], {"a1": [1], "a2": [2]}, [1, 1]),
+ ([[0, 1, 1], [0, 2, 2]], {"a1": [1], "a2": None}, [1, None]),
+ ],
+ )
+ # Verify alora_offsets are correct with adapter names
+ def test_calculate_alora_offsets_with_adapter_names(self, input_ids, alora_invocations, expected_offsets):
+ peft_config = {}
+ for alora_name in alora_invocations.keys():
+ peft_config[alora_name] = LoraConfig(alora_invocation_tokens=alora_invocations[alora_name])
+
+ adapter_names = list(alora_invocations.keys())
+ offsets = calculate_alora_offsets(
+ peft_config, adapter_names[0], torch.tensor(input_ids), adapter_names=adapter_names
+ )
+
+ assert offsets == expected_offsets
+
+ # Verify that the adapter does not modify outputs prior to invocation point
+ def test_alora_activation_matches_base_until_invocation(self):
+ transformers_class = MockTransformerWrapper
+ base_model = transformers_class.from_pretrained()
+ cfg = LoraConfig(target_modules=["linear"], alora_invocation_tokens=[2], init_lora_weights=False)
+ lora_model = get_peft_model(base_model, cfg)
+ lora_model.eval()
+
+ input_ids = torch.tensor([[0, 1, 2, 3]])
+ start = 2
+ with lora_model.disable_adapter():
+ with torch.no_grad():
+ base_out = lora_model(X=input_ids)
+
+ kwargs = get_alora_offsets_for_forward(lora_model, input_ids)
+ with torch.no_grad():
+ lora_out = lora_model(X=input_ids, **kwargs)
+ assert torch.allclose(lora_out[:, :start], base_out[:, :start])
+ assert not torch.allclose(lora_out[:, start:], base_out[:, start:])
+
+ # Verify that warning is given for alora when providing embeddings only
+ def test_input_embeds_warning(self):
+ transformers_class = MockTransformerWrapper
+ base_model = transformers_class.from_pretrained()
+ cfg = LoraConfig(target_modules=["linear"], alora_invocation_tokens=[2], init_lora_weights=False)
+ lora_model = get_peft_model(base_model, cfg)
+ lora_model.eval()
+
+ input_ids = torch.tensor([[0, 1, 2, 3]])
+ input_embeds = base_model.embed(input_ids)
+ with pytest.warns(
+ UserWarning,
+ match="Cannot calculate aLoRA offsets when only inputs_embeds are provided. Disabling aLoRA for this forward pass.",
+ ):
+ kwargs = get_alora_offsets_for_forward(lora_model, inputs_embeds=input_embeds)
+ assert kwargs.get("alora_offsets") is None
+ with pytest.warns(
+ UserWarning,
+ match="Cannot calculate aLoRA offsets during generate as input_ids are not available. Disabling aLoRA.",
+ ):
+ kwargs = get_alora_offsets_for_generate(lora_model, inputs_embeds=input_embeds)
+ assert kwargs.get("alora_offsets") is None
+
+ # Verify that error is raised when requesting num_beams > 1 for alora
+ def test_num_beams_error(self):
+ transformers_class = MockTransformerWrapper
+ base_model = transformers_class.from_pretrained()
+ cfg = LoraConfig(target_modules=["linear"], alora_invocation_tokens=[2], init_lora_weights=False)
+ lora_model = get_peft_model(base_model, cfg)
+ lora_model.eval()
+
+ input_ids = torch.tensor([[0, 1, 2, 3]])
+ with pytest.raises(ValueError) as e:
+ with torch.no_grad():
+ lora_out = lora_model(X=input_ids, num_beams=2, alora_offsets=[3])
+ assert "Beam search not yet supported for aLoRA." in str(e.value)
diff --git a/peft/tests/test_lorafa.py b/peft/tests/test_lorafa.py
new file mode 100644
index 0000000000000000000000000000000000000000..3f480049920d6982d48091c342cae98688ba8b16
--- /dev/null
+++ b/peft/tests/test_lorafa.py
@@ -0,0 +1,152 @@
+# Copyright 2025-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+from __future__ import annotations
+
+import math
+
+import torch
+from torch import nn
+
+from peft import LoraConfig, get_peft_model
+from peft.optimizers import create_lorafa_optimizer
+
+from .testing_utils import torch_device
+
+
+class SimpleNet(nn.Module):
+ def __init__(self, bias=True):
+ super().__init__()
+ self.embedding = nn.Embedding(100, 20)
+ self.layer_norm = nn.LayerNorm(20)
+ self.lin0 = nn.Linear(20, 20, bias=bias)
+ self.relu = nn.ReLU()
+ self.lin1 = nn.Linear(20, 16, bias=bias)
+
+ def forward(self, X):
+ X = self.lin0(self.layer_norm(self.embedding(X)))
+ X = self.relu(X)
+ X = self.lin1(X)
+ return X
+
+
+def test_lorafa_init_default():
+ """
+ Test if the optimizer is correctly created
+ """
+ lora_rank = 16
+ lora_alpha = 32
+ lr = 7e-5
+
+ model = SimpleNet()
+ config = LoraConfig(
+ r=lora_rank,
+ lora_alpha=lora_alpha,
+ target_modules=["lin0", "lin1"],
+ bias="none",
+ )
+ model = get_peft_model(model, config)
+ optimizer = create_lorafa_optimizer(model=model, r=lora_rank, lora_alpha=lora_alpha, lr=lr)
+
+ assert math.isclose(optimizer.param_groups[0]["scaling_factor"], lora_alpha / lora_rank, rel_tol=1e-9, abs_tol=0.0)
+
+ all_A_fixed = True
+ all_B_trainable = True
+
+ assert optimizer is not None
+
+ for name, param in model.named_parameters():
+ if "lora_A" in name:
+ all_A_fixed &= not param.requires_grad
+ elif "lora_B" in name:
+ all_B_trainable &= param.requires_grad
+
+ assert all_A_fixed and all_B_trainable
+
+
+def test_lorafa_init_rslora():
+ """
+ Test if the optimizer is correctly created when use_rslora = True
+ """
+ lora_rank = 16
+ lora_alpha = 32
+ lr = 7e-5
+
+ model = SimpleNet()
+ config = LoraConfig(
+ r=lora_rank,
+ lora_alpha=lora_alpha,
+ target_modules=["lin0", "lin1"],
+ bias="none",
+ )
+ model = get_peft_model(model, config)
+ optimizer = create_lorafa_optimizer(model=model, r=lora_rank, lora_alpha=lora_alpha, lr=lr, use_rslora=True)
+ assert math.isclose(
+ optimizer.param_groups[0]["scaling_factor"], lora_alpha / math.sqrt(lora_rank), rel_tol=1e-9, abs_tol=0.0
+ )
+
+
+def test_LoraFAOptimizer_step():
+ """
+ Test if the optimizer's step function runs without any exception and checks specific conditions on lora_A and
+ lora_B weights.
+ """
+ lora_rank = 16
+ lora_alpha = 32
+ lr = 7e-5
+ num_steps = 5
+
+ model = SimpleNet()
+ config = LoraConfig(
+ r=lora_rank,
+ lora_alpha=lora_alpha,
+ target_modules=["lin0", "lin1"],
+ bias="none",
+ )
+ model = get_peft_model(model, config).to(torch_device)
+ optimizer = create_lorafa_optimizer(model=model, r=16, lora_alpha=32, lr=7e-5)
+ loss = torch.nn.CrossEntropyLoss()
+
+ # Save initial weights of lora_A
+ initial_lora_A_weights = {name: param.clone() for name, param in model.named_parameters() if "lora_A" in name}
+ # Ensure lora_B is initialized to zero
+ for name, param in model.named_parameters():
+ if "lora_B" in name:
+ assert torch.all(param == 0), f"lora_B weights not initialized to zero for {name}"
+
+ for _ in range(num_steps): # Run the optimizer step multiple times
+ # Generate random input and label for each step
+ x = torch.randint(100, (2, 4, 10)).to(torch_device)
+ output = model(x).permute(0, 3, 1, 2)
+ label = torch.randint(16, (2, 4, 10)).to(torch_device)
+
+ # Calculate loss and perform backward pass
+ loss_value = loss(output, label)
+ loss_value.backward()
+
+ # Perform optimizer step
+ optimizer.step()
+
+ # Zero the gradients after each step to prevent accumulation
+ optimizer.zero_grad()
+
+ # Check if lora_A weights have not changed
+ for name, param in model.named_parameters():
+ if "lora_A" in name:
+ assert torch.equal(param, initial_lora_A_weights[name]), f"lora_A weights changed for {name}"
+
+ # Check if lora_B weights are non-zero
+ for name, param in model.named_parameters():
+ if "lora_B" in name:
+ assert torch.any(param != 0), f"lora_B weights are still zero for {name}"
diff --git a/peft/tests/test_loraplus.py b/peft/tests/test_loraplus.py
new file mode 100644
index 0000000000000000000000000000000000000000..64bb8bc307e58482366b63063ae1ce9cd921fe1b
--- /dev/null
+++ b/peft/tests/test_loraplus.py
@@ -0,0 +1,99 @@
+# Copyright 2024-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+from __future__ import annotations
+
+import torch
+from torch import nn
+
+from peft.import_utils import is_bnb_available
+from peft.optimizers import create_loraplus_optimizer
+
+from .testing_utils import require_bitsandbytes, torch_device
+
+
+if is_bnb_available():
+ import bitsandbytes as bnb
+
+
+class SimpleNet(nn.Module):
+ def __init__(self, bias=True):
+ super().__init__()
+ self.embedding = nn.Embedding(100, 20)
+ self.layer_norm = nn.LayerNorm(20)
+ self.lin0 = nn.Linear(20, 20, bias=bias)
+ self.relu = nn.ReLU()
+ self.lin1 = nn.Linear(20, 16, bias=bias)
+
+ def forward(self, X):
+ X = self.lin0(self.layer_norm(self.embedding(X)))
+ X = self.relu(X)
+ X = self.lin1(X)
+ return X
+
+
+@require_bitsandbytes
+def test_lora_plus_helper_sucess():
+ model = SimpleNet()
+ optimizer_cls = bnb.optim.Adam8bit
+ lr = 5e-5
+ optim_config = {
+ "eps": 1e-6,
+ "betas": (0.9, 0.999),
+ "loraplus_weight_decay": 0.0,
+ }
+ loraplus_lr_ratio = 1.2
+ loraplus_lr_embedding = 1e-6
+ optim = create_loraplus_optimizer(
+ model=model,
+ optimizer_cls=optimizer_cls,
+ lr=lr,
+ loraplus_lr_ratio=loraplus_lr_ratio,
+ loraplus_lr_embedding=loraplus_lr_embedding,
+ **optim_config,
+ )
+ assert optim is not None
+ assert len(optim.param_groups) == 4
+ assert optim.param_groups[0]["lr"] == lr
+ assert optim.param_groups[1]["lr"] == loraplus_lr_embedding
+ assert optim.param_groups[2]["lr"] == optim.param_groups[3]["lr"] == (lr * loraplus_lr_ratio)
+
+
+@require_bitsandbytes
+def test_lora_plus_optimizer_sucess():
+ """
+ Test if the optimizer is correctly created and step function runs without any exception
+ """
+ optimizer_cls = bnb.optim.Adam8bit
+ optim_config = {
+ "eps": 1e-6,
+ "betas": (0.9, 0.999),
+ "loraplus_weight_decay": 0.0,
+ }
+ model: SimpleNet = SimpleNet().to(torch_device)
+ optim = create_loraplus_optimizer(
+ model=model,
+ optimizer_cls=optimizer_cls,
+ lr=5e-5,
+ loraplus_lr_ratio=1.2,
+ loraplus_lr_embedding=1e-6,
+ **optim_config,
+ )
+ loss = torch.nn.CrossEntropyLoss()
+ bnb.optim.GlobalOptimManager.get_instance().register_parameters(model.parameters())
+ x = torch.randint(100, (2, 4, 10)).to(torch_device)
+ output = model(x).permute(0, 3, 1, 2)
+ label = torch.randint(16, (2, 4, 10)).to(torch_device)
+ loss_value = loss(output, label)
+ loss_value.backward()
+ optim.step()
diff --git a/peft/tests/test_low_level_api.py b/peft/tests/test_low_level_api.py
new file mode 100644
index 0000000000000000000000000000000000000000..0a097e2dba4928fee6f047afd4c3992832c8abf5
--- /dev/null
+++ b/peft/tests/test_low_level_api.py
@@ -0,0 +1,623 @@
+#!/usr/bin/env python3
+
+# coding=utf-8
+# Copyright 2023-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+import copy
+import re
+
+import pytest
+import torch
+from diffusers import StableDiffusionPipeline
+from torch import nn
+from transformers import AutoModel, AutoModelForCausalLM, AutoModelForSeq2SeqLM, AutoModelForSequenceClassification
+
+from peft import (
+ AdaLoraConfig,
+ IA3Config,
+ LoKrConfig,
+ LoraConfig,
+ RandLoraConfig,
+ get_peft_model,
+ get_peft_model_state_dict,
+ inject_adapter_in_model,
+ set_peft_model_state_dict,
+)
+from peft.tuners import lora
+from peft.utils import ModulesToSaveWrapper
+
+from .testing_utils import hub_online_once
+
+
+class DummyModel(torch.nn.Module):
+ def __init__(self):
+ super().__init__()
+ self.embedding = torch.nn.Embedding(10, 10)
+ self.linear = torch.nn.Linear(10, 10)
+ self.linear2 = torch.nn.Linear(10, 10, bias=True)
+ self.lm_head = torch.nn.Linear(10, 10)
+
+ def forward(self, input_ids):
+ x = self.embedding(input_ids)
+ x = self.linear(x)
+ x = self.lm_head(x)
+ return x
+
+
+class TestLowLevelFunctional:
+ # Some simple tests for the low level API
+ @pytest.fixture
+ def model(self):
+ model = DummyModel()
+
+ lora_config = LoraConfig(
+ lora_alpha=16,
+ lora_dropout=0.1,
+ r=64,
+ bias="none",
+ target_modules=["linear"],
+ )
+
+ return inject_adapter_in_model(lora_config, model)
+
+ def test_inject_adapter_in_model(self, model):
+ dummy_inputs = torch.LongTensor([[0, 1, 2, 3, 4, 5, 6, 7]])
+ _ = model(dummy_inputs)
+
+ for name, module in model.named_modules():
+ if name == "linear":
+ assert hasattr(module, "lora_A")
+ assert hasattr(module, "lora_B")
+
+ def test_get_peft_model_state_dict(self, model):
+ peft_state_dict = get_peft_model_state_dict(model)
+
+ for key in peft_state_dict.keys():
+ assert "lora" in key
+
+ def test_modules_to_save(self):
+ model = DummyModel()
+
+ lora_config = LoraConfig(
+ lora_alpha=16,
+ lora_dropout=0.1,
+ r=64,
+ bias="none",
+ target_modules=["linear"],
+ modules_to_save=["embedding", "linear2"],
+ )
+
+ model = inject_adapter_in_model(lora_config, model)
+
+ for name, module in model.named_modules():
+ if name == "linear":
+ assert hasattr(module, "lora_A")
+ assert hasattr(module, "lora_B")
+ elif name in ["embedding", "linear2"]:
+ assert isinstance(module, ModulesToSaveWrapper)
+
+ state_dict = get_peft_model_state_dict(model)
+
+ assert "embedding.weight" in state_dict.keys()
+
+ assert hasattr(model.embedding, "weight")
+
+ assert hasattr(model.linear2, "weight")
+ assert hasattr(model.linear2, "bias")
+
+
+class TestInjectAdapterFromStateDict:
+ # The inject_adapter_in_model function can determine the target modules based on the LoraConfig (default) or based
+ # on a state_dict (or rather, the state_dict keys). Here we test that the latter works as expected.
+
+ # We test a subset of model classes and PEFT configs, testing everything would be excessive
+ @pytest.mark.parametrize(
+ "model_cls_and_id",
+ [
+ (AutoModelForCausalLM, "trl-internal-testing/tiny-random-LlamaForCausalLM"),
+ (AutoModel, "hf-internal-testing/tiny-random-BertModel"),
+ (AutoModelForSeq2SeqLM, "hf-internal-testing/tiny-random-BartForConditionalGeneration"),
+ (AutoModelForSequenceClassification, "hf-internal-testing/tiny-random-RobertaForSequenceClassification"),
+ ],
+ ids=["Llama", "Bert", "Bart", "Roberta"],
+ )
+ @pytest.mark.parametrize(
+ "config",
+ [
+ AdaLoraConfig(total_step=5),
+ IA3Config(),
+ LoKrConfig(),
+ LoraConfig(),
+ RandLoraConfig(),
+ ],
+ ids=["AdaLoRA", "IA3", "LoKr", "LoRA", "RandLoRA"],
+ )
+ def test_inject_from_state_dict_and_from_config_target_same_layers(self, model_cls_and_id, config, recwarn):
+ model_cls, model_id = model_cls_and_id
+ config = copy.deepcopy(config) # since PEFT may mutate it
+
+ with hub_online_once(model_id):
+ # use config for injection
+ model = model_cls.from_pretrained(model_id)
+ model = inject_adapter_in_model(config, model)
+ sd_before = get_peft_model_state_dict(model)
+ del model
+
+ model = model_cls.from_pretrained(model_id)
+ # get other warnings, if any, out of the way
+ recwarn.clear()
+ # assure that this doesn't cause any warnings
+ model = inject_adapter_in_model(config, model, state_dict=sd_before)
+ assert not recwarn.list
+
+ sd_after = get_peft_model_state_dict(model)
+
+ # We exepct the same keys and the same shapes of the weights. Don't check the values: injection is only
+ # about creating the PEFT adapter, not about loading the actual weights
+ assert len(sd_before) > 0
+ assert sd_before.keys() == sd_after.keys()
+ for key in sd_before.keys():
+ assert sd_before[key].shape == sd_after[key].shape
+
+ def test_inject_from_state_dict_transformers(self):
+ model_id = "facebook/opt-125m"
+ config = LoraConfig()
+
+ with hub_online_once(model_id):
+ model = AutoModelForCausalLM.from_pretrained(model_id)
+ model.add_adapter(config)
+ sd_before = get_peft_model_state_dict(model)
+ del model
+
+ model = AutoModelForCausalLM.from_pretrained(model_id)
+ model = inject_adapter_in_model(config, model, state_dict=sd_before)
+ sd_after = get_peft_model_state_dict(model)
+
+ # We exepct the same keys and the same shapes of the weights. Don't check the values: injection is only
+ # about creating the PEFT adapter, not about loading the actual weights
+ assert len(sd_before) > 0
+ assert sd_before.keys() == sd_after.keys()
+ for key in sd_before.keys():
+ assert sd_before[key].shape == sd_after[key].shape
+
+ def test_inject_from_state_dict_transformers_irregular_targets(self):
+ # ensure that this works even if an "irregular" pattern is used, i.e. only targeting some modules on some layers
+ model_id = "facebook/opt-125m"
+ config = LoraConfig(
+ target_modules=r".*\.[0-5]\.self_attn\.v_proj|.*\.[4-7]\.self_attn\.k_proj",
+ )
+
+ with hub_online_once(model_id):
+ model = AutoModelForCausalLM.from_pretrained(model_id)
+ model.add_adapter(config)
+ sd_before = get_peft_model_state_dict(model)
+ del model
+
+ model = AutoModelForCausalLM.from_pretrained(model_id)
+ model = inject_adapter_in_model(config, model, state_dict=sd_before)
+ sd_after = get_peft_model_state_dict(model)
+
+ # We exepct the same keys and the same shapes of the weights. Don't check the values: injection is only
+ # about creating the PEFT adapter, not about loading the actual weights
+ assert len(sd_before) > 0
+ assert sd_before.keys() == sd_after.keys()
+ for key in sd_before.keys():
+ assert sd_before[key].shape == sd_after[key].shape
+
+ def test_inject_from_state_dict_transformers_target_parameters_raises(self):
+ # Injecting from state_dict does not correctly identify target_parameters. This is because, just from looking at
+ # the state_dict, we cannot tell if the user intends to use target_modules or target_parameters. Currently, we
+ # just assume the former, thus applying normal lora.Linear etc. layers instead of lora.ParamWrapper. When we
+ # detect that the user tries to do this, we raise an error.
+ model_id = "facebook/opt-125m"
+ config = LoraConfig(target_modules=[], target_parameters=["q_proj.weight", "v_proj.weight"])
+
+ with hub_online_once(model_id):
+ model = AutoModelForCausalLM.from_pretrained(model_id)
+ model.add_adapter(config)
+ sd = get_peft_model_state_dict(model)
+ del model
+
+ model = AutoModelForCausalLM.from_pretrained(model_id)
+ msg = "Trying to inject a PEFT adapter from a state_dict but the PEFT config uses `target_parameters`"
+ with pytest.raises(ValueError, match=msg):
+ inject_adapter_in_model(config, model, state_dict=sd)
+
+ @pytest.mark.xfail(
+ reason="Loading from state_dict with target_parameters fails", raises=AssertionError, strict=True
+ )
+ def test_inject_from_state_dict_transformers_target_parameters_fails(self):
+ # Injecting from state_dict does not correctly identify target_parameters. This is because, just from looking at
+ # the state_dict, we cannot tell if the user intends to use target_modules or target_parameters. Currently, we
+ # just assume the former, thus applying normal lora.Linear etc. layers instead of lora.ParamWrapper. When we
+ # don't detect that the user tries to do this, there is nothing that can be done.
+ model_id = "facebook/opt-125m"
+ config = LoraConfig(target_modules=[], target_parameters=["q_proj.weight", "v_proj.weight"])
+
+ with hub_online_once(model_id):
+ model = AutoModelForCausalLM.from_pretrained(model_id)
+ model.add_adapter(config)
+ # sanity check:
+ for name, module in model.named_modules():
+ if name.endswith((".q_proj", ".v_proj")):
+ assert isinstance(module, lora.ParamWrapper)
+
+ sd_before = get_peft_model_state_dict(model)
+ del model
+
+ model = AutoModelForCausalLM.from_pretrained(model_id)
+ config = LoraConfig() # no target_parameters defined, we cannot know the original intent
+ model = inject_adapter_in_model(config, model, state_dict=sd_before)
+ sd_after = get_peft_model_state_dict(model)
+
+ # this fails, we get lora.Linear instances
+ for name, module in model.named_modules():
+ if name.endswith((".q_proj", ".v_proj")):
+ assert isinstance(module, lora.ParamWrapper)
+
+ def test_inject_from_state_dict_stable_diffusion(self):
+ # same test as above, but with stable diffusion model and only testing LoRA
+ model_id = "hf-internal-testing/tiny-sd-pipe"
+ config_text_encoder = LoraConfig(target_modules=["k_proj", "q_proj", "v_proj", "out_proj", "fc1", "fc2"])
+ config_unet = LoraConfig(
+ target_modules=[
+ "proj_in",
+ "proj_out",
+ "to_k",
+ "to_q",
+ "to_v",
+ "to_out.0",
+ "ff.net.0.proj",
+ "ff.net.2",
+ ]
+ )
+ with hub_online_once(model_id):
+ pipe = StableDiffusionPipeline.from_pretrained(model_id)
+ pipe.text_encoder.add_adapter(config_text_encoder)
+ pipe.unet.add_adapter(config_unet)
+
+ sd_te_before = get_peft_model_state_dict(pipe.text_encoder)
+ sd_unet_before = get_peft_model_state_dict(pipe.unet)
+ del pipe
+
+ pipe = StableDiffusionPipeline.from_pretrained(model_id)
+ inject_adapter_in_model(config_text_encoder, pipe.text_encoder, state_dict=sd_te_before)
+ inject_adapter_in_model(config_unet, pipe.unet, state_dict=sd_unet_before)
+
+ sd_te_after = get_peft_model_state_dict(pipe.text_encoder)
+ sd_unet_after = get_peft_model_state_dict(pipe.unet)
+
+ # We exepct the same keys and the same shapes of the weights. Don't check the values: injection is only
+ # about creating the PEFT adapter, not about loading the actual weights
+ assert len(sd_te_before) > 0
+ assert sd_te_before.keys() == sd_te_after.keys()
+ for key in sd_te_before.keys():
+ assert sd_te_before[key].shape == sd_te_after[key].shape
+
+ assert len(sd_unet_before) > 0
+ assert sd_unet_before.keys() == sd_unet_after.keys()
+ for key in sd_unet_before.keys():
+ assert sd_unet_before[key].shape == sd_unet_after[key].shape
+
+ def test_inject_from_state_dict_low_cpu_mem_usage(self):
+ model_id = "facebook/opt-125m"
+ config = LoraConfig()
+
+ with hub_online_once(model_id):
+ # use config for injection
+ model = AutoModelForCausalLM.from_pretrained(model_id)
+ model = inject_adapter_in_model(config, model)
+ sd_before = get_peft_model_state_dict(model)
+ del model
+
+ model = AutoModelForCausalLM.from_pretrained(model_id)
+ model = inject_adapter_in_model(config, model, state_dict=sd_before, low_cpu_mem_usage=True)
+ # all PEFT parameters should be on meta device
+ assert {p.device.type for p in get_peft_model_state_dict(model).values()} == {"meta"}
+
+ def test_inject_from_state_dict_missing_keys_warning(self):
+ # check that if the PEFT config specifies **more** taget modules than the state_dict, we get a warning for that
+ model_id = "facebook/opt-125m"
+ config = LoraConfig()
+
+ with hub_online_once(model_id):
+ # use config for injection
+ model = AutoModelForCausalLM.from_pretrained(model_id)
+ model = inject_adapter_in_model(config, model)
+ sd_before = get_peft_model_state_dict(model)
+ del model
+
+ # delete a keys for one module from state_dict
+ del sd_before["model.decoder.layers.5.self_attn.q_proj.lora_A.weight"]
+ del sd_before["model.decoder.layers.5.self_attn.q_proj.lora_B.weight"]
+
+ model = AutoModelForCausalLM.from_pretrained(model_id)
+ msg = re.escape(
+ "While injecting the PEFT adapters, an inconsistency was discovered between the PEFT config and "
+ "the provided state_dict. This is not necessarily an issue and can be ignored if this was the "
+ "intent. The PEFT config contained these additional target modules: "
+ "['model.decoder.layers.5.self_attn.q_proj']. "
+ )
+
+ with pytest.warns(RuntimeWarning, match=msg): # as rec:#(UserWarning, match=msg) as rec:
+ model = inject_adapter_in_model(config, model, state_dict=sd_before, low_cpu_mem_usage=True)
+
+ # besides the warning, the rest of the injection should work
+ sd_after = get_peft_model_state_dict(model)
+ assert len(sd_before) > 0
+ assert sd_before.keys() == sd_after.keys()
+ for key in sd_before.keys():
+ assert sd_before[key].shape == sd_after[key].shape
+
+ def test_inject_from_state_dict_extra_keys_warning(self):
+ # check that if the PEFT config specifies **fewer** taget modules than the state_dict, we get a warning for that
+ model_id = "facebook/opt-125m"
+ config = LoraConfig()
+
+ with hub_online_once(model_id):
+ # use config for injection
+ model = AutoModelForCausalLM.from_pretrained(model_id)
+ model = inject_adapter_in_model(config, model)
+ sd_before = get_peft_model_state_dict(model)
+ del model
+
+ # remove q_proj of layer 5 from the PEFT config
+ config.exclude_modules = ["model.decoder.layers.5.self_attn.q_proj"]
+
+ model = AutoModelForCausalLM.from_pretrained(model_id)
+ msg = re.escape(
+ "While injecting the PEFT adapters, an inconsistency was discovered between the PEFT config and "
+ "the provided state_dict. This is not necessarily an issue and can be ignored if this was the "
+ "intent. The state_dict contained these additional target modules: "
+ "['model.decoder.layers.5.self_attn.q_proj']. "
+ )
+
+ with pytest.warns(RuntimeWarning, match=msg):
+ model = inject_adapter_in_model(config, model, state_dict=sd_before, low_cpu_mem_usage=True)
+
+ # besides the warning, the rest of the injection should work
+ sd_after = get_peft_model_state_dict(model)
+ assert len(sd_before) > 0
+ assert sd_before.keys() == sd_after.keys()
+ for key in sd_before.keys():
+ assert sd_before[key].shape == sd_after[key].shape
+
+
+class TestPeftStateDict:
+ # Test some edge cases around getting and setting the PEFT state_dict. There are potential sources of errors there
+ # because the adapter_name is removed from/added to the state_dict keys.
+ def test_get_peft_model_state_dict_removes_adapter_name(self):
+ # ensure that the adapter name, "default", is removed from the state_dict
+ model_id = "hf-internal-testing/tiny-random-OPTForCausalLM"
+ with hub_online_once(model_id):
+ model = AutoModelForCausalLM.from_pretrained(model_id)
+
+ # note: lora targets q_proj and v_proj; add in an auxiliary module for good measure
+ model = get_peft_model(model, LoraConfig(modules_to_save=["lm_head"]))
+ sd = get_peft_model_state_dict(model)
+ assert len(sd) > 1 # sanity check
+ assert not any("default" in key for key in sd)
+
+ def test_get_peft_model_state_dict_removes_non_defaul_adapter_name(self):
+ # ensure that the adapter name is removed from the state_dict, even if it's not "default"
+ model_id = "hf-internal-testing/tiny-random-OPTForCausalLM"
+ with hub_online_once(model_id):
+ model = AutoModelForCausalLM.from_pretrained(model_id)
+
+ model = get_peft_model(model, LoraConfig(modules_to_save=["lm_head"]), adapter_name="other")
+ sd = get_peft_model_state_dict(model, adapter_name="other")
+ assert len(sd) > 1 # sanity check
+ assert not any("other" in key for key in sd)
+
+ def test_get_peft_model_state_dict_removes_adapter_name_when_same_as_module_name(self):
+ # here the adapter is named "v_proj", which is the same name as some modules targeted with lora in the model,
+ # which is nefarious
+ model_id = "hf-internal-testing/tiny-random-OPTForCausalLM"
+ with hub_online_once(model_id):
+ model = AutoModelForCausalLM.from_pretrained(model_id)
+
+ config = LoraConfig(modules_to_save=["lm_head"], target_modules=["v_proj"])
+ model = get_peft_model(model, config, adapter_name="v_proj")
+ sd = get_peft_model_state_dict(model, adapter_name="v_proj")
+ assert len(sd) > 1 # sanity check
+ for key in sd:
+ # assert that the adapter_name was indeed removed
+ assert not key.endswith("lora_A.v_proj.weight")
+ assert not key.endswith("lora_B.v_proj.weight")
+ assert not key.endswith("modules_to_save.v_proj.weight")
+ # assert that the module name was not stripped completely from the key
+ assert ("v_proj" in key) or ("q_proj" in key) or ("lm_head") in key
+
+ def check_peft_model_weights_loaded_correctly(self, inner_model_cls, config, nested, adapter_name="default"):
+ # Runs checks that a roundtrip of get_peft_model_state_dict and set_peft_model_state_dict results in the same
+ # model (same outputs and same weights).
+ class Outer(nn.Module):
+ def __init__(self):
+ super().__init__()
+ self.inner = inner_model_cls()
+
+ def forward(self, x):
+ return self.inner(x)
+
+ if nested:
+ # add another layer of nesting
+ model_cls = Outer
+ else:
+ model_cls = inner_model_cls
+
+ x = torch.randn(1, 5)
+
+ torch.manual_seed(0)
+ base_model = model_cls()
+ with torch.inference_mode():
+ base_out = base_model(x)
+
+ torch.manual_seed(42)
+ model = get_peft_model(base_model, config, adapter_name=adapter_name)
+ with torch.inference_mode():
+ peft_out = model(x)
+ # sanity check: peft adapter has an effect
+ assert not torch.allclose(base_out, peft_out, atol=1e-6)
+
+ sd = get_peft_model_state_dict(model, adapter_name=adapter_name)
+
+ torch.manual_seed(0)
+ base_model = model_cls()
+ torch.manual_seed(42 + 1) # ensure we start with a different, randomly initialized PEFT model
+ model_new = get_peft_model(base_model, config, adapter_name=adapter_name)
+ with torch.inference_mode():
+ peft_new = model_new(x)
+ assert not torch.allclose(peft_out, peft_new, atol=1e-6)
+
+ set_peft_model_state_dict(model_new, sd, adapter_name=adapter_name)
+ with torch.inference_mode():
+ peft_out_loaded = model_new(x)
+ assert torch.allclose(peft_out, peft_out_loaded, atol=1e-6)
+
+ sd_new = get_peft_model_state_dict(model, adapter_name=adapter_name)
+ assert sd.keys() == sd_new.keys()
+ for key, val in sd.items():
+ val_new = sd_new[key]
+ torch.allclose(val, val_new)
+
+ @pytest.mark.parametrize("nested", [False, True])
+ def test_get_and_set_peft_model_state_dict_normal_names(self, nested):
+ # In this test, there is no edge case. Therefore, this test is basically the "control group" for the subsequent
+ # tests (if this test were to fail, it means the testing code itself is wrong).
+ class MyModel(nn.Module):
+ def __init__(self):
+ super().__init__()
+ self.foo_linear = nn.Linear(5, 5)
+ self.foo_baz = nn.Linear(5, 5)
+ self.baz_foo = nn.Linear(5, 5)
+ self.foo_baz_foo = nn.Linear(5, 5)
+ self.baz_foo_baz = nn.Linear(5, 5)
+
+ def forward(self, x):
+ x = self.foo_linear(x)
+ x = self.foo_baz(x)
+ x = self.baz_foo(x)
+ x = self.foo_baz_foo(x)
+ x = self.baz_foo_baz(x)
+ return x
+
+ config = LoraConfig(
+ target_modules=["foo_linear", "foo_baz", "baz_foo", "foo_baz_foo", "baz_foo_baz"], init_lora_weights=False
+ )
+ self.check_peft_model_weights_loaded_correctly(MyModel, config, nested=nested)
+
+ @pytest.mark.parametrize("nested", [False, True])
+ def test_get_and_set_peft_model_state_dict_peft_prefix_in_module_name(self, nested):
+ # Here we have a model with some modules containing "lora" in their name.
+ class MyModel(nn.Module):
+ def __init__(self):
+ super().__init__()
+ self.foo_linear = nn.Linear(5, 5)
+ self.foo_lora = nn.Linear(5, 5)
+ self.lora_foo = nn.Linear(5, 5)
+ self.foo_lora_foo = nn.Linear(5, 5)
+ self.lora_foo_lora = nn.Linear(5, 5)
+
+ def forward(self, x):
+ x = self.foo_linear(x)
+ x = self.foo_lora(x)
+ x = self.lora_foo(x)
+ x = self.foo_lora_foo(x)
+ x = self.lora_foo_lora(x)
+ return x
+
+ config = LoraConfig(
+ target_modules=["foo_linear", "foo_lora", "lora_foo", "foo_lora_foo", "lora_foo_lora"],
+ init_lora_weights=False,
+ )
+ self.check_peft_model_weights_loaded_correctly(MyModel, config, nested=nested)
+
+ @pytest.mark.parametrize("nested", [False, True])
+ def test_get_and_set_peft_model_state_dict_weight_in_module_name(self, nested):
+ # Here we have a model with some modules containing "weight" in their name.
+ # See #2772
+ class MyModel(nn.Module):
+ def __init__(self):
+ super().__init__()
+ self.foo_linear = nn.Linear(5, 5)
+ self.foo_weight = nn.Linear(5, 5)
+ self.weight_foo = nn.Linear(5, 5)
+ self.foo_weight_foo = nn.Linear(5, 5)
+ self.weight_foo_weight = nn.Linear(5, 5)
+
+ def forward(self, x):
+ x = self.foo_linear(x)
+ x = self.foo_weight(x)
+ x = self.weight_foo(x)
+ x = self.foo_weight_foo(x)
+ x = self.weight_foo_weight(x)
+ return x
+
+ config = LoraConfig(
+ target_modules=["foo_linear", "foo_weight", "weight_foo", "foo_weight_foo", "weight_foo_weight"],
+ init_lora_weights=False,
+ )
+ self.check_peft_model_weights_loaded_correctly(MyModel, config, nested=nested)
+
+ @pytest.mark.parametrize("nested", [False, True])
+ def test_get_and_set_peft_model_state_dict_bias_in_module_name(self, nested):
+ # Here we have a model with some modules containing "bias" in their name.
+ class MyModel(nn.Module):
+ def __init__(self):
+ super().__init__()
+ self.foo_linear = nn.Linear(5, 5)
+ self.foo_bias = nn.Linear(5, 5)
+ self.bias_foo = nn.Linear(5, 5)
+ self.foo_bias_foo = nn.Linear(5, 5)
+ self.bias_foo_bias = nn.Linear(5, 5)
+
+ def forward(self, x):
+ x = self.foo_linear(x)
+ x = self.foo_bias(x)
+ x = self.bias_foo(x)
+ x = self.foo_bias_foo(x)
+ x = self.bias_foo_bias(x)
+ return x
+
+ config = LoraConfig(
+ target_modules=["foo_linear", "foo_bias", "bias_foo", "foo_bias_foo", "bias_foo_bias"],
+ init_lora_weights=False,
+ bias="lora_only",
+ )
+ self.check_peft_model_weights_loaded_correctly(MyModel, config, nested=nested)
+
+ @pytest.mark.parametrize("nested", [False, True])
+ def test_get_and_set_peft_model_state_dict_adapter_name_same_as_module_name(self, nested):
+ # Here we choose a module name that is identical to the name of one of the adapters.
+ class MyModel(nn.Module):
+ def __init__(self):
+ super().__init__()
+ self.foo = nn.Linear(5, 5)
+ self.foo_baz = nn.Linear(5, 5)
+ self.baz_foo = nn.Linear(5, 5)
+ self.foo_baz_foo = nn.Linear(5, 5)
+ self.baz_foo_baz = nn.Linear(5, 5)
+
+ def forward(self, x):
+ x = self.foo(x)
+ x = self.foo_baz(x)
+ x = self.baz_foo(x)
+ x = self.foo_baz_foo(x)
+ x = self.baz_foo_baz(x)
+ return x
+
+ config = LoraConfig(
+ target_modules=["foo", "foo_baz", "baz_foo", "foo_baz_foo", "baz_foo_baz"], init_lora_weights=False
+ )
+ self.check_peft_model_weights_loaded_correctly(MyModel, config, nested=nested, adapter_name="foo")
diff --git a/peft/tests/test_mapping.py b/peft/tests/test_mapping.py
new file mode 100644
index 0000000000000000000000000000000000000000..6e204b951058ca8df79722211db19d18b9d8a233
--- /dev/null
+++ b/peft/tests/test_mapping.py
@@ -0,0 +1,55 @@
+# Copyright 2025-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+import pytest
+import torch
+
+from peft import LoraConfig, get_peft_model
+
+
+class TestGetPeftModel:
+ RELOAD_WARNING_EXPECTED_MATCH = r"You are trying to modify a model .*"
+
+ @pytest.fixture
+ def lora_config_0(self):
+ return LoraConfig(target_modules="0")
+
+ @pytest.fixture
+ def base_model(self):
+ return torch.nn.Sequential(torch.nn.Linear(10, 2), torch.nn.Linear(2, 10))
+
+ def test_get_peft_model_warns_when_reloading_model(self, lora_config_0, base_model):
+ get_peft_model(base_model, lora_config_0)
+
+ with pytest.warns(UserWarning, match=self.RELOAD_WARNING_EXPECTED_MATCH):
+ get_peft_model(base_model, lora_config_0)
+
+ def test_get_peft_model_proposed_fix_in_warning_helps(self, lora_config_0, base_model, recwarn):
+ peft_model = get_peft_model(base_model, lora_config_0)
+ peft_model.unload()
+ get_peft_model(base_model, lora_config_0)
+
+ warning_checker = pytest.warns(UserWarning, match=self.RELOAD_WARNING_EXPECTED_MATCH)
+
+ for warning in recwarn:
+ if warning_checker.matches(warning):
+ pytest.fail("Warning raised even though model was unloaded.")
+
+ def test_get_peft_model_repeated_invocation(self, lora_config_0, base_model):
+ peft_model = get_peft_model(base_model, lora_config_0)
+
+ # use direct-addressing of the other layer to accomodate for the nested model
+ lora_config_1 = LoraConfig(target_modules="base_model.model.1")
+
+ with pytest.warns(UserWarning, match=self.RELOAD_WARNING_EXPECTED_MATCH):
+ get_peft_model(peft_model, lora_config_1)
diff --git a/peft/tests/test_mixed.py b/peft/tests/test_mixed.py
new file mode 100644
index 0000000000000000000000000000000000000000..7ec18387c817e148f6346cf5f57a9a993b2d96cf
--- /dev/null
+++ b/peft/tests/test_mixed.py
@@ -0,0 +1,791 @@
+# Copyright 2023-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+import copy
+import itertools
+import os
+import platform
+import re
+import tempfile
+import unittest
+
+import pytest
+import torch
+from parameterized import parameterized
+from torch import nn
+from transformers import AutoModelForCausalLM
+
+from peft import (
+ AdaLoraConfig,
+ LoHaConfig,
+ LoKrConfig,
+ LoraConfig,
+ PeftMixedModel,
+ PrefixTuningConfig,
+ get_peft_model,
+)
+from peft.tuners.tuners_utils import BaseTunerLayer
+from peft.utils import infer_device
+
+
+class SimpleNet(nn.Module):
+ def __init__(self, bias=True):
+ super().__init__()
+ # note: out_features must be > rank or else OFT will be an identity transform
+ self.lin0 = nn.Linear(10, 20, bias=bias)
+ self.relu = nn.ReLU()
+ self.lin1 = nn.Linear(20, 16, bias=bias)
+
+ def forward(self, X):
+ X = X.float()
+ X = self.lin0(X)
+ X = self.relu(X)
+ X = self.lin1(X)
+ return X
+
+
+def _param_name_func(testcase_func, param_num, params):
+ # for parameterized tests in TextMixedAdapterTypes
+ config0, config1 = params[0]
+ name0 = config0.__class__.__name__[: -len("Config")]
+ name1 = config1.__class__.__name__[: -len("Config")]
+ if name0 != name1:
+ return f"{testcase_func.__name__}_{param_num}_{name0}_{name1}"
+ return f"{testcase_func.__name__}_{param_num}_{name0}_x2"
+
+
+class TestMixedAdapterTypes(unittest.TestCase):
+ torch_device = infer_device()
+
+ def _get_model(self, model_cls, peft_config=None, adapter_name=None, seed=0, mixed=True):
+ torch.manual_seed(0) # always use seed 0 for base model, seed for adapters may differ
+ base_model = model_cls().eval().to(self.torch_device)
+ if peft_config is None:
+ return base_model
+
+ torch.manual_seed(seed)
+ assert adapter_name is not None
+ peft_model = get_peft_model(base_model, peft_config, adapter_name=adapter_name, mixed=mixed)
+ return peft_model.eval().to(self.torch_device)
+
+ def _check_mixed_outputs(self, model_cls, config0, config1, input, *, is_commutative):
+ # This test checks different combinations of adapter0, adapter1, or combinations of the two, and whether
+ # outputs are the same/different, depending on context. If we pass is_commutative=True, it means that the order
+ # of adapters does not matter, and we expect the same output regardless of the order in which adapters are
+ # applied.
+ # We have to very careful with resetting the random seed each time it is used, otherwise the adapters may be
+ # initialized with different values, and the test will fail.
+
+ atol = 1e-5
+ rtol = 1e-5
+ seed0 = 0
+ seed1 = 1
+
+ # base model
+ base_model = self._get_model(model_cls)
+ output_base = base_model(input)
+ assert torch.isfinite(output_base).all()
+
+ # adapter 0
+ peft_model_0 = self._get_model(model_cls, config0, "adapter0", seed=seed0)
+ output_config0 = peft_model_0(input)
+
+ assert torch.isfinite(output_config0).all()
+ assert not torch.allclose(output_base, output_config0, atol=atol, rtol=rtol)
+
+ # adapter 1
+ peft_model_1 = self._get_model(model_cls, config1, "adapter1", seed=seed1)
+ output_config1 = peft_model_1(input)
+
+ assert torch.isfinite(output_config1).all()
+ assert not torch.allclose(output_base, output_config1, atol=atol, rtol=rtol)
+ assert not torch.allclose(output_config0, output_config1, atol=atol, rtol=rtol)
+
+ # adapter 0 + 1
+ peft_model_01 = self._get_model(model_cls, config0, "adapter0", seed=seed0)
+ torch.manual_seed(seed1)
+ peft_model_01.add_adapter("adapter1", config1)
+ peft_model_01.set_adapter(["adapter0", "adapter1"])
+ output_mixed_01 = peft_model_01(input)
+
+ # check the number of tuner layer types
+ tuner_layers = [mod for mod in peft_model_01.modules() if isinstance(mod, BaseTunerLayer)]
+ tuner_types = {type(tuner_layer) for tuner_layer in tuner_layers}
+ if type(config0) is type(config1):
+ assert len(tuner_types) == 1
+ else:
+ assert len(tuner_types) == 2
+
+ assert peft_model_01.active_adapters == ["adapter0", "adapter1"]
+ assert torch.isfinite(output_mixed_01).all()
+ assert not torch.allclose(output_config0, output_mixed_01, atol=atol, rtol=rtol)
+ assert not torch.allclose(output_config1, output_mixed_01, atol=atol, rtol=rtol)
+ if is_commutative:
+ delta0 = output_config0 - output_base
+ delta1 = output_config1 - output_base
+ delta_mixed_01 = output_mixed_01 - output_base
+ assert torch.allclose((delta0 + delta1), delta_mixed_01, atol=atol, rtol=rtol)
+
+ # adapter 1 + 0
+ peft_model_10 = self._get_model(model_cls, config1, "adapter1", seed=seed1)
+ torch.manual_seed(seed0)
+ peft_model_10.add_adapter("adapter0", config0)
+ peft_model_10.set_adapter(["adapter1", "adapter0"])
+ output_mixed_10 = peft_model_10(input)
+
+ # check the number of tuner layer types
+ tuner_layers = [mod for mod in peft_model_10.modules() if isinstance(mod, BaseTunerLayer)]
+ tuner_types = {type(tuner_layer) for tuner_layer in tuner_layers}
+ if type(config0) is type(config1):
+ assert len(tuner_types) == 1
+ else:
+ assert len(tuner_types) == 2
+
+ assert peft_model_10.active_adapters == ["adapter1", "adapter0"]
+ assert torch.isfinite(output_mixed_10).all()
+ assert not torch.allclose(output_config0, output_mixed_10, atol=atol, rtol=rtol)
+ assert not torch.allclose(output_config1, output_mixed_10, atol=atol, rtol=rtol)
+ if is_commutative:
+ assert torch.allclose(output_mixed_01, output_mixed_10, atol=atol, rtol=rtol)
+
+ # turn around the order of the adapters of the 0 + 1 mixed model, should behave like the 0 + 1 mixed model
+ peft_model_10.set_adapter(["adapter0", "adapter1"])
+ output_mixed_reversed = peft_model_10(input)
+
+ # check the number of tuner layer types
+ tuner_layers = [mod for mod in peft_model_10.modules() if isinstance(mod, BaseTunerLayer)]
+ tuner_types = {type(tuner_layer) for tuner_layer in tuner_layers}
+ if type(config0) is type(config1):
+ assert len(tuner_types) == 1
+ else:
+ assert len(tuner_types) == 2
+
+ assert peft_model_10.active_adapters == ["adapter0", "adapter1"]
+ assert torch.isfinite(output_mixed_reversed).all()
+ assert not torch.allclose(output_mixed_reversed, output_config0, atol=atol, rtol=rtol)
+ assert not torch.allclose(output_mixed_reversed, output_config1, atol=atol, rtol=rtol)
+ if is_commutative:
+ assert torch.allclose(output_mixed_reversed, output_mixed_01, atol=atol, rtol=rtol)
+ assert torch.allclose(output_mixed_reversed, output_mixed_10, atol=atol, rtol=rtol)
+
+ def _check_merging(self, model_cls, config0, config1, input):
+ # Ensure that when merging mixed adapters, the result is the same as when applying the adapters separately.
+ # Merging requires a bit higher tolerance for some adapters, which can also vary depending on CPU vs GPU.
+ atol = 1e-4
+ rtol = 1e-4
+ seed0 = 0
+ seed1 = 1
+
+ # adapter 0 + 1
+ peft_model_01 = self._get_model(model_cls, config0, "adapter0", seed=seed0)
+ torch.manual_seed(seed1)
+ peft_model_01.add_adapter("adapter1", config1)
+ peft_model_01.set_adapter(["adapter0", "adapter1"])
+ output_mixed_01 = peft_model_01(input)
+
+ model_merged_01 = peft_model_01.merge_and_unload()
+ output_merged_01 = model_merged_01(input)
+ assert torch.allclose(output_mixed_01, output_merged_01, atol=atol, rtol=rtol)
+
+ # adapter 1 + 0
+ peft_model_10 = self._get_model(model_cls, config1, "adapter1", seed=seed1)
+ torch.manual_seed(seed0)
+ peft_model_10.add_adapter("adapter0", config0)
+ peft_model_10.set_adapter(["adapter1", "adapter0"])
+ output_mixed_10 = peft_model_10(input)
+
+ model_merged_10 = peft_model_10.merge_and_unload()
+ output_merged_10 = model_merged_10(input)
+ assert torch.allclose(output_mixed_10, output_merged_10, atol=atol, rtol=rtol)
+
+ def _check_unload(self, model_cls, config0, config1, input):
+ # Ensure that we can unload the base model without merging
+ atol = 1e-5
+ rtol = 1e-5
+ seed0 = 0
+ seed1 = 1
+
+ base_model = self._get_model(model_cls)
+ output_base = base_model(input)
+
+ # adapter 0 + 1
+ peft_model_01 = self._get_model(model_cls, config0, "adapter0", seed=seed0)
+ torch.manual_seed(seed1)
+ peft_model_01.add_adapter("adapter1", config1)
+ peft_model_01.set_adapter(["adapter0", "adapter1"])
+ output_mixed = peft_model_01(input)
+
+ # unload
+ model_unloaded = peft_model_01.unload()
+ output_unloaded = model_unloaded(input)
+
+ assert not torch.allclose(output_mixed, output_unloaded, atol=atol, rtol=rtol)
+ assert torch.allclose(output_base, output_unloaded, atol=atol, rtol=rtol)
+
+ def _check_disable(self, model_cls, config0, config1, input):
+ # Ensure that we can disable adapters
+ atol = 1e-5
+ rtol = 1e-5
+ seed0 = 0
+ seed1 = 1
+
+ # base model
+ base_model = self._get_model(model_cls)
+ output_base = base_model(input)
+
+ # adapter 0
+ peft_model_0 = self._get_model(model_cls, config0, "adapter0", seed=seed0)
+ output_config0 = peft_model_0(input)
+ with peft_model_0.disable_adapter():
+ output_disabled0 = peft_model_0(input)
+
+ assert not torch.allclose(output_base, output_config0, atol=atol, rtol=rtol)
+ assert torch.allclose(output_base, output_disabled0, atol=atol, rtol=rtol)
+
+ # adapter 1
+ peft_model_1 = self._get_model(model_cls, config1, "adapter1", seed=seed1)
+ output_config1 = peft_model_1(input)
+ with peft_model_1.disable_adapter():
+ output_disabled1 = peft_model_1(input)
+
+ assert not torch.allclose(output_base, output_config1, atol=atol, rtol=rtol)
+ assert torch.allclose(output_base, output_disabled1, atol=atol, rtol=rtol)
+
+ # adapter 0 + 1
+ peft_model_01 = self._get_model(model_cls, config0, "adapter0", seed=seed0)
+ torch.manual_seed(seed1)
+ peft_model_01.add_adapter("adapter1", config1)
+ peft_model_01.set_adapter(["adapter0", "adapter1"])
+ output_mixed_01 = peft_model_01(input)
+ with peft_model_01.disable_adapter():
+ output_disabled01 = peft_model_01(input)
+
+ assert not torch.allclose(output_base, output_mixed_01, atol=atol, rtol=rtol)
+ assert torch.allclose(output_base, output_disabled01, atol=atol, rtol=rtol)
+
+ # adapter 1 + 0
+ peft_model_10 = self._get_model(model_cls, config1, "adapter1", seed=seed1)
+ torch.manual_seed(seed0)
+ peft_model_10.add_adapter("adapter0", config0)
+ peft_model_10.set_adapter(["adapter1", "adapter0"])
+ output_mixed_10 = peft_model_10(input)
+ with peft_model_10.disable_adapter():
+ output_disabled10 = peft_model_10(input)
+
+ assert not torch.allclose(output_base, output_mixed_10, atol=atol, rtol=rtol)
+ assert torch.allclose(output_base, output_disabled10, atol=atol, rtol=rtol)
+
+ def _check_loading(self, model_cls, config0, config1, input, *, is_commutative):
+ # Check that we can load two adapters into the same model
+ # Note that we save the adapters using a normal PeftModel because PeftMixModel doesn't support saving yet
+ atol = 1e-5
+ rtol = 1e-5
+ seed0 = 0
+ seed1 = 1
+
+ with tempfile.TemporaryDirectory() as tmp_dirname:
+ # SAVING
+ # adapter 0: note that we set mixed=False because mixed models don't support saving (yet)
+ peft_model_0 = self._get_model(model_cls, config0, "adapter0", seed=seed0, mixed=False)
+ output_config0 = peft_model_0(input)
+ peft_model_0.save_pretrained(os.path.join(tmp_dirname, "adapter0"))
+
+ # adapter 1: note that we set mixed=False because mixed models don't support saving (yet)
+ peft_model_1 = self._get_model(model_cls, config1, "adapter1", seed=seed1, mixed=False)
+ output_config1 = peft_model_1(input)
+ peft_model_1.save_pretrained(os.path.join(tmp_dirname, "adapter1"))
+
+ # adapter 0 + 1
+ peft_model_01 = self._get_model(model_cls, config0, "adapter0", seed=seed0)
+ torch.manual_seed(seed1)
+ peft_model_01.add_adapter("adapter1", config1)
+ peft_model_01.set_adapter(["adapter0", "adapter1"])
+ output_mixed_01 = peft_model_01(input)
+
+ # adapter 1 + 0
+ peft_model_10 = self._get_model(model_cls, config1, "adapter1", seed=seed1)
+ torch.manual_seed(seed0)
+ peft_model_10.add_adapter("adapter0", config0)
+ peft_model_10.set_adapter(["adapter1", "adapter0"])
+ output_mixed_10 = peft_model_10(input)
+
+ # LOADING
+ # adapter 0
+ base_model = self._get_model(model_cls)
+ # Notes:
+ # Path is tmp_dirname/adapter0/adapter0 because non-default adapters are saved in a subfolder.
+ # As a sanity check, we should set a completely different seed here. That way, we ensure that the the
+ # weights are not just randomly initialized exactly to the same values as before.
+ torch.manual_seed(123456)
+ peft_model_loaded0 = PeftMixedModel.from_pretrained(
+ base_model, os.path.join(tmp_dirname, "adapter0", "adapter0"), "adapter0"
+ )
+ output_loaded0 = peft_model_loaded0(input)
+ assert torch.allclose(output_config0, output_loaded0, atol=atol, rtol=rtol)
+
+ # adapter 1
+ base_model = self._get_model(model_cls)
+ torch.manual_seed(654321) # setting a completely different seed here should not affect the result
+ peft_model_loaded1 = PeftMixedModel.from_pretrained(
+ base_model, os.path.join(tmp_dirname, "adapter1", "adapter1"), "adapter1"
+ )
+ output_loaded1 = peft_model_loaded1(input)
+ assert torch.allclose(output_config1, output_loaded1, atol=atol, rtol=rtol)
+
+ # adapter 0 + 1
+ base_model = self._get_model(model_cls)
+ torch.manual_seed(97531) # setting a completely different seed here should not affect the result
+ peft_model_loaded_01 = PeftMixedModel.from_pretrained(
+ base_model, os.path.join(tmp_dirname, "adapter0", "adapter0"), "adapter0"
+ )
+ peft_model_loaded_01.load_adapter(os.path.join(tmp_dirname, "adapter1", "adapter1"), "adapter1")
+ # at this point, "adapter0" should still be active
+ assert peft_model_loaded_01.active_adapters == ["adapter0"]
+ output_loaded01_0 = peft_model_loaded_01(input)
+ assert torch.allclose(output_config0, output_loaded01_0, atol=atol, rtol=rtol)
+ # activate adapter1
+ peft_model_loaded_01.set_adapter(["adapter1"])
+ assert peft_model_loaded_01.active_adapters == ["adapter1"]
+ output_loaded01_1 = peft_model_loaded_01(input)
+ assert torch.allclose(output_config1, output_loaded01_1, atol=atol, rtol=rtol)
+ # activate both adapters
+ peft_model_loaded_01.set_adapter(["adapter0", "adapter1"])
+ output_loaded01 = peft_model_loaded_01(input)
+ assert torch.allclose(output_mixed_01, output_loaded01, atol=atol, rtol=rtol)
+
+ # adapter 1 + 0
+ base_model = self._get_model(model_cls)
+ torch.manual_seed(445566) # setting a completely different seed here should not affect the result
+ peft_model_loaded_10 = PeftMixedModel.from_pretrained(
+ base_model, os.path.join(tmp_dirname, "adapter1", "adapter1"), "adapter1"
+ )
+ peft_model_loaded_10.load_adapter(os.path.join(tmp_dirname, "adapter0", "adapter0"), "adapter0")
+ # at this point, "adapter1" should still be active
+ assert peft_model_loaded_10.active_adapters == ["adapter1"]
+ output_loaded10_1 = peft_model_loaded_10(input)
+ assert torch.allclose(output_config1, output_loaded10_1, atol=atol, rtol=rtol)
+ # activate adapter1
+ peft_model_loaded_10.set_adapter(["adapter0"])
+ assert peft_model_loaded_10.active_adapters == ["adapter0"]
+ output_loaded10_0 = peft_model_loaded_10(input)
+ assert torch.allclose(output_config0, output_loaded10_0, atol=atol, rtol=rtol)
+ # activate both adapters
+ peft_model_loaded_10.set_adapter(["adapter1", "adapter0"])
+ output_loaded10 = peft_model_loaded_10(input)
+ assert torch.allclose(output_mixed_10, output_loaded10, atol=atol, rtol=rtol)
+
+ if is_commutative:
+ assert torch.allclose(output_loaded01, output_loaded10, atol=atol, rtol=rtol)
+ assert torch.allclose(output_loaded10, output_mixed_01, atol=atol, rtol=rtol)
+
+ @parameterized.expand(
+ itertools.combinations(
+ [
+ LoraConfig(target_modules=["lin0"], init_lora_weights=False),
+ LoHaConfig(target_modules=["lin0"], init_weights=False),
+ LoKrConfig(target_modules=["lin0"], init_weights=False),
+ AdaLoraConfig(target_modules=["lin0"], init_lora_weights=False, total_step=1),
+ ],
+ r=2,
+ ),
+ name_func=_param_name_func,
+ )
+ def test_target_first_layer(self, config0, config1):
+ input = torch.arange(90).reshape(9, 10).to(self.torch_device)
+ self._check_mixed_outputs(SimpleNet, config0, config1, input, is_commutative=False)
+ self._check_merging(SimpleNet, config0, config1, input)
+ self._check_unload(SimpleNet, config0, config1, input)
+ self._check_disable(SimpleNet, config1, config0, input)
+ self._check_loading(SimpleNet, config0, config1, input, is_commutative=False)
+
+ @parameterized.expand(
+ itertools.combinations(
+ [
+ LoraConfig(target_modules=["lin1"], init_lora_weights=False),
+ LoHaConfig(target_modules=["lin1"], init_weights=False),
+ LoKrConfig(target_modules=["lin1"], init_weights=False),
+ AdaLoraConfig(target_modules=["lin1"], init_lora_weights=False, total_step=1),
+ ],
+ r=2,
+ ),
+ name_func=_param_name_func,
+ )
+ def test_target_last_layer(self, config0, config1):
+ # We are targeting the last layer of the SimpleNet. Therefore, since the adapters only add their activations
+ # to the output, the results should be commutative. This would *not* work if the adapters do something more
+ # complex or if we target an earlier layer, because of the non-linearity would destroy the commutativity.
+ input = torch.arange(90).reshape(9, 10).to(self.torch_device)
+
+ self._check_mixed_outputs(SimpleNet, config0, config1, input, is_commutative=True)
+ self._check_merging(SimpleNet, config0, config1, input)
+ self._check_unload(SimpleNet, config0, config1, input)
+ self._check_disable(SimpleNet, config1, config0, input)
+ self._check_loading(SimpleNet, config0, config1, input, is_commutative=True)
+
+ @parameterized.expand(
+ itertools.combinations(
+ [
+ LoraConfig(init_lora_weights=False),
+ LoHaConfig(init_weights=False),
+ LoKrConfig(init_weights=False),
+ AdaLoraConfig(init_lora_weights=False, total_step=1),
+ ],
+ r=2,
+ ),
+ name_func=_param_name_func,
+ )
+ def test_target_different_layers(self, config0, config1):
+ input = torch.arange(90).reshape(9, 10).to(self.torch_device)
+
+ config0.target_modules = ["lin0"]
+ config1.target_modules = ["lin1"]
+ self._check_mixed_outputs(SimpleNet, config0, config1, input, is_commutative=False)
+ self._check_merging(SimpleNet, config0, config1, input)
+ self._check_unload(SimpleNet, config0, config1, input)
+ self._check_disable(SimpleNet, config0, config1, input)
+ self._check_loading(SimpleNet, config0, config1, input, is_commutative=False)
+
+ # same, but switch target_modules around
+ config0.target_modules = ["lin1"]
+ config1.target_modules = ["lin0"]
+ self._check_mixed_outputs(SimpleNet, config1, config0, input, is_commutative=False)
+ self._check_merging(SimpleNet, config1, config0, input)
+ self._check_unload(SimpleNet, config1, config0, input)
+ self._check_disable(SimpleNet, config1, config0, input)
+ self._check_loading(SimpleNet, config1, config0, input, is_commutative=False)
+
+ @parameterized.expand(
+ [
+ (
+ LoraConfig(target_modules=["lin1"], init_lora_weights=False),
+ LoraConfig(target_modules=["lin1"], init_lora_weights=False),
+ ),
+ (
+ LoHaConfig(target_modules=["lin1"], init_weights=False),
+ LoHaConfig(target_modules=["lin1"], init_weights=False),
+ ),
+ (
+ LoKrConfig(target_modules=["lin1"], init_weights=False),
+ LoKrConfig(target_modules=["lin1"], init_weights=False),
+ ),
+ (
+ AdaLoraConfig(target_modules=["lin1"], init_lora_weights=False, total_step=1),
+ AdaLoraConfig(target_modules=["lin1"], init_lora_weights=False, total_step=1),
+ ),
+ ],
+ name_func=_param_name_func,
+ )
+ def test_target_last_layer_same_type(self, config0, config1):
+ input = torch.arange(90).reshape(9, 10).to(self.torch_device)
+
+ self._check_mixed_outputs(SimpleNet, config0, config1, input, is_commutative=True)
+ self._check_merging(SimpleNet, config0, config1, input)
+ self._check_unload(SimpleNet, config0, config1, input)
+ self._check_disable(SimpleNet, config1, config0, input)
+
+ @parameterized.expand(
+ [
+ (
+ LoraConfig(target_modules=["lin0"], init_lora_weights=False),
+ LoraConfig(target_modules=["lin0"], init_lora_weights=False),
+ ),
+ (
+ LoHaConfig(target_modules=["lin0"], init_weights=False),
+ LoHaConfig(target_modules=["lin0"], init_weights=False),
+ ),
+ (
+ LoKrConfig(target_modules=["lin0"], init_weights=False),
+ LoKrConfig(target_modules=["lin0"], init_weights=False),
+ ),
+ (
+ AdaLoraConfig(target_modules=["lin0"], init_lora_weights=False, total_step=1),
+ AdaLoraConfig(target_modules=["lin0"], init_lora_weights=False, total_step=1),
+ ),
+ ],
+ name_func=_param_name_func,
+ )
+ def test_target_first_layer_same_type(self, config0, config1):
+ input = torch.arange(90).reshape(9, 10).to(self.torch_device)
+ self._check_mixed_outputs(SimpleNet, config0, config1, input, is_commutative=False)
+ self._check_merging(SimpleNet, config0, config1, input)
+ self._check_unload(SimpleNet, config0, config1, input)
+ self._check_disable(SimpleNet, config1, config0, input)
+ self._check_loading(SimpleNet, config0, config1, input, is_commutative=False)
+
+ def test_deeply_nested(self):
+ # a somewhat absurdly nested model using different adapter types
+ if platform.system() == "Linux":
+ self.skipTest("This test fails but only on GitHub CI with Linux systems.")
+
+ atol = 1e-5
+ rtol = 1e-5
+ torch.manual_seed(0)
+
+ model = SimpleNet().eval().to(self.torch_device)
+ input = torch.arange(90).reshape(9, 10).to(self.torch_device)
+ output_base = model(input)
+
+ config0 = LoraConfig(r=4, lora_alpha=4, target_modules=["lin0", "lin1"], init_lora_weights=False)
+ peft_model = get_peft_model(model, config0, "adapter0", mixed=True)
+
+ config1 = LoHaConfig(r=4, alpha=4, target_modules=["lin0"], init_weights=False)
+ peft_model.add_adapter("adapter1", config1)
+
+ config2 = AdaLoraConfig(r=4, lora_alpha=4, target_modules=["lin1"], init_lora_weights=False, total_step=1)
+ peft_model.add_adapter("adapter2", config2)
+
+ config3 = LoKrConfig(r=4, alpha=4, target_modules=["lin0", "lin1"], init_weights=False)
+ peft_model.add_adapter("adapter3", config3)
+
+ peft_model.set_adapter(["adapter0", "adapter1", "adapter2", "adapter3"])
+ output_mixed = peft_model(input)
+ assert torch.isfinite(output_base).all()
+ assert not torch.allclose(output_base, output_mixed, atol=atol, rtol=rtol)
+
+ # test disabling all adapters
+ with peft_model.disable_adapter():
+ output_disabled = peft_model(input)
+ assert torch.isfinite(output_disabled).all()
+ assert torch.allclose(output_base, output_disabled, atol=atol, rtol=rtol)
+ assert not torch.allclose(output_mixed, output_disabled, atol=atol, rtol=rtol)
+
+ # merge and unload all adapters
+ model_copy = copy.deepcopy(peft_model)
+ model = model_copy.merge_and_unload()
+ output_merged = model(input)
+ assert torch.isfinite(output_merged).all()
+ assert torch.allclose(output_mixed, output_merged, atol=atol, rtol=rtol)
+
+ # merge and unload only adapter1 and adapter3
+ model_copy = copy.deepcopy(peft_model)
+ model_copy.set_adapter(["adapter1", "adapter3"])
+ output_13 = model_copy(input)
+ assert torch.isfinite(output_13).all()
+ assert not torch.allclose(output_mixed, output_13, atol=atol, rtol=rtol)
+
+ model_copy.set_adapter(["adapter0", "adapter1", "adapter2", "adapter3"])
+ model_merged_unloaded = model_copy.merge_and_unload(adapter_names=["adapter1", "adapter3"])
+ output_merged_13 = model_merged_unloaded(input)
+ assert torch.isfinite(output_merged_13).all()
+ assert torch.allclose(output_13, output_merged_13, atol=atol, rtol=rtol)
+
+ # test unloading
+ model_copy = copy.deepcopy(peft_model)
+ model_unloaded = model_copy.unload()
+ output_unloaded = model_unloaded(input)
+ assert torch.isfinite(output_unloaded).all()
+ assert torch.allclose(output_base, output_unloaded, atol=atol, rtol=rtol)
+
+ def test_delete_adapter(self):
+ atol = 1e-5
+ rtol = 1e-5
+ torch.manual_seed(0)
+
+ model = SimpleNet().eval().to(self.torch_device)
+ input = torch.arange(90).reshape(9, 10).to(self.torch_device)
+ output_base = model(input)
+
+ # create adapter0
+ torch.manual_seed(0)
+ config0 = LoraConfig(r=4, lora_alpha=4, target_modules=["lin0", "lin1"], init_lora_weights=False)
+ peft_model = get_peft_model(model, config0, "adapter0", mixed=True)
+ output_0 = peft_model(input)
+ assert not torch.allclose(output_base, output_0, atol=atol, rtol=rtol)
+
+ # add adapter1
+ torch.manual_seed(1)
+ config1 = LoHaConfig(r=4, alpha=4, target_modules=["lin0"], init_weights=False)
+ peft_model.add_adapter("adapter1", config1)
+ peft_model.set_adapter(["adapter0", "adapter1"])
+ output_01 = peft_model(input)
+ assert not torch.allclose(output_base, output_01, atol=atol, rtol=rtol)
+ assert not torch.allclose(output_0, output_01, atol=atol, rtol=rtol)
+
+ # delete adapter1
+ peft_model.delete_adapter("adapter1")
+ assert peft_model.active_adapters == ["adapter0"]
+ output_deleted_1 = peft_model(input)
+ assert torch.allclose(output_0, output_deleted_1, atol=atol, rtol=rtol)
+
+ msg = re.escape("Adapter(s) ['adapter1'] not found, available adapters: ['adapter0']")
+ with pytest.raises(ValueError, match=msg):
+ peft_model.set_adapter(["adapter0", "adapter1"])
+
+ # re-add adapter1
+ torch.manual_seed(1)
+ peft_model.add_adapter("adapter1", config1)
+ peft_model.set_adapter(["adapter0", "adapter1"])
+ output_01_readded = peft_model(input)
+ assert not torch.allclose(output_base, output_01_readded, atol=atol, rtol=rtol)
+
+ # same as above, but this time delete adapter0 first
+ torch.manual_seed(0)
+ model = SimpleNet().eval().to(self.torch_device)
+ torch.manual_seed(0)
+ peft_model = get_peft_model(model, config0, "adapter0", mixed=True)
+ torch.manual_seed(1)
+ peft_model.add_adapter("adapter1", config1)
+ peft_model.delete_adapter("adapter0")
+ assert peft_model.active_adapters == ["adapter1"]
+ output_deleted_0 = peft_model(input)
+ assert not torch.allclose(output_deleted_0, output_base, atol=atol, rtol=rtol)
+ assert not torch.allclose(output_deleted_0, output_01, atol=atol, rtol=rtol)
+
+ msg = re.escape("Adapter(s) ['adapter0'] not found, available adapters: ['adapter1']")
+ with pytest.raises(ValueError, match=msg):
+ peft_model.set_adapter(["adapter0", "adapter1"])
+
+ peft_model.delete_adapter("adapter1")
+ assert peft_model.active_adapters == []
+ output_deleted_01 = peft_model(input)
+ assert torch.allclose(output_deleted_01, output_base, atol=atol, rtol=rtol)
+
+ def test_modules_to_save(self):
+ model = SimpleNet().eval().to(self.torch_device)
+ config0 = LoraConfig(target_modules=["lin0"], modules_to_save=["lin1"])
+ peft_model = get_peft_model(model, config0, "adapter0", mixed=True)
+
+ # adding a second adapter with same modules_to_save is not allowed
+ # TODO: theoretically, we could allow this if it's the same target layer
+ config1 = LoHaConfig(target_modules=["lin0"], modules_to_save=["lin1"])
+ peft_model.add_adapter("adapter1", config1)
+ with pytest.raises(ValueError, match="Only one adapter can be set at a time for ModulesToSaveWrapper"):
+ peft_model.set_adapter(["adapter0", "adapter1"])
+
+ def test_get_nb_trainable_parameters(self):
+ model = SimpleNet().eval().to(self.torch_device)
+ params_base = sum(p.numel() for p in model.parameters())
+
+ config0 = LoraConfig(target_modules=["lin0"])
+ peft_model = get_peft_model(model, config0, "adapter0", mixed=True)
+ trainable_params0, all_param0 = peft_model.get_nb_trainable_parameters()
+
+ params_lora = sum(p.numel() for n, p in model.named_parameters() if "adapter0" in n)
+ assert trainable_params0 == params_lora
+ assert all_param0 == (params_base + params_lora)
+
+ config1 = LoHaConfig(target_modules=["lin1"])
+ peft_model.add_adapter("adapter1", config1)
+ peft_model.set_adapter(["adapter0", "adapter1"])
+ params_loha = sum(p.numel() for n, p in model.named_parameters() if "adapter1" in n)
+ trainable_params1, all_param1 = peft_model.get_nb_trainable_parameters()
+ assert trainable_params1 == (params_lora + params_loha)
+ assert all_param1 == ((params_base + params_lora) + params_loha)
+
+ config2 = AdaLoraConfig(target_modules=["lin0", "lin1"], total_step=1)
+ peft_model.add_adapter("adapter2", config2)
+ peft_model.set_adapter(["adapter0", "adapter1", "adapter2"])
+ params_adalora = sum(p.numel() for n, p in model.named_parameters() if "adapter2" in n)
+ trainable_params2, all_param2 = peft_model.get_nb_trainable_parameters()
+ # remove 2 params because we need to exclude "ranknum" for AdaLora trainable params
+ assert trainable_params2 == (((params_lora + params_loha) + params_adalora) - 2)
+ assert all_param2 == (((params_base + params_lora) + params_loha) + params_adalora)
+
+ def test_incompatible_config_raises(self):
+ model = SimpleNet().eval().to(self.torch_device)
+ config0 = LoraConfig(target_modules=["lin0"])
+ peft_model = get_peft_model(model, config0, "adapter0", mixed=True)
+
+ config1 = PrefixTuningConfig()
+ msg = "The provided `peft_type` 'PREFIX_TUNING' is not compatible with the `PeftMixedModel`."
+ with pytest.raises(ValueError, match=msg):
+ peft_model.add_adapter("adapter1", config1)
+
+ def test_decoder_model(self):
+ # test a somewhat realistic model instead of a toy model
+ torch.manual_seed(0)
+
+ model_id = "hf-internal-testing/tiny-random-OPTForCausalLM"
+ model = AutoModelForCausalLM.from_pretrained(model_id).eval().to(self.torch_device)
+ input_ids = torch.tensor([[1, 1, 1], [1, 2, 1]]).to(self.torch_device)
+ attention_mask = torch.tensor([[1, 1, 1], [1, 0, 1]]).to(self.torch_device)
+ input_dict = {
+ "input_ids": input_ids,
+ "attention_mask": attention_mask,
+ }
+ output_base = model.generate(**input_dict)
+
+ torch.manual_seed(0)
+ config0 = LoraConfig(task_type="CAUSAL_LM", init_lora_weights=False)
+ peft_model = get_peft_model(model, config0, "adapter0", mixed=True)
+ output0 = peft_model.generate(**input_dict)
+ assert torch.isfinite(output0).all()
+ assert not torch.allclose(output_base, output0)
+
+ torch.manual_seed(1)
+ config1 = LoHaConfig(task_type="CAUSAL_LM", target_modules=["q_proj", "v_proj"], init_weights=False)
+ peft_model.add_adapter("adapter1", config1)
+ peft_model.set_adapter(["adapter0", "adapter1"])
+ output1 = peft_model.generate(**input_dict)
+ assert torch.isfinite(output1).all()
+ assert not torch.allclose(output0, output1)
+
+ torch.manual_seed(2)
+ config2 = AdaLoraConfig(task_type="CAUSAL_LM", init_lora_weights=False, total_step=1)
+ peft_model.add_adapter("adapter2", config2)
+ peft_model.set_adapter(["adapter0", "adapter1", "adapter2"])
+ output2 = peft_model.generate(**input_dict)
+ assert torch.isfinite(output2).all()
+ assert not torch.allclose(output1, output2)
+
+ torch.manual_seed(3)
+ config3 = LoKrConfig(task_type="CAUSAL_LM", target_modules=["q_proj", "v_proj"], init_weights=False)
+ peft_model.add_adapter("adapter3", config3)
+ peft_model.set_adapter(["adapter0", "adapter1", "adapter2", "adapter3"])
+ output3 = peft_model.generate(**input_dict)
+ assert torch.isfinite(output3).all()
+ assert not torch.allclose(output2, output3)
+
+ torch.manual_seed(4)
+ peft_model.set_adapter(["adapter0", "adapter1", "adapter2", "adapter3"])
+
+ with peft_model.disable_adapter():
+ output_disabled = peft_model.generate(**input_dict)
+ assert torch.isfinite(output_disabled).all()
+ assert torch.allclose(output_base, output_disabled)
+
+ model_unloaded = peft_model.merge_and_unload()
+ output_unloaded = model_unloaded.generate(**input_dict)
+ assert torch.isfinite(output_unloaded).all()
+
+ with tempfile.TemporaryDirectory() as tmp_dir:
+ # save adapter0 (use normal PeftModel, because PeftMixedModel does not support saving)
+ torch.manual_seed(0)
+ model = AutoModelForCausalLM.from_pretrained(model_id).eval().to(self.torch_device)
+ torch.manual_seed(0)
+ peft_model = get_peft_model(model, config0, "adapter0")
+ output0_save = peft_model(**input_dict).logits
+ assert torch.isfinite(output0_save).all()
+ peft_model.save_pretrained(tmp_dir)
+
+ # save adapter1
+ torch.manual_seed(0)
+ model = AutoModelForCausalLM.from_pretrained(model_id).eval().to(self.torch_device)
+ torch.manual_seed(1)
+ peft_model = get_peft_model(model, config1, "adapter1")
+ output1_save = peft_model(**input_dict).logits
+ assert torch.isfinite(output1_save).all()
+ peft_model.save_pretrained(tmp_dir)
+
+ # load adapter0 and adapter1
+ model = AutoModelForCausalLM.from_pretrained(model_id).eval().to(self.torch_device)
+ peft_model = PeftMixedModel.from_pretrained(model, os.path.join(tmp_dir, "adapter0"), "adapter0")
+ peft_model.load_adapter(os.path.join(tmp_dir, "adapter1"), "adapter1")
+ peft_model.set_adapter(["adapter0", "adapter1"])
+ output01_loaded = peft_model(**input_dict).logits
+
+ atol, rtol = 1e-3, 1e-3
+ assert torch.isfinite(output01_loaded).all()
+ assert not torch.allclose(output0_save, output01_loaded, atol=atol, rtol=rtol)
+ assert not torch.allclose(output1_save, output01_loaded, atol=atol, rtol=rtol)
diff --git a/peft/tests/test_multitask_prompt_tuning.py b/peft/tests/test_multitask_prompt_tuning.py
new file mode 100644
index 0000000000000000000000000000000000000000..94a9e213834407670a3916ca4710ce0cb0f15994
--- /dev/null
+++ b/peft/tests/test_multitask_prompt_tuning.py
@@ -0,0 +1,288 @@
+# Copyright 2023-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+import os
+import tempfile
+
+import pytest
+import torch
+from torch.testing import assert_close
+from transformers import AutoModelForCausalLM
+
+from peft import get_peft_model
+from peft.peft_model import PeftModel
+from peft.tuners.multitask_prompt_tuning import MultitaskPromptTuningConfig, MultitaskPromptTuningInit
+from peft.utils import infer_device
+from peft.utils.other import WEIGHTS_NAME, prepare_model_for_kbit_training
+from peft.utils.save_and_load import get_peft_model_state_dict
+
+
+MODELS_TO_TEST = [
+ "trl-internal-testing/tiny-random-LlamaForCausalLM",
+]
+
+
+class TestMultiTaskPromptTuning:
+ """
+ Tests for the MultiTaskPromptTuning model.
+ """
+
+ @pytest.fixture
+ def config(cls) -> MultitaskPromptTuningConfig:
+ return MultitaskPromptTuningConfig(
+ task_type="CAUSAL_LM",
+ num_virtual_tokens=50,
+ num_tasks=3,
+ prompt_tuning_init_text=(
+ "classify the following into either positive or negative, or entailment, neutral or contradiction:"
+ ),
+ )
+
+ transformers_class = AutoModelForCausalLM
+ torch_device = infer_device()
+
+ @pytest.mark.parametrize("model_id", MODELS_TO_TEST)
+ def test_prepare_for_training(self, model_id, config):
+ model = AutoModelForCausalLM.from_pretrained(model_id)
+ model = get_peft_model(model, config)
+ model = model.to(self.torch_device)
+
+ dummy_input = torch.LongTensor([[1, 1, 1]]).to(self.torch_device)
+ dummy_output = model.get_input_embeddings()(dummy_input)
+
+ assert not dummy_output.requires_grad
+
+ @pytest.mark.parametrize("model_id", MODELS_TO_TEST)
+ def test_prepare_for_int8_training(self, model_id, config):
+ model = AutoModelForCausalLM.from_pretrained(model_id)
+ model = prepare_model_for_kbit_training(model)
+ model = model.to(self.torch_device)
+
+ for param in model.parameters():
+ assert not param.requires_grad
+
+ model = get_peft_model(model, config)
+
+ # For backward compatibility
+ if hasattr(model, "enable_input_require_grads"):
+ model.enable_input_require_grads()
+ else:
+
+ def make_inputs_require_grad(module, input, output):
+ output.requires_grad_(True)
+
+ model.get_input_embeddings().register_forward_hook(make_inputs_require_grad)
+
+ dummy_input = torch.LongTensor([[1, 1, 1]]).to(self.torch_device)
+ dummy_output = model.get_input_embeddings()(dummy_input)
+
+ assert dummy_output.requires_grad
+
+ @pytest.mark.parametrize("model_id", MODELS_TO_TEST)
+ def test_save_pretrained(self, model_id, config):
+ seed = 420
+ torch.manual_seed(seed)
+ model = AutoModelForCausalLM.from_pretrained(model_id)
+ model = get_peft_model(model, config)
+ model = model.to(self.torch_device)
+
+ with tempfile.TemporaryDirectory() as tmp_dirname:
+ model.save_pretrained(tmp_dirname)
+
+ torch.manual_seed(seed)
+ model_from_pretrained = AutoModelForCausalLM.from_pretrained(model_id)
+ model_from_pretrained = PeftModel.from_pretrained(model_from_pretrained, tmp_dirname)
+
+ # check if the state dicts are equal
+ state_dict = get_peft_model_state_dict(model)
+
+ state_dict_from_pretrained = get_peft_model_state_dict(model_from_pretrained)
+
+ # check if same keys
+ assert state_dict.keys() == state_dict_from_pretrained.keys()
+
+ # Check that the number of saved parameters is 4 -- 2 layers of (tokens and gate).
+ assert len(state_dict) == 3
+
+ # check if tensors equal
+ for key in state_dict.keys():
+ assert torch.allclose(
+ state_dict[key].to(self.torch_device), state_dict_from_pretrained[key].to(self.torch_device)
+ )
+
+ # check if `adapter_model.safetensors` is present
+ assert os.path.exists(os.path.join(tmp_dirname, "adapter_model.safetensors"))
+
+ # check if `adapter_config.json` is present
+ assert os.path.exists(os.path.join(tmp_dirname, "adapter_config.json"))
+
+ # check if `pytorch_model.bin` is not present
+ assert not os.path.exists(os.path.join(tmp_dirname, "pytorch_model.bin"))
+
+ # check if `config.json` is not present
+ assert not os.path.exists(os.path.join(tmp_dirname, "config.json"))
+
+ @pytest.mark.parametrize("model_id", MODELS_TO_TEST)
+ def test_save_pretrained_regression(self, model_id, config):
+ seed = 420
+ torch.manual_seed(seed)
+ model = AutoModelForCausalLM.from_pretrained(model_id)
+ model = get_peft_model(model, config)
+ model = model.to(self.torch_device)
+
+ with tempfile.TemporaryDirectory() as tmp_dirname:
+ model.save_pretrained(tmp_dirname, safe_serialization=False)
+
+ torch.manual_seed(seed)
+ model_from_pretrained = AutoModelForCausalLM.from_pretrained(model_id)
+ model_from_pretrained = PeftModel.from_pretrained(model_from_pretrained, tmp_dirname)
+
+ # check if the state dicts are equal
+ state_dict = get_peft_model_state_dict(model)
+
+ state_dict_from_pretrained = get_peft_model_state_dict(model_from_pretrained)
+
+ # check if same keys
+ assert state_dict.keys() == state_dict_from_pretrained.keys()
+
+ # Check that the number of saved parameters is 4 -- 2 layers of (tokens and gate).
+ assert len(state_dict) == 3
+
+ # check if tensors equal
+ for key in state_dict.keys():
+ assert torch.allclose(
+ state_dict[key].to(self.torch_device), state_dict_from_pretrained[key].to(self.torch_device)
+ )
+
+ # check if `adapter_model.bin` is present for regression
+ assert os.path.exists(os.path.join(tmp_dirname, "adapter_model.bin"))
+
+ # check if `adapter_config.json` is present
+ assert os.path.exists(os.path.join(tmp_dirname, "adapter_config.json"))
+
+ # check if `pytorch_model.bin` is not present
+ assert not os.path.exists(os.path.join(tmp_dirname, "pytorch_model.bin"))
+
+ # check if `config.json` is not present
+ assert not os.path.exists(os.path.join(tmp_dirname, "config.json"))
+
+ @pytest.mark.parametrize("model_id", MODELS_TO_TEST)
+ def test_generate(self, model_id, config):
+ model = AutoModelForCausalLM.from_pretrained(model_id)
+ model = get_peft_model(model, config)
+ model = model.to(self.torch_device)
+
+ input_ids = torch.LongTensor([[1, 1, 1], [2, 1, 2]]).to(self.torch_device)
+ attention_mask = torch.LongTensor([[1, 1, 1], [1, 0, 1]]).to(self.torch_device)
+ task_ids = torch.LongTensor([1, 2]).to(self.torch_device)
+
+ # check if `generate` works
+ _ = model.generate(input_ids=input_ids, attention_mask=attention_mask, task_ids=task_ids)
+
+ # check if `generate` works if positional arguments are passed
+ _ = model.generate(input_ids, attention_mask=attention_mask, task_ids=task_ids)
+
+ @pytest.mark.parametrize("model_id", MODELS_TO_TEST)
+ def test_use_cache(self, model_id, config):
+ """Test that MultiTaskPromptTuning works when Llama config use_cache=True."""
+ torch.manual_seed(0)
+ input_ids = torch.LongTensor([[1, 1, 1], [2, 1, 2]]).to(self.torch_device)
+ task_ids = torch.LongTensor([1, 2]).to(self.torch_device)
+
+ original = AutoModelForCausalLM.from_pretrained(model_id)
+ mpt = get_peft_model(original, config)
+ mpt = mpt.to(self.torch_device)
+
+ expected = mpt.generate(input_ids=input_ids, max_length=8, task_ids=task_ids)
+
+ # Set use_cache = True and generate output again.
+ mpt.base_model.config.use_cache = True
+ actual = mpt.generate(input_ids=input_ids, max_length=8, task_ids=task_ids)
+ assert_close(expected, actual, rtol=0, atol=0)
+
+ @pytest.mark.parametrize("model_id", MODELS_TO_TEST)
+ def test_bf16_inference(self, model_id, config):
+ """Test that MultiTaskPromptTuning works when Llama using a half-precision model."""
+ input_ids = torch.LongTensor([[1, 1, 1], [2, 1, 2]]).to(self.torch_device)
+ task_ids = torch.tensor([1, 2]).to(self.torch_device)
+
+ original = AutoModelForCausalLM.from_pretrained(model_id, torch_dtype=torch.bfloat16)
+ mpt = get_peft_model(original, config)
+ mpt = mpt.to(self.torch_device)
+ _ = mpt.generate(input_ids=input_ids, task_ids=task_ids)
+
+ @pytest.mark.parametrize("model_id", MODELS_TO_TEST)
+ def test_generate_text_with_random_init(self, model_id, config) -> None:
+ torch.manual_seed(0)
+ model = AutoModelForCausalLM.from_pretrained(model_id)
+ config.prompt_tuning_init = MultitaskPromptTuningInit.RANDOM
+ model = get_peft_model(model, config)
+ model = model.to(self.torch_device)
+
+ input_ids = torch.LongTensor([[1, 1, 1], [2, 1, 2]]).to(self.torch_device)
+ attention_mask = torch.LongTensor([[1, 1, 1], [1, 0, 1]]).to(self.torch_device)
+ task_ids = torch.LongTensor([0]).to(self.torch_device)
+
+ # check if `generate` works
+ _ = model.generate(input_ids=input_ids, attention_mask=attention_mask, task_ids=task_ids)
+
+ with pytest.raises(ValueError):
+ # check if `generate` raises an error if task_ids are not passed
+ _ = model.generate(input_ids, attention_mask=attention_mask)
+
+ @pytest.mark.parametrize(
+ "prompt_tuning_init",
+ [
+ MultitaskPromptTuningInit.AVERAGE_SOURCE_TASKS,
+ MultitaskPromptTuningInit.EXACT_SOURCE_TASK,
+ MultitaskPromptTuningInit.ONLY_SOURCE_SHARED,
+ ],
+ )
+ @pytest.mark.parametrize("model_id", MODELS_TO_TEST)
+ def test_generate_text_with_other_init(self, prompt_tuning_init, model_id, config) -> None:
+ # This test is flaky, hence fixing the seed. The reason is somehow related to:
+ # https://github.com/huggingface/transformers/blob/e786844425b6b1112c76513d66217ce2fe6aea41/src/transformers/generation/utils.py#L2691
+ # When an EOS token is generated, the loop is exited and the pytest.raises at the bottom is not triggered
+ # because `forward` of the PEFT model, which should raise the error, is never called.
+ torch.manual_seed(42) # seed 43 fails with transformers v4.42.3 and torch v2.3.1
+
+ with tempfile.TemporaryDirectory() as tmp_dirname:
+ model = AutoModelForCausalLM.from_pretrained(model_id)
+ model = get_peft_model(model, config)
+ model.save_pretrained(tmp_dirname, safe_serialization=False) # bc torch.load is used
+
+ config = MultitaskPromptTuningConfig(
+ task_type="CAUSAL_LM",
+ num_virtual_tokens=50,
+ num_tasks=1,
+ prompt_tuning_init_text=(
+ "classify the following into either positive or negative, or entailment, neutral or contradiction:"
+ ),
+ prompt_tuning_init=prompt_tuning_init,
+ prompt_tuning_init_state_dict_path=os.path.join(tmp_dirname, WEIGHTS_NAME),
+ )
+ model = AutoModelForCausalLM.from_pretrained(model_id)
+ model = get_peft_model(model, config)
+ model = model.to(self.torch_device)
+
+ input_ids = torch.LongTensor([[1, 1, 1], [2, 1, 2]]).to(self.torch_device)
+ attention_mask = torch.LongTensor([[1, 1, 1], [1, 0, 1]]).to(self.torch_device)
+ task_ids = torch.LongTensor([0]).to(self.torch_device)
+
+ # check if `generate` works
+ _ = model.generate(input_ids=input_ids, attention_mask=attention_mask, task_ids=task_ids)
+
+ with pytest.raises(ValueError, match="task_ids cannot be None"):
+ # check if `generate` raises an error if task_ids are not passed
+ _ = model.generate(input_ids, attention_mask=attention_mask)
diff --git a/peft/tests/test_other.py b/peft/tests/test_other.py
new file mode 100644
index 0000000000000000000000000000000000000000..7a0ca34589bc44ff65c296e48a75ca8590355b9c
--- /dev/null
+++ b/peft/tests/test_other.py
@@ -0,0 +1,532 @@
+# Copyright 2023-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+import copy
+
+import pytest
+import torch
+from torch import nn
+from transformers import AutoModelForCausalLM, AutoModelForSequenceClassification, LlavaForConditionalGeneration
+
+from peft import LoraConfig, PeftModel, VeraConfig, get_peft_model
+from peft.utils.other import ModulesToSaveWrapper, _get_no_split_modules
+
+
+class ModelWithModuleDict(nn.Module):
+ def __init__(self):
+ super().__init__()
+ self.other_layer = nn.Linear(10, 10)
+ self.module = nn.ModuleDict({"foo": nn.Linear(10, 10)})
+
+ def forward(self):
+ return self.module["foo"](torch.rand(1, 10))
+
+
+class ModelWithModuleList(nn.Module):
+ def __init__(self):
+ super().__init__()
+ self.other_layer = nn.Linear(10, 10)
+ self.module = nn.ModuleList([nn.Linear(10, 10)])
+
+ def forward(self):
+ return self.module[0](torch.rand(1, 10))
+
+
+class ModelWithParameterDict(nn.Module):
+ def __init__(self):
+ super().__init__()
+ self.other_layer = nn.Linear(10, 10)
+ self.module = nn.ParameterDict({"foo": nn.Parameter(torch.rand(10, 10))})
+
+ def forward(self):
+ return self.module["foo"]
+
+
+class ModelWithParameterList(nn.Module):
+ def __init__(self):
+ super().__init__()
+ self.other_layer = nn.Linear(10, 10)
+ self.module = nn.ParameterList([nn.Parameter(torch.rand(10, 10))])
+
+ def forward(self):
+ return self.module[0]
+
+
+@pytest.mark.parametrize(
+ "cls", [ModelWithModuleDict, ModelWithModuleList, ModelWithParameterDict, ModelWithParameterList]
+)
+def test_modules_to_save_targets_module_dict_raises(cls):
+ model = cls()
+ peft_config = LoraConfig(
+ target_modules=["other_layer"],
+ modules_to_save=["module"],
+ )
+ model() # sanity check that the model would normally work
+
+ msg = "modules_to_save cannot be applied to modules of type"
+ with pytest.raises(TypeError, match=msg):
+ get_peft_model(model=model, peft_config=peft_config)
+
+
+def test_get_peft_model_revision_warning(tmp_path):
+ base_model_id = "peft-internal-testing/tiny-random-BertModel"
+ base_revision = "v2.0.0"
+ base_model = AutoModelForCausalLM.from_pretrained(base_model_id, revision=base_revision).eval()
+ lora_config = LoraConfig(revision=base_revision)
+
+ overwrite_revision = "main"
+ overwrite_warning = f"peft config has already set base model revision to {base_revision}, overwriting with revision {overwrite_revision}"
+ with pytest.warns(UserWarning, match=overwrite_warning):
+ _ = get_peft_model(base_model, lora_config, revision=overwrite_revision)
+
+
+def test_load_multiple_adapters_different_modules_to_save(tmp_path):
+ # This tests the error described in #2422 where loading multiple adapters with different modules_to_save
+ # attributes fails (due to a regression from #2376).
+
+ model = AutoModelForCausalLM.from_pretrained("trl-internal-testing/tiny-random-LlamaForCausalLM")
+
+ def peft_config(**kwargs):
+ return LoraConfig(target_modules="all-linear", **kwargs)
+
+ original_model = copy.deepcopy(model)
+
+ peft_config_0 = peft_config(modules_to_save=["0.post_attention_layernorm"])
+ peft_config_1 = peft_config(modules_to_save=["0.post_attention_layernorm"])
+ peft_config_2 = peft_config(modules_to_save=["1.post_attention_layernorm"])
+
+ # Save adapter 0, nothing fancy, should be equal to base model weighs
+ peft_model = get_peft_model(copy.deepcopy(original_model), peft_config_0)
+ peft_model.save_pretrained(tmp_path / "adapter_0")
+
+ # Save adapter 1, modules to save weights are modified randomly, should be unique to adapter 1
+ peft_model = get_peft_model(copy.deepcopy(original_model), peft_config_1)
+ peft_model.model.model.layers[0].post_attention_layernorm.weight.data = torch.rand_like(
+ peft_model.model.model.layers[0].post_attention_layernorm.weight.data
+ )
+ adapter_1_saved = peft_model.model.model.layers[0].post_attention_layernorm.weight.data.clone()
+ peft_model.save_pretrained(tmp_path / "adapter_1")
+
+ # Save adapter 2, modules to save weights are modified randomly, should be unique to adapter 2
+ peft_model = get_peft_model(copy.deepcopy(original_model), peft_config_2)
+ peft_model.model.model.layers[1].post_attention_layernorm.weight.data = torch.rand_like(
+ peft_model.model.model.layers[1].post_attention_layernorm.weight.data
+ )
+ adapter_2_saved = peft_model.model.model.layers[1].post_attention_layernorm.weight.data.clone()
+ peft_model.save_pretrained(tmp_path / "adapter_2")
+
+ del peft_model
+
+ combined_model = PeftModel.from_pretrained(original_model, tmp_path / "adapter_0", adapter_name="adapter_0")
+ combined_model.load_adapter(tmp_path / "adapter_1", adapter_name="adapter_1")
+ combined_model.load_adapter(tmp_path / "adapter_2", adapter_name="adapter_2")
+
+ # For adapter 0 we expect every mentioned modules to save layer of this test to be equal to the original model
+ # since we didn't modify it for adapter 0 and only adapter 0 is active.
+ combined_model.set_adapter("adapter_0")
+ assert torch.allclose(
+ combined_model.model.model.layers[0].post_attention_layernorm.weight,
+ original_model.model.layers[0].post_attention_layernorm.weight,
+ )
+ assert torch.allclose(
+ combined_model.model.model.layers[1].post_attention_layernorm.weight,
+ original_model.model.layers[1].post_attention_layernorm.weight,
+ )
+
+ # For adapter 1 we expect that the modified module to save 0.post_attention_layernorm is modified, the other
+ # module to save layers mentioned above should be untouched.
+ combined_model.set_adapter("adapter_1")
+ assert torch.allclose(
+ combined_model.model.model.layers[0].post_attention_layernorm.weight,
+ adapter_1_saved,
+ )
+ assert torch.allclose(
+ combined_model.model.model.layers[1].post_attention_layernorm.weight,
+ original_model.model.layers[1].post_attention_layernorm.weight,
+ )
+
+ # For adapter 2 we expect its module to save layer (1.post_attention_layernorm) to be modified but the other
+ # module to save weights should be kept original.
+ combined_model.set_adapter("adapter_2")
+ assert torch.allclose(
+ combined_model.model.model.layers[0].post_attention_layernorm.weight,
+ original_model.model.layers[0].post_attention_layernorm.weight,
+ )
+ assert torch.allclose(
+ combined_model.model.model.layers[1].post_attention_layernorm.weight,
+ adapter_2_saved,
+ )
+
+
+class TestModulesToSaveAttributeAccess:
+ """Test attribute access on the ModulesToSaveWrapper class.
+
+ When we have modules_to_save, the original module is wrapped. As long as only forward was called on this wrapped
+ module, we were good. However, if, for instance, model parameters were directly accessed by another module, this
+ would typically fail, as the wrapper does not have this attribute. We had special properties for weight and bias,
+ but this is not enough. Therefore, attribute access is now transiently delegated to the active adapter (or original
+ module, if the adapter is disabled).
+
+ For one example, see #2099.
+
+ """
+
+ @pytest.fixture
+ def mlp(self):
+ class MLP(nn.Module):
+ def __init__(self):
+ super().__init__()
+ self.lin0 = nn.Linear(1, 2)
+ self.lin1 = nn.Linear(3, 4)
+
+ return MLP()
+
+ def test_transient_attribute_access_default_adapter(self, mlp):
+ config = LoraConfig(target_modules=["lin0"], modules_to_save=["lin1"])
+ model = get_peft_model(mlp, config)
+ assert model.lin1.weight is model.lin1.modules_to_save["default"].weight
+ assert model.lin1.bias is model.lin1.modules_to_save["default"].bias
+
+ def test_transient_attribute_access_non_default_adapter(self, mlp):
+ config = LoraConfig(target_modules=["lin0"], modules_to_save=["lin1"])
+ model = get_peft_model(mlp, config)
+ model.add_adapter("other", config)
+
+ # at this point, default is still active
+ assert model.lin1.weight is model.lin1.modules_to_save["default"].weight
+ assert model.lin1.bias is model.lin1.modules_to_save["default"].bias
+ assert model.lin1.weight is not model.lin1.modules_to_save["other"].weight
+ assert model.lin1.bias is not model.lin1.modules_to_save["other"].bias
+
+ model.set_adapter("other")
+ assert model.lin1.weight is not model.lin1.modules_to_save["default"].weight
+ assert model.lin1.bias is not model.lin1.modules_to_save["default"].bias
+ assert model.lin1.weight is model.lin1.modules_to_save["other"].weight
+ assert model.lin1.bias is model.lin1.modules_to_save["other"].bias
+
+ def test_transient_attribute_access_disabled_adapter(self, mlp):
+ config = LoraConfig(target_modules=["lin0"], modules_to_save=["lin1"])
+ model = get_peft_model(mlp, config)
+
+ # at this point, default is still active
+ assert model.lin1.weight is model.lin1.modules_to_save["default"].weight
+ assert model.lin1.bias is model.lin1.modules_to_save["default"].bias
+ assert model.lin1.weight is not model.lin1.original_module.weight
+ assert model.lin1.bias is not model.lin1.original_module.bias
+
+ with model.disable_adapter():
+ assert model.lin1.weight is not model.lin1.modules_to_save["default"].weight
+ assert model.lin1.bias is not model.lin1.modules_to_save["default"].bias
+ assert model.lin1.weight is model.lin1.original_module.weight
+ assert model.lin1.bias is model.lin1.original_module.bias
+
+ def test_transient_attribute_access_uninitialized_adapter(self, mlp):
+ # ensure that there is no weird infinite recursion when accessing a non-existing attribute on the class itself
+ with pytest.raises(AttributeError, match="has no attribute 'original_module'"):
+ ModulesToSaveWrapper.original_module
+
+ def test_transient_attribute_access_attr_does_not_exist_on_modules_to_save(self, mlp):
+ # ensure that there is no weird infinite recursion when accessing a non-existing attribute on the
+ # ModelToSaveWrapper instance
+ config = LoraConfig(target_modules=["lin0"], modules_to_save=["lin1"])
+ model = get_peft_model(mlp, config)
+
+ with pytest.raises(AttributeError, match="has no attribute 'foo'"):
+ model.lin1.foo
+
+ def test_transient_attribute_access_attr_does_not_exist_on_original_module(self, mlp):
+ # ensure that there is no weird infinite recursion when accessing a non-existing attribute on the
+ # original module of the ModelToSaveWrapper instance
+ config = LoraConfig(target_modules=["lin0"], modules_to_save=["lin1"])
+ model = get_peft_model(mlp, config)
+
+ with pytest.raises(AttributeError, match="has no attribute 'foo'"):
+ with model.disable_adapter():
+ model.lin1.foo
+
+ def test_transient_attribute_access_non_existing_adapter(self, mlp):
+ # This should normally never happen, as the active adapter should always exist, but it's a failsafe
+ config = LoraConfig(target_modules=["lin0"], modules_to_save=["lin1"])
+ model = get_peft_model(mlp, config)
+ model.base_model.model.lin1._active_adapter = "does-not-exist"
+ with pytest.raises(AttributeError, match="has no attribute 'weight'"):
+ model.lin1.weight
+
+
+class TestModulesToSaveNameSubstringBug:
+ """Test a bug that could occur with multiple modules to save where one adapter's name is a substring of another
+ adapter's name.
+
+ This bug was the result of an error in the logic of modifying the state_dict for modules_to_save in
+ set_peft_model_state_dict. The error in the logic was that it was checked if an entry from modules_to_save (a set
+ of strings) is a substring of a key of the state_dict. If it was, a new name was assigned to that key in the
+ state_dict, which would allow to load the weight later.
+
+ The issue that stems from the substring check occurs if there are multiple modules_to_save, and one of them has a
+ name that is a substring of another. So e.g. if one is named "classifier" and the other is named "classifier2",
+ there could be a false match.
+
+
+ This bug was reported in #2289.
+
+ """
+
+ def get_model(self):
+ class MyModule(nn.Module):
+ def __init__(self):
+ super().__init__()
+ self.lin = nn.Linear(5, 4)
+ # important: "classifier" is a substring of "classifier2", "classifier3", "classifier4"
+ self.classifier = nn.Linear(4, 2)
+ self.classifier2 = nn.Linear(4, 2)
+ self.classifier3 = nn.Linear(4, 2)
+ self.classifier4 = nn.Linear(4, 2)
+
+ def forward(self, x):
+ x = self.lin(x)
+ return self.classifier(x) + self.classifier2(x) + self.classifier3(x) + self.classifier4(x)
+
+ torch.manual_seed(0)
+ return MyModule()
+
+ @pytest.fixture
+ def path_merged_and_unmerged(self, tmp_path):
+ # Create 2 checkpoints:
+ # 1. merged: the model after calling merge_and_unload
+ # 2. unmerged: the PEFT model saved without calling merge_and_unload
+ path = tmp_path / "model.pt"
+
+ lora_config = LoraConfig(
+ target_modules=["lin"],
+ # important: "classifier" is a substring of "classifier2", "classifier3", "classifier4"
+ modules_to_save=["classifier", "classifier2", "classifier3", "classifier4"],
+ )
+ model = get_peft_model(self.get_model(), lora_config)
+ # mock training
+ for _ in range(5):
+ optimizer = torch.optim.SGD(model.parameters(), lr=0.01)
+ output = model(torch.randn(10, 5))
+ loss = output.sum()
+ loss.backward()
+ optimizer.step()
+
+ # save the peft model without merging
+ path_unmerged = tmp_path / "unmerged"
+ model.save_pretrained(path_unmerged)
+
+ # merge the model and save state_dict
+ path_merged = tmp_path / "merged"
+ merged = model.merge_and_unload()
+ state_dict = merged.state_dict()
+ torch.save(state_dict, path_merged)
+
+ return path_merged, path_unmerged
+
+ def test_load_merged_and_unmerged_same_weights(self, path_merged_and_unmerged):
+ # Note that this test is quasi flaky, it has a 1 in 4 chance of passing even without the bugfix. It passes when
+ # "classifier" happens to be the last element of the set model.modules_to_save. The order of the set is random.
+ # It is not possible just run this test multiple times to minimize the probability of this happening, because
+ # within the same process, the hash order is consistent. With the bug fix, this doesn't matter, as the test will
+ # always pass, but if there is a regression, there is a 1 in 4 chance of not catching it. Since the CI runs many
+ # tests, it is overall very unlikely that none will catch it though. If you see this test failing in CI, thus be
+ # aware that some of the passing tests may just pass owing to randomness.
+ path_merged, path_unmerged = path_merged_and_unmerged
+
+ # load the merged model directly
+ state_dict = torch.load(path_merged, weights_only=True)
+ model = self.get_model()
+ model.load_state_dict(state_dict)
+ sd_merged = model.state_dict()
+ del model
+
+ # load the unmerged model and merge it
+ unmerged = PeftModel.from_pretrained(self.get_model(), path_unmerged)
+ sd_unmerged = unmerged.merge_and_unload().state_dict()
+
+ assert sd_merged.keys() == sd_unmerged.keys()
+ for key in sd_merged.keys():
+ param_merged = sd_merged[key]
+ param_unmerged = sd_unmerged[key]
+ assert torch.allclose(param_merged, param_unmerged)
+
+
+class TestTargetingAuxiliaryTrainingWrapper:
+ """AuxiliaryTrainingWrapper such as ModulesToSaveWrapper and TrainableTokensWrapper are
+ in general not to be targeted by PEFT methods such as adapters. For example, a ModulesToSaveWrapper's children
+ modules should not be targeted by `LoraConfig(target_modules='all-linear')`, among other things.
+ """
+
+ @pytest.fixture
+ def plain_model_cls(self):
+ class PlainModel(nn.Module):
+ def __init__(self, i, o):
+ super().__init__()
+ self.layer1 = nn.Linear(i, o)
+
+ def forward(self, x):
+ return self.layer1(x)
+
+ return PlainModel
+
+ @pytest.fixture
+ def nested_model_cls(self, plain_model_cls):
+ class NestedModel(nn.Module):
+ def __init__(self):
+ super().__init__()
+ self.layer1 = nn.Linear(10, 20)
+ self.layer2 = nn.Linear(20, 5)
+ self.layer3 = plain_model_cls(5, 10)
+
+ def forward(self, x):
+ x = self.layer1(x)
+ x = self.layer2(x)
+ x = self.layer3(x)
+ return x
+
+ return NestedModel
+
+ def test_nested_ignores_modules_to_save(self, nested_model_cls, plain_model_cls):
+ # Make sure that `target_modules` is not targeting the nested modules of a module marked as module to save.
+ model = nested_model_cls()
+ config = LoraConfig(
+ target_modules=["layer1"],
+ modules_to_save=["layer3"],
+ )
+
+ peft_model = get_peft_model(model, config)
+ assert isinstance(peft_model.model.layer3.modules_to_save.default, plain_model_cls)
+
+ def test_targeting_module_to_save_raises(self, nested_model_cls):
+ model = nested_model_cls()
+ config = LoraConfig(
+ target_modules=["layer1"],
+ modules_to_save=["layer1"],
+ )
+ msg = "No modules were targeted for adaptation. This might be caused by a combination"
+ with pytest.raises(ValueError, match=msg):
+ get_peft_model(model, config)
+
+ def test_modules_to_save_targets_tuner_layer_raises(self):
+ # See e.g. issue 2027 and 2477
+ # Prevent users from (accidentally) targeting the same layer both with a tuner and modules_to_save. Normally, PEFT
+ # will not target the same layer with both a tuner and ModulesToSaveWrapper. However, if modules_to_save is
+ # automatically inferred, e.g. when using AutoModelForSequenceClassification, the ModulesToSaveWrapper is applied ex
+ # post, which can lead to the double wrapping.
+ model_id = "hf-internal-testing/tiny-random-OPTForCausalLM"
+ model = AutoModelForSequenceClassification.from_pretrained(model_id)
+
+ # Note: target_modules="all-linear" would also work and is closer to the original issue, but let's explicitly target
+ # "score" here in case that "all-linear" will be fixed to no longer target the score layer.
+ peft_config = LoraConfig(target_modules=["score"], task_type="SEQ_CLS")
+
+ # Since the `score` layer is in `model.modules_to_save` it should be ignored when targeted,
+ # therefore the layer should not be adapted.
+ msg = "No modules were targeted for adaptation. This might be caused by a combination"
+ with pytest.raises(ValueError, match=msg) as e:
+ get_peft_model(model, peft_config)
+
+ def test_targeting_trainable_tokens_raises(self):
+ model_id = "hf-internal-testing/tiny-random-OPTForCausalLM"
+ model = AutoModelForSequenceClassification.from_pretrained(model_id)
+
+ peft_config = LoraConfig(target_modules=["embed_tokens"], task_type="SEQ_CLS", trainable_token_indices=[0, 1])
+
+ # While this message might not be the most helpful message, at least it is not silently failing
+ msg = "trainable_token_indices cannot be applied to modules of type "
+ with pytest.raises(TypeError, match=msg) as e:
+ get_peft_model(model, peft_config)
+
+
+class TestAdapterTargeting:
+ """Make sure that already existing adapters cannot be targeted to avoid conflicts."""
+
+ @pytest.fixture
+ def base_model_cls(self):
+ class M(torch.nn.Module):
+ def __init__(self):
+ super().__init__()
+ self.l1 = torch.nn.Linear(10, 20)
+ self.l2 = torch.nn.Conv2d(1, 1, 2)
+
+ def forward(self, x):
+ return self.l2(self.l1(x))
+
+ return M
+
+ @pytest.mark.parametrize(
+ "config_cls, config_kwargs",
+ [
+ (LoraConfig, {"target_modules": "l1.*"}),
+ (LoraConfig, {"target_modules": "l2.*"}),
+ (VeraConfig, {"target_modules": "l1.*"}),
+ (VeraConfig, {"target_modules": "(l1|vera_A).*"}), # also target the shared layer
+ ],
+ )
+ def test_self_targeting_is_ignored(self, base_model_cls, config_cls, config_kwargs):
+ base_model = base_model_cls()
+ config1 = config_cls(**config_kwargs)
+ config2 = config_cls(**config_kwargs)
+
+ adapter1_name = "ADAPTER_1_512858" # sufficiently unique names to make reliable testing easier
+ adapter2_name = "ADAPTER_2_845781"
+
+ peft_model = get_peft_model(base_model, config1, adapter_name=adapter1_name)
+ state_dict_keys_1 = peft_model.state_dict().keys()
+
+ peft_model.add_adapter(adapter2_name, config2)
+ state_dict_keys_2 = peft_model.state_dict().keys()
+
+ # Ideally there should be no new modules targeted beyond existing ModuleDicts. Therefore the keys
+ # of the new state dict should only differ after the adapter name portion of the keys - not before.
+ # Expected:
+ # - a.b..xyz
+ # - a.b..xyz
+ # We're not expecting this to happen and test against it:
+ # - a.b..xyz
+ # - a..xyz
+ def remove_adapter_portion(adapter_name, key):
+ if key.endswith(f".{adapter_name}"):
+ return key.removesuffix(f".{adapter_name}")
+ return key.split(f".{adapter_name}.")[0]
+
+ adapter_invariant_keys1 = {remove_adapter_portion(adapter1_name, key) for key in state_dict_keys_1}
+ adapter_invariant_keys2 = {
+ remove_adapter_portion(adapter2_name, remove_adapter_portion(adapter1_name, key))
+ for key in state_dict_keys_2
+ }
+
+ assert adapter_invariant_keys1 == adapter_invariant_keys2
+
+
+class TestGetNoSplitModules:
+ # Ensure that children are considered when determining _no_split_modules
+ # see https://github.com/huggingface/transformers/pull/38141
+
+ def test_get_no_split_modules_simple(self):
+ # choose a model where recursively visiting children is *not* required
+ model_id = "facebook/opt-125m"
+ model = AutoModelForCausalLM.from_pretrained(model_id)
+ assert model._no_split_modules == ["OPTDecoderLayer"]
+ no_split_modules = _get_no_split_modules(model)
+ assert no_split_modules == {"OPTDecoderLayer"}
+
+ def test_get_no_split_modules_recursive(self):
+ # choose a model where recursively visiting children is required
+ model_id = "hf-internal-testing/tiny-random-LlavaForConditionalGeneration"
+ model = LlavaForConditionalGeneration.from_pretrained(model_id)
+ # sanity check: just visiting the model itself is not enough:
+ assert model._no_split_modules == []
+
+ no_split_modules = _get_no_split_modules(model)
+ assert no_split_modules == {"CLIPEncoderLayer", "LlamaDecoderLayer"}
diff --git a/peft/tests/test_poly.py b/peft/tests/test_poly.py
new file mode 100644
index 0000000000000000000000000000000000000000..8e9a2a351c8b13fd08bd21001951c04875fb789f
--- /dev/null
+++ b/peft/tests/test_poly.py
@@ -0,0 +1,100 @@
+#!/usr/bin/env python3
+
+# coding=utf-8
+# Copyright 2023-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+import os
+import tempfile
+import unittest
+
+import torch
+from transformers import AutoModelForSeq2SeqLM, AutoTokenizer
+
+from peft import PeftModel, PolyConfig, TaskType, get_peft_model
+
+
+class TestPoly(unittest.TestCase):
+ def test_poly(self):
+ torch.manual_seed(0)
+ model_name_or_path = "google/flan-t5-small"
+
+ atol, rtol = 1e-6, 1e-6
+ r = 8 # rank of lora in poly
+ n_tasks = 3 # number of tasks
+ n_skills = 2 # number of skills (loras)
+ n_splits = 4 # number of heads
+ lr = 1e-2
+ num_epochs = 10
+
+ tokenizer = AutoTokenizer.from_pretrained(model_name_or_path)
+ base_model = AutoModelForSeq2SeqLM.from_pretrained(model_name_or_path)
+
+ peft_config = PolyConfig(
+ task_type=TaskType.SEQ_2_SEQ_LM,
+ poly_type="poly",
+ r=r,
+ n_tasks=n_tasks,
+ n_skills=n_skills,
+ n_splits=n_splits,
+ )
+
+ model = get_peft_model(base_model, peft_config)
+
+ # generate some dummy data
+ text = os.__doc__.splitlines()
+ assert len(text) > 10
+ inputs = tokenizer(text, return_tensors="pt", padding=True)
+ inputs["task_ids"] = torch.arange(len(text)) % n_tasks
+ inputs["labels"] = tokenizer((["A", "B"] * 100)[: len(text)], return_tensors="pt")["input_ids"]
+
+ # simple training loop
+ model.train()
+ optimizer = torch.optim.Adam(model.parameters(), lr=lr)
+ losses = []
+ for _ in range(num_epochs):
+ outputs = model(**inputs)
+ loss = outputs.loss
+ loss.backward()
+ optimizer.step()
+ optimizer.zero_grad()
+ losses.append(loss.item())
+
+ # loss improved by at least 50%
+ assert losses[-1] < (0.5 * losses[0])
+
+ # check that saving and loading works
+ torch.manual_seed(0)
+ model.eval()
+ logits_before = model(**inputs).logits
+ tokens_before = model.generate(**inputs)
+
+ with model.disable_adapter():
+ logits_disabled = model(**inputs).logits
+ tokens_disabled = model.generate(**inputs)
+
+ assert not torch.allclose(logits_before, logits_disabled, atol=atol, rtol=rtol)
+ assert not torch.allclose(tokens_before, tokens_disabled, atol=atol, rtol=rtol)
+
+ # saving and loading
+ with tempfile.TemporaryDirectory() as tmp_dir:
+ model.save_pretrained(tmp_dir)
+ base_model = AutoModelForSeq2SeqLM.from_pretrained(model_name_or_path)
+ loaded = PeftModel.from_pretrained(base_model, tmp_dir)
+
+ torch.manual_seed(0)
+ output_after = loaded(**inputs).logits
+ tokens_after = loaded.generate(**inputs)
+ assert torch.allclose(logits_before, output_after, atol=atol, rtol=rtol)
+ assert torch.allclose(tokens_before, tokens_after, atol=atol, rtol=rtol)
diff --git a/peft/tests/test_randlora.py b/peft/tests/test_randlora.py
new file mode 100644
index 0000000000000000000000000000000000000000..5fb7edb6a5e7c1fac2e5b717fbd6ffffe2eb7154
--- /dev/null
+++ b/peft/tests/test_randlora.py
@@ -0,0 +1,301 @@
+# Copyright 2025-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+# This test file is for tests specific to RandLora, since Randlora has some specific challenges due to the shared weights.
+# These tests are copied from the test_vera.py file
+
+import os
+
+import pytest
+import torch
+from accelerate.utils.imports import is_bf16_available
+from safetensors import safe_open
+from torch import nn
+
+from peft import PeftModel, RandLoraConfig, get_peft_model
+
+
+class MLP(nn.Module):
+ def __init__(self, bias=True):
+ super().__init__()
+ self.relu = nn.ReLU()
+ self.lin0 = nn.Linear(10, 20, bias=bias)
+ self.lin1 = nn.Linear(20, 20, bias=bias) # lin1 and lin2 have same shape
+ self.lin2 = nn.Linear(20, 20, bias=bias)
+ self.lin3 = nn.Linear(20, 2, bias=bias)
+ self.sm = nn.LogSoftmax(dim=-1)
+
+ def forward(self, X):
+ X = self.lin0(X)
+ X = self.relu(X)
+ X = self.lin1(X)
+ X = self.relu(X)
+ X = self.lin2(X)
+ X = self.relu(X)
+ X = self.lin3(X)
+ X = self.sm(X)
+ return X
+
+
+# Tests copied from the TestVera class in test_vera.py.
+# Changes to the code file should be reflected here.
+class TestRandLora:
+ @pytest.fixture
+ def mlp(self):
+ torch.manual_seed(0)
+ model = MLP()
+ return model
+
+ @pytest.fixture
+ def mlp_same_prng(self, mlp):
+ torch.manual_seed(0)
+
+ config = RandLoraConfig(target_modules=["lin1", "lin2"], init_weights=False)
+ # creates a default RandLora adapter
+ peft_model = get_peft_model(mlp, config)
+ config2 = RandLoraConfig(target_modules=["lin1", "lin2"], init_weights=False)
+ peft_model.add_adapter("other", config2)
+ return peft_model
+
+ def test_multiple_adapters_same_prng_weights(self, mlp_same_prng):
+ # we can have multiple adapters with the same prng key, in which case the weights should be shared
+ assert (
+ mlp_same_prng.base_model.model.lin1.randlora_A["default"]
+ is mlp_same_prng.base_model.model.lin1.randlora_A["other"]
+ )
+ assert (
+ mlp_same_prng.base_model.model.lin1.randlora_B["default"]
+ is mlp_same_prng.base_model.model.lin1.randlora_B["other"]
+ )
+ assert (
+ mlp_same_prng.base_model.model.lin2.randlora_A["default"]
+ is mlp_same_prng.base_model.model.lin2.randlora_A["other"]
+ )
+ assert (
+ mlp_same_prng.base_model.model.lin2.randlora_B["default"]
+ is mlp_same_prng.base_model.model.lin2.randlora_B["other"]
+ )
+
+ input = torch.randn(5, 10)
+ mlp_same_prng.set_adapter("default")
+ output_default = mlp_same_prng(input)
+ mlp_same_prng.set_adapter("other")
+ output_other = mlp_same_prng(input)
+ assert not torch.allclose(output_default, output_other, atol=1e-3, rtol=1e-3)
+
+ def test_multiple_adapters_different_prng_raises(self):
+ # we cannot have multiple adapters with different prng keys
+ model = MLP()
+ config = RandLoraConfig(target_modules=["lin1", "lin2"], init_weights=False)
+ # creates a default RandLora adapter
+ peft_model = get_peft_model(model, config)
+ config2 = RandLoraConfig(target_modules=["lin1", "lin2"], init_weights=False, projection_prng_key=123)
+
+ msg = (
+ r"RandLora PRNG initialisation key must be the same for all adapters. Got config.projection_prng_key=123 but "
+ r"previous config had 0"
+ )
+ with pytest.raises(ValueError, match=msg):
+ peft_model.add_adapter("other", config2)
+
+ def test_multiple_adapters_save_load_save_projection_true(self, mlp_same_prng, tmp_path):
+ # check saving and loading works with multiple adapters and saved projection weights
+ torch.manual_seed(0)
+ input = torch.randn(5, 10)
+ mlp_same_prng.set_adapter("default")
+ output_default = mlp_same_prng(input)
+ mlp_same_prng.set_adapter("other")
+ output_other = mlp_same_prng(input)
+
+ # sanity check
+ assert not torch.allclose(output_default, output_other, atol=1e-3, rtol=1e-3)
+
+ save_path = tmp_path / "randlora"
+ mlp_same_prng.save_pretrained(save_path)
+ assert os.path.exists(save_path / "adapter_config.json")
+ assert os.path.exists(save_path / "other" / "adapter_config.json")
+
+ torch.manual_seed(0)
+ mlp = MLP()
+ peft_model = PeftModel.from_pretrained(mlp, save_path)
+ peft_model.load_adapter(save_path / "other", "other")
+
+ peft_model.set_adapter("default")
+ output_default_loaded = peft_model(input)
+ peft_model.set_adapter("other")
+ output_other_loaded = peft_model(input)
+
+ assert torch.allclose(output_default, output_default_loaded, atol=1e-3, rtol=1e-3)
+ assert torch.allclose(output_other, output_other_loaded, atol=1e-3, rtol=1e-3)
+
+ def test_multiple_adapters_save_load_save_projection_false(self, mlp, tmp_path):
+ # check saving and loading works with multiple adapters without saved projection weights
+ torch.manual_seed(1)
+ config = RandLoraConfig(target_modules=["lin1", "lin2"], init_weights=False, save_projection=False)
+ # creates a default RandLora adapter
+ peft_model = get_peft_model(mlp, config, adapter_name="first")
+ config2 = RandLoraConfig(target_modules=["lin1", "lin2"], init_weights=False, save_projection=False)
+ peft_model.add_adapter("second", config2)
+
+ input = torch.randn(5, 10)
+ peft_model.set_adapter("first")
+ output_first = peft_model(input)
+ peft_model.set_adapter("second")
+ output_second = peft_model(input)
+
+ # sanity check
+ assert not torch.allclose(output_first, output_second, atol=1e-3, rtol=1e-3)
+
+ save_path = tmp_path / "randlora"
+ peft_model.save_pretrained(save_path)
+ assert os.path.exists(save_path / "first" / "adapter_config.json")
+ assert os.path.exists(save_path / "second" / "adapter_config.json")
+
+ torch.manual_seed(0)
+ mlp = MLP()
+ peft_model = PeftModel.from_pretrained(mlp, save_path / "first", adapter_name="first")
+ peft_model.load_adapter(save_path / "second", "second")
+
+ peft_model.set_adapter("first")
+ output_first_loaded = peft_model(input)
+ peft_model.set_adapter("second")
+ output_second_loaded = peft_model(input)
+
+ assert torch.allclose(output_first, output_first_loaded, atol=1e-3, rtol=1e-3)
+ assert torch.allclose(output_second, output_second_loaded, atol=1e-3, rtol=1e-3)
+
+ def test_multiple_adapters_save_projection_true_contains_randlora_A_randlora_B(self, mlp_same_prng, tmp_path):
+ # check that the state_dicts don't contain the projection weights
+ save_path = tmp_path / "randlora"
+ mlp_same_prng.save_pretrained(save_path)
+
+ sd_default = {}
+ with safe_open(save_path / "adapter_model.safetensors", framework="pt", device="cpu") as f:
+ for key in f.keys():
+ sd_default[key] = f.get_tensor(key)
+
+ assert any("randlora_A" in key for key in sd_default)
+ assert any("randlora_B" in key for key in sd_default)
+ # default rank for RandLora is 32
+ assert sd_default["base_model.randlora_A"].shape == (32, 1, 20)
+ assert sd_default["base_model.randlora_B"].shape == (20, 1, 32)
+
+ sd_other = {}
+ with safe_open(save_path / "other" / "adapter_model.safetensors", framework="pt", device="cpu") as f:
+ for key in f.keys():
+ sd_other[key] = f.get_tensor(key)
+
+ assert any("randlora_A" in key for key in sd_other)
+ assert any("randlora_B" in key for key in sd_other)
+ assert sd_other["base_model.randlora_A"].shape == (32, 1, 20)
+ assert sd_other["base_model.randlora_B"].shape == (20, 1, 32)
+
+ def test_multiple_adapters_save_projection_false_contains_no_randlora_A_randlora_B(self, mlp, tmp_path):
+ torch.manual_seed(1)
+ config = RandLoraConfig(target_modules=["lin1", "lin2"], init_weights=False, save_projection=False)
+ # creates a default RandLora adapter
+ peft_model = get_peft_model(mlp, config, adapter_name="first")
+ config2 = RandLoraConfig(target_modules=["lin1", "lin2"], init_weights=False, save_projection=False)
+ peft_model.add_adapter("second", config2)
+
+ save_path = tmp_path / "randlora"
+ peft_model.save_pretrained(save_path)
+
+ sd_default = {}
+ with safe_open(save_path / "first" / "adapter_model.safetensors", framework="pt", device="cpu") as f:
+ for key in f.keys():
+ sd_default[key] = f.get_tensor(key)
+
+ assert not any("randlora_A" in key for key in sd_default)
+ assert not any("randlora_B" in key for key in sd_default)
+
+ sd_other = {}
+ with safe_open(save_path / "second" / "adapter_model.safetensors", framework="pt", device="cpu") as f:
+ for key in f.keys():
+ sd_other[key] = f.get_tensor(key)
+
+ assert not any("randlora_A" in key for key in sd_other)
+ assert not any("randlora_B" in key for key in sd_other)
+
+ def test_randlora_A_randlora_B_share_memory(self, mlp_same_prng):
+ randlora_A = mlp_same_prng.randlora_A["default"]
+ randlora_B = mlp_same_prng.randlora_B["default"]
+
+ # these tensors should share the same data
+ assert randlora_A.data_ptr() == mlp_same_prng.base_model.model.lin1.randlora_A["default"].data_ptr()
+ assert randlora_B.data_ptr() == mlp_same_prng.base_model.model.lin1.randlora_B["default"].data_ptr()
+ assert randlora_A.data_ptr() == mlp_same_prng.base_model.model.lin2.randlora_A["default"].data_ptr()
+ assert randlora_B.data_ptr() == mlp_same_prng.base_model.model.lin2.randlora_B["default"].data_ptr()
+ # sanity check: these tensors shouldn't share the same data
+ assert randlora_A.data_ptr() != randlora_B.data_ptr()
+
+ def test_randlora_lambda_dont_share_memory(self, mlp_same_prng):
+ # sanity check: these tensors shouldn't share the same data
+ assert (
+ mlp_same_prng.base_model.model.lin1.randlora_lambda["default"].data_ptr()
+ != mlp_same_prng.base_model.model.lin1.randlora_lambda["other"].data_ptr()
+ )
+ assert (
+ mlp_same_prng.base_model.model.lin1.randlora_lambda["default"].data_ptr()
+ != mlp_same_prng.base_model.model.lin2.randlora_lambda["default"].data_ptr()
+ )
+ assert (
+ mlp_same_prng.base_model.model.lin1.randlora_lambda["other"].data_ptr()
+ != mlp_same_prng.base_model.model.lin2.randlora_lambda["other"].data_ptr()
+ )
+ assert (
+ mlp_same_prng.base_model.model.lin1.randlora_gamma["default"].data_ptr()
+ != mlp_same_prng.base_model.model.lin1.randlora_gamma["other"].data_ptr()
+ )
+ assert (
+ mlp_same_prng.base_model.model.lin1.randlora_gamma["default"].data_ptr()
+ != mlp_same_prng.base_model.model.lin2.randlora_gamma["default"].data_ptr()
+ )
+ assert (
+ mlp_same_prng.base_model.model.lin1.randlora_gamma["other"].data_ptr()
+ != mlp_same_prng.base_model.model.lin2.randlora_gamma["other"].data_ptr()
+ )
+
+ def test_randlora_different_shapes(self, mlp):
+ config = RandLoraConfig(target_modules=["lin0", "lin3"], init_weights=False)
+ mlp_different_shapes = get_peft_model(mlp, config)
+
+ randlora_A = mlp_different_shapes.randlora_A["default"]
+ randlora_B = mlp_different_shapes.randlora_B["default"]
+
+ # sanity check
+ assert mlp.lin0.base_layer.weight.shape != mlp.lin3.base_layer.weight.shape
+
+ # lin0 has the largest output dimension, lin3 has the largest input dimension
+ # randlora_A should have the shape of (rank, largest_in), randlora_B should have the shape of (largest_out, rank)
+ assert randlora_A.shape == (config.r, 1, mlp.lin3.in_features)
+ assert randlora_B.shape == (mlp.lin0.out_features, 1, config.r)
+
+ # should not raise
+ input = torch.randn(5, 10)
+ mlp_different_shapes(input)
+
+ @pytest.mark.parametrize("dtype", [torch.float32, torch.float16, torch.bfloat16])
+ def test_randlora_dtypes(self, dtype):
+ if dtype == torch.bfloat16:
+ # skip if bf16 is not supported on hardware, see #1872
+ if not is_bf16_available():
+ pytest.skip("bfloat16 not supported on this system, skipping the test")
+
+ model = MLP().to(dtype)
+ config = RandLoraConfig(target_modules=["lin1", "lin2"], init_weights=False)
+ peft_model = get_peft_model(model, config)
+ inputs = torch.randn(5, 10).to(dtype)
+ output = peft_model(inputs) # should not raise
+ assert output.dtype == dtype
diff --git a/peft/tests/test_seq_classifier.py b/peft/tests/test_seq_classifier.py
new file mode 100644
index 0000000000000000000000000000000000000000..eb0a3d38a49c2b4309e2d9076e5b40943b470671
--- /dev/null
+++ b/peft/tests/test_seq_classifier.py
@@ -0,0 +1,306 @@
+# Copyright 2025-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License governing permissions and limitations under the License.
+
+import pytest
+import torch
+from transformers import AutoModelForSequenceClassification
+
+from peft import (
+ AdaLoraConfig,
+ BOFTConfig,
+ BoneConfig,
+ C3AConfig,
+ FourierFTConfig,
+ HRAConfig,
+ IA3Config,
+ LoraConfig,
+ MissConfig,
+ OFTConfig,
+ PrefixTuningConfig,
+ PromptEncoderConfig,
+ PromptTuningConfig,
+ PromptTuningInit,
+ RoadConfig,
+ ShiraConfig,
+ VBLoRAConfig,
+ VeraConfig,
+ WaveFTConfig,
+ get_peft_model,
+)
+from peft.utils.other import ModulesToSaveWrapper
+
+from .testing_common import PeftCommonTester
+from .testing_utils import hub_online_once
+
+
+PEFT_SEQ_CLS_MODELS_TO_TEST = [
+ "hf-internal-testing/tiny-random-BertForSequenceClassification",
+ "hf-internal-testing/tiny-random-RobertaForSequenceClassification",
+ "trl-internal-testing/tiny-LlamaForSequenceClassification-3.2",
+]
+
+
+ALL_CONFIGS = [
+ (
+ AdaLoraConfig,
+ {
+ "task_type": "SEQ_CLS",
+ "target_modules": None,
+ "total_step": 1,
+ },
+ ),
+ (
+ BOFTConfig,
+ {
+ "task_type": "SEQ_CLS",
+ "target_modules": None,
+ },
+ ),
+ (
+ BoneConfig,
+ {
+ "task_type": "SEQ_CLS",
+ "target_modules": None,
+ "r": 2,
+ },
+ ),
+ (
+ MissConfig,
+ {
+ "task_type": "SEQ_CLS",
+ "target_modules": None,
+ "r": 2,
+ },
+ ),
+ (
+ FourierFTConfig,
+ {
+ "task_type": "SEQ_CLS",
+ "n_frequency": 10,
+ "target_modules": None,
+ },
+ ),
+ (
+ HRAConfig,
+ {
+ "task_type": "SEQ_CLS",
+ "target_modules": None,
+ },
+ ),
+ (
+ IA3Config,
+ {
+ "task_type": "SEQ_CLS",
+ "target_modules": None,
+ "feedforward_modules": None,
+ },
+ ),
+ (
+ LoraConfig,
+ {
+ "task_type": "SEQ_CLS",
+ "r": 8,
+ "lora_alpha": 32,
+ "target_modules": None,
+ "lora_dropout": 0.05,
+ "bias": "none",
+ },
+ ),
+ # LoRA + trainable tokens
+ (
+ LoraConfig,
+ {
+ "task_type": "SEQ_CLS",
+ "r": 8,
+ "lora_alpha": 32,
+ "target_modules": None,
+ "lora_dropout": 0.05,
+ "bias": "none",
+ "trainable_token_indices": [0, 1, 3],
+ },
+ ),
+ (
+ OFTConfig,
+ {
+ "task_type": "SEQ_CLS",
+ "target_modules": None,
+ },
+ ),
+ (
+ PrefixTuningConfig,
+ {
+ "task_type": "SEQ_CLS",
+ "num_virtual_tokens": 10,
+ },
+ ),
+ (
+ PromptEncoderConfig,
+ {
+ "task_type": "SEQ_CLS",
+ "num_virtual_tokens": 10,
+ "encoder_hidden_size": 32,
+ },
+ ),
+ (
+ PromptTuningConfig,
+ {
+ "task_type": "SEQ_CLS",
+ "num_virtual_tokens": 10,
+ },
+ ),
+ (
+ RoadConfig,
+ {
+ "task_type": "SEQ_CLS",
+ "variant": "road_1",
+ "group_size": 2,
+ },
+ ),
+ (
+ ShiraConfig,
+ {
+ "r": 1,
+ "task_type": "SEQ_CLS",
+ "target_modules": None,
+ "init_weights": False,
+ },
+ ),
+ (
+ VBLoRAConfig,
+ {
+ "task_type": "SEQ_CLS",
+ "target_modules": None,
+ "vblora_dropout": 0.05,
+ "vector_length": 1,
+ "num_vectors": 2,
+ },
+ ),
+ (
+ VeraConfig,
+ {
+ "task_type": "SEQ_CLS",
+ "r": 8,
+ "target_modules": None,
+ "vera_dropout": 0.05,
+ "projection_prng_key": 0xFF,
+ "d_initial": 0.1,
+ "save_projection": True,
+ "bias": "none",
+ },
+ ),
+ (
+ C3AConfig,
+ {
+ "task_type": "SEQ_CLS",
+ "block_size": 1,
+ "target_modules": None,
+ },
+ ),
+ (
+ WaveFTConfig,
+ {
+ "task_type": "SEQ_CLS",
+ "n_frequency": 8,
+ "target_modules": None,
+ },
+ ),
+]
+
+
+class TestSequenceClassificationModels(PeftCommonTester):
+ r"""
+ Tests for basic coverage of AutoModelForSequenceClassification and classification-specific cases. Most of the
+ functionality is probably already covered by other tests.
+ """
+
+ transformers_class = AutoModelForSequenceClassification
+
+ def skipTest(self, reason=""):
+ # for backwards compatibility with unittest style test classes
+ pytest.skip(reason)
+
+ def prepare_inputs_for_testing(self):
+ input_ids = torch.tensor([[1, 1, 1], [1, 2, 1]]).to(self.torch_device)
+ attention_mask = torch.tensor([[1, 1, 1], [1, 0, 1]]).to(self.torch_device)
+ return {"input_ids": input_ids, "attention_mask": attention_mask}
+
+ @pytest.mark.parametrize("model_id", PEFT_SEQ_CLS_MODELS_TO_TEST)
+ @pytest.mark.parametrize("config_cls,config_kwargs", ALL_CONFIGS)
+ def test_attributes_parametrized(self, model_id, config_cls, config_kwargs):
+ self._test_model_attr(model_id, config_cls, config_kwargs.copy())
+
+ @pytest.mark.parametrize("model_id", PEFT_SEQ_CLS_MODELS_TO_TEST)
+ @pytest.mark.parametrize("config_cls,config_kwargs", ALL_CONFIGS)
+ def test_adapter_name(self, model_id, config_cls, config_kwargs):
+ self._test_adapter_name(model_id, config_cls, config_kwargs.copy())
+
+ @pytest.mark.parametrize("model_id", PEFT_SEQ_CLS_MODELS_TO_TEST)
+ @pytest.mark.parametrize("config_cls,config_kwargs", ALL_CONFIGS)
+ def test_prepare_for_training_parametrized(self, model_id, config_cls, config_kwargs):
+ self._test_prepare_for_training(model_id, config_cls, config_kwargs.copy())
+
+ @pytest.mark.parametrize("model_id", PEFT_SEQ_CLS_MODELS_TO_TEST)
+ @pytest.mark.parametrize("config_cls,config_kwargs", ALL_CONFIGS)
+ def test_prompt_tuning_text_prepare_for_training(self, model_id, config_cls, config_kwargs):
+ if config_cls != PromptTuningConfig:
+ pytest.skip(f"This test does not apply to {config_cls}")
+ config_kwargs = config_kwargs.copy()
+ config_kwargs["prompt_tuning_init"] = PromptTuningInit.TEXT
+ config_kwargs["prompt_tuning_init_text"] = "This is a test prompt."
+ config_kwargs["tokenizer_name_or_path"] = model_id
+ self._test_prepare_for_training(model_id, config_cls, config_kwargs.copy())
+
+ @pytest.mark.parametrize("model_id", PEFT_SEQ_CLS_MODELS_TO_TEST)
+ @pytest.mark.parametrize("config_cls,config_kwargs", ALL_CONFIGS)
+ def test_save_pretrained(self, model_id, config_cls, config_kwargs):
+ self._test_save_pretrained(model_id, config_cls, config_kwargs.copy())
+
+ @pytest.mark.parametrize("model_id", PEFT_SEQ_CLS_MODELS_TO_TEST)
+ @pytest.mark.parametrize("config_cls,config_kwargs", ALL_CONFIGS)
+ def test_save_pretrained_pickle(self, model_id, config_cls, config_kwargs):
+ self._test_save_pretrained(model_id, config_cls, config_kwargs.copy(), safe_serialization=False)
+
+ @pytest.mark.parametrize("model_id", PEFT_SEQ_CLS_MODELS_TO_TEST)
+ @pytest.mark.parametrize("config_cls,config_kwargs", ALL_CONFIGS)
+ def test_save_pretrained_selected_adapters(self, model_id, config_cls, config_kwargs):
+ self._test_save_pretrained_selected_adapters(model_id, config_cls, config_kwargs.copy())
+
+ @pytest.mark.parametrize("model_id", PEFT_SEQ_CLS_MODELS_TO_TEST)
+ @pytest.mark.parametrize("config_cls,config_kwargs", ALL_CONFIGS)
+ def test_save_pretrained_selected_adapters_pickle(self, model_id, config_cls, config_kwargs):
+ self._test_save_pretrained_selected_adapters(
+ model_id, config_cls, config_kwargs.copy(), safe_serialization=False
+ )
+
+ @pytest.mark.parametrize("model_id", PEFT_SEQ_CLS_MODELS_TO_TEST)
+ @pytest.mark.parametrize("config_cls,config_kwargs", ALL_CONFIGS)
+ def test_from_pretrained_config_construction(self, model_id, config_cls, config_kwargs):
+ self._test_from_pretrained_config_construction(model_id, config_cls, config_kwargs.copy())
+
+ @pytest.mark.parametrize("model_id", PEFT_SEQ_CLS_MODELS_TO_TEST)
+ @pytest.mark.parametrize("config_cls,config_kwargs", ALL_CONFIGS)
+ def test_modules_to_save_correctly_set(self, model_id, config_cls, config_kwargs):
+ # tests for a regression, introduced via #2220, where modules_to_save was not applied to prompt learning methods
+ with hub_online_once(model_id):
+ model = self.transformers_class.from_pretrained(model_id)
+ config = config_cls(
+ base_model_name_or_path=model_id,
+ **config_kwargs,
+ )
+ model = get_peft_model(model, config)
+ base_model = model.get_base_model()
+ # classifier layer is called either "classifier" or "score"
+ classifier = getattr(base_model, "classifier", getattr(base_model, "score", None))
+ if classifier is None:
+ raise ValueError(f"Could not determine classifier layer name for {model_id}, please fix the test")
+ assert isinstance(classifier, ModulesToSaveWrapper)
diff --git a/peft/tests/test_shira.py b/peft/tests/test_shira.py
new file mode 100644
index 0000000000000000000000000000000000000000..9845ee426ea85f4d2e91ce8d95dc43c54e1ce437
--- /dev/null
+++ b/peft/tests/test_shira.py
@@ -0,0 +1,278 @@
+# Copyright 2025-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+# This test file is for tests specific to SHiRA.
+
+import os
+
+import pytest
+import torch
+from accelerate.utils.imports import is_bf16_available
+from torch import nn
+
+from peft import PeftModel, ShiraConfig, get_peft_model
+
+
+def custom_random_mask_function_with_custom_kwargs(custom_arg):
+ def mask_fn(base_layer, r):
+ """
+ This mask function is similar to the random_mask provided in src/peft/tuners/shira/mask_functions.py except the
+ seed is derived from custom_kwargs. Please use this as an example to create your own custom sparse masks that
+ may use custom_kwargs. Remember, for a pretrained weight with shape m, n, mask_fn must return only one mask
+ (shape: m, n) which must be binary 0 or 1 with num_shira_parameters = r(m+n) for linear layers. Device and
+ dtype of mask must be same as base layer's weight's device and dtype.
+ """
+ new_seed = custom_arg
+ shape = base_layer.weight.shape
+ num_shira_weights = r * (shape[0] + shape[1])
+ random_generator = torch.Generator()
+ random_generator.manual_seed(new_seed)
+
+ idx = (torch.randperm(base_layer.weight.numel(), generator=random_generator)[:num_shira_weights]).to(
+ base_layer.weight.device
+ )
+ val = torch.ones_like(idx.type(base_layer.weight.dtype))
+ mask = torch.zeros_like(base_layer.weight.view(1, -1))
+ mask = mask.scatter_(1, idx.unsqueeze(0), val.unsqueeze(0)).view(shape)
+
+ return mask
+
+ return mask_fn
+
+
+class MLP(nn.Module):
+ def __init__(self, bias=True):
+ super().__init__()
+ self.relu = nn.ReLU()
+ self.lin0 = nn.Linear(10, 20, bias=bias)
+ self.lin1 = nn.Linear(20, 40, bias=bias) # lin1 and lin2 have same shape
+ self.lin2 = nn.Linear(40, 30, bias=bias)
+ self.lin3 = nn.Linear(30, 10, bias=bias)
+ self.sm = nn.LogSoftmax(dim=-1)
+
+ def forward(self, X):
+ X = self.lin0(X)
+ X = self.relu(X)
+ X = self.lin1(X)
+ X = self.relu(X)
+ X = self.lin2(X)
+ X = self.relu(X)
+ X = self.lin3(X)
+ X = self.sm(X)
+ return X
+
+
+class TestShira:
+ @pytest.fixture
+ def mlp(self):
+ torch.manual_seed(0)
+ model = MLP()
+ return model
+
+ def test_mlp_single_adapter_shapes(self, mlp):
+ # torch.manual_seed(0)
+
+ r = 2
+ config = ShiraConfig(r=r, target_modules=["lin1", "lin2"])
+ # creates a default SHiRA adapter
+ peft_model = get_peft_model(mlp, config)
+
+ shira_weight1_size = peft_model.base_model.model.lin1.shira_weight["default"].shape[0]
+ shira_weight2_size = peft_model.base_model.model.lin2.shira_weight["default"].shape[0]
+ shira_indices1_size = peft_model.base_model.model.lin1.shira_indices["default"].shape[1]
+ shira_indices2_size = peft_model.base_model.model.lin2.shira_indices["default"].shape[1]
+
+ base_weight1_size = peft_model.base_model.model.lin1.base_layer.weight.shape
+ base_weight2_size = peft_model.base_model.model.lin2.base_layer.weight.shape
+
+ delta_weight1_shape = peft_model.base_model.model.lin1.get_delta_weight("default").shape
+ delta_weight2_shape = peft_model.base_model.model.lin2.get_delta_weight("default").shape
+
+ assert shira_weight1_size == r * (base_weight1_size[0] + base_weight1_size[1])
+ assert shira_weight2_size == r * (base_weight2_size[0] + base_weight2_size[1])
+
+ assert shira_weight1_size == shira_indices1_size
+ assert shira_weight2_size == shira_indices2_size
+
+ assert delta_weight1_shape == base_weight1_size
+ assert delta_weight2_shape == base_weight2_size
+
+ return peft_model
+
+ def test_multiple_adapters_save_load(self, mlp, tmp_path):
+ # check saving and loading works with multiple adapters
+ # note, the random seeds in the below two configs are not the default values.
+ # so it will lead to different random sparse masks between saving and loading.
+ # our goal is to make sure that loaded indices are exactly the same as the saved indices regardless of what initial random mask gets generated.
+ # we will also make sure that parameters are saved and loaded correctly, and the output remains the same.
+ config = ShiraConfig(r=2, target_modules=["lin1", "lin2"], random_seed=56)
+ # creates a default SHiRA adapter
+ peft_model = get_peft_model(mlp, config, adapter_name="first")
+ config2 = ShiraConfig(r=3, target_modules=["lin1", "lin2", "lin3"], random_seed=67)
+ peft_model.add_adapter("second", config2)
+
+ assert torch.all(peft_model.base_model.model.lin1.shira_weight["first"] == 0)
+ assert torch.all(peft_model.base_model.model.lin2.shira_weight["first"] == 0)
+ assert torch.all(peft_model.base_model.model.lin1.shira_weight["second"] == 0)
+ assert torch.all(peft_model.base_model.model.lin2.shira_weight["second"] == 0)
+ assert torch.all(peft_model.base_model.model.lin3.shira_weight["second"] == 0)
+
+ shira_assign_val1_f = torch.randn_like(peft_model.base_model.model.lin1.shira_weight["first"])
+ peft_model.base_model.model.lin1.shira_weight["first"] = shira_assign_val1_f
+ shira_indices1_f = peft_model.base_model.model.lin1.shira_indices["first"]
+ shira_assign_val2_f = torch.randn_like(peft_model.base_model.model.lin2.shira_weight["first"])
+ peft_model.base_model.model.lin2.shira_weight["first"] = shira_assign_val2_f
+ shira_indices2_f = peft_model.base_model.model.lin2.shira_indices["first"]
+
+ shira_assign_val1_s = torch.randn_like(peft_model.base_model.model.lin1.shira_weight["second"])
+ peft_model.base_model.model.lin1.shira_weight["second"] = shira_assign_val1_s
+ shira_indices1_s = peft_model.base_model.model.lin1.shira_indices["second"]
+ shira_assign_val2_s = torch.randn_like(peft_model.base_model.model.lin2.shira_weight["second"])
+ peft_model.base_model.model.lin2.shira_weight["second"] = shira_assign_val2_s
+ shira_indices2_s = peft_model.base_model.model.lin2.shira_indices["second"]
+ shira_assign_val3_s = torch.randn_like(peft_model.base_model.model.lin3.shira_weight["second"])
+ peft_model.base_model.model.lin3.shira_weight["second"] = shira_assign_val3_s
+ shira_indices3_s = peft_model.base_model.model.lin3.shira_indices["second"]
+
+ input = torch.randn(5, 10)
+ peft_model.set_adapter("first")
+ output_first = peft_model(input)
+ peft_model.set_adapter("second")
+ output_second = peft_model(input)
+
+ # sanity check
+ assert not torch.allclose(output_first, output_second, atol=1e-3, rtol=1e-3)
+
+ save_path = os.path.join(tmp_path, "shira")
+ peft_model.save_pretrained(save_path)
+ assert os.path.exists(os.path.join(save_path, "first", "adapter_config.json"))
+ assert os.path.exists(os.path.join(save_path, "second", "adapter_config.json"))
+ del peft_model
+
+ torch.manual_seed(0)
+ mlp = MLP()
+ peft_model = PeftModel.from_pretrained(mlp, os.path.join(save_path, "first"), adapter_name="first")
+ peft_model.load_adapter(os.path.join(save_path, "second"), "second")
+
+ peft_model.set_adapter("first")
+ output_first_loaded = peft_model(input)
+ peft_model.set_adapter("second")
+ output_second_loaded = peft_model(input)
+
+ assert torch.allclose(output_first, output_first_loaded)
+ assert torch.allclose(output_second, output_second_loaded)
+
+ assert torch.all(shira_assign_val1_f == peft_model.base_model.model.lin1.shira_weight["first"])
+ assert torch.all(shira_assign_val2_f == peft_model.base_model.model.lin2.shira_weight["first"])
+ assert torch.all(shira_indices1_f == peft_model.base_model.model.lin1.shira_indices["first"])
+ assert torch.all(shira_indices2_f == peft_model.base_model.model.lin2.shira_indices["first"])
+ assert torch.all(shira_assign_val1_s == peft_model.base_model.model.lin1.shira_weight["second"])
+ assert torch.all(shira_assign_val2_s == peft_model.base_model.model.lin2.shira_weight["second"])
+ assert torch.all(shira_assign_val3_s == peft_model.base_model.model.lin3.shira_weight["second"])
+ assert torch.all(shira_indices1_s == peft_model.base_model.model.lin1.shira_indices["second"])
+ assert torch.all(shira_indices2_s == peft_model.base_model.model.lin2.shira_indices["second"])
+ assert torch.all(shira_indices3_s == peft_model.base_model.model.lin3.shira_indices["second"])
+
+ return peft_model
+
+ def test_save_load_custom_mask_function(self, mlp, tmp_path):
+ # we want to see if saving and loading works when a custom mask is involved
+ config = ShiraConfig(r=2, mask_type="custom", target_modules=["lin1", "lin2"], init_weights=False)
+ custom_arg = 120
+ custom_mask_fn = custom_random_mask_function_with_custom_kwargs(custom_arg)
+ config.mask_fn = custom_mask_fn
+
+ # create a custom mask SHiRA adapter
+ peft_model = get_peft_model(mlp, config, adapter_name="first")
+
+ shira_assign_val1_f = peft_model.base_model.model.lin1.shira_weight["first"]
+ shira_indices1_f = peft_model.base_model.model.lin1.shira_indices["first"]
+ shira_assign_val2_f = peft_model.base_model.model.lin2.shira_weight["first"]
+ shira_indices2_f = peft_model.base_model.model.lin2.shira_indices["first"]
+
+ input = torch.randn(5, 10)
+ peft_model.set_adapter("first")
+ output_first = peft_model(input)
+
+ save_path = os.path.join(tmp_path, "shira")
+ peft_model.save_pretrained(save_path)
+ assert os.path.exists(os.path.join(save_path, "first", "adapter_config.json"))
+ del peft_model
+
+ torch.manual_seed(0)
+ mlp = MLP()
+ peft_model = PeftModel.from_pretrained(mlp, os.path.join(save_path, "first"), adapter_name="first")
+
+ peft_model.set_adapter("first")
+ output_first_loaded = peft_model(input)
+
+ assert torch.allclose(output_first, output_first_loaded)
+
+ assert torch.all(shira_assign_val1_f == peft_model.base_model.model.lin1.shira_weight["first"])
+ assert torch.all(shira_assign_val2_f == peft_model.base_model.model.lin2.shira_weight["first"])
+ assert torch.all(shira_indices1_f == peft_model.base_model.model.lin1.shira_indices["first"])
+ assert torch.all(shira_indices2_f == peft_model.base_model.model.lin2.shira_indices["first"])
+
+ return peft_model
+
+ def test_save_load_default_random_mask_with_seed_function(self, mlp, tmp_path):
+ # we want to see if saving and loading works when a random mask is involved but the random seed is fixed.
+ config = ShiraConfig(r=2, target_modules=["lin1", "lin2"], random_seed=567, init_weights=False)
+
+ # create a custom mask SHiRA adapter
+ peft_model = get_peft_model(mlp, config, adapter_name="first")
+
+ shira_assign_val1_f = peft_model.base_model.model.lin1.shira_weight["first"]
+ shira_indices1_f = peft_model.base_model.model.lin1.shira_indices["first"]
+ shira_assign_val2_f = peft_model.base_model.model.lin2.shira_weight["first"]
+ shira_indices2_f = peft_model.base_model.model.lin2.shira_indices["first"]
+
+ input = torch.randn(5, 10)
+ peft_model.set_adapter("first")
+ output_first = peft_model(input)
+
+ save_path = os.path.join(tmp_path, "shira")
+ peft_model.save_pretrained(save_path)
+ assert os.path.exists(os.path.join(save_path, "first", "adapter_config.json"))
+ del peft_model
+
+ torch.manual_seed(0)
+ mlp = MLP()
+ peft_model = PeftModel.from_pretrained(mlp, os.path.join(save_path, "first"), adapter_name="first")
+
+ peft_model.set_adapter("first")
+ output_first_loaded = peft_model(input)
+
+ assert torch.allclose(output_first, output_first_loaded)
+
+ assert torch.all(shira_assign_val1_f == peft_model.base_model.model.lin1.shira_weight["first"])
+ assert torch.all(shira_assign_val2_f == peft_model.base_model.model.lin2.shira_weight["first"])
+ assert torch.all(shira_indices1_f == peft_model.base_model.model.lin1.shira_indices["first"])
+ assert torch.all(shira_indices2_f == peft_model.base_model.model.lin2.shira_indices["first"])
+
+ return peft_model
+
+ @pytest.mark.parametrize("dtype", [torch.float32, torch.float16, torch.bfloat16])
+ def test_shira_dtypes(self, dtype):
+ if dtype == torch.bfloat16:
+ # skip if bf16 is not supported on hardware, see #1872
+ if not is_bf16_available():
+ pytest.skip("bfloat16 not supported on this system, skipping the test")
+
+ model = MLP().to(dtype)
+ config = ShiraConfig(r=2, target_modules=["lin1", "lin2"])
+ peft_model = get_peft_model(model, config)
+ inputs = torch.randn(5, 10).to(dtype)
+ output = peft_model(inputs) # should not raise
+ assert output.dtype == dtype
diff --git a/peft/tests/test_stablediffusion.py b/peft/tests/test_stablediffusion.py
new file mode 100644
index 0000000000000000000000000000000000000000..8eb18dc9a682806bab9a1e5a120160487f525ca1
--- /dev/null
+++ b/peft/tests/test_stablediffusion.py
@@ -0,0 +1,387 @@
+# Copyright 2023-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+import copy
+from dataclasses import asdict, replace
+
+import numpy as np
+import pytest
+from diffusers import StableDiffusionPipeline
+
+from peft import (
+ BOFTConfig,
+ HRAConfig,
+ LoHaConfig,
+ LoKrConfig,
+ LoraConfig,
+ OFTConfig,
+ get_peft_model,
+ get_peft_model_state_dict,
+ inject_adapter_in_model,
+ set_peft_model_state_dict,
+)
+from peft.tuners.tuners_utils import BaseTunerLayer
+
+from .testing_common import PeftCommonTester
+from .testing_utils import set_init_weights_false, temp_seed
+
+
+PEFT_DIFFUSERS_SD_MODELS_TO_TEST = ["hf-internal-testing/tiny-sd-pipe"]
+DIFFUSERS_CONFIGS = [
+ (
+ LoraConfig,
+ {
+ "text_encoder": {
+ "r": 8,
+ "lora_alpha": 32,
+ "target_modules": ["k_proj", "q_proj", "v_proj", "out_proj", "fc1", "fc2"],
+ "lora_dropout": 0.0,
+ "bias": "none",
+ "init_lora_weights": False,
+ },
+ "unet": {
+ "r": 8,
+ "lora_alpha": 32,
+ "target_modules": [
+ "proj_in",
+ "proj_out",
+ "to_k",
+ "to_q",
+ "to_v",
+ "to_out.0",
+ "ff.net.0.proj",
+ "ff.net.2",
+ ],
+ "lora_dropout": 0.0,
+ "bias": "none",
+ "init_lora_weights": False,
+ },
+ },
+ ),
+ (
+ LoHaConfig,
+ {
+ "text_encoder": {
+ "r": 8,
+ "alpha": 32,
+ "target_modules": ["k_proj", "q_proj", "v_proj", "out_proj", "fc1", "fc2"],
+ "rank_dropout": 0.0,
+ "module_dropout": 0.0,
+ "init_weights": False,
+ },
+ "unet": {
+ "r": 8,
+ "alpha": 32,
+ "target_modules": [
+ "proj_in",
+ "proj_out",
+ "to_k",
+ "to_q",
+ "to_v",
+ "to_out.0",
+ "ff.net.0.proj",
+ "ff.net.2",
+ ],
+ "rank_dropout": 0.0,
+ "module_dropout": 0.0,
+ "init_weights": False,
+ },
+ },
+ ),
+ (
+ LoKrConfig,
+ {
+ "text_encoder": {
+ "r": 8,
+ "alpha": 32,
+ "target_modules": ["k_proj", "q_proj", "v_proj", "out_proj", "fc1", "fc2"],
+ "rank_dropout": 0.0,
+ "module_dropout": 0.0,
+ "init_weights": False,
+ },
+ "unet": {
+ "r": 8,
+ "alpha": 32,
+ "target_modules": [
+ "proj_in",
+ "proj_out",
+ "to_k",
+ "to_q",
+ "to_v",
+ "to_out.0",
+ "ff.net.0.proj",
+ "ff.net.2",
+ ],
+ "rank_dropout": 0.0,
+ "module_dropout": 0.0,
+ "init_weights": False,
+ },
+ },
+ ),
+ (
+ OFTConfig,
+ {
+ "text_encoder": {
+ "r": 1,
+ "oft_block_size": 0,
+ "target_modules": ["k_proj", "q_proj", "v_proj", "out_proj", "fc1", "fc2"],
+ "module_dropout": 0.0,
+ "init_weights": False,
+ "use_cayley_neumann": False,
+ },
+ "unet": {
+ "r": 1,
+ "oft_block_size": 0,
+ "target_modules": [
+ "proj_in",
+ "proj_out",
+ "to_k",
+ "to_q",
+ "to_v",
+ "to_out.0",
+ "ff.net.0.proj",
+ "ff.net.2",
+ ],
+ "module_dropout": 0.0,
+ "init_weights": False,
+ "use_cayley_neumann": False,
+ },
+ },
+ ),
+ (
+ BOFTConfig,
+ {
+ "text_encoder": {
+ "boft_block_num": 1,
+ "boft_block_size": 0,
+ "target_modules": ["k_proj", "q_proj", "v_proj", "out_proj", "fc1", "fc2"],
+ "boft_dropout": 0.0,
+ "init_weights": False,
+ },
+ "unet": {
+ "boft_block_num": 1,
+ "boft_block_size": 0,
+ "target_modules": [
+ "proj_in",
+ "proj_out",
+ "to_k",
+ "to_q",
+ "to_v",
+ "to_out.0",
+ "ff.net.0.proj",
+ "ff.net.2",
+ ],
+ "boft_dropout": 0.0,
+ "init_weights": False,
+ },
+ },
+ ),
+ (
+ HRAConfig,
+ {
+ "text_encoder": {
+ "r": 8,
+ "target_modules": ["k_proj", "q_proj", "v_proj", "out_proj", "fc1", "fc2"],
+ "init_weights": False,
+ },
+ "unet": {
+ "r": 8,
+ "target_modules": [
+ "proj_in",
+ "proj_out",
+ "to_k",
+ "to_q",
+ "to_v",
+ "to_out.0",
+ "ff.net.0.proj",
+ "ff.net.2",
+ ],
+ "init_weights": False,
+ },
+ },
+ ),
+]
+
+
+def skip_if_not_lora(config_cls):
+ if config_cls != LoraConfig:
+ pytest.skip("Skipping test because it is only applicable to LoraConfig")
+
+
+class TestStableDiffusionModel(PeftCommonTester):
+ r"""
+ Tests that diffusers StableDiffusion model works with PEFT as expected.
+ """
+
+ transformers_class = StableDiffusionPipeline
+ sd_model = StableDiffusionPipeline.from_pretrained("hf-internal-testing/tiny-sd-pipe")
+
+ def instantiate_sd_peft(self, model_id, config_cls, config_kwargs):
+ # Instantiate StableDiffusionPipeline
+ if model_id == "hf-internal-testing/tiny-sd-pipe":
+ # in CI, this model often times out on the hub, let's cache it
+ model = copy.deepcopy(self.sd_model)
+ else:
+ model = self.transformers_class.from_pretrained(model_id)
+
+ config_kwargs = config_kwargs.copy()
+ text_encoder_kwargs = config_kwargs.pop("text_encoder")
+ unet_kwargs = config_kwargs.pop("unet")
+ # the remaining config kwargs should be applied to both configs
+ for key, val in config_kwargs.items():
+ text_encoder_kwargs[key] = val
+ unet_kwargs[key] = val
+
+ # Instantiate text_encoder adapter
+ config_text_encoder = config_cls(**text_encoder_kwargs)
+ model.text_encoder = get_peft_model(model.text_encoder, config_text_encoder)
+
+ # Instantiate unet adapter
+ config_unet = config_cls(**unet_kwargs)
+ model.unet = get_peft_model(model.unet, config_unet)
+
+ # Move model to device
+ model = model.to(self.torch_device)
+
+ return model
+
+ def prepare_inputs_for_testing(self):
+ return {
+ "prompt": "a high quality digital photo of a cute corgi",
+ "num_inference_steps": 3,
+ }
+
+ @pytest.mark.parametrize("model_id", PEFT_DIFFUSERS_SD_MODELS_TO_TEST)
+ @pytest.mark.parametrize("config_cls,config_kwargs", DIFFUSERS_CONFIGS)
+ def test_merge_layers(self, model_id, config_cls, config_kwargs):
+ if (config_cls == LoKrConfig) and (self.torch_device not in ["cuda", "xpu"]):
+ pytest.skip("Merging test with LoKr fails without GPU")
+
+ # Instantiate model & adapters
+ config_kwargs = set_init_weights_false(config_cls, config_kwargs)
+ model = self.instantiate_sd_peft(model_id, config_cls, config_kwargs)
+
+ # Generate output for peft modified StableDiffusion
+ dummy_input = self.prepare_inputs_for_testing()
+ with temp_seed(seed=42):
+ peft_output = np.array(model(**dummy_input).images[0]).astype(np.float32)
+
+ # Merge adapter and model
+ if config_cls not in [LoHaConfig, OFTConfig, HRAConfig]:
+ # TODO: Merging the text_encoder is leading to issues on CPU with PyTorch 2.1
+ model.text_encoder = model.text_encoder.merge_and_unload()
+ model.unet = model.unet.merge_and_unload()
+
+ # Generate output for peft merged StableDiffusion
+ with temp_seed(seed=42):
+ merged_output = np.array(model(**dummy_input).images[0]).astype(np.float32)
+
+ # Images are in uint8 drange, so use large atol
+ assert np.allclose(peft_output, merged_output, atol=1.0)
+
+ @pytest.mark.parametrize("model_id", PEFT_DIFFUSERS_SD_MODELS_TO_TEST)
+ @pytest.mark.parametrize("config_cls,config_kwargs", DIFFUSERS_CONFIGS)
+ def test_merge_layers_safe_merge(self, model_id, config_cls, config_kwargs):
+ if (config_cls == LoKrConfig) and (self.torch_device not in ["cuda", "xpu"]):
+ pytest.skip("Merging test with LoKr fails without GPU")
+
+ # Instantiate model & adapters
+ model = self.instantiate_sd_peft(model_id, config_cls, config_kwargs)
+
+ # Generate output for peft modified StableDiffusion
+ dummy_input = self.prepare_inputs_for_testing()
+ with temp_seed(seed=42):
+ peft_output = np.array(model(**dummy_input).images[0]).astype(np.float32)
+
+ # Merge adapter and model
+ if config_cls not in [LoHaConfig, OFTConfig, HRAConfig]:
+ # TODO: Merging the text_encoder is leading to issues on CPU with PyTorch 2.1
+ model.text_encoder = model.text_encoder.merge_and_unload(safe_merge=True)
+ model.unet = model.unet.merge_and_unload(safe_merge=True)
+
+ # Generate output for peft merged StableDiffusion
+ with temp_seed(seed=42):
+ merged_output = np.array(model(**dummy_input).images[0]).astype(np.float32)
+
+ # Images are in uint8 drange, so use large atol
+ assert np.allclose(peft_output, merged_output, atol=1.0)
+
+ @pytest.mark.parametrize("model_id", PEFT_DIFFUSERS_SD_MODELS_TO_TEST)
+ @pytest.mark.parametrize("config_cls,config_kwargs", DIFFUSERS_CONFIGS)
+ def test_add_weighted_adapter_base_unchanged(self, model_id, config_cls, config_kwargs):
+ skip_if_not_lora(config_cls)
+ # Instantiate model & adapters
+ config_kwargs = set_init_weights_false(config_cls, config_kwargs)
+ model = self.instantiate_sd_peft(model_id, config_cls, config_kwargs)
+
+ # Get current available adapter config
+ text_encoder_adapter_name = next(iter(model.text_encoder.peft_config.keys()))
+ unet_adapter_name = next(iter(model.unet.peft_config.keys()))
+ text_encoder_adapter_config = replace(model.text_encoder.peft_config[text_encoder_adapter_name])
+ unet_adapter_config = replace(model.unet.peft_config[unet_adapter_name])
+
+ # Create weighted adapters
+ model.text_encoder.add_weighted_adapter([unet_adapter_name], [0.5], "weighted_adapter_test")
+ model.unet.add_weighted_adapter([unet_adapter_name], [0.5], "weighted_adapter_test")
+
+ # Assert that base adapters config did not change
+ assert asdict(text_encoder_adapter_config) == asdict(model.text_encoder.peft_config[text_encoder_adapter_name])
+ assert asdict(unet_adapter_config) == asdict(model.unet.peft_config[unet_adapter_name])
+
+ @pytest.mark.parametrize("model_id", PEFT_DIFFUSERS_SD_MODELS_TO_TEST)
+ @pytest.mark.parametrize("config_cls,config_kwargs", DIFFUSERS_CONFIGS)
+ def test_disable_adapter(self, model_id, config_cls, config_kwargs):
+ config_kwargs = set_init_weights_false(config_cls, config_kwargs)
+ self._test_disable_adapter(model_id, config_cls, config_kwargs)
+
+ @pytest.mark.parametrize("model_id", PEFT_DIFFUSERS_SD_MODELS_TO_TEST)
+ @pytest.mark.parametrize("config_cls,config_kwargs", DIFFUSERS_CONFIGS)
+ def test_load_model_low_cpu_mem_usage(self, model_id, config_cls, config_kwargs):
+ # Instantiate model & adapters
+ pipe = self.instantiate_sd_peft(model_id, config_cls, config_kwargs)
+
+ te_state_dict = get_peft_model_state_dict(pipe.text_encoder)
+ unet_state_dict = get_peft_model_state_dict(pipe.unet)
+
+ del pipe
+ pipe = self.instantiate_sd_peft(model_id, config_cls, config_kwargs)
+
+ config_kwargs = config_kwargs.copy()
+ text_encoder_kwargs = config_kwargs.pop("text_encoder")
+ unet_kwargs = config_kwargs.pop("unet")
+ # the remaining config kwargs should be applied to both configs
+ for key, val in config_kwargs.items():
+ text_encoder_kwargs[key] = val
+ unet_kwargs[key] = val
+
+ config_text_encoder = config_cls(**text_encoder_kwargs)
+ config_unet = config_cls(**unet_kwargs)
+
+ # check text encoder
+ inject_adapter_in_model(config_text_encoder, pipe.text_encoder, low_cpu_mem_usage=True)
+ # sanity check that the adapter was applied:
+ assert any(isinstance(module, BaseTunerLayer) for module in pipe.text_encoder.modules())
+
+ assert "meta" in {p.device.type for p in pipe.text_encoder.parameters()}
+ set_peft_model_state_dict(pipe.text_encoder, te_state_dict, low_cpu_mem_usage=True)
+ assert "meta" not in {p.device.type for p in pipe.text_encoder.parameters()}
+
+ # check unet
+ inject_adapter_in_model(config_unet, pipe.unet, low_cpu_mem_usage=True)
+ # sanity check that the adapter was applied:
+ assert any(isinstance(module, BaseTunerLayer) for module in pipe.unet.modules())
+
+ assert "meta" in {p.device.type for p in pipe.unet.parameters()}
+ set_peft_model_state_dict(pipe.unet, unet_state_dict, low_cpu_mem_usage=True)
+ assert "meta" not in {p.device.type for p in pipe.unet.parameters()}
diff --git a/peft/tests/test_target_parameters.py b/peft/tests/test_target_parameters.py
new file mode 100644
index 0000000000000000000000000000000000000000..adffbce0d5b82f85bfe1ba36f5761807a97cbd87
--- /dev/null
+++ b/peft/tests/test_target_parameters.py
@@ -0,0 +1,507 @@
+# Copyright 2025-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+import pytest
+import torch
+from torch import nn
+from transformers import AutoModelForCausalLM
+
+from peft import LoraConfig, TaskType, get_peft_model
+
+from .testing_common import PeftCommonTester
+from .testing_utils import hub_online_once, set_init_weights_false
+
+
+ALL_CONFIGS = [
+ ##########
+ # Llama4 #
+ ##########
+ # target down_proj
+ (
+ "trl-internal-testing/tiny-Llama4ForCausalLM",
+ LoraConfig,
+ {
+ "task_type": TaskType.CAUSAL_LM,
+ "target_modules": [],
+ "lora_dropout": 0.0,
+ "target_parameters": [
+ "feed_forward.experts.down_proj",
+ ],
+ },
+ ),
+ # target gate_up_proj and down_proj, but not on the same module
+ (
+ "trl-internal-testing/tiny-Llama4ForCausalLM",
+ LoraConfig,
+ {
+ "task_type": TaskType.CAUSAL_LM,
+ "target_modules": [],
+ "lora_dropout": 0.0,
+ "target_parameters": [
+ "0.feed_forward.experts.gate_up_proj",
+ "1.feed_forward.experts.down_proj",
+ ],
+ },
+ ),
+ # target down_proj and gate_up_proj on the same module
+ (
+ "trl-internal-testing/tiny-Llama4ForCausalLM",
+ LoraConfig,
+ {
+ "task_type": "CAUSAL_LM",
+ "r": 8,
+ "lora_alpha": 32,
+ "target_modules": None,
+ "lora_dropout": 0.0,
+ "bias": "none",
+ "target_parameters": [
+ "feed_forward.experts.down_proj",
+ "feed_forward.experts.gate_up_proj",
+ ],
+ },
+ ),
+ # target q_proj, v_proj as modules, and down_proj as parameter
+ (
+ "trl-internal-testing/tiny-Llama4ForCausalLM",
+ LoraConfig,
+ {
+ "task_type": TaskType.CAUSAL_LM,
+ "target_modules": ["q_proj", "v_proj"],
+ "lora_dropout": 0.0,
+ "target_parameters": [
+ "feed_forward.experts.down_proj",
+ ],
+ },
+ ),
+ ###########
+ # gpt-oss #
+ ###########
+ # target down_proj
+ (
+ "trl-internal-testing/tiny-GptOssForCausalLM",
+ LoraConfig,
+ {
+ "task_type": TaskType.CAUSAL_LM,
+ "target_modules": [],
+ "lora_dropout": 0.0,
+ "target_parameters": [
+ "mlp.experts.down_proj",
+ ],
+ },
+ ),
+ # target gate_up_proj and down_proj, but not on the same module
+ (
+ "trl-internal-testing/tiny-GptOssForCausalLM",
+ LoraConfig,
+ {
+ "task_type": TaskType.CAUSAL_LM,
+ "target_modules": [],
+ "lora_dropout": 0.0,
+ "target_parameters": [
+ "0.mlp.experts.gate_up_proj",
+ "1.mlp.experts.down_proj",
+ ],
+ },
+ ),
+ # target down_proj and gate_up_proj on the same module
+ (
+ "trl-internal-testing/tiny-GptOssForCausalLM",
+ LoraConfig,
+ {
+ "task_type": "CAUSAL_LM",
+ "r": 8,
+ "lora_alpha": 32,
+ "target_modules": None,
+ "lora_dropout": 0.0,
+ "bias": "none",
+ "target_parameters": [
+ "mlp.experts.down_proj",
+ "mlp.experts.gate_up_proj",
+ ],
+ },
+ ),
+ # target q_proj, v_proj as modules, and down_proj as parameter
+ (
+ "trl-internal-testing/tiny-GptOssForCausalLM",
+ LoraConfig,
+ {
+ "task_type": TaskType.CAUSAL_LM,
+ "target_modules": ["q_proj", "v_proj"],
+ "lora_dropout": 0.0,
+ "target_parameters": [
+ "mlp.experts.down_proj",
+ ],
+ },
+ ),
+]
+
+
+class MyAutoModelForCausalLM(AutoModelForCausalLM):
+ @classmethod
+ def from_pretrained(cls, *args, **kwargs):
+ torch.manual_seed(0)
+ model = AutoModelForCausalLM.from_pretrained(*args, **kwargs)
+
+ # check that we load the original model, not, say, a trained checkpoint
+ if args[0] == "trl-internal-testing/tiny-Llama4ForCausalLM":
+ # model contains weights with values ~1e36 or nan, so we need to reinitialize with sane values
+ with torch.no_grad():
+ for param in model.parameters():
+ param.data = torch.randn(param.shape)
+ return model
+
+
+class TestDecoderModelsTargetParameters(PeftCommonTester):
+ # This is more or less a copy of TestDecoderModels at the time of the PR being added. Unnecessary code is removed,
+ # like code required for testing non-LoRA methods. The tests being included are not selected to test specific
+ # functionality of targeting nn.Parameters, they (together with the tests in test_custom_models.py) just ensure that
+ # generally, nothing is broken.
+ transformers_class = MyAutoModelForCausalLM
+
+ def skipTest(self, reason=""):
+ # for backwards compatibility with unittest style test classes
+ pytest.skip(reason)
+
+ def prepare_inputs_for_testing(self):
+ input_ids = torch.tensor([[1, 1, 1], [1, 2, 1]]).to(self.torch_device)
+ attention_mask = torch.tensor([[1, 1, 1], [1, 0, 1]]).to(self.torch_device)
+ return {"input_ids": input_ids, "attention_mask": attention_mask}
+
+ @pytest.mark.parametrize("model_id,config_cls,config_kwargs", ALL_CONFIGS)
+ def test_attributes_parametrized(self, model_id, config_cls, config_kwargs):
+ self._test_model_attr(model_id, config_cls, config_kwargs.copy())
+
+ @pytest.mark.parametrize("model_id,config_cls,config_kwargs", ALL_CONFIGS)
+ def test_adapter_name(self, model_id, config_cls, config_kwargs):
+ self._test_adapter_name(model_id, config_cls, config_kwargs.copy())
+
+ @pytest.mark.parametrize("model_id,config_cls,config_kwargs", ALL_CONFIGS)
+ def test_prepare_for_training_parametrized(self, model_id, config_cls, config_kwargs):
+ self._test_prepare_for_training(model_id, config_cls, config_kwargs.copy())
+
+ @pytest.mark.parametrize("model_id,config_cls,config_kwargs", ALL_CONFIGS)
+ def test_save_pretrained(self, model_id, config_cls, config_kwargs):
+ self._test_save_pretrained(model_id, config_cls, config_kwargs.copy())
+
+ @pytest.mark.parametrize("model_id,config_cls,config_kwargs", ALL_CONFIGS)
+ def test_save_pretrained_pickle(self, model_id, config_cls, config_kwargs):
+ self._test_save_pretrained(model_id, config_cls, config_kwargs.copy(), safe_serialization=False)
+
+ @pytest.mark.skip(reason="Multiple adapters with target_parameters are not supported yet.")
+ @pytest.mark.parametrize("model_id,config_cls,config_kwargs", ALL_CONFIGS)
+ def test_save_pretrained_selected_adapters(self, model_id, config_cls, config_kwargs):
+ self._test_save_pretrained_selected_adapters(model_id, config_cls, config_kwargs.copy())
+
+ @pytest.mark.skip(reason="Multiple adapters with target_parameters are not supported yet.")
+ @pytest.mark.parametrize("model_id,config_cls,config_kwargs", ALL_CONFIGS)
+ def test_save_pretrained_selected_adapters_pickle(self, model_id, config_cls, config_kwargs):
+ self._test_save_pretrained_selected_adapters(
+ model_id, config_cls, config_kwargs.copy(), safe_serialization=False
+ )
+
+ @pytest.mark.parametrize("model_id,config_cls,config_kwargs", ALL_CONFIGS)
+ def test_from_pretrained_config_construction(self, model_id, config_cls, config_kwargs):
+ self._test_from_pretrained_config_construction(model_id, config_cls, config_kwargs.copy())
+
+ @pytest.mark.parametrize("model_id,config_cls,config_kwargs", ALL_CONFIGS)
+ def test_merge_layers(self, model_id, config_cls, config_kwargs):
+ config_kwargs = set_init_weights_false(config_cls, config_kwargs)
+ self._test_merge_layers(model_id, config_cls, config_kwargs.copy())
+
+ @pytest.mark.skip(reason="Multiple adapters with target_parameters are not supported yet.")
+ @pytest.mark.parametrize("model_id,config_cls,config_kwargs", ALL_CONFIGS)
+ def test_merge_layers_multi(self, model_id, config_cls, config_kwargs):
+ config_kwargs = set_init_weights_false(config_cls, config_kwargs)
+ self._test_merge_layers_multi(model_id, config_cls, config_kwargs.copy())
+
+ @pytest.mark.parametrize("model_id,config_cls,config_kwargs", ALL_CONFIGS)
+ def test_merge_layers_nan(self, model_id, config_cls, config_kwargs):
+ config_kwargs = set_init_weights_false(config_cls, config_kwargs)
+ self._test_merge_layers_nan(model_id, config_cls, config_kwargs.copy())
+
+ @pytest.mark.skip(reason="Multiple adapters with target_parameters are not supported yet.")
+ @pytest.mark.parametrize("model_id,config_cls,config_kwargs", ALL_CONFIGS)
+ def test_mixed_adapter_batches(self, model_id, config_cls, config_kwargs):
+ config_kwargs = set_init_weights_false(config_cls, config_kwargs)
+ msg = "lora.ParamWrapper does not support mixed adapter batches yet."
+ with pytest.raises(ValueError, match=msg):
+ self._test_mixed_adapter_batches(model_id, config_cls, config_kwargs.copy())
+
+ @pytest.mark.skip(reason="Multiple adapters with target_parameters are not supported yet.")
+ @pytest.mark.parametrize("model_id,config_cls,config_kwargs", ALL_CONFIGS)
+ def test_generate_with_mixed_adapter_batches(self, model_id, config_cls, config_kwargs):
+ config_kwargs = set_init_weights_false(config_cls, config_kwargs)
+ msg = "lora.ParamWrapper does not support mixed adapter batches yet."
+ with pytest.raises(ValueError, match=msg):
+ self._test_generate_with_mixed_adapter_batches_and_beam_search(model_id, config_cls, config_kwargs.copy())
+
+ @pytest.mark.parametrize("model_id,config_cls,config_kwargs", ALL_CONFIGS)
+ def test_generate(self, model_id, config_cls, config_kwargs):
+ self._test_generate(model_id, config_cls, config_kwargs.copy())
+
+ @pytest.mark.parametrize("model_id,config_cls,config_kwargs", ALL_CONFIGS)
+ def test_generate_pos_args(self, model_id, config_cls, config_kwargs):
+ self._test_generate_pos_args(model_id, config_cls, config_kwargs.copy(), raises_err=False)
+
+ @pytest.mark.parametrize("model_id,config_cls,config_kwargs", ALL_CONFIGS)
+ def test_merge_layers_fp16(self, model_id, config_cls, config_kwargs):
+ self._test_merge_layers_fp16(model_id, config_cls, config_kwargs.copy())
+
+ @pytest.mark.parametrize("model_id,config_cls,config_kwargs", ALL_CONFIGS)
+ def test_generate_half_prec(self, model_id, config_cls, config_kwargs):
+ self._test_generate_half_prec(model_id, config_cls, config_kwargs.copy())
+
+ @pytest.mark.parametrize("model_id,config_cls,config_kwargs", ALL_CONFIGS)
+ def test_training_decoders(self, model_id, config_cls, config_kwargs):
+ self._test_training(model_id, config_cls, config_kwargs.copy())
+
+ @pytest.mark.parametrize("model_id,config_cls,config_kwargs", ALL_CONFIGS)
+ def test_training_decoders_gradient_checkpointing(self, model_id, config_cls, config_kwargs):
+ self._test_training_gradient_checkpointing(model_id, config_cls, config_kwargs.copy())
+
+ @pytest.mark.parametrize("model_id,config_cls,config_kwargs", ALL_CONFIGS)
+ def test_inference_safetensors(self, model_id, config_cls, config_kwargs):
+ self._test_inference_safetensors(model_id, config_cls, config_kwargs.copy())
+
+ @pytest.mark.parametrize("model_id,config_cls,config_kwargs", ALL_CONFIGS)
+ def test_peft_model_device_map(self, model_id, config_cls, config_kwargs):
+ self._test_peft_model_device_map(model_id, config_cls, config_kwargs.copy())
+
+ @pytest.mark.skip(reason="Multiple adapters with target_parameters are not supported yet.")
+ @pytest.mark.parametrize("model_id,config_cls,config_kwargs", ALL_CONFIGS)
+ def test_delete_adapter(self, model_id, config_cls, config_kwargs):
+ self._test_delete_adapter(model_id, config_cls, config_kwargs.copy())
+
+ @pytest.mark.skip(reason="Multiple adapters with target_parameters are not supported yet.")
+ @pytest.mark.parametrize("model_id,config_cls,config_kwargs", ALL_CONFIGS)
+ def test_delete_inactive_adapter(self, model_id, config_cls, config_kwargs):
+ self._test_delete_inactive_adapter(model_id, config_cls, config_kwargs.copy())
+
+ @pytest.mark.parametrize("model_id,config_cls,config_kwargs", ALL_CONFIGS)
+ def test_adding_multiple_adapters_with_bias_raises(self, model_id, config_cls, config_kwargs):
+ self._test_adding_multiple_adapters_with_bias_raises(model_id, config_cls, config_kwargs.copy())
+
+ @pytest.mark.parametrize("model_id,config_cls,config_kwargs", ALL_CONFIGS)
+ def test_unload_adapter(self, model_id, config_cls, config_kwargs):
+ config_kwargs = set_init_weights_false(config_cls, config_kwargs)
+ self._test_unload_adapter(model_id, config_cls, config_kwargs.copy())
+
+ @pytest.mark.skip(reason="Multiple adapters with target_parameters are not supported yet.")
+ @pytest.mark.parametrize("model_id,config_cls,config_kwargs", ALL_CONFIGS)
+ def test_weighted_combination_of_adapters(self, model_id, config_cls, config_kwargs):
+ config_kwargs = set_init_weights_false(config_cls, config_kwargs)
+ msg = "add_weighted_adapter does not support targeting nn.Parameter"
+ with pytest.raises(ValueError, match=msg):
+ self._test_weighted_combination_of_adapters(model_id, config_cls, config_kwargs.copy())
+
+ @pytest.mark.parametrize("model_id,config_cls,config_kwargs", ALL_CONFIGS)
+ def test_training_prompt_learning_tasks(self, model_id, config_cls, config_kwargs):
+ self._test_training_prompt_learning_tasks(model_id, config_cls, config_kwargs.copy())
+
+ @pytest.mark.parametrize("model_id,config_cls,config_kwargs", ALL_CONFIGS)
+ def test_disable_adapter(self, model_id, config_cls, config_kwargs):
+ config_kwargs = set_init_weights_false(config_cls, config_kwargs)
+ self._test_disable_adapter(model_id, config_cls, config_kwargs.copy())
+
+ @pytest.mark.parametrize("model_id,config_cls,config_kwargs", ALL_CONFIGS)
+ def test_passing_input_embeds_works(self, model_id, config_cls, config_kwargs):
+ self._test_passing_input_embeds_works("", model_id, config_cls, config_kwargs.copy())
+
+
+class TestTargetParameters:
+ # Tests specifically designed for target_parameters
+ def test_targeting_module_and_targeting_param_equivalent(self):
+ # Test that using LoRA with target_modules vs target_parameters yields identical results.
+ # note: we purposely target the gate_proj because its weight is not square (unlike q_proj, ...), this makes it
+ # easier to catch shape errors
+ torch.manual_seed(0)
+ model_id = "hf-internal-testing/tiny-random-LlamaForCausalLM"
+ with hub_online_once(model_id):
+ model0 = AutoModelForCausalLM.from_pretrained(model_id)
+ x = torch.arange(10).view(2, 5)
+ with torch.inference_mode():
+ out_base = model0(x, output_hidden_states=True).hidden_states[-1]
+
+ # targeting the module
+ config0 = LoraConfig(target_modules=["gate_proj"], init_lora_weights=False)
+ model0 = get_peft_model(model0, config0)
+
+ # targeting the parameter
+ model1 = AutoModelForCausalLM.from_pretrained("hf-internal-testing/tiny-random-LlamaForCausalLM")
+ config1 = LoraConfig(target_modules=[], target_parameters=["gate_proj.weight"], init_lora_weights=False)
+ model1 = get_peft_model(model1, config1)
+
+ gate_proj_0_0 = model0.base_model.model.model.layers[0].mlp.gate_proj
+ gate_proj_0_1 = model0.base_model.model.model.layers[1].mlp.gate_proj
+ gate_proj_1_0 = model1.base_model.model.model.layers[0].mlp.gate_proj
+ gate_proj_1_1 = model1.base_model.model.model.layers[1].mlp.gate_proj
+
+ # ensure that the randomly initialized LoRA weights are identical
+ gate_proj_1_0.lora_A.default.weight.data.copy_(gate_proj_0_0.lora_A.default.weight.data)
+ gate_proj_1_1.lora_A.default.weight.data.copy_(gate_proj_0_1.lora_A.default.weight.data)
+ gate_proj_1_0.lora_B.default.weight.data.copy_(gate_proj_0_0.lora_B.default.weight.data)
+ gate_proj_1_1.lora_B.default.weight.data.copy_(gate_proj_0_1.lora_B.default.weight.data)
+
+ with torch.inference_mode():
+ out_lora_0 = model0(x, output_hidden_states=True).hidden_states[-1]
+ out_lora_1 = model1(x, output_hidden_states=True).hidden_states[-1]
+
+ # sanity check: basemodel outputs should be different
+ atol, rtol = 1e-6, 1e-6
+ assert not torch.allclose(out_base, out_lora_0, atol=atol, rtol=rtol)
+
+ # LoRA outputs should be the same
+ assert torch.allclose(out_lora_0, out_lora_1, atol=atol, rtol=rtol)
+
+ def test_target_multiple_parameters_on_same_module(self, monkeypatch):
+ # test that if we target multiple nn.Parameters on the same module, all of them are being used during the
+ # forward pass
+ torch.manual_seed(0)
+ model_id = "trl-internal-testing/tiny-Llama4ForCausalLM"
+ with hub_online_once(model_id):
+ x = torch.arange(10).view(2, 5)
+ model = MyAutoModelForCausalLM.from_pretrained(model_id)
+ shape_gate_up_proj = model.model.layers[0].feed_forward.experts.gate_up_proj.shape
+ shape_down_proj = model.model.layers[0].feed_forward.experts.down_proj.shape
+ num_layers = len(model.model.layers)
+
+ target_parameters = ["feed_forward.experts.gate_up_proj", "feed_forward.experts.down_proj"]
+ num_params = len(target_parameters)
+ config = LoraConfig(target_parameters=target_parameters, init_lora_weights=False)
+ model = get_peft_model(model, config)
+
+ # CHECK FORWARD CALLS
+
+ # log the weights seen during the forward call
+ weights = []
+
+ def mock_forward(self, W):
+ weights.append(W)
+ return orig_forward(self, W)
+
+ from peft.tuners.lora.layer import _LoraParameterProxy
+
+ orig_forward = _LoraParameterProxy.forward
+ monkeypatch.setattr(_LoraParameterProxy, "forward", mock_forward)
+
+ num_steps = 3
+ with torch.inference_mode():
+ for _ in range(num_steps):
+ out_base = model(x, output_hidden_states=True).hidden_states[-1]
+
+ actual_call_count = len(weights)
+ # Note: We call forward twice per step, once to create the parametrization and once for the actual forward
+ # step. This may be a bit wasteful but it's not clear how to prevent this and overall is probably negligible
+ num_forward_per_step = 2
+ # Since https://github.com/huggingface/transformers/pull/39501, one of the parameters is accessed twice per
+ # forward call, so add +1.
+ expected_call_count = num_steps * num_layers * (1 + num_params * num_forward_per_step)
+ assert actual_call_count == expected_call_count
+
+ actual_shapes = {W.shape for W in weights}
+ expected_shapes = {shape_gate_up_proj, shape_down_proj}
+ assert actual_shapes == expected_shapes
+
+ # CHECK WEIGHT UPDATES
+
+ lora_weights_before = {
+ k: v.clone() for k, v in model.named_parameters() if "lora_A.default" in k or "lora_B.default" in k
+ }
+ # sanity check:
+ assert len(lora_weights_before) == 2 * num_layers * num_params
+ # train
+ optim = torch.optim.SGD(model.parameters(), lr=0.01)
+ for _ in range(10):
+ optim.zero_grad()
+ out = model(x)
+ loss = out.logits.sum()
+ loss.backward()
+ optim.step()
+
+ lora_weights_after = {
+ k: v for k, v in model.named_parameters() if "lora_A.default" in k or "lora_B.default" in k
+ }
+ assert lora_weights_before.keys() == lora_weights_after.keys()
+ atol, rtol = 0.1, 0.1
+ for key in lora_weights_before.keys():
+ assert not torch.allclose(lora_weights_before[key], lora_weights_after[key], atol=atol, rtol=rtol)
+
+ def test_target_parameters_works_with_existing_parametrization(self):
+ # When a parameter is already parametrized, we want the LoRA parametrization to work with it correctly.
+ class MyLinear(nn.Linear):
+ # For testing purposes, define a linear layer with 2 parameters: weight and other_weight.
+ def __init__(self, *args, **kwargs):
+ super().__init__(*args, **kwargs)
+ nn.init.ones_(self.weight)
+ self.other_weight = nn.Parameter(torch.ones(self.weight.shape))
+
+ class MyModule(nn.Module):
+ def __init__(self):
+ super().__init__()
+ self.lin = MyLinear(2, 2, bias=False)
+
+ def forward(self, x):
+ return self.lin(x)
+
+ class MyParametrization(nn.Module):
+ def __init__(self):
+ super().__init__()
+
+ def forward(self, x):
+ return x + 1
+
+ # base model
+ model = MyModule()
+ x = torch.ones((2, 2))
+
+ # sanity check: result should be 1*1 + 1*1 == 2
+ output_base = model(x)
+ assert torch.all(output_base == 2)
+
+ # add parametrization to the weight
+ nn.utils.parametrize.register_parametrization(model.lin, "weight", MyParametrization())
+
+ # result should be (1+1)*1 + (1+1)*1 == 4
+ output_parametrized = model(x)
+ assert torch.all(output_parametrized == 4)
+
+ # add LoRA parametrization to the weight
+ config = LoraConfig(r=2, lora_alpha=6, target_parameters=["lin.weight"], init_lora_weights=False)
+ model = get_peft_model(model, config)
+ # manually set LoRA weights to ones
+ nn.init.ones_(model.base_model.model.lin.lora_A["default"].weight)
+ nn.init.ones_(model.base_model.model.lin.lora_B["default"].weight)
+
+ output_lora = model(x)
+ # delta_weight should be: (1+1) * lora_scale = (1+1) * (alpha / rank) = 2 * (6 / 2) = 6
+ # result should be: (1+1+6)*1 + (1+1+6)*1 == 8 + 8 == 16
+ assert torch.all(output_lora == 16)
+
+ # calling twice should yield the same result
+ output_lora2 = model(x)
+ assert torch.allclose(output_lora, output_lora2)
+
+ # add another LoRA parametrization to other_weight, should have no effect on the output
+ config = LoraConfig(r=2, lora_alpha=6, target_parameters=["lin.other_weight"], init_lora_weights=False)
+ model.add_adapter("other", config)
+
+ output_other_lora = model(x)
+ # delta_weight should be: (1+1) * lora_scale = (1+1) * (alpha / rank) = 2 * (6 / 2) = 6
+ # result should be: (1+1+6)*1 + (1+1+6)*1 == 8 + 8 == 16
+ assert torch.all(output_other_lora == output_lora)
+
+ # after unloading, the output should be the same as before LoRA was applied
+ unloaded = model.unload()
+ output_unloaded = unloaded(x)
+ assert torch.all(output_unloaded == output_parametrized)
diff --git a/peft/tests/test_torch_compile.py b/peft/tests/test_torch_compile.py
new file mode 100644
index 0000000000000000000000000000000000000000..a7ad045b91e0229dadbb2d13f9bf46925f0b2412
--- /dev/null
+++ b/peft/tests/test_torch_compile.py
@@ -0,0 +1,599 @@
+# Copyright 2024-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+# The intent of the tests contained in this file is to check as many PEFT features as possible with torch.compile. This
+# is thus a document on how well torch.compile is supported by PEFT. Currently, we know that certain features do not
+# work with torch.compile. The corresponding tests should be marked with `@pytest.mark.xfail(strict=True)`.
+#
+# When adding a new test that fails with torch.compile, please make sure first that it does NOT fail without
+# torch.compile.
+
+import gc
+import os
+
+import pytest
+import torch
+from accelerate.utils.memory import clear_device_cache
+from transformers import (
+ AutoModelForCausalLM,
+ AutoTokenizer,
+ BitsAndBytesConfig,
+ DataCollatorForLanguageModeling,
+ Trainer,
+ TrainerCallback,
+ TrainingArguments,
+)
+
+from peft import (
+ AdaLoraConfig,
+ BOFTConfig,
+ BoneConfig,
+ HRAConfig,
+ IA3Config,
+ LNTuningConfig,
+ LoHaConfig,
+ LoKrConfig,
+ LoraConfig,
+ MissConfig,
+ OFTConfig,
+ PeftModel,
+ TaskType,
+ VBLoRAConfig,
+ VeraConfig,
+ get_peft_model,
+)
+
+from .testing_utils import load_dataset_english_quotes, require_bitsandbytes
+
+
+# only run (very slow) torch.compile tests when explicitly asked to
+if os.environ.get("PEFT_DEBUG_WITH_TORCH_COMPILE") != "1":
+ pytest.skip(allow_module_level=True)
+
+
+# Mapping: name of the setting -> (Peft config instance, torch.compile kwargs)
+SETTINGS = {
+ "adalora": (AdaLoraConfig(task_type=TaskType.CAUSAL_LM, total_step=5), {}),
+ "boft": (BOFTConfig(task_type=TaskType.CAUSAL_LM), {}),
+ "dora": (LoraConfig(task_type=TaskType.CAUSAL_LM, use_dora=True), {}),
+ "ia3": (IA3Config(task_type=TaskType.CAUSAL_LM), {}),
+ "ln_tuning": (LNTuningConfig(task_type=TaskType.CAUSAL_LM, target_modules=["final_layer_norm"]), {}),
+ "loha": (LoHaConfig(task_type=TaskType.CAUSAL_LM, target_modules=["q_proj", "v_proj"]), {}),
+ "lokr": pytest.param(
+ (LoKrConfig(task_type=TaskType.CAUSAL_LM, target_modules=["q_proj", "v_proj"]), {}),
+ ),
+ "lora": (LoraConfig(task_type=TaskType.CAUSAL_LM), {}),
+ "lora-target-embeddings": pytest.param(
+ (LoraConfig(task_type=TaskType.CAUSAL_LM, target_modules=["embed_tokens"]), {}),
+ ),
+ "lora-with-modules-to-save": (LoraConfig(task_type=TaskType.CAUSAL_LM, modules_to_save=["embed_tokens"]), {}),
+ "oft": (OFTConfig(task_type=TaskType.CAUSAL_LM, target_modules=["q_proj", "v_proj"]), {}),
+ "vblora": (VBLoRAConfig(task_type=TaskType.CAUSAL_LM, target_modules=["q_proj", "v_proj"], vector_length=2), {}),
+ "vera": (VeraConfig(task_type=TaskType.CAUSAL_LM), {}),
+ "hra": (HRAConfig(task_type=TaskType.CAUSAL_LM, target_modules=["q_proj", "v_proj"]), {}),
+ "bone": (BoneConfig(task_type=TaskType.CAUSAL_LM, target_modules=["q_proj", "v_proj"], r=2), {}),
+ "bone-bat": (
+ BoneConfig(task_type=TaskType.CAUSAL_LM, target_modules=["q_proj", "v_proj"], r=2, init_weights="bat"),
+ {},
+ ),
+ "miss": (MissConfig(task_type=TaskType.CAUSAL_LM, target_modules=["q_proj", "v_proj"], r=2), {}),
+ "miss-bat": (
+ MissConfig(task_type=TaskType.CAUSAL_LM, target_modules=["q_proj", "v_proj"], r=2, init_weights="bat"),
+ {},
+ ),
+ "miss-mini": (
+ MissConfig(task_type=TaskType.CAUSAL_LM, target_modules=["q_proj", "v_proj"], r=2, init_weights="mini"),
+ {},
+ ),
+}
+
+
+@pytest.mark.single_gpu_tests
+class TestTorchCompileCausalLM:
+ """
+ Tests for using torch.compile with causal LM.
+
+ Tip: When adding a new test, set `fake_compile = True` below. With this setting, torch.compile is being skipped.
+ This is useful for two reasons:
+
+ - compile is slow, so to quickly iterate on the test, it's best to disable it and only enable it at the very end
+ - even if you expect the test to fail with compile, as compile does not work with every PEFT feature, it still MUST
+ succeed without compile, otherwise the test is incorrect.
+
+ Before creating the PR, disable `fake_compile`.
+ """
+
+ fake_compile = False
+ model_id = "hf-internal-testing/tiny-random-OPTForCausalLM"
+ max_train_loss = 15.0 # generous threshold for maximum loss after training
+
+ @pytest.fixture(autouse=True)
+ def teardown(self):
+ r"""
+ Efficient mechanism to free GPU memory after each test. Based on
+ https://github.com/huggingface/transformers/issues/21094
+ """
+ clear_device_cache(garbage_collection=True)
+ gc.collect()
+
+ @pytest.fixture(scope="class")
+ def tokenizer(self):
+ return AutoTokenizer.from_pretrained(self.model_id)
+
+ @pytest.fixture(scope="class")
+ def data(self, tokenizer):
+ def tokenize(samples):
+ # For some reason, the max sequence length is not honored by the tokenizer, resulting in IndexErrors. Thus,
+ # manually ensure that sequences are not too long.
+ tokenized = tokenizer(samples["quote"])
+ tokenized["input_ids"] = [input_ids[: tokenizer.model_max_length] for input_ids in tokenized["input_ids"]]
+ tokenized["attention_mask"] = [
+ input_ids[: tokenizer.model_max_length] for input_ids in tokenized["attention_mask"]
+ ]
+ return tokenized
+
+ data = load_dataset_english_quotes()
+ data = data.map(tokenize, batched=True)
+ # We need to manually remove unused columns. This is because we cannot use remove_unused_columns=True in the
+ # Trainer, as this leads to errors with torch.compile. We also cannot just leave them in, as they contain
+ # strings. Therefore, manually remove all unused columns.
+ data = data.remove_columns(["quote", "author", "tags"])
+ return data
+
+ def compile(self, model, compile_kwargs):
+ compile_kwargs = compile_kwargs.copy()
+ # those are only for the Trainer arguments
+ compile_kwargs.pop("torch_compile_backend", None)
+ compile_kwargs.pop("torch_compile_mode", None)
+ if self.fake_compile:
+ return model
+ return torch.compile(model, **compile_kwargs)
+
+ @pytest.mark.parametrize("settings", SETTINGS.values(), ids=SETTINGS.keys())
+ def test_causal_lm_training_trainer_compile(self, settings, tokenizer, data, tmp_path):
+ r"""Train a PEFT model with torch.compile using Trainer"""
+ tmp_dir = tmp_path / "model"
+ config, compile_kwargs = settings
+
+ torch.manual_seed(0)
+ model = AutoModelForCausalLM.from_pretrained(
+ self.model_id,
+ device_map="auto",
+ )
+ model = get_peft_model(model, config)
+
+ # record outputs before training
+ model.eval()
+ sample = torch.tensor(data["train"][:1]["input_ids"]).to(model.device)
+ with torch.inference_mode():
+ output_before = model(sample)
+ model.train()
+
+ train_kwargs = {
+ "per_device_train_batch_size": 4,
+ "max_steps": 5,
+ "learning_rate": 1e-3,
+ "logging_steps": 1,
+ "output_dir": tmp_dir,
+ "seed": 0,
+ }
+
+ if isinstance(config, AdaLoraConfig):
+ train_kwargs["learning_rate"] = 1e-2
+
+ training_args = TrainingArguments(
+ torch_compile=not self.fake_compile,
+ torch_compile_backend=compile_kwargs.get("torch_compile_backend", None),
+ torch_compile_mode=compile_kwargs.get("torch_compile_mode", None),
+ **train_kwargs,
+ )
+ trainer = Trainer(
+ model=model,
+ train_dataset=data["train"],
+ args=training_args,
+ data_collator=DataCollatorForLanguageModeling(tokenizer, mlm=False),
+ )
+ model.config.use_cache = False
+
+ if isinstance(config, AdaLoraConfig):
+
+ class OptimizerStepCallback(TrainerCallback):
+ def on_optimizer_step(self, args, state, control, **kwargs):
+ model.update_and_allocate(state.global_step)
+
+ trainer.add_callback(OptimizerStepCallback())
+
+ trainer.train()
+
+ model.eval()
+ atol, rtol = 1e-4, 1e-4
+ with torch.inference_mode():
+ output_after = model(sample)
+ tokens_after = model.generate(sample)
+ assert torch.isfinite(output_after.logits).all()
+ # sanity check: model was updated
+ assert not torch.allclose(output_before.logits, output_after.logits, atol=atol, rtol=rtol)
+ assert trainer.state.log_history[-1]["train_loss"] < self.max_train_loss
+
+ # check saving the model and loading it without compile
+ model.save_pretrained(tmp_path)
+ del model
+ torch.manual_seed(0)
+ model = AutoModelForCausalLM.from_pretrained(self.model_id, device_map="auto")
+ model = PeftModel.from_pretrained(model, tmp_path)
+ with torch.inference_mode():
+ output_loaded = model(sample)
+ tokens_loaded = model.generate(sample)
+ assert torch.allclose(output_after.logits, output_loaded.logits, atol=atol, rtol=rtol)
+ assert (tokens_after == tokens_loaded).all()
+
+ @pytest.mark.parametrize("settings", SETTINGS.values(), ids=SETTINGS.keys())
+ def test_causal_lm_training_pytorch_compile(self, settings, tokenizer, data, tmp_path):
+ r"""Train a PEFT model with torch.compile using PyTorch training loop"""
+ torch.manual_seed(0)
+ model = AutoModelForCausalLM.from_pretrained(
+ self.model_id,
+ device_map="auto",
+ )
+ config, compile_kwargs = settings
+ model = get_peft_model(model, config)
+ if isinstance(config, AdaLoraConfig):
+ model.base_model.peft_config["default"].total_step = 5
+ model = self.compile(model, compile_kwargs)
+
+ # record outputs before training
+ model.eval()
+ sample = torch.tensor(data["train"][:1]["input_ids"]).to(model.device)
+ with torch.inference_mode():
+ output_before = model(sample)
+ model.train()
+
+ model.config.use_cache = False
+ optimizer = torch.optim.AdamW(model.parameters(), lr=1e-3)
+ batch_size = 4
+ losses = []
+ max_steps = 5 * batch_size
+ for i in range(0, max_steps, batch_size):
+ batch = tokenizer.pad(data["train"][i : i + batch_size], return_tensors="pt").to(model.device)
+ # add targets
+ batch["labels"] = batch["input_ids"].clone()
+ optimizer.zero_grad()
+ outputs = model(**batch)
+ loss = outputs.loss
+ loss.backward()
+ optimizer.step()
+ losses.append(loss.item())
+ if isinstance(config, AdaLoraConfig):
+ model.base_model.update_and_allocate(i)
+
+ model.eval()
+ with torch.inference_mode():
+ output_after = model(sample)
+ tokens_after = model.generate(sample)
+ assert torch.isfinite(output_after.logits).all()
+ atol, rtol = 1e-4, 1e-4
+ # sanity check: model was updated
+ assert not torch.allclose(output_before.logits, output_after.logits, atol=atol, rtol=rtol)
+ assert losses[-1] < self.max_train_loss
+
+ # check saving the model and loading it without compile
+ model.save_pretrained(tmp_path)
+ del model
+ torch.manual_seed(0)
+ model = AutoModelForCausalLM.from_pretrained(self.model_id, device_map="auto")
+ model = PeftModel.from_pretrained(model, tmp_path)
+ with torch.inference_mode():
+ output_loaded = model(sample)
+ tokens_loaded = model.generate(sample)
+ assert torch.allclose(output_after.logits, output_loaded.logits, atol=atol, rtol=rtol)
+ assert (tokens_after == tokens_loaded).all()
+
+ @require_bitsandbytes
+ def test_causal_lm_training_lora_bnb_compile(self, tokenizer, data, tmp_path):
+ r"""Train a bnb quantized LoRA model with torch.compile using PyTorch training loop"""
+ torch.manual_seed(0)
+ model = AutoModelForCausalLM.from_pretrained(
+ self.model_id,
+ device_map="auto",
+ quantization_config=BitsAndBytesConfig(load_in_4bit=True),
+ )
+ config = LoraConfig(task_type=TaskType.CAUSAL_LM)
+ model = get_peft_model(model, config)
+ model = self.compile(model, {})
+
+ # record outputs before training
+ model.eval()
+ sample = torch.tensor(data["train"][:1]["input_ids"]).to(model.device)
+ with torch.inference_mode():
+ output_before = model(sample)
+ model.train()
+
+ model.config.use_cache = False
+ optimizer = torch.optim.AdamW(model.parameters(), lr=1e-3)
+ batch_size = 4
+ losses = []
+ max_steps = 5 * batch_size
+ for i in range(0, max_steps, batch_size):
+ batch = tokenizer.pad(data["train"][i : i + batch_size], return_tensors="pt").to(model.device)
+ # add targets
+ batch["labels"] = batch["input_ids"].clone()
+ optimizer.zero_grad()
+ outputs = model(**batch)
+ loss = outputs.loss
+ loss.backward()
+ optimizer.step()
+ losses.append(loss.item())
+
+ model.eval()
+ with torch.inference_mode():
+ output_after = model(sample)
+ assert torch.isfinite(output_after.logits).all()
+ atol, rtol = 5e-4, 5e-4
+ # sanity check: model was updated
+ assert not torch.allclose(output_before.logits, output_after.logits, atol=atol, rtol=rtol)
+ assert losses[-1] < self.max_train_loss
+
+ # check saving the model and loading it without compile
+ model.save_pretrained(tmp_path)
+ del model
+ torch.manual_seed(0)
+ model = AutoModelForCausalLM.from_pretrained(
+ self.model_id, device_map="auto", quantization_config=BitsAndBytesConfig(load_in_4bit=True)
+ )
+ model = PeftModel.from_pretrained(model, tmp_path)
+
+ with torch.inference_mode():
+ # after loading, outputs are float32 for some reason
+ output_loaded = model(sample)
+ assert torch.allclose(output_after.logits, output_loaded.logits, atol=atol, rtol=rtol)
+
+ @require_bitsandbytes
+ def test_causal_lm_multiple_lora_adapter_compile(self, tokenizer, data):
+ torch.manual_seed(0)
+ model = AutoModelForCausalLM.from_pretrained(
+ self.model_id,
+ device_map="auto",
+ quantization_config=BitsAndBytesConfig(load_in_4bit=True),
+ ).eval()
+ sample = torch.tensor(data["train"][:1]["input_ids"]).to(model.device)
+ with torch.inference_mode():
+ output_base = model(sample)
+
+ config = LoraConfig(task_type=TaskType.CAUSAL_LM, init_lora_weights=False)
+ model = get_peft_model(model, config)
+ model.add_adapter("other", config)
+ model = self.compile(model, {})
+ model.eval()
+
+ with torch.inference_mode():
+ output_default_adapter = model(sample)
+ model.set_adapter("other")
+ with torch.inference_mode():
+ output_other_adapter = model(sample)
+
+ atol, rtol = 1e-4, 1e-4
+ # outputs of the base model != output of default adapter != output of other adapter
+ assert not torch.allclose(output_base.logits, output_default_adapter.logits, atol=atol, rtol=rtol)
+ assert not torch.allclose(output_base.logits, output_other_adapter.logits, atol=atol, rtol=rtol)
+ assert not torch.allclose(output_default_adapter.logits, output_other_adapter.logits, atol=atol, rtol=rtol)
+
+ # now delete the other adapter
+ model.delete_adapter("other")
+ model.set_adapter("default")
+ with torch.inference_mode():
+ output_after_delete = model(sample)
+
+ # outputs after delete == output of default adapter
+ assert torch.allclose(output_default_adapter.logits, output_after_delete.logits, atol=atol, rtol=rtol)
+
+ def test_causal_lm_disable_lora_adapter_compile(self, tokenizer, data):
+ torch.manual_seed(0)
+ model = AutoModelForCausalLM.from_pretrained(
+ self.model_id,
+ device_map="auto",
+ quantization_config=BitsAndBytesConfig(load_in_4bit=True),
+ ).eval()
+ sample = torch.tensor(data["train"][:1]["input_ids"]).to(model.device)
+ with torch.inference_mode():
+ output_base = model(sample)
+
+ config = LoraConfig(task_type=TaskType.CAUSAL_LM, init_lora_weights=False)
+ model = get_peft_model(model, config).eval()
+ model = self.compile(model, {})
+ output_lora = model(sample)
+
+ with model.disable_adapter():
+ with torch.inference_mode():
+ output_disabled = model(sample)
+
+ atol, rtol = 5e-4, 5e-4
+ # outputs of the base model == output disabled adapter != output of lora adapter
+ assert torch.allclose(output_base.logits, output_disabled.logits, atol=atol, rtol=rtol)
+ assert not torch.allclose(output_base.logits, output_lora.logits, atol=atol, rtol=rtol)
+
+ @require_bitsandbytes
+ def test_causal_lm_merging_lora_adapter_compile(self, tokenizer, data):
+ # merge the adapter
+ torch.manual_seed(0)
+ model = AutoModelForCausalLM.from_pretrained(
+ self.model_id,
+ device_map="auto",
+ quantization_config=BitsAndBytesConfig(load_in_4bit=True),
+ ).eval()
+ sample = torch.tensor(data["train"][:1]["input_ids"]).to(model.device)
+ with torch.inference_mode():
+ output_base = model(sample)
+
+ config = LoraConfig(task_type=TaskType.CAUSAL_LM, init_lora_weights=False)
+ model = get_peft_model(model, config).eval()
+ with torch.inference_mode():
+ output_lora = model(sample)
+
+ model.merge_adapter()
+ with torch.inference_mode():
+ output_merged = model(sample)
+
+ # merging is less precise, be more tolerant
+ atol, rtol = 1e-1, 1e-1
+ # outputs of the base model != output of lora adapter == output of merged adapter
+ assert not torch.allclose(output_base.logits, output_lora.logits, atol=atol, rtol=rtol)
+ assert torch.allclose(output_lora.logits, output_merged.logits, atol=atol, rtol=rtol)
+
+ @require_bitsandbytes
+ def test_causal_lm_merging_multiple_lora_adapters_compile(self, tokenizer, data):
+ # merge multiple adapters at once
+ torch.manual_seed(0)
+ model = AutoModelForCausalLM.from_pretrained(
+ self.model_id,
+ device_map="auto",
+ quantization_config=BitsAndBytesConfig(load_in_4bit=True),
+ ).eval()
+ sample = torch.tensor(data["train"][:1]["input_ids"]).to(model.device)
+ with torch.inference_mode():
+ output_base = model(sample)
+
+ config = LoraConfig(task_type=TaskType.CAUSAL_LM, init_lora_weights=False)
+ model = get_peft_model(model, config).eval()
+ model.add_adapter("other", config)
+ with torch.inference_mode():
+ output_default = model(sample)
+
+ model.set_adapter("other")
+ with torch.inference_mode():
+ output_other = model(sample)
+
+ model.base_model.merge_adapter(["default", "other"])
+ with torch.inference_mode():
+ output_merged = model(sample)
+
+ # merging is less precise, be more tolerant
+ atol, rtol = 1e-1, 1e-1
+ # outputs of the base model != output of default adapter != output of other adapter
+ assert not torch.allclose(output_base.logits, output_default.logits, atol=atol, rtol=rtol)
+ assert not torch.allclose(output_base.logits, output_other.logits, atol=atol, rtol=rtol)
+ assert not torch.allclose(output_default.logits, output_other.logits, atol=atol, rtol=rtol)
+ # outputs of merged adapter != all others
+ assert not torch.allclose(output_base.logits, output_merged.logits, atol=atol, rtol=rtol)
+ assert not torch.allclose(output_default.logits, output_merged.logits, atol=atol, rtol=rtol)
+ assert not torch.allclose(output_other.logits, output_merged.logits, atol=atol, rtol=rtol)
+
+ @require_bitsandbytes
+ def test_causal_lm_merge_and_unload_lora_adapter_compile(self, tokenizer, data):
+ torch.manual_seed(0)
+ model = AutoModelForCausalLM.from_pretrained(
+ self.model_id,
+ device_map="auto",
+ quantization_config=BitsAndBytesConfig(load_in_4bit=True),
+ ).eval()
+ sample = torch.tensor(data["train"][:1]["input_ids"]).to(model.device)
+ with torch.inference_mode():
+ output_base = model(sample)
+
+ config = LoraConfig(task_type=TaskType.CAUSAL_LM, init_lora_weights=False)
+ model = get_peft_model(model, config).eval()
+ model = self.compile(model, {})
+ with torch.inference_mode():
+ output_lora = model(sample)
+
+ unloaded = model.merge_and_unload()
+ with torch.inference_mode():
+ output_unloaded = unloaded(sample)
+
+ # merging is less precise, be more tolerant
+ atol, rtol = 1e-1, 1e-1
+ # outputs of the base model != output of lora adapter == output of unloaded adapter
+ assert not torch.allclose(output_base.logits, output_lora.logits, atol=atol, rtol=rtol)
+ assert torch.allclose(output_lora.logits, output_unloaded.logits, atol=atol, rtol=rtol)
+
+ @require_bitsandbytes
+ def test_causal_lm_mixed_batch_lora_adapter_compile(self, tokenizer, data):
+ torch.manual_seed(0)
+ model = AutoModelForCausalLM.from_pretrained(
+ self.model_id,
+ device_map="auto",
+ quantization_config=BitsAndBytesConfig(load_in_4bit=True),
+ ).eval()
+
+ # we need at least 3 samples for this to work!
+ sample = {
+ "input_ids": torch.arange(12).reshape(3, 4).to("cuda"),
+ "attention_mask": torch.ones(3, 4).long().to("cuda"),
+ }
+
+ with torch.inference_mode():
+ output_base = model(**sample)
+
+ config = LoraConfig(task_type=TaskType.CAUSAL_LM, init_lora_weights=False)
+ model = get_peft_model(model, config).eval()
+ with torch.inference_mode():
+ output_default = model(**sample)
+
+ model.add_adapter("other", config)
+ model.set_adapter("other")
+ with torch.inference_mode():
+ output_other = model(**sample)
+
+ model = self.compile(model, {})
+
+ # set adapter_indices so that it alternates between 0 (base), lora 1, and lora 2
+ adapter_names = ["__base__", "default", "other"]
+ with torch.inference_mode():
+ output_mixed = model(**sample, adapter_names=adapter_names)
+
+ atol, rtol = 5e-4, 5e-4
+ # outputs of the base model != output of lora adapter 1 != output of other adapter
+ assert not torch.allclose(output_base.logits, output_default.logits, atol=atol, rtol=rtol)
+ assert not torch.allclose(output_default.logits, output_other.logits, atol=atol, rtol=rtol)
+ assert not torch.allclose(output_other.logits, output_mixed.logits, atol=atol, rtol=rtol)
+ # outputs of mixed adapter is mix of all 3
+ assert torch.allclose(output_base.logits[0], output_mixed.logits[0], atol=atol, rtol=rtol)
+ assert torch.allclose(output_default.logits[1], output_mixed.logits[1], atol=atol, rtol=rtol)
+ assert torch.allclose(output_other.logits[2], output_mixed.logits[2], atol=atol, rtol=rtol)
+
+ @require_bitsandbytes
+ def test_causal_lm_add_weighted_adapter_lora_adapter_compile(self, tokenizer, data):
+ torch.manual_seed(0)
+ model = AutoModelForCausalLM.from_pretrained(
+ self.model_id,
+ device_map="auto",
+ quantization_config=BitsAndBytesConfig(load_in_4bit=True),
+ ).eval()
+ sample = torch.tensor(data["train"][:1]["input_ids"]).to(model.device)
+ with torch.inference_mode():
+ output_base = model(sample)
+
+ config = LoraConfig(task_type=TaskType.CAUSAL_LM, init_lora_weights=False)
+ model = get_peft_model(model, config).eval()
+ model.add_adapter("other", config)
+ with torch.inference_mode():
+ output_default = model(sample)
+
+ model.set_adapter("other")
+ with torch.inference_mode():
+ output_other = model(sample)
+
+ model.add_weighted_adapter(["default", "other"], [0.5, 0.5], adapter_name="combined")
+ model.set_adapter("combined")
+ with torch.inference_mode():
+ output_combined = model(sample)
+
+ atol, rtol = 1e-4, 1e-4
+ # outputs of the base model != output of default adapter != output of other adapter
+ assert not torch.allclose(output_base.logits, output_default.logits, atol=atol, rtol=rtol)
+ assert not torch.allclose(output_base.logits, output_other.logits, atol=atol, rtol=rtol)
+ assert not torch.allclose(output_default.logits, output_other.logits, atol=atol, rtol=rtol)
+ # outputs of combined adapter != all others
+ assert not torch.allclose(output_base.logits, output_combined.logits, atol=atol, rtol=rtol)
+ assert not torch.allclose(output_default.logits, output_combined.logits, atol=atol, rtol=rtol)
+ assert not torch.allclose(output_other.logits, output_combined.logits, atol=atol, rtol=rtol)
diff --git a/peft/tests/test_trainable_tokens.py b/peft/tests/test_trainable_tokens.py
new file mode 100644
index 0000000000000000000000000000000000000000..38b32b06ed35f89c730af9d11945f9c7924d1f67
--- /dev/null
+++ b/peft/tests/test_trainable_tokens.py
@@ -0,0 +1,920 @@
+# Copyright 2025-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+from __future__ import annotations
+
+import copy
+
+import pytest
+import torch
+from safetensors.torch import load_file as safe_load_file
+from transformers import AutoModelForCausalLM, AutoModelForSeq2SeqLM, AutoTokenizer
+
+from peft import AutoPeftModel, LoraConfig, PeftModel, TrainableTokensConfig, get_peft_model
+from peft.tuners.trainable_tokens.layer import TrainableTokensLayer
+from peft.utils import TrainableTokensWrapper, get_peft_model_state_dict
+
+from .testing_utils import hub_online_once
+
+
+class ModelEmb(torch.nn.Module):
+ def __init__(self):
+ super().__init__()
+ self.emb = torch.nn.Embedding(100, 10)
+ self.lin0 = torch.nn.Linear(10, 1)
+
+ def forward(self, x):
+ return self.lin0(self.emb(x))
+
+ def get_input_embeddings(self):
+ return self.emb
+
+
+class ModelEmbedIn(torch.nn.Module):
+ def __init__(self):
+ super().__init__()
+ self.embed_in = torch.nn.Embedding(100, 10)
+ self.lin0 = torch.nn.Linear(10, 1)
+
+ def forward(self, x):
+ return self.lin0(self.embed_in(x))
+
+ def get_input_embeddings(self):
+ return self.embed_in
+
+
+class ModelEmbedMultiple(torch.nn.Module):
+ def __init__(self):
+ super().__init__()
+ self.embed_in = torch.nn.Embedding(100, 10)
+ self.embed_in_2 = torch.nn.Embedding(100, 10)
+ self.lin0 = torch.nn.Linear(10, 1)
+
+ def forward(self, x):
+ return self.lin0(self.embed_in(x) + self.embed_in_2(x))
+
+ def get_input_embeddings(self):
+ return self.embed_in
+
+
+class ModelEmbedInNoGet(torch.nn.Module):
+ def __init__(self):
+ super().__init__()
+ self.embed_in = torch.nn.Embedding(100, 10)
+ self.lin0 = torch.nn.Linear(10, 1)
+
+ def forward(self, x):
+ return self.lin0(self.embed_in(x))
+
+
+class TestTrainableTokens:
+ @pytest.fixture
+ def model_id(self):
+ return "trl-internal-testing/tiny-random-LlamaForCausalLM"
+
+ @pytest.fixture
+ def model_multi_embedding(self):
+ class MultiEmbeddingMLP(torch.nn.Module):
+ def __init__(self):
+ super().__init__()
+ self.emb_text = torch.nn.Embedding(10, 5)
+ self.emb_image = torch.nn.Embedding(8, 5)
+ self.lin0 = torch.nn.Linear(5, 10)
+ self.lin1 = torch.nn.Linear(10, 20)
+
+ def forward(self, x_text, x_image):
+ x_text = self.emb_text(x_text)
+ x_image = self.emb_image(x_image)
+ y = self.lin0(torch.concat([x_text, x_image], dim=1).view(-1, 5))
+ y = self.lin1(y)
+ return y, (x_text, x_image)
+
+ return MultiEmbeddingMLP()
+
+ @pytest.fixture
+ def model(self, model_id):
+ with hub_online_once(model_id):
+ # This must not be a yield fixture so that we don't carry the hub_online_once
+ # behavior over to the rest of the test that uses this fixture
+ return AutoModelForCausalLM.from_pretrained(model_id)
+
+ @pytest.fixture
+ def tokenizer(self, model_id):
+ return AutoTokenizer.from_pretrained(model_id)
+
+ def simulate_training(self, trainable_tokens_layer, adapter_name="default"):
+ """Simulates training of trainable_tokens adapter layer by assigning random
+ values to the delta tokens.
+ """
+ trainable_tokens_layer.trainable_tokens_delta[adapter_name].data = torch.rand_like(
+ trainable_tokens_layer.trainable_tokens_delta[adapter_name].data
+ )
+
+ def test_stand_alone_usage(self, model, tokenizer, tmp_path):
+ original_model = copy.deepcopy(model)
+
+ peft_config = TrainableTokensConfig(target_modules=["embed_tokens"], token_indices=[0, 1, 3])
+ peft_model = get_peft_model(model, peft_config)
+ save_path = tmp_path / "stand_alone_usage"
+
+ # simulate normal use but take care to use the tokens that we expect to be modified
+ # (+1 that we don't expect to be modified)
+ X = {
+ "input_ids": torch.tensor([[0, 1, 2, 3]]),
+ "attention_mask": torch.tensor([[1, 1, 1, 1]]),
+ }
+
+ idcs_to_modify = peft_config.token_indices
+ idcs_to_keep = [i for i in X["input_ids"][0].tolist() if i not in idcs_to_modify]
+
+ self.simulate_training(peft_model.model.model.embed_tokens)
+ output_train = peft_model(output_hidden_states=True, **X)
+
+ peft_model.save_pretrained(save_path)
+ peft_model_org = peft_model
+
+ # check whether the token indices differ from the base model after loading the model
+ # from the checkpoint.
+ peft_model = AutoPeftModel.from_pretrained(save_path)
+ output_load = peft_model(output_hidden_states=True, **X)
+ output_orig = original_model(output_hidden_states=True, **X)
+
+ # on the way, make sure that the embedding matrix itself was not modified
+ assert torch.allclose(
+ peft_model.model.model.embed_tokens.weight,
+ peft_model_org.model.model.embed_tokens.weight,
+ )
+
+ W_load = output_load.hidden_states[0]
+ W_orig = output_orig.hidden_states[0]
+ W_train = output_train.hidden_states[0]
+
+ # all PEFT model embed outputs must equal the outputs during 'training' to make sure
+ # that saving/loading works properly.
+ assert torch.allclose(W_load, W_train)
+
+ assert not torch.allclose(W_load[:, idcs_to_modify], W_orig[:, idcs_to_modify])
+ assert torch.allclose(W_load[:, idcs_to_keep], W_orig[:, idcs_to_keep])
+
+ @pytest.mark.parametrize(
+ "peft_config",
+ [
+ LoraConfig(
+ target_modules="all-linear",
+ trainable_token_indices={"embed_tokens": [0, 1, 3]},
+ ),
+ ],
+ )
+ def test_combined_with_peft_method_usage(self, model, tokenizer, peft_config, tmp_path):
+ original_model = copy.deepcopy(model)
+ peft_model = get_peft_model(model, peft_config)
+ save_path = tmp_path / "combined_usage"
+
+ # simulate normal use but take care to use the tokens that we expect to be modified
+ # (+2 that we don't expect to be modified)
+ X = {
+ "input_ids": torch.tensor([[0, 1, 2, 3, 4]]),
+ "attention_mask": torch.tensor([[1, 1, 1, 1, 1]]),
+ }
+
+ idcs_to_modify = peft_config.trainable_token_indices["embed_tokens"]
+ idcs_to_keep = [i for i in X["input_ids"][0].tolist() if i not in idcs_to_modify]
+
+ self.simulate_training(peft_model.model.model.embed_tokens.token_adapter)
+ output_train = peft_model(output_hidden_states=True, **X)
+
+ peft_model.save_pretrained(save_path)
+ peft_model_org = peft_model
+
+ # check whether the token indices differ from the base model
+ peft_model = AutoPeftModel.from_pretrained(save_path)
+ output_load = peft_model(output_hidden_states=True, **X)
+ output_orig = original_model(output_hidden_states=True, **X)
+
+ W_load = output_load.hidden_states[0]
+ W_orig = output_orig.hidden_states[0]
+ W_train = output_train.hidden_states[0]
+
+ # all PEFT model embed outputs must equal the outputs during 'training' to make sure
+ # that saving/loading works properly.
+ assert torch.allclose(W_load, W_train)
+
+ assert not torch.allclose(W_load[:, idcs_to_modify], W_orig[:, idcs_to_modify])
+ assert torch.allclose(W_load[:, idcs_to_keep], W_orig[:, idcs_to_keep])
+
+ def test_basic_training(self, model, tokenizer):
+ # ensure that the model can be trained and backpropagation works
+ config = TrainableTokensConfig(
+ target_modules=["embed_tokens"],
+ token_indices=[0, 10],
+ )
+
+ model = get_peft_model(model, config)
+ optimizer = torch.optim.AdamW(model.parameters(), lr=1)
+
+ initial_delta = model.model.model.embed_tokens.trainable_tokens_delta.default.clone()
+ initial_originals = model.model.model.embed_tokens.trainable_tokens_original.default.clone()
+
+ X = {
+ "input_ids": torch.tensor([[0, 1, 2, 3, 4]]),
+ "attention_mask": torch.tensor([[1, 1, 1, 1, 1]]),
+ }
+
+ for step in range(3):
+ optimizer.zero_grad()
+ y_pred = model(**X)
+ loss = y_pred.logits.mean()
+ loss.backward()
+ optimizer.step()
+
+ assert torch.allclose(
+ model.model.model.embed_tokens.trainable_tokens_original.default,
+ initial_originals,
+ )
+ assert not torch.allclose(
+ model.model.model.embed_tokens.trainable_tokens_delta.default,
+ initial_delta,
+ )
+
+ @pytest.mark.parametrize(
+ "peft_config",
+ [
+ LoraConfig(
+ target_modules="all-linear",
+ trainable_token_indices={"embed_tokens": [0, 1, 3]},
+ ),
+ ],
+ )
+ def test_disable_adapters_with_merging(self, model, tokenizer, peft_config):
+ X = {
+ "input_ids": torch.tensor([[0, 1, 2, 3, 4]]),
+ "attention_mask": torch.tensor([[1, 1, 1, 1, 1]]),
+ }
+
+ model = get_peft_model(model, peft_config)
+ model.eval()
+
+ outputs_before = model(**X).logits
+
+ model.train()
+ lr = 0.01
+ optimizer = torch.optim.Adam(model.parameters(), lr=lr)
+
+ # train at least 3 steps for all parameters to be updated (probably this is required because of symmetry
+ # breaking of some LoRA layers that are initialized with constants)
+ for _ in range(3):
+ optimizer.zero_grad()
+ y_pred = model(**X)
+ loss = y_pred.logits.mean()
+ loss.backward()
+ optimizer.step()
+
+ model.eval()
+ outputs_unmerged = model(**X).logits
+ model.merge_adapter()
+ outputs_after = model(**X).logits
+
+ with model.disable_adapter():
+ outputs_disabled = model(**X).logits
+
+ # check that after leaving the disable_adapter context, everything is enabled again
+ outputs_enabled_after_disable = model(**X).logits
+
+ atol, rtol = 1e-5, 1e-5 # tolerances higher than defaults since merging introduces some numerical instability
+
+ # check that there is a difference in results after training
+ assert not torch.allclose(outputs_before, outputs_after, atol=atol, rtol=rtol)
+
+ # unmerged or merged should make no difference
+ assert torch.allclose(outputs_after, outputs_unmerged, atol=atol, rtol=rtol)
+
+ # check that disabling adapters gives the same results as before training
+ assert torch.allclose(outputs_before, outputs_disabled, atol=atol, rtol=rtol)
+
+ # check that enabling + disabling adapters does not change the results
+ assert torch.allclose(outputs_after, outputs_enabled_after_disable, atol=atol, rtol=rtol)
+
+ @pytest.mark.parametrize(
+ "peft_config",
+ [
+ LoraConfig(
+ target_modules="all-linear",
+ trainable_token_indices={"embed_tokens": [0, 1, 3]},
+ ),
+ ],
+ )
+ def test_safe_merge_with_adapter(self, model, tokenizer, peft_config):
+ X = {
+ "input_ids": torch.tensor([[0, 1, 2, 3]]),
+ "attention_mask": torch.tensor([[1, 1, 1, 1]]),
+ }
+
+ model = model.eval()
+ logits_base = model(**X).logits
+
+ model = get_peft_model(model, peft_config).eval()
+ logits_peft = model(**X).logits
+
+ atol, rtol = 1e-6, 1e-6 # default
+
+ model_unloaded = model.merge_and_unload(safe_merge=True)
+ logits_unloaded = model_unloaded(**X).logits
+
+ # check that the logits are the same after unloading
+ assert torch.allclose(logits_peft, logits_unloaded, atol=atol, rtol=rtol)
+
+ @pytest.mark.parametrize(
+ "peft_config",
+ [
+ LoraConfig(
+ target_modules="all-linear",
+ trainable_token_indices={"embed_tokens": [0, 1, 3]},
+ ),
+ ],
+ )
+ def test_load_multiple_adapters(self, model, peft_config, tmp_path):
+ # tests if having more than one adpater (even with just the same config) works
+ original_model = copy.deepcopy(model)
+ model = get_peft_model(model, peft_config)
+
+ model.save_pretrained(tmp_path)
+ del model
+
+ model = original_model
+ model = PeftModel.from_pretrained(model, tmp_path)
+ load_result1 = model.load_adapter(tmp_path, adapter_name="other")
+ load_result2 = model.load_adapter(tmp_path, adapter_name="yet-another")
+
+ assert load_result1.missing_keys == []
+ assert load_result2.missing_keys == []
+
+ @pytest.mark.parametrize(
+ "peft_config_factory",
+ [
+ lambda token_indices: LoraConfig(
+ target_modules="all-linear",
+ trainable_token_indices={"embed_tokens": token_indices},
+ ),
+ ],
+ )
+ def test_multiple_adapters_different_token_indices(self, model, peft_config_factory, tmp_path):
+ # tests if multiple adapters with different token indices work
+ original_model = copy.deepcopy(model)
+
+ token_indices_1 = [0, 1, 2]
+ token_indices_2 = [2, 3, 4]
+
+ peft_config_1 = peft_config_factory(token_indices_1)
+ peft_config_2 = peft_config_factory(token_indices_2)
+
+ model = get_peft_model(model, peft_config_1, adapter_name="adapter_1")
+ model.add_adapter("adapter_2", peft_config_2)
+
+ # "train" adapter 1
+ model.set_adapter("adapter_1")
+ self.simulate_training(model.model.model.embed_tokens.token_adapter, "adapter_1")
+
+ # "train" adapter 2
+ model.set_adapter("adapter_2")
+ self.simulate_training(model.model.model.embed_tokens.token_adapter, "adapter_2")
+
+ # now we infer on adapter 1 and on adapter 2 and check if the requested indices are changed for
+ # each adapter. e.g., for adapter 1, only token indices 1 should be changed.
+ X = {
+ "input_ids": torch.tensor([list(set(token_indices_1 + token_indices_2))]),
+ "attention_mask": torch.tensor([[1] * (len(set(token_indices_1 + token_indices_2)))]),
+ }
+
+ original_output = original_model(output_hidden_states=True, **X).hidden_states[0]
+
+ # infer with adapter 1, embeddings for token indices 1 should be changed, no others.
+ model.set_adapter("adapter_1")
+ adapter_1_output = model(output_hidden_states=True, **X).hidden_states[0]
+
+ idcs_to_modify = token_indices_1
+ idcs_to_keep = [i for i in X["input_ids"][0].tolist() if i not in idcs_to_modify]
+
+ assert not torch.allclose(adapter_1_output[:, idcs_to_modify], original_output[:, idcs_to_modify])
+ assert torch.allclose(adapter_1_output[:, idcs_to_keep], original_output[:, idcs_to_keep])
+
+ # infer with adapter 2, embeddings for token indices 2 should be changed, no others.
+ model.set_adapter("adapter_2")
+ adapter_2_output = model(output_hidden_states=True, **X).hidden_states[0]
+
+ idcs_to_modify = token_indices_2
+ idcs_to_keep = [i for i in X["input_ids"][0].tolist() if i not in idcs_to_modify]
+
+ assert not torch.allclose(adapter_2_output[:, idcs_to_modify], original_output[:, idcs_to_modify])
+ assert torch.allclose(adapter_2_output[:, idcs_to_keep], original_output[:, idcs_to_keep])
+
+ @pytest.mark.parametrize(
+ "peft_config_factory",
+ [
+ lambda token_indices: LoraConfig(
+ target_modules="all-linear",
+ trainable_token_indices={"embed_tokens": token_indices},
+ ),
+ ],
+ )
+ def test_multiple_adapters_overlapping_token_indices_merging(self, model, peft_config_factory, tmp_path):
+ # tests that merging multiple adapters that have overlapping indices is not defined at the moment
+ # and would yield undefined behavior. note that merging a single adapter is fine.
+ original_model = copy.deepcopy(model)
+
+ token_indices_1 = [0, 1, 2]
+ token_indices_2 = [2, 3, 4]
+
+ peft_config_1 = peft_config_factory(token_indices_1)
+ peft_config_2 = peft_config_factory(token_indices_2)
+
+ model = get_peft_model(model, peft_config_1, adapter_name="adapter_1")
+ model.add_adapter("adapter_2", peft_config_2)
+
+ with pytest.raises(ValueError) as e:
+ model.merge_and_unload(adapter_names=["adapter_1", "adapter_2"])
+ assert "are already defined and would result in undefined merging behavior" in str(e)
+
+ @pytest.mark.parametrize(
+ "peft_config_factory",
+ [
+ lambda targets, token_indices: LoraConfig(
+ target_modules=targets,
+ trainable_token_indices={"embed_tokens": token_indices},
+ ),
+ ],
+ )
+ def test_multiple_adapters_mixed_forward(self, model, peft_config_factory, tmp_path):
+ # tests if multiple adapters with different token indices work
+ original_model = copy.deepcopy(model)
+
+ token_indices_1 = [0, 1, 2]
+ token_indices_2 = [2, 3, 4]
+
+ peft_config_1 = peft_config_factory(".*q_proj", token_indices_1)
+ peft_config_2 = peft_config_factory(".*o_proj", token_indices_2)
+
+ model = get_peft_model(model, peft_config_1, adapter_name="adapter_1")
+ model.add_adapter("adapter_2", peft_config_2)
+
+ # "train" adapter 1
+ model.set_adapter("adapter_1")
+ self.simulate_training(model.model.model.embed_tokens.token_adapter, "adapter_1")
+
+ # "train" adapter 2
+ model.set_adapter("adapter_2")
+ self.simulate_training(model.model.model.embed_tokens.token_adapter, "adapter_2")
+
+ # forward(adapter_names=...) is not available in train mode
+ model.eval()
+
+ # Build a batch of 2 items, each the same input sequence but each sequence will be passed to a different
+ # adapter via mixed batch forward.
+ input_sequence = list(set(token_indices_1 + token_indices_2))
+ X = {
+ "input_ids": torch.tensor([input_sequence, input_sequence]),
+ "attention_mask": torch.tensor([[1] * len(input_sequence), [1] * len(input_sequence)]),
+ }
+ batch_adapter_names = ["adapter_1", "adapter_2"]
+
+ original_output = original_model(output_hidden_states=True, **X)
+ mixed_output = model(output_hidden_states=True, adapter_names=batch_adapter_names, **X)
+
+ # check that the active adapter is still the last activated adapter, adapter_2
+ assert model.model.model.embed_tokens.token_adapter.active_adapter == ["adapter_2"]
+
+ adapter_1_output = mixed_output.hidden_states[0][0:1]
+ original_output_1 = original_output.hidden_states[0][0:1]
+ adapter_2_output = mixed_output.hidden_states[0][1:2]
+ original_output_2 = original_output.hidden_states[0][1:2]
+
+ idcs_to_modify = token_indices_1
+ idcs_to_keep = [i for i in X["input_ids"][0].tolist() if i not in idcs_to_modify]
+
+ assert not torch.allclose(adapter_1_output[:, idcs_to_modify], original_output_1[:, idcs_to_modify])
+ assert torch.allclose(adapter_1_output[:, idcs_to_keep], original_output_1[:, idcs_to_keep])
+
+ idcs_to_modify = token_indices_2
+ idcs_to_keep = [i for i in X["input_ids"][0].tolist() if i not in idcs_to_modify]
+
+ assert not torch.allclose(adapter_2_output[:, idcs_to_modify], original_output_2[:, idcs_to_modify])
+ assert torch.allclose(adapter_2_output[:, idcs_to_keep], original_output_2[:, idcs_to_keep])
+
+ def test_stand_alone_raises_target_layer_not_found(self, model):
+ config = TrainableTokensConfig(target_modules=["doesnt_exist"], token_indices=[0, 1, 3])
+ with pytest.raises(ValueError) as e:
+ model = get_peft_model(model, config)
+ assert "Target modules ['doesnt_exist'] not found in the base model." in str(e)
+
+ @pytest.mark.parametrize(
+ "peft_config, target_layer_name",
+ [
+ (LoraConfig(trainable_token_indices={"does-not-exist": [0, 1, 2]}), "does-not-exist"),
+ ],
+ )
+ def test_combined_with_peft_raises_target_layer_not_found(self, model, peft_config, target_layer_name):
+ # same as test_stand_alone_raises_target_layer_not_found but tests the peft method integration
+ with pytest.raises(ValueError) as e:
+ model = get_peft_model(model, peft_config)
+ assert f"Target modules {{{repr(target_layer_name)}}} not found in the base model." in str(e)
+
+ def test_multiple_targets(self, model_multi_embedding):
+ # tests the ability of targeting two modules with the same token indices
+ original_model = copy.deepcopy(model_multi_embedding)
+ config = TrainableTokensConfig(target_modules=["emb_text", "emb_image"], token_indices=[0, 1])
+ peft_model = get_peft_model(model_multi_embedding, config)
+
+ self.simulate_training(peft_model.model.emb_text)
+ self.simulate_training(peft_model.model.emb_image)
+
+ X = {
+ "x_text": torch.tensor([[0, 1, 2]]),
+ "x_image": torch.tensor([[0, 1, 2]]),
+ }
+
+ _, (emb_text_orig, emb_image_orig) = original_model(**X)
+ _, (emb_text_peft, emb_image_peft) = peft_model(**X)
+
+ assert not torch.allclose(emb_text_orig[:, [0, 1]], emb_text_peft[:, [0, 1]])
+ assert torch.allclose(emb_text_orig[:, [2]], emb_text_peft[:, [2]])
+ assert not torch.allclose(emb_image_orig[:, [0, 1]], emb_image_peft[:, [0, 1]])
+ assert torch.allclose(emb_image_orig[:, [2]], emb_image_peft[:, [2]])
+
+ @pytest.mark.parametrize(
+ "peft_config",
+ [
+ LoraConfig(
+ target_modules="all-linear",
+ trainable_token_indices={"embed_tokens": [0, 1, 3]},
+ ),
+ ],
+ )
+ def test_no_embeddings_in_save_with_combined_usage(self, model, tokenizer, peft_config, tmp_path):
+ # make sure that in combined use the only state dict key is that of the token deltas and nothing more
+
+ peft_model = get_peft_model(model, peft_config)
+ state_dict = get_peft_model_state_dict(
+ model=peft_model,
+ state_dict=None,
+ adapter_name="default",
+ )
+
+ embedding_keys = [n for n in state_dict.keys() if "embed_tokens" in n]
+ assert embedding_keys == ["base_model.model.model.embed_tokens.token_adapter.trainable_tokens_delta"]
+
+ @pytest.fixture()
+ def model_weight_untied(self, model):
+ return model
+
+ @pytest.fixture()
+ def model_id_weight_tied(self):
+ return "facebook/opt-125m"
+
+ @pytest.fixture()
+ def model_weight_tied(self, model_id_weight_tied):
+ return AutoModelForCausalLM.from_pretrained(model_id_weight_tied)
+
+ @pytest.mark.parametrize(
+ "peft_config",
+ [
+ LoraConfig(
+ target_modules="all-linear",
+ trainable_token_indices={"embed_tokens": [0, 1, 3]},
+ ),
+ ],
+ )
+ def test_weight_tying_noop_when_model_is_untied(self, model_weight_untied, peft_config, tmp_path):
+ # test if the weight tying is affected as well when we modified the embedding.
+ assert model_weight_untied._tied_weights_keys
+ assert not model_weight_untied.config.tie_word_embeddings
+
+ peft_model = get_peft_model(model_weight_untied, peft_config)
+ assert hasattr(peft_model.model.model.embed_tokens, "token_adapter")
+ assert not hasattr(peft_model.model.lm_head, "token_adapter")
+
+ @pytest.mark.parametrize(
+ "peft_config",
+ [
+ LoraConfig(
+ target_modules="all-linear",
+ trainable_token_indices={"embed_tokens": [0, 1, 3]},
+ ),
+ ],
+ )
+ def test_weight_tying_applied_when_model_is_tied(self, model_weight_tied, peft_config, tmp_path):
+ # test if the weight tying is affected as well when we modified the embedding.
+ assert model_weight_tied._tied_weights_keys
+ assert model_weight_tied.config.tie_word_embeddings
+
+ peft_model = get_peft_model(model_weight_tied, peft_config)
+
+ # make it so that the input embeddings diverge. when the weights are tied this should
+ # reflect in the output embeddings as well.
+ self.simulate_training(peft_model.model.model.decoder.embed_tokens.token_adapter)
+
+ # we have to find out if the input embedding tying is doing its job during forward.
+ # for this we can leverage the fact that emb_out(1/emb_in(x)) is embed_dim on the
+ # diagonal iff emb_in.weight == emb_out.weight.
+ token_indices = [0, 1, 2, 3]
+ emb_dim = 768
+ emb_in = peft_model.model.model.decoder.embed_tokens(torch.tensor([token_indices]))
+ emb_out = peft_model.model.lm_head(1 / emb_in)
+
+ assert torch.allclose(torch.diag(emb_out[0]), torch.tensor([emb_dim] * len(token_indices)).float())
+
+ # make sure that the state dict does not include weight-tied weights.
+ state_dict = get_peft_model_state_dict(peft_model)
+ assert not [key for key in state_dict if any(tied_key in key for tied_key in peft_model._tied_weights_keys)]
+
+ # make sure that merging and unloading restores the weight-tying.
+ merged_model = peft_model.merge_and_unload()
+
+ assert merged_model.model.decoder.embed_tokens.weight.data_ptr() == merged_model.lm_head.weight.data_ptr()
+
+ def test_weight_tying_applied_when_model_is_tied_standalone(self, model_weight_tied):
+ # since weight tying is currently not supported make sure that an error is raised when attempting
+ # to use a model that has tied input/output embeddings
+ assert model_weight_tied._tied_weights_keys
+ assert model_weight_tied.config.tie_word_embeddings
+
+ peft_config = TrainableTokensConfig(
+ target_modules=["embed_tokens"],
+ token_indices=[0, 1, 3],
+ )
+
+ peft_model = get_peft_model(model_weight_tied, peft_config)
+
+ # make it so that the input embeddings diverge. when the weights are tied this should
+ # reflect in the output embeddings as well.
+ self.simulate_training(peft_model.model.model.decoder.embed_tokens)
+
+ # we have to find out if the input embedding tying is doing its job during forward.
+ # for this we can leverage the fact that emb_out(1/emb_in(x)) is embed_dim on the
+ # diagonal iff emb_in.weight == emb_out.weight.
+ token_indices = [0, 1, 2, 3]
+ emb_dim = 768
+ emb_in = peft_model.model.model.decoder.embed_tokens(torch.tensor([token_indices]))
+ emb_out = peft_model.model.lm_head(1 / emb_in)
+
+ assert torch.allclose(torch.diag(emb_out[0]), torch.tensor([emb_dim] * len(token_indices)).float())
+
+ # make sure that the state dict does not include weight-tied weights.
+ state_dict = get_peft_model_state_dict(peft_model)
+ assert not [key for key in state_dict if any(tied_key in key for tied_key in peft_model._tied_weights_keys)]
+
+ # make sure that merging and unloading restores the weight-tying.
+ merged_model = peft_model.merge_and_unload()
+
+ assert merged_model.model.decoder.embed_tokens.weight.data_ptr() == merged_model.lm_head.weight.data_ptr()
+
+ def test_weight_tying_normally_issues_warning(self, model_weight_tied, recwarn):
+ # When using models with weight tying and targeting the embedding or the tied layer should raise a warning.
+ peft_config = LoraConfig(target_modules=["embed_tokens"])
+ peft_model = get_peft_model(model_weight_tied, peft_config)
+
+ warnings = [w.message.args[0] for w in recwarn]
+ warnings = [msg for msg in warnings if "Model with `tie_word_embeddings=True` and the" in msg]
+ assert warnings
+
+ def test_weight_tying_state_dict_ignores_tied_weights(self, model_weight_tied):
+ # since weight tying is currently not supported make sure that an error is raised when attempting
+ # to use a model that has tied input/output embeddings
+ assert model_weight_tied._tied_weights_keys
+ assert model_weight_tied.config.tie_word_embeddings
+
+ peft_config = TrainableTokensConfig(
+ target_modules=["embed_tokens"],
+ token_indices=[0, 1, 3],
+ )
+
+ peft_model = get_peft_model(model_weight_tied, peft_config)
+
+ state_dict = peft_model.state_dict()
+ peft_state_dict = get_peft_model_state_dict(peft_model)
+
+ # the state dict or the peft model state dict must not include tied adapter weights
+ state_dict_keys = [n for n, _ in state_dict.items() if "tied_adapter." in n]
+ peft_state_dict_keys = [n for n, _ in peft_state_dict.items() if "tied_adapter." in n]
+
+ assert not state_dict_keys
+ assert not peft_state_dict_keys
+
+ @pytest.mark.parametrize(
+ "peft_config",
+ [
+ LoraConfig(
+ target_modules="all-linear",
+ trainable_token_indices={"shared": [0, 1, 3]},
+ ),
+ ],
+ )
+ def test_weight_tying_applied_when_model_is_tied_encoder_decoder(self, peft_config):
+ model_id = "hf-internal-testing/tiny-random-t5"
+ base_model = AutoModelForSeq2SeqLM.from_pretrained(model_id)
+
+ peft_model = get_peft_model(base_model, peft_config)
+
+ # make it so that the input embeddings diverge. when the weights are tied this should
+ # reflect in the output embeddings as well.
+ self.simulate_training(peft_model.model.shared.token_adapter)
+
+ # we have to find out if the input embedding tying is doing its job during forward.
+ # for this we can leverage the fact that emb_out(1/emb_in(x)) is embed_dim on the
+ # diagonal iff emb_in.weight == emb_out.weight.
+ token_indices = [0, 1, 2, 3]
+ emb_dim = base_model.config.d_model
+ emb_in = peft_model.model.encoder.embed_tokens(torch.tensor([token_indices]))
+ emb_out = peft_model.model.lm_head(1 / emb_in)
+
+ assert torch.allclose(torch.diag(emb_out[0]), torch.tensor([emb_dim] * len(token_indices)).float())
+
+ # T5 has a decoder embedding layer, we can simply check if it's forward is equal to the encoder
+ # embedding forward.
+ emb_out = peft_model.model.decoder.embed_tokens(torch.tensor([token_indices]))
+
+ assert torch.allclose(emb_in, emb_out)
+
+ # make sure that the state dict does not include weight-tied weights.
+ state_dict = get_peft_model_state_dict(peft_model)
+ assert not [key for key in state_dict if any(tied_key in key for tied_key in peft_model._tied_weights_keys)]
+
+ # make sure that merging and unloading restores the weight-tying.
+ merged_model = peft_model.merge_and_unload()
+
+ assert merged_model.encoder.embed_tokens.weight.data_ptr() == merged_model.lm_head.weight.data_ptr()
+ assert (
+ merged_model.encoder.embed_tokens.weight.data_ptr() == merged_model.decoder.embed_tokens.weight.data_ptr()
+ )
+
+ @pytest.mark.parametrize(
+ "peft_config",
+ [
+ LoraConfig(
+ target_modules="all-linear",
+ trainable_token_indices={"embed_tokens": [0, 1, 3]},
+ modules_to_save=["embed_tokens"],
+ ),
+ ],
+ )
+ def test_modules_to_save_excludes_trainable_tokens(self, model, peft_config):
+ with pytest.raises(ValueError) as e:
+ get_peft_model(model, peft_config)
+ assert "The embedding layer is already marked to be trained fully" in str(e)
+
+ def test_merge_and_unload_standalone(self, model):
+ # test basic functionality of merge_and_unload for standalone TrainableTokens
+ token_indices = [0, 1, 3]
+
+ peft_config = TrainableTokensConfig(
+ target_modules=["embed_tokens"],
+ token_indices=token_indices,
+ )
+
+ peft_model = get_peft_model(model, peft_config)
+
+ self.simulate_training(peft_model.model.model.embed_tokens)
+ expected_changed_weights = peft_model.model.model.embed_tokens.trainable_tokens_delta.default.data.clone()
+
+ # make sure no TrainableTokensLayer is in the module
+ merged_model = peft_model.merge_and_unload()
+ for _, module in merged_model.named_modules():
+ assert not isinstance(module, TrainableTokensLayer)
+
+ # make sure that deltas are applied to the embedding matrix
+ assert torch.allclose(merged_model.model.embed_tokens.weight.data[token_indices], expected_changed_weights)
+
+ def test_original_module_not_in_state_dict(self, model):
+ # Every AuxiliaryTrainingWrapper has an original_module attribute. Since the TrainableTokensWrapper is wrapping
+ # a TrainableTokensLayer and it already has a base layer which serves as the original module, we don't need that
+ # and so it should not come up in the state dict to save memory.
+
+ peft_config = LoraConfig(
+ target_modules="all-linear",
+ trainable_token_indices={"embed_tokens": [0, 1, 3]},
+ )
+
+ peft_model = get_peft_model(model, peft_config)
+
+ # make sure that the original module is present and accessible even though
+ # we want to exclude it from the state dict.
+ assert peft_model.model.model.embed_tokens.original_module
+
+ state_dict = get_peft_model_state_dict(peft_model)
+
+ assert not [k for k in state_dict if ".original_module.weight" in k]
+
+ state_dict = peft_model.state_dict()
+ assert not [k for k in state_dict if ".original_module.weight" in k]
+
+ @pytest.fixture
+ def model_emb(self):
+ return ModelEmb()
+
+ @pytest.fixture
+ def model_embed_in(self):
+ return ModelEmbedIn()
+
+ @pytest.fixture
+ def model_embed_in_no_get(self):
+ return ModelEmbedInNoGet()
+
+ @pytest.fixture
+ def model_embed_multiple(self):
+ return ModelEmbedMultiple()
+
+ @pytest.mark.parametrize(
+ "model_fixture_name, getter",
+ [
+ ("model_emb", lambda model: model.emb),
+ ("model_embed_in", lambda model: model.embed_in),
+ ("model", lambda model: model.model.model.embed_tokens),
+ ],
+ )
+ def test_default_embedding_name_is_inferred_standalone(self, model_fixture_name, getter, request):
+ # make sure that the auto targeting works when `target_module=None`
+ base_model = request.getfixturevalue(model_fixture_name)
+
+ peft_config = TrainableTokensConfig(target_modules=None, token_indices=[0, 1, 3])
+ peft_model = get_peft_model(base_model, peft_config)
+
+ assert isinstance(getter(peft_model), TrainableTokensLayer)
+
+ @pytest.mark.parametrize(
+ "model_fixture_name, getter",
+ [
+ ("model_emb", lambda model: model.emb),
+ ("model_embed_in", lambda model: model.embed_in),
+ ("model", lambda model: model.model.model.embed_tokens),
+ ],
+ )
+ def test_default_embedding_name_is_inferred_combined(self, model_fixture_name, getter, request):
+ # make sure that the auto targeting works when `target_module=None`
+ base_model = request.getfixturevalue(model_fixture_name)
+
+ peft_config = LoraConfig(target_modules="all-linear", trainable_token_indices=[0, 1, 3])
+ peft_model = get_peft_model(base_model, peft_config)
+
+ assert isinstance(getter(peft_model), TrainableTokensWrapper)
+
+ def test_default_embedding_name_cannot_be_inferred(self, model_embed_in_no_get):
+ # should default to default value `embed_tokens` which is not present in this model
+ base_model = model_embed_in_no_get
+
+ peft_config = TrainableTokensConfig(target_modules=None, token_indices=[0, 1, 3])
+
+ with pytest.raises(ValueError) as e:
+ peft_model = get_peft_model(base_model, peft_config)
+
+ assert "Target modules embed_tokens not found in the base model." in str(e)
+
+ def test_embedding_name_is_used_when_given_standalone(self, model_embed_multiple):
+ peft_config = TrainableTokensConfig(target_modules="embed_in_2", token_indices=[0, 1, 3])
+ peft_model = get_peft_model(model_embed_multiple, peft_config)
+
+ assert isinstance(peft_model.model.embed_in_2, TrainableTokensLayer)
+ assert not isinstance(peft_model.model.embed_in, TrainableTokensLayer)
+
+ def test_embedding_name_is_used_when_given_combined(self, model_embed_multiple):
+ peft_config = LoraConfig(target_modules="all-linear", trainable_token_indices={"embed_in_2": [0, 1, 3]})
+ peft_model = get_peft_model(model_embed_multiple, peft_config)
+
+ assert isinstance(peft_model.model.embed_in_2, TrainableTokensWrapper)
+ assert not isinstance(peft_model.model.embed_in, TrainableTokensWrapper)
+
+ @pytest.mark.parametrize("resize_embedding", [True, False])
+ @pytest.mark.parametrize(
+ "peft_config",
+ [
+ LoraConfig(target_modules="all-linear", trainable_token_indices=[1, 2, 3]),
+ TrainableTokensConfig(target_modules=None, token_indices=[1, 2, 3]),
+ ],
+ )
+ def test_save_pretrained_auto(self, model, resize_embedding, peft_config, tmp_path):
+ # make sure that embeddings are saved alongside trainable token weights but only when
+ # the we detect the embedding to be resized (as detected by save_embedding_layers="auto")
+ if resize_embedding:
+ model.resize_token_embeddings(model.config.vocab_size + 2)
+ peft_model = get_peft_model(model, peft_config)
+
+ peft_model.save_pretrained(tmp_path, save_embedding_layers="auto")
+ state_dict = safe_load_file(tmp_path / "adapter_model.safetensors")
+
+ if isinstance(peft_config, TrainableTokensConfig):
+ contains_embedding = "base_model.model.model.embed_tokens.base_layer.weight" in state_dict
+ else:
+ contains_embedding = "base_model.model.model.embed_tokens.token_adapter.base_layer.weight" in state_dict
+
+ if resize_embedding:
+ assert contains_embedding
+ else:
+ assert not contains_embedding
diff --git a/peft/tests/test_tuners_utils.py b/peft/tests/test_tuners_utils.py
new file mode 100644
index 0000000000000000000000000000000000000000..499a4a5502ed765c4b85170fa2a2eae85a45d05b
--- /dev/null
+++ b/peft/tests/test_tuners_utils.py
@@ -0,0 +1,2182 @@
+#!/usr/bin/env python3
+
+# coding=utf-8
+# Copyright 2023-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+import dataclasses
+import re
+import unittest
+from copy import deepcopy
+
+import pytest
+import torch
+from diffusers import StableDiffusionPipeline
+from parameterized import parameterized
+from torch import nn
+from transformers import (
+ AutoModel,
+ AutoModelForCausalLM,
+ AutoModelForSeq2SeqLM,
+ AutoModelForSequenceClassification,
+ BitsAndBytesConfig,
+)
+from transformers.pytorch_utils import Conv1D
+
+from peft import (
+ AdaptionPromptConfig,
+ IA3Config,
+ LoHaConfig,
+ LoraConfig,
+ PeftModel,
+ PromptTuningConfig,
+ VeraConfig,
+ get_layer_status,
+ get_model_status,
+ get_peft_model,
+)
+from peft.tuners.lora.layer import LoraLayer
+from peft.tuners.tuners_utils import (
+ BaseTuner,
+ BaseTunerLayer,
+ _maybe_include_all_linear_layers,
+ check_target_module_exists,
+ inspect_matched_modules,
+)
+from peft.tuners.tuners_utils import (
+ _find_minimal_target_modules as find_minimal_target_modules,
+)
+from peft.utils import INCLUDE_LINEAR_LAYERS_SHORTHAND, ModulesToSaveWrapper, infer_device
+from peft.utils.constants import DUMMY_MODEL_CONFIG, MIN_TARGET_MODULES_FOR_OPTIMIZATION
+
+from .testing_utils import hub_online_once, require_bitsandbytes, require_non_cpu
+
+
+# Implements tests for regex matching logic common for all BaseTuner subclasses, and
+# tests for correct behaviour with different config kwargs for BaseTuners (Ex: feedforward for IA3, etc) and
+# tests for utility function to include all linear layers
+
+REGEX_TEST_CASES = [
+ # tuple of
+ # 1. key
+ # 2. target_modules
+ # 3. layers_to_transform
+ # 4. layers_pattern
+ # 5. expected result
+ # some basic examples
+ ("", [], None, None, False),
+ ("", ["foo"], None, None, False),
+ ("foo", [], None, None, False),
+ ("foo", ["foo"], None, None, True),
+ ("foo", ["bar"], None, None, False),
+ ("foo", ["foo", "bar"], None, None, True),
+ # with regex
+ ("foo", "foo", None, None, True),
+ ("foo", ".*oo", None, None, True),
+ ("foo", "fo.*", None, None, True),
+ ("foo", ".*bar.*", None, None, False),
+ ("foobar", ".*oba.*", None, None, True),
+ # with layers_to_transform
+ ("foo.bar.1.baz", ["baz"], [1], ["bar"], True),
+ ("foo.bar.1.baz", ["baz"], [0], ["bar"], False),
+ ("foo.bar.1.baz", ["baz"], [2], ["bar"], False),
+ ("foo.bar.10.baz", ["baz"], [0], ["bar"], False),
+ ("foo.bar.10.baz", ["baz"], [1], ["bar"], False),
+ ("foo.bar.1.baz", ["baz"], [0, 1, 2], ["bar"], True),
+ ("foo.bar.1.baz", ["baz", "spam"], [1], ["bar"], True),
+ ("foo.bar.1.baz", ["baz", "spam"], [0, 1, 2], ["bar"], True),
+ # empty layers_pattern
+ ("foo.whatever.1.baz", ["baz"], [1], [], True),
+ ("foo.whatever.1.baz", ["baz"], [0], [], False),
+ ("foo.whatever.1.baz", ["baz"], [1], "", True),
+ ("foo.whatever.1.baz", ["baz"], [0], "", False),
+ ("foo.whatever.1.baz", ["baz"], [1], None, True),
+ ("foo.whatever.1.baz", ["baz"], [0], None, False),
+ # some realistic examples: transformers model
+ ("transformer.h.1.attn.attention.q_proj.foo", ["q_proj"], None, [], False),
+ ("transformer.h.1.attn.attention.q_proj", [], None, [], False),
+ ("transformer.h.1.attn.attention.q_proj", ["q_proj"], None, [], True),
+ ("transformer.h.1.attn.attention.q_proj", ["q_proj", "v_proj"], None, [], True),
+ ("transformer.h.1.attn.attention.resid_dropout", ["q_proj", "v_proj"], None, [], False),
+ ("transformer.h.1.attn.attention.q_proj", ["q_proj"], [1], ["h"], True),
+ ("transformer.h.1.attn.attention.q_proj", ["q_proj"], [0], ["h"], False),
+ ("transformer.h.1.attn.attention.q_proj", ["q_proj"], [2], ["h"], False),
+ ("transformer.h.1.attn.attention.q_proj", ["q_proj"], [0, 1, 2], ["h"], True),
+ ("transformer.h.1.attn.attention.q_proj", ["q_proj", "v_proj"], [0, 1, 2], ["h"], True),
+ ("foo.bar.q_proj", ["q_proj"], None, [], True),
+ ("foo.bar.1.baz", ["baz"], [1], ["foo"], False),
+ # other corner cases. For ex, below is a case where layers_pattern
+ # is one of the target nn.modules
+ ("foo.bar.1.baz", ["baz"], [1], ["baz"], False),
+ # here, layers_pattern is 'bar', but only keys that contain '.bar' are valid.
+ ("bar.1.baz", ["baz"], [1], ["bar"], False),
+ ("foo.bar.001.baz", ["baz"], [1], ["bar"], True),
+ ("foo.bar.1.spam.2.baz", ["baz"], [1], ["bar"], True),
+ ("foo.bar.2.spam.1.baz", ["baz"], [1], ["bar"], False),
+ # some realistic examples: module using nn.Sequential
+ # for the below test case, key should contain '.blocks' to be valid, because of how layers_pattern is matched
+ ("blocks.1.weight", ["weight"], [1], ["blocks"], False),
+ ("blocks.1.bias", ["weight"], [1], ["blocks"], False),
+ ("mlp.blocks.1.weight", ["weight"], [1], ["blocks"], True),
+ ("mlp.blocks.1.bias", ["weight"], [1], ["blocks"], False),
+]
+
+MAYBE_INCLUDE_ALL_LINEAR_LAYERS_TEST_CASES = [
+ # model_name, model_type, initial_target_modules, expected_target_modules
+ # test for a causal Llama model
+ (
+ "HuggingFaceH4/tiny-random-LlamaForCausalLM",
+ "causal",
+ INCLUDE_LINEAR_LAYERS_SHORTHAND,
+ ["k_proj", "v_proj", "q_proj", "o_proj", "down_proj", "up_proj", "gate_proj"],
+ ),
+ # test for a Llama model without the LM head
+ (
+ "HuggingFaceH4/tiny-random-LlamaForCausalLM",
+ "base",
+ INCLUDE_LINEAR_LAYERS_SHORTHAND,
+ ["k_proj", "v_proj", "q_proj", "o_proj", "down_proj", "up_proj", "gate_proj"],
+ ),
+ # test for gpt2 with Conv1D layers
+ ("hf-internal-testing/tiny-random-gpt2", "causal", INCLUDE_LINEAR_LAYERS_SHORTHAND, ["c_attn", "c_proj", "c_fc"]),
+ # test for T5 model
+ (
+ "hf-internal-testing/tiny-random-t5",
+ "seq2seq",
+ INCLUDE_LINEAR_LAYERS_SHORTHAND,
+ ["k", "q", "v", "o", "wi", "wo"],
+ ),
+ # test for GPTNeoX. output module list should exclude classification head - which is named as "embed_out" instead of the usual "lm_head" for GPTNeoX
+ (
+ "hf-internal-testing/tiny-random-GPTNeoXForCausalLM",
+ "causal",
+ INCLUDE_LINEAR_LAYERS_SHORTHAND,
+ ["query_key_value", "dense", "dense_h_to_4h", "dense_4h_to_h"],
+ ),
+]
+
+# tests for a few args that should remain unchanged
+MAYBE_INCLUDE_ALL_LINEAR_LAYERS_TEST_INTERNALS = [
+ # initial_target_modules, expected_target_modules
+ (["k_proj"], ["k_proj"]),
+ # test with target_modules as None
+ (None, None),
+ # test with target_modules as a regex expression
+ (".*(q_proj|v_proj)$", ".*(q_proj|v_proj)$"),
+]
+
+BNB_QUANTIZATIONS = [("4bit",), ("8bit",)]
+BNB_TEST_CASES = [(x + y) for x in MAYBE_INCLUDE_ALL_LINEAR_LAYERS_TEST_CASES for y in BNB_QUANTIZATIONS]
+
+
+class PeftCustomKwargsTester(unittest.TestCase):
+ r"""
+ Test if the PeftModel is instantiated with correct behaviour for custom kwargs. This includes:
+ - test if regex matching works correctly
+ - test if adapters handle custom kwargs the right way e.g. IA3 for `feedforward_modules`
+
+ """
+
+ transformers_class_map = {"causal": AutoModelForCausalLM, "seq2seq": AutoModelForSeq2SeqLM, "base": AutoModel}
+
+ @parameterized.expand(REGEX_TEST_CASES)
+ def test_regex_matching_valid(self, key, target_modules, layers_to_transform, layers_pattern, expected_result):
+ # We use a LoRA Config for testing, but the regex matching function is common for all BaseTuner subclasses.
+ # example model_id for config initialization. key is matched only against the target_modules given, so this can be any model
+ model_id = "peft-internal-testing/tiny-OPTForCausalLM-lora"
+ config = LoraConfig(
+ base_model_name_or_path=model_id,
+ target_modules=target_modules,
+ layers_pattern=layers_pattern,
+ layers_to_transform=layers_to_transform,
+ )
+ actual_result = bool(check_target_module_exists(config, key))
+ assert actual_result == expected_result
+
+ def test_module_matching_lora(self):
+ # peft models that have a module matching method to inspect the matching modules to allow
+ # users to easily debug their configuration. Here we only test a single case, not all possible combinations of
+ # configs that could exist. This is okay as the method calls `check_target_module_exists` internally, which
+ # has been extensively tested above.
+ model_id = "hf-internal-testing/tiny-random-BloomForCausalLM"
+ with hub_online_once(model_id):
+ model = AutoModel.from_pretrained(model_id)
+ # by default, this model matches query_key_value
+ config = LoraConfig()
+ peft_model = get_peft_model(model, config)
+
+ output = inspect_matched_modules(peft_model) # inspects default adapter for peft_model
+ matched = output["matched"]
+ expected = [
+ "h.0.self_attention.query_key_value",
+ "h.1.self_attention.query_key_value",
+ "h.2.self_attention.query_key_value",
+ "h.3.self_attention.query_key_value",
+ "h.4.self_attention.query_key_value",
+ ]
+ assert matched == expected # module lists should match exactly
+
+ # no overlap with matched modules
+ unmatched = output["unmatched"]
+ for key in expected:
+ assert key not in unmatched
+
+ def test_feedforward_matching_ia3(self):
+ model_id = "hf-internal-testing/tiny-random-T5ForConditionalGeneration"
+ with hub_online_once(model_id):
+ model = AutoModelForSeq2SeqLM.from_pretrained(model_id)
+ # simple example for just one t5 block for testing
+ config_kwargs = {
+ "target_modules": ".*encoder.*block.0.*(SelfAttention|EncDecAttention|DenseReluDense).(k|q|v|wo|wi)$",
+ "feedforward_modules": ["wo", "wi"],
+ }
+ config = IA3Config(base_model_name_or_path=model_id, **config_kwargs)
+ peft_model = get_peft_model(model, config)
+ output = inspect_matched_modules(peft_model) # inspects default adapter for peft_model
+ matched = output["matched"]
+ expected = [
+ "encoder.block.0.layer.0.SelfAttention.q",
+ "encoder.block.0.layer.0.SelfAttention.k",
+ "encoder.block.0.layer.0.SelfAttention.v",
+ "encoder.block.0.layer.1.DenseReluDense.wi",
+ "encoder.block.0.layer.1.DenseReluDense.wo",
+ ]
+ expected_feedforward = [
+ "encoder.block.0.layer.1.DenseReluDense.wi",
+ "encoder.block.0.layer.1.DenseReluDense.wo",
+ ]
+ assert matched == expected # not required since we do similar checks above, but just to be sure
+ module_dict = dict(model.named_modules())
+ for key in matched:
+ module = module_dict[key]
+ if key in expected_feedforward:
+ assert module.is_feedforward
+ else: # other IA3 modules should not be marked as feedforward
+ assert not module.is_feedforward
+
+ @parameterized.expand(MAYBE_INCLUDE_ALL_LINEAR_LAYERS_TEST_CASES)
+ def test_maybe_include_all_linear_layers_lora(
+ self, model_id, model_type, initial_target_modules, expected_target_modules
+ ):
+ with hub_online_once(model_id):
+ model = self.transformers_class_map[model_type].from_pretrained(model_id)
+ config_cls = LoraConfig
+ self._check_match_with_expected_target_modules(
+ model_id, model, config_cls, initial_target_modules, expected_target_modules
+ )
+
+ @parameterized.expand(BNB_TEST_CASES)
+ @require_non_cpu
+ @require_bitsandbytes
+ def test_maybe_include_all_linear_layers_lora_bnb(
+ self, model_id, model_type, initial_target_modules, expected_target_modules, quantization
+ ):
+ if quantization == "4bit":
+ config_kwargs = {"quantization_config": BitsAndBytesConfig(load_in_4bit=True)}
+ elif quantization == "8bit":
+ config_kwargs = {"quantization_config": BitsAndBytesConfig(load_in_8bit=True)}
+
+ with hub_online_once(model_id):
+ model = self.transformers_class_map[model_type].from_pretrained(
+ model_id, device_map="auto", **config_kwargs
+ )
+ config_cls = LoraConfig
+ self._check_match_with_expected_target_modules(
+ model_id, model, config_cls, initial_target_modules, expected_target_modules
+ )
+
+ def _check_match_with_expected_target_modules(
+ self, model_id, model, config_cls, initial_target_modules, expected_target_modules
+ ):
+ """
+ Helper function for the test for `_maybe_include_all_linear_layers`
+ """
+ actual_config = config_cls(base_model_name_or_path=model_id, target_modules=initial_target_modules)
+ expected_config = config_cls(base_model_name_or_path=model_id, target_modules=expected_target_modules)
+ model_copy = deepcopy(model)
+ actual_model = get_peft_model(model, peft_config=actual_config)
+ expected_model = get_peft_model(model_copy, peft_config=expected_config)
+ expected_model_module_dict = dict(expected_model.named_modules())
+ # compare the two models and assert that all layers are of the same type
+ for name, actual_module in actual_model.named_modules():
+ expected_module = expected_model_module_dict[name]
+ assert type(actual_module) is type(expected_module)
+
+ def test_maybe_include_all_linear_layers_ia3_loha(self):
+ model_id, initial_target_modules, expected_target_modules = (
+ "HuggingFaceH4/tiny-random-LlamaForCausalLM",
+ INCLUDE_LINEAR_LAYERS_SHORTHAND,
+ ["k_proj", "v_proj", "q_proj", "o_proj", "down_proj", "up_proj", "gate_proj"],
+ )
+ with hub_online_once(model_id):
+ model_ia3 = AutoModelForCausalLM.from_pretrained(model_id)
+ model_loha = deepcopy(model_ia3)
+ config_classes = [IA3Config, LoHaConfig]
+ models = [model_ia3, model_loha]
+ for config_cls, model in zip(config_classes, models):
+ self._check_match_with_expected_target_modules(
+ model_id, model, config_cls, initial_target_modules, expected_target_modules
+ )
+
+ @parameterized.expand(MAYBE_INCLUDE_ALL_LINEAR_LAYERS_TEST_INTERNALS)
+ def test_maybe_include_all_linear_layers_internals(self, initial_target_modules, expected_target_modules):
+ model_id = "HuggingFaceH4/tiny-random-LlamaForCausalLM"
+ with hub_online_once(model_id):
+ model = AutoModelForCausalLM.from_pretrained(model_id)
+ config = LoraConfig(base_model_name_or_path=model_id, target_modules=initial_target_modules)
+ new_config = _maybe_include_all_linear_layers(config, model)
+ if isinstance(expected_target_modules, list):
+ # assert that expected and actual target_modules have the same items
+ assert set(new_config.target_modules) == set(expected_target_modules)
+ else:
+ assert new_config.target_modules == expected_target_modules
+
+ def test_maybe_include_all_linear_layers_diffusion(self):
+ model_id = "hf-internal-testing/tiny-sd-pipe"
+ with hub_online_once(model_id):
+ model = StableDiffusionPipeline.from_pretrained(model_id)
+ config = LoraConfig(base_model_name_or_path=model_id, target_modules="all-linear")
+
+ # all linear layers should be converted
+ num_linear = sum(isinstance(module, (nn.Linear, Conv1D)) for module in model.unet.modules())
+ model.unet = get_peft_model(model.unet, config)
+ num_lora = sum(isinstance(module, LoraLayer) for module in model.unet.modules())
+ assert num_lora == num_linear
+
+ def test_maybe_include_all_linear_does_not_target_classifier_head(self):
+ # See issue 2027
+ # Ensure that if a SEQ_CLS model is being used with target_modules="all-linear", the classification head is not
+ # targeted by the adapter layer.
+ model_id = "HuggingFaceH4/tiny-random-LlamaForCausalLM"
+ with hub_online_once(model_id):
+ model = AutoModelForSequenceClassification.from_pretrained(model_id, num_labels=10)
+ # sanity check
+ assert isinstance(model.score, nn.Linear)
+
+ num_linear = sum(isinstance(module, (nn.Linear, Conv1D)) for module in model.modules())
+
+ config = LoraConfig(task_type="SEQ_CLS", target_modules="all-linear")
+ model = get_peft_model(model, config)
+ assert isinstance(model.base_model.score, ModulesToSaveWrapper)
+
+ # the bug was that these were lora.Linear instances
+ assert isinstance(model.base_model.score.original_module, nn.Linear)
+ assert isinstance(model.base_model.score.modules_to_save["default"], nn.Linear)
+
+ # ensure that all but one linear layer was targeted by LoRA
+ num_lora = sum(isinstance(module, LoraLayer) for module in model.modules())
+ assert num_lora == num_linear - 1
+
+ @parameterized.expand(MAYBE_INCLUDE_ALL_LINEAR_LAYERS_TEST_CASES)
+ def test_all_linear_nested_targets_correct_layers(
+ self, model_id, model_type, initial_target_modules, expected_target_modules
+ ):
+ # See 2390
+ # Ensure that if adapter layers are already applied, we don't get nested adapter layers (e.g. LoRA targeting the
+ # lora_A, lora_B layers)
+ with hub_online_once(model_id):
+ model = self.transformers_class_map[model_type].from_pretrained(model_id)
+ config_cls = LoraConfig
+ self._check_match_with_expected_target_modules(
+ model_id, model, config_cls, initial_target_modules, expected_target_modules
+ )
+ # re-use the same model, i.e. the adapter is already applied
+ self._check_match_with_expected_target_modules(
+ model_id, model, config_cls, initial_target_modules, expected_target_modules
+ )
+
+ def test_add_second_adapter_with_all_linear_works(self):
+ # See 2390 Similar test to test_all_linear_nested_targets_correct_layers above, but using add_adapter instead of
+ # calling get_peft_model in an already adapted model
+ model_id = "HuggingFaceH4/tiny-random-LlamaForCausalLM"
+ with hub_online_once(model_id):
+ model = AutoModelForCausalLM.from_pretrained(model_id)
+
+ # important: don't reuse the first config, since config.target_modules will be overwritten, which would make the
+ # test pass trivially.
+ config0 = LoraConfig(target_modules=INCLUDE_LINEAR_LAYERS_SHORTHAND)
+ config1 = LoraConfig(target_modules=INCLUDE_LINEAR_LAYERS_SHORTHAND)
+
+ model = get_peft_model(model, config0)
+ model.add_adapter(adapter_name="other", peft_config=config1)
+
+ # both configs should result in the same target modules being chosen (remember that config.target_modules will
+ # be replaced by the actual set of target_modules)
+ assert config0.target_modules == config1.target_modules
+
+ for layer in model.base_model.model.model.layers:
+ projs = (
+ layer.self_attn.q_proj,
+ layer.self_attn.v_proj,
+ layer.self_attn.k_proj,
+ layer.mlp.gate_proj,
+ layer.mlp.up_proj,
+ layer.mlp.down_proj,
+ )
+ for proj in projs:
+ # the targted layer itself, which in the base model was the nn.Linear layer, is now a LoraLayer
+ assert isinstance(proj, LoraLayer)
+ # all children of that layer are still normal nn.Linear layers
+ assert isinstance(proj.base_layer, nn.Linear)
+ assert isinstance(proj.lora_A["default"], nn.Linear)
+ assert isinstance(proj.lora_B["default"], nn.Linear)
+ assert isinstance(proj.lora_A["other"], nn.Linear)
+ assert isinstance(proj.lora_B["other"], nn.Linear)
+
+
+class MLP(nn.Module):
+ def __init__(self, bias=True):
+ super().__init__()
+ self.lin0 = nn.Linear(10, 20, bias=bias)
+ self.relu = nn.ReLU()
+ self.drop = nn.Dropout(0.5)
+ self.lin1 = nn.Linear(20, 2, bias=bias)
+ self.sm = nn.LogSoftmax(dim=-1)
+
+
+class TestTargetedModuleNames(unittest.TestCase):
+ """Check that the attribute targeted_module_names is correctly set.
+
+ This checks LoRA and IA³, but this should be sufficient, testing all other tuners is not necessary.
+ """
+
+ def test_one_targeted_module_regex(self):
+ model = MLP()
+ model = get_peft_model(model, LoraConfig(target_modules="lin0"))
+ assert model.targeted_module_names == ["lin0"]
+
+ def test_two_targeted_module_regex(self):
+ model = MLP()
+ model = get_peft_model(model, LoraConfig(target_modules="lin.*"))
+ assert model.targeted_module_names == ["lin0", "lin1"]
+
+ def test_one_targeted_module_list(self):
+ model = MLP()
+ model = get_peft_model(model, LoraConfig(target_modules=["lin0"]))
+ assert model.targeted_module_names == ["lin0"]
+
+ def test_two_targeted_module_list(self):
+ model = MLP()
+ model = get_peft_model(model, LoraConfig(target_modules=["lin0", "lin1"]))
+ assert model.targeted_module_names == ["lin0", "lin1"]
+
+ def test_ia3_targeted_module_regex(self):
+ model = MLP()
+ model = get_peft_model(model, IA3Config(target_modules=".*lin.*", feedforward_modules=".*lin.*"))
+ assert model.targeted_module_names == ["lin0", "lin1"]
+
+ def test_ia3_targeted_module_list(self):
+ model = MLP()
+ model = get_peft_model(model, IA3Config(target_modules=["lin0", "lin1"], feedforward_modules=["lin0", "lin1"]))
+ assert model.targeted_module_names == ["lin0", "lin1"]
+
+ def test_realistic_example(self):
+ model_id = "hf-internal-testing/tiny-random-BloomForCausalLM"
+ with hub_online_once(model_id):
+ model = AutoModelForCausalLM.from_pretrained(model_id)
+ config = LoraConfig(task_type="CAUSAL_LM")
+ model = get_peft_model(model, config)
+ expected = [
+ f"transformer.h.{i}.self_attention.query_key_value" for i in range(len(model.base_model.transformer.h))
+ ]
+ assert model.targeted_module_names == expected
+
+
+class TestTargetedParameterNames(unittest.TestCase):
+ """Check that the attribute targeted_parameter_names (via target_parameters) is correctly set.
+
+ This is only implemented for LoRA. Regex matching is currently not implemented.
+ """
+
+ def test_one_targeted_parameters_list(self):
+ model = MLP()
+ model = get_peft_model(model, LoraConfig(target_parameters=["lin0.weight"]))
+ assert model.targeted_parameter_names == ["lin0.weight"]
+
+ def test_two_targeted_parameters_list(self):
+ model = MLP()
+ model = get_peft_model(model, LoraConfig(target_parameters=["lin0.weight", "lin1.weight"]))
+ assert model.targeted_parameter_names == ["lin0.weight", "lin1.weight"]
+
+ def test_realistic_example(self):
+ model_id = "trl-internal-testing/tiny-random-LlamaForCausalLM"
+ with hub_online_once(model_id):
+ model = AutoModelForCausalLM.from_pretrained(model_id)
+ config = LoraConfig(target_modules=[], task_type="CAUSAL_LM", target_parameters=["v_proj.weight"])
+ model = get_peft_model(model, config)
+ expected = [
+ f"model.layers.{i}.self_attn.v_proj.weight" for i in range(len(model.base_model.model.model.layers))
+ ]
+ assert model.targeted_parameter_names == expected
+
+
+class TestExcludedModuleNames(unittest.TestCase):
+ """Check that the attribute exclude_module is correctly set.
+
+ This checks LoRA and IA³, but this should be sufficient, testing all other tuners is not necessary.
+ """
+
+ def test_two_excluded_module_regex(self):
+ model = MLP()
+ model = get_peft_model(model, LoraConfig(target_modules=("lin.*"), exclude_modules="lin0"))
+ assert model.targeted_module_names == ["lin1"]
+
+ def test_two_excluded_module_list(self):
+ model = MLP()
+ model = get_peft_model(model, LoraConfig(target_modules=["lin0", "lin1"], exclude_modules="lin0"))
+ assert model.targeted_module_names == ["lin1"]
+
+ def test_multiple_excluded_modules_list(self):
+ model = MLP()
+ model = get_peft_model(model, LoraConfig(target_modules=["lin0", "lin1"], exclude_modules=["lin0"]))
+ assert model.targeted_module_names == ["lin1"]
+
+ def test_ia3_two_excluded_module_regex(self):
+ model = MLP()
+ model = get_peft_model(
+ model, IA3Config(target_modules=".*lin.*", feedforward_modules=".*lin.*", exclude_modules="lin0")
+ )
+ assert model.targeted_module_names == ["lin1"]
+
+ def test_ia3_multiple_excluded_modules_list(self):
+ model = MLP()
+ model = get_peft_model(
+ model, IA3Config(target_modules=["lin0", "lin1"], feedforward_modules=".*lin.*", exclude_modules=["lin1"])
+ )
+ assert model.targeted_module_names == ["lin0"]
+
+ def test_all_modules_excluded(self):
+ model = MLP()
+ with pytest.raises(ValueError, match="All modules were excluded"):
+ get_peft_model(
+ model,
+ LoraConfig(
+ target_modules=["lin0", "lin1", "relu", "drop", "sm"],
+ exclude_modules=["lin0", "lin1", "relu", "drop", "sm"],
+ ),
+ )
+
+ def test_no_modules_matched(self):
+ model = MLP()
+ with pytest.raises(ValueError, match="Target modules .* not found in the base model"):
+ get_peft_model(model, LoraConfig(target_modules=["non_existent_module"]))
+
+ def test_some_modules_excluded_some_unmatched(self):
+ model = MLP()
+ with pytest.raises(ValueError, match="No modules were targeted for adaptation"):
+ get_peft_model(model, LoraConfig(target_modules=["lin0", "non_existent_module"], exclude_modules=["lin0"]))
+
+ def test_exclude_modules_not_used(self):
+ model = MLP()
+ with pytest.warns(UserWarning, match="You have passed exclude_modules=.* but no modules were excluded"):
+ get_peft_model(model, LoraConfig(target_modules=["lin1"], exclude_modules=["non_existent_module"]))
+
+ def test_realistic_example(self):
+ model_id = "hf-internal-testing/tiny-random-BloomForCausalLM"
+ with hub_online_once(model_id):
+ model = AutoModelForCausalLM.from_pretrained(model_id)
+ config = LoraConfig(task_type="CAUSAL_LM", exclude_modules="transformer.h.2.self_attention.query_key_value")
+ model = get_peft_model(model, config)
+ expected = [
+ f"transformer.h.{i}.self_attention.query_key_value"
+ for i in range(len(model.base_model.transformer.h))
+ if i != 2
+ ]
+ assert model.targeted_module_names == expected
+
+
+class TestModelAndLayerStatus:
+ """Check the methods `get_layer_status` and `get_model_status`.`
+
+ Note that we only test LoRA here but the same logic should work for other tuner types (if they support the
+ corresponding features like merging).
+
+ """
+
+ torch_device = infer_device()
+
+ @pytest.fixture
+ def small_base_model_cls(self):
+ class SmallModel(nn.Module):
+ def __init__(self):
+ super().__init__()
+ self.lin0 = nn.Linear(10, 10)
+ self.lin1 = nn.Linear(10, 10)
+
+ return SmallModel
+
+ @pytest.fixture
+ def small_base_emb_model_cls(self):
+ class SmallEmbModel(nn.Module):
+ def __init__(self):
+ super().__init__()
+ self.lin0 = nn.Linear(10, 10)
+ self.emb = nn.Embedding(10, 10)
+
+ return SmallEmbModel
+
+ @pytest.fixture
+ def small_model(self, small_base_model_cls):
+ config = LoraConfig(target_modules="lin0")
+ return get_peft_model(small_base_model_cls(), config)
+
+ @pytest.fixture
+ def large_model(self):
+ class LargeModel(nn.Module):
+ def __init__(self):
+ super().__init__()
+ self.lin0 = nn.Linear(10, 10)
+ self.conv0 = nn.Conv2d(3, 10, 3)
+ self.emb0 = nn.Embedding(10, 10)
+ self.lin1 = nn.Linear(10, 10)
+ self.conv1 = nn.Conv2d(3, 10, 3)
+ self.emb1 = nn.Embedding(10, 10)
+
+ config0 = LoraConfig(target_modules=["lin0", "conv1", "emb0"])
+ config1 = LoraConfig(target_modules=["lin0", "lin1"], r=16)
+ model = get_peft_model(LargeModel(), config0)
+ model.add_adapter("other", config1)
+ return model
+
+ ################
+ # layer status #
+ ################
+
+ def test_layer_names_small(self, small_model):
+ layer_status = small_model.get_layer_status()
+ expected = ["model.lin0"]
+ assert [status.name for status in layer_status] == expected
+
+ def test_layer_names_large(self, large_model):
+ layer_status = large_model.get_layer_status()
+ result = sorted([status.name for status in layer_status])
+ expected = ["model.conv1", "model.emb0", "model.lin0", "model.lin1"]
+ assert result == expected
+
+ def test_module_type_small(self, small_model):
+ layer_status = small_model.get_layer_status()
+ assert [status.module_type for status in layer_status] == ["lora.Linear"]
+
+ def test_module_type_large(self, large_model):
+ layer_status = large_model.get_layer_status()
+ result = sorted([status.module_type for status in layer_status])
+ expected = ["lora.Conv2d", "lora.Embedding", "lora.Linear", "lora.Linear"]
+ assert result == expected
+
+ def test_enabled_small(self, small_model):
+ layer_status = small_model.get_layer_status()
+ assert [status.enabled for status in layer_status] == [True]
+
+ def test_enabled_large(self, large_model):
+ layer_status = large_model.get_layer_status()
+ result = [status.enabled for status in layer_status]
+ expected = [True, True, True, True]
+ assert result == expected
+
+ def test_enabled_irregular(self, large_model):
+ # this is an invalid state, but we should still test it
+ # disable a single layer
+ for module in large_model.modules():
+ if isinstance(module, BaseTunerLayer):
+ module.enable_adapters(False)
+ break
+
+ layer_status = large_model.get_layer_status()
+ result = [status.enabled for status in layer_status]
+ expected = [False, True, True, True]
+ assert result == expected
+
+ def test_active_adapters_small(self, small_model):
+ layer_status = small_model.get_layer_status()
+ assert [status.active_adapters for status in layer_status] == [["default"]]
+
+ def test_active_adapters_large(self, large_model):
+ layer_status = large_model.get_layer_status()
+ result = [status.active_adapters for status in layer_status]
+ # note: as currently implemented, the active adapter can be an adapter that does not exist on this specific
+ # layer, for instance, layer 3 (i.e. index 2) only has the "other" adapter but "default" is still shown as the
+ # active adapter
+ expected = [["default"], ["default"], ["default"], ["default"]]
+ assert result == expected
+
+ # switch to "other"
+ large_model.set_adapter("other")
+ layer_status = large_model.get_layer_status()
+ result = [status.active_adapters for status in layer_status]
+ expected = [["other"], ["other"], ["other"], ["other"]]
+
+ def test_merge_adapters_small(self, small_model):
+ layer_status = small_model.get_layer_status()
+ assert [status.merged_adapters for status in layer_status] == [[]]
+ assert [status.available_adapters for status in layer_status] == [["default"]]
+
+ # now merge "default"
+ small_model.merge_adapter(["default"])
+ layer_status = small_model.get_layer_status()
+ assert [status.merged_adapters for status in layer_status] == [["default"]]
+ assert [status.available_adapters for status in layer_status] == [["default"]]
+
+ def test_merge_adapters_large(self, large_model):
+ layer_status = large_model.get_layer_status()
+ result = [status.merged_adapters for status in layer_status]
+ assert result == [[], [], [], []]
+
+ # now merge "default"
+ large_model.merge_adapter(["default"])
+ layer_status = large_model.get_layer_status()
+ result = [status.merged_adapters for status in layer_status]
+ # default is on layer 0, 1, and 3
+ assert result == [["default"], ["default"], [], ["default"]]
+
+ # now merge "other"
+ large_model.unmerge_adapter()
+ large_model.merge_adapter(["other"])
+ layer_status = large_model.get_layer_status()
+ result = [status.merged_adapters for status in layer_status]
+ # other is on layer 0 and 2
+ assert result == [["other"], [], ["other"], []]
+
+ # now merge both
+ large_model.merge_adapter(["default", "other"])
+ layer_status = large_model.get_layer_status()
+ result = [status.merged_adapters for status in layer_status]
+ # default is on layer 0, 1, and 3, other is on layer 0 and 2
+ assert result == [["other", "default"], ["default"], ["other"], ["default"]]
+
+ def test_requires_grad_small(self, small_model):
+ layer_status = small_model.get_layer_status()
+ assert [status.requires_grad for status in layer_status] == [{"default": True}]
+
+ def test_requires_grad_large(self, large_model):
+ layer_status = large_model.get_layer_status()
+ result = [status.requires_grad for status in layer_status]
+ # default is on layer 0, 1, and 3, other is on layer 0 and 2
+ expected = [{"default": True, "other": False}, {"default": True}, {"other": False}, {"default": True}]
+ assert result == expected
+
+ # now activate "other"
+ large_model.set_adapter("other")
+ layer_status = large_model.get_layer_status()
+ result = [status.requires_grad for status in layer_status]
+ expected = [{"default": False, "other": True}, {"default": False}, {"other": True}, {"default": False}]
+ assert result == expected
+
+ # change requires grad, is now inconsistent with active/inactive adapter
+ large_model.set_requires_grad("default", requires_grad=True)
+ large_model.set_requires_grad("other", requires_grad=False)
+ layer_status = large_model.get_layer_status()
+ result = [status.requires_grad for status in layer_status]
+ expected = [{"default": True, "other": False}, {"default": True}, {"other": False}, {"default": True}]
+ assert result == expected
+
+ def test_requires_grad_irregular(self, large_model):
+ # inject an embedding layer with requires_grad=False
+ # this is an invalid state, but we should still test it
+ lora_embedding_A = nn.Parameter(torch.zeros(10, 10))
+ lora_embedding_B = nn.Parameter(torch.zeros(10, 10))
+ lora_embedding_A.requires_grad = False
+ lora_embedding_B.requires_grad = False
+ large_model.base_model.model.lin0.lora_embedding_A["default"] = lora_embedding_A
+ large_model.base_model.model.lin0.lora_embedding_B["default"] = lora_embedding_B
+
+ layer_status = large_model.get_layer_status()
+ result = [status.requires_grad for status in layer_status]
+ expected = [{"default": "irregular", "other": False}, {"default": True}, {"other": False}, {"default": True}]
+ assert result == expected
+
+ def test_available_adapters_small(self, small_model):
+ layer_status = small_model.get_layer_status()
+ result = [status.available_adapters for status in layer_status]
+ expected = [["default"]]
+ assert result == expected
+
+ def test_available_adapters_large(self, large_model):
+ layer_status = large_model.get_layer_status()
+ result = [status.available_adapters for status in layer_status]
+ expected = [["default", "other"], ["default"], ["other"], ["default"]]
+ assert result == expected
+
+ def test_devices_all_cpu_small(self, small_model):
+ layer_status = small_model.get_layer_status()
+ result = [status.devices for status in layer_status]
+ expected = [{"default": ["cpu"]}]
+ assert result == expected
+
+ def test_devices_all_cpu_large(self, large_model):
+ layer_status = large_model.get_layer_status()
+ result = [status.devices for status in layer_status]
+ expected = [
+ {"default": ["cpu"], "other": ["cpu"]},
+ {"default": ["cpu"]},
+ {"other": ["cpu"]},
+ {"default": ["cpu"]},
+ ]
+ assert result == expected
+
+ def test_with_modules_to_save(self, small_base_model_cls):
+ # check that modules_to_save are correctly reported in layer status
+ model = small_base_model_cls()
+ config = LoraConfig(target_modules=["lin0"], modules_to_save=["lin1"])
+ model = get_peft_model(model, config)
+ layer_status = model.get_layer_status()
+
+ assert len(layer_status) == 2
+ status = layer_status[1] # for modules_to_save
+
+ assert status.name == "model.lin1"
+ assert status.module_type == "ModulesToSaveWrapper"
+ assert status.enabled is True
+ assert status.active_adapters == ["default"]
+ assert status.merged_adapters == []
+ assert status.available_adapters == ["default"]
+ assert status.requires_grad == {"default": True}
+ assert status.devices == {"default": ["cpu"]}
+
+ def test_with_trainable_tokens(self, small_base_emb_model_cls):
+ # check that trainable_token_indices are correctly reported in layer status
+ model = small_base_emb_model_cls()
+ config = LoraConfig(target_modules=["lin0"], trainable_token_indices={"emb": [0, 1, 2]})
+ model = get_peft_model(model, config)
+ layer_status = model.get_layer_status()
+
+ assert len(layer_status) == 2
+ status = layer_status[1] # for trainable tokens
+
+ assert status.name == "model.emb.token_adapter"
+ assert status.module_type == "TrainableTokensLayer"
+ assert status.enabled is True
+ assert status.active_adapters == ["default"]
+ assert status.merged_adapters == []
+ assert status.available_adapters == ["default"]
+ assert status.requires_grad == {"default": True}
+ assert status.devices == {"default": ["cpu"]}
+
+ @require_non_cpu
+ def test_devices_all_gpu_large(self, large_model):
+ large_model.to(self.torch_device)
+ layer_status = large_model.get_layer_status()
+ result = [status.devices for status in layer_status]
+ expected = [
+ {"default": [self.torch_device], "other": [self.torch_device]},
+ {"default": [self.torch_device]},
+ {"other": [self.torch_device]},
+ {"default": [self.torch_device]},
+ ]
+ assert result == expected
+
+ @require_non_cpu
+ def test_devices_cpu_and_gpu_large(self, large_model):
+ # move the embedding layer to GPU
+ large_model.model.lin0.lora_A["default"] = large_model.model.lin0.lora_A["default"].to(self.torch_device)
+ layer_status = large_model.get_layer_status()
+ result = [status.devices for status in layer_status]
+ expected = [
+ {"default": ["cpu", self.torch_device], "other": ["cpu"]},
+ {"default": ["cpu"]},
+ {"other": ["cpu"]},
+ {"default": ["cpu"]},
+ ]
+ assert result == expected
+
+ def test_target_parameters(self, large_model):
+ # don't check each attribute, just the relevant ones
+ # first remove the normal LoRA layers
+ large_model = large_model.merge_and_unload()
+ config = LoraConfig(target_parameters=["lin0.weight", "lin1.weight"])
+ large_model = get_peft_model(large_model, config)
+ layer_status = large_model.get_layer_status()
+ assert [status.name for status in layer_status] == ["model.lin0", "model.lin1"]
+ assert [status.module_type for status in layer_status] == ["lora.ParamWrapper"] * 2
+
+ def test_target_parameters_and_target_modules(self, large_model):
+ # don't check each attribute, just the relevant ones
+ # first remove the normal LoRA layers
+ large_model = large_model.merge_and_unload()
+ config = LoraConfig(target_parameters=["lin0.weight"], target_modules=["lin1"])
+ large_model = get_peft_model(large_model, config)
+ layer_status = large_model.get_layer_status()
+ assert [status.name for status in layer_status] == ["model.lin0", "model.lin1"]
+ assert [status.module_type for status in layer_status] == ["lora.ParamWrapper", "lora.Linear"]
+
+ ################
+ # model status #
+ ################
+
+ def test_base_model_type_small(self, small_model):
+ model_status = small_model.get_model_status()
+ assert model_status.base_model_type == "SmallModel"
+
+ def test_base_model_type_large(self, large_model):
+ model_status = large_model.get_model_status()
+ assert model_status.base_model_type == "LargeModel"
+
+ def test_base_model_type_transformers_automodel(self):
+ # ensure that this also works with transformers AutoModels
+ model_id = "google/flan-t5-small"
+ with hub_online_once(model_id):
+ model = AutoModel.from_pretrained(model_id)
+ model = get_peft_model(model, LoraConfig())
+ model_status = model.get_model_status()
+ assert model_status.base_model_type == "T5Model"
+
+ def test_adapter_model_type_small(self, small_model):
+ model_status = small_model.get_model_status()
+ assert model_status.adapter_model_type == "LoraModel"
+
+ def test_adapter_model_type_large(self, large_model):
+ model_status = large_model.get_model_status()
+ assert model_status.adapter_model_type == "LoraModel"
+
+ def test_peft_types_small(self, small_model):
+ model_status = small_model.get_model_status()
+ assert model_status.peft_types == {"default": "LORA"}
+
+ def test_peft_types_large(self, large_model):
+ model_status = large_model.get_model_status()
+ assert model_status.peft_types == {"default": "LORA", "other": "LORA"}
+
+ def test_nb_params_small(self, small_model):
+ model_status = small_model.get_model_status()
+ assert model_status.trainable_params == 160
+ assert model_status.total_params == 380
+
+ def test_nb_params_large(self, large_model):
+ model_status = large_model.get_model_status()
+ assert model_status.trainable_params == 616
+ assert model_status.total_params == 2236
+
+ def test_num_adapter_layers_small(self, small_model):
+ model_status = small_model.get_model_status()
+ assert model_status.num_adapter_layers == 1
+
+ def test_num_adapter_layers_large(self, large_model):
+ model_status = large_model.get_model_status()
+ assert model_status.num_adapter_layers == 4
+
+ def test_model_enabled_small(self, small_model):
+ model_status = small_model.get_model_status()
+ assert model_status.enabled is True
+
+ def test_model_enabled_large(self, large_model):
+ model_status = large_model.get_model_status()
+ assert model_status.enabled is True
+
+ def test_model_disabled_small(self, small_model):
+ small_model.disable_adapter_layers()
+ model_status = small_model.get_model_status()
+ assert model_status.enabled is False
+
+ def test_model_disabled_large(self, large_model):
+ large_model.disable_adapter_layers()
+ model_status = large_model.get_model_status()
+ assert model_status.enabled is False
+
+ def test_model_enabled_irregular(self, large_model):
+ # this is an invalid state, but we should still test it
+ # disable a single layer
+ for module in large_model.modules():
+ if isinstance(module, BaseTunerLayer):
+ module.enable_adapters(False)
+ break
+
+ model_status = large_model.get_model_status()
+ assert model_status.enabled == "irregular"
+
+ def test_model_enabled_irregular_with_modules_to_save(self, small_base_model_cls):
+ # check that modules_to_save are correctly reported in layer status
+ model = small_base_model_cls()
+ config = LoraConfig(target_modules=["lin0"], modules_to_save=["lin1"])
+ model = get_peft_model(model, config)
+
+ # disable only lin0
+ model.lin0.enable_adapters(False)
+
+ model_status = model.get_model_status()
+ # since lin1 is still enabled, the overall model status is "irregular"
+ assert model_status.enabled == "irregular"
+
+ def test_model_enabled_irregular_with_trainable_tokens(self, small_base_emb_model_cls):
+ # check that trainable_token_indices are correctly reported in layer status
+ model = small_base_emb_model_cls()
+ config = LoraConfig(target_modules=["lin0"], trainable_token_indices={"emb": [0, 1, 2]})
+ model = get_peft_model(model, config)
+
+ # disable only lin0
+ model.lin0.enable_adapters(False)
+
+ model_status = model.get_model_status()
+ # since emb is still enabled, the overall model status is "irregular"
+ assert model_status.enabled == "irregular"
+
+ def test_model_active_adapters_small(self, small_model):
+ model_status = small_model.get_model_status()
+ assert model_status.active_adapters == ["default"]
+
+ def test_model_active_adapters_large(self, large_model):
+ model_status = large_model.get_model_status()
+ assert model_status.active_adapters == ["default"]
+
+ large_model.set_adapter("other")
+ model_status = large_model.get_model_status()
+ assert model_status.active_adapters == ["other"]
+
+ def test_model_active_adapters_irregular(self, large_model):
+ # this is an invalid state, but we should still test it
+ # disable a single layer
+ for module in large_model.modules():
+ if isinstance(module, BaseTunerLayer):
+ # switch a single layer's active adapter from default to other
+ if module.active_adapters == ["default"]:
+ module._active_adapter = "other"
+ assert module.active_adapters == ["other"]
+ break
+
+ model_status = large_model.get_model_status()
+ assert model_status.active_adapters == "irregular"
+
+ def test_model_active_adapters_with_modules_to_save_irregular(self, small_base_model_cls):
+ # check that modules_to_save are correctly reported in layer status
+ model = small_base_model_cls()
+ config = LoraConfig(target_modules=["lin0"], modules_to_save=["lin1"])
+ model = get_peft_model(model, config)
+ model.add_adapter("other", config)
+
+ # switch modules_to_save to "other"
+ model.lin1.set_adapter("other")
+
+ model_status = model.get_model_status()
+ # since lin0 is still on "default", the overall model status is "irregular"
+ assert model_status.active_adapters == "irregular"
+
+ def test_model_active_adapters_with_trainable_tokens_irregular(self, small_base_emb_model_cls):
+ # check that trainable_token_indices are correctly reported in layer status
+ model = small_base_emb_model_cls()
+ config = LoraConfig(target_modules=["lin0"], trainable_token_indices={"emb": [0, 1, 2]})
+ model = get_peft_model(model, config)
+ model.add_adapter("other", config)
+
+ # switch trainable tokens to "other"
+ model.emb.set_adapter("other")
+
+ model_status = model.get_model_status()
+ # since lin0 is still on "default", the overall model status is "irregular"
+ assert model_status.active_adapters == "irregular"
+
+ def test_model_merged_adapters_small(self, small_model):
+ model_status = small_model.get_model_status()
+ assert model_status.merged_adapters == []
+
+ small_model.merge_adapter()
+ model_status = small_model.get_model_status()
+ assert model_status.merged_adapters == ["default"]
+
+ small_model.unmerge_adapter()
+ model_status = small_model.get_model_status()
+ assert model_status.merged_adapters == []
+
+ def test_model_merged_adapters_large(self, large_model):
+ model_status = large_model.get_model_status()
+ assert model_status.merged_adapters == []
+
+ large_model.merge_adapter(["default"])
+ model_status = large_model.get_model_status()
+ assert model_status.merged_adapters == ["default"]
+
+ large_model.unmerge_adapter()
+ large_model.merge_adapter(["other"])
+ model_status = large_model.get_model_status()
+ assert model_status.merged_adapters == ["other"]
+
+ large_model.unmerge_adapter()
+ large_model.merge_adapter(["default", "other"])
+ model_status = large_model.get_model_status()
+ assert model_status.merged_adapters == ["default", "other"]
+
+ def test_model_merged_adapters_irregular(self, large_model):
+ # this is an invalid state, but we should still test it
+ # by merging only lin0 of "default", we end up in a irregular state, because not all "default" layers are merged
+ large_model.base_model.lin0.merge(["default"])
+
+ model_status = large_model.get_model_status()
+ assert model_status.merged_adapters == "irregular"
+
+ def test_model_requires_grad_model_small(self, small_model):
+ model_status = small_model.get_model_status()
+ assert model_status.requires_grad == {"default": True}
+
+ def test_model_requires_grad_model_large(self, large_model):
+ model_status = large_model.get_model_status()
+ assert model_status.requires_grad == {"default": True, "other": False}
+
+ large_model.set_adapter("other")
+ model_status = large_model.get_model_status()
+ assert model_status.requires_grad == {"default": False, "other": True}
+
+ # change requires grad, is now inconsistent with active/inactive adapter
+ large_model.set_requires_grad("default", requires_grad=True)
+ large_model.set_requires_grad("other", requires_grad=False)
+ model_status = large_model.get_model_status()
+ assert model_status.requires_grad == {"default": True, "other": False}
+
+ def test_model_requires_grad_model_irregular(self, large_model):
+ # inject an embedding layer with requires_grad=False
+ # this is an invalid state, but we should still test it
+ lora_embedding_A = nn.Parameter(torch.zeros(10, 10))
+ lora_embedding_B = nn.Parameter(torch.zeros(10, 10))
+ lora_embedding_A.requires_grad = False
+ lora_embedding_B.requires_grad = False
+ large_model.base_model.model.lin0.lora_embedding_A["default"] = lora_embedding_A
+ large_model.base_model.model.lin0.lora_embedding_B["default"] = lora_embedding_B
+
+ model_status = large_model.get_model_status()
+ assert model_status.requires_grad == {"default": "irregular", "other": False}
+
+ def test_model_requires_irregular_with_modules_to_save(self, small_base_model_cls):
+ # check that modules_to_save are correctly reported in layer status
+ model = small_base_model_cls()
+ config = LoraConfig(target_modules=["lin0"], modules_to_save=["lin1"])
+ model = get_peft_model(model, config)
+
+ # set modules_to_save to requires_grad=False
+ model.lin1.modules_to_save.default.weight.requires_grad = False
+
+ model_status = model.get_model_status()
+ # since lin1 is still requires_grad=True, the overall model status is "irregular"
+ assert model_status.requires_grad == {"default": "irregular"}
+
+ def test_model_requires_irregular_with_trainable_tokens(self, small_base_emb_model_cls):
+ # check that trainable_token_indices are correctly reported in layer status
+ model = small_base_emb_model_cls()
+ config = LoraConfig(target_modules=["lin0"], trainable_token_indices={"emb": [0, 1, 2]})
+ model = get_peft_model(model, config)
+
+ # set trainable tokens to requires_grad=False
+ model.emb.token_adapter.trainable_tokens_delta.default.requires_grad = False
+
+ model_status = model.get_model_status()
+ # since emb is still requires_grad=True, the overall model status is "irregular"
+ assert model_status.requires_grad == {"default": "irregular"}
+
+ def test_model_available_adapters_small(self, small_model):
+ model_status = small_model.get_model_status()
+ assert model_status.available_adapters == ["default"]
+
+ def test_model_available_adapters_large(self, large_model):
+ model_status = large_model.get_model_status()
+ assert model_status.available_adapters == ["default", "other"]
+
+ def test_model_devices_all_cpu_small(self, small_model):
+ model_status = small_model.get_model_status()
+ assert model_status.devices == {"default": ["cpu"]}
+
+ def test_model_devices_all_cpu_large(self, large_model):
+ model_status = large_model.get_model_status()
+ assert model_status.devices == {"default": ["cpu"], "other": ["cpu"]}
+
+ @require_non_cpu
+ def test_model_devices_all_gpu_large(self, large_model):
+ large_model.to(self.torch_device)
+ model_status = large_model.get_model_status()
+ assert model_status.devices == {"default": [self.torch_device], "other": [self.torch_device]}
+
+ @require_non_cpu
+ def test_model_devices_cpu_and_gpu_large(self, large_model):
+ # move the embedding layer to GPU
+ large_model.model.lin0.lora_A["default"] = large_model.model.lin0.lora_A["default"].to(self.torch_device)
+ model_status = large_model.get_model_status()
+ assert model_status.devices == {"default": ["cpu", self.torch_device], "other": ["cpu"]}
+
+ def test_model_target_parameters(self, large_model):
+ # don't check each attribute, just the relevant ones
+ # first remove the normal LoRA layers
+ large_model = large_model.merge_and_unload()
+ config = LoraConfig(target_parameters=["lin0.weight", "lin1.weight"])
+ large_model = get_peft_model(large_model, config)
+ model_status = large_model.get_model_status()
+ model_status = large_model.get_model_status()
+ assert model_status.adapter_model_type == "LoraModel"
+ assert model_status.peft_types == {"default": "LORA", "other": "LORA"}
+ assert model_status.num_adapter_layers == 2
+ assert model_status.trainable_params == 2 * (8 * 10 + 10 * 8)
+
+ def test_model_target_parameters_and_target_modules(self, large_model):
+ # don't check each attribute, just the relevant ones
+ # first remove the normal LoRA layers
+ large_model = large_model.merge_and_unload()
+ config = LoraConfig(target_parameters=["lin0.weight"], target_modules=["lin1"])
+ large_model = get_peft_model(large_model, config)
+ model_status = large_model.get_model_status()
+ assert model_status.adapter_model_type == "LoraModel"
+ assert model_status.peft_types == {"default": "LORA", "other": "LORA"}
+ assert model_status.num_adapter_layers == 2
+ assert model_status.trainable_params == 2 * (8 * 10 + 10 * 8)
+
+ def test_model_status_with_modules_to_save(self, small_base_model_cls):
+ # check that modules_to_save are correctly reported in layer status
+ model = small_base_model_cls()
+ num_base_params = sum(p.numel() for p in small_base_model_cls().parameters())
+ config = LoraConfig(target_modules=["lin0"], modules_to_save=["lin1"])
+ model = get_peft_model(model, config)
+ model_status = model.get_model_status()
+
+ assert model_status.base_model_type == "SmallModel"
+ assert model_status.adapter_model_type == "LoraModel"
+ assert model_status.peft_types == {"default": "LORA"}
+ # 2 x 80 for LoRA, 100 for modules_to_save.weight, 10 for modules_to_save.bias
+ assert model_status.trainable_params == 2 * 80 + 100 + 10
+ assert model_status.total_params == 2 * 80 + 100 + 10 + num_base_params
+ assert model_status.num_adapter_layers == 2 # lin0 + lin1
+ assert model_status.enabled is True
+ assert model_status.active_adapters == ["default"]
+ assert model_status.merged_adapters == []
+ assert model_status.requires_grad == {"default": True}
+ assert model_status.available_adapters == ["default"]
+ assert model_status.devices == {"default": ["cpu"]} # all on CPU
+
+ def test_model_status_with_trainable_tokens(self, small_base_emb_model_cls):
+ # check that trainable_token_indices are correctly reported in layer status
+ model = small_base_emb_model_cls()
+ num_base_params = sum(p.numel() for p in small_base_emb_model_cls().parameters())
+ config = LoraConfig(target_modules=["lin0"], trainable_token_indices={"emb": [0, 1, 2]})
+ model = get_peft_model(model, config)
+ model_status = model.get_model_status()
+
+ assert model_status.base_model_type == "SmallEmbModel"
+ assert model_status.adapter_model_type == "LoraModel"
+ assert model_status.peft_types == {"default": "LORA"}
+ # 2 x 80 for LoRA, 3 x 10 for trainable tokens
+ assert model_status.trainable_params == 2 * 80 + 3 * 10
+ assert model_status.total_params == 2 * 80 + 3 * 10 + num_base_params
+ assert model_status.num_adapter_layers == 2
+ assert model_status.enabled is True
+ assert model_status.active_adapters == ["default"]
+ assert model_status.merged_adapters == []
+ assert model_status.requires_grad == {"default": True}
+ assert model_status.available_adapters == ["default"]
+ assert model_status.devices == {"default": ["cpu"]} # all on CPU
+
+ def test_loha_model(self):
+ # ensure that this also works with non-LoRA, it's not necessary to test all tuners
+ class SmallModel(nn.Module):
+ def __init__(self):
+ super().__init__()
+ self.lin0 = nn.Linear(10, 10)
+ self.lin1 = nn.Linear(10, 10)
+
+ base_model = SmallModel()
+ config = LoHaConfig(target_modules=["lin0", "lin1"], init_weights=False)
+ model = get_peft_model(base_model, config)
+
+ model_status = model.get_model_status()
+ layer_status = model.get_layer_status()
+
+ assert model_status.base_model_type == "SmallModel"
+ assert model_status.adapter_model_type == "LoHaModel"
+ assert model_status.peft_types == {"default": "LOHA"}
+ assert model_status.trainable_params == 640
+ assert model_status.total_params == 860
+ assert model_status.num_adapter_layers == 2
+ assert model_status.enabled is True
+ assert model_status.active_adapters == ["default"]
+ assert model_status.merged_adapters == []
+ assert model_status.requires_grad == {"default": True}
+ assert model_status.available_adapters == ["default"]
+ assert model_status.devices == {"default": ["cpu"]}
+
+ layer_status0 = layer_status[0]
+ assert len(layer_status) == 2
+ assert layer_status0.name == "model.lin0"
+ assert layer_status0.module_type == "loha.Linear"
+ assert layer_status0.enabled is True
+ assert layer_status0.active_adapters == ["default"]
+ assert layer_status0.merged_adapters == []
+ assert layer_status0.requires_grad == {"default": True}
+ assert layer_status0.available_adapters == ["default"]
+ assert layer_status0.devices == {"default": ["cpu"]}
+
+ @require_non_cpu
+ def test_vera_model(self):
+ # let's also test VeRA because it uses BufferDict
+ class SmallModel(nn.Module):
+ def __init__(self):
+ super().__init__()
+ self.lin0 = nn.Linear(10, 10)
+ self.lin1 = nn.Linear(10, 10)
+
+ base_model = SmallModel()
+ config = VeraConfig(target_modules=["lin0", "lin1"], init_weights=False)
+ model = get_peft_model(base_model, config)
+
+ # move the buffer dict to GPU
+ model.lin0.vera_A["default"] = model.lin0.vera_A["default"].to(self.torch_device)
+
+ model_status = model.get_model_status()
+ layer_status = model.get_layer_status()
+
+ assert model_status.base_model_type == "SmallModel"
+ assert model_status.adapter_model_type == "VeraModel"
+ assert model_status.peft_types == {"default": "VERA"}
+ assert model_status.trainable_params == 532
+ assert model_status.total_params == 752
+ assert model_status.num_adapter_layers == 2
+ assert model_status.enabled is True
+ assert model_status.active_adapters == ["default"]
+ assert model_status.merged_adapters == []
+ assert model_status.requires_grad == {"default": True}
+ assert model_status.available_adapters == ["default"]
+ assert model_status.devices == {"default": ["cpu", self.torch_device]}
+
+ layer_status0 = layer_status[0]
+ assert len(layer_status) == 2
+ assert layer_status0.name == "model.lin0"
+ assert layer_status0.module_type == "vera.Linear"
+ assert layer_status0.enabled is True
+ assert layer_status0.active_adapters == ["default"]
+ assert layer_status0.merged_adapters == []
+ assert layer_status0.requires_grad == {"default": True}
+ assert layer_status0.available_adapters == ["default"]
+ assert layer_status0.devices == {"default": ["cpu", self.torch_device]}
+
+ ###################
+ # non-PEFT models #
+ ###################
+
+ def test_transformers_model(self):
+ model_id = "peft-internal-testing/gpt2-lora-random"
+ # note that loading through AutoModelForCausalLM.from_pretrained does not enable training mode, hence
+ # requires_grad=False
+ with hub_online_once(model_id):
+ model = AutoModelForCausalLM.from_pretrained(model_id)
+ model_status = get_model_status(model)
+ layer_status = get_layer_status(model)
+
+ assert model_status.base_model_type == "GPT2LMHeadModel"
+ assert model_status.adapter_model_type == "None"
+ assert model_status.peft_types == {}
+ assert model_status.trainable_params == 0
+ assert model_status.total_params == 124734720
+ assert model_status.num_adapter_layers == 12
+ assert model_status.enabled is True
+ assert model_status.active_adapters == ["default"]
+ assert model_status.merged_adapters == []
+ assert model_status.requires_grad == {"default": False}
+ assert model_status.available_adapters == ["default"]
+ assert model_status.devices == {"default": ["cpu"]}
+
+ layer_status0 = layer_status[0]
+ assert len(layer_status) == 12
+ assert layer_status0.name == "transformer.h.0.attn.c_attn"
+ assert layer_status0.module_type == "lora.Linear"
+ assert layer_status0.enabled is True
+ assert layer_status0.active_adapters == ["default"]
+ assert layer_status0.merged_adapters == []
+ assert layer_status0.requires_grad == {"default": False}
+ assert layer_status0.available_adapters == ["default"]
+ assert layer_status0.devices == {"default": ["cpu"]}
+
+ def test_model_with_injected_layers(self, large_model):
+ model = large_model.base_model.model
+ model_status = get_model_status(model)
+ layer_status = get_layer_status(model)
+
+ assert model_status.base_model_type == "other"
+ assert model_status.adapter_model_type == "None"
+ assert model_status.peft_types == {}
+ assert model_status.trainable_params == 616
+ assert model_status.total_params == 2236
+ assert model_status.num_adapter_layers == 4
+ assert model_status.enabled is True
+ assert model_status.active_adapters == ["default"]
+ assert model_status.merged_adapters == []
+ assert model_status.requires_grad == {"default": True, "other": False}
+ assert model_status.available_adapters == ["default", "other"]
+ assert model_status.devices == {"default": ["cpu"], "other": ["cpu"]}
+
+ layer_status1 = layer_status[1]
+ assert len(layer_status) == 4
+ assert layer_status1.name == "emb0"
+ assert layer_status1.module_type == "lora.Embedding"
+ assert layer_status1.enabled is True
+ assert layer_status1.active_adapters == ["default"]
+ assert layer_status1.merged_adapters == []
+ assert layer_status1.requires_grad == {"default": True}
+ assert layer_status1.available_adapters == ["default"]
+ assert layer_status1.devices == {"default": ["cpu"]}
+
+ ###############
+ # error cases #
+ ###############
+
+ def test_vanilla_model_raises(self):
+ model = nn.Linear(10, 10)
+ # note: full error message is longer
+ with pytest.raises(ValueError, match="No adapter layers found in the model"):
+ get_layer_status(model)
+
+ with pytest.raises(ValueError, match="No adapter layers found in the model"):
+ get_model_status(model)
+
+ def test_transformer_model_without_adapter_raises(self):
+ model_id = "gpt2"
+ with hub_online_once(model_id):
+ model = AutoModelForCausalLM.from_pretrained(model_id)
+ # note: full error message is longer
+ with pytest.raises(ValueError, match="No adapter layers found in the model"):
+ get_layer_status(model)
+
+ with pytest.raises(ValueError, match="No adapter layers found in the model"):
+ get_model_status(model)
+
+ def test_prefix_tuning(self):
+ model_id = "hf-internal-testing/tiny-random-BartForConditionalGeneration"
+ with hub_online_once(model_id):
+ model = AutoModelForSeq2SeqLM.from_pretrained(model_id)
+ config = PromptTuningConfig(task_type="SEQ_2_SEQ_LM", num_virtual_tokens=10)
+ model = get_peft_model(model, config)
+
+ # note: full error message is longer
+ with pytest.raises(TypeError, match=re.escape("get_layer_status() got an invalid PeftModel instance")):
+ model.get_layer_status()
+
+ with pytest.raises(TypeError, match=re.escape("get_model_status() got an invalid PeftModel instance")):
+ model.get_model_status()
+
+ def test_adaption_prompt(self):
+ model_id = "HuggingFaceH4/tiny-random-LlamaForCausalLM"
+ with hub_online_once(model_id):
+ model = AutoModelForCausalLM.from_pretrained(model_id)
+ config = AdaptionPromptConfig(adapter_layers=1, adapter_len=4)
+ model = get_peft_model(model, config)
+
+ # note: full error message is longer
+ with pytest.raises(TypeError, match=re.escape("get_layer_status() got an invalid PeftModel instance")):
+ model.get_layer_status()
+
+ with pytest.raises(TypeError, match=re.escape("get_model_status() got an invalid PeftModel instance")):
+ model.get_model_status()
+
+ def test_mixed_model_raises(self):
+ class SimpleNet(nn.Module):
+ def __init__(self, bias=True):
+ super().__init__()
+ # note: out_features must be > rank or else OFT will be an identity transform
+ self.lin0 = nn.Linear(10, 20, bias=bias)
+ self.relu = nn.ReLU()
+ self.lin1 = nn.Linear(20, 16, bias=bias)
+
+ def forward(self, X):
+ X = X.float()
+ X = self.lin0(X)
+ X = self.relu(X)
+ X = self.lin1(X)
+ return X
+
+ base_model = SimpleNet()
+ config0 = LoraConfig(target_modules=["lin0"], init_lora_weights=False)
+ config1 = LoHaConfig(target_modules=["lin0", "lin1"], init_weights=False)
+ model = get_peft_model(base_model, config0, adapter_name="adapter0", mixed="mixed")
+ model.add_adapter("adapter1", config1)
+
+ # note: full error message is longer
+ with pytest.raises(TypeError, match="get_layer_status is not supported for PeftMixedModel"):
+ model.get_layer_status()
+
+ with pytest.raises(TypeError, match="get_model_status is not supported for PeftMixedModel"):
+ model.get_model_status()
+
+
+# Tests for BaseTuner
+class MockModelConfig:
+ config = {"mock_key": "mock_value"}
+
+ def to_dict(self):
+ return self.config
+
+
+@dataclasses.dataclass
+class MockModelDataclassConfig:
+ mock_key: str
+
+
+class ModelWithConfig(nn.Module):
+ def __init__(self):
+ self.config = MockModelConfig()
+
+
+class ModelWithDictConfig(nn.Module):
+ def __init__(self):
+ self.config = MockModelConfig.config
+
+
+class ModelWithDataclassConfig(nn.Module):
+ def __init__(self):
+ self.config = MockModelDataclassConfig(**MockModelConfig().to_dict())
+
+
+class ModelWithNoConfig(nn.Module):
+ pass
+
+
+class TestBaseTunerGetModelConfig(unittest.TestCase):
+ def test_get_model_config_use_to_dict(self):
+ config = BaseTuner.get_model_config(ModelWithConfig())
+ assert config == MockModelConfig.config
+
+ def test_get_model_config_as_dict(self):
+ config = BaseTuner.get_model_config(ModelWithDictConfig())
+ assert config == MockModelConfig.config
+
+ def test_get_model_config_with_no_config(self):
+ config = BaseTuner.get_model_config(ModelWithNoConfig())
+ assert config == DUMMY_MODEL_CONFIG
+
+ def test_get_model_config_with_dataclass(self):
+ config = BaseTuner.get_model_config(ModelWithDataclassConfig())
+ assert config == MockModelConfig.config
+
+
+class TestBaseTunerWarnForTiedEmbeddings:
+ model_id = "HuggingFaceH4/tiny-random-LlamaForCausalLM"
+ warn_end_inject = "huggingface/peft/issues/2018."
+ warn_end_merge = (
+ "# Now use the original model but in untied format\n"
+ "model = AutoModelForCausalLM.from_pretrained(untied_model_dir)\n```\n"
+ )
+
+ def _get_peft_model(self, tie_word_embeddings, target_module):
+ with hub_online_once(self.model_id):
+ base_model = AutoModelForCausalLM.from_pretrained(self.model_id, tie_word_embeddings=tie_word_embeddings)
+ model = get_peft_model(
+ base_model,
+ LoraConfig(target_modules=[target_module]),
+ )
+ return model
+
+ def _is_warn_triggered(self, warning_list, endswith):
+ return any(str(warning.message).endswith(endswith) for warning in warning_list)
+
+ def test_warn_for_tied_embeddings_inject(self, recwarn):
+ self._get_peft_model(tie_word_embeddings=True, target_module="lm_head")
+ assert self._is_warn_triggered(recwarn.list, self.warn_end_inject)
+
+ def test_warn_for_tied_embeddings_merge(self, recwarn):
+ model = self._get_peft_model(tie_word_embeddings=True, target_module="lm_head")
+ model.merge_and_unload()
+ assert self._is_warn_triggered(recwarn.list, self.warn_end_merge)
+
+ def test_no_warn_for_untied_embeddings_inject(self, recwarn):
+ self._get_peft_model(tie_word_embeddings=False, target_module="lm_head")
+ assert not self._is_warn_triggered(recwarn.list, self.warn_end_inject)
+
+ def test_no_warn_for_untied_embeddings_merge(self, recwarn):
+ model_not_tied = self._get_peft_model(tie_word_embeddings=False, target_module="lm_head")
+ model_not_tied.merge_and_unload()
+ assert not self._is_warn_triggered(recwarn.list, self.warn_end_merge)
+
+ def test_no_warn_for_no_target_module_inject(self, recwarn):
+ self._get_peft_model(tie_word_embeddings=True, target_module="q_proj")
+ assert not self._is_warn_triggered(recwarn.list, self.warn_end_inject)
+
+ def test_no_warn_for_no_target_module_merge(self, recwarn):
+ model_no_target_module = self._get_peft_model(tie_word_embeddings=True, target_module="q_proj")
+ model_no_target_module.merge_and_unload()
+ assert not self._is_warn_triggered(recwarn.list, self.warn_end_merge)
+
+
+class TestFindMinimalTargetModules:
+ @pytest.mark.parametrize(
+ "target_modules, other_module_names, expected",
+ [
+ (["bar"], [], {"bar"}),
+ (["foo"], ["bar"], {"foo"}),
+ (["1.foo", "2.foo"], ["3.foo", "4.foo"], {"1.foo", "2.foo"}),
+ # Could also return "bar.baz" but we want the shorter one
+ (["bar.baz"], ["foo.bar"], {"baz"}),
+ (["1.foo", "2.foo", "bar.baz"], ["3.foo", "bar.bla"], {"1.foo", "2.foo", "baz"}),
+ # Case with longer suffix chains and nested suffixes
+ (["a.b.c", "d.e.f", "g.h.i"], ["j.k.l", "m.n.o"], {"c", "f", "i"}),
+ (["a.b.c", "d.e.f", "g.h.i"], ["a.b.x", "d.x.f", "x.h.i"], {"c", "e.f", "g.h.i"}),
+ # Case with multiple items that can be covered by a single suffix
+ (["foo.bar.baz", "qux.bar.baz"], ["baz.bar.foo"], {"baz"}),
+ # Realistic examples
+ # Only match k_proj
+ (
+ ["model.decoder.layers.{i}.self_attn.k_proj" for i in range(12)],
+ (
+ ["model.decoder.layers.{i}.self_attn" for i in range(12)]
+ + ["model.decoder.layers.{i}.self_attn.v_proj" for i in range(12)]
+ + ["model.decoder.layers.{i}.self_attn.q_proj" for i in range(12)]
+ ),
+ {"k_proj"},
+ ),
+ # Match all k_proj except the one in layer 5 => no common suffix
+ (
+ ["model.decoder.layers.{i}.self_attn.k_proj" for i in range(12) if i != 5],
+ (
+ ["model.decoder.layers.5.self_attn.k_proj"]
+ + ["model.decoder.layers.{i}.self_attn" for i in range(12)]
+ + ["model.decoder.layers.{i}.self_attn.v_proj" for i in range(12)]
+ + ["model.decoder.layers.{i}.self_attn.q_proj" for i in range(12)]
+ ),
+ {"{i}.self_attn.k_proj" for i in range(12) if i != 5},
+ ),
+ ],
+ )
+ def test_find_minimal_target_modules(self, target_modules, other_module_names, expected):
+ # check all possible combinations of list and set
+ result = find_minimal_target_modules(target_modules, other_module_names)
+ assert result == expected
+
+ result = find_minimal_target_modules(set(target_modules), other_module_names)
+ assert result == expected
+
+ result = find_minimal_target_modules(target_modules, set(other_module_names))
+ assert result == expected
+
+ result = find_minimal_target_modules(set(target_modules), set(other_module_names))
+ assert result == expected
+
+ def test_find_minimal_target_modules_empty_raises(self):
+ with pytest.raises(ValueError, match="target_modules should be a list or set of strings"):
+ find_minimal_target_modules([], ["foo"])
+
+ with pytest.raises(ValueError, match="target_modules should be a list or set of strings"):
+ find_minimal_target_modules(set(), ["foo"])
+
+ def test_find_minimal_target_modules_contains_empty_string_raises(self):
+ target_modules = ["", "foo", "bar.baz"]
+ other_module_names = ["bar"]
+ with pytest.raises(ValueError, match="target_modules should not contain an empty string"):
+ find_minimal_target_modules(target_modules, other_module_names)
+
+ def test_find_minimal_target_modules_string_raises(self):
+ target_modules = "foo"
+ other_module_names = ["bar"]
+ with pytest.raises(ValueError, match="target_modules should be a list or set of strings"):
+ find_minimal_target_modules(target_modules, other_module_names)
+
+ @pytest.mark.parametrize(
+ "target_modules, other_module_names",
+ [
+ (["foo"], ["foo"]),
+ (["foo.bar"], ["foo.bar"]),
+ (["foo.bar", "spam", "eggs"], ["foo.bar"]),
+ (["foo.bar", "spam"], ["foo.bar", "eggs"]),
+ (["foo.bar"], ["foo.bar", "spam", "eggs"]),
+ ],
+ )
+ def test_find_minimal_target_modules_not_disjoint_raises(self, target_modules, other_module_names):
+ msg = (
+ "target_modules and other_module_names contain common elements, this should not happen, please "
+ "open a GitHub issue at https://github.com/huggingface/peft/issues with the code to reproduce this issue"
+ )
+ with pytest.raises(ValueError, match=msg):
+ find_minimal_target_modules(target_modules, other_module_names)
+
+ def test_get_peft_model_applies_find_target_modules(self):
+ # Check that when calling get_peft_model, the target_module optimization is indeed applied if the length of
+ # target_modules is big enough. The resulting model itself should be unaffected.
+ torch.manual_seed(0)
+ model_id = "facebook/opt-125m" # must be big enough for optimization to trigger
+ with hub_online_once(model_id):
+ model = AutoModelForCausalLM.from_pretrained(model_id)
+
+ # base case: specify target_modules in a minimal fashion
+ config = LoraConfig(init_lora_weights=False, target_modules=["q_proj", "v_proj"])
+ model = get_peft_model(model, config)
+
+ # this list contains all targeted modules listed separately
+ big_target_modules = [name for name, module in model.named_modules() if isinstance(module, LoraLayer)]
+ # sanity check
+ assert len(big_target_modules) > MIN_TARGET_MODULES_FOR_OPTIMIZATION
+
+ # make a "checksum" of the model for comparison
+ model_check_sum_before = sum(p.sum() for p in model.parameters())
+
+ # strip prefix so that the names they can be used as new target_modules
+ prefix_to_strip = "base_model.model.model."
+ big_target_modules = [name[len(prefix_to_strip) :] for name in big_target_modules]
+
+ del model
+
+ torch.manual_seed(0)
+ with hub_online_once(model_id):
+ model = AutoModelForCausalLM.from_pretrained(model_id)
+ # pass the big target_modules to config
+ config = LoraConfig(init_lora_weights=False, target_modules=big_target_modules)
+ model = get_peft_model(model, config)
+
+ # check that target modules have been condensed
+ assert model.peft_config["default"].target_modules == {"q_proj", "v_proj"}
+
+ # check that the resulting model is still the same
+ model_check_after = sum(p.sum() for p in model.parameters())
+ assert model_check_sum_before == model_check_after
+
+ def test_suffix_is_substring_of_other_suffix(self):
+ # This test is based on a real world bug found in diffusers. The issue was that we needed the suffix
+ # 'time_emb_proj' in the minimal target modules. However, if there already was the suffix 'proj' in the
+ # required_suffixes, 'time_emb_proj' would not be added because the test was `endswith(suffix)` and
+ # 'time_emb_proj' ends with 'proj'. The correct logic is to test if `endswith("." + suffix")`. The module names
+ # chosen here are only a subset of the hundreds of actual module names but this subset is sufficient to
+ # replicate the bug.
+ target_modules = [
+ "down_blocks.1.attentions.0.transformer_blocks.0.ff.net.0.proj",
+ "mid_block.attentions.0.transformer_blocks.0.ff.net.0.proj",
+ "up_blocks.0.attentions.0.transformer_blocks.0.ff.net.0.proj",
+ "mid_block.attentions.0.proj_out",
+ "up_blocks.0.attentions.0.proj_out",
+ "down_blocks.1.attentions.0.proj_out",
+ "up_blocks.0.resnets.0.time_emb_proj",
+ "down_blocks.0.resnets.0.time_emb_proj",
+ "mid_block.resnets.0.time_emb_proj",
+ ]
+ other_module_names = [
+ "conv_in",
+ "time_proj",
+ "time_embedding",
+ "time_embedding.linear_1",
+ "add_time_proj",
+ "add_embedding",
+ "add_embedding.linear_1",
+ "add_embedding.linear_2",
+ "down_blocks",
+ "down_blocks.0",
+ "down_blocks.0.resnets",
+ "down_blocks.0.resnets.0",
+ "up_blocks",
+ "up_blocks.0",
+ "up_blocks.0.attentions",
+ "up_blocks.0.attentions.0",
+ "up_blocks.0.attentions.0.norm",
+ "up_blocks.0.attentions.0.transformer_blocks",
+ "up_blocks.0.attentions.0.transformer_blocks.0",
+ "up_blocks.0.attentions.0.transformer_blocks.0.norm1",
+ "up_blocks.0.attentions.0.transformer_blocks.0.attn1",
+ ]
+ expected = {"time_emb_proj", "proj", "proj_out"}
+ result = find_minimal_target_modules(target_modules, other_module_names)
+ assert result == expected
+
+ def test_get_peft_modules_module_name_is_suffix_of_another_module(self):
+ # Solves the following bug:
+ # https://github.com/huggingface/diffusers/pull/9622#issuecomment-2404789721
+
+ # The cause for the bug is as follows: When we have, say, a module called "bar.0.query" that we want to target
+ # and another module called "foo_bar.0.query" that we don't want to target, there was potential for an error.
+ # This is not caused by _find_minimal_target_modules directly, but rather the bug was inside of
+ # BaseTuner.inject_adapter and how the names_no_target were chosen. Those used to be chosen based on suffix. In
+ # our example, however, "bar.0.query" is a suffix of "foo_bar.0.query", therefore "foo_bar.0.query" was *not*
+ # added to names_no_target when it should have. As a consequence, during the optimization, it looks like "query"
+ # is safe to use as target_modules because we don't see that it wrongly matches "foo_bar.0.query".
+
+ # ensure that we have sufficiently many modules to trigger the optimization
+ n_layers = MIN_TARGET_MODULES_FOR_OPTIMIZATION + 1
+
+ class InnerModule(nn.Module):
+ def __init__(self):
+ super().__init__()
+ self.query = nn.Linear(10, 10)
+
+ class OuterModule(nn.Module):
+ def __init__(self):
+ super().__init__()
+ # note that "transformer_blocks" is a suffix of "single_transformer_blocks"
+ self.transformer_blocks = nn.ModuleList([InnerModule() for _ in range(n_layers)])
+ self.single_transformer_blocks = nn.ModuleList([InnerModule() for _ in range(n_layers)])
+
+ # we want to match all "transformer_blocks" layers but not "single_transformer_blocks"
+ target_modules = [f"transformer_blocks.{i}.query" for i in range(n_layers)]
+ model = get_peft_model(OuterModule(), LoraConfig(target_modules=target_modules))
+
+ # sanity check: we should have n_layers PEFT layers in model.transformer_blocks
+ transformer_blocks = model.base_model.model.transformer_blocks
+ assert sum(isinstance(module, BaseTunerLayer) for module in transformer_blocks.modules()) == n_layers
+
+ # we should not have any PEFT layers in model.single_transformer_blocks
+ single_transformer_blocks = model.base_model.model.single_transformer_blocks
+ assert not any(isinstance(module, BaseTunerLayer) for module in single_transformer_blocks.modules())
+
+ # target modules should *not* be simplified to "query" as that would match "single_transformers_blocks" too
+ assert model.peft_config["default"].target_modules != {"query"}
+
+ def test_find_minimal_target_modules_does_not_error_with_ia3(self, tmp_path):
+ # See #2429
+ # There is an issue with the compression of the target_modules attribute when using IA³. There, we additionally
+ # have the feedforward_modules attribute, which must be subset of target_modules. When target_modules is shrunk,
+ # the subset check will fail. This test ensures that this doesn't happen.
+ n_layers = MIN_TARGET_MODULES_FOR_OPTIMIZATION + 1
+
+ class InnerModule(nn.Module):
+ def __init__(self):
+ super().__init__()
+ self.query = nn.Linear(10, 10)
+
+ class OuterModule(nn.Module):
+ def __init__(self):
+ super().__init__()
+ self.blocks = nn.ModuleList([InnerModule() for _ in range(n_layers)])
+
+ target_modules = [f"blocks.{i}.query" for i in range(n_layers)]
+ feedforward_modules = [f"blocks.{i}.query" for i in range(n_layers)]
+ # the subset check happens here
+ config = IA3Config(target_modules=target_modules, feedforward_modules=feedforward_modules)
+ # the optimization step happens here, after the subset check, so at first we're fine, but we will run into an
+ # issue after a save/load roundtrip
+ model = get_peft_model(OuterModule(), config)
+ model.save_pretrained(tmp_path)
+ del model
+
+ # does not raise
+ PeftModel.from_pretrained(OuterModule(), tmp_path)
+
+
+class TestRankAndAlphaPattern:
+ @pytest.fixture
+ def model(self):
+ # we always target the foo layers, the *bar* layers are used as a control group to ensure that they are not
+ # accidentally targeted
+ class Inner(nn.Module):
+ def __init__(self):
+ super().__init__()
+ self.foo = nn.Linear(1, 1)
+ self.barfoo = nn.Linear(1, 1)
+
+ class Middle(nn.Module):
+ def __init__(self):
+ super().__init__()
+ self.foo = nn.Linear(1, 1)
+ self.foobar = nn.Linear(1, 1)
+ self.module = Inner()
+
+ class Outer(nn.Module):
+ def __init__(self):
+ super().__init__()
+ self.foo = nn.Linear(1, 1)
+ self.bar = nn.Linear(1, 1)
+ self.module = Middle()
+
+ # resulting model for overview:
+ # Outer(
+ # (foo): Linear(...)
+ # (bar): Linear(...)
+ # (module): Middle(
+ # (foo): Linear(...)
+ # (foobar): Linear(...)
+ # (module): Inner(
+ # (foo): Linear(...)
+ # (barfoo): Linear(...)
+ # )
+ # )
+ # )
+
+ return Outer()
+
+ def test_no_rank_nor_alpha_pattern(self, model):
+ # sanity check the default case, no rank or alpha pattern
+ config = LoraConfig(target_modules="all-linear")
+ model = get_peft_model(model, config).base_model.model
+ # r is the default rank and alpha, thus scaling is 1.0
+ assert model.foo.r["default"] == 8
+ assert model.foo.scaling["default"] == 1.0
+ assert model.bar.r["default"] == 8
+ assert model.bar.scaling["default"] == 1.0
+ assert model.module.foo.r["default"] == 8
+ assert model.module.foo.scaling["default"] == 1.0
+ assert model.module.foobar.r["default"] == 8
+ assert model.module.foobar.scaling["default"] == 1.0
+ assert model.module.module.foo.r["default"] == 8
+ assert model.module.module.foo.scaling["default"] == 1.0
+ assert model.module.module.barfoo.r["default"] == 8
+ assert model.module.module.barfoo.scaling["default"] == 1.0
+
+ def test_rank_and_alpha_pattern_no_matching_keys(self, model):
+ # sanity check for non-matching keys, no rank or alpha pattern
+ config = LoraConfig(target_modules="all-linear", rank_pattern={"bla": 4, "oof": 6}, alpha_pattern={"baz": 3})
+ model = get_peft_model(model, config).base_model.model
+ # r is the default rank and alpha, thus scaling is 1.0
+ assert model.foo.r["default"] == 8
+ assert model.foo.scaling["default"] == 1.0
+ assert model.bar.r["default"] == 8
+ assert model.bar.scaling["default"] == 1.0
+ assert model.module.foo.r["default"] == 8
+ assert model.module.foo.scaling["default"] == 1.0
+ assert model.module.foobar.r["default"] == 8
+ assert model.module.foobar.scaling["default"] == 1.0
+ assert model.module.module.foo.r["default"] == 8
+ assert model.module.module.foo.scaling["default"] == 1.0
+ assert model.module.module.barfoo.r["default"] == 8
+ assert model.module.module.barfoo.scaling["default"] == 1.0
+
+ # below, we test all permutations for rank_pattern of targeting outer, middle, and inner foo layers:
+
+ def test_rank_pattern_target_all(self, model):
+ config = LoraConfig(target_modules="all-linear", rank_pattern={"foo": 16})
+ model = get_peft_model(model, config).base_model.model
+ assert model.foo.r["default"] == 16
+ assert model.bar.r["default"] == 8
+ assert model.module.foo.r["default"] == 16
+ assert model.module.foobar.r["default"] == 8
+ assert model.module.module.foo.r["default"] == 16
+ assert model.module.module.barfoo.r["default"] == 8
+
+ def test_rank_pattern_target_outer(self, model):
+ config = LoraConfig(target_modules="all-linear", rank_pattern={"^foo": 16})
+ model = get_peft_model(model, config).base_model.model
+ assert model.foo.r["default"] == 16
+ assert model.bar.r["default"] == 8
+ assert model.module.foo.r["default"] == 8
+ assert model.module.foobar.r["default"] == 8
+ assert model.module.module.foo.r["default"] == 8
+ assert model.module.module.barfoo.r["default"] == 8
+
+ def test_rank_pattern_target_middle(self, model):
+ config = LoraConfig(target_modules="all-linear", rank_pattern={"^module.foo": 16})
+ model = get_peft_model(model, config).base_model.model
+ assert model.foo.r["default"] == 8
+ assert model.bar.r["default"] == 8
+ assert model.module.foo.r["default"] == 16
+ assert model.module.foobar.r["default"] == 8
+ assert model.module.module.foo.r["default"] == 8
+ assert model.module.module.barfoo.r["default"] == 8
+
+ def test_rank_pattern_target_inner(self, model):
+ config = LoraConfig(target_modules="all-linear", rank_pattern={"module.module.foo": 16})
+ model = get_peft_model(model, config).base_model.model
+ assert model.foo.r["default"] == 8
+ assert model.bar.r["default"] == 8
+ assert model.module.foo.r["default"] == 8
+ assert model.module.foobar.r["default"] == 8
+ assert model.module.module.foo.r["default"] == 16
+ assert model.module.module.barfoo.r["default"] == 8
+
+ def test_rank_pattern_target_inner_with_caret(self, model):
+ # same as before, but using the caret in the regex should also work
+ config = LoraConfig(target_modules="all-linear", rank_pattern={"^module.module.foo": 16})
+ model = get_peft_model(model, config).base_model.model
+ assert model.foo.r["default"] == 8
+ assert model.bar.r["default"] == 8
+ assert model.module.foo.r["default"] == 8
+ assert model.module.foobar.r["default"] == 8
+ assert model.module.module.foo.r["default"] == 16
+ assert model.module.module.barfoo.r["default"] == 8
+
+ def test_rank_pattern_target_middle_inner(self, model):
+ config = LoraConfig(target_modules="all-linear", rank_pattern={"module.foo": 16})
+ model = get_peft_model(model, config).base_model.model
+ assert model.foo.r["default"] == 8
+ assert model.bar.r["default"] == 8
+ assert model.module.foo.r["default"] == 16
+ assert model.module.foobar.r["default"] == 8
+ assert model.module.module.foo.r["default"] == 16
+ assert model.module.module.barfoo.r["default"] == 8
+
+ def test_rank_pattern_target_middle_inner_different_ranks(self, model):
+ # same layers targeted as in previous test, but with different ranks
+ config = LoraConfig(target_modules="all-linear", rank_pattern={"^module.foo": 16, "^module.module.foo": 24})
+ model = get_peft_model(model, config).base_model.model
+ assert model.foo.r["default"] == 8
+ assert model.bar.r["default"] == 8
+ assert model.module.foo.r["default"] == 16
+ assert model.module.foobar.r["default"] == 8
+ assert model.module.module.foo.r["default"] == 24
+ assert model.module.module.barfoo.r["default"] == 8
+
+ def test_rank_pattern_target_outer_middle(self, model):
+ config = LoraConfig(target_modules="all-linear", rank_pattern={"^foo": 16, "^module.foo": 24})
+ model = get_peft_model(model, config).base_model.model
+ assert model.foo.r["default"] == 16
+ assert model.bar.r["default"] == 8
+ assert model.module.foo.r["default"] == 24
+ assert model.module.foobar.r["default"] == 8
+ assert model.module.module.foo.r["default"] == 8
+ assert model.module.module.barfoo.r["default"] == 8
+
+ def test_rank_pattern_target_outer_inner(self, model):
+ config = LoraConfig(target_modules="all-linear", rank_pattern={"^foo": 16, "module.module.foo": 24})
+ model = get_peft_model(model, config).base_model.model
+ assert model.foo.r["default"] == 16
+ assert model.bar.r["default"] == 8
+ assert model.module.foo.r["default"] == 8
+ assert model.module.foobar.r["default"] == 8
+ assert model.module.module.foo.r["default"] == 24
+ assert model.module.module.barfoo.r["default"] == 8
+
+ def test_rank_pattern_target_outer_inner_with_caret(self, model):
+ # same as before, but using the caret in the regex should also work
+ config = LoraConfig(target_modules="all-linear", rank_pattern={"^foo": 16, "^module.module.foo": 24})
+ model = get_peft_model(model, config).base_model.model
+ assert model.foo.r["default"] == 16
+ assert model.bar.r["default"] == 8
+ assert model.module.foo.r["default"] == 8
+ assert model.module.foobar.r["default"] == 8
+ assert model.module.module.foo.r["default"] == 24
+ assert model.module.module.barfoo.r["default"] == 8
+
+ def test_rank_pattern_target_outer_middle_inner_with_caret(self, model):
+ # indicate each layer with a different rank and use the caret in the regex
+ config = LoraConfig(
+ target_modules="all-linear", rank_pattern={"^foo": 16, "^module.foo": 24, "^module.module.foo": 32}
+ )
+ model = get_peft_model(model, config).base_model.model
+ assert model.foo.r["default"] == 16
+ assert model.bar.r["default"] == 8
+ assert model.module.foo.r["default"] == 24
+ assert model.module.foobar.r["default"] == 8
+ assert model.module.module.foo.r["default"] == 32
+ assert model.module.module.barfoo.r["default"] == 8
+
+ def test_rank_pattern_target_outer_middle_inner_with_caret_dict_order(self, model):
+ # same as before, but change the order of the rank_pattern dict
+ config = LoraConfig(
+ target_modules="all-linear", rank_pattern={"^module.module.foo": 32, "^module.foo": 24, "^foo": 16}
+ )
+ model = get_peft_model(model, config).base_model.model
+ assert model.foo.r["default"] == 16
+ assert model.bar.r["default"] == 8
+ assert model.module.foo.r["default"] == 24
+ assert model.module.foobar.r["default"] == 8
+ assert model.module.module.foo.r["default"] == 32
+ assert model.module.module.barfoo.r["default"] == 8
+
+ # below, we test all permutations for alpha_pattern of targeting outer, middle, and inner foo layers:
+ # these tests are analogous to the rank_pattern tests above
+
+ def test_alpha_pattern_target_all(self, model):
+ config = LoraConfig(target_modules="all-linear", alpha_pattern={"foo": 4})
+ model = get_peft_model(model, config).base_model.model
+ assert model.foo.scaling["default"] == 0.5
+ assert model.bar.scaling["default"] == 1.0
+ assert model.module.foo.scaling["default"] == 0.5
+ assert model.module.foobar.scaling["default"] == 1.0
+ assert model.module.module.foo.scaling["default"] == 0.5
+ assert model.module.module.barfoo.scaling["default"] == 1.0
+
+ def test_alpha_pattern_target_outer(self, model):
+ config = LoraConfig(target_modules="all-linear", alpha_pattern={"^foo": 4})
+ model = get_peft_model(model, config).base_model.model
+ assert model.foo.scaling["default"] == 0.5
+ assert model.bar.scaling["default"] == 1.0
+ assert model.module.foo.scaling["default"] == 1.0
+ assert model.module.foobar.scaling["default"] == 1.0
+ assert model.module.module.foo.scaling["default"] == 1.0
+ assert model.module.module.barfoo.scaling["default"] == 1.0
+
+ def test_alpha_pattern_target_middle(self, model):
+ config = LoraConfig(target_modules="all-linear", alpha_pattern={"^module.foo": 4})
+ model = get_peft_model(model, config).base_model.model
+ assert model.foo.scaling["default"] == 1.0
+ assert model.bar.scaling["default"] == 1.0
+ assert model.module.foo.scaling["default"] == 0.5
+ assert model.module.foobar.scaling["default"] == 1.0
+ assert model.module.module.foo.scaling["default"] == 1.0
+ assert model.module.module.barfoo.scaling["default"] == 1.0
+
+ def test_alpha_pattern_target_inner(self, model):
+ config = LoraConfig(target_modules="all-linear", alpha_pattern={"module.module.foo": 4})
+ model = get_peft_model(model, config).base_model.model
+ assert model.foo.scaling["default"] == 1.0
+ assert model.bar.scaling["default"] == 1.0
+ assert model.module.foo.scaling["default"] == 1.0
+ assert model.module.foobar.scaling["default"] == 1.0
+ assert model.module.module.foo.scaling["default"] == 0.5
+ assert model.module.module.barfoo.scaling["default"] == 1.0
+
+ def test_alpha_pattern_target_inner_with_caret(self, model):
+ # same as before, but using the caret in the regex should also work
+ config = LoraConfig(target_modules="all-linear", alpha_pattern={"^module.module.foo": 4})
+ model = get_peft_model(model, config).base_model.model
+ assert model.foo.scaling["default"] == 1.0
+ assert model.bar.scaling["default"] == 1.0
+ assert model.module.foo.scaling["default"] == 1.0
+ assert model.module.foobar.scaling["default"] == 1.0
+ assert model.module.module.foo.scaling["default"] == 0.5
+ assert model.module.module.barfoo.scaling["default"] == 1.0
+
+ def test_alpha_pattern_target_middle_inner(self, model):
+ config = LoraConfig(target_modules="all-linear", alpha_pattern={"module.foo": 4})
+ model = get_peft_model(model, config).base_model.model
+ assert model.foo.scaling["default"] == 1.0
+ assert model.bar.scaling["default"] == 1.0
+ assert model.module.foo.scaling["default"] == 0.5
+ assert model.module.foobar.scaling["default"] == 1.0
+ assert model.module.module.foo.scaling["default"] == 0.5
+ assert model.module.module.barfoo.scaling["default"] == 1.0
+
+ def test_alpha_pattern_target_middle_inner_different_alphas(self, model):
+ # same layers targeted as in previous test, but with different alphas
+ config = LoraConfig(target_modules="all-linear", alpha_pattern={"^module.foo": 4, "^module.module.foo": 2})
+ model = get_peft_model(model, config).base_model.model
+ assert model.foo.scaling["default"] == 1.0
+ assert model.bar.scaling["default"] == 1.0
+ assert model.module.foo.scaling["default"] == 0.5
+ assert model.module.foobar.scaling["default"] == 1.0
+ assert model.module.module.foo.scaling["default"] == 0.25
+ assert model.module.module.barfoo.scaling["default"] == 1.0
+
+ def test_alpha_pattern_target_outer_middle(self, model):
+ config = LoraConfig(target_modules="all-linear", alpha_pattern={"^foo": 4, "^module.foo": 2})
+ model = get_peft_model(model, config).base_model.model
+ assert model.foo.scaling["default"] == 0.5
+ assert model.bar.scaling["default"] == 1.0
+ assert model.module.foo.scaling["default"] == 0.25
+ assert model.module.foobar.scaling["default"] == 1.0
+ assert model.module.module.foo.scaling["default"] == 1.0
+ assert model.module.module.barfoo.scaling["default"] == 1.0
+
+ def test_alpha_pattern_target_outer_inner(self, model):
+ config = LoraConfig(target_modules="all-linear", alpha_pattern={"^foo": 4, "module.module.foo": 2})
+ model = get_peft_model(model, config).base_model.model
+ assert model.foo.scaling["default"] == 0.5
+ assert model.bar.scaling["default"] == 1.0
+ assert model.module.foo.scaling["default"] == 1.0
+ assert model.module.foobar.scaling["default"] == 1.0
+ assert model.module.module.foo.scaling["default"] == 0.25
+ assert model.module.module.barfoo.scaling["default"] == 1.0
+
+ def test_alpha_pattern_target_outer_inner_with_caret(self, model):
+ # same as before, but using the caret in the regex should also work
+ config = LoraConfig(target_modules="all-linear", alpha_pattern={"^foo": 4, "^module.module.foo": 2})
+ model = get_peft_model(model, config).base_model.model
+ assert model.foo.scaling["default"] == 0.5
+ assert model.bar.scaling["default"] == 1.0
+ assert model.module.foo.scaling["default"] == 1.0
+ assert model.module.foobar.scaling["default"] == 1.0
+ assert model.module.module.foo.scaling["default"] == 0.25
+ assert model.module.module.barfoo.scaling["default"] == 1.0
+
+ def test_alpha_pattern_target_outer_middle_inner_with_caret(self, model):
+ # indicate each layer with a different alpha and use the caret in the regex
+ config = LoraConfig(
+ target_modules="all-linear", alpha_pattern={"^foo": 4, "^module.foo": 2, "^module.module.foo": 1}
+ )
+ model = get_peft_model(model, config).base_model.model
+ assert model.foo.scaling["default"] == 0.5
+ assert model.bar.scaling["default"] == 1.0
+ assert model.module.foo.scaling["default"] == 0.25
+ assert model.module.foobar.scaling["default"] == 1.0
+ assert model.module.module.foo.scaling["default"] == 0.125
+ assert model.module.module.barfoo.scaling["default"] == 1.0
+
+ def test_alpha_pattern_target_outer_middle_inner_with_caret_dict_order(self, model):
+ # same as before, but change the order of the alpha_pattern dict
+ config = LoraConfig(
+ target_modules="all-linear", alpha_pattern={"^module.module.foo": 1, "^module.foo": 2, "^foo": 4}
+ )
+ model = get_peft_model(model, config).base_model.model
+ assert model.foo.scaling["default"] == 0.5
+ assert model.bar.scaling["default"] == 1.0
+ assert model.module.foo.scaling["default"] == 0.25
+ assert model.module.foobar.scaling["default"] == 1.0
+ assert model.module.module.foo.scaling["default"] == 0.125
+ assert model.module.module.barfoo.scaling["default"] == 1.0
diff --git a/peft/tests/test_vblora.py b/peft/tests/test_vblora.py
new file mode 100644
index 0000000000000000000000000000000000000000..4a4801cab7904e68660a92695d0f05563d37d672
--- /dev/null
+++ b/peft/tests/test_vblora.py
@@ -0,0 +1,269 @@
+# Copyright 2024-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+import os
+
+import pytest
+import torch
+from accelerate.utils.imports import is_bf16_available
+from safetensors import safe_open
+from torch import nn
+
+from peft import PeftModel, VBLoRAConfig, get_peft_model
+
+
+class MLP(nn.Module):
+ def __init__(self, bias=True):
+ super().__init__()
+ self.relu = nn.ReLU()
+ self.lin0 = nn.Linear(10, 20, bias=bias)
+ self.lin1 = nn.Linear(20, 20, bias=bias) # lin1 and lin2 have same shape
+ self.lin2 = nn.Linear(20, 20, bias=bias)
+ self.lin3 = nn.Linear(20, 2, bias=bias)
+ self.sm = nn.LogSoftmax(dim=-1)
+
+ def forward(self, X):
+ X = self.lin0(X)
+ X = self.relu(X)
+ X = self.lin1(X)
+ X = self.relu(X)
+ X = self.lin2(X)
+ X = self.relu(X)
+ X = self.lin3(X)
+ X = self.sm(X)
+ return X
+
+
+class TestVBLoRA:
+ def get_mlp(self):
+ model = MLP()
+ return model
+
+ def test_vblora_parameters(self):
+ mlp = self.get_mlp()
+ vector_length = 2
+ num_vectors = 10
+ config = VBLoRAConfig(
+ target_modules=["lin0", "lin1", "lin3"], vector_length=vector_length, num_vectors=num_vectors
+ )
+ mlp_vblora = get_peft_model(mlp, config)
+
+ vector_bank = mlp_vblora.vblora_vector_bank["default"]
+
+ vblora_lin0_logits_B = mlp_vblora.lin0.vblora_logits_B["default"]
+ assert vblora_lin0_logits_B.shape == (mlp.lin0.out_features // vector_length, config.r, num_vectors)
+
+ vblora_lin1_logits_A = mlp_vblora.lin1.vblora_logits_A["default"]
+ assert vblora_lin1_logits_A.shape == (config.r, mlp.lin1.in_features // vector_length, num_vectors)
+
+ vblora_lin3_logits_A = mlp_vblora.lin3.vblora_logits_A["default"]
+ assert vblora_lin3_logits_A.shape == (config.r, mlp.lin3.in_features // vector_length, num_vectors)
+
+ assert vector_bank.shape == (num_vectors, vector_length)
+
+ # test if the vector bank is shared across the layers
+ assert (
+ mlp_vblora.lin0.vblora_vector_bank["default"].data_ptr()
+ == mlp_vblora.lin3.vblora_vector_bank["default"].data_ptr()
+ )
+ assert mlp_vblora.lin1.vblora_vector_bank["default"].data_ptr() == vector_bank.data_ptr()
+
+ # should not raise
+ input = torch.randn(5, 10)
+ mlp_vblora(input)
+
+ def test_save_with_topk_weights(self, tmp_path):
+ torch.manual_seed(0)
+ mlp = self.get_mlp()
+ vector_length = 2
+ num_vectors = 10
+ topk = 2
+ config = VBLoRAConfig(
+ target_modules=["lin0", "lin3"],
+ topk=topk,
+ vector_length=vector_length,
+ num_vectors=num_vectors,
+ save_only_topk_weights=True,
+ )
+ mlp_vblora = get_peft_model(mlp, config)
+ save_path = tmp_path / "vblora"
+ mlp_vblora.save_pretrained(save_path)
+ assert os.path.exists(save_path / "adapter_model.safetensors")
+
+ adapter_model_dict = {}
+ with safe_open(save_path / "adapter_model.safetensors", framework="pt") as f:
+ for k in f.keys():
+ adapter_model_dict[k] = f.get_tensor(k)
+ assert "base_model.model.lin0.vblora_logits_A_topk_indices" in adapter_model_dict
+ assert "base_model.model.lin0.vblora_logits_A_topk_weights" in adapter_model_dict
+ assert "base_model.model.lin3.vblora_logits_B_topk_indices" in adapter_model_dict
+ assert "base_model.model.lin3.vblora_logits_B_topk_weights" in adapter_model_dict
+ assert "base_model.model.lin0.vblora_logits_A" not in adapter_model_dict
+ assert "base_model.model.lin3.vblora_logits_B" not in adapter_model_dict
+
+ assert adapter_model_dict["base_model.model.lin0.vblora_logits_B_topk_indices"].shape == (
+ mlp.lin0.out_features // vector_length,
+ config.r,
+ topk,
+ )
+ assert adapter_model_dict["base_model.model.lin0.vblora_logits_B_topk_weights"].shape == (
+ mlp.lin0.out_features // vector_length,
+ config.r,
+ topk - 1,
+ )
+ assert adapter_model_dict["base_model.model.lin3.vblora_logits_A_topk_indices"].shape == (
+ config.r,
+ mlp.lin3.in_features // vector_length,
+ topk,
+ )
+ assert adapter_model_dict["base_model.model.lin3.vblora_logits_A_topk_weights"].shape == (
+ config.r,
+ mlp.lin3.in_features // vector_length,
+ topk - 1,
+ )
+
+ @pytest.mark.parametrize("save_only_topk_weights", [True, False])
+ def test_save_load(self, save_only_topk_weights, tmp_path):
+ torch.manual_seed(0)
+ mlp = self.get_mlp()
+ config = VBLoRAConfig(
+ target_modules=["lin0", "lin1", "lin3"],
+ topk=2,
+ vector_length=2,
+ num_vectors=10,
+ save_only_topk_weights=save_only_topk_weights,
+ )
+ mlp_vblora = get_peft_model(mlp, config)
+ save_path = tmp_path / "vblora"
+ mlp_vblora.save_pretrained(save_path)
+ assert os.path.exists(save_path / "adapter_config.json")
+
+ del mlp
+ torch.manual_seed(0) # make sure the base model has the same weights
+ mlp = self.get_mlp()
+ mlp_vblora_loaded = PeftModel.from_pretrained(mlp, save_path)
+
+ input = torch.randn(5, 10)
+ output = mlp_vblora(input)
+ output_loaded = mlp_vblora_loaded(input)
+ assert torch.allclose(output, output_loaded, atol=1e-8, rtol=1e-5)
+
+ def test_resume_training_model_with_topk_weights(self, tmp_path):
+ torch.manual_seed(1)
+ mlp = self.get_mlp()
+ config = VBLoRAConfig(
+ target_modules=["lin0", "lin1", "lin3"],
+ topk=2,
+ vector_length=2,
+ num_vectors=10,
+ save_only_topk_weights=True,
+ )
+ mlp_vblora = get_peft_model(mlp, config)
+ save_path = tmp_path / "vblora"
+ mlp_vblora.save_pretrained(save_path)
+
+ input = torch.randn(5, 10)
+ mlp_vblora.train()
+ # should not raise
+ mlp_vblora(input)
+
+ del mlp
+ torch.manual_seed(1)
+ mlp = self.get_mlp()
+ mlp_vblora_loaded = PeftModel.from_pretrained(mlp, save_path)
+ mlp_vblora_loaded.train()
+ msg = "Found infinity values in VB-LoRA logits. Ensure training was not resumed from a `save_only_topk_weights` model."
+ with pytest.raises(RuntimeError, match=msg):
+ mlp_vblora_loaded(input)
+
+ @pytest.mark.parametrize("dtype", [torch.float32, torch.float16, torch.bfloat16])
+ def test_vblora_dtypes(self, dtype):
+ mlp = self.get_mlp()
+ if dtype == torch.bfloat16:
+ if not is_bf16_available():
+ pytest.skip("bfloat16 not supported on this system, skipping the test")
+
+ config = VBLoRAConfig(
+ target_modules=["lin0", "lin1", "lin3"], vector_length=2, num_vectors=10, save_only_topk_weights=False
+ )
+ mlp_vblora = get_peft_model(mlp.to(dtype), config)
+ inputs = torch.randn(5, 10).to(dtype)
+ output = mlp_vblora(inputs) # should not raise
+ assert output.dtype == dtype
+
+ def test_vblora_nb_savable_params_only_topk_weights(self):
+ mlp = self.get_mlp()
+ vector_length = 2
+ num_vectors = 10
+ topk = 2
+ r = 4
+ config = VBLoRAConfig(
+ target_modules=["lin0", "lin1"],
+ vector_length=vector_length,
+ num_vectors=num_vectors,
+ topk=topk,
+ r=r,
+ save_only_topk_weights=True,
+ )
+ mlp_vblora = get_peft_model(mlp, config)
+
+ mlp_vblora.lin3.requires_grad_(True) # set lin3 to trainable
+
+ adapter_params, other_params = mlp_vblora.get_nb_savable_parameters()
+ factor = 0.25 # dtype of index is uint8
+ topk_indices_parameter = int(
+ (mlp.lin0.out_features + mlp.lin0.in_features + mlp.lin1.out_features + mlp.lin1.in_features)
+ / vector_length
+ * r
+ * topk
+ * factor
+ )
+ topk_weights_parameter = int(
+ (mlp.lin0.out_features + mlp.lin0.in_features + mlp.lin1.out_features + mlp.lin1.in_features)
+ / vector_length
+ * r
+ * (topk - 1)
+ )
+ vector_bank_parameter = num_vectors * vector_length
+ assert adapter_params == topk_indices_parameter + topk_weights_parameter + vector_bank_parameter
+ assert other_params == (mlp.lin3.in_features + 1) * mlp.lin3.out_features
+
+ def test_vblora_nb_savable_params_all_logits(self):
+ mlp = self.get_mlp()
+ vector_length = 2
+ num_vectors = 10
+ topk = 2
+ r = 4
+ config = VBLoRAConfig(
+ target_modules=["lin0", "lin1"],
+ vector_length=vector_length,
+ num_vectors=num_vectors,
+ topk=topk,
+ r=r,
+ save_only_topk_weights=False,
+ )
+ mlp_vblora = get_peft_model(mlp, config)
+
+ mlp_vblora.lin3.requires_grad_(True) # set lin3 to trainable
+
+ adapter_params, other_params = mlp_vblora.get_nb_savable_parameters()
+ logits_parameter = int(
+ (mlp.lin0.out_features + mlp.lin0.in_features + mlp.lin1.out_features + mlp.lin1.in_features)
+ / vector_length
+ * r
+ * num_vectors
+ )
+ vector_bank_parameter = num_vectors * vector_length
+ assert adapter_params == logits_parameter + vector_bank_parameter
+ assert other_params == (mlp.lin3.in_features + 1) * mlp.lin3.out_features
diff --git a/peft/tests/test_vera.py b/peft/tests/test_vera.py
new file mode 100644
index 0000000000000000000000000000000000000000..717dfb270aa823deccb28e822b6655e637b5b6be
--- /dev/null
+++ b/peft/tests/test_vera.py
@@ -0,0 +1,298 @@
+# Copyright 2024-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+# This test file is for tests specific to VeRA, since VeRA has some specific challenges due to the shared weights.
+
+import os
+
+import pytest
+import torch
+from accelerate.utils.imports import is_bf16_available
+from safetensors import safe_open
+from torch import nn
+
+from peft import PeftModel, VeraConfig, get_peft_model
+
+
+class MLP(nn.Module):
+ def __init__(self, bias=True):
+ super().__init__()
+ self.relu = nn.ReLU()
+ self.lin0 = nn.Linear(10, 20, bias=bias)
+ self.lin1 = nn.Linear(20, 20, bias=bias) # lin1 and lin2 have same shape
+ self.lin2 = nn.Linear(20, 20, bias=bias)
+ self.lin3 = nn.Linear(20, 2, bias=bias)
+ self.sm = nn.LogSoftmax(dim=-1)
+
+ def forward(self, X):
+ X = self.lin0(X)
+ X = self.relu(X)
+ X = self.lin1(X)
+ X = self.relu(X)
+ X = self.lin2(X)
+ X = self.relu(X)
+ X = self.lin3(X)
+ X = self.sm(X)
+ return X
+
+
+class TestVera:
+ @pytest.fixture
+ def mlp(self):
+ torch.manual_seed(0)
+ model = MLP()
+ return model
+
+ @pytest.fixture
+ def mlp_same_prng(self, mlp):
+ torch.manual_seed(0)
+
+ config = VeraConfig(target_modules=["lin1", "lin2"], init_weights=False)
+ # creates a default VeRA adapter
+ peft_model = get_peft_model(mlp, config)
+ config2 = VeraConfig(target_modules=["lin1", "lin2"], init_weights=False)
+ peft_model.add_adapter("other", config2)
+ return peft_model
+
+ def test_multiple_adapters_same_prng_weights(self, mlp_same_prng):
+ # we can have multiple adapters with the same prng key, in which case the weights should be shared
+ assert (
+ mlp_same_prng.base_model.model.lin1.vera_A["default"]
+ is mlp_same_prng.base_model.model.lin1.vera_A["other"]
+ )
+ assert (
+ mlp_same_prng.base_model.model.lin1.vera_B["default"]
+ is mlp_same_prng.base_model.model.lin1.vera_B["other"]
+ )
+ assert (
+ mlp_same_prng.base_model.model.lin2.vera_A["default"]
+ is mlp_same_prng.base_model.model.lin2.vera_A["other"]
+ )
+ assert (
+ mlp_same_prng.base_model.model.lin2.vera_B["default"]
+ is mlp_same_prng.base_model.model.lin2.vera_B["other"]
+ )
+
+ input = torch.randn(5, 10)
+ mlp_same_prng.set_adapter("default")
+ output_default = mlp_same_prng(input)
+ mlp_same_prng.set_adapter("other")
+ output_other = mlp_same_prng(input)
+ assert not torch.allclose(output_default, output_other, atol=1e-3, rtol=1e-3)
+
+ def test_multiple_adapters_different_prng_raises(self):
+ # we cannot have multiple adapters with different prng keys
+ model = MLP()
+ config = VeraConfig(target_modules=["lin1", "lin2"], init_weights=False)
+ # creates a default VeRA adapter
+ peft_model = get_peft_model(model, config)
+ config2 = VeraConfig(target_modules=["lin1", "lin2"], init_weights=False, projection_prng_key=123)
+
+ msg = (
+ r"Vera PRNG initialisation key must be the same for all adapters. Got config.projection_prng_key=123 but "
+ r"previous config had 0"
+ )
+ with pytest.raises(ValueError, match=msg):
+ peft_model.add_adapter("other", config2)
+
+ def test_multiple_adapters_save_load_save_projection_true(self, mlp_same_prng, tmp_path):
+ # check saving and loading works with multiple adapters and saved projection weights
+ torch.manual_seed(0)
+ input = torch.randn(5, 10)
+ mlp_same_prng.set_adapter("default")
+ output_default = mlp_same_prng(input)
+ mlp_same_prng.set_adapter("other")
+ output_other = mlp_same_prng(input)
+
+ # sanity check
+ assert not torch.allclose(output_default, output_other, atol=1e-3, rtol=1e-3)
+
+ save_path = tmp_path / "vera"
+ mlp_same_prng.save_pretrained(save_path)
+ assert os.path.exists(save_path / "adapter_config.json")
+ assert os.path.exists(save_path / "other" / "adapter_config.json")
+
+ torch.manual_seed(0)
+ mlp = MLP()
+ peft_model = PeftModel.from_pretrained(mlp, save_path)
+ peft_model.load_adapter(save_path / "other", "other")
+
+ peft_model.set_adapter("default")
+ output_default_loaded = peft_model(input)
+ peft_model.set_adapter("other")
+ output_other_loaded = peft_model(input)
+
+ assert torch.allclose(output_default, output_default_loaded, atol=1e-3, rtol=1e-3)
+ assert torch.allclose(output_other, output_other_loaded, atol=1e-3, rtol=1e-3)
+
+ def test_multiple_adapters_save_load_save_projection_false(self, mlp, tmp_path):
+ # check saving and loading works with multiple adapters without saved projection weights
+ torch.manual_seed(1)
+ config = VeraConfig(target_modules=["lin1", "lin2"], init_weights=False, save_projection=False)
+ # creates a default VeRA adapter
+ peft_model = get_peft_model(mlp, config, adapter_name="first")
+ config2 = VeraConfig(target_modules=["lin1", "lin2"], init_weights=False, save_projection=False)
+ peft_model.add_adapter("second", config2)
+
+ input = torch.randn(5, 10)
+ peft_model.set_adapter("first")
+ output_first = peft_model(input)
+ peft_model.set_adapter("second")
+ output_second = peft_model(input)
+
+ # sanity check
+ assert not torch.allclose(output_first, output_second, atol=1e-3, rtol=1e-3)
+
+ save_path = tmp_path / "vera"
+ peft_model.save_pretrained(save_path)
+ assert os.path.exists(save_path / "first" / "adapter_config.json")
+ assert os.path.exists(save_path / "second" / "adapter_config.json")
+
+ torch.manual_seed(0)
+ mlp = MLP()
+ peft_model = PeftModel.from_pretrained(mlp, save_path / "first", adapter_name="first")
+ peft_model.load_adapter(save_path / "second", "second")
+
+ peft_model.set_adapter("first")
+ output_first_loaded = peft_model(input)
+ peft_model.set_adapter("second")
+ output_second_loaded = peft_model(input)
+
+ assert torch.allclose(output_first, output_first_loaded, atol=1e-3, rtol=1e-3)
+ assert torch.allclose(output_second, output_second_loaded, atol=1e-3, rtol=1e-3)
+
+ def test_multiple_adapters_save_projection_true_contains_vera_A_vera_B(self, mlp_same_prng, tmp_path):
+ # check that the state_dicts don't contain the projection weights
+ save_path = tmp_path / "vera"
+ mlp_same_prng.save_pretrained(save_path)
+
+ sd_default = {}
+ with safe_open(save_path / "adapter_model.safetensors", framework="pt", device="cpu") as f:
+ for key in f.keys():
+ sd_default[key] = f.get_tensor(key)
+
+ assert any("vera_A" in key for key in sd_default)
+ assert any("vera_B" in key for key in sd_default)
+ # default rank for VeRA is 256
+ assert sd_default["base_model.vera_A"].shape == (256, 20)
+ assert sd_default["base_model.vera_B"].shape == (20, 256)
+
+ sd_other = {}
+ with safe_open(save_path / "other" / "adapter_model.safetensors", framework="pt", device="cpu") as f:
+ for key in f.keys():
+ sd_other[key] = f.get_tensor(key)
+
+ assert any("vera_A" in key for key in sd_other)
+ assert any("vera_B" in key for key in sd_other)
+ assert sd_other["base_model.vera_A"].shape == (256, 20)
+ assert sd_other["base_model.vera_B"].shape == (20, 256)
+
+ def test_multiple_adapters_save_projection_false_contains_no_vera_A_vera_B(self, mlp, tmp_path):
+ torch.manual_seed(1)
+ config = VeraConfig(target_modules=["lin1", "lin2"], init_weights=False, save_projection=False)
+ # creates a default VeRA adapter
+ peft_model = get_peft_model(mlp, config, adapter_name="first")
+ config2 = VeraConfig(target_modules=["lin1", "lin2"], init_weights=False, save_projection=False)
+ peft_model.add_adapter("second", config2)
+
+ save_path = tmp_path / "vera"
+ peft_model.save_pretrained(save_path)
+
+ sd_default = {}
+ with safe_open(save_path / "first" / "adapter_model.safetensors", framework="pt", device="cpu") as f:
+ for key in f.keys():
+ sd_default[key] = f.get_tensor(key)
+
+ assert not any("vera_A" in key for key in sd_default)
+ assert not any("vera_B" in key for key in sd_default)
+
+ sd_other = {}
+ with safe_open(save_path / "second" / "adapter_model.safetensors", framework="pt", device="cpu") as f:
+ for key in f.keys():
+ sd_other[key] = f.get_tensor(key)
+
+ assert not any("vera_A" in key for key in sd_other)
+ assert not any("vera_B" in key for key in sd_other)
+
+ def test_vera_A_vera_B_share_memory(self, mlp_same_prng):
+ vera_A = mlp_same_prng.vera_A["default"]
+ vera_B = mlp_same_prng.vera_B["default"]
+
+ # these tensors should share the same data
+ assert vera_A.data_ptr() == mlp_same_prng.base_model.model.lin1.vera_A["default"].data_ptr()
+ assert vera_B.data_ptr() == mlp_same_prng.base_model.model.lin1.vera_B["default"].data_ptr()
+ assert vera_A.data_ptr() == mlp_same_prng.base_model.model.lin2.vera_A["default"].data_ptr()
+ assert vera_B.data_ptr() == mlp_same_prng.base_model.model.lin2.vera_B["default"].data_ptr()
+ # sanity check: these tensors shouldn't share the same data
+ assert vera_A.data_ptr() != vera_B.data_ptr()
+
+ def test_vera_lambda_dont_share_memory(self, mlp_same_prng):
+ # sanity check: these tensors shouldn't share the same data
+ assert (
+ mlp_same_prng.base_model.model.lin1.vera_lambda_b["default"].data_ptr()
+ != mlp_same_prng.base_model.model.lin1.vera_lambda_b["other"].data_ptr()
+ )
+ assert (
+ mlp_same_prng.base_model.model.lin1.vera_lambda_b["default"].data_ptr()
+ != mlp_same_prng.base_model.model.lin2.vera_lambda_b["default"].data_ptr()
+ )
+ assert (
+ mlp_same_prng.base_model.model.lin1.vera_lambda_b["other"].data_ptr()
+ != mlp_same_prng.base_model.model.lin2.vera_lambda_b["other"].data_ptr()
+ )
+ assert (
+ mlp_same_prng.base_model.model.lin1.vera_lambda_d["default"].data_ptr()
+ != mlp_same_prng.base_model.model.lin1.vera_lambda_d["other"].data_ptr()
+ )
+ assert (
+ mlp_same_prng.base_model.model.lin1.vera_lambda_d["default"].data_ptr()
+ != mlp_same_prng.base_model.model.lin2.vera_lambda_d["default"].data_ptr()
+ )
+ assert (
+ mlp_same_prng.base_model.model.lin1.vera_lambda_d["other"].data_ptr()
+ != mlp_same_prng.base_model.model.lin2.vera_lambda_d["other"].data_ptr()
+ )
+
+ def test_vera_different_shapes(self, mlp):
+ config = VeraConfig(target_modules=["lin0", "lin3"], init_weights=False)
+ mlp_different_shapes = get_peft_model(mlp, config)
+
+ vera_A = mlp_different_shapes.vera_A["default"]
+ vera_B = mlp_different_shapes.vera_B["default"]
+
+ # sanity check
+ assert mlp.lin0.base_layer.weight.shape != mlp.lin3.base_layer.weight.shape
+
+ # lin0 has the largest output dimension, lin3 has the largest input dimension
+ # vera_A should have the shape of (rank, largest_in), vera_B should have the shape of (largest_out, rank)
+ assert vera_A.shape == (config.r, mlp.lin3.in_features)
+ assert vera_B.shape == (mlp.lin0.out_features, config.r)
+
+ # should not raise
+ input = torch.randn(5, 10)
+ mlp_different_shapes(input)
+
+ @pytest.mark.parametrize("dtype", [torch.float32, torch.float16, torch.bfloat16])
+ def test_vera_dtypes(self, dtype):
+ if dtype == torch.bfloat16:
+ # skip if bf16 is not supported on hardware, see #1872
+ if not is_bf16_available():
+ pytest.skip("bfloat16 not supported on this system, skipping the test")
+
+ model = MLP().to(dtype)
+ config = VeraConfig(target_modules=["lin1", "lin2"], init_weights=False)
+ peft_model = get_peft_model(model, config)
+ inputs = torch.randn(5, 10).to(dtype)
+ output = peft_model(inputs) # should not raise
+ assert output.dtype == dtype
diff --git a/peft/tests/test_vision_models.py b/peft/tests/test_vision_models.py
new file mode 100644
index 0000000000000000000000000000000000000000..74e5d654de26f398f8ea2562f5471d70c3f6115c
--- /dev/null
+++ b/peft/tests/test_vision_models.py
@@ -0,0 +1,156 @@
+# Copyright 2024-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+# This is not a full on test suite of vision models, since we already run many tests on dummy models with Conv2d layers
+# and on stable diffusion models. Instead, this file contains specific tests for bugs that have been found in the past.
+import gc
+
+import numpy as np
+import pytest
+import torch
+from accelerate.utils.memory import clear_device_cache
+from safetensors.torch import load_file
+from transformers import (
+ AutoImageProcessor,
+ AutoModelForImageClassification,
+ AutoProcessor,
+ LlavaForConditionalGeneration,
+)
+
+from peft import (
+ HRAConfig,
+ LoHaConfig,
+ LoKrConfig,
+ LoraConfig,
+ OFTConfig,
+ PeftModel,
+ PrefixTuningConfig,
+ get_peft_model,
+)
+
+from .testing_utils import load_cat_image
+
+
+CONFIGS = {
+ "lora": LoraConfig(target_modules=["convolution"], modules_to_save=["classifier", "normalization"]),
+ "loha": LoHaConfig(target_modules=["convolution"], modules_to_save=["classifier", "normalization"]),
+ "lokr": LoKrConfig(target_modules=["convolution"], modules_to_save=["classifier", "normalization"]),
+ "oft": OFTConfig(
+ r=1, oft_block_size=0, target_modules=["convolution"], modules_to_save=["classifier", "normalization"]
+ ),
+ "hra": HRAConfig(target_modules=["convolution"], modules_to_save=["classifier", "normalization"]),
+ # TODO: cannot use BOFT because some convolutional kernel dimensions are even (64) and others odd (147). There is no
+ # common denominator for the boft_block_size except 1, but using 1 results in an error in the fbd_cuda kernel:
+ # > Error in forward_fast_block_diag_cuda_kernel: an illegal memory access was encountered
+ # "boft": BOFTConfig(target_modules=["convolution"], modules_to_save=["classifier", "normalization"], boft_block_size=2),
+}
+
+
+# Ensure that models like Llava that pass past_key_values automatically do not fail, see #1938
+class TestPastKV:
+ def test_past_kv(self):
+ model_id = "peft-internal-testing/tiny-LlavaForConditionalGeneration"
+ prompt = "USER: \nWhat are these?\nASSISTANT:"
+
+ # prepare model and inputs
+ model = LlavaForConditionalGeneration.from_pretrained(
+ model_id,
+ low_cpu_mem_usage=True,
+ )
+ processor = AutoProcessor.from_pretrained(model_id)
+ raw_image = np.random.randint(0, 255, (224, 224, 3), dtype=np.uint8)
+ inputs = processor(text=prompt, images=raw_image, return_tensors="pt")
+
+ # get peft model
+ peft_config = PrefixTuningConfig(task_type="CAUSAL_LM", num_virtual_tokens=20)
+ model = get_peft_model(model, peft_config)
+ # check that this does not raise
+ model(**inputs, output_hidden_states=True)
+
+
+class TestResnet:
+ model_id = "hf-internal-testing/tiny-random-ResNetForImageClassification"
+ cat_image = load_cat_image() # for caching
+
+ @pytest.fixture(autouse=True)
+ def teardown(self):
+ r"""
+ Efficient mechanism to free GPU memory after each test. Based on
+ https://github.com/huggingface/transformers/issues/21094
+ """
+ clear_device_cache(garbage_collection=True)
+ gc.collect()
+
+ @pytest.fixture(scope="class")
+ def image_processor(self):
+ image_processor = AutoImageProcessor.from_pretrained(self.model_id)
+ return image_processor
+
+ @pytest.fixture(scope="class")
+ def data(self, image_processor):
+ return image_processor(self.cat_image, return_tensors="pt")
+
+ @pytest.mark.parametrize("config", CONFIGS.values(), ids=CONFIGS.keys())
+ def test_model_with_batchnorm_reproducibility(self, config, tmp_path, data):
+ # see 1732
+ torch.manual_seed(0)
+ model = AutoModelForImageClassification.from_pretrained(self.model_id)
+ model = get_peft_model(model, config)
+
+ # record outputs before training
+ model.eval()
+ with torch.inference_mode():
+ output_before = model(**data)
+ model.train()
+
+ # train the model
+ optimizer = torch.optim.AdamW(model.parameters(), lr=1e-3)
+ batch_size = 4
+ max_steps = 5 * batch_size
+ labels = torch.zeros(1, 3)
+ labels[0, 1] = 1
+ for i in range(0, max_steps, batch_size):
+ optimizer.zero_grad()
+ outputs = model(**data, labels=labels)
+ loss = outputs.loss
+ loss.backward()
+ optimizer.step()
+
+ # record outputs after training
+ model.eval()
+ with torch.inference_mode():
+ output_after = model(**data)
+ assert torch.isfinite(output_after.logits).all()
+ atol, rtol = 1e-4, 1e-4
+ # sanity check: model was updated
+ assert not torch.allclose(output_before.logits, output_after.logits, atol=atol, rtol=rtol)
+
+ # check saving the model and loading it
+ model.save_pretrained(tmp_path)
+ del model
+
+ torch.manual_seed(0)
+ model = AutoModelForImageClassification.from_pretrained(self.model_id)
+ model = PeftModel.from_pretrained(model, tmp_path).eval()
+ with torch.inference_mode():
+ output_loaded = model(**data)
+ assert torch.allclose(output_after.logits, output_loaded.logits, atol=atol, rtol=rtol)
+
+ # ensure that the checkpoint file contains the buffers
+ model_running_mean = len([k for k in model.state_dict().keys() if "running_mean" in k])
+ state_dict = load_file(tmp_path / "adapter_model.safetensors")
+ checkpoint_running_mean = len([k for k in state_dict.keys() if "running_mean" in k])
+ # note that the model has twice as many "running_mean", as there is one copy per ModulesToSaveWrapper, we need
+ # to multiply by 2 to get the same number
+ assert model_running_mean == checkpoint_running_mean * 2
diff --git a/peft/tests/test_xlora.py b/peft/tests/test_xlora.py
new file mode 100644
index 0000000000000000000000000000000000000000..724e7782cbfd508f3cb59c414a8e85f9bc438a15
--- /dev/null
+++ b/peft/tests/test_xlora.py
@@ -0,0 +1,426 @@
+# Copyright 2023-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+
+import os
+from functools import wraps
+
+import huggingface_hub
+import pytest
+import torch
+from safetensors.torch import load_file
+from transformers import AutoModelForCausalLM, AutoTokenizer
+
+from peft import LoraConfig, PeftType, TaskType, XLoraConfig, get_peft_model
+from peft.peft_model import PeftModel
+from peft.tuners.xlora.layer import XLoraLayer
+from peft.utils import infer_device
+
+
+def flaky(num_tries: int):
+ """Decorator for test functions that are flaky"""
+
+ def decorator(func):
+ @wraps(func)
+ def wrapper(*args, **kwargs):
+ for _ in range(num_tries):
+ try:
+ return func(*args, **kwargs)
+ except AssertionError as e:
+ print(f"Failed test {func.__name__} with error: {e}")
+ continue
+ raise AssertionError(f"Failed test {func.__name__} after {num_tries} tries")
+
+ return wrapper
+
+ return decorator
+
+
+class TestXlora:
+ torch_device = infer_device()
+
+ model_id = "facebook/opt-125m"
+ num_loras = 4
+
+ @pytest.fixture(scope="class")
+ def lora_dir(self, tmp_path_factory):
+ return tmp_path_factory.mktemp("lora")
+
+ @pytest.fixture(scope="class")
+ def lora_embedding_dir(self, tmp_path_factory):
+ return tmp_path_factory.mktemp("lora_embedding")
+
+ @pytest.fixture(scope="class")
+ def saved_lora_adapters(self, lora_dir):
+ file_names = []
+
+ lora_configs = [
+ LoraConfig(task_type="CAUSAL_LM", target_modules=["q_proj", "v_proj"], init_lora_weights=False)
+ for _ in range(self.num_loras)
+ ]
+ # have 1 LoRA with different target modules
+ lora_configs[-1] = LoraConfig(
+ task_type="CAUSAL_LM", target_modules=["k_proj", "q_proj", "v_proj"], init_lora_weights=False
+ )
+
+ for i, lora_config in enumerate(lora_configs, start=1):
+ torch.manual_seed(i)
+ model = AutoModelForCausalLM.from_pretrained(self.model_id)
+ peft_model = get_peft_model(model, lora_config)
+ file_name = os.path.join(lora_dir, f"checkpoint-{i}")
+ peft_model.save_pretrained(file_name)
+ file_names.append(file_name)
+ return file_names
+
+ @pytest.fixture(scope="class")
+ def saved_lora_embedding_adapters(self, lora_embedding_dir):
+ file_names = []
+ for i in range(1, self.num_loras + 1):
+ torch.manual_seed(i)
+ lora_config = LoraConfig(task_type="CAUSAL_LM", init_lora_weights=False, target_modules=["embed_tokens"])
+ model = AutoModelForCausalLM.from_pretrained(self.model_id)
+ peft_model = get_peft_model(model, lora_config)
+ file_name = os.path.join(lora_embedding_dir, f"checkpoint-{i}")
+ peft_model.save_pretrained(file_name)
+ file_names.append(file_name)
+ return file_names
+
+ @pytest.fixture(scope="class")
+ def tokenizer(self):
+ tokenizer = AutoTokenizer.from_pretrained(self.model_id, trust_remote_code=True, device_map=self.torch_device)
+ return tokenizer
+
+ @pytest.fixture(scope="function")
+ def embedding_model(self, saved_lora_embedding_adapters):
+ model = AutoModelForCausalLM.from_pretrained(self.model_id)
+ model.config.use_cache = False
+ adapters = {str(i): file_name for i, file_name in enumerate(saved_lora_embedding_adapters)}
+
+ peft_config = XLoraConfig(
+ task_type=TaskType.CAUSAL_LM,
+ peft_type=PeftType.XLORA,
+ hidden_size=model.config.hidden_size,
+ xlora_depth=8,
+ adapters=adapters,
+ )
+ model = get_peft_model(model, peft_config).to(self.torch_device)
+ return model
+
+ @pytest.fixture(scope="function")
+ def model(self, saved_lora_adapters):
+ model = AutoModelForCausalLM.from_pretrained(self.model_id)
+ model.config.use_cache = False
+ adapters = {str(i): file_name for i, file_name in enumerate(saved_lora_adapters)}
+
+ peft_config = XLoraConfig(
+ task_type=TaskType.CAUSAL_LM,
+ peft_type=PeftType.XLORA,
+ hidden_size=model.config.hidden_size,
+ xlora_depth=8,
+ adapters=adapters,
+ )
+ model = get_peft_model(model, peft_config).to(self.torch_device)
+ return model
+
+ @pytest.fixture(scope="function")
+ def model_layerwise(self, saved_lora_adapters):
+ model = AutoModelForCausalLM.from_pretrained(self.model_id)
+ model.config.use_cache = False
+ adapters = {str(i): file_name for i, file_name in enumerate(saved_lora_adapters)}
+
+ peft_config = XLoraConfig(
+ task_type=TaskType.CAUSAL_LM,
+ peft_type=PeftType.XLORA,
+ hidden_size=model.config.hidden_size,
+ xlora_depth=8,
+ adapters=adapters,
+ layerwise_scalings=True,
+ )
+ model = get_peft_model(model, peft_config).to(self.torch_device)
+ return model
+
+ def test_functional(self, tokenizer, model):
+ model.enable_scalings_logging()
+ inputs = tokenizer.encode("Python is a", add_special_tokens=False, return_tensors="pt")
+ outputs = model.generate(
+ input_ids=inputs.to(self.torch_device),
+ max_new_tokens=32,
+ )
+ assert torch.isfinite(outputs[: inputs.shape[1] :]).all()
+
+ def test_forward_hooks_are_cleaned_up(self, tokenizer, model):
+ # There was an issue that forward hooks would accumulate during generation, since one hook per forward step was
+ # being registered and generate would call forward multiple times. This is already undesirable, but to make it
+ # worse, only the last hook was removed, resulting in hooks accumulating.
+ # See https://github.com/huggingface/peft/issues/1472#issuecomment-3235817807
+ inputs = tokenizer.encode("Python is a", add_special_tokens=False, return_tensors="pt")
+ model.generate(input_ids=inputs.to(self.torch_device), max_new_tokens=10)
+ num_hooks_gen1 = len(model.base_model.model.model.decoder.layers[0].self_attn.k_proj._forward_pre_hooks)
+
+ model.generate(input_ids=inputs.to(self.torch_device), max_new_tokens=10)
+ num_hooks_gen2 = len(model.base_model.model.model.decoder.layers[0].self_attn.k_proj._forward_pre_hooks)
+ assert num_hooks_gen1 == num_hooks_gen2 == 0
+
+ def test_scalings_logging_methods(self, tokenizer, model):
+ model.enable_scalings_logging()
+
+ inputs = tokenizer.encode("Python is a", add_special_tokens=False, return_tensors="pt")
+ outputs = model.generate(
+ input_ids=inputs.to(self.torch_device),
+ max_new_tokens=32,
+ )
+ assert torch.isfinite(outputs[: inputs.shape[1] :]).all()
+
+ _ = model.get_latest_scalings()
+ # 32 is the numeber of max scalings. 3 is the number of prompt tokens.
+ assert 32 + 3 >= len(model.get_scalings_log()) > 0
+
+ model.disable_scalings_logging()
+
+ inputs = tokenizer.encode("Python is a", add_special_tokens=False, return_tensors="pt")
+ outputs = model.generate(
+ input_ids=inputs.to(self.torch_device),
+ max_new_tokens=32,
+ )
+ assert torch.isfinite(outputs[: inputs.shape[1] :]).all()
+
+ assert 32 >= len(model.get_scalings_log()) > 0
+
+ bucketed = model.get_bucketed_scalings_log()
+ keys = bucketed.keys()
+ # Once bucket for each token as we aren't using cache
+ assert len(bucketed) == 32 == len(keys)
+ seq_len = inputs.shape[1]
+ for key in keys:
+ assert len(bucketed[key][0]) == 1
+ assert len(bucketed[key][1]) == 1
+ assert bucketed[key][0][0] == key - seq_len
+
+ model.clear_scalings_log()
+ assert len(model.get_scalings_log()) == 0
+
+ def test_misc_methods(self, tokenizer, model):
+ model.set_global_scaling_weight(1.5)
+ assert model.internal_xlora_classifier.config.global_scaling_weight == 1.5
+ assert model.get_global_scaling_weight() == 1.5
+
+ inputs = tokenizer.encode("Python is a", add_special_tokens=False, return_tensors="pt")
+ outputs = model.generate(
+ input_ids=inputs.to(self.torch_device),
+ max_new_tokens=32,
+ )
+ assert torch.isfinite(outputs[: inputs.shape[1] :]).all()
+
+ assert str(model) is not None
+
+ # On CI (but not locally), this test is flaky since transformers v4.45.0.
+ @flaky(num_tries=5)
+ def test_save_load_functional(self, tokenizer, model, tmp_path):
+ inputs = tokenizer.encode("Python is a", add_special_tokens=False, return_tensors="pt")
+ outputs = model.generate(
+ input_ids=inputs.to(self.torch_device),
+ max_new_tokens=32,
+ )
+ before_logits = outputs[: inputs.shape[1] :]
+ assert torch.isfinite(before_logits).all()
+
+ model.save_pretrained(save_directory=tmp_path)
+
+ del model
+
+ model = AutoModelForCausalLM.from_pretrained(self.model_id)
+ model.config.use_cache = False
+ model = PeftModel.from_pretrained(model=model, model_id=tmp_path).to(self.torch_device)
+
+ inputs = tokenizer.encode("Python is a", add_special_tokens=False, return_tensors="pt")
+ outputs = model.generate(
+ input_ids=inputs.to(self.torch_device),
+ max_new_tokens=32,
+ )
+ after_logits = outputs[: inputs.shape[1] :]
+ assert torch.isfinite(after_logits).all()
+ assert torch.equal(after_logits, before_logits)
+
+ def test_save_load_functional_pt(self, tokenizer, model, tmp_path):
+ inputs = tokenizer.encode("Python is a", add_special_tokens=False, return_tensors="pt")
+ outputs = model.generate(
+ input_ids=inputs.to(self.torch_device),
+ max_new_tokens=32,
+ )
+ before_logits = outputs[: inputs.shape[1] :]
+ assert torch.isfinite(before_logits).all()
+
+ model.save_pretrained(save_directory=tmp_path, safe_serialization=False)
+
+ del model
+
+ model = AutoModelForCausalLM.from_pretrained(self.model_id)
+ model.config.use_cache = False
+ model = PeftModel.from_pretrained(model=model, model_id=tmp_path, safe_serialization=False).to(
+ self.torch_device
+ )
+
+ inputs = tokenizer.encode("Python is a", add_special_tokens=False, return_tensors="pt")
+ outputs = model.generate(
+ input_ids=inputs.to(self.torch_device),
+ max_new_tokens=32,
+ )
+ after_logits = outputs[: inputs.shape[1] :]
+ assert torch.isfinite(after_logits).all()
+ assert torch.equal(after_logits, before_logits), (after_logits, before_logits)
+
+ def test_topk_lora(self, tokenizer, model):
+ model.set_topk_lora(2)
+ assert model.internal_xlora_classifier.config.top_k_lora == 2
+
+ inputs = tokenizer.encode("Python is a", add_special_tokens=False, return_tensors="pt")
+ outputs = model.generate(
+ input_ids=inputs.to(self.torch_device),
+ max_new_tokens=32,
+ )
+ assert torch.isfinite(outputs[: inputs.shape[1] :]).all()
+
+ def test_softmax_topk(self, tokenizer, model):
+ # Just reach in to set the config
+ model.internal_xlora_classifier.config.top_k_lora = 2
+ model.internal_xlora_classifier.config.enable_softmax = False
+ model.internal_xlora_classifier.config.enable_softmax_topk = True
+
+ inputs = tokenizer.encode("Python is a", add_special_tokens=False, return_tensors="pt")
+ outputs = model.generate(
+ input_ids=inputs.to(self.torch_device),
+ max_new_tokens=32,
+ )
+ assert torch.isfinite(outputs[: inputs.shape[1] :]).all()
+
+ def test_set_override_scaling_pass_value(self, model):
+ # Defaults to 0
+ assert model.internal_xlora_classifier.override_scaling_pass_value == 0.0
+
+ # Set it to 2 and make sure it actually is
+ model.set_scaling_pass_value(2)
+ assert model.internal_xlora_classifier.override_scaling_pass_value == 2
+ assert model.internal_xlora_classifier.config.scaling_pass_value == 2
+
+ # Set it to None and make sure it is 1/n
+ model.set_scaling_pass_value(None)
+ assert model.internal_xlora_classifier.override_scaling_pass_value == 1 / self.num_loras
+ assert model.internal_xlora_classifier.config.scaling_pass_value == 1 / self.num_loras
+
+ def test_functional_layerwise(self, tokenizer, model_layerwise):
+ model_layerwise.enable_scalings_logging()
+ inputs = tokenizer.encode("Python is a", add_special_tokens=False, return_tensors="pt")
+ outputs = model_layerwise.generate(
+ input_ids=inputs.to(self.torch_device),
+ max_new_tokens=32,
+ )
+ assert torch.isfinite(outputs[: inputs.shape[1] :]).all()
+
+ def test_disable_adapter(self, tokenizer, model):
+ model.enable_scalings_logging()
+ inputs = tokenizer.encode("Python is a", add_special_tokens=False, return_tensors="pt")
+ with model.disable_adapter():
+ outputs_disabled = model.generate(
+ input_ids=inputs.to(self.torch_device),
+ max_new_tokens=32,
+ )
+ outputs = model.generate(
+ input_ids=inputs.to(self.torch_device),
+ max_new_tokens=32,
+ )
+ assert torch.isfinite(outputs_disabled[: inputs.shape[1] :]).all()
+ assert torch.isfinite(outputs[: inputs.shape[1] :]).all()
+ assert not torch.equal(outputs, outputs_disabled)
+
+ def test_functional_embedding(self, tokenizer, embedding_model):
+ inputs = tokenizer.encode("Python is a", add_special_tokens=False, return_tensors="pt")
+ outputs = embedding_model.generate(
+ input_ids=inputs.to(self.torch_device),
+ max_new_tokens=32,
+ )
+ assert torch.isfinite(outputs[: inputs.shape[1] :]).all()
+
+ def test_xlora_loading_valid(self):
+ # This test also simulatenously tests the loading-from-hub functionality!
+ torch.manual_seed(123)
+
+ model_id = "facebook/opt-125m"
+ model = AutoModelForCausalLM.from_pretrained(model_id)
+ model.config.use_cache = False
+
+ adapters = [
+ "peft-internal-testing/opt-125m-dummy-lora",
+ "peft-internal-testing/opt-125m-dummy-lora",
+ ]
+ adapters = {str(i): file_name for i, file_name in enumerate(adapters)}
+
+ peft_config = XLoraConfig(
+ task_type=TaskType.CAUSAL_LM,
+ peft_type=PeftType.XLORA,
+ hidden_size=model.config.hidden_size,
+ adapters=adapters,
+ xlora_depth=8,
+ xlora_size=2048,
+ layerwise_scalings=True,
+ xlora_dropout_p=0.2,
+ )
+ model = get_peft_model(model, peft_config)
+
+ downloaded = huggingface_hub.hf_hub_download(repo_id=adapters["0"], filename="adapter_model.safetensors")
+ sd = load_file(downloaded)
+ w0 = model.base_model.model.model.decoder.layers[0].self_attn.q_proj.lora_A["0"].weight
+ w1 = sd["base_model.model.model.decoder.layers.0.self_attn.q_proj.lora_A.weight"]
+
+ assert torch.allclose(w0, w1)
+
+ def test_scalings_storage(self, tokenizer, model):
+ model.enable_scalings_logging()
+ inputs = tokenizer.encode("Python is a", add_special_tokens=False, return_tensors="pt")
+ outputs = model.generate(
+ input_ids=inputs.to(self.torch_device),
+ max_new_tokens=10,
+ )
+
+ latest_scalings = model.get_latest_scalings()
+ assert latest_scalings is not None, "get_latest_scalings() should not return None after generation"
+ assert isinstance(latest_scalings, torch.Tensor)
+ assert torch.isfinite(latest_scalings).all(), "Scalings should contain finite values"
+
+ def test_per_token_normalization_with_softmax_topk(self, tokenizer, model, monkeypatch):
+ model.internal_xlora_classifier.config.top_k_lora = 2
+ model.internal_xlora_classifier.config.enable_softmax = False
+ model.internal_xlora_classifier.config.enable_softmax_topk = True
+
+ captured_data = []
+ orig_get_maybe_topk_scalings = XLoraLayer.get_maybe_topk_scalings
+
+ def mock_get_maybe_topk_scalings(self, scalings):
+ result = orig_get_maybe_topk_scalings(self, scalings)
+ if getattr(model, "internal_xlora_scalings", None) is not None:
+ captured_data.append(result)
+ return result
+
+ monkeypatch.setattr(XLoraLayer, "get_maybe_topk_scalings", mock_get_maybe_topk_scalings)
+
+ model.enable_scalings_logging()
+ inputs = tokenizer.encode("Test per token normalization", add_special_tokens=False, return_tensors="pt")
+ outputs = model.generate(
+ input_ids=inputs.to(self.torch_device),
+ max_new_tokens=1,
+ )
+
+ for scaling in captured_data:
+ weight_sums = scaling.sum(dim=-1)
+ assert torch.allclose(weight_sums, torch.ones_like(weight_sums), atol=1e-5), (
+ "Per-token scaling weights are not normalized to sum to 1."
+ )
diff --git a/peft/tests/testing_common.py b/peft/tests/testing_common.py
new file mode 100644
index 0000000000000000000000000000000000000000..9c49119bf2612946528ab5f779b1df76dace952b
--- /dev/null
+++ b/peft/tests/testing_common.py
@@ -0,0 +1,1982 @@
+# Copyright 2023-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+import copy
+import json
+import os
+import pickle
+import platform
+import re
+import shutil
+import tempfile
+import warnings
+from dataclasses import replace
+from operator import attrgetter
+
+import pytest
+import torch
+import yaml
+from diffusers import StableDiffusionPipeline
+from packaging import version
+from safetensors.torch import save_file
+
+from peft import (
+ AdaLoraConfig,
+ BOFTConfig,
+ BoneConfig,
+ CPTConfig,
+ FourierFTConfig,
+ HRAConfig,
+ IA3Config,
+ LNTuningConfig,
+ LoHaConfig,
+ LoKrConfig,
+ LoraConfig,
+ MissConfig,
+ OFTConfig,
+ PeftModel,
+ PeftType,
+ PrefixTuningConfig,
+ PromptEncoderConfig,
+ PromptLearningConfig,
+ PromptTuningConfig,
+ RandLoraConfig,
+ VBLoRAConfig,
+ VeraConfig,
+ get_peft_model,
+ get_peft_model_state_dict,
+ inject_adapter_in_model,
+ prepare_model_for_kbit_training,
+)
+from peft.tuners._buffer_dict import BufferDict
+from peft.tuners.lora import LoraLayer
+from peft.tuners.tuners_utils import BaseTunerLayer
+from peft.utils import (
+ AuxiliaryTrainingWrapper,
+ ModulesToSaveWrapper,
+ TrainableTokensWrapper,
+ _get_submodules,
+ infer_device,
+)
+
+from .testing_utils import get_state_dict, hub_online_once
+
+
+CONFIG_TESTING_KWARGS = (
+ # IA³
+ {
+ "target_modules": None,
+ "feedforward_modules": None,
+ },
+ # LoRA
+ {
+ "r": 8,
+ "lora_alpha": 32,
+ "target_modules": None,
+ "lora_dropout": 0.05,
+ "bias": "none",
+ },
+ # prefix tuning
+ {
+ "num_virtual_tokens": 10,
+ },
+ # prompt encoder
+ {
+ "num_virtual_tokens": 10,
+ "encoder_hidden_size": 32,
+ },
+ # prompt tuning
+ {
+ "num_virtual_tokens": 10,
+ },
+ # AdaLoRA
+ {
+ "target_modules": None,
+ "total_step": 1,
+ },
+ # BOFT
+ {
+ "target_modules": None,
+ },
+ # VeRA
+ {
+ "r": 8,
+ "target_modules": None,
+ "vera_dropout": 0.05,
+ "projection_prng_key": 0xFF,
+ "d_initial": 0.1,
+ "save_projection": True,
+ "bias": "none",
+ },
+ # FourierFT
+ {
+ "n_frequency": 10,
+ "target_modules": None,
+ },
+ # HRA
+ {
+ "target_modules": None,
+ },
+ # VBLoRA
+ {"target_modules": None, "vblora_dropout": 0.05, "vector_length": 1, "num_vectors": 2},
+ # OFT
+ {
+ "target_modules": None,
+ },
+ # Bone
+ {
+ "target_modules": None,
+ "r": 2,
+ },
+ # MiSS
+ {
+ "target_modules": None,
+ "r": 2,
+ },
+ # LoRA + trainable_tokens
+ {
+ "r": 8,
+ "lora_alpha": 32,
+ "target_modules": None,
+ "lora_dropout": 0.05,
+ "bias": "none",
+ "trainable_token_indices": [0, 1, 3],
+ },
+ # RandLoRA
+ {
+ "r": 32,
+ "randlora_alpha": 64,
+ "target_modules": None,
+ "randlora_dropout": 0.05,
+ "projection_prng_key": 0xFF,
+ "save_projection": True,
+ "bias": "none",
+ },
+ # CPT tuninig
+ {
+ "cpt_token_ids": [0, 1, 2, 3, 4, 5, 6, 7], # Example token IDs for testing
+ "cpt_mask": [1, 1, 1, 1, 1, 1, 1, 1],
+ "cpt_tokens_type_mask": [1, 2, 2, 2, 3, 3, 4, 4],
+ },
+)
+
+CLASSES_MAPPING = {
+ "ia3": (IA3Config, CONFIG_TESTING_KWARGS[0]),
+ "lora": (LoraConfig, CONFIG_TESTING_KWARGS[1]),
+ "prefix_tuning": (PrefixTuningConfig, CONFIG_TESTING_KWARGS[2]),
+ "prompt_encoder": (PromptEncoderConfig, CONFIG_TESTING_KWARGS[3]),
+ "prompt_tuning": (PromptTuningConfig, CONFIG_TESTING_KWARGS[4]),
+ "adalora": (AdaLoraConfig, CONFIG_TESTING_KWARGS[5]),
+ "boft": (BOFTConfig, CONFIG_TESTING_KWARGS[6]),
+ "vera": (VeraConfig, CONFIG_TESTING_KWARGS[7]),
+ "fourierft": (FourierFTConfig, CONFIG_TESTING_KWARGS[8]),
+ "hra": (HRAConfig, CONFIG_TESTING_KWARGS[9]),
+ "vblora": (VBLoRAConfig, CONFIG_TESTING_KWARGS[10]),
+ "oft": (OFTConfig, CONFIG_TESTING_KWARGS[11]),
+ "bone": (BoneConfig, CONFIG_TESTING_KWARGS[12]),
+ "miss": (MissConfig, CONFIG_TESTING_KWARGS[12]),
+ "lora+trainable_tokens": (LoraConfig, CONFIG_TESTING_KWARGS[13]),
+ "randlora": (RandLoraConfig, CONFIG_TESTING_KWARGS[14]),
+}
+
+DECODER_MODELS_EXTRA = {"cpt": (CPTConfig, CONFIG_TESTING_KWARGS[15])}
+
+
+class PeftCommonTester:
+ r"""
+ A large testing suite for testing common functionality of the PEFT models.
+
+ Attributes:
+ torch_device (`torch.device`):
+ The device on which the tests will be run.
+ transformers_class (`transformers.PreTrainedModel`):
+ The transformers class that is being tested.
+ """
+
+ torch_device = infer_device()
+ transformers_class = None
+
+ def prepare_inputs_for_common(self):
+ raise NotImplementedError
+
+ def check_modelcard(self, tmp_dirname, model):
+ # check the generated README.md
+ filename = os.path.join(tmp_dirname, "README.md")
+ assert os.path.exists(filename)
+ with open(filename, encoding="utf-8") as f:
+ readme = f.read()
+ metainfo = re.search(r"---\n(.*?)\n---", readme, re.DOTALL).group(1)
+ dct = yaml.safe_load(metainfo)
+ assert dct["library_name"] == "peft"
+
+ if hasattr(model, "config"):
+ assert dct["base_model"] == model.config.to_dict()["_name_or_path"]
+ else: # a custom model
+ assert "base_model" not in dct
+
+ # The Hub expects the lora tag to be set for PEFT LoRA models since they
+ # have explicit support for things like inference.
+ if model.active_peft_config.peft_type.value == "LORA":
+ assert "lora" in dct["tags"]
+
+ def check_config_json(self, tmp_dirname, model):
+ # check the generated config.json
+ filename = os.path.join(tmp_dirname, "adapter_config.json")
+ assert os.path.exists(filename)
+ with open(filename, encoding="utf-8") as f:
+ config = json.load(f)
+
+ if hasattr(model, "config"): # custom models don't have a config attribute
+ assert config["base_model_name_or_path"] == model.config.to_dict()["_name_or_path"]
+
+ def perturb_trainable_token_weights_if_used(self, model, config_kwargs, adapter_name="default", scale=1.0):
+ """TrainableTokensLayer is initialized to be a no-op by default. Since there's currently no way to pass
+ `init_weights=False` to the trainable tokens layer when used in conjunction with LoRA, we have to do it like
+ this to make sure that it is *not* a no-op (essentially simulating "training" of the adapter).
+ """
+ if "trainable_token_indices" not in config_kwargs:
+ return
+
+ token_wrapper = None
+
+ if hasattr(model, "get_input_embeddings"):
+ token_wrapper = model.get_input_embeddings()
+ else:
+ for module in model.modules():
+ if isinstance(module, TrainableTokensWrapper):
+ token_wrapper = module
+ break
+
+ # for a model with trainable_token_indices there should always be a trainable token wrapper somewhere.
+ # if not, then there's something broken.
+ assert token_wrapper is not None
+
+ token_wrapper.token_adapter.trainable_tokens_delta[adapter_name].data = (
+ torch.rand_like(token_wrapper.token_adapter.trainable_tokens_delta[adapter_name].data) * scale
+ )
+
+ def _test_model_attr(self, model_id, config_cls, config_kwargs):
+ with hub_online_once(model_id):
+ model = self.transformers_class.from_pretrained(model_id)
+ config = config_cls(
+ base_model_name_or_path=model_id,
+ **config_kwargs,
+ )
+ model = get_peft_model(model, config)
+
+ assert hasattr(model, "save_pretrained")
+ assert hasattr(model, "from_pretrained")
+ assert hasattr(model, "push_to_hub")
+
+ def _test_adapter_name(self, model_id, config_cls, config_kwargs):
+ with hub_online_once(model_id):
+ model = self.transformers_class.from_pretrained(model_id)
+ config = config_cls(
+ base_model_name_or_path=model_id,
+ **config_kwargs,
+ )
+ model = get_peft_model(model, config, adapter_name="test-adapter")
+ correctly_converted = False
+ for n, _ in model.named_parameters():
+ if "test-adapter" in n:
+ correctly_converted = True
+ break
+
+ assert correctly_converted
+
+ def _test_prepare_for_training(self, model_id, config_cls, config_kwargs):
+ if config_kwargs.get("trainable_token_indices", None) is not None:
+ # incompatible because trainable tokens is marking embeddings as trainable
+ self.skipTest("Trainable tokens is incompatible with this test.")
+
+ # some tests require specific tokenizers, make sure that they can be fetched as well
+ with hub_online_once(model_id + config_kwargs.get("tokenizer_name_or_path", "")):
+ model = self.transformers_class.from_pretrained(model_id).to(self.torch_device)
+ config = config_cls(
+ base_model_name_or_path=model_id,
+ **config_kwargs,
+ )
+ model = get_peft_model(model, config)
+
+ dummy_input = self.prepare_inputs_for_testing()
+ dummy_output = model.get_input_embeddings()(dummy_input["input_ids"])
+
+ assert not dummy_output.requires_grad
+
+ # load with `prepare_model_for_kbit_training`
+ model = self.transformers_class.from_pretrained(model_id).to(self.torch_device)
+ model = prepare_model_for_kbit_training(model)
+
+ for param in model.parameters():
+ assert not param.requires_grad
+
+ config = config_cls(
+ base_model_name_or_path=model_id,
+ **config_kwargs,
+ )
+ model = get_peft_model(model, config)
+
+ # For backward compatibility
+ if hasattr(model, "enable_input_require_grads"):
+ model.enable_input_require_grads()
+ else:
+
+ def make_inputs_require_grad(module, input, output):
+ output.requires_grad_(True)
+
+ model.get_input_embeddings().register_forward_hook(make_inputs_require_grad)
+
+ dummy_input = self.prepare_inputs_for_testing()
+ dummy_output = model.get_input_embeddings()(dummy_input["input_ids"])
+
+ assert dummy_output.requires_grad
+
+ def _test_load_model_low_cpu_mem_usage(self, model_id, config_cls, config_kwargs):
+ # Ensure that low_cpu_mem_usage=True works for from_pretrained and load_adapter and that the resulting model's
+ # parameters are on the correct device.
+ with hub_online_once(model_id):
+ model = self.transformers_class.from_pretrained(model_id).to(self.torch_device)
+ config = config_cls(
+ base_model_name_or_path=model_id,
+ **config_kwargs,
+ )
+ model = get_peft_model(model, config)
+
+ # note: not using the context manager here because it fails on Windows CI for some reason
+ tmp_dirname = tempfile.mkdtemp()
+ try:
+ model.save_pretrained(tmp_dirname)
+
+ model = self.transformers_class.from_pretrained(model_id).to(self.torch_device)
+ model = PeftModel.from_pretrained(
+ model, tmp_dirname, torch_device=self.torch_device, low_cpu_mem_usage=True
+ )
+ assert {p.device.type for p in model.parameters()} == {self.torch_device}
+
+ model.load_adapter(tmp_dirname, adapter_name="other", low_cpu_mem_usage=True)
+ assert {p.device.type for p in model.parameters()} == {self.torch_device}
+ finally:
+ try:
+ shutil.rmtree(tmp_dirname)
+ except PermissionError:
+ # windows error
+ pass
+
+ # also test injecting directly
+ del model
+ model = self.transformers_class.from_pretrained(model_id).to(self.torch_device)
+ inject_adapter_in_model(config, model, low_cpu_mem_usage=True) # check that there is no error
+
+ if not isinstance(config, LNTuningConfig):
+ # LN tuning does not add adapter layers that could be on meta device, it only changes the requires_grad.
+ # Therefore, there is no meta device for LN tuning.
+ assert "meta" in {p.device.type for p in model.parameters()}
+
+ def _test_save_pretrained(self, model_id, config_cls, config_kwargs, safe_serialization=True):
+ # ensure that the weights are randomly initialized
+ if issubclass(config_cls, LoraConfig):
+ config_kwargs = config_kwargs.copy()
+ config_kwargs["init_lora_weights"] = False
+ if issubclass(config_cls, IA3Config):
+ config_kwargs = config_kwargs.copy()
+ config_kwargs["init_ia3_weights"] = False
+ if hasattr(config_cls, "init_weights"):
+ config_kwargs = config_kwargs.copy()
+ config_kwargs["init_weights"] = False
+
+ with hub_online_once(model_id):
+ model = self.transformers_class.from_pretrained(model_id)
+ config = config_cls(
+ base_model_name_or_path=model_id,
+ **config_kwargs,
+ )
+ model = get_peft_model(model, config)
+ model = model.to(self.torch_device)
+
+ with tempfile.TemporaryDirectory() as tmp_dirname:
+ if safe_serialization:
+ model.save_pretrained(tmp_dirname)
+ else:
+ model.save_pretrained(tmp_dirname, safe_serialization=False)
+
+ model_from_pretrained = self.transformers_class.from_pretrained(model_id)
+ with warnings.catch_warnings(record=True) as recs:
+ model_from_pretrained = PeftModel.from_pretrained(model_from_pretrained, tmp_dirname)
+ # ensure that there is no warning
+ assert not any("Found missing adapter keys" in str(rec.message) for rec in recs)
+
+ # check if the state dicts are equal
+ if issubclass(config_cls, PromptEncoderConfig):
+ # For prompt encoding, when loading the whole state_dict, there are differences, therefore, only load
+ # adapter-specific weights for comparison.
+ # TODO: is this expected?
+ state_dict = get_peft_model_state_dict(model, unwrap_compiled=True)
+ state_dict_from_pretrained = get_peft_model_state_dict(model_from_pretrained, unwrap_compiled=True)
+ else:
+ state_dict = get_state_dict(model, unwrap_compiled=True)
+ state_dict_from_pretrained = get_state_dict(model_from_pretrained, unwrap_compiled=True)
+
+ # check if tensors equal
+ for key in state_dict.keys():
+ assert torch.allclose(
+ state_dict[key].to(self.torch_device), state_dict_from_pretrained[key].to(self.torch_device)
+ )
+
+ target_adapter_filename = "adapter_model.safetensors" if safe_serialization else "adapter_model.bin"
+
+ # check if `adapter_model.safetensors` is present
+ assert os.path.exists(os.path.join(tmp_dirname, target_adapter_filename))
+
+ # check if `adapter_config.json` is present
+ assert os.path.exists(os.path.join(tmp_dirname, "adapter_config.json"))
+
+ # check if `model.safetensors` is not present
+ assert not os.path.exists(os.path.join(tmp_dirname, "model.safetensors"))
+
+ # check if `config.json` is not present
+ assert not os.path.exists(os.path.join(tmp_dirname, "config.json"))
+
+ self.check_modelcard(tmp_dirname, model)
+ self.check_config_json(tmp_dirname, model)
+
+ def _test_save_pretrained_selected_adapters(self, model_id, config_cls, config_kwargs, safe_serialization=True):
+ if issubclass(config_cls, AdaLoraConfig):
+ # AdaLora does not support adding more than 1 adapter
+ return pytest.skip(f"Test not applicable for {config_cls}")
+
+ # ensure that the weights are randomly initialized
+ if issubclass(config_cls, LoraConfig):
+ config_kwargs = config_kwargs.copy()
+ config_kwargs["init_lora_weights"] = False
+ elif issubclass(config_cls, IA3Config):
+ config_kwargs = config_kwargs.copy()
+ config_kwargs["init_ia3_weights"] = False
+ elif hasattr(config_cls, "init_weights"):
+ config_kwargs["init_weights"] = False
+
+ with hub_online_once(model_id):
+ model = self.transformers_class.from_pretrained(model_id)
+ config = config_cls(
+ base_model_name_or_path=model_id,
+ **config_kwargs,
+ )
+ model = get_peft_model(model, config)
+ model = model.to(self.torch_device)
+
+ new_adapter_config = config_cls(
+ base_model_name_or_path=model_id,
+ **config_kwargs,
+ )
+
+ model.add_adapter("new_adapter", new_adapter_config)
+
+ with tempfile.TemporaryDirectory() as tmp_dirname:
+ if safe_serialization:
+ model.save_pretrained(tmp_dirname)
+ else:
+ model.save_pretrained(tmp_dirname, safe_serialization=False)
+
+ model_from_pretrained = self.transformers_class.from_pretrained(model_id)
+ model_from_pretrained = PeftModel.from_pretrained(model_from_pretrained, tmp_dirname)
+
+ new_adapter_dir = os.path.join(tmp_dirname, "new_adapter")
+ model_from_pretrained.load_adapter(new_adapter_dir, "new_adapter")
+
+ # check if the state dicts are equal
+ if issubclass(config_cls, PromptEncoderConfig):
+ # For prompt encoding, when loading the whole state_dict, there are differences, therefore, only load
+ # adapter-specific weights for comparison.
+ # TODO: is this expected?
+ state_dict = get_peft_model_state_dict(model, unwrap_compiled=True)
+ state_dict_from_pretrained = get_peft_model_state_dict(model_from_pretrained, unwrap_compiled=True)
+ else:
+ state_dict = get_state_dict(model, unwrap_compiled=True)
+ state_dict_from_pretrained = get_state_dict(model_from_pretrained, unwrap_compiled=True)
+
+ # check if same keys
+ assert state_dict.keys() == state_dict_from_pretrained.keys()
+
+ # check if tensors equal
+ for key in state_dict.keys():
+ assert torch.allclose(
+ state_dict[key].to(self.torch_device), state_dict_from_pretrained[key].to(self.torch_device)
+ )
+
+ target_adapter_filename = "adapter_model.safetensors" if safe_serialization else "adapter_model.bin"
+
+ # check if `adapter_model.safetensors` is present
+ assert os.path.exists(os.path.join(tmp_dirname, target_adapter_filename))
+ assert os.path.exists(os.path.join(new_adapter_dir, target_adapter_filename))
+
+ # check if `adapter_config.json` is present
+ assert os.path.exists(os.path.join(tmp_dirname, "adapter_config.json"))
+ assert os.path.exists(os.path.join(new_adapter_dir, "adapter_config.json"))
+
+ # check if `model.safetensors` is not present
+ assert not os.path.exists(os.path.join(tmp_dirname, "model.safetensors"))
+ assert not os.path.exists(os.path.join(new_adapter_dir, "model.safetensors"))
+
+ # check if `config.json` is not present
+ assert not os.path.exists(os.path.join(tmp_dirname, "config.json"))
+ assert not os.path.exists(os.path.join(new_adapter_dir, "config.json"))
+
+ self.check_modelcard(tmp_dirname, model)
+ self.check_config_json(tmp_dirname, model)
+
+ with tempfile.TemporaryDirectory() as tmp_dirname:
+ model.save_pretrained(tmp_dirname, selected_adapters=["default"])
+
+ model_from_pretrained = self.transformers_class.from_pretrained(model_id)
+ model_from_pretrained = PeftModel.from_pretrained(model_from_pretrained, tmp_dirname)
+
+ assert "default" in model_from_pretrained.peft_config.keys()
+ assert "new_adapter" not in model_from_pretrained.peft_config.keys()
+
+ def _test_from_pretrained_config_construction(self, model_id, config_cls, config_kwargs):
+ with hub_online_once(model_id):
+ model = self.transformers_class.from_pretrained(model_id)
+ config = config_cls(base_model_name_or_path=model_id, **config_kwargs)
+ model = get_peft_model(model, config)
+ model = model.to(self.torch_device)
+
+ with tempfile.TemporaryDirectory() as tmp_dirname:
+ model.save_pretrained(tmp_dirname)
+
+ model_from_pretrained = self.transformers_class.from_pretrained(model_id)
+ model_from_pretrained = PeftModel.from_pretrained(
+ model_from_pretrained, tmp_dirname, is_trainable=False, config=config
+ )
+
+ assert model_from_pretrained.peft_config["default"].inference_mode
+ assert model_from_pretrained.peft_config["default"] is config
+
+ def _test_load_multiple_adapters(self, model_id, config_cls, config_kwargs):
+ # just ensure that this works and raises no error
+ with hub_online_once(model_id):
+ model = self.transformers_class.from_pretrained(model_id)
+ config = config_cls(
+ base_model_name_or_path=model_id,
+ **config_kwargs,
+ )
+ model = get_peft_model(model, config)
+
+ with tempfile.TemporaryDirectory() as tmp_dirname:
+ model.save_pretrained(tmp_dirname)
+ del model
+
+ model = self.transformers_class.from_pretrained(model_id).to(self.torch_device)
+ model = PeftModel.from_pretrained(model, tmp_dirname, torch_device=self.torch_device)
+ load_result1 = model.load_adapter(tmp_dirname, adapter_name="other")
+ load_result2 = model.load_adapter(tmp_dirname, adapter_name="yet-another")
+
+ # VBLoRA uses a shared "vblora_vector_bank" across all layers, causing it to appear
+ # in the missing keys list, which leads to failed test cases. So
+ # skipping the missing keys check for VBLoRA.
+ if config.peft_type != "VBLORA":
+ assert load_result1.missing_keys == []
+ assert load_result2.missing_keys == []
+
+ def _test_merge_layers_fp16(self, model_id, config_cls, config_kwargs):
+ if (
+ config_cls not in (LoraConfig, IA3Config, AdaLoraConfig, LoHaConfig, LoKrConfig, VBLoRAConfig)
+ or config_kwargs.get("alora_invocation_tokens") is not None
+ ):
+ # Merge layers only supported for LoRA and IA³, and not for Activated LoRA (aLoRA)
+ if config_kwargs.get("alora_invocation_tokens") is None:
+ return pytest.skip(f"Test not applicable for {config_cls}")
+ else:
+ return pytest.skip("Test not applicable for Activated LoRA")
+ if ("gpt2" in model_id.lower()) and (config_cls != LoraConfig):
+ self.skipTest("Merging GPT2 adapters not supported for IA³ (yet)")
+
+ if (self.torch_device in ["cpu"]) and (version.parse(torch.__version__) <= version.parse("2.1")):
+ self.skipTest("PyTorch 2.1 not supported for Half of addmm_impl_cpu_ ")
+
+ with hub_online_once(model_id):
+ model = self.transformers_class.from_pretrained(model_id, torch_dtype=torch.float16)
+ config = config_cls(
+ base_model_name_or_path=model_id,
+ **config_kwargs,
+ )
+ model = get_peft_model(model, config)
+ model = model.to(device=self.torch_device, dtype=torch.float16)
+
+ model.eval()
+
+ # This should simply work
+ _ = model.merge_and_unload()
+
+ def _test_merge_layers_nan(self, model_id, config_cls, config_kwargs):
+ if (
+ config_cls
+ not in (
+ LoraConfig,
+ IA3Config,
+ AdaLoraConfig,
+ LoHaConfig,
+ LoKrConfig,
+ VeraConfig,
+ FourierFTConfig,
+ )
+ or config_kwargs.get("alora_invocation_tokens") is not None
+ ):
+ # Merge layers only supported for LoRA and IA³, and not for Activated LoRA (aLoRA)
+ return
+ if ("gpt2" in model_id.lower()) and (config_cls != LoraConfig):
+ self.skipTest("Merging GPT2 adapters not supported for IA³ (yet)")
+
+ if "gemma" in model_id.lower():
+ # TODO: could be related to tied weights
+ self.skipTest("Merging currently fails with gemma")
+
+ with hub_online_once(model_id):
+ model = self.transformers_class.from_pretrained(model_id)
+ config = config_cls(
+ base_model_name_or_path=model_id,
+ **config_kwargs,
+ )
+
+ model = get_peft_model(model, config)
+ model = model.to(self.torch_device)
+
+ self.perturb_trainable_token_weights_if_used(model, config_kwargs)
+
+ dummy_input = self.prepare_inputs_for_testing()
+
+ model.eval()
+
+ # This should work
+ logits_unmerged = model(**dummy_input)[0]
+
+ model = model.merge_and_unload()
+ logits_merged = model(**dummy_input)[0]
+
+ assert torch.allclose(logits_unmerged, logits_merged, atol=1e-3, rtol=1e-3)
+
+ model = self.transformers_class.from_pretrained(model_id)
+ config = config_cls(
+ base_model_name_or_path=model_id,
+ **config_kwargs,
+ )
+ model = get_peft_model(model, config)
+ model = model.to(self.torch_device)
+
+ for name, module in model.named_parameters():
+ if (
+ "lora_A" in name
+ or "ia3" in name
+ or "lora_E" in name
+ or "lora_B" in name
+ or "vera_lambda" in name
+ or "fourierft_spectrum" in name
+ ):
+ module.data[0] = torch.nan
+
+ with pytest.raises(
+ ValueError, match="NaNs detected in the merged weights. The adapter default seems to be broken"
+ ):
+ model = model.merge_and_unload(safe_merge=True)
+
+ for name, module in model.named_parameters():
+ if (
+ "lora_A" in name
+ or "ia3" in name
+ or "lora_E" in name
+ or "lora_B" in name
+ or "vera_lambda" in name
+ or "fourierft_spectrum" in name
+ ):
+ module.data[0] = torch.inf
+
+ with pytest.raises(
+ ValueError, match="NaNs detected in the merged weights. The adapter default seems to be broken"
+ ):
+ model = model.merge_and_unload(safe_merge=True)
+
+ def _test_merge_layers(self, model_id, config_cls, config_kwargs):
+ if issubclass(config_cls, PromptLearningConfig):
+ return pytest.skip(f"Test not applicable for {config_cls}")
+
+ if issubclass(config_cls, (OFTConfig, BOFTConfig)):
+ return pytest.skip(f"Test not applicable for {config_cls}")
+
+ if config_kwargs.get("alora_invocation_tokens") is not None:
+ return pytest.skip("Merging not applicable to aLoRA")
+
+ if ("gpt2" in model_id.lower()) and (config_cls != LoraConfig):
+ self.skipTest("Merging GPT2 adapters not supported for IA³ (yet)")
+
+ if "gemma" in model_id.lower():
+ # TODO: could be related to tied weights
+ self.skipTest("Merging currently fails with gemma")
+
+ with hub_online_once(model_id):
+ model = self.transformers_class.from_pretrained(model_id)
+ config = config_cls(
+ base_model_name_or_path=model_id,
+ **config_kwargs,
+ )
+
+ model = get_peft_model(model, config)
+ model = model.to(self.torch_device)
+
+ self.perturb_trainable_token_weights_if_used(model, config_kwargs)
+
+ dummy_input = self.prepare_inputs_for_testing()
+ model.eval()
+ logits = model(**dummy_input)[0]
+
+ model.merge_adapter()
+ logits_merged = model(**dummy_input)[0]
+ model.unmerge_adapter()
+ logits_unmerged = model(**dummy_input)[0]
+
+ model = model.merge_and_unload()
+
+ # check that PEFT layers are completely removed
+ assert not any(isinstance(module, BaseTunerLayer) for module in model.modules())
+ logits_merged_unloaded = model(**dummy_input)[0]
+
+ conv_ids = ["Conv2d", "Conv3d", "Conv2d2"]
+ atol, rtol = 1e-4, 1e-4
+ if self.torch_device in ["mlu"]:
+ atol, rtol = 1e-3, 1e-3 # MLU
+ if config.peft_type == "ADALORA":
+ # AdaLoRA is a bit flaky on CI, but this cannot be reproduced locally
+ atol, rtol = 1e-2, 1e-2
+ if (config.peft_type in {"IA3", "LORA"}) and (model_id in conv_ids):
+ # for some reason, the Conv introduces a larger error
+ atol, rtol = 0.3, 0.01
+ if model_id == "trl-internal-testing/tiny-Llama4ForCausalLM":
+ # also getting larger errors here, not exactly sure why
+ atol, rtol = 0.3, 0.01
+ assert torch.allclose(logits, logits_merged, atol=atol, rtol=rtol)
+ assert torch.allclose(logits, logits_unmerged, atol=atol, rtol=rtol)
+ assert torch.allclose(logits, logits_merged_unloaded, atol=atol, rtol=rtol)
+
+ # For this test to work, weights should not be initialized to identity transform (e.g.
+ # init_lora_weights should be False).
+ transformers_model = self.transformers_class.from_pretrained(model_id).to(self.torch_device)
+ logits_transformers = transformers_model(**dummy_input)[0]
+ assert not torch.allclose(logits_merged, logits_transformers, atol=1e-10, rtol=1e-10)
+
+ # test that the logits are identical after a save-load-roundtrip
+ if hasattr(model, "save_pretrained"):
+ # model is a transformers model
+ tmp_dirname = tempfile.mkdtemp()
+ # note: not using the context manager here because it fails on Windows CI for some reason
+ try:
+ model.save_pretrained(tmp_dirname)
+ model_from_pretrained = self.transformers_class.from_pretrained(tmp_dirname).to(self.torch_device)
+ finally:
+ try:
+ shutil.rmtree(tmp_dirname)
+ except PermissionError:
+ # windows error
+ pass
+ else:
+ # model is not a transformers model
+ model_from_pretrained = pickle.loads(pickle.dumps(model))
+
+ logits_merged_from_pretrained = model_from_pretrained(**dummy_input)[0]
+ assert torch.allclose(logits_merged, logits_merged_from_pretrained, atol=atol, rtol=rtol)
+
+ def _test_merge_layers_multi(self, model_id, config_cls, config_kwargs):
+ supported_peft_types = [
+ PeftType.LORA,
+ PeftType.LOHA,
+ PeftType.LOKR,
+ PeftType.IA3,
+ PeftType.OFT,
+ PeftType.BOFT,
+ PeftType.HRA,
+ PeftType.BONE,
+ PeftType.MISS,
+ ]
+
+ if ("gpt2" in model_id.lower()) and (config_cls == IA3Config):
+ self.skipTest("Merging GPT2 adapters not supported for IA³ (yet)")
+
+ if config_kwargs.get("trainable_token_indices", None) is not None:
+ self.skipTest(
+ "Merging two adapters with trainable tokens is tested elsewhere since adapters with "
+ "the same token indices cannot be merged."
+ )
+
+ config = config_cls(
+ base_model_name_or_path=model_id,
+ **config_kwargs,
+ )
+
+ if config.peft_type not in supported_peft_types or config_kwargs.get("alora_invocation_tokens") is not None:
+ return
+
+ with hub_online_once(model_id):
+ model = self.transformers_class.from_pretrained(model_id)
+ model = get_peft_model(model, config)
+ model = model.to(self.torch_device)
+
+ dummy_input = self.prepare_inputs_for_testing()
+ model.eval()
+
+ with torch.inference_mode():
+ logits_adapter_1 = model(**dummy_input)[0]
+
+ model.add_adapter("adapter-2", config)
+ model.set_adapter("adapter-2")
+ model.eval()
+
+ # sanity check: each adapter layer with a 'default' adapter should also have 'adapter-2'
+ containers = (torch.nn.ModuleDict, torch.nn.ParameterDict, BufferDict)
+ num_default = len([m for m in model.modules() if isinstance(m, containers) and "default" in m])
+ num_adapter2 = len([m for m in model.modules() if isinstance(m, containers) and "adapter-2" in m])
+ assert num_default > 0
+ assert num_default == num_adapter2
+
+ with torch.inference_mode():
+ logits_adapter_2 = model(**dummy_input)[0]
+
+ assert not torch.allclose(logits_adapter_1, logits_adapter_2, atol=1e-3, rtol=1e-3)
+
+ model.set_adapter("default")
+
+ with torch.inference_mode():
+ logits_adapter_1_after_set = model(**dummy_input)[0]
+
+ assert torch.allclose(logits_adapter_1_after_set, logits_adapter_1, atol=1e-3, rtol=1e-3)
+
+ model_copy = copy.deepcopy(model)
+ model_copy_2 = copy.deepcopy(model)
+ model_merged_all = model.merge_and_unload(adapter_names=["adapter-2", "default"])
+
+ with torch.inference_mode():
+ logits_merged_all = model_merged_all(**dummy_input)[0]
+
+ assert not torch.allclose(logits_merged_all, logits_adapter_2, atol=1e-3, rtol=1e-3)
+ assert not torch.allclose(logits_merged_all, logits_adapter_1, atol=1e-3, rtol=1e-3)
+
+ model_merged_adapter_2 = model_copy.merge_and_unload(adapter_names=["adapter-2"])
+
+ with torch.inference_mode():
+ logits_merged_adapter_2 = model_merged_adapter_2(**dummy_input)[0]
+
+ assert torch.allclose(logits_merged_adapter_2, logits_adapter_2, atol=1e-3, rtol=1e-3)
+
+ model_merged_adapter_default = model_copy_2.merge_and_unload(adapter_names=["default"])
+
+ with torch.inference_mode():
+ logits_merged_adapter_default = model_merged_adapter_default(**dummy_input)[0]
+
+ assert torch.allclose(logits_merged_adapter_default, logits_adapter_1, atol=1e-3, rtol=1e-3)
+
+ def _test_merge_layers_is_idempotent(self, model_id, config_cls, config_kwargs):
+ if config_kwargs.get("alora_invocation_tokens") is not None:
+ # Merging not supported for Activated LoRA (aLoRA)
+ return pytest.skip("Test not applicable for Activated LoRA (aLoRA)")
+ with hub_online_once(model_id):
+ model = self.transformers_class.from_pretrained(model_id)
+ config = config_cls(
+ base_model_name_or_path=model_id,
+ **config_kwargs,
+ )
+ model = get_peft_model(model, config)
+ model = model.to(self.torch_device)
+ model.eval()
+ torch.manual_seed(0)
+ model.merge_adapter()
+ logits_0 = model(**self.prepare_inputs_for_testing())[0]
+
+ # merging again should not change anything
+ # also check warning:
+ with pytest.warns(UserWarning, match="All adapters are already merged, nothing to do"):
+ model.merge_adapter()
+ logits_1 = model(**self.prepare_inputs_for_testing())[0]
+
+ assert torch.allclose(logits_0, logits_1, atol=1e-6, rtol=1e-6)
+
+ def _test_safe_merge(self, model_id, config_cls, config_kwargs):
+ if config_kwargs.get("alora_invocation_tokens") is not None:
+ # Merging not supported for Activated LoRA (aLoRA)
+ return pytest.skip("Test not applicable for Activated LoRA (aLoRA)")
+ torch.manual_seed(0)
+ with hub_online_once(model_id):
+ model = self.transformers_class.from_pretrained(model_id)
+ config = config_cls(
+ base_model_name_or_path=model_id,
+ **config_kwargs,
+ )
+ model = model.to(self.torch_device).eval()
+
+ inputs = self.prepare_inputs_for_testing()
+ logits_base = model(**inputs)[0]
+
+ model = get_peft_model(model, config).eval()
+ logits_peft = model(**inputs)[0]
+
+ atol, rtol = 1e-6, 1e-6 # default
+ # Initializing with LN tuning cannot be configured to change the outputs (unlike init_lora_weights=False)
+ if not issubclass(config_cls, LNTuningConfig):
+ # sanity check that the logits are different
+ assert not torch.allclose(logits_base, logits_peft, atol=atol, rtol=rtol)
+
+ model_unloaded = model.merge_and_unload(safe_merge=True)
+ logits_unloaded = model_unloaded(**inputs)[0]
+
+ if self.torch_device in ["mlu"]:
+ atol, rtol = 1e-3, 1e-3 # MLU
+
+ conv_ids = ["Conv2d", "Conv3d", "Conv2d2"]
+ if issubclass(config_cls, (IA3Config, LoraConfig)) and model_id in conv_ids: # more instability with Conv
+ atol, rtol = 1e-3, 1e-3
+
+ # check that the logits are the same after unloading
+ assert torch.allclose(logits_peft, logits_unloaded, atol=atol, rtol=rtol)
+
+ # Ensure that serializing with safetensors works, there was an error when weights were not contiguous
+ with tempfile.TemporaryDirectory() as tmp_dirname:
+ # serializing with torch.save works
+ torch.save(model_unloaded.state_dict(), os.path.join(tmp_dirname, "model.bin"))
+
+ # serializing with safetensors works
+ save_file(model_unloaded.state_dict(), os.path.join(tmp_dirname, "model.safetensors"))
+
+ def _test_mixed_adapter_batches(self, model_id, config_cls, config_kwargs):
+ # Test for mixing different adapters in a single batch by passing the adapter_names argument
+ if config_cls not in (LoraConfig,):
+ return pytest.skip(f"Mixed adapter batches not supported for {config_cls}")
+
+ config = config_cls(
+ base_model_name_or_path=model_id,
+ **config_kwargs,
+ )
+
+ torch.manual_seed(0)
+ with hub_online_once(model_id):
+ model = self.transformers_class.from_pretrained(model_id)
+ model = get_peft_model(model, config, adapter_name="adapter0").eval()
+ model.add_adapter("adapter1", config)
+ model = model.to(self.torch_device).eval()
+
+ self.perturb_trainable_token_weights_if_used(model, config_kwargs, adapter_name="adapter0")
+ self.perturb_trainable_token_weights_if_used(model, config_kwargs, adapter_name="adapter1")
+
+ dummy_input = self.prepare_inputs_for_testing()
+ # ensure that we have at least 3 samples for this test
+ dummy_input = {k: torch.cat([v for _ in range(3)]) for k, v in dummy_input.items()}
+ with torch.inference_mode():
+ with model.disable_adapter():
+ output_base = model(**dummy_input)[0]
+ logits_base = model.generate(**dummy_input, return_dict_in_generate=True, output_scores=True).scores[0]
+
+ model.set_adapter("adapter0")
+ with torch.inference_mode():
+ output_adapter0 = model(**dummy_input)[0]
+ logits_adapter0 = model.generate(**dummy_input, return_dict_in_generate=True, output_scores=True).scores[0]
+
+ model.set_adapter("adapter1")
+ with torch.inference_mode():
+ output_adapter1 = model(**dummy_input)[0]
+ logits_adapter1 = model.generate(**dummy_input, return_dict_in_generate=True, output_scores=True).scores[0]
+
+ atol, rtol = 1e-4, 1e-4
+ # sanity check that there are enough outputs and that they are different
+ assert len(output_base) == len(output_adapter0) == len(output_adapter1) >= 3
+ assert len(logits_base) == len(logits_adapter0) == len(logits_adapter1) >= 3
+ assert not torch.allclose(output_base, output_adapter0, atol=atol, rtol=rtol)
+ assert not torch.allclose(output_base, output_adapter1, atol=atol, rtol=rtol)
+ assert not torch.allclose(output_adapter0, output_adapter1, atol=atol, rtol=rtol)
+ assert not torch.allclose(logits_base, logits_adapter0, atol=atol, rtol=rtol)
+ assert not torch.allclose(logits_base, logits_adapter1, atol=atol, rtol=rtol)
+ assert not torch.allclose(logits_adapter0, logits_adapter1, atol=atol, rtol=rtol)
+
+ # alternate between base model, adapter0, and adapter1
+ adapters = ["__base__", "adapter0", "adapter1"]
+ dummy_input["adapter_names"] = [adapters[i % 3] for i in (range(len(dummy_input["input_ids"])))]
+ with torch.inference_mode():
+ output_mixed = model(**dummy_input)[0]
+ logits_mixed = model.generate(**dummy_input, return_dict_in_generate=True, output_scores=True).scores[0]
+
+ assert torch.allclose(output_base[::3], output_mixed[::3], atol=atol, rtol=rtol)
+ assert torch.allclose(output_adapter0[1::3], output_mixed[1::3], atol=atol, rtol=rtol)
+ assert torch.allclose(output_adapter1[2::3], output_mixed[2::3], atol=atol, rtol=rtol)
+ assert torch.allclose(logits_base[::3], logits_mixed[::3], atol=atol, rtol=rtol)
+ assert torch.allclose(logits_adapter0[1::3], logits_mixed[1::3], atol=atol, rtol=rtol)
+ assert torch.allclose(logits_adapter1[2::3], logits_mixed[2::3], atol=atol, rtol=rtol)
+
+ def _test_generate_with_mixed_adapter_batches_and_beam_search(self, model_id, config_cls, config_kwargs):
+ # Test generating with beam search and with mixing different adapters in a single batch by passing the
+ # adapter_names argument. See #2283.
+ if config_cls not in (LoraConfig,):
+ return pytest.skip(f"Mixed adapter batches not supported for {config_cls}")
+ if config_kwargs.get("alora_invocation_tokens") is not None:
+ return pytest.skip("Beam search not yet supported for aLoRA") # beam search not yet fully supported
+ if config_kwargs.get("trainable_token_indices", None) is not None:
+ # for some configurations this test will fail since the adapter values don't differ.
+ # this is probably a problem with the test setup and not with the implementation.
+ return pytest.skip("Trainable token indices is not supported here (yet).")
+
+ config = config_cls(
+ base_model_name_or_path=model_id,
+ **config_kwargs,
+ )
+
+ torch.manual_seed(0)
+ with hub_online_once(model_id):
+ model = self.transformers_class.from_pretrained(model_id)
+ model = get_peft_model(model, config, adapter_name="adapter0").eval()
+ model.add_adapter("adapter1", config)
+
+ # In contrast to forward, for generate, it can sometimes happen that we get the same results as the base model
+ # even with LoRA applied because the impact of LoRA is not big enough. Therefore, use this "trick" to make LoRA
+ # stronger.
+ for name, param in model.named_parameters():
+ if model.base_model.prefix in name:
+ param.data.mul_(10.0)
+
+ model = model.to(self.torch_device).eval()
+
+ dummy_input = self.prepare_inputs_for_testing()
+ # ensure that we have at least 3 samples for this test
+ dummy_input = {k: torch.cat([v for _ in range(3)]) for k, v in dummy_input.items()}
+ gen_kwargs = {**dummy_input, "max_length": 20, "num_beams": 10, "early_stopping": True}
+ with torch.inference_mode():
+ with model.disable_adapter():
+ gen_base = model.generate(**gen_kwargs)
+
+ model.set_adapter("adapter0")
+ with torch.inference_mode():
+ gen_adapter0 = model.generate(**gen_kwargs)
+
+ model.set_adapter("adapter1")
+ with torch.inference_mode():
+ gen_adapter1 = model.generate(**gen_kwargs)
+
+ def remove_padding(seq, pad_value):
+ lst = list(seq)
+ while lst and (lst[-1] == pad_value):
+ lst.pop()
+ return lst
+
+ def gens_are_same(gen0, gen1):
+ # Special function to compare generations. We cannot use torch.allclose it will raise an error when sequence
+ # lengths differ. Morevoer, we need to remove the padding from the sequences. This is because, even though
+ # normally identical sequences should have the same length, when we do mixed adapter batches, each sample
+ # will be padded to the longest sequence in that mixed batch, which can be different from the longest
+ # sequence without mixed adapter batches.
+ pad_value = model.config.eos_token_id
+ for sample0, sample1 in zip(gen0, gen1):
+ sample0 = remove_padding(sample0, pad_value)
+ sample1 = remove_padding(sample1, pad_value)
+ if (len(sample0) != len(sample1)) or (sample0 != sample1):
+ # at least one sample differs, the generations are not identical
+ return False
+ return True
+
+ # sanity check that there are enough outputs and that they are different
+ assert len(gen_base) == len(gen_adapter0) == len(gen_adapter1)
+ assert len(gen_adapter1) >= 3
+ assert not gens_are_same(gen_base, gen_adapter0)
+ assert not gens_are_same(gen_base, gen_adapter1)
+ assert not gens_are_same(gen_adapter0, gen_adapter1)
+
+ # alternate between base model, adapter0, and adapter1
+ adapters = ["__base__", "adapter0", "adapter1"]
+ gen_kwargs["adapter_names"] = [adapters[i % 3] for i in (range(len(dummy_input["input_ids"])))]
+
+ with torch.inference_mode():
+ gen_mixed = model.generate(**gen_kwargs)
+
+ assert gens_are_same(gen_base[::3], gen_mixed[::3])
+ assert gens_are_same(gen_adapter0[1::3], gen_mixed[1::3])
+ assert gens_are_same(gen_adapter1[2::3], gen_mixed[2::3])
+
+ def _test_generate(self, model_id, config_cls, config_kwargs):
+ with hub_online_once(model_id):
+ model = self.transformers_class.from_pretrained(model_id)
+ config = config_cls(
+ base_model_name_or_path=model_id,
+ **config_kwargs,
+ )
+ model = get_peft_model(model, config)
+ model = model.to(self.torch_device)
+
+ inputs = self.prepare_inputs_for_testing()
+
+ # check if `generate` works
+ _ = model.generate(**inputs)
+
+ def _test_generate_pos_args(self, model_id, config_cls, config_kwargs, raises_err: bool):
+ with hub_online_once(model_id):
+ model = self.transformers_class.from_pretrained(model_id)
+ config = config_cls(
+ base_model_name_or_path=model_id,
+ **config_kwargs,
+ )
+ model = get_peft_model(model, config)
+ model = model.to(self.torch_device)
+
+ inputs = self.prepare_inputs_for_testing()
+ if raises_err:
+ with pytest.raises(TypeError):
+ # check if `generate` raises an error if positional arguments are passed
+ _ = model.generate(inputs["input_ids"])
+ else:
+ # check if `generate` works if positional arguments are passed
+ _ = model.generate(inputs["input_ids"])
+
+ def _test_generate_half_prec(self, model_id, config_cls, config_kwargs):
+ if config_cls not in (IA3Config, LoraConfig, PrefixTuningConfig):
+ return pytest.skip(f"Test not applicable for {config_cls}")
+
+ if self.torch_device == "mps": # BFloat16 is not supported on MPS
+ return pytest.skip("BFloat16 is not supported on MPS")
+
+ with hub_online_once(model_id):
+ model = self.transformers_class.from_pretrained(model_id, torch_dtype=torch.bfloat16)
+ config = config_cls(
+ base_model_name_or_path=model_id,
+ **config_kwargs,
+ )
+ model = get_peft_model(model, config)
+ model = model.to(self.torch_device)
+
+ input_ids = torch.LongTensor([[1, 1, 1], [2, 1, 2]]).to(self.torch_device)
+ attention_mask = torch.LongTensor([[1, 1, 1], [1, 0, 1]]).to(self.torch_device)
+
+ # check if `generate` works
+ _ = model.generate(input_ids=input_ids, attention_mask=attention_mask)
+
+ def _test_prefix_tuning_half_prec_conversion(self, model_id, config_cls, config_kwargs):
+ if config_cls not in (PrefixTuningConfig,):
+ return pytest.skip(f"Test not applicable for {config_cls}")
+
+ config = config_cls(
+ base_model_name_or_path=model_id,
+ **config_kwargs,
+ )
+
+ with hub_online_once(model_id):
+ model = self.transformers_class.from_pretrained(model_id)
+ model = get_peft_model(model, config)
+ model = model.half()
+
+ assert model.base_model_torch_dtype == torch.float16
+
+ def _test_training(self, model_id, config_cls, config_kwargs):
+ if issubclass(config_cls, PromptLearningConfig):
+ return pytest.skip(f"Test not applicable for {config_cls}")
+ if (config_cls == AdaLoraConfig) and ("roberta" in model_id.lower()):
+ # TODO: no gradients on the "dense" layer, other layers work, not sure why
+ self.skipTest("AdaLora with RoBERTa does not work correctly")
+
+ with hub_online_once(model_id):
+ model = self.transformers_class.from_pretrained(model_id)
+ config = config_cls(
+ base_model_name_or_path=model_id,
+ **config_kwargs,
+ )
+ model = get_peft_model(model, config)
+ model = model.to(self.torch_device)
+
+ inputs = self.prepare_inputs_for_testing()
+
+ # check if `training` works
+ output = model(**inputs)[0]
+ loss = output.sum()
+ loss.backward()
+ parameter_prefix = model.prefix
+ for n, param in model.named_parameters():
+ if (parameter_prefix in n) or ("modules_to_save" in n) or ("token_adapter.trainable_tokens" in n):
+ assert param.grad is not None
+ else:
+ assert param.grad is None
+
+ def _test_inference_safetensors(self, model_id, config_cls, config_kwargs):
+ if (config_cls == PrefixTuningConfig) and ("deberta" in model_id.lower()):
+ # TODO: raises an error:
+ # TypeError: DebertaModel.forward() got an unexpected keyword argument 'past_key_values'
+ self.skipTest("DeBERTa with PrefixTuning does not work correctly")
+
+ config = config_cls(
+ base_model_name_or_path=model_id,
+ **config_kwargs,
+ )
+ with hub_online_once(model_id):
+ model = self.transformers_class.from_pretrained(model_id)
+ model = get_peft_model(model, config)
+ model = model.to(self.torch_device)
+
+ inputs = self.prepare_inputs_for_testing()
+
+ # check if `training` works
+ output = model(**inputs)[0]
+ logits = output[0]
+
+ loss = output.sum()
+ loss.backward()
+
+ # set to eval mode, since things like dropout can affect the output otherwise
+ model.eval()
+ logits = model(**inputs)[0][0]
+
+ with tempfile.TemporaryDirectory() as tmp_dirname:
+ model.save_pretrained(tmp_dirname, safe_serialization=True)
+ assert "adapter_model.safetensors" in os.listdir(tmp_dirname)
+ assert "adapter_model.bin" not in os.listdir(tmp_dirname)
+
+ model_from_pretrained = self.transformers_class.from_pretrained(model_id)
+ model_from_pretrained = PeftModel.from_pretrained(model_from_pretrained, tmp_dirname).to(
+ self.torch_device
+ )
+
+ logits_from_pretrained = model_from_pretrained(**inputs)[0][0]
+ assert torch.allclose(logits, logits_from_pretrained, atol=1e-4, rtol=1e-4)
+
+ def _test_training_layer_indexing(self, model_id, config_cls, config_kwargs):
+ if config_cls not in (LoraConfig,):
+ return pytest.skip(f"Test not applicable for {config_cls}")
+
+ config = config_cls(
+ base_model_name_or_path=model_id,
+ layers_to_transform=[0],
+ **config_kwargs,
+ )
+ with hub_online_once(model_id):
+ model = self.transformers_class.from_pretrained(model_id)
+ model = get_peft_model(model, config)
+ model = model.to(self.torch_device)
+
+ inputs = self.prepare_inputs_for_testing()
+
+ # check if `training` works
+ output = model(**inputs)[0]
+ logits = output[0]
+
+ loss = output.sum()
+ loss.backward()
+
+ has_trainable_tokens = config_kwargs.get("trainable_token_indices", None) is not None
+ nb_trainable = 0
+
+ for n, param in model.named_parameters():
+ if model.prefix in n or (has_trainable_tokens and "trainable_tokens" in n):
+ assert param.grad is not None
+ nb_trainable += 1
+ else:
+ assert param.grad is None
+
+ with tempfile.TemporaryDirectory() as tmp_dirname:
+ model.save_pretrained(tmp_dirname)
+
+ model_from_pretrained = self.transformers_class.from_pretrained(model_id)
+ model_from_pretrained = PeftModel.from_pretrained(model_from_pretrained, tmp_dirname).to(
+ self.torch_device
+ )
+
+ logits_from_pretrained = model_from_pretrained(**inputs)[0][0]
+ assert torch.allclose(logits, logits_from_pretrained, atol=1e-4, rtol=1e-4)
+
+ # check the nb of trainable params again but without layers_to_transform
+ model = self.transformers_class.from_pretrained(model_id)
+ config = config_cls(
+ base_model_name_or_path=model_id,
+ **config_kwargs,
+ )
+ model = get_peft_model(model, config)
+ nb_trainable_all = 0
+
+ for n, param in model.named_parameters():
+ if model.prefix in n or (has_trainable_tokens and "trainable_tokens" in n):
+ nb_trainable_all += 1
+
+ mod_list = next((m for m in model.modules() if isinstance(m, torch.nn.ModuleList)), None)
+ if mod_list and len(mod_list) == 1:
+ # there is only a single layer
+ assert nb_trainable == nb_trainable_all
+ else:
+ # more than 1 layer, i.e. setting layers_to_transform=[0] should target fewer layers
+ assert nb_trainable < nb_trainable_all
+
+ def _test_training_gradient_checkpointing(self, model_id, config_cls, config_kwargs):
+ if config_cls == PrefixTuningConfig:
+ return pytest.skip(f"Test not applicable for {config_cls}")
+
+ if (config_cls == AdaLoraConfig) and ("roberta" in model_id.lower()):
+ # TODO: no gradients on the "dense" layer, other layers work, not sure why
+ self.skipTest("AdaLora with RoBERTa does not work correctly")
+
+ if (config_cls == OFTConfig) and ("deberta" in model_id.lower()):
+ # TODO: no gradients on the "dense" layer, other layers work, not sure why
+ self.skipTest("OFT with Deberta does not work correctly")
+
+ with hub_online_once(model_id):
+ model = self.transformers_class.from_pretrained(model_id)
+
+ if not getattr(model, "supports_gradient_checkpointing", False):
+ return pytest.skip(f"Model {model_id} does not support gradient checkpointing")
+
+ model.gradient_checkpointing_enable()
+
+ config = config_cls(
+ base_model_name_or_path=model_id,
+ **config_kwargs,
+ )
+ model = get_peft_model(model, config)
+ model = model.to(self.torch_device)
+
+ inputs = self.prepare_inputs_for_testing()
+
+ # check if `training` works
+ output = model(**inputs)[0]
+
+ loss = output.sum()
+ loss.backward()
+
+ for n, param in model.named_parameters():
+ if "prompt_encoder." in n: # prompt tuning methods
+ if not issubclass(config_cls, CPTConfig):
+ assert param.grad is not None
+ elif (
+ "delta_embedding" in n
+ ): # delta_embedding is the embedding that should be updated with grads in CPT
+ assert param.grad is not None
+ elif hasattr(model, "prefix") and (model.prefix in n): # non-prompt tuning methods
+ assert param.grad is not None
+ elif "trainable_tokens_" in n: # trainable tokens layer
+ assert param.grad is not None
+ else:
+ assert param.grad is None
+
+ def _test_peft_model_device_map(self, model_id, config_cls, config_kwargs):
+ if config_cls not in (LoraConfig, VBLoRAConfig):
+ return pytest.skip(f"Test not applicable for {config_cls}")
+
+ config = config_cls(
+ base_model_name_or_path=model_id,
+ **config_kwargs,
+ )
+
+ with hub_online_once(model_id):
+ model = self.transformers_class.from_pretrained(model_id)
+
+ model = get_peft_model(model, config)
+ model = model.to(self.torch_device)
+
+ with tempfile.TemporaryDirectory() as tmp_dirname:
+ model.save_pretrained(tmp_dirname)
+
+ model_from_pretrained = self.transformers_class.from_pretrained(model_id)
+ _ = PeftModel.from_pretrained(model_from_pretrained, tmp_dirname, device_map={"": "cpu"}).to(
+ self.torch_device
+ )
+
+ def _test_training_prompt_learning_tasks(self, model_id, config_cls, config_kwargs):
+ if not issubclass(config_cls, PromptLearningConfig):
+ return pytest.skip(f"Test not applicable for {config_cls}")
+
+ with hub_online_once(model_id):
+ model = self.transformers_class.from_pretrained(model_id)
+ config = config_cls(
+ base_model_name_or_path=model_id,
+ **config_kwargs,
+ )
+ model = get_peft_model(model, config)
+ model = model.to(self.torch_device)
+
+ inputs = self.prepare_inputs_for_testing()
+
+ # check if `training` works
+ output = model(**inputs)[0]
+ loss = output.sum()
+ loss.backward()
+
+ if issubclass(config_cls, CPTConfig):
+ parameters = []
+ for name, param in model.prompt_encoder.named_parameters():
+ if name != "default.embedding.weight":
+ parameters.append(param)
+ else:
+ parameters = model.prompt_encoder.parameters()
+
+ # check that prompt encoder has grads
+ for param in parameters:
+ assert param.grad is not None
+
+ def _test_delete_adapter(self, model_id, config_cls, config_kwargs):
+ supported_peft_types = [
+ PeftType.LORA,
+ PeftType.LOHA,
+ PeftType.LOKR,
+ PeftType.IA3,
+ PeftType.OFT,
+ PeftType.BOFT,
+ PeftType.VERA,
+ PeftType.FOURIERFT,
+ PeftType.HRA,
+ PeftType.VBLORA,
+ PeftType.BONE,
+ PeftType.MISS,
+ ]
+ # IA3 does not support deleting adapters yet, but it just needs to be added
+ # AdaLora does not support multiple adapters
+ config = config_cls(
+ base_model_name_or_path=model_id,
+ **config_kwargs,
+ )
+ if config.peft_type not in supported_peft_types:
+ return pytest.skip(f"Test not applicable for {config.peft_type}")
+
+ with hub_online_once(model_id):
+ model = self.transformers_class.from_pretrained(model_id)
+ adapter_to_delete = "delete_me"
+ model = get_peft_model(model, config)
+ model.add_adapter(adapter_to_delete, config)
+ model.set_adapter(adapter_to_delete)
+ model = model.to(self.torch_device)
+ model.delete_adapter(adapter_to_delete)
+ assert adapter_to_delete not in model.peft_config
+ assert model.active_adapters == ["default"]
+
+ key_list = [key for key, _ in model.named_modules()]
+ for key in key_list:
+ _, target, _ = _get_submodules(model, key)
+ attributes_to_check = getattr(target, "adapter_layer_names", []) + getattr(
+ target, "other_param_names", []
+ )
+ for attr in attributes_to_check:
+ assert adapter_to_delete not in attrgetter(attr)(target)
+
+ # check auxiliary modules
+ for module in model.modules():
+ if isinstance(module, AuxiliaryTrainingWrapper):
+ assert adapter_to_delete not in module._adapters
+ assert module.active_adapters == ["default"]
+ if isinstance(module, ModulesToSaveWrapper):
+ assert adapter_to_delete not in module.modules_to_save
+ elif isinstance(module, TrainableTokensWrapper):
+ assert adapter_to_delete not in module.token_adapter.trainable_tokens_delta
+ assert adapter_to_delete not in module.token_adapter.trainable_tokens_original
+
+ # check that we can also delete the last remaining adapter
+ model.delete_adapter("default")
+ assert "default" not in model.peft_config
+ assert model.active_adapters == []
+
+ for module in model.modules():
+ if isinstance(module, AuxiliaryTrainingWrapper):
+ assert "default" not in module._adapters
+ assert module.active_adapters == []
+ if isinstance(module, ModulesToSaveWrapper):
+ assert "default" not in module.modules_to_save
+ elif isinstance(module, TrainableTokensWrapper):
+ assert "default" not in module.token_adapter.trainable_tokens_delta
+ assert "default" not in module.token_adapter.trainable_tokens_original
+
+ input = self.prepare_inputs_for_testing()
+ # note: we cannot call model(**input) because PeftModel always expects there to be at least one adapter
+ model.base_model(**input) # should not raise an error
+
+ def _test_delete_inactive_adapter(self, model_id, config_cls, config_kwargs):
+ # same as test_delete_adapter, but this time an inactive adapter is deleted
+ supported_peft_types = [
+ PeftType.LORA,
+ PeftType.LOHA,
+ PeftType.LOKR,
+ PeftType.IA3,
+ PeftType.OFT,
+ PeftType.BOFT,
+ PeftType.FOURIERFT,
+ PeftType.HRA,
+ PeftType.VBLORA,
+ PeftType.BONE,
+ PeftType.MISS,
+ ]
+ # IA3 does not support deleting adapters yet, but it just needs to be added
+ # AdaLora does not support multiple adapters
+ config = config_cls(
+ base_model_name_or_path=model_id,
+ **config_kwargs,
+ )
+ if config.peft_type not in supported_peft_types:
+ return pytest.skip(f"Test not applicable for {config.peft_type}")
+
+ with hub_online_once(model_id):
+ model = self.transformers_class.from_pretrained(model_id)
+ adapter_to_delete = "delete_me"
+ model = get_peft_model(model, config)
+ model.add_adapter(adapter_to_delete, config)
+ # "delete_me" is added but not activated
+ model = model.to(self.torch_device)
+ model.delete_adapter(adapter_to_delete)
+ assert adapter_to_delete not in model.peft_config
+ assert model.active_adapters == ["default"]
+
+ key_list = [key for key, _ in model.named_modules()]
+ for key in key_list:
+ _, target, _ = _get_submodules(model, key)
+ attributes_to_check = getattr(target, "adapter_layer_names", []) + getattr(
+ target, "other_param_names", []
+ )
+ for attr in attributes_to_check:
+ assert adapter_to_delete not in attrgetter(attr)(target)
+
+ # check auxiliary modules
+ for module in model.modules():
+ if isinstance(module, AuxiliaryTrainingWrapper):
+ assert adapter_to_delete not in module._adapters
+ assert module.active_adapters == ["default"]
+ if isinstance(module, ModulesToSaveWrapper):
+ assert adapter_to_delete not in module.modules_to_save
+ elif isinstance(module, TrainableTokensWrapper):
+ assert adapter_to_delete not in module.token_adapter.trainable_tokens_delta
+ assert adapter_to_delete not in module.token_adapter.trainable_tokens_original
+
+ # check that we can also delete the last remaining adapter
+ model.delete_adapter("default")
+ assert "default" not in model.peft_config
+ assert model.active_adapters == []
+
+ for module in model.modules():
+ if isinstance(module, AuxiliaryTrainingWrapper):
+ assert "default" not in module._adapters
+ assert module.active_adapters == []
+ if isinstance(module, ModulesToSaveWrapper):
+ assert "default" not in module.modules_to_save
+ elif isinstance(module, TrainableTokensWrapper):
+ assert "default" not in module.token_adapter.trainable_tokens_delta
+ assert "default" not in module.token_adapter.trainable_tokens_original
+
+ input = self.prepare_inputs_for_testing()
+ # note: we cannot call model(**input) because PeftModel always expects there to be at least one adapter
+ model.base_model(**input) # should not raise an error
+
+ def _test_delete_unknown_adapter_raises(self, model_id, config_cls, config_kwargs):
+ # Check that we get a nice error message when trying to delete an adapter that does not exist.
+ config = config_cls(base_model_name_or_path=model_id, **config_kwargs)
+ with hub_online_once(model_id):
+ model = self.transformers_class.from_pretrained(model_id)
+ adapter_to_delete = "delete_me"
+ model = get_peft_model(model, config)
+
+ msg = "Adapter unknown-adapter does not exist"
+ with pytest.raises(ValueError, match=msg):
+ model.delete_adapter("unknown-adapter")
+
+ def _test_unload_adapter(self, model_id, config_cls, config_kwargs):
+ with hub_online_once(model_id):
+ model = self.transformers_class.from_pretrained(model_id).to(self.torch_device)
+ num_params_base = len(model.state_dict())
+ dummy_input = self.prepare_inputs_for_testing()
+ with torch.inference_mode():
+ logits_transformers = model(**dummy_input)[0]
+
+ config = config_cls(
+ base_model_name_or_path=model_id,
+ **config_kwargs,
+ )
+ model = get_peft_model(model, config)
+ model = model.to(self.torch_device)
+
+ if isinstance(config, PromptLearningConfig):
+ # prompt learning does not support unloading
+ with pytest.raises(AttributeError):
+ model = model.unload()
+ else:
+ self.perturb_trainable_token_weights_if_used(model, config_kwargs)
+ with torch.inference_mode():
+ logits_with_adapter = model(**dummy_input)[0]
+
+ model.eval()
+ model = model.unload()
+ num_params_unloaded = len(model.state_dict())
+ with torch.inference_mode():
+ logits_unload = model(**dummy_input)[0]
+
+ # check that PEFT layers are completely removed
+ assert not any(isinstance(module, BaseTunerLayer) for module in model.modules())
+ assert not torch.allclose(logits_with_adapter, logits_unload, atol=1e-10, rtol=1e-10)
+ assert torch.allclose(logits_transformers, logits_unload, atol=1e-4, rtol=1e-4)
+ assert num_params_base == num_params_unloaded
+
+ def _test_weighted_combination_of_adapters_lora(self, model, config, adapter_list, weight_list):
+ model.add_adapter(adapter_list[1], config)
+ model.add_adapter(adapter_list[2], replace(config, r=20))
+ model = model.to(self.torch_device)
+
+ # test re-weighting single adapter
+ model.add_weighted_adapter([adapter_list[0]], [weight_list[0]], "single_adapter_reweighting")
+
+ # test svd re-weighting with multiple adapters
+ model.add_weighted_adapter(adapter_list[1:], weight_list[1:], "multi_adapter_svd_reweighting")
+
+ # test ties_svd re-weighting with multiple adapters
+ model.add_weighted_adapter(
+ adapter_list[1:],
+ weight_list[1:],
+ "multi_adapter_ties_svd_reweighting",
+ combination_type="ties_svd",
+ density=0.5,
+ )
+
+ # test dare_linear_svd re-weighting with multiple adapters
+ model.add_weighted_adapter(
+ adapter_list[1:],
+ weight_list[1:],
+ "multi_adapter_dare_linear_svd_reweighting",
+ combination_type="dare_linear_svd",
+ density=0.5,
+ )
+
+ # test dare_ties_svd re-weighting with multiple adapters
+ model.add_weighted_adapter(
+ adapter_list[1:],
+ weight_list[1:],
+ "multi_adapter_dare_ties_svd_reweighting",
+ combination_type="dare_ties_svd",
+ density=0.5,
+ )
+
+ # test magnitude_prune_svd re-weighting with multiple adapters
+ model.add_weighted_adapter(
+ adapter_list[1:],
+ weight_list[1:],
+ "multi_adapter_magnitude_prune_svd_reweighting",
+ combination_type="magnitude_prune_svd",
+ density=0.5,
+ )
+
+ # test cat re-weighting with multiple adapters
+ model.add_weighted_adapter(
+ adapter_list[1:], weight_list[1:], "multi_adapter_cat_reweighting", combination_type="cat"
+ )
+
+ # test linear re-weighting with multiple adapters
+ model.add_weighted_adapter(
+ adapter_list[:2], weight_list[:2], "multi_adapter_linear_reweighting", combination_type="linear"
+ )
+
+ # test ties re-weighting with multiple adapters
+ model.add_weighted_adapter(
+ adapter_list[:2], weight_list[:2], "multi_adapter_ties_reweighting", combination_type="ties", density=0.5
+ )
+
+ # test dare_linear re-weighting with multiple adapters
+ model.add_weighted_adapter(
+ adapter_list[:2],
+ weight_list[:2],
+ "multi_adapter_dare_linear_reweighting",
+ combination_type="dare_linear",
+ density=0.5,
+ )
+
+ # test dare_ties re-weighting with multiple adapters
+ model.add_weighted_adapter(
+ adapter_list[:2],
+ weight_list[:2],
+ "multi_adapter_dare_ties_reweighting",
+ combination_type="dare_ties",
+ density=0.5,
+ )
+
+ # test magnitude_prune re-weighting with multiple adapters
+ model.add_weighted_adapter(
+ adapter_list[:2],
+ weight_list[:2],
+ "multi_adapter_magnitude_prune_reweighting",
+ combination_type="magnitude_prune",
+ density=0.5,
+ )
+
+ # test linear re-weighting with multiple adapters with only first adapter having non zero weight
+ model.add_weighted_adapter(
+ adapter_list[:2],
+ [weight_list[0], 0],
+ "multi_adapter_linear_reweighting_single_enabled",
+ combination_type="linear",
+ )
+
+ with pytest.raises(ValueError):
+ model.add_weighted_adapter(
+ adapter_list[1:],
+ weight_list[1:],
+ "multi_adapter_linear_reweighting_uneven_r",
+ combination_type="linear",
+ )
+
+ with pytest.raises(ValueError):
+ model.add_weighted_adapter(
+ adapter_list[1:],
+ weight_list[1:],
+ "multi_adapter_ties_reweighting_uneven_r",
+ combination_type="ties",
+ density=0.5,
+ )
+
+ with pytest.raises(ValueError):
+ model.add_weighted_adapter(
+ adapter_list[1:],
+ weight_list[1:],
+ "multi_adapter_dare_linear_reweighting_uneven_r",
+ combination_type="dare_linear",
+ density=0.5,
+ )
+
+ with pytest.raises(ValueError):
+ model.add_weighted_adapter(
+ adapter_list[1:],
+ weight_list[1:],
+ "multi_adapter_dare_ties_reweighting_uneven_r",
+ combination_type="dare_ties",
+ density=0.5,
+ )
+
+ with pytest.raises(ValueError):
+ model.add_weighted_adapter(
+ adapter_list[1:],
+ weight_list[1:],
+ "multi_adapter_magnitude_prune_reweighting_uneven_r",
+ combination_type="magnitude_prune",
+ density=0.5,
+ )
+
+ new_adapters = [
+ "single_adapter_reweighting",
+ "multi_adapter_svd_reweighting",
+ "multi_adapter_ties_svd_reweighting",
+ "multi_adapter_dare_linear_svd_reweighting",
+ "multi_adapter_dare_ties_svd_reweighting",
+ "multi_adapter_magnitude_prune_svd_reweighting",
+ "multi_adapter_cat_reweighting",
+ "multi_adapter_linear_reweighting",
+ "multi_adapter_linear_reweighting_single_enabled",
+ "multi_adapter_ties_reweighting",
+ "multi_adapter_dare_linear_reweighting",
+ "multi_adapter_dare_ties_reweighting",
+ "multi_adapter_magnitude_prune_reweighting",
+ ]
+ for new_adapter in new_adapters:
+ assert new_adapter in model.peft_config
+
+ key_list = [key for key, _ in model.named_modules()]
+ for key in key_list:
+ _, target, _ = _get_submodules(model, key)
+ if isinstance(target, LoraLayer):
+ for adapter_name in new_adapters:
+ if "single" in adapter_name:
+ new_delta_weight = target.get_delta_weight(adapter_name)
+ weighted_original_delta_weights = target.get_delta_weight(adapter_list[0]) * weight_list[0]
+ sign = 1 if weight_list[0] > 0 else -1
+ weighted_original_delta_weights = sign * weighted_original_delta_weights
+ assert torch.allclose(new_delta_weight, weighted_original_delta_weights, atol=1e-4, rtol=1e-4)
+ elif "svd" in adapter_name:
+ assert target.r[adapter_name] == 20
+ elif "linear" in adapter_name:
+ assert target.r[adapter_name] == 8
+ elif "cat" in adapter_name:
+ assert target.r[adapter_name] == 28
+
+ dummy_input = self.prepare_inputs_for_testing()
+ model.eval()
+ for adapter_name in new_adapters:
+ # ensuring new adapters pass the forward loop
+ model.set_adapter(adapter_name)
+ assert model.active_adapter == adapter_name
+ assert model.active_adapters == [adapter_name]
+ model(**dummy_input)[0]
+
+ def _test_weighted_combination_of_adapters_ia3(self, model, config, adapter_list, weight_list):
+ model.add_adapter(adapter_list[1], config)
+ model.add_adapter(adapter_list[2], config)
+ model = model.to(self.torch_device)
+
+ # test re-weighting single adapter
+ model.add_weighted_adapter([adapter_list[0]], [weight_list[0]], "single_adapter_reweighting")
+
+ # test re-weighting with multiple adapters
+ model.add_weighted_adapter(adapter_list[1:], weight_list[1:], "multi_adapter_reweighting")
+
+ new_adapters = [
+ "single_adapter_reweighting",
+ "multi_adapter_reweighting",
+ ]
+ for new_adapter in new_adapters:
+ assert new_adapter in model.peft_config
+
+ dummy_input = self.prepare_inputs_for_testing()
+ model.eval()
+ for adapter_name in new_adapters:
+ # ensuring new adapters pass the forward loop
+ model.set_adapter(adapter_name)
+ assert model.active_adapter == adapter_name
+ assert model.active_adapters == [adapter_name]
+ model(**dummy_input)[0]
+
+ def _test_weighted_combination_of_adapters(self, model_id, config_cls, config_kwargs):
+ if issubclass(config_cls, AdaLoraConfig):
+ # AdaLora does not support adding more than 1 adapter
+ return pytest.skip(f"Test not applicable for {config_cls}")
+ if model_id.endswith("qwen2"):
+ # Qwen2 fails with weighted adapter combinations using SVD
+ return pytest.skip(f"Test does not work with model {model_id}")
+ if "gemma" in model_id.lower():
+ return pytest.skip("Combining Gemma adapters with SVD is currently failing")
+
+ adapter_list = ["adapter1", "adapter_2", "adapter_3"]
+ weight_list = [0.5, 1.5, 1.5]
+ negative_weight_list = [-0.5, -0.8, -1.2]
+ # Initialize the config
+ config = config_cls(
+ base_model_name_or_path=model_id,
+ **config_kwargs,
+ )
+
+ if not isinstance(config, (LoraConfig, IA3Config)):
+ # This test is only applicable for Lora and IA3 configs
+ return pytest.skip(f"Test not applicable for {config}")
+
+ with hub_online_once(model_id):
+ model = self.transformers_class.from_pretrained(model_id)
+ model = get_peft_model(model, config, adapter_list[0])
+
+ if isinstance(config, LoraConfig):
+ self._test_weighted_combination_of_adapters_lora(model, config, adapter_list, weight_list)
+ self._test_weighted_combination_of_adapters_lora(model, config, adapter_list, negative_weight_list)
+ elif isinstance(config, IA3Config):
+ self._test_weighted_combination_of_adapters_ia3(model, config, adapter_list, weight_list)
+ self._test_weighted_combination_of_adapters_ia3(model, config, adapter_list, negative_weight_list)
+ else:
+ pytest.skip(f"Test not applicable for {config}")
+
+ def _test_disable_adapter(self, model_id, config_cls, config_kwargs):
+ task_type = config_kwargs.get("task_type")
+ if (task_type == "SEQ_2_SEQ_LM") and (config_cls in (PromptTuningConfig, PromptEncoderConfig)):
+ self.skipTest("Seq2Seq + prompt tuning/prompt encoder does not work with disabling adapters")
+
+ def get_output(model):
+ # helper function that works with different model types
+ torch.manual_seed(0)
+
+ if hasattr(model, "generate"):
+ # let's check the scores, not the output ids, since the latter can easily be identical even if the
+ # weights are slightly changed
+ output = model.generate(**input, return_dict_in_generate=True, output_scores=True).scores[0]
+ # take element 0, as output is a tuple
+ else:
+ output = model(**input)
+
+ if hasattr(output, "images"): # for SD
+ import numpy as np
+
+ img = output.images[0]
+ return torch.from_numpy(np.array(img))
+
+ return output
+
+ # initialize model
+ with hub_online_once(model_id):
+ model = self.transformers_class.from_pretrained(model_id).to(self.torch_device)
+
+ # output from BASE MODEL
+ input = self.prepare_inputs_for_testing()
+ output_before = get_output(model)
+
+ # output from PEFT MODEL
+ if hasattr(self, "instantiate_sd_peft"):
+ # SD models are instantiated differently
+ peft_model = self.instantiate_sd_peft(model_id, config_cls, config_kwargs)
+ else:
+ config = config_cls(
+ base_model_name_or_path=model_id,
+ **config_kwargs,
+ )
+ peft_model = get_peft_model(model, config)
+
+ # trainable_token_indices doesn't have support for `init_weights` so we have to do this manually
+ self.perturb_trainable_token_weights_if_used(model, config_kwargs)
+
+ output_peft = get_output(peft_model)
+
+ # first check trivial case is not true that peft does not affect the output; for this to work, init_weight
+ # must be False (if the config supports it)
+ if isinstance(peft_model, StableDiffusionPipeline):
+ # for SD, check that most pixels have different values
+ assert (output_before != output_peft).float().mean() > 0.8
+ else:
+ assert not torch.allclose(output_before, output_peft)
+
+ # output with DISABLED ADAPTER
+ if isinstance(peft_model, StableDiffusionPipeline):
+ with peft_model.unet.disable_adapter():
+ with peft_model.text_encoder.disable_adapter():
+ output_peft_disabled = get_output(peft_model)
+ # for SD, very rarely, a pixel can differ
+ assert (output_before != output_peft_disabled).float().mean() < 1e-4
+ else:
+ atol, rtol = 1e-6, 1e-6
+ if (platform.system() == "Windows") and (model_id == "trl-internal-testing/tiny-Llama4ForCausalLM"):
+ # for some reason, Windows CI fails with stricter tolerance
+ atol, rtol = 1e-5, 1e-5
+
+ with peft_model.disable_adapter():
+ output_peft_disabled = get_output(peft_model)
+ assert torch.allclose(output_before, output_peft_disabled, atol=atol, rtol=rtol)
+
+ # after leaving the disable_adapter context, the output should be the same as with enabled adapter again
+ # see #1501
+ output_peft_after_disabled = get_output(peft_model)
+ assert torch.allclose(output_peft, output_peft_after_disabled, atol=atol, rtol=rtol)
+
+ # TODO: add tests to check if disabling adapters works after calling merge_adapter
+
+ def _test_adding_multiple_adapters_with_bias_raises(self, model_id, config_cls, config_kwargs):
+ # When trying to add multiple adapters with bias in Lora, AdaLora or BOFTConfig, an error should be
+ # raised. Also, the peft model should not be left in a half-initialized state.
+ if not issubclass(config_cls, (LoraConfig, AdaLoraConfig, BOFTConfig)):
+ return pytest.skip(f"Test not applicable for {config_cls}")
+
+ with hub_online_once(model_id):
+ config_kwargs = config_kwargs.copy()
+ config_kwargs["bias"] = "all"
+ config = config_cls(
+ base_model_name_or_path=model_id,
+ **config_kwargs,
+ )
+
+ model = self.transformers_class.from_pretrained(model_id)
+ model = get_peft_model(model, config, "adapter0")
+
+ if config_cls == LoraConfig or config_cls == AdaLoraConfig:
+ with pytest.raises(ValueError):
+ model.add_adapter("adapter1", replace(config, r=20))
+
+ if config_cls == BOFTConfig:
+ with pytest.raises(ValueError):
+ model.add_adapter("adapter1", replace(config, boft_block_num=1, boft_block_size=0))
+
+ # (superficial) test that the model is not left in a half-initialized state when adding an adapter fails
+ assert "adapter1" not in model.peft_config
+ assert "adapter1" not in model.base_model.peft_config
+
+ def _test_passing_input_embeds_works(self, test_name, model_id, config_cls, config_kwargs):
+ # https://github.com/huggingface/peft/issues/727
+ with hub_online_once(model_id):
+ model = self.transformers_class.from_pretrained(model_id)
+ config = config_cls(
+ base_model_name_or_path=model_id,
+ **config_kwargs,
+ )
+ model = get_peft_model(model, config, adapter_name="test-adapter").to(self.torch_device)
+ dummy_input = self.prepare_inputs_for_testing()
+ inputs_embeds = model.get_input_embeddings()(dummy_input["input_ids"])
+ # just check that no error is raised
+ model.forward(inputs_embeds=inputs_embeds)
diff --git a/peft/tests/testing_utils.py b/peft/tests/testing_utils.py
new file mode 100644
index 0000000000000000000000000000000000000000..ec06fb49e87622a926cbaa0d89771f7f2919f3b8
--- /dev/null
+++ b/peft/tests/testing_utils.py
@@ -0,0 +1,305 @@
+# Copyright 2023-present the HuggingFace Inc. team.
+#
+# Licensed under the Apache License, Version 2.0 (the "License");
+# you may not use this file except in compliance with the License.
+# You may obtain a copy of the License at
+#
+# http://www.apache.org/licenses/LICENSE-2.0
+#
+# Unless required by applicable law or agreed to in writing, software
+# distributed under the License is distributed on an "AS IS" BASIS,
+# WITHOUT WARRANTIES OR CONDITIONS OF ANY KIND, either express or implied.
+# See the License for the specific language governing permissions and
+# limitations under the License.
+import os
+import unittest
+from contextlib import contextmanager
+from functools import lru_cache, wraps
+from unittest import mock
+
+import numpy as np
+import pytest
+import torch
+from accelerate.test_utils.testing import get_backend
+from datasets import load_dataset
+
+from peft import (
+ AdaLoraConfig,
+ IA3Config,
+ LNTuningConfig,
+ LoraConfig,
+ PromptLearningConfig,
+ VBLoRAConfig,
+)
+from peft.import_utils import (
+ is_aqlm_available,
+ is_auto_awq_available,
+ is_auto_gptq_available,
+ is_eetq_available,
+ is_gptqmodel_available,
+ is_hqq_available,
+ is_optimum_available,
+ is_torchao_available,
+)
+
+
+# Globally shared model cache used by `hub_online_once`.
+_HUB_MODEL_ACCESSES = {}
+
+
+torch_device, device_count, memory_allocated_func = get_backend()
+
+
+def require_non_cpu(test_case):
+ """
+ Decorator marking a test that requires a hardware accelerator backend. These tests are skipped when there are no
+ hardware accelerator available.
+ """
+ return unittest.skipUnless(torch_device != "cpu", "test requires a hardware accelerator")(test_case)
+
+
+def require_non_xpu(test_case):
+ """
+ Decorator marking a test that should be skipped for XPU.
+ """
+ return unittest.skipUnless(torch_device != "xpu", "test requires a non-XPU")(test_case)
+
+
+def require_torch_gpu(test_case):
+ """
+ Decorator marking a test that requires a GPU. Will be skipped when no GPU is available.
+ """
+ if not torch.cuda.is_available():
+ return unittest.skip("test requires GPU")(test_case)
+ else:
+ return test_case
+
+
+def require_torch_multi_gpu(test_case):
+ """
+ Decorator marking a test that requires multiple GPUs. Will be skipped when less than 2 GPUs are available.
+ """
+ if not torch.cuda.is_available() or torch.cuda.device_count() < 2:
+ return unittest.skip("test requires multiple GPUs")(test_case)
+ else:
+ return test_case
+
+
+def require_torch_multi_accelerator(test_case):
+ """
+ Decorator marking a test that requires multiple hardware accelerators. These tests are skipped on a machine without
+ multiple accelerators.
+ """
+ return unittest.skipUnless(
+ torch_device != "cpu" and device_count > 1, "test requires multiple hardware accelerators"
+ )(test_case)
+
+
+def require_bitsandbytes(test_case):
+ """
+ Decorator marking a test that requires the bitsandbytes library. Will be skipped when the library is not installed.
+ """
+ try:
+ import bitsandbytes # noqa: F401
+
+ test_case = pytest.mark.bitsandbytes(test_case)
+ except ImportError:
+ test_case = pytest.mark.skip(reason="test requires bitsandbytes")(test_case)
+ return test_case
+
+
+def require_auto_gptq(test_case):
+ """
+ Decorator marking a test that requires auto-gptq. These tests are skipped when auto-gptq isn't installed.
+ """
+ return unittest.skipUnless(is_gptqmodel_available() or is_auto_gptq_available(), "test requires auto-gptq")(
+ test_case
+ )
+
+
+def require_gptqmodel(test_case):
+ """
+ Decorator marking a test that requires gptqmodel. These tests are skipped when gptqmodel isn't installed.
+ """
+ return unittest.skipUnless(is_gptqmodel_available(), "test requires gptqmodel")(test_case)
+
+
+def require_aqlm(test_case):
+ """
+ Decorator marking a test that requires aqlm. These tests are skipped when aqlm isn't installed.
+ """
+ return unittest.skipUnless(is_aqlm_available(), "test requires aqlm")(test_case)
+
+
+def require_hqq(test_case):
+ """
+ Decorator marking a test that requires aqlm. These tests are skipped when aqlm isn't installed.
+ """
+ return unittest.skipUnless(is_hqq_available(), "test requires hqq")(test_case)
+
+
+def require_auto_awq(test_case):
+ """
+ Decorator marking a test that requires auto-awq. These tests are skipped when auto-awq isn't installed.
+ """
+ return unittest.skipUnless(is_auto_awq_available(), "test requires auto-awq")(test_case)
+
+
+def require_eetq(test_case):
+ """
+ Decorator marking a test that requires eetq. These tests are skipped when eetq isn't installed.
+ """
+ return unittest.skipUnless(is_eetq_available(), "test requires eetq")(test_case)
+
+
+def require_optimum(test_case):
+ """
+ Decorator marking a test that requires optimum. These tests are skipped when optimum isn't installed.
+ """
+ return unittest.skipUnless(is_optimum_available(), "test requires optimum")(test_case)
+
+
+def require_torchao(test_case):
+ """
+ Decorator marking a test that requires torchao. These tests are skipped when torchao isn't installed.
+ """
+ return unittest.skipUnless(is_torchao_available(), "test requires torchao")(test_case)
+
+
+def require_deterministic_for_xpu(test_case):
+ @wraps(test_case)
+ def wrapper(*args, **kwargs):
+ if torch_device == "xpu":
+ original_state = torch.are_deterministic_algorithms_enabled()
+ try:
+ torch.use_deterministic_algorithms(True)
+ return test_case(*args, **kwargs)
+ finally:
+ torch.use_deterministic_algorithms(original_state)
+ else:
+ return test_case(*args, **kwargs)
+
+ return wrapper
+
+
+@contextmanager
+def temp_seed(seed: int):
+ """Temporarily set the random seed. This works for python numpy, pytorch."""
+
+ np_state = np.random.get_state()
+ np.random.seed(seed)
+
+ torch_state = torch.random.get_rng_state()
+ torch.random.manual_seed(seed)
+
+ if torch.cuda.is_available():
+ torch_cuda_states = torch.cuda.get_rng_state_all()
+ torch.cuda.manual_seed_all(seed)
+
+ try:
+ yield
+ finally:
+ np.random.set_state(np_state)
+
+ torch.random.set_rng_state(torch_state)
+ if torch.cuda.is_available():
+ torch.cuda.set_rng_state_all(torch_cuda_states)
+
+
+def get_state_dict(model, unwrap_compiled=True):
+ """
+ Get the state dict of a model. If the model is compiled, unwrap it first.
+ """
+ if unwrap_compiled:
+ model = getattr(model, "_orig_mod", model)
+ return model.state_dict()
+
+
+@lru_cache
+def load_dataset_english_quotes():
+ # can't use pytest fixtures for now because of unittest style tests
+ data = load_dataset("ybelkada/english_quotes_copy")
+ return data
+
+
+@lru_cache
+def load_cat_image():
+ # can't use pytest fixtures for now because of unittest style tests
+ dataset = load_dataset("huggingface/cats-image", trust_remote_code=True)
+ image = dataset["test"]["image"][0]
+ return image
+
+
+def set_init_weights_false(config_cls, kwargs):
+ # helper function that sets the config kwargs such that the model is *not* initialized as an identity transform
+ kwargs = kwargs.copy()
+
+ if issubclass(config_cls, PromptLearningConfig):
+ return kwargs
+ if config_cls in (LNTuningConfig, VBLoRAConfig):
+ return kwargs
+
+ if config_cls in (LoraConfig, AdaLoraConfig):
+ kwargs["init_lora_weights"] = False
+ elif config_cls == IA3Config:
+ kwargs["init_ia3_weights"] = False
+ else:
+ kwargs["init_weights"] = False
+ return kwargs
+
+
+@contextmanager
+def hub_online_once(model_id: str):
+ """Set env[HF_HUB_OFFLINE]=1 (and patch transformers/hugging_face_hub to think that it was always that way)
+ for model ids that were already to avoid contacting the hub twice for the same model id in the context. The global
+ variable `_HUB_MODEL_ACCESSES` tracks the number of hits per model id between `hub_online_once` calls.
+
+ The reason for doing a context manager and not patching specific methods (e.g., `from_pretrained`) is that there
+ are a lot of places (`PeftConfig.from_pretrained`, `get_peft_state_dict`, `load_adapter`, ...) that possibly
+ communicate with the hub to download files / check versions / etc.
+
+ Note that using this context manager can cause problems when used in code sections that access different resources.
+ Example:
+
+ ```
+ def test_something(model_id, config_kwargs):
+ with hub_online_once(model_id):
+ model = ...from_pretrained(model_id)
+ self.do_something_specific_with_model(model)
+ ```
+ It is assumed that `do_something_specific_with_model` is an absract method that is implement by several tests.
+ Imagine the first test simply does `model.generate([1,2,3])`. The second call from another test suite however uses
+ a tokenizer (`AutoTokenizer.from_pretrained(model_id)`) - this will fail since the first pass was online but didn't
+ use the tokenizer and we're now in offline mode and cannot fetch the tokenizer. The recommended workaround is to
+ extend the cache key (`model_id` passed to `hub_online_once` in this case) by something in case the tokenizer is
+ used, so that these tests don't share a cache pool with the tests that don't use a tokenizer.
+
+ It is best to avoid using this context manager in *yield* fixtures (normal fixtures are fine) as this is equivalent
+ to wrapping the whole test in the context manager without explicitly writing it out, leading to unexpected
+ `HF_HUB_OFFLINE` behavior in the test body.
+ """
+ global _HUB_MODEL_ACCESSES
+ override = {}
+
+ try:
+ if model_id in _HUB_MODEL_ACCESSES:
+ override = {"HF_HUB_OFFLINE": "1"}
+ _HUB_MODEL_ACCESSES[model_id] += 1
+ else:
+ if model_id not in _HUB_MODEL_ACCESSES:
+ _HUB_MODEL_ACCESSES[model_id] = 0
+ with (
+ # strictly speaking it is not necessary to set the environment variable since most code that's out there
+ # is evaluating it at import time and we'd have to reload the modules for it to take effect. It's
+ # probably still a good idea to have it if there's some dynamic code that checks it.
+ mock.patch.dict(os.environ, override),
+ mock.patch("huggingface_hub.constants.HF_HUB_OFFLINE", override.get("HF_HUB_OFFLINE", False) == "1"),
+ mock.patch("transformers.utils.hub._is_offline_mode", override.get("HF_HUB_OFFLINE", False) == "1"),
+ ):
+ yield
+ except Exception:
+ # in case of an error we have to assume that we didn't access the model properly from the hub
+ # for the first time, so the next call cannot be considered cached.
+ if _HUB_MODEL_ACCESSES.get(model_id) == 0:
+ del _HUB_MODEL_ACCESSES[model_id]
+ raise
 +
+ +
+ +
+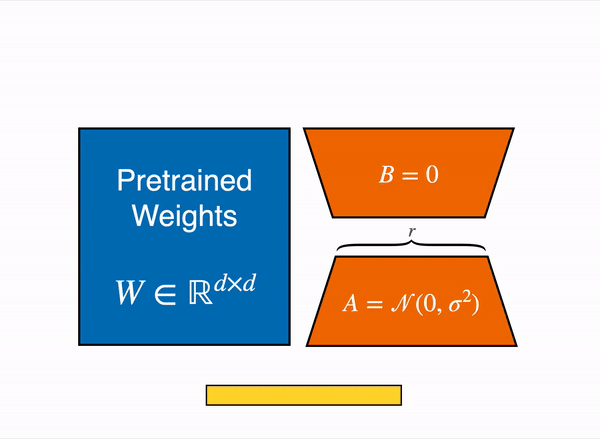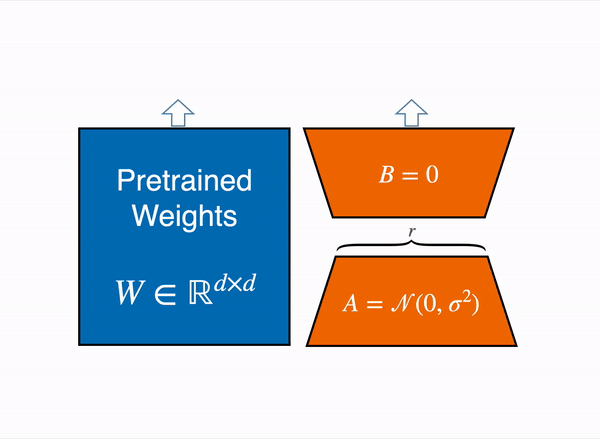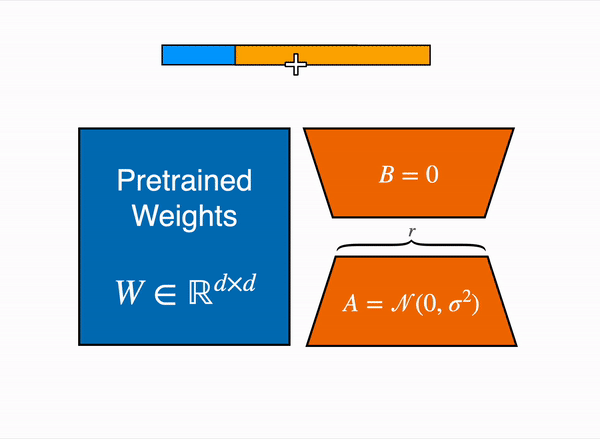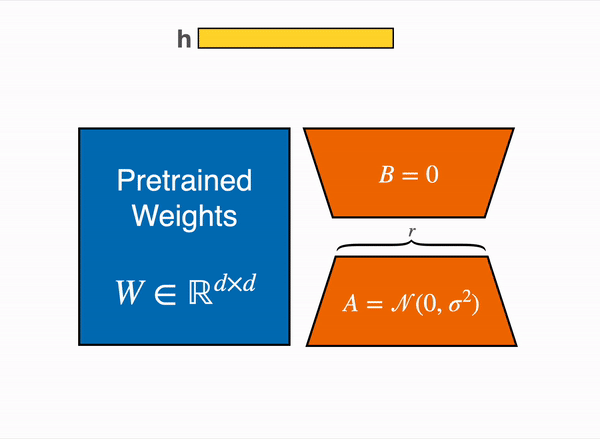 +
+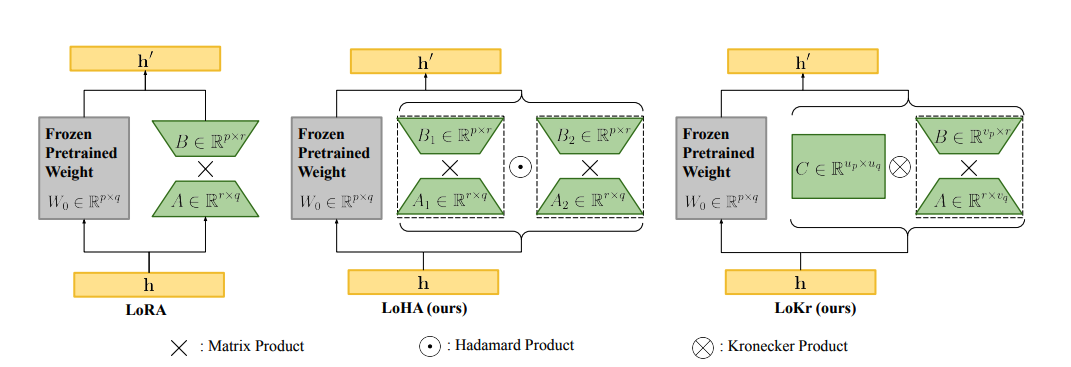 +
+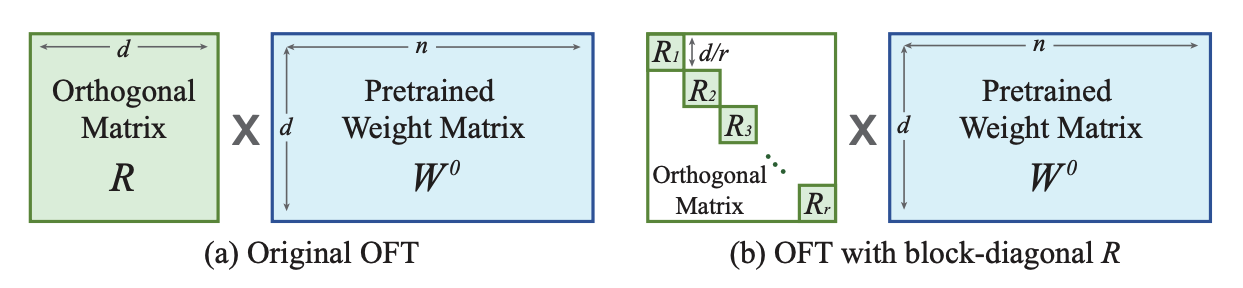 +
+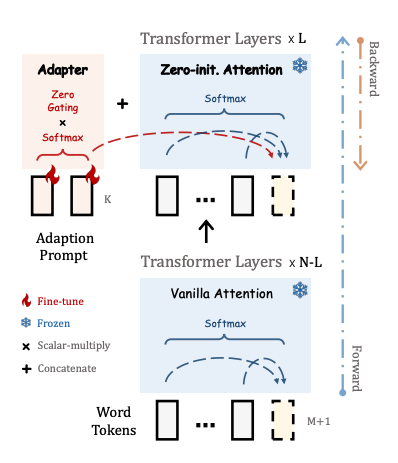 +
+ +
+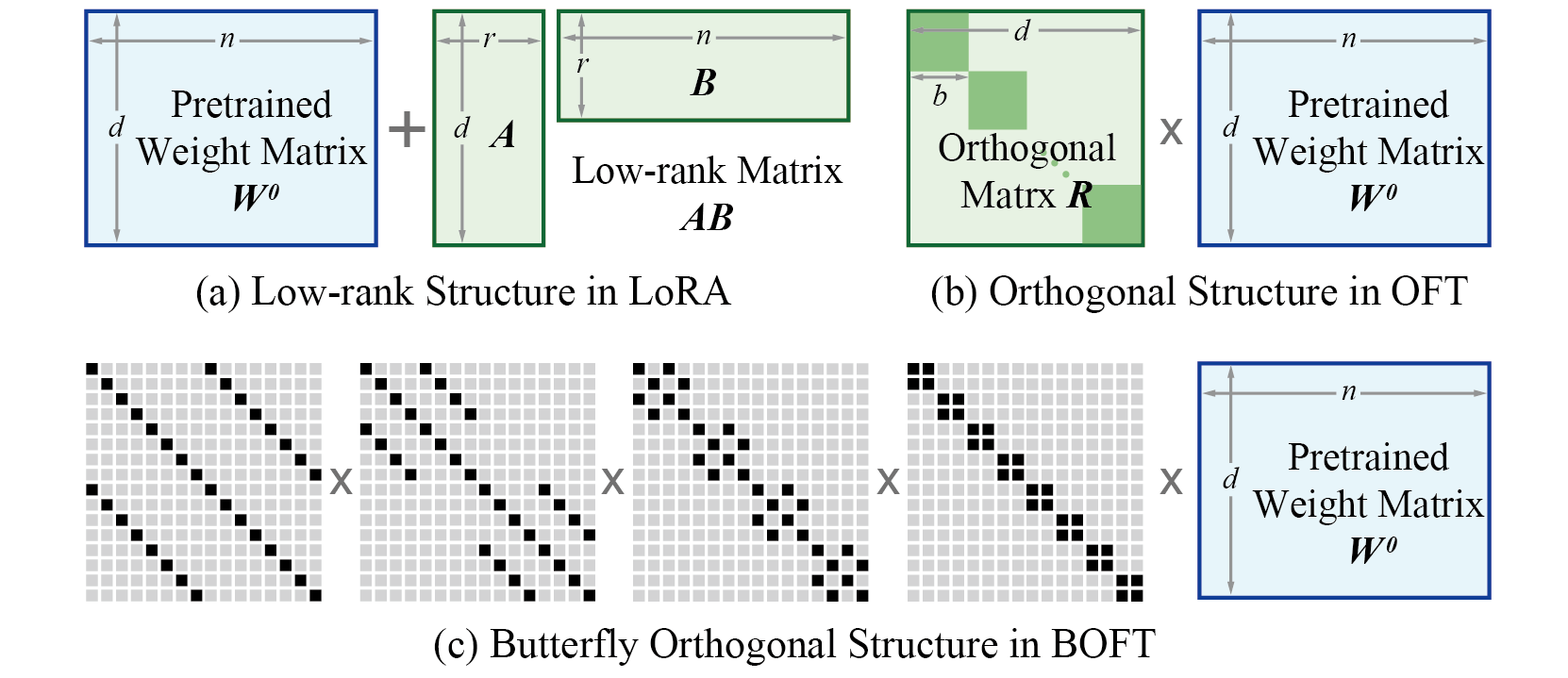 +
+ +
+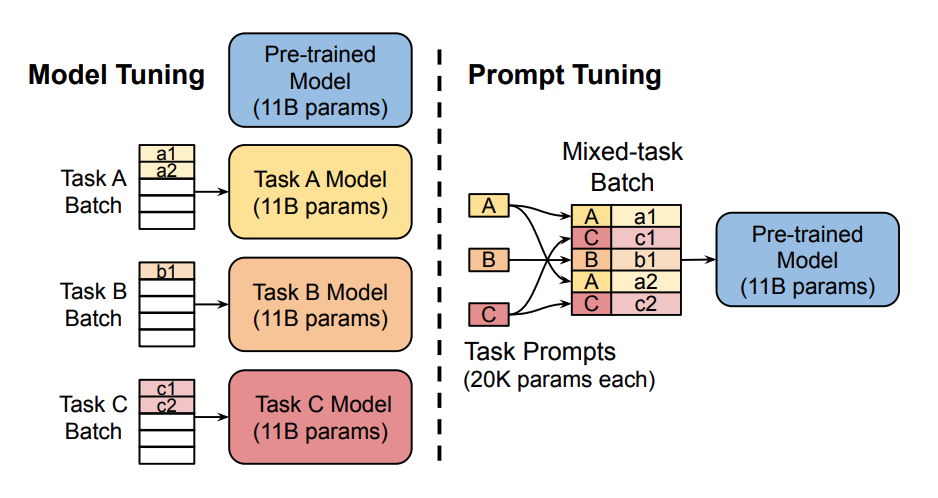 +
+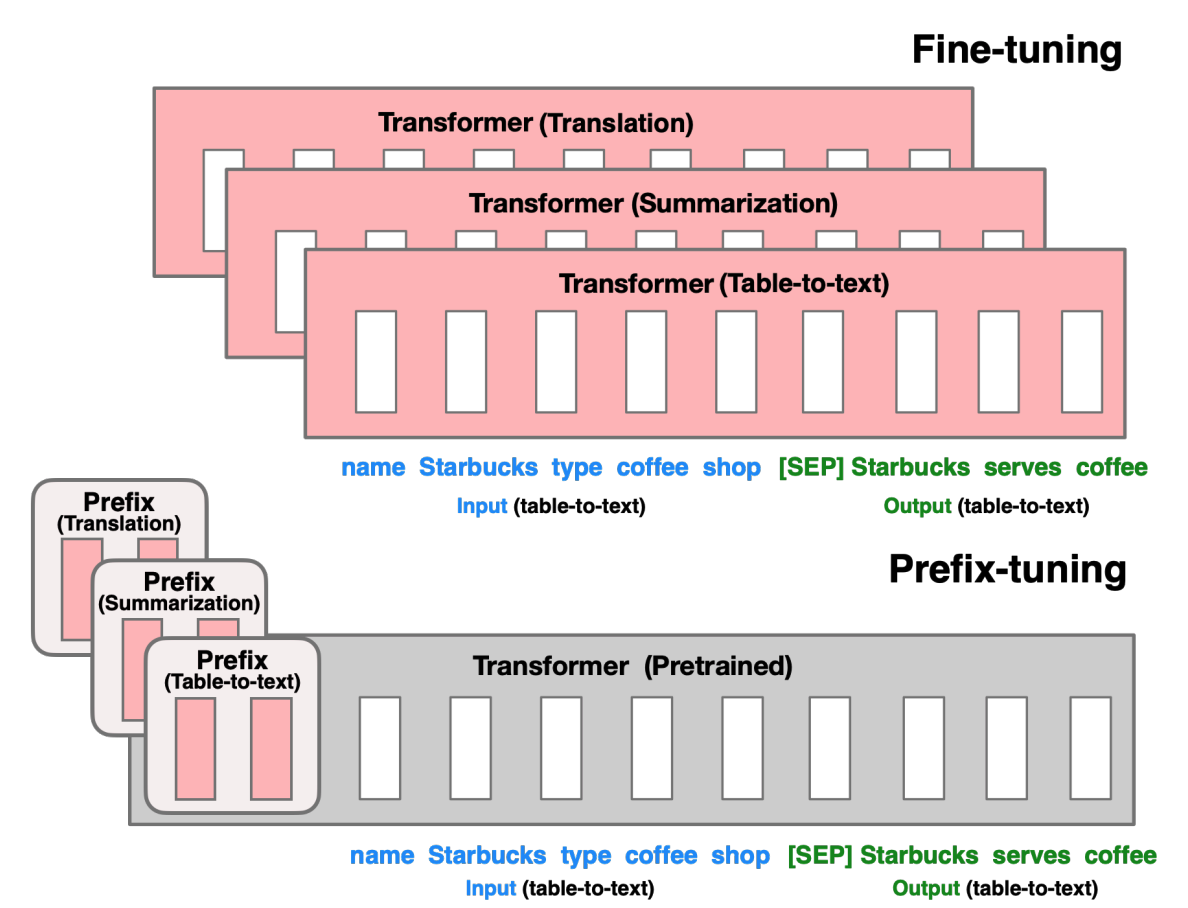 +
+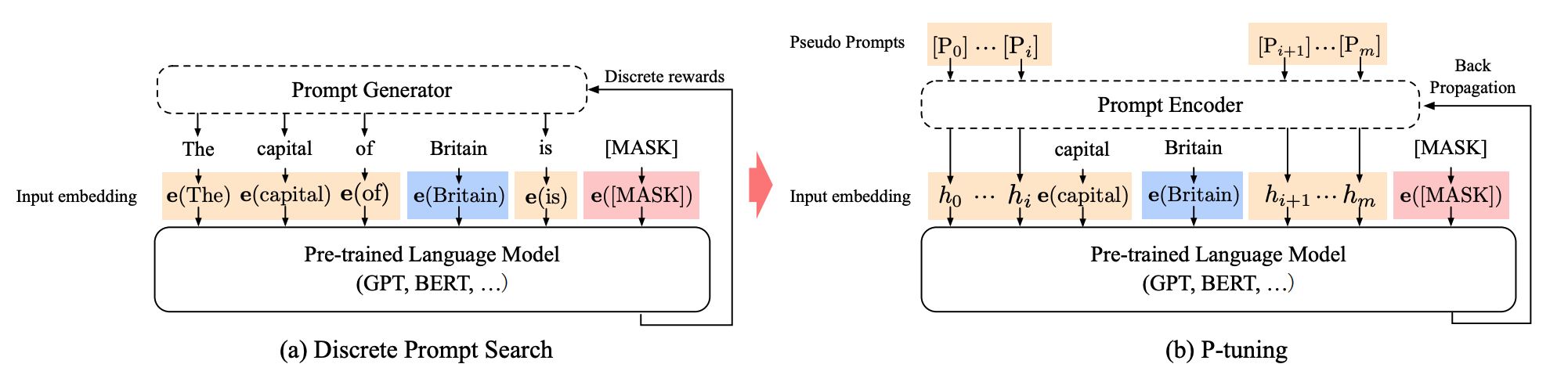 +
+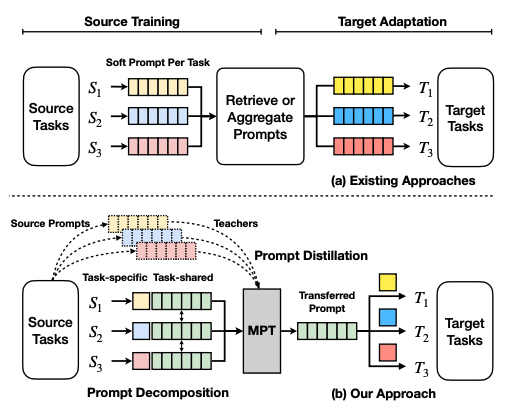 +
+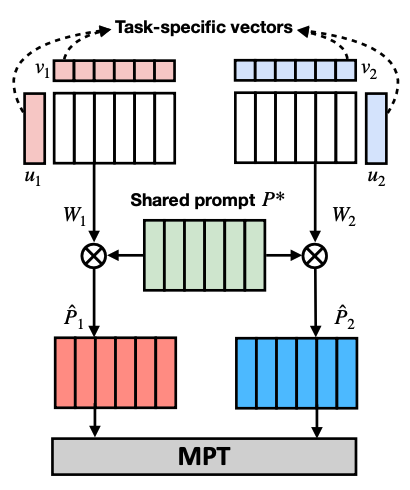 +
+ +
+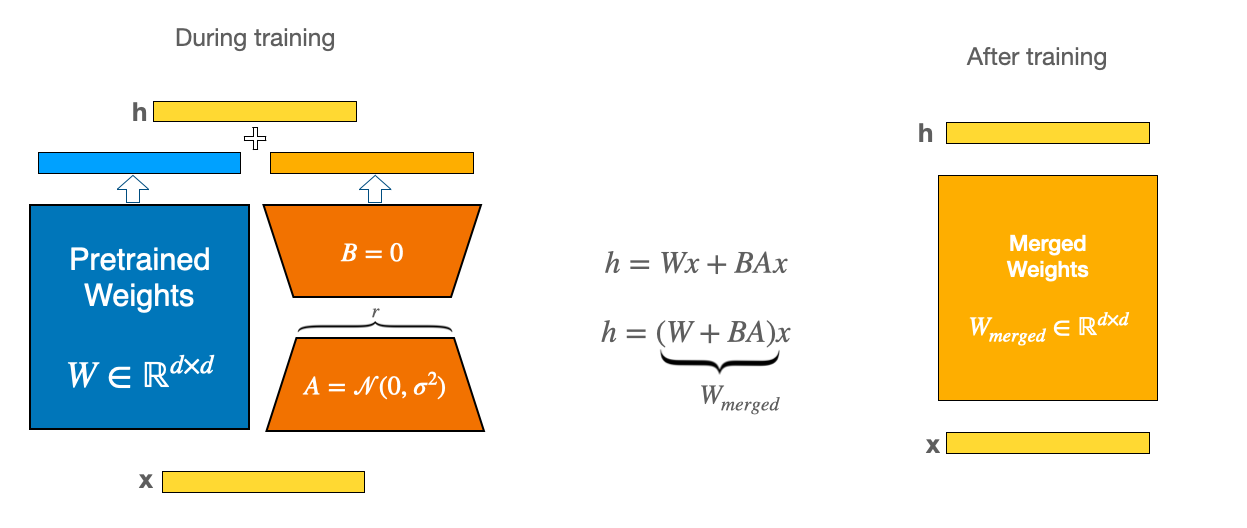 +
+ +
+  +
+ +
+  +
+ +
+ +
+ +
+Optimization in Unsloth to speed up QLoRA finetuning while reducing GPU memory usage
+
+## Multi-GPU SFT with QLoRA
+To speed up QLoRA finetuning when you have access to multiple GPUs, look at the launch command at [run_peft_multigpu.sh](https://github.com/huggingface/peft/blob/main/examples/sft/run_peft_multigpu.sh). This example to performs DDP on 8 GPUs.
+
+Note:
+1. At present, `use_reentrant` needs to be `False` when using gradient checkpointing with Multi-GPU QLoRA else it will lead to errors. However, this leads to huge GPU memory consumption.
+
+## Multi-GPU SFT with LoRA and DeepSpeed
+When you have access to multiple GPUs, it would be better to use normal LoRA with DeepSpeed/FSDP. To use LoRA with DeepSpeed, refer to the docs at [PEFT with DeepSpeed](https://huggingface.co/docs/peft/accelerate/deepspeed).
+
+
+## Multi-GPU SFT with LoRA and FSDP
+When you have access to multiple GPUs, it would be better to use normal LoRA with DeepSpeed/FSDP. To use LoRA with FSDP, refer to the docs at [PEFT with FSDP](https://huggingface.co/docs/peft/accelerate/fsdp).
+
+
+## Multi-GPU SFT with LoRA and FSDP for GPTQModel:
+As in [Multi-GPU SFT with LoRA and FSDP](https://github.com/huggingface/peft/blob/main/examples/sft/README.md#multi-gpu-sft-with-lora-and-fsdp), we also support other quantization methods like GPTQModel. You may need to install [GPTQModel](https://github.com/ModelCloud/GPTQModel) > v3.0.0 or from source. Here is the launch command for reference: [run_peft_fsdp_gptq.sh]. For the `--model_name_or_path` argument, it is important to pass a model that is already quantized with GPTQModel, like `"hugging-quants/Meta-Llama-3.1-8B-Instruct-GPTQ-INT4"`.
+
+Note: there is a bug in transformers v4.53.0 for this case, please skip this transformers version.
+
+## Tip
+
+Generally try to upgrade to the latest package versions for best results, especially when it comes to `bitsandbytes`, `accelerate`, `transformers`, `trl`, and `peft`.
diff --git a/peft/examples/sft/configs/deepspeed_config.yaml b/peft/examples/sft/configs/deepspeed_config.yaml
new file mode 100644
index 0000000000000000000000000000000000000000..56eef6e48b75727ede1d522b595b5ecde3a205a1
--- /dev/null
+++ b/peft/examples/sft/configs/deepspeed_config.yaml
@@ -0,0 +1,23 @@
+compute_environment: LOCAL_MACHINE
+debug: false
+deepspeed_config:
+ deepspeed_multinode_launcher: standard
+ gradient_accumulation_steps: 4
+ offload_optimizer_device: none
+ offload_param_device: none
+ zero3_init_flag: true
+ zero3_save_16bit_model: true
+ zero_stage: 3
+distributed_type: DEEPSPEED
+downcast_bf16: 'no'
+machine_rank: 0
+main_training_function: main
+mixed_precision: bf16
+num_machines: 1
+num_processes: 8
+rdzv_backend: static
+same_network: true
+tpu_env: []
+tpu_use_cluster: false
+tpu_use_sudo: false
+use_cpu: false
\ No newline at end of file
diff --git a/peft/examples/sft/configs/deepspeed_config_z3_qlora.yaml b/peft/examples/sft/configs/deepspeed_config_z3_qlora.yaml
new file mode 100644
index 0000000000000000000000000000000000000000..07dddcef7853b963ea64d20d39078893c4e21c33
--- /dev/null
+++ b/peft/examples/sft/configs/deepspeed_config_z3_qlora.yaml
@@ -0,0 +1,22 @@
+compute_environment: LOCAL_MACHINE
+debug: false
+deepspeed_config:
+ deepspeed_multinode_launcher: standard
+ offload_optimizer_device: none
+ offload_param_device: none
+ zero3_init_flag: true
+ zero3_save_16bit_model: true
+ zero_stage: 3
+distributed_type: DEEPSPEED
+downcast_bf16: 'no'
+machine_rank: 0
+main_training_function: main
+mixed_precision: bf16
+num_machines: 1
+num_processes: 2
+rdzv_backend: static
+same_network: true
+tpu_env: []
+tpu_use_cluster: false
+tpu_use_sudo: false
+use_cpu: false
\ No newline at end of file
diff --git a/peft/examples/sft/configs/fsdp_config.yaml b/peft/examples/sft/configs/fsdp_config.yaml
new file mode 100644
index 0000000000000000000000000000000000000000..7cccb74ca0dfa1a916b5057ceee561271c301ec5
--- /dev/null
+++ b/peft/examples/sft/configs/fsdp_config.yaml
@@ -0,0 +1,25 @@
+compute_environment: LOCAL_MACHINE
+debug: false
+distributed_type: FSDP
+downcast_bf16: 'no'
+fsdp_config:
+ fsdp_auto_wrap_policy: TRANSFORMER_BASED_WRAP
+ fsdp_backward_prefetch: BACKWARD_PRE
+ fsdp_cpu_ram_efficient_loading: true
+ fsdp_forward_prefetch: false
+ fsdp_offload_params: false
+ fsdp_sharding_strategy: FULL_SHARD
+ fsdp_state_dict_type: SHARDED_STATE_DICT
+ fsdp_sync_module_states: true
+ fsdp_use_orig_params: false
+machine_rank: 0
+main_training_function: main
+mixed_precision: bf16
+num_machines: 1
+num_processes: 8
+rdzv_backend: static
+same_network: true
+tpu_env: []
+tpu_use_cluster: false
+tpu_use_sudo: false
+use_cpu: false
\ No newline at end of file
diff --git a/peft/examples/sft/configs/fsdp_config_qlora.yaml b/peft/examples/sft/configs/fsdp_config_qlora.yaml
new file mode 100644
index 0000000000000000000000000000000000000000..f28a0f1046a735579045655dcdb9d3bf7c6ffdcc
--- /dev/null
+++ b/peft/examples/sft/configs/fsdp_config_qlora.yaml
@@ -0,0 +1,25 @@
+compute_environment: LOCAL_MACHINE
+debug: false
+distributed_type: FSDP
+downcast_bf16: 'no'
+fsdp_config:
+ fsdp_auto_wrap_policy: TRANSFORMER_BASED_WRAP
+ fsdp_backward_prefetch: BACKWARD_PRE
+ fsdp_cpu_ram_efficient_loading: true
+ fsdp_forward_prefetch: false
+ fsdp_offload_params: true
+ fsdp_sharding_strategy: FULL_SHARD
+ fsdp_state_dict_type: SHARDED_STATE_DICT
+ fsdp_sync_module_states: true
+ fsdp_use_orig_params: false
+machine_rank: 0
+main_training_function: main
+mixed_precision: 'no'
+num_machines: 1
+num_processes: 2
+rdzv_backend: static
+same_network: true
+tpu_env: []
+tpu_use_cluster: false
+tpu_use_sudo: false
+use_cpu: false
\ No newline at end of file
diff --git a/peft/examples/sft/requirements.txt b/peft/examples/sft/requirements.txt
new file mode 100644
index 0000000000000000000000000000000000000000..752b6976e62f4acff6193804c5422807bc5e8806
--- /dev/null
+++ b/peft/examples/sft/requirements.txt
@@ -0,0 +1,25 @@
+git+https://github.com/huggingface/transformers
+git+https://github.com/huggingface/accelerate
+git+https://github.com/huggingface/peft
+git+https://github.com/huggingface/trl
+git+https://github.com/huggingface/datatrove.git
+unsloth[conda]@git+https://github.com/unslothai/unsloth.git
+deepspeed
+PyGithub
+flash-attn
+huggingface-hub
+evaluate
+datasets
+bitsandbytes
+einops
+wandb
+tensorboard
+tiktoken
+pandas
+numpy
+scipy
+matplotlib
+sentencepiece
+nltk
+xformers
+hf_transfer
\ No newline at end of file
diff --git a/peft/examples/sft/requirements_colab.txt b/peft/examples/sft/requirements_colab.txt
new file mode 100644
index 0000000000000000000000000000000000000000..b8c375dc44bf85305fa53964537f4877210b10bd
--- /dev/null
+++ b/peft/examples/sft/requirements_colab.txt
@@ -0,0 +1,25 @@
+git+https://github.com/huggingface/transformers
+git+https://github.com/huggingface/accelerate
+git+https://github.com/huggingface/peft
+git+https://github.com/huggingface/trl
+unsloth[colab_ampere] @ git+https://github.com/unslothai/unsloth.git
+datasets
+deepspeed
+PyGithub
+flash-attn
+huggingface-hub
+evaluate
+bitsandbytes
+einops
+wandb
+tensorboard
+tiktoken
+pandas
+numpy
+scipy
+matplotlib
+sentencepiece
+nltk
+xformers
+git+https://github.com/huggingface/datatrove.git
+hf_transfer
\ No newline at end of file
diff --git a/peft/examples/sft/requirements_xpu.txt b/peft/examples/sft/requirements_xpu.txt
new file mode 100644
index 0000000000000000000000000000000000000000..9e5918b95180acbdc5789115ba0af71c8adf3aa5
--- /dev/null
+++ b/peft/examples/sft/requirements_xpu.txt
@@ -0,0 +1,22 @@
+git+https://github.com/huggingface/transformers
+git+https://github.com/huggingface/accelerate
+git+https://github.com/huggingface/peft
+git+https://github.com/huggingface/trl
+git+https://github.com/huggingface/datatrove.git
+deepspeed
+PyGithub
+huggingface-hub
+evaluate
+datasets
+bitsandbytes
+einops
+wandb
+tensorboard
+tiktoken
+pandas
+numpy
+scipy
+matplotlib
+sentencepiece
+nltk
+hf_transfer
\ No newline at end of file
diff --git a/peft/examples/sft/run_peft.sh b/peft/examples/sft/run_peft.sh
new file mode 100644
index 0000000000000000000000000000000000000000..8aa48648d34636eb07cd25c0abd91b943c00b49f
--- /dev/null
+++ b/peft/examples/sft/run_peft.sh
@@ -0,0 +1,41 @@
+python train.py \
+--seed 100 \
+--model_name_or_path "mistralai/Mistral-7B-v0.1" \
+--dataset_name "smangrul/ultrachat-10k-chatml" \
+--chat_template_format "chatml" \
+--add_special_tokens False \
+--append_concat_token False \
+--splits "train,test" \
+--max_seq_len 2048 \
+--num_train_epochs 1 \
+--logging_steps 5 \
+--log_level "info" \
+--logging_strategy "steps" \
+--eval_strategy "epoch" \
+--save_strategy "epoch" \
+--push_to_hub \
+--hub_private_repo True \
+--hub_strategy "every_save" \
+--bf16 True \
+--packing True \
+--learning_rate 1e-4 \
+--lr_scheduler_type "cosine" \
+--weight_decay 1e-4 \
+--warmup_ratio 0.0 \
+--max_grad_norm 1.0 \
+--output_dir "mistral-sft-lora" \
+--per_device_train_batch_size 8 \
+--per_device_eval_batch_size 8 \
+--gradient_accumulation_steps 8 \
+--gradient_checkpointing True \
+--use_reentrant True \
+--dataset_text_field "content" \
+--use_peft_lora True \
+--lora_r 8 \
+--lora_alpha 16 \
+--lora_dropout 0.1 \
+--lora_target_modules "all-linear" \
+--use_4bit_quantization True \
+--use_nested_quant True \
+--bnb_4bit_compute_dtype "bfloat16" \
+--use_flash_attn True
diff --git a/peft/examples/sft/run_peft_deepspeed.sh b/peft/examples/sft/run_peft_deepspeed.sh
new file mode 100644
index 0000000000000000000000000000000000000000..95dbf08892db530b6b5fac89c9bba5995cb6ea0b
--- /dev/null
+++ b/peft/examples/sft/run_peft_deepspeed.sh
@@ -0,0 +1,39 @@
+accelerate launch --config_file "configs/deepspeed_config.yaml" train.py \
+--seed 100 \
+--model_name_or_path "meta-llama/Llama-2-70b-hf" \
+--dataset_name "smangrul/ultrachat-10k-chatml" \
+--chat_template_format "chatml" \
+--add_special_tokens False \
+--append_concat_token False \
+--splits "train,test" \
+--max_seq_len 2048 \
+--num_train_epochs 1 \
+--logging_steps 5 \
+--log_level "info" \
+--logging_strategy "steps" \
+--eval_strategy "epoch" \
+--save_strategy "epoch" \
+--push_to_hub \
+--hub_private_repo True \
+--hub_strategy "every_save" \
+--bf16 True \
+--packing True \
+--learning_rate 1e-4 \
+--lr_scheduler_type "cosine" \
+--weight_decay 1e-4 \
+--warmup_ratio 0.0 \
+--max_grad_norm 1.0 \
+--output_dir "mistral-sft-lora-deepspeed" \
+--per_device_train_batch_size 8 \
+--per_device_eval_batch_size 8 \
+--gradient_accumulation_steps 4 \
+--gradient_checkpointing True \
+--use_reentrant False \
+--dataset_text_field "content" \
+--use_flash_attn True \
+--use_peft_lora True \
+--lora_r 8 \
+--lora_alpha 16 \
+--lora_dropout 0.1 \
+--lora_target_modules "all-linear" \
+--use_4bit_quantization False
\ No newline at end of file
diff --git a/peft/examples/sft/run_peft_fsdp.sh b/peft/examples/sft/run_peft_fsdp.sh
new file mode 100644
index 0000000000000000000000000000000000000000..63dd475f44ad062f6241ebee9c4fa9047bcace2b
--- /dev/null
+++ b/peft/examples/sft/run_peft_fsdp.sh
@@ -0,0 +1,39 @@
+accelerate launch --config_file "configs/fsdp_config.yaml" train.py \
+--seed 100 \
+--model_name_or_path "meta-llama/Llama-2-70b-hf" \
+--dataset_name "smangrul/ultrachat-10k-chatml" \
+--chat_template_format "chatml" \
+--add_special_tokens False \
+--append_concat_token False \
+--splits "train,test" \
+--max_seq_len 2048 \
+--num_train_epochs 1 \
+--logging_steps 5 \
+--log_level "info" \
+--logging_strategy "steps" \
+--eval_strategy "epoch" \
+--save_strategy "epoch" \
+--push_to_hub \
+--hub_private_repo True \
+--hub_strategy "every_save" \
+--bf16 True \
+--packing True \
+--learning_rate 1e-4 \
+--lr_scheduler_type "cosine" \
+--weight_decay 1e-4 \
+--warmup_ratio 0.0 \
+--max_grad_norm 1.0 \
+--output_dir "mistral-sft-lora-fsdp" \
+--per_device_train_batch_size 8 \
+--per_device_eval_batch_size 8 \
+--gradient_accumulation_steps 4 \
+--gradient_checkpointing True \
+--use_reentrant False \
+--dataset_text_field "content" \
+--use_flash_attn True \
+--use_peft_lora True \
+--lora_r 8 \
+--lora_alpha 16 \
+--lora_dropout 0.1 \
+--lora_target_modules "all-linear" \
+--use_4bit_quantization False
\ No newline at end of file
diff --git a/peft/examples/sft/run_peft_fsdp_gptq.sh b/peft/examples/sft/run_peft_fsdp_gptq.sh
new file mode 100644
index 0000000000000000000000000000000000000000..479a7eac834aea664f02c6b6ae6de359290ed3dd
--- /dev/null
+++ b/peft/examples/sft/run_peft_fsdp_gptq.sh
@@ -0,0 +1,36 @@
+accelerate launch --config_file "configs/fsdp_config.yaml" train.py \
+--seed 100 \
+--model_name_or_path "hugging-quants/Meta-Llama-3.1-8B-Instruct-GPTQ-INT4" \
+--dataset_name "smangrul/ultrachat-10k-chatml" \
+--chat_template_format "chatml" \
+--add_special_tokens False \
+--append_concat_token False \
+--splits "train,test" \
+--max_seq_len 2048 \
+--num_train_epochs 1 \
+--logging_steps 5 \
+--log_level "info" \
+--logging_strategy "steps" \
+--eval_strategy "epoch" \
+--save_strategy "epoch" \
+--bf16 True \
+--packing True \
+--learning_rate 1e-4 \
+--lr_scheduler_type "cosine" \
+--weight_decay 1e-4 \
+--warmup_ratio 0.0 \
+--max_grad_norm 1.0 \
+--output_dir "llama3-8B-gptq-sft-lora-fsdp" \
+--per_device_train_batch_size 8 \
+--per_device_eval_batch_size 8 \
+--gradient_accumulation_steps 4 \
+--gradient_checkpointing True \
+--use_reentrant False \
+--dataset_text_field "content" \
+--use_flash_attn True \
+--use_peft_lora True \
+--lora_r 8 \
+--lora_alpha 16 \
+--lora_dropout 0.1 \
+--lora_target_modules "q_proj,k_proj,v_proj,o_proj,up_proj,gate_proj" \
+--use_4bit_quantization False
\ No newline at end of file
diff --git a/peft/examples/sft/run_peft_multigpu.sh b/peft/examples/sft/run_peft_multigpu.sh
new file mode 100644
index 0000000000000000000000000000000000000000..dbd108d0e055c4fad1076068d15ee1560faa96ad
--- /dev/null
+++ b/peft/examples/sft/run_peft_multigpu.sh
@@ -0,0 +1,41 @@
+torchrun --nproc_per_node 8 --nnodes 1 train.py \
+--seed 100 \
+--model_name_or_path "mistralai/Mistral-7B-v0.1" \
+--dataset_name "smangrul/ultrachat-10k-chatml" \
+--chat_template_format "chatml" \
+--add_special_tokens False \
+--append_concat_token False \
+--splits "train,test" \
+--max_seq_len 2048 \
+--num_train_epochs 1 \
+--logging_steps 5 \
+--log_level "info" \
+--logging_strategy "steps" \
+--eval_strategy "epoch" \
+--save_strategy "epoch" \
+--push_to_hub \
+--hub_private_repo True \
+--hub_strategy "every_save" \
+--bf16 True \
+--packing True \
+--learning_rate 1e-4 \
+--lr_scheduler_type "cosine" \
+--weight_decay 1e-4 \
+--warmup_ratio 0.0 \
+--max_grad_norm 1.0 \
+--output_dir "mistral-sft-lora-multigpu" \
+--per_device_train_batch_size 8 \
+--per_device_eval_batch_size 8 \
+--gradient_accumulation_steps 8 \
+--gradient_checkpointing True \
+--use_reentrant False \
+--dataset_text_field "content" \
+--use_peft_lora True \
+--lora_r 8 \
+--lora_alpha 16 \
+--lora_dropout 0.1 \
+--lora_target_modules "all-linear" \
+--use_4bit_quantization True \
+--use_nested_quant True \
+--bnb_4bit_compute_dtype "bfloat16" \
+--use_flash_attn True
diff --git a/peft/examples/sft/run_peft_qlora_deepspeed_stage3.sh b/peft/examples/sft/run_peft_qlora_deepspeed_stage3.sh
new file mode 100644
index 0000000000000000000000000000000000000000..4bbc1bbcc4bd06351add38d7d5142da02787d5d4
--- /dev/null
+++ b/peft/examples/sft/run_peft_qlora_deepspeed_stage3.sh
@@ -0,0 +1,42 @@
+accelerate launch --config_file "configs/deepspeed_config_z3_qlora.yaml" train.py \
+--seed 100 \
+--model_name_or_path "meta-llama/Llama-2-70b-hf" \
+--dataset_name "smangrul/ultrachat-10k-chatml" \
+--chat_template_format "chatml" \
+--add_special_tokens False \
+--append_concat_token False \
+--splits "train,test" \
+--max_seq_len 2048 \
+--num_train_epochs 1 \
+--logging_steps 5 \
+--log_level "info" \
+--logging_strategy "steps" \
+--eval_strategy "epoch" \
+--save_strategy "epoch" \
+--push_to_hub \
+--hub_private_repo True \
+--hub_strategy "every_save" \
+--bf16 True \
+--packing True \
+--learning_rate 1e-4 \
+--lr_scheduler_type "cosine" \
+--weight_decay 1e-4 \
+--warmup_ratio 0.0 \
+--max_grad_norm 1.0 \
+--output_dir "llama-sft-qlora-dsz3" \
+--per_device_train_batch_size 2 \
+--per_device_eval_batch_size 2 \
+--gradient_accumulation_steps 2 \
+--gradient_checkpointing True \
+--use_reentrant True \
+--dataset_text_field "content" \
+--use_flash_attn True \
+--use_peft_lora True \
+--lora_r 8 \
+--lora_alpha 16 \
+--lora_dropout 0.1 \
+--lora_target_modules "all-linear" \
+--use_4bit_quantization True \
+--use_nested_quant True \
+--bnb_4bit_compute_dtype "bfloat16" \
+--bnb_4bit_quant_storage_dtype "bfloat16"
\ No newline at end of file
diff --git a/peft/examples/sft/run_peft_qlora_fsdp.sh b/peft/examples/sft/run_peft_qlora_fsdp.sh
new file mode 100644
index 0000000000000000000000000000000000000000..4ed3218c8277fd0ab8f66c2b3ea3f2fe41e7fe04
--- /dev/null
+++ b/peft/examples/sft/run_peft_qlora_fsdp.sh
@@ -0,0 +1,42 @@
+accelerate launch --config_file "configs/fsdp_config_qlora.yaml" train.py \
+--seed 100 \
+--model_name_or_path "meta-llama/Llama-2-70b-hf" \
+--dataset_name "smangrul/ultrachat-10k-chatml" \
+--chat_template_format "chatml" \
+--add_special_tokens False \
+--append_concat_token False \
+--splits "train,test" \
+--max_seq_len 2048 \
+--num_train_epochs 1 \
+--logging_steps 5 \
+--log_level "info" \
+--logging_strategy "steps" \
+--eval_strategy "epoch" \
+--save_strategy "epoch" \
+--push_to_hub \
+--hub_private_repo True \
+--hub_strategy "every_save" \
+--bf16 True \
+--packing True \
+--learning_rate 1e-4 \
+--lr_scheduler_type "cosine" \
+--weight_decay 1e-4 \
+--warmup_ratio 0.0 \
+--max_grad_norm 1.0 \
+--output_dir "llama-sft-qlora-fsdp" \
+--per_device_train_batch_size 2 \
+--per_device_eval_batch_size 2 \
+--gradient_accumulation_steps 2 \
+--gradient_checkpointing True \
+--use_reentrant True \
+--dataset_text_field "content" \
+--use_flash_attn True \
+--use_peft_lora True \
+--lora_r 8 \
+--lora_alpha 16 \
+--lora_dropout 0.1 \
+--lora_target_modules "all-linear" \
+--use_4bit_quantization True \
+--use_nested_quant True \
+--bnb_4bit_compute_dtype "bfloat16" \
+--bnb_4bit_quant_storage_dtype "bfloat16"
\ No newline at end of file
diff --git a/peft/examples/sft/run_unsloth_peft.sh b/peft/examples/sft/run_unsloth_peft.sh
new file mode 100644
index 0000000000000000000000000000000000000000..97a4a6b520e1112a85cd25387f3cb46deb465f9e
--- /dev/null
+++ b/peft/examples/sft/run_unsloth_peft.sh
@@ -0,0 +1,42 @@
+python train.py \
+--seed 100 \
+--model_name_or_path "mistralai/Mistral-7B-v0.1" \
+--dataset_name "smangrul/ultrachat-10k-chatml" \
+--chat_template_format "chatml" \
+--add_special_tokens False \
+--append_concat_token False \
+--splits "train,test" \
+--max_seq_len 2048 \
+--num_train_epochs 1 \
+--logging_steps 5 \
+--log_level "info" \
+--logging_strategy "steps" \
+--eval_strategy "epoch" \
+--save_strategy "epoch" \
+--push_to_hub \
+--hub_private_repo True \
+--hub_strategy "every_save" \
+--bf16 True \
+--packing True \
+--learning_rate 1e-4 \
+--lr_scheduler_type "cosine" \
+--weight_decay 1e-4 \
+--warmup_ratio 0.0 \
+--max_grad_norm 1.0 \
+--output_dir "mistral-sft-lora-unsloth" \
+--per_device_train_batch_size 8 \
+--per_device_eval_batch_size 8 \
+--gradient_accumulation_steps 8 \
+--gradient_checkpointing True \
+--use_reentrant True \
+--dataset_text_field "content" \
+--use_peft_lora True \
+--use_unsloth True \
+--lora_r 8 \
+--lora_alpha 16 \
+--lora_dropout 0.1 \
+--lora_target_modules "q_proj,k_proj,v_proj,o_proj,down_proj,up_proj,gate_proj" \
+--use_4bit_quantization True \
+--use_nested_quant True \
+--bnb_4bit_compute_dtype "bfloat16" \
+--use_flash_attn True
diff --git a/peft/examples/sft/train.py b/peft/examples/sft/train.py
new file mode 100644
index 0000000000000000000000000000000000000000..5a34f69357b0505e84b16436e894a2ab924ce1a7
--- /dev/null
+++ b/peft/examples/sft/train.py
@@ -0,0 +1,159 @@
+import os
+import sys
+from dataclasses import dataclass, field
+from typing import Optional
+
+from transformers import HfArgumentParser, set_seed
+from trl import SFTConfig, SFTTrainer
+from utils import create_and_prepare_model, create_datasets
+
+
+# Define and parse arguments.
+@dataclass
+class ModelArguments:
+ """
+ Arguments pertaining to which model/config/tokenizer we are going to fine-tune from.
+ """
+
+ model_name_or_path: str = field(
+ metadata={"help": "Path to pretrained model or model identifier from huggingface.co/models"}
+ )
+ max_seq_length: Optional[int] = field(
+ default=512,
+ metadata={"help": "The maximum total input sequence length after tokenization."},
+ )
+ chat_template_format: Optional[str] = field(
+ default="none",
+ metadata={
+ "help": "chatml|zephyr|none. Pass `none` if the dataset is already formatted with the chat template."
+ },
+ )
+ lora_alpha: Optional[int] = field(default=16)
+ lora_dropout: Optional[float] = field(default=0.1)
+ lora_r: Optional[int] = field(default=64)
+ lora_target_modules: Optional[str] = field(
+ default="q_proj,k_proj,v_proj,o_proj,down_proj,up_proj,gate_proj",
+ metadata={"help": "comma separated list of target modules to apply LoRA layers to"},
+ )
+ use_nested_quant: Optional[bool] = field(
+ default=False,
+ metadata={"help": "Activate nested quantization for 4bit base models"},
+ )
+ bnb_4bit_compute_dtype: Optional[str] = field(
+ default="float16",
+ metadata={"help": "Compute dtype for 4bit base models"},
+ )
+ bnb_4bit_quant_storage_dtype: Optional[str] = field(
+ default="uint8",
+ metadata={"help": "Quantization storage dtype for 4bit base models"},
+ )
+ bnb_4bit_quant_type: Optional[str] = field(
+ default="nf4",
+ metadata={"help": "Quantization type fp4 or nf4"},
+ )
+ use_flash_attn: Optional[bool] = field(
+ default=False,
+ metadata={"help": "Enables Flash attention for training."},
+ )
+ use_peft_lora: Optional[bool] = field(
+ default=False,
+ metadata={"help": "Enables PEFT LoRA for training."},
+ )
+ use_8bit_quantization: Optional[bool] = field(
+ default=False,
+ metadata={"help": "Enables loading model in 8bit."},
+ )
+ use_4bit_quantization: Optional[bool] = field(
+ default=False,
+ metadata={"help": "Enables loading model in 4bit."},
+ )
+ use_reentrant: Optional[bool] = field(
+ default=False,
+ metadata={"help": "Gradient Checkpointing param. Refer the related docs"},
+ )
+ use_unsloth: Optional[bool] = field(
+ default=False,
+ metadata={"help": "Enables UnSloth for training."},
+ )
+
+
+@dataclass
+class DataTrainingArguments:
+ dataset_name: Optional[str] = field(
+ default="timdettmers/openassistant-guanaco",
+ metadata={"help": "The preference dataset to use."},
+ )
+ append_concat_token: Optional[bool] = field(
+ default=False,
+ metadata={"help": "If True, appends `eos_token_id` at the end of each sample being packed."},
+ )
+ add_special_tokens: Optional[bool] = field(
+ default=False,
+ metadata={"help": "If True, tokenizers adds special tokens to each sample being packed."},
+ )
+ splits: Optional[str] = field(
+ default="train,test",
+ metadata={"help": "Comma separate list of the splits to use from the dataset."},
+ )
+
+
+def main(model_args, data_args, training_args):
+ # Set seed for reproducibility
+ set_seed(training_args.seed)
+
+ # model
+ model, peft_config, tokenizer = create_and_prepare_model(model_args, data_args, training_args)
+
+ # gradient ckpt
+ model.config.use_cache = not training_args.gradient_checkpointing
+ training_args.gradient_checkpointing = training_args.gradient_checkpointing and not model_args.use_unsloth
+ if training_args.gradient_checkpointing:
+ training_args.gradient_checkpointing_kwargs = {"use_reentrant": model_args.use_reentrant}
+
+ training_args.dataset_kwargs = {
+ "append_concat_token": data_args.append_concat_token,
+ "add_special_tokens": data_args.add_special_tokens,
+ }
+
+ # datasets
+ train_dataset, eval_dataset = create_datasets(
+ tokenizer,
+ data_args,
+ training_args,
+ apply_chat_template=model_args.chat_template_format != "none",
+ )
+
+ # trainer
+ trainer = SFTTrainer(
+ model=model,
+ processing_class=tokenizer,
+ args=training_args,
+ train_dataset=train_dataset,
+ eval_dataset=eval_dataset,
+ peft_config=peft_config,
+ )
+ trainer.accelerator.print(f"{trainer.model}")
+ if hasattr(trainer.model, "print_trainable_parameters"):
+ trainer.model.print_trainable_parameters()
+
+ # train
+ checkpoint = None
+ if training_args.resume_from_checkpoint is not None:
+ checkpoint = training_args.resume_from_checkpoint
+ trainer.train(resume_from_checkpoint=checkpoint)
+
+ # saving final model
+ if trainer.is_fsdp_enabled:
+ trainer.accelerator.state.fsdp_plugin.set_state_dict_type("FULL_STATE_DICT")
+ trainer.save_model()
+
+
+if __name__ == "__main__":
+ parser = HfArgumentParser((ModelArguments, DataTrainingArguments, SFTConfig))
+ if len(sys.argv) == 2 and sys.argv[1].endswith(".json"):
+ # If we pass only one argument to the script and it's the path to a json file,
+ # let's parse it to get our arguments.
+ model_args, data_args, training_args = parser.parse_json_file(json_file=os.path.abspath(sys.argv[1]))
+ else:
+ model_args, data_args, training_args = parser.parse_args_into_dataclasses()
+ main(model_args, data_args, training_args)
diff --git a/peft/examples/sft/utils.py b/peft/examples/sft/utils.py
new file mode 100644
index 0000000000000000000000000000000000000000..ea0d36bb647628561a3d447c0fdd9360caa03ba9
--- /dev/null
+++ b/peft/examples/sft/utils.py
@@ -0,0 +1,219 @@
+import os
+from enum import Enum
+
+import packaging.version
+import torch
+import transformers
+from datasets import DatasetDict, load_dataset, load_from_disk
+from datasets.builder import DatasetGenerationError
+from transformers import (
+ AutoModelForCausalLM,
+ AutoTokenizer,
+ BitsAndBytesConfig,
+)
+
+from peft import LoraConfig
+
+
+DEFAULT_CHATML_CHAT_TEMPLATE = "{% for message in messages %}\n{{'<|im_start|>' + message['role'] + '\n' + message['content'] + '<|im_end|>' + '\n'}}{% if loop.last and add_generation_prompt %}{{'<|im_start|>assistant\n' }}{% endif %}{% endfor %}"
+DEFAULT_ZEPHYR_CHAT_TEMPLATE = "{% for message in messages %}\n{% if message['role'] == 'user' %}\n{{ '<|user|>\n' + message['content'] + eos_token }}\n{% elif message['role'] == 'system' %}\n{{ '<|system|>\n' + message['content'] + eos_token }}\n{% elif message['role'] == 'assistant' %}\n{{ '<|assistant|>\n' + message['content'] + eos_token }}\n{% endif %}\n{% if loop.last and add_generation_prompt %}\n{{ '<|assistant|>' }}\n{% endif %}\n{% endfor %}"
+
+
+class ZephyrSpecialTokens(str, Enum):
+ user = "<|user|>"
+ assistant = "<|assistant|>"
+ system = "<|system|>"
+ eos_token = ""
+ bos_token = "
+
+Optimization in Unsloth to speed up QLoRA finetuning while reducing GPU memory usage
+
+## Multi-GPU SFT with QLoRA
+To speed up QLoRA finetuning when you have access to multiple GPUs, look at the launch command at [run_peft_multigpu.sh](https://github.com/huggingface/peft/blob/main/examples/sft/run_peft_multigpu.sh). This example to performs DDP on 8 GPUs.
+
+Note:
+1. At present, `use_reentrant` needs to be `False` when using gradient checkpointing with Multi-GPU QLoRA else it will lead to errors. However, this leads to huge GPU memory consumption.
+
+## Multi-GPU SFT with LoRA and DeepSpeed
+When you have access to multiple GPUs, it would be better to use normal LoRA with DeepSpeed/FSDP. To use LoRA with DeepSpeed, refer to the docs at [PEFT with DeepSpeed](https://huggingface.co/docs/peft/accelerate/deepspeed).
+
+
+## Multi-GPU SFT with LoRA and FSDP
+When you have access to multiple GPUs, it would be better to use normal LoRA with DeepSpeed/FSDP. To use LoRA with FSDP, refer to the docs at [PEFT with FSDP](https://huggingface.co/docs/peft/accelerate/fsdp).
+
+
+## Multi-GPU SFT with LoRA and FSDP for GPTQModel:
+As in [Multi-GPU SFT with LoRA and FSDP](https://github.com/huggingface/peft/blob/main/examples/sft/README.md#multi-gpu-sft-with-lora-and-fsdp), we also support other quantization methods like GPTQModel. You may need to install [GPTQModel](https://github.com/ModelCloud/GPTQModel) > v3.0.0 or from source. Here is the launch command for reference: [run_peft_fsdp_gptq.sh]. For the `--model_name_or_path` argument, it is important to pass a model that is already quantized with GPTQModel, like `"hugging-quants/Meta-Llama-3.1-8B-Instruct-GPTQ-INT4"`.
+
+Note: there is a bug in transformers v4.53.0 for this case, please skip this transformers version.
+
+## Tip
+
+Generally try to upgrade to the latest package versions for best results, especially when it comes to `bitsandbytes`, `accelerate`, `transformers`, `trl`, and `peft`.
diff --git a/peft/examples/sft/configs/deepspeed_config.yaml b/peft/examples/sft/configs/deepspeed_config.yaml
new file mode 100644
index 0000000000000000000000000000000000000000..56eef6e48b75727ede1d522b595b5ecde3a205a1
--- /dev/null
+++ b/peft/examples/sft/configs/deepspeed_config.yaml
@@ -0,0 +1,23 @@
+compute_environment: LOCAL_MACHINE
+debug: false
+deepspeed_config:
+ deepspeed_multinode_launcher: standard
+ gradient_accumulation_steps: 4
+ offload_optimizer_device: none
+ offload_param_device: none
+ zero3_init_flag: true
+ zero3_save_16bit_model: true
+ zero_stage: 3
+distributed_type: DEEPSPEED
+downcast_bf16: 'no'
+machine_rank: 0
+main_training_function: main
+mixed_precision: bf16
+num_machines: 1
+num_processes: 8
+rdzv_backend: static
+same_network: true
+tpu_env: []
+tpu_use_cluster: false
+tpu_use_sudo: false
+use_cpu: false
\ No newline at end of file
diff --git a/peft/examples/sft/configs/deepspeed_config_z3_qlora.yaml b/peft/examples/sft/configs/deepspeed_config_z3_qlora.yaml
new file mode 100644
index 0000000000000000000000000000000000000000..07dddcef7853b963ea64d20d39078893c4e21c33
--- /dev/null
+++ b/peft/examples/sft/configs/deepspeed_config_z3_qlora.yaml
@@ -0,0 +1,22 @@
+compute_environment: LOCAL_MACHINE
+debug: false
+deepspeed_config:
+ deepspeed_multinode_launcher: standard
+ offload_optimizer_device: none
+ offload_param_device: none
+ zero3_init_flag: true
+ zero3_save_16bit_model: true
+ zero_stage: 3
+distributed_type: DEEPSPEED
+downcast_bf16: 'no'
+machine_rank: 0
+main_training_function: main
+mixed_precision: bf16
+num_machines: 1
+num_processes: 2
+rdzv_backend: static
+same_network: true
+tpu_env: []
+tpu_use_cluster: false
+tpu_use_sudo: false
+use_cpu: false
\ No newline at end of file
diff --git a/peft/examples/sft/configs/fsdp_config.yaml b/peft/examples/sft/configs/fsdp_config.yaml
new file mode 100644
index 0000000000000000000000000000000000000000..7cccb74ca0dfa1a916b5057ceee561271c301ec5
--- /dev/null
+++ b/peft/examples/sft/configs/fsdp_config.yaml
@@ -0,0 +1,25 @@
+compute_environment: LOCAL_MACHINE
+debug: false
+distributed_type: FSDP
+downcast_bf16: 'no'
+fsdp_config:
+ fsdp_auto_wrap_policy: TRANSFORMER_BASED_WRAP
+ fsdp_backward_prefetch: BACKWARD_PRE
+ fsdp_cpu_ram_efficient_loading: true
+ fsdp_forward_prefetch: false
+ fsdp_offload_params: false
+ fsdp_sharding_strategy: FULL_SHARD
+ fsdp_state_dict_type: SHARDED_STATE_DICT
+ fsdp_sync_module_states: true
+ fsdp_use_orig_params: false
+machine_rank: 0
+main_training_function: main
+mixed_precision: bf16
+num_machines: 1
+num_processes: 8
+rdzv_backend: static
+same_network: true
+tpu_env: []
+tpu_use_cluster: false
+tpu_use_sudo: false
+use_cpu: false
\ No newline at end of file
diff --git a/peft/examples/sft/configs/fsdp_config_qlora.yaml b/peft/examples/sft/configs/fsdp_config_qlora.yaml
new file mode 100644
index 0000000000000000000000000000000000000000..f28a0f1046a735579045655dcdb9d3bf7c6ffdcc
--- /dev/null
+++ b/peft/examples/sft/configs/fsdp_config_qlora.yaml
@@ -0,0 +1,25 @@
+compute_environment: LOCAL_MACHINE
+debug: false
+distributed_type: FSDP
+downcast_bf16: 'no'
+fsdp_config:
+ fsdp_auto_wrap_policy: TRANSFORMER_BASED_WRAP
+ fsdp_backward_prefetch: BACKWARD_PRE
+ fsdp_cpu_ram_efficient_loading: true
+ fsdp_forward_prefetch: false
+ fsdp_offload_params: true
+ fsdp_sharding_strategy: FULL_SHARD
+ fsdp_state_dict_type: SHARDED_STATE_DICT
+ fsdp_sync_module_states: true
+ fsdp_use_orig_params: false
+machine_rank: 0
+main_training_function: main
+mixed_precision: 'no'
+num_machines: 1
+num_processes: 2
+rdzv_backend: static
+same_network: true
+tpu_env: []
+tpu_use_cluster: false
+tpu_use_sudo: false
+use_cpu: false
\ No newline at end of file
diff --git a/peft/examples/sft/requirements.txt b/peft/examples/sft/requirements.txt
new file mode 100644
index 0000000000000000000000000000000000000000..752b6976e62f4acff6193804c5422807bc5e8806
--- /dev/null
+++ b/peft/examples/sft/requirements.txt
@@ -0,0 +1,25 @@
+git+https://github.com/huggingface/transformers
+git+https://github.com/huggingface/accelerate
+git+https://github.com/huggingface/peft
+git+https://github.com/huggingface/trl
+git+https://github.com/huggingface/datatrove.git
+unsloth[conda]@git+https://github.com/unslothai/unsloth.git
+deepspeed
+PyGithub
+flash-attn
+huggingface-hub
+evaluate
+datasets
+bitsandbytes
+einops
+wandb
+tensorboard
+tiktoken
+pandas
+numpy
+scipy
+matplotlib
+sentencepiece
+nltk
+xformers
+hf_transfer
\ No newline at end of file
diff --git a/peft/examples/sft/requirements_colab.txt b/peft/examples/sft/requirements_colab.txt
new file mode 100644
index 0000000000000000000000000000000000000000..b8c375dc44bf85305fa53964537f4877210b10bd
--- /dev/null
+++ b/peft/examples/sft/requirements_colab.txt
@@ -0,0 +1,25 @@
+git+https://github.com/huggingface/transformers
+git+https://github.com/huggingface/accelerate
+git+https://github.com/huggingface/peft
+git+https://github.com/huggingface/trl
+unsloth[colab_ampere] @ git+https://github.com/unslothai/unsloth.git
+datasets
+deepspeed
+PyGithub
+flash-attn
+huggingface-hub
+evaluate
+bitsandbytes
+einops
+wandb
+tensorboard
+tiktoken
+pandas
+numpy
+scipy
+matplotlib
+sentencepiece
+nltk
+xformers
+git+https://github.com/huggingface/datatrove.git
+hf_transfer
\ No newline at end of file
diff --git a/peft/examples/sft/requirements_xpu.txt b/peft/examples/sft/requirements_xpu.txt
new file mode 100644
index 0000000000000000000000000000000000000000..9e5918b95180acbdc5789115ba0af71c8adf3aa5
--- /dev/null
+++ b/peft/examples/sft/requirements_xpu.txt
@@ -0,0 +1,22 @@
+git+https://github.com/huggingface/transformers
+git+https://github.com/huggingface/accelerate
+git+https://github.com/huggingface/peft
+git+https://github.com/huggingface/trl
+git+https://github.com/huggingface/datatrove.git
+deepspeed
+PyGithub
+huggingface-hub
+evaluate
+datasets
+bitsandbytes
+einops
+wandb
+tensorboard
+tiktoken
+pandas
+numpy
+scipy
+matplotlib
+sentencepiece
+nltk
+hf_transfer
\ No newline at end of file
diff --git a/peft/examples/sft/run_peft.sh b/peft/examples/sft/run_peft.sh
new file mode 100644
index 0000000000000000000000000000000000000000..8aa48648d34636eb07cd25c0abd91b943c00b49f
--- /dev/null
+++ b/peft/examples/sft/run_peft.sh
@@ -0,0 +1,41 @@
+python train.py \
+--seed 100 \
+--model_name_or_path "mistralai/Mistral-7B-v0.1" \
+--dataset_name "smangrul/ultrachat-10k-chatml" \
+--chat_template_format "chatml" \
+--add_special_tokens False \
+--append_concat_token False \
+--splits "train,test" \
+--max_seq_len 2048 \
+--num_train_epochs 1 \
+--logging_steps 5 \
+--log_level "info" \
+--logging_strategy "steps" \
+--eval_strategy "epoch" \
+--save_strategy "epoch" \
+--push_to_hub \
+--hub_private_repo True \
+--hub_strategy "every_save" \
+--bf16 True \
+--packing True \
+--learning_rate 1e-4 \
+--lr_scheduler_type "cosine" \
+--weight_decay 1e-4 \
+--warmup_ratio 0.0 \
+--max_grad_norm 1.0 \
+--output_dir "mistral-sft-lora" \
+--per_device_train_batch_size 8 \
+--per_device_eval_batch_size 8 \
+--gradient_accumulation_steps 8 \
+--gradient_checkpointing True \
+--use_reentrant True \
+--dataset_text_field "content" \
+--use_peft_lora True \
+--lora_r 8 \
+--lora_alpha 16 \
+--lora_dropout 0.1 \
+--lora_target_modules "all-linear" \
+--use_4bit_quantization True \
+--use_nested_quant True \
+--bnb_4bit_compute_dtype "bfloat16" \
+--use_flash_attn True
diff --git a/peft/examples/sft/run_peft_deepspeed.sh b/peft/examples/sft/run_peft_deepspeed.sh
new file mode 100644
index 0000000000000000000000000000000000000000..95dbf08892db530b6b5fac89c9bba5995cb6ea0b
--- /dev/null
+++ b/peft/examples/sft/run_peft_deepspeed.sh
@@ -0,0 +1,39 @@
+accelerate launch --config_file "configs/deepspeed_config.yaml" train.py \
+--seed 100 \
+--model_name_or_path "meta-llama/Llama-2-70b-hf" \
+--dataset_name "smangrul/ultrachat-10k-chatml" \
+--chat_template_format "chatml" \
+--add_special_tokens False \
+--append_concat_token False \
+--splits "train,test" \
+--max_seq_len 2048 \
+--num_train_epochs 1 \
+--logging_steps 5 \
+--log_level "info" \
+--logging_strategy "steps" \
+--eval_strategy "epoch" \
+--save_strategy "epoch" \
+--push_to_hub \
+--hub_private_repo True \
+--hub_strategy "every_save" \
+--bf16 True \
+--packing True \
+--learning_rate 1e-4 \
+--lr_scheduler_type "cosine" \
+--weight_decay 1e-4 \
+--warmup_ratio 0.0 \
+--max_grad_norm 1.0 \
+--output_dir "mistral-sft-lora-deepspeed" \
+--per_device_train_batch_size 8 \
+--per_device_eval_batch_size 8 \
+--gradient_accumulation_steps 4 \
+--gradient_checkpointing True \
+--use_reentrant False \
+--dataset_text_field "content" \
+--use_flash_attn True \
+--use_peft_lora True \
+--lora_r 8 \
+--lora_alpha 16 \
+--lora_dropout 0.1 \
+--lora_target_modules "all-linear" \
+--use_4bit_quantization False
\ No newline at end of file
diff --git a/peft/examples/sft/run_peft_fsdp.sh b/peft/examples/sft/run_peft_fsdp.sh
new file mode 100644
index 0000000000000000000000000000000000000000..63dd475f44ad062f6241ebee9c4fa9047bcace2b
--- /dev/null
+++ b/peft/examples/sft/run_peft_fsdp.sh
@@ -0,0 +1,39 @@
+accelerate launch --config_file "configs/fsdp_config.yaml" train.py \
+--seed 100 \
+--model_name_or_path "meta-llama/Llama-2-70b-hf" \
+--dataset_name "smangrul/ultrachat-10k-chatml" \
+--chat_template_format "chatml" \
+--add_special_tokens False \
+--append_concat_token False \
+--splits "train,test" \
+--max_seq_len 2048 \
+--num_train_epochs 1 \
+--logging_steps 5 \
+--log_level "info" \
+--logging_strategy "steps" \
+--eval_strategy "epoch" \
+--save_strategy "epoch" \
+--push_to_hub \
+--hub_private_repo True \
+--hub_strategy "every_save" \
+--bf16 True \
+--packing True \
+--learning_rate 1e-4 \
+--lr_scheduler_type "cosine" \
+--weight_decay 1e-4 \
+--warmup_ratio 0.0 \
+--max_grad_norm 1.0 \
+--output_dir "mistral-sft-lora-fsdp" \
+--per_device_train_batch_size 8 \
+--per_device_eval_batch_size 8 \
+--gradient_accumulation_steps 4 \
+--gradient_checkpointing True \
+--use_reentrant False \
+--dataset_text_field "content" \
+--use_flash_attn True \
+--use_peft_lora True \
+--lora_r 8 \
+--lora_alpha 16 \
+--lora_dropout 0.1 \
+--lora_target_modules "all-linear" \
+--use_4bit_quantization False
\ No newline at end of file
diff --git a/peft/examples/sft/run_peft_fsdp_gptq.sh b/peft/examples/sft/run_peft_fsdp_gptq.sh
new file mode 100644
index 0000000000000000000000000000000000000000..479a7eac834aea664f02c6b6ae6de359290ed3dd
--- /dev/null
+++ b/peft/examples/sft/run_peft_fsdp_gptq.sh
@@ -0,0 +1,36 @@
+accelerate launch --config_file "configs/fsdp_config.yaml" train.py \
+--seed 100 \
+--model_name_or_path "hugging-quants/Meta-Llama-3.1-8B-Instruct-GPTQ-INT4" \
+--dataset_name "smangrul/ultrachat-10k-chatml" \
+--chat_template_format "chatml" \
+--add_special_tokens False \
+--append_concat_token False \
+--splits "train,test" \
+--max_seq_len 2048 \
+--num_train_epochs 1 \
+--logging_steps 5 \
+--log_level "info" \
+--logging_strategy "steps" \
+--eval_strategy "epoch" \
+--save_strategy "epoch" \
+--bf16 True \
+--packing True \
+--learning_rate 1e-4 \
+--lr_scheduler_type "cosine" \
+--weight_decay 1e-4 \
+--warmup_ratio 0.0 \
+--max_grad_norm 1.0 \
+--output_dir "llama3-8B-gptq-sft-lora-fsdp" \
+--per_device_train_batch_size 8 \
+--per_device_eval_batch_size 8 \
+--gradient_accumulation_steps 4 \
+--gradient_checkpointing True \
+--use_reentrant False \
+--dataset_text_field "content" \
+--use_flash_attn True \
+--use_peft_lora True \
+--lora_r 8 \
+--lora_alpha 16 \
+--lora_dropout 0.1 \
+--lora_target_modules "q_proj,k_proj,v_proj,o_proj,up_proj,gate_proj" \
+--use_4bit_quantization False
\ No newline at end of file
diff --git a/peft/examples/sft/run_peft_multigpu.sh b/peft/examples/sft/run_peft_multigpu.sh
new file mode 100644
index 0000000000000000000000000000000000000000..dbd108d0e055c4fad1076068d15ee1560faa96ad
--- /dev/null
+++ b/peft/examples/sft/run_peft_multigpu.sh
@@ -0,0 +1,41 @@
+torchrun --nproc_per_node 8 --nnodes 1 train.py \
+--seed 100 \
+--model_name_or_path "mistralai/Mistral-7B-v0.1" \
+--dataset_name "smangrul/ultrachat-10k-chatml" \
+--chat_template_format "chatml" \
+--add_special_tokens False \
+--append_concat_token False \
+--splits "train,test" \
+--max_seq_len 2048 \
+--num_train_epochs 1 \
+--logging_steps 5 \
+--log_level "info" \
+--logging_strategy "steps" \
+--eval_strategy "epoch" \
+--save_strategy "epoch" \
+--push_to_hub \
+--hub_private_repo True \
+--hub_strategy "every_save" \
+--bf16 True \
+--packing True \
+--learning_rate 1e-4 \
+--lr_scheduler_type "cosine" \
+--weight_decay 1e-4 \
+--warmup_ratio 0.0 \
+--max_grad_norm 1.0 \
+--output_dir "mistral-sft-lora-multigpu" \
+--per_device_train_batch_size 8 \
+--per_device_eval_batch_size 8 \
+--gradient_accumulation_steps 8 \
+--gradient_checkpointing True \
+--use_reentrant False \
+--dataset_text_field "content" \
+--use_peft_lora True \
+--lora_r 8 \
+--lora_alpha 16 \
+--lora_dropout 0.1 \
+--lora_target_modules "all-linear" \
+--use_4bit_quantization True \
+--use_nested_quant True \
+--bnb_4bit_compute_dtype "bfloat16" \
+--use_flash_attn True
diff --git a/peft/examples/sft/run_peft_qlora_deepspeed_stage3.sh b/peft/examples/sft/run_peft_qlora_deepspeed_stage3.sh
new file mode 100644
index 0000000000000000000000000000000000000000..4bbc1bbcc4bd06351add38d7d5142da02787d5d4
--- /dev/null
+++ b/peft/examples/sft/run_peft_qlora_deepspeed_stage3.sh
@@ -0,0 +1,42 @@
+accelerate launch --config_file "configs/deepspeed_config_z3_qlora.yaml" train.py \
+--seed 100 \
+--model_name_or_path "meta-llama/Llama-2-70b-hf" \
+--dataset_name "smangrul/ultrachat-10k-chatml" \
+--chat_template_format "chatml" \
+--add_special_tokens False \
+--append_concat_token False \
+--splits "train,test" \
+--max_seq_len 2048 \
+--num_train_epochs 1 \
+--logging_steps 5 \
+--log_level "info" \
+--logging_strategy "steps" \
+--eval_strategy "epoch" \
+--save_strategy "epoch" \
+--push_to_hub \
+--hub_private_repo True \
+--hub_strategy "every_save" \
+--bf16 True \
+--packing True \
+--learning_rate 1e-4 \
+--lr_scheduler_type "cosine" \
+--weight_decay 1e-4 \
+--warmup_ratio 0.0 \
+--max_grad_norm 1.0 \
+--output_dir "llama-sft-qlora-dsz3" \
+--per_device_train_batch_size 2 \
+--per_device_eval_batch_size 2 \
+--gradient_accumulation_steps 2 \
+--gradient_checkpointing True \
+--use_reentrant True \
+--dataset_text_field "content" \
+--use_flash_attn True \
+--use_peft_lora True \
+--lora_r 8 \
+--lora_alpha 16 \
+--lora_dropout 0.1 \
+--lora_target_modules "all-linear" \
+--use_4bit_quantization True \
+--use_nested_quant True \
+--bnb_4bit_compute_dtype "bfloat16" \
+--bnb_4bit_quant_storage_dtype "bfloat16"
\ No newline at end of file
diff --git a/peft/examples/sft/run_peft_qlora_fsdp.sh b/peft/examples/sft/run_peft_qlora_fsdp.sh
new file mode 100644
index 0000000000000000000000000000000000000000..4ed3218c8277fd0ab8f66c2b3ea3f2fe41e7fe04
--- /dev/null
+++ b/peft/examples/sft/run_peft_qlora_fsdp.sh
@@ -0,0 +1,42 @@
+accelerate launch --config_file "configs/fsdp_config_qlora.yaml" train.py \
+--seed 100 \
+--model_name_or_path "meta-llama/Llama-2-70b-hf" \
+--dataset_name "smangrul/ultrachat-10k-chatml" \
+--chat_template_format "chatml" \
+--add_special_tokens False \
+--append_concat_token False \
+--splits "train,test" \
+--max_seq_len 2048 \
+--num_train_epochs 1 \
+--logging_steps 5 \
+--log_level "info" \
+--logging_strategy "steps" \
+--eval_strategy "epoch" \
+--save_strategy "epoch" \
+--push_to_hub \
+--hub_private_repo True \
+--hub_strategy "every_save" \
+--bf16 True \
+--packing True \
+--learning_rate 1e-4 \
+--lr_scheduler_type "cosine" \
+--weight_decay 1e-4 \
+--warmup_ratio 0.0 \
+--max_grad_norm 1.0 \
+--output_dir "llama-sft-qlora-fsdp" \
+--per_device_train_batch_size 2 \
+--per_device_eval_batch_size 2 \
+--gradient_accumulation_steps 2 \
+--gradient_checkpointing True \
+--use_reentrant True \
+--dataset_text_field "content" \
+--use_flash_attn True \
+--use_peft_lora True \
+--lora_r 8 \
+--lora_alpha 16 \
+--lora_dropout 0.1 \
+--lora_target_modules "all-linear" \
+--use_4bit_quantization True \
+--use_nested_quant True \
+--bnb_4bit_compute_dtype "bfloat16" \
+--bnb_4bit_quant_storage_dtype "bfloat16"
\ No newline at end of file
diff --git a/peft/examples/sft/run_unsloth_peft.sh b/peft/examples/sft/run_unsloth_peft.sh
new file mode 100644
index 0000000000000000000000000000000000000000..97a4a6b520e1112a85cd25387f3cb46deb465f9e
--- /dev/null
+++ b/peft/examples/sft/run_unsloth_peft.sh
@@ -0,0 +1,42 @@
+python train.py \
+--seed 100 \
+--model_name_or_path "mistralai/Mistral-7B-v0.1" \
+--dataset_name "smangrul/ultrachat-10k-chatml" \
+--chat_template_format "chatml" \
+--add_special_tokens False \
+--append_concat_token False \
+--splits "train,test" \
+--max_seq_len 2048 \
+--num_train_epochs 1 \
+--logging_steps 5 \
+--log_level "info" \
+--logging_strategy "steps" \
+--eval_strategy "epoch" \
+--save_strategy "epoch" \
+--push_to_hub \
+--hub_private_repo True \
+--hub_strategy "every_save" \
+--bf16 True \
+--packing True \
+--learning_rate 1e-4 \
+--lr_scheduler_type "cosine" \
+--weight_decay 1e-4 \
+--warmup_ratio 0.0 \
+--max_grad_norm 1.0 \
+--output_dir "mistral-sft-lora-unsloth" \
+--per_device_train_batch_size 8 \
+--per_device_eval_batch_size 8 \
+--gradient_accumulation_steps 8 \
+--gradient_checkpointing True \
+--use_reentrant True \
+--dataset_text_field "content" \
+--use_peft_lora True \
+--use_unsloth True \
+--lora_r 8 \
+--lora_alpha 16 \
+--lora_dropout 0.1 \
+--lora_target_modules "q_proj,k_proj,v_proj,o_proj,down_proj,up_proj,gate_proj" \
+--use_4bit_quantization True \
+--use_nested_quant True \
+--bnb_4bit_compute_dtype "bfloat16" \
+--use_flash_attn True
diff --git a/peft/examples/sft/train.py b/peft/examples/sft/train.py
new file mode 100644
index 0000000000000000000000000000000000000000..5a34f69357b0505e84b16436e894a2ab924ce1a7
--- /dev/null
+++ b/peft/examples/sft/train.py
@@ -0,0 +1,159 @@
+import os
+import sys
+from dataclasses import dataclass, field
+from typing import Optional
+
+from transformers import HfArgumentParser, set_seed
+from trl import SFTConfig, SFTTrainer
+from utils import create_and_prepare_model, create_datasets
+
+
+# Define and parse arguments.
+@dataclass
+class ModelArguments:
+ """
+ Arguments pertaining to which model/config/tokenizer we are going to fine-tune from.
+ """
+
+ model_name_or_path: str = field(
+ metadata={"help": "Path to pretrained model or model identifier from huggingface.co/models"}
+ )
+ max_seq_length: Optional[int] = field(
+ default=512,
+ metadata={"help": "The maximum total input sequence length after tokenization."},
+ )
+ chat_template_format: Optional[str] = field(
+ default="none",
+ metadata={
+ "help": "chatml|zephyr|none. Pass `none` if the dataset is already formatted with the chat template."
+ },
+ )
+ lora_alpha: Optional[int] = field(default=16)
+ lora_dropout: Optional[float] = field(default=0.1)
+ lora_r: Optional[int] = field(default=64)
+ lora_target_modules: Optional[str] = field(
+ default="q_proj,k_proj,v_proj,o_proj,down_proj,up_proj,gate_proj",
+ metadata={"help": "comma separated list of target modules to apply LoRA layers to"},
+ )
+ use_nested_quant: Optional[bool] = field(
+ default=False,
+ metadata={"help": "Activate nested quantization for 4bit base models"},
+ )
+ bnb_4bit_compute_dtype: Optional[str] = field(
+ default="float16",
+ metadata={"help": "Compute dtype for 4bit base models"},
+ )
+ bnb_4bit_quant_storage_dtype: Optional[str] = field(
+ default="uint8",
+ metadata={"help": "Quantization storage dtype for 4bit base models"},
+ )
+ bnb_4bit_quant_type: Optional[str] = field(
+ default="nf4",
+ metadata={"help": "Quantization type fp4 or nf4"},
+ )
+ use_flash_attn: Optional[bool] = field(
+ default=False,
+ metadata={"help": "Enables Flash attention for training."},
+ )
+ use_peft_lora: Optional[bool] = field(
+ default=False,
+ metadata={"help": "Enables PEFT LoRA for training."},
+ )
+ use_8bit_quantization: Optional[bool] = field(
+ default=False,
+ metadata={"help": "Enables loading model in 8bit."},
+ )
+ use_4bit_quantization: Optional[bool] = field(
+ default=False,
+ metadata={"help": "Enables loading model in 4bit."},
+ )
+ use_reentrant: Optional[bool] = field(
+ default=False,
+ metadata={"help": "Gradient Checkpointing param. Refer the related docs"},
+ )
+ use_unsloth: Optional[bool] = field(
+ default=False,
+ metadata={"help": "Enables UnSloth for training."},
+ )
+
+
+@dataclass
+class DataTrainingArguments:
+ dataset_name: Optional[str] = field(
+ default="timdettmers/openassistant-guanaco",
+ metadata={"help": "The preference dataset to use."},
+ )
+ append_concat_token: Optional[bool] = field(
+ default=False,
+ metadata={"help": "If True, appends `eos_token_id` at the end of each sample being packed."},
+ )
+ add_special_tokens: Optional[bool] = field(
+ default=False,
+ metadata={"help": "If True, tokenizers adds special tokens to each sample being packed."},
+ )
+ splits: Optional[str] = field(
+ default="train,test",
+ metadata={"help": "Comma separate list of the splits to use from the dataset."},
+ )
+
+
+def main(model_args, data_args, training_args):
+ # Set seed for reproducibility
+ set_seed(training_args.seed)
+
+ # model
+ model, peft_config, tokenizer = create_and_prepare_model(model_args, data_args, training_args)
+
+ # gradient ckpt
+ model.config.use_cache = not training_args.gradient_checkpointing
+ training_args.gradient_checkpointing = training_args.gradient_checkpointing and not model_args.use_unsloth
+ if training_args.gradient_checkpointing:
+ training_args.gradient_checkpointing_kwargs = {"use_reentrant": model_args.use_reentrant}
+
+ training_args.dataset_kwargs = {
+ "append_concat_token": data_args.append_concat_token,
+ "add_special_tokens": data_args.add_special_tokens,
+ }
+
+ # datasets
+ train_dataset, eval_dataset = create_datasets(
+ tokenizer,
+ data_args,
+ training_args,
+ apply_chat_template=model_args.chat_template_format != "none",
+ )
+
+ # trainer
+ trainer = SFTTrainer(
+ model=model,
+ processing_class=tokenizer,
+ args=training_args,
+ train_dataset=train_dataset,
+ eval_dataset=eval_dataset,
+ peft_config=peft_config,
+ )
+ trainer.accelerator.print(f"{trainer.model}")
+ if hasattr(trainer.model, "print_trainable_parameters"):
+ trainer.model.print_trainable_parameters()
+
+ # train
+ checkpoint = None
+ if training_args.resume_from_checkpoint is not None:
+ checkpoint = training_args.resume_from_checkpoint
+ trainer.train(resume_from_checkpoint=checkpoint)
+
+ # saving final model
+ if trainer.is_fsdp_enabled:
+ trainer.accelerator.state.fsdp_plugin.set_state_dict_type("FULL_STATE_DICT")
+ trainer.save_model()
+
+
+if __name__ == "__main__":
+ parser = HfArgumentParser((ModelArguments, DataTrainingArguments, SFTConfig))
+ if len(sys.argv) == 2 and sys.argv[1].endswith(".json"):
+ # If we pass only one argument to the script and it's the path to a json file,
+ # let's parse it to get our arguments.
+ model_args, data_args, training_args = parser.parse_json_file(json_file=os.path.abspath(sys.argv[1]))
+ else:
+ model_args, data_args, training_args = parser.parse_args_into_dataclasses()
+ main(model_args, data_args, training_args)
diff --git a/peft/examples/sft/utils.py b/peft/examples/sft/utils.py
new file mode 100644
index 0000000000000000000000000000000000000000..ea0d36bb647628561a3d447c0fdd9360caa03ba9
--- /dev/null
+++ b/peft/examples/sft/utils.py
@@ -0,0 +1,219 @@
+import os
+from enum import Enum
+
+import packaging.version
+import torch
+import transformers
+from datasets import DatasetDict, load_dataset, load_from_disk
+from datasets.builder import DatasetGenerationError
+from transformers import (
+ AutoModelForCausalLM,
+ AutoTokenizer,
+ BitsAndBytesConfig,
+)
+
+from peft import LoraConfig
+
+
+DEFAULT_CHATML_CHAT_TEMPLATE = "{% for message in messages %}\n{{'<|im_start|>' + message['role'] + '\n' + message['content'] + '<|im_end|>' + '\n'}}{% if loop.last and add_generation_prompt %}{{'<|im_start|>assistant\n' }}{% endif %}{% endfor %}"
+DEFAULT_ZEPHYR_CHAT_TEMPLATE = "{% for message in messages %}\n{% if message['role'] == 'user' %}\n{{ '<|user|>\n' + message['content'] + eos_token }}\n{% elif message['role'] == 'system' %}\n{{ '<|system|>\n' + message['content'] + eos_token }}\n{% elif message['role'] == 'assistant' %}\n{{ '<|assistant|>\n' + message['content'] + eos_token }}\n{% endif %}\n{% if loop.last and add_generation_prompt %}\n{{ '<|assistant|>' }}\n{% endif %}\n{% endfor %}"
+
+
+class ZephyrSpecialTokens(str, Enum):
+ user = "<|user|>"
+ assistant = "<|assistant|>"
+ system = "<|system|>"
+ eos_token = ""
+ bos_token = ""
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "ngqdEv0rP01q"
+ },
+ "source": [
+ "## Introduction\n",
+ "\n",
+ "In this notebook, we are going to fine-tune the LayoutLM model by Microsoft Research on the [FUNSD](https://guillaumejaume.github.io/FUNSD/) dataset, which is a collection of annotated form documents. The goal of our model is to learn the annotations of a number of labels (\"question\", \"answer\", \"header\" and \"other\") on those forms, such that it can be used to annotate unseen forms in the future.\n",
+ "\n",
+ "* Original LayoutLM paper: https://huggingface.co/papers/1912.13318\n",
+ "\n",
+ "* Original FUNSD paper: https://huggingface.co/papers/1905.13538\n"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "6K4S2s33ebY0"
+ },
+ "source": [
+ "## Install libraries\n",
+ "\n",
+ "Currently you have to first install the `unilm` package, and then the `transformers` package (which updates the outdated `transformers` package that is included in the `unilm` package). The reason we also install the `unilm` package is because we need its preprocessing files. I've forked it, and removed some statements which introduced some issues."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 1000
+ },
+ "id": "5cngOTr6SqEf",
+ "outputId": "6c7a2f76-682b-4f93-a3db-59ab010e5ffe"
+ },
+ "outputs": [],
+ "source": [
+ "! rm -r unilm\n",
+ "! git clone https://github.com/microsoft/unilm.git"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "RGMkEG5aRB0D"
+ },
+ "source": [
+ "## Getting the data\n",
+ "\n",
+ "Here we download the data of the [FUNSD dataset](https://guillaumejaume.github.io/FUNSD/) from the web. This results in a directory called \"data\" being created, which has 2 subdirectories, one for training and one for testing. Each of those has 2 subdirectories in turn, one containing the images as png files and one containing the annotations in json format."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": null,
+ "metadata": {
+ "colab": {
+ "base_uri": "https://localhost:8080/"
+ },
+ "id": "DTFnEZagQm4v",
+ "outputId": "97ce03ba-a6bb-4444-8eba-77eceece44e0"
+ },
+ "outputs": [],
+ "source": [
+ "! wget https://guillaumejaume.github.io/FUNSD/dataset.zip\n",
+ "! unzip dataset.zip && mv dataset data && rm -rf dataset.zip __MACOSX"
+ ]
+ },
+ {
+ "cell_type": "markdown",
+ "metadata": {
+ "id": "UrNMR64LsJXm"
+ },
+ "source": [
+ "Let's take a look at a training example. For this, we are going to use PIL (Python Image Library)."
+ ]
+ },
+ {
+ "cell_type": "code",
+ "execution_count": 5,
+ "metadata": {
+ "colab": {
+ "base_uri": "https://localhost:8080/",
+ "height": 1000
+ },
+ "id": "eG-eGcj3sNPs",
+ "outputId": "69ead0ea-15d6-4d5e-af61-a99a7533d31b"
+ },
+ "outputs": [
+ {
+ "data": {
+ "image/jpeg": "/9j/4AAQSkZJRgABAQAAAQABAAD/2wBDAAgGBgcGBQgHBwcJCQgKDBQNDAsLDBkSEw8UHRofHh0aHBwgJC4nICIsIxwcKDcpLDAxNDQ0Hyc5PTgyPC4zNDL/2wBDAQkJCQwLDBgNDRgyIRwhMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjIyMjL/wAARCAPoAvoDASIAAhEBAxEB/8QAHwAAAQUBAQEBAQEAAAAAAAAAAAECAwQFBgcICQoL/8QAtRAAAgEDAwIEAwUFBAQAAAF9AQIDAAQRBRIhMUEGE1FhByJxFDKBkaEII0KxwRVS0fAkM2JyggkKFhcYGRolJicoKSo0NTY3ODk6Q0RFRkdISUpTVFVWV1hZWmNkZWZnaGlqc3R1dnd4eXqDhIWGh4iJipKTlJWWl5iZmqKjpKWmp6ipqrKztLW2t7i5usLDxMXGx8jJytLT1NXW19jZ2uHi4+Tl5ufo6erx8vP09fb3+Pn6/8QAHwEAAwEBAQEBAQEBAQAAAAAAAAECAwQFBgcICQoL/8QAtREAAgECBAQDBAcFBAQAAQJ3AAECAxEEBSExBhJBUQdhcRMiMoEIFEKRobHBCSMzUvAVYnLRChYkNOEl8RcYGRomJygpKjU2Nzg5OkNERUZHSElKU1RVVldYWVpjZGVmZ2hpanN0dXZ3eHl6goOEhYaHiImKkpOUlZaXmJmaoqOkpaanqKmqsrO0tba3uLm6wsPExcbHyMnK0tPU1dbX2Nna4uPk5ebn6Onq8vP09fb3+Pn6/9oADAMBAAIRAxEAPwDa/wCGb/DH/QX1f/vqL/4ij/hm/wAMf9BfV/8AvqL/AOIr2WigDxr/AIZv8Mf9BfV/++ov/iKP+Gb/AAx/0F9X/wC+ov8A4ivZaKAPGv8Ahm/wx/0F9X/76i/+Io/4Zv8ADH/QX1f/AL6i/wDiK9looA8a/wCGb/DH/QX1f/vqL/4ij/hm/wAMf9BfV/8AvqL/AOIr2WigDxr/AIZv8Mf9BfV/++ov/iKP+Gb/AAx/0F9X/wC+ov8A4ivZaKAPGv8Ahm/wx/0F9X/76i/+Io/4Zv8ADH/QX1f/AL6i/wDiK9looA8a/wCGb/DH/QX1f/vqL/4ij/hm/wAMf9BfV/8AvqL/AOIr2WigDxr/AIZv8Mf9BfV/++ov/iKP+Gb/AAx/0F9X/wC+ov8A4ivZaKAPE2/Zs0HexXXdSClgVBRCQuOQTjk578Y9D1qrJ+zRYkjy/E1wo5zutFPfj+Idsf54r3aigDw+H9mvSFiUT+IL55Nx3MkKKCOwAOcHrzn8Knh/Zt8PLHifW9Ud8nmMRoMduCp/nXtNFAHisf7Nvh8TSmTW9TaIkeUqiMMoxzuODu59APxqvP8As1aWzubfxHeRqfuiS3VyOe5BGeMen9K9yooA8JX9miyAXf4muCd2Ti0UZX0+919/0ph/ZntcnHiibH/XkP8A4uveaKAPBv8Ahme2/wChpm/8Ah/8XR/wzPbf9DTN/wCAQ/8Ai695ooA8G/4Zntv+hpm/8Ah/8XR/wzPbf9DTN/4BD/4uveaKAPBv+GZ7b/oaZv8AwCH/AMXR/wAMz23/AENM3/gEP/i695ooA8G/4Zntv+hpm/8AAIf/ABdH/DM9t/0NM3/gEP8A4uveaKAPBv8Ahme2/wChpm/8Ah/8XR/wzPbf9DTN/wCAQ/8Ai695ooA8G/4Zntv+hpm/8Ah/8XR/wzPbf9DTN/4BD/4uveaKAPBv+GZ7b/oaZv8AwCH/AMXR/wAMz23/AENM3/gEP/i695ooA8G/4Zntv+hpm/8AAIf/ABdH/DM9t/0NM3/gEP8A4uveaKAPBv8Ahme2/wChpm/8Ah/8XR/wzPbf9DTN/wCAQ/8Ai695ooA8G/4Zntv+hpm/8Ah/8XR/wzPbf9DTN/4BD/4uveaKAPBv+GZ7b/oaZv8AwCH/AMXR/wAMz23/AENM3/gEP/i695ooA8G/4Zntv+hpm/8AAIf/ABdH/DM9t/0NM3/gEP8A4uveaKAPBv8Ahme2/wChpm/8Ah/8XR/wzPbf9DTN/wCAQ/8Ai695ooA8G/4Zntv+hpm/8Ah/8XR/wzPbf9DTN/4BD/4uveaKAPBv+GZ7b/oaZv8AwCH/AMXR/wAMz23/AENM3/gEP/i695ooA8G/4Zntv+hpm/8AAIf/ABdH/DM9t/0NM3/gEP8A4uveaKAPBv8Ahme2/wChpm/8Ah/8XR/wzPbf9DTN/wCAQ/8Ai695ooA8G/4Zntv+hpm/8Ah/8XR/wzPbf9DTN/4BD/4uveaKAPBv+GZ7b/oaZv8AwCH/AMXR/wAMz23/AENM3/gEP/i695ooA8G/4Zntv+hpm/8AAIf/ABdH/DM9t/0NM3/gEP8A4uveaKAPBv8Ahme2/wChpm/8Ah/8XR/wzPbf9DTN/wCAQ/8Ai695ooA8G/4Zntv+hpm/8Ah/8XR/wzPbf9DTN/4BD/4uveaKAPBv+GZ7b/oaZv8AwCH/AMXR/wAMz23/AENM3/gEP/i695ooA8G/4Zntv+hpm/8AAIf/ABdH/DM9t/0NM3/gEP8A4uveaKAPBv8Ahme2/wChpm/8Ah/8XR/wzPbf9DTN/wCAQ/8Ai695ooA8G/4Zntv+hpm/8Ah/8XR/wzPbf9DTN/4BD/4uveaKAPBv+GZ7b/oaZv8AwCH/AMXR/wAMz23/AENM3/gEP/i695ooA8G/4Zntv+hpm/8AAIf/ABdH/DM9t/0NM3/gEP8A4uveaKAPBv8Ahme2/wChpm/8Ah/8XR/wzPbf9DTN/wCAQ/8Ai695ooA8G/4Zntv+hpm/8Ah/8XR/wzPbf9DTN/4BD/4uveaKAPBv+GZ7b/oaZv8AwCH/AMXVe7/ZoYQj7H4mDS7uRNabRj8GPNfQNFAHzj/wzVqv/QxWf/fhv8aP+GatV/6GKz/78N/jX0dRQB83Tfs36pDBJKfENmQilsCBucDPrXpHwJ/5JRp//Xaf/wBGNXoN/wD8g65/65P/ACNeffAn/klGn/8AXaf/ANGNQB6TRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAV7/wD5B1z/ANcn/ka8++BP/JKNP/67T/8Aoxq9Bv8A/kHXP/XJ/wCRrz74E/8AJKNP/wCu0/8A6MagD0miiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAr3/APyDrn/rk/8AI1598Cf+SUaf/wBdp/8A0Y1eg3//ACDrn/rk/wDI1598Cf8AklGn/wDXaf8A9GNQB6TRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAZ+vXaaf4d1O9kVmS3tJZWVepCoTgflXDfAn/klGn/8AXaf/ANGNXbeI4hceGNWhMDTiSzmQxK20yZQjaD2J6ZrifgT/AMko0/8A67T/APoxqAPSaKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigCpqsMdxo97DMgeKS3kR1PQgqQRXA/An/klGn/9dp//AEY1eg3/APyDrn/rk/8AI1598Cf+SUaf/wBdp/8A0Y1AHpNFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRXP65410Lw/ObW6uzNflcpY2qGa4fjPCLk9O5wKAOgoriYvE3jDVlH9l+D/ALBHkAz6zdCPHPOI0DMRjnJI/Gs3VNW8cWdyBN4i8D2AcZSKd5MkdCQSRnmgD0iivO7HUPiFNA11b6l4O1WM/KiW7yqGbP8AeBI49KtyfEK70hwPE/hbUtLhXiS9hIurZOTg7k5wQM8qMd6AO5oqlpWsabrlkLzS76C8tyceZC4YZ9Djoau0AFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAVNVmS30e9mlbbHHbyOxxnACkmuB+BP/ACSjT/8ArtP/AOjGruddhjuPD2pwzOEiktJUdycbQUIJzxiuG+BP/JKNP/67T/8AoxqAPSaKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKRmVFLMQFAySTwBS1wfiqQ+LNZk8KR3Bg0e1jE+uXaSbSF6rb7s8FgMt6Lj1oAr3viDUfF8NxJpN6+ieFYELza82FknAzuEIb7q/8ATQjtwK8s1T4uaP4WmurPwHo8LSsPLk1q8y81we7HPzHnkbjj27Vz3xR+JL+Lb5dM0dpLXw9Zr5UMCnas2P42UduBgHoBnqa84AycCgDrI9d8deN9TWxh1LVtSuZCWEEcrbRngnaCFVfyArrtN/Z58X3tuk11Pp1iW6xSyszjjP8ACpHt1rduDqXwX0fQrGxm0y31HU4bi41C6u4Wkw6qpWJSvOP4fQk5q943+K3imx8P+GZrOe00++1Gza7uooohK8Yz+7Yh8hUYHPr19KAPPNe+D3jXwtFJf/ZUuYLb94bixm3FAMHdjhuPp2NVfDvxb8Y+HrlXXVZb+3ACtbXzGVCo7DJyv4EV7XqXi/xHqfxA0rR/Dmvab5Fxo7zu3krPbyXCNIG+YYYDK4yDx1wa8g+IOnR6ro1n40trCGzkubqWy1KG2O6H7Qh/1iEZG1x+oPXOaAPQ/CWv+H/Fl1DL4UuP+ES8TJ8zWEY/0O+I5AdQAG6kZ4YZ74Fep+FvFT61Jc6bqlkNM12zwbixaTf8h6SIf4kPqOnQ18TxyPDKksTskiEMrqcFSOhB7GvoTwN4ln+I2kIxnhg8c6EvmWV0QB9rjxjZJ6qclW9Mhh3oA95orK8Oa5D4i0K31KKN4mfKSwyDDRSKSrow9QwIrVoAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigCjrUvkaFqEweNPLtpG3ynCLhScsfT1rhPgT/ySjT/+u0//AKMau08T2xvPCes2obYZrGePcQTjMbDOByetcX8Cf+SUaf8A9dp//RjUAek0UUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQBT1XUrfRtIu9Su3CW9rE0sh9gM189+ONVuPDnwlt7G4kk/tjxZctqd5nI2I207efby1x7GvW/i1JOnw01ZLZC8s5htwgXcWEkqIQB6kMa8L/aAu/M+IEFgkflwWNjFFGgPy4OWyB26gfgKAOC8LeGdQ8XeIbbRtNVTPMSS7cLGg5Zj7Af4V9M+FPgd4V0CCJ9Qtxq98p3NLcD93njpHnGOO+etZH7O+gQ2nhC61tocXV7cNGsjKQfKTAwD3G7d07j2q/8AEb4i6z4e8WWuhaJHbm7Nstykc6bxdlnZfKGCCrfLkY65xxxkA63xH4G0zxRrmkalqDOy6csy/Z9oMcyyLtIbI9q8y8ZeE/AngyOyi1HUvElzcGB4Vt7a6VpGtF+Yo/AxEOfQ8nrji94P/aA0/VLyPT/Edj/Zlyx2CeMlot3+0D8yc8d/c1wvjS+k1XXdZ1W+ilkt7mOeGxu9vlSWkiRMDaSKcjoScdSSCDywoA9Ps/hD4S1W0stQ0zWtZNkbdo7c296NhgdmYxg7c7TuYEZ7nPNdrF4N8PR+GYPDraXbzaVAMRwTLvAPPzZPO75j83XmvDPg/wDFC08MeEtWstcuWa3ststlEoy7Fs7kX8cHJ4Gatn41eI/FEl4+nJaaDpFlH5t1ePiaVVzwq7sKXY8KuOvfHNAGh8QvgNYtpsuo+D4ZIryLLvYmQssq9TszyG9s4OMcHr4d4a1u58KeKrHVo0YS2U4Z42GCR0ZT6ZGRX2P4K12TxN4P03WZYxG91GW2ZzgBiBk9zgDPA59K+a/jp4et9C+IkklpGkcOoQi7KKScOWYMfbJBOPegD3DQLmDTPiNILMudK8VWS6nbFjgCdQN+AR/EjIccnivQ68I8JXy6j4T+GupWaFZtM1ZtNmcn7okRgwAPUMNv0r3egAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAKOtXAtNB1G5MbyCG1kk2RjLNhScAetcJ8Cf+SUaf/wBdp/8A0Y1d7qwLaNfKJjCTbyDzRjKfKfm544681wXwJ/5JRp//AF2n/wDRjUAek0UUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQBx/xPmktfAd3eRwmY2txa3LIDjKx3EbnntwprwP9oG1kg+JhmfbsubOKSPB7DK8/ipr6b1/SYte8P6hpM3Ed3bvCT6ZGAfwPNfO/xM08eIvh1ofimOF1v9KxpOpxgcIyZGcZPAfOPZxQB6n8DLmKf4UaZHG2WgkmjkGDw3mM2PyYfnVL41WWpR6Zput6VFpxktJWjna9t4HUI2NpLSjAww/Nq4L9nzxrFp2oXPhe/nCQ3jebZl2wBL0KD3YYx7r719FXdrBfWc1pcxrLBOhjkRujKRgigD5U8ReFtT8S6bca3NHYf8JDFhrm3sby2lF5GAS0qpExIcYG4Yweo5yKpeFPED3sUkN8ftDi1ltpUlCv5yeS4hbB/jibGG67WxkAYPc+LfhXpngq9TWNL0rxHdW8LrMk9hfxBrdw3HyGItwcc5PvXP6NLa6p4huta8KWjpJe209jf6SygyR+ZEVEybQBtLBcgAbWOOjCgDjvCFpJe2usWiLABeQR2gmn4SEmVZC5PYBInJPoD6jPQ3A1CSa08LeFLjSm05ZljQiWGR72Ynb57qdzd+Bj5V/Gp9Gk06HQZfBVppWs6lfXMqvqU2kTxhZWBJWLcUfKL6jALA9QAT7H8OvhRo3haVNaksblNTdPkiu7hJzbZ64Koo3dj1x2PJoA77R7H+zNFsbHj/R4EiJAAyQoB6AD8gK+ev2k7sv4n0Wz2KBFZtLuHU73Iwfps/U19HXFxDaW0lxcSpFDEpeSRzhVUckk9hXxr4p1a8+JXxKkks0Be+uFtbNDwFTO1M/zJ9zQB6r4RtG0/wAG/DXT4Chm1DWGv5UQcuqByWP+6u3Ne815zoFhHc+PrSxt/Lew8IaYtmr7MlrmVQGwcAZCIM+7+9ejUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFNCnzC287SAAuBgHnn/PpQA6iiigAooooAKKKKACiiigAooooAKKKKACiiigDD8Z/wDIi+If+wZc/wDopq5L4E/8ko0//rtP/wCjGruddgS58Palbyqzxy2sqMqjkgoQQK4b4E/8ko0//rtP/wCjGoA9JooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigArzjxBpttomv3kGowxN4U8UsIb0ltv2a7KkB89AHCqM9mAP19HqpqWmWWsafNYahbRXNrMu14pVDA/n37g9qAPjLxh4V1P4f+LGspXfdC4mtLtFKiRc5Vl9wevoRXvHwz+NVjr1mmm+JrqG01dSESZsJHc5OAeOFbPUcDuPQO8T6TbaXpseheNorrVfDnzC010jfcWTkcCUjnA7Pgg8ZHFePeIvhH4g0qE6jpKrrmiuokivbEhtynuUBJ/LIoA+pPFd99j8Ozuiyu8pWKMQXaW8hLHA2O5A3eg79MGvnn4mw3Vtplhqlw/iO1v8Af5AmvbO2h3oyYZTLDhnOBj5s5Gema8+tfGGv2dmtidQkuLFCpFneKLiEbTkfu5AVHPoKo6prF7rF1JPdyj523eVGNkanp8qDhfwFAHvvhZv+Ef0nSZNKj8StpI23CSXP2Swtip+YvK4+Z1I7MSQOK9pvdSstO0+S/vLuGC0jTe0zuAoXrnNfEmleKdT0eNktzby9PLa6tknMBHQxlwdh+noKi1fxJrevlTquqXd2qnKJLISif7q9F6dgKAPTfi78Xl8UI+gaA7DR8gzzlSGuSDkAA8hQQPckenV/w+8OP4K0pfF+q2wbWrwfZ/D+nSqQ0szgBXPTg7h17ZPpXjVekeGfibG2nQeH/GdkNW0dMrFdNzdWYIwDG5544x0I9ccUAfSvgvw5/wAI14dit5xG+pTk3GoTqOZp25ck9+Tgew7V0VeS6L4t1DwrpNpdyX58T+D2JDayhLXNkDjCzLyWAyMnqO44APqVhf2mqWEF9YzpcWs6B4pUOQwNAFiiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAp6sYl0e+NwUEIt5DIZMbdu05znjGK4L4E/8ko0//rtP/wCjGrr/ABgpfwRr6AgFtOuACxAH+rbqT0rkPgT/AMko0/8A67T/APoxqAPSaKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAGyRpNE8UqK8bgqyMMhgeoI71xVz8Pm065e+8IavcaJcMdxtQPNs39QYjwuT3XHU129FAHkuo6H4gljdPEvw/wBA8QqQzNd6dKIZWzxkq4B3nrkHjPHIrEbwH4XvbZRP8LvEdhMr5xaXSSBhjuWl/p+Ne60UAeK6b4QWK4judI+EdrbTbtpk1bU96x9CG2ZfIB9BntUPijRobq3h0r4gaDpmlCb93p2uaKjeRbOf4Zc4wCfXg5PTBNe4VXvrG01Oxmsr63juLWZSkkUi5Vh7igD4r8Y+CNZ8EamtnqkSMki74biElopBz0OOvHTrWt4I+HkviG0l17WLldM8M2jZubyQ4MgHVYxjk5wM+p7niva9f8N3nhjS7nTJdIm8TeC533ixQlruwPJ/dnOWTPTnIz9c6OheELvxJNaah4m0+Ox0mxYNpGgoAFgUcbpgB8zcKQM4HcUAUPDvh1/F2jxWENpPovgWIJ5FpkLc6kRyWlYEkIfTqcdq9Vt7eG0t47e3iSKGJQiRouFVR0AHYVJRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFAFHWrWO+0HUbSbPlT2skT4ODtZSD/ADrhPgT/AMko0/8A67T/APoxq9Bv/wDkHXP/AFyf+Rrz74E/8ko0/wD67T/+jGoA9JooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAKWsLM2iX627hJzbSCNiMgNtOD+dcH8Cf+SUaf/12n/8ARjV3OvSGLw7qciy+SyWkrCTj5MIeeQenXoa4b4E/8ko0/wD67T/+jGoA9JooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKwdU8X6Vo2qNp979pjkWD7S8gt2MaxBgrOWAxhSwz6ZyeKs/8JBYnxCNEQXEt55QmcxwO0candt3uBtXO1sZPOKANWisCPxjpMmqtpxNzHIt0bIyyQMIvPADbN+MZIYEeueK2Ly8t9PsZ727lEVtbxtLLIeiqoyT+QoAnorjW+JOlppV/qD6fqaR2lul2sbRIHuLd2wJYhvwV7nJBGRkcircfjixDa4Luxv7FdFhWa5e5RACrAsNu1zkkDvjtQB09FcbrvxBh0rRNC1az0u41C21iWKKIxyIuxpACgbk8nkcccHmrnjDxXP4Vhs5o9Hkvo7mdbfetwkQSRyAgO49z36CgDpqK871L4mahpl3LbS+EbtniD79t3H95IFmkC/3sK3UdSMCpLX4lXU2vxaHN4ZuLfUpJolFu11GWMTqzGYeqKF5I78daAPQKKZKZBE5iVWkCnYGOAT2yecCvOG+IXiODQNe1e68PafHFotybedF1BmZypG4r+79GGM4z7UAelUV5lefFpW0TxHrOj2EF7YaPJbxiRrgqZjJgNjCkDaSB155/Ft38Ur61sbSdrPRF825urd5pNUKwBoVDfLJ5fzbuQOBzgUAen0VxVx401W6toW0LRI7u5XTYtRuoLi5MLRrKCURPlO5ztfrgDA55rOu/iRfoLiS002zmRo7SbT0a4cSXcdw21CAEO0g5BHPSgD0aiuITxjqk/i278O29npz3ltMoZDcSA+SVRmk+5jI3gbc5ODXOaP8UNZ8SzabpOkx6WmtOl016LiKUwp5TYQLhgRuHPfAoA9aoryDS/ih4g1DwnqmtRxaRcPZ20MphiilQpJI6gRtub5sgt8w4BXvW1ZeNPEOvaxc22iR6YLaKOGWQ3MUnm2wZZg8cihx86yQhT0+90oA9FormvA+s6vr/h2HU9XgtYjcpHNB9mDBWjeJG5DEnIYsPwFdLQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFAGX4lnjtfCur3E0KzxRWUzvE3R1CElT9elcV8Cf+SUaf/wBdp/8A0Y1dxr8ltF4c1SS8UNapaStMCuQUCHdx34zXD/An/klGn/8AXaf/ANGNQB6TRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRSMdqk4JwM4HU0AedeOvDOreIPFVm1pYytbJp0sQuftCpCJWkRwkqbtzxkRlWG1h84444zdf8J+M9U1abVrBRZXVwiKNmqNH5UQjCvbkKhDAtvZXBBUtng1o23xB1q90TWNVh0vT1is7Ka4WE3LG4hkQjEU8RUFGK5PGRx15FOh8Y+JYLQX17b6TLb3NjZSWscIkRhPcuI1DkkjYGySQM4x1oAgHhLxJfalNa3NvbWemy64mrG6jvWkmCxoirGF2jkmMZYnueDXe65paa3oGo6U8hiS9tpLcyKMlQ6lc49s1yP/AAlPieKJNMmtdGOsz6h9hguIpma2OImkZ2QEuuAjDaTknuBzWX4l8f694e0bSbqa40UvObtbqWG3kuEJiyyeWFkGNygfePBPJAFAEFr4d1rWr/U9D8QobS5XQk061vLeNpIrhN2WlLYAVtyr8hweT161auvA3ibW9MvG1O6sIr/UL20e7WCRwhgg9CBncx5xjAqbXfF/ifSIdPhml0GxuJrEzvdXkU32WWbPEauGAj4xy55LACq/iHUfiJF4htrbTL7TIxeLIbO3MIZJfKijckuTkBmZwOmAB60AV/8AhXHia20C10W0vtMa00/Wl1KxNw8jMI1ZmEbEL6kdPU1qa54Y8ba7pEUM9/pAul1RL5SDKEiSMJsRMLn7wckn1q2154jh+Ic1lLrMR0yOx/tD7Mtmu7G4qY9+c9s7qwrfxp4lm0ez1iS5tlt9bsbua1ijgVjYyRIzoCc/vAVU5yBgjtnFAHR6xo3iu/1rw7qdvJoySacrtcJIZcO7qUcLgfdxyM8561Jc+F9Sm+J9r4njmsEs4bFrRk2N5zgtk5PTjsffpXP/AA78Za14i8QTWmqXOz7LpkUt1bNAq7ZmPDK46oUww/3/AGFNuvE/iS806XX9Lmk/s271NILaGOFHl+xxhg8sSNy7O2TjJO0DAPNAHqD7tjbCA2OCRkZrz9/AGsTaL4j06TW7ADWrg3LSJpzAxuWUkH978w2rgdMdfamWGta1rr6Hptnr8YlmtLq7uL6K0CmXy5VRE8tx8hBYbhjsQOoNM0XU9a1XX/Ck1zrMqx3umz3F1bWwjMEkkTRrlSVJ2t5hJwewxigCfW/h7qOq6brmm2+sWVjZ6mkMaRW+nbRCqHcw4cZ3En8z1rS1rwQuvNoi3tzbtBYiQXUC2g2XW9NrADPydzxkjjB4rnNY1PWYLjxS0OvXYjtNQ077L5YjwsU7IHT7pyP3hwevA/GbTbPxfD46TTrrxRNOsUC3s0LJH5bxtPKm0ERhgQgQ/wC8D2oA0rr4e3VxarGnie/glNkdPnmjijLXEA+6HJB+YZYb+vzH3zpN4G0san4evYWmh/sOEwQRo3yyJtAUP64IBHvXJyX+taNF45uzqd7cS6ICLBLiTeipJEsm5lGN5BORu6Diqviu/wBT03Ttb0vTfEN1LItpY3ttePcfOs01wYyAw/5ZsADs5HJxxxQB0z+AL5tcuNTXxXfxm4vUvJI44IlyUCqqbgM7dqKpGfmA5zVe2+GUlkulm28S3sM2nrOizJbwhnWXqD8vbtnOKPhpqM2qXXiOea41FmjvEhe2vZmf7NIsYMiJkn5d5bBGOMccCovie95BdeH3sLjUTPPcyQmzs9Ra1+0KIXfGR33KvbPbvQAsPwtdNHk0qXxLfSWpshZxIIY02AMjKx2gb2XywAWzgE+tb8Xguwt7jV7q1ury2vNWiiju7mBkVmMYI3gbcBmycnH5GuO1iS506XU7K+8SanaSaPpS3GmymdlN053lmkH/AC3KlUXac5zzknNZSTtB8Ubu4a6e1jW/tvtF094xRFktgXgaLOArOfvHhTjkcUAereHtDh8N6Jb6TbXNzPb267ImuXDMq9lyAOAOBWpXgWl6jeWninSrOS/tx4Wh8T3Edqy3bNIW/eCNH5JKgqCCTg7xnPb32gAooooAKKKKACiiigAooooAKKKKACiiigAooooAKrXVxNBLbLFZy3CyybJHRlHkrgnedxGRkAcZPPSrNFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFAGfr0c0vh3U47ckTPaSrGQcYYocc4OOfY1w3wJ/wCSUaf/ANdp/wD0Y1d9qsKXGj3sMgJjkt5EYAkZBUg8jkVwPwJ/5JRp/wD12n/9GNQB6TRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABSMu5GXJGRjI6ilooA4jTfh6YplfWdXfVRHYPp6M0AjkeJ8bvNbJ808cZ4GScE81PB4BjXQptLu9av7rMdvHbzsscb2wgbdFt2KASrc5bOe9dhRQBxkHw8ht7ObZq94NTlv/wC0f7RWGFZFm27CQoTbgqSCCCOSe5qOP4cRWdno8Gma1d2L6YZ3WWKCAmV5vvsyshXoSAAMAfQV29FAHFXXw8F7B5Fx4i1Z45bQWd4rNGwuowzsc7lO1iXPK4OBWxd+FrW61DSbxLu8tm0pClskLrtAI2kHcpLZAA5Pb15rdooA52fwhBceJxr7apqa3QQReUkqiIxg58srt5XJPXn3qpB8OtEtobiCGW+WB7eW2gi+0EraRyf6wQgj5c++fautooA4a98ANZ6TNF4evpYdQuLWLT5Lu6fe32dXJPQffCsVB7AD0zW/feE9G1DTdOsJ7VhBpzI9p5UrxNCyDapVkIIwK2qKAOam8A+HZtNgsGtJxFBJJIjpeTLKWk/1haQNvbdnnJOeKZd/Dzw1eLp6vZzxjToDbWvkXk0XlRnqBscde5PJ711FFAHNx+A/DkWoWN9HYMs9lFDFDieTbtiBEe5d2HK54LAn3q3H4V0mLxPL4jSGYapKgjeX7TJtZQMAFN23A+nXnrWzRQBzGm/D3wzpWr3Gq21hIb25R45pJ7mWbzFb7wYOxBzip4/A3heLSptMTQ7JbKd1klhEfDsvQn6dq6CigCpY6XY6Z5n2K1jg83bv2DG7aoRc/RVUfhUGqaBpOtS2kupWEF1JaP5lu0i5MbcHI/IflWlRQBQ1HQ9K1eW2l1HTrW7ktn3wtNEHMZ9Rn/PApr6Bo0s888mk2DzXClZ5GtkLSg9QxxyOB19K0aKAMlPC/h+MKE0LTFCuHULaRjDDoRx1961qKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAr3/wDyDrn/AK5P/I1598Cf+SUaf/12n/8ARjV6Df8A/IOuf+uT/wAjXn3wJ/5JRp//AF2n/wDRjUAek0UUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFAFXUlD6XdoSQGhcEqSD909COlcB8Cf+SUaf/12n/8ARjV3etXH2TQtRuSjP5VtJJsXGWwpOBmuE+BP/JKNP/67T/8AoxqAPSaKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooJABJOAOpNNR1kQOjBlPIIOQaAHUUUUAFFFFABRRRQAUVTv9X03SzGNQ1C0tDJnZ9omWPdjrjJ5q0jrIiujBkYAqynII9RQA6ik3LvCbhuIzjPOKWgAooooAKKKKACisfXfEdtoPkJJbXd3PMGZLe0QPJsXG58Ej5RkZ+oq4dUsxo51YTq9j5H2kSpyDHt3bh68UAXKK5xvGNpHfafbSafqca3vkhZ5bbZHG8oYqjFiPm+UggA4JAPJrW1PVINKhhkmDuZp47eOOPBZ3dgBgEjOMkn2BPagC7RXP2Pi/T795NkN1HAFneO4dBsnWF9shTBJ4PqAT2qbQvEtrr8k6QWt5btFHFMBcxbPMjkBKOvJ4O08HBGOQKANqiiigAooooAKKKKACiiigAooooAKKKKACiiigCvf/8AIOuf+uT/AMjXn3wJ/wCSUaf/ANdp/wD0Y1eg3/8AyDrn/rk/8jXn3wJ/5JRp/wD12n/9GNQB6TRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFUNS1rT9HezXULgQfbJxbwFlYhpDnCkgYGcHrgVfrjPiRo0uvaRpllHb3Msf9pRSTNbffiQBsuPcEg0AdBoviHS/EMVxJplw0y28phlLQvHtcdR8wGfwrTrx7VNP8bR+H7XT7jTZ7meW/uZ7+bTpNqzYQrH8okRtrsQ5wwwV6dqyn0LXruzsZtQ0LxPJfR2dtHceReGMSSIxV+koGDGF5AGT7kmgD3as/VtZtdGS0a53lru6itIUQZLO5wPwAyx9ApNeProfjy91LSJ7xNWDQ29mItjqoV4wvnCVvOGNzBjkq5YHoK9BsQfEvjefUZIlbTdEJtrJzj57ogiZx7KMIM991AFJ/izonlXjRWGrSPbeepU2u3e8IzIikkAsq5YjrgGu1sruO+sYLuMEJNGsig9QGGRn868m0LwNeS2fi25vtM1GPU5Lq/fTY5rhRD+/VlDKofG7BIJPYjFOg8Aa1aWd1aaNp0OlWt5oEMNxEtwBvvI5csCykn54yyl/Rh6YoA9ZjuYJoFnimjeFhlZFcFSPUHpUD6rp0dil8+oWq2b4C3BmURtnphs4NeU6j8PNQutDj+z+HbW3Q67b3y6QJ0KwQJGEkXd935yuSB6880av8P8AxJd3VxFaQQRaRbajcS2tgrw7XSZAN43xuowxfKsvAc7TwAQD2LqMiuV1DxsLDxLLow0W/nMXkF7iN4QgExIUgM4Y8q3ABPynitbw5Y3GmeHNOsLvb59tAsTbZjL90YHzlVJ4A5wK4zxH4P12/wDHcmv2dlp0wjjtxZvNqEsRikj3nc0axlX5k6E/w9Rk0Ad3Hq2mzOiRahau7yNEqrMpLOoyyjnkgckdqoab4v0HVtRl06z1O3e+ikkia334fMZw2B3A9RXO23hXWbXxzJr0dppJt5ruQNB5rARxlUH2hRsx57bSG7EBRnqTqeHdJ1/R7qaznfTpdM+1z3C3GXNxIsrM4UjopVmxnJyB0FAHTTTR28Ek0zqkUal3djgKAMkmmWd5b6hZw3dpMk9vMgeOVDlXU9CDVezOqNbXX25LMTedILcQsxUxZ/d78j72MZxx6U/SlvE0q1XUI7aO7WJRMlrnylbHITPO30oAt1wvjH4lWnhGXU7aW0M13bWkdzboGIE+5ipXO35SoG49fl54wa7qvM/HFje6pfazZvoV/ew3FmkNpcW1qr+RJtlVmO+VN3yzMBgcZ70AejWjyyWcD3ARZmjUyCMkqGxzjPOM0XZnFpMbXy/tAQmMS52bscZxziuMj8Va6l7aE+FtdNnHblJ4hawBnl+XDKfPOFwG49xyauyeML5onVPBviNWIIBMNuQD9POGaAM7w54/m1u70dZBYLDd6TJqFz5Mpd4GRlGwjtw69eeG4q1cfE7w/bac15ImogefHCsJs3WV/M3eW4UgHa21sE4zjFchY6dqtrb6ZbLpPiSMWWlz6WssNjbxuVk24k3faTtZSinp2NVB4K8U2139qh0iZrh5rWeSSNraIM8LSckb2yWWTBJP9MAHoNj8RNE1PSrnULKLUZ0geJPKSzcySeZ9xkXHKnnn2p0/j/TIDYp9i1SSW+tnuYYo7QliqHDg+jL3B/mQK8303wL4mtIYorzR9Ru44hAoi+2WixOIkZEEiHIcAEYz0IzzW3pujeJtMm0mSHw/qbf2ZDNbwqdQs1DRykEqdqjGCq4xjGKAN+9+KOjWhYpY6rcRJaR3zzRW3yLbOMiXJI49uvB44NduDkAjvXjr+GfFH2OW0Hh/Up4bnTV0q5M2qWgYwKXKsCE++N5HPBHXJ5retLj4mi70+WTR7ERRwmGeGbU0xI3aRisOQRg8Lwc9OKAPRCCQQDg+vpXl/gTxP4i1nWrGKbUZtQt9l0uoh9PEMcDJIViKSAAMWxyBuxz+HT/bfHf/AEA9A/8ABrL/APGKx/DeleNPDOl/YLbTNJni3vJmfVXyCzFj922Hdu+aAPQq47x5rt3oV14blga+aCfUhDcW9lEskky+W7AAEZxlRnGOM1Dpkfj3TYJY2sNKuzJM82+51iViu452r+44UdAKW/0bxF4hn02bVbDTLd9OuhdW/wBn1CRhvAOCcwjPcY9zQBTXxjP4f8IwahPHdX811eXKoNSnjtnjCyOAjfLwcKAAFPJxxkVo6j4w1I3OlW+h6RDfHVrFry0lluvKX5dhIYFcgYkUg9T0wKpXPgvU5I1aE2gulecrNNe3LfLM26RCEKEqSAQM8ED8a8Hg3xPbS6fJDNoSNp8Xk2uHvv3UZxlQPP5HyqMHsAOgoAv2/jy9l1+/01tB/d2GowWNxNHdbivnfckC7B8uSuecjPel0vx+2q+Jl0q3012hlkuIkuF8zEbRFl/eEoFAYo2NrEjjI5rFh8AeJ08RXutzXehXFxdXUV35ckVyIo5Y12qwQSAEjr82cHpitGy8FavFqS38zaGs/wBpafCR3TIjN950jabar5zyAOp9TQBq+Ftc1/XZZJbux063s7eWa0maOd2kaaJyjFAVA2ZHGTnjpXVZzXFaf4Iv9EE/9h6vbWD3DbpmNrNPubOScSzsASSckdc81FpHgzxNodrLbWPi+BYZJ5Lgq+lBtrO25sZl4GSTj3oAteP47n7Pok9q14WXVIY5YrW8MBljfKsp+ZQ3O36Yz61p+EtP1LS9D+z6rcPLL58rxiW4ad44mYlEaRuWIBxnn61z2s+BNd8QxQR6r4lsrlLeUTRBtJ27XHQ8SiptQ8G+ItVtIrW+8T2U9vFIkqRtpAwGQ5U8S84I6GgDuK8V1qx15PFlpEJg3hmbxMkrDzmDrKWCmLGeVJy+OmfTv2914b8a3KgL48W3x3h0ePJ/76c1hQ/CK5kkmOo+KWuUluftbhNJtULTc/Ocq2W5649fWgC7a+NdTufHEOlmeyOmX091b2sqQMrAxLncHZsSfMCpAQAEYDHFP8IXviPXbC+vrrxHbSwQNdWUaW9sm5njcqs7Hs2BnaPlxg96tf8ACv5/tRuv+EnvvtJJYzfYLLfk9Tu8jPNOtPANzYOz2Xim/tmYYLQWNkhI9DiAUAc/4duL3UPhTczXXjCK+lfSEd45Y4na2+TLCQ5y2RlSX579abbeIbg+C/BH9h63YWAvHh0+4it4UdUZ4ycgNyrKV6d93OeK6Bfh/OkU8SeJ75YpzmZBYWQWU+rDyPm/Gp7DwFHZnEmsXMyK4kRPsdpGEkH8Y2wj5uOtAHPah4x1cmz0q11W2S7WG9WW8PkxiSeGTy1Qh/lXqHZRzg8YFS614rvYtbtLVPE9tYNJbwXVzH5CNHbxdHALDdI7sQEUYwASe1dcnhhYs+Vq2oR7pDK/l+Su9z1ZsR/MT7+1Un8DRySM7eJPEuWJPGpMAM+gA4oA6qioraH7NawwCSSQRoE3ytudsDGWPcnualoAKKKKAOQ8d3EdrN4auJlkMMGrCaUxxNIVQQTAnCgnqwH4iuF1bVNW07whY21vFqdmXF5eWXlJNGoXzmMERESFtwQghG2p0DZ7e00UAeVawltd+I9A8Q3zeIPs9zpDxj7CLiKR598TBDHHym4buDhTgc8CrMNxrUnxHukv5dUhMV3GbKKGOZoJbUqoOcER8EncXyQenQCvTKKAMm1Np/wk+oLGl4Lv7PCZWff5JXL7dmfl3dc7fbNa1FFACEgdSB9aqXOrabZE/atQtIMEA+bMq4JGR1NRavoOk6/BHBq+n297FG29EnQMFbGMjPsayP8AhW/gr/oV9K/8BloAzPGGpaLdww3djqkT6nHHLbwyWl/bpsWUAMHMhI25CkkAsNvHoc68vNAksfDvguLxFYC0tYYZb1/tCESQwbQqbsgZZwvvhW4rqrXwF4RspfNt/Delo+NufsqHj8RU0fg3wxDPLNH4e0sSS43t9lTnHTtQByPjDWtP1bVNNjsJLf7VZ3Ec1tqv9p24gt8nEhMZk3P8m4Y2nr1FaEHiLQtZ8aSX02sWC2ejqbe1El1GBJO6gySKM9ApCA/7T49+k/4Rfw9/0AtM/wDASP8Awo/4Rfw//wBALTP/AAEj/wAKAON0e40XT/Ect7Bf2dvp1nBcRW1tLqcUhlkkkDl4xvKop28ZOTv5wBy/wZ4ms3vdRvtaW20/Ur0hpp5NSt3jZVLCONAsrEbVPJwMkk966/8A4Rfw9/0AtM/8BI/8KP8AhF/D3/QC0z/wEj/woAcPEmhMMrrWnEeouk/xqzY6pYamJjYXkF0IX8uQwyBwrYBwSO+CD+NPtrCys4BBa2kEEQJIjijCqM9eAKnChRhQAPYUALRRRQAUUUUAFFFFABRRRQAUUUUAFFFFAFe//wCQdc/9cn/ka8++BP8AySjT/wDrtP8A+jGr0DUWVNMu2YhVELkknAA2mvP/AIE/8ko0/wD67T/+jGoA9JooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKZFDHAmyKNI1yW2ooAyTkn6kkn8afRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQBW1ABtNulYAgwuCD34Nef/AAJ/5JRp/wD12n/9GNXoN/8A8g65/wCuT/yNeffAn/klGn/9dp//AEY1AHpNFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUU2SRIYnlldUjRSzMxwFA6kmgB1FUdK1nTdcs/telX1veW4YoZIHDKGHUZHfkVeoAKKKKACiiqFhrNhqd5f2lnOZJrCUQ3K+WwCORnGSMHgjpnrQBfoopCQOpxQAtFIWVVLFgFHJJPArmF+IXhw6bcXr3jxrBZrevHJCyv5LHCsoIw2TwME8ketAHUUVHFKJYo3wyF1DBHGGGR0I9aeHUnAYE/WgBaKjS4gklliSaNpIseYqsCUyMjI7cVXh1bTri3kuINQtZYIlLSSJMrKgGckkHAHB/I0AXKKpPrGmxw2szX9sIruQR27+aCsrHOAp7ng9PSq6eJdEk0xdSTVbRrFpfIFwJQUMmdu0H1zxQBq0UUUAFFcyfFU6/ERPCh0vCNZG9F59oH3Adv3Mf3uOvvXTUAFFZXiLW4/D2jvqEkXmKJEj5fYil2Chnb+FQTy3OBTtC1K61Wwe5urKK2/essRiuVnSaMdJFYAcH0IzQBp0UVwN7431a1uvFdsLbTRcaQA1pA8kgkuh5fm9MY+4GHGfmU545oA76iudtNeu5vE9to00MEcv9nC7uhiQFXJUYQldrLknvmpoPF2i3OsJpUN1K148ssKL9mlCs8X+sAfbt+XvzQBuUVyzeP9FVNQcx6gFsrYXb7rKRS8JOC6AgEgEHPAxg9qd/wnujAXPmLeRSQ+Tsilt2V5xMxWIxg9dxU4zjGOcUAdPRXMeENf1HXLnxBFqNqtsbDUmtoY9m1/K2KyluSCSGzkcdK6egAooooAKKKKACiiigAooooAKKKKACisLxmzJ4N1aRZZ4mjt2kD28xicFeeHBGOnqK4S01jUofDetWMMl+t5caqmnWFnd3pe4tyUViJJskgMA7BlZsBhg+gB6xRXlb6va+IJvDmmW17q1qtrqMum34+3ukm8W0rMjOr7mKsi4c9exPNdb4B1i91vwyLq9PmFbiWGC527ftMKsQkvb7w7jg9RQB09FeV67ravqXi5Nb1K+05rEQx2SWVyUdISM+eqb13ks2D16AYznPQW2v6rceO7rSDq2ixWkHlSC3dCbpw6sTHgSYDDbnODwelAHaUV5voXj7VNamtlCWSXF4L1TYIpaaxMOQrSfN8wLKBjC8uMH1rah8TZZbK7uNHv8AT3kh0Aan5D27MwlDYdGIcY9NvUck0Aeo0Vx+j+IbnVf7fhOqWhtbSCJ4NVgiAjUujMxOWKnZgE89+a6fTpRNplpKt2t2HhRhcqABNlR84A4GevHrQBZooooAjSeGSRo0ljZ1+8oYEj8KRLq3kuZbZJ4muIgrSRK4LIDnBI6jODj6VwsGqeG/Dni/xRdRrA1zsgaaKxtA0287ywIQZYkkMSfXnpUujTCx8d+KwGknluBA1sZYgpdwsm6MOFGVXCjknGetAHdUV5fpep+JZNG1e9tNW1C+1ddMDPpt3prRLb3fcRuUVWA5AUFskZyap3V/rw8E6lewa9rDrHdW/wBkdLZ2uMFtsqtutk3LgkjC8bRz2IB65RXm97P4ijtdV0uwv78yWepW5iuriF3aeBoVdlLRxkgbtw3KpI4BxnNRu3iPUfDugR3b6tZMftBu5AJDMJFI8osIhu2kbiAQAcDcD0IB6ZRXmmtR+K7vULGOa5uIIo9PV4bq0SRd95n5vNjjkxjgEK5KcnJ9PRIbhXgjeRlR2UFlJAIOOR1P8zQBPRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAV7/8A5B1z/wBcn/ka8++BP/JKNP8A+u0//oxq9Bv/APkHXP8A1yf+Rrz74E/8ko0//rtP/wCjGoA9JooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACsDxtbwXng7Ura6tb66gmjEckViMzbSwBKjvjqRg5AIwelb9FAHk2jvrtjaxap9kv/sVprG6Y29g9tcahA0OwySWygbir7OQOQpIHAzj3Mk9zDoiaz/wlccTahfwT20QnEs8R8yaFlVfmbAMYz22kHpXuNZ9/oWl6pfWV7fWUc9zYsXtpHzmJjjJH5D8qAPI9btfHZt9AVlvjjTVEckKyySQ3QZipkVHVd+zYMyZTIbPXNb9/4ekvfiBG+oWGvz6fcWcKTyW108UH2nkF2VZQQAu37mRnPXk16bRQB53a+DL2x8Y2trCJpNBhuG1ETzXcjOjbNgt+Wyw3ASfMSMDFXNJlnS88QWUfhvWrOG9eSVJ3MYUkRKhwfMYqSV+XjHI6V3FFAHk2k+GvFg0PVrTy5QkkdqImuZBBLOIpD5kZCSOFLrkeYCCdw47ifW/B2qahoGsQjSHlWfU4LnTrKS5TfaqmzzG37vk3BXACk43e5x6lRQBwmqWsLWlj4R0exOltqcjT30SMFaG1DDzWLIT8z8ICD/ETnisvxD4Ek1XxJq12dCWa3t9Mhh0rbcoitKiyDaVzwB5gIzxmMV6dgZzgZ6ZpaAPMtQ8LeKdT8UQeIFtdPtpBc2sphacFxDGAWjZ/LbDbiw+QqpB5zmn6d4AvdKvUu7Cy023nXX5L8SpKdwtXQqY87M9/u5x716VRQB5KnhbX/D9rq2pXNpZeQdEuoJ4tPb5pJWYuGSNY14HIG4kjJ5Peno/hVb7wxqHh/TXsjqbJa3VxeW7ZgkaPYBCSqAKrCPOPmOSSRk17NRQB5qfA2sw+A59Gt4dOeebUorzyJrmRo0RZEdlLlPmyUxwij5jx69bc2epJ4fsodO07SIruOSJ3tpMm3iwwL7CFByOSpwOea3aKACkPQ9fwpaKAPLdMuNYg8Xt4g1Tw94gvLiOx/s+Ax2cEZMe/eWf9+QXJ9ABgdBnFbtl4t1uOW7N74U16aN5i1ssdtApjjwMKx875jnPPHWu1ooA4XWtf1bVtONnZeHfEunzu6ETm1tpFwGBKspm5UjgjI4NO0ay1XRfDdxp9hp+oRXcsskv2lorYRpIx5KQibATjhc+9dxRQBg3Gsa1DaKbfwzeXNwMAh7i3iDepz5hx9K4bXPDuoeINfXWb3wPfC6WOOMCHWYY1IRiecHncCUOf4emOter0UAecTr4sl8Upr6eG7+GZbf7N5K6haGMx7gxByM5JHXNUNJ0jxfba3LqH/CPLHc3l7JNO9xewNHFE5wyRlBvU7VXkdWyTnNerUUAeaweAry1guo47Tc11ZyWErm+RSYH3Zztg+ZhuJDHk4GSaW58MeI57nzf7G0x3SCC3jmbWJFcCBi0UnFvgOCzcjjkjBFek0UAef6PpfjHRLrULmDS9Mnm1CUTXDXOtSvlwu3IAtwBwAOOwHpWv9t8d/wDQD0D/AMGsv/xiupooA5Ca7+IjPGYNI8NoozvD6hM5bjjBEQxz9c+3Wqtu/wAUnlC3EfhGKPuyG4c/lx/Ou5ooA5XyvH//AD9+Gf8AwFn/APjlHleP/wDn78M/+As//wAcrqqKAOMu7L4jXGzydZ8PWu3OfLspW3f99OaS00f4gszfbPFmloMfL5Ol7s/XLiu0ooA5T+xfGX/Q42v/AIJ1/wDjldFp8N3BYQxX10t3cqMSTrF5Yc+u3Jx+dWaKACiiigCtqGn2eq2Mtlf20VzaygCSKVdysAc8j6gVWn8PaNdWTWc+l2clu8SwtG0KkGNfuqeOgwMDtWlRQBlReGNBgt0t49F05YU+6gtkwOMenpWmiJHGscaqqKAFVRgADsBTqKAK02n2VxdRXU9nby3EP+rleJWdPoSMimf2Tpv2/wC3/wBn2n2zOftHkr5mcYzuxnpxVyigCGO0tobiW4it4kmmx5sioAz44G49Tj3qrqmjWWr6Re6Zcx7be8jaOby/lYhhgnPr71oUUAQw26xWi27s0yhdrNIAS/1wAP0qSONIYkiiRUjRQqoowFA6ADsKdRQAVzl74G0HUL2a7uIb0zTNvcpqVygz7KsgA+gFdHRQByw+HfhtSSINQBPXGq3X/wAco/4V54cxjydQx/2Frr/47XU0UAYsXhPRYUCLZlgMAb5pHPAA6lie39epqT/hGdHzn7EufXe3+Na1FAHO3PgLwpey+bd6BY3EmNu+aLe2PTJqH/hW/gv/AKFfS/8AwHWuoooAwrLwX4X04OLTw/psQfBbFsnOPqKtf8I5of8A0BtO/wDAVP8ACtOigBFVUUKqhVUYAAwAKWiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAr3/8AyDrn/rk/8jXn3wJ/5JRp/wD12n/9GNXoN/8A8g65/wCuT/yNeffAn/klGn/9dp//AEY1AHpNFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFQ3V5bWMPnXdxFbxbgu+Vwi5JwBk9yeKAJqKKiubq3sraS5up4oIIxueWVwqqPUk8CgCWikLAYyRz0oJAIBIyegoAWiiqs+o2dtfWtlNcIlzdlhBET80m0bmx9BzQBaooooAKKKKACiiigAooooAKKKKACiiigAooooAr3/APyDrn/rk/8AI1598Cf+SUaf/wBdp/8A0Y1eg3//ACDrn/rk/wDI1598Cf8AklGn/wDXaf8A9GNQB6TRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFBIAJJwB1NFZ3iCOGXw3qkdyZRA9pKshhGXClDnaPXHSgCey1Kw1FXaxvba6CHDmCVX2n3weKtV4/4VdtP0nUrjRDm3026sjLeafYGL+0bdVxIhifOGVSSSmCcDv1nuPFHiIafq1xBPqTxnWoV09DaCOa5tHUErDuTDDOTuwSFUnjrQB6zRXkGqeItdfQtC06x1a51DVZ5bmK++yIUlikQAgtiPKrGWQEbRuBHrgrq+o+KbiSxm0rU9SurVbJRbXdpbM6zXiyMsoljCAAcbQHKqOuQc0AevU1XRmZVZSyHDAHkHGefwrzi/1DXW+IMMMcOtzW/2i3Xy0gkgghXbmRhIMxyJ1yHw2eFPHN/Q7CbTPG2t/aLDWZDdXyywXIuHa3EJgUDdl8HDK4xgkbl7YwAdfZ6pZahNdw2lyk0lnN5Fwq/8s3wDtP4EVbrg7KHVIdN8VafptnqUDTGSXTZLl2zloVBxIzMQfM3EZ6fSsKfSNaGg6i2n2GvwQJNZSWdrNeM1wZFfNwwbzOFKEjBONwJGOKAPWaK89tNLlstL8WaVPourXulvIktlbG6ctNG0Ue6NZGfcpEgYnJGM8Z6V38P+oj+Ur8o+UnJHHTNAD6KKKAOe0bxppGt3jWcLXFvc+ZLGsV1A0RkMTbX2k8Ng8EA54PFX9K1u01lr8WolxZXT2kjSJtBdcbtp7jnGa4vw/oGvvrFqNS0sWNrZare6ok32hJPOMxkCxhVORgSkkn+771Fo2k+Io9A8S6Nc+FYoLfUJLmaBRqEaqVlIHlfICVOC3zAY4FAHpDzRRxPK8iLGgJZ2YAKB1JPaoJdTsIbFb6W+to7RwCs7SqIyD0w2cc159Y+BtWh8P3dkbbTVH2u2mjtZdu26jhA+SZkjCjJAIYITgLnvVmXwfqLWGnvHomiI1peT3DaSbl3tZTIuN+4x8MCWIATHPGKAO1udY0uzdkutSs4GVQxWWdVIBzg8nocH8qr3HiXRbTU00+41O0iuXhMwV5lGFBUZOT33DHrzXGWXgHU7K80gyJpl2lrpt5aSyys27MrZjRQVYmNAAgy2drH6G9pfhfXtOj0K736fLqNnpP8AZlws0jshwVIkDbcsfkGQQOvXigDpRrtu3iOXRkUNJDai5mlEseIstgKy7twJ65xjHenDxFohhllXWLBo4o2lkZblCFQdWOD0HrWcdG1VPHTa5E9kbSSzjs3ibd5mFcvuB6Z+YjH05rGh8AXI06zsZbi2WCO9vpZkhDKHhuVlBQehXzeO3yigDrv7b0vMw/tC2zBbrcy/vB8kRyQ59FODz7U/TdW0/WLb7Rp15BdQg4LROGAPofSuRbwPq93po0++1yEwixSy8yG2ZJD5bhkckP3wAwH4EZzW54Y8PyaHHeSXEkEl1eyiadofNIL7QucyO7HgDuPpQBp3+p2WlxJJe3McCyNsTeeWbBOAO5wCfwqhfeLdB06G1ludTgEd0oeFkzJuQ/xnaDhPVzhR3NO1bRHv9S07Ura6W3vLDzBGZIvMRlkUBgVBU9lIIPbvmsDUvAV3f25RNaigefTG0u8ZLBQskRYkbFDARkbmHfqPSgDob/xNpGm39vY3V3tuLjbsVY3cAMcKWZQQgJ4BYgHnHSse08Rav/ws+68NXkNl9i/s37fbSw7vMx5uzD54z7D0684GbrPw2utQ+yxWfiOa2tLNLZLWGWAyiLydpGAHVTkopJKk8HBAOK15vDOry+MLTXhr0SpBb/ZjbixHzxkozjdv4JZBg4496AOmlkEMLylXYIpYhFLMcegHJPtXL6X8Q9C1a0nvIftkdnb27Tz3M1q6xRbSdyM2Mbxjp/XiuqYMUIU7WI4OM4NcbpHga5tfCV74Z1TWvt2nXEDwp5VqIHjDlixzubJy3HHGKAJ7/wAfWNp4Vv8AXI7DUJDZOsctm9u0UyuxXaCG7EMpzyMH14p174+0zTNEi1PULPUrNZZzBHb3FtsmZgu4kKTyMA8+1Oi8FW48O6ho1zfTzw3gHziGGExkAYZRGignIB5B5HpxTNR8ELq1haR32sXVxe2ru0d7Nb27vtcAMm0xlMcL/DnjrQBDJ8StG3QfZ7XU7uOeyN9HLbWpZGhABZs5/hyAR1BOOtLN44lfxBb6dpmg32owzWKXyzwvEgaNyArAO6nHXPGc9qll8CWzPaNFqV7B5FnPZMI1iAljmOWyNmBhgCNoGMelPi8FQ26aYbbVtQgmsrNbFp4igeeBeitlcDB7rg+9AD7TUNVuPH19aSGW30y1s0ZYZYEIndmb94kgYnA24KkD171TtfiHaXcUk0elX4heKaWxkbywL9Yid3l/PxwNw3bcjkZrXbw+7eIW1f8Ate/DEKn2cGPyvLHJTG3JBPOScjkAgHFVLTwNpFkoSF7vyo45o7WJpty2qyjD+UCOOOBnOBwMDNADvD3i+DX7mKAWF1ZvPZR39uLjYfNhY43Daxxg44OD8w98aGvazHoGkvfywSTKronlxsqklmC9WIHfPXoKr6b4XsNKurG4t3nL2VgNPj3uCDCCCAeOSMDmpdS0/TPEtqLeScv9nnWVXtp9rxSKeCCp4PUUAYUPxBS/s9Km0zSLi7bVJLiG2AmjVd8RcNubJ+UhCQwzwRx2qvqHxMt7Pw5p+rxaa8n2uOWVoZLmOMxJGcPyTyeDgDrjkit208HaHYm3NtbTIba5e7iP2qUlJXBDnJbo2TkdDk8c1lXvhjwNazQaVdmC2mvIWtY7ZtQkje4jZyxTG8FxuY4HOMnFAFnV7i7tvHfhpYb24W2vhcJPbEgxtsi3KcYyDn0NNPjC6TW10V9Nt/7SN4kX2dbwk/Z2Qt9oGUGVG1hj1GM9K0Z/Cmk3NxYTypdtLYAC1b7bMDHxt7PySOCTnPfNZun3ekaj44luJNb0m51K3he1t7K2lRpYV3ZkLfxbjtUEYwu0+poAkg8ZhtV1G0uLBrdbMXBXzJMSzCLacqhUAqwbIKsenOKzNH+Ic+saXqd7baPNN5Fst1apGsieaGztjJkRRv6fdLA54J77+meDtB0e6kubOxKyOHH72aSVVDnLbVdiFyeu0DNFr4N8PWVtdW0GlwiC6UJLE5Z12A5CKGJCrnnauBntQBD4N8QXPiHS5pr1bWO6im2PDb+YCg2ggMsiqynJPbBABBINM8T+Ir3TNT0rSNLt7eS/1Ayssl4zJAiRpubcygnPTAx61tafpOn6UJvsNpFAZ38yUovMjYxlj1JwB1pmsaXpWsWQtNYtLa6ti6kR3Chl3dB178/rQBxMPj3WtVe1fSLDTVgm0htTJvJ2UjaxRlBAxjIGGPbn2rvbC6F9p1tdhdgniSULnONwBxn8ayNW0/wzbT2E2pWVoJSPsFoTDuIDgr5agDgEEj0xWzaWlvY2kNpawpDbwoI440GFRQMAAelAHIWVnbaf8XL37ODH9r0lZ5lMjENIZiN2CcA4AHFQaHeTWHiXxxJcSreXVsIZwkTOu9fJyqhCzY6YyByc+wHXNoulvetevp1o10zBzO0Kl9wAAO7GcjA/Klt9I0y0uTc22nWkM5yDLHAqsc9eQM0Acdc+L9RtvBuq6zbalo2q3ENrFNBDaK37pmOG3gvkqMggnaeDnFUpfGuuNodlctNYWLyaxHZPPKI5EMLqfmIjlZVIP+32Hriu9sbPSkSeSwtrNUnZhM0EagSMCQ27HUg7gc9805tJ057JLJ9PtWtIyCkBhUxqR0wuMCgDzvVfE3iKy0cWsOs2M97a6jNBdzw+Stw0KjKlI5GWPf8AMoYZHsDUV9421p7LRFttQhtZptJ/tBp7qGOFLl8gbGV2+Qd22En5hivRbmXSNFiM1ybSzS4nALMFQSSucDPqxpt9q9laCx3Brj7ZMsMIgUP1/i9lHc9qAON1jxVq6eIEit7qGzgiS0fypjGsd0JGzIVZvnYAfKNg+91r0SopZreMgyyRIQQAXYDk9Pzps17aW8ixz3MMTsMhXkCk/gaAPPdN8T6prOt3VhaazvlkS68o29ujxwD/AJYmRWUSRsMEEOCrEHBHFc94z8RazrHh24t7Y3jmbRI7mS1+xENBeJPDwCF+9jeSuTjbmvacAZOAKx9C8SWniD+0JLRR9ms7hrfzxNG6SlQCSNjHA574PtQBwV5rGuKPstpqeqT6empWkYvhCDKQ8UhkjJCcqGEfzY434zxxn/8ACQarqPw71x7281BtQEEE1sn2Z1k+0PCC8YXbyglDYGOMcnGK9X0zW9K1pJH0rUrS+SJtsjW0yyBD6HaTik1TXdI0QRHVdUs7ESkiM3M6x78dcbiM4yPzoA5Dxnc21/beHdYhuNQ+x2mqAXD2iS/IvlyAsUVSThtoBwfvccGs7xJDavqfhTVHPiVtLW1uYvMtmuBNuPlmLeF+cF8MOevGenHc3finQbHSY9VudXs0sJGKxz+aCrkEghSOpGDnHTB9Ko61488P6Dc6dDe3bEaghlhkhjMieWFzvJXPyngAjPLDtzQBzE+peI2+IcqvFqMNqJbd7QRRSsktuwXzVZf9WCGzlmII3cdOY1tdUTxxo99f22t3d7bancxylUc2i28iyCJ15CKArICR83BzXpsUqTwpLGco6hlOMZB5FPoAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAK9//wAg65/65P8AyNeffAn/AJJRp/8A12n/APRjV6Df/wDIOuf+uT/yNeffAn/klGn/APXaf/0Y1AHpNFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFZmtaBp+vwRRX8TkwyebDLDK0UkTYxlXUhl4JHB5FadFAHOSeBtEktoIQt7G8O/FxFfTJO4Y5YPKG3sCQDgk9B6VsaZplno+mwafYQLBawLtjjXsP6knJJPUnNW6KACiiigAooooAKKKKACiiigDm7Dxrp2o3n2eO2voy9xPaQvNEEWaaLO9Fycg4VsbgAdp9KZB40gms7nUH0nUrfTbSKd7m6njVRGYidy7d25vutyoI461keE/Bl9Z67qd/rM9wyR6vdXmm2wlRoUWXP7wADcGwzggnHzZxnmt2y8JxwWGpWF7ql/qVpqAkWSG5MYVRIWL7diKRncepPtQBGfGlmIrsGxvlu4PJC2jIvmSmbPlbSGK4YgjJIAIOcYrP8LeK9Rvb28s9Ys5opzqslnCm1MwqLdJgHKMQerYIJ7ZxWivgnS/sN3bSS30rXSwq9w9y3nKIeY9rjBG08/Uk9zVW38GaBd2VzHb395O73oupLuO/ZpknVNmQ4OVO35TjHBxQAlt48W/tIPsGjXlzqEnns9irxh4kikaJmZi23l1wACSc+gJFjVtd16DWbCy0nRrS6E9q9zKtze+Q6YKjAAVum8fX8KYvw90KGzitrb7da+TJI8UsF5IkqLIdzoHzu2FuSuevPWrd94O0e/tLC1dLmKGyVkiWC6kjJRgNyMQcspwM5PagDf7VyVl4zmuvF91okumLaxQ+b5cs9yFlmCBcuse3BQ5IDBj05Arq40WKNY0UKigKoHYCsKDw74bsNXMiwQi+uPNZY5p2fO8kyFEZiBnnO0DjI6UAYlj8QLq/tb+ZNEVGt7ZLmNXuTh1LlcbwhQ4UbsoXHOM06XxxqkFtLJNodskkd3DamP7cT/rLh7cNny/7ybseh9eKuXvhDwbpemXE19aw2tksRilllupEVUZgcFi3AyBj06Dg4qvrXw+0680q6TRo4bW8uZ4p3lnMkySbJhNhl3cgkHoR1NAGT4q1K61z4deJZpzcaZqehyypvsLx1VpERXDAjaSpDj5WH8ga6DxP4l1DSLmzs9LsY7u6khe5ZJDJ8yJtBVdisQxLD5iMDvWp/wjejyaYLC40yze3ZvMkiEQ8tnIwSQeuffNOuPDeiXcFvDcaVaTR24YQrJEG8sN94DPQHv60Acx4i8b6hp8MFxY21nHbNZxXUsl2zvsMjAKjiMExjBPzt8pxx0Nd0WUMFJG49Bnk1mT+G9EuruO7n0mykuI0WNJHhUkKpyq9OgPIHarcmn2c1/DfyWsL3cCskU7IC6K33gD1ANAFmkJwCQM0B1LMoYFl6gHkUjuI42chiFBJCgk/gByaAPLb64vbz4a6Zq0V/LZatquqWkk0yysPJkeZUKYz91B8pX/AGTkZzT9P8UTafaPv3aSbrWms7qbUZmmjsmW3VmALNjazgheQPnBx2rqtBk8Pa3pV9qFrA8trLdySTwXkJ/dTKNrjy2HyngkgDkknqTWvZyadrmjxXEdustndqJNk0G3cOMblYdRgdR2oA4G48W6lcxeDb+51eDS7O+kuRcTrCRBKygiIkvjarAFgCR25OKdrXxHu9M1K2gtEgvbZrSG5juRJGi3YZyrbVLbzjAwI1dsnp0z6NPZ21zb/Z57eGWHj93IgZeOnB4oktLaaWKWW3ieSHmJ2QEp/unt+FAGc1+n/CSWcH9qogntGdNPaIB5MEfvMnkYHGPetemeVH5wl2J5oXaHx82OuM+lCyxtK8SyIZEALoGGVz0yO2cGgDE8arqD+C9XXShMb9rZhCIM793+zjnP0rkZdV0ix0q7ufBFp9jtxPZx3t9Z2PyLGZCJCFK/M6LncSpxkZ5HHo8dxBK8qxzRu0R2yBWBKHrg+hplrfWd8rNaXcFwFOGMMgfH1xQB5xfa5rT+CybS81W5D6g8dvfpbiGSW2Vd2WIjfGeVV1TLELwM1VuNburzwR4Qv9Ytb+TUl1SKW4I0+VpESKQ7iQqcfLt7Dd2HWvWaKAIra4ju7WK5h3eXKgddyFTg+oOCD7GvJFtvL8VXt/JDdzafZ+IDdyLBpkqyozRhRIHZcvGCrhlQE9DkgjPoGr+LbXSLq6ia0ubiOxtxdXs0GwrbRknBYFgScKzYAJwp9s2D4o0Yas+lm+jF4sccnltkZEmdnPqcfyoA5XQovEreKJJtTmvITLc3Ec9ukMjwNDg+UyyFgiYAH3RuJPzc9KGnaFqWleG9YttFg1uHxB5d0IpLq6kkhH74lShc7NzKQQQCRzuOeT2Gg+LbPWJJ7WZ7e11CG6mtja+eHZjE20leASO/TpWj/bulZulF/blrVd06q4JjGSMkDnqCPwoA4BLTVU8LTbP+EjcpeWk0Uf72OZcsvnLuZ3dhtLEg/LkfL7WJdJvbyy1LT30rU7u1s9fhuLZJrlkeSEFCzI7MMqrbyoz0A7nNdppXiDS9bJ/s27FwBEkpKowAVs45Ixng5HUdwKg8S6+PD1raTtDE6XF0ls0k03lRQ7gxDu+DgZAXp1YUAY+t2d9dWehPZaTqSGz1BJXh+0IW8pG535lw2eCOWPHaqPiPS/El9e6jc2MV8s9xb240x0u1iSykViXMq7sNyQTgPkDbnpWg/jyIWXhqUWBjl18kQC5nWJIyF3AM3JO7+HC85HTIp2oeJ9Ws7vxHD9isI006GOa0kuLhkFzuVmYH5eMBH6Z5H1wAY99outJqd/dWdhqbXCaray20329Sht/3XnhUMnyg7ZPlI5yOnb0aoLWWWSxglnRVlaNWkWMlgGxkgcZI/CsCPxjYaqz2WkXDJfSxyC1lu7KZYXkXO5eQuSuMlQQcUAc9b+GtUTw3q2i2GhW2lXgjmSHU45EH2jMm5QNuXAZeCTjHYHtEnh/xC3hHVLJ7C7QXdzE8dsk9vG0CqQWCIoMZT5V+Vj84Zt2DnOt4e+IdtqHhWPUtRtrqK6jsEvJ0is5Asi4G5oc/fVSRkgnGa0ovHGjS2t1dA3K21tbQ3LzNAQpWVQ0YU92IYcDpQBzsnhHUdS8EWlpd6PpwuYNVS++xOFVHjEmSrY3IHZSQdvy8kDitS+0e5aw0VrLwrpkVzZXfmJGkyKLWMPk+WwTguAMgADsSeps6/wCK5rDwdqOs2NhcCa13qY7mAjyyv3nZdwJUDJ4PPatHVPEVrpL20MkN3czzxPMkdpbtIdiAFmIHQcgepJAGTQBx/ijwRd67f65cR6VYZ1HR44oZJWXfBdoXOfu+jqN4OflFc54lmhk+IEl1qek2d4bK4ssWZKG4eQxHcI8oWljG/dgYBaMnjHPoWtePtH0S2tbi4S6eK5tvtYZYwu2HjLEMQcjcPlGW56VJJqGow/EW0083avpt3ps04g8oAo8bxLnf1ORIePagDpa4nRtB1mzg8Sxtp2lwR6rcyzxxC5cqpMSxgMFQcNs3Eg5G49TzXbUUAcp4K8N6j4cS7ivLiB7ZxEttDGd5iCqQQZCqsw6BQc4A6kk1P4v8P3WvLo5tBZb7HUortjdAn5EzkLgHk9K6SigDgrfwTqtvql1fLdac7C9upbWGeFpIxFcFS+4ZGHG3AxxgsD97Is2fgi80u38Nf2fq0az6LbzW5M1tuSdZAuflDArgqpGD0GK7SigCO3WZLaJbiRZZggEjqm0M2OSBk4Htk1JRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAV7//AJB1z/1yf+Rrz74E/wDJKNP/AOu0/wD6MavQb/8A5B1z/wBcn/ka8++BP/JKNP8A+u0//oxqAPSaKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooA85sfF+uDxiNPvLjT5YG1aXTfs0FuwkVFh84TZ3k4+ZVIxgZzmovC3ju+126nguNRsbd7q2mkhR44xJYSIfuyIJSzADJJYR/c967TR/Dtpot7qd3DLLNNqNy1zK8wUlSQBtUhQdoCrgHPStAWdoHmYW0O6UYlIQZcf7Xr+NAHnXhrX9Q1nwPfa5f8AjTTkElqIvkgiVbKXJG5yWOWbjg4HIwKqaW0Oh+B7CbRNctyt7dQRahqtrb25+xJ5ecMsabSd2Fy4JHmZOcCvTlsLFYXhS0txExy6CNdpPuKfbwW1vGVtoookJyRGoUE/hQB5pf8AirWD4d8NX7a9HYve6jLZTTpaDypYdzqs4VxlThFI52/Pk7hVDxH4i1rRvENxp6+Mbtkt7SF0As4GaaVkmbHEf+xF04+evWZry1t2jWa5hjaUlYw8gBcgZIGevFRHVtNW2guW1C0EFwwWGUzLtkJ6BTnBP0oA84tPGmsahq1gpujb+aLOSOBYSwuoWRGmdUEZY/MzrncAuzJ71JPc6q/jPQ7jUotSmlt9auUMEVnmKC3aKRInDqnKkMhJLHGTxxgd9Jr+jQ3DW8urWCTq21omuUDA+hGc5qdtTsEuZLZ722WeNS7xGVQyqBkkjOQMc5oAyPHlvNd/D/xBb28LzTSafMsccalmZihwAByTWEg1TXdL1W0sNV1e2EEFvLa3l1B9nImwxZPupuTAQNkcEn046q28S6He3FxBa6vZTy28XnSrFOrFE/vHB6VjxeK/B3i7R7grq9vNZxRGa5X7QYikfIJcAghT6HrnpQBN4Ilvr7RpdYvmmU6nMbqG2llMn2aIgBUB6EcFsjj5sdqo+Lkvn1iBrVta8uK3SRo7BnVZP38YYHHG7Zv7g4/Cuk0bV9K1mx8/Rry2urWNvK3W7BlUgD5eOmARxT9S1jTtISJtQvIbYStsj8xsFzgkgDvwCaAPOM+NZvD6GcaquoDTQll5Qxi7EjAmYcAgr5WC3y4355qzrNt4jn8Z6dcm1v50t5bVXSOWSKEd5HQodjJk/MJF3fLgcHjrNW8a+HdEtrW4v9TRIrqLzoWjR5d0eAd+EBIXkfMeOetbkUqTRJLE4eN1DKynIIPQigDz2x0M6T8R9Tujo+sXP2y6jnt7mG6b7NGpiVX8wNIASGDkDaeNoHYD0KaQwwSSiN5CiltiDLNgdB71lHxTow1ltJ+2f6YpKlRE5XcBnZvxtL45253e1U9M8feGtX2Gy1BmR1lZXktpY0IiAMnzMoHygjNAHP8AhxpptE8T22qeGNX8m5u7i7FvLGimeORshFw/3sdRkfU1Q03Std1D4f8Ah+wu9FvXTT7gJqGnXUyxtdRbWA2tu+ZVLKcMQG2YrodP8fWl5q2oMWQaJb6Ympx3vkyoxiJYMSrKMj5SQVzke9dRYahb6lAZrbztgbb+9heI9AejAHGCOelAHnGseFNSu9E0eCDQ7j7FapPH/ZTXMMklu7MCkgkZtvygMBgkqCPeqmueBdSvZZjJokuoSnQPs0dxLeRswvVyI3JJXLBSPmC9frmvRda8R6foMlpDdGZ7m9dktbeCIu8zAZIGOBgc8kVm3HjVE1PQ7S00jULsarby3IZUCNEiAZ3K5BzllGDjr36UAcpJ4X1+88aaXqkmkTrtaza5luLqGSNRGmWK4/eKwYsMAlWPJzni3oHg7W9O8VXV7cgyyNdXMi6kbhBujlBCAoELuVwo2swUcbc12GoeJrPTdRtLG4huRJcvHGriMbFaQkKpOeTwcgZx1OMisDw14unFxNp2tvPNO+r3Gn214tuqxOUyyodp4O0HqOcdaAKXh/wTqGiWV2iWtubmTTWtGkF35aXEnOGIjiUjJ53ElhuIHrWv4G8Mz+G0v1lt7aGOdo/LWMR7wFXGGZEQMB0BILHkk84Euj6tqus6h4msHcWUtlOILctbqWjDJuVziRg+QQRwvuKj8M6trEvhrVJLpn1S/sr66tUMcccbTCOQqvGVUHA9R9aAOms3uZLOJ7yGOG5K5kjjkLqp9AxAz+QqeuDXxdqNl8MdN16KJ9XvrtoUQSqluWaWQIMhSQMFgOD9T1Nbep+Kf7G+wNqOmz28V27xmZpY/LhcKWUOd3G7bgEZGeuKAKmreHNVfUNaudJubVDq9pHbStcA5gKBl3KACG+VzwccgdRxSy6DrVj4ll1LRrjT/JuLS2tZVvEcsgiZzldpGSRIeuORWx4d1SfW/D1jqlxZNZSXUQl+zs+8op+7k4HUYPTvWF4j8exeH/ENrpRsfPEjwLLILhQ0Ylk8tSE5JAPUnaORgknFAFODwdrMV/ZSibTxFBr0+qvy5ZklDjYOBggSHnvgU/wx4L1Pw5NK63lrP9ms3tbBnaZiwLbh5gLlVwQMhAM+2MVYk8aX9vqcMNz4eeKyfUxpz3f2tG2u2PLYIBkgkgHpgnuOag0zxBf6x4x0e6hYxaLfWF08Ufm7vN2SRhJCu0FSQx4yeCOhFAG34T03VNI0OKw1RtPLQAJF9ijZV245Lbj94nJOKf4j0a81hLD7HfQ2j2l0tzmWAyh8AgKQHXj5j1z271pXxulsJzYrC10EPlCZiqFscbiASB9BXE6T4h1G08AeE7u1iju5dQMMLtqN8Q4MgJB37SXOcds47UAEvw6uTo62EOsQBpLae2unlsA6uJJDIDEN4MW1mOACRwvoKhn+FUV7ptjZXusTTLaWvkArGUEjBztdgGwTseVGz97zWPHFTz+NdbFhBFbaVZy6ot3Pa3uJZHhgMQB3AKpkYMGTkKQu75iKhfxzrZW0mit9I+zz6KdWDvPIAQmzeudvA+f5Tg9OQKAPQgAoAAwBwBXF6L4Ymk1O7ursXdtHbandXNjC/llA8gZfNBBLEEM52tjG88cDCXvjPUYvEM1pa6fbvZWstrHcyTzLEVWYZLAsQMAEY4O4hh1FXrPxLdXmrMqrYx2I1CWwKyzFJwyA/MAeCSw4Uc7SGz2oArweGo/C1lpV7bG+1B9GsXskt4kQyTxuyHpwNw2L3GcGlsfCU0nhGfT5bya0nvbhrqUiOOTy1ZsrCVcMhVUCpjGPl4pPCup3lze6lBeeILK5kW+u4ktfJ2SxFH+UDLfMoXB6fxDmsuw8Vy6b4D1TUWuIbi9g1OeGVpJXdYgboxCRlLEqirhtoIGBxgUAa8ngVG8GXHhuPV7qGO6aQ3E8cMKtIHzvXaE2qDn+ECri+Fi/9mz3Gs38mo2CSxpeoI0Z0cjKsgTYR8q/w/wg1zl346vraKOOO502XGsW+ni+CkwXCSg/cw3DpkFhkj5e2eOn8L63NrEGoxXRiN1p19LZytEMB9uCG25JXII4yaAKfiDwTpOuJI9/d3cYe0FpJIJVyY85+8ynaSTyVxu6HOBV+48OJcaza6r/AGlfR3NtbtboUMeNjFS2QUPJKLn6cYrlPiT5U+ueGNPutXs7ezurmUTWl3EkkT4hkIkdWI3BW2gA8bip6gVDr3iu80PV49P03ULFGt0tUtNKW1LNqAkOGZCPuhRnG0kDB3cYoA9Lorg4NeuZviXeaAfFNqqQmKeKyFuhlkBVy8O70AVWz975vSu4uJPJtpZc42IWztLdB6Dk/QUASUhIVSzEAAZJPavK9M8U+LLjS9a+z/aNQ1G1s0aPEMYg3seXU7FbeFO7yWXPAGSTSy3+oXPhjxNBc6jq02jiJP7P1MwbbmeR0O+LyxHkruIH3OASM8ZAB6Np2taVrAkOmanZ3wiIEhtp1l2Z6Z2k46Gr1eZXllG/gazutF1LWZobfUoJrubyDDM8KyL5gZBGjMqrkgBc8d673RXik0mGSC4vJ4nyyyXiMkjAkkZDKpx6ZHTFAGhRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAV7/AP5B1z/1yf8Aka8++BP/ACSjT/8ArtP/AOjGr0G//wCQdc/9cn/ka8++BP8AySjT/wDrtP8A+jGoA9JooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigDyS38LeJ4fEcF0NOuxCt7LIX+3J8iG7EiHbv8AmxCCm0jvWjofhLxHpF5NdRLB9vMdwtxNJOBDeuwJiZgFLkA4zkqUGQpYV1U/jLS4dfbRlS8nuY3WOVre1eRInZdyqzKOCRz6etV9L8eaXqd39nNtqFkG83ypb23MSS+USJApJ6rgkg46UAc5Y+EfEcVnrFvLBbJFqFlDbAQ3nlSI6M4d9yxnJKtkFtx+UAn0v6Z4T1TT9Pylrpa3Nvqsd5bovyhoxEsTbiqACQrvGQuOme9aum+OdP1iC6awtL15o7Y3UEM0XlNdxdA8ZYgFSccnHUetNPjI2nhI6/qukXVlGIYX8vzI5NzSYGFYNjAJHzNt6+1AHJS/D/XJ9EtYW0/RIbqHxCdT2QzMIxATlowSmcn7pGACBWj4r8C3+sXVnLYQ2S2osHs3sHlEUVsWYMZIyImJPUHG08DBGTXX+HPEFv4l0kahbQyxR+Y0RWQqcspw21lJVhnIyDg4qh4w1O+0/wDsWOynltlu9Tht5Z44kkwrH7pDHgN03DJHpQBxurfDbWL3UL26jTTJpJ/MHnTSOHcNZpBydhIIkQsOT1z1rVs/h7dWvitdSN60toL5r8pNdSt87IVI2DAyOBuJOV4K8c62ueNJtDutRSTw/qE1tp8CXM11G8ZTyTnLgbs8FXyMZwpPpnqkkSSJZFOUZQwPtQBxOgeB7rRv+Ed/fWgGlyXjSrEhUSCckjHuOBz6UWnhDWbfwbd+GpbjSLizWIQWglt5CWj3ZPmkOMnHGVxg8itvQfEo1/E9tYyrp8hlEF2XUrL5b7M4HIB5Iz2BrH0fxJLZeG/EusaiL64bTr258y33JI0apg7YyAuVxg89OeuM0AafgzQL/wAPaTcW+pagL24nuWnLjcQgKqoXLEscbepOeaj8W+GLnxG1kIL8WyQ+YsineNwdcZBR1YEY6ZwcnNULPx7Ld+GrzVRpKq8MyW8Mf2xSlxI23AR8cgBxnAJyGABI5mufGF7F4bsdVh023eS4vxYvD9pYAMZjCpVig4LYJyBgE8HpQBU1L4eTaloOn6a+rRxzWVmtpHex27pKAuBnKyjOQBlW3KSM4rtoIjDbxRGR5CiBS7nLNgdT71xOveO73wzLaWF7paXWpSWkt1Itn5zphWwqrtjY5b1YADHXmo9T8R+JpfG1jp2j/wBnQ20+kG9MWoh153oOWVfvDONoJ7k9qALtt4Ags9ekvre8At3vft/kyQCSRZj97EjE4U8/w5GThhUNt4BuINL03TW1iN7eze5D/wChgPLDNndHu3/KRuPzDrxxxQda8Sn4galp0U+kLpVtHZuVuWZXAkLhthA5YlSACcfd9TUOgePb/VvET21xpS22lSNOsNzITGyNEWBV93BYhS2B90DnNAFy38BtbSCRdfvmYacumjdDAwMKnK5BTBPJHTBB6Vs+HvD0Hh23ngt5pHilkDiLAWOLgDCIoAUcZOOpJNYng/xffa9qLWeow2tvMbX7SIIdzELvKgiQEpIhGMMp654xzWt4u8RReGNBe/keNHaRYYvMUspdj049s9SB6kdaAH+IfDy+IEgSS8eGOLfuj8mKVJNwxysisMjsRg8nsazJvAcH2TQo7LV9RsrnRoWgt7uNkeRkZQrBg6lTnaD04wMYrl5PiHqcvhW0v7fVdFiuk1g6bctOoMbqZNqyfLIQgC/N1YEDrjmrfifxd4k0KPS7azuNLvbmaBrg3TrHBBdDdhUQyTqF4IyQXPIIFAGrqnw4t9T1M6gdc1OG5PkuZE8pmEkX3XVmQlfdVIUknircHgqxs9WbU5tRvJIY7yXUUtpHVYYpnBDPwATgMQMkgV0dnObmygnYANJGrkA5AJGeK4iV7p/HmpWOpeJWSwkNusWlT2kTR3McgYFAWBZgSCDjp344ABtaR4a+x65f61Fr17crqEnmyRHyfKOF2KAVQHCrgDn+EZzzT7LwjBp9rqFvb6rqiJfSPLKROoZZHILOhC/KT7ccnjNef+DPEGo6Fo3h+1S6gvLe7sb0QWKxhCk8JDJEGBJ3MHIIPoMAd7X/AAkfi5dIn+yX0upzJYw6jJNFYqjwOJFEtqU24yULEKf3g2nPUUAdfbeAtHt/C0/hyR72602XG1Li4LmLGCuw/wAOCARjvWfqfh+Nkt/C0dza3Ftev9ou31O8ae7kCld3lowI5UAbsgL6ZNZuseN500fW7vSdTmuAtxafZGFqCwjlZFZYsqA5zuCk5GcgnioXt9UuPFHhg3WsXA1CJ7xbueKGCSS3V9hjhk2KUUle5HXODigD1ADAwOlc7qvgXw7rWoSX1/YyPcSlDI0d1LGHKY2llRgCRgYJGeB6Vxl1eahrFv4Q1K7vtds4ke7gvZre3Mb7tjKkjRhDtLYyPl43djXptjcx3dhBcRed5ciBl86NkcjH8SsAQfYgUAZNz4N0K7klea0kYy3iXzYuZVHnp91wA2B9BwepFSx+FNDi1n+1109PtwYskrOzeWSMHYCcJnvtAz3zXNwxpZfFDVZLw6sn277L9jMKztBJtQh9xUFAAcfex1pujX2uP4utbYnVH2y3Y1VbmEiCNMkwGNuFJxtA2E8E7sEUAdfrN/pthYZ1WVY7Wd1t8sCQzOdoXj1JxVZfCegJaRWq6VbC3ilSaKPb8sbpnayjsRk4x61mfEzTr7Vvh5q1npkU0t6yxvCkP3yyyK3HI5+X6+mTxWFqY8UPpuoDT01CXTBeWwVZ/MW6aEqRPswVkwCVI5BOHAOMUAddP4Q8PXMzSz6PaSSNI8rOyZJdwA5z6sAAfUCq174N0+/8R2Gp3EdvJa2Vm9rHYvbI0Y3Mp3DPTG0DAFSeDU1GLQjDqT3UjRzyLBJdR7HaHPyZBZm4HGXO44yRXOfEePWHvrJtMttXugLWdBBZ71iaRtoQs6SIUYc4Y7gOeKAO3m0nTbm5W5n0+0lnTG2V4VZhg5GCRnjtWTe6loNr4ojt5NOafVtiSGaCwaVolYlFZnVTtBwwznoD2rn/ABba+JDbaxZaXp+pXEl9HBNa3FvfKgilTaHQ7nXYMKDxw2T3zlYfC8T/ABPvNdufDM/lPDbeRdebGQs6ly7kCTOACg6fwnA9QDeTVNCbxRcWcGmyS6iGEFzdRWDMqlkDbXlC4Hy7epxyParOjwaFcJePpumW8KLK9pMRZiISbThhyBuXPGeQcGuW8K+Gl0vxlr99L4VlgW7uXe2u2liceWY1DDbvJG5lY9P4ucVBpuleI38Ma5odtos2iI87T2LvdIQYi6kw5jkZkLAONwwACMc0AdpqcOi6VoUk15Y2w06wUziMW4ZY9uTlUA69enPNWbN7AWf9oW8cUEV0qzu5QRltwGC3TnGOvNcgNFdvBetWSeD/ACo7kGSDTpbqOYtIw2k4Y+XHggMAGI6ng1mXXhfX9c8N+E7e5sXto9KIivdOnlhcXAWIIJBw6HBzgN654IFAHot1HYFlmvEti0PKvMFymSOQT05A/IVDca1pVnqMdhc31vDdvE0qRu4B2KQCfb7wrhpvAE1xrOgyXdjb3unWeky2NxFcursx/wCWeflAOPXsT+NTN4X1T7ZoOqTaHpl7cWelmymtppR/rQ8ZV/MKHIGwkfLkFvfgA9BAT7w2+uarxalYTyLHDe20kjdFSVST+ANWV+6MgA46DpXmtt4B1BNV0q6itNNsPsgjaWaE/vGYC5QkELycTI/PcY7ZoA9FiuracyCGeKQxnEgRwdp98dOlMGo2LW0tyt5bmCEFpJRKpVABkknOBxXEaR4J1bTNPmij/s2O7bS/sQuGkknDsDnJjYBQpySRhuT3HFQReCNbij8QRBNJaDUmtnihlnmbZ5W0YLKqkcDII6EAYxQB3MWtaXMsDRajaOJ5PKiKzKfMfG7aOeTjnHpSPrmkxqjPqdoqu7xqxmUBmQkOo56qQcjtiuWfwnrb6fHKbuzbUbTVTqFmkuXjC7Cmx5Aqu3DMdxBPAHQVnHwd4rXSLS0SbRHmttZbVVZzKFJZmk2EYP8AHIRn0A7ngA7hNe0l4rWQajbBbvP2fdIFMmDg4B5PJA/GpZtV0+3vo7Ga+t47uTGyFpAHbOcYHXnB/KuP8W+BL3xHqkGoxXcCSyWYsruGSWdYiu4tuAjdd4ySNjcEY5GOZ28Har/wmMutx6tDCkptw/lRMrskYG5GXdsfcd2GYFlDcGgDtaKKKACiiigAooooAKKKKACiiigAooooAKKKKAK9/wD8g65/65P/ACNeffAn/klGn/8AXaf/ANGNXoN//wAg65/65P8AyNeffAn/AJJRp/8A12n/APRjUAek0UUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQByU/gCxuvFsfiKbUb97iK4E8ce6MKuFxsDBd+zoSu7GRVTw/4Snmvbu78QQy4S5uhaWZmjeBI5mO5lCqGG5WIIYnvjGaLzU7vT/iDexXuumz05rS1a3ikiBV3aWRWVM9T9zJHI3DNQWXi3WpvEunWjRRv9qvLqC7sVjw9jFHny5GbqQwCnJAB3gCgDc0PwVpmhXP2iKW7uZEthZwG6l3/AGe3ByIk46e5yeBzwKenhK1jsJLNNR1cRMI1XF8/7tU6KvoOx/vDrmtHW9RGkaHfaiY5ZBbQtJtij8xuB2XIz9Mj615jpPxB1G68O+IFOrQm7tUgktry4gyq+ZgMG8pNoCtwDg4zyWxQB6VoWgWHh2xe009GWOSZ55C7ZLOxyT7duBgcVB4i8MWXiZLVL24vohay+dH9luWhw46MdvUjHB7VxEfifVZfBdrcwa3c+fNqZi+13FsnzQryyq8cTJzg4YoO68EZq/Z61q6aZpd5eXeuGHULGeLK6cjSQzh8xyMqJwWXIGRtOBwM0AdTceFtLuzcG6S4nNzZLYz+ZcyfvIRng4bqcnJ6nJ9TWtDClvBHDGCEjUIoLEnAGByeT+NeZXN9qOqap4e+0an4ksrK+01hefZbN49lwjKFz+7JjyfMJPGQB2IzeebxEfH4gFzdQJHOqonlTSW01rtGS2E2CQkn5t4Ix0x1AOvt/DulWt4LqGzVZVkaVPmYrG7Z3Mik7UJyclQM5OaydS8EWMuga3p+lyTWU2rI4mmaeWUM7DBYhm7gYJGCRXRXhuFsbg2iq1yI2MQboXxxn8cVyPhiPUEgP9qS6/JcSWAF7HOP3aTD7xiZeQTkgCM4wo6HFAEmgaVDraXF7fX9jqmnMUht7WBWaCBoWYFl3sfn3EjIxwq/Wtn/AIRXQPsa2n9j2f2ZZfOWLyhtEn94D175rhLea+0P4Of2attfWmpxFYYoWUxvM0k5xGjkj5mU4LA5XOeoqDztTu/DlrosS6pNeQXwOrBZ7gvbRsGaNP4JJFKYXKsvzKCT1oA9IvvD2j6nHbpfaZa3K2yMkIliDeWpABAz0BAAPqKS/wDDmiaqlsmoaTZXS2oxAJoFcRDj7uRx0H5V5yum6vc6J4Qj1iy8Rie2kmg1E207BmiCsBvKSZILFMHlsBufXd1rQ9Ra7xYWurPaw6bFHYyW96BJFMrknPmygFsBMl1bPr1BAOon0rQrvXYrmeysJtWt4w0cjxq00aZIBBPIGc/rUkGmaQuq3d/BZ2Y1B8R3E6Rr5h+UEBm6/dI/AiuWuNDvLbx7fa2NDk1AXVtaJDNHdJH5TIzb9wLDjBVuAQdvTNR6V4eudN8Z6pdy+HvtH2rUjdW+pC5TbEjQhDlC27IIYcL/AB9cUAdfp2jaXpAcabp1raBzlvIhVN31wKtT28N1C0NxDHNE33kkUMp+oNefeA/DWu6RrIudVS7WQ2Ziu5TdI8N1MGGJQoJZmwCNzbcDAx6aXxSt4p/A8rS26TiG8tZBG7hQ379ARk8DKlhzxzQBoajL4f0zUtJ0e40mE/2lK62+21QxK6puOfQkL+OPato6fYtHBGbS3KQENCpjXEZHQqMcfhXnZ8L6vPNozS6MVsf7ce9l04zRFLOAwmPaRnDfMzPtXj5mGDVS+8PytothZXS2tn4ka4uLW2iQRyMbOWRlyVGPlSM7gexQZ6kUAeove2kflb7qFfOz5e6QDfjk49fwqD+04zrg0tYZHkFuZ3lUrsT5gAp5zk5JHGMA81wPirwBfX13ax6TY6cbW2s4reP7VsZCVckhozGdowScxshY8HgAjpbmz1iDxpHqFjpOnPaSW629xctdGOYjcCTtEZ3bRnALd+1AHQrdWz3L2yTxNcIAzxBwWUHoSOoqGa+Vra7On+Te3VuCPs6TKCXxwrHnaT71yujeGNS03xM1zJp+kOqSTt/aoZhdTpJ8211AAJDY5LEYXgCqfg7wn4h0HVrrUbpdLD3NoIpYoW2h5lYkSDbGoAbPIIYj1NAGzp8lt8QPCcFzf2U9i/2iTCJPiW3likaMlZFxg5U8jsSKTULnSfh34cuLoMJJZGyDeXirLdy44BlkPJwOMngDirPhLSdS0PTpLG9+yMhnnnWSCRicyyvJggqOm/Gc84o8a6NqHiHwteaRpz2kcl2hieS6DEIhBBKhf4ulAFq/8UaJpDJHq2q2WnzNEJfKubhEYKTjPXkZ4yKjvfFui6fqFvZXF5iSe3NyjKhZDGMc7gMc54HU1lS+HdavNd0TV7w6RJPaWlxbXUfluUIkKlTHnkHCAHPZmp1l4c1+0tdDaLVbGG5sLJ7KZFtS8LKdu1lG4MCPLXvg5PAoA2pvEejW+tR6PNqMCahJjbAzYJJ5A9NxGSB1IBIHBqGLxboM2uS6LHqUTajESrQYbJIxkA4wxGRkAkjPNZh8Er/wk1zqv2i3eK4vIr1oprdnZJERV+Vt4UfdBBKkjn1rA0GxvrLxxeXTW95Jd3F9MfJuLWQxWls7/M0c27y/mCIxABOcDA5NAHXaf4z0HVpZYdOvHupYo2eRIraVim04Kt8vDZ/hPzdOOao2/jP7P4Fl8TatAhSNnHlafvlLYfYFAdVO7cMHIAHrWloWkX2kW15BJe204muJriIpa+XsaR2chvnO4AtjPB461k6d4Ini8I3vh3U9WF3bXG9kkitvJaJ2kaQsPmbPzsCAfTnOaANlvEumRfYRcPcWz303kQJPayoWkxnbyvB+vBwcZxVzTdTtNXsUvbJ3e3ckKzRsmcHB4YA9Qa5bxLpWq3WkyaSLi8vr29YNa3ohjjj090Aw5ZcMpzkgjJzkDA4rpBpbW+l2thp93JZpbeWFZVVyyLjKncD1AwT154NAGhQenFFFAHnFvr/jye+1K0mGh28lhFFNcKsEjGNJEkbAPmYZlKAdADkntitTw/4+sbnw7b3Oqme2u49Jj1G4M0JjV0K4Z0PQjd29x61ei8JSJretai+tXjjVYPIkgMcQWMAEIVIXOVDMBknOec8Vnx/DeyNtDa3mpXt1bppJ0ho3CLvhyCDlVBBGAPw5zzQBv6L4j0/XpLuKzdvNtComRsEruGV5BIORnv2qDxJ4mXw59gB0y+v3vZ/s8S2gj4cgkA72UcgH8qm0Lw9aeH4XitJJmRsfK21VXHoiKqgnqTjJ7ms/xnol9rg0SKzkEKW2pR3M0yzeXIiqrD5MqQT83Q/1oASfxosVrp08Oh6pdfbXkhEcIiLQzJuzG+XAByjDIJGR1qGfx5HZKy3mjagk1rZpeaksWx1sUb++xYbiAGOFycKfYVPdeB7GfT9PtItR1S0FlK86y21ztkllfO53ODuY7mOf9o1Nq3g3S9auY57t7sP5QhuBDOYxdxjoswXG4Z+nUjoSKAKbePIE1K4tn0q9WC2vIbSe6Zo9imbb5TABiSrb17ZG7kdaWx8bpfazbQLps6aXeTy2tpqLOAJpowxZdn3gvyPhu+2o7Xwhu8a6zqd/BHJY3EltNaqLl8b4owo3RfcOCMgnPb0Fa1t4T0a01dtTitnFyZXnAad2jSR+GdYydqseeQAeT6nIBz2lfEy31G61dJdMe0g062mum8y4Tz9sZIO+D76EgZGQeCPWn2HxItrrR9QvZdOnjktFg/doSySNMwRFV2VQTvOCRkDggkVrad4G8P6XdSXEFpLJJJA1sftV1LOBE2NyASMQAcAYHYVPaeEdFs7K4tFtZJoJwA63NxJNwDlQC7EqAeQBjB5FAFDwjqOo3eq+JrXUpw8lpqCrHEHDiFGhjcKCFUkZZsZGfriuqrM0jw/pmh+c2n23lyT7fOld2kkl2jClnYksQO5NadABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAV7/wD5B1z/ANcn/ka8++BP/JKNP/67T/8Aoxq9Bv8A/kHXP/XJ/wCRrz74E/8AJKNP/wCu0/8A6MagD0miiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAEJAOCRmjIzjIz6V5r4t8PeIL7x5ZatZ6Nb3kNrLbNFOZY1KRoxZ1+ckgknqoHAGSeg1rXQruHxqL6Xw9bTSLcTSrrL3p3iKQY2BMEkgbVCn5QBkEE0AdPba1pd5cyW1tqNrLPEzI8aSqWUrjcMZzxkZ9M1X0LxBba9ps1/DFLBbxzSRB5ioDhDjeCCflPvWB4a0K/0TWb2E6DpgtftFxMupIyLLKkrF1jVAvGCdpyQOARnPGfH4M1i48E6voTRWeni8vXu4o4pd0ex5fMMDgIMDHykr/LqAdx/bOl/Zorn+0rPyJSRHL567XxnODnBxg5+lWLe4gu4Entpo5oXGVkjYMrfQjg157c+BL+5ghlaw0kbdbi1AaaHPkQxJH5ZVW2cs2A5+UDP5113hzTJ9Kt7+CW3tbeJ76aa3S2YkeWzZBI2jaxJJIGR7mgC+2p2CzzQNfWwmgTzJYzKu6NcZ3MM5AwRyaq/27atr1vpMTJLJPam6DpMhwgIAO3duIOeCARwea5vxV4J1bWNcbUdH10aWJbYRTxrAG85xuUMx7jZJIMdM7TzitS80K+PifRtRtGtRbadbS2+yUtvcSbMngY4EYx657UAWbPXZ5/FuoaFPYCEW1tFcxXAm3ecjll5XA2kFG7ml0LXJ9VvtXsrqyS1n025WBtk/mrIGjWQMDtXHDjjFQx6RqMfji41rfam1ms4rTy8tvARnfd0xkl8Y9BTdD0fU9O1/XL66ktHg1K4EyiLcGjCxpGoOeD8qZJ9T0oA0ddi0ubRrldZgjnsAu6RJIy446EAAnOcYxznpWPouq+HdF8K6Vcg2WmWt+qNEqy7xI7KMAOQC7EAcnk4rpZ1leCRYXRJSpCs6FgD6kAjP5iuUs/Bt7Z6FoGlrq8JXRp0kjc2Z/eqiFArDzOvzE5Htx6gGrceLdCtdLg1KXUE+zTkrFsRndyDhgEUFiR3GOMHOMVHf+M9A02SCO5vjuuLf7TB5UEkoljz1QopDHvgZOOcY5rPPg68TVItRttWhingubmSFDZboxHOVZ0YbwWOVB3AjqeKnufDGoS6pod9Fq8IfSrd4gstluErOoVmO11AGAMKOlAFuXxfoUF/a2U16Y57pUaIPDIB8/3AzFcIx7KxB9ql/wCEn0j+3RopumF+XMYQwuFLBN+0PjaTt5xnOKwdT+HVpqPi9tf+0QxvKYnlVrNJJBJHwrRyNnZwFBGD0yMHmobn4dS3HjGLxH/bZS4gu/tEOLNDIEIIaJnJJK4JC4xtz3PNAHQweLNFuZbhIrpytvHJLJKYJBEFjYq5EhXacEEcHsfSl0TxHYeIhPHDDcwywhGe3vIDE+xs7H2nqp2nB9jWRafD2zivr+6vNQurz+0LSS0u0ZI4hcBzy7+Wq7nA+UN2BPqTWl4d8MR+HjKUvZLgOqphreCIAL0z5aKSevXPU0AM8cX+qaT4O1LU9Jnt4bmzge4PnwmRWVVJKgBhgn15+lTa34jsvD9jBe30M8hkBA8iLcVAXcxJ6KOO55OByam8SaIPEeg3WkPeT2kV0hjlkgClih4ZfmBHI46ZrI1DwLBq0OlLqOq3t1Jp4lXzJI4T5yycEMuzbkAAAgAgd+TQBk/8J8bLxDfXE7XV5oD6Xa6jDJBajFrHIXBZ+dxHyqe568YBrobnxda2+ttpws7uWOKaK3uLyNVMUEsgHlo3O4k7l6AgbhnGaqxfD/TIrNLVby/8r+z4tNlAlA86CMttViFyPvsMrg4rRufDFjc6ibwyXMe+WKaWGOTbHLJERsZhjORhehGdoznFAFO08XSXviC60eHQNS8yzuBDczExCOJWAZHzvyQynOACR3Apuj+N7TWdan0uKyuIp0hknj3vGfMVJAh4ViVOSCAwGQc1fsPDlvp2q6jqEd3eSSag++4jlkDIxwFGOMgBQAAD0qrpHgrS9FurG4tZbwvYwPa24knLKsLEHy8dwCARnngc8CgCvb+L7i38Kw6zrGky2/mRRMiW7rL5skpAREAOckso5x1pmpeORp+mXl0NIuJJ7C8itbu081FkQSFQjrzhgd645HfkYqyngPQf7PnsJobq5tJVVPJuLyV1jRWDKqAt8oBAII596sSeD9DmsprR7WQxTzrczn7TIHlkXBVncNubG1cZPGB6UAQ3nimTR7W0n1rTWsVuHkjMhnV4omALJvYdN4HXBAPHpnX0m7ub7SbW7u7QWk80Yd7cSCTyye24AZrO1rRp9UtbfSPLifSmKm6ead2lIRlZVHXOccsWyPfPG7QByGoeN5NP1nVLaTSs2OmPapPci4+c+eQFKx7eQCRnLCp7XxDq194g1HT4dMto7fSrhY7qd7hmMiNGJB5ahPvAMMg4HPBPZi+CoJfHV94hvSsySrAbeMSSL5bxgjLKG2P2IyDgitG28J6Naa/NrkFvMmoTuXlk+1SlXYrtyULbenA447UAYo+IUcFrBd3umvFDdadNqVssUvmStFGAxDpgbGKsp6kZyM8VnXfiXWNCk1bVriC1m3RWM/2RNQeRUheR0ZkyoAP3c4GD1z2rsrTw9o9jcTz2umWsUtwhjlZYxllJJK/TJJx05qK38J+H7RHSDRrJFeH7Ow8kHMWc7Of4c846UAYY8b3Et3e2EFlELtNXOmW7ySYiOIxJucjkcbgBj5jgDqSHah4g1yOHw4kX9nQ3l7qDWd4iuZ40KxythWGO8Y68jOK2IvCHhyCxnsotDsEtbiNY5olgULIqklQwxzgkkfWpm8N6I+i/2M2k2Z0zj/RfJXy+Dn7vrmgDIv5mu9S8MXTalaPam6ZWa2mdRJJ5UmMEPgrlcYIPWs7WPEXiWy1+50WA6f8AabqWBtKdrWRleJmYTB8PyUADEjAAI9eOsk0HR5Y4o5NKsXSFdkStboQi+g44FXDbwmSOQwx74gVjbaMoD1APboPyoA5TTbmyt/iNrUV1qdi9/PBb+REkhWQJmT5CpcgsMA5ABwRkVV8N6rrWp2mpQNrunnVIrq7jjtpbcb0CTMqFlDg7doHYcEcnv1Y0bS1vvto02zF3u3+eIF8zd67sZzS3OmxypdNasLK8uUCteQRp5ox0OWBBx2yDQBz3hHX9V1x7y7vhBBYWsaQOhhaOQXKqPPDEsQFVsrxkdfmOK1tbjsNY8L3bNcI1q0BmjuYpB8hUblkVxwCpAIPtVrTdJttM0xbGPdKh3NK8vzNM7El2b1LEkntz6Ul3oum3uknSp7OI6eQqm2UbEKgghcDHHHToehoAr+Fbu71Dwhot5fkm8uLGGWcldpLsgLcduSa16RVCqFUAKBgAdBS0AFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQBXv8A/kHXP/XJ/wCRrz74E/8AJKNP/wCu0/8A6MavQb//AJB1z/1yf+Rrz74E/wDJKNP/AOu0/wD6MagD0miiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAr3//ACDrn/rk/wDI1598Cf8AklGn/wDXaf8A9GNXoN//AMg65/65P/I1598Cf+SUaf8A9dp//RjUAek0UUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFAFe//wCQdc/9cn/ka8++BP8AySjT/wDrtP8A+jGr0G//AOQdc/8AXJ/5GvPvgT/ySjT/APrtP/6MagD0miiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiuc/wCEzsD4kbREtb95EnFtJdLB+4SXy/M2l88Hbjt3rYj1TT5Xt0jvrZ3uVLwKsykyqOpXn5gPagC3RWfba9o95JNHa6tYzvApeVYrhGMajqWAPAHvUcPiTQriGaWDWtNlihUNK6XSMIwTgFiDwM8c0AalFU5NX0yGyjvZdRtEtJDtSdp1CMfQNnB6H8qzdW8aeHdENj/aGq28SXyl4JN4KuoGdwI7dOfcUAb1FZc3iXRLe+tbGfVLWK7u1DQQySBXcHpwfXtnrVS78V2UPiGy0a3khuLiW4MFwolw0B8ppBxg5JC9MjAOaAN+io55fIt5JdjPsUttQZLYGcD3rlPDHjWXW9NutT1GwttO0+GBJxcJfLOvIJZHwo2OuBlT/eoA6+iuS1fxe8nhLUNY8Mi3vLixRpJ7a6WSORFVSxUx4DhiBwCBnOatWnjHTWg0SO+l8m/1Wx+2RQJE7ggRh3wQD0B6dTQB0dFc2/jXT2l0f7JbX17b6pFJNHPbWzuI1TGS4xuHLAYxkHrRP4jlHjXTdGjjMUFxbyyu9xA6eYwCkLGx4JAJLD09waAOkormv+E40k60dNWO9fEjwC6W2byGmUEmJX7v8p4HcYzniotE+IGka9qVrZW1vqMTXccjwSXFq0ccjR8SIGPVlPB7ccE0AdVRXJaP4tFz4Y1LxXdmQaQHkktYo4CZBBGSm49yWKsw9AR6E1I2t6h4i8LT3/h3da3sDhkS5VJEn2gMUDKxUqwO3cp4OfQ0AdTRWT/bTzeH7TVbGwmvftKROsELpuCvjnJIHGcnnsa1qACiivOdL13xDBrVxcXepR3mnf25LpbW8sccRhTG5HVgAWIPBBzxz2JoA9GorktH8XxeKcWcNpqNkt5atLBdom4BegO/BVWIIYZzkflUdvrx8N+BjeX013qUsF3LaRtNxLM32ho4wxwAO3OOgoA7GiuBvvHOqv4Tvby10pbLU7e9gsyLvcYCZZEQSI21S6/P6L0P43/EPjd/DclhZ3en+bqF75pjjtvNmjAQA4LJEWycjgLx345oA6+iqOjamus6NaaikE0AuIxJ5Uy7XQnqCPUVzeo+LNUXxNd6bpljZSW+mPb/AG97i6EchSXndGDhcKOcseegHHIB2VFcMnju5/4SIQPa2x0xtVOjgI7NcrOFJDsoGBGcfUAgnjNQaL44m8QeKJNEnjgGn3sFy1pPatKrlY3CElmC8kEkFOmOvegD0CiuP+HKJbaJqNlFNJJDa6teQxCSUyMqLK2Bkkk1c8barqWh6Iup6fc2EQgmjEyXoIWVWYLtDg/IeeuG+lAHSUV5x4l8VeI/DsdjYPe6ZLfXonmS+NuIrZQiriL55gCxY/e3Dj+E03WPEWtHVfDMo1/T9Ct77TpJZVuokngaYbPl8wSAE4YlcHopPOeAD0mivNZfHutSfEFdGtrW1XT4XhR2laNWuUcf66PMgYrzwFV845Izwui+K9bm1m4l1LV9L+x2+ty6S1qkYjO0BtshJYkOSowOhGepxgA9JpqSJICUdWAJUlTnBHUV574H1HUZry9i1jxRcS3ourqH+z7i3iQqEb5ZRhQwXZtPPy/Mfas7w/rLaN8OtVXSZ7a51C31C4DSQom4RfaNhuWReoCfNnBBwO1AHqtFeRXXjDXo7Q+Xrn+hW+r21nFqptYyuoQzAb8DbtDRncdy8HbgjrXbeCdTvtRstUhv7wXsthqc9mtz5aoZVXBBIUAZG4rx/doA3r7UbLTLf7Rf3cFrDnbvmkCLn0yfoamiljniWWGRZI3GVdDkEeoNeffEGKZ/GfguZZLyK3gnuGnlt4fMEQMWAx+VgMk459aml+0z/EE2EOs6rbaRNZRTCKGILH5wYYRX2fICgyQCM5PI6UAd9RXnFpqusnxdcQX9xq6zG8uImthaEWiWQV2jlWQLjecJzuLZJGKoeGNZ1lfEuhQTXGuyQ3EK/akvYGKIWt92CQvB8wHOTxkDjpQB6sTgZNULrWdOs7+xsri7RLm/LC2j5JkIG44x7c81Q8a2V5qPgrWLSwVnu5bVxEiOyFzj7oKkHnp75rh2tra60/w0LOw8SW1nDqkXni4Nw0kIa3mjwjElwqsQpYYHIOcc0AerUV5PNb+KJdDtLa8i1dba0vb2FmiaZ7iRQ2bd/kdGZdu5eSckKT149D8NHUz4csP7YLnUBEBMZEVGY+pVWYAkYJAJ/pQA8a7YnxCNDzML0wNcANA4RkUqDhyNpILL0Pepl1S0fWJNKDt9sjgFwybDjYSQDuxjOR0zmuU1u/urL4kabdromrXVrBp81u89tb70DyyRFecjgCNs+nFQ6Y8+n/FDXPJ0HVFs9QigX7UIx5JmTzC75LcAhkGR1K9KAO9qOCeG5hWaCVJYm+66MCD9CK888H6BrdvrN3JqtjOYrq2nL3F3IvmB3dcI6xzMjkqB8yqmAgAq18MvDknhvS/sdz4dOn3kcSxzXvnJIt0QTyoViQO/IHUcUAd7WX4g1618OaZ9uu0mlDSxwRxQgF5JHYKqrkgZye5FVfF+nS6poggSyN/EsyST2SzCI3CA52hiQM5wcEgHbgkZrhrzwvrP/CE6bYy+GzfvHrC3kVk9xFIbO2WUP5JeRgDlAVwCRzjOKAPTNNvTqOnxXZtbi1Mgz5NwFDrz32kj8ialmu7a3dEnuIomf7qu4Ut9M9ag0kbdJtgNO/s0BMfY/k/c/wCz8hK/ka4jxV4L1DW/FX9oQ2lpIitb7GudkiFUYM3Vd8eOf9WwDcZHXIB2w1rS21CWwGoW32uIqHhMoDLu+7x74NTm9tFeVDdQh4hukUyDKD1PpXPRaXqFn4uv7mLS7G4s76SKU3LyhHhKoFYbQhLH5QQSe+OABXMaZ4P8SQa//aF7ZaXKgkvjNGsyqlyJ8EHaIs/wgEOzfhigD0eG+tLksILqCUoMtskDbR74rOsfE2n3+rajp8bFWsI45ZJi6GNkcsFIYMf7jZBx2rgIfh3rX/COaTpiR2dlKmi3On3UkMpx5jPG6McKCwbyyG6HDnr31R4N1xpdVbydDt4b2zs7UW0AYx4hclhhkIAZXcDg4+XrzQB2kmuaRFawXUmqWSW9xIIoZWnULI5zhVOcE8HgelU7/wAVaTaeH31iG+s7m3Kv5DJdRqkzKDlVcnbn5TnnjB9K56Xwlq8vhe70mSLTZjPqS3QE9zIw8oSB9pYIDu+ULn0J/HR1zRdbupLK60uLR4547aa3mhug7Iok2klGUA5+XByBnNAG9o+pxazotjqkCOkV5bpcIr/eAdQwB9+au1leGNLn0TwtpWlXMkcs1laR27PGCFbYoXIzz2rVoAKKKKACiiigAooooAKKKKACiiigAooooAr3/wDyDrn/AK5P/I1598Cf+SUaf/12n/8ARjV6Df8A/IOuf+uT/wAjXn3wJ/5JRp//AF2n/wDRjUAek0UUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQB563hvXJviZ/akenWlnp4mLXF5FdFWvYfK2iOSEDDEMQdzdl+lVYPB2vabrOkXkkelSaZokl55SwbhcSW8ofagGwBSgIULuweuRivTKKAPnvwtJINJ122htrfU5LrR3gaW18xWs0ThIpAIl+YeYd2Gdjt57Vp+HfDd94l8O6vpsRtheNPb3p1SFZIYp5kIxCQYo2QAIpygON2ck17gFVc7QBk5OB1NLQB55D8Pb1NBhsTPaxSpfSXu9JpzKjupyVnLbt+4nLYAIJG3JzWhD4R1a0svDLQ6naS3+ixSxM8tuVjmDpt+6pGMYX68+tdnRQBwt98P573X7rU5b+3k+3JAbqOSKXYJYfuOiCUKR32tuwRn1Buz+F9ZbWDNba1bW9h9u+3hBZbpS5XayFi2CpGecZGfQV1tFAEc8bTW8sSyNGzoVDr1UkdRXExfDnMur3Fzq7G61G3giMtrbiELJE25ZmXJDvuwST7joa7qigDlIvCF1FZa4Tq4fU9Zws92bUBUQJsULGG7Ankk89fSq6+BrldM0NBrhXU9EDR2l8tomfKZNhRkJIPy98jkA4OK7OigDjrbwReWGk2NpZeJb2KeyaVIrpokZjBIQTGy42kjaCGxwR0xxVnUvCl9f6/pOqJ4guIhpqFY4jbxvvZgFdmOByy5HTAJyPSuoooA5mLwTZRa4uofbr1rZLp72PTmZPs8c7A5cDbuzks2N2AxJxmo9N8C22mXWlzRanfuumzXEsEb+XjE3LqcJkgEkjnPvXVUUAcnZ+DzbaNqPh5LiS10eSbzbR7OUpNGHcvJGflxt3EgdcqxB6c2E8K/2Z4d1LTtCuzaXN9IZHupFDFXYKrMFXaAdq8YwAea6SigDLutDjuNCh0mC8vbKOFY1jmtZtkoCEYG7uCBg+oJrUoooAKxbPwpo9leG7jtneczvcbpZ3kHmvwzhWJUNjjIGccVtV5jL4wvJfiX/ZMepXcdi909o8YjjIhPkkKQBGzcychmYdPu4oA7iw8NaTpjs1nbPDlWVQJpCsYY5IQFsIOf4cdvSqNx4e8M6RoGoRXqiLSZgWuhd3kjR/M2SxLsdpLHORg5rhvDHirVI7nRbzUdcv9RN4t7Bd232dMLLDgxoiqgwxBJz3yPQVb8AeKL681LUP7SubufTDYLeie5VnXeGIcK3lIowNuUUMAc4PWgDs9P0Lw1e+HHtbK2trrSb6PDMHMonXsS5JLY7HORU6+FNAS3SAaRabEl85cxgkSbQu/J53bQBnriuH0KC7l+GthHZXN/Zavoyee9qzNbLJ85by5Ny4IYKR7ZpL+41238GWGoC+1QT6jf8A28wLFNP5UDKWW2Z4gXRQNvzAdc9jQB6TZWNrptnHZ2NtFbW0QwkUSBVUdeAKp3nhrQ9Q1Bb+90ixuLsBQJpYFZ8A5HJHavLdabxnfaL4eQLqdnE9huMriaWaO83fKZPJwSduCN67OTuAPTQ8UDWb7xJYbE1rfHBbHyUimjQyA73KSRMY9xHysJRtG3g80AekLoulpq7auunWo1Jk8trsRL5pXpjd1xwKq2PhTw9pl19qsdE0+2uPm/exW6q3zDDcgZ571rOgkjZGztYEHBIOD7jpXj/gnT9XksjNpV3qw1CM6jbzzXty80JKsyQL8zFN4YIcqDwrZ6igD07SfDeiaC8r6TpNlYtKAJDbQLGWA6ZwOetP1ttJh0qa61tbY2NsPOdrhAypt/iwQef1rgtC0fWrfRNae7t9V819NWM2ryMd10u4lo2aZyxJI5G1TgY74qS+GZp/gvqlra6Jqf8Abt3axxXQu23XFzMmPmLFjlQS2OegxjtQB3+lT6Vr2kBYtMkjs1PywXdiYl9iqsoBHcEetaU1hZ3McUc9pBKkX+rV4wwT6AjiuEl0KfVtI8PCXRL46ZbCRbzSp5lR5WKDY5Bk2sFYHhm7g44FZ8vgvUpYPCZ1fSZdWktop4dSCXSljCcmKN2Zl83aSuexK5oA9PNvA1wtwYYzOqlVkKjcAeoB64pqWtvGWKQRKWfzG2oBl/7x9/evFvE/gDXZtZ1GXQ/DzxRGbdbSR3cSDYLYRrwXBB8wBhkcYyOtbun+FPEa/EQavewXDxC+kuo5/tEARIXTb5bYXzSVB2hc7MqDkUAeiyanbxazb6Y6yCe4heaNtnyEIVDDPr8w496tsyxozsQqqMlicACvOPCvhrXtF1ewW40Wyc2Znin1drvMt3HKwYPjBYsNoyrEAfwnFdh4r0mfXfC9/pttIiTTxgL5h+R8EHY2P4WxtPsTQBopfWckEc6XUDQynEciyAq554B79D+Rp9vcwXcKzW00c0TdHjYMp/EV5jP4B1Se0u7j+xtFglm1GzuYtMik/cRJCfnO7YPmkHynCDjGc113hLQ7jQJtatza2sFjcX7XVoLdsBUZVBUoAAuCvbOc0ASeI/E8vh/UNHgOlyXFvqN5HZm5WVVETuSBlep6H07c1Pe+JLa08VaZoCiOS5vUkkb9+itEqqSDsJ3NkgjgdjmqPjbTdY1O20xNHtbSd7a/hvH+03BiH7pgwAwjdeRnt71T1vS/Ed74r8Oara6bpRSwV2nMl0yvukQoyqRGcquc/wC1gdKAOk/tzSf7XGkf2laf2kV3C085fNx67c57VB/wlXh//Tf+J3p/+g/8fX+kL+45x8/PHPHNYWk+EdT0rxFez+fp1zp1zqMmorJcQu11E7qFKqc7QAMgH0PSsvwx8MX0KW5aae3ncQTW8FxvnaR1kySXVnKKScE7V5IzxQB2Nn4p0DULa5ubPWbCeC2TzJ5Y51ZY15+ZjngfK3PsaeviTRZNOmv49TtXtYXEckqSBgrEAheO53LgdTketcnbeBNRS3sIZ5dNmji0IaTPG8TsjlXUhsZGRgHPIOT2qxZ+Br6LRp7SbVwZWu47mBSsk0cOzjG538xsj1fg9OByAdBceKtDtdKi1OTUoTZyuY45I8yb2BIIAUEkjBzxxg5xg1p21xBeW0VzbSpNBMgeOSNgyupGQQR1BFcjJ4EIsrSK2urS2lgupp3EdowilEikMCvmbs9Du3ckc9a6XRtMi0bR7bToRGI4E2gRR+WvrwvYe1AEN34j0my1FbCe7xdFo1KJGz7DI21N5UEJuJwN2M1Hc+JdMigiZLoeZcXL2VuGjfD3ClgUPHHKnnoccVm6t4TvdT8QjUE1hba33wOY4rbbL+7JOPNDDcG44dWAGQOpplx4I87VftMeqzxW39pLqn2cRK2ZwoU5Y87cDoMc55oAi8PfEHTdR8NWeoalKbe5ks2u5o0tptqqhAk2kr820nBxnGCela1v4t0m/F2ljLNPcW8cjmH7NIrsUxuVQVBYjcvAyfmHrWNafDuG1sobU6tdPHbW1zBany0BhM5y79PmPJAB456Z5q3p3gv+y9RnvrbVJTPK8z5khRghlEe7bxnrGp60ARReNWi+Gr+Lrq0EuyFpmt7Xf2YrjLKCMY5JHHPpWhqvic6Zptldf2VfSyXd5HaJbhAJBuPLYyRgAE/h2qgngSI+C7rwrcancS2E8ZjVgoSSPLFycjryeh4xwc1ZufCtzfaGlje+IL+a7iuUuYL7y4kkidCCuFVApHUEEHOTmgB2qeNtI0VITqRmtpJI3mMLoN6RqcF2APT6ZJ7DrVDxX44TS9Jnk0hknuolt5Hd4i0MUcrqqlzuXBIJIGc8cjFM1b4c22tfYpr/AFW6nvreN4pLuWCB2mjdtxXayFFwehUAj1qfVvh5puqxtCb2/t4JreO2u0hkH+krHgxsxIOGUj7wwe3SgDrR0HOaWo7eH7PbRQeZJJ5aBN8jZZsDGSe5qSgAopkU0UylopEkAOCUYGn0AFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQBXv8A/kHXP/XJ/wCRrz74E/8AJKNP/wCu0/8A6MavQb//AJB1z/1yf+Rrz74E/wDJKNP/AOu0/wD6MagD0miiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAqmmrabJfGxTULRrwEg26zKZAR1+XOeKuV5VpehpqXxH8RCxsLGC3tdWt7tr3aVnjcRLuVFKYKuyurHcPvMcdKAPR4da0q4nSCDU7OWaQsqRpOrMxXqAAeSO9Pi1XTp0uHhv7WRbbPnskykRYzndg/L0PX0rjND8HXth4g12WXStIt7fULmWW3v7WQ/arcMgRQoMYCngtw3Vj1qC3+HM76Fe6bINMsDJYpYLLZQkmdVcN5ko+XlgMFcn7zfMc0AaMur+H/ABrfX2g3vmCC0liAYXirFe7wxCrsf5xhTlT+XFdE+vaNBp9xeNqdmlnauYppfOXZGw6qTnAI9K5WLwbqrajf6kx0i0mkWyFtBbwsyRm2diCScfeVivA4BA5xzJb+C9Ttr2bUEu7FrhtWOqLC0B8rc0PlMh7ggchxySTleaAN2+8XaFp0WnzXOoxLBqAZreZTuRlVC5bcOAAB1rWtrmC9tYbq2lSWCZBJHIhyrqRkEH0IrkpfCF/b2GitpU2l2t7pU00scQtGW2bzVZWG1X3DAcnOeT1611tqtwtrGt08TzhfnaJCik+wJJA/GgDPuPE2iWupDTp9UtY7wyJF5LSDdvf7i/U9h3qlY6t4S0f7XY6fcabZrA0stxFbhUCsmPMYheMjK7vTjNV5fB0j+KJtZh1BbczXEM0iRROC4jUDa37zYc4xuKbgDgHgGsr/AIV5qLTy3M/iJLi5mguIJJZrNmDLL/0z83ywQPRRnvmgDeHjnw01td3C6rE0VpE007KjHYikZPT/AGlPHUMD0INRP4qj1fQNRu/C0tvd3tmPmhu0kh2nG75lKhhleRxg+tcxqXw/1Wx8Oa8tpqaX8t3p8sS2/wBk2M8jW8UXytvwM+Sh5Bxk/Wt7S/DupNpl/fPqRi1fVLeGJ5ZbIAQIgIC+UHOW+d8nd1I7CgC5b+MNPi8IaRr2qObZdQghkWOON5WLum7aqoCx79ugqa88YaJZWtrcSXTyLdQPcwLBBJKzxoAWbaqkgDIznHJxXOTfDFb3wzpOl6jqUN5caOdtjcS2QMax7Amx4t2H4Gc5Bzg9uXat8NBfaNpulWuqxW1tYrMF3afEzK0jbt8ZXb5bLyAR65OTQB3cUizQpKudrqGGfQ0+swaZdRTaULfVbhLayQpPFIqyG7GzapdyMhgQGyOvOa06AGysUid1QuyqSFHU+1eeeHvH97Jo2qa1r5tVtrSFJZLG1t5FurMlmBWRXOWAXad4AB+Y9BXoUsfmwvGWKh1K5U4Iz6VwWr/D+dvD+uNHqN5q2sXeltp9vJeNGm1OoT5FUctgknJ460Aap8d2UVlqct5ZXdnc6fJHG9pcGNXcynERVt2zDH1bjBzjFMX4gWM2lQXNtYXlzez3bWSWEPltIZlXew3hvLwEG7cGxjvnipLXwZBcaXONWmuJtRvPIe4uPNUujxHdHsKooG05wdoJ71Y1LStKtLCGXU9Vlha2uDcQ31xcqjxOQQdpI2gbSV24xgnigDN1bxReXOgaBfafHe6b/aWoQ28pntkaSEM+0q6Mwxk8ZGcdcVqa34st9E1e00+S0nla42EyK8aqgaQRj7zAscnOFBOAadqHhqzutMtbe61C+WKzmW6Ez3ALGRDuVmZgehGccD2xVa48F6Rq14NQnu76cywJFMY7xkS5VCShfZjJBYkEYoAct5exfEddON5JJZTaW9z5DqmI3WVFG0gA9GPUmujkLLGxRQzgEqpOMn0z2rCPhGyPiWDXftmpfaoIhAqfa28soMfKR3BIBOTyRk1vMAylTnBGODg0AcfB40v49FvdZ1Xw89jp1nDI0ji7SV3dGKlUUDlcg4YlfpUqeNd1vc/8S1zdR3UNtCiyHypml+6RIVGAOd3BxjjPGZIdM8KWmhavpqzLLpsSsl/BJeSTiLOWYEFiVJ3E8YJz9KpRW3geDwXPqIkL6HdYd7iWeeViVbClWYmRSrZxjGDk8daAJdN8bTXuqW2nzaUsM0uoXVg5W53hHhj37h8gyGH0I96zpvilDHpunXA0t2uLy2nuPIVpJMCN9m0GOJiST3IUDuau6H4G0VvDstpLJ/aGmXl6dStTukRo94BXD7y547kgkEg1YXw14NW8i0CPT4I5oFa9jtow6BUchWIIwNpIAK5we4oAr6z4+Ol6vbWS6eAktuk7S3UjRKpdgAhZUYIw5zv2g8AE1Lbal4mm8d6jZK+kNpVv5GYmkcTIrBjuHy4LHgYJx8vB61sSeF9CluRcPpNoZQiJkRgfKhyq46EA9B2p134a0S/1aHVbvSrSfUINvlXMkQLptORg+xJNAGDo3jK81HxlPpFxbWlvakz/AGUl5PNmWNgu9Ts8tgeThWyMc11t19o+yyfZWiW42nyzKCUz2zjnFZun+FNA0rUX1Cw0eytryTduniiAc7jk8+9O8T3Wk2fhu+n12IS6Wkf+koYjICuR1UA5FAHD6GZ/CXhCDW5Egl1TU2hjkdruYwCSVv8AWylicDJ6gcdPejVfHniDTvCl3fIulT3um6pHY3DormC5VtnMZ3ZUjeAc7sFSOa7PTPC/hux0+eHTdHsYbS+QeckcICzKRxuHcYP60l5pXh/SPD5STSLb+zbIGZbeK08wKQCMqgBycE9s80AaGmLfpYRjU57ae7yd720RjQ88AAsx4GB159q5XX/EuqWviSawttQ0bS7a2hilLaqrA3W5jv8ALYMMBVGM4PzHGB1rq1lsdPtraPMFpFIyxQRnEYLHoijjnrxVbUn0NL+z/tMWP2v5mtjcKpcbeWKk8jHHP0oA5nUvF+oWniOe1hn090S/tbWKw8tzcSxyhC8oOei7yeFIwjZPpS0/x61z45+yz6nbrpk91NY28LIi5aMfezuL53KwywVSCMZJye/aGzN9HO0cH2zyyqSFR5mzIJAPXGcVl6v4m0rRdU0ywustcajci2jEahtjkErv5yAcdcGgDm/Ak2k2Xi3xhpGnS2EEK38TwWduoTH+jpvKgcEZU5AHBBz1r0CmhFByFAPriovttoEkf7VDsibbI3mDCH0PoaAJ6Kht7u2uwxtriKYLwTG4bH5VNQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAV7//AJB1z/1yf+Rrz74E/wDJKNP/AOu0/wD6MavQb/8A5B1z/wBcn/ka8++BP/JKNP8A+u0//oxqAPSaKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACucfxLqA8RSaQnhnUJNjIxuRNCI/KZivmcvnqp+XG7jpXR1kP4egbxGNbF7qC3GxUMS3LCFlAOAY+h+8T9TQBh6J8SdK17xTJodpDKSDIsdwJI2WQoeflDFlHBwSB+oo0bxnqFz4cvtd1XSI7bT7SO5kMkFxvdvJkdSuwgYOEPOetall4O0nT9XbUbb7WjGRplt/tcnkJIwIZxHnaCcntjmm2/gjQre6vJhbSOl2JVe3kmdoVEn+sCx52ru6nA70AYkHxKEnhy51htDu2WF4AkcDhxMszbUKOcKWBIDLng9yMEx+IvG+uaZ4Wur1NItrTU7fUYbQ289x5qMsmwghlHUhwOeAc9cDO/8A8IP4fOlT6Y1nK1nPs82NruZtwT7oyXzgemcVPceE9Eul1Bbmy85dR2falkldg5QAK2CflYADkYPHWgDA8XX3iEeGdNmeMaVcyarbQz/Y73eUieVU4Yxjdnd0wMcHJxirHijxnd6HqFxBY6bHdR6fZf2hqDyziLbCSyqsfBy5KMecDC4zkitG68E+Hr3SrfTLiwL2dvJ5safaJAQ/94sGyx9yTUreD9AeGzil02OVbMFYfNZnIU5+VixJYZOcNkZwewoA5XVviFrGmvPff2NaNokFxbJ5/wBpYyzRzY2lU2jaw3BiG9cepr0Q52nbjOOM1nXfh7R783Ju9MtZ/tRQz+ZGG8wrjaTnrjAx9Kspf2X9oNpqXMP2xIhKbcON6xk4DbeuM8ZoA4vS/EfiTT/D+r654gbTLqztUu5o47QuspMTsNmGAG0BSMnnpmmW3jPX20HWbqXT7B7q2hhlsSjvHHcmXICfvNpzkcEcMWAFdguhaSl3PdrptoLicESyeSu5weuTjv39aItC0mC1ktYtMs0t5eZIhAu1uc8jHPJNAHDXfjDV77wpNcRXltY3cetw6e1zHayFYVLR5MiSbSPvYPJHIweci34tuLqTSdIkm1SxuETXLeK5Fr5kYYNMq7crLwV3ZIbIOBkCuklGg6OLDQ/sdvDFfOY4LaO2/dsUXcc4G0YCjr6cVdOj6Y0CwHTrQwqxZYzAu0E9SBjrQByHizxVrWj3erSafcaS9tp2nJqHkSKzTSruYMvDAAfL97B7DBqJvFms6r4pg03S7mzt0MVtcSRyWxmKwyIWZmfeoU5AUDBJyDjFdt/ZWnYx9gtceX5X+pX7n93p09q43WfCnh6/8QHSLuW7J1LFw1tHCuxEiVQFEuzdGvyDChhyDjqaAO5ndo7eR0XcyqSF9TjpXmWleOtXu9AvtVj1PS769bSnvI9IiiYS2kyZyjDqV6Z3YORxwa9QAAAA6Coo7W3hnlnigiSWXHmSKgDPjpk96APN7HxbqbW+qTjXU1LTdPazuX1K3tF2lHbM0RAB4CYbIBIHU5p994k0LW/Cnio6nqdhqMFrM7WbTW4URh4h5O0EcndvAccnBNelIixqFRQqjoAMCloA888TeKbDU7ewSLV/I8O3sc0c9/DbLcLJICqiAhkYLuDNyRyVAHXB2PhojxfDjQ4ZYpopIrYRvHNE0bKykg5VgCOldXRQB53q+oavL8RLOK1utRbT47mKKSG2RolTgli4aMiVDxllcbRxgnqaJA9l8SNZivNR8QlpbwSWkDJI9rJGYE5LhNoCtuABYfdHB7+iUUAed+A9Ws7KfxJbyJqhaTUbi9SS4sJwZIdic7igyeCAv3jjoa0PDfibTBompO0Gpxx29zPM6y6dOCUkmcqUUplgQw4AyO4FdpRQBheD72O78MWEaRXMT21vFBIs9u8JDqi5ADgZHuOKy/Gemx32paa9wuteRHb3Q36S8iOHPl7QxjOcHacZ4yBmuxooA8nubDxpejTIdSbUYbqLT7eSK4six/0lTmZJNkqxknC4L5XGcHOc+roSyKWUqSMlT29qWigDzWKy1u88W3FuINYS3uHuvMubl2iWCN1KrsKyFJADgqAqsAc561TOkeMJNDg0qexv5nGgXlhdTSXcbJPcOAIm5kyejfMRn5ufb1aigDzSPR9fiiuRFpmpJZLHp6LaG+HmSMjsZ2U+b8oKFV+8M46d6x9N8N+KIvBviKxvdEvp76/06CGMS3cUu66Ebo825pDjnyznrwPSvY6KAOJ1yy1DU9G0O7/4RtLqewuUafT7sQtI6GMq2xi+zILA8nnb9Kz9a0K9vtS0HWH8GWd7DFZS2s+lSPCTbsxUoct8hUbSDjONxwDXo1FAHl+peEvEFx4ta+js4/KeO2ktWhnhjFi8ewNHvMZkKZBOFwGGQQM5JqPgvXbnxTaXZ0zSrk2+tjUF1Z5ylx9n3EiErsJIUHaPmIwo4FeoUUAVdTs31DSbyyjuHtnuIHiWdBloyykbh7jOa8wg+HOqN4d1Owm07SoGbSlsFjt5PkvplYMtzJ8o2twOu48nmvWaKAOP8MaDf6V4o1S+fT7GysL20tVSC2lz5MkakMgUKFK8nDYHTp6dhRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAV7/wD5B1z/ANcn/ka8++BP/JKNP/67T/8Aoxq9Bv8A/kHXP/XJ/wCRrz74E/8AJKNP/wCu0/8A6MagD0miiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigArznxD43fSfGYifU2t7C0ngt57YwofNMi7mYYDOwCspyNoBz97t6NRQB5RpPi7WYdUurrU9Ymnt7fxC2lfZFtUCeS+fLkLBdwIJx1x8uCM16RrdzeWeg6jc6dB9ovYbaSS3hxnzJApKrgdcnAq/RQB5jpGua7eeG9UvLrWb3zFto5YfsmnmaSGYZV05hQOS2PkxlcHJA5p9p4h8SSaGZL0anHd/2vtvhb2IJtLYkgCHKHzkyFywBYBie1el0UAee6xNrkuiaZHb6nqskb3Myz3iWht5NuSYtwWNmCj5VyFG7HOATWPf6h4gXUbC3vdR1dr99EmdIrKBkVrtZFRHZFXgHOTv8Al55wOK9aqjNo9hPrFvq0kGb62jaKKYOwKo3VcA4IPvQBxc9lfR+MYdY1Sz1V2OiQxv8A2e8m37QJGZ0wjY9OvFT20epQfFjUrtbfUf7MudNjgSV1doxOHJ4z91QG+nJru6KAPNdPg8VNpqpdSat9uTT7n+0mdjtkuAf3XkbcAc5I2ADbgHmr3hG31bT9btUuY9TNveaTDLdtcs8ii9yd/LE7OOwwvSu8ooA5nxvZteaVaAWF7exRXaSTQ2MpjmKBWBKsGU5GR0Iz071w2qad4un8M2FpDZamEkuLs28f2hmmt4zxAsxEi5wCTuZzt4yDivX6KAPK9R0nxTq+g+H7n+zb9tStNP2T29xdKqSTDCkkrKjI5wSJBuwGIxk1v6hpeo/8LE0bXLfSbkrHayQX8sVzHsbcBsUKzAsFbJzgfQ12tFAHnNl4f1v/AIWd/bEmjolss0rNeXMySPsKFFEbK24Lgg7GTAy3PSu7tbm6muruOexe3iicLDK0isJxjJYAHK4PGDirdFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQBXv/APkHXP8A1yf+Rrz74E/8ko0//rtP/wCjGr0G/wD+Qdc/9cn/AJGvPvgT/wAko0//AK7T/wDoxqAPSaKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigCvf8A/IOuf+uT/wAjXn3wJ/5JRp//AF2n/wDRjV6Df/8AIOuf+uT/AMjXn3wJ/wCSUaf/ANdp/wD0Y1AHpNFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABUe6X7Rt8tPJ2537/m3Z6Yx0x3z+FSUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAV7/8A5B1z/wBcn/ka8++BP/JKNP8A+u0//oxq9Bv/APkHXP8A1yf+Rrz74E/8ko0//rtP/wCjGoA9JooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKy7jxFpFrqNxp899Gl5b2pvJISDuEI6uOOQMds1a03UrPWNOg1CwmE9pOu+KQAgMPXnmgC1RRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFAFe//wCQdc/9cn/ka8++BP8AySjT/wDrtP8A+jGr0G//AOQdc/8AXJ/5GvPvgT/ySjT/APrtP/6MagD0miiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAMXUPFekaXqcmnXcs6XMdo94yraysPJT7zBgpBx6A5yR61oadqFtq2m22oWbs9tcxiWJmRkLKRkHDAEfjXE+MdH1PVPFsX2az1D7K+i3Vq11ayoirJIVZVYlt2P3fYdWX3xymu+HPF17aaIthpt9b3FnpFtChjmjCiVCDIGPmDYw2DaVDZ3EEgUAe10mQSQCMjqK4KXwTeS+KYriJlh0K5livrm2eZhLDPGrAKm042sWUsM4+Rv71N0Lwrqll4sGoX0LyTJc3DtepNEiTxuTsDKE3sVDYCscDaSDzigDv2ZUXczBR6k4pvnRZI8xMqMkbhwKp61babe6NdWusCA6fKmyYTsAmD6k9OcYPrivN9I8HX2teEZL10tWvru8t5EMwMQubKAqsaOU3Y3ou48dW6YxgA9UEsbbcSKd3IwetOVldQykEHoQa4aPwffWdzYahZWmmxTWuo3F0tkJmESxzRFGVX2Eg5+fAUDJPpWx4G0fUNA8J2ulaktqJ7dnANrIzIVLFh1VSPvYxjtQBs3Wo2NlJDHd3lvBJO2yJZZVUyN6KCeT7CkbUrBb/AOwNe2wvNnmfZzKvmbf723Oce9cZ4i8GX+peJL++istFvre9toIwdRMge1kjckFNgyV5zgMpJHXFQ3ngLUrvxD5xmsltW1WPVWvVLC6UqqgwqNuNny9d3Q4xQB2lrrukXzlLTVbG4YR+aRFcI5Cf3uD096z9G8a+G9fW4bTNXt5xbKzzHJXy1UkFjuxgcHnpjmueh8H6tHqGi3SWWi2z2GrXFzI1vK4LW0gYbcCMAt8/Q8fIvPJxeGgeKP7J1HSItQ0u1tZEmW2mjgZ5dzvu3OCdvRmUjBz1yM4oA24vFOgzaNNrEerWjadAxWW5Eg2IRxgn15H5iq19410Gw07Tr9r5ZrbUZlhtWgG/zWZscAdh39MGuXtvhxqQhuDdanaS3CXtvf2TtHLJtliXaFlLuWkTaOmRgkkY6V0E2gazLoixJqFjBqEd6LyHyrQi3X5slCm7cwOWJO7O4546UAX5vFmg29nbXcupwLBcxtLE/OGRSAzdOAMjJPrVLxV4ztPDUSqqLd3m+HNsGKlY5JNm8kKQBnOM4zjGaxde+Hd34jls7zUdVglvkt5La4Jt3WJo3bd8qpIpyvQbiwI6ip9X+Hs1+t1HZa19iiu4LaO4T7KJNzQEFGUlht6AY5oA7hmCIzHOAMnAzXPWnjjQL1rIQ3co+2GcRGS2kQAw/wCt3blGzbjndit9A0cKq7mR1UAtgAscdcDjmuN0bQU1XVdd1W4sZ7Ow1GLyIbWdSkgJBE0u3/lmX+Uep2AnqKANEePPDv2Oa6N5KsUQjZt9rKpKO+xHAK5KFuNw496sXvi3SNPh1KWeWbbpkiR3e2Bz5RYBgTx93BByOKx7T4dWvl3C6tqE2oM9kunQuEEPk26NuUYXhmDAHcfQcdcvm8Ard2usRXmu6hK2sJGt4wSFQSihcqNny5AGetAHSaZqSapbNPHbXcChygF1C0TMB0YA84Pb+lcf44+Ir+DL24tn05rovY+faFAcNNlso5HQbVLZ44Vh6V3FtFJDbpHLO87r1lcKC34KAP0rG1bwtDrL6j9pvZ/KvrT7K0YSMiNcMNyEqSG+d+ST96gCC58ZWemRWA1CK5MlxFA0ssMDeTEZWCLlj2LHGBkjqfWkt/HGnTX8tpJaX9v5N4tjLLPCFRJm+4pOc/MCuCBj5lzjNULn4a2N4yG51fU5QI4UIYxctFjY4Pl5VvlXO0gHHIq/L4Js5r28uXvr4/atSt9SaPcm1ZYdu0D5c7TsXIJ/hGCKALFv4u0248QPopE0V2FldRIoG9Y2CscAlgMngsAG5xmqcXj/AEh9IudXljuoNOt7RLtriRVw0bkhMAMWy2DgEA+uKbb+AtP0yaO80uaaK/t4pUtnlYMoMnJ34AZxuAPJzxwRWDoHgnUXsl0nVLCC20R4JIb62e5WZ7tztKyAqgK/NubJYtk9O9AG8njgTeG7jV7fR7m4a1b/AEm2hngdo02lt+4OUbgA4BLc4xWlHr7Q6Bd6vq+m3GlxWwZ2juHjZigGd3yMQM9ME5yKgbwdYSaXeWMl3qbi8RI5pjeP5hROAobPAxkHHXJzmmXPhaSf+xrM39xNpthObqYXMpkmnkU5iVnPVQSSc8/KvvQBzmqav4r03TrS5v5ZNMtGgmvL26ihW7a1kLEpAyKCfLVeDIATkdVFampeOzpNvq3maXPcPpVvbXEjrIiiaKXcPMXnjGxsggHjitLXfBmleINQW+upL2G4+zm1drW6eHzYiclH2nkZJ/OpNU8G+H9Zl8y/05ZWMKwNiV1DxrnarBSAwGTjOcZoAyh45mTWJLWfRZEtItTTS5LlbhWKzOEaM7MD5SHGSDkHseSF0jxzLq2sy2CaNPHHIspsrklzHKUJGJG2YiJ2kjluPQ4BdpXgS0sfFmo61cpDcedMk1pkyboCsax8gsVY/KCGxuGTzWra+E9EstSl1C3sdlzKWYsZXIUtncVUnCE5P3QOpoA5vSPGHi3VtAfWoPC1nJbeQWjhGoYlldWKuF+QjBxxnB496TV/GGoal4O8U3+hx2ywWVmz2uoJcEiQ+XvbC7eGRSPUbjjPBx1Og+GtJ8M20lvpFqbeGRtzIZncZ9txOPwp8vhzRptFm0dtNt106bdvt402IdxyT8uOSTnNAGDf+JbvT/BmjX2mxG8ku7eN/Oug7lU8veZHSMF2J4B2qcFsnArNn8farLbWEenWWnSXr6KNZuTNcMsZj6bI8AkknPJ4HGetdSnhHw8lraWw0i0MVoCLcMm4xZAU4J5GQoB9cVNceG9Eu7S2tLjSLKW3tVCwRPApWIDoFGOB7UAcw/i3Xr7xRZ6Zo9rpZtr3TY9SilvJHR0jJAKlRnLc8Y4HerZtL3/hY6GHULzasX2i4Esh8kwMCiQxxj5dwdS5fG4cDJB437nQNIvNSi1G5021lvYgojuHiBdADkAHqMHmrQsrVb974W8Qu3jETT7BvKAkhc9cZJOPegCeiiigAooooAKKK5u88G295eTXLa14giMrlzHDqkqIueyqDgD2FAHSVDd2lvfWslrdQpNBKu143GQwrmx4FtgQf7e8SnBzzq83+NdVQB5Npl7b2Gl+JNR0O6t9V1nRrX7DZpCM4t1+ZWKqPmbJIJHUpx15taV4w1zUPCeo3Md7BLcJcRJazxxvKCrY3AyLCEzww3bCE43CvT6KAMXwrqUuq6DFczi48ze6l51UFwGOGUqqhlx0baMgZxW1RRQAUUUUAFIzKi7mYKPUnFLVTUdMsdXsms9Ss4Lu2cgtDOgdSQcjg+9AE/2iD/ntH/30KckiSZ2OrY64Oa5z/hXngz/oVtH/APANP8K1NJ0DSNBSVNJ0y0sVlIMgtoVjDEdM469aAOM8V6JqN/4/iubG3mSYaUUtb4Rboo5Q7Fo5D2V0JX/gQPUCspfDfi6HRoLB4L3EOhWtvYfYr4RC0u0UBzJ843fMByAw2gjvz6zRQAgztGeveloooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigCvf/APIOuf8Ark/8jXn3wJ/5JRp//Xaf/wBGNXoN/wD8g65/65P/ACNeffAn/klGn/8AXaf/ANGNQB6TRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUANdFkUq6hlPUEZFOAwMCiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAK9/8A8g65/wCuT/yNeffAn/klGn/9dp//AEY1eg3/APyDrn/rk/8AI1598Cf+SUaf/wBdp/8A0Y1AHpNFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFU7jVtPtL+GxuLyGK6njeSOJ2wWVOWI9h3pdN1Oz1iwjvrCcT2sufLlUEBwCRkZ6jI69DQBbooooAKKMjOM81G08SRPK0qLGmSzlgAuOuT2oAkoqNJ4pXdI5UdkxuVWBK56Z9Kz9a1610SKLzY7i4uJiVhtbWPzJpccnavoByT0H4igDUorI0fxJp2s6PZ6nG7W0V47Rwx3YEUhdWZSu0nr8rce1WJNc0iK4NvJqlkk4cR+U1wgbcSAFxnOckDHvQBforNg8RaJc3gs7fWdPluixUQR3SM5I6jaDnIwfyqU6zpai6J1KzAtOLkmdf3P8Av8/L+NAF2ism68T6JaadfXzanayQ2MZkuPKmVyg56gHqSCB6nipLfxBo9zpi6lHqdp9jO3MzTKqqWxgNk8HkcHnmgDSoqlNrGmwaaNRkvrcWRZVFwJAYyWYKPmHH3iBV2gAoorhrX4jJd6lp+lR6cF1O41GexnhechYPKDNv3bcsGC/LwAeeflNAHc0VjDxVojNdKt+jG1R3k2qxyqHDlcD5wp4O3ODwagtPG3h29ivJIdRUJaQrPKZI3T903R13AblP94ZFAHQUVhN4x0RdFbVmupBbLMIGU28glEpIAQxbd+45GBtzgg9KhXxzoLadFfCe58qUyBENnMJGEYy7CMru2jucYzx1oA6OiuW1Lx7pWm39jafZdSu3v7b7TaPZ2plSdf7qkd8EHnAGRkjNdNDL50Ecux496htkgwy5HQjsaAH0UhOFJwTjsK5XRvHWn+Ip4LO2t9RspbyGZ7Wa5gCq5jba4Xk5ZTzg+lAHV0VwvhvxRPY+Ftdv/EmpfaRpeo3Ft9oeJIWdUICjaMLuJOB65FXoPHllJ4cvNWezuEazmEE1sskUjKx24O9XKbfmHzFgBg56UAdZRXJXPj21t/DljqwsZXa8keJIfPhVVZCwfMxcRADYcHdz2zUGo/EnTdOjsw9rM91NZrfSWwliDxQsQAclsOeThVJJAPtkA7SiiubtvFrXWsLaxaPfNYNcy2o1FdrRB4wdxIBJC7gy7iMZBoA6SiuNb4gRrFDMdIuhDdWk95auZE/exxYLcZypKkMOxHeq9349uW8O6vcw6YbW+t9H/ta2SeQOrRENtLbejZU/L9OeeADuqKwJ9cvbDQkvb62s1uJWiSGJLptrl8dygPGScAMcCs+DxwLxNKtrSyDapqS3DR28sjJGBCxVyXKZ5I4+XPPIFAHX0Vymo67rSeKNC0+ytbRUvLKe5niuJyCGTyxtDKrDgydRkHn2rqUbdGrHbkjPynI/A0AOorhv+Ey1VvG66QbWytrM3DQRm4Mm+cBSdyOoMecgjYTuG1sjinaJ43utTfw8s9rbR/2nZXNxKEkJMbxMo2gHsd3U+lAHb0V5x4e+IGsal4Z1nX76wsorO0skurcxtJhiULlWJHO0YBKjrnFPl8Y+ID4de9SCzD3WpR2VjMsLAeWxwZpEd125wQqkrzjJ5oA9EorznWvG+r2nhrTbqA2ENzNPMs8u6KbEUeQXSMTDcSdmVDkqCc9KffeJLufUfDV1b+JbTT9OvdMlnea4tgIJpP3e3l2VgfmJC8HCmgD0OivOpPHmqyeOjpNtZwrYxTQxh5ZYlNxG4y0qZkDEcjbsVgcHJ54s6XrV/f8AxB1bRx4ntDb2M6SLbCKIyyqyktFkHhUwcnG7JGTxggHeUVV1O7+waVeXmx3+zwPLsRdzNtUnAHc8dK8n0zxt4hvNI1f7Xrlra3VpZW1/5ojhkWJnZg8XykgoMJ33jdycmgD2KmRTRTxiSGRJEPAZGBH5ivNv+Ep1eyvr3R5dZF4lre2vn6qsEatBbSxs5JUApwUUbyMYlGema2/hmqR+FJYolkEaajd+WzRbA6NM7oy8AFSrKQVGOeKAOpvb+z023+0X13Baw5C+ZPIEXJ4AyamjkSaNZInV0YZVlOQR9a4TxtcW0PjHwwLvVbm0gb7QCiRo6bimFOGVvmJJABB74xzkvtZ1q21zU7S2aeP7NPapp1mlniK6jYIXLSbDjkuCQRt2gkeoB3tFcPaC5n8e6pbTa7rSW8M8MtvbmNVhkbYS6htnMY4GMjkHkmsPw3qnii61LT7DU7bV4RpsU8k93khb1oxsZSCpBJcqycj5aAPVKK8i0fxTq13NrMN6dea1/skXKSLbSrJ9oUncqMYowpwVG0KVPr1zq2t5cjwXDqVrc6/dzm4txq0kkUsc4RQDJ5UTKMDkA+WBkZwSRQB31hqVjqkDT6feQXUSuY2eCQOAw6gkdx6Vari/hxDNBYa15ttfxRzarNcQPfRlHljcKVbnn8wD6812lABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFAFe/wD+Qdc/9cn/AJGvPvgT/wAko0//AK7T/wDoxq9Bv/8AkHXP/XJ/5GvPvgT/AMko0/8A67T/APoxqAPSaKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooA8+8Z+F5vEPjbS5Tb3i20FhMgvbcj9zIzpkEbgTujWROOm8fUcje6L4pm8D6RosegarE9npskaGGZRsud2ELATIMAAEN8xG4/LXrmua/pvh2xF3qdwYo2cRoqoXeRj2VVBLHvwOgNZt74+8O2Fhp97LdyvDfxNPb+TbSSMY1GWYqqkqADyTjFAHCy+HNal1zWNTutG1afdaWVzYol5jbcgIJRt8wLu9c/Kdp/Gy2keKLv4m22uDTtQtrZLxfNBuF8s2xj2j/lqecnLKFABBwW79Te/ErwzYai9jPc3XmoyqWSymeP5k8wHeFK42ZbOegJ7U6P4i+HZdYGlJLeG6M5txixm2bw6ofn27cBmUE5wNw9aAPNvCwa68Y3c7TXMV7fzahFpdykibAzGVlkkUylyVUEBTGAB7810OleDNUs9E1mzm0ON0utOEL28l1Ey3FyCcSbQgGTnJdyW4Xjit+z8R+CItdujZW1uupr55aWGwIknMZ/ehGC5kIPUKSTg9cVcs/H2iajZzXFmbt9li9/GklpJEZoV6sm5RuGcDj1HrQA3wFoX9ieH4kuNFg03USiR3TxyLK1yyDHmM45JJLHnJGad4i0W8/4SDTfE2l2yXd7YxS27WjzeUJY5MchiCAVIzyOQT7Ulr44tJPC0eu3en39rE0UDCNocl2lwFVD0bkgZ4HIJwK29J1RNXsBdx29xbgsVMdwgVwR14BI/I0AcVrPgzXtYD3F9/Y+o3U+mtZslzvSO3cys4kTAJOFZV42k7AcjPEHiPwLrOqNfpaWuj7p2JjvJZmWUfuUTccRnDBk3de/rXV6z4jm0nXtI0yPSp7v+0PN/eRSIu0om7ADMMn6kD69KjuvGdhZ31xay215/oiRPezBF8u08zG0O27rggnbuwOelAHMf8IRrkmoWl59j0O3khvFumeCV95/0oylQfLHWNtv146VNp/w/wBRtbW5tp7ixuD9juLSO4mVpGlEvzbnThQd4BOd+ccEZNeiV51e+M9fvdH8VG10eWwXTPtccWpLPC4RoY9y5RskliPQgBvagC/D4NvxZeQktjYebof9mSraRk7XG7aykgAqNzcEfxHpVvVtA1rW9Ijs72608bLiKXECSx5CAnIcNuVt+1gR0245zVW38ffZdCur3W9Ku7E2tnFdL5rxk3CudoI2sQpLYGDjG4Vp+EPF9r4vsLi4t7We3e3l8qVJMMucZG1hwwwfwNAE1lpmq2Ph1LQXdpcX6ymTzZoPkIMm7BCkEsF43dSfmOelblcnrl9qV54utPDlhqR0tXsnvXuo0R5X2uECKrqVxzknBPTp3w9G+JN5cW0ltNpLzXlvpM1/5nnKi3HlTNC3bCk7S3tQB6RXIHwQx1PTdSF7AL2yu5J/NFqcyo3m4jPz/wAPnyYPuOOuWa348XStZsLGKxW4SdrcTyCcZiE0gRcKAe7A/NtBHQk8VZiL23xQmhF1dNHd6T53kNIWjVklClgCflOHHAwOuc8YAMqw+Gz2GsvqSa0zyPZT2j74Cxk8zne2XwGyFJ2hQcdBmrF14EvruZ7h/ELRXL6WummWC1CHCyB933j1xtI9CcEZrS0M6kdb8S/a7gM4njFtD5peOJPKUggEAgkkkiub8P6/451LwYNXVtBurhoTNHCFkV2AZgQQDjOBge/WgCrqXgXWdM0aa3s9QlvTfatBeTPbWkcTWuxR+8RdwzykY4YEDJHNS2ngG48R6TZDX1jgk0yWWGxWWyiffbtt3GSNi67iVypByOCckkHqvDOuX/iC5v71UtToW5Bp08e7zJxtBZmB4ABJXscg56VS8WXDz+JtA0O4u57XSr9bhrhoWaMytGqlIvNXBTOWbggnZjvQBbPg+JLjSJrbU7y3OlW7W9sqJEQFYAHIKeiqOMAY6Vp3VpqMuvafcwXpisIY5RcwcHzmIATtkY+Y5yPTBzxwp8Tz6Ho62ehX1rc2ljpsl8b7WHctcgSMAiHIJxtbLHPVP72akuPiFqkMGsytb6fB9m+wTWa3DFDLFcY3Bvm+8vI4x0zigD0iuB8EeDLrTk+06010Lu0luUsk+0K8UUcrli6BVGCc4+YsRjjAOKmg8VazJqF+WOlrZ2etJprIVcSGNtvz53YzlwMYwcE8dKTw54o1LWdat2bUdGa0uDOj6em4XVs0bEDv82QATlVAyMZyKALNr8PrCCw1Sz1DVNQ1Kz1GQzzxXZiAWXIPmKURSGyo7446VaufCWka7aQvc3t5fqtwl1DM10XUOgIUqv3Mcntz3rI8Fajo91aeJ7K5u9OnWDU7l7lWkVg0fy5kdSxAXIPPC8U/4Y6vpX/CvLVYb+0YWSStOkUqsYV8xyNwH3RgZHtQBrxeDLGCyFpHfaksYkmk/wCPknPm/fBBGCpOTjHBORikj8C6FbSWb2cNxaPawfZVa2uZIy8OSdjEHLDJJ9Qehrcsb621OxgvrOZZradBJFIvRlPQirFADIokhhSKMEIihVBJOAOByax4vCWiwaj9uitpUn+0G6wtzKE809W2btuT9K26KAMBPBXh6N3ddOALwyW4HnSYSOQ5dUG7CAn+7ipV8J6IoA+xllFmbEq80jBoOf3bAt8w+Y4znHatqigDml8AeGUsWsxp8nkmRZebqYsGUEAht+4cEjAOOaWPwF4Zi0kaWmmlbRZjOqi4l3I5GCVfduXI6gHBrpKKAMa78JaDfWdjaT6XAbexObVEBQRcYwNuOCOCOh7g1rQwx28KQwxrHFGoVEQYCgcAAdhT6KAMqLw1ocGqtqkWkWSX7OZDcrAokLEEFt2M5IJ596hufCWiTm5mj061tr2cu32yGFVmSRlKmRWxkNgnmtuigDz2z+Flta6ffWq3dtF9psBZbrPT0gzyCXkwf3hJUZB4wWH8RrZ8LeCLLw5BfK4tLh73YJlhsY7eIqudo8teCfmOSc9vSupooApyaTps0EUEmn2jwxZ8uNoVKpnrgY4qWaytbiFIZraGWKMgojxhlUjoQD0xU9FAEZt4WuFuDDGZ1UqshUbgD1APXFQx6bYxXTXUdlbJcsSTMsShznrzjPNWqKACjFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAV7//AJB1z/1yf+Rrz74E/wDJKNP/AOu0/wD6MavQb/8A5B1z/wBcn/ka8++BP/JKNP8A+u0//oxqAPSaKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAwPEfh2TWbnTL+zvPsepaZMZbeVk3oQw2urrkZBX3BBxVC88G3txNbXkPiGe31JLZrS4uVtYiJ4i27GwjCkEnBH45rrqKAPO7r4VJJIy2msvb2ojjjiha2WTYEtmthyTydjnr3xT7X4ZTWlzFcReIZY3jlkkAjs41X53ikKgc4AaFTx646V6DRQBxWmfDXTNJ1qXULSZYvnleBY7K3V4zIGDAyBNzAb/lGeMAHIqXSPAUemrpyT6rcXcdnpcml7GjRA8Tsp7DIICqOvb657CigDmk8HKmmJp41zVTbRpDFEhaLaiR9Fx5eGBGA24HIFaPh/QLLw3pn2CwUrCZHlIwqjcxycKoCqPZQB+Oa1KKAMnWtAg1prSVrm5tLq0cvBc2rhZEyMMPmBGCODx9MVRm8DaPcSSvMbt/tCRR3INwxFyIjlPN/v+hz1HByK6SigArnZfBWky3N/KWvVjv/ADftNul3IsMhkTY5KA4yR+R5HNdFRQBzreCdGkXbOlzOP7P/ALN/fXDsfJ3bu5+9kD5uvA54rQ0jQrPRVk+zPdSyShRJNdXMk8j4zjLOSeMmtKigDL1rw/Ya9FGt2sqTQ58m5t5Wimiz97bIpDAEDBGcHvWTa+BtOn0eysdctrS+ayRoIZI4jCDESPlYBsNnaNw6EjOBXVUUActN8OPCNwUMmixHYqKAJHUYThcgNyQAACeeB6Vcl8HaDNrqa3JYBtRjKlJ/NfK7cYAG7GOBxjFbtFAGDYeDPD+may+r2eniK/csWm81yTuznILY7ntxSS+GoLFbq58N2umaZqlwfnums9+4E5YEKynk89cZ5wcmt+igDP0PSINB0W10y3Z3jgXG9/vOxJLMfcsSfxqbUNMsNWtGtNSsre8tmIJiuIhIhI6HB4q1RQBTn0nTrqG3huLC1mityGhSSFWERHQqCOMe1SzWVrcSCSa2hkcDaGeMEgemT25qeigCs2n2T799pbtvIL5jB3EdCeOcVKlvDHM8yQxrLJje4UBmx0ye9SUUAV49PsoQ4itIE3rtfbGBuHoeORSw2drbo6Q20MaP95UQAN9cdanooAbHGkUaxxoqIowqqMAD2FOoooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigCvf/wDIOuf+uT/yNeffAn/klGn/APXaf/0Y1eg3/wDyDrn/AK5P/I1598Cf+SUaf/12n/8ARjUAek0UUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFNeRI0Lu6qqjJJOABQA6iqD65pEUjRyarYo6kqytcICCOoIzTf+Eg0X/oL2H/gSn+NAGjRWd/wkGi/9Bew/8CU/xo/t/Rv+gvYf+BKf40AaNFZ39v6N/wBBaw/8CU/xo/t/Rv8AoLWH/gSn+NAGjRWPd+LPDljGJLrXdNhQ93ukHp7+4oXxXoLorpq1qysMhlfII9QaANiisj/hKND/AOgpbf8AfdH/AAlGh/8AQUtv++6ANeisC68a+HbMAy6irZBP7qJ5ehA/hU+o/X0NU/8AhZHhb/n+uf8AwX3H/wAboA6uiuU/4WR4W/5/rn/wX3H/AMbrUi8S6fNGJI01BkPQjTbj6f3KANeiufvfF1pZlAuma5c7s8waVO2365UVV/4Tu2/6AHib/wAE83+FAHVUVyv/AAndt/0APE3/AIJ5v8K0IfERnhSVNF1cK4yA9sEb8VZgR+IoA2qK5+78S3duEMHhjWrrOciNYV2/XfIP0qr/AMJdqf8A0JHiD87X/wCPUAdVRXK/8Jdqf/QkeIfztf8A49WmuraiyBv+EdvhkZwZoMj/AMiUAa9FZP8Aauo/9C/ef9/4P/i6P7V1H/oX7z/v/B/8XQBrUVk/2pqP/Qv3v/f6D/4uqFtrHiqa6WOXwnDbxEn97JqiED6hUJoA6WisaG98QyJufRbKI5xtbUST9eIjUn2nXv8AoFWH/gwf/wCNUAatFZX2nXv+gVYf+DB//jVRXFz4l8h/s2l6X52Pl83UH2598Q5oA2qK5X7R4+/6Bnhv/wAGE/8A8Zo+0ePv+gZ4b/8ABhP/APGaAOqorn7STxhJv+22uhwYxt8m4llz65yi4/WrP/FRf9Qv/wAiUAa9Fc1cQ+N3nZra/wDD8UR+6klnM7D6sJRn8hUX2fx9/wBBPw3/AOC+f/49QB1VFc1b2/jfz0+06poHk/xeVp8278MzYrQ+za9/0FbD/wAF7/8Ax2gDVorBvdO8S3MSrB4htbRg2S8em7iR6fNIRVL+wfF//Q6p/wCCmP8A+KoA6uiuWj0LxYHBk8Zhk7hdKiBP45Naf9laj/0MF5/34g/+IoA1qKyf7K1H/oYLz/vxB/8AEUf2VqP/AEMF5/34g/8AiKANaishtJ1FlI/4SG9GRjIhgyP/ACHVS08MXtu7NP4r1u6UjAWRoFAPr8kQNAHRUVjroMqjB1vVWOScmVPXpwnbpS/2G/8A0GdU/wC/q/8AxNAGvRWR/Yb/APQZ1T/v6v8A8TR/Yb/9BnVP+/q//E0Aa9Fc7d+EY751ebXNeUqMDydQeIfiEwD+NV/+EEtv+g/4m/8ABxN/jQB1VFc5beDbW28zOra/NvXb+91ac7fcYYc1f/4R+y/57aj/AODK4/8Ai6ANSiuZufAPh28uHuLm2u5Zn+87ahcEnjH/AD0qL/hW/hb/AJ8bn/wYXH/xygDq6K5T/hW/hb/nxuf/AAYXH/xyprbwB4ZtJ1mj0+RnXOBLdzSLz/ss5B/KgDpaKzrbQNJs7hLi2sIIpkztdVwRxitGgAooooAKKKKACiiigAooooAKKKKACiiigCvf/wDIOuf+uT/yNeffAn/klGn/APXaf/0Y1eg3/wDyDrn/AK5P/I1598Cf+SUaf/12n/8ARjUAek0UUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQBl6z4d0fxCkKavp8F4sJLRiUZ2k9cVk/wDCtfBn/QuWP/fH/wBeuqooA5dPhx4NjkV18O2IZSGB8vPIrSXwt4fSMRjQ9N2+htUP9K1qKAMY+EPDLEk+HdJJPJJso+f/AB2k/wCEP8Mf9C5pH/gDH/8AE1tUUAYv/CH+GP8AoXNI/wDAGP8A+JrQg0ywtYEgt7G2hhQYWOOJVVR7ADirVFAEP2S2/wCfeL/vgUfZLb/n3i/74FTUUARC1tx0giH/AAAVKAAAAMAUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQBXv/wDkHXP/AFyf+Rrz74E/8ko0/wD67T/+jGr0G/8A+Qdc/wDXJ/5GvPvgT/ySjT/+u0//AKMagD0miiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACisvWdP1K/SEadrc2lshJdo7eOXzB2B3g4x7Vk/8ACOeJ/wDoebz/AMF9t/8AEUAdVRXMQ+H/ABGk6NN41vZIwcsgsbZdw9M7OK0/7KvP+hg1L/vi3/8AjVAGpRWX/ZV5/wBDBqX/AHxb/wDxqo5tEu54jGfEWqoCQcoLdTwc9RFQBsUVzEXg6SOTe/inxFKMg7XukA6g9kHpj6H1wa0P+Efh/wCghqn/AIGyf40Aa9FZH/CPxf8AQQ1T/wADZP8AGg+HoSCDqGqc/wDT9J/jQBr0VzMvgXS55DJJe65uOB8usXKjgY6B8Uz/AIQDSP8An913/wAHV1/8coA6miuat/A2k286yi51mQr/AAy6vcup+oMmDV1PDGmIgXF4cd2vpifz30AbFFczc/D7wteztPdaUs8zYzJLNIzHHA5LVF/wrTwd/wBAOD/vt/8A4qgDq6bJIkSb5HVFGBuY4HPArmIvhx4QhlSVNDt9yMGGWYjI9icGtN/C3h+Rdr6FprL6NaIR/KgC5JqenxPskvrZGGDtaVQeeR3pn9r6Z/0EbT/v+v8AjVB/BnhaRtz+GtHZvVrGIn/0Gk/4Qnwn/wBCxov/AIARf/E0AaH9saZ/0EbT/v8Ar/jR/bOl/wDQSs/+/wCv+NVrTwv4fsJTLZ6FpltIV2l4bSNCR6ZA6Vd/s2x/58rf/v0v+FAEf9s6X/0ErP8A7/r/AI0f2xpf/QSs/wDv+v8AjUn9m2P/AD5W/wD36X/Cj+zbH/nyt/8Av0v+FAGa3jHwyswhPiHS/NIUhPtabjkZHGe/apf+Eo0H/oMWP/f9f8a0Es7WI5jtoUOc5VAKmoAyf+Eo0H/oMWP/AH/X/Gj/AISjQf8AoMWP/f8AX/GtaigDn7nxv4atbZbiXV4DGx2jywztn/dUEjp6VT/4WV4R/wCgsf8AwFm/+IrrKKAOT/4WV4R/6Cx/8BZv/iKP+Fl+Ef8AoLH/AMBZv/iK6yigDFh8V6Tcb/Ja8k2NtbbYTnBwDg/J6EH8ar3njPT7SRU+wa3PkZ3QaTcOB7EhOtdFRQByv/Ce6f8A9AjxH/4Jbn/4ij/hPdP/AOgR4j/8Etz/APEV1VFAHO2njC2vWKw6TrgI/wCeumSxD83Aq3/bw/6BWqf+Ax/xrXooA52fxVPFDG6eGNemZiQY0gjDJ7ndIB+RNV/+ExvP+hM8S/8Afq3/APj1dVRQBz9n4kvb1nA8Ka3BtAOZ/s6A/T97Vv8AtW+/6F/UP+/tv/8AHa1aKAMr+1b7/oX9Q/7+2/8A8do/tW+/6F/UP+/tv/8AHa1aKAOfuda15Z40tPClxLGwO6Sa9gj2n6BmzVr7Zrv/AEB7T/wPP/xutaigDJ+2a7/0CLT/AMDz/wDG6Ptmu/8AQItP/A8//G61qKAMaS88Q+U/laPYmTB2h79gM9s4j6Vn/bfHf/QD0D/way//ABiupooA5b7b47/6Aegf+DWX/wCMUfbfHf8A0A9A/wDBrL/8YrqaKAOdiufGLeV5umaKmc+Ztv5W289v3Qzxz29PerMreJjE4ij0lZCp2s8kjAHsSMDI9sitmigDlnj8el2KXXhtUz8oa2nJA9zvGaTyvH//AD9+Gf8AwFn/APjldVRQBz1lD4xMjfb77QlTHy+RZzMc++ZRV3yNe/6CWm/+C9//AI9WpRQBl+Rr3/QS03/wXv8A/HqPI17/AKCWm/8Agvf/AOPVqUUAZT22vsjBdU05SRgMNPfj3/11U7bSPEabPtXigS43bvK0+OPPTbjJbGOc9c5HTHPQ0UAZ1tY6hDcJJNrE08YzmNoI1DceoGa0aKKACiiigAooooAKKKKACiiigAooooAKKKKAK9//AMg65/65P/I1598Cf+SUaf8A9dp//RjV6Df/APIOuf8Ark/8jXn3wJ/5JRp//Xaf/wBGNQB6TRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRUcs8UABllSMHgF2AzQBJRVf7fZ/8AP3B/38H+NJ/aVj/z+2//AH9X/GgCzRVb+0rH/n9t/wDv6v8AjTW1TT0Rna+tlVRkkzKAB69aALdFZF14r8O2Uoiu9f0qCQqGCS3kanB6HBPSof8AhNvCf/Qz6L/4Hxf/ABVAG7RWF/wm3hP/AKGfRf8AwPi/+KqWLxZ4cmTfFr+lyLnG5LyNhn8DQBsUVi3Pi7w7aW7zy63YeWgyds6sfyGSazv+Fl+Dv+g5B/3w/wD8TQB1dFcp/wALL8Hf9ByD/vh//iat2fjfw9qAJsr9rkL18m3lfHT0X3H50AdBRWIfFmkh5EDXjNGgdgtjOTg5wPudeOlU5fHekxSvGbTW2Kkjcmj3TKfoRHyKAOnorlv+E/0j/ny13/wS3X/xupofGunXCO8djrRCFQ27SbhepwMAoM/h070AdHRWOviKBwSNP1Xgkc2Mg5Bx6Uv/AAkEX/QP1T/wCk/woA16KyP+Egi/6B+qf+AUn+FQXficW0PmRaJrV02ceXDZkN9fnKj9aAN6iuY/4TGYzGNfCfiNhkgP9mjCn35kFaKaxeSRq48PaoAwBwzW4I+o83igDWorL/tW8/6F/Uv++7f/AOO0f2ref9C/qX/fdv8A/HaANSiuVPiLxNnjwNeY/wCwhbf/ABdH/CR+J/8AoRrz/wAGFt/8XQB1VFcr/wAJH4n/AOhGvP8AwYW3/wAXWmL7WyAf7EiHsb0cf+O0Aa9FYNzf+Jgh+yaDZO+BgTaiUHX2jPaqf9peOP8AoWtG/wDBw/8A8YoA6qiucs7/AMXyXkKXmgaVDbFwJZI9Ud2Ve5CmEZPtkV0dABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFAFe//wCQdc/9cn/ka8++BP8AySjT/wDrtP8A+jGr0G//AOQdc/8AXJ/5GvPvgT/ySjT/APrtP/6MagD0miiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAK9292kQNnBBNJu5WaYxgD1yFbn2xVPz9e/6Bum/+DB//AIzWpRQBy8svjvzn8mz8OCLcdge7nLY7ZxH1pvm+P/8An08M/wDgVP8A/G66qigDlfN8f/8APp4Z/wDAqf8A+N1JA/jhnIuIPDsa44Mc07nP0KiumooAxJI/E7J+7utIjbaRzbyMAccH744H6+1UPsXjv/oOaB/4Kpf/AI/XVUUAct9i8d/9BzQP/BVL/wDH6BZeOsjOuaDj20qX/wCP11NFAGOln4g2DfrFlvxztsDj/wBGVnz6F4plneRPGTQoxyI00yEqvsM5P5k11FFAHKf8I94r/wCh4l/8FkH+FH/CPeLP+h4l/wDBZBXV0UAZI0q/wM+IdQJxyfKt/wD41S/2Vff9DBqH/fq3/wDjVatFAGV/ZV9/0MGof9+rf/41VOTwzdzXouJPFOubQRmFHhSNsdsCIHn2IroaKAMj+wR/0FNU/wDAk/4Uf2CP+gpqn/gSf8K16KAMj+wR/wBBTVP/AAJP+FZ83geynmeV9W8Qb3OTs1e4QfgFYAfgK6eigDlf+EC0/wD6C/iP/wAHVz/8XT4vAunxSpJ/aniB9rA7X1m5Kn2I38iunooAyT4c08ggtfYP/UQn/wDi6yf+Fa+Ef+gSf/Aqb/4uusooA5P/AIVr4R/6BJ/8Cpv/AIuj/hWvhH/oEn/wKm/+LrrKKAMCz8FeG7GMpDpFuQf+euZD+bE+tWf+EX0H/oD2P/fhf8K1qKAMn/hF9B/6A9j/AN+F/wAKin8HeGbpQtx4f0yZQcgS2qMAfxFbdFAHO/8ACA+D/wDoVdF/8AIv/ia1f7G0v/oG2f8A34X/AAq7RQBS/sbS/wDoG2f/AH4X/Cj+x9L/AOgbZ/8Afhf8Ku0UAUv7H0z/AKB1p/34X/Cj+yNM/wCgdaf9+F/wq7RQBS/sjTP+gdaf9+F/wqzBbwW0fl28McSZztjUKM/QVJRQAUUUUAFFFFAEUFutv5u1pG8yQyHfIWwT2GTwPYcVLRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQBXv/APkHXP8A1yf+Rrz74E/8ko0//rtP/wCjGr0G/wD+Qdc/9cn/AJGvPvgT/wAko0//AK7T/wDoxqAPSaKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKoatrFjodn9r1CSSODcE3JC8mCenCAn8aw/wDhZHhb/n+uf/Bfcf8AxugDq6K5+x8a6HqRcWUt7OY8FtmnXBxnp/yzovfF1pZlAuma5c7s8waVO2365UUAdBRXK/8ACd23/QA8Tf8Agnm/wo/4Tu2/6AHib/wTzf4UAdVRXNW/jOG6lEceheIQx7yaZJGPzbAq9/bj/wDQG1T/AL9L/wDFUAa9FcxN4r1GOZ0Twbr0qKcCRfswDD1AMwP5imf8Jdqf/QkeIPztf/j1AHVUVyv/AAl2p/8AQkeIPztf/j1X7fW9SuIFlPhnUod2fklltww+oEhoA26Kyf7V1H/oX7z/AL/wf/F0f2rqP/Qv3n/f+D/4ugDWorJ/tTUf+hfvf+/0H/xdU7XVfE9xcOkvhiC2jAJWSXU1O7ngYVCQf85oA6Kisr7Tr3/QKsP/AAYP/wDGqPtOvf8AQKsP/Bg//wAaoA1aKxLq58T+Qfsml6V52RjztQk2+/SHNUPtHj7/AKBnhv8A8GE//wAZoA6qiuV+0ePv+gZ4b/8ABhP/APGau2r+K3hzdw6NDLk/LFLLIMfUqv8AKgDdorBu08WyRqLO40WF88tLDLKCPTAZcfXNU/s/j7/oJ+G//BfP/wDHqAOqorlfs/j7/oJ+G/8AwXz/APx6pYLfxt5h+06poHl7TjytPmznt1m6UAdLRWSLbX8DOq6fnvjT3/8AjtL9m17/AKCth/4L3/8AjtAGrRWS1rr5UgatYAkcEae3H/kWssaF4tCYPjMFsjn+yosY5yMZ+lAHVUVk/wBlaj/0MF5/34g/+Io/srUf+hgvP+/EH/xFAGtRWT/ZWo/9DBef9+IP/iKo3HhnU7iQuPGGtQ5OdsSWwA4AxzEfT9TQB0lFcr/wiOp/9Dv4g/K1/wDjNH/CI6n/ANDv4g/K1/8AjNAHVUVyv/CI6n/0O/iD8rX/AOM1ctfDlzBEUm8SazdNnO+R4lIHp8sYH6UAb1FYdz4a+1wGGTW9ZVSQcxXfltx/tKAf1qj/AMIJbf8AQf8AE3/g4m/xoA6qiuV/4QS2/wCg/wCJv/BxN/jWlD4as4Y9hutVk5J3SancE8nOPv8AbpQBsUVz174J0LUnR7yK8nZBhS+o3BwP+/lVf+Fb+Fv+fG5/8GFx/wDHKAOrorlP+Fb+Fv8Anxuf/Bhcf/HKvW3g3w/axlI9NQgkH967SHgAdWJPb+vUmgDdorI/4RfQ/wDoF23/AHxR/wAIvof/AEC7b/vigDWJCjJIA9TTDcQDrNH/AN9CsqTwl4fmQxy6RaOh6q8YIP4GqyeAfCEcqyr4Y0kSK24N9kTIPXPSgDcN1bjrcRf99ij7Xbf8/EX/AH2KoQeGNAtYzHBomnRoWLELbIBk9T0qT+wNG/6BNh/4DJ/hQBb+123/AD8Rf99ij7Xbf8/EX/fYqp/YGjf9Amw/8Bk/wo/sDRv+gTYf+Ayf4UAMufE2gWc7QXWuabBMuMxy3casM8jgmof+Ew8Mf9DHpH/gdH/8VVn/AIR/Rf8AoEWH/gMn+FH/AAj+i/8AQIsP/AZP8KAIF8W+G3OE8Q6Sx9Bexn+tOfxRoEcbO2t6cFUEn/SkPA/GrMGj6ZbOXg060icjBaOBVOM57D1A/KrmB6CgDlv+FleDP+hjsf8Avs/4Uf8ACyvBn/Qx2P8A33/9auqooA5ZfiP4Oc4TxDZMcE4DE8AZJ6elaKeKdGljWSO6Z0YBlZYJCCD0IO2tiigDJHiXSi6Ks0pZ2CAC2k6k4H8PTnr2rWoooAKKKKACiiigAooooAKKKKACiiigAooooAr3/wDyDrn/AK5P/I1598Cf+SUaf/12n/8ARjV6Df8A/IOuf+uT/wAjXn3wJ/5JRp//AF2n/wDRjUAek0UUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFAFe/8A+Qdc/wDXJ/5GvPvgT/ySjT/+u0//AKMavQb/AP5B1z/1yf8Aka8++BP/ACSjT/8ArtP/AOjGoA9JooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAK9/wD8g65/65P/ACNeffAn/klGn/8AXaf/ANGNXoN//wAg65/65P8AyNeffAn/AJJRp/8A12n/APRjUAek0UUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUVT1bUodH0e91O4DGG0gedwoySFBJx+Vc1oev+I9cgnEmnadaGbTory0Zbp3wZd20P8AIOgXnHce/AB2NFeYaRr2uaV8L/Dc1gsN5f3l4tnLLqE8jhS8jrvJ6kZA4yMA12HhjXp9X0+7/tCKGC8sLp7O5MLEws64+ZGPYgjjqDkHpQBv0VwHi/4gN4P16W11C4s4LSazElm7QSOxlyQd+CBsBAzjn5xgcVUufGXi3TYvtd7DoTWyRWczxJ5qyus7bCFySAVOeue30oA9KooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAK9/8A8g65/wCuT/yNeffAn/klGn/9dp//AEY1eg3/APyDrn/rk/8AI1598Cf+SUaf/wBdp/8A0Y1AHpNFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAIQGUqwBBGCD3rjLDwHDp/ifU5oY7WPQL+xFvJZI0gJcMTuOTgDBYDbjHYd67SigDh9X+G+nvoKaXoMdtYRfbYruVJ1kmjl8s5Cld4OCcZ5FdPNoOlT6PJpMlhb/YJeXt0TajHO48D35rRooAp3mk6dqIUXthbXIVGjUTRK+FbGQMjodq8ew9KyT4Ut5/GU+v3v2a7zBHFbRTWqM9sylslJDyAdxyK6KigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiimsxBUBCwJwSMfLx1P8AL8aAHUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFAFe/8A+Qdc/wDXJ/5GvPvgT/ySjT/+u0//AKMavQb/AP5B1z/1yf8Aka8++BP/ACSjT/8ArtP/AOjGoA9JooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAK9/wD8g65/65P/ACNeffAn/klGn/8AXaf/ANGNXoN//wAg65/65P8AyNeffAn/AJJRp/8A12n/APRjUAek0UUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFAFe/wD+Qdc/9cn/AJGvPvgT/wAko0//AK7T/wDoxq9Bv/8AkHXP/XJ/5GvPvgT/AMko0/8A67T/APoxqAPSaKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigCvf/8AIOuf+uT/AMjXn3wJ/wCSUaf/ANdp/wD0Y1eg3/8AyDrn/rk/8jXn3wJ/5JRp/wD12n/9GNQB6TRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRRRQAUUUUAFFFFABRXIn4n+C0uJ7eXxBaQzQSSRyJKSpDISG6jnkHHr2pZPiV4XTQbfWUvzLbXNwba2VIyHnkBxtVTjv3OByOaAOtorDg8U2T+II9Cuobmx1KWEzww3Cr+9QdSrIzKcemc8Zxism6+Knguzs7a6n1uJY7iZ4VARi6spw25QMqB6kAcigDsqKxv+Es0A2l9dpq9nJb2Eay3MscoZY1YEqSRxyBxjrWfa/ELw7dTaTGtxPH/AGuSLB5raRFnx6EjHcdfUUAdTRWPrHijSdCvLKyvZ2+2XzlLa2hjaSSQjqQqgnA9TxTNH8XaJrmm3d/Y3oaCyZ1uvNRo2hK53B1YAjGD1oA26K4yD4s+Bp7IXS+IrVU2s2x9yvwMn5SM59PXtV2H4g+F5tMk1AarFHClp9tKygpJ5JLAMEOGOSvHHOV/vDIB01Fc3pXj7wzrVlZ3djqkbx3lz9khDKys0uCdu0jI4HXp0rI1H4u+FNNvbiBpb2eG1k8q6vLa0eSC3fsHcdycgYzQB3dFY2q+KtE0Xw8uvX9/HFprqjJNgneG5XaBySRzgVjaN8U/B+vapDptjqv+lzjMSTQSReZ6BSwAJP60AdlRRRQAUUUUAFFFFABRRRQBXv8A/kHXP/XJ/wCRrz74E/8AJKNP/wCu0/8A6MavQb//AJB1z/1yf+Rrz74E/wDJKNP/AOu0/wD6MagD0miiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKRmCqWYgKBkkngClqOeFLi3kgkzskUo2PQjBoA8sstGu/BHw/vLzTB4f16C2aa7MjQlWkXJZhvBYMw6duBjtVK507S/i74L0fWbNotD1mGZ/sEUkg8syKwLDaPvA4ByBke/e1/wrHxfpvhy48MaJ4ut4NDkLhFltP3wR8lkLDtyeRz9OlX7P4M6KfBmlaLqM873mns8sd9bN5bpI5yduc8ZxgH0oA4j4l3Pja18beCHv59MW4+0gWkdi8mwyb4wxcsAcNuAwO2R3ruda0P4f+AtDiN/omn3tzcTMtuLuGJprmViWwZGACjnqcADH46emfDtIvE8PiLXdau9c1K1Ux2jXEaRpAueMKgALDJ575zgcUfEP4eQ+PV0kyXfkHT7jzCjLlZUYrvU4IIOF4IoA898Y6Lqvhj4b6/qv9i6dZnVrm2WbTbRR5VnAmcElcB2LY3cY+bvirfxItpZvgT4ZvIbTzXtIrKZpEX5oV8oAkccDOB1HavX9X0ix13SLjStRh86zuE2SR7iuR16jkcgVwUnws1K8tdP0fUvFtzd+HbGRGSxNsEaRFPyxvIrAkAYGfbp0oA5TSryfUP2oJZbhHVRZ/uElTBRDArAfXLH9aVkH/C6fiBo0L2tnb6horB5JDsjR2ijG9j0HMhJPvXoHib4fRav4msPFGl3i6drtnkCdofNSVdpUBlyOQCcH+fGKNj8MpJ9P8RnxDq323VdeVYri7ghEflxrwqoOR2GfoPTNAGPEt98O/h9HqGp6F4d1Sy022jSOWylbzJQ7qN5LoRg5BODyfatS30XwV4qsIPiBq1tC1o9ggEV0wMNqi53DHTIJYfh0zWRcfDTxtP4K/wCERfxPpjaUI1iXdZt5m1WDL8271A/Cuvk8B2zfC/8A4QtLgxR/ZBB56qPv53Fse7cn60AeYaXpOjeOLmfVfBfhwaRZ6MbiSO+RxHLdztEdiKP4QG2tkngdMEnFj4LQQ3Xwd8TrcRJKslxcBxIobd+4Q85616d8PvCb+C/B1tok08VxLE8jvLGm0OWYnofYgfhXNar8MdVt2u7fwd4iOiabqLO99aGJZFLNwTHxlPl4wCOgoA8ps9Ov/E3wS0LTbN5rjVU1qVLC2BGHUIWYZPAC5JySB1p8nj3WL/VdI8M+NNMtrO8ttTt3bUHg8qW3RXBAAAxjBIyOMH8a9nv/AIfNaeGdH0/wrf8A9l3ukOWtbmVTKPnBEu5ScEtuJzjjtisXxD8OfE/jS70tPEutaXJp1nOsskNpaNG8mAA3zEkjIz7c+wwAep0UAYGBRQAUUUUAFFFFABRRRQBXv/8AkHXP/XJ/5GvPvgT/AMko0/8A67T/APoxq9DvEaSynRBlmjYAepxXF/CHRdR8P/Dqy07VbV7W7jllLROQSAXJHT2oA7qiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKACiiigAooooAKKKKAP/2Q==",
+ "image/png": "iVBORw0KGgoAAAANSUhEUgAAAvoAAAPoCAIAAAAgFM2mAAEAAElEQVR4AezdeaB91fw+cA2SIWODsRBCipSkJJmJQgNFmTIlVMgQZShziQyJZMxchkSGMoRKRBoQSUSSKaGMvxfvb8v+nXPv+dx7P+feu++9z/nj3nXWXnvttZ61z34/63m/19pXu1o+QSAIBIEgEASCQBAYKwKf+9zn/t2nz4pj7V0qCwJBIAgEgSAQBIJA7xAI3endkKRBQSAIBIEgEASCwHgRWPl73/veeGtMbdNFYKWVVtp7773vf//777DDDu94xztWXXXV9ddf/8c//vE73/nOpz3taZ///OcvueSSFVf8HzG98sort9hiixe96EUf+9jH/va3v62yyiprr732+eeff9xxxz31qU/dZJNNZLY2qNzpe+2117rrrnvQQQf9/e9/r0PXuMY1jj32WH+PPPLILbfc8upXv/qJJ57oax1Vw1ZbbSX9la98hRi5yy67fOtb3/rpT3+qtlZzEkEgCASBILAIEPj+97/fTMMi6M5kXViBMZvsWPKDQBAIAkEgCASBRYwADmDSe9lll3Un1TPur5nzueee+5a3vEUNYnce+MAHzriqsZ+48thrTIVBIAgEgSAQBILAgkBghRVW2H333cfY1C9/+ctFd8ZY51iq+p+LZCzVpZIgEASCQBAIAkEgCPQNgdCdvo1I2hMEgkAQCAJBIAiMGYHQnTEDmuqCQBAIAkEgCASBviEQutO3EUl7gkAQCAJBIAgEgTEjELozZkBTXRAIAkEgCASBINA3BEJ3+jYiaU8QCAJBIAgEgSAwZgRCd8YMaKoLAkEgCASBIBAE+oZA6E7fRiTtCQJBIAgEgSAQBMaMQOjOmAFNdUEgCASBIBAEgkDfEAjd6duIpD1BIAgEgSAQBILAmBEI3RkzoKkuCASBIBAEgkAQ6BsCoTt9G5G0JwgEgSAQBIJAEBgzAqE7YwY01QWBIBAEgkAQCAJ9QyB0p28jkvYEgSAQBIJAEAgCY0YgdGfMgKa6IBAEgkAQCAJBoG8IhO70bUTSniAQBIJAEAgCQWDMCITujBnQVBcEgkAQCAJBIAj0DYHQnb6NSNoTBIJAEAgCQSAIjBmB0J0xA5rqgkAQCAJBIAgEgb4hELrTtxFJe4JAEAgCQSAIBIExIxC6M2ZAU10QCAJBIAgEgSDQNwRCd/o2ImlPEAgCQSAIBIEgMGYEQnfGDGiqCwJBIAgEgSAQBPqGQOhO30Yk7QkCQSAIBIEgEATGjEDozpgBTXVBIAgEgSAQBIJA3xAI3enbiKQ9QSAIBIEgEASCwJgRCN0ZM6CpLggEgSAQBIJAEOgbAqE7fRuRtCcIBIEgEASCQBAYMwKhO2MGNNUFgSAQBIJAEAgCfUMgdKdvI5L2BIEgEASCQBAIAmNGIHRnzICmuiAQBIJAEAgCQaBvCITu9G1E0p4gEASCQBAIAkFgzAiE7owZ0FQXBIJAEAgCQSAI9A2B0J2+jUjaEwSCQBAIAkEgCIwZgdCdMQOa6oJAEAgCQSAIBIG+IRC607cRSXuCQBAIAkEgCASBMSMQujNmQFNdEAgCQSAIBIEg0DcEQnf6NiJpTxAIAkEgCASBIDBmBEJ3xgxoqgsCQSAIBIEgEAT6hkDoTt9GJO0JAkEgCASBIBAExoxA6M6YAU11QSAIBIEgEASCQN8QCN3p24ikPUEgCASBIBAEgsCYEQjdGTOgqS4IBIEgEASCQBDoGwKhO30bkbQnCASBIBAEgkAQGDMCoTtjBjTVBYEgEASCQBAIAn1DIHSnbyOS9gSBIBAEgkAQCAJjRiB0Z8yAprogEASCQBAIAksWgTPPPLOffQ/d6ee4pFVBIAgEgSAQBBYeAoceemg/Gx26089xSauCQBAIAkEgCASBsSEQujM2KFNREAgCQSAIBIEg0E8EQnf6OS5pVRAIAkEgCASBIDA2BEJ3xgZlKgoCQSAIBIEgEAT6iUDoTj/HJa0KAkEgCASBILDwENhtt9362ejQnX6OS1oVBIJAEAgCQWDhIXDve9+7n40O3ennuKRVQSAIBIEgEAQWHgKHHXZYPxsdutPPcUmrgkAQCAJBIAgsPATOOOOMfjY6dKef45JWBYEgEASCQBBYeAjst99+/Wx06E4/xyWtCgJBIAgEgSCw8BBYd911+9no0J1+jktaFQSCQBAIAkFg4SGw995797PRoTv9HJe0KggEgSAQBILAwkNg22237WejQ3f6OS5pVRAIAkEgCASBhYfA1ltv3c9Gh+70c1zSqiAQBIJAEAgCQWBsCITujA3KVBQEgkAQCAJBIAj0E4HQnX6OS1oVBIJAEAgCQSAIjA2B0J2xQZmKgkAQCAJBIAgEgX4iELrTz3FJq4JAEAgCQSAIBIGxIRC6MzYoU1EQCAJBIAgEgSDQTwRCd/o5LmlVEAgCQSAIBIEgMDYEQnfGBmUqCgJBIAgEgSAQBPqJQOhOP8clrQoCQSAIBIEgEATGhkDoztigTEVBIAgEgSAQBIJAPxEI3ennuKRVQSAIBIEgEASCwNgQCN0ZG5SpKAgEgSAQBIJAEOgnAqE7/RyXtCoIBIEgEASCQBAYGwKhO2ODMhUFgSAQBIJAEAgC/UQgdKef45JWBYEgEASCQBAIAmNDIHRnbFCmoiAQBIJAEAgCQaCfCITu9HNc0qogEASCQBAIAkFgbAiE7owNylQUBIJAEAgCQSAI9BOB0J1+jktaFQSCQBAIAkEgCIwNgdCdsUGZioJAEAgCQSAILHEE3vjGN/YTgdCdfo5LWhUEgkAQCAJBYOEhcJ3rXKefjQ7d6ee4pFVBIAgEgSAQBBYeApdffnk/Gx26089xSauCQBAIAkEgCCw8BL73ve/1s9Er97NZaVUQCALLj8BZZ531l7/8ZYUVVhiu6t///vfVr371u9zlLhMeHS6fnCAQBILAVBB4zGMec+CBB06l5ByXCd2ZY8BzuSAwKwj885//XGmllfCbN73pTdKuseKKK37sYx/7wx/+MNn1Vl111Uc96lHXvva1MZ4Xv/jFa621VqjPZFglPwgEgSkiYCo1xZJzXGyF3rZsjoHI5YLAgkPgH//4x5e+9CV/EZ399tvvRz/6kfTf//73zTffXI7uXPOa10R6JuuX3/4VV1xx+umnX3bZZUjP9a9//de//vXXu971VLLlllv6OtmJyQ8CQSAITIbAl7/85a233trRz33ucw984AMnKzb3+VF35h7zXDEILC8CGMmpp55KMf7iF78ojdysvPLKu+2220Me8hD8Zptttim6M5XLnHTSSRSgc889V21qwJachTDtueee22+//SqrrDKVSlImCASBINBzBKLu9HyA0rwg8P8hwF2F6HzkIx/5/Oc/L/hml112IdI8+MEP5pbiw0J6/r/SU/7yr3/9S9nTTjvtrW9967Wuda1jjjnmN7/5zR3ucIfnPve5t7zlLe9zn/tMuaYUDAJBYEkj0Ft1J3RnSd+X6fwCQuBvf/vb3nvv/clPfvKXv/zl2muvfeihh970pjfdeOONh4WcP/3pT7/61a/IPKJz3vnOdx5//PHXuMY1Wk85sJ7ylKc86EEPuvLKK1Elh9TWjlbiBz/4wdve9rYPfOADv/3tb294wxve8573VM8aa6wxUCxfg0AQCAIDCBCJ3/e+98nsmzMrdGdgpPI1CPQRgc9+9rNvectbPvOZz2icsOJXvOIVw62k93zta1+zxxf559hjjx0uMGHO6quvzm9Fwnnc4x43UOCiiy56wAMecM4558jfdNNNtQH1GSiTr0EgCASBLgI87Pe///3lhO50YUk6CASBUQj89a9//e53v7vvvvvayuImN7nJK1/5yo022oioQ7ZxGu/V97///Ze//OXKyLn44ot///vfj6pu8mOCmtdZZx0V3uAGNxCwfNe73lXwsuLqFMj8xz/+caeddhLWI5PMI5B58ppyJAgEgSWNQG+dWTP09C/pwUzng8BcIbD//vsjH672pCc9Cc/oXlYQz2tf+9oPfehDFVzcPTSDNF7FgVUn3ute93roQx/6jGc8g8Prxv/9yOcRE8Fj8Zf4ZSLT3e52txlcJacEgSCw6BGw11c/+zjpItV+NjetCgJLBAGCzR577MGBtd1225199tkiaarjP/nJT7AN3nGEg4N8LFxnGNLjjjvOdak4HGR1CWHLLn344Yff/OY35+E6+uijL7300uETkxMEgsASR+ATn/hEPxFI7E4/xyWtWtII2E2HiMKFdOSRRz7xiU8sLIQVH3DAAR/+8IdJLFNEx0It0TZOFJVs9dYll1yCRfk6Yu/BgZrFQd/73vd23ebAEge94447nnDCCRxee+2116677jpwSr4GgSCwlBGwEuId73gHBBK7s5Rvg/Q9CCwbAYF+ts+xmw7xxnbs7YRnPvOZb37zm9vX0YnrXve6om1ufetbv+AFLyh5BnFBdCzX+vGPf8wLZrX5pz/96QsuuGB0PXVUODPG8+hHP1pCDvL0yEc+stxbVor19gXIU+laygSBIDBeBMyF+MHV2Te6czVPwHyCQBDoCQK2z8EedthhBzHI9sKpViEWXm41lT11RBwTXU488cQzzjhjmT0SrGOjnfvd735TfNjd9ra35cOqai1Q/9SnPmULZszMC5CXea0UCAJBYIkgIKCwHinoTq+6HLrTq+FIY5Y0AmiKnQMf8YhHkHYaEF/4whcoMVNkJEJ82olTTFh4JTZ5ivVvtdVWNuNpNVOJnGifeJHOLTOJIBAEljICt7rVrfpJdxKqPMXnfIoFgdlFQFCw8Bpc54Mf/GDtHCjUxjxJEM9UVjoIJcZ1nva0p023lauttprA5CnuqfOVr3xFsI4dDusqT3/6023rTCJ6+MMfLqZnupdO+SAQBILAnCEQujNnUOdCQWBSBE4++WTxv2Ji7KxTOyCLU0Z0dt55Z+rLpKd1DnitxAiuI3zHZsrqb2dIy6mwHoyHr93r06cShcPFZnPniiJSntiz++6789YL4mmVJxEEgkAQ6BsCoTt9G5G0ZykiICoZrXnve9+77rrrVv+tbsCBpojFs571rNvc5jYf/ehHP/7fD+rjjVd1LlFd7DPdyBvO73SnO9XmOt5HseGGG9pREMdCUxAd8TdeYkzmkTmVi4qbfsMb3lAl7XOo/qc+9anf+MY3pnJuygSBIBAE5gGBpexiTN+DQB8QeM5znuOX/653vas1hlgiCniKjwOe8vPPP9+2y93yQptRKBWW44l37EY3upECL3nJS2SSduoFWEKFavfke9zjHkiPQ5xT3XpGpC3yetOb3lRtxtWEPGuzLYIqJ3+DQBBYmggkdmfEYzOHgsDSRcD6poMPPpiW84QnPKFQEMRjiz/OrCmCYus/zxfRzVXeNjnWZ9lfxy7MfFVrrrmmfF4nUcbDFT75yU+mA3nP6De/+U3vzMJaNGYqS8BUxatFVbKCTJo7zIZAJCK+reGrJCcIBIGlg8B973vffnY2zqx+jktatSQQ8I6ql770pRxYz3/+86vDlm5yMImqmWL/H//4x+M3rbCAZWvFa2dCr9ZCXKxs9x4I5OmYY46RI7i4FZZAWXAjPix7NP/5z3/25lGFheZ0y4xOe59XBSnbz/CQQw4Re2Qn6NGn5GgQCAKLGIHubmG96mboTq+GI41ZWgiIm7FBzute9zr7AVbPxcRMMTZZeZoKd9Iqq6zSUDv33HO9XYtfjItKMM0KK6xgL0F75FQBC9q9Z5TTCstpp0igOJiKxE9/+lN/11577e7R0Wn8zNbPVYbYs/nmmx9xxBEzflPp6GvlaBAIAv1HwBOmn40M3ennuKRVix8B/ibbCZJbuK70FgV59rOfbcvj5ey5JeV2weHD4r3yGlHqDpfWne985zve8Y5CfG55y1t6FdfXv/71Wv9V17rwwgtL9VlvvfXk8HBtsMEGU2+GUOWvfe1rVV788plnnmkDoamfnpJBIAgsJgQ222yzfnYndKef45JWLX4EDjvsMJGML3vZy8T86i1/Fqlm6t2m3FSU8cAp3Fv8Sj//+c+PPfZYAT21+PxVr3rVfvvth1H97Gc/4zvjXK98Dfjd737n/eeIkUDj5z73uWrDhKzP4ghziYHKJ/xKy/FOie985zuObrTRRvbgsX7+y1/+8oSFkxkEgsDiRsBbhPvZwdCdfo5LWrXIEbAgnJupiI6u0lcsIZ9iny0pJwvtv//+1JrhnXJsVEhiQXRwDn6lqtMWPpxclT7llFNEJSM6vnJ7cV1VuLHAnbYK3UvXhTDTgXAXq7eW2TBvRz/vvPMUU3jTTTelJ1kXtsyzUiAIBIEgMGcIhO7MGdS5UBD4HwL2yMEnROrUgnBvxaq4mf+VmChlcx0lcRGni3EWZdwEGJJMrajyF7nhyVp11VW/9a1veQcFN5Y3hpKC6ElEF7vvCOIRtiyOx9WF/jzjGc+wNw+e1K6JRSFV9hLkhrdSzEbPt7jFLUbzHtJUbVooUHH99ddHpC6++OJWYRJBIAgEgXlGwCQvnyAQBOYSAS+FsEsN/nHqqae6LiVGhM3oBwGqQZ4RiTyinZaCv/GNb6wC/FaWffn46q+vPnWovv7n2FWfdmhE5Q615WMTNhXNoldVDQQkZWrjn9F15mgQCAKLDIGTTjqpHhF9e0Vo1J0JH93JDAKziMBFF11ETfEucX4flxHbO3otg1hmuwi+/e1vv/3tbz+iWTvttJO1UVWA6sNTVs4yfwktxCRsyVFf29H/lPjv1xHVtkMCgJ73vOe1rwMJpI3vDHOST0zCz7zDy/bNA8XyNQgEgcWNwC9+8Yt+djB0p5/jklYtZgS85EH3LGiqTopWprNM1mFvs+JLsqFOvTd0smIj8kXVeGn5Nttsg2CNKLbMQ0iSV6DXHtATFqbufPWrX3VIa+udEnImLJnMIBAEFisCwgr72bXQnX6OS1q1aBEQ1fue97zHVjckEJ0UWzPi5ZqCdWwPKEZnxnCQW4Qbe7eD615wwQXCdEZQq6lc5fWvf/0LXvCCyUo2+ed2t7udMlT6yUomPwgEgSAwlwiE7swl2rlWELjaJz7xiR/96Ef2thEsDA5xPCNA2WuvvZaH61i6JSrIXj6uVarMW9/61sZIRlx39CFereY1GyjJZVYOLBv5WA/f3FsDxfI1CASBxYqAV+L0s2uhO/0cl7RqqSAgWnmyrnpqEGMmOzqVfPspiwrCPwTotPL247H7Tvs6s4Q3iVq6NXyumpGhyud9O+200xK+M4xScoLAIkYg2wwu4sFN14LANBAQ0mtNVr3WChXwIs8JT/bWz2m9u2q4Ensrv/jFL0aYrDyXbsvCubS8V2u4/EDOH/7wB2vjvUhrIL++3v3ud3/AAx4w4aHawBDB8g52S9NtYzhhsWQGgSCwKBHo7U/+f3O+RYl7OhUEeoWASBrBOrw8XuYwumH2yJlsHRaGZNOdinceUYnNBm2Zg7XYwNCuOe09D0550Yte9P73v3+yc+2PLEDHRsne5GWDn8mK2Vmn+3bSgWLojkq46g444ICBQ/kaBILAIkagNmfvYQdDd3o4KGnSokUA+RCY3F7q6VUPE/p66jUOwygQS+yAbJtBTOIJT3iCNzagRIiLpez0m275YjlyPvCBDxx44IF2F3zsYx/bLTCw9P3yyy9Xs1AbexI+7GEPE99j84xHP/rRlCHUqntiS9OolnOpV6sqiSAQBBYNApaa9rMvoTv9HJe0akkggLX88Y9/HO6ql1h5tfhw/iWXXLLhhhtusskm++yzD+HES0Z/+MMf7rrrrt4A6r0QXf1GYA3usvrqq6vEdn/ilLvhOzK//e1vO7cuQQRChtRs9bi9eX75y1/Kt57LayW8raJeMVElB/62PZ27+SeccEJ7B3s3P+kgEASWAgK05H52M3Snn+OSVgWBiRHAMETkePmDV2J1S/A62VxHPE05zh/84Afzmnk7epVBQQbkH1uBeW+Xo5/61KdsYziwGJ4nS4XUHaHHI94d4SUYwx43vjCbKKrZYntbLS/nuvduH5MOAkEgCMwYgdCdGUOXE4PADBHwyqrRZ44oUIKK8J3yOnXrQWhQnPvf//7cW1ZF2dTY/oS27VlzzTV5wQbojhN/9atfiZj2ueKKK7r1qOFDH/qQV1LYyrmbP5zmdGuOue7Rgw8+2NeNN97YuzIGKu8WSzoIBIEgMGcIhO7MGdS5UBD4DwLUjmIDk8Hh1Z6vec1rJjta+YJ1rK7yhiwqzkBJ4srhhx/u7Z48WVjLPe95TzHFmI0gnpvf/Obdwvvttx932IDjic9r9913R5i4tywi65ZPOggEgSCwTAS+/vWvL7PMvBQI3ZkX2HPRJY0AUWR0/ycrcLOb3cyOxrZaXm+99X7/+9+LyLFBMzFmoDaPmz322IN/ijvpHve4hzXtXqflJecDoTarrbbawG6BNCH7ECrs5Q+2RRanfJe73GX0toSj3xs60LB8DQJBYNEjcOSRR/azjyv3s1lpVRAIAhMicNBBB62zzjqIiFhmr2jAYGzTbC3ViSee2C0vascuhUKh73Of+wg6Fkyz9tprb7HFFtaCtWKCnR//+Me/4x3v+MY3vlGZ0gKfaUt3u9vdvL5U/cSe9ddfv50ynBiO3VFGqPVwyeQEgSAQBOYRgdCdeQQ/lw4CM0GAACOC2PIHu/jY0+91r3vd0572tAG6o16MxwsorEIX2mzF+FlnnTX6JaOI1G677SY8ubtGfd11191zzz2n28rtt9/eKVaKfe5znxMbNN3TUz4IBIEgMHYE4swaO6SpMAgsAwE0ZRklRh62VMq2OtaHe/Gn92F5K5ZwH0HKw5v+2W5nq622outYh6XKAWcWl5kXmNf6LA6vHXfcUbxOl+s4BVWyv86I5ggJmuzoZZdd5tDAAvjJCic/CASBIDCrCITuzCq8qTwIDCJAYhFzM5g7ne+HHHJIt7iNCh/xiEf86U9/Ov7449daa63uIYvSqTXCfRw955xzBtQdtEmosjKCgU4++WT79Aht7p4+lXStOe+WtGH0hK/T6pZJOggEgSAwxwiE7swx4LlcELha21qQo2d4zbmImcneVFXYeQeFjwge/izvpZImwIjUsXOgxVYD+F500UVewC7i2DKugQhomhAaJGDZNoOEH74nL04nBfmoXP6hhx5qJflAhcv8akMgIdXLLJYCQSAIBIG5RCCxO3OJdq611BHAS4QYX3jhhQWE3ZDlCBnu4iIcZ99997VlTjezmxY7bFMc5OYGN7iBWOPa+YaDzMeycxLOwHvUrULnqxre7s8mgVZdeRkFdmUpFqdY21EQMfJOLvsWDqxd7zZjmemvfOUrylgatsySKRAEgkAQmG0EQndmG+HUHwT+hwAascsuu3hDp+CbER4fuwL+75yJUgQYL3w4//zz3/ve99q5mCCkFJ5017ve9ZWvfCX+hDBVpnz+JgqQJVcVwdPq05jb3va23m2+7bbbevl5y68EuWjCVVfdYnjSZLsI2rPn3e9+9/Wudz397Z6SdBAIAkFgXhAI3ZkX2HPRpYsAdmLLHPE3L3/5y2eMgk1xhCF7ZcTAjl6nnnoqWUg4jmVZba2WjQTf/va3Wy215ZZbtivSe0Qx86ZRm4a5DppilVYrPFnCGjGesu5RvjlL37s5SQeBIBAE+oBAYnf6MAppwxJC4CY3uYnecjz5y/Fkpfdw522lY83UcH43R+COtVTdnErTjfineLu8RnT4aMvxViyXfvWrX33KKae0zEqQgmxRaJOegfzhr9bDD2SKlW7hPtQmlE6E0ECZfA0CQWARI+D9Nv3sXehOP8clrVq0CGyzzTYbbbRRvcEK3eHYGu6qOBvCyXD+QM5LXvISzixbDgo0FsHTPrZa9jJz74Kwq3KdUsvF20J0C87tQOhFEy984Qu1oZ1IeaLrHHvssYSfgWsNf+VKe8tb3jKQr4bK8YZRC9GL2w2UydcgMGcIEDsn87fOWRuW2oWszexplzn48wkCQWAuEaiN+2yZUxd90IMeNPx0sDDqjDPOmEqruMa4q4TRdD8ynXvSSSdVzfYbtE/P1ltv7St/k2geRy0Qu/zyy9tZ0s669NJLp3JRZax+H26296s7hMx5tYXYIM61KdaWYkFgNhD4zW9+Y/IwGzWnzskQMNWpJ4NdRicrMy/5id0ZfmInJwjMLgLPfvazKSsibMqTxet0wgkn+P13r2qJuDLefN7NnDAt5Bl9ee1rX8tthGFUPf6Kd7ZJ4Gc+8xl7Lnt3hG11HFUDL5XwZAIPokPaqTpFFluWZSkWTWjCqwxk2qdneMcdZSyM9xe1su2hLX+8iWLgxHwNAnOJgBflzuXlci0I9Bbz0J3cn0FgrhHACSxBp45QX6yNsikOqmG3wIF2eNPe05/+9I033nggf/ir/ZSt+rZ0fCBw2IsjxDJ7E1YJSAiQ2rCr6173ugPsig/L6VOPMn7f+96HkA20BKMS+CyzoqS93WKgQL4GgSCw6BGwj1c/+5jYnX6OS1q1mBGwX451UjYA/NKXvqSfa6yxxt577z1hh0X2DLOK4ZIiZgTrIE9WYJWEU2UsubrXve5l0z+Xo+XQdYQy2G+wy3UEF3ur+emnn26dV4u8Gb5EN4cbDt3p5kgTmWrNuZCdww8/XKd40AbK5GsQCAKLHoHl2axrdsHx4MsnCASBOUaAM4jvyZs7iTou/b3vfW/g/Q/tZy/gRlTN1Jv38Y9/3Hoo68xbDVxmwoBsmmypVFe/wU6QJH6uqVeupD0SJ9yPx74+VY+Nf1z6sMMOm1a1KRwEgsDiQKCFDPYtdudqiwPf9CIILDgEHvrQh6IFl1xySbV8xD43FdkzrQ6KOLZyyvscbGrsJZ3eimUXZuHDrigI2lpxX+1GOK06q/Amm2zSiFRLoG6ecQrYyZDMYwnYMcccM4PKc0oQCAILHQEzn3oyhO4s9KFM+4PAeBCoDW8sCK/qfvjDHzb2MJDgkJr6JUX8PPzhD/da0FqQIl6nLUevahGgqs2lt9tuO+8rnXrlfGHtRRPdRqJuVYm18fLf9ra3Tb3OlAwCQWAxIdBbdSexO92HdtJBYO4QsDyK+iKO2BItV7VR8lFHHTUhmRBuzNVlG+WpNK4kHFHDFBef61znOr/+9a+7J1ocLt+FvP/civH2vtJumQnT9vh5zGMegz8NHBV27XIyL774Yl3YY489rAUbKJOvQSAIBIH5RSArs+YX/1x9SSPgDZ2bbbYZMcYbOq2N8r5Pi8+5mQZAodPwee2www48RJSegaMDX+22bJ/A73znO4JsuLFsIfjd735XyLPpo5JPfvKTd9ppJ24sdZJ5CD/oi9ggrGignoGvRx99tLdo1WbQA4e8kdR2gjZzoxVxZvU3UHGg3fkaBILAUkJghXoILqUup69BoEcI2JzGCx8oIrVD8QUXXGCF1HnnnTdhE4Xd2Een++qrgWJOVxvlxmosbzhvR1ElIcwieLo1H3/88T/5yU+sXbcw/qUvfWkrPJywDmuy0KLnPve5teDciy8srV9nnXUsB2vbNw9XlZwgEAQWNwJ06NrRVOyOrbz609moO/0Zi7RkKSLA+0No8ZdG4l0z9l+n9AgHprgMw2FROikIcbHRzvBROV5i9YY3vMGegVxUL3vZy+SYz1iabvmVNOmFB82KdCIN4Yf8o0KRxa961asmrE2mkGftsf3PhAX4torrqLDeeiEeKFxnQqySGQSCwPwiELozv/jn6ksdAZvTIAprrrmmEOODDz4YHOuttx5hxtcJoRHo46iXgIr18T7zgTLedSWA5txzz/3Yxz6G9DhK6TnnnHMsdJfmbzrttNMoSSKBHKUVIT2Wo0/2Zis79AgtOvvssweuUl+tv+Aak7armNhk2yjztU34ZokJT09mEAgCQWBOEVhMAeHpSxBYoAgceOCBfvZ77bVXLafCRZ761KeOfhAQUQ466CDeqG6XDz30UDvuWLhOtmn5xx13XLeqH/zgB3WIG+tb3/qWt4faZHlg3bjtmLGi7lkDaWE6rX7NdpRKNK39gdrpSQSBILCYEGivjunbQvSoOwOP8XwNAvOAgCVa4mOQFdHKFjp5lRXJRxDxu971rsla4/m43377UV+EHu+///6KXfva18ZyfvWrX/GX83nRbCy8slGygJ5uJd6CjpooTJXBeG5605vSZrw3FNOy5+Ef/vCHAw44APvx2tHuWQNp5VtO7ePsXGqTyrU//qwGThJBYKkh4LWsPe3yYiKV6UsQWLgICH+xUMtjglhSvcA/rKjyUq3Rzw4OKfSFU8zKKfHCvGAWXqmttsCZ7FwuM/sQupC3oHuNuXnYNttsoxJKz2SndPMRMlHJ1nypweV8ajNl7Iqvjdds4Q5EWh4EgsDyINC2dO+bupOVWd1neNJBYD4RsKaJMGPxFLWmAo21xguqvGuiu6JqdBMF63hTBMXFvoUjti5UideFWjROzvF60dF1TnbU6XSgDTbYwEY+ynh5BWVIQjzQu9/9bi2Z7MTkB4EgsFgRuPWtb+1Rpnd9W5kVurNYb7n0a0EiQHERxyO42AJ1b0qvFVi8UTYPxHv62aWHPexh9hXEyTTPO0o54AREP/KRj7RFkMxlqlP97FRaFQSCwMwQCN2ZGW45KwgsRQQsJt9nn30wHsu8a9c+ETkcVfxcQmR6iIjNDBEdgUfaJujHxhvieLwaff3117dRELdXD9ucJgWBIDAbCPSW7uQlErMx3KkzCCwXAvQSL73ykgc78ZSnSdyxzW8++tGPPvjBD16uqmfnZCSMwLPnnntSp2xauP3222sqD5dF7Bp80UUXzc5lU2sQCAK9Q8Dkp3dt+m+DQnf6OS5p1ZJGwPbHtv57z3veI+ZXNI+P12ZZnb7tttvaNJnSc8ghhxBOeoXRlVdeaWNoLfziF79oJ0N7Q9vVkEZlEyBNxYREXveqwWlMEAgCs4GA3Udno9ox1Lk8Adg5NwgEgVlF4MQTT7SkvH7nr3nNa7rXsp3g4YcfvsYaa1iZNYYHwdWuZvV4RRwvf202DWpNfeYzn1kV1nu7Wn4SQSAILEoEersyK/vuLP+zPTUEgdlCwKtntthiC5vZeHHE85//fKuoNtxwQ8LJDW94QzsjW3lue+XXvva13//+960h96pzWwhOtylWntszkPTiLaH2RLbfj20JPYWnW08rb7vn1VdfvX2tBK+cpg5k5msQCAJBYM4QyMqsOYM6FwoCM0fAsiyhPLWVjn38vGDL7oJeot6t0Z6B1nDxf3ltp7+115+/NsWpjb9simNTwTrFxjxOFwptzx6vRu/WY/dCGw/aj6ebOfU0FWrfffdVHmd6znOeI+wa1xGw7HVgU68kJYNAEFigCPQ2VDl0Z4HeUWn2UkTAFoJCYd7//vf/+te/tsAb6RElw1M+eumTUyybsjEgQaiIyDKx82auBz3oQV4xscyS3QJ3uMMdnvSkJ6E4Mr/61a/a8VlTZXqdlje0d0smHQSCwGJFwHOpXhicfXcW6xCnX0FgjhDwenP05b3vfW+955yn3CsdvD8L6eGQEuY8xXZYRYXWOPeDH/zgRz7yETsTCjcmID32sY9VwyWXXMLJdcopp0yxNrSGhFNue4+5HXbYwXIt0UVWmQkwmmIlKRYEgsBCR8A+FLzwehG6s9CHMu0PAr1A4MILL7QTz+mnn+5lW61BNunZcccdK/LGSi7kw9oofisFRDRjMFhRhTY7KkZn4HVainF4HX300SqR5gKzjPzb3/52q3+yBI5Fwil31Ze+9CU8ieykYcWcJjsr+UEgCCw+BEJ3Ft+YpkdBYP4REJdDofG6BgE3uAuygp1ceuml1TIOLHpPayXe4x2ivgro8dbi1VZbTZqb6dWvfrVQZbtl0HK8+uqMM86wdPzYY49de+211e/96qKhxUFPGL/srCOOOMJGOy7kunjSN7/5TSXtrdzf9agNkSSCQBAYNwKhO+NGNPUFgSAwEQLYBi8V3uMg2tHd7QbLQYDkE3hskFNvMh+ogwIkstjOyHe6050++9nPtj2dhQoRbAYKq1A4US25smqM3+rkk0/217tOt9xyy4HC+RoEgsBSQKC3dCcL0ZfC7Zc+LiEELLMaWGk1rc6Ls7Gjj7Vdb3zjG21viPHQeOzpLLjnsMMO44xvtWFURx11VLmr6Dr4E6blJV9eHxGu01BKIggEgZ4gMJ4NynrSmTQjCASB5USAYIPHHHzwwZZXeFMp+mLXH14wL/v89Kc/7U0RVb8yfFjFdcQjb7755riOl3yhR21fxOVsSU4PAkEgCIwRgdCdMYKZqoLAIkGAz+vNb37zoYceat2WyB6vJtUxFMd+PMV46Drlw7I9j5ddnHfeebiOGOdx7cu8SHBMN4JAEOgNAqE7vRmKNCQI9AyBZz/72daWC+XhxsJ4KgzIzoRnnXVWhSG/4hWvcFSoEAcWAkQZ6lkP0pwgEASCwP8hELqTWyEIBIFJEbCXz/HHH7/eeusJ5bGVjnd4WYFl3RZmYw3X/vvvLxpapoDl6DqTgpgDQSAI9ACBhCr3YBDShCDQYwSK8ey999421LG5jkgda9dPOukk0o51W95l0bd3s/cYyzQtCASBeUMgdGfeoM+Fg8BCQcBLcD75yU/ax1m8zq677lrNRnoIPxtssMFC6UXaGQSCwFJGIM6spTz66XsQmAYCu+2224c//OH73Oc+PFk777yzRVjhOtOAL0WDQBCYVwSi7swr/Ll4EFhQCAjfud/97nf22WdvttlmtWPhgmp+GhsEgsDSRSB0Z+mOfXoeBGaAwPWvf/0ttthiBifmlCAQBILAPCIQZ9Y8gp9LB4EgEASCQBAIAnOBQOjOXKCcawSBIBAEgkAQWAoIvPOd7+xnN0N3+jkuaVUQCAJBIAgEgYWHwPC7hHvSh9CdngxEmhEEgkAQCAJBYMEjsNZaa/WzD6E7/RyXtCoIBIEgEASCwMJDYNttt+1no0N3+jkuaVUQCAJBIAgEgYWHgPcK97PRoTv9HJe0KggEgSAQBIJAEBgbAqE7Y4MyFQWBIBAEgkAQCAL9RCB0p5/jklYFgSAQBIJAEFh4CPz973/vZ6NDd/o5LmlVEAgCQSAIBIGFh8CznvWsfjY6dKef45JWBYEgEASCQBBYeAg8/OEP72ejQ3f6OS5pVRAIAkEgCASBhYfAFVdc0c9Gh+70c1zSqiAQBIJAEAgCCw+BTTbZpJ+NDt3p57ikVUEgCASBIBAEFh4C3/nOd/rZ6NCdfo5LWhUEgkAQCAJBYOEhcNppp/Wz0aE7/RyXtCoIBIEgEASCwMJD4Ne//nU/Gx26089xSauCQBAIAkEgCCw8BA499NB+Njp0p5/jklYFgSAQBIJAEFh4COSdWQtvzNLiIBAEgkAQCAJBYHEgEHVncYxjehEEgkAQCAJBYP4ReNnLXjb/jZioBaE7E6GSvCAQBIJAEAgCQWD6CPzsZz+b/klzcUbozlygnGsEgSAQBIJAEAgC84hA6M48gp9LB4EgEASCQBAIAnOBQOjOXKCcawSBIBAEgkAQCALziEDozjyCn0sHgSAQBIJAEFhUCDz3uc/tZ39Cd/o5LmlVEAgC40Hg3//+93gqSi1BIAhMAYE73vGOUyg1D0VWnodr5pJBIAj0CYFf/epXF1100Yor/mfy869//esmN7nJX/7ylz/84Q/Xv/71b3vb28r88Y9//Pvf/37DDTf87W9/+8tf/rKVvOlNb3qjG93orLPOWmGFFerc9dZbb7XVVpNGMuT/7W9/k1511VXXX399Lw6U+c9//vOvf/2r8te85jWvfvWrq+Hcc891yhVXXPH3v//dBmXXvva1L7300kc/+tG77rrra17zGqdLf+tb33KuelZZZRVtU8mVV155yCGH3O1ud9t+++39ffvb3/7Zz3527733vsENbvC85z3v+c9/vl6o02edddbR5i9+8YsOqS2fIBAEliYCoTtLc9zT67lDAIFwMQbeR6J9bapDOyTHp8iEkl/60peOOeYYR+9whzs84xnPqBYr8IpXvAJBQReYfJ8nPelJn/jEJy677LKVV17ZuXLqkDQ+sdJKKz384Q8/+uijXZfIfJvb3Kbq6f5929veps6Wo9i3v/3tk046aauttvryl78sf8899zzhhBN+9KMfvfe97z3wwANbyRe/+MW77bbbJpts0nKe+tSnHn744b7+4x//eMADHnDxxRdLu+h555137LHHOtfMT4P14k1vetOFF17oKl//+tdf+tKX7rzzzpttthl+I/Ob3/zmmmuu+f73v/8pT3nKuuuuizbd6la3euQjH/nOd77zjDPO2H333e90pzshSW95y1u+8pWvAOeII45AiR784Aefeuqpr371q3Ey/MzR888//+lPfzoO9OQnP1l7WiOTCAJBYCki8J/naz5BYGkjQHj41Kc+RR74yEc+cuKJJ3bBYPiRCWa1MikQn/nMZ44//viPfexj8n/yk590Cw+njzvuOHIF/rHvvvs6+rvf/e7mN785MYNdRyboDdLK1InYAIpQ6T//+c9bbLFFPZLufe97t5q/8IUvOJEo4tDtbnc7ZT7+8Y/TPDbeeGOZ17ve9eqsO9/5zre+9a2Vka9H8l0Ib2j1dBP0Eh2k0yjzuc99zlefPfbYw+naRheRKI7yxz/+8cY3vjGVxdYamM1ee+2lnsc85jGbbropZF73utehKXJoKjvttJMa/vSnP334wx9GvF772tfKR1nuf//716VpRViU9OWXX64j3/3udwlIro57yXz84x/vol/96lc/8IEPSNTpmJD01772NZnve9/7KDpKIjoysaKf//znBksaF3zc4x7n0kiPr5jW0572tAsuuKCum79BIAjMKgKHHXaY352Pn/OsXmi6lf9Hc84nCCxxBBj7cqMceeSRG2ywwXve854C5PTTT0cC/G6xhwYRoYW9f/e7381LojA3UDvUTeArlA9iBmUFj6GyEBsUwBsQIMwDC9l88815fy655BL5XiN8y1veEjtplfz0pz91CVf/0Ic+1DIr8exnPxvtKBNem3ox7c961rPuda978R8RhPQIObjFLW5xz3vek4JCX6HTDFQy8JW+8qAHPahlvvCFL3RpT66HPexhEsVsHEXXsDe9e85znlOZeA9hxiGFi+5QWZyCdlRtsEJHUL1TTjll7bXX1veTTz4ZIK961asUwEv0GmtR5hvf+EadUnTnvve9b0lHRXcoWIbpHve4BxcbjadK0q4wPORJe84880zXhSf+Ss1CdHz19/vf/z5SVeXzNwgEgVlFgBbrd+fTN7rzH299PkFgiSOAJXCUeAQ88YlPxC1oA2QbmOAQfEO0CrynQcTcXuMa1xBZgm3gK7vssks71E2gHapCC9CI/fbbjwTCsaIA005EEcuy9dZbYyEYyRprrCH/05/+tArpE8hW1YP9YA/StJPKaX95qfiJTjvtNDnI02Mf+9gb3vCGIlp0wSHtV6eaMS3E4j73uc/tb397fWynT5jgC+Ouwrq6RxEaAk83p1xvSNvBBx/sWg5hP3gMhemZz3wmj1K3cKXREXj+5je/ufvd707CIaF973vfW2uttUTYKOC6cMYa1dPO5XsiVv3gBz+gM+lgeQDrKPBdt/ouR0mkkOTmPcxvfOMbsSg4bLTRRtpZ5RXg/FJJqzyJIBAEliACoTtLcNDT5QkQYESZSYIKTYKEwAYrtOWWWyINBx10EF3BV3oJu9vsqBw2nmjhxAlq/K8l3n///euQCjGnCYvJxI0IGDgEDxQ/F5I0WcnK5zkSiktT8ZX+xLPDL8auoztyjjrqKBEtEnxY+iWTWNJtdlUy8Fdf6E+EkMrXWpwMV+OBQptaRNETnvAEscY77rgjdYquo7CS6AXvlbTAYX8RFx8qS1WlRxLVNqKRqBqKFArYmoRQAuoFL3iBfuE9CqsTN/rgBz+IutFy5FdV8oUZiS7Cw37xi1/IVImO05zkEOeqWP4GgSAwXwi0h958NWCy64buTIZM8pcWAlQBphTbeMQjHkGDLS/SS17yEnaUfeVVET8r86Mf/Sgy1KDh1cIPqDgtp5tgicuf0s2cMP2ud72LssJ+YxKCcEUFTVhMzFCtdSJvoGWUmwmLtUy+NlG67evoBB2FM+t+97tfFUPsUBZESpTSXe9610ZNRCujUEJwqFPcTworeZ3rXEdk8UMf+lBRMnJcF0/icZM+55xzdMfiKd43X3n3hBLjdhiSr+3j6gQwIAOcDqSDKA66KeZJgj/OVT7/+c9jliBCubgXMVGxRBpJEoPG61//epU36imoWSyR+qlQfFvtQkkEgSAwqwhM8aE3q22YsPLQnQlhSeaSQ4CZJG+cffbZGI+/+k9yoGqw2TQDvhhUgN/qUY96FMPc0GGDpcsb1TJbAoWiT7SvlSDz8ENROLr5pXwgEAw86oBhdI9Wmr8GmSiVpchHXb2VdIjU1G1eO7TMhO4jGdgDN1NFBCMQNC21oReiguheP/zhDxEyoTZaK8jGSnXVUlaoOMKH+ZKsveJ94xCkEpGXLLkCph5ZWC7UhtSk/DbbbMOtBur6aoU5EonDKaCweSGiY0ma+GukU5gUpcpwUJIE8bzoRS9SAzeikuopEJQ3OuUX0wbMDBtTodcyC2BCs9SGSjoxnyAQBOYAgeGH3hxcdCqX+I9in08QCAJMOCJCHqAcWEqN1qAdMhlO9hsP2GeffcTDAoqBL7iwFuu5cBTLqYYBtGkNeiQQR+yL2BT8gLNGMcusbnazm6FQCISQ3gMOOABrsdTI1Vl0XidRKfIJS2oWvOIUtry2t6E/KSbCV6CP/He84x2WTdlmRrNFQ+MEGAndhY9JlLQC5A2KiIRFTMgBt5T08MdqL/RLVfjZXe5yFz3Fb6yoUhLHIp9UJVaEoUS0GfkuWplCgO1qQ+YhejkdX6FO6Sx/EwRQIiQMBxJdVNfVfvWLpNFmOQJ0hBg7F6pwwF18iEPWk2Ng4pddjmyjZhRHzBM25iwldQdn0jbeLkpPRVDpu09daDKFrI7mbxAIArOEAGX3la985SxVvjzVrlDTyuWpIucGgUWAANrBxHJLieoVb4vr8BzhHNwobDyrzOISaTEMv2RMRQFMiA1WrK1EGMDBj0t4MqohH5VRlbOk1UMrIp/wHBGQGG92nYiCpghkttkMk08x4lbDQjADEosyeINlTVY5KYA/yac/YRtvfvObnSXuR6tkigXmVCpqRd6wpY3auLTwAPxjoIX1FaXAS5zrqzZrJP5RkTdCghALopFDmuSK1B1pBUqekSYCIStipaXzCQLTRcD9g6k/8IEPRF6ne27K9xABfmr7SmgYgdaw9qeFoTv9GYu0ZN4QQFxs/YIoePJahEWNsMZHhCz+wU1jwZS4YIxHOIhFUhQUVp/24IPEOHFEuwUd26CPFkKesSKpNq1RnoOm6M6Ic3MoCCwFBES/0U1FyNm1cin0d9H3UWReOZdDdxb9WKeDCxIBfqJSOrlI6CjUFF8pOmPpDMJkNTglhsBjudNY6kwlQWBxIOCHZv5AIOSsXBw9WuK9sMUXRzwQ+kZ3EruzxO/MdP//EBDf2sUC4+l+Xc60HXRoPNxV4TrLiWROX3wI8JbGjbX4hrWHPQrd6eGgpEmLEIF61+Yi7FhvumQhmNkk20moE28uBquFOYuCEt4kBMqi9Ote97q1Qr43DU9DgsCiQsCb/vrZn9Cdfo5LWhUExoAA95n3Kggw4qGbrDpRz9ZVYQkK4Ae2ybF4imdB/LUtcMQnWWYlx+Y3iimsKp4+MdpWmzvLhzNCjp2LnWUtusVTVpWLbraird5BgX9YbiZq29Kwl7/85S5kOx+7AtYuzAKrRT2LibbpjgsNtFNsuLBrUdKioFzFJSy5srG1dgq+dmlB05/85CfJZl6wZXmaNlPmbI9koZldkSxhEyZlKRy6AwoLx2yhFLozAHK+BoExIlBxymOscGxVeV7kEwSCQBcBNlXwshx22sfXOsr2+8rwdwtXpvw6hUn+zzmdTztdgZZdmbbsq5dL4AeWjlvWrmZr1C2rRg5k2qqYwa7L2VTQV8XwDDnePCVtyRWW4F2bEkUyum2r96hjHupUWOS1ZdsCCauMl3H6KtTauZXZ3e/HArQqplqPG5vl2I+nXPKq2nbbbQeeQXbKsTTMzjfoi0OYjXeeW4OmEovSLb+3laJtoKtai9VREMVwlEMOOUSMFApSlxv4i6N4pbmSlphZlWaDAIgpoy8PechDrHoT4uq9Y9qGAOE3CJa1Y7iaRlZVmJm3WEjTeNSDvQ1cIl+DQBAYIwIiFP3QfKitY6x2+avKK0KXH8PUsLAREFVjzRRL743oesIAYxu2n7FNsIVUVmV7R2btrWe5lt+wXXbE4qE1Ctu/jhkmeDC0TpFj9ZZABKuyqQ5CLx1ijyufgRchJFMBNp7Jt0Scz0WdVpiTNxSuHQjL82XXYCTDSnWn89QQMCxfZ8gRFFvdoDtOca6Hi217qCzyMRuF62PzPaoJeiFmyOZ7mkTzcCE771UBvETviDHFJ1Qiv14iAYrG0vADegklxlE4qNM2YqiSq1u+LiyJZKKqer25MrUnEKzqKoQcjaxe2G+QL6neAF9vwNAkfBEsFJoqP/y3Jot2OPTOc5XrL04Domqh9XT6bi9BJ9qxkLtKAlA2/6iqkCENqO0NJUJ3hhFOThAYIwK9pTvjjMf0KMknCCwsBAgG1AIih51v6AEaTzthm1EEvIQ7hj9IJieLd4haXcmoc47QKmxFKJ+Yge540QHXDFsux27C3htqKbstfBwlLbDK8r03ijFmrW2Qo3I5lB5CUTli0AXCCfkHn9hjjz28cZM5Z7NtnMNs22zQ9hVqxkIwLRey1zD2Q95QDwOvjAtpbREgmT6UDzSCCkIW8hYFpG2HHXawS1ARLNsZoxFYgjXANmvGwFzaWauvvrq/uFFblcZzpEfaJh89ko/9oG4cTKiPr9bYQ6CVr5IK10e1WKMW+gpSaFiGc9XB/wCoNsgPnNUKSGAz/qrBNkVe8A58NEtOXdFmQqgYMOXoBSYETByo67HCI0GXV0mAKJ8gsGQRGPSUL1kg0vEliIBIFDGtDCQSQ5WRZoxZd1Cw5fw1PnQU+/hx0/D4oB2kAtxIPmLBU/PWt77VXy82dwphBo9hcX3FY+xViPQQjSxBt8UOboEtCTfxEUzDeFudbsNAtAZ1cCJfD5JB/FCVhEyyRw2KmrGusu7kGeyBROEQhclXYTG2Q6xNAqu8vyrnn7Lfj6qwBH4c+zsjKzxTPGgK8P6QgihS0mQhTKhoma/L/Ij55VarDcRMCjXemyI4jOpEQpeE/NH1iMXxulBsT1W2dcZRRpfXayBMWK09r4sSAQT3UgyH84bRqtCFbCBpo2ojawgmrGH0pXM0CASBRYBA1J1FMIjpwgwRIH5wOQmGZfsZfmG2VBx8BedgOKtSJMOnbCSRQCaygmFQg1h9XytTgtNKhRLsvc0JbS1KYyBdyLFLIX6D3BAnBKMgQPLpMQQYdtq1MBtKiZZgSMoPfOrqaFbl4zHe7YCsICgq3G677dTDCcU11k4UEawx9cJOmXxP3Gfcc6QRek8r1hLIWetyyxydaB2vYtVTaZoTHatxNR0kvYBiuDZAaSd/FrUGyMMFKqe6j3R63XpVC08ss15z4VwErhrjQt5WQQCjwKGA7XTI8KnxQqKh3m8/2YWSHwSCwCJGIOrOIh7cdG0ZCAiOYRopNMwzZsAh5QRcxxKkCaUOlpvpZaF5XrxAirKivEw2GNdhSjl9xIj4utZaa5ErhNeUqVbMjrHEleJVOBavVoX9OrTMj0sog6wgJRLIFtZCtkFQXJR0gSfJb4TDdalK3nuFUcm3DTTnl8tRqpAerjphQwNkxXushOAoPPARZ+Oi1YCBQ1P8ipAB09u7RBFxpeGIWI6YJ6FFquWwo8SggCNqQ0Md5Rzcb7/9qhiHIJ9jhUKTvrwzSyXCm37961/rOGHMaLpi8Ug7ZYvNsik2yiWHf9ArCzDOEVfMoSAQBBYfAv+ZeuYTBJYmArww6IigWoRAgAvvDCPK90E5GF4RXRApbwkSy81glyDBZsskUch0omIoCH+WF3my6N52KcAWAeIv47URqiIi2CUEzUwdc8xGe1Rbp4gUtppaWrWYhKO1ZXurUOgP6lOvzZLJZydyCDlg7ElBXgHG3gvlIVPx3wlVxnWQhuqyfjlFa71M44gjjiApuS7py9ouTMJ6MVxQtFNdC/+A2M9+9jOXqBxIiuORAw1rwi3NsECdKuM1n1gIBEhcGKFgRrwHR1R/vZpUX6qG4b+ooUyxON39PLxLFYzedKZVlmsJOXJp4U0EHsFMGuzNo8qLQ8eEKEC6wyOpy7yHrbXD10pOEAgCixYBT+p8gsDSRKDYCWlB9y38IfaI9pUW8sJGSuAHCAFWRA7xCGDdZXKLUICQAOaWxoNVyCSfoB0SPrQHMk+lLXpyljXSTmebZfJzUVZIKVVA3K5oHj4swUNEI5kMNjYgApc2gx/UmiYN48HZddddmXZtY9rZbAFGMrWW74Z0VIvJtYqgUk2tS6AyzLwGFEnCV3TcIWygyTZIAHIms2JoGtsToiQURg0kmXoIEpmqWpwGqSr/HaZYmWQnxRQuzxpqKF9sDW+a151SoYpiAoSoJodyo4C4JcFGVcPwX+0UGK6wXnePGh0BSdWXbn7SQSAIzCMCvV2ZlYXo83hX5NLzjEDRHZIAlw2BBF+phdz8Jqw1UoINUEGqlVZmtUwvCiUqyGduMYNyDAkHllOrposHFBXAbAgqFpDf8Y53lI9U0UiwHIVxJnvSYDCuIhhIRI5MdGrHHXckw/gIN3HU7n9Mu0YiEyiLSyhmnRFPEHaCA/lqPZdte5AJa9eF64qqltk+lkdZz8WZ5S/yUfnqVLNPN5Prx9fK9xcgipFeWo50nd4ylXdWZXZPl4+6tTYkEQSCwFJAoLd05z86fE3a8jcILDUEGGxrmPEVSoOFRXwrdBGMBA5+sUUL6DQCcQoZPiDmXFphykplckvVEm7ncqk4S3SISrAEBfy+LPy2nosygS3hKHQUsSZ17tj/8t3gQBw91KaxV54Kg0AQCALLREBAZAUm9u0VoaE7yxy7FFjMCBQp8ZeQM2Jx0EKBgAKEtInFoQktlDannUEgCCwmBHpLd7IyazHdZunLtBEoLaf+Tvvk/p1AduIRq60C+9e6tCgIBIEgMG8IhO7MG/S5cBAYOwLdXZXHXnkqDAJBIAgsXASyEH3hjl1aHgSCQBAIAkEgCEwJgdCdKcGUQkEgCASBIBAEgsDCRSB0Z+GOXVoeBIJAEAgCQSAITAmB0J0pwZRCQSAIBIEgEASCwMJFIHRn4Y5dWh4EgkAQCAJBIAhMCYHQnSnBlEJBIAgEgSAQBILAwkUgdGfhjl1aHgSCQBAIAkEgCEwJgdCdKcGUQkEgCASBIBAEgsDCRSB0Z+GOXVoeBIJAEAgCQSAITAmB0J0pwZRCQSAIBIEgEASCwMJFIHRn4Y5dWh4EgkAQCAJBoF8IHHXUUf1q0FWtCd25Con8DwJBIAgEgSAQBJYPgcc85jHLV8FsnR26M1vIpt4gEASCQBAIAksNgVVWWaWfXQ7d6ee4pFVBIAgEgSAQBILA2BAI3RkblKkoCASBIBAEgkAQ6CcCoTv9HJe0KggEgSAQBIJAEBgbAqE7Y4MyFQWBIBAEgkAQCAL9RCB0p5/jklYFgSAQBIJAEAgCY0MgdGdsUKaiIBAEgkAQCAJBoJ8IhO70c1zSqiAQBIJAEAgCQWBsCITujA3KVBQEgkAQCAJBIAj0E4HQnX6OS1oVBIJAEAgCQWDhIXDmmWf2s9GhO/0cl7QqCASBIBAEgsDCQ+DQQw/tZ6NDd/o5LmlVEAgCQSAIBIGFh8DWW2/dz0aH7vRzXNKqIBAEgkAQCAILD4GVVlqpn40O3ennuKRVQSAIBIEgEAQWHgI77bRTPxsdutPPcUmrgkAQCAJBIAgsPARWXnnlfjY6dKef45JWBYEgEASCQBAIAmNDIHRnbFCmoiAQBIJAEAgCQaCfCITu9HNc0qogEASCQBAIAkFgbAiE7owNylQUBIJAEAgCQSAI9BOB0J1+jktaFQSCQBAIAkEgCIwNgdCdsUGZioJAEAgCQSAIBIF+IhC6089xSauCQBAIAkEgCASBsSEQujM2KFNREAgCQSAIBIEg0E8EQnf6OS5pVRAIAkEgCASBIDA2BEJ3xgZlKgoCQSAIBIEgEAT6iUDoTj/HJa0KAkEgCASBIBAExoZA6M7YoExFQSAIBIEgMBkCf/rTnx760Ieus84622+//V//+tfhYuecc86zn/3sK6+8skre737322STTT7/+c8Pl7zsssvucpe7nH766Q49/OEPf9CDHvSQhzzkPe95T5X8wx/+8KEPfei+973vBhts8JGPfGT49OQsTQRCd5bmuKfXQSAILCQE/v3vf+MBWvz3/34WUtOvauuRRx652mqrPe1pT5Px/ve//6rs//1/2cte9olPfAITevvb3/7FL37xwAMPvPDCC3/5y1/+r8RVqb/85S+rrLLKLW95yy9/+cvf//73X/Oa17zlLW9529ve9uc//1mR1772tU95ylPe8IY3YEsu949//OOq8/J/SSMQurOkhz+dDwJLEIELLrjghBNOmNCO9hYNhn/33Xe/3e1uRxq5//3vjxCMbupvfvObr371q//6179GF5uzo7/97W8POOCAvfba64UvfOEee+zxohe96PLLL+9eHYPx+dznPnf9619fT3/84x9vttlmT3jCE9773vf+85//7JZ04pOe9KRtt9129dVX/8IXvnDta1/7zne+861udavb3OY2Z5xxhpIEpEc96lEbbrjhK17xio022uhvf/tb9/SklywCoTtLdujT8SAwiwhQI/gUGLA//vGPl156qWn3hP6LyVpwxRVX7LbbbuWtUOYDH/jAdttt97WvfW2y8hPmM/auO2Dyf/e732EM3B+f/exnJzyrn5lMOGfNJZdc8pjHPObDH/4w6YK/pjWV8IMENFqgy/icPgIf7AaiHQKskgNjcd5552EVrbbZSNCkeKBWWGEFlfuL/QyILo997GNvfOMb3+EOd1AA47n5zW/+1re+lU7z5Cc/eaWVVuo2ycB95Stfee5zn9vNlNY1PZV46lOf+o53vEPixBNP/Na3vkUHks4nCITu5B4IAgsPge985zsV0/DTn/70qKOOqkltr7rBpD396U/nvCBF7LPPPte5znU23XRTEsUUG7nyyiuzwTvssIPyQjrYwi996UtTPLcVo+KsscYaP/nJT1qOxA1veEMaw4tf/OInPvGJ3fyFksYS1lprLfzPp9xbCNy97nUvUL/pTW+qXhx99NF6h9Moea1rXesBD3gAquHQZz7zmXve855KUol+9KMftS5/7GMfe9zjHjerd5EbQCTNySef7KKnnHLKiiuu2K4u8b3vfe/Tn/70lltu2TJ/8YtfICu+fvvb326ZEnjbM5/5zMMOO2zVVVf1la6DSH3wgx+UqbybrRXGfp71rGep073UMpNY0giYhOUTBILAXCLw85///N73vrdQykc84hH3uc99iA1cD1NvAKfAjW50o2222cYpD3vYwzy/GO+pnz5nJUkLd7rTnYg0rmhGbsrOSk396my2rr3rXe869dRTJQSu1rnsPVtYH2mZxx9/PFNKDOABYc7vcY97nHTSSfK5Qpy48cYbs3n+cu7INPX39SUveYm0D5lhiy22qFAPZQyH0alDtKVHPvKR3CKgJlPJFPdq1LhakAkXeuUrX1kl5+YvS3+9611P1IvLnX/++bp21llnSWseqQMDZvvf+c53VmPEwVA1PvnJT37qU59CHGVy3t3gBjcgC+mXSJeXv/zlVdJfzAATIo20nNlIGDLIP/7xj3f3EnIwsHYVI7Xuuusai5YjQaP65je/ufnmm+tLyz/44IP5p37/+9+3HOE7H/3oRw2NO0SMc8t/1ateBatp/bLauUksDwJ+fW5OH67J5aln7OeG9ta45G8fEeC88Fg375xK40zlPd3MZX3EJ7773e+++OKLb33rW++0005TOX0uy4g28LymOjBFVHdz0zXXXJO1nmIbLEJhAKq80E7W9wUveMEyzz3zzDPxBq6BESWZT46DcigoRozBNoRQbL311m984xtpCQ984AOJNCNq6B667nWvyyVh8i2TY0WvB/xK3cLD6RIAaBg/+9nPukdZ9Ap3lWmU3R4Em9ve9rZ77rknh5dGolnsuqM3u9nN/BXSoQCpQ3t8XW+99fAesS+PfvSj73jHO5r63/Wud33f+96nGJ7E74Y7qlZJbiNcTf24KTZAavrhD3/oNhNF+4xnPINQwXIrNu8fxAUbM76/+tWvmpS1/vrr6xrYmytH0AxYrnGNa7gNfvCDH7jlWstluqna11lKGA7UxLAed9xxxpTIVBfScgqlcGPD1L00gdC9J9Nt2fJRN9MD1LnlbLXVVtLHHnssbtQ669Ghv/jTQJ3trCSWIgJjJ1CpcIoImOuwBMOF/UTpt0z18KGx53jqffeqDymbU3/sl5hWhYwQA8MyOcsEGnFhwKZYgye+ibjfsJmrU8zCpenbUzx9ZsUMYk2dp3u6UE2ChLNM2e9+97uzqVOvwYjp2te//vU6BVAiVKRNZJmNW9ziFkieGbwcRoUJR19e97rXWcbC/iFYJCWiCwaz6667YgkMedVDq+AT4fi4/e1vX9MyTgdygvIGBXExIz/iiCOq8BT/MqIYEpaw7777snam4FM8UTGhKiyWvnBbMI0aXOfuvPPO0BPFgshSCyqz1A5f/XyaPGNoAHXuuecOXBShkd9tDIj2339/xVRL/pEQy6K/1JGzzz4b3SHzyMQn/GQM+k1ucpPDDz98oNrZ/jqs7ugazcYAIV6AuulNb+pXXM3gn/LzQf5aq9BivabunHbaabgaF1g7NGcJMhK/lQVTxxxzTLuogeD3bF8lfv3rXxOrODFNYMQjG4I6SiN06w4INu4u3ZGPmlcxBVBYtzeepB7j1a086dlGoLfqztVmu+epf0IEPIj9IFmpN7/5zSIJnvOc55ib2nMC0fHw8lRqYvuEp48r0xTQtdrHlGhEzYSEroY8ouSMD3k6e0Z7UqvBxE7DpkUmyOPECUGaTi+Xf3vSebhDWORjtc2TEeweslZ2HHLIIXvvvXejegIgGDz6gUmwwqyaCABpZZT3sPYUlnje857HGKMsLB+txXO8ap7i30Z3+F/El1hpMsUTFdMGyKA1uqBTfDHFm0kOKIUGW7RSICiMzZglI4Jmz5QkOZrtdLeZND+IJS0SKAIfATPDPYSgkDpk+oAF2xiwRnVoKn9NxF2LpIRLEU6mckorY90y80ZVssRG9I/7oQ4ZSl9f+tKXAp/vqTK7zp1Ww2R0x9jZtaUVkximOwgiqoccWN1jRbRIqSoPIpbVmufu6XOT7tIdig4vD7UMtuSNaoBO6Vqli+4YTQ12M3NUcfkZC+RYASTJzYMaVmEkD6Ttx1KZY/9LfSGYaYMx7VYu4OYb3/hGN8fvVLH6VIPrqHhtzqxuSWk3sLmNp1PL9/B0rtu+avAbaYeSmAMEQnfmAOSxXcLUlijKQaBGTuXyNLfn3Vgu42FKQPb8qimXOD6zcD/Ogw46qEIW9ttvv7FcaHQl9QS0eIGgwtU9wtWqgKkzEcLslhY92s1PnVZmuuZNU7UELMxbeRMAMha6w7V/9atfnT4huEHgC75iHqxyD0omDdugjZe+ggYR24Vl0EJITZqE6yhJXWD5PFWRG/2idshUktkjYCAE3UCE0ZjXUQxJDWau+stuTQurojta7kSuJVbfjaRaZFTvzO9ZMkS2LoQJubus4mmtYlpcumQzRgLaDvHvYIoIt2p5nZj/Ko/ugK4pQK2SKSbcLdMSrrrVojsf//jHtZ9zisUqugMobIxdZzuNwoC6U7EsrZLJ6E6pO11MGt1Rv3AoNOL1r3+9GwNXUBvSgHg5RN0BLPXLRIVfpnGLdsVZTRh3dxouzuobrArTwc6luWw8piTck+hsNYNQpzyNyk2CyrhJ+OPccpx67mQdbK3F59wSZggtZzYSfiPcozhW3a51Cfcq+jhwOU8baCvpbxOoTEuAb2gGCrvtSw9u+YTeOr1qKO2zHZ0soRKjPN0f8mS1LeX83tKdxO74mQ9+6C5WLtDSqeWmj5aEeNQ2r/Bg6el/97tCazy2PJvQGo8tT1tGiAmU78fpScTM+GGXsbnmNa9ZF/HoZ5DYVx/n2k+CqMBeeg6qRyYFokpqvKc597yJVNfPPdBYj0g5ggSZeTM8Zp4qICiEj5/bQoKdoz8Jd+BAof14slAOrOmwDqItAxmo01dkTjCEEIfyKA0XmCzH44kJ118ImNVp1WQlJ8s3TBrmseX53sp4/EHGbh/66NEvrlNPSegAZzKRIVzWEiflmU/BIqI6rBMRpSGH8VAhLcFz2Y1hJgpwSglnh3zzZk4EoLVrTTHBggKZ5sHBpM4aiCmeW8WMLCYhTRliEoBmsPgpDj30UBXWitxlVoj0CHqoYowQc2LQ8Rs5brZKTFiJoy6KSE14tGUC2W3cvraE0/0KGOMRPyv1+y3Ah3l2q2ue040LTkyLMl4IB6tGeOMNdMM4yiK690zrYeur3wgGgCpV1I5BxO3cvbWE2yDylWD5fB+IkdXdhliP3Lc26sVu3fmoj8p1wU/AhMRdzbGCRvB8qUSi9WgOEtBArzXmbne7mxtGI11U71BwRlpnYQWlyneIgkhdQ9pKMJbjVmeKICAf75FTH7+OtddeG8W/KmNK/93DfllNRDGUhtt96AdimLS2HarqtNC4a6ET9UJ5aV4to6M93fukBq7OUsYhXbOdILpJp1RJt30OKeDTMov2ta8OqaR9RUSg596TaJmuCEPj61nqJmn5SSwmBEJ3JhhNDwhPNzNLDz4TOJae46AC4pRmVC666CKPBg87QaZ+ujL9sH08oLn52T85JATRFX5FSg5Yfc9KNMXaWsW6Pzlf62N6zZiJQVG5p61nhyap3Ck0ao88nAAJI4HwMihMe1CMHG2ib3mCJzJfPl5CrfEEb0rJVdUP/vegZ+TYclVpP5cHtuTqbCczo19OEOQBAZfmLpEz8MQZqJHJ4WEZ6PVAmQm/6gXkCfWmpLojEmXCYiMyNYzPXt+RM1hVSRTHQJDrmCgPR5ke03R1XFYal8VXqptGzUyX7RQQQDZvF0KPpIW24Bae45VfglwrM62Ey7H3MLcaaFontsKicIruyGE53KVuD83G1I2gjUlayQkTAJHvPgGUBLkL62UVDByNhBFVFRVE+A5I/RAwUXy60TKGDX1EOLjAJqyfjfELYsw0DO02KKS1VtINxgvDT1RCS8tvCQPkZ4LNaAbMkW+HBNCoEDvh/PUVN9U2to2JUhIable8n/ZjLqGAX6J7G6fRGPEiZcYIWmB3rt+g6QQc/AbV7Mbwc/O3UPWzdWkVKmawyCf+mmwg+jJ9zExGcLXWkTEm3G/Dt5xW1XL94Qv5wfoM5AuB8hnI5EE2QAOZy/xqksAZCv9WEs7a46tEy+wmtMctBHA4m05gro4Od8rpAzUYaPePgfOr6VYoXU/gbqbb2Keb002rym/fTWIQu/la7qHnGdjNTHoxIRC6M/FoFgshp/NlmDzVVzNmvxOeGssdzYNxDr4DSyFqmuJXZFojn4Wg2ZINKOFqJ8ULeOw+YjjOCfKmaO3arKzfPDODVch0OQ8Rxh7L8ZYZBsnjGLNRD4JFrfGUEYS7yy67MMwa4Jn+4Ac/GBER4Ox0goRZO4vC5rFnNOrJbGo9m8wCyTasvnN1gXlwCWTOQ1BoSz3TUSi12cajJsqt5RMmFCt7M+HR0ZnVd7aQHS3YR5cfOOoUM3tTzJq8MmaehuwBKkDUwQXLe6jjzJghc7pYEH/N9thXBhjzEwyL69TwVf2MvYT5JZKBAUPG18qU8GxVSa008RBXOcdZ1wxUJd2/5qkMqkc/oQKZbofcA/ynwGdNW+ZAwv0jB+f2FxEx0O4lio67BQVBdwSy8EnB0OjTDuWbtlK8UIG6wZzI5+Wo7iDWvuI6ZtjMOY4ouhPj3HHHHfXF/Y8JuSUQDgJkozvuELNhSthkdAcIBAN+H8igHSW3uFB9DJB7koB3VcZ/jBbywQKxZzVq7m1jJIpIpqsbWd3Ud82u+1YxCeUdQsSrKmbScPgB1lc8tX56LdPpdQ8oUKdTdBB0X3EmXAotluaG00gdx/+A46dH7HGT1KWrcvePscPq6utS+2s4eMO793kDpyW6mBgaD5n2APH7QoWV9Oir3063cNJBYOwIhO5MDKnJpTklwRyN8MSvp6enm583zcMv3E/ds54sTCjGgVgpM12CBF6iRj4Oj1cnkmRI6ExauwyGZL0MGtFyJEwpTFzYpzIAnvuqYqE96D1ziTSqtdaGoeVnYQN4GZgHDw6TTnTHelqPfubh+c9/vocINUiBMjCsRTNR3StWuviEaFmXQHQoRtQdz3SWz1QeZZnj+atWwU2nxNuyN75WCyVgYu6FRGKf1fjhv1W4+1cIkWmrYWK5eT0knEWfA53hQyU9bWHrilgpq+ao6yKazCc2w1obQZmYpfGl6yAZpCMcwj2AFVkSAi4FZJKIiFIOYSqIcteWK9D9oMvoIx6gsLFTeTuKdxroZo9bfjeBzTDJjIeFOZilmw270nj+O54par9D7gdI+svAaKocsPja6iF1DMh+nDs+bjk3T5kr9xiDVHqYE3WQN1CUj7tCGZZe90WVOqVV2024dV1FB+GGphe5bAXAjoRVpoahGnh5eamqTLVWs33KplYvWg3jSvjp+ZlP2AvNQxO1BBR4z8AVIdxdzj1wdNF/RaPhNuNuunXN+mZ8ek4MAtNFIHRnUsQ84F796lfzg5gHi7FQrkgPY8auePLWI1g+28BfbsbP2rENxBhGwjPatFslNNhmoVk4AbCoDEvQvbDYQ7a8m9PS7Irpo9mty9W0vkxRK9BNaJWHiBzqjgkrEibHLFxjJjyrdjRhX0n9SlrRwAOFImAVpvJUHwyMVmR2bjaPD5n9o2tsuUBR5t+FzK35BShP2GFrCecCKqDYsEzdykyY0GYMAKXTDAbStNtXNlhhO9RpD/dTA3O4BlHeoqDMwjFCOjmq568uOFdEix6hERxSzBs/BXUBVhrPfUYKYsi5sfj+cBFmTNAG0AyTvwI7ioSRTFBDJtCJOAclQD2uogDpi0SHa2IbeBXWQgoaMPCtwW4SJFgZ0ogy1JQ6VAYeC5HfMttZEgYR/cJg9IJ5VoNMyMvEQgwQUoiFSNRZA+NeX8sdgNrSgQy6zCqscl91R2dRPRTQuEvXUX91WQv9CurOVwCP4Tib8NZqdUq0S7SqJJzVzVczWMzyh+UivB9Kbumint1Klj+tyygLZXT5q0oNQSAI9BmB0J1JR8eDnoRjn65SPjADcxHPYvEfDHCtYnCyRzZOY76LJbAf0vRzxVgFhIAdxQ94HNgnRohowZp2p0QMc2uBJ28ZPM99Co34we7ckVUTN+CJrx4uMza7nWiWzBFjZs9FwmCw7kqyRibfbLB6hHC2wt1ErQ9qcyztd1RgBLcdlqbx2Ab2RvAwTVc/EuAvDQkfqnq0mVCBEXarZf4JD0xvN3Mqac4mSNIqFNY2DprmfNEjsJRZctEJayNHkTqMiA+5BX2RUFg+NEhoKCm+IsRYvsm6IePCVxWz7ai9YVyiW7N7gFWuQTGyqiq5S9ooIDcIFpcNS4zFNnnAKUa8W89wuiiCZkx4aML8Kin6QZvBa9TaFbuVCLvpfh1O645e6NowG5PJj6ZaI0gucicPn56cIBAEgsBCROD/e7gvxA7MRptNmvksiCJmzAIbuXWYN84OHi6G3+wZZXFdkRAsPac+44RnEBLIJAwGCYTZ5g1hCNkVIRqiRlhHZYSGiCMRUNyaTcOQdi49QyAFo4ujsM3Ks6A0gAqn1QBmjI2kGCmDcxQnMNF3CaKRSqwj4wvwUZLaRNXQQoyhOcvbRVtCABDb1kwvJckhvXY5woYG4Ell4OVjfiqX6OorCARvmga3OiX4wghg2FI3c5lpvfARhySaBLGAKhC0pMiNRuo4vQ3Cy6yqW0ANFIvaXYYsQcXpHl2eNN4AE/Vje+isGwOF0mz5nJUGGjUZryChcqNpaLDkWQ13EJe2PMjk3CAQBIJA3xD4//TkvjVuvtrDqFuuyb4KyxCwaRKP61A+EJEKRGXPfNhdXIHtqVkyrsAw+/BMmRYLE+HxoRZgHuy0vlBNKta1oj2qd3QFGoMaKEm8KvPV5T5cFxHBHeFZ9GtcTUJHjN103WrjunrqCQJBIAgsKQS4Nbb+7+o/jpHmOugDAqE7czQK4h74sATHCESYo0vmMkEgCASBIBAE5haBWuLqmn2jO/9bqTG3gCy5qxEtOJ56+LrKJTcS6XAQCAJBIAjMGgIj1gLP2jWnVHFid6YE0/IXEu8i7Gb560kNQSAIBIEgEAR6i0B3Q9FeNTLqTq+GI40JAkEgCASBIBAExo9A6M74MU2NQSAIBIEgEASCQK8QCN3p1XCkMUEgCASBIBAEgsD4EQjdGT+mqTEIBIEgEASCQBDoFQKhO70ajjQmCASBIBAEgkAQGD8CoTvjxzQ1BoEgEASCQBAIAr1CIHSnV8ORxgSBIBAEgkAQCALjRyB0Z/yYpsYgEASCQBAIAkGgVwiE7vRqONKYIBAEgkAQCAJBYPwIhO6MH9PUGASCQBAIAkEgCPQKgdCdXg1HGhMEgkAQCAJBIAiMH4HQnfFjmhqDQBAIAkEgCASBXiEQutOr4UhjgkAQCAJBIAgEgfEjELozfkxTYxAIAkEgCASBINArBEJ3ejUcaUwQCAJBIAgEgSAwfgRCd8aPaWoMAkEgCASBIBAEeoVA6E6vhiONCQJBIAgEgSAQBMaPQOjO+DFNjUEgCASBIBAEgkCvEAjd6dVwpDFBIAgEgSAQBILA+BEI3Rk/pqkxCASBIBAEgkAQ6BUCoTu9Go40JggEgSAQBIJAEBg/AqE748c0NQaBIBAEFgQC//znP7/61a+eeOKJX/rSl04++eSBNr/lLW+5853v/POf/3wgP1+DwEJEYOWF2Oi0OQgEgSAwMwT++te//utf/6pzr3Wta62wwgqtnr/85S///ve/W6aS2MDf//73a1zjGte85jW7JdspLfG3v/3tj3/8o9OvfvWrr7rqqsq3Q31OXHHFFQ9/+MN///vfa+TrXve6e97znq21l19++Sc+8Yk//elPl112WcucpQT0fOC28sr/M0mVueKKKxqRWbpuql1SCPzv3lpS3U5ng0AQWJoIPPjBDyZj4C6rrLLKIYccst122934xjcGxfe///373ve+DP8nP/nJhzzkIXK23nrrc845Z5NNNvnGN77xmc98xtHJEPvzn/+88847s8prrLHGWWed9bvf/e573/veZIV7la/NxJuf/OQnRxxxxHOf+9xu277+9a8/4AEPWHfddddff/1u/tlnn3366ac78WEPexiC4hBKBDTUcPPNN7/tbW+LQh177LEQRv7+8d/P7W53uy222EJJzOnTn/70lVdeudJKK8m8xz3uIROt3HHHHSG81157veENb6hrydxhhx2OP/74a1/72p/97Ge33HLLys/fIDBzBNyR+QSBILBwEfjNb35z4YUXmgov3C7MZcvf8573POpRj+K+YZIpB5/61Kfq6i94wQuOPPLIE0444ZRTTqmc9773vR6sZ5xxxsc+9jFW/KSTTpqsnewx83/JJZco8Na3vhV/kjj//PPRCNTHxwD97Gc/a6f7eu6556JWlfPTn/4UYZLGDX7xi18YUFX98Ic/lPZXSfUQmaowbnHve98bFaivY/n7xCc+cY899hioiuqj+xtttFE3f999973VrW5V2tXzn/98hzTsSU96kpzrXOc6d7jDHV75yldqIdqH7oCXXPTABz4QMapKHv/4x2OZH//4x9EXRLMyH/OYxzz72c/+7ne/+8hHPvJ5z3teZWJFT37yk/Gqj370o7vuumtl5u+CQMAvpRjJ5z73uV41OLE7NS75GwSWF4EPf/jDr3/96w866CAPbobqwAMPJB6YNFe9X/jCF/bff3/Wa3kvM3T+LrvssvbaazOKQ0eSMQECd7zjHekKlJsHPehBHE8ex60QDG9961vf/e53r5wNN9xQ4oY3vOH222+/33773ec+9/na177WCrfEd77znUc84hGGm42X6aynPOUpEjxB22yzzVZbbeVEA+RmkPnLX/7y5S9/OSbh60Mf+tDyIrkx3v/+9zt68cUX3/zmN6c/kYgY/nXWWefNb34z1vXYxz6Wp0kBH7pIdaG+juXvTW5yE9RkoCp0UFPxsJb/ox/9SObBBx9MEEJ6EEGH3vnOd9Jg+AGxHEoYHon3oGs0IXwIYn4XulkBQE6h6DgKlp122qlqRgc1QMm73OUuuvmVr3yFqOauhsa3v/1tVO9973tfs6CtMUkEgekiEGfWdBFL+QWAwEte8hIzck9wz1aP42m12IP1Fa94xY1udCNmjJ177WtfO8XT6fkf/OAHWcdb3OIWu+22G3eGNmy66aZl/Dy4UR/tWW+99aZY4RSLdQ32FE9ZysXQhV//+tf0FZaVMmG8Cg02+F3vetf1r399zIa3ReRKlwHc7GY3g7MhHvaqEIS4bzCnqofXphw3e++9N3b79v9+jDsipQChAiFg9Zl2BegZ7jeGX3scdZU999yTeIONaRv/Dva82mqr4VJHHXXUC1/4QmXoKCKI61rj+qtV73jHO4ZrK4dUy0dE/vCHP+B2cr785S9DSQJK8CTwKEzQuutd71rlffWRFvn0rW99S5f9Lt72trf5afhN6RR6RKMi9kBe2FN1WQ6JiMzmKEVt44035tXCfjC/qjZ/g8CMEVhxxmfmxAWNwJve9CZy8UAXzDg90AcyF9xX8QH8/SaUnpJ3u9vdptV+8Qoe3K9+9asZKc/xH/zgB1M/3VkKM2Ye6BLsh8f9q171KmlhDawd02Xi3q2QB6psBi+GMnXIfFoUxQEHHFARtSbHBksx3panP/3pnC9V7LzzzhPrwDZLdOtMejQCvE54ZwknNJUKzsUkLrjgAn4o6sW73/3uww47zMAp2aq66U1ver3rXa+NUcsfSNAhDIrP5z//eYfEAHGc4bsbbLCBe1IOlxa+ReyRZv65sSSYfFJQVU7dmVBDUmxuPiQcqkzdliOuqAu3uc1tFNDsNddcE0Fxw1vkdeihhw6f5YfgVpev+yQ0rAjbe+Mb31iaDeqD4ZkYoEomDD/+8Y/9Bm9/+9ufeuqpqA/FyE/AiAxXm5wgMD0EeuVa61tjGB5TN455Suzct83jgyw8S35rDxFu+Be96EXiDEzU9M6Dxq3DzM9lT2keQkRd0RPwuOOOM8etqwPcVzr2jBvDwOgOp9K0ahAowBDWWb/97W/NO6d+uke5K97vfvdzCp5EomfPzjzzTF9f9rKXMWOCGLq13ete91KYR2P11VdHy5hbR4VKyBcVaxKP8aBufC7sLnuA2ey+++4sh8pdixKAP1100UUCL1yXmNStPOnJEBAOgk0y56Q72EJYSWaVR0nCjWc4bnnLWypg7ABb96RfijSeNFwtP46xeOpTn+oQ8YMDiGJ06aWX+krSGPj9imJBo90bjopNMfoSKLLKWXe3HFZ0pzvdSWYRptNOO01aJVooUR/3J6Hlqm/L+99Nrl/QcEVsD49xv3n0aTyuhuf5JfpduNPwb0TEQ0kHcZTXvOY1ro3HPOEJT5B53etel6yFMsqkRekRGueuRuUdpWPJf8YznvG4xz1Ox7n5UEwVyhQsBQeZ4odc1KVlQpKmpQHkLvf28jwK1JbPXCJQLNYN0LfYnavNJQoL7lrUZmPmY8VBLVKdyy6Y07NtHkDTvaj5loc4fZge7iNBbO9WYhLmgW6FhYeL3m277baKmV2x9K0YMd9zUNSk2mR6EKvTpzLrkSSf1KzkPvvsY67WzqWsUDjYEhNl+VWYASDaM/kmglXSPI/PSEk2plw8hx9+eB0iemsYp1Krc7qJmdEdV8E2KDGev1wJ07qox7pnuhmqXjsdYt3wT6QEZelWyEbyShgaoj2DUYf4v775zW9KUx2YlsoUFFKGlp0DCxcJqup0FkiBolkChqpw/o5GgGNF7Iu70XorQgvDrDynCfFMwu3NbAP56KOPRjUk+DRpMNgncjlZzSJslBSjQ3sTlSJsRUkqxVprrWXsOGjIPEiqTPIhEuD2oPP5daP7Mv1e3HUmHoJ2UQ1iibb5kaoTyxHF4nT74tTV0Qts2OjX1+X/65az/Jt2Jcr4Qx/60Ec+8hG6r2q/+MUvAkFYMQ3MLV103I9dAR8EyG+/rs7xRIBRWJcrR0IZNTskR7W67xGKRLrhfTxwdMRRjxT50pUvXZn+IoU+fkcVu/2roY9AqKq/Lpq/PUGgt3QnsTseKRN//MKtiiQyM3uEFr9zj7xuUdNEDyOzMebHk8vkDDMoY1nFPMVKLWDj5bD6vkqIhaQY+xlXcIBnrh+/+T3zX795VtMvuTReMky7qOmmiyrsciZYJmQS7JwnuHmSerAHnnU8RrykYAITI88X8y3W0VSs1SP4kYrgoe9EmR7x97///V2xwgvkWKmrzbQHDyPzMLNh0gKa4pAnL1MBDdf1lVBPe1fSUQ0we5OJJopexJ+oEQDBAGjXuI4eeZTTpQFlMmeNq4mdQ2ZyZrQWo5oiO91HS3AFFqi+zuVf82ZD70n9nOc8x+ND96d4dd03WGwknQwFYQAQoBHnClaAM0DY1zbKGIzxMjpuKphMdjoASUdm3pMVSP5kCFgExMvpJ2agySrQhj8BA1nhjhRoYsUQeI0dwuGmpXf6xTn0rGc9a7I63fZIjJkJk69mt66SajBNUqEfdTtxs80280N75jOfiWGw5UWtBAxRWD1n3EJ+R2iEfPzGV5zDD9lX9VQlvjq9tJ9W7VQSKJSOdze2cZYHiN6JPpYma7miex7n8BOoXXBAoWuu7mcOLo8sNfjoHc+dwk6U6dmoKpBqthwFnO6o34IGi7x+9KMfrXKHpvJxUUzRA0FiRHkPN4873HFEmRwKAv9DwB2ZzzACnlCm1ywK0+6pVO4e1hcp8chQni2khWADMk3LiBPl6WfaPSwUOOaYY0zyzJkcZTvl0DDQEdCTiz2/8BUfOR4NDL8LldubffW8M6FEUDxEhAG25vGpU2VQBBNNps6UyCG8gV30lPEcV63W4lUccB5eHqMIFkWR7WyVcJFoQ622RdE8qmgzcmjLntqeIEriNx4iaBA+ZO8NOUWMPKz1zooJa1twJvnQMKN1UW3Ti7qKhSceVficakt10B5pOj/i5UEGpSpZZTwl6+ty/vUIVmFVMjN1B40joXvIqsROKgSqaTUJWXHPYHX6qL9oXzudVOPmaV8lymKZBGNIpeobLDdSuaVwYo9yE1ol1QY6iVJ3UElTbR3Ewt1UJAHXGu/K5G47F1naPe9uhPlAv8xAEA70gvkfODQvX90eCIR21vNk+dvg+YC11GOn+9cjyLPCp5s5YdrTzA8fq+OSMw+UmOLHI0JUwNQ/Bqg0zuXvdWqYewSi7nggL6SP54JFxX7VngLmUjVds1qS1SdF6AlDaErkecQ+oS90Fz9mhoo7xoOApTQppDlz5ViBjDGY65sp4jQ0FfMe1osPuxDhsrFIBGNAERg/E0QF0BrMgPnEXRpwqImvntcmTDiKv4QcNk/gi3WhCBAKIgSBfKJ5LCh1ihVsp0uwl7iXFShtta0fA4JFo9KkigJRjNij4+a7pmUaLIf8oFP0KgzMx0SNXi1fnKzAFEDhT9ojx8d0EMsxIUZrqO5yXMVfpytjVW0FOf6n6Fg/hkZfYGhEGC2E1VO7XYEfAe1rfWz53YRJLbpjWHFQ8juO0o76DRtinoVan9zyuwlDoIMvfelLFdMSY1FHVesOcfPIx02FYmBF7itHSXoGRc2uZbAQa9v2W4TMJ4K9uRkMtMYUPWVvBJGIY+AKMY48XCJLIFycu9uSeU+7/fwW+BrctAONMTSODmQOfFUGDpSSgfzl/0p0nLASLkWfCQ/NS6YnAD3pAx/4gEnIWBpmNlUTquXvTm3Js/z1pIYgMJcIxJk1KdoIAbc9174YGpMYBomVMkMqy82iO5O+YuMsTIUGw2vjQ/Jlbnl8TM7MvE2GCAZK4ijojgT5BNFpXEcOl5PZj/L0IcE0VbP84Q8FhbMfmxGOw6LjDaUPc52gO56JBCc2cvjElsMrj6BUSypTdxAazMZXaVdHcdAXQYJUBHaUBt5O7yZwMmRLVXQs/WWh+fhBgWFolbmyeAgLwkkdzrrBDW6AB6ifKkauBylkXJS1dlRhZ+FA6qxLwNDyFkJUc291Lz1Z2jxVJJARKRXEOibMrBXGV7SHm0wMTcscSDidTmbtOoEHzyjfXJUxNJilu2IE3VESX9Flupobpvou0zpkwhgOTbdzz4jnQGQRZWUIhHqtZlwHIUOy0SA5htKJ2C2Bx0xXVWK6tcqd46/bAAfiSQQpcqYkAuF2lZjiR2OQ7FpKg5syq3LauRop7W9V3vKnntAwg6upw6eYNuiOAsOHWg6gADIbdKddoucJP+dxsZOe9zTNCwJzg0DozqQ4swTiKhhIgSl88GbqfNVKdx/Tw5PUZn4kOFZ4iCRMcGvzlbpY1dBKogLMP8cHcYgxK5NfR/31qYsyPKb4uII1PtgAOmKtrAeitiElDtkult2qR6RZNXpBG+AQwWDK6rM9eoEk0XKqJdQgCf1CVtAappqB1192jrpDHBJjqHl64XKsKevLhtGo8AmCMzkKa0EBpcVAQEPzVOVCWAXdok5RjFahKgZM8+xcohlFsEgpGsAf5y81BQOohqFNzDxvWn2d+l86HOcORghww9cGyBCIlSFr4Totc7haS0iwNwV8Sksr/JVUs55CpvirHPxAICee2mWo0rqPdMJfok6X2eUNMkXtYMPGvUoKycJm6HkOOdHV5WONcOa3IrZhRRDGlYfbvJw5QlWGa6joddct3jNcYCo5A72uU8g2SAy/51RqSJkgEASCwLgQWKE9zcdV4+Koh9sFq2CVzcv5IMSyUCDMt5hnFp3VZJ8YJ14qEoj1NRw6nAsEAKdQRwjRPBoy/VUPBoCaMOrEFQK1WEVTczpHGftCTCgfkcY8vr7aiUt0MItbkoAZv01x1Ca8gOsKe2AL+cuIIgwhIcRZJJ+nPe1pTBQb6VykxBTZ1QUP1V55WBFCgxjVJfwlhPBJcfpwPInWtDSDVUabWH3VKoAYMb3qET4CEzk4BIvFbSSfR4btl2YUlXQvuZYuEHvEHLB29CosyiXoUsoL+vFXgJFPtQGtEZpQVMAlwFL5eBWyiGk1gaTyR//VGNt1oHrOUq1rtfLaBkn1y2+ZEybwDPqNAGqCHDJX/ZqwpNGh6mmnxIQFJsusxhhBwFYZOeKx4Anb7lnK+GA5LgHMLmfqFht7mjoFvWmBP/Y2pMIgEAQWIgKsjLmllgsbrWU6PelF6M6kA4GXEAkYSPYP2zARV5S2ISyGbsFTw91ACTC0zLklSCblbBWRBi9REikReYphsJ0V3SL8WQRPE1oYMJ6gZuCRKta67hKnm+uTRjAGhlC1loCJOaiFFZiWNVld18OkfegcEDtiHs9/QWLpZI8/afmGyBJN5bJB70Q4iUrpeoXGf8mragQUtyPutTy0wHALORIIDOdaeXdV9fkfBIJAEAgCy0AgdGcZAPXwMLOHoDCcCAcHU+MlZuScFL7iKywrIQS/QYY4HWgSJSFUd8yPaQlKln9qfvsoQkhoiNAiDZ7tlnC74Gp6TXCiBtUy19m+aOoPAkEgCASBeUcgdGfeh2C2GsDFQwwQh2Eljrjm7lKg2brkjOrFPHwEOM/o7JwUBIJAEAgCQWDZCPSW7iRUedmDN7qE0Ao+KW4UcTy95Tq6YA2zz+i+5GgQCAJBIAgEgUWJQOjO8g6rqNvuhsXLW13ODwJBIAgEgSAQBMaNwPRWlIz76qkvCASBIBAEgkAQCAKzjkDozqxDnAsEgSAQBIJAEAgC84tA6M784p+rB4EgEASCQBAIArOOQOjOrEOcCwSBIBAEgkAQCALzi0Dozvzin6sHgSAQBIJAEAgCs45A6M6sQ5wLBIEgEASCQBAIAvOLQOjO/OKfqweBIBAEgkAQCAKzjkDozqxDnAsEgSAQBIJAEAgC84tA6M784p+rB4EgEASCQBAIArOOQOjOrEOcCwSBIBAEgkAQCALzi0Dozvzin6sHgSAQBIJAEAgCs45A6M6sQ5wLBIEgEASCQBAIAvOLQOjO/OKfqweBIBAEgkAQCAKzjkDozqxDnAsEgSAQBIJAEAgC84tA6M784p+rB4EgEASCQBAIArOOQOjOrEOcCwSBIBAEgkAQCALzi0Dozvzin6sHgSAQBIJAEAgCs45A6M6sQ5wLBIEgEASCQBAIAvOLQOjO/OKfqweBIBAEgkAQCAKzjkDozqxDnAsEgSAQBJYUAv/85z//9a9/9aTLX/7yl1/72tf2pDFpxjwiELozj+Dn0kEgCASBRYjA17/+9Vve8pZvfOMbp963N73pTTe72c0uv/zy7im/+c1vfvWrX3VzpC+55JKLL754IHOyr3/5y1/23Xffd77znZMVSP7SQSB0Z+mMdXoaBILA/CPw9re/fdttt91pp50+8IEPdFvz73//+6Uvfenhhx/ezVyg6Xvd617Xv/718ZKpt3/11Vd/5Stfueqqq7ZT/vGPf+y2225f+MIX5Fx55ZWV//e//33XXXf97Gc/C66//vWv3cJ//vOf29dKqOFa17rWDjvs8Le//W3gUL4uQQRCd5bgoKfLQWBhI/D973//He94x/vf//6vfvWrC64nTK/P8ccfTwLpNl6nDjvssEMOOWRYz+gWWyjplVde+ayzzvroRz+K1elvNRt3ec973vO5z30OWZH/iU98Qv7vf/97mWefffZ5553nrCpJ5nnIQx6i5De+8Y0PfehD97nPfU455RSHnve8533+859/8pOfvOKKK2688cZV+Mwzz3zWs5615pprHnHEEb/97W8r83vf+94zn/nMFVZY4fnPf/51rnOdyszfpYxA6M5SHv30fZ4R8ND/5S9/2Z2kznODJrk8E/KABzzg8Y9//GWXXTZJkTnNvva1r/2HP/zBLJ8eMKcXHsfF2GBW/G53u1tTLNTKO7PWWmvd4x73oP3c5CY3addxb/zoRz/6yU9+wq1TmWJi8CHM4Pzzz6deyFTPy172Ml+/+c1vbrrppk972tNIIFX46KOP3myzze5+97vvscceLfNd73qXq2+xxRbnnHNOuxCiQJJ58IMfzPXTMidMKPmoRz3qSU96khq+9d+PE9/73vcq7O/mm2/uqDSd5lOf+tQb3vAGnGaTTTZRUOaLXvQiJ2rn9ttvf+qppz7lKU/54x//iOKQgtCX173udX/605/qorqmI2jKNa5xDX+f+9znrrbaag45/epXv7qvmNPb3va2KuwquilG54c//KE6ZZ577rnYko7LfOITn9j/n1h1JH9nFwEP3HyCQBCYewSYjZe//OWe3c94xjPm/uqTXdFUm4UYOPqLX/zCY4i9oaYMHJrHrwzbPe95zxk3gDH+yEc+0j395z//Of7kg3NgFd1D3bRDCij2ile84mc/+5lDOOtrXvOagw8++NWvfvVBBx105JFHdstPmL73ve/NDLdDKMgGG2xw05ve9DnPeU7LlNh5550f+chHIhZ3utOdKv/jH/+4sXjc4x6HZLioTNRHoIxMDrI999wTe3jrW98qvyjIjjvuqE6Z2izzwgsvRD722WcfBGjDDTf8wQ9+IPOnP/3pXe5yF9rSxz72sfXWW0+FMif8IFUuRDhxdLvttqPQSGg50UUC8ZJ5vetdTxrvURJXk37Qgx709Kc/XeIOd7gD3BAdoovCuvDUpz5Vvs8JJ5yw0kor4dP11V/xzqqi4bUcCaQN+6H3tEzyjwuBQvsRpvvf//4OfeUrX5GJpksbl3XWWaeVT2K2ETjppJOA71My3mxfbur1R92pccnfxYaAed53v/vdNqPtYfeue93rCtTQQka3qf3L306miDGbWcd5EBAacZ2s1BlnnEFU0B7z74suuogJR4O23HLL1kKWTxmfSy+9VCbjxKfgRBEb/A7SpT208gMJlZ922mlKcnl4YJmOs4IcOqeffvpd73rX17/+9b/+9a/rFCyEwaZ5cGB1K2Ey21fl2U42++STT9YGMommVvuPO+445pYqgDeUoKLBHsS4JhtJiiisNJvkwF7qvtpGLCxC/g488EBsVXvQDjoTjviSl7yEdHHMMce4hGs14aG1cHSCUsVI3OY2t+nG6tIwoOr2QHHud7/7VQ3ve9/70JQXvOAFAn0+85nPaLaz7njHOyrwwQ9+kMnHZqpH5enDgZ797GeTWB796EerYf/991977bWRD9oJrva1r31NJrqDTiEKaAHqNuBl67Z8lVVWuf3tb889ZNxRHJqKoxheuZAc1ZHuvVdjRBfUbCV9rZyq85rXvKYrduufcfqAAw4QpuN3xKulEtT8Rje6UQ0iyUqXATXjynPiIkFg6swoJYPAMAKeYiaUnvVXXHHFwFH2wCOVbRjIH/vXD3/4w8N1snx+onNw9eFLTz2Habzhfz8SI85CCCgZjBlNnukiKpT24Ovee+/94he/uJ1rXl724xGPeATRiPGuQ2Ij1GAmbQ4tx+TY0DBXxk4N6qx5MC2h+1yjQFThyvzOd77TLoTNNJ8LV4J8fEgxAadbbbXVQx/6UDN1PpdWfiDBtcEgsdAuXXP6T37ykw984APVwOiq8Ha3ux12UmexxNtss42m8o90Z/+601V30IWa2TsLv9GXOt16H0uEpCGAl0jouNujjooaPuqoo6Rf+MIXunqlv/SlLzGcVWDgL6upbUJJKh+32GuvvaRJNQWXNAEDHRk4ceDrgLpTR3WnqR1ykJJhDMtVVCNy4xvfGEFUsttfoS0CgGSim6SdVhL7lwkibJLggbFhdVimzK233pp7y9fKNFWQOeLz7ne/m45FMSrpxV3nKlUVfQjtcG6pOyUUud9IMjLRsle96lWl7nhiuEsF99SFRqs7CLc7RElc6gY3uIF+SWOrn/70p/m/7nznOxPGCFcItFHm53IUkvirvljzpXnor5J1rfydVQSi7tSPLn/HgICftF+7OfcY6lruKkyg3/zmN3voMACe4N36mGdkaIy6RbfyljZDFaDQvrbEfvvtR9Bm6lrOcMJjt57U2AML1+Z/OqVHBIDuPHX4dDmEBBN6H4ykFfDc51xgivCDlikSExExnbVOxIO+5U8lQUXgmMAn2GYJDdNaxsy6FX1kJ5AMXglVMedEEZdGX0RIVHAGwYCvRANwFAZGmIgyhAE2DwLIhJGiUjhdjvk6g0r/uOCCC/BImdwTTtSjrlrDi6EXjBA1Ba/1gKMiMPPUCO2Enm4iKJP1jvsDHWGZRFc4Bc66JjxIy1k1BIIBa3fOwx/+cM1TABsoeWbCat1+BDOhJ6yaQBCSQxUTzkKNcCuiUxX/gTax/WussQYBgPZTygTZgzJB8jFGhCtOxgmvQmoy6JMdrVPICRow4enTynRDUowGTrGyGhTA12x+HF0eKNC+svTGAkGkVxl0zw2HoC2kF8v0A6GHlXOKYIMuIL4ySxWb7M7XtV122UV5v/cnPOEJ5S+DKvkEzTJ2SLZfk5sNi3W5L37xi8cee6zIYrKTr5gQhMuD5oahKrm3hSU5URmnuLcf9rCHkY4UhiEShkcaJl4wspNM4hBuR2jUcb3TL0Rq9913F86FwqocQcTnlKR+/e53vzMZIFa5c1AfJeXns2QR+L8w+CXb/9EdZ0rN+TxZcGFzVk/h0eXHftQz2m/bc7lbsxmVKRR92JS3mz/FtL6wGd0Fn1M8ccJi9HZ2xTSLy59Z8ij0XPN4YnKI/B6It7rVrepE17VS1NOWJsGiePCxGTJZNZaGQT300ENve9vblp2wbkX8gbR5uRpYbo8t1sjT2eOMGeDd8LAWjsDW/vjHPxb+yRirVktchdrkMaphyrg6oy7fUc9lj1Rtc7pLO1rtZ+8f+9jHYi3YgIcvYD1V+Qhc3WS0hKLh7msMw4NzeNS6N7QZdXBpE1btgbAHujq5HtACrgQzfvSLfuD5e9/73leFrqIYQIYr7+ZABpgUGlfBSHAFR1kXPg7ylVhOF9IpmcwDyURPeUBaDUwIVmRoIMNYEofe8pa3aImWIyscEMxPLfcl2GiP7hhBn6pBjiuaK7d2uhb9QD1spA8YjSC3CNZlxr/uuus6USVlSlszugl2WiVwoBNoQDukLxrfvkpgTpqnKg12CQW6RwfSfq0QgAx468ZzV/AYso7uJfcDAQCGMv2mDK470G/BoKsH76FYIIJMtZLKEMAG6veVpYdwQXHiiSe6bzEA+YbSKW4qCffk6Ha6511XJUAwKPhHDZ9zixy4kdQAczcSO+1Xo2YtJ8OIuXH3GjtAGSOOM1c3RkaZH4eSgdx8+9vf1kHNc6IoYPxD9A9dR0lER4UYrcFCx1FSzMb94Mfl9+sGQARdVMkJPyZaWuhewoZph1xIigmyhp57CXp+aJqKY2Ebbk499YMi19XV3TN+vBqDJ7muu0XbkBInYiq+4uukwcZ0FbPm3CWQGwRawu/X9IafzqRCg11apl4g5TL9yopmyUSdISCRTxD4PwTcmvlMhoDnGphMCv1y/AgnKzZL+R4ZJqzdoDwX8lxg/NiAgYuyBMIFmu9GSITHn0cJbsTwd90QvPiqLefFQCUz+Eo5YDNIBc6tlaIsiuc+f4EwQ/PFVieD7RHsIethiuvQhBzypPMgM/fyLPPIrmhK0gJjaZaJTFhrit/wfWgzY4CUqMeImM85nc0w/aWa6I5ipnq67Oq+mm6yXnV1D31GwlAye+w9a+T56BBpnRgg4cnr0hV3ia6VJwKAThHQWpUM/8VjypHEbnnOmpIqw9hbJiOhnZDBAqU1iT1jEpgifUc+ZNbHReXoyFUZE/9nZvS6e4xR1zwWkZHj9aiYWQXcqCX1V2FdY00hTE1h5B7zmMewQw6V06Gu23XuwLkbQtuuiPa1Zrszda3Bqw3qVxKwhrhO6Tp3WiWVMBz4mQ9YimbV/YzJGcoqowuMGQz1sRpc/S1nXJUxpje/+c1RyfpafyHslBaDbCzwHvc8/YDjqfxu+u5ecg9gqLgaHulcxFdtDmEValBPt9pumjHmaFPGB6R64ajafK3uu3WlS8PonlhpdwJNy3TFp2Jo5PidIi5ELB3HPModo7z+mvAYU/W3m0Sz8R6/dydWnaibMviZr35ffk1+huZpfhQ+dBG/0yrpB+Isj5FupkM65eczkFmndP8aO9WiaO4BVXUPJR0ECoHeOrOulhEagQBby4wpIPbThEaCUanHqx88P4gpDvMp38NCmu+AH4TYUI8hmXRvqq85Cg28POKmL+Yx5ojmKO1pxep7prsWDaniLRCImg9RcWn+noCqdaHacKJrz2R6Snqm4w2iCjymXYIgYVbHoiBqJFxTcM1T0gdRYKvQo/q6nH+7dMe80FO+2V1uEc/oVr9WmXgVP2DjCdEOmRx7TBeGrFFlsjeIZj3cN9poI6TEE9YDWuV0Gmdx5TBXKpRmdG9961tLDHxkNnvsUCkNFRXL8pk6yzS+sK0T2Rsfac1Yf/31tZwkjpw1G1/Fun9pUWar3Rzpdl3No1uU/SZjsIv0CfIDEExD21ld2tEyhxNGHFDdfIaQYqFfgEIQmbc66mZQ0pTaiNegk15IZTiZ2wwhJl0oSRkCgnuYASPCAbnMdk39VUjkcKKSOAcriAJiBip0J8vktzIcuu/RRgYzIjJ9xXFN36XdZsYO2ZIe/iBYjrpW3aLuWx2BP5LK6vtxETBk+kFB7Ba3uAVGVVN5PwdtcDnyBo5lgPxkSETtEq5uBbKeVo65gSaJj8Ipxaa0YgKiURYAVpiLfL8vfJQa5/boDlA7pZsAL85BeGgXQm7kkBMUU7lDjWF0T5T2WIDtQGa+BoFFg0DozoIcSl5/Szzwkmq9J6lHvKewr8yGJ6+vHpG+4ijS/NYyPZ09u2WiNZ7Inte4iEl/8RgFBPExJKaSptpVM8PJlrA3Hr5tbu2Zrk6Ts5pOMUsKe1aK2sEk8Ko6119zShNrCfaGmE/bUJjQXWIJ/qEeXKSVH2Ni6nSHuWUjES/dN8mmt2tGN8SytQrXYczqK7ah8SxugT9GumNuWja7ZuHEjxLSOG5M9OvqQBthmRSjheiXQSF+mGE7i6BlKMkV5U4yfZdpfGkzyBa2pzvIK+VfPsWCycc+ucBM1uuiw3+xDSqRD08B94FbQhlWH89QW/liqFx1IppFG5PvU3yFIa+FynLcHqWrETz+U+JqV2OYMQYJKqAadEcMja/usWoSBNxggmlcAkcBWl2Ik8gNT0soG4+zivwgNbH6Cqif2IDOVuHhv+pBuUohwIqKbLlvcZ3hTLeZX4FKqqS/copLya9DjmIhiD6VaPhyyQkCQWBuEAjdmRucx3wVEQZkGPN10/3aasIEUbouw8KxCqXDlx4g32y1zcLZJ55ymQySuakEIsI7zkKwVSXeiB+Ub+7OdJlusq/iVOT4kATUX3Plyqm/7AHS0CagrLUrslKOImFOKSZhRlvLTOaM7nDqs4tkmGonWsOWt5YLS+RuZ3opCtwrNatmEYU+mMRrs0/1nYIlXFFhaLCyTDV7VtuUlZOCGdbNMqU8EQbIUUyIVGO2jXwYOBTTtN5MveoszxT7qj0yna5+NIKqAT1MFA1FSggMXHLsvQHVMAmxlq0LwwkihFFDzjSyfCKGA7XFFXBlXKdMMkrhRlKhSxCNaBiiJQDFqeEmkeP0AV9V91qa5ES+MzcJuagxMCPLTanj/tYN4Cy8wWod0HGutUzgK+NTVEkxpFkBOcpoCUHCzVkXRRp8beMo05CVqAOxVmcV7slfrfJ7ccMbUNJUT1qVZgSBJYhA6M4CHnRPf7aQrao+8LgzqNK1bqViO0y7WTg+LyVbtA0hnVllCz2C+SycUi/mxX4YbAbPBBfvqWqFlYgaYc/aAtqiO2V1StqpkrzmHC7cZPWVCMS+4gq+8lOwoLQQaXTHehyJojsVWeIrtsRb1E6XszyfCpUAjkAKfWcm1cb24AE4me4LI6ABsPq8gb7qHZGAZ6G0EP0iccmvD3okx+Se66dyiCXIkDqREjnFNblCpJWplhsIwY86BXAXgg8mik4hMRAuXiUYWWYxEtqbBbclQqiB2oEtSSAlzZYbC1Sg6s/f/iNA0yJtdr1a/W/z/LawJLTxtsFTbiCUarz1V21a3n0ezsYlUufyIBC6szzozdu5bG0xG5SFh6Xa0fR80QmMbjmzah0yFkLDb821QkcB7oMWWUylMDsnQpR3n9Jjam7ebO4uZpZcwWzLNBdXiVgfO0xYY8Kbhh8oKVPEhsAX7g9ra12rQgesJBKpQzRyuXJAqEooD6cGbcOMXD4fXFWLrvnqjlTb8n/wCb4b3hBiRouDwajoIoKW+KqEbfpQDhA7/IPugpMJimyRDRIQoEv5O5xZ6oh2VnhKkT8wClVpaoSjGF4rufydSg1BYHEjYMmn58B4fzImWh4sZnSzDZ1nIO22eTBn+3Kpf7oI9JburKAn7tF8JkSAtTaNEOrLSIvSKDmHQsDGi3IlkPAa8F55dpAHqDu8MMI/RdUIYhD0w0nBBYYEWHOEl6iHoiMYhdUXiczVIkH8YMKpI+y9WQt+gxs5t9ojoFgIsweTYRKAKTDT/Ilpt6Dar12MKk+KTA4vjwBeDIqO1UzCeLWnQlI8FzyGuJnoFtiYBa6iRsgbusajNGGvkxkE+oOAm1xUkPag+CP2TfHboepVs/1YlFR+jnvhuiKrzHz8rgmu47q67ltz7kc9gwoRmgqxEpTdPd0MhPjqwdXdBaBbYLpp00KqtqZ6WHnctdPbAq4RI2LFhsesUwCoHp01VasajL6Hrcke7dajVabVDGZ0tGpPMIVdrisPt+smMY8I8FRYOagBQgj46OexJYOXdoflMxkCXB5ibjASq126AQGcRH5+fttkDIIEb4v4VjQFpeD5QoyswaGv0GxkKuZH6ycqdrgu5KtfuHPbdZVRj08301EP8UxiGkpJLFwEOFtxfQvERsdCDXdQVHs9s1pI3HAZORg8ftP27GnB5hMWXv5MSqRpz4A64jlgTiIOffnrbzXolzo9MVrO1BM4hAeXxw6PM/AFqznXE8ZXHt5yf1dtZlAVRChKzM493WUQ5leeXYKi/GXGJry65x6BGR3x3Os+JwWQ0apr+DigJzxXpqkjNoYkUaMF/JmhVUmNMa8Te24/Ho7yyizvOTmZW1yEnynoZNUmf74Q6K268x9Cnc9yImBVlJ+0hS3iQAktIkg8o62KEojjq9AZkZ74kFDT5bxQTu8VAowQw8Ag8dPNbzABOaECtymOFQ2mYayvr13zM1/omYsLJ2d3TdMFrk2rGbyWNE6GjZ939Il4hhhwPt9iSEK1Wnk/wxajXZlYF5NJnQUXHtCmGUr6tZp+VDHo8QWbddBsOJfLd+yQn7wNBVyLfFs1K+NEOd3NF2T6+QstZ/hrXExpnOKeMUAC/oTey2ntHEigUxY0EGDsFOBjzWZtvmC6BRBURrXtFHFLtF7L+Hnb680MvL3kXrKQBQSc3SWHmI+hIOqkmtS5iA4qaaGoS9CVsRaydM2ykAnisY9K9Neyu3a5bkIXbBSElygGwHaIw53KBV4eru5wtAKVoD070ek0ac3znKzAPrKNQTcztKOEB2wtPoUJoajFRw5Ula99QCB0pw+jMIttsJtZTWL8xXIqSsbq4pYpdMaDbxZbkKrnHAF2q8bXHJRoP+fX/78Lsg0iuNkJ32uPXZqieC9OTA2rWfuEbWPjxVHxok54dFyZeBibp0kqZK1rf8iqnOmyz83AhTwrxbkPxInjEJzFAyUHvlp13zQApr2F/AsUs1aAZiAmvZa7Uym6fjGr/yomjEE1LTGmtV+f1hIeKBZQUjmrT9OtixbO2ulDsZeJ7zLqPERYSGsYQoxn2PDX6drAJ4481WvCaMZ2JWDRBec1dtVObAmuKFtrajb+URTEJl5W+dU2S1wGNb6YjWaX+oJYWOVQNbg3tL/S0Ea/Kk04qc0w6yvu5fRaw2hzBMym7mfytjYrw/Neu1JV+Qn/Dq8ktQcH0LRneJQHauiOr4GGKnKpSe3m5Igv8EN3BqDr4dfQnR4Oyjib5ElkpmgK6OFO6K6qabzDmeO86iKqy3PNYih2ZQH1yaCbuGMVdPj5ojvcEJwdpRyArtbby2F9mfC2eI29ZLdIGs1+aDAxgEVBAoRzmZ2zxGpgoT2tfG111oiImSAbzGDdDQeWvS6rEs2oGjAJTn27UpnTW4rfVArMAJjoETWo65DqmsOqavivKDemHQfFWpzOVFcZUfPaQKchFdAbZFIglCEFkRP8Zqvj/Ds0BhoJCQdVss5LSQVso0WvlZZpNUDVaUeDVn/l1N8uzZJjb0beGRZa2iaiOBb8Iaydtc+nqxsCYk+3km6aSEz86OYIziP5WFeo/c7le3KUBGJCpX4CjKA98NYpXbrTrWSA7miVqsq9JQqw0R2/RzwDi0Lj5HdrGE4P0x182koO0z+CjQUNRn/4rMrpji+6Y42IQRHIWARO71Ri3avCwEShED4JSNqPY4Q8Ntnlkj+rCPSW7vx/8Wvu+HxmhgAFWBSwSbbZIVm4KvHgHs6cWf2L/izWiC/AfJdKMd3O2s7RGnJneZ6OPhcJUMbHr72VFPDI9pdNkqlMhVIpJt9RHw9cXz1eBTFoap1r0E3ZXd25rTYJJT2vrcz3uG/5ysi0E494dqe0/OVJaKodmzz6LferekzfhbCIhDBHF4reYlmYPVdHd8RYoJUKs4jMW62mMa0nElS/hKQgH7ZH0lOEqTUPCSgVpOXMIMGOMpxOtLrQBgpaxZ4hGU0HtVsB1sIHZz0jsz2tS+g15Nl7iwMILZYLOB0tIF0QVlEWXic0hR3l3EFi0Cm23G+24kscZUeRPOfy9eiv040vbkGPkUaArDNAlaTdPy0qxdf28ZPXnfbVtfjvhJ7IEcXMMKPI7iKjgOq1YiMSziXUVQGDK6FtJlTUHdoJqgoomYgO/YyOosEUKfAO1KnBwGmZqnLztK+VaDkKV1pfqCyUNnwRaxwoP/C1TvFL0U13O1HN3W4QjaZtpRC77o+ue66SuBTfq/Wq8v2sqEFGyv5YfkREHSTY6LjVHQWIdbLqNHy8b1CdrNruJZIOAv9BwL2STxCYPQTID7UubMQlzHSZZ/NUNyS6wx7Uw9EpLLRVbAhHnW4yJ9zBo7AkNE/Y2g6ADWBXWKARKgsPY7150ROzfCueyxbzi+Hw3CTX1048Is1FMPA1oAserMIaSCYi1n3levDVhWq6X03qzoblsGcW61mWrx5GqNwKLkRKwS14BGrjxDp3Of/qLALRnXbDigNLp9BuGJbnSAGZjIrL0SdaDFl39+pqiU2kLIrRX1KQIBtdaC3UBePSvk490VV3jGPFGHVVB3pP83BpuRAf03p3QpOmXKs7+5/s0mx8xfdQbpRnp5UsZompsJcQQOkMkHw0CyZNBZHDfKI7LC4moUmkWZloAX5W8bA4k1aVEEW00MhyQrHoLabH+KKzTqyPmCpxMHXUvgwmQtgSENxs5QJbprpjx2pcgfl3c9qVStsoMUJ6/ViQVDDWGMHK6k6/DhNrDcNoqwGu4g5xG4sTMrL66+p+j7x+qAy2JK2P+qtr/H0SNTXnrVMD5icf28OivIxzhGO0wmvcdYaS9802V7gySkfuUpWfWHsL2P9B0/mHW/PK6YiHgGw8lSRWTjTjhQq7ZyTaGUZQO82OnIhdtfwkeoJAb9Wd0J2e3CELtRnmr2bkAifFUdpO0MNUT4RSMvlmZjwgtRCxAhWRDIW9/0hmcQuFPXA9iGkSWAjWwoQLomymjqfD87q22GF1FHCIWbJAw7nkE0bOg9IhT1irSEqkGUYT6yqe4afoeYowKeOJqXKNl/ZQrvhHa1j4KfhENMnDlFTA8nFaee6X08F0UwQoplVXGaA7jJDeedYzcjiTObFiOkUkEJGgweJ2W9+rhhn/nZDuaDYDpg3In78qN0s2Yy77rXmkhbqiJhmm7tVrp6gaDiYZyKrqFphBGt2hphRVwmUxTnKLkBQerhosaNfu2+4EPguMjcKEk3HJ1eXIEkaHEoNeTGbelDHE+Cha5m5hnokBTicDsNPojl2kxczqbw0iHNxL7CjCgYniEOgRxLATppTKKPAZpXY5aNROlcbdPVBvzMDCcY665zWsOBzXFTec28ydr8HFL91s7k86B7JLwNAkshkejGsaF+KEZnTDaIYRRrVdFzKIvkEEGrLlKjJBV93xyyKB8DbK1NpumKAGC/fxMbh+nmqQ9mNRG5z9fFQo0y/CunQQQU8mZqPvWJG4bz8uNzlk6gWCwy2UA0a1GdkJjyZzSSEQurOkhnsJddaz2xPWo5YhtwcGy1E2DGnAJIRtil7ykHWUvfFkZ9J8RVlQATB5kgqzqLci1I8ESzBp8zRngRRgV9TvyevpjPogKDJNwRWWqI/rTsUq282Z3TX/tqS26nE6s+cVS+VZ0DY5wjXqVVNMFNYyTHfUgAqMoDvMG8tHR+E/kqhGssfoDgMJhK44VEdn9ncyusN6mQ0jFiJj1EyzgSHEtJk6xTzX5Yya/Nq+UswKZmCw+MVqIi6gB0kqWqm8Q5rd9uaeeoPVg3XRHuDm0kQO58rk9xGGwiOjDWyqTFKEvRtQZJ6mcgmVBMLQKlMfPTIow1dn9asA0uwWcluy/XQRJZlw5MNwEB7clu1cF6LEyHQ/VCabzaIbdx6xWmFEbaJVGEc3GAEDWS/iDkncC8gInBu7bj9EAdlyr8p0yIirVkmaipySguQoIy2zCksbx9aq4QSmqMyAtOarUW63vYTf3UDmcFXTyik1qxDDzDDIFv09rXpSeKkhELqz1EZ8qfTXI5ucYEauw3R+Jqdmlh79rGk5DgoLz3c2TMSGr0yskkwC+ZrYUwUq1NGJZtXsU2XWK0LVYzbcJJ86VH9dmu+pmzNhmjEwt9ZCNYtoqbdI4jo4ASKFb/F6mPI6F92hn0twiMyA7pgWcwrU0rzSCVTl0hpZmWQDTo3WSADyhpRxbZlTT3BSEGlaeaoJlolMyOHvYPIlcE2eKSoFi0VXMFOv8pqK/xEk8AkLiNAR+RgqL4+IEHICQNjpKkwzMGSkmvo6rb+MMbaB32CcTQDQa1RDXKpmFEVWp3AiA8rTxL/pb7mBZFaOm8EN05rUbQPb7yhvjk8xA+Ab326ZpKeLADLqZubqJcUJW+6KRtOtKuWXDgKhO0tnrJdWTyejO1CgZDC0DY5husPG+xD5ecQUK7rDmGE8LGtFvYgbQJJcxbZGMkuKMJWXTxmqygkGDJuwBpm140i7aEswrggHdxW+xZtTThw+DubWfF2MAi4lzoDy77EuBIQkgATwX+BD1BFqkKuz2Y46XdfUzFtBB+JA0UKRH0WhcDjSFI3EvmqkiMpk0Z1u7YxiIkm7GgP9wKFa+dxaO60EZ1y9uA2rwH54T1y6fBxtATB5QFPhU3Sz1a9h+kh2ahyCOMGVQ94or00riUaUT6flJLEUEHBToY/+LoXOpo9jQSB0ZywwppLeIYCIEAzIBgwnD4K4TgxGK5Eb/gsm07y8ljSjPtYQ8VbIYfjLy+N0meQW9rXWmGAeTrc8R2yE9boYA89R0QvSgugKl7AEFxfhXik4+MW4XXgu+EoqPGIYJoxKVRiPBbEISsUYKSb6oVYaC1zQAMKSuSxRhGNLp/g1eMrwofKVYBW8ORaqFI3DIdAvObgUTUi4T10XAoI5HCIwVA7tAX/SYCgVt2stRC/kC6RtOdNNWFRMYFP/dE9M+SAQBILA2BHoLd1ZQVdNLvMJAjNDgOHnmhEl6nRrl4gH5BDxCoJ4kIPKFAsi8lRaNChXBS3EXSeGV0mZuIJl5DItJMZ7hEr4i7XUohL+DrwBKxLnoTBFh4rD/6J+X+tDDRImSXXnsrkqb8z/ebu0FulxlTFXvdzVAQfRFFchgnu5K0sFfUGAoCL6R2tEI/lpzLhZfmt8hQixn9h0KxFTbxogMJ+oyd053dNTfmkiYELbz3dmhe4szRtybL1Gd/j1KTH0DI/UWkLsSU2uEJPrUdsyx3bJ+aio6I4re/ojZPPRhFxzgSGAhXvu+wlYVk2SNOXlMbRMzKrsqfREeRsu2/UA5yBJTuWUCcvYtoc46gY2SZiwwIhMSx3FtFEfrRsgtY4omUNBoCHQW7rzn/2v8gkCy4kAOccctLiOqkxGF9nDkftMHIxZcu3Lt5xw5fTlR4DyIZCZP1EENMI9YYW8ioKjMW9BVwKzJiwzg0wMRsC7iBYypNteeBa6rx4ym8VrvIr8quQQQdncrPKtEkd3BIphMOLMKKBTuSg1kWjHl+pCUyk/WRlMxVL2KaqSugDYJuRov4WTos0mqzz5QWAhIeCnm08QmDECnsWW6Xoot6jYGVeVE6eLAPAtoiY4DZ/IstZC6OFDiyPn9a9/veesbQLQAnyidUqEO9dqfcXChUaJ96o3LbQyy5lQLUJQS/SFebn/VYgKU27kW83nonUJUWK18L6+eoWFGK8RV3eiNfltpb0F6sTReic5kaZO5PlFqmyN46u/yFZtoOCrOH2hb3JoOb7igsLd+JrtPuBWqdP9pdYoI/DcX67kyhd55l4SpI8YuaNacJtlcXCuXSFaDUkEgREIePgUB6qNJEaUnONDV5vj6+VyQaDnCAisFjnUNQ+9bTD7ZNG4J4vtcbuNtEuKzNrMppu/aNL8RNbHYTbcpgiEjZhrQyBUwNJ68WHCyYV8Fe1g7/EDuwoNhLHbF0CUdwvxRjKoKYLZmXbL3UXQD5TvoudorVMT/95eLW7BHbGnu1rbQjwB++1EUtOEGxdpm+uKbxOgprUElWIz6A5nlk2hiIu4VC1FtHGDwUVKVItLUZiswJe2w7JK+BGcXvTOPewr7qJ822jKGgLLBm1/7JB1A+qh6Djdmj6XEF1nLwMcq20FFLrThi+JKSLQW7oz8wg4P6F8gsC4ELCdoGXS9vkQDDSuOieshxLACFlsVXGgw2VsNGdNloDo4UNzlmN/oHq9wOgrWr5uqRcfoo0ZuyWtNSMk1Ma73fzlTBMwCBvdSvhlmMlujrSHnRVtta1AHeJ1MrKWx++777728hkoP4OvRAsUQUyM8Fv7A6nfRz0Mv/gY9xLCR/OoHQ3EkImap5HQWigx2IySSIm3b9qCiL+GMClH8BkYUQT3ho2LMA9LAidrG67jLhJbY98BXatiqIybCg/jPpODitkUwFgAzUpDA2oxv8YM14l2GC+R5lYFWhtolwScQ0s4hf1VidbasAC79dUhcfoS6sGQ+Mjq7Ztm0riXwCDdL5era/lquWL3ingMz5olkw5hdXaBqjhosaVYI33I2xts3dQ9JekgsEgQmCJfS7EgMHsImGebLgsR8LfWnM/etdgnGr45scXhE16FyfTbbrPhCcuMMVN7arm+raJVa/JNojDFF/xBn2C62r58k13U1kF2RGxH8QxTdvP+7uJ2a8rspsN+8+w0hdlmRSyfTKEt2IMaXBRJskcAp4z1OHZD1h75Nv1jtplhDMPOwnUt8oB9rtlau0hLVyaySIowlCijllQmtsGWs8G0inplR+XP+C8bjyK0072EwXsVfIWYset2XKaWo1kSXDyO1suYdLN2PyJ+eFtF2w/TAjdcrdU8WQIlIupgTtCo8uB1rtHUGJV7fTc+hLujpBgGAmETZ+RssvtKA4xaeeVqu068hzfKibUtZFdlUS3eZshcvXnunAt2QUUih+yc2VpOvurezzZHMLLl7WplJDTb21LLTUajirrTBSfpaSEQdccvLp8gcDUKARRMfMvAFCJm5Cas7L0HvelmZYoe6Jbxe/O1JrX+SqvKR6I+NHmfBjE2w/YwBq5VmSbZ7ATvjzBqtbWSAwnL6eUw85747XQvEGDs8SSHbMqnkSUJDJzrK0No6Za3E5ipe4kY/0XJSBppbyG8xNJ6XpI60SElUROMgfYgUyPtB8iOmtPjBzY/9I6C4auMyAEOpwYKxaPRirkuFw8Dz4uhSZXvRZKYDZGD4dQ7QGEqICJC6Cnqg8R4lZLCmoSveNcSumNzRTkGS/Cv3QSwQ/aVsa86tZZnzVGigi5UpjdDwYTnCO8BQmWO8S9ZYsSA6lcFzvNzuWiVNLJ0JjRII41C3VeOkspasydroQqpO1iUau3bRHThAHUrWsSkJcbdfaiAkaWvEI3cBhL2yaQYOWvCao27DZn8dVRV/o5YN441YlH15paSoIiRkAe7iCIvIFOVGrTTXed3JK2DVTn+pO80OZ4+dzi2Z8QRRGOkhUaHjOTSMqsGhSX8HCS6vy+Z+QSBhYVAnFkLa7z62FpKOy8AGZxs0G0fY+lhSjCvTA9xFEFQs+kmTmCKyfixPU7EAMyVbRXIIJliKs/em6rSYEw3TXPlWGVDcqgNAPkvHGLCvfFAPfWx8aDXKdTEQnu23HJL74JAF5olVhVjY85tnj2hT6HbePae2bOkhQ2TTwDQnYqJsaCXSZhsObEWmojjAUgDYgSTqsEbK5lVtEloBXIjRFS14jBYKSBYbOwtGXLYS+qO5nmlg8k9aUeF3YYtM80rIfKDwMDUVWFt0BhCEUaFvng/tnxyiOEAOP7HfGI8gmCQEsJSaWwMqvdOMJkKi2Bltq0/ohKV70aQh/pVSxnCLEWoKKbN8Hch/WJf22IouHE24ZEs8TKRrzZP/S+bzROkC1M/RUkkAPkwNCgCVaaowBRr4P1xilHGKuDpfsA5DKu7EdT4BHVEVbxpblp3KT+aktrp3naTT3gV7cc+qTV+MggTJHEp8piGEeHaKaSpSguv8TtqzNW1jJ1FanXn1I9IHwUp83A5xV3k1jIKAnRoPxrmh8B97LdjWGl+AoOwYYNeA4ccO4uz0ut+jZrAIHqSjtTV8zcILEgEPGrzCQIzRkB0p8e91TFMoycpV4UnqdpM+ukBnr84Cmsnx+yQcVWMwODh7qhHqnxHnU7dIdoT5D1tZZIWKA3l1vG8ZlA9u9kSRMfPzBTWWQywHF9Fcngiqw25sdOg09m/Wjgjk2FgmIVxECG8CLOuyOqoU3r40xX/9YUhN6lVjMLBZkiYzQv2xAOGz5Wj48icBJNvAr3ppptSUMqNUk4W9E6bkTBldEHvqDuImvUyVaGGaV6BVjmj/w44s6owccXbISqtKiC010RUJmTYOWYS7wGjGCB81CFUrPkTjdcRRxwhEycjF7G+xhf1kVOqD5MpbcgAhcyhWQwntGX6S3IAnY/R1CmXEHfCojvaPgKECQnt6xQT1BRjQUZyXb4k1NZVnFtuIBIFHmCPbHRTPpqFubp/DATkiSJKaglOgJWS0PCeOh0ddA/TxlTofSOTNYYshDpY/V7b4VSosu5z7WEPBDBck7TD3aZ5sK2wYjwG2Z2sTvluTg1GKZCMKkYPM0CosK+GAD3FL+sQHmxMkc76qncGFAtXvpVxiJvYWYbYPdB+XHVK/gaBWUKgt86s/8xC8gkCM0aAaGGJLDPjcSxUk8TCzqmNOTEvZB3NR0VamOibAXv6M8MlFTAPNQlmbExkPZTZnmoGw8w+iRexJoWRIFfQORgSoSQe8YiCAIUqKVMCXTB7xplQEHUS3mn1GI/ZqmAOfAV7QDXYyIGwzapkxF/2XnRLTf0FNzAeFYjKho3wNYyo0CFsDwWsOjEMNttUHtcBCyWsgkxbDdVsBrjlTCXBFuos4lKFywyD17SeUcQ8YEKvYvjZS+MCNPgjXqgDhAkeKIgmGVMURz3EDP47VJU8UJGt6KnREdLLA4LyqgfPQ2X46chUlAbUh1DERYIMMfN21ibsyTTc3S5gBnik63Yzl5lGN9EC1eqp+w23qJ1v1Iam4M0uqtfycSwSnWbrOwEGkyvHFjJKCNEqMUYWb+u1izqkee5MmAy0s9skFeq+G8DwqaQAIeoIRmY/ZLrfHJWWCXbKmdNxKTndegbSmo2vG5SW370ZgF+bhlMZIY/TYF1exlKFtd+AthNbAsX3aV+TCAJLGoFZ4nepdukgwFozD/pr6w6/JWaPBeJsIqTbFkVQiGl020qkqzo0iPAk0/H2FStSTwW6MlTWv2AzdfQOd7gD69hK1iobjiEciE8N9/Kp9Tgsq2p5HFhiMoOIEySDXORc01z1i6hgFFtVLVHqDqMiR7QKa9GK4QFO1KNWeDjhdRZqZjJ5uxhXIoToXV+5CZgrTbVACSDiijjpEAIWTu94iDRPO6tCBph+oBg1C9vQo+ELyRF6QjkAtYgTCZeWieRhadqJCzL/JRXgo1xUTC+LrmEQVlJ3nEVF4+NjOykcihkgOciidewSOBBgWXe0z1ftqVBfp2NU+kJE4W1pMgOs8FQXNXwkB8V8QMo8y3RuaUiV768V4+3eaJlLMIGDgpcyhJaN7j5OSUIziKOL5WgQmC8Eou54/OazJBAwx+VeoV54KAuD1WfKgcgAQR5T7D/jbW7NA8JXQp/nRjFddm699twkWFV8YXJM5f0VqWOazmq6NB1IggaD2VAa6BbkfcabkSBsmO6zuBU3wyrjUsMb8pZsQ8wgUdAPSgaolgsnIlGYW9fXCf8y7drjEkQpjxuePlzHhbjA7IyHVWAnxCFsxulcRSWQ6CBFqsWx6j5lRQEYIk8TXkgmTxlpwStaXQhZ4T2RKfKjzkU6cRTSl0y8R8MU64pSulOvPm31W9hMDillwl/usDpUrqtWrBIkFrRsIJPaMYwPpuUzULK+ooMT5i+1TG5foWzQQ+hH9x2hN6wj7orRp+doEFi6CMwXAcx1Fw0CdBTWGplg5wQ91GQdv2GGGXW8hF0UFKm/NBi/NPae66Fia/AANp6wIZqHJkF7IHsoabJLRKFGYE4lWshEbmgPZsAidUr7EaXB0UN7oDHgJVxgXEUMNoZBSuGnED1KRGlxNoQKAgYaxAkyEMui/vrQJJAAC4YF1iAu3cgS1ARF6OZcddL//mt5Ld7+X1ZSQWDhIOAmNzv3C5r7JtNiPQE8MXju0PS5b0CuOBYEeqvu/MfBvHS5Xno+DgTE7mAVljJ5VCEirUoyjGAXVAMHwkK4OQTiVKAD4YEaz1kjE1siBYly8IT1V4iDmW6rpCcJcdY6Qu/RwRY51JO2pRmzjYCHJNXQben+nO1rTbH+apKfDD/yFE+ZSjGOaeogYU+0Fv+y+KepnDWuMsRXDwqh5dA2BTKNUbN1lGY+tXv4uC6UemYVAZEAtG2XIGMLuJzVa02r8oQqTwuuFJ4AAetHzMYsuC0q00oM3OgUIAvO29FKyBTgMpDZw68ir2lCXELhOj0cneVpkkcz/Y/3s8LeJ6yKo7AUSpHXExaY1UwL+7XNIoDuVeiUIq/FTg3vat0tNq209YPmLULURUATWRGOaZ0+rcIc035QQuY55pxoEwR6qmgwAfs8ekiPuZDYO1MpsWgEV5KwYuK4ebqndaEUDgINgRVbKokgMAMEeHYsc8VahFjO4PSFcoo1zMKWrTBfKA2e7XYS6jgQzbyHL2T5vRBywh7twVHePQFPnJKWbfN4dstzZYrUFottT5pu/lym7WJgIyLOzREXxeMtUJ9V8z/i6gLSSafi2UEq0FtJCHOYigarpfXtXBHoIrR4kyuHHmkPZaMg1F0sOcmklRxOWOlGuXSKsbC03t8SWa1tFF9lMmOwyhVg6PF+3moh/3jJaL4FW25l0fromo2v6rpIFcFGnaY6NfSuJVqfE4TX2y2hciXB7kenSdieLpMKpru70nA3k7OUEYi6s5RHfwx9F4UjwMUjqVZWj6HGVDFNBBgMNpsDQqjT3ET+ckGKxba+uvYTGmivpfX8IHYSEnsrVJxa4K+GidaiSXQLWxpmZZYVfF0nkZV9TDtnSrfk7KVtoGcnpBE+fZIDFw8LXevAtURhah+0kQ+x5xI0iWoh6i84jD6hy5YlEj5FkjHSvLcKW2Mo8kxJPxnTA+bcr8bpiGOdLhMvMZRkD1FiMmuBoemEcHsL95h8a84JIbbMdmkMsqkdiE5xRyvgHBJ1juVY7YVV4GqaoRL5AxJsXddfETNEHVe3rYAy5BZfBdPwbXFMiGZTwIAaLNH9VhRiMHxPWl7yTKunmzCUIoF0CpupfagdtUbPR6aoOwE6PhqMNrk37Edga1AV1nAgVTazALuLes7oCGS69ScdBKaHgBsrnyAQBBY0AuiFnz2LMpZemK/bMGmZVU24vSGjziSX72+gBqFduEXLRIN86D0m7i3TCjsR7uwcQ2vpnCVmdh5ieu1xgFIrL1ad9ZVup3QTBAwUig0W/y6M3SHMyfo1GxbbH4hDSvS6CHT5NA/G1SonZht02EC3nm5aUDy6oIy2VT4Kwu66BFJi6Zx4fLqLQ8gEq1xr+5XHTuw4JYerl4HH/yzT4zirkpb0a4lMp+ujTGsJcRT8AC8UkVOZuKwNdbANXbOZgmL1qSV1tdOPHMW0p3bRtIwOU4GVfMoQPkTjkbb3ld0Q6vQJ/yJqmo12tKPaj474yp2EnaBTdcjyRoxnmSH5EHC6rRxwJoKf0dRsRBBLq3rK322s66sRqV7XV3/dHuhdbQLZMpPoOQK9DVWOM8sPPJ8gMIiAaS47N5g739895pg9xr7bEKbIon1WVqLlE2D4GQdKtqPdhP11WEEREpVJmyEksGecCzwLtdWQQx5hCIQZdm0uIIeGIfDFajuZyESdzpyXWTVlr5zJ/mJF5vSCZmo3gSrmcmwb4y1gxYeB5KBRIQIkQWhRwFmTzfKZf3yIGMC+0j84Ynh2UBw7F2AkouDFixAMXEvL2XUag+77CtjJ2kmPoabQnxqYNjWwDJD5t98x+61t9WIp+ChG8RJ0wu+J6ADHukLUyoaB9pBEF2pTKJ4ju2ISS8TfyKH9uDrk0QtCkW0IbMFQ0SpCdKkp+JavxbombCeWCXn3gKMifDFR73yQRjFpSyXA4D0AnPD0yTLhrEmO4hxoWUNAwq4H1cLJzpWPgfFGgYWIhR7ZMQvjBFd5OUecOOGh4Tt/wmLJDAKTIRC6MxkyyV9CCHAEcEMwqNVnptHEnRk2KTfnrn16HDLzttyM3SI8jDCQSirAmPl0ORN7ZqLPbIhjqNn5ZBDbz4axpHNwo9R12SqOCdaC8SAMiNuQz/azcCQKfMUM3rxZJq5gcs8ZhIXssMMOk11Cvshx1WI2KlRYTIbM8rb4K66Ct8IhmSpXWLwFo8VUV52MFpvtRJVw3NTmjSwcQYV97XKvKj/w16Y+LDQXCVPdDlGVpHmXyBIvfelL1UbwADiTT3vQWWoKKtPKDyQUsJURyaR2vFSzbRKtp+MiwQh91Fl7CIER03I6nG11M10DbOfoUia4aSw8rD2l8CedAprKuYRq96OBFvrK9uNJro5+oTXoDv2DLdfNGkE7MuBJbckVsjXFoDFkTv2YrvFCCqU5HLuOwuHGdHPq9G4OumPc3cNIoR9Ic5WqFv2tF1Y0DtQ9sdJeSaab9qeoHaGIW9xkTtQ1PMyd4yYBmmpxRMyPrGUsQNpCwv0MQWr03Ql77LFHvZ52+ELJCQJTQqDnsliat3AR8FhneoeFaM4Ljy1PutY1T0wrQUzEHZL2cSILpABjwGwId5XmLCDs4x/MPJHcrn1VA7JiQk8DwEXkeDQzzFz+eIAgWQGYyIF8FdItzMvNzmkPcuwiqJgdBT1q/VpUUheqp61Hc5kK1kth4ZMexCQNJT2s9U7mhB9PbWX22WcfJ+IoVYZ/R6aaGXKJ7t7QA5Xw+BADvOSIYbY+RYItrPcJsNYKYzPm3BLspapswyitC7ojwcXAStFOpEf4aByFj9NZWchYAiOgRCZvgky6iHT7qFMcBpvEetU7pxxqzixQMGCYWSuPlomubV8rMeDMqkyWTOBRK0mecXX8suVUgmkU0UwdQeMGDnW/aqTT8Q+iggS26qgONjcfbDE2mcalrksD4/yiJHXrGUi7G90JdXfVIbTMTgp1ixpKApJ8pNOCI4niDW5LaYMoaKaCiI1RZZLNuORoQvxZ7rrCih6DqPkhuL1xqdZmN7Y2o85uftG+6vTbERWkg67ovkI+ZNp40IXc7W4VVFWOnaXwJy0nYvnqt6AA5Ul6+EPuQq8VNr4YG7qmDI2zvYPCKrA6C56GG010m2Fm9ZMZrlCOwCzsU+90Vvv9rquYe4wc6FfJw1U5ukM1NGqu6xD3ZasQe6OQVXxVy0yizwhgtG5On3oK9aep/5kO5hMEZowAA0MLYfCQA89Wzz5zOCGZ3Pb4AdPuSY1bsNAu4bmsvKcwRcGDklvBE5PAztaaOyrpb8UZsIKkFFEXXCqemCboHnlskqo8Z031ah5cdTrKvnpYm8TzBbAZZTlYTZv5mlyKaTBJ9dj1zGWz2XKRp56q4jZQE01lk1gdFIod8tg1t65lL76ia4yEC3kEuwRTpP1Mu5ZPBhooyDNqY7y1gVHUWkoDo2jyylZZ+TKwpqZVhdtRWZTxYR5ci6rBu8E8WxlUPAzPqPJoELvLlrTTJRAylA4tEOta5btHu2kIUJvQKY3xSOoum2K2gd8KQx5RoJQU/2v5s5QwoUdqCWCsoI6AGoMh2BBFRi+hYqcBgsa5IbXNLeRE4oSBQAJIVoYPyWDF3WnuT1E46IWRxYD1sRSRgU4Rq+h88HF1cpRVQiiyelB2j3Uyj9ATw4Ti0Lfcpdi2m4quhhOoSuMNvdds+YpXUcJk4ql+Ne5t94a7xb0nE79BZzFypyDWBr1aojbUmahmZCvTFd2l2qwvyK5bhXxCO1Q5guuGNxNwrvIu5I7SeF/la7MrVrUDf91USJIWorZoZd3zfragK5rSVkXx4vnN1p1QTR2oqn0l2/i4OmFGj1q+X7ffY/sqYXR8ujktrReWd7WvSQSBmSPgXswnCMwYAcTFzXfggQd6fuEcLE3FIZqlsdAMSS1bJci7hMmc5z7Sg0OgRB6aMk1PRQYw6kyUGWrFKnKOlACDP6nQbjfVQo9jl2MIW4OZahditEw60RFTbbZHGVoFccW5jIH6MSo8TLQBPkQnEBLhWioR5MvIVW1MlwdrpQdUB5lMnZI2XnO6zrapapXv/mWfTMSLHJgct0Om5ria5z5nFlhafjdRs3aWiTKBf1AUIKMAYBnFKsl+A1xalAZuV5l6x1JKgwK8WB1myblTprrKDPzF/you1SwcRAZCAegxzGpj5h3FBVlQpk6XHWXLdYHplcYe8EXW1MtTAY5KymTanUjIscO14a5Ve7WSyzBBQ211M7hzjKbraiRAUJM6HWVxCcMEauzQXSHfR/1YbKUn+4u+oCPchT7cXiyokoaD8TayhBxEGWtERuVjvaJhNAnIoMaBJqyWMKO/4pQ1QALFUczoYD+UEmE3zvXRU+NiOos6Q75V5RQ3m3ueTtkykwgCixiBqDueh/ksQgSEVrBY5tCe6e5ysrm0GSHzQHUobd8UkN6AvrCCZr1eocWIMgk1gzStRFNQEyq62SS9AUxUmZqgIwdmrk3PGECQFMSDYxtWS2/QGpZSNEmd2EoywKypdrJtaIS/crTN3LqVGZ3wYNIFbWah9cu1WD7Ta5nDJ9qehJdEN9VPPmH1q4wTec3IRayvdrJ/w+fKYaEpBIiI2b+gTsoWM0x4gBUwUS4Gm00FNe7lKqb4Yln0GsWxokom02v2j8yZx5sZs/oTXkgmm/2c5zxH3AllAqEpKimYBpeSWfGtBsVry/jOlNRyFMdw08bQVpVzzRgdPIZ+VmE3Wliewde97nXMPw3PLcFHCQqaAeTRL3QKK9VI41IuIUSkdrUhg+kyCoLRYjzdMB39qhZO1h350PAZKIAr+1SmQWxHyVdTiQXRBR6idlYl3OQtB7WtNI7YMluCTKX7BrEknJafRBAIAnOMQJxZcwz4Yr4cWR7/wFfMsE3WaQ+MmZm96TtrTadhJFg1i4D4AmqrGHBQxYlAqIPwXuEFnBdMr0yeKdIFYmEvOxyCujCMHf7EMUQpwSRYSqGRam7OHe1xImagAYJgVG6qzV8gTIFFxxtYUwKGyAwzb3qAixIkmGQWHeFA0fyl4ghxFbOCo9D5sQHyCYuu8uH2yNF98g9mgJ2o0KXpClYJVZddhYklIwlGmfB0mcqjblrIu1fxwjKxCvhgCWQz7ESzsUYkA79BdDC8cpPTRWBOIVMDlsbElhtxwmtRm6BBn9AXDWvW2hDghUZE3yl2zsV+tNlVAA4ElTsFg3E56PGhYJx1CQXIUc5VALMsn6PKy73SbcYIBGpdfRUmrvi4W8hCtKVuDQsijb9yw40YhQXRizQyCCwCBFbwTFwE3UgX5gsBfIJVEwlhnw+yBEuPu/DIiG5BQZAVhtM0neU2O6fi4EDMKlbEVCMQwm4svhAMwR5wBwhG5goxn+aL4SixA5v4HgEKSAOOgmfIQU1M1jmbCCe1FNbaY1IBBFRO1RAiQ9LAURhm8RnCOZUU4oAGIUYMp/bQD5RUM17CqKtWkIHYC5YJB2KzNUPgpF8H1UrkAeNNq9AG9lt5EkLxgAlhd5ZIF1wNx5qwQDKnjgBOxodlgNCjEpCmfm5KBoEgMPcIeE7WnNMcbOBVQnPfmO4VQ3e6aCQ9bQRILwImOD6IIiJnqTike74PngIRIRQaISxkEjIAyaciOvEGAgYCQZbAWqg+EhXPS9eR45B2WKiFrziRRkIiKicUgoJw8H0oYI10lTT7pzfIcQk1ECFqeRGmolWkBdyFKlO+M7Em6izVYdq9zQlzjoB7w5ARBY3anF98Hi5ItyOPodQ4d4sWF+WGiNPMfJD7clCaHrjPu261CZsLQObH/T+ZR3jCs5IZBGaMQG/pztXMRPMJAkEgCPQWAewW352X5hEXCUvciHNzdcROkBlXKecpFyEHqOsi/WRC5L7ELYKlTDMH+iLqs8yGCQxnt1pI+zLLDxQQRCVEbG7irDEzsV+G2xSommF6U0NvDgMHkyL5Zi+EXgmOVJ5xcnIVNtFyOmdxfe1mkpM5bbv5Sc8eAglVnjFTzIlBIAgsAAQIbHQ+chobLAZ5LC1m+SypE2DEn2VHvrHUOa1KRHFZ8cflyic7rRNnVpjBthMPlmMTgTLz6mHU+XZJPkLXZRI7ZbJV/AVk1GVeSFC89YnDfkCxZQRUIedVA2e0ACwaKsANInetvltzwP8r4k17uJgNh6htstPARZESAemUJ6KUs9wJ1FNB7k5BPpyuPOW19hSQJkpZv6a8Ym6VikDHqJyC1Ylk5/XmjBb/h2vyettGS4y58DXgWKyH4vCScDrLxG/g45ZzIW3DC2m6QumxRhdCjATIS4vJI5W1dQMD7c/XpYLA7FG81BwEgsDSQYAyISLKc7N28RlLx83yrRJnhhm/4QrZsAnzh0tavsejWtrA8NHRORVnPVyG3mD1HIs7fGggB6uw/RI+QSnBJBx1Iuoggb7wSbHK0ngViw5ANhuzqY0SLOyqja0tvhNeVkvouYNtfiNODmVp1+JKttROJBynFVGq8q1/NCiIhXi1bkmEwHo6TjGqjxM1BhuotX5VHsVUnmcNvUCwbPyD5RCWJpR5QGGjBJyjlsUhprzMljGqQbC8Xaz4tdVv5WC1QTHrFi3jF2bnPVmV6XSR+NJC6NA4CYjhQzi0NOggg35VYeoXBLS8vmqA00V3oT5A4Lkj5zgEDW5QaYSscqp8/s4qAr1VdyZeXeLGyicILHEE7L9n1fQSB2F099ldC/KrjCVprDirU2+AGn1i96gnb/erdD2LJYRbmd+b7pMNfK2/VZjdZfPsrUf2QHpcuvKH/wrtMo7aKXbeejex6lXGxjliy3zwjOGzWo5oMLtlEga6JQXTMNiICDaAUrTCwwklWXoag22NeKkQCLbZPgs2F1CYp0klxRKwOiZcJq5jeV3FuZNbKuZGpq2qrNRTwHYAot+YcCJHuyIZhopDBlOJYrX7FJYDGfwDoWklLfUXhm9ZADcQKkZS0kd8Bb2gtShvj00kTHmUyJoDDUZ3kEsqC5Gm1dMSyI0eQVjNVgZgLSXzWLKg+6QaEFF0irI4C4OhltmaAUWu8DuZNBjijYWWTsGQ5CBDAraGbw+HNAktay/tQmQBq9luFSAYFBdVTJw7nyCiZhsFPZWTz5JGYFZZXioPAnOAAPHcxI61sDZ7XJfzaLaazDSxTSjHVfNAPWwtT4EudPPN6Sn8M1MjuvUMpIkl9ADr2Cufm8MUnKOEJZNg/Ep74Bfw1S58o8MdLHZDccy/GR5Wud7pYd011w96AT29YJLrWuiCIHQr7CoehW2GLfvkqMVxThfeKM1MskyUDHaarWXUZVI18B6WuDSJkjRs+cNI25aJfkAUGXjrRV20/oLR8hAkQE/1S8yvfHqDeT+La8EgG0lR6J7STeuIHYYYbN1xIX8dtUMBBUIEiWYDwcrE7indtHuSgSE5yASRXaElvAOrQnCkbXyMD9UpBkJhywzra/1lyGVidd1MaQKMt1ZVJlUDvNxGvmI2btruzeP9D1YMVEk0CPIEG++msOTQisgauFrkX+oRatJEl1rzqGF1+mR/cUElBd+gOxqjwXDGe+wV6X4zZPQtqzidTg9DYa3idPtpVbuQX5wxJfm4fyx9qLdtGJp6OcmAuqPxXGOtMTpLmrJdAp1M342Rv5QzTBHBdT+burhbeL7aKUnMHgK9VXey744fZj7zjIAfnumaRzDVfQZN8VxjyUz1ymE/gxqGT2GYTVW1pybZrYB2Slf8RGVqvKctosAkV74y5rXSnrZskjk9s62wfARCYU1lQeX4atNCj3i7SJvmMvbsjYgH0Qnssa2GZKpfJhOlTmKGar0aQp11dWaebMByIxau0vYcqqPdv+QEO+WIscBIVOUQK8gMqBmxcDnUgZ1jFWwBwIproYX9pvWTbe5HFWCnSQIUheq+Op3OPvGSOJH6gveQDWyyR4Dh5NJO1t2+hZDB8Bgnp9hWwOVQB2mmEZNAhoCgvLm+TCXpGSrEbMgkdB2Z5ARqjXHHVHwd8YEYOgV8akErphKeDpsJwRxoXluh8na0mwCLUUC5BIVA2EaRusMvI0evSUes+whtCc2qxYnqN/S4kcqZ87qRpPVUhd0rTjGt5TYoquAbLaFeIKDiVwyBm9bRCesxBJQVJNte2IYP/4PkcMl2ulCedtTtit36tJxuQo/cM0gzRgtzyo22uRlARKxy67rPUSs3PMoFScVQH3cRLuUQYN1v2Il7GymsXS7dG9Q4QTyokmuR2XRZF1Arw2EnLZfwcTnsUwLCrqvNLme4AUsxci7Gow1u9W6Dk15qCKy41Dqc/vYQAfZPhES9DsmksLWQ8RvtKaiSnrCYgcdibZRHw1BhyRjm0Cx6t85WeUuwtV5ASNuviXvle4ERLUGrWjEJdZqYehkW6qC8pSIybSFIWBIDwf5VYVfHJCzRp6trm8o9bR1ihDzQOUFY2bJwpv7lNTB5rQ+7pSTbz94wopVZPAmrYCc8u9l+fEgx83hGFEehnaAOrlUNGP4rysH+hMJBUEN2UduUQX3wCdeCnr5wIjAk1A6+AI4eWwfpCGsxXFvleH+T8BGmxY7YJJnaNtD8Xm34mUx2t6ymGb9LkzSYK0yI1sKDQxNqJh96DFW7EKGCDwJLqKhYdAfmRUeULL2hFZ5ZQsPK+KEy1nJ3rz5QIQ9Oa2c7ZKwJNnQIAgbGQFpohwYSQne5Ztw54KKgYKUKoFAwwRSl3QCGACeQJuH4O/CpTIWVBG8dRU/pH7iC8UJ5+Zjc6uKc7HTFw8XthfdUSayCjoIEKOkOQVYMEEj5nowv6cgPpF2xfiluTlwfpZOv+zbkdD8ghW6Mkppa+ZYAkSHWWee6b93naCiU/ATcSAKnXEs9hhVi5Ew8BvXBpFFtIh8ugntpqkp4SB0tXoj7qkFnzSUEJPkduXvJgVx7lDaKUf0GNcPe1r6WJgRM8JqrOEVMND7HXUgJA3trcBJLEYHZU7RS89JBwNOTNbVtIDvq2coMe8qY3NOcWcSSowsN9pvd8nRDFyqHJWB4zM88ktgPn8onj3uieY6bhY+OSCVv+Ol6xNeJpoweux6sjJDnpkPkijo0/FfLPXDpBBwBzLCZepVhMzyLNbWdooOqMgdl2skzelriPBtAbvEU1t/m/WEeFC4XRtWAoHjs1uuiqFDt/dL0D7QAC2kXkpAp+AD1aZlsA1LFaQIfFkvsrUNaaxJMKWEwRGIO+zva6apyLpPAnDhdY+oQU4RStGISQODgQEfYBpN1bKZ7dCBtSt3Gqw6J3aGUSLuiLuiINLPH0VAFqr/SzCfGg8BJo6rl3HHnGEc95bqiQNQpbgMXqrRZOw5aaSat3EDF4Vi+yh/+S0tgNY0OUYfJVMBdp3fuRg4O/XW54bMqB4dmayvW2Fgbd/neiGJ8SREoiOYZgslOZ2WVdCP5IbgtXVFJvdZyNx5aACUjAhZEgePMVwzDfYsbKYkBGGKZsHLb2DdcJn5Dr3IToqcqp2rI9FGJrxrpx9UWzyNzrlsl2w9B+4XvWPQkjKbuPT9bpxtuKCEc8ptrGAfCG5Qf4THkPPKT0Qb9Xabn67+NzZ9Fi0BvnVlXW7SQp2NziABGwpbXhJJNNZOrhyz/Oibh+VuMx7SP8WAeqND1UNZGE2uPV6+39Ng1za2HL+vCbe/hbqJmUljWfUSHWL5mckzc2VrmpJ7XwhXZACrRhKeba4oUqUPiCZjbVkzj0bX2tWyJvx7o2mY6W4fMNQk8/EQ6Xo2XbybNxpiLt9NL/GjzS2TOIeXxOZ92YpV3FRauS3f4gJAATILmZAluvT+1CpuFm69TRBizgXra1ZlVxpXMAG3mE8upQ8N0R8PU1k7kH+n2ouVXAgsxmtIm/SiLBI7Y6A4TW5EZtQCYOVcAdHQOidI2DDH02HsGnmkvhY98pZ3K1IcqRg9jTWlUYlexw3qfaI0Ikg0TQ0zYuOqMwf/MP7qjjA/CV4cJGL6iMhxkRUMHT/vvd8YeWzJ8WugOaWVQRoMis8vm29GWqGAU95Lda9w5LV/CV15FPaVHup3wDGqNv2g0PkSPUaZlGgU5CshUXsLf+rRBd+fLaV/rWr5eVfCvyH1l5m8QmD0EQndmD9vUPM8IcC6YaLKRZBUSQgVjmiyaztaTl5QtXEArBbKw4kyjtPIUaU9zaSaBS77bDQ4as3/T7poEm0N3jw6nWaNGdxz13MeoqphJP1m7yw/a6eb6QikJEpXDGJTYUF8H6I5MxIslxoFYyirD50UYYKdJ9xwuzdIM0x0ddC12F1ymzk6pGrh4oMdtBzdT5AKE1CET54OVE/1VAC1TLUXH04SSxPbjWBQsPjgdwWbQoKpz+K/YIOQDB+VHwMMwJzIJG69HqIaaUdVStvBLdeqUDx7gEsAcrrByeNCQPFCjIyU8AA2epcYZESJEySHEBu4tJbW2VDHtx1qwXkIXTEgaCBDHIjajg+p3V6jBq0bxJFzHO7NkYsYYGGSqAfQGHhyfOlqZE/7FpJ2o5qIRymAYauOKGtHBCatKZhAIAiMQ8Cv778ziaiX4jSg5x4ei7swx4IvzcsJTBLW4xck8NYVluiyuqdkkusPQ6rm9zkgLBYFMqkbN+Lt0h+1p5gdHIUjQD0oPGIHdAN1Rkr+srCYqoGHW4Ex4Oo+J0EiTbEcxAIa/nB2+0qVYa7ytnSiqtDSMlkPJIKvQSMzdERTUhC1nVrEHQSEMebkklCfVqI2WgN+oRwRPVYLJCYuupwOUinO4aL2Ti5tPSV1QWFgu9JQkKqAFcnjQgIyyYBiAYrmrzuG/uAUdy4JkTaK1+MjBujjmnChTRwR21IlYCGqicINiuMKWY7CQvK4QRa5oKoKjTaeR2ehgO30ggf1oZ2UKG+LB4RUdKJOvQSAI9BmB0J0+j07atlwIcCKYhaMmQl8ZYxP9qo5VFtKLyogtKOFBRAuhRfgLeqRki+fg7MdpKB8YBvJBdeCnwB6szVGnsB5WeUQTcSyKhVAM/KnqJCEQMwgPxBJxLWSk5sIYrkertNmltYq+Uv4Cl67oY5WjBc4SPaPNuqlHVBbOO4qLyFPEjrQgU5ikhCsKByHeUCAQCDa7rsjwYzZOqcyujKT7qIxPN1MlcirUo7WZfqaFfBOVg2QQY2g/U+ElrZI+JzA2dwJW5yOoOVynz4M1S21zhwt667qVZ+lCqXaWEOgt3VlBhz3E8wkCM0aA50XUCB6DGXArCOlFHdSGLtReapYiC4HkNJFJ3rTaAkUQ5ik2meeirosoUCwoImiEuE4F6C6IjvtTGU4QushkLcSTEAWMh2JBnhFsq6SfHHfYZKfMIN/CKLIHsuJci5hIMlwwPD4zqCqnjEAA4xFHrICQHX7DESWXwqGSx/RUgvcNp5cQiOaXZfnbokSgnhtCpsa4r8SiBKq3nfIkr2evp309jXvS1NCdngzEAm4GD4V4CHSHsCEU18IZrEXwja1dERHPaDpNozX6ad7mFErMwuqziFQ0jtMHrxKmylnG+dX2v1lYfUlrp4UAfxy9kKjG1zZizfm06pxiYa493k8/Ky5LYdrUQUqkcDRR//S/KVaysIrx5Ipys8yQKLuwWp7WFgK9pTsTbxiVYQsCU0eA7iL0daC82SdqL4TFwqWB3Ws8tX0Gyvf/qxXXgm/ISJrK7UXKwvD63+wRLcREmXDB4yPKLPMQKsD6FsddZuFuAdbaiip3AjYsnNmucd2jw2l3FH5pkzqGf/jorObg8byxIqjEPDW6Q3cU/sxniv7O0tX5VS27E+DPMcoravdFW0SaRZgwoN0zvqhBV3Pdvf4aO3/NWIij+mIgeEgFb9lewdZHxlc4mvmJGYuS5T/1kycyEVBJtgLyaE7VGCsoxewboNr6sjJ5gfm7MTbhfQLCZHJXab9iKjGgtcWOfDsfCtiXKb3Qf1zV9/ztFwKz5L1LtUscAUtmeKC4q4SbLHEo+tl9dsWac5pzrZOacSNr4+MZbLViVRcGiWwxlhWLPboNFpx7dGLPo4vhcMoscynf6EqGj1rD1cKw6igTrj3C0ocLjysHL/GeB7FZSE8t+OfzJXvgPQiHHRYsDBQ738Jc7LzAw8VZLNO5EzYDX6kNI3iKtZ8Qa5tBJYXLoB3ojrV1ZaIqur9C1qw6VJJ/WbX2iVbA9kj2uUaALMWvCyEr6JE1gIRbG0NUJq6mMLIoGMtCS4MuX/S9qHyh647aIKDC821FIS0YDhlyyohNpKrm/O0tAr2N3cnKrN7eM2lYHxGwlMzWwG3l0ew1kTeQ5R6of8LMgTJT/MrGkArYlRHruaZSle0ZyQBTKTlhGfvXacNoukNcIW/YWte2Nw15QdzGgnXk3/Epk0+KIEuokMwg0JuEIMd16U8uZBE+ytJ4ACLOvqIRaJ9YMbodkmSNm1B6UVlUHLEjItNlCrq38g5LIDxUL4SlW5FHsZDJxVmL8IlVIs8QDnvkCJO3uSJVf8JeTzez7W9UJ9aOl6Lvbf2nsxWe76KEFmE9ouZdvRGOgWsB04hb8kYlQimQtsZXBOBjnwLzzVWEqVF0OKOpLHiMu8VRIq6QGmAiNJiWmkVZYTzWFmBgWqK8TNRQJvyl4YknGSCkSn41BnR0MhSqonOMrHx16pcEeqeq0J3CaiH+7S3diTPLLyufIDBVBARS2IvWk3q2Q/BM621749NtGSNh0fuM3U8enSb3ZvBsGJ+FvQBqn1yXqHzmHD8gt2BaMgkAthUQpVSBVi5tdm6dHTPPlivAnLOLAtW7jZQmMDBa9kyi37RDdtDBMNi/2hWw8uu9H63MhAm0psI47JT9iEc8opxHmoG7iGXmM3UWjkLtsDKfcRU/rjvMtr2ISsPgQ+ELs1sg+2rVfQX5YjlCzu33g0wIhbEjok2VBKQjN5xr8LfHsYEGmrAtOWhu87CgNcgT/46VgxCrfEv67S/FzPPQaYN80E3Yo+XM1Dt7GXDtqccQ4GoS+muhgHGBj+5MdgmyEHmGA1HvoGq/AxILSmcfbSQJCBSa9nKxyhc/pDbgYIT8dzB084BFJsEGVUWGXBFBrDsBg5RZr8uw4yjobD6Jjxp6qyC13KCQcPi2dAT+hJ/h1rrxErszDEtylgeBFZfn5JwbBJYUAqQFPiAOoAGu81994ZwBKAgAPB21ksuh9hVjMPsxCxcqIZ9hUIwZwDxaDXbr8bhnZRVjzgkSDqELJArqhTk9m+GtETK5oqx6sz2PTCEXrYaBBE8QoyIC1FQeRWC0FLACDjngs8B7CAOuiFiwWFaAkysE59qLmY2vzYuRAwEZ1A4lnch6qUH8DcXFrL17OT4OJbWcfsAA1yE98pImqoleuGK3/DLTmo0nmfqLOGmF+XekqQh6zaDWGyf0kRTB5GMetjrEXZShE4AIy9FyPapNEORjdWgZx4o0gYQ5l1AGSaJSqF+mnKIyRZt8bZ9GfcSv1FGMAXrGlxXn3WPIW+E5SGiP+xMOOmvjhtbN0ZfWcjdS3TnIrgHt9hQZcofUrlQiiKHto0KZfggSbhj3HgqFUBodt40YIH4xOhBuqoDpgbvF/UANsjsDfilTgL9ldzbTwlmdVXcyBkk6cofYkVKZ8hVK5BMExobAQtTK0ua+IUDf5p73LJtxw1gI5r9cD60SmSy9T3NheCL7auLYMiXo806hvZtlVkl/0QK2lgDAwvE4lLRutsorIYcm0a4yYUJ5+z77sHlVv2K++uFRXLqn4DqsrDdPiVowOfbsdpTJ5y9QmE2td1ngNEQRH6pA/Xo5aJT0xFeGcGIuyzFUNfNEMCHWf3nBgkP6Jd/VnS6000dwBucFDYb8oIU0Bg4Cc2jGo2oY+GsDGxdFBeSbzXNjwbZsT2UiN2y/o4aAguJa0gw2QyXBeDudKZLGbxjUNiJoDZMmvz7onaiOci3Z+7G2LHIIJeKJc6Itmljiq4r/2+lqHu3MqsJGkyUuKORojBNbzJDbr4bJVag4rX4JvhslaT9ws0k0p0wdFVvGeG+33XbWOjHSlcnwI3/d0yuNbJG4uvlQciNVjkvDs9KqNZRokzuzlYdqu4ta5tQT3IW4lJvfx1n6gu/WWAuP45KTifPpZt1C0gDBHia7BEaIcIAU98VKq5i7Vw1a7lxCTmXiqTL9ajAY+ZVZ8g8Obd8HlVQmByLKRdAiL9GcKpP84/TahMKNUTgbbsqffG8U0Ze6FppIdVMDJ532tzd2VT35u4AQ6K0zK7E7C+gu6mlTuS0qnpHhZM88qsz8tJXNY+24fsgD3Uf/cDfYzpLBu5sBslKV6bEoPKLOInjwFLDxMj1t8R4TTfNyRwUQkCXq2c1zwaJ77GIh3rdAj6lHv+YRZjzQPaZbJMFweygxzAkdQj2e1PhElWFgTEmd3j2FU0BsLLNtlbKOl9ljgeCgGLtCY6jyJZOI7YWMJz6yUjRRQgG0RqcQMmkleayaBa3T9b37ri6ZbD+qRMlAVmgSTm/mv05pf13OUY2UU2KMc1kamRW74xAHh/Yo4E0g5t9m8/Bsr8uw4qbm67pm+t7a5sQu3aEr+NR19av4q/HFn4xmDSgZqQr463RtGCPdccupkA9F5eWqA6lFQEQyOSJ+YFVXZ7yB7IbBsyvHXyTSDVZaUcuUcA9wXZHQ2iFQA584hGu6WxDTKk/E0gAj2D0dPTV2vE7dzCmmrQFUoY8BwgkwntrBHLsVplPMoyAlsWBguDKcEf0RBIuvjXLjZ+V+5gGslpgh+OpyeAle2Jqn8X5i7oo26M61b5a7BTtsxRylGqL7dRdVvl+owfVxqEhw5cNZTrekfF1TsjHpVnMSCwuB3tKdxO7UkyR/Z46AObfnvvP9pUl4ZtVkTqCoJ6kpIx2btlFmYMLLCElhY2jdEpwOeIZiqA+d3C/HM7H9fsz/vIqLT4fFNb9nQswCMSrlTX+LWkl7XrPNdBQXRXfk+DCEDLzJKBpk50OGgUpfGkwVaH/Voy+MgZXnLsTM1CHWUQdRt1ZSQmc96Jl21TID0GDjNV5fxGAiQMSDKs8o+ogyYTh9ZDqFOKQkzwtixJRiGN3Kp5LWJFeHiakzQJZ5ikcntA2TDhojX+sU/ZIpDTE+MpxSNAb7J4eVpZpw8ZCXeBn0iK0SwKGn7BMWiDw5HVwUHcaYoTXXR2XEl/DTcUVhhMYXPr7qLPNJWVFtOTKwEKNsZRB8Jmw/1xJ9RfOwVcQOmShfEkeJXbMZSPIV0+sq1A71Y97aiYgjrMKDDDftDU91zxDn2u6F2LD7xIiAjgRIzUKIDT3uorNksCKRLgFeQgXOhAXaB08jdRapKo1NAQSiWm4sKG0DQVc4BHGo2jxhB0dkciMSnNxXRkprVYJJY3KIDoaNbJEJSyypH86IqloL9ZcKpYPdwkW4uzmV9hP26eZrg3ve3Wsdfsv3QyhXV8uRmOyGdAf6dEtKq7aixAby8zUIjAeBhUUb09p+ItB1dlQLuTw8+2pyz6a6WW2+PFnjGSqeFA9xBIVhqGIEfGd5IstnSiuTkiHTX06WNk334GYIFWCSPZer5ICzQ6bAAhYat7Dk1UTWWpIqOfwX5RKwOZwvh+FkYruHWiRKOYAcYvIp/96fxSQIzyxKIZ/VF8paen7VwFhSoUzEfWXveVvMhqXZMN3EEdEI2klJBegam0dI42hj/rktwILrsIV4lck3Mzzw0om6ir9IiXOF35qp0zPQPpklhNS6Kq11RTa+TlHeWKBi9bXGl+1HHxkwMa01shXz60Qflk93lNeSIojIBKce869TpAhlUCg5xgs7kWkUUA1wgcjATfbKCKwItj5KOpeG4SqiTMgYQqGF5vCgYTmYSrXWX+zEWU0n0AYMzBWbwICIGwv9UsZR8SLl1AOpHB1RuPqotsr0VcmW2a41kMDwBDsPZPbqq9vMWOB8XVlrWi0sSanuommdmMJLAYE2Oy1JtT9dvlp/mpKWLFwEhulON9ah6M6AvN86a4osjMA8FW/AJGgDdci830yaDeOJQFBkssFy2GD2nn+K8FAlGWacgD3z60JHzOnlF90xuS8bLEcjneKomBWV+FqnD/9lD6gsbDkXGFLFfVNhSQIzXZeZlM8HVLbTUQ41YoZ4oIoQ0hg5yITgG66u4liuQr9hZsgM2sZay2FZzcsxPLactIAfWOEiX83EBod4JWSWA0VHhFBoGIUDJqKGlbTCxekCYmgPZAA5E34IMAJ+qWVqwzlQK8W0RD2kGmmeMjWU98dX/UX48DNpH3FRdnyx6hgD4wsj7VQ+SiHTWXQy4g02UPm8NvABV33112jCp/lNWv58JXSHwAZD0kjdTojg8jQGDbKXjEVJnJUjvEjLc4lxnesNa8YLw5sx3TG+Br2xyXE1LPUsDgR6S3fizGKA8hkPAh5/KqITsNxIAHWHSiHt6c/QIiUTXoYJRGJM+j1/WVmWmNLD2SG0Qhgp3sC3Ui4PeoxQCdIL2RxrYY+rQm4p+SyxfL80j3J2uoJz2XJsgP6hKpbeKfwpzhJnKlPOhE2iInB8CF9AxXTK6qQ6C51Cd8gk8pk3r83i3OH7oLV4TskkvXi3KLpD3ihjL+SF2lFb5JEikBiSDwechmFC3AGNYWiJzlZ7WOKKOVVtyyT+13IbmWT/Kokpcg91cybsERHI5QgPrtsKdN2LBAkfh/QLjIZADDUyVIX1seSZdm4lcC+fgUxfhUYNZIrm9hnInMevumO88FFjQYHD/GqMZtwkI4KsQ4/4ZFhnXM8cnMgN57M8Fxoe3+WpLecGgblBYAUPyrm5Uq6yuBFgO8kzPB0cK4In+Dv4aKgyrKyVF6a8JYAPg0A54GQheLCyWIKvYnvRERZIDTIZD0qJ4FkSBTOMbcjBpYRH1PbzGAmpBqlinrElhkeCW8e1cAVKiWJluVWOObnnRVcMhw4Mt22ZObid/dNQFmE9TB0246+1P8s8cY4LUIaYKBy0NqYbcXUjxe1obxVqB11qRMlFcMi9wQEqIGY46GQR9G5EFzhJaaX4+ogyORQEZoaAdXmmhc41PyRFz6yS2TgrdGc2UE2dSwUBRId6JBiWJwjf8iHAVBhy3yCw3Aztm0zQaq1lCDl36kUBLTOJQoAyh8620PXlhEVVYquFUhHPRlfFbIiGNgFocfejyy/zKG8s2ZVZmlCcW+bpKRAERiDQW7rzf+L5iKbnUBAIApMhINBYJARvGtGIRmU1UD+5jvaLjlom11EMJQrXmXC4sROC4hg3SsZ1BGjXxjYTXrFlYidurVo31zKxUgpN+zqthJ2BxImTYCvqblrnpnAQWKAIhO4s0IFLs/uCgKm5yCETGqvfOdr60qwptIP9FuQkplgIy4jiPIDWQInDtYHNiGKL/hAcKDET7lywzL6L3LeCbKCYmHcLDIWfV771XwLYLdzz1V9ERCS4ND6NVYtFE0/WahAsTOkR/c1pK9raOjL7ThlNoe4kqDq94uvbKQMJeyUoKd6IJDlwKF+DwKJEIHRnUQ5rOhUElo0AtYB/ZIstthCaPYLKiLnm4WJZ/V12pdMsIR5chNY0TxpzcdFmXgslwn10vdag2RWmQMAk7M2DLjjFid2IKEqMLQ9sgSOMrCp0FE8S3CaS3SEF5Av5Ep6PaLa3hlEHLfXHPyxws9BPtJn3KriExYkiIUStdZsnPky0vmhr1fJzYTxWPoq5tpRPvJqdGpzubwtp757b0jbaAX7oTgMkiUWOgLDNfIJAHxCwOLxtXT977TEbtgjZbLhdwta0zAzTYlVXyyTY8OlYV2y9WMucLCEQ2OlTKTlZDfOVzyTXai/awIg2lMsDULwnRIhuSYuZhZnXPtrySSDYQ9VmkbxDbTU7kyzUSU7beUi1duuxlMkptnNsmwY5EZjoheB0dVKhLKMTBu4qFsEJo2bpXRfPqFMoH2LPEYJuw1pak/A5Q2mtGQWuNiC2GHDnnXe2Ug9dsD2BlYO1EB23s1DfvgB2s2yvm3BnyhTojRpa0qVm+x0wDLXy39ZQuAUaJF/LXUiovijvtlECpqgwZlMr+QVHK0mekS+ApraM0kfyj1PsKaDXlvrXSjolReLbWIgfTbp9dFydLtdyJFAoOpyEVY22PdTx7tHhtHX4+JB7YPhQcoLAjBHo7UL07Lsz4zHNieNEwGbHFmHZdGeZz+jlvGrtCmiFfKuH0a3dCwde08MusihiJlrJyRLmx6bj5TuYrMy48hm/tr1N1cleWmE0kGni7m2gNIZlXlcIs24O0B07yKEIIksYWjUU3bELMwrIQjPMVS1SIm7J6RaZ155DZYYFwJIuKowJdVC4xldYt0xbAtbpzC3ugsF4IwF9RUCufEv3LeIjhGAnrijHVgUohaAiK/IwDCW5DnECmz6TPRRAHYSKt9c7VOXtr00srUrDSLiKlKSm1GueECYLCe3jDNIqjEXZncie2r7iUhYDYiSislRem1KC2j6HjgLE3gTVEWvZIMAtxfdka++6tbC39v4NDVBgwpeWqK07cIWzRtpcgMzTutCu23ImpDsG0YV009iRfFrhyRKhO5Mhk/zlQSB0Z3nQy7mLCgFz9HpPU7dXzIkg0LI03fyxp03rzdpNprs141jMcNvqpg6RMWxXY8bcLTmcrqgdTgSkp45yEDBXbCqqxGjhE+0s5tOyZ+azZAnXZX3pASw92YA5Fz2qMPGJnGAFEPnBfkK1HRyrKYCGw4IZtla/VAF6mEuwmjK5Wlhcp7O41CahIcw8mapdfcLEMN1hp1lNaoeabQ8NhwoiQVaYUlsiITfVpMc97nEYqtbaxZi+oiTjrbDGoBe0B9IOQch1FbCxjYTttkFdpNbfYg+tYQy2+CduHTmApXAUi/LVWvEB/UbfqTKg49MZGLtWYSW8NNSGQ5VGkmwfIK21tk3SsFZ4wPwbF6wLTdGkEm+6tAM4NB7n2pYay5Ew3G4Y1bYKKzF1uuPdHaATwiygp+BqVdk4qsunJ6Q7CttayeiQiJqE1moYTgz0d7hAcoLADBDoLd1J7I4Hez5jQMAUmUkw52YIW3UyyfIy2YDK9Mhm0b1w0WyYRSfvyyfvs1g8SgMbgYhaEI9JTlCJYmiKcxm2ehXiQDRDuyhxnrBBGDDH1SRtoPDb/U8BlpiVst2fCXQrv5wJddIhRE6Y0FdV+stcyTRZRw4k6BMOWQvDhhEzWF8bC7FtwpwJMGQt6oW9p83ItVlJ3hlGS3QIhgElwaoydURJ5dVjOQ/mIRMmuCOCYm9Dp2M8oj0YaV9JL2qQqNMVnuIHo/I2CWqKFrKaqGGFgNBg8A8Vlu3XO9zF3tM0En3EzAy9wBHSDtKjO7ZARHo0yXWV0XiZxnTEumsEyLmUIaegvxQUXahme+xWVa0XuA5iJBqGvjJwqJUZTmhha4A6uzvu2Paat0vvnEVkEs+EgEKDY6hevGAIcDjgKACTit3RYOTD/t28XWogjMkHhXgdo6OkK6pHDiQFS8n3cwCsu5qbzDtS4Fw/EFSYRlX3qtGsxpsekNCokn4LopXLNWYgaEvkNz4+rit+xiosAFnD+OkMX+X4q8F8c1rYciQ0G7Z+Kd33XnULJB0EFhkC2VV5kQ3o/HTHo5Mhr4BNT2TTXO3wcDf7Z5XNjwUlkElkKiM8gnVkpJvVqcIEHrNSNqP6oKTTTcrVY19js3CTbPMGb3VAd0RR+Gs9bXeb4DqRzeChwIo4YhgnhIOCUmuw5SMBvmoD81zll/Mv04LfMORsZ1XlilrFOLFtuJd+oTv2saVdsZo6RfNgrspC4z10FOSG9arTqUTkB0aXxdX31jzdVy3CV+Sj8tXGKkOSaMGh5hDDydmEiFBHmGfGdVr7xBAwkCd22juVXLFdvSW4e2yQjZdgMAhNt4WtzECCwWaVhUzBHN0pg60MAsRVRNEpfQvzUKd8VpzVF1TkzhG1M1Bb96sXXamWSFPbmnUPddMuBHNWX7OxseIT3FW+UjhAbZdI96Q7B7zoNa2OfoYKYJbqwY+92wspoWARwwyiMngzoADuJsRKwYW1a7Y3l1HUUBy3AZbjdP0ylBgwiuP2dqsYETeDiCUdx5KFNHH5ufkVdnMaU8pcA9+vSTupO6AuKqaYmv1ANA/p1J3uPEEHaXvKjP4QpWiQbpLRxXI0CCweBGYgVeWUIDCAgAe9Bbp24/XxWK+jNBVmQxgvQtAyGWB8SLzqQA2+YiQiTirf/Ngju8IzBaaonHFyiHdGbVUG3RmItql8f822sQ1KEuOBV9GBvMmhjqqZbRt4gRdzMmNnlmoZIcapIkLqKibTCEelmWT2TLp7XZbPRasAEkPvqbS/8pEhAhhDTv0SQlTuMBoGE2VdD33FA8iEXmHWDmNA7EgvMklN6A77iu3hoNxMCrRg4XaJlkCt2Hsnent5hdD66yvmZOBKxuD+K30I/0BexfbycBkUlTD8dk1VP8bGypY7j/6kBiYfy9FNxQwEQobxGBe3hKO6UG0QDMR9Y7AYbK8HkYk3c/a5echa5Ac5LgofQ4lSoALNvVU14AFoZaUn+1ucCSy20m4OUwxGjr4YF9SkzkUpUBaY85EZ1pbJpUhyc2n3Yb3XzCHI4yLoJqyMfnUf4GiE02V22+NE+YVbN39caZzbMAEWD1tmnUpa3N5+FMssnwJBYOoI9NaZFXXHszef5UWAFTE99QxlZc1rqzrMhlCPRpjQtwswBma6ZbBb5nBC+IKFPCV4qJANLn8QE25CXOXtm0eKGD5XDtvJRtYWKTw7PGUDSv6EZ80404PAufVXQiNxEdpAVaiRuux9n0w+AsHECsFhk4RZCNRlO0lQHHlVA7VAsUMOOQSr4wkiA4AUHxJMjTMRP0gjuIXC1AiHaAnq59Ap34c0qQODoXbgjpiKsBLUgT5Rjfl/7d15oHXl+P9xzYMmpXlQJA3mIlMlIukbmSNTKRRKQsoYDeZMISoiZEgqkoqilMwkaUBRaVBK8/x76fJd3/3b+5x99tnPfp6z9z6f/cc+a9/rXve67/e9zro+67qutVbbt+fBcKUoFDmyIc66Jx2Hw4Bt1gj/DQcAtcHBRn75mFa23LTaSuiN/RZZs19eN5krXCBEwJ577kk3VKyE20lMiruIXOAOMbMCRvZVPSFG6ULCgumtEnUAJB24ZDSokOvL6KAgVX2abas+j8v73ve+Wp7smwTEsLLUmzqiTj7Nz1ogWyHtLJzQe6RjPlUZtFqg2n3aWvCTvOgsHGAJBU8pcryRa1M2W27Ocj5NWTkVQmA8CETujMc8zvAo2EImlk1iDtnv6g0bw/KVOuGTqDQOtopBVYcdlUCjjhN047dvhsE8cxK4U4bZ86ptZl6gwVrShwOjqhE0jW+/2bBZYGK1z55xAvEKMOdWueAmGlhT/hJX2wSTll0WW1YokYKhcluQvAcuFj4D32pyAOjtZC+QshW1IaLhETKEHXVFH5Av3vNFBHBp2CP/B3+PFGag3v72t3PeCMbROrpEx+iDsZBHJIJUGGEvDjBSj14hVogJe1dTnoou1S0/QnI8DRwewj06CSNFRR/oqpo6w98jRxgumk+Oi8IJP5JtmWH8aTWVjdGyUfDHmC+tsaC+2UUpRxO24LVoreUidBM+Jpja8KmalHHrJhw2rT8t60PrG810rNQVIehTlaXCcKtQseaL8W5roe0nqaSmQ5TSals1Nj/l98gccgD3ksYEqc/YjD0DCYFeCMzXXJL2Ujt1QmBCAmJV5IicRxfQJA6r7NEjoh6CHS6L+QNcsjOiPBY2t0pchpFTwY05PEBusXGBLheB9JHeIfVS0EpAgX5yNU89iJHJlrCt/AbqgenlP7A75pm7aMITt9thjjzySJmbLnZVEC6xOe+F3QleaJaQsiPKQ4c5OaqQdFDIZmhW1EOhzvvQIoI1E449hTNCQOKLo8VhQJBJJ+reB6EoulAcrXENdq+ftSEQAn0TcMYubyg3cF4R2jfGbDikBGSbSoklnUUfKAkWyI1R+ur2K8ELl+YCN2xSxSa4IuRSSOwgd2RpuF637N5pF/0cLQQHvwKdYXPOG6rF5gIWpWkIIzLFMkXCzWPBqiGFkm7NTQIOM/FNGrTTNTg3d5u2QyAEpiAQuTMFoKwOgRAIgRAIgRAYdQJDK3cSvh31Qyv9D4EQCIEQCIEQmIJA5M4UgLI6BEIgBEIgBEJg1AlE7oz6DKb/IRACIRACIRACUxCI3JkCUFaHQAiEQAiEQAiMOoHInVGfwfQ/BEIgBEIgBEJgCgKRO1MAyuoQCIEQCIEQCIFRJxC5M+ozmP6HQAiEQAiEQAhMQSByZwpAWR0CIRACIRACITDqBCJ3Rn0G0/8QCIEQCIEQCIEpCETuTAEoq0MgBEIgBEIgBEadQOTOqM9g+h8CIRACIRACITAFgcidKQBldQiEQAiEQAiEwKgTiNwZ9RlM/0MgBEIgBEIgBKYgELkzBaCsDoEQCIEQCIEQGHUCkTujPoPpfwiEQAiEQAiEwBQEInemAJTVIRACIRACIRACo04gcmfUZzD9D4EQCIEQCIEQmIJA5M4UgLI6BEIgBEIgBEJg1AlE7oz6DKb/IRACIRACIRACUxCI3JkCUFaHQAiEQAiEQAiMOoHInVGfwfQ/BEIgBEIgBEJgCgKRO1MAyuoQCIEQCIEQCIFRJxC5M+ozmP6HQAiEQAiEQAhMQSByZwpAWR0CIRACIRACITDqBCJ3Rn0G0/8QCIEQCIEQCIEpCETuTAEoq0MgBEIgBEIgBEadQOTOqM9g+h8CIRACIRACITAFgcidKQBldQiEQAiEQAiEwKgTiNwZ9RlM/0MgBEIgBEIgBKYgELkzBaCsDoEQCIEQCIEQGHUCkTujPoPpfwiEQAiEQAiEwBQEInemAJTVIRACIRACIRACo04gcmfUZzD9D4EQCIEQCIEQmIJA5M4UgLI6BEIgBEIgBEJg1AlE7oz6DKb/IRACIRACIRACUxCI3JkCUFaHQAiEQAiEQAiMOoHInVGfwfQ/BEIgBEIgBEJgCgKRO1MAyuoQCIEQCIF77rnn7ns/FmaExu23337zzTfrQn97t/lb3vKWs846q7/Ns9UYEIjcGYNJzBBCIATGnMAZZ5xx4okn3nrrrW3j/NOf/kQEtBUO/OeNN9747Gc/e4kllrjvfe/7kpe85Lbbbhv4LqZs8Ec/+tELX/jCBzzgAVdfffWUlTsrfP/73//e9773nOc854Ybbuhcm5LZQCByZzbMcsYYAiHwHwIu8S+//PKrrrqqbyfBdDna0Tve8Y7/+Z//ufDCC6e7bdW/9tprX/e61z33uc/daqutrrnmmtZG/vKXv2y66ab77rtva+GEy3fcccecaJTTTz/9+OOP/9znPnfkkUduueWW0xVYP/nJT374wx9O2LHeC5/xjGe8613vuvTSS++6665mK/qv+cntdN111/373/+21rflxhF1/fXXP/nJTz7ooINMfVO/aSQLs4TAgrNknBlmCITACBG48847v/rVrz7lKU9ZbbXVBtVtxm+XXXZhBZlMxu9Vr3rVOuusM6jGW9shUC6++OJHP/rRCv/4xz+ec845/Apvf/vbH/zgB7dW63F5mWWWOfDAA7fbbjvKpnOTLbbY4v73v39neVvJfvvtt8oqq7zmNa9pK+/xJ72iJs8K784jHvGIBRZYYLINL7nkEoNdaKGF0N54441VPvPMM7/whS8cddRRH/rQh+aff37lL3vZy5Zaaqm//vWv/FUm2hRzupiUY489VvtKqFKi5KlPfer6669vRxdddNHJJ59spxaa/ZKPRNi3vvWthz70ocb1oAc96J///OfKK6+stXe/+91vfetbKZ5//OMfyy677HnnnYfeE57whK985SuLLrpo00IWZh0BB18+IRACs4EA38AHP/hBwYhbbrllyMfrOt65WPBigP1kArV59tlnc/B8+9vfZpgH2HjTFCfKtttu++pXv5pHAXDeHR4F+5U1ctNNNzHqTU0Ll112GROuP62FEy7/6le/0kjr5ocffjgxYV/UVesm/CiPetSj1CdxBKGs+uxnP2tbYuWxj32sVV/+8pdb67ctP+95z3vkIx+p2g9+8INa9bWvfY3k0gIB9/CHP/wb3/hG2ybNzyuvvJImu9/97rfCCiuoz+1k1S9/+UvixjLJwkXk4/AjaDbYYINVV131hBNOIDrtgv+J+8pWD3zgA+36Ix/5yJprrokhROutt57lk046SaEKRIxmP/OZz1A2hklFfexjH1OizZ/+9KdrrbXWC17wArG/U089lWaibmmmL33pSyp86lOforf+9a9/Wc5n7hFA3jT5kLNzby99tBzvTs1LvkOgfwIuMX/96187+e666679tzL3t5R+wQzYzyabbPLa1752UDss++oyur8GXdMLSbzoRS9q3dwl+5ve9Kadd965tXCyZSc+q+abb77JKlT5+eefb4HzgA+AO8HCAQccsNhii+2xxx4UyUc/+lFm9RWveIU6HAOMqGo1od/5znfML9vJ28QnQZ3YZMkll+zcnTrUpPpWnXLKKcsvv/xOO+1EtLGyLC5PzwUXXEB18UbY7+9+97unP/3pdu3IIQXWXXfdzga7lFAAlIF9tUapuGHe8IY3PP/5z+cQ0gHJuVpQc8EFF+T/IGLsV38ma5akOPfccx0nxisAx1wZMteIwSJ22mmnSd/pEge0u4UXXpj80j7twqFiYcMNN/zkJz+5yCKLcEQ1+yVNNMjNQ+vsvvvuNJ8efv3rXyeV6BhYuKz23HNPMwu1w4OLyHQsvfTSTQs02Te/+U0Ont///vePecxjlHMp2aMe8qI98YlPrJoSfbRmR36a3zpUmkayMLsI9CGRskkITIvA3/72tzl0J7h6636h8J73vMdJTRLitDrWpfLPf/5zV8Ms0IorruhKnWmcrDJX+eMe97jllluO0ZqsTmu5K+Df/OY3rSXzbFmqB4vLBn/iE5/ostMrrriCKwIBF9w2YWmaDptKP12vN0BcnbNkfAy//e1vbeVyvFoWzVHTxTcFoIRbwloG3q7ZXZGIqsYEil8IMTDJK620kkaU23CNNdbgSLBJVfPNqFMSOs9m64aS9773vUwgySKrg+Nh7bXXbppttmoWGEVT6eS+9dZb77DDDkSG0bGOHA/6wzY/5CEPoRXUL7cB0+gAkHajRLfNLwHEIcFIcx68+MUvblpuXTBYwoVEsDtbAQWgIIv9SnzRvSOOOIIs4/Wx1W677carYVlCDHfIH/7wh9am2pY7vTsq8FRpubwdfmrKEauT1IMU5r///e+kSbWD7ac//em2Njt/Uhj6rxxt7VBOVafiU+Ur6tyqKXFsP+lJT/KPYF4+8IEPVPaMpsTRyLKmmgXd819TbjDHz/vf/36FVKaIVXmVarxakLTkIKlta7z2opwme9vb3kaWbbTRRq3Hs4OExGn2hT+5VgchXQ5+vDsNnLm0MLTenfvMpQGn2Rkk4BznVN69A8yVOvXpUtPtDC6MXIzK8utSrcsqvmjXoKLpXep0X+Uk64TIB9Cl2o9//GPXds985jMbM9ylci+rnDEf9rCHMR6slGYR6L6Vq3bpIM7srdVqIupUW+WVMskeGJTlpr4FZ3AZoK2bT7YM5stf/nJXzE0F1shZXjIKy9oU1ty99KUvbbNzIggf//jHm2qdC1pmRF1tMzw0hGWbqEYGkSB++nz+85+vDV1k31vw3y9nOuUMLXqKTFzFEUiTqqGF973vfeIL6qgpo0U5ycK5wkCW5bZKHeW0VO3FtwGKsxjLXnvtpRGmnTqhkxgw/RTZUZ/9a+p3LjCQ6tBSraue9rSnaa2JB5kXbfI3qGOChGb+/Oc/Oxgk/SgRHiJiyBRGvbWR1mU9pC1aSyqYJc6i0IGqD3ZXhf65zKahKTRTrVu1Lfcid2xCZjm6tOafDsP6d3CpoOSQQw5pa7PzJ/cM706VkyOvf/3ra7lHuSNQReE5fhwehOk73/nO2tzQeG4sc+qUIDZkiraOAXLTYWCtfwFuMMet5RqvQ06bOr/99ts7WZW3T0BWTYdQdRVDrqzakZFSWkcffXTFyxRqgYTiqeLOrGCZ/+iqnO+5RCByZy6BTbMTEDj00EN5dFvD/G2VXB65ruV25qNmyfxsq1A/nfqdlVw8Od10Ob832zrKOy+vXWiyKHvvvXdTbVoL+vCsZz1LXKNtK6f1No8R4+cisi7Qm8qGVpGmpqT3BVfw3Abqf/e730Wg8gO4H7jQXZT7rhN30+COO+4oOaP56Vz8xje+0YbaYQOqnGosmDxGbECJA74T+kMJn3yXxAgtsOuyKNghBpUUYzIV6p5lHgVz6jq4Lm0lptB/ckU333zzxz/+8eVOqD5MKXdoL11ijRxFhlm22ba6V2bJjPCmlC/NYWan3DD2K8pD2/HrsLWkCaFDx1irJjun0NhdbYtN6HDNVJn/1u5VJ827/rOy9dO3YJmMVwuGph3i0rJ0ZodxYXeQMIEKJ/tMKHe0Y+KaTdr2y/zz3vEH8AkZmuFMKXdYet1jkps2W+WO4Iu1IlyECH8SW+4QNXw2vrv/sovcKXeI3eGsweOOO07j4C+++OKlp/Wf+CDZ1fTvoKmmb20LPFuOGV4Q/7D6edhhh6lAyu+zzz5Eg4PzmGOO4SBs26r5iaTThSCaHXEOldK11lGkNX4aR6lwIciycMyvA8xBpZA4dtaiKVUTirIJt41lvjTXDDbku6Xm/T/KX+ZyI33MiP8sJN0p5mDTc4UcOSqoTwM1pwIHidjWZpttZkf8SY7ApsNZmBsEInfmBtV51yZr5F/FxcE222wjA2De7fjePTkh1nmnx/26jvRf3aWfzixOha6B+JBZiyZT0lmSe6DNinM7O+80csdJ39nZ1ZXOsGGWy2HOhjl9yxMkRMQatKMmW+gky643V8+2clZywnWSYgidGZXYxInMZbRL/DohNn1wfW/v9tKMncqhDOzIGJ1ea++11iWgM11T04JcBJs7UbYW9rjcyB31ncTLQUX/OXVy+FuQA2GM1Rq74lTbqsCcjg2QeTP88kCoaSD6w8a39oELQWtKVHZpXkxaKzTLbLPKsNNSzH/lnDZX4TpDDNVFPIAHH3ywmfVtj60qakq5U7tj6VtzWisfhS2kKmgdbTKKanaaYZrAWpaMmOYiwqGEEf3kCrsaN9GmxjKbpPL+++9f5c13m+xgpFUr81lyR0hL5Vavg+zmSs5oGmlb6EXucLDJGvGfrs8gk2iSdRQy9v6tGGkOBr4fOb9tjTc/uTMdnD7MKp8WD4cYjc5TpepU7hTzbNlMcSzRcDKEBLMcJ00jbQv+VY1XIw4A+lU3VDCn5VojZagBRp2zxJEmBkdnw67zJXdUlqVrLnwkx7T5t9r25ZxgR7wstRdr3/zmNytxvPHVWWh8Nm0b+kmjmCMBO4Nq9cw5D+iew6nRr041jigl5KOTCU1pc6LZhQTFZplEs0nbf0rnHlMyhASGVu4s6PDNpzsBAWMnuLJtzjt13dN9kwGudXJ3+pAk6LB22uXAcK7UvuUvfvGLzkGsbLM7F4hUjkIW0YmvKW9bIBEkTFAGyp0TnQSrAlFFnay++uqOVx7mtq3qpxtKqQonX6c2GTNsm6tJKhAlZ1tb0VKkj2RY7Ut3UOjE5+Tb9JOHQ7Ymg0FySVB17Wt0XAK2ZbmlUhqvjArxeHtkXFma1p6QHQb+s5/9zBnTtR3xRLFVBT7tsrVNfY4lZ96yc01hHwusBRXCeJgObeozbcHekEFkgQadtSvdsho3Ec7sjDrlZ6bMnUtkNqlz14J0TD7r4kRvIgyHfe2sViWG7KLZZTE3Bm+KrdpqCsRIv6AC2QyQaRElbXV6/2kem8rVjqCAa2tjb9s1odbMLzFkLf3qUDF3bsNmz6gfByQ52DRYC3WU1qU8hpxnlSzcVs1+HU4GRVLjbK2Ldd/MIWKEiElxBCLTtmHzkwoxBX6We0PIw/+RI83xaZhEISVnNh1+Js7uKhPZUaqmqTdkBpg9duARVRKbRGfa0qtrX/5DxYD8K9lWGJQiMXZXC9Q5hecgB6o6T7U77P2vweIeaeK46W3bgiPc/6mcX8eS3vrHUUGh1nhH/LPjTKIRuyr47/btWDKW5l+D44TotxXgpVradtH8dDw73VX7VejfqmKL9bM5XTSbNAtOCz7Nz2aBwnbx0Py0oMOt/5WVg+zf36eqGUvbJq2bZzkE+iEwhNpw2LrkZIqsk6yOOdc7qzrxOb1W8h23v3/R5srMdSpHvf95Z0/ntRqLmzCr0FnPglObchkANIEzJgtd1RgzzxNz+a41NoNlVc5w2rszl9Ou685KYaEPnEZFNFwxa7PcM5466iTyyle+0gWWM5ozaTXb+c3XQn+4J4JwEdt2KlfHcNzX6mwu9O56scIWtS2p51Rbyxwb+lNRAzEal5s0R61ikKrP9bO+NW5fBlU/7Y494PDn53DiFmdxUW4VsBwbwCp0yWsUVV8h+1fL9c0JpOe8327ZcJ3K2jVrjYspqivFprDvhVbvDlvlqpeRM3YzAgJDS0wYTtM+kdEEs6xlkySU6KGt/KxE1PLu8O3bipEzFm4YbB0tqjmWzB3j2uqyatq34KijUxndMpCVoekQYhtoJoeog6QuyoE1NfyCDkh9Jrxszi5yOcjYdYHOzPOgtDbeuky+cAM4jHk4yK9aJYYl0KC3jj2HLrefcvNr3plAhay4xBqFbvM2fHPBpLGU3BsKKRU9+fCHP2xZ9xwSdDAFKfAhAOEo4jarcJWWDcq+bC5LqdwJhmwWHHgqkwhQo0Sg8ItwPxB/FvRE4xN+zBSwnCs0B0eL41w1JZryj0NImYtmQ5Ol3KciwnSYOv7LlJhKbi3/gBVJbDZpW/Df10QwrSK2ao9t1fIzBMaPgH8T/+k+TpVDNbr7DFVvhrMzLJaZk7PJLUGR6KTznZKKGshMtFzmnwlhql0bkTIK69TvxMc2cy+7zUEhI8qqVQvMnvOpwnpABTeJZVefTD4JJcRTQFz2Oem3whGZZo2UOC/bpCwcn0ejulyiMVStm7Qts7u6xw/kao9RtJYpdfa34DxOk7lYbDbRGmNWPyWT2mONVwld0mStWp7QTvMY0WS1OXNr8+YmFD4AQKySHIBS1Wkdr4taV6h6W6vqW2yRY4n1Zd1Lq1W5vrlibq05J8s6JuKmBXpXN3wDRRGaXxPNmOlzY8PMqUvtUsDVJaaXLCOSfExf5XoTZ7pNCphxuHhByJ1KsxXoIQU4FbgWWjVc6xA4mdAjAR0exK7MWTXpgMYxoELVp3XU9BH7oJUrWFZ+kSr3Xb1tbb9ZJnaJD7EYSoKTpiknFAzfx81ETaG8k3IJiD40hWqK0VCETYlZI1wqCgl5rAAAoTtJREFUTEmctapSxBzz9c+lvp8VhTE6C1Ra04hVPs3PLIRACAwbgcidYZuRafTH2VaEyDUlj6tAT90ryw3e5M86ibuNVou/+MUvXGe7NmULmZM617OICuXwcgspdKWoJoFimYFktCw0V6UMCWPG/0EiNK6CVvNvW+aN1iEC3E/LjHEM1I74z0mlGlh3ucMsOSLVdGFt74wxS2OnTYYQJ7zISzXlu1Xu+Ekn1XiRcZXvErxqknqCApZZssaYMU7sd+PdsZarn58fB5Xd31vOA/YV20rxsWtDLuMnZKCHjdzBti7izQi3ELnWavxA88SR6kx9G6ZZ637DTmv9ZtmsmR1yh9dBZ4CqVXrLo2C+rBJ+qjuhCD4/KUKSkcOsKtMWfBhUsr0L6DTZSwINwig1QYZjmD6GYxI5eCr003SjbYH5V5NYdBDWzdhVAR/qFvNGJ1krpVShVXpS/hXSQR079W1VpdS07aJ+OsZqaBOuTWEIhEAITEYgcmcyMiNQzjyUOBBIYno5e3SaT9uy4AsT4jq47iZQztrRK5wBFEMTLOCZF3WSvcjwl4gRiLG51BZX9p55WjERHgJXvS6mXbVbW0/Z0iZzq1kL7KI0CCbNdTMJ5YKYN4Ul04i1FBhniQWmTuCAARb18LPzwy8l20bP+ULsqK7U5dxYJpiqsJSTPTKWohIElvJy4It2cRhIBahkFEOrcAPnRD3QXbjEkO2Xz1+XNKsOz1PtiNBpHnvfPNijYi6gMeTo2aQ4s9Y8GRUB0SALbVwwiq/xqwn9NP4kJrzxrzRD5u/RWjmQmsJeFvjkStf2Ujl1QmBICPiHbf4jZrBLTk1kvROg/sxgN7LrGSEwtHJnQXYln+4ExOwpCSLDJW9Ts1Ishfz9PwtzcNKQBS7lJUuKT1UKjut1Xg0WWuSeBGHa+UIU+hbIoFG4EGgaCxwAUgo4AGQn8BmUGqBsanfklNgH3wmhQGBJhiA1XLtTPGQTqcThoSZjL1IgUCK9g8uHDCKtmg63Luink5FOUgNu9SQyrOUr4jZwr4RVomyVEG1oVAVfjk3IPsm5tuJEcc+zgB0/BwXD/2F3WjAWyUNcR24Kla+jRAVkNEX9cB1VhMVAJI3iqUKlKFoQ7NMOmPI6JY7AaHTK+W90xiqhLr4Ta+WFKBcGakvCpavsSwzO2uajRBpsTVZT2MuC21t8eqmZOiEwJAT843iojAwq/y+9dEnCE8vkn84/JuduL5v0WIefW+aiixwxTf/CPW6VaiEwdwnMiPobrZ1W7o5pYGKZW//J+u/CRRIGO8pnIzpjgatGuX9ygoOp9s0ei2s4BxEBFAnTziniQySpyZGjhCuIPpAIqYRwEbshIJR4vkUTa+CG4ViS4EwJNR4j2osOaG7stLlPKRWJtPVzbL4lMkvTaSI1E44L1c5E6QlrpnC2EeDwoOzlIVHMPKNtw/cf5/bytsJR/MnZ6TRV6d699F/itpi4Rz+0Bi75mF0COZO0tiA6L4DLZ9Na2H3Z9Ynktu51snYsCcS7M3dF21xtnYeAN4VkqRfd0St2x4PipnSnUUKHDJKL48Th1l/eFy6WuldTRMm5g89G8EgL1Uk+GGkTwjF8PGJDNm/unhUDEqPpHIuWSau2clpKnkpbob51FrbVGcWfnFviZV3ugDUoSEdxaEPeZ9KZP1I0cG77uuRNuzdKGpm7AgfORIKXRDFOVsPhZ21t3zWGMKvU+9bCEV2WK6bngr899l8emGx02fdS6JpNXFO51pJX7oynKacpq6rQkzbd8gkm57RNBHxdcTmDySBsnEPuRXBidCLiFNdC02wWQmDGCSSYNfUU8N9UXktb1VbrW//Ykm1dWr373e/mmHG7Cpki38W5w4Mr6iky/MZSSdyxXE2p0NZmfk5IgKAcOVZO98KRjAH73eQqTTi64Sx0xe9AFTPlUOR9FB+ZUIsPqvMQeeKAO/jmhtzxryoE7DqEP4O1bu0zN4ZM87YJ8n8qNu1ixqVOE4txO54AsescsV0tmF8NOjJdoHN7MPCuZOqcoKacM5tzBiusk4P6TgIUCbcH7ViF+mPUMvfdvufsobXWvjXLzieSBeXMadC8uK/TlZLoLaevs5NVrqY8WYdr2SZmTQodGWdo7rV0naCaPHqb6BLHsz5U7qD4Mte1aa0Eu9qdE5dRSNdzQWX4VWiPuqfn/g01wnXtLkUJhZSisdcDCBwhxihszTlEJKmDTDOELITAzBMYS2faTA1KMEX+Cm+Ns5Jbb6SwVE+kvHCkc+26p4lTfaa6l/3OSwLO+/Xv3fcLNOZlbzv3VY/TrMgI8996B1xn5c4Sm7CLPhZa14rMdjZViXEiTSK/rZXblvkSJMA1j2B2Y6BLC4KM/0kmGd9qpdK3bdX8VJ9dpw+aEu4N+SWmST5ZUyiDTcCLTlXuLoEK6/DIelaeEkFVHhFD4PGq+VVT4j/5Uv/aEuzk9YsQ6Sr5Ul0SAfd8SJc9NIGaxJDduVWTV8ljtzhLyAiO4aYPbQs25FaRO89BJU+OzJKWJ39OXpqavGIcw3LvLNMZnpZkQea++yc4WqhVm6jj6RWy9MgUFZqzkNedcou27k78XQ/rVr6mnITynIvmpwXPTSCGuF09EoKEqoOccw6xqubJYXRVE5Fv3TbL400gwaw6M4z5t1Ond+XUudJZtRmtc4pP8zMLs4EAz790LqnTLn/7Hq9gKMPDXLXmZTNyCllZxnJCXwiTJq+c0SrBIW+sCdYI5cgTd7aVNOYKXsfcvsd2uhaXDSaFhfeCwVaBe8NaN8a7shfv4P9g+JlthzcLKiWWMRPeZdeJBrZQiaeKecivi3uuFNbdvwA/AfUgvZ0ngNrg7ERDiWoivGy8ZU8k0iBlINJUN+hNiEs/NeJRRgbOzyFPhSmlxnheWVYOFUPT23rryIQtuA4hawiXZi2DTUJxbxBhTaF7EmXzGL57DmhWMLlz3C8pKu2WBbrBExBEedxhgKrOe3yACtSPdHvV9BNJlze6WtJKy5woQBFbFnTYtRDPCteO2wwdIa6OAHQthEnTjdYFk2VbekgfKDwHA3TUISeNmx85jCkYeG3CB1MD9OgsPiR+HTk3HqLhSEDYh2xyVaadxnPTuiPLDo+Seq3lNqzjoSlUoj9cQdDh4NOsahb0s9xdTUkWQmAGCUzsO53BDo36rp0FnH1atc6oj2g299+pnI2nLcqWWGCtuSJcHDOEJEUDhz7w+AA31jGHVcicsD1iHFYpYW8YOeEGwQuGmYaw4KJZm9YKOljFH6CQh6NaoB5crLtrph5MoFB0TMzC/f8eHqjc3XxVs+2bEbLWtqIMavp4ZKU6PA3umHNjHTkibERqKHR7jleRu/uP3dU4H4lj2DBZRGtLOdUtfp6NpFnxCy5M1pe1VsGTongRdEnevWc3u+i3U/LFjiTjS6WXTKZNNWkd/ScIuDlZdy4ZhYi5GdCzGGSHuIOvizTUuF0TNDakb2gLhpwD1aBsSxe6Y0A2iTa7fHhoTERTgVwTSOIZavZrpJ56QPxRMG6rJBcEsxQSr0QA3wxnDKkBDlvOp0JTVrjK8yGx0jIyMuv5UYhU/VFZoW0Zfj23dzqJF6QKCSNZwHQYCMRc07G2BQMnjwgR/XHhBKMKjitjr5q8TaVRhLpMXxXaV+UFcrA11UyNY2xCdVJ1HAy6Wse5g7O25a+i3euQcDuFSBnZhADpRnxzbjmeqR/Hs2Pb1PjH0Q1X+UJp1Wy+Q2DGCUTuzPgUpANDSsAZ3+33dWFNDeili2nnfX4OSehcC6IJlZJlmZeFX4FtkLZZT45uG5Wzv4tswQhuCa4I1/quy+s1T+wEg6E+WaORUiHu4LU7V+qcDXwebtZTgd2lDKxi6uiJVp9E6+4ER/RNCV8C88a2cUv4SU+INRBk9kLGMZ8KZcEzzBYkmRFkQh6W+XjoAAvq881UnrKtxCx8qCJqidBRwUMmeYlUZvk4h3hKeFD4kygGAqW1hx67QMApJ4lsWObZiKT5o6qEy6QxzH62feQPEXAKmXCOpXqQQVudgf80LpKIbnAwGK/h4ElkkDhd9oWDTchWIkaMSU3zBakDgCbjKmt8HoQpBw/PkEEREJO1iaRnOpBQjhPi0iGhpgQdezFr1CTHWPlsiE761cMa9JaQknHMK8PlzGOnA3bnBkaPyqROlLjZ01acWBQMP1mpGQ/mNthS6gSfuJt90WdaNq36Sa3aL1VkFvSBnhOs564ziZSu49OR4E0j3EvCZDXLk40r5SEwLwkkVXle0s6+RokAjw5TxCeh0+IXvokbmSJMMgvNEhA95ZthSJziK3xAW4iPCEx0DtV1vw9j7+K4zIAHc3P/uMR3ocxXZENPOZIQalt3EjE/KpdzqHQDX4LcEc4VptG9MDRT516qpBwMTLW+udpmrvRZz2kszgwig3Gqt2Cqb6RSWetRSZM1qFxPiBULbB5/A2dPVVZePozWbQ3QrltLDIE2EgtjLPknqikOEuiIJAtUI+Oqk40aaN2cUedi4UYiONjmyqRRgWPDLNiXPRqInyi1btgsW6umvRME6nDb0Hy8EVKV7ZFfhISC19zxfhXbitYBaLD8OhSb+UK+YtO20pT+8/qYQWyl1/hQOeQv0WAqSUMdUJ9wpDYoSxq0YnZGbSC+9YSq5nVrutq2YLqJEqrI4ccFiGG1CQLZ4SilRO0OVS4igtX80qPUBiy8jNQPjW4reots0n8QEDBxtIumHIF2UcckZc+HpNBEOKTNi2WyhlTlrLIJdVv3YdHQxqKEymkSurkSaSnHg/iaDfMJgeEhELkzPHORngwXAfaYbXDuJh2c7nWO8XDVyzbQOn460VePeW5cXpMU6jfxi8kGwwy4j4aNFA6rxxMwFcwVGyl1wxU5K8LMMEjkiPwPNph/pTQQ0+XmF4mrjDQfEmNTdwl17ku4rSlkCAkFP7XJQkv+cBcxH1IT9Whqdl8Q7eKx0B+6gWaq+4Bsok2OIj6DiuEK2dBzZAcmbKoPd4hCWode5Aawd+NlgIWiuB8EyKhAVp9zSw+pCg6kzp5QDPiUyuFA4lFQxy5swu0hsmZ2OK60I15GkHW2YFUZcl4KasBYTBb9xOWmMoFChTD/plvurYwcLYvEEQ3WgkYgkjucK/QQ0aOQtCX7yjXFzMsgNlhzJ6EHEPE1Sc1K1KSixBNx8yEsaCOFxqIOFWhHJdcUTvihmYgh20LdOjQ+PN4dMqWUim1F0ttakBgkm6oKJVRZqOxsC3VUt9U3L52PvVDHcevTWhlGscjWklouZ2FneUpCYIYJOGXnEwIh0EmA9XXNLYrEBFbOqTqMLvtXlVk+bgDLnDSsphCVh1DTKGIHTWsEEN9A89MCo+hy3L+9e2eq3FZSHPgJuAe4E1hi5QIibKrsB+W8PuyKQs4eYRSJPrwgtILgDvFRjbR910OxJbUw26InLs1V0D65JuVF0IpN4mxQyOSLUzDALKUISLUjDaXSO1zcu9znT1LOKovFsJ2EGn8GFaXQqIk/2xJD/Ap0mJzligBqgYGkRey03pDKbDP82pTkUT3n0SE79JCek+TrQ3xUHzq/qZmqYy/VH/rDACUJoUpj+Un3VMc6NydBbK6+b26SqiDPuhoRWJxsw86mUhICITAZgaG9M2s+PZ5hwZXdh8BQEmCbXU+z3CwoGykWQADxx1Ab3C2iG3wMrrYteEQeR4u8Ct4L/1DCFtJrjImjgu1n7IkhoQFuA5faymXkaFwab4WT5K6Wm8cqYQJ3ArvsFo8Qz+KV4aepi3uawE+uCyXsPf+KK/4SJZ38+FpIEEqLlCHLWtNg3dZELbl1qDojiGNHBiJIJKRFylRrzlnlyyFE+EWaXRA9lls9Q4bMu1DnvnsdDfOpUIWtC00LWQiBEBhjAi6rODsN0FVWXdoNyWATzBqSiUg3ho4AuSCtmNDh0SFZiANxBELEzUH8MborVVOMRjU3rYjs8NZI/PQtTiRgQVKIU9icG0OIikApecFb47lwPCJN6ow7ZWSKlFzg0eH/0LjohmwVsRIuB9EHckQhmaWyEgG1pnBCcLqhXLOVBN1aR/JH60/BC5Ga1pJadsKqc1bbqlahU6sqktIIndZCy7W2rZH8DIFOAgKgLi18WyVJvP5fOqulJAT6IxDvTn/cslUITJsA9SOTQxBKLEnohLdm2k30vIGkVLcyiViJ1PS8USrOOgKCiSKV/IUyq2jrSiqaKQo6w5la6f9uHOM9nameZL9zQiDenTmhl21DYBwICDCJc/GO1N3Ic3VIcnJ5lconNFd3NK6Nc4/xe034FMdxGrKYpsww4piHksIQ6JzB0XHnyMT3byJ+ytk5gz3JrseSQIJZYzmtGdQwEnDPjvtoRMSkyMzt/g0kECBqJrIgrDa3e9vZPmsn9ViekAWpza23I3VW7r3Ejd+8a9KwPJposq3EHz0OgO13W5wH0kxWbRjK5VmTzm5Sq7vD+uiShK3jjjtOzrs08KYRzMkOak9MttqsuZBYJtNLINUdgpPNiGNGHRFMjcgbq4itTRRKR1NSsVrNcnbqv+x7dxdKX+NYspWDTba+tR5G1cdwskkIdCGQxwx2gZNVITBgAm7DngdaZ847zTi53JdA7d6uOW+tjxbkcUtOEtqQNVXPXeyjkbZNJJ7zZEi3qmfJtK1tfnpkM1XkBjQ1m8JhWBCdrCcBVmckhHn8oMR5T1SSFC8ttMpFprxw1NMKCLvKK5+w85LraT7zKyHdDYZu0Ktn50gy85Qp2D1xqiKhduHORI/ctCOPgjQv9YDKCZsVqLVtTVw9/kA1D8zUgrR9t+m5R89tdAo9DUg8V7zV0488j6CtNXc7tpXkZwjMKQEaPJ8QCIG5R8BN3R6077Erk900Pvd23XfL7JknKbNbPBwuyvtup78N4eJXcD8ak+whPV7U1bTD3jPzfA9NiVvesCVNOgvroX/8DVXZ84UpBoqn2daCSeHIkUqlMn9Ds4pikITe/JxwwQs4Rbs8XMeNeFgx3nqupnCMZxO7Ha/1kQR2LfXbg3w0+7a3vU232X4PBVCfk8MDC2Sm117cpe9OOlpEmrlEFoUOIeLAXEivcW+/CJRCaoYjhLPEnXfcLdqszb1LS7lCHj6vnqjCzm/PLfR8Rc8D1CWcwVEHQ54eSTPepMHZ41FSCj0agEZhaVT2NjG0eWs6G1TCReRhPJo1IrfkCI0pdPxwC8n6t0zFascjoyx79pLXi5JZxKUnHimpj3x/dURj/7cgf0eMwNDeiP6f+0XzCYEQmHsEXHk7fUujcdk93b0IplRAZ7obDqS+QIncamGFKVtjvOkGN6w1z7OZcpMuFSgDxDxuUR0OBo/2scA0suj16GcOGP6naoFFV9mH58zdcFXIkVCFvr21uwqZVT+FFOtnffNYKCQ7fJcZrvJe5I579CCyoQcGEj08JbYVC+MIISD4MPSTh0OhUVA5bjvSQ2vpGIUkBU1pwaeeZ2iBqXDX3r1l93ghSW2uTVKDv0053SP8VBWAqsL6Wd86U0854u+ZTJc09cX16J7mp+Hw39TPkh1UoJ/lOqLAmpoTLpBHstPaVpkpjqIqLEcdOeioJnE4gdzeaKd8Uc1WrfttCrMwQgSGVu4kmOVklU8IzEUC3PuMmUvztiQYjgqBg2bHLoI994/rokqc3Tw1x10zPAeMjYc7kxRN5bYFFsJ1s8f/eGaPc03dyuu6uQo1a19Eg+tprXliIbtLOpQO8wImF9+8FNIsmGF3xzSNCzToRvPTgk34DDgPPHhXDEKJCBEj58UCkjA8H1mSR2v9/pZ1hmvBLffekCDwxChqx7gqasNksqCeDqBQb6VD8SVw4XiVQT0OmAhgX6kc2ovzo56BpDJrTTPh3NorHaZs+Gnq3Rqtq6Zc9lQCjz7ihbIjD4qsx0zzM3nWAK3DY+TpzOBrh9zxRGMPbBQwIstIQ4Wtt+g3y56z7KmJ8ma4tegn8khNm3iDhClzCBksFVV940yqhdZvk6gFc+rg4W5pXTW3lx0GXmRRt1bZF4+R3CB9dox5/rWSkjukP0oeWMX7RRc6bIhFFwOt3Uswq5VGlgdCIKnKA8GYRsaQgGcGkgUuQ5lSYsVlNFeHQpLCad1zQXgL5Fdy3TNOTGxdUrNqzCfrRQ14wg17zOIyAJz83oolSYI18sRkjciQUI0V96wdgsa7FTnw5XKyDXWJzABohO1k5yy4Cmc+O0GzrNrUSY8xZNFVYMLV92BlxlJnPOyYp8QLB+TieHejngtYGAhLzO5SQnZEWBAZOiyMwnlQe2EyW+UO54d22CHZG/qvz5wiHpno9RfecE6dtOm5zq72WEJGEGp8ABwAsoZJPR4Rz7YW/ZECQpYBKDiiNRNEzdBD3vjBcFb7TKxYmNiQ2aHw6h0RtYqKaktn4Qu58MILKUtNeaxRjz1squFjyiq7tgrNKWHKJWZHnj1NtVR5a50q4bCxoAWbmIiSs44xs+xYclTwzYhMqWOMKoNslVkWfaucKtE3ecrmFxMHAC0lVEcgem6kqBNtJ7mn8X7VTpvveiyC/cLlaLEvmzt+HJDEotQl0tbLPRz5NtG4b3UcyXprd007rQsOVIcT75T5kssMrG5wpznwvBhE9I388l7S+l/QiN7S9x5cDoIpIIC0Zr8OJOFUUtItWuU/a91LlkOgTwKOs3xCIATaCPCXOGX7p+Lb50hgPisPgyFxClYuN4Ke4CnhaWAtmIqq6SxfKQsEgWr8Da5367qfCnHBzaLYF/tR73mgSJhGWzFpDB5zblmhOpwZFexgkJgZ5rOtk/WznP8sDf+Ni2bmqsrZEg4GLh/mkI1RKEuaE4Kx1DEN8sdombfAT5ZJBQaVEWICqwU6g21rglmcPWry7jDwLtCb1JZ6biFzLoTU5RUQ1WYv34SdXqnJdtJnUkks40kK6LZlqhF/C1SRntipWaAsq+dUo/lim1Vo+0iJpW+aQspSt9FGnlllj5tVZGIzwKawc4HYpUgcAM0qshUiLeNPalQcR7avDtPHZIo0neY9JISdJ1Y3j3kkZbRTr+Ii1KgNRw4alTojp4cSNQtETO1OkMuMwOJb+yCIClWJeXQg6V7TsbaF0hbmtzbXkwq20h/kiEb0UyzVVhx4JLLImkOXcHFEtTXV+tPmRudDrJTmq7XGSMQL/9VPB7P58jI12ULlELJ3U+ZjwSwrtMoB0Np4lkeCgFOQ48fHFdFQdfg/1xb5hEAIdBIQVvAfW3kSDJWrz6pDOjCxrUkqLIcXXVVKL5NZiQie2yYvwenbVmSHppzcGWZmtdqpRzM7oUvFJX3KVPMxiETUciN3OvvWVuI6nokVzSnfjLWshZt7vceKP4Pngw9AIY+Oml3kjjdUaGcyuePpLEYhd4SVpTNKQgmciVM4wZ100kkeKdQ8HtruyC+fyVRa2xBaf1J+BA0V4uE3XjsvBmQtuaN9nacaCSzOKoXkmgVeGaYR9sr2ZSwNXHCKUFDI9eW5ZypTA0Qh5wctxe5SnPxbjD0BQbLweHkfmaZ0WC4wk08zMfk1m63da5a9e4s85dszfWQN5laZ5XpkNvJcO56gXfWpBBKknD3qV6FIHOAGKNpFida+pMt4lQedhyodpqa4JMtx/PHHC7qhjXltzrEHiw9tJE6kkAfOoJSob9RNzarf+s19YiuzVptzPTZrwTEFpbkV6kM13lTIQgh0ITC0cifBLCfwfEJgAgKc8Aye/2rrJE/ssMMOLCjzpoSznRluthHQYfOoCiUuzSuqwtIIsrQ+ptaGLrjlW7jRhtFlvdSnnJg6gRumiy1k+cTFiCSmsWnfQnXDtXhrYS27StasPAlt0iJMqTiFMJN27MuNPLw7LtBVJlCMiAizTK+w9JqtlllHXiuhB+JAl1RwfzKRZy23lht/jN21vruN9FYwy1ofV/z0B63g2l3LhAI+1Ss2UoqJ/VInrRBqbfdveNl+H9V4pGgCC7SO9t2aZLAocZ8oVFPqDNkhpRc0zjOF0PGsEHZ8OVAQeZxkyplwdWQaeR29ctKQ+4RHynypUJ4VGghko+DSE07y07zbdsIPMcQrBqNq+qa+amKCJE5nffKXDlMOGrdHVeAdNH21XM4zy+7wojursL51z6e1pJa5psxIa7me+7SWTLbMG+Qz4VqeHp9mlQHWq9SbkiyEwEgS+M/ZLp8QCIEOAkwjAyZwwBnAfDY3+LgEd0XOJePDltvOhTJ7wJvC9gtp1S1FkhXcnCyaoJBacnYQH+E4oRXYZg4StyXTN3w8XBTiNbwUBAS3BAdJXVizeTInhFSYOoWHHHJIRx//U8BjJO7GPAs0uHGp4heyWyQYyW8VgKBjpGLII+HAsEw9+LY7twpTQkSAvlFFeq4+HaBNAQWV7Z1k0QG+q/ITcKKIa5B0PAdcL2r6NnY1dZJrpPEMWSWnR5ukgOVpfQDhWuPkINea6Bg/hH76xryL02JaO5r3lalSMGFxO/e833v2GALzgMDQenfmM/iRlGnpdAjMZQLstDwPwSb7YdHrphIRKz4bYYvaOc+HG68su8oXwiBldt99d5fvtVbAS64P34+LeM4JcoQ3QjuSS7gQRGR4SrRfLyEnDiRyuuDmdajNfYu/cD+w7lqgUZryAS6IYhBG+l+5SgNsebBNSX/hRtJJ0RzP4R1s42ltZgnwjfkHmdk+ZO+DIuBayLWc1viMh+qN6JE7g5ritDNuBMgd6ReyTYU8OC2EiozQ5QHvgrNzLbtThqenRu4WKnEWJfWzvm3IS9R5V05rnZldLrnDvSTnw61YM9uZLnvn6ZEjxdnGjVRxwy6Vs2pKAuZdTK0im1NWVkF0kuLkp6z0o1426bEOoe+xyyKtQ2Uae+x8qnUSGFq5E0HdOVkpCYH/EBA8onici911VVpHIa+MG8t5fXy4eRqtY5WkjTato5AAGmato4cG4nYhidhNEonCIfwIqxFkHFE9ah1RucqVmdtjcZBw0dld7YjA5eEjkT1ooNm1HCbOPIUyiprCzgVBTDfbS5TuXDXYEtLcs6DknkuN77FlXkaR1vJxNptwdrorrflZC24VdItfW2GXn9AZuIcudqmTVSEw5wT+k5OYTwiEQCcBCbZuEqZ1xJJka3ZWGI8Sib11n/x4DMco3Mck4CVfWHJV3WbfOjSBSDnXQieebjdZrm5r/SmXxSsJFE8fqCfE2KlUdMFBGsjT82pzqVoUhhwvCeldFA8xLV1MC1PudA4rkOZ77bWXrG39lEvUS2vSvzg73f3XWlng1VMJJKs1hbK+ZE9jK3HNeFUouU8VuXKQQW/XTWX61d1zyDQlky3Q4kQ5D5MOiCyTmDLbuFqV0JdmU/aY/LbJNk95CPyHwDxIXMouQiAExpsAI+dGqtab82dwvASNLB9W1u1Fnd1gg91o5tRXOd2dFbqUuNVLJlZbBfJFgyROazkZ0dxt3pSLH/GpND8nW5D7JaPZLeV0W5OUzQUitasKxVIn21Y5KWAiJMiTerwmNpROblu+LmvdA+hW+dqcz5ILSlflTcsSU2geVfaTh8YDEdx6Jr1MuVvTCRd6Qgp5bUtnEHk0jTqy4Ckn21rl1jmijRNOPjslLf6oUHRDoMq9/R69421iTQsez2OaqCjT0fn2iarmWwqIVHo6ybWH29ZAoH7cC2lHImtUlG3d18aF1myShRkkMLSpypE7M3hUZNchMAUBEQQGqW4In6LqPFnNoriTq21XTLKIGItVj8dtWzuDP92Vxth3dsAdcPwBngfYuaopcXc6/wf4NShBHK+XMkZPz3OPntvulKhsrVvV2OBmw2ZB6jqnTvPTgs7UQyZbCzuXm3dE6GQ9MEkdD5C0dx+ORo8b6NyqKZE7z/zvt99+MrE8DYguqQSdkneSn7Rf4sas8cR4iID7+NRxQ5zHE1AqWqAk6Bu37zWSUcqavXvyZLMjC9qn84yLxioRRk1qwRMNqhrXiwXuQ/c2WqhR0F6W3UtYTyykzLQ8mdxxdNGI9YBvW3nWIteRBY/bpjIt+LgJgPqx6/qZ75klMLRyJ7k7/zmD5BMCM06A+eTYb+sG8yMgUvdgt63q+6eMDWmh/W3uRnSX8p5kY3N+gkrZ9ixBxpWFY8CaZr0OjKljgdi2ptBZWKTGvfe+uQ3cZN6salvQMivISUNkMHi1Vn2v8pAgJQ/GJb5CD3V0wxpza9nbLQRc2tpp/cnWeiaNpGyba79LgFLfDJOwk1DiIT0akR9dLzgzF9wJxqVEOfcGf089qah1X9rneOjvDjIqx9szUCWtPBrAc4rFxYgVzh7agopqeypP634tWyuhmFtFV8V9DJOSaOpoUNJ3TQrxSknwTlE8nl3EGyS7yDONPONRH5AXeyq2NvdcJRqoaceC+BTZJDvNCy6ateUZao4EZCghTzIkjPTc46HrQUpEGK1jW+2YEQ9EaHuXWbMjTimP+qyaTaEFmXNN0rQjTbMDCU227iLLY0YgcmfMJjTDmRkCnpvMGcDIsc2+m04w8M7svpuSWlBHeVOTt99TdCVHW+vc7WauqsaRYIHxq5/1zRAyxixfUygHQiFPgMto1rEpb1sQxXAdzJYLKLigl56sD1WHu8JLr/gehC2qxFMQVWbzGCqBqhoCj4irfFf/njooPMFiqSzE41l8Mlca0+j+fG4DnZTcqlq9i1RNL7rSoJo8ItwJnlRU+2r7FsrRGe+4kKhB0Mj8VYG+EbAgqigehrneBsrQCnDYr4/n9JQGamut+cmxwax6sDIFwww3Kqqp0CwYoMcOEaDkppEql5MuR8eCpxaJ/njIYWWpS3zxbMPOdF0zK6mlNU+laXzKBQ4V08Gce5GZykQJgUWhcvLJEKIyaYsujajDfWVGLEirV7OLsGttR7OEhfmldVrLJ1vm6eFnquc2GW8dIbZFox4CqdDH5r4dD1SUgfB4wQK+uSvZ7Ugmf9u0VLNT6lZ0j9b0+AaF9lLdExoTLPPPolBTDvt6DHqzYRZCoJ2AoyefEAiBTgLMp7O2ZxO7FPbwfmfbek0EH4yfzB6fbbMV6eBfyxN0PIuZaHA2t4ovhIJhRbhDyBElHBskgkRaddRnVhW6/HXh66ezNiMqRdpzCJXTQFz0yllxP+ujHVkRnAqsqVCLwjL8NmQmXSi75GU8/rf6//dXz1nxCmFY8CwfcseHrKE/6BJhCA+2UWIzL2RggQRrPBOPaakRyf/1JEMZIUy+9I6KiZQ91nnRkNqf+31YKXIHMa/CMIR645gdMeTqeFSjzFMb/n/9+98f5QwnkhSQRDSKBR4C7RiCZfrPMJlAy1wglYzCDSD+oqT5gEwG1U9WWY4I1PVTHEQ0pKnZtqBlySImTnZLM8v1bjJHRVtls4BbWyEzbO9thTrTWdhWx0916AMLRkSpOGY4RcyvBR3DXGoOUdK5oRIbyhAyTDeZO7oQczCYOwdSjZcyVlhRNrJDtNRWJVnIBZnUDgNq0kFI3tFbUoBrR/WoaJKxdb+yeQg+q8hTj2ywSsu4ccsp5ONxYCssD5nZJ14dVB6ErdArLBzDUrPrVrsux61BmWXdVlkkruadu0uJfvovK0nKt9fatyzPFIH6/zU7kq5mqg8T7vc/YjmfEAiBTgK8C/5jmRkRAc4A5lw0QTUO/8qvJALqjVoKncHV5HtgxV2zusBly3kjPHiQnRb4EO5RjV2pq1iGmQ5gGFzaKqce2B7naypKlkNjpMv/0cgd1khnhEic8UkiV7csPQMjK9aO5Ip6Moo+d7GpnWZYaqpNNGIVE1JXzLokxiGCwCbpm/uKywBzzFA/1rZ9eEFUbuSOtfSfDS2UWSr/EAllQUxK6EH0pK2R5ie3gS65YacpsQAj21/5tvwuaJfp5abi8FCBtCph1GyFQ0PSTJk1ppHtV2juBKqamq0L1tqLcJWTNe+U4E6tLbkjgdcwqY0arNaoCprA3gmR2p1pEn4yRnJZUm1TaCv3+qlmwRHSutPWZYcNaSLh2nstHHi0o257trX3ljgSCBSxKhPdukmzbJgOD04+qpTmIIV1wFqCifIgC8hZz7pULtQly5heUciTRPuaYlqcBFGTW4gipIl9mw4RVWPEHDfZM6VENWuV+qbef4eDpLqhZajNoMHqvEL9J3SIFd5KTJrjhBfKP4sb5XyArc0n/LYJ56X/ryZBx6T7X/NBngbVjuNqwm1TOI8JRO7MY+DZXQjMKYHyPXgOimCNtgSYfNMrjA1vjUK2360lZcwEGkRVWnfp8poZELuRS1HhGNKEDSN3XOZWTW9dKFNtc+aheU9F0w67rryRO5XcU84bOokF4k9SmZbiCrLAQqvfRe4wP0bUtG+h5A5PjEe9GRHvSzlyrNpnn33YNgKI36gKDYQhZPhbW7DcRe4QUlSdplTj1sKE/4Ddamuh9WedLmWZKBRco0tkhIAgOYOXiOiUcUL21SY0okxhDRoX28yRQEmYFAuUmYBOczuVyQKH3ip/GMcAN1Xrfmu5MmNoBbqTGqieW0XE8IFpwYfXR2qRQmmz9xb894stV8jh0VpIQyisfGHCl3NOP/lgFE74kUnDWWIuCG6yqYSmAJ+Yjmky0Qx8FXZuThbwstAW5IsoZCOq1HfsUZAq8P0YeFFqColdrWnZx0itrQXflnWDbLKhZY3YqnatWf8X9Wm61BRWm601m0Ors+cpGRsCQyt3Fmz9t8xyCIRAQ4Bhtsy6Uw8WWEffLjFlvLIHzIZzN6eO61rlE35cmqtvlUQKjXDXsxbuMfEazqrPXeEcZ5kh8V2On1rV5Zt7wFoKwJUuG181q7ddtqpVghqskW7Yl5iF0VVihxI2kn+IM0YFkoIm4FvyknA/622mWiB3VHAdz48iZ4We4LBhOxljA9EllPiZ9FCWj2t6V+3WEh/Emc2lejCBXpbJZUJmsfp1E3JbtzWrfcqM+0HwTp+pOh4IXSI+ODBoRL2trcgXQROy0r3QdiRF109ah0OCG0PYi8EWWSMy6B4JUsQTuUmEkbOUXNuu/SRxnK+NWmv8K+5Oqjo8FvrPZeWnqax3evCxsf0Yqu94qEKpUcSu2cdEZFCE0SYcNkQDnWSmtNz6itlqv/nmV2uWmwUTUZkuTcmEC4ZMoVpVvsmmjunmhml+EqC13Hb0TvYIR46ZZtvWZc3W/0Wz1kLvha1bZTkE5jaB+epsO7d3k/ZDYEQJuJ4WNCnnvCHwIsg7YVw5ZoQk2DBPH7FWEq4rcmaSI4Srn1nldWDLXWS7TKdLKAm3DrEuSsgC0Sibu2VGUoIbhaRNsLJMsoxOykOCAgPPiyN/wjPc7I5h1iadZO+8BRohF9hXWUSkEtFDuHDMuPKudgQU6ubwTuzCTISOPgvZWOZ1MEDpIH4KozDGbDx1opAzSbCAoBFo03lmTGticBSMZf3Uf0ETAS8uB2ZPf2gIASCuF9X8ZHTpQo1Us9KEWXqt4WBo7pPSzwk1hx1xn9BbDDO3k9HVQGSk2hHIneNqLSEyqI3WkiyHQAjMGwLOBsP5zqz7kDv5hEAITEiAJ8BtIPIVSI1KkOS3dyM3C81JIzDhwp0Pw7asuOALK67QJb4btRSy1uJNFIw0Dq9DV8IZwFRTFaI/9Ap9Y7myX20iKCNe486jymuWJuwnOaJcykXlNWvE2YRvgFCgJPwkdygD2ohGIUE06yf/k1UTfgzBrch0Q2V1VB0b6kZr9EE5v0iJqgnbmW6hPXIM6KQN7drYSa4a6XSbSv0QCIGhJTC0wax4d+aN3s1eRo8AD4GYCBeFD6eF/M0mdYNY4Q7hPmlefm54xAd9w3VB94zeaOd+j4VyOKWk3ELkZngaTnJJBXrm/s6zhxAIgXlEYGi9O5E78+gIyG5CIAQ4daT1uCoV2xKfSrwph0QIjB+BoZU7CW+P38GWEYXAkBIQBPQZ0s6lWyEQAmNNoKenZ441gQwuBEKgVwKCUO456rX2JPXczO/hjZOsTHEIhEAIzBUCkTtzBWsaDYFhICCLWY5RPa1nzvvj4XUesSgJek6acgub+8vcoD4njWTbEAiBEJgugcid6RJL/RAYGQKe0eee8LZHsPTde7e4u1NMBnffLUj6dvu9G909J7DvRrJhCIRACPRBIHKnD2jZJASGjoCnAHtHaVu33K/utnnPAWorn/CnhwN5J4D7pyZcq9CNVB6n4cH/Xt7kXlOP12tqemqfJyZLUWx8P/KRPUzInWsezecW9KrpIdHurhfJIpuabS24P98zijy7zwOXW8uzHAIhEAKDIpBU5UGRTDvjSYDZ9kwdT9VrHkQrQuTGIo+oMWD3FnW/vci2bkfysFqbe/auZR4OPz2hxyqNK9e4Qj89/EZrHk5jbT3Tz9tJPcbQY3u8h1KJOl4T4eUG6vCyeI5wPc6L+JBV4z1KHjNoWy8xeOlLX0q7eNmFb0/oqfu97U63vXHCcwI9U8cTDptnDHp2H7Fy7rnn8rt4i0I9annCGa2H9lpFynjool7VIxbt0Qu/vL3LcxGt9eRlNXXeE5n1wVOLFNqpJxi5Xd+7J5vHInvYsXY8sNHo3OE/4U5TGAIhEAJzSCDenTkEmM3HmUC92tDT9z0t0HsSDJWw8DYDjxj2NgCag8PD2wMmQ+CdhZ477LUG3tpYL22mVDx10EOTbeL9i16PUG+EIBG8UcHLkrxuQvvlOPEySEKHRqFjFJJZNIT3anGQeAiQmt6OSaNoimrxngSSyHMRPbnYc40VelGDtyVYqDoWvHtBNe/E9moFusRjoHllPLKZuDGuM8880y48BtBTjFWe7MO1w4VDmQFiX6rZyhsbPNPZS6l0tTZUx3vCvQ7Ceyfstwq9kMHTqCk88q5p3+ae5eiNY7w7NFNTnoUQCIEQGCCByJ0BwkxT40aAy4QvhEPF+6G8CcHweF8Y8i9/+ctcGt7RTZeUDOocOSvuBQt0iUiN7BneC2krHB5eAeHN0nwbPD3eUOGZe7aVTUyseK+CNzY0TanAAUPc0B+El5iUn14u4d0LXimlZY9v5hpRn2+GU4fTiGggreiGKmzevVBtUmYeqUx+ET3yhT0A2h5tS8/Z3DOOywXFB9P0oXPBtmqSejQK0aMCP5O4lYcrGpp2ahOvpzBqr6+iqyiqqmkVqUfnceQ0LROCEHnphLfE009G3azKQgiEQAgMikDkzqBIpp0xJPDc5z7XK7Xd3MQ/UdEl1po+IAvIBX4a2kKoaMKRkzteJ0mjeGk2ZwaHkNc3quntE2I3FADdwMwrEYHi16lXUfLT+FkvzuR0oXI4TqTLcIpQORPuaLqF2q9NqBbKY1qbUzY1XkC8otyIZPzom1dheHOFhyZ7NRiNqE2pPKuvvjqBRcFwU3mHRu3IWyO8mKKJAHpLvHjcj3/8Yx4pKczqnHXWWVXTi73e9773Na6pKsx3CIRACPRHILk7/XHLVuNPgAeCe4b/RgYMu175trwXJA4jXeOXCuM91V4COiEOLXiDt3ddUTaCVqSAh+zxncgp5mKR6UJLeT+oNrlhyAJpLrSUF4iqL5mXVqAqZLpo3N5pAgtUlxYk2dhK35qXZdJGl1xyiVxgjiLvDOf14SbRlE1U430hobx4i/fIKtKKjKA86mXvRJXKXoIhJ8ljdYyOy0rlzkHZCwly2GGHqSP6xjFDvblB3WvSxeMqRMWD5QVeYl7uNucYsxe5RHV3GJ2nGrFoXOJWNkTYy7NwUAgXpxcRWfslpEok0YudPUlJCIRACEyLQOTOtHCl8iwiIGnmjDPOIEpoFDcTCWDRBGI00n4FmCTV1m1KknA5NrwBqg0N34k4zkEHHUQSseWerSfRRw6QaBQHifgUUUIucB3J55U6Q4LwGK2xxhqUBH8JuePGb3rFLVcSgLhVKt1YCMkLvDRF3BBSu+yyS+2XhCJ03AblJ2XDhaNjF198MfeSgXhxOgcMoSZH2FurvvGNb2hQPI6XhQ5zAxdxozKxxUNjF3wzE8qdZz3rWeJTek51SQyidezOgpaNl2LTpkLq8D3veQ+XlV2r6VOdFK7y8VN5s6r0XFVo/Uaje1ittXKWQyAEQqA7gbwzqzufrJ29BKgKeoXlFpaSdEyyCCeRL9wS7mxitkkfrg7ZxzREZQe3wZIo4zXj4lYHHnggoUMTsPEcJ/SEdBmCQ8t8KqUV+H64YThI/JTcU02RSiJiVAiNUiX2xZWiWdqrLTWnbe/5GQIhEALzngDPcd0xyrk7VI+WiNyZ9wdD9hgC/ROQ0ssbxD3Dy9J/K9kyBEIgBOYOgaGVO0lVnjsTnlZDYO4QcHe3fJdjjz12zt9dNXc6mFZDIARCYBgJJHdnGGclfQqByQg8897PZGtTHgIhEAIhMCGBeHcmxJLCEAiBEAiBEAiB8SEQuTM+c5mRhEAIhEAIhEAITEggcmdCLCkMgRAIgRAIgRAYHwKRO+MzlxlJCIRACIRACITAhAQidybEksIQCIEQCIEQCIHxIRC5Mz5zmZGEQAiEQAiEQAhMSCByZ0IsKQyBEAiBEAiBEBgfApE74zOXGUkIhEAIhEAIhMCEBCJ3JsSSwhAIgRAIgRAIgfEhELkzPnOZkYRACIRACIRACExIIHJnQiwpDIEQCIEQCIEQGB8CkTvjM5cZSQiEQAiEQAiEwIQEIncmxJLCEAiBEAiBEAiB8SEQuTM+c5mRhEAIhEAIhEAITEggcmdCLCkMgRAIgRAIgRAYHwKRO+MzlxlJCIRACIRACITAhAQidybEksIQCIEQCIEQCIHxIRC5Mz5zmZGEQAiEQAiEQAhMSCByZ0IsKQyBEAiBEAiBEBgfApE74zOXGUkIhEAIhEAIhMCEBCJ3JsSSwhAIgRAIgRAIgfEhELkzPnOZkYRACIRACIRACExIIHJnQiwpDIEQCIEQCIEQGB8CkTvjM5cZSQiEQAiEQAiEwIQEIncmxJLCEAiBEAiBEAiB8SEQuTM+c5mRhEAIhEB3Ah/+8IePOOKI7nWyNgTGksCCYzmqDCoEQiAEQqCTwGtf+9r5589VbieYlIw/gcid8Z/jjDAEQiAEisASSywRFCEwOwlE5s/Oec+oQyAEQiAEQmAWEYjcmUWTnaGGQAiEQAiEwOwkELkzO+c9ow6BEAiBEAiBWUQgcmcWTXaGGgIhEAIhEAKzk0Dkzuyc94w6BEIgBEIgBGYRgcidWTTZGWoIhEAIhEAIzE4CkTuzc94z6hAIgRAIgRCYRQQid2bRZGeoIRACIRACITA7CUTuzM55z6hDIARCIARCYBYRiNyZRZOdoYZACIRACITA7CQQuTM75z2jDoEQCIEQCIFZRCByZxZNdoYaAiEQAiEQArOTQOTO7Jz3jDoEQiAEQiAEZhGByJ1ZNNkZagiEQAiEQAjMTgKRO7Nz3jPqEAiBEAiBEJhFBCJ3ZtFkZ6ghEAIhEAIhMDsJRO7MznnPqEMgBEIgBEJgFhGI3JlFk52hhkAIhEAIhMDsJBC5MzvnPaMOgRAIgRAIgVlEIHJnFk12hhoCIRACIRACs5NA5M7snPeMOgRCIARCIARmEYHInVk02RlqCIRACIRACMxOApE7s3PeM+oQCIEQCIEQmEUEIndm0WRnqCEQAiEw7wn89Kc/ffrTn/7Zz362dv2a17xmm222+dCHPjTve5I9zmYCkTuzefYz9hAIgRCY6wQWWWSRX/7yl7vsssuvfvUrO/vXv/713e9+d67vNTsIgf+fQOTO/88jv0IgBIaGwF133fWXv/zlsssuG5oe9d+RAw888GlPe9omm2zy85///Nxzz33KU56y1VZbXXLJJf23ODpbbrTRRo9//OP196CDDvL92te+dr755tt5551rBH//+99///vfX3TRRTfeeOPojCk9HT0CkTujN2fpcQi0Evje9753++23t5bMyPJtt932wQ9+8OMf//gA93744Yc/6EEPevjDH843MMBmZ6Spvffem5lfbLHFHvvYx26wwQZ33333iiuu+IAHPKA6c8+9n7aOKVPNd1v5KP68+eabxbBuueWWX/ziFwsvvLAhzD///Ao/8IEPPOtZz/rqV7/60Ic+VIVRHFr6PCoEIndGZabSzxCYmMCnPvUp1sI6rgLKwIdllS0xce25VsqSveMd7/j6178+qD0ce+yxb3/7288777zPfe5zW2655ZVXXjmolmeqnec973m0y0c/+tHvf//7N9xwwwEHHFA9OfLII6W2POMZzyDvmr4dccQRW2yxBReINBderqZ8dBfomz322IO4caAueO/nd7/73dve9rb3vve973//+2X2fOMb34BldAeYng85gQWHvH/p3uwk4KLWx/nRZwYJ/OY3v6EkmKWFFlqIoXr3u99900037bfffq7RZ7BXrbs+++yzr7322le+8pWXX345u/g///M/q6222oknnrj55pu3VrOMpwiCj4H4WGBEGZ2m2r3I7/azKbzzzjuPPvpoZlj9ffbZ581vfvNKK60EhW3VgaIWbOJ6/bDDDrvjjjv233//pkEL//73v9/61rcqX3TRRd/1rnfxZyiUurHXXnuRRy9+8Yuf+cxn2ovGr776aobwwgsvxPxRj3qUrdZZZx2GcN111+W7Mkbeo9aWR3TZ4bT11ls/4hGP+Pa3v73KKqsYxTHHHLPvvvty0QFL9AD78pe/HHYkjzvuOMM/9dRT8R/R8bZ220Q/6UlPIsc/9rGPGabx+ldSYdVVV/VN0T7ucY8bBj9la5+zPE4EZtKWjBPHjGWwBFzmOhsONjLSRw+dmk8//XS22bYuQN/3vvex93NV6/zwhz88/vjjm5P+T37yE5aP/19yg4WTTjqp1fIRHLQIFaJ722677TnnnPO6171u1113lRO6/PLL//nPf7YJRwJZ8+tf//oNb3jDIYcccvHFFxNtLql9Ex8qXHfddUVmzz33xFx4xb6qRHBhu+2223HHHZ/znOd85jOfkXfyxje+cfXVV3/IQx5CwZgj5nmttdYiuWTYMNi2IoBqW99kDUHzxz/+8U9/+tOnP/1pPxWSYjYha84///znP//5+sPySexwZf+iF72I7ZfJ8Y9//EPN9dZbT/Tnb3/720tf+lJaao011mhaHt0F8/LsZz/7mmuuacJYUnmkrSBA5BlsuTee+tSnCng5/KT4LL744hCN7pCbnpeP6jvf+c7SSy9N+pDXBmjtb3/7W98O1z/84Q/jMdJmyFkYLgLOnvlMScDFpavPf/7znwyMf1pnK8u33nrrlBuOTQXmzaidofobkTsyXvjCF/ZOjAFYeeWVBUcm3B01gL+PXvEfCHPom3lRmQ/gqquu4upwPvVTTRMnBdLy9ddfr2b1wfKXvvQlIoANZtG/+MUvTrgjhfQEiXPyySezvv51v/CFLyi0Ly3svvvuvCmkg5If/ehHT3jCE1hlooF5Fk5SWB+FSjhgXMT/b9k9QhUKhSoIAptUbzXOti2wwAKSYKrmE5/4RDtdYYUVHvjAB1ogFGqYtfYjH/kI79dpp53mp4gPFwtNQ77omxI6o/wH4PzgBz+wOZlCZOiwZbEDHaNOXvKSl6hMkXA5CEUJtbDElJNC7VQHTAQrpRGFZB/BR5FYfuc732krCz5IslUVr6kSuo1TB39zBLKwlHKGXPvGa+64owiaqsznoVdmpH7Wtzbl7nzyk59sLRz1Zcftq1/96mYU5TPj7HGz0je/+U24HMOO20svvVQ474QTTnjYwx528MEHN/VHdMH/0TLLLEOL6z8Rv9xyyzkqLJPUlsl03h0oRnR06XYrAf5I/8s+rm1ay2d8+T4z3oOR6MBXvvIVF77mb7fddnP1ee9U3ufzn//8SHR+IJ3k2EDgwx/+MNvD4dG0yRvB6LoqbUrcR6OOj4UqdP3q/M6K25zD5mc/+5lyyunLX/6ynz5HHXVU1WTL5TFwPDg58iKwpk2zrQvNv9OPf/xjjd///vdntiUEqOPsSTHIBn3LW96i5JRTTjFZVIVVJAtBINPFMrXhepoC8/2KV7zCViWJWvdSy+RIXYM+5jGPqZCNcqZIs+SOnlv41re+5QqVq8My+60pMRouFjVdrOvMmWeeSWYttdRS7JlCvg01ScArrrjiZS97GQ2t0OGksDRB5TEoZPmsJSn4dRBr1YtU3ZOf/GRHo2r1ER5iMOgD7SCj8IwzzrBc0gRnuk1hpfXY3LK5E/yyQJ+Rbl/72tfcRGMTJlahzwte8AI3ENVy8y299FWvepXOI9NMPWmCDynTVLNAwJVg4nySl0riLLnkkmxb1TFHj3zkI2vZWLiRWre1zCIaex0wbatG9Ke5cIsWZeyUUsqV0KFZHYE8bbAL4Tl+KGDeLP8gPnJ4S2SP6JCr25/4xCccSyVoDNyxWuWEryOcyHP8tEr5kR7sLO98c36O3BnVI8FFrYvXska87q62uXymOxib8N532Yo9cJPqBRdcoKazgGV7FFywiQs+zl7Jfby+zgv1s2w8q+BynPnp0jLzJkNi/fXXdzdsY6KIFSXyA7g67I7t5MNgdZyVNt54Y6cndl2bruw54VlBbgY2Wzu1IwaSKHFxJlPECUshR4Lw/H3v/fDDVzXyhdZZc801uQfY/ve85z3KiSGtuWwF1pm9YOrA/e53P1kL4iPM8GTeHV4HV70kjm9N6X9ZSn6LzTbbDCVGhQairqxlv81X9YQxZuBrWXRmiSWWaFBUYec3f4lOGrsMHs4VThR1nKNdeTPDnCKAlHPIXKhG96hQqRiQWqY8qKvSTCV31LRrnac8dthhh9qpxAWbi++QhtSeU0aVkzhNnSqpb1PGAVa7UOK4YjAsyH0RpaLzLMOozZI7wkmdcocGkjmhJizUm6gZ+aiF5jzlGDDLKrR+7Gjttdd25NArTXmn3KEFCUEqhyHXDaxUNlnGzv3GC0UzGWm1QFQ5ahzqBGLTpgUHGwXcWjLSyybX/4sD3hyZwRoLTeP/i/PDfdqlXwUH/W8CyCtGFs/4kB1m/IJkevePE5eZnfHepgMzS2Bo5c44hISdSefBx/ndxWvFFJyt/PMzzPbrlERqML0suiQPLgSX8oQRp70rV0l5pAmbYVmkgGtBiIEFdQ0niDBht53fmVJJmu5iEBpwGWSBuGGeCR0dkDPh/CgUwtXEWjsBMf9iAex62ZXOZtkw/SE1dEOypKRR14su/V1nyw/VWxf3YiIsIqtjCBwVb3rTm5gZW/HlyDZgiqgH/naVm/ZduGuK20NWB03jZK0+HcPkEwQkCPXGJ0TfuGzVSc361OYGiJhC/5ksnEes0hPuxNlwww0RUAde/oxmX60LFIZ+Pve5z3VlbEHIRnanCgyqrSQ9WCZ3BFNcJVs7YTv2y+6Sa60tdy6z1uJQWnCRXbpHHYkm5IV5V84SmP3ODZV4uhoZYTYpBoGbkq3KHT/wbr/99maWH6h1WxAe/OAHa1kWy6abbjpZpjY5wt/G5cOVVZvTDYQLCWWKSVX8lVfHzBplSXkQow5OvbLKjrAy6Q5OP21FjDKxjjQ/6TDBBWJXdEkj5sVcN12VeyHRxMEm8qWyjyPTse1QJ2JUJivZdfqJijWbEKkDuG/S2XFC1dF8qhmIQsew/wvVZCjrgBRdx5tyx5J+1vHg5xh8HEIyqAwEjeaw9L/s0zo6wtpHCaXeWj5Ty04CDrBe9u5cYYp7qZk6ITCPCfyf6ZrHOx653TnpOxEzD9wYbJggSA3BJRrd4CzGsrq4oRgYide//vXMJPeGqzRea3ZLVEJNQQpXdcIc9O+EcoeYEFBgyJ36GWN7IReYDVpHpgWNwvRSXSyN8yOJw0WsGxwhLBxhNBlVCsa1I7PH1DEkrvLVVGhQAhOWCQUqSrcNjS+BslHIN0AxSKNx6cl82l2r1uFMohXEg0RP2H6G1sAZLd4d0tDmDHZTX3mbsKB1WF96BRniz0W/Tab1AYqniocDYU6dtm21zzdmFjTOZps73KiHv/71r201p/xp7MioZqE2N4+YQMelQagZnbX1DZf4i2X78iEyDJx0IOmYeVfqZgoWOpg4Vm6izzrrLBMt/Mei0IjUISFLoJCSdACdoY65EwEhQB0VLCWTqQMUWNN5bjnACQhrOYSoSasoUULWkWPZvGBFctWhSyrVnJpxa/nnyLLK5qEgDz30UIXcQuSU/BtK3fHTyB2HjdAbIVITrabeCld5Og4lZEEnFfq/oHd1HgeOnLpUkD/kn6W8pJSo2JaaHB6ONAdnHcPNYeOfRU1+QXVm/MPRwmeGRveeGDLBWmHEzprN0DB0iHZWGM4SB4//JvPYvXsEnEuR7nWyNgRmikDkTq/knZ6YB7Ekp3LODHa0tmTvXac60TtlVyyGy8TlqUscJscJ3cmdVaN1XMjy/5MvPEPKJ9uxPFB2kbtCZIGdJiPUdA517U7rWHb35nSvd5lAzfrYXDimLiuNyM/61DLL9L8F//krNuTy3bZVaPgWfNucdGAmxWhUcKHvYp25IuAoOSGeqq/NnXbaSW9ZWaE0F4j8GfI0RcqIQi0wbzQWxw9QZSBpOC2owPpyGBBDlBlnWDXY9o0k1PizxLWKUNPn8io5NdOUrDU5ghslwW9k1jghKANagVoiC+gYco2Xpa1xPzGXXMwxRsgaBZcVPhIv6CcC1JCJTsLU7jjw1a9vFfjkLBudFrg6CCCJzCogpgUKmDigOfRBnEsPzYhuaMddVLI4SSJ9Lm3hoDLXWMFOsaEHlGCTo8sR1dpnjXCtmRo7NSMkV60lSlqrWebg8U2460CzymQJbPk0JRaoJfKotaRZJmt8mp9UC8VpipsSC40Yai20zMy3CjUly977aavmJ3HQhw7ubGcgJRwt/KONXpmsTVNgNJOtHdFy10jOXSPa+XQ7BP5LgDHLpxcCLtNZJq4IlZsUS54eQQpqprJYXANVUy5J8WVEKYxK1uGYYZVZfZKI0XIV232ndfMzC10ptC79nXHoJFu5xCQLLFAYPN6sKStegSqhhAmbZR2Zf7dFcMlINGGJeW5czTP8VvEcyCxhv20r8cUoFDpr1+08HEjKGWYtiNxZa2i8QZwQFhh+F99lA2hB4QxAGGlCR2Fzh5FVoksECksgKZVAZPiNguFn+QCsZEymmmbisyFiIFXOtE84oiqkD/hOinCV6LkeMr2VQ1OFJVzQM3w3Z5kFH3FAy0RVk1JdlZtvBLRsLYFCanDk8HZowbZW+bY58g6Jmk1jV1JJSAqrWtNa64LJarJehPMYkgmzc1o3aV1+9KMfTdW1lkxrueQOKaOH09owlUMgBEJgSgJDm7vznxByPr0QoBJol0rdlWHARNmKk58KqUt2DhvZM8whW+hT4Q/36bCCaipn5rmFXLsLZEiY4Dbosl/WmiihcqqO/VIk1A9/Rt2nU+XaZLc8FoUPWU+4TyZrkwJQwTfBwTFQmcVCEi616RgjEn+xLecEmUKZMeSUB78C46qcFRczshfOBpKCkaZ4SEA+Eum3wiiWCQI1mXyqSIYQv5SfzYezSmUCpSmxwB9AeLWWTGtZei/Xy7Q2GYbK+HBaSGPic+KSEbJxVPTeMTeLgd97/baaYoj8UiZoyjTttg3zMwRCIASmJDC0cmc+XXeNnk93Ai7u5ceQCKpx73OrCFII5ZAvMipIGY59IQzXzTJ/uT0II4pHBTGpJkJPB1AV3P4CE5w38lWbVZ17d7+SduppLrXWVnwGekIG8TM1hSIy9lUpBdbSNK1RqqZlHg7VfNucl6XKzb4SyyQO0WOBOPOxUAEUm2itqa/9pma1MCPfxB+BJeVFf4itCcc7Ix3rfafidKWV3YbGxdXlSOhs05FgFjrLUxICIRACM05AoFw2gm7I3+Chn/H+NB2I3GlQdFsgC2TnlGLg7eDGEEJyge663HW2oAC3h3tbREbqqSfd2uptnRQWmc5110xvW8yiWjxP8kZNCq0zZeroLOKSoYZACITATBOI3JnpGRiR/TPk7oqS2uImL8Ggum9lRPqeboZACIRACMx2AkMrd+ISH65DU6TJgyv4LYS6onWGa27SmxAIgRAIgZElELkzXFMnh6O5hXi4epbehEAIhEAIhMDIEvhPdmo+IRACIRACIRACITDGBCJ3xnhyM7QQCIEQCIEQCIH/EIjcyXEQAiEQAiEQAiEw5gQid8Z8gjO8EAiBEAiBEAiByJ0cAyEQAiEQAiEQAmNOIHJnzCc4wwuBEAiBEAiBEIjcyTEQAiEQAiEQAiEw5gQid8Z8gjO8EAiBEAiBEAiByJ0cAyEQAiEQAiEQAmNOIHJnzCc4wwuBEAiBEAiBEIjcyTEQAiEQAiEQAiEw5gQid8Z8gjO8EAiBEAiBEAiByJ0cAyEQAiEQAiEQAmNOIHJnzCc4wwuBEAiBEAiBEIjcyTEQAiEQAiEQAiEw5gQid8Z8gjO8EAiBEAiBEAiByJ0cAyEQAiEQAiEQAmNOIHJnzCc4wwuBEAiBEAiBEIjcyTEQAiEQAiEQAiEw5gQid8Z8gjO8EAiBEAiBEAiBBYMgBEIgBEJgXAnccMMNCy200KKLLjojA7z66qsXXHDBhRde+L73ve+MdCA7DYGGQLw7DYoshEAIhMBoEPje9773uc997rrrruvS3VtvvfXLX/7yuuuu+5znPOezn/3seeed16XyXFr1jne8Y9lll33Na14zl9pPsyHQO4F4d3pnlZohEAIhMBQEDjnkkOOPP/6JT3ziMsssM1mH6JtvfvObX//612+66aZbbrllHvhX+HLuuuuulVZaqenSpz/96Ysuuuhf//pXU5KFEJgpApE7M0U++w2BEBhJAj/84Q8f9ahHcVrMYO8/9rGPkTvdO/CWt7xl1VVXfdKTntRW7e6771Yy//z/de3//ve//9rXvrbllls+7GEP++AHP7jBBhu87GUv+/CHPywCtfvuu19xxRUHH3zwfPPN98IXvvChD32oDX/yk5/Y9fOf//yNN96YijrooINuvPHGrbfe+oILLrD5WmutdcIJJ6h2xBFH/PnPf15iiSWuvPLKBz7wgW19yM8QmPcEEsya98yzxxCYmMBHP/pRV8YPetCD9thjj4lrDHGpy/pf/OIX//73v/vu4xe+8IWf//znfW8+hxteeumlP/3pT//5z3+2tvP3v//9Z/d+/vKXv1T5d77zHab9la985VlnnXX66ac3fotLLrnklFNO0f977rmnam6++ebrrbfexRdfrHz11Vf/yle+0tpy6zK5QEOIOj3ykY+0N6ve//73L7fcch/4wAce8YhHOCT23HPP0ijiUy996Utf/OIX77XXXq0ttC3feeedb3rTm/7whz8Y0c477/yKV7ziqquuUufcc8/dbrvtqJltt932bW97mxKzZl8OvG222Ua1b33rWwalcJ999ll88cWNbrHFFjOn73vf+3hufvOb32y00Ub777//yiuvLD5luq39n//5n1//+tdPfvKTv/3tb3MmcTtp9qtf/eq73vWu5z73uauttpqdSt9p62F+hsAMEPDPmU8IjBwBJ3Sf6jZLcMcddzgp33777SM3kNYOM5avfvWrnQWe97zntZYP5zLs7GLTt3/84x967rr/tttuk1Piu1apJlv25ptvbmpaqDqthddee+3jH/94MoLDwObdp1Lmyvbbb7/jjjvutNNOv/rVrzR4wAEHHH300RYEbojFKvRTTfrgta99rcqsshIfNVnr3XbbDe29995bCZVDaug/s33kkUfeW+seEuHhD3+4Qh+7q8IDDzzQT9Lkve9972Me8xjOD+V/+9vf6BK64XGPe9yhhx5aNembTTfd1KCkCdvq8MMPr/LO7x/96Efa5CbRggXuFv3fYYcdOGCU0A0KSQ0bcrEQKxb++te/KiRoOltrSggRCqb5WfGs173udUrMyGabbUaI1FqeGP0kbuqnf6UFFliAVPrIRz5C/ZgL9GqV+TVrxkuUP/OZz6xC3aDtiLb66dt4dbt+EmfPeMYzmlVZGHsCp556qoPT58QTTxyqwUZ017zke8QIuGZ1wX3ccccttdRSchQ22WQTJ1zeew72ERtJS3eZT59rrrmGRWkpvg9jfNpppwkTbLjhhq3l7Ld4AQu9/PLLVzkLzUoJPcDylKc8pQpFE2y+yCKLsL5dQjB0CT/E9ddfL4pxv/vdT2WbEzQ/+MEPFLpA52bAmcEjNF3WC15o9q1vfSsbr6Yre99yNcoistbVAW4GNQ3qjW98I9dCtUkT6DwTbvMXvehFCiXe8pc4OQqgGP4uu+zyhCc8QXnnx6RLgF1llVVoXEJhq6220uH3vOc92udOOOaYY+gGxvvRj340z4qYCyHC9cKW00Za05m3v/3t3Bj0CocEb41CqohOYsW5T97whjfw38iJsYry+NOf/rT00ktrtnry+te/HqUPfehD4lm6irO9PPWpT7U7mTQ8IhwbRMmSSy75kpe85KSTTjJB/CLyZkxKtTDZt4gPztYal9ae/exnr7/++m9+85uV6BV9dvbZZ5sLoSUlQE3WTlOuG2eeeWbz04KJe/rTn25BjMkuqL0zzjjDT4P1j9OkATlUQCN0LrzwQuJPeKsOsApsHXvssQ5I4ypxZvNf/vKXjoEmN0hv4XrVq15lVT4hMEQEhkp8jVZnnB9br26HqvP65mzr1Oak6UQ5j/vmNhChgbm6U85//0VMrL2QPpaZtGaP7CWb0fx0/nWF6uqW4fHdlDv7O3GzMU2JBT8VMs++XQTXKsaSVbO5ppRYeNaznuXqmdUUfWBcZS20NtJ9GRzbCigw/4IIlEHTW6vWWGMNjbe2wG4ZIANvpESJVfrjgltmhvLGFWRoWmNW68ZjJkdNR8LTnva0l7/85QQKYdHabNvyJz/5Sa3ZBWvn2h1DFcRTKDBNcW9omdRg7EvfiHcY/oMf/GD2T01dUkFeS2uzXD52ChpKNEStoksoD8vMJDlSheUcYtFbN59weYstthBMIXZN38knn3zZZZepJsiiWQtIsuVHHXWUZdbaiASk7M5W1ZqdlkfHiBp0XDvVAgUAVF2VfvGLX9SUDfGnI2uO+F202Xp4cywpIbl4cThFDLM5bGBv9lt7n/AbBC2QrTxAFso1hbnAUNUXS1pnnXUsE17lfKrgWndcdq0DzR4dHnpIjVUJ3XbYYYfVsvyetrOEvegJPg95yEMs1Hj9X/Oc2eTHP/6xQsdVbS6nh0Y0y/5r6vjUsgpm4Xe/+52oHIywV+V8jz2BofXuJHfHf2VPH9aUPXDpXLVd+bFJrpt72njeVmLhmFLRAZdrTFFlDs6zLpACLq9lG/SyR0EN5/TLL7+8l8qtdVybOoe6vFZYFqhZyx67ytcB1+UKOQCEM2Qq0H8uUp3WiVTlrvK5BO5///s7WbtUrc3dRaJlhWr6FltRrh2OCsmhMjCcwZUQBKzsd7/7XYYKagkKzaVttdP9m9WxR1fqpSGEEprjir1sS3Rw/V0ai7Zj3hhdjXOrMMmcE06dTGB5g9h7k87e0HacJSII7G6ZW7v4/ve/LwKi/mR9427Zd999bVjuGRf3aop3MPbGyP6tvfbarBdPBrVBV8nhYA7B7HKHs76x4m6H5kqp9BGCCckaI2eV+4Ym689k5d/4xjf861EnVN0f//hH452sZpXbu7nGoX6aKaEWUSqsPv7xj1eh49C1gRQWh66gTLlARKyEdSghUmbFFVfEvCq3fTtglNC79AQFpvHu94e3be4n9UBJMBIO6WYtRKXptcnvZbBWge8/WtJMeWVIlqZ+24L/KdN9/vnnUx6f+MQniHhHHQi09ac+9SlONYec6bOVM5uPgJSpd4pzzCikchzktKyb2JuWleBD1AqEKaQ1HYTSnG1rQ+07MFwkWEWLc7VS8zrs4DFftmrayUIIzAiBBWdkr6O409/+9reC/f6BuazlVPp/dsrw7z2QsThROuE2zmRtOhc7cTB+a665pm8lZIQzl2vlFVZYwRmf29xy595ZPmcoHgLxAmtZFJkKVY294exxpctIs0N0BinAVDsVOs8yh1z6ToJO+s5NdXplOF0O8mZrwYWda3Tn/c985jMG7gSnBakALuh1hkX50pe+5BoUFlfV2rcjg3LtSyWw0+hxzjuZOpPut99+dfpjWrjr6RWn2s6xdCmhAFhcFXganLWZ6qpMghA0TALDzGidc845UOgzP4RcCgrAWgEdZ21jYXrZSw5/16nqC0A4ffNSMCcMjBE5ZeuwrVz0My0speEw/2rCxRC6n4WrgFXo0tXOVa53zRFVwcdDSHEOcSSUCXEMYFuCzIbCK6QbVjrgMMDZ1FNvOixIpEsOBhf6LI3KJJ1qJJqxkCZm2RAMBH/lhM4DHvCAyayOwxuNEi4aBwc382jh3e9+t8YdopjX5pqqY7JzaK0lZt/hYSym3rjKYVC6sFFdBihw5mipDUsS2ZdBURsT7sXhhzkjqn1TT5USsgJtRIZoixbskRilVOrmI8cYGy8M5zKgUaUmkW/M5HLa+RcTnHJ4S0aBFzHT4VhF2JANgdCheGpbOkkmECvO9uu5w09Mx9HF12UrhOmwUuH6RhAYl6boWhG0Vjity/ZOkwntORT1CigSygUVQez/wgEgpuY/1H+rf0ZHuPa5oPRKKK21ndZl/1MOAC4i/6ekWP0766GmcOO9448p7Iam3MzW/FZNo/A/q31gYalglgWarKj6xtnNXNSYnvhpTjXSnMRIZ/UhEhdr7ViWQ2DGCDhG8+mFgLNPTZLzhetay5///OebDaUsODk6ayhhbJhwIsCpiu33sUnVdDpjQX2c0aqEcdUaA8Zwui5kTSkMq1wN1+6aDMeKIHBa1NWk01ATAamm6psht2FnbEU7wvPO1AwhwUFLuaa08M53vpNuIIMYOV11OiNZnJr55Jlkp3V71LLhMBj0kMtQ7hDddiovK0v8lXumnPAqS7xgb3TPibWc2zZ0GiXF2CRWuRI81fTT6bt6Pq1vVo0d4jx3hjU0365QtcBmgA+jkeJQTnjpDrSFtbYyZDKo9kU+qkkAOVlbpZBtIA4sGIKLYAuCLK6zywZokNUxduU+VI4oQy1P95t1ZCpqq7agQ2tqp+tmO+UgqZpgsi7mjtIiRwhTNolaqmPG3Okb5gbFzEhwIeZsXlEk2wrryCaZsKtW6Q9VxL+lTZPOhqnJZtfm7kzWVB1XjhafakfGiQPYsl0znJSHHFVyBBkSSpsOKhExmUB0CRPoqKBX9J+KcpgBSzTbnK31L8C+qkPHOyaNtHbR9l1+GplMLjwIWb43FWgayVs1WP9NFlh6WsqCY8PHQkXQyufXFDb/R5ygRk30UO21R4eNnw5XbrMKm1Y5kvQ6udAEhpQ7PzhmyO6q4xsr908ZI7VXadTNqs4FWBAgIKyq/+vWb4U19bWhalWzs52UhMCME3Ai8u/mU0HhGe9P04H7NEtZ6E7A2dP8sYXO5i59LFMzNmEmXR2645QfxQWfi34uaCdTV04uBF3ZuDCqEyhNoJABYJ/UdHq1ecXgXYdVZl+ZQNrCtqLd3NE2LxNlRwyz/ZJWtnLl7QzY2efJ5A6VQ5DVHl2DEiuWeQJ8C9C4PKXVnPq1WYUEmTM4Scf9o47RMQbO5gIoLuDqng51GC1rfTRedsulOZ0kzFfl9W0sWuCKoCFolNZV/S2jQdDYlkCBF5aSO36yxNJIeaTMQpvcUZ9brtQDI81w2oo33uYld1A1Zewi1KUhKqeEEiUyCFntU1TV5wnlDrvrAKAzqs5k36ygw4bzqeIp2leT1HBzFt1J2vIwVeyJHtUl2tSHS4OeEK3jXsKTGKp0Ud4LmzPA0nu1QF6YbsJUIdFD4XEw6DlnUmm4CXtFJLnop29UIyZKzTvSRCJAc6XOzWByyQWOKE4pql07/BYwOuos051cMo5hZPRBCVVnmT7W28c+9rGUOrelcp1Rbo4c6lwsSnyge8ELXqC3zpKWq7Dzm4iB19jJKSqtqWCC8CSgeXEEcZTLYi7lbZZdcugnDWH2ecV0w/+jqSTo1W8ayUIIhMAcEhhauZNgFkvX08fllEtPasZ1qss1Z1VXn7bk4pbdSSIwM8y8cyjbwH/AEc3tUU5pplRNjgFGzgnaZRyHuRaaHbt0ds8nYaF9hYwEjwKBxR0i0qS+QrpHB1wWO4M3G3YuuES2o+qbtXbkylL7dAy1oYQlc8FdbXZuPlmJIZAO7L0uGRpbpSafTYVgLOteSTfGXiypchVBsyMhGCkaLBxDxVi6KOc5cF1e+6IqXOLX9fdke+8sr9iKbZkuY1SB1cTK5TjpRvGYI5pMN8hTRo7xZu2IMKa0YmoSd0SpXIKXD4CvyLKOsaPkLFxVYlzcLaSAieOy4sBgpEGgQsxgBb/EXDgzSFjdYGgdIWbBqs5uNyUqC6NQBlqjGu3CKvFKXarbgCUIGxpo/HxoUz8qECKOLqwoYD4Y39rhhABZZygPQlZWB2eVgVQis45R0hQtGaHBpgOdC1wyPm3ljhaz2VqoHY03JTrfLFNdPs1PCzSlT2tJLetJZ2f8K4kldVZuK3HJ0VZSP4UIfWqZh9ICTSNHykRTihKG6C3/Vo4Nssx/onO6ucbZ8TlhgykMgRAYJwKRO9OYTRqCcfLcCyfTRk84k4qpUwMCNNrqYrZV41NxXd4pNZgQl8WuzstEseIu03nRGXWeBtesTs1dWm4dAz+TE7oL39qEneO9IHec6F3gqkmOiP2TLJbZV/qMyWRNORvIDtZawge7zhKIVZVCUpPMIrYYP33j1tIZAoLZk0PAYFB1lJBQHctK6gl/uLBmUaTLCGHwKDAw5Aj3gAYt0B/VZwaJ9RK/EIGqkh6/kbQt1wWNYix8DxQJ/xMFZl++eWVoDr3FwcDt0ailXlEYxuVyn+/KtuQXsaK3hILwEPeVsZTPgLIhQEUxxCyUc1+RpBwtSJJxrDXV6DAQPNJCE+2yuSmDpftAHANUl45xLQBblTl1SEaN+6nbjRl2yLW1pqZPW6FgpU9boZ9m1rHUWT72Jdx+VK+IEh1s0gsjB5KLCge5Y0N81mEz9hwywBAIgf8QcFbNpxcCfCRkQROIkU/KWNpQxoDTKGcAu8UTIJ1CoWt0bKkBy5IQpSJaEMPiB7IgymCtC3fL5RFxVV2OE/pDoWtcwQjGW2sEFkGgfaaR9aWWOFToA9Um+zClomOuZflRmHyCTE1ahNqQFaFlisS5nm+AFtGaEIkFTn5qRif5BjgMGGMfaRZCV8yD0bm7h2GmSygAUkObhsCuUx7EhD7TVRXkEroiEQzcN0ujJkVirRIWqDXQQysAK0l2srHMy/JywvHE1k6JG26eZsZ77AmlSHPwGHWvLwhIJIkT8cp0r5m1IRACITBCBIY2mDUfiP9RPflMRcDVPBFAQ8ic4AIR8hd0kGbLlyCdpdmaQ17OJgEhNYcngJeF24Dx4/bgV5DzqCZJIYmHP4CZF9EgMggpfgKX9UI8SlyJEgGCWRwJknj4FWzFQ8PjoiYB4TkZnbGApg8WNEUtSYDgwxfbqlUKeVY4LTTC1paTyX4dAwpJFl3y07e1BJatLFAkfDm65CeRpEv0UDWojvq2rZ+j/g0IdUhWir+4R4lTyh28XG7TGhcgiNVdPF02dHgI8IFpgkjYLjWzKgRCIARGiIDr/LpvQEDfGXV4eh6509NcsOu8IyURXPFLihTvIALc0szYywhpFIA6JBE9xE/DF0LxuF9JqgdvkJiCmBFzKBZGcJAOIjsyQ8UsXOuztbSIRBOpJ3WDaE89S6WBEjCV5s5cmEcyUYItRTLQPaSxEAiBEBhnApE74zy7czI2t+RIInHbLReLHB1yWEilXClz0my2HScCEowEQIUm5Z2M07gylhAIgfEjMLRyJ1euM3ywuaVL0IpHh6+I48edRNE6vU8JD5kblNx23gTset92ujXdFi7OyI3ndn2p5dPdvMf6HIEeG+MOI5ngtYlQqYQnwS9J5ZE7PWJMtRAIgRBoIxC50wZkXv8U5HIH+7ze6yD2R5xJ9xHLE/fpuz0t1I1IYkbTDRt5aIp8JtnQnvzbekeSUKObsGREeRZc0zHOMzua7i6azd3J5e4tcS4l0r3rVRLN2gEuyPsha5r7vLQswdzHU4DdpjfAHaWpEAiBEJhVBP6bczqrxpzBDoSA58HIOurlQSmT7U5Ot/vC3Nvlw6VB+kxWc8Jyt9y7EV0CuGcBt1agaeoJja2FHg/Tqn5aV0257MZ76VbunqOZ3EvFATPlJj1W0E93q9E3TX1PzXEfu8T2piQLIRACIRACc04g3p05ZzjvWmBu3Q7WdyKzbblkpFf312O3WAu6cZzU5h7v61b8vm2/vGwPzXOTmjRtgTxv+JIMTv2UD4MAshd3lsnpblwd9uW2bcOv+55E/dz1ZrlV7rhhXtSJw6luZ6uuulXe0/kEoYgJjXhMgDa9VsLTfkkZmTGeziIuRg+55a0NDmgeGez+uFe84hVW6W25o9R3c5zUZg0KpbmTzlMDPO9HTQ9K5rHTpuf+2S/tQtjJW0ceQw9NxtBWHtvjGUjutnPDv6bqrRcUpC65Qc/DAtp6kp8hEAIhEAJ9E4h3p290M7Chl1SX0e1v3541JyzS37YiRB4eKGHW7dkeIySbxHMRKQ9W39snvDGgXtFcjXtOjxTsJvtkwj3qDEtPDbhTkWn34GAvJaASiAO30NuEgOBK8VaH2lzyiocEegwjDSHiU4XEAe1S73moEo+PIzvcRt6IJOWkBv2kt5455D0JxIR26CoyyFoSygLR07zdsJqqb7rEKs8gqJ+eIuixipaVGCBPDMVmILrnWUdy9OpF4vYl8mU41JiheXiBcXnJhnu+KnaJj6dTuOldfjoN5Pa9at8DDnSSKq2f+Q6BEAiBEBgIgXh3po2R84BnwrNSZIfUxp65x2JxUbjKd7e55+J40E5za7qb2BWK1Mj/aH1EDQ+EEIlqlIT3M6jmWX8e7OvOrMre0CDrKDRjR/VoFm+l8ER/D/ezSjl/AMPvRUu77rorr4aH/Xh9gc+EQxJ78lxBPfeoQ1txddRjEj1zlt0lAjwjkVui6XZbIzrPqOu/h+/ZnF/k5S9/OQ3hznlignTQmhyaet2Bxwvpnqa83ku0S2Fba34aGungIYq1ijrxoEVW371ptSEp4+0Q2lHBQ43106OTeUHII3wa+Hw83CFeu1HtSFsWHiIyyJQq8S2zR3Ixz029UKzK+ZZE0Op5ifwu9mtQzSZtC028iRCxid4arwfnuKXOh2TxDEayj2Ayj7a1O2+Vkphl2XD8rCdPwuVxi9V4OaUQIIAMtm2P+RkCIRACITBAAvHuTA8mu+uxOp6m4xH+HiFoY7afv0EIQxKJC33v6PGyCD/ZzvpY9pYrr5jwbof/LfvPX5W5RlhlMqXe8cQq01ICH7JiVWAI5abYkZc32RGlwmHAM2HBQ33oG4V2p6YNWW6JIBwVCif8MLQ8B5QHnwTDXK+W5GLhqiGA5N7yozRPw+xswRNoZMsKNukh2085qUPDuTtaH4ghFTyAWCEfBtHmeULkBUT8QJ2tdZZoiiYAipITs0MGBAGpUi2EkWW6oe39TZ3tVEk9h3qytVVO4ngWFvKkqhCVt2R0qe+FGLUWOs+V1kkTyg3TbEIG0Vj8Uo3MEoaTXdRUqAXCtwQcVVSvFVNO5jqu2mpO9lMorRSVCqSkuBi9O1nllIdACIRACBSByJ1pHAm8Fy7ZGXgBHcasohI//elPGXXvkeCh4SPhafCiULZf1EloQ+vyOagB9ptDQkTDK6AVMm8MrULZG1rgDqk3+0jsYPXr7eskhRAJj4tbkdXk4CEgOAx4MrxEoiI+CldZZRUuDa+A8BJvC13Gw0j7qEA3+FhgLzVVbgaRoyYvp0sjratoFBEuJbwdyHByWOYmccO28I07pxQaZusmzTJ1iE+9ErUptGD4zHn1k7SqYJb4FG8KgUJytVbusiwC1bqWL80sVNxKCKlWmTVagQuq8mZa6zfL3GAEnJHqrewiN4KZAl4cW5GJps+Tlz05qdRS+ZxMsTcxqVyOHHBqv8YlymZEyJQSkntkHpt7vuyUGLUVxcxT2LywU/hMaM/x4AZ1arsJ3nkqt72j3fQ2CyEQAiEQAhMSSDBrQiwTF4oHuTqvmAWXjCRW9bxxWpClrtRV8NptGa8u9GVveMWVCuyl8BbVIhLETFYhO8ee0RysuG8KhkEVl2HmXb6LK9mw3vzMxvN2TNyhe+swrlJqJA6rQ77UVpPVb8o5pSg2faDGuCsEUygq/WwqdC7oW+WUcCzps0iWEltVTf2XwUMB0HmehUP0cGNIbRbx8RzqztaEpdxGLjTGY8ShpRtKVINCeEjmsiwchp8eIum0LJ+Xc8v7v9QRvINds77pD/nCcpJIPW8plzojYkVSEAFe8aFOxbm8C0LHJAl5sLUwljxl7ZgayUOWW4OMnV0lB01BPRadMNIZdTiiOLF4ffi6+MYqKYqfD0kvBRPgQ4A+rr6ZULqKJMXN6FTgjdMZIgZSSc2Oh9qvI4fiIc7EBxuHE0kka7sKObrqPbLq6xgF3AQEO3uekhAIgRAIgSIQuTONI6HyS7gcWFYmp6wOo84MC2FMln7BKLJznCisbNvOmDp+C8aM/6aSW4WTWLUu+qZakBvkWp/lIyx4EeT0kE0sMbvb5Ul0fE4MsBd80iicE5Jt6ST2kn01tD322IOFbuth60816Qz6gMKQp8ynZcg0igCZngiWcdioz5DrjwYJNeGzyl9pbaeWcfN6VHqF5DJeuqGcTCgp5BwCx47IFzXFsAAUPwKHsCA66RgeMg42PREuJJgIOC0Ti2SoLnGf8KlUofIXv/jFVKmRykrWYPWBRJOQ5OXz9bPLt5Rkj9vRT3KkqcazxX1lj4bQFPLtNcv6Zln8kVarQt47n1r2ChGaqalcCyVb2wrlaLeV1M97M7UmTtWasH4KQyAEQmD2EnAGz6dHAiIXrJ2gj2wPMRrCgr3kb+B+YHF5KaTRvOc972H/5OVIyKAnWP16qbgsGcaJhXNB72jjBHJBz67LwnHpL0JBGbjcZ8h1pjJFWHR7rPANl5JyDg974UFhMjUleMR3Yu/MIZHBbcDSdx+LF1LaO8PPm8LHwGcgXqZL3DCcHJW3O1kLxkWFCLSpqWOqGTshQnPgoEFRudpW0rFyEZnJmmrKCS/6gy8HQHnK8pebVXN1gUtGSMgouLjkHs3VfaXxEAiBEJg9BJocUNfPQzXqvCJ0ekqXd4QocbEu0EDu0Ci2ZzXdmGNBOVcNtwf7LdDDi+BbxgZHhQURE9ZdvMMj79SsAAq3gQ25LkgoUTAixk9pQG5UFpYikgRfKsOmvEeaEubQckW+VNa+EkeVCmIlSrp86uDTGZ8u1eb9KnFA+cKkYZc0mgH2SjqOHYnH8avVPVMDbDxNhUAIhMCsJSDNMW9EH5PZl20q8CRBeEzGMxzD4GsRoZPrzSs2D3pENfKNUZxJfJkHtLOLEAiB2UNgaOVOcnemfRB23l087SayQQcBKT6TZfl01B1AAfdY97vYBrCPNBECIRACITA0BKaIfQxNP9OREAiBEAiBEAiBEOiTQOROn+CyWQiEQAiEQAiEwKgQiNwZlZlKP0MgBEIgBEIgBPokELnTJ7hsFgIhEAIhEAIhMCoEIndGZabSzxAIgRAIgRAIgT4JRO70CS6bhUAIhEAIhEAIjAqByJ1Rman0MwRCIARCIARCoE8CkTt9gstmIRACIRACIRACo0IgcmdUZir9DIEQCIEQCIEQ6JNA5E6f4LJZCIRACIRACITAqBCI3BmVmUo/QyAEQiAEQiAE+iQQudMnuGwWAiEQAiEQAiEwKgQid0ZlptLPEAiBEAiBEAiBPglE7vQJLpuFQAiEQAiEQAiMCoHInVGZqfQzBEIgBEIgBEKgTwKRO32Cy2YhEAIhEAIhEAKjQiByZ1RmKv0MgRAIgRAIgRDok0DkTp/gslkIhEAIhEAIhMCoEFhwVDqafoZACIRACIwugbvv/ej//PPPb3HCgVj1r3/966Mf/eiEa/sunG+++bQ84eZ77rnn0ksvPeGqFI4ZgcidMZvQDCcEQmDMCVx11VXnn3/+AgssUOO86667br311mbMiyyyyG233db8nBsLiy666KGHHnrCCSfYV4/t6+Saa665wQYb3HHHHeedd95DH/rQe+65p3NbukTnzznnnM5VfZfceeedD3jAAw444AB96GxkscUW6yxMyVgSiNwZy2nNoEJgbAkwk0xm38OjDCZzLbS2ueCCC/7tb3/bf//9LbSWd1/WN1JAnblnRBdaaKHf//73J598ctOT9ddff9ddd7399tuVGNrXv/717bffvpcxNi30sfDoRz96ww037H1DU7bRRhttttlmNMepp566xRZb9L5taobAQAhM4z95IPtLIyEQAmNJ4Oyzz7744ounJQ5aORAKvfgkuDSuvvrqt73tba3b9r7M1m611VYrrrjihBf6re2Um+HKK6+00FrefdkQnv70p+vkC17wgsb70n2T6a4FiuIhpyzY1jcXS2s45tWvfvWSSy453WbnWX1YonXmGe3sqJVA5E4rjSyHwDQISDJwzTotc1itlyllGvvYtpf+LbzwwgceeOAf/vAHdrHqS1xYffXVWRp9VuLnUkstVfaylwanrEPl/PjHP/7zn//cn9zhilhmmWU++MEP6mH3XpEpyy233Je+9KUpuzRhBZuztcsuu+yEa8ejcJi1zngQzihGlEDkzohOXLo9BQE+gCOPPHJOrrDZ4C6ml11nni+99NIp+jHJ6sc+9rGbbLLJnARlJmn4P8VU1C233LLGGmuUnDKQJZZY4r3vfS9DePzxxyvkD2D1e/GmdNlL2yptzgltvWrEWVvL+RkCIRACc04gcmfOGY5tCzIiGTD+fM4Al8Us6KCGyrbJH9xtt92e//znH3PMMTfccEMZ5h7bZ7/ZclrBt+XOrXT4+uuvP/PMMy10ru2lRIbHLrvs8rSnPa2LJvja177WX/tgStvkbumlJ4OtI8jSNDj38kuaXWQhBEIgBIaEQOTOvJgIpr1209hm1p09PuOMMzbddFNxh2kZ+8l6zPTOyeV1W7O8FyeeeOLiiy9+2mmnWUVY7LTTToP1RnAw/Pvf/958883bdj3lT93Yeuutb7zxRt8N27atIB0gjbbG8zMEQiAEQmC0CETuTGO+dthhB66I6V4Tu5R3S4JvAmLllVe2ULtks7lPjj76aDkW0+jEJFU5IQRH3vjGN3bxRkyy6aTF2223XSVCUmlGvdpqq01adeZW9JcsMnP9zZ5DIARCIARmgEDkzjSgv+hFL3L75XTtK1mzzTbbcELYcK211prG/lI1BEIgBEIgBEJgEAQid6ZB8Rn3fqaxQaqGQAiEQAiEQAgMAYE+EzmHoOfpQgiEQAiEQAiEQAj0RCBypydMqRQCIRACIRACITC6BCJ3Rnfu0vMQCIEQCIEQCIGeCETu9IQplUIgBEIgBEIgBEaXQOTO6M5deh4CIRACIRACIdATgcidnjClUgiEQAiEQAiEwOgSiNwZ3blLz0MgBEIgBEIgBHoiELnTE6ZUCoEQCIEQCIEQGF0CkTujO3fpeQiEQAiEQAiEQE8EInd6wpRKIRACIRACIRACo0sgcmd05y49D4EQCIEQCIEQ6IlA5E5PmFIpBEIgBEIgBEJgdAlE7ozu3KXnIRACIRACIRACPRGI3OkJUyqFQAiEQAiEQAiMLoHIndGdu/Q8BEIgBEIgBEKgJwIL9lQrlUIgBEIgBEJgzgjcc889c9bA1FvPN998p5122o9+9KOFF15YbT/t1PdkW77hDW9YaqmlJlub8nEiELkzTrOZsYRACIw5gbvuuuucc865++67BzVOUuDmm2+ef/75F1100dtuu81P322NW3vjjTfuvvvuL3vZy4488sg77rijrcKUP3V79dVXf8hDHmJhyspzUmGBBRb461//evHFF995552bbrrpDjvssPPOO++77752PWG3F1lkkTnZXbYdIQKROyM0WelqCMx2AuUeqIt1y/WzRyis+FyytUzmUUcddeqppy600ELlVJhLRtTAb7311kMOOWRCy90jh85qr3nNa6666qpjjjlmiy22IH223XbbCUHtuOOOgBMQnS1MWaLDG2+88dOe9rQpaw68wp///OeBt5kGR5FA5M4ozlr6HALDQuD000+//vrrXf3PYYfYUZfjnBaT+S1Y+uuuu+6EE05Q4QUveIEAxBe/+MXvfve7PQoLjW+yySYcDBMa8jnsvOFfccUV1157LaO+5ZZb+vmiF72Im2EOm51wcxz22muvEnwTVphuIfIrrLCCnl9zzTX3u9/94F166aWn20jqh8DwE4jcGf45Sg9HmIBr5cUXX/yGG25gZVncGokL9IGYK5b+lFNOYfg32mgj5ord2nvvvRndORcf1U8NLrfccrr6r3/9a+WVV+6cBjv69re/ffXVV8+haWdiV1xxxSc+8YkPfOADN9hgA2Pp3JcSPXnWs55l4ZZ7P9tssw0/xIQ1OwvBf+pTn7raaqt1rkoJApxS973vfYMiBMaYQOTOGE/u7Bral7/85Yc97GEspW/L/Q1+MkPbX2tEwBFHHLH99tsfcMABl19++YMf/GB2XeFWW201kB0x/+y+bz4P0kQnNTtAoyX685KXvESH8Xzve99rR50cPvCBDwxEXWlkwQUX9D2HyqmzhykJgRAIAQT+k7UeECFQBG6//fbyRlx66aUT2rZeQN10002MuotFh1bjz2jdkD3bZ599LrnkEuattbz3ZVmHHBtth+5JJ53EN2CPvi333lrVLB/+Rz7yEekXbS1Pt6nW+jigKglUIQeJvbDoHBitdbIcAiEQAmNDwJ1xm2++ueGceOKJYrvDM64+7c3wDGD4e8J2zrn5ZCMPPvjgdddd94ILLrjsssuaK2Dl5TCYcw7a1PL5559vL5/+9Kf7bnDXXXddfvnlzz77bG6G9dZbb0LFQ5GstdZa/e0CTLkLdtGWhEFYKKHSfFvur/FsFQIhEAIhMJYEInemMa2vfvWrjz322MUWW6z3bWgR2Q8bbrhhm23uvYWqSdb87ne/k0goi4L7pFwvDP9OO+102GGHffCDH1xppZXmcBd2ZC88LgQKyTLdHjb111lnHQ4S/dTUkksu2ZQPfKHTOVQljRYc+B7TYAiEQAiEwIgSiNyZxsRtvfXWD3rQg9jy3rep2Mrzn//83jeZbs0999xzupvMg/qU2TzYS3YRAiEQAiEQAr0QiNzphdJ/6zz73s80NkjVEAiBEAiBEAiBISAwp0/LGIIhpAshEAIhEAIhEAIh0I1A5E43OlkXAiEQAiEQAiEwBgQid8ZgEjOEEAiBEAiBEAiBbgQid7rRyboQCIEQCIEQCIExIBC5MwaTmCGEQAiEQAiEQAh0IxC5041O1oVACIRACIRACIwBgcidMZjEDCEEQiAEQiAEQqAbgcidbnSyLgRCIARCIARCYAwIRO6MwSRmCCEQAiEQAiEQAt0IRO50o5N1IRACIRACIRACY0AgcmcMJjFDCIEQCIEQCIEQ6EYgcqcbnawLgRAIgRAIgRAYAwKRO2MwiRlCCIRACIRACIRANwKRO93oZF0IhEAIhEAIhMAYEFhwDMaQIYRACIRACMxmArfccsv8889/9913X3fddfPNN1+PKO65555FFllk2WWX7bF+qo00gcidkZ6+dD4EQiAEhpfA4Ycffu211xIic9hFusRnskYWXnjhs88+2/ett9561FFHTVZtwvItttji5JNPnnBVCseMQOTOmE1ohhMCITADBK644gpOAhbXvi+77LJVV131oosuYn179zQ0nb755pt5Ke573/vefu9n0UUXve2225q1c76w0EILvfOd77zgggsIiFe96lXf/e53r7nmmlIk9rvccsstsMACd91113rrred7TnZn7GeddZbh9AGhdb8w6PDDH/5wC63lrcuPetSjDMeO3vSmN3URRq2bWDbeZZZZpq0wP8eVQOTOuM5sxhUCs44AO9fFIsLB0n/84x//y1/+suCCfZ76tGAvbZvTByeccMLGG29cYZHjjz/+mc985qGHHkpG9DEHr33ta1dbbbX9999/yy23fMITnvC1r31t6623tt8+mppsk8c85jEbbbSRtXBxbzTV7rjjjoc97GH2ZeHFL34xNdCs6m9hzv06/e03W4VAJ4H5ehfCnRunJARCYPwIXHrppeeddx4TPtnQnDT4Lebw1CFngiFndNddd92f/OQnBx10kJLJ9thLOdtMbWy66aZdjDTre+GFF9500019+xu23357Po9tttmm8bjw6JxzzjmXX345iSODRFcNxNrFF1+8D2OPKq2jzUsuuYSjZYkllvjnP/9poe8O94IudUJggAROO+20zTffXIMnnngiyT7AluewqcidOQSYzceWAIt155139j08dquMX1sLZITAx7ve9a4+bGFbU/XTjgQ+fDONE1aYVqEr+1//+tenn376ZPbVjhZbbLH99tvPt+VpNd5WGQrSRCNQdFFXbVtN9pMKWWmllbbddtvJKsylcvs10QOBP5d6mGZDYF4SGFq506dHd16yy75CYDICp5566t///veylAwnD/xkNadb7gJdMML/bX9BBCZcC9ttt53N2zQBGaGfjW9guh3rrK+pTTbZRJt217l2uiV6y7Wg823dbm3HEJZaaqnJ9FBrzdmwfMABB9CvBx988GwYbMYYAqNLIHJndOfuPjfeeCNryjJdeeWVrN2cmx+KgT/DpzMcYC+f+9znTjnlFAt9I2NBV1999XJF9N1Is6H8CXJEEIHckYLwyEc+cu+99+6eutFs28vCHnvs8Za3vKWXmp11SjQ85SlPmXOnRWfjKRkqAlTm8ssvP1RdSmdCIAQ6CUTudDKZoxKyw3Vef3dkdNlx56W2S3DiQ5j/IQ95iOtLd3t22bzHVSussMLaa6/9wAc+cJVVVmm7KYOWMii3P8yJqAJnt912k6thoccuda9GezV6QsfmpG/dd5S1ITAZgQc/+MGTrUp5CITA8BCI3JnGXNxwww3ucuzuR6ESPAGie51p7PLeWyWpEJlfZM25557Lh7HWWmvZCwH0+Mc/nhvG8g9+8IM5TwTRoORKt2UuvfTSFqbVyelWnhMX0XT3lfohEAIhEAIhELkzjWNgySWXFNCZcoP4GKZElAohEAIhEAIhMC8JRO5Mj3akzPR4pXYIhEAIhEAIDAGBOX229xAMIV0IgRAIgRAIgRAIgW4EIne60cm6EAiBEAiBEAiBMSAQuTMGk5ghhEAIhEAIhEAIdCMQudONTtaFQAiEQAiEQAiMAYHInTGYxAwhBEIgBEIgBEKgG4HInW50si4EQiAEQiAEQmAMCETujMEkZgghEAIhEAIhEALdCETudKOTdSEQAiEQAiEQAmNAIHJnDCYxQwiBEAiBEAiBEOhGIHKnG52sC4EQCIEQCIEQGAMCkTtjMIkZQgiEQAiEQAiEQDcCkTvd6GRdCIRACIRACITAGBCI3BmDScwQQiAEQiAEQiAEuhGI3OlGJ+tCIARCIARCIATGgEDkzhhMYoYQAiEQAiEwbQL33HPPTTfdNO3NssFoElhwNLudXodACIRACIwVgR/+8IfnnnvuQgstNCejuvvuu+eff3465q677pqynTvuuOOrX/3qUUcdtfbaa09ZORVGnUDkzqjPYPofAiEwiwj84x//YM4Z9RtvvHG++eZrHfnNN9+84IILLrLIIrfeeuvtt9/etra15pwsL7DAAnvvvfcll1xiX9NqR5/XX3/96667bplllllsscUoktbNNfub3/zm73//u4XW8mkt28XOO+/8uc99bt11133Pe94DwpSbH3jggYsvvviU1VJhDAhM73gdgwFnCCEQAiFQPoA777xzQhQM+emnn37cccctvPDCE1bopbBEyZwY78696M+XvvQlWuGWW2658MIL2yq86lWv+utf//qjH/3oGc94xuMe97hejH1bCz3+3GCDDQiXHis31dDec889zznnHJuvssoqnd4X2EFr6ve9sN9++/W9bTYcYwKRO2M8uRlaCMxFArfddtuvfvUrUYCLLrpoLu2GA4DHYrLG2X4dcHXOnzFZnQnL2VRX/+edd95mm22mkTY3g01UuOKKKzgw+ra+NnzlK1/5xS9+8aCDDlp66aWpqwl7Mt1CXd12221rqzbnilVrrbUWXJdffvlqq63GgzLdxudN/VVXXbV2NFghOG86n72MNIHInZGevnR+JgkwMGL/A+mBC1/qgel1yTuHplEjZ5xxxuGHH14iQESDM6BEAxu81FJLDaTDmrr++uu/8IUvbLHFFqeccspA2uxshFB417ve1SUooxvvfOc7OzfsXmKrpzzlKbwgO+2006KLLtq98pysfeMb3zgnm/exreEsu+yyfWyYTUJg7AlE7oz9FM/qAV555ZWnnXZa23Vw70SIj8kEjTYvvvhixrjvxptu0DrrrbfeJptscvbZZ6+xxhrLLbfcnCge4uCGG264+uqrGXWCjNZ54QtfeNhhh/m58sorv+lNb5qTxps+W7CjD3zgA1TadJ0rrY10X9ZnNLrX6XttH+GYvveVDUMgBGacQOTOjE/BXO+Aq3A2qcslcu89cNMmC9p7/R5rspdHH330N7/5zTKcvNy88XPeYe1ceumlJ598cn+KROqDBIjdd98dvc6B0Cirr7662zo6V023RFPrrLPOox71KLelcPXPjTDEy172sun2KvVDIARCYJwIRO7M69l02X3kkUcOKm5dV+pdJIjQxic+8YkLLrhgzsdJNOy4446dt1TMecuUjdTLNddc04IRCbjsu+++7kftMq4ed4rznPgeeBf6k0o9dq+tmhTOtpL8DIEQCIEQGAiByJ1pYOTb2H777d0Q0YtYYap5y+973/u22mzmk6/lzDPPtDCNHU9SVcuu2vkenvOc50zogajtDj300F46PMlO/q9YnzfaaKN5af7/b99ZCoEQCIEQCIE5IBC5Mw14tMtee+317W9/m8tkys1EKF7/+teLd1horcyBMRDx0dpmlkMgBEIgBEIgBLoQiNzpAmeCVY+/9zPBismL4g6ZnE3WhEAIhEAIhMC8IDCAkMq86Gb2EQIhEAIhEAIhEAL9Eojc6ZdctguBEAiBEAiBEBgRApE7IzJR6WYIhEAIhEAIhEC/BCJ3+iWX7UIgBEIgBEIgBEaEQOTOiExUuhkCIRACIRACIdAvgcidfslluxAIgRAIgRAIgREhELkzIhOVboZACIRACIRACPRLIHKnX3LZLgRCIARCIARCYEQIRO6MyESlmyEQAiEQAiEQAv0SiNzpl1y2C4EQCIEQCIEQGBECkTsjMlHpZgiEQAiEQAiEQL8EInf6JZftQiAEQiAEQiAERoRA5M6ITFS6GQIhEAIhEAIh0C+ByJ1+yWW7EAiBEAiBEAiBESEQuTMiE5VuhkAIhEAIhEAI9EsgcqdfctkuBEIgBEIgBEJgRAhE7ozIRKWbIRACIRACIRAC/RKI3OmXXLYLgRAIgRAIgRAYEQKROyMyUelmCIRACIRACIRAvwQid/oll+1CIARCIARCIARGhEDkzohMVLoZAiEQAiEQAiHQL4HInX7JZbsQCIEQCIEQCIERIRC5MyITlW6GQAiEQAiEQAj0SyByp19y2S4EQiAEQiAEQmBECETujMhEpZshEAIhEAIhEAL9Eojc6ZdctguBEAiBEAiBEBgRApE7IzJR6WYIhEAIhEAIhEC/BCJ3+iWX7UIgBEIgBEIgBEaEQOTOiExUuhkCIRACIRACIdAvgcidfslluxAIgRAIgRAIgREhELkzIhOVboZACIRACIRACPRLIHKnX3LZLgRCIARCIARCYEQIRO6MyESlmyEQAiEQAiEQAv0SiNzpl1y2C4EQCIEQCIEQGBECkTsjMlHpZgiEQAiEQAiEQL8EInf6JZftQiAEQiAEQiAERoRA5M6ITFS6GQIhEAIhEAIh0C+ByJ1+yWW7EAiBEAiBEAiBESEQuTMiE5VuhkAIhEAIhEAI9EsgcqdfcpNs96c//emPf/zjJCtTHAIhEAIhEAIhMAMEFpyBfY7vLi+88MLNNttsoYUWOu2009Zee+3xHWhGFgIhEAIhEAKjRCDenUHO1l133TXffPPtvPPOD3rQgwbZbtoKgRAIgRAIgRCYAwLx7vQJ79///vfBBx/83Oc+99hjj33lK1+5wgorXHvttfvuu+8999yz6KKLEj3V7ic/+cnjjjtO4e23377ffvttuummE+5v7733/tWvfqXaxz72sZtuummfffaZf/75l1lmGXvR1K233nrnnXdyF336059ebLHFJmwhhSEQAiEQAiEQApMRiHdnMjLdyn/xi1+svvrqxxxzzIYbbrjXXnu9733vU/uss85afPHFF1xwQWtr49///ve77bbbKaec4ucCCyyw5ZZb/vSnP52w3a222urkk09+6lOfusEGGzz2sY999KMffcUVV+y+++6iYxpZZ5111ltvvW9+85sf+tCHJtw8hSEQAiEQAiEQAl0IxLvTBc6kqz7zmc8sv/zyBMpll1321re+dZdddlF163s/L3zhC2+55Zba8uEPf/jznve8884777vf/e7dd99tlQ2f+MQndrb7pCc9ydptttnmzW9+89JLL73ttttKAFKTovrIRz5yyCGH2ORnP/vZbbfd1rltSkIgBEIgBEIgBLoTiHenO58J1p5//vlf+MIXVl55Zbpk/fXXX2mllVZbbbUJ6t1bpNpSSy0lvMXx8/SnP/0rX/kKb01nZaGrZZdd9pnPfCZhdPTRRz/nOc8R2FJtjTXWWHjhhTvrpyQEQiAEQiAEQqB3ApE7vbP6b80lllji/ve/v6zkXrYUnJJ5c91116l81FFHvfSlL+XyqQ3POeecc889t2lk3XXX/dvf/kbl/OEPf7jqqqsEsKwig/75z3+efvrpomDXX3+9n039LIRACIRACIRACPRIIOazR1D/V23VVVf9wQ9+cOONNwo/+UgxrnVSkv2UwaNECvMRRxyhfMUVV/zd734npLXHHnvQPa973euahuQ1S9a5+OKLq8QqjqL9999/1113pXWkPyvnFiJ0JDiLdr343k9VzncIhEAIhEAIhEDvBCJ3emf1fzWlEh9++OF8Nm6Y+stf/kK4WLf55pu7bWqjjTaSc+OOqjvuuEMhx4wsHOnMbrb64Q9/+LjHPa5pZeONN37DG96w5pprVokcZ48ofPazn/3hD3+4SXY+44wzSCJ5P277cmOX2FmzeRZCIARCIARCIAR6JJBU5R5BtVcja0466SSl/C7CTBaWXHLJ8ui0ViV6RK/U4adpC0W95S1vaa1pWTJQlTT5OuJfPttttx0Z1FY5P0MgBEIgBEIgBHokEO9Oj6AmruaJgoJNso+vueaazhpk0G9+85tf/vKXolSeptNZYcoSYSzun1//+tc9pgpN2WAqhEAIhEAIhMAsJBDvTv+TToK8/vWvF7dy7xXXTmdDnrXjSTmLLLKIBXdmdVaYskS6DsXj/qwpa6ZCCIRACIRACITAZAQidyYjM3U5EfOIRzzi61//+mRV3cP1+Mc/frK1vZTbRbROL6BSJwRCIARCIAS6EEgwqwucrAqBEAiBEAiBEBgHApE74zCLGUMIhEAIhEAIhEAXApE7XeBkVQiEQAiEQAiEwDgQiNwZh1nMGEIgBEIgBEIgBLoQiNzpAierQiAEQiAEQiAExoFA5M44zGLGEAIhEAIhEAIh0IVA5E4XOFkVAiEwKwjcdttts2KcGWQIzGICkTuzePIz9BAIgXsJfOUrX7nnnnsCIwRCYIwJ5DGDYzy5GVoIhEBPBHbcccee6qVSCITAyBKId2dkpy4dD4EQCIEQCIEQ6I1A5E5vnFIrBEIgBEIgBEJgZAlE7ozs1KXjIRACIRACIRACvRGI3OmNU2qFQAiEQAiEQAiMLIHInZGdunQ8BEIgBEIgBEKgNwKRO71xSq0QCIEQCIEQCIGRJRC5M7JTl46HQAiEQAiEQAj0RiBypzdOqRUCIRACIRACITCyBCJ3Rnbq0vEQCIEQCIEQCIHeCETu9MYptUIgBEIgBEIgBEaWQOTOyE5dOh4CIRACIRACIdAbgcid3jilVgiEQAiEQAiEwMgSiNwZ2alLx0MgBEIgBEIgBHojELnTG6fUCoEQCIEQCIEQGFkCkTsjO3XpeAiEQAiEQAiEQG8EInd645RaIRACIRACIRACI0sgcmdkpy4dD4EQCIEQCIEQ6I1A5E5vnFIrBEIgBEIgBEJgZAlE7ozs1KXjIRACIRACIRACvRGI3OmNU2qFQAiEQAiEQAiMLIHInZGdunQ8BEIgBEIgBEKgNwKRO71xSq0QCIEQCIEQCIGRJRC5M7JTl46HQAiEQAiEQAj0RiBypzdOqRUCIRACIRACITCyBCJ3Rnbq0vEQCIEQCIEQCIHeCETu9MYptUIgBEIgBEIgBEaWQOTOyE5dOh4CIRACIRACIdAbgcid3jilVgiEQAiEQAiEwMgSiNwZ2alLx0MgBEIgBEIgBHojELnTG6fUCoEQCIEQCIEQGFkCkTsjO3XpeAiEQAiEQAiEQG8EInd645RaIRACIRACIRACI0sgcmdkpy4dD4EQCIEQCIEQ6I1A5E5vnFIrBEIgBEIgBEJgZAlE7ozs1KXjIRACIRACIRACvRGI3OmNU2qFQAiEQAiEQAiMLIHInZGdunQ8BEIgBEIgBEKgNwKRO71xSq0QCIEQCIEQCIGRJRC5M7JTl46HQAiEQAiEQAj0RiBypzdOqRUCIRACIRACITCyBCJ3Rnbq0vEQCIEQCIEQCIHeCETu9MYptUIgBEIgBEIgBEaWQOTOyE5dOh4CIRACIRACIdAbgcid3jilVgiEQAiEQAiEwMgSiNwZ2alLx0MgBEIgBEIgBHojELnTG6fUCoEQCIEQCIEQGFkCkTsjO3XpeAiEQAiEQAiEQG8EInd645RaIRACIRACIRACI0sgcmdkpy4dD4EQCIEQCIEQ6I1A5E5vnFIrBEIgBEIgBEJgZAlE7ozs1KXjIRACIRACIRACvRGI3OmNU2qFQAiEQAiEQAiMLIHInZGdunQ8BEIgBEIgBEKgNwKRO71xSq0QCIEQCIEQCIGRJRC5M7JTl46HQAiEQAiEQAj0RiBypzdOqRUCIRACIRACITCyBCJ3Rnbq0vEQCIEQCIEQCIHeCETu9MYptUIgBEIgBEIgBEaWQOTOyE5dOh4CIRACIRACIdAbgcid3jilVgiEQAiEQAiEwMgSiNwZ2alLx0MgBEIgBEIgBHojELnTG6fUCoEQCIEQCIEQGFkCC45sz9PxEAiBEAiBeUrg9ttvv+CCCx784AcvssgirTu++uqrL7/88tVXX33ZZZdV/u9///vMM8/8+Mc/vsoqq/h52WWXbbfddk94whNUWGyxxZT8/e9/v+eee9ZYYw3Lt95660UXXVQ/l156aSVtn+uuu+7SSy+94447brvttvnmm2/xxRdfaKGFHvKQh1hurXnnnXfq21133XXzzTers+CCC66zzjoLLLBAU+emm27685//rIerrbZaU2hB49dee+2iiy6qvq6uuuqqCrWjtbvvvlvHmvEa44orrlht2osNf/7zn3/oQx/Sk/e+973rrrvummuuufDCC7c2fuWVV1511VXzz/9fz4LWEHjQgx7UWifL84gA+vmEQAiEQAiEwJQE/vKXv7BMO+200zve8Y699trrAx/4AFmz9957b7rppso/85nPaIEo2Xrrrf3cd999q8Hzzz//AQ94gBLioEpe8pKXrLzyyn/961/9fOc732mVzwte8AIiQ8mPfvSjj3zkI1WTiHnOc55j7SabbPL+97//3e9+933ve1/y4utf/3pVaL4POeQQ1e5///vvv//+NI06u+66q103FU499VQV1ltvvbe97W0nnnii+vvss8/vfvc7MkU57UXcvPKVr6z6//rXv+xIuU8zkBe+8IVf+MIXqsKee+5Za1u/DzzwwGZ3FqiojTfeuLWC5RVWWAE97bfWHKfl4mykIA/VuO4zVL1JZ0IgBEIgBIaWwAknnNBqvDktllhiiaak5M6rXvWqKuHwaAbypje9SeFmm21WJVSFnw9/+MMpj6rsW2u8QbZaZpllHvnIR1bN173udVXh85//vBI+npVWWknJM57xDLqq6vg++OCDy4Ny3HHH+fntb3+7tmpkk8LHPvaxVei7XEQWllxyySq04aGHHmqZ68UwKZsq982TdPbZZ3/iE5+wvOOOO2qqlv182tOeRrh88YtfLHfX+uuvf80116hQn2c+85nVCIcQuca/1XikuLv+t9a4/Y3cGbcZzXhCIARCYLYRePKTn8x+c4cceeSR/ByHH344iWDB53Of+xzfzx//+EfhnrLxrXKHk4bzhiL5zne+A1rJHfEmOoDy4Eepj0hQhYoe9ahHFdtnP/vZWltrrbUa1I03qPHE2HvJCE6m66+/Xk0SZPPNN7ehPX7pS1+qbTWihOj52te+dthhh6lgw+o/LSUed8455yy//PLVefEyCqaJTDUy5TWveY1Q3SMe8YiqVsPRPhRVApHwnBJWv7QgDUR+iQOKf+G23377qXm/+92v8XVV98bme2jlTnJ36hDNdwiEQAiEQE8EvvKVrzz60Y+esOqxxx4rW6VzFf0hRCVa9KIXvUgGDPVACpxyyikPe9jD6IDW+twtBMFXv/pVhRdeeOG5557LEfK3v/3NtuW/oaJ++9vfHn/88WeccUZtyPVCK1gmLJZaaikL/EPf+ta31l57bfulKl72spcprDpa8/HTN6VlofkIkBE9HEs23G233W655RbpPgpl5AjYyeyRhUMAkVlCYLayzGFTm++www7nnXeePJ6f/OQnp5122pZbbvmHP/zhxhtvtNZ+n/SkJ9FPPttvv70SiD75yU/KDXrMYx5Tm+d7HhD4b/7UPNhTdhECIRACITAGBHgvJhvFE5/4RPpAAo0KfCd/+tOfLLD3NIooj2URKJKCL+d5z3uevBaCgzRp/XDPHHHEERKHVZYjTFf985//lNPjZ/NpnC5KSKJjjjmmWdUsaLlcMqU5lOsGf1JpHT/btI4S2oWy4b/55je/Kfb09Kc/XdrQUUcdJWdIDjXFo46u0kAWOj/VZ7KMr8jaJsxHBj3lKU/ZYostyLvaivwi3doG1dlgSgZLIN6dwfJMayEQAiEw5gR4aHbffXfxKeMkIMp78fjHP95PQkfWi7Rf2coykbfaaispvbwvgjgNlF122YWnx1ZNSbPA4SEPxoaV0/PmN7/5G9/4hrXiUOXaaWo2C1TUhP6kpoIGJQBttNFGWtBnXXrFK17BcyNXmkumqWZBlEoghuJpLWyW3U1GIdFtMpCawi4LnECf/vSnf/GLX6jD0+Pzq1/96l3vehdVJLZFNjURsS6NZNUACUTuDBBmmgqBEAiBcSYgQYcmoFSkoUhtOeigg77//e8roXKkwkiIqczfxz3ucUcffXRlGX/0ox8VxBFm4uQoiVPfTTZM8ZKD/MY3vpEOuOKKK97ylrcccMABqvGsdNIU3vrpT3+qnJPphhtumEwGtW5Ye5Ry5CZwsTOBJLvTSbe4f/azn9U9ST9um+/UMSrzHvHrSEsiwj71qU9plv+mtfEuy4JiJXeqjt1VyrafnD2RO13QzY1VkTtzg2raDIEQCIExJCC61DoqckTgiRtDvEkASMjmta99bVWQsUuXNJWJGA/dKYeQnOWmvFl4wxve4M5wCoDQKafLZKpigw02EDIjpzz2hnDZZpttmka6L7TdVqbyD3/4Q42Qbrr63Oc+lwRpa4Gea+4d4yXiFmqr0P2nm967V8jaeUkguTvzknb2FQIhEAJjRUAMi46Z1pCEk1rr8/pwDp1++unCPT/+8Y+bABO3zQc/+MHWms3yoGTEU5/61Eoz0rJ7ypr2a8HzexqtI4bVaJ0Pf/jDbTUn/EkeCV25OZ9Tx+YynVuryeOR1t1akuW5TSByZ24TTvshEAIhMA4EKJLnP//5Un15RJrxyBqWvlM/Kz5Fo8jwde9Sq3um7s1WTf228JMIkfwbakOgRwpz07IFD9eRc9NaUsvUg1ucVN522205nOr2eKvabvJqNlSTtpAc7ZlAfDlNeeuCJ/S0/uTX8TDAKpGK9NKXvrRZu9xyyzXLEy5UzrJnDHq4IneXNGc3z7tda8MNN7Sq7rS3YcXUJmwhhXODQOTO3KCaNkMgBEJg3Ah4A4MQkhuv3DzVjE1ib711QYnMGOEhT1v2NBq3c7sru6km6bhuRJIHU09Yblb97Gc/q+WzzjpLBnFTbsHDkSd838LJJ5/sbiwP+JESREDUY5HV9/Cb1lyZaurVr361atKlJQYJvTW3r7fuqHNZ/aaQqKpn9lSJR+Y89KEPbda2LUhpmtApJTOaXuTpaeJ97pDvco9bW7P5OecEInfmnGFaCIEQCIFZRKBuKTdgmcIekOOGoxq8m8w5WppYlVyc3/zmN9J6PLD4pJNOUkdqjhdQTEaKuGk8H00dz/0jaKQJf+xjH6vXZtE6bv7ipGkeCfj617++kVCVHsTN41E9lt0N7iaypjWSq3keYFNYCxO+FKJWEUytlXl3vve975Ev9iLg5WE8niQEAi3FcaUndkq3SRWi/7yES4Xa3E9iqB69o2TC8bbuKMuDJfBfJ+RgG01rIRACIRACY0bAk445VNz1LbKzxx57MO1uxfIk4homEaACvSJn2auj/vGPfxAWrU8j9ETBH/zgB80zlzvhkA6dz8IR8aGQPLXPHrmObMUJxL0kfYerqRqRvExOeZ8DiUNzcMx4VZZbrqyVcMO107ovjwJyE1YT9nJbWa1tq9a6Seey8JbQm6CeR+xorangcYJcOH66F0x2jic4ex3pAx/4QJXdfs8j5Q6vpv6E422aysLgCZiVfEIgBEIgBEJgSgICTzRN5aa0WSM5Pa2bC9NIxyF93Iy98847W+bnaK3QLBMxlJDWvvzlLzeFbQv2yzNE1ni/Jl3iI32nrc7vf/97DykWXOM14USRSCSth/ioapxMwnDNG7LaOs8jxfHT2iDBpOdVTQ5166rW5bo1varpm362rpXqVKt0RjisVczpKg9Qa+WxWR7al0jMB3HbxOdnCIRACIRACExGgC4RoGkNPMlKdkeVpJbJNpmynDPGw2/omO413bpF93hG32TVOJ9Evi666CIRN89HblNmnEByqD1op3VzMTJ6S1p0a6FlEk3QyjC5iCZLT5bPJCVIgxrR/7b3n+tDRbi0JtKnWqVpi7Jx+bj1vW2P4/FTUna9sMwb0bnlhmdQkTvDMxfpSQiEQAiEQAiMNoGhlTvJ3RntAyu9D4EQCIEQCIHhIcBF5yWyAkf8cMPTKz2Jd2eopiOdCYEQCIEQCIEQGDyB3Ig+eKZpMQRCIARCIARCYKgIRO4M1XSkMyEQAiEQAiEQAoMnELkzeKZpMQRCIARCIARCYKgIRO4M1XSkMyEQAiEQAiEQAoMnELkzeKZpMQRCIARCIARCYKgIRO4M1XSkMyEQAiEQAiEQAoMnELkzeKZpMQRCIARCIARCYKgIRO4M1XSkMyEQAiEQAiEQAoMnELkzeKZpMQRCIARCIARCYKgIRO4M1XSkMyEQAiEQAiEQAoMnELkzeKZpMQRCIARCIARCYKgIRO4M1XSkMyEQAiEQAiEQAoMnELkzeKZpMQRCIARCIARCYKgIRO4M1XSkMyEQAiEQAiEQAoMnELkzeKZpMQRCIARCIARCYKgIRO4M1XSkMyEQAiEQAiEQAoMnELkzeKZpMQRCIARCIARCYKgIRO4M1XSkMyEQAiEQAiEQAoMnELkzeKZpMQRCIARCIARCYKgIRO4M1XSkMyEQAiEQAiEQAoMnELkzeKZpMQRCIARCIARCYKgIRO4M1XSkMyEQAiEQAiEQAoMnELkzeKZpMQRCIARCIARCYKgIRO4M1XSkMyEQAiEQAiEQAoMnELkzeKZpMQRCIARCIARCYKgIRO4M1XSkMyEQAiEQAiEQAoMnELkzeKZpMQRCIARCIARCYKgIRO4M1XSkMyEQAiEQAiEQAoMnELkzeKZpMQRCIARCIARCYKgIRO4M1XSkMyEQAiEQAiEQAoMnELkzeKZpMQRCIARCIARCYKgIRO4M1XSkMyEQAiEQAiEQAoMnELkzeKZpMQRCIARCIARCYKgIRO4M1XSkMyEQAiEQAiEQAoMnELkzeKZpMQRCIARCIARCYKgIRO4M1XSkMyEQAiEQAiEQAoMnELkzeKZpMQRCIARCIARCYKgIRO4M1XSkMyEQAiEQAiEQAoMnELkzeKZpMQRCIARCIARCYKgIRO4M1XSkMyEQAiEQAiEQAoMnELkzeKZpMQRCIARCIARCYKgIRO4M1XSkMyEQAiEQAiEQAoMnELkzeKZpMQRCIARCIARCYKgIRO4M1XSkMyEQAiEQAiEQAoMnELkzeKZpMQRCIARCIARCYKgIRO4M1XSkMyEQAiEQAiEQAoMnELkzeKZpMQRCIARCIARCYKgIRO4M1XSkMyEQAiEQAiEQAoMnELkzeKZpMQRCIARCIARCYKgIRO4M1XSkMyEQAiEQAiEQAoMnELkzeKZpMQRCIARCIARCYKgIRO4M1XSkMyEQAiEQAiEQAoMnELkzeKZpMQRCIARCIARCYKgIRO4M1XSkMyEQAiEQAiEQAoMnELkzeKZpMQRCIARCIARCYKgIRO4M1XSkMyEQAiEQAiEQAoMnELkzeKZpMQRCIARCIARCYKgIRO4M1XSkMyEQAiEQAiEQAoMnELkzeKZpMQRCIARCIARCYKgIRO4M1XSkMyEQAiEQAiEQAoMnELkzeKZpMQRCIARCIARCYKgIRO4M1XSkMyEQAiEQAiEQAoMnELkzeKZpMQRCIARCIARCYKgIRO4M1XSkMyEQAiEQAiEQAoMnELkzeKZpMQRCIARCIARCYKgIRO4M1XSkMyEQAiEQAiEQAoMnELkzeKZpMQRCIARCIARCYKgIRO4M1XSkMyEQAiEQAiEQAoMnELkzeKZpMQRCIARCIARCYKgIRO4M1XSkMyEQAiEQAiEQAoMnELkzeKZpMQRCIARCIARCYKgIRO4M1XSkMyEQAiEQAiEQAoMn8P8AZJA4DPH5A3EAAAAASUVORK5CYII=",
+ "text/plain": [
+ "